Автор: Работнов Ю.Н.
Теги: механика деформируемых тел упругость деформация механика физика физика твердого тела
ISBN: 5-02-013812-6
Год: 1988
Текст
Ю.Н.РАШНОВ
MEXj t 1
ДЕ± ГО)
1Г U ^ 1
Ю. Н. РАБОТНОВ
МЕХАНИКА
ДЕФОРМИРУЕМОГО
ТВЕРДОГО ТЕЛА
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов механико-математических
и физических специальностей университетов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1988
ББК 22.251
Р13
УДК 539.3
Р а б о т н о в Ю. Н. Механика деформируемого твердого тела.— Учеб.
пособие для вузов.— 2-е изд., испр.— М.: Наука. Гл. ред. физ.-мат. лит.,
1988.— 712 с.
ISBN 5-02-013812-6
Книга представляет собой объединение элементов сопротивления мате-
материалов, теории упругости, теории пластичности, теории ползучести, вязко-
упругости и механики разрушения.
При изложении материала акцент делается на связь между физически-
физическими и механическими теориями и на общие принципы в большей мере, не-
нежели на практические расчетные методы, которые легко найти в справоч-
справочной литературе.
Для студентов университетов в качестве учебного пособия, а также
инженеров и специалистов в области механики деформируемого твердого
тела.
Табл. 2. Ил. 334 Библиогр. 17 назв.
Рецензенты:
член-корреспондент АН СССР В. В. Болотин,
доктор физико-математических наук В. Д. Клюшников
Юрий Николаевич Работное
МЕХАНИКА ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА
Редактор Н. П. Рябенькая
Художественный редактор Г. Я. Колъчепко
Технический редактор И. Ш. Акселърод
Корректоры Г. С. Вайсберг, Л. С. Сомова
ИБ № 32630
Сдано в набор 06.04.87. Подписано к печати 18.12.87. Т-25212.
Формат 60X90/16. Бумага тип. № 1. Гарнитура обыкновенная.
Печать высокая. Усл. печ. л. 44,5. Усл. кр.-отт. 44,5. Уч.-изд.
л. 44,65. Тираж 8650 экз. Цена 1 р. 80 к.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
4-я типография издательства «Наука»
630077 г. Новосибирск 77. Станиславского, 25
р 1703040000—040g688
053@2)-88 (Q) Издательство «Наука».
^—' Главная редакция
тотэтчт с no A/ioo/io а физико-математической литературы,
lbBJN O-U2-(JloolZ-b 1979; с изменениями 1988
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 9
Предисловие к первому изданию Ю
Введение И
ЧАСТЬ I. СТЕРЖНЕВЫЕ СИСТЕМЫ
Глава 1. Основные понятия 16
§ 1.1. Предмет механики деформируемого твердого тела ... 16
§ 1.2. Сплошная среда . 18
§ 1.3. Однородная среда 21
§ 1.4. Кинематическое описание сплошной среды 22
§ 1.5. Внешние силы 24
§ 1.6. Принцип Сен-Венана и статически эквивалентные системы
сил 27
§ 1.7. Внутренние силы 30
§ 1.8. Упругость 33
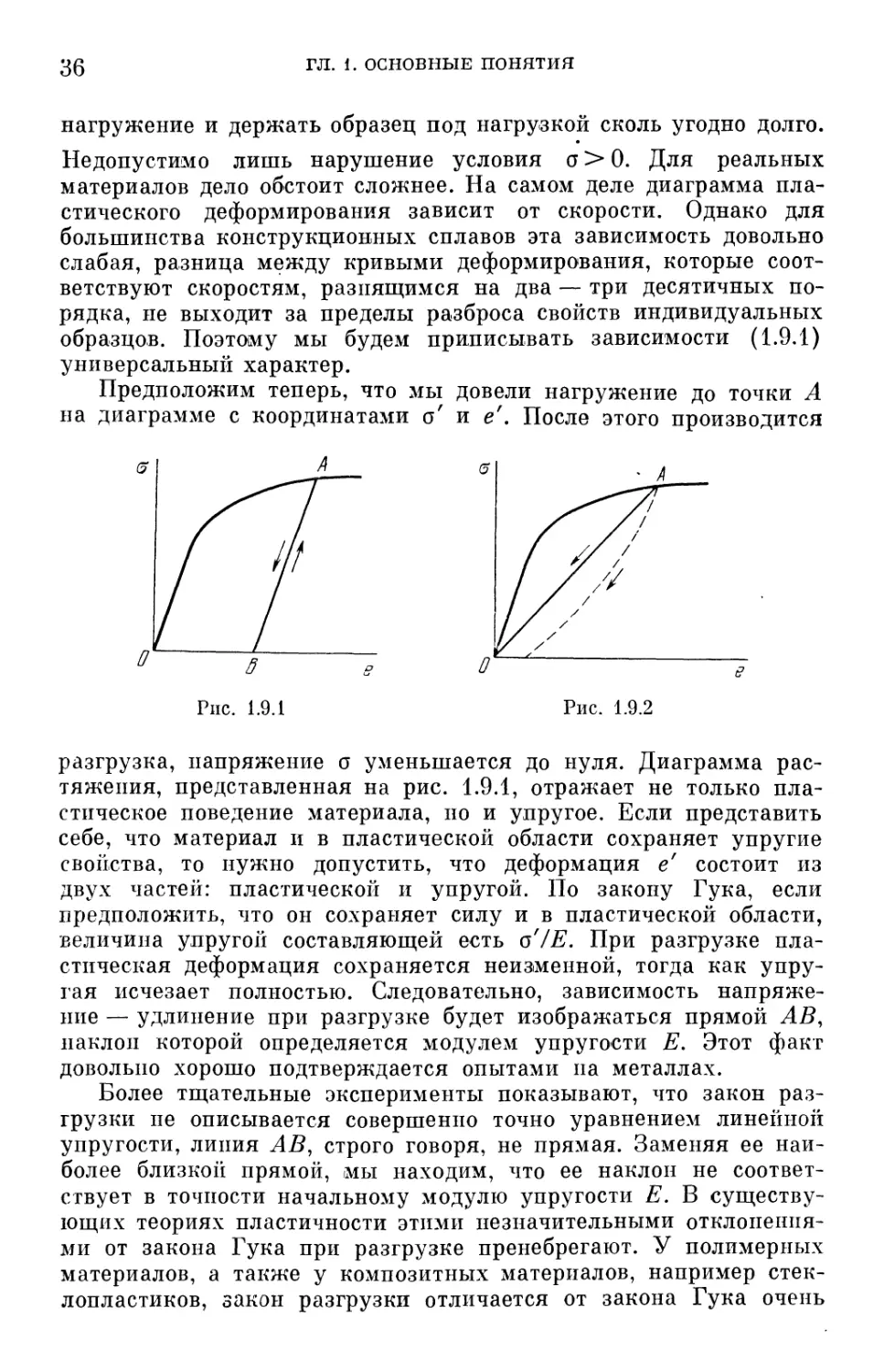
§ 1.9. Пластичность 35
§ 1.10. Последействие п ползучесть 38
§ 1.11. Тела изотропные и анизотропные 40
Глава 2. Стержни и стержневые системы — растяжение и сжатие 42
§ 2.1. Растяжение п сжатие стержней 42
§ 2.2. Напряжения п деформации при растяжении — сжатии . 45
§ 2.3. Перемещение узлов стержневых систем 48
§ 2.4. Статически неопределенные задачи на растяжение — сжатие 51
§ 2.5. Расчет стержневых систем на прочность 54
§ 2.6. Остаточные напряжения после пластической деформации 58
§ 2.7. Большая деформация 62
§ 2.8. Упругая энергия и упругие потенциалы 63
§ 2.9. Термодинамика упругой деформации ; 66
§ 2.10. Распространение упругих волн в стержнях 70
§ 2.11. Напряжения при ударе 73
Глава 3. Изгиб балок 76
§ 3.1. Действие поперечных сил на балку 76
§ 3.2. Закон плоских сечений 78
§ 3.3. Нормальные напряжения при изгибе 80
§ 3.4. Изгибающие моменты и перерезывающие силы .... 83
§ 3.5. Прочность и несущая способность при изгибе .... 87
§ 3.6. Упругопластический изгиб 91
§ 3.7. Изгиб тонкостенных стержней открытого профиля ... 93
§ 3.8. Дифференциальное уравнение изогнутой оси балки и его
интегрирование 98
§ 3.9. О решении линейных дифференциальпых уравнений с по-
постоянными коэффициентами 103
§ 3.10. Продольно-поперечный изгиб 106
§ 3.11. Изгиб балки на упругом основании 109
Глава 4. Устойчивость стержней и стержневых систем . . . . 114
§ 4.1. Постановка задач устойчивости . 114
§ 4.2. Критические силы для сжатого стержня по Эйлеру . . . 115
§ 4.3. Эластика Эйлера 118
§ 4.4. Устойчивость прямолинейной формы сжатого стержня . . 121
§ 4.5. Послекритическое поведение упругих систем .... 123
§ 4.6. Устойчивость пологой арки 127
4 ОГЛАВЛЕНИЕ
§ 4.7. Критические силы при иных видах закрепления стержня 130
§ 4.8. Устойчивость стержня в упругой среде 134
§ 4.9. Потеря устойчивости за пределом упругости — схема Кар-
Кармана 134
§ 4.10. Потеря устойчивости за пределом упругости — схема про-
продолжающегося нагружения 138
§ 4.11. Исследование поведения сжатого стержня при потере ус-
устойчивости за пределом упругости 140
§ 4.12. Внецентренное сжатие упругопластического стержня 143
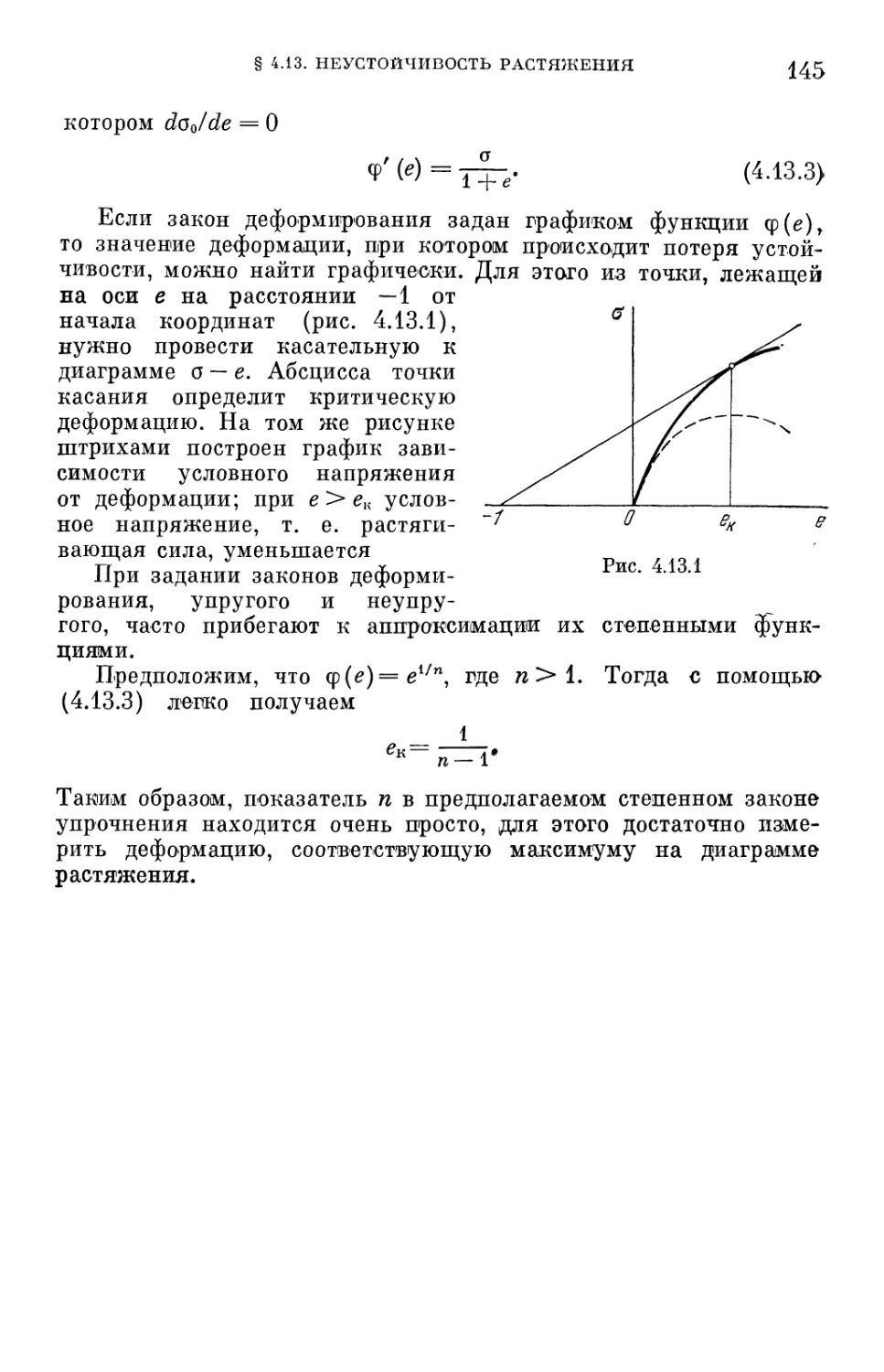
§ 4.13. Неустойчивость растяжения при большой деформации 144
Глава 5. Общие свойства упругих и пластических стержневых си-
систем 146
§ 5.1. Упругие и пластические системы 146
§ 5.2. Теоремы Лагранжа и Кастильяно 148
§ 5.3. Линейные упругие системы 151
§ 5.4. Статически неопределимые системы. Экстремальные прин-
принципы 156
§ 5.5. Метод сил и метод перемещений в строительной механике
стержневых систем 159
§ 5.6. Жесткопластическое тело 162
§ 5.7. Условие текучести и поверхность текучести .... 164
§ 5.8. Выпуклость поверхности текучести 168
§ 5.9. Статический метод определения предельной нагрузки - 170
§ 5.10. Кинематически возможные состояния и кинематический ме-
метод определения предельной нагрузки 172
Глава 6. Колебания стержневых систем 177
§ 6.1. Колебания систем с конечным числом степеней свободы 177
§ 6.2. Собственные формы колебаний 179
§ 6.3. Главные координаты 182
§ 6.4. Формула и способ Рэлея 184
§ 6.5. Нижние оценки для частоты основного тона .... 186
§ 6.6. Продольные колебания стержней 187
§ 6.7. Распространение продольных волн 191
§ 6.8. Динамический изгиб стержней 195
§ 6.9. Колебания балок постоянного сечения 199
§ 6.10. Способ Рэлея — Ритца 201
§ 6.11. Динамическая устойчивость. Следящая сила .... 205
ЧАСТЬ II. УПРУГОЕ ТЕЛО
Глава 7. Общая теория деформаций и напряжений 208
§ 7.1. Тензоры в трехмерном евклидовом пространстве . . . 208
§ 7.2. Общая теория деформаций 213
§ 7.3. Определение перемещений по заданной деформации . . . 216
§ 7.4. Теория напряжений 219
§ 7.5. Некоторые свойства полей напряжений и деформаций 221
§ 7.6. Круговая диаграмма Мора 225
§ 7.7. Разложение тензора на девиаторную и гидростатическую со-
составляющие 227
§ 7.8. Общие криволинейные, цилиндрические и сферические ко-
координаты 231
§ 7.9. Геометрически нелинейные задачи 234
Глава 8. Теория упругости. Общие уравнения и простейшие при-
примеры 236
§ 8.1. Упругое тело 236
§ 8.2. Закон Гука 238
ОГЛАВЛЕНИЕ 5
§ 8.3. Закон Гука для изотропных тел 242
§ 8.4 Формулировка задачи теории упругости. Теорема единст-
единственности решения 244
§ 8.5. Уравнения теории упругости в перемещениях и в напряже-
напряжениях 248
§ 8.6. Температурные эффекты 251
§ 8.7. Вариационные уравнения теории упругости .... 253
§ 8.8. Некоторые замечания о вариационных принципах . . . 258
§ 8.9. Обобщенные силы и перемещения 260
§ 8.10. Теоремы Клапейрона и Максвелла — Бетти 263
§ 8.11. Замечания о задачах теории упругости 265
§ 8.12. Одномерные задачи — трубы и диски 267
§ 8.13. Простейшая задача о концентрации напряжений . . . 271
§ 8.14. Концентрация напряжений у сферической полости 274
Глава 9. Антиплоская деформация, кручение, изгиб .... 278
§ 9.1. Антиплоская деформация 278
§ 9.2. Винтовая дислокация 280
§ 9.3. Трещина продольного сдвига 283
§ 9.4. Трещина конечной длины 285
§ 9.5. Освобождение энергии при раскрытии трещины . . . 286
§ 9.6. Кручение круглых стержней 290
§ 9.7. Кручение стержней некруглого поперечного сечения 292
§ 9.8. Теорема о циркуляции касательного напряжения. Тонко-
Тонкостенные стержни замкнутого профиля 296
§ 9.9. Простейшие задачи о кручении 300
§ 9.10. Теорема о максимуме касательного напряжения. Угловые
точки ... 304
§ 9.11. Концентрация напряжений при кручении 305
§ 9.12. Кручение анизотропных стержней 308
§ 9.13. Кручение тонкостенных стержпей открытого профиля 310
§ 9.14. Нормальные напряжения при кручении тонкостенных
стержней 312
§ 9.15. Стесненное кручение и изгиб тонкостенных стержней 315
§ 9.16. Касательные напряжения при изгибе стержней сплошного
сечения 318
Глава 10. Плоская задача теории упругости 323
§ 10.1. Основные уравнения плоской задачи 323
§ 10.2. Сила и момент, действующие на коптур 328
§ 10.3. Краевая дислокация 331
§ 10.4. Напряженное состояние около трещины 334
§ 10.5. Основные плоские задачи теории упругости .... 337
§ 10.6. Функция напряжений. Ортотропное тело 342
§ 10.7. Трещина в ортотропной упругой плоскости .... 346
§ 10.8. Решение задачи об упругой полуплоскости с помощью пре-
преобразования Фурье 348
§ 10.9. Сосредоточенная сила на границе полуплоскости. Контакт-
Контактная задача 351
§ 10.10. Решение для длинного прямоугольника 355
§ 10.11. Бесконечно длинная полоса 356
Глава 11. Некоторые пространственные задачи теории упругости 359
§ 11.1. Представление решения задачи теории упругости в форме
Папковича — Нейбера 359
§ 11.2. Сосредоточенная сила в изотропной неограниченной упру-
упругой среде 360
§ 14.3. Другие типы сипгулярных решений 363
6 ОГЛАВЛЕНИЕ
§ 11.4 Дислокация Вольтерра 364
§ 11.5. Теорема Вейнгартена 367
§ 11.6. Задача теории упругости для полупространства . . . 368
§ 11.7. Нормальная нагрузка на границе полупространства 371
§ 11.8. Контактная задача. Жесткий плоский штамп, круглый в
плане 372
§ 11.9. Потенциал однородного эллипсоида 374
§ 11.10. Штамп в форме параболоида 377
§ 11.11. Контактная задача Герца 378
§ 11.12. Температурные напряжения 332
Глава 12. Стержни, пластины и оболочки 386
§ 12.1. Приближенная теория изгиба балок 386
§ 12.2. Распространение вариационных методов на геометрически
нелинейные задачи 390
§ 12.3. Устойчивость сжатого стержня и родственные задачи . . 393
§ 12.4. Изгиб пластип. Основные предположения технической тео-
теории 395
§ 12.5. Линейная теория пластин 397
§ 12.6. Изотропные пластины. Дифференциальное уравнение для
прогиба и простейшие задачи 401
§ 12.7. Прямоугольная ортотропная пластина 405
§ 12.8. Прямоугольные пластины из изотропного материала 407
§ 12.9. Прямое применение вариационных принципов к задачам
изгиба пластин 409
§ 12.10. Большие прогибы -411
§ 12.11. Устойчивость пластин . 415
§ 12.12. Вариационный метод решения задач устойчивости 417
§ 12.13. Осесимметричная деформация цилиндрической оболочки 419
§ 12.14. Безмоментная теория оболочек 423
§ 12.15. Безмоментные оболочки вращения 425
§ 12.16. Уравнения краевого эффекта в теории оболочек . . . 427
Глава 13. Динамические задачи теории упругости 430
§ 13.1. Постановка динамических задач теории упругости . . . 430
§ 13.2. Свободные и вынужденные колебания 433
§ 13.3. Неравенство Рэлея и метод Ритца 436
§ 13.4. Распространение плоских волн в неограниченной упругой
среде 439
§ 13.5. Отражение волн 441
§ 13.6. Распространение волн в слое конечной толщины . . . 444
§ 13.7. Распространение волн в стержнях 448
§ 13.8. Размытие фронта сильного разрыва 451
Глава 14. Дислокации в упругом теле 453
§ 14.1. Дислокации в кристаллах 453
§ 14.2. Дислокации Бюргерса. Сингулярные члены 456
§ 14.3. Дислокации Бюргерса. Полное решение 459
§ 14.4. Прямолинейные дислокации .. 461
§ 14.5. Энергия дислокации 463
§ 14.6. Плоская дислокация 465
§ 14.7. Кольцевая дислокация 466
§ 14.8. Дислокации в телах конечного размера 469
§ 14.9. Возможные движения дислокаций 471
§ 14.10. Дислокации в теле, находящемся под нагрузкой . . . 472
§ 14.11. Сила, действующая на дислокацию 474
§ 14.12. Взаимодействие между, дислокациями 475
§ 14.13. Стенка дислокаций 478
ОГЛАВЛЕНИЕ 7
ЧАСТЬ III. НЕУПРУГОСТЬ
Глава 15. Идеальная пластичность 480
§ 15.1. Упругопластическое и жесткопластическое тело . . . 480
§ 15.2. Принцип максимума и постулат Друкера 482
§ 15.3. Диссипативная функция 485
§ 15.4. Постановка задачи теории идеальной пластичности. Тео-
Теорема единственности 487
§ 15.5. Экстремальные свойства предельных состояний текучести 491
§ 15.6. Условие пластичности для несжимаемого материала. Изот-
Изотропное тело 493
§ 15.7. Условие пластичности для анизотропных тел .... 496
§ 15.8. Плоская задача теории пластичности 500
§ 15.9. Плоская деформация , 505
§ 15.10. Простые решения. Задача Прандтля 509
§ 15.11. Линии разрыва 513
§ 15.12. Применение экстремальных принципов к задаче о плоской
деформации 515
§ 15.13. Полярно-симметричное пластическое напряженное состоя-
состояние 520
§ 15.14. Плоское напряженное состояние 523
§ 15.15. Предельное равновесие пластин 526
§ 15.16. Предельное состояние закрученного стержня .... 529
Глава 16. Упругопластическое упрочняющееся тело .... 532
§ 16.1. Деформационная теория пластичности 532
§ 16.2. Теория течения, постулат Друкера 536
§ 16.3. Теория течения, общие уравнения 538
§ 16.4. Границы применимости деформационной теории пластич-
пластичности 542
§ 16.5. Двумерная модель упрочняющегося тела 545
§ 16.6. Интерпретация соотношений пластичности в пространстве
деформаций 549
§ 16.7. Изотропное и трансляционное упрочнение 552
§ 16.8. Кусочно линейные поверхности нагружения .... 554
§ 16.9. Теория скольжения. 558
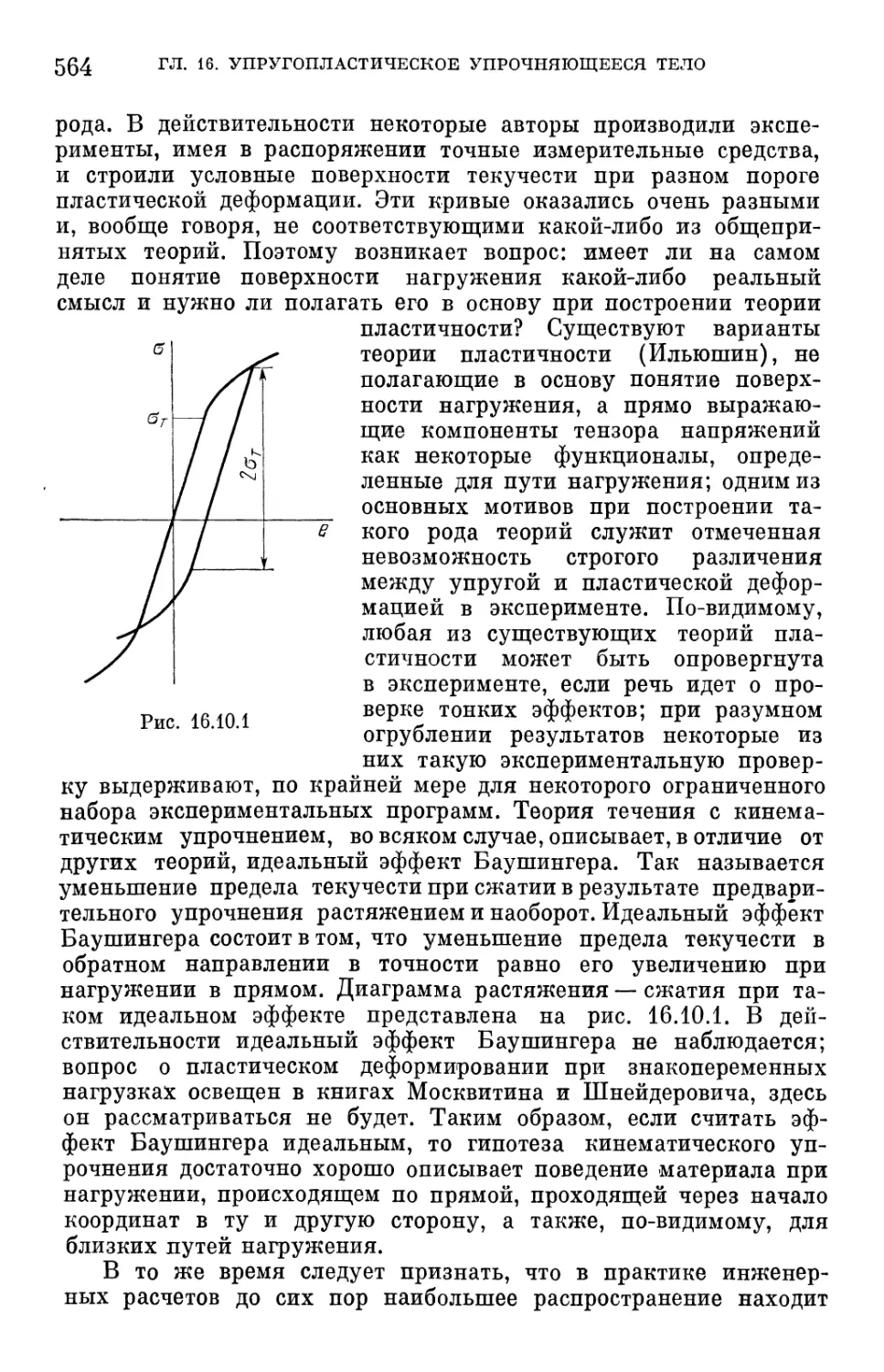
§ 16.10. Сопоставление моделей с реальностью в пластичности 563
§ 16.11. Распространение уйругопластических волн .... 565
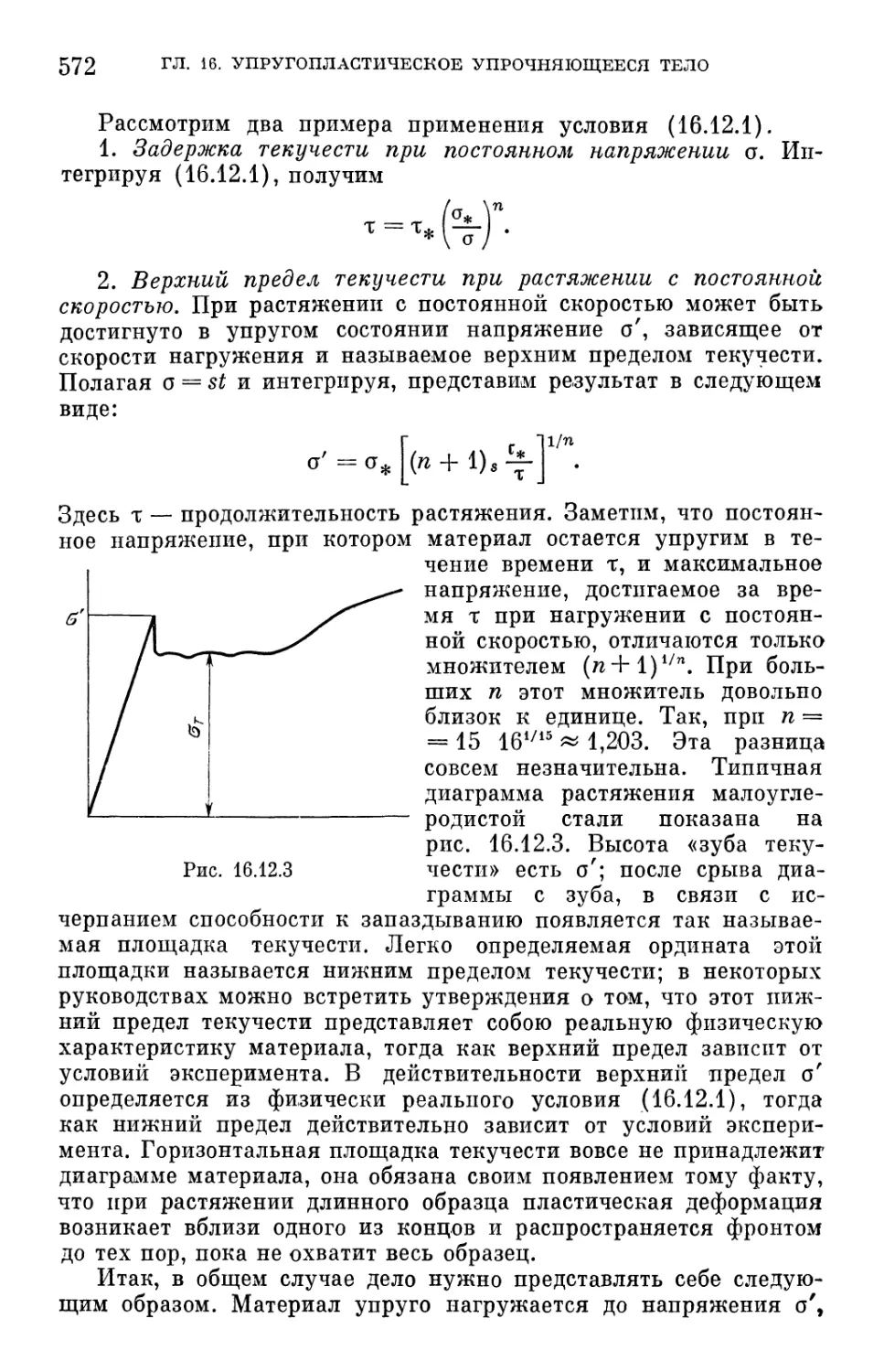
§ 16.12. Упругопластические волны. Запаздывание текучести 569
Глава 17. Наследственная теория упругости 575
§ 17.1. Линейная наследственность 575
§ 17.2. Резольвентные операторы 579
§ 17.3. Применение преобразования Лапласа 582
§ 17.4. Функции от операторов 584
§ 17.5. Линейное наследственно-упругое тело. Реологические мо-
модели 586
§ 17.6. Экспоненциальные операторы 590
§ 17.7. Наследственно-упругое тело 592
§ 17.8. Периодические нагрузки 595
§ 17.9. Принцип Вольтерра 598
§ 17.10. Устойчивость наследственно-упругих систем .... 601
§ 17.11. Вариационные принципы теории наследственной упругости 603
§ 17.12. Элементы нелинейной теории наследственности . . . 606
§ 17.13. Распространение волн в наследственно-упругом теле 608
Глава 18. Ползучесть металлов 612
§ 18.1. Испытания на ползучесть и кривые ползучести . . . 612
§ 18.2. Зависимость от напряжения и температуры .... 615
8 ОГЛАВЛЕНИЕ
§ 18.3. Кинетические уравнения ползучести * 619
§ 18.4. Простейшие теории одномерной ползучести .... 621
§ 18.5. Теория старения и расчет по изохронным кривым 624
§ 18.6. Релаксация напряжений 625
§ 18.7. Установившаяся ползучесть при сложном напряженном со-
состоянии 628
§ 18.8. Частные формы закона ползучести 632
§ 18.9. Труба под действием внутреннего давления .... 634
§ 18.10. Ползучесть вращающегося диска 636
§ 18.11. Установившаяся ползучесть пластин 639
§ 18.12. Неустановившаяся ползучесть. Изотропное упрочнение 642
§ 18.13. Устойчивость при ползучести 647
Глава 19. Механика разрушения 651
§ 19.1. Предмет механики разрушения 651
§ 19.2. Условие прочности для хрупких тел 654
§ 19.3. Хрупкое и вязкое разрушение 658
§ 19.4. Напряжения и перемещения вблизи кончика трещины 659
§ 19.5. Линейная механика разрушения 664
§ 19.6. Сила сопротивления раскрытию трещины 666
§ 19.7. Линейная модель пластической зоны 670
§ 19.8. Длительное разрушение при высоких температурах. Вяз-
Вязкое разрушение 672
§ 19.9. Хрупкое разрушение при высоких температурах . . . 675
§ 19.10. Понятие об усталостном разрушении 678
Глава 20. Механика композитов 683
§ 20.1. Композиты волокнистого строения 683
§ 20.2. Высокопрочные и высокомодульные волокна .... 636
§ 20.3. Статистическая природа прочности волокна 689
§ 20.4. Прочность пучка 693
§ 20.5. Неэффективная длина волокна в композите .... 695
§ 20.6. Однонаправленные композиты с металлической матрицей 699
§ 20.7. Композиты с полимерной матрицей 703
§ 20.8. Упругие свойства и разрушение композитов сложного стро-
строения 707
Список рекомендуемой литературы 712
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
В современной монографической и учебной литературе на-
насчитывается уже значительное количество книг по механике
сплошных сред, что с избытком покрывает требования программ
соответствующих общих курсов университетов. В то же время
имелся большой дефицит книг, специально посвященных общей
теории деформируемого твердого тела, крайне необходимых для
подготовки специалистов на университетских кафедрах соответ-
соответствующего цикла, аспирантов по специальности 01.02.04 и т. д.
Появление книги Ю. Н. Работнова по существу ликвидировало
этот дефицит, она в полной мере отвечает суммарным програм-
программам спецкурсов по указанным специальностям.
Без преувеличения можно сказать, что книга Ю. Н. Работ-
Работнова к настоящему времени является лучшей среди подобных
ей книг как у нас в стране, так и за рубежом. Впервые с еди-
единых позиций в ней дается изложение основ всех главных разде-
разделов механики деформируемого твердого тела. Книгу отличает
компактность изложения^ достигаемая за счет широкого приме-
применения таких эффективных методов исследования, как вариаци-
вариационные принципы, тензорные исчисления, теория функций комп-
комплексного переменного, интегральные преобразования и т. д. Это-
Этому также способствует и оригинальная трактовка теории на-
напряжений. Естественно, что, представляя проблему во всем ее
многообразии (стержни, пластинки, оболочки, пространственные
тела, упругость, пластичность, ползучесть, наследственность, ус-
устойчивость, колебания, распространение волн, длительная проч-
прочность, разрушение), автор сконцентрировал внимание на прин-
принципиальных вопросах. Тем не менее книга снабжена достаточно
большим количеством примеров расчета, для того чтобы читатель
мог составить представление о практических возможностях
теории.
Во многом материал книги основан на оригинальных иссле-
исследованиях автора — одного из выдающихся механиков современ-
современности. Широкая популярность недавно ушедшего от нас автора и
отмеченные выше достоинства книги привели к тому, что по ис-
истечении короткого времени после выхода в свет книга стала биб-
библиографической редкостью. Нисколько не потеряв в актуально-
актуальности, она потребовала скорейшего переиздания. Настоящее второе
издание с несущественными изменениями повторяет первое.
В. Д. Клюшников, Р. И. Мазинг
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Механика деформируемого твердого тела, как представляется
автору, должна рассматриваться как единая наука, объединяю-
объединяющая те научные дисциплины, которые по традиции излагаются
и изучаются раздельно. С другой стороны, это — именно глава
механики сплошной среды, т. е. феноменологическая теория, стре-
стремящаяся найти адекватное математическое описание совокупности
опытных фактов, устанавливаемых макроэкспериментом. Для
механики недостаточно написать определяющие уравнения, нуж-
нужно уметь их решать при данных граничных условиях и решать
возможно точно. Поэтому та картина, которую строит механик,
может иногда показаться чрезмерно упрощенной. Но механик
вынужден блуждать между Сциллой и Харибдой; с одной сторо-
стороны, его уравнения должны достаточно точно отражать действи-
действительность, с другой — быть доступными для интегрирования.
Содержание предлагаемой читателю книги состоит из глав,
материал которых практически весь излагался автором в лекциях
на механико-математическом факультете МГУ и в других уни-
университетах. Она разбита на три части. Первая из них написана
на вполне элементарном уровне. На примере простейших стержне-
стержневых систем автор стремился изложить основные идеи общей тео-
теории упругих и пластических сред. Вторая часть посвящена тео-
теории упругости и ее приложениям. Наконец третья; последняя
часть относится к проявлениям неупругости — теории пластично-
пластичности, ползучести, механике разрушения.
Автор приносит глубокую благодарность В. В. Болотину и
И. В. Гольденблатту, просмотревшим рукопись.
Советы В. В. Болотина заставили автора во многих местах
существенно переделать первоначальный текст и, как он полагает,
значительно его улучшить.
Ю. Н. Работное
ВВЕДЕНИЕ
Предлагаемая читателю книга предназначена быть учебным
пособием по дисциплине, название которой служит ее заглавием.
В технических учебных заведениях преподаются различные пред-
предметы, составляющие части механики деформируемого тела. Это —
сопротивление материалов (содержание курса не соответствует
его названию), теория упругости, теория пластичности и ряд дру-
других разделов науки, которые иногда подаются в виде дополни-
дополнительных курсов, а иногда вообще опускаются. Но в науке, как и
в практической жизни, происходит процесс переоценки ценностей.
Элементарный курс сопротивления материалов уже не удовлетво-
удовлетворяет современного инженера, во втузах иногда даются небольшие
курсы теории упругости и даже теории пластичности. Следует
заметить, что в этих курсах изложение носит нарочито элементар-
элементарный характер. Даже средняя школа стремится сейчас приучить
ученика к настоящему математическому языку и более или менее
абстрактным представлениям, свойственным современной матема-
математике. Курсы высшей математики в технической школе также
существенно приблизились к уровню науки сегодняшнего дня. По-
Поэтому чрезмерное упрощение манеры изложения кажется автору
неоправданным. Однако в этой книге автор старался не выходить
за пределы обычного втузовского курса математики, кроме от-
отдельных параграфов, которые в принципе могут быть опущены
при изучении. Сейчас нет серьезных оснований проводить резкую
границу между университетским и втузовским преподаванием,
в высшей технической школе существуют факультеты и специаль-
специальности, на которых объем сообщаемых сведений по математике
достаточен для понимания всей книги. В то же время при на-
написании ее автор имел в виду программы механико-математи-
механико-математических факультетов университетов; весь материал, содержащийся
в университетских программах по сопротивлению материалов, тео-
теории упругости и теории пластичности в книге содержится. По-
Поэтому автор надеется, что книга может послужить учебником для
университетов и учебником либо учебным пособием для учащих-
учащихся некоторых специальностей технической школы.
При написании книги необходимо было чем-то себя ограни-
ограничить. Поэтому книга не содержит расчетных методов и не может
служить руководством для практических расчетов на прочность.
Правда, в наше время никакая книга не может служить серь-
серьезным руководством такого рода; в каждой отрасли техники
накоплен свой опыт, отраженный в специфических расчетных ме-
методиках и нормах прочности. Желая представить здесь в первую
\2 ВВЕДЕНИЕ
очередь идейную сторону, автор отказался от соблазна включить
в свою книгу метод конечных элементов для решения задач тео-
теории упругости и пластичности (хотя друзья ему это настоятель-
настоятельно рекомендовали). Метод конечных элементов сейчас нашел
очень широкое применение и, вероятно, 90% выпускников ка-
кафедры теории пластичности Московского университета работают
в промышленности именно над приложениями этого метода.
На русском языке имеются многочисленные монографии,
в которых рассмотренные здесь вопросы изложены более полно
и детально, некоторые ссылки на такие монографии приводятся
в тексте, только их названия содержатся в небольшом прилагае-
прилагаемом списке литературы. Остальные упоминания о различных
результатах отдельных ученых библиографическими ссылками не
сопровождаются.
Первые шесть глав представляют собою то, что по традиции
можно было бы назвать сопротивлением материалов или эле-
элементами строительной механики. Это — механика стержней и
стержневых систем. После первой вводной главы, изучение кото-
которой рекомендуется всем, следуют две более или менее тради-
традиционно написанные главы о растяжении — сжатии и изгибе.
В гл. 4 излагается теория устойчивости стержней и стержневых
систем. Эта глава носит принципиальный характер, явление по-
потери устойчивости или выпучивания разъясняется здесь на про-
простейших примерах. Поведение более сложных объектов, например,
оболочек, доступно анализу лишь с помощью сложных и гро-
громоздких численных методов и поэтому в книге не рассматри-
рассматривается; важно отметить, что качественная картина в этих задачах
получается той же, что и в простейших примерах гл. 4. Вопрос
об устойчивости под действием следящей силы вынесен в гл. 6,
посвященную динамике стержневых систем.
В гл. 5 рассматриваются некоторые общие свойства упругих
и пластических стержневых систем. Существенно заметить, что
вариационные принципы теории упругости, ассоциированный
закон течения, свойство выпуклости поверхности нагружения для
пластической системы доказываются здесь совершенно элемен-
элементарно. Все эти теоремы будут сформулированы и доказаны
впоследствии при более общих предположениях. Автору пред-
представляется по опыту его педагогической работы, что иллюстра-
иллюстрация общих принципов на простейших примерах, где эти общие
принципы совершенно очевидны, способствует лучшему их пони-
пониманию и усвоению. Гл. 6 посвящена теории колебаний, которая
должна занять подобающее место как во втузовских, так и в
университетских программах. Кроме собственно задач о колеба-
колебаниях здесь излагается метод характеристик для решения задач
о продольных волнах в стержнях. Этот метод настолько прост
и ясен, что им можно пользоваться и его легко понять, не про-
прослушав общего курса дифференциальных уравнений математи-
ВВЕДЕНИЕ 13
ческой физики. Таким образом, материал первых шести глав
вполне доступен студенту второго курса университета или
втуза.
Следующий концентр связан с теорией упругости. В гл. 7
сообщаются элементы тензорного анализа в виде сводки основ-
основных фактов и определений. Автору представляется, что для прак-
практических целей достаточно (и вполне строго) вести изложение
общих теорем в прямоугольной декартовой системе координат.
В § 7.8, где идет речь о криволинейных координатах, говорится
о задании тензора в произвольном базисе, но эта теория даль-
дальнейшего развития не находит. Что касается тензорного языка,
который применен в гл. 7 и последующих главах, он совершенно
элементарен. Для университетов он привычен и упрощен по
сравнению с тем, что дается, скажем, в курсе дифференциальной
геометрии. Для студента втуза привыкнуть к этому языку очень
нетрудно. Автор вспоминает, как в начале тридцатых годов сре-
среди преподавателей теоретической механики шли ожесточенные
споры о том, следует ли излагать механику векторно или же
в координатах. Любопытно отметить, что акад. А. Н. Крылов
был яростным и убежденным противником векторной символики,
которая вводилась Московской школой. Автор получил воспи-
воспитание в этой школе, поэтому он особенно рад торжеству век-
векторного изложения теоретической механики и надеется, что в
учебной литературе по механике твердого тела тензорный язык
будет применяться широко и на всех уровнях.
После этого раздела следуют гл. 8—11, относящиеся к клас-
классической теории упругости. После некоторых колебаний автор
решил все же включить сюда раздел, относящийся к теории
конечных деформаций, область применения этой теории слишком
ограничена и имеющиеся решения крайне немногочисленны.
Подобранный материал в основном соответствует университетской
программе. Преподаватель всегда сможет выбрать отсюда те раз-
разделы, которые покажутся ему более интересными. В практике
преподавания теории упругости на механико-математическом
факультете МГУ автор отказался от изложения теории изгиба
Сен-Венана, считая, что вопрос о распределении касательных
напряжений при изгибе не очень важен. Однако появление ком-
композитных материалов с полимерной матрицей, которые слабо
сопротивляются сдвигу, заставило ввести опять теорию касатель-
касательных напряжений при изгибе для балок прямоугольного сече-
сечения — что нужно для практики. Вообще, применение в технике
композитных материалов заставило включить в курс элементы
теории упругости анизотропных тел.
Если в старых курсах теории упругости основной задачей
теории выдвигалось обоснование приближенных методов сопро-
сопротивления материалов, сейчас мы не можем стоять на этой точке
зрения. Действительный интерес представляют именно те задачи,
14 ВВЕДЕНИЕ
которые принципиально не могут быть решены элементарными
средствами. В последние годы сингулярные решения задач тео-
теории упругости приобрели новую жизнь, теория дислокаций, т. е.
распределенных вдоль линии особенностей, порождающих неод-
неоднозначное поле перемещений, позволила удачно и довольно точно
моделировать дефекты реальной кристаллической решетки, бла-
благодаря которым кристаллы получают возможность пластически
деформироваться. Поэтому элементы теории дислокаций вкрап-
вкраплены и в главу об антиплоском напряженном состоянии, и в
главы о плоской и пространственной задачах теории упругости.
Так же обстоит дело с теорией трещин или разрезов. При рас-
распространении трещины освобождается упругая энергия, которая
расходуется либо на увеличение поверхностной энергии трещи-
трещины, либо на производство работы пластической деформации в
концевой зоне. Эти факты лежат в основе так называемой ли-
линейной механики разрушения.
Предметом гл. 12 служит то, что принято называть приклад-
прикладной теорией упругости — стержни, пластины и оболочки. Общие
пропорции курса не позволили уделить этим важным техниче-
техническим объектам много места, да вряд ли это было бы целесооб-
целесообразно. Для практических расчетов следует обращаться к специ-
специальной литературе, изобилующей длинными формулами, табли-
таблицами и графиками. Общая точка зрения, проводимая в данной
главе, состояла в том, чтобы получать во всех случаях основные
уравнения с помощью единообразного приема, а именно отправ-
отправляясь от вариационных принципов.
Гл. 14, посвященная теории дислокаций, ни в какой мере
не относится к физике твердого тела, где эта теория находит
приложения. Это — иллюстрация методов теории упругости, дис-
дислокации предполагаются помещенными в однородную изотропную
сплошную среду. Автор предвидит возможную критику его за
то, что материал, помещенный в этой главе, соответствует со-
состоянию теории примерно в 50-х годах. Но в теории упругих
дислокаций после этого сделано не так уж много. Автору приш-
пришлось решительно противостоять соблазну изложить здесь кон-
континуальную теорию дислокаций, это завело бы его, пожалуй,
слишком далеко.
Теория пластичности излагается в двух главах, в гл. 15 —
теория идеальной пластичности, в следующей гл. 16 — теория
упрочняющихся пластических материалов. Если теория предель-
предельного равновесия пластических тел замкнута в себе, опирается
на ряд строго доказанных теорем и располагает точными мето-
методами, теория упрочняющегося пластического тела имеет еще
довольно расплывчатые контуры, предмет ее — скорее обсужде-
обсуждение и сравнение некоторых гипотез и формулировка некоторых
принципов довольно общего характера. Читатель заметит эту
разницу, объясняемую существом дела.
ВВЕДЕНИЕ 15
Наследственная теория упругости и теория ползучести метал-
металлов при высоких температурах описывают сходные внешне яв-
явления совершенно различными средствами. Как по первому, так
и по второму предмету автору принадлежат отдельные моно-
монографии довольно большого объема, поэтому выбор минимума
материала для этих глав представил определенные субъективные
трудности.
Гл. 19 относится к механике разрушения. В современной ли-
литературе часто под механикой разрушения понимается один уз-
узкий ее раздел, а именно теория распространения трещин хруп-
хрупкого и квазихрупкого разрушения. Весь формальный аппарат
для этого подготовлен ранее, поэтому здесь дается лишь неко-
некоторая сводка известных уже читателю результатов и практиче-
практические выводы из них. Большая же часть главы относится к
условиям прочности хрупких материалов, теории накопления
повреждений при длительном действии нагрузок при высоких
температурах. Здесь же сообщены краткие сведения об устало-
усталостном разрушении. Автор полагает, что вопросы прочности как
в принципиальном, так и в прикладном аспекте составляют не-
необходимый элемент образования механика-универсанта и меха-
механика-инженера, и сознает совершенно недостаточный объем из-
излагаемого им материала, но в заглавии книги фигурирует только
слово «механика», но не «прочность», не «расчеты», не «сопро-
«сопротивление материалов».
Наконец, в последней, двадцатой главе излагаются основы
теории высокопрочных композитных материалов волокнистого
строения, нашедших применение в последние годы. Эта теория
еще далека от завершения, что, вероятно, почувствует читатель.
Автор считал бы полезным дать физическое введение или
послесловие, вероятно именно послесловие, поскольку о физиче-
физических теориях и фактах нужно говорить на достаточно развитом
механическом и математическом языке. Но ограниченность объ-
объема книги не позволила сделать это.
В современной литературе по механике сплошной среды часто
излагается общая теория построения определяющих уравнений
для разного рода сред, причем подход к этому у разных ученых
различен. В данной книге обсуждаются лишь простейшие модели
и простейшие виды определяющих уравнений, относящиеся к
таким материалам и таким процессам, которые изучены доста-
достаточно хорошо экспериментально. Обсуждение наряду с реальны-
реальными моделями всего многообразия возможных мыслимых моделей
деформируемого твердого тела в рамках этого курса казалось
автору неуместным, хотя это отнюдь не означает отрицательного
его отношения к подобного рода попыткам вообще.
ЧАСТЬ I
СТЕРЖНЕВЫЕ СИСТЕМЫ
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ
§ 1.1. Предмет механики деформируемого твердого тела
Механика твердого тела, будучи одной из глав общей меха-
механики, изучает движение реальных твердых тел. Различие между
твердыми телами, с одной стороны, жидкостями — с другой,
иногда кажется интуитивно ясным (например, сталь и вода),
иногда отчетливую границу провести бывает трудно. Лед пред-
представляет собою твердое тело, однако ледники медленно сползают
с гор в долины подобно жидкости. При прокатке раскаленного
металлического листа между валками прокатного стана металл
находится в состоянии пластического течения и термин «твердое
тело» по отношению к нему носит довольно условный характер.
Неясно также, следует ли отнести к жидким или твердым телам
такие вещества, как вар, битум, консистентные смазки, морской
и озерный ил и т. д. Поэтому дать определение того, что назы-
называется твердым телом затруднительно, да пожалуй и невозмож-
невозможно. В последние годы наблюдается определенная тенденция к
аксиоматическому построению механики без всякой апелляции
к интуиции и так называемому «здравому смыслу». Таким обра-
образом, вводятся различные модели, иногда чисто гипотетические,
иногда отражающие основные черты поведения тех или иных
реальных тел и пренебрегающие второстепенными подробностями.
Для таких моделей можно установить некоторый формальный
принцип классификации, позволяющий отделить модели жидко-
жидкостей от моделей твердых тел, но эта классификация отправляется
от свойств уравнений, но не тел как таковых. Поэтому термин
«механика твердого тела» будет относиться скорее к методу ис-
исследования, чем к его объекту.
Свойства тел, окружающих нас/<в природе и создаваемых
техникой, весьма разнообразны и механика подменяет реальные
тела некоторыми идеализированными объектами, «механическими
моделями». В этой книге мы не будем следовать аксиоматиче-
аксиоматическому методу рассуждений и не будем пренебрегать соображе-
соображениями, основанными на интуиции, точнее на обобщении резуль-
§ 1.1. ПРЕДМЕТ МЕХАНИКИ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА fj
татов опыта, как повседневного, который обобщается более или
менее бессознательно (это мы и называем интуицией), так и
специального, преднамеренно запланированного.
Механика изучает движения, вызванные силами; механиче-
механическими средствами могут быть измерены только силы, вызываю-
вызывающие движение, и кинематические характеристики движения, т. е.
перемещения или изменения во времени некоторых длин. По-
Поэтому в определении модели должны фигурировать только силы
и кинематические характеристики движения; поведение модели
описывается с помощью уравнений, которые называют определя-
определяющими уравнениями. Механические теории, как праавило, носят
феноменологический характер; это значит, что в основу их пола>
гаются факты опытного происхождения; притом факты, добытые
в результате так называемого макроэксперимента, т. е. такого
эксперимента, в ходе которого измеряются только механические
величины, непосредственно входящие в определяющие уравнения:
силы и перемещения. Но при действии сил в структурных эле-
элементах тела происходят внутренние процессы, о которых можно
судить, применяя различные физические методы исследования,
например, наблюдая в оптический или электронный микроскоп,
измеряя электрическое сопротивление и т. д. Эти внутренние
процессы существенно определяют поведение материала, но изу-
изучение их служит предметом физики, а не механики. Однако
понимание физики процесса бывает полезным и для механиков,
иногда физические соображения подсказывают выбор наиболее
адекватной механической модели, они позволяют во многих слу-
случаях судить о пределах применимости тех или иных определяю-
определяющих уравнений, относящихся к данному материалу; если име-
имеются признаки того, что физический механизм деформирования
изменился, можно ожидать, что и определяющие уравнения дан-
данного типа перестают быть справедливыми. Величины, которые
измеряются не механическими, а физическими средствами, могут
фигурировать и в определяющих уравнениях, но роль их сво-
сводится к роли вспомогательных параметров, которые в принципе
могут быть исключены; для построения механической теории
данные макроэксперимента достаточны, тоща как обращение к
физике полезно лишь в качестве наводящего соображения. По-
Подобно тому как геометрия содержит в своей основе элементар-
элементарные опытные факты и результаты повседневных наблюдений,
которые резюмируются в виде систем аксиом и вытекающих из
них теорем, механика также допускает аксиоматическое построе-
построение и в этом смысле может рассматриваться как часть мате-
математики. Такая точка зрения не будет развиваться в данной кни-
книге, представляющей собою относительно элементарное руковод-
руководство, тем не менее автор хочет подчеркнуть, что он не разделяет
мнение тех, которые считают механику одним из разделов
физики.
2 Ю. Н. Работнов
18 гл. i. основные понятия
Развитие механики твердого тела в значительной степени свя-
связано с практическими целями — расчетом частей сооружений и
машин на прочность. Учебная дисциплина, излагающая способы
таких расчетов и преподаваемая в технической школе, называется
сопротивлением материалов. Содержание соответствующего курса
определяется тем уровнем и запасом сведений, который считается
в данное время необходимым для практической работы инженера.
Термин «сопротивление материалов» неточен, в соответствующем
курсе обычно больше внимания уделяется методам расчета про-
простейших элементов конструкций, чем свойствам собственно ма-
материалов и их сопротивлению действию приложенных сил.
Более точные и строгие методы, позволяющие производить
подобного рода расчеты, изучаются специальными научными
дисциплинами, которые носят название теории упругости, теории
пластичности, теории ползучести, вязкоупругости, механики раз-
разрушения и т. д. Более правильно рассматривать их не как от-
отдельные науки, а как ветви или главы механики деформируемо-
деформируемого твердого тела. Эта точка зрения и будет проведена в настоя-
настоящей книге.
Выше был употреблен термин «прочность», который требует
некоторого пояснения. В широком смысле слова под нарушением
прочности мы будем понимать достижение такого состояния, ког-
когда нарушается конструктивная функция изделия, когда оно ста-
становится непригодным для эксплуатации. В прямом и более уз-
узком смысле слава под нарушением прочности понимается раз-
разделение тела на части. Здеь термин «прочность» будет понимать-
пониматься как в том, так и в другом смысле, каждый раз с соответ-
соответствующими оговорками.
Последнее замечание будет относиться к области применения
механики деформируемого твердого тела. Хотя подавляющее
большинство исследований в этой области так или иначе свя-
связано с проблемой прочности, методы нашей науки используются,
например, в геофизике при изучении распространения сейсми-
сейсмических волн, построении моделей формирования земной коры и
рассмотрении других задач. В современной физике твердого тела
большую роль играет изучение дефектов кристаллической решет-
решетки. Строение этих дефектов часто оказывается возможным опи-
описать в терминах механики и наиболее пожалуй интересные ре-
результаты последних лет в области теории упругости относятся
именно к физике кристаллов.
§ 1.2. Сплошная среда
В основе механики лежат законы движения, открытые Ньюто-
Ньютоном и справедливые для любых материальных тел. Механика
относительности лишь уточняет законы Ньютона, эти уточнения,
существенны при очень больших скоростях, приближающихся к
§ 1.2. СПЛОШНАЯ СРЕДА 19
скорости света. При изучении движения реальных твердых тел
приближение ньютонианской механики вполне достаточно и мы
в дальнейшем ограничимся этими рамками. Заметим, что в так
называемой теории магнитоупругости рассматриваются одновре-
одновременно связанная система уравнений электродинамики и теории
упругости. Уравнения Максвелла и уравнения обычной теорип
упругости инвариантны относительно различных групп преоб-
преобразований, поэтому теория получается более стройной и логич-
логичной, если использовать в ней уравнения релятивистской теории
упругости. Практически, конечно, па результатах решения задач
эти уточнения не сказываются. Для построения конкретных ме-
механических теорий необходимо сделать следующий шаг — опре-
определить изучаемый объект. В курсах теоретической механики вво-
вводится понятие материальной точки как некоторого простейшего
идеального, т. е. не существующего в природе объекта. Матери-
Материальная точка имеет массу, но не имеет размеров, что абсурдно.
Тем не менее понятие материальной точки оказывается доста-
достаточным для решения целого ряда вопросов. Например, при изу-
изучении движения планет вокруг Солнца вполне достаточно счи-
считать как Солнце, так и планеты материальными точками, рас-
расстояния между планетами и Солнцем чрезвычайно велики по
сравнению с размерами самих небесных тел.
Общие теоремы механики формулируются для системы мате-
материальных точек, связанных силами взаимодействия или подчи-
подчиненных геометрическим связям. Простейшую систему представ-
представляет собою так называемое абсолютно твердое тело, т. е. система
конечного или бесконечно большого числа материальных точек,
расстояния между которыми остаются неизменными. После того
как наложено столь жесткое кинематическое ограничение, вопрос
о природе сил взаимодействия между точками, составляющими
твердое тело, уже не возникает, эти взаимодействия не могут
быть измерены никаким способом, они совершенно не влияют
на характер движения тела. Продолжая тот же путь рассужде-
рассуждений, можно представить себе реальное твердое тело или жид-
жидкость как систему весьма большого числа материальных точек,
взаимодействующих между собою определенным образом. Физи-
Физическая точка зрения будет состоять в том, чтобы приписывать
этим материальным точкам определенную индивидуальность,
отождествляя их с реальными атомами и молекулами. Просле-
Проследить за движением каждой физической точки совершенно невоз-
невозможно, так как число их слишком велико, поэтому, даже если
принять за отправной пункт представление об атомном строении
и об определенных законах междуатомного взаимодействия, все
равно приходится вводить некоторые осредненные характеристи-
характеристики, описывающие движение атомов и действующие между ними
силы, отказываясь от рассмотрения каждого атома в отдельности.
Методы статистической физики хорошо развиты применительно'
2*
20 гл- *• основные понятия
к простейшим системам материальных частиц, а именно к газам.
Для твердых тел получение эффективных результатов в этом на-
направлении всегда связано с дополнительными гипотезами. С дру-
другой стороны, закон Бойля — Мариотта был известен задолго до
создания кинетической теории газов как эмпирический закон,
выведенный из прямого опыта. Механические опыты в принци-
принципе производятся наблюдателем, который вооружен лишь собст-
собственным глазом и простейшими инструментами. Для невооружен-
невооруженного глаза все тела представляются сплошными, для макроско-
макроскопического описания движения тел сведения об их атомной и
молекулярной структуре совершенно не нужны. Поэтому в ме-
механике реальное твердое тело заменяется воображаемой, модель-
модельной сплошной средой. Среда называется сплошной, если любой
объем, выделенный из нее, содержит вещество, т. е. имеет массу.
Ясно, что представление о сплошной среде противоречит пред-
представлению об атомном строении вещества. Действительно, если
объемы достаточно малые, то в одном объеме может оказаться
атом, другой будет находиться в пространстве между атомами,
значит не будет содержать в себе ничего, имеющего массу.
Представление о сплошной среде до чрезвычайности упрощает
математическое описание движения тел. Так, если считать, что
среда, заполняющая в данный момент некоторый объем, пред-
представляет собой жидкость, то это значит, что каждая точка с ко-
координатами Xi принадлежит жидкости; выделяя вокруг этой точки
сколь угодно малый объем, мы найдем, что этот объем будет
содержать в себе материю, т. е. жидкость. Можно считать точку
М фиксированной точкой пространства, тогда в ней задан век-
вектор скорости I?, той скорости, которую приобретает малый объем,
окружающий эту точку в момент времени t. При этом нас со-
совершенно не смущает то, что на самом деле в момент времени t
точка может принадлежать пустому пространству. Более того,
если в точке находится атом, скорость его фактического движе-
движения нельзя отождествлять со скоростью жидкости в точке.
Атомы совершают беспорядочные движения и тоща, когда
жидкость считается находящейся в покое. Это — тепловые дви-
движения. Сами по себе тепловые движения атомов механику не
интересуют, однако температура, служащая мерой этих беспоря-
беспорядочных движений, может фигурировать в определяющих урав-
уравнениях механических теорий. Скорости сплошной среды, заме-
заменяющей реальное тело, это — некоторые осредненные скорости,
которые определяют наблюдаемые перемещения объемов. Анало-
Аналогичное положение возникает в твердых телах. Узлы кристалли-
кристаллической решетки представляют собою положения равновесия для
образующих решетку атомов, которые колеблются около этих
положений равновесия, однако средние расстояния между атома-
атомами остаются почти постоянными, и атомы лишь изредка поки-
покидают свои узлы решетки. При приложении нагрузки средние
§ 1.3. ОДНОРОДНАЯ СРЕДА 21
расстояния между атомами меняются, это изменение определяет
видимую деформацию кристалла; только эта видимая деформа-
деформация и представляет интерес для механики. Однако макроскопи-
макроскопические свойства кристалла зависят от температуры, которая оп-
определяется кинетической энергией колебательного движения ато-
атомов; таким образом, эти движения тоже учитываются в механике,
только учитываются косвенным образом, через посредство ска-
скалярной интегральной характеристики.
§ 1.3. Однородная среда
Среда называется однородной, если свойства выделенных из
нее одинаковых объемов одинаковы. Очевидно, речь здесь идет
о тех свойствах, которые доступны определению средствами ме-
механического эксперимента. Говоря о неоднородности или одно-
однородности, необходимо уточнить, о каком масштабе идет речь.
Введя представление о сплошной среде, мы
уже допустили однородность на уровне разме-
размера, порядка атомного. Обычный металл или
сплав состоит из кристаллических зерен, т. е.
кристаллов неправильной огранки, ориентиро-
ориентированных случайно, самым различным образом.
Выделяя малые элементы из поликристалли-
поликристаллического металла, мы можем оказаться в зер-
зерне одной ориентации, зерне другой ориентации,
на границе двух зерен, на стыке трех зерен
(рис. 1.3.1). Очевидно, что свойства этих объ-
объемов будут различными, металл неоднороден
на уровне размеров зерен. У технических спла- Рис. 1.3.1
вов размер зерен составляет сотые доли милли-
миллиметра, он мал по сравнению с размерами изделий из этих спла-
сплавов. Поэтому наличие микронеоднородности не влияет на пове-
поведение металла в изделии, и металл считают однородной сплош-
сплошной средой. Многие сплавы состоят из кристаллических зерен,
имеющих разный химический состав и разное строение, внутри
зерен и на границах между ними могут возникать включения
из материала иной природы. Тем не менее подобный сплав рас-
рассматривается как однородная сплошная среда. Может возник-
возникнуть другой вопрос. Предположим, что нам известны свойства
всех составляющих поликристаллической структуры и имеются
Данные об их распределении. Требуется определить свойства
композиции. Эта задача принадлежит механике, поскольку ко-
конечная цель состоит в построении модели сплошного однородного
тела со свойствами, эквивалентными свойствам неоднородного
тела, имеющего заданное строение.
Существуют неоднородные материалы с большим масштабом
неоднородности, например, бетон. Но и изделия из таких мате-
22 гл. i. основные понятия
риалов обычно имеют размеры, по сравнению с которыми раз-
размеры структурных элементов пренебрежимо малы.
Представление об однородности среды необходимо для меха-
механической теории, хотя некоторые ограничения в этом направле-
направлении могут быть сняты. Представим себе, например, пластинку
из биметалла: медь сварена со сталью, па одной стороне свойства
одни, на другой — другие. Такого рода задачи, когда свойства
меняются внезапно и остаются постоянными в довольно больших
объемах, принципиальных трудностей не представляют. Свойства
материала могут меняться по объему и непрерывным образом.
Простейший пример представляет собою неравномерно нагретое
тело. Свойства материала зависят от температуры, которая рас-
распределена по объему непрерывньш образом (или с конечным
числом разрывов). Существенно неоднородны так называемые
композитные материалы, например полимерная смола, переме-
перемешанная с рубленым стеклянным волокном. Но в механике та-
такого рода неоднородная среда заменяется эквивалентной одно-
однородной.
§ 1.4. Кинематическое описание сплошной среды
Понятие сплошной среды не так просто, как может пока-
показаться на первый взгляд и как это казалось подавляющему
большинству ученых в XIX и первой половине XX столетий.
Оказывается, что можно строить разные модели сплошной среды,
наделяя их разными свойствами. Простейшая модель, которую
мы будем называть классической моделью, вводится следующим
образом. Примем за основное первичное понятие материальную
точку. В кинематике это понятие тождественно с понятием гео-
геометрической точки. Можно представить себе точку как сферу
бесконечно малого радиуса. При стремлении радиуса к нулю
единственной величиной, индивидуализирующей точку, остается
радиус-вектор центра сферы или три числа — координаты точки.
Представляя себе некоторую замкнутую область пространства
непрерывно заполненной точками, мы получим модель сплошной
среды. Пусть xi0 — координаты некоторой точки в момент вре-
времени t0. При движении среды координаты данной точки ме-
меняются, в момент t они принимают значения хг(г). Движение
среды полиостью задано, если функции x{(t) для каждой инди-
индивидуальной точки известны. Именно так определяется кинема-
кинематика классической модели сплошной среды. До недавнего вре-
времени эта модель была единственной, на основе ее строились все
механические теории. Но можно представить себе и иные сплош-
сплошные среды, наделенные некоторой внутренней структурой. Будем
рассматривать, например, материальную точку как бесконечно
малый эллипсоид. Устремляя его размеры к нулю и сохраняя
при этом направления главных осей, мы получим среду, с каж-
§ 1.4. КИНЕМАТИЧЕСКОЕ ОПИСАНИЕ СПЛОШНОЙ СРЕДЫ 23
дой точкой которой неизменно связан ортогональный триэдр.
Для индивидуализации точки такого рода нужно задать не толь-
только ее координаты, но и направления осей триэдра, скажем —
эйлеровы углы. Кинематика такой среды строится более слож-
сложным образом, она определяется заданием не только перемещений
точек, но также и поворотов связанных с ними триэдров.
Если считать, что силы взаимодействия между атомами на-
направлены по прямым, соединяющим их центры (гипотеза цент-
центральных сил), то в уравнениях равновесия атомной решетки
будут фигурировать только координаты атомов, но не углы их
собственных вращении. Считая число атомов очень большим,
а расстояния между ними очень малыми, мы можем получить
отсюда закон упругости для сплошной среды, притом для среды,
соответствующей классической модели. Такие вычисления дей-
действительно производились, однако точные законы междуатомного
взаимодействия неизвестны и непосредственно установить их
нельзя. Поэтому в основу анализа приходится полагать более
или менее правдоподобные гипотезы.
Для целей механики происхождение закона упругости без-
безразлично, его можно рассматривать как эмпирический закон,
устанавливаемый на основе макроэксперимента, можно постули-
постулировать или принимать за определение некоторого воображаемого
объекта, который в силу неизвестных и счастливых обстоятельств
ведет себя почти так же, как многие материалы, встречающиеся
в природе. Сведения о строении кристаллической решетки тем
не менее оказываются полезными, они подсказывают соображе-
соображения о симметрии упругих свойств и позволяют вследствие этого
сократить число необходимых макроэкспериментов, а также спла-
спланировать их наиболее рациональным образом.
Взаимодействие молекул не всегда сводится к центральным
силам, хотя бы потому, что положительные и отрицательные
заряды размещены в молекуле определенным образом. Поэтому
кроме сил появляются еще моменты, стремящиеся повернуть мо-
молекулы. Адекватная модель сплошной среды, принимающая во
внимание вращательные взаимодействия, должна строиться из
ориентированных точек и для полного кинематического описания
движения такой среды наряду с перемещениями необходимо
задавать собственные вращения. Теории сплошной среды такого
типа называются моментными теориями.
Можно пойти еще дальше по пути усложнения модели и свя-
связать с каждой точкой среды еще некоторый набор кинематиче-
кинематических характеристик, изменения которых можно трактовать как
обобщенные перемещения. Им соответствуют обобщенные силы —
множители в выражении для работы. В последнее время по-
появилось много работ в указанном направлении (так называемая
микрополярная теория упругости, например). Теории такого ти-
ла еще не нашли больших практических приложений.
24 гл. i. основные понятия
§ 1.5. Внешние силы
Понятие о силе вводится в механике как первичное понятие.
Предполагается, что сила полностью определена, если задан со-
соответствующий вектор, при этом определение того, что такое век-
вектор, относится целиком к области математики. Но здесь следует
подчеркнуть, что понятие силы неразрывно связано с представ-
представлением о том объекте, на который сила действует. В действи-
действительности так называемых сосредоточенных сил, т. е. сил, при-
приложенных к точке, не существует. В теоретической механике
изучается движение материальной точки под действием сил —
векторов, но материальная точка это воображаемый объект,
абстракция.
Далее вводится понятие об абсолютно жестком теле. При
контакте двух жестких тел контакт происходит, вообще говоря,
в одной точке (если поверхности выпуклы, например). При кон-
контакте реальных твердых тел они деформируются в области кон-
контакта и образуется площадка контакта конечных размеров. На
этой площадке давление распределено непрерывным образом.
Силу тяжести считают приложенной в центре тяжести тела, но
в действительности эта сила распределена непрерывным образом
по объему, ее приводят к центру тяжести на основании теорем
статики об эквивалентности, теорем, которые справедливы только
для абсолютно жестких тел.
Возвращаясь к примеру контакта двух твердых тел, заметим,
что у достаточно прочных материалов, применяемых в технике,
размеры площадки контакта оказываются, как правило, малы
по сравнению с размерами тела. Поэтому представление о со-
сосредоточенной силе давления одного тела на другое не совсем
бессмысленно. Когда рассматривается состояние тела на доста-
достаточно большом расстоянии от площадки контакта, бывает доста-
достаточно пренебрегать ее размерами и считать давление сосредото-
сосредоточенным; в окрестности области контакта замена распределенного
давления сосредоточенной силой приводит к серьезным ошибкам.
Приведенные рассуждения о непрерывно распределенном давле-
давлении на площадке контакта, о силе тяжести, непрерывно распре-
распределенной по объему, опять-таки относятся не к реальному телу,
а к сплошной среде в том смысле, в каком было определено
это понятие выше. Можно, конечно, сказать, что в действитель-
действительности при контакте двух тел вступают в действие силы оттал-
отталкивания между атомами. Таким образом, вместо непрерывно
распределенного давления мы получим опять-таки систему со-
сосредоточенных сил, число которых неизмеримо велико. Но такое
представление будет опять-таки лишь грубым приближением к
действительности; рассматривая силы междуатомного взаимодей-
взаимодействия как силы, действующие на материальные точки, мы отвле-
§ 1.5. ВНЕШНИЕ СИЛЫ
25
каемся от реального строения атома и от квантово-механическо-
го характера межатомных взаимодействий. Отчасти по этой при-
причине мы остановимся на представлении о материи как о сплош-
сплошной среде и не будем делать дальнейших шагов.
Чтобы избежать затруднений, связанных с неоднозначностью
понятия силы, было бы более естественно принять за отправной
пункт представление о работе и ввести обобщенные силы как
множители при обобщенных перемещениях в выражении работы.
Теперь система сил, действующих на тело, будет целиком опре-
определяться заданием кинематики и, следовательно, моделью среды.
Однако наглядные представления, связанные с изображением сил
в виде векторов, сохраняют определенные преимущества, хотя
бы потому, что они привычны. Эти представления с известными
ограничениями пригодны и в механике деформируемого твердо-
твердого тела.
Теоремы геометрической статики формулируются примени-
применительно к абсолютно твердому телу или системе таких тел. Рас-
Распространение этих теорем на деформируемое твердое тело выте-
вытекает из принципа отвердения, утверждающего, что равновесие
б) В)
V////A 'Л
I
I
Ю
S)
\*в у
ZP
Рис. 1.5.1
IP
Рис. .1.5.2
механической системы не нарушается от наложения дополнитель-
дополнительных связей. Рассматривая деформируемое твердое тело как ме-
механическую систему, мы постулируем справедливость для него
принципа отвердения. В частности, равновесие тела не нарушит-
нарушится, если мы предположим, что оно сделалось абсолютно жестким.
В геометрической статике утверждается, что силу можно пере-
переносить вдоль линии ее действия (сила есть скользящий вектор).
Недопустимость такого переноса иллюстрируется примером, изо-
изображенным на рис. 1.5.1. В случае а весь стержень растяги-
растягивается силой Р, в случае б растягивается лишь заштрихованная
часть, в случае в стержень вообще не растягивается, сила при-
26 гл. i. основные понятия
ложена к месту заделки. Но реакция заделки во всех трех слу-
случаях одинакова, она равна приложенной силе и направлена в
противоположную сторону; для нахождения реакции нужно со-
составить уравнение равновесия так, как если бы стержень был
абсолютно жестким.
На рис. 1.5.2, а изображена балка, лежащая на трех опо-
опорах и нагруженная двумя одинаковыми силами в серединах про-
пролетов. Реакции опор будут RA, BB, /?с. Под действием сил балка
слегка прогнется, как показано на чертеже. Согласно принципу
отвердения равновесие системы не нарушится, если на нее нала-
налагаются дополнительные связи. Значит, мы имеем право пред-
предположить, что изогнутая балка стала абсолютно жесткой и со-
составить для нее обычные уравнения статики. Получим
Ra + Rb + Rc = 2Р, Ra = Re A.5.1)
Для нахождения трех реакций мы имеем только два уравнения
статики. Задачи такого рода называются статически неопреде-
неопределенными, а системы, подобные изображенной на рис. 1.5.2 —
статически неопределимыми. Третье, недостающее уравнение
должно быть получено из других соображений, связанных с оп-
определенными предположениями о свойствах того материала, из
которого изготовлена балка.
Заметим, что уравнения статики не изменяются, если заме-
заменить систему сил статически эквивалентной. Для случаев, изо-
изображенных на рис. 1.5.2,6 и 1.5.2, в, уравнения статики A.5.1)
сохраняются. Но совершенно очевидно, что независимо от при-
природы материала балки в случае б нагрузка будет воспринимать-
восприниматься крайними опорами и мы найдем
Ra = Re = Р, Rb — 0.
В случае в вся нагрузка воспринимается средней опорой и ре-
решение, удовлетворяющее уравнениям статики A.5.1), а также
требованиям элементарного здравого смысла, будет
Для случая а соображений, основанных на здравом смысле, не-
недостаточно. Для упругой балки метод решения будет изложен
в гл. 3, результат получается следующий:
Ra = Bc=±P, Rb-Щ-Р.
Как показывается в статике, любая система сил, действующих
на абсолютно твердое тело, эквивалентна одной силе и одной
паре сил (главный вектор и главный момент). Если система сил,
приложенная на малом участке поверхности, заменяется главным
вектором и главным моментом, мы вводим тем самым понятие
§ 1.6. ПРИНЦИП СЕН-ВЕНАНА 27
о сосредоточенном моменте, приложенном в точке. Это понятие
совершенно чуждо для статики твердого тела, где подчеркивает-
подчеркивается, что момент есть свободный век-
вектор и его можно переносить парал-
параллельно себе как угодно. Ограниче-
Ограничения, связанные с введением понятия
о сосредоточенной силе и сосредото-
сосредоточенном моменте в механику дефор-
деформируемого твердого тела, можно по-
пояснить на следующем примере.
Представим себе массивную балку,
к концу которой прикреплен стер-
стержень. На конце стержня приложена Рис. 1.5.3
сила, как это показано на рис. 1.5.3.
Перенесем силу в центр торцевого сечения балки. На основании
правил статики при этом появится момент, который мы считаем
приложенным в той же точке, что и сила.
§ 1.6. Принцип Сен-Венана
и статически эквивалентные системы сил
Результаты многочисленных точных и приближенных реше-
решений убеждают в том, что фактический способ приложения силы
и момента к концу стержня сказывается лишь в непосредствен-
непосредственной близости к этому концу. В данном случае это означает, что
если нас интересуют прогибы и удлинение балки в целом, нам
нет необходимости детально анализировать реальную ситуацию,
изображенную на рис. 1.5.3, а, при расчетах достаточно исходить
из упрощенной схемы, представленной на рис. 1.5.3, б, которая
носит совершенно условный характер, поскольку ни сосредото-
сосредоточенных сил, ни сосредоточенных (моментов не существует. Об-
Область, в которой сказывается фактический способ приложения
нагрузки, заштрихована на рисунке, границы этой области тоже
условны; вне ее состояния, соответствующие статически эквива-
эквивалентным нагрузкам, отличаются достаточно мало. Что значат сло-
слова «достаточно мало», мы пока не уточняем. Высказанное пра-
правило носит название принципа Сен-Венана, довольно расплывча-
расплывчатая формулировка связана с тем, что этот принцип не доказы-
доказывается для общего случая, а иллюстрируется многочисленными
примерами.
Представляя себе сплошную среду как предельный случай
совокупности материальных точек, мы можем трактовать так
зазываемую «распределенную» нагрузку как предельный случай
совокупности сосредоточенных сил, приложенных к точкам по-
поверхности тела, хотя такое представление в известной мере ис-
искусственно и связано с определенными привычками изложения
механики в определенной последовательности. На самом деле,
28
ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ
Рис. 1.6.1
как уже подчеркивалось, введя модель сплошной деформируемой
среды, мы должны именно распределенную нагрузку принять
как нечто первично данное, а сосредоточенная сила представляет
собою абстракцию. Для пояснения идеи нам достаточно рассмот-
рассмотреть нагрузку, распределенную по линии, нагрузки, распреде-
распределенные по поверхности либо по объему непрерывным образом,
вводятся аналогично. Предположим, что линия АВ (рис. 1.6.1)
принадлежит поверхности тела. Ра-
Разобьем ее на п равных участков
длиной б каждый, занумеруем их
границы (или середины, или любые
точки, принадлежащие участку),
приложим в каждой из точек с но-
номером к силу Рк. Положим Рк/Ь = qk.
Будем теперь безгранично увеличи-
увеличивать число сил, уменьшая расстоя-
расстояние между ними и уменьшая силу
так, что отношение PJb = qh стремит-
стремится к конечному пределу. При переходе к пределу точка линии АВ
уже не может характеризоваться номером того участка, к ко-
которому она принадлежит, этот номер также стремится к беско-
бесконечности. Вместо этого следует задавать точку ее координатой,
например длиной дуги s, отсчитываемой от точки А до заданной
точки. Итак, предельное значение qk есть q(s). Таким образом,
мы ввели понятие о нагрузке, распределенной непрерывно на
отрезке кривой АВ.
Если функция q(s) задана, то можно сделать обратный пе-
переход, разбить дугу АВ на конечное число участков As и при-
приложить в середине каждого участка сосредоточенную силу
q(s)As. Такой прием, состоящий в замене распределенной на-
нагрузки конечным числом сосредоточенных сил, иногда приме-
применяется при расчетах, особенно когда используется вычислитель-
вычислительная техника. Принцип Сен-Венана позволяет утверждать, что
такая замена может сказаться на результатах лишь в непосред-
непосредственной окрестности линии АВ.
Введем теперь понятие о распределенном моменте. Сначала
определим сосредоточенный момент следующим образом. Пусть
в точке с координатой 5 — 8 приложена сила Р, в точке с ко-
координатой 5 + е сила — Р (рис. 1.6.2). Будем уменьшать е и уве-
увеличивать силу Р так, чтобы произведение 2гР = М оставалось
постоянным. При е -*• 0 мы получим сосредоточенный момент М,
приложенный в точке, определяемой координатой s. Теперь по-
поступим так же, как при определении распределенной нагрузки.
Приложим моменты Мк в точках с номером к, будем безгранично
увеличивать число отрезков п, уменьшая их длину и уменьшая
момент так, чтобы в каждой точке s это отношение стремилось
к конечному пределу m(s).
§ 1.6. ПРИНЦИП СЕН-ВЕНАНА
29
В приведенном рассуждении весьма существен порядок пре-
предельных переходов, сначала был введен сосредоточенный момент
при е ->¦ 0, потом был определен непрерывно распределенный
момент и к нулю устремлялась величина б. Посмотрим, что
может получиться при обратном переходе. Пусть на отрезке АВ
задано распределение момента m(s). Это значит, что на участок
As действует пара сил с моментом m(s)As. Нарисуем эту пару
так, как показано на рис. 1.6.3. Одна сила, равная m(s), при-
приложена в точке с координатой s и направлена вниз, в точке
с координатой s + As приложена такая же сила, направленная
вверх. Рассмотрим следующий малый участок той же длины As.
в
Рис. 1.6.3
На концах этого участка будут приложены силы m(s + As) =
= т + Am. Складывая силы, приложенные в точке s + As, мы
найдем, что их сумма равна Am. To же самое получится на гра-
границах' всех участков длиной As, на которые можно разбить от-
отрезок АВ, на каждый участок приходится, таким образом, сила
Am. Переходя к пределу при As -*- 0, мы найдем, что распреде-
распределение момента m(s) эквивалентно распределению нагрузки
q(s)= dm/ds. При этом в точках А и В останутся сосредоточен-
сосредоточенные силы, равные m(sA) и m(sB) соответственно.
Принцип Сен-Венана позволяет предполагать, что такая опе-
операция, состоящая в замене распределенного момента распреде-
распределенной нагрузкой и двумя сосредоточенными силами (сил мо-
может быть и больше, если функция m(s) лишь кусочно непре-
непрерывна), при определенных условиях допустима, хотя в этом
примере для выяснения соответствующих условий необходим бо-
более тонкий анализ. С одним из примеров подобного анализа мы
встретимся в § 12.5.
Наконец последний пример, приводимый здесь, будет отно-
относиться к так называемой двойной силе. Выберем в теле две точ-
точки, находящиеся на расстоянии б одна от другой, соединим их
прямой и приложим в этих точках две равные и противополож-
противоположные силы, направленные вдоль этой прямой (рис. 1.6.4). Будем
неограниченно уменьшать 5, сохраняя величину силы постоян-
30 гл. i. основные понятия
ной. Очевидно, что при 6 = 0 две равные и противоположные си-
силы окажутся приложенными к одной и той же точке, они взаим-
взаимно уничтожатся и на тело не будет произведено никакого дей-
действия. Совершенно другой результат получается, если при умень-
уменьшении б сила Р увеличивается так, что произведение Р8 остается
постоянным. Оказывается, что в пределе при 6 = 0 и Р -> оо
действие сил не исчезает, в теле сохра-
^ нится некоторая совершенно определен-
определенная деформация. Убедиться в этом фак-
факте с помощью элементарных рассуж-
Рис. 1.6.4 дений вряд ли возможно, он вытекает
из точного решения уравнений теории
упругости. Мы упоминаем о нем по двум причинам: во-первых,
чтобы подчеркнуть большую осторожность, которую нужно про-
проявлять при замене системы сил статически эквивалентной, во-
вторых, чтобы показать, каким образом последовательность пре-
предельных переходов может определить окончательный результат.
§ 1.7. Внутренние силы
Сохранение формы твердого тела обеспечивается внутренними
связями, природа которых для нас безразлична. Согласно аксио-
аксиоме связей равновесие системы сохраняется, если разрушить часть
связей и заменить их силами, которые называют реакциями
связей.
Рассмотрим произвольное тело, нагруженное совокупностью
внешних сил Ри Р2, Рг, . •., Рп- Будем обозначать эту совокуп-
совокупность символом (Р). Мысленно рассечем тело поверхностью S,
проходящей через некоторую внутреннюю точку М. На левую
часть действует совокупность сил (Р)л, на правую совокупность
сил— (-Р)пр. Для того чтобы каждая из частей сохраняла рав-
равновесие, необходимо приложить на поверхности разреза S силы
взаимодействия, которые называются внутренними силами или
напряжениями.
Рассмотрим, например, как показано на рис. 1.7.1 равновесие
левой части. В классической механике сплошных сред предпо-
предполагают, что реакция отброшенной правой части представляет
собою силу, непрерывно распределенную по поверхности разреза.
В каждой точке поверхности S определен вектор 0, который мы
будем называть вектором напряжения или просто напряжением.
Это означает следующее. Окружим точку М на поверхности S
контуром «у, который заключает в себе малую площадь со. Сила,
действующая со стороны отброшенной правой части на площадку,
принадлежащую левой части, равна о (Af) со с тем большей точ-
точностью, чем меньше площадка со. Иначе говоря, напряжение есть
предел, к которому стремится вектор силы, действующей на пло-
площадку. В действительности, силы, действующие на конечную
§ 1.7. ВНУТРЕННИЕ СИЛЫ
31
(Р)
Рис. 1.7.1
площадку со со стороны отброшенной части тела, распределены
по этой площадке каким-то способом. Заменим их главным век-
вектором и главным моментом, -разделим тот и другой на величи-
величину со и устремим эту величину к нулю, т. е. стянем контур ^
в точку М. Предел отношения главного вектора сил, действую-
действующих на площадку, к величине ее площади называется напря-
напряжением. В классической теории предполагается неявно, что силы
взаимодействия распределены достаточно
равномерно и вследствие этого отноше-
отношение главного момента к величине пло-
площадки стремится к нулю вместе с этой
последней. Но в принципе можно допу-
допустить, что действие одной части тела на
другую не сводится к силам, кроме век-
вектора напряжения а на поверхности раз-
разреза появляется .также распределенный
момент jut.
Можно пойти дальше по этому пути
и предположить, что взаимодействие осу-
осуществляется также посредством некото-
некоторых образований типа рассмотренных в
конце предыдущего параграфа двойных
сил, которые распределены по поверхно-
поверхности непрерывно. В современных теориях
сплошных сред подобные предположения делаются, однако зна-
значение их состоит скорее в иллюстрации весьма большой степени
общности, которая может быть достигнута в рамках представле-
представления о сплошной среде и о потенциальной возможности значи-
значительного расширения этих рамок с тем, чтобы описать эффекты,
относимые обычно за счет дискретности строения реальных тел.
Но существующие теории, уже нашедшие применения к реаль-
реальным объектам, строятся почти искючительно на основе класси-
классической модели, которая до недавнего времени представлялась
совершенно очевидной и единственно возможной.
Через внутреннюю точку тела М можно провести бесчислен-
бесчисленное множество поверхностей S и, следовательно, выбрать бесчис-
бесчисленное множество площадок с различной ориентацией, задавае-
задаваемой, например, единичным вектором нормали к площадке п.
Для каждого вектора п или для каждой ориентации площадки
с помощью описанного выше предельного перехода мы будем
получать разные векторы напряжения а. Таким образом, нельзя
сказать, что напряжение в точке М есть вектор, это есть сово-
совокупность всех векторов напряжений для всех ориентации пло-
площадок, содержащих в себе точку М. Можно сказать, что в точ-
точке М вектор а есть функция вектора/г, в = а(п). В дальнейшем
будет показано, что это линейная вектор-функция, три компо-
компоненты вектора а получаются в результате линейного преобразо-
32
ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ
Рис. 1.7.2
вания из компонент вектора п. Очевидно, что формулы, опреде-
определяющие это линейное преобразование, содержат девять коэффи-
коэффициентов, совокупность которых определяет тензор напряжений
(матрица этих коэффициентов оказывается симметричной; таким
образом, для задания напряженного состояния
в точке нужно задать не девять величин, а
только шесть).
Вектор напряжения в точке М на площад-
площадке с нормалью п естественно разложить на
две составляющие, как показано на рис. 1.7.2,
одна из них, аЛ, направлена по вектору нор-
нормали и называется нормальным напряжением,
вторая, тп, принадлежит плоскости площадки
со и называется касательным напряжением.
Условимся считать оп положительным, если
вектор направлен по внешней нормали к поверхности S. Поло-
Положительное нормальное напряжение называется растягивающим,
отрицательное — сжимающим.
Напряженное состояние тела известно, если задан способ по-
построения вектора напряжений в любой точке тела для любой
ориентации площадки. Если во всех точках тела для площадок
одинаковой ориентации векторы напряжений одинаковы, напря-
напряженное состояние называется однородным. Приведем простейшие
примеры однородных напряженных состояний.
а. Растяжение — сжатие. На торцах призматического тела
(рис. 1.7.3) приложены равномерно распределенные нагрузки ин-
интенсивностью а. Разрезая тело плоскостью, пер-
6 пендикулярной оси, приложим в плоскости раз-
разреза равномерно распределенные нормальные на-
напряжения, равные по величине нагрузке а. Если
тело изготовлено из однородного материала, то
нет оснований предполагать, что распределение
напряжений по поперечному сечению будет не-
неоднородным, хотя, строго говоря, это необходимо
доказать. Для всех существующих моделей твер-
твердого тела такое доказательство весьма просто.
Будем говорить, что в рассматриваемом случае
призма находится в состоянии равномерного
растяжения. У однородного материала, свойства которого для
всех направлений одинаковы, растяжение или сжатие сопровож-
сопровождается удлинением или укорочением в направлении действующей
силы.
б. Чистый сдвиг. На грани прямоугольного параллелепипеда
действуют равномерно распределенные касательные усилия ин-
интенсивностью т (рис. 1.7.4). Легко убедиться, что параллелепипед
будет в равновесии только тогда, когда на всех гранях интен-
интенсивность усилий одинакова. Действительно, на верхнюю и ниж-
Рис. 1.7.3
§ 1.8. УПРУГОСТЬ
33
нюю грани действуют противоположно направленные силы тяс,
они образуют пару с плечом Ъ и моментом таЬс. Точно такую же
пару противоположного направления образуют силы, приложен-
приложенные к вертикальным граням (при суждении о равновесии тела
в целом можно применять принцип отвердения и, следовательно,
заменять распределенную нагрузку равнодействующей). Во всех
сечениях, параллельных граням ас или сб, возникают равномерно
распределенные касательные напряжения.
Равенство касательных напряжений на взаимно перпендику-
перпендикулярных площадках, действующих в направлении линии их пере-
пересечения, называют законом (или, лучше,
правилом) парности касательных напряже-
напряжений. Название «чистый сдвиг» связано с
тем, что при таком напряженном состоянии
происходит перекашивание первоначально
ортогонального элемента; изменение у пер-
первоначально прямого угла и называется де-
деформацией сдвига.
в. Гидростатическое напряженное состоя-
состояние. Если на любой площадке, проходящей
через данную точку, действует только
нормальное напряжение а для всех направлений площадок, на-
напряженное состояние называется гидростатическим. Только та-
такое напряженное состояние возможно в идеальной жидкости
(закон Паскаля), но в жидкости а отрицательно и называется
давлением. В твердых телах возможно всестороннее равномерное
растяжение. Если точка М принадлежит поверхности тела, то
одна из проходящих через нее площадок также принадлежит
поверхности. По определению на ней должно быть нормальное
напряжение, т. е. внешняя нагрузка должна быть направлена
по нормали к поверхности и интенсивность ее должна быть по-
постоянной. Таким образом, для осуществления в теле гидроста-
гидростатического напряженного состояния необходимо, чтобы на него
действовала равномерно распределенная и нормальная к поверх-
поверхности нагрузка. Очевидно, это необходимое, но недостаточное
условие.
Рис. 1.7.4
§ 1.8. Упругость
Важнейшее свойство всех без исключения твердых тел — это
упругость. В основе определения этого понятия будет находиться
модель идеального упругого тела — объекта, в природе не суще-
существующего. Идеальной упругостью называется однозначная за-
зависимость между силами и вызванными этими силами перемеще-
перемещениями. Если прикладывать к упругому телу нагрузки в различ-
различной последовательности, то конечное состояние не будет зависеть
3 Ю. Н. Работнов
34 гл. i. основные понятия
от порядка их приложения, оно определяется только конечными
значениями нагрузок. Из данного определения следует, в част-
частности, что после снятия нагрузки идеально упругое тело всегда
возвращается в исходное состояние. Данное определение упру-
упругости несколько упрощено. При более строгом подходе упругое
тело следует рассматривать как термодинамическую систему и
принимать во внимание изменение температуры, которое может
сопровождать деформацию. Далее будет показано, что однознач-
однозначная зависимость между силами и перемещениями сохраняется,
если тело теплоизолировано или если температура его поддер-
поддерживается постоянной за счет внешнего притока или оттока тепла.
Следует заметить, что для большинства твердых тел тепловые эф-
эффекты невелики, для металлов они практически неощутимы, для
полимеров иногда их приходится принимать во внимание. Мы со-
сохраняем данное определение упругости в качестве рабочего, учи-
учитывая, что оно вполне точно для адиабатического и изотермиче-
изотермического процессов и практически точно для промежуточных
случаев.
Закон упругости выполняется с очень большой степенью точ-
точности для кристаллов кварца, для термически обработанной ста-
стали, например, если нагрузки, а следовательно, и напряжения,
не слишком велики. Другие материалы считают упругими лишь
с известным приближением, сознательно пренебрегая той погреш-
погрешностью, которая связана со сделанным предположением. Суще-
Существенно, чтобы эта погрешность не выходила sa определенные
пределы, которые устанавливаются требованиями практики.
В противном случае приходится применять другие, усложненные
модели. Эти модели приходится конструировать из различных эле-
элементов; идеальная упругость и представляет один из таких эле-
элементов, фигурирующий почти во всех не слишком упрощенных
моделях твердого тела.
Основным источником сведений о механических свойствах
материалов служит опыт на растяжение. Призматический образец
растягивается напряжением а (рис. 1.7.3), измеряется его длина I
или расстояние между двумя нанесенными рисками. До растя-
растяжения эта длина равнялась Zo, приращение длины Al = l—l0 на-
называется удлинением, а отношение е = А1/10 называется относи-
тельным удлинением. (Иногда вместо слова «удлинение» мы бу-
будем употреблять более общий термин — деформация.) Если а
меняется определенным известным нам образом как функция
BpeLMeim, говорят, что задана программа испытания с(?). При
этом физическое время t не играет роли, важно не протекание
процесса во времени, а последовательность событий. Формально
это означает, что программы o(t) и а(т) тождественны, если т
есть произвольная монотонная функция t. С изменением о ме-
меняется е, если G = o(t), то e = e(t). Будем наносить в плоскости
о — е точки, соответствующие одинаковым значениям времени t.
§ 1.9. ПЛАСТИЧНОСТЬ 35
Если все эти точки при всех программах испытания окажутся
лежащими на одной и той же кривой, то материал упруг.
Уравнение полученной кривой
о = ф(е) A.8.1)
и представляет собою закон упругости. Для огромного большин-
большинства материалов закон упругости с большой точностью может
считаться линейным и его можно записать следующим образом:
с = Ее. A.8.2)
Величина Е называется модулем упругости, а соотношение A.8.2)
носит название закона Гука (Роберт Гук — английский матема-
математик и физик, 1635—1703).
Закон упругости справедлив, пока напряжение не достигает
определенного предела, называемого пределом упругости. Опре-
Определение этого предела довольно условно; располагая аппарату-
аппаратурой разной чувствительности можно обнаружить отклонение от
закона упругости при больших или меньших напряжениях. На-
Напряжение, до которого справедлив закон Гука, называют пре-
пределом пропорциональности; замечание об условности определения
относится в равной мере и к пределу пропорциональности.
§ 1.9. Пластичность
Если напряжение превышает предел упругости, зависимость
между нагрузками и перемещениями перестает быть однознач-
однозначной и перемещения, соответствующие данной системе нагрузок,
зависят от порядка их приложения. После снятия нагрузки вы-
вызванные ею деформации не исчезают, а частично сохраняются.
Эти деформации называются пластическими.
Величина пластической деформации зависит не только от ко-
конечной величины действующих сил, но также от порядка их
приложения. Вообще говоря, она зависит также от скорости на-
гружения и от времени пребывания тела под нагрузкой. Однако
при построении модели пластического тела бывает целесообразно
разделить эти эффекты.
Обратимся снова к опыту на простое растяжение. Если на-
напряжение все время монотонно возрастает и становится при
этом выше предела упругости, зависимость между напряжением
и деформацией изображается кривой, представленной на
рис. 1.9.1. Запишем уравнение этой кривой
о = ф(е), do>0. A.9.1)
При построении модели пластического тела предполагают, что
это уравнение справедливо при любой программе нагружения,
в которой напряжение монотонно возрастает. Скорость нагруже-
нагружения при этом совершенно безразлична, можно приостановить
3*
36
ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ
нагружение и держать образец под нагрузкой сколь угодно долго.
Недопустимо лишь нарушение условия а > 0. Для реальных
материалов дело обстоит сложнее. На самом деле диаграмма пла-
пластического деформирования зависит от скорости. Однако для
большинства конструкционных сплавов эта зависимость довольно
слабая, разница между кривыми деформирования, которые соот-
соответствуют скоростям, разнящимся на два — три десятичных по-
порядка, не выходит за пределы разброса свойств индивидуальных
образцов. Поэтому мы будем приписывать зависимости A.9.1)
универсальный характер.
Предположим теперь, что мы довели нагружение до точки А
на диаграмме с координатами о' и е'. После этого производится
Рис. 1.9.1
Рис. 1.9.2
разгрузка, напряжение а уменьшается до нуля. Диаграмма рас-
растяжения, представленная на рис. 1.9.1, отражает не только пла-
пластическое поведение материала, но и упругое. Если представить
себе, что материал и в пластической области сохраняет упругие
свойства, то нужно допустить, что деформация е' состоит из
двух частей: пластической и упругой. По закону Гука, если
предположить, что он сохраняет силу и в пластической области,
величина упругой составляющей есть dIE. При разгрузке пла-
пластическая деформация сохраняется неизменной, тогда как упру-
упругая исчезает полностью. Следовательно, зависимость напряже-
напряжение — удлинение при разгрузке будет изображаться прямой АВ,
наклон которой определяется модулем упругости Е. Этот факт
довольно хорошо подтверждается опытами на металлах.
Более тщательные эксперименты показывают, что закон раз-
разгрузки не описывается совершенно точно уравнением линейной
упругости, линия АВ, строго говоря, не прямая. Заменяя ее наи-
наиболее близкой прямой, мы находим, что ее наклон не соответ-
соответствует в точности начальному модулю упругости Е. В существу-
существующих теориях пластичности этими незначительными отклонения-
отклонениями от закона Гука при разгрузке пренебрегают. У полимерных
материалов, а также у композитных материалов, например стек-
стеклопластиков, закон разгрузки отличается от закона Гука очень
§ 1.9. ПЛАСТИЧНОСТЬ
37
существенно. По-видимому, это объясняется тем, что при нагру-
нагружении материала в нем образуются микротрещины. Действитель-
Действительно, о возникновении трещин на ранних ступенях деформации
судят по звуковой эмиссии, которую можно регистрировать спе-
специальной аппаратурой.
Более крупные трещины обнаруживаются визуально. На
рис. 1.9.2 изображена диаграмма деформирования гипотетическо-
гипотетического линейно упругого материала, в котором по мере растяжения
возникают трещины. Появление трещин эквивалентно уменьше-
уменьшению эффективной площади поперечного сечения, а так как при
вычислении напряжения нагрузка делится на общую площадь,
диаграмма при нагружении ничем не отличается от диаграммы
пластичности. Разница обнаруживается лишь при разгрузке, ко-
которая следует закону упругости, но как бы с уменьшенным
модулем, прямая разгрузки возвращается в начало координат,
если все трещины полностью смыкаются. Но в процессе дефор-
деформации может происходить выкрашивание перемычек между тре-
трещинами, что препятствует их полному смыканию после разгруз-
разгрузки, поэтому деформация исчезает не полностью и разгрузка
следует некоторой кривой, которая схематически показана штри-
штриховой линией. Примерно так выглядит действительная кривая
разгрузки для многих пластмасс.
Возвращаясь к обычной пластичности, т. е. к диаграмме,
изображенной на рис. 1.9.1, предположим," что образец после
разгрузки нагружается вновь. Оказывается, что повторная на-
нагрузка следует закону упругости до тех пор, пока снова не
будет достигнуто напряжение а', зависимость между айв опять
изображается отрезком ВА. После точки А, когда становится
о>о', опять вступает в силу зависимость A.9.1), образец де-
деформируется пластически, упругая же его деформация увеличи-
увеличивается в соответствии с повышением на-
напряжения по закону Гука. При о < о'
зависимость между напряжением и де-
деформацией, справедливую как при раз-
разгрузке, так и при нагружении, удобно за-
записывать в дифференциальной форме
do = Ede (o<of). A.9.2)
Соотношения A.9.1) и A.9.2) для слу-
случая растяжения определяют модель уп-
ругопластического тела. Поведение таких
материалов как сталь, алюминиевые и
титановые сплавы и другие металлические материалы, применяе-
применяемые для изготовления несущих элементов конструкций, соответ-
соответствует этой модели лишь с известным приближением. Для мно-
многих практических расчетов точность такой модели достаточна,
она полагается в основу теории пластичности.
О
Рис. 1.9.3
38
ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ
У мягкой стали, титановых сплавов и некоторых других ма-
материалов переход от упругого участка диаграммы растяжения
к пластическому происходит очень резко и пластический участок
почти горизонтален. Идеализируя действительное положение,
можно изобразить эту диаграмму так, как это показано на
рис. 1.9.3. Напряжение в таком идеализированном материале
пе может превысить величину от, называемую пределом теку-
текучести. При о = от величина пластической деформации неопреде-
неопределенна, она может расти сколь угодно, но при уменьшении де-
деформации происходит уменьшение напряжения, т. е. разгрузка,
подчиняющаяся закону Гука и описываемая уравнением A.9.2).
Теория идеальной пластичности представляет собою наиболее
законченную в математическом отношении главу теории пла-
пластичности.
§ 1.10. Последействие и ползучесть
Явление последействия типично для полимерных материалов
при невысоком уровне напряжений. Представим себе, что обра-
образец нагружен за очень короткое время до напряжения а. Дефор-
Деформация его немедленно после нагружения будет е0, это упругая
деформация. Если теперь оставить образец под действием посто-
постоянного напряжения а, мы обнаружим, что он продолжает дефор-
деформироваться и по истечении некоторого времени ?* к
начальной деформации е0 прибавится добавочная де-
деформация е , так что полная деформация будет ео + е'.
Рис. 1.10.2
Снимем мгновенно нагрузку в момент времени t#t упругая
деформация е0 исчезнет, накопленная же за время t# деформа-
деформация последействия не исчезнет. На первый взгляд может пока-
показаться, что е' — пластическая деформация, но это не так. Раз-
Разгруженный образец будет продолжать сокращаться со време-
временем, остаточная деформация будет уменьшаться, стремясь к
нулю. Этот процесс можно проиллюстрировать графиком, изобра-
изображенным на рис. 1.10.1. Здесь представлена зависимость дефор-
§ 1.10. ПОСЛЕДЕЙСТВИЕ И ПОЛЗУЧЕСТЬ 39
мации от времени для описанной выше программы испытания.
Материалы, обладающие свойством последействия, называют
наследственно-упругими или вязкоупругими. Первый термин
связан с тем, что поведение таких материалов определяется не
только тем воздействием, которое образец испытывает в данный
момент, но также историей тех воздействий, которым материал
подвергался ранее, в течение всей истории своего существования.
Второе название связано с простой механической моделью, ко-
которая качественно воспроизводит описанное поведение материа-
материала. Эта модель изображена на рис. 1.10.2. Две пружины с же-
сткостями Ci и с2 соединены последовательно, параллельно одной
из пружин установлено вязкое сопротивление — масляный демп-
демпфер. Если нагрузки прикладываются очень быстро, масло прак-
практически не успевает перетечь из одной части цилиндра в дру-
другую, пружина 2 не растягивается, мгновенно упругое поведение
системы определяется только жесткостью пружины 1. Если, нао-
наоборот, нагружение очень медленное, то сопротивление демпфе-
демпфера, пропорциональное скорости движения поршня, очень мало,
сила растягивает как пружину 1, так и пружину 2, перемещение
опять линейно зависит от силы, но теперь жесткость с опреде-
определяется из условия
С С1 С2
величина с меньше, чем ct и с2. Прикладывая постоянную на-
нагрузку в течение времени %t и затем снимая ее, мы получим
график зависимости деформации от времени, подобный представ-
представленному на рис. 1.10.1.
Нужно заметить, однако, что приведенная модель может слу-
служить лишь для качественной иллюстрации, но не для объяс-
объяснения процессов последействия в твердых телах.
Несколько иначе происходит процесс так называемой ползу-
ползучести у металлов при повышенной температуре. При мгновенном
приложении растягивающей нагрузки к образцу он приобретает
мгновенную деформацию е0, которая может быть упругой, а мо-
может состоять из упругой и пластической части, в зависимости от
температуры и напряжения. Если приложенная нагрузка сохра-
сохраняется постоянной, деформация образца продолжает увеличивать-
увеличиваться со временем, к моменту t% дополнительная деформация стано-
становится равной е\ график зависимости е от t совершенно подобен
изображенному на рис. 1.10.1. Но теперь деформация представля-
представляет собой необратимую, т. е. пластическую деформацию. В этом
можно убедиться только произведя разгрузку. Если начальная
деформация упруга, то при разгрузке произойдет мгновенное со-
сокращение на величину е0, если начальная деформация была
утгругопластической, то после разгрузки исчезает только упругая
часть о/Е. Разгруженный образец не уменьшает своей длины по-
40 гл. 1. основные понятия
еле выдержки любой длительности, деформация е', так же как
пластическая часть мгновенной деформации е0, представляет собой
необратимую, пластическую деформацию.
У реальных материалов свойства последействия и ползучести
обычно существуют одновременно. Последействие, т. е. запазды-
запаздывающая упругость, характерно для высокополимеров. Однако, ес-
если уровень напряжений достаточно высок, не вся деформация,
накопленная в результате выдержки при постоянной нагрузке,
возвращается после разгрузки. С другой стороны, если темпера-
температура испытания не слишком велика, некоторый возврат, т. е. не-
некоторое уменьшение оставшейся после разгрузки деформации со
временем, наблюдается и у металлов.
§ 1.11. Тела изотропные и анизотропные
Если свойства образца, вырезанного из материала, не зависят
от его ориентации, материал называется изотропным. В против-
противном случае материал называют анизотропным. В зависимости от
того, какой критерий принимается при отождествлении свойств
образцов, говорят о механической, оптической, тепловой и дру-
других видах анизотропии. Кристаллы, например, всегда анизотроп-
анизотропны, это определяется их внутренним строением, поскольку атомы
в кристаллической решетке располагаются совершенно определен-
определенным образом. Зная строение кристаллической решетки, можно
сделать некоторые выводы о характере анизотропии, например
указать плоскости симметрии. Образцы, вырезанные из кристалла
симметрично относительно такой плоскости, обнаружат тождест-
тождественные свойства. Технические сплавы состоят из кристалличе-
кристаллических зерен, ориентация которых беспорядочна и произвольна.
Поэтому в теле, состоящем из большого числа таких зерен, нель-
нельзя указать какое-то предпочтительное направление, отличающееся
от других. Полукристаллический металл ведет себя в среднем
как изотропное тело. При этом, конечно, предполагается, что раз-
размеры образца достаточно велики и он содержит в себе достаточно
много кристаллических зерен. Малые образцы, состоящие из не-
небольшого числа зерен, будут обнаруживать разные свойства, но
эта разница совершенно случайна, она зависит не от ориентации
образца, а от случайных ориентации составляющих его зерен.
В прокатанном металле зерна деформируются в направлении
прокатки, образуется так называемая текстура. Поэтому свойства
образцов, вырезанных в направлении прокатки и в поперечном
направлении, будут разными. Такая же анизотропия возникает
практически при всех видах обработки металлов давлением. Од-
Однако анизотропия упругих свойств, связанная с наличием тек-
текстуры, невелика; разницей в модулях упругости стержней, оси
которых ориентированы в направлении прокатки и в поперечном
направлении, можно пренебречь. Однако пластические свойства
§ 1.11. ТЕЛА ИЗОТРОПНЫЕ И АНИЗОТРОПНЫЕ 41
для этих направлений, предел упругости или предел текучести
разнятся уже заметно. Надлежащая термическая обработка де-
деформированного металла снимает анизотропию или, по крайней
мере, уменьшает ее.
Анизотропия кристаллов объясняется их атомной структурой,
но существуют материалы, у которых определяющие их анизот-
анизотропию структурные элементы имеют значительно большие раз-
размеры. Примером может служить древесина, расположение види-
видимых невооруженным глазом волокон создает относительно высо-
высокую прочность в направлении оси ствола и малую прочность в
поперечном направлении. В этом отношении можно сказать, что
природа распорядилась прочностью целлюлозы, из которой, в ос-
основном, состоит древесина, наилучшим образом. По этому прин-
принципу в технике создают так называемые композитные материалы,
примером которых могут служить стеклопластики. Тонкая стек-
стеклянная нить имеет высокую прочность, укладывая слои такой
нити, пропитывая их смолой и полимеризируя, получают моно-
монолитные пластины. Чередуя направления укладки слоев, можно
менять степень и характер анизотропии с тем, чтобы использовать
прочность волокна наивыгоднейшим образом. В последние годы
были получены и промышленно освоены высокопрочные волокна,
значительно превосходящие по своим свойствам стеклянное во-
волокно и, что особенно важно, имеющие значительно более высо-
высокий модуль упругости. Наибольшее распространение получили
волокна бора и углерода, которыми армируют пластики и ме-
металлы.
В технике широко применяют пластины и оболочки, усилен-
усиленные ребрами. Так, типичная для авиации и ракетной техники
конструкция оболочки представляет собой каркас из колец —
шпангоутов и продольных ребер — стрингеров. С каркасом соеди-
соединяется обшивка из тонкого листа. Если стрингеры и шпангоуты
расположены достаточно часто, для расчетных целей такую обо-
оболочку можно заменить сплошной анизотропной оболочкой, выбрав
надлежащим образом параметры анизотропии. Обычно такая ани-
анизотропия называется конструктивной в отличие от «физической».
На самом деле такое различение довольно условно, в том и дру-
другом случае анизотропия свойств определяется строением тела,
разница лишь в размерах дискретных структурных элементов.
ГЛАВА 2
СТЕРЖНИ И СТЕРЖНЕВЫЕ СИСТЕМЫ —
РАСТЯЖЕНИЕ И СЖАТИЕ
§ 2.1. Растяжение и сжатие стержней
Для выяснения основных идей механики деформируемого
твердого тела мы начнем с простейших задач, решение которых
основывается на непосредственном использовании данных опыта
и требует лишь элементарных соображений. В § 1.7 было рас-
рассмотрено простейшее однородное состояние растяжения, которое
возникает в цилиндрическом теле, к торцам которого приложена
равномерно распределенная нормальная нагрузка. Изменяя на-
направление внешней нагрузки на противоположное, получим од-
, \ нородное сжатие, которое
—" * формально отличается от
растяжения только зна-
знаком, который приписыва-
приписывается напряжению а.
Растяжение или сжа-
сжатие с достаточно хорошей
Рис. 2.1.1
Рис. 2.1.2
степенью точности реализуется в стержнях и стержневых систе-
системах типа ферм.
Стержнем называется цилиндрическое тело, поперечный раз-
размер которого мал по сравнению с размером в направлении обра-
образующей*). Под поперечным размером мы будем понимать рас-
расстояние между двумя параллельными касательными к контуру,
например h или h' на рис. 2.1.1. Отношение h/l < 1, эта вели-
величина представляет собой малый параметр, необходимый для оцен-
*) В учебниках сопротивления материалов для машиностроительных
специальностей слово «стержень» заменяют иногда термином «брус». В этой
книге мы будем придерживаться терминологии, принятой в литературе по
теории упругости, а также в курсах сопротивления материалов для строи-
строителей.
§ 2.1. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
кп степени точности теории. Предполагается, что huh' всегда
одного порядка, т. е. hlh' ~ 1 для всех пар касательных.
Тонкостенным называется такой стержень, у которого харак-
характерные размеры поперечного сечения сильно разнятся между
собою и из них можно скомбинировать еще один малый пара-
параметр. Простейшим примером служит стержень с сечением в фор-
форме вытянутого прямоугольника со сторонами б и /г, причем 8/h <
< 1. На рис. 2.1.1, б приведен пример тонкостенного стержня с
криволинейным профилем, для него также существует малый
параметр б/Л < 1.
Стержни встречаются как основные элементы огромного боль-
большинства инженерных конструкций. Мостовая ферма, схематиче-
схематически изображенная на рис. 2.1.2, со-
состоит из отдельных стержней, сое-
соединенных между собою заклепками
или сваркой.
Если все узлы, в которых соеди-
соединяются стержни фермы, снабжены
шарнирами и концы стержней могут
свободно поворачиваться без трения,
а также если внешние силы прило-
приложены только к узлам, все стержни
будут находиться в состоянии рас-
растяжения или сжатия.
Будем говорить, что стержень
растягивается, если к торцам его
приложены силы, статически экви-
эквивалентные одной силе, действующей
по оси стержня. Осью стержня мы
будем называть прямую, проходя-
проходящую через центры его поперечных сечений. На рис. 2.1.3
действующие нагрузки показаны в виде сил, приложен-
приложенных в центрах торцов стержня, но эти сосредоточенные силы
здесь совершенно условны. На самом деле нагрузка приклады-
прикладывается к концу стержня каким-то совершенно определенным ре-
реальным способом. На рис. 2.1.4 схематически изображены неко-
некоторые из возможных способов передачи нагрузки на стержень.
В случае а изображенная сила представляет собою равно-
равнодействующую давления со стороны заклепки или болта на стенки
отверстия, мы не очень хорошо знаем, как именно распределено
это давление. Случаи бив относятся к закреплению концов
образца в захватах машины для испытания на растяжение, об-
образец либо зажимается клиновыми губками с насечкой, либо
имеет головку. В случае г конец тяги снабжен винтовой нарез-
нарезкой. На этот конец навертывается гайка, опирающаяся на пло-
плоскость плиты, в которой просверлено отверстие для тяги. Усилие
передается от гайки к тяге, распределяясь по виткам нарезки.
44
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
Подобных конкретных способов передачи растягивающего
усилия к стержню можно указать очень много, все они будут
различны. Однако при расчете стержней на растяжение не счи-
считаются с индивидуальными особенностями, зависящими от спо-
способа приложения нагрузки, а принимают во внимание только
равнодействующие сил, приложенных к каждому из концов
стержня. Это делается на основании принципа Сен-Венана, ко-
который в данном случае может быть сформулирован следующим
образом.
Способ приложения силы к торцу стержня сказывается лишь
на расстоянии от торца порядка поперечного размера*).
Таким образом, на расстоянии порядка h от торца в случае,
изображенном на рис. 2.1.3, и от начала гладкой цилиндриче-
цилиндрической части на рис. 2.1.4, распределение нормальных напряжений
г)
Рис. 2.1.4
по сечению будет практически равномерным, тем более равно-
равномерным будет оно во всех более удаленных сечениях. Но равно-
равномерному распределению напряжений соответствует равномерное
удлинение, следовательно, первоначально плоские поперечные
сечения останутся плоскими и параллельными, они только раз-
раздвинутся при растяжении и сблизятся при сжатии. Этот фунда-
фундаментальный вывод носит название закона плоских сечений.
Этот закон иногда полагают в основу всей теории. Конечно,
плоскими остаются только те сечения, которые удалены от кон-
концов стержня или места приложения нагрузки на расстояние,
порядок которого не меньше порядка поперечного размера.
Все изложенное относится не только к растяжению, но также
к сжатию, которое отличается от растяжения формально направ-
направлением приложенной силы и, соответственно, знаком напряже-
напряжения. Фактическая разница между растяжением и сжатием гораз-
гораздо глубже, при сжатии может возникнуть новое явление — потеря
*) В дальнейшем будет показано, что принцип Сен-Венана формулиру-
формулируется иначе для тонкостенных стержней или для стержней из материала с
резко выраженной анизотропией.
§ 2.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
45
устойчивости. Центрально сжатый прямой стержень может сохра-
сохранить прямолинейную форму лишь тогда, когда сжимающая сила
меньше некоторого предельного значения, которое уменьшается
с увеличением отношения длины к поперечному размеру. Если
сжимающая сила превышает эту предельную величину, называе-
называемую критической силой, то при сколь угодно малом эксцентри-
эксцентриситете приложения силы или сколь угодно малом искривлении
оси стержня он изогнется. Это явление называется потерей ус-
устойчивости', устойчивости стержневых систем будет посвящена
гл. 4. Там же будет показано, что в области больших пластиче-
пластических деформаций наблюдается своеобразная потеря устойчивости
и при растяжении.
§ 2.2. Напряжения и деформации при растяжении — сжатии
Воспроизводя рассуждения § 1.7 применительно к растяги-
растягиваемому стержню, изображенному на рис. 2.1.3, рассечем его
мысленно плоскостью тп, перпендикулярной оси стержня (не
слишком близко к концу), и отбросим одну часть, например
верхнюю. Оставшаяся нижняя часть изображена на том же ри-
рисунке справа. Действие верхней части на нижнюю можно за-
заменить равномерно распределенными по сечению тп нормаль-
нормальными напряжениями а. После того как это
сделано, составим уравнение равновесия
нижней части стержня
Здесь F—площадь поперечного сечения.
Отсюда следует:
а =
F '
1'
t
-б
г
[ 1
в
Сделаем еще одно замечание, относящее-
относящееся к знакам. Знак внешней силы устанав-
устанавливается по отношению к той или иной
системе координат; таким образом, он со-
совершенно условен. Нельзя сказать, положи- Рис. 2.2.1
тельна или отрицательна сила Р, изображен-
изображенная на рис. 2.1.3, так как на этом рисунке ось координат от-
отсутствует. Однако для нормальных напряжений выше, в § 1.7,
было установлено совершенно определенное правило знаков, не
зависящее от выбора системы координат. Напряжение а счита-
считается положительным, если вектор напряжения направлен по
внешней нормали к поверхности, ограничивающей рассматривае-
рассматриваемый объем, и отрицательным в противном случае.
Если на тело действуют сжимающие силы (рис. 2.2.1), то
поступая по-предыдущему, можно нарисовать в сечении или
46
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
сразу сжимающие напряжения, обозначив их (—а), или, что
удобнее, положительные напряжения а. Во втором случае знак
определится автоматически из условия равновесия. В данном
случае, поступая любым из двух указанных способов, мы полу-
получим одно и то же уравнение равновесия
Отсюда
Р
Формулы для напряжений при растяжении и сжатии можно
объединить
ci=±-J-. B.2.1)
Здесь Р — внешняя сила, знак плюс или минус выбирается по
смыслу задачи.
При расчете стержневых систем бывает удобно ввести поня-
понятие о внутренней силе в стержне (иногда применяется термин
«усилие») N = +Р в случае растяжения, N = —P в случае сжа-
сжатия. Тогда в любом случае
а = -^. B.2.2)
Переходя к определению деформаций, заметим, что в усло-
условиях растяжения материал будет обязательно удлиняться в на-
направлении растяжения, в случае сжатия — обязательно укорачи-
укорачиваться. В противном случае работа силы Р была бы отрицатель-
отрицательной. Для той части стержня, которая находится в условиях
чистого растяжения, относительное удлинение
__А1_
в~ I '
оно положительно, если А1 положительно, и отрицательно, если
AZ отрицательно.
Для упругого материала по закону Гука е — о/Е, но о = N/F,
поэтому
* = ^ = ±Ж- B.2.3)
Здесь Р — абсолютная величина внешней силы, знак выбирается
по смыслу.
Заметим, что для всех материалов, применяемых в технике,
кроме резины и полимеров в каучукообразном состоянии, мо-
модуль упругости Е весьма высок по сравнению с пределом упру-
упругости или пределом текучести. Так, для стали Е = 2 • 104 кгс/мм2.
Поэтому величина упругой деформации для технических сплавов
§ 2.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ 47
составляет десятые и даже сотые доли процента, для жестких
полимеров (в стеклообразном состоянии) не больше 1—2%.
Если материал изотропен, то цилиндр, растягиваемый в на-
направлении его оси, остается цилиндром. Вообще, кроме дефор-
деформации е в направлении растяжения, будет происходить дефор-
деформация в поперечном направленин. Пусть некоторый отрезок, ле-
лежащий в поперечном сечении, имел до деформации длину 6,
длина его после деформации будет Ъ + Д6 и относительная попе-
поперечная деформация е = Ab/b. При растяжении е положительно,
а е' отрицательно, поперечные размеры образца уменьшаются.
При сжатии картина получается обратная. У изотропного мате-
материала величина е' одинакова для всех направлений в поперечном
сечении, поскольку предпочтительного направления нет. Если
деформация упруга и подчиняется закону Гука, то, как оказы-
оказывается, отношение поперечной деформации к продольной по-
постоянно
e' = _ve = —v^-. B.2.4)
Величина v называется коэффициентом Пуассона, это — констан-
константа материала. Значение v для стали, например, равно примерно
0,3. При упругопластических деформациях отношение е'/е ме-
меняется в процессе растяжения, оно зависит от напряжения.
Объем образца при растяжении и сжатии не остается постоян-
постоянным. Для изотропного материала изменение объема легко под-
подсчитать. Длина цилиндра увеличилась в отношении A + е), ли-
линейные размеры поперечного сечения уменьшились в отношении
A + е'), следовательно, площадь изменилась в отношении
A + е'у.
Относительное изменение объема равно
^- = A + еУA + е) -1. B.2.5)
Поскольку упругие деформации малы, в формуле B.2.5) следует
удержать только первые степени деформаций и мы получим
Естественно предположить, что при растяжении объем мате-
материала увеличивается, если е > О, то AF>0. Для этого нужно,
чтобы было
е'>е
Таким образом, коэффициент Пуассона упругого материала
не больше 1/2. Высказанное предположение будет строго обосно-
обосновано в § 8.4. У несжимаемого материала е' = —е/2. Пластиче-
48
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
ские деформации не сопровождаются изменением объема, поэто-
поэтому отношение —е' 1е в опыте па растяжение упругопластического
стержня возрастает с увеличением деформации от величины v
на упругом участке диаграммы, стремясь к 1/2.
Рассмотрим теперь случай анизотропного материала, но не
произвольного, а построенного определенным образом. Пусть,
например, растягивается об-
образец, вырезанный из ткане-
тканевого стеклопластика вдоль
направления основы ткани
(рис. 2.2.2). Через ось стер-
стержня проходят две плоскости
симметрии. Очевидно, что
призматический образец пос-
после деформации остается сим-
симметричным, однако дефор-
деформации в поперечных направ-
направлениях 1 и 2 будут разными,
Рис. 2.2.2
здесь
Рис. 2.2.3 е' и е" соответственно. В
упругой области е = —Vie,
v2 — различные коэффициенты Г1у-
и
е = — v2e,
ассона.
При анизотропии более общего вида, когда указать плоскости
симметрии нельзя или когда они не параллельны оси растяжения,
деформация может иметь более сложный характер, растяжение
может сопровождаться перекашиванием стержня, как показано
на рис. 2.2.3. Это легко представить себе, если выбрать образец,
состоящий из набора жестких пластин, наклонных по отношению
к оси и соединенных между собой прослойками из податливого
материала, как показано на том же рисунке.
§ 2.3. Перемещение узлов стержневых систем
Стержни, работающие на растяжение и сжатие, часто соеди-
соединяются в стержневые системы более или менее сложного строе-
строения. Соответствующий пример был приведен на рис. 2.1.2. Для
того чтобы обеспечить возникновение только растягивающих и
сжимающих напряжений, необходимо, как уже было оговорено,
чтобы соединения стержней в узле допускали свободный взаим-
взаимный поворот стержней и чтобы силы прикладывались только
в узлах. Заклепочное соединение узлов или сварка их, строго
говоря, не дает возможности свободного поворота, поэтому
в стержнях, кроме напряжений растяжения — сжатия, возникают
напряжения изгиба, о которых будет идти речь в следующей
главе. Однако эти напряжения невелики и при расчетах ими
обычно пренебрегают. Если ферма статически определима, а это
значит, что уравнения статики, составленные для каждого из
§ 2.3. ПЕРЕМЕЩЕНИЕ УЗЛОВ СТЕРЖНЕВЫХ СИСТЕМ 49
узлов, достаточны для определения всех усилий в стержнях, ве-
величины Nu где i — номер стержня, могут считаться известными.
Теперь, если все стержни упруги, то удлинение или укорочение
каждого из них будет определяться по формуле
A*i = JT-. B-3.1)
г г
при этом знак деформации (растяжение или сжатие) получа-
получается автоматически.
Следующая задача будет состоять в определении перемещений
узлов фермы. При ее решении существенно упрощающим дело
обстоятельством служит малость
деформаций отдельных стержней,
а следовательно, и малость пере-
перемещений по сравнению с длиной
стержня. Обозначая перемеще- Рис. 2.3.1
ние через и, будем считать,
что Al/l и и/1 — малые величины одного порядка малости. Так
бывает в подавляющем большинстве случаев, однако, как мы
увидим, не всегда. При сделанном предположении мы полагаем,
что перемещение, перпендикулярное оси стержня, не вызывает
его удлинения, точнее удлинение его представляет величину бо-
более высокого порядка малости, чем малая величина и/1. Дей-
Действительно, пусть правый конец стержня на рис. 2.3.1 получает
перпендикулярное его оси перемещение г/, тогда как левый конец
остается на месте. Новая длина стержня
Разлагая радикал по формуле Ньютона, получим
r-,[i + ±$ + ...
Как видно, относительное удлинение (Г — 1I1 имеет порядок
квадрата отношения и/1.
Рассмотрим теперь пример, из которого ясен принцип определения пе-
перемещений. Кронштейн, схематически изображенный на рис. 2.3.2, нагру-
нагружен в узле А силой Р, направленной, например, вертикально вниз (вообще,
направление силы может быть любым). По правилам статики определяются
усилия iVi и iV2 в стержнях. В данном примере N{ > О, N2 < 0. После этого
вычисляются удлинения А1\ и Ah (Al\ > 0, А12 < 0). Чтобы определить пе-
перемещение узла А, нужно поступить следующим образом. Предположим,
что шарнир в точке А удален и стержни разъединены. Сохраняя направле-
направления стержней, сообщим стержню 1 удлинение А/j, конец его переместится
в точку а\. Стержню 2 сообщим укорочение — А12, конец его перейдет в
точку а2.
Чтобы найти новое положение узла А, повернем стержни так, чтобы
концы их совпали в точке А" пересечения дуг, описанных концами стерж-
4 ю. н. Работнов
50
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
ней при их вращении около неподвижных шарниров. Отрезок А А" есть ис-
искомое перемещение. Нахождение перемещения АА" или его составляющих,
по каким-либо осям координат, например горизонтальной и вертикальной
оси, представляет собою задачу элементарной геометрии. Установленный
выше факт, состоящий в том, что малое перемещение, перпендикулярное
оси стержня, вызывает деформацию второго порядка малости, позволяет су-
существенно упростить решение этой геометрической задачи. Вместо того что-
чтобы перемещать концы стержней по дугам окружностей, будем двигать их
по перпендикулярам к осям стержней. Соответствующее построение пока-
показано на том же рис. 2.3.2. В результате полу-
получается несколько отличное положение узла,
а именно положение А'. Замена дуг окружно-
окружностей перпендикулярами означает, что мы как
бы дополнительно деформировали стержни,
но эта деформация имеет порядок u2/l2i тогда
как порядок основной деформации есть u/L
С другой стороны, расстояние А' А' имеет по-
порядок и2/1, если АА' = и, ошибка от замены
расстояния АА" величиной АА' есть величи-
величина порядка ujl.
Рис. 2.3.2 страдает одной несообразно-
несообразностью: в нем использованы разные масштабы
для изображения стержней и их перемеще-
перемещений. На рисунке, например, &1\ составляет
примерно одну пятую от 1и тогда как в дей-
действительности Mi/h — величина порядка 10~3.
Поэтому вся картина перемещений узла гру-
грубо искажена, дуги окружностей существенно
отличаются от перпендикуляров к осям и
точки А" и А' довольно далеки одна от дру-
другой. Чтобы избежать этой несообразности, все
построения для нахождения точки А' выпол-
выполняются в другом масштабе отдельно, как показано на том же рисунке
внизу. От некоторой точки, изображающей точку А, откладываются от-
отрезки AZi и &12 в направлениях соответствующих стержней и в произволь-
произвольном масштабе, отличном от масштаба основного чертежа. Из концов этих
отрезков к ним восстанавливают перпендикуляры, точка пересечения их
есть А'. Если бы мы пристроили к этой диаграмме сами стержни в том же
масштабе, то неподвижные шарниры оказались бы очень далеко за предела-
пределами страницы книги и дуги окружностей весьма большого радиуса были бы
на самом деле неотличимы от перпендикуляров.
Применим описанный способ к конструкции, изображенной на рис. 2.3.3.
Стержни составляют углы аире вертикалью. Требуется определить верти-
вертикальную и горизонтальную составляющие перемещения точки А. Построим
отдельно диаграмму перемещений (одной и двумя черточками отмечены
соответственно параллельные отрезки). Спроектируем ломаную ABA' на на-
направления стержней. Получим
A^i = иг sin а + Ив cos а, Ы2 = — иг sin [i + uB cos р.
Рис. 2.3.2
Отсюда находится
L sin P + A/2sina
sin (a + p)
cos P — AZ2cosa
sin (а + p)
B.3.2)
Величины AZj и A?2 легко находятся по формуле B.3.1), если указана сила,
приложенная в точке А. Усилия N\ и N2 определяются из условий статики.
Заметим, что, если а + $ = я, формулы B.3.2) становятся непримени-
неприменимыми. В этом случае перемещение точки А и удлинения стержней имеют
различный порядок малости. На рис. 2.3.4 изображена такая система: два
§ 2.4. СТАТИЧЕСКИ НЕОПРЕДЕЛЕННЫЕ ЗАДАЧИ ?1
одинаковых стержня образуют угол, равный я, к узлу приложена сила /\
перпендикулярная стержням. В предыдущей задаче мы пренебрегли изме-
изменением углов аир вследствие деформации стержней и составляли урав-
уравнения стержня для нахождения Nx и Jv2, считая эти углы теми же, что в ис-
исходном состоянии. В случае, изображенном на рис. 2.3.4, так делать нельзя,
мы вынуждены предположить, что узел пере-
переместился на величину и, стержни наклонились
на угол а каждый, так что tg а = и/1. Уравне-
Уравнение статики, составленное для деформироваввой
системы, будет
2tfsina — P = 0. B.3.3)
Удлинение стержня выразится следующим об-
образом:
cos a
Отсюда, по закону Гука
1 — cos a
= EF:
cos а
B.3.4)
Л ?г В Исключив из B.3.3) и B.3.4) усилие N, найдем
Рис. 2.3.3
Рис. 2.3.4
а как функцию Р. Поскольку упругая деформация стержня мала, переме-
перемещение и, а следовательно, и угол а тоже малые величины, только другого
порядка. Полагая приближенно sin a « tg a « a, cos а « 1 — а2/2, внося
эти выражения в B.3.3) и B.3.4) и проделывая указанное исключение,
получим
и = 13/P/(EF).
Зависимость перемещения от силы оказалась резко нелинейной.
§ 2.4. Статически неопределенные задачи
на растяжение — сжатие
Последний пример предыдущего параграфа относится к осо-
особому случаю и представляет собою исключение из общего пра-
правила. Общее же правило состоит в том, что уравнения статики
составляются в пренебрежении теми изменениями геометрии, ко-
которые связаны с деформацией. Уравнения статики линейны, со-
соотношения между перемещениями и деформациями стержней
также линейны. Если считать справедливым закон Гука B.3.1),
то в результате решения цепочки линейных уравнений переме-
перемещения окажутся линейными функциями внешних сил.
52
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
Теперь мы можем перейти к решению задач статически не-
неопределенных, понятие о которых было дано в § 1.5. Общий план
решения таких задач состоит в следующем.
1. Составить уравнения совместности деформаций, т. е. соот-
соотношения, связывающие деформации отдельных элементов при
всех возможных перемещениях узлов.
2. Заменить в уравнениях совместности деформации через
напряжения или усилия по закону Гука (или иному закону
связи).
3. Составить уравнения статики, считая геохметрию системы
определенной для иедеформированиого состояния системы.
4. Решить полученную систему линейных уравнений.
В отдельных случаях может возникнуть ситуация, подобная
той, которая была рассмотрена в конце предыдущего параграфа.
Тогда уравнения совместности деформаций окажутся нелиней-
нелинейными и уравнения статики придется составлять с учетом изме-
изменения углов из-за деформации элементов.
Поясним описанную схему на нескольких простейших примерах.
а. Система из двух стержней, изображенная на рис. 2.3.3, дополнена
третьим вертикальным стержнем. В точке А приложена сила Р, направлен-
направленная вертикально вниз (вертикальное направление стержня и силы совер-
шеБно необязательны, это сделано только для определенности).
Горизонтальное перемещение точки А не вызывает удлинения третьего
стержня, вертикальное перемещение равно удлинению этого стержня М5.
С другой стороны, первая из формул B.3.2) выражает это
у у |^ ч перемещение через Ah и А12. Таким образом, получаем урав-
II { II нение совместности
sin
sin (a + р)
B.4.1)
Рис. Z.4.1
Формулы закона Гука записываются обычным способом
Ni!i
Ы^Щр, B.4.2)
Наконец, уравнения статики для узла А будут следующими:
iVi cos a + N2 cos p + N3 — Р = О, N{ sin а — Лг2 sin р = 0.
После того как в уравнении B.4.1) удлинения будут замене-
заменены через усилия с помощью B.4.2), остается система трех ли-
линейных уравнений для определения трех усилий N{, N2 и Nz.
б. Болт с площадью сечения F\ вставлен в трубку из того же материа-
материала с площадью сечения F2, как показано на рис. 2.4.1. Приведя головку
болта и шайбу в плотное соприкосновение с трубкой, поворачивают гайку
так, чтобы она переместилась по нарезке в направлении оси на величину h.
Требуется определить напряжения в болте и трубке.
При выполнении пункта 1 плана, т. е. при составлении уравнения сов-
совместности деформаций следует помнить, что эти уравнения связывают лю-
любые возможные деформации элементов системы.
Предположил! поэтому, вопреки очевидности, что как трубка, так и
болт удлиняются, по удлинение болта больше, чем удлинение трубки на
§ 2.4. СТАТИЧЕСКИ НЕОПРЕДЕЛЕННЫЕ ЗАДАЧИ
53
величину h. Итак,
Mi — AZ2 = h. B.4.3)
Пренебрегая толщиной шайбы, полагаем l{ = Z2, заменяя A?i и А/2 через на-
напряжения по закону Гука, перепишем условие B.4.3) в виде соотношения
между напряжениями
«x-a.-f-. B-4.4)
Поскольку мы посчитали оба элемента растянутыми, при составлении урав-
уравнения равновесия нужно считать, что как в болте, так и в трубке напряже-
напряжения положительны. Рассекая систему плоскостью тп н составляя условие
равновесия любой из частей, получим
= 0. B.4.5)
Решая систему B.4.4), B.4.5), найдем
Eh F«
Eh
Совершенно очевидный результат, состоящий в том, что болт растягивается,
а трубка сжимается, получился в резуль-
результате решения автоматически.
в. В следующем примере будет приве-
приведено решение статически неопределенной
задачи, полученное несколько иным мето-
методом, который состоит в том, что у систе-
системы освобождают столько связей, сколько
нужно для превращения ее в статически
определимую. Прикладывая реакции этих
связей, выбирают величины их так. чтобы
уничтожить перемещения, ставшие воз-
возможными благодаря нарушению связей.
Эти перемещения вычисляют по отдельно-
отдельности от действующих сил и от неизвестных
реакций; вследствие линейности системы
результирующее перемещение есть сумма
перемещений от каждой из сил по отдель-
отдельности. Эту сумму приравнивают нулю, та-
таким образом, получают уравнения для на-
нахождения неизвестных реакций.
На рис. 2.4.2 изображен стержень, концы которого закреплены между
неподвижными основаниями, он нагружен двумя продольными силами.
Требуется определить усилия во всех трех участках стержня.
Освободив верхнюю заделку, мы даем возможность верхнему концу
переместиться вниз на величину 6Р, равную
Ра Р-2а ЗРа
°Р = ~"Ш ~~ EF = ~~ EF '
Приложим теперь к верхнему концу неизвестную реакцию X, которая вы-
вытягивает стержень на величину бх, равную 6Х = X-3a/(EF). Условие неиз-
неизменности длины стержня будет следующим: ЪР + 6х = 0. Отсюда, подста-
подставив выражения 6Р и бх, находим X = Р. Теперь легко подсчитать, что на
первом участке N\ = Р, на втором N2 = 0 и на третьем N3 = —Р.
г. Следующий пример будет относиться к определению так называемых
температурных и монтажных напряжений. Возвращаясь к схеме, изобра-
изображенной на рис. 2.3.3, примем для простоты, что а = р, шарнирные крепле-
Рис. 2.4.2
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
пия стержней расположены на одной горизонтали, площади сечений и моду-
модули упругости стержней одинаковы (рис. 2.4.3). Но средний стержень ока-
оказался изготовленным на величину б длиннее, чем это необходимо для сбор-
сборки системы без приложения усилий. В этом случае сборка становится воз-
возможной только за счет упругой деформации стержней. Применим общую
схему, составим уравнение совместности деформа-
ций, основываясь на диаграмме, изображенной вни-
внизу рис. 2.4.3. Условие совместности будет
= (М2 + б) cos a.
B.4.6)
Здесь AZ2 — упругая деформация, поэтому уравне-
уравнение B.4.6) переписывается следующим образом:
о Z (о I
AL
Рис. 2.4.3
Составляя уравнение равновесия и решая получен-
полученную систему, найдем
Ed cos2 а Ед 2 cos3 а
^2 :
12 1 + 2 cos3 ее
12 1 + 2 cos3 а
Совершенно такой же результат будет получен, если
система собрана без усилий при температуре t0, а после этого средний стер-
стержень нагрет до температуры t >> to. Действительно, безразлично в каком
порядке осуществляются нагревание стержня и сборка системы. Можно
представить себе, что сначала средний стержень нагрет, в результате чего
он приобрел удлинение 6 = a(t — tQ)l, и после этого произведена сборка.
Заменяя в полученных выше формулах величину б ее выражением через
температуру (см. § 2.9), получим решение задач о температурных напря-
напряжениях. Заметим, что для задач о температурных или монтажных напря-
напряжениях в статически неопределимых системах можно применять полностью
указанную в начале этого параграфа схему, т. е. составлять уравнения сов-
совместности деформаций обычным способом, но при выполнении пункта 2
учитывать, что полная деформация стержня состоит из упругой деформа-
деформации и вынужденной несовместной деформации б, которая может происходить
от температуры или от несоответствия действительного размера элемента
проектному размеру. Поэтому вместо B.3.1) нужно использовать следующие
соотношения:
Nih
B'4'7>
§ 2.5. Расчет стержневых систем на прочность
При расчетах инженерных конструкций обычно считают не-
недопустимым либо появление значительных пластических дефор-
деформаций, либо разрушение всей конструкции в целом или ее от-
отдельных элементов. Характерное напряжение, при котором пла-
пластический материал приобретает заметную пластическую дефор-
деформацию, называется пределом текучести и обозначается от. Хруп-
Хрупкие материалы ведут себя практически упруго вплоть до момента
разрушения, которое происходит при достижении напряжением
значения ов, так называемого предела прочности или временного
сопротивления. Понятие о пределе текучести ат было введено
§ 2.5. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ НА ПРОЧНОСТЬ 55
в § 1.9 применительно к идеальному упругопластическому ма-
материалу, для реальных материалов можно говорить об условном
пределе текучести. Предел прочности ов определяют также и для
пластических материалов, однако значительное изменение фор-
формы образца в области больших деформаций, при которых проис-
происходит разрыв, делает эту величину еще более условной, чем пре-
предел текучести.
При расчетах элементов конструкций необходимо иметь
некоторый запас, учитывающий неточность изготовления стерж-
стержня, возможные перегрузки в условиях эксплуатации, несоответ-
несоответствие характеристик реального материала паспортным данным,
неточность выбранной расчетной схемы. Поэтому допускаемое
напряжение [с] выбирают, деля ст или ов на коэффициент запаса
прочности п. Таким образом:
[а] = — для пластических материалов,
B.5.1)
[а] = — для хрупких материалов.
пв
Для единичного стержня, находящегося под действием растяги-
растягивающей или сжимающей нагрузки, условие прочности записы-
записывается так:
\а\ <[о]. B.5.2)
В случае сжатия возможно разрушение от потери устойчивости.
Этот вопрос будет детально рассмотрен далее, пока заметим, что
расчет на устойчивость формально сводится обычно к расчету
на сжатие при соответствующим образом пониженном допускае-
допускаемом напряжении.
Для статически определимой стержневой системы условие
прочности будет выполнено, если условие B.5.2) не нарушается
ни для одного из элементов. Действительно, если хотя бы для
одного элемента при некотором значении силы Р условие B.5.2)
нарушается, достаточно увеличить эту силу в п раз, чтобы вся
система в целом потекла или разрушилась. В статически опре-
определимой системе разрушение одного из стержней или переход
его в пластическое состояние превращает систему в механизм,
получающий свободу деформироваться неограниченно. Последнее
слово употреблено опять-таки в условном смысле. Возможность
неограниченной деформации пластического материала относится
к случаю идеальной пластичности, реальные материалы обладают
упрочнением. С другой стороны, даже система из идеально-пла-
идеально-пластических стержней при увеличении деформации меняет форму,
в результате чего иногда (не всегда) увеличение деформации
требует увеличения нагрузки.
56 ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
Поскольку в статически определимой системе напряжения во
всех стержнях представляют собою линейные функции действу-
действующих сил, запас прочности по напряжениям, обеспечиваемый
выполнением условия B.5.2), будет в то же время запасом проч-
прочности по нагрузкам. В статически неопределимых системах дело
обстоит иначе, здесь разрушение или переход в состояние теку-
текучести одного из стержней системы еще не означает разрушения
системы в целом. Поясним сказанное примером.
На рис. 2.5.1 представлена система из трех стержней, совер-
совершенно подобная рассмотренной в примере г § 2.4 и изображенной
на рис. 2.4.3. На этот раз система собрана без предварительного
напряжения, она загружена вертикальной силой в точке А.
Расчет, выполненный по правилам § 2.4 в
предположении упругости стержня, дает
NP сов'а N P 1
\
A
\\
\\
\>
Рис.
/
/j
//
//
~~t—i*
lA
p
2.5.1
1 + 2 cosd a 1+2 cos*5 a
Сразу видно, что N2>Ni и при увеличении
силы Р в среднем стержне предел текуче-
текучести будет достигнут раньше, чем в край-
крайних наклонных стержнях. Однако это не
означает исчерпания несущей способности
системы в целом. Крайние стержни, оста-
оставаясь упругими, препятствуют неограниченной пластической де-
деформации среднего стержня. Таким образом, можно различить
две стадии работы системы: упругую стадию, в которой усилия
определяются написанными выше формулами, и упругопласти-
ческую, которая наступает после перехода хотя бы одного
стержня в пластическое состояние. Значение силы Ри при ко-
котором происходит переход от первой стадии ко второй, опреде-
определяется из условия, что при Р — Pi N2 = oTF. Отсюда
COS (Xi)» y?»0.O)
Во второй стадии усилие N2 остается постоянным
iV2 = aTF
и задача определения усилия Ni решается с помощью одного
только уравнения статики
Отсюда
При дальнейшем увеличении силы и в наклонных стержнях на-
начинается* текучесть. Это уже текучесть всей системы в целом.
§ 2.5. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ НА ПРОЧНОСТЬ
57
Соответствующая сила определяет несущую способность системы
и обозначается Рт — нагрузка, при которой наступает общая те-
текучесть. Полагая в B.5.4) N{ = oTF иР = Рт, найдем
= oTF(l + 2 cos a).
B.5.5)
Зависимость перемещения и точки А от силы Р изображается
графиком, представленным на рис. 2.5.2.
Принимая один и тот же коэффициент запаса п, получим
следующие величины допускаемой нагрузки.
а. При расчете по допускаемым напряжениям B.5.3)
б. При расчете по допустимым нагрузкам B.5.5)
Р<^- A + 2cosa).
Второй способ расчета приводит к большим допустимым на-
нагрузкам, нежели первый (при а = 30° на 19%). Заметим, что
для определения предельного состояния
системы, т. е. нагрузки Рт, нет необ-
необходимости прослеживать поведение си-
системы в упругой области и последова-
последовательность перехода ее элементов в пла-
пластические состояния. В данном случае
в предельном состоянии все три стерж-
стержня текут, поэтому достаточно поло-
положить Ni = N2 = iV3 = GTF и составить
уравнение равновесия, мы получим
формулу B.5.5). Так получилось вслед-
вследствие симметрии системы, вообще же,
для возможности общего течения доста-
достаточно, чтобы напряжения достигли предела текучести в двух
стержнях. В случае, изображенном на рис. 2.3.3, заранее не из-
известно, какой стержень потечет первым, какой вторым и который
из трех остается упругим. Поэтому, казалось бы, для такой за-
задачи необходимо повторить проделанный выше анализ, который,
естественно, окажется более сложным вследствие асимметрии си-
системы. Но в предельном состоянии могут быть только три воз-
возможности:
О
Рис. 2.5.2
2) \N2\ = \N>\=oJ?,
3) \N3\ = |AM=gtF.
Для каждой из этих возможностей с помощью одного только
уравнения статики находится величина Рт, а также величина
58 ГЛ. 2. РАСТЯЖЕНИЕ II СЖАТИЕ
третьего усилия, iV3, N{ и N2 для первого, второго и третьего
случаев соответственно. Оказывается, что только в одном из
этих случаев напряжение в третьем стержне, который предпо-
предполагается упругим, оказывается по абсолютной величине меньше,
чем ст, при этом величина предельной нагрузки будет наимень-
наименьшей из трех возможных. Это утверждение пока что мы можем
только проиллюстрировать примерами, в дальнейшем оно будет
строго доказано (§ 5.9).
§ 2.6. Остаточные напряжения после пластической деформации
Рассмотрим теперь совершенно произвольную систему из п
стержней, каждый стержень мы будем отмечать индексом /.
Число уравнений статики, которые остаются после исключения
из них реакций в точках закрепления и, следовательно, содер-
содержат в качестве неизвестных только п усилий в стержнях, не
может превышать п; если это число равно п, то система стати-
статически определима, если это число есть п — р, то р называется
степенью статической неопределимости. Общая запись уравнений
статики будет следующая:
2 bijOj^Bi (i = l, 2, ...,п-р). B.6.1)
j=l
Здесь Gj — напряжение в стержне с номером /.
Если выбросить из системы р «лишних» стержней, то из
уравнений B.6.1) найдутся напряжения в каждом из оставших-
оставшихся, по формулам закона Гука через них выразятся деформации,
и мы сможем вычислить перемещения узлов; деформации остав-
оставшихся п — р стержней будут совместными. Но если лишние
стержни не выброшены, то деформации их должны быть опре-
определенным образом согласованы с деформациями тех, с которыми
они связаны. Поэтому должны быть выполнены уравнения сов-
совместности деформаций
2 а^ = 0 A = 1,2, ...,р), B.6.2)
где uij — известные постоянные коэффициенты. Теперь остается
заменить в уравнениях B.6.2) деформации через напряжения
по закону Гука с учетом возможных зазоров, натягов и тепло-
тепловых деформаций
ej^Oj/Ej + Ц]. B.6.3)
Полученная система уравнений представляет собою обобще-
обобщение тех уравнений, которые мы рассматривали на частных при-
примерах § 2.4. В B.6.1) величины Bh стоящие в правых частях,
2.6. ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ
59
представляют собою силы или линейные комбинации сил в за-
зависимости от того, как составлялись отдельные уравнения
системы. Величины г], в B.6.3) — это температурные деформации
Ц] = 0Cj(tj — to) или натяги т];- = 8//;- (см. обозначения приме-
примера г § 2.4).
Уравнения B.6.1) и B.6.2) справедливы как в упругом, так и
в упругопластическом состоянии системы, тогда как B.6.3) верно
лишь для упругих стержней. По мере
перехода стержней в пластическое со-
состояние некоторые из соотношений
B.6.3) заменяются условиями пластич-
пластичности
cs = cTS (s = I, 2, ..., к<р).
Когда число перешедших в пластиче-
пластическое состояние стержней становится
большим р, наступает общая текучесть.
Если некоторая система сил (Р),
которой соответствуют величины Bi в
уравнениях B.6.1), приводит систему
в упругопластическое ,состояние и после этого удаляется, т. е.
происходит разгрузка, претерпевшие пластическую деформацию
стержни уже не возвращаются в исходное состояние и не дают
вернуться в исходное состояние тем стержням, которые оста-
оставались упругими. Для отыскания остаточных напряжений после
разгрузки мы поступим следующим образом. Обозначим остаточ-
остаточные напряжения а,-0, остаточные деформации е,-0, последние мо-
могут быть упругими у тех стержней, которые оставались упру-
упругими, и упругопластическими у стержней, перешедших в пла-
пластическое состояние. Уравнения B.6.1), B.6.2) справедливы, как
было уже отмечено, для любого состояния системы, следова-
следовательно, и для состояния разгрузки, если принять Bi = 0. Таким
образом:
Рис. 2.6.1
= 0,
B.6.4)
= 0-
B.6.5)
Вычтем из уравнения B.6.1) уравнение B.6.4) и из B.6.2) урав-
уравнение B.6.5). Получим
п п
2 bVd (а,- — Gj0) = Вь 2 ац (ej — ej0) = 0.
jl 1
B.6.6)
Обращаясь к диаграмме пластичности, изображенной на
рис. 2.6.1, убеждаемся, что при разгрузке как из упругого, так и
60 ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
из пластического состояния
(Oj — Ojo) = ?Д^ —ej0).
Положим
Тогда уравнения B.6.6) можно переписать в форме, совершенна
тождественной B.6.1) и B.6.2)
п п
3=1 3=1
но теперь для всех стержней справедлив закон Гука
Решая эти уравнения, мы найдем oj и е$ и вычислим оста-
остаточные деформации и остаточные напряжения по формулам:
Таким образом, мы получаем следующее правило нахождения
остаточных напряжений и деформаций после разгрузки.
Для определения напряжений и деформаций, остающихся
в упругопластичеспой системе после снятия нагрузки, нужно вы-
вычесть из действительных напряжений и деформаций, соответству-
соответствующих данной нагрузке, напряжения и деформации, вычисленные
для той же нагрузки в предположении об упругом поведении
всех ее элементов.
Определим для примера остаточные напряжения в системе из
трех стержней, изображенной на рис. 2.5.1, в предположении,
что Р = Рт и, следовательно, все стержни доведены до предела те-
текучести. Фиктивные усилия, вычисленные в предположении упру-
упругости стержней, будут
N' — Р
iV2 — ±т
1\ 1 — JrT iV2 — ±т о •
l + 2cos3a 1 + 2 cos3 a
Следовательно, после разгрузки будет
N10 = oTF - Рт—CQs2a, , N20 = oTF - Рт
10 1+2 cos3 a' 20
1+2 cos3 a' 20 1 + 2 cos3 a
Предположим теперь, что разгруженная система нагружается
вторично. Усилия, соответствующие вновь приложенной силе Рг
можно определить так, как если бы остаточных напряжений не
было, а потом прибавить к ним остаточные усилия. Получаем
' l+2cos*a ' х * /l + 2cos3a*
Из этих формул ясно видно, что при Р < Рт все три стержня
§ 2.6. ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ 61
остаются в упругом состоянии, они переходят в пластическое
состояние все сразу при Р = РТ. Не составляет труда пока-
показать, что этот результат носит совершенно общий характер,
а именно:
При повторной нагрузке все элементы остаются упругими до
тех пор, пока новая нагрузка не превышает той, от которой
произведена разгрузка.
Обращаясь к рис. 2.5.2, мы видим, что разгрузка от любой
точки следует прямой, параллельной начальному участку диа-
диаграммы, и повторная нагрузка следует той же прямой до точки А,
из которой была произведена разгрузка. После того как будет
вновь достигнута точка А, соответствующая силе Р\ напряже-
напряжения в стержнях, подвергшихся пластической деформации, опять
достигают предела текучести, система опять перейдет в упруго-
пластическое состояние и дальнейшее деформирование будет сле-
следовать той же диаграмме, которой следовала бы зависимость
между Ржи при отсутствии промежуточной разгрузки.
Такое поведение упругопластической стержневой системы со-
совершенно подобно поведению образца из упрочняющегося упру-
гопластического материала, соответствующего диаграмме на
рис. 1.9.1. Только для образца диаграмма деформирования пред-
представляет собою плавную кривую, тогда как для стрежневой си-
системы, содержащей конечное число стержней, эта диаграмма бу-
будет ломаной.
Отсюда вытекает естественная мысль — моделировать упроч-
упрочняющиеся упругопластические тела набором идеально упруго-
пластических стержней, вынужденных деформироваться сов-
совместно.
Применение установленного выше правила, позволяющего
определить остаточные напряжения после разгрузки, встречает
одно ограничение. В рассмотренном примере NiQ > 0, a N20 < 0.
Может оказаться, что остаточное сжимающее напряжение N2JF
по абсолютной величине больше, чем предел текучести. В этом
случае говорят о вторичных пластических деформациях: если они
появляются, т. е. если в результате расчета оказывается, что ка-
какая-то из величин ok по абсолютной величине превышает от, то
все рассуждения, конечно, становятся неверными. Читатель легко
убедится сам, что в этом случае правило нахождения остаточных
напряжений и деформаций после разгрузки допускает очень про-
простое обобщение. Фиктивные напряжения и деформации, oj0 и ец},
нужно вычислять с учетом возможности пластических деформа-
деформаций, но при удвоенном пределе текучести. Отсюда вытекает про-
простое правило для определения того, появляются ли в системе
вторичные пластические деформации. Нужно определить напря-
напряжения во всех стержнях при Р = Рт в предположении упругости
их и проверить, не окажется ли в каком-либо стержне напряже-
напряжение большим чем 2ат.
62 гл- 2- РАСТЯЖЕНИЕ И СЖАТИЕ
§ 2.7. Большая деформация
При рассмотрении задач о растяжении упругих стержней
предполагалось, что деформации малы. Однако пластические де-
деформации металлов и упругие деформации таких материалов как
резина могут быть значительны. Посмотрим, каким образом мо-
может повлиять учет значительной величины деформаций на при-
приведенные выше рассуждения*). Прежде всего остановимся на
понятии напряжения. При растяжении поперечные размеры
стержня уменьшаются, следовательно, уменьшается площадь се-
сечения. Истинное напряжение есть сила, поделенная на факти-
фактическую площадь поперечного сечения; таким образом, оно зави-
зависит не только от величины силы, но и от величины вызванной
этой силой деформации. Чтобы построить диаграмму а — е, нужно
во время опыта непрерывно измерять поперечный размер стерж-
стержня, что бывает затруднительно. Часто под напряжением понима-
понимают силу, поделенную на первоначальную площадь поперечного
сечения, определенное таким образом напряжение называется
условным, будем обозначать его о0.
Относительная деформация е была определена как отношение
приращения длины к первоначальной длине. Такое определение
может быть сохранено и для больших деформаций, однако с ним
связано некоторое неудобство. Относительная деформация не ад-
аддитивна. Поясним это обстоятельство. Предположим, что стер-
стержень деформировался в два приема: первоначальная длина его
была Zo, после первой деформации длина стала Z4. Относительная
деформация есть е{ = (Z4 — U)/h. Теперь стержень деформирован
еще раз, длина его стала h- Длина /4 по отношению ко второму
этапу деформирования является начальной, значит относитель-
относительная деформация на втором этапе есть е2 = (h — h)/h- Полная
деформация, отнесенная к первоначальной длине е= A2 — Zo)/Zo.
Видно, что
е Ф ех + ег.
Если ei и е2 малы по сравнению с единицей, то соотношение
е = et + e2 справедливо с точностью до величин второго порядка
малости; таким образом, малые деформации аддитивны.
В механике резиноподобных материалов вместо относительной
деформации е часто используют величину А, = Z/Zo, называемую
кратностью. Очевидно,
X = 1 + е.
В качестве меры деформации, вообще говоря, можно выбрать
любую функцию от е (или от Я). Определенными преимуще-
преимуществами обладает логарифмическая деформация, определяемая
*) В литературе часто можно встретить совершенно неточный термин
«конечные» деформации.
§ 2.8. УПРУГАЯ ЭНЕРГИЯ И УПРУГИЕ ПОТЕНЦИАЛЫ gg
следующим образом:
~e = ln-± =ln(l + e).
При малых деформациях, разлагая логарифмы в ряд п удержи-
удерживая первый член, найдем
ё ~ е.
Таким образом, малая логарифмическая деформация совпада-
совпадает с обычной. Логарифмические деформации аддитивны. Дейст-
Действительно, обращаясь к приведенному выше примеру, когда дефор-
деформирование производилось в два этапа, найдем
e1 = ln-jL, e2 = In-—-, e = ln-p-.
Lo Li о
Очевидно, что
в = в i + в2.
§ 2А Упругая энергия и упругие потенциалы
В этом параграфе мы будем рассматривать упругое тело как
механическую консервативную систему, т. е. систему, для ко-
которой работа внешней силы целиком затрачивается на сообщение
кинетической энергии движения тела и накопление полностью
обратимой потенциальной энергии. Последнее свойство — способ-
способность накапливать потенциальную энергию и возвращать ее в том
или ином виде — широко использовалось ранее и, в меньшей
степени, используется в настоящее время. Примерами могут
служить лук — во времена доисторические и исторические, за-
заводная пружина часов — в наши дни.
Высказанное утверждение можно записать следующим образом:
A =f + U. B.8.1)
Здесь А — работа внешних сил, Т — кинетическая энергия дви-
движения, U — потенциальная энергия деформации. Чтобы вычис-
вычислить величину ?7, нужно предположить, что внешняя сила при-
прикладывается таким образом, чтобы кинетической энергией можно
было пренебречь. Очевидно, для этого нужно, чтобы сила при-
прикладывалась достаточно медленно и производила деформацию
с малой скоростью. В пределе, при скорости приложения нагруз-
нагрузки, стремящейся к нулю, мы получим из B.8.1)
A=U.
Заметим, что фактически для выполнения этого равенства с боль-
большой точностью нет необходимости делать скорость очень малой.
Ведь кинетическая энергия Т изменяется пропорционально квад-
квадрату скорости: уменьшая скорость в 10 раз, мы уменьшаем
величину Т в 100 раз.
64
ГЛ. 2. РАСТЯЖЕНИЕ II СЖАТИЕ
Процесс деформации стержня можно представить себе как
последовательность бесконечно малых приращений удлинения
d(AZ), вызываемых ростом силы, которая связана с удлинением
при растяжении — сжатии законом Гука. Поэтому
м
=U=\ Pd(Al).
B.8.2)
Полагая Р = oF, Al = el и замечая, что IF = F, где V — объем
стержня, найдем
U = V J ode.
о
Закон упругости связывает о и е зависимостью A.8.1): о==ф(в).
Положим
U = J ad<? =
B.8.3)
Величина U представляет собою упругую энергию на единицу
объема. Волнистая черта над символом U обозначает, что эта ве-
величина проинтегрирована по всему объему тела, в данном слу-
случае просто умножена на объем.
Для линейного упругого тела из B.8.3) следует
2? *
B.8.4)
Для упругой энергии стержня в целом путем умножения B.8.4)
на V — FI или непосредственно, интегрируя
Р
B.8.2) с учетом B.3.1), находим
I
Tt_ef(m2)
U 21
N2l
B.8.5)
Следует обратить внимание на последнее вы-
выражение для U. Условие А = V требует, чтобы
сила прикладывалась постепенно, возрастая от
нуля до конечного значения N. График за-
зависимости силы от перемещения представлен
при этом на рис. 2.8.1, и работа изобража-
изображается площадью заштрихованного треугольника. В теорети-
теоретической механике консервативными силами называются си-
силы, имеющие потенциал, только для таких сил справедливо
уравнение сохранения механической энергии B.8.1). Вообще,
зависимость п переменных уи у2, ..., уп от других п перемен-
переменных хи х2, ..., %п называется потенциальной в том случае, когда
§ 2.8. УПРУГАЯ ЭНЕРГИЯ И УПРУГИЕ ПОТЕНЦИАЛЫ C5
существует такая функция U(xk), что
Ук=—. B.8.6)
дхк
Оказывается, что если справедливы соотношения B.8.6), то об-
обратные соотношения, выражающие хк через z/s, могут быть пред-
представлены в аналогичной форме, т. е. существу-
существует функция Ф{уъ) такая, что с.
дФ /0 п 7ч
Хъ = -—. (Z.O. /)
дУъ
Переход от соотношений B.8.6) к B.8.7)
называется преобразованием Лежандра. Осу-
Осуществляется оно следующим образом.
Положим
Ф = хм - U. B.8.8) рис 282
Предполагается, что соотношения B.8.6) ре-
решены относительно xh и эти выражения внесены в B.8.8), по-
поэтому Ф = Ф(ук).
Продифференцируем B.8.8) по yh. Получим
dyk ~~ h Уг дук дхг дуК*
Вследствие B.8.6) второй и третий члены в правой части напи-
написанного равенства взаимно уничтожаются и остается соотноше-
соотношение B.8.7).
Дифференцируя B.8.3) по е, мы получаем
а = ^-. B.8.9)
Это и есть условие того, что упругая энергия U служит потен-
потенциалом напряжений. Применяя преобразование Лежандра, т. е.
полагая
мы находим
е = |р B.8.10)
Упругий потенциал U имеет непосредственный механический
смысл, это потенциальная энергия упругой деформации, накоп-
накопленная в теле. Величина Ф такого непосредственно механическо-
механического смысла не имеет. Иногда эту величину называют дополнитель-
дополнительной работой. Происхождение такого названия ясно из рис. 2.8.2,
если ?^=j °de представляет собой заштрихованную площадь,
то Ф дополняет ее до площади прямоугольника со сторонами а
и е. Для линейно-упругого материала потенциал деформаций Ф
численно равен потенциалу напряжений U, диагональ прямо-
5 10. Н. Работнов
G6 ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
угольника делит его площадь на равные части. Нз формул B.8.4)
следует:
_ аи (е) аи (о)
° ~ de ' e do '
Заметим, что вся изложенная теория не предполагает упруго-
упругости материала, пока не произведена разгрузка и, следовательно,
деформация не уменьшается, связь между деформацией и на-
напряжением а = ф(е) одинакова как для упругого, так и для
пластического тела.
§ 2.9. Термодинамика упругой деформации
Приведенное выше определение упругой деформации и, соот-
соответственно, упругого тела нуждается в уточнении. В действитель-
действительности деформация сопровождается изменением температуры по-
подобно тому, как при сжатии или растяжении газа температура
его меняется. Более общее определение упругого тела будет
следующее: работа сил, приложенных к упругому телу, на замк-
замкнутом по деформации и температуре цикле равна нулю. Разница
по сравнению с тем определением, которое было дано в § 1.8,
состоит в том, что в конце цикла температура должна быть той
же, что в начале. Очевидно, что вязкое тело (вязкая жидкость)
не подходит под это определение, силы вязкого сопротивления
совершают работу, которая переходит в тепло; чтобы цикл был
замкнутым не только по деформациям, но и по температуре, это
тепло необходимо отвести, количество отведенного тепла равно
работе сил и всегда отлично от нуля.
Рассмотрим элемент упругого тела, находящегося в однород-
однородном состоянии простого растяжения, например, в виде кубика
с ребром, равным единице. На две противоположные грани этого
кубика действуют нормальные напряжения а; так как площадь
грани равна единице, то действующая сила также есть о. По-
Поскольку длина ребра равна единице, то е представляет собою
абсолютное удлинение. Будем рассматривать силу а как внешнюю
по отношению к элементу. Если сила увеличилась на da, удли-
удлинение увеличилось на de и сила произвела при этом работу a de.
Количество тепла в объеме, вообще говоря, изменилось на dQ.
Согласно первому началу термодинамики изменение внутренней
энергии dU равно
dU = ode + dQ. B.9.1)
Второе начало термодинамики утверждает существование функ-
функции состояния S, называемой энтропией, такой что для обрати-
обратимых процессов
§ 2.9. ТЕРМОДИНАМИКА УПРУГОЙ ДЕФОРМАЦИИ 07
Здесь Т—температура. Таким образом,
dU = ode + TdS.
Это выражение должно быть полным дифференциалом, внутрен-
внутренняя энергия есть функция деформации и .энтропии
<* § T <292>
Таким образом, внутренняя энергия является термодинами-
термодинамическим потенциалом. С помощью преобразования Лежандра
строятся другие термодинамические потенциалы, а именно:
свободная энергия
U*(e,T) = U-TS, о = *-?-, 5 = -^, B.9.3)
энтальпия
<t>(o,S)=oe + U, е=д-§, Т = д-§-, B.9.4)
свободная энтальпия
Ф*(а,Т) = Ф-ТБ, е = %, S = -a^. B.9.5)
Процесс называется адиабатическим, если не происходит
теплообмена с окружающей средой, т. е. dQ = 0, а следовательно,
S = const. Для изотермического процесса Т = const. Теперь ясно,
что для адиабатического процесса потенциал напряжений пред-
представляет собою внутреннюю энергию, потенциал деформаций —
энтальпию. Для изотермического процесса эти потенциалы будут
соответственно свободная энергия и свободная энтальпия. Только
для изотермического и адиабатического процессов зависимость
между напряжением и деформацией в упругом теле однозначна.
Вообще, если существует теплообмен с окружающей средой, эта
однозначность нарушается.
Предположим, что из опыта определена зависимость между
напряжением, деформацией и температурой
о = Ее-Еа{Т~Т0). B.9.6)
Здесь а — коэффициент температурного расширения, Го — неко-
некоторая температура, соответствующая условно выбранному началь-
начальному состоянию, если Т = Го и о = 0, то е = 0.
Модуль упругости, фигурирующий в B.9.6), должен быть
определен в изотермических условиях. Если при упругом дефор-
деформировании образца его температура меняется, то упругая дефор-
деформация будет сопровождаться температурной деформацией и, не
производя непрерывного замера температуры в течение опыта,
мы не сможем отличшь упругую деформацию от температурной.
Измеряя только силу и деформацию, мы найдехМ, что зависимость
5*
68 ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
между приращением напряжения и приращением деформации пе
описывается законом Гука с модулем Е.
Предположим, что модуль упругости и коэффициент а не
зависят от температуры (это верно лишь приближенно, в узком
диапазоне температур). Выражение B.9.6) для напряжения через
деформацию и температуру получается по формулам B.9.3),
g есть производная свободной энергии по деформации. Поэтому,
интегрируя B.9.6), найдем выражение для свободной энергии
Здесь ty(T) — неопределенная пока функция от температуры. От-
Отсюда находим энтропию упругого тела
^ - дт "
Теперь вычисляется внутренняя энергия
U = ?7* + TS = ^ + ЯаеГо + -ф — Гг|/.
Если деформация равна нулю, то вследствие B.9.1) внутренняя
энергия представляет собой тепловую энергию и равна сеТ. Здесь
се — теплоемкость при постоянной деформации. Считаем, что ве-
величина се постоянна, т. е. что она не зависит ни от деформации,
ни от температуры. Полагая в найденном выражении для U ве-
величину е = 0, найдем
<ф _ 7Y = СеТ.
Это — дифференциальное уравнение для функции if)(Г), которое
легко интегрируется. Нам не нужна функция г|)(Г) сама по себе,
а нужна ее производная if)"(Г), входящая в выражение для эн-
энтропии. Так как энтропия определена с точностью до произволь-
произвольной постоянной, выберем ее таким образом, чтобы при е = 0 и
Т = То было S = 0. Опуская промежуточные выкладки, напишем
выражение для S
Т
S =Еае + се1пу~- B.9.7)
о
Выражение для внутренней энергии через деформацию и темпе-
температуру перепишется следующим образом:
U = Ц- + ЕаеТ0 + сеТ. B.9.8)
Но чтобы внутренняя энергия была потенциалом, ее нужно вы-
выразить через деформацию и энтропию. Исключая Т из B.9.7) и
§ 2.9. ТЕРМОДИНАМИКА УПРУГОЙ ДЕФОРМАЦИИ 69
B.9.8), получим
U = §-2 + ЕаТое + сеТ0 ехр 2=1*1. B.9.9)
Отсюда можно сразу получить связь между напряжением и де-
деформацией для адиабатического растяжения, когда теплообмен
отсутствует. Дифференцируя U по е, получим напряжение
j
а = g- = Ее + ЕаТ0 (i - ехр ?^j. B.9.10)
Как видно, если материал подчиняется линейному закону Гу-
ка в изотермических условиях, при адиабатическом деформиро-
деформировании зависимость между напряжением и деформацией перестает
быть линейной. Однако нелинейность эта весьма слабая. Пред-»
положим, что растяжение начато при температуре То, тогда в
начальный момент было S = 0, и весь процесс деформирования
происходит при нулевом значении энтропии. Положим S = 0
в B.9.10) и разложим экспоненту в ряд, ограничиваясь двумя
первыми членами. Получим следующий результат:
. B.9.11)
Величина ЕA + Еа2Т0/се) называется адиабатическим модулем
упругости, он больше чем изотермический модуль. При упругих
колебаниях, происходящих с большой частотой, тепло не успе-
успевает рассеиваться за время одного периода и частота собствен-
собственных колебаний определяется адиабатическим модулем. Для
металлов разница между адиабатическим и изотермическим моду-
модулями незначительна, порядка 1— 2%, для полимерных материа-
материалов эта разница может быть существенно большей. Решая урав-
уравнение B.9.7) относительно температуры, мы нашли
Очевидно, такой же результат мы получим, определяя тем-
температуру как производную от внутренней энергии по энтропии.
Разлагая в ряд экспоненту и полагая 5 = 0, найдем
B.9.12)
Из формулы B.9.12) следует, что при растяжении материал ох-
охлаждается, при сжатии нагревается. Если рассматривается, на-
например, процесс колебаний, в стержне попеременно возникают
растяжение и сжатие, т. е. понижение и повышение температуры.
Но в реальных условиях всегда происходит теплообмен с окру-
окружающей средой, т. е. утечка тепловой энергии. Внешне это
-л ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
проявляется как затухание колебаний. В длинных стержнях
могут распространяться волны типа звуковых, в один и тот же
момент некоторые участки стержня растянуты, тогда как сосед-
соседние сжаты. Вследствие теплопроводности происходит некоторое
выравнивание температур. Для анализа такого рода процессов
применяется так называемая связанная теория термоупругости,
т е одновременное рассмотрение уравнений упругости и тепло-
теплопроводности. Предсказываемые теорией эффекты похожи на эф-
эффекты внутреннего трения, и в эксперименте эти два рода явле-
явлений бывает трудно различить.
Заметим, что приведенный выше термодинамический анализ
сделан в предположении о том, что характеристики материала,
как-то Е, а, се постоянны. В действительности это не так. По-
Поэтому для реальных материалов термодинамика несколько услож-
усложняется и качественные результаты могут быть другими. Напри-
Например, многие полимеры при растяжении в упругой области не
охлаждаются, как металлы, а нагреваются. Упругое деформирова-
деформирование многих материалов сопровождается пластическим, необра-
необратимым деформированием уже при небольших нагрузках, поэтому
использование законов термодинамики обратимых процессов не
всегда может считаться оправданным.
§ 2.10. Распространение упругих волн в стержнях
Предположим, что к концу весьма длинного (полубесконеч-
яого) стержня внезапно приложена постоянная сила, которой
соответствуют напряжение о и упругая деформация е. Далее,
в гл. 6 эта задача будет рассмотрена в более общей постановке,
там мы убедимся, что напряженное состояние будет распростра-
распространяться вдоль стержня со скоростью с, величина которой для
V 1
1—i ?/—| Г~
а
Рис. 2.10.1 Рис. 2.10.2
данного материала стержня постоянна. По истечении времени t
после момента приложения силы картина будет следующая.
Участок стержня длины ct будет равномерно сжат или растянут
в зависимости от направления силы, остальная часть стержня
останется ненапряженной. Сечение ran, которое служит границей
между напряженной и ненапряженной частями стержня, называ-
называется фронтом упругой волны, этот фронт движется со скоростью с.
Зафиксируем некоторое сечение pq с координатой х, отсчиты-
отсчитываемой от конца стержня (рис. 2.10.1). В данный момент t рас-
§ 2.10. РАСПРОСТРАНЕНИЕ УПРУГИХ ВОЛН В СТЕРЖНЯХ 71
стояние его от фронта есть ct — х. Участок длиной ct — х равно-
равномерно сжат напряжением а, относительная деформация его есть
е = о/Е, следовательно, сечение pq сместилось из первоначального
своего положения на расстояние
и = e(ct — х) =-д- (ct — x).
Дифференцируя по времени, найдем скорость движения сечения
v — ?н_ — Щ. B 10 1)
dt E
Скорость, определяемая формулой B.10.1), не зависит от х, лишь
бы было х < ct. При х> ct должно быть v = 0. Таким образом,
если приложенная к концу стержня сила постоянна, то скорость
за фронтом тоже постоянна, а на фронте претерпевает разрыв,
так же как и напряжение. Если на фронте волны напряжение
и скорость претерпевают разрыв, волна называется ударной вол-
волной или волной сильного разрыва.
Из факта, устанавливаемого формулой B.10.1), можно сделать
и обратное заключение, а именно, если заставить конец стержня
двигаться с постоянной скоростью, то позади фронта волны на-
напряжения будут постоянными. Пусть, например, по концу стерж-
стержня производится удар телом очень большой массы, движущейся
со скоростью v. Тогда от конца пойдет фронт ударной волны со
скоростью с, материальная скорость частиц за фронтом будет
равна v; по формуле B.10.1) а = Ev/c. Нам осталось определить
скорость распространения фронта волны с. Для этого выделим
из рассматриваемого стержня участок длиной dx между сече-
сечениями 1—1 и 2—2 (рис. 2.10.2). Пусть в момент времени t
фронт упругой волны проходит через сечение 1—1, в момент
t + dt через сечение 2—2. Для этого нужно, чтобы dx = cdt. При-
Применим к выделенной части стержня второй закон Ньютона.
В течение времени dt в сечении 1—1 действует сила gF, тогда
как сечение 2—2 остается ненапряженным, следовательно, им-
импульс силы равен oF dt. В начальный момент t вся выделенная
часть была в покое, в момент t + dt вся она движется со ско-
скоростью у, следовательно, изменение количества движения есть
vqF dx = vpFc dt.
Здесь р — плотность материала, F — площадь поперечного сече-
сечения. Приравняем импульс силы изменению количества движения,
получим
с = vpc. B.10.2)
Более общая запись соотношения B.10.2) была бы следующей:
[а] = [v]pc. B.10.3J
Квадратные скобки обозначают скачок соответствующей вели-
72
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
чины при переходе через фронт, разницу между значениями, на-
например, а впереди фронта и позади фронта. Это станет совер-
совершенно ясным, если мы предположим, что нагрузка приклады-
прикладывается не к покоящемуся стержню, а к движущемуся и предва-
предварительно напряженному. Например, можно представить себе,
что к концу стержня приложена ступенчато меняющаяся нагруз-
нагрузка, сначала было а = а", потом напряжение на конце сразу уве-
увеличилось до а+. В результате этого будут распространяться с оди-
одинаковой скоростью два упругих фронта и на втором фронте
нужно будет записывать условие B.10.3), полагая [о] = о+ — с~,
[v] = v+ — у, при этом а+ и v+, g~ и v~ связаны уравнением
B.10.2). Уравнение B.10.2) или B.10.3) получено непосредствен-
непосредственно из уравнения количества движения и справедливо для фронта
волны, распространяющейся в любой сплошной среде. Выражая
в этом уравнении скорость через напряжение по формуле B.10.1),
которая относится именно к упругому стержню, мы найдем
с = УЯ/р.
B.10.4)
т
В)
Из формулы B.10.1) следует, что пластические деформации не-
неизбежны уже при сравнительно небольших скоростях соударе-
соударения. Для стали, например, с = 4900 м/с. Полагая Е = 2 • 106 кгс/см2
и ат = 3000 кгс/см2, мы находим, что для появления пласти-
пластических деформаций доста-
р точно, чтобы скорость удара
- превышала 7,4 м/с, что со-
соответствует высоте падения
груза 2,8 м.
2L Предположим теперь, что
постоянная сила действовала
на конец стержня не все вре-
? мя> а в течение определенного
промежутка времени т. График
зависимости силы от времени
приведен на рис. 2.10.3, а, при
t<0 о = 0, при 0<?<т о =
= const, при t > т а = 0.
На рис. 2.10.3, б изображена картина распределения напря-
напряжения по длине стержня при t < т, фронт успел продвинуться на
длину ct, за фронтом всюду напряжение постоянно и равно а.
При t > т картина меняется, на конце сила уже не действует,
значит и напряжение на конце равно нулю. Свободная от напря-
напряжений область распространяется по стержню с той же ско-
скоростью с, граница ее образует задний фронт волны. График
распределения напряжений по длине изображен на рис. 2.10.3, в,
он движется вправо со скоростью с, сохраняя неизменную форму.
Этот график повторяет график изменения во времени силы,
СТ
ct
Рис. 2.10.3
§ 2.11. НАПРЯЖЕНИЯ ПРИ УДАРЕ 73
действующей на конец стержня, с изменением масштаба по оси
абсцисс: вместо времени t за абсциссу принимается длина ct.
Сделанный вывод можно распространить и на тот случай, ког-
когда сила Р, приложенная к концу стержня, меняется во времени
по произвольному закону. Заменяя плавную кривую ступен-
ступенчатой, мы сведем задачу к рассмотрению последовательности
волн, посылаемых вдоль стержня кратковременными нагрузками
постоянной интенсивности, т. е. к уже рассмотренному случаю.
Переходя к пределу, получим перемещающееся вдоль стержня
распределение напряжений по длине, в точности повторяющее
закон изменения силы P{t) со временем. Если в некотором се-
сечении с координатой х поставить тензометр, т. е. прибор, изме-
измеряющий деформацию, по закону Гука можно определить про-
пропорциональные деформации напряжения а. Зависимость напря-
напряжения от времени в любом сечении будет повторять зависимость
от времени напряжения, приложенного на конце, со сдвигом на
время х/с.
Изложенная теория распространения упругих волн в стерж-
стержнях не вполне точна по двум причинам:
1. Продольная деформация стержня сопровождается попереч-
поперечным расширением или сокращением, в строгой теории должна
учитываться инерция поперечного движения.
2. Наличие фронта, на котором скачком меняется напряже-
напряжение, а следовательно, деформация, опять-таки вследствие попе-
поперечной деформации, сопровождающей продольную, должно при-
привести к образованию ступени на поверхности стержня, что не-
невозможно; при наличии ступени деформации в точке были бы
бесконечно велики.
Понятие о точной теории распространения волн в стержнях
будет сообщено в гл. 13.
§ 2.11. Напряжения при ударе
Если удар производится по концу весьма длинного стержня,
причем скорость ударяющего тела есть v, то напряжение в стерж-
стержне определится по формуле B.10.2), которую с учетом B.10.4)
можно переписать следующим образом:
a = ?-f. B.11.1)
Рассмотрим теперь тот случай, когда удар производится по
стержню конечной длины I и масса ударяющего груза не слиш-
слишком велика. Для определенности будем считать, что другой конец
стержня жестко закреплен и груз, например, падает на стержень
с высоты /г, как показано на рис. 2.11.1. Встречая сопротивле-
сопротивление со стороны стержня, груз будет замедлять движенпе, ско-
скорость уменьшится до нуля при наибольшем сжатии стержня,
74
ГЛ. 2. РАСТЯЖЕНИЕ И СЖАТИЕ
'///Л
Рис. 2.11.1
когда вся кинетическая энергия груза перейдет в упругую
энергию сжатого стержня и кинетическую энергию бегающих по
нему волн. После этого груз начнет снова двигаться вверх до
тех пор, пока не отделится от стержня. Если длина стержня
невелика и масса его много меньше массы груза М,
то продолжительность соударения много больше,
чем время прохождения упругой волны по длине
I стержня; за это время волна много раз пробежит
эту длину, отразится от заделанного конца, вернет-
вернется к тому концу, по которому произведен удар,
отразится снова и так далее. Сложная волновая
картина при продольном ударе будет рассмотрена
более детально в гл. 13, сейчас же мы сделаем пред-
предположение, до чрезвычайности упрощающее весь
анализ, а именно мы предположим, что плотность
материала стержня равна нулю и, следовательно,
скорость распространения продольной волны беско-
бесконечно велика. Это значит, что деформация после
удара распространяется по стержню мгновенно и в
каждый момент одинакова во всех сечениях. В такой упрощен-
упрощенной постановке задача решается прямым применением уравнения
энергии:
о
'пп I ТУ гр Ми ЮМ 9^
I + и — 1 0 — -у-. (Z.ii.z;
По мере увеличения деформации стержня скорость груза убыва-
убывает и на мгновение становится равной нулю тогда, когда величина
деформации максимальна. В это мгновение Т = О, поэтому из
B.11.2) следует
V = То = 42Mv\
Было сделано предположение о том, что стержень деформируется
так же, как и при статическом приложении нагрузки. Поэтому
упругая энергия выражается через деформацию по формуле
B.8.5). Внося это выражение в написанное выше условие, найдем
2TJ
Если груз весом Q падает с высоты ft, как это показапо на ри-
рисунке, то T0 = Qh и, следовательно:
B.11.3)
Заметим, что деформация от статически приложенного груза равна
").ст = Ql/(EF). Тогда формула для максимальной деформации
§ 2.11. НАПРЯЖЕНИЯ ПРИ УДАРЕ 75
перепишется следующим образом:
. B.11.4)
Если груз Q велик, а высота h мала, то формула B.11.3) ста-
становится неточной. Мы уже не имеем права пренебречь той до-
дополнительной работой, которую производит груз на перемещении
А/. При Al = (AZ)max уравнение работ будет следующим:
Q[h + (AZ)max] = Щ (AOmax.
Это — квадратное уравнение для (AZ)max, которое можно перепи-
переписать в виде
(AZ)Lx - 2 (AZ)CT (AZ)max - 2h (AZ)CT = 0.
Решение его
(AZ)max = (AZ)ct + /(AZ)§T + 2h (AZ)CT. B.11.5)
При решении уравнения мы выбрали знак плюс перед ради-
радикалом. Если после соударения груз окажется связанным со
стержнем, он будет совершать колебательное движение и реше-
решение со знаком минус соответствует крайнему верхнему положе-
положению. На самом деле при движении вверх груз отрывается от
стержня раньше, чем будет достигнуто это положение.
Если (А/)ст<^, отсюда следует приближенная формула
B.11.4). Другой крайний случай это тот, когда fe = 0, груз не па-
падает, а просто внезапно прикладывается всей своей величиной.
Тогда из B.11.5) следует
(AZ)max = 2(AZ)CT. B.11.6)
Наибольшие силы, действующие на систему во время удара и
складывающиеся из действующих сил и сил инерции, пропор-
пропорциональны перемещениям. Поэтому при расчетах на действие
динамических нагрузок те напряжения, которые получаются в ре-
результате статического расчета, следует умножить на динамиче-
динамический коэффициент, равный
В том анализе, который был приведен, совершенно несущест-
несущественно, что производился сжимающий удар по стержню, как
изображено на рис. 2.11.1. Формулы B.11.2) — B.11.6) справед-
справедливы для любой линейно-упругой системы, если можно допустить,
что масса ее пренебрежимо мала по сравнению с массой уда-
ударяющего груза.
В действительности процесс удара это — всегда волновой про-
процесс. В гл. 6 эта же задача будет рассмотрена применительно
к продольному удару по стержню более точно, там же будут
выяснены ограничения приближенного решения, приведенного
в этом параграфе.
ГЛАВА 3
ИЗГИБ БАЛОК
§ 3.1. Действие поперечных сил на балку
Рассмотрим стержень, находящийся под действием приложен-
приложенных к нему поперечных, т. е. перпендикулярных его оси, сил.
Такие стержни, нагруженные поперечными силами, обычно назы-
называют балками. Если тело упруго, а вначале мы будем рассмат-
рассматривать именно упругие стержни, то действие системы сил можно
рассматривать как сумму действий каждой из сил, взятых по
отдельности. Поэтому мы предположим, что на конце стержня
приложена одна единственная сосредоточенная сила Р, а другой
конец защемлен неподвижно (рис. 3.1.1). Качественные выводы
будут справедливы и для пластических стержней при произволь-
произвольной, поперечной нагрузке. Предпо-
Предположим, что все поперечные размеры
стержня имеют один и тот же поря-
порядок h, как это было оговорено в
§ 2.1, длина стержня есть Z. Оче-
Очевидно, что если стержень сломается,
то это произойдет в сечении, близ-
близком к заделке, так называемом
«опасном» сечении. Выясним, какие
напряжения возникнут в этом се-
сечении.
Ржс* 3-1*1 Прежде всего, сила стремится
срезать балку. Употребляя такое не-
неточное выражение, мы подразумеваем, что для уравновешения
силы Р в любом сечении, необязательно опасном, необходимо
приложить касательные, «срезывающие» напряжения т', кото-
которые распределены по сечению таким образом, что их равно-
равнодействующая уравновешивает силу Р. Будем называть эти на-
напряжения касательными напряжениями изгиба; они показаны
внизу рис. 3.1.1, распределение их одинаково во всех сечениях,
следовательно, по отношению к срезу все сечения изображенной
балки равноопасны.
Далее, сила Р, вообще говоря, вызывает кручение балки.
Если стержень имеет продольную плоскость симметрии, то, оче-
очевидно, напряжения кручения не возникнут тогда, когда сила
лежит в этой плоскости. Если сила параллельна этой плоскости,
§ 3.1. ДЕЙСТВИЕ ПОПЕРЕЧНЫХ СИЛ НА БАЛКУ 77
то произведение силы на расстояние линии ее действия от плос-
плоскости симметрии называется крутящим моментом. В несиммет-
несимметричном сечении можно всегда найти точку, называемую центром
изгиба. Когда поперечная сила действует в плоскости, содержа-
содержащей в себе центры изгиба всех поперечных сечений, кручения
не происходит.
Если напряжения кручения существуют, мы обозначим их т".
Как эти напряжения, так и положение центра изгиба не могут
быть найдены элементарным способом. Задача кручения отно-
относится к теории упругости или иной математической теории де-
деформируемого тела. Исключение представляет случай круглого
поперечного сечения, где решение элементарно, однако вряд ли
имеет смысл выделять этот изолированный случай из общего
контекста.
Наконец, в поперечном сечении должны возникнуть нормаль-
нормальные напряжения, создающие момент, уравновешивающий момент
силы Р относительно любой оси, лежащей в плоскости сечения.
Эти напряжения мы будем называть нормальными напряжениями
изгиба а. Очевидно, что именно нормальные напряжения макси-
максимальны в сечении, наиболее удаленном от приложенной силы.
Они то и делают это сечение опасным.
Дадим грубую оценку величии напряжений т', т" и а. Для
оценки т' заметим, что площадь сечения стержня может отли-
отличаться от величины h2 лишь числовым множителем порядка еди-
единицы. Понимая под т' среднее напряжение, мы получим
т'~-|-. C.1.1)
Формула C.1.1) дает лишь оценку порядка величины напряже-
напряжения т', но не позволяет, конечно, вычислить эту величину, для
этого в формуле C.1.1) должен был бы фигурировать еще чис-
числовой множитель.
Крутящий момент представляет собою произведение силы на
расстояние между линией ее действия и плоскостью, проходящей
через центр изгиба. Значит, порядок величины момента есть Ph.
Касательные напряжения кручения могут зависеть только от
размера h, но не от Z, следовательно, для них получается такая
же оценка
х»~^. C.1.2)
Перейдем к оценке нормальных напряжений. Момент силы
относительно оси, лежащей в опасном сечении и, например, ор-
ортогональной к направлению силы, есть PL Момент внутренних
сил, т. е. напряжений а, зависит только от а и /г. Соображения
размерности убеждают нас в том, что порядок величины этого
7g ГЛ. 3. ИЗГИБ БАЛОК
момента есть oh\ Поэтому
Если длина стержня I велика по сравнению с поперечным раз-
размером h, то касательные напряжения х и т" малы по сравнению
с нормальным напряжением о. Это нужно понимать в том смыс-
смысле, что при увеличении длины стержня с сохранением его попе-
поперечного сечения касательные напряжения остаются неизменными,
а нормальные возрастают пропорционально длине. Таким обра-
образом, всегда можно сделать отношение IIh таким, чтобы наиболь-
наибольшие касательные напряжения составили сколь угодно малую долю
от наибольших нормальных. В теории изгиба, как правило, ос-
основное внимание обращается именно на нормальные напряжения,
касательные же во внимание не принимаются. Исключения могут
быть в следующих случаях.
а. Тонкостенные стержни. Если максимальный размер попе-
поперечного сечения h много больше минимального размера 6,
в оценке C.1.1) числовой множитель в правой части может быть
порядка /г/6, а если /г/б ~ l/h, то касательные напряжения будут
того же порядка, что и нормальные.
б. Такие материалы как древесина, например, имеют малое
сопротивление межслойному сдвигу и для достаточно коротких
балок существенно меньшие по величине касательные напряже-
напряжения могут оказаться более опасными, чем нормальные. Именно
в этой связи в середине XIX столетия была развита теория ка-
касательных напряжений при изгибе. Сейчас учет касательных на-
напряжений оказался необходимым при расчете пластиков, арми-
армированных высокопрочным волокном.
§ 3.2. Закон плоских сечений
Ставя своей задачей только определение нормальных напря-
напряжений изгиба, в основу теории достаточно положить предполо-
предположение о том, что плоские до деформации поперечные сечения
балки остаются после деформации плоскими и ортогональными
к изогнутой оси. Теория изгиба, следующая из этого предполо-
предположения, носит название технической теории или теории Бернул-
ли — Эйлера. Точная теория изгиба, построенная Сен-Венаном
для случая, когда балка загружена сосредоточенными силами,
а также немногочисленные (чрезвычайно громоздкие) решения
задач об изгибе распределенной нагрузкой убеждают нас в том,
что хотя закон плоских сечений и не соблюдается, полученные
на основе его выводы оказываются весьма точными (если, конеч-
конечно, /г//< 1).
После того как мы сделали допущение о сохранении плоских
сечений, деформированное состояние стержня может быть описа-
§ 3.2. ЗАКОН ПЛОСКИХ СЕЧЕНИЙ
79
но при помощи небольшого числа параметров. Поместим начало
координат, а также оси х и у в плоскости одного из сечепий,
ось z параллельна образующей цилиндрического тела, представ-
представляющего собою балку. Выберем второе сечение, отстоящее от пер-
первого на расстоянии dz. Определим деформацию элемента тп, па-
параллельного оси z и заключенного между этими сечениями. Будем
считать, что первое сечение (левое на рис. 3.2.1) неподвижно,
тогда как правое перемещается, остава-
оставаясь плоским. Перемещение его состоит «г
из трех элементов:
а. Поступательное перемещение в
направлении оси z, равное eQdz, где
е0 — относительное удлинение элемен-
элемента, совпадающего с осью z.
б. Поворот относительно оси х па т~~
угол с/срх = x,xdz.
в. Поворот относительно оси у на
угол d(py = щ dz.
Относительное удлипение элемента
тп вследствие поступательного переме-
перемещения и поворота сечения будет
е = е0 + хху —
C.2.1)
Рис. 3.2.1
Величины хх = 1/рл и у.у = 1/ру представляют собою кривизны
проекций изогнутой оси балки на плоскости yOz и xOz соот-
соответственно.
При выводе формулы C.2.1) мы исключили возможность по-
поворота сечения около оси z, а также поступательного перемеще-
перемещения в направлении осей х и г/. Та-
Такое перемещение противоречило бы
условию сохранения ортогонально-
ортогональности плоскости сечения изогнутой оси
балки.
Для перехода к напряжениям
нам понадобится сделать еще одно
предположение, а именно допустить,
что любой призматический элемент,
образующая которого параллельна
оси 2, находится в состоянии рас-
растяжения или сжатия вдоль оси z.
Следовательно, в плоскостях, парал-
параллельных оси 2, нормальные напряжения отсутствуют. В дейст-
действительности эти напряжения могут появиться вследствие дей-
действия на балку распределенной нагрузки. На рис. 3.2.2 изобра-
изображена балка квадратного сечения со стороной квадрата 1г. Длина
балки равна Z, она загружена равномерно распределенным по
Рже. 3.2.2
80 ГЛ. 3. ИЗГИБ БАЛОК
верхней плоскости давлением д. Вся сила, действующая на балку,
есть
Р = qlh.
Используя оценку C.1.3), найдем
Рассечем теперь балку горизонтальной плоскостью. В этой плос-
плоскости будут действовать нормальные напряжения а'; если плос-
плоскость сечения близка к верхней граничной плоскости, то а' весь-
весьма мало отличается от (—д); если плоскость сечения близка
к нижней граничной плоскости, то о' мало отличается от нуля.
Поэтому а' имеет тот же порядок величины, что д:
о'-д.
Сравнивая а' и а видим, что отношение а'/а имеет порядок ма-
малости feVZ2, тогда как оценка для отношения касательных напря-
напряжений к нормальным была h/l, следовательно, напряжениями о'
и подавно можно пренебречь.
Полученная оценка, конечно, несправедлива вблизи мест при-
приложения сосредоточенных нагрузок (понятие сосредоточенной
нагрузки или силы должно определяться так, как это было разъ-
разъяснено в § 1.5). Но техническая теория балок Бернулли — Эйле-
Эйлера здесь перестает быть применимой. Исключая из рассмотрения
эти особые случаи, мы будем считать, что напряжение и дефор-
деформация связаны между собою обычным законом Гука
и, следовательно, из C.2.1) получается закон распределения нор-
нормальных напряжений по сечению
0 = Е(е0 + хху — кух). C.2.2)
Вблизи тех сечений, где приложены сосредоточенные силы,
формула C.2.2), конечно, теряет силу. Однако принцип Сен-Ве-
нана и здесь, как и при растяжении — сжатии, позволяет утвер-
утверждать, что область нарушения линейного закона распределения
напряжений изгиба простирается на длину порядка поперечного
размера сечения h.
§ 3.3. Нормальные напряжения при изгибе
Установив, что нормальные напряжения при изгибе распре-
распределяются по линейному закону в плоскости поперечного сечения,
вычислим значения этих напряжений при заданных силах. Рас-
Рассмотрим балку, загруженную произвольной системой сил, как
показано на рис. 3.3.1. Будем считать, что эти силы не вызывают
кручения, т. е. линия действия каждой из них проходит через
§ 3.3. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
81
центр изгиба соответствующего сечения (но не обязательно пер-
перпендикулярна оси балки). Желая определить нормальные напря-
напряжения в сечении тп, поместим в этом сечении оси прямоуголь-
прямоугольной системы координат хОу, как это было пояснено в предыду-
предыдущем параграфе. Мысленно рассечем балку плоскостью хОуг
отбросим одну часть балки (на рисунке правую) и рассмотрим
равновесие оставшейся части, которая изображена отдельно. Из
шести уравнений статики оставим три:
проекций сил на ось z и моментов
относительно осей х и у. Получим
условия равенства нулю
\odF=0,
- 0,
Рис. 3.3.1
C.3.1)
Индекс «л» вверху обозначает, что суммируются проекции
и моменты тех сил, действующих на стержень, которые приложе-
приложены слева от сечения.
Введем теперь следующие обозначения:
Величина Nz называется продольной силой, Мх и Му — изгибаю-
изгибающими моментами относительно осей х и у соответственно.
Внесем в уравнения равновесия обозначения C.3.2) и подста-
подставим выражение для а по формуле C.2.2). Получим
-KySy+eQF) — N2 = 0,
: - хЛу + eQSx) + Мх = 0, C.3.3)
v j 4- р S \ М =П
Е (x
E (ytx
Здесь величины Sx
и Sy представляют собой статические мо-
моменты площади сечения относительно осей х и у
Величины Ix и 1У называются осевыми моментами инерции и
определяются следующим образом:
Ix = $y*dF, Iv=\x\dF.
F F
Величина 1ху называется центробежным моментом инерции,
определяют ее следующим выражением:
1ху = ) ху dF.
Ю. Н. Работнов
:g2 гл- 3- изгиб балок
Теория моментов инерции плоских фигур представляет собою
чисто геометрическую теорию, она строится совершенно подобно
теории моментов инерции масс в механике твердого тела и здесь
излагаться не будет. Заметим только следующие свойства введен-
введенных величин.
1. Если Sx = 0, ось х проходит через центр тяжести. Если
Sx = О и Sy == 0, то начало координат совпадает с центром тяже-
тяжести сечения. Термин «центр тяжести» в отношении плоской фи-
фигуры нужно понимать условно, это понятие приобретает реаль-
реальный смысл, если представить себе, что на плоскость сечения на-
нанесен бесконечно тонкий материальный слой постоянной плот-
плотности.
2. Осевые моменты инерции всегда положительны и отличны
от нуля, если площадь сечения отлична от нуля.
3. Для любого начала координат можно выбрать такие на-
правления осей х и г/, что 1ху = 0. Такие оси называются глав-
главными осями сечения. Если начало координат находится в центре
тяжести, оси, для которых /^ = 0, называются главными цент-
центральными осями. В частности, если хотя бы одна из осей есть ось
симметрии, то 1ху = 0.
Если принять за оси координат главные центральные оси, то
формулы C.3.3) принимают совсем простой вид, а именно:
Теперь формулу для напряжений C.2.2) можно переписать сле-
следующим образом:
х у
Практически при расчетах на изгиб всегда относят сечение
стержня к главным осям и пользуются формулами C.3.4) и
C.3.5).
Заметим, что формулы C.3.4), связывающие кривизны с мо-
моментами, можно представить с помощью потенциалов, как это
было сделано в § 2.8 для растяжения — сжатия.
Положим
Ml Ml N;
ТУ X_ . V , 2^ /q q Ct\
° ~~ 2EIX ^ 2EIy "+¦ 2EF' \o.o.v)
Отсюда
_ dU __^ __ dU__ _ dU
С другой стороны
77 — f v2 j 71 v2 у ЕЕ р2 /Q Q7\
t_' JJ^ fix i о **-y i 9 c0* yUmOmi J
В данном случае, когда справедлив закон Гука, величина С/,
§ 3.4. ИЗГИБАЮЩИЕ МОМЕНТЫ И ПЕРЕРЕЗЫВАЮЩИЕ СИЛЫ 83
определяемая формулой C.3.6) или C.3.7), представляет собою
упругую энергию изгиба балки на единицу ее длины. Интегрируя
любое из этих выражений по длине, можно найти полную энер-
энергию балки
i
V - J Udz. C.3.8)
о
§ 3.4. Изгибающие моменты и перерезывающие силы
Определенные в предыдущем параграфе величины Мх п Л/„,
названные изгибающими моментами, изменяются при переходе
от одного сечения к другому, так как по мере движения слева
направо изменяются плечи и появляются новые силы, приложен-
приложенные к левой части балки. Для дальнейшего нам будет удобно
зафиксировать систему координат, поместив начало ее, например,
в крайнем левом сечении балки. Таким образом, по существу нам
нужно было бы ввести две системы координат, одну неподвиж-
неподвижную, другую подвижную с осями х ж у, расположенными в рас-
рассматриваемом сечении. Мы избежим этого за счет небольшого
изменения формулировок, как это будет видно далее. Зафиксиро-
Зафиксировав систему координат, мы задаем каждое сечение его координа-
координатой z\ следовательно, изгибающие моменты представляют собою
функции от z.
В § 3.3 нас интересовали только нормальные напряжения
при изгибе, поэтому из шести уравнений равновесия мы факти-
фактически составили только три. Проектируя силы, действующие сле-
слева от сечения на оси х и г/, мы получим величины, которые на-
называются перерезывающими силами:
2 Р*== Qx, 2j Py — Qy
Перерезывающие силы уравновешиваются касательными напря-
напряжениями в сечении, но мы не знаем закона их распределения по
сечению и поэтому не составляем уравнений равновесия внешних
и внутренних сил, подобных уравнениям C.3.1).
Для дальнейшего нам будет достаточно предположить, что все
силы действуют в плоскости, параллельной плоскости yOz; при
этом оси х и у — главные центральные оси сечения. Для упругой
балки этот случай будет совершенно общим, действие нагрузки,
параллельной плоскости xOz, учитывается точно таким же спо-
способом и результаты.просто складываются. Для пластических ба-
балок дело обстоит несколько иначе, но это будет оговорено в свое
время. Итак, мы полагаем, единственно для простоты, что
Му = 0 и Qx = 0. Заметим, что все силы, действующие на балку,
должны быть уравновешены. Поэтому
Второе уравнение справедливо для любой оси, параллельной
6*
84 гл. з. изгиб балок
оси х. Но совокупность всех сил, действующих на балку, можно
разбить на две части: силы, действующие на левую часть, и си-
силы, действующие на правую часть. Поэтому
При этом разбиение балки на левую и правые части может быть
в произвольном сечении.
Теперь, ограничиваясь стержнем, который нагружен силами,
действующими в главной плоскости yOz, сформулируем следую-
следующие определения:
Перерезывающей силой называется сумма проекций на ось у
всех сил, приложенных слева от рассматриваемого сечения, или
сумма, сил, приложенных справа, взятая с обратным знаком.
Изгибающим моментом называется момент относительно оси,
параллельной оси х и проходящей через центр тяжести сечения
всех сил, приложенных слева от сечения, или сил, приложенных
справа с обратным знаком.
Во всем изложении мы обошли молчанием вопрос о крутящем
моменте, т. е. моменте относительно оси z. Причина этого состоит
в том, что теория кручения элементарно изложена быть не может
и в этой теории основную роль играет не ось z, проходящая через
центр тяжести сечения, а параллельная ей ось, проходящая че-
через центр изгиба.
В сопротивлении материалов и строительной механике прихо-
приходится иметь дело с функциями Mx(z) и Qy(z). При этом основная
трудность состоит в том, что эти функции, как правило, оказы-
оказываются лишь кусочно гладкими. Задавая их аналитические вы-
выражения на разных участках, мы получим очень громоздкую
форму представления функций, изображаемых простыми графи-
графиками (по большей части ломаными). Поэтому в практике расче-
расчетов обычно начинают с построения графиков этих функций, или
так называемых эпюр изгибающих моментов и перерезывающих
сил. Некоторые аналитические операции, например вычисление
интегралов от кусочно линейных функций, сводятся к элементар-
элементарному вычислению площадей треугольников и трапеций. Такие
приемы, которые называют графо-аналитическими, чрезвычайно
облегчают решение многих задач, поэтому ниже будут изложены
некоторые элементарные приемы построения такого рода эпюр.
Вначале, однако, мы установим дифференциальные соотноше-
соотношения между нагрузкой, перерезывающей силой и изгибающим мо-
моментом, справедливые для тех участков, где эти функции диффе-
дифференцируемы. Рассмотрим стержень, нагруженный силами в плос-
плоскости yOz (рис. 3.4.1). Разрежем стержень по сечению тпп с ко-
координатой z и отбросим левую часть стержня. Рассматривая
оставшуюся правую часть, мы должны заменить действие сил,
отброшенных вместе с левой частью, их результирующей, равной
главному вектору, и парой, момент которой равен главному мо-
§ 3.4. ИЗГИБАЮЩИВ МОМЕНТЫ И ПЕРЕРЕЗЫВАЮЩИЕ СИЛЫ
85
менту, приведенными к центру тяжести сечения с координатой
z. По определению перерезывающей силы и изгибающего момента
главный вектор равен по величине Qy, главный момент Мх. Рас-
Рассмотрим бесконечно близкое сечение pq с координатой z + dz.
Элемент балки, заключенный между сечениями тп и pq, показан
на том же рисунке внизу. Если считать, что Qy и Мх являются
функциями. от координаты z, то с правой стороны изображен-
изображенного элемента действуют сила Qy+.dQy и момент Mx + dMx. Обо-
Обозначая интенсивность распреде-
распределенной нагрузки, т. е. силу, при- i dp /
ходящуюся на единицу длины бал- / I т\ \ р
ки, через qy, составим уравнения р\ —
равновесия элемента. Получим z
dQy = qy dz,
dMx = Qy dz.
C.4.1)
C.4.2)
q
При составлении уравнения
C.4.2) учтено, что, если qy конеч-
конечно, то момент от нагрузки qy есть
величина второго порядка мало-
малоД б
dz
Рис. 3.4.1
сти. Для изгиба в плоскости xOz, соблюдая правило знаков, полу-
получим совершенно аналогичным образом:
dQx = qx dz, dMv = -Qx dz. C.4.3)
При построении эпюр изгибающих моментов и перерезывающих
сил рекомендуется исходить только из данных выше определе-
определений, дифференциальные соотношения C.4.1) и C.4.2) полезно
использовать для контроля
1 Г Г-
правильности построения.
Рассмотрим в качестве
примера балку, изображенную
на рис. 3.4.2. Очевидно, каж-
каждая из реакций равна по ве-
величине силе Р и направлена
вверх. Точки приложения со-
сосредоточенных сил разбивают
балку на три участка.
На первом участке
Qy = -Р, Мх = -Pz,
на втором
= 0, Мх =
= —Pz + P(z — а) = —Ра,
на третьем
м.
'а Z
Рис. 3.4.2
= Р, Мх = —Pz + P(z — a) +P(z — 2a) = —PCa~z).
При вычислении перерезывающей силы и изгибающего момента на треть-
третьем участке мы в данном случав, конечно, поступили неэкономично. Проще
86 ГЛ. 3. ИЗГИБ БАЛОК
было бы вычислить проекцию и момент силы, находящейся справа от сече-
сечения, т. е. одной единственной реакции, с обратным знаком. На том же ри-
рисунке 3.4.2 изображены эпюры Qy и Мх.
Во многих случаях построение эпюр возможно и без составле-
составления аналитических выражений моментов и перерезывающих сил
по участкам. Достаточно вычислить моменты для некоторых ха-
характерных сечений, при построении же следует руководствовать-
руководствоваться следующими правилами.
а. Перерезывающая сила претерпевает разрыв только в точке
приложения сосредоточенной силы на величину этой силы,
б. На незагруженном участке перерезывающая сила постоянна.
в. На равномерно загруженном участке перерезывающая сила
есть линейная функция z, возрастающая, если нагрузка положи-
положительна.
г. Изгибающий момент претерпевает разрыв только в точке
приложения сосредоточенного момента на величину этого мо-
момента.
д. На незагруженных участках эпюра моментов есть прямая,
наклон которой пропорционален перерезывающей силе.
е. Эпюра моментов образует изломы только там, где перере-
перерезывающая сила разрывна, т. е. в точках приложения сосредото-
сосредоточенных сил.
ж. Изгибающий момент принимает экстремальное значение
там, где перерезывающая сила равна нулю.
з. На свободном конце или концевой опоре изгибающий мо-
момент равен нулю, если там не приложен внешний момент.
и. На равномерно загруженном участке эпюра изгибающих
моментов есть парабола, обращенная выпуклостью вверх, если
нагрузка положительна (направ-
^ У лена вниз).
уттутттту _^ Приложим эти правила к балке,
' * изображенной на рис. 3.4.3. Распреде-
Распределенная нагрузка направлена вниз в на-
направлении положительной оси */, сле-
следовательно, она положительна. Каждая
из реакций опор равна qa и направлена
вверх. По определению, на участке /
перерезывающая сила постоянна и рав-
равна —qa, на участке /// Qy = +qa.
Так как сосредоточенных сил нет,
то согласно правилу (а) эпюра должна
быть непрерывна. Поэтому крайние
Рпс. 3.4.3 точки эпюр на участках / и /// нужно
соединить прямой. Согласно правилу
(з) на левом и правом концах балки
изгибающий момент равен нулю, на участках / и /// по правилу (д) эпю-
эпюра прямолинейна. Поэтому достаточно вычислить изгнбающпй момент на
границе между первым и вторым, а также вторым и третьим участками.
И тут и там этот момент равен — qa(l — a). Отложим соответствующие от-
отрезки по вертикали вверх и соединим концы их прямыми с концами отрез-
отрезка, изображающего балку. В соответствии с правилом (и) на участке //
§ 3.5. ПРОЧНОСТЬ II НЕСУЩАЯ СПОСОБНОСТЬ ПРИ ИЗГИБЕ 87
эаюра моментов представляет собою параболу, направленную выпуклостью
вверх. Парабола плавно сопрягается с прямолипейными участками согласно
правилу (е). Вследствие правила (ж) абсолютная величина момента дости-
достигает максимума в середине балки, этот момент равен
qa (, ±
М = — qal +— = — qa ( ' — 2
§ 3.5. Прочность и несущая способность при изгибе
Если продольная сила отсутствует и изгиб происходит в плос-
плоскости yOz, в формуле C.3.5) сохраняется только один член,
а именно
а- М*У n^i\
а —, {6.0.1)
В точках оси х напряжения по этой формуле получаются
равными нулю, поэтому ось х называют нейтральной осью сече-
сечения, а поверхность, в которую превращается вследствие изгиба
плоскость zOz, нейтральной поверхностью.
По аналогии со стержневыми системами (§ 2.5) балки можно
рассчитывать на изгиб по допускаемым напряжениям. Для этого
нужно потребовать, чтобы наибольшее растягивающее напряже-
напряжение не превышало величины [а]р, а наибольшее сжимающее —
величины [g]c>k. Обозначим через fet и h2 расстояния от центра
тяжести сечения до его крайних точек в сжатой и растянутой
зонах соответственно. Именно в этих точках, как следует из фор-
формулы C.5.1), абсолютные величины соответствующих напряже-
напряжений максимальны. Для обеспечения прочности балки по условию
допускаемых напряжений должно быть
|Л/*|Ь<[а]Сж, |Л/*|^<[а]р. C.5.2)
Естественно потребовать, чтобы запас прочности по растяги-
растягивающим и сжимающим напряжениям был одинаков, это значит,
что знак равенства в условиях C.5.2) появляется одновременно.
Для этого нужно, чтобы было
К : hz = [а]Сж : [а]р.
Если допускаемое напряжение на растяжение и сжатие одинако-
одинаково, то расчет ведется по наибольшей абсолютной величине напря-
напряжения, значит требуется выполнение такого условия:
[CJ].
Величина /«/lyLax называется моментом сопротивления изгибу
я обозначается Wx. Таким образом, расчетная формула будет
следующая:
ГЛ. 3. ИЗГИБ БАЛОК
м„
w
C.5.3)
х j
В этой главе, так же как и в предыдущей, мы не рассматри-
рассматриваем детально вопрос о характере и об условиях разрушения.
Расчет по допускаемым напряжениям оправдан для хрупких
материалов, у которых достижение напряжением предельного
значения хотя бы в одной точке (грубо говоря) вызывает появ-
появление трещины, которая распространяется катастрофически. Мы
увидим далее, что при переменных нагрузках пластические мате-
материалы могут разрушаться хрупко и расчет по допускаемым на-
напряжениям в этом случае оправдан.
Приведем выражения моментов инерции и моментов сопро-
сопротивления для некоторых простейших форм поперечного сечения.
а. Круг диаметра d:
,4 i3
т Tid XT/ Rd
б. Круговое кольцо с наружным диаметром d и внутренним
в. Прямоугольник с высотой h и шириной Ъ:
bh*
12'
6
Если балка изготовлена из пластического материала, то рас-
расчет по допускаемым напряжениям занижает действительную не-
несущую способность балки, как это было в случае статически
неопределимых стержневых систем (§ 2.5). Так же как и в этолз
случае, бывает целесообразно производить расчет по предельному
состоянию. Чтобы пояснить идею, обратимся к рис. 3.5.1, на ко-
котором изображено сечение стержня, для простоты симметричное
относительно оси у. Рядом нарисованы эпюры распределения на-
напряжений по сечению по мере увеличения изгибающего момента.
§ 3.5. ПРОЧНОСТЬ И НЕСУЩАЯ СПОСОБНОСТЬ ПРИ ИЗГИБЕ §9
Сначала материал упруг, напряжение линейно зависит от коор-
координаты у. Когда деформация по абсолютной величине станет
больше, чем ет = от/Е, напряжение останется постоянным как
и растянутой, так и в сжатой части стержня, стержень перейдет
в упругопластическое состояние, как показано на рис. б) ив).
При этом, вообще, нейтральная ось по мере развития пластиче-
пластических зон перемещается. На рис. г) изображена эпюра, соответ-
соответствующая предельному состоянию стержня, которое, конечно, ни-
никогда не реализуется. Но эта эпюра дает верхнюю оценку для
величины изгибающего момента, который может выдержать
стержень.
Заметим, что внутренние силы в сечении, уравновешивающие
момент от внешних сил, должны приводиться к паре; следова-
следовательно, главный вектор их равен нулю. Обозначим через Ft и F2
площади частей, на которые делит сечение нейтральная ось
в предельном состоянии. Растягивающая сила равна oTFu сжима-
сжимающая сила oTF2. Вследствие сформулированного условия
отЛ - oTF2 = 0.
Отсюда Fi = F2.
Таким образом, нейтральная ось делит поперечное сечение
стержня на две равновеликие части. Пусть Сх и С2 — центры тя-
тяжести этих частей. Тогда момент внутренних сил, т. е. момент
пары, составленной растягивающей и сжимающей силами в се-
сечении, есть
Л/т = ату(С1С2).
Введем так называемый пластический момент сопротивления
W^^F(CXC2). C.5.4)
Тогда
Для того чтобы обеспечить прочность балки из идеально-пласти-
идеально-пластического материала с запасом прочности п, мы должны потребо-
потребовать, чтобы было
Но Oj/n = [а], таким образом, мы получаем следующее условие:
I М I
?У т
которое отличается от C.5.3) только тем, что вместо Wx в нем
фигурирует WT.
90
ГЛ. 3. ИЗГИБ БАЛОК
Пример ы.
а. Прямоугольное сечение высотой h и шириной и. Здесь F = bh, рас-
расстояние между центрами тяжести половинок сечения равно /г/2. Поэтому по
формуле C.5.4)
•100 = 50%.
б. Сечение в форме равнобедренного треугольника (рис. 3.5.2). В подоб-
подобных треугольниках площади относятся как квадраты сходственных элемен-
элементов. Поэтому нейтральная ось, делящая пополам площадь треугольника,
v пройдет на расстоянии h/~\'2 от вершины. Введем
I вспомогательные оси и к и, проходящие через
вершину треугольника. Обозначим через v0 ко-
координату центра тяжести треугольника, через
v\ и v2 — координаты центров тяжести его рав-
равновеликих частей. Статический момент всей пло-
площади равен сумме статических моментов ее ча-
cien, а именно
1'—. Отсюда v2 = 2уо—ии но расстояние С,С2 равно
и разности v2 — vi, поэтому •
Рис. 3.5.2
Как хорошо
= v2— vi = 2(vo —
известно vQ = "
следовательно, имеет место
С1С2 = ~=- B - Т/2) h = 0,390/г.
Пластический момент сопротивления WT « 0,0975bh2. Обычный момент со-
сопротивления Wx « 0,0417b/i2, разница между ними составляет 134%.
Если ось у не служит осью симметрии сечения, нахождение
пластического момента сопротивления и вообще рассмотрение
предельного состояния при изгибе представляет определенные
трудности. Приложение нагрузки в
плоскости, проходящей через глав-
главную ось инерции сечения, еще не
обеспечивает изгиба именно в этой
плоскости. Действительно, предста-
представим себе некоторое несимметричное
сечение, например изображенное на
рис. 3.5.3. Его можно разбить на две
равновеликие части бесчисленным
числом способов, например, проводя
прямую лгп. Центры тяжести поло-
половин сечения Cv и С2 лежат на прямой pq; чтобы ось тпп бы-
была нейтральной осью для предельного состояния стержня, необ-
необходимо, чтобы действующие силы были приложены в плоскости,
параллельной образующим стержня и проходящей через пря-
Рис. 3.5.3
§ 3.6. УПРУГ0Ш1АСТИЧЕСКИЙ ИЗГИБ
91
мую pq. Таким образом, мы легко решаем обратную задачу — оп-
определить, как нужно приложить силы, чтобы изгиб происходил
около данной нейтральной оси. Регулярные методы решения пря-
прямой задачи неизвестны.
§ 3.6. Упругопластический изгиб
Будем считать, что сечение балки имеет две оси симметрии,
п изгиб происходит в одной из продольных плоскостей симмет-
симметрии балки. При этом, очевидно, нейтральная ось не будет менять
своего положения по мере развития пластических зон (как мы
убедились в конце § 3.5, в условиях пластич-
пластичности незначительное, казалось бы, усложне-
усложнение условий задачи приводит к неизмеримо
возрастающим трудностям при ее решении).
Сохраняя гипотезу плоских сечений, положим
е = ху. Пусть для материала балки <з = ср(е),
при этом ср(е)—нечетная функция, <р(—е) =
==— ф(е). Это условие означает, что материал
ведет себя одинаково при растяжении и сжа-
сжатии. Чтобы задать форму симметричного сече-
ния балки, достаточно задать ширину его на
расстоянип у от плоскости xOz, т. е. функцию
b(y), y^[—h, +h]. Учитывая область опреде-
определения функции ft, нам будет удобнее рассмат-
ривать ее как функцию безразмерной коорди-
наты b(y/h). Если ось х также служит осью
симметрии, то b(y/k)—четная функция.
Момент относительно оси х сил, действующих на заштрихо-
заштрихованную площадку шириной b и высотой dy (рис. 3.6.1), есть
Приравнивая сумму моментов внутренних сил в сечении сумме
моментов внешних сил, действующих по одну сторону от сечения,
т. е. изгибающему моменту, получим
h
dy. C.6.1)
Вследствие симметрии относительно оси х интегрирование от —h
до +h заменено интегрированием от нуля до h и результат
удвоен.
Формулу C.6.1) можно преобразовать, приняв за переменную
интегрирования вместо у пропорциональную величину е = ку.
Если ввести еще обозначение е0 = vJn для деформации наиболее
92 гл. з. изгиб балок
удаленной от оси х точки сечения, то формулу C.6.1) легко при-
привести к виду
(ЗЛ2)
Зная функцию ф(е), можно найти Ф(е0) аналитически либо
численно.
Раосмотрим в качестве примера изгиб стержня прямоугольно-
прямоугольного сечения (b = const) при условии идеальной пластичности.
В этом случае
(о \
е<С тт I, ф(#) = с
В упругой области
-* = JLJ ъЕеЧе = -^.
0 о
Вспоминая определение предельного момента Д/т = bh2a7l перепи-
перепишем эту формулу следующим образом:
В упругопластической области
Поэтому
л т 2
График зависимости безразмерного момента MJM? от безраз-
безразмерной кривизны е0 = vJfi представлен на рис. 3.6.2. При
Мх < 2/3Мт материал остается упругим, при Мх = 2/3Мт появляет-
появляется пластическая деформация в крайнем волокне. Это состояние
(точка А) признается опасным при расчете по допускаемым на-
напряжениям. Но при этом несущая способность еще не исчерпана.
Максимальная возможная несущая способность стержня, т. е. ве-
лпчина предельного момента, выше чем момент, соответствующий
точке А, на 50%. Но, как видно из графика и нз формулы C.6.3),
это предельное значение момента будет достигнуто тогда, когда
кривизна станет бесконечно большой, что невозможно. Получен-
§ 3.7. ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
93
ная зависимость между изгибающим моментом и кривизной
справедлива до тех пор, пока изгибающий момент возрастает и,
следовательно, возрастает деформация каждого волокна. Предпо-
Предположим, что после достижения моментом некоторого значения Мх,
которому соответствует кривизна х*, началась разгрузка. Дефор-
Деформация каждого волокна будет теперь уменьшаться, значит раз-
разгрузка будет происходить в каждом волокне от напряжения о* =
= ф(х*г/) по закону упругости. Ког-
Когда изгибающий момент равен Мх <
<МХ, кривизна равна х, напряже-
напряжения находятся по закону упругой
разгрузки следующим образом:
о*-о = Е(х*х-хх)у. C.6.4)
Умножим обе части на у dF и про-
проинтегрируем по площади. Так как
то
Рис. 3.6.2
Ml - Мх = Е1Х (х* - хх). C.6.5)
Когда происходит полная разгрузка, т. е. становится М = О, кри-
кривизна не исчезает, остаточная кривизна кох находится по фор-
формуле C.6.5)
Напряжения в сечении после разгрузки также не исчезают, фор-
формула C.6.4) при кх = Хох дает
ап = а* — .
М*у
C.6.6)
Очевидно, что остаточные напряжения после разгрузки самоурав-
самоуравновешены, момент их равен нулю.
§ 3.7. Изгиб тонкостенных стержней открытого профпля
Соображения об относительных порядках величин нормаль-
нормальных и касательных напряжений при изгибе, приведенные в § 3.1,
к тонкостенным стержням неприменимы. Касательные напряже-
напряжения, возникающие вследствие изгиба и кручения, имеют в такого
рода стержнях тот же порядок величины, что и нормальные на-
напряжения, и сбрасывать их со счета нельзя. Касательными на-
напряжениями изгиба мы будем называть напряжения, распределя-
g4 гл. з. изгиб балок
ющиеся приблизительно равномерно по толщине стенки профиля
и не связанные с закручиванием стержня.
Очевидно, например, что кручения не будет, если изгибать
симметричный стержень, хотя бы двутавр или швеллер, силами,
действующими в плоскости его симметрии. Весьма большая жест-
жесткость на кручение замкнутых тонкостенных профилей делает для
них вопрос об условиях отсутствия кручения второстепенным.
В тех же случаях, когда тонкостенный стержень открытого про-
профиля изгибается в плоскости, даже являющейся главной плос-
плоскостью, но не плоскостью симметрии, необходимо принять особые
меры для предотвращения кручения. В этом параграфе мы пред-
предполагаем, что в силу тех или иных обстоятельств кручение от-
отсутствует, значит, никаких иных касатель-
касательных напряжении, кроме как от изгиба,
в стержне нет.
Сохранение плоских сечений при нали-
наличии касательных напряжений в сечении, оче-
очевидно, невозможно. Действительно, касатель-
касательные напряжения вызывают сдвиг, т. е. из-,
менение первоначально прямого угла, как
было отмечено в § 1.7. Таким образом, се-
сечение не может оставаться перпендикуляр-
Рис. 3.7.1 ньш изогнутой оси стержня, а так как на-
напряжения в сечении распределяются нерав-
неравномерно, оно не может оставаться плоским (рис. 3.7.1). Однако
если стержень загружен сосредоточенными силами, то на каждом
участке перерезывающая сила постоянна, следовательно, во всех
сечениях этого участка распределение касательных напряжений
одинаково. Одинаковы и искажения поперечных сечений. Поэто-
Поэтому длина элемента тп между двумя сечениями после деформа-
деформации равна длине того же элемента, подсчитанной по гипотезе
плоских сечений, т. е. т'п . Отсюда следует, что для балки, не-
несущей сосредоточенные силы, закон распределения нормальных
напряжений будет тем же, что по гипотезе плоских сечений
ff = _^ + ^f. C.7.1)
Для нахождения касательных напряжений будем считать, что
они распределяются по толщине стенки равномерно (рис. 3.7.2).
Положение точки на средней поверхности стержня будем опреде-
определять двумя координатами: z — расстоянием от фиксированного
сечения по образующей и s — дугой, отсчитываемой от какого-ли-
какого-либо конца средней линии открытого контура сечения. Всю длину
душ средней линии контура сечения обозначим In, толщину
стержня б будем считать функцией s, но не z. Вырежем элемент
средней поверхности двумя бесконечно близкими образующими
и двумя поперечными сечениями. Силы, действующие на грани
§ 3.7. ТОНКОСТЕПНЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
95
объемного элемента, образованного нормальными сечениями,
лроходящими через стороны элемента средней поверхности, по-
показаны на рис. 3.7.3. Уравнение равновесия элемента примет
следующий вид:
C.7.2)
oz
as
Заметим, что вследствие правила парности касательных на-
напряжений т = 0 при s = 0 и s = h. Интегрируя C.7.2), найдем
C.7.3)
Но по формуле C.7.1), учитывая независимость б от я, по-
получим
д (од) _ ду dMx . дх dMv
dz
?x dz
Iy dz *
Вспомнив дифференциальные соотно-
соотношения между изгибающими моментами
Рис. 3.7.2
Рис. 3.7.3
и перерезывающими силами, напишем последнее равенство
так:
дх п
_ by
у
oz
у
iy
Подставив это выражение в C.7.3), получим следующую фор-
формулу для закона распределения касательных напряжений:
x&ds. C.7.4)
о о
Интегралы в C.7.4) представляют собою статические моменты
части площади сечения, заштрихованной на рис. 3.7.2.
Если внешние силы действуют в плоскости симметрии сече*
ния, которую мы примем за плоскость yOz, то в формуле C.7.4)
остается один член
тб = ^
C.7.5)
«96 ГЛ. 3. ИЗГИБ БАЛОК
Формулу C.7.5) применяют иногда и для сплошных сечений,
предполагая, что вектор т параллелен оси г/, и понимая под б
ширину сечения на расстоянии у от оси х.
Эти гипотезы можно принять с большой натяжкой, точные
решения их не подтверждают.
Так, для прямоугольного сечения наибольшее напряжение
получается на нейтральной оси при у = 0, приближенная вели-
величина его
1 2 Ыъ'
Эта формула довольно точна, когда h> b, если b> h, она дает
иногда большую ошибку.
Предположим теперь, что сечение стержня несимметрично.
Покажем, что существует такая ось, параллельная оси стержня,
что силы, действующие в любой прохо-
проходящей через эту ось плоскости, не вы-
вызывают кручения. Точку пересечения
этой оси с плоскостью сечения называ-
называют центром изгиба. Если такая точка
С существует, то касательные силы в
сечении приводятся к равнодействую-
равнодействующей, проходящей через эту точку.
Отсюда следует, что сумма момен-
моментов всех касательных сил в сечении
относительно точки С равна нулю. На
элемент ds с координатами х, у дейст-
действует сила тб ds (рис. 3.7.4); момент ее
относительно точки С есть тб/? ds, где
р — длина перпендикуляра, опущенно-
опущенного из точки С на касательную. Если С есть центр изгиба, то
h
j т8р ds = 0.
о
Но р ds — это удвоенная площадь треугольника с основанием
ds и вершиной в точке С. Положим pds = da). Таким образом,
h
zdds
Рпс. 3.7.4
Применим формулу интегрирования по частям. Получим
h h
Г д (тб)
тбео
as
-cods =0.
Но т обращается в нуль при s = 0 и s = h. Воспользуемся,
§ 3.7. ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
97
кроме того, для преобразования интеграла уравнением C.7.2),
вспомнив, что
д (тб) д (об) by n ,Ьхп
как показано выше. Окончательный результат будет следующий:
h h
а так как Qx и Qy произвольны, положение центра изгиба опре-
определяется следующими условиями:
h h
s = 0,
- j
ds = 0.
C.7.6)
Совершенно элементарно находится центр изгиба для углово-
углового профиля. Если принять за полюс вершину, то секториальная
площадь со равна нулю, поэтому условия C.7.6) выполняются,
и вершина есть центр изгиба (рис. 3.7.5). Аналогично для тав-
таврового сечения центр изгиба находится в точке пересечения стен-
стенки с полкой.
Рис. 3.7.5
Рис. 3.7.6
Сделаем в заключение одно замечание о применимости прин-
принципа Сен-Венана к тонкостенным стержням. Конечно, для любой
формы сечения можно выбрать длину или расстояние от места
приложения сил настолько большим, что распределение нормаль-
нормальных напряжений будет следовать линейному закону. Но может
оказаться, что затухание местных напряжений произойдет слиш-
слишком далеко. Нижеследующий простой пример, принадлежащий
Власову, разъясняет существо дела.
Представим себе двутавровую балку (рис. 3.7.6), нагружен-
нагруженную четырьмя одинаковыми силами Pi = Р2 = Рз = Р± = Р- Каж-
Каждая из полок будет изгибаться парой РХР2 и Р3Рь в разные сто-
стороны в плоскости полки. Стенка закручивается, сопротивление ее
7 Ю. Н. Работнов
98 гл. з. изгиб балок
препятствует изгибу полок и на некотором расстоянии от торца
напряжения практически исчезнут. Но если стенка тонкая, эта
произойдет на очень большом расстоянии. Таким образом, ста-
статически уравновешенная система сил служит фактором, который
может вызвать напряжения, не носящие местного характера. Ко-
Количественной характеристикой этой четверки сил служит так на-
называемый бимомент В ==• Pbh.
Таким образом, к концу стержня можно прикладывать не
только силы и моменты, но также бимоменты; если стержень
тонкостенный, то действие бимомента простирается на достаточ-
достаточное расстояние от торца, в § 9.15 будет дана оценка для этого
расстояния.
§ 3.8. Дифференциальное уравнение изогнутой
оси балки и его интегрирование
При изгибе в главной плоскости yOz связь с кривизной
в этой плоскости дается первой из формул C.3.4), которую»
можно переписать следующим образом:
1/рх =-MJ(EIX). C.8.1)
Искривленная ось изогнутой балки представляет некоторую кри-
кривую в плоскости yOz\ задавая перемещение точек первоначально
прямой оси балки, совпадающей в на-
начальном состоянии с осью z, в виде
¦^ .z функции v(z), мы получаем по извест-
известку ной формуле анализа
1 • v" C.8.2)
Здесь штрихи обозначают производные
по z, знак плюс или минус выбирается
в зависимости от того, какую кривиз-
Рис. 3.8.1 ну мы считаем положительной. В слу-
случае, изображенном на рис. 3.8.1, изги-
изгибающий момент положителен. Выпуклость изогнутой оси обра-
обращена вверх, значит вторая производная v" тоже положительна.
Поэтому в формуле C.2.2) нужно удержать знак минус, и мы
получим следующее точное дифференциальное уравнение изогну-
изогнутой оси:
М* C.8.3)
X
X
Интегрирование этого нелинейного дифференциального урав-
уравнения довольно затруднительно, хотя л возможно. Некоторые
примеры будут приведены в § 4.11. Сейчас же мы займемся при-
§ 3.8. УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ
99
ближенной, технической теорией. Как правило, балки, представ-
представляющие собою несущие элементы конструкций, получают лишь
малые прогибы. Поэтому тангенс угла наклона касательной к уп-
упругой линии v' мал, а квадратом его, во всяком случае, можно
пренебречь по сравнению с единицей. Таким образом, вместо
C.2.3),мы будем применять следующее приближенное уравнение:
EIxv"=Mx{z). C.8.4)
Иногда бывает более удобно считать заданным не изгибающий
момент Mx(z), а нагрузку q{z). Вспомним, что из формул C.4.1)
и C.4.2) следует: M"x=q. Продифферен-
Продифференцировав C.2.4) два раза по z, получим
dz*
dzz
C.8.5)
Рис. 3.8.2
Функция, фигурирующая в правой
части, может быть, вообще говоря, обоб-
обобщенной функцией типа дельта-функции
(сосредоточенная сила) или производной
от дельта-функции (сосредоточенный мо-
момент).
Попытаемся теперь выяснить точность
приближенного уравнения C.8.4) или
C.8.3), сравнив результат его решения
с- результатом решения такого уравнения в том случае, когда оно
может быть получено без труда. Пусть защемленная балка дли-
длиной I нагружена на конце хмоментом М (рис. 3.8.2). Из точного
уравнения C.8.1) следует, что балка изогнется по дуге окруж-
окружности и прогиб на копце
/ = p(l-cos-i).
Разложим косинус в ряд, ограничившись тремя членами раз-
разложения:
cos ¦
l
•-т
Выражение для / получается следующим:
1 J_
2 р 24 рз -I"---
или
' ~ 2 1^/J ~ 24 (eiJ
C.8.6)
Решим теперь ту же задачу, интегрируя уравнение C.8.4)
100
ГЛ. 3. ИЗГИБ БАЛОК
с учетом граничных условий v@)= г/@) = 0. Получим
/0 __ J_ Ml_
Т"~ 2 Ё1Х*
Здесь через /0 обозначена величина прогиба, получающаяся
по приближенной теории. Теперь точное (до величины третьего
порядка малости) выражение прогиба мояшо представить следу-
следующим образом:
4-=т-4(-гK- <3-8-7>
Относительная ошибка при определении прогиба
|/-/ol 1 /V3
Если мы довольствуемся при определении прогиба ошибкой
в 3%, а большая точность не нужна, так как ошибка в опреде-
определении модуля упругости обычно бывает большей, то, полагая
~з~\Т) ~ юо'
мы найдем fjl = 0,3.
Такие большие прогибы бывают у пружин, для расчета кото-
которых необходима точная теория. Прогибы балок, применяемых в
качестве несущих элементов конструкций, всегда гораздо меньше
чем 30% от длины, поэтому уравнения C.8.4) или C.8.5) совер-
совершенно достаточны.
Интегрированию уравнении C.8.4) или C.8.5) посвящена очень боль-
большая литература, хотя с математической точки зрения вопрос представляет-
представляется элементарным. Вся трудность состоит в том, что правая часть обычна
м
b
—*- с
1
1
d
W
1
ч
\\
11
¦
Рис. 3.8.3
не является аналитической функцией от z, выражение ее меняется от уча-
участка к участку. Поэтому при обычном способе интегрирования приходится
на каждом участке вводить свои константы интегрирования и определять
их из условий сопряжения. Эти трудности легко обходятся, если ввести в
рассмотрение функции, принадлежащие классу Хевисайда Н. Если f(z) e
еЯ( это значит, что /B) == 0 при z < 0. Теперь мы можем построить
§ 3.8. УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ
семейство функций фп(з), определенных следующим образом:
^
При п = 0 фо(^) есть единичная функция Хевисайда, cpo(z) = H(z),
фоB) = 1 при z ^ 0, фо(^) =0 при z < 0. Очень легко доказать следующее
свойство функций фпB):
-a) (fl>0). C.8.8)
Действительно, при z < a 1 фп (z — a) dz = 0, при z > 0
о
таким образом, C.8.8) доказано. Заметим, что соотношение C.8.8) позволя-
позволяет продолжить последовательность функций фп в область отрицательных
индексов, но это будут уже обобщенные функции. Так q>-i{z — а) равна ну-
нулю всюду, кроме точки z = а. Но
с
J ф_х (* -в)^ = 1/'ае (&, с).
ъ
Очевидно, что ф-i соответствует сосредоточенной силе, ф_г — сосредоточен-
сосредоточенному моменту. В классической механике твердого тела особенности более
высокого порядка не встречаются, однако возможность их появления была
разъяснена в гл. 1.
Выражение изгибающего момента для любого сечения балки, изобра-
изображенной на рис. 3.8.3, может быть записано с помощью функций фп следую-
следующим образом:
1. От сосредоточенного момента М в сечении z = a
Мх = 0 при z < а, Мх = М при z ^ а,
таким образом,
Мх = Мфо(г — а).
2. От сосредоточенной силы Р в сечении z = b
Мх = P(pi {z — Ъ).
3. Распределенная нагрузка постоянной интенсивности д, начинающая-
начинающаяся в точке z = с, может быть задана выражением дфо(г — с). Интегрируя
два раза, получим изгибающий момент:
Эта формула верна для сечения на загруженном участке.
Если нагрузка действует только на участке [с, d], а нам нужно иметь
выражение изгибающего момента при z > d, следует продолжить положи-
положительную нагрузку вправо от точки неограниченно, а от точки d приложить
противоположную ей нагрузку —q. Тогда, при z > d
Мх = 2[ф2(B — С) — ф2(& — d)].
В общем случае, когда на балку действует несколько нагрузок разного
рода, получается
-102 ГЛ- 3- ИЗГИБ БАЛОК
Теперь дифференциальное уравнение изгиба C.8.4) очень легко интегри-
интегрируется, а именно, если момент инерции 1Х постоянен, мы получаем
J ^ — «) + ^Ф3 (^ — ^) + ^ [Ф4 (^ — ^) — Ф4 (^ —
Для практического пользования это уравнение бывает удобно записать сле-
следующим образом:
Значок «л» над символом суммы обозначает, что для каждого сечения сум-
суммируются только те величины, которые относятся к части балки, левой по
-отношению к рассматриваемому сечению. При переходе через сечение, где
приложен момент либо сила, где начинается или кончается распределенная
нагрузка, мы сохраняем все члены в формуле C.8.9) и лишь добавляем
соответствующий новый член. В этой
kffi формуле фигурируют две постоянные
2~] Ч , \~г интегрирования v@) и v'(Q), которые
1 * I iiwtjllifj) ^ должны определяться из граничных
условий.
Простейший пример представлен
на рис. 3.8.4. Реакция опоры здесь
равна gZ/2, если I — длина балки. Она
Рис. 3.8.4 направлена против оси у, следователь-
следовательно, отрицательна, тогда как направлен-
направленная вниз нагрузка положительна. Из
условия закрепления левой опоры следует, что v@) = 0. Итак, по фор-
формуле C.8.9)
EIxv (z) =EIxv' @) z- «L 4 + Ж'
Постоянная i/@) находится из условия, что v(l) =0
0= EIxv' @) I - ? + |?.
Отсюда следует
и, следовательно:
Наибольший прогиб будет при z = 1/2, а именно
_ ( I \ _ 5д1*
- V \Т - эд
§ 3.9. О РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 3.9. О решении линейных дифференциальных уравнений
с постоянными коэффициентами
Более сложные задачи, относящиеся к изгибу, как-то: продольно-попе-
продольно-поперечный изгиб, изгиб балок на упругом основании, поперечные колебания
балок — сводятся к решению линейных уравнений с постоянными коэффи-
коэффициентами более сложного вида, чем уравнение C.8.4). Трудность интегриро-
интегрирования этих уравнений заключается в том, что правая часть есть функция
от z, имеющая разные аналитические выражения на разных участках. Из-
Излагаемый ниже метод применялся еще Коши; для изгиба балок он был де-
детально разработан Крыловым.
Пусть дано линейное однородное дифференциальное уравнение поряд-
порядка п с постоянными коэффициентами
C.9.1)
Возьмем произвольную систему линейно независимых частных решений
мь м2, ..., ип
и построим из них новую систему частных решений /7&, обладающих теад
свойством, что
Uk @) = U'k @) = ... = U^-V @) = 0, U^-V @) = 1. C.9.2)
Это всегда возможно. Для этого надо взять линейную комбинацию из
частных решений т
i=l
Коэффициенты ски Ch2, . •., Ckn найдем из уравнений
n
V1 c iM-1) (Г)\ — Я (Я q 3V
xj LJiii Vu/ — ks' \o.v»oj
i=l
Детерминант этой системы есть детерминант Вронского для системы
функций mi, U2, ..., ип при z = 0, он отличен от нуля вследствие линейной
независимости функций щ, мг, ..., ип. Поэтому всегда можно найти коэф-
коэффициенты см и фактически построить функцию Uh(z).
Образуем систему таких частных решений: fri(z), U2(z), ..., Un(z).
Каждая из этих функций обладает свойством C.9.2). Составим следующую
таблицу, в которой сведены начальные значения функций и их производ-
производных:
Ui
и2
Us
17@)
1
0
0
17'@)
0
1
0
t/"@)
0
0
1
U'" @)
0
0
0
Во всех клетках этой таблицы стоят нули, лишь на главной диагонали —
единицы. Поэтому система Uk частных решений уравнения C.9.1) называ-
называется системой с единичной матрицей. Будем строить общий интеграл урав-
уравнения C.9.1) именно с помощью этой системы частных решений, линейная
независимость которой усматривается из того факта, что ее определитель
Вронского при 2 = 0 есть определитель единичной матрицы, следовательно,
?04 ГЛ. 3. ИЗГИБ БЛЛОК
равен единице. Таким образом.
Займемся теперь решением неоднородного уравнения
L(u) = /(*). C.9.4)
Докажем следующую теорему:
Интеграл уравнения C.9.4), обращающийся в нуль вместе со своими
производными до порядка п — 1 включительно при 2 = 0, дается формулой
C- C.9.5)
При этом предполагается, что в уравнении C.9.4) коэффициент при
старшей производной сделан равным единице. Вычислим последовательные
производные функции u(,z), определяемой с помощью C.9.5). Здесь z одно-
одновременно является и верхним пределом интеграла, и параметром, поэтому
по известной теореме анализа
Z
и' (*) = ип @) / (*) + J u'n (z -;о
О
Но Un@) = 0 вследствие специального выбора функций Uh(z). Продол-
Продолжая процесс дифференцирования, найдем
о
и так далее, до производной порядка п — 1 включительно. Производная же
порядка п
Z
*<n> (z) = u<f-v (о) / (*) + J и™ (z - о / (QdC,
0
причем 27^г") @) = 1.
Подставим теперь все последовательные производные функции u(z) в
уравнение C.9.4). Вследствие постоянства коэффициентов d под интегра-
интегралом получится та же комбинация производных функций Un(z), что и в опе-
операторе L(u). Учитывая же, что коэффициент при и^ есть единица, полу-
получим
Но Un есть решение уравнения C.9.1), L(Un) =0, поэтому мы полу-
получили тождество, что и доказывает теорему.
Формула C.9.5) дает не какое-нибудь частное решение уравнения
C.9.1), а решение, обращающееся в нуль вместе со своими производными
до порядка п — 1 включительно при z = 0. Это большое преимущество по-
полученного решения, упрощающее определение постоянных из начальных
условий.
§ 3.9. О РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Общий интеграл уравнения C.9.4) может быть представлен следующим
образом:
2 CkUk(z)+ Un(z-
Постоянные С\, ..., Cn имеют здесь совершенно определенные значения..
Действительно, положим z = 0. Получим
и@) = Сь
Вычислим производную от и порядка к — 1 и положим z = 0. В правой?
части обратятся в нуль все члены, кроме содержащего множителем Uhr
так как И^г) @) = 1. Получим
Таким образом,
п I
и (z) = ^ "(fe} @) Uh (z) +\Un{z-l)f (I) ft. C.9.6)
k=i 0
Формула C.9.6) представляет общий интеграл линейного дифференци-
дифференциального уравнения с правой частью в форме, наиболее удобной для прило-
приложений. Постоянные интегрирования имеют здесь простой смысл: это на-
начальные (при z = 0) значения искомой функции и ее производных. Поэто-
Поэтому метод интегрирования дифференциальных уравнений, основанный на?
формуле C.9.6) и широко применяемый в строительной механике, называ-
называется методом начальных параметров, он разрабатывался рядом советских
авторов не только в применении к балкам, но также к пластинкам и
оболочкам.
В качестве примера рассмотрим уже изученное нами уравнение C.8.4)
Соответствующее однородное уравнение
у" = 0.
Его частные решения, обладающие единичной матрицей, суть
U{ = 1, U2 = z.
Действительно, их@) = 1, и'л @) =0, U9 @) = 0, U* @) = 1- По формуле
C.9.6)
v{z) = v@)-l + vf (O)z+\(z- Q -^— d?. C.9.7)
t) X
о
По теореме Коши
г z
0 0
106
ГЛ. 3. ИЗГИБ БАЛОК
§ 3.10. Продольно-поперечный изгиб
Рассмотрим стержень, на который, кроме поперечной нагруз-
нагрузки, действует продольная сжимающая или растягивающая сила.
Пока стержень был прямым, эта сила вызывала только растяже-
р ние или сжатие стержня; как
только стержень изогнулся, сила
Р (рис. 3.10.1) создает в сечениях
изгибающий момент. В случае а\
этот момент от силы Р в сечении
с координатой z есть Pv, где v —
прогиб. В случае б) момент есть
P(v — vo) = Pv — Мо. Через Мо мы
обозначили величину Pv0. Эта
величина является неизвестной
постоянной, отнесем ее к по-
поперечным нагрузкам, момент от
которых в сечении с координатой z есть Мх. Таким образом,
полный изгибающий момент
1
p
к
z
a)
Ю
Рис. 3.10.1
Внесем это выражение в уравнение изгиба C.8.4). Получим
V"-Wv = wf- C.10.1)
X X
Это и есть уравнение продольно-поперечного изгиба. В даль-
дальнейшем нужно рассматривать отдельно два случая.
р
1. Р>0, сила растягивает стержень. Положим тгт- =к2. Пере-
пишем уравнение C.10.1) следующим образом:
м*
C.10.2)
Применим к нему метод, изложенный в предыдущем пара-
параграфе. Частные решения соответствующего однородного урав-
уравнения
ch fez, — sh kz
удовлетворяют условиям, поставленным для функций Ui(z). Дей-
Действительно, при 2 = 0 sh kz = 0, производная же этой функции,
т. е. ch kz, обращается при z==0 в единицу. Таким образом,
U1 = ch kzx
= 4" sh kz-
§ 3.10. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Ю7
По формуле C.9.6)
v(z) = v@) chkz + v' @L shkz + ±
z +
о х
C.10.3)
Это и есть общее решение уравнения продольно-поперечного из-
изгиба. Вычислим входящий в формулу C.10.3) интеграл для не-
некоторых видов нагрузок:
а. Момент М в сечении z = a
или
Мх = 0 при z < a, Ml = М при 2 ^ а,
Эта формула пригодна, если 2 > а. Если z < а, то интеграл
равен нулю.
б. Сосредоточенная сила @ в сечении z = Ь
Mx = e<Pi(*-b).
Если г < Ь, то
г
JshA;(z—?)ф1(С
О
Если z> b, то этот интеграл равен
Таким образом для балки, загруженной моментами и сосредото-
сосредоточенными силами:
v(z) = u @) ch kz + у' @) 4~ sh
/с
C.10.4)
Здесь, как и в формуле C.8.9), суммирование распространя-
распространяется на те силы или моменты, которые приложены слева от рас-
рассматриваемого сечения.
?08 ГЛ- 3- ИЗГИБ БАЛОК
2. Р < 0, сила сжимает стержень. Обозначим теперь через к2
величину —Р/(Е1Х). Уравнение продольно-поперечного изгиба
принимает вид
* + &, = <!*. C.10.5)
Решение строится буквально так же, как для растягивающей
силы, только вместо гиперболических функций будут функции
тригонометрические. Не повторяя выкладок, напишем результат:
z j
v(z) ^v@)coskz + v'@)-j- sinkz + ^
C.10.6)
Для балки, загруженной моментами и сосредоточенными си-
силами, интеграл принимает следующий вид:
v(z) = v @) cos kz + v @) -у sin kz +
{ -cos k (* -
C.10.7)
Приведем пример применения этого уравнения. Балка, лежащая на двух
опорах (рис. 3.10.2), сжимается двумя
силами, приложенными с эксцентри-
эксцентриситетом е. В концевом сечении при-
приложен, таким образом, момент Ре.
По формуле C.10.7)
v = v' @) -г sin kz + e A — cos kz).
Рис. 3.10.2
Постоянную v'@) определим из условия v(l) =0
v (i) = V—y^- sin kl + e A — cos kl) = 0.
Отсюда
1 — cos kl
Подставляя это в выражение для прогиба, получим
— sin Ая ^пГ/ ' C.10.8)
Если бы сила была растягивающей, в формуле C.10.8) следовало бы
заменить тригонометрические функции гиперболическими
C.10.9)
ch kz — 1 - sh Ь ghA.z
Явления продольно-поперечного изгиба при растяжении и
сжатии протекают качественно совершенно по-разному. Предпо-
§ 3.11. ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ Ю9
ложим, что мы увеличиваем растягивающую силу Р. Тогда уве-
увеличивается /с, гиперболические синус и косинус монотонно воз-
возрастают, но разность между ними стремится к нулю. Прогиб по
формуле C.10.9) получается отрицательным, величина его рас-
растет, но не превышает величину эксцентриситета е. Совершенно
иначе обстоит дело, если сила сжимает стержень. При значениях
параметра Ы, кратных я, обращается в нуль sin kl в знаменателе
последнего члена формулы C.10.8). Таким образом, прогиб обра-
обращается в бесконечность при некоторых значениях силы.
Не останавливаясь пока подробно на этом факте, заметим,
что он тесно связан с теорией устойчивости упругих систем, рас-
рассмотренной в гл. 4.
§ 3.11. Изгиб балки на упругом основании
Примером балки на упругом основании является железнодо-
железнодорожная шпала, нагруженная двумя силами, передаваемыми че-
через рельсы. Не имея опор, шпала передает эту нагрузку непо-
непосредственно грунту, изгибаясь при этом вследствие податливо-
податливости грунта.
Термин «упругое основание» в применении к грунту довольно
условен, ибо механические свойства грунта не тождественны со
свойствами упругого тела в обычном смысле слова. Если поста-
поставить задачу о равновесии
балки, покоящейся на мас-
массивном упругом теле,огра- 'lIH^IIII^IIIIIIIIIIII1
ничейном с одной стороны яЦШуМММ
плоскостью, мы получим
пример так называемой Рис. 3.11.1
контактной задачи теории
упругости, точное решение которой встречает большие математи-
математические трудности, Существо их состоит в том, что деформация тела
в одной какой-либо точке зависит не только от давления в этой
точке, но и от давлений в соседних точках.
Желая упростить постановку задачи и сделать ее доступной
элементарным методам, предполагают, что перемещение упругого
основания зависит только от давления в той точке, в которой
ищется перемещение. Эта гипотеза, иногда называемая гипоте-
гипотезой Винклера, как бы заменяет реальное упругое тело рядом не
связанных между собой пружин или стерженьков (рис. 3.11.1).
Считая реакцию основания пропорциональной прогибу, найдем,
что распределенная непрерывным образом по длине балки реак-
реакция есть
q = —си.
Такая упрощенная модель упругого основания довольно хоро-
хорошо воспроизводит свойства грунта, который, собственно, не мо-
ГЛ. 3. ИЗГИБ БАЛОК
жет считаться упругим телом: связность между его частицами
меньшая, нежели в сплошном упругом теле.
Заметим, что предположение о пропорциональности между
прогибом и реакцией основания выполняется совершенно строго
для плавающей балки прямоугольного поперечного сечения.
Здесь реакция представляет собою подъемную силу Архимеда.
Для составления дифференциального уравнения изгиба бал-
балки, лежащей на упругом, в смысле Винклера, основании, мы бу-
будем исходить из дифференциального уравнения изгиба в форме
C.8.5). В правой части к действующей нагрузке q мы прибавим
реакцию основания (—си) и будем считать жесткость балки при
изгибе, т. е. произведение Е1Х, постоянной. Получим
EIxviy = —си + q(z) C.11.1)
или
U ~ Е1„ [ ~~ EIV
Уравнение C.11.1) встречается не только в задаче о балке
на упругом основании, но и в других разделах строительной
механики, например, в теории цилиндрических оболочек. Зай-
Займемся сначала интегрированием однородного уравнения
vlY + Аа'и = 0. C.11.2)
Корни характеристического уравнения суть
Комбинируя соответствующие частные решения так, чтобы
избавиться от мнимостей, получим общий интеграл уравнения
C.11.2)
v = eaz (A sin az + B cos az) + e~az (С sin az + D cos az). C.11.3)
Применяя метод § 3.9, мы должны с помощью общего инте-
интеграла C.11.3) образовать систему частных решений с единичной
матрицей начальных значений.
Эти решения суть:
иг = ch az cos az, U2 = -=— (ch az sin az + sh az cos az),
t C-11.4)
U3 — —2 sh az sin OL7"> U* = —з (ch az sin az — sh az cos az).
Отметим, что
§ 3.11. ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ Щ
По формуле C.9.6)
v(z) = v@)Ui{z)+v'@)U2{z) +
+ v" @)U3(z)+v/ff@)U,{z)+vi(z). C.11.5)
Здесь
г
z — Q т^а ^* (З.и.6)
Вычислим функцию Vi(z) для случая, когда балка загружена
сосредоточенной силой в сечении с координатой z = b. Заменим
сосредоточенную силу равномерно распределенной нагрузкой на
участке от Ъ — г до Ъ + е. Интенсивность этой нагрузки примем
Q
равной Щу По формуле C.11.6) vl(z) = 01 если z<b — s.
Если z > Ъ + е, то
Ъ+г
= J
Ъ-г
Применим к этому интегралу теорему о среднем. Получим
Здесь ^^(—1, +1).
Будем теперь приближать г к пределу, равному нулю. Иско-
Искомое частное решение представится так:
vx (z) = 0 при z < &,
i>! B) ^jj-U^z — b) при z> Ь.
Желая получить решение в случае сосредоточенного момента,
приложенного в сечении с координатой а, приложим в этом сече-
сечении сосредоточенную силу величиной М/г, в сечении с коорди-
координатой а + г силу —М/г. При z > а + е, суммируя найденные
решения для двух сил, получим
Переходя к пределу при е -> 0 и вспоминая, что С/4 = f з» найдем
^i (z) ~ 0 при z <С а,
^о B) =ТТиз^ — а) ПРИ
112
ГЛ. 3. ИЗГИБ БАЛОК
Рассмотрим, наконец, случай равномерно распределенной на-
нагрузки, начинающейся при z = c. По формуле C.11.6)
о
Но, как легко проверить непосредственным вычислением,
Поэтому
v± {z) = 0 при z < с,
*>i(*)= т И - ui (z~~c)] ПРИ 2 > с-
Если нагрузка заканчивается при z = d, то считаем ее про-
продолжающейся вправо неограниченно, но прикладываем нагрузку
(—q), начиная C2 = d. При z > d получим
Окончательная формула для прогибов будет следующей:
v(z) = v @) С/, (z) + v' @) ?/2 (z) + v" @) f/3 (z) + *" @) С/4 (z) +
л
+ Шх 2 {^3 (Z - «) + ^^4 B - Ь) - ^-4 [С/х (Z - С) - ?/х (Z - д)]\.
C.11.7)
Символ суммы с индексом «л» вверху нужно понимать так
же, как в § 3.8.
Рис. 3.11.2
Рассмотрим в качестве примера задачу об изгибе полубесконечной бал-
балки силой и моментом на конце (рис. 3.11.2). В формуле C.11.5) нужно
положить
1 х ^*х
Получим
v = v@) U± (z) + и' @)U2 (z) + -У- Ud (z) + J- C74 (z).
Для определения постоянных ^@) и z/@) потребуем, чтобы прогиб на
бесконечности был равен нулю. Для этого заметим, что при больших зна-
§ 3.11. ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
чениях аргумента ch az ->- sh az ->• V2 ехр az. Следовательно, по формулам
C.11.4)
1 1
Ux (z) -+¦ "y ехр az cos az, U2 {z) -+¦ ^ exp az (sin az -f cos az),
^3 B) "* 7 exP az sin az> ^4 B) "*" Ja3 exp az ^sin az ~~ cos az)
При больших z
1 f 1
1; (z) -> -у exp az j 1; @) cos az -f ^ y' @) (sin az + cos az) +
1 M 1 Q 1
sin az + (sin az cos az) "^ °-
J
1 M 1 Q
+ T~2 7T sin az + 7~3 77" (sin az ~~ cos az)
Сравнивая коэффициенты при cos as и sinaz, найдем
Отсюда
Заметим, что прогиб v(z) меняет знак: на некоторых участках балка
приподнимается над основанием. Мы предполагаем при решении задачи,
что реакция основания возникает и при отрицательных прогибах, что су-
существенно упрощает решение.
8 ю. Н. Работнов
ГЛАВА 4
УСТОЙЧИВОСТЬ СТЕРЖНЕЙ И СТЕРЖНЕВЫХ СИСТЕМ
§ 4.1. Постановка задач устойчивости
Как оказывается, при некоторых определенных значениях
внешних сил упругая система может иметь несколько положений
равновесия, причем одни из них устойчивы, другие неустойчивы.
Для выяснения этого вопроса обратимся к примеру стержня,
сжатого силой Р (рис. 4.1.1). Предполагается, что стержень иде-
идеально прямой и сила приложена строго центрально (что практи-
практически невозможно). При указанных идеальных условиях прямо-
прямолинейная форма стержня всегда является возможной
Р формой его равновесия. Для суждения об устойчивости
уа этой формы равновесия нужно сообщить возмущение,
•^ например приложить малую поперечную нагрузку Q,
которая вызовет прогиб. При отсутствии сжимающей
силы Р малая поперечная сила вызывает малый про-
прогиб. Если сила Р невелика, то положение останется
таким же и равновесие стержня сохраняется устойчи-
устойчивым. Более строгое определение устойчивости состоит
в следующем. Равновесие стержня устойчиво, если, за-
задавшись любой величиной г) > 0, всегда можно указать
такую конечную величину е >0, что при \Q\ <e вели-
^ чина прогиба ни в одной точке не достигнет величины
г], т. е. будет Ы < г|. Оказывается, как мы увидим
Рис. 4.1.1 далее, что это условие не выполняется, если сила Р
превышает некоторое критическое значение Рк. При
Р>Р* равновесие стержня становится неустойчивым, это значит,
что сколь угодно малое возмущение достаточно для того, чтобы
возникли большие прогибы.
В данном случае возмущение создается поперечной силой.
Но можно представить себе и другой способ создания возмуще-
возмущения, например можно приложить (распределенную напрузку, не-
неравномерно нагреть стержень, вследствие чего он искривится
и т. д. Возникает естественный вопрос — будет ли зависеть кри-
критическая сила от типа возмущения. Для упругих систем, как
оказывается, критическая сила от характера возмущения не за-
зависит. Для пластических тел это не так и положение может быть
более сложным. Критическая .сила, (понимаемая ш указанном
смысле, может зависеть от характера возмущения.
§ 4.2. КРИТИЧЕСКИЕ СИЛЫ ПО ЭЙЛЕРУ
При исследовании задач устойчивости нужно иметь в виду
еще следующее обстоятельство. Реальная механическая система
для ее изучения идеализируется, и в конечном <счете мы имеем
дело не с механическим объектом, а с дифференциальным урав-
уравнением или системой дифференциальных уравнений, отражаю-
отражающих действительные ¦свойства объекта лишь приближенно т в не-
некоторой определенной области. Решение задач устойчивости —
это есть решение математической задачи, т. е. исследование
свойств уравнений. Перенос (результатов этого исследования на
реальный объект, т. е. предсказание механического эффекта,
должно делаться с осторожностью, потому что не все .свойства
решений дифференциальных уравнений являются свойствами ме-
механической системы. Мы убедимся :в отом в следующих пара-
параграфах.
§ 4.2. Критические силы для сжатого стержня по Эйлеру
Излагаемый ниже метод исследования устойчивоюти упругих
систем по отношению к малым возмущениям называется методом
Эйлера, который применил его для рассмотрения задачи об устой-
устойчивости сжатого стержня. На этом примере и будет проиллюст-
проиллюстрирован ниже этот метод, применяемый для решения задач об
устойчивости любых упругих систем.
Существо его состоит в том, что постановка задачи об устой-
устойчивости -по отношению к заданным возмущениям подменяется
несколько иной постанов-
постановкой, в известном смысле
упрощенной, а именно, ~jr
решается вопрос об устой-
устойчивости в прямом смысле
слова, а о возможности '
существования двух раз-
различных форм равновесия ^ис- ^-
стержня при одном и том
же значении силы. Простейшая задача будет относиться к слу-
случаю, изображенному на рис. 4.2.1. Очевидно, что прямолинейная
форма равновесия, когда y(z)=0, возможна. Предположим, что
наряду с прямолинейной формой возможна и представленная на
рисунке криволинейная форма. Тогда изгибающий момент в се-
сечении с координатой z есть —Pv(z). Поэтому дифференциальное
5фавнение изогнутой оси стержня будет
EIxv" +Pv = 0. D.2.1)
Присоединим ж нему граничные условия
i7@) = i7(Z) = 0. D.2.2)
Очевидно, что решение z;(z)=O удовлетворяет и уравнению
D.2.1) и граничным условиям D.2.2), но вопрос ставится так:
8*
ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
не может ли иметь уравнение D.2.1) при граничных условиях
D.2.2) нетривиальное, т. е. отличное от нуля решение. Эта по-
постановка весьма напоминает постановку задачи о нетривиальном
решении однородной системы линейных алгебраических уравне-
уравнений, которое 'Существует, как известно, если определитель систе-
системы равен нулю.
р
Положив — = к2, перепишем D.2.1) в виде
и запишем общий интеграл этого уравнения
v (z) = A sin kz + В cos kz.
Из первого граничного условия следует 5 = 0. Подставляя В = 0
во второе граничное условие, находим
Asmkl = 0. D.2.3)
Если v?=0, А Ф 0, Ы = шт, то
Формула D.2.4) определяет бесконечную последовательность
критических сил, для которых возможно искривленное состояние.
Наименьшая критическая оила Р± называется эйлеровой силой Рэ,
она равна
Р,-^. D.2.5)
Полученный результат не может удовлетворить требованиям
здравого смысла. Если Р = Рп, то константа А остается совер-
совершенно неопределенной; значит, при критическом значении силы
прогиб может быть каким угодно, равновесие оказывается без-
безразличным. Далее, если сила заключена между Рп и Pn+i, не-
нетривиального решения задачи не существует и уравнение изгиба
не может обнаружить никаких иных форм равновесия, кроме
пр ям о лине иной.
Таким образом, необходимо более детальное изучение факти-
фактического поведения сжатого стержня. Заметим, прежде всего, что
при составлении уравнения D.2.1) была допущена известная
противоречивость. До сих пор мы всегда имели дело с линейной
зависимостью между силами и перемещениями. Эта линейность,
помимо закона Гука, вытекала из предположения о малости
углов поворота, которое использовалось два раза, а именно:
1. Уравнения статики составлялись для недеформированного
состояния системы.
§ 4.2. КРИТИЧЕСКИЕ СИЛЫ ПО ЭЙЛЕРУ Ц7
2. Соотношения между перемещениями! и деформациями эле-
элементов системы линеаризовались.
Но, записывая, что Мх = Ри, мы нарушаем первое условие,
тогда как полагая 1/р = у", мы сохраняем второе. Это — очевид-
очевидная непоследовательность, за которую приходится расплачивать-
расплачиваться, получая неясный результат. Система D.2.1), D.2.2) остается
линейной относительно v(z), нам приходится интегрировать ли-
линейное уравнение, но задача по существу нелинейна и крити-
критическая сила Рп ищется как корень трансцендентного уравне-
уравнения D.2.3).
Оставаясь в рамках тех же допущений, выясним, какова
связь полученного результата с постановкой задачи об устойчи-
устойчивости по отношению к заданному возмущению. Обратимся для
этого к уравнению продольно-поперечного изгиба C.10.5),
а именно:
М*
V + кЪ = -?. D.2.6)
Если возмущение создано произвольной поперечной нагрузкой,
то для статически оиределимюй балки, изображенной на рис. 4.2.1,
всегда можно построить эпюру моментов, т. е. определить функ-
функцию M*x{z). Будем считать поэтому, что задание функции Ml
и есть задание возмущения. Ищем решение уравнения D.2.6)
в виде
сю
assm — .
Подставляя в D.2.6), получим
—+ /cJsm- = -.
Умножим обе части на sin nnz/l и проинтегрируем по z от
z = 0 до z = I. Так как
i
| . SJlZ . 71TCZ 7 I о /о тч
\ sin — sm — dz = ~y °sn {Osn — символ Кронекера),
о
то в левой части останется только один член, соответствующий
п = s, и мы получим
—
ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Здесь
I
2п
тп = — \ Мх {z) sin —у- dz.
о
Подставляя выражение для к2 ж используя формулу D.2.4),
найдем
тп
Здесь Рп — критическая сила с номером гг. Выражение для про-
прогиба получается следующим:
р-р sin—• D-2-7)
n=i n
Функция v(z), удовлетворяющая уравнению D.2.6) и граничным
условиям D.2.2), непрерывная вместе со своей первой производ-
производной, -представляется равномерно сходящимся рядом Фурье D.2.7),
содержащим только синусы кратных аргументов. Величины тп
представляют собой коэффициенты Фурье для функции Мх, од-
однако соответствующий ряд Фурье, вообще говоря, не сходится ни
в каком смысле, и функцию Мх (z) не представляет (что следует
из известной теоремы Гильберта—Шмидта, например).
Видно, что при Р = Рп прогиб обращается в бесконечность,
сколь бы ни было мало тп, т. е. возмущение. Но если РФРп,
то всегда можно выбрать достаточно малую функцию Мх, чтобы
все тп были доютаточно малы и прогиб не превосходил любую
заданную величину. Теперь становится ясным, почему реальный
смысл имеет именно первая критическая сила. В принципе, ко-
конечно, дюжно представить себе такую возмущающую нагрузку,
что //г 1 = 0, тогда потеря устойчивости произойдет при крити-
критической силе Р2. Но этот идеальный случай в действительности
неосуществим, при любой поперечной нагрузке т{ Ф 0, хотя мо-
может быть сколь угодно мало.
Обращение прогиба в бесконечность на самом деле невоз-
невозможно (в действительности |y|<Z/2), бесконечные прогибы по-
появляются опять как следствие применения линеаризованного
выражения для кривизны. Таким образом, полученный результат
скорее сигнализирует об опасности, возникающей при Р = РЭ,
чем позволяет оценить действительную степень этой опасности.
§ 4.3. Эластика Эйлера
Результаты, полученные выше с помощью линеаризованного
уравнения изгиба, неудовлетворительны в том отношении, что
они ие поз'воляют обнаружить искривленные формы оси стержня
при условии Рп<Р <Pn+i, в частности при Р>РЭ. Поэтому
§ 4.3. ЭЛАСТИКА ЭЙЛЕРА
119
мы рассмотрим задачу, поставленную в предыдущем параграфе,
в точной постановке. Напишем дифференциальное уравнение
изгиба так:
Е1хк - —Ру.
Кривизна х изогнутой оси равна dd/ds, где 8 — изображенный
на рис. 4.3.1 угол между
касательной к изогнутой
оси стержня и осью, про-
проходящей через его концы, у
Уравнение изгиба бу-
будет следующим:
f- = -/cV D.3.1)
Здесь к то же, что и в § 4.2.
Продифференцируем
уравнение D.3.1) по s,
заметив, что dy/ds = sin 8.
Получим
^ = _A;2sin9. D.3.2)
ds
Рис. 4.3.1
Уравнение D.3.2) интегрируется в квадратурах обычным спо-
способом. Запишем его так:
1 d (dO\2 79 . л
-тг -за- гз~ = — Л2 sin 0.
2 dQ \ ds j
Заметим, что преобразование левой части вполне аналогично
преобразованию левой части уравнения движения при выводе
теоремы живых сил. Разделяя переменные и интегрируя, найдем
) cos80).
Мы воспользовались здесь граничным условием при 5 = 0, х = 0
и 8 = 80.
Перейдем в этом выражении к половинным углам по формуле
€os 9 = 1 — 2 sin2 (9/2). Получим
*" = 4ft» sin«^-sin«« .
D.3.3)
Сделаем замену переменной, приняв
.9 . 6П .
sin —г- = sin -
D.3.4)
Это всегда выполнимо, потому что 9 ^ 90. Дифференцируя D.3.4),
J20 гл- 4- устойчивость стержневых систем
найдем
cos ~y d ~y = sin -j- cos ф йф.
Преобразуем к новой переменной выражение D.3.3). Полу-
Получим, разделяя переменные:
Положим sm(80/2) = m. Заметим, что при s = 0 6 = 00 и ф = я/2.
Поэтому, интегрируя левую часть от нуля до 5, правую от я/2
до ф, будем иметь
s = —
Знак минус выбран для того, чтобы было 5 > 0. Это эллипти-
эллиптический интеграл первого рода, т. е. табулированная функция.
Принимая обычные обозначения эллиптических интегралов
— га sin ф *i К 1 — m sin с
получим
При s = l/2 в силу симметрии 0 = 0, а следовательно, пф = 0.
Поэтому
F = ^ D.3.6)
Из этого уравнения определяют неизвестную величину т,
связанную с углом наклона касательной на конце стержня. Те-
Теперь можно найти координаты точек изогнутой оои стержня
х и г/, отправляясь от равенств dx/ds = sin 0, dy/ds = cos 0.
Перейдем к независимой переменной ф, пользуясь D.3.4) и
D.3.5). Получим
dx = sin Qds = г- sin
/с
= ~4" Г2
[
К 1 — т2 sin2 ф
Интегрируя и принимая во внимание, что х = у = 0 при ф = я/2,
§ 4.4. УСТОЙЧИВОСТЬ ПРЯМОЛИНЕЙНОЙ ФОРМЫ |21
получим параметрические уравнения .изогнутой оси
^ — "T"C0S(P> У — "тг [2 (?" — i? (ф)) — (F — /^(ф))]. D.3.7)
ф
Здесь Е (ф) = J "Kl — т2 sin2q)dq)— эллиптический интеграл второго
рода; Е(я/2) = Е.
Обратимся теперь к исследованию уравнения D.3.6).
Полный эллиптический интеграл F не может быть меньше
чем л/2; это значение достигается при т — 0. Поэтому если
Ы<л, то это уравнение не имеет решения; единственно воз-
возможная форма равновесия — прямолинейная. Но Ш = я, если
Р=~-Р, = ^-^.
Это — первая критическая -сила.
Таким образом, искривленная форма равновесия возможна
тогда, когда Р > Рэ. При этом каждому значению Р соответству-
соответствует совершенно определенное значение т по уравнению D.3.6)
и определенная кривая прогиба — эластика Эйлера, даваемая
уравнениями D.3.7). Прогиб растет по мере увеличения нагрузки
весьма быстро, как показано на рис. 4.3.1.
Теперь понятно, почему мы могли обнаружить криволинейные
формы равновесия при Р> Рэ только с помощью точных урав-
уравнений. Для этих форм прогибы велики, а приближенное линеа-
линеаризованное уравнение годится лишь для малых прогибов.
§ 4.4. Устойчивость прямолинейной формы
сжатого стержня
Результаты, полученные в предыдущем параграфе, еще не
дают ответа на вопрос об устойчивости в строгом смысле слова,
как это было сформулировано в § 4.1. Вместо этого мы по су-
существу ввели бифуркационный критерий устойчивости. Если
представить себе процесс нагружения стержня продольной силой
как процесс, описываемый кривой (Зависимости некоторого про-
прогиба от сжимающей силы, то на этой кривой получаются развет-
разветвления в некоторых точках, называемых .критическими или точ-
точками бифуркации. Так, на рис. 4.4.1 схематически изображен
график зависимости прогиба, например прогиба б в середине
стержня, от сжимающей силы Р; пока Р < Рэ это отрезок оси
ординат, 6 = 0. При Р > Рэ стержень может либо оставаться пря-
прямым, либо иокришгться; в соответствии с двумя возможными
формами равновесия возникает бифуркация, одному и тому же
значению силы Р соответствуют два возможных прогиба (точки
А и В). Вопрос о том, какая форма равновесия, прямолинейная
122 гл- 4- устойчивость стержневых систем
или искривленная, оказывается устойчивой, остается открытым.
Для решения его нужно было бы предположить, что стержень
находится в одном из этих состояний (А или В) и что какая-то
причина его из этого состояния вывела. Далее, нужно изучить
движение стержня и выяснить, будет ли он возвращаться в ис-
исходное состояние или, наоборот, удаляться от
него. Таким образом, вопрос об устойчивости
равновесия в принципе должен решаться в
динамической постановке, в результате анали-
анализа уравнений движения. Далее, в гл. 6 та-
такая динамическая постановка вопроса об устой-
устойчивости будет рассмотрена, сейчас же мы по-
попытаемся обойтись элементарными соображе-
соображениями. Согласно известной теореме Дирихле
в состоянии устойчивого равновесия энергия
системы имеет минимум, следовательно, всякое
отклонение от состояния равновесия должно
увеличивать энергию системы. Пусть малый
Рис. 4.4.1 прогиб v(z) и представит собой такое откло-
отклонение от прямолинейной формы равновесия.
Сжимающая сила Р совершит при этом работу на перемещении
А (см. рпс. 4.2.1), которое вычисляется по следующей формуле:
i
v'2dz, D.4.1)
вывод которой очевиден (более высокие степени v' отброшены).
Потенциальная энергия изгиба стержня находится по формулам
C.3.7), C.3.8), а именно
Таким образам, изменение полной энергии стержня вследствие
малого изгиба будет
W=U — Pb. D.4.2)
Если W>0, то по теореме Дирихле стержень устойчив, в пря-
прямолинейном состоянии, если W < О, стержень неустойчив. Для
того, чтобы прийти к этому выводу, нет необходимости ссылаться
на теорему Дирихле, если РА > Z7, сила Р производит работу
большую, чем может накопиться в виде упругой энергии стерж-
стержня, избыточная работа идет на сообщение кинетической энергии,
стержень приходит в движение, т. е. прогибается дальше, по
мере увеличения прогиба увеличивается и избыточная работа,
таким образом, {прогиб растет ускоренно. В этом и состоит по-
потеря устойчивости. Для проверки условия устойчлшости нужно
§ 4.5. ПОСЛЕКРИТИЧЕСКОЕ ПОВЕДЕНИЕ УПРУГИХ СИСТЕМ ^23
задаться видом возмущения. Положим, например,
nz
v = asm —.
После элементарных вычислений, найдем, с учетом D.2.5)
W = 2?- (Рэ — Р). D.4.3)
Очевидно, что W > О, т. е. стержень устойчив при Р < РЭ1
тогда как при Р > Рэ прямолинейная форма стержня всегда не-
неустойчива, хотя бы значение силы и попало в интервал между
ее критическими значениями.
Проведенное исследование, строго говоря, позволяет утвер-
утверждать только устойчивость прямолинейной формы по отношению
к синусоидальным возмущениям. Возникает вопрос: нельзя ли
выбрать такое возмущение v (z), по отношению к которому стер-
стержень окажется неустойчивым при действии сжимающей силы
Р < Рэ? Для того чтобы доказать, что Ро есть действительно наи-
наименьшая критическая оила, представим себе, что стержню сооб-
сообщено произвольное возмущение
оо
y(z) = 2^sinT-Z- D-4-4)
Здесь нам придется сослаться на соответствующую теорему ана-
анализа, которая применительно к данному случаю, утверждает воз-
возможность представления в виде ряда D.4.4) любой функции,
которая удовлетворяет граничным условиям v@) = v(l) = 0, не-
непрерывна вместе со своей первой производной и имеет кусочно-
непрерывную вторую производную. Учитывая ортогональность
тригонометрических функций кратных аргументов, найдем
s=l
Если Р < Pi = Рэ, то все члены суммы положительны и W > О
при любых as, т. е. для любого возмущения v (z); если Р > Рэ,
то можно выбрать такое возмущение, чтобы было W < 0 и, сле-
следовательно, по отношению к которому стержень неустойчив.
§ 4.5. Послекритическое поведение упругих систем
Приближенный анализ, основанный на линеаризованном урав-
уравнении, убедил нас в том, что при Р = Рэ стержень находится
в безразличном состоянии равновесия. На рис. 4.4.1 горизонталь-
горизонтальная штриховая прямая с ординатой Рэ изображает эти возмож-
возможные состояния. Точпный анализ § 4.3 показывает, что в действи-
действительности, при Р = Рэ стержень еще устойчив, увеличение
124
ГЛ. 1. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
сжимающей силы вызывает строго определенное увеличение про-
прогиба.
Но можно привести примеры упругих систем, которые ведут
себя после достижения критической силы совершенно иначе.
Чтобы выяснить существо дела, мы рассмотрим два примера,
которые носят совершенно модельный характер, но анализ этих
примеров предельно прост, тогда как качественные эффекты по-
получаются теми же, что и для некоторых реальных упругих си-
систем, например оболочек, где результат достигается только путем
громоздкого и трудоемкого численного счета на ЭВМ.
Пример 1. Этот пример относится к конструкции, изображенной на
рис. 4.5.1. Абсолютно жесткий стержень длиной I шарнирно закреплен на
нижнем конце, спиральная пружина удерживает стержень в равновесия
в вертикальном положении. При отклонении стержня от вертикали на угол
М.
Рис. 4.5.2
а появляется восстанавливающий момент, пропорциональный углу откло-
отклонения М = са. Если к концу стержня приложена вертикальная сила Р,
то отклоненное состояние возможно при выполнении уравнения равновесия:
PI sin a = сау или P = —
а
I sin а*
D.5.1)
Заметим, что a/sin a ^ 1, причем знак равенства выполняется лишь при
сх = 0. Таким образом, мы находим, что положение равновесия стержня,
отличпое от вертикального, возможно лишь тогда, когда
D.5.2)
График зависимости Р от а, согласно D.5.1), представлен на рис. 4.5.2
(кривая 1). Поведение такого простейшего элемента до чрезвычайности на-
напоминает поведение сжатого стержня.
Выясним теперь, как будет вести себя рассмотренная система, если в
свободном от нагрузки состоянии стержень не вертикален, а уже наклонен
по отношению к вертикали на угол oto. Все выводы сохраняют силу, разни-
разница будет состоять лишь в том, что момент М пропорционален углу a — a0,
§ 4.5. ПОСЛЕКРИТЫЧЕСКОЕ ПОВЕДЕНИЕ УПРУГИХ СИСТЕМ
поэтому вместо D.5.1) мы получим
* sin a
Кривые зависимости а от Р для разных значений осо показаны на том
же рисунке 4.5.2. При Р = Рэ никаких изменений характера этих кривых
отметить нельзя, и расчет на устойчивость при наличии начального откло-
отклонения вообще теряет смысл.
Пример 2. Точно такой же шарнирно закрепленный стержень, как
в примере 1, возвращается в исходное вертикальное положение силой со-
сопротивления R, которая пропорциональна горизонтальному перемещению и
конца стержня: R — си (рис. 4.5.3). Так
как и = I sin a, то уравнение равновесия Р
будет
PI sin а = cl2 sin a cos а. п
Отсюда, кроме тривиального решения
sin а = О, находим р^п
р = рэ cos a. D.5.3)
Теперь
Рэ = cl. D.5.4)
График зависимости а от Р в соответ-
соответствии с D.5.3) представлен на рис. 4.5.4. &
Теперь при Р = Рэ вертикальное положе-
положение стержня неустойчиво, при увеличении
а для сохранения равновесия в каждый
момент сила должна уменьшаться, а ес-
если остается постоянной, то происходит «хлопок», стержень мгновенно пово-
поворачивается на 180° и принимает положение, которое, очевидно, будет устой-
устойчивым.
Предположим теперь, что в ыспагруженном состоянии стержень был
наклонен под углом а0 к вертикали и, следовательно, Л = cl (sin a — sincc0).
Вместо соотношения D.5.3) мы получаем следующее выражение, связываю-
связывающее силу и угол:
за. D.5.5)
р 4 5 4
since
На том же рис. 4.5.4 схематически показана серия кривых, изображающих
зависимость D.5.5) при разных значениях а0. Функция от а, фигурирую-
фигурирующая в правой части D.5.5), имеет максимум при sinos=j/ sina0; таким об-
образом, максимальное значение сжимающей силы или критическая сила, со-
соответствующая заданному начальному отклонению, найдется по формуле
Ркр = P0(l - sin2/3 аоK/2. D.5.6)
В этом примере мы встретились с новым эффектом, вызванным нелиней-
нелинейностью; при некотором критическом значении силы искривленная форма
равновесия становится неустойчивой в том смысле, что при достижении
этого критического значения перемещение сразу изменяется на конечную
величину.
Следует различать два рода эффектов, которые часто объединяют об-
общим термином «неустойчивость». Мы сохраним этот термин применитель-
применительно к рассмотренной выше проблеме устойчивости прямолинейной формы
сжатого стержня, когда сила превышает критическую. Возникновение ко-
конечных перемещений при достижении силой критического значения пра-
126 гл- 4- устойчивость стержневых систем
вильнее называть «выпучиванием» или «хлопком»*). Явление выпучивания
может быть связано не только с геометрической, но и с физической нели-
нелинейностью. Вернемся к примеру 1. Если ограничиться геометрически ли-
линейной постановкой, то при малых a sin a « а и вместо D.5.1) мы получим
р = рэ при любых достаточно малых ее, т. е. тот же по существу результат,
что в задаче Эйлера об устойчивости сжатого стержня.
Предположим теперь, что зависимость между моментом и углом пово-
поворота нелинейна, например:
а — aQ — ¦
Здесь Mi, M2 и п — постоянные, М\ и М2 имеют размерность изгибающего
момента. С другой стороны, момент в шарнире должен равняться действу-
действующему моменту силы Р, т. е.
М = PI sin a « Pla. D.5.8)
Мы предполагаем, что углы достаточно малы; таким образом, задача рас-
рассматривается как геометрически линейная. Одновременный учет физиче-
физической и геометрической нелинейностей существенно усложняет исследова-
исследование, хотя позволяет обнаружить новые эффекты. Исключая М из D.5.7) и
D.5.8), мы получим связь между а и Р. Однако основной вопрос, который
мы хотим выяснить, это вопрос о существовании критической силы, т. е.
такой силы, по достижении которой угол продолжает расти без увеличения
нагрузки. Условием достижения критической силы будет равенство нулю
производной dP/da. Продифференцируем по а D.5.8) и положим в правой
части dP/da = 0.
Получим
dM M da a
— = Р1 = —, или Ш = Ж. D.5.9)
Теперь нам остается найти производную da/dM из D.5.7) и подставить
в D.5.9). Получим
М - ¦ ¦ D.5.10)
Исключив а из D.5.7) и D.5.10), найдем момент, соответствующий критиче-
критическому состоянию
1 п ч 1
кр 1 2 U
Соответствующее значение угла поворота акр находится из уравнения
D.5.10), а критическая сила
Р /а 1
Из формулы D.5.11) следует, что при а0 = 0 Ркр = М\\1. Этот результат
можно получить сразу из соображений, совершенно аналогичных тем, кото-
которые были положены в основу при решении задачи об устойчивости линейно-
*) В англо-американской литературе, как правило, это различие соблю-
соблюдается достаточно последовательно, в первом случае употребляется термин
«instability», во втором — «buckling».
§ 4.6. УСТОЙЧИВОСТЬ ПОЛОГОЙ АРКИ
127
упругой балки. Действительно, положим в D.5.7) ао = 0 и будем считать
угол отклонения весьма малым. Если а мало, то и момент по формуле
D.5.8) мал, следовательно, вторым членом в квадратных скобках D.5.7) мож-
можно пренебречь по сравнению с единицей. Мы получим
Pla
1
Это равенство возможно только тогда, когда Р = М\/1. Будем называть
критическую силу при а0 = 0 эйлеровой силой Рэ. Если нелинейность
Рис. 4.5.5
Рис. 4.5.6
отсутствует, т. е. М2 = оо, легко решить задачу и при
но, мы получаем в этом случае
Pla P
ф- 0. Действитель-
Действитель~ао "- М± ~ Рэ
Отсюда
1-р/р •
D.5.12)
Зависимость между а и Р, установленная формулой D.5.12), монотонна,
при Р-^РЭ а-^оо независимо от значения ссо- График этой зависимости
для разных а0 показан на рис. 4.5.5. В нелинейном случае, согласно D.5.11),
критическая сила убывает с увеличением эксцентриситета; графики зави-
зависимости между а и Р схематически изображены на рис. 4.5.6.
§ 4.6. Устойчивость пологой арки
Явление хлопка, т. е. мгновенного перехода из одного состо-
состояния равновесия ib другое, типично для оболочек. Как правило,
длина волны, образующейся при хлопке, невелика и поэтому
можно рассматривать элемент оболочки, претерпевающий хло-
хлопок, как дологий. Более простая задача, обнаруживающая те же
качественные особенности, это задача об устойчивости пологой
арки, например кругового очертания, как показано на рис. 4.6.1.
Пологость понимается в данноим случае в том: смысле, что угол
а < 1. Если, каск показано на рисунке, арка загружена равно-
равномерным давлением, действующим с выпуклой стороны, то, как
оказывается, при некотором значении давления q = qKV происхо-
гл- 4- УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
дит внезапное прощелкинание и арка принимает форму, показан-
показанную на рисунке штриховой линией, с выпуклостью вниз. Однако
мы здесь рассмотрим еще более простую модельную задачу. Два
стержня одинаковой длины I закреплены так, как показано на
рис. 4.6.2. В исходном состоянии каждый из них составляет угол
¦осо с горизонталью. Приложим к среднему шарниру вертикальную
силу Р, направленную вниз. Стержни укоротятся, угол наклона
Рис. 4.6.1 Рис. 4.6.2
их уменьшится, станет^равным а < а0. Будем считать а0 ^ 1, по-
поэтому sin а «а, cos а ~ 1 — а2/2. Длина стержня в исходном со-
состоянии равна l/cosa0ttl (l + al/2), после приложения силы она
равна Z/cosa ~ 1A + а2/2); таким образом, укорочение AZ =
— I (а20 — а2)/2 и относительная деформациям « (а2,— а2)/2.Из
уравнений статики найдем усилие в каждом стержне N = Р/ Bос).
По закону Гука N = EFe, следовательно,
^-=^EF{al-a?), P =--EFa(al-a*). D.6.1)
Таким образом, для нахождения величины а получилось кубиче-
кубическое уравнение. Вместо того чтобы отыскивать его корни, удобно
исследовать зависимость Р от а. Очевидно, что Р = 0 при а = О
и а = ±а0. С увеличением силы Р угол а уменьшается, но при
а = О Р = 0, следовательно, начиная с какого-то момента, угол
продолжает уменьшаться уже не при увеличении, а при умень-
уменьшении силы. Выясним, когда это происходит. Для этого вычис-
вычислим производную dP/da и приравняем ее нулю. Получим урав-
уравнение
а20 - За2 - 0.
Отсюда критическое значение угла акр = ±ао/УЗ. Когда а дости-
достигает критического значения +ao/V3, сила максимальна и равна
D.6.2)
При а = —ao/V3 значение силы то же, но знак противоположен.
График зависимости между Р и а теперь легко нарисовать, он
изображен на рис. 4.6.3. При увеличении ,силы Р угол а умень-
уменьшается, из графика можно найти значение а по заданной силе.
Когда сила становится равной критической, т. е. достигается точ-
\ч
\
\ /
V/
?
/
и
в
1
V
\
\
(Z
V
§ 4.6. УСТОЙЧИВОСТЬ ПОЛОГОЙ АРКИ 129
ка В, равновесие перестает быть устойчивым, происходит хлопок.
Стержни мгновенно переходят в положение, соответствующее
точке С, когда угол а отрицателен, конфигурация системы ста-
становится симметричной изображенной на рис. 4.6.2. Теперь сила
Р уже не сжимает стержни,
а растягивает их. Если снять
нагрузку, они несколько
сократятся и равновесие
разгруженной системы будет
соответствовать точке D на
диаграмме, т. е. углу на-
наклона —а0. Чтобы вернуть
систему в исходное состоя-
состояние, нужно приложить силу
противоположного направле-
направления, т. е. отрицательную.
Когда значение ее достигнет Рис. 4.6.3
критического (точка Е),
произойдет обратный хлопок, мы попадём в точку F диаграммы,
а если снять нагрузку, то в исходную точку А. Как видно, отре-
отрезок ЕОВ кривой Р ~ а не соответствует каким-либо реально осу-
осуществляемым состояниям системы.
Приведенные рассуждения основываются на так называемой
квазистатической постановке, допускающей мгновенные переме-
перемещения точек системы на конечные расстояния. В действитель-
действительности всякая материальная система обладает массой; поэтому по-
после достижения силой Р критического значения нужно состав-
составлять и интегрировать дифференциальные уравнения движения.
Фактически состояние, отвечающее точке В, например, реализу-
реализуется по истечении достаточного времени, когда упругие колеба-
колебания вследствие тех или иных причин затухнут.
Заметим, что в рассмотренном примере управлять движением
системы можно не путем изменения силы, а изменением длин
стержней. Формула D.6.2) позволяет не только определить кри-
критическую силу, соответствующую данному а0, но и наоборот, най-
найти значение а0, при котором данная сила Р принимает критиче-
критическое значение. Пусть на систему действует постоянная сила Р,
например натяжение пружины с малой жесткостью, такой, что
изменением силы при перемещении шарнира можно пренебречь.
Будем охлаждать стержни, считая, что концевые шарниры не-
неподвижны. Температурное сокращение стержней эквивалентно
уменьшению угла а0, при некоторой температуре угол достигает
критического значения и происходит хлопок. Этот принцип ис-
используется в некоторых регуляторах температуры, в прикурива-
прикуривателе автомобиля и др.; конструктивные формы такого рода уст-
устройств, которые производят хлопок при достижении температу-
температурой определенного значения, достаточно разнообразны.
9 10. II. Работное
130
ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
§ 4.7. Критические силы при иных видах
закрепления стержня
Сравнение точных решений с приближенным убедило нас в
том, что вопрос о критических силах в линейной постановке ре-
решается правильно. При этом реальный смысл, конечно, имеет
только первая критическая сила. Итак, для стержня с шарнирно
закрепленными концами критическая сила определяется форму-
формулой D.2.5).
При потере устойчивости на длине стержня укладывается
одна полуволна синусоиды. В действительности встречаются и
иные способы закрепления концов.
Так, если стержень жестко защем-
защемлен на одном конце, а другой конец
оставлен свободным, то задачу
можно привести к предыдущей,
как показано на рис. 4.7.1. Подстав-
Подставляя в формулу D.2.5) 21 вместо 1Г
получим
D.7.1)
На длине стержня укладывается по-
I g I ловина полуволны синусоиды.
I ^у Этими двумя примерами исчер-
! iz пываются статически определенные
{ ' задачи об определении критических
Рис 4.7.1 Рис. 4.7.2 сил. В качестве примера задачи ста-
статически неопределенной рассмотрим
следующую. Один конец стержня жестко заделан, другой закреп-
закреплен шарнирно.
При искривлении стержня в шарнире возникает реакция R,
поэтому дифференциальное уравнение изгиба принимает вид
(рис. 4.7.2). Это неоднородное уравнение продольно-поперечного
изгиба, полученное нами в § 3.10. Перепишем его так:
v" +k2
Интеграл этого уравнения
v (z) = Сг sin kz
С2 cos kz \z.
h
D.7.2)
Прогиб v линейно зависит от трех постоянных: Си С2 и Со.
В то же время прогиб удовлетворяет трем <граничиым условиям
Граничные условия однородны, т. е. не содержат свободного чле-
§ 4.7. КРИТИЧЕСКИЕ СИЛЫ ПРИ ИНЫХ ЗАКРЕПЛЕНИЯХ J31
на. Поэтому, подставляя D.7.2) в граничные условия, мы полу-
получим систему однородных уравнений для трех постоянных Со, С4
и С2. А эта система имеет нетривиальное решение тогда, когда
определитель ее равен нулю. Это и есть условие для нахождения
критической силы. Составим эти уравнения
О + С2 = О, Сх sin kl + С2 cos kl ?- = О,
Q
Су cos kl — Со sin kl ^- = 0.
Исключая постоянные, получим
tg kl — kl^ 0.
Наименьший корень этого уравнения kl = 4,49. Критическая
сила
D,49)^7,
1
Приводя ее к тому же виду, что формулы D.2.5) и D.7.1),
найдем
Рэ-^2. D.7.3)
Случай стержня, жестко заделанного на двух концах, решает-
решается совершенно так же, нужно
только ввести в рассмотре-
рассмотрение, кроме реакции, еще кон-
концевой момент. Тот же ре-
результат можно получить го-
гораздо проще, если заметить Рис. 4.7.3
(рис. 4.7.3), что упругая
линия такого стержня может быть составлена из четырех поло-
половинок полуволны синусоиды. Поэтому
^ D.7.4)
(г/2J
Объединяя все эти формулы, примем
Здесь [I — коэффициент приведения длины.
9*
гл- 4- устойчивость стержневых систем
§ 4.8. Устойчивость стержня в упругой среде
Рассмотрим задачу об устойчивости сжатого стержня, окру-
окруженного упругой достаточно податливой средой. С подобной за-
задачей встречаются, например, при расчете обсадных труб нефтя-
нефтяных скважин: длинная труба, сжимаемая собственным весом,
окружена грунтом и при выпучивании трубы со стороны грунта
возникает распределенная реакция. Однако основной интерес
этой задачи для нас состоит в другом, дифференциальное урав-
уравнение подобного типа (встречается, например, в задачах устойчи-
устойчивости оболочек, и качественный характер явления потери устой-
устойчивости в известном смысле одинаков. Будем понимать термин
«упругая среда» в том же смысле, в каком понимался термин
«упругое основание» в § 3.11, т. е. допустим, что реакция упру-
упругой среды связана с прогибом линейной зависимостью.
Обратимся теперь к дифференциальному уравнению продоль-
продольно-поперечного изгиба C.10.1). Продифференцируем два раза
по z обе части этого уравнения. Получим
»1У+ш-/' = ^&- D-8Л)
Но вторая производная изгибающего момента, вызванного
поперечной нагрузкой, равна интенсивности нагрузки с противо-
противоположным знаком; эта нагрузка представляет собою реакцию
упругой среды, следовательно,
М*х" = - д* - hv.
Подставляя последнее выражение в уравнение D.8.1),получим
EIx hIx
Положим PJ(EIX)= к2, h/(EIx) = 4а4 и перепишем это урав-
уравнение следующим образом:
vlY + k2v" +4а4г; = 0. D.8.2)
Мы не будем рассматривать приложение этого уравнения к зада-
задачам об устойчивости балок конечной длины с различными гра-
граничными условиями. Система частных решений находится стан-
стандартным методом, можно построить систему решений с единич-
единичной матрицей, как это описано в § 3.9. Вычисления при этом
оказываются довольно громоздкими, поскольку нужно находить
корни биквадратного уравнения, отделяя в них действительные
и мнимые части. Простейший пример — это устойчивость стерж-
стержня бесконечной длины. Очевидно, что постановка такой задачи
при отсутствии окружающей упругой среды лишена смысла, при
увеличении длины стержня критическая сила стремится к нулю
независимо от способа закрепления его концов. В упругой среде
§ 4.8. УСТОЙЧИВОСТЬ СТЕРЖНЯ В УПРУГОЙ СРЕДЕ
133
положение оказывается иным. Вид уравнения D.8.2) подсказы-
подсказывает характер решения, а именно z; = smXz. Подставляя это вы-
выражение в D.8.2), находим
отсюда
D.8.3)
Величина к2 пропорциональна критической силе; задавая раз-
разные Я, т. е. синусоидальные .возмущения с разной длиной волны,
мы можем получить любую критическую оилу. Однако сущест-
существует такое значение Я, три котором критическая сила минималь-
минимальна, а именно ^кр = 2а2. При этом значении X к2 = 4а2 и, следо-
следовательно,
ркр = WEIX = HEIJi. D.8.4)
Длина полуволны синусоиды, представляющей собою форму по-
потери устойчивости при минимальной критической силе, опреде-
определяемой формулой D.8.4), равна
/кр
^кр
*
D.8.5)
Найденное решение, очевидно, применимо не только к стерж-
стержню бесконечной длины, но и к шарнирно закрепленному на кон-
концах стержню, если длина
его равна критической дли- JL
не, даваемой формулой ^»
D.8.5), или кратна ей.
Действительно, если v =
= sin%z, то 1; = 1;" = О при
z кратных ZKp.
Предположим теперь, /
что длина стержня не
кратна ZKP. Принимая ре-
решения в виде v = sin Xz, q
где X = лп/l, мы удовлет-
удовлетворим и уравнению, и гра-
граничным условиям, следо-
следовательно, по формуле
D.8.3) найдем критическую силу в зависимости от целого числа
п, т. е. числа полуволн, образующихся на длине I. Будем обозна-
обозначать критическую силу для бесконечного стержня, даваемую
формулой D.8.4), символом Роо. Обозначим также через ? отно-
отношение длины стержня I к критической длине бесконечного
стержня ZKp * ? = Z/^кр. Тогда отношение критической силы стерж-
1
Ряс. 4.8.1
ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
ня конечной длины к критической силе бесконечного стержня
после очевидных преобразований формулы D.8.3) выразится сле-
следующим образом:
jZ = -t[y + ^)- Di8-6)
Теперь нужно выбрать такое целое п, при котором формула
D.8.6) дает минимальные значения Р/Роо. Очевидно, это будет
целое число, ближайшее к величине 1/? сверху или снизу. На
рис. 4.8.1 изображен график зависимости отношения PIP«, от %>•>
он состоит из кусков кривых, построенных по уравнению D.8.6)
при разных п. Следует заметить, что при ? > 1 зависимость кри-
критической силы от длины становится довольно слабой.
Легко убедиться, что в интервале т < ? < т + 1 максималь-
максимальные значения jr- = -75- т , , ,, достигаются тогда, когда фор-
/'оо * т\т-\- 1)
мула D.8.6) дает одинаковый результат при п = т и п = т+ 1.
Соответствующее значение ? равно Ут(т+1).
§ 4.9. Потеря устойчивости
за пределом упругости — схема Кармана
Формула Эйлера для критической силы D.7.5), очевидно, при-
применима только тогда, когда материал следует закону Гука. Одна-
Однако может случиться, что сила, определенная по формуле Эйлера,
вызывает в материале сжимающие напряжения, превышающие
предел пропорциональности*). Этим, в частности, объясняется
плохое совпадение с опытом, обнаруженное в ранних эксперимен-
экспериментах по проверке эйлеровой теории устойчивости. Чтобы судить
о пределах применимости формулы Эйлера, придадим ей не-
несколько иной вид. Для этого разделим обе части формулы D.7.5)
на площадь поперечного сечения стержня F. Слева мы получмм
критическое напряжение оэ. Величина г = 1/IJF, имеющая раз-
размерность длины, называется радиусом инерции сечения.
Введем безразмерную величину Я, называемую гибкостью
стержня:
Формула Эйлера перепишется следующим образом:
аэ = ^. D.9.1)
*) Мы не будем делать разницы между пределом упругости и преде-
пределом пропорциональности, оба эти термина употребляются здесь в одном и
том же смысле (см. § 1.8).
§ 4.9. ПОТЕРЯ УСТОЙЧИВОСТИ ПО СХЕМЕ КАРМАНА
Для длинных и тонких стержней X велико, следовательно,
критическое напряжение мало. Предельным для применения фор-
формулы случаем будет тот, когда оэ равно пределу пропорционально-
сти оп. Формула D.9.1) справедлива тогда, когда X > п1Е/оп.
Так, например, для малоуглеродистой стали при оп = 2000 кгс/см2
предельное значение % paiBHO приблизительно 100.
У более коротких стержней потеря устойчивости происходит
при напряжениях, превосходящих предел пропорциональности
т. е. в пластической области. Состояние пластического тела, в от-
отличие от состояния упругого тела, зависит не только от мгновен-
мгновенных значений нагрузсж, но л от порядаа их приложения. Поэто-
Поэтому, если для упругого стержня возможна лишь единственная
постановка вопроса устойчивости и сила Эйлера является един-
единственной критической силой, то в пластической области возмож-
возможны различные определения неустойчивости и, следовательно, раз-
различные критические силы.
Первые решения задачи об устойчивости сжатого стержня за
пределом пропорциональности (Энгессер, Ясинский, Карман) от-
относятся к следующей постановке. Стержень нагружается цент-
центральной сжимающей силой, принимаются меры для того, чтобы
не произошло выпучивания в процессе нагружения. Когда сила
достигает значения Р, она удерживается постоянной и стержню
сообщается малый прогиб. Равновесие стержня под действием
силы Р устойчиво, если этот прогиб исчезает после устранения
вызвавшей его причины, и неустойчиво, если прогиб увеличи-
увеличивается до тех пор, пока не установится новая форма равновесия,
стержня с искривленной осью. Приближенное исследование, осно-
основанное на линеаризованном уравнении изгиба, во существу не
позволяет решать вопрос об устойчивости или неустойчивости ка-
какой-либо формы равновесия, это исследование дает возможность
найти такое значение нагрузки, при котором равновесие является
безразличным. Именно этой задачей было фактически заменено
исследование устойчивости упругого стержня в § 4.2.
Итак, предооложим, что сжимающее напряжение в стержне
есть а. Будем считать, вопреки обыкновению, сжимающие напря-
напряжения положительными. Предположим теперь, что стержень изо-
изогнулся. Рассматривая потерю устойчивости по отношению к ма-
малым возмущениям, введем в рассмотрение изменение напряже-
напряжения бо. Так как сжимающая сила при потере устойчивости оста-
остается неизменной по предположению, то в одной части сечения
будет бо > 0, в другой бо < 0. Там, где бо > 0, мы двигаемся
вверх по диаграмме сжатия (рис. 4.9.1). Если бо достаточно ма-
мало, элемент дуги можно заменить элементом касательной и
принять
бо = Etbe. D.9.2>
Здесь Et = do/de — касательный модуль.
436
ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
В области, где бо < 0, происходит разгрузка и зависимость
между приращением напряжения и приращением деформации
изображается прямой, параллельной начальному, упругому уча-
участку диаграммы (рис. 4.9.1). Поэтому здесь
бо = ЕЬе.
D.9.3)
Будем предполагать сечение симметричным (рис. 4.9.2) отно-
относительно плоскости наименьшей жесткости. Считаем, что при
Рис. 4.9.1
потере устойчивости справедлив закон плоских сечений; поэтому
бе = кг\, где ц — расстояние точки, принадлежащей сечению, от
нейтральной оси пп, положение которой заранее неизвестно.
Так как сжимающая сила при потере устойчивости по пред-
предположению остается постоянной, то
$todF = O. D.9.4)
F
Ось пп делит сечение на две части, в одной из этих частей
справедливо соотношение D.9.2), в другой—соотношение D.9.3)
между ба и бе. Разобьем интеграл в условии D.9.4) соответст-
соответственно этому на два интеграла, заменим в них бо через бе и вос-
воспользуемся законом плоских сечений. Получим
Et J хт] dF + Е J хт] dF = 0,
или
ES2 = 0.
D.9.5)
Здесь Sx и S2 — статические моменты площадей Fv и F2 относи-
относительно оси пп (оба считаются положительными).
§ 4.9. ПОТЕРЯ УСТОЙЧИВОСТИ ПО СХЕМЕ КАРМАНА
Вычислим теперь момент относительно оси пп, создаваемый
дополнительными напряжениями бо:
8М = J 8ay dF = K (EtI± + EI2). D.9.6)
F
Здесь Л и h — моменты инерции площадей Ft и F2 относи-
относительно оси пп. Формула D.9.6) выражает зависимость между из-
изгибающим моментом и кривизной. В упругой области эта зави-
зависимость дается следующим соотношением:
8М = Е1Х%. D.9.7)
Здесь Е — модуль упругости, 1Х — момент инерции относительно*
центральной оси х. Перепишем формулу D.9.6) таким образом,
чтобы она выглядела аналогично вышеприведенной, а именное
8М = К1Х%. D.9.8)
Величина К называется приведенным модулем или модулем?
Кармана, при этом
D.9.9>
Как видно, приведенный модуль зависит не только от мате-
материала, но и от формы поперечного сечения. Теперь можно рас-
рассматривать потерю устойчивости сжатого стержня совершенно
так же, как потерю устойчивости в упругой области (§ 4.2).
В дифференциальном уравнении изгиба D.2.1) в соответствии
с D.9.8) нужно будет заменить модуль упругости Е модулем"
Кармана К. В результате для критического напряжения вместо'
формулы D.9.1) получается следующая:
oK = 4f- D.9.10)
Величина Et зависит от положения точки на диаграмме сжа-
сжатия, следовательно, от напряжения ок. Таким образам, приведен-
приведенный модуль К является также функ-
функцией ок; эта величина находится в
результате решения уравнения
D.9.10).
Вычислим приведенный модуль для
прямоугольного сечения с высотой h и
шириной Ъ (h^b). Пусть высота зоны
догрузки будет ?/г, высота зоны разгрузки
A-Е)А (рис. 4.9.3). Тогда
Рис. 4.9.3
rfCjg ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Подставляя эти выражения в уравнение D.9.5), получим
Отсюда следует
Момент инерции всего сечения относительно оси х равен Ыгг/12, момен-
моменты инерцин частей сечения относительно оси пп
г -
A — бK
По формуле D.9.9) модуль Кармана
Подставив сюда значение ?, найдем
D.9.11)
§ 4.10. Потеря устойчивости за пределом упругости —
схема продолжающегося нагружения
Исследование устойчивости сжатого стержня приводит к уста-
установлению некоторой зависимости меж1ду критическим напряже-
напряжением и гибкостью. Пока напряжение меньше предела упругости,
эта зависимость дается формулой D.9.1), за пределом упруго-
упругости— формулой D.9.10), если счи-
считать справедливой ту постанов-
постановку задачи, для которой она была
получена.
Будем откладывать критиче-
критическое напряжение по оси ординат,
гибкость — по оси абсцисс. Для
напряжений, меньших чем пре-
предел упругости, формула D.9.1)
дает кривую гиперболического
типа (рис. 4.10.1). Для напряже-
напряжений, больших чем предел упру-
упругости, кривая построена по фор-
формуле D.9.10). Для построения
нужно иметь точную диаграмму
сжатия материала; пользуясь этой кривой, можно для данного
сечения определить приведенный модуль как функцию сжимаю-
'80 10U
Л
Рис. 4.10.1
§ 4.10. СХЕМА ПРОДОЛЖАЮЩЕГОСЯ НАГРУЖЕНИЯ
щего напряжения. При построении кривой удобно вычислять
гибкость Я, задаваясь различными значениями сжимающего-
напряжения.
В первой работе Энгессера A889 г.) формула для критическо-
критического напряжения отличалась от формулы D.9.10) тем, что в ней
вместо приведенного модуля К фигурировал касательный модуль
Et. На возможность образований зон разгрузки при потере устой-
устойчивости обратил внимание Ф. С. Ясинский, после чего Энгессер
переработал свою теорию и ввел приведенный модуль К. Отно-
Относительно недавно, в 1947 г., старое решение Энгеосера, отброшен-
отброшенное самим автором, получило новое освещение в работе Шенли.
Представим себе, что стержень нагружается непрерывно возрас-
возрастающей силой; когда сила достигает некоторого значения Ро,
стержень начинает искривляться, но одновременно с искривле-
искривлением происходит дальнейшее сжатие, так как сила продолжает
увеличиваться. В результате разгрузки не происходит, напряже-
напряжения растут во всех точках сечения, быстрее с вогнутой стороны
и медленнее с выпуклой. Зависимость между приращениями на-
напряжения и деформации определяется поэтому касательным
модулем Et. В результате критическое напряжение находится иа
следующего уравнения:
ак = ^1. D.10.1)
На самом деле, как будет показано ниже, разгрузка происходит,,
по не сразу, как в схеме Кармана, а постепенно; пока прогибы
малы, зона разгрузки мала, она растет с ростом прогиба. Крити-
Критическое напряжение D.10.1) соответствует началу процесса выпу-
выпучивания, когда эффект разгрузки еще не проязвился. На рис. 4.10.1
приведена и вторая кривая, рассчитанная по уравнению D.10.1).
Опытные точки ложатся ближе к этой второй кривой.
В постановке Шенли вопрос об устойчивости сводится к воп-
вопросу о бифуркации, т. е. разветвлении форм движения. Пока сила
меньше чем Ро, при увеличении силы наблюдается одна-единст-
венная форма движения стержня, а именно его равномерное сжа>
тие. При Р > Ро возможны две формы движения: либо равномер-
равномерное сжатие, либо непрерывное выпучивание; при этом каждому
значению силы Р> Ро соответствует вполне определенное значе-
значение прогиба. Действительно, хотя при выводе формулы D.10.1)
мы воспроизводили тот же ход рассуждения, который привел нас
к формуле Эйлера для упругого состояния стержня, на самом1
деле малое приращение сжимающей силы делает возможным1
лишь малые искривления стержня, не сопровождающиеся раз-
разгрузкой. При появлении частичной разгрузки сопротивление из-
изгибу возрастает, поэтому равновесие возможно не при любом зна-
значении прогиба, а при вполне определенном его значении.
140
ГЛ. 4. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
§ 4.11. Исследование поведения сжатого стержня
при потере устойчивости за пределом упругости
Проследим более детально поведение сжатого стержня при возрастании
сжимающей силы. Будем считать материал следующим диаграмме сжатия
с линейным упрочнением (рис. 4.11.1). Приращения напряжения и дефор-
деформации при догрузке и разгрузке соответственно связаны соотношениями
D.9.2) и D.9.3), причем в формуле D.9.2) касательный модуль Et постоянен.
Обозначим через Ае укорочение оси стерж-
стержня после бифуркации, т. е. при изменении на-
нагрузки от Ро до Л через х — соответствующую
кривизну изогнутой оси стержня. Деформацию
волокна с координатой у, происшедшую после
г/ бифуркации, обозначим Ае'. Очевидно, что
Ае' = Де + ку.
D.11.1)
На нейтральной оси Ае' = 0, следовательно,
эта ось отстоит от оси х на расстоянии уо =
— =—Де/х. Внося D.11.1) в D.9.2) и D.9.3),получим
Да = Et(Ae + ny)i у > у0;
Да = Е(Ае + ку), у < у0.
В дальнейшем будем считать сечение стержня прямоугольным с высо-
высотой 2/г и шириной Ъ. Вычислим АР = Р — Ро и изгибающий момент М
Рис. 4.11.1
АР=Ъ j Aody = bEf j {Ае +ку) dy + ЪЕ J (Ае + щ) dy =
= || [- (Л* - к*J + \
D.11.2)
J
•f-n П »0
М = Ъ J Aoydy = bEt j (Ae + ку) у dy + ЪЕ J (Ае + щ) у dy =
-Л yQ -h
- _, Г Г» -1
= ?fL (xft — АеJ Bnh + Ае) + _* (кк + АеJ Bxh — Ае) . D.11.3)
бх L -Я J
Правые части в формулах D.11.2) и D.11.3) представляют собою одно-
однородные функции первой степени относительно Ае и х. Поэтому можно пе-
перейти к следующим безразмерным параметрам:
K*-2Etbh\ e*-
х --^г*. е -
2Efbh з
—-— Ае, т* = М.
АР hAP
Уравнения D.11.2) и D.11.3) примут следующий вид:
_ (e. _ %*f + ^(е* + х*J = 4 -J к*,
D.11.4)
2
Если из системы уравнений D.11.4) исключить е*, получится нелиней-
нелинейное соотношение между изгибающим моментом и кривизной. Соответствую-
§ 4.11. СЖАТИЕ СТЕРЖНЯ ЗА ПРЕДЕЛОМ УПРУГОСТИ
141
щие выкладки слишком сложны, для нас достаточно выяснить характер по-
получающейся зависимости. Заметим, прежде всего, что соотношения D.11.4)
справедливы лишь при \уо\ < /г, т. е. когда в сечении существуют зоны
догрузки и разгрузки. Вспоминая выражение для у0, найдем, что должно
б J А * * П * *
дру рру
быть yJi > Ае и, следовательно, к*
происходит догрузка, следовательно,
д у,
е*. При к* <С е* во' всем сечении
2Efbhz
Переходя к безразмерным величинам, получим
m* = >c* (к*<е*). D.11.5)
При и* = е* первое из уравнений D.11.4) дает к* = 1, следовательно,
формула D.11.5) верна при к* ^ 1. График зависимости между т* и
х* на п-ервом участке представляет собою бис-
биссектрису координатного угла от начала до точ-
точки т* = к* = 1 (рис. 4.11.2). Дальше кривую
нужно строить с помощью уравнений D.11.4).
При больших значениях к* в первом уравнении
можно пренебречь правой частью
Отсюда следует
Е
;X*.
Подставим найденное значение е*
рое уравнение. Получим
4
771* =
ВО ВТО-
A+
Рис. 4.11.2
Но по формуле D.9.11) множитель перед к* в правой части представляет
собою отношение приведенного модуля к касательному, следовательно,
К
D.11.6)
Таким образом, кривая зависимости между т* и к* имеет асимптотой
луч, выходящий из начала координат с наклоном, равным K/Et. Теперь нам
предстоит решить задачу об изгибе сжатого стержня при нелинейной за-
зависимости между моментом и кривизной, установленной графиком на
рис. 4.11.2. Если прогиб есть v(z), изгибающий момент в сечении с коорди-
координатой z равен М = —Pu(z) (см. § 4.2), кривизна изогнутой оси к = v"(z),
то отсюда следует, что
х = - -j- M".
Перейдем к безразмерным величинам. Получим
2ЕЪН3
<*"+*(*H
OJr
Заметим, что критическая сила Энгессера — Шенли
0 i9-
142 гл- 4- устойчивость стержневых систем
поэтому предыдущее уравнение можно записать следующим образом:
I2 P
*// + к* (т*)== 0# D.11.7)
Будем искать приближенное решение уравнения D.11.7). Предположим,
что стержень, шарнирно закрепленный на двух концах, изгибается по си-
синусоиде, так же как и в случае упругой потери устойчивости. Так как из-
изгибающий момент пропорционален прогибу, можно принять т*=--т0 sin (tczJI).
Подставим т* в уравнение D.11.6) и потребуем выполнения этого уравне-
уравнения только в одной точке, при z = 1/2, когда sin (nz/l) равен единице. По-
Получим
?i>m*-x*«)=0. D.11.8)
Уравнение D.11.8) легко решается графически. Для этого нужно про-
провести из начала координат луч с угловым коэффициентом, равным Р/Ро.
Точка пересечения этого луча с кривой к — т (рис. 4.11.2) имеет своими
координатами т* их* — безразмерный момент и кривизну в среднем се-
сечении стержня. Если Р < Ро, луч не пересекается с кривой, следовательно,
прогиб невозможен, стержень остается прямым. При Р = Ро значение wijj
неопределенно, луч совпадает с биссектрисой координатного угла, но АР =
= Р — Ро = 0, а при переходе от безразмер-
ных параметров к моментам и кривизнам их
нужно множить на АР. Таким образом, про-
прогиб остается равным нулю и при Р = Ро. При
Р > Ро каждому значению силы соответствует
определенное значение прогиба, которое стре-
стремится к бесконечности по мере того, как си-
сила стремится к величине Рк. Примерный гра-
график зависимости прогиба от силы приведен
на рис. 4.11.3. При Р = Ро происходит бифур-
бифуркация, прогиб непрерывно растет, стремясь
к бесконечности при Р = Рк, где Рк — крити»
К
, u о р к, д к ри
О р Рк Р ческая сила Кармана, определенная по при-
приведенному модулю. Последний результат
Рис 4113 является следствием того, что мы воспользо-
' * * вались приближенным выражением для кри-
кривизны. Если взять точное выражение кривиз-
кривизны, для каждого значения силы прогиб будет конечным, как это было пока-
показано для упругого стержня в § 4.3. Заметим, что в приведенном анализе не
учтена возможность появления пластической растянутой области в зоне
разгрузки, что обязательно будет при достаточно больших прогибах.
При испытаниях стержней на устойчивость обычно реализуются имен-
именно те условия, которые приняты при установлении критерия потери устой-
устойчивости Шенли; нагрузка, создаваемая испытательной машиной, непрерыв-
непрерывно возрастает. Однако при Р = Ро прогиб первоначально прямого стержня
равен нулю; фактически за момент потери устойчивости принимается мо-
момент, когда прогиб достигает некоторого достаточно большого значения,
поэтому измеренная критическая сила будет находиться между Ро и Рь>
притом ближе к Ро. Для реальных материалов критические напряжения,
определенные по приведенному и по касательному модулю, отличаются
друг от друга мало, как это видно из графика на рис. 4.10.1. В то же время
расчет по касательному модулю дает нижнюю границу для критического
напряжения, поэтому его и нужно рекомендовать.
§ 4.12. ВНЕЦЕНТРЕННОЕ СЖАТИЕ
143
2500
§ 4.12. Внецентренное сжатие
упругопластического стержня
В предыдущем параграфе было рассмотрено сжатие центрально-нагру-
центрально-нагруженного стержня и обсужден вопрос о поведении этого стержня после того,
как произошла бифуркация. Если сила приложена эксцентрично или стер-
стержень имеет начальную кривизну, прогиб его будет увеличиваться сразу
после приложения нагрузки. Возникает вопрос: будет ли поведение сжатого
стержня подобно поведению модели примера 1 § 4.5 или поведению модели
примера 2 того же параграфа?
Сжатый и изгибаемый упругопластический стержень представляет со-
собою физически нелинейную систему. Так же как это было показано в § 4.5,
физическая нелинейность приводит к тому, что критическая сила будет су-
существенным образом зависеть от начального прогиба или эксцентриситета
приложения нагрузки. Исследование таких задач довольно трудно, поэтому
мы изложим только идею метода, использованного Хвалла. В § 3.6 было по-
показано, каким образом устанавливается зависимость между кривизной и
изгибающим моментом в упругопластическом стержне. Если диаграмма а =
= ф(е) для материала известна, то зависимость к = к(М) может быть по-
построена хотя бы численно или графически. При наличии осевой силы ана-
анализ § 3.6 должен быть видоизменен, кривизна будет зависеть не только от
Л/, но и от силы Р, таким образом, х =
= к(М, Р). Задаваясь разными значения-
значениями Р, всегда можно построить серию кривых
зависимости к от М хотя бы графически.
При внецентренном сжатии М = Р(и + и0),
где и0 — начальный прогиб или, если vo =
= const — эксцентриситет приложения на-
нагрузки. Теперь дифференциальное уравне-
уравнение изогнутой оси стержня (в геометриче-
геометрически линейной постановке) будет следую-
следующим:
v" + x[P(» + v0), P] = 0. D.12.1)
Интегрируя уравнение D.12.1) для раз-
различных значений силы Р, можно получить
серию кривых, представляющих форму
оси стержня, и исследовать зависимость
прогиба от силы. Положение осложняется
тем, что по мере роста силы в стержне
появляются области разгрузки и зависимость х(М, Р) не однозначна.
Практически реализация описанного метода связана с большим объе-
объемом вычислительной работы. При выполнении этих вычислений приходится
задаваться кривой а = ф(е), т. е. решать задачу для некоторого совершен-
совершенно определенного материала. Для каждой формы поперечного сечения ре-
решение должно строиться заново. На рис. 4.12.1 приведены графики зависи-
зависимости критического напряжения от гибкости при разных значениях отно-
относительного эксцентриситета е/r, где г — радиус инерции сечения. Расчеты
были выполнены Хвалла для стержня прямоугольного поперечного сечения
на основании реальной диаграммы сжатия строительной мягкой стали с пре-
пределом пропорциональности 1900 кгс/см2 и пределом текучести 2400 кгс/см2.
При расчетах на устойчивость приходится иметь дело с разными материа-
материалами и разными формами поперечных сечений, поэтому обычно расчет
ведется не на основании теории, а с помощью эмпирических формул, каж-
каждая из которых справедлива для более или менее однотипных стержней из
однотипных материалов. Так, согласно действующим в СССР нормам стро-
строительного проектирования, расчет на устойчивость заменяется расчетом на
прочность при сжатии с уменьшением соответственно допускаемого напря-
напряжения. Требуют, чтобы было
Рис. 412.1
144 гл- 4- устойчивость стержневых систем
Коэффициент уменьшения основного допускаемого напряжения ф представ-
представляет собою функцию от гибкости X. Эта функция задается таблицей, кото-
которую можно найти в соответствующей справочной литературе. Так, для ста-
стали при I = 10 ф = 0,99; при X = 150 ср = 0,32.
Предполагается, что эксцентриситет или начальное искривление неве-
невелики, они находятся в пределах производственного допуска. Поэтому влия-
влияние возможного эксцентриситета по существу учитывается выбором вели-
величины ф, которая уменьшается с увеличением гибкости.
§ 4.13. Неустойчивость растяжения
при большой деформации
При изучении конечных упругих или пластических деформа-
деформаций закон деформирования естественно задавать как соотноше-
соотношение между истинным напряжением и деформацией. Выбор меры
деформации в данном случае безразличен, мы сохраним обычные
определения. Бели длина образца до деформации была Zo, а после
деформации стала Z, то е=A — U)/h, следовательно, Z = Z0(l + e).
Сила, поделенная на площадь начального поперечного сечения
образца, называется условным напряжением о0 = P/F04 тогда как
истинное напряжение о = P/F относится к фактической площади
сечения, которая уменьшается по мере растяжения. Изменение
объема при конечной деформации для всех реальных материалов
пренебрежимо мало, поэтому можно считать объем неизменным.
Из этого условия следует Fl = FolOj или F = F0/(l + е). Следова-
Следовательно, истинное напряжение будет определяться через условное
напряжение и деформацию следующим образом:
G = G0(i + e). D.13.1)
Пусть закон деформирования задан, т. е. задана зависимость
между истинным напряжением и деформацией
о = ф(е)- D.13.2)
Функция ср(е) для реальных материалов всегда оказывается мо-
монотонно возрастающей, с увеличением деформации напряжение
увеличивается. Это условие означает, что материал сам по себе
устойчив. Но в опыте на растяжение непосредственно измеряется
сила или пропорциональная ей величина о0. Может случиться,
что процесс растяжения окажется неустойчивым, это значит, что
величина о0 или Р, достигнув некоторого предельного значения,
начнет уменьшаться при дальнейшем росте деформации.
Выясним, когда это произойдет. Внесем в D.13.2) выражение
D.13.1) для о. Ползучим
а° 1 + ет
Дифференцируя это выражение по е, найдем условие, при
§ 4.13. НЕУСТОЙЧИВОСТЬ РАСТЯЖЕНИЯ
145
котором doo/de = О
D.13.3)
Если закон деформирования задан графиком функции ф(е)г
то значение деформации, при котором происходит потеря устой-
устойчивости, можно найти графически. Для этого из точки, лежащей
на оси е на расстоянии —1 от
начала координат (рис. 4.13.1),
нужно провести касательную к
диаграмме о — е. Абсцисса точки
касания определит критическую
деформацию. На том же рисунке
штрихами построен график зави-
зависимости условного напряжения
от деформации; при е > ек услов-
условное напряжение, т. е. растяги-
растягивающая сила, уменьшается
При задании законов деформи-
деформирования, упругого и неупру-
неупругого, часто прибегают к аппроксимации их степенными функ-
функциями.
Предположим, что ф(е)=е1/п, где п> 1. Тогда с помощью
D.13.3) легко получаем
О
Рис. 4.13.1
Таким образом, показатель п в предполагаемом степенном законе
упрочнения находится очень просто, для этого достаточно изме-
измерить деформацию, соответствующую максимуму на диаграмме
растяжения.
ГЛАВА 5
ОБЩИЕ СВОЙСТВА УПРУГИХ И ПЛАСТИЧЕСКИХ
СТЕРЖНЕВЫХ СИСТЕМ
§ 5.1. Упругие и пластические системы
Из стержней, которые претерпевают растяжение или сжатие
и изгиб, можно комбинировать разнообразные стержневые си-
системы. Фермами называются системы прямолинейных стержней,
соединенных шарнирно и нагруженных внешними силами в шар-
шарнирах. Элементы фермы, т. е. стержни, претерпевают растяжение
либо сжатие. Система стержней, соединенных между 1собою
жестко, называется рамой. Элементы рамы, т. е. образующие ее
стержни, находятся в состоянии изгиба и одновременного растя-
растяжения либо сжатия. Обычно продольные силы не настолько ве-
велики, чтобы было необходимо решать для элементов рамы задачу
продольно-поперечного изгиба в том смысле, как это было разъ-
разъяснено в § 3.10. Действие продольных и поперечных нагрузок на
элемент рамы учитывается по отдельности. Как в теории растя-
растяжения — сжатия, так и в теории изгиба упругих стержней в гла-
главах 2 и 3 делалось предположение о возможности рассматривать
все задачи в геометрически линейной постановке, а именно, со-
составлять уравнения равновесия для недеформированного состоя-
состояния системы и линеаризовать ура!внения связи между деформа-
деформациями и перемещениями. Для упругих систем, подчиняющихся
закону Гука, отсюда следует линейная зависимость между сила-
силами и перемещениями, для идеально упругапластических или
жесшопластических систем на отдельных примерах оказывалось
возможным достаточно просто определять предельную нагрузку.
Как будет наказано в этой главе, для геометрически линейных
систем оказывается возможным развить некоторые общие методы
и установить некоторые общие свойства, не зависящие от кон-
конкретного устройства той или иной стержневой системы.
В механике твердого тела, как и в механике вообще, удобно
пользоваться понятием обобщенной силы и обобщенного переме-
перемещения. Действительно, говоря о силах, действующих на тело,
для количественной их оценки часто пользуются некоторыми
характеристиками, не являющимися в действительности абсолют-
абсолютными величинами сил. Так, действие изгибающей пары пол-
§ 5.1. УПРУГИЕ И ПЛАСТИЧЕСКИЕ СИСТЕМЫ
147
ностью характеризуется ее моментом; говоря, что балка несет
равномерно распределенную нагрузку, мы полностью определяем
внешние силы, действующие на балку. Вообще часто приходится
иметь дело не с одной силой, а с группой их, причем эта группа
рассматривается как нечто целое. Необходимость рассмотрения
таких групп сил становится особенно очевидной, если обратиться
к изучению статически неопределимых
систем. Так, рассекая изображенную на
чертеже (рис. 5.1.1) статически неоп-
неопределимую раму, мы должны приложить
Рис. 5.1.1
Рис. 5.1.2
к краям разреза две равные и противоположные продоль-
продольные силы N, две поперечные силы Q, два момента М. Поэтому
лишними неизвестными являются группы сил, определяемые чис-
числами N, Q и М, равными продольной и поперечной силам в се-
сечении и изгибающему моменту. Иногда говорят, что за лиш-
лишние неизвестные принимаются перерезывающая сила и изгибаю-
изгибающий момент. Это неточно, так как Qy и Мх представляют собою
скалярные величины, которые не являются силой и моментом.
Сделав же сечение, мы должны для обеспечения неразрывности
тела приложить к краям разреза настоящие силы и пары Q
и Л/.
Будем называть число, определяющее группу сил, обобщенной
силой. В этом смысле момент Ж, распределенная нагрузка q
могут рассматриваться как обобщенные силы. Определим фор-
формально обобщенное перемещение как множитель при обобщенной
силе в выражении работы. Для момента обобщенным перемеще-
перемещением служит угол поворота, так как работа момента есть ЛТф.
Равномерно распределенная нагрузка, приложенная к балке, про-
прогиб которой есть v(z), производит ра|боту
А = \ qv (z) dz = q J v (z) dz =¦• gco.
Здесь обобщенное перемещение есть со, т. е. площадь, заключен-
заключенная между первоначальной осью балки и изогнутой ее осью.
В качестве последнего примера возьмем обобщенную силу,
соответствующую двум равным и противоположным силам N,
приложенным к концам разрезанного элемента фермы (рис. 5.1.2).
10*
148 ГЛ- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
Если перемещение левого конца есть ии перемещение пра-
правого м2, то работа двух сил
А = Nui — Nu2 = N'{ui — u2).
Обобщенное перемещение ut — и2 представляет собою относи-
относительное расхождение краев разреза.
§ 5.2. Теоремы Лагранжа и Кастильяно
Предположим, что к упругой системе приложено п обобщен-
обобщенных сил Qi, которым соответствуют обобщенные перемещения дг-.
Из определения упругости следует, что перемещения являются
однозначными функциями сил и обратно
<7« = ?<(?.), Qi-Qdq.)- E.2.1)
Однако вид этих зависимостей для упругого тела не может быть
вполне произволен. Дело в том, что из определения упругости
следует, что задание сил или перемещений однозначно опреде-
определяет состояние упругого тела, которое характеризуется заданием
параметров #г- или Qi, а также заданием его внутренней энер-
энергии U. Для наглядного изображения состояния системы вводят
так называемые пространство сил и пространство перемещений.
Пространство сил — это химерное пространство, в котором по
осям ортогональной декартовой системы координат откладывают-
откладываются значения сил Qi, задание совокупности сил определяет точку
в этом пространстве. Аналогичным образом определяется прост-
пространство перемещений. Формулы E.2.1) устанавливают взаимно
однозначное соответствие точек пространства сил и пространства
перемещений.
Предположим теперь, что на тело действуют силы Qi0, соот-
соответствующие перемещения равны д,-0, а внутренняя энергия 2?0.
Будем менять силы произвольным образом, но так, чтобы в конце
концов они приняли исходные значения Qi0. Изображающая точ-
точка в пространстве сил опишет при этом замкнутую кривую.
Если тело упруго, мы должны получить при этом прежнее зна-
значение перемещений и вернуться к прежнему значению внутрен-
внутренней энергии. В пространстве перемещений изображающая точка
также опишет замкнутую кривую. Согласно первому началу тер-
термодинамики в процессе деформирования все время должно вы-
выполняться следующее соотношение:
dA = dE + dQ. E.2.2)
Здесь dA — работа внешних сил, dE — приращение внутренней
энергии, dQ — количество тепла, поступившего в систему. Но
dA = Qidqi. Подставим эту величину в E.2.2) и проинтегрируем
по замкнутому пути деформирования. Так мы возвратимся к
§ 5.2. ТЕОРЕМЫ ЛАГРАНЖА И КАСТИЛЬЯНО
прежнему значению внутренней энергии, интеграл от dE равен
нулю, следовательно:
jiQ.dq^jdQ. E.2.3)
Правая часть представляет собою количество тепла, поступивше-
поступившего в систему за цикл. Для адиабатического процесса этот инте-
интеграл равен нулю. Он равен нулю также для изотермического про-
процесса, поскольку вследствие второго начала термодинамики
dQ TdS при 7 = const
j) dQ = Т j> dS = О,
поскольку энтропия S есть функция состояния и после дефор-
деформирования по замкнутому пути мы должны прийти к прежнему
значению энтропии. Таким образом, в двух указанных случаях
-- 0. E.2.4)
Отсюда следует, что подынтегральное выражение есть полный
дифференциал некоторой функции, которую мы будем называть
потенциалом сил
или
Соотношение E.2.5) состашляет содержание теоремы Лагран-
жа. Для адиабатического процесса, когда dQ = Oy из соотношения
E.2.2) сразу видно, что U = Е представляет собою внутреннюю
энергию упругого тела. Для изотермического процесса U являет-
является свободной энергией. В § 2.9 было указано, что для большин-
большинства упругих тел термические эффекты существенной роли не
играют, поэтому делать разницу между внутренней энергией и
свободной энергией нет нужды. Мы будем называть функцию U
двояко, иногда упругой энергией, иногда потенциалом сил. Вто-
Второй термин может быть предпочтителен в следующем отношении.
Представим себе, что тело состоит из упругопластических эле-
элементов и при .нагтружении его все эти элементы деформируются
активно, тогда не будет происходить разгрузка. Связь между на-
напряжениями и деформациями при активной пластической дефор-
деформации совершенно неотличима от закона нелинейной упругости
до тех пор, пока не произведена разгрузка. Очевидно, что и связь
между внешними силами и перемещениями будет такой же, как
для нелинейно упругого тела, и формулы E.2.5) будут справед-
справедливы, хотя функция U уже не будет внутренней либо свободной
энергией. Конечно, вывод этих формул, осно/ванный на рассмот-
рассмотрении замкнутого цикла деформирования и законов термодина-
термодинамики обратимых процессов, для пластического тела несправед-
150 ГЛ- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
лив. Их иногда получают из соображений термодинамики необ-
необратимых процессов; мы предпочтем ограничиться замечанием
о том, что термодинамика необратимых процессов как раз и осно-
основывается на том факте, что для определенных процессов нельзя
сказать, обратимы они или нет, пока эти процессы идут в одном
направлении.
Обращение формул E.2.5) достигается с помощью преобразо-
преобразования Лежандра (см. § 2.8). Положим
®(Qi)=Q<qi-U. E.2.6)
Следует считать, что в правой части q{ являются функциями
от Qi в соответствии с E.2.1). Повторяя вывод § 2.8, отсюда на-
находим
* = -^- E-2.7)
Функцию Ф((?г) мы будем называть потенциалом перемеще-
перемещений, формула E.2.7) составляет содержание теоремы Кастилья-
но. Потенциал Ф называют также дополнительной работой, как
и в случае простого одноосного растяжения. Вспоминая опреде-
определение основных термодинамических потенциалов, мы убеждаем-
убеждаемся, что для адиабатического процесса Ф иредставляет собою эн-
энтальпию, для изотермического — свободную энтальпию.
Заметим, что наряду с введенными упругими потенциалами
можно строить и другие. Эквивалентность соотношений E.2.5) и
E.2.7) определяется тем, что за параметры, определяющие со-
состояние упругой системы, можно принять либо перемещения,
либо силы. Но можно выбрать в качестве основной смешанную
систему определяющих параметров, например т перемещений:
?ь #2, ..., qm и п — т сил: Qm+U ..., <?„. Систему уравнений
E.2.1) всегда можно представить в таком виде:
l^i^m, m + Kr^n, l^s^ m, m +
Построим теперь следующую функцию:
U (m+i<p<n). E.2.8)
Предполагается, что правая часть представлена как функция
от qi и Qr. Теперь
J?L — o dqp ди ди дЯр
Вследствие E.2.5), dU/dqi = Qi, dU/dqP==QP, следовательно:
§ 5.3. ЛИНЕЙНЫЕ УПРУГИЕ СИСТЕМЫ 151
Продифференцируем функцию F но Qr:
dF _ 0 d(iv dU дAг
dQ ® dQr dqv dQr *
Вследствие E.2.5) два последних члена взаимно уничтожаются
и мы получим
& = -|?-. E.2.10)
Следует заметить, что смешанные потенциалы вида E.2.8)
стали применяться в механике твердого тела лишь в последнее
время, тогда как формулы Лагранжа и Кастильяно были из-
известны еще в прошлом столетии.
§ 5.3. Линейные упругие системы
Теоремы Лагранжа и Кастильяно были изложены выше для
произвольных упругих систем, не обязательно геометрически или
физически линейных. Однако наиболее просто применение их
к линейным системам. Для линейных систем как потенциал сил,
так и потенциал перемещений дредсташляют собою квадратичные
формы, и соотношения между силами и перемещениями уста-
устанавливаются при помощи линейных соотношений вида
Qi = c{jqh E.3.1)
4i = $ijQj. E.3.2)
Величины ру — (коэффициенты влияния и c{i — коэффициенты
жесткости связаны очевидными соотношениями Су= 1[}у1/|[5|,
$ч = kfjl/kl. Здесь If}I, \c\ — определители матриц fa и су,
ifiyl, \dj\ — алгебраические дополнения элементов ptj и cti соот-
соответствующих матриц. По теореме Лагранжа (?< = dU/dqh Qj ==
= dU/dqh отсюда следует •
dq. ддг
подставляя E.3.1), находим
Сц = Сд
и, аналогично,
Таким образом, из факта существования потенциалов сил и
перемещений следует симметрия матриц коэффициентов влияния
и коэффициентов жесткости.
/[52 гл- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
Выражения для потенциалов сил и перемещений записывают-
записываются очевидным образом
С другой стороны, по теореме Эйлера об однородных функциях
п — —— — —
2 dqi^i~ 2
и, аналогично,
Отсюда следует, что так же как и при простом растяжении
(§ 2.8) потенциал перемещений равен потенциалу сил и пред-
представляет собою упругую энергию, накопленную системой.
Одновременно мы получим результат, составляющий содержа-
содержание теоремы Клапейрона, а именно:
Потенциальная энергия упругой деформации линейной систе-
системы равна половине работы внешних сил ца произведенных ими
перемещениях
U = ±Qiqi. E.3.3)
Из симметрии матриц ctj или $ц вытекает еще одна теорема,
а именно теорема о взаимности работ Бетти.
Предположим, что к стержневой системе приложена система
сил Qu которым соответствуют перемещения ?$. Если к той же
стержневой системе приложена другая система сил^ь вызываю-
вызывающая перемещения Qi, то работа сил первой системы на переме-
перемещениях, вызванных действием сил второй системы, равна работе
сил второй системы на перемещениях, вызванных действием сил
первой системы,
Q'd = Qlq\. E.3.4)
Для доказательства преобразуем выражение, стоящее в левой
части, с помощью E.3.1) «и условия Сц = с^
QiQi = caqfll - cHq]q[ = Q]q\.
Последнее равенство и доказывает теорему. Для стержневых
систем как функция U(q{), так и Ф((?г) вычисляются по форму-
формулам § 2.8 и 3.3, при этом производится суммирование по всем
стержням, составляющим систему.
Теорема Кастильяно чрезвычайно удобна для нахождения
перемещений (в статически определимых системах. Действитель-
Действительно, из уравнений статики мы можем выразить усилие и изгибаю-
§ 5.3. ЛИНЕЙНЫЕ УПРУГИЕ СИСТЕМЫ
153
щий момент в каждом стержне линейным образом через внешние
силы. Поэтому усилие в любом стержне есть
7V' dN П
Ho dN/OQs можно рассматривать как усилие в стержне, вызван-
вызванное силой Q8 = l. Положим dN/dQs = N8 (в любом стержне).
Запишем выражение для потенциала перемещений в случае,
когда каждый стержень изгибается в одной плоскости, следую-
следующим образом:
Mldz
2Ё
Здесь индексы суммирования опущены, интегрирование выпол-
выполняется по всем стержням, для каждого из которых ось z совпа-
совпадает с осью стержня. Теперь перемещение, соответствующее си-
силе Qs, найдется следующим образам:
NNS
~EF
С MXMXS
E.3.5)
Формула E.3.5) была получена Мором. Как видно, это не что
иное как прямое следствие теоремы Кастильяно.
Для примера решим задачу об определении перемещения точки А кри-
криволинейного стержня, изображенного па рис. 5.3.1.
Рис. 5.3.1
Влиянием продольной силы N на перемещение можно пренебречь. Изгиба-
Изгибающий момент от силы Р есть
Мх = PR sin ф.
Обозначим номером 1 вертикальное направление, номером 2 — горизон-
горизонтальное. Приложим единичную силу в направлении 1 п в направлении 2.
Соответствующие моменты:
Мх\ = R sin ф, Мх2 = Д A —- cos ф).
Для перемещений по формуле E.3.5) получим
154 ГЛ- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
При решении этой задачи мы пользовались зависимостью между из-
изменением кривизны и изгибающим моментом, следующей из теории прямо-
прямого стержня, считая размеры сечения малыми по сравнению с радиусом R.
Этот пример очень отчетливо выявляет преимущества общих
теорем. Желая подсчитать тот же прогиб без этих теорем, мы
должны были бы составлять дифференциальное уравнение изог-
изогнутой оси криволинейного стержня, что требует геометрического
рассмотрения. Формула E.3.5) дает результат совершенно авто-
автоматически. Для систем, состоящих из прямолинейных элементов,
функции МХ8, Ns, представляющие собою изгибающий (момент
о г сосредоточенной силы и продольную силу, являются на каж-
каждом участке линейными функциями. Для вычисления интеграла
E.3.5) можно применить графоаналитический прием, состоящий
в следующем. Пусть нам нужно вычислить интеграл
Если одна из этих функций, например i|)(s), линейна, то начало
отсчета координаты s всегда можно выбрать так, чтобы было
ty(s) = ks. Итак,
Но
j Ф E) "Ф (s) ds = J ф (s) ks ds.
J ф (s) sds = QsOi ks0 = г|H.
Здесь Q — площадь, ограниченная кривой ф($) на участке
s е= [а, Ь], 1|H — ордината эпюры функции г|), соответствующая
центру тяжести площади Q, поэтому
Ф E) Ф (*) ds = Qi|H. E.3.6)
Установленное простое правило бывает очень полезно при вычислешш
интегралов в формуле E.3.5). Поясним сказанное примером. Пусть для
изображенной на рис. 5.3.2 рамы требуется определить вертикальное пере-
перемещение точки А. Построим эпюру моментов от действующих сил и от еди-
единичной силы, приложенной в точке А вертикально вниз. Принимая во вни-
внимание только изгиб, заметим, что на первом участке, считая от точки при-
приложения силы, интеграл обращается в нуль. Будем брать площади с верх-
верхней эпюры и ординаты под центром тяжести с нижней. Получим
1 fqn о 4 9 _1_ ЗРа-а г, ,2Ра-а9\__ИРа*
д = _ \ЪРа-2а.-.2а + __.2а + -?-*) - -_.
Такое графоаналитическое вычисление интеграла в формуле Мора ча-
часто называют перемножением эпюр. Не останавливаясь на конкретных при-
примерах, рассмотрим сам способ перемножения для важнейших частных слу-
случаев.
§ 5.3. ЛИНЕЙНЫЕ УПРУГИЕ СИСТЕМЫ
155
1. Две трапеции (рис. 5.3.3, а). Произведение эпюр
П = СО! г/i + со2г/2-
Здесь
al
Ы
1
1
Если ординаты одной или двух трапеций имеют разные знаки, то правило
дРа
*)
<
1
УК
1
У/
ш
с ^ ,
Рис.
сохраняется
со1 =
5.3.2
(рис.
al
z 2 »
5.3.3,
б)
п
ы
Рис. 5.3.3
= COi0! + CL
1
Рис. 5.3.4
2. О5«а из эдгю/? — параболическая. Такую эпюру представляют как ре-
результат наложения симметричной параболы со стрелой ql2/2 на трапецию.
Площадь эпюры разбивается на три площади (рис. 5.3.4):
Ы
Центр тяжести площади параболы находится посредине.
156 ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
§ 5.4. Статически неопределимые системы.
Экстремальные принципы
Принцип Лагранжа. Представим себе стержневую систему,
например ферму, на которую действует одна обобщенная сила Q,
вызывающая обобщенное перемещение q. Сделанное предполо-
предположение не нарушает общности рассмотрения, поскольку любая
система сил может рассматриваться как одна обобщенная сила.
Кроме перемещения q узлы системы получают перемещения
xi(i = l1 2, ..., п), на которых сила Q работы не производит.
Перемещения Xi не связаны какими-либо кинематическими огра-
ограничениями; приложив надлежащим образом обобщенные силы Хь
можно получить произвольные величины х{. Задание системы
перемещений д, хг позволяет вычислить деформации всех элемен-
элементов системы и, следовательно, найти потенциал U как функ-
функцию q и Xi
U=U(q,xt).
Дифференцируя U по х{, мы найдем обобщенные силы Хг, но в
действительности этих сил нет, поэтому
^7^°* E.4.1)
Уравнение E.4.1) позволяет найти х{ в функции от д, после
этого, если нам нужно найти свшь между Q и q, мы должны
воспользоваться формулой
Конечно, при выводе не обязательно и не всегда удобно выра-
выражать всю заданную нагрузку как одну обобщенную силу. Обыч-
Обычно эти силы рассматривают по отдельности и соответственно по-
получают несколько уравнений вида E.4.2).
Если система была статически определимой, то, по существу,
уравнения E.4.1) представляют собою уравнения равновесия,
полученные из начала возможных перемещений. Но статическая
определимость или неопределимость системы не имеет никакого
значения при использовании E.4.1).
Заметим, что условие равенства нулю частных производных
функции есть условие того, что функция принимает стационар-
стационарное значение. Убедимся в том, что это стационарное значение
есть минимум. Действительно, вторая вариация функции U(Xi)
равна
82?/ = -j- ддхдх dxfixj = ~y сфхгЬху
Но это есть упругая энергия системы, вычисленная для переме-
§ 5.4. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ 157
щений Ьхи 8xj. Упругая энергия всегда положительна, она обра-
обращается в нуль только при 6х{ = О, следовательно, 62i7>0. Это
и есть условие минимума функции U(Xi).
Пример. Система, изображенная на рис. 5.4.1, состоит из к стержней,
прикрепленных верхними концами к потолку и сходящихся в одной точ-
точке А. Требуется определить усилия во всех
стержнях, а также перемещения точки А,
вертикальное q и горизонтальное х. Приме-
Применяя результат § 2.3, использованный при вы-
выводе формулы B.3.2), находим
д; = g cos а —х sin а, I =
cosae
A\
\F*(Q. cos a. — x sin а„J cos a4. }
Q \
Уравнения E.4.1) и E.4.2) становятся следу-
следующими: Рис. 5.4.1
q 2 ESFS sin as cos2 as — x 2 ESFS sin2 as cos as= 0,
g У1. 2?,.F, cos3 a. — x У\ EJ?- sin a_ cos2 a, = Q.
Таким образом, задача свелась к решению системы двух линейных
уравнений с двумя неизвестными, коэффициенты которых легко вычисля-
вычисляются при любом числе стержней к. Найдя перемещения q и х, вычисляем
деформации стержней и усилия в них по закону Гука.
Принцип Кастилъяно. Рассмотрим произвольную стержневую
р раз статически неопределимую систему. Это значит, разрушив
р связей, мы превращаем ее в статически определимую. Но от-
отбрасывая каждую связь, мы должны заменить ее действие си-
силой; таким образом, вводится р неизвестных реакций связей
Хи Х2, ..., Хр. Через «лишние» неизвестные Х{ можно выразить
усилия и моменты во всех элементах системы; таким образом,
потенциал Ф будет функцией лишних неизвестных Х{. Принцип
Кастилъяно состоит в том, что величина Ф, рассматриваемая как
функция лишних неизвестных, имеет минимум для тех значений
этих неизвестных, которые существуют в действительности.
Заметим, что обобщенные перемещения, соответствующие
лишним неизвестным в статически неопределимых задачах, всег-
всегда равны нулю. Если лишняя неизвестная вводится путем отбра-
отбрасывания внешней связи, то мы требуем, чтобы соответствующее
перемещение равнялось нулю. Если неизвестная вводится за счет
нарушения внутренних связей, как в примере § 5.1 (рис. 5.1.2),
то это есть обобщенная сила, представляющая собою совокуп-
совокупность двух сил или двух моментов, приложенных к краям
разреза.
Соответствующее обобщенное перемещение — это или относи-
относительное расхождение краев разреза, или угол поворота одного
ГЛ- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
края относительно другого. Так как в действительности стержень
должен оставаться цельным, обобщенное перемещение всегда
равно нулю. Значит, по теореме Кастильяно
дф =0 D = 1,2 р). E.4.3)
ах,
Уравнения E.4.3) представляют условия экстремума функ-
функции Ф. Остается показать, что этот экстремум есть минимум.
Для этого вычислим вторую вариацию функции
Но -щкг = Р* Поэтому
Итак, 62Ф есть упругая энергия, соответствующая силам бХг.
Но упругая энергия является положительно определенной квад-
квадратичной формой, так как нельзя при-
приложить к системе такие силы, которые
сделали бы отрицательной ее энергию.
Поэтому 62Ф>0 и уравнения E.4.3)
представляют условия минимума по-
потенциальной энергии, рассматриваемой
как функция лишних неизвестных.
Условия стационарности потенциала
сил и потенциала перемещений E.4.1)
и E.4.3) справедливы не только для
Рис. 5.4.2 линейных систем, однако заключение
о том, что это стационарное значение
есть минимум, требует выполнения дополнительных условий.
Необходимое условие устойчивости равновесия по отношению
к бесконечно малым возмущениям состоит в том, чтобы квадра-
квадратичные формы
ИЛИ
были положительно определенными в той точке, где dU/dqi или
дФ/dQi обращаются в нуль. Но если линейная система устойчива
по отношению к возмущениям любой величины, поскольку соот-
соответствующие квадратичные формы положительны при любых
значениях аргумента, для нелинейных систем точка, где дости-
достигается минимум потенциала, может быть не единственной. Так,
обращаясь к примеру стержневой систехмы, рассмотренной в § 4.6,
§ 5.5. МЕТОД СИЛ И МЕТОД ПЕРЕМЕЩЕНИЕ 9
и принимая за обобщенное перемещение q величину ос, найдем
Примерный график зависимости величины U от а представлен
на рис. 5.4.2, минимальное значение U достигается при а = ±а0.
Таким образом, при отсутствии внешней силы система имеет два
состояния равновесия, разделенные потенциальным барьером
EFla^/4, Величина этого потенциального барьера соответствует
максимуму энергии при a = 0, .в этой зоне dU/da = 0, но равно-
равновесие неустойчиво.
§ 5.5. Метод сил и метод перемещений
в строительной механике стержневых систем
Строительной механикой стержневых систем обычно называют
теорию расчета более или менее сложных многократно статически
неопределимых систем. На вариационном принципе Кастильяно
основывается так называемый метод сил. Запишем выражение
потенциала перемещений статически неопределимой системы
следующим образом:
Здесь все внешние силы сведены к одной обобщенной силе Q = 1.
Теперь уравнения E.4.3) можно записать следующим образом:
№+р,д = 0. E.5.1)
Индексы ?, / относятся теперь только к «лишним» неизвестным
Хи Х2, ..., Хр; положив Q = 1, мы не нарушаем общности, фак-
фактически величины действующих сил включены в величины $iQ.
Система E.5.1) называется системой уравнений метода сил.
Будем называть статически определимую систему, полученную
из исходной отбрасыванием лишних связей, основной системой.
Перемещение, на котором производит работу сила Хг, будем
называть перемещением с номером г. Выясним, как определяются
коэффициенты в уравнениях E.4.4). Коэффициент fiy — это не
что иное, как перемещение с номером i при условии, что
к основной системе приложена сила Х5 = 1. По правилу, установ-
установленному формулой E.3.5), мы должны определить усилия и мо-
моменты для сил Xi = 1 и X, = 1, после чего находим
i
¦ dz.
ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
Точно так же
Здесь NQ, MxQ — продольная сила и изгибающий момент, соз-
созданные в основной системе внешними силами.
Рассмотрим в качестве примера раму, изображенную на рис. 5.5.1 и
имеющую форму квадрата со стороною а. Рассечем ее по оси симметрии,
9 5
М
Mliil
, ртттгп птптп ,
Рис. 5.5.1
приложим пару продольных сил Хи пару поперечных сил Х2 и пару момен-
моментов Хз. Построим эпюры моментов от нагрузки, от сил Х\ = 1, от сил Х2 =
= 1, от пары моментов Х3 = 1. Применяя правило графоаналитического
перемножения эпюр, получим
Л ^ 2 Л qc? а \ 0 , <7а2 Л 3 4
(e-2-Te—I2-TJ2-«- —-« = т?«,
а-а 2 5 о
2 +
Замечая, что величины Pi2, P23, P2Q равны нулю, мы можем высказать
общее правило, что произведение симметричной эпюры на антисимметрич-
антисимметричную равно нулю. Величина Р22 нам не понадобится, существенно лишь, что
022 Ф 0.
Составим систему уравнений E.5.1):
3Х + 22Х + 440
2а
Решение этой системы
Y q&
022*2=°.
K22 2
5 , .
= 0, X, = ^1.
2 3 24
§ 5.5. МЕТОД СИЛ И МЕТОД ПЕРЕМЕЩЕНИЙ
161
Суммарная эпюра изгибающих моментов построена на том же рис. 5.5.1.
Совершенно аналогичным образом, отправляясь от вариационного прин-
принципа Лагранжа, получают уравнения метода перемещений; это не что иное
как уравнения E.4.1) и E.4.2), записанные в форме, содержащей явно ко-
коэффициенты жесткости*). Действительно, U
есть квадратичная функция от q, я*, а именно: |
1
и = Т
Отсюда
+ ciqq = 0,
2
Т cQQq
= Q. E.5.2)
I
Ш.
I
Первый пример предыдущего параграфа по
существу представляет собою пример на приме-
применение уравнений E.5.2). Для определения вели-
величин сц следует заметить, что из E.3.1) вытекает
следующее заключение. Предположим, что на
систему наложены дополнительные связи, такие,
что все свободные перемещения xj = 0, х» = 1
и / ф s. Тогда си представляет собою реакцию
связи, запрещающей перемещение хи a dqq есть
реакция этой связи на действие внешней си-
силы. Вообще, нахождение сц и aq требует реше-
решения статически неопределенных задач с большим числом лишних неизве-
неизвестных, но в частных случаях результат получается очень простым. Рассмот-
Рассмотрим, например, изображенную на рис. 5.5.2 раму. Как легко видеть, эта
рама трижды статически неопределима (по две составляющих реакции и
Рис. 5.5.2
Рис. 5.5.4
реактивному моменту в каждой заделке— шесть неизвестных и три урав-
уравнения статики). Пренебрегая продольной деформацией стержней, убежда-
убеждаемся, что единственная кинематическая переменная, определяющая состоя-
состояние системы, есть угол поворота узла А. Будем говорить, что система один
раз кинематически неопределима. Это значит, что при применении метода
*) Мы воздерживаемся от употребления терминов «каноническая сис-
система метода сил» или «каноническая оистема метода перемещений», чтобы
избежать упрека в неканоничности обозначений.
И Ю. Н. Рабстнов
ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
перемещений нам придется решать только одно уравнение. Для составления
этого уравнения нам понадобятся решения вспомогательных задач, пред-
представленные на рис. 5.5.3. Предоставляем читателю решить эти задачи лю-
любым способом, например так, как это было разъяснено в § 3.8. Для нахож-
нахождения величины c\q наложим связь, предотвращающую поворот. Теперь
вертикальный стержень останется ненагруженным, а горизонтальный ока-
окажется в положении, изображенном на рис. 5.5.3, б. Поэтому ciq = Ql/8.
Для нахождения величины сп повернем узел на угол ф = 1, убрав си-
силу Q. Оба стержня окажутся в состоянии, изображенном на рис. 5.5.3, а,
а следовательно,
п АЕ1Х 8Е1Х
с =2 - = -.
11 ~ /
Подставляя Ciq и сц в единственное теперь первое уравнение E.5.2)t
найдем
отсюда
Теперь не составляет труда построить эпюру изгибающих моментов, изо-
изображенную на рис. 5.5.4.
§ 5.6. Жесткопластическое тело
В предыдущих разделах мы неоднократна рассматривали за-
задачи о предельном равновесии стержней и стержневых систем
из идеально-пластического материала. Основная трудность при
решении этих задач состоит в том, чтобы правильно определить
положение пластического шарнира в
балке или установить, какие именно
стержни перейдут в пластическое состо-
I ' яние, если мы имеем дело с фермой.
; Можно, конечно, как мы иногда де-
^ ^ лали, рассмотреть сначала упругое со-
, стояние системы. Наиболее напряжен-
! L ный элемент первым перейдет в пла-
к стическое состояние при возрастании
Рис. 5.6.1 внешних сил. После этого мы дол-
должны рассматривать состояние упру-
гопластическое, чтобы выяснить, какой элемент перейдет
в пластическое состояние во вторую очередь, и продолжать по-
подобным образом до тех пор, пока мы не дойдем до исчерпания
несущей способности системы. Такой путь чрезвычайно сложен
и громоздок, к тому же он вносит элемент, являющийся для
теории предельного равновесия чуждым, а именно представление
о переходе от упругого состояния к пластическому. Действи-
Действительно, в предельном состоянии те элементы, которые не достиг-
§ 5.6. ЖЕСТКОПЛАСТИЧЕСКОЕ ТЕЛО
ли предела текучести, образуют кинематически изменяемую си-
систему и малые упругие деформации этих элементов не играют
никакой роли по сравнению со сколь угодно большими деформа-
деформациями пластических элементов. Поэтому в самом начале при
определении предельного состояния мы можем принять за исход-
исходный пункт не схему упругопластического материала, а схему ма-
материала жесткопластического, который совсем не деформируется
при а < ат и получает возможность неограниченной деформации
при а = ат. Диаграмма зависимости между напряжением и дефор-
деформацией для такого материала изображена на рис. 5.6.1. Если
встать на эту точку зрения, то нахождение предельного состоя-
состояния путем анализа упругого состояния представляется крайне
искусственным.
Некоторые общие теоремы, излагаемые ниже, позволят ре-
решить поставленную задачу более прямым и простым путем.
Предварительно нам нужно несколько уточнить представле-
представление о жесткопластическом теле, которое будет лежать в основе
дальнейших рассуждений, хотя окончательные результаты при-
применимы и для увдругопласшческош тела. Рассматривая изгиб,
например балки из упрушпластического материала без упрочне-
упрочнения, мы получаем диаграмму зависимости между изгибающим
моментом и кривизной, состоящую из трех участков: упругого,
упругопластического криволинейного и горизонтального участ-
участка, соответствующего исчерпанию несущей способности (см.
рис. 2.5.2). Переход от упругого состояния к полностью пласти-
пластическому нас интересовать не будет; поэтому мы заменим эту
диаграмму подобной той, которая изображена на рис. 5.6.1. Это
значит, что мы считаем, как будто балка совсем не деформи-
деформируется, пока изгибающий момент меньше чем Мт, и получает
возможность неограниченно изгибаться, когда момент достигает
этого предельного значения.
Здесь мы будем рассматривать систему из жесткопластиче-
ских стержней, работающих на растяжение — сжатие или изгиб.
В элементах этих систем возникают усилия и изгибающие мо-
моменты, в некоторых стержнях усилия могут достигнуть величины
NT = gtF, эти стержни потескут. В некоторых сечениях изгибаемых
стержней момент достигнет предельного значения Л/т, в этих се-
сечениях образуются пластические шарниры. При некоторой ком-
комбинации внешних нагрузок QT система станет кинематически из-
изменяемой, причем для неограниченного течения системы в целом
достаточно, чтобы она превратилась в механизм с одной степенью
свободы. Для общности и единообразия рассуждений вместо уси-
усилий и моментов мы будем говорить об обобщенных внутренних
силах R3y (которые достигают предельных значений i?ST. Если
Rs = Rst, то обобщенное перемещение г8 становится неопределен-
неопределенным, как это видно из диаграммы рис. 5.6.1. Вместо того, чтобы
говорить о перемещениях, нам будет удобнее говорить о скоро-
11*
ГЛ* 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
стях перемещений, притом в тот момент, когда текучесть только
наступила, перемещения еще малы и изменение геометрии несу-
несущественно. Скорость перемещения г8 при Ra = i?3T тоже неопре-
неопределенна, поэтому термин «скорость» понимается здесь в условном
смысле: это есть производная от гв по любому монотонно возрас-
возрастающему параметру. Но каждый элемент, перешедший в состоя-
состояние текучести, связан с жесткими элементами. Поэтому соотно-
соотношение между скоростями деформации отдельных элементов бу-
будет уже не произвольным, а совершенно определенным; скорости
г« находятся е точностью до неопределенного множителя.
§ 5.7. Условие текучести и поверхность текучести
Пусть на жесткопластическую систему действует система п
внешних сил Qi. Условие достижения предельного состояния мо-
может быть записано в следующем виде:
F(Qu Qz, .... <?») = 0. E.7.1J
Уравнение E.7.1) определяет в тнмерном пространстве сил
поверхность, которую называют поверхностью текучести, это
уравнение называется условием текучести. При достижении
условия текучести точки приложения сил Qi получают скорости
<1и которые находятся между собою в определенном отношении.
Но величины этих скоростей остаются неопределенными, они
известны лишь с точностью до общего множителя. Правило, ко-
которое устанавливает распределение скоростей при наступлении
текучести, называется законом течения. Общая запись закона
течения может быть следующей:
, U & = 1, 2, ..., п. E.7.2)
Здесь % — любой неотрицательный множитель.
Существенное отличие закона течения E.7.2) от закона упру-
упругости состоит в том, что течение наступает только тогда, когда
силы Qh в точности удовлетворяют условию E.7.1). Если
F(Qi, (?2, ..., (?п)<0, никакого течения нет, д* = 0. К системе,
состоящей из упругапластических элементов, нельзя приложить
такие нагрузки, что F(Q3)>0; если такие нагрузки в действи-
действительности приложены, необходимо решать задачу уже не стати-
статики, а динамики, т. е. вводить в рассмотрение силы инерции.
В пространстве сил каждая комбинация внешних нагрузок
изображается точкой с координатами Qt\ если точка находится
внутри поверхности текучести, система остается жесткой, если
точка находится на поверхности, происходит текучесть. Состоя-
Состояния, изображаемые точками вне объема, ограниченного поверх-
поверхностью текучести, невозможны. Состояние текучести достигается
вследствие того, что достаточное число элементов системы пере-
переходит в пластическое состояние. Это значит, что обобщенное уси-
§ 5.7. УСЛОВИЕ ТЕКУЧЕСТИ И ПОВЕРХНОСТЬ ТЕКУЧЕСТИ
лие в соответствующем элементе R8 достигает предельного значе-
значения #„ и соответствующая обобщенная скорость гв становится
отличной от нуля. Пусть число этих элементов есть т. Задавая
скорости гв, мы можем всегда найти скорости точек приложения
внешних сил #*, причем они будут выражены через гв линейным
образом:
Мощность внешних сил есть Q4i, она должна равняться мощ-
мощности, необходимой для пластического формоизменения Лвтг,;
таким образом,
Q4i = Rs.K E.7.3)
Предположим теперь, что мы немного изменили величины
внешних сил, но таким образом, что они продолжают удовлетво-
удовлетворять условию текучести E.7.1). Если при этом в пластическом
состоянии остаются те же элементы, то скорости га останутся
прежними. Останутся прежними и скорости qiy но вместо E.7.3)
мы получим
= Яш*ш, E.7.4)
поскольку внутренние силы i?ST сохраняют постоянное значение.
Сравнивая E.7.3) и E.7.4), находим
С другой стороны, из условия того, что
Qi + 6Qi удовлетворяет уравнению E.7.1),
следует
6F
= о.
Таким образом,
= U?-. E.7.5)
Рис 57л
Соотношение E.7.5) называется ассоциированным законом тече-
течения. Смысл этого термина состоит в том, что закон течения тесно
связан с условием текучести, он ассоциирован с этим условием.
Величины <}г можно рассматривать как составляющие вектора
в и-мерном пространстве. Этот вектор имеет совершенно опреде-
определенное направление, устанавливаемое формулой E.7.5), но вели-
величина его неопределенна. Если строить вектор с компонентами q{
в пространстве сил, то соотношение E.7.5) означает, что вектор
скорости направлен по нормали к поверхности текучести. На
рис. 5.7.1 изображен кусок поверхности текучести; совокупность
сил, действующих на систему, изображается вектором Q; если
система находится в предельном состоянии, то точка М, конец
166
ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
У/А
¦У/А
У/А
У/А
вектора Q, лежит на поверхности текучести. Вектор q с компо-
компонентами qt направлен по нормали к поверхности текучести
в точке М.
Поясним изложенное на нескольких простых примерах.
1. Система из трех стержней (рис. 5.7.2) нагружена двумя силами Qi
ы Q2. Поскольку силы приложены в одной точке, их геометрическая сумма,
вектор Q, является вектором силы в изображающем пространстве, которое
в данном случае просто представляет собою плос-
плоскость чертежа. Точно так же вектор с компонента-
компонентами q\ и q2 представляет собою вектор скорости точ-
точки Л в обычном смысле. Для того чтобы система
превратилась в механизм, необходимо, чтобы два
стержня перешли в пластическое состояние и тем
самым получили возможность неограниченно де-
деформироваться. Третий стержень останется жест-
жестким и будет вращаться около точки закрепления.
Таким образом, существует только три направления
возможного движения точки А в соответствии с
тремя возможными попарными комбинациями пере-
перешедших в пластическое состояние стержней. Пере-
Переберем все эти возможности.
а. Стержни 1 и 2 находятся в состоянии теку-
текучести, вращается стержень 3. Вектор скорости
точки А перпендикулярен стержню 3, следова-
следовательно,
q{ = X COS P, q2 = A. sin fi.
При вращении стержня 3 против часовой стрел-
стрелки, стержни 1 я 2 будут оба растягиваться. Нам
достаточно рассмотреть только эту возможность.
Усилия в стержнях 1 и 2 при этом одинаковы и
равны NT = oTF, усилие в стержне 3 нас не интере-
интересует. Спроектируем все силы на направление, пер-
перпендикулярное к стержню 3. Получим
Qi cos р + Q2 sin p = ±iVT(sinf* + sin (a + P)). (a)
Знак минус в правой части соответствует враще-
вращению стержня 3 по часовой стрелке.
б. Стержни 1 и 3 находятся в пластическом сос-
состоянии, вращается стержень 2\ скорость точки А
направлена по горизонтали, следовательно,
q\ — А/, <?2 = 0.
Если стержень 1 удлиняется, то стержень 3 будет
укорачиваться, следовательно, усилия в них раз-
разных знаков. Проектируя все силы на горизонталь-
горизонтальное направление, найдем
<?i = ±NT (sin a + sin ji). (б)
в. Стержни 2 и 3 находятся в пластическом со-
состоянии. При вращении стержня 1 против часовой
стрелки усилия в стержнях 2 ж 3 будут сжимающими, в противном случае
Ю
У/А У
\
\
\
г
/
У/А
/
5)
Рис. 5.7.2
растягивающими. Скорость точки А
вательно,
qi = К cos a,
Условие равенства нулю проекций
перпендикулярна стержню
следо-
q2 = —X sin a.
всех сил на направление скорости
§ 5.7. УСЛОВИЕ ТЕКУЧЕСТИ И ПОВЕРХНОСТЬ ТЕКУЧЕСТИ
167
дает
cos а —• <?2 sin а = :b/VT(sina + sin(a
(в)
В зависимости от комбинаций стержней, перешедших в пластическое
состояние, мы получили три распределения скоростей и шесть условий те-
текучести, каждое из которых линейно относительно Qi и Q2. Легко прове-
проверить, что соотношение E.7.5) выполняется. Шесть прямых в плоскости Qi,
Q2 образуют шестиугольник, представляющий собою поверхность текучести.
В данном случае п = 2, пространство сил представляет собою плоскость,
а поверхность — замкнутый контур. Тем не менее мы будем сохранять об-
общую терминологию даже в двумерном
случае и говорить о поверхности те-
текучести.
На рис. 5.7.3 изображена поверх-
поверхность текучести для случая, когда
a = Р == 45°. Эта поверхность состоит
из гладких, в данном случае прямо-
прямолинейных участков, но имеет угловые
точки, в которых производная не су-
существует и, следовательно, формула
E.7.5) неприменима. Выясним, что
в действительности происходит со стер-
стержнями, когда система действующих
сил изображается угловой точкой. Рас-
Рассмотрим, например, точку т на
рис. 5.7.3. Нагрузка удовлетворяет од-
одновременно и условию текучести (а)
и условию текучести (б), следователь-
следовательно, все три стержня находятся в сос-
состоянии текучести, однако скорость точ-
точки А не вполне произвольна, она долж-
должна быть такой, чтобы стержень 1 про-
продолжал удлиняться (это относится как к условию (а), так и к условию (б),
стержень 2 удлиняется (условие (б)), а стержень 3 укорачивается (усло-
(условие (б)). Это будет выполнено, если вектор скорости точки А лежит
внутри угла, образованного прямыми, перпендикулярными к направлениям
стержней 1 и 3. На рис. 5.7.3 мы должны провести нормали к сторонам
шестиугольника, пересекающимся в точке т, направление вектора скорости
в точке т неопределенно, но он всегда находится внутри угла, образован-
образованного этими нормалями.
В общем случае поверхность текучести есть гиперповерхность
в Химерном пространстве, она может состоять из гладких кусков,
образующих в пересечении ребра. Пусть изображающая точка
находится в пересечении двух гладких поверхностей
F(Q) 0
Рис. 5.7.3
Тоода формула E.7.5) применяется два раза, и мы получаем
следующий закон течения:
dF 8F
?i = ^i-^L + ^2-^L. E.7.6)
Здесь Xi и ^2 — неопределенные множители, которые могут при-
принимать любые значения, но обязательно неотрицательные, чтобы
вектор скорости был направлен по внешней нормали к поверхно-
поверхности текучести. В противном случае мощность, затрачиваемая на
пластическую деформацию, была бы отрицательна.
168
ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
§ 5.8. Выпуклость поверхности текучести
Изложенные выше рассуждения, приведшие к установлению
ассоциированного закона течения, основывались на том, что чис-
число структурных элементов системы конечно и существует конеч-
конечное число форм перехода системы в предельное состояние. На
примере было выяснено, что поверхность текучести будет всегда
представлять собою многоугольник, поскольку для любой формы
перехода в пластическое состояние условие пластичности будет
обязательно линейным. Совершенно такое же положение возни-
возникает, например, в балке, нагруженной конечным числом сосредо-
сосредоточенных сил. Эпюра моментов для такой балки кусочно-линей-
кусочно-линейна, следовательно, максимальное значение момента может дости-
достигаться только в том сечепии, где приложена сила. Число возмож-
возможных комбинаций пластических шарниров конечно; для любой
комбинации условие статики, связывающее значение внешних
сил, будет линейным, поверхность текучести и в этом случае
представляет собою многогранник и ассоциированный закон те-
течения сохраняет силу.
Покажем, что многогранник, представляющий собою поверх-
поверхность текучести, будет всегда выпуклым. Чтобы убедиться в этом,
достаточно рассмотреть случай двух
сил. Пусть некоторой комбинации
элементов, перешедших в пластиче-
пластическое состояние в плоскости Qu Q2,
соответствует прямая аЪ (рис. 5.8.1).
Тогда полуплоскость справа от ли-
линии ab (отмечено горизонтальной
штриховкой) будет областью недо-
I
Рис. 5.8.1
Рис. 5.8.2
пустимых состояний; если конец вектора Q оказывается в этой
области, усилия в пластических элементах из условия статики
должны быть больше предельных, что невозможно. Некоторой
другой комбинации пластических элементов соответствует пря-
прямая cd. Часть плоскости, находящаяся справа от cd и отме-
отмеченная наклонной штриховкой, будет опять-таки областью недо-
недопустимых состояний. Следовательно, границей области допусти-
допустимых состояний является ломаная amd с углом в точке яг,
меньшим чем я. Продолжая это построение, мы всегда получим
.выпуклый многоугольник и выпуклый многогранник в общем
тг-мерном случае.
§ 5.8. ВЫПУКЛОСТЬ ПОВЕРХНОСТИ ТЕКУЧЕСТИ
169
Вообще, число элементов, которые могут переходить в пласти-
пластические состояния, не обязательно конечно. В балке, несущей рас-
распределенную нагрузку, момент может достигать предельного
значения в любом сечении. Мысленно заменим гладкую балку
стержнем с надрезами на расстоянии А, как показано на
рис. 5.8.2. В таком стержне пластические шарниры будут возни-
возникать только в надрезанных сечениях, число их всегда конечно,
поэтому поверхность текучести представляет собою многогран-
многогранник. По доказанному, для такой балки будет справедлив ассоции-
ассоциированный закон течения. Перейдем теперь к пределу при А ->• 0;
мы получим исходную балку, для которой поверхность текучести
будет кусочно гладкой поверхностью, и распределение скоростей
будет подчиняться ассоциированному закону.
В качестве примера рассмотрим задачу о совместном действии изгиба
и растяжения или сжатия на стержень прямоугольного сечения. Обозначим
продольную силу через Qu изгибающий момент через @2, высота сечения
пусть будет h, ширина Ь, смещение нейтральной оси ?. Тогда q\ представля-
представляет собою удлинение средней линии, q2— кривизну. Очевидно, что q\ = С^г-
Эпюра распределения напряжений показана на рис. 5.8.3. Подсчитывая про-
продольную силу и изгибающий момент, найдем
Исключая отсюда ?, получим условие предельного состояния
О2 О ы.2
= bhar.
Легко проверить справедливость ассоциированного закона течения.
8F 2<?х 8F 1 dF 8F
Действительно, щ- = —j, щ- = jp, отсюда, -щ- : -щ- =?. Поскольку
—j, щ- = j
-щ- : -щ-
мы имеем дело с двумя обобщенными силами в сечении, поверхностью
Рис. 5.8.3
Рис. 5.8.4
нагружения будет кривая в плоскости NM1 состоящая из дуг двух парабол
(рис. 5.8.4). Вектор q направлен по нормали к кривой. В точках А и В на-
направление нормали неопределенно, следовательно, вектор скорости q может
принимать любое направление внутри угла, образованного нормалями к
каждой из парабол в точке их пересечения. Действительно, если стержень
ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
переведен в пластическое состояние путем растяжения, то деформация его
будет не обязательно деформацией только растяжения. Он может одновре-
одновременно изгибаться произвольным образом, единственное органичение состоит
в том, чтобы при этом не было разгрузки, следовательно, было
<
§ 5.9. Статический метод определения
предельной нагрузки
Возможными состояниями системы, состоящей из пластиче-
пластических элементов, будут такие, для которых условие текучести не
нарушено
f(Qi)<o.
Пусть совокупность сил Qi соответствует допустимому со-
состоянию. Бесчисленное множество допустимых состояний можно
построить, например, следующим образом. Освободим столько
внутренних связей, сколько нужно для того, чтобы система стала
статически определимой, заменим эти связи их реакциями, кото-
которым припишем любые значения, но такие, чтобы ни в одном из
элементов системы усилие не превыша-
превышало предельного. После этого силы Q*
определятся из условий равновесия. Слу-
Случайно может оказаться, что допустимое
состояние является истинным, т. е. таким,
которое соответствует текучести системы.
Вообще, конец вектора Q* лежит внутри
поверхности текучести, как показано на
р с 591 Рис' 5.9.1. Истинное состояние текучести
изображается вектором Q, а соответст-
соответствующая скорость направлена по нормали
к поверхности в точке М. Вследствие выпуклости поверхности
текучести вектор Q — Q* всегда составляет острый угол с век-
*
тором q. Поэтому скалярное произведение их положительно:
(Q-Q*)q>0. E.9.1)
Из неравенства E.9.1) вытекает приближенный метод опре-
определения предельной нагрузки. Запишем неравенство E.9.1) в
следующем виде:
Qq>Q*'q. E.9.2)
Знак равенства возможен только тогда, когда выбранное ста-
статически возможное состояние совпадает с истинным. В случае,
если на систему действует только одна сила Q, неизвестная ско-
скорость q в обеих частях неравенства E.9.2) сократится и мы
§ 5.9. СТАТИЧЕСКИЙ МЕТОД 171
получим
Q>Q*.
Таким образом, нагрузка, соответствующая произвольному
статически возможному состоянию системы, меньше, чем предель-
предельная нагрузка. Этот вывод остается справедливым и для системы
сил, действующих на тело, если сравниваются нагрузки, отли-
отличающиеся пропорциональным изменением всех сил.
Рассматривая различные статически возможные состояния, мы
будем находить различные нагрузки, каждая из которых явля-
является приближением снизу для истинной предельной нагрузки.
Наилучшим приближением, согласно доказанной теореме, будет
то, для которого нагрузка получается наибольшей.
Упругое состояние системы, при котором предел текучести
достигнут в одной или нескольких точках, является по опреде-
определению статически возможным. Действительно, при решении за-
задачи о нахождении упругого состояния мы должны были поза-
позаботиться о выполнении уравнений равновесия; при этом условие
текучести нигде не было нарушено и только в отдельных точках
это условие достигнуто. Соответствующее значение внешней на-
нагрузки представляет нагрузку, определенную по способу допу-
допустимых напряжений (с запасом прочности, равным единице).
Таким образом, мы имеем совершенно строгое доказательство
того, что расчет по предельному состоянию приводит к большим
значениям допускаемой нагрузки, чем расчет по допустимым
напряжениям.
Метод приближенного определения предельной нагрузки пу-
путем подбора статически возможного состояния мы будем называть
статическим методом. Если нам представляется возможность пе-
перебрать все статически возможные состояния и найти такое со-
состояние, которому соответствует наибольшее значение нагрузки,
то это значение будет точным.
Рассмотрим в качестве примера неразрезную балку, состоящую из двух
равных пролетов и нагруженную по всей ее длине сплошной равномерно
распределенной нарузкой q (рис. 5.9.2). Величину этой нагрузки требуется
найти. Обозначим через X реакцию крайней опоры. Давая X всевозможные
вначения, мы переберем все статически возможные состояния балки. Усло-
Условие того, что наибольший изгибающий момент равен Л/т, позволит опреде-
определить для каждого значения X величину нагрузки д, максимальная нагрузка
будет соответствовать предельному состоянию. Изгибающий момент в се-
сечении с координатой z равен
M X*
Максимальное значение момента, как легко видеть, достигается при z =
¦a zi = X/g, (Jfx)max = X2lBq). Требуя, чтобы модуль этого момента не
превышал Л/т, получим
X2
*>
172
ГЛ. 5. ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
С другой стороны, максимальное значение момента может быть достиг*
нуто на средней опоре при z = I Оно равно Xl—ql2l2.Vl3 условия, что аб-
абсолютная величина этого момента не превышает Мт, найдем
X
—
Введем безразмерные величины q = ql2/MT и X •
венства перепишутся таким образом:
: Х1/Мт. Полученные нера-
1*>\х\ (а)
q* < 2 A + X). (б)
На рис. 5.9.3 штриховкой показана область, в которой выполняются нера-
неравенства (а) и (б).
Наибольшее значение нагрузки соответствует точке Л, где пересекают*
ся парабола g* = lhx2 и прямая д* = 2A + X). Абсцисса этой точки X ==
= Х\ = 2A + ]/2)," соответствующее значение
нагрузки q\ = 6 + 4f2, максимальное зна- {
чение момента в пролете достигается при
1 \
г \
1 }
1 1
1 Z 3
5 6 X
Рис. 5.9.2
Рис. 5.9.3
Анализ подобного рода становится затруднительным, если система име-
имеет более высокую степень статической неопределенности, когда приходится
искать максимальное значение предельной нагрузки как функции несколь-
нескольких параметров.
§ 5.10. Кинематически возможные состояния
и кинематический метод определения предельной нагрузки
Для того чтобы статически возможное состояние жесткопла-
стической системы было действительным состоянием предела
ного равновесия, нужно, чтобы это состояние было в то же время
кинематически возможным; это значит, что свобода пластической
деформации, связанная с переходом отдельных элементов в пла-
пластическое состояние, должна иметь возможность реализоваться
на самом деле. Обращаясь к примеру, рассмотренному в преды-
предыдущем параграфе, мы заметим, что состояния, соответствующие
внутренности заштрихованной области на рис. 5.9.3, отвечают
условию того, что система остается жесткой. Кривая а соответ-
соответствует тому случаю, когда в пролетах образовались пластические
шарниры. Этого еще недостаточно, чтобы балка получила воз-
§ 5.10. КИНЕМАТИЧЕСКИЙ МЕТОД 173
можность свободно деформироваться (рис. 5.10.1, а). Если мы
рассматриваем статически возможное состояние, удовлетворяю-
удовлетворяющее условию (б), пластический шарнир получается над средней
опорой, этого опять-таки недостаточно для того, чтобы балка
превратилась в изменяемую систему (рис. 5.10.1, б). Только
тогда, когда пластические шарниры возникнут в пролетах и над
средней опорой, что соответствует точке А диаграммы рис. 5.9.3,
балка получает возможность деформироваться так, как показано
на рис. 5.10.1, в; такое состояние ^ ^
кинематически возможно, притом JS. JL JL
совместно со статическим состоя- /г а)
нием. Последнее замечание озна-
означает, что пластические усилия 1L
должны производить положи- у///' б)
тельную работу на соответству-
ющих перемещениях, грубо говоря,
если напряжение в стержне рав-
но +ст, он должен удлиняться,
а не укорачиваться. Возвращаясь
к схеме образования пластиче-
пластических шарниров, изображенной на ^
рис. 5.10.1, а, следует заметить, Рис. 5.10.1
что она не исключает возможно-
возможности деформации по схеме, показанной на рис. 5.10.1, г, но
при этом в левом шарнире относительный поворот имеет на-
направление, противоположное моменту, работа момента отри-
отрицательна, и, следовательно, кинематически мыслимая схема
деформации несовместима с принятым статически возможным
состоянием.
Второй метод определения точного или приближенного значе-
значения предельной нагрузки для жесткопластических систем со-
состоит в том, что мы рассматриваем различные кинематически
возможные схемы перехода системы в состояние текучести и
приравниваем работу внешних сил работе внутренних сил пере-
перешедших в пластическое сотояние элементов.
Очевидно, что задаваясь различными кинематическими схема-
схемами течения системы, мы будем получать различные значения
предельной нагрузки. Оказывается, что и в этом случае можно
установить экстремальный принцип, который позволит выделить
из всех возможных схем истинную, реализуемую в конструкции,
а следовательно, определить истинную несущую способность, т. е.
предельную нагрузку.
Обозначим Q* и соответственно г* — кинематически возмож-
возможное поле скоростей, определенное с точностью до постоянного
множителя. Пусть Qi — истинные, неизвестные значения сил в
предельном состоянии. Составим уравнение равновесия в форме
гл- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
Лагранжа, приняв выбранное кинематически возможное поле
скоростей за поле виртуальных скоростей. Получим
В истинном состоянии ни в одном из элементов усилие не
может превзойти усилия текучести или момент — предельного
момента текучести. Поэтому RS^.RS = RST. Запишем следующее
неравенство:
0йГ<Д.Л. # E.10.1)
С другой стороны, определим поле внешних сил (?* так, что для
данного кинематически возможного состояния
Q*q* = i?STr;. ^E.10.2)
Очевидно, что состояние системы под действием сил Qi, вооб-
вообще говоря, не будет статически допустимым, в каком-то из эле-
элементов, для которого соответствующее г% = 0, усилие может быть
больше предельного. Сравнивая E.10.1) и E.10.2), находим
Неравенство E.10.3) служит основанием для кинематического
метода. Если на систему действует только одна обобщенная
сила, то
Q^Q* = Jb?s-. E.10.4)
q
Таким образом, кинематический метод дает верхнюю оценку
для несущей способности. Если число кинематических состояний
конечно, то наименьшая из получающихся оценок представляет
собою точную величину несущей способности.
Кинематический метод значительно более прост и удобен для
применения, чем статический метод, и поэтому находит гораздо
более широкое применение.
Рассмотрим два простых примера.
а. Жесткий брус (рис. 5.10.2) подвешен на четырех стержнях с различ-
различными сечениями или из разных материалов. Таким образом, усилия преде-
предела текучести для них даны SiT, iSW, ?зт и ^т соответственно. Сила Р при-
приложена в середине бруса. Для перехода системы в состояние текучести не-
необходимо, чтобы три стержня были в пластическом состоянии, а четвертый
оставался жестким. Рассмотрим соответственно четыре возможности, когда
деформация происходит в-результате поворота относительно точек А, В,
С n D. Очевидно, нужно рассматривать только такие состояния, когда сила
Р при повороте совершает положительную работу. Соответствующие схемы
показаны на рис. 5.10.3, а, б, в и г. Уравнение работ в этом случае тожде-
тождественно с уравнением моментов.
В случае a: -j Р* = S2V + 2S3T + 3S4Tf
в случае б: т Р* « S3T + 2S4T
§ 5.10. КИНЕМАТИЧЕСКИЙ МЕТОД
175
1
в случае в: уР* = 2?1т + S2T + ?4Т>
в случае г:
Р* = 3?1т + 252Т + S3T.
Таким образом, для четырех кинематически возможных состояний мы
получили четыре значения для предельной нагрузки
2 .4
* — Q ^orp *T" Q '
4Т»
4Т»
Теперь остается подставить числовые значения пределов текучести
для стержней и выбрать наименьшее из четырех значений силы Р*, это и
будет истинная предельная нагрузка.
Остальные три значения силы Р* со-
соответствуют состояниям кинематически
возможным, но невозможным статиче-
статически. Дело в том, что при этом усилие в
стержне, который предполагался жест-
жестким, остается превышающим предел те-
текучести для этого стержня.
ж
в
8)
I,
Рис. 5.10.2
б. В качестве второго примера рассмотрим ту же самую двухпролетную
неразрезную балку, которая была рассчитана статическим методом в § 5.9.
Зададимся координатой пластическо-
пластического шарнира в пролете (рис. 5.10.4).
Рассматривая половину балки, най-
найдем, что работа внешней нагрузки д*
равна произведению этой нагрузки
на площадь треугольника ADB, т. е.
равна •у
Момент в пролете
Рис. 5.10.4
совершает работу на угловом пере-
перемещении а + р, момент на опоре —
на угловом перемещении 2ji, но на каждый пролет приходится лишь поло-
половина этой работы. Таким образом, — a?Z2g* =MT(a + 2|3).
Заметим, что р = а|/A — |); сократив на а и введя безразмерную на-
нагрузку так же, как это было сделано в § 5.9, получим
176 ГЛ- 5- ОБЩИЕ СВОЙСТВА СТЕРЖНЕВЫХ СИСТЕМ
Условие минимума нагрузки приводит к уравнению для ?:
g2 + 2g — 1 = 0.
Отсюда g = У2 — 1 (второй корень не имеет смысла).__
Соответствующее значение нагрузки q* = 6 + 4f2 совпадает с величи-
величиной, найденной при помощи статического метода.
Без строгого обоснования кинематический метод применялся
в сопротивлении материалов достаточно давно и довольно широко.
Если возможно найти строго верхнюю грань статических оце-
оценок и нижнюю грань кинематических оценок, соответствующие
значения предельной нагрузки совпадут, и мы получим точное
решение, истинность которого подтверждается совпадением цифр,
найденных двумя разными методами. Иногда в сложных систе-
системах перебрать все допустимые статически возможные и кинема-
кинематически возможные состояния бывает затруднительно. Отыскивая
оценки в некоторых классах статически допустимых и кинема-
кинематически допустимых состояний, мы получаем верхнюю и нижнюю
оценки для несущей способности, которые не совпадают между
собою. Однако во многих случаях оказывается, что эти оценки
заключают истинное значение несущей способности в достаточно
узкий интервал, так что поиски точного решения становятся бес-
бесполезными. В этом состоит основное преимущество экстремаль-
экстремальных принципов, которые позволяют получать простыми средства-
средствами очень хорошие приближенные решения трудных задач.
ГЛАВА 6
КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
§ 6.1. Колебания систем с конечным числом
степеней свободы
Рассмотрим механическую систему, состоящую из упругого
сооружения, которое несет ряд сосредоточенных грузов. Сначала
будем представлять себе эти грузы в виде материальных точек,
которые мы занумеруем от 1 до п. Массой сооружения будем пре-
пренебрегать по сравнению с массой грузов. Обозначим ии и2, ..., ип
перемещения грузов, массы которых ти m2j ..., тп. Связь между
силами Pi, Р2, ..., Рп, приложенными к грузам, и соответствую-
соответствующими перемещениями устанавливается соотношениями
И| = 5!РЛ F.1.1)
Единичное перемещение р« определяется, например, так, как
было указано в § 5.5.
Разрешая F.1.1) относительно Pi, мы придем к следующим
соотношениям:
i>i = 2<W. F-1.2)
Коэффициенты влияния ру, как мы видели, находятся просто,
вычисление коэффициентов жесткости Сц более затруднительно.
Теперь представим себе, что система пришла в движение. На
каждый из грузов действует заданная сила (?f, которая, вообще
говоря, является функцией времени; если перемещение груза
есть Ui(t), его ускорение равно ut(?). Чтобы составить уравнение
движения, следуя принципу Даламбера, положим в соотношени-
соотношениях F.1.1) и (б-1-2) Pi = Qi — ™>\Ui. Получим
Щ + 2 $цтк = 2 h& F.1.3)
2 3
или
гпгщ + 2 Cijiij = Qi. F.1.4)
Форма F.1.4) для записи уравнений движения механической
системы более проста, но мы будем по большей части пользо-
пользоваться уравнениями в форме F.1.3) именно потому, что коэффи-
коэффициенты влияния ptj определяются проще.
12 ю. Н. Работнов
178
ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
©
©
©
"ш,
Заметим, что, по существу, нумеровать от единицы до п нужно
не грузы, а степени свободы системы. Поэтому, например, желая
решить задачу о колебаниях изображенной на рис. 6.1.1 рамы
с грузом конечных размеров на конце, мы обозначим цифрами
1, 2 и 3 степени свободы, соответствующие горизонтальному пе-
ремещению, вертикальному пе-
1 . н^ . .. Л ремещению и повороту. Соот-
^ * * ветственно т^ = т2 представ-
представляет собою массу груза, тогда
как тг есть его момент инер-
инерции, iit и и2 — это линейные
перемещения, тогда как щ —
угол поворота. Строя эпюры
Рис. 6.1.1 моментов от изображенных
единичных сил и единичного
момента и применяя графоаналитический способ вычисления
интеграла Мора, найдем необходимые для составления уравне-
уравнений движения коэффициенты влияния р#.
В технике возмущающие силы бывают известны довольно
редко, обычно задана только частота возмущающих сил и задача
расчета сводится к определению собственных частот свободных
колебаний с целью выявления возможности резонанса. Поэтому
мы положим в уравнениях движения Qi = 0 и будем искать ре-
решение в виде щ = Он sin co?. В результате подстановки этого вы-
выражения в уравнение движения получим
п\ — СО2 2 $ijmj&j = 0 F.1.5)
или
— 2 cijaj — 0.
2
F.1.6)
Будем отправляться для определенности от уравнений F.1.5),
хотя те же результаты можно получить, если использовать урав-
уравнения в форме F.1.6).
Рассматриваемая система — это система п линейных однород-
однородных уравнений для п неизвестных аи а2, ..., ап амплитуд сво-
свободных колебаний системы. При произвольных значениях со су-
существует лишь тривиальное решение: а4 = а2 = ... = ап = 0. Ус-
Условие существования нетривиального решения состоит в равен-
равенстве нулю определителя системы
••• — 7J + Pnnmn
= 0. F.1.7)
§ 6.2. СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИЙ J79
Уравнение F.1.7) представляет собою уравнение степени п
относительно со2, которое имеет п корней, каждый из которых
определяет собственную частоту системы. Таким образом, упру-
упругая система имеет столько собственных частот колебаний, сколь-
сколько у нее степеней свободы.
Мы будем предполагать, что все корни уравнения F.1.7) раз-
различны. Действительно, корни могут быть равными только тогда,
когда коэффициенты податливости и массы грузов принимают
совершенно определенные значения; достаточно немного изме-
изменить массу одного из грузов или жесткость какого-либо элемента
системы, как корни станут различными. Таким образом, случай
равных корней не может представлять каких-либо качественных
особенностей, и нам нет необходимости на нем останавливаться.
§ 6.2. Собственные формы колебаний
Условимся нумеровать корни уравнения частот в порядке воз-
возрастания, так что coi < со2 < ... < соп. Если теперь внести в урав-
уравнения F.1.5) или F.1.6) величину со = соА, эти уравнения будут
иметь отличное от нуля решение
аи а2, ..., а».
Совокупность амплитуд, соответствующих определенной собствен-
собственной частоте, называется собственной формой колебаний. Очевид-
Очевидно, что собственная форма определяется с точностью до постоян-
постоянного множителя.
Собственные формы колебаний обладают свойством ортого-
ортогональности; выбирая соответствующим образом числовой множи-
множитель, их можно сделать ортонормированными, так что
2 тМ = 6W. F.2.1)
Для доказательства заметим, что уравнения F.1.5) или
F.1.6) имеют точно такую же структуру как F.1.1) или F.1.2).
Но теперь, вместо прогибов щ, в них фигурируют амплитуды а?;
силы, вызывающие прогибы, равные амплитудам, определяют-
определяются так:
Применим теорему Бетти (см. § 5.3), принимая за первое состоя-
состояние системы собственную форму с номером к, за второе состоя-
состояние форму с номером Z. Получим по формуле E.3.4)
или
<*1 2 тга\а\ = со? 2
X
12»
180 гл- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
а так как по предположению coft Ф со/, это равенство возможно
лишь при условии F.2.1).
До сих пор мы молчаливо предполагали, что все корни урав-
уравнения частот — действительные и положительные числа. Сейчас
мы можем это доказать. Действительно, предположим, что со&—
комплексное число. Тогда обязательно найдется второй корень
со?, являющийся комплексным сопряженным числом. Амплитуды
собственной формы с номером к будут также комплексными чис-
числами вида а% = аг + ф}, амплитуды собственной формы с номе-
номером I будут комплексными сопряженными числами а\ = а* — ifa
Подставляя аг и аг в условие F.2.1), мы получим
Но это равенство невозможно, так как в левой части все слагае-
слагаемые положительные.
С другой стороны, величина со?, полученная в результате ре-
решения уравнения F.1.7), всегда положительна. Действительно,
положим в F.1.5) а*= а?, со = он, умножим на Шгпг и просумми-
просуммируем по индексу i. Получим, опуская верхние индексы,
j?i тп^а^ = соь 2j (jriiuij {ntjuj) Pij. F.2.2)
i U
Сумма, стоящая в левой части, равна единице, а сумма в пра-
правой части представляет собою удвоенную потенциальную энергию
системы, нагруженной силами тпгпи Но каковы бы ни были силы,
энергия всегда положительна, поэтому двойная сумма в правой
части положительна при любых значениях амплитуд аг-. Поэтому
сод также необходимым образом должно быть положительно.
Пример. Балка на двух опорах длиной 4J несет три одинаковые мас-
массы, расположенные на равных расстояниях между собою и от опор
(рис. 6.2.1).
Прежде всего строим эпюры моментов от единичных сил и находим
коэффициенты влияния по способу § 5.3
3 3 р,о _р,о _" 3
, === ~Т~ Я » "¦* Pi о — *^-* Pot — А 9 ** t
Запишем матрицу коэффициентов влияния следующим образом:
II 9 И 7И ~*
В8,,||= 11 16 11 X
7 И 9» i2EI
12EI 1
Обозначим о- —г- = г.
та а>
§ 6.2. СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИЙ
181
Уравнение частот F.1.7) примет следующий вид:
9 — z 11 7
11 16 -z 11
7 11 9 — z
= 0.
Раскрыв определитель, получим следующее кубическое уравнение:
а8 - 34z2 + 78z — 28 = 0.
Корни этого уравнения zx = 31,56, z2 = 2, z3 = 0,444. Соответствующие
частоты
Уравнения для амплитуд собственных форм колебаний будут такие:
9 — z) =0.
Здесь нужно последовательно принимать z = zb z = z2, z = z3. Фак-
Фактически всегда приходится рассматривать только два уравнения, в данном
случае можно взять первое и второе. Од-
1 1 Ъ на из амплитуд может быть задана по
произволу. Примем, например, аъ = 1 во
всех случаях. Получим
aj = i, «I = i,4i6, ж 4 = 1,
а\ = -1, аа2 = 0, в« = 1,
Выполнение условий ортогональности
легко проверяется. Амплитуды каждой
из собственных форм можно умножить на
Рис. 6.2.1
Рис. 6.2.2
любое число; подберем в каждом случае это число так, чтобы было выпол-
выполнено условие нормирования. Нормированные собственные формы колебаний
будут следующие:
, 0,500 л 0,708 1 0,500
0,708
4 = °»
0,708
182 ГЛ- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
„ 0,500 „ 0,708 « 0,500
__
1 ут 2
Ha рис. 6.2.2 изображены найденные собственные формы колебаний.
§ 6.3. Главные координаты
Рассмотрим произвольную конфигурацию упругой системы
с сосредоточенными грузами, имеющей п степеней свободы. Эта
конфигурация может соответствовать деформированному состоя-
состоянию от действия произвольной системы внешних сил, может быть
некоторой мгновенной конфигурацией, принимаемой системой в
процессе движения, вызванного любыми силами при произволь-
произвольных начальных условиях. Задать такую конфигурацию — это
значит задать п перемещений аи а2, ..., ап. Эти величины мы
будем называть координатами системы. По определению п коор-
координат системы произвольны и независимы между собой. Но для
того чтобы задать положение системы, существуют и другие воз-
возможности, любые п чисел, однозначно определяющих конфигура-
конфигурацию, могут быть приняты за координаты. В частности, за коор-
координаты можно принять произвольные линейные комбинации из
величин ая, лишь бы они были независимы. Предположим, что
собственные формы колебаний системы известны. Введем коор-
координаты ц,-, соответствующие данной конфигурации, следующим
образом:
аг = a\uh. F.3.1)
Для того чтобы показать законность выбора величин щ в ка-
качестве координат, нужно убедиться в том, что из уравнений
F.3.1) величины ик определяются единственным образом. Свой-
Свойство ортогональности собственных форм колебаний позволяет
очень просто решить уравнение F.3.1) относительно uh.
Для этого умножим уравнение F.3.1) на тга\ и просумми-
просуммируем по индексу i. Получим
2 тгага\ == 2 тга^а\ик.
Заменим в двойной сумме порядок суммирования. В силу
условий ортогональности и нормирования те суммы по ?, которые
относятся к неравным между собой к и s, обратятся в нули, при
s — к соответствующая сумма равна единице. В результате из
всей двойной суммы останется один только член и, и мы получим
и8 =* 2 гпгага\. F.3.2)
i
Введенные таким образом координаты и* называются главными
координатами системы.
§ 6.3. ГЛАВНЫЕ КООРДИНАТЫ
183
Рассмотрим простой пример, в котором свойство ортогональности соб-
собственных форм принимает наглядный смысл и введение главных координат
становится естественным. Изображенная на рис. 6.3.1 рама несет груз на
конце. Матрица коэффициентов влияния в этом случае будет такой:
112 3|
3 8
X
Положим
ЬЕ1 1 лг л
= о 2» Уравнение частот будет следующим:
та со
Корни его z\ = 9,24, z2 = 0,76. Нормированные главные формы колебаний
определяются величинами
4 = 0,383-^, 4 = 0,923^,
-^
а\ = - 0,923 -Л=г9 а\ = 0,383 -А=г
L ут ут
или
«i-
sin a
cos а
2
ал = —
1
cos а
sin а
а = 22°31'.
Если через центр груза провести оси координат — горизонтальную ось
х\ и вертикальную ось #2, величины а\,
(
а\ и а\,
63
будут компонентами по
\ \ \
осям х\ и х2 двух векторов «i и а2 (рис. 6.3.1).
Ортогональность собственных форм колебаний нужно понимать в этом
случае буквально как ортогональность соответствующих векторов.
Рис. 6.3.1
Направим оси координат щ и u% по векторам, соответствующим соб-
собственным формам колебаний. Для рассмотрения динамики системы оси ко-
координат щ и и2 более естественны, чем случайно выбранные оси координат
*i и х2; по оси щ цроисходят колебания с частотой ©i, по оси и2— с частотой
©а. Произвольные колебательные движения груза естественно представлять
184 ГЛ- 6* КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
как результат наложения колебаний с двумя разными частотами в двух
главных направлениях.
По формулам F.3.1) в рассматриваемом случае получаем
щ = ут (а\ sin а + аг cos а), и2 = у™, (—a^ cos а + а2 sin а).
Это не что иное, как формулы преобразования координат при переходе
от осей xi, X2 к осям щу ич\ значит, главные координаты системы — это сос-
составляющие вектора перемещения по осям щ и м2» умноженные на постоян-
постоянную величину У т.
В общем случае произвольной упругой системы главные коор-
координаты не находят такого простого и наглядного истолкования,
если не прибегать к геометрической интерпретации при помощи
многомерного пространства. Однако значение их полностью со-
сохраняется.
§ 6.4. Формула и способ Рэлея
Определение собственных частот колебаний упругой системы
становится чрезвычайно затруднительным тогда, когда число сте-
степеней свободы велико и уравнение частот имеет высокий поря-
порядок. Уже раскрытие определителя требует большого труда, не
говоря о нахождении корней уравнения частот. В то же время
для приложений часто бывает достаточно знать наименьшую
первую частоту, так называемую частоту основного тона. Ее
можно найти с достаточной для практики точностью, пользуясь
приближенным методом Рэлея.
Выпишем уравнения F.1.6)
(??т{аг — 2 c%jaj == 0.
Умножим каждое из них на а{ и просуммируем по индексу i,
после чего найдем со2 из получившегося уравнения
Если а{ = аь то по формуле F.4.1) мы получим для ю2 точ-
точное значение со?; если а* — произвольное число, то для ю2 по этой
формуле получится некоторая величина, вообще говоря, не явля-
являющаяся частотой каких-либо колебаний системы.
Представим теперь произвольную конфигурацию системы раз-
разложением ее по собственным формам: аг = a\uk. Внесем это вы-
выражение в числитель формулы F.4.1). Получим
Переменим порядок суммирования, выделив сначала сумму
По формуле F.1.6) эта сумма равна айт^. Теперь мы
§ 6.4. ФОРМУЛА И СПОСОБ РЭЛЕЯ
можем выделить сумму 2 тга\сй = б5&. Таким образом, мы по-
получим
2 Cijdiuj = 2 ©АИА«
Преобразуем теперь знаменатель формулы F.4.1)
Меняя опять порядок суммирования, найдем
Таким образом, формула F.4.1) может быть переписана так:
Так как o)i < со2 < ... < соп, то каждый член числителя боль-
больше соответствующего члена знаменателя, и мы получаем нера-
неравенство со2 > o)i или же
»'<W' F'4-2)
где пг — произвольные числа. Знак равенства возможен только
тогда, когда и2 = и3 = ... = ип = 0, т. е. конфигурация системы в
точности соответствует первой собственной форме.
Неравенство, устанавливаемое формулой F.4.2), и является
содержанием теоремы Рэлея.
Задаваясь совокупностью амплитуд аг, которая, на наш взгляд,
близка к первой собственной форме колебаний, мы находим по
формуле F.4.2) приближенное значение квадрата первой соб-
собственной частоты, представляющее собою верхнюю оценку. За-
Заметим, что числитель в формуле F.4.2) представляет собою
удвоенную потенциальную энергию системы при перемещениях
а{, знаменатель же представляет удвоенную кинетическую энер-
энергию, вычисленную в предположении, что скорости равны пере-
перемещениям. Особенно простым становится применение этой фор-
формулы тогда, когда совокупность величин аг представлена как
совокупность церемещений от действующих на систему сил Qs-
Тогда потенциальную энергию можно вычислить по теореме Кла-
Клапейрона. Обозначая перемещение от сил Q8 через v8, перепишем
формулу Рэлея следующим образом:
В числителе суммирование идет по тем точкам, где приложе-
приложены силы, в знаменателе — по точкам, где сосредоточены грузы.
186 ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
Обратимся к примеру § 6.2 и вычислим для рассмотренной там системы
первую частоту свободных колебаний приближенно, по формуле Рэлея.
Сначала зададимся формой кривой прогиба, соответствующей одной силе
Q, приложенной посередине. При этом
11 Qa3 16 Qa*
По формуле F.4.3)
, \ , 2\ = °>386 -^Т> ®i < °>622 /"-^Т-
+ v\ + v\) та х * та3
Отличие от точного решения coj = 0,617"|/.EZ/(ma3) составляет всего 0,8%.
Если взять за форму прогиба упругую линию балки, нагруженной
тремя одинаковыми силами в точках 1, 2, 3, т. е. статическую кривую про-
прогиба балки от собственного веса, то три знака приближенного решения сов-
совпадают с точным.
§ 6.5. Нижние оценки для частоты основного тона
При рассмотрении определителя F.1.7) коэффициент при неизвестной
1/со2 в старшей степени, а именно в степени п, равен (—1)п. Легко сообра-
сообразить, чему будет равен следующий коэффициент при (l/co2)™-1. Если рас-
раскрыть определитель по элементам первого столбца или первой строки, то
мы обязательно получим член §ллтл\—j (— lO1"* но аналогичные
11 х \ со /
члены получаются при раскрытии определителя по элементам любой другой
строки или столбца. Поэтому если уравнение частот имеет вид
\n-i
°
то
С другой стороны, коэффициент при втором по старшенству члене в
алгебраическом уравнении равен сумме корней его с обратным знаком
_1_ __1___ _ 1
ю? ~~ <°2 '" ^п'
Отсюда
1 - ¦ - • ¦ - / i-4--i-4- 4--±-
»22 + »s "*"¦•'¦*" <
Выражение, заключенное в скобки, всегда положительно, поэтому справед-
справедливо неравенство
—j- < Р11^г1 + Р22™2 + • • • + $пптп* F.5.1)
1
Рассматривая пример в § 6.2, мы убедились, что собственные частоты
довольно сильно разнятся по величине, поэтому формула F.5.1) может быть
использована для приближенного определения первой собственной частоты,
§ 6.6. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 187
Обращаясь к числовым данным упомянутого примера, получим
Полученная нижняя граница отличается от точного значения на 3,74%.
Формула F.5.1) (со знаком равенства вместо неравенства) была получена
из эксперимента Данкерли в середине прошлого столетия.
Нижнюю оценку F.5.1) можно как угодно улучшить, применив следу-
следующий прием. По формулам F.1.5), меняя индексы, получим aj = со2р;втвав.
Внесем это выражение в F.1.5). В результате придем к следующей линей-
линейной однородной системе, которая совершенно эквивалентна исходной
Составляя определитель системы F.5.2), получим уравнение частот,
подобное F.1.7), но содержащее уже не квадраты собственных частот, а их
четвертые степени. Повторяя буквально приведенные выше рассуждения,
найдем
-?г<$Ьтгт1 + Ппт2 + - <6-8-3>
Неравенство F.5.3) более сильное чем F.5.1), потому что сумма
1/со| -f- l/co| -|- ...меньше по сравнению с величиной 1/<о*, чем аналогич-
аналогичная сумма обратных квадратов частот по сравнению с 1/со^. Обращаясь к
тому же примеру, находим
„з \2
1 / та3
— < A21 + 256 + 121) 12Ё7
СО-. *
/EI
з*. Теперь разница с точным решением составля-
составляла
ет всего 0,32%.
Очевидно, что аналогичным образом, вместо F.5.2), можно получить
уравнение, содержащее шестые, восьмые и вообще любые четные степени со;
таким образом, точность нижней оценки можно неограниченно увеличивать.
§ 6.6. Продольные колебания стержней
Перейдем теперь к изучению колебаний систем с непрерыв-
непрерывным распределением масс. Простейшим примером здесь может
служить задача о продольных колебаниях стержня постоянного
лоперечного сечения. На рис. 6.6.1 показан элемент стержня, ко-
который в недеформированном состоянии был заключен между
сечениями тп и pq с координатами х и x + dx соответственно.
Фиксируя некоторый момент времени t, когда сечение тп зани-
занимает положение т'п', сечение pq — положение p'q , обозначим
перемещение левого сечения, первоначальная координата кото-
которого была х, через и. Смещение и является функцией двух пере-
переменных — времени t и координаты в недеформировацном состоя-
состоянии х, поэтому смещение сечения с координатой x + dx будет
188
ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
u + ~dx. На том же рис. 6.6.1 изображен элемент m'n'p'q' от-
отдельно. Обозначим напряжение, действующее в сечении т'п\
через а, тогда напряжение, действующее в сечении p'q, будет
а +— dx. Но изображенный элемент находится в движении, его
ускорение равно д2и/д?, масса pF dx, где р — плотность, F — пло-
площадь поперечного сечения. Составим уравнение движения этого
элемента
Но по закону Гука а == Ее, относительная деформация элемен-
элемента е— т р -~тР __. Jf. внося это в уравнение движения и сокра-
сокращая на F dx, получим
д2и
F.6.1)
т
п
r P
9
dx
u+du
и ^
т'
п'
р'
9'
Здесь с = Т/Е/р.
Обращаясь к § 2.10, заметим, что с есть скорость распростра-
распространения продольной упругой волны.
Дифференциальное уравнение F.6.1) называется волновым
уравнением, оно описывает всевозможные динамические процес-
процессы, в стержне, распространение
волн, а также колебания.
В § 2.10 мы рассмотрели вопрос
о распространении волн, не прибе-
прибегая к дифференциальному уравне-
уравнению, сейчас мы имеем возможность
получить те же результаты иным
путем. Действительно, уравнению
F.6.1) мы удовлетворим, положив
u = f(t± х/с), где / — произвольная
дважды дифференцируемая функция.
Но движение, описываемое найден-
найденным решением, представляет собою
распространение волн со скоростью
с. Общее решение уравнения F.6.1), принадлежащее Даламберу,
имеет следующий вид:
/ \ / \
F.6.2)
Два слагаемых представляют собой две волны, бегущие с оди-
одинаковою скоростью в противоположных направлениях.
Хотя решение F.6.2) является совершенно общим в том
смысле, что любые движения стержня могут быть представлены
Рис. 6.6.1
§ 6.6. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
таким образом, при изучении установившихся колебаний оно не-
неудобно, оно не позволяет простым способом обнаружить соб-
собственные частоты колебаний. Метод, который мы применим для
решения задач о колебаниях, называется методом разделения
переменных или методом Фурье. Заметим прежде всего, что
уравнение F.6.1) линейно и его решения обладают следующими
очевидными свойствами:
1. Частное решение уравнения F.6.1), умноженное на произ-
произвольную постоянную, представляет опять решение этого урав-
уравнения.
2. Сумма двух (а следовательно, любого числа) частных ре-
решений есть решение.
Будем теперь искать частные решения уравнения F.6.1)
в виде произведения двух функций T(t) и Х(х)
u = T(t)X(x). F.6.3)
Подставим указанное выражение для и в уравнение F.6.1):
Здесь точки обозначают дифференцирование по времени, штри-
штрихи — дифференцирование по координате.
Разделение переменных состоит в том, что уравнение это за-
записывают следующим образом:
Т с2Х" 2
F = -JT=-(O-
Первый член представляет собою функцию только времени ?,
второй член — функцию только координаты х, равенство возмож-
возможно только в том случае, если каждая из этих функций постоян-
постоянная. Таким образом, со2 — постоянная величина. Для функций
T(t) и Х(х) получаются следующие, уже обыкновенные, диффе-
дифференциальные уравнения:
У+со2Г = 0, F.6.4)
X"+4Z==0- F.6.5)
с
Общий интеграл первого уравнения
Т = A sin co? + В cos cot.
Отсюда видно, что со представляет собою круговую частоту сво-
свободных колебаний. Осталось определить функцию Х(х). Общий
интеграл уравнения F.6.5)
= Сг sin \- С2 cos —. F.6.6)
При определении констант этого уравнения из граничных
условий мы сталкиваемся с тем же положением, что и при ре-
решении задачи устойчивости. При однородных граничных уело-
190
ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
виях для определения констант d и С2 получается система одно-
однородных уравнений, имеющая тривиальное нулевое решение. Не-
Нетривиальное решение существует только при определенных зна-
значениях со, которые и являются собственными частотами.
Прежде чем перейти к примеру, выясним возможные виды
граничных условий:
а. Закрепленный конец, и==0 при любом ?, следовательно,
Х = 0.
б. Свободный конец, а = 0, следовательно, е = ди/дх = 0, а так
как T(t) вообще не равно нулю, то X' = 0.
в. На конце прикреплен груз массы М. Применяя принцип
Даламбера, приравняем силу инерции груза внутренней силе в
концевом сечении:
dt2
ИЛИ
= EFTX'.
Исключим отсюда Т с помощью уравнения F.6.4) и сократим
на общий множитель T(t). Получим
В качестве примера рассмотрим задачу о колебаниях стержня длиной J,
один конец которого закреплен, а на другом имеется груз массой М
(рис. 6.6.2).
У///////////У
Рис. 6.6.3
Помещая начало координат в точке х = 0, находим сразу, что постоян-
постоянная С2 в уравнении F.6.6) равна нулю. Подставляя значение X ==
= С\ sin (соя/с) в граничное условие на конце х = I, где прикреплен груз,
находим
со/ М со coZ'
Если С\ = 0, никаких колебаний нет, колебания возникают только тог-
тогда, когда обращается в нуль выражение, заключенное в скобки. Обозначим
§ 6.7. РАСПРОСТРАНЕНИЕ ПРОДОЛЬНЫХ ВОЛН J9J
яерез т массу стержня, т = pFl. Тогда уравнение для нахождения со при-
примет следующий вид:
coZ coZ m
— *«— =м- <6-6л>
Это трансцендентное уравнение имеет бесчисленное множество корней,
число собственных частот системы бесконечно велико. Графическое опреде-
определение корней производится так, как показано на рис. 6.6.3; значения coZ/c,
удовлетворяющие уравнению F.6.7), являются абсциссами точек пересече-
т coZ
ния кривой у = tg (cal/с) и гиперболы у= -j^ : -у*
При весьма больших значениях соZ/c гипербола проходит очень близко
к горизонтальной оси, и абсциссы точек пересечения гиперболы с танген-
тангенсоидой лишь очень немного отличаются от пп. Поэтому для высоких ча-
частот получается асимптотическая формула
При достаточно большом п собственная частота, определяемая прибли-
приближенной формулой F.6.8), сколь угодно мало отличается от ее точного зна-
значения.
Собственную частоту основного тона мы вычислим в предположении,
что масса стержня мала по сравнению с массой груза. Тогда coZ/c — малая
величина и уравнение F.6.7) в первом приближении можно записать сле-
следующим образом:
?)'-5Г-
После очевидных преобразований отсюда следует: со = УЕР/AМ). Но та-
такое значение собственной частоты мы получили бы, рассматривая колеба-
колебания системы с одной степенью свободы, а именно стержня, лишенного
массы и несущего на конце массу М. Чтобы приближенно учесть массу
стержня, удержим в уравнении F.6.7) не один, а два члена разложения
тангенса, а именно положим
юг coZ 1 (®l)s
1ё~ = + [)
Уравнение принимает вид
coZ\2 I /coz
) +(
a>lJ m if Ш
J О
(a>lJ m
Его приближенное решение у—J = м + т/3 . Отсюда ©
§ 6.7. Распространение продольных волн
Элементарное рассмотрение задачи о распространении прямой
волны в стержне было дано в § 2.10. Там было показано, что
зависимость напряжения от времени, заданная в начальном се-
сечении х = 0, будет повторяться во всех сечениях стержня со сдви-
сдвигом по времени на величину х/с, где х — расстояние сечения от
конца. С другой стороны, распределение напряжений по длине
192 ГЛ- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
стержня в любой фиксированный момент t повторяет в соответ-
соответствующем масштабе функцию времени а @, t). Первый член в
решении Даламбера F.6.2) представляет собою такую прямую
волну; перемещение и (О, ?) = /(?), заданное на конце, повторя-
повторяется в любом сечении х со сдвигом по времени. Но решение
Даламбера содержит второй член — обратную волну. Эти обрат-
обратные волны появляются в стержнях конечной длины в результате
отражения от другого конца стержня. Для решения задач такого
рода применяется метод харак-
характеристик. По классификации,
принятой в теории дифферен-
дифференциальных уравнений, уравнение
продольных колебаний F.6.1)
относится к гиперболическому
типу; характерная особенность
гиперболических уравнений со-
, стоит как раз в том, что для
О х них существуют решения ти-
типа волн.
Рис- б-7-1 Определим из F.6.2) скоро-
скорости v = du/dt и деформации
е = ди/дх. Заметим, что по закону Гука е = g/E, поэтому вместо
естественного условия, когда на конце стержня приложена сила
Р и, следовательно, напряжение равно P/F, можно говорить о том,
что на конце задана деформация е. Дифференцируя F.6.2),
получим
Умножим второе соотношение на с, после чего сложим и вычтем
получившиеся уравнения. Найдем
v + ce = 2g'(l), v-ce = 2f'(r\). F.7.1)
Здесь принято | = t + х/с, y\ = t — х/с.
Величины ? и у\ называются характеристическими координа-
координатами, а линии | = const и ц = const в плоскости х, t — характе-
характеристиками. Будем называть линию \(\\ = const) положительной
характеристикой, линию ц (| = const) — отрицательной характе-
характеристикой. Предположим теперь, что в двух точках плоскости х, t
(точки р и q на рис. 6.7.1) заданы значения vP, ep, vq, eq. Прове-
Проведем через точку р положительную характеристику г) = const,
через q отрицательную характеристику ? = const. Вдоль поло-
положительной характеристики постоянна разность у —се, вдоль
§ 6.7. РАСПРОСТРАНЕНИЕ ПРОДОЛЬНЫХ ВОЛН
193
отрицательной — сумма v + се. Таким образом,
vm — сет = vP — cep, vm + сет = vq •
ceq
F.7.2);
Из уравнения F.7.2) находятся значения скорости и дефор-
деформации в точке т, vm и ет. Уравнения F.7.2) и служат основой
метода характеристик для решения уравнения продольных коле-
колебаний при заданных начальных и граничных условиях.
Рассмотрим задачу о стержне конечной длины Z, одному концу которого
внезапно сообщаем скорость У, которая поддерживается далее постоянной.
Картину распространения волн удобно рассматривать в плоскости х, t, как
показано на рис. 6.7.2. Вся эта картина расположится в полосе ширины I.
Правый конец можно считать либо свободным, ли-
либо неподвижно закрепленным. Разберем оба эти
случая. На рис. 6.7.2 проведены характеристики g
и т|, которые разбивают полосу на треугольники.
Основания этих треугольников занумерованы, при
этом отрезки на оси х = О нумеруются четными
цифрами, а на оси х = I — нечетными. Сами тре-
треугольники обозначены буквами а, 6, с, ..., отре-
отрезок t = О, х е (О, I] отмечен индексом 0. Точки,
принадлежащие соответствующим отрезкам или об-
областям, мы будем отмечать теми же индексами.
1. Конец х = I свободен. На оси х = I а = 0,
следовательно, е0 = ех = е3 = ... =0. При х =
= 0, v2 = i>4 = ve = ... = V. На отрезке оси х
t = 0, х е= @, I], v = 0, е = 0.
Проведем характеристику положительного на-
направления 01. На ней постоянна разность v — се,
значит vi — се\ = vQ — се0. Но v0 = е0 = 0, е{ = 0,
значит v\ = 0.
Любая внутренняя точка области а соединяется
двумя характеристиками либо с отрезком 0, либо
с отрезком 2, где v = 0, е = 0. Поэтому va = 0,
еа = 0. Отрезок 2 соединяется отрицательной характеристикой либо с от-
отрезком 0, либо с отрезком 2, на каждом из этих отрезков v = 0, е = 0,
поэтому и2 + се2 = 0, отсюда е2 = —V/c.
Любая точка области Ъ соединяется двумя характеристиками с отрез-
отрезком 2> поэтому
Рис. 6.7.2
+ сеь = v2 + се2,
— сеь = v2 — се2.
F.7.3)
Отсюда следует Vb = v2i еь — е2.
Установленное правило носит совершенно общий характер; если на от-
отрезке вертикальной оси скорость и деформация сохраняют постоянные зна-
значения, то в треугольнике, ограниченном характеристиками, проходящими
через крайние точки этого отрезка, скорость и деформация сохраняют те
же значения. Вообще, если на отрезке 2 заданы переменные значения ско-
скорости и деформации, в правых частях уравнений F.7.3) будут фигуриро-
фигурировать разные значения v% и е2, соответствующие тем точкам, из которых вы-
выходят характеристики. Но решение внутри треугольника, ограниченного
характеристиками, полностью определяется заданием функций v(t), e(t)
на отрезке 2, оно не зависит ни от предшествующей истории, ни от даль-
дальнейшего изменения этих функций. Это свойство характеризует гиперболи-
гиперболические уравнения или гиперболические системы.
После сделанного замечания нам будет достаточно соединять характе-
характеристиками положительного и отрицательного направления попеременно от-
отрезки линии ж = 0 е а; = /, а именно:
13 ю. н. Работнов
ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
на линии 2—3: vz = v2 — се2 = 2 У, е3 = О,
на линии 3—4: У + се4 = ^з + сег = 2 У, е4 = У/с,
на линии 4—5: v5 = v4 — се4 = 0.
Итак, в треугольниках а, Ь, с, ... скорости п деформации чередуются
следующим образом:
а
v 0
е 0
Ь
V
V
с
с
2V
0
d
V
V
с
е
0
0
/
У
V
с
В треугольнике е будет состояние покоя, так же как в треугольнике я,
поэтому в следующих треугольниках состояния чередуются в той же после-
последовательности.
2. Конец х = I неподвижно закреплен, v = 0. На участках 0, 1, 2, а сле-
следовательно, в треугольниках а и Ъ состояние будет тем же, что и в преды-
предыдущем случае. Составляя условие на характеристики 2—5, найдем, что на
отрезке 3. а следовательно, и в треугольнике с имеем —сес = 2F, ес =
= -217с.
Заметим, что совершенно безразлично, сообщена ли концу х = 0 ско-
скорость F, или к нему приложено внезапно напряжение а = — Ее2 = —EVjc.
При отражении от закрепленного конца, как мы установили, значение при-
приложенного напряжения удваивается. Дальнейший анализ производится
точно таким же способом, как и в первой задаче, мы остановимся на пер-
первом отражении от закрепленного конца.
3. По концу стержня х = 0 производится удар грузом М, движущим-
движущимся со скоростью V. Противоположный конец стержня х = I неподвижно
закреплен. После соударения груз будет двигаться замедленно, уравнение
движения его можно записать так:
M-^--EFe = 0. F.7.4)
Обозначим время прохождения длины стержня упругой волной через
т, т = 1/с. При t < 2т, пока отраженная волна еще не возвратилась на ко-
конец х = 0, на этом конце выполняется условие е = —У/с. Через У(t) мы
будем обозначать скорость у@, ?), равную скорости груза. Перепишем
уравнение движения груза следующим образом:
dV m dV u,
М1Г~Тсе===0 жли Г+ т F==0' ^[°'2т1- <6-7.5)
Здесь \х = plFjM — отношение массы стержня к массе груза.
Интеграл уравнения F.7.5), действительный в указанном интервале и
удовлетворяющий условию У@) = Уо, есть
) F.7.6)
Скорость убывает экспоненциально, деформация или напряжение на
конце также убывают экспоненциальпо до тех пор, пока не придет отра-
отраженная волна.
В промежутке времени t e Bт, 4т] мы оказываемся на участке 4 диа-
диаграммы рис. 6.7.2. На участке 5, как мы уже выяснили, и = 0, е = —2и/с,
где величина и соответствует точке отрезка 2, лежащей на соответствую-
соответствующей характеристике. Наша задача состоит в определении движения для мо-
момента ?, соответствующего точке D участка 4 оси ординат на рис. 6.7.2,
поэтому скорость в точке В должна быть отнесена к моменту t — 2т,
§ 6.8. ДИНАМИЧЕСКИЙ ИЗГИБ СТЕРЖНЕЙ 195
следовательно, в точке С
Составляя условие на характеристике DC, получим
V{t) +ce(t) =— 2F(*-2t).
1Ттяк
ce(t) = — V(t) —2V(t — 2т). F.7.7)
Вставляя в уравнение движения выражение F.7.7) для ce(t) и заменяя
V{t — 2т) по формуле F.7.6), получим следующее уравнение:
dV \i n [i
Интеграл его, удовлетворяющий начальному условию F@) = Уо, есть
V = V0 [ехр (- у, -~j - Щ- {t - 2т) ехр (- ц ll^1)]. F.7.8)
Теперь по формуле F.7.7) можно вычислить деформацию в месте контакта
с ударяющей массой, пропорциональную силе давления груза на стержень,
се (t) = -V0 ехр ^- ji ^ j Jl + 2 ехр 2ц ^1 - ^ ij=^1)]. F.7.9)
Это решение сохраняет силу до тех пор, пока деформация e(t) не изменит
знака. Приравнивая нулю e(t), определяемое формулой F.7.9), получим сле-
следующее выражение для соответствующего момента времени t:
^ = 1+ 4j^ [2 +ехр (-2н,I.
Для того чтобы отделение груза от стержня произошло именно в интер-
интервале t е Bт, 4т), необходимо, чтобы было
[i > 0,584.
При большей массе груза следует продолжить анализ, рассмотрев интерва-
интервалы Dт, 6т), Fт, 8т) и т. д.
§ 6.8. Динамический изгиб стержней
При составлении дифференциального уравнения динамиче-
динамического изгиба стержня мы будем отправляться от дифференциаль-
дифференциального уравнения изогнутой оси балки, записанного в форме C.8.5)
Единственное различие между уравнениями C.8.5) и F.8.1)
состоит в том, что в последнем уравнении употреблен символ
частной производной по координате. Теперь, рассматривая дина-
динамические задачи, мы должны считать, что прогиб v есть функция
двух переменных — координаты z и времени t. Уравнение F.8.1)
получено для случая равновесия балки, но его можно применить
к случаю движения, воспользовавшись принципом Даламбера.
13*
196 ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
Нагрузка q(z, t) должна включать в себя силы инерции. Уско-
рение элемента балки в сечении с координатой z есть —у, сила
dt
инерции элемента длиной dz равна —pFdz—^; таким образом,
dt
сила инерции на единицу длины
Рассматривая только свободные колебания балки, когда воз-
возмущающая сила отсутствует, мы внесем это выражение q в урав-
уравнение движения F.8.1) и получим следующее дифференциальное
уравнение:
I- р/г tl = 0. F.8.2)
Уравнение поперечных колебаний в отличие от уравнения
продольных колебаний уже не гиперболическое, задачи о рас-
распространении поперечных волн носят совершенно иной характер,
чем задачи о продольных волнах. Решение типа распространяю-
распространяющейся волны для уравнения F.8.2) существует не для любой
функции f(t — z/c), а например, для функции такого вида:
v = sm со
(-т)-
Скорость поперечной волны с найдется, если подставить это вы-
выражение в F.8.2), а именно (при EIX = consl):
-
V
Как видно, скорость распространения поперечной волны не-
неограниченно растет с увеличением частоты со. Но произвольно
заданное начального возмущения вообще может быть разложено
в ряд Фурье, содержащий члены со сколь угодно высокими ча-
частотами; таким образом, существуют возмущения, которые рас-
распространяются мгновенно.
На этот результат нужно смотреть как на дефект уравнения
F.8.2), пригодного лишь для достаточно длинных волн. Если
волны короткие, то, кроме инерции поступательного движения,
следует учитывать инерцию вращения, а также влияние на про-
прогиб не только нормальных напряжении, но также и касательных
напряжений от перерезывающих сил.
Учтя эти факты, можно получить уточненное уравнение ди-
динамического изгиба, которое является гиперболическим и не до-
допускает мгновенного распространения импульсов.
§ 6.8. ДИНАМИЧЕСКИЙ ИЗГИБ СТЕРЖНЕЙ 197
Возвращаясь к уравнению F.8.2), применим к нему метод
разделения переменных, положив v(z, t)=T(t)Z(z). Получим
T{EIXZ")" + pFTZ = O. Здесь точки обозначают дифференцирова-
дифференцирование по времени, штрихи — дифференцирование по координате.
Перепишем это уравнение следующим образом:
Т pFZ ® •
Повторяя рассуждения, проведенные в аналогичном случае
применительно к продольным колебаниям, получим два обыкно-
обыкновенных дифференциальных уравнения
Т + а>2Т = О, (EIXZ")" - a>2pFZ = 0. F.8.3);
Первое уравнение показывает, что со есть частота свободных
колебаний балки. Интегрируя второе уравнение и составляя гра-
граничные условия для определения констант, мы убеждаемся, что
эти константы не все равны нулю тогда, когда со принимает опре-
определенные значения, являющиеся собственными частотами балки.
Условимся нумеровать собственные частоты в порядке возраста*
ния, так что coi < со2 < со3 < ... Каждому значению собственной
частоты он соответствует собственная форма колебаний Zh(z),
удовлетворяющая уравнению F.8.3) при со = coft, а именно:
= 0. F.8.4)
Конечно, собственная форма определена с точностью до постоян-
постоянного множителя.
Собственные формы колебаний обладают свойством ортого*
нальности, которое совершенно аналогично свойству, доказанное
му в § 6.2 для системы с конечным числом степеней свободы.
Если Zh и Zi — две собственные формы колебаний, соответствую-
соответствующие разным собственным частотам coft и со*, то
i
j pFZkZl(iz = 0. F.8.5)
о
Для доказательства заметим, что уравнение F.8.4) может
быть истолковано как уравнение статического изгиба балки рас-
распределенной нагрузкой qh, интенсивность которой равна a>kpFZh»
Точно так же Zx представляет собой статический прогиб балки
от распределенной нагрузки Qi = (ofpFZi. Применим к этим двум
состояниям балки теорему Бетти:
(z) dz = $Zl (z) qk (z) dz% F.8.6)
J98 гл- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
внеся сюда значения qh и qh получим
i i
со? J pFZhZtdz = al J pFZiZhdz. F.8.7)
о о
Так как оА ?= coz, это равенство возможно только при выпол-
выполнении условия F.8.5).
Для определенности будем нормировать собственные формы
колебаний, выбирая постоянный множитель таким образом, что-
чтобы было
г
\pFZ\dz=\. F.8.8)
о
Аналогично тому как произвольная конфигурация системы
с конечным числом степеней свободы представляется через соб-
собственные формы (§ 6.2), упругая линия балки всегда может быть
представлена в виде ряда по собственным формам ее колебаний.
Пусть v(z) есть некоторая функция, представляющая собою
прогиб балки под действием нагрузки q(z). Функция v(z) удов-
удовлетворяет дифференциальному уравнению изгиба
Представим v(z) в виде бесконечного ряда
v(z) = %Zh(z)uh. F.8.9)
Внесем этот ряд в дифференциальное уравнение
Воспользуемся теперь дифференциальным уравнением F.8.4),
чтобы исключить производные от функций Zh. Получим
= q.
Умножим обе части этого равенства на Zt и проинтегрируем
по длине балки. В силу условия ортогональности от ряда в левой
части останется только один член с индексом Z, в силу условия
нормирования этот член будет
i
= J
о
Таким образом,
г
F.8.10)
Разложение функции v(z) в ряд по функциям Zh(z) пред-
представляет собою в известном смысле обобщение разложения Фурье
§ 6.9. КОЛЕБАНИЯ БАЛОК ПОСТОЯННОГО СЕЧЕНИЯ
по тригонометрическим функциям. Если функция v(z) удовлетво-
удовлетворяет тем же граничным условиям, что и функция Zh и четы-
четырежды дифференцируема, то ряд F.8.9) сходится абсолютно и
равномерно. Но выполнение названных условий автоматически
обеспечивается тем, что v(z) является прогибом от действия на-
нагрузки q (z), причем q{z) — интегрируемая функция.
§ 6.9. Колебания балок постоянного сечения
Если жесткость постоянна, то уравнение F.8.3) принимает
следующий вид:
of
Для сокращения записи положим со2 ^— = а4. Тогда
a4Z = 0. F.9.1)
Корни характеристического уравнения будут ±а и ±ia, по-
поэтому общий интеграл уравнения F.9.1) имеет вид
Z = A ch az + В sh az + С cos az + D sin az. F.9.2)
В § 3.9 мы видели, какие преимущества дает использование
частных решений с единичной матрицей начальных значений.
Эти решения строятся с помощью общего интеграла F.9.2)
i (х) = у (сЬ х + cos х), V2 (х) = у (sh х + sin x)s
3 (х) = у (°h х — cos х)% v* (х) = у (sh ж — sin x).
Легко убедиться в том, что производная по х каждой из по-
последующих функций Vh(x) равна предыдущей функции Vh^i(x)f
причем функции нужно расположить в круговом порядке так,
что за функцией У4 следует функция У1в
Итак, общий интеграл уравнения F.9.2) мы будем записы-
записывать следующим образом:
Z = &Vi{az). F.9.3)
Рассмотрим теперь несколько примеров.
а. Балка, лежащая на двух опорах. На каждой опоре равны нулю про-
прогиб и изгибающий момент: Z@) =0, Z"@) =0, Z(l) =0, Z"(l) =0. Из
граничного условия на левом конце при z = 0 сразу следует, что С\ = С3 =
= 0. Действительно, при z = 0 все функции Vk равны нулю, кроме Vi@),
равной единице. Но при двукратном дифференцировании функция F3 пере-
переходит в V\, следовательно, коэффициенты при V\ и Уз должны обращаться
в нуль. Используя остальные граничные условия, мы получим
C2V2(al) + CAVA(al) = 0, C2V,{al) + CAV2(al) = 0.
Теперь повторяется обычное рассуждение. Если определитель системы
отличен от нуля, то С^ = С4 = 0, следовательно, никаких колебаний не про-
происходит. Если определитель равен нулю, а должно иметь совершенно опре-
200 ГЛ- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
деленное значение, а зная а, мы находим собственную частоту системы. Ус-
Условие равенства нулю определителя будет следующим:
Отсюда
V2(al) = ±V<(al)
и либо sh al = 0, либо sin al = 0. Первый случай исключается, так как
гиперболический синус не имеет действительных нулей, кроме как в нача-
начале координат. Остается вторая возможность
ап1 = пк (п = 1, 2, ...).
Вспоминая, что такое а, находим собственные частоты
pF '
Следует заметить, что собственные частоты растут пропорционально
квадрату номера, а не первой его степени, как это было в случае продоль-
продольных колебаний.
В случае балки, лежащей на двух опорах, использование общего интег-
интеграла уравнения колебаний в форме F.9.3) не очень оправдано; если обра-
обратиться к формуле F.9.2), то видно, что граничным условиям задачи удов-
удовлетворяет последний член решения, если принять а = пп/l. Соответствую-
Соответствующая собственная форма
, Г 2 . nnz
Множитель перед синусом выбран так, чтобы было выполнено условие
нормирования.
б. Балка с одним заделанным и другим свободным концом. Помещая
начало координат в заделке, получаем следующие граничные условия:
Z@) = 0, Z7@) = 0, Z"(Z) = 0, Z"'(l) = 0
(в заделке равны нулю прогиб и угол наклона, на свободном конце изги-
изгибающий момент и перерезывающая сила). Из условий в заделке следует,
что С\ = С2 = 0, из условий на свободном конце
CzVi (al) + C<V2(al) = 0, CsV<(al) + C,VX (al) = 0.
Уравнение частот
дли
icos al ch al = —1.
Приводим шесть первых корней этого уравнения:
al = 1,875; 4,694; 7,855; 10,996; 14,137; 17,279.
в. Балка с двумя свободными концами (z = 0 и z = I). Граничные ус-
условия: Z"@) = 0, Z'"@) = 0, Z"(Z) = 0, Z"'@ = 0. Из двух первых гра-
граничных условий следует С3 = С4 = 0. Из двух других
CiV3(al) + C2V4(al) = 0, ClV2(al) + C2Vz(al) = 0.
Уравнение частот
§ 6.10. СПОСОБ РЭЛЕЯ — РИТЦА 201
ИЛИ
cos cd ch al = 1.
Первые корни этого уравнения
aZ = 0; 4,730; 7,853; 10,996; 14,137; 17,279.
§ 6.10. Способ Рэлея — Ритца
Способ Рэлея, изложенный в применении к системам с конеч-
конечным числом степеней свободы, находит применение и для при-
приближенного определения частоты основного тона свободных ко-
колебаний балки. Пусть v(z)— прогиб балки под действием нагруз-
нагрузки q(z). Составим выражение
i
v(z)q (z) dz
F.10.1)
f pFv2 (z) dz
Правая часть аналогична здесь правой части формулы F.4.3),
только конечные суммы заменены интегралами. Так как v(z)
представляет собою прогиб от нагрузки g(z), эту функцию можно
представить в виде абсолютно и равномерно сходящегося ряда
v (z)= i
k=i
Преобразуем числитель выражения F.10.1)
i i
\v(z)q(z)dz~ ^uk\Zkqaz= 2
о ft==1 о
Здесь мы воспользовались формулой F.8.10). Найдем теперь
знаменатель. Нам придется возводить в квадрат ряд для v(z) и
интегрировать либо квадраты, либо попарные произведения функ-
функций Zft, умноженные на pF. Принимая во внимание условия орто-
ортогональности и нормирования F.8.5) и F.8.8), получим
Таким образом,
со2 = Щ^$. F.10.2)
Из этого равенства следует, что формула F.10.1) определяет
частоту свободных колебаний балки «Л тогда, когда функция v(z)
совпадает с соответствующей собственной формой колебаний.
202 ГЛ- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
С другой стороны, формулу F.10.2) можно переписать следую-
следующим образом:
4 + 4@^+.
1 • + • +
Каждый член числителя, начиная со второго, больше чем со-
соответствующий член знаменателя, поэтому со2 ^ (oj, или
i
J v(z)q (z) dz
? • F.10.3)
J pFu2 (z) dz
При использовании формулы F.10.3) для приближенного
определения частоты основного тона мы должны постараться
угадать первую собственную форму колебаний. В качестве тако-
таковой для балки на двух опорах, например, можно взять кривую
прогиба от собственного веса.
Обращаясь к формуле F.10.3), заметим, что числитель правой
части представляет собою удвоенную потенциальную энергию
изгиба балки, прогиб которой выражается функцией v(z), тогда
как знаменатель — это удвоенная кинетическая энергия, при вы-
вычислении которой скорости заменяются прогибами. Поэтому эту
формулу можно переписать в следующем более общем виде:
Щ F.10.4)
Такая более общая трактовка формулы Рэлея позволяет:
1. Брать в качестве v(z) функцию, выражающую прогиб ба-
балок не только от распределенной нагрузки q{z), но и от сосредо-
сосредоточенных сил Q% в точках zt. Тогда
i
2U (v) = J v{%) q (z) dz + 2QsV (z>).
о *
2. Учитывать не только непрерывно распределенную массу
балки, но также сосредоточенные массы т< в точках z*. Тогда
i
2Т (v) = J pFv2 (z) dz + 2 "IP2 Оч).
о *
3. Задаваться функцией v(zL определяя ее не как прогиб от
некоторой нагрузки, а просто подбирая непрерывную вместе с
первой производной четырежды дифференцируемую функцию,
удовлетворяющую граничным условиям задачи.
§ 6.10. СПОСОБ РЭЛЕЯ — РИТЦА 203
Воспользуемся формулой § 5.3 для упругой энергии изгиба,
заменив в ней момент через кривизну при помощи соотношения
Е1Х ту — МХ) а именно:
2U=\EIX[^\ dz. F.10.5)
Знаменатель в формуле F.10.4) сохраняет свое выражение,
Заметим, что при применении метода Рэлея требование удов-
удовлетворения функцией v(z) всех граничных условий является из-
излишним. Разрывы вторых производных функций v(z) соответ-
соответствуют приложенным сосредоточенным моментам, разрывы
третьих производных — сосредоточенным силам. Следовательно,
если функция v(z) непрерывна вместе с первой производной и
удовлетворяет граничным условиям, наложенным на прогиб и
угол поворота, она всегда может быть представлена как функция
прогиба некоторой балки под действием распределенной нагрузки,
сосредоточенных сил и моментов и доказательство теоремы Рэлея
сохраняет силу. Будем называть граничные условия, налагаемые
на v(z) и v' (z) кинематическими условиями, а на момент и
перерезывающую силу, т. е. на v" (z) и v" (z)— динамическими
условиями.
Дальнейшее развитие метода Рэлея представляет метод Ритца.
Выберем п функций (pA(z), каждая из которых непрерывна вме-
вместе со своей производной и удовлетворяет кинематическим гра-
граничным условиям. Теми же свойствами обладает линейная ком-
комбинация
Здесь си с2, ..., сп — произвольные постоянные. Выпишем вели-
величины U(v) и T(v), это будут квадратичные функции коэффици-
коэффициентов d; обозначим их U{cu с2, ..., сп) и Т(сь с2, ..., с„). Тогда
по формуле F.10.4)
«Цгу F-10.6)
Формула F.10.6) дает верхнюю оценку для со?, зависящую
от коэффициентов си с2, ..., сп, при этом наилучшей оценкой
будет самая меньшая. Вопрос об отыскании наименьшей оценки
для cl>i сводится к нахождению минимума правой части нера-
неравенства F.10.6), рассматриваемой как функция неопределенных
коэффициентов. По общему правилу составляем частные произ-
производные этого выражения по с» (г = 1, 2, ..., п) и приравниваем
204 ГЛ- 6- КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
их нулю
Сократим на множитель 1/Т и обозначим U/T через о2 в со-
соответствии с F.10.1). Получим систему п уравнений вида
?¦-» 2Ц=°- FЛ0-7)
Система F.10.7) представляет собою систему линейных одно-
однородных уравнений относительно сг, она имеет нетривиальное ре-
решение только тогда, когда ее определитель равен нулю. Но усло-
условие равенства нулю определителя приводит к уравнению степени
п относительно о2, корни этого уравнения дают стационарные
значения частот со, определяемых формулой F.10.1). Наимень-
Наименьший корень дает наилучшую при данной аппроксимации прогиба
оценку для первой собственной частоты, притом оценку сверху.
Можно показать, что второй корень будет близок к «2, и
разница между точным значением ©а и полученным приближе-
приближением уменьшается с возрастанием числа членов в выражении
для v (z). Однако нельзя сказать, будет ли это оценка сверху
или снизу.
Пример. Балка постоянного сечения длиной I защемлена на одном
конце, второй конец свободен. Точное значение собственной частоты основ-
основного тона
со?:
(alf 1 Г Е1Х з,52 Л Г Е1Х
а. Примем за функцию v{z) кривую прогиба от сосредоточенной силы
Q на конце. Уравнение упругой линии
__o_(iL A)
v "" EIX \ 2 — 6 /•
Потенциальная энергия деформации
1 1 <?2*3
Условная кинетическая энергия Т(v)
(EIxf ) IT—TV *~ 840 9F{EIxf'
По формуле F.10.4)
2 140 EIX 3,57
Разница с точным решением обнаруживается, как видно, только в третьем
знаке.
§ 6.11. СЛЕДЯЩАЯ СИЛА 205
б. Применим к рассмотренной уже задаче метод Ритца, положив
v (z) = c{lz2 + C2Z3. При этом
\ l + 12сЛ + 12с») I3,
Уравнения F.10.7) получаются следующими:
Здесь х = Ej со2.
Приравнивая нулю определитель, получим квадратное уравнение, наи-
наименьший корень его х = 12,46, поэтому
^ 3,53
Заметим, что и в том и в другом случае мы выбирали функцию y(z),
удовлетворяющей только кинематическим граничным условиям. Несмотря
на это точность оценки получается довольно высокой. Если взять в каче-
качестве v(z) функцию, выражающую прогиб балки от равномерно распреде-
распределенной нагрузки, будут выполнены и динамические граничные условия.
В точном и приближенном решениях при этом совпадают третьи знаки.
§ 6.11. Динамическая устойчивость. Следящая сила
Бифуркационный критерий устойчивости, рассмотренный в
§ 4.4, как мы выяснили там, не всегда дает ответ на вопрос об
устойчивости или неустойчивости равновесия. Неполнота этого
критерия связана с тем, что он устанавливает возможность или
невозможность смежного состояния равновесия, тогда как при
потере устойчивости, вообще говоря, может наступить не новое
состояние равновесия, а состояние движения системы. Поэтому
естественная постановка задачи устойчивости состоит именно в
изучении возможных движений механической системы. Возвра-
Возвращаясь к проблеме устойчивости сжатого стержня, напишем урав-
уравнение колебаний такого стержня следующим образом:
Вывод уравнения F.11.1) не отличается от вывода F.8.1), нуж-
нужно только заметить, что в данном случае
тогда как М = — Pv так же, как в § 4.2.
206
ГЛ. 6. КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ
Рассмотрим простейший пример балки постоянного попереч-
поперечного сечения, свободно опертой на двух концах. Если длина бал-
балки есть Z, мы удовлетворим уравнению F.11.1), приняв v =
s= sin-^-e2(D*. Подставляя это выражение в уравнение, находим
0) = -г
F.11.2)
Здесь Рэ — первая критическая сила. Формула F.11.2) показыва-
показывает, что при Р < Рд со действительна; таким образом, балка может
лишь совершать колебания около положения равновесия. При
Р>Рд о становится мнимой и движение стержня апериодично,
прогиб неограниченно растет со временем. Таким
образом, парадокс, связанный со статической по-
постановкой задачи устойчивости, оказывается раз-
разрешенным, хотя существование и величина кри-
критической силы предсказываются правильно и ста-
статическим решением.
Следующий пример будет относиться к такой
задаче, когда статическая постановка вообще ни
к какому результату не приводит. Это задача об
устойчивости под действием так называемой сле-
следящей силы, т. е. силы, приложенной на конце
стержня и направленной по касательной к его
оси (рис. 6.11.1). Дифференциальное уравнение
F.11.1) остается для этого стержня справедли-
справедливым при следующих граничных условиях:
i;@) = i/@) = 0, v"(Z)=i/"(Z) = O. F.11.3)
У///////////
Рис. 6.11.1
Последнее условие означает, что перерезывающая сила на
конце обращается в нуль. Выясним, прежде всего, недостаточ-
недостаточность статического критерия в этом случае. Для этого примем в
уравнении F.11.1) pF = 0, получим (при EIX = const)
? + »?.-о. и_
Интеграл этого уравнения
v = А + Bz + С sin kz + D cos kz.
Используя условие при z = Z, получим
-C№ sin kl - Dk* cos kl = 0,
-Ck3 cos kl+Dk3 sin ««0.
§ 6.11. СЛЕДЯЩАЯ СИЛА 207
Приравнивая нулю определитель системы, найдем
.in« со.*!
— cos kl smkl
Единственный корень этого уравнения к = 0, следовательно,
у =5 0; таким образом, критической силы в смысле Эйлера стер-
стержень, нагруженный следящей силой, не имеет, согласно стати-
статическому критерию он всегда будет устойчивым.
Будем теперь искать решение динамического уравнения
F.11.1) в виде
v = Z(z)eM.
Функция Z(z) будет удовлетворять дифференциальному урав-
уравнению
(EIXZ")" + PZ" -pFoJZ = 0. F.11.4)
Решение его
Z = A sin fa + В cos fa + С sh frz + D ch fa. F.11.5)
Здесь ^ и ip2 — корни соответствующего F.11.4) характеристи-
характеристического уравнения, которое мы здесь не выписываем. Для неиз-
неизвестной р2 получается квадратное уравнение, имеющее один по-
положительный и один отрицательный корень, которые зависят от
жесткости, длины и массы стержня, а также от силы Р. Функ-
Функция Z(z) удовлетворяет граничным условиям F.11.3). Подстав-
Подставляя F.11.5) в эти граничные условия, получаем однородную си-
систему уравнений, которая имеет нетривиальное решение, если
определитель ее равен нулю. В данном случае равенство нулю
определителя приводит к нетривиальному результату, множитель
в показателе экспоненты о находится как функция сжимающей
силы Р. Соответствующее трансцендентное уравнение мы не
выписываем, исследование его довольно сложно и может быть
выполнено лишь с помощью численных методов. Результат ис-
исследования состоит в следующем. При малых Р для о получается
два действительных значения, с увеличением Р эти корни сбли-
сближаются и при Р = Р% сливаются в один действительный корень.
При-Р>?\и величина о становится комплексной, следовательно,
прогиб неограниченно растет.
Для критической силы Р* разные авторы дают слегка отли-
отличающиеся значения. Полагая
мы сделаем ошибку, которая, по-видимому, не превысит 0,25%.
ЧАСТЬ II
УПРУГОЕ ТЕЛО
ГЛАВА 7
ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
§ 7.1. Тензоры в трехмерном евклидовом пространстве
Для механики сплошной среды вообще и механики деформи-
деформируемого твердого тела в частности аппарат теории тензоров явля-
является естественным аппаратом. В большинстве теорий выбор
системы координат, в которых ведется рассмотрение, может быть
произвольным. Проще всего, конечно, вести это рассмотрение
в ортогональных декартовых координатах. Очевидно, что доказа-
доказательство общих теорем и установление общих принципов при
написании уравнений именно в декартовых координатах не нару-
нарушает общности. Что касается решения задач, то иногда бывает
удобно использовать ту или иную криволинейную систему коор-
координат. Однако при этом почти всегда речь идет о простейших
ортогональных координатных системах — цилиндрической или
сферической для пространственных задач, изотермической коор-
координатной сетке, порождаемой конформным отображением, для
плоских задач. В некоторых случаях, когда рассматриваются
большие деформации тела, сопровождаемые существенным изме-
изменением его формы, система координат связывается с материаль-
материальными точками и деформируется вместе с телом. При построении
соответствующих теорий преимущества общей тензорной симво-
символики, не связанной с определенным выбором системы координат,
становятся очевидными. Однако в большинстве случаев эти пре-
преимущества используются при формулировке общих уравнений,
не открывая возможности для решения конкретных задач. Поэто-
Поэтому мы будем вести основное изложение в декартовых прямо-
прямоугольных координатах, случай цилиндрических координат будет
рассмотрен отдельно.
Предполагая, что читатель знаком с основами тензорной ал-
алгебры и тензорного анализа, напомним некоторые свойства тензо-
тензоров в евклидовок трехмерном пространстве. При пользовании пря-
прямоугольными декартовыми координатами исчезает разница между
ковариантными и контравариантными величинами, поэтому мы
будем пользоваться только нижними индексами. Будем обозна-
обозначать координаты точки и соответствующие оси координат одной
§ 7.1. ТЕНЗОРЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ 209
и той же буквой с разными индексами: хи х2 и х3. Соответствен-
Соответственно базисные единичные векторы будут ег, е2, е31 они образуют
правый трехгранник.
а. Определение вектора а
а = а1е1 + а2е2 + а3е3.
По повторяющемуся индексу производится суммирование от
1 = 1 до & = 3. Немой индекс, по которому производится сумми-
суммирование, может быть обозначен любой латинской буквой
агег = ару G.1.1)
б. Вектор в двумерном пространстве
а = а1е1 + а2е2 =
Условимся считать, что если немой индекс представляет собою
греческую букву, суммирование производится от единицы до
двух.
в. Преобразование компонент вектора к новому базису. Если
задан второй ортогональный базис е{, то
а = а{ег = а]е]. G.1.2)
При этом
e« = a«ej. а\ = а51а59 ац = е&. G.1.3)
г. Определение тензора ранга /с. Тензором ранга к называется
совокупность величин, зависящих от к индексов A{^ik таких,
что при преобразовании координат, т. е. переходе от базиса ег
к ej и обратно они преобразуются по формулам
Примечания. 1. В пункте (а) вектор был определен как экстенсив-
экстенсивная величина или сумма произведений вида G.1.1). Эта сумма может быть
интерпретирована геометрически как сумма векторов, но ей можно прида-
придавать и чисто формальный смысл. С другой стороны можно было не при-
прибегать к такого рода представлению, определив вектор как тройку чисел,
отнесенных к данному базису и преобразующихся при изменении базиса
по формулам G.1.3). Аналогично тензором можно называть не совокупность
скалярных величин Лг г ^, а экстенсив или символическое произ-
произведение
2. Мы будем здесь рассматривать только такие преобразования коорди-
координат, которые оставляют систему координат правой. Это избавит нас от
необходимости различать векторы и псевдовекторы, тензоры и псевдотеп-
зоры.
14 Ю. Н. Работнов
210 ГЛ> 7* 0БЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
д. Мультипликативные тензоры. Если А{^,Лк есть тензор
ранга &, Bj±j2...jp— тензор ранга р, то величины
образуют тензор ранга к + р. В частности, если заданы два век-
вектора Ъг и аи то величины аф^ представляют собою компоненты
мультипликативного тензора второго ранга.
е. Свертывание тензоров. Приравнивая два индекса, мы про-
производим суммирование по индексу, в результате получается но-
новый тензор, ранг которого на две единицы меньше. Подобная
операция получения тензора ранга к — 2 из тензора ранга к на-
называется свертыванием. Если к = 2, то в результате свертывания
получается скалярный инвариант. Так, свертывая мультиплика-
мультипликативный тензор а{Ь], получаем скалярное произведение векторов
а и 6, аЪ = аф\.
ж. Построение инвариантов. Свертывая тензор второго ранга
Aih получаем его первый инвариант Аи. Образуя мультиплика-
мультипликативный тензор четвертого ранга АцАы, можем свернуть его по
двум парам индексов: г, к и /, I или г, I и /, к. Таким образом,
получают два квадратичных инварианта АцАц и AijAju Анало-
Аналогичным образом строится кубический инвариант и следующие
за ним. Очевидно, число независимых инвариантов тензора
любого ранга ограничено. Мы не будем заниматься подсчетом
их числа.
з. Признак тензорного характера величин, зависящих от ин-
индексов. Совокупность величин -4$^...^ составляет тензор ран-
ранга к в том случае, если в результате свертки их по правилу
тензора с любым тензором Bjij2...jp ранга р мы получим тензор
ранга к — р. В частности, если ais— компоненты к произвольных
векторов, то Л^|2 >ift образуют тензор, если свертка
представляет собою скалярный инвариант. Это правило широко
применяется в приложениях.
и. Тензоры 6tj, Bijh и Т«р« Единичный тензор или тензор Кро-
некера определяется так: 6^=1 при г = /\ 6^ = 0 при i^j. Оче-
Очевидное тождество
а{
доказывает тензорный характер 6«.
Тензор третьего ранга егЛ или тензор Леви-Чивита определя-
определяется следующим образом: е*# = 0, если среди индексов по край-
крайней мере два одинаковы: e«ft = l, если порядок индексов соответ-
соответствует четной перестановке, т. е. порядок их есть 1, 2, 3, 1, 2, ...
...; Eijh = — 1, если порядок индексов соответствует нечетной пере-
перестановке 3, 2, 1, 3, 2, ...
§ 7.1. ТЕНЗОРЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ 2Ц
Исходя из данного определения, легко проверить, что
Согласно установленному выше правилу величины eijk действи-
действительно представляют собою тензор.
В двумерной области тензору Леви-Чивита соответствует тен-
тензор ^аэ такой, что Tfii = 722 = 0, *у12 = —*Y2i = 1- Легко убедиться
в том, что свертка тензора 7«р с вектором а определяет вектор,
равный по величине вектору а, но повернутый на угол л/2 по
часовой стрелке.
к. Симметричные и антисимметричные тензоры второго ранга.
Тензор называется симметричным относительно пары индексов,
если он не меняется при их перестановке. Тензор называется
антисимметричным, если при перестановке пары индексов он ме-
меняет знак (как, например, тензор Леви-Чивита). Тензор второго
ранга симметричен, если Л« = Л#, тензор B{j антисимметричен,
если Bij = —Bju Любой тензор второго ранга может быть разло-
разложен на симметричную и антисимметричную части
Ац = ± (Ац + Ан) + 1 (Ау - Ан) = АШ) + Ашу G.1.5)
Операцию выделения симметричной и антисимметричной частей
тензора мы обозначаем, заключая индексы в круглые и квадрат-
квадратные скобки соответственно. Заметим, что
GijkA(ij) ss 0, EijkAij
Если а есть произвольный вектор, то
отсюда следует
Aifliuj = A ityuiuj. G.1.6)
л. Главные оси и инварианты симметричного тензора второго
ранга. Для каждого симметричного тензора второго ранга можно
найти такой базис et (оси координат хг), для которого все со-
составляющие тензора с различными индексами исчезают. Три
отличные от нуля компоненты с двумя одинаковыми индексами
мы будем отмечать одним единственным индексом
Ац = А{ (не суммировать).
Направление оси хг будем задавать единичным вектором \и
Три вектора v< образуют ортогональный базис, величины А{ явля-
являются корнями кубического уравнения
или, в развернутом виде
А3-1ьА2
Величины Iu I2, h представляют собою инварианты тензора Ац.
14*
212 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
С другой стороны, можно построить систему инвариантов Аи Аи,
Am по общему правилу
Ai = Аи, Аи = AijAij, Ащ = AijAjkAki.
Каждая из двух систем инвариантов полна в том смысле, что
любой четвертый инвариант выражается либо через 1и /2 и /3,
либо через Ai, Au, Лш, например:
Ix = Alf /2 = 1 (At - Аи), /, = 4 (А\ - ЗА^и + 2Ат).
м. Антисимметричный тензор второго ранга как вектор. Анти-
Антисимметричный тензор coy имеет три различных отличных от нуля
компоненты: со12 = —со21, со23 = —оK2, co3i = —co3i. Положим Ph =
= 1/ггцъ<йц. Легко проверить, что
Pi = 0Jз, P21=sG>3i, Pa — ^ia.
Наоборот, вектору /?, соответствует антисимметричный тензор
Поэтому векторное произведение (о X г может быть записано
в виде <йцГ}ег.
н. Радиус-вектор и тензор инерции. Вектор х{ называется ра-
радиусом-вектором. Образуем мультипликативный тензор x{xh
умножим его на скалярную весовую функцию \х(х3) и проинте-
проинтегрируем по объему V. В результате получим тензор, называемый
тензором инерции
hi = J
v
В плоском случае при \х = 1 получаем моменты инерции пло-
плоской фигуры
Эти величины встретились нам выше при изложении теории из-
изгиба (§ 3.3).
о. Тензоры как результат дифференциальных операций. Про-
Производная от скалярной функции точки ф(#0 определяет вектор
grad ср = — ег. Обозначая -^ = ф ь мы можем обращаться с ин-
ох* ох*
дексами после запятой как с обычными тензорными индексами.
Если задано дифференцируемое векторное поле v{(xh), в резуль-
результате дифференцирования получается поле тензора второго ранга
vitj(xk). После свертывания отсюда получается скалярный инва-
инвариант — дивергенция вектора v
div v = viti.
Полагая v = grad cp или Vi = ф,<, получаем тензор второго ранга
§ 7.2. ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ 213
Ф,#, и как его свертку, дифференциальный инвариант — лапла-
лапласиан функции ф
Аф = Ф,«.
Вспоминая, что оператор rot я может быть представлен как
символическое векторное произведение оператора «набла» и век-
вектора vt и используя определение е-тензора, получим
rot V = Ъ
§ 7.2. Общая теория деформаций
Излагаемая ниже теория деформаций носит чисто геометриче-
геометрический характер и не связана с какими-либо предположениями о
свойствах деформируемой среды. Будем рассматривать точечное
преобразование евклидова пространства, в результате которого
точка М (х) сопоставляется точке М' (#'). Будем говорить, что
материальная точка М переместилась из точки пространства с
радиусом-вектором х в точку с радиусом-вектором х', хотя для
кинематической теории вводить понятие материальной точки не
обязательно. Деформация области пространства V задана, если
величины хг заданы как функции от х% ^ V. Будем считать эти
функции непрерывными и деформируемыми всюду, кроме, может
быть, некоторых поверхностей 2 в объеме V. Будем считать так-
также, что если функции x\{xs) неоднозначны, то можно выделить
однозначную ветвь.
Величины xh, т. е. декартовы координаты материальной точки
до деформации, можно сохранить в качестве индивидуальной ха-
характеристики материальной точки, меняющей свое положение в
пространстве. Поэтому они играют двойную роль: их можно рас-
рассматривать как декартовы координаты по отношению к неизмен-
неизменному базису либо как криволинейные координаты в деформиро-
деформированном пространстве; координатные линии в этом пространстве
представляют собою кривые, образованные теми точками, кото-
которые до деформации принадлежали прямым, параллельным коор-
координатным осям.
Положим
х\ — хг = щ(хк).
Вектор и называется вектором перемещения. Будем относить
этот вектор к ортогональному базису, связанному с декартовой
системой координат х{. Эта оговорка существенна для дальней-
дальнейшего, так как в принципе можно относить его к базису, образо-
образованному касательными к координатным линиям х-г в деформиро-
деформированном состоянии. Мы не будем вставать здесь на этот второй
путь.
214 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИИ
Если элемент дуги до деформации есть ds, после деформации
он станет равным ds'. Положим
?* G.2.1)
Величина е называется относительной деформацией элемента ds.
Элемент дуги в криволинейных координатах выражается следую-
следующим образом:
ds2
Элемент дуги после деформации
ds'2 = dx\dx\ = (dXi + dm) (dxi + dm) = ds2 + Ых$щ + du{dui%
Ho dui = uit jdxj, поэтому
Для вычисления произведения dm dm заменим в нем немой
индекс. Тогда
dui dm = duk duk = uh> t- uk>,- d^i d^j.
Итак,
d5/2 - ds2 = Bв«,, + uh> i uK s) dxi dxt. G.2.2)
Выражение, заключенное в скобки, представляет собою тен-
тензор, это можно утверждать на основании правила (з) § 7.1. Дей-
Действительно, левая часть G.2.1) есть инвариант по определению.
На основании правила G.1.6) в выражении G.2.2) несимметрич-
несимметричный тензор можно заменить его симметричной частью. Положим
ец = 4" (UU + Щл + uk,iUhtj). G.2.3)
Симметричный тензор ец, определенный формулой G.2.3), на-
называется тензором деформации. Теперь G.2.2) можно перепи-
переписать следующим образом:
ds2 — ds2 = 2ец dx{ dxj
или, с учетом G.2.1),
A+ .)._¦! = ?!й^. G.2.4)
as
Величину, стоящую в левой части, можно принять за меру
деформации. Почти во всех теориях, которые будут рассматри-
рассматриваться далее, деформации можно считать малыми, е < 1. Прене-
Пренебрегая е2, из G.2.4) получим следующий результат:
е = !&р.. G.2.5)
ds
§ 7.2. ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ 215
Заметим, что если направление отрезка ds задано единичным
вектором пг то dxjds = щ — направляющие косинусы этого от-
отрезка, и формула G.2.5) принимает вид
е = ецтцщ. G.2.6)
Задание тензора деформации позволяет определить изменение
длины любого линейного элемента, следовательно, полностью за-
задает геометрию деформированного тела.
Антисимметричная часть тензора, фигурирующего в формуле
G.2.2), называется тензором вращения и определяется следую-
следующим образом:
<*г> = ^(Щ,5-Щл). ' G.2.7)
Вся теория существенно упрощается, если принять, что не
только деформации е#<1, но также вращения ©у<1, а следо-
следовательно, uit j<l. По существу это предположение делалось в
части I книги, где рассматривались стержневые системы. Там же
были приведены немногочисленные примеры, когда углы поворо-
поворота и деформации имели различный порядок малости (§ 4.6).
Теперь в формулах G.2.3) можно выбросить квадратичные чле-
члены и мы получим следующие выражения для компонент дефор-
деформации:
eij = Щи) = -у (UU+ Щл)- G.2.8)
Выясним теперь геометрический смысл компонент деформа-
деформации eiS. Для этого выведем формулу, дающую изменение угла
между отрезками, направленными в исходном состоянии по еди-
единичным векторам тжп. Обозначим через dr и 8г соответствен-
соответственно эти элементы, через ds и 8s — длины элементов, через О —
угол между ними.
Тогда
drbr — ds 8s cos ft.
После деформации
dr' = dr + du = (8ij + u
и аналогично
Положим dr'8r' = cos*' A + em) A + en) ds8s. В результате по-
получим
cos О' A + em) A + en)— cos 0 = е{5\тгщ + т^щ). G.2.9)
Положим Wi = l, гс2 = гс3 = 0. Тогда по формуле G.2.6) находим
е — eti.
216 ГЛ. 7. ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
Итак, компоненты деформации с одноименными индексами
представляют собою относительные деформации элементов, на-
направленных по осям координат.
Положим теперь я4 = 1, rc2 = rc3 = 0, тгс2 = 1, яг4 = яг3 = (Х
Тогда О = я/2. Положим О' = Jt/2 — 7i2, ^^l- Пренебрегая ве-
величинами второго порядка малости, получим
Ti2 = 2е12.
Итак, компоненты деформации с разными индексами пред-
представляют собою половины изменений первоначально прямых
углов между соответствующими координатными осями. Величины
/Yi2 называют сдвигами. Вообще, если векторы т и п ортогональ-
ортогональны, то из G.2.9) следует
4" Угпп = 4^ец (тгщ + т^т) = ецтгщ. G.2.10)
§ 7.3. Определение перемещений по заданной деформации
Шесть компонент тензора деформации выражаются по фор-
формулам G.2.3) или G.2.8) через три компоненты вектора переме-
перемещения. Поэтому следует ожидать, что любые шесть функций
координат ец нельзя принять за компоненты деформации, они
должны для этого удовлетворять некоторым соотношениям. С дру-
другой стороны, если деформации заданы как функции координат и
действительно возможны в сплошном теле, нужно ожидать, что
перемещения точек тела могут быть определены, конечно — с точ-
точностью до перемещения как жесткого целого. В этом параграфе
мы выведем формулы Чезаро, решающие именно вторую задачу,
т. е. задачу определения перемещений по данной деформации.
При этом попутно мы установим те условия совместности, кото-
которым должны удовлетворять заданные компоненты деформации.
Предположим, что перемещение и\ некоторой точки тела
М0(х0) задано, ищется перемещение точки М(х). Соединим точки
Мо и М произвольной кривой, будем обозначать текущие коор-
координаты этой кривой |ь. Величины компонент деформации e{j(^k)
на этой кривой заданы. Предположим на время, что заданы так-
также компоненты тензора вращения (ог;(|й). Считая перемещения
малыми в указанном выше смысле, заметим, что из G.2.7) и
G.2.8) следует
И*, з = вц + (Иц.
Теперь перемещение точки М находится квадратурами
м
Щ = и°г+ J (eik + oift) dlk. G.3.1)
В действительности величины (otj неизвестны и наша задача
будет состоять в том, чтобы преобразовать G.3.1), исключив из
§ 7.3. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПО ДЕФОРМАЦИИ 217
этих формул компоненты вращения. Таким образом, нужно пре-
преобразовать интеграл
м м
= ] (dijd^j, G.3.2)
»о Ч
Положим d\j = —d (Xj — %]). Здесь х$ — координаты точки М,
в которой ищется перемещение. Подставляя в G.3.2) и интегри-
интегрируя по частям, получим
м м
@$j \Xj — Xj) -f- \ (&ijyk \Xj — bj/ ^bft* V' »О»О)
mo Mo
В результате интегрирования по частям в выражении G.3.3)
появились еще три константы co?j в добавление к введенным
ранее величинам и\. В формулах G.3.3) фигурируют не сами
компоненты тензора вращения, а их производные по координа-
координатам. Оказывается, что производные от со# выражаются через
производные от компонент деформации ец с помощью следую-
следующих тождественных соотношений:
(Oi}tk~eihfs—?*j, <• G.3.4)
В справедливости G.3.4) легко убедиться, подставив вместо
е{} и (Oij их выражения G.2.8) и G.2.7). Теперь формулы G.3.1)
переписываются следующим образом:
м
+ ) [tik + (xj — lj) (eik,j — ekjti)] d%k. G.3.5)
Ao
Они решают задачу об определении перемещений по заданной
деформации в том случае, когда интеграл не зависит от пути
интегрирования. Для этого нужно, чтобы подынтегральное выра-
выражение представляло собою полный дифференциал. Это будет в
том случае, если выполняются следующие соотношения:
dk, зш — ем, is — ei8t jk + e8it ik = 0. G.3.6)
Заметим, что условия G.3.6) можно было получить проще,
а именно составляя условия интегрируемости выражения для
компонент тензора (Оц, производные которых заданы формулами
G.3.4). Левая часть уравнения G.3.6) представляют собою тен-
тензор четвертого ранга, но этот тензор обладает высокой степенью
симметрии и он эквивалентен симметричному тензору второго
ранга, подобно тому как антисимметричный тензор второго ран-
ранга эквивалентен вектору. Действительно, условие G.3.6) можно
218 ГЛ- 7« ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
переписать следующим образом:
Sn = г{ктг51пеЫг ш = 0. G.3.7)
Чтобы получить условие G.3.7), следовало бы ввестп вместо
тензора вращения эквивалентный ему вектор, далее представить
тождество G.3.4) с помощью е-тензора и записать условия инте-
интегрируемости этих тождеств как условие равенства нулю ротора
вектора, используя еще раз обозначение соответствующей опера-
операции с помощью е-тензора. Мы не будем следовать этому пути,
а просто проверим, что из 81 соотношения G.3.6) на самом деле
остается только шесть.
Положим i = к = 1, / = s = 2. Получим из G.3.6)
en,22 + e22,ii-2e12,12 = 0. G.3.8)
Два других соотношения первой группы уравнений совместно-
совместности получаются круговой перестановкой индексов. Первое из
соотношений второй группы получим, приняв ? = & = 1, 7 = 2,
5 = 3. Оно будет следующим:
вц, 2з = (е12, з — e3it 2 — е23, i) ,i. G.3.9)'
Два других соотношения получаются также путем круговой
перестановки индексов. При других комбинациях индексов соот-
соотношения совместности G.3.6) выполняются тождественно. Такой
же непосредственной проверкой убеждаемся, что G.3.8) и G.3.9)
следуют из G.3.6).
Тензор Sv, образованный из тензора ем по формулам G.3.7),
называется тензором несовместности. Вообще, можно допустить,
что в теле реализуется такое деформированное состояние, когда
тензор деформации не выражается через вектор перемещений по
формулам G.2.8). Проще всего это можно представить себе сле-
следующим образом. Допустим, что из некоторых механических
соображений нам нужно разделить тензор деформации на две
части, так что е^^е^ + е^. Так, например, е^ может быть тем-
температурной деформацией, тогда как деформации е{$ носят меха-
механический характер. Условию G.3.6) удовлетворяет только сум-
суммарная деформация, тогда как S^ = — S^ Ф 0.
Отметим в заключение следующее тождество:
5«,i = 0. G.3.10)
Действительно, продифференцировав G.3.7) по х$, получим
Последний множитель симметричен относительно индексов
п, /, предпоследний антисимметричен, поэтому свертка их равна
нулю.
§ 7.4. ТЕОРИЯ НАПРЯЖЕНИЙ 219
§ 7.4. Теория напряжений
Пусть на тело, занимающее объем V и ограниченное поверх-
поверхностью S, действуют объемные силы F и поверхностные силы
Т. Это нужно понимать следующим образом. Обозначим через
АР результирующую сил, действующих на элемент объема AV.
Тогда
Аналогично, если обозначить через Аф результирующую сил,
действующих на элемент поверхности AS, то
¦-4SS),
Предположим, что эти пределы существуют. Приводя силы,
действующие на элемент объема или элемент поверхности, к не-
некоторой точке, принадлежащей этому элементу, кроме резуль-
результирующей необходимо вводить также момент AM. Предполагает-
Предполагается, что
(am)
,. (am
lim -ГТ/
\ AV
таким образом, на тело не действуют распределенные по объему
или по поверхности моментные нагрузки.
Запишем уравнение равновесия в форме Лагранжа
j FfiuidV + f Ti&itdS = 0. G.4.1)
V 8
В уравнении G.4.1) фигурируют только внешние силы, следова-
следовательно, оно выполняется не для любых перемещений 8щ а толь-
только для тех, которые не сопровождаются деформацией. Действи-
Действительно, полагая
6и = 6и0 + 6@ х г,
мы получим из G.4.1) шесть обычных уравнений статики для
равновесия абсолютно жесткого тела. В данном случае мы по-
поступим иначе и запишем условие того, что тело не деформиру-
деформируется, следующим образом:
6ец = 4" (К; + КО = 0. G.4.2)
Уравнения G.4.2) можно рассматривать как уравнения связи,
при выполнении которых справедливо G.4.1). Составим урав-
уравнения равновесия при этих условиях как уравнения Лагранжа
первого рода, введем множители Лагранжа, обозначив их (—Оу).
220 ГЛ- 7- °БЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
Применяя обычное правило, получим
ц (&Uij + бщ.д dV = 0. G.4.3)
j
S
Хорошо известно, что множители Лагранжа представляют собою
реакции связей. Соответственно на уравнение G.4.3) можно
смотреть несколько иначе. Первые два члена представляют со-
собою работу внешних сил, объемных и поверхностных. Третий
член есть работа внутренних сил, величины 6б# = i/zFuij+ 8ujti)
представляют собою обобщенные перемещения, а вц — соответст-
соответствующие обобщенные силы. Очевидно, что Оцое^ есть инвариант,
поэтому dj — симметричный тензор второго ранга, который назы-
называется тензором напряжений. Преобразуем третий интеграл в
соотношении G.4.3) интегрированием по частям. Заметим, преж-
прежде всего, что
~2 <*ц (8uitj + 6щл)
вследствие симметрии тензора о«. Теперь запишем
j OijbmrijdS — j OijtfiUidV*
S V
При преобразовании объемного интеграла в поверхностный
использована формула Гаусса — Остроградского, здесь через п
обозначен единичный вектор внешней нормали к поверхности S.
Теперь G.4.3) примет следующий вид:
f (Oijtj + Fi) SuidV - f (ацщ - T{) bu{dS = 0.
V 8
Это соотношение должно выполняться для любых Ьи„ поэтому
oijtj + Fi = 0, xzaV, G.4.4)
ацщ = Ти x<==S. G.4.5)
Формула G.4.5) устанавливает связь между определением тензо-
тензора напряжений оу и тем определением вектора напряжения о,
которое было дано в § 1.7. Действительно, уравнение равновесия
справедливо не только для тела в целом, но для любой части
тела, например, ограниченной поверхностью S, проходящей через
фиксированную точку М и имеющей в этой точке нормаль л*
По формуле G.4.5) получим:
а = OijTijei. G.4.6)
Эта формула выражает вектор <т как линейную вектор-функ-
вектор-функцию вектора пхо чем было сделано замечание в § 1.7. Нормальная
§ 7.5. СВОЙСТВА ПОЛЕЙ НАПРЯЖЕНИЙ II ДЕФОРМАЦИЙ
221
составляющая вектора
оп = on = оцщП]. G.4.7)
Последняя формула совершенно аналогична G.2.6). Если t есть
единичный вектор, лежащий на площадке с нормалью и, то со-
составляющая касательного напряжения по этому направлению
дается формулой
тп* = Oijnjti, G.4.8)
аналогичной G.2.10). Что касается самого вектора касательного
напряжения, величина его определяется следующим образом:
т=]/~а2_а2. G.4.9)
Уравнения G.4.4) называются дифференциальными уравне-
уравнениями равновесия. Заметим, что тензор несовместности Sy удов-
удовлетворяет этим уравнениям при отсут-
отсутствии объемных сил. Из формул G.4.7)
и G.4.8) непосредственно усматри-
усматривается механический смысл компонент
тензора напряжений. Полагая в G.4.7)
щ = 1? п2 = щ = 0, найдем, что аи есть
нормальное напряжение на площадке,
нормальной к оси 1; аналогично опре-
определяются а22 и 0зз. Полагая в G.4.8)
Рис. 7.4.1
найдем, что Gi2 есть касательное напря-
напряжение на площадке 1 в направлении
оси 2 или, вследствие симметрии тен-
тензора ау, касательное напряжение на
площадке 2 в направлении оси 1
(рис. 7.4.1). Из симметрии выражения G.4.8) вытекает следую-
следующий результат, который иногда называют законом парности
касательных напряжений: касательные напряжения на двух пер-
перпендикулярных площадках, действующие по нормалям к линии
их пересечения, равны между собою. Мы будем избегать слова
«закон» применительно к тривиальному следствию из условия
симметрии соответствующего тензора.
§ 7.5. Некоторые свойства полей напряжений и деформаций
В этом параграфе будут рассмотрены некоторые следствия,
вытекающие из определения симметричного тензора второго ран-
ранга в трехмерном и двумерном пространстве и оказывающиеся
полезными при формулировке механических теорий. Для опре-
определенности мы будем везде говорить о тензоре напряжений, хотя
те же самые результаты без всяких изменений переносятся на
тензор деформации, тензор инерции п т. д.
222 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
а. Инварианты, главные оси и главные значения тензора.
Применяя соображения пункта (и) § 7.1 к тензору напряжений,
мы убеждаемся в том, что уравнение для определения главных
значений будет
Здесь /3 = detlloijll, h и Д — суммы главных миноров второго и
первого ранга соответственно, /4 = Оц. Корни этого уравнения
условимся нумеровать в порядке убывания, так что
Oi ^ 02 ^ 0з.
Иногда мы будем отступать от этого правила, делая каждый
раз соответствующую оговорку. Заметим, что
h = (Ti + 02 + 0з, /2 = 0102 + 0203 + 0301, h = 010203. G.5.1)
Механический смысл приведения тензора напряжений к глав-
главным осям состоит в следующем. Около каждой точки напряжен-
напряженного тела можно выделить такой элемент в виде бесконечно
малого прямоугольного параллелепипеда, что на грани его дей-
действуют только нормальные напряжения 0Ь 02 и 03. Перефразируя
этот результат применительно к тензору деформаций, мы можем
утверждать существование такого бесконечно малого прямоуголь-
прямоугольного параллелепипеда, ребра которого удлиняются или укорачи-
укорачиваются в отношениях 1 + еи 1 + е2, 1 + ^з, но прямые углы оста-
остаются прямыми. Для инвариантов, представляющих собою коэф-
коэффициенты соответствующего кубического уравнения, сохраняются
формулы G.5.1) с заменой 0* на et.
С другой стороны, систему инвариантов тензора напряжений
можно построить по общему правилу, путем последовательного
свертывания тензорных произведений
Si = Си, 2ц = GijGij, Sin =
В главных координатах
2i = o1 + o2 + oai 2ц = о\ + а\ + aj, 2Ш = о? + о? + о5.
Инварианты Si и It просто совпадают, вообще инварианты одной
системы выражаются через инварианты другой системы по фор-
формулам, которые были приведены в пункте (л) § 7.1.
б. Главные касательные напряжения. По формуле G.4.9), ис-
используя G.4.6) и G.4.7), найдем
G.5.2)
Экстремальные значения касательного напряжения, рассмат-
рассматриваемого как функция rti, называются главными касательными
напряжениями. Уравнение G.5.2) выражает т2 через три направ-
§ 7.5. СВОЙСТВА ПОЛЕЙ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 223
ляющих косинуса п*, которые связаны известным соотношением
Таким образом, нужно решать задачу об отыскании экстре-
экстремума с дополнительным условием. Напомним, в чем состоит ме-
метод Лагранжа для решения подобных задач. Если требуется
отыскать экстремум функции Р(щ) при дополнительном условии
Ф(цг) = 0, то ищется обычным способом экстремум функции
F + ХФ, т. е. составляются уравнения
Присоединяя сюда условие Ф(щ) = 0, получаем систему урав-
уравнений, достаточную для нахождения неизвестных щ и Я. В на-
нашем случае роль функции F играет т2, определенное формулой
G.5.2), а функция Фв= п\+ п\ + nl— 1. Дифференцируя т2 по пи
получим
§? = 2аЛ [A - 2nl) о, - 2п22а2 - 2nlo3].
Используя формулу G.4.7), перепишем это выражение сле-
следующим образом:
Продифференцируем теперь дополнительное условие. Получим
дФ 9„
Производные по nt и п2 выражаются совершенно аналогичным
образом. В результате мы придем к следующей системе урав-
уравнений:
п1[о21-[2о1о]+Х] = 01
0, G.5.3)
Очевидное решение системы G.5.3) есть
rii = 1, п2 = п3 = 0.
При этом а = а4, из первого уравнения Я = а\, два другие
удовлетворяются тождественно. Аналогично можно было принять
М2 = 1 и w3 = l. Эти решения тривиальны, на главных площадках
касательное напряжение равно нулю, а для положительной вели^
чины т2 нулевое значение будет экстремальным.
224 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
Предположим теперь, что щ и п2 отличны от нуля, сократим
на эти множители в двух первых уравнениях и вычтем одно из
другого. Получим
<*i — о\ — 2 (ах"—;аа) а = 0.
Отсюда
2
Сравнивая с G.4.7), находим
л? = и! = 1/2, щ = 0.
Третье уравнение при этом выполняется. Соответствующая пло-
плоскость, в которой действует экстремальное касательное напря-
напряжение, проходит через ось х3 и делит пополам угол между плос-
плоскостями 13 и 23. По формуле G.5.2) вычислим это касательное
напряжение
Аналогично
о — а а — а
Т23 о > 131 — о
Знаки в этих формулах могут быть заменены на обратные.
Совершенно аналогичным образом определяются главные
сдвиги:
в теории деформаций.
в. Плоское напряженное состояние (плоская деформация).
В общем трехмерном случае компоненты тензора напряжения или
деформации преобразуются по формуле
G.1.4). Если Озз = 03а = 0, формулы
преобразования компонент симметрич-
симметричного тензора в двумерном пространст-
пространстве могут быть представлены в чрезвы-
чрезвычайно простом виде; некоторое графи-
графическое построение позволяет сделать
эти формулы наглядно очевидными и
избавить от необходимости запомина-
запоминания их или обращения к учебнику каж-
Рис. 7.5.1 дый раз, когда в них возникает необ-
необходимость. Предположим, что плоское
напряженное состояние задано главными напряжениями, глав-
главные оси обозначим gi и ?2. Выберем пару взаимно ортогональ-
ортогональных векторов п и и', как показано на рис. 7.5.1. Проекции их
на оси ?4 и ?2 будут следующие:
пх = cos a, n2 = sin а,
пх = — sin а, п2 = cos а.
§ 7.6. КРУГОВАЯ ДИАГРАММА МОРА
225
Нормальное напряжение на площадке п по формуле G.4.7)
ап = аг cos2 а + а2 sin2 а = * 2 2 + * 2 2 cos 2a. G.5.4)
Нормальное напряжение на площадке п'
о'п = аг sin2 а+ а2 cos2 а.
Касательное напряжение на любой площадке п по формуле
G.4.8)
G — CL
G — CL
Тя = — (стх — cr2)sin a cos а = ^""^ sin 2а- G.5.5)
Направим ось ^i по и, ось #2 по п' и перепишем предыдущие
формулы следующим образом:
G.5.6)
¦°г 2 °2 sin 2a.
§ 7.6. Круговая диаграмма Мора
Формулы G.5.4), G.5.5) допускают очень простую геометри-
геометрическую интерпретацию (О. Мор, 1882). Выберем две взаимно
перпендикулярные оси, назовем горизонтальную ось осью а, вер-
вертикальную—осью т (рис. 7.6.1). Вектор напряжения на любой
r
A
V
\
1
Л
V
r
2/
1
/
/
- ^
Рис. 7.6.1
Рис. 7.6.2
площадке с нормалью и, заданный величинами оп и тп, изобра-
изображается точкой в плоскости а, т. Будем обозначать эту точку
буквой л, так же как и нормаль к площадке, на которой дей-
действует напряжение. При переходе от одной площадки к другой
15 ю. Н. Работнов
226 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
меняется направление нормали, т. е. угол а, и изображающая
точка в плоскости а, т описывает замкнутую кривую. Формулы
G.5.4), G.5.5) задают параметрическое уравнение этой кривой,
представляющее собою окружность. Центр ее находится на оси о
в точке с абсциссой (g! + g2)/2, радиус равен (d — о2)/2. Для
построения этой окружности следует построить на оси а точки 1
с абсциссой Gi и 2 с абсциссой а2. На отрезке 1—2 как на диа-
диаметре строится окружность, называемая кругом Мора*). Сле-
Следует запомнить простое правило: если угол между нормалями
к площадкам есть а, то дуга между точками круга Мора, изо-
изображающими напряжения на этих площадках, измеряется углом
2а, отсчитываемым в противоположном направлении. Так, на
рис. 7.5.1 угол а от оси ^ к нормали п отсчитывается против
часовой стрелки, дуга 2а на рис. 7.6.1 от точки 1 к точке п
берется по часовой стрелке. Напряжение на площадке п\ со-
составляющей с площадкой п угол, равный л/2, изображается на
диаграмме точкой, диаметрально противоположной точке /г.
Круговую диаграмму можно построить и тогда, когда заданы
напряжения аар в неглавных осях координат. Построим точку хх
с координатами аи и а12 и точку х2 с координатами а22 и —а!2,
как показано на рис. 7.6.2. На отрезке, соединяющем эти точки,
как на диаметре, построим окружность. Центр ее будет лежать
на оси а на расстоянии (аи + а22)/2 от начала координат. Поме-
Пометим индексами 1 и 2 точки пересечения окружности с осью а,
дуга l#i измеряется углом 2а, направление главной оси номер 1
получим, откладывая угол а от оси х{ в противоположном на-
направлении.
Радиус круга равен (at — a2)/2, он представляет собой гипо-
гипотенузу заштрихованного треугольника. Отсюда следует
u - °ггУ + *&• G-6.1)
При выборе знака перед радикалом учтено, что о4 > а2. Теперь
получаем следующие формулы для главных напряжений:
ai.« = ^Р ± -у /(a11-ai8)« + 4a1ii. G.6.2)
-у
Из этого же треугольника видно, что
tg2a=^l^. G.6.3)
ail"~G22
Последняя формула определяет угол 2а с точностью до слагае-
слагаемого, равного л; пэтому для а получаются два значения, раз-
разнящиеся на л/2. Таким образом, мы находим сразу два угла
at и а2 между осью Xi и осями 1 ж 2 соответственно и не можем
*) Терминологическая неточность, ставшая традицией.
§ 7.7. РАЗЛОЖЕНИЕ ТЕНЗОРА НА СОСТАВЛЯЮЩИЕ
227
сделать выбор между ними. Поэтому более удобны следующие
формулы, вытекающие из рассмотрения треугольников 2х{М
или xJM:
tg a = ^i2_ = gi-gn. G.6.4)
ull w« 12
Из рассмотрения круга Мора сразу ясно, что касательное
напряжение достигает наибольшего по абсолютной величине зна-
значения на площадках, составляющих
с главными площадками угол я/4.
На круговой диаграмме им соответ-
соответствуют точки р и д. Величина этого
касательного напряжения равна
(Ot — а2)/2, как было показано в § 7.5.
Очевидно, что точно такая же
диаграмма будет изображать тензор
двумерной деформации. Если зада-
задано трехосное напряженное состоя-
состояние Gi ^ <т2 ^ 0з, круговую диаграмму
Мора можно построить для трех
плоскостей 12, 23 и 13, как показано
на рис. 7.6.3. Наружный круг проходит через точки (о4,0) и (а,, 0)
Плоскости ат и заключает внутри себя два других круга. Можно
показать, что для всех площадок, ориентированных произвольным
образом, точки, изображающие напряженные состояния, будут
находиться в заштрихованной области. Доказательство будет
приведено в § 19.2, где этот факт понадобится.
Рис. 7.6.3
§ 7.7. Разложение тензора на девиаторную
и гидростатическую составляющие
По-прежнему для определенности будем вести речь о тензоре
напряжений, хотя теория распространяется на любые симмет-
симметричные тензоры второго ранга. Положим
2л = <?« = 3a.
G.7.1)
Величина а, а также тензор o6zi называется гидростатической
составляющей тензора напряжений, а разность
Oij = Gij — GO у ( 7. /. ^ )
называется девиатором тензора напряжений. Девиатор не меня-
меняется от приложения всестороннего растяжения или сжатия. Дей-
Действительно, если дополнительно приложено гидростатическое дав-
давление /?, ТО CT$j = G^ — P&ijj СУ' = G — рг Gij = G\j.
228 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
Совершенно аналогично определяется девиатор тензора де-
деформаций. Здесь
Зе = Е1 = вн
представляет собою относительное изменение объема при дефор-
деформации. Первый инвариант девиатора вследствие определения
тождественно равен нулю
Второй инвариант девиатора определяется следующим об-
образом:
Отсюда следует:
= 2п-т2! = 2п-3«'. G.7.3)
Точно так же, опуская элементарный вывод, запишем
У - У - У У - - У3 G 7 4)
Если представить величину 2п через главные напряжения,
мы получим
Простое и наглядное истолкование этой величины можно полу-
получить следующим образом. Вычислим напряжение на площадке,
равнонаклонной ко всем трем главным осям. Будем называть
эту площадку октаэдрической, а действующие на ней напряже-
напряжения октаэдрическими напряжениями. Для октаэдрической пло-
площадки ni = n2 = n3 = 1/УЗ. По формуле G.4.7)
По формуле G.4.9)
то = 4" [<а1 - а^2 + (°* - азJ + <аз - ахJ]172- G.7.5)
Таким образом,
Ни = Зт^. G.7.6)
Величину октаэдрического сдвига мы определим по формуле
То = -§- К*! - e%f + (е2 - ezf + (еа - е^]^. G.7.7)
§ 7.7. РАЗЛОЖЕНИЕ ТЕНЗОРА НА СОСТАВЛЯЮЩИЕ
229
Поэтому
G.7.8)
Разница между формулами G.7.5) и G.7.7) связана с тем, что
компонентами тензоров являются касательные напряжения и по-
половины сдвигов, значит величина т0
соответствует уо/2. Итак, нормальное
и касательное напряжения на октаэдри-
октаэдрической площадке представляют пер-
первый инвариант тензора напряжений и
второй инвариант девиатора наиболее
простым и естественным образом.
Отметим еще одно истолкование
величины второго инварианта девиато-
девиатора тензора напряжений, принадлежа-
принадлежащее В. В. Новожилову. Вычислим сред-
среднее квадратичное значение касательного
напряжения на поверхности сферы. Рис. 7.7.1
Воспользуемся для этого формулой
G.5.2), приняв в ней пг=>х{/г. Вычис-
Вычисляя интеграл \ %2dS, мы встретимся с интегралами двух типов:
Ч-dS.
Очевидное преобразование приводит /t к следующему виду:
Отсюда следует, что
т2 dS = \ 12 [(а, - а2J + (а2 - а3J + (а, - о^J].
Таким образом, октаэдрическое касательное напряжение отли-
отличается от среднего квадратичного касательного напряжения толь-
только множителем, который легко вычисляется, но не будет нам
нужен.
Возвращаясь к октаэдрической плоскости, попытаемся зафик-
зафиксировать не только величину, но и направление октаэдрического
касательного напряжения.
Приложим к телу гидростатическое напряжение с интенсив-
интенсивностью (—а),_ тогда наплавных площадках будут действовать
напряжения oi=*ol — о, 02 = 02 — а, ог = о3 — о, а на октаэдриче-
октаэдрической площадке нормальное напряжение исчезнет, тогда как ка-
касательное сохраняет свою величину т0. Обозначим через E еди-
230 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
ничный вектор направления октаэдрического касательного напря-
напряжения. Рассмотрим равновесие тетраэдра, заключенного между
главными плоскостями и октаэдрической плоскостью (рис. 7.7.1).
Обозначим со площадь грани, принадлежащей октаэдрической
плоскости. Тогда площадь каждой из остальных граней будет
равна (о/УЗ. Из уравнений равновесия находим
Направление вектора р можно задать с помощью угла между
ним и некоторым фиксированным направлением в октаэдриче-
октаэдрической плоскости. Проведем, например, луч из центра октаэдриче-
октаэдрической грани в точку пересечения ее с главной осью 2, направле-
направление этого луча зададим с помощью единичного вектора к. По-
Положим
pfe = cosft.
Из очевидного геометрического рассмотрения следует:
Тл 2 7 7 L-
Теперь составляющие вектора р найдутся из следующих урав-
уравнений:
Pi + pJ + Pl^l, р! + Р2 + Р3 = 0, 2р1-р2-р3= /6cos*.
Первое уравнение есть условие нормирования, второе выра-
выражает тот факт, что вектор C лежит в октаэдрической плоскости,
наконец, последнее выражает условие Р& = cos О.
Решая эти уравнения относительно р4, найдем
Повернув вектор к на угол 2л/3 против часовой стрелки, т. е.
направив его в точку пересечения октаэдрической плоскости с
осью 2, мы найдем величину [}2 по совершенно аналогичной
формуле, поэтому
и, аналогично
Теперь мы можем написать следующие формулы для трех главных
§ 7.8. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 231
напряжений:
x0 cos (о - ^), G.7.9)
Угол Ф называется углом подобия девиатора тензора напряже-
напряжений. Величины о, То и Ф могут быть приняты за систему инва-
инвариантов тензора напряжений, величину Ф легко связать с тре-
третьим инвариантом девиатора. Действительно, в главных осях
2яп = К — °зK + (<*2 ~ <*iK + (аз— <*2K-
Подставляя сюда G.7.9), получим
Заметим, что формулы G.7.9) по существу представляют
собою форму представления решения кубического уравнения с
коэффициентами /4, /2, /3; это решение было известно давно вне
связи с теорией симметричных тензоров второго ранга.
§ 7.8. Общие криволинейные, цилиндрические
и сферические координаты
Вся приведенная выше теория напряжений и деформаций
сохраняется и при пользовании произвольной криволинейной, не
обязательно ортогональной системой координат. В качестве ба-
базисных векторов принимают производные от радиуса-вектора
точки по криволинейным координатам 0* = г^, по отношению
к этому базису вектор или тензор задаются контравариантными
компонентами. По отношению к взаимному базису векторы и
тензоры задаются ковариантными составляющими.
Формулы G.2.3) и G.2.8) сохраняют силу:
1
егз == у
ИЛИ
ti — 2
но теперь индексы после запятой обозначают ковариантное диф-
дифференцирование
Если вектор перемещения и тензор деформации задаются нова-
232 ГЛ 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
риантными составляющими, тензор напряжения следует задавать
контравариантными составляющими, для того чтобы в третьем
интеграле уравнения G.4.3) под интегралом был инвариант о*3ец.
Теперь уравнения равновесия G-4.4) примут вид
а граничные условия G.4.5)
Ковариантное дифференцирование контравариантного тензора
производится по правилу
c:> = ^ + lV'" + lV3. G.8.2)
Напоминаем определение символов Кристоффеля второго ро-
рода. Если ga — метрический тензор, это значит, элемент дуги
имеет вид
ds2 = gijdx* dx\
то
Г* -Г ai$ V — * (dghs 4- д8** dgk>\ /7Я^
Tkj - Th}Sg , Tkjs - T y—f + —h- —y G.8.3)
При определении символов Кристоффеля второго рода часто бы-
бывает более удобно пользоваться непосредственно геометрическими
соображениями, связанными с формулами дифференцирования
базисных векторов
а?
Именно так удобно поступать в случае декартовых или сфери-
сферических координат.
Последнее замечание в этой связи будет относиться к тому
случаю, когда криволинейные координаты ортогональны. Вместо
естественного базиса ek = rtk, векторы которого имеют разную
длину и, вообще, разную размерность, бывает удобно восполь-
воспользоваться местным базисом, образованным единичными векторами
h — eklVgkk (не суммировать). Тогда «физические» компоненты
вектора или тензора, т. е. компоненты по отношению к локаль-
локальной декартовой системе координат, определяются следующим
образом:
(не суммировать).
Имея дело со столь простыми системами координат, как ци-
цилиндрическая или сферическая, можно проделать всю намечен-
§ 7.8. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 233
ную выше цепочку выводов. В элементарных руководствах
обычно приходят к цели более коротким путем — выделяют бес-
бесконечно малый элемент, сообщают ему перемещение и находят
деформации, прикладывают к его граням напряжения и состав-
составляют уравнения равновесия. Предлагая читателю сделать соот-
соответствующий вывод формул тем или иным способом самостоятель-
самостоятельно, приведем здесь лишь окончательные результаты. Физические
компоненты векторов и тензоров мы будем отмечать не цифро-
цифровыми индексами, а буквенными нижними индексами, соответ-
соответствующими обозначениям криволинейных координат. Одноимен-
Одноименные индексы удваиваться не будут.
а. Цилиндрические координаты ds2 = dr2 + dz2 + r*dQ2. Форму-
Формулы для компонент тензора деформации:
» -д?± * -± (dUr л ди*)
вг ~ дг' ев ~~ г дв ~*~ г ' €г ~~ dz' вгг ~ 2 [dz + IF
1 / 1 ди ди0 иЛ 1 (duQ i диЛ G.8.4)
Дифференциальные уравнения равновесия:
dGrQ I dGQ dGQz ,2
darT 4 доЙТ да. 4
б. Сферические координаты ds2 ^dr^ + r2 sin2 Ф dtp2 +
Компоненты деформации:
диг 1 дМф иг А а Mfr 1 ^иф
1 / 1 диг и$ д\
Дифференциальные уравнения равновесия:
1 fZi<p , JL
r sin© Зф + г
*Ч , 1 ^°
G.8.7)
1 * ,
T1F н
234 ГЛ- 7- ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
§ 7.9. Геометрически нелинейные задачи
Откажемся от ограничения малостью компонент тензора по-
поворота, которое до сих пор всюду принималось. Теперь мы долж-
должны пользоваться нелинейными выражениями G.2.3) для ком-
компонент тензора деформации. Введем опять напряжения как мно-
множители Лагранжа и составим уравнение равновесия, совершенно
аналогичное уравнению G.4.3), а именно,
J TfiUidS - -у j <*ifi(UU + Щл +
S
или
4" Ja« Fгг*'>*+ 8им + ^w^w + M« bUk^ dV
Выражение
может быть записано в виде
( G.9.2)
Аналогично
Заменяя обозначение немого индекса и используя симмет-
симметрию тензора ац, находим, что это второе выражение равно пер-
первому, т. е. G.9.2). Поэтому условие равновесия G.9.1) можно
переписать следующим образом:
J FfiutdV + j TfiuidS - j aw (вм + икЛ) 8uktjdV = 0.
V S
Преобразуя третий интеграл путем интегрирования по частям
и приравнивая нулю выражения, стоящие под знаком объемного
и поверхностного ицтегралов, получим уравнения равновесия
[М6м + им)Ь = ^ G.9.3)
и условия на поверхности
[Мбм + ИА,,)]/1,=-Гк. G.9.4)
Для того чтобы составить уравнения G.9.3) и G.9.4), необхо-
необходимо заранее знать перемещения uk или же располагать уравне-
уравнениями связи трех перемещений с деформациями и суметь ис-
исключить компоненты поворота, так как
uk, i=*eki + ©M.
Соответствующая задача механики становится нелинейной.
§ 7.9. ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНЫЕ ЗАДАЧИ 235
В принципе можно было бы подойти к составлению уравнений
равновесия в теле, претерпевающем конечную деформацию, иным
способом. Если метрический тензор до деформации был ga, то
после деформации он станет gy. Тензор конечной деформации в
общем случае можно определить так:
При этом тензор вц можно относить как к начальному базису,
так и к базису в деформированном пространстве. Это не одно
и то же, поскольку переход к контравариантным и смешанным
компонентам будет производиться по-разному. Далее можно оп-
определить контравариантные компоненты тензора напряжений в
деформированном теле и написать уравнения равновесия обыч-
обычным способом
о^ + Р1 = 0.
Но здесь при вычислении ковариантных производных нужно ис-
использовать символы Кристоффеля, вычисленные для деформиро-
деформированного тела, и составляющие вектора F1 брать по отношению
к базису, связанному с деформированной координатной сеткой.
Таким образом, все трудности остаются, не будучи написанными
в явном виде. В этом смысле уравнения G.9.3) и G.9.4) кажут-
кажутся проще, они относятся к декартовой системе координат, не де-
деформирующейся с деформацией тела. Компоненты тензора напря-
напряжений также сохраняют механический смысл, это — обобщен-
обобщенные силы, соответствующие обобщенным перемещениям ег>
ГЛАВА 8
ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
И ПРОСТЕЙШИЕ ПРИМЕРЫ
§ 8.1. Упругое тело
Будем называть упругим телом такое тело, у которого на-
напряжение в каждой точке есть однозначная функция деформации
о» = (рц{екп). (8.1.1)
Назовем путем нагружения или соответственно путем деформи-
деформирования процесс изменения тензора напряжений или тензора
деформаций в зависимости от некоторого монотонно возрастаю-
возрастающего параметра, который мы назовем «временем». На самом
деле реальное время при определении модели упругого тела
никакой роли не играет; употребляя этот термин мы говорим
лишь о последовательности событий, но не о их временной про-
протяженности. Для наглядности тензор напряжений или тензор
деформаций можно изображать векторами, составляющие кото-
которых равны компонентам соответствующих тензоров. Положим,
например,
$1 = Gil, Sz = 022, Ss = G33, S4 = 02S, Si = 031, Sq = 012,
(8.1.2)
Тогда векторы о и в служат изображением тензоров напряже-
напряжений и деформаций в шестимерных пространствах напряжений и
деформаций соответственно. Впоследствии будет выяснено, поче-
почему в качестве е4, ^ь и eQ выбраны удвоенные компоненты тензора
еу. Такое изображение не единственно; с одной стороны, можно
было бы ввести не шестимерное, а девятимерное пространство,
если не обращать внимание на симметрию тензоров Сц и e{i,
обозначать, скажем, о12 и 02i как разные компоненты вектора о
и не умножать ец (i^j) на два. С другой стороны, нужно пом-
помнить, что представление тензора в виде вектора имеет лишь
ограниченный смысл и пригодно только для определенной фик-
фиксированной системы отнесения; формулы преобразования компо-
компонент вектора и компонент тензора при изменении осей коорди-
координат различны, поэтому, отнеся тензор напряжений или дефор-
§ 8.1. УПРУГОЕ ТЕЛО 237
маций к новым осям координат, мы получим совершенно другой
изображающий вектор. Вместо того, чтобы изображать напря-
напряженное и деформированное состояние шестимерными векторами,
мы могли бы ограничиться трехмерными пространствами, приняв
эа составляющие соответствующих векторов главные напряжения
и главные деформации. Формулировка общих закономерностей,
связывающих напряжения и деформации, для главных значений
соответствующих тензоров представляется наиболее простой и
естественной, если материал изотропен (см. § 1.11). Если мате-
материал анизотропен, преимущества такого представления утрачи-
утрачиваются.
Путь деформирования или путь нагружения, таким образом,
могут быть представлены как кривые, описываемые концами
векторов о и е в соответствующих пространствах. Закон упруго-
упругости, т. е. уравнения (8.1.1) устанавливают, в частности, что
замкнутому пути деформирования соответствует замкнутый путь
нагружения и наоборот.
Рассмотрим теперь такой класс упругих материалов, для ко-
которых работа, произведенная над элементарным объемом в зам-
замкнутом цикле по деформациям или напряжениям, равна нулю.
В классической литературе именно это определение принималось
за определение упругого материала; в современных руководствах
по отношению к ним применяется термин «гиперупругие». Со-
Сохраняя обычную терминологию, мы сохраним название «упругие»
тела для таких тел, к которым относится не только первое ус-
условие, сформулированное в начале, но также требование отсут-
отсутствия немеханических потерь энергии или, наоборот, необходи-
необходимости привлечения немеханической энергии извне при деформи-
деформировании. В § 7.4 было выписано выражение для вариации работы
внутренних сил на возможных вариациях деформаций; если ва-
вариации деформаций заменить их действительными приращения-
приращениями, мы получим элементарную работу внутренних сил на единицу
объема или изменение упругой энергии. Предположение о «ги-
«гиперупругости» исключает влияние термических эффектов. Итак,
изменение внутренней энергии равно
dU = Gijdea = skdeh.
Представление в форме скалярного произведения векторов в ше-
шестимерном пространстве и потребовало обозначений ?4 = 2е23, ...,
в девятимерном пространстве было бы просто е4 = в23. Условие
равенства нулю работы на произвольном замкнутом цикле будет
следующим:
j)dU = j)skdek = 0.
Для этого необходимо, чтобы подынтегральное выражение
238 гл-8- теория упругости, общие уравнения
представляло собой полный дифференциал, следовательно,
dU
Итак, упругая энергия U есть функция от компонент деформа-
деформации и = и(ец) и закон упругости принимает следующий вид;
а, = |^. (8.1.3)
Мы предположим, что соотношения (8.1.3) однозначно разре-
разрешимы относительно еу. С помощью преобразования Лежандра
эти обратные соотношения можно представить при помощи фор-
формул, аналогичных (8.1.2). Если и(вц) служпт потенциалом на-
напряжений, то потенциал деформаций или дополнительная работа
определяется следующим образом (см. § 2.8):
ФЫ = ог^-[/. (8.1.4$
Отсюда следует:
*i> = WZ- (8-1-5)
Происхождение термина «дополнительная работа» было разъяс-
разъяснено в § 2.8.
Требование однозначной разрешимости уравнений (8.1.3) от-
относительно деформаций эквивалентно условию выпуклости по-»
верхностей и(ец) = const в пространстве деформаций или поверх-
поверхности Ф(оц) = const в пространстве напряжений. Действительнее
соотношение (8.1.3), например, означает, что вектор о направлен
по нормали к поверхности U = const. Если эта поверхность
строго выпукла, то заданному направлению нормали соответ-
соответствует лишь одна точка поверхности. Однако требование стро-
строгой выпуклости может быть смягчено, достаточно потребовать
лишь невогнутости соответствующей поверхности. Например,
если упругий материал несжимаем и изотропен, то приложение
к нему гидростатического давления не вызывает деформации.
Наоборот^ если задана деформация, то напряженное состояние
определяется не единственным образом, а лишь с точностью до
гидростатической составляющей.
§ 8.2. Закон Гука
Опыт показывает, что, если деформации малы и тело упруго,
то соотношения (8.1.1) линейны, это значит
Оц = Етеы (8.2.1 J
и обратно
eti = Птоы. (8.2.2)
Тензор четвертого ранга Ет будем называть тензором модулей
§ 8.2. ЗАКОН ГУКА 239
упругости, а тензор Пуы — тензором упругих податливостей.
Вследствие (8.1.3) и (8.1.5)
dehl ~ de.f dakl do.f
поэтому тензоры Ет и Hijki симметричны относительно первой
и второй пар индексов
Ецы = ЕШь Нт = nfezfj. (8.2.3)
Из симметрии тензоров Оу и ец следует, что тензоры модулей и
податливостей не меняются при перестановке индексов i и /,
к и I. В результате оказывается, что из 81 компоненты тензора
четвертого ранга в трехмерном пространстве различными оста-
остаются лишь 21 компонента. Соответствующие потенциалы имеют
следующий вид:
U = -j Ете&ки Ф - 4" иаиР&м- (8-2-4)
Заметим, что для линейно-упругого тела по теореме Эйлера об
однородных функциях
е 2и'
поэтому из формулы (8.1.4) следует
и введение термина «дополнительная работа» не вызывается не-
необходимостью, функция Ф есть та же упругая энергия С/, но
выраженная через напряжения. Тем не менее в дальнейшем, во
избежание путаницы, мы будем сохранять принятую ранее тер-
терминологию и раздельные обозначения для функций Ф и U.
Материал, свойства которого одинаковы для образцов, выре-
вырезанных в любом направлении, называется изотропным. Более
точно, это определение изотропии относится к весьма малым
образцам, вырезанным в окрестности одной и той же точки. Изо-
Изотропный материал может быть неоднородным, т. е. упругие свой-
свойства его могут меняться от точки к точке. Очевидно, что потен-
потенциал напряжений или упругая энергия изотропного тела не
должен меняться при изменении осей координат, поэтому он
должен выражаться через инварианты тензора деформаций. Един-
Единственная однородная квадратичная форма, составленная из этих
инвариантов, зависит от двух констант и выражается следующим
образом:
. (8.2.5)
Модули X и \х называются упругими постоянными Ламе, они
240
ГЛ. 8. ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
полностью описывают упругие свойства изотропного тела. Пред-
Представим выражения для Е\ и Ец следующим образом:
Ej = егг = 6ij^ij, F\ =
Таким образом, (8.2.5) принимает вид
euehl.
Сравнивая с (8.2.1), находим
(8.2.6)
Очевидно, что выражения (8.2.6) для модулей упругости изо-
изотропного тела сохраняют свой вид для любой системы коорди-
координат, поскольку тензор Кронекера при изменении системы коор-
координат не меняется.
В общем случае модули упругости Еци и податливости Um
преобразуются по формулам преобразования тензора четвертого
ранга
Eijhi = Epqrsnivnjqnkrnis. (8.2.7)
Здесь nip — направляющие косинусы оси х\ по отношению к осям
хр (или наоборот, оси хР по отношению к осям х%, вследствие
высокой степени симметрии тензора Epqra это безразлично).
Часто оказывается, что анизотропное тело обладает известной
симметрией строения. Это относится, прежде всего, к кристал-
кристаллам, к композитным материалам регулярного строения, к биоло-
биологическим объектам типа древесины или кости. Используя свой-
свойства симметрии, можно выбрать такую специальную систему
координат, для которой некоторые компоненты тензора модулей
упругости обращаются в нуль или становятся тождественно рав-
равными между собой, и общее число упругих констант оказывается
меньше чем 21.
Представим совокупность модулей упругости в виде симмет*
ричной матрицы следующим образом:
Е
mi
F F
1122 1133
F F
2222 ^2233
F
^3333
2223
3323
231
тр
3331
212
312
•^
2323 ^2331 2312
^3112
^1212
Плоскость х{х2 называется плоскостью упругой симметрии тогда,
когда вид упругого потенциала не меняется при замене коор-
§ 8.2. ЗАКОН ГУКА
241
динат: хг = хг, х2= х2, х3= — х3. Плоскость симметрии сущест-
существует, когда любому структурному элементу соответствует точна
такой же структурный элемент, расположенный симметрично от-
относительно плоскости XiX2. Так, базисные плоскости кристаллов
с кубической или гексагональной решеткой будут плоскостями
упругой симметрии. При указанной замене координаты компо-
компоненты перемещения щ и и2 остаются неизменными, тогда как и*
меняет знак, становясь и3 = — и3. Индексы при обозначениях
Ецы соответствуют индексам перемещений и координат, по кото-
которым производится их дифференцирование. Производные от щ и
и2 по Хз меняют знак на противоположный так же, как производ-
производная от щ по Xi и хг. Но производная и3г3, а следовательно,
деформация е33 знака не меняет. Для того чтобы упругий по-
потенциал не изменился при указанной замене координат, нужно,
чтобы из выражения его выпали члены, меняющие знак и, сле-
следовательно, те модули, в обозначении которых индекс 3 исполь-
используется один или три раза, должны обратиться в нуль. Матрица
модулей получается следующей:
122
^2222
E.
1133
^2233
3333
0
0
0
0
0
0
Е„п„~
^1112
^2212
P
3312
0
^2323
3131
1212
Итак, при наличии одной плоскости упругой симметрии число
упругих постоянных уменьшается до тринадцати.
Если плоскость XiX3 также представляет собою плоскость
упругой симметрии, то обращаются в нуль те модули, в обо-
обозначениях которых индекс 2 встречается один или три раза.
Заменяя в предыдущей матрице соответствующие элементы ну-*
лями, получим следующую матрицу:
^1122
^2222
1133
2233
3333
0
0
0
р
2323
0
0
0
0
0
0
0
0
0
^1212
Теперь число упругих постоянных стало равно девяти. Заме-
Заметим, что те модули, в обозначениях которых индекс 1 встреча-
встречается один или три раза, также обратились в нуль. Это значит,
что если в теле имеются две взаимно ортогональные плоскости
упругой симметрии, то третья ортогональная к ним плоскость
будет также плоскостью упругой симметрии. Тело, имеющее три
16 Ю. Н. Работнов
242 rJL 8- теория упругости, общие уравнения
плоскости упругой симметрии и характеризуемое девятью упру-
упругими постоянными, называется ортотропным телом. Для обозна-
обозначения упругих констант анизотропного тела в физике кристаллов
обычно применяется не четырехиндексная система, а двухин-
дексная, основанная на соответствии, устанавливаемом форму-
формулами (8.1.2), а именно:
Si^Cifr, ei = cv\i (8.2.8)
Модули упругости Су и податливости с^1 образуют матрицы 6X6,
симметричные вследствие существования потенциала. Таким об-
образом, число упругих постоянных равно 21.
Необходимо подчеркнуть, что число упругих постоянных, фи-
фигурирующих в законе Гука, сокращается лишь тогда, когда
плоскости симметрии приняты за координатные плоскости. В дру-
других системах координат по-прежнему уравнения будут содержать
двадцать одну константу, которые выражаются через девять не-
независимых констант формулами (8.2.7).
§ 8.3. Закон Гука для изотропных тел
В приложениях часто пользуются формой записи закона Гука,
отличной от той общей формы, которая была сообщена в § 8.2,
и выбирают в качестве упругих констант некоторые комбинации
из введенных выше, которые делают формулы более удобными
или оказываются более доступными для непосредственного экс-
экспериментального определения.
Изотропное тело. Полагая Ег = Зе = 6, запишем уравнения
(8.2.1) для изотропного тела с учетом (8.2.6) в следующем виде:
oij = X06ti + 2[ieii. (8.3.1)
Если нужно записать эти уравнения разрешенными относитель-
относительно eih то бывает удобно, вместо постоянных Я и (i, воспользо-
воспользоваться так называемыми техническими постоянными
Теперь результат обращения (8.3.1) запишется следующим об-
образом:
Ч($) (8Л2)
Чтобы выяснить смысл постоянных Е и v, перепишем урав-
уравнения (8.3.2), отказавшись от последовательного сохранения тен-
тензорной формы. Для этого подставим вместо о его выражение.
§ 8.3. ЗАКОН ГУКА ДЛЯ ИЗОТРОПНЫХ ТЕЛ 243
Получим
*11 = Y 1а11 — V (а22 + <*3з)] , • • • » Vl2 = 2*12 = J а12» • • • (8.3.3)
Из формул (8.3.3) видно, что Е — модуль упругости, a v —
коэффициент Пуассона, которые были определены в § 2.2.
Свертывая (8.3.1) по индексам i и /, получим
За = (ЗХ + 2|х)в.
Положим
К = Я + -g- (A = 3A-2V)'
тогда
с = Я0. (8.3.4)
Величина Z называется объемным модулем упругости.
Закон Гука можно записать также, разбивая соответствующие
тензоры на девиаторную и шаровую составляющие. Вычтем из
обеих частей (8.3.1) обу, причем в правой части заменим а по
формуле (8.3.4). Получим
а« —об« = 2(х(ву — ебг-j), или Gli = 2|ie1> (8.3.5)
Здесь черточки над буквами, как и ранее, обозначают девиаторы
соответствующих тензоров. Заметим, что для постоянной \i часто
применяется другое обозначение, а именно ц = G. Вторая группа
формул (8.3.3) типа if = t/ji дает основание называть эту вели-
величину модулем сдвига.
Для положительной определенности квадратичной формы уп-
упругой энергии необходимо и достаточно условие К > 0, [i > 0.
Что касается технических постоянных, модуль Е должен быть
положителен. Положительны также модули К и G; отсюда сле-
следует такое ограничение возможных значений коэффициента Пу-
Пуассона
Значение v = 1/2 соответствует несжимаемому материалу. Опыт
показывает, что для всех известных изотропных материалов v>
>0. Было сделано много попыток доказать, что нижняя граница
для v равна нулю, а не —1, но достичь этого в рамках рациональ-
рациональной механики, конечно, нельзя.
Ортотропное тело. По аналогии с формулами (8.3.3) за-
закон упругости для ортотропного тела записывают следующим
16*
244 гл-8- теория упругости, общие уравнения
образом:
еи = |f (an —
(8.3.6)
*зз = J- (азз ~ V3i<*ii — ^22) ¦
3
T12 = g-"» Т23 =* 5-» Т31 = g—•
^12 V23 W31
В этих формулах фигурируют 12 упругих констант, но они не
де де
независимы; из условий --— = т-~—, ..., следует:
22 ^"ц
V12 _ V21 V13 __ V31 V23 _ V32 /о о 74
В результате число независимых упругих постоянных оказыва-
оказывается равным 9, как и должно быть для ортотропного тела.
§ 8.4. Формулировка задачи теории упругости.
Теорема единственности решения
Выпишем полную систему уравнений теории упругости, ко-
которые были по отдельности сообщены в § 7.2, 7.4 и 8.2.
Уравнения равновесия:
oiU + Fi = 0. (8.4.1)
Закон упругости: в общем случае
и для линейно-упругого тела
Оц = Етек1. (8.4.3)
Выражения компонент деформации через перемещения:
efi = u(i|i). (8.4.4)
Здесь и в дальнейшем при общих рассуждениях и доказатель-
доказательствах общих теорем мы будем предполагать заданными следую-
следующие условия на границе. Пусть поверхность тела S состоит из
двух частей: S = ST + Su. Будем считать, что в каждой точке х{
поверхности задано
щ = щ, хг е Su, (8.4.5)
о^щ = Т*, х{ е ST. (8.4.6)
Этот простейший случай далеко не исчерпывает всех возмож-
§ 8.4. ТЕОРЕМА ЕДИНСТВЕННОСТИ 245
ностей. Так, например, при вдавливании жесткого штампа в уп-
упругое тело часто считают трение отсутствующим. Тогда, если
направить ось xz по нормали к поверхности тела, граничные
условия под штампом будут такими:
В дальнейшем нам встретятся задачи подобного типа, однако
в общей теории выделять их не имеет смысла, приводимые ниже
рассуждения легко перефразируются и на такие случаи.
Итак, задача теории упругости состоит в решении уравнений
(8.4.1) —(8.4.4) при граничных условиях (8.4.5), (8.4.6).
Если S = SUJ следовательно, на всей поверхности тела заданы
перемещения, соответствующая задача называется первой основ-
основной задачей теории упругости. Если S = ST и на всей поверх-
поверхности заданы усилия 2%, мы будем говорить о второй основной
задаче. Сформулированная выше постановка относится к сме-
смешанной задаче.
Первый вопрос, который естественно поставить, состоит в том,
всегда ли существует решение. Теоремами существования реше-
решения задач теории упругости занимались многие авторы. Для
линейной теории упругости теоремы существования доказывались
Фредгольмом, Лауричелла, Коссера, Лихтенштейном и другими
авторами в начале этого столетия.
Мы не будем здесь приводить эти довольно сложные и гро-
громоздкие доказательства, а будем просто строить соответствующее
решение, удовлетворяющее как дифференциальным уравнениям,
так и граничным условиям задачи.
Заметим, что вопрос существования решения далеко не всегда
решается положительно, если закон упругости нелинеен. Так,
при степенном законе упругости, соответствующем в одномерном
случае зависимости вида
можно привести примеры задач, когда решение не существует.
Это связано с тем, что производная do/de = ааеа~1 становится
бесконечно брлыпой при е = 0.
Во всех примерах, которые будут рассмотрены ниже, вопрос
существования решения не возникает, поскольку эти решения
будут построены фактически. Однако вопрос о том, единственно
ли найденное решение, важен, и теорему единственности необ-
необходимо доказать. Это доказательство мы проведем для линейного
закона упругости (8.4.3).
Предположим, что одним и тем же объемным силам при оди-
одинаковых граничных условиях типа (8.4.5—6) соответствуют два
различных решения ai;-, ец, и{ и ai;-, е"ц, и\. Разность этих ре-
решений (Ti;- = ог — ai;-, eij = ец— ег], щ=щ— щ удовлетворяет всем
246 ГЛ- 8- ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
уравнениям (8.4.1) при F< = 0, уравнениям (8.4.3), (8.4.4) и ну-
нулевым граничным условиям: ог^ = 0, x{^ST, иг = 0, Xi^Su.
Таким образом, доказательство единственности проводится стан-
стандартным для линейных уравнений методом, оно сводится к до-
доказательству отсутствия решения однородной системы. Положим
в уравнениях (8.4.1) Fi — О, умножим на щ и проинтегрируем
по объему. Получим
л
= 0.
Преобразуем этот интеграл, заметив, что а,,-, j щ = (оцщ) ti — с*,-е#.
Итак,
J
V
= J (or^)j dV — j Gije^dV = 0.
V V
Но первый интеграл по формуле Гаусса — Остроградского пре-
преобразуется в интеграл по поверхности
Этот поверхностный интеграл равен нулю вследствие условий на
поверхности:
ггг = О, Xi^Su;
(Уф5 = 0, Xi €= ST.
Итак, остается
Если выполняются (8.4.3) и упругий потенциал U представ-
представляет собою однородную квадратичную функцию от еу, то по
теореме Эйлера об однородных функциях
Интеграл по области от положительно определенной функции
равен нулю только тогда, когда эта функция равна нулю во
всех точках, а это возможно лишь тогда, когда всюду е#, а сле-
следовательно, и Gij равны нулю. Таким образом, нулевым гранич-
граничным условиям могут соответствовать только нулевые решения.
Этим и доказывается теорема единственности.
Заметим, что перемещения определяются при этом не единст-
единственным образом, а с точностью до перемещения тела как жест-
жесткого целого. Это следует из формул Чезаро (§ 7.3), которые
определяют перемещение с точностью до шести констант и\, со?;>
§ 8.4. ТЕОРЕМА ЕДИНСТВЕННОСТИ 247
Если закон упругости (8.4.2) нелинеен, состояния, отмечен-
отмеченные одним штрихом и двумя штрихами, нужно считать бесконеч-
бесконечно близкими, тогда ец и о^ бесконечно малы. Пренебрегая вели-
величинами второго и более высокого порядка малости, представим
уравнения связи (8.4.2) следующим образом:
«* (8-4.7)
Соотношения (8.4.7) имеют совершенно ту же структуру, что
(8.4.3). Воспроизведя буквально приведенные выше рассуждения
для линейного случая, убеждаемся, что решение единственно
тогда, когда квадратичная форма
0, (8.4.8)
т. е. положительно определена. Данное доказательство позволяет
утверждать лишь единственность в малом. Условие (8.4.8) пред-
представляет собою условие выпуклости поверхности и(ец) = const
в пространстве деформаций. Но если эта поверхность выпукла
во всех точках, то условие (8.4.8) обеспечи-
обеспечивает и единственность в большом. Строгое
доказательство этого почти очевидного фак-
факта мы опускаем.
Необходимо подчеркнуть, что теорема
единственности доказана нами для геомет-
геометрически линейной постановки задачи тео-
теории упругости. Если условие (8.4.8) не вы-
выполнено, единственности может не сущест-
существовать. Это может означать одно из двух: ох f
либо принятая модель сплошной среды не-
некорректна, либо материал неустойчив. При- Рис. 8.4.1
мером такого неустойчивого материала
служит материал с падающей диаграммой растяжения, подобной
изображенной на рис. 8.4.1. Видно непосредственно, что одному
и тому же значению напряжения на этой диаграмме соответ-
соответствуют два разных значения деформации. Вопрос о действитель-
действительном существовании таких неустойчивых упругих материалов
остается открытым; диаграммы вида изображенной на рис. 8.4.1
наблюдаются при описании пластического поведения и представ-
представляют зависимость условного напряжения, т. е. растягивающей
силы от деформации. Пример неустойчивости такого рода был
рассмотрен в § 4.13. Для геометрически нелинейных систем
теорема единственности несправедлива: нарушение единственно-
единственности соответствует потере устойчивости упругого тела. Рассмотре-
Рассмотрению подобного рода задач в элементарной постановке была по-
посвящена вся четвертая глава.
248 гл- 8- теория упругости, общие уравнения
§ 8.5. Уравнения теории упругости в перемещениях
и в напряжениях
Уравнения (8.4.1) — (8.4.4) можно привести к системе трех
уравнений для нахождения трех неизвестных компонент вектора
перемещения щ. Для этого, прежде всего, комбинируя (8.4,3)
и (8.4.4), запишем
оц = -j Ет (им + иик). (8.5.1)
Внесем (8.5.1) в уравнения (8.4.1) и получим следующую си-
систему:
Ет {nht и + в,, w) + 2Fi = 0. (8.5.2)
Эти уравнения образуют систему шестого порядка. Для изотроп-
изотропного тела по формуле (8.2.6)
Подставляя в (8.5.2), вычислим по отдельности входящие туда
суммы
6<j6wWftt у = Uk> м =* 8,*.
Действительно, множитель 8^8М отличен от нуля только тогда,
когда j = i и I = к. Точно также
j = uht ih = 6>f.
В результате для изотропного тела получаем систему уравнений,
которую обычно называют уравнениями Ламе,
{% + |х) 9,1 + иЛ щ + Ft = 0. (8.5.3)
В большинстве задач теории упругости можно считать объемные
силы отсутствующими и полагать Fi = 0. Действительно, объем-
объемные силы выражаются обычно весьма простыми функциями от
координат (например, сила тяжести), и нахождение частного
решения уравнения (8.5.3) труда не составляет. Это частное
решение может быть любым, вся разница будет сводиться к из-
изменению граничных условий, которые теперь ставятся уже для
однородной системы (8.5.3). Нахождение решения этой системы
при заданных граничных условиях и составляет основную труд-
трудность.
Сделаем некоторые заключения о свойствах функций ии вы-
вытекающие из (8.5.3). Полагая Fi = 0, продифференцируем каждое
из уравнений по соответствующей координате xt и произведем
§ 8.5. УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ 249
свертку по индексу i. Получим
А0 = 0. (8.5.4)
Таким образом, объемное расширение в упругом изотропном теле
при отсутствии массовых сил есть гармоническая функция. Взяв
теперь оператор Лапласа от левой части уравнения (8.5.3) при
Fi= 0, убедимся в том, что
ДДиг = 0. (8.5.5)
Каждая из компонент вектора перемещения представляет со-
собою бигармоническию функцию от координат.
Однако не следует думать, что задача теории упругости может
быть сведена к интегрированию системы (8.5.5) или что вели-
величина 6 может быть найдена по известным методам решения
уравнения Лапласа. Величина Э никогда не бывает задана на
границе и определить ее, решая задачу Дирихле, не удается.
Система (8.5.5) представляет собою систему двенадцатого шь
рядка, тогда как исходная система (8.5.3) шестого порядка. Чтобы
определить бигармоническую функцию, на границе области не-
необходимо задать два условия, например, щ и дщ/дп, т. е. нор-
нормальную производную от ии тогда как для решения системы
(8.5.3) достаточно задать только величины щ в каждой точке
поверхности. Относительно легко построить три бигармонические
функции, принимающие на границе заданные значения, но вооб-
вообще они не будут удовлетворять уравнениям (8.5.3).
Постановка граничных условий для уравнений Ламе особенно
проста, когда речь идет о первой основной задаче теории упру-
упругости, т. е. когда на поверхности задано щ = щ. Если на гра-
границе заданы усилия, то следует по закону Гука выразить на-
напряжения через деформации, т. е. первые производные от пере-
перемещений, и внести в граничные условия (8.4.6). Таким образом,
на границе оказываются заданными некоторые линейные ком-
комбинации из первых производных функций щ, которые мы выпи-
выписывать не будем.
С другой стороны, за неизвестные можно принять компоненты
тензора напряжений. Дифференциальные уравнения равновесия,
которые мы перепишем, положив равными нулю объемные силы
в соответствии со сделанным выше замечанием
ofj>j = 0, (8.5.6)
недостаточны для определения напряженного состояния в упру-
упругом теле. Недостающие уравнения можно было бы получить
следующим образом. Выразим деформации через напряжения и
подставим полученные выражения в уравнения совместности
G.3.7) и G.3.8). Однако поскольку уравнения Ламе уже вы-
выведены, мы можем прийти к цели более коротким путем.
250 гл-8- теория упругости, общие уравнения
Перепишем уравнения Ламе в виде
Вычислим теперь оператор Лапласа от компоненты деформации
Аеу = 1 (Аии + Ди,-,{) = - *±И в и. (8.5.7)
С другой стороны, из уравнений закона Гуна (8.3.1) следует
* = aee
При написании последней формулы учтено, что АЭ = 0 (8.5.4).
Внеся выражение для Аец в (8,5.7), получим
Теперь осталось лишь заменить 6 через о с помощью (8.3.4).
Окончательно получим
= 0' или
Уравнения (8.5.8) называются уравнениями Бельтрами — Мит-
чела (более точно — Митчел получил их для отличных от нуля
объемных сил, что не вносит сколько-нибудь существенных
осложнений. По указанным выше причинам нам казалось бес-
бесполезным приводить эти более полные уравнения). Свертывая
(8.5.8) по индексу i, убеждаемся, что
Да = 0. (8.5.9)
Беря оператор Лапласа от (8.5.8), находим
AAafi = 0. (8.5.10)
Соотношения (8.5.9) и (8.5.10), конечно, немедленно следуют из
(8.5.4) и (8.5.5).
Система уравнений Бельтрами — Митчела — это система 12-го
^порядка. Произведя дифференцирование при их выводе, мы ис-
искусственно повысили порядок исходной системы. В результате
оказывается, что возможные решения системы (8.5.8) порождают
класс функций более широкий, чем возможные решения задачи
теории упругости. Решения системы (8.5.8) не обязательно удо-
удовлетворяют уравнениям равновесия. Это ясно хотя бы из сле-
следующего примера. Пусть напряжения — произвольные линейные
функции координат ati = атхк. Поскольку уравнения (8.5.8)
содержат лишь вторые производные от Оц, эти уравнения будут
выполнены тождественно при любых значениях постоянных ат.
§ 8.6. ТЕМПЕРАТУРНЫЕ ЭФФЕКТЫ 251
Но подставляя Оц = атхк в уравнения равновесия, мы найдем,
что эти постоянные связаны тремя условиями вида сцц = 0.
Если на всей поверхности тела заданы усилия, граничные
условия задают на поверхности линейные комбинации искомых
функций, т. е. напряжения. Но если заданы перемещения точек
поверхности, то сформулировать граничные условия в напряже-
напряжениях в общем виде невозможно; эти условия будут содержать не-
некоторые интегралы от напряжений и их производных, которые
получатся, если в формулы Чезаро внести выражения деформа-
деформаций через напряжения по закону Гука. Иногда, например, в
плоской задаче теории упругости соответствующие преобразова-
преобразования удается довести до конца.
§ 8.6. Температурные эффекты
Всякое твердое тело расширяется при нагревании и сокра-
сокращает свои размеры при охлаждении. Если к телу при этом при-
приложены силы, они совершают работу; таким образом, тепловая
энергия превращается в механическую. Применение к упругому
телу законов термодинамики показывает, что возможно и обрат-
обратное превращение.
Будем исходить из опытного факта, состоящего в том, что
упругая деформация и температурная деформация аддитивны.
Поэтому
о<, = Ет (ек1 - ак1№). (8.6.1)
Здесь aki — тензор коэффициентов термического расширения,
ДГ = Т — То — изменение температуры. Соотношения Дюамеля —
Неймана (8.6.1) мы будем принимать за первичный опытный
факт. Постоянные Ет определяются при Т = Го, ДУ == 0, т. е. в
изотермических условиях. Если ДГ не мало, то Ет и ам должны
рассматриваться как функции температуры; мы будем считать
разность ДГ настолько малой, что модули и коэффициенты рас-
расширения могут считаться постоянными. Таким образом, (8.6.1)
представляют собою закон термоупругости в изотермических
условиях. Для обратимого процесса
Здесь W (eih T) — свободная энергия, S — удельная энтропия.
Интегрируя (8.6.1), находим
У = у Emeijeki - Ецырыец (Т - То) + / (Т) (8.6.2)
и, следовательно,
Г(Т). (8.6.3)
Внутренняя энергия, как известно, выражается следующей
252 гл-8- теория упругости, общие уравнения
формулой:
V = У + Г5,
или
U = ^Етвцеы + Етак1ецТъ + / (Г) - Tf (Г). (8.6.4)
При фиксированной деформации изменение свободной энергии
совершается только за счет поступления в упругое тело тепла
извне, следовательно,
f(T)-Tf'(T) = ceT.
Здесь се — теплоемкость при постоянной деформации, которую
мы считаем постоянной, как и другие параметры, если прираще-
приращение температуры невелико. Дифференциальное уравнение для
функции f(T) получилось таким же, как в теории газов, инте-
интегрируя его, находим
подставляя в (8.6.3), получаем выражение для энтропии
5 = Етаыец + се Ы ~. (8.6.5)
о
Аддитивная постоянная в выражении для энтропии выбрана так,
чтобы было 5 = 0 при ец = О, Т = То.
Теперь, разрешая (8.6.5) относительно Т и подставляя
в (8.6.4), находим
се ехр
(8.6.6)
Как известно, (Ту = —, Т = jg. В адиабатическом процессе
S = const, при Т — То было 5 = 0, следовательно, в (8.6.6) следу-
следует принять 5 = 0. Соотношение между Оц и еы в этом случае по-
получается вообще говоря нелинейным, но сохранение этой нели-
нелинейности не имеет смысла, поскольку нелинейные члены имеют
тот же порядок, что и отброшенные ранее малые величины, на-
например, изменение модулей с температурой. Дифференцируя по
e»j, разлагая в ряд экспоненту и удерживая лишь первые два чле-
члена в разложении, получим
ш + т-0 EkirsE^vqar&av(l eki- (8.6.7)
Се J
Составляющие тензора четвертого ранга, заключенные в скобки
в формуле (8.6.7)т представляют собою адиабатические модули
упругости, которые больше чем изотермические. Для металлов
§ 8.7. ВАРИАЦИОННЫЕ УРАВНЕНИЯ 253
эта разница весьма мала, величина ее для одноосного растяже-
растяжения была оценена в § 2.9, эта оценка сохраняет порядок вели-
величины и для общего случая.
Дифференцируя (8.6.6) по 5, полагая 5 = 0 и удерживая два
члена разложения экспоненты в ряд, найдем изменение темпе-
температуры
TJZb = -LEmahfiv. (8.6.8)
'о Се
Разница между адиабатическим и изотермическим модулями объ-
объясняется тем, что при деформировании температура меняется и
происходит температурная деформация, приложенные напряже-
напряжения должны не только вызвать заданную деформацию, но и ком-
компенсировать температурную.
Преобразование Лежандра позволяет получить энтальпию как
функцию напряжений и энтропии и свободную энтальпию как
функцию напряжений и температуры. Таким образом, потенциа-
потенциалом напряжений для изотермического процесса служит свободная
энергия, для адиабатического — внутренняя энергия. Аналогич-
Аналогичным способом получаются различные потенциалы деформаций для
изотермического и адиабатического случаев.
Если теплоизоляция отсутствует или же процессы не на-
настолько медленны, чтобы все время существовало температурное-
равновесие с окружающей средой, часть механической энергии,
превращающейся в тепло, будет рассеиваться. Совместное рас-
рассмотрение уравнений теории упругости с температурными чле-
членами и уравнений теплопроводности позволяет ставить так назы-
называемую связанную задачу термоупругости. Обнаруживаемые при
этом эффекты незначительны и в эксперименте их трудно отли-
отличить от эффектов, связанных с внутренним трением. Поэтому ис-
исследование эффекта температуры в теории упругости почти всегда
основывается на уравнениях Дюамеля — Неймана (8.6.1), в кото-
которых модули упругости считаются постоянными и не зависящими
от характера термодинамического процесса.
§ 8.7. Вариационные уравнения теории упругости
Система уравнения теории упругости и граничные условия
представляют собою уравнения Эйлера и естественные граничные
условия некоторой вариационной задачи. Построим следующий
функционал:
^ J [Gij \ij ~~ "UiJ ~~ T Uj'V ~~ U ^ + F iUi\ dV +
+ f T*UidS + J oijnj (щ - и*) dS. (8.7.1)
254 гл-8- теория упругости, общие уравнения
Будем рассматривать в этом функционале щ, ец и Сц как не-
независимые функциональные аргументы и приравняем нулю ва-
вариацию этого функционала
«/ = J [Sou (ец - у ии -1 uitl) + ai5 (beu - у
^ 1 f dS
F + f T\bu{
+ J ^ij^j ta — и?) d5 + j OijUjbUidS. (8.7.2)
S
Приравняв нулю множитель при 6oti в объемном интеграле,
получим
т. е. уравнение (8.4.4). Приравнивая нулю аналогичный множи-
множитель в поверхностном интеграле, получим граничное условие
(8.4.5)
Точно так же, поскольку (8.7.2) справедливо при любых значе-
значениях беу, из него следует уравнение (8.4.2)
dU
Теперь преобразуем с помощью интегрирования по частям ин-
интеграл у \ (Уг} (8uitj + 8ujti) dV. Вследствие симметрии тензора о#
v
он равен
J Oij&UijdV = — j OijjSuidV + \ OijnfiUidS.
v v s
С учетом выполненного преобразования, а также уравнений
(8.4.4), (8.4.2) и условия (8.4.5) вариация функционала перепи-
перепишется следующим образом:
$j = j (aiifj + j
V 8U+8T
+ j Ti^UidS + J OiiUjbUidS, (8.7.3)
ST su
отсюда, вследствие произвольности вариаций 8м<, получается
. е. уравнения равновесия (8.4.1) и граничное условие (8.4.6).
§ 8.7. ВАРИАЦИОННЫЕ УРАВНЕНИЯ 255
Принимая часть естественных условий вариационной задачи
за предварительные условия, мы получим вариационные урав-
уравнения или вариационные принципы более частного характера,,
когда функционал зависит от меньшего числа варьируемых па-
параметров.
а. Вариационный принцип Рейснера. Предположим, что зара-
заранее выполнены условия (8.4.2), следовательно, Оц представлены
как функции деформаций ец и предполагается существование об-
обратной зависимости. При этом природа этих величин не уточня-
уточняется, т. е. не предполагается, что они выражаются через переме-
перемещения по формулам (8.4.4). Тогда входящая под интеграл комби-
комбинация Оцвц может рассматриваться как функция от Оу, так же-
как и величина U. Вследствие (8.1.4)
Теперь функционал / перепишется следующим образом:
Jua = 1 — -к Оц (Uij + UjA) + Ф (<3ij) + FiuAdV +
V
+ f T*mdS + j ацщ (и{ — щ) dS. (8.7.4)
Индексы при обозначении функционала указывают на то, что-
он выражается через независимые функции о„ и щ. Варьируя
эти аргументы, найдем
С\ 1 1
+ ^ ба^- + Ffiui] dV + f T\bu{dS +
Г / *\ jo Г
+ I OCTij^j \^ — ^i / ^-* "b 1 OijnjOUidS -
Приравнивая нулю множитель при 8оц в объемном интеграле,,
сразу получаем
дФ
Учитывая, что вследствие (8.1.5) дФ/доц = ец, это равенство-
представляет собою (8.4.4). Точно так же отсюда получается
граничное условие при х\ ^ Su
щ = и*.
Прежде чем приравнивать нулю множитель при 8и{ необходимо
выполнить интегрирование по частям, как и в предыдущем слу-
256 ГЛ- 8- ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
чае. После этого вариация функционала с учетом обращения
в нуль членов, содержащих 8вц, примет вид, в точности совпа-
совпадающий с (8.4.3); из произвольности 8щ вытекают дифферен-
дифференциальные уравнения равновесия и граничные условия при Xi^ST,
как это было показано выше.
б. Вариационный принцип Лагранжа. Предположим, что зара-
заранее выполнены уравнения (8.4.4) и геометрическое граничное
условие (8.4.5). Тогда функционал (8.7.1) приведется к следую-
следующему виду:
Ju=\[-U (ец) + FiUi\ dV + f T\UidS. (8.7.5)
v sT
Функционал (8.7.5) называется функционалом Лагранжа, он за-
зависит только от вектора перемещения ии поскольку фигурирую-
фигурирующие в выражении (8.7.5) компоненты деформации предполагают-
предполагаются выраженными через перемещения. Приравняем нулю вариацию
функционала Лагранжа
в/u = J [- |г.S^ + РЫ dV + f Т*г8и№ = 0.
у L « J ST
Положим
ди
Пока что на это равенство мы будем смотреть просто как на пе-
переобозначение для производных ди/двг,. Теперь можно написать
— 66?ij = Oifou = Oij8uu.
Подставляя в выражение для б/и и выполняя интегрирование
по частям, найдем
6/и = f (оц,1 + Fi) buxdV— j OijnfiUidS + J rJ&^dS.
V s sT
Но второй интеграл равен нулю на части поверхности *SU, так
как геометрическое граничное условие на этой части предпола-
предполагается выполненным и 8щ = 0. Поэтому из условия равенства
нулю вариации б/и вытекает уравнение равновесия
и граничное условие
в. Вариационный принцип Кастилъяно. Предположим, что вы-
выполнены дифференциальные уравнения равновесия и граничные
условия на части поверхности ST, кроме того деформации свя-
§ 8.7. ВАРИАЦИОННЫЕ УРАВНЕНИЯ 257
заны с напряжениями законом упругости. Последнее предполо-
предположение делалось при выводе функционала Рейснера (8.7.4), по-
поэтому мы примем за отправный пункт именно этот функционал,
а не самый общий (8.7.1). Преобразуем объемный интеграл
у J <?ij ("и + ujti) dV = — J о^^щ dV+ J Оцщщ dS;
V V S
подставляя его в (8.7.4), получим
Juo = J [((Ту,,- + Fi) щ + Ф (<r«)] dV - J а^щщ dS +
+ J Т*щ dS+ J GijUj(щ — щ) dS*
sT su
Считая, что уравнения (8.4.1) и граничные условия (8.4.6)
выполнены заранее, получим функционал, зависящий только от
напряжений
/e = f Ф (dij) dV — J Goulds. (8.7.6)
у su
Функционал (8.7.6) называется функционалом Кастильяно. При
варьировании этого функционала необходимо иметь в виду, что
уравнения (8.4.1) и граничные условия (8.4.6) предполагаются
выполненными. Поэтому должно быть
6оу j = 0, Ьацщ = 0, Xi «г 5Г. (8.7.7)
Покажем, что условие 6/а = 0 влечет за собою выполнение усло-
условий совместности для деформаций, которые пока что формально
определены следующим образом:
Варьируя функционал при условиях (8.7.7), мы воспользуемся
методом неопределенных множителей Лагранжа, т. е. будем рас-
рассматривать следующий функционал:
Ко = J [Ф (а«) - к (oiU + F{)] dV -
v
— \ Gijtiju'dS — f Hi (arwitj — T*) dS. (8.7.8)
S S
Теперь вариации 6а« уже можно считать совершенно произволь-
произвольными, т. е. не подчиненными (8.7.7). Приравняем нулю вариацию
17 Ю, Н. Работнов
258 гл- 8- теория упругости, общие уравнения
этого функционала
ai} dV— f tourijuldS - J |хба^ dS=- 0.
su sT
Преобразовав интегрированием по частям объемный интеграл,
перепишем это условие следующим образом:
8KG = J7i?? — ku\ бега dV+ f 8Gijnj (Хг- щ) dS +
ST
Отсюда
е (^ + ^) M иa:
Таким образом, шесть формально введенных компонент деформа-
деформации выражаются через вектор Яг- точно так же, как определен-
определенные обычным способом компоненты деформации выражаются че-
через вектор и{. Теперь, зная eih можно определить А,< интегрирова-
интегрированием по формулам Чезаро и получить обычным способом урав-
уравнения совместности G.3.5) или G.3.6). Излишне говорить, что
введенный формально, как множитель Лагранжа, вектор Я* пред-
представляет собою в действительности вектор перемещения
Кг = Щ.
§ 8.8. Некоторые замечания о вариационных принципах
Вариационные принципы Лагранжа и Кастильяно были сформулирова-
сформулированы независимо от общего вариационного уравнения б/ = 0, где / выража-
выражается формулой (8.7.1). Их называли и называют энергетическими принци-
принципами, поскольку интеграл от U по объему есть упругая энергия, а для ли-
линейно-упругого тела, для которого принцип Кастильяно был впервые сфор-
сформулирован, Ф = U. Общая точка зрения, состоящая в том, что все уравне-
уравнения теории упругости служат уравнениями Эйлера для некоторого функцио-
функционала, была высказана Вашидзу в 1958 г., принцип Рейснера был открыт
его автором в 1955 г. Правда, позже было обнаружено, что общий вариаци-
вариационный принцип (8.7.2) был сформулирован еще в 1911 г. Хеллингером, ко-
который опубликовал его в издании, редко читаемом специалистами по тео-
теории упругости. Так или иначе принципы Лагранжа и Кастильяно применя-
применяются в теории упругости чаще всего. Эти принципы имеют одно преимуще-
преимущество, состоящее в том, что они являются экстремальными. Обращение в
нуль первой вариации функционала означает, что величина этого функцио-
функционала принимает стационарное значение, которое может быть максималь-
максимальным или минимальным или ни тем, ни другим. Если вычислить вторую
вариацию функционала (8.7.1) или функционала Рейснера, мы получим
некоторую квадратичную функцию от вариаций 6aij, 6>t-j, би* в первом слу-
случае, 6iii, 6atj во втором. Вариацию этих аргументов можно всегда выбрать
так, чтобы вторая вариация функционала была по нашему желанию либо
§ 8.8. ЗАМЕЧАНИЯ О ВАРИАЦИОННЫХ ПРИНЦИПАХ 259
положительной, либо отрицательной. Поэтому обращение в нуль первой
вариации функционала не означает, что функционал достигает при этом
экстремального значения. С функционалом Лагранжа дело обстоит иначе.
Вторая вариация его выражается следующим образом:
U — о
V
Фигурирующая под интегралом квадратичная форма положительно опре-
определенна для любой разумной модели материала, для которой справедлива
теорема единственности (§ 8.4). Можно показать, что если функция U всю-
всюду строго выпукла, т. е. если эта квадратичная форма положительна всюду,
функционал имеет абсолютный максимум для истинного поля перемеще-
перемещений. Если и\ есть некоторое поле перемещений, не представляющее собою
решение рассматриваемой задачи теории упругости, а щ — истинное поле
перемещений, то
Для линейного закона упругости
1 d2U
де^деы
Эта квадратичная форма положительно определенна, третья и следу-
следующие вариации функционала Ju тождественно равны нулю; таким образом,
доказывается неравенство (8.8.1), которое носит не локальный характер.
Аналогичным образом доказывается, что функционал Кастильяно для
истинного напряженного состояния принимает минимальное значение
Вариационный принцип Лагранжа представляет собой прямой результат
применения к упругому телу начала возможных перемещений. Пусть тело
находится в равновесии под действием внешних сил Fi иГ^, которые совер-
совершают работу на перемещениях т. Внутренние силы, т. е. напряжения
—Oij, совершают работу на соответствующих им обобщенных перемещени-
перемещениях eij. Введем в рассмотрение систему возможных перемещений Ьщ, кото-
которые непрерывны вместе со своими первыми производными и обращаются в
нуль при Xi e Su. Виртуальная работа всех сил, включая внутренние, долж-
должна быть равна нулю, следовательно:
fiui dV+ j T*du. dS- f Оц&еи dV= 0. (8.8.3)
V ST V
Ho dij = dU/deij, поэтому аг-;бег-;- = &U, при x\ e Su поверхностный интег-
интеграл обращается в нуль, тогда как при xi e ST T^= 7\, поэтому (8.8.3) мож-
можно записать в виде
б/и = 0,
где 1и — функционал Лагранжа (8.7.5).
Для вывода вариационного принципа Кастильяно, рассмотрим воображае-
воображаемое напряженное состояние бац такое, что бац, j = 0, дацщ = 0, xi e ST.
Значения, которые принимают величины ба^- на части поверхности Su,
могут быть произвольны. Поскольку состояние ddj удовлетворяет условиям
равновесия, составим уравнения равновесия в форме Лагранжа, приняв за
виртуальные перемещения истинные перемещения щ и соответствующие
17*
260 ГЛ- 8- ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
деформации eij = U(i,j)- Получим
~ j догзегз dV+ J d(Si3njui dS= °» (8*8'4>
У su
а так как ец = дФ/доц, то дацец = 6Ф, и уравнение (8.8.4) может быть
записано в виде
в/а = 0,
где фунционал Ja определяется формулой (8.7.6).
§ 8.9. Обобщенные силы и перемещения
Для стержневых систем вариационные принципы Лагранжа
и Кастильяно были уже установлены выше, а именно в § 5.2.
Там же упоминалось о возможности построения смешанных ва-
вариационных принципов, в формулировке которых участвуют как
силы, так и перемещения. Способ доказательства был подобен
тому, который изложен ов § 8.8.
Во всех реальных случаях действующие на тело силы могут
быть представлены как линейные функции конечного числа или
счетного множества параметров, которые мы будем называть
обобщенными силали и обозначать Qs. Работа сил на вызванных
ими перемещениях может быть всегда представлена следующим
образом:
^ f ^ Qsqs. (8.9.1)
Здесь qs — обобщенные перемещения.
Рассмотрим несколько примеров.
1. Сосредоточенная сила. Предположим, что на части поверхности AS
приложена распределенная нагрузка постоянной итенсивности 7Y Положим
Pi = TiAS. Будем неограниченно уменьшать размер площадки AS, стяги-
стягивая ее к точке поверхности М, и одновременно будем увеличивать Г* так,
чтобы произведение TiAS оставалось постоянным. В пределе мы получим
сосредоточенную силу с компонентами Ри
Теперь по теореме о среднем
[ Т.иг dS = и. (ЛГ) f Т. dS= и. Ш') Pv
AS AS
Здесь Mf — точка, принадлежащая площадке AS. В пределе точка ЛГ совпа-
совпадает с точкой М. Таким образом.
Примечание. В линейной теории упругости перемещение в точке
приложения сосредоточенной силы бесконечно велико, как будет показано
далее (§ 11.2). Это не должно влиять на данное выше формальное опреде-
определение Qi и #г. На сосредоточенную силу можно смотреть как на совокуп-
совокупность трех сил, каждая из которых направлена параллельно одной из коор-
координатных осей. Но можно рассматривать эту силу как одно целое, приняв
§ 8.9. ОБОБЩЕННЫЕ ГИЛЫ И ПЕРЕМЕЩЕНИЯ
за обобщенную силу величину
261
Соответствующее обобщенное перемещение представляет собою проекцию
полного перемещения она направление силы
Действительно, работа может быть представлена следующим образом:
2. Сосредоточенный момент. К упругому телу прикреплена абсолютно
жесткая шайба (рис. 8.9.1). К этой шайбе приложены две параллельные
Рис. 8.9.1
и противоположно направленные силы Р и —Р, расстояние между ними
равно h. Работа этих сил
Положим Р = Q/h, тогда
А = Рщ — Ри2.
ил — ио
Величина (щ — u2)lh представляет собою угол поворота жесткой шайбы.
Перейдем теперь к пределу, увеличивая безгранично силу Р и уменьшая
плечо h так, чтобы момент Q = Ph оставался неизменным. В пределе мы
получим то, что называется сосредоточенным моментом, его можно принять
за обобщенную силу. Соответствующим обобщенным перемещением будет
угол поворота элемента, к которому приложен момент.
3. Произвольная поперечная нагрузка р{х), действующая на балку.
Как следует из результатов § 3.8 прогиб балки и (х) при любой поперечной
нагрузке представляет собою функцию, непрерывную вместе со своей про-
производной.
На рис. 8.9.2 изображена балка, свободно опертая на двух концах, для
нее функция v (х) удовлетворяет следующим граничным условиям: и@) =«
е= v(l) = 0, y"v@) = v"(l) = 0. Поэтому функция v (х) представляется в
виде равномерно сходящегося ряда синусов кратных аргументов:
V (х) = ^ qh Sin
ктсх
I "
Счетное множество коэффициентов ряда дь. может быть принято за со-
совокупность обобщенных перемещений. Если р(х) есть нагрузка, то
ктсх
При этом функция р(х) должна быть только интегрируемой, она может
262 ГЛ- 8> ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
принадлежать к классу обобщенных функций, т. е. содержать дельта-функ-
дельта-функции и их производные; функция р(х) вообще не может быть представлена
в виде тригонометрического ряда.
Поскольку все уравнения теории упругости линейны, всякое
решение задачи теории упругости, т. е. напряжения, деформации
и перемещения, выражается линейным образом через приложен-
приложенные внешние силы. А эти силы, как мы выяснили, сводятся
к конечному числу или счетному множеству обобщенных сил.
Поэтому объемный интеграл, фигурирующий в выражении функ-
функционала Кастильяно (8.7.6), есть квадратичная функция от обоб-
обобщенных сил
Поскольку Ф(о#) представляет собой положительно определен-
определенную функцию ау, интеграл от нее по объему V есть положи-
положительно определенная функция от Q8. Поверхностный интеграл
в (8.7.6) выражает работу сил, приложенных к поверхности, ее
можно также записать через обобщенные силы и перемещения.
В результате функционал (8.7.6) перепишется следующим об-
образом:
-Q.q8. (8.9.2J
Пусть сила Qm получила приращение 6(?т, тогда из условия
= О ПОЛУЧИМ
отсюда
qm = ?-. (8.9.3)
В такой формулировке теорема Кастильяно ничем не отличается
от теоремы, приведенной в § 5.2 для стержневых систем.
Точно таким же способом, если считать заданными переме-
перемещения qi, компоненты деформации представятся как линейные
функции от qu поэтому
$U(ei})dV=U(qi).
V
Функционал Лагранжа (8.7.5) принимает вид
Варьируя только одно перемещение, например qm, получим
Qm = M-. (8.9.5)
§ 8.10. ТЕОРЕМЫ КЛАПЕЙРОНА И МАКСВЕЛЛА — БЕТТИ 263
При выводе формул (8.9.3) мы считаем заданными внешние
силы, при выводе формул (8.9.5) считали заданными перемеще-
перемещения. Этим отнюдь не ограничивается общность соответствующих
выводов. Если рассматривается задача со смешанными граничны-
граничными условиями, то ее можно представить как задачу с заданными
силами, только часть этих сил известна, а часть представляет
собой силы реакции связей, которые заранее неизвестны. Будем
обозначать неизвестные силы через Xiy а соответствующие пере-
перемещения через хи Тогда по формуле (8.9.3)
*, = f|. (8.9.6)
Но если силы Хг неизвестны, то должны быть заданы перемеще-
перемещения точек их приложения х{, поэтому (8.9.6) представляет собою
систему уравнений для нахождения неизвестных Х{. Обычно не-
неизвестную реакцию можно выбрать так, чтобы соответствующее
перемещение было равно нулю; такого рода примеры были при-
приведены в § 5.2.
§ 8.10. Теоремы Клапейрона и Максвелла — Бетти
Тот факт, что упругая энергия U = Ф представляет собою
однородную квадратичную функцию от обобщенных сил или
обобщенных перемещений, позволяет немедленно доказать две
простые теоремы, а именно:
Теорема Клапейрона. По теореме Эйлера об однород-
однородных функциях
2*7 = ^ = Q.qh 2Ф = Ц Qi =
отсюда
U = <b = ±Qiqt. (8.10.1)
Упругая энергия равна половине работы внешних сил на их
перемещениях.
Если не вводить в рассмотрение обобщенные силы и обобщен-
обобщенные перемещения, то можно переписать соотношения (8.10.1)
следующим образом:
U = Ф = ТIFiUidV + TI TiuidS- (8.10.2)
V S
Теорема Максвелла. Квадратичная форма Ф имеет не-
необходимым образом следующий вид:
где brs образуют симметричную матрицу. Обобщенные перемещения
264 ГЛ- 8* ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
выражаются следующим образом:
q. = br.Qr. (8.10.3);
Свойство симметрии коэффициентов в соотношении (8.10.3J
было обнаружено Максвеллом и сформулировано в виде соот-
соответствующей теоремы.
Теорема Бетти представляет собой по существу иную
формулировку теоремы Максвелла. Пусть к одному и тому же
телу сначала приложена система сил Qs, которой соответствуют
перемещения QSf потом система сил Qs, которой соответствуют
перемещения 9s. Тогда работа сил первой системы на перемеще-
перемещениях точек их приложения, вызванных действием сил второй си*
стемы, равна работе сил второй системы на перемещениях точек
их приложения, вызванных действием сил первой системы.
Действительно,
q*Q, = brsQrQs, qsQs = bsr(?r<?s.
Вследствие симметрии матрицы Ь„ правые части равны, отсюда
следует
q& = q.. (8.Ю.4)
Это же соотношение можно записать в иной форме
J fiU\dV + f T\u\dS = J F\u\dV + [ T\u\dS. (8.10.5)
V 8 V 8
Тождество (8.10.5) представляет собой простое следствие сим-
симметрии тензора модулей упругости или тензора податливостей.
Действительно, положим в правой части (8.10.5) Т\ = а"#щ и
преобразуем поверхностный интеграл в объемный. Учитывая, что
напряжения сг# удовлетворяют вместе с силами Ft дифферен-
дифференциальным уравнением равновесия, получим
J F\u\dV + ^Tlu'idS = J аУцдУ = J Етеыег^У. (8.10.6)
V S V V
Выражение в правой части симметрично относительно верх-
верхних индексов «штрих» и «два штриха», поэтому, преобразуя ле-
левую часть (8.10.5) подобным образом, мы получим в точности
такое же выражение.
Все приведенные теоремы — Клапейрона, Максвелла и Бетти
были уже доказаны в § 5.3 для частного случая стержневых
систем.
С помощью формулы (8.10.6) можно получить очень простые
результаты, относящиеся к вычислению средних значений ком-
компонент деформации в напряженном упругом теле. Положим о# =*
s=s const. Тогда по закону Гука находятся вц = const^ а по из-
§ 8.11. ЗАМЕЧАНИЯ О ЗАДАЧАХ ТЕОРИИ УПРУГОСТИ 265
вестным значениям постоянных компонент деформации находятся
перемещения Щ. Введем обозначения для средних значений ком-
компонент деформации еу, вызванных действием сил F< и Т{,
Тогда из формулы (8.10.6) следует
J ')(8.10.7)
Нижеследующий пример взят из книги «Математическая теория упру-
упругости» Лява, который приводит его со ссылкой на оригинальную работу
Бетти.
Цилиндр высотой h произвольного поперечного сечения поставлен на
горизонтальную плоскость и деформируется под действием собственного ве-
веса. Обозначим ось цилиндра индексом 3, положим о*33 = а, а остальные ком-
компоненты напряжения примем равными нулю. Тогда е33 = о/Е9 и3 = схг/Е.
По формуле (8.10.7)
h
1
Здесь р — плотность, g — ускорение силы тяжести, F — площадь сечения.
Отсюда
п \*зз/ - 2Е •
Эта величина представляет собою укорочение цилиндра. Чтобы вычис-
вычислить изменение его объема, положим о\;- = аб^-, тогда Зе' = 6' = cJK,
щ = охгЦЗК) и по формуле (8.10.7)
h
отсюда
<в>
§ 8.11. Замечания о задачах теории упругости
В § 8.4 была сформулирована задача теории упругости, кото-
которая состоит в интегрировании системы уравнений с частными
производными при определенных граничных условиях. Общие
методы интегрирования этой системы составляют предмет мате-
математической теории упругости, этим методам посвящена огромная
литература и в настоящем курсе мы не имеем возможности идти
в этом направлении слишком далеко.
266 ГЛ- 8- ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
Однако следует отметить здесь те цели, которые имеются в
виду при отыскании решений. Приближенные методы отыскания
напряжений и деформаций в упругих телах, основанные на част-
частных гипотезах простейшего характера, принято относить к тому,
что называется сопротивлением материалов. Примером может
служить приближенная теория растяжения и изгиба стержней,
изложенная в гл. 2, 3 и 5. Теория упругости позволяет получить
точное решение задачи изгиба для определенных случаев и срав-
сравнить его с приближенным; таким образом, находится строгая
оценка погрешности элементарной теории.
Однако существенно больший интерес представляют такие за-
задачи, для решения которых элементарные гипотезы не могут
привести к цели. Типичный пример — задача о кручении призма-
призматического стержня. Если принять для кручения такую же гипо-
гипотезу плоских сечений, которая была принята для изгиба, ока-
окажется, что верный результат получится только для того случая,
когда сечение представляет собою круг или круговое кольцо;
для других форм сечения эта гипотеза приведет к очень
грубой ошибке. Точно так же никакие элементарные предпо-
предположения не позволяют найти напряжения в толстостенной тру-
трубе, подверженной действию внутреннего давления. Можно при-
привести много примеров других элементов конструкций, для
которых напряжения и деформации нельзя определить с по-
помощью элементарных приемов, а нужно использовать уравнения
теории упругости.
Не всегда удается получить точное решение задачи теории
упругости, даже если это возможно — не всегда имеет смысл им
пользоваться. Часто оказывается, что та точность, с которой из-
известны граничные условия задачи, делает практически бессмыс-
бессмысленным стремление к большой точности самого решения. Поэтому
наряду с точными методами математической теории упругости
развиваются упрощенные приближенные теории, подобные, на-
например, технической теории изгиба, рассмотренной нами ранее.
Вариационные принципы теории упругости позволяют указать
путь для построения таких приближенных теорий рациональным
образом.
В последнее время открылась новая обширная область при-
приложения теории упругости к физике твердого тела. Идеальный
кристалл с правильным расположением атомов упруг. Всякие
нарушения правильности кристаллической решетки приводят к
появлению поля напряжений, которое с достаточной степенью
точности может быть изучено методами теории упругости. В сле-
следующих главах, посвященных решению задач теории упругости,
основное внимание будет обращено именно на эту сторону, будут
приведены некоторые результаты, которые необходимы для по-
понимания современных точек зрения на механику неупругих де-
деформаций и разрушения.
§ 8.12. ОДНОМЕРНЫЕ ЗАДАЧИ — ТРУБЫ И ДИСКИ
267
§ 8.12. Одномерные задачи — трубы и диски
Наиболее простые решения задач теории упругости, как и
других механических теорий, получаются тогда, когда искомые
функции зависят от одной только координаты и дифференциаль-
дифференциальные уравнения в частных производных становятся обыкновенны-
обыкновенными дифференциальными уравнениями. Таких задач немного и они
обычно служат пробным камнем при вы-
выяснении степени эффективности той или
иной теории, решение их относительно
просто и результат решения обозрим.
В качестве одного из простейших при-
примеров рассмотрим задачу о толстостенной
трубе под действием внутреннего давле-
давления. Обозначим: а — внутренний радиус
трубы, Ъ — внешний радиус, q — давление
(рис. 8.12.1). Будем считать, что труба
очень длинная и к торцам ее приложены
растягивающие силы Р. Вследствие прин-
принципа Сен-Венана можно утверждать, что
поперечные сечения ее останутся плоскими и напряженное со-
состояние будет во всех сечениях одинаково. Очевидно, что эту
задачу следует рассматривать в цилиндрических координатах,
т. е. пользоваться уравнениями § 7.8, считая, что искомые функ-
функции зависят только от радиуса г. Тогда уравнения равновесия
G.8.5) принимают вид
Рис. 8.12.1
Jee
dr
= о,
(8.12.1)
Последнее уравнение немедленно интегрируется, мы получаем
Orz = С/г, но при г = а или г = Ъ аГ2 = 0, к поверхности трубы
приложено только нормальное давление. Поэтому должно быть
С = 0 и, следовательно, оГ2 — 0.
Поскольку сечения остаются плоскими, осевая деформация е2Х
постоянна. Деформации, радиальная и окружная, выражаются
соответственно по формулам G.8.4)
du
(8.12.2)
Заметим, что условие совместности получается из (8.12.2)
чрезвычайно просто, для этого нужно исключить из этих соот-
соотношений и. В результате получим
dr
= 0.
(8.12.3)
268 ГЛ- 8- ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
Теперь нужно написать соотношения закона Гука
*!Т = 4" l°rr — V (Ozz + Gee)],;
е&в = 4" faee — v (arP + a22)], (8.12.4)
e 4
eZz = 4" lGzz ~ v (aee + arr^ = const'
Решение системы (8.12.1), (8.12.4) и (8.12.2) или (8.12.3J
можно провести разными способами. Если нас интересуют в пер-
первую очередь напряжения, скорее всего к цели приводит следую-
следующий прием.
Заметим, что если принять
orr = -±rF, cee = -g, (8.12.5)
то уравнение равновесия будет удовлетворено тождественно. Вне-
Внесем теперь выражения (8.12.5) в (8.12.4) и подставим выраже-
выражения вгт и бее через F в условие совместности (8.12.3). В резуль-
результате получим следующее дифференциальное уравнение для функ-
функции F:
F" + i- F' - -1 F = °- (8.12.6)
Общий интеграл этого уравнения будет
следовательно, по формулам (8.12.5) получим
о„ = А + ?, ввв = А-±. (8.12.7)
Постоянные А к В определяются из граничных условий, а имен-
именно, при п = а а„ = — Ч, при г = Ъ отг = 0. Подставляя первое из
выражений (8.12.7) в граничные условия, найдем
На рис. 8.12.2 показаны графики (эпюры) распределения напря-
напряжений по толщине стенки.
Заметим, что величины огг и Gee не зависят от растягивающей
силы. Этого нужно было ожидать, уравнения теории упругости
линейны, поэтому для них справедлив принцип суперпозиции ре-
решений. Осевые напряжения aZ2 определяются теперь из последней
§ 8.12. ОДНОМЕРНЫЕ ЗАДАЧИ — ТРУБЫ И ДИСКИ
269
формулы (8.12.4)
= Eezz + 2vA.
Таким образом, напряжение czz оказывается постоянным. Про-
Произведение этого напряжения на площадь кольцевого сечения тру-
трубы л(Ь2 —а2) равно растягиваю-
растягивающей силе; если величина силы
задана, то это условие позволяет
найти ezz.
Например, если труба снаб-
снабжена доньями, на которые дей-
действует то же давление q, сила рав-
равна яа2д. С учетом найденного вы-
выражения для А, получаем
Для несжимаемого материала Рис. 8.12.2
(v = 1/2) осевая деформация за-
закрытой трубы равна нулю. Если мы теперь хотим определить
перемещение и, проще всего воспользоваться вторым уравнением
(8.12.4), из которого следует, согласно определению ее*
и = ~- [dee — v (arr + azz)].
Задача о вращающемся диске постоянной толщины решается
аналогичным образом. Если толщина диска мала по сравнению
с радиусом, можно считать напряжения равномерно распределен-
распределенными по толщине и, следовательно, не зависящими от коорди-
координаты z. Уравнение равновесия отличается от (8.12.1) только
наличием массовых сил — сил инерции Fr = pco2r. Таким образом,
dar
°тт — а99
+ pcoV = 0.
(8.12.8)
Этому уравнению можно удовлетворить, полагая
F _
Соотношения (8.12.2), (8.12.3) сохраняют силу, в (8.12.4)'
нужно принять ozz = 0; тогда, очевидно, ezz определится из третье-
третьего уравнения и уже не будет константой. Выражая деформации
через функцию F и внося в уравнение совместности, получим
270 гл- 8- теория упругости, общие уравнения
Общий интеграл этого уравнения
Отсюда
DO?.. П J I О*.
. (8.12.9)
Для сплошного диска радиусом Ъ постоянная В должна обра-
обращаться в нуль, иначе при г = 0 напряжения будут бесконечно
велики. Вторая константа А находится из граничного условия
Огг = 0 при г = Ь. Окончательный результат оказывается следу-
следующим:!
Ц 34(^). (8.12.10)
Совершенно аналогичным образом можно получить прибли-
приближенное решение задачи о вращающемся диске переменной тол-
толщины h(r). Упрощающее предположение состоит в том, что на-
напряжения Grr и Gee распределены по толщине равномерно и
напряжения azz, как и другие компоненты тензора напряжений,
равны нулю. Очевидно, что это предположение не позволяет
удовлетворить граничному условию на поверхности диска, вектор
нормали к поверхности составляет с осью угол а, тангенс кото-
которого есть dh/dr и напряжение arr дает на поверхности неуравно-
неуравновешенную силу
Чтобы уничтожить эту силу, необходимо допустить существо-
существование касательных напряжений хГ2 таких, что на поверхности
orr cos (-5- — а] + %rz cos a = 0.
Пренебрегая этой невязкой, которая мало сказывается на резуль-
результатах при условии, что \dh/dr\ < 1, заменим уравнение (8.12.8),
следующим:
~г (hOrr) + h °гг°ед + fepcoV = 0. (8.12.11)
Комбинируя (8.12.11) с (8.12.4) и (8.12.2), можно получить диф-
дифференциальное уравнение второго порядка с переменными коэф-
коэффициентами для функции w(r), ввести функцию напряжений F
и получить аналогичное дифференциальное уравнение для этой
функции. Следует заметить, что для наиболее интересного для
приложений случая — конического диска — уравнение интегриру-
интегрируется в гипергеометрических функциях. Предоставляя читателю
§ 8.13. ЗАДАЧА О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ
271
вывести соответствующее уравнение, находящее приложение при
проектировании дисков турбин, вернемся к уравнению (8.12.11)
и поставим вопрос о том, по какому закону нужно изменять про-
профиль диска, чтобы использовать материал наивыгоднейшим обра-
образом. Очевидно, что для этого нужно, чтобы во всех точках
напряжения были постоянны. Полагая Огг = Овъ = о, получим сле-
следующее уравнение для функции h (r):
Интеграл его равен
(8.12.12)
Для того чтобы в диске, профиль которого построен по урав-
уравнению (8.12.12), напряжение было постоянным, необходимо при-
приложить на наружном контуре нагрузку, вызывающую радиаль-
радиальное напряжение а. Практически это условие выполнить довольно
трудно, к тому же диск равного сопротивления, профиль которо-
которого задан формулой (8.12.2), сложен в изготовлении. Поэтому
в настоящее время диски равного сопротивления на практике не
применяются.
§ 8.13. Простейшая задача о концентрации напряжений
Очевидное решение уравнений теории упругости есть Оц =
*= const. При этом деформации по закону Гука также постоянны
и, следовательно, перемещения представляют собою линейные
функции координат. Чтобы осуществить в теле такое однородное
напряженное состояние, необходимо лишь приложить к его по-
поверхности соответствующие внешние си- *"
лы, а именно
Тг = Оф5. (8.13.1)
Предположим теперь, что в большом
теле сделана малая полость (рис. 8.13.1).
Наибольший линейный размер этой поло-
полости мал по сравнению с характерным раз-
размером тела и с расстоянием полости от
границы. Пусть на поверхности S прило-
приложены такие усилия 7\, которые создали
бы в теле однородное напряженное
состояние Oij, если бы полости не было. При наличии полости
естественно ожидать, что в большей части тела напряженное со-
состояние остается практически однородным, только в непосред-
непосредственной окрестности полости распределение напряжений будет
существенно отличаться от однородного. Это заключение пред-
Рис. 8.13.1
272 гл« 8- теория упругости, общие уравнения
ставляет собою принцип Сен-Венана, примененный к рассматри-
рассматриваемому случаю; более точная формулировка будет следующая.
Характерный размер R зоны концентрации напряжений около
полости имеет порядок характерного размера полости d и не
зависит от размера тела L, если отношение Lid достаточно велико.
Поэтому при решении задач о концентрации напряжений
часто используется прием, состоящий в том, что вместо реаль-
реального тела конечных размеров рассматривается бесконечное про-
пространство, заполненное упругим материалом, и граничное условие
на поверхности тела вида (8.13.1) заме-
заменяется требованием того, что напряжения
стремятся к заданным постоянным зна-
Р У \хг V чениям по мере удаления от источника
концентрации.
Простейший пример такого рода мож-
можно рассмотреть на основе результатов пре-
предыдущего параграфа. Пусть тонкая пла-
пластина произвольной формы в плане под-
подвергнута действию равномерно распреде-
распределенного усилия р, нормального к ее
Рис. 8.13.2 контуру Г (рис. 8.13.2). Если пластина
не имеет вырезов, в ней возникает
напряженное состояние: аи = а22 = р, а3з = oi2 = о23 = c3i = 0.
В плоскости XiX2 все оси — главные, и на любой площадке, па-
параллельной оси х3, нормальное напряжение есть р, а касательное
равно нулю. Предположим теперь, что в пластине сделано отвер-
отверстие радиусом а, и найдем распределение напряжений. Прежде
чем решать эту задачу, заметим, что схема, изображенная на
рис. 8.13.2, может быть применена и к другой задаче. Пусть мы
имеем дело не с тонкой пластиной, а с очень длинным цилинд-
цилиндром, фигура на рис. 8.13.2 представляет его поперечное сечение.
К боковой поверхности цилиндра приложены нормальные уси-
усилия р, равномерно распределенные по всей поверхности. Вдоль
оси цилиндра просверлено отверстие по всей длине. По-прежнему,
если отверстия нет, то ои = а22 = р, Oi2 = а23 = g3i = 0, но напря-
напряжение а33 ^ 0, оно найдется из условия сохранения плоских сече-
сечений. Для нахождения о33 нужно оговорить, чему равна сила,
приложенная к торцам и растягивающая либо сжимающая ци-
цилиндр. В том и другом случае распределение напряжений Он и
022 будет одним и тем же. Внешняя нагрузка такова, что в теле
нельзя указать предпочтительного направления, поэтому распре-
распределение напряжений осесимметрично и дается формулами (8.12.7).
Для определения констант получаются следующие условия: аг = 0
при г = а, аг -*• р при г -> оо. Отсюда
Orr = P l-т- , on = p 1 + -V. (8.13.2)
§ 8.13. ЗАДАЧА О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ ?73
На контуре отверстия при г = а напряжение аее достигает мак-
максимального значения
(Обб)тах= 2р.
Таким образом, наличие отверстия увеличивает максимальное
напряжение в два раза.
Число, указывающее во сколько раз максимальное напряже-
напряжение при наличии концентратора превышает напряжение в той
же точке в теле, не имеющем концентратора, называется коэф-
коэффициентом концентрации напряжений к. В рассмотренном при-
примере к = 2.
Предположение об однородности напряженного состояния при
решении задач концентрации напряжений не обязательно. Дей-
Действительно, если поле напряжений меняется в зависимости от
координат, то всегда можно указать характерную длину, на ко-
которой происходит это изменение, и если размер концентратора
достаточно мал по сравнению с этой характерной длиной, то
напряженное состояние можно считать однородным и переносить
граничные условия на бесконечность.
Проиллюстрируем это на примере вращающегося диска. Формулы
(8.12.9) указывают, что распределение напряжений в диске неоднородно,
характерная длина, на которой они меняются, есть радиус диска Ъ. При
г = 0 о*^ = о*00 = —о— Рю Ъ . Если в центре диска сделано отверстие ради-
радиусом а, причем а < &, то следует ожидать, что максимальное напряжение
будет вдвое больше. Не составляет труда решить задачу о диске с цент-
центральным отверстием точно. Для этого нужно определить константы в фор-
формулах (8.12.9) из граничных условий: ог = 0 при г = а и при г = Ъ. После
несложных вычислений, находим
При г = а
C+v)bJ
3 + V о о
Если а->0, ^ее-*—4—Р® ' т* е* оказываются ровно вдвое больше, чем
для сплошного диска.
В рассмотренном примере мы смогли оценить эффект кон-
концентрации и в том случае, когда отношение alb произвольно.
Вообще такие задачи, когда размер концентратора сравним с
размером тела и расстоянием от концентратора до границы, ока-
оказываются существенно более сложными, в большинстве случаев
результат удается получить лишь с помощью численных методов.
18 ю. Н. Работнов
274 гл- 8- теория упругости, общие уравнения
§ 8.14. Концентрация напряжений у сферической полости
Рассматриваемая ниже задача представляет собою простран-
пространственный аналог той плоской задачи о концентрации напряже-
напряжений, которая была рассмотрена в предыдущем параграфе. Беско-
Бесконечно упругое пространство растягивается во всех направлениях
равномерно, в этом пространстве содержится сферическая полость
радиусом а. Употребляя термин «упругое пространство», мы
должны представить себе тело достаточно больших размеров (ли-
(линейный размер L)_^ на границе которого приложена нагрузка,
создающая в нем равномерное растяжение во всех направлениях
с интенсивностью а. Если тело не содержит полости, т. е. нет
второго характерного размера, с которым можно сравнивать раз-
размер тела L, нет необходимости говорить о том, велик этот раз-
размер или мал. Но если речь идет о концентрации напряжений
около полости радиусом а, коэффициент концентрации будет за-
зависеть от малого параметра a/L и при стремлении этого пара-
параметра к нулю будет стремиться к некоторому конечному значе-
значению, которое не может зависеть ни от а, ни от L. В примере
с вращающимся диском в § 8.13 этот предельный переход был
сделан явно, что оказалось возможным ввиду простоты задачи.
Вообще, полагают этот малый параметр равным нулю с самого
начала, это можно сделать, либо считая размер а бесконечно ма-
малым, либо размер L бесконечно большим. Делая второе предпо-
предположение, мы приходим к представлению об упругом простран-
пространстве, т. е. об упругой среде, заполняющей все пространство.
Поставленную задачу естественно решать в сферических ко-
координатах; воспользовавшись уравнениями G.8.6) и G.8.7), мож-
можно решать ее в декартовых координатах и лишь окончательный
результат представить в сферических. Мы пойдем по этому вто-
второму пути. При наличии сферической симметрии перемещения
направлены по радиусам, выходящим из центра симметрии,
и величина перемещения зависит только от расстояния точки до
центра симметрии г. Компоненты перемещения щ будут проек-
проекциями вектора радиального перемещения иг на направления со-
соответствующих осей, т. е.
щ = иг(г)Х (8.14.1)
Дальнейший ход решения должен был бы заключаться в сле-
следующем. Выражения для щ подставляются в уравнения Ламе
при F{ = 0, каждое из этих трех уравнений приводится к одному
и тому же дифференциальному уравнению для функции ит{г).
Это будет уравнение второго порядка, следовательно, два неза-
независимых частных решения определяют его общий интеграл. Ес-
Естественно ожидать, что эти частные решения, как и в осесим-
метричной задаче, будут степенными функциями от г. Чтобы
§ 8.14. НАПРЯЖЕНИЯ У СФЕРИЧЕСКОЙ ПОЛОСТИ 275
упростить дело, будем сразу искать перемещения в виде
щ = тпхг (8.14.2)
и попытаемся удовлетворить уравнениям Ламе. Заметим предва-
предварительно, что
ч о 'V 2 дг дг xi
а) г2 = хгхг = 2d х" следовательно, r— = xi% -^ = —;
б) 6ihxh = Xi;
в) 6» = 6н + б22 + б33 = 3.
Дифференцируя (8.14.2) по xh найдем
щ. = пгп~2х^ + гябу. (8.14.3)
Отсюда
e = w,, = (n + 3)rn. (8.14.4)
Выражение для uitj симметрично относительно индексов i и /,
поэтому uitj = ujtij следовательно, ец = щъ^
Продифференцируем выражение для uiti no xk. Получим^ учи-
учитывая замечания а) и б),
uiJh = п{п- 2)гп-кхъсрк + пгп-2 (х?5к + xfin + xh8ij).
Для подстановки в уравнения Ламе нам понадобится выражение
kUi — Utjj. Произведем свертывание предыдущего равенства по
индексам / и к. После приведения получим
Подставим Э и Аи{ в уравнение Ламе. В результате получится
Это равенство возможно при п = 0 и п = —3; таким образом:
/ С Л
щ=\С1 + -^\х1. (8.14.5)
Сравнивая с (8.14.1), находим радиальное перемещение
С
-2
Ur = Схт + Ц-. (8.14.6)
Г
Получим теперь формулы для напряжений. Заметим, что при
п = — 3 0 = 0, при 7г = 0 по формуле (8.14.4) 0 = 3; эту величи-
величину нужно умножить на С\. Величины exj представляют собою сум-
суммы выражений, определенных формулами (8.14.3) при п = 0 и
/г = — 3, умноженных на соответствующие константы. Подставляя
в формулы закона Гука, найдем
<г« = С, (ЗА, + 2(i) бу + С2\к (- 3 ^ + &J. (8.14.7)
Вырежем мысленно элемент, изображенный на рис. 8.14.1.
Две грани его принадлежат поверхностям бесконечно близких
18*
276
ГЛ. 8. ТЕОРИЯ УПРУГОСТИ. ОБЩИЕ УРАВНЕНИЯ
концентрических сфер радиусом г и r + аг, остальные грани вза-
взаимно ортогональны и ориентированы произвольным образом. Нор-
Нормальные напряжения на сферических элементах мы обозначим
От, это есть радиальное напряжение. Нормальные напряжения
на других гранях одинаковы, обозначим их а*. Касательные на-
напряжения отсутствуют. Это за-
заключение есть необходимое
следствие предполагаемой цент-
центральной симметрии, в касатель-
касательной плоскости к сфере нельзя
указать предпочтительного на-
направления. Мы можем напра-
направить оси координат, как пока-
Рис. 8.14.1 зано на рисунке, ось Xi — по
радиусу, оси хг и хг — парал-
параллельно нормалям к остальным граням. Тогда координаты эле-
элемента будут хи 0, 0, г = хи an = Or, 022 = Озз = о*. Подставляя
в (8.14.7), получим
-^-. (8.14.8)
С помощью формул (8.14.8) можно решить задачу о полой
сфере под действием наружного и внутреннего давления, совер-
совершенно аналогичную рассмотренной ранее задаче о трубе. Мы не
будем выписывать относящиеся сюда формулы, которые полу-
получаются элементарно.
Отметим два частных решения, представляющих определенный интерес.
а. Концентрация напряжений около сферической полости. Положим
CiCK + 2\x) = Go. Из формул (8.14.8) следует, что при г->оо напряженное
состояние стремится к состоянию всестороннего растяжения (или сжатия)
напряжением о0. Сферическая полость имеет радиус а, при г = а о> = 0.
Отсюда следует
Напряжение а* достигает максимального значения (a*)max = V2CJ0 при г =
ч= а; таким образом, коэффициент концентрации равен 3/2.
б. Центр расширения. Положим С\ = 0 и будем считать тело неогра-
неограниченным. На поверхности сферы радиусом а перемещение и<ь по формуле
(8.14.6) равно С^а2. Умножив величину перемещения на площадь поверх-
поверхности сферы, мы получим изменение ее объема
Следовательно, С2 = AV/Djt). Таким образом, решена следующая зада-
задача. В бесконечное упругое пространство вставлена абсолютно жесткая сфе-
сфера радиусом а. Радиус ее увеличился вследствие каких-то причин так,
что объем сферы получил приращение AF. Напряжения во всем упругом
§ 8.14. НАПРЯЖЕНИЯ У СФЕРИЧЕСКОЙ ПОЛОСТИ 277
пространстве даются формулами
AV ц AF w
<8Л49>
которые имеют смысл, конечно, только при г >> а. Существенно заметить,
что в эти формулы радиус жесткой сферы а не входит, напряжения и пе-
перемещения в произвольной точке зависят только от того, как изменился
объем жесткого включения, но не зависят от размеров включения. Поэтому
радиус а можно сделать сколь угодно малым, можно даже перейти к пре-
пределу, устремив а к нулю. Однако при этом формулы (8.14.9) формально
справедливы для сколь угодно малых г и при г, стремящемся к нулю, на-
напряжения неограниченно растут. Мы получили сингулярное, т. е. обладаю-
обладающее особенностью, решение, соответствующее так называемому центру рас-
расширения. При малых г оно имеет только формальный смысл, перемеще-
перемещение, определяемое формулой (8.14.6), также растет неограниченно с умень-
уменьшением г; картина оказывается противоречащей элементарному здравому
смыслу. Существо дела состоит, конечно, в том, что при малых г предполо-
предположения линейной теории упругости становятся неверными и формальные ре-
решения перестают описывать истинное состояние тела. Однако на достаточ-
достаточно больших расстояниях от центра расширения формулы верны.
Нужно отметить, что при С\ = 0 относительное изменение объема 0
равно нулю. Это — любопытная особенность найденного решения: измене-
изменение объема жесткого включения не вызывает изменения объема какой-ли-
какой-либо части окружающей упругой среды.
В металлических сплавах при фазовых превращениях выпадают мелко-
мелкодисперсные частицы новой фазы, образование которой связано с измене-
изменением объема. В матрице, т. е. в основной массе металла, при этом возни-
возникают напряжения. Если выделения достаточно малы, их можно моделиро-
моделировать центрами расширения.
ГЛАВА 9
АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
§ 9.1. Антиплоская деформация
Здесь будет рассмотрен некоторый класс задач теории упру-
упругости, для которых решения получаются с помощью относитель-
относительно простых математических средств. Представим себе цилиндри-
цилиндрическое тело, нагруженное по боковой поверхности усилиями, рав-
равномерно распределенными вдоль образующих и направленными
вдоль образующих. Направим ось х3 по оси цилиндра, оси
xa(xi и х2) в плоскости поперечного сечения. На боковой по-
поверхности п3 = О, па — направляющие косинусы нормали к кон-
контуру сечения Г в плоскости ха. Согласно сделанному предполо-
предположению на боковой поверхности S
Га = 0, Т3 = Т(ха) (а = 1,2).
Граничными условиями на торцах цилиндра мы пока зани-
заниматься не будем, цилиндр считается очень длинным и мы рас-
рассматриваем сечения, достаточно удален-
удаленные от торцов.
Попытаемся удовлетворить уравне-
уравнениям теории упругости, приняв ut =
= и2 = 0, щ = — и (ха). Тогда по фор-
формулам закона'Гука
Оц = 022 =
= 012 == 0,
031
Рис. 9.1.1
Отличные от нуля компоненты тензора
напряжений представляют собою каса-
касательные напряжения в плоскости по-
поперечного сечения, показанные на рис. 9.1.1. Будем обозначать
их для краткости 031 = Ti, 032 = т2. Тогда
Та
Два первых уравнения равновесия (8.4.1) будут выполняться
тождественно, третье же примет следующий простой вид:
Та,а = 0.
(9.1.2):
§ 9.1. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ 279
Граничное условие на контуре Г
ъаПа. — 1 \Ь) . yu.L.O)
Усилие Т предполагается заданным как функция дуги кон-
контура s. Запишем уравнения (9.1.1) и (9.1.2) в развернутом виде
ди ди /п м А,х
"F + 5F = °- (9.1.2')
Дифференцируя первое из уравнений (9.1.1') по х2, а второе
по хи заключаем, что вследствие независимости второй смешан-
смешанной производной от порядка дифференцирования
^~^7z=Om (9.1.4)
Уравнения (9.1.2) и (9.1.4) напоминают известные соотноше-
соотношения Коши — Римана, которые связывают действительную и мни-
мнимую части функции комплексной переменной. Положим z = хг +
+ ix2 (не смешивать с обозначением координаты z). Функция
комплексной переменной w(z) может быть представлена следу-
следующим образом:
w{z) = u(xu x2)+ iv(xu x2),
где и и v — действительные функции двух переменных. Условие
дифференцируемости функции w(z) состоит в том, что частные
производные функций и и v связаны соотношением Коши — Ри-
Римана, а именно,
ди ди ди ди
Сравнивая эти соотношения с уравнениями (9.1.2') и (9.1.4),
убеждаемся, что комплексная комбинация rt — ir2 есть диффе-
дифференцируемая функция комплексной переменной z
Tl-iTa = i0'(z). (9.1.5)
Обозначение w' (z) для произвольной функции от z выбрано для
удобства.
Выражение (9.1.5), где w' (z) — любая дифференцируемая
функция, представляет собою общее решение антиплоской задачи
теории упругости, граничное условие (9.1.3) позволяет опреде-
определить функцию wr (z) единственным образо<м. Действительно, вно-
внося в это условие выражения (9.1.1) и заменяя производные
от функции и производными от функции и, заметим, что оно
280 гл- 9- АЫТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
принимает следующий вид:
dv ^xi dv d%2 m / \
¦ —— —|— ^— ' ——. _? ( S ) •
Отсюда, интегрируя, получаем
Im w = §T(s)ds. (9.1.6)
Фигурирующий в правой части интеграл есть однозначная функ-
функция от s, вследствие выполнения уравнения равновесия для тела
в целом
~ T(s)ds = O.
Однако до сих пор решение еще не полно, нам осталось
найти перемещение и(ха). Используя (9.1.1'), перепишем (9.1.51
следующим образом:
Вспомним теперь, что производная от функции комплексной
переменной z не зависит от того направления, по которому со-
сообщается приращение независимой переменной. Поэтому
, , ч ди_ . dv__ ди_ . . dv_
Вследствие соотношений Коши — Римана можно написать
также
Сравнивая это выражение с (9.1.6), замечаем, что функция и
есть действительная часть функции w(z)
j. _ г>р тG\ (Q 4 7Y
§ 9.2. Винтовая дислокация
Положим
2 2 Х9
w(z) = — Ai In z == A @ — ilnг)% r2 = xx + x2, 0 = arctg —#
xi
По формуле (9.1.7) перемещение и3 есть
и3 = — arctg -f-.
Полярный угол 0 изменяется на 2я при полном обходе вокруг
начала координат; таким образом, перемещение оказывается не-
неоднозначной функцией координат. Смысл такой неоднозначно-
9.2. ВИНТОВАЯ ДИСЛОКАЦИЯ
281
сти перемещения легко понять. Рассмотрим длинную трубу с
внешним радиусом R и внутренним радиусом с (рис. 9.2.1).
Представим себе, что труба разрезана плоскостью, проходящей
через ее ось с одной стороны, края разреза сдвинуты один от-
относительно другого в направлении, параллельном оси, на вели-
величину Ь; после этого плоскости разреза сварены или склеены
[ между собой. В трубе возникнут некоторые
напряжения, им будут соответствовать опре-
определенные деформации. Если теперь вычислять
Рис. 9.2.1
Рис. 9.2.2
перемещения по деформациям, то окажется, что при обходе
по замкнутому пути перемещения получат приращения 6,
Найденное решение как раз содержит такую особенность. Удобно
переписать его в следующем виде:
iibi, Ъ . х<> ,Л Л JV
w = — т^-lnz, и3 = ^-r arctg —. (9.2.1)
Вычислим теперь напряжения. По формуле (9.1.5)
fiLJL
2л z
2я
Отсюда
(9.2.2)
На рис. 9.2.2 показаны эти напряжения. Результирующий
вектор напряжения направлен перпендикулярно радиусу, вели-
величина его
г 2я г '
Заметим, что в точках контура вектор т направлен по каса-
касательной к окружности, поэтому выполняется граничное условие
Итак, мы действительно получили решение для трубы с раз-
разрезом, удовлетворяющее граничным условиям. Можно предста-
282 ГЛ< 9> АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
вить себе, что после сварки поверхностей разреза шов зачищен,
концы обрезаны и нет никаких внешних признаков того, что над
трубой производилась описанная операция. Однако в трубе су-
существуют напряжения, притом без внешних сил. Это можно обна-
обнаружить, если разрезать трубу, например, вдоль образующей. Она
сейчас же примет вид, изображенный на рис. 9.2.1. Напряжения,
существующие в теле, свободном от внешних сил, называются
начальными напряжениями. Начальные напряжения возникают
при неравномерном затвердевании слитков, при остывании поко-
поковок, после сварки и других технологических операций.
Полученное решение соответствует тому, что называется вин-
винтовой дислокацией.
Предположим теперь, что мы имеем дело не с трубой, а со
сплошным цилиндром. Формулы (9.2.1) и (9.2.2) можно приме-
применить и к этому случаю, на оси цилиндра при xt = х2 = 0 напря-
напряжения оказываются бесконечно большими. Таким образом, мы
получили некоторое сингулярное решение теории упругости. Бе-
Бесконечно большие напряжения в теле, конечно, невозможны.
На самом деле, если напряжения достаточно велики, уравнения
линейной теории упругости утрачивают силу. Формулы (9.2.2)
имеют смысл тогда, когда г> с, с — некоторая определенная ве-
величина. При г < с нужно строить решения, основываясь на ис-
истинных нелинейных зависимостях. Линия, на которой напряже-
напряжения, вычисленные с помощью линейной теории, обращаются в
бесконечность, называется линией дислокации, вектор 6— векто-
вектором Бюргерса (рис. 9.2.1). Область г<с, непосредственно при-
примыкающая к линии дислокации, называется ядром дислокации.
Теория упругости не дает возможности судить о том, что про-
происходит внутри ядра дислокации. Винтовая дислокация характе-
характеризуется тем, что ее линия — прямая и вектор Бюргерса направ-
направлен по линии дослокации.
Заметим, что из формул для перемещения и напряжений
(9.2.1) и (9.2.2) нельзя сделать заключения о том, в каком имен-
именно месте был произведен разрыв и последующая сварка. Это —
общее свойство дислокаций типа Вольтерра, к которому при-
принадлежит винтовая дислокация.
Вычислим теперь энергию винтовой дислокации, приходя-
приходящуюся на единицу длины цилиндра. Для этого существует два
пути. Первый путь состоит в том, что мы берем выражение для
удельной энергии U = -тг- {х\ + Тг) и интегрируем его по объему.
Второй, более простой, основан на применении теоремы Клапей-
Клапейрона. Представим себе, что труба разрезана с одной стороны
полуплоскостью XiOxz. Чтобы удержать поверхность разреза на
месте, к двум его сторонам нужно приложить продольные каса-
касательные усилия Т = т2 = ;j . Будем смотреть на усилие Т как
§ 9.3. ТРЕЩИНА ПРОДОЛЬНОГО СДВИГА 283
на внешнюю силу, приложение которой создано дислокацией,
т. е. вызвано относительным смещением поверхностей разреза
на величину Ь. Тогда, по теореме Клапейрона
_ =_in—. (9.2.3)
S с *
Величина энергии стремится к бесконечности при Л->оо и
при с -> 0. Первое кажется естественным, второе же лишний
раз подчеркивает, что для сплошного тела решение, соответству-
соответствующее линейной дислокации, физически невозможно, оно непри-
непригодно для ядра дислокации и оценка энергии ядра должна про-
производиться на основе каких-то других соображений, выходящих
за рамки линейной теории упругости.
§ 9.3. Трещина продольного сдвига
Рассмотрим функцию комплексной переменной
= Vr[— sin-|-
Посмотрим, какому решению антиплоской задачи соответству-
соответствует эта функция. Действительная часть ее с точностью до мно-
множителя, о котором мы пока не заботимся, есть перемещение
.— л
Re w (%) = — у г sin -g-.
При 0 = Jt Re w (z) = Vr, при 0 = —я Re w (z) = Vr; таким об-
образом, на отрицательной полуоси Xi перемещение претерпевает
Рис. 9.3.1 Рис. 9.3.2
разрыв. Нужно представить себе неограниченное упругое про-
пространство, разрезанное по полуплоскости х2 = 0, Xi < 0
|(рис. 9.3.1); края разреза получают перемещения в направлении
оси Xi в противоположные стороны, величина перемещения про-
пропорциональна корню квадратному из расстояния от края тре-
трещины (рис. 9.3.2).
Выясним теперь, какое при этом будет напряженное состояние
и какие внешние силы нужно приложить к телу. Производная
284 гл- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
функции w(z)
При 0 = ±я выражение м?' (z) действительно, следовательно»
по формуле (9.1.5), напряжение т2 равно нулю и на поверхности
разреза никакие силы не приложены. Очевидно, что функцию
w(z) можно умножить на любую постоянную. Обозначим эту
постоянную —КУ2/л и выпишем решение
(9.3.1)
„з = -Lj/Ir sin A, (9.3.2)
Единственный параметр, фигурирующий в решении, это вели-
величина К — коэффициент интенсивности, имеющий размерность си-
силы, разделенной на длину в степени 3/2. Существенно в этом
решении то, что напряжения обраща-
обращаются в бесконечность при г = 0. То же
самое было и в случае дислокации, од-
однако здесь особенность более слабая, а
именно вида 1/Уг, тогда как для дисло-
дислокации особенность была вида 1/г. Про-
Проделанное исследование может оставить
впечатление некоторой искусственности.
Действительно, остается неясным, как
можно на самом деле осуществить со-
состояние, описываемое (9.3.1, 9.3.2).
Рис. 9.3.3 Реальный смысл полученного ре-
результата заключается в следующем.
Представим себе упругое тело конечных размеров в пло-
плоскости хи #2, содержащее трещину конечной длины
(рис. 9.3.3). Тело подвержено действию произвольной системы
внешних сил. Нужно, конечно, помнить, что мы рассматриваем
антиплоское напряженное состояние, значит тело представляет
собой бесконечно длинный цилиндр. Трещина или щель имеет
бесконечную длину в направлении оси хг и на рис. 9.3.3 изобра-
изображено любое поперечное сечение этого цилиндра. Внешние силы,
приложенные к боковой поверхности цилиндра, а возможно и к
поверхности трещины, параллельны оси х3 и поэтому не изобра-
изображены на рисунке.
В результате решения, более или менее сложного, мы можем
найти распределение напряжений во всех точках сечения. При
этом обязательно окажется, что по мере приближения к концу
§ 9.4. ТРЕЩИНА КОНЕЧНОЙ ДЛИНЫ 285
трещины напряжения неограниченно растут. Если направить оси
координат так, как показано на рис. 9.3.3, т. е. ось Xi по каса-
касательной к оси трещины, и поместить начало координат в конце
трещины, то формулы для напряжений будут обязательно иметь
вид
^ sin+ T=icos4+ (934>
Мы ничего не можем сказать в общем случае о структуре
дополнительных невыписанных членов в этих разложениях, кро-
кроме того, что они остаются конечными при г = 0. Значит при до-
достаточно малых г выписанные главные части в формулах для
напряжений преобладают и только они имеют значение. Коэф-
Коэффициент интенсивности К будет зависеть от формы сечения, фор-
формы щели и внешних нагрузок; он находится в результате реше-
решения задачи теории упругости. При этом полное решение задачи
обычно и не интересует, основная цель состоит как раз в на-
нахождении коэффициента интенсивности.
§ 9.4. Трещина конечной длины
Рассмотрим теперь уже реальную задачу о напряжениях в
теле, содержащем трещину. Будем считать тело неограниченным;
на бесконечности задано Tt = 0, т2 = т0. Трещина занимает от-
отрезок действительной оси з:, е [-с, с] (рис. 9.4.1). Рассмотрим
функцию комплексной переменной
^?. (9.4.1)
Для точек действительной оси у z2 — с2 = ]/ х\ — с2 будет действи-
действительным, если \Xi\ > с, и чисто мнимым, если \xi\<c. Поэтому
действительная часть функции w(xi) равна нулю вне трещины
и равна ± Ау с2 — х\ на берегах трещины; значения ее на верх-
верхнем и нижнем берегу в соответствующих точках равны по вели-
величине и противоположны по знаку. Производная функции w(z)
w' (z) = ,Aiz . (9.4.2)
Vz2 — r2
• с
При z = Xi величина w'(z) будет действительной, если l#tl<c;
поэтому вследствие (9.1.5) на берегах трещины т2 = 0, поверх-
поверхность трещины свободна от напряжений. Осталось проверить
условия на бесконечности. При z -> оо w' (z)->- Ai. Таким об-
образом, должно быть Ai = 0 — ixQ. Следовательно,
А = -то. (9.4.3)
Итак, формулы (9.4.1) — (9.4.3) дают решение поставленной
задачи. Отделяя действительные и мнимые части, мы могли бы
286 ГЛ- 9* АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
выписать полные выражения для перемещения и5 и напряже-
напряжений Ti, т2. Мы ограничимся исследованием напряженного состоя-
состояния вблизи одного из концов трещины, например правого. По-
Поместим на правом конце трещины начало вспомогательной си-
системы координат |, tj, положим ? = рег'е (см. рис. 9.4.1). Тогда
Разложим это выражение в ряд по степеням ?. Получим
Для наших целей нет нужды выписывать следующие члены
степенного ряда в скобках. Существенно то, что первый член
содержит ?1/2, второй ?3/2, тре-
третий ?5/2 и так далее. При по-
почленном дифференцировании
только первый член будет со-
держать ? в отрицательной сте-
пени, а именно ?"/2, все осталь-
ные члены будут положитель-
положительными степенями ?. Следователь-
Следовательно, при ? -> О все члены разло-
Рис. 9.4.1 жения для w' (t) будут стре-
стремиться к нулю, кроме первого,
который стремится к бесконечности. Поэтому в окрестности кон-
конца трещины нам достаточно только первого члена, а именно,
(9.4.4)
Сравнивая с (9.3.1), убеждаемся, что (9.4.4) и (9.3.1) тож-
тождественно совпадают, если принять
# = ТоУ^ (9.4.5)
Выражения для напряжений вблизи конца трещины, соответ-
соответствующие приближенному выражению (9.4.4), даются формула-
формулами (9.3.3); если вычислить точные значения ti и т2, то их вы-
выражения необходимым образом будут иметь структуру формул
(9.3.4).
§ 9.5. Освобождение энергии при раскрытии трещины
Обозначим через Uo упругую энергию тела, подверженного
действию некоторой нагрузки и не содержащего трещины. Если
в теле образовалась трещина, например прямолинейная длиной
2с, энергия тела изменится и будет равна U. Кажется очевид-
очевидным, что U < UQ, появление трещины уменьшает упругую энер-
энергию. Имея дело с антиплоским напряженным состоянием в бе-
§ 9.5. ОСВОБОЖДЕНИЕ ЭНЕРГИИ ПРИ РАСКРЫТИИ ТРЕЩИНЫ ?87
сконечно длинном цилиндре, мы будем понимать под Uo или U
энергию, приходящуюся на единицу длины в направлении оси
xz. Оценить разницу между U и UQ можно из очень простых
соображений. На достаточно большом расстоянии от трещины ка-
касательное напряжение постоянно и равно т0, следовательно, энер-
энергия на единицу площади поперечного сечения есть To/B(i), В ок-
окрестности трещины напряжения в среднем уменьшаются, значит
удельная на единицу площади энергия меньше чем То/B[х). Пло-
Площадь разгруженной части около трещины необходимым образом
имеет порядок с2, так как никакого другого линейного размера,
кроме с, в условиях задачи не содержится. Итак,
Uo-U~^. (9.5.1)
В этом рассуждении не все строго. Если тело имеет конеч-
конечные размеры, то в оценке (9.5.1) фигурирует, кроме длины,
еще и некоторый характерный размер тела. Вообще говоря не
очевидно, что при безграничном увеличении размера тела при
фиксированной длине трещины разность Uo — U стремится к ко-
конечному пределу.
При фактических вычислениях мы будем исходить из реше-
решения (§ 9.3), полученного для бесконечного упругого простран-
пространства. Самый прямой и, казалось бы, естественный путь вычис-
вычисления величины Uo—U заключается в следующем. Для тела,
не содержащего трещины, Xi = 0, т2 = т0, следовательно,
Здесь dS — элемент площади поперечного сечения, интегрирова-
интегрирование распространено по всей плоскости хи х2. Для тела, содер-
содержащего трещину,
Оба эти интеграла расходящиеся, значения их бесконечно вели-
велики, но разность
оказывается конечной, ее можно вычислить непосредственно.
Этот прямой путь оказывается не самым простым. Другой
способ, которому мы и последуем, состоит в следующем. Окру-
Окружим трещину произвольным контуром Г в плоскости хи х2 и
выделим из неограниченного упругого пространства цилиндр,
основание которого ограничено контуром Г. Вектор касательного
288
ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
напряжепия в плоскости хи х2 в точке контура Г разложим на
составляющие: нормальную к контуру тп и касательную т8. На
боковой поверхности цилиндра будут действовать касательные
напряжения, равные тп и направленные вдоль образующей. Их
можно рассматривать как внешние силы по отношению к ци-
цилиндру, поэтому упругая энергия на единицу длины цилиндра
найдется по теореме Клапейрона
U = —- j xnubds.
Теперь можно сделать предельный переход, удаляя контур Г
в бесконечность. Очевидно, что U будет также стремиться к
бесконечности, но нас интересует не
величина ?/, а разность между Uo и U.
Заметим, что форма контура Г при
этом безразлична, ее нужно выбирать
из соображений удобства и простоты
интегрирования. Пусть, например, кон-
контур Г будет окружностью радиусом г
с центром в начале
(рис. 9.5.1). Тогда
тп = т4 cos 9 + т2 sin 9. (9.5.2)
В § 9.3 мы нашли, что
координат
V2
Рис. 9.5.1
На контуре окружности UI = г; если \z\ > с, то
= — ixa
?i+... • (9-5-3)
Отделяя действительную часть от мнимой, получаем
Теперь, по формуле (9.5.2)
тп = т0 sin 9 1
-^ cos 29+... . (9.5.4)
(9.5.5)
Для вычисления щ нужно разложить выражение (9.4.1) функ-
функции w в окрестности бесконечно удаленной точки, т. е. при
больших значениях \z\
w (z) = ' ' "
Удержим только первый член в этом разложении и отделим
§ 9.5. ОСВОБОЖДЕНИЕ ЭНЕРГИИ ПРИ РАСКРЫТИИ ТРЕЩИНЫ 289
действительную часть. Получим
u3=^-rsinQ+... (9.5.6)
Теперь, по теореме Клапейрона
Очевидно, что при неограниченном увеличении г величина U
стремится к бесконечности, притом за счет первого члена в скоб-
скобках. Положив в формуле для U с = 0 мы получим энергию ци-
цилиндра, не содержащего трещины,
Разница энергий
Uo-U = •%-$-<* (9.5.7)
не зависит от радиуса г, следовательно, можно считать г беско-
бесконечно большим.
При выводе формулы (9.5.7) мы удержали лишь первые чле-
члены в разложениях для т4, т2 и и3. Легко сообразить, что дало бы
удерживание следующих членов. Третий член в разложении
(9.5.5) будет содержать в знаменателе г4, второй член в разло-
разложении (9.5.6) будет содержать множитель 1/г. При вычислении
U следующие слагаемые будут поэтому обязательно содержать
отрицательные степени г, которые обращаются в нуль при пре-
предельном переходе, когда г устремляется к бесконечности.
Энергия тела, содержащего трещину, меньше чем энергия те-
тела, которое трещины не содержит. Если длина с трещины уве-
увеличивается, то происходит освобождение упругой энергии. Если
половина длины увеличилась на Ас, то из (9.5.7) следует
AU = - я ^ Ас = — — Ас. (9.5.8)
Соотношение (9.5.8), выраженное через коэффициент интен-
интенсивности К, получено нами для конкретного частного случая —
трещины длиной 2с в бесконечном теле, нагруженном равномер-
равномерно распределенными усилиями на бесконечности. Однако полу-
полученный результат совершенно универсален, он справедлив для
любой трещины, так как освобождение энергии происходит в об-
области, непосредственно примыкающей к концу трещины. Чтобы
показать это, поступим следующим образом. Сделаем разрез вдоль
оси впереди трещины на отрезке длины Ас (рис. 9.5.2). Чтобы
края разреза не разошлись, к ним нужно приложить распреде-
19 ю. Н. Работнов
290
ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
ленные силы, интенсивность которых равна касательному на-
напряжению в неразрезанном теле, т. е. вычисляется по формуле
(9.3.4) при Э = 0
К
Будем теперь уменьшать эти силы, края разреза начнут рас-
расходиться. Когда силы обратятся в нуль, мы получим ту же тре-
трещину, что в исходном состоянии, но
передвинутую вправо на длину Дс.
Берега трещины в новом положении
показаны на рисунке штриховой лини-
линией. Перемещение и3 будет определяться
формулой (9.3.2) при Э = я и при пере-
перенесенном на величину Дс начале коор-
координат; таким образом,
Рис. 9.5.2 и3 = — у — (Дс — х) .
По теореме Клапейрона, изменение упругой энергии равно
половине работы сил г на перемещении щ; таким образом,
Дс
ДС/ — — \ xu3dx.
о
Множитель 1/2 сократился, потому что расхождение берегов раз-
разно 2и3, как видно из рис. 9.5.2. Подставляя выражения т и и3,
найдем
ДС/ = 1 I/ —-— dx.
Интеграл в этой формуле легко вычислить, он равен я/2,
поэтому
ДС/--^Дс. (9.5.9)
Разница между этой формулой и формулой (9.5.8) объясня-
объясняется тем, что в первом случае изменение длины трещины рав-
равнялось 2Дс, трещина расширялась влево и вправо с сохранением
симметрии. При выводе формулы (9.5.9) предполагалось, что
трещина распространяется вправо на длину Дс, и только.
§ 9.6. Кручение круглых стержней
Рассмотрим тело, представляющее собою длинный цилиндр
с осью, параллельной оси х3, сечение его в плоскости хи х2 ог-
ограничено контуром Г или несколькими контурами ГА. Пред-
Предположим, что боковая поверхность стержня свободна от напря-
§ 9.6. КРУЧЕНИЕ КРУГЛЫХ СТЕРЖНЕЙ
291
жений, а к торцам приложены усилия, статически эквивалентные
паре сил с моментом М. Вспоминая техническую теорию изгиба
балок, основанную на гипотезе плоских сечений, предположим,
что и при кручении плоские сечения остаются плоскими, они
только поворачиваются одно относительно другого.
Будем считать, что концевое сечение х3 = 0 неподвижно. Се-
Сечение, отстоящее от него на расстоянии х3, поворачивается на
угол, пропорциональный расстоянию,
а именно fixs. Величину О можно
назвать погонным, т. е. приходящим-
приходящимся на единицу длины, углом закру-
закручивания. Из рис. 9.6.1 видно, что
Рис. 9.6.1
Отсюда следует, что ei3 = —$х2,
б2з==191^1, все остальные компоненты
деформации равны нулю. По закону
Гука все компоненты напряжения,
кроме Gi3 и а23, равны нулю; обозна-
обозначая эти компоненты так, как было
принято выше в § 9.1, найдем
Х1 = —\1$Х2, Т2 = (xO^l (9.6.1)
Напряженное состояние оказывается того же типа, что в слу-
случае антиплоской деформации, поэтому уравнения равновесия
(9.1.2) и граничные условия (9.1.3) сохраняют силу. Выражения
(9.6.1) тождественно удовлетворяют условиям равновесия. Гра-
Граничное условие на боковой поверхности (9.1.3) дает после под-
подстановки в него (9.6.1)
п^х2 — n2Xi = 0,
или
\1Ъ\ » ТЬ2 —¦ Х^ . Х2,
Это условие означает, что нормаль к контуру в данной точке
направлена так же, как радиус-вектор точки, значит — контур
представляет собою окружность. Итак, формулы (9.6.1) дают
только решение задачи о кручении стержня, сечение которого
ограничено концентрическими окружностями, значит либо сплош-
сплошного круглого стержня, либо трубы. Вектор касательного напря-
напряжения, компоненты которого даются формулами (9.6.1), направ-
направлен перпендикулярно радиусу-вектору и величина его
т _ mqr (Г2 _ ~2 , 2\ /Q д рч
Т — (jIU/ yi — Л\ -р «^2/ * \Х/m\J,?d)
На элемент площади dS — rdrdy действует сила т dS = j^Or^rdcp,
она создает момент относительно оси х3 на плече г, следова-
следовательно, усилия в каждом сечении статически эквивалентны паре
19*
292 ГЛ> 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
сил с моментом
2Я Д
Итэ4
ft3 d d ft
И
\xftr3 dr dy = \iftn
о в0
Выражение
2Я Я
-и
О Ял
называется полярным моментом инерции площади сечения. Та-
Таким образом, для трубы мы получили следующую зависимость
погонного угла закручивания от крутящего момента:
* = Wp- (9-6.3)
Теперь величина напряжения на радиусе г выражается следую-
следующим образом:
Mr /Гк а /ч
т = -jr. (9.6.4)
l
§ 9.7. Кручение стержней некруглого поперечного сечения
Предположение о том, что поперечное сечение стержня при
кручении остается плоским, вполне аналогично такому же пред-
предположению в элементарной теории изгиба балок, которая была
изложена в третьей главе. Но применительно к задачам изгиба
это предположение выполняется во всех случаях с практически
достаточной точностью, оно позволяет определить основные при
изгибе напряжения —нормальные к плоскости сечения. Некото-
Некоторое искривление поперечных сечений может происходить за счет
касательных напряжений, по эти напряжения, как было пока-
показано, относительно невелики. Для кручения, когда возникают
именно касательные напряжения, поперечные сечения действи-
действительно остаются плоскими только тогда, когда сечение ограничено
концентрическими окружностями, как это было рассмотрено в
§ 9.6. Чтобы построить решения в общем случае, добавим к на-
напряженному состоянию (9.6.1) напряженное состояние, соответ-
соответствующее антиплоской деформации по формулам (9.1.1). По-
Получим
Т4 = ил — (Г&Яг, Т2 = U>2 + \Л®Х1 (9.7.1)
и выберем функцию и так, чтобы было выполнено соответствую-
соответствующее граничное условие на поверхности цилиндра, которое
§ 9.7. КРУЧЕНИЕ НЕКРУГЛЫХ СТЕРЖНЕЙ 293
принимает следующий вид:
T^i + Т2ГС2 = 0, ха е Г, Г — контур сечения цилиндра.
Подставляя сюда (9.7.1), получим
utjti + и гПч — [I® (xzrii — xjii) = О
или
| *i--*i*i)- (9.7.2)
Таким образом, решение задачи о кручении свелось к задаче
Неймана — нахождению гармонической функции и в области,
ограниченной контуром Г, по заданному значению ее нормаль-
нормальной производной на контуре.
Пусть теперь и — функция от ха, гармонически сопряженная
с и(ха), т. е. связанная с ней соотношениями Копта — Римана,
Заменяя в (9.7.1) производные от и производными от у, по-
получим
Ti = v 2 — \фх2, т2 = —z> 1 + ixftxi.
Граничное условие (9.7.2) преобразуется к следующему виду:
Здесь символ -т- обозначает дифференцирование по дуге конту-
контура s. Выписанное граничное условие можно проинтегрировать по
дуге. В результате получим
у = цО 1 2 4- С ж sF (9 7 3)
тогда как функция v — гармоническая,
Таким образом, задача о кручении оказалась сведенной к за-
задаче Дирихле.
Формулы для т4 и т2 можно переписать следующим образом:
2 1
Здесь
Поскольку v — гармоническая функция, функция F, называемая
294 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
функцией напряжений, удовлетворяет уравнению Пуассона
AF = -2нЛ, (9.7.5)
тогда как граничное условие (9.7.3) заменяется следующим про-
простым условием:
F = Ck, Xa = Th. (9.7.6)
В этой записи учтена возможность того, что область попереч-
поперечного сечения многосвязна и граница ее состоит из ряда кон-
контуров 1\. Если сечение односвязно, то постоянную С на един-
единственном контуре Г можно выбрать по произволу, например,
положить С = 0. Для многосвязных областей далее будет уста-
установлено правило, позволяющее назначить постоянные Ck.
Заметим, что формулам (9.7.4) можно придать симметричный
вид, а именно,
Та = ТЛ- (9-7-7)
Здесь тензор ^ар определен в пункте (и) § 7.1.
Встретившийся здесь прием введения функции напряжений
с помощью (9.7.4) или (9.7.7) носит совершенно общий характер.
При построении теории сложного сдвига и кручения можно было
принять за отправной пункт не кинематическую гипотезу § 9.6,
а уравнение равновесия (9.1.2) вместе с предположением о ра-
равенстве нулю всех остальных компонент напряжения. Представ-
Представляя Ti и т2 как производные от функции F, мы удовлетворим
уравнению равновесия. Из (8.5.8) следует, что при равенстве
нулю остальных напряжений как Ti, так и т2 — гармонические
функции. Отсюда следует
AF = const.
Вычисляя теперь перемещения, мы убеждаемся, что это как раз
та константа, которая фигурирует в (9.7.5).
Нам осталось показать, что решение задачи в любой из трех
эквивалентных формулировок действительно относится к круче-
кручению призматического стержня парой сил, приложенной на тор-
торце. Прежде всего необходимо проверить, что результирующая
внутренних сил в сечении равна нулю, это значит, что
x2dS = 0. (9.7.8)
s s
Запишем первое условие следующим образом:
S ^2
Этот интеграл преобразуется в контурный, следовательно, должно
§ 9.7. КРУЧЕНИЕ НЕКРУГЛЫХ СТЕРЖНЕЙ 295
быть
\ Fn2ds - 0.
г
На каждом из контуров, образующих границу площади сечения,
F = const, следовательно, выносится из-под знака интеграла.
Оставшийся интеграл
\ n2ds = | dx2 = 0.
г г
Аналогично доказывается выполнение второго условия (9.7.8).
Вычислим теперь момент внутренних сил в сечении
М = j (х2хх — хгх2) dS = — \ (x±Ftl + x2Ft2) dS.
S 8
Перепишем это следующим образом:
М = - f [(x^U + (x2F)t2] dS + l\FdS.
S 8
Первый интеграл преобразуется в контурный, а именно,
— \ F (х1п1 + х2п2) ds= —^Ск ) (х1п1 + х2п2) ds.
г тк
Здесь сумма распространена на внутренние контуры, на внеш-
внешнем контуре Го можно зафиксировать значение Со = 0. Интеграл
\ (х1п1 + х2п2) ds= ) (x2dxx — xxdx2) = 2Qft,
где ?2k — площадь, ограниченная контуром ГА. Итак,
М = - 2 ^ С kQh +2§FdS. (9.7.9)
Для односвязной области в этой формуле остается только
интеграл
М = 2 f FdS.
s
Следует заметить, что, строго говоря, напряженное состояние
(9.7.4) будет осуществлено лишь тогда, когда на торцах стерж-
стержня приложены внешние нагрузки, определяемые этими форму-
формулами. Однако мы ограничились составлением условия равенства
нулю главного вектора и равенства заданной величине М глав-
главного момента усилий на торцах. Вследствие принципа Сен-Вена-
на, разъясненного в § 2.1, практический способ приложения кру-
296 ГЛ* 9* АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
тящего момента сказывается лишь вблизи торцов. Начиная с
некоторого расстояния, порядок величины которого равен по-
порядку поперечного размера, распределение напряжений будет
соответствовать построенному решению.
§ 9.8. Теорема о циркуляции касательного напряжения.
Тонкостенные стержни замкнутого профиля
Циркуляция вектора касательного напряжения по замкнутому
контуру y» целиком лежащему внутри области, занимаемой по-
поперечным сечением, определяется следующим образом:
^dx-L + r2dx2).
Подставляя сюда выражения для напряжений по формулам
(9.7.1), получим
/ = (j) [du — [xO {x2dxx — xxdx2)].
v
Функция u(s) представляет собою перемещение в направле-
направлении оси х3, при отсутствии дислокации (§ 9.2) это есть однознач-
однозначная функция координат, следовательно,
6 du = 0.
«/
v
Таким образом,
(— x2dxx + xxdx2).
v
Этот интеграл уже встречался нам в § 9.7, он представляет со-
собою удвоенную площадь Q, ограниченную контуром у, поэтому
/ = -2О|лО. (9.8.1)
Формула (9.8.1) и составляет содержание теоремы о цирку-
циркуляции касательного напряжения.
Если сечение односвязно, формулу (9.8.1) можно получить
сразу, применив теорему Стокса,
но в этом случае формула выражает тривиальный факт и не
представляет интереса. Для многосвязной области, если контур
Y содержит в себе один или несколько граничных контуров,
формальное применение теоремы Стокса не приведет к формуле
(9.8.1), которая выражает некоторые дополнительные требования,
а именно — требование однозначности перемещения. Действи-
§ 9.8. ТЕОРЕМА О ЦИРКУЛЯЦИИ
297
тельно, можно представить себе функции и(ха), содержащие
в себе члены вида (9.8.1), т. е. винтовые дислокации с особен-
особенностями, помещенными внутри отверстий. В этом случае пере-
перемещение не будет однозначным и формула (9.8.1) окажется не-
неверной. Представим себе, например, трубу, изображенную на
рис. 9.2.1. Ее разрезали вдоль образующей, сдвинули края раз-
разреза на величину Ъ и сварили, как было разъяснено в § 9.2.
В трубе возникнут касательные напряжения, существующие при
отсутствии внешних сил. При обходе по замкнутому контуру
перемещение получает приращение,
равное Ь, и формула (9.8.1) перестает
быть верной.
Рассмотрим кручение стержня с
многосвязным сечением при отсутствии
дислокаций. Положим С = О на
наружном контуре. Если зафиксировать
Рис. 9.8.1
б)
Рис. 9.8.2
константы Ck на внутренних контурах по произволу, решение
уравнения (9.7.5) при граничных условиях (9.7.6) всегда можно
построить, но этому решению, вообще говоря, будет соответство-
соответствовать неоднозначное перемещение. Для того чтобы перемещение
было однозначным, необходимо выбрать надлежащим образом
константы Ch. Составляя условия (9.8.1) для всех возможных
контуров, не преобразующихся один в другой путем непрерыв-
непрерывного деформирования, мы получим необходимые уравнения для
определения констант Ch.
Проиллюстрируем метод на примере задачи о кручении тонко-
тонкостенного стержня замкнутого профиля, например такого, кото-
который изображен на рис. 9.8.1. Штрихами показана средняя линия
профиля, образующая систему замкнутых многоугольников, за-
занумерованных цифрами 1, 2, 3, 4, 5. Внешнюю область мы будем
обозначать индексом нуль. Участок профиля между многоуголь-
многоугольником 1 и многоугольником 2, например, мы будем обозначать
Двойным индексом 12. Рассмотрим стенку г$, изображенную от-
298 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
дельно на рис. 9.8.2, а. Выберем локальную систему координат
х, у так, как это показано на рисунке. Толщина профиля А есть
величина переменная, но она меняется медленно. Ось стенки
криволинейна, но радиус кривизны ее велик по сравнению с
толщиной А. Поэтому мы заменим действительную стенку той,
которая изображена на j?hc. 9.8.2, б, она ограничена параллель-
параллельными прямыми, которые простираются бесконечно далеко. В этом
случае функция напряжений не зависит от х, уравнение (9.7.5)
становится следующим:
а граничное условие
F
7T 2lir (9.8.2)
dy
Решение уравнения (9.8.2) будет следующим:
Отсюда
%у = 0, т« = -|"<С* - Сг) -
Второй член, линейно зависящий от у и отражающий нерав-
неравномерность распределения напряжений по толщине стенки, в тех-
технической теории отбрасывается и касательное напряжение счи-
считается постоянным
rx = x=-Y(Cs-Cr). (9.8.3)
Величину А в формуле (9.8.3) следует считать переменной —
функцией дуги профиля A = A(s). Это изменение настолько мед-
медленно, что при выводе формулы (9.8.3) мы сочли возможным
с ним не считаться. Отброшенный член в выражении для т до-
достигает максимума при у = А/2, величина его равняется при
этом [д/дА. В дальнейшем мы покажем, что действительно
и сделанное упрощение на самом деле оправдано. Для дальней-
дальнейшего нам понадобится выбрать определенное правило зна-
знаков. Расставим предположительно стрелки, указывающие на-
направление касательного напряжения, как это сделано на
§ 9.8. ТЕОРЕМА О ЦИРКУЛЯЦИИ 299
рис. 9.8.1. Совместим ось х с предположительным направлением
т. Теперь ось у будет указывать на ту область, индекс которой
в формуле (9.8.3) нужно поставить на первое место (индекс s).
Так, на стенке 21
т21 = -т- {Сх — С2),
на стенке 34
и так далее.
Для определения констант Ск применим теорему о циркуля-
циркуляции. Пусть Qi, Q2, ..., Qs — площади многоугольников с соот-
соответствующими индексами. Тогда беря, например, контур, окру-
окружающий многоугольник 1, получим по формуле (9.8.1)
(С, - Со)J-f- + (С, - С2)\ f - (Съ - С,) J -f- = - 2A00^ (9.8.4)
01 12 15
При этом положительным считалось направление обхода про-
против часовой стрелки и учитывались предположительно выбран-
выбранные направления т на каждом участке.
Уравнение, подобное уравнению (9.8.4), можно написать для
каждого контура, окружающего один или несколько многоуголь-
многоугольников; число таких уравнений будет равно числу неизвестных
констант (величину Со можно зафиксировать по произволу, на-
например принять Со = 0).
Решая систему уравнений, подобных (9.8.4), мы найдем, что
каждая из величин Ch имеет порядок
Здесь L — характерный линейный размер стенки. Поэтому опре-
определяемая формулой (9.8.3) величина т имеет порядок fxdL, тогда
как отброшенный в выражении для т член, как мы видели, имел
порядок \xfth; таким образом, ошибка, происходящая от его от-
отбрасывания, имеет порядок
h/L « 1,
если стержень действительно тонкостенный.
Теперь нам.осталось вычислить крутящий момент. С приня-
принятой степенью точности
М 2^ С]?2ъ. ' (9.8.5)
Второй член в формуле (9.7.9), представляющий собою удво-
удвоенный интеграл от функции напряжений цо площади сечения,
при данной степени приближения следует отбросить.
300 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
§ 9.9. Простейшие задачи о кручении
Рассмотрим некоторые задачи теории кручения, решаемые
относительно элементарными средствами. Прежде всего, если мы
выберем произвольную функцию F, удовлетворяющую уравне-
уравнению (9.7.5), то условие F = const определит контур того сечения,
для которого функция F дает решение задачи кручения. Конечно,
набор сколько-нибудь полезных решений такого типа ограничен,
однако некоторые случаи оказываются интересными.
а. Кручение стержня эллиптического поперечного сечения.
Положим
Тогда
Д/ =
а*Ъй
В соответствии со сказанным выше функция
F = — |iO -^-2 f ^ + ^| - 1J (9.9.1)
решает задачу о кручении стержня, сечение которого есть эл-
эллипс
4 + 4 = 1- (9.9.2)
а Ь
Касательные напряжения выражаются следующими формулами:
Tl = -2|id-ia, т, = 2|1*-^з. (9.9.3)
Абсолютная величина вектора касательного напряжения равна
А*
т-* 2 2
Видно, что величина т монотонно растет вместе с Х\ и х2 я?
следовательно, не может достигать максимума внутри области,
наибольшее значение т достигается на контуре. Исключая из
выражения т, например, хи с помощью условия (9.9.2) нахоДйм,
что на контуре
а + о
§ 9.9. ПРОСТЕЙШИЕ ЗАДАЧИ О КРУЧЕНИИ
301
Положим для определенности а> Ь, тогда т достигает макси-
максимального значения при х2 = Ь, а именно,
2 «.
а -г о
Вычислим теперь крутящий момент, интегрируя F по площа-
площади эллипса,
X
b
i' (9.9.4)
Из результатов этого параграфа получаются как частный слу-
случай известные уже результаты для стержня кругового сечения.
б. Кручение стержня прямоугольного поперечного сечения.
Пусть сечение стержня есть прямоугольник со сторонами 2а и
26, Ь>а. Примем за оси хх и хг оси сим-
симметрии сечения, как показано на рис. 9.9.1,
и положим
F = 2d Y*> (*2) cos *w*i» ^n =
71=0
м
(9.9.5)
При таком выборе функции напряжений
граничное условие при х^ = ±а будет авто-
автоматически выполнено. Кроме того, эта функ-
функция четна относительно хи следовательно,
dF/dXi нечетна по этой же переменной,
напряжения т2 в точках М и Ми рас-
расположенных симметрично по отношению
к оси #2, равны по величине и противопо-
противоположны по знаку. Подставим (9.9.5) в условие (9.7.5). Получим
оо
2 уУ'п — ^пУп) cos Xn^i = — 2|1$ч
п=о
Умножим обе части этого равенства на cosA,A#i и проинтег-
проинтегрируем по #i*b пределах от —а до +а. Заметим, что
Рис. 9.9.1
Т
+а
J
2 (—
Поэтому для функций Yk получается следующая последователь-
последовательность дифференциальных уравнений:
302 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
Интеграл каждого из этих уравнений, удовлетворяющий усло-
условию УЛ(±Ь)=О, есть
Таким образом, функция напряжений для кручения стержня
прямоугольного сечения получается следующей:
При выводе этой формулы безразлично какой размер принять
за размер а, а какой обозначить буквой Ъ. Поставленное выше
условие Ъ> а совершенно необязательно для вывода формулы
(9.9.6), однако если принять это допущение, выражение для
функции F может быть представлено в несколько иной форме.
Представим себе, что сечение стержня представляет очень
вытянутый прямоугольник, так что Ъ > а. Тогда, очевидно, в боль-
большей части сечения функция F практически не зависит от х2.
Это значит, что касательные напряжения почти параллельны
длинной стороне. Итак, примем F = F0(xiI уравнение (9.7.5)
становится обыкновенным дифференциальным уравнением
Решение его, удовлетворяющее условию F0(±a)=0, есть
В действительности F зависит как от хи так и от х2, и мы
примем
F = F0+Fi(xi, хг).
Теперь функция Fx есть гармоническая функция:
AF, = 0.
Положим по-прежнему, что Fx представляется рядом (9.9.5),
функции Yk будут теперь удовлетворять однородным дифферен-
дифференциальным уравнениям
Нам нужно рассматривать только четные решения, поэтому
с»
Yn = Ап ch A,n#2, Fx= 2 An ch Xnx2 cos ^nXv
Теперь нужно выбрать величины Ак так, чтобы удовлетворить
§ 9.9. ПРОСТЕЙШИЕ ЗАДАЧИ О КРУЧЕНИИ
303
граничному условию при хг = ±6, а именно,
F (х±, ± Ь) =
Л ch Xn6 cos Кх1 = 0.
Умножим на cos XkXi и проинтегрируем от аг4 = —а до #i = +а.
В результате получим
Ап =
Окончательная формула для F принимает следующий вид:
(9.9.7)
Ряд (9.9.7) отличается от ряда (9.9.6) тем, что часть его
просуммирована. Последнюю формулу можно было бы получить
и путем прямого преобразования (9.9.6); мы специально привели
два различных решения одной и той же задачи для того, чтобы
проиллюстрировать полезный прием, применяемый при интегри-
интегрировании линейных дифференциальных уравнений в частных про-
производных методом Фурье; прежде чем отыскивать решение в
виде ряда, выделяется некоторое частное решение, обычно поли-
полином. Ряд в формуле (9.9.7) представляет собою некоторую по-
поправку к полиномиальному решению, этот ряд сходится весьма
быстро, особенно если Ъ > а, и допускает дифференцирование,
необходимое для определения т4 и т2.
Не выписывая здесь легко получающиеся из (9.9.7) формулы
для крутящего момента и касательных напряжений, представим
их в следующем виде:
Tmax — "
М
(9.9.8)
Коэффициенты к{ и к2 зависят от отношения Ъ : а, значения их,
рассчитанные Сен-Венаном, приводятся в следующей таблице:
Ъ/а
1
1,2
1,5
2,0
2,5
0,1406
0,166
0,196
0,229
0,249
k2
0,208
0,219
0,231
0,246
0,253
Ъ/а
3
4
5
10
оо
hi
0,263
0,281
0,291
0,312
0,333
k2
0,267
0,282
0,291
0,312
0,3?3
304 ГЛ- 9- АЫТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
§ 9.10. Теорема о максимуме касательного напряжения.
Угловые точки
На примере стержня эллиптического сечения мы убедились в том, что
касательное напряжение достигает максимума в точке, принадлежащей
контуру сечения. Если решение представлено в виде ряда, как например
для прямоугольного сечения, то сделать подобное заключение, основываясь
непосредственно на анализе найденного решения, затруднительно. Однако,
опираясь на известные свойства гармонических функций, можно доказать,
что величина касательного напряжения не может принимать максимального
(так же как и минимального) значения во
внутренней точке области, следовательно,
наибольшая величина достигается на контуре.
В теории гармонических функций существу-
существует теорема о том, что гармоническая функция
не может иметь экстремума внутри области,
эту теорему мы считаем известной и будем
на нее опираться. Пусть в некоторой точке
области сечения М касательное напряжение
есть т. Направим ось х\ параллельно векто-
вектору т в точке Л/, тогда %ш = т = dF/dx2. По-
Поскольку F удовлетворяет уравнению Пуассо-
Рис. 9.10.1 на, dF/dx2 есть гармоническая функция, ко-
которая не может принимать экстремальное зна-
значение во внутренней точке области своего оп-
определения. Поэтому в окрестности точки М всегда найдется такая точка Q,
для которой Tiq > Tim. Но абсолютная величина касательного напряжения
т =5 ]/ х\ + х* ^ тх, поэтому xQ > Tim. Таким образом, доказано, что ни в
одной внутренней точке области касательное напряжение не может достигать
максимума (так же как и минимума).
Что касается поведения касательного напряжения на контуре сечения,
некоторые особенности могут возникнуть тогда, когда контур имеет угло-
угловые точки. Полагая u(z) = и + iv, как это было сделано в § 9.1, мы удов-
удовлетворим условию того, что функции и(ха) и и(ха) —гармонические сопря-
сопряженные. Формулы (9.7.1) или эквивалентные им (9.7.2) могут быть пере-
переписаны следующим образом:
х = Ti — ix2 = u'(z) — фОг. (9.10.1)
Теперь граничное условие для комплексной функции кручения запишется
следующим образом:
1
Im и = у \iftzz + Ch, 2еГй, (9.10.2)
Пусть точка О контура представляет собою угловую точку, касатель-
касательные к контуру образуют в этой точке угол а (рис. 9.10.1). Если а < я, как
изображено на рисунке, будем называть угол выступающим, если а >• зх —
входящим. Продолжим касательные и рассмотрим вместо реального сече-
сечения область в виде угла, образованного касательными, направим ось х вдоль
одной из сторон угла. Характер особенности в точке О от такой замены,
очевидно, не меняется. Функция
§ 9.11. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ПРИ КРУЧЕНИИ
305
удовлетворяет условию (9.10.1). Действительно,
cosB9-
2"""
1
1тио= у
cos a
(z = re*
При 9 = 0 и 9 = а1тио = -2 Or2 + Ck, что соответствует выполнению ус-
условия (9.10.1). К функции но может быть добавлена аналитическая внутри
угла функция щ, обращающаяся в нуль на сторонах угла 9 = 0 и 9 = а.
Представим эту функцию в виде
«х-2-*
(9.10.3)
k=i
Если аи — вещественные числа, Im щ = 0 при 9 = 0; чтобы выполня-
выполнялось условие Im щ = 0 при 9 = а, нужно, чтобы было sin Кка = 0, следо-
следовательно, Я = зх/а.
Чтобы удовлетворить условию (9.10.2) в ряде (9.10.3), следует сохра-
сохранить только положительные степени zx, так как щ @) = 0. По форму-
формуле (9.10.1)
i
Для выступающего угла а < я, следовательно, X > 1 и т@) = 0. Для
входящего угла а > я, следовательно, Я<1 ит@) = оо.
§ 9.11. Концентрация напряжений при кручении
Пусть задача кручения решена для некоторой области S
(рис. 9.11.1, а). Рассмотрим теперь стержень, сечение которого
представляет плоскую область 6", которая отличается от обла-
области S наличием концентратора напряжений. Так называется,
например, канавка на поверхности стержня (рис. 9.11.1, б) или
внутренняя цилиндрическая полость, пересекающая плоскость
сечения по контуру y (рис. 9.11.1, в). Концентратор напряжений
не должен образовывать входящих углов. В противном случае,
Рис. 9.11.1
по-предыдущему, касательное напряжение в угловой точке равно
бесконечности, и задача о концентрации напряжений становится
беспредметной.
Будем считать, что концентратор напряжений мал. Это озна-
означает следующее. Проведем окружность наименьшего радиуса б,
20 ю. Н. Работнов
ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
полностью заключающую в себя концентратор. Проведем окруж-
окружность радиусом р с тем же центром. Такую же окружность про-
проведем в сечении стержня без концентратора, она выделит из
области S область со, ограниченную или одной окружностью
радиусом р, или дугой окружности радиусом р и частью дуги
контура Г области 5, как показано на рис. 9.11.1, б, в. Концент-
Концентратор считается малым в том случае, когда выполнены следую-
следующие условия.
а. Решение задачи кручения для области S дает в области со
значения Ti и т2, мало отличающиеся от постоянных т? и т?.
б. Характерный размер концентратора мал по сравнению
с размером области
8<р.
Тогда задача о концентрации напряжений при кручении
может быть заменена задачей о концентрации напряжений при
антиплоской деформации для бесконечного или полубесконеч-
полубесконечного тела. В этом теле сделана цилиндрическая полость или
вырез с края, напряжения Ti и т2 стремятся к т? и т% при х{, х2,
стремящихся к бесконечности, поверхность полости или гранич-
граничная поверхность в случае полубесконечного тела свободны от
напряжений. Для определения комплексной функции кручения,
мы имеем
1пиф)=С, г^ч + Г, (9.11.1)
xi — ix2 = u(z). (9.11.2)
При ЭТОМ и' (оо) = Т? — ix\.
Рассмотрим задачу о концентрации напряжений около полости,
имеющей форму кругового цилиндра радиусом а. Поместим начало
координат в центре кругового сечения полости; таким образом,
на контуре у z = aeiQ. Положим
?
При z = aeiQ
f(aeie) = 2а cos в.
Следовательно, Im / = 0 при z ^ f. Итак, функция f(z) удовлет-
удовлетворяет граничному условию (9.11.1). Далее
Не нарушая общности, можно потребовать, чтобы при z = °°
было хг = tJ= т, т2 = 0, поэтому функция
(9.11,3)
§ 9.11. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ПРИ КРУЧЕНИИ 307
решает поставленную задачу о концентрации напряжений около
круглого отверстия.
Из (9.11.3) следует
/ 9 \
(9.11.4)
Максимальное значение касательного напряжения в согласии
с теоремой § 9.10 достигается на контуре отверстия, т. е. при
z=*aeiQ. Подставляя последнее выражение в (9.11.4), получим
т1 = тA — cos 26), T2==Tsin26.
Наибольшая величина касательного напряжения получается при
6 = ± л/2, а именно,
Множитель, показывающий во сколько раз максимальное напря-
напряжение больше, чем напряжение на бесконечности, называется ко-
коэффициентом концентрации напряжений.
Учитывая сделанные в начале параграфа оговорки о малости
концентратора, позволившей заменить задачу кручения задачей
об антиплоской деформации, мы можем определить коэффициент
концентрации иначе; это множитель, показывающий во сколько
раз увеличивается напряжение при наличии концентратора по
сравнению с тем, которое было бы в этом же месте при круче-
кручении стержня без концентратора.
В данном случае коэффициент концентрации равен 2. Заме-
Заметим, что при 6 = 0 т2 = 0. Поэтому, если рассечь тело плоскостью
хи хъ, эта плоская граница будет свободна от напряжений.
Таким образом, найденное решение будет справедливо не только
для бесконечной плоскости с круговым отверстием, но также
для полуплоскости с вырезом в форме полуокружности или для
стержня с полукруглой канавкой на поверхности; если радиус
кривизны контура сечения много больше чем а, решение для
бесконечной полуплоскости будет мало отличаться от истинного.
Для отверстий, форма которых отличается от круговой, реше-
решение получается с помощью конформпого отображения. Пусть
функция z=cd(?) осуществляет конформное отображение области,
внешней по отношению к контуру f, на внешность единичного
круга в плоскости ?. Потребуем, чтобы при ? ->¦ <х> со(?) -> ?, тогда
будет со'(оо) = 1. Теперь функция
f-^) (9.11.5)
дает решение задачи о концентрации напряжения. Действительно,
du = 1 du _ 1 Л 1_\
dz со7 (?) dt, ~ Тсо' (Q[ ~t?)'
При z ->¦ оо du/dz-^x, поэтому условие (9.11.2) выполняется.
308 ГЛ- 9* АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
С другой стороны, на единичной окружности ? = eia Im и = 0.
Теперь напряжения находятся по следующей формуле:
Желая определить напряжения в произвольной точке сече-
сечения, мы должны в формуле (9.11.6) перейти к переменной z.
Однако для нахождения коэффициента концентрации в этом нет
необходимости, максимум т = у т? + xjjj будет всегда достигаться
при I « eia.
Пример. Полость в виде эллиптического цилиндра с полуосями а и
6, направленными вдоль х\ и Х2 соответственно. Отображение внешней об-
области эллипса на плоскость с выброшенным единичным кругом дается
формулой
m а — Ъ
со(Й = ? + Т, * = 7+7-
2
По формуле (9.11.6) при ? = i получаем т1 = ^ , m x. Поэтому коэффи-
коэффициент концентрации
* 1 + ^И7)
Мы опустили достаточно простое, но требующее некоторых выкладок
доказательство того, что наибольшее касательное напряжение возникает
именно при ? = =Ы или @, ±&) в плоскости х\, х%\ что в этих точках на-
напряжения экстремальны, следует из соображений симметрии.
§ 9.12. Кручение анизотропных стержней
Мы рассмотрим здесь простейший случай кручения ортотропного стерж-
стержня, для которого координатные плоскости служат плоскостями упругой
симметрии. Согласно § 8.2 в этом случае
Ti = Hi (из, 1 — ®х2), т2 = M-2(w3,2 + <b;i). (9.12.1)
Здесь, в соответствии с обозначением упомянутого параграфа, Ц\ =
1*2 = #2323-
Напряжения Ti и Тг по-прежнему выражаются через функцию напряже-
напряжений по формулам (9.7.4). Внесем эти выражения в (9.12.1), исключим функ-
функцию и3. Получим
Это уравнение можно разными способами привести к виду (9.7.5), т. е.
к уравнению кручения изотропного стержня. Один из таких способов со-
состоит в следующем. Сделаем замену координат по формулам
§ 9.12. КРУЧЕНИЕ АНИЗОТРОПНЫХ СТЕРЖНЕЙ 309
Тогда уравнение для функции напряжений примет следующий вид:
d2F d2F
Это уравнение совпадает с (9.7.5) (за исключением множителя в пра-
правой части); таким образом, задача о кручении ортотропного стержня све-
свелась к задаче о кручении изотропного стержня, сечение которого подверг-
подвергнуто аффинному преобразованию (9.12.3), т. е. ограничено в плоскости |,
х\ контуром Г7, который получается из контура Г в плоскости ха путем рас-
растяжения или сжатия в направлении координатных осей. Граничное условие
в плоскости ха на контуре Г остается прежним: F = С. Это же условие вы-
выполняется и на преобразованном контуре Г", поскольку между Ги Г су-
существует точечное соответствие.
Ограничиваясь случаем односвязной области, перепишем выражение
(9.7.9) для крутящего момента в виде интеграла по площади S' в плоско-
плоскости |, т|:
4 у jiir f
а. Стержень эллиптического сечения. Полагая
.2 2
как и для изотропного стержня, убеждаемся, что уравнение (9.12.2) будет
\р2
выполнено при А = — Ф —% ¦—%—• Определим теперь крутящий момент
а Н^ + Ь fx2
по обычной формуле (9.7.9), опустив знак,
tt (9Л2-5)
б. Стержень прямоугольного сечения. Уравнение (9.12.4) решается те-
теперь для прямоугольника со сторонами
с учетом приведенных выше формул, связь между углом закручивания и
крутящим моментом дается следующей формулой:
М = кг[11'&Bа)Ц2Ь). (9.12.6)
Здесь ki определяется по-прежнему таблицей § 9.9, но зависит не от отно-
отношения 6/а, а от отношения
а а \
Для армированных материалов типа стеклопластиков, углепластиков и
боропластиков важно определить по отдельности модули p,i и цг — сдвига в
плоскости пластины и межслойного сдвига. Это можно сделать, испытав на
кручение два плоских образца с различными отношениями Ь\а.
310 ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
§ 9.13. Кручение тонкостенных стержней
открытого профиля
Если сечение имеет форму весьма длинного, вытянутого
прямоугольника с размерами сторон I и 8, 8/1 < 1, то формулы
(9.9.8) принимают вид
Действительно, как видно из таблицы § 9.9, коэффициенты kt
и к2 стремятся к величине 1/3 при неограниченном уменьшении
отношения 8/1; при 8/1 =1/10 погрешность формул (9.13.1) со-
составляет около 6%. Вспомним второй способ, при помощи кото-
которого была решена задача о кручении стержня прямоугольного
сечения в § 9.9. Сначала предполагалось, что касательные на-
напряжения параллельны длинной стороне прямоугольника. При
этом на концах не будет выполнено гра-
граничное условие, состоящее в том, что век-
вектор касательного напряжения в точках
контура направлен по касательной к нему.
Необходимая поправка была построена
в виде ряда. Если прямоугольник очень
вытянутый, то эта поправка будет сказы-
сказываться лишь на расстоянии d от конца,
при этом, очевидно, размер d имеет по-
Рис. 9.13.1 рядок ширины профиля б. Если 6/Z<
< 1, то d/Z<l, и для очень вытянутых
профилей поправка перестает быть существенной. Профили про-
прокатных балок из металла обычно бывают составлены из узких
прямоугольников. На рис. 9.13.1 изображены так называемые
тавровый, двухтавровый и зетовый профили. Если профиль в це-
целом закручивается на угол Ф, то в каждом из составляющих его
прямоугольных стержней возникает момент, определяемый фор-
формулой (9.13.1), где бг и U относятся к элементу с номером г.
Таким образом, получается формула
***- (9.13.2)
Определим отсюда $ и, находя по формуле (9.13.1) крутящий
момент М в каждом из прямоугольных элементов, получим
б3/
M^M^i: (9ЛЗ-3>
Теперь но формуле (9.13.1) находим наибольшее касательное
§ 9.13. ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 311
напряжение в элементе с номером s
(9.13.4)
Из последней формулы следует, что наибольшее касательное
напряжение будет там, где толщина 6S максимальна. Очевидно,
найденные формулы дают погрешность тем большую, чем боль-
больше отношение 6гА; при выводе их мы пренебрегали взаимнвш
влиянием элементов в зонах, обведенных кружками на
рис. 9.13.1.
Предположим теперь, что профиль тонкостенного стержня
имеет криволинейное очертание, как показано на рис. 9.13.2.
Штрихами изображена средняя линия про-
профиля, s — дуговая координата, измеряемая
вдоль этой средней линии, 8(s)—пере-
8(s)—переменная толщина. Более точно нужно
считать, что задана средняя линия, в каж-
каждой точке М к ней проведена нормаль,
по нормали отложены отрезки 6(s)/2
в каждую сторону, множество концов та-
таких отрезков образует границу контура.
Будем считать, что 8/1 < 1, при этом I есть
длина дуги средней линии. Сделаем еще
предположение о том, что радиус кривизны средней линии р
имеет тот же порядок, что Z, т. е. велик по сравнению с б.
Отдельные изломы, которые возможны здесь, так же как в при-
примерах, приведенных на рис. 9.13.1, вносят такую же погреш-
погрешность; теория перестает быть справедливой в окрестности точки
излома. Записывая формулу, связывающую момент с погонным
углом закручивания, в виде
Рис. 9.13.2
будем называть величину С геометрической жесткостью. Для
криволинейного стержня фигурирующая в уравнении (9.13.2)
сумма будет заменена интегралом и мы получим
(9.13.5)
тогда как касательное напряжение в точке, примыкающей к гра-
граничной поверхности,
(9.13.6)
312 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
§ 9.14. Нормальные напряжения
при кручении тонкостенных стержней
Как следует из общей теории, поперечные сечения стержня
остаются при кручении плоскими только тогда, когда стержень
представляет собою круговой цилиндр. Во всех других случаях
происходит искажение поперечного сечения, так называемая де-
планация. Однако формулы (9.7.5) по-
показывают, что контур сечения не ис-
искажается в своей плоскости, а пово-
поворачивается как целое; депланация,
т. е. буквально выход из плоскости,
связана только с перемещением точек
- в направлении оси х3. Для того чтобы
изложенная теория кручения была при-
применима, необходимо, чтобы внешние
связи не препятствовали депланации.
В противном случае ставится задача
о так называемом стесненном кручении.
Рис. 9.14.1 Эта задача решается относительно эле-
элементарными средствами для тонкостен-
тонкостенных стержней открытого профиля, для которых она и представ-
представляет особый интерес.
Чтобы пояснить существо дела, определим жесткость при кру-
кручении тонкостенной трубы с радиусом R и толщиной стенки б
(рис. 9.14.1). По формуле (9.6.3) для малых отношений 8/R
приближенно
Сл = 2nR38.
Разрежем теперь трубу вдоль образующей. Вычисляя жесткость
по формуле (9.13.5), найдем
1
и отношение
С, 1 б2
Для тонкостенной трубы, когда 8/R < 1, уменьшение жест-
жесткости за счет сделанного разреза чрезвычайно сильно. Причина
этого ясна: в сплошной трубе возникают касательные напряже-
напряжения в сечениях ее вдоль образующей, в разрезанной трубе эти
напряжения снимаются и она получает возможность деплани-
ровать.
А теперь обратимся к случаю, изображенному на рис. 9.14.2.
Разрезанная вдоль образующей труба заделана одним концом,
к другому концу приложен крутящий момент. Жесткость такой
трубы будет больше, чем в предыдущем случае, но меньше, чем
9.14. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ КРУЧЕНИИ
313
у сплошной трубы. Заделка предотвращает депланацию торцового
сечения, в результате жесткость увеличивается при этом в тем
большей степени, чем короче труба. Для сплошного стержня
эффект стеснения депланации убывает быстро по мере удаления
от заделки; если единственный характерный размер есть /?, то
зона концевого эффекта имеет длину поряд-
порядка R. В этом состоит принцип Сен-Венана,
разъясненный применительно к задаче о кру-
кручении в § 9.7. Однако для тонкостенных
стержней оценка области концевого эффек-
эффекта оказывается иной. Дело в том, что, кроме
малого параметра R/1, появляется второй
Рис. 9.14.2
Рис. 9.14.3
малый параметр 6/й, и простые соображения размерности ока-
оказываются недостаточными для того, чтобы выяснить истинное
положение дел.
Сохраняя основную гипотезу теории кручения, представим ве-
величину касательного напряжения т следующим образом:
cos a
as
(9.14.1)
Формула (9.14.1) представляет собою не что иное, как другую
запись общих формул (9.7.1); первый член соответствует поворо-
повороту сечения на угол ft на единицу длины относительно некоторого
центра О (рис. 9.14.3); здесь р — радиус-вектор, а — угол между
радиусом-вектором и нормалью к траектории касательного напря-
напряжения. Величина dujds представляет собою депланацию, ds есть
элемент дуги траектории касательного напряжения т, т. е. линии,
в каждой точке которой вектор т направлен по касательной. Но
на средней линии контура т = 0; применяя формулу (9.14.1) к
средней линии, найдем '
ftp cos a ds + du3 = 0.
Произведение р cos ads = p ds представляет собою удвоенную пло-
площадь заштрихованного треугольника <2со, таким образом,
ft dco + duz = 0.
Интегрируя это дифференциальное соотношение, найдем
Ms, x3)=-ft(x3)«>(s). ' (9.14.2)
Величина co(s) называется секториальной площадью, она заштри-
314 ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
хована на рис. 9.14.3. Дифференцируя перемещение щ по коор-
координате х3, мы найдем величину относительного удлинения в на-
направлении оси 3
')
Таким образом, в плоскости поперечного сечения, кроме ка-
касательных напряжений т, появляются нормальные напряжения
а = Ее33 = — ЕЪ' (х3) со (s). (9.14.3)
В формуле (9.14.3) остается неопределенность, связанная с вы-
выбором точки О, принимаемой за центр вращения, а также с вы-
выбором начала отсчета секториальной площади вдоль дуги контура.
Чтобы устранить эту неопределенность, выясним, как изменяется
вид формулы (9.14.3), если принять за полюс другую точку,
например точку В. Из очевидного геометрического рассмотрения
(известного в теоретической механике при выводе интеграла
площадей для движения точки под действием центральной силы)
мы можем записать
d(uc = — (х1С — Xi)dx2 + (х2С — x2)dxi.
Здесь хас — координаты точки С, ха — текущие координаты точки
дуги s. Аналогично
dcoB = — (xiB — xt)dx2 + {х2В — x2)dxi.
Отсюда
d(oc = d(dB — (#ic — %ib) dx2 + (x2C — x2B) dxt.
Интегрируя, находим
сос = сов + (^2с — x2B)Xi —{xiC — xiB)x2. (9.14.4)
Таким образом, секториальная площадь определена с точ-
точностью до линейной функции от координат. Записывая формулу
(9.14.3) в виде
о = Ах, + Вх2 + С - ЕЪ' (х3) со (s), (9.14.5)
мы можем выбрать точку С и начало отсчета секториальной пло-
площади по произволу, руководствуясь лишь соображениями удоб-
удобства. Примем за оси ха главные центральные оси инерции, так
что
J Xa8 ds=O, J хххф ds=O (9.14.6)
о о
(см. § 3.3). Выберем точку С так, чтобы было
i i
zaco6 ds = 0, j соб ds = 0. (9.14.7)
Определенная таким образом точка С называется центром изги-
изгиба, происхождение этого термина будет ясно из дальнейшего.
^ § 9.15. СТЕСНЕННОЕ КРУЧЕНИЕ И ИЗГИБ СТЕРЖНЕЙ 315
Составим теперь уравнения равновесия, как это делалось
в § 3.7:
— Мх, J oxfids ^ М2.
Подставляя выражения (9.14.4) для о и учитывая (9.14.5) и
(9.14.6), находим
Здесь F = j б ds —- площадь сечения, h и /2 — моменты инерции
относительно осей #i и х2 соответственно. Теперь формулу (9.14.5)
можно переписать следующим образом:
а„^ + ^+" Я*'а>. (9.14.8)
Полученная формула для нормального напряжения отличается
от той, которая относится к элементарной теории изгиба, нали-
наличием последнего члена, содержащего секториальную площадь.
Этот член появляется тогда, когда погонный угол закручивания
$ меняется с координатой х3-
§ 9.15. Стесненное кручение и изгиб тонкостенных стержней
Предположив, что изгиб отсутствует и продольная сила равна
нулю, мы получим формулу (9.14.3) для нормальных напряже-
напряжений, связанных только с кручением. Рассматривая равновесие
малого элемента, изображенного на рис. 3.7.3, мы найдем, что
нормальные напряжения, меняющиеся с координатой х3, влекут
за собою появление касательных напряжений, и дифференциаль-
дифференциальное уравнение рановесия элемента будет
д (тб) . д (од) __ п
ds "^ дх„ ~~
о
Отсюда
Т6 = - j (o6)i8<k. (9.15.1)
о
Заметим, что вывод этой формулы буквально повторяет вывод
формулы касательных напряжений при изгибе в § 3.7, но теперь
величина о связана с кручением и определяется формулой
(9.14.3). Внося это выражение в (9.15.1), находим
(9.15.2)
316 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
Теперь крутящий момент в сечении будет состоять из двух частей:
М3=Мк+М«. (9.15.3)
Первая составляющая Мк находится обычным способом, по фор-
формуле Мк = jj/OC, где жесткость С определяется формулой (9.13.6),
тогда как вторая составляющая это — момент от напряжения т,
даваемого выражением (9.15.2),
I S
о о
Интегрируя по частям с учетом последнего из условий (9.14.6),
получим
M.^—EIA". (9.15.4)
Здесь величина
i
называется секториальным моментом инерции. Если крутящий
момент М3 задан, то, подставляя Мк и Л/« в соотношение (9.15.3),
получим следующее дифференциальное уравнение стесненного
кручения:
Eh®" - СрЪ = -М3(х3). (9.15.5)
Решение однородного уравнения может быть представлено в виде
= ехр I ± -11 X const.
Здесь линейный размер d представляет собою то расстояние от
торца, на котором концевой эффект заметно ослабевает. Из урав-
уравнения (9.15.5) следует
Возвращаясь к примеру с трубой (§ 9.14), мы легко находим,
что секториальный момент инерции имеет порядок R58, геомет-
геометрическая жесткость С — порядок Дб3, следовательно,
Как видно, второй малый параметр б/Л, о котором шла речь
в § 9.14, появляется в знаменателе и значительно увеличивает
зону концевого эффекта по сравнению с той, которую предпо-
предполагает принцип Сен-Венана.
Полагая —Е1Л' =2?, перепишем формулу для нормальных на-
напряжений в виде
о-В©//.. (9.15.6)
Эта формула до чрезвычайности похожа на формулу для напря-
§ 9.15. СТЕСНЕННОЕ КРУЧЕНИЕ И ИЗГИБ СТЕРЖНЕЙ 317
жений при изгибе. Роль координаты играет секториальная пло-
площадь, роль момента инерции — секториальный момент инерции.
Величину В называют бимоментом. Условие ортогональности
четырех функций от s, а именно,
б, хи аг2, со,
устанавливаемое формулами (9.15.6), (9.14.7), позволяет предста-
представить нагрузку /?, заданную на торце стержня, следующим образом:
2 2
Здесь R — некоторый остаток, ортогональный к четырем перечис-
перечисленным функциям. Умножая на соб и интегрируя, вследствие ус-
условий ортогональности, получаем
? = — jpco6ds. (9.15.8)
Бимоментная нагрузка, таким образом, характеризует самоурав-
самоуравновешенную систему сил, приложенных на конце стержня. Пер-
Первые три члена формулы (9.15.7) определяют напряженное состоя-
состояние, распространяющееся сколь угодно далеко от торца, бимо-
бимоментная нагрузка в тонкостенных стержнях вызывает напряже-
напряжения, затухающие на характерной длине d, наконец, оставшаяся
самоуравновешенная нагрузка вызывает напряжения, которые в
рассматриваемой приближенной теории не принимаются во вни-
внимание.
Пример 1. Трубка радиусом R с толщиной стенки б разрезана вдоль
образующей на длине I. Концы трубки остаются неразрезанными. Требу-
ется определить жесткость ее при кручении.
Принимая за начало отсчета секториальной площади точку А
(рис. 9.14.1), получим со а = #2Ф, #2 = #sincp. По формуле (9.14.4)
Ос = /?2ф + aR sin ф.
Чтобы точка С была центром изгиба, необходимо выполнение условия
+я
2 = 0.
—я
Выполняя интегрирование, находим отсюда а = 2R и, следовательно,
сое = Я2(ф + 2 sin ф).
Секториальный момент инерции находится как интеграл от G)? по дуге
контура, результат получается следующий:
Теперь находим размер
rf = nl/2(l + v)Y^= 5,06 -сг-
318 ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
(при v = 0,3) и переписываем уравнение (9.15.5) в виде
Граничные уравнения должны выражать тот факт, что в сечениях ^ = 0и
х3 = I депланация отсутствует, следовательно, О@) = О(/) = 0. Интеграл
этого уравнения
О = Оо + A ch -~- + В sh -j-.
Из граничных условий находим
. а „ » Ch (Z/d) — 1
я"ио» *-uo sh(l/d) •
Интегрируя О (#3) от ж3 = 0 до ^3 = h получим полный угол закручивания.
После подстановки найденных констант, окончательный результат получа-
получается следующим:
d Ch (lid)
1 ]
* I sh (lid)
Величина О0 представляет собою погонный угол закручивания разрезанной
трубы без стеснения депланации.
Пример 2. Четыре силы, равные по абсолютной величине Р и при-
приложенные к торцу двухтаврового стержня, как показано на рис. 3.7.6, слу-
служат примером чисто бимоментной нагрузки. Если к торцу приложены сосре-
сосредоточенные силы Qi, то интеграл в формуле (9.15.8) заменяется конечной
суммой
Здесь Qi — секториальная площадь, определяющая положение силы (?г-.
В случае, изображенном на рис. 3.7.6, элементарный расчет приводит к ре-
зультату
В = Pbh.
Этот пример привел Власов, чтобы пояснить медленное затухание бимо-
ментных напряжений. Если стенка балки исчезает, каждая из полос оказы-
оказывается в состоянии чистого изгиба моментом РЬ, напряжения изгиба пере-
передаются сколь угодно далеко без всякого ослабления. Связывающая полки
стенка закручивается, поэтому изгибающий момент в каждой из полок по-
постепенно уменьшается и на некотором расстоянии от торца нормальные на-
напряжения в сечении балки становятся пренебрежимо малыми. Но это рас-
расстояние определяется соотношением между большой изгибной жесткостью
полки и малой крутильной жесткостью стенки, это расстояние во всяком
случае много больше, чем размеры Ъ и h.
§ 9.16. Касательные напряжения при изгибе стержней
сплошного сечения
Элементарная теория касательных напряжений при изгибе
относится к сечениям балок, изгибаемых в плоскости симметрии
x2Oxz. В основу ее полагаются следующие грубые предположения.
а. Касательное напряжение т = о2з направлено по оси х2,
составляющая Oi3 = 0.
§ 9.16. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ СТЕРЖНЕЙ
319
б. Величина т зависит только от х2.
Выделим элемент балки, изображенный на рис. 9.16.1, он
ограничен плоскостями: х3 = const, х3 + dx3 = const. В плоскости
Мл
х3 = const действует нормальное напряжение сг = -^ х2, в плоско-
1 М +dM
сти х3 + dx3 = const — нормальное напряжение а + ао=^ j х2;
таким образом, в направлении оси появляется сила
Величина интеграла представляет собою статический момент
площади той части сечения, которая отстоит от оси Xi на расстоя-
расстоянии, большем чем х2. Обозначим этот статический момент ?4. По-
Появившаяся сила уравновешивается каса-
касательными напряжениями т, равномерно
распределенными по нижней граничной
площадке b(x2)dx3. Уравнение равновесия
получается следующим:
dM-]?- = xbdx3.
i
Отсюда, вспоминая, что dM/dx3 = Q есть
перерезывающая сила, получаем формулу
т = ^. (9.16.1)
Рис. 9.16.1
Эта формула была выведена Журавским в середине прошлого
века и применена при проектировании деревянных мостов. Дере-
Дерево слабо сопротивляется сдвигу в продольной плоскости и для
коротких деревянных балок касательные напряжения могут быть
более опасными, чем нормальные. Деревянные балки, как прави-
правило, имеют прямоугольное сечение, для прямоугольника с высотой
2h формула (9.16.1) дает следующий результат:
Здесь F — площадь поперечного сечения.
По этой формуле наибольшее касательное напряжение ттах =
О Q
= ~2F ДОСТИгается ПРИ ^2 = 0, т. е. на нейтральном слое балки,
где нормальное напряжение равно нулю.
В действительности, для касательных напряжений должно
быть выполнено граничное условие (9.1.3). Это значит, что в точ-
точках контура вектор касательного напряжения должен быть на-
320
ГЛ. 9. АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
правлен по касательной к контуру. Предположение (а) удовлет-
удовлетворяет этому условию для прямоугольного сечения, поэтому
можно ожидать, что именно для прямоугольного сечения элемен-
элементарная теория окажется точной. Для других форм поперечного
сечения нарушение граничного условия приводит к серьезной
погрешности.
Рис. 9.16.2
Заметим, что при выводе формулы для касательных напря-
напряжений при изгибе тонкостенных стержней (§ 3.7) был использо-
использован совершенно тот же способ рассуждений, что и при выводе
формулы (9.16.1). У тонкостенных стержней, действительно, ка-
касательные напряжения могут иметь тот же порядок величин, что
и нормальные. В сплошных стержнях касательные напряжения
малы, для металлических балок они, как правило, несуществен-
несущественны, поэтому и теория касательных напряжений в таких балках
лишена практического значения. Нужно признать, что в течение
ряда десятилетий элементарная теория, приводящая к формуле
(9.16.1), излагалась скорее по традиции. Реальная область ее
применения для металлических конструкций относится к расчету
составных балок, подобных тем, которые изображены на
рис. 9.16.2. Касательное усилие в плоскости разъема концентри-
концентрируется в крепежных элементах — болтах или заклепках — или
передается через сварной шов. Расчет деревянных балок, пред-
представлявший важность во времена Журавского, утратил свою ак-
§ 9.16. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ СТЕРЖНЕЙ 321
туальность. Однако проблема определения касательных напряже-
напряжений при изгибе возникла вновь в последние годы в связи с при-
применением новых композитных материалов, теории которых будет
посвящена гл. 20. Поэтому мы изложим здесь схему построения
точной теории изгиба, ограничиваясь наиболее важным для при-
приложений случаем, когда сечение балки прямоугольно.
Если балка длиной I заделана одним концом и нагружена на
другом конце силой, лежащей в плоскости симметрии, мы пред-
предположим, что нормальное напряжение изгиба определяется так
же, как в элементарной теории, а именно,
азз — 7 •
При этом координата хъ отсчитывается от заделки. Предположим
также, что все компоненты напряжения, кроме оаз, равны нулю.
При этом первые два уравнения равновесия удовлетворяются
тождественно, тогда как третье становится следующим:
Та,« + Ц* = 0.
Здесь, как и ранее принято, оза = та. Этому уравнению можно
удовлетворить, приняв
Ti = —Ф,2, т2 = фд + w (fe2~~- **)• (9.16.3)
Легко проверить, что член, пропорциональный Р, в выражении
для т2 представляет собою элементарное решение. Подставив
(9.16.3) в уравнения Бельтрами — Митчела (§ 8.5), получим
Отсюда следует
Рхл
Для прямоугольника xt = ±6, х2 = ±fe граничные условия бу-
будут следующими: при xt*=±b т1=<р,2!=0, при x2 = ±h т2 =
= ф>4 = 0. Таким образом, на контуре прямоугольника ф = const
или ф = 0. Решение уравнения (9.16.4) ищется совершенно таким
же способом, как для задачи кручения в § 9.9. Частное решение
уравнения (9.16.4), обращающееся в нуль при х = ±.Ь, есть
Теперь полагаем ф = ф0 + <р4, где ф0 — гармоническая функция,
удовлетворяющая условиям: ф0 = 0 при Xi = d-b, ф0 + фA = 0 при
21 Ю. Н. Работнов
322 ГЛ- 9- АНТИПЛОСКАЯ ДЕФОРМАЦИЯ, КРУЧЕНИЕ, ИЗГИБ
х2 = ±h. He приводя выкладок, почти буквально повторяющих
выкладки § 9.9, запишем окончательный результат
я3 / *\ х
з Ъ J ?г k (/)
(9.16.5)
Теперь распределение напряжения на отрезке х2 = 0 будет не-
неравномерным, в центре сечения напряжения уменьшаются по
сравнению с величиной, даваемой элементарной формулой
(9.16.2). Наибольшее значение напряжений достигается при
Xi = ±6, разница по сравнению с элементарным решением уве-
увеличивается с уменьшением h/b, для квадрата она составляет
12,6%, при h/b = 1/4 эта разница достигает почти 100%. Как
оказывается, для анизотропных композитных материалов поправ-
поправка к элементарной теории, даваемая формулой, аналогичной
(9.16.5), может быть весьма существенна.
ГЛАВА 10
ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
§ 10.1. Основные уравнения плоской задачи
Состоянием плоской деформации называется такое состояние
упругого тела, когда
а) перемещение вдоль одной из осей, например xs, равно нулю
ц3 = 0; A0.1.1)
б) компоненты перемещения uY и и2, а также компоненты
тензора напряжений зависят только от xt и х2
1га = 1га(хр), Оу = а«(яр), а, [1 = 1,2. A0.1.2)
Отсюда немедленно следует, что для изотропного тела а4з = о2з =
= 0. Действительно, деформация е13, например, равна
*1з = у (М1.з + Изд) = 0,
так как uY не зависит от х3, a и3 = 0.
Для того чтобы в теле осуществить плоскую деформацию,
нужно, чтобы граничные условия не зависели от координаты хг.
Представим себе длинный цилиндр с осью, параллельной оси х3,
на боковой поверхности цилиндра п3 = 0, так как нормаль к по-
поверхности перпендикулярна оси хг. Если в каждой точке боковой
поверхности приложены усилия 7\ и Т2, лежащие в плоскости
поперечного сечения, граничное условие для напряжений име-
имеет вид
оа?щ = Та. A0.1.3)
При этом уже нет необходимости рассматривать всю боковую
поверхность, условие A0.1.3) можно считать выполненным на
контуре Г любого поперечного сечения цилиндра плоскостью хи
#2, например в плоскости х3 = 0. Уравнения теории упругости для
перемещений иа или напряжений оар образуют замкнутую си-
систему. После решения ее условие щ = 0 (и, следовательно, егг =
= 0) позволяет определить компоненту напряжения а33, а именно,
о33 = vcw
Рассмотренная в § 8.12 задача о равновесии длинной трубы слу-
служит примером задачи о плоской деформации. Действительно,
21*
324 гл- 10- плоская задача теории упругости
накладывая на состояние плоской деформации равномерное рас-
растяжение или сжатие в направлении оси х3, можно сделать де-
деформацию в33 равной произвольной постоянной величине и соот-
соответственно сообщить результирующей нормальных напряжений в
сечении любое заданное значение.
В теории антиплоского напряженного состояния мы убеди-
убедились, какие удобства связаны с представлением решения через
функцию комплексной переменной. В теории плоской деформа-
деформации применим аналогичный метод, но соотношения оказываются
более сложными. Положим, как обычно,
z = xt + ix2i z = Xi — ix2.
На эти формулы можно смотреть как на формулы преобразова-
преобразования координат, поскольку они устанавливают взаимно однознач-
однозначное соответствие между парами переменных х^ и х2 с одной сто-
стороны, z и z с другой. Любая функция двух переменных х± и х2
может быть представлена как функция переменных z и z. Пусть
f(z, z)— такая функция. Если нужно продифференцировать ее
по х{ или х2, следует применить правило дифференцирования
сложной функции. По этому правилу
(*?) <10Ы)
Оператор Лапласа от функции / преобразуется следующим об-
образом:
^4 A0.1.5)
Д/ 4.
dzdz
Выпишем теперь уравнения Ламе для плоской деформации,
когда и3 = 0:
\iAUi = — (К + \i) Э>4, [ХДМ2 == — (X + li) Э>2, 6 = Ua, a.
Будем считать, что и{ и и2 представлены как функции от z и z,
воспользуемся формулой A0.1.5) и заменим два уравнения Ламе
одним уравнением
4fx-^r = — (К + |i) (в х + Ю 2), w = ut + iu2. A0.1.6)
dzdz '
В § 8.5 было показано, что Э — гармоническая функция, следо-
следовательно, она может рассматриваться как действительная часть
аналитической функции комплексной переменной
8 +*(, = /(*).
Из соотношений Коши — Римана Эд = \f>J, Э,2 = —ip.i следует
§ 10.1. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ЗАДАЧИ 325
Здесь ]'{z)—функция, комплексно сопряженная с f(z). Урав-
Уравнение A0.1.6) принимает вид
Проинтегрируем обе части по переменной z, получим
4\id? = -(b + ix)](z) + g'(z). A0.1.7)
Здесь g(z)—произвольная функция комплексной переменной z.
Интегрируем еще раз по переменной z и приходим к следующе-
следующему результату:
A\iw = -(X + [i)zf(z) + g(z) + h(z). A0.1.8)
Вследствие A0.1.4) можно написать следующие очевидные тож-
тождества:
, . dw , dw . . (dw dw \
«1,1 + 1Щ.1 = ~z + -= , «i,2 - *«,., = *(-k- Tz}
отсюда получается
(wi.i + u2t2) + i (u2,i + г/1,2) = 2^.
dz
Следовательно, Э = uit t + u2,2 = 2 Re dw/dz. Таким образом, дей-
действительные части выражения A0.1.7) и функции 2\if(z) равны
Но функции f(z) и f (z) отличаются только знаком при мнимой
части, действительные части их одинаковы, поэтому из написан-
написанного равенства следует
-(X + li)f(z)+g'(z)=2iif(z)
с точностью до чисто мнимой постоянной. Отсюда
/=-4-.
и формула A0.1.8) принимает следующий вид:
4\iw = — ^±^ zg' (z) + g(z) + h(z).
Эта формула получена Колосовым и Мусхелишвили иным путем,
она представляет общее решение задачи о плоской деформации,
выраженное через две произвольные аналитические функции
комплексной переменной. Обычно найденное решение записыва-
записывается в следующем виде: __ _
+ Ш2) = Хф (z) — ?ф7 (z) — \f) (z) ,
A0.1.9)
326 ГЛ- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
Функции ф и г|) отличаются от g и h лишь постоянными множи-
множителями, а именно,
Такое представление удобно в том отношении, что формулы для
напряжений оказываются не содержащими упругих констант.
Из формул закона Гука
Он = А,6 + 2[Ш!,!, о22 = ЯЭ + 2\т2,2
следует
но
Таким образом,
Он + о22 = 4 Re q/ (z). A0.1.10)
Рассмотрим теперь следующую комплексную комбинацию из ком-
компонент тензора напряжений:
0*22 Оц ZlOi2 ==: ^[^ (^2, 2 Ui, i IWl, 2 — IU2> i) .
Произведем перегруппировку членов в правой части
dw dw dw
. dw dw dw
Таким образом,
<?22 — <*11 ~ 2fcr12 = — 2 ^- = 2 (*p* A) + ф' E)) A0.1.11)
и аналогично
Кривая в плоскости хи х2 задается уравнением xa = Xa{s) или
в комплексной форме z = z(s), или z=z(s). За параметр s всегда
можно выбрать длину дуги этой кривой, отсчитываемую от про-
произвольной точки. Пусть кривая z = z(s) есть след пересечения с
плоскостью хи х2 цилиндрической поверхности, образующая ко-
которой параллельна оси #3. Компоненты усилия на этой поверхно-
поверхности равны
J- а === Оар*^Э
ИЛИ
Ti ds = Gn dx2 — О12 dxu T2 ds == o12 dx2 — o22 dxiu
§ 10.1. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ЗАДАЧИ 327
Образуем комплексную комбинацию 7\ + iT2. Полагая dx1 =
1 — i —
= -* {dz + dz), dx2 = ^- (dz — dz), получим
ir2)ds = (On + o22)dz + (o22 - olt - 2o12)dz
или по формулам A0.1.10), A0.1.11)
^(Г1 + ^Г2)^ = (ф/ + ф/)^ + Bф// + ^/)й1
Выражение, стоящее в правой части, есть полный дифференциал
функции двух комплексных переменных: ф + 2ф' + \|); таким об-
образом,
i J G\ + iT2) ds = Ф + V + ф. A0.1.13)
Полученные формулы применимы не только к состоянию
плоской деформации, но также к плоскому напряженному состоя-
состоянию, которое характеризуется условиями
Озз = 0, Оза = 0.
Такое состояние с известным приближением реализуется в пла-
пластине толщиной 2/г, нагруженной силами, лежащими в ее средней
плоскости, которую мы примем за плоскость Х\, х2. Тогда гранич-
граничные плоскости будут плоскостями х3 = ±h. Если понимать под
напряжениями их средние значения по толщине пластины,
а именно величины
+л
<<Уц> = Yh .1 aHdx^
-л
то напряжения <оза> из уравнений равновесия выпадут. Действи-
Действительно, выпишем первое уравнение равновесия
Оц, 1 + Oi2, 2 + О13, 3 = 0
и проинтегрируем его по х3 от —h до +h. При интегрировании
третьего члена получим
J ^13,3 dx3 = o13 \th,
но граничные плоскости пластины по условию свободны от ка-
касательных напряжений. Таким образом, мы получаем только два
Уравнения равновесия, такие же, как в задаче о плоской дефор-
деформации
оаР,р = 0. A0.1.14)
При написании уравнений A0.1.14) угловые скобки, символизи-
символизирующие осреднение по толщине, опущены.
328 гл-10- плоская задача теории упругости
В уравнениях закона Гука мы положим о33 = 0, поэтому
Л# + 2\ie33 = О (О = еп + е22 + е33).
Отсюда находим
Теперь оставшиеся уравнения закона Гука можно переписать
следующим образом:
I* =
Вся дальнейшая теория развивается так же, как в § 10.1 для
плоской деформации; разница состоит в том, что постоянная X
заменена постоянной Я* и величина к выражается следующим
образом:
3 —v
§ 10.2. Сила и момент, действующие на контур
Если усилие Та задано на замкнутом граничном контуре од-
носвязной или многосвязной области, то по формуле A0.1.13)
можно определить главный вектор R{ + iR2 усилий, приложенных
к контуру. Действительно,
§?! + гт2) ds,
отсюда _ __
i (Rx + Ш2) = [ф + V + t]r. A0.2.1)
Прямые скобки с индексом Г внизу обозначают приращение за-
заключенного в скобки выражения при обходе контура по часовой
стрелке. Из формулы A0.2.1) следует, что если область много-
многосвязна и главный вектор сил, приложенных к одному из гра-
граничных контуров, отличен от нуля, то функции ф или ф, или и
та и другая должны быть неоднозначными. Тело, сечение кото-
которого представляет собой односвязную область, должно быть в
равновесии под действием внешних сил, поэтому, если во внут-
внутренних точках не приложены сосредоточенные силы, RY + iR2 = 0
и функции ф, г|) однозначны. Вычислим теперь главный момент
приложенных к контуру Г сил по формуле
М = ф {х1Т2 — х2Тг) ds = —Rej)i(T1 + iT2) ~z ds.
С помощью A0.1.13) представим это выражение следующим об-
образом:
М = — Re j) I d (ф + 2фг + яр).
§ 10.2. СИЛА И МОМЕНТ, ДЕЙСТВУЮЩИЕ НА КОНТУР 329
Выполним интегрирование по частям, заметив при этом, что
Re 2ф = Re z<p, поэтому соответствующие члены, появляющиеся
при интегрировании, взаимно уничтожаются. В результате полу-
получим следующую формулу:
М = Re [ J г|) dz — z d^ — ziq/ (z)]r. A0.2.2)
Если область ?, представляющая сечение тела плоскостью х3 = 0,
многосвязная, мы обозначим, как и прежде, наружный контур
Го, внутренние ГА. В частности, контур Го может быть стянут
к бесконечно удаленной точке, тогда область S представляет со-
собой бесконечную плоскость с отверстиями, ограниченными кон-
контурами ГА. Пусть Rik и R2h—составляющие главного вектора
усилий, приложенных к контуру 1\. Функции ф и \f>, голоморф-
голоморфные в области сечения S, должны обладать такими особенностями
в области Sh, ограниченной контуром 1\ и не принадлежащей
телу, чтобы при обходе контура 1\ выполнялось условие A0.2.1).
В то же время напряжения и перемещения, а следовательно,
правая часть A0.1.10), A0.1.11) и A0.1.9) должны оставаться
однозначными. Примем
Ф = A In (z — zh) + ф1? я|) = В In (z — zh) + ifi.
Здесь zh — произвольная точка, zk ^ Ski ф4 и ф4 — однозначные
функции, голоморфные в S. Поскольку производные от ф и -ф
однозначны, требование однозначности напряжений удовлетворя-
удовлетворяется автоматически. Заметим, что [InB — zk)\T = 2ni, [ln(z — zh)]r =
= — 2ni. Условие однозначности перемещения приводит к следую-
следующему равенству:
2(А + H, A0.2.3)
тогда как из условия A0.2.1) следует
i{Rih + iR2h) = ~2ni{А-В). A0.2.4)
Находя А ж В из A0.2.3) и A0.2.4), получим
¦w-
-iR \ A0.2.5)
4 ¦-<—^+*
Если неуравновешенные силы приложены и к другим контурам,
то соответствующие логарифмические члены просто добавляются
к выражениям A0.2.5).
Представим теперь себе, что контур 1\ стягивается в точку,
тогда как главный вектор Rt + iR2 остается неизменным. Форму-
Формулы A0.2.5) сохраняют силу, лишь бы было zh^Sh. В пределе,
когда контур 1\ стягивается к точке zh, мы получаем сосредото-
сосредоточенную <жгу в точке zh. Таким образом, формулы A0.2.5) дают
330 гл- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
решение для сосредоточенной силы, приложенной внутри об-
области.
Обратимся теперь к тому случаю, когда область S представ-
представляет собою всю плоскость переменной z, содержащую либо от-
отверстия Sk, либо сосредоточенные силы в точках zh. В этом об-
общем случае
N N
¦Ф= S Akln(z-zk) + ^, ф= 2 Я* I* (*-**) +IV (Ю-2.6)
Здесь ф^ и 1))^—аналитические и однозначные в области S функ-
функции. Вне круга радиусом R, заключающего в себе все контуры Г*,
Ф* = 2«пЛ Ф# = 2Ь«2П. (Ю.2.7)
—оо —оо
Потребуем, чтобы компоненты тензора напряжений остались на
бесконечности ограниченными. Для этого нужно, чтобы в разло-
разложении A0.2.7) исчезли все члены, соответствующие положитель-
положительным тг>2; таким образом,
Ф* = Yz + Фо B), яр* = T'z + г|э0 (z).
Здесь ф0 и фо — функции, голоморфные на бесконечности. При
z + °o из A0.1.10) и A0.1.12) следует
oTi + °7. = 2 (Г + Г), аГ2 - аГх + 2toS = 2Г.
Отсюда
Г = 1 (аП + аГ2) + iC, Г = 4 (<хГ. - afi + 2гаГ2). A0.2.8)
Что касается величины перемещения при z -> °о? то По формуле
A0.1.9) оно равно нулю лишь тогда, когда
г2(Д* + *Д2*) = о, г = о, г = о.
Это значит, что главный вектор приложенных к телу сил и на-
напряжения на бесконечности равны нулю.
Выясним теперь, в какой мере определены введенные функ-
функции ф и \|). Если заданы напряжения, мы отправляемся от фор-
формул A0.1.10) — A0.1.12). В них входят только производные от
функций ф и ф, следовательно, сами функции определены с точ-
точностью до постоянных a + ?fJ и a' + ф' соответственно. Более
того, от производной ф' входит только действительная часть,
следовательно, сама функция ф определяется с точностью до
слагаемого
В формуле A0.2.8) опять-таки появляется мнимая константа iC,
§ 10.3. КРАЕВАЯ ДИСЛОКАЦИЯ 331
соответствующая щ. Таким образом, если задавать напряжения,
то функции ф и ф могут содержать пять произвольных констант
7, а, р, а и {}'. Теперь комплексное перемещение по формуле
A0.1.9) определяется с точностью до слагаемого, соответствую-
соответствующего перемещению тела как твердого целого,
Накладывая определенные связи, например, закрепляя элемент,
мы подчиняем пять констант трем условиям, две постоянные по-
прежнему остаются неопределенными и их можно зафиксировать
произвольным образом. В дальнейшем, если не оговаривается
противное, мы будем полагать а = Р = 0, следовательно, ф@) = 0.
§ 10.3. Краевая дислокация
При рассмотрении винтовой дислокации (§ 9.2) мы встреча-
встречались с примером сингулярного решения уравнений теории упру-
упругости, соответствующего особенности во всех зонах прямой —
оси х3. Аналогичным образом можно построить сингулярное ре-
решение уравнений теории упругости для
плоского деформированного состояния,
которому соответствует неоднозначное по-
поле перемещений. Будем называть краевой
дислокацией такую дислокацию, для
которой вектор Бюргерса перпендикуля-
перпендикулярен оси дислокации. Это значит, что если
принять ось х3 за линию дислокации, пере-
перемещение при обходе контура, окружающе-
окружающего ось х3, получает приращение, равное 6.
Мы предположим, что и2 при этом оста-
остается однозначным, но это предположение Рис. 10.3.1
не нарушает общности, направление оси
Xi всегда можно выбрать совпадающим с направлением век-
вектора Ь. Образование краевой дислокации можно предста-
представить себе так. В бесконечной упругой среде вырезан ци-
цилиндр, ось которого есть ось х3. Рассечем среду полуплоскостью,
параллельной.оси х3 и пересекающей поверхность цилиндра, как
показано на рис. 10.3.1, раздвинем края разреза на расстояние
Ь вдоль оси Xi и заполним образовавшуюся щель материалом.
После того как дислокация создана, никаких следов от разреза
не оказалось, материал снова стал сплошным и однородным.
Чтобы найти точное решение поставленной задачи, мы должны
еще удовлетворить граничным условиям на поверхности цилинд-
цилиндрической полости. Вместо этого мы поступим следующим обра-
образом. Будем стягивать контур основания цилиндра в точку ха = 0.
В пределе мы получим уже сплошное упругое пространство,
в котором осуществлено некоторое напряженное состояние. Сле-
332 ГЛ- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
дует ожидать, что на оси х3 напряжения обладают особенностью.
Для получения необходимой неоднозначности и здесь, так же как
при решении задачи о сосредоточенной силе или о внутреннем
контуре, несущем неравномерную нагрузку, следует выбрать
функции ф(г) и if) (z) содержащими логарифмические члены, но
теперь уравнения для коэффициентов при них изменятся, усло-
условие неоднозначности перемещений примет вид
2ф = 2п1{кА + В), A0.3.1)
а в уравнении A0.2.4) нужно принять силу, равной нулю, и мы
получим
0 = 2ni(A-B). A0.3.2)
Таким образом, краевой дислокации соответствуют следующие
функции фиф:
* = м?Тх)ln (z -Zh) + *•• A0'3-4)
Дислокации рассмотренного типа, соответствующие поступатель-
поступательному относительному перемещению краев разреза, мы будем на-
называть дислокациями Бюргерса. Вольтерра рассмотрел более об-
общий тип дислокаций, когда кроме относительного поступательного
перемещения имеется еще относительный поворот краев разреза.
Положим
ф == CZ In (z — Zk) + ф2, Яр = i|J.
Здесь ф2 и ф2 — функции, определенные формулами A0.3.3),
A0.3.4). Теперь производная (р (z) неоднозначна. На самом деле,
ф' (z) = с In (z - zh) + ..., ![ф' (z) ]г = 2nic,
но действительная часть ф'B) остается однозначной, если с дей-
действительно. Вторая производная ф" (z) остается однозначной, по-
поэтому условие однозначности напряжений выполняется. Добавляя
к функции ф2 слагаемые с ln(z — zft), мы должны потребовать,
чтобы главный вектор силт приложенных к контуру, по-прежнему
равнялся нулю. По формуле A0.2.1) мы проверяем, что условие
выполняется тождественно, если оно выполнено для функций фг
и г|J. Теперь дополнительное приращение перемещения при об-
обходе контура, заключающего в себе точку zft, будет
2\ii [u1 + iu2]Tk = 2nic (I + к) z.
Таким образом, кроме поступательного относительного перемеще-
перемещения краев разреза, происходит поворот их на угол ясA + х)/|х.
Возвращаясь к дислокации Бюргерса, приведем явные формулы
для перемещений и напряжений в случае напряженной упругой
§ 10.3. КРАЕВАЯ ДИСЛОКАЦИЯ 333
среды, когда Ф^гр^О. Подставляя A0.3.3), A0.3.4) в A0.1.9)
и отделяя действительную часть от мнимой, мы получаем выра-
выражения для перемещений, а именно,
}
х\
Обращаясь к выражению для А и вспоминая, что х = 3 —4v, пе-
перепишем эти формулы следующим образом:
2(l-v) r2
а = arctg —, г2 = я? + ^2.
Переходим к вычислению напряжений. Для подстановки в фор-
формулы A0.1.10) и A0.1.11) нам понадобятся следующие величины:
/ / \ iA . л хл 1Х9 . г / \ // / \ 2iA
'() A * 2 = -^ (z), ф/B) = -г$
13
г г r*
В результате подстановки находим напряжения, а именно,
ri ' Г* A0.3.6)
Формулы A0.3.5) и A0.3.6) определяют поля перемещений и
напряжений в зависимости от вектора Бюргерса &. При этом со-
совершенно безразлично, по какой поверхности производился раз-
разрез и была ли эта поверхность плоскостью, как показано на
рис. 10.3.1. В частности, разрез можно произвести по полупло-
полуплоскости #2 = 0, %i > 0 и сдвинуть нижний край разреза относи-
относительно верхнего на величину Ь. Такой способ создания краевой
дислокации не требует удаления либо добавления материала.
Энергию упругого объема, содержащего краевую дислокацию,
можно вычислить точно таким же способом, как вычислялась
энергия винтовой дислокации в § 9.2. Касательное напряжение
334
ГЛ. 10. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
в плоскости х2 = 0 есть
По теореме Клапейрона
и = -7 \ то dS = 7—n : ^n —
2 J 4л A — v) с
с
A0.3.7)
Рассуждения здесь в точности совпадают с теми, которые были
приведены в § 9.2 применительно к винтовой дислокации. Точно
так же интеграл оказывается расходящимся, если подставлять
пределы интегрирования 0 и °°. Выражение A0.3.7) отличается
от (9.2.3) только множителем A —v) в знаменателе.
§ 10.4; Напряженное состояние около трещины
Теперь мы в состоянии решать более реальную задачу о на-
напряженном состоянии при наличии трещины или щели, чем за-
задача о трещине продольного сдвига, рассмотренная в § 9.3, 9.4.
Упругое пространство разрезано на части
плоскости —а ^ xt < а, х% == 0, на беско-
бесконечности а2г = ст, аи = (Ti2 — 0. В плоскости
^i^2 трещине соответствует изображен-
изображенный на рис. 10.4.1 разрез между зонами
Xi = ±а. Из условий симметрии оче-
очевидно, что на оси Xi должно быть о12 =
= 0. Мы удовлетворим этому условию,
если примем
. A0.4.1)
\ t
I I
t \
\
Подставим это выражение if) (г) в форму-
формулу A0.1.9). Получим
Рис. 10.4.1 "~ ¦"/ ~" — /~"
Отделяя действительную и мнимую части, находим следующие
выражения для перемещений:
\iUi = A — 2v) Re ф + х2 Im фл,
\ш2 = 2A — гIи1ф — хг Кеф'.
A0.4.2)
По формуле A0.1.12)
— ои + 2ioi2 == —2(z —г)ф" (z).
§ 10.4. НАПРЯЖЕННОЕ СОСТОЯНИЕ ОКОЛО ТРЕЩИНЫ 335
Из этого соотношения и A0.1.10) находим
ац = 2(Кеф/ + ж21тф"), о22 = 2A1еф' -х21т ф"),
A0.4.3)
а12 = —2х2 Re ф".
Формулы A0.4.2) и A0.4.3) определяют поле перемещений и на-
напряжений с помощью одной только функции комплексной пере-
переменной ф (z). При #2 = 0 о12 = 0, Он = 2 Re ф' = а22,
= A — 2v)Reф, \хи2 = 2A —
Желая решить с помощью найденных формул поставленную
задачу о трещине, следует выбрать функцию ф(з) таким обра-
образом, чтобы Re ф' была равна нулю на отрезке —а < xt < +a. Так
же, как и в соответствующей задаче для антиплоского состояния,
положим
У Z —~ CL
A0.4.4)
Выясним, к чему стремятся компоненты напряжения при z ->- °°.
В формулы для напряжений входит ф'(з), при этом ф'(°°) = С
Произведение x2q>" (z) при z->~°°, как легко показать, стремится
к нулю. Действительно,
Cz2
как x2(z2 — a2)~in, так и x2z2(z* — a2)~3/2 стремятся к одному и
тому же пределу xz/z, следовательно, произведение x2q>" (z) стре-
стремится к нулю.
Таким образом, при z ->¦ °о
Он = ст22 = 2СЛ Gi2 = 0.
Если принять 2С==а, функция q(z) = Cl/z2 — а2 служит решени-
решением задачи о всестороннем растяжении тела, содержащего трещи-
трещину. Эта задача отличается от той, которая была поставлена вна-
вначале. Действительно, мы потребовали, чтобы на бесконечности
было а22 = а,* а ои = 0. Но это несущественно. Предположим, что
тело, содержащее трещину, растягивается вдоль трещины. Тогда,
очевидно, наличие трещины никак не влияет на напряженное
состояние, которое остается однородным. Поэтому, для того чтобы
перейти от найденного решения к решению первоначально по-
поставленной задачи, достаточно прибавить к напряжению аи, да-
даваемому первой из формул A0.4.3), постоянное сжимающее на-
напряжение — а. Нас будет прежде всего интересовать распределе-
распределение напряжений около конца трещины, где напряжения велики.
Поэтому указанная поправка никакой роли не играет и мы ее
вводить не будем. Вычисление поля перемещений и напряжений
336 rJL 10* ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
приводит к довольно громоздким выражениям, и мы ограничим-
ограничимся нахождением напряжения о2г и перемещения и2 для точек
плоскости #2 = 0. По формулам A0.4.2) и A0.4.3) получаем
A0.4.5)
В непосредственной близости кончика трещины \xt — a\=r<
< а, разлагая выражения для иг и о22 по степеням г, мы получим
для главных членов разложения следующие формулы:
. (ю.4.6)
Как видно, характер особенностей у конца трещины совершенно
такой же, как в случае трещины продольного сдвига. Коэффи-
Коэффициент интенсивности Кг определяется точно так же, с заменой
т на а.
Похожим способом решается задача о трещине в поле чистого
сдвига, расположенной на оси хи как и в предыдущем случае,
но при следующих условиях на бесконечности:
СО СО СО f\
а12 = т, Оц = a22 = U.
Примем теперь вместо A0.4.1) следующее выражение для функ-
функции if:
\|) = —ф — zq/.
Подставляя его в A0.1.9), получим
2\х (ul + iu2) = хф — (z — z) ф7 (z) + ф (z).
Отделим действительную часть от мнимой, получим формулы для
перемещений
\хиг = 2A — v)Req + x2 Im фл,
A0.4.7)
|ш2 = A — 2v) Im ф — хг Re ф'.
По известным формулам вычислим напряжения
О22 = 2х21ту", A0.4.8)
Oi2 = 2 (—Im ф7 — х2 Re ф ").
Заметим, что теперь при х2 = 0 выполняется условие о22 = 0.
Положим
Ф = С/а^^ ч> = -<*= A0.4.9)
У а — z
§ 10.5. ОСНОВНЫЕ ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 337
Так же как и выше, убеждаемся в том, что произведение #2ф" (z)
стремится к нулю при z-^°°, тогда как q/(°°) = Ci. Таким обра-
образом, при z -> оо
(Гц = 022 == 0, di2= —2С = т.
Полагая Кп = тУяа, убеждаемся в то^ что все компоненты на-
напряжения имеют особенность типа 1/Уг около кончика трещины
и на оси Xii
Последние формулы имеют ту же структуру, что при антипло-
антиплоском состоянии и для трещины в поле растягивающих напря-
напряжений.,
§ 10.5. Основные плоские задачи теории упругости
Первая основная задача. Так называется задача об определе-
определении перемещений по заданным на контуре усилиям. Если на
каждом из контуров 1\ заданы составляющие усилия Т± и Г2,
вычисляются функции
s
s
h = /ift + if a = i J {?x + W,) ds.
Задача состоит в нахождении функций ф и г|), удовлетворяющих
граничным условиям:
Л = /и+1/2к = фB) + «флG)+ф(Г), zeTk. A0.5.1)
Наружный контур Го может стянуться в бесконечно удаленную
точку, в этом случае функции ф и г|) ведут себя на бесконеч-
бесконечности так, как это было выяснено в § 10.2, а именно,
где фоB) и ifH (z) голоморфны на бесконечности и в области 5,
тогда как постоянные Г и Г7 определяются формулами A0.2.8).
Вторая основная задача. Если на границе заданы перемеще-
перемещения, на каждом из контуров 1\ известна функция дуги s
Задача сводится к нахождению функций ф и if), удовлетворяю-
удовлетворяющих граничному условию
gu = giu + ig2k = Ky{z)-zlp'G)-yb{zI z^Tk. A0.5.2)
Кроме двух оснрвных задач встречаются смешанные задачи,
когда на части границы заданы усилия, а на другой части —
перемещения или на одном и том же участке границы задана
некоторая линейная комбинация из усилий и перемещений,
22 10. Н. Работнов
338 ГЛ- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
Задача о трещине, например, по существу представляет собой
первую основную задачу, область, ограниченная контуром Г,
превратилась в щель, поверхность этой щели свободна от уси-
усилий, на этой поверхности, т. е. на верхней и нижней сторонах
разреза Д + if 2 = 0. Но примененный в § 10.4 искусственный
прием сводит дело по существу к смешанной задаче; зафиксиро-
зафиксировав функцию if)(z) с помощью A0.4.1), мы выбираем функцию
так, чтобы было а22 = cJi2 = 0, #2 = 0 при \xl\<a и и2 = 0 при
l#il > а. Последнее условие вытекало из симметрии задачи.
Здесь мы рассмотрим в первую очередь основные задачи для
трех случаев:
а) для односвязной конечной области;
б) для бесконечной плоскости, из которой выброшена часть,
ограниченная контуром Г;
в) для полубесконечной области, лежащей по одну сторону
незамкнутой кривой.
Задача для многосвязных областей представляет значительно
большие трудности, для решения их применяются специальные
методы, изложение которых вышло бы за рамки данной книги.
При решении задачи типа а) и б) обычно бывает удобно пре-
преобразовать область S либо на круг единичного радиуса (слу-
(случай а), либо на плоскость с выброшенным кругом единичного
радиуса (случай б). В том и другом случае функция z = co(E;),
осуществляющая конформное отображение областей, устанавли-
устанавливает соответствие между точками контура г^Г и точками ок-
окружности единичного радиуса ? = а = е™ в плоскости ?. Функции
Ф и \|) будут теперь функциями переменной ?. Для краткости
мы будем употреблять для них те же символы, т. е. вместо
ф[со(?)] будем писать просто ф(^), хотя строго говоря это и не-
некорректно. Нужно было бы писать
причем функции ф и ф! различны.
Чтобы преобразовать граничные условия, заметим, что
dz dl dz со' (?)'
Теперь граничные условия будут выполняться на контуре ок-
окружности g = а и функции /i + if2, так же как gt + ig2 должны
рассматриваться как функции а или, что то же, угла д. Вместо
A0.5.1) и A0.5.2) мы теперь получим
/(») = /i(<>) + */.(») = Ф(а) + |Ц-?Н + *И, A0.5.3)
g @) = ft @) + ig* @) = *Ф И - §гщ ? (о) - * (а). A0.5.4)
Метод решения первой и второй задачи для круговой области
§ 10.5. ОСНОВНЫЕ ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 339
или плоскости с выброшенным кругом один и тот же; поскольку
условия A0.5.3) и A0.5.4) имеют совершенно одинаковую струк-
структуру, этот метод основывается на применении интеграла Коши.
Напомним некоторые свойства интеграла Коши. Пусть контур Г
делит плоскость комплексной переменной z на внутреннюю ко-
конечную область S+ и внешнюю бесконечную область S~. Если
функция f(z) голоморфна в S+ и непрерывна в 5+ + Г, то
A0.5.6)
г
Если f(z) голоморфна в5'и непрерывна в *S+ + Г, то
yidt=f(ooL z<=S+, A0.5.7)
г
Интегралом типа Коши называется выражение следующего вида:
Здесь ht(t) и h2(t) —функции, заданные на контуре Г, при этом
комплексная комбинация ht + ih2 не является контурным значе-
значением какой-либо функции комплексной переменной.
Идею применения интегралов Коши к решению плоской за-
задачи теории упругости мы проиллюстрируем на примере первой
краевой задачи для круговой области. Пусть радиус круга равен
единице, условие A0.5.1) выполняется при z = a = e1'*. Умножим
обе части A0.5.1) на 2^[о__ z и проинтегрируем по окружности.
Получим
2KiJ o-z
_ 1 Гф(<г)*у , 1 ГофЧоК . 1 №(S)do
~2niJ o-z +2mj a - za ° + 2ni J o-z *
Интеграл в левой части представляет собою интеграл типа Коши,
он всегда может быть вычислен, поскольку /t и /2 — известные
функции от д. Функция ф голоморфна в S+, первый интеграл
в правой части есть интеграл Коши, по формуле A0.5.5)
Второй интеграл на первый взгляд не есть интеграл Коши. Од-
22*
340 ГЛ- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
нако на самом деле он приводится к интегралу Коши. Это при-
приведение основывается на том, что
0 = 1. A0.5.9)
Голоморфная в S+ функция ф может быть представлена в виде
ряда
Ф = uiZ + a2z2 + ...
(мы принимаем, как было условлено ранее, ф@) = 0), следова-
следовательно,
ср' (а) =а± + 2а2о + За3а2 + .. 9, ср' (а) = а± + -^ + — + ...
Произведение аф'(а) задается, таким образом, следующим рядом:
^сг + 2аа + -^ + ...,
следовательно, оно представляет собою контурное значение ана-
аналитической функции ___
3aQ
2 ^
Первый член этого ряда представляет собою функцию, голоморф-
голоморфную в S+, вследствие A0.5.5) интеграл Коши от ata есть a^z
при z e S+. Остальная часть ряда голоморфна во внешней обла-
области *S~, значение ее при z -+¦ <*> есть 2а2, поэтому по формуле
A0.5.7) интеграл Коши от нее равен 2а2. Итак,
i' (°)da _ г „ i or
Поступим точно таким же образом с последним интегралом, по-
положим
у$ = Ь0 + Ьхг + b2z2 + ...
Тогда _
Ф (о) = К + ^ + . ..
Эту функцию можно рассматривать как контурное значение ана-
аналитической функции, получающейся путем замены а на z. Она
голоморфна в S~ и принимает значение Ьо при z -> «э, поэтому
(а) da _ т
Итак, мы получили
^1^7-2^0-^-2^-Г«'- A0-5Л0)
§ 10.5. ОСНОВНЫЕ ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 341
Из^ этого соотношения необходимо исключить постоянные аи а2
и Ьо. Для этого разложим в ряд интеграл в правой части A0.5.10)
1 Cf(o)da_ 1 Г f(a)da = J_ Г/^?.— ^f
2niJ o — z ' 2ni J а A — z/o) 2ni J а "*" 2ni J
Внесем это разложение в A0.5.10) и представим функцию ср
также в виде ряда. Получим
Сравнивая коэффициенты при одинаковых степенях z, найдем
Вторая из этих формул определяет действительную часть коэф-
коэффициента аи Выше было показано (§ 10.2), что мнимая часть
его может быть выбрана произвольной. Положим ее равной нулю,
тогда
1 Cfda
Теперь A0.5.10) можно переписать следующим образом:
Y v ' 2 J 4 J 2 2J
-I fli?l_JLff _ №. (ю.5.11)
2т J a — z 4m J a2 2mJ a v '
Последний член в формуле A0.5.11) есть постоянная, которую
можно опустить. Но тогда не будет выполнено условие (впрочем
произвольное и необязательное) ф@) = 0.
Чтобы определить функцию i|)(z), перейдем от граничного
условия A0.5.1) к комплексно сопряженному и разрешим его
относительно i|)(z). Получим
* (о) =7(а) - ф (о) - аф' (о).
Вычислим от обеих частей интеграл типа Коши, который в каж-
каждом случае будет сводиться к интегралу Коши вследствие A0.5.9).
Не приводя Детальных рассуждений, выпишем результат
(Ю.5.12)
2_
2ni j о — z
Очевидно, что решение задачи теории упругости возможно лишь
тогда, когда приложенные силы статически уравновешены. Глав-
Главный вектор сил равен нулю тогда, когда функция / есть одно-
однозначная функция дуги контура граничной окружности. Выше мы
убедились, что ^ ] ~Т есть действительное число. Легко пока-
342 гл- 10- плоская задача теории упругости
зать, что это есть условие равенства нулю главного момента.
Заметим, что
*_-„(!) —
поэтому
„(
Заменяя df его выражением 1(Т^ + Иг), выпишем условие равен-
равенства нулю мнимой части контурного интеграла, а именно,
Это и есть условие равенства нулю главного момента.
Если функция со(?), отображающая окружность единичного
радиуса на контур Г границы упругого тела, рациональна, ме-
метод остается по существу тем же самым и решение задачи всегда
может быть доведено до конца и представлено в замкнутом виде.
Выражения, фигурирующие в равенствах A0.5.3) и A0.5.4), при
этом всегда могут быть представлены как контурные значения
рациональных аналитических функций переменной ? и интегралы
типа Коши вычисляются как интегралы Коши. Метод комплекс-
комплексной переменной применительно к плоским задачам очень хороша
представлен в ряде монографий и учебной литературе (Мусхели-
швили, Савин, Новожилов, Амен-Заде и др.)? поэтому здесь он
не будет развиваться более подробно и иллюстрироваться дру-
другими примерами.
§ 10.6. Функция напряжений. Ортотропное тело
Уравнения равновесия плоской задачи при отсутствии объем-
объемных сил
Gap, Р = 0
будут тождественно удовлетворяться, если принять
Cap = Т«в W^ A0.6.1)
или
Ou = F22, o22 = FH, o12 = -F12. A0.6.2)
Функция F называется функцией напряжений. Выражая компо-
компоненты деформации через напряжения, а следовательно, через
функцию F и подставляя эти выражения в единственное теперь
условие совместности из системы G.3.5)
^11,22 + ^22,11 ~~ 2012,12 = 0, A0.6.3)
мы получим единственное дифференциальное уравнение для функ-
§ 10.6. ФУНКЦИЯ НАПРЯЖЕНИЙ. ОРТОТРОПНОЕ ТЕЛО 343
ции F. Вся изложенная выше теория, связанная с применением
функций комплексной переменной, может быть построена (и стро-
строится обычно) на этой основе. Как оказывается, общая теория
становится более простой тогда, когда материал анизотропен, из-
изложенная выше теория для изотропного материала представляет
собою вырожденный случай.
Рассмотрение произвольной анизотропии не представляет ка-
каких бы то ни было принципиальных трудностей, вся техническая
трудность состоит в необходимости решения алгебраического
уравнения четвертой степени, корни которого, вообще говоря,
комплексны. Для приложений нам будет достаточно ограничить-
ограничиться плоской задачей для ортотропного материала. Будем записы-
записывать уравнения закона Гука по отношению к осям упругой сим-
симметрии материала следующим образом:
1
Щ " "' (Ю.6.4)
^12 — ~g Gl2*
В обозначениях (8.3.6)
1-Я, ^ _1_ 1+Я, = J_ JV_ = ^12 = ^21 2 A + К) = J_
/^ jjj gjj hj tii № tii tii Cx n
Часто употребляются также следующие обозначения:
—2j- = cii\ -^g— = С221» "^-= сГгХ = Cn1! —jf: = c6<i1t (Ю.6.5)
Разрешим соотношения A0.6.4) относительно оаР. Получим
1 —
A0.6.6)
Ограничения на параметры анизотропии очевидны. Должно быть
1 - V - v2 > 0, % > -1. A0.6.7)
Заменим теперь в A0.6.4) аар с помощью A0.6.2) и подставим
в A0.6.3). Получим
A + X)Ftun + 2A + %-v)F1121 + A -X)F92222 = 0. A0.6.8)
Решение этого уравнения ищем в виде F = f(xi +тх2). Подстав-
Подставляя это выражение в A0.6.8), находим, что уравнение будет
удовлетворено при любой четырежды дифференцируемой функции
344 гл- 10- плоская задача теории упругости
f{z), если (о удовлетворяет следующему уравнению:
Решение этого биквадратного уравнения
± У^^Ш- <•»¦••<»
Для древесины, стеклопластиков, углепластиков и боропластиков,
т. е. практически для всех применяемых в практике ортотроп-
ных материалов, значения со2, даваемые формулой A0.6.9), дей-
действительны и, очевидно, положительны. Обозначим эти корни ±р
и ±q (p>q). Заметим, что pq = у jZTx'
Поскольку функция F должна быть действительной, то общее
решение уравнения A0.6.8) может быть записано следующим
образом:
F{xa) = F(z,) + F{!,) + H(z2) + H(z2),
A0.6.10)
zl = xi + ipx2, z2==Xi + iqx2.
Полагая 2F' = f, 2H' = h, по формулам A0.6.2) найдем
ИЛИ
o22 = Re f (Zi) + Re V (z2), A0.6.11)
0i2 = —p Ina /' (z^ — q Im h' (z2).
Так как e^ — u^i, е2г = и2,2, перемещения иа найдутся, если под-
подставить A0.6.1) в первые две формулы A0.6.4) и проинтегриро-
проинтегрировать. В результате получаем
и± = - [р2 A + Ц + v] Re/ (Zl) - [g2 A + I) + v] Re/*(z2),
u2 = у [A - Ц + vp2] Im / (zx) + ± [A - X) + v<?2] Im Л (z2).
A0.6.12)
Для изотропного тела A, = 0, x=v и формула A0.6.9) дает рав-
равные корни, следовательно, р == q = 1 и представление функции
напряжений в виде A0.6.10) перестает быть справедливым. Та-
Таким образом, случай изотропии — вырожденный, требующий осо-
особого исследования. Это исследование было выполнено другим
методом в § 10.1, поэтому мы только наметим основную идею выг
вода тех же формул, отправляясь от бигармонического уравнения,
§ 10.6. ФУНКЦИЯ НАПРЯЖЕНИЙ. ОРТОТРОПНОЕ ТЕЛО 345
которому удовлетворяет функция напряжений:
AAF = Ft ни + 2F1122 + F>2222 = 0. A0.6.13)
Сделаем в этом уравнении замену переменных z = xt + ix2, z =
= #4 — ix2. В новых переменных бигармоническое уравнение запи-
запишется следующим образом:
Это уравнение интегрируется непосредственно четыре раза под-
подряд по всем аргументам, при этом учитывается, что &F =
d2F
=4 _— аи+ а22A0.1.4) есть действительная величина и сама
dz dz
функция напряжений также действительна. В результате получа-
получается известная формула Гурса, дающая представление бигармо-
нической функции через две произвольные функции комплексной
переменной
F = zf{z) + zf {z) + h{z) + h(z). A0.6.14)
Теперь формулы A0.1.10) —A0.1.12) получаются путем диффе-
дифференцирования и образования соответствующих комбинаций из
вторых производных функции F с надлежащими переобозначе-
переобозначениями, перемещение находится путем последующего интегрирова-
интегрирования, как и для анизотропного тела.
Возвращаясь к анизотропному телу, сформулируем постановку
первой и второй основных задач.
Первая задача. На контуре заданы усилия Ti(s) и T2(s).
Внесем в выражения
Ti = 011^1 + 012^2, Т2 = 021^1 ~Ь 022^2
величины направляющих косинусов нормали к контуру
а также выражения 0аР через функцию напряжений по формулам
A0.6.2). Получим
Таким образом, функция напряжений F должна удовлетворять
следующим двум контурным условиям:
,2 = J Txds = fu F9l = -\ T2ds = - /2.
346 ГЛ- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
Обращаясь к выражению A0.6.10) для функции напряжений,
перепишем эти граничные условия для функций /(Zi) и h(z2)
A0.6.15)
1Ы+ f &)+ h{z2)+h(z2)= -2f2(s).
Вторая задача. Величины перемещений, определяемые форму-
формулами A0.6.12), принимают на границе заданное значение
Ui = gu U2 = g2.
§ 10.7. Трещина в ортотропной упругой плоскости
Упругая ортотропная плоскость растягивается напряжением а22 = сг0
на бесконечности, на отрезке [—а, а] оси х\ сделан разрез. Положим
?
у z{ — a
Для точек действительной оси z\ = х\. Имеем при |a:i| >• а
Axi
Re/ = ,-r—S Im/=0.
при |a;i | < а
Ах
Re/'=0, '^
Функция h(z2) определяется подобным же образом:
По формулам A0.6.11) находим, что на поверхности разреза х2 = 0,
Приравнивая нулю величину т, получаем
pA + qB = 0. A0.7.1)
При zi-)-oo и z2->oo f-+A, h'-+B. Таким образом, при х\ -> оо ац->-
->• — /?2Л — g2B, O22-+A+B. Если на бесконечности задано растягивающее
напряжение о22 = Оо, то
Л + В = оо. A0.7.2)
Решая уравнения A0.7.1) и A0.7.2), находим
А = — -i^2-f В=-?^2_. A0.7.3)
При этом на бесконечности оказывается приложенным также растягиваю-
растягивающее напряжение оц = pqoo; чтобы снять его, на полученное решение на-
накладывается равномерное сжатие вдоль оси х\.
§ 10.7. ТРЕЩИНА В ОРТОТРОПНОЙ УПРУГОЙ ПЛОСКОСТИ 347
Вычислим теперь распределение напряжений аи и 022 для точек дейст-
действительной оси вне разреза. Получим
A0.7.4)
Поскольку нас интересует напряженное состояние в непосредственной ок-
окрестности кончика трещины, введем локальную систему координат \ =
= хх — а, х\ = х2. При g < а из A0.7.4) получаем
«„- J
Коэффициент К\ интенсивности напряжений О22 определяется так же, как
для изотропного материала, тогда как коэффициент интенсивности напря-
напряжений ац отличается от него множителем pq = УA — М/A + М-
В ортогонально армированном материале опасными направлениями воз-
возможного разрушения будут направления осей х\ и #2, поэтому мы рассмот-
рассмотрим поле напряжений около кончика трещины более детально. Положим
& = % + iP4, h=l + Щ, ?\ = I2 + рУ, р| = ? + дУ• 9Х =arctg^,
g^
©2 =arctg-?-. При р < а получим
Отсюда по формуле A0.6.11)
A A А 0 1
A0.7.6)
При |=0,
A0.7.7)
В сечении, проходящем через ось ?2, кроме напряжения ai2, действует нор-
нормальное сжимающее напряжение
A0.7.8)
Рассмотрим теперь задачу о распространении трещины при сдвиге. За-
Заменяя в выражениях для / и g А на iA, В на Ш, найдем, что граничное
условие для О\2 на поверхности трещины выполняется автоматически; ус-
условия 022 = 0, х е [—а, а] и ai2 = То, ги2-+°° приведут к следующей
системе:
А + В = 0, рЛ + д? = т0.
В результате вычислений убеждаемся, что на оси х\ касательное напряже-
напряжение ai2 имеет ту же особенность, что в изотропном случае, а именно,
= -^jL., Кп = т0 Уш. A0.7.9)
348 гл- 10- плоская задача теории упругости
§ 10.8. Решение задачи об упругой полуплоскости
с помощью преобразования Фурье
Применение интегральных преобразований позволяет свести
задачу об интегрировании дифференциальных уравнений в част-
частных производных к интегрированию системы обыкновенных диф-
дифференциальных уравнений для изображения искомых функций.
Для иллюстрации этой идеи мы приведем здесь решение задачи
об упругой полуплоскости с помощью преобразования Фурье; для
областей другого вида оказываются удобными другие интеграль-
интегральные преобразования. Напомним, что в § 10.4 были изложены
приемы, позволяющие получить относительно простое решение
этой задачи; формулы A0.4.2) и A0.4.3) относились к случаю,
когда на границе о12 = 0, а формулы A0.4.7) и A0.4.6) —к слу-
случаю, когда равно нулю нормальное давление g22 при х2 = 0. Та-
Таким образом, задача о полуплоскости может быть сведена к оп-
определению одной единственной функции cp(z) по заданным зна-
значениям ее действительной или мнимой части на границе. Огра-
Ограничиваясь теми примерами, которые были рассмотрены в § 10.4,
перейдем к изложению метода интегральных преобразований.
Напомним определение и основные свойства преобразования
Фурье. Если f(x) —интегрируемая функция, х^{—°°, +°°), то
ее образом Фурье называется функция действительной пере-
переменной р
-f-OO
I
Обратно, если образ Фурье некоторой функции / (р) известен, то
сама функция восстанавливается по формуле
+ ОО
/(*)=-!= J ](p)e-**dp.
— оо
Рассмотрим теперь следующую задачу. Упругая среда запол-
заполняет полуплоскость —°° <х2<0, ось Xi есть граница полупло-
полуплоскости. Для удобства в этом параграфе мы вернемся к обычным
обозначениям осей координат, полагая Xi = x, х2 = у. Пусть на
границе задано
0) = -g(*), M*, 0) = 0. A0.8.1)
Совершенно аналогичным образом можно задать другие гранич-
граничные условия, выкладки при этом изменятся лишь незначительно
и совершенно очевидным образом. Поэтому мы ограничимся рас-
рассмотрением задачи с граничными условиями A0.8.1).
§ 10.8. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 349
Выпишем уравнения равновесия
^ + — = 0, ^р + — = 0. A0.8.2)
Умножим уравнения A0.8.2) на eipx и проинтегрируем по а; в пре-
пределах от —оо до +оо. Заметим, что, если g(±oo) = 0, то интегри-
интегрирование по частям дает
+ 0О +ОО
j g' (x) eb*dx =-.-iptg (x) e*v*dx = — lp~g (p)
— CX) —ОС
и аналогично
+ C3O
gW (x) eipxdx = (— ip)ng (p).
Таким образом, мы получим уравнения равновесия
— ipa±1 + с12 = 0, — ipo2l + а22 = 0. AU.8.3)
Здесь штрихи обозначают дифференцирование по переменной у.
Подвергая преобразованию Фурье граничные условия A0.8.1),
получим
М/?, 0) = —д"(/?), "о12(р, 0) = 0. A0.8.4)
Как было показано в § 8.5, каждая из компонент тензора напря-
напряжений есть бигармоническая функция, поэтому
Применяя к этому уравнению преобразование Фурье, получим
для образа Фурье а2г следующее обыкновенное дифференциальное
уравнение:
<?21 — 2р2ааа + р%22 = 0.
Запишем решение его следующим образом:
Ъ2 = (А+Ву)еМ». A0.8.5)
По существу это есть склейка двух решений, +р и —р представ-
представляют собою двойные корни характеристического уравнения, ре-
решение рассматривается в нижней полуплоскости о22(р, —°°) = 0,
поэтому, если р > 0, то нужно брать решение, соответствующее
корню +р, а если р < 0, то решение, соответствующее корню —р.
Дифференцируя A0.8.5) по у, получим
350 ГЛ- 10- ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
Подставляя в граничные условия A0.8.4), с учетом A0.8.3)
найдем
A = ~q(p), B=\p\q(p).
Теперь A0.8.5) можно переписать следующим образом:
^22 = -q(p) A - \р\у)е^\ A0.8.6)
С помощью A0.8.3) найдем последовательно
о» = -iq(p)pyelply, ц = 1(Р) A + \р\у)еЫ*. A0.8.7)
По формуле обращения находятся сами напряжения. Мы приве-
приведем подробные вычисления для одного из них, например а22:
а22 = - ^= J q (р) A - | р | у) e\v\y-iv*dp,
где q{p)=^—= \ q^)eiv^dE,. Внеся это выражение в формулу для
Т/2я J
* — СХ)
О22, мы можем переменить порядок интегрирования. Получим
+ сх> +сх>
а™ = Ш J ? №) dg j (I -1PI У) e\v\v-i^-%)dp. A0.8.8)
—оо —оо
Вычислим первую половину внутреннего интеграла:
+ оо 0
f
-—L-—
- y + t (x - I) |0 j/ + i (x - I)
¦ 1
Здесь г2 = (ar —1J +i/2. Аналогичным образом вычисляется вторая
половина внутреннего интеграла
+ 00
г4 '
Проделав подобным же образом все вычисления, мы получим
следующие формулы, представляющие собою решение первой
§ 10.9. СИЛА НА ГРАНИЦЕ ПОЛУПЛОСКОСТИ 351
основной задачи для полуплоскости:
+ ОО +ОО
'• +. 2 °° ' (Ю.8.9)
<*12 — — — J J3
§ 10.9. Сосредоточенная сила на границе
полуплоскости. Контактная задача
Пусть на участке — е ^ | ^ е, #Ш = ^/Bе), тогда как на
остальной границе q(^) = 0. Переходя к пределу при е -> 0,
найдем
Эти формулы дают решение задачи о сосредоточенной силе, при-
приложенной к границе упругой полуплоскости. Найденное решение,
как и всякое другое решение задачи о действии сосредоточенной
силы, не должно пониматься буквально в том смысле, который
вытекает из названия параграфа. Действительно, при х = у = 0
напряжения оказываются бесконечно большими.
Формулами A0.9.1) можно пользоваться в двух случаях:
а. Нагрузка большой интенсивности распределена на малом
+8
участке, например, на участке — е<#^е, причем] qdx=P,
—е
тогда формулы A0.9.1) верны в области Ы > е, \у\ > е.
б. Из формул A0.9.1) обратным переходом можно получить
A0.8.9). Для этого нужно в A0.9.1) заменить координату х па
х — |, т. е. получить решение для сосредоточенной силы, прило-
приложенной в точке х — %. Далее, эта сила Р полагается равной
0(Ю^! и производится интегрирование по |. Хотя мы и отправ-
отправлялись от решения для сосредоточенной силы, получающиеся
в результате формулы A0.8.9) содержат сходящиеся интегралы
и напряжения оказываются конечными, если функция д(?) ог-
ограничена.
Иногда такой обратный путь оказывается более эффективным,
решение для сосредоточенной силы можно бывает получить неза-
независимо, иногда просто путем подбора. Так, напряженное состоя-
состояние, описываемое простыми формулами A0.9.1), оказывается еще
более простым, если преобразовать компоненты тензора о«р к по-
полярным координатам, приняв точку приложения силы за начало.
Вместо этого мы сразу выведем соответствующие формулы в
352 гл- 10- плоская задача теории упругости
полярных координатах. Положим
^^ а0е = О, <^е = 0. A0.9.2)
Здесь угол G отсчитывается от линии действия силы, как пока-
показано на рис. 10.9.1. Непосредственной проверкой убеждаемся, что
уравнения равновесия G.8.5) будут при этом выполнены тож-
тождественно. Уравнения совместности Бельтрами — Митчела (8.5.8)
приведутся к единственному условию
Аогг = 0,
которое также выполняется тождественно.
Непосредственной проверкой убеждаемся в том, что форму-
формулы A0.9.1) и A0.9.2) совпадают.
Вообще говоря, способ подбора, пример которого был приве-
приведен, нужно применять с известной осторожностью, существует
опасность того, что при этом в точке приложения сосредоточен-
сосредоточенной силы появится дополнительная излишняя особенность. Пре-
Предельный переход, использованный при выводе
формул A0.9.1), исключает эту опасность.
Для нахождения перемещений следовало
бы применить тот же способ, что и при выво-
де формул A0.9.1), т. е. проинтегрировать со-
соотношения для образов Фурье и перейти к ори-
оригиналам. Однако мы вычислим перемещение
и2 другим, более простым способом. Вследствие
закона Гука
Рис. 10.9.1 ди2 _ е _ JL (G _ VG \
Мы приняли для определенности, что осуществлено плоское на-
напряженное состояние. При плоской деформации изменяются зна-
значения констант. Интегрируя это соотношение, получим
*. 0)= jj (а22 - wu) dy.
Применим эту формулу к тому случаю, когда на границе прило-
приложена сосредоточенная сила, следовательно, напряжения выража-
выражаются формулами A0.9.1). Вычислим первый интеграл
§ 10.9. СИЛА НА ГРАНИЦЕ ПОЛУПЛОСКОСТИ 353
Положим у2/х2 = z. Тогда
л О л
+ -5- A0.9.3)
При подстановке нижнего предела правая часть в этом равен-
равенстве обращается в бесконечность при любом х, таким образом,
сосредоточенная сила в плоской задаче вызывает бесконечные
перемещения не только в точке ее приложения, что было бы
естественно, но всюду. Это обстоятельство представляется пара-
парадоксальным, но оно есть неизбежное следствие самой постановки
плоской задачи. Как мы увидим далее (§ 11.7), если сосредото-
сосредоточенная сила приложена к границе упругого полупространства,
а не полуплоскости, парадокс исчезает, перемещения оказываются
конечными всюду кроме точки приложения силы.
Интеграл от ои в тех же пределах оказывается конечной ве-
величиной, независимой от координаты х, мы не выписываем зна-
значение этого интеграла и возвращаемся к рассмотрению обраща-
обращающейся в бесконечность части, даваемой формулой A0.9.3).
Продифференцируем найденное выражение и2(х, 0) по х. По-
Получим
ди2 (х, 0) _ р д I /\° _ _ _р_ \_ (_z\ 1° =Л_!
дх 2пЕ дх \ х2) —оо п^ х V1 "t"z' I"0 п^ х
Таким образом, хотя перемещение бесконечно всюду на линии
у = 0, производная от перемещения или угловой коэффициент
касательной к деформированной границе конечна всюду кроме
точки х = 0.
Пусть теперь граница полуплоскости несет нормальную на-
нагрузку #(?), угол наклона касательной к искривленной границе
а(х) определяется путем суперпозиции
Контактной задачей для полуплоскости называется смешанная
задача теории упругости, когда одна часть границы свободна
от усилий или на ней действуют заданные усилия, тогда как на
другой части границы осуществляется контакт с упругим или
жестким телом, вдавливаемым в полуплоскость. Здесь мы рас-
рассмотрим простейшую контактную задачу: на участке же[-а, а]
в полуплоскость вдавливаетеся жесткий штамп без трения; таким
образом, на участке контакта и2{х, 0) = g(x), a12 = 0 всюду, о2г
равно нулю вне участка контакта, на участке контакта а2г =
= — q(x). Полагая а(х) = gr(x) и подставляя в A0.9.4), получим
23 ю. Н. Работнов
354 гл-10- плоская задача теории упругости
интегральное уравнение для функции q(x)
A0.9.5)
о
Решение уравнения вида \ »_/ d?, = f (x) дается формулой
а
Ъ
~]/(х — а) (х— Ъ) J ? — * ~V(x — а) (х — Ъ)
а
A0.9.6)
Как видно, решение не единственно, второй член содержит про-
произвольную постоянную с, которая определяется из дополнитель-
дополнительных условий, например, если задана действующая на штамп сила.
Рассмотрим задачу о действии на полуплоскость загруженного
плоского жесткого штампа, так что g (х) = const, g/==0. Приме-
Применяя к решению уравнения* A0.9.5) формулу A0.9.6), найдем,
что интегральный член будет равен нулю и давление дается
следующим выражением:
4{х)= ' X const.
V а — х
Постоянный множитель легко определяется из условия.
—а
где Р — действующая на штамп сила. Отсюда получаем
<?(*)= Р .-. A0.9.7)
п V а * — х*
Следует обратить внимание на то, что особенность у края штам-
штампа получается точно такой же, как в задаче о трещине, рассмот-
рассмотренной в § 10.4. В действительности, эти задачи совершенно
идентичны, задача о трещине нормального разрыва ставится как
смешанная задача, разница состоит лишь в том, что в задаче
о штампе задано равное нулю перемещение вне отрезка [—а, а]
оси х и напряжение на бесконечности конечно, в задаче о штам-
штампе перемещение постоянно и отлично от нуля на этом отрезкег
на бесконечности напряжение отсутствует. Формулу A0.9.7)
можно без труда получить по методу § 10.4, мы предоставляем
сделать это читателю.
§ 10.10. РЕШЕНИЕ ДЛЯ ДЛИННОГО ПРЯМОУГОЛЬНИКА 355
§ 10.10. Решение для длинного прямоугольника
Часто применяемые на практике балки таврового, двутаврово-
двутаврового, зетового, коробчатого и других тонкостенных сечений могут
рассматриваться как состоящие из длинных прямоугольных по-
полос, соединенных между собой вдоль краев. Элементарная теория
изгиба применительно к таким профилям может быть неточной;
более правильные расчеты получаются, если строить для каждой
из полос решение плоской задачи теории упругости и эти реше-
решения сопрягать между собою. Таким образом, возникает естествен-
естественная необходимость построения решения плоской задачи для
длинного, вытянутого прямоугольника. Оговорка о том, что пря-
прямоугольник должен быть вытянут, существенна. Дело в том,
что метод разделения переменных, который будет применен
в этой задаче, не позволяет удовлетворить двум граничным усло-
условиям на каждой стороне. Поэтому при решении добиваются
точного удовлетворения граничных условий на длинных сторо-
сторонах, тогда как на коротких сторонах граничные условия выпол-
выполняются лишь интегрально. Вспомним, что такая же ситуация
встречается в теории кручения и изгиба. Пусть ширина балки
есть 26, длина Z, оси координат выбраны так, что границами
служат линии хх = 0, хх = Z, х2 = ±Ь.
Будем искать функцию напряжений в одной из следующих
форм:
F = 2 U (*?) cos ^± (решение Рибьера)^ A0.10.1)
1
п=1
F = 2 ^п fca) sin^Ti (Решение Файлона). A0.10.2)
n=l
Подставляя в уравнение для функции напряжений A0.6.8), мы
получим дифференциальное уравнение четвертого порядка для
функций /п, одинаковое как для решения Рибьера, так и для
решения Файлона. Каждая из функций /„ будет зависеть от че-
четырех констант. Представляя заданные при х2 = =Ь& нагрузки
или перемещения формально рядами по косинусам или синусам
аргумента, кратного nxjl, мы находим эти константы; таким об-
образом, граничные условия на длинных сторонах оказываются
удовлетворенными. Подчеркнем еще то, как это уже делалось
неоднократно, что ряды Фурье для заданных величин нагрузок
вовсе не обязательно должны быть сходящимися, нагрузки мо-
могут быть разрывными и даже содержать дельта-функции или
производные от них (сосредоточенные силы и моменты).
Функция F(xu x2) в решении Рибьера четна относительно хи
поэтому можно представить себе, что оно относится не к одной
23*
356
ГЛ. 10. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
полосе, а последовательности любого числа полос длиной Z, как
показано на рис. 10.10.1. Из этого рисунка видно, что при ^4 = 0
и Xi = I концы полосы не могут поворачиваться, значит, щ = 0.
Из симметрии следует, что в этих сечениях момент экстремален,
поэтому поперечная сила Q = dM/dxx равна нулю. Действительно,
012 = --^ 12, подставляя сюда A0.10.1), мы находим, что ai2 = 0,
тогда как Оц = F,22 ^ 0. То, что ^ = 0, можно показать точными
Рис. 10.10.1
Рис. 10.10.2
вычислениями, однако приведенные выше соображения симмет-
симметрии кажутся нам достаточными.
Обращаясь к решению Файлона, мы убеждаемся, что при
распространении его на бесконечную цепочку одинаковых балок
картина будет такая, как показано на рис. 10.10.2. При ^ = 0,
Xi = l равен нулю изгибающий момент. Действительно, из фор-
формул A0.10.2) следует, что Оц = Р>22 обращается в нуль в ука-
указанных сечениях.
Принципиальная возможность решения задачи теории упру-
упругости для прямоугольной области состоит в следующем. Сложим
функции Рибьера и Файлона A0.10.1) и A0.10.2). Прибавим
вторую такую же сумму, в которой координаты х{ и х2 поменяем
местами. Для постоянных коэффициентов функций /п при удов-
удовлетворении граничных условий получаются бесконечные системы
линейных алгебраических уравнений. Для построения фактиче-
фактического численного решения эти бесконечные системы приходится
где-то обрывать. При этом возникает трудный вопрос о том,
в какой мере решение указанной системы из конечного числа
уравнений приближает истинный результат.
§ 10.11. Бесконечно длинная полоса
Ограничившись сделанными замечаниями, относящимися к
прямоугольникам длинным, но имеющим конечную длину, мы
перейдем к случаю, когда длина полосы чрезвычайно велика по
сравнению с ее шириной, так что I можно считать бесконечно
большой. Тогда ряды Фурье по косинусам или синусам заменя-
§ 10.11. БЕСКОНЕЧНО ДЛИННАЯ ПОЛОСА 357
ются соответствующими интегралами Фурье. Положим, например,
cos (XtfJ <»,. A0.11.1)
Это решение соответствует нагрузке, расположенной симметрично
относительно оси х2. Заменяя в A0.11.1) косинус через синус,
мы получим решение для обратно-симметричной нагрузки. По-
Поскольку любая нагрузка может быть разложена на симметричную
и обратно-симметричную части, комбинация двух таких выраже-
выражений позволяет решить любую задачу. Здесь мы ограничимся
симметричным случаем, т. е. уравнением A0.11.1). Обратно-сим-
Обратно-симметричный случай рассматривается совершенно аналогично. Если
материал изотропен, функция напряжений бигармонична, она
удовлетворяет уравнению
AAF = 0.
Подставляя сюда выражение A0.11.1) для функции F, найдем,
что она удовлетворяет уравнению
fv - 2Я2/" + ^7 = °- A0.11.2)
Общий интеграл его
= A ch %х2 + В sh hx2 + Скх2 ch U2 + D Kx2 sh kx2. A0.11.3)
Здесь величины А, В, С и D представляют собою функции от К,
Общий метод проще всего пояснить на примерах.
Пример 1. Перерезывание полосы. Как показано на рис. 10.11.1, рав-
равномерно распределенная нагрузка q приложена с двух сторон полосы ши-
шириной 2Ъ на участке длиной 2а. Вследст-
Вследствие симметрии задачи относительно оси #i,
нужно принять в выражении A0.11.3)
В = С = 0, тогда f(kx2) будет четной
функцией х2. Теперь граничным условиям
достаточно удовлетворить на верхней сто-
стороне полосы, эти условия будут
Ч
г
ai2 = 0, а22 = —#(#1 е [—a, aj), l
с22 = 0(*1?[-а>а]). Рис. 10.11.1
Из формулы A0.11.1) следует, что имеет место
= - 2 f ХУ (Хх2) si
- 2
(вследствие четности подынтегральной функции интеграл от —оо до +°°
заменен удвоенным интегралом от нуля до бесконечности). Из первого гра-
граничного условия следует
Г(Щ = 0,
а из второго
cos
К|>а.
358 гл- 10- плоская задача теории упругости
По формулам обратного косинус-преобразования Фурье находим
а
X2/ (Щ = ~ [ соз UA% = ± sin Яд.
о
Теперь для функций Л (К) и ?>(А,) получается следующая система уравне-
уравнений:
) shW
Отсюда
А 2sinXaChXb+XbchXb) D =
Теперь выражения Л(Х) и D(h) нужно внести в A0.11.3) и вычислить ин-
интеграл A0.11.1) или вторые производные от него по xi, x% т. е. напряже-
напряжения. Фактическое нахождение величин напряжений требует выполнения
численных квадратур.
ГЛАВА И
НЕКОТОРЫЕ ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
§ 11.1. Представление решения задачи теории упругости
в форме Папковича — Нейбера
Основная идея изложенного в гл. 10 метода комплексной пе-
переменной для решения плоской задачи теории упругости состоя-
состояла в том, чтобы представить искомые напряжения и перемеще-
перемещения через функции комплексной переменной, т. е. по существу
через гармонические функции действительных переменных ха.
Для этих функций формулируются те или иные краевые задачи,
методы решения которых и составляют содержание соответству-
соответствующего раздела теории упругости. Большая часть эффективных
методов решения пространственных задач теории упругости
представляет собою развитие той же идеи. Здесь мы приведем
и будем в дальнейшем использовать одно такое представление
решения задачи теории упругости через четыре гармонические
функции. Это представление было открыто Папковичем в 1932 г„
и независимо Нейбером в 1933 г. Будем отправляться от урав-
уравнений Ламе при отсутствии объемных сил
0 A1.1.1)
и будем искать решение этих уравнений в следующем виде:
Wi = <p< + t,<. A1.1.2)
Здесь ср* — три гармонические функции, тогда как гр подбирается
с тем, чтобы удовлетворить уравнениям Ламе. Из формул A1.1.2)
следует
Подставляя последнее выражение в A1.1.1»), получим
Мы удовлетворим этому уравнению, приняв заключенное в скобки
выражение равным нулю. Отсюда следует уравнение, которому
удовлетворяет функция ф
^ + г(Т^Т)Фм = 0. A1.1.3)
Здесь мы заменили отношение постоянных Ламе через коэффи-
коэффициент Пуассона по формулам § 8.3.
360 ГЛ- И- ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Уравнение A1.1.3) представляет собою уравнение Пуассона,
решение его может быть представлено как сумма любого частно-
частного решения и общего решения однородного уравнения, т. е. про-
произвольной гармонической функции. Будем искать частное реше-
решение в виде г|) = г|)* =Aq>hxk. Находим последовательно производные
функции г|)*:
*Ф* = А (Фг + Щ,гхк), ^*ij = A (<pi,j + ф;\г + 4
Отсюда следует
(при свертывании учтено, что функции фг гармонические). Срав-
Сравнивая последнюю формулу с A1.1.3), найдем
4<l-v)e
Поэтому решение уравнения A1.1.3) будет следующим:
где ф0 — четвертая гармоническая функция. Окончательно, ком-
комбинируя A1.1.2) и A1.1.4), получаем
(№+ Фо),г. A1.1.5)
Формула A1.1.5) определяет так называемое решение Папкови-
ча — Нейбера. Термин «решение» в данном случае не совсем
удачен, это есть некоторое функциональное представление для
вектора перемещения в линейно-упругом теле, которое можно
использовать для построения уже конкретных решений опреде-
определенных задач. Мы не будем здесь касаться вопроса о том, может
ли любое решение уравнений Ламе быть представлено в виде
A1.1.5). Можно доказать, что это так, и, более того, введение
четырех гармонических функций излишне; не нарушая общно-
общности, можно принять ф0 = 0, если только v Ф 1/4. В тех задачах,
которые мы будем рассматривать, произвол, содержащийся в фор-
формулах A1.1.5), достаточно широк для того, чтобы позволить
удовлетворить граничным условиям.
§ 11.2. Сосредоточенная сила в изотропной
неограниченной упругой среде
Касаясь вопроса о сосредоточенных силах, мы установили,
что соответствующие решения позволяют найти решение для на-
нагрузок, произвольным образом распределенных по поверхности
или объему. Излагаемое ниже решение относится к случаю еди-
единичной сосредоточенной силы, приложенной в начале координат
§11.2. СИЛА В НЕОГРАНИЧЕННОЙ УПРУГОЙ СРЕДЕ 361
и направленной по оси xh. Соответствующие перемещения мы
будем отмечать двумя индексами, первый относится к направ-
направлению силы, второй индекс — компоненты с номером i вектора »•
Таким образом, определяются перемещения иы и напряжения
Gun, которые удовлетворяют следующим условиям:
1. uhi — однозначные функции координат xs.
2. Всюду кроме точки xs = 0 выполняются уравнения:
°hijtj = 0, ekij = (uhU + ukj,i)> tii 0 -v
A1.Z.I;
3. uhi = О при xs = oo.
4. Если 2 — замкнутая поверхность, заключающая в себе на-
начало координат, то
|б^ A1.2.2)
Рассмотрим теперь неограниченное упругое пространство
с произвольным распределением массовых сил Fu Решение за-
задачи теории упругости для пространства дается следующими
формулами:
щ(х8) = H(l)(l),
Jp (И.2.3)
<Jij (*.) = J ош (xs - Is) Fh (Is) dV.
Строение формулы A1.2.3) указывает на то, что uhl представляют
собою компоненты тензора второго ранга, тогда как akij образуют
тензор третьего ранга. Эти тензоры называются тензорами Грина
для перемещений и напряжений соответственно.
Покажем, что тензор uki симметричен
uhi{xs - Is) = uih(xs - Is). A1.2.4)
Заметим прежде всего, что величины иы могут зависеть только
от абсолютных величин разностей xs —18, поэтому аргументы
можно заменить на |s — x8. Единичная сила, направленная по оси
координат xk и приложенная в точке |в, вызывает в точке xs пе-
перемещение uhi(xs — ?s). Единичная сила, приложенная в точке xs
и направленная по оси хи вызывает в точке ?s перемещения
C& — xs). По теореме Бетти
Заменяя в правой части разность |8 — xs величиной xs — gs, при-
приходим к условию симметрии A1.2.4).
Условие A1.2.2) указывает на то, что величины chij должны
возрастать с уменьшением г как 1/г, только в этом случае инте-
интеграл по поверхности сферы радиусом г от Gkij может оказаться
362 ГЛ* И* ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
независящим от радиуса г. Попытаемся выбрать в качестве функ-
функций ф| в формулах A1.1.5) следующие гармонические, всюду
кроме начала коордпнат, функции:
-~'
Положим временно
4A ~v)
Для вычисления щ по формулам A1.1.5) заметим, что
Подставляя эти выражения в A1.1.5), получим
»« = A-с)^ + с^. A1.2.5)
Переходим теперь к вычислению напряжений. Вычислим первые
производные от uki% При этом используется очевидное тождество
d/d 8ki. Дифференцируя A1.2.5) по xh получим
Выражения для компонент деформации будут следующими:
2eMj = иш + иш = - A - 2с) *«* + V« + 2С^ - 6С
Свертывая по индексам i и у, находим
После подстановки в формулы закона Гука находим
Вернемся к обычным обозначениям упругих констант и приведем
подобные члены. Получим
j + Vi+VJ
? J-
Чтобы проверить выполнение условия A1.2.2), примем за поверх-
поверхность S сферу радиусом г, для которой п{ = xjr. Подынтегральное
§ 11.3. ДРУГИЕ ТИПЫ СИНГУЛЯРНЫХ РЕШЕНИЙ 363
выражение в этом условии будет следующим:
Это выражение нужно интегрировать по поверхности сферы. За-
метим, что \ -«• = 4я. Интеграл от хкХх1гк обращается в нуль
ir
при i Ф /с, при i = к он одинаков для всех значений индексов и,
очевидно,
J
2 2
В результате получаем
J okijnjdl> = —
s
Таким образом, найденное решение соответствует не единичной
силе, а силе равной — 4n\iShi, приложенной в начале координат.
Решение для единичной силы или тензор Грина запишется теперь
следующим образом:
hxi
р ох
§ 11 3. Другие типы сингулярных решений
Отправляясь от формул A1.2.7) и A1.2.8), можно построить
другие типы решений с особенностями, как-то:
а. Двойная сила и сосредоточенный момент. В точке |,- = О
приложена сила —Pi, в точке §j = Aj приложена сила Рг. По фор-
формулам A1.2.7) перемещение равно
uk = -PiUhi @) + PiUki (Д,) = PAjih
Перейдем теперь к пределу, устремляя к нулю Д,- и неограни-
неограниченно увеличивая силу Рг-, так что произведение РгД^ стремится
к конечному пределу Р<Д,- -> пг{5. Получим следующее решение
с особенностью в начале координат:
ик = тцик{>5. A1.3.1)
Если i = /, то rrtj называется двойной силой без момента
(рис. 11.3.1). Система двух равных и противоположно направлен-
направленных сил, вообще говоря, эквивалентна нулю, но в данном случае,
364 ГЛ. 11. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
когда силы неограниченно возрастают с уменьшением расстояния
между ними, в упругой среде возникает напряженное состояние.
Если i?=j, то произведение тпц представляет собою момент пары
-p *—г
-p
Рис. 11.3.1 Рис. 11.3.2
и в пределе мы получаем решение, соответствующее сосредото-
сосредоточенному моменту (рис. 11.3.2).
Напряжения будут выражаться теперь совершенно аналогич-
аналогичным образом
a*e = m«okf«.j. A1.3.2)
Мы выпишем здесь в явном виде только выражения A1.3.1), бо-
более громоздкие формулы A1.3.2) выписывать не будем,
о
xkxixj
A1.3.3)
Особенность, соответствующая двойной силе, имеет более высо-
высокий порядок, а именно, 1/г2 — для перемещений и 1/г3 — для на-
напряжений.
б. Центр растяжения (сжатия). Свернем тензор ukjij по ин-
индексам i и /. Соответствующие формулы дают перемещения от
трех единичных двойных сил, направленных по координатным
осям. Из формул A1.3.3) следует
Формула A1.3.4) определяет полярно-симметричное поле переме-
перемещений, уже рассмотренное в § 8.14, т. е. соответствующее центру
сжатия. Таким образом, центр расширения или центр сжатия
может рассматриваться как результат наложения трех двойных
сил без моментов. Более детальное обсуждение этой задачи со-
содержится в названном параграфе и мы к нему возвращаться не
будем.
§ 11.4. Дислокация Вольтерра
Здесь будет рассмотрен другой тип сингулярных решений, когда на-
напряжения и перемещения обращаются в бесконечность не в одной точке,
а на некоторой линии. Мы уже встречались с примерами таких сингуляр-
сингулярных решений, рассматривая в § 9.2 винтовую дислокацию, в § 10.3 — крае-
§ 11.4. ДИСЛОКАЦИЯ ВОЛЬТЕРРА 365
вую дислокацию. Особенности поля напряжений и перемещений в том и
другом случаях были равномерно распределены вдоль прямой — линии^ дис-
дислокации. Здесь мы рассмотрим задачу о дислокации в неограниченной уп-
упругой среде в самой общей форме. Пусть дан некоторый замкнутый кон-
контур Г (рис. 11.4.1). Построим поверхность 2, проходящую через этот кон-
контур, сделаем по этой поверхности разрез. Берега разреза обозначим 2+ и
2-. Теперь представим себе, что берега разреза раздвинуты на одну и ту
же величину b в произвольном направлении. Таким образом, относитель-
относительное смещение краев разреза задано вектором Ъ.
В оригинальной теории Вольтерра вектор Ь мо-
может быть не постоянным, а линейной функцией ко-
координат. Для приложений к физике твердого тела
особое значение имеет тот случай, когда Ь = const;
рассмотрением этого случая мы и ограничимся.
Итак, берега разреза раздвинуты на величину
вектора Ь. Может случиться, что при этом нам
придется удалить часть материала; там где об- рис ц 41
разуется пустота, заполним ее мысленно тем же
материалом и восстановим сплошность тела. Ана-
Аналогичным образом уже строились винтовые и краевые дислокации, сейчас
же мы рассматриваем общий случай.
Излагаемое ниже решение было дано самим Вольтерра в 1907 г., позд-
позднее Бюргере A939 г.), Питч и Келер A950 г.) и другие авторы представили
его в иной форме, более удобной для приложений. Теория упругих дисло-
дислокаций служит предметом отдельной гл. 14 этой книги, теория Вольтерра в
общих чертах излагается ниже.
Будем смотреть на формулы A1.2.7) и A1.2.8), дающие решение для
сосредоточенной силы, как на предельный случай решения, соответствующе-
соответствующего некоторым массовым силам, распределенным в конечном объеме, при без-
безграничном уменьшении объема. Результирующая этих сил остается все
время равной единице, а главный момент стремится к нулю.
До сих пор мы избегали пользоваться в нашем изложении аппаратом
теории обобщенных функций и если сейчас будет записано уравнение, со-
содержащее функцию Дирака, то это нужно понимать именно в указанном
выше смысле, символ дельта-функции в дифференциальном уравнении обо-
обозначает то, что решение ищется для заданной функции, определенной в ко-
конечном объеме, а после этого производится предельный переход.
Напомним определение трехмерной функции Дирака &(ха — ?«), состоя-
состоящее в следующем: интеграл Г А (я8 — g5) dV равен единице, если объем V
v
заключает в себе точку ?,, и этот интеграл равен нулю в противном слу-
случае. Тогда определенные формулами A1.2.8) напряжения удовлетворяют
следующим уравнениям:
aw, i + 8hiA(x8 - Is) = 0. A1.4.1)
Здесь, в отличие от A1.2.8), точка приложения силы есть |8. Запись A1.4.1)
нужно понимать в том слысле, что объемные силы равны нулю вне объема
У, содержащего в себе точку ?в и, скажем, постоянны по величине и рав-
равны 1/F внутри этого объема. При такой постановке задачи решение сущест-
существует, оно будет непрерывным и ограниченным, при переходе к пределу при
У->0 мы должны получить формулы A1.2.8). Заметим, что такой путь вы-
вывода этих формул представляется более строгим, чем способ подбора реше-
решения с особенностью нужного характера, который был использован в § 11.2.
Определим теперь поле перемещений следующим образом:
¦.-!¦
3G6 ГЛ< И' ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Здесь ns — единичный вектор нормали к поверхности 2. Покажем, что фор*
мулы A1.4.2) дают решение задачи о дислокации. Для этого нужно убе-
убедиться в следующем:
1. Перемещение и{ при переходе черев поверхность 2 изменяется скач-
скачком на величину Ь{.
2. Поле перемещений и* удовлетворяет уравнениям теории упругости
при нулевых объемных силах.
3. На поверхности 2 и на контуре Г не приложены силы.
Для доказательства первого утверждения поступим следующим обра-
образом. Проведем через контур Г вторую поверхность Е' и определим переме-
перемещение и\ формулой, аналогичной A1.4.2),
2'
Теперь S — 2 + 2' представляет собой замкнутую поверхность; если п, есть
внешняя нормаль к S, то ns есть внутренняя нормаль, и наоборот, поэтому
В этом соотношении интеграл берется на замкнутой поверхности S, поэто-
поэтому его можно преобразовать в объемный интеграл по формуле Гаусса —
Остроградского, а именно,
Щ — Щ = ) oikS}SbkdV
v
или, вследствие A1.4.1),
и. — и\ = Ъг § AdV. A1.4.3)
v
По определению функции Дирака А правая часть A1.4.3) равна 6* или рав-
равна нулю в зависимости от того, находится точка ха
внутри объема V, ограниченного поверхностью 5,
или вне этого объема. Таким образом, левая часть
получает скачкообразное приращение при перехо-
переходе через поверхность S. Но при переходе через по-
поверхность 2 может получить приращение только
перемещение ис, таким образом, первое утвержде-
утверждение доказано. Более того, поверхность 2 и соот-
соответственно 2' — любые поверхности, проходящие че-
через контур Г, и рассуждения, связанные с соотно-
... 0 шением A1.4.3), всегда сохраняют силу. Отсюда
Рис. 11.4.2 следует, что в уравнении A1.4.2) интегрирование
можно вести по любой поверхности 2; выражения
для Ui и, следовательно, вц определяются только заданием контура Г —
линии дислокации и вектора Бюргерса Ь. Многозначность и% связана с об-
обходом по контуру, окружающему линию дислокации Г (см. рис. 11.4.2),
а не с пересечением какой-то определенной поверхности 2. Отсюда ясног
что щ, j и он представляют собою непрерывные функции координат.
Переходим к проверке второго утверждения. По закону Гука
§ 11.5. ТЕОРЕМА ВЕЙНГАРТЕНА 3G7
НО Opka = EksmnUpm, n, ПОЭТОМу
гэ = J
2
Используя симметрию тензора Грина мрт, заметим, что
EijpqUpm, nq == EijpqUmp, qn = Omij, n
и, следовательно,
<V
[¦
Ho Omij, n, как было показано в § 11.3, есть напряжение, соответствующее
двойной силе в точке |. Таким образом, решение A1.4.2) для перемещений
и A1.4.4) для напряжений есть решение задачи теории упругости, соответ-
соответствующее распределению двойных сил на поверхности 2. Это решение
A1.4.4) по самому своему построению удовлетворяет однородным уравне-
уравнениям равновесия во всей области, кроме поверхности 2, а так как поверх-
поверхность 2 может быть заменена любой другой, проходящей через контур Г,
то и на этой поверхности никаких сил действовать не может. Проверка
третьего утверждения по существу излишня, легко проверить, что, как это
и должно быть, по поверхности 2 распределены двойные силы без момента.
Действительно, из A1.4.4) следует, что интенсивность распределения двой-
двойных сил есть
™тп = Ekamnbkn8.
Момент единичной двойной силы в плоскости хтхп равен векторному про-
произведению базисных векторов етХ еп* Таким образом, момент, приходя-
приходящийся на единицу площади, есть
т = Eksmnbknsem Х en-
Тензор Екжтп симметричен относительно индексов т и л, а так какетХ еп=
= — епХ ет, то иг = 0. Таким образом, на поверхности 2 не приложены
ни усилия, ни моменты.
§ 11.5. Теорема Вейнгартена
При изложении теории дислокаций в предыдущем параграфе мы в
большей мере следовали статье Лейбфрида, чем оригинальной работе Воль-
терра. Вывод о том, что выбор поверхности разреза 2 не существен, а поле
перемещений и напряжений определяется лишь контуром Г и вектором 6,
приведет неизбежным образом к выводу о том, что в формулах § 11.4 по-
поверхностные интегралы могут быть преобразованы в интегралы по конту-
контуру Г. Для изотропного тела это было сделано частично в работах Бюргерса
A939 г.); в формулах Бюргерса, кроме контурных интегралов, остался еще
телесный угол, под которым виден контур Г из данной точки пространства.
Пич и Келер в 1950 г. сумели представить телесный угол, также с помощью
контурных интегралов. Для анизотропного тела решение в явной форме по-
лучпть не удалось.
Метод Вольтерра при всем своем изяществе производит впечатление
некоторой искусственности, решение оказалось угаданным как бы случайно
и оправдано последующей проверкой. Теорема Вейнгартена устанавливает
принципиальную возможность решений, соответствующих многозначным пе-
перемещениям с сохранением непрерывности деформаций и их производпых,
и накладывает определенные ограничения на характер неоднозначности.
ggg ГЛ. 11. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Выберем две бесконечно близкие точки М^ и М~ на разных сторонах по-
поверхности 2 на рис. 11.4.1 и две другие бесконечно близкие точки М+ и М~.
Соединим точки М* и М+, Af ~ и ЛГ~бесконечно близкими кривыми, одна
из которых находится на стороне 2+, другая на стороне 2~\ Положим в фор-
формулах Чезаро G.3.5)
Вследствие сделанного предположения о непрерывности аи и их производ-
производных т]+ = т|- для бесконечно близких точек на двух сторонах поверхно-
поверхности 2, но в точках М* и М~ как перемещения м^, так и повороты со^,
вообще говоря, различны. По формуле G.3.5) получаем
м
»?•=«г+<(**-*?)+
м
Криволинейные интегралы разнятся на бесконечно малую величину, поэто-
поэтому пределы их обозначены буквами Мо и М без индексов плюс и минус.
Вычитая одно уравнение из другого, получим
К] = К] + KJ (*;-*;)• t11-5-1)
В формуле A1.5.1) квадратные скобки обозначают, как обычно, разры-
разрывы соответствующих величин. Это соотношение и составляет содержание
теоремы Вейнгартена: если напряжения и их производные непрерывны, то
разрывы непрерывности перемещений могут быть только такими, которые
соответствуют перемещению жесткого тела.
§ 11.6. Задача теории упругости для полупространства
Формулы A1.1.5) представляют перемещения в упругом теле
через четыре гармонические функции. Однако в общем случае
в граничных условиях фигурируют комбинации этих функций,
и воспользоваться известными решениями задач теории гармони-
гармонических функций, как правило, не удается. Однако в некоторых
случаях задача теории упругости сводится к той или иной зада-
задаче для уравнения Лапласа; таким образом, удается построить
эффективные решения. Одной из таких задач служит задача об
упругом полупространстве. Пусть упругая среда занимает область
пространства #зе[0, оо)? плоскость х3 = 0 является границей, на
которой заданы те или иные условия. Здесь мы ограничимся
изучением наиболее простого случая, когда на граничной пло-
плоскости равны нулю касательные напряжения оа3 (а = 1, 2).
В этом случае, как будет показано, все перемещения и напряже-
напряжения выражаются через одну гармоническую функцию. Условим-
Условимся сохранять индексные обозначения только для осей Xi и х2у
ось х9 будем обозначать как ось z. Как уже было принято раиеег
§ 11.6. ЗАДАЧА ТЕОРИИ УПРУГОСТИ ДЛЯ ПОЛУПРОСТРАНСТВА 369
индексы, принимающие значения 1, 2, будем отмечать гречески-
греческими буквами. Перепишем теперь формулы A1.1.5) следующим
образом:
Ua = фа — / н — vl КЩЧ + Фо),сс + *Фз,сс],
1 Та *М A1'6Л>
«з = Фз - 4(l-v) Ы ((рРЖР + ^ + фз + Z~e
Касательные напряжения вш выражаются формулами
( ди<х\
(Тза = И ("з.а + -гг).
После подстановки сюда выражений A1.6.1), находим, что при
z = О должно быть
d<ta i-2v I
+ ф
IF + 2(l-v) фз-а 2(l-v
Этому условию можно удовлетворить, если принять
5фа 1 —2v ^Фо дфр 1—2v
Ф *f
Первое условие A1.6.2) утверждает тождественное равенство
двух гармонических функций на плоскости z = 0. Но если две
гармонические функции совпадают в некоторой области, они сов-
совпадают всюду. Что касается второго равенства A1.6.2), левая
часть его есть значение при z = 0 гармонической функции dtpo/dz,
тогда как правая часть есть граничное при z = 0 значение функ-
функции Жг-фз,*. В § 11.1 при выводе формул A1.1.4) мы убедились,
что если грг- — гармонические функции, то
A {Xi^i) = 2^i, i.
В нашем случае -ф< = ф3) г-, следовательно,
поскольку фз — функция гармоническая.
Таким образом, получаются соотношения, справедливые для
всего полупространства,
5(Ра l-2v ЗФ0 l_2v
ф
A1-6-4)
Если ввести обозначение
1 — 2v дер*
то формулы A1.6.3) выражают все функции фь. через одну
24 ю. н. Работнов
370 ГЛ> И' ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
гармоническую функцию <р*, а именно,
фос = — ф,а, фо=^аф,а + 2-^~ ф* A1.6.5)
(при выводе последнего соотношения следует произвести инте-
интегрирование по частям). Теперь по формулам A1.6.1) находятся
перемещения
Для простоты записи здесь сделано еще одно переобозначение,
а именно,
_ 3 —4v *
ф "~ 4 A - v) A - 2v) ф 4
Через единственную гармоническую функцию ф вычисляются
также все напряжения. Мы не будем выписывать здесь все фор-
формулы, приведем лишь выражение о33, а именно,
Возможные краевые задачи при поставленном заранее условии
<Таз = 0 на граничной плоскости S при 2 = 0 будут следующие:
а) первая задача: о33 = — <?(#<*), xa^S\
б) вторая задача: u3 = w(xa), xa^S;
в) смешанная или контактная задача:
щ = w (ха), ха е= Si, a33 = — q (#a), x* €= S2, S4 + S2 = S.
Поскольку в граничных условиях всех этих трех задач будут фи-
фигурировать только производные функции ф по z, а не сама
функция или ее производные по ха, при математической форму-
формулировке перечисленных краевых задач удобно принять в каче-
качестве неизвестной производную от ср по z, положив
д(р - F (х z)
— - t (ха, z).
Тогда при z = 0
«8 = 2(l-v)F, a33 = 2ii^-. A1.6.8)
Первая задача сводится, таким образом, к определению гармони-
гармонической функции по заданному на границе значению ее нормаль-
нормальной производной (задача Неймана), вторая задача — к опреде-
определению гармонической функции по заданному ее значению на
границе (задача Дирихле). Контактная же задача формулируется
следующим образом: требуется найти гармоническую в верхнем
полупространстве функцию F, если на части S4 граничной пло-
§ 11.7. НОРМАЛЬНАЯ НАГРУЗКА НА ГРАНИЦЕ 371
скости задано перемещение w; значит, F= 2A~ v) > тогда как на
dF g ф
оставшейся части-т—=—ttj. Термин «контактная задача» связан
с тем, что заданное перемещение uz = w может быть осуществле-
осуществлено путем вдавливания абсолютно жесткого штампа без трения,
хотя некоторые другие задачи, например задача о напряженном
состоянии около плоской трещины, приводят к точно такой же
математической формулировке.
§ 11.7. Нормальная нагрузка на границе полупространства
Здесь будет рассмотрено общее решение первой основной за-
задачи для упругого полупространства, вторую задачу, как мала
реальную, мы рассматривать не будем. Решение задачи Неймана
для полупространства, как известно, дается следующей формулой:
Здесь г2 = (xt - hJ + (х2 - Ъ%J + ъ\ dS = d\, d%2. Функция $(xai z):
определяемая формулой A1.7.1), где интеграл берется по всей
плоскости z = 0, удовлетворяет уравнению Лапласа и нормаль-
нормальная производная ее (d^/dz)z=u = —m(xa). Интеграл A1.7.1)
называется потенциалом простого слоя плотности т(ха). Функ-
Функция if> — гармоническая, так как
Г — гармоническая функция коор-
координат #«, z, а интегрирование ве-
ведется по переменным |«. Вычислим
теперь производную /d
dz
mz dS 1 I'm cos a
2л
s
— 1 Г
2л J
На рис. 11.7.1 показан угол а. Заметим, что cos a dS/r2 — телес-
телесный угол, под которым виден из точки М элемент поверхности
dS\ обозначим этот телесный угол dco. Разобьем границу полу-
полупространства на две части: 54 — круг радиусом р с центром в точ-
точке А — основании перпендикуляру опущенного из точки М на
граничную плоскость, и *S2 — внешность этого круга. Предста-
Представим теперь выражение для производной dty/dz в виде суммы двух
интегралов
24*
372 ГЛ* И* ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Применим к первому интегралу теорему о среднем и будем при-
приближать z к нулю, при этом
h s2
Следовательно,
I = — 771.
\ dz Jz=zQ
Итак, формула A1.7.1) действительно дает решение задачи Ней-
Неймана для полупространства. Теперь мы можем написать решение
первой основной задачи для упругого полупространства, а именно,
S
В частности, если к поверхности приложена сосредоточенная
Р, то F - ^
Нормальные перемещения точки границы выражаются следу-
следующим образом:
В отличие от плоской задачи, рассмотренной в § 10.9, здесь пе-
перемещение обращается в бесконечность только в точке прило-
приложения силы. При стремлении г к бесконечности, перемещение
на поверхности стремится к нулю. С помощью A1.6.6) легко
убедиться, что перемещение стремится к нулю по мере удаления
от точки приложения силы по любому направлению.
§ 11.8. Контактная задача. Жесткий плоский штамп,
круглый в плане
Рассмотренный ниже пример представляет собою трехмерный
аналог плоской контактной задачи, решенной в § 10.9. В отли-
отличие от плоского случая мы не сумеем представить в замкнутой
форме, подобной A0.9.6), решение для штампа произвольного
профиля. Для плоского штампа результат может быть получен
разными способами; излагаемый ниже метод принадлежит Рос-
Ростовцеву и, кажется, приводит к цели наиболее коротким путем.
Положим х\ + х\ = р2 и рассмотрим функцию
производная ее по z
§ 11.8. КОНТАКТНАЯ ЗАДАЧА 373
*есть гармоническая функция. Действительно, выражение
(z + iaJ + р2 отличается от величины r2 = z2 + p2 только тем, что
к координате z добавлено постоянное слагаемое, а функция 1/г
есть гармоническая. Отсюда следует, что г|>(р, z) есть гармони-
гармоническая функция координат ха, z\ действительные и мнимые части
функций о|з и dty/dz также будут гармоническими. При z = О
(я/2 (Р<а),
1пиЬ = . ;г^ A1.8.1)
т larcsm(a/p) (p>a), v '
0 (,>.).
Положим теперь
Вследствие A1.8.1) на граничной поверхности при р<а выпол-
выполняются условия
q
„ ск w OF с
2 A — v) я dz i/"T~
тогда как при р > а
dz 2\л
Если принять с = гс , _ , то функция F даст решение задачи
о плоском штампе, имеющем в плане форму круга радиуса а,
который вдавливается симметрично на глубину w в поверхность
упругого тела. При этом вели-
величина вдавливания w считается
заданной. Давление под штам-
штампом при этом определяется
следующей формулой: ш'////ШбШ
я A — v) у а2 __ 2 * Рис. 11.8.1
Интегрируя давление по площади круга, найдем силу, вдавли-
вдавливающую штамп. Удобнее представить результат в виде, разре-
разрешенном относительно w,
Давление, выраженное через силу, будет при этом
374 ГЛ- И- ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Как видно, давление обращается в бесконечность на контуре
штампа, характер особенности при этом совершенно тот же, что
в плоской задаче. Эта особенность отражается также и на кар-
тине перемещений, при р = а — О -^- = -~ = О, при р > а, соглас-
согласно A1.8.1), угловой коэффициент касательной к меридиану де-
деформированной поверхности пропорционален производной
d . a a
-г- arcsin — = >.
При р = а + О эта величина обращается в бесконечность, разрез
участка, примыкающего к краю штампа, имеет вид, показанный
на рис. 11.8.1.
§ 11.9. Потенциал однородного эллипсоида
Содержание этого параграфа связано с приемом, который при-
применяется для решения смешанных задач теории упругости для
полуплоскости. Рассмотрим потенциал U непрерывного распре-
распределения масс в некотором объеме, предполагая объем и распре-
распределение масс симметричными относительно плоскости z = 0. Этот
потенциал будет необходимым образом четной функцией z, сле-
следовательно, производная dU/dz обращается в нуль при z = 0 вне
заполненного массой объема. Будем теперь сплющивать объем
и, переходя к пределу, получим потенциал простого слоя, на-
нанесенного на некоторую область 54 е S. В области 54 величина
потенциала будет некоторой функцией координат ха. Теперь,
если принять построенный таким образом потенциал за функцию
F, мы получим решение некоторой контактной задачи. Действи-
Действительно, в области S = S — Si dF/dz = 0, следовательно, эта часть
граничной плоскости свободна от напряжений. В области SY F
есть некоторая функция координат, определяющая форму штампа.
Напомним определение и некоторые свойства потенциала.
Пусть в объеме V задана некоторая функция р(#г-), которую мы
будем называть плотностью. Обозначим через V+ множество то-
точек, заключенных в объеме У, и через V~ множество точек, на-
находящихся вне этого объема. Потенциалом называется функция
p-^, A1.9.1)
Здесь г2 = (х{-11J + (х2-ЪJ + (хз-ЪJ- Функция U(Xi) и ее
производные Uj непрерывны на границе объема У+, но вторые
производные претерпевают разрыв. В теории потенциала дока-
доказывается следующее свойство:
0, ^еГ, ДС/=-4яр, я<еу*. A1.9.2)
§ 11.9. ПОТЕНЦИАЛ ОДНОРОДНОГО ЭЛЛИПСОИДА 375
Фактическое нахождение потенциала путем прямого вычисления
интеграла A1.9.1) обычно встречает существенные трудности,
поэтому часто подбирают функцию С/, удовлетворяющую урав-
уравнениям A1.9.2).
Классическим примером такого подбора служит формула для
потенциала однородного эллипсоида, принадлежащая Дирихле.
Пусть уравнение эллипсоида будет
и плотность р = const.
Составим кубическое уравнение относительно К:
2-=-* 1 = / (хь %) = 0. A1.9.3)
Это уравнение имеет три действительных корня. На самом деле
при X -> ±<х> / == —1, при X = — а\ f =± оо. График функции /(А,)
пересекает ось X три раза, независимо от значений Хи Обозначим
через Xt наибольший корень уравнения A1.9.3) и определим
функцию и(х() следующим образом:
U = ярвло, J [п(а|Д}У2 Л, A1.9.4)
при этом
и = 0, если Xi s У+, и = Я4, если хг е У-.
Если точка ^ принадлежит поверхности эллипсоида, то уравне-
уравнение A1.9.3) имеет корень Л = 0, причем этот корень будет наи-
наибольшим. Действительно, попытавшись построить примерный
график функции /(А,), мы убеждаемся, что два корня уравнения
A1.9.3) всегда отрицательны. Отсюда следует, что U есть не-
непрерывная функция координат. Вычислим теперь производную
dU/dxh = Uth. Получим
A1.9.5)
Член, содержащий множителем производную dU/dxk, исчезает,
так как другой множитель при этом члене есть /(яг, и); при
u = %i он равен нулю в силу A1.9.3), при и = 0 равна нулю
производная. Непрерывность производных Uth на границе обла-
областей V+ и V~ устанавливается, как и для функции U. Нам по-
376 ГЛ- И* ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
надобятся также вторые производные U}km. Дифференцируя:
A1.9.4), находим
J ди_
A1.9.6)
Свернув по индексам кит, получим
At/ = — 2npa1a2a3 I
Интеграл в этом выражении вычисляется; непосредственной про-
проверкой легко убедиться в том, что подынтегральное выражение
есть производная по X от функции 2[П(а| + К)]" , поэтому
Если Хх ^ У+, то гг = 0 и из A1.9.7) следует
AU = — 4лр, я,-€=У+.
Если ^ s У то и = Х, где X — один из корней уравнения
A1.9.3). Заменим в нем X через и и продифференцируем по хк*
Получим
2*ft V 5i a« _0
e2 + « T(*i+*Ja*fc
Умножим на — и просуммируем по индексу к. Получим
at + u
Отсюда следует
§ 11.10. ШТАМП В ФОРМЕ ПАРАБОЛОИДА 377
следовательно, правая часть A1.9.7) обращается в нуль и мы
имеем
Таким образом, действительно формула A1.9.4) представляет
выражение для потенциала однородного эллипсоида, получить
>ее путем прямого интегрирования из формулы A1.9.1) было бы
весьма затруднительно.
§ 11.10. Штамп в форме параболоида
Из формулы A1.9.4) следует, что для внутренних точек эл-
эллипсоида потенциал представляет собою квадратичную функцию
координат Xi. Будем теперь сплющивать эллипсоид в направле-
направлении оси х3 = z, т. е. будем устремлять к нулю полуось а3, одно-
одновременно увеличивая плотность р. В пределе мы получим про-
простой слой, распределенный по площади эллипса с полуосями
•ui = а и а2 = Ъ. Плотность этого слоя
т
/2 2
Потенциал этого простого слоя получается предельным перехо-
переходом по формуле A1.9.4) (здесь мы возвращаемся к обычным
обозначениям координат и полуосей эллипса а, Ъ и с)
л
U ff
= npabc f f + X b* + X /П. A1.10.2)
I /(а2+Я)(ьа + Ь)Х ^ '
Теперь в соответствии с результатами § 11.7 мы находим
Принимая во второй из формул A1.6.8) F=U, Озз = —g, на-
находим:
j а о
Давление q распределено по площади эллипса с полуосями а
и Ь, результирующая сила Р найдется интегрированием по
площади:
F F
Но интеграл от т по площади эллипса равен интегралу от р по
378 ГЛ- И- ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
объему исходного эллипсоида, именно с соблюдением этого усло-
условия производился предельный переход. Таким образом,
jm dF = -у pabc.
SP
Внося в выражение для Р, мы находим [Jtpc = и, следова-
следовательно,
г -4-4- A1-ю.з)
Перемещение щ при z = 0 и внутри эллипса определяется теперь
первой из формул A1.6.8), а именно,
х
Найденное решение соответствует задаче о вдавливании жесткого
штампа, имеющего форму параболоида. Если штамп достаточно
пологий и поверхность его гладкая, при этом в точке первона-
первоначального контакта радиус кривизны отличен от нуля, то пере-
перемещение и3 может быть разложено в ряд Тейлора и при удер-
удержании первых членов разложения его следует рассматривать
как квадратичную функцию координат, а именно,
щ = Ах2+Ву2 + С. A1.10.5)
Подставляя в A1.10.4) и приравнивая коэффициенты при х2, у2
и свободных членах, мы получим три уравнения для нахождения
глубины вдавливания при х = у = 0, т. е. константы С, а также
для размеров площадки контакта а и 6. Однако прежде чем вы-
выписать эти уравнения и извлечь из них некоторые следствия,
мы переформулируем саму постановку задачи.
§ 11.11. Контактная задача Герца
Как показал Герц A881 г.), изложенная выше теория рас-
распространяется без всяких изменений на случай контакта двух
произвольных упругих тел. Два изотропных упругих тела, име-
имеющие, вообще говоря, разные упругие постоянные, ограничены
выпуклыми поверхностями. Будем отмечать индексом «плюс»
величины, относящиеся к одному из этих тел, и индексом «ми-
«минус» величины, относящиеся ко второму телу. Эти тела приво-
приводятся в соприкосновение так, что точка О+ первого тела совпа-
совпадает с точкой О~ второго тела. Теперь одно тело прижимается к
§ 11.11. КОНТАКТНАЯ ЗАДАЧА ГЕРЦА
379
другому силой Р, вследствие упругой деформации вместо точеч-
точечного контакта в точке О образуется площадка контакта конеч-
конечных размеров. Теория Герца основывается на следующих пред-
предположениях.
1. В окрестности точки О уравнение каждой из поверхностей,
ограничивающих контактирующие тела в их первоначальном со-
состоянии (до наступления контакта),
может быть записано следующим обра-
образом (рис. 11.11.1):
A1.11.1)
= А'х2 + В~у2 + 2С~ху.
Оси х+ и аг, у+ и у выбраны парал-
параллельными, поэтому в формулах A1.11.1)
при обозначении координат х и у ин-
индексы опущены.
2. Размеры площадки контакта ма-
малы по сравнению с радиусами кривиз-
кривизны поверхностей контактирующих тел,
поэтому в разложениях функций Рис. 11.11.1
z+(x, У) и z~(xi У) достаточно удер-
удержать квадратичные члены, кап это сделано в формулах 'A1.11.1).
3. Поскольку нас интересует напряженное и деформированное
состояние на площадке контакта и вблизи ее, можно прибли-
приближенно считать, что это напряженное и деформированное состоя-
состояние практически не отличается от то-
того, которое возникает в упругом полу- ] п
пространстве, поэтому изложенная вы-
ine теория сохраняет силу.
Заметим, что величины А, В и С в
формулах A1.11.1) могут быть равны-
равными нулю. Тогда разложение функций
z+ и z~ начинается с членов четвертой '
степени относительно х и у (при есте- Рис. 11.11.2
ственном предположении о четности
функции х и у). Соответствующая контактная задача была полу-
получена Штаерманом.
После приложения силы Р тела приведены в соприкоснове-
соприкосновение, как показано на рис. 11.11.2. Точки О+ и О" совпали, сов-
совпали также оси х+ и х~, у* и у~. Точки а и Ъ служат границами
площадки контакта в изображенном сечении, точка ш+ совпала
с точкой т~. Обращаясь опять к рис. 11.11.1, видим, что для
этого должно быть выполнено геометрическое условие
I i
i
z+ + ut + z + и J" = a = const.
A1.11.2)
380 ГЛ- И- ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Заметим, что рис. 11.11.1 для упрощения сделан неточно,
В действительности точки поверхности контакта получают не толь-
только перемещения и? и щ, но также ut и щ , и? и щ, которые,
вообще говоря, различны для двух контактирующих тел. Поэто-
Поэтому точки т+ и т~, сливающиеся после деформации в одну точ-
точку т, на рис. 11.11.1 нельзя помещать на одной вертикали.
Однако легко убедиться, что учет смещений в плоскости осей
х, у приведет к появлению в условии A1.11.2) членов вида
и\/BВ), ..., где R — один из радиусов кривизны. Эти члены
имеют второй порядок малости по сравнению с теми, что фигу-
фигурируют в левой части A1.11.2), и при принятой степени точно-
точности теории должны быть отброшены.
Величина а представляет собою сближение тел при упругом
контакте. Подставляя выражения A1.11.1) в соотношение
A1.11.2), получим
и+ + щ = а - (А+ + А~) х2 - (В+ + В") у*-2 (С+ + С~) ху.
A1.11.3)
Квадратичная форма, стоящая в правой части A1.11.3), может
быть преобразована надлежащим поворотом осей в сумму квад-
квадратов, поэтому A1.11.3) можно переписать следующим образом:
ut + щ = а — Ах2 — By2. A1.11.4)
В выражении A1.11.4) оси х и у уже не совпадают по на-
направлению с первоначально произвольным образом выбранными
осями х± и у±. Соотношение A1.11.4) заменяет полученные в
конце предыдущего параграфа выражения A1.10.5) для прогиба
и3 под жестким штампом. Вследствие сформулированного выше
третьего предположения теории Герца как u?f так и щ (при
z+ = 0, ?~ = 0) выражаются по формуле A1.10.4), следовательно,
A1.11.4) можно переписать так:
х dX = а - Ах2 - By*.
)
Уравнение A1.11.5) распадается на три уравнения, позволяю-
позволяющие вычислить а, а и Ъ. Мы выпишем эти уравнения, положив
§ 11.11. КОНТАКТНАЯ ЗАДАЧА ГЕРЦА 381
Получим
ро Г
a= — \ -
a J
A1.11.6)
в
oo
CL v
0
Каждый из интегралов представляет собою функцию отношения
осей эллиптической площадки контакта /с, все они приводятся
к эллиптическим интегралам и, следовательно, могут быть вы-
вычислены. Мы не будем здесь приводить это решение, ограничив-
ограничившись некоторыми качественными выводами и анализом простей-
простейших случаев.
Поделив второе из уравнений A1.11.6) на третье, мы найдемг
что отношение А/В есть функция к, но А и В зависят только
от геометрии соприкасающихся тел, это заданные постоянные.
Поэтому отношение Ыа = к не зависит от нагрузки и упругих
свойств контактирующих тел, это отношение определяется только
их геометрией.
Следующее заключение, которое можно сделать, состоит в
следующем. Отношение Р/а3 должно оставаться постоянным при:
изменении нагрузки, что следует из второго или третьего урав-
уравнения, поэтому
а ~ Р1/3.
Размер площадки контакта меняется пропорционально корню
кубическому из нагрузки.
Теперь из первой формулы A1.11.6) следует
а ~ Р2/3.
Сближение контактирующих тел пропорционально нагрузке в
степени 2/3.
Последний факт был положен Герцем в основу теории соуда-
соударения упругих тел. Было сделано допущение о том, что зави-
зависимость между нагрузкой и перемещением при ударе остается
той же, что и в статике. Более точный анализ требует учета
сил инерции в самих уравнениях теории упругости.
Обратимся теперь к рассмотрению простейших случаев, когда
интегралы в формулах A1.11.6) вычисляются элементарно.
а. Контакт двух сфер радиусами Н+ и Н~. Очевидно, что
уравнение сферы вблизи точки О есть z = r2/BR), поэтому
~ 2R+ 2R- 2Я+Д-
382 ГЛ* и- ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Интеграл в первой формуле A1.11.6) для а при Х = 1
со
Интеграл во второй или третьей формуле A1.11.6) для А—В
iJ 2'
Отсюда получаем следующий результат:
a=y^iJ^, a = V2ai*P*&2A. A1.11.7)
б. Контакт двух круговых цилиндров одинакового радиуса R
с перпендикулярными осями. Как легко убедиться, в этом случае
площадка контакта будет кругом, формулы A1.11.7) сохраняют
силу и в этом случае, но теперь
A~D 2R-
§ 11.12. Температурные напряжения
Деформация тела, вообще говоря, не обязательно должна
быть только упругой, она может быть вызвана какими-либо
иными причинами. Как мы увидим дальше, при пластическом
деформировании полная деформация оказывается состоящей из
двух частей: упругой, связанной с напряжением закона Гука,
и пластической, необратимой.
Другой, самый простой пример такой вынужденной неуцругой
деформации представляет собою деформация, связанная с изме-
изменением температуры. В общем случае температурное расшире-
расширение анизотропно и температурная деформация е^ определяется
так:
Здесь af,- — тензор коэффициентов термического расширения,
Т — текущая температура, То — условно зафиксированная темпе-
температура, при которой предполагается, что деформация равна ну-
нулю. Тензор е-%) вообще не удовлетворяет уравнениям совместно-
совместности, поэтому возникают упругие деформации ejj. Полная де-
деформация
удовлетворяет условиям совместности, т. е. выражается через
компоненты перемещения по известным формулам.
§ 11.12. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ 383
Таким образом, мы имеем
A1.12.1)
Упругое изотропное тело, как правило, изотропно и по отноше-
отношению к температурной деформации, тензор ац = абу, где а — обыч-
обычный линейный коэффициент теплового расширения, и формулы
A1.12.1) принимают вид
Оц = Ш« + 2|хс« - (ЗЯ + 2|i) а (Г - То) 6«.
Внося это выражение в уравнение равновесия, получим
(к + \i) в.* + \iAui - а (ЗА, + 2|х) Г.* = 0. A1.12.2)
Эти уравнения имеют тот же вид, что уравнения Ламе, роль
объемных сил Ft играет градиент температуры.
Заметим, что уравнения A1.12.2) непригодны в том случаег
когда материал несжимаем; множитель при Tti обращается в бес-
бесконечность. Но для несжимаемого материала X = °° и уравнения
закона Гука нужно записывать следующим образом:
Здесь гидростатическая составляющая тензора напряжений пред-
представляет собою независимую величину в том смысле, что она
не связана с деформированным состоянием тела. При наличии
температурной деформации мы получаем
оц = ав« + 2|х^ - 2^ха (Т - То) «<,,
а после подстановки в уравнения равновесия вместо A1.12.2)
получается следующая система:
а г + мА^ - 2|лаГ, = 0, uit t = 0. A1.12.3)
Возвращаясь к общему случаю, заметим, что частное решение
системы A1.12.2) есть
После подстановки в дифференциальные уравнения найдем
Отсюда, переходя к техническим постоянным, т. е. выражая
множитель в правой части через коэффициент Пуассона vt
найдем
Аг|)=|±~аГ. A1.12.4)
Достаточно найти любое частное решение этого уравненияг
после чего задача сводится к нахождению решения уравнений
Ламе, удовлетворяющего соответствующим образом измененным
384 ГЛ< 14- ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
граничным условиям. Если распределение температур стацио-
стационарно, то, как правило, частное решение для функции г|) нахо-
находится достаточно просто, путем подбора. Вообще же уравнению
A1.12.4) удовлетворяет потенциал непрерывного распределения
массы плотностью — -г— ,_ v aT. Это замечание можно исполь-
использовать в тех случаях, когда нагревается какая-то часть упругого
тела, при этом существует граница между нагретой и ненагретой
частями.
Так, например, используя формулу A1.9.4) для потенциала
однородного эллипсоида, можно без труда решить задачу о тем-
лературных напряжениях в теле, содержащем в себе мгновенно
нагреваемую область, имеющую форму эллипсоида. Теперь пере-
перемещения будут определяться по формулам A1.9.5) с точностью
до множителя, который читатель легко восстановит. Комбинируя
формулы A1.9.5), мы найдем компоненты деформации, а следо-
следовательно,— напряжения. Производные от потенциала тяготения
представляют собою силы тяготения, которые убывают по мере
удаления от начала координат как 1/г2, следовательно, напря-
напряжения убывают как l/rs, т. е. так же как перемещения и напря-
напряжения от центра расширения. Поэтому формулы щ = \р,г дают
полное решение для неограниченной среды. В § 8.14 было разъ-
разъяснено, что центр расширения моделирует напряжения, возни-
возникающие при выпадении новой фазы. Очевидно, что изменение
объема может быть вызвано не только изменениями температуры,
но и фазовыми превращениями, поэтому формулы A1.9.5) могут
«быть применены к тому случаю, когда частица выпавшей фазы
имеет форму эллипсоида; эти выражения пригодны как для то-
точек, принадлежащих внутренности включения (при m = 0), так
ж для точек матрицы (и Ф 0). Заметим, что внутри включения
перемещения представляют собою линейные функции координат
и, следовательно, напряжения постоянны. При этих рассуждени-
рассуждениях предполагалось, что упругие свойства включения и матрицы
одинаковы. Можно построить решение и для того случая, когда
упругие постоянные различны (Эшелби).
Возвращаясь к температурным задачам, вспомним, что рас-
распространение тепла описывается уравнением теплопроводности
а .
Здесь к — коэффициент теплопроводности, с — теплоемкость, р —
плотность.
Продифференцируем A1.12.4) по t и внесем в правую часть
вместо dT/dt выражение этой производной через ДГ из уравне-
уравнения теплопроводности. Получим
§ 11.12. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ 385
Этому уравнению можно удовлетворить, приняв
A1.12.5)
Если величины аг-,- постоянны, то распределение температуры,
линейно зависящее от координат, не вызывает напряжений в
теле. Действительно, уравнения совместности содержат только
вторые производные от компонент деформации, следовательно,
они будут удовлетворены тождественно, если е^ = е) представ-
представляют собою линейные функции от х8. Конечно, при этом предпо-
предполагается, что поверхность тела не закреплена, в противном слу-
лае может оказаться, что перемещения, соответствующие данной
системе деформаций и определенные по формулам Чезаро (§7.3),
окажутся недопустимыми вследствие граничных условий; тогда
в местах закрепления возникнут реактивные силы, которые вы-
вызовут напряжения в теле,
J3 анизотропных телах положение осложняется в тех случаях,
когда анизотропия криволинейна. Например, цилиндр, изготов-
изготовленный из стеклопластика или углепластика путем намотки,
ортотропен, но упругие свойства его обладают цилиндрической
симметрией, в цилиндрических координатах модули упругости
и коэффициенты температурного расширения постоянны. Но при
переходе к декартовым координатам тензоры Ет и ац будут
уже не постоянными, а функциями координат #а; поэтому даже
равномерное температурное поле вызовет напряжения. Эта задача
легко решается методом, совершенно подобным тому, который
был применен в § 8.12 для трубы из изотропного материала.
Присваивая радиальному направлению индекс единицы, мы за-
запишем уравнение упругости в форме A0.6.4). Теперь уравнение
для функции напряжений оказывается следующим:
** + *"р ЕТ\ A1Л26)
Не останавливаясь на элементарном решении этого уравнения
при граничных условиях ап = — F = О при г = а и г = Ь, т. е. на
внутренней и на наружной поверхностях трубы, заметим, что
для армированных пластиков, как правило, cti > ct2. Из решения
следует, что при охлаждении трубы в ней возникают растяги-
растягивающие радиальные напряжения, которые могут привести к раз-
разрыву по цилиндрической поверхности. Такие повреждения на-
наблюдаются в процессе изготовления труб с горячей полимериза-
полимеризацией, при охлаждении после полимеризации возникает кольцевая
трещина.
25 ю. Н. Работнов
ГЛАВА 12
СТЕРЖНИ, ПЛАСТИНЫ И ОБОЛОЧКИ
§ 12.1. Приближенная теория изгиба балок
Элементарная теория, изложенная в гл. 3 и 4, основывалась
на гипотезах, введенных ad hoc и обоснованных лишь некоторы-
некоторыми соображениями качественного характера. Здесь мы получим
те же уравнения, отправляясь от общих законов теории упруго-
упругости. Наиболее надежный путь построения приближенных теорий,
который будет использован в настоящей главе, состоит в том,
что за основу принимаются вариационные уравнения теории
упругости в одной из форм, приведенных в § 8.7. После этого
делаются некоторые предположения о характере распределения
перемещений или напряжений (или того и другого независимо).
Дифференциальные уравнения приближенной теории получаются
как уравнения Эйлера вариационной задачи для функций от
переменных, число которых меньше трех.
Как уже было сказано выше, балкой называется призмати-
призматическое тело, длина которого много больше поперечных размеров.
Выберем оси координат следующим образом. Поместим начало
координат в центре тяжести одного из поперечных сечений, рас-
расположим оси Xi и х2 в плоскости поперечного сечения, тогда х3
будет осью призмы. Направления осей Xi и х2 всегда можно
выбрать так, чтобы было
x±x%dF = 0.
F
Оси Xi и х2, удовлетворяющие этому условию, называются глав-
главными центральными осями инерции поперечного сечения. В ча-
частности, если одна из осей есть ось симметрии сечения, оси бу-
будут главными.
Предположим, что балка несет поперечную нагрузку в плос-
плоскости #2, #з, действующую в направлении оси х2. Обозначим
интенсивность этой нагрузки р(х3). Функция р(х3) может при-
принадлежать классу обобщенных функций, т. е. включать в себя
дельта-функции (сосредоточенные силы) и производные от дель-
дельта-функций (сосредоточенные моменты). Сделанное предположе-
предположение о том, что нагрузка лежит целиком в плоскости х2, х3, не
нарушает общности. Действительно, любая нагрузка может быть
разложена на составляющие в плоскостях хи х3 и #2, #з| для
§ 12.1. ПРИБЛИЖЕННАЯ ТЕОРИЯ ИЗГИБА БАЛОК 387
второй плоскости приводимые ниже соображения повторяются
буквально, и принцип суперпозиции позволяет рассматривать две
независимые задачи по отдельности. Предположим также, что к
торцам балки в центрах сечений приложены равные силы Р,
растягивающие или сжимающие балку.
Заметим, что нагрузка р(х3) не обязательно должна лежать
в плоскости х2х$, она может действовать в параллельной плоско-
плоскости. Величины прогибов и нормальных папряжений при изгибе
от этого не меняются, как будет видно из приводимого ниже
вывода. Однако касательные напряжения зависят от положения
плоскости действия сил, они могут потребовать для своего урав-
уравновешивания приложения к торцам балки крутящих моментов.
Если ось х2 есть ось симметрии сечения, то, очевидно, крутящий
момент не потребуется, если нагрузка лежит в плоскости #2, #з,
нагрузка в любой параллельной плоскости будет вызывать кру-
кручение. Однако, если ось х2 есть главная центральная ось сече-
сечения, но не ось симметрии, и нагрузка лежит в плоскости х2, #3,
изгиб, как правило, будет сопровождаться кручением; чтобы
кручения не было* ось х2 должна проходить не через центр се-
сечения, а через некоторую точку, называемую центром изгиба.
Элементарная теория, позволяющая найти центр изгиба для тон-
тонкостенных стержней открытого профиля, была изложена в § 3.7,
распространение ее на стержни произвольного сечения служит
предметом теории изгиба Сен-Венана, которая в этой книге из-
излагаться не будет.
Естественно предположить, что изгиб балки будет происхо-
происходить в плоскости х2хъ, т. е. что первоначально прямая ось балки
станет лежащей в этой плоскости плоской кривой. В дальнейшем,
как и в гл. 3, мы будем полагать х2 = г/, хг = z. Пусть точка N
оси балки с координатой z до
деформации перешла в положе- "
яие N\ получив перемещение ^
w(z) в направлении оси z и v(z) I ^\
в направлении оси г/. Координа- у
ты точки N' будут @, v, z+w).
На рис. 12.1.1 изображены эти ?
точки, первоначально прямая v '
ось балки и кусочек изогнутой w
оси, которой принадлежит точ- Рис. 12.1.1
ка N'.
Сделаем теперь основное упрощающее весь дальнейший ана-
анализ предположение, называемое гипотезой плоских сечений. Как
нам кажется, слово «гипотеза» в данном случае не вполне умест-
уместно. Мы вовсе не предполагаем справедливость этой гипотезы,
а строим воображаемый объект, который ведет себя заведомо не
так, как реальная балка, у которой сечение вовсе не остается
плоским. Но поведение этого воображаемого искусственно по-
25*
388 гл- 12- стерший, пластины и оболочки
строенного объекта мало отличается от поведения реальной балки
при определенных условиях. Итак, мы рассматриваем такие де-
деформации балки, когда плоские сечения, перпендикулярные оси
балки, остаются плоскими, перпендикулярными оси и после
деформации. На рис. 12.1.1 показана некоторая точка М, при-
принадлежащая плоскому сечению, проходящему через точку Лт
оси. Радиус-вектор точки М можно записать следующим образом:
г = хег + уе2 + ze3.
Радиус-вектор точки М\ в которую перешла точка М в резуль-
результате деформации, вследствие предположения о сохранении плос-
плоского сечения будет
г' = хе1 + (у + v) e2 + (z + w — yv')ez.
При этом выводе, геометрически ясном из рассмотрения
рис. 12.1.1, мы считали, что v' = dv/dz < 1.
Компоненты перемещения точки М будут, таким образом,
И1 = 0, м2 = у, Us = w — yv'. A2.1.1)
Вычисляя компоненты деформации, мы находим, что все они
равны нулю, кроме одной
eii = w'_yv»4 A2.1.2)
Поскольку мы наложили геометрические ограничения на харак-
характер деформации балки и предопределили заранее поле деформа-
деформаций, заданное формулой A2.1.2), содержащей две неизвестные
функции одной только переменной z, для получения уравнений
изгиба естественно применить вариационный принцип Лагранжа.
Построим функционал Лагранжа по формуле (8.7.5)
i i
Ju = - j | \ Е (wf - yv"J dFdz+ \vpdz + P[w{l)-w @)]
OF 0
или, выполнив интегрирование по площади сечения,
i
vp\ dz + P[w(I) - w@)]. A2.1.3)
Здесь F — площадь сечения, / — момент инерции площади сече-
сечения относительно оси х (см. § 3.3), / = j y2dF. Вариация функ-
функционала Лагранжа должна обращаться в нуль при варьирова-
варьировании независимых аргументов w и v. Варьируя w, получим
i
— j EFw'hwdx + [6м; (I) — би; @)] Р =0.
§ 12.1. ПРИБЛИЖЕННАЯ ТЕОРИЯ ИЗГИБА БАЛОК 389
Преобразуем интеграл путем интегрирования по частям. Резуль-
Результат будет следующий:
— EFw' {I) 8w (I) + EFw' @) 8w @) +
i
+ [8w (Z) — 8w @)] P + J EFw"8w dz.
0
Так как 8w(z)— произвольная функция, то отсюда следует
w" = 0, w' = const = ?-. A2.1.4)
Проварьируем теперь прогиб tf(z). Получим
f (—
Проинтегрировав первый член по частям два раза, преобразуем
это равенство к следующему виду:
г
J (— EIv™ + p) 8v dz + EIv" (I) 8v' A) — EIv" @) 6i;' @) —
о
- EIv"' (I) 8v (I) + EIv"' @) 8v @) = 0. A2.1.5)
Предполагая, что 8v(z) — произвольная дважды дифференцируе-
дифференцируемая функция, мы должны считать, что 8v(z), ze[0, I] есть про-
произвольная функция такая, что 8v и 6i/ принимают при 2 = 0
и z = l произвольные значения. Поэтому из A2.1.5) следует диф-
дифференциальное уравнение
EIv1Y-p = 0 A2.1.6)
и естественные граничные условия
v"(l) = v" @) = 0, !/"(*) =iT@) = 0. A2.1.7)
Эти условия относятся к балке со свободными концами. Они
изменятся, естественно, если на конце балки приложена сосредо-
сосредоточенная сила или момент. Тогда соответствующие члены не-
необходимо включить в функционал Лагранжа как работу внешних
сил. Если на деформацию балки на ее концах наложены некото-
некоторые кинематические ограничения, например, у@) = 0 (конец
2 = 0 свободно оперт) или v@) = z/@) = 0 (конец балки защем-
защемлен), то эти ограничения представляют собой предварительные
условия, которые служат граничными условиями для A2.1.7),
тогда как при варьировании мы должны подчинять тем же ус-
условиям 6у@) = 0 и (или) 6г/@) = 0 вариацию 8v(z) и соответ-
соответствующие члены в A2.1.5) выпадают. Величина EIv" (z) назы-
называется изгибающим моментом, величина EIvm (z) — перерезыва-
390 гл- 12- стержни, пластины и оболочки
ющей силой; более детальный анализ конкретных примеров был
дан в гл. 3. Существо данного параграфа состоит в том, чтобы
показать, каким образом элементарная теория может быть полу-
получена из точных уравнений теории упругости, если подчинить
поле деформаций некоторым ограничениям.
§ 12.2. Распространение вариационных методов
на геометрически нелинейные задачи
В гл. 4 была рассмотрена в элементарном изложении теория
устойчивости упругих стержней. Особенность этих задач состоя-
состояла в том, что уравнения равновесия составлялись для деформи-
деформированного состояния стержня, т. е. по существу речь шла о гео-
геометрически нелинейных задачах. Вариационные уравнения, опи-
описанные в § 8.7, эквивалентны геометрически линейным урав-
уравнениям теории упругости, для которых доказана теорема
единственности. Поэтому никакие задачи устойчивости с по-
помощью этих вариационных уравнений решать нельзя. Здесь мы
постараемся распространить вариационные уравнения на геомет-
геометрически нелинейные задачи. Существо дела состоит в том, что
уравнения статики должны составляться не в исходной системе
координат, например декартовой, а в той криволинейной систе-
системе координат, в которую превращается исходная вследствие
деформации. Прямой путь получения таких уравнений довольно
сложен, поэтому нам будет удобно вернуться к выводу § 7.4, где
напряжения определялись по существу как обобщенные силы,
для которых компоненты тензора деформации служили обобщен-
обобщенными перемещениями. Пусть тело, ограниченное поверхностью
S = ST + Su, находится под действием массовых сил F{ и по-
поверхностных сил 7*1, заданных на 5Г. Составим уравнения рав-
равновесия в форме Лагранжа, учтя также виртуальную работу
внутренних сил, т. е. напряжений, имеющих потенциал U(ea),
б fj [Ргщ - U (е^)] dV + f Tilths] = 0.
Это уравнение по форме не отличается от того, которое полу-
получается в результате варьирования (8.7.5), но теперь для компо-
компонент тензора деформации мы сохраним точные нелинейные вы-
выражения G.2.3)
еИ = 4 (иМ + иМ + иыиы)- A2.2.1)
Граничные условия на части поверхности Su
щ — щ=0 A2.2.2)
мы будем считать выполненными заранее; это значит, что пере-
§ 12.2. ВАРИАЦИОННЫЕ МЕТОДЫ ДЛЯ НЕЛИНЕЙНЫХ ЗАДАЧ 391
мещения варьируются с учетом A2.2.2), т. е. так, что би» = 0,
Чтобы учесть дополнительные условия A2.2.1) и A2.2.2),
мы введем, как это делалось в § 8.7, множители Лагранжа Оц
и |Х*, тогда условие равновесия будет представлять собой равен-
равенство нулю вариации следующего функционала:
= J [оц [ец — -j Щ* — ^Щл - -jUkjUkj) — U (ей) + FfU|J dV +
v
— uDvudS. A2.2.3)
ST Su
Проварьируем перемещения иг. Получим
б/ = J |-у °ч $ии + 8из,г + ukMkj + uktfiukti)
V
Выражение
может быть записано в виде
j ^ A2.2.4)
О J1
+ ukt
Аналогично
Оц (8ujt г + uht} 8uht г) = оц FW + uht,) 8uht i =
= on (fifti + uh> i) 6uht j = skj8uht j.
Поэтому уравнение A2.2.4) можно записать следующим образом:
§{—SkjbuktS + Fkbuk}dV+ ^Tt8u{dS+ J bu^dS = 0.
V sT su
Преобразуя объемный интеграл обычным способом, получим
уравнения равновесия
*<и = 0 A2.2.5)
и условие на поверхности
вцщ = Г*, хг е ST, SijTij = \iu Xi e Su. A2.2.6)
Здесь
8ц = оиF*+щ.к). A2.2.7)
Заметим, что тензор ^несимметричен, 5У=^5^. Существо сделан-
сделанного вывода заключается в следующем. Тензор напряжений (fy
отнесен к метрике, определенной для недеформированного тела.
При составлении дифференциальных уравнений равновесия в
392 гл- 12- стержни, пластины и оболочки
обычной форме то обстоятельство, что координатные плоскости
декартовой системы координат искривляются в результате дефор-
деформации и становятся координатными поверхностями некоторой
криволинейной системы координат, во внимание не принимается.
Вместо того чтобы рассматривать эти изменения геометрии, мы
просто определим напряжения как обобщенные силы, соответст-
соответствующие компонентам деформации, определенным точными нели-
нелинейными формулами. Действительно, варьируя компоненты де-
деформации e(j в функционале A2.2.3), мы снова придем к извест-
известным уравнениям связи
аи
В заключение перепишем функционал A2.2.3) с учетом A2.2.6)
J = J [°ij Yij"~~ Тщ>>"~~ 4" и>*"~~4" Uh>*Uk'j)"" U(^«) + ^J^ +
v
+ J TiUidS + J (щ - и*) okj (8ik + uitk) rijdS. A2.2.8)
S s
Условие стационарности функционала A2.2.8) эквивалентно вы-
выполнению всех уравнений геометрически нелинейной теории уп-
упругости, этот функционал вполне аналогичен функционалу
(8.7.1), в который он и превращается после отбрасывания чле-
членов, вносящих нелинейность.
Поступая точно так же, как в § 8.7, мы можем получить от-
отсюда функционал Рейснера, а именно,
dV
+ j TiUidS + J (щ — и*
Здесь варьируются независимо напряжения с^ и перемещении щ.
Функционал Лагранжа, записываемый через щ, и деформации
ец, выраженные через щ по формулам A2.2.1), послужил отправ-
отправной точкой для всех выводов. Прямое распространение на гео-
геометрически нелинейные задачи вариационного принципа типа
Кастильяно невозможно. Действительно, в линейной теории было
использовано то обстоятельство, что беу выражается через Ьщ по
тем же формулам, по которым ец выражаются через щ. Поэтому
преобразование объемного интеграла можно было произвести до
варьирования функционала. В нелинейной теории этого сделать
нельзя.
§ 12.3. УСТОЙЧИВОСТЬ СЖАТОГО СТЕРЖНЯ 393
§ 12.3. Устойчивость сжатого стержня
и родственные задачи
При тех же предположениях, которые были приняты за ос-
основу в § 12.1, составим точное выражение деформации по фор-
формулам A2.2.1)
Второй член мал по сравнению с первым, но последний может
быть того же порядка, что первый. Поэтому мы опускаем второй
член и записываем
е х = w' + —у'2 — yv". A2.3.1)
В нелинейной теории остальные компоненты деформации уже не
обращаются все в нуль, но они малы по сравнению с е1и Пред-
Предположим теперь, что стержень сжимается продольной силой Р,
как это было показано на рис. 4.1.1, концы стержня для про-
простоты будем считать шарнирно опертыми. Составим функционал
Лагранжа так же, как это делалось в § 12.1, но с учетом вы-
выражения A2.3.1) для деформации еи
i
ju = _ j Ц- EF (w' + 4 У'2)' + 4 EIv\ dz - ^ @ - w
Варьируя перемещение w, найдем, что
w' + -|-i/2 = — -^ = const. A2.3.2)
Существенно заметить, что это соотношение нелинейно относи-
относительно прогиба и. Варьируя перемещение и и преобразуя резуль-
результат интегрированием по частям, с учетом A2.3.2) придем к сле-
следующему дифференциальному уравнению:
+ Pv = 0. A2.3.3)
При закреплении стержня по схеме, приведенной на рис. 4.1.1,
выполняются следующие граничные условия:
i7@)= i7(Z) = 0, v" @)= v" (l) = 0. A2.3.4)
В § 4.2 уравнение A2.3.3) уже было рассмотрено. Было показа-
показано, что при граничных условиях A2.3.4) нетривиальное решение
существует лишь тогда, когда сила Р принимает одно из сле-
следующих дискретных значений:
D n2n2EI
394 ГЛ. 12. СТЕРЖНИ, ПЛАСТИНЫ И ОБОЛОЧКИ
Наименьшая критическая сила, соответствующая w = l, была на-
названа эйлеровой силой. Вся задача об определении критической
силы оказалась линейной в том смысле, что она свелась к интег-
интегрированию линейного дифференциального уравнения A2.3.3).
Однако для определения критических сил оказалось необходимо
решать трансцендентное уравнение.
Рассмотрим теперь другую задачу, нелинейный характер ко-
которой совершенно очевиден. Предположим, что концы балки не-
неподвижно закреплены так, что w@) = w(l) = 0. Балка несет по-
поперечную нагрузку q(z)= qosm(nz/l). Добавляя к функционалу
i
Ju работу внешних сил j qvdz и выбрасывая работу силы Р на
о
перемещениях w, получим вместо A2.3.3)
_ pv" = Qo sin 2L. A2.3.5)
Уравнение A2.3.2) сохранится, но величина Р в этом уравнении
представляет собой неизвестную, подлежащую определению про-
продольную силу. Очевидно, что знак минус в A2.3.2) следует за-
заменить на плюс, сила Р будет растягивающей. Положим v =
= asin(nz/l); тогда, подставляя в A2.3.5), найдем
a = •
Р/Рд'
Интегрируя A2.3.2) от z = 0 до z = ! (с заменой — Р на Р) и
подставляя найденное выражение для и, получим следующее
уравнение:
которое всегда может быть решено графически или численно.
Если нагрузка q(z) представляет собой более сложную функ-
функцию, она раскладывается в ряд Фурье и уравпение для Р/Р9
оказывается существенно более сложным; в общем случае левая
часть его представляет собою бесконечный ряд. В случае исче-
исчезающей изгибной жесткости отсюда получается решение для
упругой струны
^
п —
а-
§ 12.4. ИЗГИБ ПЛАСТИН 395
§ 12.4. Изгиб пластин.
Основные предположения технической теории
Пластиной называется тело, ограниченное двумя плоскостями
2 = ±h и цилиндрической поверхностью, образующие которой
параллельны оси z. В плоскости z = 0, называемой срединной
плоскостью, выбираются произвольным образом координаты ха
(а = 1,2). Предполагается, что размеры пластины в плане зна-
значительно больше, чем толщина 2h (рис. 12.4.1). Так же, как в
§ 2.1, где речь шла о стержнях, будем принимать за наимень-
наименьший поперечный размер наименьшее расстояние между каса-
касательными к контуру пластины. Под контуром пластины пони-
понимается контур сечения цилиндрической поверхностью плоскости
z = 0. Так же, как теория изгиба балок,
теория пластин может быть построена при
помощи любого из вариационных принци-
принципов. Если при выводе уравнения изгиба мы
отправлялись от вариационного принципа
Лагранжа, то здесь мы примем за основу
вариационный принцип Рейснера (не в си-
силу каких-то его преимуществ, а Для иллю-
иллюстрации метода). Дело в том, что в физи-
физически нелинейной теории пластин, изготов- Рис. 12.4.1
ленных из нелинейно-упругого или пласти-
пластического материала, реализация вычислений на основе принципа
Лагранжа приводит к очень большим трудностям, тогда как
принцип Рейснера позволяет получить приближенное решение
задачи относительно просто.
Основное кинематическое ограничение, принимаемое в техни-
технической теории пластин, называется обычно гипотезой прямых
нормалей. Оно вполне аналогично гипотезе плоских сечений
теории изгиба (и также мало имеет оснований называться «гипо-
«гипотезой»). Предполагается, что прямолинейные элементы, нормаль-
нормальные к срединной плоскости пластины до деформации, остаются
после деформации прямыми, нормальными к деформированной
срединной поверхности и длины этих элементов не меняются.
Обозначим через р радиус-вектор точки срединной плоскости
р = хаеа.
Тогда радиус-вектор любой материальной точки плоскости М
может быть представлен в виде
г = р + zv,
где v = e1xe2— единичный вектор, направленный по оси z.
После деформации точка М перейдет в положение М' с радиу-
радиусом-вектором
г' = р' + zv'.
396 ГЛ. 12. СТЕРЖНИ. ПЛАСТИНЫ И ОБОЛОЧКИ
Обозначим через иа, w перемещения точки срединной плоскости
N, которая имела до деформации радиус-вектор р. Новый ра-
радиус-вектор этой точки
р' = р + иаеа + wv.
Согласно гипотезе прямых нормалей вектор v' представляет со-
собою единичный вектор нормали к деформированной срединной
поверхности, заданной радиусом-вектором р. Поэтому
, P,lXP,2 A24Л)
|РдХР,21 V
Производные вектора р' выразятся следующим образом:
рд = ех + и1Лег + и2Ле2 + wtl\,
Р,2 = e2 + ult 2ег + u2t2e2 + h>,2v-
Векторное произведение, входящее в формулу A2.4.1),
W,2
- A2.4.2)
В формуле A2.4.2) опущены члены, содержащие более высокие
степени производных от перемещений. Следует заметить, что
при этом отбрасываются, например, такие произведения как
^2,1^,2, малые по сравнению с и2Л. Но произведения и квадраты
величин wtl и wt2 не появляются и их отбрасывать не прихо-
приходится. Это замечание сделано в связи с тем, что производные
от прогибов пластины w могут значительно превышать произ-
производные от перемещений иа так, что м?,ам?,э может быть того же
порядка малости, что ма, р. Действительно, полагая порядок иа, р,
равным 8 и w^w^ имеющим тот же порядок 8, находим, что
порядок tota равен Уе и порядок ма> рм>т равен е3/2<е. В даль-
дальнейшем при построении геометрически нелинейной теории мы
встретимся с такими обстоятельствами, однако, приближенное
равенство A2.4.2) с вытекающими из него следствиями сохранит
силу. Теперь мы можем записать
г' = р + иаеа — zwtaea + xz.
Сравнивая выражение для г' с исходным выражением для ра-
радиуса-вектора г точки М, найдем, что компоненты перемещения
этой точки
Ua =Ua — ZWta.
Теперь по обычным формулам геометрически линейной теории
вычисляются компоненты тензора деформации
4 = eap-zw,aP) e? = e% = 0. A2.4.3)
§ 12.5. ЛИНЕЙНАЯ ТЕОРИЯ ПЛАСТИН
397
Здесь еар представляют собою компоненты деформации срединной
плоскости: 2еа($ = иа, р + щ, а. Формулы A2.4.3) достаточны для
построения общей теории. Составляя функционал Лагранжа и
приравнивая нулю его вариацию, мы получим некоторые диф-
дифференциальные уравнения для иа и w с соответствующими гра-
граничными условиями, т. е. построим
техническую теорию изгиба пластин,
заранее предполагающую выполне-
выполнение известных кинематических огра-
ограничений. Но мы будем пользоваться
вариационным принципом Рейснера
и зададимся следующим законом ^^ 'аа
распределения напряжений по тол-
толщине:
(Tq/y 0^4
A2.4.4)
Рис. 12.4.2
Симметричные тензоры ГаР и Мар называются тензорами усилий
и моментов соответственно. Действительно,
+h +h
-h -/i
Это значит, что на единицу длины сечения пластины плоскостью,
параллельной осям ха и 2, действует нормальная сила Г»», ка-
касательная сила Гар, изгибающий момент Maa и крутящий мо-
момент Л/аР (рис. 12.4.2).
§ 12.5. Линейная теория пластин
Заметим, что для тела, подчиняющегося закону Гука, соот-
соотношения A2.4.3) и A2.4.4) эквивалентны; принимая линейную
зависимость деформаций от координаты 2, мы автоматически по-
получаем линейную зависимость напряжений от координаты z. Для
физически нелинейного тела соотношения A2.4.3) и A2.4.4)
взаимно противоречивы, однако при построении приближенной
теории это противоречие сознательно допускается.
В линейной теории упругости потенциал деформации выра-
выражается следующим образом (§ 8.2):
Ф (<r«j) = у IWrfeZars. A2.5.1)
Для изотропного упругого тела, находящегося в условиях плос-
плоского напряженного состояния, получим
Ф==Ш forii + aw ~ 2vanaM + A + v) (ax22 + o^)]. A2.5.2)
398 гл. 12. стержни, пластины и оболочки
Составим функционал Рейснера, выполнив интегрирование по
координате z. Получим по формуле (8.7.4)
s
i^3ф
dxx dx2 + j T^ntfUads — J Ma$n$wtads — j R*w d$.
+ qw
J v v v
Здесь в первом интеграле интегрирование ведется в области S>
занимаемой плартиной в плоскости хи х2, тогда как контур *f
ограничивает область S в этой плоскости; единичный вектор п
представляет собою вектор нормали к контуру «у в плоскости
2 = 0 и ds — элемент дуги этого контура. В формуле A2.5.3)
фигурируют усилия и моменты, задаваемые на контуре у. Пока
что мы не уточняем виды необходимых граничных условий, по-
поэтому контурные интегралы оставляем в их общей форме; по
ходу вывода мы установим, что именно должно быть задано на
контуре пластины. Через q обозначена нагрузка на единицу
площади, действующая в направлении оси z, через Л* — дей-
действующие в атом направлении усилия на контуре. Варьируя Г
и МаР, получаем
_ * дФ _ 3 дФ ,,0
или в случае изотропного тела
»и =—-=Ч (Ми -
¦ О ГЧ.О ^ J--L
M12. A2.5.5)
В теории пластин формулы A2.5.5) часто записываются разре-
разрешенными относительно Маъ, а именно,
Mil = -D (WM + VWt22) , Мгг = -D (W 22 + VM7fii) , М2 5 6)
Mi2 = — D(l — x)wtiz.
Здесь величина
2Ehs
называется цилиндрической жесткостью пластины. Заметим, что
при изгибе пластины по цилиндрической поверхности, когда
§ 12.5. ЛИНЕЙНАЯ ТЕОРИЯ ПЛАСТИН 399
= w(Xi), из A2.5.6) следует
2Eh?
Обычная теория изгиба балок, примененная к полоске единичной
ширины, дала бы следующее соотношение:
Разница объясняется тем, что при изгибе балки происходит сво-
свободная поперечная деформация, сокращение поперечного размера
в растянутой области и увеличение его в сжатой области. В ши-
широкой пластине такая деформация контура сечения ее плоскостью
2, х2 невозможна, стеснение поперечной деформации эквивалент-
эквивалентно увеличению модуля упругости, величина Е заменяется на
величину E/(l— v2). При v = 0,3 эффект стеснения поперечной
деформации увеличивает жесткость на 9,9%.
Варьируя перемещение иа, мы получим, следуя тому же пу-
пути, что в § 8.7, такие уравнения равновесия и граничные условия:
Т*м =0, Гартгр = К или и* = и?, х« е= у. A2.5.7)
Уравнения A2.5.7) вместе с уравнениями связи A2.5.4) или
A2.5.3) для общего случая анизотропного линейно-упругого тела
тождественны с уравнениями плоской задачи теории упругости.
Итак, усилия в срединной плоскости и перемещения точек сре-
срединной плоскости пластины находятся из уравнений плоской
задачи независимо от того, изгибается пластина или не изги-
изгибается.
Будем теперь варьировать прогиб w. Интегрируя один раз
по частям, получим
1 dx2 = J Ma^8wt(Xt^dx1 dx2 =
s s
= J [(Ma$wa)fi — Ма^фш%а] dxx dx% =
s
= J Ma$wtan?>ds — J Mat$$
V S
Преобразуем второй интеграл таким же способом. Получим
JMa^8wtadx1 dx2 = J Mар,р/га 8w ds — JMa^a^8wdx1 dx2.
s v s
Таким образом, вариация функционала при варьировании одного
400
ГЛ. 12. СТЕРЖНИ, ПЛАСТИНЫ И ОБОЛОЧКИ
только прогиба w будет следующая:
q) 8w dxx dx2
+ j R8wds = 0.
Вследствие произвольности вариации 8w отсюда следует, прежде
всего, дифференциальное уравнение, ко-
которому удовлетворяют моменты
Д/аР,аР + д = О. A2.5.8)
Что касается контурных интегралов, мы
преобразуем первый из них с тем, чтобы
выделить интегрируемую часть dbwjds и
оставить производную от bw по нормали.
Это необходимо, поскольку независимо
можно задавать 8w и dbw/dn, тогда как
dbw/ds определяется заданием 6w на кон-
контуре. Обращаясь к рис. 12.5.1, где показана часть дуги контура
с единичными векторами п и t нормали и касательной соответ-
соответственно, находим
д д д д д , д
n п п + n
Рис. 12.5.1
дхл
дп
ds
Поэтому после очевидной перегруппировки членов получаем
. = (M^nl + М22п\ + 2М12п1п2) -т^ -—
Г Л/Г т\/г I Л/Г / 2 2\1 дЬш
— {1V111П1П2 — М 22П1П2 -f- М 12 \П>2 — ^1/J ~~Z~
Положим
М1Хп\ + М22п\ + 2М12п1п2 = G,
М12 {п\ — nl) == Н.
A2.5.9)
Величину G будем называть изгибающим моментом, величину
Н — крутящим моментом. Итак,
71/Г S< /~1 WU7 ту и\)Ш
ОТЬ uS
При интегрировании этого выражения по дуге второй член мо-
может быть преобразован интегрированием по частям
^Hd-^ds = H8wB-^dJLbwds. A2.5.10)
V Л v
Если величина Я задана как непрерывная функция на всем
замкнутом контуре у, то первый член исчезает, он появляется
§ 12.6. ИЗОТРОПНЫЕ ПЛАСТИНЫ 40f
тогда, когда величина Н непрерывна лишь на участке АВ дуги
контура Y- Теперь с учетом выполнения A2.5.8) мы можем
написать
V V V Y
Здесь
Q = Qana = Mat,tna. A2.5.11)
Для того чтобы было 6/ua = 0, как оказывается, нет необходи-
необходимости задавать все моменты Afap» достаточно задать изгибающий
момент G* и поперечную силу /?*, тогда на той части контура,
где заданы усилия и моменты, должно быть
G = G*, ?L + Q = R*. A2.5.12)
OS
Для пояснения смысла второго из условий A2.5.12) следует
обратиться к § 1.6, где была показана элементарным способом^
эквивалентность непрерывного распределения момента и линей-
линейной нагрузки.
С учетом отмеченного выпишем окончательное точное выра-
выражение функционала Рейснера
Juo ==
= J Г- 7V«p + Tk/ap^ap + -^Ф {T<$) + ^ф{М<х») + Qw\ dxxdx% +-
s
J
*d?ds-l R*w ds- A2.5.13)
Выражения для моментов MaP через производные от прогиба w^
в общем случае получаются обращением уравнений A2.5.3).
§ 12.6. Изотропные пластины. Дифференциальное
уравнение для прогиба и простейшие задачи
Предполагая решенной известными методами первую задачу
о нахождении усилий Гар и перемещений иа, обратимся к ре-
решению задачи об изгибе. Подставим в уравнение A2.5.8) вы-
выражения для моментов A2.5.6) и придем к следующему диффе-
дифференциальному уравнению для прогиба:
J-. A2.6.1)
Здесь АЛ — повторенный два раза оператор Лапласа. В декар-
декартовых координатах
ДА*/; = Wtilll + 2М7.Ц22 + ^,2222-
10. Н. Работнов
402 гл- 12- стержни, пластины и оболочки
Для перерезывающих сил Qa по формулам A2.5.11) и A2.5.6)
получаем
Qa = -DAw>a. A2.6.2)
Уравнение A2.6:1) записано в инвариантной форме, поскольку
оператор Лапласа инвариантен при преобразовании координат.
В полярных координатах, как известно,
Выписывать выражение для два раза повторенного оператора
Лапласа ДДш мы не будем, способ получения его очевиден. Рас-
Рассмотрим теперь некоторые простейшие задачи изгиба.
а. Цилиндрический изгиб. Положим w = м?(#1), юЛ = w'wtii =
= w"', ..., м?э2 = 0. Уравнение A2.6.1) приводится к виду
Это уравнение отличается от уравнения изгиба балки только
тем, что модуль Е заменен величиной E/(l — v2), как уже было
разъяснено в § 12.5. Интегрируя обычным способом это урав-
уравнение, найдем прогиб w и изгибающие моменты
М и = -DlV ", Мгг = VDW " = -vMn.
Появление поперечного момента М22 указывает на то, что ци-
цилиндрический изгиб возможен в двух случаях: либо когда пла-
пластина простирается в область х2^(—°°, +°°), либо когда к ее
«свободным краям приложены надлежащим образом внешние мо-
моменты, например, если пластина прямоугольна и занимает об-
область х2^(а, Ъ)\ при х2 = а и х2 = Ь приложены изгибающие
моменты G = —М22.
б. Чистый изгиб. Положим w = — г/2А {х\ + х%). Уравнение
A2.6.1) выполняется тождественно при # = 0, по формулам
A2.5.6)
Мп = М22 = AD (I + v), Mi2 = 0.
По формулам A2.5.9) находим
К контуру у любой части пластины оказываются приложенными
только изгибающие моменты G (рис. 12.6.1).
в. Кручение прямоугольной пластины. Положим w = — Ах^х2%
Уравнение A2.6.1) опять-таки будет удовлетворено при д = 0,
но теперь
Предположим, что пластина имеет прямоугольную форму со сто-
сторонами, параллельными осям хг и х2, как показано на рис. 12.6.2.
§ 12.6. ИЗОТРОПНЫЕ ПЛАСТИНЫ 403>
На стороне АВ щ — 1, п2 = 0 по формуле A2.5.9) Н = —М12 =
= — АщA— v). На стороне ВС лг± = 0, гг2 = 1, по той же формуле
M = +AD(l — v). Точка В представляет собою точку разрыва
непрерывности функции H(s), поэтому, преобразуя распределе-
распределение момента в распределение нагрузки на контуре по формуле
A2.5.10), мы должны сохранить первый член в правой части.
Для участка АВ точка В слу-
ясит верхним пределом, для С^
участка ВС — нижним, поэтому 4 ^-^^С \lABd-»I
Рис. 12.6.1 Рис. 12.6.2
в точке В появляется удвоенная сила, равная 2AD(l — v). На
каждом из участков dH/ds = 0. Таким образом, края пластины
свободны от нагрузок, но в каждом из углов приложена сосре-
сосредоточенная сила, как показано на рисунке. Для осуществления
такого загружения достаточно опереть пластину в точках А, С
и D и приложить силу в точке В. Такая схема эксперимента
применяется для определения крутильной жесткости пластины
D(l-v).
г. Круглая симметрично загруженная пластина. Главные кри-
кривизны срединной поверхности пластины при осесимметричном ее
изгибе будут
d2w 1 dw 1
Подставляя в формулы A2.5.6) вместо wtli и ш2г, получим соот-
соответственно выражение для радиального момента Мтг и окружно-
окружного момента Мт
Мгг = ~ D(wirr + v^-r), Mm = - D (^ + vm>,rr). A2.6.3)
Решение однородного уравнения A2.6.1), записанного в поляр-
полярных координатах, ищется в виде w = rn. Полагая ДДш = 0,
получим
гс2 = 0, (тг-2J = 0.
Таким образом, характеристическое уравнение имеет два двой-
двойных корня и решение его
w = Ci + C2r2 + C3 In г + Скгг In r. A2.6.4)
26*
404 гл- 12- стержни, пластины и оболочки
Если пластина сплошная и прогиб при г = 0 ограничен, то
d = 0. Член С4г2 In г остается конечным при г = 0, но при диф-
дифференцировании его достаточное число раз появляется особен-
особенность, она соответствует сосредоточенной силе, приложенной в
центре пластины. Действительно, перерезывающая сила Qr на
окружности радиусом г получается по формуле A2.6.2), которая
в полярных координатах примет вид
Полагая w = г2 In г, получим
Умножая на длину окружности 2лг и приравнивая результат
приложенной в центре силе Р, найдем, что
Г Р
Выражение для прогиба A2.6.5) нам будет удобно переписать
в виде, не содержащем логарифмов размерной величины. Поло-
Полошив радиус внешнего контура пластины равным а, с учетом
найденного выражения для С4 перепишем формулу A2.6.4) для
сплошной пластины следующим образом:
i A A2.6.5)
Постоянные d и С2 находим из граничных условий при г = а.
Так, если пластина свободно оперта по контуру, то w(a) = 0 и
М22(а) = 0. В результате получается следующая формула для
прогиба:
a
Наибольший прогиб в центре
/n\ 3 + v Pa2
Если пластина защемлена по контуру, то w(a)=w'(a) = 0 и вы-
выражение прогиба будет следующим:
w =
Если пластина несет распределенную нагрузку д, частное
решение уравнения A2.6.1) иногда можно просто подобрать.
Если q (г) задана разными аналитическими выражениями на раз-
разных участках или содержит особенности типа дельфа-функции
§ 12.7. ПРЯМОУГОЛЬНАЯ ОРТОТРОПНАЯ ПЛАСТИНА 405
(линейная нагрузка, распределенная по окружности), для интег-
интегрирования соответствующего уравнения в полярных координатах
существует техника, вполне аналогичная той, которая была из-
изложена в § 3.8 применительно к более простому дифференциаль-
дифференциальному уравнению изгиба балок. Описание этой техники выходит
за рамки нашего курса.
§ 12.7. Прямоугольная ортотропная пластина
Рассмотрим прямоугольную пластину из ортотропного мате-
материала с осями упругой симметрии, параллельными сторонам
пластины. Потенциал перемещений, соответствующий уравнениям
A0.6.4) для плоского напряженного состояния, будет следующим:
Ф Ы ~ [A - К) oh + A + X) a222-2va11a22 + (l + x) (aj,
A2.7.1)
Ло формулам A2.5.3) получим
1/7I1 = ~~ 2EhF[A
^,22 = - т|-з [A
или после обращения
Мп = -D [ A + Я) wM + vh7i22], M2Z = -D [ A - К) ш>22 + VM7,и],
A2.7.2)
и—y+k—w
>12'
Здесь D = — 2 2у. Для изотропного материала Я = 0, % = v
и формулы A2.7.2) переходят в A2.5.6). Внося выражения для
моментов A2.7.2) в уравнение равновесия A2.5.8), получим
A + Я) Wtll}1 + 2 (v + 1Я^2) ^,1122 + A -
^,2222 =
A2.7.3)
Точное решение в виде рядов получается в двух случаях, а именно:
а. Пластина оперта по контуру х\ = 0, х\ = а, Х2 = 0, #2 = Ъ. Из усло-
условия w(x, 0) = 0 следует w)u(x\, 0) =0, поэтому условие равенства нулю
момента ^22(^1, 0) = 0, вследствие A2.7.2) приводится к условию
A, 0) = 0.
Будем искать прогиб в виде
. пгтсх . ппх ... . ..
mn sm l sin —г*- A2.7.4)
a 0
m,n
406
гл- 12- стержни, пластины и оболочки
При этом все граничные условия для прогибов и моментов будут выпол-
выполняться. Подставляя выражение для прогиба в A2.7.3), получим
rnx snxo
Умножим на sin i-sin L и проинтегрируем по площади. пластины. За-
аи
метив, что
а ъ
о о
положим
Я. тпх ппх
йа
гпхл
snx.
а Ь
^ e sr J Jg sin ^гsin
о о
Теперь коэффициенты в разложении прогиба A2.7.4) будут определяться
следующими формулами:
птп
D [A + X) (^L + 2
^J {^ + A - X, (-J-
Полученное решение не очень удобно, поскольку вычисление прогиба тре-
требует суммирования двойного ряда. Излагаемый ни-
ниже способ позволит представить решение той же-
задачи в виде одинарного ряда. Выберем оси коор-
координат так, как показано на рис. 12.7.1. Предполо-
Предположим, что:
б. Стороны л?1 = 0 и х\ = а свободно оперты^
а на двух других сторонах заданы какие угодно»
граничные условия. Положим
sin
A2.7.5>
р 12 7 1
Р Таком выборе функции прогиба граничные ус-
ловия w = 0 и м>,п = 0 при х\ = 0 и a:i = а бу-
будут выполнены. Подставив A2.7.5) в уравнение A2.7.3), получим
D
^)Vm - 2 (v
Умножим на sin (rnx\ja) и проинтегрируем. Положив
а
2 Г
«г (*г) = — J
Sin
§ 12.8. ПРЯМОУГОЛЬНЫЕ ИЗОТРОПНЫЕ ПЛАСТИНЫ 407
еайдем, что каждая из функций Yr удовлетворяет следующему дифферен-
дифференциальному уравнению:
- 2 (v
A2.7.6)
Решение однородного уравнения A2.7.6) ищем в виде
Для величины ? получается характеристическое уравнение:
A — Я) Р4 — 2 fv+1~^""v2) f + A + Я) =0. A2.7.7)
V 1 + к I
Это биквадратное уравнение, корни могут быть либо действительными, ли-
либо комплексными. В первом случае действительные корни ±Pi и ±Рг, по-
поэтому
Во втором случае эти корни попарно сопряженные, а именно, fi, 2,3,4 =
= zt P ± гд, а следовательно,
л тпха тПх
m= chp—i^cos Л + Л i
тлхл ( тпха тПхЛ
Ym= chp—i^cos q—Л + Л2 sing —1] +
ткх ( тпх . тпх
+ sh р 5 Л_ cos g ? + ASinq 1
a \ 3 a 4 a
Может случиться, что биквадратное уравнение имеет два двойных корня
dr§. Для изотропного материала, например, Р = 1. Случай изотропного ма-
материала будет специально рассмотрен в следующем параграфе.
В заключение, рассмотрим задачу о кручении ортотропной
прямоугольной пластины. Полагая, как и в пункте (в) § 12.6,
iv = — Axtx2, находим, что уравнение A2.7.3) тождественно удов-
удовлетворяется; по формуле A2.7.2) получаем
Здесь Р — одна из четырех сосредоточенных сил, приложенных
в углах пластины, как показано на рис. 12.6.2.
§ 12.8. Прямоугольные пластины из изотропного материала
Если материал изотропен, т. е. % = v, К = 0, то дифферен-
дифференциальный оператор в уравнении A2.7.3) превращается в двукрат-
двукратно повторенный оператор Лапласа и мы получаем опять уравне-
уравнение A2.6.1). Применяя к задаче о пластине, две противоположные
стороны которой оперты, изложенный в § 12.7 метод, найдем,
408 гл- 12- стержни, пластины и оболочки
что характеристическое уравнение приводится к виду
Р4 - 2j}2 + 1 = 0.
Оно имеет двойные корни р = ±1, поэтому
I71TLX ITlTtX
Ym = (Ах + А3х2) ch —^ + (А2 + А±х2) sh —^. A2.8.1)
Уравнение A2.7.6) содержит еще правую часть. Если нагрузка q
зависит только от координаты хи то всегда можно представить
прогиб в виде
W = Wo + Wit
Здесь w0— решение однородного уравнения A2.6.1), построенное1
в виде ряда A2.7.5), где функции Ym даются выражениями
A2.8.1), тогда как wt — частное решение уравнения изгиба, ко-
которое удовлетворяет граничным условиям на опертых сторонах
пластины. В качестве такого частного решения можно взять
решение задачи о цилиндрическом изгибе. Так, например, если
q = const, то
Чтобы удовлетворить граничным условиям при х2 = ±6/2, раз-
разложим wy в ряд Фурье. Получим
Поскольку поверхность прогиба симметрична относительно оси xt
в выражении A2.8.1) следует принять Л3==^12 = 0. Выражение
для прогиба получается следующем:
\ . тпх
х
Симметрия поверхности изогнутой пластины относительно оси
х{ = а/2 заставляет удерживать в этом разложении только члены,
т-г тпЪ
соответствующие нечетным т. Положив -т,—— ат5 получим сле-
следующие условия для нахождения констант:
а : Alm ch ат + атАш sh ат = О,
( im + 2Ш ch am + атАш sh am = 0.
Найдя Aim и Akm из этих уравнений, получим следующий
§ 12.9. ВАРИАЦИОННЫЕ ПРИНЦИПЫ В ЗАДАЧАХ ИЗГИБА 409
результат:
w = тг
(т = 1, 3, 5, ...)• A2.8.2)
Ряд в формуле A2.8.2) сходится чрезвычайно быстро, практиче-
практически в нем достаточно удержать один первый член. Не останав-
останавливаясь на деталях, приведем значения прогиба и изгибающего
момента в центре квадратной пластины (а = Ь)
aw = 4,06.10~3^-4, Mmax = 4,79.1(rV (v = 0,3).
Эти числа понадобятся нам для оценки точности приближенных
решений, которые будут получены далее,
§ 12.9. Прямое применение вариационных принципов
к задачам изгиба пластин
Как было выяснено в § 12.5, задачи деформации срединной поверхно-
поверхности и задача изгиба решаются отдельно и независимо. Поэтому при при-
приложении вариационных методов можно составлять необходимые функцио-
функционалы отдельно для плоского напряженного состояния Гар, иа и изгиба
Jlfap, w. Выпишем соответствующие функционалы для изгиба.
а. Функционал Рейснера. Из формулы A2.5.13) следует
[а^М + Я? ° (М^) + Н ^2 ~ J G* д?- ds - J R*wds.
S V V
A2.9.1)
б. Функционал Лагранжа. Из общей формулы (8.7.5) вследствие кине-
кинематической гипотезы A2.4.3) следует
Ad = j (- u (wm) + И ^Л ~ j G* ^г ds"" JR*wds* A2-9>2)
S j V V
Здесь C/(eaP) = ЧтРа^вхввх.
Для изотропного тела
U = V.D [^ + е|а + 2гвпв22 + A + v) (ej, + el)].
в. Функционал Кастилъяно. Полагая распределение напряжений по тол-
толщине линейным, согласно A2.4.4), находим
/м = j Ф (Map) dx±dx2 ~^G*?Lds-^ Rw*ds, A2.9.3)
8 V V
при этом моменты должны удовлетворять уравнению равновесия A2.5.8)
и статическим граничным условиям.
410 гл. 12. стержни, пластины и оболочки
Приложение прямых методов вариационного исчисления к решению эа-
дач изгиба мы проиллюстрируем на примере вариационного принципа Рейс-
нера. Положим
^ap-2»J#"»V A2-9.4)
Здесь фь — функции, удовлетворяющие кинематическим граничным усло-
условиям, т?р — функции, удовлетворяющие статическим граничным условиям
для моментов. Подставляя в A2.9.1), получим
Варьируя параметры аъ, b?p, получим систему уравнений
?L = 0, JL = 0. A2.9.5)
dak <z
Функция F содержит квадратичную часть относительно аи, Ь^$ и линей^
ную часть, соответствующую нагрузке q и силам, приложенным к краям
пластины. Поэтому уравнения A2.9.5) будут линейными. Бесконечная си-
система A2.9.5) укорачивается; заменяя ее конечной системой, получим после
решения приближенный результат. Если функции щ и т^ образуют пол-
полные системы, при увеличении числа членов приближенное решение стре-
стремится к точному. Для иллюстрации рассмотрим ту же самую задачу, кото-
которая была решена в предыдущем параграфе, а именно задачу об изгибе сво-
свободно опертой квадратной пластины равномерно распределенной попереч-
поперечной нагрузкой. Полагая
= С cos —L cos ——
a a
получим по формуле A2.9.1)
В2 , С2 \j4a2
—
Приравнивая нулю производные по Л, Б и С, получим следующую систему
уравнений:
/2 4
отсюда А = l2i. = 4,16-10~3 2?_ , В = 5,4-10"ga2. Такой результат мы
n6D D
получим, если удержим в двойном ряде A2.7.4) лишь первый член. Ошибка
при определении прогиба составляет 2,4%, ошибка при определении наи-
наибольшего изгибающего момента несколько больше, она равна 12%. Выбрав
выражения для прогиба и для моментов в виде произведений синусов, мы
обеспечили точное выполнение соотношений A2.5.6), поэтому результат
совпал с тем, который получился бы в результате удержания первого чле-
члена в двойном ряде, представляющем точное решение. Поэтому, если бы
вместо принципа Рейснера мы использовали принцип Лагранжа, то, при-
приняв такое же выражение для w, мы нашли бы ту же величину А и путем
§ 12.10. БОЛЬШИЕ ПРОГИБЫ 411
дифференцирования по формулам A2.5.6) пришли бы к точно тем же вы-
выражениям для моментов. Решим теперь ту же задачу при несколько более
грубых предположениях. Положим
w = Ах\(а — Х\)х2(а — х2).
Для определения прогиба нам будет достаточно воспользоваться вариаци-
вариационным принципом Лагранжа. Вычисляя интеграл A2.9.2), получим
w 2 30 ^36
Отсюда, дифференцируя по Л и приравнивая результат нулю, получим
А = 0,0801 _«., u>max = 5,008-1<Г3?^.
Последний результат отличается от точного на 23%.
Описанная процедура, состоящая в том, что вместо решения диффе-
дифференциального уравнения ищется непосредственно стационарное значение
некоторого функционала, а представление искомых функций — в виде
A2.9.7), сводит задачу к нахождению значений коэффициентов ад и Ь^р »
при которых квадратичная функция от них принимает стационарное значе-
значение, называется процедурой или методом Ритца. Строго говоря, метод Рит-
ца развит применительно к тому случаю, когда исходным функционалом
служит функционал Лагранжа, поэтому необходимо лишь представление
црогиба в виде w= 2 аьУкт Следует заметить, что для истинного значения
прогиба функционал Лагранжа принимает максимальное значение. Это сле-
следует из того, что вторая вариация функционала Jw есть
и вследствие выпуклости функции U подынтегральное выражение положи-
положительно определенно. Точно так же показывается, что функционал Кастилья-
но принимает минимальное значение для истинного распределения момен-
моментов. Относительно функционала Рейснера подобное заключение сделать
нельзя.
§ 12.10. Большие прогибы
Для решения задач устойчивости, как мы уже выяснили,
уравнения равновесия должны составляться для деформирован-
деформированного состояния упругого тела. Соответственно, применяя вариа-
вариационное уравнение, в нем необходимо удерживать квадратичные
члены в формулах для деформаций, как это было сделано для
общей теории в § 12.2 и для задачи об устойчивости стержня
в § 12.3. В задачах изгиба пластин достаточно удерживать те
квадратичные члены, которые зависят от прогиба w, производ-
производные от перемещений иа мы сохраним лишь в первой степени.
Повторяя вывод § 12.4, мы найдем, что формулы A2.4.3) сохра-
сохранят силу и в этом случае, но компоненты деформации средин-
срединной поверхности нужно будет вычислять по формулам
" Щ>а + WpWj. A2.10.1)
412 гл. 12. стержни, пластины и оболочки
Перепишем теперь функционал Рейснера следующим образом:
= \ \ — "о- Та$ (на,р + Ыр,а + ^,а^,р) +
Jug
s
53
S" Ф (Га^ + 53?
J K$na4ds _ JG*|? <fe - j R*w dSt A2.10.2)
Варьируя усилия ГаР, мы получим уравнения связи A2.5.4), где
?ар определяются формулами A2.10.1), варьируя перемещения z/a,
получим снова дифференциальные уравнения и граничные усло-
условия A2.5.7). При варьировании прогиба мы поступаем так же,
как в § 12.5, с той разницей, что производные от прогиба вхо-
входят в множитель при Гар. Поэтому нам придется дополнительно
преобразовать интегрированием по частям вариацию
x2 = — ) TafrW^bWftdXidXei =
s
Но первый интеграл преобразуется в контурный
— J TafiWian$w ds,
а второй вследствие уравнений равновесия A2.5.7) принимает
вид
— J Ta$W,a$lV dxxdx2.
s
В результате уравнение равновесия A2.5.8) ' заменится сле-
следующими
Ма$% aP — Ta^wM + q == 0.
Выражая изгибающие моменты через м>>ар, получим для изотроп-
изотропной пластины
DAAw - raP^,ap + q = 0, A2.10.3)
и в граничном условии A2.5.12) добавится составляющая усилий
в срединной поверхности, направленная по оси z; второе из ус-
условий A2.5.12) примет вид
|f + 0 - Та$и;,ащ = R*. A2.10.4)
Для того чтобы удовлетворить дифференциальным уравнениям
равновесия A2.5.7), мы введем функцию усилий, подобно тому,
§ 12.10. БОЛЬШИЕ ПРОГИБЫ
как в гл. 10 была введена функция напряжений. Положим
1 ар ~ 'Yao'TЭх**,<"
ИЛИ
Tn = Ft22, T22 = FMi ri2 = -F12, A2.10.5)
при этом уравнения равновесия будут удовлетворены тождествен-
тождественно. Если деформации связаны с усилиями формулами A2.5.4)
и компоненты деформации зависят только от иа1 функция F бу-
будет бигармонической, как и в обычной плоской задаче. Но те-
теперь компоненты деформации заданы формулами A2.10.1). Об-
Образуя из них комбинацию, фигурирующую в левой части уравне-
уравнения совместности A0.6.3), мы найдем, что она уже не обращается:
тождественно в нуль, теперь уравнепие совместности будет сле-
следующим:
^11,22 + ^22,11 —¦ 2^12,12 = ^,12 — ^,11^,22-
Подставляя выражение деформаций через функцию усилий F па
формулам A2.5.4) и A2.10.4), получим
AAF ^ 2Eh (u?J12 — wA1w,22). A2.10.6)
Система уравнений A2.10.3), A2.10.5) и A2.10.6) описывает де-
деформацию пластины с большими прогибами. Эти уравнения на-
называются уравнениями Кармана. Вывод соответствующих урав-
уравнений для анизотропных пластин не встречает никаких затруд-
затруднений, выписывать эти довольно громоздкие выражения мы здесь
не будем. Система оказывается нелинейной, поэтому известны
только численные решения ее для отдельных частных случаев
путем непосредственного отыскания стационарного значения:
функционала A2.10.2) по способу, аналогичному тому, который
был описан в § 12.9. Сложность состоит в том, что коэффициен-
коэффициенты в предполагаемом выражении для прогиба w или функции:
напряжений F теперь ищутся из нелинейных алгебраических
уравнений. Для симметричной деформации круглой пластинки
уравнения A2.10.2) и A2.10.6) становятся обыкновенными диф-
дифференциальными уравнениями, которые можно интегрировать лю-
любым численным методом.
Заметим, что если D = 0, полученные уравнения описывают прогиб ж
напряженное состояние мембраны, не сопротивляющейся изгибу. Приведем
результаты численного решения задачи о круглой мембране радиусом о:
и толщиной 2Д, нагруженной равномерным давлением q, полученные Хенкиг
тах
or@)= 0.42s'j/|V, cr (.) = 0.328J/|V
Заметим, что удовлетворительное приближенное решение этой задачи мо-
может быть получено совершенно элементарно. Предположим, что поверхность
мембраны после деформации становится сферической с радиусом р. Стрела
прогиба / = Wmax, радиус кривизны сферы и половина центрального угла
414
ГЛ. 12. СТЕРЖНИ, ПЛАСТИНЫ И ОБОЛОЧКИ
меридионального сечения поверхности мембраны связаны следующими оче-
очевидными соотношениями (см. рис. 12.10.1):
a a ol асх,
р ^ Жа ^ "а ' f = atg — & —.
Сфера находится в состоянии равномерного всестороннего растяжения с
напряжением о. Уравнение равновесия будет следующее:
Отсюда
2he-2na-a « дяа2.
Aha'
A2.10.7)
Легко убедиться в том, что полученное нами непосредственно уравнение
равновесия представляет собою уравнение A2.10.3). Действительно, в ок-
окрестностей средней точки уравнение изогнутой
по сферической поверхности пластины запишет-
запишется так:
При этом локальные оси координат выбраны так,
что плоскость х\, хч касается сферы, ось хъ на-
направлена но нормали. Предположив поверхность
изогнутой мембраны сферической, мы постави-
поставили все ее элементы в одинаковые условия, по-
поэтому такая же локальная система координат мо-
может быть привязана к любой точке. Подставляя
в A2.10.3) w)U = w,22 = 1/р, Тп = Т22 = 2/ш,
wЛ2 = Т\2 = 0, получим выражение A2.10.7).
Относительное удлинение е, одинаковое для
всех направлений, представляет собою разность
Рис. 12.10.1
между длиной дуги и, длиной хорды, поделенную на длину хорды,
е =
pa — psina ^ а__
ра 6
В упругой мембране а и е связаны между собой законом Гука
1 —v
Е
¦а.
Поэтому
Отсюда находим
а _ 1 — v qa
. — v да
Е 2h
Стрела прогиба / дается следующей формулой:
V Е 2h
При v = 0,3, получаем
2Eh
§ 12.11. УСТОЙЧИВОСТЬ ПЛАСТИН 415
Полученный результат меньше точного на 3,3%, такая ошибка, конечно,
очень мала. Напряжения, одинаковые повсюду, получаются следующими;
а = 0,390
1/Ж?-
V BfeJ
Эта величина на 7,8% меньше, чем наибольшее напряжение в центре и на
19% больше, чем минимальное напряжение на краю. Оценка для макси-
максимального напряжения тоже оказывается удовлетворительной.
Построенное грубо приближенное решение содержит в себе явное про-
противоречие; из условия равенства напряжений с неизбежностью вытекает
равенство всех деформаций, но контур мембраны закреплен и величина
деформации контурной линии равна нулю.
§ 12.11. Устойчивость пластин
Представим себе, что пластина нагружена таким образом, что
усилия Гар отличны от нуля, а прогиб w и, следовательно, мо-
моменты Л/аР равны нулю. Будем называть такое плоское напря-
напряженное состояние в пластине начальным напряженным состоя-
состоянием. В отношении него будем употреблять термин безмоментное
состояние. Поставим задачу об устойчивости пластины по отно-
отношению к весьма малым (бесконечно малым) искривлениям сре-
срединной плоскости. При определении усилий Та$ мы должны были
пользоваться обычными уравнениями плоской задачи теории уп-
упругости, а следовательно, линеаризированными выражениями для
еа*. Если пластина получает малое изгибное возмущение м>, тог
конечно, величины w%aw^ малы по сравнению с иа,р, но при
варьировании прогиба в A2.10.2) именно эти члены, являющие-
являющиеся множителями при больших Гар, должны варьироваться.
Таким образом, уравнение A2.10.3) сохраняет силу. Мы пере-
перепишем его, опустив величину поперечной нагрузки
DAAw - rV,cte = 0- A2.11.1)
Это уравнение служит основным уравнением теории устойчиво-
устойчивости изотропных пластин. Здесь усилия Т&$ считаются заданными^
т. е. найденными в результате предварительного решения плоской
задачи теории упругости. Заметим, что обычно начальное напря-
напряженное состояние бывает достаточно простым, анализ уравнения:
A2.11.1) в случае, когда Г?р суть функции координат, оказы-
оказывается затруднителен.
К уравнению A2.11.1) нужно присоединить однородные гра-
граничные условия, например:
и> = 0, — = 0 на защемленном контуре,
G = 0, w = 0 на свободно опертом контуре,
6 = 0, — + Q — Ta$w%OLn$ = 0 на свободном крае.
гл- 12- стержни, пластины и оболочки
Здесь G, Н и Q представляют собой линейные дифференциаль-
дифференциальные операторы над прогибом, которые вычисляются по форму-
формулам, приведенным выше.
Такая постановка задачи, совершенно аналогична постановке
задачи Эйлера об устойчивости сжатого стержня. Требуется най-
найти критическое значение параметра нагрузки, т. е. множителя
при Гар, при котором линейное однородное уравнение A2.11.1)
при однородных граничных условиях имеет нетривиальное реше-
решение, т. е. решение, отличное от тождественного нуля. Ограни-
Ограниченность и неполнота анализа подобного рода были разъяснены
в гл. 4 и мы не возвращаемся к сделанным там разъяснениям.
Здесь в качестве примера мы рассмотрим одну только задачу
устойчивости: прямоугольная пластина длиной а в направлении
оси хи шириной Ъ в направлении оси х2 равномерно сжимается
вдоль оси Xi усилием Тп = —Т. Уравнение A2.11.1) примет вид
Если пластина шарнирно оперта по контуру, то граничным усло-
условиям ш = 0иС = 0на контуре, как в примере (а) § 12.7, мы
можем удовлетворить, приняв
2ткх ппх
amnSin—^sin-j-*.
Подставляя это выражение в дифференциальное уравнение, мы
лридем к серии равенств
отсюда
т л2Д/ Ъ п2 а
b* \ a { m b
Минимальное значение, получаемое для Т при целых п и пг,
будет критическим сжимающим усилием для пластины, анало-
аналогичным силе Эйлера для стержня. Очевидно, что минимум будет
достигаться при п = 1. Положив alb = р, найдем
Гкр=^ [iL + 1.J = ^ k (m, P). A2.11.2)
При фиксированном ? минимизируем к(т1 ^) по т. Получим
отсюда следует, что минимум достигается при т = $; если [} —
§ 12.12. ВАРИАЦИОННЫЙ МЕТОД ДЛЯ ЗАДАЧ УСТОЙЧИВОСТИ 417
целое число, то действительно, полагая т = [}, получаем
По этой формуле определяется критическое усилие для квадрат-
квадратной пластины и пластины, которую можно разбить на целое чис-
число квадратов. Если [J — нецелое число, то в формулу A2.11.2)
подставляются вместо ш ближайшие к р сверху и снизу целые
числа. В качестве критической принимается меньшая из получа-
получающихся сил. Формула A2.11.2) дает одинаковый результат при
m и т + 1, если
k(m, $)=
Отсюда легко находим
) = У2, У6, Ш, ...
Таким образом, если РеA, 2)_, то при [}<У2« 1,414 нужно
принимать тгс = 1, при |3>У2 следует вносить в формулу
A2.11.2) значение w = 2. График зависимости коэффициента 74&
от параметра т был показан на рис. 4.8.1, он состоит из пересе-
пересекающихся дуг кривых, соответствующих разным значениям т.
В точках пересечения коэффициент к принимает максимальные
значения; считая т индексом левой кривой, легко находим
&тах - 4 + m{m + iy
Уже при f}^D, 5) можно считать & = 4 независимо от [}, ошибка
составит при этом не более 1,25%.
§ 12.12. Вариационный метод
решения задач устойчивости
Пренебрежение членами wtawt& по сравнению ска,рв A2.10.1)
означает, что прогибы пластины считаются малыми и не влияют
существенно на деформацию срединной поверхности. Однако из
этого не следует, что их можно отбросить в выражении функ-
функционала A2.10.2). Действительно, предположим, что уравнения
A2.5.7) выполнены заранее и проинтегрируем в A2.10.2) члены
вида i/2TafiUa,fi. Будем считать также, что поперечные нагрузки
на поверхности и краевые моменты на кромках пластины отсут-
отсутствуют, как это было принято выше. Функционал A2.10.2) при-
примет вид
J = I I T TUW&W$ + ^ccpw,aj3 + Д Ф (Map)] dxxdx%
27 ю. н. Работнов
418 гл- 12« стержни, пластины и оболочки
или, если считать, что выполнены уравнения связи A2.5.3),
J = J [~ Т *V.«"M» - U (w^\ dxidx*- A2.12.1)
s
Это — однородный квадратичный функционал, для которого в изо-
изотропном случае уравнение A2.11.1) служит уравнением Эйлера.
Вместо того чтобы искать критическую нагрузку путем интегри-
интегрирования этого уравнения, можно применить прямой метод,
а именно, аппроксимировать прогиб при помощи линейного
агрегата
из функций, удовлетворяющих кинематическим граничным усло-
условиям, т. е. использовать процедуру Ритца. Функционал при
этом обратится в однородную квадратичную функцию от ак и
условие б/ = 0 приведет к системе линейных однородных урав-
уравнений вида
ж? = °- A2Л2-2>
Эта однородная система имеет нетривиальное решение лишь при
определенных значениях параметра нагрузки, обращающих в
нуль детерминант системы.
Предположим, что силы Г?р изменяются пропорционально,
так что Гар = — KTafa где Та$ — фиксированная величина. Бу-
Будем искать критическое значение параметра X. Положим
•у J T^wiaw^dx1dx2 = Т (ak), J U {wM) dxxdx2 == U {ah),
s s
T(ah) и U(ak) —известные квадратичные формы. Тогда
J = -KT(ak)+U(ak).
Уравнения A2.12.2) запишутся телерь следующим образом:
— Я^ + ^ = 0. A2.12.3)
dah ^ дак ^
Приравнивая нулю определитель этой системы, мы получим для
параметра % алгебраическое уравнение, степень которого равна
числу членов в представлении прогиба w; таким образом, если
/с = 1, 2, ,.., п, мы получаем п значений X и п «критических»
нагрузок. Но мы видели, что в действительности число крити-
критических нагрузок и соответственно форм потери устойчивости бес-
бесконечно велико. Поэтому естественно поставить вопрос о том,
в каком отношении находятся приближенные значения Л, най-
найденные описанным методом, и точные величины критических
§ 12.13. ИЗГИБ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 419
нагрузок. Соответствующую оценку легко дать для первой, т. е.
наименьшей критической нагрузки.
Заметим, что уравнение A2.12.3) можно получить с помощью
следующего формального приема. Положим / = 0, найдем из
этого условия
Х = Щ A*12.4)
Будем теперь искать минимум % как функции от ak. Получим
следующую систему уравнений:
dak T2\ dak да1
Если ТФО, эта система эквивалентна системе A2.12.3); таким
образом, задача о нахождении критических значений параметра
К сводится к нахождению экстремальных значений К как функ-
функции от ак, заданной выражением A2.12.4). Отсюда следует, что
наименьшее критическое значение параметра К оценивается сле-
следующим образом:
^min<^N- A2.12.5)
Здесь ак — произвольный набор чисел. Таким образом, верхняя
оценка для наименьшей критической силы дается формулой
A2.12.5).
§ 12.13. Осесимметричная деформация
цилиндрической оболочки
Оболочкой называется тело, ограниченное двумя эквидистант-
эквидистантными поверхностями. Чтобы сделать определение более точным,
выберем некоторую поверхность S. В каждой точке М этой по-
поверхности проведем нормаль и отложим по одну и по другую
сторону поверхности отрезки, равные h, так что MtM = М2М = h.
Совокупность точек М{ образует одну сторону оболочки, совокуп-
совокупность точек М2 — другую сторону, 2h — толщина оболочки, S —
ее срединная поверхность. Оболочка считается тонкостенной,
если h < /?, где R — наименьший из главных радиусов кривизны
срединной поверхности. Техническая теория оболочек основыва-
основывается на точно такой же гипотезе прямых нормалей, что и тех-
техническая теория пластин. Предполагается, что линейный элемент,
нормальный к срединной поверхности до деформации, остается
нормальным к деформированной срединной поверхности. Если
отнести поверхность к ортогональной системе криволинейных
координат и выбрать локальные оси ха в касательной плоскости
к срединной поверхности, направив ось z по нормали, то для
27»
420 гл- 12- стержни, пластины и оболочки
деформации еар можно сохранить формулы A2.4.3), записав их
в следующем виде:
A2.13.1)
Величины хар теперь следует назвать параметрами изменения
кривизны; вопрос о том, как выразить в общем случае деформа-
деформации еа& и параметры изменения кривизны х«э через перемещения
точек срединной поверхности или каким уравнениям совместно-
совместности они удовлетворяют, изучается в общей теории оболочек, ко-
которая здесь рассматриваться не будет. Следует заметить, что
формула A2.13.1) не является точным следствием гипотезы пря-
прямых нормалей. Это ясно из рис. 12.13.1,
абсолютное удлинение элемента тп есть
отрезок пп =yizds, но длина этого эле-
элемента есть не ds, a ds(l + z/R), как вид-
видно из чертежа. Поэтому относительное
удлинение будет
е =
1+zJR'
Аналогичным образом нужно было бы
исправить и общие формулы A2.13.1),
но ошибка, которая получается, если пре-
Рис. 12.13.1 небречь этой поправкой, имеет порядок
h/R по сравнению с единицей. Доказано
(в результате достаточно сложных вычислений, выходящих за
рамки нашего курса), что сама гипотеза прямых нормалей
вносит погрешность порядка h/R по сравнению с точным
решением задачи теории упругости, поэтому удержание членов
такого порядка в приближенной теории лишено смысла.
Введем в рассмотрение усилия Г«р и моменты Ма$, предполо-
предположив, что распределение напряжений по толщине по-прежнему
линейно, т. е. дается формулами A2.4.4). При вычислении функ-
функционала Рейснера, строго говоря, при интегрировании по тол-
толщине необходимо учитывать кривизну, т. е. производить инте-
интегрирование по площади элемента, изображенного на рис. 12.13.1.
Если пренебречь этим обстоятельством, то, как легко показать,
ошибка будет опять иметь порядок h/R, Таким образом, с точ-
точностью до членов указанного порядка малости функционал
Рейснера для оболочки имеет в основном структуру функциона-
функционала A2.5.13) с той разницей, что вместо величин м;>аЭ в нем будут
фигурировать параметры изменения кривизны иар.
Простейшим примером, на котором можно проиллюстрировать
некоторые общие особенности поведения оболочек служит круго-
круговая цилиндрическая оболочка. Предположим, что цилиндриче-
цилиндрическая оболочка со средним радиусом Я, толщиной стенки 2h и
длиной L нагружена внутренним давлением q(x). Сделаем вна-
§ 12.13. ИЗГИБ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 421
чале предположение о том, что длина L много больше радиуса
R и что давление q(x) меняется по длине оболочки достаточно
медленно. Вырежем из оболочки кольцо длиной dx, разрежем
его пополам и рассмотрим равновесие изображенного на
рис. 12.13.2 полукольца. Из уравнения немедленно получаем
Таким образом, предполагаемое напряженное состояние в обо-
оболочке
Г! = 0, T2 = q{x)R, Mt=:Jlf2 = 0. A2.13.2)
Принятая система обозначений в данном случае упрощена по
сравнению с обычной, касательные усилия и крутящие моменты
отсутствуют вследствие симметрии обо-
оболочки и действующей нагрузки, для обо-
обозначения сил и моментов достаточно те-
теперь одного индекса 1 для продольного
направления и 2 для поперечного. На-
Напряженное состояние, даваемое формула-
формулами A2.13.2), называется безмоментным
состоянием, изгибающие моменты равны
нулю, в оболочке действуют только уси-
усилия Та- В действительности безмомент- Рис. 12.13.2
ное состояние в оболочке реализовано
быть не может. В самом деле, усилие Т2 растягивает кольцо,
относительное удлинение в окружном направлении е2 = -^Ц=:
= 2Екч следовательно, срединная поверхность оболочки получает
радиальное перемещение
w = eR = Ш- A2.13.3)
Если кривизна в окружном направлении была 1/R до нагруже-
ния, она станет равной 1/(Д + w) ~ 1/R — w/R2; таким образом,
изменение кривизны в окружном направлении есть w/R2. По
формуле A2.13.1)
Отсюда видно, что неучет изменения кривизны в окружном на-
направлении влечет за собою ошибку, порядок которой не превы-
превышает величины h/R, поэтому в дальнейшем мы будем полагать
^2 = 0. Но если q(x) меняется с координатой х достаточно быст-
быстро, то радиальные перемещения соседних колец окажутся раз-
различными, образующие цилиндра будут изогнутыми. Соответству-
Соответствующая кривизна определяется так же, как для балки или для
422 гл- 12- стержни, пластины и оболочки
пластинки, а именно,
Ki = w"(x).
Составим теперь функционал Рейснера, точнее ту часть функ-
функционала, которая не зависит от граничных условий,
2 R x "** 4Л. 2
_ Jl (Ml + Mt- 2vMxM2) - qw] dx.
Ah J
Варьируя Ми М2, Т2 и w и выполняя обычные преобразования
члена, содержащего 8w", путем интегрирования по частям по-
получим
2h
Отсюда путем последовательного исключения Ми М2 и Тг полу-
получим следующее дифференциальное уравнение:
w1Y + 4a4 (w — w0) = 0. A2.13.4)
Здесь 4a4 = 2~V , тогда как w0 есть величина, пропорциональ-
пропорциональная нагрузке q(x) и определяемая формулой A2.13.3).
Уравнение A2.13.4) совершенно подобно изученному в § 3.11
уравнению изгиба балки на упругом основании. Граничные усло-
условия здесь совершенно очевидны,
они те же, что и для балки. Это
становится ясным, если рассмот-
рассмотреть выделенную из оболочки по-
полосу, как показано на рис. 12.13.3.
Вследствие кривизны полоски дей-
действующие с двух сторон усилия
Т2 дают составляющую, направ-
направленную по радиусу, а так как Т2
Рис. 12.13.3 пропорционально прогибу ш, то
эта полоска находится в тех же
условиях, что и б&лка на упругом основании. Именно так вы-
выводится уравнение A2.13.4) в элементарных руководствах. При-
Приближенное решение уравнения A2.13.4) есть w = w0, оно при-
пригодно тогда, когда первый член A2.13.4) мал по сравнению со
вторым, т. е. функция wo(x) заметно изменяется на длине много
большей, чем характерная длина
С другой стороны, если q(x) меняется достаточно медленно, то
§ 12.14. БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК 423
для удовлетворения граничным условиям необходимо к частному
решению w = w0 добавлять решение однородного уравнения, ко-
которое затухает на длине порядка X. Таким образом, общая кар-
картина поведения круговой цилиндрической оболочки под действием
осесимметричной нагрузки рисуется следующим образом. На
большей части длины оболочки в ней реализуется безмоментное
напряженное состояние. Изгиб проявляется лишь вблизи концов
и в местах резкого изменения нагрузки: он носит характер
краевого эффекта, т. е. область, где напряжения изгиба суще-
существенны, простирается лишь на некоторую определенную длину
порядка X.
§ 12.14. Безмоментная теория оболочек*)
На примере цилиндрической оболочки мы убедились в том,
что при плавно меняющейся нагрузке в большей части оболочки
можно пренебречь изгибом и напряжениями от изгибающих мо-
моментов по сравнению с равномерно распределенными по толщине
напряжениями от усилий Гар. Моментное напряженное состояние
реализуется только в зоне краевого эффекта, протяженность кото-
рой оценивается характерным линейным размером % = УД/fc. Для
оболочки положительной гауссовой кривизны этот результат но-
носит совершенно общий характер, схема расчета таких оболочек
строится следующим образом. Сначала находится усилие в обо-
оболочке, которую представляют как тонкую, нерастяжимую мембра-
мембрану, совершенно не сопротивляющуюся изгибу. Эта задача решает-
решается с помощью одних только уравнений статики и, собственно
говоря, не относится к теории упругости. Соответствующая тео-
теория называется безмоментной теорией оболочек. Решение, най-
найденное по безмоментной теории, как правило, не позволяет удов-
удовлетворить всем граничным условиям, поэтому вблизи границы
рассматривается краевой эффект, связанный с изгибом. Ввиду
малости области краевого эффекта, уравнения теории оболочек
для этой области принимают относительно простую форму. Для
вывода уравнений безмоментной теории нам понадобятся некото-
некоторые сведения" из теории поверхностей, которые предполагаются
известными и сообщаются для справки.
Поверхность отнесена к криволинейной системе координат и1,
и2 и задана радиусом-вектором r(u1?u2). Векторы rfi образуют
на поверхности ковариантный базис, вектор единичной нормали
к поверхности есть п. Метрический ковариантный тензор есть
ёгз = r$irj, кривизна поверхности задается тензором Ъц = г^п =
= г\%пг Любой вектор может быть задан в локальном базисе
*) Читатель, не знакомый с теорией поверхностей, может опустить этот
параграф без ущерба для понимания дальнейшего.
424 гл- 12- стержни, пластины и оболочки
rti, n, в частности,
r.V = Г«г|Ь + Ьуп, itfi = - Ь{г^. A2.14.1)
Первая группа формул носит название деривационных формул!
Гаусса, вторая — деривационных формул Вейнгартена. Здесь
Т% —символы Кристоффеля для поверхности, поднятие индекса
у тензора Ь\ производится с помощью метрического контрава-
риантного тензора gi}.
Наряду с метрическим тензором опускание индексов может
производиться в результате свертки с дискриминантным тензором
"*'П^ где Yi2 = 1, Т21 = -1, Ти = Т22 = 0, g = gxlg22 — g212.
Предположим, что точка поверхности получает перемещение
W, так что радиус-вектор деформированной поверхности есть
г+м?. Условие нерастяжимости при бесконечно малых перемеще-
перемещениях можно записать следующим образом:
dr dw = 0
или
^дгд = 0, юлг2 + wt2rt2 = 0, w,2J\2 = 0. A2.14.2)
Так же как при выводе дифференциальных уравнений равнове-
равновесия сплошной среды мы введем контравариантные компоненты
усилия ГаР как множители Лагранжа. Выделим некоторую часть
оболочки 2, ограниченную контуром Г. На единицу площади
действует сила q, на контуре приложено усилие интенсивности Т
на единицу длины линии контура. Приравняем нулю работу сил
на виртуальных перемещениях, подчиненных условиям A2.14.2).
Получим
\ (
(qw - r*wtarti) dZ+\Twds = 0.
Г
Преобразуем поверхностный интеграл, используя тождество
исключая с помощью A2.14.1) вторые производные от радиуса-
вектора г и вводя вектор нормали v к контуру Г в касательной
плоскости
v -
В результате получаем
f (q + Vprapr,a + Ta^n)w dZ + J (T - Ta\ria) ds = 0. A2.14.3)
s ' г
J
s г
Здесь символ \7т^аР обозначает, как обычно, ковариантную про-
производную тензора
§ 12.15. БЕЗМОМЕНТНЫЕ ОБОЛОЧКИ ВРАЩЕНИЯ
425
Из A2.14.3) следуют уравнения равновесия
VpT^ + q« = 0, ГаРЬаР + qn = 0
и граничное условие
A2.14.4)
Система из двух дифференциальных уравнений и конечные соот-
соотношения A2.14.3) позволяют определить три компоненты Та*.
Альтернативная форма записи уравнений A2.14.3) получится,
если опустить у тензора ГаР индексы двукратным свертыванием
его с дискриминантным тензором, т. е. принять
Теперь уравнения равновесия можно записать следующим об-
образом:
5ц,а - 512il - 5ПГ2\ + S12 (i^ - Г?а) + S^T
22A
21t2
12
(Г222 - r;a) - S22Y\2
q2g = О,
qig = 0, A2.14.5)
2&12 = qn.
§ 12.15. Безмоментныс оболочки вращения
Оболочки вращения представляют собою наиболее простой
объект для приложения безмоментной теории. Примем за направ-
направление 1 направление вдоль меридиана, за направление 2 — окруж-
окружное направление. На рис. 12.15.1
изображен кусок дуги меридиана. За
координатные параметры мы при-
примем длину дуги меридиана s, отсчи-
отсчитываемую от произвольной паралле-
параллели, и угол ф между плоскостями
меридиональных секций, также от-
отсчитываемый от произвольной плос-
плоскости. Радиус параллели, на которой Рис. 12.15.1
лежит точка М, т. е. расстояние
этой точки до оси симметрии, есть заданная функция дуги s.
При таком выборе координат
Символы Кристоффеля вычисляются по обычным формулам, вы-
выражения для них получаются следующими:
? } j Г|х = 0,
Г2 sinG
A 12 ~—
Гоо 0.
¦ 12 > A 22
Угол 0 образован касательной к меридиану и осью симметрии.
426 гл- 12- стержни, пластины и оболочки
Коэффициенты второй квадратичной формы равны
Ь = — Ъ =— Ь = О
Здесь радиус кривизны меридиана /?4 = ds/dQ, радиус кривизны
нормального сечения, имеющего общую касательную с парал-
параллелью R2 = r/cosQ. Первое из уравнений A2.14.5) удовлетворяет-
удовлетворяется тождественно, второе и третье соответственно принимают вид
Перейдем теперь к физическим компонентам усилий
с
1У1 — ~i iV2 ~ °и-
Система уравнений равновесия преобразуется следующим об-
ра)зом:
A2.15Д)
Систему уравнений A2.15.1) можно получить элементарным спо-
способом, второе уравнение иногда называют уравнением Лапласа,
оно справедливо не только для осесимметричной оболочки, но
для любой оболочки:/ отнесенной к линиям кривизны. Первое
уравнение можно получить, рассматривая равновесие кольца,
заключенного между двумя бесконечно близкими параллелями.
В это уравнение войдет величина qn, которая исключается с по-
помощью второго уравнения, отсюда появление усилия N2 в этом
уравнении. Но для интегрирования системы A2.15.1) мы пойдем
по прямо противоположному пути, а именно, исключим из пер-
первого уравнения N2. Получившееся уравнение содержит только Nu
оно легко интегрируется и мы получаем следующий результат:
N1 = -
A2.15.2)
§ 12.16. КРАЕВОЙ ЭФФЕКТ В ТЕОРИИ ОБОЛОЧЕК
427
§ 12.16. Уравнения краевого эффекта в теории оболочек
Если характерный размер области краевого эффекта есть
Я = 1/Rh, соответствующий небольшой кусок оболочки можно рас-
рассматривать как плоскую предварительно изогнутую пластину.
Это значит, что метрика срединной поверхности оболочки при-
приближенно отождествляется с метрикой плоскости, касательной
к срединной поверхности в ее недеформированном состоянии.
Линии кривизны поверхности спроектируются на эту плоскость
приблизительно как ортогональные прямые, которые можно при-
принять за координатные линии. В окрестности точки касания М
в декартовых координатах ха, z,
выбранных так, что оси ха лежат I
в касательной плоскости, а ось z
нормальна к ней, уравнение поверх-
поверхности можно записать следующим
образом:
_fl
/1
Pirc. 12.16.1
Здесь Ri и R2 — главные радиусы
КРИВИЗНЫ, Хю = 1/Ri И Х2о = 1/^2 —
начальные кривизны. При изгибе точки поверхности приобре-
приобретают дополнительные перемещения в направлении оси z, как
показано на рис. 12.16.1 и, соответственно, меняются кривиз-
кривизны, становясь равными l/i?t + wtiu 1/R2 + w>22. Теперь мы можем
модифицировать вывод § 12.10, предположив, что изменения
кривизн wM и w22 малы по сравнению с начальными кривизна-
кривизнами l/Ri и l/i?2. Заменим в уравнении A2.10.3) кривизны их
новыми выражениями и сохраним лишь линейную часть. Получим
DAAw — j± — ^ + ? = 0. A2.16.1)
При выводе второго уравнения рассуждения должны быть не-
несколько изменены. Задавая поверхность уравнением z = z(xa),
мы как бы предполагаем, что поверхность получилась в резуль-
результате деформации из плоскости. Соответствующие компоненты
деформации* мы обозначим ?ар- Они удовлетворяют такому же
уравнению совместности, как то, которое было использовано при
выводе A2.10.6), вместо кривизн м?>ар в правой части будут фи-
фигурировать заданные начальные кривизны l//?t и 1/Д2. Получим
1
11,22
i
~1~?
22,11
9р° —
— ^12,12 —
A2.16.2)
Начальные деформации е&$ определяют геометрию ненагружен-
ной поверхности и, следовательно, не связаны с напряжениями.
Упругие деформации еа$ добавляются к начальным, поэтому
428 гл- 12- стержни, пластины и оболочки
в уравнение совместности нужно подставлять величины ва$ + еа$
в левую часть и l/ffi + M>,n, I/R2 + ^,22 в правую. Пренебрегая
вторыми степенями изменений кривизн w^ и учитывая A2.16.2),
получим следующее уравнение совместности:
^11,22 + ^22,11 — 2^12Д2 = d п~"-
Л11 2
Поступая далее точно так же, как при выводе уравнения
A2.10.6), получим
AAF + 2Eh fyl + ^] = 0. A2.16.3)
Определим дифференциальный оператор второго порядка L сле-
следующим образом:
Внося в A2.16.1) выражения для усилий через функцию уси-
усилий F, перепишем систему уравнений следующим образом:
= 0, AAF + 2EhL(w) = 0. A2.16.4)
В литературе принято называть эти уравнения уравнениями тео-
теории пологих оболочек. Соответствующие решения оказываются
затухающими на расстоянии по дуге порядка % = TlRh. Многие
авторы рекомендуют применять их и для оболочек, размер кото-
которых в плане существенно больше, чем X. Так, Власов рекомен-
рекомендовал эти уравнения для оболочек, у которых стрела подъема не
превышает 1/5 пролета, никак не оговаривая при этом относи-
относительную толщину. Многочисленные расчеты с помощью прибли-
приближенных уравнений A2.16.4) и уравнений точной теории, кото-
которые мы здесь не приводим, показали, что для оболочек, приме-
применяемых обычно в строительной практике, разница сравнительно
невелика и рекомендация Власова может считаться практически
обоснованной, хотя строгий анализ подтверждает пригодность
уравнений A2.16.4) лишь для оболочек, размер которых в плане
имеет порядок X, или для исследования краевых эффектов в обо-
оболочках положительной гауссовой кривизны. Последняя оговорка
существенна. В оболочках отрицательной кривизны состояния
изгиба могут простираться сколь угодно далеко вдоль асимпто-
асимптотических линий. В оболочках нулевой кривизны, например ци-
цилиндрических, изложенная в § 12.13 теория применима далеко
не всегда. Действительно, приближенная теория изгиба и кру-
кручения тонкостенных стержней открытого профиля, изложенная
в § 9.15, по существу представляла собою некоторый упрощен-
упрощенный вариант теории оболочек. Краевой эффект от бимоментной
§ 12.6. КРАЕВОЙ ЭФФЕКТ В ТЕОРИИ ОБОЛОЧЕК 429
нагрузки, как было там выяснено, простирается на длину <3 =
= Д2М, которая гораздо больше, чем характерная длина % = УШг.
Характерная особенность решений общей и точной теории обо-
оболочек состоит в том, что если такое решение удается найти, то
оно, как правило, имеет сложный вид и содержит большое число
членов. Однако элементарный анализ показывает, что из этих
членов существен только один, все остальные малы и могут быть
без ущерба отброшены. Поэтому следует стремиться к тому, что-
чтобы заранее упростить сами исходные уравнения теории с тем,
чтобы в результате решения получить именно необходимую его
главную часть. Построение таких упрощенных вариантов и ана-
анализ пределов их применимости составляет в значительной мере
предмет современной теории оболочек, которая не будет изла-
излагаться в нашем курсе, носящем общий и скорее вводный ха-
характер.
Заметим, что предположение о малости изменений кривизн
w,a$ по сравнению с 1/Ra не обязательно. Не составляет труда
вывести уравнения, подобные уравнениям A2.16.4), но содержа-
содержащие нелинейные части, как уравнения § 12.10. Такие уравнения
применяются, например, для решения задачи о прощелкивании
пологой оболочки под действием распределенного давления или
сосредоточенной силы. Качественные результаты получаются
чрезвычайно похожими на те, которые были получены в § 4.6
для простейшей системы из двух стержней. Но здесь эти резуль-
результаты могут быть получены только путем применения численных
методов.
ГЛАВА 13 ;
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§ 13.1. Постановка динамических задач теории упругости
В § 8.4 были выписаны общие уравнения статической теории
упругости и соответствующие граничные условия, там же была
сформулирована постановка задачи теории упругости. В общем
случае движение упругого тела происходит во времени и элемен-
элементы его обладают ускорениями, поэтому более общей будет по-
постановка динамической задачи теории упругости. В декартовых
координатах эти ускорения представляют собою вторые произ-
производные от перемещений по времени. Применяя принцип Далам-
бера, мы получим уравнения движения упругого тела, добавив
к действующим силам Ft силы инерции:
Fi -* Fi - рй{.
Таким образом, уравнения движения, заменяющие (8.4.1), будут
следующие:
Gijj-pui + Ft^O. A3.1.1)
Остальные уравнения (8.4.2)—(8.4.4) и граничные условия
(8.4.5), (8.4.6) сохраняются, но теперь к ним нужно добавить на-
начальные условия, а именно,
щ = и?, щ = v\, t = 0. A3.1.2)
Оставляя в стороне вопрос о доказательстве существования ре-
решения, докажем теорему единственности, при этом мотивировка
остается той же, что и для статической задачи в § 8.4. Ход
доказательства остается в основных чертах тем же самым. Пред-
Предположим, что одним и тем же начальным условиям A3.1.2) и
граничным условиям удовлетворяют два различных решения си-
системы A3.1.1) и (8.4.2) —(8.4.4), а именно, "i, **а\ Щ, о"ц. Тог-
Г » Г /Г
да разность этих решений щ=щ — иг, о# = о#—о^ удовлетво-
удовлетворяет однородным уравнениям движения
<b;,i-pui = O, A3.1.3)
нулевым начальным условиям
щ ¦= 0, щ = 0 при t = 0
§ 13.1. ПОСТАНОВКА ДИНАМИЧЕСКИХ ЗАДАЧ 431
и однородным граничным условиям
= 0, хг е ST, щ = О,
(обозначения здесь те же, что в § 8.4).
Умножим A3.1.3) на й{, свернем по индексу i и проинтегри-
проинтегрируем по объему. Первый интеграл преобразовывается интегриро-
интегрированием по частям
щ),; — OijUU] dV = J
S
Но интеграл по поверхности обращается в нуль вследствие одно-
однородных граничных условий.
Заметим, что
8U • dU " ' d ( P"i ui\ dT
6 pW^ V
^7ir V~2—у = ir-
Здесь символом Г обозначена кинетическая энергия, приходя-
приходящаяся на единицу объема. Таким образом, из A3.1.3) мы по-
получаем
Проинтегрируем это выражение по времени, заметив, что вслед-
вследствие нулевых начальных условий при ? = 0, Р = 0 и Г = 0,
Получим
§U + T)dV=0. A3.1.4)
Но Т есть положительно определенная квадратичная функция
от скоростей йи U — вследствие предположения о выпуклости
потенциала — положительно определенная функция от деформа-
деформаций вф Поэтому равенство A3.1.4) будет выполнено лишь в том
случае, если
ei3 = 0, щ = 0.
Первое условие означает, что перемещения отвечают движению
твердого тела без деформации, из второго следует, что скорости
равны нулю, а так как при t = 0 было и{ = 0, то перемещение
остается равным нулю все время. Отсюда следует
г п г п
Щ = UU Gij = ay.
Сформулировав общую постановку динамической задачи тео-
теории упругости и доказав теорему единственности, мы перейдем
к постановке задач более частного характера, которые и будут
рассмотрены в нашем курсе.
432 ГЛ' 13* ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
а. Свободные колебания. Упругое тело свободно от действия
внешних сил, Ft = 0, Ог$щ = 0 на ST. Часть поверхности Su мо-
может быть неподвижно закреплена, на ней щ = 0. Заданы началь-
начальные условия A3.1.2). Таким образом, тело приводится в движе-
движение сообщением ему начального распределения перемещений и
скоростей.
б. Вынужденные колебания. Если объемные силы Fu поверх-
поверхностные силы Т{ и заданные перемещения точек поверхности щ
представляют собою периодические функции времени такие, что
и величины, отмеченные индексом «нуль», от времени не зависят,
то в качестве типового представителя функции ф(?) можно при-
принять
ф@ = ехр(^). A3.1.5)
Действительно, любая периодическая функция может быть пред-
представлена рядом Фурье. Построив решение для одного члена
этого ряда A3.1.5), мы можем воспользоваться принципом су-
суперпозиции для построения полного решения.
в. Распространение волн. Если в некоторой части тела вне-
внезапно создается возмущение, оно распространяется с конечной
скоростью. Это значит, что в точке, находящейся на расстоянии L
от источника возмущения, в течение некоторого времени т будет
сохраняться покой. Периодическое возмущение, создаваемое в
точке, будет вызывать в другой точке, отстоящей от нее на рас-
расстоянии L, также периодическое движение, но сдвинутое по фазе.
Задачи подобного типа называют волновыми задачами.
Подобно тому как статические задачи теории упругости до-
допускают вариационную формулировку, решение динамической
задачи может быть сведено к отысканию стационарного значения
интеграла действия
§dt$(T-U)dV. A3.1.6)
О V
В выражении A3.1.6) Т есть кинетическая энергия на единицу
объема Т = 72рйгй,-, а
U = U(eij), e(j = 72
При составлении интеграла действия мы считали, что к телу
не приложены внешние силы, объемные или поверхностные, ко-
которые совершают работу на каком-либо из кинематически допу-
допустимых полей перемещений и.
§ 13.2. СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 433
§ 13.2. Свободные и вынужденные колебания
Будем искать решение уравнений движения в следующем
виде:
щ = Ui exp icot.
Здесь Ui — функции только координат, но не времени. Аналогич-
Аналогичным образом представятся, очевидно, компоненты деформации и
напряжения. Обозначая теперь через ии а# амплитуды перемеще-
перемещений и напряжений, так что щ=и{, мы получим вместо A3.1.3)
следующую систему:
aii(j-poJ^ = 0. A3.2.1)
Граничные условия в случае свободных колебаний должны быть
однородными, при этом множитель exp icot сокращается. Вопрос
о начальных условиях мы пока оставляем в стороне. Уравне-
Уравнения связи между амплитудами напряжений и деформаций сохра-
сохраняют форму обычных уравнений закона Гука
ац = ЕтиК1. A3.2.2)
Система уравнений A3.2.1) и A3.2.2) при однородных граничных
условиях имеет очевидное тривиальное решение щ = О, atj = 0.
Однако при некоторых значениях параметра со = он возможно и
ненулевое решение
иг = <Pi» aij = s\r
Соответствующие значения параметра ык называются собствен-
собственными частотами упругого тела, а функции ср определяют соб-
собственные формы колебаний. Заметим, что в A3.2.1) войдут квад-
квадраты собственных частот, которые сохранятся при всех даль-
дальнейших выкладках, поэтому корню о)& будет всегда соответство-
соответствовать второй, равный по величине и противоположный по знаку
корень — Oft. Мы не будем вводить для этих отрицательных кор-
корней специальную нумерацию, но следует помнить, что кроме
решения щ ехр шг всегда присутствует и второе решение
Ичвхр(—itot). Это замечание позволяет образовывать из них дей-
действительные комбинации, которые одни только имеют механиче-
механический смысл. *
Выпишем теперь уравнения, связывающие s\j с ф^ и вытека-
вытекающие из A3.2.1),
4" j - Р«>2ф1 = 0. A3.2.3)
Очевидно, что вследствие однородности системы уравнений и
граничных условий, функции ср* и соответственно Sy определены
с точностью до произвольного множителя. Уравнения A3.2.1) и
A3.2.3) могут рассматриваться как уравнения статической зада-
задачи теории упругости с массовыми силами —ро2ггг. Пусть о = cok
28 ю. Н. Работнов
434 ГЛ- 13- ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
есть какая-либо из собственных частот. Тогда иг = ф^ представ-
представляет собою перемещение, вызванное действием распределенных
по объему сил Pi = — <Одрф$. Аналогичным образом при частоте
cos иг = ф* есть перемещение, вызванное силами Р\ = — ^
Но по теореме Бетти (§ 8.10)
или
Но он ?= (Os и вышенаписанное равенство возможно только тогда,
когда интеграл равен нулю, следовательно,
fpqMcpJdV=0 (кф$). A3.2.4)
v
Равенство A3.2.4) выражает свойство ортогональности собствен-
собственных форм колебаний, установленных для элементарной теории
стержневых систем в § 6.2. Из условия ортогональности следует,
в частности, что частоты coft всегда действительны. Чтобы дока-
доказать это, предположим противное, а именно, допустим, что Oi =
= а + ф. Уравнение для нахождения собственных частот будет
обязательно иметь еще один комплексно сопряженный корень
(о2 = ос — ф. Соответствующие собственные формы будут также
комплексно сопряженными
<Pi = Pi + i(lb Ф? = Pi ~ iQi-
Из условия ортогональности следует
Но это равенство возможно лишь тогда, когда pi = 0, #i = 0; та-
таким образом, движений с комплексными частотами быть не мо-
может. Очевидно, что этим исключается и случай чисто мнимых
частот.
Поскольку ф^ определены лишь с точностью до произволь-
произвольного постоянного множителя, их можно нормировать произволь-
произвольным образом. Обычно принимают
V= 6As. A3.2.5)
v
Соотношения A3.2.5) выражают условия нормирования и одно-
одновременно повторяют условия ортогональности собственных форм.
§ 13.2. СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Принцип суперпозиции позволяет представить общее выраже-
выражение для перемещений при свободных колебаниях упругого тела
следующим образом:
оо
и* = 2 {Ak sin <М + Bk coscoft?) ф^ (xs). A3.2.6)
Здесь Ak и Bk — неопределенные константы. Соотношение A3.2.6)
получается путем комбинации выражений для перемещений, со-
содержащих множители ехр(±?ю?). Дифференцируя A3.2.6) по
времени, находим
оо
Щ = 2 И*©А COS (Oht — Bh(Ok Sin (Okt) ф| (Xs).
k=l
Приравнивая при t = О значения перемещений и скоростей их
заданным начальным значениям, получим
2 я*ф* (*.) = А (ха), 2 Л©лФ? (*.) - у? («в).
Умножаем каждое из этих равенств на Рфг и интегрируем по
объему. Вследствие A3.2.5) в левой части от каждого ряда оста-
остается лишь по одному члену и мы получим
Bk = f puUdV, Ak=±- \pv\y\dV. A3.2.7)
V k V
Следует заметить, что соотношения A3.2.6) не предполагают
возможности разложения функций и\ и v\ в ряды по собственным
формам колебаний или фундаментальным функциям ф*. Началь-
Начальное распределение скоростей вообще может быть даже не непре-
непрерывным, и если говорить о сходимости, то речь может идти лишь
о сходимости в среднем.
Предположим теперь, что на тело действуют периодические
силы с круговой частотой р. Для простоты будем считать, чта
/^ = 0, Тi — ^° exp ipt на всей поверхности S; рассмотрение бо-
более общего случая дополнительных трудностей не встречает. По-
Полагая перемещения и напряжения также пропорциональными
exp ipt и сохраняя обозначения щ и afj для амплитуд перемеще-
перемещений и напряжений, получим следующие уравнения:
Оц,5-рР2Ъ = 0 A3.2.8)
при граничном условии
Т°и xs€=S. A3.2.9)
Представим искомое решение в виде
щ = щ + и\, о ц = о у
28*
436 ГЛ- 13- ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Здесь u°i, o°ij — решение статической задачи теории упругости,
удовлетворяющее уравнениям равновесия
ofcj = О,
уравнениям связи и граничным условиям A3.2.9). Тогда первая
часть решения uh a^ удовлетворяет следующим уравнениям дви-
движения:(
<4;-PP2«'i = PP2«i- A3.2.10)
Положим и$ = 2<ЗДгИ соответственно o^j = 2аь5гг Подставляя
эти выражения в A3.2.10) и исключая производные s^j с по-
помощью A3.2.3), получим
Умножая на фГ и интегрируя по объему, с помощью A3.2.5)
найдем
Отсюда следует
ат = ^-^ j р«?ФГ dV. A3.2.11)
Если р = (ош, т. е. частота возмущающей силы совпадает с одной
из собственных частот упругого тела, соответствующий коэффи-
коэффициент обращается в бесконечность, т. е. наступает резонанс. До-
Доказательство того, что непрерывные и дважды дифференцируе-
дифференцируемые функции uh удовлетворяющие кинематическим граничным
условиям, могут быть представлены абсолютно и равномерно
сходящимися рядами фундаментальных функций или собственных
форм колебаний выходит за рамки этой книги.
§ 13.3. Неравенство Рэлея и метод Ритца
Умножим обе части уравнения A3.2.1) на щ, проинтегрируем
по объему и разрешим полученное равенство относительно о2.
Найдем
A3.3.1)
Преобразуя числитель интегрированием по частям при однородных
§ 13.3. НЕРАВЕНСТВО РЭЛЕЯ И МЕТОД РИТЦА. 437
граничных условиях, получим
''HUeif
pu\dV
A3.3.2)
Если W| = ф|, то уравнение A3.2.1) выполняется при со = o)ft и
формула A3.3.1) либо A3.3.2) даст точное значение квадрата
собственной частоты с номером к. Но если щ — произвольные
функции, то уравнение A3.2.1) не вьшолняется, формула A3.3.2)
определяет некоторое число о2, которое, вообще говоря, не пред-
представляет собою квадрат частоты каких-либо свободных колебаний
системы. Покажем, что функционал, фигурирующий в правой
части A3.3.1) или A3.3.2), позволяет получить оценку по край-
крайней мере для наименьшей из собственных частот. Условимся ну-
нумеровать собственные частоты в порядке возрастания, так что
0)i <¦ 0J < (Оз < . . .
Выберем в качестве щ произвольную систему трех дифференци-
дифференцируемых и непрерывных функций, удовлетворяющих кинематиче-
кинематическим граничным условиям. Тогда, в соответствии с замечанием,
сделанным в конце § 13.2,
Щ = 2 яьф?-
А так как вследствие A3.2.3)
ТО
J ах^щ dV= aham(ol J pq%q)? dV= 2 <&*%-
Совершенно аналогично вследствие ортогональности главных форм
Теперь соотношение A3.3.1) можно переписать следующим об-
образом:
ИЛИ
Но каждый член ряда в числителе не меньше соответствующего
члена ряда в знаменателе, так как (o)ft/o)iJ > 1, поэтому со? ^со2
438 ГЛ- 13- ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
и A3.3.2) можно заменить следующим неравенством:
®;<-?. A3.3.3)
Здесь U — упругий потенциал, вычисленный для заданной систе-
системы перемещений щ, Т — выражение кинетической энергии, в ко-
котором скорости заменены перемещениями ии
Неравенство A3.3.3) дает верхнюю оценку для низшей часто-
частоты колебаний упругого тела. Если функции щ содержат некото-
некоторое число к неопределенных параметров cs, то O = U(cs) и f =
= T(cs). Наилучшим приближениям для а>1 будут соответствовать
значения cs, минимизирующие дробь в правой части A3.3.3), по-
поэтому должно быть
Отсюда
или, полагая VIT = со2,
0J _. 0# A3.3.4)
дс дс v '
Наиболее простой результат получается тогда, когда параметры
cs входят в выражение щ линейно, а именно,
щ = S cj\. A3.3.5)
Тогда уравнения A3.3.4) линейны и однородны; для существо-
существования нетривиального решения необходимо, чтобы детерминант
системы был равен нулю. Это условие приводит к алгебраическо-
алгебраическому уравнению степени к относительно со2. Вследствие неравен-
неравенства Рэлея наименьший корень этого уравнения будет давать
верхнюю оценку для со2, которая может только улучшиться
с увеличением к. При увеличении к корень уравнения с номе-
номером т будет стремиться к величине о)^, при этом нельзя сказать
сверху или снизу. Доказательство этой теоремы мы не приводим,
заметим лишь, что для ее выполнения необходима полнота си-
системы функций /V т. е, возможность представления любой до-
допустимой системы перемещений и{ в виде A3.3.5). Описанная
приближенная процедура определения частот носит название ме-
метода Ритца. -...--•.
§ 13.4. РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН 439
§ 13.4. Распространение плоских волн
в неограниченной упругой среде
Выражая в A3.1.3) напряжения через компоненты перемеще-
перемещения с помощью закона Гука, получаем для общего случая тела
с произвольной анизотропией следующие дифференциальные урав-
уравнения движения:
-тг Eijki (uktlj + ultkj) — риг = 0. A3.4.1)
Будем называть плоской волной такое решение системы A3.4.1),
которое описывает перемещение неизменной конфигурации в на-
направлении единичного вектора п со скоростью с. Как оказывает-
оказывается, решения такого типа, соответствующие постоянной скорости
с, не зависящей от конфигурации, возможны лишь в неограни-
неограниченной упругой среде. Согласно определению поле перемещений,
соответствующее плоской волне, дается следующими выраже-
выражениями:
щ = и№-пвхл). A3.4.2)
Подставляя его в A3.4.1), получим
E (Utfun + и]пкщ)— pU'[c2=0.
— Em (
Полагая иг = 8isUs, приведем эту систему к следующему виду:
[—
— Ет (riinfito + rifjifiis) — pSi>2J Us =0.
Эта система однородных линейных уравнений имеет нетривиаль-
нетривиальное решение тогда, когда определитель ее равен нулю. Условие
det 14-#ii«>znA, + nknfiu) - p6isc21 = 0 A3.4.3)
представляет собою кубическое уравнение относительно с2, ре-
решение которого определяет для каждого направления п три ско-
скорости распространения плоских волн. В частном случае, если
тело изотропно, то, как было показано в § 8.2, тензор модулей
упругости имеет следующий вид:
Внесем эти выражения в уравнение A3.4.3). Заметим, что
6,-j6w6ft8W/Wj = 6iAAsraft/ij = 8ikbji6ianknj = пгп81
Sik&jlSksriinj = 6;s.
Теперь уравнение A3.4.3) для скоростей плоских волн примет
следующий вид:
det II {К + |i) ил + |i6ie - pc26jl = 0. A3.4.4)
нять,
шется
например
, щ = 1, щ =
следующим образом:
Х + 2|Л — рс2
0
0
ГС3 = 0.
0
ц-рс2
0
Теперь
0
0
\i-pc2
440 гл- 13- ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Для изотропного тела, очевидно, скорости распространения волн
во всех направлениях одинаковы, поэтому в A3.4.4) можно при-
-0.
Как видно, оно имеет двойной корень, следовательно, в изотроп-
изотропном теле получается не три, а две скорости распространения
плоских волн, а именно,
в1 = 1Л±*. с,= У±-. A3.4.5)
Заметим, что для изотропного тела уравнения движения можно
было сразу записать в следующей форме:
{X + \i) е,« + рЬщ - рщ = 0. A3.4.6)
Не нарушая общности, мы можем рассмотреть волны, распрост-
распространяющиеся вдоль оси хи а именно:
а) продольные волны: ul = u(ct — xl), uz = w3 = 0, 0 = u'; пер-
первое уравнение движения приводится к следующему:
(X + 2\i-рс2)и" =0.
Уравнение удовлетворяется, когда с = с^
б) поперечные волны: Ui = u3 = 0, u2 = u(ct — xl). Подстановка
во второе уравнение движения приводит к результату
Таким образом, с2 есть скорость распространения поперечных
волн.
Заметим, что для поперечных волн 0 = 0, распространение их
не сопровождается изменением объема. С другой стороны, для
продольных волн rot и —0. Поэтому их называют, соответственно,
эквиволюминальными и безвихревыми или волнами искажения и
расширения.
В § 2.10 была рассмотрена задача о распространении продоль-
продольной волны в стержне. Скорость ее, согласно элементарной тео-
теории, давалась выражением с0 = УЕ/р. Эта скорость отлична как
от d, так и от с2. В действительности волны вида A3.4.2) в
стержне, представляющем собою ограниченное тело, распростра-
распространяться не могут, возмущение, переносимое вдоль оси стержня,
меняет свою конфигурацию.
Заметим, что сделанный вывод о возможности существования
двух типов волн, распространяющихся со скоростями с{ и с2, но-
носит в известном смысле менее общий характер, чем упомянутый
результат в § 2.10. Действительно, отыскивая решение в виде
§ 13.5. ОТРАЖЕНИЕ ВОЛН 441
Ui(ct — x), мы предполагаем, что функции щ по крайней мере
дважды дифференцируемы, в противном случае подстановка их
в уравнения движения была бы бессмысленна. Первые произ-
производные от функций щ по времени — это скорости. Напряжения
выражаются через первые производные от перемещений по коор-
координатам. Эти первые производные должны быть непрерывны,
следовательно, волны рассматриваемого типа не могут нести раз-
разрывов скоростей или разрывов напряжений. Для стержня мы
сразу предположим, что на фронте волны скорость и деформация,
а следовательно, напряжение, меняются скачком, и получим ско-
скорость фронта в этом предположении. Волны, несущие разрывы
производных от перемещений, т. е. скоростей и напряжений,
называются волнами сильного разрыва или ударными волнами.
Возможность распространения ударных волн в неограниченной
упругой среде со скоростями cY и с2 требует дополнительного
обоснования. Для продольных волн сильного разрыва применение
этого обоснования получается в результате буквального повто-
повторения анализа § 2.10 для стержня. Совершенно аналогичные
рассуждения, основанные на теореме о количестве движения, по-
позволяют установить возможность распространения ударных волн
искажения. Таким образом, уравнения движения упругой среды
допускают решения, содержащие разрывы первых производных
от перемещений.
§ 13.5. Отражение волн
Продольная волна, распространяющаяся в направлении оси
хи есть, как мы видели, следующее решение уравнений дви-
движения:
7/ — 4 ('у» __ /» /• \ 7/ — 7/ — С\ I \ О С \ \
W'l — J \^i W'/ j 2 — ^3 — *J, { LO.O. L }
Предположим теперь, что плоская волна распространяется не
вдоль оси xi, а вдоль некоторой пря- ^
мой, лежащей в плоскости х{х2 и со-
составляющей угол а с направлением оси
Xi (рис. 13.5.1). Направляя ось | по
этой прямой, мы найдем по формулам
преобразования координат
Ъ ;— /У» ПЛО Г/ ~f- Т Ч1Т1 Г/
w *^ 1 V^v/O чЛ • *л^2 OXXJ. чЛ•
Перемещение U направлено вдоль оси
I и равно '"
U = f(Xl cos a + xz sin a - Cit). Ржс< 135>1
Теперь это перемещение можно спроектировать на оси Xi и х2,
мы получим
ui = /(#i cos ос+ #2 sin a — c^cosa,
uz = f(xt cosa + ^sina — ct^)sina, A3.5.2)
442 гл- 13- динамические задачи теории упругости
Совершенно аналогичным образом можно записать величины пе-
перемещений щ, связанных с плоской волной искажения, распрост-
распространяющейся вдоль луча, лежащего в плоскости х^ х2 и состав-
составляющего угол р с осью Xi. Теперь
V = g(xi cos p + х2 sin р — c2t)
есть перемещение, перпендикулярное к направлению распростра-
распространения, и составляющие этого перемещения по осям координат
lit = g (xi cos p + x2 sin p — c2t) sin p,
U2 = g (xi cos p + x2 sin p — c2t) cos p, A3.5.3)
Теперь рассмотрим следующую задачу. Упругая среда зани-
занимает полупространство xt > 0, граница полупространства жестко
закреплена таким образом, что на ней перемещения равны нулю
(рис. 13.5.2). Справа под углом а0 к оси
Xi идет волна расширения Uo = /0. Пере-
Перемещения Ui и и2 в падающей волне да-
даются формулами A3.5.2), в которых нуж-
нужно заменить а через а0 и с± через — си
так как направление движения волны
на рис. 13.5.2 противоположно тому, ко-
которое было принято при выводе этих
формул. В акустике и оптике волна, па-
падающая на плоскую преграду, отражается
от нее. То же происходит и с упругими
волнами, но если на преграду падает
волна расширения, то отражаются уже
Рже. 13.5.2 две волны: волна расширения и волна
искажения. Сделаем это предположение
и покажем, что оно единственное возможное. Итак, предполо-
предположим, что на стенку падает волна расширения под углом ао>
отражается волна расширения U = f под углом а и отра-
отражается волна искажения V = g под углом р. Компоненты
полного перемещения найдутся как суммы компонент пере-
перемещений от этих трех волн. Комбинируя формулы A3.5.2)
и A3.5.3) и учитывая сделанные замечания о разнице направ-
направлений падающей и отраженной волн, получим
Ui = /о (xi cos а0 + х2 sin а0 + cj) cos а0 +
+ f(Xi cos а + х2 sin а — c^cosa — g(xi cosp + х2 sinp — c2t)sinp,
u2 = /о (xi cos a0 + Xz sin a0 + cYt) sin a0 +
+ / (#i cos a + x2 sin a — CJ) sin a + g (#i cos p + x2 sin p — c2t) cos p,
§ 13.5. ОТРАЖЕНИЕ ВОЛЫ 443
Перемещения должны обращаться в нуль на жесткой стенке при
Xi = 0. Следовательно,
/0 (х2 sin а0 + Cit) cos а0 + / (х2 sin а — cj) cos а —
—g (x2 sin p — c2t) sin p = 0,
A3.5.4)
/0 (х2 sin а0 + с^) sin а0 + / (#2 sin а — с^) sin а0 +
+ g (x2 sin р — c2t) cos p = 0.
Эти равенства должны выполняться для любых значений х2 и t,
а это возможно только тогда, когда аргументы всех функций
одинаковы. Это значит, что
х2 sin а0 + c{t = — х2 sin а + c±t = (— х2 sin |3 + c2t) -^-.
Отсюда
sin а = — sina0, sin|3 = -sina0. A3.5.5)
Таким образом, волна расширения отражается по закону геомет-
геометрической оптики, угол падения равен углу отражения. Кроме
этого возникает волна искажения, отражающаяся под углом р,
при этом 1р| < laol, как показано на рис. 13.5.2. Если известна
форма падающей волны, т. е. функция /0, из уравнений A3.5.4)
находятся функции / и g, определяющие форму отраженных волн.
Как видно, они отличаются от функции /0 лишь постоянным
множителем, а для функции g также масштабом аргумента.
Мы рассмотрели для простоты довольно искусственную задачу
об упругой среде, скрепленной с абсолютно жесткой стенкой. Бо-
Более реальная задача это, конечно, задача об отражении волны
от свободной поверхности. Решается она точно таким же спосо-
способом, только вместо условия и{ = и2 = 0 при хх = 0 нужно исполь-
использовать условие Он = а12 = 0. Напряжения выражаются через пер-
первые производные от перемещений, вместо A3.5.4) получатся не-
некоторые равенства, содержащие производные функций /0, / и g.
Совершенно такие же рассуждения убеждают в том, что функ-
функции должны зависеть от аргументов, отличающихся лишь мно-
множителем, и мы неизбежным образом приходим к соотношениям
A3.5.5),
Предположим теперь, что на плоскую стенку падает волна
искажения под углом р0. Все построение производится совершен-
совершенно аналогично, нет надобности его повторять. Мы находим, что
от стенки отражаются две волны, волна искажения под углом р
и волна расширения под углом а, при этом
sinf} = —sinpo, sina = ^-sinBo.
C2
444 гл- 13- Динамические задачи теории упругости
Но Ci > с2, поэтому угол а больше, чем угол [}, и решение спра-
справедливо лишь до тех пор, пока Isinal < 1. Для этого необходимо,
чтобы угол р0 не превосходил критического значения
Если коэффициент Пуассона v = 1/3, cjc2 = 2, %р = 30°. Задача
о взаимодействии с преградой волны искажения, падающей под
углом большим чем критический, решается совершенно иными
средствами и совсем не элементарна.
Установленные в этом параграфе факты проливают свет на те
волновые процессы, которые могут происходить в ограниченной
упругой среде. Даже если начальное возмущение было таково,
что оно порождало лишь простые волны одного какого-либо рода,
продольные или поперечные, в результате отражений будут воз-
возникать и продольные, и поперечные волны, распространяющиеся
с разными скоростями. Поэтому решение типа рассмотренных
в § 13.4, когда одно и то же деформированное и напряженное
состояние переносится без изменения с постоянной скоростью,
для ограниченных упругих тел, вообще говоря, невозможно.
§ 13.6. Распространение волн в слое конечной толщины
Сделанное в конце § 13.5 замечание не исключает возможно-
возможности распространения с постоянной скоростью волн специального
вида. Особую роль для теории играют синусоидальные волны / =
= sin к(х — ct) X const. Здесь к = 2n/L, L — длина волны, со =
= кс — круговая частота колебательного движения фиксированной
точки. Ясно, что вместо синуса можно взять косинус; поскольку
уравнения линейны, решения можно складывать, поэтому мы бу-
будем задавать синусоидальную волну с помощью комплексного
представления / = exp ik(x — ct)X const, суперпозиция двух таких
комплексных волн всегда позволит выделить действительную
функцию. Обратимся теперь к уравнениям A3.4.6). Дифферен-
Дифференцируя по х{ и суммируя, найдем
или
с?Лв — ?-| = 0- A3.6.1)
дГ
Теперь, продифференцируем первое из уравнений A3.4.6) по «г2,
второе по Xi и вычтем одно из другого. Вспоминая определение
§ 13.6. ВОЛНЫ В СЛОЕ КОНЕЧНОЙ ТОЛЩИНЫ 445
антисимметричного тензора <0у, получим
я2©.,
01
Вместо индексов 1 и 2 мы написали i и /, потому что из A3.4.6)
можно получить три уравнения для всех возможных комбинаций
индексов. Перепишем последнее уравнение так:
о
^0. A3.6.2)
^Г0.
dt
По виду уравнений A3.6.1) и A3.6.2) можно предположить, что
величина Э распространяется со скоростью си величина со^- со
скоростью с2. Но это не совсем так, мы не можем поставить раз-
раздельные граничные условия для Э и для cozi, поэтому фактиче-
фактически уравнения оказываются связанными между собой. Однако
эти соображения играют определенную наводящую роль при вы-
выборе структуры предполагаемых решений тех или иных задач.
Сейчас мы рассмотрим следующую задачу. Бесконечная плита
ограничена плоскостями #2 = =^. Нужно выяснить вопрос о воз-
возможности распространения синусоидальных волн в направлении
оси Xi. Предполагается, что перемещение и3 = 0. Граничные пло-
плоскости х2 = ±h свободны от напряжений. Таким образом, нужно
найти перемещения щ(хи х2, t) и и2(хи х2, t). Положим
ut = <pfl + i|)j2, u2 = Ф,2 —it>,i. A3.6.3)
Вместо неизвестных функций uY и и2 мы ввели две другие не-
неизвестные функции ф и я|). Вычисляя Э и со 12 = со, получим
0 = Аф, со = Аг|).
Потребуем, чтобы ф и if удовлетворяли уравнениям A3.6.1) и
A3.6.2), а именно, чтобы было
*2ДФ—^=0, 0^-^1=0. A3.6.4)
ot ot
Если ф и i|) удовлетворяют уравнениям A3.6.4), то 0 и со удов-
удовлетворяют A3.6.1) и A3.6.2). Вопрос об общности такого пред-
представления остается открытым, во всяком случае формулы A3.6.3)
будут определять некоторое решение уравнений динамической
теории упругости, а если мы сумеем удовлетворить граничным
условиям — мы найдем некоторое возможное движение упругой
среды. Вопрос о том, как создать это движение, также остается
открытым.
Будем искать решение уравнений A3.6.4) в виде
ф = /(я2)ехр ik(xl -ct), ф = g(x2)ex]) ik{xi — ct).
446 ГЛ- 13- ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Подставляя выражение для ф в A3.6.4), получим уравнение для
/"_а2/==0, a = kU
Общий интеграл этого уравнения
/ = A ch ах2 + В sh ax2.
Совершенно аналогичным образом находим
g = С ch $х2 + D sh ря2, р2 = A:2 (l — c2/4).
Ограничимся рассмотрением волновых движений, симметричных
относительно плоскости х2 = 0. При этом ut должно быть четной
функцией от я2, а м2 — нечетной. Для этого необходимо, чтобы
/(#2) была четной, a g(x2) —нечетной. Следовательно, J9 = C = 0,
поэтому
f(x2) = A ch а#2, г (Ж2) = Z) sh [ta2. A3.6.5)
Теперь по формулам A3.6.3) мы можем найти выражения для
перемещений, а именно,
')exp ik(x, - ct),
w2 = (/' — ikg) exp гй; (xY — ct).
Вследствие симметрии достаточно, чтобы граничные условия были
удовлетворены при х2 = +/&, условия при а:2 = — А- выполняются
при этом автоматически. На свободной поверхности должно быть
G22 = а12 = 0, следовательно,
Mlia + M2il = 0, Я9 + 2\хи2> 2 = 0, ar2 = fe. A3.6.7)
Внесем выражения м4 и и2 по формулам A3.6.6) в граничные
условия, подставим туда значения A3.6.5) для функций fug.
Получим
A2ika sh ah + D ([52 + к2) sh $h = 0,
Л [c2a2 — (cj — 2cf) /b2] ch afe — D2c\ik§ ch рл = О.
Эта система допускает для А и D ненулевое решение тогда,
когда определитель системы равен нулю. Запишем это условие,
заметив предварительно, что
с\а? - (с* - 2с2) &2 = с\ (Л* - Р2).
Получим
Поскольку а и р зависят от с, уравнение A3.6.8) есть уравне-
уравнение, определяющее скорость распространения синусоидальных
§ 13.6. ВОЛНЫ В СЛОЕ КОНЕЧНОЙ ТОЛЩИНЫ 447
волн в плите. При выводе мы предполагали, что с < с2 < ct, по-
поэтому аи р действительны. Но это предположение несуществен-
несущественно; может оказаться, что уравнение A3.6.8) имеет и такие
решения для с, при которых либо р, либо а и р становятся
мнимыми.
Исследование корней уравнения A3.6.8) затруднительно и мы огра-
ограничимся двумя крайними случаями.
а. Длинные волны. Если длина волны L велика по сравнению с h, то
р/г и ah малы по сравнению с единицей и гиперболические тангенсы мож-
можно заменить первыми членами их разложений. Получим
Очевидное решение этого уравнения есть Р = О, следовательно, с = с2, в
пластине возможно распространение волн сдвига. Предполагая $ Ф 0, по-
получим
Ак2а2 = (&2 + Р2J. A3.6.9)
Подставляя сюда выражения а и Р и разрешая относительно с, находим
с2 — с2
с« = 4с!Л 2
Заменив ь\ и с\ их выражениями через упругие константы и плотность и
переходя к техническим постоянным Е и v, представим этот результат в
следующем виде:
2) . A3.6.10)
Скорость, определяемую формулой A3.6.10), можно назвать «пластиночной».
Ее можно получить по элементарному способу § 2.10, рассматривая распро-
распространение плоского фронта разрыва. Стесненность деформации условием
е3з = 0, как мы знаем, приводит к увеличению жесткости в отношении
1: A-v2).
б. Короткие волны. Гиперболический тангенс с увеличением аргумента
стремится к единице, поэтому для коротких волн A3.6.8) принимает вид
Раскрывая скобки, получим кубическое уравнение для с2, которое мы не
будем выписывать в развернутом виде. Оно имеет три корня, из которых
только один определяет скорость с <С сг. При с >> сг величина Р оказывается
мнимой и приведенный выше анализ теряет силу. В результате вычисле-
вычислений оказывается, что при v = 1/4 с = 0,9194 с2, а при v = 1/2 с = 0,9553 с%
При малых а и р возмущение проникает на малую глубину от поверх-
поверхности пластины и взаимное влияние двух свободных поверхностей практи-
практически отсутствует. Если рассмотреть задачу не об упругом слое конечной
толщины, а об упругой полуплоскости, уравнение A3.6.11) будет определять
скорость распространения поверхностных волн — так называемых волн
Рэлея.
448
ГЛ. 13. ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Возвращаясь к общему уравнению A3.6.8), мы убеждаемся,
что скорость распространения синусоидальной волны зависит от
ее длины. Поэтому заданное возмущение произвольной формы,
которое можно представить как сумму гармонических состав-
составляющих, будет распространяться по стержню, меняя свою форму.
Это явление, т. е. зависимость скорости от длины волны и, как
следствие, искажение формы импульса, называется дисперсией,
в данном случае геометрической дисперсией, происходящей от
наличия свободных границ.
§ 13.7. Распространение волн в стержнях
Задача о распространении продольных, крутильных и попе-
поперечных волн в длинных стержнях круглого сечения была рас-
рассмотрена в 70-х годах прошлого столетия одновременно и неза-
независимо Похгаммером и Кри; относительная сложность получен-
полученных ими общих формул делала в течение долгого времени их
результаты мало обозримыми, лишь в 30-х — 40-х годах были
произведены расчеты и построены графики зависимости фазовой
скорости от длины волны для случая, когда поле перемещений
осесимметрично.
Весь анализ для случая цилиндрического стержня аналогичен
анализу задачи о распространении волн в пластине, но соотно-
соотношения A3.6.3) заменяются соответствующими соотношениями
в цилиндрических координатах; уравнения A3.6.4) также запи-
записываются в цилиндрических координатах. Вместо функций f(x2)
и g(x2) появляются соответству-
соответствующие функции от радиуса, ко-
которые удовлетворяют уравне-
уравнениям Бесселя и скорости волн
определяются из трансцен-
трансцендентного уравнения, заменяю-
заменяющего A3.6.8), но содержаще-
содержащего бесселевы функции. Как и
для пластины, весьма длинные
волны распространяются со
«стержневой» скоростью с0 =
1,0
— У2?/р, тогда как весьма ко-
** роткие волны идут по поверх-
Рис. 13.7.1 ности со скоростью волн Рэлея.
На рис. 13.7.1 представлена за-
зависимость скорости волны, поделенной на с0, от отношения а/Ь —
радиуса цилиндра к длине волны. Горизонтальная асимптота
соответствует скорости волн Рэлея.
Следует заметить, что эта кривая представляет собою не един-
единственное возможное решение соответствующего уравнения, оно
справедливо для так называемой первой моды. Для того чтобы
§ 13.7. РАСПРОСТРАНЕНИЕ ВОЛН В СТЕРЖНЯХ 449
пояснить существо дела, обратимся к формулам A3.6.6), кото-
которые сохраняют для стержня примерно такую же структуру.
В результате суперпозиции волн, идущих в прямом и обратном
направлении, получаются стоячие волны, т. е. решение типа
и= U (r) sin кх sin kct.
Для перемещений иг и их формула имеет одинаковую структуру,
поэтому индексы не поставлены. При колебаниях по первой мо-
моде перемещения в зависимости от длины волны либо направлены
в одну сторону при всех г, либо меняют знак один раз при не-
некотором определенном значении радиуса, который определяет
узловой цилиндр. При следующих модах появляется несколько
узловых цилиндров.
Сложность точного анализа этой задачи вызвала появление
различного рода приближенных теорий, которые обычно стро-
строятся следующим образом. Делается некоторое кинематическое
предположение о характере распределения перемещений, состав-
составляется функционал действия по Гамильтону, варьированием
этого функционала получается дифференциальное уравнение или
система дифференциальных уравнений задачи (идея чрезвычай-
чрезвычайно близкая к той, которая лежит в основе построения техниче-
технической теории изгиба балок и пластин). Простейшая теория, ко-
которая будет изложена ниже, основывается на уравнении, выве-
выведенном еще Рэлеем. Это уравнение содержит предположение
элементарной теории о сохранении плоских сечений, но прини-
принимает во внимание инерцию поперечного движения элементов
стержня. Направим ось Xi по центральной оси стержня произ-
произвольного поперечного сечения, тогда оси х2 и х3 будут лежать в
плоскости поперечного сечения. Полагая деформацию еп = и1} i
независящей от х2, #3, найдем ег1 = е3з = —viii, 4, следовательно,
перемещения равны
U2 = — VM4| i#2, Щ = —VMt, i#s.
Кинетическая энергия на единицу длины балки будет
Здесь F — площадь сечения, 1Р — полярный момент инерции.
Опуская индексы при щ и хи напишем выражение для
действия:
МЯ[(*Г(&П(?И- A3-7Д)
Здесь г — радиус инерции сечения, /р = Fr1. Проварьируем функ-
функционал A3.7.1). При этом воспользуемся тем обстоятельством,
что символы варьирования и дифференцирования переставимы,
29 ю. н. Работнов
450 ГЛ- 13- ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
поэтому
ди\2 ди дЬи д (ди к \ д2ия
(ди \ ди дби д I ди * \ д и *
2 \da; 9«/ ~~ ^ 5^ 5д; ^^ ~ дх \дх dt dt ) qx* dt dt
д ( д2и д8и) д ( дъи * \ * д*и
[)[0u) +
Вследствие симметрии левой части относительно t и х в правой
части можно поменять местами t и х и получить путем сложе-
сложения этих результатов симметричное выражение. Мы не будем
это делать, а просто внесем найденные вариации квадратов про-
производных в выражение функционала Н и выполним интегриро-
интегрирование по # и по t. Получим
Ш = F\dt\ — р-о + pv2r2 2 2 +E
J J \ 2 2
Вследствие произвольности вариации 8и для всех t ж х отсюда
следует дифференциальное уравнение
*г-?+лЧ&-0- A3-7-2)
Это уравнение было получено Рэлеем и приведено в его книге
«Теория звука», оно воспроизводится в курсе Лява [7]. В стерж-
стержне, движение которого описывается уравнением A3.7.2), воз-
возможно распространение прогрессивных гармонических волн. По-
f 2зх , . Л
лагая и = exp -g- (ct — х)\ и подставляя это выражение в
уравнение, мы найдем
с = с0 ^ а. A3.7.3)
0 1 + 4n2v2 (r/Lf v '
На рис. 13.7.1 штрихами показана зависимость фазовой скорости
от отношения радиуса к длине волны для круглого стержня, для
которого г2 = а2/2. Как видно, для волн, длина которых равна
или превышает диаметр стержня, совпадение с точным реше-
решением очень хорошее.
§ 13.8. РАЗМЫТИЕ ФРОНТА СИЛЬНОГО РАЗРЫВА 451
§ 13.8. Размытие фронта сильного разрыва
Поправка Рэлея повышает порядок уравнения до четвертого, линии
ct ± x уже не служат характеристиками уравнения A3.7.2), поэтому рас-
распространение сильных разрывов вдоль характеристик теперь оказывается
невозможным. Очевидно, что перемещение и не может быть разрывным,
сильным разрывом в нашем случае будет разрыв деформации е = ди/дх
или скорости v = du/dt. Вследствие линейности A3.7.2) и постоянства коэф-
коэффициентов как деформация, так и скорость удовлетворяют тому же самому
уравнению, поэтому в дальнейшем мы будем рассматривать это уравнение,
в котором и заменено через v. Если граничное условие на конце, например,
полубесконечного стержня задано как ступенчато изменяющаяся функция
от времени, в плоскости х, t мы уже не получим разрывного решения, раз-
разрыв будет размываться. Заметим, что в уравнении A3.7.2) имеется малый
параметр при старшей производной. Если длина волны L значительно боль-
больше, чем г, то дифференцирование по х эквивалентно по порядку делению
на L, и безразмерный малый параметр (r/LJ появляется явным и очевид-
очевидным образом. Для исследования размытия фронтов мы поступим иным обра-
образом. Перейдем от переменных х и t к характеристическим переменным
обычной задачи о продольных волнах
| = х + cot, ц = х — cot.
Прямая волна распространяется в направлении |; если в обычной теории
это волна сильного разрыва, то скорости и деформации не меняются в на-
направлении |, производные по § равны нулю. Но в перпендикулярном на-
направлении ц эти величины претерпевают скачок, грубо можно сказать, что
производные их обращаются в бесконечность. Естественно ожидать, что и
решение A3.7.2) будет обладать сходными особенностями, функция v будет
медленно меняться в направлении | и быстро меняться в направлении г).
Поэтому производные по т] будут по величине значительно больше, чем
производные по |, и при преобразовании четвертой смешанной производной
в уравнении A3.7.2) мы удержим только один, самый большой член, соот-
соответствующий четырехкратному дифференцированию по г\. В результате по-
получим
+ °
или в результате интегрирования по г\
Из этого уравнения можно сделать немедленно качественный вывод о раз-
размере области размытия фронта, который был задан при х = 0 как разрыв-
разрывная функция времени. Оценим протяженность этой области линейным раз-
размером d. Сравнивая порядки величин двух членов уравнения A3.8.1), по-
v 2 v
лучим (числовые множители опущены) — = г -д. Отсюда следует оценка
d^V^x. A3.8.2)
Уравнение A3.8.1) допускает автомодельное решение. Введя новую пере-
переменную
29*
452 гл- 13- динамические задачи теории упругости
мы преобразуем его в обыкновенное дифференциальное уравнение
a v аи
зГй^ 0 A3.8.3)
dv
или, если обозначить "Tv = F,
dv
= F,
d2v
Это — известное уравнение Эри, ограниченное решение которого записыва-
записывается следующим образом:
F = CAi(E). A3.8.4)
Здесь Ai (?) — функция Эри, которая выражается следующим образом че-
через функцию Бесселя:
Разрывное решение в случае, когда концу полубесконечного стержня вне-
внезапно сообщается скорость vQi удовлетворяет условиям v = 0 при г\ < 0 и
и = г;о при т] > 0. Подчиним решение уравнения A3.8.3) условиям у(оо) =
= vq, v(—оо) = 0. Не приводя детальных выкладок, выпишем окончатель-
окончательный результат (Кукуджанов, 1970)
На рис. 13.8.1 показана форма размытого фронта в зависимости от безраз-
безразмерной координаты ?. Переход к характеристическим координатам ?, г|
и натуральным координатам #, t производит-
производится без труда. Изображенная на рисунке кар-
^^^ тина растягивается по мере продвижения
/>— фронта в соответствии с оценкой A3.8.2). Су-
щественно отметить первый максимум, орди-
ордината которого превышает высоту заданного
скачка примерно на 25%.
Миндлин и Херрман предложили более
(J г точную и сложную систему приближенных
р .„-. уравнений, учитывающих поперечную инер-
гис. lo.o.l цию и сдвиг. Любопытно отметить, что, как
показал Кукуджанов, эта более точная тео-
теория при применении описанного выше асимптотического метода приводит
к тому же результату.
Недостаток уравнения A3.7.2) состоит в том, что оно соответствует
бесконечно большой скорости распространения импульсов, волнистая кри-
кривая, изображенная на рис. 13.8.1, уходит вперед бесконечно далеко. В дей-
действительности передний фронт образован волной расширения, которая дви-
движете^ вдоль оси стержня с наибольшей скоростью, но очень быстро ослабе-
ослабевает с расстоянием. Далее, по-видимому, возникает сложная комбинация
продольных и поперечных волн, отражающихся от боковой поверхности,
и наиболее возмущенная область продвигается со скоростью с0.
Приведенный анализ представляет интерес для правильной интерпре-
интерпретации результатов динамических испытаний стержней из упруго-пластиче-
упруго-пластического материала. Обычно при этом в основу полагается элементарная тео-
теория гл. 2, видоизмененная в результате введения тех или иных гипотез
о пластическом поведении. Эффекты, связанные с поперечной инерцией, ча-
часто искажают результаты и делают сомнительными аргументы, приводимые
в пользу той или иной из конкурирующих гипотез.
ГЛАВА 14
ДИСЛОКАЦИИ В УПРУГОМ ТЕЛЕ
§ 14.1. Дислокации в кристаллах
За последние десятилетия в физике твердого тела получило
широкое распространение представление о несовершенствах кри-
кристаллической решетки, называемых дислокациями. Этим несо-
несовершенствам приписывается основная роль при объяснении ряда
особенностей поведения реальных кристаллов. Механизм пласти-
пластической деформации, ползучести, разрушения, рассеяния энергии
при циклическом деформировании связываются большинством
современных авторов с перемещением дислокаций внутри кри-
кристалла. Дислокационные представления используются также для
объяснения механизма роста кристалла. Возможные дефекты
кристаллической решетки не ограничиваются, конечно, одними
дислокациями; этим термином называются дефекты особого рода,
обладающие совершенно определенными свойствами. Однако
дислокационные представления, как оказалось, имеют настолько
общий характер, что на их основе можно построить очень боль-
большое количество разного рода моделей, объясняющих те или иные
свойства реального кристалла, и выбрать из этих моделей те,
которые наилучшим образом отвечают опытным данным.
Необходимо заметить, что дислокационные модели для одного
и того же явления можно бывает строить различным образом,
привнося каждый раз различные физические гипотезы. Поэтому
на теорию дислокаций нужно смотреть не как на физическую
теорию, направленную на объяснение определенного круга яв-
явлений, а скорее как на формальный аппарат, позволяющий кон-
конструировать большое количество разнообразных физических тео-
теорий. Преимущество дислокационных схем состоит в том, что они
позволяют сформулировать гипотезу в точных терминах, не при-
прибегая к интуитивным и зачастую не очень ясным соображениям,
и дают возможность произвести расчет, т. е. получить количест-
количественный результат.
При построении теории кристаллических дислокаций чрезвы-
чрезвычайно плодотворной оказалась идея замены дискретной кристал-
кристаллической решетки сплошной упругой средой. Дело в том, что
всякий дефект кристаллической решетки нарушает равновесие
между атомами, в результате чего расстояния между ними ме-
меняются. Смещения атомов по отношению к тем положениям,
454 гл- 14- дислокации в упругом теле
которые они занимают в идеальной решетке, быстро уменьша-
уменьшаются по мере удаления от дефекта. Поэтому кристалл можно
условно разделить на две области: малая область, непосредствен-
непосредственно примыкающая к дефекту, где искажение решетки значитель-
значительно, и весь остальной кристалл, где искажения малы. Эта вторая
область с достаточной степенью точности может рассматриваться
как сплошная упругая среда. В теории дислокаций делается еще
следующий шаг по пути схематизации; несовершенства структу-
структуры считаются локализованными вдоль некоторой линии, так на-
называемой линии дислокации, и напряженное состояние описыва-
описывается как результат решения некоторой задачи теории упругости,
соответствующей распределению определенного вида особенно-
особенностей вдоль линии дислокации.
Такое приближение не всегда достаточно и в ряде случаев
в рассмотрение вводится более сложная схема, когда для первой
области принимается во внимание реальный характер между-
междуатомного взаимодействия.
Теория упругих дислокаций, т. е. построение и изучение ре-
решений уравнений теории упругости, соответствующих некоторо-
некоторому распределению особенностей на заданных линиях, создана
достаточно давно. Основные результаты здесь принадлежат Воль-
терра. Эта теория носила довольно формальный характер и не
имела сколько-нибудь серьезных приложений до тех пор, пока
к дислокационным представлениям не прибегла физика кристал-
кристаллов. С тех пор появилось очень большое количество исследова-
исследований, направленных на развитие формальной теории дислокаций,
и к настоящему времени она приобрела достаточно законченный
характер. Здесь будут излагаться лишь элементы формальной
теории упругих дислокаций, непосредственные же прило-
приложения к физике кристаллов носят чисто иллюстративный ха-
характер.
Для того чтобы ввести понятие о кристаллической дислока-
дислокации и установить ее связь с упругой дислокацией, рассмотрим
модель простейшего кристалла, решетка которого такова, что
соседние атомы помещены в вершинах куба. На рис. 14.1.1 изо-
изображена одна атомная плоскость такой решетки, линии, соеди-
соединяющие соседние атомы, образуют одинаковые квадраты. Такое
расположение атомов возможно тогда, когда кристалл свободен
от дефектов. При наличии дефектов сохранение правильной
квадратной сетки уже невозможно, силы, действующие на каж-
каждый атом со стороны его соседей, становятся неодинаковыми и
решетка искажается. На рис. 14.1.2 изображена атомная плос-
плоскость искаженной решетки. Вне области, ограниченной конту-
контуром Г, искажение, как видно, невелико. Кристалл с таким не-
незначительным искажением решетки называется «хорошим» кри-
кристаллом, точнее, область вдали от дефекта называется «хорошей»
областью. Но внутри контура Г, заключающего в себе дефект,
§ 14.1. ДИСЛОКАЦИИ В КРИСТАЛЛАХ
455
искажение сильнее. Область кристалла с сильно искаженной ре-
решеткой называется «плохой».
Осталось дать формальный признак, позволяющий отличать
хороший кристалл от плохого. Выберем в идеальной или, как
мы будем говорить, эталонной решетке некоторый путь обхода,
начинающийся от какого-либо узла, например замкнутый путь
abcda. Воспроизведем тот же путь в реальном хорошем кристал-
кристалле, отправляясь от произвольно выбранного узла а. Кристалл
считается хорошим, если этот путь может быть воспроизведен
1
\
i T
<l I
у
9
—к-
т
I
I
l\ 1 I
—о
j I
I
Рис. 14.1.1
а' е' Ьт
Рдс. 14.1.2
единственным и несомненным способом. Действительно, сравни-
сравнивая рис. 14.1.1 и рис. 14.1.2, мы не сомневаемся в том, какой узел
искаженной решетки соответствует тому или иному узлу эта-
эталонной решетки, достаточно только выбрать соответствующие
пары соседних атомов, чтобы установить отправную точку и на-
направление выхода; после этого мы без всяких колебаний прово-
проводим контур а'Ъ'с&'а. Если путь обхода а'Ъ'с'&'а не окружает
плохой области, т. е. не включает в себя контур Г, он будет
замкнутым, и при возвращении в точку а эталонной решетки
мы вернемся в точку а1 реальной решетки, из которой был на-
начат обход. Но если, как показано на рис. 14.1.2, путь обхода
окружает плохую область, то может случиться, что путь закон-
закончится не в точке а\ а в точке е\ как показано на чертеже.
В этом случае дефект решетки, заключенный внутри контура Г,
называется дислокацией. Вектор а'е', представляющий собою
величину незамыкания, называется вектором Бюргерса. Более
удобно определять вектор Бюргерса не на искаженной решетке,
а на эталонной, тогда величина его и направление не зависят
от выбора исходной точки обхода и пути, лишь бы он окружал
плохую область.
В рассмотренном случае говорят, что в теле произведена дис-
дислокация, характеризуемая вектором Бюргерса Ь. Легко предста-
представить себе, каким образом можно создать в кристалле дислока-
456 гл- 14- дислокации в упругом теле
цию. Возьмем лист резины, разграфленный на клетки, разрежем
его вдоль одной из нанесенных линий, сместим верхний край
разреза относительно нижнего и начнем склеивать края разреза,
заботясь о том, чтобы вертикальные линии совпадали. Сначала
это можно делать без больших усилий, за счет незначительной
деформации резины, по мере приближения к концу разреза это
становится все более трудным, резину приходится сильно дефор-
деформировать. Наконец, когда расстояние до конца остается совсем
небольшим, мы вынуждены склеить края как попало, не забо-
заботясь о совпадении линий, так как сверху оказываются лишние
линии.
Таким образом, конец разреза оказывается окруженным пло-
плохой областью. Если теперь воспроизвести на деформированном
и склеенном листе замкнутый путь, заданный на листе недефор-
мированном или эталонном, этот путь окажется разомкнутым,
причем вектор Бюргерса равен величине произведенного сдвига.
Хорошая область кристалла может рассматриваться как склеен-
склеенная упругая среда, поэтому формальная теория упругих дисло-
дислокаций, рассмотренная в общих чертах в § 11.4, а также для
частных случаев в § 9.2 и 10.3, находит приложение в физике
металлов.
Однако, как уже было подчеркнуто, предметом этой главы
служат не физические приложения, а дальнейшее развитие фор-
формальной теории.
В частности, для металлов модель простой кубической решет-
решетки, положенная здесь в основу рассмотрения, мало реальна.
Наибольший интерес представляют дислокации, расположенные
в кристаллографических плоскостях скольжения с вектором
Бюргерса, направленным в сторону возможного скольжения. Для
гранецентрированной кубической решетки, например, таких си-
систем скольжения (плоскость и направление в этой плоскости)
всего двенадцать. Геометрическая теория поведения дислокаций
в пересекающихся системах скольжения представляет собою
раздел физики твердого тела, она излагается в многочисленных
руководствах и здесь затронута не будет (см. например Ван
Бюрен).
§ 14.2. Дислокации Бюргерса. Сингулярные члены
В § 11.4 были получены общие формулы, определяющие поле переме-
перемещений для дислокаций простейшего вида, а именно таких, которые соот-
соответствуют лишь поступательному относительному перемещению сторон раз-
разреза. Как это явствует из теоремы Вейнгартена и как предполагается в
общей теории Вольтерра, относительное перемещение, вообще говоря, долж-
должно соответствовать движению твердого тела, т. е. содержать наряду с посту-
поступательным перемещением еще поворот.
В физике твердого тела особую роль играют именно простейшие дисло-
дислокации рассмотренного типа, которые мы будем называть дислокациями Бюр-
§ 14.2. ДИСЛОКАЦИИ БЮРГЕРСА. СИНГУЛЯРНЫЕ ЧЛЕНЫ
457
герса*). Общие формулы § 11.4 выражают поле перемещений через поверх-
поверхностные интегралы по поверхности 2, проходящей через контур Г. Посколь-
Поскольку на поверхности 2 напряжения непрерывны, то можно ожидать, что вы-
выбор той или иной контрольной поверхности, проходящей через контур Г,
несуществен. Поэтому поверхностные интегралы, фигурирующие в форму-
формулах A1.4.2), должны преобразовываться в интегралы по контуру Г. Соот-
Соответствующий вывод можно найти, например, в статье Де Вита, изданной в
качестве приложения к книге Эшелби. Здесь мы изложим другой вывод
формул для перемещений, соответствующих дислокаций, который принад-
принадлежит Бюргерсу. Будем отправляться от решения для сосредоточенной си-
силы Р, приложенной в произвольной точке неограниченной среды, которое
мы запишем в первоначальном, непреобразованном виде так, как это сле-
следует из представления Папковича — Нейбера
и —
grad
A4.2.1)
Здесь i|? — непрерывная функция, удовлетворяющая уравнению Пуассона.
Задача состоит в определении вектора и смещения в неограниченном упру-
упругом теле таким образом, чтобы при обходе по любому контуру, окружающе-
окружающему трубку дислокации, этот вектор получал приращение, равное постоян-
постоянному вектору Бюргерса Ь. Трубкой дислокации мы будем называть торо-
тороидальную полость, окружающую замкнутую линию дислокации Г и такую,
что вне этой полости кристалл может считаться хорошим. В переводе на
язык механики сплошной среды это значит, что
путь обхода не должен приближаться к линии Г
настолько, чтобы уравнения линейной теории
упругости потеряли силу.
Позаботимся прежде всего о том, чтобы по-
получить требуемую многозначность. Гармониче-
Гармоническая функция, претерпевающая заданный разрыв
при переходе через поверхность 2, натянутую
на контур Г, известна; это интеграл Гаусса или
потенциал двойного слоя постоянной интенсив-
интенсивности, нанесенного на поверхность,
Рис. 14.2.1
Здесь г — расстояние от произвольной точки пространства до точки поверх-
поверхности 2, v — нормаль к этой поверхности.
Будем обозначать координаты точек поверхности через ?*, радиус-век-
радиус-вектор точки поверхности через %, соответственно координаты произвольной
точки пространства с радиусом-вектором х будут х%. Фигурирующая в
A4.2.2) производная от 1/г по нормали будет
Но (хх — |г)/г — это направляющие косинусы радиуса-вектора, выходяще-
выходящего из точки \ к точке х (рис. 14.2.1), следовательно,
cos a
dv '""""' —
*) В современной физической литературе термин «дислокация» приме-
применяется именно к дислокациям Бюргерса. Дислокации Вольтерра, соответ-
соответствующие поворотам краев разреза, называют дисклинациями.
458
ГЛ. 14. ДИСЛОКАЦИИ В УПРУГОМ ТЕЛЕ
Выражение, стоящее под знаком интеграла в формуле A4.2.2), представля-
представляет собою телесный угол, под которым виден из точки | элемент поверхно-
поверхности 2, а функция ф есть телесный угол, под которым виден из точки х кон-
контур Г. Таким образом,
Q
Полагая
6Q
A4.2.3)
V I
мы выделим ту часть вектора перемещения и, которая обусловливает тре-
требуемую неоднозначность. Легко убедиться в том, что формула A4.2.3) пред-
представляет собою главную часть перемеще-
перемещения, вызванного непрерывным распреде-
распределением двойных сил. Действительно, если
в некоторой точке поверхности 2 прило-
приложена сила — 6q, а в точке г', находящейся
на нормали и отстоящей от поверхности
на расстоянии 5s, приложена сила + 6#
(см. рис. 14.2.2), то главная часть переме-
перемещения по формуле A4.2.1) выразится
следующим образом:
dgds
4я|д,
d_ M \
dv\r J'
Рис. 14.2.2
Уменьшая 6s и увеличивая модуль 8q так,
чтобы произведение 6g5s оставалось по-
постоянной величиной порядка малости d2, получим двойную силу. Итак,
формула A4.2.3) даст перемещение от распределения на поверхности
двойных сил интенсивностью 6q ds—biid?,. Момент, приходящийся на еди*
ницу площади, есть' 6# X v5s или \ib x v d 2. Интегрируя по поверхности,
найдем главный момент всех сил, действующих на поверхность,
Л/=
A4.2.4)
Но по смыслу функция ф должна зависеть лишь от выбора контура Г, но
не от натянутой на его поверхности 2. Поэтому момент М должен свестись
к моменту от некоторых сил, распределенных по контуру Г, следовательно,
интеграл по поверхности, определяющий момент М, должен преобразовы-
преобразовываться в контурный интеграл. Чтобы выполнить это преобразование, будем
отправляться от формулы Стокса
2
Положим в этой формуле v = /в, где е — постоянный вектор, / — скаляр-
скалярная функция координат. Тогда " ' i:
rot i? = Vx/e = V/Xe = grad fXe.
v в формул'}
юлучим
;Ь= — Г grad/Xv d2.
Внося выражения для v и rot v в формулу. Стокса и сокращая на постоян-
постоянный векторный множитель ef получим
A4.2.5)
г
§ 14.3. ДИСЛОКАЦИИ БЮРГЕРСА. ПОЛНОЕ РЕШЕНИЕ 459
Вектор Бюргерса Ъ может быть представлен как градиент скалярного про-
произведения Ъ§, поэтому формулу A4.2.4) можно переписать следующим об-
образом:
M = -\i§(bl)dl. A4.2.6)
г
Итак, момент М есть момент от сил, приложенных к контуру. Чтобы оп-
определить сами эти силы, воспользуемся тождеством
Интеграл по замкнутому контуру от второго члена правой части равен ну-
нулю, поэтому A4.2.6) можно переписать следующим образом:
Теперь видно, что на каждый элемент d% линии контура действует сила,
равная —\ibxd%. Второе слагаемое решения будет соответствовать рас-
распределению равных и противоположных сил по формулам A4.2.1)
- A4-2'7)
Выражение ю** может быть представлено также в виде поверхностного ин-
интеграла по формуле A4.2.7)
и** = - 4я" ) bx%mdTx v ^ = 4S" J Urad 7 Fv) ~~ v Г grad Til dI"
A4.2.8)
Сумма w* -f- и** представляет собою ту часть вектора w, которая обеспечи-
обеспечивает выполнение условий требуемой неоднозначности перемещения и от-
отсутствия сил на поверхности дислокационной трубки. Однако вектор и* +
+w** не удовлетворяет уравнениям теории упругости; в соответствии со
структурой решения для сосредоточенной силы к нему нужно добавить гра-
градиент некоторой функции Ч*. Итак,
и = и* +'и** + grad Т. A4.2.9)
§ 14.3. Дислокации Бюргерса. Полное решение
Для того чтобы определить функцию Ч?, подставим A4.2.8) в уравне-
уравнения Ламе
0.
Учитывая, что и* и ю** — гармонические векторы, отсюда получим
Здесь 0=div w, постоянная в правой части A4.3.1), принята равной нулю,
поскольку нам достаточно выбрать любое частное решение A4.3.1), веду-
ведущее себя надлежащим образом на бесконечности и непрерывное вместе со
своими производными на поверхности 2, т. е. представимое в виде контур-
контурного интеграла, не зависящего от выбора контрольной поверхности. Выпол-
Выполнение этого второго условия встречает наибольшие трудности. Вычислим
теперь дивергенции векторов и* и и**.
460 гл- 14- дислокации в упругом теле
а. Дивергенция вектора в*. Отправляясь от выражения для а* в ви-
виде поверхностного интеграла (формулы A4.2.2) и A4.2.3)), найдем
б. Дивергенция вектора и**. Будем отправляться от представления
этого вектора в виде поверхностного интеграла A4.2.8). Получим
Но 1/г есть гармоническая функция:
Поэтому
е** = - jz Гъ. д* (-) ds = е*.
4jlJ ldx.dv\rJ
2
2
Теперь уравнение A4.3.1) может быть записано следующим образом:
Частное решение этого уравнения можно найти следующим образом. За-
Заметим, что Дг = 2/г. Отсюда следует
dv~~2 дх
2- д
1 Я+ ц
Умножим обе части этого равенства на jj-. , 2» &$t свернем по индек-
индексу j и проинтегрируем по поверхности. Получим
J 2
Сравнивая с уравнением A4.3.2), мы убеждаемся, что частное решение это-
этого уравнения есть
Но это частное решение претерпевает разрыв нормальной производной на
поверхности 2 и не может быть преобразовано в контурный интеграл. Что-
Чтобы исправить дело, к функции Ч1" необходимо добавить надлежащим об-
образом выбранную гармоническую функцию. Воспользуемся для этого сле-
следующей вспомогательной формулой векторного анализа:
rot (vXw) = Vx (vxw) = (m>V) » — (i?V) w — w div v -f v div>.
§ 14.4. ПРЯМОЛИНЕЙНЫЕ ДИСЛОКАЦИИ
Положим в этой формуле v = Ъ, ио = (х — |)/г. Получим
b +
rot FX- „ i— a ui~r r •
Здесь e;. — единичные векторы координатных осей.
Преобразуем теперь подынтегральное выражение в формуле A4.3.3)
ь.у.
Выражение, заключенное в квадратные скобки, отличается от величины
rot (bx{x — 1)/г) только знаком перед вторым членом. Определим теперь
функцию W следующим образом:
Она отличается от функции^! на величину -^ « -l-2ili \ Т"^' ^та Функ"
ция представляет собою потенциал простого слоя на поверхности 2, т. е.
гармоническую функцию с разрывом нормальной производной, который ком-
компенсирует соответствующий разрыв у функции ^Fi.
Дадим теперь сводку окончательных формул:
и = и* + и** + grad ?
или
С помощью формул предыдущего и настоящего параграфов это выражение
может быть представлено через поверхностные интегралы.
Остается сделать некоторые уточнения, относящиеся к выбору знаков.
Будем считать, что система координат правая. Положительное направление
нормали к поверхности 2 и положительное направление обхода контура Г
таковы, что со стороны положительной нормали обход представляется про-
происходящим против часовой стрелки. При переходе через поверхность 2 со
стороны положительной нормали телесный угол получает отрицательное
перемещение, равное — 4л;, и соответственно перемещение изменяется на
величину вектора Бюргерса Ь. Следовательно, вектор Бюргерса представ-
представляет собою перемещение отрицательной стороны поверхности разреза по
отношению к ее положительной стороне.
§ 14.4. Прямолинейные дислокации
Винтовая дислокация, рассмотренная в § 9.2, и краевая дислокация,
построенная в § 10.3 как пример решения некоторой плоской задачи теории
упругости путем представления решения через функции комплексной пере-
переменной, служат примерами дислокаций, для которых линия дислокации —
прямая. Те же результаты могут быть получены и путем применения об-
общих формул § 14.3; это и будет сделано в настоящем параграфе.
462
ГЛ. 14. ДИСЛОКАЦИИ В УПРУГОМ ТЕЛЕ
а. Винтовая дислокация. Направим линию дислокации по оси я3, при-
примем за поверхность 2 левую полуплоскость на рис. 14.4.1. Телесный угол,
под которым видна левая полуплоскость из точки М с координатами яа,
равен
G4
Для винтовой дислокации вектор Бюргерся имеет составляющие (О, О, Ь),
поэтому
В данном случае вектор d% направлен по оси #3, так же как вектор &, их
векторное произведение равно нулю, следовательно, и** = 0. Векторное про-
д изведение Ъх{х — %) направлено
7 перпендикулярно оси х3, поэтому
при скалярном умножении его на
d% получится также нуль и ^? = 0.
Итак, единственная отличная от ну-
нуля компонента вектора перемеще-
перемещения и есть
Все компоненты напряжения кроме
tfi3 и а2з обращаются в нуль, для ка-
касательных напряжений получаются следующие выражения:
2л
2л
A4.4.2)
б. Краевая дислокация. Направим по-прежнему ось дислокации по оси
«з, вектор Бюргерса — по оси х\. Телесный угол Q мы уже нашли при рас-
рассмотрении винтовой дислокации, следовательно,
Обозначая через d% элемент оси я3, найдем, что векторное произведение
bXd% имеет единственную отличную от нуля составляющую по оси х2,
равную — bd%. Таким образом,
** _ л ** _ __ — Г J^k ** _ л
и1 ~ ' и2 4л J г • из
Из теории потенциала известно, что интеграл в выражении и2 приводит-
приводится к величине In (я^ -f- x^), таким образом,
Л-Лв О /О Ci\
Переходим к вычислению функции Ч?. Произведение [6х(# — 1)]
§ 14.5. ЭНЕРГИЯ ДИСЛОКАЦИИ 463
сводится в данном случае к величине 6x2^1; таким образом,
1 Х+У +Г bx2dt
* = ~Ы Я + 2ц. J —Т~-
Дифференцируем Y по a;i и по я2:
Теперь мы можем выписать формулы для перемещений
ь \ *.
|1+
Ь Г Е ,2, ,ч , h+H Ж2
М2 ~~ 2я I 4- 2а 1п ^1 *" Х2У "Г я + 2|х д.2 . ^2 •
L 1 ' 2J
Не приводя очевидных вычислений, выпишем формулу для вращения
°*12=-Jk ^2^2- A4'4'4)
Формулы для напряжений уже были приведены в § 10.3. Если вектор Бюр-
герса положителен, дислокация также считается положительной. Точку пе-
пересечения положительной дислокации с плоскостью д
х\0х2 принято изображать значком в форме пере-
вернутой буквы Т, как показано на рис. 14.4.2.
Краевую дислокацию можно создать разными спо-
способами, например сдвигая края разреза по левой
или правой полуплоскости ххОхъ, разрезая по верх-
верхней или нижней полуплоскости Х20хъ и перемещая
края разреза, в одном случае с добавлением слоя
материала, в другом —- с его удалением. Условное
«XU Л. V,/ k/ JLL1A«/X1A* JJ r~Sjr J VA'Jt V/ К/1 \J Jf ^UVlVXXll V1U( V WJ.VJJ1XW ^
обозначение краевой дислокации расшифровывает^ 1
ся следующим образом. Горизонтальная переклади- Рис. 14.4.2
на указывает на направление вектора Бюргерса,
вертикальная черточка символизирует слой материала, который нужно вве-
ввести в разрез, чтобы создать дислокацию.
§ 14.5. Энергия дислокации
Для создания дислокации должна быть затрачена некоторая работа, на-
накапливаемая в виде упругой энергии дислокации. Наиболее простой спо-
способ подсчета этой энергии заключается в следующем. Предположим, что в
теле сделан разрез и к поверхностям разреза прикладываются внешние си-
силы, распределенные точно таким же образом, как распределяются напря-
напряжения на поверхности 2, когда дислокация уже создана. Работа этих сил
на перемещении Ь по теореме Клапейрона, равна удвоенной энергии дисло-
дислокации. Таким образом,
-¦я
464
ГЛ. 14. ДИСЛОКАЦИИ В УПРУГОМ ТЕЛЕ
здесь S—вектор напряжения на поверхности 2, S = ff^v
тельно,
Следова-
СледоваПрименим эту формулу к винтовой дислокации. Предположим, что разрез
произведен по полуплоскости х2 = 0 (хх > 0). Касательное напряжение по
формуле A4.4.2) равно
6 1
Умножим на вектор Бюргерса Ъ и проинтегрируем по х\ в пределах от хх
= с до х\ = R. Получим выражение энергии на единицу длины
п R _ п
A4.5.2)
Величина с — это радиус ядра дислокации, имеющий порядок Ъ. Желая вы-
вычислить энергию более точно, мы должны были бы прибавить сюда энергию
ядра, которая уже не может быть найдена методами теории упругости, для
ее подсчета необходимо прибегать к атомным моделям. Величина R пред-
представляет собою размер тела, для тела бесконечных размеров и энергия дис-
дислокации становится бесконечно большой. В связи с этим можно сделать
следующее замечание. При построении дислокации мы исходили из неог-
неограниченной среды, в предположении бесконечных размеров тела были вы-
вычислены напряжения. В теле конечных размеров, вообще говоря, возникает
дополнительная система напряжений, которая находится из условия ра-
равенства нулю сил, действующих на свободную поверхность. Для винтовой
дислокации как раз дело обстоит просто, поверхность кругового цилиндра,
имеющего осью линию дислокации, свободна от
напряжений. Поэтому формулы A4.4.2) и выра-
выражение для энергии A4.5.2) совершенно точ!ны,
если линия дислокации совпадает с осью кру-
} гового цилиндра радиусом R. В тех случах, ког-
~~ да напряжения от дислокации не оставляют
границу свободной от усилий, появляется до-
дополнительная энергия (положительная или от-
отрицательная), которая называется энергией вза-
взаимодействия дислокации со свободной поверх-
поверхностью. Пример дислокации в теле ограничен-
ограниченных размеров будет рассмотрен ниже.
Вычислим теперь энергию краевой дислока-
дислокации. Касательное напряжение в плоскости х2 =
= 0 по формуле A0.3.6) равно
Ъ\х 1
Рис. 14.5.1
2лA —v) х
В правой полуплоскости оно направлено так же,
как вектор Бюргерса Ъ, следовательно, энергия
найдется совершенно таким же способом, как в случае винтовой дисло-
дислокации
A4.5.3)
Вместо того чтобы делать разрез в плоскости х2 = 0 и сдвигать две сто-
стороны разреза одну относительно другой (рис. 14.5.1, а), можно было еде-
§ 14.6. ПЛОСКАЯ ДИСЛОКАЦИЯ 465
лать разрез по плоскости хх = 0, раздвинуть края разреза на величину Ъ,
заполнить образовавшуюся щель добавочным материалом и спаять (см.
рис. 14.5.1, б). Работа, затрачиваемая при этом, есть
R
J
Знак «минус» стоит здесь потому, что положительная нормаль к верх-
верхней полуплоскости х2Ох3 направлена влево, при этом, если смотреть со сто-
стороны нормали, обход полуплоскости по оси хъ представляется происходя-
происходящим против часовой стрелки. По формуле A0.3.6) при х\ = 0
_ Ь\х 1
an — — 2я A — v) х2 '
Легко убедиться, что таким способом для энергии дислокации опять полу-
получается выражение A4.5.3).
§ 14.6. Плоская дислокация
Предположим теперь, что линия дислокации лежит в плоскости хз = 0
и вектор Бюргерса находится в той же плоскости и направлен по оси х\.
Определим касательные напряжения в плоскости дислокации; для большин-
большинства приложений только эти напряжения представляют интерес. В ходе
вычислений нам понадобятся производные от перемещений щ, 3, из, и и2, з
и из, 2. Для нахождения производных от составляющих вектора и* мы вос-
воспользуемся тем обстоятельством, что функция qp = —Q/Dji) представляет
собою потенциал скоростей в неограниченной жидкости при наличии вихре-
вихревой нити единичной интенсивности. Скорость жидкости выражается при
этом формулой Био — Савара
1 Г* dl
г
В нашем случае отлична от нуля только компонента перемещения
Следовательно,
г
Вычисляя вектор и** по формулам A4.3.5), найдем
tt« = 0, u**=0, и3** = ^
г
Здесь г2 = {х\ — \{J-{-(х2 — 1гJ. Вычислим теперь функцию Ч*":
—L с i
/ ' с~~ 2A — v) '
г
30 Ю. Н. Работнов
466 ГЛ- 14- ДИСЛОКАЦИИ В УПРУГОМ ТЕЛЕ
Соответствующие составляющие перемещения равны
г г
Продифференцируем Ч^ и Ч'.г по я3, а 4е,3 по хх и х2 и положим xz = 0.
Получаем
сЬ
Подсчитывая сдвиги ег\ и е32, найдем следующие выражения для касатель-
касательных напряжений:
*2~h
A4.6.1)
Формулы A4.6.1) имеют особенно простой вид тогда, когда коэффициент
Пуассона среды принят равным нулю,
&Р* ^г^/^ следовательно, с = 1/2. В этом случае
a3i =
A4.6.2)
Рис. 14.6.1
Формула для отличного от нуля напря-
напряжения Оз1 может быть истолкована таким образом: величина
представляет собою удвоенную площадь треугольника, изображенного штри-
штриховкой на рис. 14.6.1, сторонами которого являются элемент дуги контура Г
и две прямые, соединяющие концы элемента с точкой х. Выражение для
(Тз1 можно переписать теперь следующим образом:
%-. A4.6.3)
§ 14.7. Кольцевая дислокация
На основе вышеивложенной теории плоских дислокаций мы можем
рассмотреть напряженное состояние, создаваемое дислокацией в форме
кругового кольца радиусом р. Ограничимся рассмотрением случая, когда
v = 0; все вычисления можно довести до конца и для общего случая, од-
однако выкладки при этом более сложны. При сделанном допущении каса-
§ 14.7. КОЛЬЦЕВАЯ ДИСЛОКАЦИЯ
467
тельное напряжение направлено по вектору Бюргерса и постоянно в точ-
точках, равноудаленных от центра кольца дислокации, как ясно по виду фор-
формул A4.6.2). Поэтому нам достаточно вычислить т для точки оси xi, отстоя-
отстоящей на расстояние г от центра. Вводя обозначения, показанные на
рис. 14.7.1, и применяя формулу A4.6.2),
найдем
2Я
T=4ttJ(
pr cos ф— р"
A4.7.1)
Введем обозначение
J (Г, Р) = j (р2
/ y"~'
\ \
\ \
-N
P/
A9
V
1*
¦
/
/
?
/
/'
"
\ \
\ \
i I
, /
' — 2грсозфI/2-
A4.7.2) Рис. илл
Формулу A4.7.1) можно теперь записать следующим образом:
h»-9J Ъ» д ¦'-« A4.7.3)
Интеграл A4.7.2) — эллиптический, полагая ф = 2гр + я, приводим его к
обычному виду полного эллиптического интеграла первого рода и получаем
К
A4.7.4)
Пользуясь формулой A4.7.3), мы можем без труда получить явное выраже-
выражение для касательного напряжения через эллиптические интегралы первого
и второго рода, однако этот вывод для наших целей бесполезен.
Некоторый интерес представляет зато вопрос о характере распределе-
распределения касательных напряжений вблизи самой линии дислокации, когда г
весьма близко к р. При этом модуль эллиптического интеграла A4.7.4) ста-
становится близким к единице и для К (к) применимо следующее разложение:
к (к) = in-y + \ (hi~y -1j к'2 + ...
Здесь к' — дополнительный модуль, к'2 = 1 — к2. В нашем случае к = 2>'гр/
1(г + р) и, с точностью до первой степени разности р — г, к' = (р — г)/Bр).
Ограничиваясь первым членом в разложении К (к) и используя формулу
A4.7.3), получим
Здесь выписаны члены, обращающиеся в бесконечность при г -> р. Первый
член дает обычную для дислокации особенность, но наряду с ним еще име-
имеется член, обращающийся в бесконечность как логарифм (р — г).
Займемся теперь вычислением энергии кольцевой дислокации. По фор-
формуле A4.5.1)
2Я р-С
С
р
Ь [' С
о о
30*
468 ГЛ.14. ДИСЛОКАЦИИ В УПРУГОМ ТЕЛЕ
В качестве верхнего предела при интегрировании по г выбран не радиус
дислокации р, а величина р — с. Так же как при вычислении энергии ли-
линейной дислокации мы считаем, что формулы для напряжений справедли-
справедливы на расстоянии от линии дислокации, превышающем радиус «плохой»
области с.
Воспользуемся вторым выражением для т по формуле A4.7.3) и проин-
проинтегрируем по частям. Получаем
W = ±JL [A/]P-C~ J rJdr\. A4.7.6)
Применяя уже использованную нами выше формулу для полного эллип-
эллиптического интеграла первого рода при значении модуля, близком к единице,
найдем, что первый член в фигурных скобках в формуле A4.7.6) равен
Интеграл, являющийся вторым членом в фигурных скобках, не расходится
при верхнем пределе, равном р, поэтому мы будем вместо него вычислять
интеграл
Jr/dr.
о
Воспользуемся первоначальным выражением A4.7.2) для 7, внесем его под
знак интеграла и переменим порядок интегрирования. Вычислим сначала
С rjr / . Ф l+sin(q)/2)\
г* + р2 _ 2ф cos фI/2 = Р B S1H Т + COS ф Ш cos (ф/2) J.
о
J
Осталось проинтегрировать это выражение по ф в пределах от нуля до 2я.
Соответствующие интегралы вычисляются элементарно (второй берется ин-
интегрированием по частям) и мы получаем
Р
rJ dr = 8р.
о
Окончательное выражение для энергии будет следующим:
2 / \
W = 2яр Jgjj- (in ? + 3 In 2 — 2J.
Энергия, приходящаяся на единицу длины окружности, оказывается равной
i-^- + 31n2 —I
Конечно, оценка величины с не настолько точна, чтобы следовало сохра-
сохранять множитель 1,08, и линейную плотность энергии кольцевой дислокации
можно определять по формуле
§ 14.8. ДИСЛОКАЦИИ В ТЕЛАХ КОНЕЧНОГО РАЗМЕРА 469
Заметим, что при v = 0, как было принято, энергия винтовой и краевой
дислокации одинакова. Расчет, сделанный без этого предположения, приво-
приводит к формуле, отличающейся от формулы A4.7.7) лишь множителем
11 1
2 + 2 1 —v*
Таким образом, линейная энергия кольцевой дислокации равна среднему
значению энергии краевой и винтовой дислокаций в блоке, размер которого
равен радиусу кольцевой дислокации.
Очевидно, что кольцевая дислокация в ненапряженном теле существо-
существовать не может, энергия монотонно возрастает с возрастанием радиуса и не
существует конечного значения радиуса, для которого энергия минимальна.
Если в плоскости скольжения действует касательное напряжение т0, усло-
условие равновесия дислокации будет следующим:
0W
Это условие представляет собою результат применения начала возможных
перемещений к телу, содержащему дислокацию. Отсюда получается
§ 14.8. Дислокации в телах конечного размера
Если известно напряженное состояние, соответствующее дислокации в
неограниченной упругой среде, то решение задачи о дислокации в теле
конечных размеров приводится к статической задаче теории упругости для
этого тела при заданных усилиях на поверхности; эти усилия и напряже-
напряжения, вызванные дислокацией, должны взаимно уничтожаться.
Энергия дислокации по-прежнему будет выражаться формулой A4.5.1),
но компоненты напряжения в этой формуле определяются в результате ре-
решения задачи теории упругости с удовлетворением граничным условиям;
поэтому величина энергии будет зависеть от
положения дислокации в теле. Здесь мы рас-
рассмотрим простейший пример — винтовую дис-
дислокацию в круговом цилиндре бесконечной
длины, ось которой параллельна оси цилинд- . н^д ^ , „ -
ра, но не совпадает с ней. Пусть будет ради- \у^ 1 j z 7
ус цилиндра R, расстояние винтовой дислока-
дислокации от оси ОС\ = р. Проведем ось х\ через
центр сечения и ось дислокации, как пока-
зано на рис. 14.8.1, и поместим вторую дисло- гжс. 14.о.1
кацию противоположного знака в точке С2,
находящейся на оси х\ на расстоянии R2!p от начала координат. По форму-
формулам A4.4.2) напряжения в неограниченной среде для такой пары дислока-
дислокаций выражаются следующим образом:
Здесь пиг2 — расстояния точки М от точек С\ и Сч. соответственно.
Нормальная к контуру составляющая касательного напряжения на ок-
окружности радиусом р определяется так:
470 гл- 14- дислокации в упругом теле
Подставляя сюда значения напряжений по формулам A4.8.1) и замечая,
что из подобия соответствующих треугольников
г2: п = R : р,
мы убеждаемся, что хп = 0, следовательно, формулы A4.8.1) определяют
напряженное состояние от винтовой дислокации в круговом цилиндре, тор-
торцевые сечения которого закреплены от поворота. Последнее обстоятельство
вытекает из тех предположений, которые были приняты при выводе основ-
основных формул для винтовой дислокации в § 9.2 и 14.4. В сечениях такого
закрепленного цилиндра возникает крутящий момент, равный моменту от
напряжений о'31 и о^. Величина этого момента
Вычисляя соответствующие интегралы, находим
M=-^-(R2-p2). A4.8.2)
Если торцы цилиндра не закреплены, в нем возникают напряжения круче-
кручения от момента, равного и противоположного моменту 71/, значение которо-
которого дается формулой A4.8.2), и цилиндр закручивается на некоторый угол,
который находится по обычной формуле теории кручения. Эти дополни-
дополнительные напряжения кручения
Энергия такого цилиндра, содержащего дислокацию, получается по формуле
R
=!W
р+с
Здесь т = о2+ o\j'2 при х2 = 0. Окончательный результат получается сле-
следующим:
w = wo + "и" Iln A - ?)- A - ?2J] • A4.8.4)
Здесь Wo — энергия винтовой дислокации в неограниченной среде, опреде-
определяемая по формуле A4.5.2), второй же член формулы может быть назван
энергией взаимодействия со свободной поверхностью. В формуле принято
? = р/#. Энергия дислокации, рассматриваемая как функция ее относитель-
относительной координаты ?, имеет минимум при ? = 0 и максимум при ? =
= | / 2 = 0,541. Таким образом, при ? = 0 дислокация находится в
состоянии устойчивого равновесия, при ? = 0,541 — в состоянии неустойчи-
неустойчивого равновесия.
За последние годы уделялось большое внимание изучению так называе-
называемых нитевидных кристаллов, обладающих исключительно высокой проч-
прочностью. Одна из теорий образований подобного рода кристаллов предпола-
предполагает, что в нем содержится одна единственная винтовая дислокация, на-
направленная вдоль оси. Соответствующее закручивание может быть обнару-
обнаружено экспериментально при помощи рентгенографии. В ряде случаев это
закручивание было обнаружено. Сделанный в этом параграфе вывод пока-
показывает, что действительно винтовая дислокация, направленная по оси ци-
цилиндра, будет сохраняться; чтобы вывести ее, необходимо преодолеть по-
потенциальный барьер, равный разности энергий в положении максимума в
минимума. При этом неясно, каким образом можно это сделать.
§ 14.9. ВОЗМОЖНЫЕ ДВИЖЕНИЯ ДИСЛОКАЦИЙ 471
§ 14.9. Возможные движения дислокаций
В неограниченной среде поле напряжений, соответствующее дислока-
дислокации, не зависит от положения линии дислокации. Энергия дислокации так-
также не зависит от положения; следовательно, перемещение линии дислока-
дислокации как целого не требует дополнительной работы, дислокация свободна
перемещаться как угодно, если считать, что в ядре дислокации также
действуют консервативные силы и при перемещении ее в ядре не происхо-
происходит диссипации энергии. В действительности это, конечно, не так и для
перемещения дислокации необходимо затратить известную работу, но в
теории упругости все силы предполагаются консервативными.
С другой стороны, в кристаллической решетке, которую мы моделируем
сплошной средой, энергия дислокации будет меняться в пределах одного
междуатомного расстояния. Для того чтобы вывести ее из положения, со-
соответствующего минимуму энергии, необходимо преодолеть потенциальный
барьер. Говоря о движении дислокаций, мы имеем в виду движения бес-
бесконечно медленные. Движущаяся с конечной скоростью дислокация обла-
обладает не только потенциальной энергией, но также и кинетической и для
сообщения этой скорости дислокации, быв-
бывшей в покое, нужно затратить некоторую
энергию.
Перемещение линии дислокации соответ-
соответствует конечному относительному перемеще-
перемещению частиц материала по обе стороны от той
поверхности, по которой движется линия ди-
дислокации. При этом возможны только та-
такие движения, которые не приводят к нару-
нарушению сплошности тела. Это значит, что от-
носительное перемещение представляет собою
скольжение частиц по поверхности, ометае-
мой движущейся дислокацией. Те движения, р 14 9 1
при которых частицы перемещаются в об- * ' '
ласть, уже заполненную материалом, оче-
очевидно невозможны. Мы исключаем из рассмотрения и такие случаи, ког-
когда за движущейся дислокацией образуются пустоты. Чтобы отделить воз-
возможные движения дислокаций от невозможных, предположим, что элемент
линии дислокации d% с вектором Бюргерса Ь перемещается на величину
da (рпс. 14.9.1). Относительное перемещение частиц по обе стороны разре-
разреза, сделанного по заштрихованной площадке с нормалью v, есть &, следо-
следовательно, перемещение элемента дислокации вызывает изменение объема
Это изменение объема происходит за счет образования полости в теле, если
оно положительно, и попросту невозможно, если оно отрицательно. Таким
образом, возможны только такие движения дислокации, когда
= 0 A4.9.1)
и, следовательно, движение элемента d% происходит в плоскости, определя-
определяемой направлением этого элемента и вектором Бюргерса. У винтовой дис-
дислокации направления линии дислокации и вектора Бюргерса совпадают,
следовательно, любая плоскость, проходящая через ось, является плос-
плоскостью ее возможного движения. Краевая дислокация может двигаться
только в направлении ее вектора Бюргерса или противоположном; другие
движения для нее невозможны.
Рассмотренная в § 14.6 плоская дислокация может двигаться как угод-
угодно в своей плоскости, но не может выходить из нее. Эта плоскость назы-
называется плоскостью скольжения дислокации (не смешивать с кристаллогра-
кристаллографическими плоскостями скольжения).
472 гл- 14- дислокации в упругом теле
Движения дислокации, при которых нарушается условие A4.9.1), на-
называются неконсервативными. Эти движения принципиально возможны
вследствие того, что в кристаллической решетке имеются дефекты — вакан-
вакансии и внедренные атомы, которые перемещаются в результате неравномер-
неравномерного распределения между атомами энергии их тепловых колебаний. Можно
представить себе, что дефект, находящийся вблизи дислокации, движет-
движется, это движение носит диффузионный характер, т. е. описывается матема-
математически с помощью уравнения диффузии, и дислокация следует за ним,
выходя из своей плоскости скольжения. Подобные диффузионные движе-
движения дислокаций возможны, главным образом, при высоких температурах,
за их счет относят некоторые механизмы ползучести.
§ 14.10. Дислокации в теле,
находящемся под нагрузкой
Дислокация, созданная в неограниченной упругой среде, может в ней
свободно перемещаться, если выполнено условие A4.9.1). Действительно,
энергия дислокации не зависит от ее положения, следовательно, движение
линии дислокации с сохранением конфигурации не требует затраты допол-
дополнительной работы. В теле конечных размеров дислокация уже не свободна,
упругая энергия тела зависит от положения дислокации и естественным
направлением ее движения будет то, которое приводит к уменьшению
энергии. Так, в примере § 14.8 дислокация, находящаяся на расстоянии от
оси цилиндра р < 0,541, будет двигаться к оси, стремясь занять положе-
положение устойчивого равновесия. Дислокация, удаленная от оси на расстояние,
превышающее р = 0,541, будет двигаться от оси, стремясь выйти на по-
поверхность.
Предположим теперь, что к телу, содержащему дислокацию, приложе-
приложены произвольные внешние силы. Всякое перемещение дислокации внутри
тела приводит к перемещениям точек его поверхности; действующие на
поверхности внешние силы производят работу на этих перемещениях. Если
перемещения при этом направлены противоположно силам и работа отрица-
отрицательна, общая энергия системы увеличивается, что невозможно, так как
никакой дополнительной энергии в тело поступить не может. Таким обра-
образом, движения дислокаций, при которых внешние силы производят отри-
отрицательную работу, невозможны.
Наоборот, если при перемещении дислокации силы производят поло-
положительную работу, общая энергия системы уменьшается, а так как общая
энергия всегда стремится принять минимальное значение, прикладывая
внешние силы к телу, мы как бы действуем на дислокацию, заставляя ее
двигаться. Воспроизведем приведенные рассуждения в более точной
форме.
Пусть оц, Ui — система напряжений и перемещений, соответствующая
дислокации в теле, ограниченном поверхностью S, линия дислокации есть
замкнутая кривая Г, вектор Бюргерса есть Ь.Как мы видели, энергия дис-
дислокации равна
Здесь S — произвольная поверхность, проведенная через контур Г, v — еди-
единичный вектор нормали к поверхности 2.
Представим теперь себе, что в теле вырезана тороидальная полость,
окружающая контур Г, но дислокация еще не произведена. Приложим на
наружной поверхности тела систему сил Р', соответствующие напряжения
будут а^«, перемещения щ. Область концентрации напряжений вблизи то-
тороидальной полости простирается на расстояние порядка поперечного раз-
§ 14.10. ДИСЛОКАЦИИ В НАГРУЖЕННОМ ТЕЛЕ 473
мера полости, при предельном переходе эта область исчезает. Таким обра-
образом, напряжения %• и соответствующие перемещения определяются так
Ж6' Сд^ае^те™р^раезрез по поверхности 2 и переместим стороны разреза
на величину вектора Бюргерса. Производимая при этом работа найдется
следующим образом:
W
= \ a'^-dZ + Г PfiUidS + | J orffodZ.
i s s
Первый член представляет собою работу тех внутренних сил, которые уже
были приложены к поверхности разреза, второй - работу внешних сил на
дополнительных перемещениях, связанных с дислокацией наконец тре-
третий - это работа сил, создающих дислокацию, т. е. энергия дислокации Wo.
Сумма двух первых членов представляет собою энергию взаимодействия
дислокации и поля напряжений от внешних сил
С другой стороны, эта энергия взаимодействия может быть вычислена
путем подсчета работы внутренних сил по всем элементам объема тела
Но по теореме Бетти
Система напряжений ai5 представляет собою самоуравновешенную систе-
систему, система деформаций е[. является кинематически возможной в сплош-
сплошном теле, следовательно, согласно начала
возможных перемещений
Таким образом, энергия взаимодейст-
взаимодействия Wi равна нулю. Отсюда следует
А= f P'u.dS=-=— fa'.v.b.dZ. A4.10.1)
Рис. 14.10.1
Эта формула принадлежит Колоннетти.
Работа внешних сил на перемещениях, вызванных дислокацией, нахо-
находится по этой формуле через напряжения, соответствующие заданной си-
системе сил. При движении дислокации эта работа получает приращение ЪА,
для возможных движений должно быть 6\4 > 0.
Обратимся к простому примеру. На рис. 14.10.1 изображен блок конеч-
конечной длины I, содержащей положительную краевую дислокацию. На блок
действуют такие силы, что в плоскости хх0хъ существует только касатель-
касательное напряжение Oi3 = т, величина которого постоянна.
По формуле Колоннетти величину А можно определить, интегрируя по
части плоскости хх0хъ, находящейся впереди дислокации. Тогда на едини-
единицу длины линии дислокации
"~~~ Л = —%Ъ{1 — и).
474 гл- 14- дислокации в упругом теле
Можно считать, что дислокация получена путем разреза части плоскости
х\Ох3, находящейся слева от линии дислокации. Тогда положительным нуж-
нужно считать направление нормали вниз, v3 = —1 и мы получим
А = тЬи.
Два выражения для А разнятся на постоянную величину. Предположим,
что дислокация переместилась на величину du. Тогда
dA = %Ь du.
Работа положительна тогда, когда положительно du, следовательно, при-
приложенные силы двигают дислокацию вправо до тех пор, пока она не вый-
выйдет на поверхность. В результате этого произойдет показанный на
рис. 14.10.1 штриховой линией сдвиг одной части блока относительно дру-
другой на величину &, т. е. элементарная пластическая деформация.
Отрицательная дислокация в тех же условиях стала бы двигаться влево.
§ 14.11. Сила, действующая на дислокацию
В приведенном примере перемещению дислокации на величину du
соответствовала работа %Ъ du. Множитель при перемещении в выражении
работы естественно назвать силой, действующей на единицу длины линии
дислокации. Заметим, что такое определение силы является чисто стати-
статическим. Можно говорить о равновесии дислокации, если действующая на
нее сила равна нулю. В противном случае направление силы указывает на
направление движения, но не позволяет определить, например, ускорение.
К более общему определению силы, действующей на дислокацию, мож«
но подойти следующим образом. Представим себе элемент линии дислока-
дислокации df, этот элемент переместился на расстояние du (рис. 14.9.1). В ок-
окрестности элемента имеется поле напряжений ац. Обозначая через v еди-
единичный вектор нормали к плоскости движения элемента d%, по формуле
A4.10.1) найдем приращение работы внешних сил
dA = —OijVj
Здесь dco — площадь, ометаемая вектором d\ при его движении. С другой
стороны, dA можно представить как скалярное произведение некоторого
вектора dF и перемещения dw
dA= dFdu.
Вектор dF мы будем называть силой, действующей на элемент d% дисло-
дислокации. Положим Oijbj = pi. Вектор р представляет собою вектор напряже-
напряжения на площадке, нормальной к вектору Бюргерса, умноженный на вели-
величину последнего. А так как vd(d~duXd%, то
dA = — p(duXdl)
или, переставляя сомножители в смешанном произведении,
dA = du(pXd%).
Таким образом, мы нашли силу, действующую на дислокацию,
dF = pXdl. A4.11.1)
Эта сила всегда перпендикулярна линии дислокации.
В действительности, нам нужно знать не силу, действующую на дис-
дислокацию, а ту составляющую этой силы, которая действует в плоскости
скольжения. Обозначим эту составляющую dQ, она равна силе dF за
вычетом той ее части, которая направлена по нормали к d(a:
dQ=dF— (vdF)v.
§ 14.12. ВЗАИМОДЕЙСТВИЕ МЕЖДУ ДИСЛОКАЦИЯМИ 475
Легко проверить, что эта формула может быть записана в виде тройного
векторного произведения
dQ = vxdFxv.
Вычислим отдельно произведение
vXdF = vxpxdl = p(v d%) — d\ (vp) = — dg (v/?).
Таким образом,
dQ = (vp) (xxdl)
или
d<? = (<VA'Hvxd5>- A4.11.2)
Первый множитель представляет собою скалярное произведение век-
вектора Бюргерса на вектор напряжения в плоскости скольжения, второй ука-
указывает, что сила dQ направлена по нормали к линии дислокации в плос-
плоскости скольжения.
§ 14.12. Взаимодействие между дислокациями
Пусть в теле созданы две дислокации, линии которых суть Г и Г', век-
векторы Бюргерса Ъ и Ъ' соответственно. Этим дислокациям соответствуют
системы напряжений Oij и ог- и деформации ец и ег>. Энергия взаимодей-
взаимодействия может быть подсчитана двояким способом; либо нужно предполо-
жить, что первая дислокация уже существовала в теле к моменту, когда в
нем создается вторая, либо наоборот. Работа напряжений ац на относи-
относительном перемещении Ъ\ краев разреза 2', проведенного через контур Г',
представляет собою энергию взаимодействия
2'
Если дислокации создаются в обратном порядке, то
Энергия взаимодействия между двумя дислокациями не равна нулю
подобно энергии взаимодействия между дислокацией и полем напряжений
от внешних сил. По-прежнему эта энергия может быть вычислена путем
суммирования работ, произведенных в элементарных объемах,
Напряжения Oij и о^ самоуравновешены, но деформации е%$ и е^ не
представляют собою деформаций, возможных в сплошном теле, при созда-
создании дислокации сплошность нарушается. Поэтому W% не является вирту-
виртуальной работой самоуравновешенной системы сил и не должна обращаться
в нуль.
Предположим теперь, что элемент d\ линии дислокации Г перемещает-
перемещается на расстояние du. Соответствующее изменение энергии взаимодействия
есть —dWi. Возможное движение дислокации должно сопровождаться
уменьшением энергии взаимодействия; представляя это уменьшение в виде
476 гл- 14- дислокации в упругом теле
произведения вектора перемещениями на вектор dF
— dW.= dF du,
мы приходим к определению силы dF, действующей со стороны второй
дислокации на элемент d% первой. Эта сила выражается формулой A4.11.2)
предыдущего параграфа, если напряжения оц от внешних сил заменить
напряжениями о^, создаваемыми второй дислокацией.
Особый интерес для приложений представляют прямолинейные дисло-
дислокации; взаимодействие прямолинейных дислокаций мы рассмотрим более
подробно.
а. Две параллельные винтовые дислокации. Винтовая дислокация
(О, О, Ъ) создает поле напряжений, симметричное относительно оси хъ, она
не имеет определенной плоскости сколь-
скольжения и сила взаимодействия между
двумя такими дислокациями не зависит
от их расположения относительно осей
ха. Направим по оси х3 дислокацию
(О, О, Ь\), вторая дислокация (О, О, Ь2)
^ пусть проходит через точку (§, О, 0)
~~*~ (рис. 14.2.1). Предположим, что дисло-
кация Ь\ уже существовала, в плоскости
%1 Х2 = 0 ей соответствует касательное на-
Ь
Рис 1412 1 пряжение <J23= -^ —. Создавая вто-
вторую дислокацию, мы производим отно-
относительное смещение в направлении оси х$ на величину Ъ2 краев разреза в
плоскости х2 = 0 от х\ = ? до х\ = Я. Соответствующая работа на единицу
длины линии дислокации
2л х 2 х 2jx | "
I 1
Сила взаимодействия между дислокациями
Г = — —1 = — \1Ь-&А-. A4.12.1)
Формула для силы взаимодействия между двумя винтовыми дислокациями
оказывается такой же, как для силы взаимодействия между двумя линей-
линейными зарядами. Она положительна, если дислокации одного знака, и от-
отрицательна, если дислокации разных знаков. Таким образом, дислокации
одного знака отталкиваются, дислокации разных знаков притягиваются,
стремясь слиться в одну дислокацию с вектором Бюргерса Ъ\ — Ь2. В част-
частности, две дислокации с равными и противоположными векторами Бюргер-
Бюргерса, сливаясь, уничтожают друг друга.
б. Две краевые дислокации в общей плоскости скольжения. Рассмотрим
две краевые дислокации, лежащие в плоскости х2 = 0, одна из них направ-
направлена по оси хъ и имеет вектор Бюргерса Ъ\ в направлении оси хи другая
параллельна ей, проходит через точку (?, 0, 0) и имеет вектор Бюргерса Ьг
того же направления, что первая. Энергия взаимодействия подсчитывается
здесь точно так же, как в случае двух винтовых дислокаций, так как каса-
касательное напряжение в плоскости х2 = 0 от первой дислокации есть
012~2лA-^)"~Г'
§ 14.12. ВЗАИМОДЕЙСТВИЕ МЕЖДУ ДИСЛОКАЦИЯМИ
477
Формула взаимодействия имеет следующий вид:
Р-
ЩТ^)' A4Л2-2>
и в случае краевых дислокаций дислокации одного знака отталкиваются,
разных знаков — притягиваются.
в. Две краевые дислокации в параллельных плоскостях скольжения.
Рассмотрим две краевые дислокации так, как это показано на рис. 14.12.2.
Первая дислокация вызывает в плос-
плоскости скольжения второй дислока-
дислокации касательное напряжение
2л
Для нахождения силы, действующей
на вторую дислокацию, нет необхо-
необходимости вычислять энергию взаимо-
взаимодействия, можно просто воспользо-
воспользоваться формулой A4.11.2) (так же,
как и в ранее рассмотренных случа-
случаях). В точке (gi, ?2), где помещена
вторая дислокация, на плоскости
скольжения действует касательное
напряжение
Рис. 14.12.2
2л A - v)
направленное так же, как вектор Бюргерса. Для вычисления силы, дейст-
действующей^ плоскости скольжения, достаточно знать величину т, в формулу
для этой силы входит скалярное произведение вектора напряжений, дейст-
действующего на плоскости скольжения, на вектор Бюргерса. Это скалярное про-
произведение равно %Ь2. Следовательно, величина силы есть
2л A - v) р4
м Заметим, что gi/p = cos 6, ?2/р = sin 6. После очевидных преобразова-
преобразовании представим формулу для силы взаимодействия в таком виде:
A4Л2-3)
Картину взаимодействия между дислокациями можно представить себе
следующим образом. Состояние равновесия осуществляется при 6 = jt/4 и
Э = л/2. Если дислокации одного знака, они стремятся удалиться, когда
Э < л/4, и сблизиться, если 6 > л/4. Состояние равновесия при 6 = л/4 не-
неустойчиво, при 6 = л/2 устойчиво. Это показано схематически на рис. 14.12.2,
здесь же приведен примерный график зависимости силы F от координа-
координаты g2. Если дислокации имеют разные знаки, картина получается противо-
противоположной, при 6 < л/4 дислокации стремятся сблизиться, при 6 > л/4
стремятся удалиться. Устойчивое равновесие оказывается при 6 = л/4.
Степень устойчивости взаимного расположения дислокаций определяет-
определяется энергией активации, т. е. величиной работы, которая необходима для
того, чтобы разрушить возникшее образование. Пусть, например, мы имеем
две дислокации одного знака, расположенные одна над другой (8 = л/2).
Фиксируя нижнюю дислокацию, будем перемещать верхнюю вправо до тех
пор, пока сила не обратится в нуль, т. е. 6 не станет равным л/4. Работа
силы F на этом пути и есть энергия активации; после того как эта работа
478 гл- 14- дислокации в упругом теле
произведена, дислокации будут отталкиваться, и первоначальное состояние
уже не восстановится. Подсчитаем энергию активации
dQ
Но li = ?2ctg 6, dg = — l2 . 2q * следовательно,
sin и
Л/4
U — W_ f 5!2« ,e ^ 0Д53 W_. A4.12.4)
8лA —v) J sin^0 2яA —v)
Jl/2
§ 14.13. Стенка дислокаций
Предположим теперь, что вдоль оси х2 на равных расстояниях d рас-
расположен ряд одинаковых краевых дислокаций F, 0, 0). Основываясь на
результатах предыдущего параграфа, следует ожидать, что такое располо-
расположение будет устойчивым. В последующем мы вернемся к вопросу об ус-
устойчивости подобного расположения, пока что ограничимся соответствую-
соответствующим допущением. Если мы хотим рассматривать напряженное состояние
в точках, отстоящих от оси х2 на расстояние, достаточно большое по срав-
сравнению с расстоянием d между дислокациями, мы можем заменить дискрет-
дискретный ряд дислокаций непрерывным их распределением, слоем дислокаций.
Представим себе, что на каждый бесконечно малый элемент d%2 оси х2 при-
приходится краевая дислокация с вектором Бюргерса Р d\2. На больших рассто-
расстояниях от оси х2 такой слой вызывает напряженное состояние, не отличаю-
отличающееся от напряженного состояния, вызванного рядом дислокаций на рас-
расстоянии d одна от другой, если р = b/d. Слой дислокаций может прости-
простираться неограниченно вдоль оси х2 или может быть расположен на части
плоскости х\ = 0 от Х2 = —L до х2 = +L. Рассмотрим сначала случай бес-
бесконечной стенки. Вращение, вызванное краевой дислокацией F, 0, 0), про-
проходящей через начало координат, дается формулой A4.4.4):
Ъ *,
Следовательно, дислокация [J d%2 в точке @, %2) создает в точке (хи х2)
вращение
ю21
Ш —rt оГ*
2я г2
Подсчитаем вращение, создаваемое бесконечной стенкой дислокаций:
Из рис. 14.13.1 видно, что x\\r = cos 6, следовательно,
Интеграл в формуле для со представляет собою угол, под которым из точ-
точки М видна бесконечная ось х2, этот угол равен +п справа от оси х2 и
—я слева от оси.
Таким образом,
со = -у sign x1 = 2^" sign x^. A4.13.1)
Итак, стенка дислокаций может служить моделью плоской границы, раз-
разделяющей области кристалла, повернутые одна относительно другой на
§ 14.13. СТЕНКА ДИСЛОКАЦИЙ
479
угол b[d, или моделью границы мозаичных блоков. Так называются су-
существующие в любом реальном кристалле области, отличающиеся слабой
относительной разориентацией.
Рассмотрим теперь напряженное состояние в теле при наличии беско-
бесконечной стенки дислокаций. Исходя из формулы A0.3.6), для касательного
напряжения Oi2 получим следующее выра-
выражение:
а =
12
=
12 2я A
jx x F »;-(*,-
\212
12 2я A
Переходя к введенному выше углу 8, най-
найдем
S \ cos26Je==0. A4.13.2) | f
~V)J/2 А Ц
Таким же образом можно убедиться в том,
что и остальные напряжения обращаются в
нуль. Итак, бесконечная стенка дислокаций
оставляет тело ненапряженным, разделяя его
на области, повернутые одна относительно
другой.
В действительности, если мы рассматри-
рассматриваем не непрерывно распределенные дислока-
дислокации, а дискретный ряд, в непосредственной
близости от оси х2 получится напряженное состояние, быстро затухающее по
мере удаления от оси. Если мы захотим соединить две части кристалла со
слегка разнящейся ориентацией атомных плоскостей, мы обязательно полу-
получим несовпадение рядов атомов в плоскости соединения; чтобы добиться
необходимого совпадения нужно деформировать решетку, но эти деформа-
деформации будут носить чисто местный характер. Таким образом, более точная
модель границы блока должна быть построена из дискретных дислокаций,
расположенных на конечных расстояниях.
Рассмотрим теперь стенку ограниченной длины, занимающую прост-
пространство от ?2 = —Т* до \2 = +L.
Формула A4.13.2) для О\2 сохраняет силу, но пределы интегрирования
будут
Рис. 14.13.1
0 = arccos
0О = arccos
Интегрируя, подставляя пределы и производя некоторые простые преобра-
преобразования, получим
о = My. *i (Х1 ~ х\ — L )
12 rr(i лЛ /„2 „2 . г2\2
Касательное напряжение принимает бесконечно большие значения при х\ =
= 0, х2 = ±1/, оно обращается в нуль на линии
Это — гипербола, проходящая через концы отрезка х\ = 0, х2 е [-L, L].
Она разбивает плоскость х\, х2 на две области, в которых в\2 имеет раз-
различные знаки. Дислокация того же знака, попавшая в незаштрихованную
область (рис. 14.13.1), будет отталкиваться от оси х2, в заштрихованной
области дислокации того же знака притягиваются к оси х2, за счет чего
происходит рост стенки.
ЧАСТЬ III
НЕУПРУГОСТЬ
ГЛАВА 15
ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
§ 15.1. Упругопластическое и жесткопластическое тело
В главе 5 было дано определение идеального упругопласти-
ческого и жесткопластического тела и выяснены некоторые об-
общие свойства стержневых систем, составленных из идеальных
упругопластических или жесткопластических элементов. Термин
«идеальная» пластичность понимается здесь, как и в гл. 5, в том
смысле, что материал не обладает упрочнением, т. е. при о = ох
стержень может деформироваться неограниченно. Напомним, что
рассматривалась задача о предельном равновесии, т. е. о нахож-
нахождении нагрузки, при которой наступает общая текучесть. При
этом деформации стержней, перешедших в пластическое состоя-
состояние, как это заранее оговорено, могут быть сколь угодно велики,
если не принимать во внимание геометрических ограничений.
Учитывая эти последние, более осторожно было бы говорить о
мгновенных скоростях пластической деформации; эти мгновен-
мгновенные скорости могут быть совершенно произвольны и действи-
действительно сколь угодно велики. Напомним, что исчерпание несущей
способности стержневой системы, как правило, соответствует
превращению ее в механизм с одной степенью свободы. Поэтому
соотношения между скоростями пластической деформации ее
элементов остаются жестко фиксированными, эти скорости опре-
определяются с точностью до общего произвольного множителя. На-
Напомним также фундаментальный результат, полученный в § 5.7
и 5.8. Если стержневая система нагружена системой обобщенных
сил Qi, то в предельном состоянии выполняется условие
F(Qi) = 0. A5.1.1)
При F < О система остается жесткой, состояние, при котором
F > 0, невозможно. При этом обобщенные скорости перемещений
qu соответствующие обобщенным силам Qti определяются ассо-
ассоциированным законом течения
Ь = Ьщ* A5Л'2)
где Я — произвольный множитель. Соотношения между скоро-
§ 15.1. УПРУГОПЛАСТИЧЕСКОЕ И ЖЕСТКОПЛАСТИЧЕСКОЕ ТЕЛО 481
стями qi фиксированы, если Qt не соответствует ребру поверх-
поверхности нагружения, в противном случае возникает известная не-
неопределенность. Как было показано в § 5.8, функция F не вогну-
вогнута. Это значит, что если ~Q*% таковы, что F (Q*)^.0x то справед-
справедливо следующее неравенство:
{Qi-Q'i)Qt>0 или @f_tf).J*L>O. A5.1.3)
В рассмотренных примерах, относящихся к стержневым си-
системам — фермам, функция F была кусочно линейной, уравнение
F(Q) = 0 в w-мерном пространстве сил Qi определяло многогран-
многогранник, ограниченный гиперплоскостями. На ребрах пересечения
этих гиперплоскостей направление нормали неопределенно, соот-
соответственно вектор qt может занимать произвольное положение
в плоскости, нормальной к ребру, и внутри угла, образованного
пересекающимися граничными гиперплоскостями. Еще большая
свобода выбора направления вектора qt имеется в вершинах
многогранника, где пересекаются несколько гиперплоскостей.
Наша задача теперь будет состоять в том, чтобы получить
условие пластичности и закон течения для общего случая произ-
произвольного напряженного состояния. Рассмотрим элемент в декар-
декартовых прямоугольных координатах, компоненты тензора напря-
напряжения Оц можно принять за обобщенные силы, действующие на
этот элемент. Соответствующие обобщенные скорости будут ег>
Если деформации малы, то вц = ёц, но это предположение не
обязательно. Естественно предположить, что пластическое состоя-
состояние будет достигнуто тогда, когда некоторая функция от компо-
компонент тензора напряжений достигнет предельного значения
F(a,,) = 0. A5.1.4);
Такие состояния g*j, для которых F(o*j)^0, будем называть
допустимыми.
Условие пластичности A5.1.4) может быть геометрически ин-
интерпретировано как уравнение поверхности в шестимерном или
девятимерном пространстве, где координатами точек служат ком-
компоненты напряжений о#. В первом случае учитывается симмет-
симметрия тензора <3ц и координат остается всего шесть, во втором слу-
случае равенства Oi3 = oj{ не используются. Будем называть гипер-
гиперповерхность, определяемую уравнением A5.1.4), поверхностью
текучести. Для изотропного тела условия перехода в пластиче-
пластическое состояние должны определяться только главными напряже-
напряжениями независимо от ориентации главных осей, поэтому условие
пластичности можно записать в виде
u a2, G3) = 0.
Геометрическая интерпретация в этом случае вполне наглядна:
31 Ю. Н. Работнов
482 гл-15- идеальная пластичность
выписанное условие определяет поверхность в трехмерном евкли-
евклидовом пространстве. В отдельных частных случаях бывает доста-
достаточно рассматривать условие пластичности не в общем шестимер-
шестимерном пространстве, а в каком-либо из его подпространств с мень-
меньшим числом измерений.
Теперь нам необходимо принять некоторую систему предполо-
предположений, которая позволила бы сделать общие заключения о виде
функции F и распределении скоростей пластического течения гц.
При этом результаты, полученные для стержневых систем и
сформулированные в виде соотношений A5.1.2) и A5.1.3), дол-
жны быть использованы в качестве наводящих соображений.
Может быть, наиболее простой путь состоял бы в том, чтобы
просто постулировать невогнутость функции Р(оц) и справедли-
справедливость ассоциированного закона течения; однако представляется
соблазнительным положить в основу теории некоторый общий
принцип, допускающий достаточно простую формулировку и со-
содержащий в себе все необходимые следствия. Такого рода прин-
принципы или постулаты формулировались разными авторами в раз-
различной форме; мы приведем здесь два принципа, приводящих к
совершенно эквивалентным результатам.
§ 15.2. Принцип максимума и постулат Друкера
Принцип максимума Мизеса формулируется следующим об-
образом. Пусть задано распределение скоростей е«, которому соот-
соответствует поле напряжений аг> Мощность диссипации D опреде-
определяется следующим образом:
D = оце%. A5.2.1)
Здесь efj — тензор скоростей пластической деформации.
Утверждается, что для истинного напряженного состояния
мощность диссипации не меньше, чем для любого допустимого
состояния o*j, т. е. такого, что во всех точках тела F(o*j) ^
<0. Итак,
Это условие обычно записывают следующим образом:
(°«-<UK>0. A5-2.2)
Неравенство A5.2.2) совершенно аналогично неравенству
A5.1.3); оно устанавливает по крайней мере невогнутость по-
поверхности нагружения. Теперь, предполагая, что функция F(dj)
непрерывна и кусочно дифференцируема, составим локальное
условие максимума диссипации D как функции Оц при условии
соблюдения условия пластичности A5.1.4). Для этого, как хорошо
§ 15.2. ПРИНЦИП МАКСИМУМА И ПОСТУЛАТ ДРУКЕРА 483
известно, нужно искать условия экстремума функции
ф = в — %F = аме& — X
где % — неопределенный множитель Лагранжа. Следуя обычному
правилу, приравниваем нулю производные от функции Ф по Оц.
Отсюда следует
10 dGij'
Это — ассоциированный закон течения, совершенно аналогичный
закону A5.1.2), установленному для стержневых систем.
Так же как и в случае стержневой системы, где функция
была только кусочно гладкой, точнее — состояла из линейных
участков, можно предположить, что и в условии A5.2.4) функ-
функция F — кусочно гладкая и в некоторых «угловых точках» одно-
одновременно выполняется к условий
F.(o«)«0 E = 1, ..., к). A5.2.4)
Применяя ассоциированный закон течения к каждому из условий
A5.2.4), найдем
h
Из условия положительности мощности диссипации, которое бу-
будет установлено в § 15.3, следует, что к$ ^ 0.
Если тензор скоростей деформации Ец представить себе сво-
свободным вектором в том же пространстве напряжений, в котором
строится поверхность текучести, т. е. откладывать компоненту е#
этого вектора по той же координатной оси, по которой отклады-
откладывается соответствующая компонента а#, и напряженное состоя-
состояние изображается точкой М поверхности текучести, то вектор
скорости пластической деформации направлен по нормали к по-
поверхности в точке М. Если поверхность текучести строго выпук-
выпукла, то задание компонент е?? определяет точку М, а следователь-
следовательно, и напряженное состояние, единственным образом.
В вышеприведенных рассуждениях мы применяли векторный
язык, ведя разговор о тензорах. Для простоты и краткости
в дальнейшем мы будем часто пользоваться и векторной симво-
символикой, обозначая через а напряженное состояние, а через s —
распределение скоростей деформаций. Однако нужно помнить,
что любые векторные операции для векторов а я г совершенно
незаконны, их нельзя, например, преобразовывать к другим осям
координат, формулы преобразования компонент тензора и век-
вектора различны.
Друкер положил в основу построения теории пластичности
следующий постулат. Пусть а* — некоторое допустимое напря-
31*
484
ГЛЛ 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
женное состояние в указанном выше смысле, а — истинное на-
напряженное состояние. Назовем о — о* дополнительным напряже-
напряжением. Постулат Друкера утверждает, что работа дополнительно-
дополнительного напряжения на замкнутом цикле по напряжениям неотри-
неотрицательна
A5.2.6)
Интегрирование ведется в пространстве напряжений по пути,
выходящему из точки о* и возвращающемуся в эту же точку.
Заметим прежде всего, что для упругопластического тела
de = de9 + dev,
где ее — упругая деформация, ер — пластическая деформация.
Соответственный интеграл разобьется на две части. Заметим
также, что
(а — а*) dee = (j) а de9 — а* j) de9 = 0.
Действительно, первый интеграл в правой части представляет
собою работу упругой деформации на замкнутом пути, равнут >
Рис. 15.2.1
Рис. 15.2.2
нулю, второй же интеграл обращается в нуль потому, что упру-
упругая деформация однозначно определяется действующим напря-
напряжением. Итак, должно быть
<J)(a —
Рассмотрим путь, изображенный на рис. 15.2.1. На участке
MN пластическая деформация не происходит, на участке NP
напряжение получает приращение da, отрезок NP принадлежит
поверхности F = 0, пластическая деформация получает прира-
приращение dev» Работа дополнительного напряжения есть (а—о*) dep»
§ 15.3. ДИССИПАТИВНАЯ ФУНКЦИЯ 485
На участке РМ происходит разгрузка, значит, соответствующая
часть интеграла опять равна нулю, пластическая деформация
при разгрузке не меняется. Итак, из A5.2.6) следует
(a-a*)dep>0. A5.2.7)
Соотношение A5.2.7) совершенно тождественно с соотношением
A5.2.2), только оно записано в векторной форме, во-первых, и не
в скоростях, а в приращениях пластической деформации, во-
вторых.
Ассоциированный закон течения также следует из постулата
Друкера. Для доказательства выберем точку М на самой поверх-
поверхности текучести по одну и по другую сторону от точки N (точ-
(точки М' и М" на рис. 15.2.2). Теперь должно быть
(а — a*') dev > 0, (а — о*") dev > 0.
Беря точки М' и М" сколь угодно близко к точке N, убеждаем-
убеждаемся, что одновременное выполнение выписанных неравенств воз-
возможно лишь тогда, когда вектор dev направлен по нормали к по-
поверхности текучести, т. е.
dep = dX-~. A5.2.8)
Заметим, что для жесткопластической модели все оговорки,
связанные с выделением пластической части деформации, не
нужны, а индексы «р» и «е» при е и е излишни.
§ 15.3. Диссипативная функция
Поскольку напряжения определяются через скорости дефор-
деформации либо единственным образом в случае строго выпуклой
поверхности текучести, либо с известной степенью произвола,
диссипативная функция A5.2.1) может быть выражена через
скорости пластической деформации
Z) = Z)(8fi). A5.3.1)
Будем считать, что рассматриваемое тело жестко-пластическое,
значит, By — скорости пластической деформации.
Продифференцируем A5.3.1). Получим
дР
Но вследствие ассоциированного закона течения
= л dG{ 2 — a dF = О.»
86 ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
поскольку выполняется условие идеальной пластичности. Итак,
"« - щ. A5-3.2)
Соотношения A5.3.2) взаимны по отношению к ассоциирован-
ассоциированному закону течения A5.2.3), однако они уже не содержат не-
неопределенного множителя, напряжения Оц определяются един-
единственным образом, если D — строго выпуклая функция от скоро-
скоростей. Но функция диссипации сама определена с точностью до
произвольного множителя Я, что ясно из структуры выражения
A5.2.1). Для того чтобы формула A5.3.2) давала определенные
величины Оц при неопределенном с точностью до множителя за-
задании скоростей деформации, необходимо, чтобы D была однород-
однородной функцией первой степени от еу, тогда производные dD/дгц
будут однородными функциями нулевой степени, т. е. будут за-
зависеть лишь от отношений скоростей. Действительно, подставляя
A5.3.2) в A5.2.1), находим
а отсюда по теореме Эйлера об однородных функциях и следует
необходимый результат.
Заметим, что если dD/дгц представляют собою однородные
функции нулевой степени от е#, они зависят уже не от шести
независимых аргументов, а только от пяти, например от отноше-
отношения каждой из компонент Ец к любой, произвольно выбранной
из них. Итак, формулы A5.3.2) выражают шесть величин а«
через пять независимых аргументов. Отсюда следует, что между
ними существует тождественное соотношение. Это тождествен-
тождественное соотношение и есть условие пластичности.
Уравнение 23(е#) = const определяет поверхность постоянной
диссипации в пространстве скоростей деформации ег> Соотноше-
Соотношения A5.3.2) показывают, что вектор напряжения а направлен
по нормали к поверхности диссипации; этот результат представ-
представляет собою прямую, параллель с ассоциированным законом те-
течения, или, скорее, его перефразировку. Некоторая кажущаяся
разница состоит в том, что поверхность F = 0 в пространстве на-
напряжений фиксирована, тогда как поверхность постоянной мощ-
мощности диссипации может быть выбрана по произволу. Чтобы нор-
нормировать эти поверхности, можно поступать совершенно произ-
произвольным образом, например можно принимать
1. A5.3.3)
Для нормированных таким или подобным образом поверхностей
постоянной диссипации можно сформулировать принцип макси-
максимума, состоящий в следующем. Пусть о« — заданное напряжен-
напряженное состояние, Ец — соответствующее истинное поле скоростей
§ 15.4. ТЕОРИЯ ИДЕАЛЬНОЙ ПЛАСТИЧНОСТИ
деформации, нормированное в смысле A5.3.3), е^— произволь-
произвольное поле скоростей деформации такое, что?)(е^) = 1. Тогда
0. A5.3.4)
Для доказательства неравенства A5.3.4), перепишем его следую-
следующим образом:
Но левая часть равна 2)(е«)=1, остается доказать, что правая
часть не больше единицы. Пусть о^ — пластическое напряжен-
напряженное состояние, соответствующее полю скоростей деформации ?ц.
Тогда A5.2.2) можно переписать следующим образом:
или
Но e*j(j*j = D (e*j) = 1, следовательно,
Этим доказывается неравенство A5.3.4). Из этого неравенства
следует невогнутость поверхности постоянной диссипации.
§ 15.4. Постановка задачи теории
идеальной пластичности. Теорема единственности
Постановка задачи теории идеальной пластичности сущест-
существенно отличается от постановки задачи теории упругости. Не
претендуя на исчерпание всех возможностей, упомянем здесь
три проблемы.
1. Предельное равновесие жесткопластического тела. С зада-
задачами подобного рода мы уже встречались применительно к
стержневым системам. Общая постановка будет состоять в сле-
следующем. На части поверхности Sv заданы мгновенные скорости
перемещений vu на части поверхности ST заданы усилия fx7\, где
\i—неопределенный множитель. Требуется определить несущую
способность тела, т. е. то значение параметра нагрузки \хт, при
котором наступает общая текучесть, это значит, что тело полу-
получает возможность неограниченно пластически деформироваться.
Вообще при \i < \1Т в теле могут возникать пластические зоны,
но примыкающие к ним жесткие области ограничивают свободу
пластического течения.
На рис. 15.4.1 пластические области заштрихованы. При уве-
увеличении нагрузки пластические области расширяются и, нако-
наконец, сливаются, отделяя жесткие части А ж В друг от друга, как
488
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
показано на рис. 15.4.2. Теперь части А и В могут свободно пе-
перемещаться друг относительно друга. Это и значит, что наступи-
наступило состояние общей текучести.
Можно представить себе, что заданы только скорости переме-
перемещений. Например, на рис. 15.4.3 изображен образец с боковыми
вырезами, растягиваемый с постоянной скоростью. При этом об-
образец деформируется, в нем наступает состояние общей текуче-
текучести, как показано на рисунке. Требуется определить величину
силы, которую нужно приложить, чтобы образец действительно
деформировался. Участок образца, захваченный зажимом, оста*
ется жестким, он весь перемещается со скоростью v, но распре-
распределение усилий в месте захвата остается совершен-
совершенно неопределенным, можно искать только величину
суммарной силы.
2. Стационарные задачи о пластическом формоиз-
формоизменении. При решении вопросов о предельном равно-
Рис. 15.4.1
\Р
Рис. 15.4.3
весии рассматриваются только мгновенные распределения скоро-
скоростей в момент исчерпания несущей способности, тогда как дефор-
деформации считаются бесконечно малыми. В задачах о пластическом
формоизменении деформации велики. Но в теории идеальной пла-
пластичности деформации сами по себе не фигурируют, в уравнения
входят лишь мгновенные скорости материальных точек. Поэтому в
рамках модели жесткопластического тела возможно рассмотрение,
например, такой задачи. Стержень (проволока) диаметром D про-
протягивается через коническую фильеру, в результате диаметр
уменьшается до величины d, соответственно увеличивается дли-
длина. В заштрихованной области материал находится в пластиче-
пластическом состоянии (границы этой области на рис. 15.4.4 показаны
совершенно условно). При анализе процесса фиксируется точка
пространства, для этой точки пишутся уравнения пластичности,
которые относятся не к какому-то определенному материальному
элементу, а к тому элементу, который в данный момент прохо-
проходит через фиксированную точку пространства и в следующий
момент ее покидает.
§ 15.4. ТЕОРИЯ ИДЕАЛЬНОЙ ПЛАСТИЧНОСТИ
489
Совершенно аналогично изучаются стационарные движения
жидкости в координатах Эйлера, идеально-пластическое тело,
подобно жидкости, совершенно лишено памяти о предшествую-
предшествующих воздействиях. В рассмотренном примере можно определить
силу Р, необходимую для осуществления протяжки, можно опре-
определить давление на стенки фильеры.
3. Нестационарные задачи о пластическом формоизменении.
Задачи такого рода сложны, и примеры решения немногочислен-
немногочисленны. Жесткий штамп, внедряющийся
в пластическое полупространство,
встречает все большее сопротивле-
сопротивление по мере увеличения площади
контакта и останавливается на не-
некоторой глубине (рис. 15.4.5). В ре-
результате пластической деформации
стержня с выточкой, изображенного
на рис. 15.4.3, конфигурация выточ-
выточки меняется по мере растяжения. Сф
Естественный, хотя и крайне трудо-
трудоемкий путь решения таких задач состоит в следующем. Зная
мгновенные значения скоростей, можно определить малые
перемещения Аи = v At, где At — приращение параметра нагруз-
нагрузки (или любая малая величина). Приращения Аи известны и
на контуре выточки, следовательно, можно построить новый кон-
контур выточки, близкий к исходному, решить задачу пластичности
для этого нового контура, определить
новые распределения мгновенных ско-
скоростей и повторить всю процедуру. Так
постепенно, шаг за шагом, можно най-
найти изменение геометрии, связанное
с пластической деформацией. Когда в #
полуплоскость внедряется клин, зада-
задача оказывается автомодельной и находится замкнутое решение.
Но это едва ли не единственный пример.
Специфическая особенность идеального жесткопластического
тела состоит в том, что в нем, вообще говоря, чередуются плас-
пластические и жесткие области, в пластических областях неопре-
неопределенно распределение скоростей, в жестких — распределение на-
напряжений. Поэтому теорема единственности носит ограниченный
характер: она утверждает только единственность распределения
напряжений в пластических областях, не фиксируя их границы.
__ t 9 t П ft ft
Пусть (Jij, Vi, 8|j и cr$j, У{, 8|j — два решения, удовлетворяющие
условиям равновесия, статическим и кинематическим граничным
условиям. Тогда разность напряжений <т^ — о\-2 удовлетворяет
уравнениям равновесия и нулевым граничным условиям на SV.
Поле скоростей деформации г — е# кинематически возможно,
490 rjL 15- идеальная пластичность
оно соответствует нулевым скоростям на части поверхности SV.
Составим уравнение равновесия в форме Лагранжа
J Wi, - <й) (e'u - 4) d7 = 0. A5.4.1)
v
Правая часть должна была бы равняться мощности приложен-
приложенных внешних сил, но эта мощность тождественно равна нулю
вследствие сделанных выше оговорок, касающихся граничных
условий для Оц и Vu Если поверхность текучести строго вы-
выпукла, то
(ОЦ ~ <?•) 4- > 0, (<*Ь ~ Oil) *ii > 0,;
причем равенство выполняется только тогда, когда сг# = а^. Сле-
Следовательно, условие A5.4.1) влечет за собою равенство напря-
напряжений
Итак, в пластических областях распределение напряжений опре-
определяется единственным образом. Интеграл в уравнении A5.4.1)
распространяется на весь объем тела, в жесткой области е^ = е$;-,,
поэтому интеграл по жестким областям обращается в нуль авто-
автоматически. Но из этого следует, что распределение напряжений
в жесткой области неопределенно.
Полным решением задачи теории идеальной пластичности на-
называется такое решение, которое удовлетворяет уравнениям рав-
равновесия, условию пластичности в пластических областях, где на-
напряжения и скорости деформирования связаны ассоциированным
законом, и граничным условием, статическим и кинематическим.
При этом должно выполняться еще одно условие, относящееся
к возможному распределению напряжений в жестких зонах. По
доказанному в жесткой зоне может существовать любое напря-
напряженное состояние, удовлетворяющее условиям равновесия, гра-
граничным условиям и условиям сопряжения с пластическими за-
законами. Необходимо, чтобы напряженное состояние, возможное
в жесткой зоне, удовлетворяло условию Р(оц)^0, т. е. было до-
допустимым для жесткопластического тела. При этом достаточно,
чтобы можно было найти хотя бы одно точное распределение
напряжений. В отношении распределения скоростей и конфигура-
конфигурации жестких зон полное решение не единственно, однако из
теоремы о единственности распределения напряжений следует
единственность предельной нагрузки, переводящей тело в пла-
пластическое состояние, если условие пластичности строго выпукло.
Если поверхность текучести только не вогнута, то предельная
нагрузка определяется неединственным образом; как правило,
природа этой неединственности находит простое объяснение.
§ 15.5. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА 491
§ 15.5. Экстремальные свойства
предельных состояний текучести
Две теоремы, приведенные ниже, позволяют получить ниж-
нижнюю и верхнюю оценку для параметра нагружения \х. Эти тео-
теоремы были впервые сформулированы и доказаны Гвоздевым в
малодоступной публикации 1936 г.; они многократно переоткры-
переоткрывались независимо разными авторами.
1. Теорема о нижней оценке несущей способности. Пусть а«,
е«, Vi — неизвестное нам истинное решение задачи о предельном
состоянии тела, подверженного действию системы поверхностных
сил 7\, (Tij—некоторое допустимое напряженное состояние, соот-
соответствующее поверхностным силам Тг . Напомним, что для до-
допустимого напряженного состояния выполняются уравнения рав-
равновесия и условие F(o*j)^0. Составим уравнения равновесия
в форме Лагранжа как для истинного, так и для допустимого
состояния, принимая за поле виртуальных скоростей истинное
поле скоростей (заранее неизвестное),
= J TpidS + j TpidS, A5.5.1)
Sv ST
^ \ T^v^S + ^T^dS. A5.5.2)
Здесь Ti = CijUj — истинные поверхностные силы, соответствую-
соответствующие предельному состоянию тела, Т\ = Офъ — поверхностные
силы, соответствующие допустимому состоянию ai;-. Вычитая
A5.5.1) из A5.5.2), получим
J TiVidS — [ T*VidS = J (a{i — о*,) e^dV.
sv sv v
Но вследствие A5.2.7) правая часть неотрицательна, поэтому
T*VidS. A5.5.3)
Неравенство A5.5.3) служит для нижней оценки несущей спо-
способности. Если внешняя нагрузка сводится к одной обобщенной
силе Q, которой соответствует обобщенная скорость д, то
в неравенстве A5.5.3) неизвестная скорость q сокращается и
получается оценка несущей способности
Q>Q*. A5.5.4)
Возвращаясь к той форме постановки задачи, которая была сфор-
492 гл-i5- идеальная пластичность
мулирована в § 15.4, примем, что нагрузки заданы в виде \iT°it
и статически допустимое состояние удовлетворяет статическим
граничным условиям вцщ = ц*Г* на 5Г. Тогда можно принять ji
за обобщенную силу, а обобщенная скорость будет равна
J T°iVidS; неравенство A5.5.4) принимает вид
Немедленное следствие доказанной теоремы состоит в следую-
следующем: расчет по допустимым напряжениям дает значения допу*
стимой нагрузки не больше, чем расчет по предельному состоя-*
нию. Действительно, решая задачу теории упругости и требуя,
чтобы предел текучести ни в одной точке не был превзойден,
мы вводим в рассмотрение допустимое напряженное состояние
в смысле, который был установлен выше.
2. Теорема о верхней оценке несущей способности. Пусть
viieij — произвольное кинематически допустимое поле скоростей
и скоростей деформации, т. е. такое поле, которое удовлетворяет
граничным условиям v-x = у$ на части поверхности Sv. По задан-
заданным скоростям деформации гц определяются напряжения Оц
единственным образом, если поверхность напряжения строго вы-
выпукла. Напряжения g*j вообще не удовлетворяют уравнениям
равновесия. Выпишем уравнения равновесия в форме Лагранжа,
принимая v* за поле виртуальных скоростей
Прибавим и вычтем в правой части этого равенства величину
мощности пластического формоизменения, соответствующего ки-
кинематически допустимому полю V{, а именно, интеграл от ОЪ
Получим
f T^dS = J o^ldV - J (eft -
S V V
Но второй член в правой части неотрицателен, поэтому
J TiV*dS < J Oifi^dV. A5.5.5)
S V
Если по-прежнему внешняя нагрузка представляется одной обоб-
обобщенной силой Q, то
Правая часть известна, если задано кинематически возможное
поле скоростей.
§ 15.6. ИЗОТРОПНОЕ ТЕЛО 493
Применяя оценки A5.5.4) и A5.5.6), можно получить интер-
интервал, в котором заключено истинное значение предельной нагруз-
нагрузки Q. Если верхняя оценка и нижняя оценка совпадают, то мы
получаем точное решение задачи о несущей способности, что
следует из доказанной выше теоремы единственности. Элемен-
Элементарные примеры применения статического и кинематического
методов оценки несущей способности уже были приведены в
гл. 5, далее будут рассмотрены примеры более сложные.
Нахождение кинематически возможных полей скоростей, кото-
которые не обязательно должны быть непрерывными, обычно не
встречает трудностей; варьируя эти поля, находят нижнюю грань
inf(?, определяемую формулой A5.5.6). Эта величина inlQ мо-
может совпадать с точным решением, а может являться наилучшим
приближением в определенном классе возможных кинематиче-
кинематических схем пластического деформирования.
Построение статически допустимых полей встречает большие
трудности, связанные главным образом с тем, что определенные
в пластических областях поля напряжений должны допускать
продолжение в жесткие зоны, притом такое, что условие пластич-
пластичности нигде не превышается.
§ 15.6. Условие пластичности
для несжимаемого материала. Изотропное тело
Опыт показывает, что пластическая деформация металлов не
сопровождается заметным изменением объема, таким образом,
скорость объемной деформации равна нулю
е« = е?1 + е22 + е?3 = °-
Подставляя сюда выражения A5.2.3) для скоростей пласти-
пластического течения, получим
dF dF dF n
Общий интеграл этого дифференциального уравнения в частных
производных первого порядка получается стандартным способом.
Составляется система обыкновенных дифференциальных урав-
уравнений
<*aii _ <*а22 _ <*азз _ dau __da м^(М\
Перебирая три интегрируемые комбинации, найдем
сти — а = Ci, а22 — о = с2, 03з — с — с3.
Таким образом, функция F зависит не от самих напряжений,
494
гл-15- идеальная пластичность
а от девиаторнои составляющей тензора напряжений
F(au - сб«) = F (о«) = 0. A5.6.2)
Шесть компонент девиатора симметричного тензора не незави-
независимы, а связаны между собою условием Si = Си = 0. Поэтому
можно выбрать такой способ геометрического представления ус-
условия A5.6.2), при котором оно изображается поверхностью в
пятимерном пространстве. Мы не будем вставать на этот путь,
а сразу перейдем к случаю изотропного материала. В этом случае
достаточно рассматривать условие пластичности, выраженное
через главные напряжения
а2, а3) = 0. A5.6.3)
Это условие допускает уже наглядную геометрическую интер-
интерпретацию в трехмерном пространстве главных напряжений. Учи-
Учитывая условие несжимаемости, следует считать функцию теку-
текучести зависящей от компонент девиатора напряжений или же
от трех разностей главных напряжений
01 — а2, а2 — а3, а3 — ои из которых не-
независимы только две. Сохраняя сим-
симметрию записи, мы будем принимать
условие пластичности для несжимаемо-
несжимаемого материала в следующем виде:
Fid — Gz, а2 —Оз, а3~а1) = 0. A5.6.4)
Уравнение A5.6.4) представляет собою
Уравнение цилиндра с осью, равнона-
клоненной к трем координатным осям.
Действительно, от изменения каждой
из координат си а2, а3 на одну и ту же
величину уравнение A5.6.4) не нару-
нарушается, а это изменение как раз и соответствует движению
по образующей цилиндра. Очевидно теперь, что условие
A5.6.4) нет необходимости изображать поверхностью в трех-
трехмерном пространстве, достаточно начертить контур основания
цилиндра или след пересечения его с октаэдрической плос-
плоскостью.
Теперь мы подойдем к такому представлению с другой сто-
стороны. Для изотропного материала условие пластичности можно
записывать очевидным образом, как соотношение между тремя
инвариантами
2ц, Sin) = 0'.
Если материал несжимаем, то от 2i условие пластичности по до-
доказанному зависеть не может, и, следовательно, в нем могут
фигурировать только второй и третий инварианты девиатора.
§ 15.6. ИЗОТРОПНОЕ ТЕЛО
495
Следуя идее § 7.7, будем представлять второй инвариант через
посредство октаэдрического касательного напряжения, а участие
третьего инварианта — через угол подобия девиатора. Теперь
предельное состояние текучести будет изображаться контуром
в эктаэдрической плоскости, уравнение которого в полярных ко-
координатах будет
т. = ф(#). A5.6.5)
На рис. 15.6.1 представлена октаэдрическая плоскость и про-
проекции на нее главных осей, сплошные лучи соответствуют поло-
положительным полуосям, штриховые — отрицательным. Если предел
текучести при растяжении и сжатии одинаков, как это обычно
бывает, и равен ат, то на каждом из лучей отсекается отрезок
T0=J1o—ат = тт. Соединяя концы этих отрезков, мы получаем
шестиугольник, соответствующий условию наибольшего касатель-
касательного напряжения. Действительно, наибольшее касательное напря-
напряжение равно полуразности наибольшего и наименьшего из глав-
главных напряжений; таким образом, если за критерий пластичности
принять достижение наибольшим касательным напряжением
предельного значения, в пространстве главных напряжений ус-
условие пластичности будет изображаться призмой с гранями
<Ji —а2 = ±ат, а2 —а3 = ±ат, а3 — Oi = dbaT. A5.6.6)
Каждая из этих полскостей отсекает отрезок, равный ат на одной
из главных осей и —ат на другой главной оси; проекции этих
Л/2
отрезков на октаэдрическую плоскость и равны как раз i-^V-ffTt
т. е. соответствуют отрезкам, соединяющим вершины шестиуголь-
шестиугольника с цилиндром.
Условие пластичности наибольшего касательного напряжения,
выражаемое формулами A5.6.6), называется условием Треска —
Сен-Венана. Очовидно, что из всех выпуклых контуров, прохо-
проходящих через шесть точек АВ'СА'ВС, шестиугольник Треска —
Сен-Венана будет внутренним.
Внешний из семейства выпуклых контуров, проходящих через
эти же точки, будет шестиугольник, стороны которого делятся
в названных точках пополам. Соответствующее условие пластич-
пластичности называется условием постоянства наибольшего приведен-
приведенного напряжения и записывается в виде шести равенств, каждое
из которых выполняется на одной из сторон шестиугольника,
о1 — о = ± -|orT, a2 — а = ± -| ат, а3 — а = ± § стт. A5.6.7)
Условие выпуклости поверхности текучести и несжимаемости
материала накладывает, как видно, очень жесткие ограничения
на вид возможных условий пластичности, которые представля-
представляются выпуклыми контурами, заключенными между двумя шести-
496
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
угольниками. Это значит, что если предел текучести при растя-
растяжении и сжатии одинаков, то влияние третьего инварианта на
достижение пластического состояния относительно невелико.
Теперь, пожалуй, наиболее простое и естественное предполо-
предположение будет состоять в том, чтобы выбрать в качестве контура
пластичности просто окружность
т0 = const =
A5.6,8)
по отношению к которой шестиугольник Треска — Сен-Венана
будет вписанным, а шестиугольник максимального приведенного
напряжения описанным. Условие пластичности A5.6.8) называ-
называется условием пластичности Мизеса.
Возвращаясь к общему представлению тензора напряжений,
мы можем переписать условие A5.6.8) следующим образом:
2ju =
= Const = -о" СГТ.
A5.6.9)
В пятимерном пространстве девиаторов это — уравнение гипер-
гиперсферы; таким образом, в этом пространстве поверхность текуче-
текучести строго выпукла. В пространстве
напряжений Оц, так же как в про-
пространстве главных напряжений а*,
поверхность текучести представляет
собою цилиндр, она только не вогну-
вогнута. В случае плоского напряженного
состояния, когда одно из главных
напряжений, скажем а3, равно ну-
нулю, естественно вести рассмотрение
не в октаэдрической плоскости, а в
плоскости а3 = 0. На рис. 15.6.2
представлен шестиугольник, полу-
получающийся в пересечении этой плос-
плоскости с призмой Треска — Сен-Вена-
Сен-Венана и описанный вокруг него эллипс
Мизеса. В первом случае выполняется одно из следующих
условий:
ai = dbaT, Oz = ±Gt, сг± — а2 = =Ьат. A5.6.10)
Эллипс Мизеса описывается следующим уравнением:
ol + о1 — о1о1 = о$. A5.6.11)
§ 15.7. Условие пластичности для анизотропных тел
Всякая анизотропия по существу представляет собою кон-
конструктивную анизотропию: она определяется строением материа-
материала, т. е. наличием тех или иных ориентированных структурных
элементов. В теории упругости физическая анизотропия не отли-
Рис. 15.6.2
§ 15.7. АНИЗОТРОПНЫЕ ТЕЛА
497
чима от конструктивной анизотропии, если вообще противопо-
противопоставление этих терминов имеет какой-то смысл. Вероятно, мож-
можно считать, что физическая анизотропия это та же конструктив-
конструктивная, но на атомном уровне. Так или иначе, если мы имеем в
распоряжении коробку в виде куба, например, и внутри этой ко-
коробки находится сколь угодно сложное нагромождение упругих
элементов, связанных механическими устройствами без трения,
то в самом общем случае связь между силами, прикладываемыми
к граням куба, и его деформациями описывается в линейной
области через посредство 21 константы, никакой эксперимент не
позволяет нам судить о том, что именно содержится внутри ко-
коробки. Если элементы, заключенные в коробку, могут переходить
в пластическое состояние, то пластическое поведение рассматри-
рассматриваемого куба может быть очень различным в зависимости от
того, какова внутренняя структура коробки.
Многие авторы строили теорию пластичности анизотропного
материала, отправляясь от квадратичного условия пластичности,
представляющего собою обобщение A5.6.9), а именно,
AiWGifiki = const1 A'vbiotfihi = const. A5.7.1)
Существуют формулировки условия анизотропной пластичности
в виде кусочно линейных соотношений типа теории Треска —
Сен-Венана или теории наибольшего приведенного напряжения.
Здесь, однако, будет использован другой подход, который кажет-
кажется более реалистичным для конструктивно-анизотропных элемен-
элементов, например, пластин и оболочек, подкрепленных ребрами,
а также для композитных материалов, армированных непрерыв-
непрерывным волокном.
Чтобы разъяснить основную идею, вернемся к той форме рас-
рассуждений, которая была проведена в § 5.7, 5.8 применительно
к стержневой системе; пусть будут д* — обобщенные скорости
деформации некоторых элементов, Qi — соответствующие обоб-
обобщенные силы. Представим себе теперь, что две системы, которые
будут соответственно отмечаться индексами 1 и 2, соединены
между собою так, что некоторые элементы их деформируются
одинаково, будучи связаны между собой. Тогда g$ = q\2) = ?*.
С другой стороны, суммарные усилия Qi = Q^ + Q[2\ Условия
текучести для системы 1 и 2 записываются соответственно сле-
следующим образом:
FM^^kl РМ*) = Ь1 A5-7.2)
Когда система переходит в пластическое состояние, оба условия
A5.7.2) выполняются одновременно. В соответствии с ассоцииро-
32 ю. Н. Работнов
498
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
ванным законом течения
п. — aW = аФ —
dF>1
дРл
Отсюда следует пропорциональность частных производных от
функций Ft и F2 в состоянии текучести
ЯР ЯР
A5.7.3)
Примем теперь @$ = Qi — Q^K Если число обобщенных сил
есть п, система A5.7.2) и A5.7.3) состоит из п + 2 уравнений,
исключая из них п+ 1 величину Q{^ и /?, получим условие пла-
пластичности для составной системы
F(Qi) = k\ A5.7.4)
Геометрическая интерпретация этого результата чрезвычайно
проста. В пространстве сил Qi строится поверхность Fx (Qi) =
= &i, поверхность
42) (&) = F2 (Qi - <#>) = к\ A5.7.5)
представляет собой поверхность текучести F\ (Q) = &2» пере-
перенесенную параллельно себе так, чтобы центр ее оказался на пер-
первой поверхности. Такое построение можно выполнить для любой
точки первой поверхности, уравнение A5.7.4) представляет со-
собою уравнение огибающей семейства поверхностей. Очевидно,
Ю
/
Рис. 15.7.1
Рис. 15.7.2
что поверхности F1 = k\ и F2 = к\ можно поменять местами, т. е.
в качестве поверхности текучести можно принять огибающую
поверхностей F1(Qi — Qt2)) = k\f эта огибающая будет та же,
что и в первом случае. Приведем некоторые простейшие примеры.
1. Пластина us изотропного материала, подчиняющегося усло-
условию пластичности Мизеса, усилена ортогональной решеткой. Уси-
Усилия приложены вдоль стержней решетки. Условие пластичности
решетки в плоскости <jt, a2 изобразится прямоугольником; теку-
§ 15.7. АНИЗОТРОПНЫЕ ТЕЛА 499
честь решетки наступает тогда, когда усилия в той или другой
системе ортогональных стержней достигают предела текучести.
Этот прямоугольник изображен на рис. 15.7.1, а. На рис. 15.7.1,6
представлен эллипс Мизеса для пластины, уравнение которой
дается формулой A5.6.11). Поместим центр эллипса Мизеса в
точку контура прямоугольника и будем
его двигать, обходя контур. В результате
получим фигуру, изображенную на
рис. 15.7.2, контур ее состоит из четырех
прямолинейных отрезков, соединенных
дугами эллипса. Здесь мы предположили,
что оси <Ji и а2 являются главными осями,
поэтому все построение ведется на плос-
плоскости. Предположим теперь, что оси d и
а2 не главные, так что заданы напряже-
напряжения аи, а22, а12. Решетка не может вы- Рис. 15.7.3
держивать каких бы то ни было касатель-
касательных напряжений, поэтому поверхность текучести для решетки в
трехмерном пространстве аи, а22, а12 останется прямоугольником
в плоскости ai2 = 0. Условие пластичности Мизеса запишется те-
теперь следующим образом:
°и + а|я — аХ1а22 + 3aJa = a?. A5.7.6)
Это — уравнение эллипсоида. Двигая эллипсоид параллельно себе
так, чтобы центр его оставался на площади прямоугольника, мы
получим поверхность, изображенную на рис. 15.7.3 и напоми-
напоминающую диванную подушку, она состоит из двух плоских гра-
граней, четырех участков поверхности эллиптического цилиндра и
частей поверхности эллипсоида по углам.
2. Треугольная стержневая решетка. Напряженное состояние
аи, а22, ai2 может быть осуществлено в системе, состоящей из
одной системы стержней, составляющих угол ф4, с осью ои тогда
и только тогда, когда это напряженное состояние представляет
собою простое растяжение или сжатие в направлении стержней.
На рис. 15.7.4 представлен соответствующий круг Мора. Обозна-
Обозначая растягивающее напряжение через а и откладывая угол 2ср4
в обратном направлении, найдем из рисунка
1 1
Оц = -о- a A + cos 2ф!), a22 = _ a (I — cos 2фх),
2 A5.7.7)
При фиксированном угле q>4 в пространстве an, a22, ai2 изобра-
изображающая точка пробегает отрезок, вообще говоря, наклонный
по отношению ко всем трем осям (рис. 15.7.5). Величина а огра-
ограничена условием достижения текучести в стержнях при растя-
растяжении или сжатии. Для простоты можно считать эти пределы
32*
500
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
одинаковыми, хотя это совсем не обязательно. Если имеется
вторая система стержней, ориентированная под другим углом ф2,
то допустимые напряженные состояния будут изображаться точ-
точками другого отрезка, также симметричного относительно начала
координат. Перемещая второй отрезок параллельно самому себе
так, чтобы середина его все время находилась на первом отрезке,
Рис. 15.7.4
Рис. 15.7.5
мы получим параллелограмм, подобно тому как в примере 1 для
ортогональной системы стержней предельная поверхность вырож-
вырождалась в прямоугольник. Наконец, добавим третью систему стер-
стержней, ориентированную под углом ф3. Соответствующий отрезок
перемещается по площади параллелограмма, очерчивая грани
параллелепипеда. В результате получается параллелепипед,
внутренность которого соответствует допустимым состояниям,
а граница — предельным состояниям, когда одна из систем
стержней переходит в состояние текучести. Добавляя еще систе-
системы стержней, будем получать последовательно многогранные
поверхности текучести; при этом не играет никакой роли то об-
обстоятельство, что тройная система статически определима, а си-
система стержней четырех и более направлений статически не-
неопределима.
Приведенные примеры показывают, что при решении задач
предельного равновесия применение условий типа A5.7.1) не
может считаться более оправданным, чем всякого рода кусочно
линейные аппроксимации, широко распространенные в лите-
литературе.
§ 15.8. Плоская задача теории пластичности
Под термином «плоские задачи» мы будем понимать такие,
которые вводят в рассмотрение только три компоненты тензора
напряжений аар и соответственно три компоненты тензора ско-
скоростей деформации еар и две компоненты вектора скорости va*
Это не означает, что поле напряжений или поле скоростей на
§ 15.8. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ ПЛАСТИЧНОСТИ 501
самом деле представляют собою плоские поля; просто оставшиеся
компоненты, если они отличны от нуля, не вводятся в рассмот-
рассмотрение. В случае необходимости их, как правило, можно найти
после того, как задача уже решена. Условие пластичности может
быть выражено в виде соотношения между главными напряже-
напряжениями Gi и а2 в плоскости ха> Третье напряжение а3 предполага-
предполагается либо вообще не входящим в условие пластичности, либо ис-
исключенным тем или иным способом (при принятой системе обо-
обозначений условие at > G2> a3, вообще говоря, не выполняется).
Вместо at и а2 нам будет удобно ввести в рассмотрение величины
Р = -Т(<*1 + Ош), т = у((Т1-(Т2)- A5.8.1)
С помощью обозначений A5.8.1) любое условие пластичности
для изотропного материала может быть записано в виде
т = т(/?). A5.8.2J
Обозначая через ф угол между первым главным направлением
и осью хи выразим компоненты тензора а«р через /?, т и г|), на-
например, с помощью построения круга Мора следующим образом:
а11 = р + тсоз2<ф, а22 = р — тcos 2г|), ai2 = тsin2-ф. A5.8.3J
Поскольку т есть функция от р согласно A5.8.2), компоненты
тензора напряжений выражаются всего через две величины: р
и ф. Подставляя в уравнения равновесия выражения A5.8.3),
получим
A + т' cos 2if>) рл — 2т sin 2i|n|)fl + х'р>2 sin 2г|) + 2т cos 2г|л|)>2 = 0,
A — х cos 2г|)) /7i2 + 2т sin 2фф|2 + t'/?,i sin 2г|) + 2т cos 2ЩЛ = 0.
A5.8.4J
Здесь %' = dxfdp.
Для интегрирования квазилинейной системы A5.8.4) приме-
применим метод характеристик, заключающийся в следующем. При-
Присоединим к уравнениям A5.8.4) следующие очевидные тождества:
рл dxi + p>z dx2 = dp, г]),! dxi + г|)>2 dxz = йг|). A5.8.5)
Тождества A5.8.5) вместе с уравнениями A5.8.4) представляют
собою систему четырех линейных уравнений для четырех неиз-
неизвестных: ptiJ pt2y i|),i, if>J. Решение этой системы для ptU напри-
например, может быть представлено следующим образом:
/>.! = %!. A5.8.6)
Здесь D — определитель системы, DPt i — тот же определитель,
в котором столбец, содержащий коэффициенты при /?fl, заменен
столбцом из правых частей. Определитель D содержит дифферен-
дифференциалы dxt и dx2, следовательно, зависит от выбранного в плос-
502 гл-15- идеальная пластичность
кости ха направления. Может случиться, что для некоторого на-
направления, составляющего угол ср с осью хи так что tgcp =
= dx2/dxi, знаменатель в формуле A5.8.6) обращается в нуль.
Это направление называется характеристическим направлением,
а линии, пересекающие ось Xi под углом ср, характеристиками.
Для того чтобы соотношение A5.8.6) имело смысл, необходимо,
чтобы числитель также обращался в нуль для того же направле-
направления. Но определитель DPt i содержит дифференциалы dp и d-ф,
следовательно, уравнение Dp> i == 0 представляет собою соотноше-
соотношение между dp и d\|), выполняющееся вдоль характеристики.
Иногда это соотношение оказывается возможным проинтегриро-
проинтегрировать, и мы получаем в замкнутом виде интеграл вдоль характе-
характеристики. Итак, положим D = 0. Опуская элементарные выкладки,
связанные с раскрытием определителя четвертого порядка, при-
придем после упрощений к следующему дифференциальному урав-
уравнению характеристик:
dx\ (cos 2-ф + т') + 2dx± dx2 sin 2ф + (cos 2ф — т') dx\ = 0.
Отсюда
Из формулы A5.8.7) следует, что при |х'| -< 1 существует два
семейства характеристик, соответствующих знакам плюс и минус
в формуле A5.8.7). В этом случае система A5.8.4) называется
гиперболической. Если |т'1 >1, то формула A5.8.7) определяет
мнимые направления, и система A5.8.4) называется эллиптиче-
эллиптической. Метод характеристик, т. е. отыскание соотношений вдоль
характеристик из условия DPt i = 0, для эллиптической системы
не приводит к цели. Наконец, промежуточный случай, когда
|т'| = 1 и оба семейства характеристик сливаются, соответствует
параболической системе исходных дифференциальных уравнений.
В зависимости от вида условия пластичности в теории пластич-
пластичности встречаются все три случая; при этом гиперболическая
задача оказывается наиболее простой, для нее разработаны эф-
эффективные методы решения. Дальнейшее изложение будет огра-
ограничено почти исключительно случаем гиперболичности уравне-
уравнений пластичности.
Будем называть семейство характеристик, соответствующее
знаку минус в формуле A5.8.7), характеристиками ?, а соответ-
соответствующее знаку плюс — характеристиками т|, понимая под этим
то, что можно выбрать параметры ? и т], определяющие положе-
положение точки по отношению к системе криволинейных координат,
образованных характеристическими линиями. Фактический вы-
выбор этих координатных параметров в каждом случае определяет-
определяется соображениями удобства, соответствующие примеры будут
§ 15.8. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ ПЛАСТИЧНОСТИ 503
рассмотрены ниже. Предположим, что ось xt направлена по ка-
касательной к характеристике ?, тогда угол ср равен нулю и из
A5.8.7) мы получаем
sin2i|) = +Vl — т'2 на линии ?.
Аналогично
sin2i|) = — VI — т'2 на линии т|.
Из этих двух соотношений следует, что
\|) = t'. A5.8.8J
Знак минус в этом соотношении исключен, так как в противном
случае знаменатель в формуле A5.8.7) обратился бы в нуль.
Поэтому в каждой точке характеристики
составляют углы ±г|) с первым главным на-
направлением, как показано на рис. 15.8.1. Из /у
A5.8.8) следует
A5'8'9)
Вместо того чтобы искать соотношения'
вдоль характеристик стандартным способом,
приравнивая нулю соответствующий опре-
определитель, мы придем к цели более корот-
коротким путем, отправляясь непосредственно
от уравнений A5.8.4). Умножим первое из них на sin 2гр, второе
на —cos 2i|) и сложим. Получим
sin 2^,1 — (cos 2xf> — т')pt2 — 2xipfl = 0.
Направим теперь ось Xi по касательной к линии ?. Вследствие
A5.8.8) коэффициент при втором члене исчезнет, sin 2\f> мы заме-
заменим на VI — т'2 и, разделив на 2т, получим следующее диффе-
дифференциальное соотношение, выполняющееся в любой точке харак-
характеристики ?:
у]/ 1 — %'2dp — d\|) = 0
на линии
Аналогичным образом находим
•?— у 1 — т'2 dp + d\|) = 0 на линии tj.
Эти соотношения интегрируются. Положим
Теперь интегралы вдоль характеристик записываются следующим
504 ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
образом:
-ф = const на линии |, A5 811)
= const на линии г\.
Перейдем теперь к рассмотрению поля скоростей. Условие пла-
пластичности A5.8.2) может быть записано в стандартной форме так:
( )
Вследствие ассоциированного закона пластичности мы находим
скорости деформации для главных направлений в следующем
виде:
e^Ml-т'), е2 = -ЯA + т'). A5.8.12)
При этом скорость сдвига равна нулю. Если материал изотропен,
то из ассоциированного закона течения следует, что главные оси
тензоров Gij и гц всегда совпадают. Выберем локальные оси де-
декартовой прямоугольной системы координат xt и х2, направлен-
направленные по главным осям тензора а«р, обозначим у4 и v2 компоненты
скорости по этим осям, тогда &i = vit i, е2 = v2>2. Из соотношений
A5.8.12) следует тождество
Заменяя 8i и е2 их выражениями и записывая условие равенства
нулю скорости сдвига, получим следующую систему:
A + т/)у1,1+A~т/)у2,2 = 0, i;i., +!7а,1 = 0. A5.8.13)
Вследствие A5.8.9) первое уравнение A5.8.13) можно заменить
следующим:
cos2 г|) vit 1 + sin2 г|) vZt 2 = 0.
Прибавим к этому уравнению второе уравнение A5.8.13), умно-
умноженное на sin -ф cos \|), и сложим. Замечая, что
где dsi — элемент касательной к характеристике |, представим
результат следующим образом:
•—- (vt cos if» + i;2'sin я|)) = 0. A5.8.14)
Но заключенное в скобки выражение представляет собою состав-
составляющую скорости по направлению характеристики |, которую
мы обозначим через Pg. Совершенно аналогичный результат по-
получается для скорости по направлению характеристики т], iv
Таким образом, мы получаем
dvi = Q на касательной к линии g, . .
(lo.o.lo)
dVn — О на касательной к линии tj.
Этот результат истолковывается очень просто: при пластическом
§ 15.9. ПЛОСКАЯ ДЕФОРМАЦИЯ
505
течении элементы, принадлежащие характеристикам, не меняют
длины.
Следует подчеркнуть, что в уравнении A5.8.14) ds* представ-
представляет собою дифференциал локальной декартовой системы коор-
координат, а не дифференциал дуги характеристики. Поэтому при
дифференцировании угол г|) считается постоянным. Соотношения,
выраженные через производные по характе-
характеристическим параметрам, можно получить
следующим образом. Обозначим через t и п
единичные векторы: касательный к линии \
и нормальный к ней; представим вектор v
следующим образом:
Здесь Vi и Vni соответственно — проекции
вектора v на касательную к линии g и на
нормаль к ней. Заметим, что dt = п chf),
dn = — ?<#ф, как это легко установить из
рис. 15.8.2. Продифференцировав вектор v по дуге характеристи-
характеристики, найдем
рис. 15.8.2
В»
ди„
— v*\n.
С другой стороны, дифференцируя тот же вектор, заданный в
неподвижной локальной системе координат г/а, получаем
Проделывая те же выкладки для второго семейства характери-
характеристик, мы заменим соотношения A5.8.15) следующими дифферен-
дифференциальными соотношениями, содержащими производные по харак-
характеристическим параметрам:
1 — Vn
дг\
= 0.
A5.8.16)
§ 15.9. Плоская деформация
Если скорость деформации в направлении оси хг е3 = 0, то
условия пластичности Мизеса и Треска — Сен-Венана приведут
к одному и тому же результату. Действительно, условие Мизеса
в главных напряжениях записывается следующим образом:
- о-2J + (а, - ст3J + (о-з - ах)
2ст?.
A5.9.1)
506 гл- 15- ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
Вследствие ассоциированного закона пластичности имеем
83 = А, Bа3 — Oi — а2) = 0,
поэтому
Подставляя в A5.9.1), получим следующее условие пластично-
пластичности, связывающее главные напряжения в плоскости at, a2:
Если принять условие пластичности Треска — Сен-Венана, то
равенство нулю скорости е3 означает, что в это условие не вхо-
входит напряжение а3, напряжение d есть наибольшее, напряже-
напряжение а2 — наименьшее и условие пластичности принимает вид
(Jl — 02 = (Тт.
Переходя к обозначениям § 15.8, убеждаемся, что как в том, так
и в другом случае условие пластичности A5.8.2) принимает са-
самую простую форму, а именно,
Постоянная к называется пластической постоянной, она состав-
составляет 1/2 предела текучести при критерии Треска — Сен-Венана и
ат/УЗ « 0,56ат для критерия Мизеса. Очевидно, что эта разница
никак не сказывается на ходе решения задачи.
По формуле A5.8.9) tga = ±l. Это значит, что характеристи-
характеристики ортогональны и пересекают траектории главных напряжений
под углом ±я/4. Но на площадках, равнонаклонных к главным
осям, достигают максимального значения касательные напряже-
напряжения. Следовательно, характеристики — это траектории главных
касательных напряжений. Вследствие A5.8.14) вдоль характе-
характеристик удлинения равны нулю, поэтому вся деформация пред-
представляет собою чистый сдвиг в осях |, т]. Конечно, последнее
замечание относится к бесконечно малой деформации, связанной
с мгновенным распределением скоростей деформации.
По формуле A5.8.10) мы находим, что
Поэтому интегралы A5.8.11) принимают вид
A5.9.2)
jj-— г|) = const на линии ?,
JL + tb = const на линии ti.
Интегралы уравнений теории пластичности A5.9.2) были полу-
получены Хенки в 1923 г. и носят его имя.
§ 15.9. ПЛОСКАЯ ДЕФОРМАЦИЯ 507
Формулы A5.9.2) подсказывают естественный выбор коорди-
координатных параметров характеристических линий
Как будет показано дальше, существуют вырожденные случаи,
когда величины ? и г) не могут приниматься за криволинейные
координаты точки в плоскости ха, но пока мы эти случаи рас-
рассматривать не будем.
Дифференциальные уравнения характеристик в плоскости мы
получим, записав
dx dx
—е = tgi|) на линии g, -г-* =ctg if> на линии ц.
1 1
Вследствие A5.8.9) при т' = 0 а = я/4. Поскольку угол а на-
наклона характеристик к линиям главных напряжений отличается
от угла ф на постоянную величину я/4, мы заменили в соотно-
соотношениях A5.9.2) угол ф на угол ср. Таким образом, мы получаем
Введем новые переменные по формулам
Xi = #i cos ф — х2 sin ф, х2 = Xi sin ф + х2 cos ф.
Подставляя их в A5.9.3), получим следующую систему:
Уравнения для скоростей A5.8.16) имеют точно такую же фор-
форму. Действительно, для ортогональной сетки характеристик vni =
вУч, vny] — — vi и уравнения принимают вид
??-4-*,-0, ^! + 4-»б-О. A5.9.5)
Уравнения A5.9.5) носят название уравнений Гейрингер.
Исключая из A5.9.4) или A5.9.5) любую из переменных, мы
находим, что каждая из величин хи х2, V*, иц удовлетворяет те-
телеграфному уравнению
k -rf=:0- A5-9-6)
С помощью найденных уравнений может быть решена следующая
основная задача или задача Коши для уравнений теории пла-
пластичности. На участке дуги АВ контура тела, находящегося в
условиях плоской деформации, заданы усилия (рис. 15.9.1). По-
Положим в формулах A5.8.3) г|) = ф + я/4, они примут следующий
508
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
вид:
— Tsin2q>, а22 = р + т sin 2<p, а12 =
A5.9.7)
Поскольку на дуге АВ контура в каждой точке выполнено усло-
условие СарЯр = Га, а аар выражаются через две величины, р и ф, то
каждой точке контура М можно сопоставить точку т в плоскости
характеристик ?, tj, а отрезку АВ в плос-
плоскости ха будет соответствовать отрезок
аЪ в плоскости характеристик, как пока-
показано на рис. 15.9.2. Для каждой точки т
граничной кривой аЪ в плоскости харак-
характеристик по формулам A5.9.4) можно
вычислить величины Xi и х2. Далее про-
производится интегрирование линейной си-
системы A5.9.4) в плоскости характери-
характеристик. Решение определено в треугольнике
abc, образованном дугой аЪ и крайними
характеристиками, проведенными через точки а, Ь. Простейшая
численная схема будет состоять в том, что треугольник в плоско-
плоскости |, г\ разбивается ортогональной сеткой координатных линий,
а дифференциальные уравнения заменяются разностными
(#
Рис. 15.9Л
Здесь индексы т нумеруют вертикальные ряды точек, индексы
п — горизонтальные. По этим формулам последовательно вычис-
вычисляются Ха в точках ряда, ближайшего
к линии аЬ, затем следующего ближай-
ближайшего ряда и так далее до точки с.
Для каждого угла в плоскости ?, г\,
таким образом, находятся величины хл
и по формулам A5.9.4), координаты
точек в физической плоскости. Нанося
соответствующие точки в плоскости ха,
мы получаем криволинейные характе-
характеристики; каждой точке Q в физической
__ плоскости соответствует точка q в
? плоскости характеристик, координаты
которой § и к\ определяют величины р
и ф, а следовательно, компоненты тен-
тензора напряжений аар для точки Q.
Совершенно аналогичным способом рассчитывается поле ско-
скоростей, если на линии АВ заданы компоненты скорости.
Как мы убедились, решение задачи Коши определяет един-
единственным образом поле напряжений в криволинейном треуголь-
\
\
\
Рис. 15.9.2
§ 15.10. ПРОСТЫЕ РЕШЕНИЯ. ЗАДАЧА ПРАНДТЛЯ 509
нике ABC. Вообще говоря, это решение может быть продолжено:
к характеристике АС или ВС может примыкать новая пласти-
пластическая область. Именно таким образом строятся перечисленные
в § 15.4 задачи жесткопластического анализа, примеры которых
будут приведены ниже. Как правило, пластические зоны грани-
граничат с зонами, которые остаются жесткими.
Это последнее обстоятельство указывает на то, что задачи
теории идеальной пластичности не оказываются статически опре-
определенными, как это может показаться на первый взгляд и как
считалось в ранние периоды развития теории пластичности. На-
Наличие жестких зон означает кинематическое стеснение пласти-
пластического течения: на границе жесткой зоны нормальная состав-
составляющая скорости должна обращаться в нуль. Поэтому, после
того как построено статическое решение по методу, изложенному
выше, необходимо проверить, возможно ли для данного поля
характеристик построить кинематически возможное поле скоро-
скоростей. В случаях, изображенных на рис. 15.4.3 или 15.4.4 (в по-
последнем случае стенки фильеры играют роль границ жестких
областей), может оказаться, что линия разрыва скрости упи-
упирается в границу жесткой зоны,— такое решение недопустимо.
Но даже если кинематически возможное поле скоростей удается
построить, может оказаться, что скорость диссипации энергии D
в некоторой области окажется отрицательной, что также невоз-
невозможно. Наконец, устанавливая границы жестких и пластических
зон, мы всегда располагаем определенной свободой выбора. Мо-
Может оказаться, что та часть материала, которую мы предполагали
жесткой, на самом деле перейдет в состояние текучести. Теперь
мы можем сформулировать требования, которые должны предъ-
предъявляться к истинному или так называемому полному решению
плоской задачи теории пластичности, а именно:
1) возможность построения кинематически допустимого поля,
скоростей;
2) неотрицательность диссипации;
3) непревышение условия пластичности в жестких областях.
Для проверки выполнимости последнего требования обычно
бывает достаточно удовлетвориться проверкой возможности про-
продолжения пластических полей в жесткие области. Полученное
поле напряжений будет статически допустимым, поэтому верхняя
и нижняя оценки предельной нагрузки совпадают, давая точное
решение.
§ 15.10. Простые решения. Задача Прандтля
В предыдущем параграфе существенным образом предполага-
предполагалось, что часть границы тела отображается на плоскость ?, ц
как некоторая линия, не параллельная оси ? или оси tj, т. е.
не являющаяся характеристикой. Так бывает не всегда. Пред-
510
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
положим, что на участок прямолинейной границы действуют
равномерно распределенные нормальные усилия а и касательные
усилия т (рис. 15.10.1). Нормаль п к границе образует угол а
с осью xi. По формулам A5.9.7), вычисляя нормальное и каса-
касательное напряжения на площадке с нормалью/г, получим
<5п = р — к sin 2 (ф — а), тп = к cos 2 (ср — ос). A5.10.1 J
Отсюда находятся постоянные значения ф и /?, а следовательно,
Рис. 15.10.1
Рис. 15.10.2
?о и Tio. Отрезок АВ границы изображается в плоскости ?, г\
одной только точкой (go, Ло)' Угол наклона характеристик ф
постоянен, поэтому пластическое поле представляет собою тре-
треугольник; внутри этого треугольника величина р постоянна, она
сохраняет то же значение, что и на границе.
Другое простое решение мы получим тогда, когда пласти-
пластической области соответствует отрезок характеристической линии
в плоскости характеристик, на-
например линии | = const, как по-
показано на рис. 15.10.2. Каждая
точка этой линии имеет координа-
координаты go и т]. Пусть в точке т ц = т]0,
значит, ей соответствует в плоско-
плоскости xi, x2 ^-характеристика, вдоль
ф = -у- A0 + Ло). -^ =
Рис. 15.10.3
которой
= ~2" (?о — Ло)- Итак, g-характери-
стики представляют собою прямые, в каждой точке которых на-
напряженное состояние одинаково, т. е. все три компоненты тензора
напряжений сохраняют постоянные значения. Совершенно анало-
аналогичным образом отрезку линии л = const в плоскости хи х2 соот-
соответствуют прямолинейные ^-характеристики.
По-видимому, первое решение задачи теории идеальной пла-
пластичности принадлежит Прандтлю. В прямолинейную границу
вдавливается прямолинейный штамп без трения, так что под
штампом возникает распределенное давление q (рис. 15.10.3).
§ 15.10. ПРОСТЫЕ РЕШЕНИЯ. ЗАДАЧА ПРАНДТЛЯ 511
Как мы выяснили, треугольная область под штампом соответ-
соответствует точке в плоскости характеристик, в этой области возни-
возникает постоянное напряженное состояние такое, что 022 = —?.
Характеристики подходят к поверхности под углом я/4, назовем
^-характеристикой линию, проведенную из некоторой точки под
углом —я/4. Подставляя в A5.9.7), находим
022 = -g = />-&;
отсюда
p = k-q
в области, отмеченной римской цифрой /. Пристроим к тре-
треугольнику справа центрированный пучок линий т], который со-
соединит область / с треугольной областью ///. Характеристика
семейства | выходит из области / под углом —я/4, превращается
в дугу окружности, ортогональной к прямолинейным характе-
характеристикам семейства т] и продолжается в области /// как отрезок
прямой, пересекающей границу под углом +я/4. В области ///
022 = О, и, следовательно, A5.9.7) дает О^р + к; отсюда
р = —к.
Но вдоль ^-характеристик величина т], определяемая формулой
A5.9.2), остается постоянной. Поэтому
/г — д п _ к я
Отсюда
q = B + я) к. A5.10.2);
Прандтль строил изображенную на рис. 15.10.3 симметричную
картину. При этом поле скоростей получается следующим обра-
образом. Центральный треугольник
движется вниз как жесткое целое.
На линии АВ тангенциальная со-
составляющая скорости претерпевает
разрыв, но нормальная к АВ состав-
составляющая, равная WV2, сохраняется рис ^10 4
неизменной вдоль каждой из дуг
окружностей, представляющих собою
^-характеристики в области //. В результате весь треугольник
ACD движется как жесткое целое в направлении, указанном
стрелкой, скользя по границе жесткой зоны CD.
Полученное решение полно, найдено кинематически допусти-
допустимое поле скоростей, диссипация, очевидно, не отрицательна,
возможно продолжение решения в жесткие зоны как угодно
далеко. Предельная нагрузка, при которой наступает течение
материала, определяется формулой A5.10.1). Но конфигурация
пластических зон и кинематика течения единственным образом
не определяются. Альтернативная схема, предложенная Хиллом,
512
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
представлена на рис. 15.10.4. Два жестких треугольника сколь-
скользят направо и налево под углом я/4, вытесняя материал в сек-
ториальных областях и крайних треугольниках. Теперь поле
скоростей во всей пластической области EBCDA непрерывно,
скольжение происходит по границе жесткой зоны. Очевидно, что
предельное значение нагрузки q вычисляется точно так же по
формуле A5.10.2). Заметим, что, отправляясь от решения
Прандтля, мы можем продолжать пластическое поле вниз, как
d
Рлс. 15.10,5
показано на рис. 15.10.5. На том же рисунке представлена кар-
картина в плоскости характеристик. Точка Ъ соответствует точке В
в физической плоскости и всему жесткому треугольнику, отрезки
be и bd соответствуют дугам ВС и BD. Построение характери-
характеристик в физической плоскости производится путем интегрирования
уравнений A5.9.5) с помощью разностной схемы, которая ничем
не отличается от описанной вы-
выше схемы решения задачи Ко-
ши. Расширяя веер пучков пря-
прямолинейных характеристик,
т. е. продолжая симметричным
образом дуги ВС и BD, мы бу-
будем продвигать все дальше и
дальше точку О, где встречают-
встречаются крайние характеристики. Ре-
Реальный смысл этой задачи со-
состоит в схеме перерезывания
полосы толщиной 2h. Нужно
представить себе, что к полосе симметричным образом с двух сто-
сторон приложены нагрузки, равномерно распределенные на длине I
каждая, когда пластические поля от этих нагрузок встречаются в
точке О, пластическая область пронизывает всю толщину полосы
насквозь, и происходит ее перерезывание. Заметим, что диффе-
дифференциальное уравнение A5.9.6) может быть проинтегрировано по
методу Римана; функцией Римана для него служит некоторое
выражение, содержащее функцию Бесселя; мы здесь не приводим
этого выражения. Хилл рассчитал таблицы координат точек, по ко-
Рис. 15.10.6
§ 15.11. ЛИНИИ РАЗРЫВА
513
торым может быть построено поле характеристик, продолжающее
поле, ограниченное двумя характеристиками в форме дуг окруж-
окружности.
Заметим, что решение задачи Прандтля допускает немедлен-
немедленное и совершенно очевидное обобщение. Рассмотрим тупой угол,
загруженный равномерно распределенной нагрузкой на одной
из сторон, как показано на рис. 15.10.6. Выполняя построение
так же, как в задаче Прандтля, мы строим два треугольника /
и /// и соединяющий их сектор //. В результате точно таких же
вычислений мы находим
д = B + я-26)Л. A5.10.3)
§ 15.11. Линии разрыва
Формула A5.10.3) и соответствующая конфигурация пласти-
пластической области относятся только к случаю тупоугольного клина.
Если угол б > я/2 и клин остроуголен, области / и /// нала-
налагаются друг на друга. В этом случае строится решение с линией
разрыва напряжений, как показано на рис. 15.11.1. Характери-
Характеристики в областях АОС и ВОС прямолинейны, они отходят от
сторон угла, составляя с ним
углы ±я/4 (на рисунке пока-
показаны только характеристики од-
одного семейства). На линии ОС
должны быть непрерывны нор-
нормальное к этой линии напря-
напряжение оп и касательное тп,
тогда как напряжение от, пока-
показанное на том же рисунке
справа, может претерпевать раз-
разрыв. Составим поэтому те об-
общие условия, которые должны
выполняться на линии разрыва
напряжений. Будем обозначать
индексами плюс и минус вели-
величины, относящиеся к разным сторонам линии разрыва. Условия
непрерывности оп и хп по формулам A5.10.1) могут быть запи-
записаны следующим образом:
р+ — к sin 2 (ф+ — а) = р~ — к sin 2 (ф~ — а),
cos (ф+ — а) = cos (ф~ — а).
Из второго уравнения следует
Ф+ — а = — (ф~ — а) ± шт,
так как, удержав в этом равенстве знак плюс перед скобкой в
правой части, мы получили бы ф+ = ф~ и, следовательно, не-
33 ю. Н. Работнов
514 гл- 15- идеальная пластичность
прерывность всех компонент напряжения. Теперь из первого
уравнения получаем
/>+-/r = ±2&sin2(cp--a). A5.11.1)
Знак плюс или минус в уравнении A5.11.1) выбирается по смыс-
смыслу. Возвращаясь к задаче об остроугольном клине с углом ра-
раствора 2у = я — 6, принимаем прямую ОС за ось х2, тогда а = 0.
Так же, как в задаче Прандтля p+~k—q1 р~ = — ft, угол ф+,
который составляет идущая слева характеристика с горизонталью
Ф+ = я/4 —у. Подставляя в A5.11.1), находим
2к - q = ±2к cos 2-у.
Для характеристик, изображенных на рис. 15.11.1, в этом
соотношении следует выбрать знак плюс, и мы найдем предель-
предельную нагрузку следующим образом:
g = 2&(l-cos2Y). A5.11.2)
Выбор знака в данном случае подчинен условию того, что при у,
стремящемся к нулю, предельная нагрузка должна также стре-
стремиться к нулю.
Из условия пластичности A5.9.2), которое можно переписать
так:
следует
к2 - т*, A5.11.3)
а поскольку оп и тп непрерывны, разрыв напряжения ot может
происходить только за счет изменения знака перед радикалом.
На характеристике тп = к и радикал обращается в нуль. Отсюда
вытекает фундаментальный результат, а именно: характеристики
или линии скольжения не могут служить линиями разрыва для
напряжений.
С другой стороны, тангенциальная составляющая скорости
может претерпевать разрыв только вдоль характеристики. Это
ясно из процедуры построения поля скоростей по характеристи-
характеристикам, отправляясь от линии АВ, на которой скорости заданы.
Очевидно, что если распределение скоростей на границе имеет
разрыв, претерпевать разрыв может только абсолютная величина
скорости, но не ее направление, в противном случае произошло
бы нарушение сплошности тела. Характеристика, выходящая из
точки разрыва граничных условий, будет нести разрыв танген-
тангенциальной составляющей скорости. Таким образом, тангенциаль-
тангенциальная составляющая скорости течения может претерпевать разрыв
только на характеристике или на особой линии, служащей оги-
огибающей семейства характеристик.
§ 15.12. ЗАДАЧА О ПЛОСКОЙ ДЕФОРМАЦИИ
515
Возвращаясь к примеру остроугольного клина, обратимся к
§ 3.6, где было дано элементарное рассмотрение задачи об из-
изгибе стержня из упруго-идеально-пластического материала. На
рис. 3.5.1 представлены эпюры напряжений в сечении. По мере
роста изгибающего момента пластические зоны охватывают все
большую часть сечения, упругая область суживается, и в пре-
пределе, когда М -> А/т, упругая область обращается в плоскость
(на чертеже в линию), отделяющую растянутую область от сжа-
сжатой. Таким образом, линия разрыва напряжений может рассмат-
рассматриваться как предельная конфигурация упругой области, если
рассматривать полностью пластическое состояние тела как пре-
предельное состояние для тела упругопластического. Но в приве-
приведенном выше изложении теории предельного равновесия подоб-
подобного рода соображения могут иметь лишь наводящий характер.
§ 15.12. Применение экстремальных принципов
к задаче о плоской деформации
Экстремальные принципы теории идеальной пластичности,
изложенные в § 15.5, позволяют весьма просто получить верх-
верхние оценки для несущей способности. Обычный способ получе-
получения таких оценок заключается в том, что предполагаемая пласти-
пластическая область разрезается на жесткие блоки, которые могут
скользить друг относительно друга, преодолевая силу трения
% = k. Одна из возможных схем приближенного решения задачи
case:
Рис. 15.12.1
о вдавливаний штампа представлена на рис. 15.12.1. Блоки обо-
обозначены большими латинскими буквами, вдавливающийся штамп
обозначен буквой А, оставшаяся жесткой часть массива — бук-
буквой О. Рядом построена диаграмма относительных скоростей;
на этой диаграмме точки соответствуют блокам, отрезок CD,
например, представляет относительную скорость скольжения бло-
блока С относительно D. Из соображений симметрии диаграмма по-
построена только для одной половины пластической области.
Элементарный подход, получающийся в результате сложения
произведений длин границ на их относительные скорости и при-
33*
516
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
равнивания этого произведения мощности внешних сил, при-
приводит к следующей оценке для предельной нагрузки:
1
q<2
sin a cos а
+
A5.12.1)
При а = 30°, получаем
q < 5,77&,
что превышает точное значение A5.10.2) на 12%. Минимизируя
оценку по углу, можно ее немного уменьшить (на 2%). Для
задачи о тупом клине, нагруженном на одной из сторон
(рис. 15.10.6), кинематически возможная схема состоит в том, что
часть материала просто соскальзывает по плоскости, наклонной
Рис. 15.12.2
к горизонту под углом р (рис. 15.12.2). Будем считать, что спол-
сползает часть угла, занимающая отрезок, равный единице, и вер-
вертикальная скорость тоже равпа единице. Из нарисованной справа
диаграммы скоростей находим, что скорость скольжения есть
1/sin p, длина, по которой происходит скольжение, найдется по
sin у -гт
теореме синусов, она равная—( ' . Поэтому
sin \у р)
sin у
sin E sin (у — P)*
Как нетрудно убедиться, минимум этого выражения достигается
при р = у/2, таким образом,
Q< slny . • A5.12.2)
sin2 (y/2) '
Знак равенства получается тогда, когда у = я/2, и схема соскаль-
соскальзывания под углом я/4 соответствует точному решению.
Следующий пример относится к протяжке полосы. Половина
толщины ее до протяжки равнялась единице, после протяжки А.
Простейшая кинематическая схема представлена на рис. 15.12.3,
положение точки F выбирается так, чтобы получилась минималь-
минимальная верхняя оценка для натяжения р. Положение точки F будем
задавать расстоянием ее т до границы EG.
§ 15.12. ЗАДАЧА О ПЛОСКОЙ ДЕФОРМАЦИИ
517
Диаграмма скоростей представлена на том же рисунке. Из
элементарной геометрии следует:
vAb
-VIZ
2 cos a
+ 1,
" ]/ rr?
2 cos а
1
При этом принято, что лист поступает в матрицу со скоростью,
равной единице, и выходит со скоростью 1/й. Вычисляя длины
отрезков EF и FG и состав-
составляя выражение мощности,
развиваемой при взаимном
скольжении блоков, получим
Полученное выражение до-
достигает минимума, когда т =
= Уй, и, следовательно,
2к sin a I
— 2ctga. A5.12.3)
Ha рис. 15.12.4 представ-
представлены графики зависимости
величины р/Bк) от степени
редукции h. Очевидно, что
решение имеет смысл тогда, Рис. 15.12.3
когда р < 2/с. На рисунке
приведены только те части получающихся при расчете по урав-
уравнению A5.12.3) кривых, которые удовлетворяют этому условию.
Если угол а невелик, а степень редукции значительна, то мень-
меньшая оценка для усилия р получится, если принять более слож-
сложную схему разбивки пластической области на блоки, а именно
ту, которая показана на рис. 15.12.5. Часть кривой для а = 30°
справа от точки излома рассчитана именно по этой схеме (Кал-
ладайп).
Для нахождения нижних оценок несущей способности необ-
необходимо строить статически допустимое поле напряжений. Эта
задача, как правило, оказывается более сложной, чем задача по-
построения кинематически возможного поля. Действительно, строя
кинематически возможное поле скоростей, мы можем выбрать
границу с жесткой областью по произволу и совершенно не дол-
должны заботиться о том, может ли эта область на самом деле
оставаться жесткой, тогда как статически возможное состояние
должно распространяться на всю область, занятую телом. Один
простой способ построения статически возможных полей напря-
напряжений мы покажем. Заметим прежде всего, что статически воз-
518
ГЛ. 15. ИДЕАЛЬНАЯ ПЛАСТИЧНОСТЬ
можное напряженное состояние изображается кругом Мора с
радиусом, меньшим или равным пластической постоянной к.
Если линия, нормаль к которой есть п, служит линией разрыва
напряжений, на этой линии непрерывны ап и тп, тогда как а<
претерпевает разрыв в соответствии с формулой A5.11.3). Точка
с координатами оп и хп оказывается, таким образом, общей для
кругов Мора, изображающих напряженное состояние по две сто-
стороны линии разрыва. Для определенности рассмотрим опять
задачу о штампе. Под штампом
возникает состояние двухсторон-
двухстороннего сжатия, которое изображает-
изображается кругом Мора / (рис. 15.12.6).
Л
4
ОЛ 0,5 0,8 0,9 0,95
(Г-/1)
Рис. 15.12.4
Рис. 15.12.5
Точка F соответствует сжатию от приложенной нагрузки д, так
что абсцисса ее есть — д. Круг /// изображает состояние сжатия
в области, находящейся под свободной поверхностью, главные
оси тензора напряжений направлены по вертикали и по гори-
горизонтали, вертикальное напряжение равно нулю, поэтому круг
Рис. 15.12.6
Мора проходит через начало координат. Состояние внутри угла,
стороны которого составляют угол ±ф с вертикалью, проходя-
проходящей через граничную точку погруженного участка, изображается
малым кругом Мора //. Точки т и п пересечения круга II с
кругами / и III определяют разрывы напряженного состояния.
15.12. ЗАДАЧА О ПЛОСКОЙ ДЕФОРМАЦИИ
519
Вспоминая правило, согласно которому углам в физической плос-
плоскости соответствуют удвоенные дуги кругов Мора, проходимые в
противоположном направлении, заметим, что углу я/2 — ф между
прямыми С и М в области /// соответствует дуга Cm круга ///,
измеряемая углом я — 2ф. Аналогичным образом, дуга Fn на кру-
круге / измеряется также центральным углом я — 2ф. Точки тип
круга // соответствуют прямым, угол между которыми равен 2ф,
поэтому центральный угол, определяющий дугу тщ равен 4ф.
Отсюда следует, что радиусы круга / и круга //, проходящие
через точку п, пересекаются в этой точке под прямым углом,
это же относится к радиусам кругов II и ///, проходящим че-
через точку п. Таким образом, если положение точки F задано,
Рис. 15.12.7
Рже. 15.12.8
радиус круга // этим определен. Самое дальнее положение точки
F, т. е. самое большое значение нагрузки q получается в том
случае, когда в клиновидной области II также осуществляется
пластическое состояние, т. е. радиус круга /7 равен к. Этот
случай изображен на рис. 15.12.7; для величины q получается
следующая оценка:
п *> кО 4- 9У9"\ « Л ЯЧА* М^19Л\
Идя далее по этому же пути, мы можем провести из граничной
точки загруженного участка несколько лучей и ввести в рас-
рассмотрение соответственно несколько клиновидных зон. В резуль-
результате оценка для q будет увеличиваться, а в пределе мы получим
центрированный пучок характеристик, соответствующий точному
решению.
Проведенный анализ относился к упрощенной задаче, когда
нагрузка простирается вправо бесконечно далеко. Но полученная
оценка A5.12.4) будет справедлива и для штампа конечной ши-
ширины. Действительно, обращаясь к рис. 15.12.8, мы убеждаемся,
что на границе между областями II и IV выполняются те же
условия, что и на границе областей II и ///, например. Поэтому
в области IV возникает напряженное состояние, изображаемое
кругом Мора 777 на рис. 15.12.6.
520 гл- 15- идеальная пластичность
§ 15.13. Полярно-симметричное пластическое
напряженное состояние
Если часть границы плоского тела образована дугой окруж-
окружности радиусом а и действующая нагрузка направлена по нор-
нормали к этой дуге, т. е. по радиусу окружности, поле напряже-
напряжений мы получим, предположив его полярно-симметричным с по-
полюсом в центре окружности. Напишем уравнение равновесия в
полярных координатах, предполагая, что аг и аф — главные на-
напряжения:
Условие пластичности имеет вид о^ — ог = ±2/с. Выбирая для
определенности знак плюс, получим
dr ~~ г '
Отсюда
ar = -g + 2fcln-j-f аф = — g + 2fe/^1 + In^-^ A5.13.1)
Здесь через q обозначено нормальное давление, приложенное на
границе: таким образом, использовано граничное условие ar(a) =
= — q. Траектории главных напряжений — это лучи и концентри-
концентрические окружности, поэтому траектории главных касательных
напряжений образуют с радиусом углы ±я/4 в каждой точке,
т. е. представляют собою логарифмические спирали.
Простейшая задача, которую можно решить с помощью фор-
формул A5.13.1),— это задача о предельном равновесии трубы, на-
находящейся под действием внутреннего давления. Обозначим че-
через а внутренний радиус, через Ъ наружный радиус трубы. По-
Полагая в первой из формул A5.13.1) аг(Ь) = О, находим
Что касается поля скоростей в данном случае, оно находится
элементарно, без применения метода характеристик. Поскольку
поле скоростей тоже полярно-симметрично, оно задается при
помощи одной только радиальной компоненты скорости и. Скоро-
Скорости в радиальном и осевом направлениях будут соответственно
du и
ег — -jgr, еФ — —•
Мы не приводим вывода этих формул, отсылая читателя к § 8.12,
где аналогичные выражения были получены не для скоростей
деформации, а для деформаций. Поскольку скорость деформации
в осевом направлении ez = 0, а материал несжимаем, мы полу-
§ 15.13. ПОЛЯРНО-СИММЕТРИЧНОЕ СОСТОЯНИЕ
521
чаем для функции v{r) следующее дифференциальное уравнение:
Отсюда следует
: — Х const.
A5.13.2)
Формулы A5.13.1) применимы и тогда, когда имеется незагру-
незагруженный участок границы, образованный дугой окружности;
в этом случае нужно положить q = 0. Решение будет определяться
единственным образом в криволинейном треугольнике, обра-
образованном граничной дугой и выходящими из ее концов логариф-
логарифмическими спиралями. Конечно, это верно лишь тогда, когда мы
на самом деле уверены в том, что материал в области, примы-
примыкающей к круговой границе, находится в пластическом состоянии.
В качестве примера рассмотрим задачу о растяжении полосы с
симметричными круглыми вырезами (рис. 15.13.1). Из уравне-
уравнения логарифмической спирали г = а ехр ср следует, что крайние
характеристики встретятся на оси симметрии полосы тогда, когда
точки выхода этих характеристик будут определяться углами ±^т
причем
В сечении pq распределение напряжений дается второй из фор-
формул A5.13.1), а именно:
и удваивая результат,
Интегрируя в пределах от г = а до
522 гл-15- идеальная пластичность
получим
^ Н + т-} <15ЛЗ-3>
Здесь Akh — несущая способность гладкой полосы, ширина кото-
которой равна минимальной ширине надрезанной полосы. Выражение,
стоящее в правой части формулы A5.13.3), всегда больше еди-
единицы, оно называется коэффициентом поддержки. При любом
виде надреза несущая способность полосы с концентратором бу-
будет больше, чем несущая способность полосы с той же минималь-
минимальной шириной. Это следует из статического экстремального прин-
принципа. Если предположить, что в заштрихованной на рис. 15.13.2
полосе растягивающее напряжение равно пределу текучести,
а в остальной части полосы напряжения равны нулю, мы полу-
получим некоторое статически возможное напряженное состояние;
соответствующая нагрузка будет служить оценкой для предель-
предельной нагрузки снизу. Что касается поля скоростей для полосы
с двумя круговыми вырезами, расчет его оказывается далеко не
элементарным. Разделенные пластической зоной части полосы
движутся поступательно вдоль оси, удаляясь одна от другой с
относительной скоростью V; на граничных характеристиках нор-
нормальная составляющая скорости задана и выполнены условия
A5.8.16). Эти данные позволяют или строить поле скоростей
численно, или же решать задачу аналитически по методу Рима-
на, представляя результат в виде некоторых интегралов, содер-
содержащих функции Бесселя. Что касается полноты построения
решения, этот вопрос остается открытым. Возможность построе-
построения поля скоростей доказывает лишь кинематическую допусти-
допустимость решения, следовательно, формула A5.3.3) дает наверняка
верхнюю оценку. Но могут существовать и другие кинематически
возможные схемы, например скольжение по прямой тп, пока-
показанной на рис. 15.13.1 штриховой линией, которые дадут для Р
оценку более низкую, чем оценка A5.13.3).
Рассмотрим теперь полосу, ослабленную круглым отверстием
(рис. 15.13.3). Можно и здесь строить поля характеристик из
логарифмических спиралей от контура отверстия до выхода на
боковую сторону. Но треугольники, образованные прямолиней-
прямолинейными характеристиками, выходящими с боковой стороны, соот-
соответствуют равномерному полю растягивающих напряжений. По-
Полученная оценка несущей способности
P = 2kBh-2a)
будет точной, так как статически возможное поле, построенное
по тому же принципу на рис. 15.13.2, дает точно ту же вели-
величину предельной нагрузки^
§ 15.14. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
523
§ 15.14. Плоское напряженное состояние
В случае плоского напряженного состояния условия пластич-
пластичности Мизеса и Треска — Сен-Венана приводят к разным резуль-
результатам. Рассмотрим сначала условие Мизеса. Для плоского напря-
напряженного состояния оно принимает вид
Мы удовлетворим этому уравнению тождественно, если примем
ох = 2kcos((d — ~], Go = 2/ccosfco + 5jr]. A5.14.1)
I о / l и /
Отсюда следует
p = кУЗ cos со, т = к sin a).
Для подстановки в формулу A5.8.7), определяющую наклон ха-
характеристик, вычислим производную
, йт 1_
После подстановки в A5.8.7), получаем
t — УЗ" sin 2г|з sin со + 1^3 — 4 cos2 со
"j/З cos 2г|? sin со — cos со
A5.14.2)
Для того чтобы характеристики были действительны, должно
быть cos2 со < 3/4. Формулы A5.14.1) представляют собою пара-
параметрическое уравнение эллипса в координатах ои а2. Этот эллипс
Рис. 15.141
Рис. 15.14.2
изображен на рис. 15.14.1, цифры, стоящие около четырех точек
эллипса, обозначают соответствующие значения а). Жирными ли-
линиями от со = я/6 до 5я/6 и от 7я/6 до Ия/6 обозначены те об-
области, для которых характеристики действительны и уравнения
524 гл-15- идеальная пластичность
гиперболические. В отмеченных четырех точках характеристики
совпадают и система уравнений становится параболической,
оставшиеся небольшие участки соответствуют области эллиптич-
эллиптичности.
Функцию G(p), определенную формулой A5.8.10), удобнее
представить как функцию параметра со, а именно,
Интегралы вдоль характеристик записываются теперь в форме
A5.8.11). Из соотношения A5.14.2) следует, что характеристики
не ортогональны. По формуле A5.8.9) можно вычислить угол
±<х, который составляют характеристики с первым главным на-
направлением
В частности, если напряженное состояние представляет собою
простое растяжение, то со = л;/3, как это видно из рис. 15.14.1,
и tga = Y2, a = 55°44/. Предположим, что полоса просто растя-
растягивается напряжением <3i и pq — одна из характеристик, отделя-
отделяющих верхнюю жесткую область от пластической нижней. Неза-
Независимо от общей теории покажем, что характеристика pq служит
также характеристикой для поля скоростей. Выберем локальные
оси координат, как показано на рис. 15.14.2; напряжения в этих
осях будут определяться по формулам A5.8.3), а именно,
<*ii=f(l — cos2\|)), a22=y(l + cos2\|)), a12 =-Jsin2ap. A5.14.5)
Здесь мы посчитали угол a|) неизвестным, наша задача состоит
в том, чтобы показать, что линия pq есть на самом деле харак-
характеристика и а|) = я/2 — а. Условие пластичности Мизеса запишет-
запишется в координатах ха следующим образом:
<*и + <4 - <*па22 + у ((& + aL) = 3/с2.
Вследствие ассоциированного закона течения
8ц = Я Bан — a22), е22 = Я B<з22 — 0п)» 2е12 = Y а = %вц.
Но вдоль характеристик скорость деформации должна равняться
нулю. Подставляя A5.14.5) в условие 2<3ц — а2г = 0, мы найдем,
что угол а|) действительно дополняет угол а до прямого, т. е. а|) =
= 35°16/. В отличие от случая плоской деформации, на границе
может претерпевать разрыв не только тангенциальная составля-
составляющая, но и нормальная к характеристике составляющая. Теперь
§ 15.14. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
525
сумма главных удлинений в пластической области уже не равна
нулю, следовательно, происходит изменение толщины пластинки.
Формулы A5.14.1) показывают, что при плоском напряжен-
напряженном состоянии величины главных напряжений ограничены ве-
величиной 2/с, в отличие от плоской деформации, где они могут
быть сколь угодно велики, лишь бы их разность оставалась по-
постоянной. В задаче о трубе под действием внутреннего давления,
рассмотренной в § 15.13, наружный радиус Ъ можно было брать
сколь угодно большим, всегда можно приложить настолько боль-
большое давление q, чтобы труба полностью перешла в пластическое
состояние. Аналогичным образом в задаче о
растяжении полосы с двумя круговыми выре-
вырезами протяженность пластической зоны опре-
определялась лишь возможным углом у, определя-
определяющим ту точку, из которой выходит крайняя
характеристика. При плоском напряженном
состоянии дело обстоит иначе. К контуру от-
отверстия в пластине можно приложить лишь та-
такое давление, которое не превышает 2&, так
как на контуре ar = — q, a аг по модулю не
больше чем 2/с, как мы уже выяснили. Со-
Соответственно пластическая область, имеющая
форму кольца, простирается лишь на конечное
расстояние. Аналогичная ситуация возникает
при решении задачи о растяжении полосы с
симметричными круговыми вырезами (рис.
15.13.1). Эту задачу мы и рассмотрим. Полагая aT = ai, <Jr = a2,
подставим A5.14.1) в уравнение равновесия. Получим
Т
При r = a со = я/3, как следует из рис. 15.14.1. Интегрируя урав-
уравнение при данном граничном условии, найдем
A5.14.6)
С возрастанием г величина со убывает, при со = jt/6 мы достига-
достигаем точки параболичности на изображающем эллипсе, характери-
характеристики сливаются при г » 2,07а. Если ширина полосы больше чем
та, которая необходима для встречи гиперболических областей,
идущих от противоположных вырезов. Хилл предложил соеди-
соединять концы областей гиперболических характеристик прямой,
соответствующей параболической точке эллипса Мизеса ср = я/6,
для которой аф = 2&, ог = к (рис. 15.14.3). В наших опытах на
титановом сплаве, поведение которого очень близко к поведению
идеального упругопластического материала, мы никогда не
Рис. 15.14.3
526 гл- 15- идеальная пластичность
получали этих параболических перемычек. Типичная картина при-
приведена на фотографии рис. 15.14.4; здесь в результате специаль-
специальной техники выявлены пластические области, на фотографии они
Рис. 15.14.4
серые. Как видно, вместо пластической аеремычки в середине
остается упругий ромб, стороны которого образуют углы с осью
стержня порядка 55°, что и следует из теории.
§ 15.15. Предельное равновесие пластин
В предельном состоянии пластины, подверженной действию
изгибающей нагрузки, срединная плоскость служит плоскостью
разрыва напряжений. По ту и другую сторону от этой плоскости
реализуется плоское напряженное состояние такое, что aaP(z) =
= const, 2^@, h) и Oaf$(—z) = — oap(z). Умножая Gap на z и ин-
интегрируя по толщине оболочки, мы получим тензор изгибающих
моментов
+h
Map = J o^(z)zdz,, A5.15.1)
-h
Поскольку величины оар кусочно постоянны, моменты будут
удовлетворять условию пластичности, которое совершенно по-
подобно условию пластичности для напряжений. Тензор моментов
можно привести к главным осям, и предельное состояние пласти-
пластины будет изображаться либо эллипсом Мизеса, либо шестиуголь-
шестиугольником Сен-Венана. Поскольку при изучении плоского напряжен-
напряженного состояния мы пользовались первым условием, здесь мы рас-
рассмотрим одну простейшую задачу при помощи условия Треска.
§ 15.15. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИН
527
Графическое представление этого уравнения для моментов не
отличается от соответствующего представления для напряжений
(рис. 15.15.1). Уравнение равновесия для моментов в декартовых
координатах будет, очевидно, иметь вид A2.5.8); для получения
этого уравнения в полярной системе координат для полярно-
симметричного распределения моментов мы сделаем независимый
вывод, отправляясь от начала возможных перемещений. При по-
полярно-симметричном изибе прогиб (или
скорость прогиба) пластины есть w(r),
кривизна радиального сечения равна
d2w/dr2, кривизна сечения в плоскости,
перпендикулярной радиусу, есть утр- По-
Последний результат можно получить путем
непосредственного геометрического рас-
рассмотрения, а можно сослаться на формулы
(8.8.2) для радиальной и окружной де-
деформации в случае полярной симметрии.
Напишем теперь функционал
Рис. 15.15.1
Приравнивая нулю вариацию этого функционала и преобразо-
преобразовывая результат интегрирования по частям, мы получим естест-
естественные граничные условия, которые здесь не выписываются,
и дифференциальное уравнение
Е
J3
"г
/
Мт
А
"г
С
Интегрируя один раз, получим
dMr Mr—Mm i С ,
dr г ~ г J
0.
A5.15.2)
Величина —\qrdr = Q представляет собою поперечную силу,
приходящуюся на единицу длины окружности радиусом г. Те-
Теперь мы можем непосредственно решать задачи о предельном
равновесии круглых симметрично загруженных пластин.
а. Пластина загружена распределенной нагрузкой q и оперта
по контуру. Положим Mi = Л/ф, М2 = Мг. В центре Мг = М^ и
напряженное состояние изображается точкой А на рис. 15.15.1.
На контуре при г = а Мг = 01 следовательно, состояние пластины
изображается точкой В диаграммы. Предполагая, что состояние
пластины в целом соответствует стороне АВ шестиугольника,
положим в A5.15.2) М9 = МТ1 Q = i/2qr. Подставляя в уравнение
528 гл- 15- идеальная пластичность
A5.15.2) и интегрируя, получим
Mr=MT-^qr*.
Из граничного условия Мг(а) = 0 находится предельная нагрузка
б. Пластина загружена сосредоточенной силой Р и оперта по
контуру. В этом случае точка г = 0 оказывается особой точкой
и выполнение условия Мг = М9 в центре не обязательно. Полагая
М9 = МГ и интегрируя уравнение A5.15.2) при Q = P/BnrI мы
находим
Итак, момент Мг сохраняет постоянное значение, которое должно
быть равным нулю вследствие граничного условия Мг(а) = 0.
Отсюда находим предельное значение нагрузки Р
Р = 2яМг.
Напряженное состояние во всей пластине изображается точкой В
диаграммы. Заметим, что вследствие ассоциированного закона
течения в этом случае форма искривления
пластины остается неопределенной, тогда
как под действием распределенной нагруз-
нагрузки вдоль стороны АВ скорость прогиба пла-
пластины такова, что момент Мг = М2 не про-
производит работу, следовательно, d2w/dr2 = О
и плоская поверхность пластины превраща-
превращается в коническую.
Для задач, отличных от полярно-симмет-
Рис 1515 2 ричных, точные решения отсутствуют. Одна-
Однако верхняя оценка, основанная на рассмот-
рассмотрении кинематически возможных форм дви-
движения, получается довольно просто при помощи некоторого еди-
единообразного приема, в особенности пригодного для пластин, по-
полигональных в плане. Предположим, что полигональная пластина
свободно оперта по контуру и нагружена в точке С сосредоточен-
сосредоточенной силой Р (рис. 15.15.2). Одна из возможных схем потери
несущей способности будет следующая. По линиям, соединяющим
точку приложения силы с вершинами контура, происходят изло-
изломы, плоская срединная поверхность превращается в поверхность
пирамиды, ребра которой образованы указанными линиями, а гра-
грани остаются плоскими. Обозначим прогиб в точке приложения
силы через б, длины ребер излома Zs, двугранные углы между
гранями примыкающими к соответствующим ребрам, cos. Изги-
§ 15.16. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ ЗАКРУЧЕННОГО СТЕРЖНЯ 529
бающий момент на единицу длины линии излома есть Мт,
поэтому
Чтобы найти двугранный угол cos, проведем через точку прило-
приложения силы С прямую АВ, перпендикулярную линии СС%
(рис. 15.15.3), и продолжим примы-
примыкающие к вершине С8 стороны кон- 4-
тура пластинки до пересечения с
этой прямой в точках А и В. Левая
грань поворачивается около прямой
BCSJ правая—около прямой ACS,
прямая АСВ изламывается, как по-
показано на том же чертеже во второй
проекции, на этой проекции виден
угол cos. Он равен 8/АС + 8/ВС. Но Рис. 15.15.3
АС = Zetg\f>e, J5C = l8tg<ps. Вычисляя
cos и подставляя в неравенство для несущей способности Р, по-
получим
Р<МТ 2 (ctg cps + ctgi|)s). A5.15.3)
Рассмотрим несколько простых примеров:
а. Прямоугольная пластина со сторонами а, Ъ, нагруженная в центре.
Для нее ctg ф = b/a, ctg \\> = а/Ъ. Следовательно, по формуле A5.15.3)
б. Пластина в форме правильного п-уголъника, нагруженная в центре,
Предельная нагрузка дается формулой
T
При п ->¦ оо мы получаем в пределе
Р = 2лМт.
А это есть найденное выше точное значение предельной нагрузки для
круглой пластины.
§ 15.16. Предельное состояние закрученного стержня
Полагая все компоненты тензора напряжений равными нулю,
кроме двух
мы получим напряженное состояние, которое в упругом теле
соответствовало антиплоской деформации или кручению. Условие
34 ю. Н. Работнов
530 гл- 15- идеальная пластичность
пластичности в этом случае приведется к условию постоянства
касательного напряжения
t-tJ + t^*8. A5.16.1)
Константа &, как мы уже видели, по-разному выражается через
предел текучести при растяжении в зависимости от того, поль-
пользуемся ли мы условием пластичности Мизеса или Сен-Венана.
Мы удовлетворим уравнению A5.16.1), приняв
Ti = — &sin0, T2 = fccos0. A5.16.2)
На рис. 15.16.1 видно, что вектор т, имеющий постоянную вели-
величину, перпендикулярен лучу, составляющему угол 0 с осью х^
Подставим выражения A5.16.2) в уравнения равновесия та, «==
= 0. Получим
9 i cos 0 + 0>2 sin 0 = 0. A5.16.3)
Уравнение A5.16.3)—это линейное дифференциальное уравне-
уравнение в частных производных первого порядка. Для интегрирова-
интегрирования его применяется метод характеристик, т. е. составляются
Рис. 15.16.1 Рис. 15.16.2
дифференциальные уравнения характеристик обычным способом,
cos0 sin0 0 #
Отсюда следует
х2 + Xi tg 0 = с @), 0 = const.
Таким образом, характеристики прямолинейны. Так как в точке
контура вектор т должен быть направлен по касательной к кон-
контуру, то характеристики представляют собою прямые, нормаль-
нормальные к контуру. Очевидно, что для односвязных сечений поле на-
напряжений оказывается разрывным. При кручении стержня кру-
кругового сечения характеристики будут радиусами и центр сече-
сечения будет особой точкой, в которой направление вектора т не
определено. Если контур сечения имеет выступающий угол, как
показано на рис. 15.16.2, элементарные геометрические сообра-
§ 15.16. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ ЗАКРУЧЕННОГО СТЕРЖНЯ 531
жения убеждают нас в том, что из угла будет выходить линия
разрыва, на которой пересекаются характеристики, выходящие
с двух сторон угла. В окрестности угловой точки касательная к
линии разрыва представляет собою биссектрису угла, образован-
образованного касательными к сторонам угла.
На рис. 15.16.3 показано построение пластического поля на-
напряжений в стержне прямоугольного сечения. Линии разрыва
делят прямоугольник на две трапеции и два треугольника, в каж-
каждом из этих элементов вектор касательного напряжения сохра-
сохраняет постоянное направление, указанное на рисунке.
Вводя функцию напряжений, как это было сделано в теории
упругого кручения, т. е. полагая ti=JF>i, т2 = —F,2, мы получим
для функции F следующее дифференци-
дифференциальное уравнение:
F\ + F% = к\
Это — уравнение поверхности равного ска- Рис. 15.16.3
та. Граничное условие для функции F,
так же как в § 9.7, оказывается таким: F = const на контуре; для
односвязного сечения можно принять F = 0. Функция F изобража-
изображается, таким образом, построенной на контуре линейчатой поверх-
поверхностью, прямолинейные образующие которой нормальны к линии
контура и имеют постоянный наклон к к плоскости поперечного
сечения. Для круга это будет поверхность конуса, для прямо-
прямоугольника — поверхность в виде крыши, ребра которой проекти-
проектируются на плоскость как линии разрыва. И здесь, как в теории
плоского напряженного состояния, линии разрыва напряжений
следует рассматривать как выродившиеся упругие области.
Величина предельного момента, так же как и для упругого
стержня, выражается формулой
= 2JjFdz1dz2,
т. е. измеряется удвоенным объемом, ограниченным плоскостью
сечения и надстроенной над нею поверхностью равного ската к.
ГЛАВА 16
УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
§ 16.1. Деформационная теория пластичности
Как мы видели, согласно теории пластического течения, осно-
основанной на условии пластичности Треска — Сен-Венана с ассоци-
ассоциированным законом течения, пластическая деформация представ-
представляет собою простой сдвиг в плоскости, определяемой осями
наибольшего и наименьшего главных напряжений. Если дефор-
деформации малы, то скорость деформации равна производной от
деформации по времени. С другой стороны, если упрочняющийся
материал оказывается в состоянии чистого сдвига, то величина
пластического сдвига представляет собою совершенно определен-
определенную функцию от касательного напряжения
Тр = ф(т). A6.1.1)
Естественно предположить, что и при сложном напряженном
состоянии зависимость A6.1.1) сохраняет силу. Считая, что
полная деформация представляет собою сумму упругой и пла-
пластической деформации, и замечая, что
= 4-к—
e2P = 0 и пластическая объемная деформация отсутствует, мы
получаем следующие зависимости между напряжениями и де-
деформациями:
— — Г — ( 4- ^1 4- —
^ = ^[^2-v(a3 + a1)], A6.1.2)
При этом должно быть с1>о2>о3. Уравнения A6.1.2) пред-
представляют собою конечные соотношения между напряжениями и
деформациями, хотя в основу было положено предположение
о том, что пластичность представляет собою именно течение
материала. Первичный опытный факт, выражаемый уравнением
A6.1.1), можно истолковать и таким образом, что пластическое
течение представляет собою чистый сдвиг, но величина дефор-
§ 16.1. ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ 533
мации не произвольна, как это было в теории идеальной пла-
пластичности, а зависит от действующего напряжения. Уравнение
A6.1.1) справедливо тогда, когда т не убывает, более точная
запись его будет следующая. Если т изменяется произвольным
образом во времени § от ? = 0 до ? = t, то
[T(?)], |е [О,*].
Это значит, что при разгрузке пластическая деформация сохра-
сохраняется. Здесь мы не предусмотрели возможность появления
вторичных пластических деформаций при приложении больших
касательных напряжений противоположного знака. Учет со-
соответствующих эффектов требует введения дополнительных
гипотез.
Чрезвычайно простые уравнения A6.1.2) записаны в главных
напряжениях. Если направления главных осей заранее неизвест-
неизвестны, уравнения нужно записать в произвольных осях. При этом
вся простота исчезает, результирующие уравнения становятся
сложными до чрезвычайности. Более того, если главные оси из-
известны, мы должны знать заранее, по какой оси будет действовать
наибольшее напряжение о4, по какой — наименьшее а3. Но может
случиться, что в процессе нагружения соответствующее нера-
неравенство нарушается, следовательно, меняется та плоскость, в ко-
которой происходит сдвиг. Таким образом, изложенная теория
имеет лишь ограниченную область применения.
Так называемая деформационная теория пластичности пред-
представляет по существу распространение на пластическое тело того
закона связи между напряжениями и деформациями, который
устанавливается нелинейной теорией^ упругости. Пластический
потенциал, который заменяет здесь упругий потенциал, для изо-
изотропного тела есть функция инвариантов тензора деформаций.
Обычно при этом применяются следующие гипотезы:
1. Объемная деформация подчиняется закону линейной уп-
упругости
о = ЗКе. A6.1.3)
2. Упругопластический потенциал U завист только от вто-
второго инварианта тензора деформаций, например от октаэдриче-
ского сдвига
U=U(b).
Из второй гипотезы следует, что
а«-2СЫ7«. A6.1.4)
Здесь Оц и ец — девиаторы соответствующих тензоров, Ga(^0) —
функция октаэдрического сдвига, появляющаяся при диффе-
дифференцировании потенциала U(^Q). Свертывая обе стороны равен-
равенства A6.1.4) и вспоминая определения т0 и ^о (см. § 7.7), мы
534 ГЛ- 16* УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
находим
Соотношение A6.1.5) означает существование единой кривой
to ~~ То для всех видов напряженных и деформированных состо-
состояний, точнее для всех путей нагружения или деформирования.
Таким образом, существование этой кривой должно быть при-
принято за первичный опытный факт, выполнение или невыполнение
его при эксперименте служит критерием правильности пли не-
неправильности теории в целом. Величина пластического модуля
сдвига Gs, определенная как функция октаэдрического сдвига у0,
может рассматриваться и как функция октаэдрического касатель-
касательного напряжения т0. Заметим, что принятая гипотеза, выражон-
ная уравнениями A6.1.4) и A6.1.5), не предполагает разделения
деформации на упругую и пластическую. Действительно, закон
Гука для девиаторных составляющих тензоров напряжений и де-
деформаций записывается так:
Здесь \х — упругий модуль сдвига. Диаграмма зависимости т0 — То»
по предположению, одинаковая для всех путей деформирования,
включает в себя упругую сдвиговую деформацию, тогда как
упругая объемная деформация определяется уравнением A6.1.3).
Вид функции т0(То) проще всего определить из опы*га на
чистый сдвиг, например, при кручении тонкостенной трубки
кругового сечения. Действительно, при чистом сдвиге
Здесь тит — касательное напряжение и сдвиг. Таким образом,
диаграмма т0 — То получается из диаграммы чистого сдвига т — т
путем простого изменения масштаба. Получить искомую зави-
зависимость из опыта на растяжение несколько сложнее. Дело в том,
что растяжение сопровождается изменением объема, поэтому для
нахождения функции то(То) нужно знать объемный модуль упру-
упругости К и производить пересчет, основываясь на уравнениях
пластичности. Мы не будем здесь описывать эту процедуру,
отсылая к специальной литературе.
Основной опытный факт, наблюдаемый при одноосном на-
гружении — растяжении или сжатии, а также при кручении,
заключается в следующем. Пока мы движемся по кривой де-
деформирования от начала координат так, как показано на
рис. 16.1.1 стрелкой, т. е. пока напряжение и деформация, в дан-
данном случае ти], возрастают, связь между т и т дается диаграм-
диаграммой пластического деформирования. Зависимость между напряже-
§ 16.1. ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ
535
О
Рис. 16.1.1
нием и деформацией однозначна в том смысле, что она не за-
зависит от скорости деформирования или приложения нагрузки,
но она нарушается при движении в обратном направлении, т. е.
при изменении знака т или у. Опыт показывает, что при
уменьшении напряжения материал возвращается в упругое со-
состояние, зависимость между напряжением и деформацией при
разгрузке изображается на диаграмме прямой, проходящей через
ту точку кривой деформирования, от которой произведена раз-
разгрузка. Закон упругости при разгрузке — это не точный физиче-
физический закон, на самом деле диаграмма раз-
гру/эки не вполне прямолинейна, и сред-
средний модуль, получаемый при замене ис-
истинной диаграммы разгрузки наиболее
близкой к ней прямой, может незначи-
незначительно отличаться от начального модуля
щ определяющего наклон первого участка
диаграммы нагружения. Но теория плас-
пластичности всегда имеет дело с гипотетиче-
гипотетической идеальной средой, которая воспроиз-
воспроизводит поведение реального тела лишь с
некоторым приближением. Теперь для об-
общего случая естественно принять следую-
следующее допущение. Если октаэдрическое на-
напряжение или соответственно октаэдриче-
ский сдвиг возрастает, то происходит пластическая деформация,
описываемая уравнениями A6.1.4). Если при некоторых зна-
значениях т0 =^т0 и y0 = у0 происходит разгрузка, то изменения
девиатороъ оу и ец связаны законом упругости, который удобно
записывать в дифференциальной форме:
dGij = 2\ideij, T0<CtQ. A6.1.6)
Уравнения A6.1.6) заменяют при разгрузке уравнения A6.1.4),
тогда как уравнение A6.1.3), естественно, всегда сохраняет силу.
В записи условия, при котором справедливо A6.1.6), содержится
нечто большее, чем только закон разгрузки, при повторной
нагрузке материал будет деформироваться упруго до тех пор,
пока октаэдрическое напряжение не достигнет величины т0, от
которой производилась разгрузка. При дальнейшем нагружении
зависимость т0 — fo следует по продолжению первоначальной
кривой и уравнения A6.1.4) снова вступают в силу, продолжая
действовать так, как если бы разгрузки и повторной нагрузки
не было. Подчеркнем еще раз, что при реверсировании нагрузки,
т. е. при смене растяжения сжатием или после изменения на-
направления крутящего момента мы можем снова выйти в пласти-
пластическую область. Здесь этот вопрос пока не обсуждается.
536 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
§ 16.2. Теория течения, постулат Друкера
Альтернативная точка зрения на процесс пластической де-
деформации материала с упрочнением состоит в том, что пласти-
пластическая деформация представляет собою именно пластическое
течение материала, происходящее в общем так же, как пласти-
пластическое течение идеально пластического материала, описанное в
§ 15.9. Но теперь поверхность нагружения в изображающем
пространстве напряжений не остается неизменной, она меняет
свою форму по мере движения изображающей точки в простран-
пространстве напряжений, которое было описано в § 15.2. Как и в теории
идеальной пластичности, в основу теории пластичности с упроч-
упрочнением можно положить тот или иной принцип или постулат.
Такие постулаты вводились по-разному разными авторами, но все
они приводят к одному и тому же следствию, а именно к допу-
допущению закона течения, ассоциированного с данной мгновенной
поверхностью нагружения.
Здесь мы рассмотрим наиболее известный из них, а именно
постулат Друкера, который формулируется так же, как и в тео-
теории идеальной пластичности. Итак, представим себе напряже-
напряжение cr*j, изображаемое в шестимерном (или девятимерном) про-
пространстве напряжений точкой Л/* — концом вектора напряже-
напряжения о*. Через точку М* проходит поверхность
нагружения 5*, т. е. поверхность, отделяющая
область упругих состояний или разгрузки от
области пластических состояний. В теории
идеальной пластичности путь нагружения, со-
сопровождающегося пластической деформацией,
. мог проходить только по поверхности 5*, этот
\у** путь сопровождался только упругой деформа-
Рис. 16.2.1 Цией, если проходил внутри объема, ограни-
ограниченного поверхностью S*. Выход пути нагру-
нагружения за пределы поверхности ?* предполагался невозможным.
Для упрочняющегося материала движение конца вектора о* за
пределы поверхности S* возможно. Так, например, возможно
состояние а, отвечающее точке Л/, через которую проходит новая
поверхность нагружения S, как показано на рис. 16.2.1. Пред-
Предположим теперь, что мы вышли из точки М* и возвратились в
нее по некоторому замкнутому пути «у, который может частично
выходить за пределы поверхности 5*, например проходить через
точку М, не выходя за пределы поверхности S. Постулат Дру-
Друкера формулируется совершенно так же, как и для идеальноц
пластичности. Если о — вектор напряжения на пути «у, то о-
— о* — дополнительное напряжение, и работа его на замкнутом
пути неотрицательна. В индексных обозначениях имеем
A6.2.1)
§ 16.2. ТЕОРИЯ ТЕЧЕНИЯ, ПОСТУЛАТ ДРУКЕРА 537
Рассмотрим именно тот замкнутый путь, который изображен на
рис. 16.2.1. Точка Л/*, соответствующая напряжению о*, лежит
внутри поверхности S* или в крайнем случае на этой поверх-
поверхности, как показано на рисунке. Из точки М* можно прийти в
любую точку Ми лежащую на ?*, по любой кривой, соединяю-
соединяющей эти две точки и находящейся целиком
внутри поверхности S*. После этого мы со-
сообщаем напряжению о' приращение do, вы-
ходящее за пределы поверхности S*, и по-
попадаем в бесконечно близкую точку М. Че-
Через нее проходит ногаая поверхность текуче-
текучести S; на пути М^М произошло приращение
пластической деформации dep. Из точки М
в точку М* можно вернуться по пути, за-
заключенному целиком внутри новой поверх- 16.2.2
ности нагружения S, т. е. без дополни-
дополнительной пластической деформации. На участках M^Mi и ММ*
деформация упруга, на участке ММ малая деформация de со-
состоит из упругой и пластической частей
de = de + dep.
Работа дополнительного напряжения на упругой деформации,
как было установлено в § 15.2, для замкнутого пути нагруже-
нагружения равна нулю, поэтому из A6.2.1) следует
(<ту-<?¦)&&>(>. A6.2.2)
Условие A6.2.2) означает, что вектор в —а*, где а* — радиус-
вектор любой точки внутри поверхности S*, образует тупой угол
с направлением вектора dev. Если поверхность нагружения глад-
гладкая, то, повторяя рассуждения § 15.2, мы убеждаемся в том,
что вектор dev направлен по нормали к поверхности нагружения.
Сама поверхность располагается целиком по одну сторону каса-
касательной гиперповерхности и, следовательно, является выпуклой
или по крайней мере невогнутой.
Предположение о гладкости поверхности S в точке М не обя-
обязательно, в некоторых вариантах теории пластического течения
принимается, что точка М может быть угловой. Это значит,
что касательные в точке М образуют конус с вершиной в этой
точке (рис. 16.2.2). Из неравенства A6.2.2) следует, что вектор
dev должен лежать внутри конуса, образованного нормалями к
поверхности S в окрестности точки М.
Допустим теперь, что ai;- = cr^; мы выходим из точки М5 в
бесконечно близкую точку М\ при этом происходит пластическая
деформация dep; после этого возвращаемся в точку М по тому
же пути, совершая упругую разгрузку. Из постулата Друкера
538 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
следует
dGijdel > 0. A6.2.3)
Последнее неравенство характеризует известную устойчивость
материала, которую легко проиллюстрировать на примере про-
простого растяжения. Если диаграмма зависимости о — е такова, что
с увеличением деформации е напряжение о возрастает, то do de >
> 0. Но если свойства материала характеризуются падающей
диаграммой, как на рис. 16.2.3, то после
точки А — максимума кривой — неравен-
неравенство A6.2.3) нарушается. Такой материал
неустойчив, он продолжает деформиро-
деформироваться при падающей нагрузке.
Постулат Друкера, как неоднократно
и настойчиво подчеркивал сам автор, от-
# s нюдь не вытекает из законов термодина-
р igo3 мики. Сам Друкер употребляет для него
термин «К'вазитермодинамический». По-
Поэтому на требование выполнения посту-
постулата Друкера следует смотреть как на определение класса устой-
устойчивых материалов. Подчеркнем, что в данном случае речь идет
об устойчивости именно материала, а не образца, подвергнутого
растяжению. В § 4.13 был рассмотрен пример неустойчивости
растяжения образца из материала, подчиняющегося степенному
закону упрочнения, т. е. устойчивого по Друкеру; неустойчивость
процесса деформирования была связана с изменением площади
поперечного сечения. Существуют материалы, деформирование
которых сопровождается появлением внутренних дефектов, что
эквивалентно уменьшению площади эффективного, т. е. несу-
несущего фактически нагрузку, сечения. При макроскопическом
описании поведения таких материалов постулат Друкера не вы-
выполняется.
Заметим, что результаты этого параграфа совершенно недо-
недостаточны для того, чтобы фактически построить теорию пласти-
пластического течения. Они лишь устанавливают некоторые разумные
рамки, ограничивающие определенным образом выбор системы
допущений, отличающих тот или иной вариант теории пласти-
пластического течения.
§ 16.3. Теория течения, общие уравнения
Запишем уравнение поверхности ?*, проходящей через точку
o%j, следующим образом:
Ы/с2 = 0. A6.3.1)
В общем случае функция /(aaj) и величина к2 могут зависеть^от
деформации и от путей нагружения и деформирования любым,
§ 16.3. ТЕОРИЯ ТЕЧЕНИЯ, ОБЩИЕ УРАВНЕНИЯ 539
сколь угодно сложным образом. Величины ozi удовлетворяют
уравнению A6.3.1); при движении по пути нагружения поверх-
поверхность деформируется и уравнение A6.3.1) меняет свой вид, но
таким образом, что конец вектора напряжения всегда лежит на
поверхности S. Будем называть нагружение активным, если при-
приращение вектора а направлено в наружную сторону поверхности
S и, следовательно, сопровождается пластической деформацией.
Если вектор da направлен внутрь объема, ограниченного поверх-
поверхностью S, и, следовательно, происходит лишь упругая деформа-
деформация, будем называть нагружение пассивным или разгрузкой.
Наконец промежуточный случай, когда da лежит на поверхности
нагружения, мы будем называть нейтральным нагружением. Сде-
Сделаем два следующих предположения.
1. Нейтральное нагружение не сопровождается пластической
деформацией. Это условие выражает требование непрерывности
при переходе от пассивного нагружения к активному. Заметим,
что в теории идеальной пластичности дело обстоит совершенно
иначе, там величина пластической деформации или скорости
деформации неопределенна и становится отличной от нуля при
достижении вектором о поверхности текучести. В деформацион-
деформационной теории, как она была сформулирована выше, непрерывности
при переходе от пассивного нагружения к активному нет; при
активном нагружении, бесконечно мало отличающемся от ней-
нейтрального, происходит пластическая деформация, при бесконечно
близком пассивном пути нагружения дефогромац'ия упруга. Это
обстоятельство служит серьезным доводом, препятствующим рас-
расширенному использованию деформационной теории.
2. Приращения пластической деформации представляют собою
линейные функции от приращений напряжения.
Заметим, что хотя мы назвали излагаемую теорию теорией
пластического течения, на самом деле до сих пор речь шла не
о скоростях течения, а о бесконечно малых приращениях ком-
компонент тензора пластической деформации. Но если мы примем,
что напряженное состояние меняется в зависимости от какого-ли-
какого-либо монотонно возрастающего параметра, мы можем назвать этот
параметр временем и ввести в рассмотрение скорости деформа-
деформации, как это делалось в теории идеальной пластичности. Нужно
только помнить, что физическое время не играет в теории пла-
пластичности никакой роли, существенна последовательность собы-
событий, но не действительная скорость, с которой они происходят.
Поэтому можно, как и в теории идеальной пластичности, запи-
записать закон пластического течения следующим образом:
> - 1 df
Но теперь % уже не произвольная величина, а совершенно опре-
определенная функция. Чтобы уточнить структуру этого множителя,
540 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
мы воспользуемся двумя введенными выше гипотезами. Разложим
приращение вектора а на две составляющие: do', направленную
по касательной к поверхности нагружения, и do", направленную
по нормали. Согласно второму предположению вклады в вели-
величину dev от этих двух составляющих суммируются, но величина
do' соответствует нейтральному нагружению и, согласно первой
гипотезе, вклада в приращение пластической деформации не вно-
вносит. Следовательно, приращение пластической деформации должно
быть пропорционально нормальной составляющей вектора do,
которая в свою очередь пропорциональна величине ^—deki. По-
dGki
этому множитель % должен быть тоже пропорционален этой ве-
величине. В результате получаем
'е%=н^кАгйом- A6-3-2)
Величина Н в формуле A6.3.2) может быть функцией напряже-
напряжений и деформаций или функционалом от пути нагружения. Во
всяком случае, общая форма записи уравнений A6.3.2) оставляет
очень большой простор для выбора частных предположений.
Один вариант теории пластического течения с упрочнением
мы уже разобрали в § 16.1. Предполагая, что поверхность тече-
течения есть призма Треска — Сен-Венана, и считая, что мы нахо-
находимся все время на одной и той же грани этой призмы, мы
проинтегрировали по существу уравнения A6.3.2) и пришли к
некоторому варианту деформационной теории. Другой вариант
был предложен Прагером, он основан на предположении, что
как функция /, так и функция Н зависят лишь от второго ин-
инварианта девиатора тензора напряжений, например
/ = 2ц = 2ц —-jSj.
Теперь
Выражение j^- oki представляет собою производную по времени
от /, т. е. от 2П, или, если перейти к октаэдрическому касатель-
касательному напряжению,
/ = 2ц = 6тото.
Поэтому уравнения A6.3.2) примут вид
е% = 0^(то)то. A6.3.3)
В качестве параметра нагружения или времени в том смысле, в
§ 16.3. ТЕОРИЯ ТЕЧЕНИЯ, ОБЩИЕ УРАВНЕНИЯ 541
каком это было разъяснено выше, можно принять величину т0,
при активном нагружении эта величина монотонно возрастает.
Можно указать случай, когда уравнения A6.3.3) можно проин-
проинтегрировать, это случай так называемого пропорционального
нагружения, когда все компоненты девиатора тензора напряже-
напряжений изменяются в одном и том же отношении. Величина т0 есть
однородная функция первой степени от о#, поэтому при про-
пропорциональном нагружении о«/т0 = const. В таком случае, интег-
интегрируя A6.3.3), получаем
о
Оказывается, что при пропорциональном нагружении уравнения
теории течения типа Прагера и уравнения деформационной тео-
теории совпадают. Вычитая из компонент девиатора тензора дефор-
деформации, определяемых формулами A6.1.4), упругие компоненты,
находим
-р _ 1 /1 1
**' - Т [Gs |i
Таким образом,
Г
1|то^(то)йто = 1
Величина Gs определяется как функция от у0 или т0 по диа-
диаграмме т0 — Чо с помощью формулы A6.1.5). Для того чтобы
найти функцию А(т0), продифференцируем полученное соотно-
соотношение по to, переписав его предварительно в виде
о
В результате получим
^й) A6'3-4)
Величины Gs и Gt называются соответственно секущим и каса-
касательным модулями. Величина Gs, согласно формуле A6.1.5),
представляет собою угловой коэффициент луча, выходящего из
начала координат в точку (т0, "f0), тогда как Gt = dxjd^ есть уг-
угловой коэффициент касательной к кривой в этой точке. Таким
образом, функция h(r0) легко находится, если известна диаграм-
диаграмма пластичности, полученная при каком-либо одноосном деформи-
деформировании образца из данного материала.
542 гл- 16- упругопластическое упрочняющееся тело
Теперь, добавляя упругую деформацию, мы можем записать
полные уравнения рассматриваемого варианта теории течения
следующим образом:
е» = ±oi} + з^<*« + ^(^- ?) т„. A6.3.5)
§ 16.4. Границы применимости деформационной теории
пластичности
Опытные данные, относящиеся к условиям пропорциональ-
пропорционального нагружения, довольно хорошо подтверждают существование
единой для всех видов напряженных состояний кривой зависи-
зависимости октаэдрического напряжения от октаэдрического сдвига, а
также устанавливаемую формулами A6.1.4) пропорциональность
между девиатором напряжений и девиатором деформаций. Так
обстоит дело, во всяком случае, для углеродистой и низколеги-
низколегированной стали, для титановых сплавов. Однако для некоторых
сплавов, например алюминиевых и магниевых, а также высоко-
высокопрочных сталей, уже диаграмма растяжения не совпадает с диаг-
диаграммой сжатия, а в плоскости т0 — Чо опытные точки, соответ-
соответствующие разным напряженным состояниям, не ложатся на одну
кривую. Положение можно исправить, допустив, что пластический
потенциал U зависит не только от второго инварианта девиатора,
но, возможно, от третьего инварианта и от гидростатической
составляющей тензора. Заметим, что уже уравнения A6.1.2)
фактически вводят зависимость от третьего инварианта, поверх-
поверхность нагружения в виде шестигранной призмы задается урав-
уравнением вида A5.1.5).
Термин «пропорциональное» нагружение был определен в
§ 16.3, он относится к соотношениям между компонентами девиа-
девиатора тензора напряжений. При простых опытах, которые произ-
производятся главным образом над тонкостенными трубками под дей-
действием растяжения, внутреннего давления и кручения, пропор-
пропорциональность нагружения обеспечивается пропорциональным
изменением внешних сил, приложенных к образцу. Но в общем
случае произвольного тела пропорциональное изменение внешних
сил не обязательно влечет за собою пропорциональное нагруже-
нагружение, для этого необходимо выполнение некоторых условий, кото-
которые нам предстоит выяснить.
Положим Т = Т°а, F = F°a, здесь Г° и F0 — постоянные век-
векторные поля, заданные соответственно на поверхности тела и в
его объеме, а — параметр нагружения, возрастающий монотонно.
Мы удовлетворим дифференциальным уравнениям равновесия и
граничным условиям, положив сг^- = а^а. Объемная деформация
связана с гидростатической компонентой тензора напряжений
§ 16.4. ПРИМЕНИМОСТЬ ДЕФОРМАЦИОННОЙ ТЕОРИИ 543
законом Гука
е ~ — о°а + е°а.
С другой стороны, из A6.1.4) следует
Поэтому
-е°(а — P)fi4i. A6.4.1)
В общем случае эти величины не будут удовлетворять урав-
уравнениям совместности. Действительно, если, например, величины
e\j удовлетворяют этим уравнениям, величины A6.4.1) не будут
им удовлетворять, поскольку, во-первых, множитель fi есть
функция координат, во-вторых, добавляется второй член, про-
пропорциональный разности a — fi. Для того чтобы действительно
осуществлялось простое нагружение, достаточными условиями
будут следующие: во-первых, материал " несжимаем, во-вторых,
р не зависит от координат. Последнее условие будет выполнено,
если Gs(t0) является степенной функцией от т0. Действительно,
если 70 = ато, то Gs = — xi~fe и |i = а\ При /с = 1 а=^ и требова-
требование несжимаемости материала отпадает, но это тривиальный слу-
случай линейно упругого материала.
Таким образом, достаточные условия того, чтобы при про-
пропорциональном изменении внешних сил осуществлялось пропор-
пропорциональное нагружение, состоят в следующем (теорема Илью-
Ильюшина) :
1) зависимость между октаэдрическим напряжением и окта-
эдрическим сдвигом степенная;
2) материал несжимаем.
Первое условие весьма стеснительно, поскольку зависимость
должна быть степенной с одним и тем же показателем степени
во всем диапазоне изменения т0 и f0, а не кусочно степенная
аппроксимация истинной зависимости, которая иногда приме-
применяется. Реальные материалы имеют линейно упругий участок
диаграммы, поэтому для них первое условие заведомо не выпол-
выполняется.
Хотя при непропорциональном нагружении деформационная
теория дает результаты, отличные от предсказаний логически
более оправданной теории течения, при нагружении, близком к
пропорциональному, она может удовлетворительно согласоваться
с опытом. Само понятие нагружения, близкого к пропорцио-
пропорциональному, в достаточной мере неопределенно, если в качестве
критерия точности деформационной теории при пропорциональ-
пропорциональном нагружении мы приняли согласование ее с простейшей тео-
544 гл- 16- упругопластическое упрочняющееся тело
рией течения, то кажется естественным допустить применимость
ее в тех случаях, когда не нарушаются некоторые общие прин-
принципы, полагаемые в основу теории течения любого вида. По-
Поэтому Будянский поставил задачу выяснения тех условий, при
которых уравнения деформационной теории согласуются с посту-
постулатом Друкера.
Как было показано в § 16.3, уравнения деформационной тео-
теории можно записать в виде
Вычислим приращение пластической деформации при изменении
величин (Зц
Ъ* + 4 ъ*й (?)¦ A6-4-2)
Но 1/GS = Yo/to, поэтому
Вспоминая, что dxo/d^o = Gt — касательный модуль, перепи-
перепишем, A6.4.2) следующим образом:
Т [Gs - J) d°» + S [Gt
~ ds
a
Здесь мы ввели обозначение s2 — Еп = 1/3to.
Если обратиться к геометрической интерпретации соотношений
пластичности в девятимерном пространстве девиаторов напряже-
напряжений, где напряженное состояние изображается вектором а, то
величина s представляет собою длину этого вектора. Заметим,
что независимых компонент девиатора всего пять, поэтому неко-
некоторые авторы изображают напряженное состояние вектора в пя-
пятимерном пространстве, поскольку гидростатическая компонента
тензора на пластическое поведение не влияет. Проверим теперь
выполнение неравенства A6.2.3), вытекающего из постулата
Друкера. Поскольку пластическая деформация не сопровождается
изменением объема, на приращениях defj производит работу
только девиаторная часть тензора напряжений и неравенство
принимает вид
dOitdefy^O. A6.4.4)
Подставляя сюда A6.4.3), получим
[ ) ЯА + т
При этом учтено, что a^atey = s ds.
§ 16.5. ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА 545
Для реальных материалов диаграмма деформирования всегда
направлена выпуклостью кверху и не имеет точек перегиба, по-
поэтому |x>Gs>Gf. Вследствие этих неравенств выражения, за-
заключенные в скобки, положительны, а поэтому условие A6.4.4)
всегда выполняется.
Другое следствие из постулата Друкера состоит в том, что
вектор dep либо нормален к поверхности нагружения, если она
гладкая, либо находится внутри конуса, образованного норма-
нормалями к поверхности, если точка нагружения представляет собою
угловую точку. При формулировке деформационной теории было
сделано предположение, что уравнения ее сохраняют силу тогда,
когда То возрастает; при убывании октаэдрического напряжения
происходит разгрузка. Таким образом, поверхность нагружения
в девиаторном пространстве представляет собою сферу s = const.
Это предположение, как оказывается, противоречит постулату
Друкера. Действительно, обращаясь к выражению A6.4.3), мы
замечаем, что второе слагаемое определяет составляющую век-
вектора dep, нормальную к поверхности сферы. Но первое слагаемое
зависит от дифференциалов ddj, поэтому вектор dev меняет свое
направление в зависимости от соотношения между этими диффе-
дифференциалами или непосредственно от вектора da. Отсюда следует,
что точка М, конец вектора о, является угловой точкой поверх-
поверхности нагружения. Если эта точка коническая и касательные к
поверхности нагружения образуют конус с углом раствора 2[},
уравнения деформационной теории справедливы до тех пор, пока
вектор dev не выходит за пределы конуса, образованного нор-
нормалями к поверхности нагружения, угол раствора этого конуса
равен я — 2р. Необходимы специальные дополнительные гипотезы
для того, чтобы выяснить связь между приращениями напряже-
напряжений и деформаций, если последние выходят за пределы двух
указанных конусов. При этом, конечно, переход от активной
деформации к разгрузке происходит непрерывно.
§ 16.5. Двумерная модель упрочняющегося тела
Мы не закончили изложения теории Будянского в § 16.4. Для построе-
построения полной модели тела, подчиняющегося уравнениям деформационного ти-
типа для некоторых путей нагружения, отличных от пропорционального, не-
необходимы дополнительные гипотезы. Один факт существен, и его следует
еще раз подчеркнуть: соотношения деформационной теории могут быть
справедливы для непропорциональных нагружений только тогда, когда по-
последующие поверхности нагружения, ограничивающие область упругой
разгрузки, имеют угловую точку, перемещающуюся по пути нагружения
вместе с концом вектора а. Чтобы выяснить некоторые свойства упруго-
пластических систем, которые, вероятно, принадлежат и упругопластическо-
му телу, рассмотрим некоторую простую модель. В качестве такой модели
выберем круглую тонкостенную трубу из упругопластического материала,
не обладающего упрочнением. Труба изгибается моментами Mi и М2 в пер-
перпендикулярных плоскостях хи хъ и х2, я3. Обозначим радиус трубы #, тол-
3 5 ю. Н. Работпов
546
ГЛ. 16. УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
щину стенки б, модуль упругости Е, предел текучести от. Будем называть
пропорциональным такое нагружение, когда М\ и М2 изменяются пропор-
пропорционально. В этом случае нейтральная ось сохраняет свое положение, и,
очевидно, можно просто рассматривать изгиб трубы моментом М =
=1/ МJ + Mg, приложенным в неизменной плоскости. Очевидно, что, пе
нарушая общности, можно принять за эту плоскость х2, хз, тогда нейтраль-
нейтральной осью будет ось х\ и М = М\. Пока напря-
напряжение нигде не превышает предела текуче-
текучести, кривизна изогнутой оси К\ = к зависит
от момента следующим образом:
М
Рис. 16.5.1
Пластические деформации возникают сначала
в точках, наиболее отдаленных от оси х{; при
увеличении момента образуются симметрич-
симметричные дуговые пластические области (дуга А В
на рис. 16.5.1 и симметричная с ней внизу).
Полярный угол, определяющий границу плас-
пластической зоны, мы обозначили через 0. Де-
Деформация в точках А и В, а также в сим-
симметричных с ними относительно оси хи по аб-
абсолютной величине равна от/Е, следовательно,
xi? sin G = —-.
В упругой зоне в точке, определяемой полярным углом if < 0, величи-
величина напряжения определяется следующим образом:
A6.5.1)
Вычислим теперь изгибающий момент по формуле
Я/ 2
2 sin г|> ^г|>.
/
= 4 f
При этом в пластической области, при if> > 0 а = ат, а в упругой области
справедлива формула A6.5.1). В результате интегрирования получим
т sin 0
Введем теперь вместо моментов и изменений кривизн безразмерные
величины
м,
ER
Полученная связь между М ж к может быть с новыми обозначениями пред-
представлена следующим образом:
Q = щ в упругой области при q < 1,
Q = B0 + sin 20) q в упругопластической области A6.5.2)
при q = 1/sin 0 > 1.
Пластическая деформация появляется при Q = я, исчерпание несущей
§ 16.5. ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА 547
способности наступает при Q = QT = 4 (в последней из формул A6.5.2)
мы не стали выражать правую часть через q для сокращения записи). Оче-
Очевидно, что диаграмма зависимости Q от q будет до чрезвычайности напо-
напоминать диаграмму деформирования упругопластического материала с уп-
упрочнением.
Рассматриваемая модель соответствует телу с начальной изотропией,
соотношения A6.5.2) не зависят от того, в какой плоскости производится
изгиб или как была выбрана ось хх. Теперь нам легко вернуться к общему
случаю, когда изгиб происходит около произвольной оси и на трубу дейст-
действуют пропорционально возрастающие моменты М\ и М2. Соответствующие
кривизны будут х,\ и Иг, при пропорциональном нагружении, очевидно,
X! : к2 = М\ : М2. Переходя к соответствующим безразмерным величинам,
мы можем написать:
Qi=*Gequ Q2 = Gsq2. A6.5.3)
При этом, если <?2 = Q\ + Q\ < л:2 или q2 = q\ + q\ < 1 Gs = щ при
Ge (я, 4) Gs = 20 + sin29 и 0 = arcsin(l/g). Мы получили полный ана-
аналог деформационной теории пластичности; уравне-
уравнения A6.5.3) описывают как упругое поведение тру-
трубы, так и ее упругопластическое поведение. Очевид-
Очевидно, что пластический модуль G8 представляет со-
собою отношение Q/q, он может быть выражен как
через величину Q, так и через величину #, кото-
которые играют роль соответствующих октаэдрических
составляющих напряжения и деформации.
Но соотношения деформационного типа A6.5.3)
справедливы не только для пропорционального на-
гружения. Предположим, например, что мы дове-
довели пропорциональное нагружение путем изгиба в
плоскости #2, #з до некоторого значения Q > л, ™ис" 16.5.2
которому соответствует пластическая зона с гра-
границей, определяемой углом 0. После этого будем одновременно изменять и
Q\, и (?2, но так, чтобы при этом не происходила разгрузка. Теперь новой
нейтральной осью будет прямая пп', составляющая угол а с осью х\, как
показано на рис. 16.5.1. Рассмотрим крайний случай, когда точка В остается
на месте, а точка А движется в направлении, указанном стрелкой. Когда ле-
левый конец пластической области придет в точку А', прямая пп' окажется
параллельной хорде А'В. Изгибающий момент относительно оси пп' опре-
определится по формулам A6.5.2), в которых угол 0 следует заменить через
0 -— р. Таким образом, мы получаем
—р) cosp, <?2 = <?@-P)sinp. A6.5.4)
Уравнения A6.5.4) представляют собою параметрические уравнения пре-
предельного пути нагружения, выходящего из точки Q, для которого соотноше-
соотношения деформационной теории пластичности A6.5.3) еще остаются справедли-
справедливыми. Заменив р на —р, мы получим симметричную кривую, соответствую-
соответствующую тому случаю, когда точка А остается на месте, а движется точка В.
Проводя касательные к линиям A6.5.4), мы получим угол //, ограничен-
ограниченный прямыми, составляющими утлы ±а с осью х\ (рис. 16.5.2). Для прира-
приращений параметров (?i и Q2, которые изображаются векторами, лежащими
внутри этого угла, уравнения деформационного типа сохраняют силу. Оп-
Определим угол а. Для этого продифференцируем соотношения A6.5.4). По-
Получим
В непосредственной окрестности точки Q ? имеет тот же порядок, что Ар,
35*
548 гл- 16- упругопластическое упрочняющееся тело
поэтому
Здесь
dQ^dQd^^ d_Q_ e
d9 dq dQ dq Ч ё
Ho dQ/dq представляет собою касательный модуль на кривой деформиро-
деформирования Gt. Теперь мы можем написать:
&Q{ = — Gtq Ctg 9 Ар, Д<?2 = Gsq А|3.
Наклон предельных путей, проходящих через точку Q, определяется сле-
следующим образом:
^|| A6.5.5)
В результате простых вычислений находим, что а = л/2 при 0 = 0 и 0 =
= я/2, его минимальное значение, равное 76°28', достигается при 0 = 57°30'.
Выясним теперь условия разгрузки в упругую область после пропор-
пропорционального нагружения. Очевидно, что упругая разгрузка также может
произойти не только в результате уменьшения безразмерного момента Q\,
трубка возвратится в упругое состояние, если сечения повернутся каждое
относительно оси, не пересекающей пластическую область. Пусть эта ось
разгрузки составляет угол ф с осью х\. Должно быть ф ^ 0. Область / на
рис. 16.5.2, заключенная между лучами, составляющими угол 20, будет той
областью, в которую следует направить вектор dQ для упругой разгрузки.
Таким образом, контур, играющий роль поверхности нагружения, который
вначале был окружностью Q = л, приобретает угловую точку. Чтобы вы-
выяснить форму этого контура вдали от точки (?, поступим следующим обра-
образом. Обозначим через Q1 n Q2 изменения безразмерных изгибающих мо-
моментов вследствие разгрузки, так что
Q = (? + (?i» Q — Q + (?2« A6.5.6)
Поскольку при разгрузке материал деформируется упруго, Qx и Q2 пред-
представляют собою составляющие момента, направленного по оси разгрузки.
Поэтому можно принять
Q't = — лсо cos ф, Q'2 = — лсо sin ф.
В точке, определяемой полярным углом ф, изменение напряжения вслед-
вследствие разгрузки будет
а' = — со ат sin (ij) — ф).
Если фиксировать значение ф и менять параметр со, то разгрузка будет
происходить вдоль прямой, проходящей через точку Q. Мы выяснили, что
разгрузка будет упругой тогда, когда ф <С 0. Складывая то напряжение,
которое было до момента начала разгрузки, с напряжением а', мы получим
а = сгт[1 —cosin М— ф)], if> > 0,
fsinip I
о == о —.—q — со sin D) — ф) и vP < 9.
TLsinU J
Граница контура нагружения получится из условия, что напряжение до-
достигнет предела текучести при сжатии. Если это произойдет в той части
§ 16.6. ИНТЕРПРЕТАЦИЯ В ПРОСТРАНСТВЕ ДЕФОРМАЦИЙ 549
сечения, которая была в пластическом состоянии, мы должны обратиться
к первой формуле A6.5.7). Наибольшая абсолютная величина а достигается
при я|) — ф = л/2, тогда а = атA — со). Полагая а = — ат, получаем 0=2
и по формулам A6.5.6)
<?i = Q — 2я cos ф, (?2 = ~2л sin ф. A6.5.8)
Это — уравнение окружности с радиусом 2л и центром в точке (Q, 0).
Выясним теперь возможность появления пластической деформации при
разгрузке в той области, которая оставалась при первом нагружепии уп-
упругой. Условие достижения экстремального значения величиной а, опреде-
определяемой второй формулой A6.5.7) и рассматриваемой как функция \|), будет
sin 0
Условие того, что это экстремальное напряжение равно пределу текучести
при сжатии
sin
sin 6
— cosing — 9) = — 1.
Возводя эти равенства в квадрат и складывая, мы исклю-
исключим угол \|) и получим следующее соотношение между
со, ф, 9:
1 о COS ф
Это соотношение эквивалентно следующему:
-Q* = л2. A6.5.9) Рис. 16.5.3
Мы получили уравнение окружности радиусом л с центром в точке
(Q — я/sin 9, 0). Таким образом, контур нагружения ограничен двумя пря-
прямыми и дугами одной окружности A6.5.8) при 9 < 43°30' и двух окружно-
окружностей A6.5.8) и A6.5.9) при 9 > 43°30'. На рис. 16.5.3 эти контуры изобра-
изображены для некоторых значений 9.
Следует обратить внимание на то, что по мере уменьшения 9, т. е.
продвижения угловой точки вправо, точка пересечения поверхности нагру-
нагружения с осью Q\ движется влево. Этот результат можно сформулировать
следующим образом: увеличение предела текучести при изгибе в одном на-
направлении сопровождается уменьшением предела текучести при изгибе в
противоположном направлении.
§ 16.6. Интерпретация соотношений пластичности
в пространстве деформаций
В упругой области, а следовательно, внутри поверхности нагружения
изменения деформаций связаны с изменениями напряжений законом Гука,
поэтому в девятимерном изображающем пространстве деформаций поверх-
поверхности нагружения S можно поставить в соответствие поверхность деформа-
деформаций s. Обращаясь к модели § 16.5, замечаем, что в плоскости qu qi началь-
начальная граница пластичности изображается окружностью q\-\- q\ — 1, точка
(Q, 0) соответствует точке (q, 0), где q = 1/sin 9. Отсюда видно преиму-
преимущество наглядности такого представления. В плоскости Q\, Q2 все пласти-
пластические состояния были заключены между близко лежащими концентриче-
концентрическими окружностями с радиусами Q = л и Q = 4, поэтому мы даже не
550
ГЛ. 16. УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
строили соответствующих графиков, ограничившись схематическим изобра-
изображением на рис. 16.5.2. В плоскости q\, q^ пластические состояния занима-
занимают всю область, внешнюю по отношению к единичному кругу.
При упругой разгрузке т~ = ттр но предельные прямые упругой раз-
разгрузки составляют угол 0 с осью Q\ в плоскости Qi, Q2, такой же угол со-
составляют с осью q\ предельные прямые в плоскости qi, #2. Но здесь этот
результат допускает очень простую геометрическую интерпретацию. На
рис. 16.6.1 можно видеть, что поскольку отрезок ON равен 1/sin 0, предель-
предельные прямые упругой разгрузки каса-
касаются начальной окружности текучести.
Выясним теперь, что соответствует об-
области // применимости деформацион-
деформационной теории в этом новом представле-
1
нии. Полагая q± = -q- Q±, будем счи-
S
тать, что Gs задано как функция Q =
+ Q\. Тогда
Рис. 16.6.1
Чтобы найти ~$п\'~о~)'> продифференцируем по Q величину q = Q/G8. По-
Получим ^
dq 1 . . d ! 1
dq 1
Ho -^q = -Q~, поэтому
Внося это выражение в формулу для
Аналогично
В окрестности точки (q, 0) следует принять @i = Q, Q2 = 0; таким образом,
Отношение приращений деформаций равно
, получим
= ¦? д<?2 + (± - ¦?) %
A6.6.1)
§ 16.6. ИНТЕРПРЕТАЦИЯ В ПРОСТРАНСТВЕ ДЕФОРМАЦИЙ 55
Подставляя отношение д7Гиз A6.5.5), получим
Таким образом, область // представляет собою внешний угол, образован-
образованный касательными к окружности начальной текучести. Как видно, изобра-
изображение в пространстве деформаций в данном случае отличается простотой
и симметричностью.
Заметим, что по крайней мере для изотропного материала неравенства
A6.2.2) и A6.2.3), вытекающие из постулата Друкера, могут быть перепи-
переписаны следующим образом:
<16-6-2>
^ft A6.6.3)
Это следует из того, что на приращении пластической деформации, не
сопровождающейся изменением объема, совершает работу только девиатор-
ная часть тензора напряжения, а
= 2\x
Из A6.2.2) вытекает, что вектор а направлен по нормали к поверхности де-
деформирования, если она гладкая.
Применительно к описанной двумерной модели можно показать спра-
справедливость ассоциированного закона. Если мы выйдем из угловой точки в
упругую область и достигнем контура нагружения изнутри либо там, где
он прямолинеен, либо где. образован дугой окружности, то в первый момент
вектор приращения пластической деформации будет направлен по норма-
нормали к контуру в соответствии с требованием, вытекающим из постулата
Друкера. Мы не будем здесь доказывать это свойство, так же как не бу-
будем выводить довольно сложное соотношение между Aqi и AQi для тех
случаев, когда путь нагружения продолжается в область, не принадлежа-
принадлежащую областям / или //. Смысл проведенного для простой модели анализа
заключается в следующем. Точка зрения на упрочняющийся материал как
на совокупность упругих и идеально-пластических элементов, скомбиниро-
скомбинированных каким-то образом, имеет определенный смысл, поэтому некоторые
общие принципы, справедливые для модели, естественно допустить и для
упрочняющегося тела. Эти принципы состоят в следующем.
а. Существует некоторый конус такой, что для приращений напряжен
ний, заключенных внутри этого конуса, справедливы соотношения дефор-
деформационного типа.
б. Из справедливости деформационной теории для некоторых нагруже-
ний, отличных от пропорционального, следует существование угловой точ-
ки на поверхности нагружения.
в. Для гладкой части поверхности нагружения справедлив ассоцииро~
ванный закон или принцип градиенталъностщ состоящий в том, что век-
вектор приращения пластической деформации направлен по нормали к по-
поверхности.
г. Упрочнение при деформировании в одном направлении сопровожда-
сопровождается разупрочнением при деформировании в противоположном направле-
направлении. Этот эффект называется эффектом Баушингера.
552 гл- 16- упругопластическое упрочняющееся тело
§ 16.7. Изотропное и трансляционное упрочнение
Простейшая теория течения, которая формулируется с по-
помощью уравнений A6.3.3) или A6.3.5), была названа теорией
изотропного упрочнения. Действительно, согласно этой теории
поверхность нагружения, определяемая уравнением A6.3.1),
сохраняет свою форму, т. е. изменяется с сохранением подобия.
Если откладывать по осям координат в девятимерном простран-
пространстве напряжений компоненты девиатора, то эта поверхность
будет сферой, которая увеличи-
увеличивает свой радиус к. Очевидно,
что при изотропном упрочне-
упрочнении эффект Баушингера не на-
наблюдается. Наоборот, равномер-
равномерное расширение сферы по мере
увеличения напряжения озна-
означает, что упрочнение при рас-
растяжении, например, влечет за
собой точно такое же упрочне-
упрочнение при сжатии (рис. 16.7.1,а).
Согласно простейшей идеали-
Рис. 16.7.1 зации опытных данных предел
текучести при сжатии должен
уменьшаться ровно настолько, насколько увеличился предел те-
текучести при растяжении. Будем говорить в этом случае об иде-
идеальном эффекте Баушингера. Очевидно, мы получим идеальный
эффект Баушингера, если допустим, что поверхность нагружения
перемещается параллельно самой себе, следуя за точкой нагру-
нагружения, как показано на рис. 16.7.1, б. Будем называть соответ-
соответствующую теорию пластичности теорией трансляционного упроч-
упрочнения. Бели уравнение начальной поверхности нагружения было
/@u)=fc2, то при параллельном переносе уравнение последую-
последующей поверхности нагружения будет
}(оц-в«) = к2. A6.7.1)
Здесь Sij — тензор, составляющие которого служат в простран-
пространстве напряжений координатами центра поверхности нагружения,
а величина к остается постоянной. Тензор sZj обеспечивает то,
что поверхность нагружения всегда проходит через точку на-
нагружения, но этого условия недостаточно, необходимы еще до-
дополнительные гипотезы. Простейшее предположение, сделанное
Ишлинским, состоит в том, что
A6.7.2)
где с — постоянный множитель и в качестве функции ()
принят второй инвариант девиатора. При одноосном напряжен-
§ 16.7. ИЗОТРОПНОЕ И ТРАНСЛЯЦИОННОЕ УПРОЧНЕНИЕ 553
ном состоянии A6.7.1) и A6.7.2) приводят к линейной связи
между напряжением и деформацией; таким образом, эти урав-
уравнения описывают пластичность с линейным упрочнением.
Независимо от Ишлинского и почти одновременно с ним
Прагер предложил аналогичную гипотезу, назвав ее гипотезой
кинематического упрочнения, потому что она может быть про-
проиллюстрирована на простой кинематической модели. Для на-
наглядности обратимся к двумерному случаю, когда поверхности
нагружения соответствует контур нагружения. Представим себе,
что изготовлена рамка с вырезом, имеющим форму контура
нагружения; эта рамка может свободно перемещаться по плос-
плоскости напряжений, причем специальные направляющие обеспе-
обеспечивают поступательное перемещение, предотвращая поворот.
В плоскости движется палец, воспроизводящий путь нагружения.
Если между пальцем и вырезом рамки нет трения, то при пе-
перемещении пальца в произвольном направлении, составляющем
острый угол с направлением внешней нормали к контуру выре-
выреза, рамка переместится по направлению нормали. Таким обра-
образом, перемещение центра рамки будет направлено так же, как
приращение пластической деформации, величина этого переме-'
щения как раз такая, какая нужна для того, чтобы контур
нагружения все время проходил через точку нагружения. А те-
теперь нужно представить себе, что аналогичная кинематическая
модель построена в девятимерном пространстве.
Заметим, что при рассмотрении отдельных частных задач
теории пластичности вместо всего пространства напряжений
можно рассматривать подпространства с меньшим числом изме-
измерений. Но здесь приходится проявлять известную осторожность.
Так, например, при плоском напряженном состоянии пласти-
пластическая деформация будет трехмерной и использование двумер-
двумерной кинематической модели типа Прагера может привести к не-
неверным результатам, как отметил Будянский в дискуссии по
статье Прагера. Эти трудности не возникают, если воспользо-
воспользоваться вариантом гипотезы трансляционного упрочнения, кото-
который был предложен Циглером. Согласно этой гипотезе тензор Sy
определяется следующими дифференциальными уравнениями:
Sit = ^ (ац - s{j)
с естественным начальным условием ^ = 0, при ? = 0, т. е. до
начала пластической деформации. Теперь при Оц = 0 соответст-
соответствующее Sij также равно нулю и кинематическая модель сохра-
сохраняется в любом подпространстве пространства напряжений.
Остановимся, наконец, на варианте теории трансляционного
упрочнения, принадлежащем Новожилову и Кадашевичу. Эти
авторы предполагают, что тензоры si5 и е% связаны соотноше-
соотношениями типа соотношений деформационной теории пластичности,
554 гл- 16- упругопластическое упрочняющееся тело
а именно,
^ = 26*^. A6.7.3)
Здесь G* — функция инвариантов тензора siS или е%. При рас-
рассмотрении конкретных примеров авторы считали, что G* зави-
зависит только от второго инварианта девиатора тензора sxi и в
уравнении A6.7.3) фигурируют компоненты девиаторов. При ин-
интерпретации этого уравнения тензор Sy рассматривают как тен-
тензор «внутренних» самоуравновешенных напряжений, точнее —
как некоторую интегральную меру этих напряжений, возникаю-
возникающих в кристаллических зернах.
§ 16.8. Кусочно линейные поверхности нагружения
Существенная нелинейность соотношений A6.7.3) позволяет
описать поведение реального материала значительно лучше, чем
это делается с помощью других гипотез.
Теперь мы можем вернуться к той простейшей теории пла-
пластичности, с рассмотрения которой мы начали § 16.1. При изу-
изучении границ применимости деформационной теории и при ана-
анализе простейшей модели мы встретились с такой ситуацией, когда
начальная поверхность нагружения была гладкой, а последую-
последующие поверхности становятся сингулярными, коническая точка
появляется в точке нагружения и следует за нею по пути на-
нагружения. Сейчас речь будет идти об особенностях другого рода.
Начальная поверхность нагружения может состоять из частей
нескольких гладких поверхностей, образующих при пересечении
ребра. Простейший пример, рассмотренный в § 16.1, это призма
Сен-Венана, ограниченная шестью гранями. Эта призма в про-
процессе деформации может расширяться с сохранением подобия;
в этом случае следует говорить об изотропном упрочнении,
а может переноситься параллельно без изменения размеров
в случае трансляционного упрочнения. При выводе формул
A6.4.2), когда было заранее оговорено, что точка нагружения
остается все время на одной и той же грани призмы, разницу
между изотропным и трансляционным упрочнением при активном
нагружении обнаружить нельзя и элементарные рассуждения,
положенные в основу при выводе этих формул, не были связаны
с какими-либо предположениями о поведении поверхности на-
нагружения. Сейчас, вставая на ту или иную точку зрения, мы
можем получить более общие соотношения, пригодные для тех
случаев, когда точка нагружения переходит с одной грани призмы
на другую или остается на ребре, образованном пересечением
двух граней. Сделаем, например, предположение о том, что упроч-
упрочнение изотропно. Нам будет удобно видоизменить обозначения
по сравнению с § 16.1, а именно, обозначить главные напряже-
§ 16.8. КУСОЧНО ЛИНЕЙНЫЕ ПОВЕРХНОСТИ НАГРУЖЕНИЯ 555
ния а?, От, и а;. Предположим, что мы находимся на грани приз-
призмы, соответствующей условию gs — сц = к. Тогда / = а? — ап,
^- = 1, ^- = — 1, -^- = 0. Подставляя в A6.3.2), получим
-oJ, if = 0. A6.8.1)
Эти соотношения можно проинтегрировать, и мы получим
nI ev- = 0. A6.8.2)
Формулы A6.8.2) отличаются от A6.1.2) только тем, что в них
не добавлена упругая деформация и не-
незначительно изменены обозначения. Оче-
Очевидно, что конечные соотношения A6.8.2)
справедливы не только для пропорцио-
пропорционального нагружения, но в гораздо более
широких пределах изменения угла, под
которым направлен вектор нагруже-
нагружения а. В этом состоит серьезное преиму-
преимущество теории пластического течения
с кусочно линейной поверхностью на-
нагружения. Предположим теперь, что мы
вышли на другую грань призмы, напри- Рис* 16>81
мер на ту, которая соответствует условию
06 — 0; = к. Тогда, интегрируя соотношения, совершенно аналогич-
аналогичные тем, которые были выписаны для первой грани, получим
е|=Ч*6-<^ + е!\ <* = #, 4 = -h(al-al). A6.8.3)
Здесь штрихами отмечены величины пластической деформации,
накопленные на той части пути нагружения, которая соответ-
соответствовала первой комбинации, а именно, / = as — с^; они вычисля-
вычисляются по формулам A6.8.1).
Особого рассмотрения требует тот случай, когда точка нагру-
нагружения остается на ребре поверхности нагружения. Предположим,
например, что О1 = оц?^а?, тогда одновременно выполняются два
условия: os — Gi = ±2k и Gt,— a?=s±2fe, причем величина к уве-
увеличивается в процессе нагружения. На рис. 16.8.1 показано се-
сечение призмы октаэдрической плоскостью в окрестности ребра;
в этой плоскости лежат нормали к поверхности призмы. Нормали
к граням призмы в точке пересечения ребра с октаэдрической
плоскостью образуют угол, внутри которого лежат возможные
приращения пластической деформации. Этот угол составляет 60°,
Вычисляя по отдельности скорости пластической деформации,
соответствующие тем граням, которые пересекаются на ребре, по
556
ГЛ. 16. УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
формулам типа A6.8.1) и складывая эти скорости, получим
'4 = #i(org- k)> el =
A6.8.4)
Здесь вместо ал написано а§. Состояние, при котором gs = ап, нуж-
нужно рассматривать как сжатие в направлении оси ? напряжением
а$ —а;; на это сжатие накладывается гидростатическое напряжен-
напряженное состояние a = a$, которое вследствие несжимаемости матери-
материала не должно влиять на скорость пластической деформации. По-
Поэтому следует считать, что как Ни так и Н2 зависят от разно-
разности as — G;. При этом сумма Я! + Н2 есть заданная, т. е. опре-
определяемая из опыта функция, соотношение же между Я4 и Н2
остается неопределенным. Поэтому результат интегрирования
уравнений A6.8.4) можно представить следующим образом:
= — h (с>? —
е\ =
A6.8.5)
При g? = 0 el = —h(—oz); таким образом, функция h(—Gz)
представляет непосредственно зависимость между пластической
деформацией е9 и напряжением gs при простом сжатии. В дан-
данной теории диаграмма сжатия совпадает с диаграммой растяже-
растяжения, уравнение которой получается
путем простой перемены знаков:
M
В уравнениях деформационного ти-
типа A6.8.5) остается один неопределен-
неопределенный параметр А,. Эта неопределенность
есть неизбежное следствие жесткого
предположения о том, что напряженное
состояние изображается точкой ребра
призмы пластичности. Такое условие
ограничивает выбор возможных напря-
напряженных состояний. Для того чтобы
при этом были выполнены условия сов-
совместности деформаций, необходимо
иметь известную кинематическую сво-
свободу. Но с другой стороны, можно при-
привести примеры, когда вывод о неопределенности деформации на
ребре поверхности нагружения противоречит опыту и, может быть,
здравому смыслу. Так при простом растяжении или сжатии в на-
направлении оси поперечные деформации могут быть произвольными,
лишь бы выполнялось условие постоянства объема. Этот непри-
неприемлемый результат представляет собою неизбежное следствие
слишком далеко идущей идеализации. Реально можно было бы
Рис. 16.8.2
§ 16.8. КУСОЧНО ЛИНЕЙНЫЕ ПОВЕРХНОСТИ НАГРУЖЕНИЯ 557
говорить, вероятно, о значительной неустойчивости поперечной
деформации. Это значит, что, прикладывая малую поперечную
нагрузку в каком-либо направлении, мы достигнем того, что
вся или почти вся поперечная деформация будет происходить
в этом направлении. Опытов подобного рода не существует, и
нам представляется правильным смотреть на теорию течения
с кусочно линейной поверхностью нагружения как на аппрок-
аппроксимацию более реальной в механическом смысле теории с глад-
гладкой поверхностью нагружения. Впрочем, по этому вопросу име-
имеются и другие точки зрения.
Как всегда, можно привести примеры крайних следствий из
принятой аппроксимации, но во многих случаях результаты
расчета по кусочно линейной теории достаточно близки к ре-
результатам теории с гладкой поверхностью нагружения, возмож-
возможная погрешность окупается несравненной простотой.
Мы не будем здесь рассматривать в деталях вопрос о модели
трансляционного упрочнения с кусочно линейной поверхностью
нагружения. Простая схема, приведенная на рис. 16.8.2, иллю-
иллюстрирует эту разницу. Двигаясь в октаэдрической плоскости по
радиальному пути нагружения при изотропном упрочнении, мы
будем все время находиться на одной и той же стороне расши-
расширяющегося шестиугольника, представляющего собою след пере-
пересечения октаэдрической плоскости с расширяющейся призматиче-
призматической поверхностью нагружения. При кинематическом упрочнении
шестиугольник сначала будет двигаться вправо по нормали к той
стороне, на которой находится конец вектора нагружения. В мо-
момент, когда шестиугольник займет положение, показанное штри-
штриховой линией, конец вектора нагружения окажется в вершине,
которая будет следовать по прямолинейному пути нагружения,
увлекая за собою перемещающийся параллельно шестиугольник.
Радиус-вектор s центра шестиугольника изображает в некотором
масштабе пластическую деформацию, вызванную напряжением а
при заданном радиальном пути нагружения. Конечно, это отно-
относится к случаю линейного упрочнения.
Следует заметить, что в случае пропорционального нагру-
нагружения гипотеза трансляционного упрочнения не приводит к урав-
уравнениям деформационной теории. Эта оговорка необходима в связи
с распространенным мнением об универсальной значимости де-
деформационной теории для пропорциональных нагружений.
Использование в качестве поверхности нагружения призмы
Сен-Венана — это далеко не единственная возможность. В § 15.6
мы видели, что в качестве поверхности текучести может быть
выбрана шестигранная призма, описанная около цилиндра Ми-
зеса, а не вписанная как призма Сен-Венана. Соответствующий
вариант теории строится совершенно аналогичным образом, неко-
некоторые авторы использовали его для решения конкретных задач;
здесь мы ограничимся лишь упоминанием. В § 15.7 было пока-
558 гл- 16- упругопластическое упрочняющееся тело
зано, сколь сложный вид могут принимать поверхности текучести
для анизотропных тел; при решении задач пластичности для
таких тел естественно выбирать некоторые кусочно линейные
аппроксимации хотя бы не для всей поверхности, а для той ее
части, на которой, как можно ожидать, окажется конец век-
вектора нагружения в данной конкретной задаче.
§ 16.9. Теория скольжения
Рассмотренные до сих пор теории пластичности основывались
на гипотезах формального характера; реальная структура поли-
поликристаллического материала и хорошо известная картина пласти-
пластического деформирования кристаллических зерен при этом совер-
совершенно не принимались во внимание. Такой подход имеет свои
преимущества и недостатки. С одной стороны, общие законы
пластичности, сформулированные для произвольного тела безот-
безотносительно к его физической природе, позволяют охватить едино-
единообразным способом широкий круг явлений — пластичность метал-
металлов, предельное равновесие грунтов, хрупкое разрушение горных
пород и бетона и так далее. Такая общность чрезвычайно подку-
подкупает; действительно, экспериментатор с удивлением обнаружива-
обнаруживает, что макроскопическое поведение тел самой разнообразной
физической природы оказывается поразительным образом сход-
пым. Оказывается, что это поведение еще более поразительным
образом может быть приблизительно хорошо описано при помощи
уравнений, полученных из некоторых априорных гипотез доста-
достаточно формального характера. Но при более детальном изучении
опытных данных оказывается, что при внешнем глобальном сход-
сходстве обнаруживаются и различия в поведении разных материа-
материалов. Эти различия связаны с тем, что микромеханизмы не только
неупругой, но даже упругой деформации не одинаковы. Поэтому
естественно стремление к тому, чтобы положить в основу теории
пластичности некоторые физические представления о протекании
пластической деформации. Нужно признать, что мы еще далеки
от возможности построения макроскопической теории, основан-
основанной на анализе и описании процессов, происходящих на микро-
микроуровне. Теория скольжения Батдорфа и Будянского, которая
будет схематически изложена ниже, отнюдь не может быть на-
названа «физической» теорией. Однако положенные в ее основу
гипотезы в определенной мере отражают процессы, происходя-
происходящие внутри отдельных кристаллических зерен, хотя и не вос-
воспроизводят их точным и полным образом. Пластическая дефор-
деформация единичного кристалла происходит за счет сдвига в
определенной кристаллографической плоскости в определенном
направлении. Совокупность плоскости скольжения и направле-
направления скольжения в этой плоскости называется системой сколь-
скольжения. Система скольжения задается парой ортогональных еди-
§ 16.9. ТЕОРИЯ СКОЛЬЖЕНИЯ 559
ничных векторов: вектора п — нормали к плоскости скольжения
и вектора (J — направления скольжения. Если касательное напря-
напряжение тпр превышает предел текучести, кристалл пластически
деформируется, причем эта деформация представляет собою
деформацию чистого сдвига. При пластической деформации ве-
величина сдвига ^аР есть вполне определенная функция от тар
в активном процессе, когда ^ар растет. Плоскости скольжения —
это плоскости наиболее плотной упаковки атомов, направления
скольжения — это те, для которых расстоя-
расстояния между центрами соседних атомов наи-
наименьшие. Так, в кристаллах с кубической
гранецентрированной решеткой (рис. 16.9.1)
имеется четыре плоскости скольжения и
три направления, всего 12 систем сколь-
скольжения. На рисунке темными кружками
обозначены атомы, лежащие в одной из
таких плоскостей, и стрелками показаны на-
направления, для которых расстояния между
атомами наименьшие. Эти факты надежно
установлены из опытов над монокристалла- Рис. 16.9.1
ми. Обычно скольжение происходит в не-
нескольких системах скольжещш одновременно; при этом сдвиг,
происходящий в одной системе скольжения, оказывает упрочняю-
упрочняющее действие на другие системы. Количественное описание этих
эффектов взаимного упрочнения пока отсутствует. Следует иметь
в виду, что атомные плоскости не перемещаются одна относитель-
относительно другой как целое, для этого нужно было бы слишком большое
напряжение. Фактически движутся дислокации, при выходе одной
дислокации на поверхность кристалла, т. е. при ее исчезновении,
две части кристалла, расположенные с двух сторон от плоскости
движения дислокации, оказываются смещенными на величину
вектора Бюргерса Ь.
Простейшая схема, принятая Батдорфом и Будянским, со-
состоит в том, что для каждого зерна предполагается существова-
существование одной только системы скольжения. В более поздней работе
тех же авторов было сделано предположение о существовании
нескольких систем скольжения, что до чрезвычайности усложни-
усложнило анализ и привело в общем к тем же качественным выводам.
Если даже принять схему первой работы Батдорфа и Будянского,
т. е. допустить существование одной-единственной системы сколь-
скольжения, то действительная картина будет достаточно сложной.
Для того чтобы пластическая деформация поликристаллического
объекта могла произойти на самом деле, необходимо, чтобы
соседние зерна не препятствовали этому. Макроскопический эф-
эффект пластической деформации тела в целом будет обнаружен,
когда в теле появятся цепочки пластически деформированных зе-
зерен. На ранних ступенях пластической деформации большие бло-
560 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
ки зерен остаются в упругом состоянии, перемещаясь и повора-
поворачиваясь как целое. Поэтому пластическая деформация чрезвычай-
чрезвычайно неоднородна; лишь с увеличением общей деформации
происходит выравнивание локальной деформации. В особенности
это относится к материалам с незначительным упрочнением.
В теории скольжения эта сложная картина не воспроизво-
воспроизводится, трудности обходятся введением некоторых упрощающих
предположений. Зафиксируем по произволу два
взаимно перпендикулярных направления п
и р, определяющих предположительную си-
систему скольжения. Если число зерен в объе-
объеме тела велико, то всегда найдется некоторое
число зерен, для которых нормаль к плоско-
плоскости возможного скольжения — по предположе-
предположению единственная — будет находиться внутри
конуса с осью п и телесным углом при верши-
вершине dQ (рис. 16.9.2). Материал предполагается
Рже 16.9.2 статистически изотропным, поэтому число та-
таких зерен пропорционально dQ и не зависит
от п. Будем называть их зернами с плоскостью скольжения
п§ Если число зерен с плоскостью скольжения п достаточно
велико, то среди них существуют такие, для которых направле-
направление скольжения лежит внутри угла d$ с биссектрисой р. Будем
называть такие зерна зернами с системой скольжения яр. Для
статистически изотропного материала относительный объем зе-
зерен с системой скольжения wp пропорционален dQd$. В систе-
системе скольжения п§ действует касательное напряжение тпР, соот-
соответствующие зерна претерпевают деформацию чистого сдвига
7^р = ^(тпр)- Здесь была сделана гипотеза о том, что напряжен-
напряженное состояние однородно и не меняется от зерна к зерну. Вто-
Вторая гипотеза состоит в том, что деформация зерен с системой
скольжения яр вызывает такую же общую деформацию тела,
пропорциональную относительному объему соответствующих зе-
зерен, а именно:
Итак, деформация тела в целом представляет собою результат
наложения бесконечно большого числа чистых сдвигов для всех
возможных систем скольжения #гр. Чтобы вычислить эту дефор-
деформацию, перейдем к составляющим тензора деформации относи-
относительно фиксированных осей хг по формулам преобразования
компонент тензора второго ранга (§ 7.1). Принимая направления
п и р за направления 1 и 2 новой системы координат, мы
должны принять все e{j равными нулю, кроме ei2 = 4n&/2. Тогда
de
12.
§ 16.9. ТЕОРИЯ СКОЛЬЖЕНИЯ 561
Но pii = л*, p2i = ft, следовательно,
del = -г <*'P' + ^pi) F (T^ dQ *'
Интегрируя, получим формулы для пластических деформаций
A6-9Л)
1
Q —Я/2
Здесь Q — поверхность единичной сферы. Касательное напряже-
напряжение тпр вычисляется по обычной формуле
т», = о«га&. A6.9.2)
При этом использована первая гипотеза, заключающаяся в том,
что напряженное состояние однородно и, следовательно, тпР в
любом зерне выражается через компоненты тензора Сц по
обычным формулам. Если эта гипотеза с известной натяжкой
и может быть принята, то предположение о возможности сум-
суммирования деформаций, приводящее к формулам A6.9.1), пред-
представляет собою далеко идущую идеализацию.
Для фактического вычисления деформаций направления лир
задаются с помощью эйлеровых углов, по которым и ведется
интегрирование. Основная трудность связана с тем, что функ-
функция F(x) отлична от нуля только при т>тт, поэтому интегралы
в формулах A6.9.1) распространяются не на всю поверхность
сферы, а лишь на некоторую ее область.
Согласно теории скольжения начало пластической деформа-
деформации связано с достижением предела текучести в какой-то из
систем скольжения. Но если ттах = тТ, то всегда найдутся такие
зерна, для которых это напряжение будет касательным напря-
напряжением в системе скольжения. Поэтому начальная поверхность
соответствует условию максимального касательного напряжения
Треска — Сен-Венана. Для последующих поверхностей точка на-
гружения будет конической точкой.
Вычисления по формулам A6.9.1) довольно сложны и громоздки. Чи-
Чикала смог довести до конца рассмотрение простейшего случая, когда обра-
образец сначала растягивается, а потом закручивается. Не воспроизводя вы-
выкладки, мы приведем лишь окончательный результат. Поскольку в опыте
участвуют два напряжения а и т, его можно представить графически в
плоскости, как это сделано на рис. 16.9.3. Начальная поверхность нагруже-
ния есть эллипс, уравнение которого
,а2 + 4т2 = const.
При растяжении точка нагружения движется по оси абсцисс, пересекает
начальную поверхность, доходит до точки М и движется дальше по лучу,
выходящему из этой точки. Оказалось, что касательные, проведенные к на-
начальному эллипсу из точки Af, делят плоскость а, т на четыре области.
Если приращения напряжений таковы, что точка нагружения попадает в
область /, происходит упругая разгрузка. Приращения деформаций при
36 ю. Н, Работпов
562 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
движении точки нагружения в область // определяются по формулам типа
формул деформационной теории, интегралы A6.9.1) не зависят от пути на-
нагружения, а только от конечных значений а и т. Для путей нагружения,
направленных в области /// и IV, соотношения между деформациями и на-
напряжениями оказываются довольно сложными, законченный результат по-
получен автором для ортогонального нагружения, показанного стрелкой на
рисунке, т. е. для закручивания при постоянной осевой нагрузке. При ма-
малых Дт было получено
4 G* -f ГТ A693)
Г
Здесь Еш и Et — соответственно секущий и касательный модули, определен-
определенные по диаграмме растяжения для точки М. Опыт на кручение при посто-
постоянной растягивающей силе выявляет разницу между различными теориями
пластичности наиболее контрастным образом. По теории течения с гладкой
поверхностью текучести началь-
начальный модуль G* = р- — модуль уп-
упругости при сдвиге. По деформа-
деформационной теории, соответствующей
закону A6.1.4), G = Gs(a); это
значит, что начальный модуль оп-
определяется степенью растяжения
перед приложением крутящего
момента. Опытные данные пока-
Рпс 16 9 3 зывают, что при небольшой плас-
пластической деформации начальный
модуль догрузки G* приблизи-
приблизительно равен модулю упругости; при увеличении пластической деформа-
деформации предварительного растяжения величина G* несколько уменьшается,
однако формула A6.9.3) все же дает заниженный результат. Деформацион-
Деформационная теория приведет к существенно меньшей величине G* и, таким обра-
образом, резко противоречит эксперименту, что и неудивительно, рассматривае-
рассматриваемое нагружение наиболее далеко от пропорционального.
Качественная картина, представленная на рис. 16.9.3, весьма похожа па
ту, которая была найдена нами для модели, рассмотренной в § 16.5. Рас-
Расположение областей на рис. 16.9.3 и 16.6.1 совершенно одинаково, правда
рис. 16.6.1 относится к плоскости деформаций, а рис. 16.9.3 —к плоскости
напряжений. Такое сходство качественных результатов не должно вызы-
вызывать удивления. Теория Батдорфа —- Будянского, так же как и наша модель,
представляет тело в виде собрания упругопластических элементов; в тео-
теории скольжения таким элементом служит зерно, наделенное одной-единст-
всиыой системой скольжения. При активной пластической деформации
касательное напряжение и сдвиг в зерне связаны однозначной функцио-
функциональной зависимостью и соотношения деформационной теории оказываются
справедливыми до тех пор, пока во всех элементах продолжается актив-
активная деформация. При этом с увеличением напряжения пластическая де-
деформация распространяется на новые элементы, но разгрузка нигде не
происходит. Такое положение соответствует догрузке внутрь угла //. При
догрузке в области /// и IV часть элементов может догружаться, в плас-
пластическую деформацию могут втягиваться новые элементы, но некоторые
из пластически деформированных зерен разгружаются, возвращаясь в уп-
упругое состояние. Этим определяется сложность анализа для указанных
областей.
Существуют и другие варианты скольжения — Бишопа и Хилла, Лина,
Малмейстера, Клюшникова, которые здесь рассматриваться не будут. За-
Заметим только, что теория Клюшникова построена для некоторой модельной
двумерной среды, поэтому она проще, чем описанная модель Батдорфа —
§ 16.10. СОПОСТАВЛЕНИЕ МОДЕЛЕЙ С РЕАЛЬНОСТЬЮ 563
Будянского. Даже простейшая модель, рассмотренная в § 16.5, приводит к
достаточно сложным зависимостям для общего случая, уравнения, полу-
полученные для этой модели, не позволяют сделать даже качественный вывод
о характере изменения поверхности нагружения при более или менее слож-
сложных путях нагружения. Тем более трудно это сделать для изложенной вы-
выше теории скольжения, которая, по-видимому, правильно отражает основ-
основной механизм пластической деформации поликристаллического металла.
Хотя вводимые гипотезы чрезмерно упрощают действительное положение
дела, уравнения все же получаются слишком сложными. Это обстоятельство
приводит нас к довольно пессимистическим выводам относительно возмож-
возможного прогресса теории пластичности, основанной на наглядных механиче-
механических представлениях.
§ 16.10. Сопоставление моделей с реальностью
в пластичности
В послевоенное время значительные усилия ряда исследова-
исследователей в разных странах были направлены на построение теории
упругопластического деформирования при произвольном виде
нагружения. В настоящее время можно считать надежно подт-
подтвержденными уравнения деформационной теории при пропорцио-
пропорциональном нагружении. Для нагружений, близких к пропорцио-
пропорциональному, предсказания этой теории также оказываются удов-
удовлетворительными, хотя мера необходимой «близости» по существу
не определена. Вопрос о существовании или, наоборот, отсут-
отсутствии конической точки на поверхности нагружения, если встать
на точку зрения теории течения, также остается открытым и
вообще вряд ли может быть решен в результате эксперимента.
Любая теория пластичности представляет лишь модель явле-
явления и проверке могут подлежать только следствия из этой тео-
теории, притом с определенной степенью точности, зависящей от
характера рассматриваемой задачи. Определение поверхности те-
текучести требует точной фиксации момента перехода от пласти-
пластической деформации к упругой, тогда как в действительности
этот переход совершается постепенно. В практике эксперимента
положение предельной поверхности текучести приходится опре-
определять, задаваясь некоторым допуском, некоторой пороговой ве-
величиной пластической деформации, которая соответствует вы-
выходу на эту поверхность. Но этот порог, вообще говоря, произво-
произволен, он зависит от воли экспериментатора и от точности имею-
имеющейся в его распоряжении измерительной аппаратуры.
Другое осложняющее обстоятельство состоит в следующем.
Предположим, что мы установили допуск пластической дефор-
деформации при растяжении и сжатии. Спрашивается: как ограничить
эквивалентную пластическую деформацию при каком-либо ком-
комбинированном напряженном состоянии? Ответить на этот вопрос
можно, задавшись определенной теорией пластичности, т. е.
сделав предположение о связи тензоров efj и Оц. Но задача
экспериментатора состоит именно в установлении связи такого
36*
564
ГЛ. 16. УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
рода. В действительности некоторые авторы производили экспе-
эксперименты, имея в распоряжении точные измерительные средства,
и строили условные поверхности текучести при разном пороге
пластической деформации. Эти кривые оказались очень разными
и, вообще говоря, не соответствующими какой-либо из общепри-
общепринятых теорий. Поэтому возникает вопрос: имеет ли на самом
деле понятие поверхности нагружения какой-либо реальный
смысл и нужно ли полагать его в основу при построении теории
пластичности? Существуют варианты
теории пластичности (Ильюшин), не
полагающие в основу понятие поверх-
поверхности нагружения, а прямо выражаю-
выражающие компоненты тензора напряжений
как некоторые функционалы, опреде-
определенные для пути нагружения; одним из
основных мотивов при построении та-
такого рода теорий служит отмеченная
невозможность строгого различения
между упругой и пластической дефор-
деформацией в эксперименте. По-видимому,
любая из существующих теорий пла-
пластичности может быть опровергнута
в эксперименте, если речь идет о про-
проверке тонких эффектов; при разумном
огрублении результатов некоторые из
них такую экспериментальную провер-
проверку выдерживают, по крайней мере для некоторого ограниченного
набора экспериментальных программ. Теория течения с кинема-
кинематическим упрочнением, во всяком случае, описывает, в отличие от
других теорий, идеальный эффект Баушингера. Так называется
уменьшение предела текучести при сжатии в результате предвари-
предварительного упрочнения растяжением и наоборот. Идеальный эффект
Баушингера состоит в том, что уменьшение предела текучести в
обратном направлении в точности равно его увеличению при
нагружении в прямом. Диаграмма растяжения — сжатия при та-
таком идеальном эффекте представлена на рис. 16.10.1. В дей-
действительности идеальный эффект Баушингера не наблюдается;
вопрос о пластическом деформировании при знакопеременных
нагрузках освещен в книгах Москвитина и Шнейдеровича, здесь
он рассматриваться не будет. Таким образом, если считать эф-
эффект Баушингера идеальным, то гипотеза кинематического уп-
упрочнения достаточно хорошо описывает поведение материала при
нагружении, происходящем по прямой, проходящей через начало
координат в ту и другую сторону, а также, по-видимому, для
близких путей нагружения.
В то же время следует признать, что в практике инженер-
инженерных расчетов до сих пор наибольшее распространение находит
Рис. 16.10.1
§ 16.11. РАСПРОСТРАНЕНИЕ УПРУГОПЛАСТИЧЕСКИХ ВОЛН 565
простейшая деформационная теория. Для активного нагружения
уравнения этой теории представляют по существу уравнения
нелинейной теории упругости. Эти уравнения по форме совпа-
совпадают с уравнениями теории установившейся ползучести, где их
применимость кажется более обоснованной. Некоторые задачи,
решение которых будет рассмотрено в гл. 18, совершенно совпа-
совпадают с аналогичными задачами деформационной теории пластич-
пластичности.
§ 16.11. Распространение упругопластических волн
Распространение упругих однородных волн в стержнях было
рассмотрено в элементарной постановке в § 2.10 и 6.7. В § 13.7,
13.8 были выявлены те ограничения, при которых элементарная
теория применима (длинные волны) и в первом приближении
те поправки, которые нужно внести в результаты элементарной
теории, относящейся к предполагаемой возможности распростра-
распространения фронтов, несущих разрыв деформаций, напряжений и ско-
скоростей. Эти ограничения естественным образом снимаются, если
рассматривать не волны в стержнях, а плоские волны в полу-
полубесконечном теле, возникающие в том случае, когда к границе
полубесконечного тела внезапно прикладывается нормальное
давление или этой границе сообщается мгновенная скорость.
Практически эксперименты подобного рода делаются на толстых
плитах, заряд взрывчатого вещества укладывается, на поверхцо-
сти плиты и подрывается либо вторая плита бросается путем
взрыва на первую так, что контакт возникает по всей поверх-
поверхности одновременно. Создание действительно плоского фронта
при этом довольно трудно, с одной стороны. С другой — изме-
измерения перемещений и скоростей возможны только на второй
свободной поверхности плиты, от которой отражается приходя-
приходящая ударная волна. Поэтому информация, извлекаемая из опытов
подобного рода, довольно ограничена.
Эти замечания существенны в связи с тем вопросом, который
будет рассмотрен ниже, а именно вопросом о распространении
упругопластических волн. Большая часть экспериментальных
данных, сюда относящихся, получена в опытах по распростра-
распространению волн именно в стержнях. С другой стороны, пластическая
деформация связана с диссипацией энергии, и вопрос, скажем,
о прогрессивных волнах для упругопластических тел лишен
смысла, возбужденные с одного конца волны быстро затухнут
и не дойдут до второго конца. Большая часть опытов произво-
производилась при импульсном нагружении на одном конце, измерялись
либо остаточные деформации после прохождения пластического
фронта, либо изменение деформации во времени в каком-либо
сечении образца. Даже приближенный анализ, подобный сделан-
сделанному в § 13.8 для упругого стержня, для упругопластических
566 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
стержней отсутствует, поэтому при интерпретации результатов
измерений допускается некоторая погрешность. Мы подчеркиваем
это обстоятельство, поскольку различные авторы при построении
теории распространения упругопластических волн полагали в
основу разные гипотезы об определяющих уравнениях материала.
При сравнении теоретических предсказаний с результатами экс-
эксперимента далеко не всегда ясно, объясняются наблюдаемые рас-
расхождения природой исходных гипотез или же вторичными эф-
эффектами типа рассмотренных в § 13.8. Здесь мы встанем на точку
^1 зрения простейшей теории деформационного
типа, принадлежащей Тейлору, Карману и
Рахматулину. В основу этой теории пола-
полагается гипотеза о существовании так на-
называемой динамической диаграммы дефор-
деформирования. Производя деформирование при
разных скоростях деформации или разных
скоростях нагружения для металлов, мы
gi -_. будем получать разные диаграммы с — еу
при больших скоростях диаграммы распо-
Рис. 16.11.1 лагаются выше. Основная гипотеза, по-
полагаемая в основу теории, заключается в
том, что с увеличением скорости диаграмма не поднимается не-
неограниченно, а приближается к некоторой предельной диаграм-
диаграмме. Можно сказать, что эта диаграмма соответствует бесконечно
большой скорости деформации, но такое утверждение имеет
смысл только для завершения логической схемы. В действитель-
действительности утверждается, что при достаточно высоких скоростях де-
деформации диаграмма становится мало чувствительной к изме-
изменению скорости и воображаемая «мгновенная» или «динамиче-
«динамическая» диаграмма фактически определяет зависимость между
напряжением и деформацией при тех скоростях, которые
реализуются при распространении пластических волн. Итак,
предположим, что уравнение динамической кривой одномерного
деформирования есть
а = ф(е). A6.11.1)
Соответствующий график представлен на рис. 16.11.1. Суще-
Существенно, что кривая, изображающая уравнение A6.11.1), направ-
направлена выпуклостью вверх, вторая производная <р"(е) всюду отри-
отрицательна. Для реальных металлов дело всегда обстоит именно
так. Обращаясь к выводу уравнения продольных колебаний
стержней, запишем выведенное там уравнение движения в сле-
следующем виде:
Здесь v — скорость движения сечения в целом, v = du/dt, где и —
перемещение, принятое за искомую переменную в § 6.6 и далее.
5 16.11. РАСПРОСТРАНЕНИЕ УПРУГОПЛАСТИЧЕСКИХ ВОЛН 567
Вместо закона Гука мы должны использовать уравнение
A6.11.1). Вводя обозначение
а{е) = /1Ш, A6.11.2)
перепишем уравнение движения следующим образом:
а2(*)-|-17 = 0- A6Л1-3>
Присоединим к этому уравнению следующее тождество:
il-f = 0, A6.11.4)
вытекающее из того, что е = ди/дх, и = du/dt.
Для интегрирования системы A6.11.3), A6.11.4) мы приме-
применим метод характеристик, уже описанный в § 15.8, применитель-
применительно к плоской задаче. Присоединим к уравнениям этой системы
два соотношения
*Ldx + dvdt==dUi pdx+dLdt = de. A6.11.5)
и*С ut OX ut
Мы получим систему из четырех уравнений A6.11.3) — A6.11.5)
для четырех частных производных ди/дх, du/dt, де/дх, de/dt.
Приравнивая нулю определитель системы, мы получаем соот-
соотношение между дифференциалами dx и dt, определяющее харак-
характеристические направления.
Совершенно аналогично, заменяя один из столбцов определи-
определителя столбцом правых частей уравнений, приравняем получив-
получившийся определитель нулю. Подставляя в результат соотношения
между dx и dt для первого и второго характеристического урав-
уравнения, получим соотношения между du и de, выполняющиеся
вдоль характеристик. Опуская выкладки, приведем окончатель-
окончательный результат.
Характеристики первого направления
dx — a(e) dt = 0, du + a(e) de= 0. A6.11.6)
Характеристики второго направления
dx + a(e)dt = 0, du -a{e)de = 0. A6.11.7)
Заметим, что соотношения на характеристиках интегрируются.
Положим
е
q>(e) = J a(e) de,
о
Тогда в результате интегрирования получаем
v ± ф (е) = const. A6.11.8)
Интеграл A6.11.8) выполняется на характеристиках первого се-
568 ГЛ- 16- УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
мейства с верхним знаком, на характеристиках второго семейства
с нижним.
Простейшая задача, решаемая с помощью найденных интегра-
интегралов, состоит в следующем. Концу полубесконечного стержня в
момент ? = 0 сообщается скорость v = V(t), при t^O весь стер-
стержень находится в покое. Будем рассмат-
рассматривать картину в плоскости х, t, как по-
показано на рис. 16.11.2. В точке р ско-
скорость vp — V(tp)=Vp известна. Проведем
через р характеристику второго семейства
с отрицательным наклоном, она пересечет
ось х в точке q. На линии pq v — qp =
=*const, но в точке q у = 0и е = 0, сле-
следовательно, ф = 0. Поэтому
^р-Фр = 0, <f>[ep)=Vp.
Проведем теперь характеристику положи-
положительного направления из точки р в неко-
некоторую точку п. На этой характеристике v + ф = const, следова-
следовательно,
vn + <p(en)=2VP.
Соединим точку п с точкой т оси х характеристикой второго
семейства. Из условия vm — фт == 0 найдем
1?я-ф(еп) = 0.
Поэтому
()У A6119J
Оказывается, что во всех точках характеристики, выходящей
из точки р оси t, скорость и и деформация е сохраняют постоян-
постоянные значения. Но наклон характеристики определяется величи-
величиной а(е), которая сохраняет на характеристике постоянное зна-
значение, следовательно, характеристики прямолинейны. Если
V(t) — неубывающая функция времени, характеристики образу-
образуют расходящийся пучок, как показано на рис. 16.11.3. Этот ри-
рисунок относится к тому случаю, когда скорость растет постепен-
постепенно от куля и, следовательно, выходящая из начала координат ха-
характеристика соответствует минимальной скорости распростране-
распространения волны а@), которая определяется наклоном касательной к
диаграмме деформирования в начале координат. Если внезапно
концу сообщается отличная от нуля скорость, картина оказы-
оказывается несколько иной. Для того чтобы выяснить ее, предполо-
предположим, что скорость нарастает от нуля до величины V в течение
короткого времени т, а после остается постоянной. Из точек
отрезка [0, т] оси t выходят прямолинейные характеристики,
нижняя из них соответствует скорости а@), верхняя — скорости
а(е), где е — деформация, соответствующая скорости V согласно
§ 16.12. ЗАПАЗДЫВАНИЕ ТЕКУЧЕСТИ
569
уравнению A6.11.9). Из точек оси t^(x, °°) будут выходить
параллельные характеристики с той же скоростью а(е). Перейдем
теперь к пределу, устремляя т к нулю. В результате мы получим
центрированный пучок (рис. 16.11.4)
z-a(e)t = 0.
Наклон каждой характеристики этого пучка определяет а(е),
а следовательно, деформацию е и скорость V по уравнению
A6.11.9). Штриховая прямая тп соответствует фиксированному
сечению стержня, в котором можно прикрепить датчик и осцил-
лографировать деформацию. На участке пр е = 0, в точке р еще
п = 0, но на участке рт деформация, а следовательно, и скорость
монотонно возрастают, достигая конечного значения в точке т
и сохраняя это значение на участке qm% Волны, соответствующие
центрированному пучку характеристик, называются волнами
Римана.
Рпс. 16.11.3
Рис. 16.11.4
Располагая осциллограммами деформации, полученными для
нескольких датчиков, наклеенных на образце, можно найти ди-
динамическую диаграмму деформирования. Для этого нужно от-
отметить в плоскости х, t точки, соответствующие одним и тем же
значениям е. По доказанному эти точки лежат на одной и той
же характеристике. Проведя прямую и измеряя ее наклон, мы
находим скорость а(е) и а = ср(е).
§ 16.12. Упругопластические волны.
Запаздывание текучести
Диаграмма деформирования иа рис. 16.11.1 не имела упругого
участка. Выясним, как будет обстоять дело в том случае, когда
существует отличный от нуля предел пропорциональности. В этом
случае а @) = с0 — скорость продольной упругой волны. Для на-
наглядного выяснения существа дела рассмотрим случай упруго-
пластического тела с линейным упрочнением, соответствующая
диаграмма изображена на рис. 16.12.1. Предположим, что ско-
570
ГЛ. 16. УПРУГОПЛАСТИЧЕСКОЕ УПРОЧНЯЮЩЕЕСЯ ТЕЛО
рость V монотонно возрастает до некоторой величины У4, после
чего остается постоянной. Пока было V < соет, по стержню шли
упругие волны со скоростью с0, характеристики х — cot = const
были параллельны. Как только становится V > соет, вступают
в силу уравнения пластической динамики. Но при линейном
упрочнении скорость пластических волн а{ определяется накло-
наклоном пластического участка диаграммы деформирования и оста-
остается постоянной. Характеристики сразу поворачиваются вверх и
Рис. 16.12.2
идут параллельно с наклоном а1# Точка т на рис. 16.12.2 соот-
соответствует точке предела текучести М на рис. 16.12.1. Возникает
вопрос: что же делается внутри пучка, образованного лучами
тр и mq? Каждый из этих лучей представляет собою крайнюю
характеристику упругой и пластической области соответственно,
на линии mq сохраняется значение деформации еТ и скорость
V = соет. В точке т
1
Ф = J code = соеТ,
поэтому и скорость, и деформация на луче тр будут теми же,
что на луче mq. Отсюда с неизбежностью следует, что угол
qmp представляет собою область постоянных значений е = еТ,
V = соет. На эту область можно смотреть как на своеобразное
вырождение пучка волн Римана, проводя лучи внутри этого пуч-
пучка, мы не можем рассматривать их как волны, потому что
в точке М не существует касательной, производная ф'(ет),
а следовательно, а(ет) не определены.
Характерная особенность малоуглеродистых сталей — это так
называемое запаздывание текучести. Как оказывается при крат-
кратковременном действии нагрузки, вызывающей напряжения, зна-
§ 16.12. ЗАПАЗДЫВАНИЕ ТЕКУЧЕСТИ 571
чительно превышающие статический предел текучести, материал
может оставаться некоторое непродолжительное время в упругом
состоянии. Под статическим пределом текучести здесь мы пони-
понимаем условную величину, измеряемую в обычных опытах на
стандартном оборудовании. Непродолжительное время нужно
понимать в том смысле, что эффект запаздывания заметен при
временах порядка микро- и миллисекунд, т. е. главным образом
в волновых процессах. Объяснение механивма этого явления,
относящееся к области физики металлов, дается различно раз-
разными авторами. Точка зрения Котрелла, которая до недавнего
времени была почти общепризнанной, состоит в том, что в угле-
углеродистой стали дислокации блокируются растворенными атомами
углерода. Под действием напряжения и при наличии тепловых
флуктуации дислокация постепенно высвобождается из облака
растворенных атомов, а освободившись, сразу продвигается на
большое расстояние, что означает большую пластическую дефор-
деформацию. Сравнительно недавно была выдвинута альтернативная
точка зрения, объясняющая пластическую деформацию после
задержки размножением дислокаций. Оставляя в стороне дисло-
дислокационный язык, заметим, что для материала постулируется
определяющее уравнение того же типа, что уравнение, которое
применяется для описания ползучести металлов при высоких
температурах (см. § 18.4 уравнение A8.4.1)). Соответствующим
выбором входящей в это уравнение функции можно добиться
удовлетворительного качественного объяснения наблюдаемых
явлений, связанных с запаздыванием текучести. Не вставая на
какую-либо из этих точек зрения, мы примем в качестве основ-
основного условия наступления текучести следующее условие Кот-
Котрелла — Екобори:
т
j<p(a)<tt = l. A6.12.1)
о
Здесь т — время запаздывания текучести при заданной программе
нагружения o(t). Пока величина интеграла в соотношении
A6.12.1) меньше единицы, материал остается упругим, при до-
достижении равенства A6.12.1) он переходит в пластическое со-
состояние. Вопрос о том, как происходит этот переход, будет
затронут ниже. В качестве функции ф обычно применяют сте-
степенную функцию
ife)n <16Л2-2>
В этой формуле, конечно, фигурируют две независимые постоян-
постоянные, а не три, но нам удобно зафиксировать, например, харак-
характерное время т* и определять из опыта напряжение от* и по-
показатель степени п. Заметим, что показатель п довольно велик,
он достигает значений от 10 до 20.
572 гл- 16- упругопластическое упрочняющееся тело
Рассмотрим два примера применения условия A6.12.1).
1. Задержка текучести при постоянном напряжении а. Ин-
Интегрируя A6.12.1), получим
2. Верхний предел текучести при растяжении с постоянной
скоростью. При растяжении с постоянной скоростью может быть
достигнуто в упругом состоянии напряжение о', зависящее от
скорости нагружения и называемое верхним пределом текучести.
Полагая о = st и интегрируя, представим результат в следующем
виде:
a =
г Wn
Здесь т — продолжительность растяжения. Заметим, что постоян-
постоянное напряжение, при котором материал остается упругим в те-
течение времени т, и максимальное
напряжение, достигаемое за вре-
время т при нагружении с постоян-
постоянной скоростью, отличаются только
множителем (гг+1I/п. При боль-
больших п этот множитель довольно
близок к единице. Так, при п =
= 15 161/15» 1,203. Эта разница
совсем незначительна. Типичная
диаграмма растяжения малоугле-
малоуглеродистой стали показана на
рис. 16.12.3. Высота «зуба теку-
Рис. 16.12.3 чести» есть о'; после срыва диа-
диаграммы с зуба, в связи с ис-
исчерпанием способности к запаздыванию появляется так называе-
называемая площадка текучести. Легко определяемая ордината этой
площадки называется нижним пределом текучести; в некоторых
руководствах можно встретить утверждения о том, что этот ниж-
нижний предел текучести представляет собою реальную физическую
характеристику материала, тогда как верхний предел зависит от
условий эксперимента. В действительности верхний предел о'
определяется из физически реального условия A6.12.1), тогда
как нижний предел действительно зависит от условий экспери-
эксперимента. Горизонтальная площадка текучести вовсе не принадлежит
диаграмме материала, она обязана своим появлением тому факту,
что при растяжении длинного образца пластическая деформация
возникает вблизи одного из концов и распространяется фронтом
до тех пор, пока не охватит весь образец.
Итак, в общем случае дело нужно представлять себе следую-
следующим образом. Материал упруго нагружается до напряжения о',
§ 16.12. ЗАПАЗДЫВАНИЕ ТЕКУЧЕСТИ
573
которое тем выше, чем больше скорость. При выполнении усло-
условия A6.12.1) он мгновенно переходит в пластическое состояние,
соответствующее некоторой точке N на диаграмме деформирова-
деформирования (рис. 16.12.4). Учитывая сказанное в § 16.11, мы принимаем
за эту диаграмму мгновенную или динамическую диаграмму.
Положение точки N и путь перехода определяются целиком ус-
условиями эксперимента.
t
A
Рис. 16.12.4
Рис. 16.12.5
Теперь мы можем выяснить особенности распространения
упругопластических волн в стержнях, материал которых обла-
обладает свойством запаздывания текучести. Приложим к концу по-
полубесконечного стержня напряжение o(t) или сообщим ему ско-
скорость V(t), что одно и то же. В течение времени т, определяе-
определяемого из уравнения A6.12.1), от конца стержня будут распро-
распространяться только упругие волны, переносящие заданное на
конце изменение напряжения вдоль стержня. В каждом сечении
условие A6.12.1) будет выполняться при одном и том же зна-
значении t, поэтому упругое состояние в координатах #, t будет
соответствовать точкам полосы на рис. 16.12.5. Верхняя граница
полосы представляет собою фронт разгрузки из упругого состоя-
состояния в пластическое. Этот фронт движется со скоростью упругой
волны, следовательно, разгрузка может происходить только по
закону Гука. Действительно, в § 2.10 было показано, что раз-
разрывы напряжений и скоростей на фронте, движущемся со ско-
скоростью с, связаны условием
[о] = [v]pc.
С другой стороны, разрыв скорости и разрыв деформации свя-
связаны очевидным кинематическим соотношением
М = Ис
574 гл- 16- упругопластическое упрочняющееся тело
Исключая из этих двух условий [v], находим
Этим и доказывается, что при распространении волны от точки
М происходит упругая разгрузка в точку Р. Дальше все проис-
происходит так же, как и без запаздывания. Образуется область
постоянных значений rpq, а далее идут пластические волны, со-
соответствующие динамической диаграмме.
Явление упругой разгрузки после прохождения волны упру-
упругого перенапряжения, как можно назвать упругое состояние с
напряжением, превышающим предел текучести от, было обна-
обнаружено экспериментально.
ГЛАВА J7
НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
§ 17.1. Линейная наследственность
Принцип наследственности, сформулированный Больцманом
и получивший значительное математическое развитие в работах
Вольтерра, состоит в следующем. Предположим, что некоторый
физический или механический процесс определяется воздействи-
воздействием, т. е. заданием некоторой функции у(т), т^(—°°, t]. Реак-
Реакция рассматриваемого тела или системы определяется некоторой
функцией u(t). В общем случае величина функции u(t) в на-
настоящий момент времени t определяется не только значением
воздействия в данный момент t, но всей историей изменения
функции и в указанном выше промежутке времени. Говорят,
что и есть функционал от г; и записывают его символически
следующим образом:
и= Т (и). A7.1.1)
— оо
Функционал ЗГ называется линейным, если
где с —константа. Связь между напряжениями и деформациями
в тердом теле не обязательно должна иметь характер упругой
связи или вид соотношений теории пластичности. Закон связи
вида A7.1.1) определяет то, что называется вязкоу пру гостью
или вязкопластичностъю; при специальном выборе линейного
функционала ?Г можно получить уравнения так называемой ли-
линейной вязкоупругости. Термин «вязкоупругюсть» обязан своим
происхождением тому обстоятельству, что при некоторых част-
частных предположениях относительно вида функционала соотноше-
соотношение A7.1.1) можно записать в виде дифференциального соотно-
соотношения, связывающего линейным образом производные различных
порядков от и и v по времени. Линейная связь между а и е
есть закон Гука, линейная связь между а и е есть закон вязко-
вязкости Ньютона. Получающееся линейное соотоношение между про-
производными от а и от е в известном смысле обобщает эти про-
простейшие модели; поэтому тело, описываемое с помощью этого
соотношения, называют вязкоупругим.
В последнее время этот термин получил распространение в
применении к телам, поведение которых не может быть описана
576 ГЛ- 17- НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
при помощи дифференциальных уравнений конечного порядка.
Мы предпочитаем в данном случае принадлежащий Вольтерра
термин «наследственная упругость», как более точно и более
образно передающий существо дела. Однако в этом параграфе
и в ближайших следующих собственно наследственная теория
упругости излагаться не будет, мы рассмотрим общие формы
наследственных зависимостей между любыми физическими вели-
величинами.
Достаточно общее выражение линейного функционала A7.1.1)
будет следующее:
и (t) - и (t) + К ] К (*, т) v (т) dx. A7.1.2)
— ОО
Функция K(t, х) называется ядром наследственности. Параметр л
может быть принят равным единице, однако в дальнейшем нам
будет удобно сравнивать зависимости типа A7.1.2) с одинако-
одинаковыми ядрами К при различных X. Ядро наследственности харак-
характеризует степень «забывания» к моменту времени t о тех воз-
воздействиях, которые были совершены в момент времени т. Поэто-
Поэтому, если свойства материала со временем не меняются, то есте-
естественно предположить, что мера «памяти» и «забывания» зависит
от разности t — т. Это интуитивно очевидное предположение было
сформулировано Вольтерра в виде условия замкнутого цикла,
которое состоит в следующем.
Если v(t)—периодическая функция, то необходимое и до-
достаточное условие того, чтобы и u{t) была также периодической,
состоит в том, что ядро К зависит от разности t — т
K(t,x) = K(t-x). A7.1.3)
Предположим, что v(t) —периодическая функция с периодом со:
)= v(t).
Внесем в A7.1.2), заменив в этом уравнении t на ?+со. По-
Получим
и (t + со) = v {t + со) + A, J К (t + со, т) и (т) dx.
Заменим теперь переменную интегрирования т на т + со, получим
t
и (t + со) = v (t + со) + A, j К (t + со, т + со) и (т + со) dx.
— оо
Учитывая периодичность v (t), найдем, что последнее уравнение
совпадает с A7.1.2) в том и только в том случае, когда
со, т + со) = #(?, т).
§ 17.1. ЛИНЕЙНАЯ НАСЛЕДСТВЕННОСТЬ 577
Дифференцируя по параметру со и полагая со = 0, получим
дК . дК п
Общий интеграл этого уравнения в частных производных
первого порядка есть произвольная функция от разности t — т;
этим и доказывается равенство A7.1.3).
В уравнении A7.1.2) нижний предел интегрирования принят
равным —°°. В действительности, всякая история начинается
с некоторого конечного момента времени — времени создания
материала или изготовления изделия, или первого нагружения.
Поэтому мы будем записывать интегральное соотношение A7.1.2)
с разностным ядром следующим образом:
t
u = v + xlK(t-T)v{x)dx. A7.1.4)
о
Представим A7.1.1) следующим образом:
о t
и = и+ j К (t — т) v (т) dx + \ К {t — т) v (т) dx.
-эо О
Применим к первому интегралу теорему о среднем. Получим
о о
\ K(t — %)v(%)dx = v(t1) J K{t-x)dx, гге(—Т,0).
-г -г
Если интеграл
-г
стремится к нулю при неограниченном возрастании Г, t, то ядро
удовлетворяет условию затухающей памяти, и замена нижнего
предела, равного — °°, на значение его, равное нулю, позволяет
применять уравнения A7.1.4) вместо A7.1.1). Заметим, что при
этом нижний предел был взят конечным, равным —Т. Таким
образом, принцип затухающей памяти утверждает не столько
возможность замены нижнего предела — °° нулем, сколько не-
несущественность выбора начального момента отсчета времени т =
= 0. Очевидно, что при периодической функции v(t) функция
u(t) не будет периодической, но отклонение от периодичности
или апериодический добавок к функции u(t) стремится к нулю
с возрастанием t.
Вместо полной записи A7.1.4) мы будем пользоваться сокра-
сокращенной записью
A7.1.5)
Умножение на оператор К* означает вычисление фигурирующего
37 ю. Н. Работнов
578 гл- 17- наследственная теория упругости
в A7.1.4) интеграла. Для операторов К* можно ввести опера-
операцию умножения следующим образом. Произведением двух опе-
операторов L*M* называется оператор, ядро которого определяется
формулой
J L(t — s)M(s — x) ds.
Делая простую замену переменных, убеждаемся, что умножение
операторов коммутативно:
Очевидно, что таким же способом можно определить умножение
неразностных операторов, но в этом случае умножение не ком-
коммутативно. В приложениях для так называемых стареющих ма-
материалов вводятся и неразностные ядра. Некоммутативность
умножения сильно осложняет в этом случае решение конкретных
задач.
На уравнение A7.1.5) можно смотреть как на интегральное
уравнение Вольтерра второго рода, определяющее функцию v(t)
при заданной u(t). Как известно, решение интегрального урав-
уравнения записывается так:
1>=-A-ЛГ*(А,))и. A7.1.6)
Здесь Г* (X) — резольвентный оператор, ядро которого определя-
определяется рядом Неймана. Этот ряд можно получить чисто формаль-
формально. Решая A7.1.5) относительно v так, как если бы это было
алгебраическое уравнение, и сравнивая с A7.1.6), получим
__!_- = l._a,r*(A,). A7.1.7)
Если бы в левой части вместо %К* стояло число, меньшее еди-
единицы по модулю, мы могли бы разложить дробь в ряд, пред-
представляющий собою геометрическую прогрессию. Сделаем это с
операторной дробью, понимая возведение в степень оператора
так, как было определено умножение операторов. Получим
Г* = X* - ХК*2 + Х2Я*3 + ... A7.1.8)
Это операторное тождество вполне эквивалентно известному ря-
ряду Неймана для резольвенты. В теории интегральных уравнений
доказывается сходимость ряда Неймана для любых ограниченных
ядер К. Здесь мы заметим, не приводя доказательства, что ряд
Неймана сходится, если итерированные ядра становятся ограни-
ограниченными, начиная с некоторого номера. В частности, если ядро
имеет особенность вида (t — т)"а, 0=^а<1, то ряд Неймана
сходится.
§ 17.2. РЕЗОЛЬВЕНТНЫЕ ОПЕРАТОРЫ 579
§ 17.2. Резольвентные операторы
В задачах наследственной теории упругости приходится вво-
вводить несколько операторов Вольтерра и выполнять некоторые
операции, состоящие в решении интегральных уравнений, ядра
которых представляют некоторые комбинации исходных ядер
и их резольвент. Правило умножения операторов и соотноше-
соотношения A7.1.7) позволяют записать и выполнить промежуточные
операции преобразований по правилам алгебры, однако заклю-
заключительный этап будет состоять в решении интегрального урав-
уравнения. Ряд Неймана при этом скорее указывает на принципиаль-
принципиальную возможность решения интегрального уравнения, чем слу-
служит эффективным средством для такого решения. На практике
положение облегчается тем фактом, что ядра наследственности,
характеризующие свойства материала, выбираются в результате
обработки опытных данных, а опытные данные лежат внутри
некоторой полосы разброса. Поэтому, как правило, оказывается
возможным искать операторы наследственности внутри некото-
некоторого класса, достаточно широкого для удовлетворительного вос-
воспроизведения опытных данных, с одной стороны^ допускающего
явное выполнение обращения A7.1.7), с другой. Выберем неко-
некоторый оператор /?*, который будем называть порождающим опе-
оператором. Тогда оператор Г*(^) будем называть резольвентным
оператором, порождаемым оператором К*. Из A7.1.7) следует
такое явное выражение для резольвентного оператора Г*(Я):
Рассмотрим теперь следующее интегральное уравнение:
u = (l + \iT*(X))v. A7.2.2)
Находя отсюда по правилам обычной алгебры функцию v, по-
получим
A7.2.3)
Мы убедились, что если ядро принадлежит к резольвентному
типу, то его резольвента будет опять-таки резольвентным ядром,
порождаемым также оператором Z*, но при другом значении
параметра. Операторное тождество
можно переписать, полагая Х = х, А, + ц = г/, в следующем виде:
Г* (х) Г* (у) = ^-м [Г* (х) - Г* (у)]. A7.2.4)
Соотношение A7.2.4) выражает теорему об умножении резоль-
резольвентных операторов. При х = у путем предельного перехода
37*
580 гл- 17- наследственная теория упругости
получаем
дТ*
дх
Продолжая этот процесс, найдем выражение для любой степени
резольвентного оператора Г*()
г* "ог^яЬ^- A7-2-5)
Таким образом, формула A7.2.4) указывает на то, что система
резольвентных операторов, порождаемых любым оператором Ку
образует поле, причем операция возведения в степень недопу-
недопустима в том смысле, что результат ее выводит за пределы поля.
Для наследственной теории упругости особое значение имеют
резольвентные ядра, порождаемые ядром Абеля:
, , -1<ос<0.
Ядро Абеля, очевидно, удовлетворяет условию затухающей па-
памяти. В определении A7.2.6) величина ГA + а) представляет
собою гамма-функцию указанного аргумента. Напомним ее опре-
определение и основные свойства
х
Г (х) = J s*-ie~*ds, Г A + х) = хТ (х), Г A) = 1.
о
Через гамма-функции выражается так называемый интеграл Эй-
Эйлера или бета-функция
В (р, q) = jVi A -уу-Чг =
о
Используя эту формулу, мы легко получим следующее правило
умножения операторов Абеля:
Для этого нужно воспользоваться общим определением умноже-
умножения операторов, которое было дано в § 17.1, и ввести новую
переменную интегрирования z = (s — r)/(t — т). Отсюда следует,
в частности, правило возведения оператора Абеля в произволь-
произвольную степень
la = An-i+mcc A7.2.7)
1 т*771
Если а<0 и тп>-. , , то индекс оператора /а становится по-
положительным и особенность исчезает.
§ 17.2. РЕЗОЛЬВЕНТНЫЕ ОПЕРАТОРЫ 581
Построим класс резольвентных операторов, порождаемых опе-
оператором Абеля. Будем называть их дробно-экспоненциальными
операторами Эа(Р) и определять следующим образом:
_* = 1 + рэ:(Р). A7.2.8)
* 7
Разлагая в ряд фигурирующую в левой части равенства дробь,
мы получим выражение для Эаф) в виде ряда A7.1.8), на этот
раз знакопостоянного. С учетом A7.2.7) мы можем написать
явное выражение для ядра оператора Эаф):
Эа ф, t) - t ^
При а < 0 и при малых t первый член ряда оказывается пре-
преобладающим, поэтому
Этот член определяет главную часть особенности. При р > 0 чле-
члены ряда, соответствующие положительным степеням t, неогра-
неограниченно растут вместе с ?, поэтому
Таким образом, при р>0 дробно-экспоненциальное ядро не
удовлетворяет условию затухающей памяти. Вопрос о поведе-
поведении Э-функции при [}<,0 будет рассмотрен позже; здесь эле-
элементарные соображения уже недостаточны.
Заметим, что при а = 0 /а = 1, Э0(Р, f) = exp ^f. Хорошо из-
известно, что если ядром интегрального уравнения служит экспо-
экспоненциальная функция, то резольвента будет также экспоненци-
экспоненциальной функцией. Теорема умножения A7.2.4) легко проверяется
непосредственно, так же, как формула A7.2.5).
Дробно-экспоненциальные функции и интегралы от них про-
табулированы, эти таблицы описаны и частично приведены в
книге Работнова A977). Следует заметить, что дробно-экспонен-
дробно-экспоненциальные функции оказались чрезвычайно удобными для описа-
описания линейной наследственности в горных породах, полимерах и
армированных пластиках. Принимая ядро ползучести в виде од-
одной дробно-экспоненциальной функции
удается, как правило, достаточно хорошо описать данные по
ползучести, возврату и релаксации. Показатель а при этом обыч-
обычно оказывается близким к —0,7, хотя это не может служить
общим правилом.
532 ГЛ. 17. НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
§ 17.3. Применение преобразования Лапласа
Напомним, что изображением по Лапласу функции f(t) на-
называется функция / (р) параметра р, определенная следующим
образом:
оо
l A7.3.1)
Параметр р может принимать любые комплексные значения. За-
Заметим, что для определения f (р) необходимо знать функцию f(t)
только для положительных значений аргумента, для отрицатель-
отрицательных значений ее можно доопределить произвольным образом,
например, положив /@ = 0 ПРИ * < 0. Функция, тождественно
равная нулю при отрицательных значениях аргумента, назы-
называется функцией, принадлежащей к классу Хевисайда.
Зная изображение f(p), можно восстановить оригинал или
функцию f(t) по формуле Меллина
a+ioo
A7.3.2)
a—ioo
Здесь прямая Rep = a выбирается таким образом, чтобы все осо-
особые точки функции f(p) располагались слева от этой прямой.
Для отрицательных значений t интеграл A7.3.2) равен нулю,
поэтому формула Меллина автоматически дает функцию, при-
принадлежащую к классу Хевисайда. Мы не приводим здесь необ-
необходимых условий для того, чтобы преобразование Лапласа
A7.3.1) существовало, и для того, чтобы функция / (р) служила
изображением некоторой функции /(?). Эти условия выполняют-
выполняются для всех тех случаев, с которыми нам придется иметь дело.
Напомним теорему о свертке. Если
то
7(р) = ё(р)Щр). A7.3.3)
Отсюда легко получаются известные формулы преобразования
Лапласа от интеграла и, следовательно, от производной, если
h{p)
Применяя преобразование Лапласа к интегральному уравнению
A7.1.4) и используя теорему о свертке, получим
§ 17.3. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 583
Точно так же, вычисляя интеграл Лапласа от равенства A7.1.6),
найдем _
Отсюда следует
1_ХГ=—L=r. A7.3.4)
1 + КК v
Соотношение A7.3.4) совершенно сходно по форме с A7.1.7), но,
в отличие от него, представляет собою не символическое, а обыч-
обычное алгебраическое равенство. В задачах наследственной теории
упругости ряд авторов применяет технику преобразования Лап-
Лапласа, здесь мы будем следовать другой системе изложения,
а именно, примем за основу изложенную в § 17.2 теорию ре-
резольвентных операторов. Однако преобразование Лапласа нам
понадобится для выяснения асимптотических свойств введенных
выше дробно-экспоненциальных функций. Вычислим сначала
преобразования Лапласа функции /а. Вспоминая определение
гамма-функции, находим
Принимая в формуле A7.3.4) К = — р/а, Г = — ?Эа, находим
Э(РР) A7
Подставляя в формулу Меллина, приходим к следующему ин-
интегральному представлению для функции Э«(Р, t):
a+ioo
j
a-ioo F H
Для того чтобы получить интегральное представление для ин-
интеграла от Эа-функции или для произведения Эа-1, нужно раз-
разделить подынтегральное выражение на р. Получим
a+ioo
э:(Р)-1=^ J ,
Известно (см. Дёч), что асимптотическое поведение интеграла
Меллина, определяемого формулой A7.3.2), описывается следу-
следующим образом. Пусть функция f(p) имеет простые полюсы с
неотрицательной действительной частью и р0 — тот полюс, у ко-
которого действительная часть наибольшая. Следовательно, в ок-
окрестности полюса р0 функция f(p) может быть представлена
584 rJL 17- наследственная теория упругости
следующим образом:
Тогда при больших значениях t главный член в асимптотиче-
асимптотическом разложении функции f(t) будет
Если действительные части полюсов отрицательны, функция f(t)
стремится к нулю при t ->¦ <*>, если полюс с наибольшей дейст-
действительной частью находится в начале координат, функция f(t)
стремится к постоянному значению, равному А. Если функция
f(p) неоднозначна, то рассматривается та ветвь функции, кото-
которая однозначна в плоскости, разрезанной вдоль отрицательной
1
полуоси. При р > 0 из формулы [17.3.5) следует, что р0 = Р 1+а
поэтому
Эа(Р, *)~
Мы убедились еще раз в том, что дробно-экспоненциальная функ-
функция при р > 0 неограниченно возрастает с увеличением t. Более
того, теперь мы знаем, что эта функция растет как обычная
экспонента.
При р<0 положим р = |р|в'я, pQ = rei(p. Вследствие того, что
рассматривается полуплоскость с выброшенной отрицательной
полуосью —п < ф < я. Подставляя в уравнение р\ — Р = О,
находим
При а<0 найденное значение ф больше, чем я, поэтому рас-
рассматриваемая ветвь функции полюсов не имеет и Эа(р, t)->-0
при р<0 и ^->оо. Что касается изображения функции Эа(Р)«1,
оно имеет единственный полюс р=0, вычет для этого полюса
А =— 1/р, поэтому
Э*(Р)-1^— -1- (Р<0,*->оо). A7.3.8)
Установленные свойства элементарно проверяются для обычных
экспоненциальных функций.
§ 17.4. Функции от операторов
Формула A7.1.8) определяет некоторую функцию от опера-
оператора К*, заданную в виде ряда. Этот ряд был получен в ре-
результате разложения левой части соотношения A7.1.7). Анало-
Аналогичным образом может быть определена произвольная функция
§ 17.4. ФУНКЦИИ ОТ ОПЕРАТОРОВ 585
от оператора. Пусть f(x) есть произвольная функция комплекс-
комплексной переменной х, аналитическая в окрестности точки х = 0.
Представим ее в виде ряда
По определению этот ряд имеет отличный от нуля радиус схо-
сходимости г. Функция f{K*) оператора Вольтерра определяется
следующим образом:
/ {К*) = / @) + /' @) Я* + -|- Г @) Я*2 + ... A7.4.1)
Вольтерра доказал следующую теорему. Если степенной ряд име-
имеет отличный от нуля радиус сходимости, то операторный ряд,
получающийся из него заменой переменной оператором с огра-
ограниченным ядром К*, сходится всюду. Операторный ряд мы будем
называть сходящимся, если ряд для его ядра сходится абсолют-
абсолютно. Мы не будем здесь приводить доказательство этой теоремы,
которое можно найти, например, в книге Работнова [11]. Заме-
Заметим, что условие ограниченности ядра можно заменить условием
ограниченности его итераций, начиная с некоторого номера.
Поэтому теорема справедлива для слабо сингулярных ядер типа
дробно-экспоненциальных. Будем называть ограниченными такие
операторы, которые удовлетворяют условию
(К*-1)г-„=К„?>оо. A7.4.2)
Таким образом, у ограниченного оператора ограничено не только
ядро, но и интеграл от ядра. Предельное соотношение A7.3.8)
указывает на то, что Э-операторы при отрицательных р ограни-
ограничены, но оператор Абеля, соответствующий случаю, когда (J = 0,
не ограничен. Приведем опять-таки без доказательств со ссылкой
на книгу Работнова [11] следующие теоремы, относящиеся к пре-
предельным значениям комбинаций из операторов.
1. Если операторы L* и М* ограничены и iV* = L*ilf*, то
iVoo^JI/oo. A7.4.3)
2. Если функция g(t)^G такова, что при любом выборе по-
положительной величины т) существуют такое число #«, и такое
значение t = ttf что для t>t^
ТО
(K*g)m=K»g». A7.4.4)
3. Произведение оператора К* в степени п на единицу стре-
стремится при t ->¦ оо к величине произведения 7?* на единицу
586 ГЛ- 17- НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
в степени п:
A7.4.5)
Умножая оператор, определенный рядом A7.4.1), на функ-
функцию g(t)^G, получим как результат применения предыдущих
теорем следующую.
4. Произведение аналитической функции /(#*) от ограничен-
ограниченного оператора Волътерра на функцию g^G стремится при не-
ограниченном возрастании t к величине функции f от произве-
произведения Koogoo
Гоо). A7.4.6)
Очевидно, что этот ряд имеет тот же радиус сходимости, что
и исходный ряд для функции /(#). В частности, из формулы
A7.4.6) следует, что из интегрального уравнения A7.1.5) при
условии, что u<^G, вытекает такая величина предельного зна-
значения переменной v:
Формула A7.4.7) составляет содержание известной теоремы Пэ-
ли — Винера, она становится неприменимой при \ХКОО\=1.
§ 17.5. Линейное наследственно-упругое тело.
Реологические модели
При одноосном напряженном состоянии, например при про-
простом растяжении, основное определяющее соотношение наслед-
наследственной теории упругости мы будем записывать следующим
образом:
± . A7.5.1)
Разрешая относительно напряжения, получим
а = ЯA-Г*)е. A7.5.2)
Здесь Г* — резольвента ядра К* или, наоборот, К* — резольвента
ядра Г*. Будем называть ядро К* ядром ползучести, а Г* — яд-
ядром релаксации. Соответственно рассмотрим две возможные экс-
экспериментальные схемы.
а. Опыт на ползучесть. К телу прикладывается нагрузка, со-
соответствующая напряжению а. При мгновенном приложении на-
нагрузки возникает мгновенная деформация е0 = о/Е. Далее тело
деформируется во времени по закону
Соответствующий график представлен на рис. 17.5.1. Если опе-
оператор К* ограничен, то величина деформации не превосходит
§ 17.5. РЕОЛОГИЧЕСКИЕ МОДЕЛИ
587
некоторого верхнего предела
модуль упругости
Здесь /?«> — длительный
Обычный модуль Е следует называть теперь мгновенным моду-
модулем. Оператор ползучести не обязательно должен быть ограни-
ограниченным. Ползучесть многих ма-
материалов описывается ядром
Абеля К = Х1а. При этом вели-
величина деформации сверху ничем
не ограничена, но скорость де-
деформации все время убывает.
Существуют эксперименты по
ползучести пластиков, продол- &
жавшиеся 100 000 часов (около ч
12 лет). Зависимость e(t) на всем
протяжении испытания была сте-
степенной без какой-либо тенденции
к выходу на горизонтальную
асимптоту. Если в момент времени t = Т произведена разгрузка,
то немедленно возвращается мгновенная упругая деформация е0,
накопленная же деформация ползучести убывает постепенно.
Для любого момента t>T уравнение A7.5.1) дает
т
Рис. 17.5.1
Если ядро удовлетворяет условию затухающей памяти, то при
t ->• оо е ->¦ 0, значит происходит полный возврат.
б. Отгыт на релаксацию. Растянем быстро образец напряже-
напряжением а0 и зафиксируем его деформацию е = о0/Е. При постоян-
постоянной деформации
а = аоA_Г*.1).
Из теоремы 4 предыдущего парагра-
параграфа следует, что Ее
= ^A-Г.). A7.5.3)
Процесс релаксации состоит в том,
что напряжение, которое было рав- Рис- 17.5.2
но в начальный момент Ее, постепенно убывает до ве-
величины Е„>е. Если ядро ползучести неограниченно, то, как сле-
следует из A7.5.3), Есо = 0 и напряжение в процессе релаксации
стремится к нулю. Примерная кривая релаксации представлена
на рис. 17.5.2. Заметим, что технически осуществить совершенно
чистый опыт на релаксацию невозможно. Для полимерных мате^
588 гл- 17- наследственная теория упругости
риалов обычно последовательно с образцом включается доста-
достаточно жесткий силоизмеритель. При релаксации напряжения в
образце меняется деформация силоизмерителя, по ней судят о
величине напряжения. Но вследствие деформации силоизмерите-
силоизмерителя и деформация образца не остается постоянной, таким образом,
в этой схеме можно приближаться к условиям чистой релакса-
релаксации, но нельзя выполнить эти условия вполне точно. Другая
система испытаний состоит в том, что установленный на образце
тензометр управляет механизмом, изменяющим нагрузку. По-
Поскольку всякий тензометр имеет определенный порог чувстви-
чувствительности, испытание на релаксацию по существу заменяется
испытанием на ступенчатую ползучесть, в конце каждой ступе-
ступени деформация образца восстанавливается до первоначального
значения. Можно уменьшить величину этих ступеней, но нельзя
их совершенно уничтожить.
Соотношения A7.5.1) и A7.5.2) часто записывают в несколь-
несколько иной форме.
Определим оператор ползучести
4 A7-5.4)
и оператор релаксации
G* = Е(Г0- Т*1*о). A7.5.5)
Здесь /0 — оператор обычного интегрирования, ядра операторов
К*10 и Г*/о соответственно — это проинтегрированные один
раз ядра К и Г. Теперь закон наследственной упругости может
быть записан следующим образом:
е = /*а, c = G*e. A7.5.6)
Ядро оператора /* называется функцией ползучести, ядро опера-
оператора G* — функцией релаксации. Они непосредственно опреде-
определяются из опытов на ползучесть и релаксацию, тогда как для
нахождения функций K(t) и Г (it) соответствующие кривые бы-
бывает необходимо дифференцировать. В современной литературе
соотношения A7.5.6) часто записывают в виде так называемых
сверток Стилтъеса, а именно,
— т) dor(t), or = G*de = JG(* — %)de (т).
о
A7.5.7)
Здесь интегралы понимаются в смысле Стилтьеса, что позволяет
рассматривать непосредственно, не делая предельных переходов,
§ 17.5. РЕОЛОГИЧЕСКИЕ МОДЕЛИ
те случаи, когда нагрузка прикладывается или деформация про-
производится мгновенно.
Свойства наследственно-упругого тела, обнаруживаемые при
испытаниях на ползучесть или релаксацию и проиллюстриро-
проиллюстрированные графиками на рис. 17.5.1 и 17.5.2, легко воспроизвести на
модели, изображенной на рис. 1.10.2. Если обозначить через е
перемещение, на котором производит работу сила а, то, как со-
совершенно очевидно, при мгновенном приложении нагрузки сна-
сначала растянется только пружина 1; жесткость пружины, или
модуль Еи представляет собою мгновенный модуль. По истече-
истечении достаточно большого времени система приблизится к состо-
состоянию равновесия, когда скорость, а следовательно, и сопротив-
сопротивление движению поршня в цилиндре с вязкой жидкостью стано-
становятся равными нулю. В предельном состоянии податливости
пружин складывается, следовательно, длительный модуль опре-
определяется следующим образом: Е~^ = Е^1 + Е^1. Обозначая через
т] коэффициент вязкости, который определяет силу сопротивле-
сопротивления движению поршня а' в зависимости от скорости по формуле
а' = цё и вводя обозначения
мы получим дифференциальное уравнение движения системы
в следующем виде:
о + Хо = Е(е + \хе). A7.5.8)
При большой скорости нагружения отсюда следует о = Ее или
о = Ее для мгновенной деформации. В предельном состоянии
покоя а =4г Ее = Е^е, отсюда Е** = E\i/X. Поскольку Е^ < Е,
должно быть \х < К, что видно и из формул, определяющих эти
величины. Если теперь отвлечься от изображенной на рис. 1.10.2
модели, скомбинированной из пружин и вязкого сопротивления,
мы можем принять дифференциальное соотношение A7.5.8) за
определяющее уравнение для некоторого материала. Этот модель-
модельный материал сейчас принято называть стандартным вязкоупру-
гим телом. Уравнение A7.5.8), как мы видели, качественно пра-
правильно описывает поведение реальных материалов в условиях
ползучести или релаксации. Однако для количественного описа-
описания свойств каких бы то ни было реальных твердых тел, как
выяснилось, модель стандартного вязкоупругого тела непригодна.
Реология, наука о течении разного рода тел (от греческого
рео— теку), широко пользуется обобщениями рассмотренной
простейшей модели, которые вводят в рассмотрение производные
более высоких порядков. Общее уравнение типа A7.5.8) будет
590 ГЛ. 17. НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
иметь следующий вид:
P(°) = Q(e). A7.5.9J,
Здесь Р(о) — линейная функция от а и производных о до по-
порядка п включительно с постоянными коэффициентами, Q(e) —
такая же функция от деформации е. К соотношению вида
A7.5.9) можно прийти, если рассмотреть модель, составленную
из большого числа пружин и вязких сопротивлений, соединенных
в разных комбинациях последовательно и параллельно. Конечно,
было бы достаточно наивно искать в структуре материала соот-
соответствующие упругие и вязкие элементы, однако способ, осно-
основанный на построении реологических моделей, обладает некото-
некоторым преимуществом. Мы убедились, что в уравнении A7.5.8)
должно быть \х < А,, при этом не было необходимости в обраще-
обращении к модели, условие 2?«> < Е, из которого следует первое не-
неравенство, означает только то, что приложенная сила совершает
положительную работу, расходуемую на накопление энергии де-
деформации, а частично рассеиваемую в виде тепла. В общем слу-
случае A7.5.9) тоже должны быть выполнены некоторые неравен-
неравенства, которые могут быть не столь очевидны. Но если построена
эквивалентная реологическая модель из стержней, накапливаю-
накапливающих энергию, и вязких сопротивлений, рассеивающих ее, то у нас
есть полная уверенность в том, что для соответствующего мо-
модельного тела законы термодинамики будут выполняться. Второе
преимущество модельных представлений состоит в том, что для
любой заданной конфигурации системы может быть вычислена
внутренняя энергия, представляющая собою энергию упругих
пружин, и скорость необратимой диссипации энергии вязкими
элементами. Имея в распоряжении закон наследственной упру-
упругости A7.5.1), A7.5.2), мы можем подсчитать полную работу
деформирования, но не можем отделить накопленную энергию
от рассеянной. Поэтому, например, Блонд целиком строит изло-
изложение теории на модельных представлениях.
§ 17.6. Экспоненциальные операторы
Несмотря на то, что уравнение стандартного вязко-упругого
тела может быть применено к описанию свойств реальных тел
лишь с большой натяжкой, несколько более детальное изучение
этого уравнения все же может оказаться интересным. С другой
стороны, следует иметь в виду, что старые работы по вязко-
упругости C0-е — 40-е гг.) в значительной мере основывались
на модели стандартного тела. В более поздних работах оно так-
также применялось из-за простоты и возможности эффективного
решения некоторых задач, которые не удается довести до конца
при более сложных определяющих уравнениях. В § 17.2 мы вве-
ввели интегральный оператор /0, соответствующий обычному инте-
§ 17.6. ЭКСПОНЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
591
грированию и порождающий класс резольвентных операторов,
ядрами которых служат экспоненциальные функции. Умножим
обе части уравнения A7.5.8) на/0- Получим
Отсюда, применяя обычные алгебраические действия, найдем
а = я|\ + (и_Я)-Л—1 A7.6.1)
или, с учетом A7.2.8),
{-Ще. A7.6.2)
Наоборот, выражая деформацию е через напряжение а, найдем
в = -тг [1 + (^ — \i) Э* (— Н*)] ОТ»
Переход от A7.6.1) к A7.6.2) можно произвести по формуле
A7.2.3). Если один экспоненциальный член, фигурирующий в
уравнении A7.6.2), недостаточно хорошо воспроизводит опытные
данные, естественно попытаться добавить еще несколько экспо-
экспоненциальных членов и выбрать оператор ползучести следующим
образом:
** = S fc|9Z(-Pi). A7.6.3)
Если все [}« и кг положительны, то /?«, = 2 &i и ^°° < ?. Обраще-
Обращение этого оператора будет выражаться следующим образом:
Г* =2 ™,9*O(-YS). A7.6.4)
Величины ms и у8 можно найти следующим образом. Из соотно-
соотношения между оператором X* и резольвентным оператором Г*
A7.1.7) следует
*Г*
Подставляя сюда выражения A7.6.3) и A7.6.4) и принимая тео-
теорему умножения резольвентных операторов A7.2.4), получаем
следующую серию равенств:
(.7.6.5)
Отсюда следует, что ч* находятся как корни алгебраического
уравнения степени п, после чего т8 определяются из системы
линейных уравнений. Можно показать, что все f« действительны
и положительны.
592 гл-17- наследственная теория упругости
Не составляет груда убедиться в том, что интегральное урав-
уравнение с ядром A7.6.3) эквивалентно дифференциальному соот-
соотношению A7.5.9). Для этого интегральное уравнение A7.5.1)
дифференцируется п раз по времени t\ получившаяся система
из w + 1 уравнений содержит линейным образом е, о и их про-
производные до порядка п включительно, а также п различных ин-
интегралов вида Эо(—C) а. Исключая эти интегралы, мы прихо-
приходим к дифференциальному соотношению вида A7.5.9). Обратно,
для того чтобы перейти от дифференциального закона к инте-
интегральному представлению, можно использовать ту же процедуру,
которая была применена к стандартному вязкоупругому телу.
Нужно умножить соотношение A7.5.9) на/0 > тогда Р и Q об-
обратятся в полиномы степени п от оператора /0, частные двух
полиномов следует разложить на простые дроби, каждая из ко-
которых расшифровывается как экспоненциальный оператор. При
этом необходимо, чтобы корни каждого полинома были различ-
различны, действительны и в результате получалось к{ > 0 и [5* > 0.
Заметим, что эти достаточные условия положительности работы
не необходимы. Можно представить себе, что некоторые к{ отри-
отрицательны и некоторые корни $t комплексны. Появляющиеся в
последнем случае осциллирующие ядра в принципе допустимы,
хотя при представлении с помощью реологических моделей обыч-
обычного типа они появиться не могут. Но в принципе реологическая
модель может быть и динамической, она может включать в себя,
кроме упругих и вязких элементов, массы, могущие совершать
колебания. Для описания свойств реальных материалов модели
такого рода, насколько нам известно, не применялись.
§ 17.7. Наследственно-упругое тело
Для дальнейшего сокращения записи введем упругий опера-
оператор Е, представляющий собою сумму постоянного слагаемого и
оператора Вольтерра,
r^. A7.7.1)
Теперь уравнения A7.5.1) и A7.5.2) можно переписать в совсем
простом виде
Эта запись открывает совершенно естественный путь обобщения
уравнений закона Гука на наследственно-упругое тело. Примем
A7.7.2)
Здесь Я и jx — упругие операторы, построенные так же, как
§ 17.7. НАСЛВДСТВЕННО-УПРУГОЕ ТЕЛО 593
оператор Е, а именно,
Здесь Л* и М* — два, вообще говоря, различных оператора, опи-
описывающие наследственные свойства изотропной среды. Вместо
операторов Я и \i можно ввести «технические» операторы Е и v,
из них можно скомбинировать операторный модуль сдвига [х ^
= —. Расшифровка этого выражения проста, когда Е и v
содержат операторные части, принадлежащие к одному и тому
же классу резольвентных операторов.
Опытные данные показывают, что объемное последействие не-
незначительно и объемную деформацию можно считать упругой.
Поэтому операторный объемный модуль обращается в постоян-
постоянную. Записывая это уравнение
Е _ Е
l_2v l-2v>
найдем выражение для операторного коэффициента Пуассона
v^v + Ц-^Г*. A7.7.3)
Вычисляя операторный модуль сдвига для материала без объем-
объемного последействия, найдем
fW) {i7JA)
Обращение этой формулы, т. е. получение явного выражения
для оператора |Л, достаточно просто тогда, когда К* — резоль-
резольвентный оператор. В противном случае необходимо решать тем
или иным способом интегральное уравнение.
Для анизотропного тела вводятся тензор-операторы четвертого
ранга, заменяющие упругие константы в законе Гука. Соответ-
Соответственно закон наследственной упругости записывается в одной
из следующих форм:
A7.7.5)
или
* * * *
aij -Gabies, eij = Jijk^kh A7.7.6)
Связь между операторами G\ib\ и Jijkii с одной стороны, 2?<jW
и Щ7А, с другой, та же, что и связь, установленная формулами
A7.5.5), A7.5.6) для одномерного случая. Положим в операторе
Ет слагаемое, содержащее интегральный оператор, равным ну-
нулю, получим тензор мгновенных модулей Етг. С другой стороны,
38 ю. Н. Работнов
594 гл- 17- наследственная теория упругости
произведение ЕцМ • 1 при t ->• оо стремится к постоянному тензору
длительных модулей. Заметим, что тензоры мгновенных и дли-
длительных модулей необходимым образом симметричны, тогда как
симметрия операторных модулей, вообще говоря, не вытекает
яз каких-либо механических соображений. Это становится ясным,
если поставить в соответствие наследственно-упругому телу ди-
динамическую модель, содержащую вращающиеся массы. Гироско-
Гироскопические силы не связаны с перемещением симметричной мат-
матрицей. Однако в большинстве приложений симметрия матрицы
операторных модулей или податливостей постулируется, при
этом оказываются справедливыми некоторые теоремы взаимно-
взаимности и вариационные принципы. Если конструировать модели из
упругих и вязких элементов, эта симметрия получается необхо-
необходимым образом. Она следует также, если принять некоторые
принципы необратимой термодинамики, например принцип Он-
загера. Однако мы предпочитаем избегать подобного рода ар-
аргументов.
Единственное условие, которому должны удовлетворять тен-
тензоры наследственно-упругих операторов, состоит в том, что ра-
работа при произвольном пути деформирования должна быть
неотрицательна. Выразим напряжение через деформации по пер-
первой из формул A7.7.6). Функции Gm{t — т) определены только
для положительных значений аргумента, нам будет удобно до-
доопределить их для отрицательных значений следующим образом:
Теперь выражение для работы W может быть записано следую-
следующим образом:
t t
2W (t) = j J Gm (s - т) detj (s) dekl (т). A7.7.7)
о о
Представим функции Gijhi через их косинус-преобразования
Фурье
оо
Gw(s — т) = J- J G\m (со) cos со (s - т) dco.
о
Подставляя их в A7.7.7) и меняя порядок интегрирования, по-
получим
w = IT
О
Здесь Ац и Bij — функции времени, определяемые следующим
образом:
Ац —: J cos (os dey (s), B{j — J sin asdeu (s).
§ 17.8. ПЕРИОДИЧЕСКИЕ НАГРУЗКИ 595
В зависимости от программы нагружения величины Ац и В и мо-
могут принимать любые значения, поэтому необходимое и достаточ-
достаточное условие положительности работы состоит в знакоположи-
тельности, фигурирующей под интегралом квадратичной формы:
GWMw>0- A7-7.9)
Полученное неравенство составляет содержание теоремы Брейера
и Оната. В одномерном случае это неравенство приводится к
условию положительности косинус-преобразования Фурье функ-
функции релаксации, Gc > 0. Нетрудно показать, что это условие эк-
эквивалентно условию положительности синус-преобразования ядра
релаксации, Г8 > 0.
§ 17.8. Периодические нагрузки
Возвращаясь к одномерным задачам, рассмотрим поведение
наследственно-упругого тела под действием периодического воз-
возмущения, например периодического деформирования. Положим
е = е0 exp icot. A7.8.1)
Если принять в соотношении наследственности нижний предел
интеграла равным минус бесконечности, то вследствие условия
замкнутого цикла напряжение будет также периодической функ-
функцией времени. Поэтому здесь нам будет удобно выбирать нижний
предел именно так. Если интегрирование ведется не от — °°, а от
нуля, то выражение для а будет содержать апериодический до-
добавок, стремящийся к нулю по мере возрастания времени t.
Итак, положим
а = а0 exp [i (cot + ф) ]. A7.8.2)
Подставляя выражения а и в в закон наследственной упругости,
записанный, например, в виде A7.5.2), получим
аоехр [i ((ot + ф)] = Ее0 exp icot — J Г (t — т) exp imdx \.
Заменим переменную интегрирования, положив t — x = z1 и пред-
представим exp icox как сумму cos ©т + i sin ©т. Получим
а0 exp [i (tot + ф) ] = Ee0 exp iat A — Гс + iT8).
Здесь введены следующие обозначения:
оо оо
Гс = J Г (z) cos mdz, Ts = ] Г (z) sin coz dz.
о о
Эти величины отличаются от косинус- и синус-преобразований
Фурье только множителями.
38*
596 ГЛ- 17* НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
Определим теперь комплексный модуль упругости E' + iE",
зависящий от частоты со. Действительная и мнимая части комп-
комплексного модуля выражаются формулами
Е'=Е{1-ТС), Е"=ЕТ8. A7.8.3)
Теперь соотношение между напряжением и деформацией может
быть записано следующим образом:
o = (E' + iE")e. A7.8.4)
Очевидно, что уравнение A7.8.4) справедливо лишь тогда, когда
e(t) задано выражением A7.8.1) и от момента начала воздей-
воздействия прошло достаточно много времени, так что апериодический
добавок к выражению A7.8.2) для напряжения может считаться
пренебрежимо малым.
Уравнение A7.8.4) может быть переписано также следующим
образом:
во = еоУЕ'2 + Е = ео\Е\, tg<p = §1 = г^-. A7.8.5)
При выводе этих соотношений мы могли бы использовать закон
наследственности, записанный в форме A7.5.1). Повторяя бук-
буквально те же вычисления, мы получим
Е' = Е 1±ф—-, Е" =-- Е ^Ц г. A7.8.6)
Вычислим теперь работу, совершаемую напряжением A7.8.2) на
деформации A7.8.1). Переходя к действительным функциям, по-
положим, например, е = е0 sin со?, o = o0sin((o? + ф). Работа за вре-
время от t = 0 до настоящего момента t определяется следующим
образом:
А = J a de.
о
Проделав необходимые элементарные вычисления, которые мы
здесь не приводим, получим следующий результат. Работа будет
состоять из двух частей, первая часть — периодическая функция
от t, т. е. полностью обратимая работа упругих тел. Но вторая
часть оказывается пропорциональной времени t, следовательно,
это та часть работы, которая рассеивается необратимым образом,
превращаясь в тепло. Величина необратимой работы в единицу
времени называется мощностью диссипации D; выделяя из инте-
интеграла работы множитель при t, получим
D = -к- (оо0е0 sin ф.
§ 17.8. ПЕРИОДИЧЕСКИЕ НАГРУЗКИ 597
Отсюда с помощью A7.8.5) получаем
D = ± wjIK, = 4 EmlY&. A7.8.7)
Необходимое и достаточное условие положительности диссипации
состоит в том, чтобы синус-преобразование ядра ползучести К
или ядра релаксации Г было положительно. Но по теореме
Брейера — Оната, приведенной в § 17.7, выполнение этого усло-
условия обеспечивает положительность работы при любом виде де-
деформирования или нагружения; это есть единственное термоди-
термодинамическое ограничение, налагаемое на ядро наследственности.
С помощью комплексного модуля легко решаются задачи
о вынужденных колебаниях наследственно-упругих систем.
Пусть, например, колебания системы с одной степенью свободы
описываются уравнением
v + со* A — Г*) v = (o20 exp ipt. A7.8.8)
Будем искать его решение в виде v = aexp[i(pt + (p)]. Подстав-
Подставляя это выражение в A7.8.8), выполняя интегрирование при
помощи замены переменной t — r = z и сокращая множитель
exp ipt, получаем
а [— р2 + ©J A - Гс + iT&)] = со* exp (— fф).
Отделяя действительную часть от мнимой и вводя обозначения Е'
и Е" вместо Гс и Г, соответственно по формулам A7.8.3), по-
получаем
<17-8-8)
со2
Это решение не зависит от начальных условий, значит рассмат-
рассматриваются действительно установившиеся колебания, когда сла-
слагаемое в решении, соответствующее свободным колебаниям, за-
затухает практически до нуля. Для решения задачи о свободных
колебаниях необходимо исследовать строго интегро-дифферен-
циальное уравнение A7.8.8), что, в общем, затруднительно.
Решение этого уравнения можно представить как линейную ком-
комбинацию двух функций, которые играют роль синуса и косинуса,
но представляются довольно сложными двойными рядами. На-
Насколько нам известно, никто не пытался построить таким образом
фактическое решение, т. е. просуммировать и протабулировать
эти ряды. Однако некоторое суждение о характере затухания
свободных колебаний по истечении достаточно большого времени
от их начала, т. е. тогда, когда затухание уже практически не
зависит от того, каким образом были возбуждены колебания
вначале, можно получить, используя ту же технику. Положим
ГЛ. 17. НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
в уравнении A7.8.8) правую часть равной нулю и будем искать
решение однородного уравнения в виде v = exp ipt. Подставляя
в A7.8.8) и проделывая те же вычисления, что и в случае вы-
вынужденных колебаний, получим
- Р2 + со2о E'+EiE" = 0. A7.8.10)
Отсюда видно, что р есть комплексное число. Действительное
решение уравнения можно записать, например так:
v = e~~ht sin cat.
Отделяя в следующем из A7.8.10) выражении для р действи-
действительную и мнимую части, получаем
со
/\Е\+Ё' ,
1 2Е ' h==@*
Здесь величина \Е\ — абсолютная величина комплексного моду-
модуля— определяется первой из формул A7.8.5).
§ 17.9. Принцип Вольтерра
Уже в ранних работах Вольтерра было отмечено, что при ре-
решении задач наследственной теории упругости операции, связан-
связанные с решением дифференциальных уравнений, аналогичных
обычным уравнениям теории упругости, и операции интегриро-
интегрирования по времени, связанные с вычислением операторов Воль-
Вольтерра, могут выполняться в произвольном порядке. Отсюда
вытекает следующее правило, которое можно назвать принципом
Вольтерра.
Для решения задачи наследственной теории упругости нужно
построить решение задачи обычной теории упругости и в окон-
окончательном результате заменить упругие постоянные операторами,
расшифровав полученные комбинации операторов по известным
правилам.
Этот принцип применим при соблюдении определенных усло-
условий, которые будут выяснены далее, расшифровка операторных
комбинаций также требует некоторых пояснений.
В сороковые — пятидесятые годы, когда наследственная теория
упругости получила новое развитие в работах американских
авторов, для решения задач получил широкое распространение
метод, основанный на применении преобразования Лапласа. Для
этого метода был сформулирован принцип соответствия, который
по существу представляет собою простую перефразировку прин-
принципа Вольтерра. Применяя к основным соотношениям закона
наследственной теории упругости A7.7.2) преобразование Лап-
Лапласа, мы получим на основании теоремы о свертке следующие
§ 17.9. ПРИНЦИП ВОЛЬТЕРРА 599
уравнения:
о« =~Ш« + 2jxi«. A7.9.1)
Здесь черточки над буквами обозначают преобразования Лапласа
соответствующих функций. Уравнения A7.9.1) имеют форму
обычных уравнений закона Гука. Выполняя преобразования Лап-
Лапласа над уравнениями равновесия, соотношениями связи между
деформациями и перемещениями и граничными условиями, мы
получим для изображений систему уравнений, совпадающую
с системой уравнений теории упругости. Ее решение ничем не
отличается от решения задачи обычной теории упругости; изо-
изображения напряжений и перемещений оказываются выраженны-
выраженными явно через изображения заданных на границе усилий и пере-
перемещений и функций наследственности. Теперь последний этап
будет заключаться в том, чтобы перейти от изображений к ори-
оригиналам. Эта процедура буквально повторяет ту, которая предпи-
предписывается принципом Вольтерра, но в других терминах.
Необходимое ограничение применения принципа Вольтерра,
равно как и метода, основанного на преобразовании Лапласа,
состоит в следующем. В каждой точке поверхности тела должно
быть задано либо усилие, либо перемещение, либо какая-нибудь
комбинация этих величин, но тип граничных условий не должен
меняться. Так, например, принцип Вольтерра неприменим к за-
задаче о движущемся штампе. Пусть штамп длиной L движется
со скоростью V по границе полуплоскости. Если штамп гладкий,
то касательное _усилие Г4 равно нулю всюду на поверхности,
следовательно, Tt = 0. Но со вторым граничным условием дело
обстоит сложнее. Перемещение u2(t) в фиксированной точке гра-
границы М известно только в течение конечного промежутка вре-
времени ?^[8, 0 + L/F], если 9 — тот момент, когда конец штампа
приходит в точку М. Для других значений времени u2(t) неиз-
неизвестно, поэтому вычислить изображение по Лапласу п2(р) не
представляется возможным. Такое же положение возникает и при
прямом применении принципа Вольтерра. Действительно, при
окончательной расшифровке полученных операторных соотноше-
соотношений неизбежным образом придется вычислять интеграл
Здесь R — ядро некоторого результирующего оператора. Но функ-
функция и2(х) известна только для указанного выше интервала вре-
времени.
Заметим, что для решения некоторых задач с переменными
границами принцип Вольтерра все же оказывается применимым,
эти задачи будут отмечены далее.
гл- 17« НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
Если операторы К и \л относятся к одному и тому же классу
резольвентных операторов и в решении задачи теории упругости
появляется рациональная комбинация упругих констант, заме-
заменяемых операторами, то описанные выше правила алгебры опе-
операторов позволяют свести эту комбинацию к одному оператору
того же класса. В противном случае выкладки становятся до-
довольно сложными в такой же мере, в какой сложно обращение
преобразования Лапласа. В современной литературе можно найти
многочисленные примеры численных решений, основанных на
численном обращении преобразования Лапласа.
В некоторых случаях решение задачи теории упругости ока-
оказывается таким, которое содержит трансцендентные функции от
операторов. В качестве примера можно привести построенное
в § 12.13 решение задачи об осесимметричном изгибе круговой
цилиндрической оболочки. Решение соответствующего однородно-
однородного уравнения для упругой оболочки строится из частных ре-
решений
exp (=b[kc) cos p#, exp (±$x) sin §x.
Здесь (З4 = . а 2—• В задаче наследственной теории упругости
4а h вЩф
постоянная р заменяется оператором [J, который получается в ре-
результате замены коэффициента Пуассона v соответствующим
оператором. Но v» = (v • I)*, = 1/2, тогда как v0 можно принять
равным 0,3. Отсюда следует, что отношение f5oo/p0 = 0,95. Совер-
Совершенно очевидно, что при практическом расчете оболочек следует
считать коэффициент Пуассона постоянным. Заметим, что транс-
трансцендентные функции от операторов всегда представляют собою
функции от коэффициента Пуассона — единственной безразмер-
безразмерной упругой постоянной для изотропного материала. Поэтому
в приложениях часто вместо условия отсутствия объемного после-
последействия, которое приводит к формуле A7.7.3), принимают ко-
коэффициент Пуассона просто постоянным, v = v. Такое предполо-
предположение до чрезвычайности упрощает решение всевозможных за-
задач. Действительно, распределение напряжений в упругом теле
обычно зависит от коэффициента Пуассона, если этот коэффи-
коэффициент заменяется оператором, в теле происходит перераспределе-
перераспределение напряжений во времени даже при постоянных нагрузках.
Но если коэффициент Пуассона постоянен, то распределение на-
напряжений определяется только действующими в данный момент
нагрузками; при постоянстве нагрузок распределение напряже-
напряжений остается неизменным. Перемещения точек тела при этом ме-
меняются, их изменение целиком определяется операторным моду-
модулем упругости Е, точно так же как этим модулем определяется
релаксация напряжений в теле, точки поверхности которого удер-
удерживаются неподвижными. Возвращаясь к задаче о цилиндриче-
цилиндрической оболочке, заметим, что в выражении для прогиба в знаме-
§ 17.10. УСТОЙЧИВОСТЬ НАСЛЕДСТВЕННО-УПРУГИХ СИСТЕМ 601
нателе появляется цилиндрическая жесткость и = —¦: ^-. Ес-
3A — v ;
ли-^-= -g-[l + иЭ*(-—|3)]и v определяется формулой A7.7.3), то
в результате стандартных вычислений, основанных на теореме
умножения резольвентных операторов, получаем
1 —v2
A7.9.2)
При выводе этой формулы сохранение v в качестве оператора
не вносит серьезных осложнений.
Трансцендентные функции операторов, так же как иррацио-
иррациональные комбинации, можно бывает представить в виде рядов
и построить таким образом точное решение задачи. Некоторые
примеры такого рода приведены в книге Работнова [11].
§ 17.10. Устойчивость наследственно-упругих систем
Уравнение изогнутой оси стержня, находящегося под дей-
действием продольной сжимающей силы и поперечной нагрузки,
получается из уравнения C.10.1) поперечного изгиба путем
простой замены модуля упругости Е оператором ЕA — Г*). Это
интегро-дифференциальное уравнение в общем случае переменной
жесткости имеет вид
^)+Р^-д0-Р^. A7.10.1)
дх2) дх2 ° дх2 V
Здесь учтено, что стержень может иметь начальный прогиб vo(x).
Для решения этого интегро-дифференциального уравнения ис-
используем метод разложения по собственным функциям. Рассмот-
Рассмотрим обыкновенное дифференциальное уравнение
(Е1и*)" +Ри" =0 A7.10.2)
и присоединим к нему те граничные условия, которые были
поставлены для интегро-дифференциального уравнения A7.10.1).
Мы получили обычную задачу об устойчивости продольно сжа-
сжатого упругого стержня, изученную в гл. 4. Собственные значения
Рь. уравнения A7.10.2) образуют неограниченную последователь-
последовательность; каждому собственному значению соответствует фундамен-
фундаментальная функция uk. Для однородных граничных условий, не
связанных с введением внешних по отношению к системе
упругих элементов, справедлива теорема об ортогональности
ГЛ- 17< НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
фундаментальных функций, а именно:
i
J
Это условие служит в то же время условием нормировки фун-
фундаментальных функций, которые определены с точностью до по-
постоянного множителя. Будем теперь искать решение интегро-
дифференциального уравнения A7.10.1) в виде ряда
Подставим этот ряд в A7.10.1), умножим на EIus и проинте-
проинтегрируем по длине балки. Используя A7.10.2) и условия орто-
ортогональности и нормированное™ функций uh, получим серию
уравнений для функции Ts
[-Ps(l-T*) + P]Ts = P8qs(t). A7.10.3)
Здесь
S
О
При исследовании задач устойчивости интерес представляет лишь
первая форма, соответствующая Pi = Pd. Сила Рэ называется
эйлеровой силой. Положив Р/Рэ = p(t), перепишем интегральное
уравнение A7.10.3) при s = l следующим образом (индексы опу-
опущены) :
A - р) Т - Г*Г = -д. A7.10.4)
Решение этого уравнения может быть представлено следующим
образом:
Предположим сначала, что рассматривается поведение стержня
при малых значениях времени. Интегральный член Г*Г в A7.10.4)
при этом пренебрежимо мал, и мы получаем обычную формулу
теории продольно-поперечного изгиба упругой балки
гр
1-р-
Отсюда видно, что при весьма кратковременном приложении
нагрузки по мере приближения силы Р к эйлеровой силе ампли-
амплитуда прогиба Т может быть сколь угодно большой. При этом
интегральный член Г*Г остается сколь угодно малым, если
время достаточно мало. Этот результат можно резюмировать еле-
§ 17.11. ВАРИАЦИОННЫЕ ПРИНЦИПЫ 603
дующим образом: при мгновенном приложении нагрузки проис-
происходит упругая потеря устойчивости по Эйлеру.
Если, начиная с некоторого времени t, способ приложения
нагрузки перестает играть роль, это значит q ^ G в смысле, ого-
оговоренном в § 17.4, то вследствие теоремы Пэли — Винера
Но 1 — Гто = i?00/?l; таким образом, при р<Еоо/Е стержень асимп-
асимптотически устойчив в том смысле, что прогиб его под действием
продольной силы и произвольной поперечной нагрузки стремится
к конечному пределу. Этот предел неограниченно возрастает,
когда р стремится к величине отношения EJE\ при р^Е^/Е
предельная теорема перестает быть справедливой. Общий вывод
из рассмотренного примера следующий. Система мгновенно не-
неустойчива, когда нагрузка превосходит эйлерову, вычисленную
по мгновенному модулю. Система асимптотически неустойчива,
если нагрузка превышает эйлерову нагрузку, соответствующую
длительному модулю. При меньших нагрузках система устойчива.
Этот результат относится не только к случаю сжатого стержня,
но п к любой наследственно-упругой системе, устойчивость ко-
которой может быть исследована на основе геометрически линейной
постановки задачи типа Эйлера.
§ 17.11. Вариационные принципы теории
наследственной упругости
В обычной теории упругости вводятся потенциалы напряже-
напряжений и перемещений следующим образом (§ 8.2):
1 1
Введем наряду с упругими потенциалами следующие потенциалы
наследственности:
&1 = eij^ijkl^kli ^i = GijKijklGhl- A7.11.1)
При варьировании потенциалов наследственности условимся при-
применять символ вариации только к множителю, стоящему впереди
интегрального оператора, так что, например,
Операторы Г^ и К^, вообще говоря, могут быть несиммет-
несимметричными относительно пар индексов ij и Ы, но нам будет удобно
принять такую симметрию. Если Г да = Г^-, например, то
604 ГЛ- i7* НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
Отметим еще следующие тождества:
а.А, = 2U0 - СЛ = 2Ф0 + Ф1в A7.11.2)
С помощью введенных потенциалов и с учетом принятого прави-
правила варьирования мы можем переписать основной закон наслед-
наследственной теории упругости A7.7.5) следующим образом:
°И = JT.. (^о - U,), ei} = ±- (Фо + Фх). A7.11.3)
Теперь совершенно так же, как это было сделано в обычной
теории упругости (§ 8.7), можно построить функционал
- i- ии - ± Щл) - Uo (erf + U, (ei}) + F{u\ dV +
+ f T*UidS + j а^щ (щ — щ) dS. A7.11.4)
ST Su
Этот функционал совершенно аналогичен известному функцио-
функционалу Хеллингера — Вашизу; варьируя напряжения, перемещения
и мгновенные значения деформаций, мы получим уравнения на-
наследственной теории упругости и граничные условия как урав-
уравнения Эйлера и естественные граничные условия для функцио-
функционала A7.11.4).
Вариационные принципы типа Рейснера, Лагранжа и Кастиль-
яно получаются отсюда совершенно так же, как в обычной тео-
теории упругости. При выводе уравнения Рейснера заметим, что
вследствие A7.11.2)
ц - Uo + Ui = [/„,
но в функционале Рейснера в качестве независимых аргументов
принимаются щ и а^, поэтому UQ должно быть выражено через Оц.
Вычислим производную от С/о по Оц
Но матрицы Е и П взаимно обратные, поэтому
Таким образом,
и вследствие A7.11.3)
Теперь функционал Рейснера может быть записан следующим
§ 17.11. ВАРИАЦИОННЫЕ ПРИНЦИПЫ 605
образом:
Jua = J [— cTij \ ^fi + aifl) Ч-Фо + Ф^ FiM|] аУ +
+ J Г?М|й5 + J a^ (щ — uj) dS. A7.11.5)
Функционалы Лагранжа и Кастильяно получаются из соответ-
соответствующих функционалов для упругого тела простой заменой U
на UQ — UU О на Ф0 + Оь Мы не выписываем соответствующие-
выражения, отсылая к § 8.7.
Проиллюстрируем применение одного из вариационных прин-
принципов, например принципа типа Рейснера, на примере задачи о(>
изгибе балки. Для одноосного напряженного состояния
Положим е = ку, a = Mz/I, т. е. зададимся независимо линейным
законом распределения как напряжений, так и деформаций по
сечению. Подставляя в A7.11.5) и выполняя интегрирование па
площади, получим
i
Jua =
Мк + 41г + WMK*M + qv)dz'
о
Здесь x = i/', v(z)—прогиб балки. Варьируя прогиб v(z),
лучим
= J (- Mbif + qbv) dz =0.
о
Если на концах балки не приложены силы, производящие ра-
работу на перемещениях или углах поворота концов, то в резуль-
результате двукратного интегрирования по частям получаем
i
о
Отсюда сдедует уравнение равновесия
M'=q(z).
Теперь варьируем момент M(z). Получаем
о
Отсюда находим
х = 1/' = 1+^М. A7.11.6)
rjL 17* НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
Полученные следствия из вариационного принципа типа Рейс-
нера носят, конечно, достаточно тривиальный характер. Эти
уравнения можно было получить из обычных уравнений изгиба
балки простой заменой модуля упругости соответствующим опе-
оператором. Но можно представить себе более сложный случай,
когда Е и X* представляют собою функции координаты г/. Так
будет, например, если балка неравномерно нагрета по толщине;
ядро наследственности в сильной степени зависит от темпера-
температуры. Уравнение A7.11.6) в этом случае сохраняет силу, только
вместо 1/Е и X* нужно подставить приведенные величины,
а именно,
1 _ 1 CifdF • _ДП
р F F
Таким образом, расчет балки должен производиться по осред-
ненному операторному модулю, при этом вариационный принцип
фиксирует совершенно определенный способ такого осреднения,
которое, вообще говоря, не единственно. При использовании
принципа типа Лагранжа, например, мы придем к точно тем же
уравнениям, но при зависимости операторного модуля от коор-
координаты необходимый способ осреднения окажется иным.
Заметим, что вариационные принципы наследственной теории
упругости допускают и иную трактовку. Вследствие принципа
Вольтерра можно применять любой метод для решения задачи
обычной теории упругости, и лишь в окончательном результате
упругие константы следует заменить операторами. Отсюда сле-
следует, в частности, что для нахождения точного или приближен-
приближенного решения задачи теории упругости может быть применен
любой из известных вариационных методов; если в результате
решения в окончательном результате появится некоторая ком-
комбинация упругих констант, ее можно заменить такой же ком-
комбинацией из операторов и расшифровать по известным правилам.
§ 17.12. Элементы нелинейной теории наследственности
Еще Вольтерра, основываясь на теории, развитой Фреше,
представил нелинейный функционал вида A7.1.1) рядом, напо-
напоминающим в известной мере ряд Тейлора. Для одномерного
•случая и применительно к наследственно-упругому телу, это раз-
разложение имеет следующий вид:
t
«= I /i(*-t1)dcr(T1) +
—оо
t t
+ J J /a (* - *i, * - т2) da (Tl) da (т2) + ... A7.12.1)
— 00 —СЮ
§ 17.12. ЭЛЕМЕНТЫ НЕЛИНЕЙНОЙ ТЕОРИИ НАСЛЕДСТВЕННОСТИ 607
Приложение формулы A7.12.1) к обработке опытных данных
было начато больше чем через пятьдесят лет после появления
работы Вольтерра. Следует отметить, что во всех этих новейших
работах исследовались материалы, поведение которых мало от-
отличалось от линейного. Поэтому в разложении A7.12.1) была
достаточно удержать два члена, соответствующих однократному
и тройному интегралам. Двукратный интеграл обычно отбрасы-
отбрасывается, так как поведение материала при растяжении и сжатии
предполагается одинаковым. Даже при таких упрощениях опре-
определение вида ядра, зависящего от трех независимых аргументов,,
довольно затруднительно. Обращение соотношения A7.12.1) име-
имеет тот же вид, но фактическое выполнение такого обращения
встречает существенные трудности. Лишь относительно недавна
A957 г.) кратно-интегральное представление было распростране-
распространено на случай трехмерного напряженного состояния. При сохране-
сохранении интегралов до трехкратных включительно поведение изотроп-
изотропного материала описывается при помощи 12 независимых ядер.
Многие авторы поэтому стремились упростить полученные соот-
соотношения, делая те или иные предположения. Мы не будем здесь
касаться этих вопросов.
Возвращаясь к одномерному случаю, сделаем упрощающее-
предположение, касающееся структуры последовательных ядер
в A7.12.1), а именно, положим
k
Jk (t - т19 * - т2, ... ,t - xh) = ak П / {t - т«). A7.12.2)
Положим теперь
s=
0
Здесь мы заменили нижний предел т = — °° пределом т = 0 по
причинам, которые были обсуждены выше. Теперь A7.12.1) пе-
перепишется следующим образом:
е = axs + a2s2 + a3s3 + ... A7.12.3)
Ряд A7.12.3) онределяет е как функцию s. Обозначая через
ф(е) обращение этой функции, получим
<р(е) = A + К*)а. A7.12.4).
Функция ф(е) определяется непосредственно из эксперимента.
При а = const из A7.12.4) следует
1 + ?*•Г (l/.iz.o>
Уравнение а = ф(е) определяет кривую мгновенного деформиро-
деформирования; кривые ползучести, перестроенные в координатах а, е для
gO8 ГЛ- 17- НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
фиксированных значений времени t, называются изохронными
кривыми. Задаваясь видом ядра или определяя его из опытов
при малых напряжениях, когда справедливы уравнения линейной
наследственности и, следовательно, (р(е) = Ее, мы можем вос-
восстановить вид мгновенной кривой, т. е. найти функцию ф(е).
Для этого необходимо, чтобы в эксперименте подтвердился факт
подобия изохронных кривых ползучести, следующий из A7.12.5).
Действительно, изохронные кривые ползучести оказываются по-
подобными с достаточной степенью точности для различных мате-
материалов. При обработке опытных данных неточность в определе-
определении ядра К может быть компенсирована надлежащим выбором
функции ф, поэтому более простое ядро Абеля можно принимать
вместо дробно-экспоненциальной функции.
Заметим, что нелинейность поведения материала, если она
выражена достаточно заметно, обычно бывает связана с необра-
необратимостью. Поэтому на уравнение A7.12.4) можно смотреть как
на уравнение наследственной пластичности, т. е. считать его
справедливым тогда, когда е > 0. Тогда закон разгрузки должен
быть сформулирован иначе, например вместо функции ср(е)
в уравнение A7.12.4) нужно ввести некоторую функцию а|)(е, е*),
где е*-—величина деформации в момент начала разгрузки.
§ 17.13. Распространение волн
в наследственно-упругом теле
Здесь мы ограничимся рассмотрением одномерных волн и для
простоты будем говорить о распространении продольной волны
в стержне, хотя правильнее было бы рассматривать плоский
фронт в неограниченной среде. Те уравнения, с которыми мы
€удем иметь дело, совершенно точны для такого плоского фрон-
фронта, тогда как для стержня они лишь приближенны, так как в них
не учитываются поперечная инерция и деформация сдвига. Диф-
Дифференциальное уравнение распространения волн в упругом
стержне, как мы видели в § 6.7, имеет следующий вид:
2 д\ д2и __ п
дх2 dt2
Здесь с2 — Е/р. Для волн расширения в неограниченной среде Е
заменяется на % + 2\х, для волн искажения на [х, таким образом,
математическая теория оказывается совершенно тождественной.
Заменяя Е через наследственно-упругий оператор, получим сле-
следующее интегро-дифференциальное уравнение:
Л Л* = 0 A7.13.1)
дх2
§ 17.13. РАСПРОСТРАНЕНИЕ ВОЛН 609
Прогрессивные волны. Положим
и = exp i(o(t + q -|Л A7.13.2)
Если q, как мы в этом убедимся, комплексное число, q = #i + Щг,
то вышеприведенное выражение можно переписать следующим
образом:
и = exp (- ^а) exp m (t + Ql -J-). A7.13.3)
Первый множитель определяет затухание, т. е. убывание ампли-
амплитуды с расстоянием, величина c/qi представляет собою скорость
распространения волны. Подставляя A7.13.2) в уравнение дви-
движения A7.13.1), найдем
q
Для каждого конкретного вида ядра в этом выражении можно
отделить действительную часть от мнимой и, следовательно,
найти qt и q2. Если затухание невелико и Г« < 1 + Гс, то можно
получить приближенное соотношение
q = ?i + iq* «A + Гс)-1/2 + *Г/A + Гс)-3/2. A7.13.4)
Ho qi = A + ГС)~1/2 = 1/Е/Еоо, таким образом, скорость прогрес-
прогрессивных волн
с _
Тх ~Соо~
Это — скорость упругих волн, определяемая длительным модулем.
Полученное решение может быть найдено совершенно фор-
формальным путем, в результате простой замены в обычном реше-
решении задачи о распространении прогрессивных волн в твердом
теле модуля упругости Е комплексным модулем E' + iE". Сле-
Следует заметить, однако, что решения типа A7.13.2) носят несколь-
несколько условный характер. Предполагается, что волны движутся пз
точки х = —оо7 в этой точке амплитуда бесконечно велика. Имен-
Именно так должно обстоять дело, если понимать решение A7.13.2I
или A7.13.3) в буквальном смысле. На самом деле нужно пред-
предположить, что волны возбуждаются где-то достаточно далеко
и решение A7.13.3) описывает приближенно скорость прохожде-
прохождения гребня волны через некоторую точку и разницу амплитуд
Двух соседних гребней.
Возможность получения решения задач о распространении
наследственно-упругих волн прямой заменой обычных модулей
комплексными модулями составляет содержание так называемого
принципа соответствия для динамических задач. Мы уже при-
39 Ю, Н. Работнов
610 гл- 17« НАСЛЕДСТВЕННАЯ ТЕОРИЯ УПРУГОСТИ
меняли принцип соответствия для решения задачи о свободных
колебаниях системы с одной степенью свободы. Как здесь, так
и там мы убедились в том, что этот принцип применим лишь
для описания таких процессов, которые можно назвать в извест-
известном смысле стационарными.
Ударные волны. Задача о распространении возмущения, не-
несущего разрыв некоторых параметров процесса, решается, по-
пожалуй, проще всего при помощи преобразования Лапласа. При-
Применим преобразование Лапласа по времени к уравнению A7.13.1)
и, воспользовавшись тождеством
представим результат в следующем виде:
и"—^A + К)й = 0.
Здесь штрихи обозначают дифференцирование по х. Интеграл
этого уравнения, стремящийся к нулю при х -> °°, будет сле-
следующий:
Аналогичные выражения, отличающиеся только множителем, по-
получаются и для производных от и, в частности для а. Предпо-
Предположим, что на конце прикладывается постоянное напряжение о0
в момент ? = 0; тогда а@, p)=ojp и, следовательно,
(*, Р) = ^-ехр (_ а. УГП?). A7.13.5)
Обращение выражения A7.13.5) встречает серьезные трудности,
которые удается преодолеть лишь для немногих частных видов
ядер, однако асимптотические оценки позволяют сделать некото-
некоторые выводы. Прежде всего при малых t и, следовательно, боль-
больших р справедливо асимптотическое представление
К (р) - -?Л
Поэтому
5 [хх р) ~ Ц- ехр (- Я. - ±-К @) f-).
Отсюда следует
Итак, волна распространяется со скоростью упругой волны, он-
8 17.13. РАСПРОСТРАНЕНИЕ ВОЛН
ределяемой мгновенным значением модуля. Экспоненциальный
множитель определяет затухание.
С другой стороны, при t ->- °°, р -* о становится справедливым
следующее предельное соотношение:
Примем F — К* • 1, F = К/р. Поэтому при малых р
K(p)~F(oo) = ±.
Соотношение A7.13.5) принимает вид
Отсюда следует
При достаточно больших значениях t возмущение распростра-
распространяется без затухания со скоростью с*. < с. Итак, картину рас-
распространения волны в наследственно-упругом теле нужно пред-
представить себе следующим образом. Сначала идет упругая волна
с мгновенной скоростью с, за фронтом сигнал быстро затухает
по экспоненциальному закону. По мере приближения к фронту
упругой волны, распространяющейся с длительной скоростью сх,
интенсивность сигнала должна возрастать до величины о0 на
фронте, а за этим фронтом остается постоянной. Такая доволь-
довольно очевидная картина может быть получена и в результате более
строгого анализа.
39*
ГЛАВА 18
ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
§ 18.1. Испытания на ползучесть и кривые ползучести
Внешнее протекание процесса ползучести металлов и сплавов
при повышенных температурах весьма напоминает ползучесть
полимерных материалов или проявление наследственной упру-
упругости, рассмотренной в гл. 17. Однако ползучесть металлов не
может рассматриваться как наследственно-упругий эффект; де-
деформация ползучести в основном необратима, это с одной сто-
стороны, с другой — зависимости между напряжением и деформацией
или скоростью деформации резко нелинейны. В наследственной
теории упругости создание более или менее законченной мате-
математической теории предшествовало накоплению опытного мате-
материала. Можно только удивляться тому, что построения, продик-
продиктованные в большей мере внутренней логикой развития науки,
чем непосредственными запросами практики, оказались столь
хорошо пригодными для описания поведения горных пород,
пластмасс, древесины и других материалов. В теории ползучести
материалов дело обстояло как раз наоборот. Диски паровых
турбин испытывают значительные напряжения от центробежных
сил и находятся в условиях относительно высоких температур.
Инерционные напряжения не могут быть уменьшены путем уве-
увеличения толщины, некоторое снижение напряжений может быть
достигнуто за счет выбора рационального профиля, однако здесь
имеется совершенно определенный предел. Оказалось, что инер-
инерционные напряжения вызывают медленное деформирование дис-
диска—увеличение его наружного диаметра и изменение формы
профиля. Это явление было названо «ползучестью», по-английски
«creep». (В первых русских публикациях это английское слово
«крип» употреблялось в транслитерации без перевода.) Усилия
металлургов были направлены на получение новых сталей и спла-
сплавов, стойких в отношении ползучести. Перед инженерами встала
задача расчета на ползучесть, т. е. определения расчетным путем
времени, по истечении которого деформация достигнет некоторой
наперед задаваемой величины, которая считается предельно до-
допустимой.
Первые теории ползучести создавались именно инженерами,
а не механиками-теоретиками, они относятся к середине 20-х го-
годов. В это время уже были сформулированы основные положе-
положения теории пластичности, поэтому, естественно, теория ползучести
§ 18.1. ИСПЫТАНИЯ НА ПОЛЗУЧЕСТЬ g J3
полагала в основу уже известные законы пластичности, модифи-
модифицируя их надлежащим образом.
Четко выраженная практическая направленность характери-
характеризует развитие теории ползучести в последующие годы, вплоть
до настоящего времени. В 50-е — 60-е годы эта теория сформи-
сформировалась как самостоятельная ветвь механики сплошной среды;
в это время был накоплен очень
большой экспериментальный матери-
материал. Были поставлены опыты спе- /
циально для проверки и уточнения
основных гипотез теории, с одной
стороны. С другой — в промышлен-
промышленности был выполнен огромный объем
экспериментов, направленных на О
получение данных по ползучести
отдельных сплавов, предназначен- Рис- *&\А
ных для применения их в конструк-
конструкциях. Не доставляя достаточно полного материала для про-
проверки математической теории ползучести, эти результаты все же
смогли быть использованы теоретиками. Особый интерес пред-
представляют эксперименты, выполненные на моделях более или ме-
менее сложных изделий — трубах, дисках, диафрагмах турбин и т. д.
Сравнение данных опыта с предсказаниями расчета, построен-
построенного на основе той или иной теории, могло служить качественным
подтверждением ее правильности.
Стандартный метод испытаний на ползучесть — это испытание
на растяжение постоянной нагрузкой цилиндрического образца.
Современные жаропрочные сплавы разрушаются под действием
постоянной нагрузки при относительно малой деформации, по-
поэтому деформации ползучести, измеряемые в эксперименте, неве-
невелики. С другой стороны, конструктор не может допустить сколь-
сколько-нибудь большие деформации ползучести (обычно не свыше
1%), поэтому изучение ползучести представляет интерес только
в пределах изменения деформации не свыше 1—2%. При этом
изменение площади поперечного сечения невелико и постоянство
нагрузки можно отождествлять с постоянством деформации. В ста-
старых работах^ принимались специальные меры для того, чтобы
компенсировать уменьшение площади сечения при растяжении
соответствующим уменьшением нагрузки; для этого создавались
специальные конструкции нагружающих устройств. В современ-
современной испытательной технике эти меры не принимаются.
На рис. 18.1.1 представлена типичная кривая ползучести,
т. е. диаграмма зависимости деформации е от времени t при
постоянном напряжении о. Здесь е0 — мгновенная деформация,
зависящая только от приложенного напряжения. Она может
быть чисто упругой, а может включать в себя мгновенную пла-
пластическую деформацию. Римской цифрой / отмечен первый уча-
Ю. Н. Работнов
ГЛ- 18- ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
сток кривой ползучести, скорость ползучести de/dt постепенно
убывает до минимального значения v(а). На участке // скорость
ползучести сохраняет постоянное значение de/dt = v(a). Ha
третьем участке скорость начинает возрастать и ползучесть за-
заканчивается обрывом образца.
Приведенная диаграмма представляет собою схему. В дей-
действительности картина ползучести может быть самой разнооб-
разнообразной. Может отсутствовать первый участок, после непродолжи-
непродолжительного периода ползучести с относительно постоянной ско-
скоростью она начинает увеличиваться, таким образом, вся диаграм-
диаграмма состоит из третьего участка. Участок // часто бывает трудно
выделить, это может быть просто некоторая область около точки
перегиба, отделяющей участки / и ///. Наконец, при низком
уровне напряжений даже при очень длительных испытаниях не
будет достигнута минимальная скорость и не произойдет разрыва
образца, вся диаграмма ползучести будет состоять из одного
первого участка. Именно такой результат был получен в опытах
Робинсона, продолжавшихся 100 000 часов (около 12 лет).
Иногда кривые ползучести выглядят и более сложным обра-
образом, периоды замедления и ускорения чередуются не так, как
это показано на идеальной диаграмме рис. 18.1.1. Как правило,
такое поведение свидетельствует о фазовых переходах в сплаве.
Теория, которая будет излагаться ниже, применима к материа-
материалам структурно устойчивым, и в принципе фазовые переходы
исключаются из рассмотрения.
Уменьшение скорости деформации на первом участке кривой
ползучести определяется эффектом упрочнения; ползучесть со-
сопровождается такими структурными изменениями, которые уве-
увеличивают сопротивление материала ползучести. При исчерпании
способности материала к упрочнению скорость ползучести стано-
становится постоянной, кривая ползучести выходит на второй участок.
Если деформации ползучести велики и, следовательно, изме-
изменение площади сечения образца значительно, при постоянной
нагрузке напряжение будет возрастать и, следовательно, скорость
будет, увеличиваться. Таким образом, на диаграмме появится
третий участок. Для некоторых материалов такое чисто геомет-
геометрическое объяснение появления третьего участка оказывается
точным. Однако третьи участки наблюдаются на кривых ползу-
ползучести жаропрочных материалов, которые разрушаются при очень
малом удлинении. Причина этого состоит в том, что ползучесть
сопровождается образованием микротрещин и микрополостей на
границах кристаллических зерен. В результате эффективная пло-
площадь сечения, воспринимающая нагрузку, уменьшается и скорость
ползучести увеличивается. С увеличением скорости ползучести
увеличивается скорость образования новых микротрещин и роста
уже имеющихся; наконец в каком-то месте образца микротре-
микротрещины сливаются, образуя большую трещину разрушения.
§ 18.2. ЗАВИСИМОСТЬ ОТ НАПРЯЖЕНИЯ И ТЕМПЕРАТУРЫ 615
§ 18.2. Зависимость от напряжения и температуры
При проектировании изделий, работающих в условиях по-
повышенных температур, конструктор встречается с задачами раз-
различного характера в зависимости от назначения и условий
эксплуатации изделий. Так, элементы стационарных паровых
турбин рассчитываются на сроки службы порядка десяти и более
лет, соответственно напряжения и температуры должны быть не
слишком высоки. Сопло реактивного
двигателя ракеты подвергается дей-
действию весьма высоких температур и
больших давлений, но продолжитель-
продолжительность работы двигателя составляет
несколько минут. Соответственно ос-
основные механические модели и рас-
расчетные методы в этих двух крайних
случаях оказываются неодинаковы- и Т
ми, хотя общие принципы построе-
построения теории остаются теми же. Поэто- Рпс' 1821
му для начала нам будет удобно
руководствоваться следующей довольно условной классификацией
областей применения теории ползучести:
1. Длительная ползучесть — месяцы и годы.
2. Ползучесть средней длительности — часы и дни.
3. Кратковременная ползучесть — секунды и минуты.
Каждая из этих областей характеризуется определенным диа-
диапазоном температур и напряжений, который удобно рассмотреть
на диаграмме рис. 18.2.1. Здесь по оси абсцисс откладывается
температура Г, по оси ординат — напряжение а. В результате
кратковременного испытания на разрыв определяется предел
прочности ов. Верхняя кривая 1 соответствует зависимости пре-
предела прочности от температуры, область, лежащая выше этой
кривой и обозначенная буквой Р, есть область мгновенного раз-
разрушения. Предел прочности ов зависит от скорости испытания,
особенно при высоких температурах, но мы не принимаем во
внимание эти эффекты при рассуждениях качественного характе-
характера. Штриховая кривая 2 определяет ту границу, ниже которой
ползучесть вообще не наблюдается. Эта кривая также довольно
условна. Многочисленные попытки определения истинного преде-
предела ползучести, т. е. такого напряжения (при данной температу-
температуре), ниже которого материал вообще не ползет, не привели ни
к каким результатам и в настоящее время оставлены. Под дей-
действием постоянного напряжения о образец при данной темпера-
температуре разорвется по истечении времени t. Наоборот, задаваясь
временем ?, можно определить напряжение, при котором образец
в это время разорвется. Назовем. это напряжение длительной
прочностью Of. Очевидно, что'величина длительной прочности за-
40*
616 ГЛ. 18. ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
висит от t и эта зависимость довольно сильная. Вопросы разру-
разрушения при ползучести будут рассмотрены детально в гл. 19, пока
что мы ограничимся сообщенными краткими сведениями. Кри-
Кривая 3 представляет собою кривую зависимости длительной проч-
прочности от температуры при фиксированном t.
Очевидно, что расчет на ползучесть имеет смысл производить
тогда, когда деформация ползучести, накопленная за время ?,
не слишком мала, например, составляет
10% от упругой деформации. Ошибка
в 10% для инженерных расчетов до-
допустима, поэтому будем считать, что
если деформация ползучести меньше
10% от упругой, с ползучестью вообще
можно не считаться. Кривая 4 соответ-
соответствует тем значениям напряжений и
температур, при которых деформация
ползучести за время t составляет оп-
Рис. 18.2.2 ределенную заданную заранее долю от
упругой деформации, например, 10%,
5% или какая-то иная доля. Заштрихованная область П между
кривыми 3 и 4 представляет собою ту область, где должна
быть справедлива выбранная теория ползучести, если расчеты
производятся на длительность службы, равную t. Очевидно,
что конфигурация и размеры области П в сильной степени
зависят от времени t; поэтому, если сравнивать длительную и
кратковременную ползучесть, может возникнуть ситуация, по-
подобная изображенной на рис. 18.2.2, когда область ITi соответ-
соответствует длительной ползучести, область П2 — кратковременной и
эти области не имеют общих точек. Диаграммы типа изображен-
изображенных на рис. 18.2.1 и 18.2.2 фактически удается построить лишь
в редких случаях, обычно оказывается возможным выделить лишь
некоторые подобласти, для которых определены константы и
функции, фигурирующие в законе ползучести, границы же обла-
областей обычно точно неизвестны. Однако схематические представ-
представления, отраженные этими диаграммами, бывают полезными для
того, чтобы ориентировочно оценить границы применимости того
или иного варианта теории.
Что касается фактической зависимости скорости ползучести от
напряжения и температуры, заметим, что для практических це-
целей бывает удобно задать эти зависимости в аналитической
форме. Разброс экспериментальных данных для различных об-
образцов при испытаниях на ползучесть довольно велик, поэтому
различные аналитические аппроксимации зависимости скорости
ползучести от напряжения дают практически одинаково хороший
результат, при выборе этих аппроксимаций следует руководство-
руководствоваться также и соображениями удобства применения их при
расчетах. Наиболее надежные данные, основанные на обработке
§ 18.2. ЗАВИСИМОСТЬ ОТ НАПРЯЖЕНИЯ И ТЕМПЕРАТУРЫ 617
большого экспериментального материала, относятся к зависимо-
зависимости от напряжения минимальной скорости ползучести v(о). При-
Приведем некоторые наиболее употребительные зависимости.
1. Степенной закон:
v (о) = га
ol
п—1
A8.2.1)
В этой формуле фигурируют три константы е„, оп и п, хотя не-
независимые из них только две. Постоянную еп? например, можно
выбирать по произволу, это некоторая характерная скорость де-
деформации, которую следует фиксировать наиболее удобным спо-
способом. При невысоких температурах показатель п может быть
очень большим, порядка п = 8 -ь 12. Тогда постоянная оп играет
роль, сходную с ролью предела ползучести, если о < оп? хотя бы
не намного, скорость v очень мала, если а превышает ап, ско-
скорость v сразу становится очень большой.
Недостаток степенного закона состоит в том, что dv/dc = О
при о = 0. Аналогичный факт в нелинейной теории упругости при
степенном законе приводит к бесконечно большой скорости рас-
распространения волны. В задачах теории ползучести также иногда
возникают противоречивые ситуации, устранение которых, впро-
впрочем, труда не составляет. Зато при решении задач о ползучести
при сложном напряженном состоянии степенной закон имеет ряд
серьезных преимуществ, благодаря которым он очень широко
применяется в настоящее время.
2. Степенной закон с пределом ползучести. Положим
v (о) = гп j-^ 1) , о>о'П1
^°п * , A8.2.2)
v (о) = 0, а < а'п.
Теперь постоянная оп может быть на самом деле названа преде-
пределом ползучести. С другой стороны, такое толкование не имеет
четкого механического смысла или экспериментального под-
подтверждения. Просто, имея в распоряжении три независимые кон-
константы вместо двух констант уравнения A8.2.1), можно описать
экспериментальные данные несколько лучше. Показатель п' ока-
оказывается значительно меньше, чем показатель п в формуле
A8.2.1).
3. Экспоненциальный закон:
v (о) = 8сехр (-2-Y A8.2.3)
Зависимость A8.2.3) появляется во многих физических теориях
пол(зучести. Она не пригодна для малых значений о. Действи-
Действительно, при о = 0 из A8.2.3) следует у(о) = ее^О. Чтобы испра-
исправить этот недостаток, экспоненциальный закон часто заменяют
ГЛ. 18. ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
законом гиперболического синуса
i;(a) = 2eesh~-. A8.2.4)
Формула A8.2.4) при больших значениях о/ое дает результаты,
не отличающиеся от результатов формулы A8.2.3), при малых
же значениях о из A8.2.4) следует
т. е. линейная зависимость скорости от напряжения. Область ма-
малых напряжений обычно мало интересует конструктора, произ-
производящего расчет изделия, поэтому экспоненциальным законом
A8.2.3) можно пользоваться, не обращая внимания на формаль-
формальные противоречия в окрестности точки, где a = О, или устраняя
эти противоречия при помощи того или иного искусственного
приема..
Что касается зависимости от температуры, все параметры an
и n, oe и 8е представляют собою функции температуры. С извест-
известной степенью приближения можно считать, что множители перед
функциями от напряжения, например, ?п^п в формуле A8.2.1)
или ге в формуле A8.2.3) пропорциональны величине
Здесь Uo — некоторая энергия активации, к — постоянная Больц-
мана, Т — абсолютная температура. В небольшом диапазоне из-
изменения температур такая аппроксимация может быть удовлет-
удовлетворительна. Но от температуры зависят и другие константы. Так,
величина п в степенном законе A8.2.1) уменьшается с темпера-
температурой. Дать какие-либо аналитические зависимости для измене-
изменения констант уравнений A8.2.1) — A8.2.4) в зависимости от тем-
температуры затруднительно, поэтому в книге Работнова и Милейко,
содержащей довольно большой опытный материал, эти зависи-
зависимости представлецы просто графиками. В физической литературе
можно встретить зависимости скорости ползучести от напряжения
и температуры, претендующие на универсальность и имеющие
вид
Л
v = ехр •
кТ
Нужно признать, что формулы подобного рода мало пригодны
для описания поведения технических сплавов и даже чистых ме-
металлов в области напряжений и температур, интересующей кон-
конструктора. Тем более не обоснованы рекомендации по использо-
использованию формул подобного типа для экстраполяции данных по
ползучести на более длительные сроки.
§ 18.3. КИНЕТИЧЕСКИЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ 619
§ 18.3. Кинетические уравнения ползучести
Рассматривая ползучесть как некоторый вид квазивязкого те-
течения металла, мы должны допустить, что в каждый момент
скорость ползучести при данном структурном состоянии опреде-
определяется однозначно действующим напряжением и температурой.
Структурное состояние — это термин, чуждый по существу ме-
механике, поэтому применение его в данном контексте должно
быть пояснено более детально. Понятие о структурном состоянии
связано с теми или иными физическими методами фиксации
этого состояния — металлографическими наблюдениями, рентге-
ноструктурным анализом, измерением электрической проводимо-
проводимости и т. д. Обычно физические методы дают лишь качественную
характеристику структуры, выражающуюся, например, в словес-
словесном описании картины, наблюдаемой на микрофотографии шли-
шлифа. Иногда эта характеристика может быть выражена числом,
но это число бывает затруднительно ввести в механические оп-
определяющие уравнения. В современной физической литературе,
относящейся к описанию процессов пластической деформации и
особенно ползучести, в качестве структурного параметра, харак-
характеризующего, например, степень упрочнения материала, прини-
принимается плотность дислокаций. Понятие плотности дислокаций
нуждается в некотором пояснении. Линейная дислокация харак-
характеризуется совокупностью двух векторов — направленного вдоль
оси дислокации и вектора Бюргерса. Можно заменить прибли-
приближенно распределение большого числа близко расположенных дис-
дискретных дислокаций их непрерывным распределением и опреде-
определить, таким образом, плотность дислокаций, которая представляет
собою тензор. Экспериментальных методов для измерения тензо-
тензора плотности дислокаций не существует. Однако некоторую отно-
относительную оценку можно получить, например, путем подсчета
так называемых ямок травления. Когда линия дислокации выхо-
выходит на поверхность, в окрестности точек выхода имеется кон-
концентрация напряжений. При травлении реактивами поверхности
кристалла окрестность точки выхода дислокаций растравливается
более интенсивно, около этой точки образуется ямка. Таким об-
образом, определяется некоторая скалярная мера плотности дисло-
дислокаций, которая вводится в определяющие уравнения как струк-
структурный параметр. Условность такого приема очевидна.
Здесь мы будем вводить параметры состояния в определяю-
определяющие уравнения более или менее формальным образом. Иногда мы
будем называть их параметрами упрочнения или параметрами
повреждения, но будем воздерживаться от более детальной их
интерпретации. Связь с физической идентификацией структурных
состояний материала и вводимыми нами параметрами можно
установить, например, следующим образом. Предположим, что
над образцом из данного материала проводится некоторая про-
620 гл- 18- ползучесть металлов
грамма механических испытаний А, в ходе испытаний фиксиру-
фиксируются структурные состояния любым физическим методом, напри-
например, снимаются микрофотографии шлифов Аи А2, ..., Ап. У нас
нет никаких средств для количественной оценки этих фотогра-
фотографий, но мы ясно различаем их; мы можем утверждать, что фото-
фотография Ап+1 отличается от фотографии Ап. Будем записывать это
так:
Более того, мы можем утверждать, что фотография An+i отвечает
стадии процесса деформирования, следующей за Ап. Введем сле-
следующее обозначение:
Пусть теперь над образцом производится испытание по другой
программе В и снимается серия микрофотографий Ви В2, ..., Вт.
Будем называть материал однопараметрическим, если для каж-
каждой фотографии Bs можно найти тождественную фотографию
Ak, Bs = Ak, и если из Bs+i>Bs следует Ah+l>Ak. Теперь в ка-
качестве структурного параметра можно принять любую монотон-
монотонную функцию q от к, q = q(k).
Приведенные рассуждения отнюдь не означают, что нужно на
самом деле нумеровать фотографии, это есть лишь некоторая ра-
рациональная основа, позволяющая перекинуть мост между физи-
физикой и механикой.
В действительности число структурных параметров, исполь-
используемых в теории ползучести, невелико.
Теперь естественно записать сделанное в начале параграфа
утверждение следующим образом:
p = v(o, T, qu g2, ..., qn). A8.3.1)
Здесь через р мы обозначили деформацию ползучести р = е — е0,
Уи #2, ..., qn — структурные параметры, которым при желании
можно приписывать определенный физический смысл, а можно
удовлетвориться указанной выше принципиальной возможностью
связи с картиной, регистрируемой физическими методами. К урав-
уравнению A8.3.1) следует добавить некоторые кинетические урав-
уравнения, описывающие изменение структурных параметров qs. Это
могут быть, например, дифференциальные неинтегрируемые соот-
соотношения типа
ф = Фг(о, Г, р, t, qu g2, .., qn). A8.3.2)
Явная зависимость от времени функции фг- может отражать на-
наличие некоторых процессов, которые происходят во времени не-
независимо от процесса деформирования. Это может быть выпа-
выпадение новых фаз, диффузионное движение дислокаций и примес-
примесных атомов или что-нибудь другое.
§ 18.4. ПРОСТЕЙШИЕ ТЕОРИИ ОДНОМЕРНОЙ ПОЛЗУЧЕСТИ 621
§ 18.4. Простейшие теории одномерной ползучести
Теория упрочнения. Простейшее и наиболее, может быть, есте-
естественное предположение о характере упрочнения состоит в том,
что за меру упрочнения принимается просто величина накоплен-
накопленной деформации ползучести q^ = р. Теперь основное определяю-
определяющее уравнение имеет следующий вид:
p = v(a,T,p). A8.4.1)
Уравнение A8.4.1) иногда называют уравнением состояния при
ползучести, но этот термин в теориях, использующих термоди-
термодинамику, имеет несколько иной смысл. Существенно подчеркнуть,
что параметром упрочнения является именно деформация ползу-
ползучести р\ в ранних работах эта оговорка часто не делалась и за
параметр упрочнения принималась полная деформация (иногда
за вычетом упругой части). Опыты показывают, что мгновенная
пластическая деформация, если она невелика — порядка 1—2%,—
не оказывает упрочняющего влияния на последующую ползу-
ползучесть. Это можно объяснить некоторой разницей механизма мгно-
мгновенной пластической деформации и пластической деформации,
происходящей в процессе ползучести. В первом случае, если пла-
пластическая деформация невелика, она происходит в результате
локализованного скольжения по пачкам плотно расположенных
плоскостей скольжения в кристаллических зернах, при этом
большая часть объема металла остается недеформированной,
а следовательно, неупрочненной. Ползучесть происходит в резуль-
результате скольжения по атомным плоскостям, распределенным по
объему равномерно и на близких расстояниях; величина сдвига
в каждой плоскости невелика, но достаточна для создания рав-
равномерного упрочнения.
Первые участки кривых ползучести удовлетворительно опи-
описываются степенной функцией времени, так что деформация
ползучести пропорциональна tm. В соответствии с этим закон
упрочнения можно задать в следующем виде:
A8.4.2)
В первых опытах Эндрейда A910 г.) было найдено, что т = 1/3
и, следовательно, а = 2. Этот автор считал показатель т = 1/3
универсальной константой; для подтверждения этого были по-
построены различные физические теории. В действительности вели-
величина а для разных материалов непостоянна, она может зависеть
от температуры и даже от напряжения. Уравнение A8.4.2) не
описывает перехода ко второй фазе. Чтобы объяснить появление
второй фазы, следует допустить, что при некоторой величине р
способность материала к упрочнению исчерпывается. Для этого
в уравнении A8.4.2) функцию пластической деформации р~а
622
ГЛ. 18. ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
нужно заменить некоторой другой функцией. Так, некоторые ав-
авторы принимают
Рс
Рс
Здесь рс — константа. Что касается функции /(о), она может вы-
выбираться в том же виде, что функция v(g) в § 18.2; все приве-
приведенные там аппроксимации дают в общем одинаково хороший
результат.
Теория упрочнения — второй вариант. Вместо того чтобы при-
принимать за меру упрочнения величину деформации ползучести,
можно определить параметр упрочнения q как работу, рассеян-
рассеянную вследствие ползучести
= v(o, T,q).
A8.4.3)
Рис. 18.4.1
Результаты предсказаний этого второго варианта теории упроч-
упрочнения немного отличаются от результатов первой теории. Чтобы
выяснить характер отличия, обра-
обратимся к опытам на ползучесть
при ступенчатом изменении на-
нагрузки. На рис. 18.4.1 представле-
представлены две кривые ползучести, соот-
соответствующие напряжениям о4 и
02, ^2 > 01. Для ясности отложена
только деформация ползучести р.
Представим себе теперь следу-
следующий опыт. Сначала было при-
приложено напряжение а4, ползу-
ползучесть происходила до момента
времени ?4 или до точки А на
нижней кривой. При t = ?4 на-
напряжение внезапно увеличивается до о2. Согласно уравнению
A8.4.1) мерой упрочнения служит деформация ри поэтому на
кривой ползучести, соответствующей напряжению о2, нужно най-
найти точку В, для которой деформация ползучести р = ри и просто
передвинуть часть кривой ползучести вправо параллельно себе,
чтобы совместить точку В с точкой А. Согласно A8.4.3) при
о = const мерой упрочнения служит произведение ор. Поэтому на
кривой ползучести нужно найти такую точку С, для которой
произведение G2p2 = GiPi, и переместить параллельно себе часть
кривой «2, находящуюся выше точки С. По второму варианту
теории кривая ползучести, соответствующая измененной нагруз-
нагрузке, проходит несколько выше. Опытные данные в общем доста-
достаточно хорошо подтверждают обычную теорию, соответствующую
уравнению A8.4.1), хотя предсказания уравнения A8.4.3) может
быть несколько лучше. Столь осторожная оценка связана с тем,
§ 18.4. ПРОСТЕЙШИЕ ТЕОРИИ ОДНОМЕРНОЙ ПОЛЗУЧЕСТИ 623
что разница в результатах, получаемых с помощью двух различ-
различных Сравнений, сравнительно невелика, а экспериментальные
даннь!е по ползучести обнаруживают разброс.
Теория течения. Принимая в качестве параметра упрочнения
произвольную функцию времени или просто время, мы получим
уравнение ползучести в следующем виде:
p = v(a,T,t). A8.4.4)
Такое чрезвычайно упрощенное предположение не выдерживает
критики просто в логическом отношении, что касается экспери-
экспериментальной проверки, в некоторых случаях результаты оказыва-
оказываются удовлетворительными, в других — грубо неверными. Обра-
Обращаясь к рассмотренному выше случаю ползучести при ступенча-
ступенчатом изменении нагрузки, заметим, что в точку А необходимо
сместить участок кривой 2, продолжающийся вправо от точки Д
соответствующей моменту времени tlt При этом скорость пол-
ползучести после увеличения нагрузки оказывается резко занижен-
заниженной по сравнению с вышеизложенными теориями и с данными
эксперимента.
Особенно простой вид принимает уравнение A8.4.4) в том
случае, когда его можно записать в следующем виде:
p = v(a, T)x{t).
Здесь функция т(?)—экспериментально определяемая функция
времени. Принимая за<кон ползучести в таком виде, при посто-
постоянном напряжении и постоянной температуре мы находим
р = е — eo = v(G, T)x{t).
Последнее уравнение устанавливает подобие кривых ползучести.
В ограниченном диапазоне напряжений такое подобие прибли-
приближенно соблюдается, поэтому для кривых ползучести при посто-
постоянном напряжении можно получить вполне удовлетворительную
аппроксимацию. Мы перепишем уравнение A8.4.4) при условии
подобия кривых ползучести следующим образом:
% = v(o,T). A8.4.5)
Но это есть уравнение нелинейно-вязкого течения жидкости при
том условии, что скорость определяется по отношению к видо-
видоизмененному времени. Такая простая трактовка делает эту тео-
теорию достаточно удобной для практических приложений, хотя
явное введение времени в определяющие уравнения лишено ме-
механического смысла и приводит к легко обнаруживаемым проти-
противоречиям.
g24 гл- 18- ползучесть металлов
§ 18.5. Теория старения и расчет по изохронным кривым
Сделав первый шаг по пути отступления от механического
здравого смысла и сформулировав теорию течения с помощью
A8.4.4) или A8.4.5), мы можем сделать следующий шаг, просто
предположив, что е и о связаны между собою функциональной
зависимостью, содержащей явно время
e = f(a, t). A8.5.1)
Уравнение A8.5.1) записано для изотермических условий, тем-
температуру можно ввести в правую часть в качестве третьего ар-
аргумента. Единственное достоинство столь примитивной теории
состоит в ее простоте, но это достоинство нельзя сбрасывать со
счета. Кривые ползучести многих конструкционных материалов
оказываются весьма причудливыми, особенно если процесс пол-
ползучести сопровождается фазовыми переходами. Описать эти кри-
кривые при помощи какой-либо логически безупречной теории, на-
например теории упрочнения, в том или ином варианте было бы
чрезвычайно сложно. С другой стороны, гипотеза упрочнения,
принимающая материал однопараметрическим и меняющим струк-
структурное состояние (но не фазовый состав) только вследствие де-
деформации, к таким сложным материалам просто непригодна; для
них следует строить кинетическое уравнение по типу A8.3.1) и
A8.3.2). Уравнение A8.5.1) позволяет воспроизвести опытные
кривые пластического деформирования и последующей ползуче-
ползучести во всем их своеобразии, и погрешность при расчете, связан-
связанная с несовершенством исходной точки зрения, может быть часто
компенсирована с избытком тем выигрышем, который получается
за счет точного воспроизведения первых опытных данных.
Для использования формулы A8.5.1) бывает удобно пере-
перестраивать первичные кривые ползучести в виде так называемых
изохронных кривых. Серия кривых ползучести при разных на-
напряжениях о представляет собою графическое изображение функ-
функциональной зависимости между тремя переменными а, е и t.
При этом е и t откладываются по осям координат, величины о
служат пометками кривых. Очевидно, что этот график можно
перестроить, можно принять за оси координат ось е и ось а,
тогда значения времени t будут пометками изохронных кривых.
Схема такой перестройки показана на рис. 18.5.1 и вряд ли
нуждается в пояснении.
При обработке довольно большого опытного материала было
обнаружено, что для многих материалов изохронные кривые пол-
ползучести подобны и уравнение изохронных кривых может быть
представлено следующим образом:
а = -*« A8.5.2)
§ 18.6. РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ
625
Параметры а и р определяются из обработки кривых ползучести,
величина [J для металлов и сплавов близка к 0,3. Уравнение
о = <р(е) A8.5.3)
определяет мгновенную кривую деформирования, которая в дейст-
действительном эксперименте получена быть не может, но может быть
восстановлена из серии изохронных кривых ползучести. Опыты
показывают, что мгновенная кривая, определяемая уравнением
A8.5.3), достаточно близка к кривой быстрого деформирования
(за время порядка 1—2 секунды). По-
Поэтому вся серия кривых ползучести для
разных о может быть восстановлена
в результате испытания на кратковре-
кратковременное растяжение и испытания на
ползучесть при одном только уровне
•напряжений, что достаточно для нахож-
нахождения параметров а и [J, если функция
ф(е) известна.
Заметим, что соотношение A8.5.2)
вытекает из нелинейно-наследственной
теории, описанной в § 17.12, а именно,
из уравнения
A8.5.4)
Частный вид зависимости A8.5.2) по-
получается при условии, что оператор К*
имеет ядро Абеля, К ~ (t — т)р"*. Урав-
Уравнение A8.5.4), по-видимому, достаточно Рис. 18.5.1
хорошо описывает наблюдаемые эффек-
эффекты и в этом смысле может конкурировать с уравнением теории
упрочнения. Более того, уравнение наследственного типа описы-
описывает некоторые вторичные эффекты, которые гипотеза упрочне-
упрочнения во внимание не принимает, например, возврат после снятия
нагрузки, который наблюдается и у металлов, хотя далеко не
в такой степени, как у полимеров.
§ 18.6. Релаксация напряжений
Если элемент, в котором может происходить ползучесть, свя-
связан с упругими элементами, которые стесняют его возможные
деформации, происходит перераспределение напряжений в эле-
элементах системы. Собственно для решения задач о перераспреде-
перераспределении напряжений нужны теории ползучести, описанные в § 18.4.
Если «перемещения точек системы удерживаются постоянными, то
реакции закреплений будут со временем изменяться; этот про-
процесс называется релаксацией реакций. Релаксацией напряжений
называется процесс падения со временем напряжения в элемен-
626 ГЛ- 18- ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
те, длина которого (поддерживается (постоянной. Простейшая за-
задача релаксационного типа соответствует схеме, представленной
на рис. 18.6.1. Стержень единичной длины с единичной пло-
площадью поперечного сечения соединен последовательно с пружи-
пружиной, жесткость которой есть с. В начальный момент стержню
WH.
Рис. 18.6.1
сообщено удлинение е0, при этом напряжение в нем равно а0.
Удлинение пружины соответственно равно о0/с В дальнейшем
суммарная деформация, т. е. сумма удлинений стержня и пру-
пружины, поддерживается постоянной, следовательно, выполняется,
условие
e + -^- = eo + -f = const.
Если материал стержня ползет, то за счет удлинения стержня
укорачивается пружина, соответственно напряжение о уменьша-
уменьшается со временем. Измеряя удлинение упругой пружины, можно
определить закон релаксации или функцию o(t).
Когда жесткость пружины мала, удлинение стержня практи-
практически не влияет на величину усилия в пружине и схема испы-
испытания мало отличается от обычной схемы испытания на ползу-
ползучесть. Другой крайний случай — это случай бесконечно жесткой
пружины, когда с = оо и следовательно,
е = const. A8.6.1)
Будем называть этот крайний случай чистой релаксацией. Опыт
на чистую релаксацию в принципе неосуществим, в действитель-
действительности можно говорить лишь о некотором приближенном (воспро-
(воспроизведении соответствующих условий. Действительно, при с = оо
нельзя измерять напряжение путем измерения деформации пру-
пружины, но можно сделать эту жесткость чрезвычайно большой,
настолько большой, чтобы можно было, с одной стороны, пре-
пренебречь незначительным нарушением условия A8.6.1) и, с дру-
другой, иметь возможность измерять очень малые деформации упру-
упругого элемента с необходимой точностью.
Другая возможность и чаще применяемая на практике схема
эксперимента состоит в том, что образец ползет при постоянной
нагрузке. Установленный на нем прибор фиксирует отклонение
величины деформации от первоначально заданной и управляет
действием сервомеханизма, который уменьшает нагрузку так,
чтобы упругое сокращение восстановило первоначальную дефор-
деформацию образца. Любой прибор имеет определенный порог чув-
§ 18.6. РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ 627
стви^гельности, таким образом, опыт на релаксацию заменяется
опытом на ползучесть при ступенчато меняющейся нагрузке с
обеспечением постоянства деформации лишь в отдельные диск-
дискретные моменты.
Испытания на релаксацию по описанным причинам сложны,
дороги и не всегда надежны. Механические теории ползучести
позволяют рассчитывать процесс релаксации по данным испыта-
испытаний на ползучесть. Приведем соответствующий анализ, исполь-
используя разные теории.
Теория упрочнения. Запишем уравнение ползучести A8.4.2)
при 'степенной зависимости /(о) следующим образом:
рра = оп. A8.6.2)
Здесь безразмерное напряжение о отнесено к модулю упруго-
упругости /?, поэтому
р = е — о.
Масштаб времени изменен таким образом, что множитель в пра-
правой части перед оп сделан равным единице. Полагая е = const =
= в0, находим р = о0 — а, р =' —о. Внося эти значения в A8.6.2),
разделяя переменные и интегрируя, найдем
A~J)ac%. A8.6.3)
Формула A8.6.3) определяет время релаксации ют напряжения а0
до напряжения о. Очевидно, что и при других видах функции
/(о) задача решается квадратурами, которые ни при одном из
принятых законов ползучести не выражаются через элементар-
элементарные функции. При втором варианте теории упрочнения, чтобы
получить тот же закон ползучести при постоянном напряжении,
необходимо заменить уравнение A8.6.2) следующим:
pqa = оп+ав A8.6.4)
Здесь в случае релаксации
q == J a dp = — J a da = — (о* — а2).
Внося в A8.6.4) и выполняя интегрирование, получаем
Подынтегральное выражение в формуле A8.6.5) отличается от
гл. is. ползучесть металлов
соответствующего выражения в формуле A8.6.3) множителем
При ? < 1 и а > 1 эта величина больше единицы, поэтому фор-
формула A8.6.5) предсказывает более медленный ход кривой ре-
релаксации.
Теория наследственности. Применяя уравнение A8.5.4) к
случаю релаксации, когда е = const и, следовательно, ф = ф0, по-
получаем
а = j-^; = A — Г*) ф0. A8.6.6)
Здесь, как и в гл. 17, Г* — резольвентный оператор по отноше-
отношению к оператору X*. Проверка уравнения A8.6.6) для металлов,
по-видимому, не делалась, а для стеклопластиков она дает до-
довольно хороший результат.
Не составляет труда рассчитать ход кривой релаксации на
основе теории течения или теории старения. По существу эти
теории совершенно не приспособлены ~для описания ползучести
при переменных нагрузках, а именно так и следует рассматри-
рассматривать процесс релаксации. Тем более может показаться удивитель-
удивительным, что предсказания этих малоудовлетворительных теорий дают
не слишком большую погрешность. Нужно заметить, что назван-
названные теории для своего применения не требуют каких-либо анали-
аналитических аппроксимаций, тогда как уравнения типа A8.6.2)
удовлетворительно описывают лишь первые участки кривых пол-
ползучести структурно устойчивых сплавов.
§ 18.7. Установившаяся ползучесть при сложном
напряженном состоянии
Под установившейся ползучестью мы будем понимать такой
процесс, когда скорость накопления необратимой деформации
представляет собою функцию только напряжения и температуры,
поэтому при постоянных напряжении и температуре скорость
ползучести постоянна. Полагая
е = е0 + р,
мы будем считать, что
P = v(c, Г).
Что касается величины е0 мгновенной деформации, по предло-
предложению Удквиста в нее можно включать также дополнительную
деформацию ползучести, накопленную на первом неустановив-
неустановившемся участке, как это показано на рис. 18.7.1.
§ 18.7. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
629
Следует иринять, например, что
eo = ПГ + i
A8.7.1)
Здесь Omax — наибольшее значение напряжения, достигнутое в
процессе нагружения. Пользование формулой A8.7.1) можно по-
пояснить следующим образом. Предположим, что приложенное на-
напряжение меняется в соответствии с графиком рис. 18.7.2.
На участке ОА напряжение возрастает, величина деформации
g(o) определяется в каждый момент действующим напряжением
о. После точки А напряжение сначала убывает, потом начинает
возрастать. Пока о ^ оА, величина пластической (или условно
пластической) деформации остается постоянной, равной g(cA)-
После точки В, когда становится о > оА, пластическая дефор-
деформация по-прежнему будет определяться действующим напряже-
напряжением о.
" t
Рис. 18.7.1
Рис. 18.7.2
Уравнения установившейся ползучести достаточно хороша
отражают действительное поведение материала в двух случаях:
а. Процессы большой длительности {десятки и сотни тысяч
часов) при умеренных напряжениях и температурах. На кривых
ползучести вторые участки весьма протяженны и можно прини-
принимать во (внимание только их.
б. Кратковременная ползучесть {секунды и минуты) при вы-
высоких температурах и напряжениях. В этих условиях упрочне-
упрочнение не происходит, ползучесть начинается с постоянной ско-
скоростью, которая потом начинает увеличиваться вследствие тре-
щинообразования. Описание соответствующего механизма будет
дано в гл. 19, трактующей вопросы разрушения.
Для произвольного напряженного состояния мы сделаем еще
один шаг по пути упрощения теории и будем пренебрегать мгно-
мгновенной деформацией, как упругой, так и пластической. Полагая
Рч = ?ij, запишем закон течения следующим образом:
Единственное условие, налагаемое на функции у#, состоит в том,
41 Ю. Н. Работнов
630 ГЛ- 18' ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
чтобы мощность диссипации была положительной
VijGij > 0.
Обычно предполагается, что зависимость скоростей ползучести
от напряжений потенциального типа, т. е. существует потенциал
скоростей ползучести Ф(о>«) такой, что
е„~^-. A8-7.2)
Отсюда преобразованием Лежандра получаются обратные соот-
соотношения
а« = -^-, и = о&ц-Ф. A8:7.3)
dei}
Существование потенциалов Ф и С/, строго говоря, не является
следствием каких-либо общих принципов механики или термо-
термодинамики. Некоторое обоснование принятой гипотезы может
быть сделано в результате применения принципа типа Онзагера
или Циглера в термодинамике необратимых процессов. С другой
стороны, можно соответствующим образом переформулировать
постулат Друкера, чтобы получить требуемую потенциальную
зависимость. Здесь мы не будем развивать ни ту, ни другую
точку зрения. Соотношения вида A8.7.2) и A8.7.3) содержат в
себе достаточно широкие возможности для воспроизведения экс-
экспериментальных данных, с одной стороны, с другой — обладают
серьезными аналитическими преимуществами. Если заменить в
A8.7.2) и A8.7.3) скорости деформации через деформации, мы
получим соотношения нелинейной теории упругости или теории
пластичности деформационного типа. Для этих теорий справед-
справедливы известные вариационные принципы, которые просто пере-
перефразируются на случай ползучести. Методы решения задач: де-
деформационной теории пластичности и теории установившейся
ползучести совершенно одинаковы. Именно поэтому мы не при-
приводим каких-либо примеров решения задач по деформационной
теории пластичности, имея в виду изложить некоторые простей-
простейшие задачи здесь, применительно к случаю ползучести.
Необходимо сделать, однако, одну оговорку. Принимать ско-
скорость деформации ползучести равной производной от самой де-
деформации можно только, когда деформации малы. В противном
случае нужно вводить скорости деформации е^- каким-либо иным
способом. Здесь мы не будем рассматривать вопрос о ползучести
при больших деформациях и не будем пытаться построить соот-
соответствующие уравнения.
Что касается выбора структуры зависимости, например, по-
потенциала Ф от компонент тензора напряжений, естественно пред-
предположить, что потенциал зависит от некоторой однородной
функции компонент тензора oti. Эта однородная функция s(o>y)
§ 18.7. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ 631
без нарушения общности может быть выбрана как функция пер-
первой степени, так что
Полагая Ф'(s)= v(s), перепишем уравнения A8.7.2) следующим
образом:
Частные производные ds/doy представляют собой однородные
функции нулевой степени от oti. Это значит, что шесть частных
производных зависят не от шести аргументов, а от пяти, напри-
например от отношений компонент ozj к одной из них. Отсюда следует,
что, исключая эти отношения, мы найдем тождественное соотно-
соотношение между ds/dGn, которое всегда можно записать следующим
образом:
(%) A8-7.5)
Полученное тождественное соотношение необходимым образом
однородно относительно своих аргументов, поэтому функция мо-
может быть принята однородной функцией первой степени.
Применяя оператор со к обеим частям соотношений A8.7.4)
и учитывая наложенное условие однородности, получим
ю(е«)= v = v{s). A8.7.6)
Величина s представляет собою приведенное напряжение, вели-
величина v — приведенную скорость деформации. Уравнение A8.7.6)
определяет связь между и и s совершенно так же, как при рас-
растяжении, когда устанавливается связь между скоростью дефор-
деформации 6 и напряжением о:
е = v(g).
Бывает удобно определять приведенное напряжение s так, чтобы
при простом растяжении было s = о, и функцию v(s) так же
следует определять из опыта на ползучесть при растяжении.
Тогда приведенная скорость z; = G)(etj) автоматически обратится
в скорость деформации растяжения. Умножая A8.7.4) на <5ijy
найдем мощность диссипации
D = Оцгъ = sv(s).
При этом учтено, что по теореме Эйлера Gijds/dGij = s. Определяя
потенциал напряжений по формуле A8.7.3), найдем
Вследствие A8.7.6) этот потенциал выражается через v и, следо-
воречиям.
а* = *М-щ;- <18-7-7>
41*
632 . гл-18- ползучесть металлов
§ 18.8. Частные формы закона ползучести
Рассмотрим некоторые наиболее применяемые частные формы,
которые принимают зависимости предыдущего параграфа.
1. Приведенное напряжение s пропорционально октаэдриче-
скому касательному напряжению. Положим
„--i-^ij. A8.8.1)
Определенная таким образам величина s = а0, называемая ин-
интенсивностью напряжений, связана с т0 следующим образом:
Tq g Oq.
Легко проверить, что при простом растяжении напряжением а
s = а. Дифференцируя A8.8.1) по ati, получим
Возводя 1в квадрат и свертывая, находим, что
2 ds ds .
з "^-^7=1-
Итак,
N1/2
) . A8.8.3)
При простом растяжении несжимаемого материала 8ц = е, е22 —
= взз = — 72е, 6tj = 0 {i^=j) и из формулы A8.8.3) следует
у = 6. Величину у, определяемую формулой A8.8.3), называют
интенсивностью скоростей деформации.
2. Приведенное напряжение пропорционально наибольшему
касательному напряжению. Относя тензор напряжений к глав-
главным осям, положим
s = Gi — a3 (gi > a2 > a3). A8.8.4)
Производные ds/dci^l, ds/do3 = — 1, они связаны тождествен-
тождественным соотношением
2
Таким образом,
у=4-(81-8з)- A8-8-5)
При этом скорость ползучести е2 в направлении промежуточного
по величине главного напряжения а2 равна нулю. Особо следует
рассмотреть тот случай, когда два главных напряжения равны
§ 18.8. ЧАСТНЫЕ ФЮРМЫ ЗАКОНА ПОЛЗУЧЕСТИ 633
между собою. Пусть, напршмер, ct = а2 > а3. Приложим к телу
всестороннее сжатие интенсивностью р = Gi = a2. Поскольку по-
потенциал ползучести принятг независимым от гидростатической
составляющей, распределение скоростей ползучести от этого не
изменяется. Но теперь напряжения в направлениях 1 и 2 обра-
обратятся в нуль, остается только сжимающее напряжение —р + а3
в третьем главном направлешии. Считая функцию v(s) нечетной,
т. е. допуская, что поведенже материала при растяжении и сжа-
сжатии одинаково, получим
е3=- — v(p — а3). A8.8.6)
Что касается скоростей в двух других направлениях, их вели-
величины могут быть произвольными, они связаны только условием
несжимаемости со скоростью е3. Следует напомнить, что совер-
совершенно аналогичное положение было в теории идеальной пластич-
пластичности при условии лластичшости Треска — Сен-Венана. Условие
равенства двух главных на.пряжений слишком частно, за него
приходится расплачиваться допущением известной кинематиче-
кинематической свободы.
Несколько более сложные зависимости, например, учитываю-
учитывающие роль не только второгоо инварианта девиатора напряжений,
но также третьего инварианта, иногда применяются для интер-
интерпретации опытных данных, ,для решения задач они оказываются
слишком сложными. Так, мо»жно принять
J A8.8.7)
Такой выбор параметра ? ошределяется очень простым выраже-
выражением его через угол подобия: девиатора Ф (см. § 7.7), а именно,
? = cos 30.
Представим главные напряжения по формулам G.7.9):
2
&i = а -й- -у а0 cos О, ...
Найдем, что скорости деформации по формулам A8.7.4) выра-
выразятся таким образом:
?i = v(s)(gcos # + 3g'sin3dsmd), ... A8.8.8)
Следующие формулы получаются заменой Ф на О — 2я/3 и
О — 4я/3 соответственно. Прои этом аргумент функции g, а имен-
именно ? = cos 30, не меняется. Вывод соотношений A8.8.8) очевиден
в принципе, но требует проюедения выкладок, которые мы здесь
опускаем.
634 гл- 18- ползучесть металлов
§ 18.9. Труба под действием внутреннего давления
Решение этой задачи особенно просто в том случае, когда тру-
труба имеет донья и внутреннее давление вызывает осевую растяги-
растягивающую силу. В этом случае деформация оказывается плоской,
т. е. скорость деформации в направлении оси трубы ег = 0. Со-
Сохраним обозначения § 8.12. Предположим заранее, что ez = 0.
Как мы увидим, это упрощающее предположение несущественно.
Очевидно, что скорости деформации будут выражаться через ра-
радиальную скорость ползучести и по тем же формулам, по кото-
которым в § 8.12 были выражены деформации через радиальное пе-
перемещение, а именно, er = dv/dr, еф = v/r. Из условия несжимае-
несжимаемости
Отсюда, интегрируя, находим v = l/3c/Br) и, следовательно,
р _ V3" с __ 1/3" с
Здесь с — неопределенная пока постоянная интегрирования, мно-
множитель УЗ/2 введен для удобства. Определим по формуле A8.8.3)
величину у, а именно, v = c/r2. Следует заметить, что если ггФ0у
то для достаточно длинной трубы эта величина постоянна, ввести
в условие несжимаемости еще одно постоянное слагаемое и про-
проинтегрировать получившееся уравнение не составило бы ника-
никакого труда. Вследствие условия гг = 0 должно быть в соответ-
соответствии с законом ползучести A8.7.4) при условии A8.8.1) аг =*
в V2(ar + оФ) и по формуле A8.8.3)
s = -V- К - ог) = s -V , A8.9.1)
где s{v)— известная функция, определяющая закон ползучести.
Уравнение равновесия в цилиндрических координатах имеет вид
5Г+ г
Внося сюда A8.9.1), получим
1 s(v),
ctv.
йсс 2_ / cVdr 1 s(v
Уз \ ?) * Уз »
Интегрируем это уравнение при граничном условии аг(я) = —9-
j. A8.9.2)
§ 18.9. ТРУБА ПОД ДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ 635
Теперь легко находим оф и сг:
l^^M- A8-9-3)
Величина v зависит от неопределенной пока константы с, кото-
которую можно найти из второго граничного условия сг(Ь) = О. Это
условие приводит к следующему уравнению:
<!i*? = 0. A8.9.5)
va
При любом задании функции s(v) квадратуры могут быть выпол-
выполнены хотя бы численно. Таким образом, формулы A8.9.2) —
A8.9.5) полностью решают задачу. Остается проверить утверж-
утверждение о том, что состояние плоской деформации осуществляется
в трубе с доньями. Вычислим осевую силу
Ъ vb
Р = 2к \azr dr = — пс\ az —.
Внесем сюда выражение A8.9.4) для а2. Заметим, что при ин-
интегрировании первого члена, равного —q, нет необходимости
переходить к переменной интегрирования у, этот член дает со-
составляющую осевой силы, равную — nq(b2 — а2). Проинтегри-
Проинтегрируем оставшуюся часть
*ь *ъ vb
С dv Сs (v) j Сs {v) j
J у2 J у J v2
vb
Таким образом,
Р = — яд(Ь2 — а2)+ щЪ2 = яда2,
что и доказывает сделанное ранее предположение.
Заметим, что приведенное элементарное решение путем про-
простой перефразировки переносится на случай расчета пластиче-
пластической трубы, просто функция s определяет в этом случае не ско-
636 ГЛ- 18' ПОЛЗУЧЕСТЬ МЕТАЛЛОВ
рость ползучести, а величину напряжения, соответствующую де-
деформации v. Уравнение A8.9.5) позволяет определить констан-
константу с, а следовательно, и радиальное перемещение.
При степенном законе ползучести решение выписывается
в замкнутом виде; полагая в уравнениях A8.9.2) — A8.9.5)
получим в результате элементарных вычислений следующие
формулы:
\ ( Ь \]
) '
A8-9.6)
P = b/a.
В задачах теории пластичности степенной закон редко дает
удовлетворительное описание экспериментальных кривых. Как
правило, приходится решать упруголластическую задачу; в рам-
рамках деформационной теории пластичности нет разницы между
формулами, описывающими упругое и пластическое состояния,
но функция s(v) оказывается линейной для достаточно малых
значений v и нелинейной после достижения предела текучести.
Это обстоятельство, естественно, усложняет решение задачи, хотя
трудности не носят принципиального характера. Более серьезным
моментом служит то, что предположение о несжимаемости ма-
материала для упругопластических тел, строго говоря, не выпол-
выполняется. Имеются многочисленные решения, учитывающие эффект
сжимаемости, нам не кажется, что получаемое при этом уточ-
уточнение настолько серьезно, чтобы была необходимость излагать
соответствующие результаты.
§ 18.10. Ползучесть вращающегося диска
Задача о расчете на ползучесть вращающегося диска паровой
турбины была первой серьезной технической задачей, которая
вызвала необходимость разработки теории ползучести, что было
отмечено в начале этой главы. Эта задача не стала менее акту-
актуальной и в наше время, коода газовая турбина служит необходи-
необходимым элементом турбовинтового и турбореактивного самолета. По-
Повышение рабочих температур влечет за собою разработку новых
жаропрочных сплавов, для которых задачи расчета на прочность
ставятся и решаются примерно теми же методами, что и для
паровых турбин.
Число публикаций, посвященных методам расчета вращаю-
вращающихся дисков, исключительно велико. В то время, когда кон-
конструктор не располагал электронно-вычислительной техникой,
§ 18.10. ПОЛЗУЧЕСТЬ ВРАЩАЮЩЕГОСЯ ДИСКА 637
усилия специалистов были направлены на разработку методов
последовательных приближений, пригодных и достаточно удоб-
удобных для ручного счета. В реальном диске всегда существует не-
неоднородное температурное поле, поэтому параметры, фигурирую-
фигурирующие в принятом законе ползучести, представляют собою функции
радиуса. Диск имеет переменную толщину ft (г), при этом из
технологических и конструктивных соображений профиль де-
делается таким, что функция h (r) не допускает простого аналити-
аналитического задания вЬ всей области ее определения.
Не останавливаясь на описании метода последовательных
приближений, которое следует искать в специальной литературе,
поясним его идею. Из дифференциального уравнения равновесия,
составленного с учетом переменности толщины, радиальное на-
напряжение Gr определяется как некоторый функционал от аф:
После этого из уравнения совместности деформаций и закона
ползучести определяется аф как функционал от аг и аф, содер-
содержащий неизбежным образам константу С:
аФ = /г2(аг, оФ, С).
К решению полученной системы уравнений применяется метод
последовательных приближений, за исходное приближение вы-
выбирается некоторое заданное распределение напряжения аФ. Если
функционал Fi определяется единственным образом, то функцио-
функционал F2 может быть представлен в различных формах, от выбора
вида этого функционала зависит быстрота сходимости процесса
последовательных приближений. Нужно отметить, что в некото-
некоторых вариантах этот метод дает поразительно быструю сходимость.
Здесь мы изложим идею метода прямого численного интегри-
интегрирования, который при современных вычислительных средствах
реализуется достаточно быстро и просто. В диске возникает
плоское напряженное состояние, характеризуемое главными на-
напряжениями аф и аг. Введем вместо них две другие переменные,
а именно, s = а0 и угол Э так, что
2(+-?). A8.10.1)
Внося в выражение для а0
ffo = <?г + сГф — агсгф,
мы получим тождество s = а0. Вычисляя компоненты скорости
деформации по формулам A8.8.2), найдем
+ -|Л еф =-|-i; cos (в--?-). A8.10.2)
При а0 = const формулы A8.10.1) определяют в плоскости сг, аф
638 гл- 18- ползучесть металлов
эллипс, каждая точка которого может быть помечена определен-
определенным значением 0. На рис. 18.10.1 показана часть этого эллипса
с пометками значений 0 для некоторых точек. Эта схема бывает
полезной при установлении области изменения угла 0. Диффе-
Дифференциальное уравнение равновесия в предположении постоянства
распределения напряжении по толщине получается так же, как
в § 8.12, с той разницей, что вместо величин а
в уравнения входят величины ha. Кроме того,
добавляются силы инерции. В результате урав-
уравнение получается следующим:
1Г (hor) + h ^^- + рсо%г = 0.
Примем за независимую переменную величину
e = in-?- = ing.
Рис. 18.10.1
Здесь через Ъ обозначен наружный радиус диска.
Вместо толщины h введем безразмерную функцию
Здесь hQ — произвольная константа, имеющая размерность длины,
некоторая характерная толщина диска. Внесем выражения
A8.10.1) в уравнение равновесия, заменим дифференцирование
по г дифференцированием по 5 и вшедеод переменную г\ вместо h.
После некоторых преобразований получим следующее уравнение:
к.
6
я
/
4
т
ж
/Т
'fir e&
т ViexpB?-i|)) = 0, -ф = 1п-|-, т = ^ A8.10.3)
(а*— произвольная константа). Поскольку еф = v/r, zr =
скорости гг и еф удовлетворяют следующему уравнению сов-
совместности:
Положим z=In (и/г^), где е* — произвольная константа, имеющая
размерность скорости деформации. Внося в уравнения совмест-
совместности выражения A8.10.2) и учитывая введенное обозначение,
получим
i| Sin (e - -J-) - |g- cos (б - -?-) - /3 cos 0 = 0. A8.Ю.4)
Система уравнений A8.10.3) и A8.10.4) достаточно проста для
ее численного решения. Неудобство состоит в том, что гранич-
§ 18.11. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН 639
яые условия поставлены на внутреннем радиусе г = а и наруж-
наружном радиусе r==b, поэтому приходится применять метод прогон-
прогонки, задаваться вторым граничным условием при г = а, например,
и повторять расчет до тех пор, пока не окажется выполненным
условие при г=Ъ. Для расчетов подобного рода существуют
стандартные программы. Подобные методы, основанные на пред-
представлении напряжений и перемещений формулами типа A8.10.1)
и A8.10.2), применялись для задач пластичности и ползучести
Соколовским и Малининым.
§ 18.11. Установившаяся ползучесть пластин
Принимая для пластины гипотезу нормальных элементов
Кирхгофа, положенную в основу технической теории изгиба
упругих пластин (см. § 12.4), мы представим поле скоростей
деформаций © пластине следующим образом:
Здесь е^р — скорости деформации срединной поверхности, иар —
скорости изменения кривизны, которые связаны с прогибом
w(Xa) следующим образом:
Если закон ползучести для материала известен, то известен по-
потенциал напряжений ?/(еар), так что напряжения выражаются
следующим образом:
dU
a
Вследствие принятого выражения для еар функцию U можно
рассматривать как функцию е?р и иар, содержащую z как пара-
параметр. При этом, очевидно,
dU dU 1 dU
,, ,
Теперь мы можем написать
dU
a
Проинтегрируем обе части этого равенства по z от —h до +h.
В левой части получится усилие Гар, которое выражается сле-
следующим образом:
]J!LJ!?. A8.U.2)
640 гл- 18- ползучесть металлов
Здесь
+ h
U* = J и(8ор__ ZKa^ dZt A8.11.3)
—Л
Совершенно аналогичным образом, вводя изгибающие моменты
по формулам
+ h
Ма$ = j zoa$ dz
—h
и используя соотношение A8.11.1), получим
Мар = ^. A8.11.4)
Очевидно, что, применяя преобразование Лежандра, можно
построить потенциал скоростей деформации
Ф (Г«р, Мар) - Г^б^ + М^Ъц ~ U
такой, что
0 дФ дФ /ло лл rv
е«р = ^' ^=Ш7Р- A8л1-5)
Фактическое вычисление потенциала С/* по формуле A8.11.3)
встречает затруднения, получить явное его выражение не удает-
удается. Обычный путь, по которому идут разные авторы в тех слу-
случаях, когда и усилия Та$ и моменты Л/аР играют одинаковую роль
и ни теми, ни другими пренебрегать нельзя, состоит в той или
иной аппроксимации потенциала (обычно потенциала скоро-
скоростей Ф) с помощью некоторого подходящего выражения, напри-
например квадратичной формы относительно Г«р и Ма$. Если Уар = О
или Жар = 0, то потенциал легко вычисляется. В первом случае
получается обычный случай плоского напряженного состояния;
мы рассмотрим только случай изгиба. Если еар == — zxap, то v — zk
вследствие однородности, к представляет собою выражение, обра-
образованное из компонент тензора хар точно таким же способом,
как v было образовано из компонент тензора е«р. Потенциал мо-
моментов будет теперь определяться следующей формулой:
hh
A8.11.6)
При этом считалось, что ползучесть материала при растяжении
и сжатии описывается одинаковым законом, поэтому ?/(?)—чет-
?/(?)—четная функция своего аргумента. Теперь
M** = U*'(k)?-. A8.11.7)
Функция к есть однородная функция первой степени, следова-
§ 18.11. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН 541
тельно, дк/дка$ связаны тождественным соотношением и сущест-
существует такой инвариант первой степени от компонент Д/аР, т(Ма$),
что
** = Ф№щ2 A8.11.8)
Величины тик связаны однозначной зависимостью, которая
может быть установлена, например, из опыта на цилиндрический
изгиб.
Если принять критерий 1 § 18.8, то
W2 = М2 = М^ + М22 _ MiiM22 + _|__ (M22 + М2г) A8.Ц.9)
и соответственно
ft» = XS = 4" [xi'l + «22 + ХцХ,, + 4 (*» + "")]• A8.11-10)
Формулы, выражающие скорости изменения кривизн через мо-
моменты, будут следующие:
1м
1м ) у, (М Ljfcf
О 1VI22h Х22 — я^ liK/22 о JKi
U / 0 ^
xu = -|-^^-Afu. A8.11.11)
Точные решения, полученные © результате численного интегри-
интегрирования, удается найти только для круглых симметрично загру-
загруженных пластинок. Умножая уравнения равновесия в цилиндри-
цилиндрических координатах на z и интегрируя по толщине, мы получим
следующее дифференциальное уравнение для изгибающих мо-
моментов:
Здесь iVr — перерезывающая сила, которая в свою очередь опре-
определяется через поперечную нагрузку q(r) в результате интегри-
интегрирования уравнения
Это уравнение отличается от уравнения равновесия для вращаю-
вращающегося диска только видом свободного члена. Скорости измене-
d2w I dw v
ния кривизн хг — —2~, хф = -г—, эти формулы совершенно тож-
тождественны с теми формулами, которые выражают ег и еф через
радиальную скорость, поэтому уравнение совместности буквально
совладает с соответствующим уравнением для диска. Моменты
выражаются через т и ф по формулам, совершенно подобным
642 гл-18« ползучесть металлов
формулам A8.10.1), а выражения для скоростей изменения кри-
кривизны аналогичны A8.10.2). Отсюда следует, что процедура чис-
численного интегрирования, предложенная для вращающихся дис-
дисков, целиком переносится на задачи об изгибе пластинок. Нам
нет необходимости рассматривать еще раз в деталях эту лишь
слегка видоизмененную процедуру. Заметим, что введение в ка-
качестве независимой переменной логарифма радиуса и в качестве
искомой функции логарифма т подобно тому, как это было сде-
сделано в § 18.10, совсем не обязательно; все рассмотрение можно
вести в исходных естественных переменных.
Применения критерия наибольшего касательного напряжения
(пункт 2 § 18.8) приводит к тому, что т принимает одно из трех
возможных значений:
Для каждого из участков, на которых выполняется одно из этих
трех услсхвий, решение строится весьма просто. Так, например,
i л/г i I dw л .
если т = \Мг\, то кф = -гг = и и, следовательно, w не зависит
от г. Если 7тг= |Мф|, то Kr = d2w/dr2 = 0 и пластинка изгибается
по конической поверхности. Вся трудность состоит в том, что
границы участков по радиусу пластины заранее неизвестны и
нахождение этих границ встречает определенные трудности, ко-
которые иногда преодолеваются сравнительно легко, а иногда их
преодоление требует труда и изобретательности. Во всяком слу-
случае каждая задача при таком подходе требует специального рас-
рассмотрения и для решения таких задач необходимы каждый раз
особые приемы. В 40-х—50-х годах как в теории ползучести, так
и в теории пластичности решалось очень много осесимметричных
задач для дисков и пластин по критерию приведенного напряже-
напряжения, заданного кусочно линейной функцией (автор также не из-
избежал этого всеобщего увлечения). При современной вычисли-
вычислительной технике, по-видимому, более правильно и рационально
пользоваться критерием типа Мизеса, один раз составленная и
отлаженная программа выдает результаты совершенно единооб-
единообразным способом для всевозможных нагрузок и всевозможных
граничных условий. Решения, использующие кусочно линейные
функции, сейчас представляют скорее исторический интерес и
здесь рассматриваться не будут.
§ 18.12. Неустановившаяся ползучесть.
Изотропное упрочнение
Естественное распространение сформулированной в § 18.4
теории упрочнения на общий случай трехосного напряженного
состояния заключается в том, что потенциал напряжений Ф
считается зависящим не только от напряжений, но также от
§ 18.12. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ 643
некоторого скалярного параметра упрочнения q:
Ф = Ф(«, q). A8.12.1)
В этой записи мы сохранили предположение о том, что зависи-
зависимость от напряжений otj сводится к зависимости от приведенного
напряжения s, представляющего собою однородную функцию
первой степени от Oij. Параметр упрочнения может быть опре-
определен различными способами. В соответствии с тем анализом,
который был приведен в § 18.4, мы рассмотрим два варианта,
а именно,
Qi = ^(Pij)dt1 A8.12.2)
о
t
A8.12.3)
Здесь pij — скорость пластической деформации, pi5 = ei5 — яыы
В задачах неустановившейся ползучести необходимо (выделять
деформацию ползучести из полной деформации, поэтому закон
течения будет записываться следующим образом:
Возвращаясь к определениям параметра упрочнения A8.12.2) и
A8.12.3), замечаем, что при одноосном растяжении <7i=p, сле-
следовательно, первый критерий служит обобщением первого ва-
варианта теории упрочнения. Величина q2 представляет собою рас-
рассеянную работу и обобщает естественным образом меру упрочне-
упрочнения во втором варианте теории, рассмотренной в § 18.4. При
определении величин рц мы сделали самое общее предположение
о том, что материал анизотропен, для изотропного случая и не-
сжимающего материала
_ - \_-
Pij — eij 2|X °ti'
Учет сжимаемости не вызывает, очевидно, затруднений.
Рассмотрение двух вариантов выбора параметра упрочнения
производится совершенно одинаково и приводит к чрезвычайно
близким результатам, поэтому мы проделаем анализ лишь для
¦случая первого, обычного варианта теории упрочнения, соответ-
соответствующего уравнению A8.12.2). Простейшее предположение
о структуре уравнения A8.12.4) будет состоять в том, что пра-
правая часть его есть степенная функция от q (индекс опущен) и s.
Итак,
h)ik- {18Л2-5)
644 гл- 18- ползучесть металлов
В одномерном случае s = const отсюда следует
р =
т. е. степенной закон ползучести как по напряжениям, так и по
времени. Предположим теперь, что тело нагружено некоторой
системой сил Qi, которым соответствуют перемещения q{. Неко-
Некоторые из перемещений qk могут быть зафиксированы, соответ-
соответствующие реакции Qk релаксируют. Другие силы Qs заданы как
функции времени, например постоянны. Перемещения qs ищутся
как функции времени.
Решение задач неустановившейся ползучести с помощью оп-
определяющего уравнения A8.12.5) достаточно сложно, оно может
быть выполнено лишь численно шагами по времени, притом на
каждом шаге необходимо решать задачу о неустановившейся
ползучести при постоянном д, зависящем от координат. Однако
для определения перемещений отдельных точек и нахождения
закона релаксации связей можно применять излагаемый ниже
приближенный метод.
Положим
Это соотношение представляет собою разложение перемещения q{
на две части: pt — связанную с ползучестью и упругую $aQj. Та-
Такое разложение в действительности невозможно, ползучесть ме-
меняет распределение напряжений в теле и, следовательно, его
упругую деформацию. Тем не менее мы сделаем такое допуще-
допущение; величины $ц, коэффициенты влияния, находятся из решения
обычной задачи теории упругости.
Предположим теперь, что для рассматриваемого тела решена
задача установившейся ползучести в соответствии с определяю-
определяющим уравнением
PlJ~s *V
В результате этого решения найден потенциал ползучести Q,
выраженный через силы Q{. Этот потенциал будет однородной
функцией степени п от Q{, поэтому может быть представлен как
Qn, где Q — однородная функция первой степени. После этого
скорости обобщенных перемещений выразятся следующим об-
образом:
Ь = (?Пщ- A8-12-7)
Предположим теперь, что для нашего тела, для которого мы хо-
хотим решать приближенную задачу неустановившейся ползучести,
предварительно решены две (вспомогательные задачи.
§ 18.12. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ 645
а. Задача теории упругости, в результате которой найдены ко-
коэффициенты [iy в формуле A8.12.6).
б. Задача установившейся ползучести, в результате чего из-
известна функция Q{Qi), определяющая скорости установившейся
ползучести по формулам A8.12.7).
Построим теперь следующую систему уравнений:
Д-- A8Л2-8)
Она имеет ту же структуру, что и система A8.12.5), но в ней
фигурируют только внешние силы и скорости точек их прило-
приложения. Осталось определить функционал Р первой степени от-
относительно скоростей пластического течения р{. Применяя ту
же идею, которая была использована при определении парамет-
параметра gt формулой A8.12.2), заметим, что частные производные
dQ/dQi представляют собою однородные функции нулевой степе-
степени относительно Qi, поэтому между ними существует тождествен-
тождественное соотношение
Функция Q может быть сделана однородной функцией первой
степени своих аргументов. Теперь положим
A8.12.9
Типичная проблема релаксационного типа формулируется следу-
следующим образом: к системе приложены две обобщенные силы —
сила (>i, которая остается постоянной, и реакция закрепления
Q2, которой соответствует зафиксированное перемещение д2. Оп-
Определим функцию Q таким образом, чтобы было Q(Qi, 0) = (?i,
(?@> (?2)=(?2- Уравнения ползучести A8.12.8) запишутся сле-
следующим образом:
Pi = iii-Р12Ф2 = T+^Qn^ л = -P22<?2-r+^QnW2'
A8.12.10)
Положим x(t)=Q2/Qu Q = Qif(x). Тогда
-^ = /(*)-*/'(*), wrnx)m
Вследствие однородности функции Q
p2
Разделим первое уравнение A8.12.10J на второе и учтем
546 гл 18- ползучесть металлов
введенные обозначения х и f(x). Получим
С другой стороны,
Теперь выражение параметра упрочнения запишется следующим
образом:
Р = р^ Ja^-Zjf, ijdx = $22QlS(x). A8.12.11)
При этом интегрировании было учтено условие (V@) = Qu сле-
следовательно, при ? = 0 х = \. Это условие всегда можно поставить,
определив надлежащим образом обобщенные силы. Теперь второе
из уравнений A8.12.10) может быть проинтегрировано, а именно,
мы получаем
¦
¦ L A8.12.12)
Это и есть искомый закон релаксации. Что касается перемещения
qu оно легко находится в результате интегрирования первого
уравнения A8.12.10).
Последнее замечание будет относиться к возможности выбора
функции Q однородной первой степени относительно Qlm Если
показатель п достаточно велик, то в качестве функции Q можт.о
бывает принять функцию текучести для задачи предельного со-
состояния. Так, для балки, изгибаемой моментом М и растягивае-
растягиваемой силой Г, условие предельного состояния будет
М + Р = const. A8.12.13)
Здесь меры момента и силы выбраны таким образом, чтобы
в условии пластичности не фигурировали явно какие-либо кон-
константы. Левая часть этого условия неоднородна относительно М
и Г, поэтому нам следует найти эквивалентное однородное вы-
выражение.
Рассмотрим уравнение
Полагая о = ±1, мы получим A8.12.13). Разрешим это уравне-
уравнение относительно о и положим о = ±1. Получим
j(M+ VM* + 4Г2) = ± 1.
§ 18.13. УСТОЙЧИВОСТЬ ПРИ ПОЛЗУЧЕСТИ 647
Теперь мы можем принять
Q = у (М + VM* + 42'2). A8.12.14)
Выражение A8.12.14) будет однородным первой степени относи-
относительно Ж" и Г.
§ 18.13. Устойчивость при ползучести
Поскольку ползучесть неограничена и деформация при сколь
угодно малом напряжении за достаточное время может достичь
сколь угодно большой величины, то любой процесс ползучести
может быть охарактеризован как неустойчивый. Рядом авторов
(и автором этой книги в том числе) делались попытки построе-
построения некоторых условных критериев устойчивости бифуркацион-
бифуркационного типа. В применении к сжатому стержню это означает сле-
следующее. Предположим, что под действием посто-
постоянной сжимающей силы стержень равномерно IF
сжимается. В некоторый момент времени он от-
клоняется от прямолинейной формы. Если откло-
отклонение мало, то уравнения теории ползучести ли-
линеаризируются. Вообще говоря, созданный прогиб
будет неограниченно расти, но при использова-
использовании уравнений теории упрочнения может возник-
возникнуть такое положение, что прогиб будет снача-
сначала убывать до некоторой величины и только
потом начнет расти. Условие начального убыва- -F
ния прогиба может трактоваться как условие
устойчивости в некотором условном смысле. Вы- Рис. 18.13.1
бирая другие типы возмущения, например, пред-
предполагая стержень начально искривленным или эксцентрично
сжатым, авторы принимали за достижение критического состоя-
состояния момент, когда на кривой прогиб — время обнаруживалась не-
некоторая характерная точка перехода от медленного его измене-
изменения к быстрому. Не касаясь этих результатов, рассмотрим здесь
приближенное решение задачи о выпучивании сжатого стержня
с сечением в форме идеального двутавра. Это сечение схемати-
схематически изображено на рис. 18.13.1. Две полки с одинаковой пло-
площадью поперечного сечения F/2 соединены стенкой, которая вос-
воспринимает перерезывающую силу, но не принимает участия в
сопротивлении изгибу. Будем считать, что расстояние между
полками велико по сравнению с их толщиноч и распределение
напряжений в них равномерно, о = о+ в верх1 ей полке и о=*о~
в нижней. Тогда
648 гл- 18- ползучесть металлов
Принимая закон уотановившейся ползучести в виде
е =
положим
Fon* M~ 1
тогда
Если 8 — скорость деформации оси стержня, х — скорость из-
менения кривизны, то скорости деформации верхней и нижней
полок будут 8 + xh и е — xfe соответственно. Учитывая возмож-
возможность положительных и отрицательных знаков напряжений и
знаков скоростей соответственно, нам будет удобно записывать
основной закон ползучести в виде A8.2.1), а именно,
8 =
Поэтому
е = -i [\N + МI71 (N + М) + \N — М\п~г (N —
, A8.13.1)
yh = ±[\N + МI71 (N + M) - \N-M Г (N- М)].
Идеальный двутавр заменяет реальный стержень, имеющий две
оси симметрии. Площадь F должна быть, очевидно, та же, что
у реального стержня. Осталось подобрать размер h так, чтобы
при изгибе идеальный двутавр вел себя так же, как реальный
стержень. Предположим, что последний имеет две оси симметрии,
высота его // и переменная ширина Ъ. Положим
Здесь у — расстояние от оси, проходящей через центр тяжести.
Тогда
л
A8.13.2)
Рассмотрим теперь стержень с сечением в форме идеального
двутавра длиной Z, шарнирно опертый по двум концам и сжатый
силой Р. Подобно тому как это делалось в § 4.2 при выводе
критической силы Эйлера, мы должны принять N = —Р, М = Pw,
к = —d3w/dz2dt. Возвращаясь к обычным обозначениям N ж М
в формулах A8.13.1), мы получим из второй из них следующее
§ 18.13. УСТОЙЧИВОСТЬ ПРИ ПОЛЗУЧЕСТИ 649
дифференциальное уравнение:
Введем безразмерный прогиб w = w/h и безразмерную коорди-
координату ? = zM, тогда уравнение перепишется следующим образом:
|Д1 -J- WJ — | 1 — W \ \i — uJj\' \1O.LO.O)
dfdt
Здесь а = PJF.
Для приближенного решения этого уравнения применяются
различные приемы. Мы рассмотрим наиболее простой случай
гг = 3. Заметим, что множитель (о/сп)п представляет собою ско-
скорость укорочения стержня от действия силы Р, обозначим эту
скорость 80 и перепишем A8.3.3) при п = 3 следующим образом:
— = -eoCw + w>). A8.13.4)
Будем искать его приближенное решение в виде
w = с (t) sin -2JL.
Подставив в A8.13.4), получим
{^ff csin ^ = б0 (Зс sin i^L + сз sin3 «*Lje A8.13.5)
Дальше можно поступать по-разному. Можнод например, потре-
потребовать, чтобы A8.13.5) выполнялось в среднем на всем стержне.
Для этого уравнение A8.13.5) умножается на sin(jtfe?/Z) и интег-
интегрируется по длине балки. Мы поступим проще, а именно, потре-
потребуем выполнения A8.13.5) в одном сечении — в середине балки.
При z = h^ = 1/2 получается
Разделим переменные и проинтегрируем. Получим
Здесь Со — начальный безразмерный прогиб. Величина безраз-
безразмерного прогиба стремится к бесконечности при стремлении t
к конечной величине, называемой критическим временем. Из
формулы A8.13.6) следует
с
Применяя другие методы определения критического времени, мы
42 Ю. Н. Работнов
650 гл- 18- ползучесть металлов
будем получать несколько отличные оценки, но уточнения здесь
вряд ли необходимы. Величина е0, зависящая от о3, очень чув-
чувствительна к величине нагрузки, поэтому при определении кри-
критического времени из опыта получается большой разброс. Этот
разброс существенно уменьшается, если определять не критиче-
критическое время, а напряжение, соответствующее данному критическо-
критическому времени. Это тем более так, что показатель п = 3, выбранный
нами для модельной задачи, сильно занижен до сравнению
с реальными значениями показателя ползучести. Что касается
правой части формулы A8.13.7), она дает тоже лишь ориенти-
ориентировочную оценку, величина с0 редко бывает известна точно, при
проектировании реальных конструкций исходят из статистиче-
статистических данных, позволяющих оценить наибольшую возможную
величину эксцентриситета при данной технологии изготовления
изделия.
Следует заметить, что конечное критическое время, понимае-
понимаемое в указанном смысле как время обращения прогиба в беско-
бесконечность, обязано своим существованием нелинейности опреде-
определяющего уравнения. Действительно, при тг= 1 уравнение A8.13.5)
становится следующим:
Применяя ту же технику разделения переменных, мы получим,
на этот раз уже точно,
. / л/Л ,
?ot= — In с,
\ * /
и прогиб достигает бесконечной величины лишь при t = o°.
Сделаем в заключение несколько замечаний об учете мгно-
мгновенной пластической деформации. В § 4.11 было выяснено, что
начально искривленный стержень из упругопластического мате-
материала мгновенно выпучивается при достижении нагрузкой кри-
критического значения, которое зависит от начального прогиба.
Можно сказать наоборот, каждой силе соответствует критический
прогиб, при котором стержень выпучивается от действия этой
силы. Если сила Р сжимает стержень, прогиб его растет со вре-
временем до тех пор, пока не достигнет критического значения,
соответствующего данной силе Р. Это время и будет критическим
временем, но при достижении критического времени обращается
в бесконечность не прогиб, а скорость изменения прогиба во
времени. Приведенное рассуждение не вполне строго: ползучесть
меняет распределение напряжений в поперечных сеченпях и, сле-
следовательно, изменяет зависимость между критической силой и
прогибом. Однако погрешность невелика и разъясненная схема
сейчас получила признание.
ГЛАВА 19
МЕХАНИКА РАЗРУШЕНИЯ
§ 19.1. Предмет механики разрушения
В восемнадцати предшествующих главах были изложены раз-
различные разделы механики деформируемого твердого тела, при
втом практическая направленность каждого из них не очень
акцентировалась. Но основная область приложения механики
твердого тела — это оценка прочности реальных элементов кон-
конструкций в реальных условиях эксплуатации. С этой точки зре-
зрения различные главы приближают нас к решению этого основ-
основного вопроса в разной степени. Классическая линейная теория
упругости формулирует свою задачу следующим образом: дано
некоторое тело, на это тело действуют заданные нагрузки, точки
границы тела претерпевают заданные перемещения. Требуется
определить поле вектора перемещений и тензора напряжений
во всех точках тела. После того как эта задача решена, возни-
возникает естественный и основной вопрос — что это, хорошо или
плохо? Разрушится сооружение или не разрушится? Теория
упругости сама по себе ответа на этот вопрос не дает. Правда,
зная величину напряжений, мы можем потребовать, чтобы в каж-
каждой точке тела выполнялось условие прочности, т. е. некоторая
функция от компонент Оц не превосходила допускаемого зна-
значения. В частности, можно потребовать, чтобы нигде не дости-
достигалось условие пластичности, более того, чтобы по отношению
к этому локальному условию сохранялся некоторый запас проч-
прочности, понятие о котором было сообщено в гл. 2 и 3. Мы знаем,
что для пластичных материалов выполнение условия пластич-
пластичности в одной точке еще не означает потери несущей способно-
способности, что было детально разъяснено на простом примере в § 3.5.
Поэтому расчет по допустимым напряжениям для пластичного
материала безусловно гарантирует прочность изделия. Для хруп-
хрупких материалов условие локального разрушения отлично от
условия наступления текучести и локальное разрушение может
послужить началом разрушения тела в целом. Поэтому расчет
по допускаемым напряжениям для хрупких материалов более
оправдан. Аналогичная ситуация возникает при переменных
нагрузках и при действии высоких температур. В этих условиях
даже пластические материалы разрушаются без заметной пла-
пластической деформации и микротрещина, возникшая в точке, где
42*
ГЛ- 19« МЕХАНИКА РАЗРУШЕНИЯ
была достигнута опасная комбинация напряжений, может очень
быстро распространиться на большое расстояние и привести к
разрушению конструкции в целом. В большинстве случаев сле-
следует считать разрушенной конструкцию, когда в ней появился
первый очаг разрушения, поэтому методы расчета по допускае-
допускаемым напряжениям могут считаться оправданными.
В то же время теория упругости содержит в себе некоторые
разделы, которые отвечают на вопрос о возможности разруше-
разрушения прямым и непосредственным образом, а именно:
1. Теория устойчивости упругих систем. Достижение нагруз-
нагрузкой величины критической эйлеровой силы может считаться за
момент разрушения. Правда, как мы выяснили на примере сжа-
сжатого стержня и на некоторых упрощенных искусственных при-
примерах (§ 4.5), достижение критической силы не всегда означает
потерю несущей способности. Но при Р>РЭ прогибы начинают,
как правило, расти чрезвычайно быстро, поэтому практически
эйлерову силу можно принимать за разрушающую нагрузку.
В отдельных случаях допускается и работа конструкций в после-
критической области. В крыле самолета, например, под действи-
действием сжимающих напряжений, обшивка в эксплуатационных
условиях может терять устойчивость, но силовая конструкция
крыла — лонжероны и нервюры — продолжают сохранять несу-
несущую способность.
2. Теория колебаний. Как мы видели, эта теория позволяет
найти спектр собственных частот свободных колебаний упругой
системы. Если частота возмущающей силы совпадает с одной из
собственных частот свободных колебаний, наступает резонанс.
Для линейно-упругого тела в постановке линейной теории упру-
упругости амплитуды вынужденных колебаний становятся бесконечно
большими. На самом деле так не бывает. Во всех материалах
существует внутреннее трение. Теория упругих колебаний с зату-
затуханием, пропорциональным скорости, рассматривается в курсах
теоретической механики, основной качественный результат со-
состоит в том, что резонансная амплитуда конечна. В реальных
материалах внутреннее трение подчинено более сложным зако-
законам, даже если его можно считать линейным (см. гл. 17), но
качественный результат остается тем же. Поэтому резонансы на
высоких гармониках, как правило, не страшны. Для турбинных
лопаток, например, гармоники выше пятой-шестой во внимание
не принимаются. Но резонанс на основном тоне или на первых
гармониках может считаться причиной неминуемого разрушения.
Отмеченные два аспекта мы зафиксировали, но далее развивать
не будем.
3. Линейная механика разрушения. В гл. 9, 10 и 11 приме-
применительно к антиплоскому и плоскому состоянию были даны ре-
решения для трещин и получены выражения для коэффициентов
интенсивности К. Для суждения о том, будет ли трещина рас-
§ 19.1. ПРЕДМЕТ МЕХАНИКИ РАЗРУШЕНИЯ 653
пространяться, необходимо знать единственную константу мате-
материала — так называемую вязкость разрушения или эффективную
поверхностную энергию Gc. Оказалось, что величина Ge выра-
выражается через критический коэффициент интенсивности напря-
напряжений К, которым (см. гл. 9—11) называется коэффициент при
сингулярном члене с особенностью вида Bяг)~1/2 для напря-
напряжения около кончика трещины. Таким образом, расчет по ли-
линейной механике разрушения на прочность сводится к расчету
по допускаемым напряжениям, но эти напряжения могут быть
бесконечно большими, условие К<Ке как раз и означает огра-
ограничение, налагаемое на степень интенсивности напряжения, стре-
стремящегося к бесконечности по мере приближения к концу тре-
трещины. В действительности концевая зона, где уравнения теории
упругости теряют силу, имеет конечный размер. Если этот раз-
размер сравним с размером трещины или с расстоянием от ее конца
до свободной поверхности тела, теория линейной механики раз-
разрушения становится неприменимой. Вопросы, связанные с фак-
фактическим определением вязкости разрушения Ge или Кс и с
выявлением ограничений теории, будут рассмотрены ниже.
Следует отметить, что в последние годы появилось очень
большое число монографий по механике разрушения. Упомянем
семитомный переводной труд энциклопедического характера
«Разрушение», монографии Морозова и Партона, Черепанова, ряд
переводных сборников. Многие авторы понимают под механи-
механикой разрушения именно и только механику распространения
трещины. Но в теории трещин предполагается, что материал
остается упругим и не меняет своих свойств всюду, кроме окре-
окрестности конца трещины, которая или стягивается в точку в ли-
линейной механике, или рассматривается как пластическая область
или область больших упругих деформаций. Такая точка зрения
далеко не исчерпывает многообразия реальных процессов раз-
разрушения. При переменных нагрузках, например, уже после
относительно небольшого числа циклов в материале появляются
субмикроскопические трещины, которые растут и сливаются в
макроскопические трещины, приводящие к видимому разруше-
разрушению. Не вдаваясь в детали микроскопической картины, этот
процесс можно представить как накопление поврежденности,
характеризуемой некоторым параметром состояния. Кинетика
изменения этого параметра должна быть включена в определяю-
определяющие уравнения среды. Такая точка зрения лежит в основе того,
/что можно назвать механикой рассеянного разрушения. Соответ-
Соответствующая теория развивается применительно к усталости метал-
металлов и длительной прочности при высоких температурах.
До сих пор все изложение носило чисто детерминистский
характер, свойства материала считались заданными и совер-
совершенно определенными. В действительности упругие, пластиче-
пластические и прочностные характеристики обнаруживают разброс, для
C54 rJL 19- МЕХАНИКА РАЗРУШЕНИЯ
одного и того же материала можно говорить не о постоянной
характеристике, а о ее статистическом распределении. Если мо-
модуль упругости и предел текучести меняются в узких пределах
и расчет по средним значениям достаточно достоверен, то проч-
прочность хрупких материалов и их структурных составляющих
должна рассматриваться как случайная величина и отвлечься от
ее статистического характера принципиально невозможно. Имен-
Именно статистическая теория позволяет объяснить и оценить количе-
количественно так называемый масштабный эффект; прочность большо-
большого изделия всегда оказывается меньше, чем прочность малой его
модели (после пропорционального перерасчета, конечно). Изло-
Изложение современных статистических теорий прочности заняло бы
слишком много места, однако некоторые сведения нам представ-
представлялось необходимым сообщить. Эти сведения особенно суще-
существенны для понимания природы прочности современных компо-
композитных материалов, состоящих из полимерной или металлической
матрицы, армированной угольным, борным или иным высоко-
высокопрочным волокном. Разброс свойств армирующих волокон до-
довольно велик и для понимания того, в какой мере эти свойства
могут быть реализованы в композите, необходимо некоторое
представление о статистической природе его прочности. Именно
поэтому изложение элементов статистической теории будет дано
ниже, в гл. 20.
§ 19.2. Условие прочности для хрупких тел
Для хрупких тел, примерами которых могут служить стекла,
силикаты, полимеры в стеклообразном состоянии, бетон, зака-
закаленные стали, графит и другие материалы, критерий разруше-
разрушения может быть сформулирован в принципе так же, как крите-
критерий пластичности, в виде некоторого соотношения между компо-
компонентами тензора напряжений
й(о«)=0. A9.2.1);
Если Д(а#)<0, материал не разрушается; при выполнении ус-
условия A9.2.1) хотя бы в одной точке, в этой точке происходит
локальное разрушение. Что нужно понимать под термином «ло-
«локальное разрешение», зависит от объекта: это либо разрыв,
раздавливание или срез некоторых структурных элементов, либо
появление зародышевой трещины, которая или распространяется
далее как трещина типа Гриффитса, или сливается с трещинами,
возникшими в соседних точках, где выполнено условие A9.2.1).
Заметим, что область локального разрушения служит источником
концентрации напряжений, поэтому весьма вероятно появление
новых очагов разрушения по соседству с уже возникшими.
Не касаясь многочисленных уточненных применительно к спе-
специальным материалам форм соотношения A9.2.1), остановимся
§ 19.2. УСЛОВИЕ ПРОЧНОСТИ ДЛЯ ХРУПКИХ ТЕЛ
655
на простейшем и достаточно универсальном условии — условии
Мора. Оно формулируется следующим образом:
Разрушение происходит тогда, когда на некоторой площадке
с нормалью п величина касательного напряжения достигает кри-
критического значения, зависящего от действующего на этой пло-
площадке нормального напряжения
т„ = /(а„). A9.2.2)
Чтобы сформулировать условие A9.2.2) в терминах главных на-
напряжений, например, нам будет удобно прибегнуть к геометри-
геометрической интерпретации с помощью круговой диаграммы Мора
г
Рис. 19.2.1
Рис. 19.2.2
(§ 7.6). Если главные напряжения ai>a2>a3, то мы можем
построить три окружности Мора, как это показано на рис. 19.2.1.
В указанном параграфе было сделано замечание о том, что на-
напряженное состояние на любой площадке изображается точкой
с координатами сп и тп, лежащей в заштрихованной области.
Там мы упомянули об этом факте без доказательства. Здесь нам
понадобится только одно, а именно то, что изображающая точка
не может выйти за пределы большого круга, построенного на
напряжениях о4 и с3. Для доказательства предположим против-
противное. Тогда отрезок МС (рис. 19.2.2) больше радиуса круга Мора,
и мы имеем следующее неравенство:
оп —
A9.2.3)
После элементарных преобразований это неравенство примет сле-
следующий вид:
а2 - ап (а4 + а3) + otG3 > 0.
Здесь а2 = о2п + т*.
По определению ап и тп представляют собою нормальное и
касательное напряжения на некоторой площадке, следовательно,
G2n22
о\п\
g56 ГЛ- 19- МЕХАНИКА РАЗРУШЕНИЯ
Внеся эти выражения в неравенство A9.2.3), получим
ог^з A — л? — п\) + [о\ — ог2 (аг + ог3)] wl > 0.
Но направляющие косинусы связаны соотношением
Поэтому выражение в первых скобках равно п\. Сокращая на
эту величину, придем окончательно к следующему неравенству:
g\ — ог2 (аг + а3) + ахстз > 0. A9.2.4)
Но это неравенство невозможно. Действительно, квадратный
трехчлен относительно с2 в левой части неравенства имеет корни
с2 = о4 и а2=<Тз, при а2 = ±°° этот трехчлен равен +°°, поэто-
поэтому в интервале d > с2 > а3 он отрицателен. Таким образом, ис-
исходное предположение привело к противоречию.
Проводя аналогичные рассуждения, мы можем доказать, что
эта точка лежит вне каждого из двух малых кругов Мора, но
это нас сейчас не интересует. Условие тп = /(ап) изображается
некоторой кривой в плоскости а, т, той же плоскости, в кото-
которой построены круги Мора; эта кривая изображена на рис.. 19.2.1.
Теперь проверка прочности производится просто, если окруж-
окружность большого круга Мора не касается предельной кривой, как
показано на рисунке, разрушение не произойдет, условие проч-
прочности останется ненарушенным. Если круг Мора коснется пре-
предельной кривой, то происходит локальное разрушение. Теперь
ясно, как построить кривую тп = /(ап). Нужно произвести испы-
испытания до разрушения при однородном напряженном состоянии
при различных отношениях Ci: a3 и построить соответствующие
окружности Мора. Огибающая этих предельных окружностей бу-
будет предельной кривой.
Существенно заметить, что промежуточное по величине глав-
главное напряжение о2 совсем не фигурирует в условии прочности.
Это не вполне соответствует данным опыта и служит определен-
определенным недостатком теории. В действительности семейство предель-
предельных окружностей Мора не всегда имеет огибающую. Однако
ошибка, связанная с пренебрежением ролью а2, обычно не слиш-
слишком велика.
Условие того, что окружность Мора, построенная на главных
напряжениях с4 и а3, касается некоторой предельной кривой,
может быть записано в виде
д(а1? а3) = 0. A9.2.5)
Подобно тому, как это делалось для плоской задачи теории пла-
пластичности, можно принять за базисные переменные величины
p = (oi + о3)/2 и t = (gi — g3)/2 и записать условие прочности
§ 19.2. УСЛОВИЕ ПРОЧНОСТИ ДЛЯ ХРУПКИХ ТЕЛ
657
Мора в виде
x = g{p). A9.2.6)
Совершенно аналогично записывалось условие пластичности для
плоского напряженного состояния в § 15.8 (уравнение A5.8.2)).
Обычно проще всего бывает определить прочность при растяже-
растяжении свр и прочность при сжатии свс. Построив предельные
окружности Мора для растяжения и сжатия, проведем к ним
Рис. 19.2.3
Рис. 19.2.4
касательную и предположим, что эта прямолинейная касатель-
касательная служит предельной огибающей Мора. Рассматривая всевоз-
всевозможные окружности, касающиеся, например, прямой АВ на
рис. 19.2.3, найдем, что функция g в этом случае линейна. Дей-
Действительно, из подобия треугольников ОАВ и КСВ следует
Но СК = (d - с3)/2 = т, СВ = ОВ - ОС = ОБ - р, отрезки А О, ОВ
и АВ фиксированы заданием предельной кривой. Написанная
выше пропорция принимает следующий вид:
Отсюда и следует линейное соотношение между тир или между
а4 и а3. Это соотношение иногда бывает удобно записывать еле*
дующим образом:
авр
ог — — (т3 = авр. A9.2.7)
Развивая ту же идею, которая заставила перейти от условия
пластичности Треска к условию пластичности Мизеса, можно
предположить, что предельное состояние осуществляется тогда,
когда возникает неблагоприятная комбинация октаэдрического
касательного напряжения и октаэдрического нормального напря-
напряжения. Условие A9.2.6) при этом заменяется следующим:
то = /(с). A9.2.8)"
Соответствующие теории развивались Шлейхером, Надаи, Ягном,
658
ГЛ. 19. МЕХАНИКА РАЗРУШЕНИЯ
Уравнение A9.2.7) дает удовлетворительные результаты для на-
напряженных состояний, заключенных между одноосным растяже-
растяжением и сжатием. Далекая экстраполяция его за эти пределы
сомнительна. Опыты на сжатие при наложенном гидростатиче-
гидростатическом давлении позволяют уточнить форму предельной огибаю-
огибающей слева, в области всесторонних сжимающих напряжений
(рис. 19.2.4). Однако здесь возникает трудность и известная
неопределенность, которая разъяснена в следующем параграфе.
Опыты с наложением всестороннего растяжения осуществить не
удается, во всяком случае положение точки М, которая должна
была бы определять искомое сопротивление отрыву при всесто-
всестороннем растяжении, определить экспериментально невозможно.
§ 19.3. Хрупкое и вязкое разрушение
Свойство разрушаться вязко или хрупко, с заметной пласти-
пластической деформацией или без нее, не может рассматриваться как
абсолютное и неотъемлемое свойство материала. При наложении
всестороннего сжатия такие хрупкие в обычных условиях мате-
материалы, как мрамор или песчаник, деформируются пластически
1
i
r
1
2
Рис. 19.3.1
Рис. 19.3.2
или текут, разрушение их происходит после большой пласти-
пластической деформации. Определение тех истинных напряжений, при
которых происходит разрушение в пластической области, с одной
стороны, встречает экспериментальные трудности, с другой —
применимость критерия типа A9.2.1) для разрушения в пласти-
пластической области вызывает определенные сомнения. По-видимому,
здесь существенную роль играет величина пластической дефор-
деформации, которая в уравнение A9.2.1) не входит. Таким образом,
строя предельные круги Мора для разных напряженных состоя-
состояний, мы получим огибающую, касание которой окружности Мора
соответствует разным физическим явлениям. Левая часть кри-
кривой, показанная на рис. 19.3.1, соответствует наступлению пла-
пластического состояния, правая — хрупкому разрушению. Соединя-
Соединяющий их участок не вполне определен.
§ 19.4. СОСТОЯНИЕ ВБЛИЗИ КОНЧИКА ТРЕЩИНЫ 659
В работах Иоффе, Давиденкова, Фридмана и других авторов
развивалась мысль о том, что существует два типа разрушения —
разрушение вследствие среза — пластическое и вследствие отры-
отрыва — хрупкое. Схематически это можно показать на графике,
приведенном на рис. 19.3.2. Если окружность Мора касается
вертикальной прямой 1—1 и не пересекает горизонтальную пря-
прямую 2—2, разрушение происходит вследствие отрыва и крите-
критерий разрушения записывается следующим образом:
ffi = op, q1>0.
Сопротивление отрыву ср считается постоянной материала, под-
подлежащей опытному определению. Если окружность Мора касается
горизонтальной прямой, то наступает текучесть при касательном
напряжении течения тт. Некоторые авторы вводят представление
о сопротивлении сдвигу тв > тт, т. е. о касательном напряже-
напряжении, при котором происходит разрушение. Из физических сооб-
соображений делается заключение о том, что сопротивление отрыву
слабо зависит от температуры и скорости испытания, когда как
сопротивление пластической деформации от этих факторов зави-
зависит сильно. Понижая температуру или увеличивая скорость,
можно поднять прямую 2—2 и добиться того, чтобы хрупкое
разрушение наступало уже при простом растяжении.
Другой путь состоит в том, чтобы создать в «образце такие
концентраторы напряжений, которые создают локальное напря-
напряженное состояние типа всестороннего растяжения. Следует заме-
заметить, что изложенная простая схема носит довольно грубый и
приближенный характер. Нет увереннее™ в том, что сопротив-
сопротивление отрыву действительно представляет собой константу и
не зависит от вида напряженного состояния. В действительности
чистый отрыв, т. е. разделение тела по исходной поверхности,
по-видимому, не наблюдается. Прилегающая к поверхности от-
отрыва зона, хотя бы и очень небольшой глубины, оказывается
пластически деформированной. Различные экспериментальные
определения сопротивления отрыву не дали надежных резуль-
результатов, поэтому изложенная здесь схема в значительной мере при-
принадлежит истории. Однако представление о существовании со-
сопротивления сдвигу и сопротивления отрыву сыграло опреде-
определенную роль для разъяснения физической стороны вопроса о
разрушении.
§ 19.4. Напряжения и перемещения
вблизи кончика трещины
Основные идеи так называемой линейной механики разруше-
разрушения уже были сформулированы ранее в главах, относящихся
к теории упругости. Так, в § 9.4 была рассмотрена трещина
конечной длины в поле сдвига, было выяснено, что вблизи тре-
660
ГЛ. 19. МЕХАНИКА РАЗРУШЕНИЯ
щины на оси, служащей продолжением трещины, напряжения
выражаются следующей формулой:
T = :fe- + O(l),: A9.4.1)
1/2яг
тогда как перемещения имеют следующий вид:
A9.4.2)
Здесь г — расстояние от кончика трещины, измеренное вдоль
линии, на которой расположена трещина, в формуле A9.4.1)
это расстояние отсчитывается от кончика вперед, т. е. в нераз-
неразрушенный материал, в формуле A9.4.2) оно отсчитывается назад.
Совершенно аналогичным образом в § 10.4 было показано,
что трещина в теле, находящемся в условиях плоского напря-
. . женного или плоского дефор-
yL |Л^1Д мированного состояния, имеет
ту же особенность для напряже-
напряжений, что и в формуле A9.4.1).
Соответствующие формулы для
растяжения в направлений,
перпендикулярном трещине,
будут
птт
A9.4.3)
(формулы A0.4.6)). В том же
Рис. 19.4.1 § 10.4 была рассмотрена тре-
трещина в поле сдвига в плоско-
плоскости трещины. Формулы для этого случая имеют точно такой
же вид, что и формулы A9.4.3), а именно,
^ 1 — v
Индексы I, II и III принято относить к различным схемам на-
гружения, изображенным на рис. 19.4.1. В § 9.5 для трещины,
находящейся в условиях антиплоского напряженного состояния,
было показано, что освобождение энергии выражается через Кш.
Говоря об освобождении энергии, мы имеем в виду то, что при
увеличении длины трещины упругая энергия тела уменьшается.
Производная от энергии по длине
щхеет размерность силы, поэтому величину Q можно назвать
силой сопротивления продвижению трещины, не вкладывая в это
§ 19.4. СОСТОЯНИЕ ВБЛИЗИ КОНЧИКА ТРЕЩИНЫ
6.61
понятие какое-либо содержание, выходящее за рамки того, что
дается в данном определении. Анализ § 9.5 повторяется букваль-
буквально для условий нагружения типа / и типа //. Если одновре-
одновременно действуют растяжение и сдвиги в двух направлениях,
соответствующие работы совершаются независимо и мы полу-
получаем общую формулу
±
A9.4.4)
Рис. 19.4.2
Асимптотические формулы A9.4.1) — A9.4.3) и следующее из
них уравнение A9.4.4) пригодны не только для того простей-
простейшего случая, для которого они были выведены. При произволь-
произвольной нагрузке и при произвольной форме трещины особенность
для напряжений вблизи кончика будет иметь вид г~1/2, а коэф-
коэффициент интенсивности, конечно, будет зависеть от нагрузки
и от формы трещины. В рассмот-
рассмотренном ранее случае для первой
формы было найдено
Кг = all па,
где 2а — длина трещины. Совер-
Совершенно такую же структуру сохра-
сохраняет выражение коэффициентов
интенсивности Ки и Кш с соот-
соответствующей заменой нормально-
нормального напряжения на бесконечности
а касательным напряжением т.
Трещина в поле растягивающих
напряжений представляет, пожалуй, наибольший интерес с точки
зрения приложений, поэтому сейчас мы рассмотрим более общую
задачу о трещине, края которой небут произвольную нагрузку
p(#i), одинаковую как на верхнехМ, так и на нижнем крае раз-
разреза (рис. 19.4.2). В § 10.4 были получены формулы для пере-
перемещений и напряжений в полуплоскости, содержащей симмет-
симметрично нагруженную трещину. На участке оси х{, xl^[—a, а],
задано напряжение а2г = — p(%i), вне этого отрезка и2 = 0. Из
формул A0.4.2) и^ A0.4.3) следуют такие граничные условия
для функции ф (z):
Re q/ (z) = ?, хг е= [— а, + а],
Im ф (z) =-• 0, хх ф. [— а, + а].
Второе условие можно продифференцировать: в результате мы
приходим к краевой задаче для производной ф'; на участке, за-
занятом трещиной, задана ее действительная часть, вне этого уча-
участка мнимая часть равна нулю. ~
gg2 ГЛ. 19. МЕХАНИКА РАЗРУШЕНИЯ
Задача о нахождении аналитической в полуплоскости функ-
функции комплексной переменной z при условии, что на отрезках
границы хг = 0 заданы попеременно действительная или мнимая
часть функции, решается с помощью формулы Келдыша — Се-
Седова (см., например, Лаврентьев, Шабат). Разобьем границу на
отрезки чередующимися точками ак и fefe, положим
(Re/ (хг), хх €= [ак, 6ft],
1/2 n
П
Тогда в верхней полуплоскости
It + To + V+---+7n-iz _ A9.4.5)
В нашем случае а4 = —а, Ь4 = +а, s (хг) = у р (х^), xY e [—а, а],
5(^i) = 0 вне этого отрезка и формула A9.4.5) приводится к сле-
следующей:
= J- 1/1+^. Г р(t) У*=±~*- + ^А_; A9.4.6)
при z -> оо
+а
ф' (оо) = - -Д- Г р @ \f±=±dt + ?±.
^ v ' 2mz J ^v ' * t + a ' z
—а
Для того чтобы перемещение было однозначно, вычет функции
(p'(zj в бесконечно удаленной точке должен быть равным нулю,
в противном случае в формулах A0.4.2) неизбежно появятся
логарифмические члены. Из этого условия находим
Нас будет интересовать особенность в кончике трещины, напри-
например при z = а. Заметим, что в формуле A9.4.6) интегральный
член остается ограниченным при z = а, слабые особенности типа
(z — a)i/z в подынтегральном выражении и перед интегралом вза-
взаимно компенсируются. На самом деле всегда можно выбрать
такую функцию p(z) комплексной переменной z, что p(t) пред-
представляет ее значение на отрезке [—а, а] действительной оси.
Тогда этот интеграл представляет собою интеграл Коши, его
§ 19.4. СОСТОЯНИЕ ВБЛИЗИ КОНЧИКА ТРЕЩДНЫ
663
значение равно значению подынтегральной функции при f = z и
-сингулярный множитель исчезает.
По формуле A0.4.3) напряжение а2г на оси xt равно удвоен-
удвоенной действительной части q/ (z):
Положим
Следовательно, в окрестности кончика трещины сингулярная
часть напряжения а2г есть
„ 2У0 О-
Внося сюда выражение для Yo A9.4.7) и сравнивая с A9.4.3),
находим
+а
VUF <19-4-8>
Для правого конца трещины подынтегральное выражение за-
заменится на />(?)J/ aQZ_tt • Если p(t) —
четная функция, то, умножая числитель \р
и знаменатель подынтегрального выраже-
выражения на Уа — t и замечая, что интеграл от
нечетной функции
J
преобразуем выражение A9.4.8) к следующему виду:
Рассмотрим два простейших примера.
а
1. р = const
а
Г dt n
= а, \ _г : = "«г» К1 =
мы получили уже
известный результат.
2. Трещина растягивается двумя симметрично приложенными силами
(рис. 19.4.3). По формуле A9.4.9)
К Р
664 ГЛ- 1S- МЕХАНИКА РАЗРУШЕНИЯ
§ 19.5. Линейная механика разрушения
Основное предположение линейной механики разрушения
состоит в том, что трещина распространяется тогда, когда вели-
величина коэффициента интенсивности достигает критического значе-
значения, характерного для данного материала. Совершенно эквива-
эквивалентная формулировка этого предположения состоит в том, что
сила G, движущая трещину, превосходит критическое значение —
сопротивленвд распространению трещины. Формула A9.4.4) ут-
утверждает эквивалентность двух этих формулировок. Что каса-
касается механического содержания принятой гипотезы и всей теории
в целом, на этот вопрос можно ответить по-разному, а в рамках
формальной теории вообще его можно не ставить. Тем не менее
некоторые соображения могут быть высказаны. В оригинальной
работе Гриффитса предполагалось, что освобождающаяся при
росте трещины упругая энергия расходуется на увеличение по-
поверхностной энергии: если ^ есть поверхностная энергия на еди-
единицу площади, то сила сопротивления движению трещины Gc = 2^.
Анализ Гриффитса в течение долгих лет считался безупречным,
хотя в нем содержится некоторый органический дефект. Энергия
поверхностного натяжения вводится в уравнения теории как
нечто данное и постороннее по отношению к упругому телу. На
самом деле, поверхностная энергия есть энергия поверхностного
слоя, свойства которого в той или иной мере отличаются от
свойств остального материала и при решении задачи теории уп-
упругости этот поверхностный слой нужно как-то моделировать.
Простейшая схема будет состоять в том, чтобы рассматривать
поверхностный слой как бесконечно тонкую пленку с постоян-
постоянным натяжением f- Если контур свободного отверстия имеет
кривизну, то поверхностное натяжение дает нормальную состав-
составляющую силы на контуре. При переходе к разрезу, в вершине
которого кривизна становится бесконечно большой, поверхност-
поверхностное натяжение создаст сосредоточенные силы. В результате осо-
особенность у кончика трещины оказывается более высокого по-
порядка, а именно, вида 1/г, а не 1/Уг. На это обстоятельство было
обращено внимание Гудьером, однако полное решение задачи
было опубликовано Умного позже. В связи с этим можно выра-
выразить сомнение, связанное с тем, в какой мере пригодно пред-
представление о поверхностном натяжении в твердом теле как о на-
натянутой бесконечно тонкой пленке, а особенно в какой мере эта
идеализация сохраняет смысл при переходе к пределу, когда от-
отверстие превращается в бесконечно тонкий разрез.
Измеренные методом раскрытия трещины значения поверх-
поверхностной энергии удовлетворительно совпадают с другими ее оцен-
оценками для стекол. Для металлов измеренная величина Gc оказы-
оказывается на три порядка выше, чем поверхностная энергия. Поэтому
здесь приходится искать другие механизмы. У пластичных ме-
§ 19.5. ЛИНЕЙНАЯ МЕХАНИКА РАЗРУШЕНИЯ
665
таллов в окрестности кончика трещины появляется пластическая
область. Протяженность ее d можно грубо оценить по первой
формуле A9.4.3). Полагая в ней а22 = сгт, К — Ки, r = d, полу-
получаем следующую оценку:
<**-^. A9-5.1)
Конечно, в формуле A9.5.1) должен фигурировать числовой мно-
множитель, который нельзя получить из формулы A9.4.3); для этого
нужно решать соответствующую упругопластическую задачу.
Необходимое условие применимости линейной механики разру-
разрушения к расчету металлических элементов состоит в том, чтобы
размер d был много меньше, чем длина трещины, толщина об-
образца и расстояния от конца трещины до свободной поверхно-
поверхности. Тогда можно считать, что освобождающаяся упругая энер-
энергия расходуется на работу пластического деформирования, со-
совершаемую в малой пластической зоне перед кончиком трещины.
Пластически деформируемый
материал образует тонкий
слой вблизи поверхностей
трещины. У хрупких мате-
1 !
1
1
/
/
/
:
Рис. 19.5.1
Рис. 19.5.2
риалов, например, у графита, продвижению магистральной тре-
трещины предшествует распространение направленных в разные сто-
стороны и ветвящихся микротрещин. Затруднительно подсчитать
из рациональных соображений затрачиваемую на это работу, од-
однако суммарную работу на единицу длины или силу можно
непосредственно определить из макроэксперимента. Символом Ки
принято обозначать критический коэффициент интенсивности,
определенный в условиях плоской деформации. Для того чтобы
в пластической зоне действительно с достаточно хорошим при-
приближением воспроизводились условия плоского деформированного
состояния, необходимо, чтобы толщина образца была значитель-
значительно больше, чем размер пластической зоны d. Так, проект бри-
британского стандарта и некоторые ведомственные нормы, приня-
43 ю. Н. Работнов
ggg ГЛ. 19. МЕХАНИКА РАЗРУШЕНИЯ
тые в Советском Союзе, рекомендуют в качестве достоверных
определения КТс на образцах, у которых толщина, длина тре-
трещины и расстояние от кончика трещины до свободной поверхно-
поверхности не меньше, чем 2^5 (/?1с/атJ. Наиболее распространенный
тип образца, применяемый для определения Кю, показан схема-
схематически на рис. 19.5.1. Это — массивный образец, испытываемый
на внецентренное растяжение. Первоначальный надрез продол-
продолжается усталостной трещиной, которая создается в результате
приложения пульсирующей нагрузки. Фиксируется нагрузка, при
которой происходит страгивание трещины. Для того чтобы оп-
определить величину Кгс, соответствующую моменту страгивания
трещины, нужно иметь решение задачи теории упругости для
образца принятой формы. Для стандартных образцов такие ре-
решения были получены численными методами, результаты пред-
представлены в виде аппроксимирующих формул, графиков или таб-
таблиц. Если обозначить через Рс силу, при которой страгивается
трещина, то критический коэффициент интенсивности находится
по формуле
Размеры Z, Ъ и t показаны на рис. 19.5.1. На рис. 19.5.2 приведен
типичный график этой функции применительно к схеме испы-
испытания рис. 19.5.1.
Изложенный способ хорошо проходит для вполне хрупких
материалов, например для графита. У стали началу неустойчи-
неустойчивого роста трещины предшествует некоторое ее незначительное
подрастание при слабо меняющейся нагрузке, происходящее
одновременно с формированием пластической зоны около ее кон-
конца. Поэтому диаграмма зависимости раскрытия трещины А от
силы Р перестает быть линейной и фиксация критической силы
Рс носит в известной мере условный характер. Соответствующие
правила, обеспечивающие по крайней мере воспроизводимость
результатов, оговорены в нормативных документах и здесь, естест-
естественно, рассматриватья не будут.
§ 19.6. Сила сопротивления раскрытию трещины
В предположении о том, что пластическая зона или зона раз-
разрушения у конца трещины очень мала, была получена формула
A9.4.4), выражающая силу сопротивления раскрытию трещины
Gc через Кс. Ограничиваясь первой модой, перепишем ее сле-
следующим образом:
Ge=i^-iCje. A9.6.1)
Если пластическая зона значительна и распределение напряже-
напряжений существенно отличается от того распределения напряжений,
§ 19.6. СИЛА СОПРОТИВЛЕНИЯ РАСКРЫТИЮ ТРЕЩИНЫ 667
которое соответствует слабой сингулярности типа Bлг)~/2, то
формула A9.6.1) утрачивает силу и сама величина критического
коэффициента интенсивности теряет смысл. Но сила Gc, соот-
соответствующая освобождению упругой энергии при движении тре-
трещины, сохраняет смысл и может быть определена непосредст-
непосредственно. Один из методов экспериментального определения силы Gc
состоит в следующем. Рассмотрим, например, схему испытания
надрезанного образца на изгиб сосредоточенной силой Q. Пере-
Перемещение под действием силы Q точки ее приложения есть и.
Поскольку стержень упруг, перемещение пропорционально силе,
и = (?б. Величина б, податливость, зависит от геометрии образца
и, конечно, от глубины начальной трещины Z. Существенно знать
эту зависимость 8A), ее можно определить экспериментально,
испытывая образцы с разными пропилами. По теореме Клапей-
Клапейрона при действии силы Q упругая энергия
Если при некоторой постоянной силе Q = QC трещина придет
в движение, освобождение упругой энергии будет
ь*г" IT'
Отсюда
Если испытание производится на машине с постоянной скоростью
захвата, то трещина устойчиво растет с ростом прогиба при
падающей нагрузке; регистрируя длину трещины и соотнося ее
с величиной прогиба, из одного опыта можно определить подат-
податливость б как функцию длины трещины I и сразу найти Gc. Но
это будет величина Gc, соответствующая движению трещины,
а не страгиванию ее с места. У пластичных материалов эти
величины разнятся, у хрупких, например графитов, разница
невелика.
В недавнее время концепция силы сопротивления продвиже-
продвижению трещины получила некоторое новое развитие и новую ин-
интерпретацию. В работах Эшелби, Раиса, Черепанова было пока-
показано, что величина G при определенных предположениях может
быть представлена в виде некоторого интеграла по пути, не за-
зависящего от этого пути. Пусть и(вг5) —упругая энергия на еди-
единицу объема тела. Будем рассматривать движение плоской тре-
трещины и относить все величины к слою единичной толщины.
Рассмотрим интеграл
в
в
J = J [udy - a^njds), A9.6.3)
А
43*
E68 Гл- 19- МЕХАНИКА РАЗРУШЕНИЯ
взятый по некоторому пути, соединяющему точки А и В. Пока-
Покажем, прежде всего, что этот, так называемый «джей-интеграл»
не зависит от пути. Очевидно, для этого достаточно показать,
что он обращается в нуль для любого замкнутого пути. Заме-
Заметив, что dy = riids, преобразуем интеграл но формуле Гаусса —
Остроградского
§ [о * - *>? «*) - Я [# - {"•> тЫ * *¦ («-8-")
Но
OU 8U де.} de{j / ди. \ ди{ du{j
дх дег. дх w« дх ' Гг' дх )ti "гд>д дх [ "гз дх
Поскольку выполняются уравнения равновесия
правая часть A9.6.4) обращается в нуль и контурный интеграл
равен нулю. Таким образом, /-интеграл не зависит от пути ин-
интегрирования. Это свойство сохраняется, если точки А и В на-
находятся на двух сторонах разреза или трещины. Выясним теперь
связь /-интеграла, взятого по произвольной дуге АВ, и силы
сопротивления движению трещины. Выделим площадь S, огра-
ограниченную дугой АВ и берегами трещины, которую будем пред-
предполагать достаточно длинной. Полная энергия части тела (слоя
единичной толщины), заключенной в области S, есть
W = \ Udx dy— ]
АВ
Предположим теперь, что конец трещины продвинулся на рас-
расстояние А, при этом совершена работа раскрытия третцины GCA.
Эта работа равна изменению энергии части тела S:
GcA = 6PF. A9.6.5)
Чтобы вычислить 6W, заметим, что поля напряжений и пере-
перемещений около продвинутой трещины останутся теми же самы-
самыми; эти поля можно вычислить, заменив координату х на х — Д.
Таким образом,
Выполняя интегрирование по координате х и подставляя в
§ 19.6. СИЛА СОПРОТИВЛЕНИЯ РАСКРЫТИЮ ТРЕЩИНЫ QQQ
A9.6.5), находим
Gc = -/. A9.6.6)
/-интеграл инвариантен, т. е. не зависит от пути интегрирования
лишь в том случае, когда существует потенциал С/(е#), т. е.
когда тело либо упруго, либо подчиняется уравнениям дефор-
деформационной теории пластичности. Если считать, что материал
в пластической области деформируется в соответствии с уравне-
уравнениями теории течения, например, то /-интеграл уже не будет
инвариантен и соотношение A9.6.6) потеряет силу. Условие
независимости /-интеграла от пути интегрирования позволяет
оценить характер особенности у конца трещины для нелинейного
материала. Пусть, например, напряжения и деформации связа-
связаны степенной зависимостью а ~ еа. Тогда
U ~ ее ~ о а .
Пусть на расстоянии г от кончика трещины а ведет себя как rnt
Тогда первая часть интеграла A9.6.3) будет иметь порядок
(интегрирование по у эквивалентно умножению на г). Чтобы
интеграл не зависел от пути, показатель должен быть равен ну*
лю, отсюда
п = —•
1+а'
При а = 1 отсюда получится прежний результат 72 = —1/2, для
идеально-пластического материала а = О, п = О и особенность от-
отсутствует.
Если пластическая зона впереди трещины велика, диаграмма
зависимости перемещения и от силы Q не будет линейной и фор-
формула A9.6.1) становится неприменимой. Однако соотношение
G«—г-f- A9-6-7>
остается верным. Определяя U для разных значений I просто
как площадь, органиченную диаграммой сила — перемещение, по
формуле A9.6.7) можно найти величину Gc — силу сопротивле-
сопротивления движению трещины. В современной литературе часто гово-
говорится, что таким способом находится экспериментально вели-
величина /-интеграла. Это неточно, для упругопластического мате-
материала значение интеграла A9.6.3), вообще говоря, зависит от
пути ж не может считаться механической характеристикой, тогда
как величина Gc всегда сохраняет некоторый объективный
смысл.
670
ГЛ. 19. МЕХАНИКА РАЗРУШЕНИЯ
§ 19.7. Линейная модель пластической зоны
Почти одновременно Дагдейл, с одной стороны, Леонов и
Панасюк, с другой, предложили формально эквивалентные модели
концевой зоны трещины. Предположение Дагдейла относилось к
задаче о трещине в тонком листе, когда можно представить
пластическую зону в виде узкой полосы впереди трещины. Дей-
Действительно, пластическая деформация представляет собою сдвиг
в плоскостях, составляющих угол л/4 с граничными плоскостями
пластины, в терминах теории
пластичности при плоском напря-
напряженном состоянии локализация
пластического течения в узкой
полосе соответствует параболиче-
параболической точке в решении уравнений
-$ теории пластичности. Математи-
Математическая модель соответствует схе-
схеме, изображенной на рис. 19.7.1,
относящемся к случаю равномер-
равномерного растяжения вдоль оси у
напряжением а». Трещина с пер-
первоначальной длиной 2а при растяжении порождает пластиче-
пластические зоны, мыслимые как отрезки нулевой толщины. В этих
пластических зонах действует постоянное напряжение, равное
пределу текучести от. Будем рассматривать вместо трещины дли-
длиной 2а трещину длиной 2с, отрезки которой а< \х\ <с загруже-
загружены постоянной нагрузкой р{х) = От. По формуле A9.4.9) коэф-
коэффициент интенсивности
v ___ 2 Ус
Рис. 19.7.1
От напряжения а» коэффициент интенсивности на конце тре-
трещины длиной 2с будет по той же формуле
Требуя, чтобы при х = ±с напряжения оставались конечными,
мы придем к следующему уравнению:
Отсюда
A9.7.1)
Положим c — a — d, где d — протяженность пластической области.
Если d < а, то а/с « 1 — dla. При малых d справедливы предпо-
предположения линейной механики разрушения; значит, имеет опре-
определенный смысл величина коэффициента интенсивности. Разла-
§ 19.7. ЛИНЕЙНАЯ МОДЕЛЬ ПЛАСТИЧЕСКОЙ ЗОНЫ 671
гая в A9.7.1) правую часть в ряд и удерживая лишь два члена
разложения, получим следующую приближенную формулу для
оценки малой протяженности пластической зоны:
Эта оценка совпадает с той, которая была получена в § 19.5 из
соображений теории размерностей. В условиях плоской дефор-
деформации или в более сложных случаях, когда толщина плиты не
очень мала, но и не слишком велика, оценка сохраняет силу,
но числовой коэффициент меняется.
Используя формулы плоской задачи теории упругости, можно
определить величину бс или раскрытие трещины. Мы приведем
здесь соответствующую точную формулу без вывода:
6< = ^i^^1» [sec
Отсюда при малых значениях а«>/ат, когда пластическая область
мала, следует приближенная формула
6« = ^1-v2) = 2V A9-7.4)
Заметим, что эту формулу легко получить с помощью инвари-
инвариантного /-интеграла. Выберем путь интегрирования так, как по-
показано на рис. 19.7.2 жирной линией. На этом пути dy = О,
аЩ = огп2, n2ds = dx, в интеграле A9.6.3) остается только про-
процЩ г2, 2 , ерале (
изводная от перемещения dujdx и
по формуле A9.6.5) мы получаем т
,
Сс = -(Ыл-Ы,]аг, ~{ { { } {' оГ
откуда немедленно следует формула б>
.A9.7.4).
В действительности острый конец Рис. 19.7.2
трещины перед началом ее продви-
продвижения затупляется, величина раскрытия, предшествующего
распространению трещины, может быть измерена. В реаль-
реальных условиях структура соотношения A9.7.4) сохраняется, ме-
меняется лишь числовой коэффициент, который зависит от формы
и размеров образца. Поэтому существует пропорциональность
между силой сопротивления движению трещины Gc или квадра-
квадратом коэффициента интенсивности Kl, с одной стороны, и вели-
величиной критического раскрытия трещины бс, с другой. Были пред-
предприняты значительные усилия по разработке методов определе-
определения критического раскрытия трещины для пересчета величин
Gc или Кс. Большие надежды, возлагавшиеся на этот метод, свя-
связаны с тем, что бс можно определять на малых образцах, тогда
E72 ГЛ- 19« МЕХАНИКА РАЗРУШЕНИЯ
как для определения К1с необходимо выполнение условий, ого-
оговоренных в § 19.5. Эти условия для сталей с невысоким пределом
текучести могут быть очень стеснительными. Волна энтузиазма,
связанного с методом бс, достигла максимума около 1970 г., но
в последнее время пошла на убыль. Корреляция между бс и
характеристиками вязкости разрушения устанавливается лишь
для определенных классов материалов при жесткой стандарти-
стандартизации условий испытаний, и вряд ли можно говорить о 6С как
о константе материала.
§ 19.8. Длительное разрушение
при высоких температурах. Вязкое разрушение
Теория длительного разрушения или длительной прочности
металлов при высоких температурах является в известной мере
контрастной по сравнению с описанной выше теорией распро-
распространения трещин в хрупких или упругопластических телах.
При длительном действии нагрузок при повышенной температуре
металл ползет, явление ползучести было описано и проанализи-
проанализировано в гл. 18. Там было отмечено, что если уровень напря-
напряжений достаточно высок, то, начиная с некоторого момента, ско-
скорость ползучести начинает возрастать (третья фаза ползучести)
и процесс ползучести заканчивается разрушением образца.
Основная информация о длительной прочности материала
получается в результате испытания на длительную прочность
при растяжении. Образец нагружается растягивающей силой,
определяется время, по истечении ко-
которого образец разрушается. Результа-
Результаты испытаний представляются в виде
так называемой диаграммы длительной
прочности, типичная диаграмма пред-
представлена на рис. 19.8.1. По оси ординат
откладывается логарифм разрушающе-
разрушающего напряжения а, по оси абсцисс —
логарифм времени до разрушения. В
i 7-~г логарифмических координатах эта ди-
диаграмма состоит обычно из двух пря-
Рис. 19.8.1 молинейных участков, участок АВ с
меньшим наклоном соответствует вяз-
вязкому разрушению, сопровождаемому большой пластической де-
деформацией. На участке ВС при меньших напряжениях и соот-
соответственно больших длительностях деформации разрушения не-
невелики и разрушение можно назвать хрупким или квазихруп-
квазихрупким. Заметим, что напряжение а относится к первоначальной
площади поперечного сечения, поэтому на участке вязкого раз-
разрушения по оси ординат в логарифмической шкале откладыва-
откладывается условное напряжение.
§ 19.8. ДЛИТЕЛЬНОЕ ВЯЗКОЕ РАЗРУШЕНИЕ
673
В действительности приведенная на рис. 19.8.1 схема реали-
реализуется не всегда, у некоторых материалов отсутствует участок
вязкого разрушения, у других, наоборот, во всем диапазоне на-
напряжений разрушение носит вязкий характер. Не всегда пере-
переход от вязкого разрушения к хрупкому происходит сразу в точке
В диаграммы. В окрестности этой точки обычно бывает область
смешанных разрушений, которой на
диаграмме соответствует показанная
штриховой линией кривая.
Линейный характер зависимости
разрушающего напряжения от времени
до разрушения подсказывает выбор
определяющих уравнений при анализе
процесса разрушения. Эти уравнения
должны быть такими, чтобы оконча-
окончательные зависимости представлялись
степенными функциями. Рассмотрим
способы феноменологического описания
того и другого типа разрушений.
Если разрушение происходит при
большой деформации, с участком не-
неустановившейся ползучести можно не считаться и предполагать
скорость ползучести зависящей только от напряжения. При этом
удобно принять логарифмическую меру деформации
~е = In —.
Рис. 19.8.2
Здесь х — длина некоторого отрезка, направленного вдоль оси рас-
растяжения, х0 — его начальная длина.
Уравнение ползучести, как и в § 18.7, мы запишем в следую-
следующем виде:
J = g'(o)o + v(o). A9.8.1)
Если образец растягивается постоянной силой Р, то условное,
т. е. отнесенное к первоначальной площади сечения, напряжение
есть Go = P/FQ. Из условия несжимаемости материала
Отсюда
Поэтому истинное напряжение равно
а = аоехрG). A9.8.2);
Исключая с помощью A9.8.2) скорость деформации е из A9.8.1),
g74 ГЛ- 19' МЕХАНИКА РАЗРУШЕНИЯ
получим дифференциальное уравнение для а, которое легко ин-
интегрируется, а именно,
Диаграмма деформирования реальных материалов обычно такова,
что при некотором напряжении а = о% числитель подынтеграль-
подынтегрального выражения обращается в нуль. Соответствующее значение
t по формуле A9.8.3) мы обозначим через ?*. Это время и следует
принять за время разрушения. Действительно, график зависимо-
зависимости а от t по уравнению A9.8.3) подобен изображенному на
рис. 19.8.2 (кривая i), при t = t% скорость удлинения становится
бесконечно большой. Заметим, что условие
~ *'<*•) = о
встречалось нам при рассмотрении вопроса об устойчивости рас-
растяжения пластического стержня в § 4.11. Критическому напря-
напряжению Qjj. соответствует определенная критическая деформация
е*, определяемая из формулы A9.8.2), Таким образом, процесс
ползучести устойчив до того момента, когда будет достигнута
вследствие ползучести критическая деформация еф. Это — дефор*
мация равномерного растяжения. Фактически при е>е# происхо-
происходит образование шейки и мгновенный разрыв.
Пренебрегая мгновенной пластической деформацией, мы по-
получим вместо A9.8.3) следующее уравнение:
Здесь верхний предел интегрирования принят равным бесконеч-
бесконечности, что соответствует превращению образца в бесконечно длин-
длинную и бесконечно тонкую нить. График зависимости о от t по
уравнению A9.8.4) представлен на том же рис. 19.8.2. За кри-
критическое время теперь можно принять лишь то конечное время,
при котором перемещение и напряжение становятся бесконечно
большими. Фактически, конечно, разрыв происходит при неко-
некотором конечном перемещении, но кривая а — t в конце идет вверх
чрезвычайно круто и абсцисса асимптоты ?* дает достаточно хо-
хорошую оценку времени до разрушения. Если принять степенной
закон ползучести и = Аоп, то по формуле A9.8.4) получается
A9.8.5)
Апо-
§ 19.9. ХРУПКОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ 675
Степенная зависимость между ?# и а0 хорошо описывает первый
прямолинейный участок на диаграмме длительной прочности
(рис. 19.8.1).
§ 19.9. Хрупкое разрушение при высоких температурах
Длительное действие нагрузки относительно небольшой ин-
интенсивности вызывает в металле образование трещин. При доста-
достаточно высоких температурах эти трещины имеют закругленные
концы и образуются в результате слияния пор, возникающих
на границах зерен. Один из предположительных механизмов об-
образования этих пор — диффузия вакансий из тела зерна к его
границам. У технических сплавов, содержащих различные при-
примеси, возможна диффузия примесей к границам и образование
хрупких фаз. Ориентировка микротрещин в значительной мере
случайна, она определяется ориентировкой граней кристаллов,
но по преимуществу трещины возникают на тех гранях, плоско-
плоскости которых ближе всего к плоскостям, перпендикулярным дейст-
действию растягивающего напряжения. Этот факт, а также прямые
эксперименты на трубчатых образцах при различных видах на-
напряженного состояния приводят к заключению, что интенсив-
интенсивность трещинообразования, а следовательно, и длительная проч-
прочность зависят от наибольшего нормального напряжения. Поэтому
если на диаграмме рис. 19.8.1 откладывать по оси ординат лога-
логарифм наибольшего нормального напряжения, то участок, соот-
соответствующий хрупкому разрушению, остается неизменным для
всех видов напряженных состояний. Более точный анализ экс-
экспериментальных данных привел некоторых авторов к уточнению
критерия длительной прочности и введению эквивалентного на-
напряжения, несколько отличного от отах. Получающаяся поправка
невелика и здесь рассматриваться не будет. Задача о вязком
разрушении, т. е. об устойчивости вязкого течения, будет ре-
решаться по-разному для разных форм образцов, поэтому первый
участок диаграммы, стремящийся к вязкому разрушению, харак-
характеризует лишь те условия, в которых были получены опытные
точки, т. е. условия растяжения цилиндрического образца.
Возвращаясь к вопросу о хрупком разрушении, примем, что
наличие микротрещин: ослабляет поперечное сечение образца,
уменьшая его эффективную площадь. Обозначим через о) степень
уменьшения эффективной площади вследствие растрескивания.
Если геометрическая площадь поперечного сечения есть F, то
эффективная площадь, воспринимающая нагрузку, есть F(l — о).
Поэтому истинное напряжение
Здесь рассматривается схема хрупкого разрушения в чистом
g76 гл- 19- МЕХАНИКА РАЗРУШЕНИЯ
виде, поэтому изменение площади сечения, связанное с удлине-
удлинением образца и учтенное в § 19.8, во внимание не принимается,
считается, что удлинение очень мало.
Будем считать, что скорость трещинообразования есть функ-
функция от истинного напряжения
0)=-Ф(о). A9.9.2)
Из уравнения A9.9.1) находится о как функция а, и после диф-
дифференцирования получаем
Внесем это выражение для со в A9.9.2), разделим переменные и
проинтегрируем. Получим
оо
J^. A9.9.3)
Верхний предел интегрирования здесь принят равным бесконеч-
бесконечности, как и при рассмотрении вязкого разрушения в § 19.8.
В действительности при некотором конечном напряжении, кото*
рому соответствует площадь трещин о < 1, происходит внезап-
внезапный отрыв. Однако из тех же соображений, что и ранее, мы
сохраняем в формуле A9.9.3) бесконечный верхний предел, уточ-
уточнение этого предела мало сказывается на результате, т. е. на
величине t%— времени до разрушения. Если считать, что ф (а) —
степенная функция ф(о) = саь, то из A9.9.3) получается
**= сA + к)оьт (ШК4>
Зависимость A9.9.4) отличается от A9.8.5) только показателем
ft, в логарифмических координатах она изображается также
прямой.
В промежуточной области необходимо учитывать как накоп-
накопление поврежденности о, так и изменение площади сечения с
удлинением образца. Соответствующий анализ может быть про*
делан (Работнов, 1966), мы его здесь не приводим. Приняв за
эффективное напряжение величину а, определяемую формулой
A9.9.1), мы естественным образом должны прийти к заключению
о том, что скорость ползучести определяется тем же эффектив-
эффективным напряжением:
A9.9.5)
Подставляя сюда найденное из A9.9.3) и A9.9.1) выражение-
§ 19.9. ХРУПКОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ 677
для со как функции времени t, мы найдем, что уравнение A9.9.4)
будет описывать кривую ползучести с увеличивающейся ско-
скоростью. Более общее предположение состоит в том, что скорость
ползучести зависит кроме напряжения от двух структурных па-
параметров — параметра упрочнения и параметра поврежденности
со. В качестве параметра упрочнения можно принять, как это
было сделано в § 18.4, величину накопленной деформации пол-
ползучести р. Тогда уравнения одномерной ползучести могут быть
записаны, например, следующим образом:
В результате интегрирования этой системы мы получим кри-
кривую ползучести с первым участком замедляющейся ползучести,
где основную роль играет упрочнение, и с третьим участком ус-
ускоренной ползучести, когда параметр поврежденности становится
значительным и эффективное напряжение существенно возра-
возрастает.
В заключение этого раздела выясним, как определяется дли-
длительная прочность при переменных напряжениях. Если <р(о) —
( о \h
степенная функция, ф =-- с I j^—I, то в уравнении A9.9.2)
можно разделить переменные:
Интегрируя от со = 0 до со = 1, получим
t
1 = A + к) j cokdt.
о
Если а = const, то t = t% (а) есть время до разрушения при дан-
данном напряжении, причем A + к) cok = l/t% (а). Поэтому условие
разрушения при переменных нагрузках запишется следующим
образом:
I
5-^ = 1. A9.9.6)
О
Уравнение A9.9.6) выражает так называемый принцип линей-
линейного суммирования поврежденности.
При экспериментальной проверке принципа линейного сумми-
суммирования поврежденности обнаруживаются некоторые систематиче-
систематические отклонения, которые, впрочем, не очень велики. Как пра-
правило, ошибка получается в сторону занижения долговечности, т. е.
повышения запаса прочности.
ГЛ- 19« МЕХАНИКА РАЗРУШЕНИЯ
§ 19.10. Понятие об усталостном разрушении
При действии периодических нагрузок, меняющихся очень
большое число раз (тысячи и миллионы раз), материалы, разру-
разрушающиеся в обычных статических условиях вязко, обнаружи-
обнаруживают картину разрушения, совершенно подобную хрупкому раз-
разрушению. После некоторого числа циклов на поверхности изде-
изделия или образца появляется трещина, которая прорастает все
далее и далее до момента разрушения. Ограничиваясь пока слу-
случаем простого растяжения — сжатия, будем обозначать среднее
напряжение цикла от, амплитуду переменной составляющей аи.
Таким образом, например,
G = Gm + ov sin cot. A9.10.1)
To, что в качестве периодической функции выбран синус, не
существенно, форма цикла мало влияет на условия разрушения,
существенно число циклов п, после которого происходит разру-
разрушение. Закон изменения напряжения по уравнению A9.10.1)
осуществляется, например, при изгибе вала, несущего тяжелый
маховик. Элементы материала вала испытывают попеременно рас-
растяжение и сжатие одинаковой интенсивности, при постоянной
угловой скорости о напряжение есть о = ov sin co?. Такой цикл
называется симметричным. Степень асимметрии цикла принято
характеризовать параметром г, который определяется как отно-*
шение минимального напряжения цикла к максимальному
A9.10.2)
Для симметричного цикла г==—1, при постоянной нагрузке
г = +1.
Описанная выше схема нагружения вращающегося вала весом
маховика, т. е. силой постоянного направления, используется
при устройстве наиболее распространенных испытательных ма-
машин. Образец круглого поперечного сечения зажимается в шпин-
шпиндель, на другом конце образца помещается подшипник, к нему
подвешивается груз. Максимальное напряжение подсчитывается
по обычным формулам теории упругого изгиба в предположении
о том, что материал следует закону Гука. Это не совсем точно,
в действительности при циклическом нагружении диаграмма за-
зависимости деформации от напряжения представляет собою криво-
криволинейную замкнутую петлю, как схематически показано на
рис. 19.10.1. Однако погрешность в определении а обычным спо-
способом невелика и ею можно пренебречь. Прикладывая нагрузки
разной величины и фиксируя число циклов до разрушения п,
строят диаграмму, которая схематически показана на рис. 19.10.2.
По оси абсцисс откладывается число циклов до разрушения, по
оси ординат — напряжение. Эта диаграмма носит имя Вёлера
§ 19.10. ПОНЯТИЕ ОБ УСТАЛОСТНОМ РАЗРУШЕНИИ
679
A870 г.), который опубликовал первые экспериментальные дан-
данные по исследованию усталости. Диаграмма Вёлера для стальных
образцов, как оказывается, имеет горизонтальную асимптоту, при
п ~ 107 кривая практически выходит на асимптоту, соответствую-
соответствующее напряжение называется пределом
выносливости и обозначается o_i для
данного случая симметричного цикла
(г = —1). Особенно хорошо выявляет-
ея асимптота, если построить график
в полулогарифмических координатах, —
как показано на рис. 19.10.3.
У цветных металлов и у сталей при
повышенных температурах диаграм-
диаграмма Вёлера не имеет асимптоты, предел
выносливости определяется условно,
как величина напряжения, при котором
образец разрушается после заданного
числа циклов. Это число, называемое базой испытаний, устанав-
устанавливается в зависимости от назначения изделия, т. е. от его требу-
требуемой долговечности.
Существуют и другие схемы испытания на усталость, при
г е [0, +1], т. е. при одностороннем нагружении, плоский обра-
образец изгибается вращающимся эксцентриком. Существуют машины
Рис. 19.10.1
Рис. 19.10.2
Рис. 19.10.3
для испытания на растяжение и сжатие с разным коэффициентом
асимметрии цикла, пульсирующая сила создается либо механи-
механическим путем, либо при посредстве электромагнита, возбуждаю-
возбуждающего продольные колебания. В машинах резонансного типа ча-
частота возмущающей силы принимается близкой к собственной
частоте системы, состоящей из образца и присоединенных к нему
масс, система автоматического регулирования поддерживает по-
стояйство амплитуды. Основная техническая трудность при ис-
испытании на растяжение — сжатие состоит в центровке образцов;
незначительный эксцентриситет приложения нагрузки создает на-
напряжения изгиба, которые практически не поддаются учету. Прд
о
680 ГЛ- 19« МЕХАНИКА РАЗРУШЕНИЯ
обработке и интерпретации результатов усталостных испытаний
необходимо иметь в виду следующее.
1. Большой разброс экспериментальных данных. При испыта-
испытании большого числа образцов результаты этих испытаний вовсе
не укладываются на единую кривую Вёлера, а занимают целую
область, схематически показанную штриховкой на рис. 19.10.4.
Поэтому кривая Вёлера представля-
представляет собою лишь некоторую среднюю
линию. Если число опытов достаточ-
достаточно велико, их можно обработать ме-
методами математической статистики
и построить кривые, соответствую-
соответствующие данной вероятности разрушения.
На рис. 19.10.4 показаны кривые,
j соответствующие вероятности раз-
разрушения 1% и 99%. Теперь предел
Рис. 19.10.4 выносливости следует определять
как напряжение, при котором веро-
вероятность усталостного разрушения при достаточно большом числе
циклов не превышает некоторую заданную величину. В действи-
действительности для получения достаточно полной статистической ин-
информации нужен очень большой экспериментальный материал,
поэтому под a_i понимают среднее значение предела выносливо-
выносливости и производят расчет на прочность при симметричном цикле
по формуле
(W<^-, A9.10.3)
где к — запас прочности, достаточно большой, чтобы учесть воз-
возможный разброс величины о_4. Статистическая теория кривой
усталости изложена в книге Болотина.
2. Масштабный эффект. Для образца диаметром 100 мм из
стали предел выносливости может оказаться примерно на 40%
ниже, чем для образца диаметром 10 мм. Это объясняется тем,
что разрушение начинается от некоторого дефекта, слабого места.
Чем больше объем образца, тем больше вероятность нахождения
в нем опасного дефекта. Статистическая теория прочности, объ-
объясняющая масштабный эффект, будет изложена в § 20.3 приме*
нительно к иным объектам, а именно, тонким хрупким волокнам.
Приведенный там анализ переносится на задачу об усталостном
разрушении, для зависимости прочности от напряженного объема
получается следующая формула:
Здесь (т«! есть значение предела выносливости образца с объ-
объемом VQ, a — константа, подлежащая определению из опыта, как
19.10. ПОНЯТИЕ ОБ УСТАЛОСТНОМ РАЗРУШЕНИИ
681
это будет разъяснено в § 20.3. Нам казалось, что тонкие волок-
волокна — это более чистый объект для применения статистической
теории слабого звена, именно поэтому изложение ее отнесено к
гл. 20.
Соотношение A9.10.4) позволяет понять, почему предел вы-
выносливости при растяжении — сжатии даже при максимально чи-
чистой постановке эксперимента оказывается ниже, чем предел
2,8
10
0,8
0,5
\
\
\NSJ
\
\
V
\ 1
V
ч
ч
N.
70 10г
70
7О7
Рис. 19.10.5
выносливости при изгибе. Во втором случае максимальные напря-
напряжения действуют в небольшом объеме, примыкающем к поверх-
поверхности образца. В случае, когда напряжение переменно по сече-
сечению, прямое применение формулы A9.10.4) конечно невозможно,
но теория § 20.3 позволяет дать количественную оценку разницы
между пределом выносливости при изгибе и при растяжении —
сжатии.
Что касается механизма усталостного разрушения, некоторые
суждения о нем можно вынести из рассмотрения графика, пред-
представленного на рис. 19.10.5 (Хантер и Фрике, 1953 г.) и отно-
относящегося к испытаниям алюминиевых образцов при симметрич-
симметричном цикле. По оси ординат отложено напряжение, отнесенное
к условному пределу выносливости of, определенному на базе
2 • 107 циклов, по оси абсцисс — число циклов. Кривые соответ-
соответствуют:
1) появлению первых следов пластической деформации в кри-
кристаллических зернах;
2) появлению первых микротрещин, обнаруживаемых элект-
электронным микроскопом;
3) началу соединения субмикротрещин в микротрещины, ви-
видимые под оптическим микроскопом;
4) появлению первой видимой трещины;
5) разрушению.
44 ю. Н. Работнов
682 ГЛ- 19- МЕХАНИКА РАЗРУШЕНИЯ
Как видно, процесс разрушения можно разбить на два этапа:
инкубационный период, когда внутри материала накапливаются
микроскопические повреждения, и этап продвижения магистраль-
магистральной трещины, который заканчивается разрушением. Картина до
чрезвычайности напоминает ту, которая наблюдается при дли-
длительном разрушении в условиях высоких температур, разница
состоит в том, что субмикро- и микротрещины появляются в ре-
результате попеременных пластических сдвигов в теле зерна, а не
на границах зерен. Существуют теории накопления поврежден-
ности при переменных нагрузках (Костюк), которые мы здесь
не затрагиваем. Что касается роста трещины, то, как оказывается,
скорость его определяется коэффициентом интенсивности напря-
напряжений, поэтому можно принять
? = /(АЯ). A9-10.5)
Здесь I — длина трещины, АК = АКг — амплитуда изменения ко-
коэффициента интенсивности, который определяется методами тео-
теории упругости. Для функции f(AK) обычно применяют степен-
степенную аппроксимацию f(AK) = АКтХ const. Показатель т в зави-
зависимости от материала принимает значения от т = 2 до т = 6.
Если цикл изменения напряжений несимметричен, то предел
выносливости или максимальное напряжение, соответствующее
заданному числу циклов до раз-
разрушения, или асимптота кри-
кривой Вёлера обозначается аг. Ре-
Результаты определения предела
выносливости при асимметрич-
асимметричных циклах бывает удобно пред-
представлять в координатах от — аг,
как показано на рис. 19.10.6.
Проведенная кривая отделя-
? ет область состояний, прпводя-
т щих к разрушению в прямом
или условном смысле, от обла-
Pirc. 19.10.6 сти допустимых состояний. Точ-
Точка пересечения кривой с осью
gv соответствует пределу выносливости при симметричном цикле
g_i, на оси абсцисс она отсекает отрезок, равный статическому
пределу прочности ав. На этом же графике штриховой линией
проведена прямая отах = от + ov=> aT. Область, заключенная между
этой прямой и предельной кривой разрушения, будет областью
больших пластических деформаций; такие состояния недопусти-
недопустимы. Различные авторы предлагали разные способы для установ-
установления вида границы допустимых состояний, основываясь на ог-
ограниченном числе опытных данных; изложение этих способов
выходит за рамки данной книги.
ГЛАВА 20
МЕХАНИКА КОМПОЗИТОВ
§ 20.1. Композиты волокнистого строения
В последние десятилетия наряду с традиционными материа-
материалами появились новые искусственные материалы — так назы-
называемые композиты. Строго говоря, термин «композитный мате-
материал» пли «композит» следовало бы относить ко всем гетероген-
гетерогенным материалам, состоящим из двух или большего числа фаз.
Сюда относятся практически все сплавы, применяемые для из-
изготовления элементов конструкций, несущих нагрузку. Соеди-
Соединение хаотически ориентированных зерен пластичного металла
и второй более прочной, но хрупкой фазы позволяет в извест-
известной мере регулировать свойства конечного продукта, т. е. по-
получать материал с необходимой прочностью и достаточной пла-
пластичностью. Усилиями металлургов созданы прочные сплавы на
основе железа, алюминия, титана, содержащие различные леги-
легирующие добавки. Достигнутый к настоящему времени предел
прочности составляет примерно 150 кгс/мм2 для сталей, 50 кгс/мма
для алюминиевых сплавов, 100 кгс/мм2 для титановых сплавов.
Эти цифры относятся к материалам, из которых можно путем
механической обработки получать изделия разнообразной формы.
Теоретический предел прочности атомной решетки металла, пред-
представляющий собою верхнюю границу того, к чему можно в идеале
стремиться, по разным моделям оценивается по-разному, в сред-
среднем это 1/10—1/15 от модуля упругости материала. Так, для же-
железа теоретическая прочность оценивается значением примерно
1400 кгс/мм2, что в десять раз выше названной для сплава на
железной основе цифры. В настоящее время существуют спосо-
способы получения тонкой металлической проволоки или ленты с
прочностью порядка 400—500 кгс/мм2, что составляет около од-
одной трети теоретической прочности. Однако применение таких
проволок или лент в конструктивных элементах неизбежным об-
образом ограничено.
Одним из крупнейших достижений экспериментальной физи-
физики последних десятилетий было получение бездислокационных
нитевидных кристаллов из металлов, окиси алюминия, карбида
кремния, нитрида бора и некоторых других соединений. На этих
кристаллах была достигнута теоретическая прочность, что имело
огромное принципиальное значение. Надежды на возможность
44*
ГЛ- 20* МЕХАНИКА КОМПОЗИТОВ
практической реализации теоретической прочности в конструк-
конструкциях в общем не оправдались, нитевидные кристаллы слишком
малы, диаметр их составляет несколько микрон, а длина 1 —
2 миллиметра. Наконец обычное стекло в виде тонких нитей диа-
диаметром несколько микрон, как оказалось, имеет прочность, рав-
равную или превышающую прочность высокопрочных легированных
сталей. Из такого тонкого волокна можно делать нити, изго-
изготовлять стеклоткань. С увеличением диаметра прочность волок-
волокна резко падает, прочность же массивных изделий из стекла в
сильнейшей степени зависит от состояния поверхности и пол-
полностью теряется при появлении мельчайших дефектов. Исполь-
Использование высокопрочных волокон и нитей для несущих элементов
конструкций возможно только путем соединения их в -монолит-
-монолитное целое некоторым связующим или погружением их в одно-
однородную матрицу. Такой матрицей может служить металл, поли-
полимерная смола или что-либо иное. Таким образом, получаются
композиты волокнистого строения. В этой главе мы ограничим
наше рассмотрение композитами волокнистого строения, армиро-
армированными прочным волокном.
Первым примером такого рода композитов, получивших до-
достаточно широкое практическое применение, служат стеклопла-
стеклопластики (мы не говорим здесь об известных с глубокой древности
саманных постройках, т. е. о композитах глина — солома, ме-
механические свойства которых совсем не плохи). Перемешивая
полимерную массу с мелко изрубленным стеклянным волокном,
мы получаем первый пример композита с хаотическим армиро-
армированием. Прочность такой пластмассы выше, чем прочность неар-
мированного материала, однако потенциальная прочность стек-
стеклянного волокна используется при этом далеко не полностью,
разрушение всегда происходит по матрице, стеклянные волокна
не разрываются, а выдергиваются из пластмассы. Следует за-
заметить, что изделия из хаотически армированных пластиков,
например полиэтилена, изготовляются обычными способами — пу-
путем формования, выдавливания, литья. Поэтому стандартное
технологическое оборудование оказывается пригодным для полу-
получения таких изделий.
Стеклотекстолиты получаются из стеклянной ткани, которая
пропитывается полимерной смолой — эпоксидной, полиэфирной
или какой-либо иной. Куски этой ткани укладываются в форму,
смола полимеризуется тем или иным способом. Таким образом,
можно получить очень просто сложные изделия типа тонкостен-
тонкостенных оболочек; для изготовления деталей кузова автомобиля, на-
например, нет необходимости в дорогостоящих сложных штампах
и мощном прессовом оборудовании, пропитанная смолой стекло-
стеклоткань может выкладываться на деревянную или гипсовую фор-
форму. Разрушение стеклотекстолитов начинается с того, что хруп-
хрупкая матрица трескается в местах перегиба нитей, образующих
§ 20.1. КОМПОЗИТЫ ВОЛОКНИСТОГО СТРОЕНИЯ 685
стеклоткань. Поэтому прочность стеклянных волокон использует-
используется далеко не в полной мере.
При изготовлении осесимметричных оболочек из стеклопла-
стеклопластиков наилучшие результаты получаются при намотке изделия
под натяжением. Стеклянные нити из нескольких катушек со-
собираются в ленту, которая проходит через ванну со смолой и
наматывается на оправку на специальном станке. При изготов-
изготовлении цилиндрической, например, оболочки соли стекловолокна
могут укладываться в продольном и окружном направлении, а
могут наматываться под разными углами к образующим ци-
цилиндра. Меняя порядок укладки армирующих слоев, можно
изготовить оптимальное в известном смысле изделие, например,
обеспечить его равнопрочность в продольном и поперечном на-
направлении.
Мы не приводим здесь цифр, характеризующих прочность и
жесткость стеклянного волокна, эти величины колеблются в
довольно широких пределах; зная их, можно вынести лишь
весьма относительное суждение о прочности или жесткости ком-
композита.
Приведем некоторые сравнительные данные для хороших стек-
стеклопластиков, армированных в одном направлении хорошо ориенти-
ориентированным волокном: прочность при растяжении 100 кгс/мм2,
модуль упругости Е = 4,2 • 103 кгс/мм2. При плотности около
2 г/см3 удельная прочность, т. е. прочность на единицу массы
у стеклопластика оказывается примерно в четыре раза выше, чем
у стали, и в полтора раза выше, чем у титанового сплава. Однако
низкое значение модуля упругости до чрезвычайности ограни-
ограничивает возможность использования стеклопластиков в кон-
конструкциях, особенно тогда, когда они комбинируются с ме-
металлами.
Конструкции из стеклопластиков имеют недостаточную жест-
жесткость, использование всего ресурса прочности их часто оказывается
невозможным вследствие недопустимо больших перемещений. Тон-
Тонкостенные конструкции разрушаются обычно вследствие потери
устойчивости, а критические нагрузки определяются не проч-
прочностью, а модулем упругости. Если соединить титановый элемент
с элементом из стеклопластика, например, усилить полку
титановой балки элементом из стеклопластика, получится сле-
следующее.
Модуль упругости титана равен 11 • 103 кгс/мм2, т. е. в 2,6 раза
больше, чем у стеклопластика. Поэтому при совместной работе
напряжения в титане будут в 2,6 раза больше. Передел проч-
прочности титана и стеклопластика почти одинаков, в результате
окажется, что когда напряжения в титановом сплаве равны
100 кгс/мм2, в стеклопластиковой накладке они составляют всего
37 кгс/мм2, т. е. усиление титановой балки накладкой из стекло-
стеклопластика весьма малоэффективно.
686
ГЛ. 20. МЕХАНИКА КОМПОЗИТОВ
§ 20.2. Высокопрочные и высокомодульные волокна
В сравнительно недавнее время были разработаны и промыш-
промышленно освоены новые непрерывные волокна, обладающие примерно
той же или более высокой прочностью, чем стеклянные волокна,
и имеющие существенно более высокий модуль упругости. В ни-
нижеследующей таблице приводятся данные о прочности и модуле
упругости наиболее распространенных и промышленно освоенных
видов волокон.
Приводимые здесь цифры носят сугубо ориентировочный ха-
характер. На мировом рынке имеется множество видов волокон
с чрезвычайно разнообразными механическими характеристиками
и не всегда бывает возможно отличить рекламные данные от фак-
фактических. Если значения модуля более или менее устойчивы, то
цифры прочности весьма условны, они характеризуют относитель-
относительные преимущества того или иного вида волокна, но не фактиче-
фактическую реализацию прочности в композите. В таблице приведены
некоторые характерные значения этих величин.
Вид волокон
Стеклянные
Борные
Угольные
Органические
а, кгс/мм2
2^0
350
150—300
280
Е • 10—3, кгс/мм2
7,2
40
20—45
13
Как будет разъяснено далее, прочность волокна зависит от
случайных дефектов, поэтому можно говорить не об абсолютной
величине прочности, а о статистическом распределении величин
прочности, определяемых в данных условиях на образцах данной
длины (обычно 10 мм). Приводимые в таблице цифры представ-
представляют собою среднее значение прочности, для задания прочности
как случайной величины нужно задать по меньшей мере вели-
величину дисперсии, а лучше — истинную кривую распределения
прочности. На образце малой длины вероятность встретить опас-
опасный дефект меньше, поэтому следует ожидать, что средняя проч-
прочность увеличивается с уменьшением длины образца. Такого рода
масштабный эффект действительно довольно сильно выражен у
волокнистых материалов.
В других главах этой книги мы не касались свойств отдель-
отдельных материалов и тем более не затрагивали вопросов, связан-
связанных с физической или структурной природой прочности. Кон-
Конструктор выбирает материалы из имеющегося ассортимента, рас-
расчетчик, применяющий методы теории упругости или теории
пластичности к оценке прочности, использует лишь весьма скупую
§ 20.2. ВЫСОКОПРОЧНЫЕ И ВЫСОКОМОДУЛЬНЫЕ ВОЛОКНА 687
информацию о свойствах применяемого материала, заимствуя ее
из справочников или, редко, из результатов лабораторных ис-
испытаний. Строгое распределение функций конструктора и мате-
материаловеда накладывает определенный отпечаток на традиционный
образ мышления инженера, работающего с металлами. Особен-
Особенность композитов заключается в том, что материал создается в
процессе изготовления конструкции. Располагая различным об-
образом волокна, меняя их плотность, т. е. процентное содержание
в матрице, можно в принципе получить элементы, обеспечиваю-
обеспечивающие необходимую прочность при наименьшей затрате материала,
т. е. оптимизировать конструкцию. Однако реализация оптималь-
оптимального проекта встречает подчас технические трудности, которые
могут оказаться непреодолимыми. В результате находится неко-
некоторое промежуточное, компромиссное решение. Именно поэтому
в настоящей главе, посвященной механике новых материалов,
изложению собственно механических представлений будут пред-
предпосланы краткие сведения об армирующих волокнах и ма-
матрицах.
а. Борные волокна получаются в результате осаждения бора
из газовой фазы на раскаленную вольфрамовую проволоку. Диа-
Диаметр проволоки около 10 мкм, диаметр борного волокна бывает
обычно 100—150 мкм. Высокая стоимость вольфрамовой прово-
проволоки определяет в значительной мере дороговизну борного во-
волокна, поэтому существует тенденция к увеличению диаметра.
Однако более толстое и более жесткое волокно становится мало-
малопригодным, например, для намотки.
Кристаллические зерна бора растут на поверхности вольфра-
вольфрамовой нити, образуя поликристаллическую структуру с радиаль-
радиальной ориентацией. Дефекты поверхности нити порождают непра-
неправильности кристаллической структуры и создают дефекты волок-
волокна, снижающие его прочность. Отсюда — высокие требования к
чистоте поверхности вольфрамовой нити. Возможность замены
вольфрама нитями из стеклоуглерода обсуждалась в литературе,
некоторый практический опыт в этом направлении имеется,
однако после нескольких лет работы и большой рекламы (фир-
(фирма АВКО в США) борного волокна на угольной подложке на
рынке практически нет.
После получения волокна вольфрамовая подложка практически
исчезает, превращаясь в бориды вольфрама, таким образом, цент-
тральная часть волокна обладает очень малой прочностью. Упру-
Упругие свойства волокна анизотропны, но какие-либо прямые данные
о характере этой анизотропии и о величине упругих постоянных
отсутствуют, известны только модуль упругости при растяжении
вдоль оси волокна и модуль сдвига, определяемый методом кру-
крутильных колебаний. Последняя величина является комплексной,
т. е. представляет собою некоторую комбинацию основных упру-
упругих констант.
688 гл-20- механика композитов
Прочность борного волокна в поперечном направлении, по-
видимому, невелика. Об этом можно судить потому, что на микро-
микрофотографиях шлифов разорванных композитов обнаруживаются
продольные трещины.
б. Углеродное волокно получается обычно в результате карбо-
карбонизации полиакрилнитрильного волокна. Процесс изготовления
этого волокна довольно сложен и содержит несколько стадий:
окисление при умеренной температуре, карбонизация и высоко-
высокотемпературная обработка. Как известно, решетка углерода пред-
представляет собою плоскую гексагональную решетку с минимальным
о
расстоянием между атомами 1,42 А. Атомы соединены между
собою валентными связями, и модуль упругости в плоскости
решетки равен 105 • 103 кгс/мм2, т. е. превышает модуль упруго-
упругости стали в пять раз. Поэтому и теоретическая прочность также
очень высока. Атомные плоскости, отстоящие друг от друга при-
о
мерно на 3,5 А, связаны между собою относительно слабыми си-
силами, у монокристалла графита модуль упругости в направлении,
перпендикулярном атомным слоям, примерно в 200 раз меньше,
чем модуль в плоскости слоя. В угольном волокне атомные пло-
плоскости ориентированы таким образом, что они содержат в себе
прямые, приблизительно параллельные оси волокна.
Средний угол разориентации составляет у хорошего волокна
8—10°. Поэтому модуль упругости при растяжении волокна ока-
оказывается в 2,5—5 раз меньше, чем модуль при растяжении в
плоскости атомной решетки. При одинаковой степени разориен-
разориентации материалы, полученные по разной технологии, обнаружи-
обнаруживают разные значения модуля. Это связано, по-видимому, с тем,
что пучки атомных плоскостей объединяются в слегка искрив-
искривленные фибриллы, видимые под электронным микроскопом.
Межфибриллярные связи, определяющие эффективный модуль
сдвига, могут быть более сильными и менее сильными. Соответ-
Соответственно и характер разрушения моноволокна при разрыве может
быть различным, при слабых межфибриллярных связах волокно
рассыпается при разрыве в пыль, при сильных — разделяется на
две части более или менее гладкой поверхностью.
В зависимости от температуры обработки получаются волокна
либо с высокой прочностью, либо с высоким модулем. При из-
изготовлении углеродных волокон они соединяются в пряди, а пряди
в нити. Прядь может содержать 30 моноволокон, а нить 50 пря-
прядей, нить слегка подкручивается.
в. Органические волокна. В обычных полимерах длинные цеп-
цепные молекулы образуют клубки. Специальные методы позволяют
получить полимерное волокно с практически прямолинейными
длинными цепными молекулами, ориентированными параллельно
оси волокна. При растяжении в этих волокнах реализуется вы-
высокая прочность, указанная в табл. 1. Модуль упругости при-
§ 20.3. СТАТИСТИЧЕСКАЯ ПРИРОДА ПРОЧНОСТИ ВОЛОКНА 689
мерно вдвое выше, чем у стеклянного волокна, но существенно
меньше, чем у углеродного и борного. Боковые связи между
цепными молекулами органического волокна очень слабы, по-
поэтому в композите оно может расщепляться. Композиты, арми-
армированные органическим волокном, очень плохо сопротивляются
сжатию.
Стеклянные, борные и углеродные волокна следуют закону
Гука до момента разрыва, поэтому удлинение при разрыве неве-
невелико и энергия, затрачиваемая на разрушение, низкая. Органи-
Органические волокна обнаруживают некоторые пластические свойства,
диаграмма растяжения в конце искривляется, уменьшая свой на-
наклон, и площадь под диаграммой, т. е. работа разрушения, может
быть больше, чем у более жестких борных и углеродных волокон.
§ 20.3. Статистическая природа прочности волокна
Так называемые статистические теории прочности были раз-
разработаны первоначально в целях описания результатов испыта-
испытаний на усталость и предсказания прочности элементов машин,
находящихся под действием переменных нагрузок. Краткие све-
сведения об усталости были сообщены в одном из параграфов пред-
предпоследней главы (§ 19.10). Здесь мы заметим, что результаты
испытаний обнаруживают большой разброс, и поэтому современ-
современная точка зрения на расчет изделий состоит в том, что мы не
можем с абсолютной достоверностью гарантировать прочность
изделия, а можем лишь утверждать, что вероятность его разру-
разрушения достаточно мала. В основе одной из таких статистических
теорий лежит гипотеза слабого звена. Существо этой гипотезы
состоит в следующем. Тело мыслится составленным из большо-
большого числа структурных элементов, каждый из которых имеет свою
локальную прочность. Разрушение всего тела в целом происходит
тогда, когда выходит из строя хотя бы один структурный эле-
элемент. Для массивных тел такое предположение чрезмерно упро-
упрощает фактическое положение дел; для разрушения тела как це-
целого, вероятно, необходимо, чтобы вышла из строя некоторая
группа элементов, именно так строятся более сложные и совер-
совершенные теории. Но для моноволокна гипотеза слабого звена пра-
правильно отражает существо дела. Прямое микроскопическое обсле-
обследование поверхности волокна — борного, угольного или иного —
показывает, что на волокне всегда имеются разного рода дефек-
дефекты — мелкие и крупные. Эти дефекты расположены случайным
образом. Прочность образца волокна длиной I определяется проч-
прочностью его наиболее слабого дефектного места и, таким образом,
является случайной величиной. Результаты испытаний партии
из некоторого достаточно большого числа волокон п представля-
представляются при помощи диаграмм, подобных изображенной на
рис. 20.3.1. Число волокон, разорвавшихся при напряжении, ле-
690
ГЛ. 20. МЕХАНИКА КОМПОЗИТОВ
жащем между аг и oi+i, есть щ, соответствующий прямоугольник,
заштрихованный на рисунке, имеет стороны а1+1 — аг- и щ Изме-
Изменим масштаб диаграммы, будем откладывать по оси ординат
вместо
величину ^т-—__,а у тогда суммарная площадь фи-
фигуры, ограниченной ломаной и осью абсцисс, будет равна еди-
единице. Уменьшая интервалы по оси абсцисс, мы получим в пре-
\-П;
Рис. 20.3.1
Рис. 20.3.2
деле плавную кривую (рис. 20.3.2) плотности р(о) распределе-
распределения прочности волокон длиной I, подчиненную условию норми-
нормирования
+ 00
j p(o) d(J = 1.
— 00
Теперь величина
Р(о)= j p(o)da
—оо
представляет собою относительное количество волокон, прочность
которых не больше а.
Аппроксимируя непосредственно установленное из опыта
дискретное распределение прочности непрерывным, мы можем
определить:
1) среднюю величину прочности волокна
+ ОО
<а>= j op (о) do; B0.3.1)
— 00
2) дисперсию прочности D или среднее квадратичное откло-
отклонение
+ СО
D2= j (a —<<7»2p(a)da.
§ 20.3. СТАТИСТИЧЕСКАЯ ПРИРОДА ПРОЧНОСТИ ВОЛОКНА 691
Из этой формулы следует
-J-0O
D2 = j огр (a) do - <o>2. B0.3.2)
Отношение
w = D/<a>
называется коэффициентом вариации.
Задание средней прочности <о> и в некоторых случаях дис-
дисперсии D часто считается достаточным для того, чтобы охаракте-
охарактеризовать прочность волокна. Во всяком случае в технических
условиях на волокно фиксируется величина <о> (при заданной
длине образца), а иногда ставится требование, чтобы коэффи-
коэффициент вариации w не превосходил некоторого предела. В дейст-
действительности эти данные совершенно недостаточны для суждения
о реальной прочности композита, как будет показано ниже.
Характер зависимости прочности от длины волокна можно
установить, не делая каких-то специальных предположений о
механизме разрушения и о статистике распределения дефектов.
Если F(l) — вероятность отсутствия на участке длиной I таких
дефектов, которые соответствуют разрушающему напряжению,
меньшему чем а, так что F = 1 — P(g) при фиксированном а, то
для участка длиной V та же вероятность будет F{V). Предполо-
Предположим теперь, что участки I и V соединены последовательно. По
теореме об умножении вероятностей вероятность неразрушения
участка длины I + V равна
B0.3.3)
Возьмем логарифмические производные по I от обеих частей
равенства B0.3.3). Получим
<""<' +О = dinF(l) = _ с> 0<3.4)
Величина с должна быть постоянной, поскольку она не меняется
от прибавления к длине I произвольной длины Г'. Интегрируя
B0.3.4), получим
F(Z) = exp(-cZ). B0.3.5)
При этом учтено, что F@) = l и соответственно F(oo) = 0. Отсю-
Отсюда следует
Z, о)=1 —exp(-cZ).
Величина с должна быть функцией действующего напряжения.
Делая некоторые дополнительные гипотезы, ряд авторов полу-
получали для функции с (о) следующее выражение:
с = (а — Со)а X const при о> о01 с = 0 при а ^ а0.
Соответствующее распределение обычно записывается в следующем
692 гл. 20. механика композитов
виде:
B0.3.6,
Формула B0.3.6) обычно называется, не вполне правильно, рас-
распределением Вейсбулла. Фактически эта формула содержит три
константы, выделение характерной длины Lo представляет опре-
определенные удобства для приложений, это может быть, например,
длина стандартного образца для испытаний. Напряжение а0 пред-
представляет собою пороговое напряжение, при g<g0 разрушение не-
невозможно. В действительности определение трех констант по дан-
данным эксперимента приводит к неустойчивым результатам и
величину а0 часто полагают равной нулю, так будем поступать и
мы. Дифференцируя B0.3.6), находим плотность распределения
)
Здесь принято ао = О. Вычислим по формуле B0.3.1) среднюю
прочность
Сделав замену переменной
мы приходим к интегралу, определяющему гамма-функцию
и получаем следующую формулу для средней прочности:
Совершенно аналогичные вычисления приводят к следующему
выражению для дисперсии прочности (по формуле B0.3.2)):
( !)( |) B0.3.9)
и для коэффициента вариации
w = у Y2 'a -1- B0.3.10)
Существенно заметить, что коэффициент вариации не зависит
§ 20.4. ПРОЧНОСТЬ ПУЧКА
693
от о%. Этот результат получается вследствие того, что в фор-
формуле B0.3.6) было принято Go = O. В противном случае вели-
величина w будет зависеть как от <т0, так и от а^. На рис. 20.3.3
представлен график зависимости и; от а по формуле B0.3.10).
Зависимость средней прочности <о> от длины образца L, да-
даваемая формулой B0.3.8), описывает масштабный эффект. В ло-
логарифмических координатах зависимость между средней проч-
прочностью и длиной L по формуле B0.3.8) изображается прямой
w
0,2
\
X
\
к
*—
¦
— I.
10
Рис. 20.3.3
Рис 20.3.4
линией, наклон которой увеличивается с увеличением коэффици-
коэффициента вариации. Отсюда следует, что может возникнуть положение,
схематически изображенное на рис. 20.3.4. Материал / обнару-
обнаруживает большую среднюю прочность, чем материал // при длине
образца LQ. Но a2<ab поэтому у материала // масштабный эф-
эффект выражен сильно и для более коротких образцов длины Z/
картина оказывается обратной, средняя прочность материала //
выше.
§ 20.4. Прочность пучка
Задача о прочности пучка волокон с различной прочностью
его индивидуальных составляющих была полностью исследована
в работе Даниелса A945 г.), относящейся к текстильным нитям.
Схема Даниелса с незначительным изменением была перенесена
на проблему прочности при растяжении однонаправленного ком-
композита, армированного непрерывным волокном. В основу этой
схемы полагаются некоторые упрощающие предположения,
а именно, считается, что модуль упругости всех волокон одина-
одинаков. При выводе соответствующих формул, если число волокон
весьма велико, нам нет необходимости даже вставать на вероят-
вероятностную точку зрения. Представим себе пучок детерминирован-
детерминированным, пусть Р{о)—отношение числа волокон, разрывающихся
694 гл- 20- механика композитов
при напряжении, меньшем (или равном) о, к общему числу
волокон. Предполагая, что волокна распределены в пучке равно-
равномерно и диаметр их в среднем одинаков, мы находим, что при
напряжении, равном а, Р(о) представляет собою долю (относи-
(относительную площадь) сечения пучка, в котором волокна уже разор-
разорваны, поэтому нагрузка передается на относительную площадь
1 — Р{о). Обозначим через о0 условное напряжение, т. е. силу,
отнесенную к первоначальной пло-
площади сечения неразрушенного пучка.
Тогда истинное напряжение равно
Q = — #
Отсюда следует
Оо = оA-Р(о)). B0.4.1)
Рис. 20.4.1 Поскольку волокна следуют закону
Гука, а = Ее, поэтому уравнение
B0.4.1) может рассматриваться как уравнение диаграммы
растяжения пучка (рис. 20.4.1). Максимальное значение прочности
пучка От соответствует максимуму этой диаграммы. Дифферен-
Дифференцируя B0.4.1) по а и приравнивая результат нулю, получим
1 - Р (а7) - огр (а') = 0. B0.4.2)
Здесь р(а) = Р'(а)— плотность распределения прочности воло-
волокон. Из B0.4.2) находится величина а' и в результате подста-
подстановки в B0.4.1) прочность пучка о0 = от. Величина от всегда
оказывается меньше средней прочности <а>. Для иллюстрации
рассмотрим очень простой пример, когда плотность распределе-
распределения р{о) постоянна в интервале g^(g~, g+) и вследствие усло-
условия нормировки р = 1/(а+ — а-).
Интегральная плотность распределения имеет вид
Подставляя в B0.4.2), получаем следующее уравнение:
о+ - 2о' = 0.
Отсюда
п по формуле B0.4.1)
Если а+ = 2а_, то от = о-, при а_>а+/2 нужно принять о~ = о'
и опять-таки от = о-, т. е. реализуется наименьшее значение
§ 20.5. НЕЭФФЕКТИВНАЯ ДЛИНА ВОЛОКНА В КОМПОЗИТЕ 695
прочности пучка. В крайнем случае а+ = 2а-, <а> = За_/2, таким
образом, прочность пучка в полтора раза меньше средней проч-
прочности образующих его волокон.
Теперь поставим следующий вопрос. Пусть известно распре-
распределение прочности моноволокон, определенное на некоторой дли-
длине Lo. Требуется определить прочность пучка волокон длиной L.
Если L < Lo (а для композитов, как будет показано ниже, вы-
выполняется именно это условие), то в силу вступают два противо-
противоположных фактора. С одной стороны, масштабный эффект при
большом коэффициенте вариации выражен более сильно, поэтому
средняя прочность на длине L растет по сравнению с прочно-
прочностью, определенной на длине Lo. С другой стороны, реализация
прочности в пучке от оказывается ниже средней прочности и
это снижение прочности увеличивается с ростом коэффициента
вариации. Поэтому не вполне ясно, какому волокну следует от-
отдать предпочтение, с большим разбросом прочности или с малым
разбросом. Во всяком случае, предъявляемые иногда к постав-
поставщикам волокна требования ограничить дисперсию прочности не-
некоторым узким пределом не могут считаться оправданными.
Предположим, что распределение прочности волокон опреде-
определяется формулой Вейсбулла B0.3.6) при а0 = 0. Подставляя в
B0.4.2), находим
L ( о у* 1
LQ \ с* / а
и по формуле B0.4.1)
(Т. \1/ос / 1 м/а
B0.4.3)
В этой формуле е есть основание натуральных логарифмов. Срав-
Сравнивая с формулой B0.3.8), запишем это выражение в виде
от = к(о>.
Коэффициент
можно назвать коэффициентом реализации средней прочности
в пучке. Приведем некоторые значения его:
а 5 10 20
к 0,646 0,754 0,841
§ 20.5. Неэффективная длина волокна в композите
Обозначим через vf объемное содержание волокна в композите
и соответственно vm = 1— vf — объемное содержание материала
матрицы. Получим следующее выражение для среднего напря-
напряжения в однонаправленном композите:
а = G<Vf + Gmvm. B0.5.1)
696
ГЛ. 20. МЕХАНИКА КОМПОЗИТОВ
Здесь G/ — напряжение в волокне, ат — напряжение в матрице.
Пренебрегая эффектом поперечной деформации, связанной с не-
неодинаковостью коэффициента Пуассона, найдем, что при сов-
совместной и одинаковой деформации волокна и матрицы напря-
напряжения относятся как модули упругости. Полимерная матрица
упруга вплоть до момента разрушения, отношение модуля упру-
упругости угольного волокна к модулю упругости эпоксидной смолы
Ef :i?m== 40 000 : 350 = 114, когда напряжение в волокне равно
пределу прочности порядка О/ = 300 кгс/мм2, от = 300:114==
= 2,6 кгс/мм2, тогда как предел прочности смолы порядка 7—
8 кгс/мм2. Этот простой подсчет, имеющий целью лишь оценку по-
порядка величины, показывает, что волокна рвутся раньше, чем
матрица. Это тем более относится к материалам с металлической
Рис. 20.5.1
матрицей, способной деформироваться пластически. Если компо-
композит состоит из п волокон, то в идеальном случае прямолинейных
волокон с одинаковым модулем и одинаковой площадью попе-
поперечного сечения усилия распределяются между этими волокнами
равномерно. Если одно волокно оборвется, то в том сечении,
где произошел обрыв, нагрузка распределится на п — 1 волокон,
напряжение в волокнах увеличится и далее разрушение будет
происходить по схеме пучка. Распределение усилий между разор-
разорванным волокном и соседним, еще не разорванным, осуществля-
осуществляется в результате сдвиговой деформации матрицы, и на некото-
некотором расстоянии U от места обрыва наличие обрыва практически
не будет сказываться на распределении усилий, величина уси-
усилия в оборванном волокне будет почти та же, что и в соседних
необорванных волокнах. Длина /0 называется неэффективной
длиной, длина 2/0 принимается за длину пучка, к которому при-
применяется изложенная в § 20.4 теория. Для оценки неэффек-
неэффективной длины применяются различные схемы, которые мы и
рассмотрим.
1. Сдвиговый анализ. Рассмотрим волокно, помещенное в
трубку из упругого материала матрицы, как показано на
рис. 20.5.1. Радиус волокна пусть будет г, радиус трубки /?.
Наружная поверхность трубки жестко закреплена. Предполо-
Предположим, что материал трубки работает только на сдвиг, смещение
сечения, находящегося на расстоянии х от места обрыва, пусть
§ 20.5. НЕЭФФЕКТИВНАЯ ДЛИНА ВОЛОКНА В КОМПОЗИТЕ 697
будет и (х). Уравнение равновесия элемента длиной dx запишет-
запишется следующим образом:
ЯГ2 g + 2ягт = 0.
Но а = ? ди/дх, вследствие сделанного предположения о том, что
матрица работает только на сдвиг, т = [я^г/ (/? — г), поэтому по-
получим следующее дифференциальное уравнение:
-^Г+-а = 0 или _ + __ = 0. B0.5.2)
Здесь
Решение уравнения B0.5.2), удовлетворяющее условию о@) = 0
и о(°°) = а0, есть
а==аоA_е-*/0). B0.5.4)
Определение неэффективной длины, конечно, может быть
только условным, например,
а) длина, на которой напряжение достигает 90% своего пре-
предельного значения (Розен),
оо
б) длина Z, на которой интеграл j (а0 — a) dx = laOi
о
Касательное напряжение т определяется из условия равновесия,
они принимает максимальное значение при х = 0, а именно,
tmax = ^O^ft"*
Как правило, это напряжение оказывается выше, чем предел
прочности материала матрицы при сдвиге.
2. Решения теории упругости. Более строгая схема решения
той же задачи состоит в том, что оборванное волокно рассматри-
рассматривается включенным в анизотропную упругую среду, упругие
постоянные которой находятся в результате определения харак-
характеристик составляющих гетерогенной системы волокно — матрица.
Мы не приводим здесь это довольно сложное решение, при
построении которого волокно рассматривается как стержень и гра-
граничные условия на плоскости обрыва удовлетворяются интеграль-
интегрально. Оценки неэффективной длины оказываются близкими к тем,
которые были получены выше, но распределение касательных
45 ю. Н. Работнов
698
ГЛ. 20. МЕХАНИКА КОМПОЗИТОВ
напряжений оказывается существенно иным. На рис. 20.5.2 пред-
представлены примерные графики условия х(х) для решения, найден-
найденного по схеме пункта 1, и в результате применения методов тео-
теории упругости. Наибольшее значение касательного напряжения
достигается на некотором расстоянии от конца и оно существен-
существенно больше, чем это следует из упрощен-
упрощенного сдвигового анализа. Поэтому обрыв
неизбежным образом сопровождается от-
отслоением матрицы от волокна. Но такое
отслоение, на какие малые расстояния
оно бы ни распространялось, неизбежно
создает сингулярность для напряжений.
Картина получается совершенно подобной
той, которая изображена на рис. 20.5.3:
¦ трещина распространяется вдоль плоской
границы двух материалов с разными
Рис. 20.5.2 упругими свойствами. Решение этой пло-
плоской задачи обнаруживает тот же характер
особенности, что и для трещины в однородном материале, напря-
напряжение на кончике трещины обращается в бесконечность, как
г~1/2, решение соответствующей реальной осесимметричной зада-
задачи неизвестно.
3. Определение неэффективной длины с учетом силы трения.
Есть основания предполагать, что при вытаскивании волокна
из матрицы не происходит сразу полного освобождения волокна
«Го
h
Рис. 20.5.3
Рис. 20.5.4
по всей поверхности. Существует некоторая сила, остающаяся
постоянной на определенном, притом не столь малом пути, ко-
которая оказывает сопротивление движению волокна. Будем назы-
называть эту силу силой трения и обозначим через т величину силы
на единицу площади поверхности. Теперь идеальная расчетная
схема должна была бы носить такой характер. Цилиндрическая
трещина продвинулась на длину 10 (рис. 20.5.4), вследствие
растяжения матрицы на поверхность цилиндра длиной 10 и ра-
радиусом г действует сила трения 2яг/0т; эта сила равна растяги-
растягивающему усилию в волокне. Но по определению эффективной
длины при #>Z0 напряжение в волокне постоянно и равно о0,
следовательно, усилие есть яг2<т0. Разность усилий по левую и
§ 20.6. КОМПОЗИТЫ С МЕТАЛЛИЧЕСКОЙ МАТРИЦЕЙ
по правую сторону сечения х = 10 создает сингулярность поля
напряжений, и коэффициент интенсивности пропорционален этой
разности. Если бы мы умели вычислять величину этого коэф-
коэффициента интенсивности Ки и знали значение критического коэф-
коэффициента интенсивности, мы смогли бы найти величину 10. Верх-
Верхняя оценка для U получится в предположении о том, что КПс — О,
таким образом,
2лх/0т =л;г2а,
откуда
*o=g. B0.5.5)
Величина т вообще неизвестна, и пути ее экспериментального
определения неясны. Во всяком случае она меньше, чем сопро-
сопротивление композита разрушению при сдвиге. Принимая т =
= 2 кгс/мм2, а = 240 кгс/мм2 (ориентировочные оценки для угле-
углепластика), получим U ^ 30d при d = 10 мкм, Zo = 0,3 мм. При
разрыве композита поверхность разрыва напоминает щетку, из
разлома матрицы, как щетинки, торчат кончики оборванных во-
волокон. Средняя длина этих вытянутых кончиков равна неэф-
неэффективной длине волокна. Результаты таких измерении показы-
показывают, что величина неэффективной длины в сильной степени
зависит от технологии изготовления композита, определяющей
величину т в формуле B0.5.5), для композитов углерод — эпок-
эпоксидная смола величина U может достигать 0,5—1 мм. При этой
длине большая дисперсия прочности волокон приводит к сниже-
снижению прочности пучка за счет коэффициента реализации /с, опре-
определяемого формулой B0.4.4), который не перекрывается увели-
увеличением средней прочности вследствие масштабного эффекта.
§ 20.6. Однонаправленные композиты
с металлической матрицей
Композит, армированный строго параллельными волокнами
одного направления, обнаруживает в направлении армирования
наибольшую прочность. В поперечном направлении сопротивле-
сопротивление его очень невелико, сопротивление сдвигу в плоскости, со-
содержащей волокна, также низкое. Модуль упругости в направ-
направлении армирования определяется достаточно точно по правилу
смесей, вытекающему непосредственно из формулы B0.5.1). Если
деформации волокна и матрицы одинаковы, то
E*Efv, + Envn. B0.6.1)
Эта формула приближенна по двум причинам. Во-первых, волок-
волокна и матрица имеют разный коэффициент Пуассона, поэтому про-
происходит неравномерная поперечная деформация и возникает поле
45*
700 гл- 20- механика композитов
микронапряжений. Во-вторых, угольные и органические волокна
объединяются в слегка подкрученные нити и параллельность
укладки нарушается. Однако формула B0.6.1) дает приемлемые
результаты, хотя пользоваться ею следует лишь для ориентиро-
ориентировочных предварительных Прикидок при проектировании мате-
материала. Определить модуль упругости Е на готовом композите
технически гораздо проще, чем набирать статистику модулей мо-
моноволокон. В еще большей степени это относится к другим уп-
упругим постоянным.
Что касается предсказания прочности композита по данным
о прочности его компонент, результаты многочисленных работ
разных авторов привели пока к результатам в общем негативным.
Теория пучка, изложенная в § 20.4, даст лишь материал для
ориентировочных суждений, уточнение этой теории требует ис-
исчерпывающей статистической информации не только о прочности
моноволокон, но и о распределении модуля упругости. Распре-
Распределение Вейсбулла не описывает достаточно точным образом рас-
распределение прочности моноволокон, фактически распределение
оказывается бимодальным, т. е. функция имеет два максимума.
Поэтому экстраполяция прочности на малые разрывные длины,
основанная на распределении Вейсбулла, совершенно ненадежна.
Определение неэффективной длины в большой мере условно.
Поэтому здесь будут изложены лишь некоторые наполовину ка-
качественные соображения, принадлежащие Милейко и позволяю-
позволяющие объяснить наблюдаемое изменение прочности и характера
разрушения композита в зависимости от объемного содержания
волокна. В некоторых случаях эти соображения подсказывают
меры, необходимые для улучшения свойств композита.
Пластичная матрица. Если материал матрицы пластичен, а во-
волокно хрупко, при достижении удлинения, соответствующего
пределу прочности волокна, последнее рвется, тогда как матрица
продолжает вытягиваться. В некоторых старых работах (Келли
и др.) делается вывод о том, что при малой, концентрации хруп-
хрупких волокон прочность композита может оказаться ниже проч-
прочности матрицы. Волокна разрываются при сравнительно низком
среднем напряжении, а дальше вся нагрузка воспринимается
матрицей, относительная площадь сечения которой vm меньше,
чем площадь сечения исходного материала, vm = 1 — vf. Это умень-
уменьшение прочности происходит до тех пор, пока vf меньше неко-
некоторого критического значения vKV. При vf > i?Kp большая часть
нагрузки воспринимается прочными волокнами и прочность ком-
композита растет с увеличением Vf. Эта схема была бы верна, если
бы разрушение всех волокон происходило в одном и том же
сечении. В действительности при малых значениях vf по мере
удлинения матрицы происходит беспорядочное дробление. Рас-
Распределение растягивающего усилия в каждом кусочке длины
1>210 будет таким, как показано на рис. 20.6.1, а, при даль-
20.6. КОМПОЗИТЫ С МЕТАЛЛИЧЕСКОЙ МАТРИЦЕЙ
701
нейшей вытяжке возможен разрыв в той средней части, где на-
напряжение максимально.
Если Z^2Z0, график распределения усилия будет соответст-
соответствовать рис. 20.6.1,6, вероятность разрыва такого кусочка волокна
уже мала. В результате оказывется, что все волокна раздро-
раздробятся на отдельные куски длиной от Zo до 210. Величина 10 опре-
определяется в данном случае максимальным напряжением, которое
в
.1
\
О)
б)
Рис. 20.6.1
Рис. 20.6.2
может выдержать отрезок волокна установленной длины, т. е.
прочностью волокна, экстраполированной на длину 10. В резуль-
результате средняя прочность кусочков раздробленного волокна будет
иметь порядок <g(Z0)>, она соответствует, например, L = l0 в фор-
формуле B0.3.6), если считать справедливой гипотезу слабого звена
при распределении Вейсбулла. Теперь прочность композита будет
определяться формулой, следующей из B0.5.1):
а = avf {Of (Zo)> + A — vf) am.
B0.6.2)
Здесь а — коэффициент, учитывающий то, что в одно и то же
сечение композита попадают разные сечения оборванных воло-
волокон. На конце волокна напряжение равно нулю, в середине оно
равно <G/(Z0)>, поэтому коэффициент а равен примерно 1/2. Ве-
Величина о'т—это то напряжение в матрице, при котором рвутся
или выдергиваются короткие волокна, оно меньше чем от, если
материал матрицы способен к упрочнению. На рис. 20.6.2 в ко-
координатах о — vf уравнению B0.6.2) соответствует прямая 1.
Другой возможный механизм разрушения композита состоит
в следующем. При существующей технологии изготовления во-
волокнистых композитов нельзя быть уверенным в том, что во-
волокна распределятся в матрице равномерно. Всегда возможны
образования, подобные показанным схематически на рис. 20.6.3.
Несколько волокон оказываются плотно сомкнутыми между со-
собою, образуя цепочку длиной с. Если разорвется одно волокно
702 гл- 20- механика композитов
цепочки, вблизи разрыва появится концентрация напряжений в
соседнем волокне, оно разорвется в свою очередь и так далее,
пока в композите не образуется трещина длиной с. Может слу-
случиться, что она остановится, а может быть и так, что она пойдет
дальше и образец разделится на две части. Предполагая вторую
возможность, определим прочность композита следующей фор-
формулой:
а = VfOfmm + A — Vf) о"т. B0.6.3)
Здесь G/min — некоторое относительно небольшое напряжение,
при котором разрывается одно волокно цепочки. Следует ожи-
ожидать, что эта величина уменьшается с возрастанием vf, поскольку
при этом увеличивается число волокон, на-
находящихся в цепочках. Мы не будем учиты-
учитывать этой возможности и представим урав-
уравнение B0.6.3) прямой 2 на рис. 20.6.2.
Строго говоря, конечно, отфот, но мы
пренебрегли этой разницей на чертеже,
точно так же, как мы приняли предельное
значение У/ = 17 тогда как при плотной упа-
упаковке круговых цилиндров одинакового
диаметра vf = 0,907. Теперь нам предстоит
выяснить, когда вступает в силу второй ме-
механизм разрушения, которому соответствует меньшая прочность.
Обозначая через Кс критический коэффициент интенсивности,
заметим, что для изотропного материала
о
о
0
о
о
О
чГХ
'О
Рис. 20.6.3
о
о<
\°
пс
. 2
При этом было G = ~^v K2Ci где G — работа продвижения тре-
трещины на единицу длины или сила сопротивления ее движению.
Для анизотропного материала можно было бы вывести анало-
аналогичные точные формулы, которые в данном случае для нас бес-
бесполезны, существенно то, что
а<]/|х (...)• B0.6.4)
Заключенное в скобки и обозначенное точками выражение
представляет собою функцию упругих констант, которая зависит
от vf. Но эта зависимость не должна нас интересовать. Сущест-
Существенно то, что сопротивление раскрытию трещины происходит за
счет пластической деформации матрицы, оно уменьшается с
уменьшением объемной доли матрицы, т. е. увеличением vf. При
vf = 1 следует считать G = 0, что мы и делали по существу, пред-
предположив, что разрыв одного волокна в цепочке приводит к раз-
§ 20.7. КОМПОЗИТЫ С ПОЛИМЕРНОЙ МАТРИЦЕЙ
рыву всех волокон и образованию трещины длиной с. Таким об-
образом, границей неравенства B0.6.4) служит на рис. 20.6.2 па-
падающая кривая 5. Ломаная ABCD изображает зависимость проч-
прочности о от объемного содержания волокна У/, характерное паде-
падение прочности после точки В отмечалось в экспериментах. Опыт-
Опытные точки на участке АВ мало отклоняются от прямой, на
участке BCD разброс опытных данных существенно больше. Это
легко понять, если заметить, что величина с случайна и условия
образования трещины размером с также не вполне определенны.
Для композиции углерод — алюминий, например, оптимальное
содержание угольного волокна, соответствующее точке В, оказа-
оказалось равным примерно 0,2—0,3.
§ 20.7. Композиты с полимерной матрицей
Полимерная матрица следует закону Гука почти до момента
разрушения, незначительные отклонения от закона упругости
могут не приниматься во внимание. Как правило, удлинение
матрицы при разрыве в несколько раз больше, чем удлинение
волокна, поэтому качественная картина поведения такого ком-
композита в известной мере напоминает поведение композита с ме-
металлической матрицей: при малом объемном содержании волокна
возможно его дробление. Однако малая прочность матрицы по
отношению к касательным напряжениям и довольно слабая связь
между волокном и матрицей вносят свою специфику. В компо-
композите органическое волокно — эпоксидная смола, наоборот, раз-
разрывное удлинение смолы меньше, чем удлинение волокна. Ввиду
малой прочности матрицы происходит ее дробление на мелкие
частички, которые легко отваливаются, обнажая пучки волокон,
которые уже относительно легко обрываются.
В армированном высокопрочными волокнами композите тре-
трещина не будет распространяться поперек волокон, а приведет
к расслоению. Этот механизм впервые был описан и объяснен
Гордоном и Куком, которые проделали следующий анализ. Была
рассмотрена пластина с эллиптическим отверстием с полуосями
а и Ь. Пластина растягивается в направлении малой полуоси.
Напряжение а2г достигает максимального значения в точке xt =
= ?2 = 0 (рис. 20.7.1), напряжение Оц достигает максимума в не-
некоторой точке с координатами Xi=x*, х2 = 0. Отношение макси-
максимального напряжения Оц к максимальному напряжению о22 было
вычислено для разных отношений Ъ/а. Оказалось, что с умень-
уменьшением этого отношения величина (он) max/@22) та* стремится к
некоторому пределу, который для изотропного материала равен
1/(ЗУЗ)« 0,192 (этот точный результат найден Полиловым, Гор-
Гордон и Кук считали на ЭВМ и получили отношение около 1/5).
Из этого был сделан вывод о том, что если прочность в направ-
направлении оси Xt меньше,, чем примерно 1/5 прочности в направле-
704
ГЛ. 20. МЕХАНИКА КОМПОЗИТОВ
нии укладки волокон, образуется показанная на рисунке про-
продольная трещина, которая воспрепятствует росту поперечной.
С другой стороны, Полилов показал, что в некоторой точке
контура эллиптического отверстия, отмеченной крестиком на
рис. 20.7.1, достигают максимума касательные напряжения Oi2,
при этом для изотропного материала отношение (Gi2)max/@22)max
оказывается равным приблизительно 0,324 при Ъ/а -> 0. Каса-
Касательные напряжения на контуре щели оказываются более опас-
опасными, чем нормальные напряжения перед кончиком трещины,
и картина расслоения скорее напоминает ту, которая показана
на рис. 20.7.2.
Т-
Рис. 20.7.1
Рис. 20.7.2
Мы не приводим здесь решения для распределения напря-
напряжений около эллиптического отверстия, оно может быть полу-
получено по методу, схематически описанному в § 10.5, это решение
можно найти в книгах Мусхелишвили [8], Савина [13], Амен-
Заде. Для анизотропного материала решение также построено,
отношение @12I^/@22) max получается меньшим, чем для изотроп-
изотропного, но оно почти всегда больше, чем отношение пределов
прочности матрицы на сдвиг и композита на разрушение вдоль
волокон. Можно определить ту величину объемного содержания
волокон, при котором распространение поперечной трещины и
продольное раскалывание равновероятны. Для композиции
стеклянное волокно — эпоксидная смола соответствующее значе-
значение vf колеблется от 0,2 до 0,3. В реальных стеклопластиках
значение vf равно приблизительно 0,7.
На рис. 20.7.3 приведена фотография разорванного образца
из однонаправленного углепластика. Видно, что короткие по-
поперечные разрывы разделяются длинными продольными трещи-
трещинами и схема пучка, описанная в § 20.4, может быть применена
лишь с большой натяжкой. Таким образом, прочность однона-
однонаправленного композита даже при растяжении в значительной
мере определяется сдвиговой прочностью матрицы и прочностью
адгезии, которую в свою очередь можно характеризовать кри-
критическим коэффициентом интенсивности Ки с. Определение проч-
прочности матрицы на сдвиг обычно производят путем опыта на изгиб
§ 20.7. КОМПОЗИТЫ С ПОЛИМЕРНОЙ МАТРИЦЕЙ
705
сосредоточенной силой по схеме, изображенной на рис. 20.7.4.
По элементарной теории (§ 9.16) наибольшее касательное напря-
напряжение в сечении будет в срединной плоскости и оно равно
Экспериментально определяемые значения ть, как оказывается,
Рис. 20.7.3
зависят от отношения l/h, опытные точки в координатах ттах,
l/h располагаются примерно
так, как это показано на I
рис. 20.7.5. В области / тре- |
щина образуется ниже сере-
середины сечения и сопровожда-
сопровождается разломом, в области //
происходит действительно
разрушение от сдвига в нейт-
нейтральной плоскости, наконец
в области /// — разлом от
нормальных напряжений и
ный характер. Очевидно,
Рис. 20.7.4
ТОЧКИ ДЛЯ Ттах НОСЯТ фиКТИВ-
что достоверные значения пре-
предела прочности при сдвиге соответствуют определению его
в области //, границы которой устанавливаются визуально по
характеру разрушения (обычно l/h от 4 до 6). Характер раз-
разрушения в области / объясняется, по-видимому, тем, что у очень
коротких балок сжимающие нормальные напряжения в плоско-
плоскостях, параллельных нейтральной, увеличивают сопротивление
сдвигу. Действительно, давление передается, как показано схе-
схематически на рис. 20.7.4, через ролики довольно большого ра-
радиуса, чтобы уменьшить местное смятие. С другой стороны, для
балки из материала с резко различающимися между собою мо-
модулями нормальной упругости и сдвига концевой эффект зату-
затухает не по Сен-Венану. Действительно, в § 20.5 на основе сдви-
сдвигового анализа было показано, что для волокна радиусом г на-
706
ГЛ. 20. МЕХАНИКА КОМПОЗИТОВ
пряженная зона вблизи его конца простирается на глубину [5,
определяемую формулой B0.5.3). Поэтому следует ожидать, что
если поперечный размер стержня из композитного материала
г
I
° О
О
о
1
|
1
1
1
1 °
1 '
1*
I
1 1
¦7"
э
1 о о
ж
О
0 °
0 о °
Рис. 20.7.5
есть А, длина зоны краевого эффекта будет иметь порядок не /г,
а /г, умноженное на корень квадратный из отношения Е/\х.
Для коротких балок из однонаправленных композитов величины
% и I оказываются одного порядка, поэтому теория поперечного
изгиба, описанная в § 9.16, для них неприменима.
Малая жесткость по отношению к межслойному сдвигу при-
приводит к тому, что кроме прогиба, определяемого по обычной
теории изгиба (§ 3.8), появляется дополнительный прогиб, свя-
связанный со сдвиговой деформацией. Соответствующая приближен-
приближенная теория была дана еще Тимошенко, последующие уточнения
мало что к ней прибавили. Мы изложим идею этой теории на
простом примере балки на двух опорах, загруженной сосредо-
сосредоточенной силой Р посредине (z = l/2). Прогиб в точке прило-
приложения силы / состоит из двух частей / = Д + /2, величина Д на-
находится из обычной теории изгиба. По способу, изложенному
в § 3.8, мы легко находим
/ - Pl* (т — bJ^_
7l "" 48?/ [ 12
Перерезывающая сила Q по абсолютной величине всюду равна
Р/2, она меняет знак в точке приложения силы. Касательное
напряжение в сечении от перерезывающей силы x = Qty(x, у),
где i|)(#, у)—функция, определяющая распределение касательных
напряжений по сечению и удовлетворяющая условию
Теперь потенциал перемещений от поперечной силы выразится
§ 20.8. КОМПОЗИТЫ СЛОЖНОГО СТРОЕНИЯ 707
следующим образом:
V О F О
Здесь а есть интеграл от "ф2 по площади. В теории Тимошенко,
который принимал в стержне прямоугольного сечения парабо-
параболическое-распределение напряжений, зависящих только от вер-
вертикальной координаты г/, получается
а = 6/5. B0.7.1)
Определяя прогиб /2 по теореме Кастильяно, легко найдем
Складывая /t и /2, находим, что первая, основная часть прогиба
увеличивается пропорционально кубу длины, тогда как /2 зави-
зависит от длины в первой степени. Отсюда следует, что, испытывая
на изгиб балки разной длины, можно выделить величину /2 и,
следовательно, найти модуль межслойного сдвига [х. Фактически
для стеклопластиков получить таким способом надежные резуль-
результаты не удалось, мелкие экспериментальные ошибки неизбеж-
неизбежным образом накладываются и вносят большую погрешность.
Пока что, как нам представляется, единственный надеж-
надежный способ определения \х состоит в испытании на кручение
двух стержней прямоугольного сечения с разными отношениями
сторон. Способ обработки, описанный в § 9.12, позволяет опре-
определить по отдельности модуль сдвига в плоскости листа и мо-
модуль межслойного сдвига. Так, для однонаправленного угле-
углепластика было найдено, что модуль межслойного сдвига рав-
равняется 230 кгс/мм2, тогда как модуль сдвига в плоскости слоя
570 кгс/мм2.
§ 20.8. Упругие свойства и разрушение композитов
сложного строения
В авиации и реактивной технике, где главным образом при-
применяются современные композитные материалы, обычная техника
изготовления листов и пластин состоит в том, что сначала из-
изготовляется так называемый препрег. На барабан под натяжением
наматывается лента из волокна, пропитанного смолой. Лента
может быть изготовлена заранее с очень редким и слабым утком,
а может формоваться непосредственно в процессе намотки —
нити с нескольких катушек просто укладываются рядом, образуя
сплошную ленту. После намотки лист разрезается по образую-
образующей и укладывается на плоскость. Из этих листов или препре-
708 гл-20- механика композитов
гов собирается пластина, которая полимеризуется под давлением.
Монослои препрега укладываются под разными углами, таким
способом можно получить желаемую анизотропию. Иногда слои
однонаправленного препрега чередуются со слоями ткани или
материалами типа бумаги или даже металлической фольги. Здесь
мы изложим только общую схему определения упругих постоян-
постоянных и расчета на прочность таких сложных пластин, фактическое
проведение вычислений без применения ЭВМ затруднительно,
а вопросы, связанные с техникой разного рода расчетов, в этой
книге не излагаются.
Принимая за основной элемент структуры монослой, будем
задавать его упругие свойства тензором модулей упругости 2?да,
который для ортотропного материала может быть задан так, как
это сделано в § 10.6. Однако для расчетов нам будет удобно
задавать тензор Е\щ (г, /, /с, Z=l, 2) по отношению к произ-
произвольной системе координат. Все слои деформируются одинаково,
поэтому напряжения в слое номер s будут
оЬ = E\jhlekl. B0.8.1)
Теперь средние напряжения в композите определятся по
формулам
а« = Emekh Ет - =±- E8mh9> B0.8.2)
где hs — толщина слоя с номером s.
Результат обращения соотношений B0.8.2) запишем следую-
следующим образом:
Здесь EJjli — тензор податливости или матрица, обратная мат-
матрице Ет. При конкретных расчетах бывает удобно переходить
на матричный язык, представляя тензор модулей упругости как
симметричную матрицу 3X3. Внеся выражения для вц в фор-
формулы B0.8.2), получим
°Ь — RijhlGkh Rijhl = EifrqEpqki. B0.8.3)
Теперь проверяется выполнение условия прочности
/s(ct«)<0 B0.8.4)
для каждого слоя по отдельности. Обычно разрушение какого-
либо слоя принимается за разрушение конструкции. Но, вообще
говоря, выход из строя одного слоя не означает еще потери не-
несущей способности оболочки или пластины. После разрушения
в каком-либо смысле одного из слоев его упругие константы
изменяются, соответственно, изменяется величина -Яда и мы
должны последовательно проверять оставшиеся слои.
§ 20.8. КОМПОЗИТЫ СЛОЖНОГО СТРОЕНИЯ
709
Что касается условия прочности монослоя, здесь возможны
два вида разрушения: скалывание матрицы и разрыв волокон.
Если обозначить напряжение вдоль волокон оп, напряжение в
перпендикулярном направлении оп и
касательное напряжение тп, то разру-
разрушение произойдет при нарушении од-
одного из следующих двух условий:
On<ob, f(o'n,Tn)<k. B0.8.5)
Второе условие с достаточной степенью
точности аппроксимируется линейной
функцией, а именно,
Рис. 20.8.1
* т„
rn + mo'n<:k. B0.8.6)
На рис. 20.8.1 приведены опытные точ-
точки и прямая, соответствующая уравнению B0.8.6). Опыты про-
производились на растяжение образцов, вырезанных под углом к
направлению армирования. Величина к, как видно, представляет
собою сопротивление сдвигу матрицы. По-видимому, этот способ
определения к дает наиболее точные результаты.
При растяжении стержня напряжением а под углом ф к нап-
направлению армирования мы имеем оп== о cos2 ф, оп= a sin2 ф,
тп =-2-зт2ф. Если угол ф мал, то приблизительно ап=аA—ф2),
ап=аф2, тп = (Уф. Для углепластика было определено
к = 5,6 кгс/мм2, тогда как оь = 80—100 кгс/мм2. Пренебрегая
квадратом угла ф, найдем, что разрушение от скола не произой-
произойдет в том случае, когда ф< ~4°.
Укладка слоев волокна с небольшой разориентировкой ±5°,
как оказывается, дает определенные преимущества. Прочность на
разрыв почти не меняется по сравнению с однонаправленным
материалом, но перекрестное армирование тормозит развитие
возникших на случайных дефектах трещин. В результате диспер-
дисперсия прочности оказывается существенно меньшей, чем у одно-
однонаправленного материала при той же средней прочности.
Система из нитей трех различных направлений будет геомет-
геометрически неизменяема, поэтому современные композиты выкла-
выкладываются таким образом, чтобы было не менее трех направле-
направлений армирования. Если принять за ось xt среднюю линию пла-
пластины, то обычная укладка — это укладка в четырех направле-
направлениях под углами к этой оси 0, я/2, ±ф. При чередовании слоев
следует сохранять симметрию относительно средней плоскости,
чтобы растяжение не сопровождалось изгибом. Варьируя коли-
количество слоев той или иной ориентации и меняя угол ф, можно
в известном смысле оптимизировать конструкцию, выбирая же-
710 гл- 20- механика композитов
лаемую степень анизотропии. При оценке такого композита
условие B0.8.6) становится малосущественным, разрушение
слоя — это разрыв его волокон, после чего слой просто выключа-
выключается из работы. Упругие свойства композита теперь мало зависят
от упругости смолы, модуль упругости в направлении пг и мо-
модуль сдвига малы по сравнению с модулем упругости Е в на-
направлении волокон. Поэтому тензор модулей упругости слоя,
волокна которого составляют угол ер с осью хи определится
следующим образом. Деформация в направлении п есть еп =
= еа^пащ. Потенциал напряжений для слоя
U = -^Ее\ = y Епап$ПуЩ.
Поэтому
EUv6 = ЕпаЩПуЩ. B0.8.7)
Здесь, как обычно, па, ...— направляющие косинусы волокон
слоев с номером s по отношению к осям координат xt и х2.
Для системы 0, я/2, ±ср при относительных толщинах h0,
Ля/2, К после элементарных вычислений находим
F Е
^1111 =Ji(h0 + К COS4 ф)> ^2222 = ff (hn/2 + К Sin4 ф)>
^1122 =-^-cos2 cpsin2 ф = E12l2, H = h0 + А„/2 + Аф.
Теперь при оценке прочности нужно проверять только условие
B0.8.5) и в случае его нарушения повторять расчет, полагая
в формулах B0.8.8) толщину разрушенного слоя равной нулю.
Конечно, такая схема расчета довольно груба. Уточнение ее
связано с довольно громоздкими выкладками.
В заключение остановимся на вопросе о влиянии концентра-
концентраторов напряжений на прочность армированных пластиков. На-
Напомним, что теоретическим коэффициентом концентрации назы-
называется отношение наибольшего нормального напряжения в не-
некоторой точке к величине среднего напряжения, которое при
растяжении, например, получается путем деления силы на ос-
ослабленную площадь поперечного сечения. Эффективный коэф-
коэффициент концентрации — это отношение нагрузки, разрушающей
гладкий образец, к нагрузке, разрушающей образец с концентра-
концентратором, при условии, что минимальная площадь сечения в том и
другом случае одинакова. Очевидно, что теоретический коэф-
коэффициент концентрации и эффективный коэффициент не долж-
должны совпадать, вовсе не обязательно, чтобы разрушение про-
происходило в результате достижения нормальным напряжением
предельного значения в одной только точке. У металлов обра-
образование пластических зон перераспределяет напряжения и,
§ 20.8. КОМПОЗИТЫ СЛОЖНОГО СТРОЕНИЯ
711
л-
как мы видели в гл. 15, наличие концентратора может даже
повысить несущую способность по сравнению с гладким образ-
образцом. Композиты с полимерной матрицей ведут себя упруго
вплоть до разрушения, и разрушение действительно происходит
вследствие отрыва. Однако эффективный коэффициент концен-
концентрации оказывается для них значительно меньше, чем теоретиче-
теоретический. По формулам § 10.5 мы можем после некоторых сравни-
сравнительно несложных вычислений определить поле напряжений
около круглого отверстия, растягиваемого приложенным на бе-
бесконечности напряжением ст.
Оказывается, что наиболь-
наибольшие нормальные напряжения
возникают в точках А и В
(рис. 20.8.2), при этом тео-
теоретический коэффициент кон-
концентрации равен 3. Но в не-
которых точках С и D (и
симметричных с ними), по-
положение ""которых определя-
определяется полярным углом -ф, до-
достигают максимального зна-
значения касательные напряже-
напряжения Gi2. Величина угла гр
близка к 20°. Для анизот-
анизотропного материала решение
более сложно, но результат
получается сходным. Коэффициент концентрации оказывается
больше 3. Угол г|), определяющий положение точки мак-
максимума касательного напряжения, сравнительно мало за-
зависит от степени анизотропии. Но композит плохо сопро-
сопротивляется сдвигу, поэтому в точках, где достигает максимума
касательное напряжение, появляются показанные на рисунке
трещины. В однонаправленном материале эти трещины распро-
распространяются вдоль штриховых линий на всю длину образца и
приводят к общему разрушению. При перекрестном армировании
они продвигаются неглубоко и практически не раскрываются;
разрушается бмола, но не волокна. Но возникновение этих не-
небольших трещин разгружает материал в окрестности опасных то-
точек А и В, Схематически можно представить дело так, как если
бы растягивалась изображенная на рис. 20.8.2 сбоку полоса с
неглубокой выточкой. Для коэффициента концентрации напря-
напряжений в такой полосе существует приближенная формула Ней-
бера, по этой формуле для теоретического коэффициента кон-
концентрации к получается оценка к = 1,4— 1,6. Такие же значения
получаются для эффективных коэффициентов концентрации на-
напряжений для образцов из стеклопластиков и углепластиков с
круглым отверстием.
Рис. 20.8.2
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Болотин В. В. Статические методы в строительной механике.— М.: Строй-
издат, 1961.
Д е Вит Р. Континуальная теория дисклинаций. Механика.— М.: Мир,
1977.— (Новое в зарубежйой технике.)
Закономерности ползучести и длительной прочности: Справочник/Под ред.
С. А. Шестерикова.— М.: Машиностроение, 1983.
Ив л ев Д. Д. Теория идеальной пластичности.— М.: Наука, 1966.
Качан о в Л. М. Основы механики разрушения.— М.: Наука, 1974.
К л ю ш н и к о в В. Д. Математическая теория пластичности.— М.: Изд-во
МГУ, 1979.
Л я в А. Математическая теория упругости.— М.: ОНТИ, 1935.
Мусхелишвили Н. И. Некоторые основные задачи математической
теории упругости.— М.: Наука, 1966.
Новожилов В. В. Теория упругости.— М.: Судпромгиз, 1958.
П а р т о н В. 3., М о р о з о в Е. М. Механика упругопластического разру-
разрушения.— М.: Наука, 1974.
Победря Б. Е. Механика композиционных материалов.— М.: Изд-во МГУ,
1984.
Р а б о т н о в Ю. Н. Ползучесть элементов конструкций.— М.: Наука, 1966.
Работнов Ю. Н. Элементы наследственной механики твердых тел.— М.:
Наука, 1977.
С а в и н Г. Н. Распределения напряжений около отверстий.— Киев: Hay-
кова думка, 1968.
Тимошенко С. П., Войновский-Кригер С. Пластинки и оболоч-
оболочки.— М.: Физматгиз, 1963.
Хил л Р. Математическая теория пластичности.—М.: Гостехиздат, 1956.
Черепанов Г. П. Механика хрупкого разрушения.— М.: Наука, 1974.