Текст
Основы проектирования
цифровых схем
Барри Уилкинсон
Университет штата Северная Каролина, США
Издательский дом “Вильямс”
Москва ♦ Санкт-Петербург * Киев
2004
Издательский дом “Вильямс”
Зав. редакцией С. И. Тригуб
Перевод с английского М.В. Бойко
Под редакцией А.А. Голубченко
Уилкинсон, Барри.
У36 Основы проектирования цифровых схем. : Пер. с англ. — М. :
Издательский дом “Вильямс”, 2004. — 320 с.: ил. — Парал. тит. англ.
ISBN 5-8459-0685-7 (рус.)
Эта книга посвящена вопросам проектирования цифровых ло-
гических схем. В краткой, но строгой форме в ней излагаются ме-
тоды проектирования основных классов логических схем — от вен-
тилей до схем на программируемых логических матрицах. Данная
книга будет особенно полезной для студентов, изучающих электро-
нику и вычислительную технику. Великолепная методика изложе-
ния, наличие большого количества примеров и заданий для само-
проверки с ответами делает ее незаменимой для тех, кто совершает
первые шаги в области проектирования сложных цифровых систем.
ISBN 5-8459-0685-7 (рус.)
ISBN 0-13-570110-4 (англ.)
© Издательский дом “Вильямс”, 2004
© Prentice Hall Europe, 1998
Оглавление
Предисловие 14
Глава 1. Цифровые системы и представление
информации 19
Глава 2. Логические вентили 51
Глава 3. Проектирование комбинационных схем 99
Глава 4. Триггеры и счетчики 153
Глава 5. Проектирование последовательных схем 195
Глава 6. Проектирование устройств
на программируемых логических
интегральных схемах (ПЛИС) 233
Глава 7. Тестирование логических схем 275
Ответы на задания для самопроверки 303
Предметный указатель 315
Содержание
Предисловие м
Глава 1. Цифровые системы и представление
информации 19
1.1. Цифровые системы 19
1.1.1. Управляющие системы 20
Логические сигналы и функции 21
Положительная и отрицательная логика 22
Логические функции 22
Вычисления 24
Цифровой компьютер 24
1.2. Представление чисел в цифровых системах 26
1.2.1. Двоичные числа 26
1.2.2. Преобразование чисел 30
1.2.3. Шестнадцатеричные и восьмеричные числа 31
1.3. Арифметические операции над двоичными числами 34
1.3.1. Сложение 34
1.3.2. Отрицательные числа и вычитание 36
Вычитание 38
Обратный код 42
1.3.3. Двоично-десятичное представление
десятичных чисел 42
1.4. Представление алфавитно-цифровых символов 44
1.5. Пример цифровой логической схемы 45
1.6. Резюме 47
1.7. Упражнения 48
1.8. Список дополнительной литературы 50
Глава 2. Логические вентили 51
2.1. Логические сигналы 51
Алгебраические операции над двузначными
переменными 52
2.2. Базовые логические функции 53
2.2.1. Вентиль НЕ 53
2.2.2. Вентиль И 54
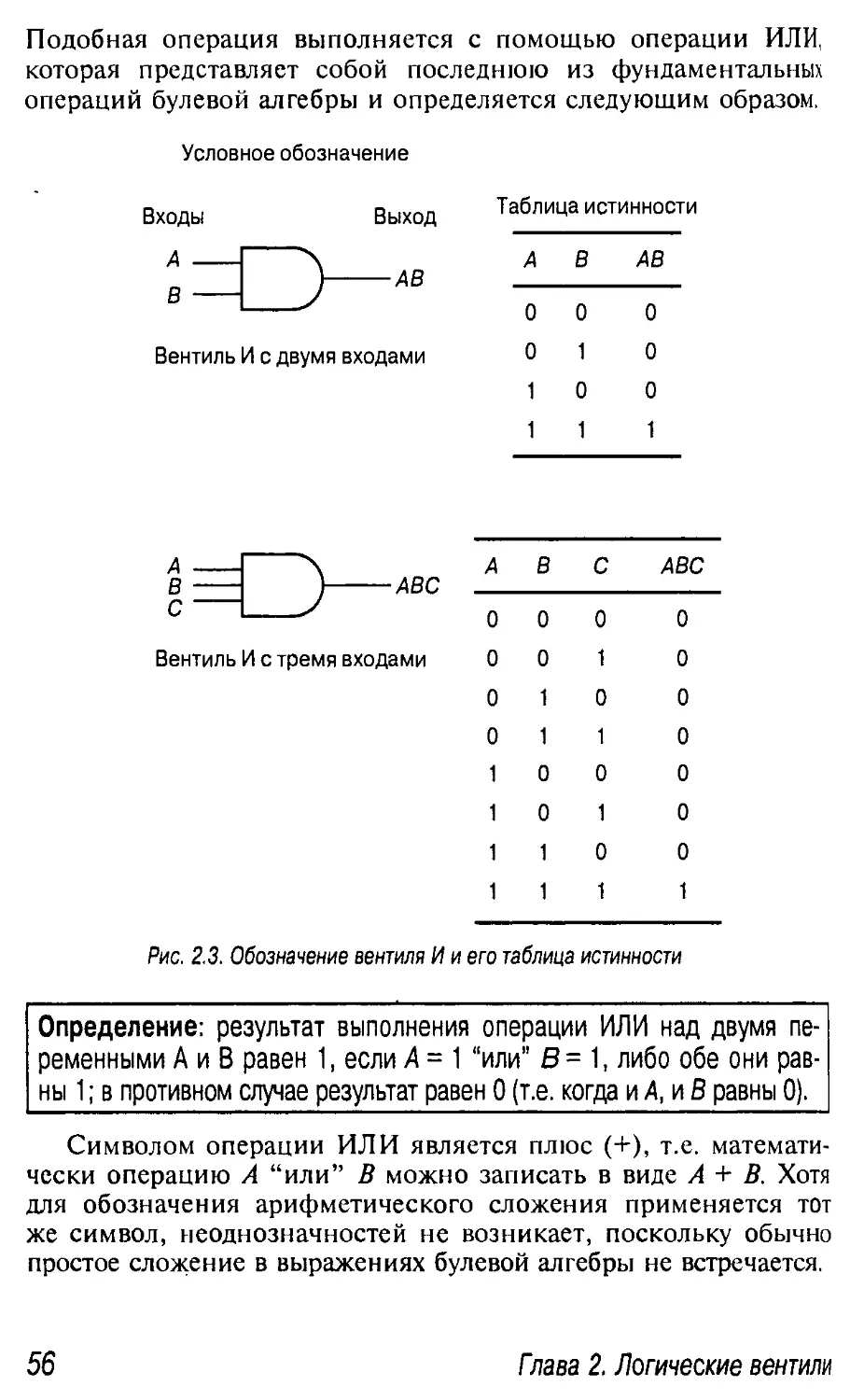
2.2.2. Вентиль ИЛИ 55
2.3. Основные соотношения булевой алгебры 58
2.3.1. Тождества и их применение 58
Применение соотношений 59
2.3.2. Основные алгебраические правила 62
Применение основных законов булевой
алгебры в логическом проектировании 65
2.3.3. Принцип дуализма 67
Дуальные функции 67
Дуальные равенства. Принцип дуализма 69
2.3.4. Теорема де Моргана 70
2.4. Универсальные вентили 73
2.4.1. Вентиль И-НЕ 73
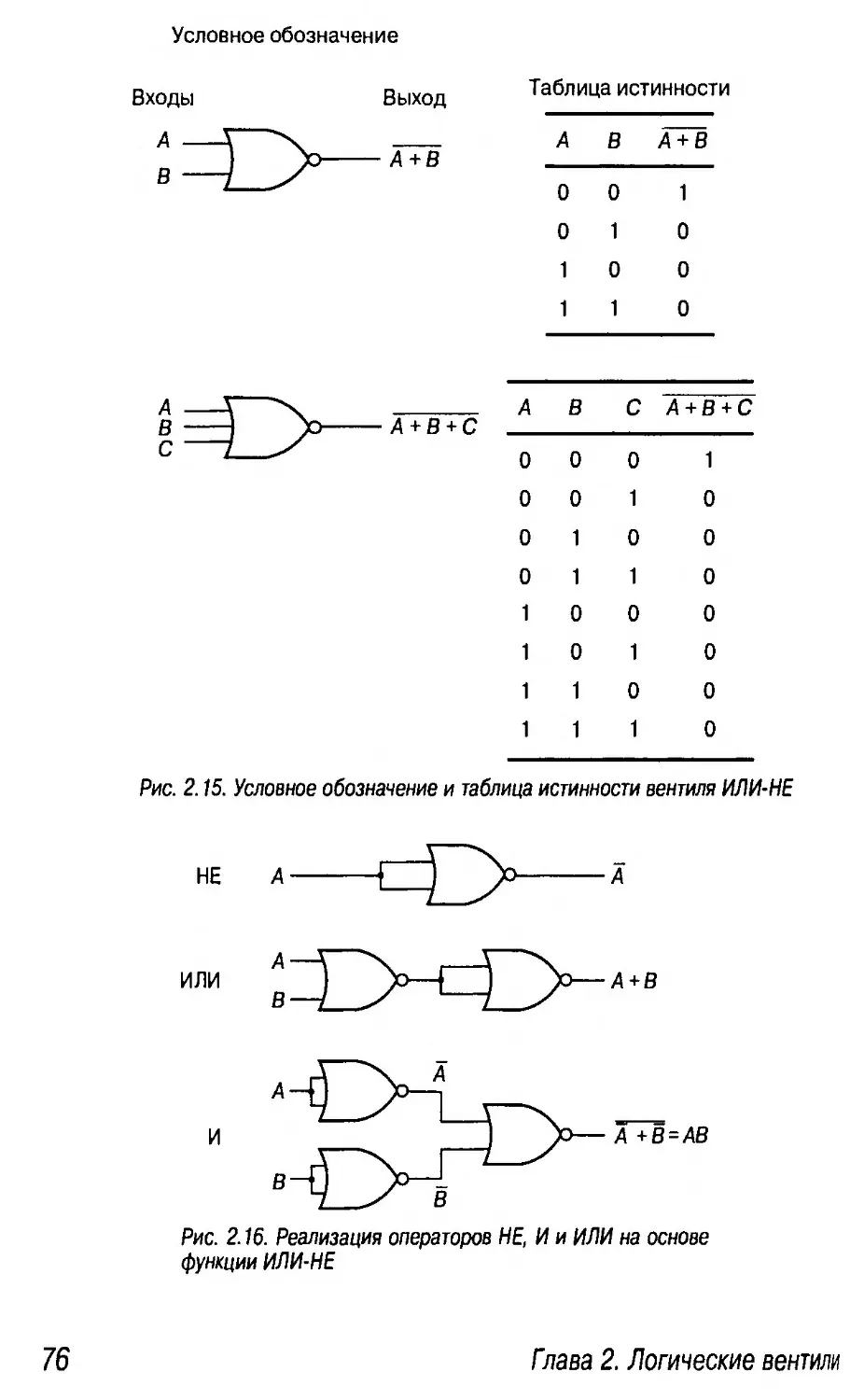
2.4.2. Вентиль ИЛИ-НЕ 75
2.5. Другие вентили 77
2.5.1. Вентиль исключающее ИЛИ 77
2.5.2. Вентиль исключающее ИЛИ-НЕ 79
2.5.3. Коммутативные функции 80
2.6. Проектирование вентилей 81
2.6.1. Комбинационные логические ТТЛ-схемы 81
2.6.2. Мсталл-оксид-полупроводниковые (МОП) вентили 85
Ключи на МОП-транзисторах 85
Базовые КМОП-ветили 91
Комбинационные функции 91
Произвольные функции 94
2.7. Резюме 94
2.8. Упражнения 95
2.9. Список дополнительной литературы 97
Содержание
7
Глава 3. Проектирование комбинационных схем 99
3.1. Комбинационные схемы 99
3.2. Реализация булевых выражений 102
3.2.1. Дизъюнктивная форма логических выражений 102
Выражения в канонической форме 103
Описание с помощью таблиц истинности 104
Преобразование выражений в каноническую форму 104
3.2.2. Выражения в конъюнктивной форме 105
Преобразование в каноническую форму 107
3.3. Альтернативные реализации 108
Выражения в дизъюнктивной форме 108
Выражения в конъюнктивной форме 109
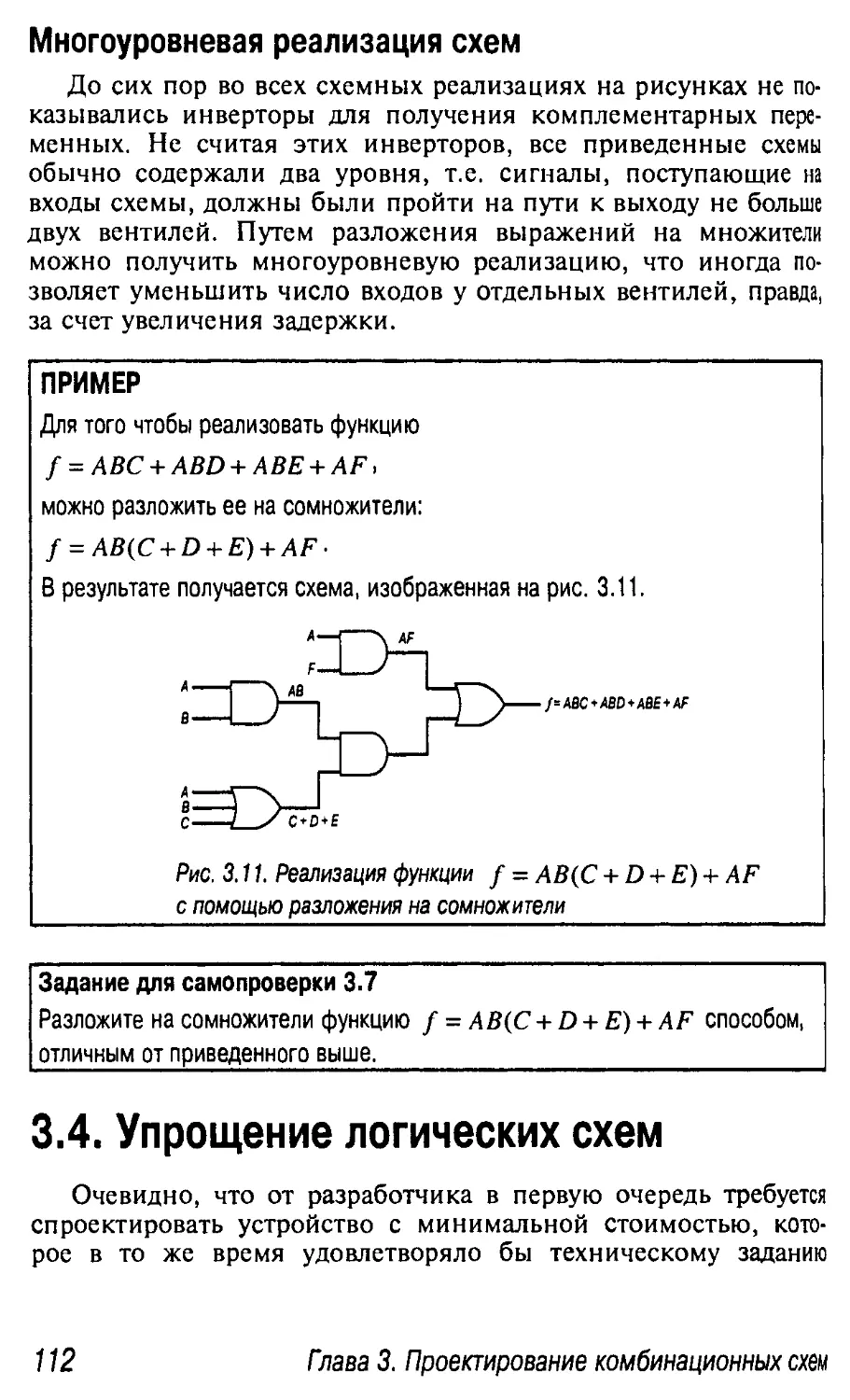
Многоуровневая реализация схем 112
3.4. Упрощение логических схем 112
3.4.1. Алгебраическое упрощение булевых выражений 113
1. Группировка членов с последующим
применением тождеств ИЗ
2. Приведение выражения в каноническую
форму с последующим упрощением 115
3. Использование теоремы де Моргана 116
3.4.2. Метод минимизации с помощью карт Карно 117
Алгоритм минимизации 120
Группирование ячеек по краям карты Карно 121
Большие группы 122
Карты Карно для четырех переменных 123
Выбор оптимальных групп 124
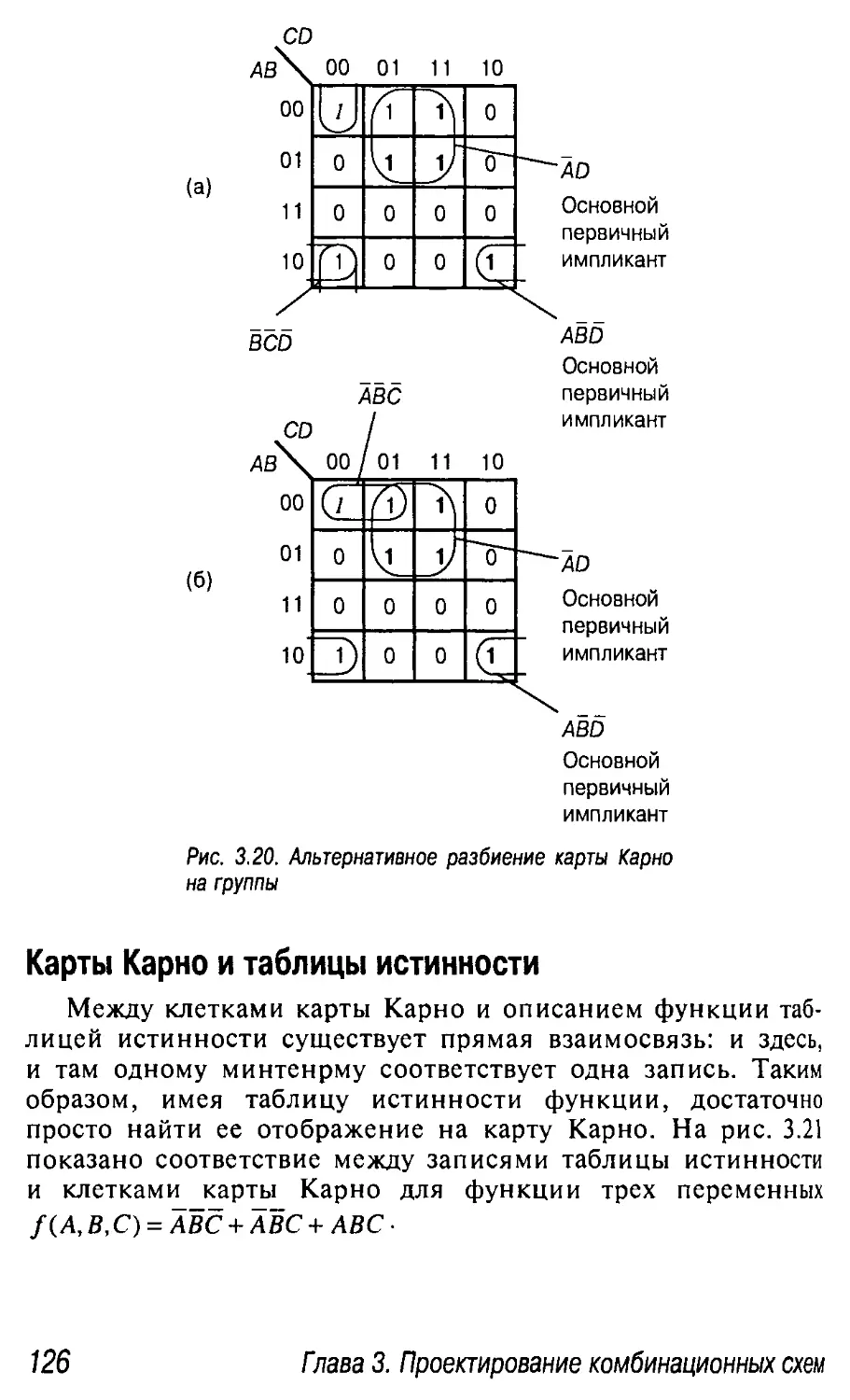
Карты Карно и таблицы истинности 126
Нумерация минтермов в карте Карно 127
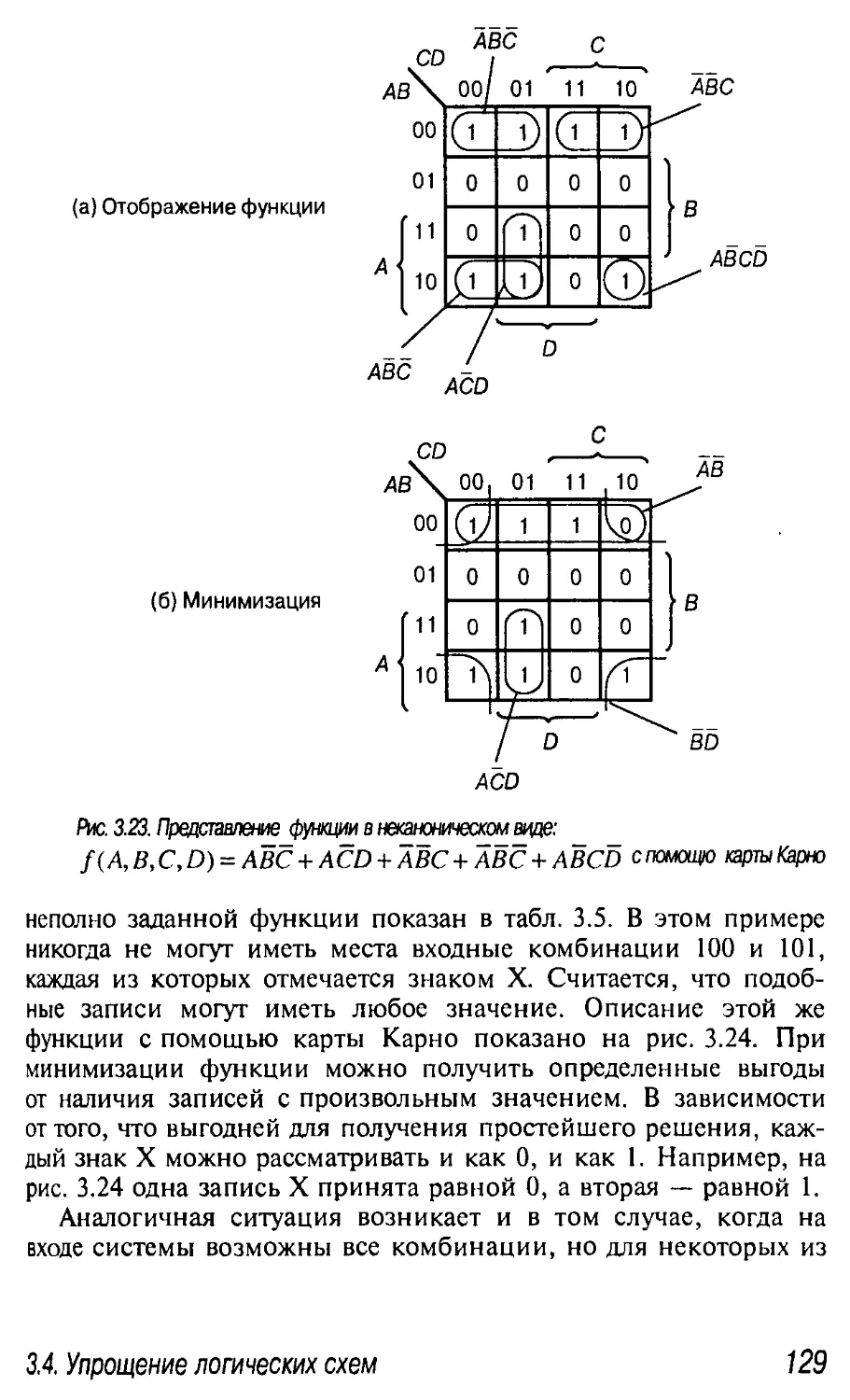
Функции в неканонической виде 127
Неполно заданные функции 128
Примеры входных комбинаций, которые
никогда не случаются 130
Минимизация с использованием нулей на
карте Карно 132
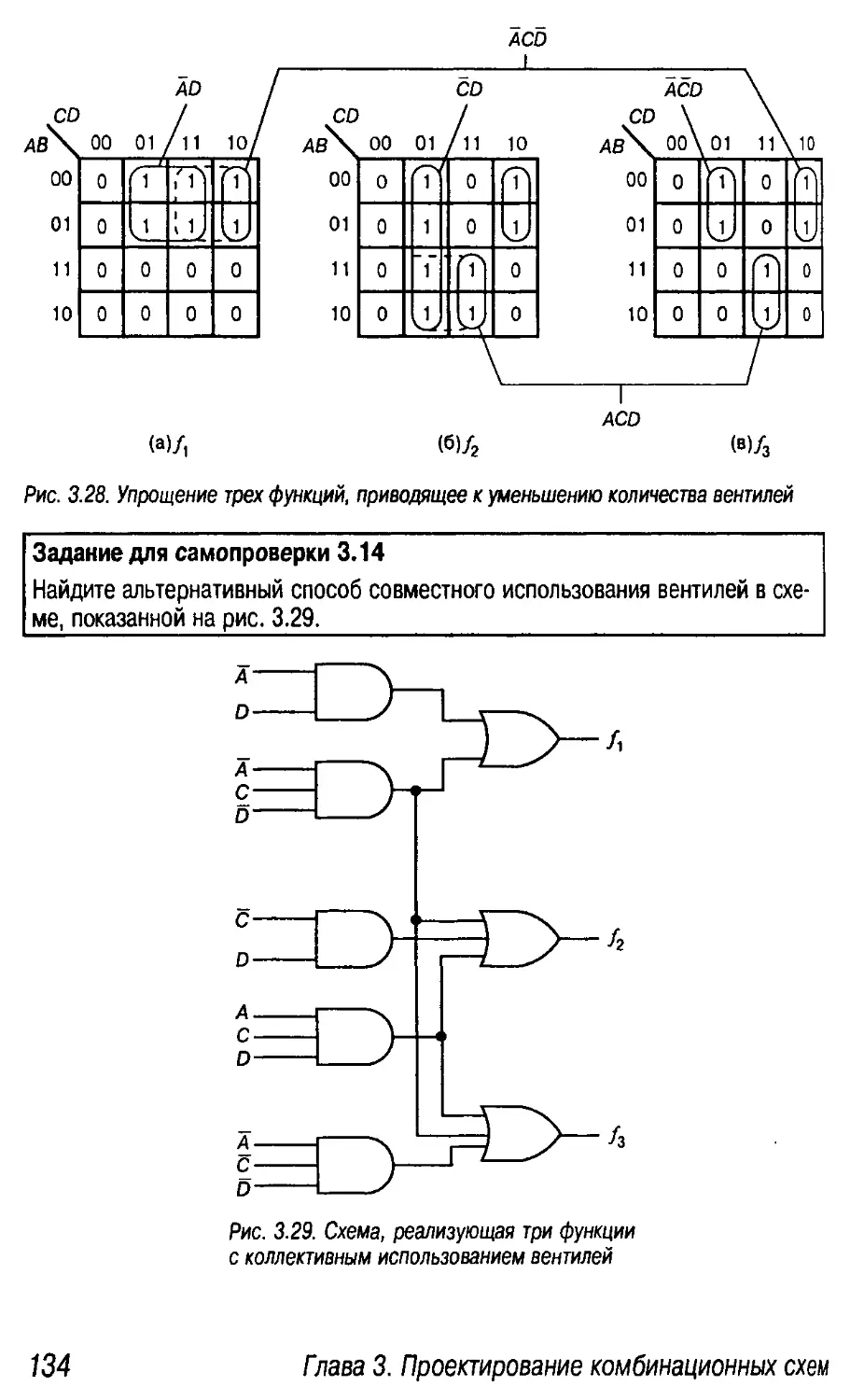
Минимизация систем со многими выходами 133
Карты Карно большего размера 135
8
Содержание
3.5. Комбинационные логические микросхемы средней
степени интеграции 135
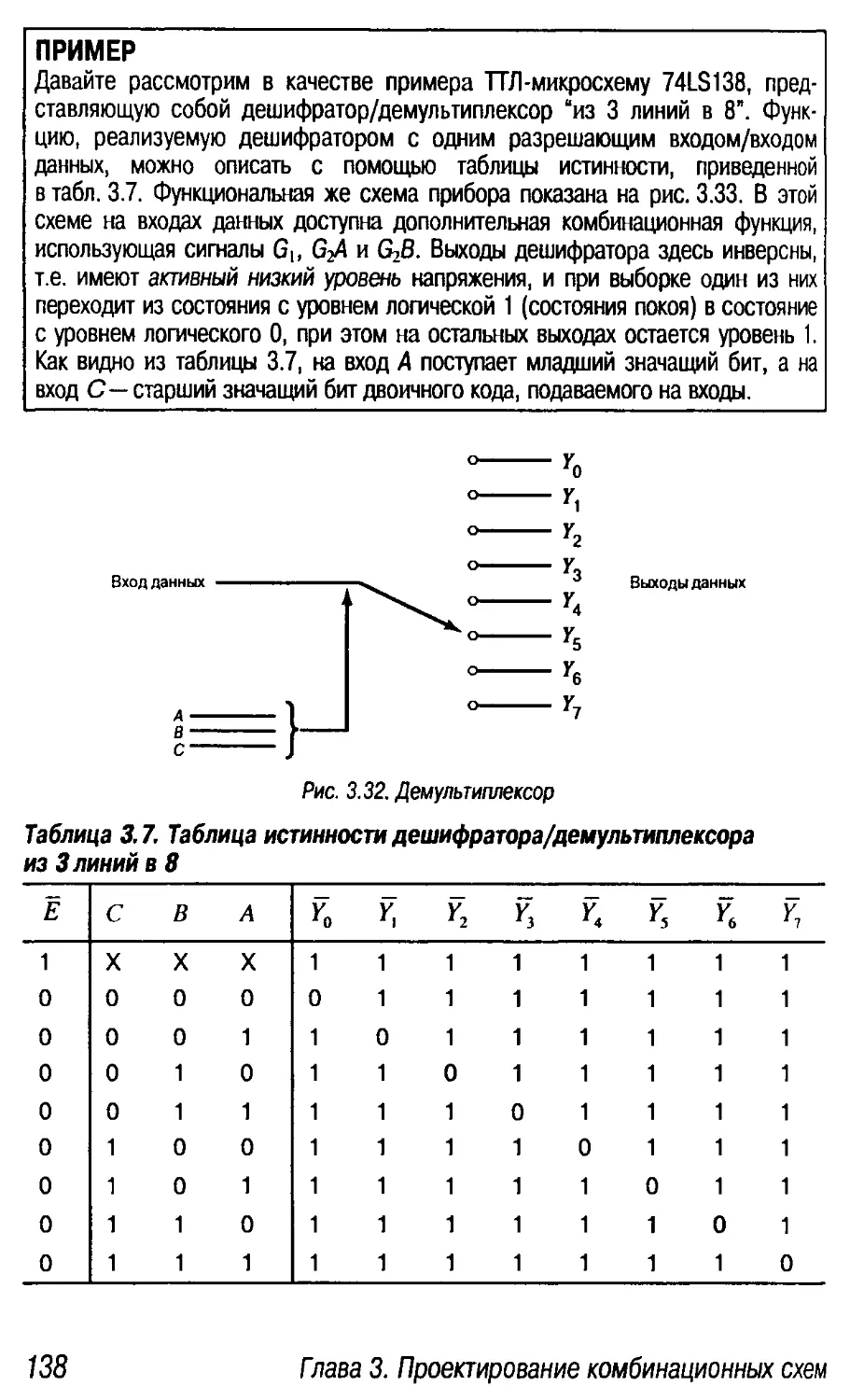
3.5.1. Дешифраторы/демультиплексоры 136
Области применения
дешифратора/демультиплексора 139
3.5.2. Мультиплексоры 141
Области применения селекторов
данных/мультиплексоров 144
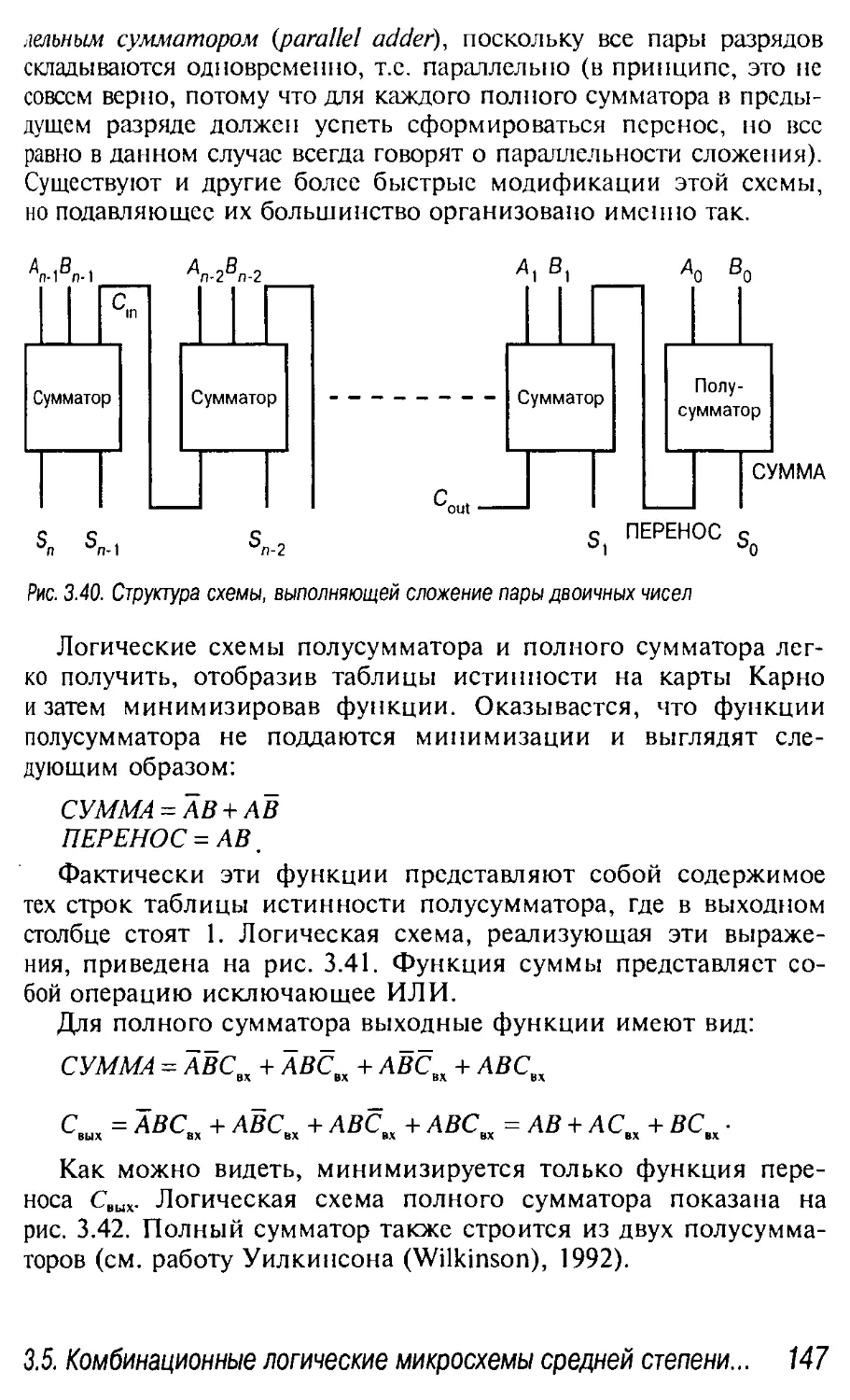
3.5.3. Арифметические схемы 145
Сложение 146
Вычитание 148
3.6. Резюме 149
3.7. Упражнения 149
Глава 4. Триггеры и счетчики 153
4.1. Последовательные схемы 153
4.2. Проектирование элементов с памятью на основе вентилей 155
4.3. Триггеры 157
4.3.1. RS-триггер 158
Таблица истинности 158
Характеристическое уравнение триггера 159
Переключение по уровню 159
4.3.2 D-триггер 161
Переключение по фронту 162
Асинхронные входы установки и сброса 165
Диаграмма состояния триггера 165
4.3.3. JK-триггер 167
4.4. Регистры 169
4.4.1. Регистры сдвига 170
Области применения регистров сдвига 172
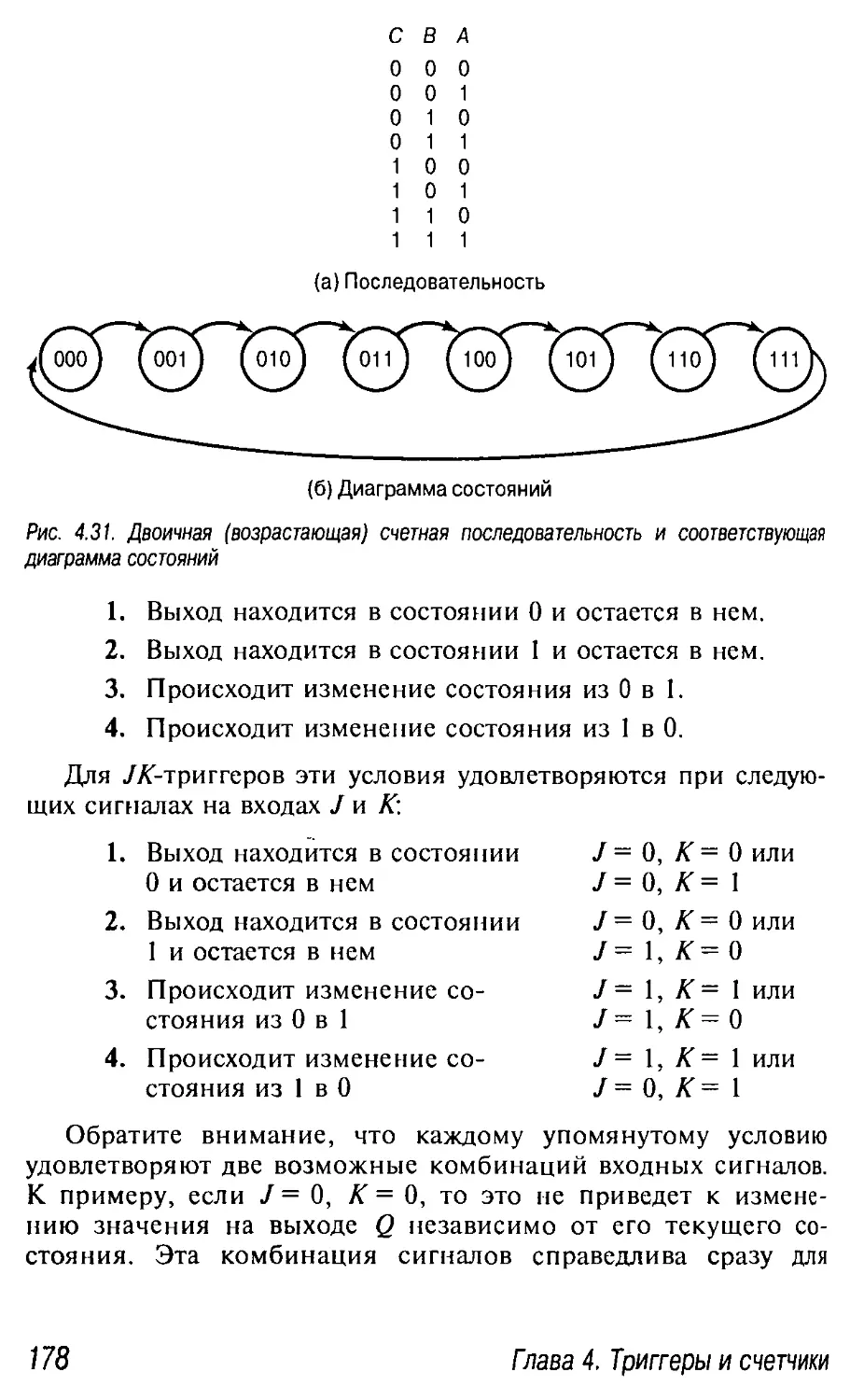
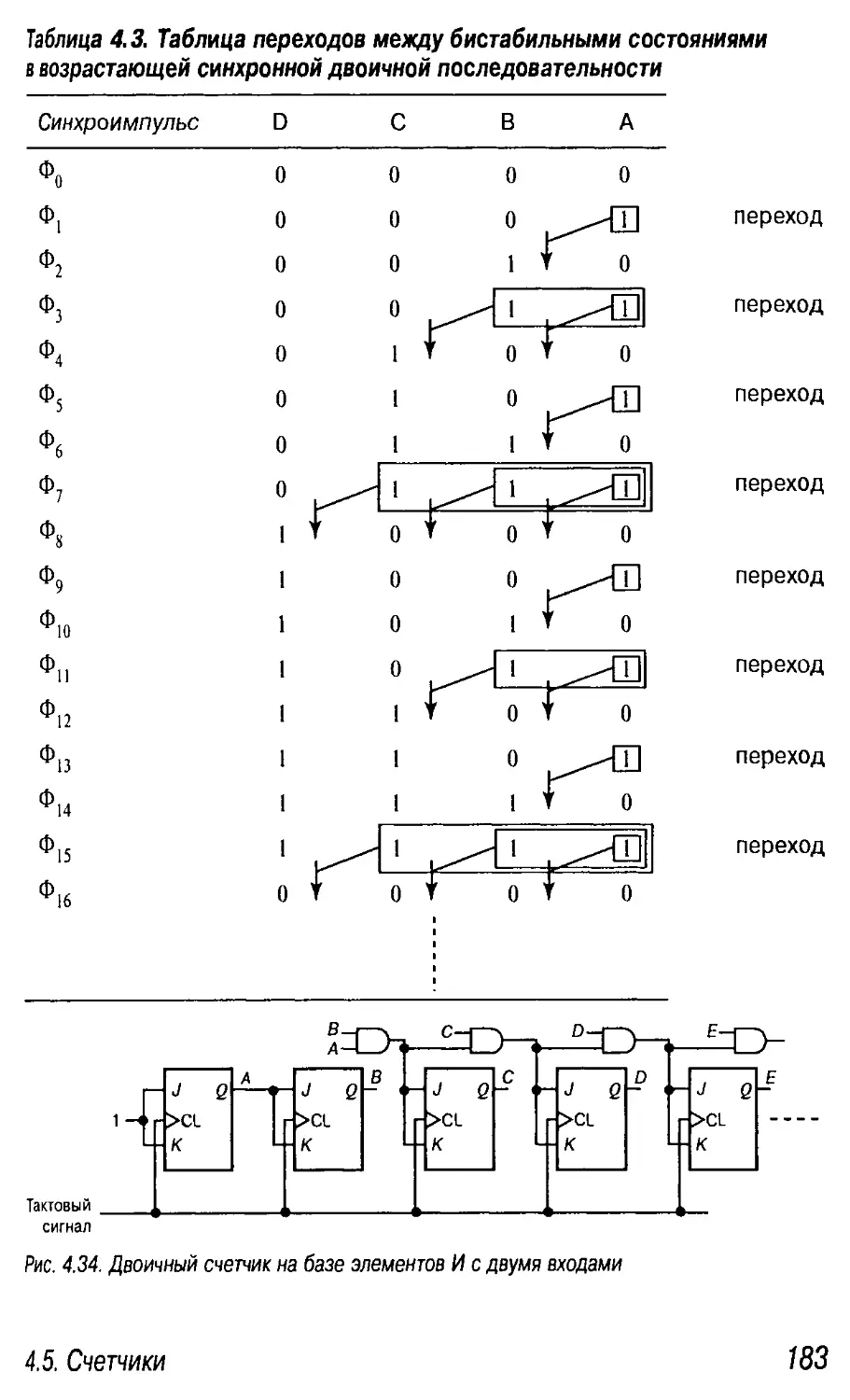
4.5. Счетчики 176
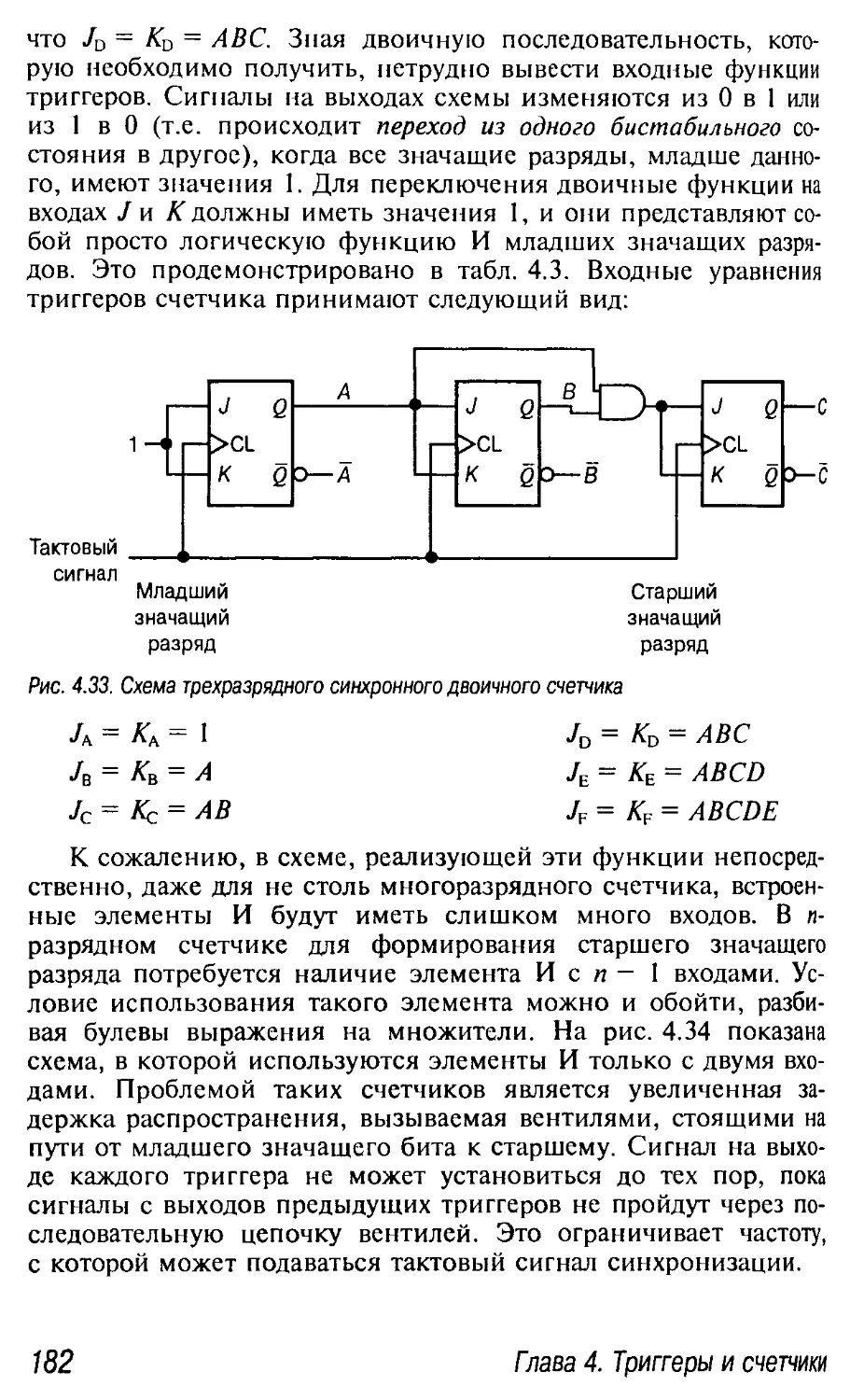
4.5.1. Счетчики на JK-триггерах 177
Нахождение функций на входах триггеров 177
Таблица возбуждения 179
Таблица (переходов) состояний 179
4.5.2. Счетчики на D-триггерах 184
Содержание
9
4.5.3. Начальные условия 186
4.5.4. Двоичные счетчики с обратным счетом 186
4.5.5. Двоичный счетчик со сквозным переносом 188
4.6. Резюме 190
4.7. Упражнения 190
Глава 5. Проектирование последовательных схем 195
5.1. Модель синхронной последовательной схемы 195
5.2. Проектирование синхронных последовательных схем 198
5.2.1. Задача 1: счетчик с двумя произвольными
счетными последовательностями 199
Диаграмма состояний 199
Таблица (переходов) состояний 199
Назначение состояниям значений переменных 200
Входные функции триггеров 200
5.2.2. Задача 2: детектор последовательности 202
Алгоритм проектирования 203
Диаграмма состояний 203
Таблица (переходов) состояний 204
Назначение состояниям значений переменных 205
Входные функции триггеров 208
Выходная функция 209
Логическая схема 209
5.2.3. Использование JK-триггеров 210
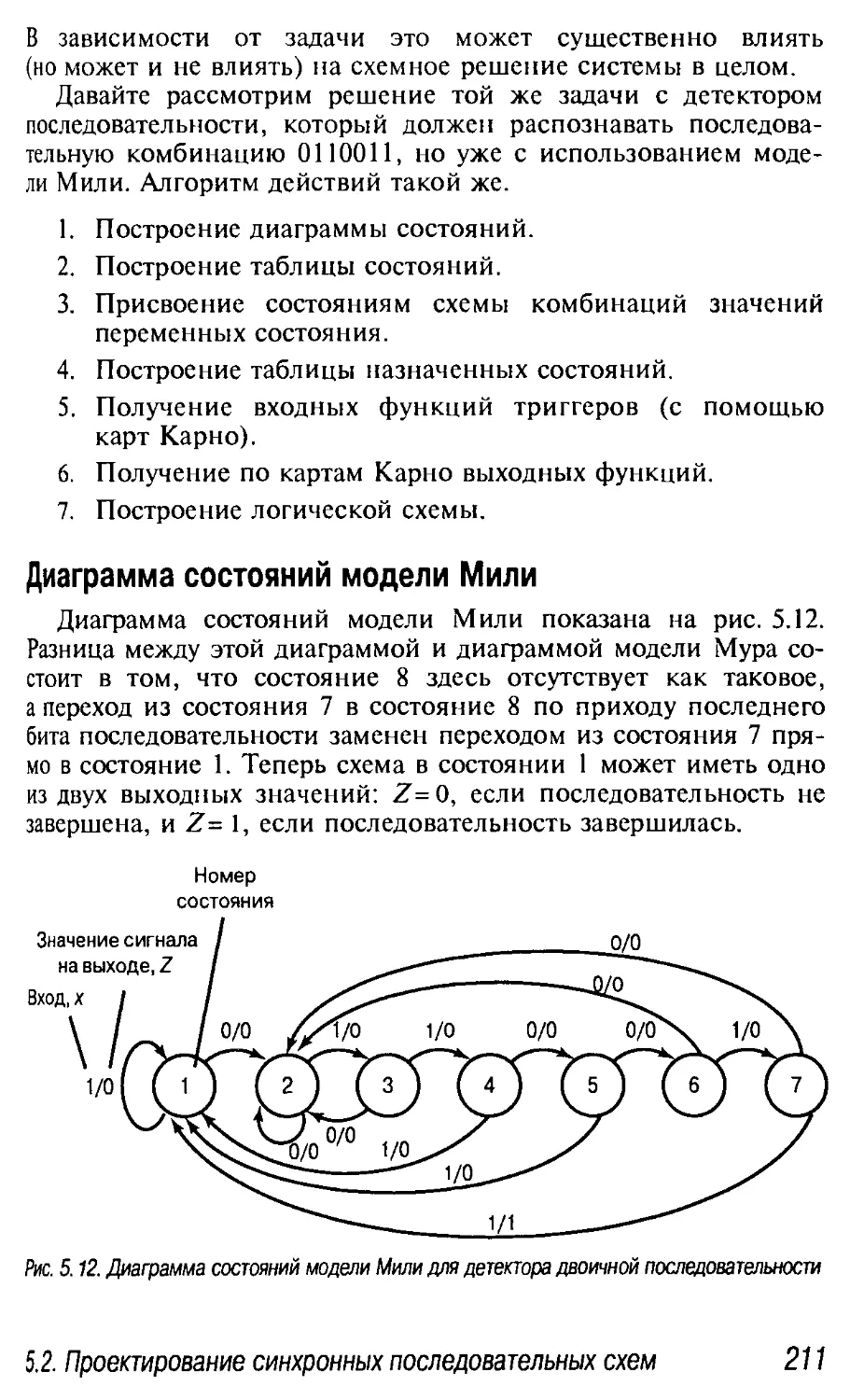
5.2.4. Проектирование на основе модели Мили 210
Диаграмма состояний модели Мили 211
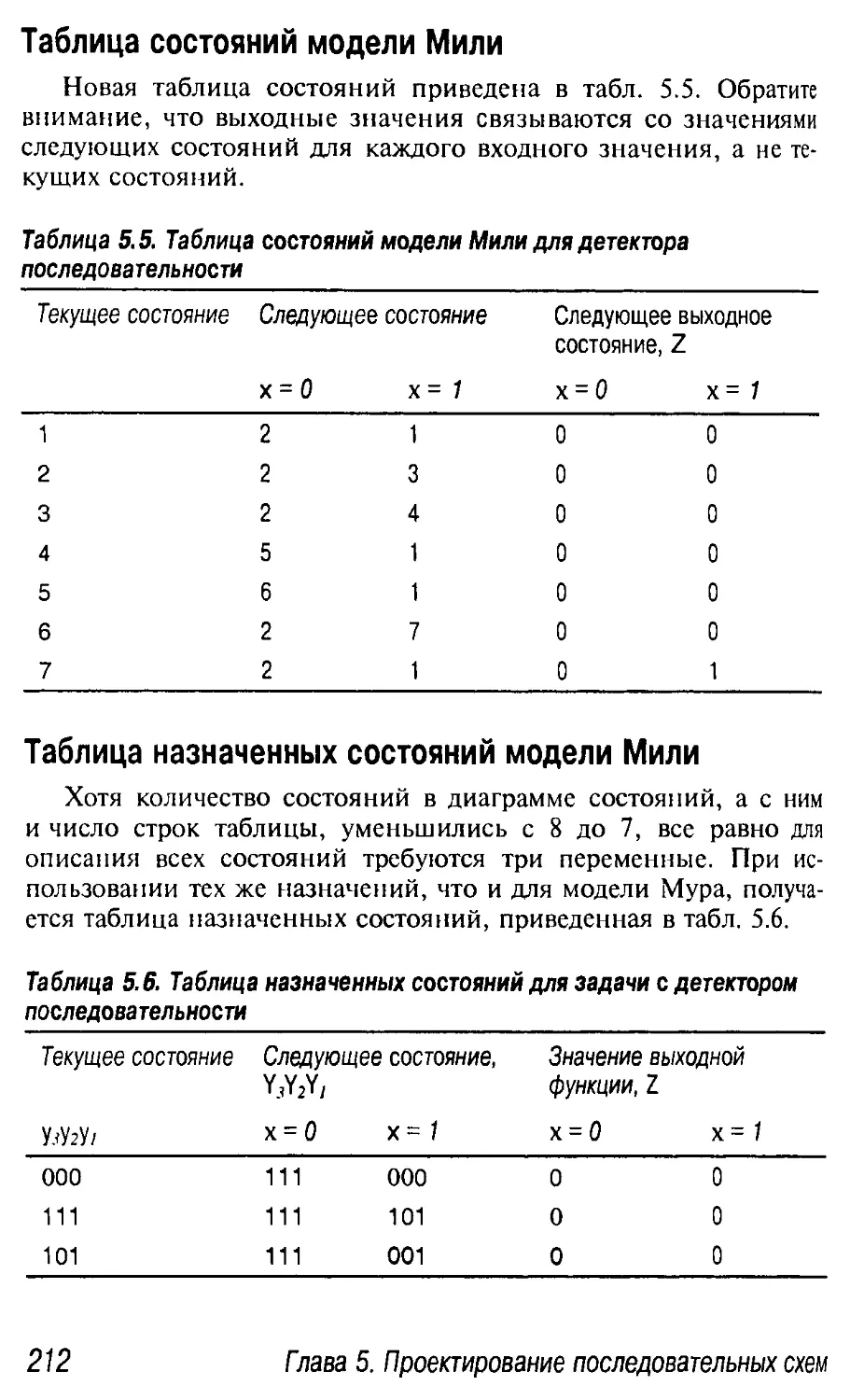
Таблица состояний модели Мили 212
Таблица назначенных состояний модели Мили 212
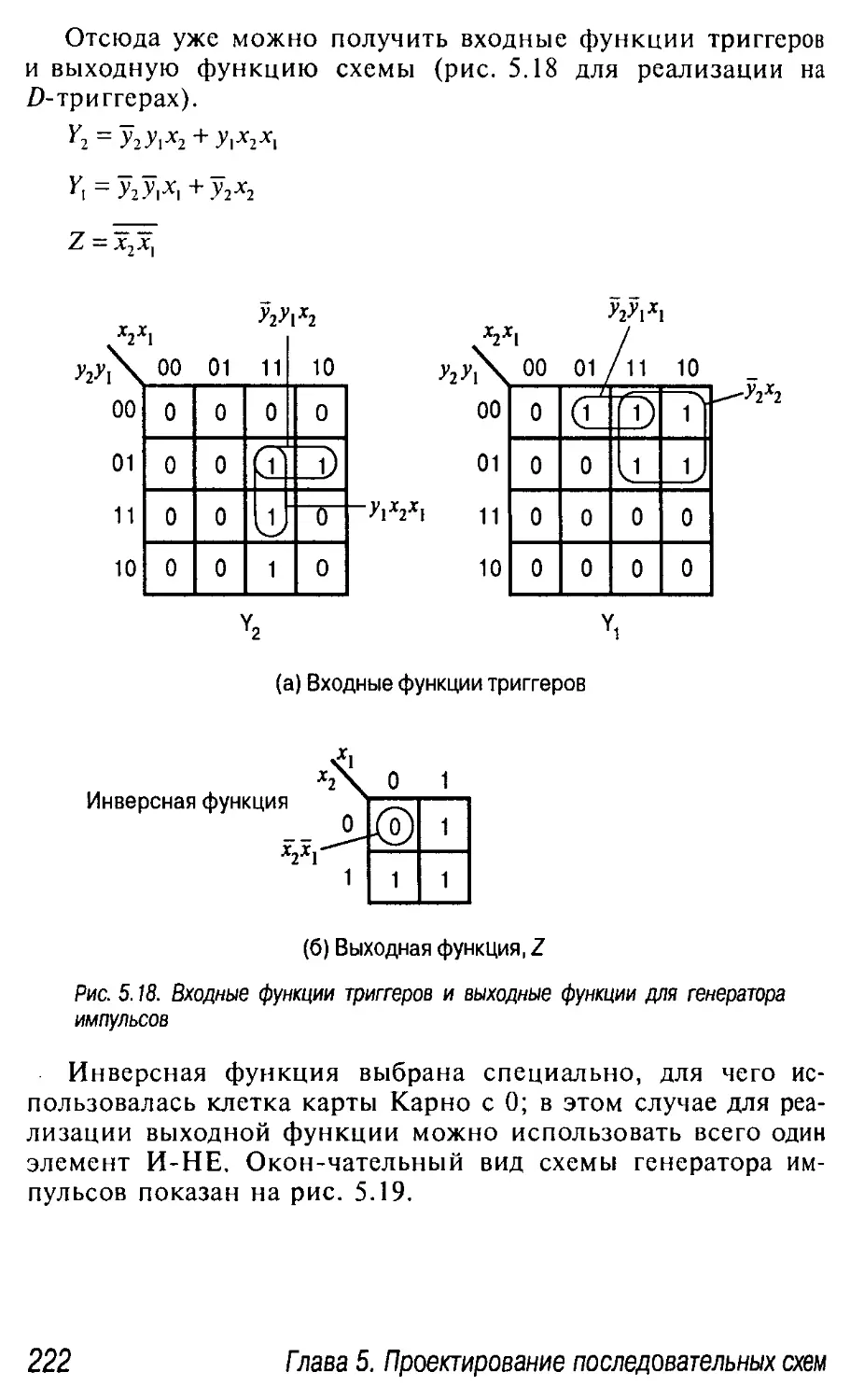
Входные функции триггеров 213
Выходная функция 214
5.2.5. Минимизация количества состояний 214
Эквивалентные состояния 215
Минимизация таблиц состояний модели Мили 218
5.2.6. Диаграммы состояний с использованием
выражений перехода 218
Пример: проектирование генератора импульсов
переменной длительности 219
10
Содержание
Таблица состояний с использованием
выражений переходов 223
5.2.7. Неполно заданные системы 224
Задача: проектирование интерфейсной логики 225
5.2.8. Прямое назначение переменных 229
5.3. Резюме 230
5.4. Упражнения 230
Глава 6. Проектирование устройств
на программируемых логических
интегральных схемах (ПЛИС) 2зз
6.1. Программируемые логические интегральные схемы 233
6.2. Комбинационные ПЛИС 235
6.2.1. Программируемые логические матрицы (ПЛМ) 235
6.2.2. Программируемая матричная логика (ПМЛ) 240
6.3. ПЛИС для реализации последовательных логических схем 246
6.3.1. Регистровые ПЛИС 247
6.3.2. Макроячейки 251
6.4. Инструментальные средства программирования ПЛИС 252
6.4.1. Структура файла с исходным кодом языка ABEL 253
Независимое от архитектуры проектирование 255
6.4.2. Комбинационные функции 255
Операторы множеств и отношений 259
Метод таблиц истинности 262
Тестовые векторы 262
6.4.3. Последовательные функции 263
Метод уравнений 263
Метод диаграмм состояний 264
Метод таблиц истинности 266
Тестовые векторы 266
Архитектурно независимое проектирование 266
6.5. Использование постоянных запоминающих устройств (ПЗУ) 268
6.6. Резюме 273
6.7. Упражнения 273
Содержание / /
Глава 7. Тестирование логических схем 275
7.1. Необходимость тестирования электронных схем 275
7.2. Неисправности 276
Константные неисправности 277
Другие неисправности 277
Одиночная константная неисправность 278
7.3. Формирование тестовых векторов для
комбинационных схем 280
7.3.1. Табличный и алгебраический методы 281
7.3.2. Метод активизации пути 281
Установка сигнала на выходе базовых вентилей
с заданным логическим уровнем 283
Активизация пути 285
Активизация пути благодаря проходу в прямом
и обратном направлении 286
Эквивалентные неисправности в элементах 288
Полное тестирование базовых вентилей 289
Схемы с одной нагрузкой 289
Схемы с многочисленными нагрузками 290
Необнаруживаемые неисправности 293
7.4. Тестирование последовательных схем и сложных
электронных систем 296
7.4.1. Метод сканирования пути 296
7.4.2. Встроенное самотестирование 298
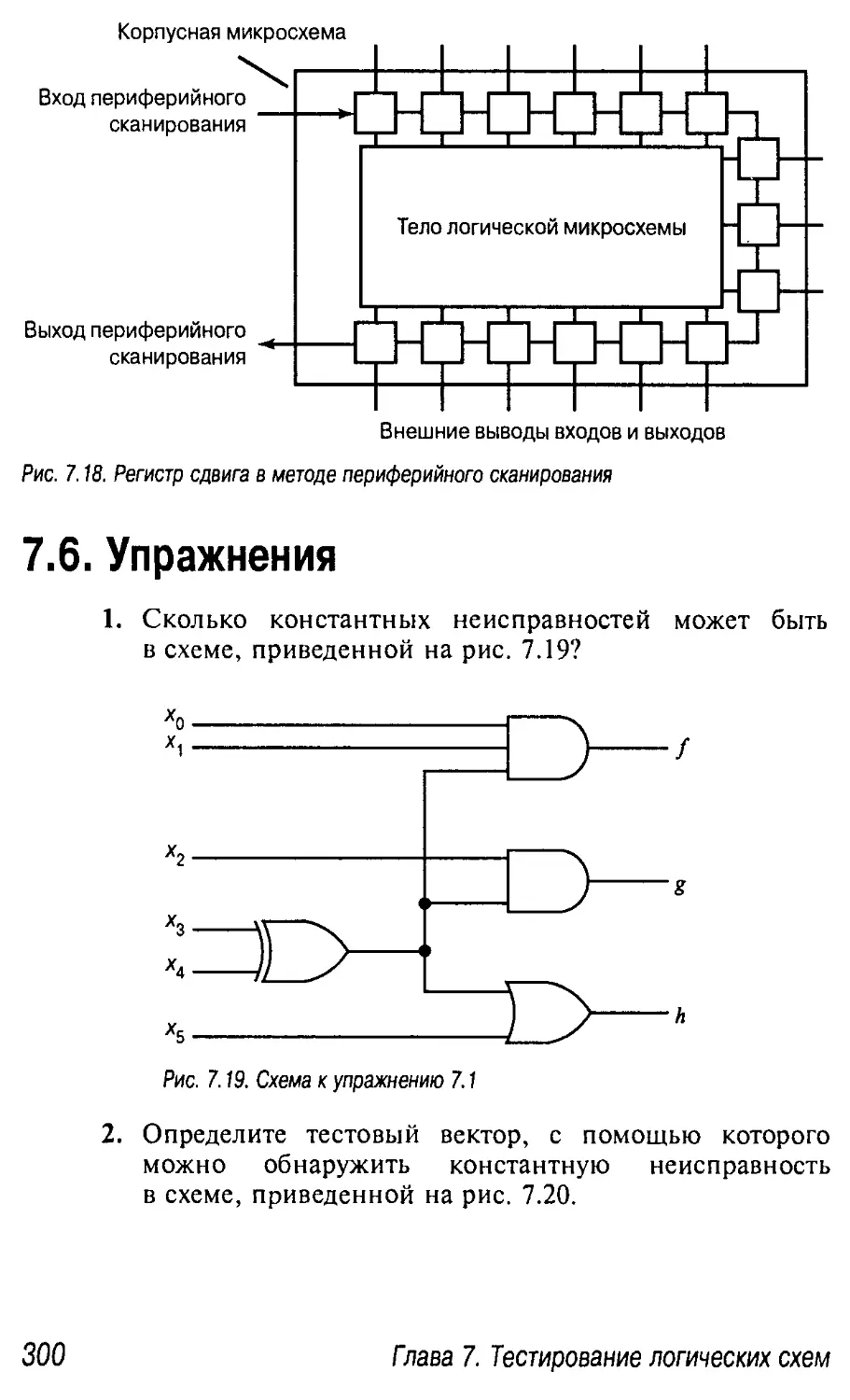
7.4.3. Периферийное сканирование 299
7.5. Резюме 299
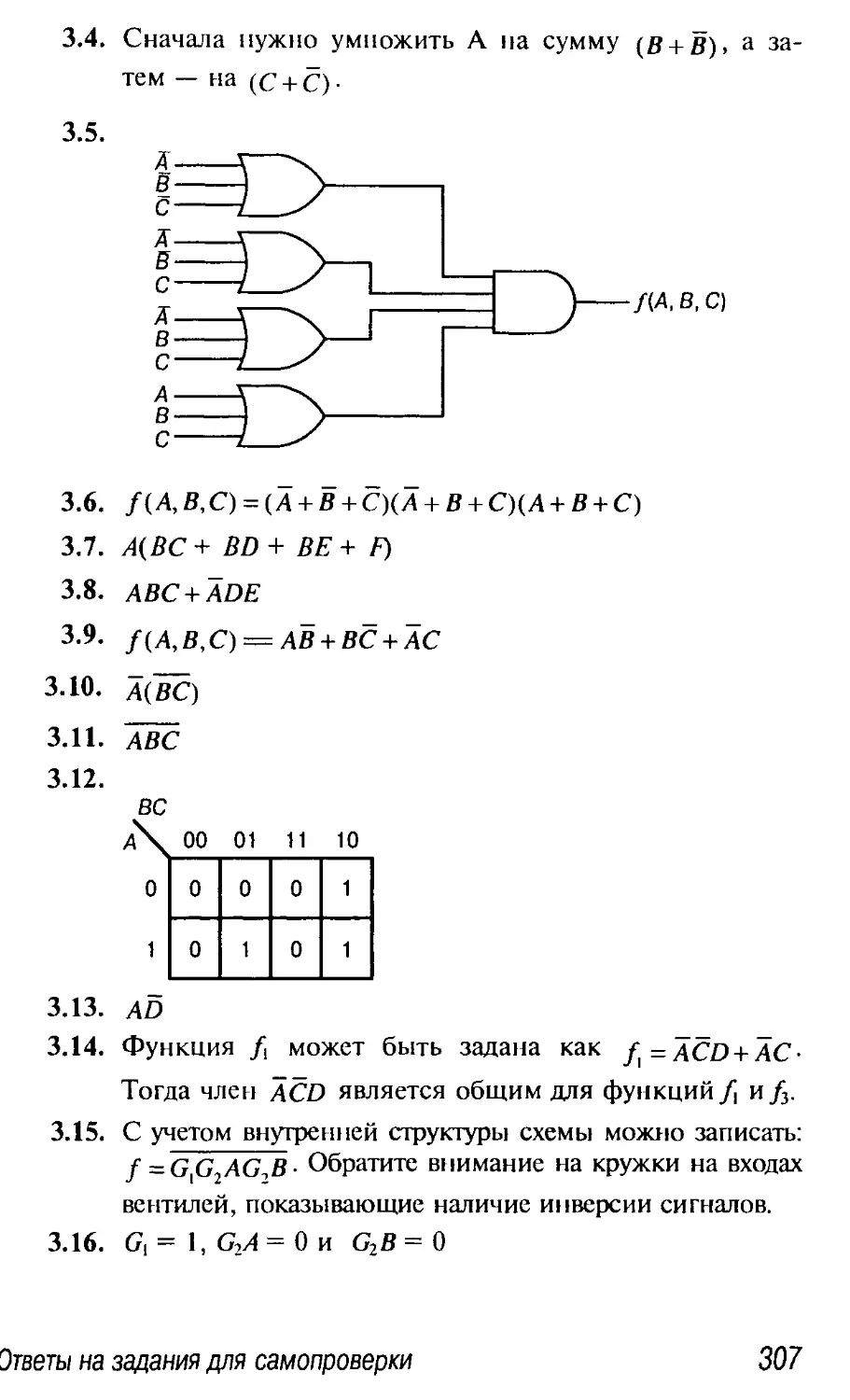
7.6. Упражнения 300
Ответы на задания для самопроверки зоз
Предметный указатель 315
12
Содержание
Предисловие
Эта книга написана для того, чтобы дать представление
о ключевых аспектах проектирования логических схем студен-
там электротехнических и компьютерных специальностей.
Структура материала была специально разработана таким обра-
зом, чтобы изложить курс за один семестр.
В главе 1 вы ознакомитесь с общими концепциями построе-
ния цифровых систем и основными областями их применения.
Здесь вводится понятие логического сигнала, имеющего два
возможных состояния. Такие сигналы используются во всех
цифровых системах; они могут принимать одно из двух значе-
ний — 0 или 1 — и применяться либо для управления, либо для
представления чисел (в двоичной форме). В этой же главе
в общих чертах в рамках вопросов проектирования цифровых
схем поясняются двоичная система счисления и двоичная
арифметика. Поскольку книга посвящена только основам, то
преобразование чисел из одной системы счисления в другую
описано весьма поверхностно. Однако в книге приводятся
ссылки на литературу, в которой можно найти более подробное
описание затрагиваемых в ней тем.
Математическим базисом цифровых систем является булева
алгебра, которая в данном контексте определяет выполнение
операций над бинарными переменными. Именно эти операции
реализуются в логических вентилях, делая такие вентили фун-
даментом любой цифровой системы. Различные типы логиче-
ских вентилей вместе с соответствующими функциями булевой
алгебры описываются в главе 2. В конце главы кратко рассмат-
риваются простейшие схемотехнические решения логических
вентилей. Данный материал будет интересен прежде всего ин-
женерам-электрикам; студенты компьютерных специальностей
могут опустить этот раздел без ущерба для целостности изложения.
Логические вентили часто называют комбинационными ло-
гическими схемами, поскольку состояния на их выходах зависят от
комбинаций значений входных сигналов. В главе 3 описывается
методика проектирования более сложных комбинационных
цифровых систем на основе вентилей. Одним из ключевых ас-
пектов при проектировании цифровых систем является количе-
ство и типы используемых вентилей. Часто желательно, чтобы
количество вентилей в системе было минимальным. В этой
же главе описываются методики уменьшения количества вен-
тилей, в частности метод минимизации с использованием
карт Карно. Минимизация очень сложных логических схем
часто выполняется с помощью специализированных компью-
терных программ. Описание методов, более пригодных для
программной реализации, можно найти в литературе, список
которой приведен в конце главы.
Большинство цифровых систем имеет память, в которой
хранится информация о прошлых событиях. От этих событий
может зависеть реакция таких систем. Базовыми логическими
компонентами, обладающими свойством памяти, являются
триггеры, которым посвящена глава 4. Триггеры составляют ос-
нову более сложных схем “последовательной логики”, на выходе
которых могут формироваться последовательности различных со-
стояний. Еще одной широко распространенной последователь-
ной логической схемой является счетчик, состояния па выходе
которого воспроизводят числовые последовательности, например
возрастающую двоичную последовательность. Принципы по-
строения счетчиков описываются в этой же главе. Сведения
о внутренней структуре триггеров можно найти в дополнитель-
ной литературе, хотя зачастую это и необязательно, так как в по-
давляющем большинстве случаев используются уже готовые
триггеры или стандартные схемотехнические решения.
В главе 5 продолжается описание проектирования последо-
вательных схем. Значительное внимание уделено методу диа-
грамм состояний, который поясняется с помощью практиче-
ских примеров. Все рассматриваемые устройства относятся
к так называемым синхронным последовательным схемам, ко-
торые управляются с помощью внешнего тактового сигнала.
Благодаря простоте организации временных диаграмм выпол-
нения операций при наличии тактового сигнала подобные схе-
мы составляют подавляющее большинство цифровых устройств.
Описание проектирования асинхронных последовательных
схем, в которых такой сигнал отсутствует, можно найти в лите-
ратуре, список которой дан в конце главы.
Глава 6 целиком посвящена программируемым логическим
интегральным схемам (ПЛИС). ПЛИС представляют собой
логические компоненты с изменяемой внутренней структурой
Предисловие
15
связей, которые позволяют создавать различные устройства на
базе одной микросхемы. ПЛИС широко используются для
уменьшения количества компонентов и общей стоимости ко-
нечного изделия. Для получения необходимой внутренней
структуры связей такие ИС должны “программироваться”.
Процедура программирования описывается с использованием
языка программирования ПЛИС, синтаксис которого представ-
лен в главе 6. Здесь же приведены все детали, необходимые для
практического программирования. Более подробные сведения
о языках программирования ПЛИС можно найти в предложен-
ном списке литературы.
В главе 7 представлены методики тестирования логических
схем для выявления ошибок, которые могли появиться в про-
цессе производства или эксплуатации устройства. Тестирование
является крайне важным моментом, но почему-то до сих пор
в имеющейся литературе по проектированию логических схем
эта тема опускалась. К изготовлению работоспособной систе-
мы, как и к проектированию, следует относиться со всей серь-
езностью, и в этом контексте тестирование устройств является
неотъемлемой частью процесса проектирования.
Как видно из краткого описания материала, есть несколько
ключевых моментов, на которых строится изложение. Для препо-
давателей имеется специальный раздел с ответами к упражнениям.
Автор хотел бы выразить глубокую признательность Кристо-
феру Гленни (Crostopher Glennie) из издательства Prentice Hall за
постоянную помощь в ходе подготовки этой книги и конструк-
тивную критику рукописи. Также автор считает своим долгом
поблагодарить Жаклин Харбор (Jackueline Harbor) за работу над
рукописью, а весь коллектив Prentice Hall — за профессионализм.
Наконец, отдельное спасибо анонимным рецензентам за прило-
женные ими усилия и ценные комментарии. Автор оценит лю-
бые пожелания или предложения по исправлению материала, ко-
торые можно присылать по электронному адресу abw@uncc.edu;
они будут учтены в последующих изданиях книги.
Барри Уилкинсон
16
Предисловие
От издательства
Вы, читатель этой книги, и есть главный ее критик и ком-
ментатор. Мы ценим ваше мнение и хотим знать, что сделано
правильно, что можно было сделать лучше и что еще вы хотели
бы увидеть изданным. Нам интересны любые ваши замечания
по поводу книги.
Мы ждем ваших комментариев. Вы можете прислать нам
обычное или электронное письмо либо просто посетить наш
Web-сервер и оставить свои замечания там. Одним словом, лю-
бым удобным для вас способом дайте нам знать, нравится или
нет вам эта книга, а также выскажите свое мнение о том, как
сделать наши книги более интересными для вас.
Посылая письмо или сообщение, не забудьте указать назва-
ние книги и ее авторов, а также ваш обратный адрес. Мы вни-
мательно ознакомимся с вашим мнением и обязательно учтем
его при отборе и подготовке к изданию последующих книг.
Наши координаты:
E-mail: inf oSwilliamspublishing . com
WWW: http:/ /www.williamspublishing.com
Информация для писем из:
России: 115419, Москва, а/я 783
Украины: 03150, Киев, а/я 152
Глава 1
Цифровые системы
и представление
информации
Цели и задачи
В этой главе описаны основные элементы цифровых систем
и области их применения. Большая часть материала по-
священа представлению информации в таких системах.
Здесь вводится понятие логического сигнала, имеющего
всего два возможных значения, и показывается, как подоб-
ные сигналы могут использоваться для представления
управляющих сигналов и числовых данных.
1.1. Цифровые системы
Как правило, цифровые системы разрабатываются для ре-
шения двух тесно взаимосвязанных задач:
• управления устройствами;
• выполнения вычислений.
Цифровая система может сначала выполнять вычисления и
на основе полученных результатов предпринимать определен-
ные действия по управлению. В качестве примеров таких сис-
тем можно назвать: а) системы управления промышленным
оборудованием и б) автомобильные системы.
1.1.1. Управляющие системы
Давайте рассмотрим простой пример управления количест-
вом материала в бункере (рис. 1.1). Целью является поддер-
жание количества материала в бункере между уровнями L1
и L2, причем известно, что материал отбирается с определен-
ными интервалами. Цифровая система управляет клапаном
подачи материала в бункер. В системе имеются два датчика,
один из которых определяет момент достижения материалом
уровня L1, а второй — момент достижения уровня L2. Каж-
дый датчик при прохождении материалом заданного уровня
формирует сигнал. Как правило, такой сигнал представляет
собой некоторый уровень напряжения, скажем, 5 вольт, когда
уровень материала пересекает линию датчика, и 0 вольт, когда
этого не происходит. Таким образом, входной сигнал имеет
два состояния: одно индицирует прохождение материалом оп-
ределенного уровня, а второе — отсутствие данного события.
Клапан подачи материала также управляется сигналом, имею-
щим всего два состояния, в нашем случае это состояния ВКЛ
и ВЫКЛ. Например, сигнал напряжением 50 вольт может
открывать клапан, а сигнал напряжением 0 вольт — закрывать
Выходной
сигнал
Сигнал об
ошибке
Рис. 1.1. Контроль расхода материала в бункере
20
Глава 1. Цифровые системы и представление информации
его. Клапан должен открываться, когда уровень материала
в бункере опускается ниже отметки L1, и оставаться откры-
тым до тех пор, пока уровень материала не поднимется выше
отметки L2, после чего он должен закрыться. Кроме того,
клапан остается закрытым, пока уровень материала не падает
ниже отметки L1. Наша цифровая система должна вырабаты-
вать сигнал, реализующий такой “алгоритм”, при этом сигнал
имеет два состояния: для включения и для выключения кла-
пана подачи материала.
В системе индицируются два уровня, поэтому подача материала
в бункер осуществляется через определенные интервалы времени.
Если бы система решала задачу поддержания объема материала
на одном фиксированном уровне, закрывая клапан при превы-
шении этого уровня и открывая его, когда уровень опустится
ниже отметки, то клапан постоянно закрывался бы и открывался.
Логические сигналы и функции
В последующих главах будут рассмотрены законы проекти-
рования цифровых систем, в том числе и таких, как показанная
на рис. 1.1, а пока отметим, что входные и выходные сигналы
таких систем имеют лишь два значения, обычно передаваемых
в виде двух уровней напряжения. Внутри самой цифровой сис-
темы могут использоваться, скажем, 5 вольт для передачи од-
ного значения и 0 вольт — для передачи второго. Чтобы не
привязываться к конкретным величинам напряжений, далее
такие сигналы с двумя возможными значениями будут назы-
ваться логическими. Любая проектируемая цифровая система
разрабатывается на основе компонентов, которые восприни-
мают и формируют на выходе двузначные логические сигна-
лы. В приведенном выше примере значения сигнала соответ-
ствовали состояниям “включено” (ВКЛ) и “выключено”
(ВЫКЛ). Иногда могут использоваться термины ИСТИННЫЙ
(TRUE) и ЛОЖНЫЙ (FALSE): скажем, сигнал с первого
датчика считается ИСТИННЫМ, когда уровень материала
выше отметки 1, и ЛОЖНЫМ, если уровень материала ниже
ее. Значение ИСТИНННЫЙ здесь соответствует состоянию
ВКЛ, а ЛОЖНЫЙ — состоянию ВЫКЛ. Обычно при проекти-
ровании логических схем вместо терминов используют число-
вые значения 1 (ИСТИНННЫЙ) и О (ЛОЖНЫЙ). Ниже при-
ведена таблица для рассматриваемой ситуации с указанием со-
ответствующих “логических” сигналов.
1.1. Цифровые системы
21
Таблица 1.1. Логические сигналы
Ситуация Логическое напряжение Состояние ключа Логическое значение
Ниже уровня ОВ ВЫКЛ ЛОЖНЫЙ (0)
Выше уровня 5В ВКЛ ИСТИННЫЙ (1)
Положительная и отрицательная логика
В реальных системах, как правило, используются напряже-
ния 0 и 5 вольт, хотя для внутренних вентилей таких сложных
устройств, как микропроцессоры, эти уровни могут быть суще-
ственно ниже. Имея два напряжения, скажем, эти же 0 и 5 вольт,
необходимо решить, какое из них приписать каждому логиче-
скому значению. К примеру, можно использовать напряжение О
вольт для представления логической 1 и 5 вольт — для представ-
ления логического 0, но какое бы напряжение ни было выбрано,
оно должно быть одинаковой величины во всей системе. Обычно
для представления логической 1 выбирается более высокое на-
пряжение, а для представления логического нуля — более низкое
(т.е. 5 вольт = 1 и 0 вольт — 0). Такая логика получила название
положительной (positive logic representation). Можно использовать
и обратное представление, когда высокое напряжение соответству-
ет логическому 0, а низкое — логической 1. Такая логика назы-
вается отрицательной. Возможно также и одновременное исполь-
зование в одной системе обеих логик (при этом по-прежнему
должны использоваться только два напряжения). Использование
двух представлений в одной логической системе получило назва-
ние смешанной логики. В этом случае для именования логических
сигналов требуются специальные условные обозначения (см. ра-
боты Флетчера (Fletcher), 1980 или Тиндера (Tinder), 1991).
Логические функции
Для того чтобы разработать “алгоритм” или выходную логиче-
скую функцию цифровой системы, логическим сигналам необхо-
димо присвоить имена, как переменным в алгебре. Например,
входные сигналы от изображенных на рис. 1.1 датчиков можно
назвать 5, и S2 (от первого и от второго, соответственно). Выход-
ной управляющий сигнал пусть называется Z. На рисунке также
показан второй выходной сигнал, который указывает на наличие
в работе системы ошибки. Такая ошибка может возникнуть,
22
Глава 1. Цифровые системы и представление информации
например, в том случае, если первый датчик показывает, что ко-
личество материала ниже отметки L1, в то время как второй, —
что уровень материала превышает отметку L2, что, понятно, при
правильной работе всех компонентов системы невозможно. Обо-
значим этот выходной сигнал ошибки Е. Алгоритм генерации
сигнала ошибки можно записать в следующем виде:
Е — 1, если 5, = 0 и 5, = 1
Данная логическая функция может быть записана в виде
выражения булевой алгебры:
e = s[s2
В данной записи переменная будет равна нулю, если
5, = 1, и единице, если 5, = 0. Символ точки (•) обозначает
логическую операцию И.
В общем случае в системе может быть более одного сигнала
ошибки, например Е,, Е2, Е3 и т.д., каждый из которых указы-
вает на возникновение того или иного сбоя в работе системы.
Если необходимо, чтобы при выполнении условия Е, = 1 или
Ег = 1, или Е3 = 1 звучал сигнал тревоги, то алгоритм генера-
ции такого сигнала будет выглядеть так:
Тревога = 1, если Е, = I, или Е2 = I, или Е3 = 1
Логическая функция данного условия в булевой алгебре за-
писывается следующим образом:
Тревога = Е, + Е2 + Е3
Здесь символ (+) соответствует операции булевой алгебры
ИЛИ. Итак, рассмотренный пример познакомил с тремя ос-
новными операциями булевой алгебры: И (), ИЛИ (+) и НЕ
(—). Пользуясь ими, можно создать любую логическую функ-
цию. Полнее возможности булевой алгебры будут описаны
в главе 2. Таким образом, для решении задачи управления не-
обходимо иметь логическую схему с двумя входными сигнала-
ми, 5, и S2, и одним выходным сигналом, Е, который будет
принимать значение 1, если 5, = 0 и 52 = 1, в противном случае
Е = 0. Выполнение данного условия требует применения ком-
бинационных логических схем, поскольку значение на выходе
системы зависит от комбинации сигналов на входе. Функция
генерации сигнала тревоги также реализуется с использованием
схем комбинационной логики.
Выходная функция Z носит более сложный характер, по-
скольку требует наличия в схеме памяти для запоминания
1.1. Цифровые системы
23
логических значений. Z будет равна 1 при 5, = 0, но не перей-
дет обратно в 0, когда 5, станет равным 1, а сделает это только
при S2= 1. Схемы, на основе которых можно реализовать по-
добную функцию, носят название последовательных логических
схем, поскольку в общем случае сигналы на их выходах следуют
некоторым последовательностям. Проектирование таких логи-
ческих схем рассматривается в главе 4.
Вычисления
Более сложные задачи управления часто связаны с приме-
нением измерительных датчиков. Например, это могут быть
датчики измерения температуры. Скажем, необходимо, чтобы
с помощью нагревательных элементов температура материала
в бункере поддерживалась на определенном уровне. К примеру,
нагреватель должен включаться, если температура материала
опускается ниже 40°С, и работать до тех пор, пока температура
не поднимется до 45°С, после чего он должен отключиться до
того момента, пока температура вновь не опустится до 40°С.
Этот алгоритм очень похож на используемый для контроля ко-
личества материала в бункере, за исключением того, что теперь
необходимо работать с числовыми данными, а не с простыми
сигналами типа ВКЛ и ВЫКЛ. В этой и других задачах могут
иметь место многочисленные измерения и сложные расчеты,
основанные на полученных данных. Например, современный
автомобильный двигатель управляется с помощью цифровой
системы. В этом случае управленческие воздействия для полу-
чения оптимального режима работы зависят от значений не-
скольких переменных, включая текущую скорость, нагрузку,
температуру и т.д. Совершенно ясно, что в этом случае придет-
ся иметь дело не только с логическими двузначными перемен-
ными, но и с числовыми данными.
Цифровой компьютер
Полуавтоматическое выполнение вычислений для облегче-
ния тяжелых ручных расчетов долго оставалось мечтой. Но
в 1850-х годах Ч. Бэббиджем была изобретена механическая
счетная машинка, электронные версии которой начали разра-
батываться во время второй мировой войны и использовались
для расчетов траектории реактивных снарядов. Бэббидж пер-
вым сформулировал идею универсального программируемого
24
Глава 1. Цифровые системы и представление информации
калькулятора, электронная версия которого сейчас называется
“цифровым компьютером”. Такие компьютеры находятся на
вершине цифровых систем и представляют собой сложные
устройства, которые оперируют числами и с помощью про-
грамм, хранящихся в памяти, вычисляют необходимые вы-
ходные значения. Наиболее сложные задачи управления, на-
пример управление автомобилем, в настоящее время решают-
ся уже не специализированными контроллерами, а с помо-
щью именно цифровых компьютеров.
На рис. 1.2 показана обобщенная структурная схема циф-
рового компьютера. Процессор способен выполнять различ-
ные арифметические операции над числами, после чего при-
нимать основанные на результатах расчетов решения. Выпол-
няемые компьютером действия кодируются в числовой форме
и записываются в память в виде команд. Для этой цели чаще
всего используется двоичная числовая форма, которая будет
описана ниже. Закодированные команды последовательно по-
даются в процессор для выполнения. Конечно, последова-
тельность этих команд (программа) создается человеком
(программистом). Процессору необходимо абсолютно точно
указывать, какие вычисления он должен выполнить и какие
решения принять в зависимости от полученного результата,
что и делается в процессе разработки программы.
Рис. 1.2. Структура программируемого компьютера
1.1. Цифровые системы
25
1.2. Представление чисел в цифровых
системах
1.2.1. Двоичные числа
Имеем ли мы дело с полностью программируемым компью-
тером или с узкоспециализированной управляющей системой,
в любом случае приходится оперировать числами, а значит,
представлять их в виде напряжений. Предположим, использу-
ются десятичные числа, при этом каждому разряду соответству-
ет один сигнал. В этом случае каждый сигнал должен представ-
ляться десятью различными уровнями напряжения — по одно-
му для каждого возможного значения цифры в каждом разряде.
Например, цифра 0 могла бы представляться напряжением О
вольт, цифра 1 — напряжением 1 вольт и т.д. Тогда электрон-
ные схемы должны проектироваться таким образом, чтобы они
могли воспринимать и генерировать десять различных уровней
напряжения, по одному для каждого разряда числа.
Десятичная система счисления является позиционной. В ней
используются цифры, умноженные на степень числа 10, при
этом величина показателя степени зависит от положения
цифры в числе. Например, возьмем десятичное число
235 = 2 х 102 + 3 х 10' + 5 х 10°. Здесь 10 является основанием
системы счисления и показывает, что для представления любой
числовой величины требуется 10 различных цифр: 0, 1, 2, 3, 4,
5, 6, 7, 8 и 9. Само число десять было выбрано, вероятно, бла-
годаря тому, что у человека на руках десять пальцев, однако
в качестве основания можно выбрать любое число. В общем
случае «-разрядное число в системе счисления с основанием b
может быть представлено в виде:
дп.1дп_2...ц...д2д|ц) = a^lF' + У*2 +- + а$+... + а-fi + аф' + д#,
где а, — z-тый разряд числа.
Если бы люди использовали в качестве основания число 9,
то применялось бы только девять цифр: 0, 1, 2, 3, 4, 5, 6, 7
и 8, и любое число выражалось бы исключительно с их по-
мощью. Число 235 в этой системе счисления представляло
бы величину 2 х 92 + 3 х 9' + 5 х 9° = 194. Если бы исполь-
зовалась восьмеричная система (с основанием 8), то цифр
было бы, соответственно, 8: 0, 1, 2, 3, 4, 5, 6 и 7, а число 235
равнялось бы 2 х 82 + 3 х 8' + 5 х 8° = 157. Для однозначно-
сти определения основания системы счисления его можно
26
Глава 1. Цифровые системы и представление информации
показывать справа от числа в виде нижнего индекса. Таким об-
разом, запись 235|О указывает на использование десятичной сис-
темы, 2359 — системы с основанием 9, 2358 — восьмеричной.
С уменьшением величины основания системы уменьшается
и количество цифр. При уменьшении основания до трех (так на-
зываемая троичная система счисления) придется оперировать
цифрами 0, 1 и 2, а при уменьшении основания до 2 (двоичная
система) остаются только цифры 0 и 1. Эти цифры двоичной
системы называются битами (от англ. nary digits — двоичные
разряды). Бит может принимать только одно из двух значений:
О или 1. В качестве примера двоичного числа можно, например,
назвать число 1100012, которое в десятичной системе счисления
равно 1 х 25 + 1 х 24 + 0 х 23 + 0 х 22 + 0 х 2' + 1 х 2° = 49.
Задание для самопроверки 1.1
Чему равно двоичное число 11012 в десятичной системе счисления?
Числа могут быть не только целыми, но и дробными. Разряды
дробной части представляют собой основание, показатели степе-
ни которого не положительны, а отрицательны. Например, за-
пись в десятичной системе выглядит так: 0,12,0 = 1 х КГ1 + 2 х 1(Г2,
а в двоичной системе: 0,1012 = 1 х 2~' + 0 х 2-2 + 1 х 2-3.
Задание для самопроверки 1.2
Чему будет равно двоичное число 1101,1012 в десятичной системе счисления?
Двоичная система счисления идеально подходит для систем,
оперирующих двузначными управляющими сигналами типа
ВКЛ/ВЫКЛ, однако еще более важным ее преимуществом пе-
ред другими системами счисления является то, что с ее помо-
щью любые числа можно выразить с помощью всего двух цифр:
0 и 1. Для выражения любого разряда необходимы лишь два
уровня напряжения. Например, значение 0 вольт может пред-
ставлять двоичный ноль, а 5 вольт — двоичную единицу. Все
это существенно упрощает проектирование цифровых систем,
в частности проектирование электронных схем. Использование
всего двух напряжений также облегчает борьбу с колебанием их
уровней, которые могут возникать вследствие изменения харак-
теристик компонентов схемы, внешних электромагнитных по-
мех и электрических шумов.
1.2. Представление чисел в цифровых системах
27
Часто в цифровой системе необходимо запомнить числовые
значения. В таком случае для хранения каждого разряда пона-
добится одна “ячейка” памяти. В этом смысле двоичное пред-
ставление информации также обладает преимуществом, по-
скольку большинство современных запоминающих устройств
естественным образом позволяют хранить два значения. На-
пример, в памяти на магнитных носителях (дискеты и жесткие
магнитные диски) двузначная информация может храниться
в виде двух направлений вектора намагниченности — вдоль или
поперек материала с магнитными свойствами. Каждому биту
выделяется участок носителя, вектор намагниченности которого
может находиться в одном из двух состояний, соответствующих
двум направлениям намагниченности1. Существует еще один
широко используемый тип запоминающих устройств, основан-
ный на полупроводниковых технологиях, когда для представле-
ния информации используется заряд конденсатора. Присутствие
заряда соответствует наличию единицы, а его отсутствие — нулю.
В оптических системах для представления информации может
использоваться присутствие или отсутствие светового пучка, при
этом присутствие пучка света будет соответствовать 1, а отсутст-
вие — 0. Даже простейшие механические переключатели или ре-
ле могут находиться в двух состояниях, то есть быть включенны-
ми или выключенными. Преимущество использования только
двух состояний было взято за основу и в одном из старейших ме-
тодов храпения информации — на перфорированных лентах
и картах. Отверстие в определенном месте перфокарты означало
1, а отсутствие — ноль. Можно сказать, что присутствие или от-
сутствие “чего-либо” является достаточно универсальным прин-
ципом для представления значений двоичной логики.
По описанным выше причинам двоичная система полу-
чила всеобщее распространение и нашла самое широкое
применение в цифровых системах2.
1 Не только направления вектора магнитного поля представляют со-
бой логические значения; к примеру, логическую единицу может представ-
лять и изменение направления этого вектора, а ноль — отсутствие из-
менений. Более полное описание различных методов хранения информации
на магнитных носителях можно найти в книге Уилкинсона (Wilkinson)
и Хоррокса (Horroks), 1987.
2 Вообще говоря, для наиболее экономичного представления информа-
ции величина основания системы счисления должна стремиться к числу е
(основанию натурального логарифма), равному 2,71828. — Прим, перев.
28
Глава 1. Цифровые системы и представление информации
Задание для самопроверки 1.3
Какие еще методы вы можете предложить для хранения информации в двоим-
ной форме?
Однако преимущества двоичной системы не даются даром.
Поскольку размер основания уменьшается, при этом уменьша-
ется и количество используемых цифр, но это же увеличивает
количество разрядов, требующихся для представления чисел.
В табл. 1.2 показано, что происходит при изменении основа-
ния от 10 до 2 (2 — это наименьшее возможное основание).
Видно, что с уменьшением основания количество разрядов
увеличивается. Например, представление числа 15 в десятич-
ной системе требует лишь двух разрядов, в то время как
в троичной оно записывается тремя, а в двоичной — четырь-
мя цифрами. Количество разрядов зависит от величины числа.
При использовании системы счисления с основанием b для
представления любого числа имеется b различных цифр, и для
записи числа х понадобится [log^x] разрядов. Представление
чисел в двоичной системе счисления обычно требует в три
раза больше разрядов, чем в десятичной, и, таким образом,
использование двоичной логики дается ценой тройного уве-
личения количества проводов и схемных элементов, так как
для каждого разряда обычно требуется свой провод/элемент.
Однако сами схемы при этом оказываются значительно проше.
В цифровой системе или компьютере двоичные числа, как
правило, состоят из фиксированного числа битов. Группа из
восьми битов называется байтом (byte) и является удобной
единицей для представления буквенно-цифровой информа-
ции; подробно см. в разделе 1.5. Числа довольно часто пред-
ставляются с использованием больших групп битов. В компь-
ютерах, например, для представления чисел часто выделяются
тридцать два бита; при необходимости представления не столь
больших положительных чисел в старшие разряды просто до-
бавляются нули (способ представления отрицательных чисел
будет рассмотрен ниже).
Задание для самопроверки 1.4
Какое наибольшее положительное двоичное число может быть представ-
лено байтом?
1.2. Представление чисел в цифровых системах
29
Таблица 1.2. Представление чисел в различных системах счисления
Основание
2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1
10 2 2 2 2 2 2 2 2
11 10 3 3 3 3 3 3 3
100 11 10 4 4 4 4 4 4
101 12 11 10 5 5 5 5 5
110 20 12 11 10 6 6 6 6
111 21 13 12 11 10 7 7 7
1000 22 20 13 12 11 10 8 8
1001 100 21 14 13 12 11 10 9
1010 101 22 20 14 13 12 11 10
1011 102 23 21 15 14 13 12 11
1100 110 30 22 20 15 14 13 12
1101 111 31 23 21 16 15 14 13
1110 112 32 24 22 20 16 15 14
1111 113 33 30 23 21 17 16 15
1.2.2. Преобразование чисел
Итак, почему двоичная система счисления заняла доми-
нирующее положение в электронике, понятно. Однако на
практике намного удобнее пользоваться привычной десятич-
ной системой (даже если не пользоваться для счета пальца-
ми). Поэтому чаще всего числовые данные вводятся
в электронные системы в десятичном виде. Результаты вычис-
ления также предпочтительно иметь в десятичной форме. По-
этому необходим способ преобразования двоичных чисел
в десятичные, и наоборот, но только такой, чтобы его мог
использовать компьютер.
Небольшие десятичные числа довольно легко преобразовать
в двоичный вид, зная значения степеней двойки:
30
Глава 1. Цифровые системы и представление информации
Десятичное 64 32 16 8 4 2 1
число
26 25 24 23 22 21 2°
Двоичное 1000000 0100000 0010000 0001000 0000100 0000010 0000001
число
Если необходимо преобразовать десятичное число 25 в дво-
ичную систему, то следует просто разложить его на числа, являю-
щиеся степенями двойки, начиная со степени, наиболее близкой
по значению, но меньшей 25:
25 = 16 + 8 + 1 = 10000 + 01000 + 00001 = 11001
Более формальный метод преобразования можно вывести на
основе определения “позиционной” системы счисления (см.
работу Уилкинсона (Wilkinson), 1992).
Задание для самопроверки 1.5
Как выглядит число 23410 в двоичной системе счисления?
Неформальный способ преобразования двоичных чисел
в десятичные заключается в суммировании степеней двойки,
начиная с наибольшей степени, меньшей десятичного числа,
и заканчивая наименьшей (нулевой), например:
11001 = 16 + 8 + 1
Более формальный алгоритм можно найти, взяв за основу оп-
ределение позиционных систем счисления (см. работу Уилкин-
сона (Wilkinson), 1992).
1.2.3. Шестнадцатеричные и восьмеричные
числа
Позиционная система счисления, основание которой равно
16, называется шестнадцатеричной. Эта система имеет шестна-
дцать различных цифр, и для обозначения значений первых де-
сяти значений от 0 до 9 используются цифры 0, 1,2, 3, 4, 5, 6,
7, 8 и 9. Остальные значения, а именно: 10, 11, 12, 13, 14
и 15, записываются в виде больших букв латинского алфавита:
А= 10, В = 11, С = 12, D = 13, Е = 14 и F = 15. На англий-
ском часто слово “шестнадцатеричный” (hexadecimal) сокра-
щают до “hex”. Цифры шестнадцатеричной системы счисления
и их двоичные эквиваленты приведены в табл. 1.3.
1.2. Представление чисел в цифровых системах
31
Таблица 1.3. Двоичные, десятичные и шестнадцатеричные числа
Десятичная система Двоичная система Шестнадцатеричная система
0 0000 0
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 0110 6
7 0111 7
8 1000 8
9 1001 9
10 1010 А
11 1011 В
12 1100 С
13 1101 D
14 1110 Е
15 1111 F
Шестнадцатеричная система счисления играет важную роль
в электронике, поскольку позволяет очень просто преобразовы-
вать числа в двоичную систему и обратно. Благодаря тому что
основание шестнадцатеричной системы (16 = 24) равно двум
(основанию двоичной системы) в четвертой степени, одному
шестнадцатеричному разряду соответствует четыре двоичных.
Для того чтобы преобразовать двоичное число в шестнадцате-
ричное, нужно просто разбить двоичное число на группы по
четыре цифры и преобразовать каждую такую группу в шестна-
дцатеричный разряд. Переведем, к примеру, двоичное число
101001112 в шестнадцатеричную систему счисления:
101001112 = А716
(10102 = 10 в десятичной системе или А в шестнадцатерич-
ной). Количество разрядов полученного шестнадцатеричного
эквивалента вчетверо меньше, чем у исходного двоичного числа
при условии, что количество двоичных битов было кратно
32
Глава 1. Цифровые системы и представление информации
четырем. Следовательно, двоичные числа легко записать в ше-
стнадцатеричном виде с меньшим количеством разрядов, при-
чем картина распределения “1” и “0” исходного двоичного
числа остается прозрачной. Именно по этой причине шестна-
дцатеричное написание используется в технической документа-
ции значительно чаще, чем двоичное.
Метод преобразования чисел из шестнадцатеричной систе-
мы в двоичную можно получить все из того же определения по-
зиционной системы счисления. В качестве примера рассмотрим
преобразование шестнадцатеричного числа IАС16:
1АС16 = (00012) х 162 + (10102) х 161 + (11002) х 16",
что равняется
(О х 23 + 0 х 22 + 0 х 2' + 1 х 2") х 162 + (1 х 23 + 0 х 22 + 1 х
х2' + 0 х 2°) х 16' + (1 х 23 + 1 х 22 + 0 х 21 + 0 х 2") х 16".
Пользуясь тем, что 162 = 28, 161 = 24, 16° = 2", можно записать:
(О х 2" + 0 х 2'° + 0 х 29 + 1 х 28) + (1 х 27 + 0 х 26 + 1 х 25 +
+ 0 х 24) + (1 х 23 + 1 х 22 + 0 х 21 + 0 х 2°), что эквивалентно за-
писи 0001 101011002.
Задание для самопроверки 1.6
Преобразуйте шестнадцатеричное число ЗР|6 в двоичное.
Задание для самопроверки 1.7
Преобразуйте двоичное число 1000010101000102 в шестнадцатеричное.
Метод преобразования из восьмеричной системы счисления
в двоичную также достаточно прост. Следует принять во вни-
мание, что основание 8 представляет собой 2 в третьей степени,
поэтому три двоичных бита соответствуют одному восьмерич-
ному разряду. Например, восьмеричное число 345м преобразует-
ся в двоичный эквивалент следующим образом:
3458 = (011 100 101)2.
Однако восьмеричная система по столь удобна как шестнадца-
теричная, поскольку в большинстве систем используются двоич-
ные слова, количество битов в которых кратно байту, а один байт
записывается в виде двух шестнадцатеричных разрядов. Восьме-
ричная система была удобна в старых компьютерных системах,
где использовались 24-битовые слова, и в этом случае восемь
восьмеричных разрядов как раз и составляли одно такое слово.
1.2. Представление чисел в цифровых системах
33
1.3. Арифметические операции над
двоичными числами
1.3.1. Сложение
Понятно, что, поскольку внутри цифровой системы исполь-
зуются двоичные числа, над ними необходимо выполнять ариф-
метические операции. К счастью, двоичная математика предель-
но проста. В школе мы сталкиваемся с таблицами десятичного
сложения, вычитания и умножения, в которых приведены различ-
ные комбинации чисел, включающие все десять используемых
цифр. Точно такие же таблицы можно построить и для двоичной
системы счисления, но в данном случае существует всего четыре
возможных комбинации из двух цифр: 0 и 0, 0 и 1, 1 и 0, 1 и 1.
Возьмем, например, сложение: 0 + 0 = 0, 0+1 = 1, 1+0=1,
1 + 1 = 10. Если сравнить с десятичной арифметикой (0 + 0 = 0,
0+1 = 1, 0 + 2 = 2... 9 + 9= 18), то налицо явное упрощение.
Правила двоичного сложения представлены в табл. 1.4.
Таблица 1.4. Сложение двоичных цифр
А В Сумма Десятичная система
0 0 0 0 0
0 1 0 1 1
1 1 0 1 0 1 1 0 1 2
Предположим, необходимо просуммировать два двоичных
числа, каждое из которых состоит из нескольких битов. Снача-
ла, как и в десятичной системе счисления, складываются млад-
шие значащие биты чисел. В десятичной системе, если резуль-
тат сложения превышает цифру 9, то появляется перенос, при-
бавляющийся к следующему по величине разряду (например,
7 + 8 = 5 и перенос в разряд десятков). Для двоичной системы
справедливо то же самое, только перенос формируется при по-
явлении числа, большего 1 (например, 1 + 1 = 0 и перенос 1
в следующий по величине разряд). В следующем же разряде,
как для десятичной системы, складываются уже три числа: со-
ответствующие биты слагаемых плюс бит переноса. Всего, та-
ким образом, как показано в табл. 1.5, возможны восемь ком-
бинаций сложения трех двоичных цифр.
34
Глава 1. Цифровые системы и представление информации
Таблица 1.5. Сложение трех двоичных цифр
А В Сах ^вых Сумма Десятичная система
0 0 0 0 0 0
0 0 1 0 1 1
0 1 0 0 1 1
0 1 1 1 0 2
1 0 0 0 1 1
1 0 1 1 0 2
1 1 0 1 0 2
1 1 1 1 1 3
Для того чтобы сравнить операции сложения в десятичной
и двоичной системах, давайте сложим десятичные числа 22](1 и 2810:
Десятичная система Двоичная система
2 2 10 110
2,8 ,1,1,1 0 0
5 0 110010
Итак, основные правила, по существу, не меняются и не за-
висят от того, какая система используется (это справедливо для
любого основания). Кратко их можно сформулировать так:
слагаемые суммируются поразрядно, начиная с младшего зна-
чащего разряда. Если результат сложения разряда равен или
превышает число b (величину основания), то формируется пе-
ренос, который складывается с цифрами в следующем по стар-
шинству разряде. Единственное отличие в том, что для деся-
тичной системы счисления перенос возникает в случае превы-
шения числа 9, а для двоичной — единицы.
Задание для самопроверки 1.8
Сложите в двоичной системе числа 81 w и 63,0. Проверьте правильность отве-
та, преобразовав полученный результат в десятичную систему.
Для того чтобы реализовать сложение с помощью электрон-
ных компонентов, необходимо использовать схему, на первый
каскад которой поступают биты двоичных слагаемых, а па выходе
1.3. Арифметические операции над двоичными числами
35
формируются бит суммы и бит переноса, поступающий в следую-
щий каскад. Каждый же последующий каскад такой схемы дол-
жен складывать уже три бита: два бита соответствующих разрядов
двоичных чисел и бит переноса предыдущего каскада. Пример
проектирования подобной схемы будет рассмотрен в главе 3.
1.3.2. Отрицательные числа и вычитание
Двоичное вычитание может выполняться по таким же прави-
лам, как и в десятичной системе, т.е. с “заимствованием” в случае
необходимости из предыдущего разряда. В десятичной системе та-
кое заимствование происходит в том случае, когда вычитаемое
(число, которое вычитается) больше уменьшаемого (числа, из кото-
рого вычитают). К примеру, чтобы отнять 7 от 6, нужно взять 10
из предыдущего разряда и вычесть 7 уже из 16. Однако из сооб-
ражений простоты реализации схемы вычитание обычно выпол-
няется как “сложение с дополняющим числом”. Такой метод
применим в любой системе счисления и основан на замене от-
рицательного числа его дополнением. В десятичной системе чис-
ло, дополнительное данному, вычисляется следующим образом:
10" - А,
где п — количество разрядов десятичного числа. Предположим,
есть число с тремя разрядами, и пусть это будет 235. Тогда до-
полнительное ему число находим как 1000 — 235 = 765.
Аналогичным образом можно найти и дополнительное чис-
ло в двоичной системе счисления:
2" - А,
где п — количество разрядов двоичного числа. Предположим,
есть трехразрядное число 011 (3|0). Найдем число, дополнитель-
ное ему: 1000 - 011 = 101.
В двоичной системе счисления дополнительное число или
дополнительный код (2’s complement) служит для представле-
ния отрицательных чисел. Например, представление числа —3
в двоичном виде будет выглядеть как 101. Положительные же
числа, как, скажем, +3, представляются обычным образом:
011. Для того чтобы можно было выражать как положитель-
ные, так и отрицательные числа, необходимо иметь достаточ-
ное количество разрядов, так как перед положительными числа-
ми будет стоять как минимум один ноль. Отрицательные же чис-
ла всегда будут начинаться с I. В табл. 1.6 приведены двоичные
36
Гпава 1. Цифровые системы и представление информации
эквиваленты десятичных чисел от —8 до +7 с использованием 4
разрядов. Обратите внимание, что положительные числа не ме-
няют свой “двоичный вид”. Также стоит отметить, что количе-
ство всех отрицательных чисел в заданном диапазоне всегда на
одно больше, чем положительных, и максимальное по модулю
отрицательное число (в нашем случае —8) не имеет положи-
тельного эквивалента и не подчиняется сформулированному
выше правилу, в соответствии с которым —8 можно получить
как 23 — 8 (мы получим 0). Однако данное представление отри-
цательного числа абсолютно правильно, и, прибавив, напри-
мер, к —8 единицу, мы получим —7: 1000 + 0001 = 1001.
Таблица 1.6. Представление отрицательных двоичных чисел с помощью
дополнительного кода
Десятичная система Двоичная система
+7 0111
+6 0110
+5 0101
+4 0100
+3 0011
+2 0010
+1 0001
0 0000
-1 1111
-2 1110
-3 1101
-4 1100
-5 1011
-6 1010
-7 1001
-8 1000
Как правило, все числа в системе выражаются с помощью
заданного фиксированного количества разрядов; часто встреча-
ются системы, где для чисел отводится, скажем, 32 разряда
(бита). При использовании дополнительного кода с помощью п
1.3.2. Отрицательные числа и вычитание
37
разрядов можно задать любые числа, значения которых лежат
в диапазоне от -2" до +2" — 1, включая ноль. Чтобы добрать ко-
личество разрядов до заданного, в случае положительных чисел
к ним впереди при необходимости дописываются нули. Для от-
рицательных чисел впереди дописываются единицы. Например,
число —6 в случае использования четырех разрядов имеет вид
1010, а при использовании восьми разрядов — 11111010.
В большинстве цифровых систем и компьютеров отрицатель-
ные величины представляются именно в виде дополнительного
кода, так как такое представление значительно упрощает сложе-
ние и вычитание. Давайте на примерах рассмотрим, в чем же
преимущества дополнительного кода для двоичной арифметики.
Следует отметить, что все описанные ниже ситуации одинаково
справедливы и для десятичных чисел, в чем легко убедиться.
Вычитание
Для того чтобы вычесть из числа X число У, нужно найти
дополнительный код числа У, т.е. получить —У Затем X и ~¥
складываются:
X- У= Х+ (-Y) = X + (2" - У) = X- Y+ 2".
Если X больше, чем У, то их разность, X — У, окажется поло-
жительной. Член 2” представляет собой число, которое выражает-
ся 1 и л нулями (1000...000). Если оставить в результате только п
битов, то этот член можно игнорировать, и тогда получим кор-
ректный положительный результат. Если же разность X— У от-
рицательная, то корректное отрицательное число в форме допол-
нительного кода формируется естественным образом: 2П — (У— X).
Чтобы убедиться, что представление чисел в дополнитель-
ном коде всегда адекватно, нужно доказать, что при любой
комбинации положительных и отрицательных чисел результат
будет верным. Если число У уже отрицательно, то отрицание
отрицательной величины даст положительное число:
-(-У) = 2" - (2П - У) = 2" - 2" + У= У
Таким образом, видно, что пользоваться дополнительным
кодом можно всегда.
ПРИМЕРЫ
(а) X и У — положительные числа, Х> У Результат положи-
тельный.
38
Гпава 1. Цифровые системы и представление информации
Пусть Х = 0110(6), a Y = ООН (3). Тогда ~Y= 1101 (-3),
и 6 — 3 можно вычислить следующим образом:
Десятичная система Двоичная система
6 0 110
-3 .1.1 0 1
3 0 0 11
Обратите внимание, что соответствующий члену 2П бит пе-
реноса в последнем разряде формируется, но игнорируется.
б) X и Y— положительные числа, Х<. Y. Результат отрица-
тельный.
Пусть Х = 0011(3), a Y= ОНО (6). Тогда-Y = 1010 (-6),
и разность 3 — 6 определяется так:
Десятичная система Двоичная система
3 0 0 11
-6 1,0 1 0
-3 110 1
В данном случае перенос в последнем разряде не появ-
ляется, и ответ представляет собой отрицательный ре-
зультат — число —3.
в) X — положительное, а У — отрицательное числа. Резуль-
тат всегда положительный.
Пусть Х= ООН (3), а У= 1101 (-3). Тогда -У = 0011
(+3), и 3 — (—3) вычисляется таким образом:
Десятичная система Двоичная система
3 0 0 11
-(-3) 0 0,1,1
6 0 110
1.3.2. Отрицательные числа и вычитание
39
г) X — отрицательное, a Y — положительное числа. Резуль-
тат всегда отрицательный.
Пусть Х = 1101 (-3), a Y= 0011 (3). Тогда-Г = 1101 (-3),
а —3 — 3 вычисляется так:
Десятичная система Двоичная система
-3 110 1
-3 ,1,1 0,1
-6 10 10
Соответствующий члену 2П бит переноса в последнем
разряде формируется, но игнорируется.
Очевидно, что во всех приведенных случаях остается опера-
ция вычитания, необходимая для получения числа — У из числа
+ Y (вычитание Y из 2"). Если бы это вычитание выполнялось
обычным методом (с помощью заимствования), то вычитания
избежать бы не удалось. К счастью, дополнительный код числа
можно получить, не вычитая его из 2П. Число 2" представляет
собой единицу с п нулями, то есть 2П = 100...00. Таким образом,
2"— 1 записывается как 011...11. Если вычитать из числа
011...11 любое другое двоичное число, то результат будет пред-
ставлять собой вычитаемое, только все его биты будут проин-
вертировапными (т.е. все 1 поменяются на 0, а все 0 — на 1).
Например, при вычитании ОНО из 1111 получаем 1001 ((« — 1)-й
бит обычно игнорируется). Операция инвертирования битов
чрезвычайно проста, но следует помнить о том, что в итоге
нужно вычитать число из 2", а не из 2" — 1. Именно поэтому
к получаемому результату необходимо прибавить единицу, т.е.
2" — Х= (2П — 1) — X + 1. Таким образом, мы имеем простой
способ получения дополнительного кода числа, который фор-
мулируется в виде простого правила: для получения дополни-
тельного кода числа необходимо проипвертировать все его раз-
ряды и прибавить к результату единицу. В главе 3 будет пока-
зано, что этот метод может быть легко реализован па
аппаратном уровне. Стоит отметить, что данное правило пред-
ставляет собой только способ получения числа в нужном виде,
по не является определением дополнительного кода как тако-
вого: дополнительный код числа определяется как 2" — N.
40
Гпава 1. Цифровые системы и представление информации
Задание для самопроверки 1.9
Преобразуйте двоичное число 0101010 в дополнительный код отрицательного
числа, используя сформулированное выше правило.
Задание для самопроверки 1.10
Используя тот же метод, преобразуйте ответ из предыдущего задания в по-
ложительное число.
Существует и альтернативный алгоритм преобразования чи-
сел в дополнительный код, заключающийся в копировании всех
разрядов справа налево, включая первую встретившуюся 1, после
которой все остальные биты слева инвертируются (доказать это
утверждение предлагается самостоятельно; см. упражнение 1.10).
Дополнительный код можно рассматривать с разных точек
зрения. Например, можно считать, что разряды числа имеют
следующие “весовые” коэффициенты:
_2п-| 2П-2 2П-3 21 2°
Например, число —6 выглядит так:
_23 22 21 2°
1 0 1 0 = —23 + 21 = -6
Подобный подход вытекает непосредственно из определения
дополнительного кода (см. упражнение 1.11).
Задание для самопроверки 1.11
Преобразуйте двоичное число 0101010 в дополнительный код отрицательного
эквивалента, используя правило “копирования разрядов справа налево, вклю-
чая первую 1, с инверсией всех остальных разрядов слева". Покажите, что
полученный результат правильный.
Наконец, заметим, что использование дополнительного кода
исключает необходимость в специальной обработке чисел при вы-
читании, когда вычитаемое больше уменьшаемого, в отличие оттого,
к чему мы привыкли при вычитании десятичных чисел на бумаге.
Задание для самопроверки 1.12
Отнимите 6310 от 14)0 в десятичной системе счисления. Повторите для их
двоичных эквивалентов.
1.3.2. Отрицательные числа и вычитание
41
Обратный код
Результат инверсии всех разрядов двоичного числа называ-
ется обратным кодом (l’s complement) и определяется как
—Х = (2" - 1) - Y.
Оказывается, что арифметические операции можно выпол-
нять непосредственно и над обратным кодом, не используя до-
полнительный, хотя в этом случае появление переноса в по-
следнем разряде показывает, что к полученному результату сле-
дует добавить 1. Это следует из определения обратного кода
(упражнение 1.12). Однако в большинстве компьютеров для
представления отрицательных чисел используется именно до-
полнительный код. Десятичный вариант двоичного обратного
кода (на английском носит название 9’s complement) определя-
ется следующим образом:
-Х = (10" - 1) - Y.
1.3.3. Двоично-десятичное представление
десятичных чисел
В некоторых практических задачах применения арифметики,
например в калькуляторах и кассовых аппаратах, необходимо
осуществлять простые операции над десятичными числами
и выводить результат на экран или индикатор в десятичном ви-
де. В этом случае десятичные числа вводятся с клавиатуры,
и полученные результаты в десятичном же виде выводятся на
экран устройства отображения. Понятно, что десятичные числа
можно преобразовать в двоичные, а полученный двоичный ре-
зультат можно снова преобразовать в десятичный и вывести на
экран. В качестве альтернативы можно сохранить информацию
внутри системы в десятичном виде, воспользовавшись двоично-
десятичным представлением (binary-coded decimal — BCD). В дво-
ично-десятичном представлении каждый десятичный разряд
представляется в виде 4-разрядного двоичного кода. Далее эти
4-разрядные группы просто ставятся друг за другом, образуя еди-
ную цепочку. Например, десятичное число 234510 можно пред-
ставить в двоично-десятичном коде как 0010 0011 0100 0101.
Числа в таком представлении можно суммировать как двоич-
ные, соблюдая, правда, при этом определенные правила. Пусть
необходимо сложить два десятичных числа: 243110 и 5425,п:
42
Глава 1. Цифровые системы и представление информации
2431
5425
7856
0010 0100 ООН 0001
0101 0100 0010 0101
0111 1000 0101 ОНО
Можно видеть, что сложение двоично-десятичных кодов чи-
сел по методике сложения обычных двоичных чисел дает пра-
вильный двоично-десятичный результат. Однако данный при-
мер был тщательно подобран, чтобы ни в одном десятичном
разряде сумма не превысила 10. Если же такое превышение все-
таки произойдет, то для получения верного результата необходи-
мо произвести так называемую коррекцию. Поправочный коэф-
фициент, который обязательно нужно учесть, равен 6, и его надо
прибавить к полученному числу. Такой прыжок позволяет
“перескочить” шесть неиспользуемых кодовых комбинаций дво-
ично-десятичного кода, которые представляют числа 10, 11, 12,
13, 14 и 15 (а именно: 1010, 1011, 1100, 1101, 1110 и 1111).
Если получаемый в результате сложения двух разрядов чисел
разряд суммы будет находиться между 10 и 15, то достаточно
просто работать с четырьмя битами двоично-десятичного разряда:
36
2 5
5 11
6 — поправочный коэффициент
6 1
ООН оно
0010 0101
0101 1011
оно
ОНО 0001
Если же результирующий разряд суммы оказывается равным
16, 17 или 18, то четыре бита двоично-десятичного разряда
принимают вид 0000, 0001 и 0010, соответственно. Возникнет
перенос, который прибавится к следующему по старшинству
двоично-десятичному разряду. Здесь уже недостаточно работы
только с четырьмя битами двоично-десятичного разряда, и не-
обходимо распознавать возникновение бита переноса:
3 8
2 9
6 1
6 — поправочный коэффициент
67
ООН 1000
0010J001
ОНО 0001
ОНО
ОНО 0111
Компьютеры, спроектированные для выполнения операций над
двоично-десятичными числами, имеют специальные команды для
1.3.2. Отрицательные числа и вычитание
43
автоматической коррекции результатов. При вычитании поправоч-
ный коэффициент в случае необходимости просто отнимается.
В прошлом, когда использовались однокристальные 4-разрядные
микропроцессоры, двоично-десятичный код был очень удобен,
но в наши дни спектр его применения уже не столь широк.
1.4. Представление алфавитно-цифровых
символов
Кроме чисел компьютеры должны представлять буквы алфа-
вита и другие символы, которые могут вводиться с клавиатуры
или выводиться на монитор либо принтер. Для описания таких
символов часто используется термин буквенно-цифровые символы,
поскольку они включают в себя и десятичные цифры от 0 до 9.
Для их кодирования специалистами был разработан стандартный
код, получивший название ASCII-код (от англ. American Standard
Code for Information Interchange — Американский стандартный
код для обмена информацией); этот код показан в табл. 1.7.
В соответствии с этой таблицей, 7-разрядный код получается пу-
тем взятия трех битов b7,bb,b5 из верхней строчки, к которым под-
ставляются справа четыре бита Ь^,Ь3,Ьг,Ьу, стоящие в правом
крайнем столбце. Например, ASCII-код буквы В будет 1000010.
Таблица 1.7. 7-разрядный ASCII-код
bzbebs ООО 001 010 011 100 101 110 111
Ь^ЬзЬгЬ^ 0 1 2 3 4 5 6 7
0000 0 NUL DLE SP 0 @ Р Р
0001 1 SOH DC1 ! 1 А Q а q
0010 2 STX DC2 U 2 В R b Г
0011 3 ЕТХ DC3 # 3 С S С s
0100 4 EOT DC4 $ 4 D т d t
0101 5 ENQ NAK % 5 Е и е u
0110 6 АСК SYN & 6 F V f V
0111 7 BEL ЕТВ 7 G W 9 w
1000 8 BS CAN ( 8 Н X h X
1001 9 НТ ЕМ ) 9 I Y I У
44
Гпава 1. Цифровые системы и представление информации
Окончание табл. 1.7
bzbsbs ООО 001 010 011 100 101 110 111
Ь^зЬгЬ 0 1 2 3 4 5 6 7
1010 10 LF SUB t J Z j z
1011 11 VT ESC + < К [ k {
1100 12 FF FS 1 < L \ I I
1101 13 CR GS - = M ] m }
1110 14 SO RS > N n -
1111 15 SI US / ? 0 0 DEL
Задание для самопроверки 1.13
Как выглядит ASCII-код буквы w?
Задание для самопроверки 1.14
Как заменить коды строчных букв на коды прописных букв независимо от са-
мой буквы?
1.5. Пример цифровой логической схемы
В этом разделе мы рассмотрим простой пример применения
цифровой логики, который послужит своеобразным введением
к более детальному изучению материала последующих глав.
Этот пример раскроет особенности двух базовых типов логиче-
ских схем: комбинационных и последовательных. Каждому из
них в книге посвящены отдельные главы.
Клавиатура компьютера организована таким же образом, как
у печатной машинки, и вмещает все символы алфавита, цифры, зна-
ки препинания и специальные символы1. Обычно клавиши кла-
виатуры электрически объединяются в двумерную матрицу, имею-
щую, скажем, п столбцов и т строк (см. рис. 1.3). Сигнал с уров-
1 Расположение клавиш печатной машинки было придумано много лет
назад с целью замедлить работу машинистки, поскольку старые механи-
ческие машинки не могли печатать со столь высокой скоростью, которая
была бы доступна оператору, если бы клавиши располагались удобным для
набора образом! Подобное выдуманное расположение клавиш продолжает
использоваться и сегодня, хотя современные клавиатуры выдерживают
любую скорость набора.
1.5. Пример цифровой логической схемы
45
нем логической единицы поступает поочередно на каждую строку
матрицы и при нажатии клавиши передается на столбец, в пересе-
чении которого со строкой находится эта клавиша. Затем определя-
ется номер столбца, т.е. идентифицируется нажатая клавиша. (Для
того чтобы избежать возникновения ошибочных путей прохожде-
ния сигнала при одновременном нажатии сразу нескольких кла-
виш, необходимо использование дополнительных компонентов.)
Клавиша
Ключ
Строка
Столбец
Выбор
столбца
Идентификатор нажатой клавиши
Рис. 1.3. Дешифратор клавиатуры
Предположим, что в описанной выше матрице имеется четыре
строки. Тогда для определения номера строки будет достаточно
двух битов. Это двухразрядное число должно быть преобразовано
в 4-разрядную кодовую группу, положение единицы в которой по-
кажет номер строки с нажатой клавишей (табл. 1.8). Электронная
схема, которая преобразует 2-битовые кодовые комбинации в 4-
битовые, называется дешифратором “из 2 направлений в 4” (2-line-
46
Глава 1. Цифровые системы и представление информации
to-4-line decoder). Его название говорит о том, что комбинация
сигналов на двух входах определяет выбор одного из четырех вы-
ходов. Проектирование дешифраторов будет описано в главе 3.
Таблица 1.8. Кодовые комбинации определения номера строки
Строка Яз я2 Ri Ro
0 0 0 0 0 1
0 1 0 0 1 0
1 0 0 1 0 0
1 1 1 0 0 0
Для того чтобы последовательно проходить все эти кодовые
комбинации, можно воспользоваться 2-разрядным счетчиком:
логической схемой, сигналы на выходе которой последователь-
но принимают значения: 00, 01, 10 и 11. Тема проектирования
счетчиков будет рассмотрена в главе 4.
Наконец, необходима логическая схема, которая бы принима-
ла сигналы от столбцов и формировала двоичное число, опреде-
ляющее номер столбца с активным логическим сигналом. Пред-
положим, у нас есть шестнадцать столбцов. Тогда понадобится 4-би-
товое число и шифратор из 16 направлений в 4. Такая схема
осуществляет операцию, обратную той, которую выполняет де-
шифратор из 4 направлений в 16. Шифратор реализует функцию,
таблица истинности которой имеет вид, показанный в табл. 1.9.
Это еще один пример логической схемы, проектирование кото-
рой будет рассмотрено позже. Из рис. 1.3 видно, что результа-
том работы системы является адрес строки и столбца, на пере-
сечении которых находится нажатая клавиша. В действительно-
сти каждому символу клавиатуры присваивается уникальный
ASCII-код, и необходимо дополнительное преобразование.
1.6. Резюме
Бесспорно, нет человека, который бы не сталкивался с ком-
пьютером. Наиболее важным моментом в данной главе являет-
ся вывод о том, что для представления числовых и логических
значений в компьютерах и других цифровых системах должны
использоваться сигналы, имеющие всего два состояния.
Из прочитанной главы необходимо усвоить следующее.
Сигналы с двумя состояниями являются наиболее удобными
и универсальными для использования в цифровых системах.
1.5. Пример цифровой логической схемы
47
Таблица 1.9. Таблица истинности шифратора “из 16 направлений в 4”
С15 Cl4 Ci3 С,2 C11 Сю c9 c8 c7 Ce c5 c4 Сз c2 Ci Co Состояние на выходе
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 oooo
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0001
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 00 1 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 00 1 1
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 00
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 101
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 111
0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 000
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 001
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 10 11
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1100
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1101
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1110
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1111
Двузначные сигналы используются для решения двух основ-
ных задач: для управления (включение/выключенис самых раз-
нообразных приводов) и для представления чисел в двоичной
системе счисления.
Шестнадцатеричные числа очень удобны для промежуточ-
ного представления информации.
Сложение двоичных чисел подобно сложению десятичных.
Вычитание двоичных чисел удобнее всего выполнять, пред-
ставляя отрицательные числа с помощью дополнительного кода.
1.7. Упражнения
1. Напишите первые тридцать чисел в системах счисле-
ния с основаниями 11 и 12.
2. В 1951 году Тьюринг (изд. Hodges, 1983) в одной из
первых работ по проектированию компьютеров ис-
48
Глава 1. Цифровые системы и представление информации
пользовал систему счисления с основанием 32. На-
пишите первые тридцать два числа этой системы. Как
вы думаете, почему автор выбрал именно эту систему?
3. Преобразуйте в двоичную форму следующие десятич-
ные числа:
. 56
. 102
4. Преобразуйте в десятичную форму следующие целые
двоичные числа:
. 1011
• 11111
5. Преобразуйте в двоичную форму следующие шестна-
дцатеричные числа:
. 77
• АА
6. Преобразуйте в шестнадцатеричную форму следую-
щие двоичные числа:
• 1010101010
• 1111111111
7. Преобразуйте в дополнительный двоичный код сле-
дующие отрицательные десятичные числа:
• -12
. -345
8. Преобразуйте в десятичную форму следующие 8-раз-
рядные отрицательные двоичные числа:
• 111111111
. 10010000
9. Преобразуйте следующие десятичные числа в двоичную
форму и выполните указанные арифметические операции,
используя там, где необходимо, дополнительный код:
. 32 + 32
. 67 + 132
. 67-32
. -24 + 43
. -88 - 99
1.7. Упражнения
49
10. Докажите, что число действительно может быть пре-
образовано в дополнительный код по следующему
алгоритму: “копирование всех разрядов справа нале-
во, включая первую встретившуюся 1, после которой
вес остальные биты слева инвертируются”.
11. Покажите, что дополнительный код можно получить с по-
мощью следующих “весовых” коэффициентов разрядов:
______2п-1 2П~2 2П~3 21 2°
12. Пользуясь определением обратного кода, докажите, что
формат может быть использован при вычитании, если
прибавлять к результату 1 в случае появления переноса в
последнем разряде (так называемый циклический перенос).
13. Определите, какие действия с клавиатурой (ее функ-
циональная схема описана в разделе 1.6) приведут
к возникновению ошибочных путей прохождения
сигнала и ошибкам в работе (предполагается, что до-
полнительных элементов нет).
1.8. Список дополнительной литературы
1. Fletcher, W.I., An Engineering Approach to Digital Design,
Prentice Hall: Englewood Cliffs, New Jersey, 1980.
2. Hodges, A., Alan Turing: The Enigma, Simon and Schuster:
New York, 1983. (В этой книге приводится замечатель-
ная биография Алана Тьюринга (советуем прочесть пе-
ред выполнением упражнения 1.2), которую просто
обязаны знать студенты факультетов, связанных с вы-
числительной техникой!)
3. Karam, G.M. and Bryant, J.C., Principles of Computer
Systems, Prentice Hall: Englewood Cliffs, New Jersey, 1992.
4. Page, E.S. and Wilson, L.B., Information Representation and
Manipulation in a Computer, Cambridge University Press:
Cambridge, England, 1973. (Немного старая (но никак не
устаревшая) книга, посвященная исключительно вопро-
сам представления информации.)
5. Tinder, R.F., Digital Engineering Design, A Modem Ap-
proach, Prentice Hall: Englewood Cliffs, New Jersey, 1991.
6. Wilkinson, B. and Horrocks, D., Computer Peripherals, 2nd
edition, Hodder and Stoughton: London, 1987.
7. Wilkinson, B., Digital System Design, 2nd edition, Prentice
Hall: London, 1992.
50
Глава 1. Цифровые системы и представление информации
Глава 2
Логические вентили
Цели и задачи
В этой главе описаны основные компоненты цифровых
систем — логические вентили. Здесь будут подробно рас-
смотрены различные типы логических вентилей, исполь-
зующихся в системах. Также будут описаны базовые
функции булевой алгебры — математической основы логи-
ческого проектирования систем.
2.1. Логические сигналы
Сначала давайте вкратце повторим наиболее важные положе-
ния из теории логических сигналов, о которых говорилось в главе
1. Во всех цифровых системах для управления (включения или вы-
ключения приводов) и представления двоичных чисел используют-
ся сигналы, способные принимать только два значения. Каждое
из логических значений таких сигналов выражается с помощью
определенного уровня напряжения. Цифровую систему можно
изобразить в виде, показанном на рис. 2.1. Сами логические сиг-
налы могут изменяться во времени (как, например, сигналы сис-
темы управления, описанной в главе 1). В главе 1 упоминалось, что
для обозначения уровня логической единицы может использовать-
ся уровень напряжения +5 В, и О В — для обозначения логиче-
ского нуля. Использование более высокого из двух уровней сигна-
ла для обозначения логической 1 и более низкого — для обозначе-
ния логического 0 называется положительной логикой. Наоборот,
если для обозначения логического 0 применяется более высокое
напряжение, а логическая 1 представляется менее высоким, то
такое представление сигналов называется отрицательной логи-
кой. Как правило, в рамках одной системы стараются обходиться
только одной из двух логик, обычно положительной.
Выходные напряжения
— _г
Выходы
Входные напряжения
1
О
Логическая
схема
1_
1
О
Время
Рис. 2.1. Логическая схема, принимающая и выдающая логические сигналы
Алгебраические операции над двузначными
переменными
Эта книга написана для того, чтобы научить проектировать
логические схемы, состояние на выходах которых изменяется
в соответствии с требованиями к устройству. Каждая задача
имеет уникальные особенности, поэтому наиболее приемлемый
подход к проектированию сложных логических функций за-
ключается в их реализации на основе простых стандартных вы-
ражений. Подобно тому как сложные математические выраже-
ния строятся на основе четырех фундаментальных арифметиче-
ских операций (сложения, вычитания, умножения и деления),
так и логические функции можно создавать из более простых.
Логические функции можно считать алгебраическими выраже-
ниями, переменные в которых могут принимать только одно из
двух значений. Правила, описывающие операции над перемен-
ными с двумя возможными значениями, были разработаны ма-
тематиком Булем в XIX веке. В то время, естественно, никто не
помышлял о создании цифровых систем. Главной задачей логи-
ческой математики того времени было определение истинности
или ложности утверждений. Однако между разделом математи-
ки, разработанным Булем (булевой алгеброй), и “ключевыми”
схемами' (их определение впервые дал Шеннон в 1938 году)
существует самая непосредственная связь.
' Термин ключевая схема (switching circuity сложился исторически
и происходит от электромеханических ключей, которые использовались
для реализации логических функций на заре вычислительной техники. Од-
нако он применяется до сих пор, особенно при рассмотрении внутренней
структуры логических вентилей, речь о которой пойдет в разделе 2.6.2.
52
Гпава 2. Логические вентили
2.2. Базовые логические функции
Булева алгебра декларирует три фундаментальные операции,
на основе которых могут быть построены любые логические
функции:
НЕ (NOT)
И (AND)
ИЛИ (OR)
Эти и несколько других простых функций реализуются
в простейших схемах — вентилях. На вентиль поступает один
или более входных сигналов, а на его выходе генерируется вы-
ходной сигнал, значение которого зависит от реализуемой вен-
тилем логической функции. В главе 1 приведено неформальное
описание базовых логических операций; теперь давайте рас-
смотрим их более формально.
2.2.1. Вентиль НЕ
Логическая переменная может иметь только два значения:
ИСТИНА или ЛОЖЬ (1 или 0). Часто возникает необходимость
изменить одно из этих значений на другое, т.е. заменить еди-
ницу на ноль, или наоборот. Такая логическая операция явля-
ется фундаментальной операцией булевой алгебры и называется
операцией НЕ.
Определение: операция НЕ выполняется над одной переменной, и ее
результатом является логическое значение, противоположное исход-
ному. Если, к примеру, А = 1, то НЕ А = 0, и если А = 0, то НЕ А = 1.
Операция НЕ, выполненная над переменной А, записывает-
ся как А. Ниже будут рассмотрены базовые электронные схе-
мы, на основе которых формируют логические элементы, вы-
полняющие операцию НЕ. Однако при проектировании систем
значительно удобнее показывать нс реальную структуру таких
схем, а их условные обозначения и рисовать готовую систему,
используя общепринятые символы вентилей. На рис. 2.2 пока-
зано обозначение логического вентиля НЕ и таблица истинно-
сти реализуемой им функции. В таблице истинности указыва-
ются состояния всех выходных сигналов при любых комбина-
циях входных сигналов. Так как в нашем случае вентиль имеет
2.2. Базовые логические функции
53
только один вход, то на выходе могут наблюдаться два состоя-
ния, и запись соответствий выходных состояний входным в ви-
де таблицы оказывается очень удобной. Элемент НЕ часто на-
зывают инвертором, потому что он инвертирует переменную,
т.е. формирует дополнительную ей величину. Кружок на выходе
в символе элемента как раз и служит для обозначения инвер-
сии. Такие кружки часто используются в символах, чтобы ука-
зать на наличие инверсии, и, как будет показано дальше, могут
стоять как на входе, так и па выходе.
Условное обозначение Таблица истинности
Рис. 2.2. Обозначение вентиля НЕ и его таблица
истинности
Задание для самопроверки 2.1.
Каким будет результат операции НЕ над переменной А?
2.2.2. Вентиль И
Еще одной фундаментальной операцией, широко исполь-
зуемой при разработке цифровых систем, является операция,
определяющая, когда два или более логических сигнала одно-
временно равны 1. Например, необходимо спроектировать сум-
матор, который складывает два двоичных разряда, А и В,
и формирует бит суммы и бит переноса. Бит переноса равен 1
лишь в том случае, когда и А, и В одновременно равны 1 (см. главу
1, раздел 1.3.1). Можно найти множество задач по управлению,
когда требуется выполнить то или иное действие при одновре-
менном выполнении нескольких условий. Все эти ситуации
описываются с помощью функции И.
Определение: Результат операции И, выполняемой над перемен-
ными А и В, равен 1, если А = 1 “и” В = 1; в противном случае ре-
зультат равен 0.
54
Гпава 2. Логические вентили
В математике операция И обычно показывается с помощью
символа т.е. выражение А “и” В записывается как АВ,
it А В = 1 при А = I и В = 1; в любом другом случае А В = 0.
Иногда знак умножения просто опускают, так же, как делают
это в обычной, не логической, алгебре или арифметике, т.е.
А В можно записать и как АВ. При этом, однако, следует пом-
нить, что имена переменных могут состоять из более чем одной
буквы, т.е. запись АВ может с таким же успехом служить име-
нем одной переменной. Более того, использование многобук-
венных имен переменных и функций часто предпочтительнее,
так как они более информативны Например, переменная
МОТОР_ВКЛ, сразу говорит о назначении сигнала. Однако,
поскольку опускать символ умножения принято повсеместно,
далее он будет опускаться, если только не возникнет необходи-
мость разъяснить характер операции.
Как и обычное умножение, операция И применима к любому
числу переменных. Можно выполнить, например, операцию А
“и” В “и” С, т.е. А В С, или просто АВС. Результат будет равен 1
лишь тогда, когда все три переменные будут одновременно равны
1, иначе результат равен 0. Таким образом, АВС равно 1 только
в единственном случае, когда все переменные равны 1. Операто-
ром И можно объединять любое количество переменных, но
опять же результат равен 1 тогда и только тогда, когда все пере-
менные равны 1, в любом другом случае результат будет равен 0.
Вентиль И может иметь конечное количество входов. Их
может быть два, три, четыре или больше. Обозначения венти-
лей И с двумя и тремя входами, а также их таблицы истинно-
сти показаны на рис. 2.3. Показанные на рисунке условные
обозначения иногда называют отличительными (distinctive
shapes'), потому что их формы были разработаны таким образом,
чтобы по ним можно было безошибочно определить тип вентиля.
Задание для самопроверки 2.2
Определите результат логического умножения АА.
2.2.2. Вентиль ИЛИ
Часто разработчик должен показать, что из нескольких усло-
вий хотя бы одно выполняется, т.е. истинно (равно 1). В главе
1 был приведен пример, когда было необходимо сформировать
сигнал ошибки при наличии одного из сигналов ошибки.
2.2. Базовые логические функции
55
Подобная операция выполняется с помощью операции ИЛИ,
которая представляет собой последнюю из фундаментальных
операций булевой алгебры и определяется следующим образом.
Условное обозначение
Входы
Выход
-АВ
Вентиль И с двумя входами
Таблица истинности
А В АВ
0 0 0
0 1 0
1 0 0
1 1 1
АВС
Вентиль И с тремя входами
АВС АВС
ООО О
0 0 1 0
0 10 0
0 11 0
10 0 0
10 1 0
110 0
111 1
Рис. 2.3. Обозначение вентиля И и его таблица истинности
Определение: результат выполнения операции ИЛИ над двумя пе-
ременными А и В равен 1, если А = 1 “или” В= 1, либо обе они рав-
ны 1; в противном случае результат равен 0 (т.е. когда и А, и В равны 0).
Символом операции ИЛИ является плюс (+), т.е. математи-
чески операцию А “или” В можно записать в виде А + В. Хотя
для обозначения арифметического сложения применяется тот
же символ, неоднозначностей не возникает, поскольку обычно
простое сложение в выражениях булевой алгебры не встречается.
56
Гпава 2. Логические вентили
Как и в случае функции И, функция ИЛИ применима
к сколь угодно большому числу переменных. Скажем, можно
записать операцию А “или” В “или” С в виде А + В + С. Ре-
зультат будет равен 1, когда хотя бы одна (или более — в любой
комбинации) из этих переменных равна 1. Функция ИЛИ мо-
жет быть равна 0 только в том случае, если все переменные од-
новременно равны нулю. На рис. 2.4 показаны обозначения
вентилей ИЛИ с двумя и тремя входами, а также соответст-
вующие им таблицы истинности.
Условное обозначение
Входы Выход
Вентиль ИЛИ с двумя входами
Таблица истинности
А В Д + В
0 0 0
0 1 1
1 0 1
1 1 1
Вентиль ИЛИ с тремя входами
Д + В + С
А В С д + в + с
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Рис. 2.4. Обозначение вентиля ИЛИ и его таблица истинности
Задание для самопроверки 2.3
Определите результат логического сложения Д + Д.
2.2. Базовые логические функции
57
2.3. Основные соотношения булевой
алгебры
2.3.1. Тождества и их применение
После каждого их подразделов этой главы, посвященных
описанию вентилей НЕ, И и ИЛИ, приводилось задание для
самопроверки. По сути, ответы па них представляют собой
часть набора важнейших тождеств логической алгебры. Вот
список этих тождеств:
АЛ = А
АО = О
А-А = А
А + 1 = 1
А + 0 = А
А + А = А
АА=О
А + А = 1
А = А
Эти соотношения, как уже было сказано, называются ос-
новными булевыми тождествами. Их легко доказать, для чего
достаточно записать все возможные значения переменных
в таблицу истинности (табл. 2.1) и убедиться, что любая ком-
бинация значений переменных всегда даст один и тот же ре-
зультат по обе стороны знака равенства. Запомните этот метод,
ибо он будет использован в разделе 2.3.4 при доказательстве
теоремы де Моргана.
Таблица 2.1. Доказательство основных тождеств булевой алгебры
с помощью таблицы истинности
А А А-1 АО АА А н и 1 А + 0 А+А А-А А + А А
0 1 0 0 0 1 0 0 0 1 1
1 0 1 0 1 1 1 1 0 1 0
58
Гпава 2. Логические вентили
Приведенные выше основные тождества могут быть распро-
странены и на большее количество переменных:
Л51 = АВ
А-ВО = О
АВА = АВ
/< + 5+1 = 1
А+В+0=А+В
А + В+ А = А + В
А-ВА=0
А+В+А=}
Задание для самопроверки 2.4
Докажите тождество А В-1 = A-В, используя таблицу истинности.
Применение соотношений
А теперь давайте рассмотрим области применения приве-
денных выше тождеств булевой алгебры на “аппаратном уров-
не”. Как правило, эти тождества используются для упрощения
логических выражений, но об этом речь пойдет далее.
Неиспользуемые входы вентиля И
Часто с помощью логических соотношений необходимо оп-
ределить, что произойдет, если часть входов вентиля останется
незадсйствованной. Предположим, имеется вентиль И с тремя
входами, но необходимо реализовать функцию только двух пе-
ременных, А и В. Эти переменные подаются на два входа вен-
тиля, а что делать с третьим входом, С? Давайте рассмотрим
следующие возможные ситуации.
1. Вход С подключен к постоянной логической 1 (+5 В).
2. Вход С подключен к постоянному логическому О (О В).
3. Вход С подключен к одному из двух остальных входов
логического элемента (А или В).
4. Вход С оставлен неподключенным.
Отметим сразу, что последний вариант нужно оценивать, ис-
ходя из фактического схемного решения, так как для разных ти-
пов схем результат может кардинально отличаться, и на входе С
2.3. Основные соотношения булевой алгебры
59
может установиться как 0, так и 1. Неподключенный вход также
подвержен влиянию внешних помех, например электромагнитных
излучений. Так что четвертый вариант рассматриваться не будет,
поскольку он непрактичен или по крайней мере нежелателен.
Давайте рассмотрим остальные варианты из приведенного
выше перечня. Если неиспользуемый вход подключается к ло-
гической 1, то в результате получается функция АВ1 = АВ. Если
же вход С присоединить к логическому нулю, то получается
функция АВО = 0. Подключение входа С ко входу А дает функ-
цию АВА = АВ. Таким образом, чтобы сохранить неизменным
исходное требование к логическому элементу — осуществлять
операцию И только над двумя переменными А и В, — имеется
только два варианта.
1. Вход С подключен к постоянной логической 1 (+5 В).
2. Вход С подключен к одному из остальных входов вентиля
(А или В).
Выбор будет зависеть от системных факторов. Подключение
входа С к источнику питания +5 В оказывает на систему наи-
меньшее влияние. Скажем, его же подключение ко входу А (или
В) увеличит нагрузку на тот вентиль, с выхода которого приходит
сигнал на вход А (В), потому что теперь ему придется управлять
уже двумя входами. Вентили могут подключаться только к огра-
ниченному количеству других вентилей, и это число называется
коэффициентом разветвления (fan-out). На рис. 2.5 показана си-
туация, когда вход С подключен ко входу А. При этом вентиль G,
должен управлять состояниями уже на двух входах вентиля б>
Рис. 2.5. Подключение неиспользуемого
входа вентиля И (GJ
Неиспользуемые входы вентиля ИЛИ
Предположим, имеется вентиль ИЛИ с тремя входами, но
необходимо реализовать функцию переменных А+В. Эти пере-
менные подаются на два входа элемента. Давайте рассмотрим
три возможных варианта.
60
Гпава 2. Логические вентили
1. Вход С подключен к постоянной логической 1 (+5 В).
2. Вход С подключен к постоянному логическому О (О В).
3. Вход С подключен к одному из остальных входов (А или В).
Если подать на неиспользуемый вход логическую 1, то в ре-
зультате получается функция А + В + 1 = 1. Если подать 0, то
реализуется функция А + В+ 0 = А +В. И, наконец, подклю-
чение входа С к одному из остальных входов дает функцию
А+В + А = А+В. Очевидно, что для реализации функции
ИЛИ переменных А и В остается только два варианта.
1. Вход С подключен к постоянному логическому О (О В).
2. Вход С подключен к одному из остальных входов (А или В).
Подключение неиспользуемого входа к напряжению О В яв-
ляется простейшим решением, хотя на рис. 2.6 показан вари-
ант, когда вход С подключен ко входу А. В этом случае вентиль
(7/ должен управлять двумя входами вентиля G2.
Рис. 2.6. Подключение неиспользуемого
входа вентиля ИЛИ (G2)
Возможные неисправности вентилей
Еще одной важной областью применения основных тождеств
логической алгебры является определение влияния на вентиль
возможных неисправностей. Информация о потенциальных не-
исправностях, которые могут возникнуть в схеме, очень важна
для разработчика. Неисправности (нс ошибки проектирования!)
могут возникнуть как на этапе изготовления, так и в процессе
эксплуатации. Очень часто неисправности можно смоделировать,
предположив наличие на сигнальной линии постоянной логиче-
ской единицы или постоянного логического нуля (это так назы-
ваемая модель залипания уровня — stuck-at fault model)'.
1 Более подробно неисправности логических схем будут рассматриваться
в главе 7.
2.3. Основные соотношения булевой алгебры
61
Предположим, имеется двухвходовой вентиль И с входами Л
и В. Что происходит в случае неисправности? Предположим,
что на входах вентиля возможны три неисправности.
1. На входе А наблюдается постоянный уровень логической 1.
2. На входе А наблюдается постоянный уровень логического 0.
3. На обоих входах элемента наблюдается уровень сигнала^.
Используя базовые тождества булевой алгебры, чрезвычайно
просто установить, что будет наблюдаться на выходе вентиля.
Все три ситуации и соответствующие им таблицы истинности
приведены на рис. 2.7. Постоянная логическая единица на од-
ном из входов приведет к тому, что сигнал на выходе будет
в точности повторять входной. Постоянный 0 вызовет наличие
на выходе постоянного логического 0. Наконец, короткое за-
мыкание двух входов (третья ситуация) окажет такое же воздей-
ствие на выход элемента, как и постоянная логическая едини-
ца, т.е. сигнал на выходе будет повторять сигнал на входе А.
Предположим теперь, что имеется двухвходовой вентиль
ИЛИ. Пользуясь теми же базовыми тождествами, можно оце-
нить влияние различных неисправностей на входах вентиля
ИЛИ на его выход. Соответствующие таблицы истинности по-
казаны на рис. 2.8. Постоянная логическая 1 на входе установит
на выходе вентиля такой же постоянный уровень; постоянный
О заставит выходной сигнал повторять состояния на исправном
входе, а короткое замыкание входов будет эквивалентно подаче
на один из входов постоянного нуля, т.е. выходной сигнал бу-
дет в точности повторять сигнал на нормальном входе. Полу-
ченные здесь результаты будут неоднократно использованы при
тестировании логических схем, о котором пойдет речь в главе 7.
2.3.2. Основные алгебраические правила
В обычной алгебре существуют правила, которые принимаются
без доказательств. Например, А+В=В+Ап АВ = ВА, где знак
“+” обозначает арифметическое сложение и знак — арифме-
тическое умножение. Оказывается, что это правило справедливо
и для операторов ИЛИ и И булевой алгебры, но только благодаря
тому, что таблицы истинности этих операторов симметричны,
т.е. в таблице всегда можно поменять местами переменные А
и В, получив правильную таблицу функции. Таким образом, в
булевой алгебре справедливы следующие соотношения:
62
Гпава 2. Логические вентили
Вентиль И с двумя входами
Входы
Выход
J-------- А1 =А
Таблица истинности
А В АВ
0 1 0
0 1 0
1 1 1
1 1 1
А В АВ
0 0 0
0 0 0
1 0 0
1 0 0
А В АВ
0 0 0
0 0 0
1 1 1
1 1 1
Рис. 2.1. Возможные неисправности на входах вентиля И
А + В= В+ А
АВ= ВА
Формально это правило носит название закона коммута-
тивности.
В обычной математике порядок вычисления выражения, со-
стоящего из нескольких переменных, между которыми стоит
один и тот же оператор, не важен. Например, известно, что
АВС = (АВ)С = А(ВС); скобки здесь показывают, над какими
переменными действия осуществляются в первую очередь.
В булевой алгебре порядок действий также не имеет значе-
ния, т.е. снова же можно записать: АВС = (АВ)С = А(ВС). Это
2.3. Основные соотношения булевой алгебры
63
правило называется законом ассоциативности. Запишем его еще
раз для обеих операций:
АВС = (АВ)С = А(ВС)
А + В + С — (А + В) + С — А + (В + С).
Вентиль ИЛИ с двумя входами
Входы
Выход Таблица истинности
А В А + В
Д + 1=Д ________________
О 1 1
О 1 1
1 1 1
1 1 1
Рис. 2.8. Возможные неисправности на входах вентиля ИЛИ
В обычной арифметике скобки используются для того, чтобы
показать порядок вычислений; это необходимо, если операторы
различны. В булевой алгебре скобки выполняют ту же роль.
64
Гпава 2. Логические вентили
В обыкновенной алгебре у них есть еще одно важное назначение:
показывать, когда умножение относится не к одной переменной,
а к группе. К примеру, запись А(В + Q означает, что переменная
А умножается на сумму В + С. Можно разложить это выражение
на сумму двух произведений: АВ+ АС, т.е. показать, что умно-
жение относится к обоим слагаемым внутри скобок. Подобное
преобразование справедливо и в булевой алгебре для операторов
И и ИЛИ. Данное свойство носит название закона дистрибутив-
ности. В булевой алгебре закон дистрибутивности гласит:
А(В + 0 = АВ + АС
А + (ВС) = (А + В)(А + 0.
Обратите внимание, что операция ИЛИ во втором выраже-
нии распространяется на оба члена в скобках. К арифметиче-
скому сложению закон дистрибутивности неприменим, т.е.
в обычной математике А + (ВС) * (А + В)(А + С).
Применение основных законов булевой алгебры
в логическом проектировании
Приведенные выше законы и соотношения позволяют про-
ектировать логические выражения и создавать альтернативные
варианты решений. Например, вследствие действия закона ас-
социативности выражения можно раскладывать па сомножите-
ли, получая разные реализации функции, как показано на
рис. 2.9 для функции /= ABCD. Это важно еще и в тех случаях,
когда имеются вентили только с определенным количеством
входов (у выпускаемых вентилей количество входов может быть
от 2 до 8). На рис. 2.9(a) показана реализация функции /= ABCD
на основе четырехвходового вентиля. На рис. 2.9(6) и (в) тот же
результат достигается уже с использованием двухуровневой
структуры. В таких схемах сигналы проходят от входа до выхода
уже два вентиля. Двухуровневые схемы широко используются для
реализации выражений; об этом пойдет речь в главе 3.
Закон дистрибутивности позволяет реализовать функцию
вида/= АВ + АС по крайней мере двумя способами (рис. 2.10).
Видно, что в схеме, изображенной на рис. 2.10(6) удалось обой-
тись меньшим количеством вентилей. Теория создания элек-
тронных устройств с наименьшим возможным числом компо-
нентов является очень важной и носит название логической ми-
нимизации (logic minimization). Более подробно вопросы
логической минимизации будет рассматриваться в главе 3.
2.3. Основные соотношения булевой алгебры
65
Рис. 2.9. Использование закона ассоциативности для получения аль-
тернативных вариантов реализации функции f = ABCD
(б)
А(В + С)=АВ + АС
Рис. 2.10. Использование закона дистрибутивности для реализации
функции f = АВ + АС
66
Гпава 2. Логические вентили
Задание для самопроверки 2.5
Нарисуйте две альтернативных реализации логической функции
f = ABC+BD.
Безусловно, существуют и другие законы булевой алгебры,
которые очень часто помогают при минимизации и перегруп-
пировке элементов цифровых схем. Они будут изучены в по-
следующих разделах главы.
2.3.3. Принцип дуализма
Дуальные функции
Если в таблице истинности операции И заменить все нули
на единицы, а все единицы — на нули, то получится таблица
истинности операции ИЛИ. Таким образом, если имеется
схема, реализующая функцию И в рамках позитивной логики,
когда логический 0 представлен напряжением О В, а логиче-
ская 1 — напряжением +5 В, то та же схема в случае исполь-
зования отрицательной логики (логический 0 представлен на-
пряжением +5 В, а логическая 1 — О В) при работе с указан-
ными уровнями напряжения будет реализовать функцию
ИЛИ. При этом в схему не потребуется вносить никаких из-
менений. Точно так же вентиль ИЛИ из схемы с положитель-
ной логикой превратится в вентиль И, когда его перенесут
в схему с отрицательной логикой. Вентиль НЕ остается ин-
вертором независимо от типа логики.
Предположим, имеется логическая схема, которая реализует
функцию f = A + BC в устройстве с положительной логикой.
При изменении логического представления на отрицательное
она уже будет выполнять функцию f = А(В + С), т.е. все опера-
торы, входящие в функцию, поменяются местами (И поменяет-
ся на ИЛИ, а ИЛИ поменяется на И). Это явление проиллюст-
рировано на рис. 2.11. Вообще, если есть сколь угодно сложная
логическая схема, на основе которой реализуется некоторая
функция f(A, В, С... •, +, 0, 1), работающая в системе с поло-
жительной логикой (т.е. функция с переменными
А, В, С..., операциями И, ИЛИ и постоянно существующими О
и 1), то в системе с отрицательной логикой она же будет осу-
ществлять функцию f(A, В, С... +, •, 1, 0), т.е. в функции все
2.3. Основные соотношения булевой алгебры
67
операции “+” заменятся на операции все операции за-
менятся на операции “+”, все постоянные 1 заменятся на О,
а все постоянные 0 заменятся на 1. Причем совсем не обяза-
тельно, чтобы схема состояла только из вентилей И, ИЛИ
и НЕ; она может включать и более сложные по структуре ком-
поненты, по эффект будет иметь место и в этом случае, по-
скольку любую схему можно свести к базовым вентилям, на
входы которых подаются напряжения, а с выходов снимаются.
(а) Схема
(б) Представление
в системе с
положительной
логикой
(в) Представление
в системе с
отрицательной
логикой
А+ВС
А+ВС
А(В + С}
Рис. 2.11. Дуализм схем
Функция, реализуемая в системах с отрицательной логикой,
дуальна (dual) функции, которая реализуется в системе с поло-
жительной логикой. Таким образом, если есть функция
/= f(A, В, С... -, +, 0, 1),
то дуальная ей функция будет иметь вид;
/=Ж В, С... +, ., 1, 0).
Задание для самопроверки 2.6
Найдите функцию, дуальную функции f = A + B(C + АР).
68
Гпава 2. Логические вентили
Дуальные равенства. Принцип дуализма
Предположим, есть доказанное равенство
f(A, В, С ... , +, 0, 1) = g(A, В, С ... , +, 0, 1).
Тогда следует, что справедливо и дуальное ему равенство, т.е.
f(A, В, С... , +, 0, 1) = £(А, В, С... , +, 0, 1).
Этот принцип носит название принципа дуализма (principle of
duality). Его можно доказать математически, рассматривая пред-
ставления в положительной и отрицательной логике. Пусть
имеются две логических схемы L, и L2, которые в системе с по-
ложительной логикой реализуют эквивалентные функции /()
и g(). Тогда в системе с отрицательной логикой они тоже будут
реализовать эквивалентные функции/() и £*() (рис. 2.12).
Представление
в системе
с положительной
Представление
в системе
с отрицательной
логикой
Ла, В,...)
Тогда Равно
/И,В,...)
Рис. 2.12. Дуальные равенства
Для получения дуального равенства следует просто заменить
все операции ИЛИ “+” на операции И а все операции И
— на операции ИЛИ “+”, а также все нули на единицы,
а единицы — на нули.
Примеры
(а ) Предположим, есть доказанное равенство
А + 0 = А
Согласно принципу дуализма, выражение, дуальное ле-
вой части (А + 0), должно быть равно выражению, дуаль-
2.3. Основные соотношения булевой алгебры
69
ному правой части (А). Выражение, дуальное члену /1+0,
имеет вид А1, а переменной А дуальна сама же перемен-
ная А. Следовательно, мы имеем дуальное равенство
/11 = А,
и оно верно без доказательства.
б) Предположим, доказано, что
А+АВ=А.
Это было довольно легко, ведь А + АВ = А(1 + В) = А2-
Поменяв местами операторы, можно сразу записать ду-
альное равенство:
А(А + В) = А-
В этом примере интересно то, что при разложении ле-
вой его части снова получается исходное выражение,
т-е. А(А + В) = АА + АВ = А + АВ = А-
Задание для самопроверки 2.7
Запишите равенство, дуальное равенству АВ + АС + ВС = АВ + АС
(теорема о консенсусе, см. главу 3),
2.3.4. Теорема де Моргана
Функция А + В (операция ИЛИ) может равняться 0 только
в одном случае: когда обе переменные, Л и В, одновременно
равны 0. Во всех других случаях А + В = 1. Точно так же функ-
ция АВ (операция И) может быть равна 1 только тогда, когда
и переменные А и В равны 1; при любых других комбинациях
АВ = 0. Очевидно, что между операциями И и ИЛИ должно
существовать простое соотношение. Равенство А + В = 0 верно
только в том случае, когда А = 1 и В= 1. АВ = 0 только при
А = 1 и В = 1. Следовательно, выражение
А + В= ~АВ
и дуальное ему выражение
АВ = А + В
2 Тут были использованы алгебраическое разложение на сомножители
и базовое тождество.
70
Гпава 2. Логические вентили
будут справедливы. Эти важные соотношения известны под
названием теоремы де Моргана (DeMorgan theorem) и здесь
приведены для двух переменных. Эта теорема может быть
легко доказана, если записать каждую функцию в виде табли-
цы истинности, с помощью которой можно быстро убедиться,
что для любых комбинаций А и В значения обеих функций
будут в точности совпадать, что и видно из табл. 2.2. Кстати, это
еще раз подтверждает, что при небольшом количестве перемен-
ных использование таблиц истинности для доказательства то-
ждеств вполне оправданно и является мощным средством.
Таблица 2.2. Доказательство теоремы де Моргана для двух переменных
k В А + В АВ д + в ~дв
О 0 0 0 1 1
О 1 1 0 1 1
10 10 11
111 1 0 0
Теорема де Моргана может быть распространена на сколь
угодно большое число переменных. Например, для трех пере-
менных можно записать
А + В + С = АВС
АВС = А + В + С.
Или в общем случае:
А + В + С... = АВС...
АВС...= А + В + С...
Доказательство теоремы де Моргана для любого числа пере-
менных может быть начато с ее доказательства для двух перемен-
ных с использованием подхода на основе таблицы истинности,
показанной в табл. 2.2. В этой таблице приведены все возмож-
ные комбинации переменных и соответствующие им результи-
рующие значения. Доказав равенство, его можно будет использо-
вать для переменных с другими именами без доказательства.
Подставим в равенство А + В = АВ вместо переменной
В переменную ВС, где С — третья переменная. Тогда получим:
А + (ВС) = А(ВС)-
2.3. Основные соотношения булевой алгебры
71
___Поскольку уже известно, что, согласно теореме де Моргана
ВС = В + С, то после подстановки сразу получается выражение
теоремы де Моргана для трех переменных:
А+В+С=АВС
Ясно, что этот процесс может быть повторен для четырех и бо-
лее переменных, и, следовательно, теорема де Моргана справедли-
ва для любого числа переменных (доказательство методом матема-
тической индукции). Похожий подход может быть применен
и для доказательства дуального равенства, если вдруг кому-нибудь
вздумается проверить его, не полагаясь на принцип дуализма.
Задание для самопроверки 2.8
Докажите дуальную форму теоремы де Моргана для трех переменных, т.е. что
АВС = А + В + С.
Теорему де Моргана можно записать в еще более общем ви-
де, включив в обе стороны равенства операции И и ИЛИ.
Обобщенная форма теоремы де Моргана может быть записана
в следующем виде:
7(А,В,С...+,) = f (А, В,С...,+)
или
/(Д,В,С...+,-)=7(АВ,С...-,+)-
Эта запись означает, что функция f включающая перемен-
ные и операторы И и ИЛИ, эквивалентна инверсной функции
от инверсных (комплементарных) переменных с взаимно пере-
ставленными операторами (И меняется на ИЛИ, а ИЛИ, соот-
ветственно, — на И).
Не следует путать теорему де Моргана с принципом дуализ-
ма. Принцип дуализма позволяет записать равенство, как ду-
альную форму другого равенства. При этом ни одна перемен-
ная не инвертируется. Теорема же де Моргана говорит о спра-
ведливости равенства в прямой и дуальной формах, которые
могут использоваться для упрощения логических выражений.
Задание для самопроверки 2.9
Примените теорему де Моргана в общей форме для функции
/ = A + B + CD-
72
Гпава 2. Логические вентили
2.4. Универсальные вентили
2.4.1. Вентиль И-НЕ
Теорема де Моргана устанавливает взаимосвязь между опе-
рациями И и ИЛИ. Следовательно, из трех фундаментальных
операций булевой алгебры (И, ИЛИ и НЕ) строго обязатель-
ными являются только две (И и НЕ либо ИЛИ и НЕ), посколь-
ку третья может быть заменена функцией двух других. Соглас-
но теореме де Моргана,
А + В = 1в.
Значит, функцию А + В можно заменить функцией АВ, т.е.
оператор ИЛИ заменить на И и НЕ. Очевидно, что, комбини-
руя соответствующим образом операции И и НЕ, можно сфор-
мировать “универсальную” функцию, И-НЕ (NOT-AND или
NAND), на основе которой реализовать все три фундаменталь-
ные операции, а значит, и любую логическую функцию. Вот
как выглядит функция И-НЕ для двух переменных:
А "И-НЕ" В = АВ.
Условные обозначения вентилей И-НЕ с двумя и тремя вхо-
дами и их таблицы истинности приведены на рис. 2.13.
Довольно просто показать, что все три базовые операции —
И, ИЛИ и НЕ — могут быть получены из функции И-НЕ. Опе-
рацию НЕ можно получить, заменив переменную В на А , что
в результате дает АА:
АА = А.
Операцию ИЛИ можно получить, используя такую же под-
становку для обеих переменных сразу:
а+в=(аа)(вв)-
Ну, и, наконец, операцию И можно получить так:
АВ = (АВ)-
Результаты этих подстановок показаны на рис. 2.14. Отсю-
да следует, что с помощью функции И-НЕ (АВ), можно реа-
лизовать любую функцию, включающую операции
И/ИЛИ/НЕ. С этой точки зрения функция И-НЕ является
2.4. Универсальные вентили
73
универсальной, и вентиль, который ее реализует, также будет
универсален в том смысле, что для реализации любой логиче-
ской схемы достаточно иметь только вентили этого одного
типа. На складе обычно имеются вентили только одного типа,
и па замену используются тоже только вентили одного типа,
Концепция универсального вентиля была чрезвычайно при-
влекательной в то время, когда логические системы должны
были проектироваться на основе вентилей в виде микросхем.
Кроме того, оказалось, что внутренняя структура вентиля,
реализующего функцию И-НЕ, немного проще, чем у схем И
и ИЛИ. Наконец, совсем не обязательно делать прямые под-
становки, показанные на рис. 2.14; вся схема сразу может
разрабатываться с учетом свойств элементов И-НЕ.
Условное обозначение
Входы
Таблица истинности
А В АВ
О 0 1
О 1 1
1 О 1
1 1 о
0 0 1 1
0 10 1
0 11 1
10 0 1
10 1 1
110 1
111 о
Рис. 2.13. Условное обозначение и таблица истинности вен-
тиля И-НЕ
74
Гпава 2. Логические вентили
Рис. 2.14. Реализация операторов НЕ, И
и ИЛИ на основе функции И-НЕ
2.4.2. Вентиль ИЛИ-НЕ
В качестве универсального элемента можно использовать не
только элемент И-НЕ, но и ИЛИ-HE (NOT-OR или NOR),
реализующий функцию А + В Из теоремы де Моргана следует, что
АВ = А + В-
Следовательно, функцию АВ можно заменить функцией А + В
Оператор НЕ может быть получен путем замены в члене А + В пе-
ременной В на А, в результате чего получается А+А=А. Таким
образом, видно, что вентиль ИЛИ-HE также является универ-
сальным. Условные обозначения вентилей ИЛИ-HE с двумя
и тремя входами, а также соответствующие таблицы истинности
приведены на рис. 2.15. Формирование функций И и НЕ из опе-
ратора ИЛИ-HE показано на рис. 2.16. В электронике нет специ-
ального символа для обозначения универсальных операций И-НЕ
и ИЛИ-HE, но в математике они существуют (знаки Т для И-НЕ
и i для ИЛИ-НЕ).
Функции И-НЕ и ИЛИ-НЕ дуальны друг другу, т.е. вен-
тиль, который в системе с положительной логикой реализует
функцию И-НЕ, в системе с отрицательной логикой будет вы-
полнять операцию ИЛИ-НЕ, и наоборот. Это можно доказать,
изучив таблицы истинности обоих вентилей. Если заменить
в них все нули на единицы, а единицы — на нули, то как раз
и получится таблица дуального вентиля, что показано в табл. 2.3.
2.4. Универсальные вентили
75
Условное обозначение
Входы Выход
Таблица истинности
А В А + В
0 0 1
0 1 0
1 0 0
1 1 0
А В
С А + В + С
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 0
Рис. 2.15. Условное обозначение и таблица истинности вентиля ИЛИ-НЕ
Рис. 2.16. Реализация операторов НЕ, И и ИЛИ на основе
функции ИЛИ-НЕ
76
Глава 2. Логические вентили
Таблица 2.3. Дуализм операторов И-НЕ и ИЛИ-НЕ
И-НЕ ИЛИ-НЕ
Входы Выход Входы Выход
0 0 1 1 1 0
0 1 1 1 0 0
1 0 1 0 1 0
1 1 0 0 0 1
Задание для самопроверки 2.10
Покажите, как получить функцию ИЛИ-НЕ на основе вентилей И-НЕ и, наобо-
рот, как на базе вентилей ИЛИ-НЕ реализовать функцию И-НЕ.
2.5. Другие вентили
2.5.1. Вентиль исключающее ИЛИ
Операция ИЛИ (А + Б) равна 1 в трех случаях, в том числе
и тогда, когда обе переменные равны 1. Более точно этот опе-
ратор можно назвать функцией включающее ИЛИ. Однако су-
ществует оператор ИЛИ, который не формирует 1 в случае, ес-
ли А и В одновременно равны 1. Т.е. при А = 1 или В= 1 эта
функция принимает значение 1, но если обе переменных равны
1, то результат будет равен 0. Данная операция получила назва-
ние исключающего ИЛИ {exclusive-OR). Условное обозначение
вентиля исключающего ИЛИ и его таблица истинности показа-
ны на рис. 2.17. Обратите внимание, что условное обозначение
этого вентиля напоминает обозначение вентиля, реализующего
функцию обычного (включающего) ИЛИ. Операцию исклю-
чающее ИЛИ принято обозначать с помощью символа Ф. Для
операндов Ли В эту операцию можно записать в виде
А®В = АВ + АВ,
откуда легко вычислить, что она равна 1, когда единице равна
только одна из переменных (АВ при А= 1 и 5=0; АВ при
А = 0 и В= 1). Эти два условия отображены и в таблице истин-
ности в ячейках, где стоят единицы. В тех ячейках результи-
рующего столбца таблицы истинности, где стоят единицы, со-
держится информация о виде результирующей функции,
а соответствующие комбинации переменных формируют ее члены.
2.5. Другие вентили
17
Условное обозначение
Таблица истинности
А В А®8
0 0 0
0 1 1
1 0 1
1 1 0
Рис. 2.17. Условное обозначение и таблица истинности венти-
ля исключающее ИЛИ
Вентиль (включающее) ИЛИ может иметь и больше двух вхо-
дов. Оператор же исключающее ИЛИ ограничен двумя перемен-
ными. Да и могло ли быть иначе? Была бы эта функция равной
нулю, если две переменные из трех равны 0 или все три?..
Задание для самопроверки 2.11
Предположим, что вентиль исключающее ИЛИ с тремя входами действитель-
но существует и формирует на выходе 1, когда А = 1 или В = 1, или С = 1, но
если хотя бы две любые переменные одновременно равны 1, то с выхода
снимается 0. Опишите эту функцию математически.
Операция исключающее ИЛИ не рассматривается как фун-
даментальный оператор булевой алгебры, так как ее можно раз-
ложить на операции И, ИЛИ и НЕ, но для нее также сущест-
вуют базовые тождества:
А Ф 0 = А
А®1 = А
А Ф А = О
АФА = 1
А® В = АФВ = (А® В)-
Кроме того, операция исключающее ИЛИ подчиняется
законам коммутативности, ассоциативности и дистрибу-
тивности.
78
Глава 2. Логические вентиля
Закон коммутативности: А Ф В = В Ф А
Закон ассоциативности: (А® В) ®С=А® (В ®С) =
= А® В® С
Закон дистрибутивности: А(В Ф Q = АВ ® АС
Доказать справедливость этих законов для операции исклю-
чающее ИЛИ можно, воспользовавшись таблицей истинности
или разложив ее на базовые операции.
2.5.2. Вентиль исключающее ИЛИ-НЕ
Операция, инверсная функции исключающее ИЛИ, называ-
ется операцией исключающее ИЛИ-НЕ (exclusive NOR). Обозна-
чение и таблица истинности реализующего ее вентиля приведе-
ны на рис. 2.18. Для двух переменных она записывается в виде:
(АФВ) = АВ + АВ’
т.е. данная функция принимает значение 1 при А = 1 и В = 1
(АВ) либо при А = 0 и В = О (АВ). Эта операция используется
для сравнения двух двоичных разрядов: она дает 1 только в том
случае, когда значения обоих разрядов равны (независимо от то-
го, пули это или единицы), и поэтому на се основе легко реали-
зовать компаратор или функцию эквивалентности. Сравним ис-
ключающее ИЛИ-НЕ с простой операцией исключающее ИЛИ:
вторая принимает значение 1 в том случае, если переменные от-
личаются (функция неэквивалентности). Оператор исключаю-
щее ИЛИ-НЕ также подчиняется законам коммута тивности и ас-
социативности; а как обстоит дело с законом дистрибутив пости,
Условное обозначение
АФВ
Таблица истинности
А В АФ8
0 0 1
0 1 0
1 0 0
1 1 1
Рис. 2.18. Условное обозначение и таблица истинности венти-
ля исключающее ИЛИ-НЕ
2.5. Другие вентили
79
предлагается выяснить самостоятельно. Как и в случае универ-
сальных элементов И-НЕ и ИЛИ-НЕ, операция исключающее
ИЛИ-НЕ не имеет собственного символа.
2.5.3. Коммутативные функции
Итак, уже описаны шесть базовых функций двух перемен-
ных, а именно: И, ИЛИ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ
и исключающее ИЛИ-НЕ. Всего можно определить шестна-
дцать функций, аргументами которых являются две булевы пе-
ременные, в том числе постоянный логический 0 и постоянная
логическая 1 (табл. 2.4). Из всех этих функций только функции
F6, F7, Fs, F4 и F,4 являются коммутативными, т.е. перемен-
ные внутри них могут быть переставлены местами без измене-
ния результата; сюда не входят функции Fn (постоянный логи-
ческий ноль) и F,s (постоянная логическая единица). Что каса-
ется перечисленных функций, то F, — это операция И, F6-
операция исключающее ИЛИ, F, — ИЛИ, Fs — операция ИЛИ-
НЕ, F9 — операция исключающее ИЛИ-НЕ и F[4 — операция
И-НЕ. Остальные же функции не обладают свойством комму-
тативности. Таким образом, шесть приведенных выше функций
формируют полный набор коммутативных операций. Для реа-
лизации коммутативных операций выпускаются соответствую-
щие вентили, тогда как для реализации некоммутативных
функций вентили обычно не выпускаются и могут встречаться
разве что в виде части специального компонента. Преимущест-
вом наличия вентилей только для коммутативных функций яв-
ляется то, что входы таких вентилей могут использоваться
в любом порядке и при желании взаимозаменяться.
Таблица 2.4. Функции двух переменных
А В Fo Fi Гг Гз Гд Fs Fe F? Fs Fg F« Fn F12 F13 F14 F15
00000000001 i i i i i i Г
010000111100 0 0 1 1 1 1
100011001100 1 1 0 011
110101010101 0 1 0 1 0 1
Задание для самопроверки 2.12
Какие свойства функций F2l F3, F4, F5l F10, Fn, F|2 и F13, приведенных
в табл. 2.4, позволяют сказать, что они некоммутативны?
80
Гпава 2. Логические вентили
2.6. Проектирование вентилей
В этом разделе будут в общих чертах описаны свойства
и внутренняя структура вентилей. В начале будет приведено
описание устаревших, но все еще используемых ТТЛ-вентилей,
затем будут более подробно описаны МОП-вентили. Этот раз-
дел может быть опущен без особого ущерба для целостности
изложения материала.
2.6.1. Комбинационные логические ТТЛ-схемы
Вентили изготавливаются на основе технологии полупро-
водниковых интегральных схем. Их не изготавливают по оди-
ночке, поскольку технология интегральных схем позволяет по-
лучать в одном корпусе сразу большое количество вентилей.
Первым получившим широкое признание типом интегральных
микросхем стало семейство ТТЛ-вентилей (так называемая
транзисторно-транзисторная логика). Оно появилось в 1960-х
годах и используется до сих пор для построения небольших
цифровых систем и в качестве интерфейса к более серьезным
интегральными схемами. Во многих случаях ТТЛ-технология
была заменена технологией КМОП (см. раздел 2.7), но функ-
циональные свойства микросхем остались теми же.
Приборы ТТЛ-логики, как правило, содержат несколько
вентилей в одном корпусе, обычно от 2 до 100. Если количество
вентилей в одном корпусе не превышает 12, то такие микро-
схемы называются микросхемами малой степени интеграции,
или МИС (small-scale integration — SSI). Микросхемы с количе-
ством вентилей в одном корпусе от 12 до 100 называют мик-
росхемами средней степени интеграции, или СИС (medium-
scale integration — MSI). Термин “большие интегральные схе-
мы”, или БИС (large-scale integration — LSI), применяется
в отношении микросхем с количеством вентилей в одном
корпусе от 100 до 1000; сверхбольшими интегральными схе-
мами, или СБИС (very large-scale integration — VLSI), называют
микросхемы, содержащие более тысячи вентилей. На этом
уровне чаще приводится не количество вентилей, а общее ко-
личество транзисторов в одном приборе. В зависимости от
типа технологии и реализуемой функции один вентиль может
требовать от 2 до 6 транзисторов. Скажем, для построения
ТТЛ-вентиля И-НЕ требуется четыре транзистора.
2.6. Проектирование вентилей
81
Микросхемы транзисторно-транзисторной логики чаще
всего поставляются в корпусах с двухрядным расположением вы-
водов или корпусах типа DIP (от англ, dual-in-line). Длина самых
маленьких корпусов — около 0,75 дюйма, ширина — 0,25 дюйма;
они имеют по семь ножек с каждой стороны (в каждом ряду)
при шаге между ними 0,1 дюйма. Высота корпуса составляет
примерно 0,2 дюйма. Такие корпуса используются для разме-
щения небольшого количества вентилей (рис. 2.19). Показан-
ные примеры относятся к ТТЛ-микросхемам серии 74LSXX.
Существуют и более длинные DIP-корпуса с большим количе-
ством выводов вдоль каждой из сторон. Перечень популярных
устройств и некоторые их характеристики приведены
в табл. 2.5. Конечно, кроме перечисленных в таблице, есть
множество других микросхем малой и средней степени инте-
грации, относящихся к семейству ТТЛ-схем, некоторые из ко-
торых реализуют более сложные функции, например, декодиро-
двухвходовых вентиля И инверторов
вентиля И-НЕ
Рис. 2.19. Состав ТТЛ-микросхем в корпусах с двухрядным расположением выводов
В транзисторно-транзисторной логике номинальное значе-
ние напряжения логической 1 составляет +3,4 В, хотя может ге-
нерироваться в пределах от +2,4 до +5 вольт. Обычно с уровнем
логической 1 ассоциируют напряжение +5 В. Напряжение ис-
точника питания ТТЛ-схем тоже +5 В. Номинальное значение
напряжения логического 0 составляет +0,2 В, но на практике
82
Глава 2. Логические вентили
также может колебаться от 0 до +0,4 В. Обычно говорят, что
уровню логического нуля соответствует напряжение 0 вольт.
Величины номинальных напряжений могут слегка изменяться
в зависимости от типа прибора. В общем случае напряжения
выше +2 В распознаются как логическая 1, а ниже +0,8 В —
как 0, что позволяет допустить наличие в системе внешнего
электрического шума. Степень перекрытия диапазона распо-
знаваемых напряжений и диапазона генерируемых напряжений
показана на рис. 2.20.
Таблица 2.5. Перечень первых ТТЛ-микросхем
Маркировка микросхемы Тип элемента Количество входов Количество вентилей в одном корпусе
74LS04 НЕ 1 6
74LS08 И 2 4
74LS11 и 3 3
74LS21 и 4 2
74LS32 или 2 4
74LS00 И-НЕ 2 4
74LS10 И-НЕ 3 3
74LS20 И-НЕ 4 2
74LS30 И-НЕ 8 1
74LS133 И-НЕ 13 1
74LS02 ИЛИ-НЕ 2 4
74LS27 ИЛИ-НЕ 3 3
74LS260 ИЛИ-НЕ 5 2
74LS86 исключающее ИЛИ 2 4
74LS266 исключающее ИЛИ-НЕ 2 4
74LS51 2И-ИЛИ-НЕ 2
74LS54 4И-ИЛИ-НЕ 1
Шумом называют нежелательные электрические сигналы,
возникающие в проводящих линиях системы. Своим воз-
никновением они обязаны нормальным переключениям вен-
тилей в процессе работы, в результате чего в соседних при-
борах и линиях связи могут появляться помехи. Эти помехи
2.6. Проектирование вентилей
83
передаются как посредством электромагнитного поля, так
и колебаниями напряжения питания. Несколько реже встре-
чается ситуация, когда источник шума находится вне самой
системы. Логические устройства должны работать правильно
даже при воздействии на них шумов. Величина напряжения,
вызываемого электрическим шумом, которое система может
выдержать без ухудшения работоспособности, называется
запасом помехоустойчивости (noise margin). Этот запас фак-
тически представляет собой максимальное напряжение шу-
ма, которое, будучи прибавленным или отнятым от сгенери-
рованного логического сигнала, еще не приводит к тому, что
вход вентиля перестает воспринимать его в качестве задан-
ного логического уровня. Для ТТЛ-приборов запас помехо-
устойчивости как для высокого, так и для низкого логиче-
ских уровней составляет +0,4 В. Эта величина относится
к непрерывному низкочастотному шуму. Поведение логиче-
ских устройств в условиях воздействия импульсных или
сверхвысокочастотных шумов может значительно отличаться
от работы в условиях наличия низкочастотных шумов и ха-
рактеризуется уже не запасом помехоустойчивости на посто-
янном токе, а другим параметром — запасом помехоустойчи-
вости на переменном токе (а.с. noise margins).
3
Напряжение,
В 2
Генерируемые
выходные
напряжения
Рис. 2.20. Уровни напряжения в ТТЛ-приборах
Диапазон логического О
Распознаваемые
входные
напряжения
84
Гпава 2. Логические вентили
2.6.2. Металл-оксид-полупроводниковые (МОП)
вентили
В этом разделе дается краткое описание внутреннего строе-
ния МОП (металл-оксид-полупроводник) вентилей. МОП-
вентили вытеснили ТТЛ-вентили в большинстве применений и,
благодаря намного более низкому энергопотреблению, широко
используются в схемах со сверхвысоким уровнем интеграции.
Ключи на МОП-транзисторах
Логический вентиль воспринимает напряжения двух уров-
ней и генерирует напряжения двух уровней. Поэтому говорят,
что напряжение может иметь высокий (в литературе на англий-
ском — HIGH) и низкий (LOW) логические уровни. Каждое из
этих напряжений можно получить с помощью простейшей схе-
мы на механических ключах (рис. 2.21). Один ключ располага-
ется таким образом, что соединяет источник с высоким уров-
нем напряжения и выход, а второй устанавливается между вы-
ходом и источником напряжения низкого уровня. В каждый
момент времени может быть замкнут только один ключ. Для
того чтобы создать на выходе схемы высокий уровень напряже-
ния, нужно замкнуть верхний ключ, а нижний разомкнуть,
а чтобы установить низкий уровень, следует замкнуть нижний
ключ и разомкнуть верхний. Естественно, в современных элек-
тронных схемах механические ключи не используются, но логи-
ка, которой подчиняются процессы в электронных вентилях,
приблизительно соответствует ситуации, показанной на рис. 2.21.
Давайте рассмотрим принцип работы МОП-транзистора и
сравним его с работой ключа1. МОП-транзистор имеет три вы-
вода: исток, сток и затвор. Исток и сток транзистора соответ-
ствуют клеммам механического ключа. Сам транзистор, как
и ключ, имеет два состояния: проводящее и такое, когда прово-
димость между клеммами отсутствует. Для того чтобы изменить
состояние механического ключа, нужно поставить его плечо
в необходимое положение; чтобы изменить состояние МОП-
транзистора, на его затвор подается напряжение определенного
уровня. Когда транзистор “включается”, между выводами стока
1 Познакомиться более детально с различными типами логических
схем транзисторно-транзисторной и других типов логик можно в лите-
ратуре, ссылки на которую приведены в конце главы.
2.6. Проектирование вентилей
85
(а) Ключи
(б) Формирование напряжения
высокого логического уровня
Высокий
уровень
напряжения
Низкий
уровень
напряжения
Высокий
уровень
напряжения
Низкий
уровень
напряжения
Замкнут
'1 Выход
Ч Разомкнут
(в) формирование напряжения
низкого логического уровня
Высокий
уровень
напряжения
Разомкнут
Выход
Низкий
уровень
напряжения
Рис. 2.21. Комплементарные ключи, формирующие разные логические уровни
напряжения
и истока устанавливается состояние проводимости. В выклю-
ченном состоянии проводимость между стоком и истоком от-
сутствует. Таким образом, с помощью напряжения на затворе
86
Глава 2. Логические вентили
можно управлять состоянием транзистора. Это напряжение из-
меряется относительно потенциала истока и обозначается Узи.
Различают два типа МОП транзисторов: «-канальный
(л-МОП) и р-канальный (p-МОП). Давайте сначала рассмотрим
л-канальный транзистор. Для нормального режима работы
МОП-структуры с «-каналом требуется, чтобы потенциал стока
был более положителен, чем потенциал истока. Напряжение О
В между затвором и истоком “запирает” транзистор
(препятствует прохождению тока между истоком и стоком), и,
чтобы снова “включить” его, на затвор требуется подать поло-
жительное напряжение относительно истока, причем его вели-
чина должна превышать пороговое напряжение (threshold voltage).
Конструкция транзистора выбирается таким образом, чтобы ве-
личина порогового напряжения имела заданное значение.
Обычно для схем с напряжением питания +5 В величина поро-
гового напряжения составляет около +1,5 В. На рис. 2.22 показан
символ, которым принято обозначать л-канальный МОП-
транзистор2 на принципиальных схемах, и уровни напряжений,
необходимые для переключения транзистора в каждое из состоя-
ний, т.е. его открытия или запирания. Здесь принимается, что для
отпирания транзистора используется уровень напряжения +5 В.
Для правильной работы МОП-транзистора p-типа необхо-
димо, чтобы потенциал стока был более отрицательным, чем
у истока. Напряжение между затвором и истоком, которое вы-
ключает, или “запирает” транзистор (т.е. создает между исто-
ком и стоком большое сопротивление), также равно О В. Одна-
ко чтобы открыть транзистор (создать проводящий канал между
истоком и стоком), теперь нужно подать между затвором
и истоком не положительное, а отрицательное напряжение, аб-
солютная величина которого должна превышать пороговый
уровень, обычно составляющий примерно —1,5 В. Условное
обозначение и напряжения, которые подаются на МОП-
транзистор с каналом p-типа, показаны на рис. 2.23. В данном
примере транзистор открывается напряжением —5В. Обратите
внимание, что символ МОП-транзистора с каналом р-типа
имеет кружочек на затворе, что, как и в обозначениях логиче-
ских вентилей, свидетельствует об инверсии.
2 Условное обозначение, приведенное на рисунке, относится к п-канальнаму
МОП-транзистору с обогащенным каналом. Существует еще одна разновид-
ность МОП-устройств — с обедненным каналом, но в ключевых режимах
они используются относительно редко.
2.6. Проектирование вентилей
87
(а) Условное обозначение
(б) Открытое состояние
(в) Закрытое состояние
Разомкнут
Рис. 2.22. Работа п-канального МОП-транзистора в ключевом режиме
Показанную на рис. 2.21 ключевую схему можно реализовать,
взяв МОП-транзистор с каналом w-типа и МОП-транзистор с
каналом p-типа (рис. 2.24)3. Когда на вход такой схемы подается
напряжение +0 В, напряжение затвор-исток «-канального тран-
зистора также оказывается равным 0 В, и оно запирает транзи-
стор. В то же время напряжение затвор-исток р-канального
МОПО-транзистора становится равным —5 В, так как потенциал
на истоке относительно затвора равен +5 В, в результате чего
транзистор открывается. При этом на выходе пары появляется
3 В данном примере напряжение источника взято равным +5 В, чтобы бы-
ло легче понять работу цепи. Реально оно может быть и ниже +5 В. В лите-
ратуре принято обозначать напряжение источника питания символом а
напряжение О В — символом V®
88
Глава 2. Логические вентили
напряжение +5 В, и в целом данная ситуация соответствует той,
что изображена на рис. 2.21(6). Если же на вход транзисторной
пары подать положительное напряжение +5 В, то потенциал
затвора «-канального МОП-транзистора относительно его ис-
тока окажется равным тем же +5 В и включит транзистор, а О В
между затвором и истоком р-канального транзистора (т.е. их
потенциалы стали равны), наоборот, закроет его. Такая ситуа-
ция эквивалентна положениям ключей, показанным на
рис. 2.21(b), при этом на выходе установится напряжение О В.
Затвор
(а) Условное обозначение
Сток
Исток
(б) Открытое состояние
Замкнут
(в) Закрытое состояние
Разомкнут
Рис. 2.23. Работа МОП-транзистора с каналом p-типа в ключевом режиме
Показанная на рис. 2.24 схема называется комплементарной
(complementary) парой МОП-транзисторов, поскольку два тран-
зистора как бы дополняют друг друга; в каждый момент време-
ни один из них открыт, а второй закрыт. Обычно уровни на
входах и выходах логических схем рассматриваются только
2.6. Проектирование вентилей
89
в плане того, соответствует ли он логической 1 или логическо-
му 0. Таким образом, все логические схемы в зависимости от
состояния входов могут формировать либо уровень логического
0 (0 В), либо уровень логической 1 (+5 В). В описанной схеме
па комплементарной паре МОП-транзисторов (КМОП-паре)
логический ноль на входе приводит к формированию на выходе
логической 1, и, наоборот, логическая 1 устанавливает на выхо-
де уровень, соответствующий логическому 0.
Рис. 2.24. Ключевая схема на комплементарных МОП-транзисторах
90
Гпава 2. Логические вентили
Базовые КМОП-ветили
Изображенная на рис. 2.24 схема фактически представляет
собой вентиль НЕ, на основе которого можно легко построить
вентили И-НЕ и ИЛИ-НЕ. На рис. 2.25 показан КМОП-
вентиль И-НЕ с двумя входами — А и В. Здесь «-канальные
транзисторы включены последовательно напряжению О В,
а транзисторы с р-каналом — параллельно напряжению +5 В.
Когда на входы А и В одновременно подается логическая 1, оба
транзистора «-типа открываются, и на выходе устанавливается
напряжение О В. При этом оба транзистора с каналом р-типа
закрыты. Если на один из входов подать логическую 1, то от-
кроется соответствующий р-канальный транзистор, и на выходе
установится уровень логической 1, а по крайней мере один из
транзисторов с каналом «-типа будет заперт. КМОП-вентиль
ИЛИ-НЕ изображен на рис. 2.26. В данном случае последова-
тельно и параллельно включенные транзисторы из предыдущей
схемы меняются местами. КМОП-вентиль И легко получить из
вентиля ИЛИ-НЕ, подключив к его входами инверторы
(т.к. АВ = А + В). Аналогично, КМОП-вентиль ИЛИ можно по-
лучить из вентиля И-НЕ, если предварительно проинвертиро-
вать его входные сигналы (А + В = АВ).
Комбинационные функции
Путем применения последовательных и параллельных вклю-
чений транзисторов можно придумать КМОП-схемы, реали-
зующие произвольные функции с операторами И/ИЛИ. На
транзисторах с «-каналом создаются компоненты схем, которые
реализуют в булевых выражениях условия формирования логи-
ческого 0, поскольку через них выход схемы привязывается
к уровню 0. На транзисторах же с p-каналом создаются схем-
ные узлы, которые реализуют условия для формирования логи-
ческой 1, так как с их помощью потенциал выхода привязыва-
ется к 1. Эти два условия булевой алгебры должны дополнять
друг друга, и, если, скажем, схема привязки к 1 реализует
функцию Fup, то схема привязки к 0 реализует комплементар-
ную ей инверсную функцию, Fdown,
Задание для самопроверки 2.13
Что произойдет, если Fup * FJown?
2.6. Проектирование вентилей
91
Схема
Моделирование
ключами
Рис. 2.26. КМОП-вентиль ИЛИ-НЕ
Выход
Моделирование
ключами
92
Гпава 2. Логические вентили
Существуют две базовых конфигурации, которые могут ис-
пользоваться для реализации любой из этих функций: последова-
тельное или параллельное включение. Последовательное включе-
ние транзисторов создает такое соединение, которое проводит
только в том случае, когда все транзисторы переключаются в от-
крытое состояние (т.е. представляет операцию И). Параллель-
ное включение задает соединение, которое проводит при откры-
тии любого из транзисторов (т.е. реализуется операции ИЛИ).
Функция Fup реализуется на транзисторах p-типа, и, следова-
тельно, на них нужно подавать комплементарные переменные
(на что и указывают кружки на затворах таких транзисторов).
Давайте еще раз посмотрим на уже знакомые схемы венти-
лей И-НЕ и ИЛИ-НЕ и разберемся, как в них реализуются
функции Fup и Fdown. Для вентиля И-НЕ условия можно запи-
сать в следующем виде:
привязать к 0, когда А = 1 и В = 1;
привязать к 1, когда А = 0 и В = 0.
или через две комплементарные булевы функции Fdown и Fup:
Edown = АВ
^Р = А + В’
где
^down = Eup-
Функция Fup реализуется на параллельно включенных транзи-
сторах (т.е. в конфигурации ИЛИ), а функция Fdown реализуется
на последовательном соединении транзисторов (в конфигурации
И). Первую функцию легче получить, подавая прямые сигналы А
и В, а не инверсные А и В, поскольку используются полевые
транзисторы p-типа. Поэтому достаточно подавать на верхние
и нижние транзисторы сигналы А и В (см. рис. 2.25).
Для вентиля ИЛИ-НЕ условия выглядят так:
привязать к 0, когда А — 1 или В = 1
привязать к 1, когда А = 0 и В = 0
или в виде булевых функций Fup и Fdown:
/\lown = Л + В
2.6. Проектирование вентилей
93
где снова же
Л1о»п = ^"“Р '
Ввиду использования транзисторов p-типа для реализации
функции Fup опять же лучше подавать сигналы А и В, а не ин-
версные А и fl (см. рис. 2.26).
Произвольные функции
Теперь рассмотрим, как реализовать логическую функцию.
Пусть нужно построить вентиль, на выходе которого реализует-
ся булева функция
F=AB+AC-
Тогда функцию привязки к 1 можно задать в виде:
Fur = AB + AC>
а инверсную ей функцию привязки к 0 — в виде
Tdown = ^В + АС = (АВ) (ас) = (А + В) (А + С) •
В результате получается схема, показанная на рис. 2.27. Обра-
тите внимание, что здесь появилась необходимость использовать
последовательное и параллельное включение как верхних, так
и нижних транзисторов. Также необходимы схемы для инверти-
рования входных переменных (на рисунке не показаны). В об-
щем случае реализация функции f = AB + AC на вентильном
уровне требует двухуровневого решения, т.е. на первом уровне
должны стоять два вентиля И, а на втором — один вентиль
ИЛИ. Однако, как видно, эту же функцию в рамках КМОП-
логики можно реализовать и с помощью одного “уровня” тран-
зисторов (если не учитывать инверторы) (рис. 2.27).
2.7. Резюме
После изучения этой главы читателю необходимо знать сле-
дующее.
• Базовые логические вентили: И, ИЛИ и НЕ.
• Когда использовать вентили И-НЕ и ИЛИ-НЕ.
94
Глава 2. Логические вентили
Входы
+5 В
Рис. 2.27. КМОП-схема, реализующая функцию АВ + АС
• Функции, реализуемые вентилями исключающее ИЛИ
и исключающее ИЛИ-НЕ.
• Булевы тождества и законы, включая принцип дуализма
и теорему де Моргана.
• Внутреннюю структуру и функции, выполняемые венти-
лями, которые изготавливаются по КМОП-технологии.
2.8. Упражнения
1. Используя таблицы истинности, докажите приведен-
ные ниже тождества:
(А + В)(А + CD) = АВ + ACD
АВ + АС + ВС = АВ + АС
2. При каких условиях справедливо следующее выраже-
ние булевой алгебры?
А + ВС=(А + В)С
2.8. Упражнения
95
3. Определите, справедливы ли приведенные ниже тож-
дества:
XY + XZ + YZ = XY + XZ
X Ф Y = (XYZ)(XYZ)
4. Определите значение переменной X для каждой из
логических схем, изображенных на рис. 2.28.
Рис. 2.28. Схемы к упражнению 2.4
5. Определите вид дуальных функций для приведенных
ниже выражений:
f(A,B,C) = АВ + АВС
f(A,B,C) = АВС(А + ВС)
96
Гпава 2. Логические вентили
6. Напишите равенства, дуальные приведенным ниже:
А+АВ+=А+В
А+АВ=А
7. Упростите следующие выражения, используя теорему
де Моргана:
АВС + АВС
(А + В)(А + В + С)
8. Пусть схема реализует функцию f = (A + B)CD в сис-
теме с положительной логикой. Какой сигнал она бу-
дет формировать в системе с отрицательной логикой?
9. Докажите приведенные ниже базовые тождества для
операции исключающее ИЛИ:
А®В = А
А©1 = А
А©А = 0
А©А = 1
А®В = А© В = (А®В)
10. Спроектируйте КМОП-схемы, реализующие следую-
щие функции:
/ = АВС+АС
f = (А+В)(А + С)
11. Какую булеву функцию реализует КМОП-схема, при-
веденная на рис. 2.29?
2.9. Список дополнительной литературы
97
Входы
Рис. 2.29. Схема к упражнению 2.11
2.9. Список дополнительной литературы
1. В книге Дж. Уокерли (Wakerly) содержится очень много
материала, посвященного логическим схемам различ-
ных семейств (включая ТТЛ, ЭСЛ, МОП и др.).
2. Wakerly, J.F., Digital Design Principles and Practices,
2nd edition, Prentice Hall: Englewood Cliffs, New Jersey, 1994.
98
Глава 2. Логические вентили
Глава 3
Проектирование
комбинационных схем
Цели и задачи
В этой главе будет рассмотрено применение описанных ранее
базовых вентилей для разработки несложных логических схем,
сигналы на выходах которых зависят от состояний на вхо-
дах в конкретный момент времени. Такие схемы называются
комбинационными, поскольку значения выходных сигналов не-
посредственно зависят от комбинации сигналов на входах
схемы. Вентили, описанные в главе 2, представляют собой
комбинационные схемы, на основе которых можно строить бо-
лее сложные комбинационные функции. Так как часто перед
разработчиком стоит задача реализовать логическую функцию
с помощью минимального числа элементов или при минималь-
ной стоимости, то в данной главе большое внимание будет
уделено способам перекомпоновки и упрощения комбинационных
логических схем.
3.1. Комбинационные схемы
Любую комбинационную функцию можно описать с помо-
щью булева выражения. Например, имеется такая функция:
/ = АВ + С
Очевидно, что она равна 1 в том случае, когда либо АВ = 1,
либо С = 1. Проще всего реализовать эту функцию, используя
один элемент И, который формирует произведение переменных
А и В, и один элемент ИЛИ, с выхода которого снимается сум-
ма АВ+С (рис. 3.1). Эта комбинационная схема имеет три вхо-
да, А, В и С, и один выход,/.
Логические функции могут включать и комплементарные
компоненты, как, например, функция
f2=AB + C,
которая равна 1, когда одновременно А = 1 и В = 0, или при
С= 1. Реализация этой схемы, при условии, что инвертиро-
ванной переменной В нет, требует применения вентиля НЕ
(рис. 3.2).
Рис. 3.1. Реализация функции
fi = АВ + С на вентилях И и ИЛИ
Рис. 3.2. Реализация на вентилях функции f2~ АВ + С
На рис. 3.1 показана двухуровневая схема, поскольку сигналы
на пути от входа к выходу проходят через два вентиля. Схема,
изображенная на рис. 3.2, является трехуровневой, если вклю-
чить и вентиль НЕ, хотя иногда вентиль НЕ и не считают за
отдельный уровень схемы, поэтому ее также можно рассматри-
вать как двухуровневую. Двухуровневые схемы являются очень
важными элементами цифровых систем, поскольку позволяют
реализовать функции И-ИЛИ (и ИЛИ-И) с минимальными за-
держками прохождения сигналов со входа на выход. Позже будут
рассмотрены альтернативные варианты реализации подобных
схем, требующие, однако, большего количества уровней.
Как и фундаментальные операции И, ИЛИ и НЕ, более
сложные функции также можно представлять с помощью
100
Глава 3. Проектирование комбинационных схем
таблиц истинности. Для функции / — это табл. 3.1. Можно ви-
деть, что / принимает значение 1 в пяти случаях: когда А = О,
В = 0 и С = 1; когда Л = О, В = 1 и С = 1; когда А = 1, В = О
и С — 1; когда Л = 1, В= 1 и С= 0 и, наконец, когда А = 1, В = 1
и С= 1. Следовательно, функция/ может быть записана как
/ = АВС + АВС + АВС + АВС + АВС ,
где каждый член соответствует одной из записей таблицы ис-
тинности. Если в результате вычисления член оказывается рав-
ным 1, то и все выражение примет значение 1.
Задание для самопроверки 3.1
Заполните таблицу истинности для функции f2.
Таблица 3.1. Таблица истинности функции f; = АВ + С
А в с АВ + С
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
С помощью таблицы истинности можно записать любую
функцию, взяв каждую запись в качестве члена выражения.
Однако при таком подходе может оказаться, что записанная
функция имеет количество членов больше минимально необхо-
димого, и, следовательно, для ее реализации понадобится
больше вентилей или вентили с большим количеством входов
(или и то, и другое). Очевидно, что желательно получить выра-
жение, которое позволило бы построить схему с минимальной
общей стоимостью. Упрощение выражений как основной способ
минимизации функций будет рассмотрено позже, а сначала да-
вайте изучим алгебраические свойства логических выражений.
3.1. Комбинационные схемы
101
3.2. Реализация булевых выражений
3.2.1. Дизъюнктивная форма логических
выражений
Итак, вы уже знаете, что существует несколько способов
описания логической функции. Однако есть “стандартная”
форма, которой пользуются очень часто, — запись, состоящая
из булевых переменных, объединенных оператором И, с по-
следующим соединением полученных членов-произведений
с помощью функции ИЛИ. Выражения, приведенные в пре-
дыдущем разделе, записаны именно в таком виде. Операцию
И, как известно, можно рассматривать в булевой алгебре как
умножение; член, полученный посредством применения этого
оператора, называется произведением. Операция ИЛИ в буле-
вой алгебре представляет собой сложение и связывает между
собой слагаемые. Выражение, состоящее из суммы отдельных
произведений переменных, называется дизъюнкцией конъюнк-
ции (т.е. суммой произведений), или дизъюнктивной формой
записи. Следующая функция, к примеру, записана именно
в дизъюнктивной форме:
/(А, В, С) = АВ + АВС + АС-
Переменные А, В и С данного выражения указываются
в скобках после функции. Функции, записанные в дизъюнктив-
ной форме, реализуются на базе вентилей И и ИЛИ (рис. 3.3).
Рис. 3.3. Двухуровневая реализация функции f = АВ + АВС + АС
102
Глава 3. Проектирование комбинационных схем
Выражения в канонической форме
В предыдущем примере некоторые члены записанного вы-
ражения содержали только часть переменных. Если в каждом
члене выражения, записанного в дизъюнктивной форме, со-
держатся все переменные (или их комплементарные величины),
как, например, здесь:
/(А, В,С)-АВС + АВС + АВС + АВС.
то такая запись называется канонической формой дизъюнктивного
выражения. Произведения, из которых состоит функция, за-
писанная в канонической форме, носят названия минтермов
(minterms).
Задание для самопроверки 3.2
Нарисуйте логическую схему, реализующую функцию
f(A, В, С) = АВС + АВС + АВС + АВС
Каждый минтерм выражения в канонической форме может
быть описан с помощью двоичного числа, каждый разряд кото-
рого принимает значение 1 в том случае, когда соответствую-
щая переменная минтерма стоит в истинном виде, и — 0, когда
переменная инверсна. Таким образом, для каждого минтерма
существуют уникальные двоичные числа, т.е. две = 000= Ро,
АВС = 001 = 7] и т.д. (табл. 3.2).
Таблица 3.2. Нумерация минтермов
Минтерм Номер Обозначение
АВС 000 Ро
АВС 001 Pi
АВС 010 Р2
АВС 011 Рз
АВС 100 Р<
АВС 101 Рз
АВС 110 Р6
АВС 111 Р1
3.2. Реализация булевых выражений
103
Каноническую форму дизъюнктивного выражения можно
записать, используя стандартный алгебраический символ сло-
жения, X, т.е.
/(А, В, С) = АВС + АВС + АВС + АВС = Ро + Р2 + Р3 + Р5 = £(0,2,3,5) •
Задание для самопроверки 3.3
Напишите логическое выражение для функции у(д1в1С) = У (0,3,7)'
Описание с помощью таблиц истинности
Проблемы, связанные с проектированием, могут начаться уже
с описания таблицы истинности схемы. Очевидно, что такой вид
записи естественным образом представляет собой канониче-
скую форму дизъюнктивного выражения, поскольку каждая за-
пись таблицы истинности соответствует одному минтерму. На-
пример, табл. 3.3 является таблицей истинности для функции
f(A,B,C) = АВС + АВС + АВС + АВС- Каждая 1 в столбце значе-
ния функции соответствует одному минтерму.
Таблица 3.3. Таблица истинности функции
f (А,В,С) = АВС + АВС + АВС + АВС
А в с f
0 0 0 1 <-АВС
0 0 1 0
0 1 0 1 «—АВС
0 1 1 1 «-АВС
1 0 0 0
1 0 1 1 «—АВС
1 1 0 0
1 1 1 0
Преобразование выражений в каноническую форму
Каноническая форма дизъюнктивных выражений может
быть получена из неканонической умножением каждого члена
104
Глава 3. Проектирование комбинационных схем
на произведение (X + Х)(У+ У)(...), где X, К и т.д. — перемен-
ные, отсутствующие в данном члене.
ПРИМЕР
Выражение
/(А, В, С) = АВ + АС + АВС.
записанное в неканонической дизъюнктивной форме, преобразуется в кано-
ническое следующим образом:
/(А, В, С) = АВ(С + С) + АС(В + В) + АВС =
= АВС + АВС + АВС + АВС + АВС =
= АВС + АВС + АВС + АВС.
Повторяющиеся члены, как, например, второе произведение АВС, просто
убираются (так как АВС + АВС = АВС, что следует из базового тождест-
ва А + А = А).
Задание для самопроверки 3.4
Как преобразовать в каноническую форму функцию f(A, В, С) = А?
Выражения, записанные в канонической форме, легко снова
преобразовать в неканонические, повторно раскладывая их на
сомножители и убирая сомножители типа (Х+Х), появляю-
щиеся в том случае, когда в одном члене стоит переменная X,
а в другом — X . Этот процесс, как будет показано позже, пред-
ставляет собой основу метода упрощения булевых выражений.
3.2.2. Выражения в конъюнктивной форме
Существует еще одна, правда, не столь распространенная
форма записи логических выражений, когда переменные (или
инверсные им величины) объединяются между собой операто-
рами ИЛИ, а между полученными таким образом членами сто-
ят операторы И. Член выражения, сформированный с помо-
щью оператора ИЛИ, называется, естественно, суммой, а вы-
ражение, состоящее из подобных членов, — произведением сумм,
или конъюнктивной формой (product-of-sum). Оно может быть
каноническим, если в каждом члене присутствуют все пере-
менные данной функции (или их инверсии). Ниже приведен
пример конъюнктивного выражения в неканонической форме:
3.2. Реализация булевых выражений
105
f(A, B,C) = (A + B + C)(A + B)(A + C) ;
а вот выражение
/(A,B,C) = (A + B + C)(A+B + C)(A + B + C)
представляет собой уже каноническую форму записи. Члены
выражения в канонической форме называются макстермами
(maxterms).
Выражения, записанные в конъюнктивной форме, могут
быть реализованы с помощью вентилей ИЛИ и И, как показа-
но на рис. 3.4 для функции, заданной выше.
Рис. 3.4. Двухуровневая реализация функции
/(А,В,С) = (А + В + С)(А + В)(А + С)
Задание для самопроверки 3.5
Нарисуйте схему, которая реализовывала бы функцию
f (А,В,С) = (А + В+ С)(А + В+ С)(А +В + С)(А +В+ €)
Каждый макстерм записанного в канонической форме вы-
ражения можно представить в виде двоичного числа, единицы
которого будут представлять истинную переменную, а нули —
комплементарную. Например, макстерм А + В + С можно пред-
ставить в виде А + В + С = 101 = $, • Нумерация макстермов при-
ведена в табл. 3.4. Конъюнктивную функцию, записанную
в канонической форме, можно записать и просто с помощью
алгебраического символа умножения, П:
/(А, В, С) = (А + В + С)(А + В + С)( А + В + С) = S2S5S6 = fj (2,5,6)
106
Глава 3. Проектирование комбинационных схем
Таблица 3.4. Нумерация макстермов
Макстерм Номер Обозначение
А + В + С ООО So
А + В + С 001 Si
А + В + С 010 Si
А + В + С 011 s3
А + В + С 100 S4
А + В + С 101 s5
А + В + С 110 s6
А + В + С 111 s7
Задание для самопроверки 3.6
Напишите логическое выражение для функции /(Д,в,С) = J"J(O,3,7)
Преобразование в каноническую форму
Метод, дуальный преобразованию в каноническую форму
дизъюнктивных выражений, т.е. умножение на член XX =0, не
срабатывает в случае преобразования конъюнктивных выраже-
ний. Поэтому используется следующий способ: с помощью
теоремы де Моргана формируется инверсная функция J. Ре-
зультирующее выражение будет, естественно, иметь дизъюнк-
тивную форму. Затем полученное выражение преобразуется
в каноническую форму, и теорема де Моргана применяется еще
раз, чтобы вернуть функции исходную конъюнктивную форму,
после чего она будет иметь канонический вид.
Для того чтобы разработать более формальный метод преоб-
разования выражения, можно использовать обозначения мин-
термов и макстермов (см. работу Уилкинсона (Wilkinson), 1996).
3.3. Альтернативные реализации
Над булевыми функциями можно осуществлять практически те
же алгебраические операции, что и над обычными алгебраическими
выражениями: раскладывать на множители, вставлять в них скобки
для обозначения порядка действий и т.п. Варианты логических вы-
ражений могут подсказать способ аппаратной реализации функции.
3.2. Реализация булевых выражений
107
ПРИМЕР
/(А,В,С) = (А + В + С)(А + В)
7(А, В, С) = (А + В + С)(А + В) =
= (А + В + С) + (А + В) =
=АВС+АВ=
= АВС + АВ(С + С) =
= АВС + АВС + АВС
f(A, В, С) = АВС + АВС + АВС =
= (АВС')(АВС')(АВС') =
= (А + В + С)(А + В + С)(А + В + С)
Выражения в дизъюнктивной форме
Как было показано ранее, функции, записанные в дизъюнк-
тивной форме, предусматривают совершенно очевидную воз-
можность реализации на основе вентилей И для получения
произведений и— вентилей ИЛИ для формирования конечной
суммы. Запишем такое выражение:
/(А, В,С) = АВС + АВС + АВС,
при взгляде на которое, сразу становится очевидным один из
способов реализации такой функции на базе элементов И
и ИЛИ, проиллюстрированный на рис. 3.5. Однако, если при-
менить теорему де Моргана, можно получить выражение вида:
/(А, В, С) = (АВС)(АВС)(АВС),
реализуемое, как показано на рис. 3.6, только на вентилях И-
НЕ. Кстати, рис. 3.6 показывает интересное и чрезвычайно
полезное свойство реализации функций на вентилях И-
НЕ: вентили И-НЕ просто заменяют вентили И и ИЛИ в И-
ИЛИ-реализации, приведенной на рис. 3.5. Первый ряд вен-
тилей И-НЕ реализует логическую функцию И, как и записа-
но в исходном выражении. Последний вентиль И-НЕ, соби-
рая выходные сигналы вентилей первого ряда, осуществляет
логическую операцию ИЛИ. Сигналы на выходе каждого из
108
Глава 3. Проектирование комбинационных схем
вентилей первого ряда имеет уровень логического 0 (низкий)
в том случае, если на все входы вентиля поступает сигнал
с уровнем логической 1 (высокий), при этом, как видно из
схемы, любой из нулей приведет к формированию на выходе f
логической 1.
Для более четкого определения целевой функции существует
альтернативный символ вентиля И-НЕ, который показан на
рис. 3.6. Обратите внимание на кружочки инверсии на входах
символа обычного вентиля ИЛИ, которые показывают, что реа-
лизуется функция X+Y+Z (то же, что и функция И-НЕ
XYZ), где X, Y, Z — сигналы на входах вентиля. В принципе
можно считать, что кружочки инверсии на выходах вентилей
И-НЕ и на входах альтернативного символа как бы уничтожают
друг друга. Альтернативный символ обычно используется в тех
случаях, когда хотят подчеркнуть, что выполняется именно
операция ИЛИ. Если бы в качестве выходного использовался
вентиль И, то в его символе на выходе присутствовал бы до-
полнительный кружочек инверсии.
Рис. 3.5. Реализация функции /(д, в, С) = АВС + АВС + АВС
на базе вентилей И и ИЛИ
Выражения в конъюнктивной форме
Выражения, записанные в конъюнктивной форме, проще
всего реализовать на аппаратном уровне с использованием вен-
тилей ИЛИ для получения сумм и — вентиля И для формиро-
вания результирующего произведения. К примеру, выражение
/(А,В,С) = (А + В + С)(А + В + С)(А + В + С)
3.3. Альтернативные реализации
109
Рис. 3.6. Реализация функции
f(A, В, С) = АВС + АВС + АВС на базе вентилей И-НЕ
Рис. 3.7. Реализация функции
f (А, В,С) - АВС + АВС + АВС на базе венти-
лей И-НЕ (используется альтернативное обозначение)
легко реализовать с помощью простой схемы (рис. 3.8). Если
же к нему применить теорему де Моргана, то можно записать:
f (А, В, С) — (А 4- В 4- С) + (А 4- В 4- С) 4- (А 4- В 4- С)
Это выражение уже реализуется только на вентилях ИЛИ-НЕ
(рис. 3.9). Опять же можно видеть одно полезное свойство: вен-
тиль ИЛИ-НЕ непосредственно заменяет вентили И и ИЛИ
в И-ИЛИ-реализации функции. Здесь также иногда может
применяться альтернативный символ, подчеркивающий вы-
полняемую операцию (рис. 3.10). В данном случае желательно
показать, что последней выполняется именно операция И.
В этом символе кружочки обозначения инверсии ставятся на
входах символа вентиля И.
110
Глава 3. Проектирование комбинационных схем
Рис. 3.8. Реализация функции
f(A, В, С) = (А + В + С)(А + В + С)(А + ~В + С)
на базе вентилей ИЛИ и И
Рис. 3.9. Реализация функции
f(A, В,С) = (А + В +С)(А + В + С')(А+~В + С)
на базе вентилей ИЛИ-НЕ
ktlnoKj
Рис. 3.10. Реализация функции
f(A,B,C) = (A + B + C)(A + B + C)(A + B + C)
на базе вентилей ИЛИ-НЕ (используется аль-
тернативное обозначение)
3.3. Альтернативные реализации
111
Многоуровневая реализация схем
До сих пор во всех схемных реализациях на рисунках не по-
казывались инверторы для получения комплементарных пере-
менных. Не считая этих инверторов, все приведенные схемы
обычно содержали два уровня, т.е. сигналы, поступающие на
входы схемы, должны были пройти на пути к выходу не больше
двух вентилей. Путем разложения выражений на множители
можно получить многоуровневую реализацию, что иногда по-
зволяет уменьшить число входов у отдельных вентилей, правда,
за счет увеличения задержки.
ПРИМЕР
Для того чтобы реализовать функцию
/=АВС + ABD + АВЕ + AF,
можно разложить ее на сомножители:
f = АВ(С + D + Е) + AF
В результате получается схема, изображенная на рис. 3.11.
Рис. 3.11. Реализация функции f = АВ(С + D + E) + AF
с помощью разложения на сомножители
Задание для самопроверки 3.7
Разложите на сомножители функцию f = АВ(С + D + Е) + AF способом,
отличным от приведенного выше.
3.4. Упрощение логических схем
Очевидно, что от разработчика в первую очередь требуется
спроектировать устройство с минимальной стоимостью, кото-
рое в то же время удовлетворяло бы техническому заданию
112
Глава 3. Проектирование комбинационных схем
(т.е. реализовывало необходимую функцию, имело допустимую
задержку, нужное быстродействие, эффективность и т.п.). Если
схема разрабатывается на вентилях в корпусном исполнении, то
обычно речь идет о минимизации количества микросхем с уче-
том общей задержки распространения сигналов и доступных
типов вентилей. Если же разработка выполняется в виде сверх-
большой интегральной схемы (СБИС), то стоит задача мини-
мизации количества используемых транзисторов.
Предположим, устройство разрабатывается на основе вентилей
в корпусном исполнении. Существует несколько путей упрощения
схемы. Все они, однако, начинаются с описания функции устрой-
ства с помощью булевых выражений. Упрощение этого выраже-
ния подразумевает уменьшение количества используемых пере-
менных в каждом из членов функции и числа членов выражения
в целом (в какой-то мере эти два требования могут противоре-
чить друг другу). Процесс упрощения часто называют минимиза-
цией (minimization). В практическом смысле целью минимизации
логической схемы является получение выражения, реализация ко-
торого обойдется в наименьшую сумму или позволит увеличить
быстродействие по сравнению с устройством, реализованным на
основе исходного выражения. В некоторых случаях желательным
является уменьшение количества уровней схемы, хотя при этом
и может потребоваться использование большего количества вен-
тилей. Объясняется это тем, что задержка распространения схе-
мы непосредственно связана с количеством уровней вентилей.
3.4.1. Алгебраическое упрощение булевых
выражений
Алгебраическое упрощение логических выражений в первую
очередь заключается в применении тождеств и законов булевой
алгебры. Ниже описываются основные методы упрощения, ко-
торые используются в зависимости от вида исходной функции.
В большинстве случаев наилучший метод выбирается интуи-
тивно. Более формальные методы будут описаны позднее.
1. Группировка членов с последующим
применением тождеств
Метод заключается в применении закона ассоциативности
для правильной группировки членов, после чего к сгруппиро-
ванным членам применяются известные тождества типа
А + 1 = 1, которые позволяют сократить выражение.
3.4. Упрощение логических схем
113
ПРИМЕР
f(A,B,C) = А + АС + ABC =
= A(l + C + BC) =
= A.
Для создания дополнительных групп и получения нужных
тождеств можно вводить повторяющиеся члены (поскольку
А + А = А).
Существует еще одно тожество, которое обычно не относят
к базовым, но зачастую оно очень полезно при упрощении
уравнений:
А+АВ =А+В
Доказывается оно с помощью таблицы истинности и при-
меняется в любых удобных ситуациях.
ПРИМЕР
В примере ниже тождество А + АВ = А + В применяется дважды:
f(A,B,C) = А + В + ABCD =
=A+ABCD+B=
=A+BCD+B=
= A + B + CD.
Теорема о непротиворечивости
Другое тождество из той же общей категории, что и тожде-
ство А + АВ = А+В, имеет вид:
АВ + АС+ВС = АВ + АС-
Здесь член ВС может быть сокращен. Это тождество также
несложно доказать с помощью таблицы истинности. Вместе
с дуальным ему тождеством
(А + В)(А + С)(В + С) = (А + В)(А + С)
оно представляет собой так называемую теорему о непротиво-
речивости (Consensus theorem). “Лишний” член уравнения на
самом деле представляет собой элемент, общий для двух ос-
тальных членов.
114
Глава 3. Проектирование комбинационных схем
Задание для самопроверки 3.8
Упростите выражение
f = ABC+ ADE + BCDE,
используя теорему о непротиворечивости. (Подсказка: сгруппируйте члены
ВО и РЕ)
2. Приведение выражения в каноническую форму
с последующим упрощением
Как уже было показано, выражение, записанное в дизъюнк-
тивной форме, можно привести к каноническому виду путем
умножения на множители типа Х + Х. Члены канонического
выражения могут быть перегруппированы так, что в результате
получается упрощенное выражение. Таким образом, сначала
выражения преобразуются в канонический вид. Затем они
группируются с целью упрощения. При необходимости для
формирования групп можно ввести повторяющиеся члены.
ПРИМЕР
/(А, В, С) = АВ + АВС + АВС + АВС =
= АВ(С + С) + АВС + АВС + АВС =
= АВС + АВС + АВС + АВС + АВС =
= АВ(С + С) + АС (В + В) + АВ(С + С) =
= АВ + АС + АВ.
Этот метод позволяет минимизировать выражения в дизъ-
юнктивной форме. Для упрощения выражений в конъюнктив-
ной форме необходимо сначала получить инверсную функцию
(она, естественно, будет иметь дизъюнктивную форму). После
этого функция минимизируется и с использованием теоремы де
Моргана снова переводится в конъюнктивную форму.
Задание для самопроверки 3.9
Каким еще способом можно минимизировать функцию
/(А, В,С) = АВ + АВС + АВС + АВС ?
3.4. Упрощение логических схем
115
3. Использование теоремы де Моргана
Теорема де Моргана является чуть ли не основным спосо-
бом уменьшения логических выражений. Как правило, она
наиболее эффективна в тех случаях, когда приходится иметь
дело со сложными функциями, включающими многоуровневые
инверсии. Многократное применение теоремы де Моргана по-
зволяет значительно уменьшить число уровней.
Чтобы запомнить порядок действий при применении теоре-
мы де Моргана, следует усвоить простое правило: если над вы-
ражением, включающим члены, связанные оператором (И или
ИЛИ), есть общая длинная черта инверсии, то можно разбить
ее на две части, одновременно изменив оператор между члена-
ми (оператор И заменяется на ИЛИ, а оператор ИЛИ — на И).
Аналогично, если над разными членами выражения, связанны-
ми оператором, стоит несколько отдельных символов инверсии,
то можно объединить их и изменить оператор.
ПРИМЕР
Упрощение функции
f(A, В,С) = (ABD + BCD)BC + АС
можно начать с “разбиения" длинного знака инверсии на два:
= ^ABD + ВСо)вс^(ас)'
Продолжая в том же духе, получим
= ^аво+(всо)+(вс^(а + с) =
= ((АВО)(ВС£>) + (В + С))( А + С) =
= ((A + B + D)(BCD)+B + C)(A + C).
Перемножая члены, записанные в скобках (с учетом того, что вв = О
и DD = 0), легко получить
= (АВСО+В + С)(А + С)'
Продолжая перемножение (вспомним, что СС = С), получим:
= АВ + АС + ABCD + ВС + С-
Наконец, после заключительной перегруппировки:
= AB + C(A + ABD + В + 1) =
= АВ + С.
116
Гпава 3. Проектирование комбинационных схем
Теорема де Моргана может применяться к различным чле-
нам выражения, и способы ее использования изменяются в за-
висимости от вида выражения. Например, в одном выражении
можно применить как объединение символов инверсии, так
и их разделение, и решить, что лучше в каждом конкретном
случае, довольно непростая задача. Ну и следует, конечно же,
помнить, что сама теорема де Моргана не является самодоста-
точной — она всегда работает совместно с базовыми тождест-
вами булевой алгебры.
Задание для самопроверки 3.10
“Разбейте” символ инверсии над указанной функцией: у = д + sc
Задание для самопроверки 3.11
“Объедините” символы инверсии над функцией д + ВС
3.4.2. Метод минимизации с помощью карт Карно
Хотя с помощью алгебраической минимизации можно значи-
тельно сократить выражение и привести его к простейшему виду
(или к любому нужному виду), успех ее применения самым не-
посредственным образом зависит от умения инженера применять
соответствующие правила булевой алгебры. Как было показано,
в случае дизъюнктивного выражения в канонической форме су-
ществует одно правило, которое может использоваться для ми-
нимизации многократно, а именно: РЛ + РЛ = Р(Л + А) = Р. где
Р— член в виде произведения переменных, а А — переменная,
общая для нескольких заданных членов выражения (этот метод
описан под номером 2 выше). Однако этот метод требует умения
определять, какие члены могут быть сгруппированы. Существует
простой визуальный метод, называемый методом карт Карно
(Karnaugh тар method), дающий возможность определять члены
логического выражения, которые можно объединить.
Карта Карно состоит из двухмерного массива клеток. Каждая
клетка соответствует одному минтерму. Минтермы соседних
клеток — все равно, по горизонтали или по вертикали — со-
держат одинаковые переменные, только в одном минтерме пе-
ременная стоит в прямой форме, а в другом — в инверсной.
3.4. Упрощение логических схем
117
Клетка обозначается 1 для тех минтермов, которые присутствуют
в минимизируемой функции. Минимизация производится объеди-
нением прилежащих клеток, отмеченных 1, в группу, содержащую
общий член-произведение, при этом исключается переменная, ко-
торая присутствовала в минтермах в разных формах (согласно тож-
деству Р(А+А) = р). Причем, как будет показано далее, если два
минтерма в результате объединения дают более простое произведе-
ние, то это вовсе не означает, что группа не может быть затем
объединена с соседними группами того же размера.
На рис. 3.12 показана карта Карно для трех переменных.
Всего можно записать восемь комбинаций из трех переменных,
и каждой комбинации соответствует одна клетка карты Карно. Все
клетки по двум краям карты нумеруются цифрами, которые пред-
ставляют используемые переменные. Здесь 0 означает инверсную
(комплементарную) форму соответствующей переменной, а 1 -
отсутствие инверсии. Так как соседние клетки карты отличаются
только одной переменной, то по верхнему краю карты нумерация
будет следующей: 00, 01, 11, 10. Эта последовательность по сущест-
ву представляет собой так называемый код Грея (Gray code). Обо-
значения карты по вертикали строятся таким же образом. В дан-
ном случае вертикаль обозначается только одной цифрой, соот-
ветствующей третьей переменной функции. Таким образом,
каждая клетка идентифицируется в соответствии с обозначения-
ми по вертикали и горизонтали. Верхняя левая клетка, например,
будет обозначаться как ООО, что соответствует минтерму АВС
(см. текст)
Рис. 3.12. Карта Карно для трех переменных
118
Гпава 3. Проектирование комбинационных схем
Можно пользоваться и альтернативной формой обозначения
клеток карты Карно, также приведенной на рис. 3.12; здесь
фигурные скобки по краям карты показывают, каким клеткам
соответствуют переменные в истинной (нс инверсной) форме.
Пользуясь таким обозначением, легче определить клетки, в ко-
торых переменная не инверсна.
Порядок переменных может быть и иным, например та-
ким, как показан на рис. 3.13, где переменная С располагает-
ся по вертикали, а переменные АВ — по горизонтали. Однако
в данной книге будет использоваться первый способ обозна-
чения переменных в картах Карно, поскольку легче найти
клетку, соответствующую члену, читая карту слева направо,
т.е. так же, как записан сам член выражения (например, АВС:
А — по вертикали и ВС — по горизонтали). Однако, второй
способ тоже используется достаточно широко, и какой из них
удобнее — дело личного предпочтения.
ч да
00 01 11 10
АВС АВС АВС АВС
АВС АВС АВС АВС
Рис. 3.13. Карта Карно для трех переменных с аль-
тернативным обозначением хлетох
Наличие 1 в клетке карты Карно указывает на то, что вся
функция равна 1. В остальные ячейки можно записать нули,
показав, что функция в этих случаях равна 0. Часто эти нули
опускают, так как они не нужны для дальнейшей работы. На
рис. 3.14 показана карта, заполненная для функции
f(A, В, С) = АВС + АВС + АВС-
Задание для самопроверки 3.12
Нарисуйте карту Карно для функции у = две + АВС + АВС
3.4. Упрощение логических схем
119
Рис. 3.14. Представление функции
f(A, В, С) = АВС + АВС + АВС
с помощью карты Карно для трех переменных
Алгоритм минимизации
Обычно алгоритм минимизации начинает работать с того
момента, когда уже имеется подлежащее минимизации выра-
жение, записанное в дизъюнктивной форме. Для начала пред-
положим, что это выражение будет сразу иметь канонический
вид. Тогда алгоритм можно разбить на три шага.
1. Проставляются 1 в те клетки карты, которые соответст-
вуют членам заданного выражения.
2. Объединяются в группы наибольшего возможного разме-
ра ячейки с единицами.
3. Определяются по карте новые члены выражения, соот-
ветствующие выделенным группам.
Рис. 3.15. Карта Карно с тремя переменными для
функции f(A,B,C) = ABC + АВС + АВС
120
Гпава 3. Проектирование комбинационных схем
ПРИМЕР
Предположим, нужно минимизировать следующее выражение:
/(А, В, С) = АВС + АВС + АВС •
Карта Карно этой функции изображена на рис. 3.15. В выражении всего три
члена, поэтому на карте должно быть три клетки с вписанными единицами.
Две из них прилегают друг к другу, следовательно, эти два члена можно
сгруппировать. Группируясь, АВС и АВС дают просто АВ- Последняя
клетка карты с 1 не соседствует ни с какой другой клеткой с 1 и не может
быть объединена в группу. Группы показаны на рисунке линиями, обведен-
ными вокруг соответствующих клеток. Переменную, которую можно убрать,
легко определить, глядя на обозначения клеток. В одной клетке группы такой
переменной соответствует 0, а в соседней — 1. Альтернативное обозначение
ячеек с помощью фигурных скобок в данном случае удобно для определения
общего члена. Пользуясь им, вы сразу видите, что вся нижняя строка соот-
ветствует истинной переменной А, два правых столбца — истинной перемен-
ной В, а два центральных — истинной переменной С. Итак, минимизирован-
ное выражение имеет вид: АВ + АВС-
Группирование ячеек по краям карты Карно
Очень важным свойством крат Карно является то, что клет-
ки по краям карты рассматриваются как прилегающие к клет-
кам противоположного края (например, верхний и нижний
края или правый и левый являются соседними), поскольку они
также отличаются только одной переменной.
ПРИМЕР
На рис. 3.16 показано, как сгруппировать клетки на противоположных краях
карты Карно. В данном случае минимизация имеет следующий вид:
/(А, В, С) = АВС + АВС = АС(В + В) = АС •
Рис. 3.16. Свойство кругового пе-
рехода карт Карно
3.4. Упрощение логических схем
121
Большие группы
До сих пор рассматривались ситуации, когда объединялись
только два члена, что позволяло сократит^ всего одну пере-
менную. Если в двух полученных таким образом уже сокра-
щенных членах снова будет отличаться только одна перемен-
ная, их можно объединить еще раз и сократить вторую пере-
менную. Однако это проще сделать сразу при использовании
карт Карно, формируя как можно большие группы таким же
образом, как это делалось в случае двух прилежащих клеток.
Примеры формирования больших групп клеток показаны на
рис. 3.17. Возле каждой карты внизу показан результирующий
член, который представляет собой переменную, общую для
всех клеток группы. Если группа из двух клеток позволяет со-
кратить одну переменную, то в случае группы из четырех кле-
ток можно убрать две переменные, а из восьми — три. Для
формирования групп можно использовать и свойство круго-
вого перехода карт Карно (рис. 3.17(b)). В последнем приме-
ре, показанном на рис. 3.17(г), получаемая в результате ми-
нимизации выходная функция представляет собой константу 1
и не зависит от значений переменных. Обратите внимание, что
/22
Гпава 3. Проектирование комбинационных схем
размер групп клеток карты Карно, участвующих в минимиза-
ции, может быть равен только 2, 4, 8, ..., 2", и клетки в группе
могут располагаться только в виде квадрата или прямоуголь-
ника. Число клеток по каждой стороне такого прямоугольни-
ка (квадрата) также должно быть равно степени 2.
Карты Карно для четырех переменных
Для функций четырех переменных требуются карты Карно
с шестнадцатью клетками (рис. 3.18). Методика минимизации
такова же, как и в случае меньших карт Карно. Прилегающие
клетки, которые содержат 1, группируются таким образом,
чтобы сформировать области как можно большего размера.
Карты Карно для четырех переменных позволяют сформиро-
вать группы из двух, четырех, восьми или всех шестнадцати
клеток (в последнем случае результирующая функция будет
представлять собой константу 1).
00 01 11 10
ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
D
Рис. 3.18. Карта Карно для функции четырех переменных
3.4. Упрощение логических схем
123
ПРИМЕР
Предположим, имеется функция
/(А, В, С, D) = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD +
ABCD + ABCD,
которую требуется минимизировать. Отображение функции на карту Карно
показано на рис. 3.19. Это позволяет получить следующий минимизирован-
ный вид функции:
f(A,B,C,D) = AD + CD + ABD-
Рис. 3.19. Карта Карно для функции четырех переменных
f(A, В, С, D) = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD +
+ABCD + ABCD
На последнем примере видно, что группы объединяемых
клеток могут перекрываться. Это делается специально с целью
получения групп наибольшего размера и, следовательно, для
получения членов с минимальным количеством переменных.
На карте Карно можно найти и альтернативные группы клеток
с единицами. Обычно выбираются максимально большие группы,
но иногда можно выбрать разные группы одинакового размера.
Выбор оптимальных групп
Группы клеток на карте Карно (включая и отдельный клетки с 1)
называются импликантпами (implicants). Группы, которые не содер-
жат других групп, входящих в состав более крупных групп, назы-
ваются первичными импликантами (prime implicants). Первичные
124
Гпава 3. Проектирование комбинационных схем
импликанты не могут быть объединены с другими первичными
импликантами с целью увеличения размера. Основная задача —
правильно выбрать первичные импликанты, которые бы наилуч-
шим образом покрывали функцию. Те из первичных импликантов,
которые содержат как минимум одну клетку с 1, не накрываемую
другим первичным импликантом, называются основными первичны-
ми импликантами (essential prime implicants), и именно они необхо-
димы для решения задачи. Те же из них, которые нс являются ос-
новными, но содержат клетки с 1, не накрываемые другими ос-
новными первичными импликантами, носят называние неосновных
первичных импликантов (non-essential prime implicants) и также могут
потребоваться. Могут быть и такие первичные импликанты, кото-
рые включают только клетки, уже входящие в состав одного или
нескольких основных первичных импликантов; они называются
(суто) избыточными первичными импликантами ((essentially)
redundant prime implicants). Подобные группы пи при каких об-
стоятельствах не участвуют в минимизации.
Общая стратегия минимизации заключается в нахождении
прежде всего основных первичных импликантов. Эти импликан-
ты обязательно будут присутствовать в решении, и их можно
найти, выявив как минимум одну клетку с единицей, которую
нельзя перекрыть никаким другим способом. Затем необходимо
выбрать наилучший набор неосновных первичных импликантов,
которые включат в себя оставшиеся непакрытые единицы.
ПРИМЕР
Предположим, имеется функция
f(A. В, С, D) = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD.
которую нужно минимизировать. На рис. 3.20 показано ее отображение на кар-
ту Карно. В данном случае одни единицы могут накрываться разными груп-
пами, тогда как другие могут входить в состав только одной группы. Здесь
можно выделить два основных первичных импликанта: AD и ABD.. поскольку
они содержат клетки с 1, выделенными утолщенным шрифтом. Таким обра-
зом, с помощью этих двух импликантов могут быть накрыты шесть клеток с 1,
при этом остается ненакрытой одна клетка с 1, выделанной курсивом. Она может
войти в состав одного из двух первичных импликантов: BCD или АВС \ та-
ким образом, в данном случае задача минимизации имеет два решения:
f(A, В,С, D) = AD + ABD + BCD
или
f(A,В,С, D) = AD + ABD + ABC
3.4. Упрощение логических схем
125
(a)
Рис. 3.20. Альтернативное разбиение карты Карно
на группы
Карты Карно и таблицы истинности
Между клетками карты Карно и описанием функции таб-
лицей истинности существует прямая взаимосвязь: и здесь,
и там одному минтенрму соответствует одна запись. Таким
образом, имея таблицу истинности функции, достаточно
просто найти ее отображение на карту Карно. На рис. 3.21
показано соответствие между записями таблицы истинности
и клетками карты Карно для функции трех переменных
/(А, В,С) = АВС + АВС + АВС
126
Глава 3. Проектирование комбинационных схем
Таблица истинности
Карта Карно
Рис. 3.21. Соответствие междуописаниями функции f(A, В,С) = АВС + АВС + АВС
с помощью карты Карно и таблицы истинности
Нумерация минтермов в карте Карно
Иногда удобно обозначать минтермы, соответствующие
клеткам карты Карно, с помощью номеров. Такие номера для
карт Карно функций трех и четырех переменных показаны на
рис. 3.22 (в предположении указанного порядка расположения
переменных).
CD
Ав\ 00 01 11 10
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
Четыре переменных
Три переменных
Рис. 3.22. Нумерация минтермов на карте Карно
Функции в неканонической виде
До сих пор рассматривалась минимизация логических
функций с помощью карт Карно для тех случаев, когда выра-
жение имело дизъюнктивную форму канонического вида. Каж-
дый член такого выражения представлял собой произведение
3.4. Упрощение логических схем
127
всех переменных функции в прямой или инверсной формах,
и ему соответствовала одна клетка карты. Функции, записан-
ные в неканонической форме, также могут минимизироваться
с помощью карт Карно, для чего выражение преобразуется в
канонический вид и затем отображается на карту Карно. Однако
клетки, которые будут накрываться преобразуемыми членами,
можно определить, не выполняя преобразования. Например, ес-
ли в выражении для функции четырех переменных f(A, В, С, В)
присутствует член АВС, то ему будут соответствовать две при-
легающие клетки карты Карно: ABCD и ABCD (поскольку
ABCD + ABCD = ABC(D + D) = АВС)- Такие прилегающие клетки
легко определить по обозначениям (особенно, если пользовать-
ся способом обозначения с применением фигурных скобок, по-
казанным на рис. 3.18). Если соседних клеток две, то в соответ-
ствующем члене будет теряться одна переменная — та, которая
имеет разную форму в каждой из клеток. Аналогично, если
прилегающих ячеек четыре, то будут исключаться две перемен-
ные, причем эти четыре ячейки могут быть сгруппированы как
в виде квадрата 2x2, так и в виде прямоугольника 4x1.
ПРИМЕР
Отображение функции в неканоническом виде
/(А, В,С, D) = ABC + ACD + АВС + АВС + ABCD
на карту Карно показано на рис. 3.23. Минимизированная функция будет вы-
глядеть следующим образом:
f(A, В, C,D) = ACD + BD + AB
Обратите внимание, что процедура отображения функции на карту обратна
процедуре минимизации, и клетки, соответствующие каждому члену логическо-
го выражения, могут перекрываться точно так же, как они группируются при
минимизации. Следует запомнить использование четырех угловых клеток карты
для формирования одной группы, соответствующей произведению BD
Неполно заданные функции
Некоторые комбинации входных значений не случаются ни-
когда. Функция обычно задается только для тех значений, ко-
торые могут иметь место. Подобные функции называются не-
полно заданными (incompletely specified functions). Пример такой
128
Глава 3. Проектирование комбинационных схем
ABC
С
(а) Отображение функции
(б) Минимизация
Рис. 3.23. Представление функции в неканоническом виде:
f(A,B,C,D) = ABC + ACD + АВС + АВС + ABCD спомощо карты Карно
неполно заданной функции показан в табл. 3.5. В этом примере
никогда не могут иметь места входные комбинации 100 и 101,
каждая из которых отмечается знаком X. Считается, что подоб-
ные записи могут иметь любое значение. Описание этой же
функции с помощью карты Карно показано на рис. 3.24. При
минимизации функции можно получить определенные выгоды
от наличия записей с произвольным значением. В зависимости
оттого, что выгодней для получения простейшего решения, каж-
дый знак X можно рассматривать и как 0, и как 1. Например, на
рис. 3.24 одна запись X принята равной 0, а вторая — равной 1.
Аналогичная ситуация возникает и в том случае, когда на
входе системы возможны все комбинации, но для некоторых из
3.4. Упрощение логических схем
129
них состояния на выходах не имеют
значения. Опять же, при задании опре-
деления выходной функции могут быть
использованы значения X, обладающие
описанным выше свойством.
Рис. 3.24. Пример отображения на карту
Карно неполно заданной функции
Таблица 3.5. Пример неполно заданной функции
А В с f (А, В, С)
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 X
1 0 1 X
1 1 0 1
1 1 1 0
Примеры входных комбинаций, которые никогда
не случаются
Неиспользуемые комбинации входных сигналов могут воз-
никнуть, когда две подсистемы соединяются между собой так,
как показано на рис. 3.25; при этом подсистемы могут быть
полностью заданными. На первую подсистему поступают ло-
гические сигналы А, В и С, а на ее выходах формируются
сигналы F и G. Оба этих выходных сигнала являются полно-
стью заданными функциями сигналов А, В и С (табл. 3.6), но
в этой подсистеме могут формироваться не все комбинации F
и G: в данном примере состояния F= 0 и G= 1 не появляют-
ся никогда, и эта комбинация как раз и представляет собой ту
запись, значение которой безразлично при проектировании
второй подсистемы.
130
Глава 3. Проектирование комбинационных схем
А ► Я - F G Н
с ►
Рис. 3.25. Появление в логической системе состояний, которые могут считаться
произвольными
Таблица 3.6. Функции подсистем
А В С F G
"о О О О о"
О О 1 1 О
О 1 О О О
0 1111
1ОООО
10 10 0
110 11
11111
Еще одним широко приводимом в литературе примером явля-
ется ситуация, когда числа в системе представляются в виде дво-
ично-десятичного кода (см. главу 1, раздел 1.3.3). При двоично-
десятичном представлении каждый десятичный разряд записыва-
ется в виде четырех двоичных разрядов, т.е. ОООО2 = 0,и,
00012 = 1|0, ОО1О2 = 210, ОО112= 310, ... 1ОО12 = 9,0. Двоичные ком-
бинации от 10102до 11112 при этом не используются и могут рас-
сматриваться как состояния, вид которых не имеет значения.
ПРИМЕР
Предположим, необходимо спроектировать логическую схему, которая бы
формировала 1, когда на выходе появляется двоично-десятичных код восьми
(1000) или девяти (1001). Карта Карно такой функции изображена на рис. 3.26,
и она минимизируется в элементарную функцию f = А. Все не используемые
при двоично-десятичном кодировании кодовые комбинации на карте помече-
ны как такие, значение которых неважно. Обратите внимание, что здесь по-
лезно применять нумерацию минтермов, приведенную на рис. 3.22.
3.4. Упрощение логических схем
131
Рис. 3.26. Функция детекти-
рования двоично-десятичных
кодов цифр 8 и 9
Задание для самопроверки 3.13
Как изменится функция из предыдущего примера, если нужно детектировать
только двоично-десятичный код цифры 8?
Минимизация с использованием нулей на карте Карно
Единицы на карте Карно показывают комбинации входных
сигналов, при которых функция принимает значение 1; нули
показывают комбинации переменных, при которых функция
равна 0. Следовательно, инверсная функция f, может быть по-
лучена группировкой не единиц, а нулей.
ПРИМЕР
При минимизации функции f = АВС + АВС + АВС получается отображе-
ние на карту Карно, приведенное на рис. 3.27. В результате: f = АВ + АС
при минимизации с использованием 1 и f = А + ВС при минимизации
с использованием 0.
В данном случае инверсная форма даже несколько проще.
Если для функции существуют состояния, значения которых
неважны, то их можно рассматривать и как 0, и как 1, но если при
рассмотрении прямой формы функции,/, и инверсной формы, J,
учитывать эти состояния по-разному, то полученные в результате
выражения уже не будут комплементарными друг другу, т.е. f *f-
132
Глава 3. Проектирование комбинационных схем
(а) Прямая форма (б) Инверсная форма
функции
функции
Рис. 3.27. Группировка нулевых клеток карты Карно для получения
инверсной функции
Минимизация систем со многими выходами
До сих пор рассматривалась минимизация одной функции.
Однако может потребоваться реализация сразу нескольких функ-
ций одних и тех же переменных. В таких случаях возможно кол-
лективное использование вентилей, т.е. использование выхода
вентиля в реализации нескольких функций одновременно. Чтобы
подобное совмещение было возможным, часто полная миними-
зация логических функция становится даже нежелательной.
ПРИМЕР
Пусть в системе нужно реализовать сразу три логических функции:
/j = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD,
f2 = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD,
/3 = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD.
Карты Карно для этих функций показаны на рис. 3.28. Обратите внимание,
что для коллективного использования вентилей группы, позволяющие полу-
чить максимальную минимизацию (на рисунке выделены пунктирными ли-
ниями), используются не всегда.
/=AD+ACDt
f2=CD + ACD + ACD,
f}=ACD + ACD + ACD.
Полученная в результате логическая схема показана на рис. 3.29.
3.4. Упрощение логических схем
133
Рис. 3.28. Упрощение трех функций, приводящее к уменьшению количества вентилей
Рис. 3.29. Схема, реализующая три функции
с коллективным использованием вентилей
134
Глава 3. Проектирование комбинационных схем
Карты Карно большего размера
Карта Карно для трех переменных состоит из двух карт для
двух переменных, расположенных рядом, причем вторая из них
является зеркальным отражением первой. Аналогично, карта
Карно для четырех переменных состоит из двух зеркальных и
объединенных между собой карт Карно для трех переменных
(одна над другой). Карта для функции пяти переменных стро-
ится на базе двух карт для четырех переменных, расположен-
ных бок о бок и также симметричных, как показано на
рис. 3.30. Таким образом, зная свойства карт Карно, можно по-
строить карту для функции из п переменных, используя две
карты для (л — 1) переменных. Однако на практике метод карт
почти не используется для функций с более чем пятью пере-
менными, но и при таком количестве переменных работать с
картой крайне неудобно, потому что могут объединяться не
только прилегающие клетки с единицами, но и группы из од-
ной половины карты с группами, расположенными зеркально
в другой половине. Для функций с количеством переменных
больше четырех-пяти используется метод ввода переменных
в карту (для пяти или шести переменных) либо метод Куайна-
МакКласки (Quine-McCluskey), но чаще всего — компьютерная
программа минимизации, основанная на методе Куайна-
МакКласки или любом другом методе, пригодном для механи-
стической компьютерной программы. Боле подробную инфор-
мацию по данной теме можно найти в дополнительной литера-
туре, список которой приведен в конце главы.
3.5. Комбинационные логические
микросхемы средней степени интеграции
Среди функций булевой алгебры есть стандартные, которые
очень часто встречаются на практике и потому реализуются
многими фирмами-производителями в виде отдельных микро-
схем средней степени интеграции (СИС). В этом разделе будут
описаны два подобных устройства: дешифратор/демультиплексор
и селектор данных/мультиплексор. Здесь также будут рассмотре-
ны арифметические схемы, реализуемые в виде СИС.
3.5. Комбинационные логические микросхемы средней степени... 135
с
Рис. 3.30. Карта Карно для пяти переменных
3.5.1. Дешифраторы/демультиплексоры
Дешифратором называется устройство, предназначенное
для распознавания комбинаций входных сигналов. Для каж-
дой возможной двоичной комбинации на входе дешифратора
активируется всего один его выход. Поясним это на примере.
Предположим, есть дешифратор с тремя входами. На трех
входах может быть восемь (23 = 8) комбинаций сигналов, и,
следовательно, необходимо иметь восемь выходов. Такой де-
шифратор называют дешифратором “из 3 линий в 8"; его ус-
ловное обозначение показано на рис. 3.32'. Выходы дешифра-
тора обычно работают в режиме с активным низким уровнем,
т.е. в нормальном состоянии они находятся в состоянии
' Для таких распространенных логических устройств, как дешифраторы,
имеются стандартные символы (см. спецификацию стандартных графических
символов для обозначения логических функций IEEE — IEEE Standard Graphic
Symbols for Logic Functions [IEEE, 1984]). Однако эти обозначения не явля-
ются общепринятыми в функциональных схемах, поэтому в данной книге
использоваться не будут. Заинтересовавшиеся читатели могут обратиться
к соответствующим работам из списка в конце главы.
136
Глава 3. Проектирование комбинационных схем
с уровнем логической 1, а при активации на них возникает
состояние с уровнем логического 0. В дешифраторе логиче-
ский 0 на каждом выходе появляется только тогда, когда на
вход подается соответствующая комбинация входных сигна-
лов. Выходы с активным низким уровнем здесь показываются
наличием черты инверсии над их обозначениями. В микро-
схемах подобного назначения почти всегда присутствует спе-
циальный “разрешающий” вход, обозначаемый латинской ли-
терой Ё (рис. 3.31). Этот вход разрешает работу микросхемы
и позволяет выходным сигналам изменяться. Чтобы микро-
схема работала, на разрешающем входе (при условии, что он
тоже работает в режиме активного низкого уровня) следует ус-
тановить уровень логического 0.
Рис. 3.31. Дешифратор “из 3
линий в 8’
Демультиплексором {demultiplexor) называется схема, на-
поминающая дешифратор, но несколько иного назначения
(функцио-нальная схема показана на рис. 3.32). В данном
случае имеется одна входная линия данных, которая может
подключаться к тому выходу, номер которого зависит от ко-
довой комбинации на входах. Логические схемы дешифрато-
ра и демультиплексора, по сути, не отличаются. Вход дан-
ных демультиплексора фактически эквивалентен разрешаю-
щему входу дешифратора.
3.5. Комбинационные логические микросхемы средней степени... 137
ПРИМЕР
Давайте рассмотрим в качестве примера ТТЛ-микросхему 74LS138, пред-
ставляющую собой дешифратор/демультиплексор “из 3 линий в 8”. Функ-
цию, реализуемую дешифратором с одним разрешающим входом/входом
данных, можно описать с помощью таблицы истинности, приведенной
в табл. 3.7. Функциональная же схема прибора показана на рис. 3.33. В этой
схеме на входах данных доступна дополнительная комбинационная функция,
использующая сигналы G,, бгД и СЬВ. Выходы дешифратора здесь инверсны,
т.е. имеют активный низкий уровень напряжения, и при выборке один из них
переходит из состояния с уровнем логической 1 (состояния покоя) в состояние
с уровнем логического 0, при этом на остальных выходах остается уровень 1.
Как видно из таблицы 3.7, на вход А поступает младший значащий бит, а на
вход С— старший значащий бит двоичного кода, подаваемого на входы.
Выходы данных
Рис. 3.32. Демультиплексор
Таблица 3.7. Таблица истинности дешифратора/демультиплексора
из 3 линий в 8
Е с в А Уо у, У, У< У, Уь Уу
1 X X X 1 1 1 1 1 1 1 1
О О О О О 1 1 1 1 1 1 1
О О О 1 1 О 1 1 1 1 1 1
0 0 1 0 1 1 О 1 1 1 1 1
0 О 1 1 1 1 1 О 1 1 1 1
О 1 О О 1 1 1 1 0 1 1 1
0 1 О 1 1 1 1 1 1 О 1 1
О 1 1 О 1 1 1 1 1 1 О 1
О 1 1 1 1 1 1 1 1 1 1 О
138
Гпава 3. Проектирование комбинационных схем
Задание для самопроверки 3.15
Какую функцию реализуют сигналы Gb и G2B в схеме, изображенной на
рис. 3.33?
Входы
разрешения/
данных
Входы
выборки
Выходы
Рис. 3.33. Функциональная схема дешифратора/демультиплексора из 3 линий в 8
Задание для самопроверки 3.16
Какие логические значения необходимо подать на входы Gb G2A и G2B, чтобы
активировать дешифратор/демультиплексор?
Области применения дешифратора/демультиплексора
Дешифратор адреса
Основным назначением дешифратора является декодирование,
или “дешифрация” двоичного кода, т.е. он должен распознать
3.5. Комбинационные логические микросхемы средней степени... 139
определенную комбинацию битов на своих входах и показать
ее, активируя тот или иной выход. Подобная функция часто
встречается в схемах компьютерного интерфейса, решающих за-
дачу определения “адресов” модулей памяти. Для того чтобы
можно было использовать дешифратор в такой ипостаси, на его
входы подаются сигналы адреса микросхем памяти, и один из
выходов дешифратора активирует нужный модуль.
ПРИМЕР
Предположим, необходимо активировать модуль памяти, адрес которого 010.
В этом случае будет использован вход у2 (рис. 3.34).
Рис. 3.34. Дешифрирование адреса памяти
Использование дешифратора/демультиплексора для реализа-
ции комбинационных логических функций. Каждый выходной
сигнал дешифратора/демультиплексора соответствует одному
минтерму дизъюнктивного логического выражения. К приме-
ру, дешифратор “из 3 линий в 8”, входы которого обознача-
ются как А, В и С (где А — младший значащий бит кодовой
комбинации), а выходы — как у, у, у, у. у , у. у и у,
01234 5 6 7
реализует следующую функцию:
140
Гпава 3. Проектирование комбинационных схем
Уо = СВ A
Уо = СВ A
У, = СВ А
У, = СВ А
У2 = СВ А
У, = СВ А
У, = СВ А
У, = СВ А
У4 = СВ А
или
У4 = СВ А
У5 = СВ А
У6 = СВ А
У7 = СВ А
У5 = СВ А
У6 = СВ А
У7 = СВ А
Выбирая необходимые выходы устройства и объединяя их
с помощью вентиля ИЛИ, можно сформировать любое выра-
жение, записанное в дизъюнктивной форме.
ПРИМЕР
Предположим, необходимо реализовать следующую логическую функцию:
/(С, В, А) = СВА + СВА + СВА.
Для формирования этой функции нужно снять активные сигналы с выходов
У3, У, и (те- получить минтермы СВА, СВА и СВА), а потом объеди-
нить их с помощью трехвходового вентиля ИЛИ. Выходы у большинства де-
шифраторов имеют низкий активный уровень напряжения, так что схема при-
нимает вид, показанный на рис. 3.35, где используется вентиль И-НЕ.
3.5.2. Мультиплексоры
Мультиплексором называется логическая схема, которая по-
зволяет выбирать только один из набора входных сигналов
и передавать его на единственный выход. Функциональная
схема мультиплексора изображена на рис. 3.36. Он имеет во-
семь входов данных, Do, Dt, D2, D3, Dt, D5, D6 и D-,, и всего один
выход, У. Дополнительные входы А, В и С служат для выбора
одного из восьми входных сигналов и его передачи на выход.
Если подать на вход кодовую комбинацию СВА = ООО, то будет
3.5. Комбинационные логические микросхемы средней степени... 141
выбран первый по порядку вход данных, т.е. Y = Do. При
СВА = 001 будет передан сигнал У= £>, и т.д. (при условии, что
А — младший значащий бит кода). Мультиплексор, имеющий
восемь входов и один выход данных, как в этом примере, назы-
вается селектором данных, или мультиплексором “из 8 линий в Г’
(8-line-to-l-line data selector/multiplexer).
Рис. 3.35. Использование дешифратора для реализации дизъюнктивного выражения
Входы данных
»о
Рис. 3.36. Модель мультиплексора
142
Глава 3. Проектирование комбинационных схем
Рис. 3.37. Селектор данных/мультиплексор “из 8 линий в 1
3.5. Комбинационные логические микросхемы средней степени... 143
Области применения селекторов
данных/мультиплексоров
Дешифратор адреса
Селектор данных/мультиплексор можно использовать для
дешифрования адреса (рис. 3.38). Здесь селектор данных пока-
зан в виде блок-схемы, а кружки обозначают наличие инверсии.
Обычно для активации модуля памяти необходим именно ин-
версный сигнал. В данном примере на адресных входах А, В
и С распознается наличие комбинации 010. Один из входов
данных, помер которого соответствует требуемой комбинации
сигналов АВС, устанавливается в состояние с постоянной логи-
ческой 1, а все остальные входы данных — в состояние с посто-
янным логическим 0. (Входы ТТЛ-схем, на которых требуется
наличие логического 0, могут подключаться к напряжению 0 В,
а входы с 1 — к напряжению 5 В.) На рисунке схематично по-
казаны и ключи, с помощью которых можно организовать вы-
бор различных адресов. Эти соединения могут быть
и “аппаратно реализованными”, т.е. представлять собой жест-
кое соединение с логическим 0 или логической 1.
Применение селектора данных для реализации логических функций
Кроме основной функции — выбора одного из нескольких
входных сигналов с последующей передачей на выход — селек-
торы данных можно использовать и для реализации логических
выражений, записанных в дизъюнктивной форме. Если на вход
данных подать постоянный высокий логический уровень и вы-
брать его при помощи соответствующего кода на входах выбор-
ки, то на выходе Y появится логическая 1. Таким образом, же-
стко подключив все входы данных к 0 или 1 (в зависимости от
того, фигурирует ли данный член в дизъюнктивном выраже-
нии), на выходе Y можно сформировать требуемую функцию.
ПРИМЕР
Пусть необходимо реализовать следующую логическую функцию:
f(C, В, А) = СВА + СВА + СВА .
Для этой цели необходимо использовать селектор данных “из 8 линий в Г
(рис. 3.37), так как в данном примере имеются три переменные А, В и С. Для
получения на выходе требуемой функции, нужно подать на входы данных D,
(для получения члена СВА), Ds (для получения СВА) и D, (СВА) высокие
уровни напряжения, а остальные входы подключить к 0. Обозначение устрой-
ства, реализующего подобную функцию, показано на рис. 3.39.
144 Гпава 3. Проектирование комбинационных схем
Селектор данных
из 8 линий в 1
Рис. 3.38. Дешифратор адреса памяти, реализованный на базе селек-
тора данных
Селектор данных
из 8 линий в 1
О
1
О
О
О
1
О
1
Выходы
ДС.В.А)
ДС, В, А)
Переменные
--- А
, — в
функции — с
Рис. 3.39. Формирование дизъюнктивного выражения
с помощью селектора данных
3.5.3. Арифметические схемы
Очевидно, что для выполнения сложения и других арифмети-
ческих операций компьютеры должны содержать специальные
логические схемы; иногда арифметические схемы требуются
в других цифровых системах. В этом разделе будут рассмотрены
схемы для выполнения двоичного сложения, которые часто реа-
лизуются в виде микросхем средней степени интеграции (СИС).
3.5. Комбинационные логические микросхемы средней степени... 145
Сложение
Один из путей аппаратной реализации двоичного сложения ос-
нован на воспроизведении на бумаге алгоритма сложения, описан-
ного в разделе 1.3.1 главы 1. Для его реализации необходимо иметь
схему, которая бы умела складывать два младших значащих двоич-
ных разряда слагаемых чисел. Такая схема называется полусумма-
тором (half adder). Полусумматор имеет два входа и два выхода и
реализует функцию, таблица истинности которой показана ниже.
Таблица 3.8. Таблица истинности полусумматора
А в СУММА ПЕРЕНОС
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Также необходима схема, которая суммировала бы два сле-
дующих двоичных разряда и бит переноса от результата сложе-
ния предыдущего разряда. Такая схема называется полным сум-
матором (full adder). Полный сумматор имеет уже три входа
и два выхода; его таблица истинности показана ниже.
Таблица 3.9. Таблица истинности полного сумматора
А в С„, СУММА р ''-'вых
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
Таким образом, если необходимо спроектировать схему, кото-
рая бы складывала два «-битовых числа, то для этого понадобится
один полусумматор и п -1 полных сумматоров, включенных, как
показано на рис. 3.40. Такая логическая схема называется парал-
146
Гпава 3. Проектирование комбинационных схем
дельным сумматором (parallel adder), поскольку все пары разрядов
складываются одновременно, т.е. параллельно (в принципе, это не
совсем верно, потому что для каждого полного сумматора в преды-
дущем разряде должен успеть сформироваться перенос, но все
равно в данном случае всегда говорят о параллельности сложения).
Существуют и другие более быстрые модификации этой схемы,
Рис. 3.40. Структура схемы, выполняющей сложение пары двоичных чисел
Логические схемы полусумматора и полного сумматора лег-
ко получить, отобразив таблицы истинности на карты Карно
и затем минимизировав функции. Оказывается, что функции
полусумматора не поддаются минимизации и выглядят сле-
дующим образом:
СУММА = АВ + АВ
ПЕРЕНОС = АВ.
Фактически эти функции представляют собой содержимое
тех строк таблицы истинности полусумматора, где в выходном
столбце стоят 1. Логическая схема, реализующая эти выраже-
ния, приведена на рис. 3.41. Функция суммы представляет со-
бой операцию исключающее ИЛИ.
Для полного сумматора выходные функции имеют вид:
СУММА = АВСп + АВСвх + АВСвх + АВСвх
Свих = АВСвх + АВСвх + АВСвх + АВСвх = АВ + АС„ + ВСК
Как можно видеть, минимизируется только функция пере-
носа Свых. Логическая схема полного сумматора показана на
рис. 3.42. Полный сумматор также строится из двух полусумма-
торов (см. работу Уилкинсона (Wilkinson), 1992).
3.5. Комбинационные логические микросхемы средней степени... 147
СУММА
или
ПЕРЕНОС
СУММА
Рис. 3.41. Полусумматор
Рис. 3.42. Полный сумматор
Вычитание
Вычитание числа В из числа А выполняется путем сум-
мирования отрицательного числа В в дополнительном коде
с числом А. Представление отрицательного двоичного числа
можно получить путем инвертирования всех битов числа й
и добавлением 1. Прибавление этой 1 эффективно реализу-
ется в параллельном сумматоре путем замены его первого
каскада (полусумматора) па полный сумматор, вход переноса
которого подключается к напряжению с уровнем логической
1. Таким образом, операция вычитания может выполняться
с использованием параллельного сумматора, включенного,
как показано на рис. 3.43.
748
Гпава 3. Проектирование комбинационных схем
On On-1 On,2 D, Cout D(
Рис. 3.43. Схема для вычитания пары двоичных чисел
3.6. Резюме
В этой главе раскрыты следующие вопросы.
• Различные пути реализации булевых выражений, запи-
санных в дизъюнктивной и конъюнктивной формах.
• Упрощение булевых выражений с использованием ал-
гебраических методов.
• Упрощение булевых выражений с использованием
карт Карно.
• Мультиплексоры и демультиплексоры на микросхемах
средней степени интеграции (СИС).
• Простейшие схемы сложения и вычитания.
3.7. Упражнения
1. Пусть сигнал на выходе схемы принимает значение ло-
гической 1 только тогда, когда на трех ее входах появля-
ются следующие кодовые комбинации:
ООО, 001, 010, ОН, НО.
Составьте таблицу истинности выходной функции. По-
лучите минимальное булево выражение для нее и спро-
ектируйте логическую схему, которая бы реализовывала
эту функцию.
2. Какую булеву функцию реализует схема, показанная на
рис. 3.44?
3.7. Упражнения
149
3. Преобразуйте в канонический вид следующие выражения:
АВ+АВ+С;
(А + В)(А + С)С-
4. Преобразуйте следующие выражения из дизъюнктив-
ной формы канонического вида в конъюнктивную
форму канонического вида:
/( А, В, С) = АВС + АВС + АВС + АВС;
/(А,В,С,£>) = ^(0,3,5,9)-
5. Постройте схемы, которые бы реализовали записанные
ниже функции только на вентилях И-НЕ:
У (А, В, С) = АВС + АВС + АВС + АВС
У(А,В,С) = (А + В + С)(А + В + С)(А + В + С)-
6. Повторите предыдущее упражнение, но только с венти-
лями ИЛИ-НЕ.
7. Для каждой из записанных ниже функций нарисуйте
двухуровневую логическую схему, предполагая, что все
инверсные величины уже имеются:
/(А, В, С) = АВ(С + АВС) + АВ + С
/(А, В, С) = (А + В + С)(А + В + С)(А + В + С) •
/50
Гпава 3. Проектирование комбинационных схем
8. Реализуйте следующие выражения, используя только
элементы И-НЕ с 2 входами:
f (А, В, С, D) = ABCD + ABCD + ABCD;
/(A,B,C,D) = (A + B + C + D)(A+B + C + D)(A + B + C +
+D)(A + B + C+D)
9. На рис. 3.45 использованы альтернативные символы
обозначения логических вентилей. Какой вид имеет
выходная функция /•’этой схемы?
10. Минимизируйте записанные ниже выражения алгеб-
раическими методами:
/(А, В, С) = (А + ВС)(В + С)(АВС + ВС);
f(X,Y,Z)=(X+YZ)(XY(Z + YZ)-
11. Докажите алгебраически теорему о непротиворечивости.
12. Упростите следующие выражения, пользуясь только
теоремой о непротиворечивости:
АВС + ABD + BCD + ACD + ACD\
(А + В)(А + С)(А + D)(B + С)(В + D)(C + D)
13. Найдите более простое решение для реализации логи-
ческой функции схемы, показанной на рис. 3.46.
14. На входы логической схемы приходят два 2-битовых
числа, а с выхода снимается сигнал Z, который прини-
мает значение 1 в том случае, когда числа равны между
собой. Спроектируйте двухуровневую схему, используя
только вентили И и ИЛИ, при условии, что как пря-
мые, так и инверсные входные сигналы доступны.
3.7. Упражнения
151
10. Спроектируйте двухуровневую логическую схему, ко-
торая бы складывала вместе четыре 1-битовых разря-
да, используя только вентили И и ИЛИ. (Начните
с составления таблицы, в которой будут записаны
входные и выходные сигналы.)
3.8. Список дополнительной
литературы
1. IEEE, Standard Graphic Symbols for Logic Functions, Std.
94-1984, New York: IEEE, 1984.
2. Roth, C.H., Fundamentals of Logic Design, 3rd Edition, West
Publishing Company: St. Paul Minnesota, 1985.
3. Wilkinson, B., Digital System Design, 2nd edition, Prentice
Hall: London, 1992.
152
Глава 2. Проектирование комбинационных схем
Глава 4
Триггеры и счетчики
Цели и задачи
В этой главе описываются логические компоненты, сигналы
на выходах которых зависят не только от текущих значе-
ний входных сигналов, но и от предыдущих состояний, при-
чем как на входах, так и на выходах. Такие компоненты
могут запоминать события и реагировать в зависимости
от их характера, что очень важно для построения слож-
ных логических систем.
4.1. Последовательные схемы
До сих пор рассматривались логические схемы, выходные
сигналы которых зависели только от текущих значений вход-
ных сигналов. Например, выход логического вентиля И примет
состояние 1, когда на его входах появятся две единицы. Такие
схемы назывались комбинационными, поскольку выходные
значения определялись комбинациями сигналов на входах. Час-
то, однако, возникает нужда в такой схеме, значения на выхо-
дах которой зависят от предыдущих выходных состояний
(а значит, и от предыдущих входных значений). В качестве при-
мера такой схемы можно назвать двоичный счетчик, состояния
на выходах которого изменяются в соответствии с двоичной чи-
словой последовательностью: ООО, 001, 010, ОН, 100, 101, ... .
После комбинации 000 следует комбинация 001, после 001 —
010 и т.д. Изменение одной комбинации на выходах схемы на
другую инициируется специальным сигналом, который называ-
ется тактовым (clock signal) и подается на отдельный вход уст-
ройства. Этот сигнал непрерывно изменяется из 0 в 1 и из 1 в 0
через одинаковые интервалы времени, и изменение выходных
состоянии счетчика происходит как раз в момент перехода так-
тового сигнала из одного состояния в другое, а по какому
именно переходу: из 0 в 1 или из 1 в 0 зависит уже от особен-
ностей конкретной схемы. На рис. 4.1 показаны временные
диаграммы возрастающей двоичной последовательности для
случая, когда изменения выходных состояний счетчика проис-
ходят в момент перехода тактового сигнала из 0 в 1. Выходные
сигналы на диаграммах обозначены как QjGiG’-
Тактовый
сигнал
е0 I____I—i_i—i__i—l_t
0 ____________________I----------------1_________________I----------------L
ез ;____________________________i----------------------l
Рис. 4.1. Двоичная возрастающая последовательность на выходе счетчика
Задание для самопроверки 4.1
Переделайте рис. 4.1 для случая, когда изменения выходных состояний про-
исходят в момент перехода тактового сигнала из 1 в 0.
Показанная графически на рис. 4.1 двоичная возрастающая
последовательность имеет три разряда, что требует наличия трех
выходов — по одному на каждый бит. То, какое значение при-
мет выходной бит (0 или 1), будет зависеть от предыдущих со-
стояний на всех трех выходах. Младший значащий бит будет
принимать значение 1 после чисел: ООО, 010, 100 или ПО,
и значение 0 — после чисел 001, 011, 101 или 111.
Счетчики относятся к схемам, которые, согласно общей
классификации, называются последовательными логическими
схемами (sequential logic circuits'). Такие схемы характеризуются
тем, что их выходные значения зависят не только от входных
состояний в текущий момент времени, но и от предыдущих со-
стояний на входах/выходах. Последовательные логические схе-
мы, изменение значения выходных сигналов которых иниции-
руется входным тактовым сигналом и в которых собственно
изменение выходного состояния происходит в момент перехода
154
Гпава 4. Триггеры и счетчики
тактового сигнала из одного состояния в другое, называются
синхронными последовательными логическими схемами (synchronous
sequential logic circuits). В этой главе будут изложены основы про-
ектирования таких схем, составляющих львиную долю семейства
последовательной логики, поскольку наличие тактового сигнала
для синхронизации выходов существенно упрощает проектирова-
ние. Например, компьютеры большей частью представляют со-
бой именно синхронные последовательные системы. Однако бы-
вают ситуации, когда использование тактовых импульсов для
синхронизации затруднено или вовсе невозможно. Логические
схемы, в которых синхронизирующие тактовые сигналы отсутст-
вуют, называются асинхронными последовательными логическими
схемами (asynchronous sequential logic circuits). Проектирование
асинхронных схем подробно описано в специальной литературе
(см., например, работы Уокерли (Wakerly, 1990) или Вилкинсо-
на (Wilkinson, 1992)). Однако в данной книге будут рассматри-
ваться только синхронные схемы, хотя следует заметить, что по
существу базовые синхронные последовательные логические
схемы являются асинхронными, а вход тактовых импульсов
представляет собой просто еще один асинхронный вход.
Чтобы запоминать предыдущие состояния, последовательная
логическая схема должна обладать своего рода памятью. Для
начала давайте рассмотрим, как построить элементарную ячей-
ку памяти и как затем ввести ее в состав базовых строительных
блоков последовательных схем.
4.2. Проектирование элементов с памятью
на основе вентилей
На выходе логической схемы сигнал с постоянным уровнем
напряжения можно поддерживать сколь угодно долго, если
воспользоваться обратной связью, когда выход соединяется со
входом таким образом, что на выходе принудительно сохраня-
ется заданное значение сигнала. Предположим, что на все вхо-
ды элемента И подается логическая 1. В результате на выходе
тоже появляется 1. Если подать эту 1 обратно на вход при усло-
вии, что и на других входах будет сохраняться 1, то сигнал на
выходе останется равным 1 (рис. 4.2). Если же на выходе пер-
воначально был 0, то подача его обратно на вход приведет
к принудительному поддержанию на выходе нуля. То, в каком
состоянии находится выход, в общем случае не известно, т.е.
4.2. Проектирование элементов с памятью на основе вентилей 155
в момент начального включения он может быть равным как О,
так и 1, что зависит от внутренней структуры вентилей, и вы-
ходное значение останется неизменным, если на остальных
входах вентиля И будут присутствовать 1.
Если бы на одном из других входов вентиля И был установ-
лен 0, то выходной сигнал также установился бы в 0 и оставал-
ся бы таким все время, так как установить его в 1, используя
только эти входы, нельзя. Для того чтобы иметь возможность
принудительно устанавливать на выходе вентиля 0 или 1, требу-
ется схема, показанная на рис. 4.3. В этой схеме использованы
два вентиля И-НЕ, и имеются два входа, обозначенных Я
(reset — сброс) и 5 (set — установка). Их присутствие дает воз-
можность принудительно выставлять на выходе схемы либо
логический 0 (подачей 0 на вход сброса R при 5=1), либо ло-
гическую 1 (соответственно, подачей 0 на вход 5 при R = l\
Обратите также внимание, что над обозначениями обоих входов
стоят знаки инверсии, которые показывают, что активным
уровнем напряжения является низкий уровень, т.е. действие про-
исходит при поступлении на вход 0. Эти сигналы противопо-
ложны сигналам с активным высоким уровнем, где любое дейст-
вие осуществляется при подаче 1. Как только сигнал на выходе
принудительно устанавливается в 0 или 1, значение на входе
(как R, так и S) может возвращаться в состояние 1, но выход-
ной сигнал при этом останется неизменным.
Рис. 4.2. Возможный ва-
риант элемента с памятью
Рис. 4.3. Элемент с памятью, обладающий возмож-
ностью установки-сброса
Часто удобно иметь не только “прямой” выход, Q, но и ин-
версный, Q, на котором при нормальном функционировании
схемы с памятью наблюдается сигнал, комплементарный сигналу
Q, т.е. если Q = 0, то 2 = 1, и если Q = 1, то Q = Q- Этот инверс-
ный сигнал легко получить с выхода первого вентиля И-НЕ схе-
мы, показанной на рис. 4.3. Обычно эту схему изображают так,
как показано на рис. 4.4. Иногда также удобнее иметь входы
с активными высокими уровнями, что достигается введением до-
полнительных вентилей И-НЕ (в роли инверторов) (рис. 4.5).
156
Гпава 4. Триггеры и счетчики
Такие простейшие схемы с памятью, аналогичные приведенным на
рис. 4.3—4.5, называются защелками (latches) и входят в состав
более сложных элементов с памятью, называемых триггерами.
Рис. 4.4. Элемент с памятью, имеющий
прямой и инверсный выходы
Рис. 4.5. Элемент с памятью, имеющий прямой и инверсный
выходы и входы с активными высоким уровнем
Задание для самопроверки 4.2
Что произойдет при одновременной подаче на входы схемы, изображенной на
рис. 4.5, сигналов S = 0 и Я = О?
4.3. Триггеры
Схема защелки, приведенная в предыдущем разделе, может
хранить одно двоичное значение, но имеет тот недостаток, что
выходные сигналы изменятся после того, как сигнал на одном
из входов перейдет в 0. В последовательных логических схе-
мах же желательно, чтобы состояния на выходах изменялись
синхронно с приходом тактового сигнала. Такие схемы с па-
мятью обычно называют триггерами (flip-flops). Триггер также
может хранить один бит, формируя па выходе непрерывный сиг-
нал 0 или 1, пока не изменятся условия на входах и одновремен-
но не произойдет изменение состояния тактового импульса.
4.3. Триггеры
157
Английский термин “flip-flop”, обозначающий триггер, что в воль-
ном переводе означает “щелк-щелк”, происходит от способа
работы триггера, сигнал на выходе которого резко, “со щелч-
ком” переключается из 0 в 1 или из 1 в 0. Как и в случае заще-
лок, сигнал на выходе триггера обычно обозначается латинской
заглавной буквой Q, а инверсный (состояние которого в обыч-
ном режиме работы триггера противоположно прямому) — Q.
Триггер представляет собой базовый “кирпичик” всех по-
следовательных схем. Аналогично тому, как существует не-
сколько типов базовых вентилей, существует и несколько типов
триггеров. Каждый тип триггера характеризуется своей табли-
цей истинности, описывающей взаимосвязь между состояния-
ми на входах и выходах. Обычно в таблице указываются только
состояния для выхода Q.
4.3.1. RS-триггер
ЛЗ’-триггер (иногда его называют 5Л-триггером), как и защел-
ка, имеет два входа: установки (6) и сброса (Л). Если подать на
вход Алогическую 1, то сигнал на выходе также установится в 1,
а если подать 1 на вход R, то выходной сигнал сбросится в 0. От-
личие состоит в том, что синхронная работа триггера требует на-
личия дополнительного входа тактовых импульсов. Изменение
состояния на выходе будет происходить только в момент перехо-
да тактового сигнала из одного состояния в другое. До изменения
состояния тактового сигнала напряжение на выходах изменяться
не будет, даже если состояния на входах S и R изменятся.
Таблица истинности
s r е+
о о е.
0 1 о
1 0 1
1 1 X
Рис. 4.6. Табли-
ца истинности
RS-триггера
Триггеры можно описывать с помощью таб-
лиц истинности. Таблица истинности RS-
триггера показана на рис. 4.6, где в столбце £)+
приведены значения сигнала на выходе Q триг-
гера после активирующего изменения состояния
тактового сигнала. Иногда для обозначения зна-
чения сигнала на выходе Q до момента измене-
ния состояния тактового сигнала используется
знак Q_. Символом X обозначено неопределен-
ное состояние.
758
Гпава 4. Триггеры и счетчики
Характеристическое уравнение триггера
Работу триггера можно описать и с помощью так называе-
мого характеристического уравнения (characteristic equation), ус-
танавливающего взаимосвязь между сигналом на выходе Q
и входными сигналами триггера. Характеристическое уравнение
Я5-триггера выглядит так:
Q,=QR + S-
Зная характеристическое уравнение, можно построить логи-
ческую схему.
Задание для самопроверки 4.3
Покажите, что приведенное выше характеристическое уравнение действи-
тельно соответствует логической схеме и таблице истинности триггера R-S.
Переключение по уровню
Самой простой формой активации с помощью тактового
сигнала является установление уровня тактового сигнала рав-
ным уровню логической 1, т.е. состояния на выходах изменя-
ются согласно значениям на входах 5 и R в момент установле-
ния уровня тактового сигнала равным 1. Это так называемый
режим с переключением по уровню. На рис. 4.7 показана схема
Я5-триггера с переключением по уровню, в основе которой ле-
жит элемент с памятью, изображенный на рис. 4.5. Пока вход
тактовых импульсов CL находится в состоянии 0, на выходах
первого ряда вентилей И-НЕ будет уровень 1 независимо от
логических уровней на входах 5 и R. Когда же вход CL перехо-
дит в состояние с уровнем 1, сигналы на управляющих входах 5
и R проходят в схему и устанавливают выход в соответствующее
состояние. Подразумевается, что, пока CL = 1, значения 5 и R
не изменяются, иначе могут поменяться и значения на выходах
схемы. При CL = 0 сигналы 5 и R могут изменять свои состоя-
ния, не оказывая немедленного воздействия на выходные сиг-
налы, хотя для сохранения синхронизирующей природы такто-
вых импульсов нежелательно, чтобы они менялись непосредст-
венно в момент перехода сигнала CL в состояние 1. Иногда
подобные схемы называют прозрачными защелками.
Временные диаграммы режима с переключением по уровню
изображены на рис. 4.8. Обратите внимание, насколько важно,
чтобы сигналы на управляющих входах триггера оставались
4.3. Триггеры
159
стабильными в течение всего интервала времени, пока сигнал
синхронизации CL находится в состоянии 1 (с высоким уров-
нем). Также следует отметить, что значения 5 и R могут ме-
няться и до перехода тактового импульса в состояние 1.
Рис. 41. Схема RS-триггера с переключением по уровню
Сигналы S/R должны
Сигналы S/R должны
оставаться постоянными
оставаться постоянными
Рис. 4.8. Пример временных диаграмм работы RS-триггера с переключением по уровню
Если необходимо просто хранить значение одного двоич-
ного бита (который может быть 0 или 1), то совсем не обяза-
тельно иметь схему с двумя входами управления, 5 и R. Доста-
точно иметь один вход данных, который будет определять зна-
чение на выходе (ну и, конечно, вход тактового сигнала). На
рис. 4.9 показано, как реализовать эту задумку с помощью за-
щелки, изображенной на рис. 4.7. Таким образом, проблема
одновременной подачи на оба управляющих входа активных
сигналов (S = R= 1), сформулированная в задании для само-
проверки 4.1, автоматически снимается.
160
Гпава 4. Триггеры и счетчики
s
Переключение по уровню напряжения на практике оказыва-
ется далеко не таким удобным, как кажется на первый взгляд,
потому что такая логика работы накладывает ограничения на
момент изменения входных сигналов. Состояния на входах
триггера, переключаемого по уровню, не должны изменяться на
протяжении всего времени, пока тактовый сигнал имеет уро-
вень 1, а также в момент собственно изменения состояния так-
тового сигнала из 0 в 1 или из 1 в 0. Существуют более слож-
ные механизмы запуска срабатывания триггеров, которые сни-
мают указанные ограничения, правда, достигается это за счет
увеличения стоимости (в частности, из-за увеличения числа
компонентов). Обычно подобные механизмы запуска срабаты-
вания ассоциируются с двумя типами триггеров: D-триггерами
и /А'-триггерами, которые описаны ниже.
4.3.2 D-триггер
D-триггером называется триггер, эквивалентный D-защелке,
схема которой показана на рис. 4.9. После активирующего пере-
хода тактового сигнала из одного состояния в другое на выходе Q
этого триггера просто устанавливается значение, соответствую-
щее состоянию на входе D. Таблица истинности D-триггера при-
ведена на рис. 4.10; здесь снова обозначение Q+ показывает со-
стояние на выходе после изменения состояния тактового сигнала.
Характеристическое уравнение D-триггера предельно просто:
Q+ = D.
(В данном случае характеристическое уравнение не D Q+
дает прямого представления о конфигурации схемы.) “ ”
Рис. 4.10. Таблица истинности D-триггера 1 1
4.3. Триггеры
161
Переключение по фронту
Необходим механизм, который бы обеспечивал изменение
выходного сигнала триггера во время перехода уровня тактового
сигнала (так называемое переключение по фронту) и позволял
поступающим на входы схемы сигналам изменяться, не влияя
на состояния выходов в другие моменты времени. Первый под-
ход к решению этой задачи состоял в использовании каскад-
ного соединения двух защелок. При этом первая, ведущая, за-
щелка в момент времени, когда тактовый сигнал равен 1, захва-
тывает входные значения, после чего вторая, ведомая, защелка,
использует в качестве входных сигналов сигналы с выходов ве-
дущей, причем активным для нее является нулевой уровень
тактового сигнала. Сигналы на выходах всей схемы в целом
меняются по отрицательному переходу тактового сигнала. Ло-
гическая схема организованного подобным образом Д-триггера
показана на рис. 4.11, а временные диаграммы — на рис. 4.12.
Схема триггера типа ведущий-ведомый требует наличия двух
полных защелок и тем не менее не снимает ограничения неиз-
меняемости входных сигналов во время высокого уровня такто-
вого сигнала. Кроме того, сигнал на выходе задерживается до
момента прихода отрицательного фронта тактового сигнала.
Подробности функционирования схем данного типа можно
найти в литературе, список которой приведен в конце главы.
(Структура типа ведущий-ведомый наиболее характерна для JK-
триггеров, которые описаны в разделе 4.3.3.)
Рис. 4.11. Схема D-триггера со структурой ведущий-ведомый (устаревший вариант)
Более удобной и современной формой триггеров является
схема, действительно переключающаяся по фронту, в которой
162
Глава 4. Триггеры и счетчики
изменение уровней на выходах происходит (если оно должно
происходить) именно в момент перехода тактового сигнала
с одного заданного уровня на другой. В любое другое время со-
стояния на выходах остаются неизменными, и значения на вхо-
дах (в данном случае на одном входе данных D) могут изме-
няться практически когда угодно. Значение на входе (входах)
триггера в момент поступления фронта тактового сигнала опре-
деляет выходное значение. Схемная реализация такой логики
достаточно сложна, да и с практической точки зрения не столь
уж важно ее знать, поскольку в большинстве случаев использу-
ются уже готовые микросхемы триггеров, в то время как защел-
ки иногда строят и на отдельных вентилях.
Рис. 4.12. Временные диаграммы D-триггера со структурой ведущий-ведомый
Существуют две формы переключения триггеров по фрон-
ту. При переключении по положительному фронту активным
фронтом является переход от 0 к логической 1, а при пере-
ключении по отрицательному фронту, соответственно, пере-
ход из 1 в 0. Широко используются обе этих формы. На
рис. 4.13 показаны временные диаграммы работы Д-триггера
с переключением по отрицательному фронту для случая
D= 1. Состояние на выходе этого триггера будет изменяться
только в момент отрицательного фронта тактового сигнала,
и это изменение зависит от значения сигнала на входе данных
D в этот самый момент. На практике непосредственно перед
отрицательным фронтом синхроимпульса должен быть не-
большой период времени, называемый временем установления
данных, во время которого сигнал на входе данных не должен
изменяться. Иногда также указывают, что сразу после перепада
4.3. Триггеры
163
тактового сигнала должен быть еще один короткий период
времени, называемый временем удержания данных, в течение
которого сигнал D тоже должен оставаться неизменным. Дли-
тельность этого периода зависит от внутренней структуры
триггера. Переключение по положительному фронту импульсов
осуществляется аналогично, за исключением только того, что
указанные периоды установления и удержания данных распо-
лагаются вокруг положительного фронта тактового сигнала.
О или 1
Время Время
Рис. 4.13. Временные диаграммы D-триггера с переключением
по отрицательному фронту
Триггеры являются базовыми компонентами любой логиче-
ской системы. На рис. 4.14 показаны условные обозначения D-
триггера. Всегда указывается форма переключения: кружок обо-
значает переключение отрицательным фронтом (триггеры со
структурой ведущий-ведомый обычно изображаются по-другому).
Иногда форма переключения не указывается.
С переключением по С переключением по
положительному фронту
отрицательному фронту
Рис. 4.14. Условные обозначения D-триггеров
164
Гпава 4. Триггеры и счетчики
Асинхронные входы установки и сброса
Все триггеры могут иметь отдельные (асинхронные) входы
сброса и установки, сигналы на которых позволяют непосред-
ственно устанавливать выход в состояние 1 или 0 вне зависи-
мости от наличия тактового сигнала синхронизации. Триггеры
с подобными свойствами незаменимы при создании счетчи-
ков (о них речь пойдет позже). Обычно асинхронные входы
сброса и установки имеют активные низкие уровни (т.е. дей-
ствие происходит при нулевом уровне сигнала на них). Эти
входы, как правило, показываются сверху и снизу символа
триггера (см. рис. 4.15 для О-триггера).
R R
С переключением по С переключением по
положительному фронту отрицательному фронту
Рис. 4.15. Условные обозначения D-триггера с асинхрон-
ными входами установки и сброса
В качестве примеров микросхем D-триггеров с переключе-
нием по положительному фронту можно назвать следующие
ТТЛ-микросхемы: 74LS74 — сдвоенный О-триггер, 74LS175—
четыре О-триггера в одном корпусе, 74LS174 — шесть О-триг-
геров в одном корпусе и, наконец, 74LS374 — восемь О-
триггеров в одном корпусе. В микросхемах с количеством
триггеров более двух все триггеры обычно имеют общий вход
тактовых импульсов.
Диаграмма состояния триггера
Последовательные схемы могут находиться только в опреде-
ленных состояниях. Все реальные последовательные схемы
имеют конечное число таких состояний и иногда, называются
конечными автоматами. Триггер может находиться в одном из
4.3. Триггеры
165
двух состояний: когда на выходе 0 или 1. Изменение состояния
инициируется при определенных условиях на входах и поступ-
лении активирующего фронта тактового импульса (для син-
хронных последовательных схем). Состояния последовательной
схемы и условия для их изменения могут иллюстрироваться
с помощью специальной диаграммы состояний.
Диаграмма состояний D-триггера показана на рис. 4.16.
Диаграммы подобного вида называются диаграммами состояний
модели Мура (Moore model state diagram). Каждое состояние на
такой диаграмме показывается в виде окружности с двумя чис-
лами внутри, одно из которых показывает номер произвольного
состояния схемы, например 1, 2 и т.п., а второе — значение на
выходе (выходах) в этом состоянии. Состояния с различными
номерами могут иметь как разные, так и одинаковые выходные
значения. Триггер, например, имеет два состояния, для каждого
из которых есть свое значение на выходе. В состоянии 1 вы-
ходной сигнал равен 0, а в состоянии 2—1. Переходы из од-
ного состояния в другое показаны в виде дуг между кружками,
и эти дуги помечаются цифрами, которые обозначают входные
сигналы, приводящие к подобному изменению выходного со-
стояния (при этом сигнал синхронизации обычно не указывает-
ся, так как в синхронных схемах условие поступления его фронта
является само собой разумеющимся). Для триггера, диаграмма
состояний которого изображена на рисунке, текущим состоя-
нием является первое (при котором Q= 0), а при подаче на
вход данных сигнала D = 1 происходит переключение в состоя-
ние 2 (Q — 1). Аналогично, если в состоянии 2 (Q= 1) подать
на вход данных сигнал D = 0, то триггер вернется в состояние 1.
При подаче некоторых входных сигналов не происходит изменения
Значение сигнала на выходе Q
Рис. 4.16. Диаграмма состояний модели Мура D-триггера
166
Глава 4. Триггеры и счетчики
состояния, поэтому обозначающие их дуги показываются в ви-
де петли. Для D-триггера такими сигналами являются D = О
в состоянии 1 и D= 1 в состоянии 2. Соответствующие петли
показаны на рис. 4.16.
Альтернативным типом диаграммы состояний является диа-
грамма состояний модели Мили (Mealy model state diagram), кото-
рая будет описана в главе 5. Для сложных схем обычно требуется
использование не самих значений булевых переменных, а выра-
жений, которые дают значения, соответствующие цифрам над
дугами. Подобные обозначения также будут описаны в главе 5.
4.3.3. JK-триггер
Очень часто требуется схема, сигнал на выходе которой мог
бы изменяться как из 0 в 1, так и из 1 в 0, т.е. необходимо,
чтобы схема реализовала так называемый бистабильный режим
работы. В качестве примера такой схемы можно назвать двоич-
ный счетчик, последовательность состояний которого описана
в разделе 4.1. Реализацию подобного режима работы обеспечи-
вает JA'-триггер, который дополнительно позволяет также уста-
навливать выход в 1 и сбрасывать его в 0. Таблица истинности
//(-триггера приведена на рис. 4.171. Иногда для того, чтобы
показать значение сигнала на выходе триггера до прихода ак-
тивного фронта импульса синхронизации, используется обозна-
чение Q_, но здесь будет использоваться просто символ Q. Ко-
гда /= К = 0, состояние на выходе не изменяется. Вход / соот-
ветствует входу S AS-триггера: если J = 1 (а К= 0), на выходе
устанавливается 1. Вход К соответствует входу R AS-триггера:
если К = 1 (a J = 0) на выходе устанавливается 0. При
1= К = 1 выход переходит из одного бистабильного состояния
в другое: при Q = 0 Q+ = 1 и при Q = 1 Q+ = 0.
Характеристическое уравнение /А'-триггера выглядит сле-
дующим образом:
Q^=JQ + KQ-
на основе которого и строится схема JA'-триггера, хотя прямая
реализация такого уравнения и не дает нужного решения
(подробнее см. работу Уилкинсона (Wilkinson), 1992).
' Существует триггер, который работает исключительно как биста-
бильный элемент и называется Т-триггером. Его единственный вход данных
Т соответствует входам J и К, накоротко замкнутым между собой. Т-
риггеры довольно редко встречаются в виде готовых корпусных микросхем.
4.3. Триггеры
167
Условные обозначения JA-триггеров с переключением по по-
ложительному и отрицательному фронтам приведены на рис. 4.18.
Как и в случае D-триггеров, обычно в разработках используются
готовые корпусные микросхемы, так что внутренняя реализация
(а это, по существу, асинхронная последовательная схема)
в контексте данной книги интереса не представляет. Но, конечно,
внешние временные диаграммы работы JA-триггера важны.
J к
0 0 Q
0 1 0
1 0 1
1 1 Q
Рис. 4.17. Таблица
истинности JK-
триггера
С переключением по С переключением по
положительному фронту
отрицательному фронту
Рис. 4.18. Условные обозначения JK-триггера
Примером корпусного /^-триггера является принадлежащая
к ТТЛ-семейству микросхема 74LS109, представляющая собой
сдвоенный /^-триггер с переключением по положительному
фронту. В этой микросхеме схеме вход К сделан инверсным
(К). Микросхемы 74LS73, 74LS76, 74LS78, 74LS112, 74LS113
и 74LS114 представляют ряд сдвоенных JA-триггеров с пере-
ключением по отрицательному фронту. Микросхемы, содержа-
щие большее количество триггеров в одном корпусе, встреча-
ются редко. (Тут следует заметить, что каждый /^-триггер име-
ет в два раза больше входов данных, чем тот же D-триггер, что
ограничивает их возможное количество в одном корпусе, по-
скольку количество выводов у корпуса имеет предел.
Диаграмма состояний модели Мура /A-триггера показана на
рис. 4.19. Следует отметить, что теперь уже имеется два вход-
ных сигнала и не одно условие смены состояния триггера.
К примеру, для изменения состояния на выходе триггера из
первого (2=0) во второе (2=1) может выполняться как усло-
вие J = 1, К = 0, так и условие J = 1, К = 1.
JK- триггер может эмулировать работу D-триггера, для чего
просто нужно на J-вход подавать сигнал D, а на А-вход — сиг-
нал D , используя для этого инвертор (рис. 4.20). В общем, это
аналогично тому, как ААза шелка преобразовывалась в D-защелку.
768
Глава 4. Триггеры и счетчики
Значение сигнала на выходе Q
Рис. 4.19. Диаграмма состояний модели Мура J К- триггера
Рис. 4.20. 4К-триггер в режиме D-
триггера
Задание для самопроверки 4.4
Как D-триггер может работать в режиме JK-триггера? (Подсказка: вниматель-
но изучите характеристическое уравнение JK-триггера.)
4.4. Регистры
Триггер может хранить только один двоичный разряд. Од-
нако часто возникает необходимость хранить группу битов —
так называемое двоичное слово (binary word) — скажем, из 8 бит
(1 байта). Для хранения восьми битов можно использовать во-
семь триггеров. Наиболее удобным вариантом для решения
данной задачи будет использование D-триггеров (хотя можно
использовать и JA'-триггеры, включенные по схеме, показан-
ной на рис. 4.20). На рис. 4.21 показаны восемь Д-триггсров,
организованных в 8-разрядный регистр. Такие схемы обычно
размещаются в одном корпусе и имеют вид микросхемы ма-
лой степени интеграции. Регистры широко используются
в компьютерах для хранения двоичных чисел.
4.4. Регистры
169
Выходы данных
Входы данных
Рис. 4.21. Восьмиразрядный регистр данных
Иногда возникает необходимость в установке во всех регистрах
определенных значений, при которых система инициализируется.
Этого легко добиться, используя асинхронные входы установки
и сброса (см. рис. 4.15). Например, для установки на всех выходах
О достаточно просто соединить между собой входы сброса всех реги-
стров и подать на них сигнал общей инициализации системы.
Задание для самопроверки 4.5
Как выставить на выходе 8-разрядного регистра комбинацию битов
010101010?
4.4.1. Регистры сдвига
В регистре сдвига (shift register) сигналы с выходов состав-
ляющих регистр триггеров поступают на входы соседних триг-
геров. В схеме, приведенной на рис. 4.22, присутствует только
один входной сигнал, который подается на вход данных пер-
вого триггера, и каждый поступающий тактовый импульс заста-
вит данные сдвигаться вправо на одну позицию. Таким обра-
зом, если начальное значение на выходах триггеров регистра
было, скажем, 00000000 и на вход схемы была подана 1, то при
подаче тактовых сигналов в регистре последовательно будут на-
ходиться значения 10000000, 11000000, 11100000, ППОООО,
11111000, 11111100, 11111110 и 11111111 (если предположить,
что на входе первого триггера в момент прихода каждого акти-
вирующего тактового импульса будет находиться логическая 1).
Если же после первого тактового импульса 1 снимается
(т.е. начинает подаваться 0), то на выходах регистра будет полу-
чена новая последовательность: 10000000, 01000000, 00100000,
00010000, 00001000, 00000100, 00000010 и 00000001. Если, нако-
/70
Глава 4. Триггеры и счетчики
нец, подавать на вход регистра данные в последовательной фор-
ме (т.е. набор нулей и единиц, следующих в заданном порядке),
то они бит за битом будут введены в регистр. Данные, которые
вводятся в регистр, зависят от логических значений на линии
данных при поступлении тактовых импульсов.
На рис. 4.22 показан регистр сдвига с последовательным вво-
дом и параллельным выводом. Информация в такой регистр вво-
дится последовательно (по одному биту), а считывается
“параллельно” (т.е. все биты считываются одновременно).
В альтернативных регистрах с последовательным вводом и после-
довательным выводом данные последовательно вводятся и по-
следовательно снимаются с выхода последнего триггера
(рис. 4.23). (Регистры сдвига с параллельными вводом-выводом —
это обычные регистры данных; они показаны на рис. 4.21.)
Выходы данных
Вход данных
Рис. 4.22. Восьмиразрядный регистр сдвига с последовательным вводом и параллель-
ным выводом
Выход данных
Вход данных
Рис. 4.23. Восьмиразрядный регистр сдвига с последовательным вводом и последова-
тельным выводом
Регистры сдвига можно сформировать на основе JK-
триггеров, если соединить выходы Q каждого из них со входами
/каждого последующего триггера и входы Q со входами К, как
показано на рис. 4.24.
4.4. Регистры
171
Выходы данных
Рис. 4.24. Восьмиразрядный регистр сдвига с последовательным вводом и параллель-
ным выводом, собранный на JK-триггерах
Области применения регистров сдвига
Сдвиговые регистры находят чрезвычайно широкое приме-
нение в логических системах. Здесь будут упомянуты только
некоторые способы их использования.
Умножение и деление
Регистры часто используются для хранения данных, т.е. на-
бора битов, который представляет двоичное число. Однако
сдвиговый регистр может быть использован для деления на лю-
бую величину, являющуюся степенью 2, что достигается про-
стым сдвигом числа в регистре на нужное количество позиций
вправо. Предположим, в 8-разрядном регистре хранится деся-
тичное число 10 (в двоичной форме — 00001010). Сдвиг числа
на одну позицию вправо, т.е. по направлению к старшему зна-
чащему биту, даст результат 00000101, т.е. десятичное число 5.
Задание для самопроверки 4.6
Какой результат будет получен после следующего сдвига числа 00000101
вправо?
Если хранящиеся в регистре числа сдвигать не вправо,
а влево (что подразумевает соединение триггеров справа налево,
а не слева направо), то, соответственно, можно выполнять ум-
ножение на степень 2.
Формирование управляющих импульсов
Регистры сдвига находят применение и в системах управле-
ния, где они используются для формирования последовательно-
стей импульсов. Для этого последний выход регистра сдвига со-
единяется со входом первого триггера, образуя так называемый
кольцевой счетчик (ring counter). Предположим, с помощью
асинхронных сигналов на триггерах 8-разрядного регистра,
172
Гпава 4. Триггеры и счетчики
показанного на рис. 4.25, выставлена кодовая комбинация
10000000. Тогда последовательная подача тактовых импульсов
приведет к генерации повторяющихся комбинаций:
10000000
01000000
00100000
00010000
00001000
00000100
00000010
00000001
Управляющие импульсы
Тактовый
сигнал
Сигнал
инициали-
Рис. 4.25. Кольцевой счетчик с соединением входов сброса и установки, обеспечиваю-
щим начальное состояние 10000000
зации
Диаграмма состояний модели Мура показана на рис. 4.26.
Обратите внимание, что для счетчиков на диаграмме состояний
входные сигналы отсутствуют, поскольку единственным вход-
ным сигналом для них является тактовый сигнал, благодаря ко-
торому и происходит смена состояний. На каждом выходе коль-
цевого счетчика — Ро, Рх, Р2, Р3, Р4, Р$, Ли Р7 — формируется
импульс 1 с длительностью в один период тактового сигнала, ко-
торый возникает в разные моменты времени (рис. 4.27). Эти им-
пульсы могут использоваться для управления частями цифро-
вой системы, например внутренними блоками компьютеров.
Рис. 4.26. Диаграмма состояний кольцевого счетчика
4.4. Регистры
173
Рис. 4.27. Формирование управляющих импульсов с помощью кольцевого счетчика
Если сигнал с последнего выхода схемы, показанной на
рис. 4.25, сначала проинвертировать и только затем подать на пер-
вый триггер, то получится перекрестный кольцевой счетчик, или,
как его еще называют, счетчик Джонсона (Johnson counter). Его
схема приведена на рис. 4.28.
Выходы данных
Тактовый
сигнал
Рис. 4.28. Перекрестный кольцевой счетчик
Перекрестный кольцевой счетчик, инициализированный
в нулевом состоянии, позволяет получить чрезвычайно удобную
для многих областей применений повторяющуюся последова-
тельность: 00000000, 10000000, 11000000, 11100000, ННОООО,
11111000, 11111100, 11111110, 11111111, 01111111, 00111111,
00011111, 00001111, 00000111, 00000011, 00000001, 00000000, ....
Все члены такой последовательности отличаются от соседних
кодовых групп только одним битом. Эта особенность полезна
174
Глава 4. Триггеры и счетчики
при использовании выходных сигналов счетчика в схемах де-
шифрации. К примеру, для распознавания каждой комбинации
можно воспользоваться одним восьмивходовым вентилем И
и получить шестнадцать импульсов Р. При изменении числа на
следующее задержки в триггерах не будут вызывать кратковре-
менного появления других комбинаций, что могло бы случать-
ся, если бы при переходе от одного числа к следующему изме-
нялось состояние не одного выхода, а нескольких. Логические
выражения для импульсов Р имеют такой вид:
Ро = D0D1D2D3D4D5D6D7
Pt=D0blb2b}b4b5b6b1
Р2 = О0О}Ь2Ь3Ь4Ь5Ь6Ь7
p5 = d0d,d2d3d4d5d6d7
P^D^D.D^D.b.b,
Рт = D0D]D2D3D4D5D6D-i
Pt = О0О,О2О3О4О5О6О7
po = DoD,D2D3D4D5D6D7
рю = DaDiD2D-iDiD.iDfpi
Pu = D^b.D^D^D,
Pn = b^D^D^D.D,
Pn = DoD,D2D3D4D5D6D7
^4 = DoD,D2D3D4D,D6D7
/’5 = DoD1D2D3D4D5D6D7
Задание для самопроверки 4.7
Напишите последовательность состояний на выходах 8-разрядного перекре-
стного кольцевого счетчика, если его начальное состояние 01010101?
Задание для самопроверки 4.8
Как создать перекрестный кольцевой счетчик на основе JK-триггеров?
Последовательные операции: исторические аспекты
В главе 3 описывалась операция параллельного сложения,
когда пары двоичных разрядов складываются между собой
с помощью отдельных полных сумматоров. Однако можно вос-
пользоваться и альтернативным способом сложения двоичных
чисел, записывая их в регистры сдвига и складывая последова-
тельно с использованием одного полного сумматора (рис. 4.29).
Обратите внимание, что перенос, возникающий после одного
сложения, используется при вычислении суммы следующей
4.4. Регистры
175
пары битов. Такая схема, правда, работает очень медленно по
сравнению с параллельным сумматором, но более экономична
в плане числа используемых компонентов, так как для сложе-
нии «-разрядных чисел требуется иметь не п полных суммато-
ров, а всего один (что позволяет выполнять и операцию вычи-
тания). В первых компьютерах образца 1960-х использовались
именно последовательные сумматоры.
Тактовый
сигнал
Сдвиговые регистры
Рис. 4.29. Последовательный сумматор (устаревшее решение)
4.5. Счетчики
Счетчиком называется последовательная схема, на выходе ко-
торой формируется заданная повторяющаяся последовательность
состояний. Счетные последовательности уже упоминались в пре-
дыдущем разделе при изучении регистров сдвига. Счетчики стро-
ятся на основе все тех же триггеров, каждый из которых соответ-
ствует одному биту счетной последовательности. Наиболее гиб-
кими для построения счетчиков являются JA'-триггеры,
поскольку на их основе можно получать дополняющие сигналы,
подавая комбинацию J = К = 1; кроме того, они дают возмож-
ность устанавливать или сбрасывать триггеры в нужные состоя-
ния (с помощью сигналов J = 1, К= 0 и J=0, К= 1, соответст-
венно). Можно использовать и D-триггеры, но при этом для
получения нужной счетной последовательности часто прихо-
дится вводить дополнительные элементы. Однако, хотя тригге-
ры D-типа и не являются наиболее естественным выбором, ино-
гда они предпочтительнее, особенно при проектировании СБИС,
потому что базовый .D-триггер состоит из меньшего количества
776
Гпава 4. Триггеры и счетчики
транзисторов, чем JA'-триггер. Более того, количество взаимных
связей при использовании Р-триггсров может быть меньшим,
чем в случае применения /А'-триггеров. Потому давайте начнем
с рассмотрения реализации счетчиков на /Л'-триггерах, а затем
рассмотрим возможные схемы на £>-триггерах.
4.5.1. Счетчики на JK-триггерах
Для синхронной работы схемы, т.е. для достижения одновре-
менного изменения сигналов на всех выходах, все триггеры
должны управляться одним и тем же тактовым сигналом, как по-
казано на рис. 4.30. При таком решении проблема сводится к оп-
ределению логической функции на входе каждого триггера, кото-
рая требуется для получения нужной последовательности. Давай-
те попробуем подойти к этой задаче формально, что позволит
определить общий подход для формирования произвольной дво-
ичной последовательности. Возьмем в качестве примера возрас-
тающую 3-разрядную двоичную последовательность. Табличный
вид этой последовательности и соответствующая диаграмма со-
стояний показаны на рис. 4.31, где А — младший, а С — старший
значащий биты. На рис. 4.30 показаны триггеры с выходами А, В
и С. Выход А представляет младший значащий разряд, а выход
С — старший значащий разряд последовательности.
Тактовый
сигнал
Младший
значащий
Старший
значащий
разряд
разряд
Рис. 4.30. Входы 3-разрядного счетчика на JK-триггерах
Нахождение функций на входах триггеров
Имея схему из трех триггеров, необходимо определить три
пары функций: (JA, А"а), (Jb, ^в) и (Jc, Кс). Существует четыре
возможных сценария поведения выходов каждого из триггеров
(что справедливо для любого счетчика).
4.5. Счетчики
177
СВА
ООО
О О 1
О 1 О
О 1 1
1 о о
1 О 1
1 1 о
1 1 1
(а) Последовательность
(б) Диаграмма состояний
Рис. 4.31. Двоичная {возрастающая) счетная последовательность и соответствующая
диаграмма состояний
1. Выход находится в состоянии 0 и остается в нем.
2, Выход находится в состоянии 1 и остается в нем.
3. Происходит изменение состояния из 0 в 1.
4, Происходит изменение состояния из 1 в 0.
Для /А'-триггеров эти условия удовлетворяются при следую-
щих сигналах на входах J и К:
1. Выход находится в состоянии 0 и остается в нем J = 0, К = 0 или J= 0, К= 1
2. Выход находится в состоянии 1 и остается в нем J = 0, К = 0 или / = 1, К= 0
3. Происходит изменение со- стояния из 0 в 1 J — 1, К = 1 или / = 1, К = 0
4. Происходит изменение со- стояния из 1 в 0 S S II II —” сГ II II
Обратите внимание, что каждому упомянутому условию
удовлетворяют две возможные комбинаций входных сигналов.
К примеру, если J = 0, К= 0, то это не приведет к измене-
нию значения на выходе Q независимо от его текущего со-
стояния. Эта комбинация сигналов справедлива сразу для
178
Гпава 4. Триггеры и счетчики
двух условий: когда выход находится в состоянии 0 и остается
в нем и когда выход находится в состоянии 1 и остается
в нем. Аналогично, комбинация J = О, К = 1 приведет к уста-
новлению на выходе 0 независимо от начального выходного
значения. Она также справедлива для двух условий: когда
происходит изменение состояния из 0 в 1 и когда происходит
изменение состояния из 1 в 0.
Таблица возбуждения
Число входных комбинаций для выполнения приведенных
выше условий можно уменьшить, вводя состояния, значения
которых можно считать произвольными (табл. 4.1). Она носит
название таблицы возбуждения (excitation table) триггера.
Таблица 4.1. Таблица возбуждения JK-триггера
0-э0+
О —»О
1 -»1
0-э1
1 —»О
J к
О X
X о
1 X
X 1
Таблица (переходов) состояний
Табл. 4.1 можно использовать для вывода требуемых буле-
вых функций на входах каждого триггера. Давайте для начала
построим таблицу состояний (state table), или, как ее иногда
еще называют, таблицу переходов состояний (state transition
table). В этой таблице приводится каждое возможное состоя-
ние вместе с последующим; ее можно вывести, используя
диаграмму состояний. Таблица состояний счетчика из рас-
сматриваемого примера показана в виде табл. 4.2. Если взгля-
нуть на столбец переменной А, то оказывается, что нет ни од-
ного случая, когда переменная А должна оставаться в текущем
состоянии, будь это 0 (переход “0 —> 0”) или 1 (“1 —> 1”). Пере-
менная изменяет свое значение из 0 в 1 (“0 -> 1”) в момент
прихода следующего тактового импульса, когда на выходах С, В
и А присутствуют комбинации ООО, 010, 100 и 110. Согласно
таблице возбуждения JA'-триггера (см. табл. 4.1), такого поведения
4.5. Счетчики
179
переменной А можно добиться, установив на входе JA сигнал
/А = 1 (при этом на входе А"л сигнал может быть как 0, так
и 1). Переменная А изменяется из 1 в 0 (“1 —> 0”) тогда, когда
комбинация СВА имеет вид 001, 011, 101 и 111. Опять же,
согласно таблице возбуждения JA’-триггера, для этого нужно
выставить на входе Кл сигнал = 1 (JA находится в произ-
вольном состоянии и может быть как 0, так и 1). Таким обра-
зом, получены функции сигналов JA и Л"А от переменных С, В
и А. Очень удобно отобразить эти функции на карты Карно,
получив карты Карно входных функций всех триггеров счет-
чика в виде, показанном на рис. 4.321.
Таблица 4.2. Таблица состояний двоичного счетчика, показанного
на рис. 4.31
Текущее состояние Следующее состояние
С в А с+ в+ А+
0 0 0 0 0 1
0 0 1 0 1 0
0 1 0 0 1 1
0 1 1 1 0 0
1 0 0 1 0 1
1 0 1 1 1 0
1 1 0 1 1 1
1 1 1 0 0 0
4 = = 1
4 = 4. = А
Jc= Кс = АВ
В результате схема счетчика будет иметь вид, показанный на
рис. 4.33. Итак, чтобы построить счетчик, необходимо выпол-
нить следующую последовательность шагов.
1 Порядок переменных А, В и С приведенных в картах Карно, был из-
менен специально, поскольку переменная А представляет младший знача-
щий бит. Однако в минимизированных выражениях логических функций
все переменные записаны в нормальном порядке.
180
Гпава 4. Триггеры и счетчики
Рис. 4.32. Карты Карно для сигналов на входах J и К двоично-
го счетчика
1. Нарисовать таблицу (переходов) состояний.
2, Нарисовать карту Карно для сигналов на входах каж-
дого триггера.
3. Получить минимизированные функции для сигналов
на входах триггеров.
4. Нарисовать результирующую логическую схему счетчика.
Этот алгоритм может использоваться для получения счетчи-
ка с любой числовой последовательностью. К примеру, можно
получить схему для любого количества переменных. В случае,
скажем, четырех переменных — А, В, С и D — можно вывести,
4.5. Счетчики
181
что JD = KD = ABC. Зная двоичную последовательность, кото-
рую необходимо получить, нетрудно вывести входные функции
триггеров. Сигналы на выходах схемы изменяются из 0 в 1 или
из 1 в 0 (т.е. происходит переход из одного бистабильного со-
стояния в другое), когда все значащие разряды, младше данно-
го, имеют значения 1. Для переключения двоичные функции на
входах / и Д'должны иметь значения 1, и они представляют со-
бой просто логическую функцию И младших значащих разря-
дов. Это продемонстрировано в табл. 4.3. Входные уравнения
триггеров счетчика принимают следующий вид:
значащий
разряд
значащий
разряд
Рис. 4.33. Схема трехразрядного синхронного двоичного счетчика
Л = К А = 1
/в = = А
Jc= Кс = АВ
JD= KD = ABC
JE= КЕ = ABCD
Jv= Kv = ABCDE
К сожалению, в схеме, реализующей эти функции непосред-
ственно, даже для не столь многоразрядного счетчика, встроен-
ные элементы И будут иметь слишком много входов. В л-
разрядном счетчике для формирования старшего значащего
разряда потребуется наличие элемента И с п — 1 входами. Ус-
ловие использования такого элемента можно и обойти, разби-
вая булевы выражения на множители. На рис. 4.34 показана
схема, в которой используются элементы И только с двумя вхо-
дами. Проблемой таких счетчиков является увеличенная за-
держка распространения, вызываемая вентилями, стоящими на
пути от младшего значащего бита к старшему. Сигнал на выхо-
де каждого триггера не может установиться до тех пор, пока
сигналы с выходов предыдущих триггеров не пройдут через по-
следовательную цепочку вентилей. Это ограничивает частоту,
с которой может подаваться тактовый сигнал синхронизации.
182
Глава 4. Триггеры и счетчики
Таблица 4.3. Таблица переходов между бистабильными состояниями
а возрастающей синхронной двоичной последовательности
Синхроимпульс D с в А
фо 0 0 0 0
ф1 0 0 0 ^-{~П переход
Ф2 0 0 1 У 0
фз 0 0 ъ*'"' 1 ^ТП переход
Ф4 0 1 У 0 * 0
Ф5 0 1 0 ^JT| переход
Ф6 0 1 1 У 0
Ф7 0 Ь'"'' 1 1 ^-ГП переход
Ф8 1 у 0 + 0 + 0
Ф9 1 0 0 ^ЛП переход
ф ^10 1 0 1 у 0
фп 1 0 1 ^4~j~| переход
Ф12 1 1 т 0 1 0
Ф13 1 1 0 ^--ГП переход
Ф14 1 1 1 У 0
Ф15 1 1 1 переход
Ф16 0 у 0 У 0 У 0
Рис. 4.34. Двоичный счетчик на базе элементов И с двумя входами
4.5. Счетчики
183
Задание для самопроверки 4.9
Измените уравнения входных сигналов JX-триггеров 8-разрядного двоичного
счетчика таким образом, чтобы использовались вентили И с количеством
входов не более трех. Нарисуйте схему включения вентилей.
4.5.2. Счетчики на D-триггерах
Давайте теперь посмотрим, как построить двоичный счетчик
на Р-триггсрах. Процедура, .отработанная для /Л'-триггеров,
может быть перенесена па любой тип триггеров. Естественно,
при этом должна использоваться таблица возбуждения, соответ-
ствующая данному типу триггеров. В табл. 4.4 приведена таб-
лица возбуждения Р-триггера. В пей присутствует только один
столбец входных состояний (по количеству входов данных),
в котором пет условно произвольных состояний. Фактически
на вход D подается сигнал, который должен соответствовать
новому значению на выходе Q независимо от текущего значе-
ния: 0, если на выходе должен установиться 0, и 1, если нужно,
чтобы на выходе установилось значение 1.
Таблица 4.4. Таблица возбуждения D-триггера
Отображение входных функций Р-триггеров на карту Карно
сводится к перечислению последующих значений на каждом
выходе (рис. 4.35). В итоге получаются следующие выражения
входных функций:
da = a,
Dti — АВ + АВ 5
Dc = АВ + ВС + АВС.
184
Глава 4. Триггеры и счетчики
Аппаратная реализация этих логических функций показана
па рис. 4.36. Обратите внимание, что выход q первого каскада
этой схемы (соответствующего младшему значащему биту) со-
единен с помощью обратной связи со входом D, что приводит
к появлению у триггера свойства бистабильности, необходимого
для создания счетчика. Остальные входные функции триггеров
имеют более сложный вид, чем для счетчика на /А'-триггсрах,
и в целом можно сказать, что счетчик на О-триггерах требует
более сложной входной логики. Однако, как указывалось ранее,
структура О-триггера проще, к тому же меньшее количество
входов заметно сокращает количество требуемых связей.
Старший значащий разряд
Младший значащий разряд
Рис. 4.35. Карты Карно для входных функций двоичного счетчика на D-триггерах
Тактовый
сигнал
Рис. 4.36. Схема синхронного двоичного счетчика на D-триггерах
Описанная в этом разделе методика проектирования может
использоваться при разработке счетчиков, генерирующих лю-
бую рекурсивную последовательность. Еще один пример ее ис-
пользования будет дан в следующем разделе, а также в главе 5.
4.5. Счетчики
185
4.5.3. Начальные условия
При подаче питания на логическую схему выходы всех
триггеров находятся, как правило, в произвольных состояниях.
Что же происходит в счетчике, когда на его вход синхрониза-
ции приходит первый синхроимпульс? Все зависит от началь-
ных состояний выходов и входных функций составляющих его
триггеров. В некоторых решениях бывает так, что не все воз-
можные комбинации состояний выходов принадлежат требуе-
мой последовательности, и возникает возможность генерации
новой последовательности состояний, которая не будет вклю-
чать в себя ни одной комбинации из нужной последовательно-
сти. Вероятность такой работы схемы зависит от того, каким
образом учитывались условно произвольные состояния при ми-
нимизации входных функций. Если на выходе появится хотя
бы одна из комбинаций, входящих в нужную последователь-
ность, то счетчик начнет работать правильно.
Проблема начальных условий счетчика может решаться либо
таким отображением выходных значений, когда любая неопре-
деленная комбинация выходных состояний рано или поздно
переходит в одну из заданных выходных комбинаций при по-
ступлении очередного тактового импульса, либо путем исполь-
зования асинхронных входов сброса/установки для принуди-
тельной, установки нужных начальных состояний.
Давайте рассмотрим первый метод, спроектировав счетчик, на
выходе которого повторяется последовательность ООО, 001, ОН, ПО,
ООО, ... . Диаграмма состояний такого счетчика приведена на
рис. 4.37, где показано, что все неопределенные кодовые комбина-
ции переходят в состояние ООО при поступлении следующего же
тактового импульса. Карты Карно входных функций О-триггеров
изображены на рис. 4.38, а схема счетчика — на рис. 4.39.
4.5.4. Двоичные счетчики с обратным счетом
Двоичным счетчиком с обратным счетом (binary-down counter)
называется счетчик, последовательность комбинаций на выхо-
дах которого имеет вид 111, НО, 101, 100, 011, 010, 001, 000,
111, ... . Для того чтобы спроектировать счетчик с обратным
счетом, нужно изучить схему счетчика. Если сравнить возрас-
тающую двоичную последовательность с убывающей двоичной по-
следовательностью, то можно увидеть, что убывающая последова-
тельность может быть получена из возрастающей путем инверсии
всех разрядов последней. Таким образом, счетчик с обратным
186
Гпава 4. Триггеры и счетчики
счетом можно получить, снимая сигналы не с прямых выходов Q,
а с инверсных Q. Счетчик с обратным счетом можно построить
и иначе, а именно: используя в качестве аргументов входных
функций сигналы с комплементарных выходов, т.е. 1 (первый
триггер работает в бистабильном режиме в счетчиках обоих ти-
пов), А, АВ, АВС, ... При использовании второго подхода вы-
ходы счетчика с обратным счетом останутся теми же выходами
триггеров, что и для счетчика с прямым счетом.
Рис. 4.37. Последовательность состояний счетчика, в которой
все неопределенные комбинации переходят в состояние ООО
Рис. 4.38. Входные функции D-триггеров счетчика
Тактовый
сигнал
Рис. 4.39. Схемная реализация счетчика
4.5. Счетчики
187
Из сказанного выше следует, что можно построить такой
счетчик, который будет считать как в прямом направлении, так
и в обратном. Подобный счетчик называется двунаправленным,
или реверсивным двоичным счетчиком (bidirectional binary counter).
Для указания направления счета может использоваться двоич-
ный управляющий сигнал, скажем, нулевое состояние которого
заставляет счетчик работать в прямом направлении, а единич-
ное — в обратном. Управляющий сигнал будет определять по-
дачу на стоящие на входах следующего триггера вентили сигна-
ла либо с прямого выхода Q, либо с инверсного Q. Устройство
такого счетчика показано на рис. 4.40.
Рис. 4.40. Реверсивный двоичный счетчик
4.5.5. Двоичный счетчик со сквозным переносом
Если не требуется, чтобы сигналы на выходах всех триггеров
изменялись строго синхронно, т.е. короткие задержки между по-
явлением выходных сигналов приемлемы, то можно создать схе-
му с меньшими затратами. Счетчик, работающий подобным об-
разом, называется счетчиком со сквозным переносом (ripple
counter), поскольку сигналы как бы переносятся сквозь схему из
одного конца в другой. Иногда такой тип счетчиков называют
еще асинхронным двоичным счетчиком (asynchronous binary counter),
хотя, строго говоря, такая схема не относится к классу асин-
хронных логических схем. Тактовый сигнал также выполняет
здесь синхронизирующую роль, но внутри отдельные триггеры
“тактируются” сигналами с выходов предшествующих триггеров
188
Гпава 4. Триггеры и счетчики
(кроме первого). В результате могут появиться небольшие за-
держки между появлением сигналов на выходах триггеров.
Прямой счетчик со сквозным переносом можно создать,
изучив двоичную последовательность, которая показана
в табл. 4.5. Сигнал, соответствующий младшему значащему би-
ту, А, переключается (меняет свое состояние из 0 в 1 или из 1
в 0) с приходом каждого тактового импульса. Следующий наи-
меньший значащий бит, В, изменяется только в том случае,
когда А переходит из 1 в 0. Аналогично, бит С, меняет свое со-
стояние только при переключении из 1 в 0 бита В. JA'-триггсры
работают в бистабильном режиме при установке на их входах
сигналов J= К= 1, a D-триггеры — при соединении входа
данных D с инверсным выходом q. Если имеется три рабо-
тающих в бистабильном режиме триггера с выходами A, S и С,
то можно заставить переключиться выход В, подключив выход
А ко входу синхронизации второго триггера (при условии пе-
реключения по переднему фронту). Выход С можно заставить
переключаться сигналом с выхода В, подав последний на вход
синхронизации третьего триггера. Полученная схема двоичного
счетчика с прямым счетом на D-триггерах показана на
рис. 4.41. Вместо D-триггеров можно использовать и JK-
триггеры, просто подавая 1 на оба входа, J и К, одновременно.
Таблица 4.5. Таблица переходов между бистабильными состояниями для
двоичного счетчика со сквозным переносом
Синхроимпульс С в А
% 0 0 0 переключение / из 1 в 0
Ф1 0 0
Ф2 0 1 * 0 1
фз 0 —ц ,11
Ф4 1 0 ’ 0 ’
Ф5 1 0 ,11
Ф6 1 1 0 ’
Ф7 1 —ц ,1 1
Ф* 0 0 ' 0 '
Ф9 0 0
4.5. Счетчики
189
Рис. 4.41. Двоичный счетчик со сквозным переносом
В качестве примера двоичных счетчиков со сквозным пере-
носом, реализованных в корпусных ТТЛ-микросхемах, можно
назвать 4-разрядные асинхронные двоичные счетчики 74LS294
и 74LS197.
Задание для самопроверки 4.10
Как соединить D- или Ж-триггеры с переключением по отрицательному
фронту, чтобы получить двоичный счетчик со сквозным переносом?
4.6. Резюме
В этой главе были рассмотрены следующие темы.
• Свойства триггеров как базовых блоков последова-
тельных логических схем.
• Концепция диаграмм состояний (модель Мили)
и таблица состояний.
• Принципы построения регистров.
• Счетчики как последовательные схемы, на выходах
которых формируются повторяющиеся двоичные
поел едо вател ьн ости.
• Принципы создания синхронных счетчиков с про-
извольными счетными последовательностями
4.7. Упражнения
1. Составьте таблицу истинности триггера, схема кото-
рого приведена на рис. 4.42.
190
Гпава 4. Триггеры и счетчики
Рис. 4.42. Схема х упражнению 4.1
2. Дорисуйте не показанную временную диаграмму для
выхода /Л’-триггера с переключением по положитель-
ному фронту (рис. 4.43).
Рис. 4.43. Временные диаграммы к упражнению 4.2
3. Что произойдет с /Л’-триггером, если подать на его вход
синхронизации серию активирующих тактовых импуль-
сов, при условии, что значение на выходе Q в начальный
момент времени равно 0, а входные функции имеют вид:
J= 1
K=Q
4. Спроектируйте синхронный двоичный счетчик на D-
триггерах, комбинации на выходах которого следуют
3-разрядному коду Грея (рис. 4.44).
47. Упражнения
191
5. Повторите предыдущее упражнение, но для JK-
триггеров.
6. Спроектируйте двоичный счетчик, состояния кото-
рого циклически изменяются от 0 до 4 (т.е. от ООО до
100 в двоичной системе). Обеспечьте, чтобы этот
счетчик не мог перейти на другую циклическую по-
следовательность, введя отображение всех неисполь-
зуемых комбинаций таким образом, чтобы после пер-
вого активного фронта тактового импульса счетчик
переходил в состояние ООО. Используйте /)-триггеры.
7. Повторите предыдущее упражнение, используя JK-
триггеры.
8. Определите вид последовательности на выходах счет-
чика, показанного на рис. 4.45.
Рис. 4.45. Счетчик к упражнению 4.8
9. Спроектируйте схему двоичного счетчика, который
бы реализовал диаграмму состояний, показанную
на рис. 4.46.
Рис. 4.46. Диаграмма состояний к упражнению 4.8
192
Гпава 4. Триггеры и счетчики
4.8. Список дополнительной
литературы
При рассмотрении материала были опущены детали
внутренней структуры JK- и ZJ-триггеров с переключе-
нием по фронту. Эти детали можно найти в соответст-
вующей литературе, например у Уокерли (Wakerly),
1994 и Катца (Katz), 1994. Там же можно получить бо-
лее подробную информацию и о строении триггеров
типа ведущий-ведомый.
1. Katz, R. Н., Contemporary Logic Design, Benjamin/Cummings:
Redwood City, California, 1994.
2. Wakerly, J.F., Digital Design Principles and Practices, 2nd
edition, Prentice Hall: Englewood Cliffs, New Jersey, 1994.
4.7. Упражнения
193
Глава 5
Проектирование
последовательных схем
Цели и задачи
В предыдущей главе были описаны базовые кирпичики по-
следовательных схем — триггеры, а также показано, как
использовать триггеры для создания регистров и счетчиков.
Здесь будет представлен формальный способ описания
и проектирования последовательных схем произвольного ти-
па. Как и ранее, будут рассматриваться только синхронные
схемы, в которых переход из одного состояния в другое про-
исходит в момент изменения уровня тактового импульса. В
данной главе описаны также различные проблемы, возни-
кающие при проектировании, и методы их решения.
5.1. Модель синхронной
последовательной схемы
Как было показано в главе 4, в реальных последовательных
схемах существует конечное число логических состояний. По
этой причине такие схемы еще называют конечными автомата-
ми. Давайте рассмотрим обобщенную модель синхронных по-
следовательных схем, которая может служить отправной точкой
при проектировании любых подобных схем. Состояния схемы
можно представить двоичными сигналами, называемыми пере-
менными состояний (state variables). Каждое состояние характе-
ризуется однозначной для него комбинацией значений таких
переменных, хранящихся в триггерах и активирующихся по
внешнему тактовому сигналу. На рис. 5.1 показана модель
последовательной логической схемы на D-триггерах1, носящая
название модели Мили (Mealy model). Схема имеет п входов: X,,.!
... Хо и т выходов: Z,,^ ... Zq. Также существуют два набора из к
внутренних сигналов — ук_, ... у0, и Кк_| ... Yo. Сигналы у опреде-
ляют текущее состояние схемы. Это так называемые перемен-
ные текущих состояний (present state variables')', их значения
хранятся в триггерах. Сигналы Y — переменные следующих со-
стояний (next state variables) — формируются с целью измене-
ния текущих состояний схемы и являются входными сигнала-
ми триггеров. Сигналы Y представляют собой комбинацион-
ные функции входных сигналов схемы, Х„_| ... Хо, и текущих ее
состояний, Vk-i ••• Уо- Выходные сигналы схемы, Zn^ ... Zq, также
являются комбинационными функциями входных сигналов
и текущих состояний. Для того чтобы на основе этой модели
построить синхронную последовательную схему, необходимо
получить комбинационные функции переменных следующих
состояний, Гк_| ... Yo, и выходные сигналы, Zn)_|... Zq.
Тактовый
сигнал
Выходы
Входы
х0
Рис. 5.1. Модель синхронной последовательной схемы (модель Мили)
' С таким же успехом можно было бы использовать и УК-триггеры,
но в таком случае пришлось бы иметь дело с удвоенным количеством
входных сигналов триггеров.
196
Глава 5. Проектирование последовательных схем
Прежде всего необходимо определить количество триггеров,
требующихся для построения конкретной схемы (т.е. найти к).
Если схема должна находиться только в двух состояниях, то дос-
таточно одной переменной состояния, которая для одного со-
стояния будет принимать значение 0, а для другого — 1. Если же
нужно обеспечить работу схемы в трех или четырех состояниях,
понадобятся уже две переменные, поскольку только в таком слу-
чае удастся получить четыре различных кода: 00, 01, 10 и 11 — по
одному для каждого состояния. Для обеспечения 5 или 6 состоя-
ний необходимо уже три переменных, и т.д. В общем случае, при
количестве состояний от 2к-1 + 1 до 2к необходимо иметь к пере-
менных состояний и, следовательно, к триггеров. Если исполь-
зуются триггеры с переключением по положительному фронту,
то все изменения состояний будут происходить во время перехо-
дов уровня тактового сигнала из 0 в 1. Если же применяются
триггеры с переключением по отрицательному фронту, то изме-
нения будут происходить по заднему фронту тактового сигнала.
В любом случае, после прихода активирующего перехода такто-
вого импульса необходимо обеспечить достаточную задержку до
момента поступления перехода следующего тактового импульса,
чтобы сигналы успели пройти схемы комбинационной логики
и установить значения переменных следующего состояния.
Обратите внимание, что сами по себе изменения сигналов на
входах (первичных) никак не влияют на текущее состояние схе-
мы, поскольку факт наличия или отсутствия изменения состояния
будет определяться сигналами на входах и текущим состоянием
в момент поступления активирующего перехода тактового им-
пульса (с учетом задержек в схеме). Поскольку выходные сигналы
схемы представляют собой комбинационные функции, вклю-
чающие и входные сигналы, то изменения состояний на входах
могут привести к немедленному изменению состояний на выходах,
причем без синхронизации с приходом тактового импульса. Этой
проблемы легко избежать, если комбинационные функции выход-
ных сигналов будут зависеть только от переменных текущих со-
стояний. Подобный подход реализуется в модели Мура (Moore
modet), которая уже рассматривалась ранее на примере триггеров
(см. главу 4, разделы 4.3.2 и 4.3.3). Обобщенная структура после-
довательной схемы данного типа показана на рис. 5.2.
Начинать проектирование синхронной последовательной
схемы можно как с использованием модели Мили, так и с ис-
пользованием модели Мура, но в первом случае изменения
5.1. Модель синхронной последовательной схемы
197
входных сигналов могут влиять на состояние выходов непо-
средственно в момент изменения, а не синхронно с приходом
тактового сигнала. Таким образом, в этом аспекте поведение
моделей может отличаться. Счетчики по своей сути есть схемы,
поведение которых описывается моделью Мура, так как у них
выходами служат непосредственно выходы триггеров, т.е. Z=y.
Выходы
сигнал
Рис. 5.2. Модель синхронной последовательной схемы (модель Мура)
Задание для самопроверки 5.1
Сколько нужно триггеров для построения конечного автомата с сорока восе-
мью возможными состояниями?
5.2. Проектирование синхронных
последовательных схем
При использовании модели конечного автомата (все равно —
модели Мили или Мура) есть два набора функций, которые не-
обходимо определить: функции переменных следующих состоя-
ний, Хк_,... Yo, и функции выходных состояний, Z,,^] ... Zq. Давайте
попробуем выработать универсальную процедуру получения
этих функций на примерах и начнем, скажем, с модели Мура.
198
Гпава 5. Проектирование последовательных схем
5.2.1. Задача 1: счетчик с двумя произвольными
счетными последовательностями
Предположим, требуется создать синхронный счетчик, с вы-
ходов которого в зависимости от состояния входа управления С
должна сниматься одна из двух заданных повторяющихся по-
следовательностей. Пусть при С=0 формируется последова-
тельность 00, 01, 11, а при С= 1 — последовательность 00, 11, 01.
Диаграмма состояний
Обычно первым шагом является построение диаграммы со-
стояний на основе технического задания. В данном случае под-
ходит модель Мура, поскольку выходами схемы служат выходы
триггеров (переменные состояний). Диаграмма состояний мо-
дели Мура для рассматриваемой задачи приведена на рис. 5.3.
В последовательности имеются всего три состояния, однако при
включении может возникнуть и четвертое, поэтому в диаграмме
состояний необходимо отобразить, что оно должно перейти в со-
стояние 1. Номера состояний в показанной на рисунке диа-
грамме обозначаются цифрами в кружках; следующие цифры
показывают соответствующие значения на выходах схемы; над
каждой дугой стоят значения сигнала управления С, необходи-
мые для перехода из одного состояния в другое. В данном слу-
чае номера состояний были выбраны произвольно, но позже
будет рассмотрен формальный метод их выбора и нумерации.
Рис. 5.3. Диаграмма состояний модели
Мура для счетчика
Таблица (переходов)состояний
Таблица состояний строится на основе диаграммы состоя-
ний (табл. 5.1). (Правильней эту таблицу называть таблицей
переходов состояний, поскольку в ней отображены именно
5.2. Проектирование синхронных последовательных схем
199
переходы между состояниями.) Для четырех возможных со-
стояний, 1, 2, 3 и 4, необходимо иметь 2 триггера с выходными
сигналами у2 и у, (это и есть переменные текущих состояний).
Таблица 5.1. Таблица состояний для задачи со счетчиком
Текущее состояние Следующее состояние С = 0 С= 1
1 2 3
2 3 1
3 1 2
4 1 1
Назначение состояниям значений переменных
Для каждого состояния необходимо выбрать значения пере-
менных текущих состояний. В целях удобства присвоим состоя-
нию 1 комбинацию значений переменных уу/, = 00, для состояния
2 — У2У1 ~ 01, Для состояния 3 — У2У1 = 11 и для состояния
4 — У2У\ = 10, поскольку это соответствует и требуемым вы-
ходным состояниям. Результаты назначения каждому состоя-
нию определенных значений переменных удобно записать
в виде так называемой таблицы назначенных состояний
(assigned state table) (табл. 5.2).
Таблица 5.2. Таблица назначенных состояний для задачи со счетчиком
Текущее состояние Следующее состояние У2¥у
УгУ/ С = 0 С = 1
00 01 11
01 11 00
11 00 01
10 00 00
Входные функции триггеров
Давайте, как и в модели на рис. 5.2, будем использовать 21-
триггеры. Требуемые входные сигналы триггеров Y2Y\ могут
быть определены из таблицы назначенных состояний. Для
200
Гпава 5. Проектирование последовательных схем
D-триггеров входные значения У представляют собой значения
состояний на выходах у, которые должны установиться после
прихода очередного импульса тактового сигнала. (По сути,
в данном случае используется таблица возбуждения £)-триггера,
которая приводилась в главе 4, поэтому, если бы счетчик стро-
ился на ./Х'-триггерах, то использовалась бы таблица возбужде-
ния JX'-триггера. Вариант с использованием УАГ-триггеров ос-
тавлен в качестве упражнения для самостоятельной работы).
Карты Карно для обеих входных функций показаны на
рис. 5.4. Функции имеют следующий вид:
у2 = УгУ^ + У1У\С
= УгС + У1У\С+ y2ytC
Поскольку выбрана клетка угуС> а не обведенная пунк-
тирной линией группа, минимизация функции KJ неполная.
Член у у С выбран потому, что он встречается и в выражении
для функции У2, а значит, для его получения можно исполь-
зовать один и тот же вентиль. Конечный вид логической схе-
мы счетчика показан на рис. 5.5.
Рис. 5.4. Карты Карно входных функций D-триггеров
Задание для самопроверки 5.2
Пользуясь рис. 5.4, найдите альтернативные выражения для входных функций
О-триггеров с другим общим членом.
5.2. Проектирование синхронных последовательных схем
201
Выходы
Вход
С
сигнал
Рис. 5.5. Конечный вид схема счетчика
5.2.2. Задача 2: детектор последовательности
В предыдущей задаче переменными состояний служили вы-
ходные сигналы схемы. Теперь построим синхронную последо-
вательную схему, выходные сигналы которой представляют собой
функцию этих переменных, а кодирование ее состояний не столь
очевидно вытекает из условий задачи. (Для счетчика, например,
совершенно ясно, что переменные состояний должны следовать
заданной в условии счетной последовательности.)
Давайте рассмотрим синхронную последовательную схему,
которая бы детектировала определенную кодовую последова-
тельность, поступающую через единственный вход данных.
Логическое значение на этом входе может меняться после каж-
дого тактового импульса. Схема имеет один выход, состояние
которого равно 1 только тогда, когда на входе появляется за-
данная последовательность. Обобщенный вид такой схемы по-
казан на рис. 5.6, где, кроме входа тактовых импульсов, имеется
вход данных х и выход данных Z. Предположим, нужно опреде-
лить наличие на входе кодовой последовательности 0110011,
причем состояние на выходе Z должно устанавливаться в 1 при
появлении на входе последнего бита последовательности. Схе-
мы данного типа могут применяться для решения разных задач,
например для обнаружения синхронизирующей комбинации
битов, записываемой на магнитный диск до или после данных,
или для детектирования синхронизирующих кодов в системах
передачи данных. Детекторы двоичных последовательностей
можно встретить и в других устройствах. Например, комбина-
ционный электронный замок открывает дверь только при вве-
дении заданной последовательности чисел. Хотя при разработке
202
Глава 5. Проектирование последовательных схем
такого замка на основе последовательной комбинационной
схемы потребуется еще и сигнал синхронизации. (Вообще-то,
комбинационные замки представляют собой асинхронные уст-
ройства, поскольку сигналы на их входах могут изменяться
и в отсутствие тактового сигнала, так что обычно они и проек-
тируются как асинхронные устройства.)
Вход данных
х ----
Синхронная
последовательная
схема
Выход
Z
Тактовый сигнал
Рис. 5.6. Детектор двоичных последовательностей
Алгоритм проектирования
Можно выделить следующие шаги проектирования элек-
тронной схемы.
1. Построение диаграммы состояний.
2. Построение таблицы состояний.
3. Присвоение состояниям схемы комбинаций значений
переменных состояния.
4. Построение таблицы назначенных состояний.
5. Получение входных функций триггеров (с помощью
карт Карно).
6. Получение по картам Карно выходных функций.
7. Построение логической схемы.
Диаграмма состояний
Диаграмма состояний строится, исходя из условий задачи.
Как показано на рис. 5.7, в рассматриваемом случае последова-
тельность реализуется за восемь шагов, что предполагает нали-
чие восьми состояний. Диаграмма является диаграммой состоя-
ний модели Мура, в которой каждому состоянию соответствует
конкретное значение выходного сигнала. Начальным состояни-
ем является состояние 1, в котором на выходе присутствует
5.2. Проектирование синхронных последовательных схем
203
значение 0. Схема изменяет свое состояние, если на входе по-
является 0 (точнее, если логический 0 имеется на входе во вре-
мя прихода тактового импульса). Это первый 0 последователь-
ности, который требуется обнаружить, и при его появлении
схема переходит в состояние 2. При этом на выходе сохраняет-
ся значение 0. Поступление следующих значений входной по-
следовательности приводит к переходу схемы в состояния 3, 4,
5, 6, 7 и, наконец, 8. И только в последнем, восьмом состоя-
нии, после приема последнего бита заданной последовательно-
сти, на выходе схемы устанавливается значение 1. После этого
следующая 1 возвращает схему в начальное состояние с номером
1. Если же принимается 0, то он может быть первым нулем но-
вой последовательности, поэтому происходит переход в состоя-
ние 2. Все остальные переходы на диаграмме состояний, имею-
щие место до приема последнего бита последовательности, явля-
ются либо переходами в состояние 1, если принимается 1,
либо — в состояние 2, если принимается 0 (который рассматри-
вается в качестве первого 0 последовательности). В целом, если
в условии нет дополнительных ограничений, в качестве воз-
можной последовательности необходимо рассматривать все ча-
стные последовательности битов, которые могут появиться до
приема последнего бита заданной последовательности.
Рис. 5.1. Диаграмма состояний детектора двоичной последовательности
Таблица (переходов) состояний
Таблица переходов состояний приведена в табл. 5.3. Здесь
приведены не только последующие состояния, но и значения
на выходе схемы, соответствующие каждому из текущих со-
стояний. В модели Мура, которая здесь используется, каждому
204
Глава 5. Проектирование последовательных схем
состоянию отвечает связанное с ним выходное значение.
В данном случае на выходе может появиться только одно зна-
чение: 0 или 1. Для определения выходной функции будет ис-
пользоваться столбец выходных состояний, но прежде необхо-
димо назначить состояниям значения переменных.
Таблица 5.3. Таблица состояний детектора последовательности
Текущее состояние Следующее состояние Выходное состояние
х=0 х=1 Z
2 2 3 0
3 2 4 0
4 5 1 0
5 6 1 0
6 2 7 0
7 2 8 0
8 2 1 1
Назначение состояниям значений переменных
Для описания восьми различных состояний требуются три
переменных состояния, скажем, УзУзУУ Следующим шагом явля-
ется выбор и присвоение каждому из состояний определенных
значений переменных. Назначение значений переменных может
быть произвольным. К примеру, пусть состояние с номером 1
описывается комбинацией 001, состояние 2 — 010, состояние 3 —
ОН, состояние 4 — 100, состояние 5 — 101, состояние 6 — НО,
состояние 7— 111 и состояние 8 — 000. Существует огромное
количество возможных вариантов такого присвоения значений
переменным, и каждый из них приводит к получению своей вы-
ходной функции и последовательности смены состояний. При-
сваивать значения переменным следует так, чтобы выходные
функции имели наиболее простую форму, но, к сожалению, об-
щего способа выбора оптимального варианта не существует. Бо-
лее простую функцию можно получить, если на карте Карно
имеются прилегающие ячейки с единицами, а этого уже в той
или иной степени можно добиться. Назовем первый пункт алго-
ритма получения простейшей функции “правилом № 1”.
5.2. Проектирование синхронных последовательных схем
205
Правило № 1. Состояниям, которые переходят в одно и то же следую-
щее состояние, нужно назначать коды, отличающиеся значением только
одной переменной.
На рис. 5.8 (а) показан пример применения правила 1 для
формирования обозначения двух состояний, не изменяющихся
при переходе. Если первое правило применить не удается, то
существует “правило № 2”.
Правило № 2. Следующим состояниям, в которые может перехо-
дить текущее, назначаются коды, отличающиеся значением только од-
ной переменной.
(а) Правило № 1: При переходе в
одинаковое следующее состояние
назначаются коды, отличающиеся
значением только одной
переменной.
(б) Правило № 2: Следующим
состояниям, в которые может
переходить текущее состояние,
следует назначать коды,
отличающиеся значением только
одной переменной.
(в) Состояниям с одинаковым
значением на выходе следует
назначать коды, отличающиеся
значением только одной
переменной.
Значение
Код: ООО 001
Рис. 5.8. Назначение переменных трем различным состояниям
Правило № 2 продемонстрировано на рис. 5.8 (б). Нако-
нец, “правило № 3”, которого следует придерживаться в тех
206
Глава 5. Проектирование последовательных схем
случаях, когда нельзя применить два предыдущих, можно
сформулировать так.
Правило № 3. Состояниям с одинаковым значением на выходе (с одинако-
выми входными значениями) следует назначать коды, отличающиеся значе-
нием только одной переменной.
Правило № 3, продемонстрированное на рис. 5.8 (в), служит
для получения наиболее простой выходной функции. Правила
№ 1 и 2 позволяют получить простейшие функции следующего
состояния. Однако все эти правила представляют собой лишь
рекомендации и не могут гарантировать получение схемы с ми-
нимальным количеством вентилей.
Код, называемый кодом Грея, характеризуется тем, что все
его соседние кодовые комбинации отличаются значением толь-
ко одного бита. Код Грея, например, используется при обозна-
чении ячеек карт Карно. Для трех переменных комбинации ко-
да Грея выглядят следующим образом: ООО, 001, 011, 010, НО,
111, 101, 100. Поэтому код Грея пригоден для кодирования по-
следовательности состояний, в которой одно состояние перехо-
дит в другое. Для рассматриваемой задачи, применив правило
№ 1 для состояний 4, 5 и 8 (все они переходят в состояние 1)
и состояний 3, 6 и 7 (они также переходят в одно и то же со-
стояние 2), можно сделать следующие назначения:
Состояние 1 = 000
Состояние 4 = 001
Состояние 5 = 010
Состояние 8 = 100
Состояние 2=111
Состояние 3 = 101
Состояние 6=110
Состояние 7 = 011
Присвоение состоянию 1 кода 000 облегчает инициализацию
триггеров в этом состоянии. (Хотя на представленной дальше
схеме это не показано, предполагается, что все триггеры имеют
входы сброса, которые могут быть использованы для установки
в состояние 000.) Из состояния 8 возможны переходы либо
в состояние 1, либо в состояние 2, но в данном случае прекрас-
но подходит вариант с переходом только в состояние 1.
(Возможность других (неэквивалентных) назначений или ис-
пользование других правил для получения более удобного на-
значения переменных предлагается изучить самостоятельно.)
Таблица назначенных состояний приведена в табл. 5.4.
5.2. Проектирование синхронных последовательных схем
207
Таблица 5.4. Таблица назначенных состояний детектора
последовательности
Текущее состояние УзУзУ/ Следующее состояние х = 0 х= 1 Значение на выходе Z
ООО 111 000 0
111 111 101 0
101 111 001 0
001 010 000 0
010 110 000 0
110 111 011 0
011 111 100 0
100 111 000 1
Входные функции триггеров
Входные функции трех триггеров схемы можно получить,
отображая переменные следующих состояний из таблицы
назначенных состояний на карте Карно (рис. 5.9) (предпо-
лагается, что используются Т)-триггеры).
Рис. 5.9. Входные функции триггеров детектора двоичной последовательности
Процедура отображения очевидна: значение каждого сле-
дующего состояния просто вносится в карту. В результате полу-
чаются функции следующего вида:
У3 = ху,+хуз + у2у]
208
Глава 5. Проектирование последовательных схем
= Х + УзЛ»
= УзУ + У>УгУ\ + ху2у{+ху2у{
Обратите внимание, что для функции У, выбрано решение,
которое позволяет использовать общий вентиль для формиро-
вания члена у у2у функции У2.
Задание для самопроверки 5.3
Какой вид имеет максимально минимизированная функция У]?
Выходная функция
Вид выходной функции получается непосредственно из
столбца выходных значений таблицы состояний после отобра-
жения его на карту Карно (рис. 5.10), в результате получается
следующее выражение:
z = y3y2y1
Рис. 5.10. Выходная функция Z
Логическая схема
Наконец, пользуясь полученными выше функциями, можно
нарисовать конечную схему (рис. 5.11).
Задание для самопроверки 5.4
Имеются четыре состояния: 1, 2, 3 и 4, для которых известно, что состояние
1 переходит в состояние 2, состояние 2 переходит в состояние 3, состояние 3
переходит в состояние 4 и состояние 4 переходит в состояние 1. Покажите,
как двумя различными способами назначить значения переменных состояний
в предположении, что первому состоянию присваивается код 00.
5.2. Проектирование синхронных последовательных схем
209
Вход
Выходы
сигнал
Рис. 5.11. Логическая схема детектора двоичной последовательности
5.2.3. Использование JK-триггеров
Вместо /^-триггеров можно использовать JA'-триггеры. Для
получения из таблицы состояний функции следующих состоя-
ний воспользуемся уже знакомой таблицей возбуждения, при-
веденной в главе 4, раздел 4.5.1. Как было сказано, для JK-
триггеров можно получить функции более простого вида, чем
для D-триггеров, но, поскольку входных сигналов и, следова-
тельно, входных функций в два раза больше, то логика может
быть более сложной.
5.2.4. Проектирование на основе модели Мили
Вспомним, что модель состояний Мили отличается от моде-
ли Мура тем, что каждому состоянию не обязательно соответст-
вует один набор выходных значений. Сигналы на выходе зави-
сят не только от текущего состояния, но и от сигналов на вхо-
дах, приводящих в данное состояние. На диаграмме состояний
модели Мили над дугами, направленными к состоянию, указы-
ваются как выходные, так и входные сигналы, которые приво-
дят к переходу в данное состояние. Часто для одной и той же
задачи диаграмма состояний модели Мили имеет меньше со-
стояний, чем диаграмма состояний модели Мура, поэтому пе-
ременных состояний и триггеров состояний меньше. Однако
выходные функции могут иметь более сложную форму, по-
скольку в них используются не только переменные состояний,
но и входные переменные. Существеннее то, что в случае из-
менения входных сигналов в промежутках между поступлением
тактовых импульсов могут изменяться и значения на выходах.
2/0
Глава 5. Проектирование последовательных схем
В зависимости от задачи это может существенно влиять
(но может и не влиять) на схемное решение системы в целом.
Давайте рассмотрим решение той же задачи с детектором
последовательности, который должен распознавать последова-
тельную комбинацию 0110011, но уже с использованием моде-
ли Мили. Алгоритм действий такой же.
1. Построение диаграммы состояний.
2. Построение таблицы состояний.
3. Присвоение состояниям схемы комбинаций значений
переменных состояния.
4. Построение таблицы назначенных состояний.
5. Получение входных функций триггеров (с помощью
карт Карно).
6. Получение по картам Карно выходных функций.
7. Построение логической схемы.
Диаграмма состояний модели Мили
Диаграмма состояний модели Мили показана на рис. 5.12.
Разница между этой диаграммой и диаграммой модели Мура со-
стоит в том, что состояние 8 здесь отсутствует как таковое,
а переход из состояния 7 в состояние 8 по приходу последнего
бита последовательности заменен переходом из состояния 7 пря-
мо в состояние 1. Теперь схема в состоянии 1 может иметь одно
из двух выходных значений: Z=0, если последовательность не
завершена, и Z= 1, если последовательность завершилась.
Номер
состояния
Рис. 5.12. Диаграмма состояний модели Мили для детектора двоичной последовательности
5.2. Проектирование синхронных последовательных схем
211
Таблица состояний модели Мили
Новая таблица состояний приведена в табл. 5.5. Обратите
внимание, что выходные значения связываются со значениями
следующих состояний для каждого входного значения, а не те-
кущих состояний.
Таблица 5.5. Таблица состояний модели Мили для детектора
последовательности
Текущее состояние Следующее состояние Следующее выходное состояние, Z
х = 0 х= 1 х = 0 х= 1
1 2 1 0 0
2 2 3 0 0
3 2 4 0 0
4 5 1 0 0
5 6 1 0 0
6 2 7 0 0
7 2 1 0 1
Таблица назначенных состояний модели Мили
Хотя количество состояний в диаграмме состояний, а с ним
и число строк таблицы, уменьшились с 8 до 7, все равно для
описания всех состояний требуются три переменные. При ис-
пользовании тех же назначений, что и для модели Мура, получа-
ется таблица назначенных состояний, приведенная в табл. 5.6.
Таблица 5.6. Таблица назначенных состояний для задачи с детектором
последовательности
Текущее состояние УтУгУ/ Следующее состояние, Ч.Ж Значение выходной функции, Z
х = 0 х = 1 х = 0 х= 1
ООО 111 ООО 0 0
111 111 101 0 0
101 111 001 0 0
212
Гпава 5. Проектирование последовательных схем
Окончание табл. 5.6
Текущее состояние Следующее состояние, Y.(Y2Y; Значение выходной функции, Z
001 010 000 0 0
010 110 000 0 0
110 111 011 0 0
011 111 000 0 1
Входные функции триггеров
Функции следующих состояний можно получить из табли-
цы назначенных состояний. Одна комбинация переменных,
jyw = ЮО не используется, поэтому на карте Карно соответ-
ствующее ей состояние обозначено как условно произвольное.
(Предполагается, что при включении все триггеры схемы
можно обнулить общим сигналом сброса до состояния ООО,
поэтому состояние у3у2У1 = ЮО никогда не появится.) Карты
Карно входных функций приведены на рис. 5.13 (включая
общие группы). В результате получаются выражения, очень
похожие на полученные ранее:
У3=%у,+ху3 + у3у2у1+ту2у|
Рис. 5.13. Входные функции для детектора двоичной последовательности, полученные
с использованием модели Мили
5.2. Проектирование синхронных последовательных схем
213
Выходная функция
Выходная функция является функцией переменной х и пе-
ременных текущих состояний У3У2У1, которые можно взять из
таблицы назначенных состояний и отобразить на карте Карно,
как показано на рис. 5.14. Отсюда получим:
Z = xy3y2y,
Структура схемы следует из всех перечисленных уравнений.
Задание для самопроверки 5.5
Изменится ли (если изменится) что-либо на выходе Z, если переменная х поме-
няет свое значение из 1 в 0, когда выход будет находиться в состоянии Z = О?
5.2.5. Минимизация количества состояний
Количество переменных и, соответственно, количество
триггеров, определяется количеством состояний диаграммы со-
стояний. Если количество состояний лежит в интервале от 2n~' + 1
до 2П, то требуется п переменных состояний и, соответственно,
п триггеров (при условии кодирования всех состояний). Понят-
но, что хотелось бы уменьшить количество состояний до мини-
мума, поскольку это упростит схему устройства. В простых слу-
чаях диаграмма состояний, полученная на основе технического
задания, как правило, уже содержит минимальное число со-
стояний, но для более сложных задач диаграммы состояний,
построенные “на глазок”, часто могут получаться значительно
сложнее, чем того требует решение. Возможность избежать
этого зависит от навыков и умения разработчика. В любом
случае, составленная диаграмма не должна содержать ошибок,
2/4
Глава 5. Проектирование последовательных схем
и часто ее правильность легче определить как раз по диаграмме
с избыточным числом состояний.
В данном разделе будут рассмотрены способы уменьшения
количества состояний схемы. Идентичные состояния (identical
states), то есть состояния с одним и тем же следующим состоя-
нием и теми же выходными сигналами, явно могут быть объе-
динены в одно состояние. (Хотя такие состояния встречаются
достаточно редко, но они есть в примере, приведенном в разде-
ле 5.2.7.) После этого необходимо выявить состояния, которые
можно свести к одному, если в схеме уже имеются другие такие
же состояния или были сделаны таковыми. Подобные состоя-
ния называются эквивалентными (equivalent states).
Эквивалентные состояния
Эквивалентные состояния прежде всего необходимо распо-
знать . Два состояния называются эквивалентными и, следова-
тельно, могут быть заменены одним состоянием, если выпол-
няются следующие условия:
• выходные сигналы1, связанные с этими двумя состоя-
ниями, одинаковы;
• соответствующие следующие состояния также одинаковы
или эквивалентны.
Если эти условия удовлетворяются, то такие два состояния
можно объединить в одно, присвоив ему новое имя. Первое ог-
раничение сразу исключает из рассмотрения пары состояний,
выходные значения в которых отличаются. Такие состояния на-
зываются несовместимыми по выходу (output incompatible). Для
объединения состояния обязательно должны быть совместимы-
ми по выходу. После того как исключены пары состояний, не-
совместимые по выходу, среди оставшихся можно начать поиск
тех, которые удовлетворяют второму условию эквивалентности.
Рассмотрим, например, таблицу состояний модели Мура,
показанную в табл. 5.7. Как видно из этой таблицы, схема име-
ет два входа, X] и х2, и один выход, Z Формально идентичных
состояний нет. Состояния 3 и 7 имеют одинаковые выходные
значения, поэтому совместимы друг с другом по выходу, но при
этом они несовместимы по выходу со всеми остальными со-
стояниями, 1, 2, 3, 4, 5 и 6. Зато состояния 1, 2, 3, 4, 5 и 6 совмес-
' Текущие выходные состояния для модели Мура и следующие выход-
ные состояния для модели Мили.
5.2. Проектирование синхронных последовательных схем
215
тимы по выходу между собой. Таким образом, в качестве по-
тенциально эквивалентных состояний можно рассматривать пару
состояний 3 и 7 и пары, образуемые состояниями 1, 2, 4, 5 и 6.
Таблица 5.7. Таблица состояний модели Мура с эквивалентными состояниями
Текущее состояние Следующее состояние, х,х2 Выходное значение, Z
00 01 11 10
1 5 3 2 1 0
2 5 3 1 4 0
3 3 4 4 5 1
4 5 3 2 2 0
5 6 7 1 1 0
6 3 3 1 7 0
7 7 1 1 5 1
“Потенциально эквивалентные” состояния можно записать
в одну строку со следующими состояниями, которые, исходя из
таблицы, должны быть эквивалентными (табл. 5.8). Требуемые эк-
вивалентные пары выбираются непосредственно из таблицы со-
стояний. Например, для того, чтобы при %1х2 = 10 были эквива-
лентны состояния 1 и 2, состояние 1 должно быть эквивалентно
состоянию 4. (Остальные записи либо совпадают, либо совпадут,
если будет 1 = 2.) Продолжая работу с таблицей подобным обра-
зом, можно получить список пар состояний, которые должны
быть эквивалентны друг другу, чтобы “потен-циально” эквива-
лентные пары стали действительно эквивалентными. Иногда тре-
буемые пары несовместимы по выходу. Лучше сделать отметки
напротив таких пар в последнем столбце таблицы, потому что та-
кие “потенциально” эквивалентные пары не могут быть эквива-
лентными. После этого таблица просматривается еще раз на пред-
мет выяснения, нет ли в списке этих вновь выявленных несовмес-
тимых по выходу пар. Если — да, то они снова помечаются как
несовместимые. Этот процесс повторяется до тех пор, пока в таб-
лице не останутся одни только совместимые по выходу пары2.
В рассматриваемом случае совместимы по выходу и эквивалентны
2 Процедура нахождения эквивалентных пар может быть упрощена
путем использования так называемой импликационной диаграммы
(implication chart) (подробнее см. в работе Каца — Katz, 1994).
216
Глава 5. Проектирование последовательных схем
пары (1, 2), (2, 4), (1, 4) и (3, 7). Состояния 5 и 6, не объединен-
ные ни с каким другим, остаются. Поскольку 1=2, 2 = 4
и 1 = 4, то можно сказать, что 1=2 = 4. (Даже если бы оказа-
лось, что 1=2 и 2 = 4, то все равно можно было бы вывести,
что 1=2 = 4; однако это может быть не так, если в таблице
присутствуют условно произвольные состояния, см. ниже.)
Остались четыре состояния, которые можно переименовать
в А (для состояний 1, 2 и 4), В (для состояний 3 и 7), С (для состоя-
ния 5) и D (для состояния 6). Если выполнить эти подстановки,
то получается минимизированная таблица состояний, показан-
ная в табл. 5.9. Теперь можно проектировать схему, используя
эту таблицу, которая требует наличия только двух переменных
состояний, а не трех.
Таблица 5.8. Пары эквивалентных состояний из табл. 5.7
Потенциально эквивалентные пары Требуемая эквивалентность пар Несовместимость по выходу
1,2 (1,2), (1,4)
1,4 (1,2)
1,5 (5, 6), (3, 7), (1,2) X
1,6 (3, 5), (1,2), (1,7) X
2,4 (1,2)
2,5 (5, 6), (3,7), (1, 4) X
2,6 (3, 5), (4, 7) X
3,7 (3,7), (1,4)
4,5 (5, 6), (3,7), (1,2) X
4,6 (3,5), (1,2), (2, 7/) X
5,6 (3,6), (3,7), (1,7) X
Таблица 5.9. Минимизированная таблица состояний модели Мура
Текущее состояние Следующее состояние, хук? Выходное значение, Z
00 01 11 10
~А С В А А О
В В А А С 1
С D В А А О
D В В А В О
5.2. Проектирование синхронных последовательных схем
217
Задание для самопроверки 5.6
Составьте соответствующую таблицу назначенных состояний для схемы, опи-
сываемой табл. 5.9.
Минимизация таблиц состояний модели Мили
Для минимизации таблиц состояний модели Мили исполь-
зуется та же процедура, что и в случае модели Мура. Единст-
венное отличие состоит в том, что для совместимости по выхо-
ду состояний необходимо, чтобы выходные значения их сле-
дующих состояний совпадали во всех столбцах.
5.2.6. Диаграммы состояний с использованием
выражений перехода
Если переход из одного состояния в другое задастся несколь-
кими входными переменными, как это имеет место в сложных
цифровых системах, то описанные рапсе диаграммы состояний
становятся слишком громоздкими и неудобными. Возьмем для
примера схему с тремя отдельными входами — а, b и с. Предпо-
ложим, что переход из состояния 1 в состояние 2 осуществляется
при abc = 001 иначе ничего не происходит. Если использовать
прежнюю систему обозначений, то диаграмма состояний выгля-
дела бы так, как показано па рис. 5.15(a). Однако есть более
удобный вид записи, при котором условие, необходимое для
осуществления или отсутствия перехода, просто указывается в
виде так называемых выражений перехода (transition expressions)
(рис. 5.15(6)). Каждое выражение перехода может быть сведено к
простейшему виду или записано в любой корректной с точки
зрения булевой алгебры форме. Например, выражение abc мож-
но записать и в виде a+b + 'с- При использовании выражений
перехода очень важно, чтобы па диаграмме учитывались все ком-
бинации значений переменных. Кроме того, каждая конкретная
комбинации значений переменных не должна вызывать более
одного перехода, поскольку это породит неоднозначность.
На рис. 5.16 показан пример диаграммы состояний для JK-
триггера с использованием других обозначений.
Задание для самопроверки 5.7
Нарисуйте диаграмму состояний D-триггера с использованием выражений
перехода.
218
Гпава 5. Проектирование последовательных
abc
ООО
(а) Обозначение с использованием двоичных кодов
Если записать в более
удобной форме: а + Ь + с (см. текст)
(б) Диаграмма состояний, использующая выражения переходов
Рис. 5. /5. Обозначения на диаграммах состояний
JK
JK
Рис. 5.16. Диаграмма состояний модели Мура JK-триггера с ис-
пользованием выражений перехода
Пример: проектирование генератора импульсов
переменной длительности
Для того чтобы па примере показать использование диа-
грамм состояния с выражениями переходов, рассмотрим сле-
дующую практическую задачу. Пусть требуется разработать
синхронную последовательную схему с двумя входами (х2 и х,)
и одним выходом (Z). Сигнал на выходе должен принимать
значение 1 и оставаться таким на протяжении стольких перио-
дов тактовых сигналов, количество которых задается сигналами
5.2. Проектирование синхронных последовательных схем
219
на обоих входах. Например, если x2Xt = 01, то Z= 1, и в этом со-
стоянии выход остается па протяжении еще одного периода
тактовых импульсов после изменения входных сигналов. Если
х2Х] = 10, то Z= 1 в течение двух периодов тактовых сигналов,
и если x2Xi = Ю, то Z= 1 целых три периода. При изменении же
входных состояний в момент, когда выходной сигнал находится
в единичном состоянии, выход немедленно сбрасывается в 0.
Такое устройство представляет собой один из типов генерато-
ров импульсов и естественным образом описывается с помо-
щью диаграммы состояний модели Мура, так как можно опи-
сать состояния, в которых на выходе должна наблюдаться 1.
Необходимо описать четыре состояния:
состояние 1 — начальное состояние;
состояние 2 — на выходе 1 в течение первого периода
тактовых импульсов;
состояние 3 — па выходе 1 в течение второго периода
тактовых импульсов;
состояние 4 — на выходе 1 в течение третьего периода
тактовых импульсов.
Диаграмма состояний с использованием выражений перехо-
дов показана на рис. 5.17. Обратите внимание, что состояние 4
переходит в состояние 1 независимо от условий па входах. Все
комбинации переменных х2хн необходимые для того или иного
перехода, записаны в виде дизъюнктивных выражений перехо-
дов, что уменьшает вероятность случайно не учесть одну из
входных комбинаций. Продолжив процесс проектирования,
можно построить таблицу состояний, показанную в табл. 5.10.
Рис. 5.17 Диаграмма состояний, построенная с использованием выражений переходов
220
Глава 5. Проектирование последовательных схем
Таблица 5.10. Таблица состояний для генератора импульсов
Текущее состояние Следующее состояние, х,х2 Выходное значение, Z
00 01 11 10
1 1 2 2 2 0
2 1 1 3 3 1
3 1 1 4 1 1
4 1 1 1 1 1
Попробуем минимизировать таблицу состояний. Результат
выполнения этой процедуры показан в табл. 5.II. Обратите
внимание, что состояние I несовместимо по выходу с осталь-
ными тремя состояниями, поэтому минимизация невозможна.
Таблица 5.11. Эквивалентные пары состояний, полученные из табл. 5.10
Потенциально эквивалентные пары Требуемые эквивалентные пары Несовместимость по выходу
2,3 (1,3), (3,4) X
2,4 (1,3) X
3,4 (1,4) X
Следующим шагом назначаются переменные состояний
с использованием двух переменных, в результате чего получает-
ся такое представление: состояние I = 00, состояние 2 = 01, со-
стояние 3 = И и состояние 4 = 10. (Из состояний 2, 3 и 4 воз-
можен переход в состояние 1, поэтому правило I 1 можно
применить к состояниям 2, 3 и 4.) Эта процедура дает таблицу
назначенных состояний, показанную в табл. 5.12.
Таблица 5.12. Таблица состояний для генератора импульсов
Текущее состояние У?У/ Следующее состояние, Y,Y; х2х, Выходное значение, Z
00 01 11 10
00 00 01 01 01 0
01 00 00 11 11 1
11 00 00 10 00 1
10 00 00 00 00 1
5.2. Проектирование синхронных последовательных схем
221
Отсюда уже можно получить входные функции триггеров
и выходную функцию схемы (рис. 5.18 для реализации на
D- триггерах).
= УгУЛ + >1*2*1
I7! = + У1Х2
Z = x2xt
(а) Входные функции триггеров
Инверсная функция
(б) Выходная функция, Z
Рис. 5.18. Входные функции триггеров и выходные функции для генератора
импульсов
Инверсная функция выбрана специально, для чего ис-
пользовалась клетка карты Карно с 0; в этом случае для реа-
лизации выходной функции можно использовать всего один
элемент И-НЕ, Окон-чательный вид схемы генератора им-
пульсов показан на рис. 5.19.
222
Глава 5. Проектирование последовательных схем
Входы
xi ----
Выход
X,
У1
Х2
л
Х2
*1
Рис. 5.19. Схема генератора импульсов
Таблица состояний с использованием выражений
переходов
При использовании переходных выражений, описывающих из-
менения состояний, удобно пользоваться таблицей состояний,
в которой особым образом перечисляются все выражения перехо-
дов, как показано в табл. 5.13 для задачи с генератором импульсов.
Выражения переходов располагаются в этой таблице по вертикали.
Таблица 5.13. Таблица состояний с перечислением выражений переходов
Текущее состояние Выражения переходов Следующее состояние Y2Y; Выходное значение, Z
УгУ/
1 00 V, 1 00 0
2 01
2 01 Х,Х| +х2х, 1 00 1
х2х[ + х2х. 3 1 1
3 11 х2х. 1 00 1
х2х, + x2xt + х2х, 4 1 0
4 1 0 1 1 00 1
5.2. Проектирование синхронных последовательных схем
223
Из такой таблицы состояний можно непосредственно запи-
сать “неминимизированные” уравнения следующих состояний,
выбирая записи, соответствующие условию равенства 1 каждой
переменной Y, и используя следующее равенство:
Y- = ^{(текущее состояние, при котором У" = 1) • ( выражение перехода)
т.е.:
^2 = (У2У1)(х2^| + %2х1) + (у2у|)(х2х1)
У, = (Ь У1)(.Г2Л, + Х2Х| +х2л-|) + (у2.у|)(х2Т| +х2х,);
Эти выражения и служат входными функциями для тригге-
ров Р-типа. Упростив их, можно получить тот же результат.
5.2.7. Неполно заданные системы
Концепция неполно заданных систем в схемах комбинаци-
онной логики уже рассматривалась в главе 3 (раздел 3.4.2).
В таких системах используются так называемые условно произ-
вольные состояния, которые показывают, что существуют неоп-
ределенные значения, каждое из которых в процессе миними-
зации можно принять равным как 0, так и 1.
Проектирование неполно заданных систем в общих чертах
повторяет описанное ранее, за исключением только того, что
теперь при минимизации таблицы состояний условно произ-
вольным состояниям можно приписывать такие значения, ко-
торые позволят уменьшить количество состояний. Это ана-
логично тому, как условно произвольные состояния в картах
Карно позволяют получить более простое решение. Если
в системе есть условно произвольные состояния, то они поя-
вятся и в таблице состояний в виде записей, помеченных
значком “X”. Два состояния могут быть объединены при ус-
ловии, что они совместимы по выходу, и по выходу совмес-
тимы эквивалентные пары. При появлении знака “X” его
можно рассматривать как любой номер состояния и объеди-
нять с другими состояниями. Однако, как и в картах Карно,
знаку X может быть присвоено только одно значение. При
использовании выражений переходов состояния, выражения,
записанные в виде набора функций относительно какого-то
состояния, не обязательно должны накрывать все возможные
комбинации переменных. Некоторые комбинации значений
переменных могут быть условно произвольными.
224
Гпава 5. Проектирование последовательных схем
Задача: проектирование интерфейсной логики
Рассмотрим задачу разработки некоторой интерфейсной схе-
мы компьютера. Пусть требуется спроектировать схему, па кото-
рую поступают два входных сигнала: RD (от read — читать) и WR
(от write — записать) и которая должна на выходе /формировать
импульс длительностью два периода тактовых сигналов, если
RD = 0, или три периода тактовых сигналов, если WR = 0- Из-
вестно, что одновременно эти два сигнала равны 0 быть не могут
(т.е. чтение и запись не могут осуществляться одновременно). Та-
ким образом, ситуация RD = 0 и WR = 0 записывается в виде ус-
ловно произвольного состояния. Обратите внимание, что в данной
задаче на входы приходят сигналы с активным низким уровнем
напряжения, т.е. действие происходит при поступлении на вход
логического 0, а не 1. (В интерфейсных системах компьютеров
сигналы управления довольно часто имеют активный низкий уро-
вень. При таком обозначении можно считать, что вызывать дей-
ствие будут и прямые сигналы RD, и WR с активным уровнем 1.)
Эта задача чем-то напоминает создание генератора импуль-
сов из предыдущего раздела, но отличается в начальных допу-
щениях. Здесь предполагается, что после того как со входов RD
или WR произошла активация выходного импульса, сигналы на
входах могут возвращаться в неактивное состояние (с уровнем
1) до его окончания, т.е. после начала выходного импульса зна-
чения на входах RD и WR условно произвольны. Давайте по-
строим диаграмму состояний модели Мура (рис. 5.20). Для на-
чала это можно сделать интуитивно, чтобы доказать на практи-
ке эффективность алгоритма минимизации диаграммы
состояний. Диаграмма построена с использованием выражений
переходов. На рис. 5.21 изображена та же диаграмма, но с ис-
пользованием булевых значений. Для минимизации количества
состояний удобней пользоваться второй версией диаграммы.
Таблица состояний приведена в табл. 5.14. Рассматривая все
несовместимые между собой пары состояний, можно построить
таблицу, показанную в табл. 5.15. Состояние 1 является несо-
вместимым по выходу со всеми остальными состояниями, и его
можно дальше не рассматривать. Видно, что только одна пара
состояний эквивалентна, а именно: состояния 3 и 6 (факти-
чески они одинаковы), что приводит к диаграмме состояний,
изображенной на рис. 5.22.
5.2. Проектирование синхронных последовательных схем
225
Рис. 5.20. Диаграмма состояний для задачи интерфейсной логики с использованием вы-
ражений переходов
Рис. 5.21. Диаграмма состояний для задачи интерфейсной логики с использованием бу-
левых значений
226
Глава 5. Проектирование последовательных схем
Таблица 5.14. Таблица состояний для задачи с интерфейсной логикой
Текущее состояние Следующее состояние, RD, WR Выходное значение, Z
00 01 11 10
1 1 4 X 2 0
2 3 3 X 3 1
3 1 1 X 1 1
4 5 5 X 5 1
5 6 6 X 6 1
6 1 1 X 1 1
Таблица 5.15. Эквиаалентные пары состояний, полученные из табл. 5.14
Потенциально эквивалентные пары Требуемая эквивалентность пар Несовместимость по выходу
2,3 (1,3) X
2,4 (3,5) X
3,5 (3,6) X
2,6 (1,3) X
3,4 (1,5) X
3,5 (1,6) X
3,6
4,5 (5, 6) X
4,6 (1,5) X
5,6 (1,6) X
Можно сформулировать задачу иначе и получить другую
диаграмму состояний. Например, диаграмма, представленная па
рис. 5.23, также удовлетворяет техническому заданию. Здесь для
того, чтобы показать, что переход имеет место при RD = 1 или
WR = 1, но не в случае равенства 1 обоих сигналов, было ис-
пользовано выражение перехода RD ® IVR (т.е. операция
“исклю-чающее ИЛИ”)- На этой диаграмме также задаются
входные значения для последующих переходов — если эти зна-
чения не остаются неизменными, то импульс прерывается
5.2. Проектирование синхронных последовательных схем
227
раньше времени, как и в задаче с генератором импульсов, опи-
санной выше. Однако на диаграмме, показанной на рис. 5.23,
присутствуют не все возможные комбинации переменных, по-
скольку предполагалось, что есть некоторые комбинации, кото-
рые вообще не могут появиться, в частности комбинация
RD = IVR = 1. На этой диаграмме также показываются в скоб-
ках значения переменных, необходимые для переходов между
состояниями. Возможна ли минимизация этой диаграммы со-
стояний, читателю предлагается выяснить самостоятельно.
Рис. 5.22. Минимизированная диаграмма состояний для задачи интерфейсной логики
Рис. 5.23. Альтернативная диаграмма состояний для задачи интерфейсной логики
(при других допущениях)
В системе, имеющей условно произвольные состояния, если
состояние 1 = состоянию 2 и состояние 2 = состоянию 3, то со-
стояние 1 s состоянию 3 только в том случае, если для каждой
эквивалентной пары условно произвольные состояния интер-
228
Гпава 5. Проектирование последовательных схем
претируются одинаково. Обычно это наблюдается только тогда,
когда удается показать, что состояние 1 е состоянию 2, состоя-
ние 2 = состоянию 3 и состояние 1 = состоянию 3 (т.е. имеет
место полная круговая тождественность).
5.2.8. Прямое назначение переменных
До сих пор при проектировании всех схем делалась попытка
уменьшить количество триггеров до минимума, кодируя состоя-
ния с помощью переменных. Альтернативой такому подходу яв-
ляется метод, когда состояния не кодируются, а для каждого из
них используется своя переменная состояния. Например, если
имеется система с восемью состояниями, то используются восемь
переменных, УоУхУгУзУАУзУбУч- Для каждого состояния только одна
переменная равна 1, то есть у0 принимает значение 1 для состоя-
ния 1, У! — для состояния 2 и т.д. Таким образом, таблица назна-
ченных состояний будет выглядеть следующим образом:
То .Vi У1 Уз Уа Уз Уб Уч
Состояние 0= 10000000
Состояние 1= 01000000
Состояние 2= 00100000
Состояние 3= 00010000
Состояние 4= 00001000
Состояние 5= 00000100
Состояние 6= 00000010
Состояние 7= 00000001
Такая форма назначения называется прямым назначением (one-
hot assignment). Подобное присвоение переменных увеличивает
количество триггеров состояний (до восьми в рассматриваемом
примере), но при этом в общем случае упрощается вид функций
следующих состояний. Широко распространенным вариантом
прямого назначения является так называемое квазипрямое назна-
чение (almost one-hot assignment), при котором за начальным со-
стоянием резервируется кодовая комбинация 00... 00. При по-
добном назначении переменных легко обеспечить инициализа-
цию триггеров в начальном состоянии. Кроме того, в этом случае
для описания восьми состояний достаточно семи переменных.
5.2. Проектирование синхронных последовательных схем
229
Задание для самопроверки 5.8
Назначьте состояния для системы с восемью состояниями, используя метод
квазипрямого назначения.
5.3. Резюме
В этой главе были рассмотрены следующие вопросы.
• Общие модели синхронных последовательных схем
(модели Мили и Мура).
• Проектирование синхронных последовательных схем.
• Методы эффективных разработок.
• Способы уменьшения количества используемых
компонентов путем минимизации числа состояний.
• Диаграммы состояний с выражениями переходов,
которые более практичны при проектировании
сложных последовательных схем.
5.4. Упражнения
1. Имеется синхронная последовательная схема со вхо-
дом х и выходом Z. Сигнал на выходе должен прини-
мать значение 1 в том случае, если на вход приходит
кодовая последовательность 0110100, иначе на выходе
должен быть 0. Нарисуйте диаграмму состояний мо-
дели Мура для этой схемы.
2. Повторите предыдущее задание, используя диаграмму
состояний модели Мили.
3. Имеется синхронная последовательная схема с двумя
входами (xi и х2) и одним выходом, Z. Выходной сиг-
нал должен принимать значение 1 только на время
присутствия па входах последнего числа из последова-
тельности 00, 11, 00, 11, подаваемой на входы. Нари-
суйте диаграмму состояний модели Мура для этой схе-
мы и составьте таблицу состояний. Затем спроектируй-
те схему, которая бы реализовала заданную функцию
с минимальным количеством триггеров £>-типа.
230
Гпава 5. Проектирование последовательных схем
4. Повторите предыдущее задание, используя JK-
триггер.
5. Имеется синхронная последовательная схема со вхо-
дом х и выходом Z. Значение на выходе должно быть
равно 1 только тогда, когда на вход приходит одна из
двух числовых последовательностей: 1100 или ООН.
Нарисуйте диаграмму состояний модели Мура для
этой схемы и составьте таблицу состояний. Затем
спроектируйте схему, которая бы реализовала задан-
ную функцию с использованием минимального коли-
чества триггеров />-типа.
6. Повторите предыдущее задание, используя диаграмму
состояний модели Мили.
7. Спроектируйте схему генератора импульсов, который
бы формировал импульс длительностью и периодов
тактового сигнала, где п — кодовая комбинация, при-
ходящая на три входа (0 < п < 7).
8. Минимизируйте таблицу состояний модели Мили,
приведенную в табл. 5.16.
Таблица 5.16. Таблица состояний к упражнению 5.8
Текущее состояние Следующее состояние, *1*2 Выходное значение, Z
00 01 11 10
1 2 3 2 1 0
2 1 3 1 4 1
3 3 4 3 5 1
4 5 3 2 2 0
5 6 7 1 4 1
6 3 7 1 1 0
7 1 1 1 2 1
9. Минимизируйте таблицу состояний модели Мили,
приведенную в табл. 5.17.
5.4. Упражнения
231
Таблица 5.17. Таблица состояний к упражнению 5.9
Текущее состояние Следующее состояние, xtx2 Следующее значение на выходе, Z
00 01 11 10 00 01 11 10
1 1 2 2 4 0 0 0 0
2 1 3 1 4 0 0 0 0
3 1 3 2 4 0 0 0 0
4 1 8 7 5 0 0 0 0
5 1 5 6 5 0 0 1 0
6 3 8 7 5 0 0 0 0
7 2 8 6 5 0 0 0 0
8 3 8 7 8 0 0 1 0
5.5. Список дополнительной
литературы
1. Katz, R. Н., Contemporary Logic Design, Benja-
min/Cummings: Redwood City, California, 1994.
2. Nelson, V. P., Nagle, H. T., Carroll, B. D. and Irwin, J. D.,
Digital Logic Circuit Analysis and Design, Prentice Hall:
Englewood Cliffs, New Jersey, 1995.
3. Wakerly, J.F., Digital Design Principles and Practices, 2nd
edition, Prentice Hall: Englewood Cliffs, New Jersey, 1994.
4. В этой книге опущена тема проектирования асинхронных
последовательных схем; впрочем, и в большинстве других
книг она упоминается вскользь. Вопросы проектирова-
ния асинхронных последовательных схем достаточно
подробно изложены в работе Уэйкерли (Wakerly, 1994).
232
Гпава 5. Проектирование последовательных схем
Глава 6
Проектирование устройств
на программируемых
логических интегральных
схемах (ПЛИС)
Цели и задачи
В предыдущих главах рассматривались фундаментальные
логические компоненты электроники, из которых состоят
цифровые системы: вентили, простые комбинационные схе-
мы на основе вентилей (дешифраторы, триггеры) и, нако-
нец, последовательные логические схемы, состоящие из
триггеров и вентилей. В этой главе будут описаны гибкие
логические компоненты, которые называются программи-
руемыми логическими интегральными схемами или ПЛИС
(PLD — programmable logic devices). Структура стандартной
ПЛИС может конфигурироваться, позволяя получать раз-
личные комбинационные или последовательные схемы.
ПЛИС широко используются для уменьшения количества
компонентов в сложных логических системах.
6.1. Программируемые логические
интегральные схемы
Программируемые логические интегральные схемы содер-
жат вентили и иногда триггеры, располагаемые таким обра-
зом, что взаимные связи между ними могут быть изменены,
позволяя реализовывать нужную логическую функцию. Ком-
бинационные логические ПЛИС содержат только базовые
вентили и обычно организованы в виде матрицы из вентилей
И или вентилей ИЛИ, на основе которых легко реализовать
любую функцию дизъюнктивной формы. В последовательных
ПЛИС па выходах добавляются триггеры.
Какой бы ни была логическая структура ПЛИС, ко всем по-
добным приборам предъявляется общее требование: все они
должны обладать средствами изменения взаимных связей между
элементами, обеспечивающими формирование требуемых логи-
ческих конфигураций. В первых вариантах ПЛИС это достига-
лось за счет изготовления интегральных схем с полупроводнико-
выми плавкими перемычками внутри, позволявшими осуществ-
лять только однократное программирование. В исходном
состоянии эти перемычки проводят ток, обеспечивая тем самым
избыточное количество связей между элементами микросхемы.
Затем для получения требуемой картины отдельные перемычки
пережигались пользователем, для чего использовалось специаль-
ное устройство, называвшееся программатором (programmer).
Обычно программатор ПЛИС подключался к небольшому ком-
пьютеру, программное обеспечение которого преобразовывало
требуемые логические функции в соответствующие изменения
конфигурации межсоединений ПЛИС. Конечно, после разру-
шения перемычка не могла быть восстановлена. ПЛИС, подоб-
ные описанным выше схемам на плавких перемычках, носят
название программируемых пользователем (field programmable).
ПЛИС с плавкими перемычками появились в 1970-х годах.
В настоящее время существуют варианты ПЛИС, в которых ис-
пользуется технология электрически стираемых постоянных за-
поминающих устройств (ЭСПЗУ)1. В таких приборах наличие
или отсутствие связи зависит от хранимой в двоичной форме
информации. Возле каждой точки соединения имеется ячейка
памяти, в которой хранится, скажем, 0, когда соединение должно
существовать, и 1, если соединение должно отсутствовать. Полу-
проводниковые ПЛИС с памятью обеспечивают возможность
быстрого и многократного изменения конфигурации связей.
Существуют также варианты ПЛИС, межсоединения в кото-
рых формируются в процессе изготовления прибора в соответ-
ствии с требованиями заказчика и не подлежат изменению.
Чтобы получить фиксированную конфигурацию связей, необ-
' Более подробную информацию о технологии ЭСПЗУ можно найти
в дополнительной литературе, список которой приведен в конце главы.
234
Глава 6. Проектирование устройств на программируемых...
ходимо создать специальный комплект фотошаблонов (масок),
с помощью которых и производится интегральная схема. По-
добная технология масочного программирования слишком до-
рога для изготовления единичных устройств, по в полной мере
окупает себя при массовом производстве одинаковых схем.
Все три перечисленных выше типа ПЛИС (на плавких пе-
ремычках, с ячейками памяти или с масочным программирова-
нием) выпускаются в корпусах с одинаковым расположением
выводов, так что в системе можно с легкостью заменять один
тип ПЛИС другим. Для экспериментов вначале могут исполь-
зоваться микросхемы репрограммируемого типа, хотя они яв-
ляются самыми дорогостоящими и наиболее медленными. За-
тем в малых сериях их можно заменить на однократно про-
граммируемые ПЛИС и, наконец, после запуска в серийное
производство возможен переход на ПЛИС с масочным про-
граммированием с фиксированной структурой связей.
Далее ПЛИС будут рассматриваться как устройства
с “программируемыми соединениями”, что справедливо в от-
ношении всех типов подобных микросхем вне зависимости от
того, используются ли в них плавкие перемычки, ячейки с па-
мятью или масочное программирование. Логические структуры
ПЛИС разных типов мало отличаются друг от друга. Для начала
давайте рассмотрим комбинационные ПЛИС.
6.2. Комбинационные ПЛИС
6.2.1. Программируемые логические матрицы
(ПЛМ)
Стандартная логическая структура комбинационной ПЛИС
позволяет реализовать выражения в дизъюнктивной форме.
Структура связей ПЛИС представляет собой двухмерную матрицу
с программируемыми соединениями в точках пересечения. На
рис. 6.1 показан пример функциональной схемы комбинацион-
ной ПЛИС с шестнадцатью входами (70, 7Ь /2, 73, /4, 75, 76, /7, /8, 79,
/10, Аь Аг. Аз. Ад, As) и восемью независимыми выходами (70. Fb
А, F3, Л. А5, F6, F7). Комбинационные ПЛИС такого типа назы-
ваются программируемыми логическими матрицами, или ПЛМ
(programmable logic arrays— PL А). Количество входов и выходов
в таких ПЛМ может варьироваться в широких пределах.
6.2. Комбинационные ПЛИС
235
16 вентилей НЕ
Рис. 6.1. Функциональная схема программируемой пользователем логической матрицы
Из рис. 6.1 видно, что для приведенного случая на каждом
выходе может быть реализовано дизъюнктивное выражение,
содержащее до сорока восьми членов-произведений, каждый
из которых, в свою очередь, может состоять из шестнадцати
переменных в прямой или инверсной форме. Количество
произведений в результирующем выражении определяется
числом вентилей И, а количество переменных в каждом из
этих произведений — количеством входов всей схемы. На
входы вентилей И могут поступать переменные как в прямой,
так и в инверсной формах.
Реально ПЛМ организована так, что каждый из 48 вентилей
И и 8 вентилей ИЛИ имеет не две, как показано на рис. 6.1,
входных линии, а только одну. Соединения в точках пересе-
чения представляют собой полупроводниковые перемычки,
236
Глава 6. Проектирование устройств на программируемых...
включенные последовательно с диодом (или эквивалентное со-
единение); они и являются входами вентилей2. Поэтому обычно
структура ПЛМ имеет такой вид, как рис. 6.2.
Рис. 6.2. Упрощенная функциональная схема программируемой логической матрицы
Для каждой входной переменной существует четыре
состояния (рис. 6.3). В начальном (незапрограммированном)
состоянии все внутренние связи оставлены целыми, и ко вхо-
дам вентилей оказываются подключенными как прямые, так
и инверсные формы переменных. Пережиганием одной из
перемычек можно выбрать нужную форму переменной, а пе-
режиганием обеих — вообще отменить ее выбор, т.е. исклю-
чить переменную из произведения. Если уничтожить все свя-
зи, ведущие к вентилю И, то обычно на его выходе генериру-
ется логическая 1.
2Более подробную информацию о реализации вентилей можно найти
в дополнительной литературе, список которой приведен в конце главы.
6.2. Комбинационные ПЛИС
237
(б) Выбор переменной в прямой форме
(в) Выбор переменной в инверсной форме
(г) Переменная не выбрана
Рис. 6.3. Различные состояния связей вентилей И в программируемой логической матрице
Как правило, обе формы переменной, прямая и инверсная, не
фигурируют в одном члене логического выражения, поскольку он
автоматически становится равным 0 (т.е. переменные и / не
используются вместе, так как piJ = о, где Р — остальные пере-
менные, входящие в этот же член). Исключением является слу-
чай неиспользуемых вентилей И, когда все связи к такому вен-
тилю остаются в изначальном, незапрограммированном состоя-
нии, т.е. соответствующее произведение равно нулю. (При этом
теоретически существует возможность возникновения логиче-
ских сбоев, если все переменные изменяются одновременно, но
такая ситуация крайне маловероятна.) В качестве альтернативы
можно на один из входов подавать логическую 1. Затем этот
вход подключается к каждому из неиспользуемых вентилей И.
Чтобы не усложнять материал, вопросы, связанные с неисполь-
зуемыми вентилями И, далее просто опускаются.
238
Глава 6. Проектирование устройств на программируемых...
ПРИМЕР
Предположим, необходимо реализовать на ПЛМ следующие логические
функции:
/, = АВС
/, = АС+ВС
f^AB + ACD + ABC-
Требуемые электрические соединения внутри ПЛМ для этих функций пока-
заны на рис. 6.4. Значками X показаны программируемые связи, которые
должны остаться нетронутыми. Обратите внимание, что, если функции со-
держат одинаковые произведения переменных, то их можно получать
с помощью одних и тех же связей, как это делалось при реализации на
обычных вентилях И-ИЛИ. Ввиду ограниченности количества доступных
вентилей упрощение логических выражений может оказаться полезным
и при реализации системы на программируемых логических матрицах. На
практике ПЛМ лучше всего подходят для тех случаев, когда требуется
реализация нескольких выражений в дизъюнктивной форме, особенно, ес-
ли они содержат много отдельных членов, количество которых значитель-
но больше, чем в приведенном выше примере.
Задание для самопроверки 6.1
Нарисуйте нормальную функциональную схему устройства на ПЛМ, изобра-
женного на рис. 6.4.
Если функция, которую требуется реализовать, не является
дизъюнктивной, то ее необходимо привести к этому виду.
ПРИМЕР
Чтобы реализовать функцию вида /= С(А Ф В), сначала необходимо при-
вести ее к дизъюнктивному виду:
f = С(А Ф В) = С(АВ + АВ) = АВС + АВС,
а затем реализовать нормальным образом. (Существует программное обес-
печение, которое автоматически преобразует булевы выражения в требуе-
мую форму (подробнее см. ниже).)
6.2. Комбинационные ПЛИС
239
Рис. 6.4. Использование ПЛМ для формирования функций f = ABC' f2 = АС + ВС
и f} = АВ + ACD + АВС
6.2.2. Программируемая матричная логика
(ПМЛ)
ПЛМ, описанные в предыдущем разделе, имеют програм-
мируемые связи как на входах вентилей И, так и на входах
вентилей ИЛИ. Фирма Advanced Micro Devices (AMD) произ-
водит целое семейство ПЛИС, электрические связи которых
программируются только на входах вентилей И. Такие уст-
ройства фирма назвала программируемой матричной логикой,
или ПМЛ (programmable array logic— PAL); этот термин ныне
240
Глава 6. Проектирование устройств на программируемых...
применяется для всех типов подобных микросхем3. В ПМЛ
каждый вентиль И имеет непосредственную связь со входом
одного вентиля ИЛИ. Как правило, ко входам каждого
(восьмивходового) вентиля ИЛИ подключено восемь вентилей
И. Причиной ограничения числа элементов является стремле-
ние увеличить общее быстродействие, поскольку программи-
руемые электрические связи вносят существенно большую за-
держку, чем фиксированные.
Первые образцы ПМЛ, появившиеся в 1970-х годах, разраба-
тывались на основе биполярной логики и имели полупровод-
никовые плавкие перемычки. Сегодня, однако, доступны
и электрически стираемые микросхемы ПМЛ на КМОП-
транзисторах, совместимые с первыми сериями по выводам.
Хотя вначале внедрение ПМЛ было достаточно медленным, те-
перь они практически повсеместно используются для замены
стандартных компонентов малой и средней степени интеграции
в интерфейсных схемах компьютеров. В настоящее время такие
устройства изготавливаются многими производителями
(включая Texas Instruments и Signetics Corporation). На основе ПМЛ
существуют и последовательные логические схемы (регистровые
ПМЛ; подробнее см. в разделе 6.3.1).
На рис. 6.5 показан пример комбинационной ПМЛ AMD
PAL16L8. Буква L в названии микросхемы означает, что сни-
маемые с выходов сигналы инверсны (т.е. имеют активный
низкий уровень). Микросхема PAL16L8 может иметь до 16 вхо-
дов и до восьми выходов, однако некоторые из выходов могут
играть роль входов, поскольку приходится учитывать ограниче-
ния по количеству выводов у корпуса4. Наличие внутренних
связей между входами и выходами обеспечивает возможность
реализации обратной связи. Выходы ПМЛ снабжены буферами
с тремя состояниями, которые могут переводиться в рабочее
состояние функцией входных переменных и переменных об-
ратной связи. Совмещенные входы и выходы могут использо-
ваться в качестве входов, при этом буфер данного выхода пере-
водится в высокоимпедансное (третье) состояние.
3 Сокращение PAL является зарегистрированной торговой маркой
фирмы Advanced Micro Devices Inc.
4 Чаще всего устройства ПМЛ поставляются в 20- или 24-выводных
корпусах типа DIP; схема PAL16L8, к примеру, имеет 20 выводов.
6.2. Комбинационные ПЛИС
241
Программируемые соединения
Входы/выходы
242
Глава 6. Проектирование устройств на программируемых...
Как видно из рис. 6.5, имеется десять независимых входов
(Д, /2, /3, Ц, /5, /6. /7, /8, /9, /10), каждый из которых по выбору
может быть прямым или инверсным. Имеется восемь выходов,
шесть из которых (IO2, IO3, IO4, IOS, IO6, IO-,) также могут слу-
жить входами, а два — только выходами (О, и О8). Данная мик-
росхема позволяет формировать до восьми различных выраже-
ний в дизъюнктивной форме, в каждом из которых, в свою
очередь, может содержаться до семи произведений, включаю-
щих до 10 переменных в каждом. Как вариант, имеется воз-
можность сформировать два независимых дизъюнктивных вы-
ражения из семи произведений каждое, при этом в каждом
произведении может присутствовать до шестнадцати перемен-
ных (по шесть дополнительных переменных добавляется в ре-
зультате использования совмещенных входов/выходов). Между
прочим, благодаря такому совмещению выводов можно реали-
зовать и другие многочисленные комбинации. В ПМЛ не уда-
ется получить выигрыш от наличия в двух или более выраже-
ниях одинаковых членов, поскольку для каждого вентиля ИЛИ
каждый член должен формироваться отдельно. В микросхеме
PAL16L8 выходные сигналы инверсны, т.е. функции имеют вид
И-ИЛИ-НЕ. В номенклатуре комбинационных ПМЛ имеются
микросхемы и с большей размерностью. Например, микросхема
PAL20L8 имеет четырнадцать входов, шесть совмещенных вхо-
дов/выходов и два некоммутируемых выхода, т.е. она позволяет
иметь в 24-вы водном корпусе до двадцати входов.
ПРИМЕР
На рис. 6.6 показано, как на одном из выходов устройства PAL16L8 может
быть реализована функция f = АВС + ABC + АС Обратите внимание,
что электрические связи всех неиспользуемых входов вентилей И не трону-
ты, что приводит к установлению на их выходах постоянных нулевых уровней.
Нулевые уровни с выходов вентилей И поступают на входы вентиля ИЛИ и,
таким образом, никак не влияют на него. Выход f переводится в активный
режим путем удаления всех электрических связей со входом вентиля И,
управляющего выходным буфером. Это приводит к появлению на выхо-
де этого вентиля постоянной 1, требующейся для перевода буфера в ак-
тивное состояние.
6.2. Комбинационные ПЛИС
243
м вв сс
Входы
Рис. 6.6. Реализация логической функции f = АВС + АВС + АС на ПМЛ
Выражение, записанное в дизъюнктивной форме, может быть
реализовано с помощью нескольких уровней. Обычно такая ситуа-
ция возникает, когда выражение необходимо реализовать с помо-
щью конкретной микросхемы ПМЛ, возможности которой не по-
зволяют этого сделать в рамках двух уровней. Для этого выходной
сигнал подастся обратно на один из входов микросхемы, как по-
казано на рис. 6.7. К примеру, чтобы реализовать функцию вида
А + В+ С+ D+ Е+ F+ G+ Н+ 1+ J, можно сделать так, что первый
каскад будет формировать сумму Х= А + В+ С+ D+ Е+ F+ G,
а второй — Х+ Н+ 1+ J. В целях наглядности соединения с неис-
пользуемыми вентилями И не показаны.
Соединения с неиспользуемыми
вентилями И не показаны
Рис. 6.7. Многоуровневая реализация дизъюнктивной логической функции
244
Глава 6. Проектирование устройств на программируемых...
Задание для самопроверки 6.2
Какое максимальное число переменных может содержаться в одном члене-
произведении для микросхемы PAL16L8?
Задание для самопроверки 6.3
Какое максимальное число переменных может содержаться в одном члене-
произведении для микросхемы PAL16L8 при использовании обратной связи?
Показанная на рис. 6.5 микросхема AMD PAL16L8 содержит
инвертирующие буферы с активным низким уровнем выходных
сигналов (это можно видеть и по букве L в названии схемы).
Существуют также и ПМЛ с пеипвертирующими выходными
каскадами (в их названии присутствует буква Н, что говорит об
отсутствии инвертирования на выходах). Собственно, если есть
микросхема с инвертирующими выходами, а необходимо полу-
чить функцию в прямой форме, то можно просто преобразовать
ее в обратную, правда, при этом количество членов-
произведений может превысить максимальное их количество
для данной ПМЛ. Наиболее простой способ получения обрат-
ной функции в виде дизъюнктивного выражения заключается
в группировке на карте Карно ячеек, содержащих нс 1, а 0.
В некоторых микросхемах существует возможность получить
на выходе либо прямой, либо инверсный сигнал, что достигает-
ся благодаря наличию программируемой цепочки, подобной той,
что показана на рис. 6.8. Если оставить программируемую связь,
то с выхода будет сниматься сигнал в прямой форме (т.е. на вы-
ходе элемента будет наблюдаться сигнал, поданный на вход),
а если удалить ее, то выходной сигнал станет инверсным входно-
му. Схема, изображенная па рис. 6.8, обычно размещается после
вентиля ИЛИ, но до выходного буфера. ПМЛ с такой структурой
иногда называются микросхемами типовой матричной логики
(generic array logic devices— GAL5) и относятся к категории уни-
версальных ПЛИС (universal PLD). В качестве примера универ-
сальной ПЛИС с возможностью программирования типа вы-
ходного каскада (т.е. с инверсией или без) можно привести
микросхему AMD PALCE16V8, которая имеет ту же структуру
вентилей И-ИЛИ, что и PAL16L8 (здесь буква С обозначает
КМОП, Е — электрическое стирание, V — переменный выход).
5 Название GAL является зарегистрированной торговой маркой компа-
нии Lattice Semiconductor Corp.
6.2. Комбинационные ПЛИС
245
Вход
Выход
Программируемое
соединение >:
О В (логический 0)
Рис. 6.8. Цепь, позволяющая получать на выходе
прямой либо инверсный сигнал
6.3. ПЛИС для реализации
последовательных логических схем
ПМЛ/ПЛМ могут использоваться и для создания на их ос-
нове последовательных схем. Теоретически обратная связь по-
зволяет сформировать триггеры, но на практике более вероятно
использование отдельных триггеров, как показано на рис. 6.9.
ПЛМ или комбинационная ПМЛ
Рис. 6.9. Синхронная последовательная схема на ПМЛ/ПЛМ
246
Глава 6. Проектирование устройств на программируемых...
Поскольку такая структура является общей для всех после-
довательных схем, очень заманчиво включить в состав ПЛИС
триггеры. И такие ПЛИС действительно существуют. Они на-
зываются регистровыми ПЛИС.
6.3.1. Регистровые ПЛИС
В регистровых ПЛИС D-, RS- или /Л'-триггеры встроены
непосредственно в микросхему. Термин регистровый подразу-
мевает, что все выходные каскады тактируются единым сигна-
лом синхронизации, и, следовательно, в микросхеме все входы
тактовых импульсов триггеров подключены к общей линии
сигнала синхронизации.
На рис. 6.10 показана структура типовой регистровой ПЛИС
AMD PAL16R6. В этой микросхеме восемь независимых вхо-
дов, шесть О-триггеров и два совмещенных входа/выхода, по-
добных выходам ПЛИС PAL16L8. Сигналы с выходов триггеров
также могут использоваться в качестве переменных обратной
связи, что дает возможность иметь до шестнадцати перемен-
ных, как и в микросхеме PAL16L8. (ИС PAL16L8 входит в со-
став семейства PAL16R8.) С помощью этой схемы можно реа-
лизовать до восьми членов дизъюнктивного выражения. Следо-
вательно, в случае конечного автомата, это устройство может
обеспечить максимум восемь входов х, шесть переменных со-
стояний y/Y и два отдельных выхода Z, с которых могут сни-
маться значения выражений в дизъюнктивной форме.
ПРИМЕР
Рассмотрим первый пример из главы 5, раздел 5.2.1, а именно: схему син-
хронного счетчика, с выходов которого в зависимости от уровня сигнала на
управляющем входе снимается одна из двух повторяющихся последователь-
ностей. При С = 0 последовательность выглядит как 00, 01, 11, а при
С= 1 — 00, 11, 01. Входные уравнения для О-триггеров выглядят следую-
щим образом:
D2 = У2У1С + уЛС
Пх=угС + угу,С + у2ууС-
6.3. ПЛИС для реализации последовательных логических схем 247
CLK
Рис. 6.10. Регистровая ПМЛ AMD PAL16R6
248
Глава 6. Проектирование устройств на программируемых...
Предположим, что этот счетчик необходимо реализо-
вать на основе ПЛИС PAL16R6. Хотя на триггеры этой
схемы поступают входные сигналы функций в прямой
форме (в отличие от PAL16L8, в которой генерируются
обратные функции), выходные сигналы все равно будут
инверсными. Поэтому если реализовать эти уравнения
“в лоб”, то биты в генерируемых последовательностях
будут проинвертированы, т.е. будут генерироваться по-
следовательности 11, 10, 00 и 11, 00, 10. Если еще раз
воспользоваться методикой, описанной в главе 5, но
с учетом того, что биты проинвертированы, можно по-
лучить диаграмму состояний, показанную на рис. 6.11,
а из нее — следующие выражения для функций:
О2 = у1С + у,у1С+у2
^=у2С + угу}+у2у}С-
В целях удобства в картах Карно можно обозначать
комбинации 11, 10, 00, 01, вместо традиционных 00, 01,
11, ГО, поскольку такая последовательность также пред-
ставляет собой код Грея (при переходе от одной комби-
нации к соседней изменяется только один бит). Однако
при использовании ПАЛ нет необходимости минимизи-
ровать функции. Реализация счетчика на регистровой
ПЛИС показана на рис. 6.12. Обратите внимание, что
использование для обратной связи входных выводов со-
всем не обязательно, поскольку на выходах у2 и у, име-
ется внутренняя реализация такой связи.
Рис. 6.11. Диаграмма состояний модели Мура
синхронного счетчика для инвертированных
битов последовательностей
Компанией AMD выпускаются и другие регистровые ПМЛ,
например микросхемы PAL20X10, предназначенные для реали-
зации счетчиков. Эти микросхемы имеют комбинации вентилей
6.3. ПЛИС для реализации последовательных логических схем 249
типа И-ИЛИ-исключающее-ИЛИ (рис. 6.13), что позволяет
добиться непосредственной реализации функций переменных
состояний вида (дизъюнктивное выражение 1) Ф (дизъюнк-
тивное выражение 2), при этом каждое дизъюнктивное выра-
жение может иметь два члена, каждый из которых может со-
держать до 16 переменных (как и в ПЛИС PAL16R6, здесь
вступает в силу ограничение общего количества выводов вхо-
дов/выходов корпуса).
Рис. 6.12. Реализация счетчика на основе регистровой ПМЛ
Соединения с неиспользуемыми
вентилями И не показаны
Рис. 6.13. Комбинация операций И-ИЛИ-исключающее-ИЛИ в ПЛИС AMD PAL20X10
250
Гпава 6. Проектирование устройств на программируемых...
Существуют и ПЛМ со встроенными выходными триггера-
ми, т.е. в них вентили И-ИЛИ имеют программируемые связи
с вентилями И и с вентилями ИЛИ, а также имеются
“регистровые” выходы (т.е. с триггерами, синхронизируемыми
общим тактовым сигналом). Такие микросхемы называют про-
граммируемыми логическими генераторами последовательностей
(programmable logic sequencer— PLS).
6.3.2. Макроячейки
Макроячейками (macrocells) называются повторяющиеся уча-
стки структуры ПЛИС с программируемыми связями. Пример
такой макроячейки, в которой можно выбрать электрическую
связь через выходной триггер или обходным путем, приведен
на рис. 6.14. В данном случае триггер становится физически
дальше от выходного вывода микросхемы и интегрирован
в макроячейку. Такие триггеры называются скрытыми (buried
flip-flops). В приведенном примере показана ячейка с двумя
мультиплексорами, каждый из которых управляется програм-
мируемой связью. Если удалить эту связь, то выбирается вход,
обозначенный 1, а если оставить ее, то выбирается вход, обо-
значенный 0. В макроячейке, изображенной на рис. 6.14, один
мультиплексор позволяет подавать на выход микросхемы либо
сигнал с выхода Q триггера, либо сигнал с вентиля И-ИЛИ —
в обоих случаях с дополнительной инверсией, осуществляемой
выходным буфером. Второй мультиплексор служит для выбора
пути обратной связи к массиву И-ИЛИ — это опять может быть
либо выход Q триггера, либо выход буфера. В сложных ПМЛ
могут встречаться и другие вариации подобной структуры.
В качестве примера ПМЛ с макроячейками можно привести
микросхемы PAL22V10 и PAL32VX10.
Макроячейки могут также служить для описания других
комбинационных/последовательных логических схем с повто-
ряющейся структурой, организованной в виде массива с двух-
мерной программируемой сеткой электрических связей (так на-
зываемые матрицы логических ячеек — logic cell arrays). Термин
“макроячейка” может иметь разные значения, в частности его
используют для обозначения библиотек типовых структур, ис-
пользующихся при проектировании СБИС.
6.3. /7ЛИС для реализации последовательных логических схем 251
Рис. 6.14. Пример макроячейки со скрытым триггером
6.4. Инструментальные средства
программирования ПЛИС
Для того чтобы запрограммировать ПЛИС, необходимо сна-
чала определить, какие связи уничтожить, а какие оставить.
В простых схемах это можно сделать и вручную, прорабатывая
все связи между элементами с помощью электрической прин-
ципиальной схемы, однако в большинстве случаев применяют-
ся специальные программы. Программное обеспечение воспри-
нимает в качестве входных данных описание логической функ-
ции, которую требуется реализовать. Это описание может быть
в виде булева выражения, таблицы истинности или (для после-
довательных схем) диаграммы состояний. Результатом работы
ПО является файл, в котором содержится информация обо всех
требующихся электрических связях (так называемая карта
программирования — programming тар). Этот выходной файл ис-
пользуется непосредственно для управления программатором.
Некоторые программы включают в себя средства логического
моделирования, позволяющие проверить работоспособность
логической схемы до программирования ПЛИС. Пожалуй, од-
ними из наиболее популярных пакетов программного обеспече-
ния являются PALASM2 (PAL assembler) от AMD Inc. и ABEL
(Advanced Boolean Expressions Language — улучшенный язык бу-
левых выражений) от Data I/O Corporation. Давайте остановимся
на последнем как на наиболее распространенном и признанном
во всем мире средстве для создания логических схем.
252
Глава 6. Проектирование устройств на программируемых...
6.4.1. Структура файла с исходным кодом
языка ABEL
Следуя правилам языка ABEL, пользователь пишет програм-
му для компьютера, в которой описывается логическая функ-
ция, реализуемая на ПЛИС. Операторы языка позволяют задать
тип используемой микросхемы и присвоить имена ее выводам.
Выходные функции обычно описываются булевыми выраже-
ний, но возможны и другие способы описания.
Как правило, программа делится на несколько частей
(рис. 6.15). Ключевые слова самого языка ABEL нечувствительны
к регистру букв, но имена переменных подобной нечувствительно-
стью не обладают. ABEL допускает “свободное” форматирование
с использованием пробелов и символов перевода каретки (ввода
новой строки). Программа должна начинаться с ключевого слова
module и имени модуля, а заканчиваться ключевым словом end.
Оператор title просто указывает заголовок для формируемых
файлов, указываемый в виде строки символов в одиночных ка-
вычках. Ниже следуют различные декларации. Оператор device,
Заголовок
Декларативная часть
module modele_name
title 'Name to be printed in file'
device_id device device_type;
@ALTERNATE
identifiers pin pin_nubders;
Описание логики схемы
equations
Тестовые векторы
test vectors
Завершающая часть
end module name
Рис. 6.15. Пример структуры файла с исходным кодом на языке ABEL
6.4. Инструментальные средства программирования ПЛИС
253
например, идентифицирует программируемую микросхему. Она
обязательно должна поддерживаться компилятором, а используе-
мое имя должно соответствовать ее имени в языке ABEL.
Для изменения способа интерпретации или обработки компи-
лятором файла с исходным кодом могут использоваться специ-
альные “директивы”. Директива ©alternative, например, по-
зволяет распознавать альтернативный набор символов (см. ниже).
Назначение имен сигналам/выводам ПЛИС инициируется
оператором pin, с помощью которого каждому выводу микро-
схемы присваивается свой идентификатор. Выводы микро-
схемы могут быть входами и выходами, а соответствующие
идентификаторы используются в следующем разделе выра-
жений при описании сигналов на входах и выходах. Все
операторы декларирования типа микросхемы и выводов за-
вершаются точкой с запятой.
Затем следует раздел описания логики схемы. При ис-
пользовании булевых уравнений раздел equation содержит
список выражений булевой алгебры, определяющих выход-
ные функции, аргументами которых являются входные сиг-
налы. Каждое выражение также оканчивается точкой с запя-
той. В качестве альтернативных описаний логических функ-
ций могут использоваться таблицы истинности или
текстовые варианты диаграмм состояний (для последова-
тельных схем). В файл с исходным кодом можно вставлять
комментарии, заключая их в двойные кавычки (разрешается
также только начинать строку с комментариями символом ка-
вычек, а заканчивать символом перевода каретки).
Файл может содержать раздел с описанием тестовых векто-
ров, определяющих набор входных значений, и ожидаемые вы-
ходные состояния. Этот раздел используется средствами моде-
лирования языка ABEL для определения правильности логиче-
ского описания схемы.
Компилятор (compiler) языка ABEL использует файл исход-
ного кода для создания на его основе документации и карты
электрических связей, позволяющей запрограммировать кон-
кретную ПЛИС. Картина программируемых связей содержится
в одном файле, который загружается в ПЛИС. Документация
включает в себя список булевых выражений схемы, упрощен-
ных или перегруппированных из исходных таким образом, что-
бы они могли быть реализованы в рамках конкретной ПЛИС,
и оформляется в виде отдельного файла.
254
Глава 6. Проектирование устройств на программируемых...
Независимое от архитектуры проектирование
Оказывается, совсем не обязательно указывать тип микро-
схемы и номера ее выводов; эта информация может быть вре-
менно опущена, что позволяет получить решение, не зависящее
от архитектуры. Выбор типа микросхемы может быть предло-
жен пакетом ABEL непосредственно перед программированием
ПЛИС. При этом необходимым требованиям может удовлетво-
рять сразу несколько типов микросхем. Иногда, если тип мик-
росхемы не указывается в начале работы, исходная программа
должна также включать дополнительные детали о сигналах, ис-
пользуя назначения атрибутов сигналов (оператор istype)
и расширения через точку {dot extensions'), описывающие свойства
сигналов. К примеру, сигнал на выходе Qo триггера О-типа
можно описать с помощью строки qo istype 'reg_d'. Рас-
ширение может быть приписано к имени сигнала, если нужно,
например, указать, что сигнал па данном входе используется
для очистки триггера (.RE). Во всех приводимых далее приме-
рах будет предполагаться, что тип микросхемы задан заранее.
6.4.2. Комбинационные функции
Комбинационные функции содержат входные переменные,
соединенные логическими операторами И, ИЛИ и НЕ, и при-
сваиваются выходным переменным при помощи знака равенства.
В языке ABEL операторам И, ИЛИ, НЕ, исключающее ИЛИ
и исключающее ИЛИ-НЕ по умолчанию присвоены следующие
символы: &, #, !, $ и !$, соответственно. Такие обозначения не
очень понятны, поэтому допускается использование альтернатив-
ных символов: * (для оператора И), + (для ИЛИ), / (для НЕ), :+:
(для оператора исключающее ИЛИ) и :*: (для оператора исклю-
чающее ИЛИ-НЕ). Альтернативный набор символов выбирается
путем ввода директивы ©ALTERNATE. Обратите внимание, что
альтернативный набор символов исключает возможность исполь-
зования традиционных арифметических операторов сложения,
умножения и деления, которые также разрешены к применению
в языке ABEL. Для описания комбинационной функции вида
/ = AB + CD
на языке ABEL пишется следующая конструкция:
f = А * /В + С * D;
или, используя принятый по умолчанию набор символов
f = А & !В # С & D;
6.4. Инструментальные средства программирования ПЛИС
255
Порядок выполнения операторов определяется списком
приоритетов, которые могут принимать значения от 1 до 4 (см. ру-
ководство Data I/O Corp., 1990); его можно изменять с помо-
щью скобок. В приведенном выше простом примере скобки нс
нужны, поскольку оператор НЕ и так имеет наивысший при-
оритет, затем следует оператор И и, наконец, оператор ИЛИ,
поэтому все действия автоматически выполняются в нужном
порядке. Выходная переменная, f и переменные А, В, С и D
должны быть заданы в разделе описаний переменных
(declarations) и ассоциированы с конкретными выводами устрой-
ства (если не требуется решение, не зависящее от архитектуры).
ПРИМЕР
ПЛИС часто применяют для реализации логических схем дешифраторов, ко-
торые чрезвычайно распространены в компьютерных системах. Предполо-
жим, нужно спроектировать дешифратор с четырьмя входами, А, В, Си D,
и четырьмя выходами, Qo, Qt, Q2 и Q3. Сигнал на выходе Qo должен при-
нимать значение 0, когда Л = О, 5 = 0, С = 0 и Z) = 0. Сигнал Q1 должен
принимать значение 0, когда Л = 0, 5 = 0, С = 0 и D = 1. Q3 должен стано-
виться равным 0, когда Л = 0, 5=0, С = 1 и Z) = 0. Наконец, Q3 становится
равным 0, когда Л = 0, 5=0, С = 1 и Z) = 1.
Запишем все четыре функции в виде булевых выражений:
20 = ABCD
Q} = ABCD
Q, = ABCD
Qy = ABCD
Ясно, что реализовать эти функции на ПЛИС не составляет труда — напри-
мер, на PAL16L8. Их описания с помощью операторов языка ABEL приве-
дены на рис. 6.16. В программе тип устройства задан в первом разделе
файла. Каждый входной и выходной сигнал ассоциирован с конкретным вы-
водом ПЛИС в разделе описания переменных. Обратите внимание, что, по-
скольку используется ПЛИС с инвертирующими выходами (т.е. с активным
низким уровнем), имена выводов также содержат знак инверсии. Знаки ин-
версии также стоят и в именах выходных функций, поскольку реализуемые
выражения подразумевают инверсию.
256
Глава 6. Проектирование устройств на программируемых...
module decoder
title '4-to-8-line_decoder'
decoder device 'P16L8'
@ALTERNATE
A,B,C,D pin 1,2,3,4;
/Q0,/Ql,/Q2,/Q3 pin 12,13,14,15;
equations
ZQO = /А ★ /в ★ /с * /D.
/Q1 = /А ★ /в ★ /с * D;
/Q2 = /А ★ /в ★ с * /D;
/Q3 = /А * /в ★ с * D;
end module name
Рис. 6.16. Программа для дешифратора, написанная на
языке ABEL
Естественно, никто не будет использовать ПЛИС для реали-
зации такой простой схемы, как дешифратор, которых и так
существует громадное количество на стандартных микросхемах
(например, 74LS154 — дешифратор из 4 линий в 16). Предпо-
ложим, однако, что сигнал на одном из выходов дешифратора
должен принимать значение 0, когда на входах появляется одна
из двух заданных комбинаций: ABCD или A.BCD Такой сигнал
можно описать выражением в дизъюнктивной форме:
ё0 = ABCD + ABCD,
которое на языке ABEL записывается следующим образом:
/Q0 = /А * /В * /С * D + /А * В * С * D;
Синтаксис языка предлагает несколько дополнительных
средств для описания. К примеру, уравнения необязательно за-
писывать в формате ПЛИС. Булевы выражения можно записать
с использованием символики языка ABEL в любом виде
(включая использование скобок для задания очередности дей-
ствий), лишь бы это были корректные булевы выражения.
Компилятор ABEL будет пытаться самостоятельно упростить
6.4. Инструментальные средства программирования ПЛИС
257
эти выражения до вида, подходящего для заданной ПЛИС.
Иногда заранее трудно определить количество членов, которые
будут входить в конечное выражение, поэтому использование
выбранной ПЛИС оказывается невозможным.
Одним из наиболее распространенных методов перегруппи-
ровки является инверсия выходной функции. К примеру, зада-
на функция
f = ABCD + ABCD
В разделе описания выражений в файле языка ABEL ее
можно записать следующим образом:
Q0 = /А * /В * /С * D + /А * В * С * D;
Если бы для использования была задана ПЛИС PAL16L8, то
компилятор ABEL должен был бы сформировать инверсную
функцию, которая в неминимизированном виде имела бы че-
тырнадцать членов-произведений (четыре переменных дают
шестнадцать возможных комбинаций). Результирующее мини-
мизированное выражение, полученное путем объединения кле-
ток с пулями в карте Карно (рис. 6.17), выглядит так:
<20 = А + D + ВС + ВС >
и его уже легко реализовать с помощью ПЛИС PAL16L8. (Для
реализации исходного уравнения можно использовать и ПМЛ
с активными высокими уровнями выходных сигналов, но ПЛИС с ак-
тивными низкими уровнями все же распространены шире.)
Рис. 6.17. Объединение ячеек с нулями
для получения инверсной функции
258
Гпава 6. Проектирование устройств на программируемых...
Операторы множеств и отношений
В языке ABEL под множеством понимается группа сигналов,
имеющих общее имя. Это имя может использоваться в разделе
описания уравнений файла для замены отдельных имен сигна-
лов. Множества задаются в декларативной части файла. Предпо-
ложим, входные сигналы /0, /,, /2 и /3 формируют множество с
именем X, входные сигналы /4, /5, /6 и /7 формируют второе мно-
жество Y и, наконец, группа выходных сигналов Оа, Oh О2 и О3
формируют множество Z Множества сигналов в файле с исход-
ным кодом языка ABEL описываются следующим образом:
X = [10, II, 12, 13] ;
Y = [14, 15, 16, 17] ;
Z = [00, О1, 02, 03] ;
Здесь используются квадратные скобки и точки с запятой.
После задания множеств их можно использовать почти со все-
ми операторами языка. При этом имеется только одно ограни-
чение: размерность множеств должна совпадать, и тогда опера-
торы применяются к соответствующим членам каждого множе-
ства. Например,запись
Z = X + Y;
эквивалентна записи
ОО = 10 + 14;
01 = II + 15;
02 = 12 + 16;
03 = 13 + 17;
Еще одним очень полезным свойством языка ABEL является
наличие группы операторов отношений, которые могут исполь-
зоваться вместе с множествами. Пользователю доступны сле-
дующие операторы отношений: == (равно), != (неравно), <
(меньше), <= (меньше или равно), > (больше), >= (больше или
равно). Эти операторы могут использоваться с выражениями
булевой алгебры; в результате будет получена функция, для ко-
торой заданное отношение истинно.
Операторы отношений могут использоваться и в выражени-
ях булевой алгебры наряду с обычными операторами. К приме-
ру, если требуется получить сигнал Q, равный 1, только в том
случае, когда двоичное число на входах X (/0, Ц, Л и /3) равняет-
ся 0100 или 0101 (т.е. 4 или 5), можно записать:
Р = (X == 4) + (X == 5) ;
6.4. Инструментальные средства программирования ПЛИС
259
где 4 и 5 — десятичные числа. Можно использовать и другие
системы счисления, например шестнадцатеричную, если ука-
зать перед числом префикс Ah. Такие конструкции очень по-
могают при описании схем дешифраторов адресов памяти, ко-
торые должны реагировать на появление на шине адреса оп-
ределенных чисел.
ПРИМЕР
Сигнал на выходе Р должен принимать значение 1 (истина) при X меньше
Y (т.е. когда 4-разрядное число, подаваемое на входы /0, Ц, Ли /3,
меньше, чем 4-раз-рядное число, подаваемое на входы /4, /5, /6 и /7).
В этом случае можно записать:
Р = X < Y;
или
Р = [10, II, 12, 13] < [14, 15, 16, 17];
Это уравнение трансформируется в соответствующее выражение в дизъюнк-
тивной форме (достаточно длинное и с большим числом членов с восемью
переменными в каждом).
Задание для самопроверки 6.4
Сколько именно членов содержится в выражении из предыдущего примера?
В разделе описаний можно определять и константы:
limitl = 4; "задаем константу"
Р = (X == limitl) ,-
Знак равенства используется как при задании констант, так
и при описании уравнений.
Обозначение множества позволяет также задавать диапазон
номеров сигналов, не указывая промежуточных членов множе-
ства. Допустима запись вида [хо . . х5], которая обозначает,
соответственно, [хо, xl, х2, хЗ, х4, х5]. Такая запись
удобна в тех случаях, когда множество объединяет группу сиг-
налов, обозначения которых имеют “индексы”.
Символы множества особенно удобны, когда приходится
иметь дело с большим количеством “шинных” сигналов, что
характерно для микропроцессорных систем.
260
Глава 6. Проектирование устройств на программируемых...
ПРИМЕР
Имеется схема с шестью входами, Д,. А2, А3, Л4, Л5, и шестью выходами,
Оо, О,, О2, О3, О3, О5. Сигналы со входов передаются на выходы, когда на
управляющем входе С наблюдается нулевой логический уровень. Если же на
входе появляется 1, то с выходов снимаются сигналы , д д^, дз, д
д,. Программа, написанная на языке ABEL, показана на рис. 6.18. Компилятор
языка ABEL должен преобразовать эту запись в отдельные выражения для каж-
дого выходного сигнала. В данном случае выражение
Q = /С * А + С * /А;
соответствует системе
QO = /с * АО С * /АО
Q1 = /С * А1 С * /А1
Q2 = /С * А2 ь С * /А2
Q3 = /С * АЗ ь С * /АЗ
Q4 = /С * А4 ь С * /А4
Q5 = /С * А5 ь С * /А5
module complementer
title 'complementer'
decoder device 'P16L8'
@ALTERNATE
AO, Al, A2, АЗ, A4 , A5 pin 2, 3, 4, 5, 6, 7;
QO, QI, Q2, Q3, Q4, Q5 pin 12,13,14, 15, 16, 17;
C pin 1;
equations
Q = /С * A * C * /А;
end
Рис. 6.18. Программа на языке ABEL для схемы инвертора
6.4. Инструментальные средства программирования ПЛИС
261
Метод таблиц истинности
Кроме возможности использовать для описания комбинаци-
онных функций булевы выражения, язык ABEL позволяет зада-
вать их при помощи таблиц истинности, в которых каждому зна-
чению функции соответствует определенный помер. Общая фор-
ма такой записи начинается с ключевого слова truth_table, за
которым в скобках перечислены имена всех входов и выходов.
Тем самым создается заголовок таблицы истинности. В после-
дующих строках задаются значения сигналов на этих входах
и выходах. К примеру, если имеется таблица истинности для
схемы с тремя входами, А, В и С, и тремя выходами, О0, О, и 02,
то сигналы на них можно описать следующим образом:
truth_table ([А, В, С] -> [ОО, О1, 02])
[О, 0, 0] -> [0, 0, 0] ;
[О, 0, 1] -> [1, 0, 1] ;
[О, 1, 0] -> [0, 0, 0] ;
[0, 1, 1] -> [0, 1, 1] ;
[1, 0, 0] -> [1, 1, 0] ;
[1, 0, 1] -> [0, 1, 1] ;
Эта таблица истинности является неполной, поскольку в ней
не заданы некоторые состояния системы (АВС= 110 и 111). Для
того чтобы пометить эти состояния как условно произвольные,
необходимо записать в начале программы директиву ®dcset
(определяющую множество условно произвольных состояний).
Задание для самопроверки 6.5
Какой набор булевых функций описывает таблица истинности, приведенная выше?
Тестовые векторы
Раздел файла, в котором задаются тестовые векторы, являет-
ся опциональным, но при совместном использовании с входя-
щими в пакет ABEL средствами моделирования он очень удо-
бен для проверки соответствия спроектированной схемы задан-
ной спецификации. Оформляется он точно так же, как и раздел
уравнений при использовании описания в виде таблицы ис-
тинности. После заголовка ставится ключевое слово, в данном
случае это test_vectors, и следует перечисление значений
входных и требуемых выходных сигналов.
262
Глава 6. Проектирование устройств на программируемых...
6.4.3. Последовательные функции
Метод уравнений
Для того чтобы запрограммировать регистровую ПЛИС,
кроме описания сигналов па всех выходах следует отдельно
учесть последовательность функционирования таких схем. На-
значение сигналам переменных выполняется с помощью специ-
ального оператора регистрового присваивания (registered
assignment operator). Он обозначается парой символов := и ис-
пользуется в уравнениях для описания выходных функций
триггеров. Если необходимо, чтобы сигнал на выходе триггера
Qo повторял сигнал на входе /0 после каждого тактового импуль-
са (т.е. речь идет о простом D-триггере), то в разделе описания
уравнений можно просто записать:
Q0 := 10;
ПРИМЕР
Для того чтобы запрограммировать на основе ПЛИС 3-разрядный двоич-
ный счетчик (см. главу 4, раздел 4.5.2), необходимо задать входные функ-
ции £)-триггеров, из которых, собственно, и состоит счетчик:
ЯЛ=А
D„ = АВ + АВ
Dc = АС + ВС + АВС,
где ОА, DB и Dc — сигналы на входах триггеров, а А, В, С — на их выхо-
дах. Таким образом, исходный файл с программой на языке ABEL для та-
кого счетчика мог бы выглядеть так, как показано на рис. 6.19. (Конечно,
если бы задача сводилась к реализации простого 3-раз-рядного счетчика,
то куда логичнее и эффективнее было бы использовать готовую микро-
схему средней степени интеграции, например 4-разрядный счетчик
74LS163, но в случае применения ПЛИС остальную ее часть можно запро-
граммировать для других нужд.)
6.4. Инструментальные средства программирования ПЛИС
263
module three-bit_counter title 'three-bit_counter' decoder device 'P16R8' 0ALTERNATE
A,B,C pin 2, 3, 4, 5, 6, 7;
QO, QI, Q2 pin 12,13,14, 15, 16, 17;
CLK pin 1;
equations
QO : = /А;
QI : = A * /В + /А * B;
Q2 : = /А * С + /В * С + A * В /С;
test vectors ([А, В, C] -> [QO, QI, Q2])
(0, 0, 0] -> [0, 1, 1];
[0, 0, 1] -> [0, 1, 0];
[0, 1, 0] -> [0, 1, 1];
[0, 1, 1] -> [1, 0, 0];
[1, 0, 0] -> [1, 0, 1];
[1, 0, 1] -> [1, 1, 0];
[1, 1, 0] -> [1, 1, 1];
[1, 1, 1] -> [0, 0, 0];
end
Рис. 6.19. Программа на языке ABEL для 3-разрядного двоич-
ного счетчика
Метод диаграмм состояний
Альтернативный метод описания последовательных схем на
языке ABEL заключается в использовании диаграмм состояний.
Иными словами, указываются состояния и условия (в виде бу-
левых уравнений), при которых происходит переход из одного
состояния в другое. Для этого используются условные конст-
рукции типа IF-THEN-ELSE и CASE, метки GOTO.
Каждому состоянию присваивается уникальное имя (а не но-
мер, в отличие от примеров в предыдущих главах) и значения пе-
ременных состояний, которые задаются с помощью уравнений
еще до описания диаграммы состояний. Задание последней на-
чинается с ключевого слова state_diagram, за которым следуют
описания переменных состояния (обычно в виде множества).
264
Глава 6. Проектирование устройств на программируемых...
В последующих строках указываются состояния, соответствую-
щие им выходные сигналы, а также выражения, описывающие
условия перехода в другое состояние (состояния). В рассматривае-
мом примере нет специфически формируемых выходных сигналов,
и выходы схемы представляют собой просто выходы триггеров.
ПРИМЕР
Рассмотрим диаграмму состояний, полученную в главе 5, раздел 5.2.1, для
счетчика, с выходов которого, в зависимости от сигналов на управляющем
входе Р, снимаются две различные повторяющиеся кодовые последователь-
ности. Программа на языке ABEL для этого счетчика показана на рис. 6.20, а
слева для удобства изображена его же диаграмма состояний.
module three-bit_counter
title 'three-bit_counter'
decoder device 'P16R8'
0ALTERNATE
Р
QO,
CLK
Q1
pin
pin
pin
2, 3, 4, 5, 6, 7;
12,13,14, 15, 16, 17;
1;
Диаграмма состояний
D/10
A =
В =
C =
D =
0;
2;
3;
state_diagram
state
state
state
state
end
A:
B:
C:
D:
IF
IF
IF
GOTO
[QO,
THEN
THEN
THEN
A;
QI]
C
A
B
ELSE
ELSE
ELSE
B;
C;
A;
Р
Р
Р
Рис. 6.20. Программа на языке ABEL для счетчика с двумя последовательностями
и описанием в виде диаграммы состояний
6.4. Инструментальные средства программирования ПЛИС
265
Метод таблиц истинности
Последовательную схему можно описать и в формате таб-
лиц истинности. В этом случае приводится описание теку-
щего состояния, входные значения переменных и соответст-
вующего следующего состояния (по сути это таблица перехо-
дов состояний). Таблица истинности описанного выше
счетчика с двумя двоичными последовательностями показана
на рис. 6.21. Список начинается с ключевого слова
truthtable, после которого записываются имена всех
столбцов таблицы, что похоже на описание таблиц истинно-
сти для обычных комбинационных схем. Единственное отли-
чие состоит в том, что используется символ :>, а не ->. Обра-
тите внимание, что для обозначения условно произвольных
состояний в языке ABEL применяется символ .X.
Тестовые векторы
Для последовательных схем тестовые векторы записываются
практически так же, как и для комбинационных. Обычно до-
полнительно указывается входной сигнал сброса, переводящий
схему в известное состояние. Записываемые справа выходные
сигналы должны генерироваться в момент прихода активного
фронта тактового сигнала.
Архитектурно независимое проектирование
Если в предыдущих примерах потребовалось бы опустить
тип устройства и номера выводов, чтобы иметь возможность
выбрать ПЛИС в конце проектирования, то пришлось бы
столкнуться с неоднозначностью, возникающей в результате
неполноты описания. Когда ранее описывался сигнал, прихо-
дящий на вход синхронизации, он присваивался выводу кон-
кретной микросхемы с определенным номером. В отсутствие
этой информации необходимо задать сигнал синхронизации
как таковой. Это можно сделать следующим образом:
[QO,Ql].clk = clock;
Такая запись говорит о том, что входной сигнал синхрониза-
ции триггеров Qo и будет называться clock. Расшире-
ние . elk представляет собой уже упоминавшееся расширение,
записываемое через точку. Аналогично, может понадобиться
266
Глава 6. Проектирование устройств на программируемых...
указать, что Qo и Qt являются сигналами с выходов триггеров
определенного типа, например D-триггеров. Для этой цели
служит специальный оператор признака istype:
[QO, QI] Istype 'reg_d';
где 'reg_d' представляет собой атрибут для указания того, что
сигнал снимается с выхода именно D-триггера.
module three-bit_counter
title 'three-bit_counter'
decoder device 'P16R8'
@ALTERNATE
pin 2;
QO, QI
CLK
RESET
pin 12,13;
pin 1;
pin 3;
A = 0;
B = 1;
C = 2;
D = 3;
truth table
(P.
0
1
0
1
0.
1
X.
[QO, QI])
A
A
В
В
с
с
D
> [QO,Q1])
В;
С;
С;
А;
А;
В;
А;
end
Рис. 6.21. Программа на языке ABEL для двоичного счет-
чика с двумя последовательностями, написанная с исполь-
зованием формата таблиц истинности
6.4. Инструментальные средства программирования ПЛИС
267
6.5. Использование постоянных
запоминающих устройств (ПЗУ)
Эту главу мы завершим описанием полупроводниковых по-
стоянных запоминающих устройств, которые, строго говоря, не
относятся к классу ПЛИС, но также могут быть запрограмми-
рованы как комбинационные логические схемы. Постоянные
запоминающие устройства, или ПЗУ (read-only memory — ROM),
представляют собой тип памяти, содержимое которой в нор-
мальных условиях можно только считывать, но не изменять.
Полупроводниковые ПЗУ так же, как и ПЛИС, являются
энергонезависимыми, т.е. информация в них не теряется даже
при отключении питания. Основной областью применения та-
ких устройств в компьютерных системах является хранение
информации, имеющейся на момент включения. Однако по-
стоянные запоминающие устройства находят чрезвычайно ши-
рокое применение и в других электронных логических схемах.
Базовая структура ПЗУ (как и любого полупроводникового
запоминающего устройства) представляет собой двухмерный
массив ячеек памяти, в каждой из которых может храниться
один двоичный разряд (0 или 1) — рис. 6.22. В функциональ-
ной схеме, приведенной на рисунке, память организована
в структуру типа “xl”, т.е. в каждый момент времени доступ-
ным может быть только один бит. Каждая ячейка имеет в мас-
сиве уникальную позицию, задаваемую строкой и столбцом,
в пересечении которых она лежит. В приведенной на рис. 6.22
схеме имеются 2Г строк и 2s столбцов. Чтобы выбрать нужную
строку, необходимо задать r-разрядное число, а для выбора ад-
реса столбца — ^-разрядное число. Полный адрес ячейки зада-
ется путем конкатенации (присоединением одного числа
к концу другого) этих двух чисел. Для заданного количества
ячеек памяти минимальное количество строк и столбцов может
быть получено в случае квадратного массива.
Ячейки памяти могут создаваться с помощью различных
технологий, включая технологию масочных постоянных запоми-
нающих устройств (fixed read-only memory), информация в кото-
рых не может изменяться после изготовления схемы. Есть и та-
кие типы памяти, которые позволяют изменять содержимое
при помощи стирания и последующей записи данных в вы-
бранных ячейках. Это так называемые программируемые ПЗУ,
268
Глава 6. Проектирование устройств на программируемых...
или ППЗУ (programmable ROM— PROM) и стираемые програм-
мируемые ПЗУ, или СППЗУ (erasable programmable ROM—
EPROM)1. Запись новой информации представляет собой отно-
сительно медленный процесс, который, как правило, требует
извлечения микросхемы из системы.
Для того чтобы прочесть информацию, записанную в ячейку
памяти, задается адрес строки, который позволяет выбрать
только одну из строк. Затем так же выбирается столбец,
и в результате оказывается выбранной определенная ячейка памя-
ти. В процессе считывания информация проходит из ячейки по
столбцу до определенного вывода микросхемы. (В процессе запи-
си, если эта возможность предусмотрена в данном ПЗУ, инфор-
мация поступает в выбранную ячейку в обратном направлении.)
1 В отечественной литературе ПЗУ с возможностью изменения запи-
санной информации иногда называют полупостоянными запоминающими
устройствами или ППЗУ. (Прим, перев.)
6.5. Использование постоянных запоминающих устройств (ПЗУ)
269
Часто ячейки бывают организованы в наборы слов, и все
биты одного слова считываются одновременно. Этого можно
добиться дублированием структуры типа х1 для каждого бита
слова (рис. 6.23), которая называется организацией типа хи, где
и — количество битов в каждом слове. В данной структуре ор-
ганизации памяти используется один дешифратор номера стро-
ки, но для каждого бита слова используются отдельные схемы
выборки столбца. При этом из-за существующих ограничений
на количество выводов в одном корпусе может оказаться про-
блематичным получение в одной микросхеме структуры с вы-
соким значением числа п. Однако структура типа х8 является
стандартной для однокорпусной микросхемы.
Рис. 6.23. Организация полупроводниковой памяти типа хп
Задание для самопроверки 6.6
Какая максимальная емкость памяти типа х1 может быть реализована в 20-
выводном корпусе?
Постоянное запоминающее устройство можно рассматри-
вать как корпус микросхемы с зонами хранения информации,
270
Глава 6. Проектирование устройств на программируемых...
каждая из которых обладает уникальным адресом. Микросхе-
ма имеет входы (входы адреса) и выходы (выходы данных).
Рассматривая ПЗУ под таким углом зрения, можно считать,
что на микросхему подается набор входных сигналов, а с ее
выходов снимается набор выходных сигналов. Значения вы-
ходных сигналов зависят от (постоянного) содержимого кон-
кретных ячеек памяти, выбираемых с помощью входных сиг-
налов. Таким образом, запоминающее устройство можно счи-
тать комбинационной логической схемой.
Задание для самопроверки 6.7
Какая максимальная емкость памяти типа х8 может быть реализована в 20-
выводном корпусе?
ПРИМЕР
На базе постоянного запоминающего устройства необходимо реализовать
комбинационную функцию, заданную с помощью табл. 6.1. Запись информа-
ции в ячейки памяти этого ПЗУ должна выглядеть, как показано на рис. 6.24.
Здесь не делается попыток минимизировать функцию, поскольку реализация
на ПЗУ этого не требует. (Минимизация может оказаться необходимой только
в том случае, если количество переменных слишком велико и превышает воз-
можности микросхемы.) Из рис. 6.24 видно, что используется только один вы-
ход запоминающего устройства, поскольку согласно условию требуется полу-
чить только одну булеву функцию.
Таблица 6.1. Таблица истинности логической функции, реализуемой на ПЗУ
ABCD f(A. В, С, D)
ООООО
0 0 0 1 1
0 0 10 0
0 0 111
0 10 0 0
0 10 11
0 110 1
0 1111
1 0 0 0 0
6.5. Использование постоянных запоминающих устройств (ПЗУ)
271
Окончание табл. 6.1
А В с D f ГА, В, С. D;
1 0 0 1 0
1 0 1 0 1
1 0 1 1 1
1 1 0 0 1
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0
Содержимое
области
Данные
f(A,B,C,D)
Рис. 6.24. Использование постоянного за-
поминающего устройства в качестве комби-
национной схемы
Так как множество микросхем постоянной памяти имеет
организацию типа хи, то ясно, что такие ПЗУ пригодны и для
реализации нескольких логических функций одновременно.
При и = 8 можно получить восемь независимых функций од-
272
Глава 6. Проектирование устройств на программируемых...
них и тех же входных переменных, действуя так же, как
и в случае обычной ПЛИС. Даже если и не использовать все п
выходов, такое решение все равно остается очень выгодным
с точки зрения стоимости схемы. Единственным недостатком
постоянных запоминающих устройств является то, что их быст-
родействие гораздо ниже по сравнению с ПЛИС или обычными
корпусными логическими элементами.
6.6. Резюме
В этой главе были рассмотрены следующие вопросы.
• Концепции построения ПЛИС.
• Программируемые логические матрицы (ПЛМ).
• Устройства программируемой матричной логики
(ПМЛ).
• Последовательные ПЛИС.
• Схемы, реализуемые на основе ПЛИС.
• Программные инструментальные средства работы
с ПЛИС, в частности некоторые аспекты языка ABEL.
• Использование постоянных запоминающих устройств
в качестве комбинационных логических схем.
6.7. Упражнения
1. Реализуйте функцию f = ACD + ВС + Ё на основе
ПЛМ. Покажите структуру внутренних связей.
2. Реализуйте функцию f = ACD + BC + E на основе
ПМЛ. Покажите структуру внутренних связей.
3. В главе 5, раздел 5.2.2, описан детектор двоичной по-
следовательности, имеющий один вход данных и один
выход, сигнал на котором принимает значение 1, ко-
гда на входе появляется последовательность битов
0110011. Уравнения входных функций триггеров де-
тектора имеют вид:
6.7. Упражнения
273
Y2 = x + УзУ1У1
Г1 = УзУ1 + УзУзУ, +лу2У, н-ТУзЛ
При этом выходное уравнение выглядит следующим
образом:
z = У3У2У1
Реализуйте этот детектор последовательности на ос-
нове регистровой ПМЛ. Покажите структуру внутрен-
них связей.
4. Напишите на языке ABEL программу для реализации
па ПЛИС схемы, которая бы сравнивала два 6-
разрядных двоичных числа, А и В, и формировала бы
три выходных сигнала, один из которых принимал бы
значение 1, когда А < В, второй — когда А = В, и тре-
тий — когда А > В.
5. Напишите программу на языке ABEL для схемы, ко-
торая бы решала задачу из упражнения 6.3.
6. Докажите, что минимальное число строк столбцов
массива ячеек памяти ЗУ можно получить в том слу-
чае, когда этот массив имеет квадратную форму.
6.8. Список дополнительной
литературы
1. Advanced Micro Devices, Product Line & Selector Guide,
Sunnyvale, CA, 1990.
2. Data I/O Corp., ABEL™ Design Software User Manual,
Redmond, Washington, 1990.
3. Pellerin, D. and Holley, M., Digital Design Using ABEL,
Prentice Hall: Englewood Cliffs, New Jersey, 1994.
4. Wakerly, J.F., Digital Design Principles and Practices, 2nd
edition, Prentice Hall: Englewood Cliffs, New Jersey, 1994.
274
Глава 6. Проектирование устройств на программируемых...
Глава 7
Тестирование логических
схем
Цели и задачи
В последней главе будут рассмотрены общие методы по-
иска неисправностей в комбинационных логических схе-
мах, а также в очень краткой форме изложены методы
выявления неполадок в более сложных последовательных
схемах и системах.
7.1. Необходимость тестирования
электронных схем
Необходимость испытания логического устройства или сис-
темы возникает сразу после изготовления, поскольку требуется
как можно раньше обнаружить все ошибки, возникшие в про-
цессе производства или те, что могут возникнуть при после-
дующей эксплуатации. (Подразумевается, что проект электрон-
ного устройства выполнен абсолютно правильно, что доказало
логическое моделирование.) Тестирование электроники имеет
огромное значение и должно учитываться еще на стадии проек-
тирования, поскольку процесс производства несовершенен.
Схемы могут иметь физические дефекты (отказы — faults), ко-
торые появляются на этапе производства и непредвиденным
образом изменяют поведение устройства. Кроме того, даже по-
следующие манипуляции с уже готовой микросхемой в корпусе
также могут повредить ее. Целью тестирования является выяв-
ление отказов и идентификация неисправных микросхем. Ре-
зультаты тестирования могут передаваться производителю с це-
лью улучшения технологического процесса.
Тестирование представляет собой серьезную интеллектуаль-
ную задачу, поскольку в схеме может происходить громадное
количество отказов. Единственный известный способ узнать,
исправно ли работает корпусная микросхема —- подать на ее
первичные входы (primary inputs— входные выводы корпуса мик-
росхемы) известные тестовые сигналы и проследить за сигна-
лами на первичных выходах (primary outputs— выходных выводах
корпуса микросхемы). Если эти сигналы отличаются от ожи-
даемых, значит, что-то в схеме работает не так, как надо, т.е.
возможны неисправности или ошибки проектирования. Ошиб-
ки проектирования выявляются довольно быстро путем подачи
тестовых сигналов на эмулятор; тестовый вектор строится на ос-
нове требуемой логической функции. Для нахождения отказов
па схему подаются тестовые вектора, благодаря которым можно
распознать, какие проблемы возникли. Насколько сложно вы-
явить причину неисправности, зависит от контролепригодности
и степени наблюдаемости внутренних узлов схемы. Часто, однако,
требуется найти не определенную неполадку в схеме, а только
убедиться в том, что опа имеется (если, конечно, не исследует-
ся определенный этап технологического процесса).
7.2. Неисправности
Прежде чем начать поиск неисправности схемы, желательно
получить хотя бы общее представление о том, какие из них
могут возникнуть в данном устройстве. Существует достаточно
много различных типов физических неисправностей, влияющих
на работу электронных схем. Чтобы упростить тестирование,
удобно смоделировать возможные неполадки. В общем случае
модель может основываться на эффекте, который данная неис-
правность оказывает на схему. Неисправности можно разделить
па две большие категории: логические модели неисправностей
и модели параметрические. Первые описывают неисправности,
которые влияют на логическую функцию схемы. Вторые — не-
исправности, которые изменяют параметры схемы, например
величину напряжения, тока, нагрузочной способности или за-
держки. В данной главе будут рассматриваться только логиче-
ские неисправности.
276
Гпава 7. Тестирование логических схем
Константные неисправности
Многие неисправности можно промоделировать, считая что
они приводят к появлению на сигнальной линии — фактически
на входе или выходе вентиля — постоянного логического уровня
напряжения (0 или 1). Неисправность, приводящая к установле-
нию на линии постоянного сигнала носит название константной
(на жаргоне ‘"залипание" в 0 или в 1 (stuck-at-O, stuck-at-l)).
Другие неисправности
Кроме ситуаций, когда на линии принудительно появляется
постоянный логический уровень 1 или 0, часто возникают
и другие сбои в работе. Иногда внутреннее короткое замыкание
или разрыв цепи могут приводить не к появлению постоянного
О или 1, а к возникновению па выходе некоторого промежуточ-
ного уровня логического сигнала. Такой тип неисправностей
называется константной неисправностью с залипанием в откры-
том состоянии (stuck-on fault), или константной неисправностью
транзисторного уровня (transistor level stuck-at fault). Найти такие
неполадки всегда тяжело, и здесь они рассматриваться не будут.
Существуют неисправности, которые присущи только
КМОП-схемам и которые нельзя промоделировать в виде про-
стой константной неисправности: это так называемые кон-
стантные неисправности типа обрыва (stuck-open fault), когда
транзистор ведет себя как разомкнутая цепь (т.е. имеет высокий
импеданс). Это может привести к тому, что выходной сигнал
будет сохранять предыдущие значения на короткие интервалы
времени (обычно порядка миллисекунд) при том, что как тран-
зистор подтяжки, так и нагрузочный транзистор закрыты.
Короткое замыкание между двумя частями схемы так и на-
зывается: неисправность типа замыкания, или перемычка
(bridging fault). Влияние КЗ па вентиль зависит от технологии
изготовления последнего и местоположения. Может оказаться,
что будет изменена булева функция или сигнал па линии
“залипнет” на постоянном уровне, а могут возникнуть и другие
ошибки функционирования схемы. Например, замыкание меж-
ду входом и выходом комбинационной логической схемы мо-
жет привести к формированию последовательной схемы. Соз-
дание перемычки между двумя выходами может вызвать изме-
нение уровня напряжения в линии, причем величина этого
напряжения будет зависеть от отношения мощностей разных
вентилей и их способности управлять сигналом в линии.
7.2. Неисправности
277
Одиночная константная неисправность
Модель константной неисправности наиболее популярна
ввиду се простоты. Она используется в большинстве пакетов
моделирования. И именно ей будет уделено основное внимание
в настоящей главе. На рис. 7.1 показаны точки возникновения
константных неисправностей на входах стандартного двухвхо-
дового вентиля И и результирующий сигнал на его выходе. Са-
ма неисправность возникает, вероятно, внутри элемента. Мо-
дель константной неисправности описывает влияние физиче-
ской неисправности на входные/выходные сигналы вентиля.
Залипание в О
Д—X-
Залипание в 1
Залипание в О
Залипание в 1
А
В
Залипание в О
А
В
1
Залипание в 1
Рис. 7.1. Константные неисправно-
сти на входах/выходах вентиля И
278
Гпава 7. Тестирование логических схем
Для вентиля И с двумя входами существует шесть возмож-
ных константных неисправностей — по одной из двух каждого
типа для каждой из трех линий вентиля. Для к сигнальных ли-
ний существует 1к различных комбинаций потенциальных оди-
ночных неисправностей. При возникновении множественных
неисправностей каждая сигнальная линия может находиться
в трех состояниях: быть свободной от неполадок, находиться
в состоянии с постоянным уровнем логического 0 и в состоянии
с постоянным уровнем логической 1. Для к различных сигналь-
ных линий имеется всего Зк различных комбинаций трех со-
стояний. Из них только одно свободно от ошибок, следователь-
но, существует 3k — 1 различных состояния с неисправностями.
Таким образом, число комбинаций ошибок может быть очень
велико. В данной главе будут рассматриваться только одиноч-
ные неисправности, поскольку анализ множественных неис-
правностей в явном виде — задача весьма сложная. К счастью,
подавляющее большинство множественных неисправностей об-
наруживается во время поиска одиночных ошибок.
На рис. 7.2 показана простейшая логическая схема, у кото-
рой три первичных входа, А, В и С, и один первичный выход,/
В ней также имеется всего одна внутренняя линия, обозначен-
ная х. Неполадка может проявиться на любой из сигнальных
линий схемы, поэтому на рисунке крестиками показаны пять
возможных участков их появления: линии А, В, С, f х. Сигналы
на каждой из этих линий могут перейти в состояние с постоян-
ным логическим уровнем — 0 или 1. Следовательно, всего в дан-
ной схеме возможно 10 разных константных неисправностей.
Внутренний
сигнал х
Рис. 1.2. Места возможного возникновения константных
неисправностей в простой логической схеме
Если выход вентиля соединен с несколькими входами сле-
дующего вентиля, то каждый путь прохождения сигнала необ-
ходимо рассматривать отдельно, так как модель константной
неисправности представляет собой отражение внутренней
7.2. Неисправности
279
неполадки, которая, возможно, не является отказом непосред-
ственно сигнальной линии, влияющим на все входы, подклю-
ченные к данному выходу. На рис. 7.3 показана схема, в кото-
рой выходной сигнал одного вентиля управляет входами двух
других. В этом случае может возникнуть сразу восемь различ-
ных константных неисправностей. Здесь неполадка на выходе
вентиля И может привести к “залипанию” уровней на входах
обоих последующих вентилей ИЛИ и НЕ. Эти вентили также
могут иметь константные неисправности на входах, по они уже
будут влиять на функционирование только их самих.
Рис. 7.3. Места возможного возникновения константных
неисправностей в логической схеме с коэффициентом
разветвления больше единицы
7.3. Формирование тестовых векторов
для комбинационных схем
Простейшие схемы легко протестировать, подавая на все
входы определенные значения уровней и сравнивая выходные
сигналы с таблицей истинности схемы. Например, чтобы про-
вести полное тестирование вентиля И с двумя входами, доста-
точно подать на них кодовые комбинации 00, 01, 10 и 11 и убе-
диться, что выходные значения равны, соответственно, 0, 0, 0
и 1. Если же хоть в одном случае значение на выходе отличает-
ся от ожидаемого, то это значит, что в схеме вентиля имеется
неисправность. Входные комбинации, используемые для обна-
ружения неисправностей, носят название тестовых векторов
(test vectors). Тестовые векторы, которые подаются на схему для
проверки ее работоспособности, называются тестовым набором
(test set). К примеру, исчерпывающие испытания двухвходового
вентиля И заключаются в подаче на этот элемент тестовых век-
торов 00, 01, 10 и 11, составляющих тестовый набор. Количест-
во комбинаций, которые необходимо подать на входы схемы
280
Гпава 7. Тестирование логических схем
для ее полного тестирования, зависит, конечно же, от числа
входов. Для п входов имеется 2п различных входных комбина-
ций. Следовательно, с увеличением сложности схемы и количе-
ства входов подавать на них все возможные комбинации вход-
ных сигналов становится непрактично.
Покрытием неисправностей (fault coverage) теста называется
относительное число ошибок, которые с его помощью можно
выявить. Основной проблемой данного подходя является нахо-
ждение минимального количества тестовых векторов при за-
данном покрытии неисправностей.
7.3.1. Табличный и алгебраический методы
Если известна булева функция схемы, то сравнение функции
с ошибкой вследствие неисправности и ожидаемой функции
позволит получить булевы выражения для тестовых векторов.
Это можно сделать, сравнивая таблицы истинности, содержа-
щие значения выходных сигналов при наличии ошибки и без
нее. Имея булеву функцию, можно также путем выполнения
определенных алгебраических манипуляций (например, по ме-
тоду булевых разностей), добиться получения тестового набора.
Здесь эти методы рассматриваться нс будут, потому что они
подходят только для поиска неисправностей в небольших схе-
мах, работа которых описывается простыми логическими урав-
нениями. Заинтересованным читателям рекомендуется обра-
титься к работе Лала (Lala, 1996).
7.3.2. Метод активизации пути
Метод активизации пути (path sensitization method) подходит
для более сложных комбинационных логических схем и заклю-
чается в проверке неисправности в заданной точке путем пода-
чи в нее значения сигнала, противоположного тому, которое
вызывается неисправностью. Если тестируется неисправность
типа “залипания в 1”, то в точку неисправности подается 0. Ес-
ли же тестируется константная неисправность с постоянным
низким уровнем (“залипание в 0”), то в точку подается 1. Пу-
тем подачи на вход сигналов с соответствующими уровнями ак-
тивизируется путь передачи логического уровня сигнала в точке
неисправности сквозь схему до выхода, где его можно наблюдать.
7.3. Формирование тестовых векторов для комбинационных схем 281
ПРИМЕР
На рис. 7.4 показан пример тестирования схемы по
описанному выше методу. Здесь стоит задача обнаруже-
ния неисправности типа “залипание в 0” на выходе
вентиля И. Согласно методике, следует подать в точку
неисправности логическую 1 (уровень, противополож-
ный неисправному). Это можно сделать, если подать 1
на входы вентиля И. Затем сигнал необходимо передать
на первичный выход; этого можно добиться, подав 0 на
второй вход вентиля ИЛИ. В итоге на выходе вентиля
ИЛИ появится сигнал с уровнем, соответствующим
логическому уровню сигнала на выходе вентиля И: ло-
гический 0 в случае, если последний неисправен, и ло-
гическая 1, если он исправен.
Залипание в 0 Подача логической 1
Рис. 7.4. Пример использования метода активизации пути для
нахождения неисправности
В некоторых схемах логические уровни могут инвертиро-
ваться — например, если в схеме, показанной на рис. 7.4, вме-
сто вентиля ИЛИ используется вентиль ИЛИ-НЕ. Чтобы облег-
чить описание действий по обнаружению неисправностей, вво-
дится обозначение сигнала: большая латинская литера D
показывает, что выходной сигнал равен 1, когда схема исправ-
на, и 0, если она неисправна. Аналогично, обозначение D по-
казывает, что в исправном состоянии выходной сигнал равен О,
а в неисправном — I1. На рис. 7.4 выходной сигнал f обозна-
чался бы буквой D.
Символы D и D изначально использовались в так называемом D-
алгоритме (см. работу Рота (Roth et al., 7967), разработанном специально
для получения тестовых векторов методом активизации пути. Использо-
вание такого обозначения подразумевает, что больше ни один нормальный
сигнал в схеме нельзя обозначать как D.
282
Гпава 7. Тестирование логических схем
Установка сигнала на выходе базовых вентилей
с заданным логическим уровнем
На рис. 7.5 показаны сигналы, которые необходимо подать
для того, чтобы получить на выходе каждого из базовых венти-
лей сигнал с логическим уровнем 0 или 1. Знаком X отмечены
условно произвольные сигналы, которые могут иметь значение
как 0, так и 1. Базовые вентили по своей природе симметрич-
ны, поэтому их входные сигналы можно менять местами, не
боясь, что выходная функция изменится.
Залипание в О
Залипание в 1
Залипание в О
Залипание в 1
Залипание в 1
Залипание в 1
Рис. 7.5. Получение на выходах базовых логических вентилей сигналов с уровнем
логического 0 или логической 1
7.3. Формирование тестовых векторов для комбинационных схем 283
На рис. 7.6 показаны сигналы, которые требуется подать на
входы вентилей для того, чтобы передать на их выходы сигнал,
возникающий в результате неисправности на одном из входов.
В этом плане очень полезным свойством обладают вентили ис-
ключающее ИЛИ и исключающее ИЛИ-НЕ: сигнал ошибки
в них передается на выход независимо от состояния на другом
входе. (Естественно, при этом надо знать, является ли значение
этого сигнала прямым, D, или инверсным, D.)
Залипание в О
Залипание в 1
Залипание в О
Залипание в 1
Залипание в О
О
D/D
Залипание в 1
(а) Неисправность типа
"залипание в 0"
Рис. 7.6. Активизация пути в вентилях
D/D
0/1
(б) Неисправность типа
“залипание в 1 ”
284
Гпава 7. Тестирование логических схем
Активизация пути
Каждый вентиль на пути до первичного выхода должен быть
активизирован (sensitized). Для этого используется та же методи-
ка подачи определенных входных сигналов, как показанная на
рис. 7.6, только теперь отслеживается передача по пути сигна-
лов D и D (рис. 7.7). Следует обратить внимание, что активи-
зация пути для вентилей, показанных на рис. 7.6 и рис. 7.7,
достигается подачей на входы вентилей И и И-НЕ логических
1, а на входы вентилей ИЛИ и ИЛИ-НЕ — логических 0 (за
исключением, конечно, самих мест неисправности). Для венти-
лей исключающее ИЛИ и исключающее ИЛИ-НЕ активизи-
рующими могут быть любые сигналы.
Рис. 1.1. Активизация пути в вентилях для сигналов DID
7.3. Формирование тестовых векторов для комбинационных схем 285
ПРИМЕР
Чтобы воспользоваться методом активизации пути для обнаружения кон-
стантной неисправности типа “залипания в 1" на первичном входе схемы,
которая изображена на рис. 7.8, нужно подать на ее входы следующие
сигналы: = 0, х, = 1, хг = 1, х3 = 0 и х4 = 0. Это позволит передать
возникающий в результате неисправности сигнал на первичный выход.
Сигнал = 0 пытается принудительно установить логический уровень
в месте неисправности в 0, а остальные сигналы служат для образования
пути активизации вплоть до первичного выхода. Если выходной сигнал ра-
вен 1, то это говорит о том, что схема исправна, а если он равен 0, то на-
лицо наличие неисправности.
Рис. 7.8. Активизация пути в логической схеме
Активизация пути благодаря проходу в прямом
и обратном направлении
В показанной на рис. 7.8 схеме первичные входные сигналы
позволяют активизировать все вентили, стоящие на пути до ее
первичного выхода. На практике так происходит далеко не
всегда, и приходится задавать определенные логические уровни
и на входах внутренних вентилей. Это можно сделать, подавая
соответствующие сигналы на первичные входы. Общая проце-
дура заключается в определении сначала логических значений,
которые необходимо получить на входах каждого логического
вентиля для передачи сигнала D/D на выход. На втором этапе,
идя по пути в обратном направлении, задаются логические зна-
чения на входах и выходах всех вентилей, стоящих до тех, что
принадлежат пути. Таким образом, процесс активизации пути
состоит из двух этапов: прямого и обратного прохода пути
(forward trace и backward trace).
286
Гпава 7. Тестирование логических схем
ПРИМЕР
Рассмотрим схему, изображенную на рис. 7.9. Нужно выявить константную
неисправность типа “залипание в 0" в точке, помеченной крестиком. Сна-
чала попытаемся установить в месте потенциального возникновения неис-
правности противоположный логический уровень — в нашем случае 1.
Чтобы сделать это, нужно подать на входы схемы следующие сигналы:
х() =1 или х, = 1, или хп = х, = 1. Если идти в прямом направлении, то
необходимо активизировать путь до выхода, а для этого потребуется вы-
ставить уровень напряжения в еще одной точке внутри схемы: а = 1, по-
сле чего на выходе вентиля И-НЕ появится сигнал D. Чтобы он мог прой-
ти на выход/схемы, необходимо, чтобы в точках b и с были уровни, соот-
ветственно, 6=1 и с = 0. Если двигаться в обратном направлении (от
выхода к входу), то сигналы в точках бис будут иметь требуемый логиче-
ский уровень 0, если на входах х4 и х5 выставить сигналы х4 = 1 и х5 = 0.
Сигнал в точке а можно перевести в 1, если выставить на входах х2
и х, логические единицы. Следовательно, входной тестовый вектор имеет
вид ХоХ|Х2ХзХ4х5 = 011110 или 101110 или 111110.
Рис. 7.9. Обнаружение константной неисправности методом прямого и об-
ратного прохода пути
Задание для самопроверки 7.2
Какое значение сигнала на выходе схемы, приведенной на рис. 7.9, будет сви-
детельствовать о наличии неисправности “залипание в 0” в указанном месте?
Эквивалентные неисправности в элементах
Эквивалентными неисправностями (equivalent faults) называют-
ся неисправности, которые детектируются одними и теми же
7.3. Формирование тестовых векторов для комбинационных схем 287
тестовыми векторами. Соответственно, неисправности неэкви-
валентны, если существует хотя бы один тестовый вектор, кото-
рый обнаруживает одну из них, но не обнаруживает остальные.
Давайте для удобства ограничимся рассмотрением логических
вентилей не более чем с тремя входами. (Ясно, что полученные
результаты можно будет распространить и на вентили с большим
количеством входов.) Пусть необходимо протестировать трехвхо-
довый вентиль И на предмет залипания в 0 одного из его входов.
Как видно рис. 7.6, тестовый вектор будет представлять собой
111, т.е. не имеет значения, какой вход тестируется на наличие
неисправности. Поэтому все константные неисправности
с “залипанием в 0” на входах вентиля И будут эквивалентными.
Тестовый вектор 111 также дает возможность проверить, нет ли
“залипания в 0” на выходе вентиля (см. рис. 7.5), поэтому и эта
неисправность является эквивалентной неполадкам на входах
вентиля И. Таким образом, для вентиля И все неисправности на
входах и выходе типа “залипания в 0” эквивалентны, так что
достаточно тестировать только одну из них. Тестовый вектор не
позволяет отличить их друг от друга. Аналогично, для вентиля
ИЛИ с тремя входами тестовый вектор ООО покажет, присутст-
вует ли константная неисправность типа “залипание в 1” на
любом из трех входов и на выходе вентиля, т.е. эти неисправ-
ности также эквивалентны друг другу. Эквивалентные неис-
правности присутствуют и в вентилях И-НЕ и ИЛИ-НЕ.
Задание для самопроверки 7.3
Определите эквивалентные неисправности для вентилей И-НЕ и ИЛИ-НЕ.
Для вентилей исключающее ИЛИ/исключающее ИЛИ-НЕ
эквивалентных неисправностей не существует, что, впрочем,
можно было заключить из рис. 7.5 и рис. 7.6. Чтобы неисправ-
ности были эквивалентны друг другу, все тестовые наборы для
каждой из них должны совпадать. Хотя тестовый вектор 11
и покажет обе константные неисправности с “залипанием в О”
на обоих входах исключающего ИЛИ, они не будут эквивалент-
ны, поскольку второй вектор (01) выявит одну из неисправно-
стей, а третий (10) — другую. Аналогично, неисправность
с “залипанием в 0” на входе и неисправность с “залипанием в 1”
на выходе неэквивалентны друг другу, потому что еще один
вектор — а именно, 00 — обнаруживает только неисправность
288
Гпава 7. Тестирование логических схем
на выходе, пропуская неисправность на входе. Те же самые ар-
гументы имеют силу и для вентиля исключающее ИЛИ-НЕ.
Полное тестирование базовых вентилей
Для того чтобы полностью проверить работоспособность
вентиля И с тремя входами, нужно подать на его входы тесто-
вые векторы 111 (для выявления константных неисправностей
с постоянным нулевым уровнем), ОН, 101 и НО (для выявления
“залипания в 1” на каждом из входов и, следовательно, на вы-
ходе). Чтобы полностью протестировать вентиль ИЛИ, нужно
подать на него тестовые векторы ООО (для обнаружения кон-
стантных неисправностей с постоянным единичным уровнем),
100, 010 и 001 (для обнаружения константных неисправностей
с постоянным нулевым уровнем, соответственно, на первом, вто-
ром и третьем входах и выходе). Чтобы протестировать любой
вентиль с п входами, достаточно использовать п + 1 вектор, хотя
различных неисправностей в нем может быть 2п + 2. Обратите
внимание, что полное тестирование всех входных неисправно-
стей дает полное представление и о выходных неполадках. Это
справедливо для всех базовых элементов электроники. Следова-
тельно, можно исследовать только входные неисправности.
Задание для самопроверки 7.4
Определите тестовый набор для полного тестирования вентиля И-НЕ с тремя
входами и такого же вентиля ИЛИ-НЕ. (Сперва придется решить задание для
самопроверки 7.2.)
Схемы с одной нагрузкой
Под нагрузочной способностью, или коэффициентом разветв-
ления (fan-out) вентиля понимают количество входов других вен-
тилей, которые могут быть подключены к выходу данного вен-
тиля. Нагрузочная способность, равная 8, свидетельствует
о том, что к выходу вентиля можно подключить не более 8 вхо-
дов других элементов. Коэффициент разветвления указывает,
что сигнал с данного выхода может управлять несколькими
входами других компонентов схемы.
Если элемент схемы не имеет разветвления, т.е. сигнал с его
выхода проходит на один вход другого элемента, то неисправность
на входе данного элемента может попасть на первичный выход
только по одному пути. Активизируя этот путь, можно обнару-
7.3. Формирование тестовых векторов для комбинационных схем 289
жить любые ошибки на всем его протяжении, что и показано
на рис. 7.10. Все пути в такой схеме могут быть прослежены
и обратно — с выхода на вход. Следовательно, для того, чтобы
выявить все неисправности схемы, достаточно подать тестовый
вектор, позволяющий обнаруживать только неисправности на
первичных входах схемы. Этот факт значительно уменьшает ко-
личество тестовых векторов, но это справедливо только для
схем без разветвления. К сожалению, на практике такие схемы
почти не встречаются.
Рис. 1.10. Тестированием на входе схемы можно обнаружить все неисправности схемы
Задание для самопроверки 7.5
Почему в предыдущих главах книги наличие большого коэффициента раз-
ветвления считалось преимуществом, а не недостатком электронных схем?
Схемы с многочисленными нагрузками
Для схем с коэффициентом разветвления больше единицы
полное тестирование всех входов нс даст исчерпывающей ин-
формации о неисправностях схемы; более того, зачастую про-
верить входы всех элементов схемы невозможно. При активи-
зации одного пути может активизироваться и другой, поэтому
сигналы от неисправности проходят по обоим путям и объеди-
290
Гпава 7. Тестирование логических схем
няются до достижения ими первичного выхода. Такой объеди-
ненный сигнал может оказаться неотличимым от сигнала, по-
лучаемого в отсутствие неисправностей. На рис. 7.11 изображе-
на общая схема того, как может происходить одновременная
активизация нескольких путей. На рис. 7.11(a) показано нали-
чие двух путей к первичному выходу, один из которых активи-
зируется, а другой “деактивизируется”. Однако иногда
“деактивизировать” один путь нельзя просто потому, что оба
пути используют одни и те же сигналы для активизации. На-
пример, на рис. 7.11(6) активизированы уже оба пути, но оба
сигнала могут взаимодействовать, никак не влияя на результи-
рующий сигнал на первичном выходе схемы. К примеру, если
оба полученных сигнала D попадают на вентиль ИЛИ, то с его
выхода будет снят один сигнал D, и, следовательно, неисправ-
ность удастся обнаружить. Однако на рис. 7.11(b) можно видеть
ситуацию, когда сигналы взаимодействуют друг с другом, так
что на первичном выходе получается одинаковый сигнал как
при наличии неисправности, так и без таковой.
Пример единственного пути активизации при наличии раз-
ветвления в схеме показан на рис. 7.12. Подача тестового век-
тора 100 однозначно определит константную неисправность ти-
па-“залипание в 1” на одном из входов. Однако в той же схеме,
но с вентилями ИЛИ (рис. 7.13) обнаружить неисправность
можно, только активизируя сразу два пути тестовым вектором
010. Если попытаться активизировать лишь один путь, подавая,
скажем, тестовый вектор 010, этот путь оказался бы блокиро-
ванным единицей на входе вентиля ИЛИ второго уровня. На-
конец, в схеме на рис. 7.14 активизация двух путей вообще
приводит к пропаданию сигнала от неисправности.
Задание для самопроверки 7.6
Какой тестовый вектор можно было бы подать на схему, приведенную на рис. 7.14?
Для нахождения подходящего тестового вектора приходится
использовать метод проб и ошибок, начиная с активизации
только одного пути и продолжая в случае необходимости искать
более сложные решения. Для решения этой непростой задачи
имеются компьютерные программы, разработанные специально
для определения неисправностей методом активизации пути.
7.3. Формирование тестовых векторов для комбинационных схем 291
Логическая схема
О или 5
Логическая схема
а) Одиночный активизированный путь от места неисправности к первичным выходам
Логическая схема
б) Множественные взаимоусиливающие активизированные
пути от места неисправности к первичным выходам
Первичные
входы
Логическая схема
Первичный
выход
в) Множественные взаимоподавляюшие активизированные
пути от места неисправности к первичным выходам
Рис. 7.11. Активизация одного или нескольких путей
292
Гпава 7. Тестирование логических схем
Тестовый вектор
Рис. 1.12. Схема с разветвлением, в которой для определения не-
исправности достаточно активизировать один путь
Тестовый вектор
Рис. 1.13. Схема с разветвлением, в которой для определения не-
исправности необходимо активизировать не менее двух путей
Рис. 7.14. Схема с разветвлением, в которой активизация двух пу-
тей приводит к пропаданию сигнала вследствие неисправности
Необнаруживаемые неисправности
В схеме, приведенной выше, удается активизировать все
пути. Однако существует огромное количество схем, в кото-
рых подобная методика отнюдь не дает ответа на вопрос,
7.3. Формирование тестовых векторов для комбинационных схем 293
каким должен быть тестовый вектор. Рассмотрим, например,
схему, показанную на рис. 7.15. Для того чтобы обнаружить
константную неисправность типа “залипание в 0” в месте,
отмеченном крестиком, нужно попытаться принудительно ус-
тановить в этом месте противоположный (высокий) уровень
напряжения, подавая на входы схемы сигналы х0 = 1 и х2 = 1.
Активизировать путь до выхода можно, установив а = b = 0.
Для того чтобы получить 0 на связи а, нужно подать сигналы
х0 = 0 или Х| = 0. Чтобы получить b = 0, нужно подать сигна-
лы X] = 1 или х2 = 0. Эти условия, однако, являются взаимо-
исключающими, поскольку сигналы х0 и х2 должны быть ус-
тановлены в 1, чтобы в месте возможной неисправности из-
менить уровень на противоположный. Если же выбрать для
установки а в 0 сигнал х0 = 0, не удастся установить в 0 сиг-
нал Ь. И наоборот: если установить в нулевой уровень сигнал
Ь с помощью х() = 1, установить в 0 сигнал а уже не получит-
ся. Следовательно, обнаружить неисправность в этой схеме
методом активизации пути невозможно.
Рис. 1.15. Схема с необнаруживаемой неисправностью
Есть и другие виды необнаруживаемых неисправностей. На-
пример, константная неисправность с переходом сигнала в по-
стоянный единичный уровень (“залипание в 1”) на связи Ь
также нельзя выявить: для этого требуется подать сигналы
xb = 0, х,=0 и х2 = 0, чтобы выставить нули на входах вентиля
ИЛИ. А принудительная установка связи с константной неис-
правностью в 0 требует подачи сигналов Х| = 1 и х2 = 0, т.е. опять
возникает конфликт.
Причина, по которой неисправности переходят в разряд не-
обнаруживаемых, кроется в том, что приведенная схема облада-
294
Глава 7. Тестирование логических схем
ет избыточностью. Это единственный фактор, в результате ко-
торого такие схемы становятся нечувствительными к тестиро-
ванию (см. работу Нельсона и др. (Nelson et al., 1995). Взгляните:
данная схема реализует функцию
f = xoxl + xQx2+xlx2-
Но ведь ее можно упростить до вида
f = xoxl+xix2-
В этом можно убедиться, внимательно изучив карту Карно
(рис. 7.16). Можно видеть, что член ХоХ2 был лишним, потому
что каждая соответствующая ему клетка с 1 на карте Карно мо-
жет быть накрыта областями других групп. Если удалить из
схемы соответствующий вентиль И, то получится полностью
тестируемая схема (такая же, как на рис. 7.12). Хотя этот лиш-
ний член и не нужен с функциональной точки зрения, он мог
быть введен намеренно во избежание “эффекта гонки”'. Ино-
гда, если под рукой имеются вентили только определенного ви-
да, например только с двумя входами, выгоднее реализовать
неминимизированную функцию. Если такая реализация дейст-
вительно необходима, то для обеспечения возможности пря-
мого наблюдения сигналов внутри схемы может понадобиться
дополнительное количество выходов.
Рис. 1.16. Карта Карно для функции
f = хох,+хох2+х,х2
1 См. список рекомендуемой литературы.
7.4. Тестирование последовательных схем...
295
7.4. Тестирование последовательных
схем и сложных электронных систем
До сих пор рассматривался поиск неисправностей только
в простых комбинационных логических схемах. Однако по-
следовательные логические схемы и полные электронные сис-
темы представляют собой более сложные объекты тестирова-
ния. В этом разделе будут очень кратко рассмотрим особенно-
сти проверки таких схем. Тестирование последовательных
схем можно разделить на два этапа. Во-первых, последова-
тельная схема должна быть установлена в известное состоя-
ние. Во-вторых, после подачи входных сигналов это состоя-
ние должно измениться в другое известное состояние. Такая
постановка вопроса требует контролепригодности
(controllability) схемы. При этом оба — текущее и следующее —
состояния схемы должны поддаваться наблюдению (be
observable). В главе 5 была представлена общая модель элек-
тронной последовательной схемы (см. рис. 5.1). К сожалению,
переменные состояний не могут быть наблюдаемы непосред-
ственно; чтобы добиться этого, необходимо прибегнуть к ме-
тоду сканирования пути (scan-path method).
7.4.1. Метод сканирования пути
Метод сканирования пути предусматривает ввод в схему
дополнительных узлов, которые позволяют получить последо-
вательную загрузку и выгрузку данных из триггеров состоя-
ний. Для этого по специальному сигналу выборки между со-
седними триггерами организуются пути прохождения сигна-
лов, которые формируют своеобразный регистр сдвига
с последовательным вводом и последовательным выводом.
Если еще добавить входные и выходные выводы этого регист-
ра, которые позволят загружать и выгружать данные, то полу-
чится примерно такая схема, как на рис. 7.17.
Возможны два режима работы такой схемы.
1. Нормальный режим, в котором схема конфигурируется
согласно техническим требованиям. Логика следующего
состояния служит для загрузки данных в триггеры со-
стояний и формирования выходной функции Z.
296
Гпава 7. Тестирование логических схем
2. Режим сканирования пути, в котором триггеры состоя-
ний конфигурируются как регистр сдвига с последова-
тельным входом и последовательным выходом.
Выбрать режим можно с помощью мультиплексоров “из 2
линий в 1”, установленных на входах триггеров состояний, как
показано на рис. 7.17. Все мультиплексоры управляются с по-
мощью сигнала выбора режима mode_selecT. скажем, при
mode_select = 0 схема функционирует в нормальном режиме,
а при mode_select = 1 — в режиме сканирования пути. Во время
тестирования режимы используются попеременно.
сканирования
Рис. 1.17. Модель последовательной схемы с путями сканирования
7.4. Тестирование последовательных схем...
297
Для проверки работоспособности последовательной схемы
необходимо выполнить следующее.
1. Тестирование регистра сдвига, т.е. тестирование допол-
нительной логики по методу сканирования пути. Этот
тест проводится в режиме сканирования путем сдвига по
регистру известного кода, например 0101010 ..., и его
сравнения с кодом на выходе.
2. Тестирование комбинационной логики следующего со-
стояния. Для ее проверки необходим доступ ко входам
и выходом этого участка схемы. Входы доступны, по-
скольку являются первичными входами схемы, а вот
выходы комбинационной логики могут быть частично
доступны как первичные выходы (при условии ис-
пользования модели Мили) и частично — через реги-
стры сдвига в нормальном режиме работы схемы. Что-
бы получить доступ к выходам, необходимо сначала
выбрать нормальный режим работы устройства, чтобы
загрузить триггеры, а затем перейти в режим сканиро-
вания пути, чтобы путем сдвига вывести содержимое
триггеров из схемы.
3. Тестирование таблицы состояний, т.е. проверка правиль-
ности ее реализации. Для такой проверки необходимо
задать тестовую последовательность. Можно переводить
схему из каждого текущего состояния, указанного в таб-
лице состояний, в следующее по порядку, т.е. провести
комплексное испытание. Для этого, еще до специфиче-
ского изменения входных сигналов, триггеры состояний
сначала загружаются в режиме сканирования пути соот-
ветственно текущему состоянию, чтобы можно было пе-
рейти из него в следующее, а затем выгружаются.
7.4.2. Встроенное самотестирование
При встроенной функции самотестирования в электронном
устройстве предусматриваются дополнительные схемные эле-
менты, которые не только позволяют организовать тестовый
режим, но и служат для задания тестовых последовательностей
и имеют в своем составе компараторы, сравнивающие эти по-
следовательности с правильными выходными кодами. К приме-
298
Глава 1. Тестирование логических схем
ру, приведенная выше методика сканирования пути вполне
может применяться в виде встроенного самотестирования, если
разместить внутри микросхемы генератор последовательностей,
сигнал с которого будет поступать на входы сканирования,
а также компараторы, присоединенные к линиям выходов ска-
нирования. Вместо генератора специальной последовательности
можно использовать и генератор псевдослучайной последова-
тельности. Более детальное описание техники встроенного са-
мотестирования можно найти в работах Нельсона и др. (Nelson
et al., 1995) и Лала (Lala, 1996).
7.4.3. Периферийное сканирование
Метод периферийного сканирования расширяет область
применения техники сканирования пути на целые системы
микросхем. Каждый чип оснащается входом и выходом пери-
ферийного сканирования. Триггеры считывают информацию
с обычных выводов входных и выходных сигналов и формиру-
ют регистр сдвига, как показано на рис. 7.18. Выход перифе-
рийного сканирования каждой микросхемы соединен со входом
сканирования следующей микросхемы, что и позволяет постро-
ить длинный сдвиговый регистр. Все микросхемы могут инди-
видуально отключаться от теста схемы благодаря наличию на-
страиваемых линий связи с регистром сдвига. Этот метод был
принят в качестве стандарта тестирования электронных плат
IEEE 1149.1 (Institute of Electrical and Electronics Engineers —
Институт инженеров по электротехнике и электронике). В со-
став каждой микросхемы входит не только регистр сдвига, но
и дополнительная логика, которая позволяет контролировать
сам процесс тестирования. Более подробную информацию
можно найти в описании стандарта IEEE 1149.1 (1990).
7.5. Резюме
В этой главе были раскрыты следующие вопросы.
• Концепция модели константной неисправности.
• Концепция тестовых векторов.
• Концепция метода активизации пути.
• Тестирование последовательных схем (кратко).
7.4. Тестирование последовательных схем...
299
Корпусная микросхема
Внешние выводы входов и выходов
Рис. 1.18. Регистр сдвига в методе периферийного сканирования
7.6. Упражнения
1. Сколько константных неисправностей может быть
в схеме, приведенной на рис. 7.19?
2. Определите тестовый вектор, с помощью которого
можно обнаружить константную неисправность
в схеме, приведенной на рис. 7.20.
300
Гпава 7. Тестирование логических схем
3. Определите тестовые векторы для тестирования логи-
ческих схем, приведенных на рис. 7.21, на предмет
константных неисправностей.
Рис. 7.21. Схема к упражнению 7.3
7.7. Список дополнительной
литературы
1. IEEE, Test Access Port and Boundary-Scan Architecture,
IEEE Standard 1149.1, IEEE: New York, 1990.
2. Lala, P. K.., Practical Digital Logic Design and Testing, Pren-
tice Hall: Englewood Cliffs, New Jersey, 1996.
7.7. Список дополнительной литературы
301
3. Nelson, V. P., Nagle, H. T., Varroll, B. D. and Irwin, J. D.,
Digital Logic Circuit Analysis and Design, Prentice Hall:
Englewood Cliffs, New Jersey, 1995.
4. Roth, J. P., Bouricius, W. G. and Schneider, P. R.,
“Programmed algorithms to compute tests to detect and
distinguish between failures in logic circuits,” IEEE Trans.
Comput., EC-16, no. 5, pp. 567-80, 1967.
5. Wilkins, B. R., Testing Digital Circuits. An Introduction, Van
Nostrand Reinhold: Wokingham, England, 1986.
302
Гпава 7. Тестирование логических схем
Ответы на задания
для самопроверки
Глава 1
1.1. 11012 = 1310 (в десятичной системе)
1.2. Дробная часть, 0,1012 = О,61251О (0,1, = 0,510;
0,0012 = 0,12510). Следовательно, двоичное число
1101,1012 = 13,61251О.
1.3. “Галочка” карандашом в квадратике в анкете: если
есть = 1, нет = 0.
1.4. 255 (т.е. 11111111, или 28 - 1)
1.5. 11101010, (т.е. 128 + 64 + 32 + 8 + 2)
1.6. 00111101,
1.7. 42А2,6
1.8.
Десятичная система Двоичная система
81 1 0 1 0 0 0 1
63 0,1,1,1,1,1,1
144 10 0 1 0 0 0 0 =128 + 16
1.9. 1010101 + 1 = 1010110
1.10. 0101001 + 1 = 0101010
1.11. 1010110: Обратное преобразование в положительный
эквивалент, используя метод “инвертирования всех
разрядов плюс 1”: 0101001.
1.12.
Десятичная система Двоичная система
14 0 0 0 111 0
-63 1 0 0 0 0 0 1
-49 1 0 0 1111
1.13. 1110111
1.14. Изменением бита Ь6 из 1 в 0. В качестве альтерна-
тивы можно вычитать из кода шестнадцатеричное
число 20|6.
Глава 2
2.1. А
2.2. А
2.3. А
2.4.
Таблица 1. Таблица истинности, доказывающая, что А В 7 = А В
АВС + BD = В(АС + D)
304
Ответы на задания для самопроверка
2.1. А(В + CAD) = АВ + ACD
2.2. (Д + В)(Д + С)(В + С) = (Д + В)(Д + С)
2.3. Первое доказательство:
АВ=А+В
согласно таблице истинности (см. таблицу 2)
Таблица 2. Доказательство тождества АВ = А + В
А В АВ А + В
0 0 1 1
0 1 0 0
1 0 0 0
1 1 0 0
Затем в выражение АВ = А + В подставляем вместо
переменной В сумму В + С и получаем:
А(В + С) = А + (В + С)
АВС = А + В + С
2.9. f = AB(C + D)
2.10.
2.11. АВС + АВС + АВС
Ответы на задания для самопроверки
305
2.12. Во всех случаях, значения функций при А = О,
а В = 1 отличаются от значений при А = 1, а В = 0.
2.13. Одновременно включатся и верхняя, и нижняя схе-
мы, что приведет к заземлению на 0 источника пита-
ния +5 В. При этом через схему потечет чрезмерно
большой ток. Величина напряжения на выходе будет
зависеть от внутренних сопротивлений частей схемы.
Глава 3
3.1.
Таблица 3. Таблица истинности функции f2=AB + C
А В с АВ + С
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 1
3.2.
3-3. f = ABC + ABC + ABC (=ABC + BC)
306
Ответы на задания для самопроверки
3.4. Сначала нужно умножить А на сумму (В + В), а за-
тем — на (С + С)-
3.5.
3.6. /(А, В, С) = (А + В + С)(А + В + С)(А + В + С)
3.7. А(ВС + BD+ BE + F)
3.8. АВС + ADE
3.9. f(A, В, С) = АВ + ВС + АС
ЗЛО. А(ВС)
3.11. АВС
3.12.
3.14. Функция /| может быть задана как ft=ACD + AC-
Тогда член ACD является общим для функций / и/.
3.15. С учетом внутренней структуры схемы можно записать:
f =GIG2AG2B Обратите внимание на кружки на входах
вентилей, показывающие наличие инверсии сигналов.
3.16. (7|=1,G2A = 0h G2B=0
Ответы на задания для самопроверки
307
Глава 4
4.1.
Тактовый
сигнал
4.2. q - q -1, т.е. сбой схемы.
4.3. Из рис. 4.3 и теоремы де Моргана следует, что
QR + R- Мы также можем сказать, что
Q= 1 при 5= 1 (т.е. сигнал 5 выставляет выход
в единичное состояние) или Q=l, если выходной
сигнал уже находился в этом состоянии и Я=0
(qr). Это характеристическое уравнение также мож-
но доказать, сформировав таблицу, в которой пере-
числены текущие состояния сигналов 5, R и Q,
а также новое значение Q (2+). Из этой таблицы мо-
жет быть получена результирующая функция, а затем
минимизирована с помощью карты Карно. Необхо-
димо только убедиться, что новые значения сигнала
Q согласуются с существующими записями для этого
значения Q в качестве входного сигнала.
4.4. Следует подать прямо на вход D сигнал q =jq + kq,
т.е.
D Q
--->CL Q
308
Ответы на задания для самопроверки
4.5. Имея триггеры Fo, F\, F2, F3, Ft, Fs, F6 и F2 и подклю-
чив входы сброса триггеров Fo, F, F4, F6 и входы ус-
тановки Ft, F$, Fs и F7 к источнику управляющего
сигнала с активным низким уровнем напряжения.
4.6. Код 00000010 или 2 в десятичной системе. При
сдвиге вправо будет округляться дробная часть числа.
4.7. Повторяющуюся последовательность вида:
01010101 -> 00101010 -> 10010101 -» 01001010 10100101
4.8. Так же, как и при реализации на D-триггерах, с той лишь
разницей, что сигнал с выхода Q последнего триггера
подается на вход К первого триггера, а сигнал с выхода
Q последнего триггера — на вход J первого триггера.
4.9. /А = КА = 1
/в = = А
Jc= Кс = АВ
JD= KD = ABC
JE= КЕ = (ABC)(D)
JF= (ABC)(DE)
JG= KG = {ABC)(DEG)
/н = Кц = (ABC)(DEG)H
в результате получается такая схема:
4.10. Следует подать выходной сигнал Q одного триггера
на вход синхронизации следующего.
Ответы на задания для самопроверки
309
Глава 5
5.1. Шесть (так как 26 = 64 — ближайшее число, являю-
щееся степенью 2).
5.2.
Wic
У2 =У2У1С+У2У1С
у, =У2У1^ + У2У1 + У2У>С
5-3. У, = У3У, + УзУг+хУг^+^У,
5.4.
1 00 00
2 01 10
3 И и
4 10 01
5.5. Это будет зависеть от значений на входах у3, у2 и уь
пока Z= 0. Только если УзУзУ^ = 011 выходная функ-
ция немедленно изменится (из 0 в 1), в чем можно
убедиться, изучив ее карту Карно.
5.6. Как всегда, удовлетворить все правила полностью
невозможно. Состояния А, В и С приводят к группе
тех же следующих состояний. Состояния А и С так-
же имеют одинаковые выходные значения. Одно из
возможных назначений состояний, если использо-
310
Ответы на задания для самопроверки
вать правила 1 и 3, выглядит так: А = 00 и С= 01
(отличаются только одним битом). Состояния А и D
также в большинстве случаев приводят к одним
и тем же следующим состояниям и имеют одинако-
вые выходные значения, поэтому мы можем при-
своить состоянию D код 10, в результате чего оста-
ется назначить состоянию В код И. Обратите вни-
мание, как уменьшение количества состояний
усложняет применение “правил”.
5.7.
5.8.
Уо У1 У2 Уз У> Л Уб
Состояние 0 = 0 0 0 0 0 0 0
Состояние 1 = 1 0 0 0 0 0 0
Состояние 2 = 0 1 0 0 0 0 0
Состояние 3 = 0 0 1 0 0 0 0
Состояние 4 = 0 0 0 1 0 0 0
Состояние 5 = 0 0 0 0 1 0 0
Состояние 6 = 0 0 0 0 0 1 0
Состояние 7 = 0 0 0 0 0 0 1
Ответы на задания для самопроверки
311
Глава 6
6.2. 16 (10 входов устройства плюс 6 входов/выходов, кото-
рые также могут быть использованы в качестве входов).
6.3. Каждая выходная функция может содержать до 7 чле-
нов-произведений. Есть всего 8 выходов. При усло-
вии использования всех обратных связей, можно
сформировать до 7 х 8 = 56 членов-произведений.
6.4. 15+14+13+12+11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 +
3 + 2 + 1 = (15 х 14)/2 = 320
6-5- Qa = ABC+ABC
Q, - АВС + АВС + АВС
Q2=ABC + ABC + ABC
С учетом условно произвольных состояний функции
можно минимизировать до вида:
Qa = ABC+AC
Q,=A + BC
в2=С
6.6. 217 битов (2 вывода питания, 1 вывод для выхода дан-
ных и 17 выводов для битов адреса).
6.7. 210 битов (2 вывода питания, 8 выводов выхода дан-
ных и 10 выводов для битов адреса).
312
Ответы на задания для самопроверки
Глава 7
7.1.
Залипание в О
Д—X—
Залипание в 1
7.2. Логический 0(D)
7.3. Для элемента И-НЕ:
Все входные константные неисправности типа
“залипания в 0” и выходная константная неисправ-
ность типа “залипания в 1” (тестовый вектор 111).
Для элемента ИЛИ-НЕ:
Все входные константные неисправности типа
“залипания в 1” и выходная константная неисправ-
ность типа “залипания в 0” (тестовый вектор ООО).
Ответы на задания для самопроверки
313
7.4. Для элемента И-НЕ: 111 плюс ОН, 101, ПО (для тес-
тирования всех входов на предмет константных не-
исправностей типа “залипания в 1”).
Для элемента ИЛИ-НЕ: ООО плюс 100, 010, 001 (для
тестирования всех входов на предмет константных
неисправностей типа “залипания в 0”).
7.5. Использование общих выходных сигналов вентилей
позволяет уменьшить количество вентилей в систе-
мах с большим количеством выходов.
7.6. 011
314
Ответы на задания для самопроверки
Предметный указатель
А
Advanced Boolean Expressions
Language, 252
American Standard Code for
Information Interchange, 44
ASCII-код, 44
D
DIP-корпус, 82
I
IEEE, 299
Institute of Electrical and
Electronics Engineers, 299
A
Американский стандартный
код для обмена
информацией, 44
Атрибут сигнала, 255
Б
Байт, 29
БИС, 81
Большие интегральные
схемы, 81
Буквенно-цифровые
символы, 44
Булева алгебра, 23
В
Вентиль, 53
Время
удержания данных, 164
установления данных, 163
Выражения перехода, 218
д
Двоично-десятичное
представление, 42
Двоичное слово, 169
Двоичный счетчик, 153
асинхронный, 188
реверсивный, 188
с обратным счетом, 186
со сквозным переносом, 188
Двухуровневая схема, 100
Демультиплексор, 755; 137
Детектор двоичных
последовательностей, 202
Дефект, 275
Дешифратор, 136
Диаграмма состояний, 166
модели Мили, 167
модели Мура, 166
Дизъюнктивная форма, 102
Дизъюнкция, 102
Дополнительное число, 36
3
Закон ассоциативности, 64
Закон дистрибутивности, 65
Закон коммутативности, 63
Залипание, 277
Запас помехоустойчивости, 84
на переменном токе, 84
Затвор, 85
Защелка, 157
ведомая, 162
ведущая, 162
прозрачная, 159
И
Идентичные состояния, 215
Импликант, 124
первичный, 124
избыточный, 125
неосновной, 125
основной, 125
Импликационная
диаграмма, 216
Инвертор, 54
Институт инженеров
по электротехнике и
электронике, 299
Исток, 85
К
Каноническая форма, 103
Карта Карно, 117
Карта программирования, 252
Квазипрямое назначение
переменных, 229
КМОП-технология, 81
Код Грея, 118-, 207
Кольцевой счетчик, 172
перекрестный, 174
Комбинационные логические
схемы, 23
Компилятор, 254
Комплементарная пара, 89
Конечный автомат, 195
Контролепригодность, 276; 296
Конъюнктивная форма, 105
Конъюнкция, 102
Коэффициент разветвления,
60-, 289
Л
Логическая минимизация, 65
Логическая функция, 100
Логический сигнал, 21
М
Макроячейка, 257
Макстерм, 106
Малая степень интеграции, 81
Матрица логических ячеек , 251
Метал-оксид-полупроводник, 85
Метод
активизации пути, 281
карт Карно, 117
Куайна-МакКласки, 135
сканирования пути, 296
Минимизациия, 113
Минтерм, 103
МИС, 81
Модель
Мили, 196
Мура, 197
МОП-вентиль, 85
Мультиплексор, 755; 141
Н
Нагрузочная способность, 289
Начальные условия, 186
316
Предметный указатель
Неисправность константная, 277
с залипанием в открытом
состоянии, 277
типа замыкания, 277
типа обрыва, 277
транзисторного уровня, 277
Необнаруживаемая
неисправность, 294
Неполно заданная функция, 129
О
Обратный код, 42
Оператор регистрового
присваивания, 263
Описание переменных, 256
Основание системы
счисления, 26
Отказ, 275
Отрицательная логика, 22
П
Параллельный сумматор, 146
Первичный вход, 276
Первичный выход, 276
Переменные следующих
состояний, 196
Переменные состояний, 195
Периферийное
сканирование, 299
ПЗУ, 268
масочное, 268
программируемое, 268
стираемое
программируемое, 269
ПЛИС, 233
программируемая
пользователем, 234
регистровая, 247
универсальная, 245
ПЛМ, 235
ПМЛ, 240
Покрытие неисправностей, 281
Полный сумматор, 146
Положительная логика, 22
Полусумматор, 146
Пороговое напряжение, 87
Последовательные логические
схемы, 24\ 154
асинхронные, 155
синхронные, 755
Постоянное запоминающее
устройство, 268
Потенциально эквивалентные
состояния, 216
ППЗУ, 269
Принцип дуализма, 69
Программатор, 234
Программируемая логическая
матрица, 235
Программируемая матричная
логика, 240
Программируемые логические
интегральные схемы, 233
Программируемый генератор
последовательностей, 251
Прямое назначение
переменных, 229
Р
Расширение через точку, 255
Регистр, 169
Регистр сдвига, 170
с параллельным
вводом/выводом, 171
с последовательным вводом
и параллельным
выводом, 171
с последовательным вводом
и последовательным
выводом, 171
Предметный указатель
317
с
Самотестирование, 298
СБИС, 81\ 113
Сверхбольшая интегральная
схема, 81, 113
Сверхбольшие интегральные
схемы,
Селектор данных, 755; 142
Синхронная последовательная
схема, 195
СИС, 81
Система счисления
восьмеричная, 33
двоичная, 27
позиционная, 26
шестнадцатеричная, 31
Скрытый триггер, 251
Смешанная логика, 22
Состояния несовместимые по
выходу, 215
СППЗУ, 269
Средняя степень интеграции, 81
Сток, 85
Счетчик Джонсона, 174
Т
Таблица
возбуждения, 179
назначенных состояний, 200
переходов состояний, 199
переходов состояний, 179
состояний, 199
Тактовый сигнал, 153
Теорема
Де Моргана, 77; 116
о непротиворечивости, 114
Тестовый вектор, 280
Тестовый набор, 280
Типовая матричная логика, 245
Транзисторно-транзисторная
логика, 81
Триггер, 157
D-триггер, 161
JK-триггер, 167
RS-триггер, 158
с переключением по
уровню, 159
с переключением
по фронту, 162
Т-триггер, 167
ТТЛ-вентиль, 81
У
Улучшенный язык булевых
выражений, 252
Условно произвольные
состояния, 224
X
Характеристическое
уравнение, 159
III
Шифратор, 47
э
Эквивалентная
неисправность, 288
Эквивалентные состояния, 215
ЭСПЗУ, 234
Я
Язык ABEL, 252
318
Предметный указатель