Текст
Н. М. Иванов
А. И. Мартыноз
ДВИЖЕНИЕ
КОСМИЧЕСКИХ
ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
В АТМОСФЕРАХ
ПЛАНЕТ
МЕХАНИКА КОСМИЧЕСКОГО ПОЛЕТА
Н.М. ИВАНОВ, А.И. МАРТЫНОВ
ДВИЖЕНИЕ
КОСМИЧЕСКИХ
ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
В АТМОСФЕРАХ
ПЛАНЕТ
МОСКВА ’’НАУКА”
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 85
39.62
И 18
УДК 629.787
Иванов Н.М., Мартынов А. И. Движение космических летатель¬
ных аппаратов в атмосферах планет. — М,: Наука. Главная редакция фи¬
зико-математической литературы, 1985. — 384 с.
Книга посвящена комплексному исследованию оптимальных траекто¬
рий и режимов движения в атмосфере Земли и других планет Солнечной
системы, имеющих атмосферу (Марс, Венера, Юпитер, Сатурн, Уран, Неп¬
тун) .
С единых позиций анализируется проблема спуска; выявляются общие
и специальные задачи торможения; с использованием различных методов
оптимизации проводится решение наиболее важных и характерных задач
движения в атмосфере, Выводятся некоторые критерии подобия, позво¬
ляющие обеспечить определение оптимальных траекторий при движении
в атмосферах различных планет и при использовании различных критери¬
ев оптимальности. Даются рекомендации по применению методов опти¬
мизации для поиска решения тех или иных задач спуска в зависимости
от их характера и специфики.
Ил. 179. Библиогр. 150 назв.
Рецензент доктор технических наук Ю.Г. Сихарулидзе
Николай Михайлович Иванов
Александр Иванович Мартынов
ДВИЖЕНИЕ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
В АТМОСФЕРАХ ПЛАНЕТ
(серия ’’Механика космического полета”)
Редактор Ю.Г. Гу реви ч
Технический редактор В.В. Лебедева
Корректоры Т.В. Обод, Т.А. Печко
Набор осуществлен в издательстве на наборно-печатающих автоматах
ИБ № 12317
Сдано в набор 11.07.84. Подписано к печати 05.11.84. Т — 21 332
Формат 60 X 90 1 /16. Бумага офсетная № 2. Гарнитура Универе
Печать офсетная. Усл.печ.л. 24,0. Усл.кр.-отт. 24,0. Уч.-изд.л. 26,61
Тираж 1650 экз. Тип зак. 2069. Цена 4р. 30 к.
Издательство "Наука”
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени 1-я типография издательства "Наука",
199034 Ленинград В-34, 9-я линия, 12
1 703030000-005
И 93-85
053 (02)-85
© Издательство "Наука”
Главная редакция
физико-математической
литературы, 1985
ОГЛАВЛЕНИЕ
Предисловие 1
Введение 9
РАЗДЕЛ I
ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО ДВИЖЕНИЯ КОСМИЧЕСКОГО
ЛЕТАТЕЛЬНОГО АППАРАТА В АТМОСФЕРЕ 11
Глава 1. Физические характеристики планет и их атмосфер 11
§ 1.1. Общие сведения 11
§ 1.2. Поверхности планет 15
§ 1.3. Атмосферы планет 18
Глава 2. Характеристика проблемы спуска в атмосфере 25
§ 2.1. Основные задачи спуска 25
§ 2.2. Условия входа в атмосферу 30
§ 2.3 Аэродинамические формы космических летательных аппаратов 31
§ 2.4. Способы управления 37
§ 2.5. Основные типы системы тепловой защиты 38
§ 2.6. Системы мягкой посадки 42
Глава 3. Постановка задачи оптимального управления в атмосфере 43
§ 3.1. Математическая модель движения 43
3.1.1. Уравнения движения без учета уноса массы теплозащитно¬
го покрытия (45). 3.1.2. Уравнения движения, учитывающие
унос массы и изменение формы КЛА в процессе обгара тепло¬
защитного покрытия (47).
§ 3.2. Критерии оптимальности, используемые при решении задачи
спуска , 55
§3.3. Современные методы теории оптимального управления 58
3.3.1. Классификация методов решения задачи оптимизации
( 58 ). 3.3.2. Классические методы решения ( 60 ). 3.3.3. Метод
достаточных условий В.Ф. Кротова ( 68 ) . 3.3.4. Характеристика
задач оптимального управления ( 71 ).
3
РАЗДЕЛ II
СПУСК КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА НА ПОВЕРХНОСТЬ
ПЛАНЕТЫ 76
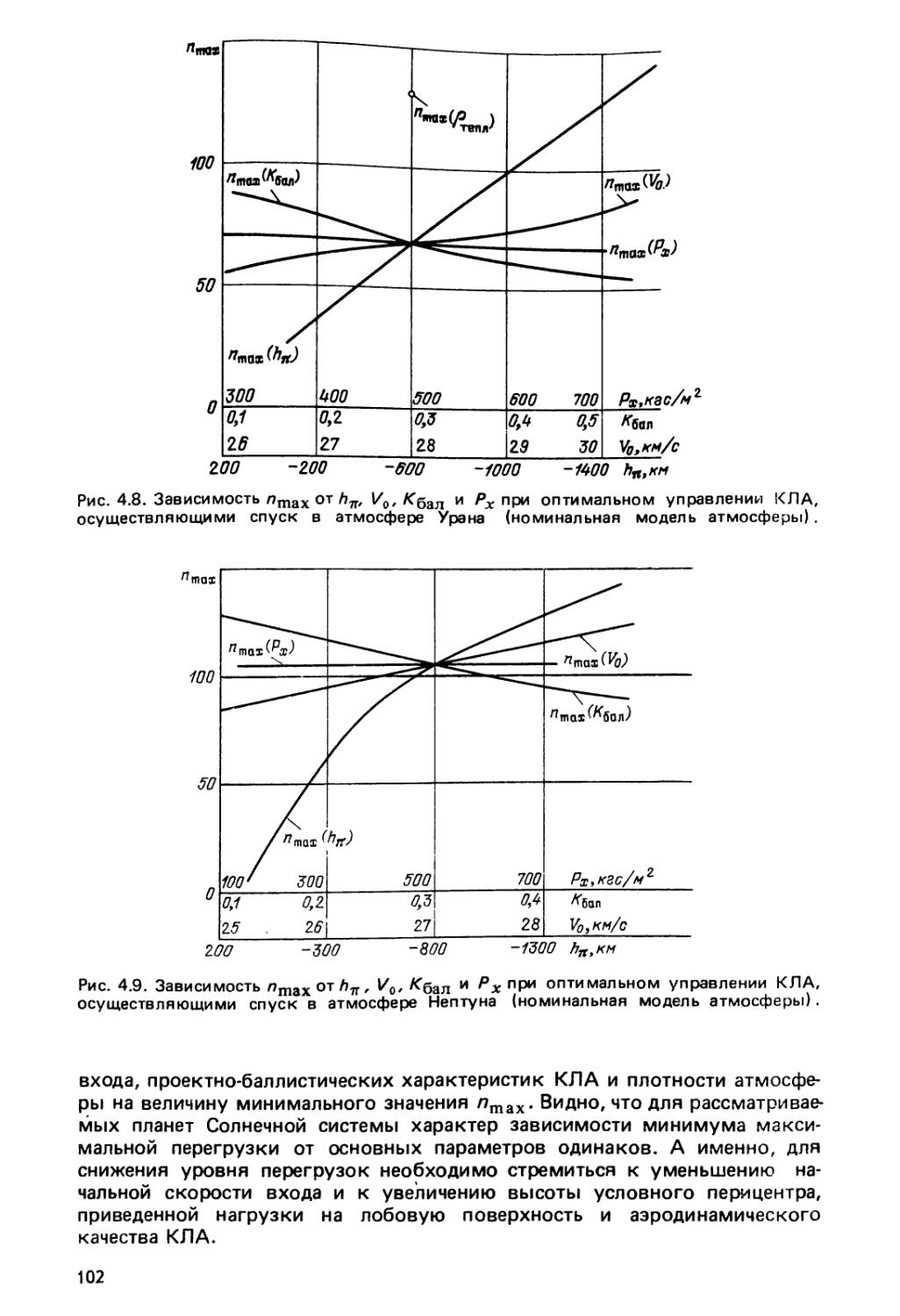
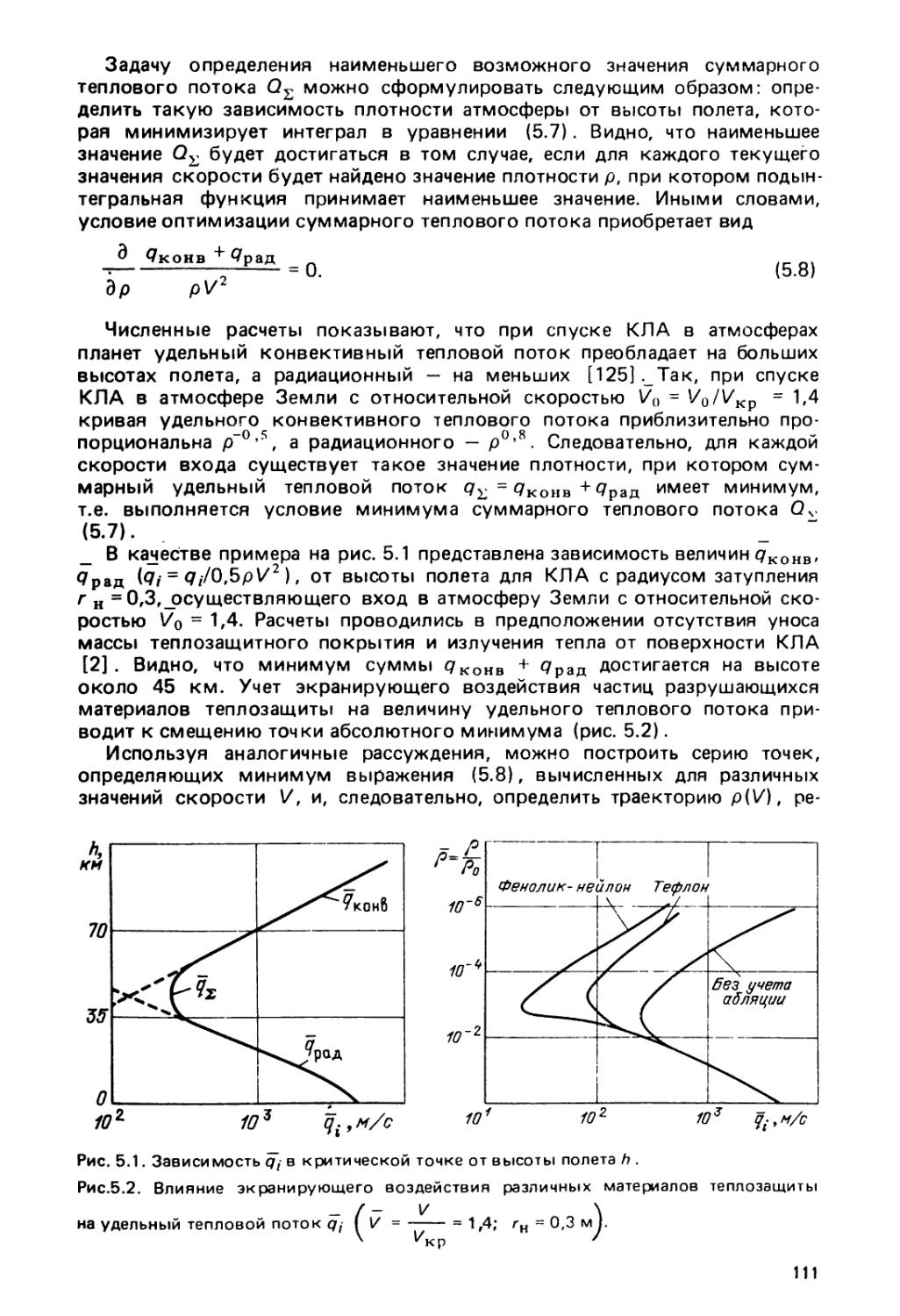
Глава 4. Максимизация коридора входа в атмосферу планеты и миними¬
зация максимальной перегрузки 76
§4.1, Постановка задачи 76
§ 4.2. Максимизация верхней границы коридора входа 78
§ 4.3. Минимизация нижней границы коридора входа 85
§ 4.4. Анализ коридоров входа для различных планет Солнечной сис¬
темы 87
§ 4.5. Приближенные оценки коридоров входа . 91
§ 4.6. Минимизация максимальной перегрузки при заданной ширине
коридора входа 94
Глава 5. Минимизация массы тепловой защиты космического летательно¬
го аппарата 104
§5.1. Критерии оптимальности 104
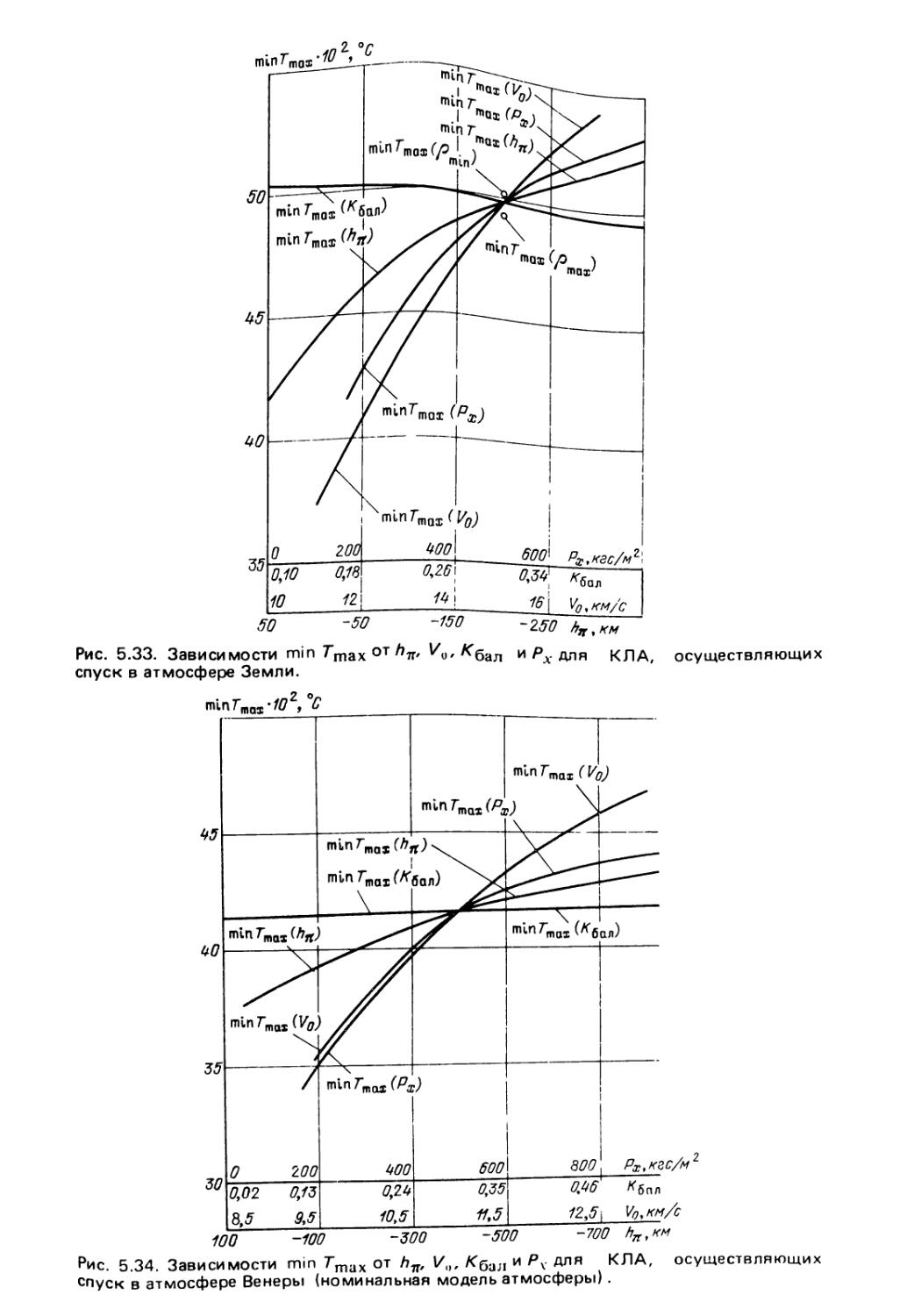
§ 5.2. Оптимизация траекторий спуска из условия минимума суммар¬
ного теплового потока 110
5.2.1. Нижняя граница минимального суммарного теплового
потока ( 110). 5.2.2. Учет реальных ограничений (117). 5.2.3. Ог¬
раничение на дальность полета (131 ). 5.2.4. Управление баллисти¬
ческим параметром ( 133 ). 5.2.5. Анализ результатов решения
задачи минимизации суммарного теплового потока (137).
§ 5.3. Оптимизация траекторий спуска из условия минимума объеди¬
ненного критерия по тепловым нагрузкам и перегрузкам 143
§ 5.4. Минимизация максимальной температуры поверхности косми¬
ческого летательного аппарата 145
5.4.1. Ограничение на конечную скорость спуска (145). 5.4.2. Уп¬
равление аэродинамическими силами и тягой двигательной уста¬
новки (155).
§ 5.5. Оптимизация траекторий спуска из условия минимума обобщен¬
ного теплового критерия 163
Глава 6. Оптимизация траекторий спуска из условия минимума массы
системы мягкой посадки 168
§ 6.1. Минимизация конечной скорости спуска 168
§ 6.2. Анализ результатов решения задачи минимизации конечной
скорости спуска 171
§ 6.3. Оценка влияния неопределенности параметров атмосферы на
оптимальное управление 173
§ 6.4. Оптимизация траекторий спуска из условия минимума характери¬
стической скорости
§ 6.5. Оптимизация траекторий спуска из условия максимума конечной
высоты ул
6.5.1. Оптимальное управление при отсутствии ограничений на
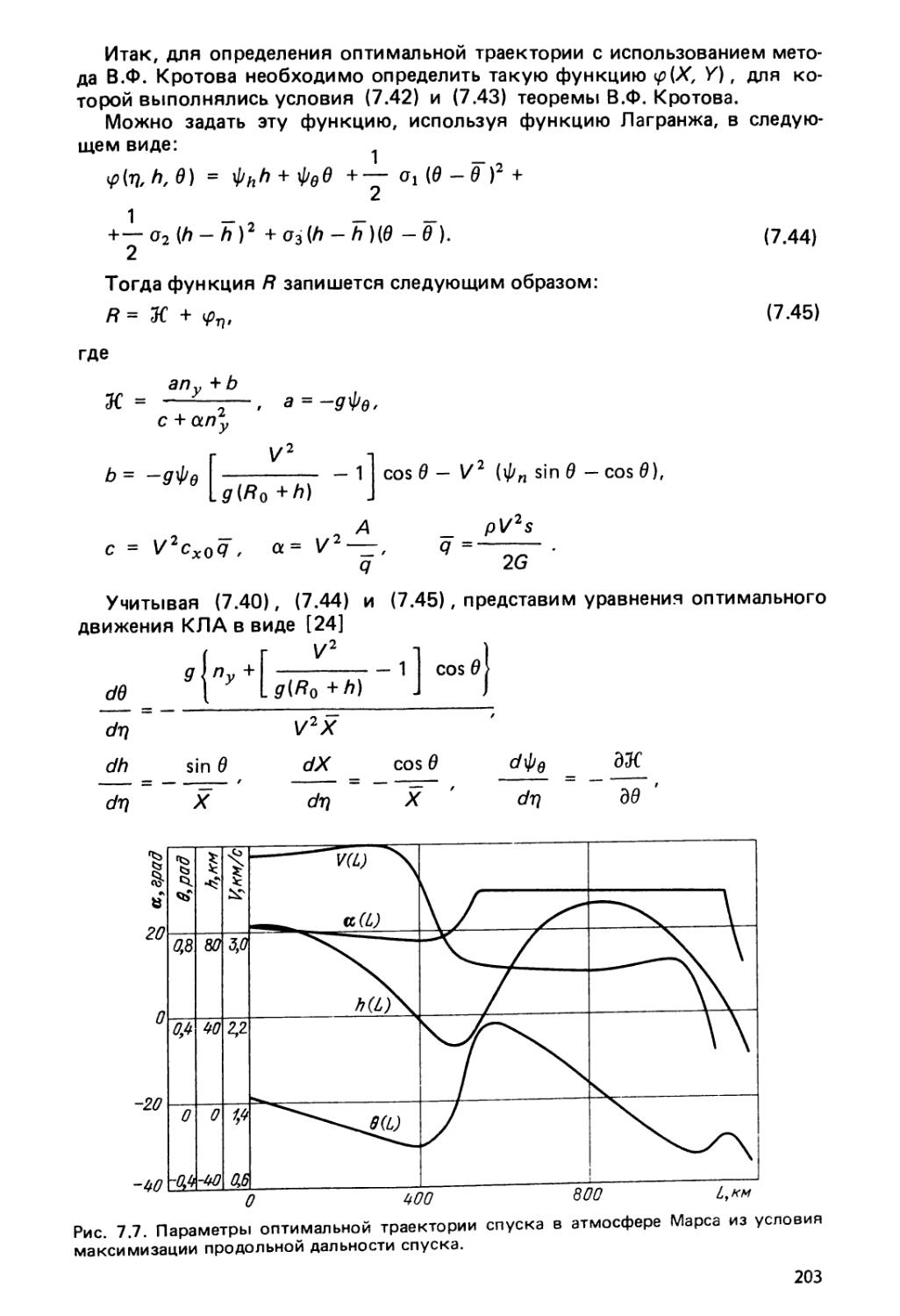
фазовые координаты ( 177 ), 6;5.2. Оптимальное управление
при наличии ограничений на фазовые координаты (182).
4
Глава 7. Оптимальное управление дальностью полета в атмосфере 189
§ 7.1. Минимизация дальности спуска 189
§7.2. Максимизация дальности спуска 198
7.2.1. Максимизация дальности спуска с использованием прин¬
ципа максимума Понтрягина ( 198 ). 7.2.2. Максимизация даль¬
ности спуска с использованием достаточных условий Кро¬
това (201).
§7.3. Анализ результатов решения задачи максимизации дальности
полета 204
§7.4. Приближенно-оптимальное управление 209
§ 7.5. Управление боковой дальностью полета 213
РАЗДЕЛ III
ВЫВЕДЕНИЕ КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА НА ОРБИ¬
ТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ С ИСПОЛЬЗОВАНИЕМ
АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ 220
Глава 8. Синтез оптимального управления при комбинированном способе
выведения на орбиту 220
§ 8.1. Обсуждение проблемы 220
§ 8.2. Постановка задачи 224
§ 8.3. Оптимальное управление в атмосфере 232
Глава 9. Приближенно-оптимальные законы управления из условия мак¬
симизации скорости вылета из атмосферы 252
§ 9.1. Оптимальное управление подъемной силой при постоянном
коэффициенте лобового сопротивления 252
§ 9.2. Максимизация конечной скорости без учета влияния гравита¬
ционных и центробежных сил 257
§ 9.3. Случай нулевого значения угла курса 265
§ 9.4. Влияние гравитационной и центробежной сил 273
§ 9.5. Максимизация конечной скорости при произвольном законе
изменения плотности атмосферы 282
§ 9.6. Общий случай оптимального управления из условия максимиза¬
ции конечной скорости 289
Глава 10. Примеры решения задач выведения на орбиты Юпитера, Марса
и Венеры комбинированным способом 294
§10.1. Общие закономерности решения задачи 294
§ 10.2. Выведение на орбиту искусственного спутника Юпитера 296
10.2.1. Максимизация конечной скорости (296 ). 10.2.2. Миними¬
зация суммарного теплового потока ( 301 ). 10.2.3. Минимиза¬
ция максимальной температуры (304).
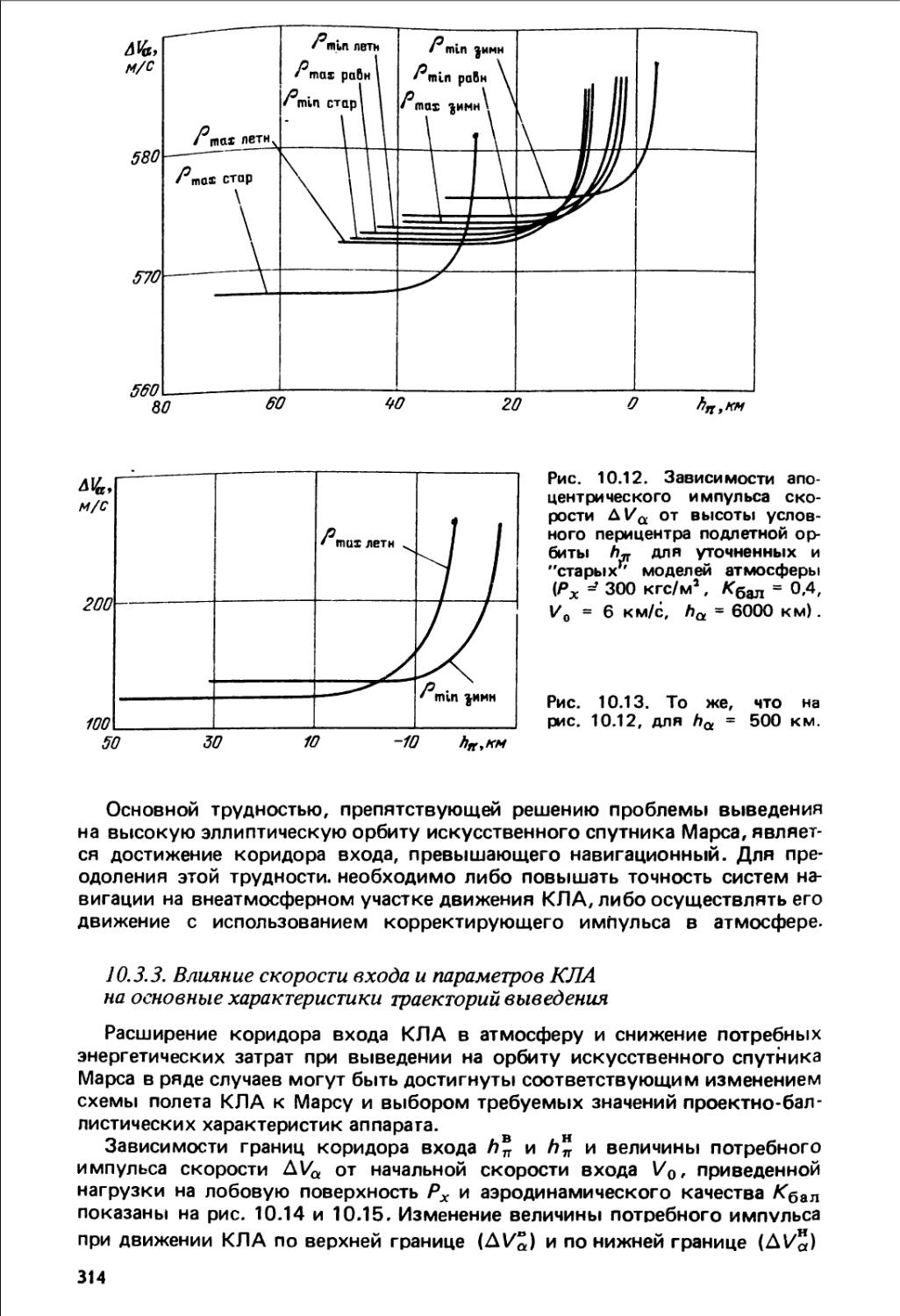
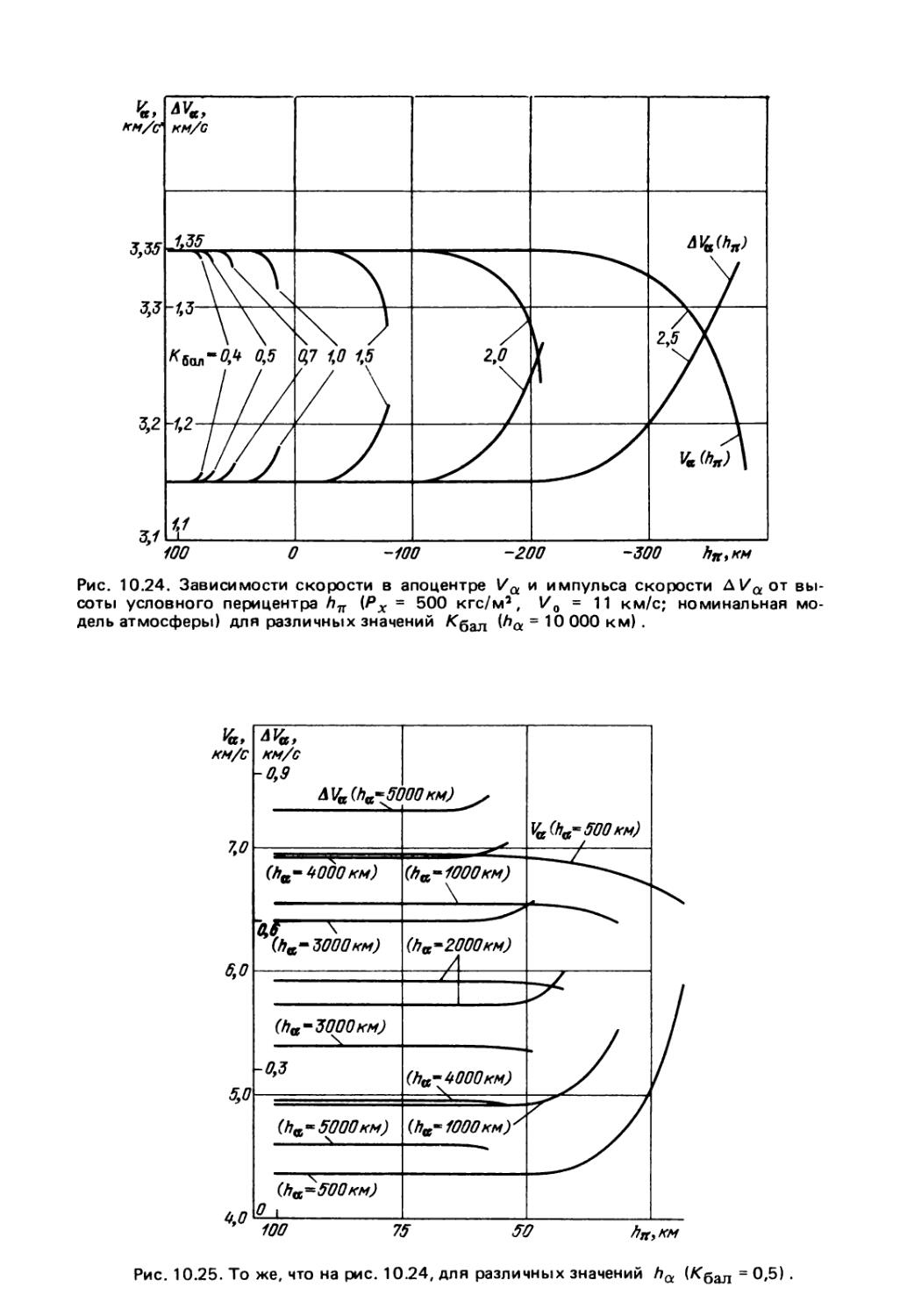
§ 10.3. Выведение на орбиту искусственного спутника Марса 309
10.3.1. Исходные предпосылки (309). 10.3.2. Влияние уточне¬
ния моделей атмосферы на параметры траекторий выведения
(312). 10.3.3. Влияние скорости входа и параметров КЛА на
основные характеристики траекторий выведения (314).
5
§ 10.4. Выведение на орбиту искусственного спутника Венеры 320
10.4.1. Исходные предпосылки (320). 10.4.2. Управление с ис¬
пользованием эффективного качества (322), 10.4.3. Учет ограни¬
чения на величину максимально допустимой перегрузки (326).
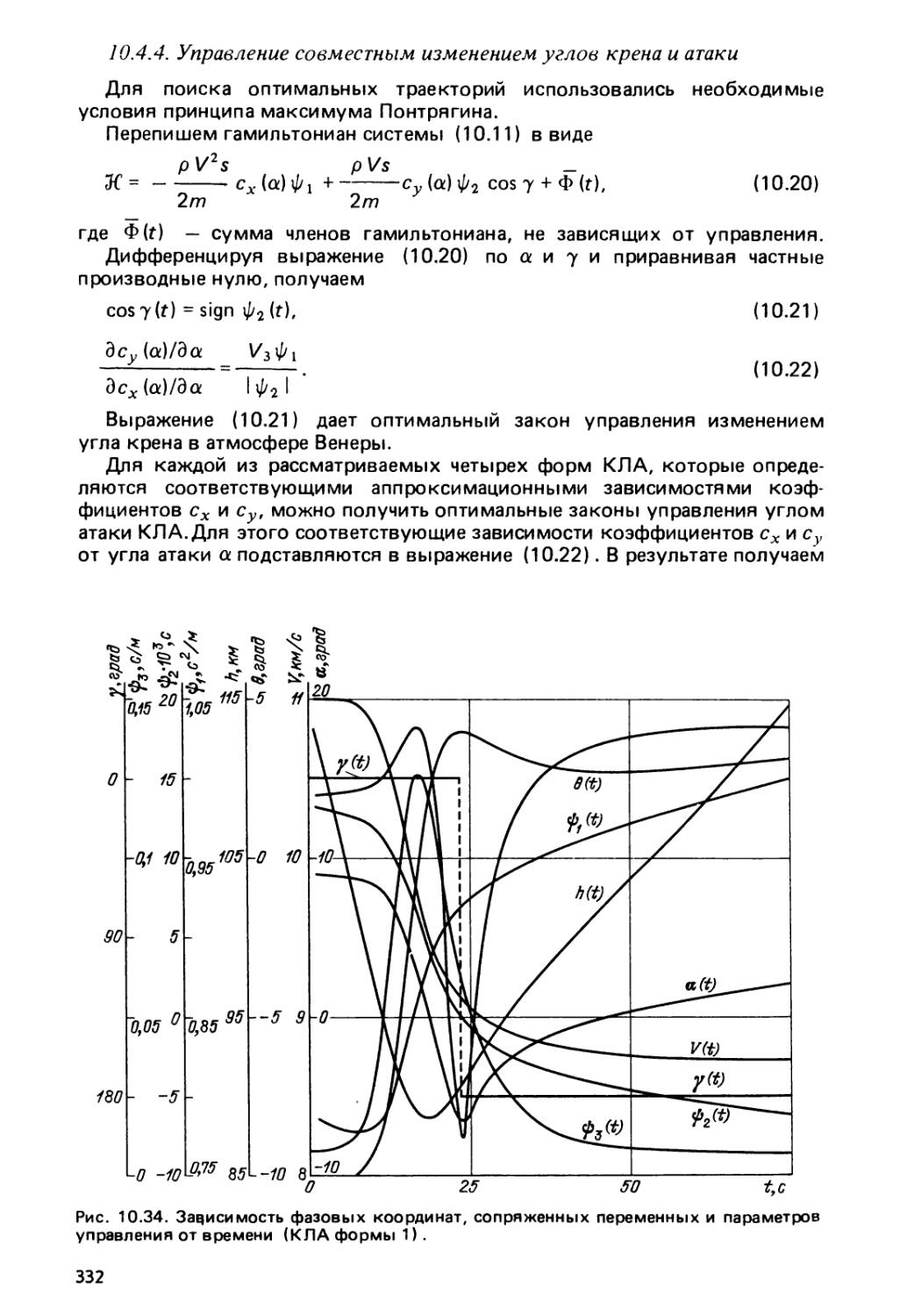
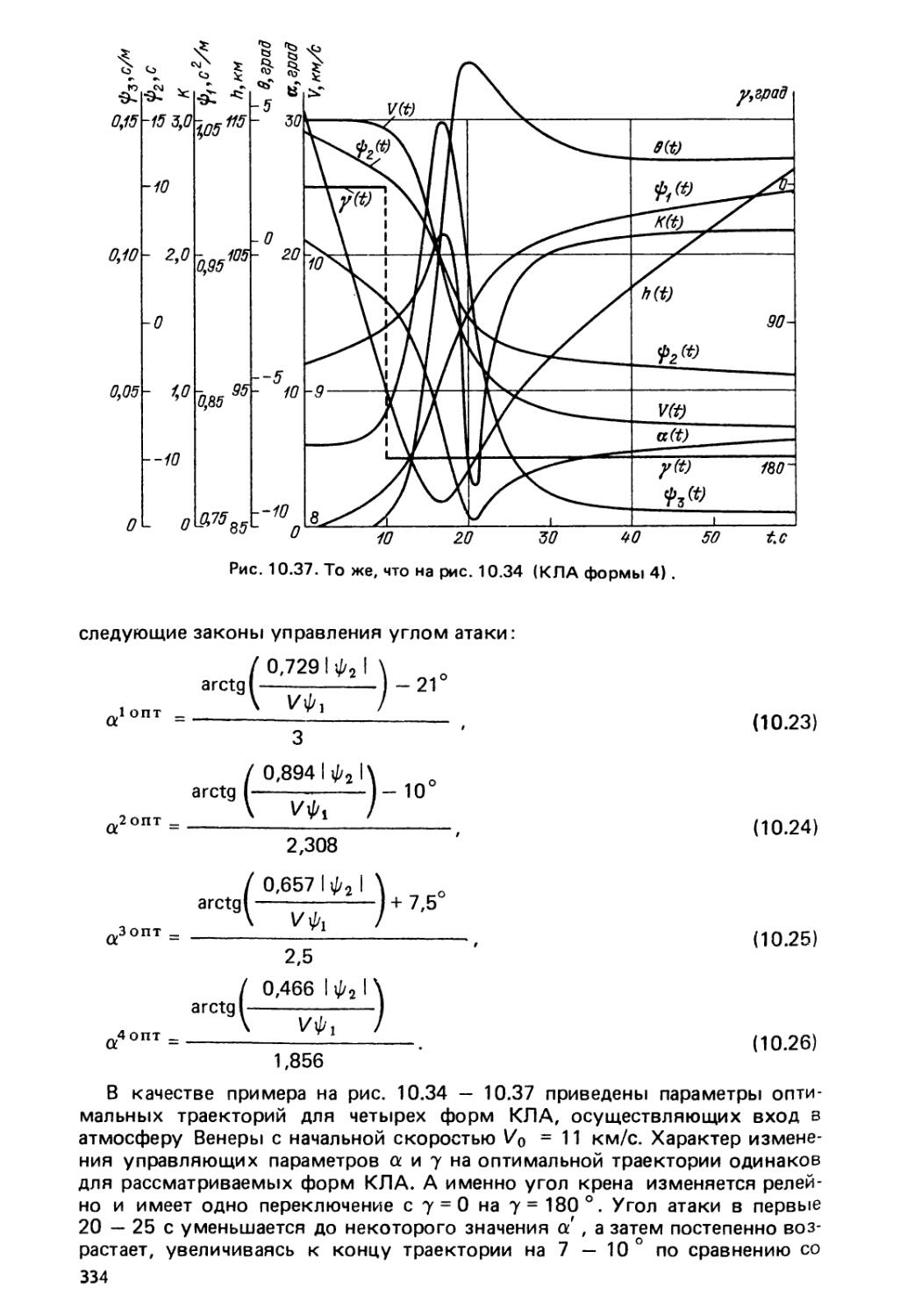
10.4.4. Управление совместным изменением углов крена и ата¬
ки (332). 10,4.5. Эффективность применения комбинированно¬
го способа выведения ...... 335
§ 10.5. Выведение на орбиту искусственного спутника Венеры с исполь¬
зованием многократного прохождения атмосферы 336
Г лава 11, Использование корректирующего импульса в атмосфере при
выведении на орбиту комбинированным способом 347
§ 11.1. Оптимальное управление при выведении на орбиту с использо¬
ванием корректирующего импульса 347
§ 11.2. Максимизация коридора входа 357
11.2.1, Общие замечания (357), 11.2.2. Постановка задачи (358).
11.2.3. Качественные результаты решения оптимальной задачи
(360). 11 2.4. Максимизация коридора входа в атмосферу Юпите¬
ра (361)* 11*2.5. Максимизация коридора входа в атмосферу
Марса (365). 11.2.6. Максимизация коридора входа в атмосферу
Венеры (372).
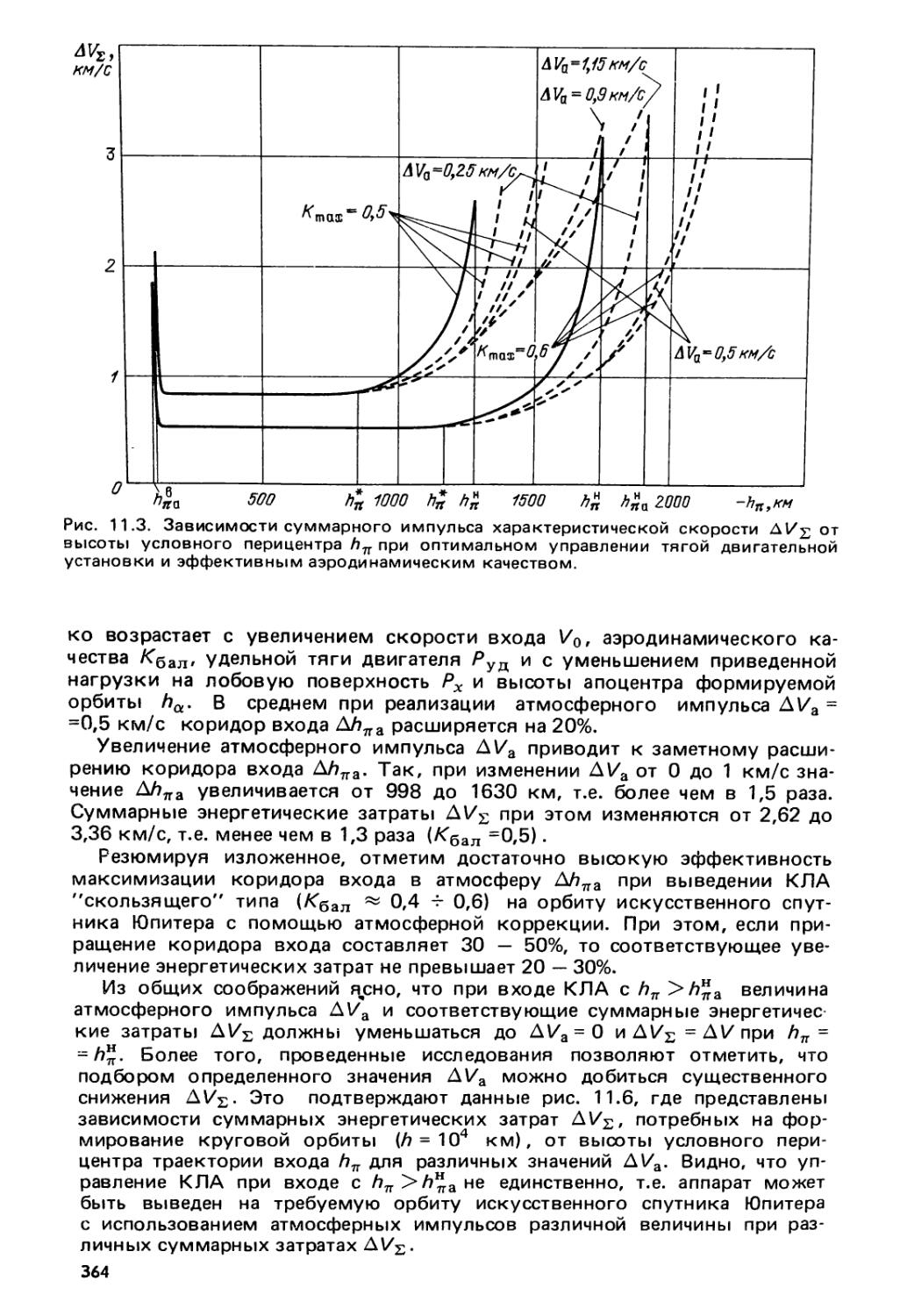
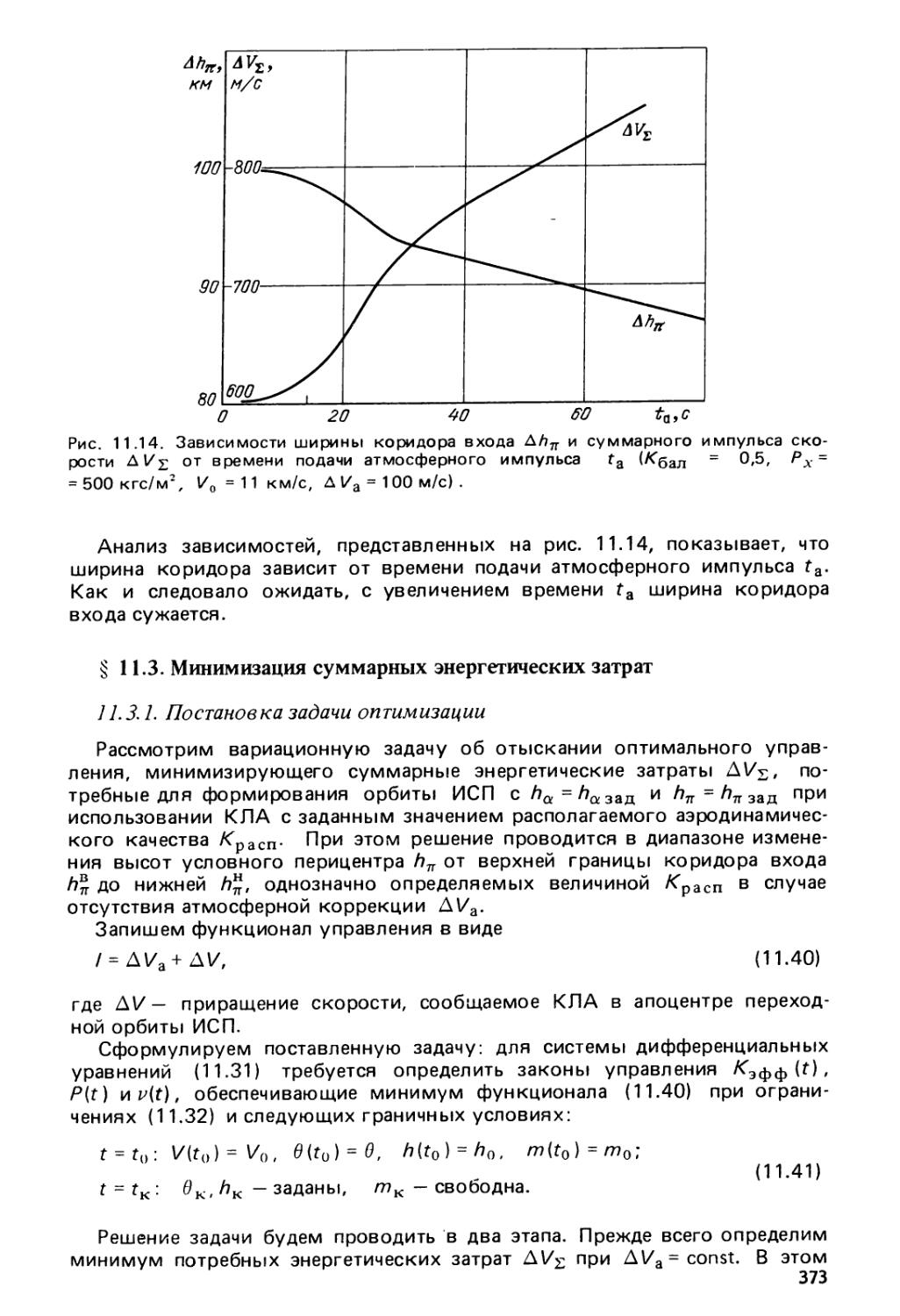
§ 11.3. Минимизация суммарных энергетических затрат 373
11.3.1. Постановка задачи оптимизации (373). 11.3,2. Некоторые
качественные результаты (374). 11.3.3. Некоторые численные
результаты для случаев выведения на орбиты спутников Юпи¬
тера, Марса и Венеры (375) *
377
Основные обозначения
Слисок литературы * ■
379
ПРЕДИСЛОВИЕ
В настоящее время исследованию вопросов оптимального движения
космических летательных аппаратов (КЛА) в атмосферах некоторых
планет посвящено значительное число работ советских и зарубежных ав¬
торов. Как правило, это либо статьи, рассматривающие лишь отдельные
стороны обсуждаемой проблемы, либо монографии, имеющие сравнительно
узкое целевое назначение.
Обилие публикаций объясняется как значением рассматриваемой проб¬
лемы, так и большим многообразием возможных методических подходов к
решению задач оптимизации, различием физических условий движения КЛА
в атмосфере, схем полета, типов КЛА, функционалов управления, видов
управляющих параметров и типов систем теплозащиты и мягкой посадки,
выбранных моделей движения и т.д.
Отсутствие в опубликованных к настоящему времени работах единого
методического подхода к решению проблемы оптимизации траекторий
движения КЛА в атмосфере с четко обоснованными допущениями, ис¬
ходными предпосылками и единой терминологией вызывает необходимость
обобщения и систематизации исследований задач движения КЛА в ат¬
мосфере Земли и атмосферах других планет Солнечной системы.
Систематизация материала потребовала от авторов ряда новьк раз¬
работок, анализа и обобщения отдельных частных результатов опубли¬
кованных ранее исследований./ Структурно книга построена следующим
образом.
Очень кратко описываются основные физические характеристики планет
Солнечной системы, обладающих атмосферой, и рабочие модели атмосфер,
необходимые для решения задач оптимального управления спуском КЛА.
Рассмотрены особенности спуска, определяемые спецификой физических
условий снижения КЛА в атмосфере каждой из рассматриваемых планет.
Дается характеристика основных задач спуска и выявляются задачи, общие
для всех планет, обладающих атмосферой.
С использованием современных методов оптимизации (динамическое
программирование, классическое вариационное исчисление, достаточные
условия В.Ф. Кротова, принцип максимума Л.С. Понтрягина, "машинные"
методы и т.д.) решены основные и специальные задачи оптимизации тра¬
екторий спуска КЛА в атмосферах всех рассматриваемых планет. Это в
первую очередь задачи оптимизации перегрузочного режима, минимизации
массы тепловой защиты и системы мягкой посадки, максимизации конеч¬
ной скорости вылета КЛА из атмосферы при выведении на орбиту ис¬
кусственного спутника планеты с использованием предварительного аэро¬
динамического торможения. Рассмотрен также ряд специальных задач,
таких, как максимизация зоны маневра, оптимизация траекторий спуска из
7
условия обеспечения заданных конечных значений фазовых координат
и т.д. Дается анализ эффективности используемых методов решения ва¬
риационных задач спуска и приводятся рекомендации по выбору пред¬
почтительного метода оптимизации.
Книга снабжена большим количеством фактического материала. Прово¬
дятся систематизация и обобщение численных результатов решения основ¬
ных вариационных задач для всех рассматриваемых планет.
Книга рассчитана на научных работников, инженеров и аспирантов,
специализирующихся в области оптимального управления и механики
космического полета. Она может быть также полезна студентам вузов
соответствующих специальностей.
Авторы выражают благодарность Н.Л. Соколову, А.А. Щетинникову,
Г.В. Гребенщиковой, В.П. Копытовой и Т.Ф. Соколовой за помощь в со¬
здании книги, а также Ю.Г. Сихарулидзе и Ю.Г. Гуревичу, доброжелатель¬
ные критические замечания которых во многом способствовали улучшению
содержания книги.
ВВЕДЕНИЕ
Интенсивное изучение Вселенной и прежде всего планет Солнечной
системы объясняется желанием получить ответ на ряд фундаментальных
проблем, интересующих человечество на протяжении всей истории его
существования: когда и как возникла Солнечная система и как проходи¬
ла ее эволюция; каково строение материи; каковы истоки возникновения
и эволюции жизни в Солнечной системе и т.п.
В последние годы эти вопросы приобретают большой практический
интерес, так как на современном уровне развития цивилизации заметно
возросло влияние человека на окружающий мир. В этих условиях неразум¬
ное использование достижений цивилизации может оказать неблагоприят¬
ное воздействие на естественный ход эволюции планеты и разумной жизни
на ней. Поэтому особое значение приобретают вопросы, связанные с изуче¬
нием планет Солнечной системы, пониманием законов их формирования
и естественной эволюции.
Солнечная система представляет собой огромную лабораторию, в ко¬
торой природа проводит эксперименты по эволюции материи под воз¬
действием различных внешних факторов, и изучение объектов этой систе¬
мы позволит понять основные законы их эволюции и наметить пути даль¬
нейшего развития нашей цивилизации, обеспечивающие наилучшие условия
существования разумной жизни на Земле.
До недавнего времени изучение Вселенной проводилось с помощью
астрономических средств, позволивших получить большой объем инфор¬
мации о планетах. Но, как стало ясно, эти средства не могли дать ответа
на все интересующие людей вопросы в силу ограниченности своих воз¬
можностей. Кроме того, факты, полученные с помощью этих средств, до¬
пускают неоднозначную интерпретацию, и зачастую выводы, сделанные
на их основе, оказывались неверными. Так, например, возникли ошибоч¬
ные гипотезы, объясняющие существование "марсианских каналов";
был "получен" широкий диапазон изменения периода вращения Венеры
вокруг ее оси; с помощью радиотехнических методов был "измерен*
диапазон изменения температуры на поверхности Венеры от —40 С до
+400 °C и т.д.
С наступлением космической эры человек получил новое могучее средст¬
во для непосредственного изучения планет и космического пространства.
С помощью автоматических межпланетных станций (АМС) были по¬
лучены однозначные и достоверные сведения об условиях на плане¬
тах, позволившие глубже понять процессы, происходящие в Солнечной
системе.
Основными направлениями научных исследований планет сегодня явля¬
ются:
9
фотографирование поверхности планет с орбиты искусственного спут¬
ника, пролетной траектории или непосредственно с поверхности планеты
с передачей полученных изображений на Землю;
прямые измерения параметров атмосферы (температуры, давления
и т.д.) и их изменения по высоте при спуске космического летательного
аппарата (КЛА) в атмосфере;
определение относительного содержания химических элементов в ат¬
мосфере и их изотопногасостава;
определение химического состава атмосферы с помощью газоанализа¬
торов различных типов;
изучение верхних слоев атмосферы по методу "радиопросвечивания";
спектральные наблюдения свечения газов атмосферы в ультрафиолето¬
вых лучах (этот участок спектра недоступен для наблюдений с Земли) ;
измерение содержания заряженных частиц в атмосфере и околопланет¬
ном пространстве, измерение скорости и потока заряженных частиц в
магнитосфере планеты;
измерение напряженности магнитного поля планет и изучение струк¬
туры ее магнитосферы;
изучение рельефа поверхности, физических свойств и состава грунта
планеты;
сравнение различных характеристик планет и их спутников;
исследование гравитационного поля планет путем анализа траектории
движения их искусственных спутников или пролетных КЛА;
изучение теплового и радиоизлучения планет с близких расстояний
в широком диапазоне длин волн.
Даже из этого далеко не полного перечня можно видеть разнообразие
задач, связанных с исследованиями планет, и те большие возможности,
которые они представляют. Видно также, что многие из указанных на¬
правлений могут быть реализованы лишь с использованием аппаратов,
осуществляющих спуск на поверхности планет, или выведенных на орби¬
ты искусственных спутников планет назначения. Таким образом, комплекс¬
ное исследование, осуществляемое космическими летательными аппарата¬
ми в атмосферах планет, представляет собой актуальную проблему.
Однако следует иметь в виду следующую принципиальную особенность
создания современных КЛА и особенно аппаратов ближайшего будущего.
С каждым годом усложняются стоящие перед КЛА целевые задачи, в
связи с чем резко увеличивается доля научной аппаратуры в общем весо¬
вом балансе КЛА.
Существенным резервом в решении этих задач является организация
движения КЛА в атмосферах по оптимальным траекториям.
РАЗДЕЛ I
ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО ДВИЖЕНИЯ
КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА
В АТМОСФЕРЕ
Глава 1
ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛАНЕТ
И ИХ АТМОСФЕР
§1.1. Общие сведения
Из восьми планет Солнечной системы, обладающих атмосферой, услов¬
но выделяются две группы: планеты земной группы (Венера, Земля,
Марс);
планеты юпитерианской группы, или планеты-гиганты (Юпитер, Са¬
турн, Уран, Нептун).
Особое место занимает восьмая планета — Плутон. По своим физи¬
ческим свойствам она ближе к планетам земной группы, но удалена от
Солнца дальше всех, замыкая планеты-гиганты. Среднее гелиоцентри¬
ческое расстояние (большая полуось орбиты вращения Плутона вокруг
Солнца) составляет 39,439 а.е. Пока имеется немного данных для того,
чтобы ответить на вопрос, обладает ли Плутон атмосферой. Спектральные
и спектрофотометрические измерения не показали следов поглощения
метана в газовой фазе (который мог бы находиться в виде насыщенных
паров в равновесии с поверхностным льдом) или каких-либо других ат¬
мосферных составляющих.
Главное различие между двумя группами планет состоит в их размерах,
массе и плотности, что объясняется различиями в соотношениях трех
основных типов вещества планет — газов, льдов и горных пород (среди
последних основное место занимают железо, силикаты и окислы магния,
алюминия, кальция и других металлов).
Планеты земной группы имеют меньшие размеры и массу, они более
плотные, медленнее вращаются вокруг своих осей, почти все их вещество
сосредоточено в литосфере, а атмосфера составляет очень малую долю
общей массы. Внутренние источники тепла слабы и практически не влия¬
ют на тепловой баланс поверхности и атмосферы. Эти планеты близки
друг к другу по химическому составу, внутреннему строению, количеству
тепла, поступающего от Солнца. Процессы, протекающие в атмосферах
этих планет, также близки. Сравнительное исследование планет земной
группы представляет особый интерес, поскольку это помогает лучше
понять процессы, протекающие на Земле.
Планеты-гиганты обращаются на больших расстояниях от Солнца, имеют
значительные массы и малые плотности, характеризуются быстрым вра¬
щением вокруг своих осей. Средняя плотность планет-гигантов близка
к плотности воды, а периоды вращения составляют 10—15 часов. Быстрое
вращение планет приводит к появлению значительной центробежной силы
в экваториальных областях и, следовательно, к значительному сжатию
этих планет у полюсов. Отметим, что в отличие от планет-гигантов планеты
земной группы имеют при сравнительно небольшой массе большие среднюю
плотность и период вращения.
11
Таблица 1.1
Основные элементы орбит планет Солнечной системы
Планета
Среднее рас¬
стояние от
Солнца,
млн. км
Сидериче¬
ский период
обращения
Т, сут.
Синодиче¬
ский период
обращения
Т5, сут.
Эксцен-
триситет
е
Расстояние от Зем¬
ли, млн. км
мини¬
мальное
макси¬
мальное
Венера
108,2
224,7
583,92
0,007
39
260
Земля
149,6
365,26
—
0,017
—
Марс
227,9
686,98
779,94
0,093
56
400
Юпитер
778,3
4332,59
398,88
0,048
591
965
Сатурн
1427
10759,2
378,09
0,054
1199
1653
Уран
2871
30685,93
369,66
0,046
2586
3153
Нептун
4498,6
60187,64
367,48
0,009
4309
4682
Плутон
5908,9
90471,85
366,72
0,250
4249
7558
Оси вращения планет-г и гантов расположены различным образом. Ось
вращения Юпитера практически перпендикулярна к плоскости его орбиты.
Угол наклона оси вращения Сатурна близок к земному и марсианскому
углам наклона и составляет 63° 15 . Ось вращения Урана наклонена к
плоскости орбиты на очень малый угол (около 2°), т.е. лежит практи¬
чески в плоскости орбиты. Направление вращения Урана, как и Венеры,
является обратным направлению вращения всех остальных планет. Такое
необычное положение оси Урана приводит к тому, что за длительный пе¬
риод обращения этой планеты вокруг Солнца (84 года) на небе Урана
наблюдается перемещение Солнца от Северного небесного полюса до Юж¬
ного и далее снова до Северного полюса через экватор.
В табл. 1.1 приведены основные элементы орбит планет Солнечной
системы, а в табл. 1.2 — их основные физические характеристики.
Таблица 1.2
Основные физические характеристики планет
Планета
Масса,
1024 кг
Отноше¬
ние массы
планеты к
массе Зем¬
ли
Средняя
плотность
р, г/см3
Г равитационный
параметр д,
км3/с2
Ускорение
силы тяже¬
сти на по¬
верхности
в едини¬
цах
9 = 9,81м/с2
Венера
4,27
0,81
5,25
324858,8
0,9
Земля
5,97
1
5,52
398600,5
1
Марс
0,64
0,107
3,95
42828,48
0,38
Юпитер
1901
317,88
1,35
126712000
2,68
Сатурн
568
95,17
0,7
37934100
1,16
Уран
87
, 14,54
L3
5803160
0,93
Нептун
103
17,25
1,65
6871308
1,41
Плутон
0,01
0,002
1,4
1040
0,06
12
Отметим, что в настоящее время основное внимание исследователей
привлекают три планеты Солнечной системы: Марс, Венера и Юпитер. Имен¬
но к этим планетам в последние годы были осуществлены полеты совет¬
ских и американских автоматических межпланетных станций. Ниже при¬
водятся более подробные сведения об этих планетах, необходимые для
дальнейшего изложения материала.
Марс. Эта планета обращается вокруг Солнца по эллиптической орбите
с большой полуосью, равной 1,524 а.е., и эксцентриситетом е = 0,093. Си¬
дерический период обращения Т = 686,98 земных суток. Наиболее удоб¬
ными для наземных наблюдений Марса являются периоды перигелийных
или афелийных противостояний. В первом случае расстояние между Марсом
и Землей минимально и составляет 56 млн. км (великое противостояние) .
При афелийных противостояниях расстояние между планетами достигает
400 млн. км.
Интервал времени между двумя последовательными противостояниями
(синодический период обращения Марса) составляет в среднем 7"5~780сут.
Противостояния происходят каждые два земных года, со сдвигом на50сут.
позже предыдущего. Период вращения Марса, приводимый в астрономи¬
ческих ежегодниках,представляет собой сидерический период, отнесенный
к точке весеннего равноденствия этой планеты, и составляет Г =
= 24 ч 37 мин 22,663 с ± 0,004 с среднего солнечного времени.
Как видно, марсианские сутки близки к земным (долгота центрального
меридиана в 0 ч для некоторой даты отличается всего лишь на 9 от преды¬
дущей или последующей даты). Для того чтобы проследить за полным обо¬
ротом Марса вокруг оси, наблюдатель, находящийся в какой-либо опреде¬
ленной точке поверхности Земли, должен затратить около 40 сут.
Положение оси вращения Марса обычно задается небесными экватори¬
альными координатами его северного полюса, составляющими [66]
а0 1950,0 = 317,32° — 7" • 0,1011°,
60 1950,0 = 52,68°- Т 0,0570°,
Отношение объе¬
ма планеты к
объему Земли
Экваториаль¬
ный диаметр,
км
Отношение эк¬
ваториального
диаметра пла¬
неты к эква¬
ториальному
диаметру Зем¬
ли
Период враще¬
ния вокруг
оси со
Наклонение
плоскости эк¬
ватора к плоско¬
сти орбиты 7
о
0,90
12100
0,95
243 сут 03 ч
50 мин (вра¬
щение обрат¬
1
12800
1
ное)
23,9 ч
0,15
6800
0,53
24,6 ч
1318
142700
11,11
9,9 ч
755
120800
9,43
10,2 ч
63
47600
3,98
10,8 ч (враще¬
58
44400
3,82
ние обратное)
15,8 ч
0,01
3000
0,20
6,4 ч
23° 27'
25° 12'
3° 07'
26° 45'
98° 00’
29° 36'
13
Таблица 1.3
Характеристика марсианских сезонов
Ареоцентрическая
долгота Солнца,
град
Сезон
Продолжительность
северное полу¬
шарие
южное полу¬
шарие
земные сутки
марсианские
сутки
0-90
весна
осень
199
194
90-180
лето
зима
183
178
180-270
осень
весна
147
143
270-360
зима
лето
158
154
где а0 — прямое восхождение северного полюса, 60 — склонение север¬
ного полюса, Т — время в юлианских столетиях, отсчитываемое от юлиан¬
ского дня I.D. 2433282,5.
Плоскость экватора Марса наклонена к плоскости его орбиты под углом
25 12 (для сравнения отметим, что наклонение 7 для Земли составляет
23°27).
Смена сезонов на Марсе во многом подобна смене сезонов на Земле.
В табл. 1.3 приведены некоторые сведения о длительности марсианских
сезонов и соответствующие им интервалы ареоцентрических долгот Солн¬
ца [66] (ареоцентрическая долгота Солнца в момент весеннего равно¬
денствия равна нулю).
Физическая поверхность Марса может быть аппроксимирована трехос¬
ным эллипсоидом с осями
А = 3400,12 км, В = 3394,18 км, С = 3372,45 км.
Для проведения расчетов траекторий снижения КЛА в атмосфере Марса,
а также в ряде других случаев важным является использование другой мо¬
дели поверхности Марса - эквипотенциальной. Так, эквипотенциальная
поверхность, соответствующая уровню с давлением 6,1 мбар, может быть
задана трехосным эллипсоидом с осями
А = 3396,67 км, В = 3395,23 км, С = 3377,22 км.
Уровень с давлением 6,1 мбар условно^прини мается во многих^лучаях
за исходный уровень отсчета высот на Марсе. ~~ '
Расстояние от центра Марса до его поверхности в функции широты
определяется выражением
= А^1 —— sin2^.
Венера. Вторая (после Меркурия) по удалению от Солнца планета. Среднее
расстояние Венеры от Солнца 108,2 млн.км (0,72333 а.е.). Сидерический
период обращения Венеры вокруг Солнца равен 224,7 земных суток. Вра¬
щение Венеры вокруг Солнца происходит со средней скоростью 34,99 км/с.
Среди планет Солнечной системы Венера имеет самый малый эксцентриси¬
тет орбиты: е- 0,007 (т.е. орбита почти круговая). Синодический период
обращения Венеры в среднем составляет 583,92 земных суток. Эквато¬
риальный радиус Вэ - 6050 км, полярный радиус R = 6049 9 км
е оВеТп*0 окРУжает довольно плотная атмосфера. Ее масса ‘составляет
' кг. Венера, как и Уран, имеет обратное вращение — с
14
востока на запад. Угловая скорость вращения Венеры очень мала и
равна 2,99 • 10'7 рад/с.
Юпитер. Самая большая планета Солнечной системы, существенно отли¬
чающаяся от планет земной группы по многим основным характеристикам
(масса, состав и строение атмосферы и т.д.).
Большая полуось эллиптической орбиты, по которой вращается Юпитер
вокруг Солнца, составляет 5,203 а.е. [76], эксцентриситет орбиты ра¬
вен 0,0484.
Фигура Юпитера может быть представлена геометрически в виде эллип¬
соида вращения. Величина экваториального радиуса /?э, отнесенная к экви¬
потенциальному уровню Р= 1 атм, составляет 71 455 км. Ошибка опреде¬
ления величины /?э составляет ±30 км и включает в себя ошибки измере¬
ний и неопределенность в знании параметров атмосферы. Полярный радиус
Юпитера /? = 66 832 ± 30 км, геометрическое сжатие е = 0,0647 ± 0,0001.
Радиус планеты на широте у? может быть определен из соотношения
R^ = ЯЭИ — е sin2 <р).
Значительное изменение радиуса Юпитера в зависимости от широты
приводит к существенному влиянию широты точки поверхности на величи¬
ну ускорения силы тяжести. А именно на экваторе величина д минималь¬
на и составляет 22,6 м/с2, на полюсе она максимальна и равна 28,38 м/с2.
Отношение массы Солнца к массе Юпитера может быть принято равным
1047,355 с наибольшей ошибкой ±0,025, величина гравитационного пара¬
метра Юпитера м = 126 712 000 ± 3000 км3/с2, масса Юпитера М =
= 1,901 • 1024 кг.
Период вращения Юпитера равен 9,9 ч, линейная скорость вращения
на экваторе 12,3 км/с. Наклонение плоскости экватора Юпитера к плоско¬
сти орбиты мало (3°07'), вследствие чего смена времен года отсутствует.
§ 1.2. Поверхности планет
Марс. При рассмотрении поверхности Марса с Земли легко выделяются
три основных типа деталей [66] :
полярные шапки, которые имеют максимальные размеры зимой и силь¬
но уменьшаются летом;
светлые области - относительно яркие участки планеты, расположенные
преимущественно вблизи северных широт и занимающие около 2/3 поверх¬
ности Марса;
темные области - относительно темные участки планеты, расположенные
вблизи южной тропической зоны.
После полетов к Марсу КЛА типа "Марс", "Маринер" и "Викинг" были по¬
лучены детальные фотографии поверхности планеты, на которых была
обнаружена масса топографических деталей разного типа. Номенклатура
наименований этих деталей может быть представлена следующим образом:
кратеры диаметром более 20 км (таких кратеров около 6000) ;
кратеры диаметром более 100 км (их около 180);
цепочки кратеров;
каньоны (протяженные депрессии с крупными склонами) ;
хребты;
протяженные узкие депрессии, обычно встречающиеся группами;
пересекающиеся долины;
плоскогорья с крупными склонами;
горы;
кратеры неправильной формы;
5
15
10
0
Lr
II. п
Рис. 1.1. Гипсометрическая диаграмма
поверхности Марса.
низменные и возвышенные рав¬
нины;
холмы.
Подробное наименование всех
отмеченных деталей и координа¬
ты их расположения на поверхнос¬
ти Марса можно найти, напри¬
мер, в работе [66].
На рис. 1,1 приведены результа¬
ты статистической обработки гип¬
сометрической карты Марса в ви¬
де так называемой гипсометричес¬
кой диаграммы [66], которая по¬
казывает, как зависит относитель¬
ная полощадь S участков поверх¬
ности, имеющих высоту/?, от вели¬
чины последней. Видно, что диаг¬
рамма имеет два максимума:
вблизи h = 0 и h = —3 км. Основ¬
ной вклад в первый максимум
вносит часть поверхности, расположенная к югу от параллели +45° во
второй максимум — часть, расположенная к северу.
Около половины поверхности Марса составляют кратерные области,
остальная часть покрыта молодыми вулканическими образованиями
либо равнинными отложениями. Больше всего кратеров находится в юж¬
ном полушарии планеты. Максимальная плотность кратеров наблюдается
в областях, попадающих на нулевой максимум гипсометрической диаграм¬
мы (см. рис. 1.1). к
Кратеры по происхождению подразделяются на метеоритные и вулкани¬
ческие. Они заметно отличаются по форме. Метеоритный кратер почти
круглый, имеет кольцевой вал с характерной грубой структурой, внутрен¬
ние и внешние террасы, при достаточно больших размерах - центральную
горку, при еще больших - внутренний вал; вокруг простирается равнина
Вулканический кратер - гладкий по краям. Его окружают застывшие
лавовые потоки и каналы.
Иногда оказывается достаточно сложным определить по фотографиям
происхождение кратера, особенно когда он сильно разрушен. Тем не менее
можно с уверенностью сделать вывод, что подавляющее большинство
марсианских кратеров относится к числу метеоритных.
Температуру верхнего слоя грунта, данные о его тепловых свойствах
и косвенные сведения о структуре грунта можно получить, исследуя яр¬
кость Марса в инфракрасной области спектра при помощи наземных теле¬
скопов [66]. Средняя температура на освещенной части диска планеты
составляет около 230 К, максимальная температура — около 300 К.
Многочисленные исследования показывают, что поверхностный слой
марсианского грунта представляет собой тонкодисперсную раздроблен¬
ную среду. Она во многом похожа на лунный грунт — реголит, который
сформировался под действием длительной обработки мелкими метеорита¬
ми. Фотографии мест посадки американских КЛА "Викинг-1,2" показы¬
вают наличие камней различных размеров. В местах посадки этих КЛА
16
присутствовал грунт двух типов: песчаный и каменистый. Одна из двух
опор КЛА "Викинг-1" попала на песчаный грунт, другая на каменистый.
Первая опора погрузилась на глубину 16,5 см, вторая, оказавшись на ка¬
менистом грунте, совсем не погрузилась. Здесь термины "песчаный" и
"каменистый" понимаются условно. Каменистый грунт не является сплош¬
ным скальным образованием, просто частицы грунта сцеплены более проч¬
но, и их средние размеры больше.
Предполагается (с большой степенью вероятности), что на широте
~ 45 начинается зона вечной мерзлоты. Распространено мнение, что за¬
пасы воды в форме вечной мерзлоты на Марсе могут быть значительными.
Учитывая наличие грунтового льда, можно допустить, что незначительное
количество воды в жидкой фазе может появиться и вблизи поверхности,
хотя в среднем марсианский грунт очень сухой.
Венера. Плотный облачный покров, окружающий Венеру, не позволяет
применять для изучения рельефа оптические измерения формы края ее
диска и размера теней, отбрасываемых горными массивами и изменяющих¬
ся при различных высотах Солнца над венерианским горизонтом. Един¬
ственным возможным методом изучения рельефа Венеры в настоящее
время является радиолокация. В результате радиолокационных измерений
были обнаружены разные в геологическом отношении структуры поверх¬
ности Венеры [52]. Было установлено, что максимальный перепад высот
на поверхности этой планеты может достигать 18 км. Проведенные впослед¬
ствии измерения высот поверхности Венеры с помощью автоматических
КЛА подтвердили этот вывод. При этом оказалось, что углы наклона по¬
верхности небольшие (максимальные углы наклона на расстоянии 100 км
в среднем составляют 1,2°). Кроме того, были обнаружены кратеры, диа¬
метр наибольшего из которых составляет 160 км при сравнительно неболь¬
шой глубине (около 500 м). Всего определено более десятка кратеров
диаметром, превышающим 30 км.
Интересно отметить, что из трех тел Солнечной системы — Луны, Марса
и Венеры, поверхность которых сильно кратерирована, наиболее глубокие
кратеры обнаружены на Луне, более мелкие — на Марсе и самые мелкие —
на Венере. Выявленная последовательность дает основания предполо¬
жить, что отмеченное различие глубин кратеров на этих небесных телах
обусловлено в основном влиянием атмосферы [52].
Представляет интерес большая каналообразная структура шириной
около 120 км, длиной 1500 км и глубиной 1,5 км. Она проходит в районе
экватора в области планетоцентрических долгот 240—250°. Аналогичный
разлом меньшей длины (около 860 км) отмечен также вблизи экватора
в области планетоцентрических долгот 350—360 . Были обнаружены приз¬
наки тектонической деятельности на Венере, не исключается возможность
также и современной вулканической деятельности на этой планете.
Информация о структурных образованиях рельефа более мелкого мас¬
штаба была получена с помощью спускаемых аппаратов (СА) АМС "Вене¬
ра-9, 10, 13, 14". Районы посадки существенно отличаются по своим морфо¬
логическим характеристикам. Так, в районе посадки СА станции "Венера-9"
зафиксирована россыпь камней, имеющих острые углы, с преобладающими
размерами в несколько десятков сантиметров. В районе посадки СА стан¬
ции "Венера-10" наблюдался более сглаженный рельеф со слабовозвышаю-
щимися каменными глыбами. Выявилось, что поверхность между глыбами
покрыта слоем мелкозернистого грунта.
Через толщу венерианской атмосферы проникает лишь небольшая доля
солнечной радиации, достаточной, однако, для сильного нагрева поверх¬
ности планеты. Это объясняется действием так называемого "парникового"
2. Зак. 2069 17
эффекта (атмосфера Венеры является практически непрозрачной для
теплового излучения поверхности в космическое пространство).
По результатам наземных наблюдений, а также непосредственных изме¬
рений в местах посадки СА станций "Венера" был сделан вывод, что темпе¬
ратура ночной стороны планеты составляет 7"0 = 740 ± 30 К. Интересно
отметить, что температура поверхности и приповерхностной атмосферы
освещенной стороны Венеры мало отличается от температуры ее темной
стороны. Суточное изменение температуры поверхности и околоповерх-
ностной атмосферы также незначительно и не превышает 1 К. Наличие
массивной теплосодержащей плотной атмосферы Венеры не предполагает
также значительных изменений температуры по широте (уменьшение тем¬
пературы от экватора к полюсам не превышает 12 К).
О веществе поверхностного покрова Венеры в настоящее время имеется
очень мало сведений. Тем не менее имеющиеся данные показывают, что
грунт на этой планете более плотный, чем на Луне и Марсе (в слое одина¬
ковой толщины). Радиолокационные измерения поверхности Венеры,
проводившиеся с помощью СА станций "Венера-8, 9, 10, 13, 14", показали^
что средняя плотность грунта для слоя толщиной 2—3 м составляет величи¬
ну, в среднем равную 2,56 г/см3.
Юпитер. В отличие от планет земной группы, основная масса вещества
Юпитера не отличается по химическому составу от атмосферы. Нижняя
граница атмосферы к настоящему времени четко не определена.
Поток внутреннего тепла, излучаемый Юпитером, очень большой (срав¬
ним по величине с потоком, получаемым планетой от Солнца) и создает
в недрах Юпитера высокие температуры. Поэтому во всей толще над грани¬
цей раздела водородно-гелиевая смесь находится в сверхкритическом
состоянии.
§ 1.3. Атмосферы планет
Марс. Марсианская атмосфера по результатам масс-спектрометричес¬
кого анализа на КЛА "Викинг-1" [66] имеет следующий состав: углекис¬
лый газ - 95%, азот - 2-3%, аргон - 1-2%, кислород - 0,1-0,4%.
Локальные вариации давления, связанные с топографическими особен¬
ностями Марса, весьма значительны. Минимальные высоты на поверхности
Марса составляют примерно 4 км, максимальные на больших площадях
(20 X 20 ) — около 8 км, а высоты вершин больших вулканов достигают
27 км. При этом топографические вариации давления изменяются от 8
до 5 мбар. Поскольку безопасная мягкая посадка КЛА с применением па¬
рашютной системы при низких давлениях является трудной задачей, учет
данных о топографических вариациях давления оказывается исключитель¬
но важным.
Суточные вариации давления по данным КЛА "Викинг-1" имеют ампли¬
туду ±0,1 мбар. В местах посадки КЛА "Викинг-1,2" было обнаружено
систематическое изменение давления (рис. 1.2). При этом амплитуда се¬
зонных изменений давления составляла около ±0,5 мбар. Сезонные колеба¬
ния давления, по-видимому, вызваны процессами конденсации и сублима¬
ции углекислого газа, содержащегося в полярных шапках Марса. На Марсе
не могут существовать открытые водоемы вследствие низкого атмосферно¬
го давления. Возможны два резервуара накопления воды на этой планете:
грунт и полярные шапки, в которых, вероятно, сосредоточено довольно
большое количество льда. Результаты наземных наблюдений в течение дли¬
тельного времени показывают [66], что и в атмосфере Марса также имеют¬
ся водяные пары, однако их содержание очень мало. В среднем оно состав-
18
Рис. 1.2. Сезонные изменения давления
атмосферы Марса.
ляет 15—20 мкм осажденной воды
(это в 100 раз меньше, чем в очень
сухих районах Земли). Общее ко¬
личество воды в атмосфере Марса
не превышает нескольких кубичес¬
ких километров. Содержание воды
в атмосфере Марса меняется во
времени (в зависимости от сезона
и времени суток), при этом макси¬
мальное количество воды достигает
60 мкм, но в ряде случаев оно
уменьшается до 10 мкм и ниже.
Средняя по широтам и сезонам
температура нижней атмосферы
Марса составляет Го = 210 К. Имеются суточные колебания температуры,
которые заметно сглаживаются с ростом высоты. На высоте 1 —2 км от экви¬
потенциальной поверхности Марса суточные колебания температуры нахо¬
дятся в пределах 10—20 К. В период протекания пылевых бурь температу¬
ра атмосферы вблизи поверхности и на других уровнях заметно возрастает.
При проектировании К Л А, осуществляющих спуск в атмосфере Марса,
очень важное значение имеет выбор достоверной инженерной модели атмос¬
феры, учитывающей возможное разнообразие условий и соответствующей
современному уровню знаний.
В работах [66, 75] предложены две группы рабочих моделей атмосферы
Марса для высот от 0 до 80 км. Это модели для всей планеты и модели для
экваториального пояса. Средний молекулярный вес атмосферы принят
равным 43,5 г/моль.
Таблица 1.4
Основные характеристики рабочих моделей атмосферы Марса
Параметр
Модель 1
(основная,
средняя по
сезонам
для сред¬
них широт)
Модель 2
(минималь¬
ная по 7”0
и макси¬
мальная по
Ро>
Модел ь 3
(макси маль-
ная по 7"0
и минималь¬
ная по р0)
Модель 4
(максималь¬
ная по 7"0
и по Р80км>
Модель 5
(минималь¬
ная по 7*0 и
по Р80км>
Давление у по¬
6,0
7,5
4,5
7,5
4,5
верхности Ро,
мбар
Средний моле¬
43,0
43,6
42,4
42,4
43,6
кулярный вес д,
г/моль
Температура у
210
150
260
260
150
поверхности То, К
Плотность атмо¬
1,48 • Ю"2
2,67 • 10" 2
8,82 • 10’3
1,47 • 10"2
1,6 • 10"2
сферы у поверх¬
ности р0, кг/м3
Градиент темпе-
2,5
0,7
1,0
1,0
0,7
ратуры по высо¬
те, К/км
19
Таблица 1.5
Модели атмосферы Марса
Основная
Минимальная по То, мак¬
симальная по р0
h, км
Т, К
Р, мбар
р, кг/м3
Г, К
р, кг/м3
-5
222
9,37
2,18
■ ю-2
153
4,95 ■ 10-’
0
210
6,0
1,48
• 10"2
150
2,67 ■ 10-’
10
185
2,28
6,36
• 10"3
143
7,36 ■ 10-’
20
160
7,58 • 10”1
2,45
• 10’3
136
1,94 • 10-’
30
150
2,19 • 10'1
7,56
• 10-4
129
4,84- 10~4
40
150
6,29 • 10’2
2,17
• 10“4
122
1,13 • 10"4
50
150
1,83 • IO’2
6,31
■ 10’5
115
2,54 • IO'5
60
150
5,41 • 10-’
1,86
• 1СГ5
108
5,07 • 10‘
70
150
1,62 • 10~’
5,59
• 10_б
101
9,47 • 10-’
80
150
4,93 • IO'4
1,7 •
10’6
94
1,57 • 10-’
В первом случае рассматриваются три температурных профиля: основ¬
ной, минимальный и максимальный. Для оценки всего возможного диапа¬
зона изменения плотности необходимо использовать пять моделей, полу¬
ченных путем комбинации каждого из температурных профилей с макси¬
мальным и минимальным давлением у поверхности. В соответствии с ра¬
ботами [66, 75] приведем основные характеристики пяти моделей, полу¬
ченных подобным образом (табл. 1.4), и зависимости температуры Т, дав¬
ления Р и плотности рот высоты h (табл. 1.5).
Во второй группе моделей задаются среднесуточные профили для широ¬
ты ±15 на период летнего равноденствия, летнего и зимнего солнцестоя¬
ния (табл. 1.6), а также суточные вариации профиля для периода равноден¬
ствия.
Таблица 1.6
Основные характеристики рабочих моделей атмосферы Марса с учетом сезонных и
суточных вариаций
Параметр
Среднесуточные профили (»р = ± 15°)
Суточные вариации (про¬
филя для периода) равно¬
денствия (<р = ±15°)
равноден¬
ствие
лето
зима
макси маль-
ная модель
минималь¬
ная модель
Давление у поверх¬
5,7
5,1
4,5
5,9
5,5
ности Ро, мбар
Температура у по¬
220
250
190
230
210
верхности То, К
Плотность атмо¬
1,34 • 10“ 2
1,06- 10’2
1,23- 10“ 2
1,32 • 10“2
1,35 ■ 10
сферы у поверх¬
ности р0, кг/м3
Градиент темпе-
2,5
3
2
2,5
2,5
ратуры в тропо¬
сфере, К/км
20
Максимальная по То, мини¬
мальная по р0
Максимальная по То и
по Ро
Минимальная по То и по р0
Т, К
р, кг/м3
т, К
р, кг/м3
т, К
р, кг/м3
265
1,24 • 10-2
265
2,08 • 10’2
153
2,97 ■
10"2
260
8,82 ■ IO’3
260
1,47 • 10’2
150
1,6 •
ю-2
250
4,38 • 10’3
250
7,3 • 10_3
143
4,42 •
10“3
240
2,13 • 10'3
240
3,55 • 10~3
136
1,17 •
10'3
230
1,02 • 10’3
230
1,7 • 10'3
129
2,9 •
10-4
220
4,71 • 10'4
220
7,86- 10“4
122
6,79 •
10'5
210
2,14 • 10'4
210
3,56 • 10'4
115
1,52 •
ю-5
200
9,39 ■ 10“5
200
1,57 • 10'4
108
3,04-
10_б
190
3,99 • 10'5
190
6,65 • 10'5
101
5,68 •
10“7
180
1,64 • 10“5
180
2,72 • IO’5
84
9,44 ■
10"8
Венера. Анализ данных, полученных при помощи АМС "Венера7', позволил
определить следующее объемное содержание основных составляющих
атмосферы Венеры [60] : углекислый газ — около 97%; азот — не более 2%;
кислород — менее 0,1%; вода - около 12 мг/л « 1%) .
Приведенному газовому составу соответствует величина среднего моле¬
кулярного веса /л = 43,4 г/моль.
Рассматриваются три модели атмосферы: номинальная, максимальная
и минимальная [60]. Минимальной модели соответствуют То = 747 К,
Ро = кгс/см2; максимальной — То = 753 К, Ро = 95,2 кгс/м2 (табл. 1.7).
Профиль скорости ветра на Венере имеет ряд характерных особенностей
[66]. Возможно возрастание скорости ветра с высотой от 0,5 м/с вблизи
поверхности до 100—140 м/с на высотах около 50 км. Наиболее заметное
изменение скорости ветра [с градиентом до 4—6 (м/с)/км] наблюдалось
в диапазонах высот от 11 до 18 км и от 42 до 50 км.
Юпитер. Наблюдения с помощью научных приборов, установленных на
КЛА "Пионер" и "Вояджер", показывают, что основными компонентами
атмосферы Юпитера являются молекулярный водород и гелий (наиболее
вероятное соотношение: 86% водорода и 14% гелия [76]). Кислород, угле¬
род и азот связаны в основном в молекулах Н2О, СН4 и NH3 и их суммар¬
ное содержание не превышает 0,2%. Однако теоретические исследования и
наблюдения не исключают увеличенного по сравнению с приведенными
цифрами содержания гелия. Максимально допустимая величина объемных
отношений Не : Н2, по-видимому, не превышает единицы.
В соответствии с работой [76] в табл. 1.8 приведены три модели атмос¬
феры Юпитера, которые учитывают имеющиеся к настоящему времени дан¬
ные о вертикальном разрезе атмосферы этой планеты и их разброс. Пер¬
вая модель (номинальная) дает наиболее вероятную зависимость парамет¬
ров от высоты. Вторая модель (минимальная по температуре — "холод¬
ная") позволяет получить верхнюю границу плотности в нижней атмосфе¬
ре и нижнюю границу в высоких слоях атмосферы. Третья модель (мак¬
симальная по температуре — "теплая") дает нижнюю границу плотности в
нижней атмосфере и верхнюю границу в ее высоких слоях. Средний моле¬
кулярный вес в первой и третьей моделях принимался равным д =
=2,28 г/моль, во второй модели /л = 3,00 г/моль.
21
СП чГ
<о
•0
Л
-
о
-
о о
о
о
Г'
1
о
7
о
о
О 1
1
1
V— т—
г—
т—
о
ч—
о
г-
г—
<- о
о
о
00
со
•
СМ
00
см
см
со
00 см
см
00
L0
8
00
СМ •
СМ
1П
00
сч
см
<э
L0
СП
CD
СП
CD
in
in
Г\1П
оо
1П
о'
о”
сп
о'
о"
со" см”
см"
тг
in
СМ Г-'
оо”
in
О)
L0
СМ
т—
о о
1 о
о
о
о
о
о
о о
1 о
со
т— V—
О т-
г—
т—
г—
т— г—
О г-
in
со
•
ш со см
со
О)
• с-
со
О)
см
г*
• О)
Таблица 1.7
Модели атмосферы Венеры
со
г—
г-
7 7
о
о
о
о
о
о
о о
I
о
со in
см
о
о
*“
т_
О
ш
со со
о
о
§
СП
со
см
со о
о
о
г*
со
О)
СМ.’Ф г-
in
со
т-
г-
00
О)
Т—
CN
о о
сэ
сэ
сэ
СМ
о
in
СП
in
ш см
ш
со
о?
см
in
о"
СП
Г-'
о"
6“ 6*
о'
6“
о'
Г-'
см
тг
Т—'
in
CN г-'
СП
СП
О)
ш
см
т—
210 650 1,73-10-“ 1,73-10-“ 900 3,3-10-“ 1,9-10'“ 500 5,66-10'“ 5,8 • 10'1
220 650 8,94-10'“ 8,94-10'“ 900 2,1-10'“ 1,18-10-“ 500 2,4-10-“ 2,46-10"
ГО
с
го
2
У
-с
7 7 7 о о о о о 7 о о
OOOr-1-^^^Or-^
• • • LD LD CN М • СП 04
О4_ 00 СП г- CN г- CD LO .0* СО
<-' оо' со LO ОО' 04 1П Т-' СП I I
040004»— ОС0000)Ш0404С0
О) СО <D * - - СО О <0 - W *>
(Nr- 04 04 СО г- Щ г- СО
8 т- О СО О
00 (Я 1П 04
CD 1П СО СО 04
Т- СО СО со о о
1П О) 04 СО СО
Г- т- Г- 04 04 04 04
I
I
о
’3-
cooioi’^ojcoo'ooo'
с< CD О) СО г-
04 т- 00 1П СО 04
ся о
« «П ' ’ г-
I I О О I
О О т- т- о
тГ in
I
Ч <4 Q
04 О* Т-
со
• • О* СО¬
СО 04 О in 04
00 CN (D сч со
1П со" СЧ Г"-'
I
сосог*сооооооо
СООГ^т-Шт-СОСОСОСО
’t’^OlOJr-T-r-r-^r-
I
СО •1ПО4О4С0СО-1ПО)Г'00т-
ся СП -е in in CD т-к in СП in СХ) in 00^
т-' »-"• со' СП т-' СП СП тф Т-' Г-' 1-‘ CN СП
о 7> о о о о
in
in
СО
о
’3-
СО
»“
со
о
1П
о
00
00
СЯ 00
04
тг
о-'
оо'
СП
Oj'
оГ
СП
0)
CN
СЭ СХ)
04
г-7
О)
»— т—
оо*-’ео4оО’еооооооо1
О1’ФС0Г*00О11ПС0С0С0С0С000С0
СОЩСООЧт— г-т— Г-Т— г-г-т— Г-О4
ОООООООООООО1ПО
О СО 00 ’З- ’JOOCNCDOlDO’tO
04 Т- | | т— Т- 04 04 СО СО
Таблица 1.9
Модели атмосфер Сатурна, Урана и Нептуна
Планета
Модель
р0, кг/м3
/3, м-1
"Теплая”
0,75
2,42 • 10'5
Сатурн
Номинальная
0,711
3,68 ■ 10"5
"Холодная"
0,655
5,55 • 10's
"Теплая"
0,071
2,23 ■ 10'5
Уран
Номинальная
0,487
3,67 • 10'5
"Холодная"
0,522
8,11 • 10'5
Нептун
Номинальная
0,48
5,7 -10's
Газовый состав по объему для каждой модели составляет:
86% Н2 и 14% Не для основной и "теплой" моделей;
50% Н2 и 50% Не для "холодной" модели.
Температура на уровне Р = 1 атм для основной модели атмосферы при¬
нимается равной 180 К, а для "холодной" и "теплой" соответственно 150 К
и 220 К.
Средний градиент температуры в тропосфере составляет: 2,2 К/км для
основной модели, 1,6 К/км для "холодной" и 2,2 К/км для "теплой".
Сатурн, Уран, Нептун. В настоящее время имеется слишком мало све¬
дений о параметрах атмосфер этих планет. При исследовании траекторий
спуска КЛА в атмосферах этих планет-гигантов может быть использова¬
на экспоненциальная зависимость плотности от высоты [144]
Р = Ров~р1',
гдеро — плотность атмосферы у поверхности планеты, а /3 — градиент плот¬
ности.
В табл. 1.9 приведены значения р0 и 0 для трех моделей атмосфер Сатур¬
на и Урана и для номинальной модели атмосферы Нептуна.
Таблица 1.10
Параметры атмосферы Земли
h , км
т, К
Г, °C
Р, мбар
р, кг/м3
—2
0
10
20
30
40
50
60
70
80
90
100
110
120
301,1
28,0
288,15
15,0
223,25
-49,9
216,65
-56,5
226,51
-46,64
250,35
-22,8
270,65
—2,5
247,02
-26,13
219,58
-53,56
198.64
486.65
-74,51
196,6
255,49
334,42
1,278
• 10s
1,478
1,01
• 10s
1,225
2,65 •
104
.4,135
• 10’*
5,53 •
103
8,89 •
10‘2
1,197
■ 103
1,84 •
10'2
2,871
• 102
3,99 •
10~3
7,978
• 101
1,03 •
10~3
2,19 •
101
3,1 • 1
О"4
5,22
8,28 •
10“5
1,05
1,84 •
10“5
1,83 •
10’1
3,418
• 10“6
3,186
• 10“2
5,549
• ю-7
7,36 ■
10_3
9,34 •
10“8
2,666
2,44 •
10'8
24
Следует отметить, что приведенные значения р0 и /3 являются сугубо
предварительными и в дальнейшем возможно их существенное изменение
по мере уточнения наших знаний о параметрах атмосфер этих планет.
Земля. Атмосфера нашей планеты является, естественно, наиболее изу¬
ченной по сравнению с другими планетами Солнечной системы. Выше при¬
водятся основные параметры атмосферы Земли в соответствии с ГОСТ
4401—81 [86]. Этот стандарт устанавливает числовые значения основных
параметров атмосферы в функции высоты в диапазоне от —2 км до 120 км.
Данные, приведенные в табл. 1.10, определяют средние значения парамет¬
ров атмосферы для широты = 45О32 33” и соответствуют среднему уров¬
ню солнечной активности. Этот стандарт может быть использован при
проектировании летательных аппаратов, осуществляющих спуск в атмосфе¬
ре Земли.
Атмосфера Земли представляет собой смесь газов, водяного пара и неко¬
торого количества аэрозолей. Основными составляющими атмосферы Зем¬
ли являются: азот — 78,084%, кислород — 20,948%, аргон — 0,934%, угле¬
кислый газ — 0,0314%.
Глава 2
ХАРАКТЕРИСТИКА ПРОБЛЕМЫ СПУСКА В АТМОСФЕРЕ
§ 2.1. Основные задачи спуска
Под спуском на поверхность планеты в общем случае понимают про¬
ведение всех операций, связанных с организацией подхода КЛА к плот¬
ным слоям атмосферы, безопасным и надежным прохождением атмосфе¬
ры и мягкой и точной посадкой в выбранном районе. Основные трудности
решения этой проблемы определяются тем, что в ходе спуска должна
быть погашена вся энергия (потенциальная и кинетическая), уровень
которой исключительно высок: удельная энергия (в расчете на 1 кг массы
КЛА) исчисляется десятками миллионов джоулей при спуске с орбиты
искусственного спутника Земли (ИСЗ) до миллиардов джоулей при по¬
садке на Юпитер.
В настоящее время для спуска на поверхности планет, имеющих атмо¬
сферу, единственно целесообразным является комбинированный способ
гашения скорости: путем сообщения небольшого корректирующего или
тормозного импульса (при спуске с орбиты искусственного спутника
планеты) КЛА переводится на траекторию, пересекающую плотные слои
атмосферы, при движении в которых происходит пассивное гашение ско¬
рости за счет сил сопротивления атмосферы, затем при сближении КЛА
с поверхностью планеты следует активное или пассивное гашение оста¬
точной скорости. Эффективность указанного пути решения задачи спуска
определяется тем, что затраты на активное торможение составляют (в за¬
висимости от планеты назначения) от долей до единиц процентов по отно¬
шению к полностью активному способу торможения. С другой стороны,
комбинированный способ выдвинул ряд дополнительных задач, решение
которых определило новые направления исследований, составляющих
существо проблемы спуска.
Из приведенного определения нетрудно видеть, что траектория спуска
разделяется на три взаимосвязанных участка:
подход к плотным слоям атмосферы;
25
движение в атмосфере;
мягкая посадка на поверхность планеты назначения.
Обычно, когда говорят о спуске КЛА, имеют в виду прежде всего вто¬
рой участок — участок основного аэродинамического торможения, кото¬
рый в значительной степени определяет существо и основные особенности
рассматриваемой проблемы. Действительно, именно здесь гасится подав¬
ляющая доля энергии, а КЛА подвергается интенсивному воздействию
механических и тепловых факторов. Физическая сущность процессов,
протекающих на этом участке, достаточно ясна: в результате того, что
воздушная среда препятствует движению КЛА, возникают аэродинами¬
ческие силы сопротивления. Скорость аппарата гасится, но при этом КЛА
и окружающая его среда сильно нагревается, т.е. механическая энергия
движения переходит в тепловую энергию торможения, которая рассеива¬
ется в окружающем пространстве и поглощается КЛА. Кроме того, нали¬
чие сил торможения приводит к возникновению перегрузок, действую¬
щих на КЛА, величины которых тем больше, чем интенсивнее проходит
гашение энергии. Итак, определились первые две задачи, которые необ¬
ходимо решить в ходе спуска, — преодоление перегрузок и защита КЛА
от теплового воздействия.
Снижение уровня тепловой нагрузки. При пассивном торможении КЛА
с использованием аэродинамических сил энергия движения практически
полностью переводится в тепловую. Тепловая энергия, подводимая к
КЛА, частично рассеивается за счет излучения от нагретой поверхности
или за счет уноса теплозащитного покрытия, частично поглощается систе¬
мой теплозащиты и частично аккумулируется за счет теплоемкости кон¬
струкции КЛА. Последнее обстоятельство при недостаточно надежной
теплозащите может вызвать увеличение температуры силовых элементов,
ухудшить условия работы аппаратуры и затруднить решение проблемы
жизнеобеспечения экипажа КЛА или надежного функционирования уста¬
новленной на нем научной аппаратуры. В результате возникает задача
защиты КЛА от чрезмерного нагревания. Степень важности этой проблемы
может быть различной в зависимости от планеты, на которую осуществля¬
ется спуск, от величины начальной скорости входа и аэродинамической
формы КЛА. Так, при спуске КЛА с орбиты искусственного спутника в
атмосферах планет земной группы (Земля, Венера, Марс) необходимая
масса теплозащитного покрытия составляет не более 5-10% массы
КЛА. В частности, для КЛА, осуществляющего спуск по траектории со
сравнительно малой дальностью полета в атмосфере, степень теплонапря-
женности траектории спуска не является определяющим фактором, и,
как правило, выбор траектории снижения осуществляется, исходя из
других условий. Затем рассчитываются тепловые нагрузки, действую¬
щие на КЛА, снижающийся по такой траектории, и обеспечивается потреб¬
ная тепловая защита КЛА.
При параболических и гиперболических скоростях входа, а также при
спуске с орбиты искусственного спутника внешних планет Солнечной
системы (Юпитер, Сатурн, Уран) потребная масса теплозащиты может
достигать 30—50% от массы КЛА. В этом случае многие траектории мо¬
гут оказаться непригодными для спуска вследствие невозможности ор¬
ганизации тепловой защиты КЛА при ее приемлемой массе хотя дру¬
гие условия и будут выполняться. Отсюда возникает одна из наиболее
сложных задач космической техники - задача минимизации массы тепло¬
вой защиты КЛА.
Решение этой задачи обычно ведется по двум направлениям:
совершенствование системы теплозащиты •
26
выбор оптимальной траектории снижения, позволяющей для заданного
типа системы теплозащиты обеспечить наименьшую ее массу (при этом
предполагается, что вид используемого теплозащитного материала, фор¬
ма КЛА и его аэродинамические характеристики известны).
Оба направления оптимизации взаимосвязаны, но степень корреля¬
ции между ними не столь существенна, чтобы исключить независимое
их рассмотрение.
Перегрузочный режим. Снижение уровня перегрузок, действующих
на КЛА в процессе спуска, относится к числу основных требований. Чрез¬
вычайно высокие перегрузки при спуске автоматического КЛА могут
привести к его разрушению или нарушению нормальной работы аппара¬
туры. Во избежание этого необходимо проводить мероприятия по улучше¬
нию прочностных характеристик элементов конструкции КЛА и его ап¬
паратуры, что, как правило, приводит к их утяжелению. Это в свою оче¬
редь вызывает уменьшение массы полезной нагрузки КЛА при одинако¬
вой начальной массе. Поэтому при прочих равных условиях предпочтение
отдается траекториям, при спуске по которым величины перегрузок, дейст¬
вующих на КЛА, минимальны.
Задача снижения уровня перегрузок становится еще более принципиаль¬
ной при спуске пилотируемых КЛА. Реакция космонавтов на воздейст¬
вие перегрузок определяется рядом факторов, среди которых особое
значение имеют величина перегрузки, время ее действия, скорость нараста¬
ния и направление вектора перегрузки по отношению к туловищу, а также
исходное функциональное состояние организма. Нарушениям гемодина¬
мики принадлежит одно из ведущих мест в генезе физиологических сдви¬
гов при перегрузках. Определенное значение имеют и такие факторы, как
смещение внутренних органов и их деформация, что может нарушить
функции этих органов. Изменение функций центральной нервной системы
сопровождается снижением не только физической, но и умственной рабо¬
тоспособности членов экипажа летательных аппаратов. Кроме того, пере¬
грузки оказывают значительное влияние на дыхание, газообмен и работу
сердёчно-сосудистой системы.
Относительно "легкий" перегрузочный режим имеет место при спуске
с орбиты искусственного спутника в атмосферах планет земной группы.
Так, даже при баллистическом спуске автоматических КЛА с орбиты
ИСЗ величина максимальной перегрузки не превышает 8—10 единиц. Это
позволяет при условии организации входа КЛА в атмосферу по пологой
траектории вблизи границы захвата исключить из рассмотрения (по край¬
ней мере из числа первоочередных) проблему минимизации перегрузоч¬
ного режима для КЛА, осуществляющих спуск с орбиты ИСЗ.
При возвращении же пилотируемых КЛА из межпланетного полета в
силу больших начальных скоростей входа и продолжительного пребы¬
вания экипажа в космосе задача снижения уровня перегрузок имеет прин¬
ципиальное значение. Несмотря на то, что это требует существенных до¬
полнительных затрат массы, в настоящее время анализируются даже такие
схемы полета, которые предполагают гашение скорости до первой косми¬
ческой активным путем с последующей посадкой КЛА с орбиты ИСЗ.
Даже поверхностное рассмотрение первых двух задач спуска показы¬
вает, что количественные характеристики величин перегрузок, темпера¬
туры и теплового потока в значительной степени определяются траекто¬
рией снижения КЛА, т.е. зависят от того пути, по которому он подходит
к поверхности планеты. Однако организация движения КЛА по единствен¬
ной оптимальной траектории в общем случае невозможна, хотя бы в силу
того, что условия входа в плотные слои атмосферы не могут быть реали¬
27
зованы абсолютно точно. Разброс начальных условий входа зависит от
типа системы навигации на первом участке траектории — участке подлета
к плотным слоям атмосферы (внеатмосферная навигация). Очевидно,
что чем выше требования по обеспечению точности входа, тем сложнее и,
как правило, тяжелее система внеатмосферной навигации. Возникает
противоречивая ситуация: с целью выбора и реализации оптимальной
траектории на атмосферном участке требуется организация точного вхо¬
да, а для упрощения системы внеатмосферной навигации требования про¬
тивоположны. Рассмотрение атмосферного участка спуска позволяет
сформулировать задачу максимизации коридора входа.
Коридор входа КЛА в атмосферу в общем случае определяется диапа¬
зоном высот условного перицентра (или углов входа 0О на высоте hQ),
при входе с которыми возможен безопасный спуск КЛА с выдерживанием
основных ограничений на фазовые координаты траектории снижения.
Как видно, варьируемый параметр единственный — высота ибо на¬
чальная скорость входа Vo определяется в основном выбранной схемой
полета и практически не зависит от конкретной величины Ьл.
На практике все решается компромиссным путем — сравнением имею¬
щихся возможностей и соответствующих массовых затрат на каждом из
участков спуска. Следует указать, что проблема внеатмосферной нави¬
гации имеет в значительной степени самостоятельное значение и ей посвя¬
щены отдельные публикации. В настоящей книге подробно рассматрива¬
ется лишь задача максимизации коридора входа.
Для создания относительно простой и легкой системы навигации КЛА,
функционирующей на участке подлета к плотным слоям атмосферы пла¬
неты, необходимо, чтобы ширина коридора входа была максимальной.
Это объясняет целесообразность постановки задачи о максимизации ко¬
ридора входа путем управления на атмосферном участке, т.е. для КЛА
определенной аэродинамической формы и с заданными проектно-баллис¬
тическими характеристиками необходимо найти такое управление, ко¬
торое позволило бы выполнить все поставленные условия при входе з воз¬
можно широком коридоре. Можно отметить, что соответствующим выбо¬
ром проектно-баллистических характеристик КЛА коридор входа в атмо¬
сферу можно сделать достаточно большим. Однако этим обстоятельством
не всегда оказывается возможным воспользоваться, поскольку сущест¬
вуют разного рода ограничения на диапазон реализуемых значений про¬
ектно-баллистических характеристик КЛА.
Рассмотрение заключительного участка спуска - мягкой посадки -
выдвигает еще одну важную задачу, которую необходимо решать на этапе
основного аэродинамического торможения - задачу минимизации массы
системы мягкой посадки (СМП). Необходимость и самостоятельный ха¬
рактер этой задачи объясняются тем, что работы сил сопротивления недос¬
таточно для полного гашения скорости КЛА. Например, скорость встречи
Г2тд ’
с поверхностью Земли V — \/ = 2 ~ 4 м/с может быть достигнута
сх§Ро
при величине приведенной нагрузки на лобовую поверхность КЛА Рх =
т 2
“ cxs _ ~ 2 кгс/м , что неосуществимо без применения специальных
устройств.
Организация движения на заключительном участке спуска зависит от
цели полета, типа КЛА, характеристик атмосферы и рельефа поверхности
планеты назначения, а также от особенностей и характера движения на
участке основного аэродинамического торможения. Имея в виду достав¬
ку на поверхность планеты научной аппаратуры, мы будем говорить толь¬
ко о "мягкой" посадке, когда скорость встречи КЛА с поверхностью
не превышает нескольких метров в секунду. Исходя из этого, для авто¬
матических КЛА в настоящее время можно выделить четыре основных
типа систем мягкой посадки: активную с использованием двигателей
мягкой посадки, парашютную, парашютно-реактивную и пассивную (с ис¬
пользованием тормозных юбок, щитков, баллонов, разрушающихся ферм
и т.п.).
Тип СМП, характер и эффективность ее работы принципиальным обра¬
зом зависят от начальных условий движения на этом участке — вектора
состояний Х^3) . Достаточно очевидно, что если имеется возможность
выбора Хо(3) , то существуют также их значения, которые позволяют наи¬
лучшим образом и с наименьшими затратами решить задачу мягкой по¬
садки. Но Xq3^ формируются на участке основного аэродинамического
торможения, ибо Х^ = Xq3\ Отсюда следует, что необходимо органи¬
зовать торможение таким образом, чтобы обеспечить вполне определен-
(2)
ные фазовые координаты Хк .
Рассмотрение сформулированных четырех задач (снижение уровня теп¬
ловой нагрузки, минимизация перегрузки, максимизация коридора входа
в атмосферу и минимизация массы СМП) является обязательным при
реализации спуска на поверхность любой планеты, имеющей атмосферу.
В итоге определяется одна траектория или семейство траекторий, по ко¬
торым должно проходить движение КЛА. Но вид этих траекторий зависит
от ряда факторов и условий. Здесь имеются в виду:
тип ЛА, его конструктивное решение и аэродинамические характерис¬
тики;
способ управления и возможности системы управления;
вид системы теплозащиты;
тип системы мягкой посадки и т.д.
Кроме того, очевидно, что решение основных задач спуска зависит
также от физических характеристик планеты назначения и ее атмосферы.
Отметим, что этими задачами не ограничивается их перечень. Можно ука¬
зать ряд дополнительных специальных задач, важность и сложность реше¬
ния которых определяется поставленной конечной целью полета:
задача точной посадки;
полет на минимальную или максимальную продольную или боковую
дальность;
поиск оптимальной траектории и оптимального управления на участке
мягкой посадки и т.п.
Особое место занимает задача выведения КЛА на орбиту искусствен¬
ного спутника планеты (ИСП). Космический летательный аппарат с меж¬
планетной траектории перелета входит в плотные слои атмосферы пла¬
неты, гасит скорость приблизительно до первой космической и вылетает
из атмосферы. Затем следует или формирование требуемой орбиты ИСП
активным путем, или повторный вход и посадка. Эта задача имеет много
общего с указанными выше, но имеет и ряд специфических особенностей
(см. раздел III).
29
§ 2.2. Условия входа в атмосферу
Начальные условия входа КЛА в атмосферу планеты определяются па¬
раметрами подлетной траектории на условной границе плотных слоев
атмосферы. Под условной границей понимается то максимальное зна¬
чение высоты Ла над поверхностью планеты, на которой аэродинамические
силы торможения КЛА становятся соизмеримыми с силой притяжения
планеты (значения /?а приведены в табл. 2.1).
Для проведения качественного анализа траекторий и решения основ¬
ных и дополнительных задач спуска во многих случаях нет необходимости
рассматривать пространственное движение и "привязываться" к конкрет¬
ной точке входа, а достаточно рассматривать лишь продольное движение
в плоскости подлетной орбиты. Как известно, для определения продоль¬
ного движения необходимо задать три параметра траектории: начальные
высоту h0 = /?а, скорость Уо и угол 0о наклона траектории к местному
горизонту на высоте h0. Вместо угла 0о часто используют высоту услов¬
ного перицентра Между этими параметрами имеется однозначное со¬
ответствие [24]. При спуске КЛА в атмосферах "больших" планет (Юпи¬
тер, Сатурн, Уран, Нептун) скорость входа относительно вращающейся
планеты может быть существенно уменьшена при входе в атмосферу в
направлении, совпадающем с направлением вращения планеты. Так, при
входе КЛА в атмосферу Юпитера начальная скорость входа уменьшается
на 12,6 км/с. Это оказывает значительное влияние на параметры траекто¬
рии спуска и в целом на облик КЛА.
Скорость входа КЛА в атмосферу определяется выбранной схемой
полета. В табл. 2.2 приведены значения возможных скоростей входа 1/0
для разных схем полета, которые предусматривают спуск КЛА в атмо¬
сфере.
Точность обеспечения расчетного значения Vo в настоящее время доста¬
точно высока и составляет величину порядка нескольких метров в се¬
кунду. Такая погрешность обычно не оказывает заметного влияния на
траекторию спуска.
Угол 0о входа КЛА в атмосферу или высота условного перицентра
траектории входа могут быть обеспечены любыми независимо от выбран¬
ной схемы полета. Точность реализации номинального значения угла входа
оказывает большое влияние на режим движения КЛА в атмосфере. Ве¬
личина возможного разброса угла входа (ширины навигационного кори¬
дора) Д0оав или высоты условного перицентра Д/?”ав относительно но¬
минального значения определяется точностью работы систем навигации и
коррекции КЛА на подлетном участке траектории.
В настоящее время при проектировании КЛА, осуществляющих спуск
в атмосфере, можно ориентироваться на следующие значения навигацион¬
ных коридоров входа:
Таблица 2.1
Условная граница плотных слоев атмосферы
Планета
Высота условной
Планета
Высота условной
границы /?а, км
границы /7а, км
Венера
100
Сатурн
500
Земля
100
Уран
500
Марс
100
Нептун
400
Юпитер
400
30
Таблица 2.2
Диапазон возможных скоростей входа в атмосферу
Планета
Скорость 1/0 при
спуске с низкой
околокруговой
орбиты, км/с
Скорость 1/0 при
спуске с вытянутой
эллиптической ор¬
биты, км/с
Скорость Vo при
спуске с траекто¬
рии прямого меж¬
планетного переле¬
та, км/с
Венера
7,7-8
8,3-9,2
10,4-13
Земля
7,9-8
8,5-9,5
11,2-17
Марс
3,3-3,6
3,8-4,7
5,6-8
Юпитер
43—45
48-55
60,4-70
Сатурн
25-27
27-32
35-39
Уран
15-16
20-24
26-30
Нептун
16,5-17,5
19-23
25-29
спуск с орбиты спутника планеты: Д0” ав «±15';
спуск на Землю при возвращении от Луны: Д/7вав ~±3^-10 км;
спуск на Землю при возвращении от планет Солнечной системы: Д/7вав
~±20 км;
спуск на Марс и Венеру с траектории прямого перелета: Д/?”ав « ±20 +
-^50 км;
спуск на планеты юпитерианской группы с траектории прямого перелета
и с применением автономных средств навигации: Д/?”ав 400 ^600 км.
§ 2.3. Аэродинамические формы космических
летательных аппаратов
В связи с многообразием задач, которые могут ставиться перед косми¬
ческими летательными аппаратами, снижающимися в атмосфере, предъяв¬
ляется ряд важных требований к их аэродинамическим характеристикам.
Для удовлетворения этих требований, зачастую противоречивых, косми¬
ческие спускаемые летательные аппараты разрабатываются различной
формы. Приведем краткое описание наиболее характерных типов КЛА,
классифицируя их в зависимости от способа получения аэродинамичес¬
ких сил.
1. Большинство разработанных к настоящему времени КЛА обеспе¬
чивает необходимые для торможения или маневра аэродинамические
силы с помощью мощного тормозного щита (КЛА "скользящего" типа).
Такие КЛА обладают хорошими тормозными свойствами, имеют малую
конвективную теплопередачу, характеризуются высоким значением ко¬
эффициента полезного использования объема и компактностью.
Недостатками таких КЛА являются сравнительно небольшое аэродина¬
мическое качество, которое может быть на них получено, и повышен¬
ное значение тепловых потоков при больших скоростях входа за счет
увеличения доли лучистого теплообмена в общем балансе.
2. У космических аппаратов второго типа аэродинамические силы созда¬
ются с помощью несущего корпуса (КЛА типа "несущий корпус") . На
них имеется возможность реализовать достаточно большие значения аэро¬
динамического качества. Однако следует отметить, что эти аппараты утра¬
чивают такие достоинства, как большая величина коэффициента сопро¬
тивления, малые конвективные теплопотоки и компактность.
31
3. Для получения больших значений аэродинамического качества мо¬
гут быть использованы крылатьье конфигурации КЛА (КЛА типа "косми¬
ческий самолет"). Практическое применение их затруднено, так как свя¬
зано с необходимостью обеспечения надежной теплозащиты и прочности
крыльев при движении КЛА с гиперзвуковыми скоростями.
Приведенная классификация носит условный характер. Имеется целый
ряд промежуточных форм КЛА, которые обладают теми или иными свой¬
ствами в зависимости от того, к какому типу компоновки они относятся.
С точки зрения решаемых проектно-баллистических задач спуска, одной
из определяющих характеристик КЛА является величина максимального
аэродинамического качества [2]. По мере увеличения сложности задач,
стоящих перед космическим летательным аппаратом, снижающимся в
атмосфере, возникает необходимость увеличения маневренных возмож¬
ностей КЛА и, следовательно, его максимального аэродинамического ка¬
чества /Стах. Однако увеличение Ктах сопряжено с решением ряда слож¬
ных технических проблем. Поэтому во многих случаях, когда это оказы¬
вается допустимым, для спуска выбираются КЛА, имеющие по возмож¬
ности более простую геометрическую форму.
Космические летательные аппараты, обладающие небольшим аэроди¬
намическим качеством (Ктах < 0,5—0,7), имеют возможность осущест¬
влять некоторый управляемый маневр на траектории с целью сниже¬
ния уровня перегрузок, уменьшения нагрева, компенсации разбро¬
са начальных условий входа, уменьшения массы системы мягкой
посадки и т.д.
Космические летательные аппараты с большим значением аэродина¬
мического качества (Ктах > 1—1,5) обладают широкими маневренными
возможностями при одновременном выдерживании невысокого допусти¬
мого уровня перегрузок и интенсивности нагрева. При спуске КЛА с боль¬
шим значением аэродинамического качества можно выбирать точку по¬
садки в широких пределах изменения начальных условий входа в атмо¬
сферу и осуществлять посадку "по-самолетному".
Ниже приводится краткое описание наиболее распространенных аэро¬
динамических форм КЛА.
Наиболее простой формой КЛА, осуществляющего спуск по баллисти¬
ческой траектории, является сфера. В качестве примера на рис. 2.1 пред¬
ставлена характерная зависимость коэффициента лобового сопротивления
сх от числа Маха М« для КЛА баллистического типа.
Аэродинамические компоновки КЛА первого типа (с развитым тор¬
мозным теплозащитным лобовым щитом) позволяют получить величину
аэродинамического качества К ъ 0,5—0,6. У таких КЛА именно лобовая
часть является не только тормозной, но и несущей поверхностью.
Среди КЛА первого типа наи¬
более распространенными яв¬
ляются сегментно-конические
формы. КЛА такой формы сос¬
тоят из лобового щита в виде
сферического сегмента и распо¬
ложенного за ним корпуса в виде
Рис. 2.1. Зависимость коэффициента
лобового сопротивления Сх от числа
Маха Моо для КЛА баллистического
типа.
32
обратного конуса с затупленной по сфере кормовой частью (рис. 2.2).
Для таких форм характерными параметрами являются: угол $с между
касательной к поверхности сегмента и его осью, угол полураствора
конуса и его удлинение Хк = lK/dM. На рис. 2.2 приведена зависимость
аэродинамического качества от угла атаки сегментно-конического тела
(£0 =65°, ак =5°, Хк = К М = 6).
Величина Ктах увеличивается с уменьшением удлинения обратного
конуса, т.е. с увеличением его притупления. В предельном случае конус
вырождается в сферический сегмент, а КЛА приобретает дискообразную
форму.
У КЛА с тормозным щитом аэродинамическое качество будет наиболь¬
шим в том случае, если его часть, расположенная за лобовым щитом, не вы¬
ходит из аэродинамической тени. Такие КЛА носят название зонтообраз¬
ных. Эти КЛА при сверхзвуковых скоростях полета обладают динами¬
ческой устойчивостью, но в трансзвуковом и дозвуковом диапазонах
скоростей, как и КЛА сегментно-коническои формы, теряют ее.
При аэродинамических компоновках с тормозным щитом наибольшее
аэродинамическое качество реализуется у КЛА зонтообразной и диско¬
образной форм. Но их существенным недостатком являются плохие мо¬
ментные характеристики. Кроме того, при относительно небольшой пло¬
щади миделева сечения такие формы характеризуются пониженным ко¬
эффициентом полезного использования объема корпуса КЛА. Поэтому
при выборе аэродинамической компоновки КЛА для решения ряда задач
спуска целесообразно помимо указанных выше форм рассматривать и
такие, которые представляют собой в какой-то степени компромиссное
решение между сегментно-коническими и зонтообразными формами.
Примером одной из таких форм являются аппараты в виде конуса с
косым срезом хвостовой части (рис. 2.3). При больших углах полураствора
конуса и среза б их форма приближается к первому типу и, наоборот,
при малых значениях этих углов напоминает формы с несущим корпусом.
У таких КЛА оказывается возможным получить за счет несимметрии
хвостовой части необходимое значение аэродинамического качества при
нулевом угле атаки. Поскольку в этом случае обтекание КЛА симметрично,
то расчет аэродинамических характеристик значительно упрощается. При
симметричном обтекании также устраняется несимметричность обгара
КЛА во время движения в плотных слоях атмосферы. Кроме того, при
3. Зак. 2069
33
Рис. 2.3. Космический летательный аппарат в виде ко¬
нуса с косым срезом хвостовой части.
использовании таких КЛА представляется воз¬
можным существенно уменьшить радиацион¬
ную составляющую суммарного теплового по¬
тока. При этом полезную нагрузку можно рас¬
полагать и за пределами корпуса, в аэродина¬
мической тени за его донным срезом. Стаби¬
лизация полета КЛА на заданном угле атаки
достигается путем соответствующего размеще¬
ния его центра масс. Очень важным при этом
является то, что разворот КЛА вокруг про¬
дольной (или скоростной) оси по углу крена
приводит к изменению вертикальной составляющей аэродинамического
качества (или подъемной силы) практически без изменения его полного
значения. Появляется возможность управления подобными аппаратами,
которое получило название управления креном или управления эффектив¬
ным качеством.
Проведенные исследования показывают, что у КЛА, имеющих форму
конуса с косым срезом хвостовой части, при устойчивом полете, нулевом
угле атаки, приемлемых тормозных свойствах и реально достижимых
положениях центра масс можно обеспечить величину аэродинамического
качества до /Стах = 0,6—0,7.
Практическая реализация /Стах > 0,7 у КЛА первого типа является
весьма сложной задачей. Значение /Стах > 0,7 может быть .получено на
КЛА типа "несущий корпус". Например, могут быть использованы КЛА
с несущей поверхностью в виде конического сегмента (рис. 2.4). Основ¬
ная идея их компоновки заключается в том, что при полете на балансиро¬
вочном угле атаки а или в некоторой его окрестности корпус КЛА це¬
ликом располагается в аэродинамической тени от несущей поверхности
и при гиперзвуковых скоростях полета практически не оказывает влия¬
ния на аэродинамику КЛА.
Располагаемое аэродинамическое качество конических сегментов рас¬
тет с уменьшением углов полураствора £к, затупления X и атаки а. Уве¬
личение угла среза 5 также ведет к увеличению аэродинамического ка¬
чества, так как при этом несущая поверхность все более приближается
к плоской, которая при равной площади обеспечивает получение макси¬
мального значения аэродинамического качества.
Космические летательные аппараты с несущей поверхностью в виде
затупленных конических сегментов с углами полу раствора конуса =
= 15-25 и умеренными значениями угла среза 6 способны обеспечить
аэродинамическое качество ЛГтах = 0,7-1,0 при реально достижимых ба¬
лансировочных углах атаки, позволяющих располагать в аэродинамической
тени от несущей поверхности (при a = абал) корпус достаточного объема.
Для получения более высоких значений аэродинамического качества
у КЛА такого типа необходимо уменьшать угол полураствора конуса
и величину угла атаки (рис. 2.5), однако это приводит к ухудшению объем¬
ных характеристик КЛА.
Проведенные исследования показывают, что для КЛА типа "несущий
корпус , имеющих различную форму, увеличение аэродинамического
качества сопряжено с ухудшением объемных характеристик. При этом
максимальное значение аэродинамического качества полуконусов с плос-
34
к
Рис. 2.4. Зависимость аэродинамического качества К от коэффициента лобового со¬
противления Сх для КЛА типа "несущий корпус" (несущая поверхность в виде ко¬
нического сегмента).
кой несущей поверхностью выше соответствующих значений для полу кону¬
сов с плоским верхним срезом.
Исследования показывают, что на КЛА типа "несущий корпус", имею¬
щих острый носок и острые угловые кромки, можно получить более вы¬
сокие значения /Стах. Однако в реальных условиях при движении КЛА
в плотных слоях атмосферы необходимо по тепловым соображениям
носовую часть притуплять, а острые кромки скруглять.
Рис. 2.5. Зависимость аэродинамического качества К от угла атаки а для КЛА в виде
затупленного конического сегмента.
35
В общем случае КЛА типа "несущий корпус" с учетом эффекта от за¬
тупления могут обеспечить величину аэродинамического качества до
^тах ~ 1,5—1,8. Управление полетом таких КЛА можно осуществлять
как изменением угла крена, так и угла атаки. Для получения величины
располагаемого аэродинамического качества /Стах > 2 следует исполь¬
зовать КЛА со специальными развитыми несущими поверхностями. На¬
пример, может быть использован КЛА, имеющий конфигурацию в виде
комбинации треугольного крыла с полуконусом (рис. 2.6). Изменение
угла стреловидности передней кромки крыла к оказывает существенное
влияние на величину максимального аэродинамического качества. А имен¬
но, увеличение угла к при постоянном объемном параметре приводит
к росту /Стах. Соответствующим выбором формы поперечного сечения
корпуса, расположенного на верхней поверхности крыла, можно добиться
некоторого увеличения /Стах по сравнению с комбинацией крыла с по¬
луконусом. В качестве примера на рис. 2.6 приведена характерная зави¬
симость величины аэродинамического качества от угла атаки для КЛА,
представляющего собой комбинацию полуконуса ($к = 7°) с треуголь¬
ным крылом (Ж = 60°).
При решении задач спуска КЛА с большим значением аэродинамичес¬
кого качества может быть использовано аналитическое выражение по¬
ляры. При малых углах атаки (а < 15—20°) поляра приближенно может
быть представлена в виде
сх=ВСу+сх0, су=Суат+су0, (2.1)
где при М > 5 коэффициенты т = 2, п = 3/2.
При больших углах атаки могут быть использованы следующие со¬
отношения:
сх =Схо +#isin3az су = Aisin2acosa. (2.2)
В табл. 2.3 [2] представлены значения сх0/ В, cyQ из уравнений (2.1)
и значения сх0, Alz из уравнений (2.2) для типичного КЛА с большим
значением аэродинамического качества.
Изложенное в настоящем параграфе позволяет получить представление
о наиболее характерных аэродинамических формах КЛА, используемых
# \\
-4 0
/ 4
8
16
а,гр ад
Рис. 2.6. Зависимость аэродинамического качества К от угла атаки а для КЛА в виде
комбинации треугольного крыла с полуконусом.
36
Таблица 2.3
Значения параметров, определяющих аэродинамические характеристики КЛА
Число
Маха М
Коэффициенты из уравнений (2.1)
Коэффициенты из уравнений (2.2)
сх0
I су0
l В
сх0
Аг
Вг
5
0,008
1,04
0,9
0,036
3,4
3
10
0,0112
1,04
0,32
0,03
2,2
2
15
0,0112
1,04
0,40
0,028
1,8
1,6
20
0,0112
1,04
0,44
0,026
1,75
1,58
для спуска. Числовые значения аэродинамических коэффициентов (в за¬
висимости от числа Маха) приводятся ниже при рассмотрении конкрет¬
ных задач спуска.
§ 2.4. Способы управления
Как известно, при пассивном торможении КГ1А в атмосфере управле¬
ние траекторией спуска практически может осуществляться только пу¬
тем изменения коэффициентов аэродинамической подъемной силы су,
лобового сопротивления сх и значения миделя $. Однако при этом
варьирование s связано с разработкой и использованием специальных
устройств (щитки, тормозные юбки и т.п.), в то время как изменение
аэродинамических коэффициентов происходит в результате поворота
КЛА вокруг его осей, т.е. при изменении прежде всего углов атаки а
и крена у.
Отмеченные особенности и предопределили три основные способа управ¬
ления, характерные для трех типов КЛА. Аппараты "баллистического"
типа, у которых величина аэродинамического качества К = су!сх = 0 в те¬
чение всего времени полета, могут управляться только с использованием
баллистического параметра ох = (cYs)/G; при этом не имеет значения,
изменяется ли сх или s, важен только диапазон варьирования ох. Эффек¬
тивность этого способа управления проявляется лишь при возможнос¬
ти изменения ох в 7—10 раз, что практически выполнить достаточно
сложно.
Управление траекторией полета КЛА типа ''космический самолет" с
большим значением аэродинамического качества (К > 1) может осущест¬
вляться "по-самолетному" — путем изменения углов атаки и крена, что
ведет к изменению величины аэродинамических коэффициентов. Возмож¬
ности управления такими аппаратами достаточно велики в виду больших
значений управляющих сил и диапазона их изменения.
В настоящее время наиболее распространенными КЛА являются аппа¬
раты "скользящего" типа. Основной особенностью таких аппаратов явля¬
ется то, что при сравнительно малом значении аэродинамического качества
(К & 0,2 -г 0,6) они имеют большие значения коэффициентов подъемной
силы и лобового сопротивления. Космические летательные аппараты
"скользящего" типа путем специального размещения грузов по объему
аппарата балансируются в полете на постоянном угле атаки (абал = const)
и управляются поворотом вокруг продольной или скоростной оси (путем
изменения угла крена у). Следовательно, составляющие аэродинамичес¬
кого качества в вертикальной плоскости и в боковом направлении явля-
37
ются функцией угла крена 7:
~ ^эфф = ^бал cos У•
Кб =^6anSin7.
(2.3)
(2.4)
В этом случае управление траекторией в вертикальной плоскости дви¬
жения осуществляется за счет изменения величины /Св = /<6ancos7, а в бо¬
ковом направлении для управления можно использовать знак угла крена.
Следует отметить, что при абал = const в ходе торможения коэффициенты
су и сх практически не меняются, по крайней мере в диапазоне чисел Маха
М > 4. Это позволяет переписать выражение (2.3) в виде
_ ^эфф “ ^6ancos7z
где /в - вертикальная составляющая в подъемной силе; Хбал — значение
подъемной силы при балансировочном угле атаки.
Как уже указывалось, такой способ управления называется управле¬
нием креном или управлением эффективным качеством. Его основной
недостаток заключается в наличии "паразитной" боковой составляющей,
которая затрудняет управление при необходимости выдерживать точное
значение боковой дальности. Этот недостаток компенсируется многими
преимуществами, главным из которых являются чрезвычайно малые
расходы топлива на развороты КЛА, так как во многих случаях аппараты
практически нейтральны по крену.
В заключение отметим, что для стабилизации КЛА около центра масс
используются в основном газореактивные двигатели малой тяги. Для
аппаратов типа "космический самолет" наряду с указанным могут при¬
меняться аэродинамические рули. Специальная стабилизация КЛА баллис¬
тического типа ввиду их простых аэродинамических форм во многих
случаях не применяется, а динамическая устойчивость при спуске дости¬
гается путем выбора необходимого запаса статической устойчивости,
т.е. специальной компоновкой КЛА.
§ 2.5. Основные типы системы тепловой защиты
Системы теплозащиты могут быть классифицированы по конструктив¬
ному исполнению и по типу используемого материала. Рассмотрим кратко
основные конструктивные схемы систем теплозащиты, а также номенкла¬
туру и основные свойства материалов теплозащитного покрытия.
Конструктивные схемы теплозащиты. В настоящее время при проек
тировании КЛА рассматривается несколько основных систем теплозащиты:
абляционная;
радиационная неохлаждаемая;
радиационная, охлаждаемая материалом с изменяющимся фазовым
состоянием;
радиационная, охлаждаемая водой;
радиационная комбинированная;
с панелями многократного применения.
При использовании абляционной системы большая часть теплового по¬
тока, поступающего к поверхности КЛА, идет на изменение агрегатного
состояния оплавляемого материала, а остальное тепло поступает внутри
корпуса.
Абляционная система теплозащиты по сравнению с радиационной имеет
следующие недостатки :
исключается повторное использование КЛА;
38
для КЛА с большим значением аэродинамического качества из-за воз¬
растания времени спуска требуется большое количество вещества с низ¬
кой температурой изменения агрегатного состояния, что увеличивает
массу системы теплозащиты.
Конструктивно радиационные системы теплозащиты строятся следую¬
щим образом.
Радиационная неохлаждаемая система состоит из наружного теплоза¬
щитного экрана и теплоизоляционного слоя, устанавливаемого между
наружным теплозащитным экраном и основной конструкцией. Масса
такой системы зависит в основном от вида используемого материала теп¬
лозащитного экрана и теплоизолятора.
Радиационная охлаждаемая система в общем случае содержит радиа¬
ционный экран, обшивку-изолятор и активную систему внутреннего ох¬
лаждения.
Для минимизации массы такой системы теплозащиты необходимо
соответствующим образом подбирать материал для теплозащитного эк¬
рана и обшивки изолятора, а также минимизировать массу хладагента.
Последнее зависит как от величины тепловых потоков, действующих
на КЛА и проходящих через теплозащитный экран и обшивку-изолятор,
так и от выбранной системы расположения хладагента в конструкции
КЛА. Анализ характеристик охлаждаемой и неохлаждаемой радиацион¬
ных систем теплозащиты показал, что для охлаждения поверхности КЛА
с большим значением аэродинамического качества можно использовать
комбинированную радиационную систему теплозащиты. В этом случае
на небольших участках верхней поверхности фюзеляжа и крыла и на по¬
верхности киля используется неохлаждаемая радиационная система тепло¬
защиты. Остальная часть верхней поверхности, на которой температура
не превышает допустимого для конструкции значения, экранами не по¬
крывается. Для охлаждения нижней поверхности КЛА используется ра¬
диационная охлаждаемая система теплозащиты. Использование комби¬
нированной системы в ряде случаев может привести к существенному
уменьшению массы теплозащиты.
Система теплозащиты с панелями многократного применения угганав-
ливается на силовых панелях, изготовленных из жаропрочных сплавов
(титановых, никелевых, кобальтовых и др.). Ее общая масса слагается
из массы многократно используемых панелей, внешнего защитного на¬
пыления, yfrioB крепления, силовой панели и изоляции, а также из массы
элементов бистемы охлаждения, если она используется.
Таблица 2.4
Теплофизическив характеристики материалов теплозащиты
Теплофизическая характеристика
Материал
тефлон
рефразил
фенолик-фибер-
глэсс
Эффективная энтальпия
1 700-2000
3500-3600
1000-1100
т?эфф' ккал/кг
Температура разрушения Гр,°С
427
1530
1650
Удельный вес р, кгс/м3
2210
2100
1600
Теплоемкость С, ккал/ (кг • град)
0,25
0,28
0,4
Теплопроводность X,
ккал/ (м-страд)
5,84-1 СТ5
6,93-1 О'5
1,054 • 10~4
39
Характеристика материалов теплозащитного покрытия. Номенклатура
материалов теплозащитного покрытия может быть довольно обширной.
В общем случае по виду используемых материалов системы теплоза¬
щиты можно разделить на два больших класса: неметаллические и метал¬
лические.
В первом случае для систем теплозащиты с уносом массы поверхность
КЛА необходимо защищать материалами, способными поглощать большое
количество энергии при сублимации. Хорошо работают в этих условиях
Рис. 2.7. Конструктивная схема систе¬
мы неметаллической теплозащиты: 1~
силовая конструкция; 2 — клеевой
слой; 3 — защитное покрытие; 4 —
изоляция.
обугливающиеся разрушающиеся материалы, содержащие большое коли¬
чество углерода. Кроме того, могут быть использованы такие материалы,
как фенолик-нейлон, тефлон, рефразил, фенолик-фиберглас. Теплофизи¬
ческие характеристики некоторых неметаллических материалов приве¬
дены в табл. 2.4.
Для неметаллической системы теплозащиты без уноса массы внешний
теплоизолирующий слой на основе волокнистых или керамических ма¬
териалов наносится на силовую металлическую обшивку. Рабочая тем¬
пература этой обшивки существенно меньше температуры, достигаемой
на наружной поверхности КЛА при спуске в атмосфере.
На рис. 2.7 приведена конструктивная схема системы неметаллической
теплозащиты. Крепление изоляционных панелей к силовой конструкции
осуществляется с помощью пластично-упругого клея, обеспечивающего
равномерное распределение напряжений в изоляции и клеевом шве. По¬
скольку наряду с высокими температурами поверхности на систему тепло¬
защиты действуют также аэродинамические силы и вибрации, то к мате¬
риалам теплоизолирующего слоя предъявляются следующие требования:
высокая температура плавления;
высокая механическая прочность;
стойкость к окислению;
незначительная теплопроводность X;
большая теплоемкость С;
минимальный удельный вес р.
Таблица 2.5
Характеристики материалов теплозащиты
Сплав
Максимально
допустимая
температура Т,
Плотность р,
г/см3
Сплав
Максимально
допустимая
температура Г,
°C
Плотность р,
г/см3
Алюминиевый
150
2,7 - 2,8
Кобальтовый
980
9,13
Титановый
450 - 500
4,4 - 4,6
Ниобиевый
1370
9 — 10
Никелевый
700 -1100
8,2 -8,5
40
Согласно этим требованиям эффективность теплоизоляции обратно
пропорциональна величине Л=Хр/С, называемой характеристическим
числом теплоизоляции.
Характеристическое число выводится из дифференциальных урав¬
нений, описывающих процесс теплопередачи, и служит критерием для
выбора материала теплозащиты. При этом наилучшему теплозащит¬
ному материалу соответствует наименьшее значение характеристического
числа Л.
Рис. 2.8. Конструктивная схема системы металлической теплозащиты: 1 — силовая
конструкция; 2 — изоляция; 3 — металлический радиационный экран.
В общем случае выбор материала для внешнего теплоизолирующего слоя
системы неметаллической теплозащиты оптимально удовлетворяющего
всем перечисленным требованиям, представляет собой довольно сложную
задачу. Выход здесь может быть найден в создании теплоизоляции, сос¬
тоящей из многих слоев различных материалов. При этом специфические
требования предъявляются к каждому слою теплоизоляции. Так, внешний
слой должен противостоять окислению, а также термическим и механичес¬
ким нагрузкам. По мере углубления в слои теплозащиты тепловые на¬
грузки уменьшаются.. Основанием для оптимального выбора материалов
последующих слоев служит как можно более точное знание закона рас¬
пределения температуры в материале теплозащиты. Для каждого диапа¬
зона изменения температуры может выбираться оптимальный по массе
материал теплозащитного слоя.
Проведенные исследования показали, что в большинстве случаев масса
системы теплозащиты, близкая к минимальной, реализуется при использо¬
вании трехслойной изоляции. При этом оптимально удовлетворяются все
перечисленные требования к системе теплозащиты. Можно отметить также,
что наиболее перспективными материалами системы неметаллической
теплозащиты с точки зрения стоимости, массы и простоiw конструкции
являются керамические материалы. Они химически инертны при повы¬
шенной температуре, имеют низкую теплопроводность и малый объем¬
ный вес.
В системе металлической теплозащиты теплоизолирующий слой распо¬
лагается между внешней обшивкой и силовой конструкцией (рис. 2.8).
При проектировании системы металлической теплозащиты необходимо:
определить действующие нагрузки и тепловые потоки;
исследовать характеристики возможных материалов;
выбрать материалы для радиационного (теплоизучающего) экрана,
изоляции и силовой конструкции.
Панели радиационных экранов должны выдерживать динамические
нагрузки и иметь достаточную жесткость для предотвращения возникно¬
вения флаттера. Узлы навески панелей, передающие нагрузку на силовую
конструкцию, должны обеспечивать перемещение панелей в случае тепло-
41
Рис. 2.9. Зависимость максимального 3h
чения температуры наружной поверхНос а'
Гтах в точке торможения 1 и на бокОвп-
кромке 2 от радиуса затупления носоа^
части г н.
вого расширения. При этом обяза.
тельным условием является сохране-
ние требуемых механических свойств
конструкции системы теплозащиты
при выдерживании заданного огра.
ничения по допустимой температуре
конструкции КЛА на траектории
спуска.
В качестве примера на рис. 2.9 для
КЛА типа "несущий корпус", осу¬
ществляющего спуск с орбиты искус¬
ственного спутника Земли, приве¬
дены максимальные значения темпе¬
ратуры наружной поверхности в точ¬
ке торможения и на боковой кромке
в зависимости от радиуса закругле¬
ния носовой части. Знание закона распределения температуры по поверх¬
ности КЛА позволяет оптимальным образом подобрать материал для сис¬
темы металлической теплозащиты.
В табл. 2.5 приведены некоторые характеристики материалов теплоза¬
щиты.
§ 2.6. Системы мягкой посадки
При спуске КЛА на поверхность планеты, окруженной атмосферой, в
основном рассматриваются три типа систем мягкой посадки:
пассивная тормозная система с амортизацией;
реактивная тормозная система;
комбинированная система мягкой посадки, предполагающая последова¬
тельное использование пассивного и активного торможения.
Пассивная тормозная система (без двигателей мягкой посадки) пред¬
ставляет собой наиболее простой тип системы мягкой посадки. Она может
иметь различное конструктивное исполнение. К пассивной тормозной сис¬
теме относятся парашютные системы, тормозные зонтичные устройства,
парабалонные системы, разрушающиеся фермы и т.д. Наиболее эффектив¬
ным тормозным устройством является парашют. Его основные достоинст¬
ва: конструктивная простота, высокое лобовое сопротивление, относитель¬
но небольшая масса и малый компоновочный объем. Для достижения
допустимых перегрузок при контакте с поверхностью планеты в случае
использования парашюта необходимо применять амортизирующие устрой¬
ства (надувные мешки, колесное или лыжное шасси с амортизацией и пр.).
Система посадки получается достаточно легкой и простой, однако при
реальных величинах хода амортизатора ударные перегрузки достаточно
велики (лтах > 50). Следует также отметить, что посадка на шасси (амор¬
тизаторы) при боковом сносе под действием ветра (простая амортизация
в виде баллонов) может привести к опрокидыванию КЛА. Использование
же систем с амортизаторами самолетного типа приводит к их усложнению.
42
Парашютные системы имеют и ряд недостатков, особенно проявляющихся
при спуске на планеты, имеющие разреженную и неспокойную атмосферу.
Основными из них являются:
трудность управления процессом спуска КЛА на парашюте;
возрастание массы парашюта с увеличением скорости парашютиро¬
вания;
возрастание площади парашюта с увеличением массы КЛА.
В силу этого парашютная система с амортизаторами может быть исполь¬
зована только для простейших автоматических КЛА малой массы
с аппаратурой, выдерживающей большие ударные перегрузки при по¬
садке.
Снизить перегрузки в момент касания практически до нуля (и тем
самым обеспечить комфортабельную мягкую посадку) можно при исполь¬
зовании реактивной системы мягкой посадки. Для этой цели возможно
применение жидкостных или твердотопливных ракетных двигателей.
Отметим, что можно создать и комбинированную реактивную систему
мягкой посадки: на основном участке торможения использовать твердо¬
топливный двигатель, а на участке предпосадочного маневра и посадки —
жидкостный двигатель.
Исследования, проведенные в процессе разработки КЛА "Марс-3,6",
"Викинг-1,2", "Восток", "Союз", показали, что комбинированная (пара¬
шютно-реактивная) система мягкой посадки является наиболее распрост¬
раненной. Предварительное торможение КЛА парашютом позволяет сущест¬
венно снизить потребные запасы топлива на активное торможение, а следо¬
вательно, и массу системы мягкой посадки. Это обстоятельство, однако,
не дает права сделать однозначный выбор в пользу системы парашютно¬
реактивного типа для любых КЛА, осуществляющих спуск на поверхности
планет, ибо помимо выигрыша в массе необходимо учитывать и другие
факторы. Так, при сравнительно большой массе КЛА использование пара¬
шютно-реактивной системы может оказаться недостаточно надежным,
хотя и выигрышным в отношении массы. Это объясняется тем, что с увели¬
чением начальной массы КЛА существенно возрастает площадь парашюта,
что влечет за собой большие трудности по обеспечению устойчивой и безо¬
пасной работы системы парашютно-реактивного типа. Поэтому при реше¬
нии проблемы безопасной мягкой посадки КЛА на поверхности планет,
окруженных атмосферой, необходимо в каждом конкретном случае про¬
водить специальный анализ по выбору наиболее рациональной системы
мягкой посадки.
Глава 3
ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
В АТМОСФЕРЕ
§ 3.1. Математическая модель движения
Успех решения любой задачи в значительной степени определяется ее
правильной постановкой, отражающей все реально происходящие процессы,
учитывающей необходимые ограничения и вместе с тем не заслоняющей
главной цели исследования. Изучение движения КЛА в атмосфере в этом
смысле не составляет исключения. Подстановка и решение этой задачи
включает три основных этапа.
43
1. Разработка математической модели движения КЛА в атмосфере,
т.е. формальное представление объекта оптимизации, позволяющее иссле¬
довать проблему с привлечением современного математического аппарата
и быстродействующих ЭВМ.
2. Формулировка критерия оптимальности, т.е. определение некоторых
условий, которые отражают основную цель управления и характеризуют
эффективность выполнения поставленных перед КЛА задач.
3. Выбор метода решения задачи, который, с одной стороны, давал бы
искомое решение задачи, а с другой — являлся бы наиболее рациональным
с точки зрения его применимости, корректности и потребных ресурсов
ЭВМ. А это в свою очередь определяется свойствами рассматриваемой
математической модели и зависит от сложности оптимизируемых пара¬
метров, накладываемых ограничений и т.д.
Перейдем к более подробному рассмотрению каждого из них примени¬
тельно к изучаемой проблеме.
Исследование движения КЛА в атмосфере следует начинать с построе¬
ния математической модели, которая позволяет отразить и описать по край¬
ней мере основные процессы, происходящие с КЛА в его реальном полете
в атмосфере.
Процесс математического моделирования движения КЛА в общем слу¬
чае включает:
формулировку законов, связывающих основные объекты модели (аэро¬
динамика КЛА, окружающая среда, массово-инерционные характеристи¬
ки, ограничивающие факторы - температура, перегрузки, тепловые потоки
и т.д.) ;
получение в результате анализа модели движения КЛА выходных данных
(теоретических) для дальнейшего их сопоставления с результатами экспе¬
риментальных наблюдений процесса спуска (послеполетного анализа);
последующий анализ модели движения КЛА в связи с накоплением дан¬
ных об изучаемом процессе снижения КЛА в атмосфере и модернизацию
модели движения КЛА.
В процессе развития науки и техники данные о процессе спуска все более
и более уточняются и может наступить такой момент, когда выводы, полу¬
чаемые на основании существующей математической модели, в некоторых
случаях не будут соответствовать нашим знаниям о рассматриваемом яв¬
лении. В результате возникает необходимость построения новой, более со¬
вершенной математической модели движения КЛА.
Используя материалы предыдущих глав, можно приступить к составле¬
нию конкретных математических моделей движения КЛА в атмосфере.
Но прежде следует сделать замечание о том, что если степень приближе¬
ния модели к реальным процессам определяется в основном уровнем на¬
ших знаний об изучаемой проблеме, то сложность модели зависит не толь¬
ко от изучаемого предмета, но и от требуемой точности искомых резуль¬
татов, отведенного ресурса времени решения на ЭВМ и т.п. Этим и объяс¬
няется многообразие математических моделей и соответственно большое
многообразие представления уравнений движения КЛА (см., напоимер,
[1,2, 14, 16,24]).
Ниже приводятся только наиболее распространенные системы уравнений
движения КЛА, записанных как для наиболее простого случая, когда не
учитывается унос массы теплозащитного покрытия КЛА, так и с учетом
этого процесса.
44
3.1.1. Уравнения движения без учета уноса
массы теплозащитного покрытия
При исследовании траекторий снижения КЛА в атмосферах планет
наиболее общим случаем является запись уравнений движения КЛА в инер¬
циальной системе координат [2] , связанной с центром планеты назначения:
m(Vx + Vz GOy — Vycoz) = X, m(Vy + Vxgoz - Vzgjx) = Y,
m(Vz + Vycox - Vxcoy) = Z,
/ x + (/z /у) COyCDz / Xy ^x ^z) ! xz t^z ^x +
+ !yz (“z - wj) =MX.
Iу CO у 4" (/x Iz) COX C0z Ixy (^x + ^y ! xz ^^x ^z )
yz <“^X ~ My ,
Iz Uy — x ) <“*^x ^y xz U*Ox 03y G0z) IyZ G0x ^z )
+ fXy(GOy - G0X) = MZ.
Здесь zn— масса КЛА; !x, !y, tz, IxyJxzJyz — осевые и центробежные
моменты инерции КЛА; Vx, Vy,Vz — составляющие вектора скорости
движения центра масс КЛА; оох, Goy, goz — составляющие вектора угловой
скрости поворота выбранной системьТкоординат/Л^У,Z — проекции рав-
нбДействующей внешних сил и реактивной силы тяги на оси инерциальной
системы координат; M^My.Mz — моменты внешних и реактивных сил
относительно соответствующих осей координат.
Как известно, любая инерциальная система координат помимо распо¬
ложения начала координат характеризуется основной плоскостью и основ¬
ным направлением. В планетоцентрической системе координат за основную
плоскость может быть принята экваториальная. Тогда за основное направ¬
ление при этом выбирают точку весеннего равноденствия, т.е. точку пере¬
сечения эклиптики с небесным экватором, в которой центр Солнца перехо¬
дит из южной половины небесной сферы в северную.
Уравнения движения в планетоцентрической системе координат име¬
ют вид
+ m(R + h)Goz cos2 +
R+h
+ 2m<jjz VxgCQ$ip,
m Vze =Z2 -m
zg 8 R+h
+ m(R + h)co2 sin p cos <£,
Vxg
h=vyg, *=—T-tS^
R+h
— tg + 2mgo l/XgSin(p +
R + h
• ^zg
= -
R+h
Здесь Xg,Yg,Zg - проекции равнодействующих внешних сил и реактив¬
ной силы тяги на оси системы координат, связанной с поверхностью плане¬
ты V — составляющие скорости КЛА относительно инерциаль¬
ной системы отсчета в проекциях на оси системы координат, связанной с
45
поверхностью планеты; у>- широта, к - долгота, R - радиус планеты h -
высота полета.
В некоторых случаях оказывается более удобным пользоваться системой
уравнении движения КЛА, записанных при некоторых упрощающих предпо¬
ложениях. В частности, если пренебречь суточным вращением планеты
кривизной ее поверхности и ускорением центра масс планеты в абсолют¬
но неподвижном пространстве, то систему координат, связанную с поверх¬
ностью планеты, можно считать инерциальной. В этом случае получим
следующую систему уравнений движения КЛА:
т VXg = *g. т Vyg = Yg, т Vzg = Zg.
Для проведения качественных исследований и предварительных расчетов
траекторий спуска КЛА часто оказывается удобным пользоваться упро¬
щенными уравнениями движения КЛА, записанными в скоростной системе
координат без учета вращения планеты:
cos 0
p(h)V
2РХ
V cos 0
R+h
Psin(tf-0)
+
m
(3.1)
0 “ ^эфф
• • V cos 0
h = V sin 9. L = R, m = -C,
R+h
Здесь
glh) = g0
R2
(R+h)2
m
Px = , p = 0 npnt0<t<rK;
m
px = — , , p=o npnto<t<t,;
сп ' n
m
p.x- p = Q npntj^f^tj;
cnpn
px = , p=pw*o, a = приг>г:,
где t0, tK - моменты начала и конца участка основного аэродинамического
торможения; t0-момент начала спуска КЛА на парашюте; t* = t* -момент
разрифовки парашютов, tj- момент сброса парашютов и включение тормоз-
нои двигательной установки; cntFп— коэффициент лобового сопротивления
и площадь зарифованного парашюта; сп, Fn — jo же для разрифованного
парашюта, тп с — масса парашютной системы; п?кла “Секундный расход
массы топлива, принимаемый постоянным; Р (t) —тягадвигателя, варьируе-
мая в диапазоне О (t) ^Рщах; д (г) - угол тангажа, изменяемый в пре¬
делах 0 (t) <2я.
Следует отметить, что при расчете траекторий спуска на участке мягкой
посадки второе уравнение системы (3.1) может быть несколько упрощено
46
I/ cos О
за счет пренебрежения членом , величина которого чрезвычайно
R + h
мала и практически не оказывает влияния на точность решения задачи.
В уравнениях (3.1) вращение планеты и окружающей ее атмосферы
не учитывается. Вообще говоря, скорость вращения атмосферы является
довольно значительной величиной. Она может достигать около 6% от круго¬
вой орбитальной скорости для Земли и -около 20% для Юпитера. Однако
для упрощения анализа ее можно не учитывать.
Сжатие планеты также не учитывается, т.е. планета и ее атмосфера
считаются сферическими. Как известно, сжатие планеты достаточно заметно
проявляется на длительных операциях, таких, как орбитальный полет КЛА.
Маневр выведения КЛА на орбиту ИСП совершается при небольшой угло¬
вой дальности по отношению к поверхности планеты. Поэтому при реше¬
нии поставленной задачи планету можно считать сферической и исполь¬
зовать постоянное значение величины радиуса.
В заключение приведем уравнения движения КЛА, записанные в поляр¬
ной системе координат [2]. Пусть полюс будет размещен в центре планеты.
Угол поворота радиус-вектора отсчитывается от некоторого начального,
неизменного в пространстве радиуса-вектора. Тогда получим следующие
уравнения движения:
m(VT + Ур/с) = Р cos $ — X cos 0 — У sin О,
m(Vp — VT к) = Р sin у — mg — X sin 6 + У cos 0,
где Ур и VT — соответственно радиальная и тангенциальная составляющие
скорости; угол между осью двигателя и продольной осью КЛА; Р — тяга
двигателя; X — сила лобового сопротивления; У — подъемная сила.
3,1.2, Уравнения движения, учитывающие унос массы
и изменение формы КЛА в процессе обгара теплозащитного покрытия
Вход КЛА в атмосферы Земли и планет с большими начальными ско¬
ростями сопровождается интенсивным термохимическим разрушением их
теплозащитного покрытия до газообразного состояния и резким увеличе¬
нием количества разрушающегося и уносимого материала покрытия. Так,
для КЛА, возвращающегося от Марса и имеющего в момент входа в атмос¬
феру Земли скорость около 20 км/с, потеря массы теплозащитного пок¬
рытия может достигать 30% первоначальной массы [63]. Еще более зна¬
чительной может быть потеря массы теплозащитного покрытия при входе
КЛА в атмосферы "больших" планет, где начальная скорость составляет
30 —60 км/с. Исследования процесса разрушения теплозащитного покры¬
тия КЛА, обтекаемого водородно-гелиевой смесью, моделирующей атмос¬
феру Юпитера, показывают, что суммарный унос массы на траектории сни¬
жения в атмосфере Юпитера может составить величину, сравнимую с на¬
чальной массой КЛА.
Интенсивный обгар теплозащитного покрытия приводит к заметному
изменению исходной формы КЛА. Это, естественно, влияет на аэродинами¬
ческие характеристики КЛА и на величину и распределение тепловых пото¬
ков по его поверхности. Таким образом, при исследовании вопросов дина¬
мики КЛА, осуществляющих вход в атмосферы планете большими началь¬
ными скоростями, необходимо учитывать явления, связанные с о гаром
сублимирующего материала теплозащитного покрытия поверхности К
Следует отметить, что при разрушении теплозащитного материала проис¬
ходит ряд процессов, находящихся в сложной взаимосвязи. Это процессы.
блокировки конвективного потока, вызванной влиянием паров покрытия;
экранирования лучистого потока, преобладающего при больших скоростях
входа, за счет поглощения излучения продуктами разрушения; разложения
материала; поглощения энергии газообразными продуктами разложения
при их прохождении через обуглившийся слой; переноса и аккумуляции
тепла в материале теплозащитного покрытия. Полный учет отмеченных про¬
цессов даже при исследовании самых несложных конфигураций КЛА яв¬
ляется чрезвычайно сложной и во многом еще плохо изученной проблемой
и требует численного решения громоздкой системы уравнений, в том
числе уравнений энергии, динамики, химических, кинематических и других
соотношений (см., например, [11]). При выводе дифференциальных урав¬
нений изменения формы КЛА и массы теплозащитного покрытия обычно
вводится ряд упрощающих предположений. В общем случае независимо от
конкретной исходной конфигурации КЛА может быть принята следующая
модель процесса обгара теплозащитного покрытия.
1) Предполагается, что величина суммарного удельного теплового по¬
тока в каждой точке поверхности КЛА задана в виде некоторой зави¬
симости от плотности р, скорости V, температуры Т и других параметров
набегающего потока, от координат точки на поверхности КЛА и величин,
определяющих геометрию его поверхности.
2) Перемещение произвольного бесконечно малого элемента поверх¬
ности КЛА вследствие обгара сублимирующего материала теплозащитно¬
го покрытия за бесконечно малый, промежуток времени dt происходит в
направлении нормали п к этому элементу.
3) Скорость уноса массы теплозащитного покрытия с единицы площади
поверхности КЛА пропорциональна суммарному удельному тепловому
потоку qe и обратно пропорциональна значению эффективной энтальпии
теплозащитного покрытия ??Эфф:
dm _
dt г/эфф ’ <3,2)
4) Характеристики материала теплозащитного покрытия (плотность*
Ртз.п и эффективная энтальпия 7?эфф) в процессе обгара остаются неизмен¬
ными либо описываются в виде функций параметров набегающего потока,
координат точки поверхности КЛА и геометрии его исходной формы.
Даже с учетом сделанных допущений и
упрощений не всегда удается вывести урав¬
нения изменения формы и положения в
пространстве произвольного элемента по¬
верхности КЛА. В качестве примера рас¬
смотрим одну из возможных [40] конфи¬
гураций КЛА —сферически затупленный ко¬
нус с косым донным срезом (рис.3.1) .Уп¬
равление таким КЛА осуществляется пу¬
тем изменения угла крена при постоян¬
ном (равном нулю) балансировочном угле
атаки. Это позволяет считать процесс обте¬
кания носовой части КЛА осесимметрич¬
ным. Точный расчет обгара даже такой
Рис. 3.1. Сферически затупленный конус с ко¬
сым донным срезом.
48
несложной конфигурации при сделанных выше упрощающих предположе¬
ниях затруднителен. Поэтому введем еще несколько допущений для КЛА
рассматриваемой формы:
толщины унесенных слоев материалов теплозащитного покрытия в кри¬
тической точке (5^ и на боковой конической поверхности (62) пропорци¬
ональны:
62 = 51 к sin $к, (3.3)
здесь к < 1 — постоянный коэффициент, $к — угол полураствора конуса;
приближенное значение к может быть определено из работы [40] (обычно
эта величина в большинстве расчетов принимается равной 0,1 — 0,2);
углы полураствора конуса $к и наклона донного среза е в процессе
обгара остаются постоянными; при этом носовая часть поверхности КЛА
остается сферической, а радиус ее меняется таким образом, чтобы точка
сопряжения сферы и конуса не имела излома.
Учитывая изложенное, можно записать из геометрических соотношений
уравнение изменения радиуса затупления в критической точке носовой
части гн в зависимости от толщины обгораемого слоя теплозащитного пок¬
рытия в критической точке 51
sin
Дл„ —(1 —«)«!. (3.4)
1 — sin $к
Иными словами, предлагаемая модель пропорционального обгара
позволяет заменить интегрирование локального уноса массы по всей по¬
верхности КЛА вычислением перемещения поверхности в критической точ¬
ке. Толщина обгораемого слоя теплозащитного покрытия в критической
точке зависит от величины тепловых потоков, которые могут быть
определены по приближенным формулам, приводимым ниже.
Уравнения плоского движения КЛА с учетом уноса массы теплозащит¬
ного покрытия в проекциях на направления касательной и нормали к
траектории запишутся в следующем виде:
dV poe~@hsV2
= —сх — д sin 0,
dd рое @hsV
~ Су
dt У 2т
COS 7 11 I COS в,
V \ gR /
(3.5)
dh dm dU
= V sin 0, = pT3 n —,
dt dt dt
где Ртз.п — плотность материала теплозащитного покрытия; U — объем
КЛА; т — масса КЛА.
На рис. 3.1. видно, что геометрическая форма КЛА определяется углом
е наклона донного среза, углом полураствора конуса $к, радиусом гн
сферического затупления носовой части КЛА и базовым радиусом R В
этом случае объем КЛА может быть записан в виде функции четырех этих
параметров:
U=U (е, ,rn , R). (3.6)
Здесь только параметры гн и R изменяются в процессе обгара.
Учитывая перечисленные допущения и соотношения (3.2) - (3.4) и
(3.6), можно последнее уравнение (3.5) для уносимой массы теплоза-
4. Зак. 2069
49
щитного покрытия переписать в виде
dm
Ay drn (fr sin £K
- ———F (еЛк,Гн —^ = — J———d -«),
dt
^7эфф Ртз.п^эфф SintrK)
dR
Qs
dt
KtgaK, (3.7)
Ртз.п ^?эфф
где через
F (e, 0Kt rn, R) обозначена производная изменения объема как
сложной функции перемещения поверхности при обгаре теплозащитного
покрытия:
dU г / *9е + *9 \3/2 о 1
F = = л Я2 к+г2 (1 - sin 0К)(1 -к) . (3.8)
L \tge-tg£K/ J
При этом величина суммарного удельного теплового потока
2 / р \ mi / V \ ni
U ■ |3-91
где конвективному тепловому потоку соответствует индекс 7=1,3 радиа¬
ционному 7= 2; а, т, п — постоянные коэффициенты, зависящие от харак¬
теристик материала теплозащитного покрытия и конструктивных особен¬
ностей КЛА.
Приближенные формулы для оценки массы уносимого теплозащитного
покрытия. При проведении предварительных инженерных расчетов могут
оказаться полезными простые приближенные соотношения для оценки
массы уносимого теплозащитного покрытия КЛА. Величина, потери массы
теплозащиты по всей поверхности КЛА может быть определена из диффе¬
ренциального уравнения
— = J о'$п- (3.10)
dt Sn т?эфф
С учетом соотношения [40]
1 з з
выражение (3.10) примет вид
dm
dt
%фф sn
f ПХ
где Sn — площадь поверхности КЛА; пх — продольная перегрузка; gv0 —
тепловой поток в критической точке КЛА.
Скорость КЛА при спуске в атмосфере определяется уравнением
dV
т = —X—Gsinfl,
dt
где G — вес КЛА; О — угол наклона вектора скорости к местному гори¬
зонту.
Предполагая, что траектории движения КЛА в атмосфере при сверх¬
круговых скоростях входа достаточно пологи, введем допущение 0=0.
Тогда вторым членом в этом уравнении можно пренебречь.
50
Полная аэродинамическая сила лобового сопротивления X космичес¬
кого летательного аппарата направлена по вектору набегающего потока.
В этом случае для X может быть записано следующее выражение [41]
Х= pV2 f nxdSn.
С учетом этого выражения уравнение для скорости примет вид
dV
dt
Используя в качестве независимой переменной массу КЛА, путем неслож¬
ных преобразований с учетом уравнений в критической точке КЛА для кон¬
вективного теплового потока
1,291 • 10
Qk о НВ “ /—1
и радиационного теплового потока
получим следующее выражение для скорости уноса массы КЛА [40]:
— =—— (1,31 Ю2 г'0’5 е0-5^?1-25 +
т ^?эфф
+ 3,07 • Ю4гне_0,ЗХЙ V6}dV ,
где V = V/VKp.
При получении соотношения (3.11) предполагалось, что атмосфера
изотермична, т.е. имеет место экспоненциальная зависимость плотности р
от высоты h:
Р = Po«Kh-
Если известны зависимость высоты полета от скорости h(V) и измене¬
ние радиуса затупления в критической точке rH(V) вдоль траектории по¬
лета КЛА, то соотношение (3.11) можно использовать для оценки потерь
массы теплозащитного покрытия КЛА. В частности, на изовысотных участ¬
ках полета (/? = /?i) в случае, когда радиус гн может рассматриваться как
постоянная величина (rH = rt), соотношение (3.11) интегрируется следую¬
щим образом:
-°~тк. = 1 — ехр ( — [58,22o0’se0,5Xhi(i72’2S - У2,25) +
I Пэфф
+ 4,4-103г1е-°’Ш1(?л71 - У07)]] , (3.12)
где /п0 и Л7К — соответственно начальное и конечное значения массы.
Нетрудно найти приближенное выражение для определения уносимой
массы теплозащитного покрытия и для других конфигураций КЛА. Приве¬
дем для сравнения формулу, аналогичную (3.12), позволяющую проводить
оценку величины уносимой массы теплозащитного покрытия на участке го¬
ризонтального полета КЛА, имеющего форму сферически затупленного
51
Рис. 3.2. Зависимость относительной величины уноса массы теплозащитного покрытия
Дтот скорости полета И: а) пэфф 3 2,1 • Ю4 кДж/кг; б) пэфф = 4,2 • 104 кДж/кг.
/,0м С4
18 У,км/с
гя-2,0м^
1,5м
1,0
0,5у6
конуса [40] :
= ехр
аг(гн)
а2 (rH) = Brnf
2F £ /Р1 \ т< Ио”'_1) - ]
схР1517эфф 1 = 1 \ Ро /
ni~ 1
^конв
где 1/0 - безразмерная скорость входа в атмосферу; Ук- конечная ско¬
рость движения КЛА в атмосфере; А и В — постоянные коэффициенты.
Влияние условий входа и параметров КЛА на величину уносимой
массы теплозащитного покрытия. Для КЛА сегментной формы, осущест¬
вляющего вход в атмосферу Земли, на рис. 3.2 для двух значений эффек¬
тивной энтальпии приведены значения Д7й = (mQ - полученные из
соотношения (3.12) при некоторой постоянной высоте h*t на которой вели¬
чина принимает минимальное значение [40]. Высота /?* определяется
следующим образом
1,25
X
Проведенные расчеты показывают, что для диапазонов 10 км/с < Vh
<25 км/с и 0,5 м < г < 2 м значение Л* находится в пределах 30 км
< h* < 100 км.
_Из рассмотрения представленных зависимостей следует, что величина
Д/п существенно зависит от начальной скорости Уо входа КЛА в атмосфе¬
ру, радиуса затупления в критической точке гн и эффективной энтальпии
%фф. А именно, с уменьшением VQ и гн, а также с увеличением т?эфф
/Л/Л
52
3 3 Зависимость от-
ипсительной потери массы
ппозашитного покрытия
от начальной скоро¬
ди’входа в атмосферу Ио
Сплошная линия - точное
решение, штрихован-при¬
ближенное) .
I {
/vo=20 км/с
I /
I /
I /
I /
' / '
I /
/
/
\
15 км/с
11км/с
о, в
1,2
Рис. 3.4. Зависимость от¬
носительной потери массы
теплозащитного покрытия
Ал?! от радиуса затупле¬
ния - носовой части г н
(сплошные линии — точ¬
ное решение, штриховые —
приближенное).
нппй 3*5* Зависимость от-
теппТеЛЬН0Й потеРИ массы
^защитного покрытия
кон'ум Угла, полураствора
нии 'сплошные ли-
Точное решение,
ное) Ь,е “■ приближен¬
ия
т^град
происходит уменьшение уносимой массы теплозащитного покрытия.
Например, при Vo = 15 км/с и заданном значении т?Эфф уменьшение
радиуса _затупления гн с 2 м до 0,5 м приводит к снижению вели¬
чины Ат на 20%; при увеличении эффективной энтальпии с 2,1-104
до 4,2-104 кДж/кг относительное значение уносимой массы также умень¬
шается на 20% (при прочих равных условиях).
Для КЛА, имеющего форму сферически затупленного конуса, при фик¬
сированных гн = 2 м, £к = 30 , 1? = 0,1 и качестве К = 0,5 (величина качест¬
ва определяется комбинацией параметров гн, и е) на рис. 3.3—3.6
представлены зависимости- [40], показывающие влияние начальной ско¬
рости входа 1/0, радиуса затупления ги, угла полураствора конуса #к и
эффективной энтальпии т?эфф на относительную потерю массы теплоза¬
щитного покрытия КЛА Д/7?! =/пк/л70. При этом предполагалось, что на¬
чальная масса КЛА т0 = 5000 кг, эффективная энтальпия т?эфф =
= 2,51 • 104 кДж/кг и коэффициент к = 0,1.
Видно, что уменьшение скорости входа приводит к снижению относи¬
тельной потери массы теплозащитного покрытия КЛА. Так, при уменьше¬
нии скорости входа от 20 км/с до 15 км/с величина Атх изменяется от
0,29 до 0,105.
Изменение радиуса затупления гн влияет неоднозначно на унос массы.
А_именно, при больших скоростях входа (У0>14 км/с) зависимость
(гн) имеет ярко выраженный минимум, причем с увеличением ско¬
рости 1/0 этот минимум смещается в сторону меньших значений гн. При
скоростях входа 1/0 < 14 j<m/c минимум величины Д/nj практически от¬
сутствует, а величина Д/7?! с увеличением радиуса затупления гн от 0,1
до 0,5 м уменьшается и остается практически постоянной при дальнейшем
возрастании гн.
Интересно отметить, что при больших скоростях входа (Уо ~
~18 -^20 км/с) существенного уменьшения уносимой массы теплозащит¬
ного покрытия можно достигнуть на КЛА с большими значениями угла
полураствора конуса £к. Так, при скорости входа в атмосферу 1/0 =
= 20 км/с увеличение угла от 15° до 40° приводит к снижению величи¬
ны Д/7?! с 0,7 до 0,24. Как и следовало ожидать, уменьшение эффективной
\
v
Vq~ 20 км/с*
». \
15 км/с К
. а х.
х
X
11,2км/с*^
2500 5000 п • 4,2"' л-Дж/л-г
'Эфф
Рис. 3.6. Зависимость относительной потери массы теплозащитного покрытия от
эффективной энтальпии Пэфф (сплошные линии — точное решение, штриховые — при¬
ближенное) .
54
энтальпии приводит к увеличению уносимой массы теплозащитного покры¬
тия КЛА. Причем, этот эффект существенно усиливается при больших ско¬
ростях входа в атмосферу (см. рис. 3.6).
В заключение параграфа отметим следующее. Часть членов правых
частей представленных уравнений движения записана в самом общем виде
и их необходимо расшифровывать в каждом отдельном случае. Прежде всего
следует конкретизировать данные по плотности атмосферы p(h), гра¬
витационному ускорению g(h) и аэродинамическим коэффициентам
сх(М, а), су (М, а).
Данные по плотности и ускорению силы тяжести приведены в главе 1.
Зависимость плотности от высоты полета представлена в виде экспоненты
или таблично, а ускорение свободного падения — в виде g(h) = р! (R + А)2,
т.е. рассматривается случай только центрального поля тяготения. Некото¬
рые данные по аэродинамике приведены в главе 2, а в дальнейшем в каж¬
дом конкретном случае зависимости аэродинамических коэффициентов
от угла атаки и скорости полета будут оговариваться по мере необходи¬
мости.
§ 3.2. Критерии оптимальности, используемые
при решении задачи спуска
Правильный выбор критерия оптимальности оказывает существенное
влияние на надежность и корректность решения задачи спуска. При выборе
критерия руководствуются принципом строгого соответствия избранного
критерия той цели, которая должна быть достигнута в результате функ¬
ционирования объекта. Формулировка этого принципа достаточно проста,
однако при его применении в конкретных задачах возникают существенные
трудности, которые видны из следующих соображений. Во-первых, к кри¬
териям предъявляются, как правило, противоречивые требования. С одной
стороны, критерий должен быть простым и достаточно полно отражать фи¬
зическую сущность исследуемого процесса и с другой, должен учитывать
все существенные особенности решаемой задачи оптимизации траекторий
спуска КЛА. Кроме того, критерий должен заметным образом реагировать
на изменение параметров. Во-вторых, во многих задачах спуска из-за неяс¬
ности в оценке наилучшего результата критерий может принимать вектор¬
ную форму, по которой трудно оценить эффективность оптимизации траек¬
торий спуска КЛА. Кроме того, часто оказывается трудным оценить
степень соответствия частных задач спуска эффективности общей за¬
дачи.
В общем виде задача оптимального управления спуском КЛА оценивает¬
ся скалярными критериями /Iz /2,. . . , !St которые являются составляющи¬
ми вектора эффективности /. В процессе предварительного анализа рас¬
сматриваемой задачи спуска могут быть найдены различные варианты
построения скалярных критериев /г, определенных в допустимой области
1х, образованной соответствующими ограничениями. Необходимо среди
различных вариантов найти такие скалярные критерии Г Е lXl которые
обеспечивают оптимальное значение вектора эффективности /.
Здесь возникают следующие основные проблемы:
выбор принципа оптимальности, определяющего весовое отношение меж¬
ду компонентами вектора эффективности;
приведение к одному масштабу измерений компонент вектора эффек¬
тивности;
учет приоритета (степени важности компонент), определяющего зна¬
чимость достижения совершенства по отдельным компонентам.
55
Для принятия решения, оптимального в смысле векторного критерия,
выделяется в первую очередь область компромиссов. Эта область опреде¬
ляется как некоторое подмножество, принадлежащее множеству допусти¬
мых решений и обладающее тем свойством, что внутри этой области одна
компонента вектора эффективности не может быть улучшена без ухудше¬
ния хотя бы одной другой компоненты. Задача нахождения области ком¬
промиссов сводится к задаче нахождения глобального экстремума линей¬
ной формы, справедливого для выпуклого допустимого множества. При
отсутствии выпуклости производятся определение всех локальных экстре¬
мумов и их проверка по условиям доминирования. Выделение области
компромиссов существенно сужает области поиска оптимального вектора
критериев и тем самым ускоряет процесс оптимизации. После выделения
этой области выбор оптимального вектора эффективности производится на
основе какой-либо схемы компромисса, имеющей оЪщие принципы. Одним
из широко распространенных принципов является принцип априорного
ранжирования. Он сводится к выбору компонент вектора эффективности
(векторного критерия), ранжированию этих компонент по важности путем
введения весовых коэффициентов и определению числовых значений каж¬
дой компоненты (как по объективным, так и по субъективным факторам).
После этого производится свертывание вектора эффективности в скаляр и
выбирается вариант с наибольшим (или наименьшим) значением этого
скаляра. Последнее приводит во многих случаях к существенному упроще¬
нию задачи.
Самым простым способом свертывания вектора эффективности в ска¬
ляр является суммирование компонент с соответствующими весовыми
коэффициентами, т.е. построение обобщенного критерия качества в адди¬
тивной форме:
/ = ?lsfs,
где 1$ — критерий эффективности s-й операции; fs — весовой коэффициент
s-й операции.
Именно этим способом свертывания векторного критерия в скаляр
и будем пользоваться в дальнейшем.
При проектировании космических летательных аппаратов, осуществляю¬
щих посадку на поверхность какой-либо планеты, в качестве основного
критерия, характеризующего оптимальность того или иного варианта
решения, часто используется критерий максимума полезного груза, достав¬
ляемого на поверхность:
Л7п.г плах. (3.13)
Обычно полезный груз включает научную аппаратуру, отсеки с оборудова¬
нием, используемые для работы на планете, планетоход или ракету возвра¬
щения и т.д.
Выбор критерия (3.13) в качестве основного определяется значительной
стоимостью доставки одного килограмма массы груза на поверхность пла¬
неты, а также теми научными данными, которые предполагается получить
с помощью аппаратуры, размещенной на КЛА. Критерий оптимальности
(3.13) имеет ясный физический смысл и является всеобъемлющим. Однако
при решении задач оптимального управления спуском использовать этот
критерий "напрямую" оказывается ‘ затруднительным. Действительно,
масса полезного груза, являющегося составной частью массы КЛА, зависит
/
от массы остальных систем ( S ) , обеспечивающих его доставку на
56
поверхность:
тп.г = тКЛА — mi-
i~ 1
При заданной массе /пКла максимум полезного груза соответствует
условию
i
min S mif (3.14)
f= 1
т.е. критерий (3.13) является векторным и имеет много составляющих.
Укрупненно можно выделить четыре основных составляющих сумм (3.14):
конструкция КЛА;
система тепловой защиты;
система мягкой посадки;
системы управления, терморегулирования, телеметрические датчики,
радиоаппаратура и т.п.
Наилучшее удовлетворение условия (3.14) достигается двумя путями.
Во-первых, необходимо наилучшим образом решить все специальные зада¬
чи, возникающие при разработке указанных выше систем, т.е. совершенст¬
вовать конструкцию КЛА и его тепловую защиту, систему мягкой посадки,
систему управления и т.д. Во-вторых, провести комплексную оптимизацию,
чтобы в рамках возможных технических решений и возникающих противо¬
речивых требований найти компромисс в создании отдельных систем,
приводящих к наилучшему удовлетворению условия (3.14).
Проведение комплексной оптимизации является довольно сложной
проблемой. Поэтому при решении задачи спуска КЛА в атмосфере какой-
либо планеты проводят предварительное исследование по оценке влияния
каждой из перечисленных выше составляющих на оптимизируемый функ¬
ционал (3.13). Для этого выделяют одну из составляющих сумм (3.14)
в качестве критерия оптимальности, а остальные переводят в разряд ограни¬
чений. Сравнивая результаты оптимизации по отдельным составляющим,
определяют тем самым вес каждой из них.
Опыт решения задач' спуска КЛА в атмосфере Земли и других планет
показывает, что, как правило, удается выделить одну из составляющих
векторного критерия (3.13), которая имеет существенно больший вес по
сравнению с другими составляющими. Эту составляющую обычно и исполь¬
зуют в дальнейшем в качестве критерия оптимальности для решаемой
задачи спуска. Так, например, при спуске КЛА в разреженной атмосфере
Марса основную роль играет масса системы мягкой посадки [24], а при
спуске КЛА в атмосфере Юпитера — масса системы теплозащиты [25, 63].
Следует отметить, что для удовлетворения условию минимизации выделен¬
ной главной составляющей суммы (3.14) оказывается затруднительным ис¬
пользовать прямые критерии оптимальности. Поэтому часто применяются
так называемые косвенные критерии, которые позволяют провести предва¬
рительный сравнительный анализ траекторий и выбрать наилучшую из них.
Например, в качестве косвенных критериев оптимальности часто исполь¬
зуются следующие:
коридор входа (его максимизация приводит к уменьшению массы систе¬
мы управления КЛА);
максимальная перегрузка (ее уменьшение приводит к снижению массы
конструкции КЛА) ;
суммарный тепловой поток, максимальное значение температуры по¬
верхности КЛА, минимальное время спуска (уменьшение этих параметров
приводит к снижению массы системы теплозащиты КЛА) ;
57
минимизация конечной скорости спуска, максимизация конечной высо¬
ты (уменьшение VK или увеличение hK приводит к снижению массы си¬
стемы мягкой посадки).
Анализ траекторий движения КЛА в атмосферах планет показывает,
что именно указанные критерии находят самое широкое применение.
Хотя они и носят косвенный характер, однако использование их особенно
удобно для проведения сравнительных оценок, и, как правило, удовлетво¬
рение им создает самые благоприятные предпосылки для оптимизации
основного критерия тахл?п г. Вместе с тем ими далеко не исчерпывается
класс возможных критериев. Например, во многих случаях решающую
роль играет условие точной посадки КЛА в заданном районе поверхности
планеты назначения, что выдвигает требование по минимизации рассеива¬
ния точек посадки. Применение этого критерия заведомо ухудшает условия
по максимизации массы полезной нагрузки, так как в этом случае выдви¬
гаются дополнительные требования к системе управления, условиям входа
в плотные слои атмосферы, форме КЛА, его компоновке, аэродинамике
и т.п. Таким образом, возможны ситуации, в которых объективно сущест¬
вуют более сильные требования, удовлетворение которым строго обяза¬
тельно. С подобными случаями приходится считаться.
§ 3.3. Современные методы теории оптимального управления
3.3.1 Классификация методов решения задачи оптимизации
Эффективное решение задач оптимального управления спуском, т.е.
получение конечного численного результата, является проблемой перво¬
степенной важности. Однако надежных и универсальных методов решения
нет, а известные методы приспособлены для решения лишь определенного
класса задач. Появление и совершенствование ЭВМ способствовало разра¬
ботке специализированных численных методов решения, расширивших
общее число и круг задач оптимального управления, решаемых до конца.
Все известные методы решения принципиально можно разбить на два
самостоятельных класса: аналитические и численные.
Характерной особенностью аналитических методов является выведение
совокупности условий, которым экстремальное решение обязательно
должно удовлетворять. Другими словами, в этом методе выводятся анали¬
тические условия (признаки) оптимальности, однако не указываются спо¬
собы нахождения искомого оптимального решения. Вместе с тем для по¬
лучения конечного решения (в том числе, численного) на основе аналити¬
ческих методов требуется применение регулярных вычислительных алго¬
ритмов, ибо аналитическим путем получить решение в замкнутой форме
для большинства практических задач не представляется возможным. Ис¬
пользование аналитических методов, хотя и не гарантирует получение
конечного численного результата исходной оптимальной задачи, но являет¬
ся инструментом качественного исследования исходной задачи, а в ряде
случаев позволяет получить аналитические зависимости, реализуемые,
правда, только с участием ЭВМ.
Широкое использование и распространение численных методов решения
связано в основном с появлением ЭВМ. Методы численного решения задач
оптимального управления и соответствующих вариационных задач разде¬
ляются на прямые и непрямые.
Принципиальная особенность прямых методов заключается в построении
итерационных процедур последовательного изменения (увеличения, умень¬
шения) функционала /(х, и, г) . В вариационном исчислении получил
58
распространение ряд прямых методов (метод Ритца, метод Галеркина),
известных из теории приближенных вычислений. Однако наибольшее
число прямых методов возникло в связи с необходимостью решения совре¬
менных задач оптимального управления. Фактическое содержание прямых
методов решения задач оптимального управления, естественно, отличается
от классических прямых методов. Основная особенность современных пря¬
мых методов заключается в том, что выводятся аналитические зависимости
вариации управления, которые в результате последовательного применения
регулярного вычислительного алгоритма должны обеспечить получение
экстремума исходного функционала. Указанные методы будем называть
алгоритмическими в отличие от классических прямых методов. Непосред¬
ственным критерием оценки, работы любого из прямых (в том числе и ал;
горитмических) методов является численное значение исходного функ¬
ционала !, причем в результате регулярного применения численной проце¬
дуры решения получается последовательность чисел (значений функциона¬
ла /), которая должна сходиться к исходному экстремуму. Заметим, что
принятая классификация методов решения является, хотя и достаточно
удобной, но не вполне исчерпывающей. Известны, в частности, комбиниро¬
ванные методы, в которых используется сочетание прямых методов реше¬
ния с анализом необходимых условий оптимальности, например [73].
Фактическая вычислительная процедура по-прежнему соответствует проце¬
дуре типового прямого метода.
Нахождение эффективного решения с использованием прямых (в том
числе и алгоритмических) методов тесно связано с проблемой существова¬
ния искомого оптимального решения. Если не всякая минимизирующая
последовательность сходится к искомому (притом заранее неизвестному)
минимуму, то исходная (в том числе и вариационная) задача называется
некорректной [25]. Для задач оптимального управления некорректность
является типичным явлением [21] , и построены иллюстративные примеры,
в которых минимизирующая последовательность по а. существует, но тем
не менее искомый минимум / не достигается. Разработке методов решения
некорректно поставленных оптимальных и вариационных задач в настоящее
время уделяется серьезное внимание и известен ряд работ (см., напри¬
мер, [35]), в которых развиваются методы регуляризации некорректных
задач.
Принципиальная особенность непрямых методов заключается в использо¬
вании необходимых условий экстремума исходного функционала /(X, и, г).
В результате получается п дополнительных дифференциальных уравнений
(п — порядок исходной системы дифференциальных уравнений движения),
гарантирующих равенство нулю первой вариации 5/. При этом исходная за¬
дача трансформируется в краевую задачу для системы 2п+к уравнений с раз¬
деленными краевыми условиями, причем к дополнительных уравнений (ал¬
гебраических или дифференциальных) соответствуют исходным ограниче¬
ниям на фазовые координаты. Непосредственным критерием оценки ра¬
боты любого из непрямых методов является численное значение некоторо¬
го условного функционала Pv, характеризующего степень выполнения
краевых условий (в начальной точке г0 или в конечной точке гк). Пока¬
затель качества решения РЕ, называемый в дальнейшем приведенным
функционалом, является косвенным критерием оценки и математически
определяется как функция (чаще всего квадратичная) невязок краевых
условий. В конечном итоге должно выполняться условие = 0. Эффек¬
тивность использования непрямых методов в большой степени зависит
от умения решать краевые задачи для исходных дифференциальных уравне¬
ний движения КЛА и дополнительных (дифференциальных, алгебраичес¬
59
ких) уравнений, соответствующих необходимым условиям оптимальности
и ограничениям на фазовые координаты. К группе непрямых методов ре¬
шения относятся также и некоторые аналитические методы, использование
которых естественным образом приводит к необходимости решения крае¬
вой задачи.
Вопрос о преимуществе методов той или иной группы (прямых, непря¬
мых) при выборе некоторого метода для решения конкретной задачи в
настоящее время является открытым.
3.3.2. Классические методы решения
Здесь кратко рассматриваются аналитические методы, ставшие достаточ¬
но известными и распространенными — принцип максимума Понтрягина и
метод динамического программирования Беллмана. Представленные мето¬
ды решения задач оптимального управления являются аналитическими как
в смысле принципиального получения замкнутого решения, так и в смысле
получения функциональных зависимостей, на основании которых численны¬
ми методами возможно получение искомого решения. Заметим, что в силу
характерных нелинейностей заданных дифференциальных уравнений движе¬
ния КЛА (см. §3.1) получение аналитического решения (в традиционном
смысле) исходной задачи в настоящее время не представляется возможным.
Этим объясняется широкое использование регулярных вычислительных
процедур при численном решении оптимальных задач на ЭВМ.
Основная задача вариационного исчисления. Рассматривается типовая
вариационная задача с минимизируемым функционалом вида
т
/ = JF(X,uzt)cft+ Ф[Х(г)].
о
Функционал / является скалярной величиной. Начальные условия
х0 =Х(ГО), хоевйх,
при этом величина Хо задана.
Решение (поиск оптимального значения управления и= и*) строится
согласно известной процедуре Эйлера - Лагранжа. Вводится множитель
Лагранжа, являющийся векторной функцией X(t), и в результате ищется
безусловный экстремум функционала / , записываемый в виде
т т .
/ = Ф[Х(Г)] + f F(X, и, t)dt — f < X(t), [X-f(X, u,t)]>dt,
или
о о
т
/ = Ф[Х(Г)] + /£(XzuzXzf)cft,
(3.15)
о
где подынтегральная функция L представляется в форме
L —XX + 3((X,u,X,t). (3.16)
Функция К (X, и, X, t), называемая гамильтонианом, определяется в виде
(3.17)
Из классического вариационного исчисления непосредственно следует,
что уравнения Эйлера - Лагранжа имеют вид [применительно к (3.15)]
(3.18)
60
После вычисления частных производных системы (3.18), для чего
используется запись (3.17) для расширенного гамильтониана К и подста¬
новка этих частных производных Э J(/dX,. . . , дЖ/дй в исходную систему,
непосредственно получаются необходимые условия оптимальности
d
— Х = -
dt
~ЬМДХ,и, Xzt)
ЭХ
d d
— X = f(X, и, t}, —Jf = 0.
dt du
(3.19)
t
Уравнения (3.19) можно записать в более компактной форме
эк*1
t
'ЭЗГ'
х= —
, х = -
L эх
. эх
(3.20)
где К* (X, X, t) = (Xz £/*z \z t), а £/* удовлетворяет необходимому условию
оптимальности №/ди= 0. Уравнения в форме (3.20) известны под назва¬
нием канонических уравнений Гамильтона.
Граничные условия для уравнений (3.20) задаются исходным значением
Хо = X(t0) = Х( 0) и вычисленным значением
ЭФ [X(t)J '
В результате поставленная вариационная задача сводится к краевой задаче
для системы обыкновенных дифференциальных уравнений.
Ограничение на управление в задаче вариационного исчисления. Исход¬
ной вариационной задачей является задача с минимизируемым функциона¬
лом вида
/(Хо, to) = If(X, и, t) dt + Ф[X(t), t] (3.21)
о
и с ограничением и^Ви. В интеграле (3.21) начальный момент t0 = 0,
конечный fK = Т. Предполагается, что существует оптимальное значение
критерия /* (X, t), являющееся функцией, дважды дифференцируемой по
X и f, и что £7*(Х, Э/*/ЭХ, f) есть искомое оптимальное управление, мини¬
мизирующее некоторую функцию К:
+ F(Xz£7zt).
Минимальным значением является
В результате преобразований функционала (3.21) и в силу предположе¬
ний относительно существования / * и £7* может быть получено соотношение
/ (Хо, to ) — / * (Хо, to)
П * 9/*(Xzf)
= 0 = / br +
о 9f .
c/t = J^F°c/t =/°.
о
Отсюда следует, что если /* (X, f) есть оптимальное значение исходного
функционала (3.21), то оно должно удовлетворять следующему уравнению
в частных производных:
Э/*(Хх t)
9f
Э/(Х, f)
эх
(3.22)
61
при граничном условии
/*[Х(П, Л =Ф[Х(Л, Г].
Уравнение (3.22), полученное непосредственно из (3.21), есть известное
в вариационном исчислении уравнение Гамильтона — Якоби, которое явля¬
ется необходимым и достаточным условием оптимума. Решение уравнения
(3.22) в общем виде не получено.
Из-за трудностей, возникающих при решении уравнений в частных произ¬
водных, уравнение Гамильтона — Якоби желательно привести к более
удобному виду. Для оптимальной траектории должны выполняться диффе¬
ренциальные соотношения
— X(t) = f(X,u*t) =
dt
Г дЭТ*(Х,р,Г)
L Эр
(3.23)
d
— p{t) = -
dt
ЬМ(Х,р, t)
дх
называемые также каноническими уравнениями Гамильтона. Здесь p(t) =
= [Э/* (X, Г)'] /ЪХ,. где производная берется на оптимальной траектории;
К = Г(Х,и, t) +<Х, р >; = minJC = p'f(X, и\ t) + F(X, и*, t).
Как и в случае системы уравнений (3.19), к уравнениям (3.23) должно
быть присоединено уравнение ЭК*/Эи* =0. Граничные условия для уравне¬
ний (3.23) разделенные:
X(tQ)=XQ,
p(tK)=p(T) =
т.
Условия оптимальности, характеризующие двухточечную краевую
задачу (3.23), тождественны задаче (3.20). Параметр р называется векто¬
ром сопряженного состояния, а дополнительная система уравнений
для р(г)
d
dt
P(t) = -
dF(X,u*,t)'
дХ
bf(X,u\t}
ъх
p
— сопряженной системой. Отметим, что в случае отсутствия ограничений,
накладываемых-на управление и, вектор p(t) отождествляется с вектором
X(t) множителей Лагранжа в основной задаче вариационного исчисления.
Динамическое программирование. Методы теории динамического прог¬
раммирования получили достаточно широкое развитие в решении задач
спуска КЛА в атмосфере. Основой метода является широко известный
принцип оптимальности [6]. Оптимальное поведение обладает тем свойст¬
вом, что каковы бы ни были первоначальное состояние и решение в началь¬
ный момент, последующие решения должны составлять оптимальное
поведение относительно состояния, получающегося в результате первого
решения. Принцип оптимальности фактически утверждает, что отрезок
некоторой оптимальной траектории есть снова оптимальная траектория.
Как отмечается в [1], это утверждение справедливо для широкого класса
процессов. Поэтому, в частности, он справедлив для многих задач об опти¬
мальном управлении и в том числе для задач об экстремуме конечно-интег¬
рального функционала задачи Больца.
Основу собственно метода динамического программирования составляет
допущение о существовании функции V(x, t), которая имеет смысл экстре¬
62
мума оптимизируемого функционала I (X, и, г):
V(X,t} = min !(t, X, и) = /(t,X), (3.24)
гдеи = а(Г); t>t0 — текущий момент времени, tQ — начальный и tK —
конечный моменты протекания управляемого процесса X = X(t). Иначе,
V(X, f) рассматривается как функция от начальных временно фиксируе¬
мых условий tz X = X(Г).
Рассмотрим проблему минимизации функционала
/ =JK F(X, и, t|tf + $[tK,X(tK)l (3.25)
* о
при связях X = f(X, и, t) и начальном условии Хо - X{tQ). Определим функ¬
цию V(X, t) согласно (3.24). В соответствии с принципом оптимальности
можно записать следующее дифференциальное уравнение для функции
У(ХЛ):
V(X,t) = min [FAt + V(X + AXt + At) + O(4t)]. (3.26)
u
Предполагая, что существует разложение функции V( X,t) в ряд Тейлора,
и осуществляя предельный переход при 4t->0, получаем соотношение
Г bV(X,t) bV(X,t} .
О = min F(X, и, t} + + X
и L dt дХ
или
bV(X,t)
~ dt
= min F(X, и, t) +
u
bV(X,t) .1
x •
bX 1
(3.27)
Уравнение (3.27) для функции V в общем виде может быть представле¬
но как
(3.28)
что формально является записью уравнения Гамильтона — Якоби. Символ
К означает функцию Гамильтона, причем для оптимальной задачи с миними-
зируемым интегральным функционалом = f F(X, u,t)dt при связях
X = f{X, и, t) функция Гамильтона имеет вид
bV
f+F^ — f
bt
bV Z dV '
где f есть скалярное произведение 2 tz .
ЬХ / = i °Xj
Уравнения Гамильтона — Якоби вида (3.28), согласно [1] называются
уравнениями Веллмана. Уравнения Веллмана можно свести к каноничес¬
ким уравнениям Гамильтона в предположении существования оптимально¬
го управления
d ГЭК*1'
d
dt
(3.29)
63
с раздельными граничными условиями X(f0) = Хо и
p(tK)=p(T) =
Э/*(ХК< 7~)'
ЭХК
В результате уравнения Веллмана (в случае обоснованности предположе¬
ния о непрерывной дифференцируемости функции V) принципиально
допускают представление условий оптимальности в форме двухточечной
краевой задачи. Однако при практическом решении задач методом динами¬
ческого программирования используются специальные вычислительные
схемы, реализующие функциональные уравнения типа (3.26), наиболее
приспособленные для решения на ЭВМ.
Эффективное численное решение современных задач методом динамичес¬
кого программирования во многом определяется возможностями памяти
существующих ЭВМ. Это связано с существом вычислительной процедуры
самого метода, согласно которому происходит оценка (по /у) всех воз¬
можных состояний X управляемой системы при всех возможных управле¬
ниях и с обязательным запоминанием оценок /у и соответствующих им
областей (X, и).
Объем памяти современных ЭВМ, необходимый для хранения информа¬
ции о возможных вариантах решения вариационных задач и соответствую¬
щих значениях оценок /у, накладывает требования на характер решаемых
задач, в частности по величине размерности, и допускает решение задач
лишь сравнительно небольшой размерности.
Использование методов динамического программирования эффективно
только в случае соответствующей подготовки исходной задачи (учета
ограничений по размерности, числу просматриваемых вариантов, шагу
дискретности) и сводится к отысканию экстремума основного аддитивного
N
функционала/ = S Д/у(tz_ lz fz) по всем возможным реализациям (X, Г).
i = 1
Так, для отыскания глобального минимума функционала / предложена
следующая схема решения, известная под названием "киевский веник"
[34, 35]:
S0(XK,) = min {So(%;.!> + /,(X,•_!ZXK()} . (3.30)
Г
Здесь So (Хк,) есть значение функционала вдоль траектории, соединяющей
начальную точку с текущей точкой ХК1. При решении по схеме (3.30)
n-шаговый процесс отыскания экстремума преобразовывается в п одноша¬
говых процессов принятия решений, связанных рекуррентными соотноше¬
ниями.
Для задачи минимизации функционала
т п- 1
/ = / F(X,u}dt^ S F(XitUi} Д, Т = пА
о i = о
при ограничениях X/+ ! = f (Xif uif Д), Хо =Х(Г0)из принципа оптимальнос¬
ти получается система рекуррентных соотношений, описывающих п-шаго-
вый процесс, при котором ищутся п векторов управления uQ, uif. . . , ип_{,
минимизирующих /(Хо)- Пусть 1п(Хп} есть оптимальное значение искомого
аддитивного функционала / л-шагового процесса, начинающегося при Хо.
Тогда система рекуррентных соотношений принимает вид
/«(Хо) = min [F(X0, u0) Д + /„ _ i (X!)], Xi = f(X0, uQ, A);
64
|(X,) = min [Л(Х,, u, )Д +/„ 2(X2]],X2 =ЦХ{,щ,\};
“ i
(3.31)
/2(Х„_2) = min [F(X„ 2, u„ _ 2) Д + !\<Xn - t )1.
un-2
*„ — 1 = f(X„ — 2/ un - 2 • Д)>
/j (X,,_ I) = min [F(X„_ lzu„_ 1) Д ].
"n- 1
Процедура решения по методу динамического программирования вклю¬
чает два этапа. На первом этапе происходит определение всех возможных
состояний (X, и) , производится численная оценка допустимых состояний
по величинам соответствующих функционалов/7 и получается последова¬
тельность оценок /j (Хп_х], /2(^-2)/ • • • / 1п(Хъ}, причем характерная
особенность процедуры получения оценок /, заключается в осуществле¬
нии обратного движения — от некоторого конечного состояния (в момент
tK) с шагом дискретности А до возможного начального состояния
(в момент to) - В результате оптимальные решения становятся известными
не для одного конкретного начального условия, а для некоторого набора
начальных условий из интересующего диапазона. На втором этапе, при
естественном движении от начала процесса в конец, для любого конкретно¬
го начального значения XQ может быть осуществлен однозначный выбор
искомого оптимального решения, что обеспечивается соответствующей
вычислительной процедурой принятия решения.
В заключение следует отметить, что, несмотря на ряд известных недос¬
татков и ограничений (в частности, ограничение рассматриваемых функцио¬
налов из-за требования аддитивности), методы динамического программи-
рования достаточно широко используются при решении ряда задач об опти¬
мальном управлении. Это связано как с большой универсальностью самого
метода, так и с появлением различных модифицированных методов реше¬
ния, базирующихся на идеях динамического программирования.
Принцип максимума Понтрягина. Теоретической основой большого
круга оптимальных задач программного управления считается математи¬
ческая теория оптимальных процессов [8, 72]. Эта теория, получившая
большое признание, базируется на принципе максимума, указывающем
необходимые условия оптимальности для задач программного управления.
Сущность принципа максимума заключается в том, что он дает возмож¬
ность (по крайней мере аналитическую) решать вариационные задачи с
ограничениями типа неравенств, наложенными на управляющие функции,
когда методы классического вариационного исчисления становятся непри-
менимыми.
Рассмотрим случаи, когда правые части в дифференциальных уравнениях
движения КЛА явно не зависят от времени t (так называемый случаи
автономности)
X = f(X и). (3.32)
В качестве минимизирующего функционала рассматривается функционал
задачи Лагранжа, также соответствующий случаю автономности:
/ = / f°[X(t),u(t)] dt.
Го
5. Зак. 2069
65
Основная задача, заключающаяся в отыскании оптимальных управлений,
формулируется следующим образом [72].
В фазовом пространстве Вх даны две точки XQ и Х^. Среди всех допусти¬
мых управлений и = u(t), переводящих фазовую точку из положения XQ
в положение Х^ согласно (3.32), найти такое, для которого функционал
(3.33) принимает наименьшее возможное значение. В процессе решения
задачи нахождения оптимального управления и* (г) кроме основной систе¬
мы уравнений (3.32), расширенной за счет преобразования интегрального
функционала
dXi
= fj(X,u) (/ = 0,1,2 л), (3.34)
dt
рассматривается дополнительная система дифференциальных уравнений
d Ф1 ” df.(X,u}
=- s — ф; (/ = 0,1,2 п) (3.35)
dt о ^Xf
относительно вспомогательных переменных ф' = (i//0, ^lz. . . , фп}. Если
выбрано некоторое допустимое управление и (t), и имеется
соответствующая фазовая траектория X(t) системы (3.34) с начальным
условием XQ = X{tQ), то система (3.35) принимает вид
d\h « df;[X(t),u(t)]
S — Ф/ (/ = 0,1,2 n). (3.36)
ar j = о oXi
Система (3.36) линейна и однородна, поэтому при любых начальных
условиях для имеется единственное решение -0' = (i//0, Ф1, . . . , фп),
определенное на всем отрезке tQ < ti, на котором определены управле¬
ния u(t) и траектория X(t).
Вводится функция переменных X, ф, и
М(ф,Х, и) = ( ф, f(x, и)),
с помощью которой системы уравнений (3.34) и (3.36) могут быть запи¬
саны в виде следующей гамильтоновой системы:
dt L Эф J
d газе
— «// = - — .
dt Lax
(3.37)
(3.38)
При фиксированных постоянных значениях ф и X функция 1К становится
функцией управляющего параметра и фЕВи]. Точную верхнюю грань
значений этой функции обозначим через М(ф, X):
М(ф,Х)= sup К(ф,Х,и).
ви
Если точная верхняя грань значений непрерывной функции достигается в
некоторой точке области управления BU1 то М{ф, X) есть максимум значе¬
ний функции при фиксированных фи X.
Таким образом, для оптимальности управления и (г) и траектории XI t)
необходимо существование такой ненулевой непрерывной вектор-функции
Ф№) = (i//0 (t), фх (Г), ..., соответствующей функциям и (г) и X(t),
что
66
1) при любом t, функция К(ф (t), X(t}, и) переменной и G Ви
достигает в точке и = и (t) максимума
W(t), Х{ t).u(t)) = /И(ф(Г),Х(Г)); (3.39)
2) в конечный момент выполнены соотношения
Фо (*Ч КО, М(ф (Гх), X(tY)) = 0. (3.40)
Если величины ф (t), X(t)f и (t) удовлетворяют гамильтоновой системе
уравнений (3.37) и (3.38) и условию 1), то функции ф0 (f) и Л4(ф (t), X(t})
переменной t являются постоянными, так что проверку соотношений
(3.40) можно проводить в любой момент времени t, tQ <t<ti (не обяза¬
тельно в момент ).
Необходимо отметить, что равенство (3.39) в приведенной формули¬
ровке составляет главное содержание принципа максимума Понтрягина.
Непосредственное использование принципа максимума для решения задач
оптимального управления заключается в следующем.
Исходная система дифференциальных уравнений (3.32) преобразовыва¬
ется к виду (3.34) введением дополнительной фазовой переменной XQ.
Составляется функция
К(Ф, Х,и) = S ф^РС"),
i = О
причем вектор-функцию ф' = (ф0, Ф1, Фи) всегда нормируют, полагая,
например, фо = — 1. В этом случае
ЗС(ф, Х,и) = £
Z = 1
Составляется вспомогательная система дифференциальных уравнений
для функций фг = (Фо, Ф1, Фи) согласно (3.38), причем ф0 = 0. Пред¬
полагается, что функция JT является выпуклой функцией по и, поэтому
условие (3.39) принципа максимума в каждый момент t дает г соотноше¬
ний между неизвестными функциями для определения управлений и =
= (ult иг ) . Таким образом, заранее предполагается, что оптимальное
управление существует и что производные
Э5С(ф(г),Х(Г),^)
(7=1,2 г)
и = и(Г)
могут быть выражены аналитически. В результате решение исходной опти¬
мальной задачи сводится к решению двухточечной краевой задачи для га¬
мильтоновой системы уравнений (3.37) и (3.38) . При этом необходимо
обеспечить переход фазовой системы из заданного начального положения
Xq в заданное конечное положение Х\, что достигается соответствующим
выбором вектор-функции ф' = (—1, Ф1, ..., фЛ/).
В настоящее время принцип максимума распространен на все типы опти¬
мальных задач программного управления, однако при практической реали¬
зации по-прежнему необходимо решать по крайней мере двухточечную
краевую задачу для системы дифференциальных уравнений структуры
(3.37) и (3.38) .
Известно значительное количество обобщений рассмотренной задачи:
задачи с подвижными концами, задача в случае неавтономности (3.32) и
67
(3.33), задача с ограничениями на фазовые координаты, задача со статисти¬
ческими условиями. Принцип максимума был распространен также на си¬
стемы, качественно отличные от первоначально изучавшихся: на дискрет¬
ные системы, системы с распределенными параметрами и др.
Метод решения оптимальных задач программного управления, основан¬
ный на использовании принципа максимума, является в настоящее время
наиболее строгим математически обоснованным и популярным методом.
Это связано, во-первых, с естественным характером исходных положений
постановки задачи, не требующих априори непрерывности и дифференци¬
руемости искомой функции экстремума, как того требует метод динами¬
ческого программирования в отношении функции V (t, х) . Во-вторых,
использование принципа максимума позволяет (хотя бы формально)
решать сложные технические задачи с соответствующими реальными огра¬
ничениями на управление и фазовые координаты, тогда как методы клас¬
сического вариационного исчисления здесь становятся неработоспособны¬
ми. Однако практическое использование принципа максимума в случае
численного решения на ЭВМ зависит от эффективности вычислительного
алгоритма соответствующей краевой задачи.
Таким образом, использование принципа максимума в качестве метода
решения задач оптимального программного управления считается наиболее
обоснованным теоретически и удобным практически, поскольку процедура
решения с использованием принципа максимума является легко стандарти¬
зуемой. Тем не менее в силу вычислительных затруднений решения соот¬
ветствующих краевых задач метод принципа максимума не является уни¬
версальным средством получения численного решения и поэтому в послед¬
нее время получают развитие методы, принципиально не сводящиеся к
необходимости решения краевых задач.
3.3.3. Метод достаточных условий В.Ф. Кротова
В течение последних лет сформировались новые направления, позволяю¬
щие подходить к решению вариационных задач с нетрадиционных позиций.
В этом параграфе представлен метод, получивший широкое распростране¬
ние, — метод достаточных условий В.Ф.Кротова.
При исследовании современных технических задач, являющихся менее
идеализируемыми, чем первоначально изучавшиеся, потребовалось обобще¬
ние проблем оптимального управления, связанное с такими управляющими
воздействиями u(t) на траекториях движения X(t), которые не удается
описать обычными функциями времени и которые требуют обобщающих
математических конструкций. Были обнаружены нерегулярные случаи
оптимальных управлений и движений, в частности случаи импульсных опти¬
мальных управлений (когда оптимальным управлением оказывается после¬
довательность мгновенных импульсов, описываемых 6-функциями) и слу¬
чаи нерегулярных режимов (скользящих режимов, режимов особого управ¬
ления) .
Под скользящим режимом управляемой системы понимается такое ее
движение, которое получается как предельный случай обычного движения
этой системы при бесконечно частых, следующих друг за другом скачко¬
образных изменениях управляющих воздействий. Движения, которые отве¬
чают скользящим режимам, как правило, осуществляются вдоль поверхно¬
стей переключения. Известно, что указанные нерегулярности оптимального
управления и* (г) часто обусловливаются характером минимизируемой ве¬
личины (в том числе аналитическим видом функционала /) и характером
ограничений на фазовые координаты. В число нерегулярных режимов вхо-
68
дят и режимы особого управления, к которым в связи с изучением сколь¬
зящих режимов [10] в последнее время значительно возрос интерес. Ситуа¬
ция, характерная для особых управлений, если использовать функцию К
принципа максимума, заключается в том, что функция 5€или явно не зави¬
сит от управления и, или является постоянной на конечном интервале вре¬
мени и также не зависит от и. Случаи неоднозначности и постоянства функ¬
ции возникают также из-за трудностей качественного анализа исходной
задачи (с точки зрения существования оптимального управления). Заме¬
тим, что если в некоторой задаче для каждого момента времени существует
несколько значений управления и, при которых значение функции Ji макси¬
мально, то в таком случае можно говорить о существовании скользящего
режима. Понятно, что в указанном случае применение общепринятых необ¬
ходимых условий невозможно принципиально и оптимальное управление не
может быть определено однозначно. Тем не менее и в этих случаях опти¬
мальная траектория может быть найдена и быть единственной [9].
Общий подход к теории нерегулярных оптимальных движений и, в част¬
ности, движений типа скользящего режима связан с введением обобщенных
понятий экстремали и новых принципов оптимальности. Один из таких
принципов, основанный на достаточных условиях абсолютного минимума,
представлен в работах В.Ф.Кротова и его сотрудников и на основании этого
принципа развит метод решения [46 — 48].
Рассматривается проблема минимума функционала задачи Больца
G
/= / f°[X(t), u(t), t]dt + F(X(t0), XltiYi (3.41)
*0
при условиях
X = f(X,u,t), (342)
причем множество допустимых пар вектор-функций X(t) и u(t) образует
множество D. Относительно X(t) и U(t) предполагается также выполнение
условий X(t0) G ВХо и X(tK) G ВХк; кроме того считается, что они подчи¬
няются требованиям измеримости, кусочной непрерывности, кусочной
гладкости и т.д.
Метод состоит в доопределении функционала / до некоторого нового
функционала L на множестве Е пар вектор-функций X(t) и u(t), не подчи¬
няющихся уравнениям связи (3.42) . Конструкция должна подбираться та¬
ким образом, чтобы существовала последовательность {Xs (t), us (t)} £ D,
на которой выполняется соотношение
lim / [Х5, ys] = inf L. (3.43)
s -► oo
Для задачи (3.41), (3.42) функционал / доопределяется до функциона-
ла L при помощи равенства
I ]
L = Ф(Х0, ) - f Я[*(Г), u (t), t]cfr,
е
Я(Х, U, Г) = ЦХ, и, t)-f°(X,u,t)+ — .
ЪХ ot
Ф(Х0, Xt) = F(X0, Xi) + Xi) - 4>(t0, Xo),
(3.44)
(3.45)
(3.46)
69
причем <p(f, X) — непрерывная дифференцируемая функция, подбираемая
таким образом, чтобы выполнялось условие (3.43).
Принцип оптимальности формулируется следующим образом. Пусть име¬
ется последовательность {Xs (t), us (t)) ED. Для того чтобы эта последова¬
тельность была минимизирующей, необходимо и достаточно существование
такой функции (t, X} , непрерывной и кусочно-дифференцируемой при
каждом фиксированном t Е (г0, ), чтобы при $ -> оо выполнялись
условия
R(XS, us, И МW, t е (t0, гх),
Xu) -> тТФ(Х0, ), XiEBiti),
pAt} = supfi(X, u, t), X, и Ep(t).
(3.47)
(3.48)
(3.49)
Если существует минимальное значение X(t), и (t) Е D, то условия (3.47)
и (3.48) принимают вид
R(X{t}, и (г), Г) = Д'(t), t Е (tOz tx),
Ф(Хо, Хх) = inf Ф(Х0, Хх), XQEB(tQ), Хх EBltA-
Экстремальное значение функционала L, определяемое равенством
(3.43), ищется в форме фундаментальной минимизирующей последователь¬
ности. В случаях, когда предельный элемент этой последовательности в
исходной области D отсутствует, получается специальная математическая
конструкция, сводящаяся к движению (скольжению) управляемой систе¬
мы вдоль некоторого приближенного решения (называемого функцией
нулевой близости} с бесконечно частыми переключениями с одного из
управлений Uj (г) (/ = 1, ..., к + 1) на другое, где число к называется
вырождением оптимального режима. Фактическое построение обобщенной
экстремали осуществляется на основании условий (3.47) и (3.48) и опреде¬
ляется, следовательно, экстремальными свойствами функции R(Xfu.t)
при каждом фиксированном значении t Е (гОлгх). Необходимо подчерк¬
нуть, что на основании предложенного принципа оптимальности возможно
получение известных методов решения — классических формализмов Лаг¬
ранжа, Понтрягина и Веллмана, что достигается соответствующим выбором
функции (t,X) . Другими словами, в достаточно регулярных случаях ус¬
ловия (3.47) и (3.48) принципа оптимальности близки известным соотно¬
шениям принципа максимума и метода динамического программирования.
Так, сравнивая выражение (3.28) и соотношение (3.44), нетрудно заме¬
тить, что в регулярных случаях роль функции может играть функция V,
фигурирующая в уравнении (3.28).
Для решения вырожденных задач, когда имеет место многозначность
функции К по управлению и, разработан специальный метод решения, полу¬
чивший название метода кратных максимумов. Основная особенность этого
метода заключается в том, что искомое минимальное значение определяется
при каждом значении t выбором точки фазового пространства Х= X, обес¬
печивающей sup/?, в то время как максимум по и гарантируется в силу
заранее осуществленного выбора функции (t, X).
Как отмечается в [13, 46], основным преимуществом метода кратных
максимумов является его простота. При наличии полного вырождения
(когда к = п} решение X(t) получается непосредственно в виде конечного
выражения. Отмеченное упрощение принципиально обусловлено соотноше¬
нием (3.43), осуществляющим трансформацию исходной оптимальной
70
задачи (3.41), (3.42), в силу которого допустимыми решениями являются
функции Х(Г) и u(t), не связанные уравнением (3.42).
В настоящее время метод решения, основанный на использовании доста¬
точных условий экстремума, получил заметное развитие. Известно значи¬
тельное число публикаций, в которых с помощью указанного метода иссле¬
дуются современные задачи оптимального управления (см., например,
[13, 46] ) . Согласно указанным работам, при управлении углом атаки а
спускаемого аппарата наличие скользящих режимов является типичным .:
характерным случаем (особенно при квадратичной зависимости Кота),
что, однако, нельзя считать полностью доказанным фактом. В частности,
в работе [84] в составе оптимального решения скользящий режим отсут¬
ствует.
Необходимо обратить внимание на качественную сторону принципа опти¬
мальности В.Ф.Кротова. Принцип постулирует возможность сведения задачи
об абсолютном минимуме функционала к задаче о безусловном максимуме
функции R(X,u, t) (п + 2) переменных Xt (/ = 1, 2, ..., п) и ut (I =
= 1,2, ..., г ) при каждом фиксированном t G (t0, t J . Однако соотноше¬
ние (3.45) для функции R (X, u,.t), являющееся уравнением в частных про¬
изводных для неизвестной функции (f, X), в общем случае не делает
исходную оптимальную задачу более простой в решении.
3.3.4. Характеристика задач оптимального управления
Каждую конкретную оптимальную задачу программного управления до¬
пустимо решать любым из известных методов. Однако к сожалению, отсут¬
ствуют сравнительный анализ различных методов и соответствующие реко¬
мендации относительно того, какой из методов решения является наиболее
эффективным для определенного класса задач. Как показывает практика,
чаще всего на выбор того или иного метода решения влияют степень из¬
вестности самого метода и личные вкусы исследователя. Заметим, что в тех
случаях, когда выбор сделан в пользу методов, использующих необходи¬
мые условия экстремальности, трудности численной реализации, связанные
с решением соответствующей краевой задачи, должным образом и заранее
не оцениваются. Использование любого из аналитических или алгоритмиче¬
ских методов редуцирует (в случае численного решения) исходную вариа¬
ционную задачу к некоторой новой эквивалентной задаче, для решения
которой могут быть использованы известные приемы поиска экстремума,
которые, однако, не являются универсальными и стандартными. В этом
параграфе показывается, что независимо от метода, используемого при ре¬
шении исходной задачи оптимизации, численное решение любой задачи опти¬
мального программного управления сводится в конечном итоге к нахожде¬
нию решения некоторой многопараметрической задачи математического
программирования.
Рассмотренные выше классические методы решения (в форме задачи ва¬
риационного исчисления на условный экстремум, в форме принципа макси¬
мума Понтрягина) приводят к одной и той же основной системе
обыкновенных дифференциальных уравнений (двухточечной краевой зада¬
че) как необходимому условию оптимальности. Решение по методу динами¬
ческого программирования в принципиальном отношении сводится к полу¬
чению гамильтоновой системы и связано с необходимостью решения крае¬
вой задачи. Таким образом, от возможности и эффективности решения си¬
стем уравнений (3.23) , (3.29) , (3.37) , (3.38) зависит успех решения исход¬
ной вариационной задачи для каждого из рассмотренных аналитических
методов.
71
Решение двухточечной краевой задачи заключается в нахождении таких
значений переменных и* (к = 1,2, ...,т?; т?<л) в одной из граничных точек
(допустим, в момент времени tQ = 0), чтобы в другой граничной точке
(в момент tк = Г) обеспечивалось выполнение или заданных соотношений
между переменными, или заданных значений самих переменных. В число
искомых переменных oKq в общем случае входят некоторые фазовые пере¬
менные Хс (с = 1,2, ..., кх) и вспомогательные переменные vd (d = У ,2, ...
..., к2), суммарное число которых к = ki + к2 = т?, и, таким образом, а* =
= °к0 (Кс' • Вспомогательными переменными vd являются (в зависимо¬
сти от метода решения) или множители Лагранжа X, или сопряженные пере¬
менные гамильтониана К.
Пусть в конечный момент tK должны выполняться п соотношений
X(tK) = ХК, где X(tK) — заданные по условиям конкретной задачи значе¬
ния фазовых переменных X в момент tKt а ХК — численные значения пере¬
менных X в результате решения соответствующей гамильтоновой системы
для известных в момент t0 начальных значений Х[, v? и некоторых вы¬
бранных значений о/о = (Х*с, vd) ‘ Здесь размерности векторов X/ и vj со¬
ответственно равны г 1 = п— к\ и г2 — п — к2, где размерность п соответ¬
ствует размерности фазбвого вектора X исходной оптимальной задачи. Вы¬
полнение соотношения Х(гк) = ХК сводится к решению системы алгебраи¬
ческих уравнений, заданных неявным образом:
ДХ(Гк) = и/(аКо), (3.50)
где ДХ(ГК) = X(tK) — XKl a w(oKo) — некоторая функция искомого векто¬
ра °к0 (к =Ъ2, ..., г}) недостающих начальных значений Хс и рd в момент
времени tOl причем аналитический вид функции и/(аКо) не известен. Следо¬
вательно, решение уравнения (3.50) заключается в отыскании нулей век-
тор-функции
= (3.51)
Таким образом, проблема решения двухточечной краевой задачи сводится
к отысканию решения алгебраического уравнения (3.51).
Процедура решения краевой задачи состоит из ряда последовательных
итераций, на каждой из которых происходит целенаправленное изменение
переменных oKq согласно некоторому регулярному алгоритму, призванно¬
му обеспечить решение уравнения (3.51) и, следовательно, выполнение
(3.50). Необходимость в указанной процедуре решения связана с практиче¬
ской невозможностью определения искомых начальных значений Хс и vd.
В качестве меры выполнения конечных соотношений ДХ(ГК) = 0 часто при¬
нимается соответствующая функция невязок [функция конечных значений
фазовых переменных X(tK} ] согласно известному методу штрафных функ¬
ций. В этом случае мерой эффективности решения краевой задачи считается
текущее значение приведенного функционала
ръ = S cm[Xm(tK) - Хкт]2 ст>0 (3.52)
т = 1
на каждом шаге итерационного процесса. Следовательно, решению краевой
задачи, т.е. минимуму функционала исходной оптимальной задачи, должна
отвечать сходящаяся последовательность приведенных функционалов
pz ">0< гДе верхний индекс ц соответствует номеру итерации.
72
Отметим, что для успешного решения краевой задачи необходимо иметь
вычислительный алгоритм, определяющий аналитическую зависимость меж¬
ду требуемым изменением функционала Р% и соответствующими значе¬
ниями искомых начальных переменных Хс и Pj. Однако процедура решения
краевой задачи практически не может быть стандартизована в силу нелиней¬
ных дифференциальных связей в прикладных задачах, что приводит к необ¬
ходимости разработки в каждом конкретном случае соответствующего
вычислительного алгоритма.
Фактическое решение краевой задачи сводится к решению некоторой
экстремальной задачи, в частности и в том случае, когда ищется минимум
приведенного функционала (3.52) = 0. Процедура решения включает
в себя последовательность решений задачи Коши, соответствующую целе¬
направленно изменяемому вектору недостающих начальных значений oKq .
В общем виде запись результирующей экстремальной задачи может быть
представлена следующим образом:
Ф = Ф(ак,ар), (3.53)
где ок и (Jp — переменные редуцированной вариационной задачи в моменты
времени tQ и Гк. В случае разделенных краевых условий (когда ок соответ¬
ствует, например, моменту t0) приходим к экстремальной задаче поиска
минимума функции конечного числа начальных переменных
G = min w(aKo )• (3.54)
Именно такая задача минимизации типична для случаев численного реше¬
ния гамильтоновых систем, характеризуемых двухточечной краевой зада¬
чей, поскольку решение уравнения (3.51) даже в результате длительного
итерационного процесса возможно лишь в пределах заданной наперед точ¬
ности. Если же величина допустимой погрешности задается вне связи с ха¬
рактером решения гамильтоновой системы, то потребные затраты машин¬
ного времени будут совершенно нереальными.
Решение исходной оптимальной задачи методом динамического програм¬
мирования принципиально сводится к решению гамильтоновой системы
(3.29) и, следовательно, к решению характерной задачи минимизации вида
(3.54). Метод динамического программирования, непосредственно исполь¬
зуемой как вычислительный метод, приводит к необходимости решения
соотношений вида (3.32), позволяющих для каждого узла tK временной
сетки определить допустимые фазовые переменные ХК1- и соответствующие
допустимые управления ик/ . Затем для интересующих начальных условий и
в результате организованного перебора находится такая последовательность
XKi и ик1 ' которая должна обеспечивать экстремум исходного функциона¬
ла /. Таким образом, в результате использования вычислительной процеду¬
ры метода динамического программирования происходит преобразование
исходной задачи оптимального управления в некоторую эквивалентную
задачу нелинейного программирования, после чего остается определить
минимум функции конечного числа переменных
/ = /(Х0,*1 XnV (355)
соответствующих узлам {к = 0, 1,...,/V) временной сетки. Индекс/Vсо¬
ответствует числу интервалов разбиения заданного временного интервала
(0, Т).
Решение оптимальной задачи программного управления на основе доста¬
точных условий абсолютного минимума сводится в общем случае к необхо¬
димости нахождения экстремума функции R(X,u,t) в каждый момент
73
времени t G (t0, tK) . Следовательно, исходная задача минимизации функ¬
ционала / = l(X,u,t) преобразуется в последовательность экстремальных
задач для функции (3.45) R (X, и, t)что в обобщенном виде может быть
представлено так:
L = L(Y0, Л Yn).
(3.56)
Здесь Yj (/ = 0,1, ...,/V) означает последовательность решений экстремаль¬
ных задач для функции R (Х,и, t) для соответствующего момента t из за¬
данного временного интервала (tQ, fK). Как отмечалось при рассмотрении
метода кратных максимумов, в случае полного вырождения (к = п) ука¬
занное преобразование исходной задачи в задачу (3.56) является наиболее
эффективным, поскольку непосредственно должно приводить к конечным
соотношениям для определения оптимального решения X(t).
Использование методов, основанных на варьировании в пространстве со¬
стояний, сводит исходную вариационную задачу к эквивалентной задаче не¬
линейного программирования. В результате остается найти решение экстре¬
мальной задачи определения минимума функции (3.55) в пространстве фа¬
зовых переменных XKif соответствующих узлам Гк временного интервала
(О, Т) и определяемых на решениях системы дифференциальных уравнений
движения КЛА. Отличие от метода динамического программирования за¬
ключается в том, что для осуществления регулярной вычислительной
процедуры решения здесь требуется задание некоторого нулевого прибли¬
жения Х° с соответствующей оценкой функционала /°. В силу вычислитель¬
ной процедуры происходит регулярное измерение приближения Xм-1,
которое приводит к улучшению функционала /м_1. Таким образом, если
в вычислительном аналоге метода динамического программирования опре¬
деляются все допустимые фазовые переменные ХК1-, соответствующие воз¬
можным оптимальным решениям, то в методах варьирования в пространст¬
ве состояний оцениваются только такие фазовые переменные Хк/, которые
могут привести к улучшению функционала , известного в предыдущем
(д — 1)-м приближении.
При использовании функциональных градиентных методов [12, 96, 105]
вариация 5/ связывается с вариациями 6 Y(t) согласно соотношению
(3.57)
где Ф (t) - аналитически известная функция влияния, а 6 Y(t) могут быть
как вариациями du(t), так и вариациями 6X(f) в зависимости от типа
задачи. В методах этого направления условия скорейшего спуска опреде¬
ляются на каждом шаге итерационного процесса, что приводит к
целенаправленному выбору допустимых вариаций 5 Y(t), которые должны
обеспечивать сходящуюся минимизирующую последовательность F-+G,
где G — искомый минимум, ад— номер итерации. Указанные функцио¬
нальные методы разделяются на две группы: градиентный спуск в фазовом
пространстве (в случае вариаций 6 Y = 6Х) и градиентный спуск в прост¬
ранстве управлений (когда 6 Y = ди).
Использование градиентных функциональных методов приводит к необ¬
ходимости решения экстремальной задачи поиска минимума функции ко¬
нечного числа переменных
/ = /(<?! Cj).
(3.58)
Здесь параметр спуска С/, размерность которого совпадает с размерностью
74
г управляющего воздействия и, определяет длину шага вдоль направления
движения к искомому минимуму G исходной задачи оптимизации. Итера¬
ционная процедура определения минимума G сводится к нахождению на¬
правления градиента функционала и отысканию каким-либо регулярным
способом длины шага спуска С. Практическим и достаточно эффективным
способом определения длины шага С является аппроксимация нескольких
итерационных решений (например, использование параболической аппрок¬
симации) с последующей проверкой найденного экстремального значения
С* на возможный текущий минимум функционала / для некоторого за¬
крепленного направления градиента. После исчерпания возможностей мини¬
мизации текущего направления к минимуму осуществляется переход к но¬
вому направлению, для которого также исследуется возможность отыска¬
ния шага С*. В результате нахождения экстремальных параметров спуска
С* (для каждого текущего направления движения к минимуму G) прин¬
ципиально определяется сходящаяся минимизирующая последовательность
/м -> G. Степень сходимости, характеризующаяся величиной общего числа
итераций д, в большой степени зависит от возможности и эффективности
нахождения экстремального параметра С*, фактическая процедура отыска¬
ния которого устанавливается только при численном машинном решении
исходных оптимальных задач.
Рассмотренные современные методы решения оптимальных задач про¬
граммного управления приводят к необходимости решения эквивалентных
задач математического программирования. На основании описанных вычис¬
лительных алгоритмов можно сделать вывод, что принципиально вычисли¬
тельная процедура решения имеет одну и ту же структуру. В зависимости
от выбранного метода решения конкретной оптимальной задачи указанная
общая задача математического программирования представляет или
экстремальную задачу (3.53) и (3.58), или задачу нелинейного программи¬
рования (3.55) , или последовательность экстремальных задач (3.56).
Следовательно, эффективность решения задач оптимального управления
фактически определяется уровнем развития соответствующих методов
решения экстремальных задач математического программирования.
Рассмотренные в этом параграфе современные методы решения задач
оптимального управления предполагают использование достаточно слож¬
ных вычислительных процессов получения решения. Поэтому эффектив¬
ность каждого метода в конечном счете зависит от обоснованно выбранного
способа решения соответствующей задачи математического программирова¬
ния. Вместе с тем достаточно распространенным является мнение о всесиль-
ности известных методов оптимизации для решения прикладных задач
оптимального управления, в силу которого считается, что выбор метода
решения и использование известных приемов формализации и численного
решения должны достаточно быстро и гарантированно приводить к успеху.
Несмотря на известные сложности решения прикладных оптимальных
задач и отсутствие эффективных вычислительных процедур численного
решения, использование методов теории оптимального управления остается
на сегодняшний день наиболее обоснованным и универсальным средством
исследования. Разработка специальных методов решения задач математиче¬
ского программирования, соответствующих исходным вариационным
задачам, позволит значительно повысить эффективность методов теории
оптимального управления в процессе численной реализации.
РАЗДЕЛ II
СПУСК КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА
НА ПОВЕРХНОСТЬ ПЛАНЕТЫ
Глава 4
МАКСИМИЗАЦИЯ КОРИДОРА ВХОДА В АТМОСФЕРУ ПЛАНЕТЫ
И МИНИМИЗАЦИЯ МАКСИМАЛЬНОЙ ПЕРЕГРУЗКИ
§ 4.1. Постановка задачи
Шириной коридора входа КЛА в атмосферу планеты называется раз¬
ность углов входа
A0=0?-0S
или разность высот условного перицентра
АЛ 7Г = - Л" ,
соответствующих верхней и нижней границы коридора. Нижняя граница
коридора входа соответствует такому наименьшему значению угла входа
0О = Oq (или высоты условного перицентра = h ”), при входе с кото¬
рым на траектории спуска еще возможно обеспечить выполнение постав¬
ленных ограничений и конечных условий; верхняя граница соответствует
такому наибольшему значению угла входа 0О = (или высоты = /?®),
при входе с которым на траектории спуска также выдерживаются задан¬
ные ограничения и конечные условия. Таким образом, при входе КЛА в
любую точку коридора входа обеспечивается безопасный спуск с выдер¬
живанием основных ограничений на фазовые координаты траектории
спуска.
Одним из основных ограничений, накладываемых на траекторию спуска
КЛА в атмосфере планеты, является ограничение на величину допусти¬
мой перегрузки
П<ЛдоП. (4.1)
Кроме того, в ряде случаев может возникнуть необходимость в удовлет¬
ворении некоторых других условий (ограничение на минимально допусти¬
мую высоту пролета КЛА над поверхностью планеты, посадка в заданный
район, выдерживание заданных значений конечной скорости спус¬
ка и т.д.).
Задача максимизации коридора входа заключается в поиске таких оп¬
тимальных законов управления КЛА, которые реализуют максимальное
значение верхней границы коридора входа (/7®->тах) и минимальное зна¬
чение нижней границы коридора входа (/?£->min) при выдерживании на
траектории спуска поставленных ограничений.
Запишем уравнения движения центра масс КЛА без учета вращения пла¬
неты в виде
dV cx(a)pV2s g0RQsm6
dt 2m (RQ+h)2
76
dO cy(a)pVs g0RQCos6 VcosO
= ■ cos у +
dt 2m V(R0+h)2 Ro +h
dh
= l/sin e,
dt
где p = Ръе~$н — плотность атмосферы; a — угол атаки; у — угол крена,
сх и су — соответственно коэффициенты силы лобового сопротивления и
аэродинамической подъемной силы; /?0 — радиус планеты; V — скорость
полета; 0 — угол наклона траектории к местному горизонту; h — высота
полета.
Введя, безразмерные переменные [84] ух, у2, Уз, v > т с помощью соот¬
ношений
V
У2=6' Уз=№' и = cos у,
систему уравнений движения запишем следующим образом:
—2
=-cx(a)c0/?e‘J'3-(l) siny2=/lr
dr \ 0Яо >
dy2
dr
(4.2)
=0Яо Ki sin у2 =f3,
dr
где с0 = PqS Ro/2т .
Условие (4.1) в безразмерных переменных запишется в следующем
виде: ,
Я1(У1.Уз,сх(а), су(а)}=п — с0у1е~Уз\/сх+Су<0. (4.3)
Сформулируем следующие задачи Майера по определению нижней и
верхней границ коридора входа:
найти траекторию, удовлетворяющую уравнениям (4.2), краевым ус¬
ловиям
И1<0) = К1, Кз(0)=Уз ■ У1(Т)=у1к, Уз(Т} = Узк (4-4)
(О < Т, Т — свободно) и ограничениям
д,(т)<0 '(/=1,2 т) <4-5>
(где т— количество ограничивающих факторов), которой соответствует
max(О *
найти траекторию,удовлетворяющую связям (4.2), краевым условиям
(4.4) и ограничениям (4.5), которой соответствует miny2 (0).
Приведем в общем виде необходимые условия экстремума для сформу¬
лированных задач Майера, предполагая, что управление КЛА осуществляет¬
ся путем изменения углов атаки а и крена 7 [84]. При этом будем считать,
что на величину угла крена ограничений не накладывается, но функция
u =cos7 ограничена I и I <1. Рассматриваются только положительные
значения угла атаки 0 <а <а0-
77
Запишем функции Гамильтона и Лагранжа в виде
К = + X2f2 + X3f3,
F = JC + jzqz + Mi (1 - u) + (1 + i/) + /л3а + (a0 — a),
(4.6)
(4.7)
где X/, Fi ~ множители Лагранжа.
Необходимые условия оптимальности могут быть описаны следующим
образом [25] :
d\i
dr
djf dQz
+ 111
d/z d/z
(/ = 1,2,3,...);
(4.8)
dF
= 0,
da
gzgz = 0, ^3a = 0, M4<ao-a) = O,
dF
=0, gl(1-u)=0, м2(1 +у)=0. (4.9)
du
На оптимальной траектории спуска должно удовлетворяться условие
Вейерштрасса
max Jf(y (f), X (t), a, v} = X(t), a(t), u(t)). (4.10)
a,v
§ 4.2. Максимизация верхней границы коридора входа
Определение верхней границы из условия захвата КЛА атмосферой.
Для КЛА "скользящего" типа, управление которыми осуществляется из¬
менением угла крена у, сформулированная вариационная задача о макси¬
мизации верхней границы коридора входа из условия захвата КЛА
атмосферой и при отсутствии каких-либо ограничений на траектории спуска
имеет достаточно тривиальное решение, а именно, верхняя граница опреде¬
ляется с использованием программы /Сэфф = ~^бал-
В табл. 4.1 —4.7 приведены численные результаты решения задачи мак¬
симизации для КЛА, имеющих различные проектно-баллистические
характеристики и осуществляющих вход с траекторий прямого перелета
в атмосферы планет Солнечной системы. Видно, что изменение величины
аэродинамического качества Кбал, приведенной нагрузки на лобовую
поверхность Рх, а также плотности атмосферы р оказывает одинаковое
качественное влияние на величину max А®. Возрастание аэродинамического
качества и увеличение плотности атмосферы приводят к смещению верхней
границы коридора в сторону ее увеличения. Тот же эффект достигается
и при уменьшении величины приведенной нагрузки на лобовую поверхность
и начальной скорости VQ входа КЛА в атмосферу.
Следует отметить, что степень влияния перечисленных факторов1 на
величину тахй^ существенно отличается для различных планет
(табл. 4.8). Данные, приведенные в этой таблице, показывают, что для всех
планет Солнечной системы, обладающих атмосферой, наиболее эффектив¬
ным способом смещения верхней границы коридора входа является из¬
менение величины аэродинамического качества, а наименее эффективным —
изменение величины приведенной нагрузки на лобовую поверхность.
Видно также, что наибольшее изменение величины max/?* за счет варьиро¬
вания основных факторов (начальной скорости входа VQ, аэродинамичес-
1 В диапазонах их изменения, приведенных в табл. 4.1 —4.7.
78
Таблица 4.1
Параметры траекторий спуска в атмосфере Земли
(исходные параметры: Ло = 100 км, = 11 км/с, Рх = 500 кгс/м2, К"бал = 0,3; Р = Рном)
см
CDCMOOOt-CD'oO
О CD XI X г- со
т- СО г- см г-
Т- см г- М- со
00 <- ср in о
77 '77
in
03
LD СО Г" со см
CD (XI 00
I II-
CM
t—
x-
CD
CD
r—
co
in
»—
CM
CM
*—
,(М
T—
x-
Г"
in
co
CM
1
1
CM
co
LD
CM
CD^
co
CM
oo'
in
co'
CD
r-'
cm'
cm'
co'
co
Г"
CD
CD
CD
CD
•'fr
1"-
CM
00
CM
CO
T—
CM
CM
ш
CM CD со
г-' оз' ю
in ю
r^LDCMCO^fr^^fOO
COCM’tlOCOOCDr-
Т- 00 I я- см CD I (XI
I I I I I I
1П (N (D СО.
Г**' Г^' 00
Ш 1П 1П
X
rt
Е
с:
ID СЮ Ю ID Ф Ф Г- см
ю см х" ю in in in oo'
S
II
co
in
°4
03
<o
oo'
о
o'
оз'
оз'
r-'
re
xt
о
CD
in
CD
о
CM
CM
CM
CM
CM
CM
*
Я k
С
CO
in CM 03 C*3
Г*? I< СК)' Kf r-
in in in
in
о
CD
CD
о
00
xt
03
о
00
CM
re
CD
in
re
CM
CD
re
re
in
1—
CO
00
00
in
00
in
CD
Г"
00
CD
о
in
re
re
in
CD
Г"
re
xt
co
xr
*
I I I I I I I I
ID
00
CM 03
00
x-
LD
00
00
00
co <-
x-
Г"
CM
CM
у
1 °?
1
CM
re
CM
I I II
ry. 00
in CD
00
CD
xr
CM
^r
CD
’tf-
03
xr
03
1 re
CM
CM
00 00
r- co
7? 1
X- 00
o' V-' о
X-
r^- CD
CM r*
CM «-
CM
I
I
CD
xt
CO
I
in CD r-
1П CO co'
x (O x
X CO (N st Щ CD <-
О o' V-' oo' оз' in oo' co'
XXXincOXCDX
LO
Г*
I
00
со о О 00 О СМ
<- оо со st со <-
СМ т— т-
00 со о со «-
СМ 'С >
00 г* со
00 st см
'7 |
г*
г*
I
со
st
I
СО
г*
7
оо со со со
7777
Г"
со
7
СЮ
st СО СО st СО
СО со St СО <-
St
со
I
О)
LO о' СО Г"** СО
CM st О) см со
I III
г- оо см о) st
LO со' o' 1Л Г*' см' Г"-'
00 Г* СМ СО st t-
00 <- <-
Ю О
О) LO
см
sr аэ
см' со'
со <-
аэ сп см^ о\
st LO г-'
00 00 st co
St
аэ
см
г*
со'
St
CD О st st СЮ
оо' o' оо' О)
СО st 00 см оо
см_ о) о) аэ О) о о сп ld
’-' см' Г-' см' ,—' ' см' '
00^ СО CN О St О st st аэ
со' <-' <-' О) Г-' St О) to со' St Г-' со'
СМ 00 СО СО Т- Г- оо см см о г*
т— СМ <- см
г*
I
со
Г"
7
оо со со
77?
00
г*
г*
00
7
5
*
д £
с
сю
СП
СМ
о
st
Г"
О)
st
st
00
St
in
st
оо'
со'
оо'
о'
Т-'
оо'
О)
00
СО
St
00
СМ
st
00
St
СО
СМ
00
ф
л
S
ф
>
о.
S
л
о.
(□
со
о.
(-
ф
S
I II II
о С II II II II
Ь Ь Q. Q. Q. Q.
U
I—
¥
О
о
ID
II
ОМ
о °
и 11
5 §
II X X ю ю
о. а. а.
00
st
CM
co
00
in
Г'»
St
Г'»
о
00
CM
о
Таблица 4.6
Параметры траекторий спуска в атмосфере Урана
(исходные параметры Ло = 500 км, 1/0 = 28 км/с, Рх = 500 кгс/м2, Kgan = 0,3; р = РцОМ)
S
о
я
Q.
II
Q.
= 29 км/с 75,5 -462 537,5 6,7 75,5 8 77,5 -462 -462 0
= 200 кгс/м2 85,2 -716 801,2 5,5 85,2 -2812 2897,2 85,2 -716 801,2
= 700 кгс/м2 53,8 -734 787,8 5,5 53,8 -382 435,8 -734 -734 0
эал = 0,2 46,1 -536 582,1 7,5 46,1 -643 693 -338 -536 192
□ал = 0,5 74,3 -1262 1336,3 4,2 74,3 -739 813,3 -545 -1262 7 77
кого качества /Сбал и приведенной нагрузки на лобовую поверхность Рх)
достигается при спуске КЛА в атмосфере Сатурна, а наименьшее: по началь¬
ной скорости входа — при спуске в атмосфере Земли, по величине аэроди¬
намического качества — при спуске в атмосфере Венеры, по величине приве¬
денной нагрузки на лобовую поверхность— при спуске в атмосфере Земли.
В табл. 4.1 — 4.7 приведены также значения максимальной перегрузки
лтах, достигаемой КЛА при движении по верхней границе коридора входа.
Видно, что наибольшие значения максимальной перегрузки достигаются при
движении КЛА в атмосфере Юпитера (пт а х ~ 10-^20) , а наименьшие - при
движении в атмосфере Марса (лтах ~ 1,2^2,7) .
Ограничение на суммарный тепловой поток. Движение КЛА вблизи
верхней границы коридора входа, определенной из условия захвата КЛА
атмосферой планеты при полете с /Сэфф — "“^бал, может сопровождаться
большими тепловыми нагрузками, причем величина суммарного теплового
потока возрастает с увеличением Л®. Поэтому в ряде случаев оказывается
необходимым при определении верхней границы коридора входа, наряду с
условием захвата КЛА атмосферой, учитывать и ограничение на величину
суммарного теплового потока < ^Едоп) • Данные по оценке верхней
границы коридора входа в атмосферу планет Солнечной системы для КЛА
"скользящего" типа при ограничении на величину суммарного теплового
потока также приведены в табл. 4.1 — 4.7.
Представленные в них материалы позволяют оценить влияние основных
факторов — начальной скорости входа, приведенной нагрузки на лобовую
поверхность, аэродинамического качества, параметров атмосферы — на
верхнюю границу коридора входа. Тем самым оказывается возможным
выявить основные пути расширения коридора входа за счет соответствую¬
щего смещения верхней границы Л®. Анализ численных результатов пока¬
зывает, что для рассматриваемых планет характер зависимости Л® от приве¬
денной нагрузки на лобовую поверхность Рх и аэродинамического качест¬
ва К'бал одинаков. А именно смещение верхней границы коридора входа в
сторону увеличения Л® может быть достигнуто при уменьшении Рх и увели¬
чении ЛГбал- Аналогичный эффект имеет место для всех планет и при умень¬
шении начальной скорости входа.
Проведенные исследования показывают также, что существенное влия¬
ние на величину Л® оказывает изменение допустимой величины суммарного
теплового потока. Так, например, для КЛА, осуществляющего спуск в ат¬
мосфере Земли (Уо = 11 км/с, Рх = 500 кгс/м2 и К'бал = 0,3), изменение
ОЕдоп на 10 кВт/см2 ведет к смещению верхней границы коридора входа
примерно на 150 км, а при спуске в атмосфере Юпитера (Vo =65 км/с,
Рх = 300 кгс/м2 и Х'бал = 0,3) аналогичное изменение Оедоп приводит к
смещению /?® примерно на 60 км.
Совместное управление углами атаки и крена. Рассмотрим КЛА "сколь¬
зящего" типа и типа "несущий корпус". Зависимость аэродинамических
коэффициентов от угла атаки для первого типа КЛА имеет вид [84]
сх = 0,1363 + 1,624 | sin3a |, су = 1,624 | sina | sinacosa. (4.11)
Для второго типа КЛА эти зависимости могут быть приближенно
аппроксимированы следующими формулами:
сх = 0,2175 + 2,364о? = сх0 + k^a2, су = 1,41а = ^,а; (4.12)
сх = 0,116 + 2;7a2, су = 1,6а; (4.13)
сх =0,0725 + 2,84а2, су = 1,7а. (4.14)
83
Таблица 4.8.
Изменение верхней границы коридора входа
Э/7*
ЭЛ®
ЭЛ®
Планета
г
км
, км • м“ /кГС
а '
Э ^бал
Венера
-0,9
16,425
-0,0322
Земля
0,225
22,75
-0,0166
Марс
0,45
32,25
-0,0312
Юпитер
3,924
141,925
-0,15
Сатурн
39,62
194,75
-0,151
Уран
7,1
146,5
-0,099
Нептун
8,15
89,02
-0,0627
Используя (4.8) — (4.10), для КЛА типа "несущий корпус" получим сле¬
дующий закон оптимального управления углом крена и атаки при движе¬
нии по верхней границе коридора входа:
• ч / к / 9 / Xi /] \
v = sign Х2 (т), tga =——— + V — — + 2,
21Х2 I 4x^2
(4.15)
0<а<7г/2.
Численные расчеты оптимальных траекторий спуска показали, что для
КЛА типа "несущий корпус" характерным является следующее оптималь¬
ное управление [84]. Аппарат входит в атмосферу с максимальным отрица¬
тельным значением управляющего параметра v = — 1. Угол атаки в момент
входа в плотные слои атмосферы составляет некоторое значение мень¬
шее угла атаки а, соответствующего максимальному значению коэффициен¬
та cv. Затем в процессе снижения в атмосфере угол атаки а уменьшается до
значения а2, соответствующего коэффициенту сх, близкому к его мини¬
мальному значению (сх ~0,1 -?0,15) . [Отметим, что на некоторых оптималь¬
ных траекториях, соответствующих небольшим допустимым перегрузкам,
угол атаки а может сначала несколько увеличиться, а затем уменьшиться.
При этом оптимальная траектория может содержать участки движения по
ограничению (4.1) , а угол атаки а2 может стать равным нулю.] В дальней¬
шем до конца траектории спуска происходит непрерывное увеличение уг¬
ла атаки а; второй управляющий параметр v на всей траектории спуска
остается неизменным (и =— 1).
Оптимальное управление КЛА "скользящего" типа при движении по
верхней границе коридора входа определяется следующими выражениями
[84] :
1/ = sign{Л2 (т)}, (4.16)
а = а0, если
I Х2 I
2£2/Л1
*1 |Х2 I
2£2У1а0
если
Х1(т),
< Ai (т).
(4.17)
(4.18)
к 1 I ^2 I
2^2 И1
Численные расчеты показали, что для КЛА "скользящего" типа типич¬
ным является следующий закон управления углом атаки а и параметром v.
84
С момента входа в атмосферу имеется некоторый интервал времени
в течение которого поддерживается постоянное значение обоих
управляющих параметров: а = aQ и v(t) = — 1. Угол атаки а0 близок к
углу атаки а , соответствующему максимальному значению коэффициен¬
та Су. В некоторый момент времени t = G начинается уменьшение угла
атаки а в соответствии с (4.18) . После достижения значения а = alf кото¬
рое может стать и нулевым, происходит возрастание угла атаки до величи¬
ны а = aQ при v (т ) = — 1. Близкое к нулю значение угла атаки а = а0 и
значение второго параметра v(t) = — 1 выдерживаются постоянными до
конца оптимальной траектории спуска. Как показали исследования, пре¬
дельное значение перегрузки при движении КЛА по верхней границе кори¬
дора входа достигается не всегда.
§ 4.3. Минимизация нижней границы коридора входа
Ограничение на максимально допустимую перегрузку. Решение задачи
минимизации нижней границы для КЛА "скользящего" типа, управляемого
углом крена, при ограничении на величину максимальной допустимой пере¬
грузки сводится к поиску оптимального управления аэродинамическим
качеством, обеспечивающего минимальное значение высоты условного
перицентра, при входе с которой достигается максимальная перегрузка
/7т ах = лдоп- В общем случае для КЛА "скользящего" типа сформулиро¬
ванная задача решается как и в случае максимизации h%, достаточно три¬
виально: нижняя граница определяется с использованием программы
Кэфф = ^бал- Следует отметить, что при полете с /Сэфф = по нижней
границе в ряде случаев может не выполняться условие по захвату КЛА
атмосферой планеты.
Для расчета нижней границы коридора входа с учетом ограничения по
перегрузке и выполнения условия захвата КЛА атмосферой используется
оптимальная программа, заключающаяся в двухразовом переключении
эффективного аэродинамического качества [25] :
^эфф ” ^^бал/ ^бал/ + ^бал-
Заметим, что полет КЛА до момента достижения максимума перегрузок
протекает с постоянным положительным значением /Сэфф = Кбгп. Момен¬
ты последующих переключений /^Зфф на —/<бал, а затем снова на +/<бал
выбираются из условия захвата КЛА атмосферой.
В табл. 4.1 — 4.7 приведены дополнительно некоторые результаты реше¬
ния задачи минимизации нижней границы коридора входа для КЛА с
различными значениями проектно-баллистических характеристик, осу¬
ществляющих вход в атмосферы планет Солнечной системы с различными
значениями начальной скорости входа. Видно, что уменьшение нижней гра¬
ницы коридора входа достигается при уменьшении начальной скорости Vo
и увеличении основных проектно-баллистических характеристик КЛА: при¬
веденной нагрузки на лобовую поверхность Рх и аэродинамического качест¬
ва К'бал • Эта закономерность остается неизменной при входе КЛА в атмо¬
сферу любой из рассматриваемых планет.
Кроме того, проведенные исследования показали, что существенное сме¬
щение нижней границы коридора входа может быть достигнуто при измене¬
нии величины допустимой перегрузки. Так, при входе КЛА в атмосферу
Земли (Vo = 11 км/с, Рх = 350 кгс/м2 и /Сбал = 0,3) изменение величины
Лдоп на 100 единиц приводит к смещению /?“ примерно на 350 км, а при
85
Таблица 4.9
Нижняя граница коридора входа при спуске в атмосфере Марса
1/0, км/с
6 ■
5
7
6
6
6 j
6
6
6
^бал
0,3
I
0,3
0,3
0,3
0,3
г 1
0,3
0,3
0,2
0,4
Рх, кгс/м2
350
350
350
200
500
350
350
350
350
^ДОП' км
6
6
6
6
6
3
9
6
6
h™, км
-182
-215
-162
-228
-130
-260
-120
-128
-280
км
227
280
220
173
333
307
133
338
142
входе КЛА в атмосферу Юпитера (Vo = 65 км/с, Рх = 300 кгс/м2 и
^бал = 0/3) — примерно на 900 км.
Ограничение на минимально допустимую высоту полета. При снижении
КЛА на планету, обладающую разреженной атмосферой (в первую очередь
на Марс), одним из важных является ограничение на минимально допусти¬
мую высоту полета над поверхностью планеты. Оптимальной программой
управления, реализующей минимальное значение нижней границы коридора
входа при наличии этого ограничения, является программа полета с по¬
стоянным максимальным значением эффективного качества [24] /СЭ(Ь(Ь =
= +*бал.
В табл. 4.9 приведены некоторые численные результаты расчета нижней
границы коридора входа для КЛА, осуществляющих спуск в атмосфере
Марса.
Приведенные данные показывают, что нижняя граница коридора входа
h* существенно зависит от основных рассматриваемых параметров: приве¬
денной нагрузки на лобовую поверхность Рх, аэродинамического качества
^бал/ начальной скорости входа Уо и минимально допустимой высоты
полета Лдоп. Нижняя граница коридора входа возрастает при увеличении
Уф И При уменьшении Кбал-
Ограничение на максимально допустимую температуру. При снижении в
атмосфере планет аппаратов, имеющих радиационную систему теплозащи¬
ты, важную роль играет ограничение на максимально допустимую темпера¬
туру поверхности КЛА. В табл. 4.1 — 4.7 приведены некоторые результаты
решения задачи минимизации нижней границы коридора входа при ограни¬
чении на Гт ах для КЛА, осуществляющих спуск в атмосфере планет Сол¬
нечной системы. Видно, что расширение коридора входа за счет соответ¬
ствующего смещения нижней границы h* при наличии ограничения на мак¬
симально допустимую температуру поверхности КЛА может быть
достигнуто за счет уменьшения начальной скорости входа в атмосферу и
величины приведенной нагрузки на лобовую поверхность. Изменение вели¬
чины аэродинамического качества оказывает слабое влияние на нижнюю
границу коридора входа.
Следует отметить, что заметное уменьшение нижней границы коридора
входа достигается при увеличении допустимой температуры на поверхности
КЛА. Так, при спуске в атмосфере Земли (Уо = 11 км/с,Рх = 500 кгс/м2,
Кбал = 0,3) изменение величины Тдоп на 100 °C приводит к смещению h*
на величину около 60 — 80 км, а при спуске в атмосфере Юпитера (Уо =
= 65 км/с, Рх = 300 кгс/м2, Кбал = 0/3) — на величину около 180 —
200 км.
86
Совместное управление углами атаки и крена. При движении по нижней
границе коридора входа КЛА "скользящего" типа или типа "несущий кор¬
пус" оптимальное управление определяется выражениями (4.15) — (4.18).
Расчеты показали, что для КЛА типа "несущий корпус", типичным является
следующий закон управления [84].
Летательный аппарат входит в атмосферу при I/ = 1 и с углом
атаки Qi, удовлетворяющим условию а < < а, где а соответ¬
ствует величине /Стах, а а — величине сутак. После момента входа
(т > 0) угол атаки а(т) уменьшается, угол крена становится равным
нулю (v = 1) . В процессе спуска перегрузка нарастает и в некоторый мо¬
мент достигает предельно допустимого значения. В дальнейшем угол атаки
а(т) уменьшается до нуля с целью выдерживания допустимого значения
перегрузки. После достижения углом атаки нулевого значения имеется не¬
который произвол в управлении обоими параметрами (а и у) .Этот произ¬
вол обычно используют для обеспечения поставленных в задаче требований
по конечным условиям снижения в атмосфере.
Для КЛА "скользящего" типа оптимальное управление при движении по
нижней границе коридора заключается в следующем [84]. Летательный ап¬
парат входит в атмосферу при v = 1, а = aQ. На некотором начальном
интервале времени (0, т) КЛА движется с постоянным начальным углом
атаки а(т) = а0. Далее угол а(т) уменьшается до некоторого значения, при
котором достигается максимально допустимая перегрузка. Для того чтобы
удовлетворить условию движения с постоянным значением перегрузки,
угол атаки уменьшают до нуля. Как и для КЛА типа "несущий корпус",
после достижения углом атаки значения а = 0 в управлении углами атаки
и крена остается некоторый произвол, зависящий от величины (лта х)ДОп-
§ 4.4. Анализ коридоров входа для различных планет
Солнечной системы
Ограничение на максимально допустимую перегрузку. В табл. 4.1 - 4.7 и
на рис. 4.1. приведены некоторые результаты решения задачи максимизации
коридора входа в атмосферы планет КЛА "скользящего" типа при
ограничении на максимально допустимую перегрузку. Анализируя пред¬
ставленные материалы, можно сделать ряд выводов, справедливых для
всех рассмотренных планет и случаев подхода к плотным слоям атмос¬
феры.
1. Коридор входа практически не зависит от нагрузки на лобовую по¬
верхность, а только смещается по высотам условного перицентра. При этом
ббльшим значениям Рх соответствует более низкое по расположение
коридора.
2. Использование КЛА, обладающих даже малым значением аэродинами¬
ческого качества, приводит к значительному расширению коридора входа
по сравнению с баллистическими КЛА, что свидетельствует об эффектив¬
ности использования КЛА "скользящего" типа.
3. С увеличением Кбал происходит расширение коридора входа, причем
это достигается в основном за счет снижения нижней границы в сторону
меньших высот услдвного перицентра.
4. Увеличение начальной скорости приводит к существенному сужению
коридора входа в атмосферу.
5. Значительное расширение коридора входа достигается при увеличении
максимально допустимой перегрузки. Ширина коридора входа становится
равной ширине навигационного коридора (см. гл. 2) при следующих значе¬
87
ниях величины максимально допустимой перегрузки:
для Венеры лдоп = 2СН25,
для Земли Лцоп — 25-гЗО,
для Марса лдоп = 5-НО,
для Юпитера лдоп = 8СН100,
для Сатурна лдоп = 5СН-70,
для Урана лдоп = 6СИ80,
для Нептуна лдоп = 9СН100.
Следует отметить, что использование двухпараметрического управления
(углами атаки и крена) по сравнению с однопараметрическим (углом кре¬
на) позволяет значительно расширить коридор входа ЛА в атмосферы пла¬
нет. В табл. 4.10 приведены максимальные коридоры входа в атмосферу
Земли аппаратов типа "несущий корпус" и "скользящего" типа для различ¬
ных значений относительной начальной скорости входа и допустимой вели¬
чины максимальной перегрузки. Здесь приняты следующие обозначения:
(а, 7 = var) — максимальная ширина коридора входа при двухпара¬
метрическом управлении аппаратом; Д/?я (а = const) — то же при управ¬
лении только углом крена; ДЛ”Р — ширина коридора входа, рассчитанная
по приближенным зависимостям.
Используя эти данные, можно оценить эффективность двухпараметри¬
ческого управления по сравнению с однопараметрическим. Видно, что с
увеличением относительной скорости входа эффективность двухпараметри¬
ческого управления падает для КЛА любого типа. Так, например, для КЛА
Рис. 4.1. Зависимость ширины коридора входа от аэродинамического качества
^бал ПРИ входе КЛА в атмосфеоу Земли [|/() = 1,2; сплошные линии — численные
расчеты на ЭВМ, штриховые — расчеты по формуле (4.19) ].
88
Таблица 4.10
Эффективность двухпараметрического управления
CXf су
1/()
Ио =
Чср
лдоп
(а,7 =var), км
Д/7Я (а = const), км
ALnP
Д/7Я , КМ
1,2
8
316
102
298
1,5
8
140
46
152
—
3
1,8
8
86
78
33
<л
о
2,5
8
38
18
32
С
(Л
3
1,2
10
406
143
387
с
1„5
10
189
61
172
СМ
—
1,8
10
108
35
96
CD
3
с
2,5
10
42
26
38
+
СО
сл
1,2
15
582
226
560
со
со
см
со
1,5
1,8
15
15
263
126
83
44
251
114
о‘
II
2,5
15
55
34
47
И
>>
1,2
20
787
318
753
о
CJ
1,5
20
356
122
341
1,8
20
181
57
170
2,5
20
78
39
69
%
1,2
10
264
158
251
S
1,5
10
138
41
126
со
1,8
10
56
35
48
См"
+
2,5
10
33
16
27
LD
Гч
3
1,2
20
590
310
572
СМ
5
1,5
20
228
91
214
о'
II
и*
II
CJ
1,8
20
140
52
129
2,5
20
43
18
36
сч
1,2
10
438
160
422
1,5
10
192
68
178
см
+
1,8
10
92
38
80
CD
d
2,5
10
43
18
36
CD
1,2
20
842
316
816
о'
II
II
1,5
20
362
110
349
к
о
о
1,8
2,5
20
20
183
78
62
38
172
69
гч
3
1,2
10
510
162
490
’Т
со
1,5
10
220
78
203
СМ
1,8
10
121
42
110
+
Ю
2,5
10
58
31
44
СМ
Гч
3
1,2
20
975
165
945
<э
о'
II
г\
II
1,5
1,8
20
20
418
246
146
53
395
232
и
о
О
2,5
20
85
42
73
= 1,2 до Vo = 2,5 величина (а, у = var) - (а = const)
уменьшается с 214 км до 20 к;м (лДОп = 8) •
Ограничение на минимально допустимую высоту полета. В табл. 4.9
приведены данные по расчету коридора входа КЛА в атмосферу Марса ДЛЯ
при ограничении на минимально допустимую высоту полета над поверх¬
ностью планеты, которые позволяют оценить парциальное влияние основных
89
параметров (начальной скорости входа, аэродинамического качества, при¬
веденной нагрузки на лобовую поверхность и минимально допустимой
высоты полета) на ширину коридора входа. Видно, что коридор входа рас¬
ширяется при уменьшении /Сбал, и ^доп и увеличении Рх.
Полет на заданную дальность. Определим коридор входа при полете КЛА
на заданную дальность следующим образом [21]. Пусть Л® — высота услов¬
ного перицентра траектории входа, имеющей заданную дальность /_к (от¬
считываемую по поверхности планеты от линии апсид) при спуске с
постоянным отрицательным значением аэродинамического качества
^эфф — — АСбал, Q — высота условного перицентра траектории входа, ко¬
торая имеет ту же дальность при спуске с постоянным положительным зна¬
чением аэродинамического качества /СЭфф = Кбал- Диапазон высот услов¬
ного перицентра /?° < /?я < /?” определяет максимальный коридор входа
для заданной дальности £к и аэродинамического качества Кбал- Это озна¬
чает также, что для любого значения Е (Л°,Л”) можно подобрать такое
постоянное качество АГбал G (—+Кбзп) при спуске с которым даль¬
ность полета будет равна заданной. Приведенное определение коридора
входа исходит только из условия получения заданной дальности полета.
Если на траекторию спуска накладываются дополнительные ограничения,
например из соображений теплового режима или перегрузки, то это приво¬
дит к сужению коридора входа и к изменению программ управления КЛА
на границах коридора.
В табл. 4.11 приведены результаты численных расчетов коридора входа
в зависимости от величины допустимых перегрузок при спуске в атмосфере
Земли (Vo = 11 км/с, Рх = 500 кгс/м2) с постоянным качеством и заданной
дальностью полета в атмосфере.
Как и следовало ожидать, увеличение аэродинамического качества,
дальности полета в атмосфере и допустимой перегрузки приводит к расши¬
рению коридора входа.
Ограничение на суммарный тепловой поток. В табл. 4.1 — 4.7 приведены
результаты решения задачи максимизации коридора входа в атмосферы
планет при наличии ограничений на величину максимально допустимой пере¬
грузки и суммарного теплового потока. Эти материалы позволяют сделать
следующие основные выводы.
1. С увеличением начальной скорости VQ коридор входа сужается.
2. Увеличение приведенной нагрузки на лобовую поверхность также при¬
водит к сужению коридора входа.
3. Изменение аэродинамического качества не однозначно влияет на
ширину коридора входа. А именно, при входе КЛА в атмосферы Земли,
Юпитера, Урана и Нептуна возрастание аэродинамического качества приво¬
дит к расширению коридора входа. При снижении в атмосфере Венеры уве¬
личение А^бал приводит к сужению коридора входа. Увеличение аэродинами¬
ческого качества для КЛА, осуществляющих спуск в атмосфере Марса,
Таблица 4.11
Коридор входа при ограничении на заданную дальность
^бал
0,5
0,3
0,7
0,5
0,5
0,5
0,5
L, км
5000
5000
5000
2000
10 000
5000
5000
пдоп
20
20
20
20
20
10
30
А Л я, км
120
102
147
105
143
40
198
90
приводит сначала к некоторому уменьшению ширины коридора входа, а за¬
тем к ее увеличению. Для КЛА, осуществляющих спуск в атмосфере Сатур¬
на, наблюдается обратная картина, т.е. с увеличением аэродинамического
качества коридор входа сначала расширяется, а затем сужается.
Кроме того, исследования показали, что существенное расширение кори¬
дора входа достигается при увеличении допустимой перегрузки и уменьше¬
нии допустимой величины суммарного теплового потока.
Ограничение на максимально допустимую температуру. Данные, позво¬
ляющие оценить влияние всех основных факторов на ширину коридора
входа при ограничении на максимально допустимую температуру поверх¬
ности КЛА, приведены в табл. 4.1 — 4.7. Видно, что при оптимальном управ;
лении ширина коридора входа возрастает при уменьшении начальной
скорости входа, приведенной нагрузки на лобовую поверхность и при уве¬
личении максимально допустимой температуры. Изменение величины аэро¬
динамического качества не однозначно влияет на ширину коридора входа
при спуске в атмосферах различных планет. Так, при спуске в атмосфере
Земли, Юпитера, Сатурна, Урана и Нептуна увеличение аэродинамического
качества приводит к расширению коридора входа, а при спуске в атмосфе¬
рах Венеры и Марса, наоборот, к сужению коридора входа.
§ 4.5. Приближенные оценки коридоров входа
Управление углом крена. Определим ширину коридора входа в атмосфе¬
ру летательных аппаратов, управляемых углом крена, используя прибли¬
женные соотношения [1]:
Здесь
Лщах
(4.20)
(4.21)
Сравнение результатов расчета по формуле (4.19) с результатами числен¬
ного интегрирования показывает, что для КЛА, осуществляющих спуск в
атмосфере планет земной группы, формула (4.19) дает вполне удовлетво¬
рительные результаты. Причем точность расчетов повышается с увеличе¬
нием аэродинамического качества (см. рис. 4.1) .
При входе КЛА в атмосферы планет-гигантов расхождение между точны¬
ми численными расчетами коридора входа и приближенными по формуле
(4.19) достаточно велико (около 40 — 50%), что делает неприемлемым ис¬
пользование формулы (4.19) для практических расчетов величи¬
ны для.
Ниже приводятся приближенные соотношения, позволяющие с приемле¬
мой точностью проводить оценки коридора входа при ограничении на
91
величину допустимой перегрузки при входе в атмосферы планет-гигантов.
Основными параметрами, определяющими величину Д/?я при заданных
характеристиках атмосферы, как уже указывалось, являются: начальная
скорость входа 1/0, приведенная нагрузка на лобовую поверхность PXt
аэродинамическое качество /<бал и величина допустимой перегрузки лДОп-
Имеем:
— f( Уо, Рх, Кбзп, /?доп )• (4.22)
Разлагая (4.22) в ряд Тейлора и ограничиваясь членами первого порядка
малости, получаем
= ДЛ°"( У°", Р°п, К^п, ) + A Vo +
О У о
ЭД/?я .
+ ~ Д^доп •
О^ДОП
гпо 1/ОП РОП ^ОП «ОП
где Vo , Рх , К^п, лдоп
Частные производные определим следующим образом:
ЭД/?Я
— = Д1 (У0 )Д/7лрибл ( Уо, К™, лд°опп ),
(4.23)
(4.24)
опорные (исходные) значения параметров.
эд/?я
I/;", р,. I.
(4.25)
ддля
=Дз (Кбал) ДЛ"рибл(1/°п, Р™, К5ал, ),
О^бал
ЭД/7Я _
— -/МЛдоп^тг (V'o ,Рх '^бал'Лдоп)-
^доп
(4.26)
(4.27)
Для получения коэффициентов Д,- достаточно провести расчеты величи¬
ны коридора входа численным методом и по формуле (4.19) в трех точках,
которые для каждого варьируемого параметра задаются, как правило, на
концах интервала варьирования и в его середине (опорное значение) .
Используя найденные значения коэффициентов Д,- в трех точках, можно
получить достаточно точную аналитическую аппроксимацию (до 1%)
функций Д1 (VQ), А2 (Рх) , Д3 (Х'бал) и ^4 (ЛдОП) в виде полинома
Лагранжа второй степени.
В качестве примера получения приближенной зависимости по оценке ши¬
рины коридора входа летательных аппаратов, управляемых углом крена,
рассмотрим случай спуска КЛА в атмосфере Сатурна. Предположим, что
основные варьируемые параметры изменяются в следующих пределах:
35 км/с < Vo < 38 км/с,
50 кгс/м2 <600 кгс/м2,
0,2 <АГбал<0,8
(4.28)
50 < "доп <300.
92
В качестве опорных будем рассматривать следующие значения пара¬
метров :
Vgn = 36,5 км/с, Р°п = 300 кгс/м2, К£“л = 0,5, л°"п = 100. (4.29)
Представление зависимостей Аг (VQ) , А2(РХ), А3 (Кбал) и /А4(/7ДОП)
в виде полинома Лагранжа дает следующие аналитические выражения:
>41 (Vo) = 0,5391-Ю"9 - 0,0005294 1/0 + Ю,109165, А2 (Рх) = 0,6,
Дз(К'бал) =0,9472 К|ал - 1,8477 Кбал + 1,2823,
(4.30)
Д4 (лдоп) = 0,04305-10"4 п 2ОП - 0,2223-10"2 лдоп + 0,7908.
Исследования показывают, что использование приближенных выражений
(4.23) — (4.27), (4.30) позволяет получить достаточно высокую точность
(6—8%) при оценке ширины коридора входа КЛА ''скользящего'* типа.
Управление углом атаки. Эффект управления углом атаки для расшире¬
ния коридора входа можно оценить по следующей приближенной формуле
[1,2]:
Д/?я(а = var)
где а0 “ начальный угол атаки; а* — максимально допустимый угол атаки;
С2 — \/сх + Су *.
Исследования показали, что при спуске с переменным углом атаки
ширина коридора входа может быть значительно увеличена в основном за
счет уменьшения /?”. При этом наибольшее значение реализуется в
случае, когда начальный угол атаки близок к углу атаки, соответствующе¬
му суmax ,аа* соответствует С2 min •
В качестве примера рассмотрим спуск в атмосфере Земли. Предположим,
что КЛА типа "несущий корпус" обладает максимальным аэродинамичес¬
ким качеством /<бал = 1/54 при а = 0 и максимальным коэффициентом
подъемной силы сутах 0'5 при а = 30°. Расчеты показали, что использова¬
ние управления по углу атаки при входе в атмосферу Земли с гиперболи¬
ческими скоростями (Vo > 13 км/с) позволяет расширить коридор входа
по сравнению с управлением по углу крена. Так, при входе в атмосферу
Земли с начальной скоростью Vo = 13 км/с коридор входа расширяется
на 18—20 км, а при Vo = 18 км/с — на 8—9 км.
Совместное управление углами атаки и крена. В табл. 4.10 для сравнения
приведены коридоры входа при неоптимальном (приближенном) законе
управления углом атаки. Этот довольно простой закон управления заклю¬
чается в следующем [84] . На нижней границе КЛА входит в атмосферу при
некотором угле атаки а = eq , подбираемом эмпирически из условия полу¬
чения максимального по модулю угла входа. Движение КЛА с найденным
значением продолжается до достижения предельной перегрузки
п = лдоп. Далее происходит уменьшение угла атаки с целью поддержания
постоянного значения допустимой перегрузки.
93
Рассмотренный закон управления достаточно эффективен по сравнению
с оптимальным законом управления, так как существенно сокращаются
затраты машинного времени потребного для расчета нижней границы кори¬
дора входа, при незначительном ухудшении точности расчетов •/?” (вели¬
чина h^f полученная при расчете по приближенным формулам, отличается
от величины h*t полученной при оптимальном управлении, на несколько
процентов).
В случае движения КЛА по верхней границе коридора входа аналогичные
результаты (хуже оптимальных на несколько процентов) получаются при
движении КЛА с постоянными значениями углов атаки и крена (а = аь
у = 180°).
§ 4.6. Минимизация максимальной перегрузки
при заданной ширине коридора входа
Рассмотрим задачу минимизации максимальной величины перегрузки,
действующей на КЛА в процессе спуска в атмосфере. Особенностью этой
задачи является то, что минимизируемый функционал
“ лтах (4.31)
не является традиционным [25, 73, 97] . Это существенно затрудняет
формальную запись необходимых условий оптимальности.
В предположении, что поле тяготения планеты центральное, запишем
уравнения плоского движения центра масс КЛА с учетом вращения планеты
и уноса массы теплозащитного покрытия в виде
dV cxs pV2
= = — —————— — gsin0 + co rsinв,
dt m0 — CxSynmyH 2
dO cys pV2 3 -
f2 =— = cos 7 cost/ +
dt mQ — CxSynmyH 2 V
V co2r
+ — cos# + 2 co + cos0,
г V
dh (7/7? yH Qkohb
f3 =— = l/sinfl, /4 = =
dt dt t)
где
Ci = 0 при T(t) < Tp, C\ = d при 7"(t) > 7"p;
r(t) = Vta KOHB +адрад)/еа;
myn — масса теплозащитного покрытия, уносимая с единицы площади
поверхности КЛА; SyH — площадь поверхности КЛА, с которой происходит
унос массы; а — усредненный коэффициент, учитывающий неравномер¬
ность распределения уносимой массы на поверхности по сравнению с расчет¬
ной точкой, е— коэффициент, характеризующий излучательную способ¬
ность материала теплозащитного покрытия, а— постоянная Стефана —
Больцмана; А — коэффициент, характеризующий поглощательную способ¬
ность материала теплозащитного покрытия; В — коэффициент, зависящий
от газового состава атмосферы.
94
Трансформируем рассматриваемую задачу в задачу Майера, используя
замену переменных
CXS
К ~ = const.
2^о
Тогда система уравнений движения запишется в следующем виде [25] :
б/0 _ сур /рп~?
fi =— v cos7 — д
V =
кр
fi-
fs ~
f< =
si па,
gsin0 + 2
.32)
1 ,64^0,94
r— sin0 —2
С учетом сделанных преобразований сформулируем следующую вариа¬
ционную задачу: на участке основного аэродинамического торможения
требуется определить программу управления минимизирующую
функционал / = minnx(tK) при следующих граничных условиях:
0(Го) = ^о, Л(^о)=ЛО/ myH(t) = лх(Г0) = t0=const, (4.33)
0(ГК), - свободны.
(4.34)
Конечное время Гк определяется из условия dnx!dt I - 0.
1 Г - Гк
Введем в рассмотрение гамильтониан
сур !рпхт'
К = 1//! 0 + 1//2 Л + i//3^vh + ^4пх V
2т к
ф i cosy + F(t),
(4.35)
где F(t} — функция, не зависящая в явном виде от управляющего парамет¬
ра у. Сопряженные переменные i//z определяются следующими выраже¬
ниями:
d&i ЭК /кр ' /пхт' sin0 ,
— =_gyj—- ^1Sin0 + sj— +
dt Э0 nxm кр г
02COS0 + ^nlx,S
co2 r^tcosf),
d^2 ЭК /п~//р* , 2F-
= =cysy/ /301COS7-V -
dt dn кт nxm r
ф! cos 0 —
95
ЪгПу н
c-ylJEZm-^s.
4 к
COS0 пх
2г кр,
sin0 Гт
1,5
В
ri
/ кр
пх m
РФз
V
COS0 /nxm' COS0
Ф i T’ — v ЗФ i —
Г кр 2r
a)2cos0 /nxm' sin0
—— -V 0ф2 —
2 кр 2
n^5™1’5
Р'Ь +
К1 ’p
/кр' /кп xp' р
у/ (Зф4 + 4V ip4sin0 +
т т гл
/кпхр' . /кпх р'
— 2>/ co2^4sin0 + у/ co2r(3\p4sin 0 ,
m m (4.36)
gcos0 [кр^ .
yH^l^lCOS^ “ V m $уНС1Ф1
Z пх
- n*x’5 да у/крт 3l2SyiiCi^ -ду/к.рпхт 3/2SyHC! 4/4sin0 +
j пх
+ и2гу/крпхт~3128упС\^4Ып6 +—г £унС1ф4,
т
ЭК cvs /рпх gcosO /кр' _3/2
= -—V—- ip1cos7 V "х1 Ф1-
дпх 4 кт 2
cos0 / т 1
V
крпх
/ т ’
/ Ф 2 А 1 64 о 94
КрПх TJ K^V’^
m1’5 /тпх} , л /*РпГ .
В—-т- п°'5ф3 + 1,5|3у/ \p4sin0 + 3g0V Ф*-
к1,ьр кр т
Гкр'-' 1
• gsin0 — V co2r\p4sin0 +— ф4.
тпх т
с/ф4
c/t
2г
CyS /рпх
V 1P1COS7 —
4 кт
co2rcos0 /кр ’ _^/о
+ у/ п/'1
2 т х
т1’64
X
т
-
1,64
„0,64 ,i,
п х V3 -
тпх
96
Из условий трансверсальности находим граничные значения сопряжен¬
ных переменных при t = tK:
Ф1 (Ge) = V'sUk) = 0, iMrJ = - 1- (4*37)
Принимая во внимание, что система уравнений (4.32) автономна и вре¬
мя tK свободно, получаем
K(t)=0. (4.38)
Тогда с учетом (4.35) и (4.37) из уравнения (4.38) имеем
^2 (Гк )
dnx/dt
dh/dt
= 'к
Из выражения (4.35) видно, что максимальное значение гамильтона К по
величине эффективного качества достигается при
^эфф ^бал sign i//1.
Итак, на оптимальной траектории, реализующей min/?max, управление
по К'эфф релейно, а переключение /Сэфф с одного значения на другое долж¬
но происходить в те моменты времени, когда функция меняет знак.
Количество переключений эффективного качества определяется числом
нулей функции и выявляется лишь в результате численного решения
краевой задачи для систем (4.32), (4.36) и условий (4.33), (4.34), (4.37).
Следует отметить, что в том случае, когда оказывается возможным
использование более простых моделей движения (например, при спуске в
атмосферах Земли и Марса), в которых не учитываются такие факторы, как
унос массы КЛА, вращение планеты и т.д. (см. § 4.1), целесообразно
использовать другой путь преобразования исходной задачи [97], который
позволяет определить структуру оптимального управления на основе
анализа уравнений оптимального движения без решения краевой задачи.
Для этого используется приближенная форма записи уравнений движения
КЛА при следующих предположениях:
закон изменения плотнрсти по высоте имеет экспоненциальный вид;
угол наклона траектории к горизонту мал, а составляющая силы тяжести
вдоль направления полета много меньше сил аэродинамического тормо¬
жения:
sin0~0, cos0~1, I sin0 | < I nx |;
управление КЛА осуществляется путем изменения угла крена, а коэф¬
фициент лобового сопротивления на траектории спуска постоянен.
Учитывая изложенное,а также используя новые переменные
у=—, х = -1пй, ,кр=ТХ
2т Хр УКр 9°
уравнение движения КЛА можно записать в виде [97]
,, и
У = U,
У
где и = х/гХ’К'эфф/ у'
Проведя замену переменных у' = ух, у" = Уъ. уравнение (4.39) запишем
следующим образом:
(4.39)
(4.40)
7. Зак. 2069
97
Критерий оптимальности вариационной задачи о минимуме максималь¬
ной перегрузки может быть представлен в виде
9о г
причем предполагается, что максимум перегрузки на траектории спуска
единствен.
Для того чтобы свести рассматриваемую вариационную задачу к какой-
либо известной формальной записи (например, к задаче Майера) , исполь¬
зуется следующий прием [97]. Вводится некоторая вспомогательная функ¬
ция (/?, связанная с продольной перегрузкой соотношением -hx D (пх).
Функция возрастает вместе с пх при D = 1 и сохраняет нулевое постоянное
значение при 0= 0. При этом (tK) « maxпх. Учитывая выражение для
производной
п* = (и -2у2)егх, (4.42)
запишем систему сопряженных дифференциальных уравнений в виде
^'1 =. _ ф2 _ ф3е~2х D,
(4.43)
В соответствии с принципом максимума оптимальное управление обеспе¬
чивает гамильтониану
JC = -^iu + 3(1(xfy1/y2) • (4,44)
абсолютный максимум.
Анализ гамильтониана (4.44) показывает, что структура оптимального
управления определяется функцией ^(х). Как показано в работе [97],
поведение функции (х) и соответственно структура оптимального управ¬
ления могут быть различными в зависимости от характера граничных
условий. Так, в частности, если ограничения на конечные параметры
траектории отсутствуют, то функция i//j(x) на всей траектории спуска
остается отрицательной, и, следовательно, оптимальной программой управ¬
ления, реализующей минимальное значение максимальной перегрузки,
является программа полета с постоянным максимальным значением аэро¬
динамического качества:
^эфф + ^бал°
Если в конце траектории спуска задана конечная скорость Ук, то для
получения минимального значения пх необходимо использовать программу
двухразового переключения эффективного качества:
^эфф + ^бал/ ^бал' + ^бал-
При движении КЛА вблизи верхней границы коридора входа для предот¬
вращения его вылета из атмосферы, используется программа одноразового
переключения /СЭфф:
^эфф ^бал/ + ^бал-
При этом момент переключения КЭфф зависит от высоты условного пери-
98
^Эфф
Ф 5,
' км
-5
500
1?
«Ъ- £
ио
^зфф ft)
—т—— ~
0,5
-0
-~5
-ъ
20
IX.
1 \
1
-цз
^9
150
—10
-15 0
-5
-7
.^'“Х (t)
О 25 50 75 t.c
Рис. 4.2. Характер изменения параметров оптимальной траектории спуска КЛА в
атмосфере Юпитера из условия минимизации лтах.
^тах^бал)
^тах
Уо)
~т
^та®
^та® &0)
П та® х)
п талиба л)
/ 200
^та® (hff)
400
i
ООО
I
800
, Рх,*гс/м
0 0,1
8,5 9,5
0,2
10,5
0,5
11,5
0,4
12,5
0,5 /(бал
Vq,km/c
100 -100 -500 -500 -700 h^KM
Рис.4.3. Зависимость лтах от Ля, Ио, Кбал и Рх при оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Венеры (номинальная модель атмосферы).
центра внутри навигационного коридора входа. Чем круче вход КЛА в атмо¬
сферу (т.е. чем меньше величина h^), тем раньше наступает момент переключе¬
ния эффективного качества с отрицательного значения на положительное,
а при движении вблизи нижней границы коридора входа в некотором диапа¬
зоне высот условного перицентра /?* оптимальная программа
управления вырождается в программу Колета с постоянным максимальным
значением аэродинамического качества КЭфф = + ^бал-
В качестве примера на рис. 4.2 приведены параметры оптимальной
траектории спуска КЛА в атмосфере Юпитера. На рис. 4.3—4.9 приведены
результаты численного решения задачи минимизации /7тах при спуске КЛА
в атмосферах рассматриваемых планет Солнечной системы (Венера, Земля,
Марс, Юпитер, Сатурн, Уран, Нептун). Показано влияние начальных условий
99
^tTIQX
50 -75 -200 ~Ъ25 ЪП)км
Рис. 4.4. Зависимость максимальной перегрузки лтах от высоты условного пери¬
центра Ьц, начальной скорости входа 1/0, аэродинамического качества /Сбал и приве¬
денной нагрузки на лобовую поверхность Рх при оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Земли (номинальная модель атмосферы).
Кружочками обозначены значения лтах при номинальных значениях варьируемых па¬
раметров и крайних отклонениях плотности атмосферы от номинальной.
\
|"тая5%1п %имн^
|а®(/та® ^имнА^
35 пип летн^\
^тах (Ц))
^тах
пи1 рабн^
лтах
^тах ^rt)
^"тах %)
К ^тах (Р
\ 4 тах рс
^тах (Р )
' тах летн7
0tf^
150
250
S50 450
Рх,кгс/мг
0,1
0,2
0J 0,4
^бал
5
6
7 8
Vq>km/c
-250 Ья,км
Рис. 4.5. Зависимость лтах от ЛЯ/ VQf Kfan и Рх при оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Марса (минимальная модель атмосферы для
весеннего равноденствия). Кружочками обозначены значения лтах при номиналь¬
ных значениях варьируемых параметров и различных отклонениях плотности атмо¬
сферы от минимальной для весеннего равноденствия: nmax(pmin летн) _ мини¬
мальная летняя модель; птах(ртах летн) - максимальная летняя модель;
лтах1Рттзимн)-минимальная зимняя модель; лтах(ртахзимн)-максимальная зим-,
няя модель;/7тах(ртахравн)—максимальная модель для весеннего равноденствия.
Рис. 4.6. Зависимость лтах от ^о/^бал и ?х ПРИ оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Юпитера (номинальная модель атмосферы).
Рис. 4.7. Зависимость nmax от Ио, Кбал и Рх при оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Сатурна (номинальная модель атмосферы).
Рис. 4.8. Зависимость лтах от 1/0, Кбал и при оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Урана (номинальная модель атмосферы).
Рис. 4.9. Зависимость n^OT^, И0/ Кбал и рх ПР” оптимальном управлении КЛА,
осуществляющими спуск в атмосфере Нептуна (номинальная модель атмосферы).
входа, проектно-баллистических характеристик КЛА и плотности атмосфе¬
ры на величину минимального значения лтах. Видно, что для рассматривае¬
мых планет Солнечной системы характер зависимости минимума макси¬
мальной перегрузки от основных параметров одинаков. А именно, для
снижения уровня перегрузок необходимо стремиться к уменьшению на¬
чальной скорости входа и к увеличению высоты условного перицентра,
приведенной нагрузки на лобовую поверхность и аэродинамического
качества КЛА.
102
Следует отметить, что при достаточно крутом входе КЛА в атмосферу
планеты (вблизи нижней границы навигационного коридора входа) может
возникнуть опасность низкого пролета над поверхностью планеты. Это
может привести (особенно при полете над гористой местностью) к "жест¬
кой" посадке КЛА на поверхность планеты и, следовательно, к разрушению
научных приборов, находящихся на его борту. В связи с этим в ряде случа¬
ев при решении задачи минимизации лтах необходимо принимать во
внимание ограничение на минимально допустимую высоту полета над
поверхностью планеты.
Исследования показали, что в первую очередь это ограничение должно
приниматься во внимание при спуске КЛА в атмосфере Марса. Действитель¬
но, при снижении в разреженной атмосфере этой планеты минимальная
высота пролета над поверхностью может составлять 3—5 км (вход по ниж¬
ней границе навигационного коридора). А при спуске в атмосферах других
планет высота /?mjn соответственно составляет для Венеры 35—45 км, для
Земли 20 — 30 км, для Юпитера 120 — 140 км, для Сат\<рна 160- 180 км,
для Урана 140— 160 км, для Нептуна 70 — 90 км.
Оценим эффективность оптимального управления (Дл) из условия
minnmax. Сравнение оптимального управляемого спуска будем прово¬
дить с неуправляемым баллистическим спуском на примере спуска в
атмосфере Юпитера. В табл. 4.12 представлены данные, позволяющие
оценить величину
Дл = лтах|Кэфф = 0-/7тах|Кэфф =к°^ф. (4.45)
Заметим, что наибольшая эффективность управления достигается при
движении КЛА по нижней границе коридора входа. Так, если при входе
КЛА вблизи границы захвата его атмосферой Юпитера уменьшение пере¬
грузки по сравнению с баллистическим спуском составляет всего лишь
5—10 единиц, то при движении по нижней границе коридора входа пере¬
грузка уменьшается на 70—150 единиц.
С учетом- этого факта в табл. 4.12 приведены данные по оценке эффек¬
тивности оптимального' управления именно для случая движения по кижней
границе навигационного коридора входа. Видно, что с увеличением началь¬
ной скорости входа VQ и аэродинамического качества /Сбал эффективность
оптимального управления возрастает, в то время как изменение приведен-
Таблица 4.12
Эффективность оптимального управления
и,,
км/с
рх.
кгс/м 2
К бал
Модель
атмосферы^
Абсолютный
экстремум
Экстремум с уче¬
том ограничений
А
An
км
rnin nmax
км
min nmax
60
200
0,3
ном.
-244
49
-1444
121
95
60
200
0,3
"холГ
-273
79
-1473
155
126
60
200
0,3
"тепл."
-188
31
-1388
88
72
60
200
0’2
ном.
-246
52
-1446
132
77
60
200
0,4
ном.
-242
46
-1442
110
108
60
100
0,3
ном.
-237
48
-1437
119
94
60
300
0,3
ном.
-250
51
-1450
122
96
55
200
0,3
ном.
-190
38
-1390
111
90
65
200
0,3
ном.
-285
61
-1485
132
107
103
ной нагрузки на лобовую поверхность практически на нее не влияет. При
этом следует отметить, что характер влияния основных параметров на
эффективность управляемого спуска остается неизменным для различных
моделей атмосферы, однако величина разности Ал существенно зависит от
выбранной расчетной модели атмосферы. А именно, для "холодной" моде¬
ли атмосферы эффективность оптимального управления наибольшая, а
для "теплой" — наименьшая.
Итак, в настоящей главе определен методический подход к решению
(и приведены результаты численного решения) задач максимизации кори¬
дора входа и минимизации максимальной перегрузки для КЛА, осуществ¬
ляющих спуск в атмосферах планет Солнечной системы. Решение задач про¬
водилось с использованием принципа максимума Понтрягина. Показано, что
структура оптимального управления остается неизменной при входе КЛА в
атмосферы всех рассматриваемых планет в широком диапазоне изменения
начальных условий входа и основных проектно-баллистических характерис¬
тик КЛА. Для летательных аппаратов "скользящего" типа, управляемых уг¬
лом крена, оптимальная программа управления, реализующая максималь¬
ный коридор входа при ограничении на максимально допустимую перегруз¬
ку, заключается: 1) в полете КЛАс максимальным отрицательным значени¬
ем /Сэфф = —/Сбал при движении по верхней границе коридора входа, 2) в
полете с двумя переключениями /Сэфф = + ^бал/ - ^бал, + ^бал при движе¬
нии по нижней границе коридора входа. Оптимальная программа управле¬
ния, реализующая min/7maXf состоит в полете с максимальным положитель¬
ным значением эффективного аэродинамического качества.
Глава 5
МИНИМИЗАЦИЯ МАССЫ ТЕПЛОВОЙ ЗАЩИТЫ
КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА
§ 5.1. Критерии оптимальности
Имеется большое количество работ, посвященных проблеме оптими¬
зации траекторий спуска в атмосфере из условия минимума массы систе¬
мы тепловой защиты КЛА (см., например, [23, 118, 135] ). Даются различ¬
ные постановки задачи min/nT3 п и приводятся примеры ее решения с
использованием различных методов оптимизации. При этом практически
отсутствуют результаты решения задачи minn?T3>n с использованием пря¬
мого критерия оптимальности. Как правило, используются косвенные
критерии, которые позволяют достаточно легко получить численные ре¬
зультаты для КЛА, осуществляющих спуск в атмосферах планет Сол¬
нечной системы, и провести сравнительный анализ оптимальных траекто¬
рий спуска при различных исходных предпосылках. Выбор достаточно
простого косвенного критерия оптимальности для задачи min/nT3 п требу¬
ет специального предварительного анализа и зависит от многих факторов
(типа системы теплозащиты, материала теплозащитного покрытия и т.д.).
Ниже приводятся расчетные формулы для различных типов систем тепло¬
вой защиты и указываются соответствующие им косвенные критерии
оптимальности.
Расчет массы системы теплозащиты с сублимирующим покрытием.
Масса системы теплозащиты с сублимирующим покрытием может быть
104
определена в виде
^тз.п ~ тун +
(5.1)
где/77ун — уносимая масса; П7пр — прогреваемая масса теплозащиты.
Как уже отмечалось (см. гл. 3), расход уносимой массы теплозащитно¬
го покрытия определяется в основном эффективной энтальпией, темпера¬
турой разрушения и тепловыми потоками, поступающими от ударного
слоя газа. Масса унесенного в процессе разрушения слоя теплозащиты
с 1 м2 поверхности КЛА определяется интегралом
/Пун= f mdt= f vxpcdt,
где pc — плотность сублимирующего материала; Vx — линейная скорость
уноса; to, tK — моменты начала и конца уноса материала теплозащитного
покрытия, fh— удельный расход массы с единицы поверхности.
Момент начала уноса массы теплозащитного покрытия определяется
условием, когда температура поверхности Тп достигает температуры
разрушения Гр материала теплозащиты. Температура Тп может быть оп¬
ределена из следующего уравнения:
где А и е — коэффициенты поглощательной и излучательной способности
материала теплозащитного покрытия: 0= 5,67032 • 10"8 Вт • м-2 • К“4 —
постоянная Стефана — Больцмана.
Удельный расход массы с единицы поверхности можно оценить по фор
муле [2, 78]
• ^рад + Qkohb —
m = —
^?эф ф
Следует отметить, что для некоторых простых конфигураций КЛА для
расчета величины m могут быть использованы упрощенные аналитические
зависимости, приведенные в главе 3.
До начала уноса массы нет особой необходимости в определении вели¬
чины прогреваемой массы системы теплозащиты. Расчет массы Л7пр про¬
изводится после окончания процесса разрушения материала теплозащит¬
ного покрытия, определяемого условием Тп-Тр (в момент Гк). Для
расчета массы прогреваемого теплозащитного покрытия сначала опреде¬
ляется толщина прогреваемого слоя Ах. Зная Д х, площадь поверхности,
покрытой слоем теплозащиты ST3.n, и удельный вес материала теплоза¬
щиты р, легко определить величину тпр по формуле
^пр Д* ^ТЗ.пР*
Для расчета толщины прогреваемого теплозащитного покрытия в дан¬
ной точке поверхности КЛА обычно решается одномерная задача теплопро¬
водности. Уравнение теплопроводности, описывающее распределение
температуры по глубине материала теплозащитного покрытия в направ¬
лении, перпендикулярном к« поверхности КЛА, может быть записано в
виде [78]
Э
Эх
105
где Хи С — теплопроводность и теплоемкость материала соответственно;
х — координата, отсчитываемая от наружной поверхности КЛА вглубь
прогреваемого материала теплозащитного покрытия.
Для решения этого уравнения с целью определения глубины прогрева
Дх необходимо учитывать граничное условие
-X
д Лтр
Эх
Qkohb +^<7рад еог^"п
х=0
на внешней поверхности материала и граничное условие Гпр < 7ДОП
(Тдоп — допустимая температура нагрева силовой конструкции КЛА)
на внутренней поверхности в месте стыка теплозащитного пакета и си¬
ловой конструкции КЛА.
Распределение температуры по глубине материала в конце процесса
разрушения можно определить по формуле
f VxdtxCp
ro
гпр = 7"о + (Гр - Г0)ехр— — ,
(Гк - tQ )Х
где То — начальная температура материала теплозащитного покрытия.
Толщина прогреваемого слоя определяется следующим образом [2] :
где fHarp — время нагрева внутренней поверхности теплозащиты; tnp —
температура прогреваемого слоя; Тм — температура окружающей среды;
АТвн — повышение температуры на внутренней поверхности за время
^нагр- Зная толщину прогреваемого материала и его плотность, легко
определить прогреваемую массу теплозащиты /ппр и, следовательно, сум¬
марную массу системы теплозащиты с сублимирующим покрытием по
формуле (5.1).
Анализ приведенных расчетных формул для системы теплозащиты
с сублимирующим теплозащитным покрытием показывает, что в качестве
косвенных критериев оптимальности в задаче минимизации /птзп могут
служить величина суммарного теплового потока, поступающего к поверх¬
ности КЛА, и температура на внешней поверхности теплозащитного пок¬
рытия.
Ниже приводятся основные теплофизические характеристики некото¬
рых материалов теплозащитного покрытия [2] :
тефлон: 1?эфф = 1?00 - 2000 ккал/кг, Гр =427аС, р = 2210 кгс/м3, С=
= 0,25 ккал/ (кг • град), X = 5,84 • 10 5 ккал/(м • с • град) ;
рефразил: т?эфф =3500 4- 3600 ккал/кг, 7"р=1530°С, р = 2100 кгс/м3,
С = 0,28 ккал/ (кг • град), X = 6,93 • 10"5 ккал/ (м • с • град) ;
фенолик-фибергласс: 1?эфф=1°00 - 1100 ккал/кг, 7*р=1650 °С, р =.
= 1600 кгс/м3, С= 0,4 ккал/(кг • град), Х= 1,054 • Ю"4 ккал/(м • с • град).
Расчет массы системы теплозащиты с внешним неметаллическим теп¬
лоизолирующим слоем. Несублимирующая система теплозащиты с внеш¬
ним неметаллическим теплоизолирующим слоем, как правило, рассчиты¬
вается для использования на КЛА, обладающих большим значением аэро¬
динамического качества [143]. При этом учитывается неравномерность
распределения температуры (в процессе снижения в атмосфере) по по¬
верхности КЛА, которую представляют в виде суммы отдельных участков
106
(панелей). Если температура на каком-либо участке не превышает допус¬
тимого значения для металлической силовой обшивки КЛА, то внешняя
теплоизоляция на этой панели не используется. Масса системы теплоза¬
щиты в таком случае может быть представлена в виде суммы двух сос¬
тавляющих
т = mi + т2, (5.2)
где
/771 = Ci Z?i jSi j , ГП2 ~ (1 — Cl )^2 i$2 i • (5.3)
, i= 1 i- 1
Здесь /7?! — масса панелей теплозащиты, не имеющих внешней теплоизо¬
ляции; т2 — масса панелей, имеющих внешнюю теплоизоляцию; п —
число панелей поверхности КЛА; = 1 при 7"max z < 7^, Ci = 0 при
Гтах, > и — массы участков поверхности КЛА площадью 1 м2
соответственно с внешней теплоизоляцией и без нее, $2,и$1£- — площади
панелей с внешней теплоизоляцией и без нее, Тх — предельная температу¬
ра поверхности КЛА, при которой еще возможно использование для теп¬
лозащиты панелей, не имеющих внешней теплоизоляции.
Масса теплозащиты b2i на единицу площади s2i определяется величиной
суммарного теплового потока приходящего на единицу площади
7-й панели в процессе спуска КЛА в атмосфере.
Выражение (5.2) для массы системы теплозащиты с неметаллическим
изоляционным покрытием можно записать в виде
т= S s2ib2i -С^ + тг.
i= 1
Суммарное количество тепла, поступающего на /*-ю панель, определя¬
ется обычным образом:
f q^dt,
ч
где = Qkohb +<7рад — суммарный удельный тепловой поток.
Установлено, что для различных материалов теплозащиты характер из¬
менения функции b2i(Q^tl одинаков, с увеличением суммарного тепло¬
вого потока Qsz происходит монотонное увеличение b2i.
Таким образом, масса системы теплозащиты с внешним неметалличес-
ским теплоизолирующим слоем для КЛА заданной конфигурации опре¬
деляется величиной суммарного теплового потока, приходящегося на
единицу поверхности КЛА.
Расчет массы системы теплозащиты с внешним металлическим тепло¬
изолирующим слоем. Будем рассматривать две возможные схемы систе¬
мы металлической теплозащиты [118, 138]:
радиационный экран + изолятор + силовая конструкция КЛА;
радиационный экран + изолятор + активная система внутреннего ох¬
лаждения.
Как и ранее, для более точного представления геометрии наружной
поверхности КЛА ее целесообразно разбить на большое число панелей
(для аппаратов с большим значением аэродинамического качества, осу¬
ществляющих спуск с орбиты искусственного спутника Земли, число
панелей может доходить до 30 на одну сторону относительно оси сим¬
метрии) .
107
Общая масса системы металлической теплозащиты первой из рассматри¬
ваемых схем равна сумме масс внешней металлической обшивки
и теплоизолирующего слоя S/772/:
п
т = Z (mli + m2i).
i= 1
Масса панели металлической обшивки обусловливается величиной
максимальной температуры на траектории спуска:
тп = ^ЛИЛтах )si'
где dxi— масса участка металлической панели площадью 1 м2 . Характер
изменения функции б/1г(7}тах) аналогичен характеру изменения функции
: с возрастанием Г,тах увеличивается и значение функции
^1 ДЛ’шах) •
Масса теплоизоляции m2i определяется аналогично выражению (5.3).
Таким образом, масса системы металлической теплозащиты первой
схемы зависит от максимальной температуры на поверхности панелей и
величины аккумулируемого тепла. Решение вариационных задач по отыс¬
канию оптимального управления на траектории снижения с целью мини¬
мизации массы системы металлической теплозащиты сразу по двум кри¬
териям (7"max-> min и -> min) затруднено, а в некоторых случаях
и невозможно. Поэтому обычно в качестве функционала управления ис¬
пользуется какой-либо один из рассматриваемых критериев, а второй
используется как ограничение. Чаще всего вводится ограничение на ве¬
личину Гтах, позволяющее поддерживать максимальную температуру
на поверхности панели, не превышающую исходную, и, следовательно,
определять необходимый материал внешнего радиационного экрана.
Для второй из указанных схем системы металлической теплозащиты
с активной системой внутреннего охлаждения суммарная масса тепло¬
защиты, приходящаяся на единичную площадь поверхности, может быть
определена по формуле
т = + т2 + т3, (5.4)
где тх = рб — приведенная масса изолятора (6 —его толщина), т2 -
гк
= 5 9охл°^ ~ приведенная масса потребного количества хладагента,
т3 — масса теплозащиты с активной системой внутреннего охлаждения,
приходящейся на единичную площадь поверхности.
Предполагая, что система внутреннего охлаждения автоматически под¬
держивает заданное значение температуры внутри отсека (7"отс = const),
можно получить следующее выражение для величины теплового потока,
приходящегося на систему внутреннего охлаждения:
<7охл _ (7”п — 7”отс> •
где а0 - постоянный коэффициент, Гп - температура на стыке изолятора
и системы внутреннего охлаждения, которая может быть определена из
решения уравнения теплопроводности следующим образом. Предположим,
чтодГ/Э/~ ЭГ/ЭхОГ/дг, т.е. будем считать что процесс прогрева обшив¬
ки-изолятора описывается одномерным уравнением теплопроводности
Э7~(х, Г) д2Т(х, Г)
ъг а дХ2
108
с граничными условиями
Т(х, О) = Го,
ЭТ(х,Г)
~ Qkohb + <7рад <7изл/
х = 6
ЭГ(хД)
Эх
Qoxn •
х = 0
Г>0, 0<х<5.
Здесь а - постоянный коэффициент, зависящий от теплофизических ха¬
рактеристик используемого материала изолятора; дизл — излучаемый
радиационным экраном тепловой поток.
Уравнение теплопроводности, характеризующее распределение тем¬
пературы по толщине изолятора 5, может быть аппроксимировано систе¬
мой обыкновенных дифференциальных уравнений:
СТ1 4 ^1 -г
Ci 71 ~~~ 1 _^конв+^рад“’еог^1 7 <^1 ~ 2 ),
С272
dT2 Xi Х2
— Дх2 = (Г, -Т2}- — (Т2-Т3),
dt Дх! Дх2
dTn_.
dt
^хп_
Ki-2
^п-2
(Т„_
Ki- 1
(Тп-1 - Тп),
(5.5)
п —
7п-1
Тп) — ео~ «о (Тп Тотс),
С
Дх! + Дх2 + Ах3 + . . . + Дхп_ ! + Ахп = 5.
Здесь п — количество слоев изолятора, в каждом из которых температу¬
ра предполагается постоянной (Ть Т2, . . . , Тп = const); Дх, — толщины
слоев изолятора; С7 — постоянные коэффициенты. Количество слоев оп¬
ределяется требуемой точностью аппроксимации температуры 7". Решая
систему уравнений (5.5), можно получить требуемую величину темпера¬
туры на внутренней стороне изолятора Гп. Таким образом, формулы
(5.4) и (5.5) для расчета массы системы теплозащиты с внешним метал¬
лическим теплоизолирующим слоем (с активной системой внутреннего
охлаждения) показывают, что масса этой системы определяется вели¬
чиной суммарного теплового потока и максимальной температурой на
поверхности КЛА 1\, а также интегралом от температуры внутренней
гк
поверхности изолятора f Tndt.
? о
Заканчивая анализ расчета массы систем теплозащиты различных типов
(с сублимирующим покрытием и с внешним неметаллическим и метал¬
лическим теплоизолирующим слоем), отметим, что во всех рассмотрен¬
109
ных случаях масса /пТЗЛ1 в основном определяется величиной суммарного
теплового потока, действующего на КЛА, и максимальной температу¬
рой поверхностного слоя его изолятора. Эти параметры имеют ясный
физический смысл и могут быть использованы в качестве косвенных
критериев при решении вариационных задач спуска КЛА в атмосферах
планет Солнечной системы из условия min/nT3 п.
§ 5.2. Оптимизация траекторий спуска из условия минимума
суммарного теплового потока
5.2.1. Нижняя граница минимального суммарного теплового потока
Рассмотрим задачу определения наименьшего возможного значения
суммарного теплового потока в критической точке КЛА, управляемых
углом крена. При этом будем предполагать, что ограничение на величину
управляющего параметра — аэродинамического качества — отсутствует.
Такое упрощение условий оптимизации позволяет получить достаточно
простым способом [125] нижнюю оценку для траекторий спуска в атмос¬
ферах планет в смысле указанного выше критерия оптимальности. Полу¬
чаемая в результате траектория абсолютного минимума не является
реальной траекторией, так как не учитывает физических ограничений,
накладываемых на траекторию спуска.
Суммарный тепловой поток, поступающий к критической точке КЛА
со сферическим затуплением, как отмечалось (см. гл. 3), может быть
записан в виде
S (Qkohb + ^рад)°^-
(5.6)
О
Предполагая, что при спуске КЛА угол наклона траектории к местному
горизонту мал, так что выполняется неравенство
и ускорение свободного падения д(Л) постоянно и равно
9ih)^g0,
уравнение для скорости движения КЛА
dV pV2
~~~ —g(h) <?(A)sin0
Л 2РХ
запишем в виде
dV cxs ,
— =* pV2.
dt 2m
Для КЛА, управляемых углом крена, баллистический параметр ох =
- cxs/m в первом приближении можно считать постоянным на траектории
спуска.
С учетом последней формулы получаем из (5.6) следующее выражение
для величины суммарного теплового потока:
9конв+9рад
J ; dv.
cxs vK pv2
(5.7)
PV2
110
Задачу определения наименьшего возможного значения суммарного
теплового потока можно сформулировать следующим образом: опре¬
делить такую зависимость плотности атмосферы от высоты полета, кото¬
рая минимизирует интеграл в уравнении (5.7). Видно, что наименьшее
значение Qx будет достигаться в том случае, если для каждого текущего
значения скорости будет найдено значение плотности р, при котором подын¬
тегральная функция принимает наименьшее значение. Иными словами,
условие оптимизации суммарного теплового потока приобретает вид
ДОконв_^Д=0 (58)
pV2
Численные расчеты показывают, что при спуске КЛА в атмосферах
планет удельный конвективный тепловой поток преобладает на больших
высотах полета, а радиационный — на меньших [125] . Так, при спуске
КЛА в атмосфере Земли с относительной скоростью Уо = ^о/^кр = М
кривая удельного конвективного теплового потока приблизительно про¬
порциональна р”0,5, а радиационного — р0,8. Следовательно, для каждой
скорости входа существует такое значение плотности, при котором сум¬
марный удельный тепловой поток = QKOHB + <7рад имеет минимум,
т.е. выполняется условие минимума суммарного теплового потока
(5.7).
_ В качестве примера на рис. 5.1 представлена зависимость величин рконв,
драд (9/= 9//0,5рУ2 ), от высоты полета для КЛА с радиусом затупления
г н = 0,3,-Осуществляющего вход в атмосферу Земли с относительной ско¬
ростью Уо = 1,4. Расчеты проводились в предположении отсутствия уноса
массы теплозащитного покрытия и излучения тепла от поверхности КЛА
[2] . Видно, что минимум суммы Qkohb 4 <7рад достигается на высоте
около 45 км. Учет экранирующего воздействия частиц разрушающихся
материалов теплозащиты на величину удельного теплового потока при¬
водит к смещению точки абсолютного минимума (рис. 5.2).
Используя аналогичные рассуждения, можно построить серию точек,
определяющих минимум выражения (5.8), вычисленных для различных
значений скорости V, и, следовательно, определить траекторию p(V), ре¬
Рис. 5.1. Зависимость в критической точке от высоты полета h .
Рис.5.2. Влияние экранирующего воздействия различных материалов теплозащиты
_ / - V
на удельный тепловой поток q, ( V = = 1,4; гн = 0,3 м
' ^кр
111
авизующую абсолютное минимальное значение суммарного теплового
потока для КЛА с заданным радиусом затупления г н.
Следует отметить, что в ряде случаев, позволяющих использовать уп
рощенные аналитические зависимости qkohb и 9рад от плотности, ско
рости и радиуса затупления, процедура получения абсолютного минимума
может быть существенно упрощена.
Так, при спуске КЛА в атмосфере Земли удельные конвективный и
радиационный тепловые потоки могут быть выражены следующими ап¬
проксимирующими зависимостями:
р0,5 ^3,25
QkOHB • (5.9)
ГН
(5.11)
т
)
где Ро — плотность воздуха на уровне моря, а значения коэффициентов
приведены в табл. 5.1.
Используя (5.9) и (5.10), из соотношения (5.8) получаем уравнение
оптимальной траектории, реализующей абсолютный минимум суммарно
го теплового потока:
1
[Л рЗ ,2 5 I/ ч 3 ,2 5 -П
± г
2 rJ’5C(/n-1) \В J
Подставляя значения QKOHB, 9рад и р из (5.9) — (5.11) в выражение (5.7),
получаем величину суммарного теплового потока, подводимого к крити¬
ческой точке на оптимальных траекториях при различных значениях радиу¬
са затупления носовой части гн:
I — 0,5/и
Qv ,
где
tn - 1 1 ,2 5 т т 0,5 п - 2 ,2 5
d_ 2PV C(2m - 1) г Д/?3-25 p(?-s I к/1/
ffo PoS2 L 2C(m —1) J i „
В качестве примера на рис. 5.3 поедставлены траектории абсолютного
минимума суммарного теплового потока в виде зависимостей p(V) для
трех случаев: без учета абляции и излучения поверхности КЛА; с учетом
абляции (материал — тефлон); с учетом абляции и излучения поверхнос¬
ти КЛА (материал — фенолик-нейлон). _
Видно, что при больших скоростях входа (V = V/VKp > 1,8) все оп¬
тимальные траектории приближаются к изовысотным траекториям. При
Таблица 5.1
Значения коэффициентов .4, В, С, т и п
V, м/с
А
В
С
т
п
< 8550
2,1 10"
3050
3,03 • ю2
1,68
7,4
8550 - 11600
2,1 • 10"
3050
1,91 10"
1,41
20,0
> 11600
2,1 • 10"
3050
9,33 102
1,3
8,0
112
Рис. 5.3. Зависимость- относительной
скорости полета КЛА V от относитель¬
ной плотности атмосферы р"на траекто¬
рии абсолютного минимума Qv
уменьшении скорости (V < 1,8) про¬
исходит уменьшение плотности р
(или высоты h) на оптимальной
траектории. Можно заметить также,
что для уносимой теплозащиты аб¬
солютные минимумы проходят на
больших высотах, чем в случае от¬
сутствия^ абляции и излучения, во всем рассматриваемом диапазоне ско¬
ростей V.
На рис. 5.4 приведены параметры оптимальной траектории для лета¬
тельных аппаратов, имеющих различную аэродинамическую форму. Все
конфигурации имеют одинаковый характерный размер (г =2 м). Видно,
что для КЛА с большим углом полураствора конуса оптимальные тра¬
ектории проходят на больших высотах.
Учет ограничения на перегрузку. Используя выражения (5.9) и (5.10)
для удельных конвективного и радиационного тепловых потоков, полу¬
чим следующее выражение для продольной перегрузки:
—2-
2РХ
В2
2РХ
. \ 2т — м + 2 ,2 5 _
X»Po"'S3’2S(y)
2С(т - 1 )гн‘ >5
1/(т - 0,5)
Видно, что величина перегрузки возрастает с уменьшением радиуса
гн. Проведенные расчеты показывают, что при движении КЛА по тра¬
ектории абсолютного минимума в атмосфере Земли продольная перегруз¬
ка может достигать величины пх -850 (ол. = МРХ = 0,008; гн = 1 м). По¬
этому представляется интересным рассмотреть траектории абсолютного
минимума Qv для выявления таких участков траектории, на которых
будет достигаться абсолютный минимум величины Qv при выдерживании
ограничения на величину допустимой перегрузки. Для этого на зависимости
р0ЛТ (V) или Аопт (V), соответствующие абсолютному минимуму, нано¬
сится зависимость рдоп (Ю или АДОп(И, соответствующая заданному
значению допустимой перегрузки /7ДОП. Кривые ропт {V) илиЛопг(1/),
лежащие выше зависимостей рдоп (W или /7ДОП (И» будут удовлетворять
ограничению по допустимой перегрузке [67] .
На рис. 5.5 показана допустимая область для траекторий абсолютных
минимумов Qv при спуске в атмосфере Земли КЛА с аэродинамическим
качеством /СП1ах = 1 и приведенной нагрузкой на лобовую поверхность
Рх = 500 кгс/м2.
Учет ограничения на величину подъемной силы, допустимую перегруз¬
ку, удельный тепловой поток и высоту полета. Рассмотрим задачу о мини¬
мизации суммарного теплового потока в критической точке КЛА
Qv = ? KqP°'5 V^lSdt
8. Зак. 2069
113
Рис. 5А Параметры оптимальной траектории КЛА, имеющих различную аэродинами¬
ческую форму (материал теплозащитного покрытия — фенолик-нейлон).
(kq — постоянный коэффициент) при следующих ограничениях на тра¬
екторию снижения:
Cj,^Cymax, (5.12)
п2 (h, V, Су) < ЛдОП, (5.13)
41Ь,У,СуХс/яоп, (5.14)
Л>ЛДоп- (5.15)
Допустимые значения ограничивающих факторов (5.12) — (5.15) задают¬
ся из соображений прочности конструкции и обеспечения условий нормаль¬
ной работы аппаратуры и экипажа (при пилотируемом полете) .
Предполагается [2], что q(h, V, су) при любых заданных значениях
высоты и скорости полета является четной и монотонной функцией су.
Кроме того, функции п2 и q имеют минимум по су, достигаемый при
су =0.
/7,6 1,0 2,2 V
Рис. 5.5. Допустимая область для траекторий абсолютных минимумов Q^.
114
Учитывая это, перепишем ограничение (5.13) в виде двух следующих
неравенств:
(п2)Су = 0 < п2яоп, |с, | < c*y{h, и, (5.16)
где Cy(h, V) — положительное решение уравнения r?(h, V, су} = ЛдОП.
Аналогично условие (5.14) эквивалентно следующим двум ограничениям:
{q)Cy = о < <7ДОП, су <c*y*(h, V), (5.17)
где Су* (h, V.) — положительное решение уравнения
q(h, V, су) = 9ДОП.
Анализ выражений [л2 (h, У)]Су = о и [q(h, У)]Су = о показывает
[2], что они монотонно убывают по высоте и возрастают по скорости.
В этом случае условия (5.16) и (5.17) могут быть представлены в виде
h>h*(V), h>h**(V),
где h * (V) — решение уравнения
[л2 (/?, У)]су = о = Лдоп /
a h ** (V) — решение уравнения
^Jcy = О QДОП
при любых заданных значениях V.
Приведем ограничения (5.12) и (5.15) к виду
Су max
при
* * ♦
Су max Су, Су ,
|су|<с?р(Л,У) =
c*y(h,V)
при
Су<Сутлх, Су ,
k*
(htV)
при
с*-
Су \ Uy max * »
^ДОП
при
^доп
>h*, h**.
Л>Лпр(У) =
л*
(V)
при
Л’>Лдоп/ л”.
h**(V}
при
А*’>АДОП, Л*.
(5.18)
(5.19)
Используя замену 1? = h
*К
= f kqP°*s V3»iSdt в виде
*9
представим функционал
’’к p°'s V3'is
l = ~kq S—y dr),
n. -%-X(h,V,cy)
(5.20)
rue X(h, V,cy) = glh)
115
Рис. 5.6. Характерный вид зависимости к (Л).
Рис. 5.7. Структура оптимальной траектории.
Минимум функционала (5.20) дает такое решение Ь(т]) и су (т?), при ко¬
тором для каждого фиксированного значения т? Е (?70, ??к) подынтеграль¬
ное выражение в (5.20) достигает минимума при ограничениях (5.18) и
(5.19). Поскольку подынтегральная функция положительна, ее минимум
по су при любых заданных значениях т? и h реализуется при | =
= c^p(hrn) [2].
Подставляя значение |су | = с"р(Л, я) в (5.20), исследуем на минимум
по Л функцию
0,5 уЗ,15
К(т?, Л) = ~ту
jX(h, V,CyP(h,ri))
в области высот h >Лпр(т?).
Характерный вид функции к (h) при 77 = const показан на рис. 5.6. Про¬
веденные исследования показали [2], что минимальное значение функции
к (А ) достигается в точке перехода с одной границы [су = су тах) на дру¬
гую (су = су или су = Су*), т.е., другими словами, в точке выхода на огра¬
ничение (5.14) или (5.15).
На рис. 5.7 показана структура оптимальной траектории, состоящей из
участков полета на предельных значениях сур, участков полета по ограниче¬
ниям и участков скользящего режима. В зависимости от начальных условий
входа, проектно-баллистических характеристик КПА и параметров атмо¬
сферы отдельные участки могут отсутствовать.
В качестве примера на рис. 5.8 ( [2] ) приведены параметры траектории,
реализующей абсолютный минимум суммарного теплового потока в крити¬
ческой точке для гипотетического КЛА со следующими данными:
начальная масса т0 = 5000 кг;
нагрузка на крыло m/S — 150 кг/м2;
аэродинамические коэффициенты
сх = 0,1 + 1,83 | sin3a |, су = ± 1,83 sin3acosa;
граничные условия: т?0 = 2,93-106 м, h0 = 80-Ю3 м, 0о = — 1 14° =
= 15-Ю3 м;
ограничения: лпр = 5 и 2, с"р = 0,645;
ограничения на высоту полета и удельный тепловой поток не учиты¬
вались.
116
Таким образом, представленные в настоящем параграфе данные позво¬
ляют определять траекторию, на которой достигается абсолютное мини¬
мальное значение суммарного теплового потока в критической точке КЛА.
5.2.2. Учет реальных ограничений
Общая постановка задачи. В предположении, что поле тяготения планеты
центральное, запишем уравнения плоского движения центра масс КЛА с
учетом вращения планеты и уноса массы теплозащитного покрытия в сле¬
дующем виде:
dV
~dt~
cxs pV2
= —— tzsin 0 + co rsin0,
mQ — с1^унтун 2
dO
CyS pV g
„ „ _ cosy COS0 +
dt ~
/77q ^1^ун^ун 2 V
(5.21)
dh
dt
V'sin 0,
dt
^конв+^рад-еРТ'р
^эфф
Cl = 0 при T„(t)<Tp,
Ci=K при T„(t)>Tp,
Tnlt) =
+
KOHB
рад
ea
T
Где к — усредненный коэффициент, учитывающий неравномерность распре¬
деления уносимой массы с поверхности КЛА по сравнению с расчетной точ¬
кой, а остальные обозначения аналогичны приведенным в главе 3.
При записи уравнений движения (5.21) предполагалось, что в процессе
снижения в атмосфере планеты на КЛА действуют радиационный и конвек¬
тивный теплопотоки, однако вначале они незначительны и полностью отра¬
жаются от его поверхности. По мере углубления КЛА в плотные слои атмо¬
сферы величины тепловых потоков монотонно возрастают и, начиная с
некоторого момента времени t', определяемого условием достижения тем¬
пературы на поверхности Тп = Т^, тепловые потоки достигают такого
Рис. 5.8. Параметры оптимальной траек¬
тории: 1 — = 5; 2 — лпР = 2.
117
значения, что полностью не могут быть отражены от поверхности КЛА.
С этого момента начинается процесс уноса массы, который продолжается
до момента времени t", когда на КЛА, существенно погасивший скорость,
воздействие тепловых потоков уменьшается, и они снова полностью отра¬
жаются от его поверхности.
Таким образом, параметры траектории спуска в моменты времени t' и
t имеют разрывы непрерывности первого рода.
Предполагается, что плотность атмосферы изменяется по экспоненциаль¬
ному закону
Значения р0 и р для каждой из планет приведены в главе 1.
Будем рассматривать КЛА трех типов: "скользящего", с "несущим кор¬
пусом" и "космический самолет".
В первом случае управление КЛА осуществляется путем изменения эф¬
фективного аэродинамического качестра /СЭфф = ^6ancosT» где 7 — угол
крена. При этом величина эффективного качества может изменяться
в пределах
^бал ^эфф + ^бал •
В процессе снижения КЛА в атмосфере могут накладываться следующие
ограничения:
на высоту условного перицентра траектории входа
< /?*, (5.22)
где /?£ и — соответственно нижняя и верхняя границы навигационного
коридора входа;
на максимально допустимую перегрузку
<h = nmax - лдоп < 0; (5.23)
на минимально допустимую высоту полета над поверхностью планеты
g2(t) =Л(г)-Ъдоп > 0; (5.23')
на максимально допустимую температуру конструкции
<7з(^) - Гтах — ГдОП С 0. (5.24)
Сформулируем задачу оптимального управления общего вида: для про¬
цессов снижения КЛА в атмосфере, описываемых системой дифференциаль¬
ных уравнений (521), требуется определить программу управления КЛА,
обеспечивающую минимум функционала
гк
/ = ОГ= f (<7К0НВ + <7рад)сУГ (5.25)
при ограничениях (522) - (524), управлении |Кэфф| = ЛГбал и следую-
щих краевых условиях:
t = t0; V=VQ, h=hQ, тун =0, во— свободно;
при t = tK фазовые координаты могут быть либо свободными, либо
принимать какие-либо конкретные значения.
Необходимые условия оптимальности. Сформулированную вариацион¬
ную задачу будем решать с использованием необходимых условий опти-
118
мальности принципа максимума Понтрягина [95]. Оптимальный закон
управления в этом случае определяется из условия максимума гамиль¬
тониана
i = 1
(5.26)
где — правые части дифференциальных уравнений (5.21), — сопря¬
женные переменные, определяемые из уравнений
.chk.
—2 = - при qAt) ¥=0, (5.27)
dt bxi 7
dt
Эх,-
dtp
Эх/
при Qy = 0.
(5.28)
bnq • ЭК /d<p
Здесь Ф = A = / ; n — порядок производной функции q-
dt ди/ du '
при которой управление КЛА при движении по ограничению может быть
получено в явном виде.
Сопряженные переменные в момент выхода на ограничение q- (t х) скач¬
ком меняют свою величину:
л dq. dqf
(5.29)
где Mi и р2 — постоянные множители.
Как отмечалось, в моменты tf и t,r фазовые координаты имеют разры¬
вы непрерывности первого рода. Из анализа уравнений (5.26) — (5.29) сле¬
дует, что сопряженные переменные и гамильтониан в этих точках тоже
имеют разрывы первого рода. Согласно теореме Вейерштрасса [72], имеем
в точках t ' и t" :
ф^' + Ат) = ф^' - Ат), K(t' + Ат) = JC(t' - Ат),
ф^" 1-Ат) = ф^" - Ат), K(t"+Ат) = K(t'Ат),
где Ат — сколь угодно малая величина.
Необходимые и достаточные условия прохождения экстремали вдоль
ограничений (5.22) —(5.24) имеют вид
dtn
Граничные значения сопряженных переменных определяются из условий
трансверсальности:
5
5/-К5Г+ S =
i = 1
Определение оптимального закона управления, реализующего минималь¬
ное значение суммарного теплового потока, на основе необходимых усло¬
вий принципа максимума Понтрягина сводится к решению двухточечной
краевой задачи для систем обыкновенных дифференциальных уравнений
(5.21), (5.26) — (5.28). Возможный выход оптимальной траектории на
119
ограничение приводит к появлению дополнительных параметров в краевой
задаче, и порядок ее существенно возрастает. Имеется большое количество
достаточно хорошо разработанных методов численного решения краевых
задач. В частности, при решении вариационных задач спуска КЛА в атмо¬
сфере хорошо зарекомендовал себя метод последовательных приближений.
При использовании этого метода (как и любого другого) скорость ре¬
шения краевой задачи во многом определяется правильным выбором на¬
чального приближения. Возможны два пути задания первого приближения.
В первом случае используются различные физические соображения и задает¬
ся некоторое допустимое управление и1 (Г) . Во втором случае проводится
качественный анализ структуры оптимальных траекторий некоторой моде¬
ли упрощенного движения КЛА. Эффективность второго подхода к выбору
начального допустимого управления в основном определяется возмож¬
ностью создания модели движения КЛА, которая была бы,с одной стороны,
сравнительно простой и допускала возможность качественного исследова¬
ния оптимальных траекторий, с другой стороны, достаточно полно отражала
основные свойства исследуемого процесса.
Ниже приводятся примеры численного решения вариационной задачи о
минимуме суммарного теплового потока для КЛА, осуществляющих спуск
в атмосферах Земли и Юпитера.
Оптимальное управление летательным аппаратом "скользящего" типа,
осуществляющим спуск в атмосфере Земли. Рассмотрим задачу минимиза¬
ции суммарного теплового потока в критической точке КЛА "скользящего"
типа, осуществляющего спуск в атмосфере Земли со сверхкруговой началь¬
ной скоростью VQ > 1.
На траекторию спуска накладывается ограничение на величину макси¬
мально допустимой перегрузки (5.23). Для качественного анализа структу¬
ры оптимального управления [123] сделаем некоторые упрощения уравне¬
ний движения (5.21). Будем предполагать, что уноса массы теплозащитного
покрытия не происходит, вращение планеты отсутствует (со = 0), угол
наклона траектории мал, так что
sin0 ~ 0, cos0 1,
а проекция сил тяжести на направление полета много меньше сил аэродина¬
мического торможения
I 9о sin0 | < |g0"x I.
Используя принятые выше допущения и вводя новые переменные
y=^r^R°^p' ^=VT' x=lnV' = V ro9o,
уравнения движения КЛА (не учитывающие вращение планеты)
dV cxpV2s gQR2s\nO
dt
2т
(/?о+А)2 '
dO
сур Vs cos 7
9oR2o V2
dh . n
~v~ = Vsinfl,
dt
~dt
2т
V(R0+h) ' R()+h'
можно представить в виде нелинейного уравнения второго порядка
d2y _ е2х — 1
120
где
-J = у/Т^в, и = y/~R^Kcosy.
at
В общем случае оптимальные траектории, реализующие min Q^, могут
быть двух типов: проходящие внутри допустимой области фазовых коор¬
динат и содержащие участок движения по ограничению (5.23) .
Сначала проведем анализ структуры оптимального управления при отсут¬
ствии участка движения по ограничению (первый тип траекторий) . Из рас¬
смотрения уравнения (5.30) видно, что управление и входит в его правую
часть линейно. Оптимальное управление, найденное из условия максимума
гамильтониана (5.26), гранично и определяется следующим образом:
и(х) =итах signal (х). (5.31)
Здесь Ф1 (х) определяется из решения линейного неоднородного дифферен¬
циального уравнения второго порядка [19]
^-+ g?(x, у2)Ф\ = £(*, Ziz К2 ), (5.32)
dxz
где
Как видно из (5.31), оптимальное управление принимает предельные
значения t/max и -t/max, а моменты переключения оптимального управле¬
ния соответствуют нулям функции ф\ (х) . Таким образом, анализ опти¬
мального управления сводится к анализу числа нулей и последовательности
смены знака в решении уравнения (5.32) .
Анализ критерия оптимальности (5.25) показывает, что для летательных
аппаратов "скользящего" типа, осуществляющих спуск в атмосфере Земли,
функция % из условия (5.33) является знакопостоянной. Это означает, что
максимальное число нулей уравнения (5.32) равно двум. Следовательно,
возможны пять типов оптимального управления на траекториях, не содер¬
жащих участки движения по ограничению (рис. 5.9) :
полет с постоянным максимальным значением /Сэфф ~ +^балг
121
одноразовое переключение эффективного аэродинамического качества
с максимального отрицательного значения /<эфф = ”^бал на максимальное
положительное /Сэфф = +^бал;
двухразовое переключение эффективного аэродинамического качества
с максимального отрицательного значения КЭфф ~ на максимальное
положительное К’эфф= +^бал и затем опять на максимальное отрицательное
^эфф — ^бал,’
одноразовое переключение эффективного аэродинамического качества с
максимального положительного значения Кэфф = +^бал на максимальное
отрицательное КЭфф = ~^бал;
полете постоянным минимальным значением ^эфф = — Kq&ji,
Рассмотрим теперь структуру оптимальной траектории, содержащей
участок движения по ограничению (5.23) . Дифференциальное уравнение
для сопряженной переменной V/i при полете КЛА с постоянной перегрузкой
имеет вид [123]
d2^i Г , d2<pv 1 d ldf°\ 9f°
— 2 - + w2(x,k2)+-— 2-kj =— I —)—— .
dx L dyi<Pv J dx i Ъуг
У 2
(5.34)
Анализ условий разрыва вспомогательных переменных (5.29) и уравне¬
ния (5.32) показывает, что функция (х) в момент выхода на ограниче¬
ние (5.23) и схода с него обращается в нуль. Этот вывод значительно
облегчает поиск структуры оптимального управления. А именно, для траек¬
торий, содержащих один участок движения по ограничению, имеется лишь
одна точка переключения оптимального управления на участке выведения
КЛА на ограничение. Эта точка переключения однозначно определяется
условием выхода на изоперегрузочную траекторию.
Рис. 5.10. Параметры оптимальной траектории спуска КЛА в атмосфере Земли.
122
Для траекторий, содержащих два участка движения по ограничению,
имеются три точки переключения, гёричем две из них определяются усло¬
вием касания ограничения при первом и втором выходах на него соответ*
ственно, а третья следует из минимума функционала (5.25).
Итак, анализ позволил определить структуру оптимального управления
из условия minQs, не прибегая к интегрированию сопряженной системы
дифференциальных уравнений. Использование найденных законов управле¬
ния в качестве первого приближения позволяет достаточно быстро получить
искомую оптимальную траекторию. В качестве примера на рис. 5.10приве¬
дены параметры оптимальной траектории спуска [5, 20J КЛА, осущест¬
вляющего вход в атмосферу Земли с начальной скоростью Уо = 11 км/с,
углом входа = — 6° и максимально допустимой перегрузкой лдоп =
= 10.
Из представленных на рис. 5.10 зависимостей видно, что для рассматри¬
ваемых условий входа и величины допустимой перегрузки оптимальное
управление КЛА заключается в следующем. Вход в атмосферу осущест¬
вляется с максимальным отрицательным качеством /Сэфф = — =
= —0,2. На 36-й секунде полета происходит переключение кЭфф на макси¬
мальное положительное значение К'эфф = 0,2. На 68-й секунде полета пере¬
грузка достигает допустимого значения, и полет до 130-й секунды происхо¬
дит с переменной величиной /Сэфф, удовлетворяющей условию движения
КЛА с постоянным значением перегрузки п = лдоп. Заключительный
участок траектории спуска после "схода" КЛА с ограничения от 130-й до
150-й секунды протекает с максимальным отрицательным значением
^эфф = ^бал-
Оптимальное управление летательным аппаратом "скользящего" типа,
осуществляющим спуск в атмосфере Юпитера- Рассмотрим задачу миними¬
зации суммарного теплового потока для КЛА, снижающегося в атмосфере
Юпитера при выдерживании ограничения (5.23) на величину допустимой
перегрузки и на высоту условного перицентра траектории входа (5.22)
[25].
Будем считать, что на КЛА действуют конвективные и радиационные
тепловые потоки. При этом величины удельных тепловых потоков опреде¬
ляются следующими выражениями:
Необходимо отметить, что решение задачи minqE проводится в предпо¬
ложении равновероятного входа КЛА в коридор (5.22) . Сравнение резуль¬
татов решения задачи, полученных при свободном значении hn [абсолютное
минимальное значение функционала (5.25) ] и с учетом условия (5.22) по¬
зволяет оценить влияние этого фактора на оптимизируемый функционал.
Используя необходимые условия оптимальности и уравнения (5.21),
запишем систему уравнений для сопряженных переменных при gjt) < 0:
cxs cys p g cos“ L
=- — pVrpx i/^cosy -i//2cos0 — i//2 ’ +
m m О V/2 Г
dt m m
123
- 3,28Др0’7 V2’28^o-3fip°’5V2^o,
~~~ = ff’/'icosfl — «Micosfl i//2sin0 +—i//2sin0 +
dt V 2
0,7
+ ^2sin0 — Videos#,
di//3 = cxs pV2(i _
dt m21
2pcosd V -
— ф2 + т V^cose ip2cos0 + — aAp
Vr3 r2 V 7)
0 5
+ — bBp°'sV3^4 +O,7p°’1V3’26^o + 0,5Bp°’s V3^0,
Я
^^4 CXS 2^1®ун . cy° ... с1®ун
— =— pV2—4>i- — pV^2—cos 7,
dt 2 m2 2 rrr
2/zsin0 cys pfiV
: co i/^sina + i//2cosy —
r3 m2
a?
°-7V3-28^4 +
где i//0 — сопряженная переменная, получаемая при введении в систему диф¬
ференциальных уравнений движения (521) переменной fo = dQ^/dt.
Закон изменения угла крена при движении по изоперегрузочному участ¬
ку имеет вид
cost ={(£ - у ~^-Г)со50 +{ pfiV2 Vsin6 - 2р у[- (77 -
- (д- co2r)sin0^| - 4pVV — 2pV2+j}phV2j /(—0pV3cos6-2pVcos6}.
Оптимальное управление на участке движения внутри допустимой области
фазовых координат определяется из условия максимума гамильтониана
JC = -
cxs pV2
т 2
cys pV
Ф1-(д-ыг)ф1 sin в +— -7—i//2cos7 + 2соф2 -
— — 7—i//2cos0 + Vi//3sin0 + 7 (аДр0’7У3’28+ер0,5У3)ф4 +
+ Ар0,7 У3,28ф0 +Вр°’5 У3ф0 =-^y^2cos7 + <I>(r)
и имеет вид
^эфф ~ ^бал ^2/
где Ф (t) — функция времени, не зависящая в явном виде от управляющего
параметра.
Видно, что оптимальный закон управления на участке движения внутри
допустимой области фазовых координат представляет собой кусочно-по¬
стоянную функцию. Количество переключений эффективного качества
выявляется после решения краевой задачи и определяется числом нулей
функции ф2-
В качестве первого приближения допустимого управления при решении
краевой задачи можно использовать оптимальные законы управления, най-
124
Рис. 5.11. Параметры оптимальной траектории спуска КЛА в атмосфере Юпитера
(тип I).
денные при решении задачи min для КЛА, осуществляющих спуск в
атмосфере Земли (см. рис. 5.9) . Решение краевой задачи показало, что при
спуске в атмосфере Юпитера оптимальное управление в зависимости от
начальных условий входа и проектно -баллистических характеристик КЛА
может быть двух типов:
тип I имеет место, когда траектория спуска проходит внутри допусти¬
мой области фазовых координат (рис. 5.11 и 5.12); управление заключает¬
ся в одноразовом переключении эффективного аэродинамического качест¬
ва /^эфф С ^бал Н8 _*_^балг
&
Пх
CMZ
3012
500
855
208
200
570
nx(t)
10 4
100
2.85
q А*) У,
*конб хЛХУ
Рис. 5.12. Параметры оптимальной траектории спуска КЛА в атмосфере Юпитера
(тип I).
125
Рис. 5.13. Параметры оптимальной траектории спуска КЛА в атмосфере Юпитера
(тип II).
тип II соответствует траекториям спуска, содержащим участок движе¬
ния по ограничению (5.23); при выведении КЛА на изоперегрузочный
участок, а также после схода е него используется программа одноразового
переключения /Сэфф с —/Сбал на +/Сбал (рис. 5.13).
Отметим, что оптимальное управление типа I характерно для КЛА, осу¬
ществляющих спуск в атмосферу вблизи верхней границы коридора входа
и с возможно меньшими начальными скоростями VQ. Так, например, для
КЛА, входящего в атмосферу со скоростью Уо = 60 км/с (/Сбал = ОД*
Рх — 200 кгс/м2), для диапазона высот условного перицентра от Лл =
= —244 км до Ля = —380 км характерно оптимальное управление типа I,
а для Л< — 380 км — оптимальное управление типа II.
В случае входа КЛА в атмосферу при Ля = —350 км (/Сбал = 0,3; Рх =
= 200 кгс/м2) и Vq < 65 км/с характерно оптимальное управление типа I,
а при Vo > 65 км/с — оптимальное управление типа II.
Результаты решения краевой задачи показали (рис. 5.14), что абсолют¬
ное минимальное значение теплового потока имеет место при входе ЛА в
атмосферу с минимальным значением высоты условного перицентра (hn =
= ^япип) * при котором еще возможно выдерживание ограничения на вели¬
чину максимально допустимой перегрузки. Так, при номинальных значе¬
ниях начальной скорости входа и проектно-баллистических характеристик
КЛА имеем: minQs = 670 кДж/см2 при ЛяпИп = -1747 км. Как и следо-
вале ожидать, при движении КЛА внутри навигационного коридора входз
(в том случае, если его нижняя граница /?“ совпадает с h„min) величина
теплового потока min02 монотонно возрастает с увеличением высоты
условного перицентра траектории входа и достигает величины minQ^ =
= 975 кДж/см2 при Ля = Л® = —248 км.
Оптимальное управление КЛА с большим значением аэродинамического
качества. Рассмотрим эту задачу на примере аппарата, осуществляющего
спуск с орбиты ИСЗ, из условия minQs. На траекторию спуска наклады¬
вается ограничение на величину максимально допустимой температуры
126
Рис. 5.14. Зависимость суммарного теплового потока и максимальной перегрузки
лтах от высоты условного перицентра (сплошные линии — с учетом ограничения
на лтах, штриховые — без учета этого ограничения).
(5.24). Управление КЛА ведется путем изменения угла крена. Следует от¬
метить, что возможности определения структуры оптимального закона
управления на основе анализа решений вспомогательного уравнения (5.34)
для КЛА с большим значением аэродинамического качества очень ограни¬
чены. При движении в атмосфере со скоростью, меньшей круговой, реше¬
ние вспомогательного уравнения (5.34) для сопряженной переменной
^i(t) может иметь ярко выраженный колебательный характер, а количест¬
во переключений /СЭфф довольно большим. Однако если неоднородная
часть этого уравнения — знакопостоянная функция, то решение вспомога¬
тельного уравнения может не иметь нулей [46].
Анализ структуры оптимального управления для рассматриваемой зада¬
чи можно провести, используя особенности траектории снижения. На участ¬
ке движения с постоянной температурой нетрудно получить аналитическое
выражение для величины суммарного теплового потока [46]
ДОЕ =
Ciml/p5-3
сх5<7(7”дОП )
F-(T'
(5.35)
где Сх — постоянный коэффициент; q(Гдоп) — удельный тепловой поток,
соответствующий допустимой температуре поверхности КЛА; — ско¬
рость в начале интервала движения с постоянной температурой; V2 — ско¬
рость в конце этого*интервала.
Выражение (5.35) позволяет оценить долю суммарного теплового
Потока ДОе от общего суммарного теплового потока на траектории
спуска в различных диапазонах скоростей (табл. 52.).
Рассмотрение данных, представленных в табл. 5.2, показывает, что для
Получения наименьшей величины теплового потока на траекториях, содер*
127
Таблица 5.2
Распределение суммарного теплового потока на траектории снижения
V/V., %
AQ^/Q^, %
v/va.%
100-90
90-80
44 80-70
26 70 - 60
14
7
жащих участок полета с постоянной температурой, целесообразно осу¬
ществлять наискорейшее выведение КЛА на этот участок в самом начале
траектории снижения.
Учитывая изложенное, примем в качестве первого приближения следую¬
щую программу управления /СЭфф:
одноразовое переключение К'эфф с — Кбал на +Кбал на участке выве¬
дения;
управление, поддерживающее постоянное значение Гдоп в течение макси¬
мально возможного интервала времени;
одноразовое переключение КЭфф с -Кбал на +Кбал на участке схода с
ограничения Т = Тдоп.
Решение краевой задачи показало (рис. 5.15), что оптимальная програм¬
ма управления практически полностью совпадает с программой первого
приближения. При этом длительность отдельных участков полета для рас¬
сматриваемого примера составляет Atj = 180 с (выведение на ограниче¬
ние) , At2 = 870 с (движение по ограничению), At3 = 450 с (сход с ограни¬
чения) . Видно, что наибольшая длительность полета по оптимальной траек¬
тории приходится на участок полета с постоянной температурой. Причем
выведение КЛА на режим полета с Т= Таоп осуществляется с максимально
возможной скоростью = 7790 м/с при начальной скорости входа Уо =
= 7820 м/с.
Режим особого управления. Выше были рассмотрены примеры решения
задачи минимизации суммарного теплового потока minQs в предположе-
128
нии, что сопряженная переменная (х), определяющая структуру опти¬
мального управления, не равна тождественно нулю. Как известно, случай
g/j (х) = 0 на отдельных участках траектории носит название особого и тре¬
бует специального дополнительного анализа для выявления оптимального
закона управления на этих участках [9, 13]. Учитывая обобщенные выраже¬
ния для удельных конвективного и радиационного потоков (см. главу 3),
запишем в переменных х и у2 выражение для оптимизируемого функ¬
ционала
хк
QS = f [9К0НВ(^ И2)+<7рад(^ (5.36)
Х„
в следующем виде:
(5.37)
где
С,
Аконв 2т\т' mi)
VT КР \cxs> VV Л /
кр
С2
(5.38)
(5.39)
rii, п2,mh т2, Дконв/ 5рад _ постоянные коэффициенты.
Перепишем уравнение (5.32), определяющее оптимальное управление,
в виде
d2i//i Э
-- + g?(x, у2}фх =-—r[<7S(*z/2)b
dx2 ду2
Где ^конв +^рад'
Условием особого управления в рассматриваемой задаче является равен¬
ство нулю выражения
[<7S(X,K2)J = 0. (5-40)
Равенство (5.40) соответствует условию стационарности подынтеграль¬
ного выражения критерия (5.36) по координате у2 и определяет траекто¬
рию абсолютного минимума Qs. Проведенные исследования показали, что
траектории абсолютного минимума представляют собой монотонно воз¬
растающие /г(х) в плоскости ху2, которые не соответствуют заданным
начальным условиям Уоь Уо2- В то же время можно подобрать такие на¬
чальные условия входа КПА в атмосферу, что оптимальная траектория
будет содержать участки особого управления [46]. Учитывая (537) —
(5.39) , а также то, что значения тг < 1, а т2 > 1, получим из выражения
(5.40) следующее решение у2 (х), соответствующее экстремали особого
управления:
уЦх) = аеЬх,
9. Зак. 2069
129
где
1
т 1 ~mi
(l-znJCi
а =
(п?2 — 1 ) С2 .
п2 —П1
ГП2 —fTIl
Постоянные коэффициенты а и b положительны, поскольку тх < 1,
т2 > 1 и п2 > П\. Оптимальное управление при движении по участку особой
экстремали определяется из условия равенства нулю младшей из производ¬
ных функции сопряженной переменной (х), в которую в явном виде
входит управление К (х). Для рассматриваемой задачи — это четвертая
производная:
/С*(х) =
е2х -1 -а2Ь2е2Ьх
ае
Ьх
Величина суммарного теплового потока, подведенного к критической
точке КЛА при движении по участку особой экстремали (хх<х<х2),
равна
01 =<4 ? + Сг f1y^m2-1)e(1-n>)xdx.
xi х,
После несложных преобразований [46] получим
=A(Vi - ЙД
где
—1
1
X
1 + Д
X ,
(л2 —п1) — (п2т1—п1т2 }
(т2 — тх)
д — постоянный коэффициент.
Следовательно, суммарный тепловой поток при движении КЛА по
участку особого управления определяется лишь скоростями КЛА в момен¬
ты выхода на этот участок Ух и схода с него V2.
Рассмотрим теперь оптимальное управление КЛА на участке выхода
на особую экстремаль. Будем считать, что этот участок расположен
в области сверхкруговых скоростей. Качественный анализ структуры ре¬
шений уравнения (5.32) показывает [46], что в этом случае они имеют
апериодический характер. Допустим, что оптимальная траектория неодно¬
кратно пересекает участок особого управления. Тогда на последнем участ¬
ке между пересечениями, который предшествует выходу на особую экстре¬
маль, решение уравнения (5.32) имеет не более двух нулей. При этом один
нуль расположен в точке выхода на участок особой траектории.
Анализ оптимальной траектории на последнем участке между переклю¬
чениями показал [46], что при подходе к точке выхода на особую экст¬
ремаль оптимальное управление обязательно имеет одно переключение
(рис. 5.16). Аналогичный закон оптимального управления имеет место и
на всех предшествующих участках между переключениями оптимальной
траекторией особой экстремали.
130
Уг
/
/
/
<*7
л
X
л
J
1
1
1
1
к
X
1 _
х* 1
X
\
Рис. 5.16. Параметры оптимальной траектории спуска, со¬
держащей участок особого управления (Кбал = 0/3) •
Рис. 5.17. Параметры оптимальной траектории спуска, со¬
держащей участок особого управления (Кбал =1).
Таким образом, на основании проведенных рассуждений можно сравни¬
тельно просто организовать численную процедуру поиска оптимального
управления на траекториях, содержащих участки особого управления,
без интегрирования уравнения (5.32). В качестве примера на рис. 5.17
приведены параметры оптимальной траектории спуска, содержащей участок
особого управления. Рассматривался КЛА с величиной аэродинамического
качества /Сбал = 1 и приведенной нагрузкой на лобовую поверхность Рх =
^ 500 кгс/м2, осуществляющий вход в атмосферу Земли со скоростью
|/0 = 2. Видно, что первоначально КЛА движется в атмосфере с максималь¬
ным положительным значением/Сэфф = 1; затем, для того чтобы обеспе¬
чить выход КЛА на особую экстремаль, происходит переключение /Сэфф
на максимальное отрицательное значение /Сэфф = ~1- Движение^по особой
экстремали происходит в интервале скоростей от V = 1,8 до V = 1,5, при
этом величина аэродинамического качества постепенно изменяет свое
значение от максимального отрицательного до максимального положи¬
тельного. В дальнейшем с уменьшением скорости полета траектория спуска
переходит с особой экстремали на участок движения по ограничению (вели¬
чина допустимой перегрузки лдоп = 10) и схода с ограничения.
5.2.5. Ограничение на дальность полета
Будем предполагать, что вход КЛА в атмосферу осуществляется в плос¬
кости траектории с малыми начальными углами входа.
В этом случае уравнения движения могут быть записаны в следующем
виде [2] :
dV scxpV2 d6 _ sCypV
dt 2m ' dt 2m '
,, (5.41)
dh dL _
= l/sin0, = Vcos0,
dt dt
где h - высота полета; L - расстояние по горизонтали (дальность полета).
131
Определим суммарное количество тепла, подводимого к лобовой по¬
верхности КЛА, следующим соотношением:
tK
Q^=A f pV3dt, (5.42)
Ч
где А — постоянный коэффициент.
Уменьшим порядок системы уравнений (5.41), используя вместо пере¬
менной t высоту/?. Получим
dV scxpV d6 scv p
= —— , = y- . (5.43)
dh 2m sin 6 dh 2m sin 6
Используя обозначения dV/dh = Vf и scx/m = ox, получим [2]
sin 0 = oxpV/V'.
Перепишем (5.42) в виде
2A , 2А
Qz= f V]/dh = f Fxdh.
Ox °x
После несложных преобразований из последнего уравнения (5.41)
получим выражение для переменной L
L =
*0
/
Лк
2V’
(jxpV
oxpV
4 И
*0
f
Лк
F2dh.
Решим вариационную задачу определения минимума функционала
(5.42) при условии заданной дальности спуска L =1. Эта вариационная
задача относится к классу изопериметрических задач с подвижным правым
концом [2], поскольку скорость при конечной высоте/?к не задана.
Составим вспомогательный функционал
2^V\
2V' /
dh,
где X* — постоянный коэффициент.
Принимая экспоненциальный закон изменения плотности атмосферы,
с помощью уравнения Эйлера получим
„ (3 , (V')2
V + V
2 V
2(V')30e2l3h
■ , -2--j = 0. (5.44)
а2х pl V2
Уравнение (5.44) позволяет получить закон оптимального изменения
скорости движения КЛА на траектории спуска в виде
V = С2 exp f
cfh
4e-0h \
а2Ро /
1/2
(5.45)
где постоянные С\ и С2 определяются из условия h = h0, V= Vo.
Используя найденное выражение для оптимальной скорости полета
(5.45), определим закон изменения угла наклона траектории к местному
горизонту.
Предположим, что отношение аэродинамических коэффициентов сх и
су на траектории спуска постоянно. Разделим одно из уравнений (5.43) на
132
рис. 5.18. Зависимость скорости полета
от высоты h при оптимальном управ¬
лении из условия Q^min и ограничении
на дальность полета.
другое и, интегрируя полученное
уравнение при 0 = 0О и V = VQ,
получим
,5-46'
Для определения требуемого зна¬
чения отношения Су/сх такого,
при котором закон изменения угла 0
используется изопери метрическое условие
f ctg 0 dh = I.
(5.46) совпадал бы с оптимальным,
(5.47)
В качестве примера на рис. 5.18 представлена зависимость скорости по¬
лета V от текущей высоты h при оптимальном соотношении аэродина¬
мических коэффициентов су!сх для КЛА, осуществляющих спуск с орбиты
ИСЗ (VQ =7,8 км/с, 0О = -1°, I = 2000 км).
5.2.4. Управление баллистическим параметром
Рассмотрим задачу оптимизации траектории спуска КЛА баллистичес¬
кого типа, имеющего изменяемую геометрическую форму. Примем следую¬
щие допущения:
планета считается плоской и невращающейся;
ускорение силы тяжести постоянно;
траектория спуска близка к вертикальной (0 0 ~ 90 ) ;
сила тяжести, действующая на КЛА, пренебрежимо мала по сравнению с
силой лобового сопротивления;
сила лобового сопротивления задается формулой
1
X = — cxp(h)sV2;
коэффициент лобового сопротивления сх в сверхзвуковом режиме
полета не зависит от чисел Маха и Рейнольдса.
С учетом этих допущений движение КЛА баллистического типа описы¬
вается дифференциальными уравнениями [62]
h + V = 0,
. cxp(h)sV2
V + = 0.
2т
(5.48)
Используя высоту в качестве переменной величины, запишем уравнения
(5.48) в несколько другой форме:
dt_ = _ 1 dV _ cxp{h)sV (5 49)
dh V dh 2т
Предполагается, что КЛА снабжен устройствами, изменяющими его
геометрическую форму таким образом, что коэффициент лобового сопро¬
тивления может изменяться программным образом на траектории сниже-
133
ния в атмосфере. Текущее значение коэффициента лобового сопротивления
ограничено нижним и верхним пределами:
сх min сх сх max • (5.50)
Класс допустимых траекторий. Допустим, что в данный момент времени
КЛА имеет скорость V и находится на высоте h. В плоскости фазовых
координат скорость — высота (рис. 5.19), это положение определяется
точкой Р. Точка Р' соответствует новому положению КЛА, после его пе¬
ремещения за бесконечно малое время со скоростью V' = V + d V на высоту
h' = h + dh. В результате бесконечно малое смещение КЛА в этой плоскос¬
ти будет характеризоваться вектором РР’ .
Для каждого значения коэффициента сх существует единственное бес¬
конечно малое смещение, которое, однако, не всегда является физически
возможным из-за ограничения (5.50). Будем считать, что в плоскости
Vh класс допустимых траекторий ограничен двумя предельными вектора¬
ми [62]:
вектором PR, соответствующим минимальному значению коэффициен¬
та лобового сопротивления cxmin;
вектором РТ, соответствующим максимальному значению коэффициен¬
та лобового сопротивления схтах.
Таким образом, два предельных вектора PR и РТ делят плоскость ско¬
рость — высота на две области: область Н, заключенную внутри угла TPR и
достижимую для КЛА и область Н *, лежащую вне этого угла и недоступ¬
ную для КЛА.
Область допустимых траекторий. Пусть КЛА переводится из начального
состояния 1/0, hQ в конечное состояние VK, /?к. При заданной программе
изменения коэффициента лобового сопротивления второе уравнение (5.49)
может быть проинтегрировано [62]. Например, если коэффициент лобового
сопротивления постоянен, то будем иметь
V ехр
Г сх5
L 2т
h
f p(h)dh
о
= const.
(5.51)
Используя начальные условия, получим две граничные траектории,
соответствующие предельным значениям коэффициента лобового сопро¬
тивления (сх = cxmin и сх = схтах)и исходящие из точки / (рис. 5.20).
Определяя постоянную интегрирования по заданным конечным условиям,
можно построить две другие граничные траектории, которые заканчивают¬
Рис. 5.19. Класс допустимых траекторий в плоскости скорость — высота.
Рис. 5.20. Область допустимых траекторий.
134
ся в точке F. Эти четыре граничные траектории образуют область IDF С!,
которая содержит все допустимые траектории. При этом не существует
такой траектории, соединяющей граничные точки / и F, которая может
пересечь границу этой области без нарушения условия (5.51).
Оптимальное управление коэффициентом лобового сопротивления.
Примем следующий обобщенный закон теплопередачи:
= крх Vy.
Перепишем его в виде
с/ Qs 1
—L (5.52)
dh
где — количество тепла, переходящего от пограничного слоя к поверх¬
ности КЛА, имеющей площадь S; к — постоянная; хи у — безразмерные
показатели степени. Значения показателей степени х и у могут быть различ¬
ными в зависимости от площади поверхности КЛА. Если S — полная пло¬
щадь обтекаемой поверхности, то
х=1, у = 3.
Если рассматриваемая площадь относится к носовой части КЛА, то
х=0,5, у = 3.
Из уравнения (5.52) следует, что бесконечно малое приращение коли¬
чества тепла, поступающего к поверхности КЛА, записывается в виде:
dQ^. = ^dh,
где
^ = ^Kp^Vy-\
Полное количество тепла, поступающего к поверхности КЛА за время
полета от точки / до точки F, равно
f
0^ = f 'I'dh, (5.53)
i
где индексы 7 и f соответствуют параметрам траектории в начальной и ко¬
нечной точках.
В соответствии с изложенным задача об отыскании оптимального
управления коэффициентом лобового сопротивления может быть сформу¬
лирована следующим образом: в классе траекторий V (h ), удовлетворяю¬
щих заданным граничным условиям, определить такую траекторию, на
которой реализуется минимум функционала (5.53). Уравнение замкнутого
контура, который ограничивает все допустимые траектории (см. рис. 5.20),
может быть символически записано в виде [62]
e(V,h) = 0.
В граничных точках / и F получим
elVi'hj) = c(Vf.hf) =0.
В соответствии с "теоремой Грина о преобразовании линейных интегралов
в поверхностные изучение свойств функции
u(V,h) = = к (у - 1) pxVy
dV
(5.54)
позволяет сделать важные заключения о выборе оптимальной траектории.
135
I
F
И
,/
таз
fi)
Рис. 5.21. а) Траектории, доставляющие экстремум теплопередаче и времени полета
UCF ■-= tmin; IDF = Gamin' rmaxH 6} распределение знаков расширенной
функции ш*(У, Л) {IABF = Q^min) .
Анализ выражения (5.54) показывает, что функция a>(V,h) повсюду
отрицательная, поэтому оптимальная траектория состоит только из таких
отрезков, которые идут вдоль границы допустимой области [62]. Оказы¬
вается, что минимальное значение суммарного теплового потока реализу¬
ется при движении по пути IDF (рис.5.21,а). Этот путь состоит из отрезка
ID, проходимого с максимальным значением коэффициента лобового соп¬
ротивления сх = схтах, и отрезка DF, проходимого с минимальным зна¬
чением сх = cxmin Таким образом, можно сделать вывод, что оптимальной
программой управления коэффициентом лобового сопротивления является
программа одноразового переключения сх с максимального значения на
минимальное.
Оптимальное управление КПА из условия minQz ПРИ заданном времени
полета. Рассмотрим задачу минимизации суммарного теплового потока
для случая, когда время полета задано. Эта задача относится к классу
линейных изопериметрических задач. Она может быть также решена с по¬
мощью теоремы Грина. Согласно методике, изложенной в [62], для реше¬
ния задачи minO^ при tK = const необходимо провести исследование рас¬
пределения знаков расширенной функции со* (У, h, X) внутри допустимой
области изменения фазовых координат. Эта функция может быть запи¬
сана следующим образом:
di//*
со* (У, Л, X) = —— ,
Э V
где Л — постоянный множитель Лагранжа, а
Учитывая (5.54), представим функцию со* в виде
136
Рис. 5.22. Множество дуг, доставляющих экстре¬
мум количеству тепла, переданного телу в те¬
чение заданного времени.
Функция со* ( V, /?, X) положительна при
движении КЛА слева от линии постоянной
скорости теплопередачи (5.55) и отри¬
цательна при движении справа от нее (см.
рис. 5.21,6). Таким образом, расширен¬
ная функция co*(l<6, X) меняет знак
внутри допустимой области. Оптимальная
траектория, следовательно, состоит из от¬
резков, проходимых КЛА вдоль границы
допустимой области (полет с предель¬
ными значениями Cx=CvminH Cxmax) И
отрезков, удовлетворяющих условию равенства нулю расширенной функ¬
ции со*. Способ соединения этих отрезков и, следовательно, структура опти¬
мального закона управления могут быть различными и определяются задан¬
ными граничными и изопериметрическими условиями. В качестве примера
на рис. 5.22 приведены возможные типы оптимального управления при пе¬
реведении КЛА из начальной точки / в конечную точку F.
5.2.5. Анализ результатов решения задачи
минимизации суммарного теплового потока
Приведем численные результаты решения вариационной задачи мини¬
мизации суммарного теплового потока для КЛА "скользящего" типа,
управляемых углом крена и осуществляющих спуск в атмосферах Земли,
Венеры, Марса, Юпитера, Сатурна, Урана и Нептуна. Расчеты проводились
при следующих значениях начальных условий входа в атмосферу и проект¬
но-баллистических характеристик КЛА:
для Земли
11 км/с < Vo < 17 км/с, — 400 км < <40 км,
150 кгс/м2 </\ <700 кгс/м2, 0,1 <Кбал ^0,5;
для Венеры
8.5 км/с < Vo <13 км/с, — 800 км <6Я <50 км,
100 кгс/м2 </\<900 кгс/м2, 0,1 <Кбал ^0,6;
для Марса
5.5 км/с < Уо <9 км/с, —300 км </?я <30 км,
150 кгс/м2 </\ <550 кгс/м2, 0,1 </Сбал ^0,5;
для Юпитера
57 км/с < Vq <75 км/с, —3000 км </ц <180 км,
100 кгс/м2 </\<500 кгс/м2, 0,1 </Сбал <0,6;
для Сатурна
35 км/с < Vо <40 км/с, 0 <ЛЯ <—3000 км,
200 кгс/м2 <РХ <750 кгс/м2, 0,1 <Кбал ^0,5;
для Урана
26 км/с < Vq <30 км/с, -1600 км<^ <150 км,
137
Рис. 5.23. Зависимости суммарного теплового потока от h^,
КЛА , осуществляющих спуск в атмосфере Земли.
Рис. 5.24. Зависимости суммарного теплового потока Qj; от 1/0, /Сбал и для
КЛА, осуществляющих спуск в атмосфере Венеры (номинальная модель атмо-
сфеоы).
кВт
см2
^бал)
(
Рmax равн)
0ГС^
0s OW \
(hit)
г^-
Qt<P^
sSv Q's, (p
$\\ z ma® ле-
гн)
\\ ^P I )
\\ * ma® ^имн'
\ (p . I)
\ ' тьп лети7
W
(p •
• min %и>
и
X
Qz (^b)
150
250
550
450
Рх,кгс/м
0,1
0,2
0,3
Op
^бал
5
6
7
8
Vo, км/с
,2.
hrt'KM
Рис. 5.25. Зависимости суммарного теплового потока от hn, 1/0, Кбал и^хЛля
КЛА, осуществляющих спуск в атмосфере Марса (минимальная модель атмосферы
для равноденствия) .
Рис. 5.26. Зависимости суммарного теплового потока Qj; от Ьл, 1/0, ^бал
КЛА, осуществляющих спуск в атмосфере Юпитера (номинальная модель атмосферы).
Рис. 5.27. Зависимости суммарного теплового потока от h^, l/0, Kgan и для
КЛА, осуществляющих спуск в атмосфере Сатурна (номинальная модель атмосферы) .
Рис. 5.28. Зависимости суммарного теплового потока от h^, V{), и Рх для КЛА,
осуществляющих спуск в атмосфере Урана (номинальная модель атмосферы) .
300 кгс/м2 </\<750 кгс/м2, 0,1 </Сбал <0,6;
для Нептуна
25 км/с<1/0 <29 км/с, —1500 км </?я <90 км,
100 кгс/м2 </\<800 кгс/м2, 0,1 </Сбал <0,5.
На рис. 5.23 — 5.29 приведены результаты расчетов оптимальных траек¬
торий спуска КЛА в атмосферах планет Солнечной системы. Показано влия¬
ние приведенной нагрузки на лобовую поверхность, аэродинамического
качества, начальной скорости входа в атмосферу и высоты условного пери¬
центра траектории входа на величину суммарного теплового потока.
Анализ представленных зависимостей показывает, что характер изменения
величины Q% от перечисленных параметров для рассматриваемых планет
Солнечной системы остается неизменным. А именно, уменьшение вели¬
чины может быть достигнуто при уменьшении начальной скорости
входа в атмосферу и высоты условного перицентра. Аналогичный эффект
достигается и при уменьшении значений основных проектно-баллисти¬
ческих характеристик КЛА — величины приведенной нагрузки на лобовую
поверхность и аэродинамического качества.
Следует отметить, что для каждой из рассматриваемых планет степень
влияния перечисленных факторов на величину оказывается различной
Рис. 5.29. Зависимости суммарного теплового потока от ^бал и ?х A°R
КЛА, осуществляющих спуск в атмосфере Нептуна.
141
Таблица 5.3
Влияние основных параметров на суммарный тепловой поток
Планета
"эй;'
кВт с/ (см2 км)
кВт/(см2 км)
Э Q v
Ъ?х
кВт м2/(см2 кгс)
Э^бал
кВт/см2
Венера
5,5
0,02
0,03
11
Земля
5
0,05
0,08
19
Марс
2,2
0,021
0,018
8
Юпитер
24
0,18
19,5
220
Сатурн
70
0,09
1,5
460
Уран
26
0,1
0,65
270
Нептун
20
0,07
0,4
95
(табл. 5.3). Так, изменение величины начальной скорости 1/0 наиболее
заметно проявляется при спуске в атмосфере Сатурна (увеличение 1/0 на
1 км/с приводит к возрастанию суммарного теплового потока
70 кВт/см2), а наименее заметно — при спуске в атмосфере Марса (увели¬
чение Vo на 1 км/с приводит к возрастанию всего лишь на 2,2 кВт/см2) .
Изменение высоты условного перицентра оказывает наибольшее влияние
д
на величину при входе в атмосферу Юпитера «0,18 кВт/(см2 - км) ,
La/,,
д
а наименьшее — при входе в атмосферу Венеры «0,02 кВт/(см2 - км) .
Увеличение приведенной нагрузки на лобовую поверхность оказывает
га
наибольшее влияние на при спуске в атмосфере Юпитера «
L аях
, а наименьшее — при спуске в атмосфере Ве-
Г d Qs
неры
L ьрх
«0,03 кВт • м2/(см2 • кгс)
х
аэродинамического качества наиболее заметно влияет на при спуске
/ d 1
в атмосфере Сатурна I
' 3 ^бал
/ dQz \
Марса I «8 кВт/см2 I.
\а/сбал /
5.29, позволяют также оценить
от номинального значения на t _t
Анализ^ этих зависимостей показывает, что при снижении КЛА в более
плотной атмосфере суммарный тепловой поток увеличивается.
и, наконец, изменение величины
«460 кВт/см2^, а наименее — в атмосфере
Зависимости, представленные на рис. 5.23 —
влияние отклонения плотности атмосферы
величину суммарного теплового потока.
142
§ 5.3. Оптимизация траекторий спуска из условия минимума
объединенного критерия по тепловым нагрузкам и перегрузкам
Рассмотрим задачу определения оптимального управления КЛА из ус¬
ловия минимума объединенного критерия по суммарному тепловому по¬
току и перегрузке [2, 126]
гк 1 /о , Г~ъ Г» Р
/ = / ДцР /2v3 +Д12\Ах + Су — , (5.56)
to 2т
ГД® Дц и ^12 “ весовые коэффициенты (Ar { > Q, А12^ 0), которые
определяются из инженерных соображений и отражают свойства системы
теплозащиты и конструкции КЛА.
Запишем уравнения движения центра масс КЛА в виде
• р V2 s
f{ = V + сх — + д sin в = О,
2 т
f3 = h - V sin <9 = О,
pV2
2
f4 = L — V cos 0 = 0.
Система включает четыре переменные V,0 ,h и L. Начальные и конеч¬
ные условия движения в атмосфере фиксированы:
приГ = Г0; V=VOt 0=0о, h-hQl L = Lo; (5.57)
npnf = fK: V= VK, h ~ ^K, L = LK. (5.58)
Время полета t = tK определяется достижением заданных граничных ус¬
ловий.
Предполагается, что за счет использования каких-либо аэродинамичес¬
ких устройств возможно независимое управление аэродинамической
подъемной силой (Су) и-силой лобового сопротивления (Сх).
Таким образом, в рассматриваемой задаче два управления: их = су и
и2 - сх. В частном случае возможно управление одним параметром при фик¬
сированном другом.
Сформулируем следующую вариационную задачу: на траектории спуска
КЛА в атмосфере определить программу управления параметрами и и2,
минимизирующую функционал (5.56) при заданных начальных (5.57) и
конечных (5.58) условиях.
Запишем функцию Гамильтона в виде
/ cxs pV2 л\ , 9
ЗС=Ф1( — 0 5(п0)+ф2 —
\ т 2 / ’
1 cys pV2
V L g m 2
— cos 0^1 V sin 0 + i//4 Vcos 0 + фofо (Z- 0• h, L, cx, Cy\.
Здесь функция определяет подынтегральное выражение критерия опти¬
мальности траектории спуска (5.56)
-7
/ = f fo(V,0,h, L, сх, Су) dt.
* о
Как известно, решение системы уравнений для сопряженных переменных
при неизвестных граничных условиях для затруднено. В этом случае
143
целесообразно использовать достаточно эффективный прием введения не¬
вязок по конечным условиям в функционал критерия оптимальности [2] :
/= Mn₽l/2V3 +Д12х/с2+4 + ^Г {v~ Vk}2 +
^0
(5.59)
-вк)2 +-^- (h - hK)2 +~^-{L- LK}2,
гдеДо1, —/^04 — постоянные коэффициенты.
Как видно из (5.59) , смысл функционала (5.56) не изменился, однако
при этом оказывается возможным считать конечные значения соответст¬
вующих переменных свободными и использовать для определения конеч¬
ных значений сопряженных переменных условия трансверсальности
[66].
С учетом введенных невязок по граничным условиям получим
f0ycn =Л11Р1/2У3 +а^(^2~— ) Vc2 +с2у +
+ AOi(V-VK^-C-^-S-gsine)
_cos^_^
2т
у + A03(h -hK)(Vs\nO +Ao4(L - £K)Vcos0).
Тогда функция Гамильтона принимает вид
-А02(е-вк)^ ± CypV s
2т
Vc2 +c2y + A0, (V- VK +gsine) -
- (, .rpj +
+ Д03(Л -/JKiV'sine + A04(L - LK)Vcos6 - + ffsinfl) +
, 1 cyspV2 / V2\ 1
+ ^2 V [ g ~2m V _ ~gr)cos0 + Usin/? +
Как следует из принципа максимума, для получения минимального значе¬
ния функционала (5.59) необходимо, чтобы гамильтониан JC имел макси¬
мум по управлению и в допустимой области изменения u^U.
При неограниченных значениях сх и су будем иметь (66]
dJC _ 3Jf
дсу °’ Эсх ’ °‘
Отсюда получаем следующие выражения для управляющих параметров:
СуЛТ-^Г2[А^в-^-^
144
Рис. 5.30. Оптимальное изменение пара¬
метров h, Q, Сх и Cv на траектории
спуска.
При учете ограничений на величину
сх или су на оптимальной траекто¬
рии появляются участки полета
КЛА с граничными значениями па¬
раметров управления сх и су:
сх ”cxmaxz сх =czmin и
су = су m ах z Су = Су m in •
Переменные ф, определяются обыч-
ным образом:
: ЭК
Фг =
ЭК
эе'
3 dh ’
ф4 =
эк
Э£ ■
Таким образом,
поставлен-
ная вариационная задача сводится к
двухточечной краевой задаче, имеющей для фазовыл координат граничные
условия (5.57), (5.58) и для сопряженных переменных условия
(fx) ^2(tK) = ’Аз(^к)= ’//4(fK) = 0.
В качестве примера рассмотрим задачу входа КЛА в атмосферу с круго¬
вой скоростью при независимом управлении двумя параметрами: силой
аэродинамического сопротивления и подъемной силой. Для простоты при¬
мем, что До 1 = Ао2 = Аоз = Ао4 = 0, т.е. правый конец траектории спуска
полагается свободным. На рис. 5.30 представлена типичная оптимальная
траектория, соответствующая входу КЛА в атмосферу с круговой скоро¬
стью VQ = Укр = 7,78 км/с и углом входа 6Q = —2,2° на высоте hQ —
= 75 км. Из рассмотрения этих зависимостей видно, что траектория
спуска состоит из участка пикирования, сравнительно пологого участка
и участка крутого снижения в конце траектории.
§ 5.4. Минимизация максимальной температуры
поверхности космического летательного аппарата
5.4.1. Ограничение на конечную скорость спуска
Рассмотрим следующую задачу: при заданных условиях входа в атмо¬
сферу (Vo, 0o,hQ) найти закон управления углом крена ?, минимизирую¬
щий величину
/ = max Т. (5.60)
В конце траектории спуска накладываются ограничения
npnf = tK: У=УК, 0К и — свободны.
10. Зак. 2069
145
Используя в качестве аргумента относительную длину дуги траектории
V
dl-~Rdt'
плоское движение КЛА в атмосфере опишем системой дифференциальных
уравнений вида
dV = _ pV _ sin 0 dO = grpcosy / gr А
dl = 9Г2Рх 9Г V ' dl~ 2Py )' .....
dp
dl
= —ftorsinfl,
где
m
cxs
Температуру поверхности КЛА определим из уравнения теплового
баланса (см. главу 3)
ПП1 \/П2
А — (!е - ) - еаГ4 = 0.
ГН ^0
(5.62)
Здесь А и nf — постоянные коэффициенты, зависящие от формы КЛА, по¬
ложения рассматриваемой точки на поверхности КЛА и т.д.; /Oz le, —
энтальпии, являющиеся функциями скорости, температуры поверхности
КЛА и температуры окружающей среды; гн — радиус затупления, 6 —
коэффициент излучательной способности, о — постоянная Стефана —
Больцмана.
Заменим в уравнениях движения (5.61) функцию р на Т, используя вы¬
ражение (5.62) . Тогда получим [100]
сП/
dl
= -Vfxw,T}^—gr
'х
sinfl
У '
de
dl
= -fl (v, T )sine + pf, (V, T) + gr
T).
где fj(V, T) — некоторые функции скорости полета и температуры кон¬
струкции.
В общем случае на траектории спуска возможно появление нескольких
максимумов температуры Т = Т* (рис. 5.31), причем минимальное значе¬
ние максимума Т* реализуется в неко¬
торой внутренней точке траектории (Z =
= /*). Кроме того, может существовать
такая область начальных условий входа в
атмосферу и проектно-баллистических ха¬
рактеристик КЛА, при которых после дос-
Рис. 5.31. Характер изменения температуры по¬
верхности КЛА на траектории спуска.
тижения минимального значения функционала (5.60) необходимо осущест¬
влять движение с постоянным значением Т= min(max Г) = Г*. В этом случае
предупреждается возможность увеличения минимизируемого функционала
относительно найденного экстремального значения в процессе дальнейшего
полета в атмосфере.
При использовании принципа максимума для решения подобных задач,
как известно [66], имеет место разрыв сопряженных переменных и га¬
мильтониана Кв точке I = /* достижения минимума функционала (5.60)
[или, что одно и то же, в момент выхода КЛА на режим полета с постоян¬
ным значением температуры Т = min( max7") ].
Условия разрыва сопряженных переменных можно записать в виде
JC+=JC'-|p, ФГ = < + (/=1,2 п), (5.63)
п
где К = S ф1х1 — гамильтониан; ф1 — сопряженные переменные, опре-
i = 1
деляемые обычным образом:
(7=1,2 л),
(5.64)
х, — фазовые координаты, неразрывные в точке Z*:
xf = xf (7=1, ..., n).
Как следует из принципа максимума, оптимальное управление в каждой
точке траектории обеспечивает максимум гамильтониана (5.63) .
Поскольку угол крена у входит в уравнения движения (5.61) только в ви¬
де cos у, целесообразно использовать вместо у непосредственно величину
cos у = и, имеющую ограниченный диапазон изменения:
-1 < и < 1.
Анализ гамильтониана (5.63) показывает, что параметр и входит в него
линейно. Из принципа максимума следует, что в этом случае оптимальное
управление будет иметь вид
уОПТ = 1 (7опт = 0) при > q
г/опт=_1 (уОПТ=я) при 1//2<0.
Следует отметить [100], что управление КЛА после достижения точки
I = /*, соответствующей оптимизируемому значению максимальной тем¬
пературы, оказывается неопределенным. В самом деле, из рассмотрения
сопряженной системы дифференциальных уравнений
, ЭК , эк , эк
*<="эй' ^=-эГ' ^=~1т
(5.65)
с учетом их граничных значений ф2 = 0, Фз — 0 и условия К = 0, соответст¬
вующего свободному значению аргумента I, имеем
ф2 = 0. (5.66)
Выполнение условия (5.66) означает, что вектор сопряженных перемен¬
ных ф тождественно равен нулю на участке траектории спуска, соответст¬
147
вующем интервалу изменения аргумента
lK < I < Г. (5.67)
т.е. в интервале движения (5.67) принцип максимума не дает информации
о законе управления КЛА и, следовательно, на этом участке полета допу¬
стимо любое управление углом крена [100].
Таким образом, решение поставленной вариационной задачи об отыска¬
нии оптимального управления КЛА из условия минимума максимального
значения температуры сводится к решению краевой задачи для системы
шести дифференциальных уравнений (5.64) и (5.65) с начальными усло¬
виями для фазовых координат
У=1/о, 0 = 0О/ T=TQ при Z = 0.
Решение краевой задачи заключается в выборе начальных значений со¬
пряженных переменных таким образом, чтобы удовлетворить на правом
конце траектории (Z = I *), определяемом равенством
Г=0, (5.68)
граничным условиям для сопряженных переменных
Ф1 = 0г ^=0, ^=-1. (5.69)
В силу линейности и однородности сопряженной системы дифферен¬
циальных уравнений (5.65) и существования первого интеграла гамильто¬
ниана 0 краевая задача по отысканию начальных значений сопряженных
переменных сводится к однопараметрической [100]. Для этого может
быть использован следующий прием. Будем считать, что начальные значения
сопряженных переменных 0О i и ф02 могут быть выражены через некото¬
рый параметр 6 в виде
’/'oi = sin8 и 1//02 = cos8.
Определяя ^03 из условия равенства нулю гамильтониана будем иметь
начальное направление вектора i//0 в функции одного параметра 8. В этом
случае для решения краевой задачи достаточно выбрать параметр 8 таким
образом, чтобы при 1 = 1* (7=0) выполнялись условия = 0 и Ф3 < 0.
Сопряженная переменная = 0, поскольку = 0.
Как уже отмечалось, в общем случае на траектории спуска возможно по¬
явление нескольких максимумов температуры Т и, следовательно, равен¬
ство (5.68) может выполняться в нескольких точках траектории. При этом
положение точки I = Z* на траектории спуска заранее определить нельзя.
Существует несколько возможных способов преодоления подобной труд¬
ности при решении вариационных задач снижения КЛА в атмосфере с функ¬
ционалом типа (5.60) (смлнапример, [2, 63, 135]). В частности, можно
применить методику для минимизации первого максимума температуры,
который появится на траектории спуска. Далее, если это оказывается воз¬
можным, необходимо продолжать движение с постоянным значением тем¬
пературы Т = Т*.
Оказалось, что в силу ограниченности управления и полет КЛА на режиме
постоянной температуры возможен лишь при значениях Г*, не меньших не¬
которой минимально допустимой температуры Гдоп. В самом деле, при
движении КЛА в атмосфере с постоянным значением температуры управле¬
ние и* определяется из условия равенства нулю старшей производной
ЪпТ/Ы ", в которую в явном виде войдет управление. В нашем случае поря-
148
Рис. 5.32. Типичный вид зависимости управляющего параметра и* от скорости
полета V.
док этой производной равен двум. Тогда из условия Т = 0 будем иметь
(5.70)
Поскольку при полете с постоянным значением температуры производ¬
ная Т = 0, можно исключить из выражения (5.70) одну из фазовых коорди¬
нат — угол 6. В этом случае управление полетом КЛА на режиме 7"* —
= const является только функцией скорости V:
U* =COSy* =^2(7^onz И.
Характерный вид этой зависимости приведен на рис. 5.32. Анализ этих
зависимостей показывает, что если Г* < Таоп, то существует такой диа¬
пазон скоростей полета
Vj < V < V2l
при полете с которыми режим Т = Т* = const не может быть реализован
из-за ограниченности управления.
Величина допустимой температуры, при которой еще оказывается воз¬
можным полет с постоянной температурой во всем диапазоне изменения
скорости V, может быть определена из системы уравнений
^(7-доп, И = 1, 0.
Отсюда также можно определить значение критической скорости VKp,
при которой управляющий параметр и принимает наибольшее значение
при Т = 7”доп.
Величины ГдОП и Укр могут быть различными и определяться несущими
свойствами КЛА (параметром Ру}, положением рассматриваемой точки на
поверхности КЛА, его формой и т.д.
149
Численные результаты решения краевой задачи показали, что для КЛА
при различных условиях входа с орбиты искусственного спутника Земли и
с различными конфигурацией и проектно-баллистическими характеристика¬
ми сопряженная переменная на интервале 1о <1 < /к остается все вре¬
мя положительной. Следовательно, для получения минимальной температу¬
ры в первом ее максимуме необходимо осуществлять полете углом крена
Отметим одно важное обстоятельство. Численный анализ результатов ре¬
шения краевой задачи показал, что величина Тлоп оказывается очень близ¬
кой к максимальному значению температуры поверхности КЛА, которая
реализуется при полете на режиме квазистационарного планирования'.
0=0. При этом можно получить достаточно простые аналитические выра¬
жения, позволяющие с приемлемой степенью точности определять величи-
ер
(Яо^о)
где Тпп,тах — максимальная температура, достигаемая на режиме квази¬
стационарного планирования; У пл — критическая скорость, достигаемая
на режиме квазистационарного планирования.
Следует отметить, что для получения траектории движения КЛА в атмо¬
сфере, совпадающей с достаточной степенью точности с траекторией квази¬
стационарного планирования, достаточно обеспечить на траектории спуска
следующие условия:
Результаты численного решения краевой задачи показали, что в ряде
практически важных случаев минимальная температура в первом максиму¬
ме (7"*) будет меньше 7"доп (или, что одно и то же, меньше ТПл.пгах)-
В этом случае нельзя утверждать однозначно, что при дальнейшем движении
в атмосфере существует управление, реализующее температуру поверхно¬
сти КЛА, меньшую чем Т* . Можно отметить, что имеется по крайней ме¬
ре один закон управления, обеспечивающий всюду в процессе управления
температуру не выше Тдоп.
Исследуем отдельно вопрос, существует ли закон управления, позволяю¬
щий реализовать на траектории снижения в атмосфере температуру, всюду
меньшую Тдоп. Для этого рассмотрим следующую вариационную задачу.
Предположим, что КЛА движется с некоторым постоянным значением
температуры Т = 7"дОП. Требуется определить такой закон управления
после схода с режима Т= ТЛОП, который обеспечивает минимум температу¬
ры в ближайшем максимуме. Эта задача аналогична рассмотренной выше и
отличается только тем, что начальные значения фазовых координат не
постоянные, а определяются условиями движения КЛА на режиме
7”доп-
150
Рис. 5.33. Зависимости min 7"max от ^бал и Рх для КЛА, осуществляющих
спуск в атмосфере Земли.
Рис. 5.34. Зависимости min 7"max от У,„ Кбая и для КЛА, осуществляющих
спуск в атмосфере Венеры (номинальная модель атмосферы) .
mlnFmas'^ , С
mln Г,
т*,п Лпа®/7
па® (^о)
т*>п Лпс
Лпс
m^Tna® (^бал)
Л(Р .
‘ • тип $ими)
ls та® гимн)\
п^тах^я'^ \
^бал)^
^ma® V*)
\\mln 7maiGo
\ \ • min
\ mln (р
\ • та®
"tnrmaxQ3
* та®
лети)
1 )
летн^
1 рабн)
min Г,
150 250
та® Щ)
550
450
1
Рх.кгс/м
0,1 0,2
5 6
0,5
7
о,1>
, в:
^*бол
! Vo, К м/с
-250 h^, км
2
Рис. 5.35. Зависимости тш7"тахот h^, Vtt,K^nv\ Рх&пг\ КЛА, осуществляющих
спуск в атмосфере Марса (минимальная модель атмосферы для равноденствия) .
Соответственно изменяются и граничные условия для сопряженных
переменных в начале траектории схода с режима Т = TJlxtn\
I и \ Э7~ . . . ЪТ , . ЪТ
’/'l (fcx) ’Mtcx) = V's(^x) = +
где^и ир — постоянные коэффициенты. Отсюда получим [5, 22] с учетом
условия JT = О
^i(tcx) = 0< ^2(fcx) = 0, Фз(^сх) = 1- (5.72)
Решение краевой задачи, к которой сводится поставленная вариационная
задача, при граничных условиях для сопряженных переменных (5.69) и
(5.72) показало [100], что после схода КЛА с режима полета Т -
принципиально возможно получение максимальной температуры, меньшей
чем 7"ДОГ1. При этом оказывается, что снижение температуры весьма незна¬
чительно и не превышает нескольких градусов при min (Тщах)
1200-^1700 °C для КЛА, осуществляющих спуск с орбиты ИСЗ.
Таким образом, можно сделать следующий вывод о структуре управле¬
ния, обеспечивающего наименьшее значение максимальной величины тем¬
пературы поверхности КЛА:
вход в атмосферу с нулевым углом крена (у * = 0) и полет до первого
максимума температуры Tf;
полет от момента достижения максимума температуры Т* с некоторым
постоянным значением угла крена 7*^0, выбираемым из условия обеспе¬
чения выхода КЛА на режим стационарного планирования (5.71) ;
152
полет по траектории с Т = Гдоп (или по траектории квазистационарного
планирования, определяемого условием 0 = 0);
сход КЛА с режима квазистационарного планирования, когда оказывает¬
ся невозможным выдерживание этого режима движения при существующих
для рассматриваемого КЛА ограничениях на величину управляющего
параметра;
полет после схода с нулевым значением угла крена.
При использовании описанного закона управления в зависимости от
проектно-баллистических характеристик КЛА и условий входа в атмосферу
максимальной температурой может оказаться либо температура в первом
максимуме Г* , либо максимальная температура на участке квазистацио¬
нарного планирования.
В качестве примера на рис. 5.33 — 5.39 представлены зависимости мини¬
мального значения максимальной температуры от высоты условного пери¬
центра, начальной скорости входа и основных проектно-баллистических
характеристик летательных аппаратов, осуществляющих вход в атмосферы
планет Солнечной системы.
Начальные условия входа и проектно-баллистические характеристики
КЛА варьировались для каждой планеты в тех же диапазонах, что и в зада¬
че Qvni in (см. п. 5-2.5) . Анализ представленных материалов показывает,
Рис. 5.36. Зависимости mm 7"max от V,if К^п и Рх для КЛА, осуществляющих
-пуск в атмосфере Юпитера (номинальная модель атмосферы) .
153
mlnTmal-fO3, °C
200 SOO -1Н -3000 Ья,кн
Рис. 5.37. Зависимости min 7max от h^, Уо, Кбал _v ля КЛА, осуществляющих
спуск в атмосфере Сатурна (номинальная модель атмосферы) .
Рис. 5.38. Зависимости min7"max от /7Я, l/0, Kffan и ?х Для КЛА, осуществляющих
спуск в атмосфере Урана (номинальная модель атмосферы) .
Рис. 5.39. Зависимости minTmax от h^, VQ, Кбзл и Рх для КЛА, осуществляющих
спуск в атмосфере Нептуна (номинальная модель атмосферы) .
что для рассматриваемых планет характер зависимости минимального зна¬
чения максимальной температуры от варьируемых параметров остается
неизменным. А именно, заметное уменьшение величины min7"max может
быть достигнуто при увеличении и уменьшении У о и Рх. Изменение
величины аэродинамического качества в рассмотренных пределах практи¬
чески не влияет на величину minTmax.
5.4.2. Управление аэродинамическими силами
и тягой двигательной установки
Постановка задачи. Для решения задачи минимизации максимальной
температуры конструкции КЛА могут быть использованы так называемые
прямые методы вариационного исчисления. К ним может быть отнесен,
в частности, метод, основанный на использовании формулы Блисса для
Фиксированной номинальной траектории [92, 93].
Будем предполагать, что снижение максимального значения температуры
на траектории спуска может быть достигнуто за счет использования малых
аэродинамических тормозных устройств, двигательной установки, тормоз¬
ных парашютных устройств и небольших изменений несущих свойств КЛА.
Предположим также, что траектории входа в атмосферу характеризуются
наличием одного явно выраженного максимума температуры.
155
Уравнения движения центра масс КЛА для случая плоского движения
запишем в следующем виде:
c/V
e~0hv2
P COStf
sin0
- Рх-
+
—
dt
m
m
r2 '
Fi
dO e
-^V2 Psin<^> 1
+ 4-
1 1/COS0
dt y
m
mV '
< V2r) r
(5.73)
F3=^ = Vsin0,
c _dL _ l/cos0 c dm _ P
4 dt r ' 5 dt c
Здесь V — скорость полета; 6 — угол наклона траектории к местному гори¬
зонту; h — высота полета; L — дальность полета; т — масса КЛА; t — вре¬
мя полета; г — расстояние от центра масс КЛА до центра планеты; Р ~
тяга двигательной установки; — угол отклонения вектора тяги относи¬
тельно вектора скорости; с — скорость истечения рабочего тела,
9oPoRoS
Рх = cx(v; iiy = су w; со =— z
где Rq — средний радиус планеты; gQ — гравитационное ускорение на по¬
верхности планеты.
Переменные в уравнениях (5.73) являются безразмерными. Они связаны
с размерными величинами (отмеченными индексом "р") следующими соот¬
ношениями:
/л р
/7?о
гдет0 — начальная масса КЛА.
Оптимизируемый функционал запишем в виде [114]
Ф= max Т(Х) = тах(е”0,125^л у0,8125),
tK)
гдеХ — фазовый вектор. При этом
dT{X[t))
max Г(Х) = T[X(tJ), - - * ■ = О,
(5.74)
где t* — время, соответствующее достижению max Т.
Определение оптимальной коррекции управления. Обозначим вектор
управления КЛА через и и определим влияние на функционал (5.74) изме¬
нения вектора управления Ьи относительно значения и, соответствующего
опорной траектории:
Ьи = и - и.
Полное приращение функционала (5.74) в каждый момент времени t
может быть представлено следующим образом:
£/7-=6Г(г)+^(Г)Л.
156
Для фиксированного момента времени t*f соответствующего достиже¬
нию максимума температуры Т(Х) на опорной траектории, получим сле¬
дующее выражение для приращения функционала (5.74) :
dT = 5T(tJ.
Отсюда следует, что в рамках первой вариации задача определения влияния
управления на величину максимальной температуры эквивалентна задаче
с функционалом Т, заданным в фиксированный момент времени F*.
Определение величины 67"(г#) можно осуществить с использованием
формулы Блисса [114] :
6Г(Г,) = ( J (JbF)dt.
ч
Здесь i//— вектор сопряженных переменных, определяемый для номиналь¬
ной траектории следующим образом:
= 8F = F(X,u+8и)—F(X,u);
at оХ
Fty — скалярное произведение векторов; индексы 7 и f соответствуют
параметрам траектории в начальной и конечной точках-
Граничные условия для сопряженных переменных получим в виде
= 0,8125 У-0,1875e-°,i2S0h = ^4(t.) = i//5(F,) =0,
Фз(Г,) =-0,125^-°’125/ЗЛ У0’8125.
Учитывая изложенное, условие оптимальной коррекции номинальной
программы управления для минимизации величины максимальной темпе¬
ратуры (5.74) можно записать в виде
1//6Г(61/опт) = min( ipdF).
Отсюда после несложных преобразований [114] нетрудно получить
Э(^Г)
6«опт = - S«maxsign——.
На участках траектории спуска, где управление КЛА осуществляется
путем изменения коэффициента подъемной силы (при фиксированном
значении коэффициента лобового сопротивления сх) будем иметь
6с°пт =—6cymaxsigni//2. (5.75)
При этом эффективность снижения величины 7’тах
соответствующая интервалу времени [f, t J , находится из выражения
WbCy = ^ s \ ^1\ e-phVdt.
157
При управлении КЛА, путем изменения коэффициента лобового сопро¬
тивления (при фиксированном су) получим
6с£пт = 5cxmaxsigni//lz W&Cx = f \ фг \ e~^V2dt. (5.76)
t
Введение тормозных парашютов можно представить в виде импульсного
изменения коэффициента лобового сопротивления сх. Тогда эффективность
снижения максимальной температуры будет определяться соотношением
[114]
1 3 Q
IV =-min- —
х Сп-с ЭГ f=fnc
где fn.c ~ оптимальный момент подачи тормозного импульса; сПеС — коэф¬
фициент аэродинамического сопротивления парашютной системы.
Оптимальный закон отклонения вектора тяги двигательной установки
относительно вектора скорости центра масс КЛА определяется следующим
образом:
\р2 я ф2
i//onT = arctg - = (1 + signi//x )sign , (5.77)
Ф1У 2 ф1
а эффективность оптимального использования двигательной установки в
момент времени для снижения величины максимальной температуры
записывается в виде
эг V (фг и)2 + ф2' ф5
w = + —,
Э^хар V С
Приближенное аналитическое решение. Для синтеза оптимального управ¬
ления (5.75) — (5.77) получим приближенное аналитическое решение со¬
пряженной к (5.73) системы уравнений для номинальной программы
управления в виде функции текущих фазовых координат [92]. Для опре¬
деленности примем, что номинальная траектория определяется в предполо¬
жении спуска КЛА без работающей двигательной установки с постоянными
значениями аэродинамических коэффициентов.
Представим траекторию спуска в виде двух участков:
первый участок, на котором аэродинамические силы пренебрежимо ма¬
лы по сравнению с гравитационными силами;
второй участок, на котором аэродинамические силы являются опреде¬
ляющими.
Рассмотрим сначала второй участок. Уравнения движения представим
в виде [114]
dV 1/2 dO dh ... а dm n tr_
— = = — = Vs.nfl, — =0. (5.78)
Функция Гамильтона для уравнений (5.78) и дифференциальные уравне¬
ния для сопряженных переменных запишутся в виде
^ = —+ $2PypV + \{j3VsinOt
d^i
~JT~= 2^хРУФ1 - PyP^2 - Фз sin0,
158
d\p2
= — \/ф3 cos О,
dt
<^4
dt
= -рхрУ2Ф1
Учитывая, что на траектории спуска для автономной системы (5.78)
гамильтониан равен нулю (J( = 0), получим [114] (значком "плюс"
отмечены переменные, соответствующие второму участку траектории)
а!=0,8125Ф, ^2 = а2р, а2=—0,125Ф—,
Pf
sinfl), ^4 = а3+—$, а3=0,125Ф,
Рх / Р
где/с = ру/рх.
Значения максимальной температуры Ф= max Г и плотности р? в момент
t = tf определяются из решения системы уравнений (5.78) и граничного
условия на правом конце траектории. В нашем случае для номинальной
траектории полета (рх = const, ру = const) получим
0f- 0
V = Vfexp — ,
Р
Р = Р/+—
Vy
(cosO — cosOf),
0,8125
Of =
0,25му
На первом участке траектории спуска движение КЛА определяется
системой уравнений
dV _ sin0 <У0 = _ y2z,| CQs0
dt r2 dt Vr2
— = l/sin0,
dt
dm
dt
0.
(5.79)
Уравнения (5.79) имеют аналитические решения. Функция Гамильтона
для уравнений (5.79) и уравнения для сопряженных переменных записы¬
ваются в виде [114]
3C = -V'111V’-V'2(1 — V2r)
г*
cos О
Vr2
Фз sin0,
. .,2 X COS0 , . „
—— = -i//2 (1 + V r) ~ i//3sin0,
dt V2 r 2
(5.80)
d^3 _
dt
2sin0
d\p4
= 0.
dt
159
Предположим, что сопряжение первого и второго участков траектории
производится непрерывным образом:
(знаком "минус" обозначены параметры, соответствующие первому участ¬
ку траектории, а звездочкой — параметры траектории в момент сопряжения
участков) . Будем считать в качестве условия, определяющего момент со¬
пряжения участков траектории, достижение заданной величины суммарной
перегрузки
(5.81)
Учитывая, что пх = pV2px и пу = pV2py, из (5.81) получим условие сопря¬
жения участков траектории
В точке сопряжения участков траектории сопряженные переменные
терпят разрыв:
tf'i. = ’/'б. Фз. = ’/'з.
ф4'. = ф5\+7- =
Постоянная v определяется следующим образом:
sin О*
0,8125Ф 0,25 1 sin0z
0,8125 Ф
1 + _ __+
r2V2(l+u) 0,8125 pf со к tg О*
r2*V2(l + со)
2
Учитывая условие Jf = 0 и уравнения (5.79) и (5.80) получаем следую¬
щие выражения для сопряженных переменных на первом участке:
_ BV2 — 1
Wi = А - , В = const, ф2 = 4tg0, А = const,
const.
(5.82)
Константы А, В и С определяются следующим образом:
ф I sin0* \
А = 0,8125 — 1 -——-)ctg0#>O,
к \ sin0y7
1
У*(1 + со)
sin 0у
> 0,
160
С = 0,125Ф
0,8125 со
0,25(1 +<о)
0/25 р,
0,8125 pf
25 Ф.
1 +
Анализ структуры оптимального закона управления КЛА, обладающим
аэродинамическим качеством. Используя результаты аналитического реше¬
ния для сопряженной системы уравнений, исследуем структуру оптималь¬
ного закона управления КЛА. Оптимальный закон изменения коэффициен¬
тов аэродинамической подъемной силы и лобового сопротивления из
условия min Лп ах может быть записан с учетом (5.75), (5.76), (5 80) и
(5.82) .
Для коэффициента аэродинамической подъемной силы на всей траекто¬
рии спуска имеем
5conT = -5Cymaxsign0.
Для коэффициента лобового сопротивления получим:
на первом участке > 0, и полет протекает с постоянным значением
£гопт _
ut.xmax/
на втором участке оптимальная программа управления может иметь
переключение, причем количество переключений не превышает двух. Усло¬
вие существования переключений
имеет вид
BVl <1. (5.83)
Учитывая тот факт, что значе¬
ние постоянной В может быть од¬
нозначно определено по началь¬
ным условиям и интегралам кеп-
лерова движения, можно пост¬
роить области начальных значений
фазовых координат, удовлетво¬
ряющих неравенству (5.83).
В качестве примера на рис. 5.40
для КЛА, осуществляющих спуск
в атмосфере Земли и имеющих
различные значения аэродинами¬
ческого качества, представлены
зависимости Уо = ^о(^о)/ справа
от которых выполняется нс-
равенсво (5.83).
Рис. 5.40. Зависимость относительной
начальной скорости входа Ио = У/УКр
от начальной высоты входа hQ.
11. Зак. 2069
161
Рис. 5.41. Характер изменения оптимального угла отклонения вектора тяги </>опг.
При управлении вектором тяги двигательной установки на втором участ¬
ке будем иметь [114]
+ ОПТ
(5.84)
Отсюда видно, что при изменении 0+ от 0* до 0/ оптимальный угол от¬
клонения вектора тяги </?опт возрастает от значения <р + опт Е (я72, я) до
<£°пт = я (рис. 5.41,3). При этом оказывается, что ip~onT нечетная функ¬
ция 0. Структура оптимального управления во многом определяется харак¬
тером изменения сопряженной переменной Ф1~. Рассмотрим возможные
варианты поведения функции "(0):
а) > 0 на всем интервале изменения угла 0; в этом случае структура
оптимального управления углом отклонения вектора тяги имеет вид, изо¬
браженный на рис. 5.41, а;
б) = 0; этот случай характерен для достаточно больших скоростей
полета, и оптимальное управление углом имеет структуру, показанную
на рис. 5.41,6.
Оценки влияния начальных условий входа КЛА в атмосферу на оптими
зируемый функционал min 7"тзх. Величина максимальной температуры од¬
нозначно определяется двумя параметрами: скоростью Va и высотой поле¬
та ha в условном апоцентре, которые легко находятся по начальным усло¬
виям Vo, Oq, hQ. Влияние начальных условий на максимальную температуру
характеризуется значениями сопряженных переменных
, ЭФ , ЭФ , ЭФ
^02= — . ^ОЭ=ГТ- (5.85)
в условном апоцентре траектории.
Анализ выражения (5.85) показывает, что функционал min7max изме¬
няется ^немонотонно при изменении относительной начальной скорости
полета Vo. В качестве примера на рис. 5.42 приведены зависимости мини¬
мального значения максимальной температуры от VQ и hQ для КЛА, осу¬
ществляющего спуск в атмосфере Земли.. Видно, что увеличение высоты
полета h0 при заданной начальной скорости Уо приводит к возрастанию
максимальной температуры. Сравнение численных результатов, получен¬
ных на основе использования приближенных аналитических решений и
путем численного интегрирования точных уравнений движения, указывает
на их хорошее согласование.
162
Рис. 5.42. Зависимость m i n Tm ах от относительной начальной скорости Ио = И/Икр
(сплошные линии соответствуют высоте Ло = 180 км, штриховые — высоте /?0 =
= 120 км; 1 — приближенное аналитическое решение; 2 — точное решение).
§ 5.5. Оптимизация траекторий спуска из условия минимума
обобщенного теплового критерия
Рассмотрим задачу об отыскании оптимального управления КЛА из
условия минимума обобщенного теплового критерия [33]
/ = f (A^T + A^qW.
Этот критерий при 4ц =0 сводится к условию минимального подвода
тепла в заданную точку поверхности КЛА, а при Ai2 к условию минималь¬
ного прогрева его обшивки.
Соотношение между весовыми коэффициентами Аг г/Аг 2 определяется
из инженерных соображений и зависит от выбранного типа системы тепло¬
защиты и материала теплозащитного покрытия.
Будем рассматривать КЛА с большим значением аэродинамического
качества, управление которым осуществляется путем изменения угла
атаки а.
На величину угла атаки накладывается ограничение
amin а атах* (5.86)
Зависимость коэффициентов су и сх от угла атаки а может быть
записана в виде
сх ~ схо + sin3a, су = A j sin2acosa,
где сх0, А}, В.! — коэффициенты, зависящие от числа Маха (рис. 5.43).
Решение задачи будем проводить с использованием методов классическо¬
го вариационного исчисления. Поскольку эти методы пригодны лишь для
163
шим значением аэродинамического качества.
Рис. 5.44. К определению функции а (17) .
неограниченного множества допустимых функций фазовых координат
X(t) и управления u(t), то рассматриваемая задача может быть решена
только в том случае, если удастся перевести замкнутое множество
R[X(t}, u(t)] в открытое путем преобразования координат. Выполнить та-
кое преобразование можно [33], если ограничение на управление (5.86)
свести к ограничению на управление а вида
^min (^) Л йщах (X),
где amjn(X) и атах(Х) — непрерывные и дифференцируемые функции
всех своих аргументов Xit
Введем новые переменные т?(Х) такие, при которых функция а(т?)
будет непрерывной и равной:
ah) = amin при —со < п < 77J,
O!h) = O!max При Т?2 < 7? < +оо;
на интервале т?4 < 7?< т?2 Функция а(т?) монотонная (рис. 5.44).
Известно, что при использовании классического вариационного исчисле¬
ния искомая экстремаль должна удовлетворять необходимым условиям
оптимальности — уравнениям Эйлера — Лагранжа
d zdF \ bF
dt \dXt ЭХ,- (5.87)
9F
— =0 (/=1 1).
OUj
Здесь F — вспомогательная»функция
F = /o+ S
i = 1
где — множители Лагранжа.
При использовании указанной замены переменных уравнение (5.87)
заменяется уравнением для новой переменной т?, записанным в следующем
виде:
dF да
да дт?
(5.88)
164
Из (5.88) имеем в общем случае на оптимальной траектории либо
3F
— =0,
да
что соответствует изменению а(Г) внутри заданной области (5.86), либо
да
т=о'
дт?
что соответствует предельным значениям amin и amax.
В точке соединеня эйлеровых участков экстремали и участков движения
с граничными значениями а необходимо учитывать условие Эрдмана —
Вейерштрасса
При этом в момент соединения различных участков траектории может
иметь место разрыв непрерывности управления a
а/ + о at-о-
Если известны граничные условия, то оптимальная траектория может
быть найдена путем совместного решения уравнений (5.87) и (3.1). Если
же некоторые граничные условия неизвестны, то они могут быть определе¬
ны из условия трансверсальности:
Дополним систему уравнений (3.1) следующими уравнениями для пере¬
грузки п, удельного теплового потока q и температуры поверхности Г:
1
=q - a) = о,
где Ф — постоянный коэффициент.
При введении ограничений на величины п, q и управление а в соответст¬
вии с изложенным выше методом можно перейти к неограниченным вспо¬
могательным переменным qn, qq и т?а.
Для рассматриваемой задачи уравнения Эйлера-Лагранжа относительно
переменных V, (), h, L, n,T,q \л управления а могут быть записаны в таком
виде [33] :
mg
165
+ x5(Cj+4)1/2p^2j_
2 mg
- -X7 - g(p)(Az У,а) =X3,
h h
X4 = 0,
dn
ba
Д = 0,
Эт?а
, bq
X5=Q, 4Х6еоТ3 = ФХ6, X7=0,
д=[х14“)—— -M— --Х7<7(О1)(Л, К a)l.
L 2 mg y 2 m J
В нашем случае функционал F не зависит в явном виде от времени t.
Поэтому первый интеграл исследуемой системы может быть записан в виде
п bF .
S — X/-F = C1. (5.89)
i = 1
Раскрывая (5.89), будем иметь
Хх V + X20 +Х3/? + Х4£ + (Х6Ф-Д11)7’-Д12д = С1. (5.90)
Условия трансверсальности запишутся следующим образом:
[CiSt + XiSV + X^fl +X35/7+X46z. + (Х6 -Дц)6Т]> =0.
*0
Таким образом, для рассматриваемой задачи оптимальная траектория
находится из решения краевой задачи для системы из 15 уравнений с 15
Рис. 5.45. Оптимальные траектории
спуска при отсутствии ограничений:
а) вид траекторий; б) программа
управления по углу атаки.
Ч 65°
*4-66°
3 4
5
6
7
VtKM/C
Рис. 5.46. Оптимальные траектории
спуска при ограничениях по углу ата¬
ки (lai < 75° ) : а) вид траекторий;
6) программа управления по углу
атаки.
о?
166
неизвестными. Для проверки правильности численного решения краевой
задачи может быть использован интеграл (5.89).
Очевидно, решение краевой задачи для полученной системы уравнений
требует большого количества вычислений. Следует отметить, что система
из 15 уравнений для оптимальной траектории охватывает практически
все возможные ограничения на фазовые координаты и на конечные условия
движения КЛА для рассматриваемой задачи. На практике часто приходится
Рис. 5.47. Оптимальная программа изменения угла атаки а: 1 — оптимальная траекто¬
рия без ограничений на фазовые координаты; 2 — оптимальная траектория при ограни¬
чении на максимально допустимую перегрузку (лдоп = 2); 3— оптимальная траекто¬
рия при ограничении на температуру несущей поверхности КЛА (7"доп = 1600 °C).
рассматривать только часть из указанных ограничений. В этом случае реше¬
ние краевой задачи и, следовательно, определение оптимальной траектории
существенно упрощается. В частности, при решении можно заменять усло¬
вия, фиксирующие значения естественными граничными условия¬
ми. При этом множители Лагранжа Лд и определяются из условий транс¬
версальности, и порядок исходной краевой задачи уменьшается.
В качестве примера на рис. 5.45—5.47 представлены результаты решения
краевой задачи [33] для гипотетического КЛА с величиной нагрузки на
несущую поверхность rfi/s= 15 кг/м2 и максимальной величиной аэродина¬
мического качества ^тах= 1,2. Граничные условия движения КЛА в
атмосфере принимались следующими:
при t = to - /?о=82,5км, Уо=О,95, 0О= —2°;
при t = tK: = 0,5.
Остальные параметры считались свободными. Кроме того, предполагалось,
что Ац = 0, т.е. минимизировался суммарный тепловой поток в критичес¬
кой точке.
Рассматривались три возможных случая оптимизации траектории спуска:
при отсутствии ограничений (рис. 5.45),
с учетом ограничений по углу атаки (рис. 5.46),
с учетом ограничений по углу атаки, перегрузкам и тепловым потокам
(рис. 5.47).
Видно, что при отсутствии ограничений на фазовые координаты мини¬
мум функционала может быть достигнут за счет резкого уменьшения
времени спуска. Введение ограничения по углу атаки ( I а | < 75 , угол
крена 7=0) приводит к более пологим траекториям с предельным положи¬
тельным значением а = атах на основной части траектории. Дополнитель¬
ные ограничения по перегрузкам или температуре обшивки приводят к
появлению на траектории спуска участков с п = лдоп или Т = 7"доп (см.
рис. 5.47).
167
Глава 6
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ СПУСКА
ИЗ УСЛОВИЯ МИНИМУМА МАССЫ
СИСТЕМЫ МЯГКОЙ ПОСАДКИ
§ 6.1. Минимизация конечной скорости спуска
При реализации полетов КЛА к планетам Солнечной системы наряду со
многими другими задачами следует решать сложную и ответственную
задачу организации безопасной мягкой посадки. Особый интерес эта задача
представляет при спуске на поверхности планет, обладающих разреженной
атмосферой. Действительно, как было показано (см., например, [24]),
в этом случае существенно возрастает масса, потребная для обеспечения
мягкой посадки на поверхность планеты, и, следовательно, уменьшается
масса полезной нагрузки, в состав которой входит и исследовательская
аппаратура. Имеются два основных направления минимизации массы
системы мягкой посадки (СМП) КЛА:
выбор рационального типа СМП;
оптимизация траекторий спуска КЛА для создания наилучших условий
(с точки зрения минимума массы системы мягкой посадки) при вводе
в действие СМП.
В настоящей главе рассматривается второе направление, т.е. предполага¬
ется, что тип системы мягкой посадки задан (реактивная либо па¬
рашютно-реактивная) , а задача заключается в выборе такой траекто¬
рии спуска, которая обеспечивает минимум массы для определен¬
ного типа СМП.
Анализ участка мягкой посадки для реактивной и парашютно-реактив¬
ной СМП позволил определить достаточно простые критерии оптимальнос¬
ти для участка основного аэродинамического торможения [24].
Так, при использовании реактивной системы мягкой посадки для умень¬
шения энергетических затрат на активное торможение КЛА при работе
СМП необходимо стремиться к получению в конце участка основного
аэродинамического торможения минимального значения характеристичес¬
кой скорости Ухар, потребной для последующего торможения КЛА актив¬
ным путем. Однако использование этого критерия в ряде случаев оказыва¬
ется не совсем удобным, поскольку он связан с параметрами траектории
спуска на участке мягкой посадки и определенной программой управления
КЛА на этом участке. Поэтому часто для анализа используется еще более
простой критерий — минимум скорости спуска на заданной конечной
высоте:
VK = min VK, hK задано, 0K свободно. (6.1)
При использовании парашютно-реактивной системы мягкой посадки
требования к конечным параметрам участка аэродинамического торможе¬
ния заключаются в следующем:
если задана высота раскрытия парашютной системы (hK =/?q), то прог¬
рамма управления на траектории аэродинамического торможения
должна обеспечивать минимум скорости (min Ук = Vq) к моменту достиже¬
ния высоты h0 = Лк;
в общем случае минимум массы парашютно-реактивной системы при
прочих равных условиях достигается тогда, когда высота включения систе¬
мы максимальна, т.е.
max Лк = h о. (6 2)
168
Выбранные критерии (6.1) и (6.2) позволяют приступить к исследова¬
нию основного участка траектории спуска КЛА.
Рассмотрим вариационные задачи об отыскании оптимальных законов
управления на участке основного аэродинамического торможения при
использовании различных способов организации мягкой посадки КЛА на
поверхности планет и проведем сравнительный анализ результатов решения
этих задач при спуске в атмосферах различных планет.
Оптимальное управление КЛА. Рассмотрим следующую задачу: на участ¬
ке основного аэродинамического торможения определить программу
управления эффективным аэродинамическим качеством /Сэфф(Й, миними¬
зирующую функционал
/ = VK
(6.3)
при ограничениях на управление
^бал ^эфф < ^бал
(6.4)
и на фазовые координаты
Q1 (г) =Лдоп - Л (Г) <0,
(6.5)
Q2U) = Лдоп - n(t) >0
(6.6)
при следующих краевых условиях:
при t = : V=Vo, 0=0Q, h=hQ, (6.7)
приГ = Гк: h=hK, 0K—свободно. (6.8)
Предположим, что в общем случае оптимальная траектория содержит не
более одного участка движения по каждому из ограничений. Пусть и
f(3) _ моменты выхода КЛА соответственно на ограничения (6.5) и (6.6),
a f(2)n — моменты схода КЛА с этих ограничений.
Согласно принципу максимума Понтрягина, условием минимума функ¬
ционала (6.3) является условие максимума гамильтониана
dV dO dh
К = + ^2 + Фз •
dt dt dt
(6.9)
Здесь , ф2, Фз “ сопряженные переменные, которые определяются
следующим образом: при qx (t) < 0 и q2 (f) > О
di//! ЭК dty2 _ ЭК di//3 _ ЭК
dt dV ' dt ЪО ' dt ЭЛ
при (t) =q2(t) = 0
ЭК
dJC
Э/^эфф
д<р
dt
“ ЭИ +
д^р
~dV
ЭКдфф
ЭК
d^3 ЭК ЭКэфф д<р
= + , где
dt dh д<р dh
ЭК
_ЭК [ ЭКэфф э^
dt де э^ де
Э/^эфф
ip = d2qi2ldt1.
Э/^эфф
169
В момент выхода КЛА на ограничение сопряженные переменные скач
ком меняют свою величину:
0:(г(1’з))-^1(г(1-з))=д1-^ +
о V о V
ф2*(/1’3))-ф2(Г(1>3))=Д1-^+
О V ои
Ф'з^1-3') - <A3(f(1’3)) = Дх
о V дп
где Ml,2 — const.
Кроме того, должно быть выполнено условие касания оптимальной
траектории при выходе на ограничения:
*Ь2-.О.
dt
Сопряженные переменные в конце траектории спуска определяются из
условий трансверсальности: i//1K = — 1, ф2к = 0, Фзк = •
Из выражения (6.9) следует, что оптимальное управление на участке
движения внутри допустимой области фазовых координат является гранич¬
ным [24] :
^эфф ~ ^бал s*9n $2 •
Управление КЛА при движении вдоль ограничений определяется из выра¬
жения
В общем случае возможно существование следующих типов оптималь¬
ных траекторий, реализующих минимальное значение конечной скорости
спуска и соответствующих им законов управления (табл. 6.1):
оптимальная траектория содержит участки выхода на каждое из рассмат¬
риваемых ограничений (сначала на изоперегрузочный, а затем на изо-
высотный участок), движения по этим ограничениям и последующего
схода с ограничений внутрь допустимой области фазовых координат
(тип 1) ;
оптимальная траектория содержит один участок движения по ограниче¬
нию п = лдоп и последующего схода с ограничения внутрь допустимой
области фазовых координат (тип 2);
оптимальная траектория содержит один участок движения по ограниче¬
нию h = hj^QTi и последующего схода с ограничения внутрь допустимой
области фазовых координат (тип 3);
оптимальная траектория целиком лежит внутри допустимой области
фазовых координат (тип 4);
оптимальная траектория касается ограничения п =пДОП (тип 5) ;
оптимальная траектория касается ограничения h = /?доп (тип 6) ;
оптимальная траектория касается двух ограничений h = ЛДОП и п = лдоп
(тип 7);
оптимальная траектория содержит участок движения по ограничению
п, - "доп, а другого ограничения h = Л касается в одной точке
(тип 8);
170
Таблица 6.1
Вид законов управления /Сэфф для оптимальных траекторий спуска КЛА
Тип
траекто¬
рии
Структура оптимального управ¬
ления
—
Тип
траекто¬
рии
Структура оптимального управ¬
ления
1
^бал
0
^эфф
П /1 FVLL
^бал
Л'эфф
: J !
“^бал
7
0
ill
Я~/7дол
t
~^бал
1 1 1
• 1 1
2
^бал
0
~^бал
Л'эфф
- ; г'О'!
- •—* Я = Лд0П
^бал
^Эфф Л=Лд0П
1 1 1 •
^эфф
t
8
0
“^бал
: И
• i
i i
i i
Кбал
0
~^бал
t
3
■ 1 J
- !
! ^-^доп
^Эфф
t
^бал
1 i i
^бал
Л'эфф
5
9
0
“^бал
1 I 1 1
-ill,
■ i i ;
i i i
/^h
"~"доп
4-6
0
!
t
t
оптимальная траектория содержит участок движения по ограничению
/? = /?доп, а другого ограничения п = лдоп касается в одной точке
(тип 9).
Исследования показали, что выбор типа оптимального закона управле¬
ния КЛА определяется в зависимости от физических характеристик плане¬
ты и ее атмосферы, начальных условий входа в атмосферу, проектно-бал¬
листических характеристик КЛА, величин ограничений лдоп и Лдоп«
§ 6.2. Анализ результатов решения задачи
минимизации конечной скорости спуска
В табл. 6.2. приведены некоторые результаты численного решения вариа¬
ционной задачи о минимуме конечной скорости спуска КЛА, осуществляю¬
щих посадку на поверхность планет.
Анализ многочисленных результатов показал, что величина конечной
скорости VK практически не зависит от начальной скорости /о и высоту
условного перицентра траектории входа в атмосферу любой из рассматри¬
ваемых, планет при движении вблизи границы захвата КЛА атмосферой.
Следует отметить, что диапазон высот условного перицентра траекторий
входа в атмосферу kh'^, для которого сохраняется свойство независимости
величины конечной скорости от h^, при оптимальном управлении сущест-
171
Т а б л и ц а 6.2
Численные результаты решения задачи l/K= l/Kmjn
Исходные
параметры
Варь ируемый
параметр
Ис min/
м/с
Исходные
параметры
Варьируемый
параметр
Hemin /
м/с
Земля
-
128
Венера
-
14
1/0 = 11 км/с
Рх = 700 кгс/м2
151
Ио = 11 км/с
Рх = 200 кгс/м2
9
h0 = 100 км
^бал = 0,5
123
ho = ЮО км
Рх = 700 кгс/м2
17
/?к = 5 км
Р = Pmin
136
Лк = 5 км
*бал = 0,5
15
Рх = 500 кгс/м2
Р =Ртах
120
Рх = 500 кгс/м2
Р "Ртах
14
Кбал=0>3
hK= 10 км
196
^бал = 0,3
hK = 10 км
25
Р ~ Рном
Р=Рном
Марс
-
549
Юпитер
—
109
1/0 = 7 км/с
Рх = 200 кгс/м2
416
Ио = 65 км/с
Рх = 100 кгс/м2
61
/?0- = 100 км
Рх = 500 кгс/м2
654
h0 = 400 км
Рх = 500 кгс/м2
140
hK = 5 км
Кбал ~ 0,5
531
Лк = 5 км
*бал = 0,7
99
Рх = 350 кгс/м2
Р =Ртах равн
538
Рх = 300 кгс/м2
Р “Ртепл
117
^бал =0/
Лк = 10 км
718
^бал = 0,3
Р = Рхол
93
Р = Pmin равн
Р = Рном
Лк= 10 км
122
Сатурн
-
131
Уран
—
140
1/0 = 37 км/с
Рх = 200 кгс/м2
83
1/0 = 28 км/с
Рх = 200 кгс/м2
88
h0 = 400 км
Рх = 700 кгс/м2
155
h0 = 400 км
Рх = 700 кгс/м2
165
hK = 5 км
^бал = 0,5
127
Лк = 5 км
^бал ~ 0,5
135
Рх = 500 кгс/м2
Р ~ Рхол
143
Рх = 500 кгс/м2
hK = 5 км
153
^бал = 0,3
hK = 10 км
144
^бал = 0,3
Р=Рном
Нептун
-
167
1/0 = 28 км/с
Рх = 200 кгс/м2
103
Ло = 400 км
Рх = 700 кгс/м2
198
hK = 5 км
^бал = 0,5
161
Рх = 500 кгс/м2
^бал = 0,3
венно зависит от величины аэродинамического качества. При этом оказыва¬
ется, что даже небольшое увеличение /Сбал приводит к заметному расшире¬
нию диапазона высот ДЛ^. Так, при спуске КЛА в атмосфере Марса с
начальной скоростью Vq = 6 км/с изменение Кбал от 0/3 до 0,5 приводит
к возрастанию Д/^. с 230 км до 330 км.
Свойство независимости величины конечной скорости от /?я в диапазоне
Д/?я является определяющим при выборе потребной величины аэродинами¬
ческого качества. Действительно, при заданной ширине навигационного
коридора входа Д/?нав для обеспечения минимального значения конечной
скорости целесообразно выбирать величину Кбал таким образом, чтобы
выполнялось условие
дл;>дл«в. (ело)
Следует подчеркнуть, что при спуске КЛА в атмосферах рассматривае¬
мых планет выполнение условия (6.10) достигается при небольших значе¬
ниях аэродинамического качества (^бал % 0/3 4- 0,5). Величина конечной
172
скорости спуска при оптимальном управлении КЛА для этих значений Кбал
приведена в табл. 6.2.
Наиболее существенное уменьшение конечной скорости спуска при
оптимальном управлении может быть достигнуто за счет снижения приве¬
денной нагрузки на лобовую поверхность. Так, уменьшение Рх на 200 кгс/с2
приводит к снижению конечной скорости спуска на 20 — 30% при спуске
КЛА в атмосфере всех рассматриваемых планет. Существенное уменьшение
величины конечной скорости спуска при оптимальном управлении может
быть также получено при уменьшении конечной высоты /?к.
Как и следовало ожидать, наибольшее значение конечной скорости спус¬
ка, превышающее в 3—4 раза величину полученную при спуске на
поверхности других планет, реализуется при снижении КЛА в атмосфере
Марса. Это объясняется исключительной разреженностью атмосферы этой
планеты.
Учитывая, что задача минимизации массы системы мягкой посадки КЛА
в атмосфере Марса имеет первостепенное значение при решении проблемы
безопасного спуска на поверхность этой планеты, рассмотрим более подроб¬
но особенности решения задачи поиска оптимального управления КЛА с
учетом влияния неопределенности параметров атмосферы, а также с учетом
использования критерия оптимальности, более полно отражающего харак¬
тер задачи мягкой посадки на поверхность с использованием реактивной
СМП.
§ 6.3. Оценка влияния неопределенности параметров атмосферы
на оптимальное управление
При движении КЛА в атмосфере Марса конечные параметры оптималь¬
ной траектории спуска очень чувствительны к возможным отклонениям
плотности атмосферы. Так, изменение давления у поверхности планеты от 4
до 7 мбар [24] приводит к уменьшению конечной скорости примерно на
100 м/с. Возможный большой разброс параметров атмосферы Марса приво¬
дит к целесообразности решения задачи об отыскании оптимального управ¬
ления КЛА из условия минимума конечной скорости спуска в игровой
постановке [81]. Сформулируем задачу следующим образом. Требуется
определить оптимальный закон управления эффективным аэродинамичес¬
ким качеством /Сэффг который при заданных ограничениях на управление
(6.4) и фазовые координаты (6.5), (6.6) и граничных условиях (6.7),
(6.8) обеспечивал бы минимальную конечную скорость КЛА на заданной
высоте при наиболее неблагоприятном воздействии атмосферы.
Функционал минимаксной задачи определения наихудшей модели атмо¬
сферы и оптимального управления, который обеспечивает гарантированный
минимум конечной скорости спуска КЛА на заданной высоте, записывается
в виде
/ = min max l/K.
эфф
В соответствии с принципом максимума для конфликтных ситуаций [81]
необходимое условие оптимальности может быть записано следующим
образом:
JC = sup inf JC (Кэфф, p). (6.11)
К- эфф P
Здесь гамильтониан и сопряженные переменные имеют обычный вид (6.9).
Анализ выражения (6.11) показал [81], что структура оптимального
управления эффективным аэродинамическим качеством определяется
173
знаком сопряженной переменной ф2 и имеет вид /Сэфф = ^бал sign ^2 . а
структура наихудшей модели атмосферы определяется знаком функции
е(г) = -1//1\/ + /Сэфф1//2.
При этом минимальная модель атмосферы р = pmjn соответствует поло¬
жительным значениям функции JC, а максимальная — отрицательным.
Таким образом, вариационная задача о минимуме конечной скорости
спуска в игровой постановке сводится к решению двухточечной краевой
задачи для основной и сопряженной систем дифференциальных уравне¬
ний при заданных граничных условиях (6.7) и (6.8).
В работе [81] приведены результаты численного решения минимаксной
вариационной задачи о минимуме конечной скорости спуска КЛА в ат¬
мосфере Марса. При этом предполагалось, что ограничения на фазовые
координаты движения в атмосфере отсутствуют. Решение задачи показало,
что оптимальная программа управления эффективным аэродинамическим
качеством представляет собой релейную функцию с однократным переклю¬
чением К'эфф с максимального отрицательного значения на максимальное
положительное.
Кроме того, решение задачи позволило выявить следующую интерес¬
ную особенность. Наихудшей моделью атмосферы, при которой реализу¬
ется наибольшее значение конечной скорости спуска, является модель,
состоящая из отрезков Pmin(h) и pmax(/?l. Причем на некотором начальном
интервале t0 < t < G критической является модель атмосферы pmin(^), на
следующем интервале — максимальная модель Pmax(^) и, нако¬
нец, на последнем /интервале t2 < г3 - снова минимальная модель
Pmin(^) • При этом оказалось, что превышение величины гарантированной
конечной скорости КЛА, полученной из решения минимаксной задачи,
относительно величины конечной скорости, найденной из решения обыч
ной задачи оптимизации траектории спуска в предположении использо¬
вания минимальной модели атмосферы (р = pmin), составляет 5—7%. Эта
погрешность является допустимой при проведении проектно-баллисти¬
ческих исследований на первом этапе проектирования КЛА.
§ 6.4. Оптимизация траекторий спуска из условия минимума
характеристической скорости
Как известно [24], при использовании реактивной системы мягкой
посадки на поверхность планеты, окруженной атмосферой, величина ха¬
рактеристической скорости однозначно определяет потребные запасы
топлива, а следовательно, и массу реактивной СМП. Поэтому представля¬
ется интересным решить задачу оптимизации траекторий спуска КЛА в
атмосфере из условия обеспечения минимума характеристической ско¬
рости на участке работы реактивной СМП и сравнить полученные резуль¬
таты с результатами решения задачи о минимуме конечной скорости cnvc-
ка (см. § 6.2).
Итак, ставится следующая задача [82] : определить закон изменения
управляющего параметра (/Сэфф) на траектории спуска КЛА в атмосфе¬
ре, который обеспечивает минимум характеристической скорости, тре¬
буемой на активном участке при заданной тяговооруженности двигатель¬
ной установки. При этом будем предполагать, что на активном участке
направление вектора тяги противоположно направлению скорости спус¬
ка КЛА, т.е. двигатель работает по программе гравитационного разворота
[24]. Влияние атмосферы на движение на участке гравитационного разво
рота не учитывается.
Г//;
Запишем уравнения движения КЛА в безразмерном виде, нормализован¬
ном по V и h [82] :
dO 1 [ д VQV \
_ = ft. к,фф1.
dV 1 g
— = pVoV2ox sin0 = f2(0, V,h},
dt 2 Vo
•dh Vo _
— = V/sin= f3 (V, 9),
dt ho
где l/= V/Vo и h = h/hQ.
Уравнения движения КЛА на участке гравитационного разворота за¬
пишем следующим образом:
de
9
dV
9
=
— COS0,
=
(n + sin 0),
dt
vov
dt
Vo
(6.12)
dh
Vo -
— =
Vsin0,
dt
h0
где п = Р/тд — тяговооруженность КЛА.
Уравнения (6.12) могут быть проинтегрированы аналитически [82] :
__ п(п — sin0 J)
= ipi (0i, Vi) — — hK) - ^(0i, V'i,/?i,Лк) - 0,
(6.13)
где индексы 1 и "к" соответствуют временам окончания участков аэроди-
дп
намического и активного торможения; Ухар =—(tK — tx) безразмерная ха-
Vo
рактеристическая скорость.
В конечной точке траектории спуска (гк) необходимо выдерживать
следующие значения параметров:
0(гк) = -9Оо, Йгк) = 0, /Йгх) = *к-
Запишем функцию Гамильтона в виде
Г 1 _ / 9 VQV \
^6 + ^3G-
+
Уравнения сопряженных переменных имеют вид [82]
_/ Vo v
• dt \ R +hoh
9_
vov
i//!sin0 +—i//2cos0 —
Vo
V\) —
—-Ui//3cos0,
ho
175
VO \ a
=--1 cos и
Ф1 +
d^2
dt
1
~P Vo tfx ф ф
V0V
+(R +hoh)2
COS0
Ф1
В конечный момент времени (tK) должны быть выполнены условия
трансверсальности
sv'xap - + + ф2ь\7 +i//3б/7=о.
Необходимым условием минимума функционала 1/хар является усло¬
вие максимума гамильтониана JC При этом функция достигает верхней
грани по /Сэфф при К'эфф = ЛСбалsign i//!. Таким образом, структура оп¬
тимального закона управления эффективным аэродинамическим качест¬
вом из условия получения минимального значения характеристической
скорости совпадает со структурой управления КЛА из условия минимума
конечной скорости спуска. Численные результаты решения краевой зада¬
чи, к которой сводится поставленная вариационная задача, показали, что
при отсутствии ограничений на траектории спуска функция ^^опреде¬
ляющая число переключений эффективного качества из условия minUxap/
имеет один нуль. Следовательно, оптимальная программа управления
заключается в одноразовом переключении эффективного качества с ми-
и
км/с
К
^Эфф
Дед
~50
1
7 I 1 /
Л
/Гэфф(О
s'
1 * / 1
I |/
~20
~и
Я
\ \
и ед
дед
10
-1
-1 \
-2
I
i
fl 25 75 125 tfC
Рис. 6.1. Параметры оптимальной траектории спуска в атмосфере Марса из условия
минимума характеристической скорости.
176
иимального значения ^эфф = — ^бал на максимальное ^эфф =+^бал-
0 качестве примера на рис. 6.1 приведены параметры оптимальной тра¬
ектории спуска КЛА в атмосфере Марса из условия минимума Ухар.
В заключение сделаем одно замечание. Критерий УхарШ1П полнее отра-
жаег физический смысл рассматриваемой задачи, но он является более
громоздким по сравнению с критерием VK min. В работе [24] приведены
численные результаты решения задачи оптимального управления из ус¬
ловия V'xap min и ^Kmiiv полученные при одинаковых исходных предпо¬
сылках. При этом наблюдалось практически полное совпадение найден¬
ных оптимальных траекторий для двух рассматриваемых критериев оп¬
тимальности. Поэтому в зависимости от поставленных задач нужно ис¬
пользовать тот или иной критерий оптимальности, заведомо отдавая пред¬
почтение критерию VK min при проведении поисковых исследований.
§ 6.5. Оптимизация траекторий спуска
из условия максимума конечной высоты
6.5.1. Оптимальное управление при отсутствии ограничений
на фазовые координаты
При использовании парашютно-реактивной системы мягкой посадки
наиболее благоприятные условия для ее работы создаются при реализации
максимальной высоты полета на участке аэродинамического торможения
при заданной скорости ввода парашютной системы. Ниже рассмотрим
задачу поиска оптимального управления КЛА с использованием принципа
максимума Понтрягина.
Критерий оптимизации рассматриваемой задачи может быть представ¬
лен в виде
/ = тах/?(Гк), (6.14)
и
гдеи — управляющий параметр.
Будем предполагать, что управление КЛА осуществляется путем из¬
менения эффективного значения аэродинамического качества
^эфф ~ ал COS 7*
Движение КЛА вокруг центра масс не учитывается, т.е. предполага¬
ется, что переключение угла крена осуществляется мгновенно. Величина
эффективного аэродинамического качества ограничена:
- ^бал < ^эфф < + ^бал • (6.15)
Решение задачи будем проводить в два этапа.
Вначале исследуем оптимальные траектории спуска при отсутствии
ограничений на фазовые координаты. В общем случае это не совсем вер¬
но, поскольку снижение КЛА в атмосферах планет может сопровождаться
большими перегрузками. Кроме того, при спуске на планеты с разреженной
атмосферой весьма важным является ограничение на минимально допусти¬
мую высоту полета над поверхностью планеты. Однако, учитывая тот
факт, что спуск в атмосферах планет осуществляют в основном автома¬
тические КЛА, а также то, что учет дополнительных ограничений на траекто¬
рии приводит к снижению эффективности управляемого спуска, представ¬
ляется интересным оценить предельные возможности таких КЛА по управ¬
лению конечной высотой спуска и тем самым сформулировать разумные
требования к величине допустимых значений ограничивающих факторов.
12. Зак. 2069
177
На втором этапе решается задача максимизации конечной высоты
учетом ограничений, накладываемых на фазовые координаты.
Уравнения плоского движения центра масс КЛА записываются в ско¬
ростной системе координат в виде (5.21) в предположении отсутствия
уноса массы теплозащитного покрытия (л?ун = 0).
При анализе оптимальных траекторий спуска будем предполагать экспо¬
ненциальный закон изменения плотности по высоте
Р
= Ро*
Сформулируем задачу оптимального управления следующим образом:
определить программу изменения эффективного качества /Сэфф (t), ми¬
нимизирующую функционал (6.14) при ограничении на управление (6.15),
дифференциальных связях (5.21) и краевых условиях
1/ = 1/0, 0 = 0О, = Г=Го,
\/=1/к,0к свободно, гк свободно.
С помощью гамильтониана системы (5.21)
dV dB dh pV2
Ж = ф i + Ф2 + Фз = Ф1 — [0 ~ г\ ф 1 sin 0 +
dt dt dt 2PX
pV Г 9 I/
+ Ккал Ф2 cosy + 2<лф2 — — +
6ал 2PX [v R+h
запишем уравнения сопряженных переменных в виде
dфl
dt
рУФх
Рх
COS0 со2 г
Ф2 +—— COS0 - i//3sin0,
/?+/? V2
йф 2
9Ф 1COS0 — со2 гф 1COS0 ф'2 sin 0 +
30 V
(6.16)
dф3 3Jf pV2 2gsin0 _ t
— = = вфх — ф1 - cj2i//1sin0 +
dt dh 2PX r3
pVfi 2gi//2cos0 VcosO co2
+ *6an—CO5>h —3 + —~Г Ф2-— ^2COS0.
Необходимым условием максимума функционала (6.14) является усло¬
вие минимума функции К как функции управления /Сэфф.
Управление К^фф входит в правую часть системы (5.21) линейно. В
этом случае оптимальное управление, найденное из условия минимума
гамильтониана, принимает граничное значение и определяется следующим
образом:
Кэфф = K6ansignih- (6-17)
178
Условие трансверсальности в конечной точке траектории имеет вид
6/ - К5Г + + ф38Ь = 0.
Поскольку величина hK максимизируется, а величины и tK не зада¬
ны, получаем
Ф2к = 0, ^Зк = 1-
(6.18)
Из условия J£ = 0 можно представить переменную фi (t) как функцию
V,6 и/?:
h
^(r)=v
Vs\nO
— asin# + U)2rsin0
2PX
С учетом (6.18) получим в конце траектории спуска
^Ks’n^K
X
Таким образом, поставленная вариационная задача определения опти¬
мального управления из условия /7ктах сводится к двухпараметрической
краевой задаче.
Решение краевой задачи существенно облегчается, если предварительно
провести исследование характера поведения функции ф2 (t) и тем самым
определить структуру оптимального управления. Как следует из (6.17),
оптимальное управление принимает на траектории спуска свои предельные
значения ^эфф = + ^бал» ~^бал» а моменты смены знака, или моменты
переключения оптимального управления, соответствуют нулям функции
ф2 (Г). Отсюда следует, что анализ структуры оптимального управления
сводится к анализу числа нулей и последовательности смены знака решения
второго уравнения (6.16). Видно, что это уравнение представляет собой
линейное относительно ф2 (t) неоднородное дифференциальное уравнение
первого порядка, которое не интегрируется в аналитическом виде и не
отделяется от основной системы.
Для анализа характера поведения функции ф2 (г) на траектории спус¬
ка воспользуемся приближенными уравнениями движения КЛА [19].
Введем некоторые упрощающие предположения. Будем считать, что вра¬
щение планеты отсутствует (со = 0), угол наклона траектории к горизон¬
ту мал, так что можно допустить
sin в и со$0 « 1,
а проекция сил тяжести на направление полета много меньше сил аэроди¬
намического сопротивления
I^osin0| <
Используя эти допущения и вводя новые переменные
X v кр
уравнения движения (5.21) можно записать в виде [19]
d2y е2х-г
V
179
Рис. 6.2. Параметры оптимальной траектории спуска в атмосфере Марса из условия
максимизации конечной высоты.
где
и = х/^ХЛ'бал COS?, —“ = — 6.
dx
Итак, плоское движение КЛА в атмосфере планеты описывается нели¬
нейным уравнением второго порядка, причем управляющий параметр
^э^)ф = ^6ancos? входит в это уравнение линейно. В этом случае крите¬
рии оптимальности и краевые условия при х=хк могут быть записаны
в виде
/ = min у2 (хк),
и
гдехк задано требуемой величиной конечной скорости.
Произведем замену переменных у = И,/" = у2 и запишем уравнения
движения в следующем виде:
dyx dy2 е2х - 1
— =^(х, у2)~и, ——=/1, f(x, У2) = . (6.19)
dx dx у2
Сопряженная к (6.19) система дифференциальных уравнений записы¬
вается следующим образом:
с/ф1 d\}j2 bf
dx 2' dx Э/2
Краевые условия для сопряженных переменных на правом конце траекто¬
рии имеют вид
Ф1 (*к) = О, Ф2(*к) = 1.
Вспомогательная система (6.19) может быть приведена к одному линейно-
180
Рис. 6.3. Изменение траекторных параметров V,0,h сопряженных переменных
ф2, ф3 и эффективного качества Кэфф ПРИ оптимальном управлении из условия мак¬
симизации конечной высоты при спуске в атмосфере Юпитера (Ля = —460 км, Кбал=
= 0,2, Рх — 200 кгс/м2; номинальная модель атмосферы).
му неоднородному дифференциальному уравнению второго порядка
с/ф ?
—— + со2 (х, у2 }ф 1 = о, (6.20)
dx2
где
е2х - 1
Из записанного выше гамильтониана системы (5.21) следует, что его
максимум достигается при граничных значениях управления К^фф и опре¬
деляется следующим образом:
и(х) = - t/max sign 1//! (х) .
Таким образом, анализ оптимального управления сводится к анализу
числа нулей и последовательности смены знака решения уравнения (6.20).
Рис. 6.4. Изменение траекторных параметров V, 6, h, сопряженных переменных
Ф2, ф3 и эффективного качества К’эфф ПРИ оптимальном управлении из условия мак¬
симизации конечной высоты при спуске в атмосфере Юпитера = —1175 км,
Кбал = 0,2, Рх = 200 кгс/м2; номинальная модель атмосферы) .
Ь £
400
е- ?
40
си k
40
0,6
-14
0
\s\v(t)
Л*эфф (t)
20
200
20
0,2
-32
-20
0
0
181
Коэффициент со2 этого уравнения обладает рядом свойств, позволяющих
провести качественный анализ структуры оптимального управления, т.е.
определить число нулей функции фг и последовательность смены знака
решения уравнения (6.20) без интегрирования основной системы [19].
В частности, на участке движения в атмосфере со сверхкруговой скоростью
решение уравнения (6.20) имеет апериодический характер, поскольку
со2 (х, у2) < 0, а на участке движения с докруговой скоростью — колеба¬
тельный характер. Поэтому на участке движения со сверхкруговой ско¬
ростью решение уравнения (6.20) имеет не более одного нуля независимо от
того, на какую планету Солнечной системы осуществляется спуск КЛА,
а оптимальное управление соответственно имеет не более одного пере¬
ключения.
На участках траектории спуска коэффициент со2 (х,у2)> 0, поэтому
решение уравнения (6.20) может иметь колебательный характер. Для
выяснения структуры решения уравнения (6.20) в этом случае в соот¬
ветствии с методикой, изложенной в [19], необходимо оценить возмож¬
ные перегрузки на траектории спуска. Величина перегрузки, при которой
решение уравнения (6.20) имеет апериодический характер, равна
л/ях1
зк Т
Проведенные исследования показали, что для КЛА, осуществляющих
спуск в атмосферах планет, величина перегрузки пх, как правило, пре¬
вышает значение ,и1, следовательно, число переключений /^эфф не пре-
вышает одного. В тех случаях, когда пх<пх, число нулей не превышает
двух. Поскольку один нуль расположен в конце траектории, будем иметь
на участке движения с докруговой скоростью не более одного переклю¬
чения. При этом на последнем участке получим
Ф 1 (х) 0 И /^эфф ~~ + ^бал*
Таким образом, на оптимальной траектории спуска число переключе¬
ний эффективного аэродинамического качества не превышает двух. Для
проверки оптимального числа переключений /Сэфф в каждом конкрет¬
ном случае необходимо проводить интегрирование вспомогательной систе¬
мы уравнений (6.16) вдоль траектории с соответствующим числом пере¬
ключений.
В качестве примера на рис. 6.2 —6.4 приведены результаты расчетов
оптимальных траекторий спуска КЛА с траектории- прямого перелета
в атмосферах Марса и Юпитера.
6.5.2. Оптимальное управление при наличии ограничений на
фазовые координаты
Проведем анализ структуры оптимального управления при ограниче¬
нии на фазовые координаты [19]. Оптимальная траектория в общем слу¬
чае состоит из участков движения по ограничениям и участков движения
внутри допустимой области фазовых координат. Запишем условие дви¬
жения КЛА вдоль ограничения в виде
? (xz/i,y2) = 0/ (6.21)
<p(ipi,... ,^п) — вектор, размерность которого в общем случае определя¬
ется числом ограничивающих факторов.
182
Если вектор <р имеет размерность больше единицы, то КЛА движется
по ограничениям последовательно. Между участками движения по огра¬
ничению оптимальная траектория будет иметь участки перехода с одного
ограничения на другое. Управление эффективным аэродинамическим
качеством при движении КЛА вдоль ограничения полностью определя¬
ется из условия равенства нулю полной производной от выражения (6.21)
р-го порядка [19] :
^(х, У1, Уг, и) = о. (6.22)
Здесь и — порядок производной, начиная с которого управляющий пара¬
метр Кэфф явным образом входит в производную. В задаче о максими¬
зации конечной высоты спуска величина v = 2. Тогда из (6.22) получим
следующие выражения для управления при движении КЛА по ограничению
[19] :
1
Uf = f + ~^~ tex ★'Ру, и), ^=1,
= f + —— кр’х +У1А h *> = 2.
гу2
Сопряженные переменные и гамильтониан в момент выхода КЛА на
ограничение имеют разрыв:
<Pi - = Mgrady/P — = jugradxi/p Ч
Для случая р=1 условие разрыва сопряженной переменной ф} может
быть записано следующим образом:
(Ф+\ - = Ф^и+ ~ Ф 'и •
(6.23)
Анализируя (6.23), легко показать, что вспомогательная переменная
в момент выхода КЛА на ограничение равна нулю: ф{ - 0. При v = 2 в мо¬
мент выхода на ограничение условие разрыва сопряженных переменных
может быть представлено в виде
1
= ф\и+ - ф_! U’.
(6.24)
Используя (6.24), легко показать, что в момент схода КЛА с ограни¬
чения функция равна нулю. Это обстоятельство (равенство нулю функ¬
ции фх в момент выхода на ограничение и схода с него) существенно
упрощает анализ структуры оптимального закона управления на участках
движения вне ограничений. Действительно, наличие даже одного участка
движения по ограничению приводит к уменьшению максимального числа
переключений на участках движения вне ограничения на два по сравнению
с числом переключений для траекторий без ограничения. Это имеет нема¬
ловажное значение, поскольку в рассматриваемой задаче максимизации
конечной высоты общее число переключений невелико.
Покажем, что при
типа
наличии участка движения КЛА по ограничению
Q = лдоп ~ = 0 или q = лдоп - n(t) = 0,
Для которых у = 2, в задаче максимизации конечной высоты характер
траектории на участке, предшествующем движению по ограничению, не
183
влияет на величину Лктах. Действительно, в конце участка выхода КЛА
на ограничение выполняются следующие два условия [19] :
ф(х) = 0, qx +и^2 = 0.
Выполнение условия разрыва сопряженных переменных может быть
достигнуто путем подбора двух свободных параметров: начальных зна¬
чений вспомогательных переменных ф](х0) и ф2 <*о)• Величина функци¬
онала управления / = Лктах после схода с ограничения также определя¬
ется двумя сопряженными переменными ф\ и ф2, поскольку после схода
с ограничения имеется разрыв сопряженных переменных. Отсюда ясно,
что функционал h к тах не зависит от участка выведения КЛА на ограни¬
чение. Отметим также, что в большинстве рассматриваемых случаев на
интервалах перехода с одного ограничения на другое максимальное число
нулей функции (х) равно двум. А поскольку на концах интервала пере¬
хода с одного ограничения на другое i//j =0, то, следовательно, на этом
интервале оптимальное управление /Сэфф не должно иметь переключе¬
ний. Однако учитывая, что в момент схода КЛА с ограничения происходит
разрыв сопряженной переменной, можно сделать вывод, что это приводит
к смене знака функции ф] (х). Вторая смена знака реализуется
на конце интервала перехода КЛА между ограничениями и обеспе¬
чивается собственным решением уравнения для сопряженных пере¬
менных (6.20).
Ниже в качестве примера приводятся результаты численного решения
задачи об отыскании оптимального управления КЛА, осуществляющего
спуск в атмосферах Марса и Юпитера. При этом в первом случае ограни¬
чивающим фактором является минимально допустимая высота полета
над поверхностью планеты, а во втором — максимально допустимая пе¬
регрузка.
Решение задачи будем проводить в предположении наличия одного участ¬
ка движения КЛА по ограничению. Приведенные выше результаты качест¬
венного анализа структуры оптимального управления были использованы
в качестве первого приближения при решении краевых задач, к которым
сводится поставленная задача максимизации конечной высоты полета.
Рассмотрим задачу об отыскании оптимального управления КЛА в
атмосфере Марса из условия максимума конечной высоты при ограниче¬
нии (6.5) на допустимую высоту полета над поверхностью планеты. Это
ограничение позволяет учитывать возможности рельефа поверхности Мар¬
са и исключает возможность "жесткой" посадки КЛА при полете его в
нижних слоях атмосферы.
В предположении, что поле тяготения Марса центрально и атмосфера
не вращается, уравнения плоского движения центра масс КЛА запишем
в виде
p(h)V2
p(h)V
cos# У cos#
V =
— gihjsinO,
0 = Кэфф
-g{h) + ,
2РХ
2РХ
V г
R2
(6.25)
h = l/sin 6, g(h) = до— .
Пусть оптимальная траектория содержит единственный интервал дви¬
жения по ограничению (6.5). При движении КЛА внутри допустимой об¬
ласти фазовых координат гамильтониан системы (6.25) и сопряженные
184
переменные могут быть представлены следующим образом:
pl/2
JC=-0,—
2РХ
р(/
- ф ipsin# + Фгкэфф-тг
gcosd
VcosB
(6.26)
-ф2 v +
ф2 + ф3 l/sin0,
г
фурУ
dt
Рх
— Ф2
geos 9 cos0\
—+—;
0^2
dt
фгдсоз0 - ф2
l/siп 0 \
]— ФзУсозО,
(6.27)
йфз
~dt~
2<7cos0
г
2gcos0 Vcos0\
ф з sin 0,
Оптимальное управление при q < 0, определенное из условия макси¬
мума гамильтониана Ж как функции управления /Сэфф, имеет вид
^эфф — ^бал5’9пФ2-
На изовысотном участке полета (движение по ограничению) получим
следующий закон управления эффективным аэродинамическим качеством:
2PJ1 — У2)
Кэфф - у2р*(Я+/,доп ) '
где V= V/VKp.
Сопряженные переменные в точке касания (ti)
ния h = Лдоп скачком меняют свою величину:
Ф1(Т1)-Ф1 U1) = О/ Ф*2 U1) - ф2 U1) = М2 V,
Фз^ 1) — Фз (^ 1) = Mi •
(6.28)
траекторией ограниче-
(6.29)
где звездочкой отмечены параметры при движении КЛА по ограничению.
Момент схода КЛА с ограничения (6.5) определяется условием ф2УЛ -
= 0. На участке движения по ограничению уравнения сопряженных пере¬
менных записываются следующим образом:
йф\ _ рУф*!
dt Рх
/5.
ltPV2
=
dt 2РХ
В конце траектории спуска из условий трансверсальности получаем
= 0.
(6.30)
(6.31)
Учитывая, что на траектории спуска гамильтониан равен нулю, для
третьей сопряженной переменной будем иметь
^эфф °хРк Укгк^к ~ 2м cos + ^KCOS^KrK^K
Фзк= 2r2V2sin0K
185
Выше было показано, что для задачи максимизации конечной высоты
участок траектории полета, предшествующий ограничению, не влияет на
функционал управления. Отсюда следует, что на участке выведения КЛА
на ограничение управление /Сэфф не определено и может быть любым,
но приводящим КЛА на ограничение со скоростью, не меньшей некоторой
скорости схода с ограничения Vcx, обеспечивающей максимальное значение
/7К- На участке движения после схода с ограничения максимальное число
нулей функции ф2 не превышает двух. Учитывая, что оба нуля расположены
на концах этого участка, можно сделать вывод, что оптимальное управление
после схода КЛА с ограничения не имеет переключений и, следовательно,
он совершает полет с постоянным максимальным положительным или
отрицательным значением /Сбал.
Таким образом, поставленная вариационная задача сводится к проверке
на оптимальность с использованием уравнений (6.25) - (6.31) законов
управления /Сэфф = -Кбал или ^эфф = +^бал- Проведенные численные
исследования в широком диапазоне варьирования исходных данных (проект¬
но-баллистических характеристик КЛА, условий входа в атмосферу и пара¬
метров атмосферы) показали, что на участке схода КЛА с ограничения
оптимальной программой управления является программа полета с мак¬
симальным положительным значением /Сэфф, В качестве примера на
рис. 6.5 приведены параметры оптимальной траектории спуска КЛА в ат¬
мосфере Марса из условия максимума конечной высоты.
Оптимальное управление КЛА, осуществляющих спуск в атмосфере
Юпитера, при ограничении на максимально допустимую перегрузку. Анализ
необходимых условий оптимальности принципа максимума Понтрягина
[19] для задачи максимизации конечной высоты спуска КЛА в атмосфере
Юпитера при ограничении на максимально допустимую перегрузку показал,
что решение вариационной задачи, как и в предыдущем случае, сводится
к выбору одного из двух возможных законов управления КЛА (/Сэфф =
= ~^бал или ^эфф = +^бал) на участке полета после схода с ограничения.
186
Численные результаты решения показывают, что оптимальной програм¬
мой управления на этом участке является программа полета с /Сэфф =
= +Кбал. Выведение КЛА на изоперегрузочный режим может осуществлять¬
ся произвольным образом при выполнении лишь одного условия: скорость
КЛА в момент касания ограничения не должна быть меньше оптимальной
скорости схода с него. При полете КЛА по ограничению управление эффек¬
тивным качеством определяется однозначно [82] :
Кд V со2г \ . .
— - - — cos0J + p0V2Vsine +
+ 2р v( — — 2sin0(<7 — со2/? — w2h)p V — 4pVV —
\2РХ /
— 2р V2 + fipli \Z2jy<—/Зр l/3cos в —2pVcos в).
В качестве примера на рис. 6.6 приведены параметры оптимальной
траектории спуска КЛА в атмосфере Юпитера из условия максимума ко¬
нечной высоты при ограничении на максимально допустимую перегрузку.
Некоторые результаты решения задачи максимизации конечной высо¬
ты при спуске КЛА в атмосферах планет. Найденные программы оптималь¬
ного управления КЛА позволяют провести анализ траекторий спуска из
условия /?к тах методом численного интегрирования для различных планет.
Будем рассматривать прежний диапазон основных варьируемых парамет¬
ров Рх и /Сбал (см. п. 5.2.5). Величина скорости при вводе пара¬
шютной системы может изменяться в пределах:
200 м/с < VK доп <850 м/с.
Рассмотрим влияние основных варьируемых параметров на величину
максимальной конечной высоты. При этом в дальнейшем величину конеч¬
ной высоты, полученной при оптимальном управлении из условия (6.14),
будем обозначать через /?ктах. Величина максимальной высоты мало зави-
Рис. 6.6. Параметры оптимальной траектории спуска в атмосфере Юпитера из условия
максимизации конечной высоты при ограничении на максимально допустимую пере¬
грузку = —1175 км, Кбал = 0,2, рх = 200 кгс/м2; номинальная модель атмо¬
сферы) .
187
Таблица 6.3
Численные результаты решения задачи Лк = Лктах
Исходные пара¬
метры
Варьируемый
параметр
^ктах/
км
Исходные па¬
раметры
Варьируемый
параметр
^ктах»
км
Земля
—
25,1
Венера
50,8
Уо = 11 км/с
Рх = 700 кгс/м2
22,4
1/0 = 11 км/с
Рх = 200 кгс/м2
55,6
h0 =100 км
^бал = 0,5
38,5
Ло =100 км
Рх = 700 кгс/м2
49,0
1/к = 0,7 км/с
Р = Pmin
26,7
Ик = 0,7 км/с
Р ~ Pmin
43,0
Рх = 500 кгс/м2
Р = Ртах
31,9
Рх = 500 кгс/м2
Р ~ Ртах
62,8
^бал ~ 0,3
1/к = 0,5 км/с
25,0
^бал = 0,3
^бал = 0,5
71,2
1/к = 0,2 км/с
18,3
Ик = 0,5 км/с
47,2
Ик = 0,2 км/с
40,4
Марс
-
17,3
Юпитер
—
89,1
VQX= 7 км/с
Рх= 200 кгс/м2
22,6
1/0 = 65 км/с
Рх = 500 кгс/м2
' 79,0
hQ =100 км
Рх = 500 кгс/м2
14,0
h0 = 400 км
^бал = 0,5
122,2
1/к = 0,7 км/с
^бал = 0,5
26,2
1/к = 0,7 км/с
Р = Ртепл
107,1
Рх = 350 кгс/м2
Р = Ртах равн
18,4
Рх = 300 кгс/м2
Р = Рхол
58,6
К бал = 0,3
1/к = 0,5 км/с
11,0
*бал = 0,3
Ик = 0,5 км/с
74,4
1/к = 0,2 км/с
-
1/к = 0,2 км/с
56,2
Сатурн
-
104,1
Уран
-
99,1
1/0 = 37 км/с
Рх = 200 кгс/м2
139
1/0 = 28 км/с
Рх = 200 кгс/м:
1 124,0
h0 = 400 км
Рх = 700 кгс/м2
105
hQ = 400 км
Рх = 700 кгс/м:
г 89,8
1/к = 0,7 км/с
^бал = 0,5
136
1/к = 0,7 км/с
^бал = 0,5
130,8
Рх = 500 кгс/м2
Р = Ртепл
80,3
Рх = 500 кгс/м2
1/к = 0,5 км/с
80,5
*бал = 0'3
Р = Рхол
72,3
^бал = 0,3
1/к = 0,2 км/с
57,1
Р ~ Рном
1/к = 0,5 км/с
95,8
1/к = 0,2 км/с
81,3
Нептун
-
63,3
Vo = 28 км/с
Рх = 200 кгс/м2
79,3
h0 = 400 км
Рх = 700 кгс/м2
57,4
Ик = 0,7 км/с
*бал = 0,5
92,7
Рх = 500 кгс/м2
1/к = 0,5 км/с
50,1
^бал = 0,3
Ик = 0,2 км/с
34,8
сит от высоты условного перицентра траектории входа: с увеличением
внутри навигационного коридора входа, расположенного вблизи гра¬
ницы захвата КЛА атмосферой, происходит незначительное уменьшение
^ктах/ а увеличение начальной скорости входа VQ приводит к незначи¬
тельному возрастанию /?ктах- Характер зависимостей /JKmaxW и
^ктах (Уо) остается неизменным для различных моделей атмосферы и
разных планет, но сама величина /7ктах существенно зависит от модели
атмосферы и физических характеристик рассматриваемой планеты.
Сравнение величин /?ктах, рассчитанных для двух предельных моделей
атмосферы при оптимальном управлении, показывает, что увеличение плот¬
ности от минимальной до максимальной приводит к возрастанию hKmax
в среднем на 5 км для Земли, 1,5 — 2 км для Марса, 20 км для Венеры,
50 км для Юпитера и 32 км для Сатурна (табл. 6.3).
В целом можно отметить, что для рассматриваемого диапазона изме¬
нения Vo и /?я максимальная высота при минимальной плотности лежит
выше 25 км для Земли, 10 км для Марса, 40 км для Венеры, 55 км для
Юпитера, 70 км для Сатурна, 55 км для Урана и 30 км для Нептуна. Замет¬
188
ное влияние на максимальную конечную высоту оказывает изменение ве¬
личины приведенной нагрузки на лобовую поверхность и аэродинамичес¬
кого качества КЛА. При этом увеличение Кбал <и уменьшение Рх) приво¬
дит к возрастанию /?ктах Для всех рассматриваемых планет (см. табл.6.3).
Как и следовало ожидать, заметное влияние на величину Лк тах оказывает
изменение допустимой скорости введения парашютной системы Ук. При
увеличении VK происходит возрастание /?ктах Для всех рассматриваемых
планет (см. табл. 6.3).
Таким образом, анализ оптимальных траекторий спуска показал, что во
всем диапазоне варьируемых параметров имеет место достаточный запас
по высотам для работы парашютно-реактивной системы. При этом даже
при спуске на Марс, обладающий наиболее разреженной атмосферой, мак¬
симальная конечная высота составляет hK max >10 км.
Глава 7
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ДАЛЬНОСТЬЮ ПОЛЕТА
В АТМОСФЕРЕ
§ 7.1. Минимизация дальности спуска
Задача обеспечения посадки КЛА в выбранном районе поверхности пла¬
неты назначения является во многих случаях одной из важнейших. Требо¬
вание обеспечения точной посадки пилотируемого корабля настолько оче¬
видно, что не требует специальных доказательств. Наряду с этим можно
констатировать, что в космической технике давно прошло и то время,
когда автоматические КЛА могли садиться куда попало. Достаточно
вспомнить спуск КЛА "Викинг", когда была применена энергетически невы¬
годная орбитально-десантная схема полета ради того, чтобы иметь возмож¬
ность "сесть" в наиболее благоприятном районе Марса. Советские АМС
"Венера" наводятся таким образом, чтобы в каждом полете исследовать
определенные новые районы Венеры. Однако ни КЛА "Викинг", ни АМС
"Венера" не имели возможности осуществлять спуск с управляемой даль¬
ностью полета на атмосферном участке. Задача посадки в выбранном райо¬
не решалась путем выбора и последующей реализации соответствующих
требуемых начальных условий входа. Подобный путь решения, даже при
большом допуске на рассеивание точек посадки, не всегда может быть реа¬
лизован. Действительно, рассмотрим самый простой вид спуска — возвра¬
щение с орбиты. Если продольная дальность по трассе полета может быть
обеспечена соответствующим выбором времени включения тормозной дви¬
гательной установки, величиной и направлением тормозного импульса,
то боковой промах относительно точки посадки может быть скомпенсиро¬
ван, как правило, только управлением на атмосферном участке спуска.
В крайнем случае надо дожидаться такой ситуации, когда трасса посадоч¬
ного витка строго пройдет через район посадки. Еще более критичной вы¬
глядит задача при подходе к планете назначения по параболической траекто¬
рии. Оперативно поменять район посадки в ходе полета КЛА технически
очень сложно, а иногда и невозможно. Например, спустя некоторое время
после запуска АМС "Венера-13" и "Венера-14" были получены новые инте¬
ресные данные о поверхности Венеры и в свете этого желательно было
поменять районы посадки. Ценой огромных усилий большого коллектива
инженеров, ученых и специалистов по оперативному управлению полетом
189
АМС, проведших специальную исследовательскую работу, удалось решить
эту задачу, применив специальную коррекцию и последующий сложный ма¬
невр АМС, чтобы не нарушить требуемое строгое относительное движение
СА и АМС. При этом точка посадки каждой из станций была смещена всего
на несколько градусов по широте и долготе.
Учитывая сказанное, в дальнейшем всегда будем предполагать, что в
каждом конкретном случае могут быть обеспечены наиболее благоприят¬
ные начальные условия и исследуется управление дальностью полета КЛА
только на атмосферном участке снижения с использованием аэродинамичес¬
ких подъемных сил. В такой постановке на передний план выходит задача
определения маневренных возможностей КЛА. Под зоной маневра будем
понимать область достижимых дальностей в продольном и боковом нап¬
равлениях аппаратом определенной геометрической формы при заданных
начальных условиях входа. Успех решения задачи точной посадки при уп¬
равляемом спуске зависит от того, насколько зона маневра превышает
возможный разброс точек посадки из-за действия разного рода возмущаю¬
щих факторов, включая и ошибки начальных условий. В самом общем слу¬
чае для нахождения зоны маневра необходимо прежде всего определить
максимальные (Z-np max/ L бтах) и минимальные (£Прmin/min) продоль¬
ные и боковые дальности полета. В этом случае появляется необходимость
в решении четырех в известной мере независимых частных задач поиска
^•пртах/ ^-npmin/ ^бтах и ^-6min-
Результаты решения задачи максимизации зоны маневра показывают
потенциальные возможности маневрирования того или иного КЛА, однако
в ряде случаев указанные выше частные задачи приобретают самостоятель¬
ное значение. Наиболее наглядно это можно продемонстрировать на при¬
мере возвращения КЛА на Землю после облета Луны. Как известно, траек¬
тория полета КЛА по облетному маршруту Земля — Луна — Земля пред¬
ставляет собой очень вытянутую эллиптическую кривую с фокусом в цент¬
ре Земли и перицентром, лежащим в диапазоне от 25° с.ш. до 25° ю.ш.
в зависимости от склонения Луны в момент полета КЛА.
Если говорить о посадке КЛА на Землю, не имея в виду строго заданный
район, то для этого достаточно обеспечить только приведение аппарата в
определенный коридор по высотам перигея подлетной траектории. В этом
случае вход аппарата в атмосферу можно проводить с любой стороны от¬
носительно Земли: с севера ("северное" сближение) или с юга ("южное"
сближение). Принципиально это можно выполнить путем задания соответ¬
ствующего направления полета КЛА по облетной (возвратной) траектории.
При этом следует иметь в виду, что "северный" вариант возвращения по
облетной траектории "Земля —Луна — Земля" имеет ряд несомненных пре¬
имуществ. Во-первых, полет по такой схеме дает существенный энергети¬
ческий выигрыш, в результате чего появляются дополнительные возмож¬
ности по установке научной аппаратуры; во-вторых, несколько облегчает¬
ся управление полетом на участках полета к Луне и от Луны. И, в-третьих,
при такой схеме полета появляется возможность управлять КЛА с назем¬
ных стационарных пунктов, расположенных на территории СССР, почти
до входа его в плотные слои атмосферы. Это очень существенное преиму¬
щество, так как в этом случае происходит максимальное уточнение под¬
летной траектории и при необходимости может быть проведена коррек¬
ция этой траектории непосредственно перед входом в плотные слои атмос¬
феры; система управления спуском получает точные сведения об условиях
входа и работает в сравнительно благоприятных условиях. Однако для по¬
садки КЛА на территории Советского Союза исполнение "северного" ва¬
рианта связано с большими, зачастую неразрешимыми трудностями. Это
190
объясняется тем, что при входе с "севера" проекция перигея траектории
на поверхность Земли практически лежит ниже южной границы территории
СССР, а так как полет КЛА происходит с севера на юг, то КЛА удаляется
от территории СССР. В результате возникает задача минимизации продоль¬
ной дальности полета (Z-npmin) с тем, чтобы посадка КЛА осуществлялась
севернее проекции перигея на поверхность Земли. Если не рассматривать
ограничение по перегрузкам, то решение задачи достигается увеличением по
модулю угла входа, что ведет к уменьшению дальности полета и посадке
на территории СССР.
Введение ограничения по допустимым перегрузкам существенно ослож¬
няет решение задачи, которое возможно, как показали соответствующие
исследования, только в некоторых случаях при определенном склонении
Луны и введении изоперегрузочного участка снижения, при этом макси¬
мальные перегрузки достаточно велики (лтах > 10). Единственным пу¬
тем облегчения перегрузочного режима является переход на реализацию
"южного" варианта входа. В этом случае появляется другая крайность:
протяженность участка траектории от точки входа до точки посадки на
территории Советского Союза составляет 6000 — 11000 км в зависимости
от склонения Луны. Преодолеть такие расстояния в атмосфере на КЛА,
управляемых только с использованием ограниченных аэродинамических
сил, не представляется возможным и просто исключено для КЛА "сколь¬
зящего" типа. Однако было найдено интересное и оригинальное решение,
успешно реализованное для возвращения советских автоматических стан¬
ций "Зонд". Впервые спуск аппарата проходил по так называемым рико¬
шетирующим траекториям, когда спускаемый аппарат после кратковре¬
менного погружения в атмосферу, совершает полет по баллистической
траектории, затем опять входит в плотные слои атмосферы и совершает
посадку. Как видно, в этом случае имеют место три участка траектории
снижения (рис. 7.1). Участок первого, погружения — самый короткий по
дальности и непродолжительный по времени движения — является наиболее
ответственным и принципиальным при обеспечении посадки в заданном
районе. Например, для спускаемого аппарата станции "Зонд" (АГбал ~ 0,3)
время полета на этом участке = 100 ч-150 с, дальность полета L ! — 700 —
1200 км, а максимальные перегрузки не превышают 5—6 единиц. На вто¬
ром участке спускаемый аппарат движется практически только под дейст¬
вием сил тяготения по эллиптической кривой. Дальность полета, отсчиты¬
ваемая по поверхности Земли, полностью определяется условиями вылета
из плотных слоев атмосферы, т.е. скоростью Vi и углом наклона вектора
Рис. 7.1. Траектория управляемого движения спускаемого аппарата в атмосфере:
/ — участок первого погружения в атмосферу; // — участок движения вне плотных
слоев атмосферы; /// — участок второго погружения в атмосферу.
191
скорости к местному горизонту в1
Земли :
на границе плотных слоев атмосферы
/_2 = 2г arctg
Нетрудно видеть, что, во-первых, одна и та же дальность Z_2 может
быть получена при разных сочетаниях V{ и 0Х; во-вторых, варьированием
Vi и 0! может быть реализована сколь угодно большая дальность L 2.
Третий участок — участок повторного погружения — близок по своим
характеристикам к аналогичному участку спуска с орбиты ИСЗ. При этом
начальные значения скорости V3 и угла входа 03 по модулю практически
равны соответственно Vx и 0j. Дальность полета для спускаемого аппара¬
та "скользящего" типа равна 1000 — 1500 км, а маневренные возможности
весьма ограничены и составляют всего несколько сотен километров по
продольной и несколько десятков километров по боковой дальности поле¬
та. В силу этого принципиальное значение имеет управление на первом
участке спуска, которое должно обеспечивать очень высокую точность ус¬
ловий вылета (Vi и 0j) . Действительно, ошибка А V t = ± 1 м/с или Д0 j =
= ± Г приводит к промаху в дальности полета Д£ = ± 30^40 км. Следова¬
тельно даже при возможности маневрирования на участке повторного
входа погрешность в скорости вылета Vi более 0,1% (при отсутствии
каких-либо других возмущений) приводит к некомпенсируемому промаху
в точке посадки.
Таким образом, применение рикошетирующих траекторий дает возмож¬
ность практически неограниченно максимизировать продольную дальность
полета. Это следует иметь в виду и прибегать к этому способу, когда другие
пути нерациональны или просто невозможны. Для определенности в даль¬
нейшем мы будем рассматривать задачу максимизации ^пртах только
для случаев полностью атмосферного движения, оговаривая все отличи¬
тельные особенности, связанные со схемой полета.
Ниже будем рассматривать вариационную задачу об отыскании оптималь¬
ного управления КЛА из условия минимальной продольной дальности на
траектории спуска. При этом учитываются ограничения на максимально
допустимую перегрузку лдоп и на минимально допустимую высоту полета
над поверхностью планеты (ЛдОп), имеющей разреженную атмосферу.
Оптимальное управление углом крена КЛА. Для анализа структуры оп¬
тимального управления воспользуемся приближенными уравнениями дви¬
жения [19]
d2y е2х -1 dy . ,
= и, — =ч/я^( (7.1)
dx у dx
где
(7.2)
Предполагается, что угол крена у варьируется в пределах 0<у<я, а
величина аэродинамического управления изменяется в диапазоне
УЖбал <</<-Уя0кбал. (7.3)
Функционал управления и ограничения на фазовые координаты записы¬
ваются следующим образом:
(7.5)
(7.6)
<Р1 (х, У 2 ) = vWh - Лдоп <0,
V’zU, /2> =УгМ -Кдоп<0.
Начальные условия задаются в виде
У1(хо> = К1, У2(х0)=У2, (7.7)
а конечные значения параметров траектории ух (хк) и /2 (хк) считаются
произвольными.
Сформулируем следующую задачу: определить такую программу управ¬
ления эффективным аэродинамическим качеством (7.2) с учетом ограниче¬
ния (7.3), которая обеспечивает минимальную величину дальности полета
КЛА при выдерживании заданной величины перегрузки (7.5) и минимально
допустимой высоты полета (7.6).
В общем случае оптимальная траектория спуска состоит из трех участ¬
ков: выхода на ограничение, движения по ограничению и схода с огра¬
ничения.
Условие касания траекторией спуска ограничений (7.5) и (7.6) записы¬
вается следующим образом [19] :
d<p
= У! —2/2 = 0- (7.8)
dx
На изоперегрузочном участке траектории управление имеет вид
и =
лдоп
(1 -е~гх) — 4
лдоп
2х
(7.9)
е
а на изовысотном — вид
- 1
и =
/2
(7.10)
Как показано в работе [19], для удержания КЛА на изоперегрузоч¬
ном и изовысотном участках траектории в диапазоне перегрузок Лцоп =
= 2-МО и высот Лдоп = 3-М0 км оказывается достаточным, чтобы КЛА
обладал величиной аэродинамического качества /Сдоп = 0,3 + 0,5.
Поскольку управление и входит в правую часть системы уравнений (7.1)
линейно, то в соответствии со стандартной процедурой принципа максиму¬
ма получим следующий закон оптимального управления КЛА из усло¬
вия £min:
и = \/ Я/Гк sign (х),
где сопряженная переменная i//i
(х) определяется из уравнения
dx2
(7.11)
Ф1
Анализ (7.11) показал, что на участке выхода КЛА на ограничение мак¬
симальное число нулей функции ф> (х) не превышает одного, причем непо¬
средственно перед выходом на ограничение Ф1 (х) < 0. Отсюда можно сде¬
лать вывод, что оптимальное управление имеет либо одно переключение
K's** с максимального отрицательного на максимальное положительное
значение, либо вообще не содержит переключений (предельный случай
входа КЛА по нижней границе коридора). На участке полета после схода с
ограничения оптимальное управление не имеет переключений и КЛА осу-
13. Зак. 2069
193
Рис. 7.2. Параметры оптимальной траектории спуска в атмосфере Земли из условия
минимизации продольной дальности спуска при управлении углом крена.
У,
KM/G
h,
км
”x
Rx(t)
0(t)l
-1,0
10
100
10
y(t)
-0,5
5
50
5
-
i 1
! ! 1
1
200 t,c
ществляет полет с максимальным отрицательным значением
Кэфф = (7.12)
после схода с изоперегрузочного участка полета и с максимальным поло¬
жительным значением
^эфф = \/ Я Х‘/Сбал (7.13)
после схода с изовысотного участка траектории.
Приведенное исследование структуры оптимального закона управления
существенно упрощает численное решение поставленной задачи: необходи¬
мо подобрать момент переключения эффективного аэродинамического
качества таким образом, чтобы в. момент достижения заданного значения
ограничения (7.5) или (7.6) выполнялось условие касания (7.8). Дальней¬
шее движение КЛА по ограничениям (7.5) и (7.6) осуществляется одно¬
значно в соответствии с (7.9) или (7.10).
Движение по изоперегрузочной или изовысотной траектории происходит
до момента достижения величиной /Сэфф своего крайнего граничного
значения
^эфф — X ^бал*
В качестве примера на рис. 7.2 приведены параметры оптимальной траек¬
тории КЛА, осуществляющего вход в атмосферу Земли со скоростью
11 км/с.
Оптимальное управление углом атаки. Приведем результаты решения
задачи об отыскании оптимальной траектории спуска КЛА, управляемого
углом атаки, из условия получения минимальной конечной дальности* поле¬
та с учетом ограничения на величину перегрузки [19]
г~г 7 pV'2®
"s = V<\ + —. (7.14)
Допустим, что зависимость коэффициента лобового сопротивления от
коэффициента подъемной силы имеет вид
Сх = СхО + «Су-
(7.15)
194
где к — постоянный коэффициент. При этом величина коэффициента
подъемной силы удовлетворяет следующему ограничению:
Су min су сушах- (7.16)
Запишем уравнения движения КЛА в атмосфере в
dV pV2s dG pV2s / V
= —с* — 9 sin 0, — = cv + (
dt 2m dt y 2mV \Rq +h
dh dL Rq V cos 0
= V sin 0Z — .
dt dt Rq +h
следующем виде:
(7.17)
Для системы уравнений (7.17) в начальный момент времени t0 имеем
V(tQ)=VQt 0(tQ)=0o, h(tQ) = /?Oz L(t0) = /-о-
Сформулируем задачу следующим образом: определить такой закон
управления углом атаки, при котором дальность полета КЛА от начальной
высоты h о до некоторой фиксированной достаточно малой конечной вы¬
соты h к была бы минимальной. При этом на траектории спуска должны вы¬
держиваться ограничения (7.14) — (7.16).
В общем случае оптимальная траектория спуска может состоять из
участков, на которых выполняется условие регулярности [19]
Ъпъ
Ъсу
* О,
(7.18)
и участков, на которых это условие не выполняется:
= 0
Ьсу
(7.19)
Рассмотрим оптимальную траекторию, на которой выполняется условие
(7.18). Запишем гамильтониан системы уравнений (7.17) в виде
Г cvpVs
о +
L 2m
( V cos el + Фг v sin в -
\R0+h Vj J
(7.20)
Сопряженная с (7.17) система дифференциальных уравнений записы¬
вается следующим образом:
/ V д\ , п , RoVsinO
= ф. I 1 sin в - Фг У cos в + Фз 9 cos в + -
dt Vi\R0+h V)
dy2 IfiCypVs VcosO 2gcos6
~dt ' 2m + (Яо +Л)2 ~ V2
&cxPV2
2m
s
2g sin 0 \ Rq V cos 0
+ I + i//4
R0+h> (Яо+Л)2
-X(t)
2/npo
(7.21)
195
dty3 (cvPs cos в
“Ф1 I +
eft '2m R0+h
0^4 л
= 0.
dt
- ^4
Ro cos 0
Rq + h
pVs f—z 77
+ 2X(t) yjc2 + c2
2mg0
Здесь X(tj — множитель Лагранжа, определяемый выражением
r
В конце траектории спуска имеем следующие граничные условия
h(tK) = hK; L(tK), 0(tK) и V(tK) — var, tK - свободно,
Ф1 = = 0, i/ц = —1.
Учитывая, что конечное время не задано, будем иметь
К = 0.
Теперь можно определить ф2 fco) ,если задать i//10 и i//30. В этом случае
поставленная вариационная задача сводится к двухпараметрической двухто¬
чечной краевой задаче для системы обыкновенных дифференциальных
уравнений (7.17) и (7.21).
Оптимальное управление обеспечивает максимум гамильтониану (7.20)
по су.
На участке движения по ограничению постоянство перегрузки обеспечи¬
вается изменением величины cy(t} в соответствии с условием = /7доп.
В качестве примера на рис. 7.3 приведены параметры оптимальной траек¬
тории для КЛА, снижающихся в атмосфере Земли, из условия Z.np -+ min.
Вход в атмосферу осуществлялся с околокруговой орбиты с начальной
скоростью Vq = 7,9 км/с и углом 0О = —3,8 . Величина максимально до¬
пустимой перегрузки бралась равной лдоп = 20.
Рассмотрим вариационную задачу об отыскании оптимального управле¬
ния углом атаки при полете на минимальную дальность, когда оптимальная
траектория содержит конечное число нерегулярных точек. Система сопря¬
женных уравнений движения КЛА в этом случае запишется следующим
Х(г)
(7.22)
(7.23)
(7.24)
Рис. 7.3. Параметры оптимальной траектории спуска в атмосфере Земли из условия
минимизации продольной дальности спуска при управлении углом атаки.
196
образом:
, ( v
— = Ф1
dt \R0+h
д\ flol/sin0
— I sin в — ф2 V cos 0 + ф2д cos 0 + Ф4 —,
V' R0+h
d^2 Г 0cx pV2s
Ф1 —
dt L 2m
2g cos в
(/?o +^)U
fcxPV2s
2m
2g sin в
+ 4
+
где звездочкой отмечена нерегулярная точка траектории.
Из (7.26) видно, что, в отличие от регулярного случая, в нерегулярных
точках оптимальной траектории сопряженные переменные ф2 и Фз будут
иметь скачки соответственно на величины д — и д •
При этом на оптимальной траектории должны быть выполнены следую¬
щие условия [19]:
f X(t)dt<°°,
*0
-ф4 + f X(t) dt = C > 0.
*0
(7.27)
(7.28)
Из (7.27) и (7.28) получаем условия, которым должна удовлетворять
197
оптимальная траектория в нерегулярной точке t *:
q - Лдоп Q (ЛдОП/схо)<
dt
1ЬГ) = 0.
(7.29)
Таким образом, для получения оптимальной траектории в нерегуляр¬
ном случае [см. условие (7.19)] необходимо одновременно удовлетворять
краевым условиям (7.23), (7.24) и условиям (7.29) в нерегулярной точке.
Итак, если количество нерегулярных точек равно п, то поиск оптимальной
траектории сводится к последовательному поиску л + 1 отрезков оптималь¬
ной траектории.
В качестве примера рассматривался случай входа КЛА в атмосферу Зем¬
ли с начальной скоростью Уо = 7,9 км/с и углом входа 0О = —3,8 . Макси¬
мально допустимая перегрузка на траектории спуска принималась равной
лдоп = Решение вариационной задачи из условия получения Z.npmin по¬
казало [19], что оптимальная траектория, построенная по описанной мето¬
дике, содержит одну нерегулярную точку (рис. 7.4).
§ 7.2. Максимизация дальности спуска
7.2.1. Максимизация дальности спуска
с использованием принципа максимума Понтрягина
Рассмотрим вариационную задачу об отыскании оптимального закона
управления КЛА из условия получения максимума продольной дальности
полета (L пр max). Прежде всего рассмотрим КЛА, управляемые углом
крена.
Управление углом крена. Сформулируем задачу следующим образом:
определить такой закон управления углом крена или эффективным аэро¬
динамическим качеством /Сэфф, который обеспечивает максимальную даль¬
ность полета при ограничении на максимально допустимую перегрузку
(7.5) или минимально допустимую высоту полета (7.6). Будем использо¬
вать уравнения плоского движения КЛА, записанные в виде (7.17).
Имеем следующие начальные значения параметров движения:
r = toz V(t0)= Vo, 0(to) = 0О,
Л(Го)= h0, L(t0) = L0. *7-3°)
Конечные значения фазовых координат траектории спуска могут быть
различными в зависимости от физических характеристик планеты, на кото¬
рую совершается посадка. Так, если планета окружена достаточно плотной
атмосферой, тормозные свойства которой позволяют снизить скорость по¬
лета КЛА до требуемого значения без использования каких-либо специаль¬
ных маневров в атмосфере, то в конце траектории спуска можем записать:
f = rK, V(fK) И 0(ГК) - свободны, /7(гк) = /7К. (7.31)
Если тормозных свойств атмосферы недостаточно для гашения избытка
скорости КЛА (например, при посадке на Марс), то в конце траектории
имеем
f = V(tK) < VK,
0(tK} - свободно, /?(tK) = hK. (7.32)
198
Запишем уравнения сопряженных переменных при движении КЛА внут¬
ри допустимой области фазовых координат:
d^i ЭК pV \ Кз&ьР 9qRqCos0 cos 0 -i
= = J/j - \b2 ■ + + -
dt bV Px L 2PX (/?o+/?)2U2 Ro + h J
R cos 0
— ф3 sin 0 — ^4 ,
Rq + h
b^2 ЭК
dt b0
— Фз V cos 0 +
d\p3 ЭК
dt bh L 2PX (Ro +h)3 J
Г pV V cos в 2ffo^ocos^'l U/?ocos0
+ Ф1 [Кэфф 2PX^ + (до +л)2 V(Ro +/?)3 ] + (/?0 +/J)2
C/1//4 ЭЗС
0.
dt bL
На участке движения вдоль ограничения будем иметь
dt
ЭК
_ bV
by
е bV '
d^2
dt
bX
b0
Э</>
+ еэё~'
dt
где
bh
by
e
bh
d^
dt
bL
by
е ,
bL
(7.34)
d2g
&К/ЬКэ$ф
by/Ь Кэфф
В частности, при движении
d^* _ рУф* _ Ro
dt~ Рх 4 Rq + />'
КЛА по изовысотному участку получаем
(1Ф1 Rl PV
Ф i 9о
dt
(Яо+Ь)2 2РХ
d^3 _
—
dt 2РХ
VR0
1^ = о.
dt
В момент ti выхода
меняют свою величину:
р V2
(i + Фь ~ту /
(Яо +Л)2
на ограничение сопряженные переменные скачком
(7.35)
+
+
bq
iKfri) - Ф1(п)= ^i”^r +
bq
Фз (f 1) - ’МП) = Mi “Г” +
oh
. bq
bq
М2 ЭЛ '
bL
199
Рис. 7.5. Параметры оптимальной траектории спуска в атмосфере Марса из условии
максимизации продольной дальности спуска при управлении углом крена (Рх =
— 250 кгс/м2, Кбал — ОД 1/0 = 6 км/с, 0О = —20° ).
Сопряженные переменные в конце траектории спуска удовлетворяют
условию трансверсальности [20]. В качестве примера на рис. 7.5 приведе¬
ны параметры оптимальной траектории спуска из условия Z-npmax Для
КЛА, осуществляющих спуск в атмосфере Марса. Видно, что максимальное
значение дальности полета при ограничении на минимально допустимую
высоту полета реализуется при использовании программы двухразового
переключения эффективного качества:
^эфф “ + ^бал / “ ^бал* + ^бал*
Рис. 7.6. Параметры оптимальной траектории спуска в атмосфере Марса из условия
максимизации продольной дальности спуска при управлении углом атаки.
град
м/с
ъ
КМ
Л, V,
км км/с
lAt)y
90
6
6
0,55
90 6
к «ф
h(t)
/hw]
a(t) 1
60
-4
0
-0,05
60 4
50
0
-14
-24
-5
-6
-0,65
-1,25
50 2
0
200
Управление углом атаки. Методика получения оптимальной траектории
спуска, реализующей максимальную дальность полета в атмосфере при
управлении углом атаки с использованием принципа максимума Понтря¬
гина, полностью аналогична рассмотренной выше для КЛА, управляемых
углом крена. Отличие получаемых здесь законов управления обусловлено
различным представлением аэродинамических характеристик КЛА. В част¬
ности, для КЛА типа "несущий корпус", имеющего аэродинамические
характеристики
сх(а) = 0,2+ 2,3 sin2 (1,125а + 5,625°),
суМ = -0,1 + 2,3 sin (1,125 а + 5,625°) cos (1,125а.+ 5,625°),
получим следующий закон оптимального управления [24]:
(7.36)
Параметры траектории спуска КЛА в атмосфере Марса для найденного
оптимального закона управления приведены на рис. 7.6.
7.2.2. Максимизация дальности спуска
с использованием достаточных условий Кротова
Использование необходимых условий оптимальности принципа макси¬
мума Понтрягина позволяет найти траектории, которые могут оказаться
оптимальными. Окончательное решение в том, являются ли эти траекто¬
рии действительно оптимальными, может быть в общем случае принято
лишь после того, как будет проверено выполнение достаточных условий
оптимальности на этих траекториях. Эту проверку можно осуществить,
используя метод Кротова.
Рассмотрим в качестве примера задачу максимизации продольной даль¬
ности спуска КЛА в атмосфере, решенную выше с использованием принци¬
па максимума Понтрягина. Задача решается при следующих исходных
предпосылках. Рассматривается плоское движение КЛА, при этом силы
инерции, связанные с вращением планеты, не учитываются, а ускорение силы
тяжести считается постоянным. Аэродинамические характеристики КЛА
имеют вид
Су = Су ot, сх = cxq +АСу,
где А — постоянный коэффициент.
В этом случае уравнения
следующим образом:
dV
движения КЛА в атмосфере
= -g (X + sin в)
dt
d0
dt
можно записать
cos в
dh
= У sin в,
dt
dL
= I/COS0,
dt
(7.37)
X =
s.
201
Уменьшим размерность задачи, используя переход к новому аргументу
(энергии) :
V2
V Ь‘ (7,38)
Дифференцируя (7.38) по времени г, получаем [24]
dr} _
~T=~VX- (7.39)
Теперь уравнения движения КЛА (7.37) запишутся следующим образом:
пу + [ — il cos в
— = Т= ,
dti у2Х
dh sin 0 dX
dri X ' dr}
cos 0
X
(7.40)
V2 =2g{T)-h).
Управляющим параметром в (7.40) является перегрузка nv, на кото-
рую наложены ограничения у
I пу I Пу max»
< су amaxPV2S
2G
(7.41)
где атах — максимальный допустимый угол атаки.
На концах траектории имеем следующие граничные условия:
У2о У2
т?0 = —+ hQf +
2д
Теорема В.Ф. Кротова, определяющая достаточные условия оптималь¬
ности, заключается в следующем [24].
Пусть имеется пара (У, и) GМ, где фазовые координаты Хи У и управле¬
ние и связаны соотношениями
У = ^(Х, У, у), у е F(X, У).
Для того чтобы функционал управления /(У, у) имел абсолютный мини¬
мум на множестве М, достаточно существования такой функции ^(Х, У),
для которой
R (X, Y, й) = д(Х), X е (Хо, Хх),
Ф(Уо, У1) = 1пТФ(У0, Ух),
Ф = ^(Уо, У1)+^(ХЬ У1)-^(У0/Х0),
где (У, и) — искомая оптимальная траектория.
Функция R записывается следующим образом:
R = ipyf — fQ +<pXf
р(Х)= sup Я(Х, У, у).
Y,u
(7.42)
(7.43)
202
Итак, для определения оптимальной траектории с использованием мето¬
да В.Ф. Кротова необходимо определить такую функцию <р(Х, Y), для ко¬
торой выполнялись условия (7.42) и (7.43) теоремы В.Ф. Кротова.
Можно задать эту функцию, используя функцию Лагранжа, в следую¬
щем виде: 1
(Р (7)z h, 6) = л + 1//0 0 + — О1 (0 — 0 )2 4-
1 - о - -
+— о2 (h — h )2 + oj(h — h ) (0 — 0 ).
2
(7.44)
Тогда функция R запишется следующим образом:
Я =
(7.45)
где
с + ап2у
г V2 1
b = -дфй - 1 cos 0 - V2 sin 0 - cos 0),
Lgftfo +^) J
, _ 1 А - Pv*s
с = V cxoq , а- V _, q -
q 2G
Учитывая (7.40), (7.44) и (7.45), представим уравнения оптимального
движения КЛА в виде [24]
g\nv +Г 11 cos0l
de 1 Lsr(A?o+^) J J
dq ~ V2X
dh sin e dX cos 0 dtye dJC
Рис. 7.7. Параметры оптимальной траектории спуска в атмосфере Марсо из условия
максимизации продольной дальности спуска.
203
d$h _
, ЯК
диг₽
dri
” ~bh~
bh
(/ = 0,
если
ny Ф ;
j = 1, если пу = ПуР),
ЗЦ0, /7, nv, 77) = supjf(0, h, nVt T]).
zz л
Вариационная задача максимизации дальности полета КЛА в атмосфере с
использованием достаточных условий В.Ф. Кротова сводится к двухточеч¬
ной краевой задаче по определению недостающих начальных значений со¬
пряженных переменных и
Описанная в этом параграфе методика решения задачи максимизации
продольной дальности спуска КЛА в атмосфере носит универсальный ха¬
рактер и может быть использована для КЛА, осуществляющих спуск в
атмосферу любой планеты. На рис. 7.7 в качестве примера приведены пара¬
метры оптимальной траектории КЛА, снижающегося в атмосфере Марса.
§ 7.3. Анализ результатов решения задачи
максимизации дальности полета
Численные результаты решения вариационной задачи максимизации даль¬
ности полета КЛА, управляемых креном и осуществляющих спуск в ат¬
мосферах планет, приведены на рис. 7.8—7.14. Для каждой из рассматрива¬
ние. 7.8. Зависимости максимальной дальности полета Lnp в атмосфере Земли отЛя,
ио* * бал и Рх-
204
Рис. 7.9. Зависимости максимальной дальности полета £Пр в атмосфере Венеры от
л/ ^бал и Рх-
емых планет можно проследить частное влияние на величину максимальной
дальности спуска следующих параметров: начальной скорости входа Vo, вы¬
соты условного перицентра приведенной нагрузки на лобовую поверх¬
ность Рх и величины аэродинамического качества /Сбал .
Для определенности рассматривался случай входа КЛА в атмосферу пла¬
нет с траектории прямого перелета.
В качестве номинальных принимались следующие значения варьируемых
параметров:
для Венеры
Vo = 11 км/с, h* = —400 км, /<бал = 0,3, Рх = 500 кгс/м2;
для Земли
Vq = 15 км/с, h* = -200 км, /Сбал = 0/3, Рх = 500 кгс/м2;
для Марса
Vo = 7 км/с, h* = -150 км,
для Юпитера
Vq = 65 км/с, = -12000 км
для Сатурна
Vq = 37 км/с, /7^ = —1400 км,
для Урана
l/J = 28 км/с, = —600 км,
'бал = 0,3, Рх = 350 кгс/м2;
^бал = 0,3, Р* = 300 кгс/м2;
Кбал = 0,3, Р* = 500 кгс/м2;
А^бал =0,3, Рх = 500 кгс/м2;
205
Рис 7.Ю. Зависимости максимальной дальности полета Lnp в атмосфере Марса от
h^c VQ, Кбал и рх-
?ис* 7,12/ Зависимос™ максимальной дальности полета Z_nD в атмосфере Юпитера от
П^. I/- _ Кс LA Р-. Н
Рис. 7.12. Зависимости максимальной дальности полета L пр в атмосфере Сатурна от
^бал и Рх-
для Нептуна
Vq = 27 км/с, h* = —800 км, /('бал = 0,3, Р* = 500 кгс/м2.
Диапазон изменения указанных параметров для различных планет Сол¬
нечной системы составляет:
для Венеры
9 км/с < Уо < 13 км/с, —800 км </7я < -50 км, 0,1 </Сбал 0,45,
100 кгс/м2 <РХ <800 кгс/м2;
для Земли
10 км/с < Уо < 18 км/с, -400 км </?я < 0, 0,1 < /Сбал < 0,5,
50 кгс/м2 <РХ <800 кгс/м2;
для Марса
5,5 км/с < \Z0 < 8,5 км/с, —300 км < hn < 25 км, 0,1 < Кбал < 0,5,
200 кгс/м2 < Рх < 400 кгс/м2;
для Юпитера
57 км/с < < 70 км/с, —3400 км < < 180 км, 0,1 </<бал ^0,6,
207
ЛИСи '1Кк3аиИрИМОСТИ максилальной Дальности полета Lnp в атмосфере Нептуна от
100 кгс/м2 СР.г < 500 кгс/м2;
для Сатурна
35 км/с < Vo < 39 км/с, -3500 км < < 15 км, 0,1 < /Сбал < ОД
200 кгс/м2 <PY <800 кгс/м2;
для Урана
26 км/с < VQ < 32 км/с, —1500 км < < 130 км, 0,1 < /<бал < 0/5,
300 кгс/м2 <РХ < 700 кгс/м2;
для Нептуна
25 км/с< Уо <29 км/с, -1600 км<Рх <20 км, 0,1 </Сбал <0,5,
100 кгс/м2 <PY<800 кгс/м2.
Из анализа представленных данных видно, что характер зависимости
максимальной дальности спуска КЛА от основных варьируемых парамет¬
ров остается неизменным для всех рассматриваемых планет. А именно, уве¬
личение дальности спуска КЛА при оптимальном управлении может быть
достигнуто за счет увеличения скорости входа в атмосферу, высоты услов¬
ного перицентра, приведенной нагрузки на лобовую поверхность и аэроди¬
намического качества.
Отметим, что значения продольной дальности спуска КЛА при оптималь¬
ном управлении существенно отличаются для каждой из рассматриваемых
планет. Так, для КЛА, осуществляющих спуск в атмосфере Сатурна, вели¬
чина /_Пр наибольшая и составляет /_пр~6-^8 тыс. км (см. рис. 7.12),
а для КЛА, снижающихся в атмосфере Венеры, дальность наименьшая и
составляет /_пр — 350 450 км (см. рис. 7.9).
§ 7.4. Приближенно-оптимальное управление
Изучение оптимальных траекторий и исследование эффективности их
использования представляют собой сложную проблему из-за большой
трудоемкости получения семейства экстремалей, соответствующих различ¬
ным значениям условий входа КЛА в атмосферу и его проектно-баллисти¬
ческих характеристик. Решение этой проблемы может быть существенно
облегчено, если использовать приближенно-оптимальные законы управ¬
ления, обеспечивающие незначительные погрешности по величине оптими¬
зирующего функционала. В работах [16, 70, 71] предлагается достаточно
эффективный способ построения приближенно-оптимальных законов
управления, опирающийся на использование общего функционала управле¬
ния (независимо от того, является ли он максимизируемым либо миними¬
зируемым). Приведем некоторые результаты решения задачи максимиза¬
ции продольной дальности полета при использовании указанного способа
получения приближенно-оптимального закона управления КЛА. Предва¬
рительно кратко опишем метод получения таких траекторий [71 ].
Запишем уравнения пространственного движения КЛА в следующем
виде:
dV
de
1
[ °y ,
/ u2>
1 J
— =
pV2 -
£7 sin d?,
=
= —
g0 — pv cosy -
-\g
dt
2
dt
V I
2
\ r i
' J
dh
dl
Яо
(7.46)
— =
V sin0,
— =
V cqsO
dt
dt
r
14. Зак. 2069
209
dt
1 ( °У
Vcos9\° 2
pV2 sin у —
V2 cos 0 tg p cos ??
Ro + h
)■
dp Ucos0sin?7
dt Ro +h
dX Ucos0cos?7
dt (Rq + h)cosp
CXS CyS Rq _Qh
Здесь ox = ; oy = ; g = g0 ~; p = poe pn; rj - угол
G G (Ro+h)2
курса (угол между проекцией вектора скорости на плоскость местного
горизонта и местной параллелью); р, X— широта и долгота; у — угол
крена.
Используя обозначения
_ h
h = —
Ro
. dh - I
h-—=r, I =
dl Ro
Ro VcosO
dl= dt,
R0 + h
допущение
1
Ro + ~ Rq (g » go) и учитывая, что —
cos О
= tg20 + 1, из
системы уравнений (7.46) получаем
Тогда 0 может быть записано в виде
* °У -RR h ffRo
6= gRo ;Рое^ 0 cosy — +1.
2 cos0 V'
Введем в рассмотрение некоторую опорную траекторию Z?* (г), которой
соответствуют фазовые координаты 0*, 0* и управление и*. Уравнение
в вариациях относительно этой опорной траектории принимает вид
- . _ BRoe~PR°h — Aue~PR<>h _
ДА — 20* Д/ид0 + — ' и'М = — , (7.47)
cos 0* cos 0
где
Оу 1 _ gRo
и = 9Ro — Рогозу - В= —Т--1-
2 cos 0 V
Уравнение (7.47) является линейным относительно ДА пописывает ко¬
лебательный процесс, который возникает при воздействии управляющего
параметра Ду.
Предполагая, что колебательный процесс регулируется по закону
Ду= -СДА = — C(tg0 - tg0*),
можно сделать вывод, что независимо от величины у* вариации управле¬
ния Дуопт должно соответствовать оптимальное значение демпфирующе¬
го параметра С°пт. Тогда для КЛА, управляемого углом крена [16],
получаем
cosyonT = cosy* - Сопт CQS<9 - (tg0 - tg0*); (7.48)
_ Po ф
gRo Oy
для КЛА, управляемого изменением характерной площади поверхности
210
S имеем
$опт _ £* £onT
(7.49)
4 cos 0 *
-(tgfl-tgfl*).
gRо PoOy cos у
Выражения (7.48) и (7.49) приближенно могут быть представлены в виде
cosy0"1 = cos?* — ConT(tg0 — tgO*),
(7.50)
(7.51)
2fZ
I/2
S°nT =S* - Сопт (tg0 — tg0*).
cos 7
При управлении углом атаки будем иметь следующее выражение для
приближенно-оптимального закона:
Asin ot ~~ С(tg0 tgflnn) /
где Asin3a = sin3a — sin3a#max-
Таким образом, видно, что процедура поиска приближенно-оптимально¬
го управления сводится к определению оптимальной системы демпфирова¬
ния отклонений высоты полета относительно некоторой заранее заданной
опорной траектории.
Как показали исследования [16], траекторией максимального демпфи¬
рования яляется такая, на которой выполняется условие dti/dt & 0, т.е. так
называемая траектория квазистационарного планирования. Ее целесообраз¬
но использовать в качестве опорной. Большим удобством также является
тот факт, что траектория квазистационарного планирования может быть
выражена аналитически
2д 1
tg0nn(\< w*) = - — — •
/ Оу \ 1/2 2$ Ro
I cos 7 1 V2 + -
\ 0Х / ffR0 - V2
Если в качестве основной регулируемой величины использовать ха¬
рактерную площадь поверхности S, то качественный характер структуры
оптимального закона управления характерной площадью становится опре¬
деленным. А именно, закон оптимального управления имеет релейный
характер и моменты переключения SonT с одного граничного значения на
другое определяются выполнением следующего условия:
о = 0ПЛ.
Численные результаты решения задачи показали, что эффективность
использования приближенно-оптимального закона управления (7.50)
достаточно высока. Так, для рассматриваемого примера точное решение
задачи дает значение функционала Z.Kmax ~ 888,5 км, в то время как при¬
ближенно-оптимальное решение обеспечивает значение функционала
^•ктах ~ 883,5 км [70]. На оптимальной траектории спуска возможны
участки полета с режимами управления, близкими к скользящему. На
этих участках управление КЛА заключается в многократном переключении
величины Sonr с одного граничного значения на другое.
В качестве примера на рис. 7.15 приведены параметры оптимальной
траектории. Видно, что приближенно-оптимальной программой управления
КЛА является программа двухразового переключения SonT на большей
части траектории
SonT _ с о Q
°тах/ °min/ °тах
211
Рис. 7.15. Параметры оптималь¬
ной траектории спуска в атмо¬
сфере Земли из условия макси¬
мизации конечной дальности
полета при использовании при¬
ближенно-оптимального закона
управления характерной пло¬
щадью КЛА.
с последующим переходом
на режим скользящего поле¬
та на некотором интервале в
конце траектории спуска.
После окончания поле¬
та КЛА в скользящем ре¬
жиме |
участок
= 5 min’
следует конечный
полета с SOITT =
Как показано в
работе [70], момент пе¬
реключения SonT с мак¬
симального значения на мини¬
мальное близок к моменту
достижения минимальной вы¬
соты полета,а момент перек¬
лючения cSmjn на Smax — к
моменту достижения максимальной высоты полета КЛА. Поскольку
приближенно-оптимальное управление носит демпфирующий характер,
то максимальные и минимальные колебания высоты в конце траекто¬
рии спуска становятся близки к диапазону высот полета, ограниченному
условием
Рпл($тах> Р Pnn(Smin)*
(7.52)
При попадании траектории спуска в диапазон (7.52) в каждой точке
(р, V} возможен полет КЛА на режиме квазистационарного планирования
при одновременном удовлетворении условия 0 = 0ПЛ. Таким образом,
если при 0 (tf) = 0пл выполняется условие
Рпл. min ($max> < < Рпл. max (^min) *
где
gRQ \ 2cos0
$max gRo
gR0 \ 2cos0
/ ^^.xO ^m in 0^0
то это является признаком, определяющим начало возможного скользяще¬
го режима.
Проведенные исследования показали также, что результаты решения
вариационной задачи о максимизации конечной дальности полета КЛА
могут быть улучшены (т.е. более приближены к оптимальным), если
использовать для определения величины SOITT формулу
5опт s* __ Со пт (sin 0 — eOITTsin 0ПЛ),
где еопт = const — поправочный коэффициент. Так, для рассматриваемого
212
Рис. 7.16. Параметры оптимальной траек¬
тории спуска в атмосфере Земли из
условия максимизации конечной даль¬
ности полета при использовании прибли¬
женно-оптимального закона управления
углом атаки.
примера величина еогтт = 2,2. При
этом максимальная дальность будет
составлять 887,4 км, т.е. всего лишь
на 1,1 км отличаться от оптималь¬
ного (точного) решения.
Приведем численные результаты
решения задачи максимизации про¬
О 3000 0000 L,km
дольной дальности спуска КЛА, управляемого углом атаки а [71]. Пред¬
полагается, что КЛА входит в атмосферу с начальной скоростью =
= 7870 м/с и углом наклона траектории к местному горизонту 0О = —0,18
на начальной высоте /?0=91,5км. Зависимости аэродинамических коэф¬
фициентов от угла атаки имеют вид
сх = 0,042 + 1,461 sin3 а |, су = 1,82sinacosa| sina |.
(7.53)
Нагрузка на характерную площадь поверхности составляет
G/Sb= 133 кгс/м2.
Величина максимального аэродинамического качества достигается при угле
атаки а = 20,5° и составляет /Стах = 2.
Подбор оптимального значения параметра Сопт для приближенно-опти¬
мальной формулы (7.51) проводился с использованием численных расчетов
и дал следующий результат:
Сопт =11.
Параметры приближенно-оптимальной траектории спуска приведены
на рис. 7.16.
Таким образом, приведенная в настоящей главе методика решения
вариационных задач из условия минимизации и максимизации продольной
дальности спуска позволила определить оптимальные законы управления
КЛА как в случае управления углом крена, так и при управлении углом
атаки. Описанная методика носит универсальный характер и может быть
использована для решения задачи максимизации зоны маневра КЛА при
спуске в атмосфере любой планеты Солнечной системы.
§ 7.5. Управление боковой дальностью полета
Максимизация боковой дальности спуска КЛА, управляемых углом
крена. Независимо от того, будем ли мы управлять при полете КЛА в ат¬
мосфере продольной или боковой дальностью, при изменении угла крена
всегда будут иметь место две составляющие подъемной силы: вертикальная
или эффективная Уэфф = ^6anCOS7, и боковая /б = Убал^нТ/ где
рУ2
^бал “ ?у бал $ ~“ •
Нетрудно видеть, что диапазон изменения Уэфф и Yq одинаков, причем
если Уэфф = ^бал = ^тах* то Уб = 0, и наоборот. Важное значение имеет
и тот факт, что при полете в атмосфере подъемная сила Убал всегда отлич¬
213
на от нуля, а ее величина зависит от аэродинамической формы КЛА, выб¬
ранного значения абал и от реализуемого режима снижения, т.е. от величи¬
ны скоростного напора.
При отмеченных условиях определение предельной зоны маневра без уче¬
та ограничений сводится к расчету траекторий снижения при разных углах
крена 7, причем в каждом конкретном случае 7 = const. Величина зоны
маневра зависит от начальных условий и величины располагаемого значения
аэродинамического качества, расширяясь при увеличении скорости входа
Рис. 7.17. Зоны маневра КЛА при оптимальном управлении углом крена для различ¬
ных значений балансировочного угла атаки (Vo = 6 км/с, 279 км, VK = 1/Kmjn).
и величины Красп = ^бал и ПРИ уменьшении по модулю угла входа. Качест¬
венный характер зависимости £б(^-пр) одинаков для спуска в атмосфере
любой планеты назначения.
Для примера на рис. 7.17 представлены зоны маневра КЛА, осущест¬
вляющих спуск в атмосфере Марса. Возможности бокового маневрирова¬
ния, особенно для КЛАл'скользящего" типа, незначительны. Введение раз¬
ного рода ограничений (по величине максимальной перегрузки, конечной
скорости спуска и т.п.) не меняет общей картины, а лишь несколько сокра¬
щает зону маневра.
Отмеченные обстоятельства предопределили тот факт, что на аппаратах
"скользящего" типа ведется управление лишь продольной дальностью
полета с использованием угла крена. Для уменьшения возможного боко¬
вого отклонения траектории спуска осуществляются перевороты КЛА
"с боку на бок" с целью смены знака угла крена и, следовательно, измене¬
ния направления действия боковой составляющей подъемной силы. При
этом следует иметь в виду, что частый переворот КЛА "с боку на бок"
недопустим, так как это приводит к увеличению потребных запасов топли¬
ва на стабилизацию КЛА и, что особенно важно, к "размыканию" управле¬
ния по продольной дальности в момент переворота, ведущему к увеличе¬
нию конечного промаха. Поэтому усилия исследователей направлены
на поиск таких алгоритмов управления, использование которых позволяло
бы парировать боковое отклонение при минимальном числе переворотов.
Максимизация боковой дальности при совместном управлении углами
атаки и крена. При осуществлении бокового маневрирования в атмосфере
в предположении фиксированных начальных условий входа продольная
дальность заведомо уменьшается по сравнению с tnpmax ПРИ прочих рав¬
ных условиях и будет изменяться в диапазоне £пр mjn < £пр ^-пр max-
Нетрудно видеть, что каждому значению £пр из диапазона
[£пр min/ ^-npmaxi соответствует вполне определенное значение Lq и
при некотором /_„р достигается Z-бтах-
В ряде важных случаев возникает необходимость полета с максималь¬
ной боковой дальностью. Если одновременно выдвигается и условие точно¬
го выдерживания Дпр, то возникают противоречивые требования. Дей¬
ствительно, максимальное значение боковой дальности спуска для КЛА
214
с заданными проектно-баллистическими характеристиками может быть
получено при одном определенном значении продольной дальности спуска
(см., например, рис. 7.17) . Тем не менее получить требуемое значение мак¬
симальной боковой дальности спуска можно соответствующей коррекцией
межпланетной траектории или выбором времени включения тормозной
двигательной установки при спуске с орбиты ИСП. С учетом этого замеча¬
ния задачу сформулируем следующим образом. Путем совместного измене¬
ния углов атаки и крена определить управление КЛА, обеспечивающее
достижение Lgmax для каждого значения /_пр из диапазона
[£Пр min/ ^-npmaxJ при заданных начальных условиях и поставленных
ограничениях.
Для решения задачи воспользуемся упрощенными уравнениями прост¬
ранственного движения КЛА
dV cx(a)pV2s
= : д sin в,
dt 2т
de
cy (a)pVs
—
= cos
dt
2m
dh
dL
—
= Vsinfl, =
dt
dt
дcos в V
+ cos
V Ro +/?
de cy(a)pVs sin у
dt 2т cos в
VR0
cosecos0
Ro + h ^6
(Ro +^)cos
Ro
\/cos0cose tg ——
Ro
Rq +h
(7.54)
<УДб VR0
= COS0 sin 6,
dt Rq + h
где e — угол между плоскостью подлетной траектории и текущей пло¬
скостью движения. Гамильтониан и сопряженные переменные на участке
движения внутри допустимой области фазовых координат имеют вид
dV dO dh dL dL6 de
+ 4*2 + 03 +04— + 05~ +|Дб— J
dt dt dt dt dt dt
(7.55)
Vcxps
d^ dJC
dt ~ bV
gcosO
02 — 03 Sin0 —
V2
CypS
2m
*02
dt
CyPScosy
2m
cos e cos 0
cos
*0,
а £б
cos 0 cose tg —
+ -°
Ro +A
£sin0
0!COS0 —
V
Ro
Ro + h
02
COS0
Г ^2 -
Ro
Ro
ф4 05cos0sine —
Rq + h
l/sin0
+ ф2 — l/i^cos# —
Ro + h
m
02 ~
^6,
VRq cosesin 0 VR0
ф4 + d/5 sine sin 0 —
Ro + h ^-6 Ro + h
cos
Ro
215
. L6
vcosetg
Cy,pVs sinyosin0 Rq
— Фб ^6sin0,
CXV2 S Ph cvVscosy
Po№h Ф1 +
2m
2gsin 0
cos20
9J€
2m
4Фз
~dt~
Vcost?
+ J/ 9 Ф . lb 9
(Я0+Л)2 (/?o+ft)3 V(R0+h)3
(7.56)
bh
2ptcos0
Pofie ^нф2
HoVcosflsine cvVs
+ :— Ф5 + ■2—
(Ro + h)2 2m
siny ai.
—- Poe eh(ty6
cost?
2т
V/? 0 cose cos 0
+
Z-б
(RQ+h}2 cos
Ro
Vcos0cose tg——
Ro
(Ro +h)2
+
Фа +
Фб
dJC
=
— =
const.
dt
dL
dJC
VRo
dt
Ro +h
V cost)
cose
+
06,
Lq
Rq(Rq +/))cos
Ro
a . L6
cose coso sin
Ro
2
cos
Ro
dJC
"de
1
—ф4
tt0
+
с1ф6
~dt~
VRo
Rq + h
L6
Ro . .
06 sine.
Rq +h
cos0sin e
cos
Ro
Фа -
Vcos0 tg
VR0
\b s cos 0 cos e —
Ro+h
Представим гамильтониан в виде
pV2s pVscv cvpVs sin у
K= Схфх + 02 COSy +
2m 2m 2m cosO
(7.57)
06 +^3/
где A3 — сумма членов гамильтониана, не зависящих от управления.
Рассмотрим в качестве примера КЛА, аэродинамические характеристики
которого аппроксимируются следующими зависимостями:
сх(а) = 0,2 + 2,3 sin2 (1,125а + 5,625°),
су(а) = -0,1 + 2,3sin (1,125а + 5,625°)cos(1,125а + 5,625°).
Из условия максимума гамильтониана (7.57), учитывая (7.58), получим
закон оптимального управления по углам атаки и крена
а = -5° + 0,89arctg / — +J— ТА
I sin у / sin-y \2 Г
\ ф 2 cos у + ~ Фь H/2cosy+ фА ) /
4 COS0 \ cost? 6/ /
(7.59)
(7.60)
(7.58)
Фб
у = arctg
ф2 cos 6
216
При введении разного рода ограничений, например по высоте полета,
сопряженные переменные в точке ti скачком меняют величину:
ФР Ui) - ’/'i(ti)
) - ^2 (fl )
^5Р(Г1) - Ф4 Ui)
Э<7
bq r.
= Ml- + Pi
— =0,
bV
bV
bq
bq
= Mi
— + М2
— = М2
b0
be
bq
bq
= Mi
— + М2
— = Mb
bh
bh
bq
bq
= Mi
~ + М2
— =0,
bL
bL
bq
bq
= Mi
+ М2
— = 0,
Э/-6
dZ_6
Эд
bq
:Mi
— + М2
— =0,
be
be
где ац и ц2 = const, ад — функция, ограничивающая допустимую область
фазовых координат.
Законы управления по а и 7 при движении КЛА по изовысоте записы¬
ваются в виде
7
гр
= arctg
ФГ6Р
ф 2Р COS 0
(7.61)
агр = —5° + 0,44arcsin
т
1,74
р Vs
V \ 1
™ + 0,087
Ro+hl фг6р
arct9 —J
Фгр
(7.62)
Уравнения сопряженных переменных с учетом (7.61) и
h = hrp имеют вид
(7.62)
при
Vps г . 1 (д V
i//ip[0,2 + 2,3sin2 (0.5S2!)] фТ2р I-
т V \V R0+h
cose
До
Ro + h
R
ф\р — 1Д5Psin e —
/?0 +
cos e tg
^iptg £2 я +
217
dф¥ rn r« PVs
= di//ip -1/ф3р+ ^iptgi2i [0,2 + 2,3 sin2 (0,5121) ] -
dt 2m
p Vs r
- [03+2,3sin2 (0,5S2i) ] ф$р -
2m
p Vs \bf.p
- [Q3 + 23sin2 (ОЗЯЛ 06P-4-,
2m фг2р
dф\p V2s ig V \
= -[03 + 2,3sin2 (0,5 S21) ] pP Ф\р + I ) P Фгр +
2m \|/ R0 + hj
Ф5р + -^Ц^р-^ +
(Яо+Л)2 £б
cos
*O
У cos е tg
/?о
—^ер +
(Я0 + Л)2
dt
V „„ 2д
+ Г Ф2Р Z
(R0+h)2 V(R0+h)3
V \ Фт6р
+ 7^F^sine4v-^)7Tp^r6P-
+ (— - ^ptg£21-(- —\Рф'р_
\IZ R0+h) R0+h)
2Д „„ 2д ф£р
т Ф ip tg £2! + +
(Я0 + Л)3 (Яо + Л)3 V
V — Z 9 V \ O^P / rp
V R0+hl p 6
*6P Ф? V ,rp W ,rp
——Г7Т Т7Г' = const’
(Я0+Л)2 ф2р
L5
sin
R° »?<■ Vc°se
^^0 (ГО ■ /
-*spsine+^— -
(Яо+Ь)2^2 ('
2д
(Яо+Л)3 V фт2р
VR0
cos e
dt
Ro+h
2^-6
Я cos2
Ro
d ФбР
VR0 sine
, ГР VH>
dt
о
Rq + Ь
где
Ro + h Lq
cos
Ro
cose
(7.63)
-0г6р,
/?0+Л Lq
R cos
Ro
[Lq\
\Zsine tgl I
Ф$Р O XA •— ^₽'
n о • л
= arcsin
m / g
1,74 —
pVs \U
R0+h I
1
+ 0,087
ФТ6Р
Рис. 7.18. Зависимость управляющих параметров а и у, аэродинамического качест¬
ва К, высоты полета h и скоростного напора q от времени спуска t (Lq = L gmax)-
Из условия трансверсальности в конце траектории спуска (в точке
схода с ограничения) получим 05к = 1, ф6к = 0.
Остальные сопряженные переменные не определены.
Таким образом, поставленная задача сводится к четырехпараметри¬
ческой краевой задаче для систем дифференциальных уравнений (7.54),
(7.56) и (7.63) .
В качестве примера на рис. 7.18 представлен характер изменения управ¬
ляющих параметров, а также высоты полета и скоростного напора для
КЛА, осуществляющего полет на максимальную боковую дальность (Z.R =
= 2350 км) при спуске сорбиты ИСЗ (0О = — 0,9°, Уо ^7,57 км/с) . На
рис. 7.19 показаны зоны маневра при оптимальном управлении (из усло¬
вия Lq- L б max) углами атаки и крена для КЛА типов "несущий корпус"
и "космический самолет", осуществляющих спуск в атмосфере Марса.
Рис. 7.19. Зоны маневра при оптимальном управлении (из условия Lq = L^grnax)
углами атаки и крена для КЛА типа "несущий корпус" (7) и "космический само¬
лет" (2) , осуществляющих спуск в атмосфере Марса (1/0 = 6 км/с, = —79 км) .
РАЗДЕЛ III
ВЫВЕДЕНИЕ КОСМИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА
НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ
С ИСПОЛЬЗОВАНИЕМ АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ
Глава 8
СИНТЕЗ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
ПРИ КОМБИНИРОВАННОМ СПОСОБЕ ВЫВЕДЕНИЯ НА ОРБИТУ
§ 8.1. Обсуждение проблемы
Применение искусственных спутников позволяет эффективно решать
широкий круг задач по изучению планет. К числу исследуемых вопросов
в первую очередь относятся: картографирование поверхности; определение
параметров атмосферы и фигуры планет; изучение магнитного поля, ра¬
диационных поясов, магнитосферы, ионосферы, инфракрасного излуче¬
ния, взаимодействия солнечного ветра с ионосферой и атмосферой. При¬
менение радиолокационных приборов на борту КЛА создает возможность
для изучения рельефа поверхности в том случае, если планета окружена
плотным слоем облаков. Использование приборов, устанавливаемых на
борту спутников, позволяет исследовать целый ряд явлений, не получив¬
ших до настоящего времени объяснения (сезонные волны потемнения по¬
верхности Марса, изменение скорости вращения атмосферы Юпитера с
широтой, радиоизлучение Юпитера в дециметровом диапазоне и др.) .
Летательный аппарат, находящийся на орбите искусственного спутника
планеты (ИСП), может быть использован как ретранслятор для передачи
на наземные станции научной информации, поступающей с КЛА, совер¬
шившего посадку на поверхность планеты.
Выведение КЛА на орбиту ИСП в ряде случаев может быть одним из
этапов решения сложной технической проблемы — посадки КЛА на по¬
верхность планеты. Действительно, помимо схемы посадки непосред¬
ственно с подлетной траектории может быть совершена посадка ЛА на
поверхность планеты с использованием орбитально-десантной схемы (та¬
ким образом была организована посадка КЛА "Викинг" на поверхность
Марса) . В этом случае КЛА первоначально выводится на орбиту ИСП
с использованием тормозной двигательной установки или с использова¬
нием комбинированного маневра, включающего предварительное аэро¬
динамическое торможение в атмосфере и доразгон с помощью двигатель¬
ной установки для выхода на орбиту. Затем весь КЛА или его часть (спу¬
скаемый аппарат) совершает спуск с орбиты на поверхность планеты.
Описанный маневр имеет и самостоятельное значение, если конечной целью
является только выведение КЛА на орбиту ИСП (без последующего спус¬
ка на поверхность) .
Следует отметить, что в настоящее время все большее распространение
получает идея использования так называемых аэростатно-спутниковых
систем для изучения параметров атмосферы планет. КЛА, находящийся на
орбите ИСП, содержит в состыкованном состоянии один или несколько СА,
каждый из которых, в свою очередь, может иметь на борту несколько аэро¬
статных зондов. По мере необходимости осуществляется отделение очеред¬
ного СА от орбитального аппарата и вход его в плотные слои атмосферы.
220
По мере гашения скорости спуска производится последовательный сброс
аэростатных зондов, их наполнение легким газом и выход на заданную
высоту дрейфа. В гондоле аэростатного зонда помещаются научные прибо¬
ры, предназначенные для измерения параметров атмосферы планеты на
различных высотах.
При использовании аэростатно-спутниковых систем зондирования атмос¬
феры существенно возрастает роль КЛА, выводимых на орбиту ИСП. С
помощью этих орбитальных КЛА решаются задачи дистанционного зондиро¬
вания атмосферы, ретрансляции полученных данных научных измерений
на Землю, прием и обработка информации с приборов, установленных на
аэростатных зондах, навигация аэростатных зондов (определение коорди¬
нат и скорости перемещения) и т.д.
Разделение процесса посадки на два этапа — выведение на орбиту ИСП
и спуск с орбиты — позволяет решать ряд смежных задач. В первую оче¬
редь следует отметить, что при полетах КЛА к планетам Солнечной системы
посадка КЛА с экипажем на поверхность может быть не обязательной,
а в ряде случаев даже недопустима в силу существующих условий на пла¬
нете. В этом случае может быть использовано только выведение КЛА
на планетоцентрическую орбиту. При этом кинетическая энергия КЛА
рассеивается не полностью, и энергетические затраты, потребные для обрат¬
ного перелета, будут меньше, чем в случае посадки на поверхность.
Во-вторых, при полете КЛА к планетам (а также при возвращении на
Землю) разделение посадки на два этапа позволяет расширить диапазон
параметров траекторий сближения при посадке в заданный район, что в
свою очередь позволяет облегчить проблему точной посадки в заданный
район поверхности планеты.
При полярной ориентации орбиты достижимым является любой район
поверхности планеты. Поскольку орбита искусственного спутника пла¬
неты может быть определена с достаточно высокой точностью, то точность
посадки будет существенно выше в случае двухэтапной посадки, чем при
спуске КЛА с траектории прямого перелета.
Отметим также следующее. Наличие вблизи Земли и некоторых других
планет поясов повышенной радиации делает наиболее безопасным для
человека проникновение в околопланетное пространство со стороны
полюсов.
При осуществлении прямой посадки на территорию СССР необходи¬
мым оказывается "южное" сближение. При этом наблюдение за КЛА
со станций, расположенных в северном полушарии, прекращается задолго
до входа КЛА в атмосферу. Это вызывает уменьшение точности коррекции
траектории сближения.
При использовании схемы спуска, предусматривающей выведение КЛА
на промежуточную орбиту, допустимо "северное" сближение КЛА с Зем¬
лей, что повышает точность коррекции. Кроме того, важным является
то, что при прямой посадке требуется корректировать кроме высоты
условного перицентра подлетной траектории еще и геоцентрические ко¬
ординаты перигея и наклонение плоскости орбиты, а при выведении КЛА
на орбиту ИСП достаточно в большинстве случаев корректировать лишь
один параметр — высоту условного перицентра.
Таким образом, различие между двумя схемами посадки сводится
в основном к тому, что в одном случае задачи о "динамической" точности
полета в атмосфере и "географической" точности места посадки решаются
одновременно, а в другом случае — последовательно.
Различие также есть и с конструктивной точки зрения. При переходе
на промежуточную орбиту необходимо использовать реактивные двигатели,
221
т.е. КЛА должен иметь двигательную установку с необходимым запасом
топлива, в то время как при прямой посадке осуществляется лишь пассив¬
ное торможение в атмосфере.
Кроме отмеченных различий и особенностей существует и ряд других,
о которых будет сказано ниже.
Способы перевода КЛА на орбиты ИСП. Можно выделить три возмож¬
ных способа перевода КЛА на орбиту ИСП:
с помощью двигателя большой тяги;
с применением двигателя малой тяги;
с использованием предварительного аэродинамического торможения
КЛА атмосферой планеты и последующим формированием требуемой
орбиты ИСП активным путем.
Для анализа возможностей реализации каждого из этих способов не¬
обходимо установить потребные затраты характеристической скорости.
Опишем кратко перечисленные способы переведения КЛА на орбиту ИСП
и сравним их по затратам характеристической скорости.
Предположим, что орбита спутника задана радиусами перицентра г и
апоцентра г а. Величина импульса характеристической скорости Д1/хар
при одноимпульсном переходе КЛА с гиперболической траектории на
требуемую орбиту определяется выражением [101]
Видно, что потребны^ импульс Д 1/хар уменьшается с ростом га, т.е.
переведение КЛА на более вытянутые орбиты при заданной высоте пери¬
центра приводит к уменьшению затрат характеристической скорости.
Численные расчеты показывают, что при переведении КЛА на низкие кру¬
говые орбиты потребный импульс ДУхар может достигать значительных
величин. Так, при переведении КЛА с траектории прямого гиперболи¬
ческого перелета на круговые орбиты искусственных спутников Марса
и Венеры с высотой h = 500 км и Юпитера с высотой h = 7000 км потреб¬
ная величина импульса характеристической скорости тормозного импульса
Д 1/хар составляет для Марса 2—4,5 км/с, для Венеры 3,4—5 км/с, для Юпи¬
тера около 17 км/с. Учитывая, что у двигателей большой тяги удельная
тяга ограничена, для реализации потребных значений характеристической
скорости при переводе КЛА на низкие орбиты нужны значительные затраты
топлива. В частности, расчеты показывают, что уменьшение скорости полета
КЛА (с начальной массой 5—8 т, осуществляющих выведение на орбиту
искусственного спутника Марса) на каждые 100 м/с требует примерно
150—200 кг дополнительной массы КЛА (массы топлива и конструктив¬
ных элементов двигательной установки) . Уменьшить эти затраты можно,
применив другие способы перехода КЛА на орбиту ИСП.
Двигатели малой тяги, как известно, имеют более высокие значения
удельного импульса. Однако недостатком этого способа является слишком
большое время перехода, что приводит к необходимости предварительного
торможения КЛА двигателем большой тяги.
Способ перевода КЛА на орбиту ИСП, предусматривающий аэродина¬
мическое торможение в атмосфере планеты, заключается в таком выборе
высоты условного перицентра подлетной траектории и такого закона
управления движения в атмосфере, чтобы КЛА после входа в атмосферу
тормозился до необходимой величины скорости, а затем вылетал из ат-
мдсферы. Для предотвращения повторного входа КЛА в атмосферу сле¬
дует прикладывать импульс скорости, повышающий перицентр орбиты.
222
Рис. 8.1. Основные этапы выведения КЛА на
орбиту искусственного спутника планеты с
предварительным аэродинамическим тормо¬
жением.
Условная граница атмосферы
Конечная орвита вывевания КЛА
В том случае, когда допускается нес¬
колько погружений КЛА в атмосферу,
необходимо производить включение
тяги двигательной установки для уп¬
равления высотой перицентра при сле¬
дующих за первым погружениях в ат¬
мосферу.
На рис. 8.1 представлены основ¬
ные этапы схемы выведения КЛА на
орбиту ИСП с предварительным аэро¬
динамическим торможением. Ле¬
тательный аппарат входит в плотные
ростью Уо под углом 0О- После аэродинамического торможения (учас¬
ток 7—2) он вылетает из плотных слоев атмосферы и осуществляет дви¬
жение по переходному эллипсу с высотой апоцентра h а t и высотой пери¬
центра Понятно, что должно быть меньше высоты условной
границы атмосферы (h nl < h а) .
Очевидно, что выведение КЛА на орбиту ИСП с предварительным аэро¬
динамическим торможением в атмосфере во многих случаях должно при¬
вести к существенному энергетическому выигрышу. Однако для форми¬
рования орбиты ИСП указанным способом приходится решать ряд новых
сложных технических задач, из которых в первую очередь можно указать
слои атмосферы (точка 7) со ско-
следующие.
1. Обеспечение высокой точности навигации на подлетном участке с
целью организации точного входа КЛА в требуемый коридор по высоте
условного перицентра (поскольку даже при использовании управляемого
движения в атмосфере ширина коридора входа КЛА в атмосферу планет
мала) .
2. Создание КЛА, который должен функционировать в течение длитель¬
ного времени после прохождения плотных слоев атмосферы. Это требует
обеспечения надежной теплозащиты, соответствующего выбора проектно¬
баллистических характеристик КЛА и его компоновки.
3. Разработка совершенной системы управления КЛА, которая должна
функционировать на участках подлета к планете, прохождения плотных
слоев атмосферы и на внеатмосферном участке с целью формирования
орбиты ИСП. Такая система должна быть полностью автономной и быть
комбинированной, т.е. способной функционировать как на участке, где
в качестве основной управляющей силы используется аэродинамическая
сила, так и на участке ра кето динамического маневра, где в качестве ак¬
тивной управляющей силы используется тяга двигательной установки.
Отмеченные трудности могут быть преодолены, если использовать
для перевода. КЛА на низкую орбиту ИСП комбинацию двух описанных
способов [120]. В этом случае осуществляется предварительный ракето¬
динамический перевод КЛА на эллиптическую орбиту с большим эксцент¬
риситетом и перицентром, расположенным несколько выше уровня ат¬
мосферы. В дальнейшем КЛА осуществляет несколько последователь¬
ных погружений в атмосферу в районе перицентра с использованием им¬
пульсов тяги двигательной установки, выдаваемых на внеатмосферном
Участке полета.
Этот процесс продолжается до тех пор, пока высота апоцентра оску-
лирующей орбиты не достигнет заданной величины. После этого с исполь¬
зованием тяги двигательной установки осуществляется подъем пери¬
центра орбиты на высоту, обеспечивающую заданное время существо¬
вания искусственного спутника планеты.
Отметим, что в общем случае целесообразность использования маневра
перевода КЛА на орбиту ИСП определяется с учетом многих факторов,
в частности с учетом того, что выведение на орбиту спутника планеты явля¬
ется одним из многочисленных маневров КЛА, совершающего перелет.
Однако постановка изолированной задачи исследования свойств воз¬
можных траекторий выведения на орбиту ИСП на участке аэродинами¬
ческого торможения позволяет наиболее просто получить практически
важные количественные результаты.
В литературе многократно рассматривались различные аспекты про¬
блемы выведения на орбиту ИСП с использованием предварительного
аэродинамического торможения, однако число работ, обобщающих эту
проблему для случая выведения КЛА на орбиту любой планеты Солнеч¬
ной системы, незначительно.
Настоящий раздел посвящен изучению основных особенностей решения
задачи о выведении КЛА на орбиты планет и обобщению полученных ре¬
зультатов для всех планет Солнечной системы, окруженных атмосферой.
S 8.2. Постановка задачи
Общая схема маневра перевода КЛА с траектории межпланетного пере¬
лета на орбиту искусственного спутника планеты с использованием пред¬
варительного аэродинамического торможения в атмосфере представлена
на рис. 8.2. Задача маневра заключается в переводе КЛА из начального
положения S] в заданное конечное положение s2 с минимальными затра¬
тами топлива.
Пусть для чисто реактивного маневра, проводимого целиком вне атмо¬
сферы, оптимальной является траектория С, а расход топлива на прове¬
дение этого маневра составляет величину/(С). А для комбинированного
маневра оптимальной является траектория Ci + С * + С2, где Ci и С2 —
участки реактивного маневра, а С* — участок траектории, проходящий
в атмосфере планеты. Пусть при этом /(CJ и /(С2) суть величины затрат
топлива на траекториях Сх и С2. На участке аэродинамического тормо¬
жения С* затраты топлива принимаются нулевыми. Тогда условие опти¬
мальности комбинированного маневра запишется следующим образом:
/(CJ + /(С2) < /(С)
Для оптимизации затрат топлива при комбинированном маневре не¬
обходимо использовать теорию оптимальных аэродинамических маневров.
Рис. 8.2. Общая схема маневра перевода
КЛА с траектории межпланетного перелета
на орбиту искусственного спутник?
планеты.
224
Ниже приводятся результаты исследования оптимальных траекторий дви¬
жения КЛА в атмосферах планет.
Прежде чем исследовать проблему оптимизации комбинированного
маневра выведения КЛА на орбиту ИСП, приведем краткое изложение
основных исходных предпосылок и ограничений на параметры траектории
движения КЛА в атмосфере.
Критерии выбора орбиты спутников планет. Выбор орбиты спутника
планеты определяется двумя основными факторами: научными задачами,
которые решаются с помощью ИСП и возможностями космической тех¬
ники.
С точки зрения научных исследований планет и окружающего их про¬
странства наиболее удобными являются низкие круговые или низкие
эллиптические орбиты (картографирование поверхности планеты, изуче¬
ние химического состава и свойств ее атмосферы, исследование грави¬
тационного поля и т.д). и высокие эллиптические (изучение магнитосфе¬
ры, ионосферы, радиационных поясов планеты, ее естественных спутни¬
ков и т.д.) .
С точки зрения возможностей космической техники вубор потребной
орбиты ИСП определяется на основе анализа энергетических затрат, по¬
требных для выхода на орбиту ИСП, оценки затрат для обеспечения спус¬
ка КЛА на поверхность и при необходимости возвращения взлетной сту¬
пени на орбиту ожидания, простоты и точности выполнения космических
операций, разрешающей способности аппаратуры, возможности радио¬
связи с Землей, времени существования КЛА на орбите ИСП, районов
посадки на поверхности планеты и т.д.
Движение КЛА по орбите ИСП зависит от ее параметров - высоты
апоцентра h а и перицентра Как известно, энергетически оптималь¬
ная орбита ИСП должна иметь минимально допустимую высоту пери¬
центра h я и максимально допустимую высоту апоцентра h а (под энерге¬
тически оптимальной понимается такая орбита, для формирования ко¬
торой требуются минимальные энергетические затраты при переходе с
подлетной гиперболической траектории на требуемую эллиптическую
орбиту ИСП). Высота перицентра h п определяется из условия потреб¬
ного времени существования КЛА на орбите ИСП и точности наведения
на межпланетной траектории. Максимально допустимая высота апоцентра
ha при заданной высоте перицентра может определяться из потребного
периода Т обращения КЛА по орбите спутника планеты. При выборе ве¬
личины Т, кратной периоду обращения планеты, КЛА будет перемещаться
над одними и теми же районами поверхности планеты, что может проти¬
воречить требованиям картографирования планеты. Выбор периода /,
кратного земным суткам, обеспечивает сеансы связи с КЛА в одно и то же
время. Из этого условия обычно и выбирают высоту апоцентра орбиты
ИСП.
Существенным достоинством орбит с большим эксцентриситетом яв¬
ляется сравнительная малость энергетических затрат на их формирование
при использовании ракетодинамического маневра. При переводе КЛА
на низкую круговую (или низкую эллиптическую) орбиту также активным
путем энергетические затраты существенно возрастают. Однако такие
орбиты имеют ряд очень важных достоинств. В частности, они значительно
упрощают операцию спуска КЛА на поверхность планеты и возвращение
на орбиту ИСП. При формировании таких орбит наиболее полно проявля¬
ются достоинства метода выведения с предварительным аэродинамическим
торможением в атмосфере.
15. Зак. 2069
225
Учитывая изложенное, будем проводить исследование траекторий выве
дения КЛА на следующие орбиты ИСП:
низкие круговые с /?кр = 500-М ООО км для планет земной группы и
с /?кр = 1000^5000 км для планет-гигантов;
низкие эллиптические орбиты с h л = 500-^1000 км и Rq < h а < 5/?0,
высокие эллиптические орбиты с > 5/?0 и с 5О/?о < 120Rq.
Аэродинамические характеристики КЛА, выводимого на орбиту ИСП.
Будем рассматривать два основных режима движения КЛА в атмосфере
[101,120] :
перевод на орбиту ИСП с траектории гиперболического перелета с ис¬
пользованием однократного погружения в атмосферу планеты;
перевод на низкую орбиту ИСП с вытянутой эллиптической орби¬
ты с использованием многократных касаний атмосферы в районе пери¬
центра.
Как известно, в общем случае аэродинамические коэффициенты зави¬
сят от формы КЛА, числа Рейнольдса и числа Маха. При переводе КЛА
с траектории гиперболического перелета на орбиту ИСП скорость полета
его в атмосфере соответствует числам Маха, значительно превышающим
величину М = 3-М, начиная с которой аэродинамические характеристики
ЛА практически не зависят как от числа Маха, так и от числа Рейнольдса,
если его величина больше 1000 [24]. Однако исследования показывают,
что на траектории выведения возможно наличие участков полета, на ко¬
торых сказывается зависимость аэродинамических коэффициентов от
числа Re. Эти участки соответствуют большим высотам .полета, т.е. мо¬
ментам входа КЛА в атмосферу и выхода из нее.
При выведении на орбиту ИСП могут быть использованы КЛА различ¬
ной конфигурации (см. главу 2); сегментно-конической формы ("Союз",
"Аполлон") или имеющие форму затупленного конуса ("Марс-1"). Как
уже отмечалось, аэродинамическое качество таких КЛА не превышает
величины /Сбал % 0J5. Могут быть также использованы и перспективные
КЛА с большим значением аэродинамического качества. При этом следует
отметить, что массы конструкции и теплозащитного покрытия пропор¬
циональны площади поверхности КЛА, которая возрастает с увеличением
аэродинамического качества, а так называемая объемная эффективность
формы КЛА (отношение объема в степени 2/3 к площади поверхности)
с ростом качества уменьшается от 0,2 для сферы (К = 0) до 0,1 для КЛА
с величиной /Стах = 1,5 и до 0,05 для КЛА с величиной ^тах=3. Учитывая
изложенное, в настоящей главе при анализе траекторий выведения на ор¬
биту ИСП диапазон возможных значений аэродинамического качества
ограничивается величиной /Стах = 2,5. Способ перевода КЛА на низкую
орбиту ИСП, использующий многократное погружение в атмосферу, наи¬
более целесообразно применять в том случае, когда газодинамический
нагрев поверхности КЛА достаточно мал, так что необходимость в созда¬
нии специального КЛА, обладающего системой теплозащиты, отсутствует.
При реализации такого способа торможения КЛА происходит в разрежен¬
ных слоях атмосферы, так что число Re при минимальных высотах поле¬
та меньше 1000. В этом случае с увеличением высоты полета и соответ¬
ствующим ему снижением числа Re коэффициент аэродинамического
сопротивления растет и может быть определен в соответствии с выраже¬
нием [23]
c.v = <\о[1 + cYe-151°6^~<1+Fx)],
где R - характерный размер тела, см; рж - плотность газа в невозму¬
щенном потоке, г/см3; Ех — коэффициент, характеризующий форму
Рис. 8.3. Зависимость коэффициента ло¬
бового сопротивления сх от числа Re
для сферы.
тела (для сферы Ех = 0); сх0 —
коэффициент аэродинамического
сопротивления в сплошном потоке.
В качестве примера на рис. 8.3
приведена зависимость коэффици¬
ента сопротивления от числа Re для
сферы. Видно, что с уменьшением
числа Re от 1000 до 1 коэффициент
лобового сопротивления ^ возрас¬
тает почти в два раза.
При движении КЛА на больших высотах вследствие разреженности
атмосферы происходит изменение его аэродинамических характеристик
по сравнению с их значениями при движении в плотной среде. Будем пред¬
полагать, что поляра КЛА описывается параболой вида
Сх = с*х0 + А*с fa2.
Для учета эффекта разрежения потока на большой высоте полета могут
быть использованы следующие зависимости:
Схо= сх0[1 + 1,8 • 10”3 (ДА )2], А* = А [1 + 6,14 • 1СГ4 (ДА )1,s],
d* = d[1 +23 Ю_6 (ДА)3].
Здесь ДЛ — величина отклонения высоты полета от некоторого расчет¬
ного номинального значения, а коэффициенты cxQ, And соответствуют
поляре КЛА при его движении в плотной среде. Хотя с увеличением высоты
полета происходит возрастание коэффициентов с* и су, однако их изме¬
нение таково, что в целом величина /Стах заметно уменьшается с ростом
высоты h . Так, если в диапазоне высот 0 < h <50 км аэродинамическое
качество /Стах практически остается неизменным и равным трем, то при
увеличении h > 50 км аэродинамическое качество уменьшается, и
^тах = 1 3 на высоте около 90 км для КЛА, осуществляющего движение
в атмосфере Земли. Учитывая, что выведение КЛА на орбиту ИСП про¬
исходит, как правило, при прохождении плотных слоев атмосферы на
высоте h > 40-^50 км, фактор зависимости аэродинамических коэффи¬
циентов от высоты полета может оказать значительное влияние на тра¬
екторию полета и его необходимо принимать во внимание. Это замеча¬
ние распространяется на все планеты, имеющие атмосферу.
Ограничения на параметры траектории и ширину коридора входа. Под
шириной коридора входа для КЛА, выводимого на орбиту ИСП, понима¬
ется разность высот условного перицентра, при входе с которыми в ат¬
мосферу планеты при заданных ограничениях на фазовые координаты
и на управление обеспечивается попадание в заданную область фазовых
координат после выхода из атмосферы.
Общим требованием для любых способов проведения маневра выве¬
дения КЛА на орбиту ИСП является достижение заданной высоты апо¬
центра после пролета им атмосферы планеты.
В общем случае на траекторию движения в атмосфере могут накла¬
дываться те же ограничения, что и для КЛА, осуществляющего посадку
на поверхность планеты (см. главу 2) . Если КЛА пилотируемый, то обя¬
зательным является ограничение на величину максимальной перегрузки.
227
Как уже отмечалось, величина максимальной переносимой человеком
перегрузки зависит от времени и направления ее действия. При этом за¬
метное влияние оказывает и время пребывания космонавта в невесо¬
мости до момента входа КЛА в атмосферу планеты. Обычно при оценках
ширины коридора входа рассматривают как максимально допустимые
значения перегрузок, лежащие в интервале от 5 до 10 единиц.
Более высокий уровень перегрузок допустим при выведении на ор¬
биту ИСП беспилотного КЛА. В настоящее время успешно функциони¬
руют КЛА, конструкции которых рассчитаны на величину максималь¬
ной допустимой перегрузки nmax = 200-^250. Учитывая, что у КЛА, кон¬
струкция которых рассчитана на выдерживание больших перегрузок,
существенно возрастает масса конструкции, можно отметить, что и для
беспилотных КЛА уровень максимальной перегрузки может быть су¬
щественным ограничивающим фактором. Однако траектории выведения
КЛА на орбиту ИСП являются более пологими, чем для КЛА, осуществляю¬
щих посадку на поверхность планеты. Как следствие этого, траектории
выведения характеризуются меньшими значениями максимальной пере¬
грузки. Соответственно уменьшается роль этого фактора (по сравнению
со спускаемыми аппаратами) при оценке ширины коридора входа для
КЛА, выводимых на орбиты ИСП. С другой стороны, несколько возрастает
роль ограничения по максимальным тепловым потокам, а также по сум¬
марному подводу тепла в процессе торможения в атмосфере.
В числе возможных ограничений, существенно влияющих на ширину
коридора входа, следует учитывать ограничение на величину импульса
скорости, потребного для поднятия перицентра орбиты за пределы ат¬
мосферы. Величина разгонного импульса определяется параметрами орбиты
после прохождения КЛА атмосферы. В том случае, когда радиус пери¬
центра этой орбиты мал, потребная величина разгонного импульса в пе¬
ресчете на скорость может оказаться даже больше, чем при ракетодина¬
мическом способе перевода КЛА на орбиту ИСП. Величина потребного
импульса определяет нижнюю границу допустимых значений высоты услов¬
ного перицентра траекторий входа, т.е. нижнюю границу коридора входа.
Если после вылета из атмосферы КЛА обладает энергией, превышающей
заданную, и для ее уменьшения необходимо использовать ракето¬
динамический маневр, то величина располагаемой характеристичес¬
кой скорости может определять также и верхнюю границу коридо¬
ра входа.
Существенное влияние на ширину коридора входа оказывает ограниче¬
ние сверху на допустимые апоцентрические расстояния после выхода
КЛА из атмосферы. Высота апоцентра переходной орбиты определяется
требуемыми параметрами формируемой орбиты ИСП.
Анализ внеатмосферного участка траектории перехода КЛА на орбиту
спутника планеты. Будем предполагать, что КЛА после торможения в
атмосфере вышел на некоторую орбиту с перицентром, лежащим ниже
границы плотных слоев атмосферы. Требуется определить такую траек¬
торию перехода на заданную орбиту, чтобы сумма импульсов характеристи¬
ческой скорости была минимальной. Траектория перехода определяется
классом исходных орбит [42], ограниченного начальной орбитой Ро и
конечной (заданной) орбитой Рк, на которую нужно перейти за счет им¬
пульсов скорости, сообщаемых двигателем. Начальная орбита Ро может
лежать целиком внутри заданной орбиты либо пересекать ее. В том случае,
когда начальная орбита Ро пересекает заданную орбиту Рк,оптимальным
переходом является, как показано в [42, 111 ], двухимпульсный переход.
Первый импульс сообщается в апоцентре орбиты PQ, второй — в перицентре
228
орбиты Рк. Среди всех возможных орбит Ро с одним и тем же гaQ, на
которые КЛА переходит в результате торможения в атмосфере, оптималь¬
ная орбита имеет гя0 = Gromax- Это объясняется тем, что первый импульс
минимален при гп0 = тах, а второй при фиксированном г а от г я0 не
зависит.
Если начальная орбита лежит внутри заданной (ra0 < г ак). ™ опти¬
мальным переходом является двухимпульсный или трехимпульсный пере¬
ход. Для двухимпульсного перехода первый импульс подается в точке
пересечения начальной орбиты Ро с условной окружностью, ограничиваю¬
щей атмосферу планеты, а второй — в апоцентре орбиты Рк, с которым
совпадает апоцентр переходной орбиты. Для трехимпульсного перехода
первый импульс подается в той же точке, второй - в апоцентре получен¬
ной орбиты и третий — в перицентре орбиты гяк. Величина третьего им¬
пульса не зависит от параметров начальной орбиты. Доказательство того,
что сумма первых двух импульсов уменьшается с ростом высоты пери¬
центра орбиты Pq (при фиксированной высоте апоцентра), приведено в
ряде работ [43,101,111,120].
В некоторых случаях число допустимых включений тяги двигательной
установки может быть ограничено. В частности, может быть поставлено
требование, чтобы после прохождения плотных слоев атмосферы КЛА
переводился на заданную орбиту одним импульсом. В этом случае для
получения минимальных затрат импульса характеристической скорости
движение КЛА в атмосфере должно быть организовано так, чтобы
raQ = гак. Таким образом, при подаче импульса скорости в апоцентре
орбиты мы имеем вырожденный случай двухимпульсного перехода и,
следовательно, реализуется минимальное значение ДУхар. Рассмотрим
этот случай подробнее.
Определение потребных энергетических затрат на внеатмосферном
участке при одноимпульсном переходе. Предположим, что орбита, реа¬
лизовавшаяся после выхода ЛА из атмосферы, задана (т.е. параметры
ук, 0К, = /?а - зафиксированы, см. рис. 8.1). Требуется использовать
наилучшим образом располагаемый запас рабочего тела, чтобы при
заданных параметрах конечной орбиты он мог бы быть сделан мини¬
мальным.
Учитывая требование длительного существования искусственного спут¬
ника планеты, требуется при заданной величине импульса Д Ухар обеспе¬
чить максимальное увеличение высоты перицентра. Или для заданного
времени существования искусственного спутника планеты необходимо
определить минимальные энергетические затраты, что в первую очередь
сводится к заданному увеличению высоты перицентра.
Определим параметры орбиты после приложения импульса, используя
уравнения энергии и момента количества движения [111]. Пусть после
подачи импульса параметры орбиты характеризуются радиусом перицентра
гя1 и радиусом апоцентра га1. Тогда будем иметь
где Vi и г ! - скорость КЛА и радиус текущей точки орбиты, полученной
после подачи импульса.
Параметр может быть вычислен через параметры орбиты, реализо¬
вавшиеся после вылета КЛА из атмосферы ( Ук> 0К, Лк),и величину
229
скорости:
^тг1 ~ 1 + 2 {н0 + Го—Д Vxap cos и* +
Г~- ~Ro Ro ' -
+ 7 2Н0+2—-Г20-± ДУ:
Здесь Но — безразмерная полная энергия КЛА
мо сферы
- (VI ЯЦ 1
Но = I—— - д0 ) ——;
X 2 гк/ g0R0
Го — безразмерный момент количества движения КЛА после его вылета
атмосферы:
VVkCQs0k
floV<7o*o
Д^хар
—zzz; безразмерная величина приращения скорости; г
\/ 9 о
радиус-вектор орбиты в момент приложения импульса.
Для заданной величины скорости ДУхар из уравнения (8.1) можно
определить истинную аномалию а* и угол наклона вектора тяги к мест¬
ному горизонту и таким образом, чтобы высота перицентра была макси¬
мальна 1Хя1
R0
2Н0 + 2——
г
Г . . , Д^хар
хар SIH U +
Г
)х
AVxapcosu*j . (8.1)
после его вылета из
ат-
из
Го =
ДУхар
*
........ (.
дХя1 _
Та* '
Истинная
о.
Ro
>min
г я 1
дХЯ1
ди*
= 0.
аномалия
Ro 1 + V1 + 2H0n'cos д ‘
X* =
г *
d* связана с радиусом-вектором г* соотношением
р2
А О
v Учитывая, что
дХях _ ЭХЯ1
да* дХ*
dX*
= О,
da*
определим искомое решение одной из двух систем уравнений:
э2д1 = о
эх*
^2.= о-
ди*
(8.2)
ЭХ*
— = о,
эа*
=0.
ду*
(8.3)
230
Путем их несложных преобразований (см. [111]) легко получить
\л0 •
Таким образом, при переходе с орбиты, реализовавшейся после вылета
КЛА из атмосферы, на орбиту с максимальным возможным радиусом пе¬
рицентра при одноимпульсном переходе включение двигательной установ¬
ки следует проводить в апоцентре траектории.
Высота перицентра новой орбиты при одноимпульсном апоцентриче-
ском переходе не может быть получена больше высоты апоцентра исход¬
ной орбиты при сколь угодно большой величине скорости Д V\ap. Иными
словами, одноймпульсный переход при скорости AV\ap, превышающей
некоторую предельную величину Д Упр, заведомо неоптимален.
При* ДУхар = Д Ухар совершается переход КЛА на круговую орбиту
при апоцентрическом включении двигательной установки. При заданных
параметрах орбиты выведения после прохождения аппаратом плотных
слоев атмосферы планеты (hao и ^ло) потребное приращение скорости
А Ухар, сообщаемое в апоцентре орбиты для переведения его на круговую
орбиту, определяется по формулам [111]
-хМ
Критерий оптимальности при управлении движением КЛА на атмосфер¬
ном участке. Итак, задача заключается в поиске такого управления аэроди¬
намическими силами, которое реализует максимальную величину высоты
перицентра траектории после вылета КЛА из атмосферы при заданной вы¬
соте апоцентра орбиты.
Параметры орбиты, реализовавшейся после вылета КЛА из атмосферы
(/?ai и ЛЯ1), могут быть выражены через скорость полета следующим об¬
разом [139] :
2^о *S
(8.4)
2>° я. +Лк vl
Учитывая, что hal = const, из (8.4) следует, что максимизация высоты
условного перицентра эквивалентна максимизации суммы hai +h.nl,
которая определяется только скоростью VK в момент вылета КЛА из ат¬
мосферы, т.е. максимально возможная высота перицентра КЛА реализует¬
ся при достижении максимальной скорости в момент его вылета из атмо¬
сферы :
/ = l/K-> max.
(8.5)
При этом должна учитываться связь между скоростью и углом
траектории к местному горизонту на высоте
наклона
7-
(8.6)
Найденный критерий оптимальности очень прост и нагляден, так как
позволяет проводить решение задачи без учета внеатмосферного участка
полета после прохождения плотных слоев атмосферы. Вместе с тем, зная
1/к и 6К на границе атмосферы hQ = hK, нетрудно рассчитать все парамет¬
231
ры переходной орбиты, в том числе скорости в апоцентре Va и перицентре
Vn. Случай апоцентрического одноймпульсного перехода и будем рассмат¬
ривать в дальнейшем.
§ 8.3. Оптимальное управление в атмосфере
Рассмотрим задачу об отыскании оптимального закона управления
КЛА на участке аэродинамического торможения для случая управления
эффективным аэродинамическим качеством
^эфф ~ ^бал cos 7,
где /Сбал — значение аэродинамического качества на балансировочном угле
атаки; у — угол крена. При этом величина эффективного качества может
изменяться в пределах
-Кбал ^К'эфф Кбал • (8.7)
При исследовании траектории движения в атмосфере будем использо¬
вать уравнения плоского движения центра масс КЛА с учетом вращения
планеты и уноса массы теплозащитного покрытия:
dV cxspV2
— = д sin 6 + со 2 г sin 6,
dt 2(тц - CiSyiIn?yH)
d6 cxsp Vcos у geos 6 V cos 6 co2rcos0
+ 2 co +- (8 8)
dt 2(n?0 - CiSyH myH) V г V'
dh _ I/ • д drriy^ Qkohb +а*7рад —
— v sin a, = —
dt dt V '
где
a -Br~lf2nl/2V3 a -Ar n°>7l/3»28
Чконв~°лн P V , Чрад,~АГнр V ,
Ci=O при 7”(t) < 7"p, <?!=/< при nt) > Гр ,
) _4 J ^KOHB + а 9радГ •
e a
Задача об отыскании оптимального управления в атмосфере при выведе¬
нии КЛА на орбиту ИСП может быть сформулирована следующим образом:
в интервале (8.7) определить закон изменения /Сэфф, переводящий КЛА
из начального положения (Vo, 60, hQ) в конечное положение (0KlhK),
обеспечивая значение VK = Уктах. Выполнение условий в конце участка
основного аэродинамического торможения позволяет реализовать наимень¬
шее значение величины приращения скорости ДУхар, потребной для фор¬
мирования заданной орбиты ИСП.
Решение вариационной задачи об отыскании оптимального управления
КЛА из условия минимума приращения скорости Д1/хар при фиксиро¬
ванных начальных условиях
V(tQ) = VQl 6(tQ)=6Ql h(tQ)=hOr m(t0}=mQ
и конечных условиях
V'k = max, 0К = f(VK); tKfhK,mK - свободны
будем проводить с использованием принципа максимума Понтрягина.
232
В этом случае поставленная задача сводится к трехпараметрической
краевой задаче для системы дифференциальных уравнений движения (8.9)
и сопряженных переменных по поиску недостающих значений сопряжен¬
ных переменных в начальный момент времени tQ. При этом система урав¬
нений для сопряженных переменных и гамильтониан ЗС имеют такой же вид,
как и для вариационных задач спуска КЛА в атмосфере, рассмотренных
в главе 5.
Краевая задача. В качестве вычислительного метода для решения крае¬
вой задачи может быть использован описанный выше (см.главу 3) метод
последовательных приближений. Для сходимости итерационного процесса
большую роль играет выбор первого приближения. При решении постав¬
ленной вариационной задачи об отыскании оптимального закона управле¬
ния из условия максимума конечной скорости выбор первого приближе¬
ния осуществляется двумя путями. С одной стороны, на основе некоторого
упрощения системы уравнений движения КЛА проводится анализ сопря¬
женной системы дифференциальных уравнений и из условия минимума
гамильтониана определяется структура оптимального закона управления
движением. Знание структуры оптимального закона управления существен¬
но упрощает поиск первого приближения, однако при этом процедура
решения краевой задачи все еще остается достаточно громоздкой и требую¬
щей больших затрат машинного времени. С другой стороны, для выбора
первого приближения могут быть использованы аналитические методы
расчета траекторий движения КЛА в атмосфере, которые позволяют су¬
щественно сократить время решения краевой задачи по сравнению с числен¬
ным решением при незначительных погрешностях вычислений.
Рассмотрим оба пути определения начального приближения для рас¬
сматриваемой задачи максимизации конечной скорости.
Анализ структуры оптимального управления в общем случае. Для ис¬
следования структуры оптимального управления введем ряд общеприня¬
тых допущений [19] :
а)
cxs
2т
PV2
> I (р — co2r) sin ОI;
б) sin 6^0, cos 0 ~ 1, г-Ro’’
apV3
в) •
Исключая из системы дифференциальных уравнений
(8.8) время Г, по¬
лучаем
dd cv 2т / д V u?R0
-— cos 7 + ; I — —'— —
d V cxV cxspV2\V Rq V
dh 2m0 dm CiSyVLamV
dV cxspV dV cxsri
— 2 co.
(8.9)
Гамильтониан и система сопряженных уравнений имеют вид
dh dm
2 ~dV~ ~ ~dV~'
dO
- Ф
JC= -
■ 01
dV
2m
•02,
dV
cxsp V
(8.10)
233
V
'dV
2m6
cxspV2
dp
dh
2т
*o
g?/?o „ \ dp V/i
2w| - ,
V ' dh p2
d^3 _ 2 f g V
dV TxspV2 \V 77
u?2 R о
\7~
(8.11)
cxspV cxsri
Оптимальное управление, доставляющее максимум гамильтониану
(8.10), имеет вид
Кэфф =^бал sign 01-
Отсюда следует, что число переключений /СЭфф равно числу нулей функ¬
ции (V) на интервале VK < V < 1/0. Проведем исследование функции
i//(V). Из первого уравнения системы (8.11) выразим переменную
С/0! cxspV
dV 2т
(8.12)
Продифференцируем (8.12) по скорости V, учитывая (8.11) получим сле¬
дующее уравнение для :
С/2Ф1 1 ( V
-1- + —
dV2 V dV \ R
co2 Ro g \ 4P2 dP
■ + + 2w —=0, (8.13)
V V 1 V3p3 dh
т
где Рх = ——.
cxs
Произведем замену переменной [101]
/ 1 v d^ \
V/1(V)=Z(V)exp f
\ 2г0 £ /
и призедем уравнение (8.13) к виду
d2Z
+ B(V)Z = Q,
dV2
где
B(V)
1
4У2
/ V co2R0
/ + +
\ rq V
g \ dp 4P2
V / dh p3 V3
Функции Фх (V) и Z (V) обращаются в нуль одновременно. Если функ¬
ция В {V) C1/4V2, то любое нетривиальное решение уравнения для В (V)
имеет не более одного нуля.
dp 1 о
Поскольку < 0, то B(V) <— V2 при условии
dh 4
V2
+ со2 Rq + 2cpV — g>Q
rq
или
234
что является справедливым для любых траекторий выведения КЛА на
орбиту ИСП. Отсюда следует, что оптимальный закон управления эффек¬
тивным аэродинамическим качеством Кэфф при отсутствии ограничений
имеет не более одного переключения.
Резюмируя изложенное, отметим, что специфика движения КЛА в атмо¬
сфере при формировании орбиты ИСП комбинированным способом не при¬
водит к качественным изменениям структуры оптимального управления
К'эфф ПРИ движении КЛА в атмосферах различных планет и представ¬
ляет собой одноразовое переключение Кэф(Ь С + ^бал на ~^бал-
Следовательно, решение краевой задачи сводится к определению вре-.
мени t' переключения эффективного качества Л^эфф на атмосферном
участке.
При этом существуют два таких значения высоты условного перицентра
траектории, соответствующих верхней и нижнеи границам коридора входа
/?® и Л®, при входе с которыми в атмосферу планеты оптимальная
программа управления вырождается в программу полета с постоянными гра¬
ничными значениями эффективного аэродинамического качества соответ¬
ственно /^эфф ^бал И ^эфф “ ^’^бал*
Анализ структуры оптимального управления КЛА в некоторых частных
случаях. В ряде практически важных случаев исследование движения в^
атмосфере можно проводить, используя более простые модели движения
КЛА, чем система (8.8). В частности, можно не учитывать унос массы
теплозащитного покрытия КЛА либо принимать модель атмосферы изо¬
термической, что допускает описание закона изменения плотности ат¬
мосферы с высотой в виде экспоненты. Проведем анализ структуры опти¬
мального закона управления для этих двух случаев.
dm
А) =0.
dt
Запишем уравнения движения КЛА в вертикальной плоскости в следую¬
щем виде:
dV
dt
-oxpV2
(Ro + h)2
sin 0,
dh
= V sin B,
dt
de
dt
cxs
2m
V2
(Ro +h)2
где ox
—_ масса КЛА; s - характерная площадь. Введем сле-
2 т
дующие упрощения:
д sin е
sin в ~В, cos 0 ~ 1, — ~ 0.
(/?о+Л)2
V2 IJL V2 11
/?о + h {Rq + h)2 Rq Rq
Получим следующую систему уравнений:
dV , dh dB 1 / 9
- = -oxpv2, —=ve. — [кэфф oxpv +
dt dt dt V \
Ro
235
Уменьшим порядок системы, исключив время f:
dh
dV
6
axpV'
de_ i r_ _i
dV ~ V [ Кэфф + oxpV2 \ Rl Ro AT
(8.14)
Итак, задача оптимального управления сводится к выбору управления
Кэфф = ^эфф на интервале -Кбал ^э<Ьф ^+^бал, переводящего ЛА
из начальной точки (hQt0o) при скорости V = VQ в положение (Лк, 0К) и
обеспечивающего VK = Уктах. Величина 0К удовлетворяет условию
) haK.
Запишем гамильтониан системы (8.14) в виде
где сопряженные переменные ф\ и 02 определяются системой уравнений
dy^ dJC 0 dp ф1 / р V2 \ dp ф2
dV dh oxV dh р2 \ Rq Ro I dr oxp2V3 '
(8.15)
d\p2 dJC Ф1
dv de oxpv
Оптимальное управление, доставляющее максимум гамильтониану при
любом значении V в интервале VK < V < Уо, запишется в виде
Видно, что число переключений /Сэфф равно числу нулей функции ф2 на ин¬
тервале VK < V < VQ. Исключая ф1 из второго уравнения (8.15), запишем
уравнение второго порядка для ф2
d2\jj2 1 d\)s2 ( V2 р2
dp фг
(8.16)
о n ~ 0-
dV2 V dV \ Ro Ro 1
dh oxp2V3
Используя подстановку
/1^1 X
^2(l/)=Z(l/)exp( f — d$),
' 2 к0 ? )
приведем уравнение (8.16) к виду
d2Z
— +S(V)Z = 0,
dV2
(8.17)
где
1 1 V2 u. \ dp
4 V2 V Ro Rl> dh
1
o2xp2V2
Функции ф2 (V} и Z (V) обращаются в нуль одновременно. Согласно
[101, 120] имеем В <1/41/2, а в этом случае уравнение (8.17) имеет не
более одного нуля. Следовательно, оптимальное управление в рассмотрен¬
ной задаче имеет не более одного переключения, если скорость в конце
торможения не ниже круговой.
236
Проведенные численные расчеты показали, что для оптимального закона
управления величина /Сэфф в момент переключения изменяется от макси¬
мального значения Кэфф = +Кбал Д° минимального /Сэфф = “^бал ПРИ М0‘
нотонном уменьшении скорости от V = Vo до V = VK.
Б) р =рое 0Н
Приведем результаты анализа структуры оптимального закона управле¬
ния КЛА, следуя А.А. Шилову [30]. Пусть движение КЛА описывается
системой дифференциальных уравнений вида
Для определения структуры оптимального управления преобразуем систе¬
му дифференциальных уравнений, используя следующие упрощающие
предположения:
О 0qO
-— «1, sin0«0, cos0~1, 0(/?)=const, —r-<1.
R0+h Pv
Тогда получим 1
(8.18)
где
X — новая независимая переменная, имеющая смысл относительной потери
полной энергии и удовлетворяющая уравнению
где
Задача формулируете^ следующим образом: требуется обеспечить
максимум функционала Ук одновременно с выполнением граничных ус¬
ловий
Ук = Угк. ha(YiK, YiK, VK) = ha, Хк-свободно.
(8.19)
Для решения задачи используется принцип максимума Понтрягина, соглас¬
ью которому оптимальное управление при каждом фиксированном значе¬
нии независимой переменной X обеспечивает абсолютный минимум гамиль-
тониана
(8.20)
237
Здесь ф1 и ф3 — сопряженные переменные, определяемые системой диф¬
ференциальных уравнений
Фзк +С3
Ф 1К
V'ik-К>0.
(8.22)
х=хк
*’■ + ,8-2”
су сх~ коэффициенты подъемной силы и лобового сопротивления, изме¬
нением которых осуществляется управление полетом КЛА в атмосфере;
часть гамильтониана, не зависящая от управляющих функций
СУ и сх-
Согласно [26], траектория сопряженных переменных должна удовлет¬
ворять условиям
3^
ЗЛ
где С3 — положительная постоянная. Из последнего выражения получаем:
3/?а
з/?а
3X1
Поскольку правые части системы уравнений (8.18) не зависят от аргумента
X явно и, кроме того, учитывая, что Хк свободно, будем иметь первый
интеграл системы (8.18) и (8.21)
ЗС(Х) = °. (8.23)
Таким образом, поставленная вариационная задача сводится к решению
двухточечной краевой задачи по определению начальных значений двух со¬
пряженных переменных i//10 и 1//2о так, чтобы удовлетворялись условия
(8.19) и (8.22). Недостающее начальное значение третьей сопряженной
переменной ф30 определяется из условия (8.23).
В зависимости от применяемого способа управления КЛА возможны
два.случая:
полет осуществляется на постоянном балансировочном угле атаки
а “ абал, а управляющий параметр су ограничен
cymin ; (8.24)
полет осуществляется путем изменения углов крена и атаки, при этом
величины коэффициентов лобового сопротивления и подъемной силы
связаны некоторым соотношением, аппроксимирующим поляру КЛА:
с*=схо+кс2. (8.25)
Из анализа гамильтониана (8,10) следует, что в первом случае (а = )
управление должно быть всегда граничным по су. Знак сопряженной пере¬
менной i/zj определяет, какое из граничных значений должен принимать
управляющий параметр су. Для функции можно записать следующее
линейное однородное дифференциальное уравнение:
o^i > /
—~2 ■ +5Ф1 =о,
dr
238
(1/V2) —1
где ? - переменный коэффициент ~ J . Анализ показывает,
что на всем интервале полета КЛА со сверхкруговой скоростью (V> 1)
переменный коэффициент £ остается отрицательным. Отсюда можно сде¬
лать вывод, что функция обращается в нуль на этом интервале не более
одного раза, а управляющий параметр су имеет не более одного переклю-
чения с одного граничного значения на другое.
Во втором случае, когда аэродинамические коэффициенты сх и су связа¬
ны соотношением (8.25), оптимальное управление КЛА может быть как
граничным, так и неграничным.
При этом для любых значений сх0 и к , т.е. для любых поляр класса
(8.25), величина су на участке движения со сверхкруговой скоростью
может изменить знак только один раз. Кроме того, на участках траектории
полета, где выполняется условие
к 0з >0,
управление по су будет всегда граничным.
Как и в рассмотренном ранее случае, знак оптимального значения су
определяется знаком сопряженной переменной 01, а смена знака происхо¬
дит в момент, когда функция становится равной нулю. Таким обра¬
зом, проведенный анализ дает представление о структуре оптимального
управления в некоторых частных случаях. Так, можно сделать вывод
о том, что при управлении КЛА путем изменения угла крена оказывается
возможным избежать интегрирования системы сопряженных уравнении,
так как задача заключается лишь в поиске момента переключения Кэфф
с одного предельного значения на другое.
Метод определения первого приближения. Приведем приближенный
аналитический метод решения системы дифференциальных уравнений
(8 8) с учетом вращения планеты и уноса массы теплозащитного покры¬
тия с поверхности КЛА, [27]. Введем следующие допущения, несущест¬
венно влияющие на точность получаемых решений :
cxspV2
2т
> j<7cos01 + Iо?2 rsin,
sin0^0, cos0~1, сх = const,
Су
К =—- = const,
Сх
p(h} = poe 0Н,
где к — коэффициент, зависящий от системы единиц измерений. С их
учетом система уравнений (8.8) перепишется в следующем виде:
dv- c*spv2( ^L=^+PVM'
dt 2m dt 2m
dm KpV3 dL
= _ — = v
dt 2 ' dt
dp
— V&p0,
dt
239
где
CtSyHaa { дг Ш2Г2 2w \
к ■ M =1 1 + - + )
V X V2 V2 у )
-кусочно-постоянная функция на конечных интервалах изменения ар¬
гумента Vq.
Исключая время t, получаем
de
К
2mM
dp 2m0fi
~dV
V
cxsV '
dV cxsV
dm
KVm
dL
2m
(8.26)
dV
cxs
dV
cxspV’
Интегрируя третье уравнение системы (8.26), определяем изменение мас¬
сы КЛА в зависимости от скорости движения V:
miVj^Ae81'2, (8.27)
где
A=/n0e2cx5 , В = -
2сх$
Для получения закона изменения угла наклона вектора скорости к
местному горизонту 0 в зависимости от V проинтегрируем первое урав¬
нение системы (8.26) :
V 2МА
0(V) = 0О - Kin /) . (8.28)
v0 cxs
tBV2
dV может быть вычислен с помощью разложения
ряд по аргументу BV2:
— (BV2)n + . . .
п\
v е1
Интеграл /j = f —
Vo V
экспоненциальной зависимости eBV в степенной
— (ЯУ2)2+ — (£У2)3 + .. . +
2! 3!
= 1 +BV2 +
2!
1
.. +— (BV2)
/!
тогда
v ( 1 1 1 1 ч
/1= / —+SU+—Я2У3 +—B3V5+...+ —Bnv2n~l -г \dV =
v. I V 2\ 3! п\ ’■’ /
V 1 I Bn(V2n-Vtn)
= In + — s —
VQ 2 n= 1 n n\
где / - число членов разложения экспоненциальной зависимости.
Окончательно уравнение (8.28) принимает вид
V
o(V) = eQ -/cin—
2МА V 1 i
In—+ — S
cxs Uo 2 n= 1
(8.29)
Подставляя зависимости (8.27) и (8.29) во вторую формулу системы
(8.26), можно определить соотношение между скоростью движения ап¬
парата V и плотностью атмосферы р, соответствующей той высоте h, на
240
которой происходит полет КЛА:
2/Х40О WAK
p(V) = pQ + /, /2
cxs
АРМА2
11,
cxs
(8.30)
V
/з= f
где
v
/2= f ~ dV,
V. V
Подчеркнем, что при использовании экспоненциальной зависимости
плотности от высоты формула (8.30) фактически определяет изменение
высоты от скорости полета.
Интеграл /2 также вычисляется с использованием разложения функции
в степенной ряд:
In2 V- In2 Vo
— +
/2
2
I
S
п= 1
1 / „ In У „ InUo
Вп \V2n V^n
п\ \ 2п 2п
V2n
Tn2
^o2”\
+ W
Интеграл /3 берется по частям
/ v е3^ \ /,(П / V е3^
,3 = ,'\ ' dV ~ ! / -T7~d
\ к0 v ; л(г0)\г0 v
Окончательно зависимость (8.30) имеет вид
,„Л
/2040o 204 Kin Vo
p(V) - p0 +l +
\ CXS CXS
I
S
п= 1
Bn(V2n - l/02w)l
пп\
2&АК Г In2 У— ln2U0 /
+ S
cxs L 2 n= 1
n\ \
v2n
In V 7
- v20
2n
,2n ,nV/0
J 2„
1/2 n
~An2~ +
ЗМА2 Г V 1
In — + —
L Vo 2
Таким образом, формулы (8.27), (8.29) и (8.31) дают возможность
определить параметры траектории движения в атмосфере при известных
начальных условиях, характеристиках КЛА и параметрах атмосферы. Для
нахождения траекторий движения КЛА баллистического типа можно ис¬
пользовать формулы (8.27), (8.29) и (8.31) с учетом того, что
+ J_ £ Bn(V2n — Vo”)l
п • п\
nix2 2MA
m(V}=AeBy , 0(V)=0O
20Д0О
p(V) =p0 +
cx$
In
. Vo
п • п\
п • п\
20MA2 £
V 1
In + —
cxs L Vo 2
16. Зак. 2069
п • п\
+
['
V 1
+ —
1
+ —
2
241
Целесообразность использования расчетных формул (8.27), (8.29),
(8.31) и (8.32) зависит от потребного числа членов экспоненциального
ряда I, удовлетворяющих заданным условиям точности. Поэтому пред¬
ставляется интересным исследовать влияние числа I на точность ре¬
шения.
g табл. 8.1 - 8.6 приведены результаты расчетов траекторий выведения
КЛА на орбиты искусственных спутников различных планет для широ¬
кого--диапазона изменения начальных условий входа КЛА в атмосферу
й его проектно-баллйстических характеристик. Расчеты проводились по
уравнениям движения_18.»В1. и_лриближенным зависимостям~~Т8.29) \ "(8.31)
IT'78.32). Число членов экспоненциального ряда I принималось равным
двум.'
Из рассмотрения численных результатов, представленных в табл. 8.1 —
8.6, видно, что точность определения основных траекторных параметров
(угла наклона траектории к местному горизонту и скорости КЛА) сущест¬
венно зависит от начальных условий входа КЛА в атмосферу, его проектно¬
баллистических характеристик, плотности атмосферы и высоты апоцентра
переходной орбиты.
Погрешность вычисления угла 0К и скоростей Ук и Va по приближен¬
ным формулам определялась следующим образом:
100%,
где индексом "ч" обозначены параметры, полученные численным интегри¬
рованием уравнений (8.8), а индексом "пр" — при использовании прибли¬
женных уравнений (8.29), (8.31) и (8.32).
Отметим, что для каждой из рассматриваемых планет и для всего диапа¬
зона варьируемых параметров погрешности Д0к,Д Уки Д Va не превышают:
Д0К = 2%,
Д0К = 1,5%,
Д0К = 3,9%,
Д0К = 4,52%,
Д0К = 3%,
Д0К = 1,1%,
ДУК =4%,
ДУК =2,9%,
ДУК =4,5%,
Д VK = 3,3%,
Д1/к = 1,2%,
ДУК = 2,9%,
ДУй = 2,4%
Д Va = 5%
Д Va = 6,4%
Д Va = 3%
Д = 3%
ДУа = 3,9%
— для Земли;
— для Венеры;
— для Марса;
— для Юпитера;
— для Сатурна;
— для Урана.
При этом время счета Гсч сокращается в 15 — 20 раз по сравнению с числен¬
ным способом расчета на ЭВМ траекторных параметров по уравнениям
(8.8).
Аналогичные расчеты для I > 2 показали, что увеличение числа членов
ряда I позволяет добиться снижения погрешностей вычисления параметров
0К, и V&- Так, при /=3 погрешности не превосходят (3 4-5)%, при I =
= 5 — (2,5 4-4) %, а I = 20 — (2,2 4- 2,5) %. Однако в этом случае расчетные
формулы принимают весьма громоздкий вид и продолжительность решения
уравнений (8.27), (8.29), (8.31) и (8.32) значительно возрастает: в 7 — 10
раз при изменении I от 2 до 20.
Анализ точности расчета траекторных параметров с помощью предложен¬
ного приближенного метода (при /= 2) и при использовании других извест¬
ных аналитических методик решений [28, 137] показал, что при рассмотре¬
нии движения в атмосфере любой планеты Солнечной системы использова¬
ние предлагаемого аналитического метода дает наиболее точные результаты.
242
Таблица 8.1
Параметры траекторий выведения КЛА на орбиту искусственного спутника Земли
(исходные параметры: Ио = 13 км/с, Кбал = 0,5, Рх = 300 кгс/м2, р0 = 1,23 кг/м3, /3= 0,165 км х, ha = 1000 км)
в5
4м О
*-> о
<1
Р.‘
к« s
ь *
о
STS's
Ь *
2
ф
§
Ф L
d
Л «
3* X о.
Ф U
*
<1
сг
к a s
Ь *
о
? i's
ь У.
h S
< *
Варьируемые
параметры
О)
М- d- d-
d-
d- d- d-
d-
d’ d" 00
О)
со
о
г*
см г*
о
о
co
CO
co
см
со
см
см
со
co см
co
CM
CM
CO
CM
0
d-
со
CD 0
CD
r*
0
см
о
1
Г-' О
7
см
со
г*
О)
r- r*
d-
d’
co
co
r*
г*
со
г*
со
r* r*
r*
0)
d’
O)
со
со
со
со
со
CD CD
cd
CD
CD
cd
CD
^-ХТЮСОГ^СОСМ^-СМЮГ^ОО
оог^оостсооооооооооосоо
СОСОСОСОСОСОСОСОСОСОСОГ*
00 СМ СО Г* СО 0 СМ 10
6 6 Г- Г-' <- Г-' N о Г-' О О N
I I I I I I II I
0 СО СО 10 00 т- Г* СО 00 СМ СО
г- 04 СО Г* CM г- CM St О)
00 О) г^' 0 Г- об об 00 00 00 г< 04
СМ 00 10 00 СМ СО СО L0 00
<- СМ 10 СО СМ О) О г- г- 0 О СО
co oi > ю г-‘ г< об об со об г* см
г*
00 со СО 10 СМ СМ СО 10
СО СМ сб СМ *4- см со со см см o’
I I I I I I I I I I I
об
10 СО ю т- О) -<Г
'-'-CNCQr-Or-r-
об об об г^ об об об об
10 г- О)
0 СМ О
г^.об об
^ТГ^Г^Г'СО0М’М’^Г0С0ОО
ООГ*ООО)С0ООООООООСООО
Г< !<!<!< Г< Г< !< Г< |< об 00
СО 0 а) «- со
со г*' со' О) ю о см
ср со со см d- -о-
111 1111
'г
со г* О) со
Т-- об об г-'
ю со со ю
I I I
5
0 00
о о
II II
Ф. СП
243
пр
сч *
с
*- Q
<1 £
v£p,
км/с
о
Ь ¥
i
<1
* cf
th а
Ф 1-
СХ
sri &
Ф L-
*3 С)^
^р.
км/с
rd
ь *
варьируемые
параметры
оососососососососососоо
in
СОСОГ'СООШОГ^ОО
смсосм^смсмспсмспсо
CO in 00
CD 00 CXI in Г* r*
О О О О г-' о О ш
CD CD in О) СО Xt Ш
СО СО CM Xt СМ СО Л СО СО CD
CDCDCDCDCDCDCDCDCD'in
CD г- О) xf О) 00 Q) 1П
СО Xt СО Xt CM C*) i*5 co co
CDCD<D<D<DCD<D<D<D<D
CO Xt 00 Г"- Г*
CM Г* 1П О CD
CD Xt !< Xt 00
O) 00 CD Ш
CO Г- CD О 00
CD Xt Г< Xt 00
00
ID f CD CD
О *- о о
SOI Ol in CD
CO CM CM CT)
CD CD CD CD 1П
00 CO О) O) <-
Г- co см см о
CD CD CD CD CD
CT) CT) CO Г*. in Ш CM
Q CM CM ° CM CM г-' г-' CM CM
Til I I I I I I
CM CD <- 00 CD CD CD
Xt in Ш Xt CO 1П Xt xt in Г*
Г* l< !< Г** Г< !< Г"*' Г<
Щт-оосот-тютшсо
CO Xt CM xt CM CO CO CO CO 1П
[< |< r< l< !< !< Г*» Г* Г"»
CD CO CD
00 CM xt
CD CM 00
Ла= 1500км 30 6,98 7,13 -2,1 6,85 6,81 0,5 6,27 6,59 4,7 19
Кэфф=-0,5 103,3 7,49 7,49 0 0,84 0,81 0,3 6,55 6,55 0 450
244
Таблица 83
Параметры траекторий выведения КЛА на орбиту искусственного спутника Марса
(исходные параметры: 1/0 = 6 км/с, Кбал = 0» 5, Рх = 300 кгс/м2, р0 = 0,0133 кг/м3, /3= 0,093км”1,ha = 1000 км)
a”
кГ q
V и
b
<1 c£
^p,
км/с
V4a.
км/с
i
Ф L-
e<
ri a
Ф I—
i
<1 c£
о/
b *
км/с
Варьируемые
параметры
«-ШШОФСМСМСЛ
00 Г" CD Г** О) Г"» О) г**
CD 00 in
00 г- СМ
CXI
CD CD 00 M- CO w- CD r*. 00
CO CO CO CD Cxi” CO CXJ о M-'
CXI r* r- co 00
Г» r>.CD CD Г* Г* Г* in 00^
CXJ CxT CM Cxi CM CM CXJ CM CO CM ex?
СМГ‘ООГ*Г‘СОСМСМ CM CM
oo oo oo r- oo oo oo to cd
CM CM CM CM CM CM CM CM CO CM CM
r*
M- CO O> CD 00 CD 00
in co CO CXJ T-' CM* T-' cm' cm cm
I I I I I I I I I I I
in CD ID
со
см
co
T—
г*
ш
CD т- О
CD
o'
о
CM
о
см
doo
CD о
T—
00
об
Г- т—
CD Г* Г* M- 00 CD
r* CD Г** r* r> CO 00
CD Г* rC CM CD CD CD
00 oo
г* г*- CM
CD CD
Г* Г"- Г* in co r* r* r* 00 CD
CM CM CM CM CM CM CM CM
I I I I I I I I I о
CM 00
ÑÑГ*ООГ‘Г*Г*Г*‘1ПООГ>«
cococococococdcococdco
CO CD
CDCDCDCDinCDCDCD^tr*r*
co co co co co co co' co' co' co' co
ООООГ'^СМСМШ^Г CM 00
о CD l< CD CD M-' см' op
CO I 1П Г* T- CO CO M’ CM "T
I I I I I I I I
s
¥
CD
о
o'
in
o'
I
•e*
e
Л
245
г» оооог-г^^ооог^г-оооо
9*Ju U
О (J)mO>'-CD^OCNCO
СО ^■OCNr-r^LDOM-r^in
CXI ГМГМГМГМГМГМГМСМГМГМ
ч-
СО
т-
т-
V-
со
гм
I
т—
гм'
I
со
*“
СхГ
I
ГМ
гм
Гм'
o' см'
со
О)
со
ГМ
in
со
г*
О)
00 00
о>
00
со
Т—
О)
О)
<□
со
00^04
8
Г"»
со
со
г*'
со"
со
г*"
со'
оо' in
со
со
со
со
со
со
со
со
со со
ЧГ
ш
00
г^
00
гм
гм
со оо
г*.
°ч
ф
г\
со
г*
г*
г»'
г*-'
г*.'
г*'
г*'
г*'
г*'
г*
Г'-
СП
СО
со
со
со
со
со
со
со
со
со
со
со
<1
СО Г- ID СО О) СО LD Г- О СО
о' т-' o' o' o' o' о" г-“ о' о" о"
<3-
ГМ ГМ СО
оо со т-
Г"
Ш Oi М-
О)
гм
’е
со
сэ
со
со
со
со'
Кэфф = - 0,5 -253 43,02 43,74 -1,6 3,38 3,43 1,3 37,89 37,34 1,4 140
246
Таблица 8.5
Параметры траекторий выведения КЛА на орбиту искусственного спутника Сатурна
(исходные параметры: Ио = 37 км/с, = 0,5, Рх = 300 кгс/м2, р0 = 0,711 кг/м2, /3 =0, 0368 км-1, ha = 10 000 км)
со
со
CD
co
co
co
г-
со
СП
co
CD
co
г*
Сх
r*
CM
о
in
от
о
ID
LD
о
00
00
00
о
г-
о
см
со
CM
CD
г»
CM
см
со
*~
co
00
co
от
00
о
CD
о'
о'
o'
o'
o'
7
о'
о'
о'
o'
o'
*“
00
r-
cd
со
со
00
ID
cd
т—
00
о
о
О)
О)
см^
0°,
о
CD
CD
Т—*
см'
T—*■
T—'
см'
«—**
см'
т—‘
co'
o'
см
см
CM
CM
CM
CM
см
см
см
CM
CM
CM
■3-
CD
LO
co
co
CD
см
О
о
CD
CD
Т—
t—
o
«—
<—
T—
<“•
со
о
r—
O^
T—
см'
см'
cm'
cm'
см'
см'
см'
см'
co'
cm'
см
см
CM
CM
CM
CM
см
см
см
CM
CM
CM
со
co
о
см
CM
co
co
а
о'
o'
o'
o'
o'
о'
со
о
o'
o'
м-
со
co
st
со
от
ID
со
co
00,
СО
О)
О)
СО
о
£
CM'
’Т
LD
’sf
’Г
*■"
in'
id'
со
00
о
co
co
LD
ID
CM
co
с*
(О
CD'
00
cd
о~
от
o%
in
00'
in
’Г
см'
id'
in'
00
CM^
ОЭ
r^-
от
С'
о"
I
o'
I
7
o'
I
o'
I
о'
1
о'
1
о'
1
o'
1
7
o'
1
7
см
со
8
co
co
ш
О
°°L
CD
Ю
о
о
Т—
от
CM'
00'
LD
LD
in'
in
in
in
in
ID
со'
in'
in'
co'
ID
СМ
CM
CM
CM
CM
см
см
см
CM
CM
CM
CM
см
co
’t
co
со
со
CD
CM
CD
r*
CD,
r*
r*
г*
с-
CD
in
cd
CM'
Г*»
LD
ID
in
ID
in
in
in'
in
ID
co'
in'
СМ
CM
CM
CM
CM
см
см
см
CM
CM
CM
CM
Г»
см
CM
CM
т—
KT
T—
co
c-
см
LD
г^.
■=T
r—,
. T—
in
о
CM
in
co
о
о
о
CM
ID
CD
т—
co
о
1—
0?
см
»—
CP
Г"*»
247
CD to СП СО (N CD О) (Ю СМ
СМ* См" См" со" со" См" См" СО См" со" со" <-"
5
*
о
о
о
о
II
а
S
*
СО
00
си
3
S
CZ
1D
(О
I-
X
СЕ>
<1 #
СО О* «- 04 СП М- LD т- Г»
си о>, сч П. <4 Ч СЧ
т-" т-' т-' Т-" г-‘ Г-" 04 о"
О» СО Г"- со со ю
Ч о*,т_, 00 ч
о" о" о" Т-" о" о" о о" о" о" о
I I I I
ю
О) СМ СМ СО СО г* СО О О) со см
СЭ 04 СЭ Т-; СО Г* CM LD Г* СП СП
СП оо" о" оо" о" со" о" со" О) СП со"
00
со
со
со
со
о»
см
о
сэ
г*
см
ю
00
со
СТ)
си" оо"
о"
оо"
о"
со"
ст>"
со"
СТ)"
СТ)"
оо"
ф
см"
I
Ч *1 °0.
см" см" см"
I I I
СП СО
см см" см"
I I I
о-
см
со
см
О)
г*
3
о»
ОУ
ю
LD
ю
со
ю"
ю
LO
ю"
ю"
ю"
ш"
ю"
ш"
<з-"
in"
см
ю
со
со
00
г*
со
*3-
СП
со
см
о
со
т—
§
со
’З-
г—
г*
00
00
см
см
см
СТ)
т—
см
г—
со
см
т—
О' U
о
L.
1—
¥
L.
¥
5
¥
х
О *
II о
¥
О
04
СМ
о
о
о
о
о
о
о
о
о
to
ф’-
to
о"
to"
in
<—
ф||
II
II
II
и
и
, m X
X
о
о
а
а
к о.
о.
Q.
Q. С
Кэфф = -0,5 -108 15,6 15,75 -0,9 6,256 6,19 1 11,47 11,86
248
Итак, исследования показали, что на этапе предварительного проектиро¬
вания для расчета траекторий движения КЛА в атмосферах планет с
помощью предлагаемого метода можно ограничиться числом I = 2. В этом
случае расчетные выражения (8.27), (8.29), (8.31) и (8.32) имеют следую¬
щий вид:
при спуске с постоянной величиной аэродинамического качества
WT/2 V 2МА
m(V)=AeBV , e(V)=e0-K\n фх (V), (8.33)
Vo cxs
р(Ю=Ро +^~ {Ф1(У)10О +KlnV0-MAGl(V)] -КФ^У)} ;
cxs
при баллистическом спуске
m(V) = AeBl/\ 0(V) = eo-^-G{V),
cxs
2QA (834)
p( K) = Po + Ф1 (Ю[0о - МАФХ (V)].
Здесь
Ф,(У) = 1п77- + | (V2 - vg)(4 + ev2 +SVg),
Vo о
, / BV2 BV20
$2<v)= 2Vn2V_ln2'Z° +5'/2|nU_BV'o|nV'° 2~*+ _2~ +
B2VA\nV £21фпУо B2V* B2V*A
+ 4 4 16-+ 16 /’
При вычислении параметров траекторий движения КЛА в атмосферах
планет, когда унос массы теплозащитного покрытия незначителен, и, следо¬
вательно, может не учитываться (например, для некоторых случаев движе¬
ния в атмосфере Марса), расчетйые формулы (8.34) преобразуются к еще
более простому виду
0(У) = 0О
(8.35)
р( V) = ро +
V
Зависимости (8.31) - (8.35) дают возможность найти решение диффе¬
ренциальной системы уравнений <8.26) в фазовом пространстве перемен¬
ных Vв, р, т. При необходимости знания времени t движения КЛА в атмо¬
сфере, его можно вычислить интегрированием уравнения
_2_
cxs Го pMV1
которое получается путем преобразования первой формулы исходной си¬
стемы дифференциальных уравнений.
Резюмируя изложенное, отметим, что предложенный приближенный ана¬
литический метод является достаточно эффективным для расчета траекто-
249
Таблица 8.7
Результаты решения задачи оптимизации траекторий движения КЛА
в атмосфере Юпитера при использовании численных методов (1) и предлагаемого
метода с введением поправочных полиномов (2) (3 — погрешность вычислений)
км
min /7тах
Qmim кДж/см2
1
2
3
1
2
3
-220
48 Я
48,9
0
995
995
0
-500
61,6
60,5
1,79
734
739
-0,68
-750
76,1
74,8
1,71
578
582
-0,69
-1000
92,0
90,2
1,96
466
472
-1,29
-1200
106,5
104,4
1,97
389
392
-0,77
-1400
122,3
120,0
1,88
337
338
-о,з
рий движения КЛА в атмосферах планет, когда имеет место унос массы
теплозащитного покрытия с поверхности аппарата (Венера, Юпитер, Сатурн,
Уран). Он может быть также использован для вычисления параметров
траекторий движения в атмосферах планет, когда влиянием уноса массы
можно пренебречь (см. таблицы 8.1—8.6).
Применение предложенного аналитического метода расчета траекторий
движения КЛА в атмосфере наиболее целесообразно при проведении
большого объема параметрических исследований и при решении много¬
итерационных краевых задач, возникающих при оптимизации заданного
функционала. Как было отмечено выше, предложенный метод може+ быть
использован для случаев, когда КЛА движется с постоянным или нулевым
значением аэродинамического качества. Тем не менее это не исключает
возможность решения с его помощью сложных вариационных задач. Дело
в том, что, как показывают имеющиеся результаты многочисленных иссле¬
дований (см., например, [19]), решение задач оптимального управления
КЛА "скользящего" типа, как правило, сводится к поиску моментов
переключений управляющего параметра — аэродинамического качества с
одного экстремального значения на другое. Это в принципе позволяет по¬
следовательно проводить расчеты для тех участков движения, на которых
полет осуществляется с постоянным значением аэродинамического качест¬
ва, а затем сопрягать такие участки. При наличии ограничений на траектор¬
ные параметры или при двухканальном управлении по углам крена у и
атаки а предложенный аналитический метод можно использовать при
поиске первого приближения.
При проведении сравнительного анализа результатов расчета траекторий
движения КЛА в атмосферах планет, полученных с использованием предло¬
женного приближенного аналитического метода и точным решением с по¬
мощью численных методов, была обнаружена интересная закономерность,
состоящая в том, что в зависимости от решаемой конкретной задачи при¬
ближенные данные либо всегда больше, либо меньше соответствующих
результатов, вычисленных с помощью ЭВМ [27]. Это обстоятельство натал¬
кивает на мысль о введении в расчетные выражения поправочных полино¬
мов, компенсирующих систематические ошибки и повышающих точность
решения задач. Для этого необходимо проанализировать погрешности (А),
получаемые при приближенном решении, найти обуцие закономерности
этих погрешностей от условий входа (УО,0О) > параметров КЛА (/Сбал,
250
max» км
Va max , к
1
2
3
1
2
3
59,4
59,4
0
38,42
38,42
0
59,8
59,97
-0,28
38,4
38,38
0,05
60,5
60,71
-0,35
38,25
38,2
0,13
61,45
61,69
-0,39
62,5
62,7
-0,32
63,75
63,8
-0,08
Рх) и характеристик атмосферы (ро,0), а затем вычислить поправочные
полиномы, аппроксимирующие выявленные зависимости.
Итак,
Л = f( Уо, 0о, А'бал, Рх, Ро, (8-36)
В общем случае выражение (8.36) можно представить в виде полинома
/7-й степени по всем варьируемым параметрам
"з
"4
«5
П6
S At t j j t j V'n'i X
* 1 *2 '3 *4 *5 *6 UZ j
Ь = 1
*4= 1
«5 = 1
Z6 = 1
(8.37)
Вычисление всех коэффициентов полинома (8.37) требует весьма гро¬
моздких расчетов и значительных затрат времени. Однако, как показали
исследования широкого класса задач движения КЛА в атмосферах планет,
достаточно вводить в расчетные выражения поправочные полиномы второго
порядка, что позволяет существенно повысить точность расчета траекторий
движения (погрешности 1 вычислений не превышают 2%; табл. 8.7) . Такая
аппроксимация требует расчета 64-х поправочных коэффициентов. Расчет¬
ные трудности, возникающие при этом, не принципиальны, ибо определение
коэффициентов поправочных полиномов проводится с использованием
весьма простых вычислительных алгоритмов. Суммарные затраты машин¬
ного времени не превышают 8—10 секунд.
Следует иметь в виду, что поправочные полиномы вычисляются для каж¬
дого конкретного класса задач. Очевидно, что наиболее целесообразно и
эффективно вводить их в расчетные формулы при исследовании большого
семейства траекторий, когда требуется высокая точность расчетов (напри¬
мер, при решении многоитерационных краевых задач, при проведении пара¬
метрических исследований и т.д.) .
1 Погрешность вычисления (3) определяется отношением разности значений опти¬
мизируемых параметров, полученных с помощью точного численного (1) и прибли¬
женного (2) методов, к значению параметра, вычисленного с помощью точного чис¬
ленного (1) метода (в процентах) .
251
Глава 9
ПРИБЛИЖЕННО-ОПТИМАЛЬНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ
ИЗ УСЛОВИЯ МАКСИМИЗАЦИИ СКОРОСТИ ВЫЛЕТА
ИЗ АТМОСФЕРЫ
§9.1. Оптимальное управление подъемной силой
при постоянном коэффициенте лобового сопротивления
В предыдущей главе основное внимание уделялось численным методам
анализа траекторий выведения КЛА на орбиту ИСП. Аналитические реше¬
ния этой сложной проблемы получить очень трудно вследствие существен¬
ной нелинейности динамических уравнений, описывающих движение КЛА
в атмосфере. Как правило, аналитические решения являются менее точны¬
ми по сравнению с численными методами, поскольку они предполагают
введение некоторых упрощений, но тем не менее обладают определенными
преимуществами, поскольку форма решения получается более наглядной.
Анализ решений приводит к явным характеристикам, которые в дальней¬
шем можно достаточно полно исследовать с помощью численных методов.
Кроме того, аналитические решения позволяют провести быстрый сравни¬
тельный анализ различных траекторий. Важным является также то, что в
областях пространства состояний они обеспечивают полное описание дина¬
мики системы. Последнее обстоятельство имеет большое значение при син¬
тезе алгоритмов управления КЛА.
В этой главе приводятся аналитические решения в явном виде задачи
максимизации конечной скорости выведения КЛА на заданную высоту
апоцентра переходной орбиты. Задача формулируется как общая оптималь¬
ная задача Майера и заключается в определении программ управления,
осуществляющих выведение КЛА на требуемую орбиту ИСП.
Как отмечалось, аналитическое решение задачи в общем виде представ¬
ляет известную трудность. Поэтому исследователи при решении задачи
максимизации конечной скорости для конкретных условий движения КЛА
в атмосфере планеты вводят те или иные упрощающие предположения, ко¬
торые позволяют существенно облегчить получение аналитического реше¬
ния для рассматриваемого случая. Ниже приводятся некоторые частные
случаи решения задачи максимизации конечной скорости вылета КЛА из
атмосферы, полученные при различных упрощающих предположениях.
Затем описывается общее аналитическое решение, включающее результаты
частных решений.
В этом параграфе приводятся результаты аналитического исследования
оптимального управления подъемной силой КЛА [136] из условия VKmax
в предположении постоянства коэффициента лобового сопротивления.
Будем считать, что управление КЛА осуществляется путем изменения вели¬
чины подъемной силы. Использование упрощающего предположения о по¬
стоянстве коэффициента лобового сопротивления при решении задачи мак¬
симизации конечной скорости в ряде случаев дает результаты, достаточно
близкие к оптимальным. Объясняется это тем, что для многих поляр КЛА
оптимальным является такое изменение су, которое происходит вблизи
максимальной величины су = с^тах в достаточно слабом диапазоне изме¬
нения коэффициента лобового сопротивления сх.
Основные уравнения движения КЛА в атмосфере можно записать
в форме
dV X gR^sinO / dO do\ Y gRlcosd
eft m (Ro+h}2 ' \dt dt) m (R0+h}2
252
dh
—-= \/sin0,
dt
do
= VcosO
dt
Яр
Re + h'
(9.1)
где а— продольная угловая дальность полета КЛА.
Если принять h/RQ < 1 и L = RqO, то уравнения движения (9.1) упрощают¬
ся и приводятся к виду
dt
dh
dt
(9.2)
Vsin 0,
-37 = Ucos0.
dt
Учитывая предположение об экспоненциальной зависимости плотности
атмосферы от высоты (изотермическая атмосфера), можно записать
dp
Траектория спуска может быть разбита на два участка: верхний (движе¬
ние на больших высотах), где справедливо предположение
« 3sin0,
и нижний (движение на малых высотах), где справедливо предположение
757 > ^sinfl.
С учетом этих предположений гамильтониан системы уравнений для пере¬
менных состояний (9.2) и множителей Лагранжа , ф2. Фз и Фа запишется
в виде
+ ф3 \Zsin0 + Фа VcosO.
(9.3)
Из необходимых условий оптимальности принципа максимума Понтряги¬
на для КЛА, управляемых углом атаки, получаем
_ ф2 ЭУ _ о
да mV да
где Y = ^p0V2scy(a)e ph.
В общем случае функция су(а) является периодической с периодом 2л.
Она содержит единственный максимум и единственный минимум и не име¬
ет горизонтальных точек перегиба в интервале
л , л
2 2
Уравнение необходимого условия оптимальности может быть удовлетво¬
рено одним из условий:
Ф2 = О И ymin < У < Утах, (9.4)
253
либо
^2*0 и Г=Гтах или r=rmin. (9.5)
Для КЛА заданной конфигурации верхняя и нижняя границы управления
задаются условиями
Су (а) = Су тах, Су (а) = — Су тах .
Итак,оптимальная траектория состоит из двух участков: расположенных
внутри области допустимых значений управления и определяемых усло¬
виями (9.4), и расположенных на границах допустимых значений управле¬
ния, определяемых условиями (9.5).
Будем предполагать, что время полета КЛА в атмосфере не ограничено.
В этом случае
К = 0. (9.6)
Учитывая выражения (9.3) и (9.4) , запишем уравнения для сопряженных
переменных при полете КЛА с переменным значением подъемной силы
1
= фг2Х — 03sinв - i//4cos0,
d^2 , d$3 рХ <У04
—— = — VcosO + i//4Usin0 = 0, = —, = 0.
dt dt т dt
Дифференцируя второе уравнение системы (9.7) , получаем
d2ty2
—-— = cos0 + (0з sin 0 + 04cos0)0 = 0.
dt2 dt
(9.7)
(9.8)
Таким образом, управление подъемной силой можно рассчитать по уравне¬
ниям (9.3), (9.6) — (9.8) следующим образом [136]:
|9.9)
Исследования показывают, что первый член в уравнении (9-9) всегда
является доминирующим.
Как показано в [136] полет КЛА внутри допустимой области возможен
только в том случае, если выполняется условие
PqSCу max
2т
(9.10)
На основании условия (9.10) можно отметить, что большинство оптималь¬
ных траекторий, как правило, начинается с участка максимальной или
минимальной подъемной силы.
Дифференциальные уравнения для скорости полета КЛА и угла наклона
траектории с учетом (9.9) для участка полета на малых высотах внутри
допустимой области управлений записываются в виде
X
т'
dV
dt
— = — 0Xcos0.
dt
(9.11)
254
Из второго уравнения (9.11) и последнего уравнения системы (9.2)
получаем
^.-3.
dL
или
e-df = -Q(L- Li)' (9.12)
где индекс / означает начальные условия для каждого участка траекторий
внутри допустимой области управлений.
С учетом (9.1), (9.2) и (9.12) будем иметь следующие решения:
б/Л гл о/> of/? _ 1 л
dL - tg[0 - 0(L - £,)], м tg0<
(9.13)
или
(9.14)
Отсюда
1 | cos 0 |
h-hi = 4 In .
P | COS0/I
Аналогичным образом получим уравнения для плотности р и скорости
полета V.
Уравнения (9.2) и (9.11) позволяют определить соотношение между
скоростью и высотой полета в виде
Приведем результаты решения задачи при полете КЛА на граничных
участках оптимальной траектории, т.е. на участке полета либо с максималь¬
ной либо с минимальной подъемной силой. На них выполняется условие
[136]
к-я
Y
. 'max
COS 0 <
m
Основные уравнения для переменных состояния на граничных участках
можно записать следующим образом:
—ycose,
dt m dt y dt dt
(9.15)
где Ку = poscy max 2~ Для участков полета с максимальной подъемной си¬
лой. Тогда из уравнений (9.15) получаем
Кх
V = l/,exp[ —-— 1
L Kjie-wi
к; v
e-e^—-in—.
Kx Vt
или
255
Аналогичным образом из уравнений (9.15) будем иметь
dO _ Kye~&h
dh sin 0
(9.16)
cosO = ~p~e — Ce,
(9.17)
где
Cq = ^hi ” COS0f.
(9.18)
С учетом (9.17) из уравнений (9.15) получаем
^ = [/3(cos0 + Ce)-^j.
(9.19)
Интегрируя (9.19), будем иметь
(9.20)
В уравнении (9.20) интеграл в правой части может быть вычислен в
замкнутой форме следующим образом:
(Cfl
(9.21)
если Св > 1,
de
1
(1 -Ce)tg| - (1 -С2)1/2
(9.22)
если Св = 1.
В качестве примера применения описанного приближенного метода реше¬
ния задачи максимизации конечной скорости вылета КЛА из атмосферы
рассмотрим задачу его выведения на орбиту ИСЗ. В этом случае число
участков полета с переменным и постоянным (граничным) значениями
управляющего параметра зависит от положения конечной скорости относи¬
тельно начальной. Ниже будет рассмотрена не вся оптимальная траектория
выведения, а только та ее часть, конечная точка которой достигается при
использовании двух участков.
Рассмотрим КЛА, обладающий максимальным аэродинамическим ка¬
чеством /Стах = 3 и входящий в атмосферу Земли с начальной скоростью
256
Vo — Ю/98 км/с, углом наклона траектории 0О =-3° и Ло = 109,8 км;
примем, что конечные высота hK = 35,08 км, а дальность LK = 83,57 км.
Результаты решения задачи показали, что оптимальная траектория начинает¬
ся участком минимальной подъемной силы [136]. Точка перехода от гра¬
ничного участка траектории к участку траектории, лежащему внутри допу¬
стимой области, может быть найдена следующим образом.
Пусть в точке перехода фазовые координаты КЛА имеют значения Lx
и hx. Тогда из уравнений (9.13) и (9.14) получим следующие соотношения
для участка траектории, расположенного внутри допустимой области:
hx
I cos[0K - PU1 - Z-к )] I
ICOS0K I
(9.23)
dh
dL
= tg[0K - 0(Z_
L = Li
/-к )].
(9.24)
Таким образом, получили семейство участков траекторий внутри допусти¬
мой области управлений, зависящее от конечного значения угла наклона
траектории О к.
Аналогичные соотношения можно получить для граничных участков
траектории, используя уравнения (9.16), (9.18) — (9.20):
1
In
0
(9.25)
о,
PIL. -Z-K) = 0i -0К -Св f
0К
de
CQ + cos0'
dh
dL
(9.26)
Очевидно, в момент перехода координаты h^L^vi наклон траектории
dh/dL |L = L для указанных выше участков должны совпасть. Проводя
сравнение уравнений (9.23) с (9.25) и (9.24) с (9.26) и исключая L,
получаем
cos0K = —т~е^Лксо5 0i (Се + cos0i),
Ку
е. (9‘27)
0К = 20! +P(L! - LK) - 0К - Се
Итак, решение задачи свелось к двум алгебраическим уравнениям с дву¬
мя неизвестными 0К и 0Ь
§ 9.2. Максимизация конечной скорости без учета влияния
гравитационных и центробежных сил
Рассматривается движение гиперзвукового КЛА в атмосфере планеты,
имеющей центральное поле тяготения. Предполагается, что снижение КЛА
в атмосфере происходит с постоянной массой (двигатель не работает и
унос массы теплозащитного экрана отсутствует).
Состояние КЛА в пространстве задается вектором положения г и векто¬
ром скорости V. Вектор г определяется тремя компонентами: модулем
17. Зак. 2069 257
вектора г , долготой к, широтой р. Вектор скорости V также определяется
тремя компонентами: модулем скорости V, углом курса относительно на¬
правления на Северный полюс планеты ф, который измеряется в плоскости
местного горизонта, и углом наклона траектории к местному горизонту 0.
В этом случае уравнения движения КЛА могут быть записаны в следующем
виде [147] :
dV Рг0 X
= — ffo“rsin9 ,
dt г m
dO Y V2
V — =—go —ycosO + — cosy + COS0Z
dt r m r
d\)j Xsiny V2
(9.28)
dr dp dK Usini//cos0
— =Vsine, r—= Ucos0cosi//, r-r-= .
dt dt dt cosy?
Итак, в общей постановке задачи оптимального управления КЛА
рассматривается полное шестимерное состояние. Система уравнений (9.28)
позволяет определить параметры траектории полета КЛА, если для каждого
момента времени задана функция лобового сопротивления X, программа
изменения подъемной силы Х(Г) и угла крена у (t) .
Примем следующее обобщенное выражение для поляры КЛА:,
Сх схо ксу, п > 1.
При этом предполагается, что коэффициент лобового сопротивления сх0
при нулевой подъемной силе, коэффициент к и показатель степени п для
всего диапазона скоростей и для всех рассматриваемых планет Солнечной
системы не зависят от скорости полета (числа Маха) и от числа Рейнольдса.
В уравнениях системы (9.28) подъемная сила Y и сила лобового сопро¬
тивления Хопределяются известными соотношениями
X = ~— р У2 Су s, X = ~ р V2 сх s,
а изменение плотности атмосферы с высотой описывается экспоненциаль¬
ной зависимостью
Р~Рое
Вводится параметр управления подъемной силой [147]
(п-1)к
с х Q
(9.29)
п
У
Коэффициенты подъемной силы и лобового сопротивления в этом случае
определяются следующим образом:
* [(п-1) + Хя]
су ~ су сх ~ сх , (9.30)
где Су и Сх — значения коэффициентов, соответствующие максимальной
величине аэродинамического качества /<тах. Учитывая (9.29) и (9.30),
258
получаем
СхО У1" . ПСх0
{п — 1 J ' х п — 1
СУ
IS —z -
лтах ~ #
сх
1 /л — 1 \(”-1)/”/1X1/”
П\ сх0 J \к/
При этом максимальному аэродинамическому качеству соответствует зна¬
чение параметра управления X = 1.
Величина п для КЛА типа "космический самолет" близка к 3/2, а для
КЛА типа "несущий корпус"/7 ~2.
При анализе траекторий выведения КЛА на орбиту ИСП могут быть
использованы также следующие упрощающие предположения:
аэродинамические силы существенно превышают составляющие силы
тяжести (нормальную и тангенциальную к траектории полета), т.е. гравита¬
ционными силами в уравнениях движения можно пренебречь;
продольная и боковая дальности полета невелики, т.е. можно использо¬
вать уравнения движения в предположении плоской планеты.
В этом случае уравнения движения (9.28) могут быть упрощены и
записаны следующим образом [147]:
VcosOcos^,
eft
—j— = V/cos 0 sin i//,
eft
dZ
dt
= l/sin0,
dV X dty Xsiny dO Ycosy
— = у—= у—=
dt m' dt mcosQ' dt m '
где X, Y. и Z —продольное, боковое и вертикальное перемещения КЛА.
Положительная ось X правой ортогональной системы координат XYZ,
связанной с центром масс КЛА, направлена по проекции начального векто¬
ра скорости Уо на плоскость местного горизонта. В этом случае начальное
значение угла курса всегда равно нулю, а изменение угла ф измеряется
относительно оси X. Используя безразмерные переменные
SCу р
2т ft'
(9.31)
а также выбирая в качестве независимой переменной вместо времени t
угол наклона траектории к местному горизонту 0, будем иметь безразмер¬
ные уравнения движения КЛА в виде
d% cos0cosi// drj cos0sini// dco sin0
dO coXcosy ' dO coXcosy dO Xcosy
(9.32)
dV (n-D + X" d$ tgy
dO Xcosy ' d6 cos0
где £ — безразмерная продольная дальность; ri — безразмерная боковая
дальность, со — безразмерная плотность атмосферы, Ro — средний радиус
планеты, V — безразмерная скорость полета КЛА.
Переход к записи уравнений движения в безразмерном виде позволяет
получить решение поставленной вариационной задачи в общей форме.
259
Начальные условия входа КЛА в атмосферу при 6 = для системы
уравнений (9.31) имеют вид
£(^о) = £о=О/ 7?(0О ) = 7?0 = 0/ Со(0о) = ^о,
(9 33)
V(60)=V0, ЖМо=0.
Функционал качества рассматриваемой задачи о максимизации конечной
скорости записывается следующим образом:
/=V(0K)=VK. (9.34)
Необходимые условия оптимальности. Для решения поставленной вариа¬
ционной задачи будем использовать принцип максимума Понтрягина. Запи¬
шем гамильтониан системы уравнений в виде
созвсозф cos0sin0 sin0
JC = Ф1 + ф2 — ф3
COACOS7 CoXcOS 7 XCOS 7
(л—1) + Х" tg7
“ Фа ~ + Фб ~ •
XcOS 7 cos 0
Сопряженные переменные определяются обычным образом:
4фг _ ЭК_ 0^2 _ ЭК_
dO ' d0 drj '
dф3 dJf (Фгсоз ф + i//2sin ф)соз0
dB Эсо со2 X cos 7
dф4 dJf .
dO dV
(9.35)
(9.36)
dф5 dJf (i/^sin ф — ф2созф)соз0
dO дф coXcos7
В соответствии с принципом максимума для определения оптимальной
программы изменения подъемной силы и угла крена необходимо решить
систему дифференциальных уравнений движения (9.32) и дифференциаль¬
ных уравнений (9.36) для сопряженных переменных Ф1 таким образом,
чтобы при начальных условиях (9.33) и заданных конечных условиях до¬
стигался максимум функционала качества (9.34) при минимизации гамиль¬
тониана (9.35).
Рассмотрение системы уравнений (9.36) показывает, что четыре из пяти
уравнений интегрируются в явном виде:
Ф1=а1, Ф2~а2, Ф4=а4< (9.37)
Ф5 = а1т?-а2^ + а5, (9.38)
где alza2za4,а5 — постоянные.
Учитывая (9.37) и (9.38), получаем уравнение для сопряженной пере¬
менной ф3
dфз (алсозф +a2sin i//)cos0
—— = 7; • (9.39)
du со X cos 7
260
Численные значения констант (9.37), (9-38) могут быть определены из
условия трансверсальности
(-Кс/0 +
(9.40)
где Х= Х(£, т?, со, У, ДО.
Введем вертикальную и горизонтальную компоненты управления подъ¬
емной силой:
a1=Xcos7, а2 = Xsin72, ai+a2<Xmax. (9.41)
Учитывая (9.41), перепишем выражение для гамильтониана (9.34)
в виде
JC = — и (a? + а|)”/2 + Ва2 +С],
^1
где
А =-а4,
& cos0 '
(a! cos<p + а2 sin i//)
со
cos0 — sin0 — (л — 1 )а4.
(9.42)
(9.43)
С =
Видно, что коэффициенты А, В и С от параметров управления ai и а2 не
зависят в явном виде. Чтобы найти оптимальные законы управления углом
крена 7 и параметром подъемной силы X, приравняем нулю частные произ¬
водные гамильтониана от составляющих управления Qi и а2:
ЭК ЭК
= 0, = 0.
3^1 Эа2
(9.44)
Решая совместно уравнения (9.44), получаем в общем виде оптимальные
законы управления КЛА при неограниченных значениях Хи 7:
X" =
С
(n-l)A'
sin7 = —
В
лАХ"-1
(л - 1)£?Х
пС
(9.45)
(9.46)
Выражения (9.45) и (9.46) описывают оптимальный закон управления
в наиболее общем виде. При этом, как видно из (9.45) и (9.46) аналитиче¬
ские решения возможны только в том случае, если коэффициенты В и С
являются функциями только угла наклона траектории к местному гори¬
зонту 0. Это имеет место, когда конечные значения продольной и боковой
дальностей не заданы, т.е. ах и а2 равны нулю.
Для нахождения константы а4 перепишем условие трансверсальности
(9.40) в виде
-K(eK)ddK + Ф1КС^К + ^2к^к + Фзк^к +
+ ^4KdVK +ф5кс/фк +dVK = 0.
Откуда 1Д4к = — 1, и а4 = ф4 = —1.
261
Уравнение (9.38) упрощается до ф5 = а5, а уравнение (9.39) для сопря¬
женной переменной ф3 интегрируется в явном виде:
Фз ~ аз-
Теперь из уравнения (9.44) получим значения коэффициентов А, В.\л С
д $
>4=—а4 = 1, В = —— , С = — a3sin0 + (п - 1),
а оптимальные законы управления параметром подъемной силы и углом
крена (9.45) и (9.46) запишутся в виде
X" = 1 —-—-— sin0,
(л - 1)
“ а5
nX”-1cos0
(9.47)
(9.48)
Итак, найденные оптимальные законы управления (9.47) и (9.48) выра¬
жаются в явном виде через независимую переменную 0. При известных
константах а3 и а5 оптимальные траектории могут быть получены для
поляры общего вида и для любой планеты Солнечной системы.
Определение констант а3 и а5. Рассмотрим методику определения кон-
ртант а3 и а5 в общем случае,т.е. когда конечная скорость VK максимизи¬
руется при заданных конечных значениях угла наклона траектории, высоты
и угла курса:
е = ек, а>(0к) = а>к, 1//(0к) = Фк.
Выпишем из (9.31) уравнения движения для со и ф
doo = _ sin 0
dO Xcos7Z
d\p _ tgy
dd cos0
(9.49)
(9.50)
Определим параметры управления из (9.47) и (9.48)
/ эз \1/п
/ ’
<9.51)
tg? = ±
fs
у/п2\2^-^cos2в-a2s
(9.52)
Учитывая (9.51) и (9.52), из выражений (9.49) и (9.50) получаем [147]
«к
сок- со0=+п J
*0
' a3sin0\<"-2>/"
1 1 sin0cos0<70
. п- 1 /
a3sin0V2"-2)/"
1 cos20— a2
n-1 /
(9.53)
262
(9.54)
Используя замену переменной т = sin0, преобразуем уравнения (9.53) и(9.54)
к виду
(9.55)
Фк = ±а5 / • 0.56)
Неизвестные константы а3 и а5 могут быть определены из уравнений (955)
и (9.56). При использовании КЛА,для поляры которыхл = 2, интегральные
уравнения (9.55) и (9.56) приводятся к нормальным эллиптическим интег¬
ралам Вейерштрасса [147]
гк тс/т
сок - coo = ±2 f - — - -- , (9.57)
то у 4а3т3 - 4т4 — 4а3т + (4 — а])
гк dr
Фк = ±а5 f , • (9.58)
То (1 -т2)у4а3т3 -4т4 -4а3т+(4—а2)
Оценка величины конечной скорости при оптимальном управлении для
случаев п=2. Подставляя оптимальный закон(9.47)управления параметром
подъемной силы X в дифференциальное уравнение для безразмерной ско¬
рости V (9.32), получаем
dV a3sin0 л
dO (л — 1 )Xcosy Xcosy
После несложных преобразований (см. [147] ) найдем для л = 2 величину
потерь скорости ЛА на атмосферном участке:
_ _ eK cosOdO
Ук — =аз1^к — <^о) — 4 f • (9.59)
0О \А(1 — a3sin0)cos20 — а|
Последний член уравнения (9.59) представляет собой эллиптический
интеграл
г0 V4а3т3 — 4т2 — 4а3т + (4 —а2 )*
263
Окончательно имеем для величины конечной скорости при оптимальном
управлении
Vk = “ аз (^к — ) — 4 /.
Простые аналитические результаты могут быть получены в предположе¬
нии малости угла наклона траектории к местному горизонту. Это предполо¬
жение справедливо для большинства траекторий выведения КЛА на орбиту
ИСП. В этом случае с большой степенью точности можно принять
sin0 « в, cos0 « I.
Тогда эллиптические интегралы (9.57) и (9.58) сводятся к интегралам
стандартного вида
0 к
сок - со0 - ~ —2 f
*0
ede
-4а3в + (4 - а2)
(9.60)
0R
фк - Фо = Д|// = -а5 f
во
de
-4а3е + (4 — а2)
(9.61)
Выражения (9.60) и (9.61) легко интегрируются [147]
9(Д^)М + (Асо )2 [8а! (в3к + 03Q) + 6а23(62к62Q)(4-а25) - (4 - aj)3]-^
+ [ | а3 (бк - Go) + (4 - al)(61 - е20)j = 0, (9.62)
al (Дф)4 + al (Д i// )2 [2а3 (0О _ 0К) - (4 - af)] + af (0К - 0О )2 = 0. (9.63)
В уравнениях (9.62) и (9.63) предполагается, что величины До;, Аф, 0к и
0О известны и заданы, а константы а3 и а5 неизвестны. Анализ уравнений
(9.62) и (9.63) показывает, что константы а3 и а5 имеют по четыре воз¬
можных значения, которые удовлетворяют этим уравнениям. Часть корней
может быть комплексной. Они отбрасываются, как не имеющие физическо¬
го смысла. Для окончательного выбора констант а3 и а5 необходимо про¬
верить каждую группу вещественных констант с точки зрения получения
максимальной величины конечной скорости.
При л = 2 и cos 7 « 1 уравнение (9.59) легко интегрируется. В резуль¬
тате получаем
_ 4 _
VK = а3 Дсо + — Д ф — VQ
а5
при
#5 ¥= 0
и
VK = а3Дсо + — (1 — а30к ~ V 1 ~аз@о ) ~
при а5 = 0.
Таким образом, поставленная вариационная задача о максимуме конеч¬
ной скорости при выведении на орбиту ИСП летательного аппарата с за¬
данным значением угла курса и с параболической полярой (п = 2), сводит-
264
л
град
0\
-д О 4 в,град
Рис. 9.1
Рис. 9.1. Зависимость угла крена 7
от угла наклона траектории к мест¬
ному горизонту 6 при оптимальном
управлении.
Рис. 9.2. Зависимость параметра
подъемной силы X от угла наклона
траектории 6 при оптимальном уп¬
равлении.
Рис. 9.3. Зависимость констант а3 и
a s от конечного угла курса iJ>K.
ся к решению двух совместных алгебраических уравнений (9.62) и (9.63)
для определения констант а3 и а5.
В качестве примера на рис. 9.1 и 9.2 приведены оптимальные программы
управления углом крена у и параметром подъемной силы X для КЛА, осу¬
ществляющего вход в атмосферу Земли с начальным углом во = —5°. Ко¬
нечное значение угла наклона траектории принималось равным = 7°.
Зависимости приведены для различных конечных значений угла курса фк.
Соответствующие значения констант а3 и а5 приведены на рис. 9.3.
§ 9.3.‘Случай нулевого значения угла курса
Рассмотрим важный с точки зрения практического применения случай
выведения КЛА на орбиту ИСП при нулевом значении угла курса (0К = 0),
т.е. будем предполагать, что КЛА осуществляет движение в вертикальной
плоскости [120].
Будем считать, что аэродинамические силы значительно превышают со¬
ставляющие силы тяжести в направлениях, нормальном и касательном к
траектории полета. Кроме того, учитывая, что диапазон скоростей и высот
маневра выведения КЛА на орбиту ИСП относительно мал, будем исполь¬
зовать уравнения движения, записанные в предположении плоской и невра-
265
(9.64)
щающейся планеты:
d% cos0 daj sin0 dV n — 1 + X”
dO coX ' dO X ' dO X
где
l/=lg
m^CypoS
ехр(-т?),
V
V (&д)пКтл*
L — горизонтальная дальность.
Задача заключается в определении такого оптимального закона управле¬
ния параметром подъемной силы Хопт, который обеспечивает максималь¬
ное значение функционала (9.34) при начальных условиях
0 “ 00/ ? = ?0 = 0/ О? = О?0/ У= Уо
и конечных условиях
0 = 0Kz f=^K/ CO = GJR.
Составим гамильтониан
1//1COS0 i//2sin0 ^з(л~ 1+Х")
сК = — —-
соХ X X
(9.65)
Сопряженные переменные Фз определяются вспомогательными
уравнениями
dxpt dJC d\p2 i//icos0
dO d0 dco co2 X
cf&3 _ dJf _
d6 ’ bV ~
(9.66)
Оптимальным является такое управление Хопт, которое в каждый мо¬
мент времени обеспечивает минимум гамильтониана (9,65) .
Первое и третье уравнения системы (9.66) имеют следующие интегралы:
- const, ф3 = const.
Из условия стационарности гамильтониана будем иметь
Ф1COS0
со
- i//2sin0 = (п - 1 )«р3[ 1 - (Хопт)"].
(9.67)
Дважды дифференцируя уравнение (9.67) и учитывая (9.64), получаем
[120]
0isin0 t л с/(Хопт)”
—— +i//2cos0 = (n- 1)i//3 — ' (9.68)
, .1( </2(Х°ПТ)" , . п ф1С05в
(/7 — 1)^'з Т + l//2Sin0
d2e о
W2 (ХОПТ)1/и °’
(9.69)
266
Решая совместно уравнения (9.67) и (9.68) , будем иметь
(n-1)!sin0 -(X°"T)"+[1 - (XonT)"]cosflL
(9.70)
= (п- 1
dO
1 _d(XonT)"
dO
(9.71)
где е = Ф1/Ф2 = const.
Подставляя уравнения (9.70) и (9.71) в уравнение (9.69), получаем сле¬
дующее нелинейное дифференциальное уравнение второго порядка для
оптимального закона управления:
е
- П~\: (sing d(X°n--^ + [1 - (XonT)n]cos6>l . (9.72)
(Лопт)1/"1 de I
Уравнение (9.72) интегрируется в квадратурах при свободной конечной
дальности полета КЛА- В этом случае Ф1 = е = 0, а оптимальный закон
управления будет иметь вид
(Хопт)” = 1 + asin0,
где а = const и определяется из граничных условий по высоте или скорос¬
ти. Интегрируя второе уравнение системы (9.64) получаем
ок
Дсо = СОК - GJ0 = —f
00
—s-^-—de.
(1 + asin0)1/n
(9.73)
Отсюда можно найти величину постоянной а. Ее знак определяется следую¬
щим образом. Если подъемная сила положительна, то траектория полета
КЛА выпукла вверх и угол наклона траектории 0 увеличивается. Если
подъемная сила отрицательна, то траектория вогнута вниз и угол 6 умень¬
шается. Если параметр подъемной силы X меняет знак, то траектория
имеет точку перегиба. В этой точке sin#* = — 1/а.
Принимая во внимание, что маневр выведения КЛА на орбиту ИСП со¬
вершается практически при малых углах наклона траектории к местному
горизонту, можно аппроксимировать уравнение (9.73) следующим соотно¬
шением:
(п — 1)(2 — 1/л)а2До; = ±[п — (п - 1 )адк](1 + аОк)1~1!п -
(п- 1 )а#0](1 +а<90)1_1М,
где знак "минус" соответствует траектории с точкой перегиба, а знак
"плюс" — траектории без точки перегиба. Так, для п = 2 постоянная а
определяется из уравнения четвертого порядка
(81/16) Да/а4 - (9/12)До?(02 + 0з)дз +
+ [(27/2)До>2(02 + 0g) + (0к - 0о)2]а2 -
-6(02 - 0§)(02 - 0о)а —36Да>2 +9(02 - 0J)2 =0.
267
Рис. 9.4. Зависимость Дсо= со0 — сок от угла наклона траектории 0К при оптимальном
управлении для различных значений константы а.
Некоторые результаты решения вариационной задачи о максимуме ко¬
нечной скорости вылета КЛА из атмосферы приведены на рис. 9.4 [120].
Начальный угол входа КЛА в атмосферу Земли принимался равным
Оо =-10°.
Видно, что пространство допустимых оптимальных траекторий полета
КЛА разделено на две области А и В кривой MN. Оптимальные траектории,
лежащие в области А, не содержат точек перегиба. Траектории же, лежащие
в области В, содержат точки перегиба, по которым и происходит пересече¬
ние оптимальных траекторий с кривой MN. Проведенные численные расчеты
показали, что существуют две оптимальные траектории с различными ви¬
дами управления подъемной силой, обеспечивающие одну и ту же макси¬
мальную конечную скорость. На одной из траекторий точка перегиба отсут¬
ствует, и полет протекает с большим значением коэффициентов подъемной
силы и силы лобового сопротивления. Это позволяет КЛА за более корот¬
кий промежуток времени осуществить пролет плотных слоев атмосферы
планеты. Полет по траектории, содержащей точку перегиба, протекает с
меньшим коэффициентом подъемной силы, что приводит к большему вре¬
мени полета КЛА в атмосфере.
В качестве примера на рис. 9.5 представлена зависимость величины
d = п^т axkj (Ц>/Ук) от конечного значения угла наклона траектории
полета при оптимальном управлении для различных значений До; (выведе¬
ние КЛА осуществляется на орбиту ИСЗ) [120]. Когда конечная высота
полета в атмосфере больше или равна начальной (Дсо < 0) , существует
268
единственное значение угла 0Kl при котором потери скорости на оптималь¬
ной траектории минимальны. Это значение определяется соотношением
da _ d Г 0К п + asinfl
c/0K ^KL (l+asinfl)1/"
ао
(9.74)
Учитывая (9.73), получаем
da
(1 +as\ne)1 + lfn
п
(1 + asin0K)x^
(9.75)
f
00
После несложных преобразований уравнения (9.75) находим
sin 0К = — 1 /а = sin0* .
(9.76)
Зависимость (9.76) показывает, что оптимальный угол наклона траекто¬
рии в конечной точке, обеспечивающий абсолютный минимум потерь ско¬
рости для каждого значения Дсо < 0, равен значению угла 0К = 0*, при ко¬
тором точка перегиба совпадает с конечной точкой.
Когда конечная высота меньше начальной, существуют относительный
максимум и относительный минимум потерь скорости. Максимум имеет
место в том случае, когда осуществляется переключение с оптимальной
Рис. 9.5. Зависимость отношения скоростей от конечного значения угла наклона траек¬
тории 0К при оптимальном управлении [d= nKmaxlg (^о/^к) 1 •
269
Оптимальные траектории, найденные выше из условия минимума потерь
скорости, не учитывали возможные ограничения на величину подъемной
силы. Рассмотрим методику определения оптимального закона управления
КЛА в аналитическом виде для случая, когда имеется ограничение на
управление
(9.77)
Функция Гамильтона записывается в виде
- (1/0)[(/7 — 1 )(1 + a sin 0) + X”).
(9.78)
Анализ выражения (9.78) показывает, что если начальное значение X
положительно, то существует точка перегиба, в которой X изменяет знак
на отрицательный. Поскольку переменная 0 заточкой перегиба уменьшает¬
ся, необходимо изменить знак в правой части соотношения (9.78) . Таким
образом, гамильтониан (9.78) достигает минимума при положительном
начальном значении параметра управления X. Характер изменения функ¬
ции в зависимости от X показан на рис. 9.6. Абсолютный минимум дости¬
гается при значении управляющего параметра X = (1 + a siп0) 1/и.Эта кри¬
вая асимптотически приближается к кривой JC = X"-1 для КЛА, поляра
которых имеет показатель степени п> 1.
Характер оптимального изменения параметра управления Хп = 1 +а sin0
в зависимости от угла наклона траектории 0 для положительных значений
константы а показан на рис, 9.7. Зависимость Xй (0) пересекает прямую
“ \пах не более чем в одной точке, находящейся между значениями
Хо и Ак- В этом случае точка перегиба отсутствует. Таким образом, на
оптимальной траектории управление, удовлетворяющее условию (9.77),
состоит из участков переменного (Xvar) и ограниченного (Xmjn) управле¬
ний. Для расчета постоянной а и угла наклона траектории 0Sf при котором
происходит переключение режимов управления, используется соотношение
Хщах 1 +asin0. (9.79)
Интегрируя второе уравнение системы (9.64) в пределах от 0О до 0S при
оптимальном управлении (9.79), получаем значение высоты cos, на которой
осуществляется переключение режимов управления:
Рис. 9.7. Характер оптимального изменения параметра управления Кп в зависимости от
угла наклона траектории 0 (а > 0) . °
270
(9.80)
Рис. 9.8. Структура оптимального управления при а < О.
Рис. 9.9. Структура оптимального управления при а < О и 0К < О.
Если это же уравнение проинтегрировать в пределах от 6S до вк при X
= Хтах, то будем иметь
Ык-Ц = (cos вк - COS 0s)/Xmax •
Итак в момент переключения режимов управления можно рассчитать
с помощью уравнений (9.79) - (9.81) значения постоянной а, угла tis и
ВЫСОТЫ
Если принять допущение о малости угла наклона траектории к местному
горизонту, то тогда из уравнений (9.79) - (9.81) получим следующие
формулы, характеризующие параметры оптимального управления в точке
переключения с X = Xvar на X = Хтах.
= 1X2/7 — 1)а2] {[/7 -(/7-1)а0,](1+а0/ 1/и-
- [л - (п - 1)а0о]1 _i 1п ) - (9-82)
сок — = (0$ ~ .
Для КЛА, у которого зависимость сх от су описывается параболой (л-
= 2), уравнение (9.82) будет уравнением четвертой степени относительно
постоянной а.
Рассмотрим структуру оптимального управления при отрицательной ве¬
личине постоянной а. Характер изменения управляющего параметра X” от
угла наклона траектории в для этого случая показан на рис. 9.8. Видно,
что кривая Xй (0) пересекает линию Х = ХДх в одной точке. На оптималь¬
ной траектории может существовать точка перегиба, так как X может при¬
нимать нулевое значение. Последовательность оптимального управления
при 0К > 0 , следующая :
X = Хтах X = Xvar.
Для получения постоянной а, угла 0, и высоты a)s в момент переключе¬
ния режимов управления проводится интегрирование второго уравнения
системы (9.64) в пределах от 0О до 0, при X = Хтах, а затем в пределах от
0, до 0К при оптимальном переменном управлении (9.79).
Для малых углов наклона траектории к местному горизонту будем
иметь следующую систему уравнений для параметров оптимального
271
управления:
Amax = 1+a0s, ws-w0 =(0o -^)/2Лтах,
Wk -ws= [n/(n-1)(2n-1)a2]{+[n-(n-1)a0K. ] (1 +а0к )1-1/»_
(9.83)
-In (n - 1 )a0s] [1 +30J1-1/"}.
Знак "плюс" в третьем уравнении системы (9.83) соответствует оптималь¬
ной траектории, не содержащей точки перегиба. Для параболической поляры
(л-2) третье уравнение системы (9.83) является уравнением четвертой
степени относительно постоянной а. При отрицательном значении постоян¬
ной а может оказаться, что граничные условия и значения Хтах будут та¬
ковы, что 6К < 0s. Этот случай изображен на рис. 9.9. Как видно, на кривой
оптимального управления имеется точка перегиба, а последовательность
участков полета с X = Xvar и X = Хтах следующая:
Х ~ Хтах = \/аг ”*■ ^ = Хтах . (9.84)
Оптимальные параметры управления для последовательности (9.84)
рассчитываются интегрированием второго уравнения системы (9 64)
Учитывая предположение о малости угла наклона траектории к местному
горизонту, получаем следующую систему дифференциальных уравнений:
^тах ~ 1 + a 6S, - О>0 = (0§ -02)/2Хтах ,
WJ2 = —[2л/(л —1)(2л — 1)а2] [л —(л — 1)a0J (1 +ав!!)1-11п1
wsl - = (02 - 0>)/2Хтах , (9-85)
(9.86)
режимов управления°°риГэ JO)*™ ПбРВаЯ И ВТорая ВЬ1СОТЫ, переключения
Щим°оСбр«омЮ[120]°:ЖНО °ПРвДеЛИТЬ И3 СИСтемь| Уравнений (9.85) следую-
a = (1 -n>Xmax + 2(2л - 1 )X”max + (Л - 1 )(2л - 1)'
(л - 1) (2л - 1) (0g + 02 2Х До)
Зная величину а, определенную с помощью (9.86), можно рассчитать пара¬
метры оптимального управления 0ir wilr Р
Таким образом, выше представлено аналитическое решение задачи
КЛА Н3 °РбИТУ ИСП С максимальным значением величины
характеоные^Е^Гг ПРИ Нулевом значении угла курса (^ = 0). Показаны
характерные свойства оптимальных траекторий в общей форме с примене¬
Рис. 9.10. Оптимальная траектория с двумя переключениями режимов управления
272
нием обобщенной поляры. Оказалось возможным получить оптимальный
закон управления в замкнутой форме при свободной дальности полета.
Для этого закона управления установлено существование двух классов
оптимальных траекторий с различными стратегиями управления: класса
траекторий с использованием большой подъемной силы (а следовательно,
и большого аэродинамического сопротивления), обеспечивающих вы¬
ведение КЛА на орбиту ИСП за меньшее время, и класса траекторий с ма¬
лым углом атаки (для поддержания малого аэродинамического сопротив¬
ления) , но требующих большого времени для достижения тех же конечных
условий.
Показано, что для достижения максимальной конечной скорости закон
управления определяется однозначно, если известны начальные и конеч¬
ные значения высоты и угла наклона траектории к местному горизонту.
При наличии ограничения на величину подъемной силы и свободной даль¬
ности полета число переключений режимов управления на оптимальной
траектории не превышает двух, а ограничение на управление существует
всегда на концах оптимальной траектории.
§ 9.4. Влияние гравитационной и центробежной сил
Выше были приведены результаты решения задачи максимизации конеч¬
ной скорости КЛА, выводимого на орбиту ИСП, в предположении плоской
и невращающейся планеты, а также при допущении, что аэродинамические
силы намного превосходят по величине гравитационную силу. С исполь¬
зованием угла наклона траектории к местному горизонту в качестве неза¬
висимой переменной и преобразования остальных переменных состояния
показано, что уравнения движения представляют собой явную функцию
только параметра управления X и угла наклона траектории 0. При этих
предположениях множители Лагранжа постоянны на траектории дви¬
жения в атмосфере.
Функциональная фо0ма параметра управления для КЛА, имеющего
параболическую поляру, достаточно проста:
X = ( 1 +3i sin 0)1/2.
Для определения постоянной ai из условия выполнения требуемых значе¬
ний конечной высоты и угла наклона траектории к местному горизонту
необходимо в общем случае решать уравнения, содержащие эллиптичес¬
кие интегралы. При этом оказалось, что для траекторий движения КЛА в
атмосфере, для которых допустимо предположение о малости угла 0
sin 0^0, cos 0^1, (9.87)
постоянная ах может быть вычислена аналитически.
Без введения каких-либо новых дополнительных предположений эти
результаты могут быть расширены и для пространственного случая (с
учетом достижения в момент вылета КЛА из атмосферы заданного значения
угла курса). В этом случае, как было показано, движение КЛА зависит от
явной функции управляющих параметров X и у и от угла наклона траекто¬
рии 0 таким образом, что множители Лагранжа остаются постоянными
вдоль оптимальной траектории его полета. Оптимальный закон управления
по углу крена для КЛА, имеющего параболическую поляру, записывается
в виде
sin у = a2/X2cos 0. (9.88)
Параметр X определяется уравнением (9.79), а постоянные а^ и а2 нахо¬
273
18. Зак. 2069
дятся из условия совместного решения двух уравнений, содержащих эл¬
липтические интегралы. Для малых значений 0 можно получить решения
в явном виде.
Проведенные исследования показали, что оптимальные законы управле¬
ния справедливы для КЛА с большими значениями аэродинамического ка¬
чества или для траекторий с малыми углами наклона к местному горизон¬
ту. В других случаях, представляющих интерес для разработчиков КЛА
(например, для КЛА с малым значением аэродинамического качества,
для планет, обладающих значительным гравитационным полем, и т.д),
могут возникать большие ошибки при использовании приближенных
решений по сравнению с точными численными решениями.
Приведем аналитические решения задачи максимизации конечной ско¬
рости вылета КЛА из атмосферы с учетом влияния гравитационной и цен¬
тробежной сил на траекторию для плоского и пространственного случа¬
ев [139].
Запишем уравнения движения КЛА в трехмерном пространстве в ат¬
мосфере сферической невращающейся планеты в следующем виде:
do
dt
dV
dt
V cos 0 cos ф dx
(Rq +/7) sin к ' dt
X go Ro sin 0
" (RQ +A)2
V sin ф cos 0
Ro +h
d0 Ycos 7
dt mV
dh
= V sin 0,
dt
V goRlcos0
Ro+h V(RQ+h)2p
d$ = У sin 7 V cos 0 sin ф ctg к
dt mV cos 0 Ro +h
(9.89)
где о — продольная угловая дальность полета, к — боковая угловая даль¬
ность полета.
Перепишем уравнение для 0 из системы (9.59) в виде
d0 /cvscos7
— = pV[^
dt \ 2m
9gRq \
V2(R0+h) )
COS 0
p(Ro + h}
Результаты численного моделирования показывают, что величина Мнечув¬
ствительна к интегрированию по рили по 0 и поэтому может рассматри¬
ваться как постоянная. Введем следующие допущения:
будем считать, что величинар0 sin 0 существенно меньше величины
Х/т и поэтому ею можно пренебречь;
V cos 0 sin ф ctg к
величина —— - существенно меньше единицы и ею также
Ro +h
можно пренебречь.
С-учетом сделанных допущений уравнения движения КЛА (9.89) прини¬
мают следующий вид:
dV _ cxV2s
dt 2jd
d0 / cvs cos 7
=pvl -y- -
dt \ 2m
dh
= V sin 0,
dt
d\jj
dt
p VCyS sin 7
(9.90)
2m cos 0
274
Здесь величины продольной и поперечной угловых дальностей считаются
свободными, в уравнения движения не включаются и в следующем ниже ана¬
лизе не рассматриваются.
Проведем преобразование переменных состояния:
h
РоРсуЗе л
- „ / СУ \,
/ V \
V =— ,
СО =
У =21 — 1
п —— ,
(9.91)
Р
2т
\c‘J
\ /
где со — безразмерная высота, V — безразмерная скорость, сх и су — коэф¬
фициенты силы лобового сопротивления и подъемной силы, соответствую¬
щие максимальному аэродинамическому качеству. Используя второе урав¬
нение системы (9.90), заменим независимую переменную t на в. Тогда с
учетом (9.91) получим уравнения движения (9.90) в виде
dV
2с х
da>
Те
С* | —— cos у + М )
\ с* /
~d6
sin в
cos
d\p
СУ
dO
су cos у + /И sin у cos в
где
2тМ
M =
CyS
(9.92)
9
Видно, что уравнения (9.92) являются явными функциями управляющих
параметров су и у и независимой переменной 0. Важно отметить, что угол О
не является монотонной функцией, и поэтому необходимо проводить спе¬
циальные исследования при переходе через точки, где угол 0 меняет знак
(точки перегиба).
В общей формулировке задача состоит в нахождении таких программ
управления подъемной силой су и углом крена у на интервале О Е (0О, дк),
которые максимизировали бы функционал = VK при условии вы¬
полнения уравнений движения (9.92) с заданными начальными и конеч¬
ными условиями и при ограничениях на управления
Cymin Су Сушах • 7m in 7 7тах*
Запишем гамильтониан системы (9.92) в виде
iZ/iCySiny сх
' / - - Фг sin в - 2 —
Ср cos 0 сг
X = —У
Су -
cos у + М
Су
и расширенный функционал в виде
/ — ! J + к £2 .
Здесь множители Лагранжа Фз суть сокращенные переменные сис¬
темы (9.92) . Вектор-строка к множителей Лагранжа связана с конеч¬
ными ограничениями уравнением
(0К), оЯ0к ), Ф(ок), ек ] =о. (9.93)
275
(9.94)
Уравнения Эйлера — Лагранжа запишутся следующим образом:
_ Э5С _ Э5С _ дф3 _ Э5С _
dO дф ' dO да) ' dO ди
Из рассмотрения уравнений (9.94) ясно видно достоинство применяемо¬
го преобразования уравнений движения КЛА, а именно: множители Ла¬
гранжа постоянны вдоль оптимальной траектории движения. Условия транс
версальности в конце траектории выведения запишутся в виде
ЭФ ЭФ
v/1(0k) =
Эф
0=0К’
Ф2(0К ) =
Эсо
ЭФ
ЭФ
Фз (0к )
=
, JC(0K) =
—
Э1/
0 = 0К
де
(9.95)
Если управляющие параметры су и у лежат внутри допустимой области
управления, то необходимые условия оптимальности можно представить
следующим образом:
Э5С дМ
= 0, = 0.
дсу Э cos у
Раскрывая (9.96), получаем:
(9.96)
Ф ! sin у
cos 0
ф2 sin в cos у + 2ф3
cv dcY
— cosy-
сх дсу
После несложных • преобразований из
получить уравнение, связывающее угол
фициентами:
(9.97)
21//3сл
2 sin 0 + = 0. (9.98)
С*х
уравнений (9.97) и (9.98) можно
крена с аэродинамическими коэф-
с*
sin у = ф, —- . (9.99)
Эс\.
2ф3 Су cos О
дсу у
Подставив уравнение (9.99) в (9.97), будем иметь
-/ дсх с* М/2 1
±М\21 cos0 ^3-^1) - =
\ д cv сх / cos#
, / дсх \ 1
= ^2 sin(9 + 2ф3[сх-су ) — .
\ У дсу ) (9.100)
Введем в уравнения (9.99) и (9.100) две новые постоянные: фх = Ф1/ф3 и
Ф2 — Функциональную зависимость между коэффициентом силы
лобового сопротивления и коэффициентом подъемной силы представим
в явном виде
С.х = сх0 + кСу , п > 1.
276
В общем случае анализ оптимального управления можно проводить
для произвольного п, однако для удобства мы в дальнейшем ограничим¬
ся случаем /7 = 2. Как и ранее, будем использовать в качестве переменной
управления параметр
/
Коэффициенты подъемной силы и лобового сопротивления запишутся сле¬
дующим образом:
1
су=с*к c^ycJd+X2),
(9.101)
где
«2
= 2сх .
хо
(9.102)
Уравнение (9.100) перепишется в виде
± М (4X2cos20 — i//1) sin 0 + (1 - X2 ).
cos 0
Отсюда получаем выражение для оптимального значения управляющего
параметра Хопт [139]
Х°пт
(-М +11!2)2 - —
4 cos 0
1/2
(9.103)
где
/ = М2 + ф2 sin 0 + 1 — Ф1 77" •
4 cos 0
Используя зависимости (9.101) и (9.102), получим из уравнения (9.103)
выражение для оптимального значения угла крена
sin-уопт = ] (9.104)
2Х cos0
Видно, что полученные выражения для оптимальных законов управле¬
ния (9.103) и (9.104) определяются двумя сопряженными переменными
i//i и ф2 и углом наклона траектории к местному горизонту 0 . Причем
величина sin у в уравнении (9.104) обратно пропорциональна управляю¬
щему параметру X. Это означает, что X = 0 в том случае, если константа соп¬
ряженной переменной ф1 = 0. Постоянные и ф2 определяются из усло¬
вий (9.93) и (9.95).
Проинтегрируем уравнения движения КЛА (9.92) с учетом выражений
(9.103) и (9.104). Получим конечные значения параметров движения
V, со и ф при 0 = 0К :
— — 0 к/ — —2 1 \ dO
vteK)-v{e0) = 2M(eK-e0)+f ± f h+M2+i + ^ -—-
о0 о* \ 4cos0/
1
со(0к ) -со(0о) = + f ±f ——sin0<70,
0 о 0*
277
0*
1
(9.105)
Ф, — dO.
2\/Гcos20
0*
Ф(ок)-Ф(е0} = ±/
е0
Если величина I в уравнениях (9.105) приближается к нулю, то это озна¬
чает, что угол наклона траектории к местному горизонту 0 принимает
экспериментальное значение 0* (т.е. достигается точка перегиба). Поэтому
в интегралах (9.105) интервал интегрирования разделяется в точке переги¬
ба. Выражения для конечных значений параметров движения КЛА (9.105)
сводятся к табличным эллиптическим интегралам. Для траекторий движе¬
ния в атмосфере с малыми углами в, для которых справедливо допущение
cos 0~1 и sin 0^0, выражения (9.105) могут быть проинтегрированы в
конечном виде [139] :
_ _ 2
V (0К )-U(0o)=+ v
i//2
+
(9.106)
±
±(2ф20о -4ЬН<Мо +6)1/2 -X
3^1
1
зП.
(9.107)
знак, если
-О 1 -о 1
где a=/W2+1+i//2 — , Ь = М2+1— ф^ — .
4 4
Правые части уравнений (9.107) имеют положительный
величина 0 возрастает, и отрицательный, если 0 уменьшается на траектории
спуска. Знаки "плюс — минус" перед вторыми членами во втором и третьем
уравнениях (9.107) показывают наличие точки перегиба. Если точка пере¬
гиба существует, то используется знак "плюс", если такая точка отсут¬
ствует, то применяется знак "минус". Сочетания различных комбинаций
знаков могут привести к четырем различным действительным значениям
постоянных , i//3 и 0К, для которых удовлетворяются граничные ус¬
ловия и условия трансверсальности. Граничные условия могут быть запи¬
саны в виде функций указанных постоянных [139].
В результате получим четыре нелинейных условия, которые удовлет¬
воряются четырьмя константами фх, ф2 • Фз и 0К. Нормализуя величины ф{
и ф2 можно уменьшить число постоянных до трех:^ , ф2, Фз-& общем слу¬
чае для их определения необходимо решать нелинейные алгебраические
уравнения. При этом могут получиться четыре различных действительных
значения постоянных. Одно из них будет обеспечивать глобальный макси¬
мум (наилучшее значение рассматриваемого функционала Уктах). Другие
решения будут определять либо локальный максимум, либо экстремаль¬
ные траектории, которые не удовлетворяют необходимым условиям второ¬
го порядка (нарушается условие Лежандра — Клебша или критерий Якоби
в точке сопряжения) .
В рассматриваемой задаче максимизации конечной скорости выведе¬
ния КЛА на орбиту ИСП величина сопряженной переменной ф3 = 1. Поэто¬
му задача заключается в определении двух постоянных фг и ф2 из уравне¬
ний (9.107) . После этого можно получить программы оптимального управ¬
ления из уравнений (9.108) и (9.104), а величина приведенной конечной
278
скорости при оптимальном управлении определяется первым уравнением
системы (9.107).
Отметим, что форма выражения для оптимального управления углом
крена у зависит от конкретной аппроксимации управляющего параметра
X (9.103) . Для аппроксимации первого порядка будем иметь для X выра¬
жение [см. (9.79) ]
Х = ± ( 1 + ^2 sin 0)1/2.
Управляющий параметр X изменяет знак в точке перегиба угла наклона
траектории в.
Проведенные исследования показывают, что в тех случаях, когда на
управляющие параметры X и 7 накладываются ограничения, множители
Лагранжа остаются постоянными при движении КЛА с граничными зна¬
чениями управлений. Действительно, если угол крена является гранич¬
ным (7гр), то управляющий параметр X для КЛА, имеющего параболи¬
ческую поляру, будет равен
М / М2 _ _ М \1/2
X = ± ( - + 1 + 02 sin & + Ф1 7гр ) • (9.108)
cosyrp \ cos27rp cos(7 '
Подставляя X из (9.108) в уравнения движения (9.92), получаем алгеб¬
раические уравнения для определения конечных значений параметров дви¬
жения КЛА. Для малых углов наклона траектории они могут быть проин¬
тегрированы в конечном виде, т.е. можно получить решения, аналогичные
уравнениям (9.107). Если значение коэффициента подъемной силы ограни¬
чено, то управление по углу крена, определяемое уравнением (9.99), за¬
пишется следующим образом:
C0S7= (-/WcJP ± >4 [ Д2+Л42—(СуР)2 J 1/2! 1-2- , (9.109)
( л ) М + А
причем 1
А = (02 sin^ + 2*с^р ) cos 0, (9.110)
где <р — величина отношения су!с^, соответствующая граничному значе¬
нию су, а СдР — значение отношения схГс£, соответствующее граничному
значению сх. Подставляя выражения для cos 7 в уравнения движения
(9.92), получаем интегралы, которые даже для малых значений угла накло¬
на траектории к местному горизонту будут иметь очень сложный вид.
Используя в качестве независимой переменной не угол 0, а угол крена
7, можно существенно упростить эти интегралы. Действительно, из уравне¬
ния (9.109) для малых значений 0 получим следующее дифференциальное
соотношение между 0 и А :
1
d0 = dA —— . (9.111)
Используя уравнение (9.98) и определение величины А из (9.110), можно
найти зависимость между параметром А и углом крена у в виде
А-( М cos 7 + с£р) . (9.112)
sin 7
Учитывая соотношение (9.111) и используя уравнение (9.112), будем иметь
d0 = — | 01 (cfp cos 7 + М ) — -— I dy. (9.113)
L 02 sin2y J
279
(9.113) уравнения движения (9.92)
С учетом выражений (9.111)
перепишутся в виде
dV
— =2ф1С^
dy
1
1Д2 sin27
doo _ 1 _ 1
—— = 0? (Mcos 7 + с£р )-=у—Т~ - 20 1 р — ,
dy 02 sin 7 02 sin27
(9.114)
d0 _ 1
= -сгр 0] -■ cosec7.
</7 02
Уравнения (9.114) легко интегрируются в конечном виде:
1/(0к)
— 0 I
V(0o) =-2-£0
02
1 I
Л(Як)
СИ)
= f* (3)
си»
Л(0о)
01 ( - Г 1
о>(0к)-о>(0о) =-=- 01c£pln SH)
20и у L 1+cw)
(9.115)
-0! {М + стрС{А) ]—!— + 4с£рСИ) —— ]
У СИ)2 СИН
= f2(0)
(О.,)
<>«
<>«
W - 0(0о) = -4^ Сгур In(sM)- -1 )
02 I [1 + СИ)])
■4(0к)
^3(0)
>4 (<?„ )
«к
0„
где
S(A) = sin7=M<p ±М[А2 +М2 - (с’.1’)2] ,/2} .
• М2 +А2
(9.116)
а С (А ) = cosy и определяется уравнением (9.109).
Уравнения (9.115) и (9.116) справедливы для траекторий, у которых
отсутствуют точки перегиба. Точки перегиба имеют место, когда подкорен¬
ное выражение в уравнениях (9.109) стремится к нулю, т.е.
Д2(0.) = (<р)2-М2. (9.117)
Здесь 0* — значение угла наклона траектории в точке перегиба. Его можно
определить, если воспользоваться уравнениями (9.110) и (9.117). Для
траектории, на которой имеется точка перегиба, получим из уравнений
движения (9.114)
viej - viol}) = 2f} io j - [г, (ej+ft юл,
со(в к) — со(0()) = 2f2 (0 J - [Л(0К) +Л(^о)],
Ф (0к) -Ф(0„) = 2ме.) - [f.Aej+f.io»)]'
где fj(O) — правые части уравнений (9.115) .
Некоторые результаты сравнения приближенной оптимальной траекто¬
рии, найденной по приведенным аналитическим зависимостям, сточной
оптимальной траекторией приведены на рис. 9.11—9.15 [139]. В [139] рас¬
сматривалась задача максимизации конечной скорости при конечных огра¬
ничениях на высоту и угол наклона траектории для КЛА, выводимых на
280
Рис. 9.11. Зависимость параметра М от скорости полета V.
Рис. 9.12. Зависимость угла атаки а от угла наклона траектории к местному горизон¬
ту 6 (сплошная линия — точный численный расчет ^штриховая — приближенный рас¬
чет, штрих-пунктирная — приближенный расчет при М = О) .
орбиту ИСЗ (нагрузка на несущую поверхность mg/S = 300 кгс/м2). Управ¬
ление КЛА осуществлялось путем изменения угла атаки при нулевом значе¬
нии угла крена. В точных и в приближенных расчетах оптимальной траекто¬
рии использовались аэродинамические характеристики КЛА, приведенные
Рис. 9.13. Зависимость угла атаки а от скорости полета V обозначения те же, что на
рис. 9.12).
Рис. 9.14. Зависимость высоты h от скорости полета V (обозначения те же, что на
рис. 9.12) .
281
Рис. 9.15. Зависимость угла наклона
траектории в от скорости полета V
(обозначения те же, что на рис. 9.12).
на рис. 9.16. Начальные условия входа КЛА в атмосферу Земли принима¬
лись следующими: VQ = 10351 м/с, в0 =- 1,57°, Ло = 58 км.
Приближенное решение задачи определения оптимальной траектории
проводилось по описанному выше методу с учетом.влияния параметра М
(см. рис. 9.12 — 9.15). Представленные зависимости показывают, что
приближенная оптимальная траектория хорошо согласуется с точной опти¬
мальной траекторией.
Сравнение приближенных программ изменения угла атаки а от угла 0 с
точной оптимальной траекторией приведено на рис. 9.12. Видно, что
наибольшее отличие приближенного управления углом атаки от точного
достигается вблизи точки перегиба кривой а(0). Для рассматриваемых
приближенных и точной оптимальной программ управления на рис. 9.14 —
9.15 приведены зависимости высоты и угла наклона траектории от скорос¬
ти, которые показывают, насколько приближенная траектория близка к
трчной в фазовом пространстве. Видно, что траектории, полученные для
/И = 0, значительно отличаются от точного решения всюду, кроме граничных
участков. Отличие в конечной скорости не превышает 6 м/с для описанного
приближенного метода и не превышает 24 м/с при М = 0.
§ 9.5. Максимизация конечной скорости при произвольном законе
изменения плотности атмосферы
Рассмотрим возможность получения аналитического решения задачи
максимизации конечной скорости в предположении, что гравитационное
поле планеты центрально, а плотность атмосферы является произвольной
функцией высоты. Будем использовать метод стыковки асимптотических
разложений [136]. Траектория движения КЛА в атмосфере рассматривает¬
ся в двух областях — внешней (кеплеровой) и внутренней. Во внешней
области преобладают гравитационные силы, а во внутренней — аэродинами¬
ческие. В каждой области получаются аналитические решения в замкнутой
форме, после чего строится общее решение, пригодное для обеих об¬
ластей.
282
Запишем уравнения движения КЛА в атмосфере планеты в следующем
виде:
dV
= - (2e)~1cxpV2 — (1 +/7)'2sin0,
dt
c(0 . o n dh
— = (2e)"1cvpV'+[(1 +Л)"1 - (1+Л«)”2\Л2] VcosO, Usin0.
dt y dt
Плотность атмосферы предполагается произвольной функцией высоты,.
так что
f(e,h)
p=p(0)f(ez/?)>0, lim 0.
€-*о е
Будем предполагать, что управление КЛА Осуществляется путем изменения
угла атаки, который входит в выражения для коэффициентов подъемной
силы су =су(а) и силы аэродинамического сопротивления сх =cXq + т)с2(а)
(сЛо и rj— постоянные). Начальные условия движения КЛА в момент tQ
считаются заданными, г.е. при t= tQ
V=V0, 0=0О, h=h0. (9.118)
В конечный не фиксированный момент времени tK на заданной высоте Лк
задан угол наклона траектории к местному горизонту 0К, т.е. при t = tK
6=eKf h=hK. (9.119)
Задача заключается в отыскании такого закона управления, при котором
максимизируется конечная скорость или, что то же самое, минимизируется
энергия, потерянная КЛА на участке движения в атмосфере. Запишем
гамильтониан приведенной системы дифференциальных уравнений в виде
JC = ^v[-(2e)~1cxV2p- (1 +A)'2sin0] +
+ $в {(2e}~1cyVp + [(1 +ЛГ1-(1 + Л)'2 I/-2] l/cosfl} +^hVsine.
Из условия максимума гамильтониана по управлению а определим
оптимальное соотношение для величины коэффициента подъемной силы
[136]
. кУфв
Су(а) = —— ,
у Фу
где к = (2т?)'1 •
Учитывая,что время полета свободно, а гамильтониан на оптимальной
траектории постоянен, получаем
JC = O. (9.120)
Из условий трансверсальности будем иметь для сопряженной переменной
V/K=1. (9.121)
Принимая в качестве независимой переменной высоту полета КЛА
запишем систему уравнений для фазовых координат и множителей Лагран¬
жа в следующем виде:
283
de
, 1
(2e) lcyp—-
+ [(1 +Л)-1
- (1 + h)’2 U’2]
I ctg0.
dh
sin0
d^y _
1 Э5С
d^e
1 dJC
dh
Usin0 bV
dh
l/sin# be '
dh
I/sin# bh
(9.122)
1
Таким образом, задача оптимального управления сведена к решению
системы дифференциальных уравнений (9.122) и уравнения (9.120) с крае¬
выми условиями (9.118), (9.119) и (9.121).
Приведем решение задачи в области, где преобладают гравитационные
силы (внешняя область). Запишем фазовые координаты и множители
Лагранжа в виде
2' = 20(Л)+ег1(Л) +О(е2), (9.123)
где через Z обозначены параметры V, #, фн, фу, фв. Для нулевых членов
разложения получим следующие уравнения:
dV0 VQ deQ л о
dxb у
—^Г=-—Т - Фе, К1 +Л)"1 +(1 + Л)’2 Ко2 ] К1 ctg0o,
ап 1/0
<^о фу ctg#0
~dh~= й~+'а)2у0 ctg0° +V/e»[(1 +h}~l~(1 +h}~2 (9’124)
d^h 2фу г 1
dh (1+Л)31/0 Ч(1+Л)2
(9.125)
Wo sin0o~^ + h}2 + 1 — (1 +Л) 2 V"2 ] l/ocos0o +
+ Фи„ Vosin90 =0.
Интегрирование первых двух уравнений (9.124) дает
_ 2
У о - = Si, (1 +Л) VqCOS0o =В2. (9.126)
1 + h
Для остальных трех уравнений системы (9.124) получим интегралы
Фе0 =#з I tg0o I =±£3tg0o,
, _ 1 1
Фи = + B3h r- + S4 -
(1 +Л)2 4(1 +Л)2
(9.127)
+
1 + h
4
Верхний знак в уравнениях (9.126) - (9.127) соответствует положитель¬
ному значению угла наклона траектории 0О, а нижний — отрицательному.
Величины Bi —В5 являются постоянными интегрирования. Связь между
этими постоянными может быть получена путем подстановки уравнений
(9.127) в уравнение (9.125):
В3 — Bi (В3— В$) — В5 =0.
284
Начальное значение сопряженной переменной
в виде *
1
Фул = [S3(1 - Уо ) + в4 Vo2 ].
V'o
может быть записано
(9.128)
Уравнения (9.124) не учитывают влияния атмосферы, поэтому они не
могут быть использованы в области полета КЛА на малых высотах, где
аэродинамические силы преобладают над гравитационными. Видно также,
что в полученном приближении первого порядка отсутствует управление
КЛА. Следует отметить, что фазовые переменные и множители Лагранжа,
определяемые во внешней области, оказывают влияние на фазовые пере¬
менные, множители Лагранжа и управление во внутренней области.
Проведем исследование движения КЛА в области, где аэродинамические
силы преобладают над гравитационными (внутренняя область). Запишем
уравнения движения в виде
dV
dt^
V cos 0 *
e2h*2V2 9
dO
dt^
1
1 +e/?*
dh
= V sin 0.
de
Проведем масштабирование гамильтониана и множителей Лагранжа
Представим разложение параметров движения КЛА и сопряженных пере¬
менных во внутренней области следующим образом:
Z = Z$(h*} + eZ*(h*} + О(е2).
Тогда для нулевых членов этого разложения получим следующие уравнения:
dVQ 1 d0Q _ су ^Фу0 »♦ 1
cxpV0 2sjn0o ■ “2sin0o ' dh* СхР 2sin0S '
(9.129)
(9.130)
(9.131)
d^e . . dP
—ctgflj, —JbL = _2<l ;
dh* h° dh* p dh*
3€o =y K0CxpV^2 cyvo + K, Vo si"0o =0.
Оптимальное управление подъемной силой определяется из условия
максимума гамильтониана JTq
с -
у фу„^'
Перепишем систему (9.129) суметом (9.131) в виде
ф*у v;=kC0, ф* =Cop{O)f(h*) = C1f(h*),
к о о
sin 0о =- кС0фд2 + С2, “ Г--
0 2Ct
Ч=±[:
(9.132)
11/2
2Cj (C2-sin0o‘) ,
kCa J
кСа
где Со, Ci, С2 — постоянные интегрирования.
285
133)
Учитывая (9.132), из уравнения (9.130) получим связь между постоян¬
ными интегрирования
C0CiC2 = ккх.
В этом случае оптимальный закон управления КЛА можно переписать
следующим образом:
су = ± I f 1 — sin 0Q
\ С2
Здесь
/2 = kxlk^ =cxJt]>0,
где кх и к^ — постоянные коэффициенты.
Знание конечной высоты полета позволяет определить величину постоян¬
ной С2. В результате получим оптимальный закон управления КЛА в виде
явной функции угла наклона 0q. Подставляя (9.133) в (9.129), получаем
[136]
(9.134)
ff(h*)dh* = + (l——Vh sin 02} 1/2sin0od0o +C4. (9.135)
\ 2kk* J \ C2 /
Уравнения (9.134) и (9.135) могут быть проинтегрированы в эллиптичес¬
ких функциях. В зависимости от знака параметра С2 возможны различные
решения. Рассмотрим каждое из них подробно.
а) С2 > 0. Тогда будем иметь
/ 1 \1/2 1
11 sin 0о = (1 -02sin2i>)1/2, (9.136)
\ С2 / Dj
где
о 1 / я \ /1 \1/2
/З2 = 2(1+С2) >0, p=2(-+0oj, • (9.137)
Из (9.136) и (9.137) видно, что в свою очередь решение а) имеет три
возможных случая, определяемых величиной коэффициентов 0 и С2.
Случай 1:0<1,С2>1. Уравнения (9.134) и (9.135) записываются
в виде
V'o = У0*(Г0)ехр {
0(л*)=0(л;н(-^-]|о1Г(0,0)--|в
\ klk^ /I Dj J ’ 0О
о
Здесь F — эллиптический интеграл первого рода с амплитудой v и модулем
3; Е — эллиптический интеграл второго рода
0(Л*) = -/
286
о
Случай 2: 0 = 1, С2 = 1. Имеем
Vq = Vo (0o)exp [ln(secp +tgi^) + 2sinр]|
g(h*} = g(ho} +(—=; I In (sec v + tgp) - 2sinp] .
X^klk^J ldo
Случай 3: 0 > 1, C2 < 1. Введем следующие обозначения:
1
a = —, sin ip = 0sin0.
0
Тогда решение уравнений (9.134) и (9.135) запишется в виде
Vo* = Vo(to)exp |+ (-^=г^[(2С2 - 1)F(<p, а) + 2E(ip, а)])
<7(Л*) = <7(Л‘) Т (х/С?-)[F(<д а) - 2Е(д>, а)] £ ,
б) С2 < 0. Введя обозначение С2 = — С2 > 0, получим
^о'
(l -sin0o*— Г* =-=~(1 -0 2sin2p)1/2.
\ С2 / О,
D,
в
Здесь
_ /_ 1 \1/2 _ 2
п1=с2—; 0=—
\ 1+С2/ 1+С2
Как и в решении j) , здесь также возможны три случая.
Случай 1: 0 < 1, С2 > 1. Имеем
VJ = VS (to) exp |±-i- [d, F(p70) 4 -J-F(70_) j }
<7(л*) =р(л5) ± ^«0» —■=- f <^0>]
Случай2: 0= 1, Сг = 1. Имеем
Vo* = V0(t0)exp^ ±-^|jn(sec0 + tg 0) + 2sin ,
glh*) =g{hS ) ± ( ) In(sec7 + tg 7) - 2sin v |
\ 2klkv /I Jl0o
1 / 7Г \
»--(7 -«»)•
во
e
e0
_ _ _ 1 -
СлучайЗ: 0 > 1, С2 < 1. Обозначив а =у < 1, sin = 0 sin р, получим
(2С2 -1)F(£a) + 2E(£a)
i/s’,/;i'”iexp{±^b
^0
Условия стыковки частей оптимальной траектории, расположенных
287
во внешней и внутренней областях, могут быть записаны в виде [136]
Vo(0) = Vo* (~) = Bt + 2 = Уоо, 0o(O)=e;(°o) = cos-1
\ ч/Si + 2 /
Здесь I/qq и 0оо соответствуют значениям Уо и 0Q, найденным из раз¬
ложения во нешней области при h = 0. Приравнивая (9.127) и (9.132)
при h -> 0, будем иметь
к
-2(В3 -в4)+в5 = — .
Со
Таким же образом получим
I / sin 0оо \1/2 к 1
5з=-—— |1 —I , = —5-— -e3d - Уо2о > .
C0tg(?oo V / V00C0 Voo
Bs = B3(1
Как показано в работе [136], постоянные внешнего разложения можно
определить через постоянные внутреннего разложения. В результате можно
записать общее решение, справедливое для обеих областей, в следующем
виде:
0С = 0О + 0о* - 0оо + 0(e), Vc = Vo + I/; - VQ0 + 0(e),
1
1 + Л
+
к
С Q vs
1
[—2(S3 -S4)+e5] +0(6),
Vqq
I ( Sin 02 V/2 _
Фес =±S3 tg0o ±— (1 I +£3tg0oo +O(e),
Oq \ C2 J
=^h„ +0<e).
где индексом "с" отмечены параметры на границе внешней и внутренней
областей разложения.
Анализ аналитических зависимостей для оптимальных траекторий, полу¬
ченных с использованием метода стыковки асимптотических разложений,
показывает, что в зависимости от величины конечной высоты возможны
следующие четыре типа управления КЛА в атмосфере:
1) подъемная сила вначале положительна, а затем становится отрица¬
тельной;
2) подъемная сила вначале отрицательна, а затем становится положи¬
тельной;
3) подъемная сила всегда положительна и убывает от максимального
значения в начальной точке до минимального в конечной. Минимальное
значение постоянно, а максимальное значение стремится к бесконечности
при С2 -*0. Учитывая, что в общем случае подъемная сила ограничена не¬
которым максимально допустимым для данного КЛА значением, следует
отметить, что существуют участки траектории полета с граничным значе¬
нием подъемной силы. При С2 -+°° величина максимальной подъемной силы
стремится к своему наименьшему значению, т.е. при больших С2 подъем¬
ная сила практически постоянна на траектории;
288
4) подъемная сила всегда положительна и возрастает от минимального
значения в начальной точке до максимального в конечной. Ее максимальное
значение постоянно. Минимальная величина подъемной силы изменяется
от нуля до наибольшего значения при убывании С2 от sin0o до —°°. Итак,
при больших отрицательных значениях коэффициента С2 подъемная сила
почти постоянна на траектории.
§ 9.6. Общий случай оптимального управления
из условия максимизации конечной скорости
В предыдущих параграфах этой главы были приведены некоторые
частные решения задачи максимизации конечной скорости КЛА, выводи¬
мых на орбиту ИСП, при использовании различных упрощающих предполо¬
жений. Очевидно, для того чтобы более полно исследовать проблему опти¬
мизации траекторий выведения КЛА на орбиту ИСП, необходимо разви¬
вать общую теорию оптимальных аэродинамических маневров. Эта общая
теория, с одной стороны, должна по возможности более полно отражать
действительную физическую картину движения в атмосфере, а с другой
стороны, должна быть достаточно универсальной, т.е. применимой к ат¬
мосфере любой планеты, не зависеть от выбора модели атмосферы и физи¬
ческих характеристик КЛА (масса, геометрические размеры и форма).
Результаты исследования этой проблемы многими авторами (см., на¬
пример, [108, 110, 113, 136]) показывают, что ее общее решение во мно¬
гом зависит от удачного выбора подходящего комплекса безразмерных
параметров движения. Ниже приводится один из возможных путей построе¬
ния общей теории оптимального маневрирования КЛА [110], осуществ¬
ляющего выход на орбиту ИСП.
Запишем уравнения движения КЛА в атмосфере планенты следующим
образом:
dr do VcosOcosxIs d<p У cos 0 sin
dt ' dt r cos ' dt r
dV pV2scx dO psCyV2 I V2\
= g sjn Qt у = cos 7 —h I cos 0,
dt 2m dt 2m \ r /
pscx V2 V2
V = sin 7 cos 0 cos ф tg <p,
dt 2m cos 0 r
где r — радиус текущей траектории; о— продольная угловая дальность
полета; — широта, i// — угол курса.
Положение КЛА, рассматриваемого как материальная точка с постоян¬
ной массой, определяется шестью переменными г , о, V, 0 и ф, Управление
осуществляется путем изменения угла крена у и коэффициента подъемной
силы Су. Однако вместо величины су оказывается более удобным исполь¬
зовать параметр управления подъемной силой
А = Су/Су .
Учитывая, что Су — коэффициент подъемной силы, соответствующий макси¬
мальному качеству /Стах получим при К= Ктах величину А = 1. Для коэф¬
фициента сх запишем
f(A)=cx/cx ,
19. Зак. 2069
289
где с*х — коэффициент силы лобового сопротивления при максимальном
аэродинамическом качестве.
На управляющие параметры Ли у наложены следующие ограничения:
(9.138)
Используя в качестве независимой переменной параметр г. вместо t,
уменьшим число уравнений движения КПА до пяти [110] :
do
COS 0
dip sin ip
dr
r cos tp tg 0
dr г tg 0
/
dxp
psCy sin 7
cos ф tg <p
dr
2m sin 0 cos 0
rig в
9
dV
pscx V
9
dt~
2m sin 0
V '
d6
pscy cos 7
COS 0
dt
2m sin 0
I V1 r
sin в
(9.139)
Введем две новые переменные [110]
psCy ГГ У 2 cos20
Z V — , и = .
2л? (3 дг
Дифференцируя по г второе уравнение (9.140), будем иметь
du _ cos20 d(V2} 2V2sin0cos0 dO V2cos20
dr gr dr gr dr gr2
(9.140)
Используя уравнения движения (9.139) с переменными (9.140), получаем
du
2zu
yr
■ f(A)
+ A cos 7 tg 0 + -
sin 0
]
dr
sin 0
r
^max
2\/Prz
J'
de
z
/Г Г
V r A cos 7 +
cos 0
- A cos
4 \1
(9.141
dr
sin 0
V’ и
Я
d\[j
z
cos2 0 cos ф tg P 1
dz
= — fiza,
dr
dr
У 1 1 1 Ol 1 1 J
sin 0 cos 0 r L
1 r
где
1 dp 1 1 d0
рР ~dT ~2&7 2^17
Проведенные исследования показывают, что для рассматриваемых планет
Солнечной системы коэффициент а очень близок к единице,так что в боль¬
шинстве случаев можно принять а ~ 1.
Переходя к независимой переменной z„ перепишем уравнения (9.141)
в виде
do
dz
cos ф d<p
Prz cos <ptg 0 ' dz
sin i//
Prztg0
290
d\[/
dz
1
du 2u Г
dz y/Prsind [
(9.142)
dO
dz
где
Acosy + G
у/pF sin 6
cosO / cos20 \
и
Для планет, обладающих атмосферой, при выведении КЛА на орбиту
ИСП величина г колеблется около среднего значения во всем представляю¬
щем интерес диапазоне высот полета. Поскольку в правых частях уравне¬
ний (9.142) величины Р и г появляются только в виде произведения Рг,
можно предположить без существенного искажения конечного результата,
что Рг = const. Это позволяет ликвидировать зависимость правых частей
уравнений (9.142) от параметра г .
Таким образом, в результате использования двух переменных z и и полу¬
чены уравнения (9.142), полностью не зависящие от физических характе¬
ристик КЛА. Эти уравнения применимы к описанию движения любого
типа КЛА, имеющих различные вес, диаметр и форму. Они могут быть ис¬
пользованы при расчете траекторий движения КЛА в атмосфере любой пла¬
неты, определяемой соотношением между плотностью и высотой (либо
средним значением произведения (Зг ). В отличие от ранее рассмотренных
случаев в уравнениях (9.142) не накладывается никаких ограничений на
величину угла наклона траектории к местному горизонту и на величину
максимального аэродинамического качества.
Сформулируем задачу оптимального управления в общем виде: при за¬
данном начальном состоянии и частично заданном конечном состоянии
Хк определить такие законы управления параметром подъемной силы
A(z) и углом крена у (z), подчиненные ограничениям (9.138), при кото¬
рых минимизируется функционал /(XK,zK).
Для определения оптимального закона управления КЛА воспользуемся
необходимыми условиями принципа максимума Понтрягина. С помощью
пятикомпонентного вектора 0, связанного с вектором состояния X запи¬
шем гамильтониан Х’в виде
02 sin 0 03 / COS20COS0tg^ \
=——(Asiny = I +
prztgO x/prsinflcos 0\ у prz /
Ф 1 COS ф
JC =
Prz cos tg 0
Фз
J HA)
sin 0
+ A cosy tg0 +
05 (Acosy + G)
• (9.143)
V0r sin 0
t 204^
VjSrsinfl L /Стах Z\ prz Л
Связь между компонентами вектора состояний и сопряженными пере¬
менными 0/ записывается в канонической форме следующим образом:
dXt дХ d& дХ
= (7=1,2 5), = (7=1,2 5).
dz дф/ dz bXi
Необходимым условием оптимальности является достижение гамильто-
291
нианом (9.143) абсолютного максимума в каждой точке траектории.
При этом возможны следующие типы оптимальной траектории:
1) оба управляющих параметра находятся внутри допустимой области
управления (9.138) :
Л = A (z) — переменная, у = у (z) — переменная;
2) изменение параметра подъемной силы происходит внутри допустимой
области (9.138), а значение угла крена постоянно и равно его максималь¬
ному граничному значению:
Л - A(z) — переменная, lyI = утах - постоянная;
3) оптимальное значение угла крена находится внутри допустимой об¬
ласти (9.138), а значение параметра подъемной силы постоянно и равно его
максимальному граничному значению:
1Л1=Лтах- постоянная, 7 = 7 (z) - переменная;
4) оба управляющих параметра находятся на границе допустимой облас¬
ти управления (9.138) :
I А| = Атах ~ постоянная, |у| = утах - постоянная.
Для первых двух типов управления из условия максимума гамильто¬
ниана по А
ЭК
= О
ЭА
получим
c/f /Стах / ^3Siny \
~ + /<тахСО57^ = — — + ^5COS0 . (9.144)
dA 2ф4и \cos0 /
Для первого и третьего типов управления из условия максимума га¬
мильтониана по углу крена
— = о,
Эу
найдем
^maxsinytg0 =
2ф4и \ cos0
ф$ sin
(9.145)
Решение уравнений (9.144) и (9.145) дает оптимальные законы управле¬
ния параметром подъемной силы и углом крена. Видно, что оптимальные
законы управления для Аи у являются функциями сопряженных пере¬
менных ф з , ф4 и ф5.
В общем случае для нахождения оптимальных законов управления
необходимо решать краевую задачу для двух систем из пяти дифферен¬
циальных уравнений. Покгцкем, что для рассматриваемой задачи выведе¬
ния КПА на орбиту ИСП оптимальные законы управления могут быть
определены аналитически при некоторых упрощающих предположениях,
не существенно влияющих на конечные результаты решения. Запишем
уравнения для первых трех сопряженных переменных
&ф1 Q c/i//2 i//icosi//sin^ фзсоьф
dz ' dz 0rz cos2 <^tg0 firz cos2 <£tg0
(9.146)
^Фз _ фуьтф i//2cosi// фз sin ф tg<£
dz 0rzcos^tg0 0rztg0 firztgO
292
Уравнения (9.146) могут быть проинтегрированы в явном виде:
=3], ф2 = a2cosp + a3sino,
ф3 = Si sirup — (а2 sino — a3coso)cos(p.
Анализ показывает, что для всех планет, обладающих атмосферой, па¬
раметр G в уравнениях системы (9.142) сохраняет практически постоян¬
ное значение. Учитывая это, получаем следующий интеграл для сопряжен¬
ной переменной ф4:
ф4=а4/и. (9.147)
Таким образом закон оптимального управления параметром подъемной
силы записывается в виде
df ajsin<p - (a2sino -a3coso)cos^
— si n 7 , (У. I )
d\ 2cos0
где
К m ax &2
a2 =
З4
^max a3
a3 =
34
Сопряженная переменная ф5 может быть определена следующим об¬
разом. Запишем дифференциальное уравнение для гамильтониана (9.143) :
dM фхсоьф ф2ыпф
dz 0rz2cos^tg0 0rz2tg0
ф 3 cos ф tg<p?
/kz2 tg 0
Отсюда найдем
Л
\/j37sin0
Фз sin 7
COS0
2ф4и Г f(A)
+ , + Л cos 7 tg в
sin в L^max
(9.149)
Для определения сопряженной переменной ф5 из (9.149) воспользуем¬
ся законом оптимального управления параметром подъемной силы (9.144)
ЛА) - А
dA
df
Анализ всех известных решений задачи максимизации конечной ско¬
рости показывает, что для любой поляры изменение су при оптимальном
законе управления происходит вблизи точки, соответствующей /Стах
(т.е. в линейной области изменения поляры КПА). Поэтому получаем
ЛА) - Аи
dX
z + = О,
dz
293
что после интегрирования дает
Prz
гдеа5 — постоянная интегрирования.
Учитывая выражения для гамильтониана (9.143) и для закона опти¬
мального управления по крену (9.145) находим
^таха5
а5 * П1 ух •
а4
Глава 10
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ВЫВЕДЕНИЯ НА ОРБИТЫ ЮПИТЕРА,
МАРСА И ВЕНЕРЫ КОМБИНИРОВАННЫМ СПОСОБОМ
§ 10.1. Общие закономерности решения задачи
Анализ имеющихся результатов исследования рассматриваемой проб¬
лемы позволяет выявить ряд общих закономерностей, справедливых для
всех планет, обладающих атмосферой.
-1. При проведении исследований с целью определения принципиальной
возможности и технической целесообразности применения комбиниро¬
ванного способа перевода КЛА с гиперболической траектории на орбиту
ИСП удобным является использование критерия максимума скорости
после прохождения атмосферного участка VK max при заданных значениях
высоты апоцентра переходной орбиты ha и угла наклона вк, определяемого
соотношением (8.6).
Помимо простоты и наглядности, критерий VK max существенно упро¬
щает, как отмечалось выше, решение краевой задачи при поиске оптималь¬
ного управления, а знание параметров VK, 6К, hK = ha позволяет без тру¬
да рассчитать скорости КЛА в апоцентре и перицентре Vn переходной
орбиты, оценить разгонный импульс для формирования требуемой ор¬
биты ИСП и провести сравнение энергетических затрат при полностью
активном и комбинированном способах перевода КЛА на орбиту спут¬
ника.
2. В случае управления КЛА на атмосферном участке полета путем
изменения эффективного аэродинамического качества специфика пла¬
нет, особенности их атмосфер, проектно-баллистические характеристи¬
ки аппарата не влияют на структуру оптимального управления в атмо¬
сфере: КЛА входит в атмосферу планеты и движется с максимальным
значением аэродинамического качества Ктах = + Кбал (у = 0), а затем
следует переключение на /Cmin = — ^бал (? = 180°). Точка переключения
управления определяется в каждом случае конкретными условиями дви¬
жения.
Существуют два предельных случая, соответствующий входу по верх¬
ней и нижней границам коридора. В первом случае КЛА движется в ат¬
мосфере все время с минимальным значением аэродинамического ка¬
чества, во втором — с максимальным. Такая закономерность может быть
нарушена лишь введением дополнительных ограничений и условий при
решении оптимальной задачи (например, ограничение по максимально
294
допустимой перегрузке, температуре и т.п.). Этот вывод существенно
упрощает исследование рассматриваемой проблемы, так как в каждом
конкретном случае алгоритм решения краевой задачи сводится только
к поиску момента переключения управления с Kmax на ^min-
При применении управления путем изменения углов атаки и крена
оптимальное решение реализуется при однократном изменении угла кре¬
на (с 7 = 0 на 7= 180°) и непрерывного изменения угла атаки. При этом
характер зависимости a(t} зависит прежде всего от конкретных условий
движения и характеристик КЛА. Это затрудняет решение задачи. Однако
выявлена следующая особенность: такое управление при сопоставимых
условиях не дает существенного (и тем более принципиального) выиг¬
рыша по сравнению с управлением эффективным качеством — потребная
величина разгонного импульса на формирование требуемой орбиты умень¬
шается всего на несколько процентов. Это во многих случаях освобож¬
дает от необходимости исследования сложного двухпараметрического
управления и допускает ограничиться лишь всесторонним изучением воз¬
можностей управления одним параметром — эффективным качеством.
3. При реализации комбинированного способа выведения минимальные
энергетические затраты, потребные на формирование заданной орбиты
ИСП, соответствуют входу по верхней границе коридора входа (A\/Iriiri =
= ДУВ), а максимальные — по нижней (ДУтах = ДУН). При этом вели¬
чина корректирующего1 импульса ДУтах в несколько раз превышает
импульс увеличиваясь с ростом аэродинамического качества.
4. При использовании оптимального управления в пределах всего фи¬
зически возможного коридора входа наблюдается имеющая важное прак¬
тическое значение зависимость величины потребного приращения скорости
от высоты условного перицентра входа ДУ(ЛЯ). Величина ДУ в значи¬
тельной части коридора входа (более 60 — 70% полной ширины кори¬
дора) остается практически неизменной и численно близкой к ДУт|П-
Лишь вблизи нижней границы происходит резкое возрастание ДУ. Вели¬
чина "полки” в зависимости ДУ(/?Я) тем больше, чем больше величина
располагаемого аэродинамического качества.
5. Характер зависимости величины корректирующей скорости ДУ
от высоты апоцентра формируемой орбиты ha практически одинаков
для всех планет: с повышением ha потребные энергетические затраты
на подъем перицентра орбиты КЛА резко возрастают. В среднем увели¬
чение ha в четыре - пять раз приводит к росту ДУ более чем в три раза.
При возрастании ha до некоторого значения комбинированный способ
становится нецелесообразным, т.е. для каждой планеты существует опре¬
деленный класс орбит, в котором принципиально можно рассматривать
указанный способ.
6. Имеются оптимальные параметры орбит ИСП, формируемых с ис¬
пользованием комбинированного способа, дающие максимальный энер¬
гетический эффект по сравнению с чисто активным способом перевода
КЛА на орбиту, причем для каждой из рассматриваемых планет эти ор¬
биты следует искать среди низких круговых орбит.
7. Центральное место в изучаемой проблеме занимает задача максими¬
зации ширины коридора входа. Как обычно, наиболее кардинальным
путем расширения коридора Д/?я является увеличение величины распо¬
лагаемого аэродинамического качества /Стах, так как влияние других
факторов на ДАЯ не столь существенно. Однако это автоматически ве-
1 Имеется в виду импульс характеристической скорости, однако для упрощения
записи индекс "хар" здесь и далее опущен.
295
дет к резкому увеличению ДУ, соответствующему входу вблизи нижней
границы коридора. В силу этого следует искать и другие пути. В частности,
хорошие результаты во многих случаях дает применение атмосферной кор¬
рекции (см. главу 11).
Отмеченные особенности, естественно, не исчерпывают всех нюансов,
связанных с реализацией рассматриваемого способа и зависящих от кон¬
кретных планет, проектно-баллистических характеристик КЛА и условий
движения. Приводимые ниже материалы подтверждают сказанное.
Подробно будут рассматриваться задачи выведения КЛА на орбиты
Юпитера, Марса и Венеры. И этот выбор не случаен, ибо в настоящее вре¬
мя именно для них комбинированный способ представляет наибольший
практический интерес. С другой стороны, резко отличающиеся данные
этих планет и условий движения в их атмосферах позволяют выявить
и нагляднее подчеркнуть все характерные особенности, достоинства и не¬
достатки комбинированного способа, перевода КЛА с гиперболической
орбиты на орбиту ИСП.
§ 10.2. Выведение на орбиту искусственного спутника Юпитера
10.2.1. Максимизация конечной скорости
Специфика движения КЛА в атмосфере Юпитера накладывает ряд осо¬
бенностей на решение этой задачи. Это в первую очередь большие ско¬
рости подлета к планете, значительная скорость вращения атмосферы
и необходимость учета уноса массы теплозащитного покрытия ЛА.
Эти особенности приводят к необходимости (наряду с решением зада¬
чи минимизации энергетических затрат, потребных для формирования
заданной орбиты искусственного спутника Юпитера) изучения возмож¬
ностей облегчения теплового режима путем поиска соответствующих
траекторий движения в атмосфере. Учитывая это, ниже рассмотрим зада¬
чи минимизации потребной характеристической скорости, теплового по¬
тока и максимальной температуры при заданной величине ДУ.
Численное решение задачи максимизации конечной скорости проводи¬
лось при варьировании начальных условий входа и основных проектно¬
баллистических параметров КЛА в следующих пределах:
50 км/с< Уо < 70 км/с,
(10.1)
100 кгс/м2 ^Рх <400 кгс/м2, 0,3 </Сбал <0,6.
Рассматривались три модели атмосферы с экспоненциальной зависи¬
мостью плотности от высоты
p(h) = р()е~^,
где р0 =0,152 кг/м3, 0 = 0,046 км'1 — для номинальной модели;
Ро ~ 0,124 кг/м3, 0 = 0,0328 км'1 — для "теплой" модели;
Ро = 0,24 кг/м3, 0 = 0,055 км'1 — для "холодной" модели.
В зависимости от целей, стоящих перед КЛА, рассматривались низкие
круговые орбиты с высотами h < 10 тыс. км и эллиптические с высотами
апоцентра > 104 км.
В качестве примера на рис. 10.1 приведены зависимости фазовых ко¬
ординат V, в и h, сопряженной переменной и аэродинамического ка¬
чества /Сэфф от времени t при оптимальном управлении из условия VK max.
296
£
Г
■s£
-1
400
-0
■хпп
1
со
-0
45
■ ■ 1
V(t)
-4
-2
40
\ !
!
\
\ 1
\ 1
к®
оии
0
\
s \ 1
9(t)
-2
~4
35
О ' 200 400 000 t,c
Рис. 10.1. Зависимость фазовых координат V, 0, h сопряженной переменной и аэро¬
динамического качества Кэфф от времени полета t при оптимальном управлении из
условия максимизации конечной скорости (Рх = 200 кгс/м2, Кбал = 0,4, ha =
= 3000 км) .
Из рассмотрения представленных зависимостей видно, что учет специ¬
фики движения в атмосфере Юпитера не оказывает влияния на структу¬
ру оптимального закона управления КЛА. А именно функция фх (t), опре¬
деляющая момент переключения эффективного качества, изменяется
монотонно: с увеличением времени полета ЛА в атмосфере она возрастает
и один раз обращается в нуль. При этом момент переключения /Сэфф зави¬
сит от местоположения КЛА внутри коридора входа: с уменьшением
высоты условного перицентра траектории входа время переключения
^эфф с +^бал на ^бал возрастает.
На рис. 10.2 приведена зависимость потребных энергетических затрат
на формирование комбинированным способом круговой орбиты искус¬
ственного спутника Юпитера от высоты условного перицентра траекто¬
рии входа при оптимальном управлении КЛА на атмосферном участке.
Анализируя эти данные, отметим значительную энергетическую эффектив¬
ность использования рассмотренного способа выведения по сравнению
с газодинамическим. Так, энергетические затраты ДУ составляют вели¬
чину, в 10—30 раз меньшую, чем при реализации соответствующих орбит
искусственного спутника Юпитера с помощью активного маневра.
Нетрудно видеть, что величина разгонного импульса ДУ для всего ди¬
апазона начальных условий и характеристик КЛА [см. (10.1)] возрастает
с уменьшением высоты условного перицентра /?я и экстремальные зна¬
чения ДУ приходятся на границы коридора входа: ДУт|п — при /?я = h*,
А'бпах — при /?я = /?”. При этом ДУпнп уменьшается с ростом аэродина¬
мического качества /Сбал, а ДУтах увеличивается. Так, изменение /('бал
от 0,3 до 0,6 приводит к снижению минимальных энергетических затрат
A in от 1,28 км/с до 0,51 км/с и увеличению максимальных ДУтах
от 2,08 км/с до 3,2 км/с.
Как отмечалось выше, в значительной части коридора входа величина
ДУ практически не зависит от высоты /?я и близка к своему минимальному
297
Рис. 10.2. Зависимость потребного импульса скорости ДИ от высоты условного пери¬
центра траектории входа hn (VQ = 60 км/с,Рх= 200 кгс/м2, ha= 10 000 км; сплош¬
ные линии — номинальная модель атмосферы, штриховые — "холодная" модель атмо¬
сферы, штрихпунктирные — "теплая" модель атмосферы, штриховые линии со звез¬
дочкой — номинальная модель атмосферы, полет с постоянным качеством) .
значению AV^nin- Протяженность этого участка увеличивается с ростом
аэродинамического качества /Сбал. Так, при /Сбал =0,3 этот участок за¬
нимает примерно 2/3 коридора входа и составляет около 340 км, в то
время как при /Сбал = 0,6 эти цифры соответственно равны 3/4 и 1200 км.
При этом, если величина ДУтах составляет 1,5 Al/min для КЛА с /Сбал =
=0,3, то для КЛА с/^бал =0,6 величина ДУтах = 6,3Al/min,
Отсюда следует важный вывод, что при увеличении аэродинамического
качества использование всего физически возможного коридора
входа не всегда представляется целесообразным ввиду резкого увеличения
потребных энергетических затрат ДИ По этой же причине не представля¬
ется приемлемым использование некоторых простых программ управ¬
ления К3фф на атмосферном участке {например программы/Сэфф = const,
где /^эфф выбирается в зависимости от реализуемой величины и требу¬
емого значения ha), эффективность которых была показана, например,
при формировании комбинированным способом орбит искусственных
спутников Марса [101].
Как и следовало ожидать, ширина коридора входа ДЛЛ увеличивается
с ростом аэродинамического качества /Сбал. Так, если для КЛА с/Сбал=
= 0,3 величина Д/?я составляет около 500 км, то для КЛА с/Сбал =0,6 вели¬
чина Д/?я возрастает более чем втрое и достигает примерно 1600 км.
При выборе потребной величины KQajl следует учитывать в первую
очередь ширину навигационного коридора входа и возможный разброс ха¬
рактеристик атмосферы. Из рассмотрения рис. 10.2 видно, что верхняя
граница1 коридора входа Л® практически не зависит от принятой модели
атмосферы, тогда как нижняя граница для "холодной" модели атмо¬
сферы сдвигается в сторону меньших (по модулю) значений Ля, что приво¬
дит к сужению коридора Д/7Я на 10—15%. Энергетические затраты оста-
1 На рис. 10.2 верхняя граница соответствует началу кривых, а нижняя граница —их
концу.
298
Рис. Ю.З. Зависимости потребного им¬
пульса скорости ДИ от начальной скоро¬
сти входа Уо, аэродинамического качества
/<бал и приведенной нагрузки на лобовую
поверхность Рх (сплошные линии —
дЛя = 1100 км, штриховые — ДЛ^ =
= 800 км).
ются практически без изменения
для всех трех рассмотренных мо¬
делей атмосферы. Если исходить из
величины навигационного коридора
входа Д/7яав = 1100 км 550 км
относительного прицельного значе¬
ния Ля), то для реализации выве¬
дения КЛА на орбиту искусствен¬
ного спутника Юпитера комбини¬
рованным способом требуется ап¬
парат с аэродинамическим качест¬
вом Кбал >0,5.
Проведем анализ влияния усло¬
вий входа КЛА в атмосферу и его па¬
раметров на величину энергетических затрат, характеризуемых величиной
приращения скорости ДУ. При этом будем считать, что потребная ширина
коридора входа =/?в -/# определяется с учетом разброса параметров
атмосферы и ограничена величинами навигационного коридора входа
ДЛяав, равными 1100 км и 800 км. На рис. 10.3 представлены зависи¬
мости'потребного импульса ДУ от скорости входа Vo, аэродинамического
качества /Сбал и приведенной нагрузки на лобовую поверхность Рх. t
Величина ДУ значительно уменьшается при использовании КЛА с боль¬
шими значениями аэродинамического качества Кбал- Так* изменение /<бал
от 0 51 до 0,6 приводит к снижению энергетических затрат ДУ от 2,64 до
0,7 км/с, т.е. в 3,8 раза (Д/?£ав = 1100 км). Изменение варьируемых пара¬
метров Уо и Рх достаточно слабо влияет на величину ДУ.
На рис. 10.4 представлены зависимости потребного импульса скорости
ДУ от высоты апоцентра формируемой орбиты искусственного спутника
Юпитера ha при использовании КЛА с К бал =0^ для различных величин
навигационных коридоров входа. Видно, что для всех рассмотренных слу¬
чаев характер зависимости ДУ(Ла) одинаков. А именно, при увеличении
высоты ha до некоторого значения h'a, зависящего от ширины навигаци¬
онного коридора ДЛяав, величина потребного разгонного импульса Д У
сначала практически не изменяется, а затем при ha > ha существенно воз¬
растает. Так, при изменении ha от 2000 км доЛа=9000 км
= 1100 км) величина ДУ составляет около 0,51 км/с, при дальнейшем
увеличении ha до h* =20 000 км величина ДУ возрастает до 3,2 км/с. При
ha>h*a коридор входа в атмосферу ДА^. = ft? — ft? становится меньше
величины ДЛ?а®. Соответствующие этому случаю (Дйя < ДЛд- ) участки
зависимостей ДУ(йа) обозначены на рис. 10.4 штрихпунктирной линией.
Выведение на такие орбиты комбинированным способом не представля¬
ется возможным. В этом случае необходимо или увеличивать^ точность
навигации на внеатмосферном участке подлета (уменьшать ДЛЯ ), или
использовать иную схему формирования орбит.
Данные, приведенные на рис. 10.4, показывают, что даже при умень¬
шении ДЛ?а® до 500 км возможно выведение КЛА комбинированным
" 299
Рис. 10.4. Зависимости потребного импульса скорости ДИ от высоты апоцентра ha
формируемой орбиты искусственного спутника Юпитера при оптимальном управлении
(Уо = 60 км/с, Рх = 200 кгс/м2, Кбал = 0,6; сплошные линии — комбинированный
способ выведения, штриховая — газодинамический способ выведения, штрихпунктир-
ные — комбинированный способ с дальнейшим активным подъемом орбиты) .
способом на эллиптические орбиты с высотами ha только до 47 000 км.
При необходимости получения больших значений ha требуются допол¬
нительные энергетические затраты, поскольку сначала осуществляется
выведение на орбиту с высотой апоцентра ha=h^, а затем с помощью
одно- или двухимпульсного газодинамического маневра КЛА переводится
на орбиту с требуемыми значениями высот ha Потребные энергети¬
ческие затраты в этом случае существенно увеличиваются с ростом высо¬
ты ha. Так, при изменении ha от 20000 км до 40000 км величина A V
возрастает от 3,2 до 11,4 км/с (Д/?вав = 1100 км).
Проведем сравнение скоростей ДУ, потребных для формирования ор¬
бит искусственных спутников Юпитера комбинированным и газодинами¬
ческим способами.
Из рис. 10.4 видно, что для достаточно широкого класса орбит искус¬
ственных спутников Юпитера комбинированный способ выведения при¬
водит к огромному энергетическому выигрышу. Так, для КЛА с =
= 0,6 и Рх =200 кгс/м2, подлетающего к атмосфере Юпитера с начальной
скоростью Уо =60 км/с (ДЛ»ав =1100 км), энергетические затраты более
чем в 20 раз меньше по сравнению с газодинамическим способом выве¬
дения на орбиты с высотой апоцентра ha < 15 000 км (при этом величи¬
на ДУ не превышает 800 м/с).
Представленные материалы показывают принципиальную возможность
и большой энергетический выигрыш комбинированного способа выведе¬
ния КЛА на орбиты искусственного спутника Юпитера аппаратов "сколь¬
зящего" типа, однако во всех рассуждениях мы не затрагивали вопро¬
сов обеспечения тепловой защиты КЛА при прохождении плотных слоев
атмосферы. Имеющиеся материалы исследований (см., например, [102])
показывают, что эта проблема играет существенную роль при движении
в атмосфере Юпитера, ибо потребная масса системы тепловой защиты
может достигать 30—40% от массы КЛА. В силу этого представляется
целесообразным рассмотреть задачу о поиске оптимальных траекторий
из условия минимума массы тепловой защиты КЛА.
Прежде всего отметим следующее: использование прямого критерия
min л7Тз.п связано с необходимостью рассмотрения КЛА конкретной фор¬
300
мы, конкретного типа теплозащитного материала и требует проведения
сложных и трудоемких расчетов. Вместе с тем целью исследования не
является оптимизация массы теплозащитного покрытия какого-то кон¬
кретного КЛА, а изучение принципиальных возможностей облегчения
теплового режима путем поиска соответствующих траекторий движения
в атмосфере Юпитера. В силу этого ниже рассматриваются две вариацион¬
ные задачи: задача минимизации суммарного теплового потока, действу¬
ющего на КЛА (Qsmin)/ которая однозначно характеризует массу тепло¬
защитного покрытия, и задача минимизации максимального значения
температуры. Такая постановка существенно облегчает решение задач
и в то же время позволяет получить качественные выводы об эффектив¬
ности оптимизации траекторий по тепловому критерию.
10.2.2. Минимизация суммарного теплового потока
Решение задачи о минимизации суммарного теплового потока проведем
при следующих предпосылках: будем считать, что заданы параметры фор¬
мируемой орбиты ha = ha3aa, /7Я = ^язад и затраты на коррекцию для
построения итоговой орбиты ДУ = АУзад > В этом случае конеч¬
ные условия в момент вылета КЛА из атмосферы имеют вид
У(ГК)=УК, 0(ГК) = 0К- h{tK}=hK. (10.2)
Итак, сформулируем вариационную задачу: найти оптимальное управ¬
ление эффективным качеством на атмосферном участке полета КЛА,
доставляющее минимум функционалу
гк
I ~ = f <*7рад + *7конв
^0
удовлетворяющее системе дифференциальных уравнений (8.8), конеч¬
ным (10-2) и начальным условиям
V(t0)=V0, 0(to} = 0o, h(to) = hQf m(to)=mQt Qs(to) = O,
при этом масса КЛА в момент t = tK не задана.
Используя необходимые условия оптимальности [137], запишем систе¬
му уравнений для сопряженных переменных:
^-0.
dt
d\ln cYspV cxsp gcosO cos0 oj2 r
= Ф\ — К'эфф ^2 “У" ^2 Ф2 + — -^2COS0 -
dt m 2m V2 r V"
— i//3sin0 +
7?
i//4 +
- 3,28/4rH p°’7\/2’28i//o - 3Br~y2pi/2V2\pOt
d\b2 g o)r
= РФ i COS0 — co2 cos0 Ф2 sin0 + Ф2 sin0 — \/ф3со$6,
dt v V
dt
2m
2m
301
2gcos0 Vcosfl w2cos0 0 7C.S„„
^-^2 —Ф2-—Г1 УИаАгнУ3'™р°^-
d^4 cxspV2 cxspV
dt ~ 2m2 ф1+К^Ф~^~^-
где фо — сопряженная переменная, получаемая при введении в систему
дифференциальных уравнений движения переменной f0 =—£.
dt
Оптимальное управление определяется из условия максимума гамиль-
тониана
-р dV , d6 dh dm dQ т
+ ^/J2 + —-ф0
dt dt dt dt dt
и имеет вид
/^эфф “ ^”бал'3'9р Ф2 г
т.е. оптимальный зако^ управления Кэфф представляет собой кусочно¬
постоянную функцию. Количество переключений эффективного качества
выявляется после решения краевой задачи и определяется числом нулей
функции ф2 (Г). ’
задача Решалась методом последовательных приближений
LbiJ. Результаты ее решения позволили выявить структуру оптимального
управления эффективным качеством, которая в общем случае представля-
Гпят^а +ДТГ°тВ.:е П^7)еГИ+е/ЭфФ К +к^на затем
(,пл . эфф I / ^бал> ^бал» +^бал- При этом если
КЛА входит в атмосферу с граничными значениями высот условного пе¬
рицентра /7Я и h^, то программа управления вырождается в программу
кДж/см 2
K.W
м, и
хг км/с
~ h,
км
иоо
,
№00
000
00
юоо
200
-0
ООО
-0
jod
200
0
-8
~00
массЬ11°кп1аВ™ИМ0СТИ фазовЬ1Х координат V, е, h, суммарного теплового потока От
качгс!н^гА ' перегрУзки пх. сопряженной, переменной и аэродинамического'
ЭФФ °Т времени полета f при оптимальном управлении из условия миними-
кбал=оТаГЛо"олко:° :°потока при Ик=Vk =60 км/с< =200 -с/м’.
302
2
ЛИ ^^кДж/см1
км/с
3
Е'=" й. г =“ж 3== г”== ==:: ”=
минимизации импульса скорости, РЛ1/ мП . . ттпихпх/нктионые — оптималь*
заданной величины импульса скорости ДУзад иО£т1п, штРих"у^Рн1ь,е
^управление из условия минимизации суммарного теплового потока).
полета при постоянном значении аэродинамического качества: *эфф
=_ is и /< , , =+ КПятт соответственно.
в качеств* примера на рис. 10.5 приведены зависимости фазовых ко¬
ординат V 0и h суммарного теплового потока Qv, массы т,перегрузи
п «пряженной переменной и аэродинамического качества Кэфф
от'времени полета t при оптимальном управлении из условия Os min-
нГ рис 10.6 показаны зависимости суммарного теплового потока Q^,
потоебного разгонного импульса ДУ и скорости КЛА в апоцентре фор¬
мируемой орбиты искусственного спутника Юпитера Уа от высоты У^°в
ного перицентра Видно, что абсолютный минимум значения теплово^
го потока O r min реализуется при входе КЛА в атмосферу по верхней
танице коридора входа = а максимальная величина Q^min дости
гается в середине коридор 1 oi ж* g q — 679 кДж/см^при
q = 426 кДж/см2 при =йя -- 131 км, a Qs max 679 кДж/с р
h = - 1115 км (Л£ = - 2120 км). Данные рис. 10.6 показывают, что опти¬
мизация траекторий КЛА с точки зрения минимума тепловых потоков
О£ неэффективна, так как при этом величина Ог уменьшается
тельно а потребные энергетические затраты на формирование орбиты
существенно возрастают. Например, если сравнить оптимальные траекто¬
рии из условий ДУщт и Qsmin» то можно отметить, что в пеРв°^учае
Qv « 695 кДж/см2 (ДУ = ДУтщ = 0,51 км/с), а во втором случае суммар¬
ные тепловые потоки уменьшаются весьма незначительного о/У кдж/см ),
в то время как потребные энергетические затраты ДУ увеличиваются
примерно в три раза по сравнению с ДУт1п (ДУ - 1,52 км/с).
Однако при реализации всего возможного коридора входа (т.е. если
д/)п = — /?” ~ Д/?”ав) оптимизация тепловых потоков не приводит
303
Рис. 10.7. Зависимости суммарного теплово¬
го потока 0% от начальной скорости входа
Уо аэродинамического качества /Сбал и при¬
веденной нагрузки на лобовую поверхность
Рх при оптимальном управлении (сплошные
ДЛ
линии — зависимость QSmin с учетом огра-
ничения на величину Д/?вав, штриховые —
зависимости абсолютного минимума тепло¬
вого потока) .
к увеличению энергетических затрат,
так как в любом случае
Д1/тах=Д|/(Ая=Ляи)>ДУ(Л„#=Л« )
при /7? .
Следует отметить, что величина
суммарного теплового потока min'
полученная с учетом возможной точ¬
ности входа, для рассматриваемого
КЛА с /Сбал = 0,6 практически не из¬
меняется приуменьшении навигацион¬
ного коридора входа Д/?вав от 1100 км до 800 км и равна соответственно
695 кДж/cm^ и 692 кДж/см2. “Дальнейшее уменьшение Д/?£ав до 400 км
приводит к снижению Q^min до 637 кДж/см2.
Данные, приведенные на рис. 10.7, позволяют оценить влияние ско¬
рости входа Уо и проектно-баллистических характеристик КЛА на вели¬
чины Q% min и ^E^min • Видно, что уменьшение приведенной нагрузки
на лобовую поверхность Рх скорости входа Vo и увеличение аэродинами¬
ческого качества /Сбал способствуют некоторому снижению минималь-
ных теплопотоков OLn,in и Q^min-Так, изменение Кбал от 0,5 до 0,6,
Рх от 300 до 100 кгс/м и Уо от /0 до 50 км/с приводит к уменьшению
величины Qs min соответственно от 810 до 695 кДж/см2, от 965 до
587 кДж/см2 и от 787 до 705 кДж/см2 (Д/?£ав = 1100 км).
Итак, для рассмотренных основных проектно-баллистических характе¬
ристик КЛА оптимизация траекторий движения в атмосфере Юпитера
по тепловому критерию ОепнппРи реализации комбинированного спо¬
соба построения орбиты искусственного спутника Юпитера практически
неэффективна, так как при незначительном уменьшении тепловых потоков
потребные энергетические затраты на формирование орбиты ДУ воз¬
растают весьма существенно. Однако при использовании всего коридора
входа можно добиться некоторого уменьшения тепловых потоков (на
2 — 5%) при энергетических затратах ДУ < ДУ(А£).
10.2.3. Минимизация максимальной температуры
Рассмотрим вариационную задачу минимизации максимальной темпе¬
ратуры поверхности КЛА в процессе движения в атмосфере Юпитера. Осо¬
бенностью этой задачи является то, что оптимизируемый функционал / =
- т _4 /а^рад + Qkohb
'max - v является нетрадиционным, поскольку пере-
304
менная Т в явном виде не входит в систему дифференциальных уравне¬
ний (5.21) и момент достижения Гтах не определен. С целью упрощения
решения примем во внимание следующее обстоятельство: выведение
КЛА на орбиту искусственного спутника всегда происходит по рикоше¬
тирующим траекториям, на которых достигается единственный макси¬
мум температуры. Это позволяет привести поставленную исходную зада¬
чу к задаче Майера, считая, что концом рассматриваемых траекторий яв¬
ляется точка достижения максимума температуры в некоторый момент
времени t*.
Введем в систему дифференциальных уравнений (8.8) дополнительную
координату Z = еоТ4, так что
f0 =— = - 0,7аДгн p0’73U3’28 + 3,28аДгнР0’7'/2’28 -
dt
-0,5Br„°’5p°'5pV3 4- ЗВг^’5p°'s V2. (10.3)
Очевидно, что переменные Т и Z достигают максимума одновременно,
что позволяет минимизировать функционал
_ ^шах _ <ЭДрад + Qkohb )max*
Поставленная вариационная задача может быть сформулирована следую¬
щим образом: на участке движения КЛА в атмосфере требуется определить
программу управления, минимизирующую функционал / = Z(t*) при диф¬
ференциальных связях (8.8) и (10.3) и следующих граничных условиях:
при t = t0 : V(t0)=VQl 0(ГО) = 0О, h(t0)=h0, m(tQ) = m0/ Z(tQ) = ZQ;
(10.4)
при t = f*: 0(t*) = 0*, h(t*)=h*, m(t*) -свободна, U(f*) = f(h*, Z*),
где t* определяется из уравнения dZ/dt = 0 и соответствует, как указыва¬
лось выше, моменту достижения 7"тах .
Как и ранее, будем использовать необходимые условия оптимальности
принципа максимума Понтрягина. Запишем систему уравнений сопряжен¬
ных переменных и гамильтониан:
,0,
dt
д cos 0 cos О
+
V2 г
С1Ф1
dt
CxSpV ^эфф^х^Р
m 2m
Ф2
+ 3ClSyH ^-0,5^,1/2^^^2 296^0.7^2.28^ _
П
- 7,4784aArHp°-1Vl'2s^0 + 1,58r„°'Sp1/20V2 фс - 6Br~0’5p112 Уф0,
d^2 9 V
9Ф1 cos 0 — cd2 гф1 cos 0 Ф2 sin 0 + — ф2 sin 0 +
dt V r
+ ф2 sin 0 — \/ф3 cos 0,
V
20. Зак. 2069
305
cxsV2 2ц sin 0 _ cxsV
= - ~Z P^1 3 0i - “> 01 sin 6 + /Сэфф р^з -
dt 2m r3 vv 2m
2ucos0 , l/cosO w2 cos 0
_ -Z_-— 02 + —2— 02
Vr3 r v
_ ^h^aArHV3'26pc^ _ CiS^..
rj 27?
-QAQaApo’1P2V3'2*'h+2,29QaArKp°’1pV2'2*to ~
^2-Br^°’SP112^ У30о + 1,5Sr"o,5pl/20V20o.
4
d4>4 cxspV
dt 2m2 ФФ
dV dd dh
№ 01 + — 02 +-—03 + 04 + — 00 =
dt dt dt dt dt
02~
(105)
Br~°’5V3pll2W4 -
cxspV
02.
2m2
dm dZ cxspV
: /^эфф +F(t),
dt dt 2m фф
где F(t) - функция, не зависящая в явном виде от управляющего парамет¬
ра Кдфф .
Из рассмотрения гамильтониана JC определим оптимальный закон управ¬
ления аэродинамическим качеством
Кэфф =^бал Sign 02-
Итак, на траектории, реализующей минимум величины Zmax, а следова¬
тельно, и минимум максимальной температуры 7"гпах, управление по ^эфф
кусочно-постоянное, а переключение с одного экстремального значе¬
ния на другое должно происходить в те моменты времени, когда функция
ф2(О меняет знак. Количество переключений /Сэфф, как и в предыдущих
задачах, определяется числом нулей функции i//2fr) и выявляется в резуль¬
тате численного решения краевой задачи для систем (8.8) и (10.5) и усло¬
вий (10.4).
Исследование оптимальных траекторий показало, что для всего рассмат¬
риваемого коридора входа КЛА в атмосферу программой управления,
реализующей rnin^ax, является программа движения КЛА с максималь¬
ным положительным качеством: КЭфф = + ^бал-
При этом для всего диапазона скоростей входа Vo и параметров КЛА
Рх и Кбал абсолютный минимум максимальной температуры Гтах достига¬
ется при входе КЛА по верхней границе коридора А®. На рис. 10.8 приведе¬
ны зависимости максимальной температуры 7"тах от высоты условного пе¬
рицентра /7Я при оптимальном управлении. Видно, что с увеличением высо¬
ты величина min 7"max монотонно уменьшается, достигая абсолютного
минимума 7min = 4310 °C при hn = А® = — 131 км.
Поскольку после достижения Гтах (при г = Г*) КЛА продолжает движе¬
ние в атмосфере, то представляется интересным исследовать управление
аппаратом на участке полета от Г* до момента вылета из атмосферы (t =
= tK) , обеспечивающее оптимальное по энергетическим затратам выведение
на орбиту искусственного спутника Юпитера с заданными параметрами.
Будем решать задачу определения оптимального закона изменения /СЭфф(t)
при <fK, который минимизирует энергетические затраты, потребные
на формирование заданной орбиты (AVmin), для систем дифференциаль-
306
Рис. 10.8. Зависимости скорости в апоцентре формируемой орбиты Va, потребного
импульса скорости Д1/ и максимальной температуры 7"тах от высоты условного
перицентра (1/0 = 60 км/с, Рх = 200 кгс/м2, Кбал = 0,6, ha = 5000 км; сплошные
линии — оптимальное управление из условия минимизации импульсов скорости Д1/,
штриховые — оптимальное управление из условия минимизации максимальной
температуры).
ных уравнений (8.8) и (10.3) . В качестве начальных условий примем зна¬
чения параметров V*, 0 *, h*, т* при t = t* . Конечные условия будут иметь
вид: ha — задано, <n(fK) — свободно.
Для достижения минимума ДУ достаточно реализовать максимум ско¬
рости КЛА при вылете из атмосферы (при отмеченном условии ha — зада¬
но). Поэтому в качестве критерия оптимальности используем / = Ук тах.
Решение будем проводить аналогично рассмотренной выше задаче о миними¬
зации 7"тах, воспользовавшись уравнениями для гамильтониана и системы
сопряженных переменных (10.5). Поставленная задача не имеет решения
вблизи верхней границы коридора входа /?° > /?я > так как при полете
с оптимальной программой /^эфф = + ^бал аппарат вылетает либо на гипер¬
болическую орбиту искусственного спутника Юпитера, либо на эллипти¬
ческую с h >/7а3ад (здесь — минимальная высота условного перицентра,
при входе с которой в атмосферу КЛА не может быть выведен на заданную
орбиту с h а </?азад) • При входе КЛА в атмосферу с высотами >
> h™ программа оптимального управления /Сэфф(Г) , реализующая выведе¬
ние КЛА на заданную орбиту искусственного спутника Юпитера с ДУт1п,
представляет собой одноразовое переключение /Сэфф с + К^ал на ~^бал-
На рис. 10.9 в качестве примера показано изменение фазовых координат
V, 0 и h, массы аппарата т, температуры Т в критической точке КЛА, сопря¬
женной переменной i//2, аэродинамического качества /С'эфф и перегрузки
пх в зависимости от времени движения КЛА в атмосфере Юпитера при
оптимальном управлении /Сэфф из условия min 7"max на участке от f0 до f*
и из условия ДУт1П на участке от Г* до Гк.
На рис. 10.8 представлены зависимости потребного разгонного импульса
скорости ДУ на формирование орбиты искусственного спутника Юпитера и
скорости КЛА в апоцентре переходной орбиты Va от высоты условного
перицентра подлетной траектории при оптимальном управлении из усло¬
вия min Гтах с последующей минимизацией ДУ (штриховые линии) .
Для сравнения приведены аналогичные зависимости для задачи нахождения
307
Рис. 10.9. Зависимости фазовых координат V, в, Л,величин т, T,.nXi сопряженной пере¬
менной и аэродинамического качества Кэфф от времени спуска t при оптимальном
управлении из условия минимизации максимальной температуры Ттах (1/0 = 60 км/с,
hn = —1015 км, Рх = 200 кгс/м2, Kgan = ^,6, ha = 5000 км; номинальная модель
атмосферы).
A^min (сплошные линии), рассмотренной выше (но без оптимизации
по ^тах) • Видно, что при движении КЛА в коридоре от h'^ = —1775 км до
Л” = —2130 км результаты решения обеих задач совпадают по Ттлх и
A^min, а в области /7Я от Ля = —350 км до /?я = —1775 км отличаются по
величинам AVmin не более чем на 1 — 2%.
На рис. 10.10 показаны зависимости минимальной величины Ттах от
скорости входа Vo, аэродинамического качества К'бал и приведенной
нагрузки на лобовую поверхность Рх. Видно, что величины min 7*max и
min 7” max уменьшаются при увеличении аэродинамического качества /Сбал
и уменьшении скорости входа Уо, а изменение приведенной нагрузки Рх
практически не оказывает влияния на min 7"max и min Т^ах. Так, измене¬
ние Уо от 70 км/с до 50 км/с приводит к снижению температуры min 7*^х
от 14520 °C до 7000 °C, а увеличение аэродинамического качества /Сбал
от 0,3 до 0,6 уменьшает min 7"^х от 9400 °C до 7920 °C.
Резюмируя изложенное, укажем, что использование управления из усло¬
вия min Утах не приводит к существенному снижению температуры по
сравнению со значениями Гтах, полученными для оптимальных траекторий
из условия AVmin. В силу этого минимизация максимальной температуры
при решении задачи выведения КЛА на орбиту комбинированным способом
самостоятельного значения не имеет.
Рассмотренные решения некоторых оптимальных задач движения КЛА
в атмосфере Юпитера при комбинированном способе построения орбиты
искусственного спутника Юпитера позволяют сделать следующие выводы:
1) имеется принципиальная возможность комбинированного способа
формирования орбит искусственного спутника Юпитера с ha до 20 -
40 тыс.км аппаратами "скользящего" типа;
2) оптимизация траекторий КЛА "скользящего" типа из условия Q^min
неэффективна, так как незначительное снижение суммарного теплового
308
рис. 10.10. Зависимости минимума макси¬
мальной температуры 7"т ах от начальной
скорости входа 1/0, аэродинамического
качества К^п и приведенной нагрузки на
лобовую поверхность Рх при оптимальном
/ •
управлении (сплошные линии — m in7max
с учетом ограничения на величину
штриховые — абсолютный минимум Ттах).
100
, К бал
300 кгс/м2
р Лт'1П
I Is
\ 1 х к
«5ал)Л'
/Л
v; “ “ - \
minFmoxW
50 60
0 0,it
70
о,в\
200
потока Ov ведет к существенному
возрастанию потребных энергетичес¬
ких затрат;
3) хотя масса теплозащитного пок¬
рытия Л7Т3.П и может достигать 30—
40% от массы КЛА, тем не менее реа¬
лизация орбит искусственного спут¬
ника Юпитера с использованием ком¬
бинированного способа характеризу¬
ется достаточно высокой энергетичес¬
кой эффективностью,так как затраты
топлива во многих случаях (/<бал > 0/5, < 20 000 км, Д/?”ав =
= 1100 км) не превышают 10 — 15% от массы КЛА, т.е. суммарные затраты
не будут превышать примерно 50% от /пКЛА, в то время как для чисто
ракетодинамического способа выведения КЛА на орбиту искусственного
спутника Юпитера потребуются затраты топлива /лт > 90% от л?КЛА;
4) при использовании комбинированного способа выведения КЛА на
орбиту искусственного спутника Юпитера наибольший энергетический
выигрыш наблюдается при движении КЛА вблизи верхней границы коридо¬
ра, так как решение всех рассмотренных задач дает оптимальный результат
при входе КЛА в атмосферу по верхней границе /7Я = .
§ 10.3. Выведение на орбиту искусственного спутника Марса
10.3.1. Исходные предпосылки
Известен ряд работ (см., например, [29, 68]) , посвященных исследова¬
нию проблемы выведения КЛА на орбиту искусственного спутника Марса
с использованием предварительного аэродинамического торможения в
атмосфере. В них рассматриваются вопросы поиска оптимальных траекто¬
рий КЛА, выбора его основных проектно-баллистических характеристик,
синтеза алгоритмов управления и т.д. При этом расчеты траекторий прово¬
дились для моделей атмосферы, составленных на основании имеющейся
информации о Марсе на период 1972— 1975 гг. Как уже отмечалось (см.
главу 1), за последние годы произошло существенное уточнение парамет¬
ров атмосферы планеты. Длительное исследование атмосферы Марса, в
частности с помощью КЛА "Викинг", функционирующих на орбитах
искусственного спутника Марса, показало, что зависимости параметров
атмосферы от высоты полета отличаются для различных времен года.
Были получены новые сезонные модели атмосферы Марса: зимняя, летняя
и в период равноденствия. Для каждого сезона в свою очередь предложено
по два варианта атмосферы: максимальной и минимальной по плотности.
Вследствие этого возникла необходимость нового подробного изучения
309
траекторий движения КЛА в атмосфере при выведении на орбиту искусст¬
венного спутника Марса с учетом уточненных моделей атмосферы.
Будем рассматривать два класса орбит искусственного спутника Марса:
низкие круговые с высотами апоцентра hg-др 1000 км и высокие эллипти¬
ческие c^/^'oFK^nO^ flo TO^KMr-^kicneHHb^ анализ оптимальных траекто¬
рий выведения КЛА будем проводить при следующих исходных пред¬
посылках:
начальная скорость входа КЛА в атмосферу Марса варьируется в диапа¬
зоне 6 км/с < 1/0 < 8 км/с;
величина аэродинамического качества изменяется в пределах 0,3 <
<Кбал ^ОД-
величина приведенной нагрузки на лобовую поверхность лежит в диапа¬
зоне 100 кг^м2 < 1000 кгфм2 ;
движение КЛА происходит в пределах всего коридора входа;
рассматриваются КЛА, управляемые углом крена. Как отмечалось выше,
оптимальной программой управления КЛА является программа одноразо¬
вого переключения эффективного значения аэродинамического качества
с максимального на минимальное значение. Момент переключения /СЭфф
выбирается из условия обеспечения требуемых параметров Траектории на
выходе КЛА из атмосферы.
“' Для рассматриваемой программы управления существуют два таких
значения высоты условного перицентра траектории {h* и /?£), при входе
с которыми в атмосферу Марса оптимальная программа управления вы¬
рождается в программу' полета с постоянными граничными значениями
эффективного качества /Сэфф = + К’бал и ^эфф= — ^бал- Учитывая, что
во всем диапазоне изменения высоты условного перицентра от /?£ до
Л® и для всех моделей атмосферы величины максимальной перегрузки и
минимальной высоты полета не являются критичными (/7тах < 6, /7mjn>
>20 км), можно отметить, что при заданных параметрах КЛА, скорости
входа и точном знании атмосферы Марса эти значения определяют нижнюю
и верхнюю границы коридора входа.
При исследовании траекторий выведения КЛА на орбиту во многих слу¬
чаях (особенно при решении задач оптимизации) представляется удобным
использовать зависимость плотности атмосферы от высоты над поверх¬
ностью планеты, заданную в аналитическом виде. Учитывая, что траектории
выведения КЛА на орбиту искусственного спутника Марса проходят на вы¬
сотах h > 20 30 км, будем рассматривать аналитические зависимости, ап¬
проксимирующие табличные модели атмосферы (см. гл. 1) наиболее точно
именно в диапазоне высот 20 км <Л <100 км.
Более точная аппроксимация зависимости p(h) достигается при исполь¬
зовании полиномов вида
p(h)= Z Afh1,
i = 1
где 7 — номер участка аппроксимации. Определение коэффициентов этих
зависимостей (7 = 0, 1, .. . , п) не представляет принципиальных труд¬
ностей и может быть осуществлено с помощью известных вычислительных
процедур (см., например, [30]) . Точность в определении плотности атмо¬
сферы р, рассчитанной при использовании полинома, зависит от его поряд¬
ка п. Так, проведенные численные расчеты показали, что при /7 = 5 погреш¬
ность в определении плотности Др при изменении высоты h в рассматри¬
ваемом диапазоне не превышает 1,5 — 2%, а при п = 20 величина Др для
тех же высот h не превышает 1% относительно табличных значений. Менее
310
Таблица 10.1
Параметры экспоненциальных зависимостей уточненных моделей атмосферы
Параметры
атмосферы
Зимняя
Равноденствие
Летняя
макси¬
мальная
мини¬
мальная
макси¬
мальная
мини¬
мальная
макси¬
мальная
| мини-
| мальная
р0, кг/м3
0,0123
0,0125
0,0133
0,0136
0,0106
I
0,0106
Д,м-’
1,04- 10-4
1,22 • 10-“
0,93- 10'4
1,06 ■ 10-4
0,84 • 10’4
0,94 - 10" 4
точная аппроксимация табличных моделей атмосферы Марса достигается
при использовании экспоненциальной зависимости
p(h) = рое~е'г.
В табл. 10.1 приведены параметры экспоненциальной зависимости р0 и 0,
полученные для шести уточненных моделей атмосферы Марса (см. главу 1).
Расчеты показывают (рис. 10.11), что в диапазоне высот h от 20 км до
100 км плотность атмосферы р, определенная в соответствии с экспонен¬
циальной зависимостью, отличается от табличной не более чем на 3% для
всех рассматриваемых моделей атмосферы. Эти модели атмосферы (см.
табл. 10.1) и будем использовать при проведении исследований, имея в
виду, что применение экспоненциальной зависимости плотности атмосфе¬
ры р от высоты h позволяет получать вполне удовлетворительную точность
вычислений и существенно упрощает решение задачи определения оптимальг
ного закона управления КЛА в атмосфере.
Основными параметрами, определяющими принципиальную возмож¬
ность выведения КЛА на орбиту ИСП, являются коридор входа КЛА в ат¬
мосферу Д/?я и энергетические затраты (приращения скорости ДИ, потреб¬
ные на формирование орбиты. Поэтому при анализе траекторий выведения
основное внимание будем уделять именно параметрам и Д\/. Кроме
Рис. 10.11. Зависимость плотности атмосферы р от высоты над поверхностью плане¬
ты h (сплошные линии — экспоненциальный закон, штриховые - табличные значения).
311
10.3.2. Влияние уточнения моделей атмосферы
на параметры траекторий выведения
Численные результаты по оценке влияния уточнения моделей атмосферы
Марса относительно "старых" моделей (составленных на период 1973 —
1975 гг.) представлены на рис. 10.12, 10.13 и в табл. 10.2. Видно, что пара¬
метры nmax и /?min не являются критичными при проектировании КЛА.
Действительно, во всем диапазоне изменения высот условного перицентра
от /?” до и для всех моделей атмосферы величина лтах достаточно
мала и не превышает 5—6 единиц, а высота /?min во всех случаях более
18 км, что существенно превышает обычное ограничение на минимально
допустимую высоту пролета КЛА над поверхностью планеты (Amin >
^доп ~ 5~10 км).
На рис. 10.12 помимо зависимостей, рассчитанных по уточненным моде¬
лям атмосферы, представлены данные, полученные для "старых" моделей.
Видно весьма заметное изменение величин и = h* — h^. Наиболь¬
шее расхождение наблюдается при сравнении с результатами, соответствую¬
щими "старой" максимальной модели. В этом случае верхняя h* и нижняя
границы коридора входа смещаются в сторону меньших значений
При этом величина h* уменьшается на 40 — 60 км, a — на 30 — 50 км, в
результате чего ширина коридора входа Д/7Я при использовании уточненных
моделей атмосферы сужается на 20 — 35% по сравнению с величиной Д/7Я/
полученной для "старой" максимальной модели. Численные результаты,
полученные для "старой" минимальной модели, очень близки к результа
там, соответствующим Ртах летн и Рщахравн- На величину потребных
энергетических затрат уточненные модели атмосферы влияют очень слабо:
расхождение в величине скорости на коррекцию Д1/ не превышает 1%.
Важно отметить, что неточность знания параметров атмосферы Марса
приводит к значительному сужению коридора входа ДЛЯ. Так, при фор-
Таблица 10.2
Влияние уточнения моделей атмосферы Марса на основные характеристики траек¬
торий выведения
(исходные параметры: Ио = 6 км/с, Кбал = рх= 300 кгс/м2 )
Модели атмосферы
.В
пп, км
, н
км
ДЛЯ, км
ha = 5600 1
км
^тах зимн
39;02
1,57
37,45
^min зимн
39,41
- 3,41
34,82
ртах равн
46,18
6,75
39,43
^min равн
39,09
1,95
37,14
^тах летн
49,54
8,27
41,27
^min летн
42,84
3,63
39,2
^тах стар
70,85
26,56
44.29
^min стар
47,88
7,87
40,01
h о■ = 500 км
^min зимн
31,29
- 26,72
58,01
^тах летн
49,24
- 18,12
67,37
312
мировании высоких эллиптических орбит искусственного спутника Марса
(см. рис. 10.12) разброс параметров атмосферы приводит к уменьшению
величины ДЛЛ примерно на 40%. Это вызывает повышенные требования к
точности навигации на участке подлета КЛА к атмосфере планеты. Такой
разброс обусловливает точное знание сезона, во время которого КЛА
достигает Марса. Однако при рассмотрении долгосрочных программ трудно
указать точно сезон подлета КЛА к Марсу. Кроме того, в этом случае нужно
создавать КЛА с характеристиками, позволяющими осуществлять движе¬
ние в атмосфере в определенный сезон (зима, лето и т.д.), что создает до¬
полнительные трудности. Целесообразнее, очевидно, допуская некоторое
усложнение системы управления и увеличение массы, создавать КЛА, рас¬
считанный на реализацию полета в любой период. Это приводит к необхо¬
димости принимать во внимание максимальный возможный разброс пара¬
метров атмосферы вне зависимости от времени подлета к планете. Тогда
определение проектно-баллистических характеристик КЛА будет осущест¬
вляться исходя из минимальной ширины коридора входа Д/7Л и максималь¬
ной скорости ДУа, потребной на формирование орбиты.
Характер зависимостей остается неизменным для орбит с раз¬
личными значениями /7Л и ha (низкие круговые и высокие эллиптические
орбиты искусственного спутника Марса) . Однако величина ДУ существен¬
но зависит от высоты ha формируемой орбиты. При этом следует отметить,
что при выведении КЛА на круговую орбиту высотой h = 500 км наблюда¬
ется значительное отличие между величинами Д Уа, полученными при входе
в атмосферу с /?л = Лл и с /)я = /?л. Величина ДУа(/7л) в два раза превышает
величину ДVa(hл). При выведении КЛА на высокую эллиптическую орбиту
с ha = 6000 км величина ДУа меняется незначительно внутри коридора
входа: ДУа(Лл) больше, чем ДУа(/?л), на 1,5 - 2%. При этом возможный
коридор входа Д/7Л при выведении на низкие круговые орбиты искусствен¬
ного спутника Марса, составляющий (с учетом возможного разброса пара¬
метров атмосферы) около 50 км, более чем в два раза превышает величину
Д/?л, полученную при формировании высоких эллиптических орбит.
1 Д1/в,м/с
Д1/Н, м/с
в
''max
и
"max
^min* км
^mirp км
/7а =
5600 км
574,3
586,1
1,06
2,91
39,31
29,07
576
587
1,1
3,27
33,33
24,26
573
585,3
1,02
2,7
45,09
34,23
574,4
586
1,06
2,95
39,47
29,36
572,2
585,1
1,0
2,51
47,53
36,05
573,6
586
1,03
2,71
42,17
31,38
568
582
0,95
2,24
65,94
53,12
572,5
585
1,02
2,63
46,43
35,37
ha = 500 км
137,6
261,3
1,13
5,52
32,88
18,45
124,1
266,3
1,04
4,1
46,58
28,26
313
Рис. 10.12. Зависимости апо-
центрического импульса ско¬
рости от высоты услов¬
ного перицентра подлетной ор¬
биты для уточненных и
"старых'' моделей атмосферы
{Рх 300 кгс/м2, Кбал = 0,4,
Vo = 6 км/с, = 6000 км).
Рис. 10.13. То же, что на
рис. 10.12, для ha = 500 км.
Основной трудностью, препятствующей решению проблемы выведения
на высокую эллиптическую орбиту искусственного спутника Марса, являет¬
ся достижение коридора входа, превышающего навигационный. Для пре¬
одоления этой трудности необходимо либо повышать точность систем на¬
вигации на внеатмосферном участке движения КЛА, либо осуществлять его
движение с использованием корректирующего импульса в атмосфере.
10.3.3. Влияние скорости входа и параметров КЛА
на основные характеристики траекторий выведения
Расширение коридора входа КЛА в атмосферу и снижение потребных
энергетических затрат при выведении на орбиту искусственного спутника
Марса в ряде случаев могут быть достигнуты соответствующим изменением
схемы полета КЛА к Марсу и выбором требуемых значений проектно-бал¬
листических характеристик аппарага.
Зависимости границ коридора входа h® и /jJ и величины потребного
импульса скорости от начальной скорости входа Vo, приведенной
нагрузки на лобовую поверхность Рх и аэродинамического качества К’бал
показаны на рис. 10.14 и 10.15. Изменение величины потребного импульса
при движении КЛА по верхней границе (ДУ^) и по нижней границе (ДУ”)
314
Рис. 10.14. Зависимость апоцентри чес кого импульса скорости Д1/аи границ коридора
входа в атмосферу от проектно-баллистических характеристик КЛА и начальной ско¬
рости входа 1/0 (Рх = 300 кгс/м2, ^бал = 0А =6 км/с, = 6000 км) для р0 =
= 0,0125 кг/м3, 0 =1,22 Ю-4 м"1.
несущественно в широком диапазоне варьирования К^ал, Pxv\ V q. Это гово¬
рит о том, что добиться значительного снижения величины потребного им¬
пульса за счет изменения проектно-баллистических характеристик КЛА и
начальной скорости его входа в атмосферу не представляется возможным.
Вместе с тем видно, что изменение величин Кбал и приводит к значи¬
тельным вариациям ширины коридора входа Д/>я. Так, увеличением началь¬
ной скорости входа в плотные слои атмосферы Vo можно добиться расши¬
рения коридора входа, причем преобладающее влияние оказывает умень¬
шение нижней границы коридора входа /?”. Зависимость (Уо) практи¬
чески линейная во всем рассматриваемом диапазоне значений VQ (незна¬
чительная нелинейность начинает наблюдаться лишь при скоростях, близких
к Vo = 8 км/с). Так, изменение 1/0 на каждые 0,5 км/с уменьшает /7Я
Примерно на 7 км, и при 1/0 = 8 км/с величина Д/7Я достигает 62 км.
Другим параметром, существенно влияющим на ширину коридора
входа, является аэродинамическое качество К^ал. Увеличение аэродинами¬
ческого качества Кбал дает возможность расширить коридор входа как
за счет уменьшения нижней границы /7Я, так и за счет некоторого увеличе¬
ния верхней границы /7Я. Смещение обеих границ происходит практически
линейно. Так, изменение величины Кбал на 0*1 расширяет коридор входа
примеоно на 11 км, и при К^лл = 0,75 величина Д/7Я достигает ± 35 км.
Изменение приведенной нагрузки на лобовую поверхность приводит к
параллельному смещению границ коридора входа и, следовательно, замет¬
ного увеличения коридора входа не происходит.
315
Рис. 10.15. То же, что на рис. 10.14, где р0 = 0,0106 кг/м3 , 0 = 0,84 • 10"4 м"1 .
Рис. 10.16. Зависимости апоцентрического импульса скорости Д Va и границ коридо¬
ра входа в атмосферу от проектно-баллистических характеристик КЛА и начальной
скорости входа Ио (Рх = 300 кгс/м2, = 0,4, 1/0 = 6 км/с, ha = 6000 км) для
Ро =0,0125 кг/м3, 0 =1,22 -10“4 м"1 .
Рис. 10.17. То же, что на рис. 10.16, для р0 = 0,0106 кг/м3, 0 = 0,84 • 10"4 м”1.
Таким образом, представленные результаты численного расчета опти¬
мальных траекторий выведения КЛА на высокие эллиптические орбиты
искусственных спутников Марса показывают принципиальную возможность
расширения коридора входа за счет увеличения начальной скорости
входа Vo и аэродинамического качества Кблл. При этом даже при использо¬
вании КЛА с К'бал 0,6 -г 0,7, входящих в атмосферу Марса со скоростью
VQ ~ 8 км/с, коридор входа Д/?я больше навигационного коридора
Д/?яав =±25 км.
Проведем анализ траекторий выведения КЛА на низкие круговые орби¬
ты искусственного спутника Марса. Соответствующие зависимости, пока¬
зывающие влияние начальной скорости входа и проектно-баллистических
характеристик КЛА на величины ДУ”, ДУ^, h* и h*, приведены на
рис. 10.16 и 10.17. Видно, что характер этих зависимостей такой же, как и
Для случая выведения КЛА на высокие эллиптические орбиты. Изменяя
соответствующим образом скорости входа Уо и проектно-баллистические
параметры КЛА, можно добиться значительного расширения коридора
входа. Так, при увеличении начальной скорости 1/0 с 6 км/с до 8,5 км/с
коридор входа превосходит по ширине навигационный и составляет ДЛП =
= 102 км для КЛА с аэродинамическим качеством Кбал = ОД и приведенной
нагрузкой на лобовую поверхность Рх = 300 кгс/м2. При этом при выведе¬
нии на низкую круговую орбиту искусственного спутника Марса преобла¬
дающее влияние начальной скорости входа в атмосферу планеты сказывает¬
ся на изменении нижней границы коридора входа hувеличение скорости
на каждый 1 км/с приводит к расширению коридора входа примерно на
18 км за счет смещения нижней границы коридора Д/?я. Наибольшее влия¬
317
ние на изменение ширины коридора входа при выведении КЛА на низкие
круговые орбиты оказывает изменение величины аэродинамического
качества. Если принять ширину навигационного коридора входа равной
ДЛ"ав = 60 км, то даже при К'бал = 0,4 коридор входа превосходит
навигационный. Расширение коридора входа с увеличением К'бал происхо¬
дит за счет смещения обеих границ Лв и причем нижняя граница изме¬
няется более значительно, чем верхняя. Приведенная нагрузка на лобовую
поверхность Рх практически не влияет на ДЛП. Таким образом, имеется
принципиальная возможность формирования низких круговых орбит
искусственного спутника Марса комбинированным способом при исполь¬
зовании КЛА с /^бал ОД, осуществляющих вход в атмосферу планеты
со скоростью Уо > 6,0 км/с. При этом достигается значительный энергети¬
ческий выигрыш по сравнению с чисто активным способом перевода аппа¬
рата с гиперболической орбиты на орбиту спутника.
Следует отметить, что изменение начальной скорости входа Уо и аэроди¬
намического качества К^ал оказывает значительное влияние на величину
5 ДУа = ДУВ — ДУ£. Увеличение Уо и Кбал приводит к возрастанию 6 ДУа
в основном за счет изменения потребного импульса ДУ® при движении
КЛА по нижней границе коридора входа, тогда как величина ДУ® при этом
практически не изменяется. Наиболее существенно влияет на 8 Д<У® аэроди¬
намическое качество К'бал- Например, при изменении К’бал от 0,2 до 0,7
величина 8ДУа изменяется от 50 м/с до 320 м/с, а потребный импульс
ДУ а на формирование низкой круговой орбиты искусственного спутника
Марса по нижней границе коридора входа возрастает от 195 м/с до 450 м/с.
Подобного влияния на величину 8ДУа можно достичь за счет изменения
начальной скорости входа Уо на 3,5 — 4 км/с. Например, для КЛА с величи¬
ной аэродинамического качества К'бал = ОД и приведенной нагрузкой на
лобовую поверхность Рх = 300 кгс/м2 изменение начальной скорости входа
Уо от 5 км/с до 8,5 км/с приводит к возрастанию величины 8ДУа от 70 м/с
до 320 м/с. Величина приведенной нагрузки на лобовую поверхность Рх не
оказывает заметного влияния на потребный разгонный импульс при движе¬
нии КЛА по нижней и верхней границам коридора входа.
Резюмируя изложенное, отметим, что увеличение начальной скорости
входа Уо и аэродинамического качества Кбал приводит, с одной стороны,
Рис. 10.18. Зависимости а по цен три чес ко го импульса скорости AV& и границ коридо¬
ра входа в атмосферу от высоты апоцентра переходной орбиты ha (Рх = 300 кгс/м3,
1/0 = 6 км/с, Кбал = 0,4) для р0 = 0,0125 кг/м3 , 0 = 1,22 • 10"4 м"1 .
318
Рис. 10.19. То же, что на рис. 10.18, где р0 =0,0106 кг/м3, 0=0,84-10 4 м"1.
Рис. 10.20. Зависимости апоцентрического импульса скорости Д1/аи границ коридора
входа в атмосферу от высоты апоцентра переходной орбиты ha (Рх = 300 кгс/м2,
Vo = 6 км/с, Кбал = 0,4) для р0 = 0,0125 кг/м3, 0 = 1,22 • 10"4 м"1.
к расширению коридора входа Д/?п, а с другой — к росту величины потреб¬
ного разгонного импульса на формирование заданной орбиты искусствен¬
ного спутника Марса. Это обстоятельство нужно учитывать при выборе
оптимальных условий входа КЛА в атмосферу Марса и его проектно-бал¬
листических характеристик Рх и /Сбал-
Оценим влияние высоты апоцентра формируемой орбиты ha на ширину
коридора входа и потребные энергетические затраты на формирование
круговой орбиты искусственного спутника Марса с /?кр = ha. Соответ¬
ствующие зависимости представлены на рис. 10.18 и 10.19 (для низких
круговых орбит) и на рис. 10.20 и 10.21 (для высоких эллиптических
орбит). Видно, что расширение коридора входа ДЛЯ происходит при умень¬
шении высоты апоцентра переходной орбиты практически только за счет
смещения нижней границы /?”• Зависимость нелинейная, и величина
коридора входа приближается к значению Д/?я 20 км при возрастании
высоты апоцентра переходной орбиты до значений ha 20000 км.
Величина потребного импульса скорости Д1/а существенно зависит от ha
как при движении КЛА по нижней, так и по верхней границе коридора
входа. При этом, как и следовало ожидать, увеличение ha приводит к
319
Рис. 10.21. То же, что на рис. 10.20, для р0 = 0,0106 кг/м3 , 0 = 0,84 • 10’4 м’1 .
возрастанию импульсов скорости ДУ® и ДУ®, Видно, что наиболее заметное
изменение величин ДУ® и ДУ® происходит при возрастании высоты ha
примерно до 14 000 км. Так, для КЛА с К^п = 0,4 увеличение от
2000 км до 14 000 км приводит к изменению ДУ® от 370 м/с до 672 м/с.
Дальнейшее увеличение /?а приводит к незаметному возрастанию импульсов
скорости ДУ® и ДУ®. Так, при увеличении /7а с 14 000 км до 20 000 км ве¬
личина ДУ® возрастает всего лишь с 672 м/с до 677 м/с. Это можно объяс¬
нить тем, что при выведении КЛА на высокие эллиптические орбиты глуби¬
на погружения КЛА в атмосферу и, следовательно, время его движения в
атмосфере уменьшаются таким образом, что влияние аэродинамического
торможения при выведении КЛА на орбиты с высотами апоцентра /)а >
> 14 000 км становится незначительным.
По другому ведет себя зависимость ДУ®(/?а) при выведении КЛА на низ¬
кие круговые орбиты: при возрастании /?а от 200 км до 450 км происходит
уменьшение величины потребного импульса ДУ®. На высоте ha — 450 км
наблюдается минимум зависимости ДУ®(/?а), составляющий около 250 м/с.
При дальнейшем увеличении ha величина ДУ® возрастает.
Таким образом, для формирования орбит искусственного спутника
Марса с использованием предварительного аэродинамического торможения
в атмосфере наиболее рациональной с точки зрения минимизации энергети¬
ческих затрат является область высот апоцентра переходной орбиты h& =
= 400-^500 км.
§ 10.4. Выведение на орбиту искусственного спутника Венеры
10.4.1. Исходные предпосылки
Основные особенности решения этой задачи определяются чрезвычай¬
ной плотностью атмосферы Венеры (на два порядка превышающей зем¬
ную) . С одной стороны, это обстоятельство способствует решению постав¬
ленной задачи. Действительно, при использовании комбинированного спо¬
соба торможения оказывается достаточным организовать движение КЛА
в верхних слоях атмосферы Венеры на высотах h > 70 км. Тем самым
отпадает необходимость выдерживания ограничения на траектории спуска
по минимально допустимой высоте полета над поверхностью планеты с
320
целью исключения движения в облачном слое, расположенном на высотах
40 — 50 км. Дело в том, что облака Венеры содержат частицы агрессивной
серной кислоты и длительное пребывание КЛА в облачном слое потребо¬
вало бы принятия специальных мер по его защите от разрушения. С другой
стороны, наличие плотной атмосферы приводит к возникновению достаточ¬
но тяжелого перегрузочного режима (лтах > 30). Это обстоятельство
необходимо учитывать при расчете траекторий выведения КЛА на орбиту
искусственного спутника Венеры, вводя ограничение по максимальной
перегрузке.
Численное решение задачи максимизации конечной скорости при выве¬
дении КЛА на орбиту проводилось при следующих исходных значениях
начальной скорости входа, проектно-баллистических характеристик КЛА и
высоты апоцентра переходной орбиты:
Vo = 11 км/с, Рх = 500 кгс/м2, Кбал = 0,5, ha = 500 км.
При исследовании траектории выведения эти параметры варьировались в
пределах
9км/с<У0 <15 км/с, 300 кгс/м2 <РХ <700 кгс/м2,
0,3<К'бал<0,7, 500 км <Ла <10 000 км.
Предполагалось, что управление такими КЛА возможно как путем измене¬
ния одного из параметров (угла атаки или угла крена), так и совместным
изменением этих углов.
При решении задачи выведения КЛА на орбиту искусственного спутника
Венеры рассматривались четыре возможные формы аппаратов, характеризуе¬
мые различными зависимостями аэродинамических коэффициентов от угла
атаки и различными величинами максимального аэродинамического качест¬
ва. Зависимости аэродинамических коэффициентов от угла атаки прини¬
мались в виде
сх=А + В cos(aa + Ь) - для всех форм,
су = D sin (аа + Ь) - Для форм 1,3, 4,
cv=D sin (— а + —A cos (— а +—- для формы 2,
у \2 2/ \2 2/
где значения постоянных коэффициентов А, В, D, а и Ь равны:
а
для формы 1 А = 1,08,
для формы 2 А = 1,46,
В = -0,96,
D = 0,3,
д = 21;
для формы 3
А =0, 73,
для формы 4
А = 0,89,
В = -1,23,
В = - 0,67,
В = 0,87,
£2 = 2,2, а = 2,308, b = 10;
D = 0,44 а = 2,5, b = - 7,5;
D = 0,405, а = 1,856, b = 0.
Для каждой из рассматриваемых форм максимальное аэродинамичес¬
кое качество равно: /Стах =1,4 для формы 1; /Стах =2,8 для формы 2;
Ктах = 1 /5 ДЛЯ формы 3; /Стах = 2,15 для формы 4.
При проведении расчетов использовалась номинальная модель атмосфе¬
ры, задаваемая в виде экспоненциальной зависимости плотности от высоты
р = poe~(ai+bih+c^h^h,
где р0 =4,28 кг/м3, aj =-0,0873, bx =0,002361, сх = - 0,411 • 10-5 .
В отличие от рассмотренного выше случая выведения КЛА на орбиты
искусственных спутников Юпитера и Марса возможные отклонения харак¬
теристик плотности атмосферы от номинального значения не приводят к
21. Зак. 2069 321
существенному изменению характеристик траектории выведения на орбиту
искусственного спутника Венеры. Так, при изменении плотности атмосфе¬
ры от максимального значения до минимального наибольшее отклонение
конечной скорости выведения от величины скорости, реализовавшейся
при использовании номинальной модели атмосферы, не превышает 1%.
При поиске оптимальных траекторий выведения КЛА на орбиту искусст¬
венного спутника Венеры на первом этапе решения задачи не будем учиты¬
вать ограничение на величину максимально допустимой перегрузки.
10.4.2. Управление с использованием эффективного качества
Решение вариационной задачи по поиску оптимальной программы управ¬
ления КЛА из условия максимума конечной скорости в апоцентре переход¬
ной орбиты Vamax привело к известному результату: оптимальной прог¬
раммой управления углом крена является его одноразовое переключение
со значения у = 0 (Кэфф = +Кбал) на у = 180°(/Сэфф = -Кбал)- В качестве
примера на рис. 10.22 и 10.23 приведены зависимости фазовых координат
V, в и h, сопряженных переменных и ф3 и угла крена у от времени t
для КЛА типов "несущий корпус" и "космический самолет" при оптималь¬
ном управлении из условия Vamax. Видно, что характер изменения фазо¬
вых координат и сопряженных переменных аналогичен для обоих рассматри¬
ваемых типов КЛА. Исследования показали, что, как и во всех преды¬
дущих случаях, момент переключения угла крена зависит от положения
высоты условного перицентра траектории внутри коридора входа: чем бли¬
же высота hn расположена к нижней границе, тем дольше протекает полет
КЛА с 7 = 0. При движении КЛА по верхней и нижней границам коридора
Рис. 10.22. Зависимости фазовых координат V, 0 и h, угла крена у и сопряженных
переменных и от времени полета t при оптимальном управлении КЛА
типа "несущий корпус".
322
входа оптимальная программа управления вырождается в программу полета
с постоянным углом крена: у = 0 для = h* и у = 180 для = Л®.
Следует также отметить, что отличие условий движения КЛА в атмосфе¬
ре Венеры от условий движения в атмосферах Юпитера и Марса не приводит
к качественному изменению характера зависимости оптимизируемого
функционала от основных варьируемых параметров (начальных условий
входа КЛА в атмосферу, проектно-баллистических характеристик КЛА и
высоты апоцентра формируемой орбиты). Но, естественно, количествен¬
ные результаты будут существенно определяться физическими особен¬
ностями Венеры и ее атмосферы.
На рис. 10.24 и 10.25 представлены зависимости характеристической
скорости Д1/а, потребной для формирования комбинированным спосо¬
бом круговой орбиты искусственного спутника Венеры (hKр = 500 км),
и скорости в апоцентре переходной орбиты Va от высоты условного пери¬
центра траектории входа hn при оптимальном управлении КЛА на участке
аэродинамического торможения. Как обычно, на большей части коридора
входа при уменьшении от /?® величина импульса характеристической
скорости Д Va практически не зависит от высоты hn. Лишь вблизи нижней
границы коридора входа уменьшение приводит к заметному возраста¬
нию величины потребного импульса ДУа. Протяженность участка ДУа =
= const связана с величиной аэродинамического качества и высотой апо¬
центра переходной орбиты ha, причем с увеличением Кбал и уменьшением
ha длительность участка полета с Д1/а = const возрастает (см. рис. 10.24 и
10.25).
Проведем анализ влияния проектно-баллистических характеристик КЛА,
начальной скорости входа и высоты апоцентра переходной орбиты на ши¬
рину коридора входа и величину импульса скорости, потребного для пере¬
вода КЛА на круговую орбиту искусственного спутника Венеры высотой
h =ha. Как и в рассмотренных выше случаях, с возрастанием /Сбал и Уо
коридор входа расширяется, а с увеличением ha — сужается (см.
323
Рис. 10.24. Зависимости скорости в апоцентре и импульса скорости Д1/аот вы¬
соты условного перицентра (Рх = 500 кгс/м1, 1/0 = 11 км/с; номинальная мо¬
дель атмосферы) для различных значений Kffan (ha = 10 000 км) .
Рис. 10.25. То же, что на рис. 10.24, для различных значений ha (Kq^ = 0,5) .
Рис. 10.26. Зависимости границ коридора входа и скорости в апоцентре переходной
орбиты Va от проектно-баллистических характеристик КЛА и условий входа (Рх =
= 500 кгс/м2, Кбал = ^,5, ha = 500 км, Vo = 11 км/с; номинальная модель атмо¬
сферы) .
рис. 10.24—10.26). Изменение приведенной нагрузки на лобовую поверх¬
ность практически не влияет на ширину коридора входа: с возрастанием Рх
происходит малозаметное увеличение На рис. 10.26 представлены
зависимости скорости Va и высоты от проектно-баллистических харак¬
теристик КЛА Рх и Кбал начальной скорости входа Уо и высоты апоцентра
переходной орбиты ha. Видно, что величина скорости при движении
КЛА вблизи верхней границы коридора входа практически постоянна во
всех случаях. При движении КЛА вблизи нижней границы коридора входа
величина скорости V” существенно зависит от Кбал, У о и Причем с
увеличением Кбал, Уо и ha происходит уменьшение величины ско¬
рости 1/ан.
Наличие плотной атмосферы, окружающей планету, в сочетании с высо¬
кими скоростями входа приводит к появлению достаточно больших зна¬
чений максимальных перегрузок на траектории движения КЛА в атмосфе¬
ре (лтах^30 — 60), хотя минимальная высота полета КЛА над поверх¬
ностью планенты достаточно велика:
^min > 80 км (рис. 10.27) .
325
Рис. 10.27. Зависимость максимальной перегрузки nmax и минимальной высоты
полета /?mjn от проектно-баллистических характеристик КЛА /Сбал и началь¬
ной скорости входа в атмосферу 1/0 и высоты апоцентра переходной орбиты ha.
Представляет практический интерес исследование задачи выведения КЛА
на орбиту искусственного спутника Венеры комбинированным способом
с учетом ограничения на величину максимально допустимой перегрузки.
10.4.3. Учет ограничения на величину
максимально допустимой перегрузки
Сформулируем следующую вариационную задачу: на участке движения
КЛА в атмосфере, описываемого системой дифференциальных уравне¬
ний (8.8), требуется определить программу управления углом крена у,
максимизирующую функционал / = Ук при условиях
У(£о)“^о, h(t0)-h0,
(10.6)
VK = max, Лк=/)0=Ла
(10.7)
и ограничениях
0<y <180°,
(10.8)
nx ^Пдоп*
(10.9)
326
Как и ранее, при решении задачи будем использовать необходимые ус¬
ловия оптимальности принципа максимума Понтрягина. Уравнения для
сопряженных переменных и гамильтониана при полете КЛА внутри допус-
тимой области фазовых координат запишутся в виде
d^i scxpV
= l//j +
dt т
, f scyP
\ 2m
d^z / cos0
г—
dt
sin0 _ sin0 \
— sin 0 + V + cA —T" ^2 “ V'^/3cos0/
Vr2 г V2 /
— со2sin в
dt
+
\/COS0
+—
2 cos 0 '
V
dV de dh
M = i//i + ^2 + •
dt dt dt
(10.10)
(10.11)
Для достижения экстремума функционала I - VK необходимо сущест¬
вование ненулевого непрерывного сопряженного вектора ф, описываемого
системой дифференциальных уравнений (10.10), при котором гамильто¬
ниан (10.11) достигает минимальной величины. При этом в конечной
точке траектории выполняется условие трансверсальности
6/- jf6r+Ф15У++'МЛ =0. (10.12)
Отсюда будем иметь граничное значение сопряженной переменной 1Д1 (fK>
ф1(гк) = 1. (10.13)
Принимая во внимание, что система уравнений движения (8.8) не содер-
жит в явном виде время Гк, получаем
Jf(T)=O.
Учитывая
(10.14)
Фз UK) =
(10.11) и (10.13), из уравнения (10.14) находим
1 [ cxspV2
\/sin 0 I
2т
sin0 _
+ и „ — gj2 (/?()+/))sin 0—
(Яо + h)
Г CySpV
[ 2m
cos у — p
+ g?(/?0 +/?)
i//2(tK)
cos 0
cos 0
+ V + 2gj +
/?о +Л
(/?0 +h)2V
327
Уравнения для сопряженных переменных при движении КЛА по огра-
ничению (10.9) запишутся следующим образом:
ЭК dJC/dy
b<p
d\^2
dK dX/dy
dt
dV dp/dy
bv '
dt
Ь0 Ь<р/Ьу b0
d^*3
dJC ЭЗС/Э?
b<p
(10.15)
+
—
dt
bh btp/by
bh
Необходимые и достаточные условия прохождения экстремали вдоль
границы допустимых значений фазовых координат имеют вид
—^-=0 (р = 0,1,2 к), (10.16)
dt
где к — порядок производной функции q (f), которая содержит в явном
виде управляющий параметр у (Г) ; в нашем случае к = 2.
При этом
d2q d2h crs „ . •
у> = = ——- = (pV2 + 4pVV+2pV2 + 2pVV) . (10.17)
dt2 dt2 2go3m
Из уравнений (10.16) и (10.17) получаем закон изменения угла крена
при движении по изоперегрузочному участку:
[ / д У\ Г . . / cxs pV2\
cos у = | j cos в +|_pj3 V2 V sin в + 2p —J —
— 2gp V sin 0 1 — 4p VV — 2p V2 + fiph V21 (—ftp U3cos 0 — 2pV cos 0 )_1.
’ (10.18)
Сопряженные переменные в момент tx выхода на изоперегрузочный ре¬
жим скачком меняют свою величину:
0ПП
bq bq
cxspV
+
дозт
cxspV cxspV cxsp
b2V \
2ffo3 5'оэ"’ 2^03m
btbV /'
dq dq
= o,
(10.19)
03 U1
bq bq
) -03(r,)=pl — +p2—- =
bh bh
cxsp(3V2
-Д1
2gOtm
cxsp/3 cxsV2 d2p
-р2 VV+ .
Роз т 2go3m btbh
Таким образом, поставленная вариационная задача максимизации конеч¬
ной скорости вылета КЛА из атмосферы при ограничении на величину мак¬
симально допустимой перегрузки сводится к краевой задаче для систем
дифференциальных уравнений (8.8), (10.10), (10.11) , (10.15) и гранич¬
ных условий (10.6) - (10.9), (10.13), (10.14).
328
Рис. 10.28. Зависимости скорости V высоты h и перегрузки пх от времени С при
оптимальном управлении из условия максимизации скорости 1/а при пх < лдоп
(сплошные линии — без ограничения на пх, штриховые — с учетом этого ограни¬
чения) .
В качестве примера на рис. 10.28 - 10.29 представлены зависимости фа¬
зовых координат V и h, перегрузки пхи аэродинамического качества/Сэфф
от времени полета t при оптимальном управлении. Анализ зависимостей
показывает, что структура оптимального управления /Сэфф (г) состоит в
следующем: полет КЛА с постоянным качеством КЭфф = ^бал от мо"
мента Го входа в атмосферу до момента Гп переключения /Сэфф с ^эфф
= + ^бал на ^эфф =“^бал, движение с минимальным значением /Сэфф
=—Кбал Д° момента достижения допустимого значения перегрузки rlz
полет по изоперегрузочному участку, где изменение управляющего пара¬
метра происходит в соответствии с (10.18) и полет с /Сэфф = — ^бал Д° вь,‘
лета из атмосферы.
На рис. 10.30 - 10.32 приведены зависимости импульса скорости & Va,
потребного для перевода КЛА на орбиту искусственного спутника Венеры
ha = 500 км, от h^. Величина допустимой перегрузки варьировалась в диа¬
пазоне от 15 до 40.
и и
Рис. 10.29. Зависимости аэродинамического качества ^эфф от времени t при опти¬
мальном управлении из условия минимизации потребного импульса скорости
при пх < лдоп (обозначения те же, что на рис. 10.28) .
329
15
Рис. 10.30. Зависимости потребного импульса скорости ДИа от высоты условного
перицентра при оптимальном управлении и ограничении по допустимой перегруз¬
ке лдоп (Ио =11 км/с, Рх = 500 кгс/м2 , ha = 500 км) для Кбал = 0,5.
Рис. 10.33. Зависимости интегрального теплового потока от высоты условного
перицентра траектории входа
Представленные зависимости показывают, что введение ограничения
на величину пх приводит к сужению возможного коридора входа КЛА в
атмосферу и возрастанию величины потребной скорости для КЛА
всех рассмотренных типов. Причем ширина коридора входа уменьшается,
а величина импульса скорости увеличивается тем сильнее, чем мень¬
ше величина лдоп- Так, например, уменьшение лдОп от 30 до 15 единиц
приводит к изменению Д/7Я от 84 км до 48 км, аД1/а—от 0,48 км/с до
0,64 км/с.
Оценка интегральных тепловых потоков. В процессе решения основной
задачи по определению величины потребного импульса скорости для КЛА,
переводимых на орбиту искусственного спутника Венеры были проведены
расчеты интегральных тепловых потоков для различных значений ha и Х'бал-
На рис. 10.33 приведены зависимости величины интегрального теплового
Г
потока Оу = f q^dt от высоты условного перицентра траектории входа
t о
для КЛА, обладающих различной величиной аэродинамического качества
(радиус затупления носовой части обоих КЛА принимался равным гн -
= 0,5 м). Видно, что величина <3£ возрастает с увеличением 6Я, а макси¬
мальная величина теплового потока соответствует полету с h„ = что
объясняется увеличением времени движения КЛА в атмосфере с ростом
Л„. Так, при имеем Qsmax «0,28 • 109 Дж/м , а при ЛЯ=АЯ
Q£min -0,13.109 Дж/м2 = 0,5,/?а = 500 км).
Уменьшение высоты ha приводит к возрастанию Q±. Так, для ha
= 500 км (Кбал =0,5) Qmax «0,5 • 109 Дж/м2. При выведении на орбиту
искусственного спутника Венеры КЛА различных типов величина
больше для КЛА типа "несущий корпус", обладающего большим значением
/Сбал и меньшим значением гн, по сравнению с КЛА "скользящего типа.
Так, для КЛА типа "несущий корпус" Q^max -0,127 • 10 Дж/м , а для
КЛА "скользящего" типа Q^max «0,28 -10 Дж/м2, т.е. почти в шесть
раз меньше (ha = 10 000 км).
331
10.4.4. Управление совместным изменением углов крена и атаки
Для поиска оптимальных траекторий использовались необходимые
условия принципа максимума Понтрягина.
Перепишем гамильтониан системы (10.11) в виде
pV2s pVs _
JC = -сх(а)ф14- су (а) ф2 cos у + Ф (г), (10.20)
2т 2т
где Ф(г) — сумма членов гамильтониана, не зависящих от управления.
Дифференцируя выражение (10.20) по а и 7 и приравнивая частные
производные нулю, получаем
cos у (f) = sign (10.21)
Эсу(а)/Эа
— = - (10.22)
дсх(а)/да I I
Выражение (10.21) дает оптимальный закон управления изменением
угла крена в атмосфере Венеры.
Для каждой из рассматриваемых четырех форм КЛА, которые опреде¬
ляются соответствующими аппроксимационными зависимостями коэф¬
фициентов сх и су, можно получить оптимальные законы управления углом
атаки КЛА. Для этого соответствующие зависимости коэффициентов сх и су
от угла атаки а подставляются в выражение (10.22). В результате получаем
Рис. 10.34. Зависимость фазовых координат, сопряженных переменных и параметров
управления от времени (КЛА формы 1) .
332
h<c/M
следующие законы управления углом атаки:
а3опт=
а4 опт =
а2опт =
а1 опт
! 0,729 1i//2 1
arctg
■J —21°
(
3
0,894 I02h
\ о
arctg I-
)
- 10°
/
2,308
0,657 1 1
/
\ О
arctg!
4+7,5°
(10.23)
(10.24)
(10.25)
1,856
(10.26)
В качестве примера на рис. 10.34 — 10.37 приведены параметры опти¬
мальных траекторий для четырех форм КЛА, осуществляющих вход в
атмосферу Венеры с начальной скоростью Vo = 11 км/с. Характер измене¬
ния управляющих параметров а и у на оптимальной траектории одинаков
для рассматриваемых форм КЛА. А именно угол крена изменяется релей-
но и имеет одно переключение с у = 0 на у = 180°. Угол атаки в первые
20 — 25 с уменьшается до некоторого значения а , а затем постепенно воз¬
растает, увеличиваясь к концу траектории на 7 — 10° по сравнению со
334
Рис. 10.38. Зависимости потребного импульса скорости AVа от высоты условного
перицентрз hn при оптимальном управлении (сплошные линии — управление по у,
штриховые — управление по а и 7) .
значением а = а .Сравнение двух рассмотренных выше способов управления
КЛА показывает (рис. 10.38), что эффективность использования двух¬
параметрического управления (а + 7) невысока по сравнению с однопара¬
метрическим (7). Возможный выигрыш в величине конечной скорости
при двухпараметрическом управлении не превышает 3 — 5% по сравнению
с однопараметрическим .
10.4.5. Эффективность применения комбинированного
способа выведения
Приведем результаты сравнения двух способов выведения КЛА на ор¬
биту искусственного спутника Венеры: комбинированного (с использо¬
ванием предварительного аэродинамического торможения) и газодинами¬
ческого. На рис. 10.39 представлены зависимости массы полезного груза
л?п.г от начальной массы КЛА.
Расчет массы полезного груза проводился по следующей формуле:
^п.г ^тз.п ^с.у,
д г
где т0 — начальная масса КЛА; тт - т(} (1 — е с ) — масса топлива;
П7тзп = 0,1 /по — масса теплозащитного покрытия; тс у —масса системы
управления, принимаемая постоянной и равной 200 кг. Видно, что в диа¬
пазоне начальной массы КЛА 1000 кг </77 0 <6000 кг использование комби¬
нированного способа выве¬
дения на орбиту искусствен¬
ного спутника Венеры явля¬
ется более выгодным. При
этом с увеличением началь¬
ной массы КЛА эффектив¬
ность использования ком¬
бинированного способа вы-
Рис. 10.39. Зависимости массы
полезного груза тп г от на¬
чальной массы КЛА ш0 (ha =
= 1000 км, Рх = 500 кгс/м2,
*бал ” 0,5, VQ = 11 км/с;
сплошные линии — ha
= 1000 км, штриховые —
= 500 км) .
О
т0,кг
335
ведения возрастает. Так, если при ш0 = 1000 кг и ha = 1000 км масса полез¬
ного груза,выводимого на орбиту искусственного спутника Венеры газодина¬
мическим способом /т?п г = 340 кг, а комбинированным — /т?п г = 670 кг,
то при возрастании mQ до 5000 кг масса полезного груза для обоих спосо¬
бов составляет соответственно 810 кг и 4000 кг.
§ 10.5. Выведение на орбиту искусственного спутника Венеры
с использованием многократного прохождения атмосферы
Рассмотренный выше комбинированный способ выведения КЛА на ор¬
биту искусственного спутника Венеры, предполагающий однократное
прохождение атмосферы с последующей подачей небольшого разгонного
импульса для поднятия перицентра формируемой орбиты, оказывается
эффективным при выведении КЛА на орбиты, высоты апоцентра которых
не превышают ha = 8000 -г 8500 км. Формирование орбит искусственного
спутника Венеры с большей высотой ha этим способом затруднено из-за
повышенных требований, предъявляемых к точности работы системы авто¬
номной навигации и коррекции на припланетном участке полета. Приме¬
нение другого (активного) способа перевода КЛА на эти орбиты оказы¬
вается эффективным лишь при высотах апоцентра Ла >105 км, так как
для реализации меньших значений ha требуются большие затраты топлива.
Одним из возможных путей формирования орбит искусственного спут¬
ника Венеры с высотами апоцентра 8000 км^ ha 105 км является исполь¬
зование способа с многократным прохождением атмосферы [102]. Этот
способ предполагает предварительный ракетодинамический перевод КЛА с
гиперболической траектории на опорную эллиптическую орбиту с большим
эксцентриситетом и перицентром, расположенным несколько выше уровня
атмосферы, определяющего допускаемый конструкцией КЛА газодинами¬
ческий нагрев (ha=h°n и = h £п). Далее, КЛА путем многократного
погружения в атмосферу в районе перицентра переводится на переходную
орбиту с заданной высотой апоцентра ha=ha3aa и высотой перицентра
^тг </?°п.Для поддержания необходимой высоты перицентра на внеатмос¬
ферных участках полета подаются корректирующие импульсы тяги дви¬
гательной установки, а, после того как высота апоцентра переходной орби¬
ты достигнет заданной величины, перицентр орбиты поднимается за счет
импульса двигательной установки на заданную высоту /?я = Лязад.
Для определения эффективности описанного способа необходимо иметь
оценки потребных суммарных затрат характеристической скорости А1/Ххар
и времени , затрачиваемого для перехода на требуемую орбиту, при за¬
данных ограничениях на максимальную температуру 7"П1ах и перегруз
ку лтах.
Ниже рассматриваются две вариационные задачи по определению опти¬
мального управления тягой двигательной установки, реализующего мини¬
мум затрат характеристической скорости А^хар и времени перехода t%
при учете указанных ограничений.
Следует отметить, что эти две задачи являются взаимозависимыми. Дей¬
ствительно, время перехода КЛА и величина суммарного импульса
Д^Ехар во многом определяются параметрами опорной орбиты h&n и
h°n. При этом известно, что чем меньше величина импульса скорости, пере¬
водящего КЛА с гиперболической траектории перелета на высокоэллипти¬
ческую орбиту искусственного спутника Венеры* тем больше период обра¬
щения КЛА по этой орбите и, следовательно, больше суммарное время fv.
Поэтому при решении каждой из сформулированных задач необходимо
336
дрполнительно учитывать ограничение либо на период обращения КЛА по
опорной орбите ti <ГдОП (для задачи минимизации Al/vxap) , либо на ве¬
личину импульса скорости ДУ* <ДУ{доп (для задачи минимизации t2) .
1 Отметим также, что один из возможных методов оценки величин
Д^Ехар и приведен в работе [101]. Результаты расчетов величин
ДУ^хар и по этому методу могут служить первым приближением для
решения сформулированных вариационных задач.
Будем использовать уравнения плоского движения центра масс КЛА с
учетом вращения планеты и уноса массы теплозащитного покрытия:
dV cxspV2 р . Р
- sin в + co2rsin0 + — cos(p — 0),
dt 2т г2 т
dO р V <л2г Р
— cos0 + — cos0 + 2со + sin0 + sin(v — в), (10.27)
dt r2V г V mV
dh dm Ci SyH P
~dt" Vs'n6' ~dT~ ~ (<,KOHB +э<7рад - еаГр>_ Рудд03 '
где
у 7
V3'25, q^ = BsTprHV3'2,
гн
С1 = 0 при T(t)<Tp, Ci = к при T(t)>Tp,
T(t) = у/ (<7КОНВ + a<Zpafl)/60.
Будем также предполагать, что управление движением КЛА осущест¬
вляется путем изменения величины P(t) и направления v(t) тяги двига¬
тельной установки. При этом значения управляющих параметров могут
изменяться в пределах
0<P(t)</’max. 0<Р<2л. (10.28)
Поставленные задачи будем решать с учетом ограничений на максималь¬
но допустимые значения температуры и перегрузки:
g(t) = Т- 7дОП < 0, £(f) = п - пдоп < 0. (10.29)
Приведем общую формулировку задач: для системы дифференциальных
уравнений (10.27) найти законы изменения P(t} и v(t), которые реали¬
зуют минимум следующих функционалов управления:
/ = min ДУЕ хар = min(AV? + 2ДУТ + ДУ р) (10.30)
или
/ = mints = rninCtj + St') (10.31)
при ограничениях (10.28), (10.29) иограничении
П<ГДоп (Ю.32)
Для функционала (10.30) и при ограничении
ДУ7 < д Vi доп (10.33)
22. Зак. 2069
337
для функционала (10.31) при краевых условиях
V(t0) = V0f 0(to) = 0o, h(tQ) = hQ, = (10.34)
Игк)=Ук, вкк) = вк, Л(ГК)=ЛК, /П(ГК) = Л7К. (10.35)
Начальные условия фиксируются в момент подлета к планете (до приложе¬
ния импульса ДУ[) , а конечные условия соответствуют параметрам тре¬
буемой формируемой орбиты искусственного спутника Венеры.
При записи функционалов управления (10.30) и (10.31) использованы
следующие обозначения:
AVj — тормозной импульс, потребный для перевода КЛА с траектории
перелета Земля — Венера на высокую эллиптическую орбиту искусствен¬
ного спутника Венеры;
Д1/р — разгонный импульс, потребный для формирования заданной
орбиты;
- корректирующие импульсы скорости, подаваемые для формиро¬
вания перицентра промежуточных орбит с целью выдерживания ограниче¬
ния (10.29) на величину допустимой перегрузки или температуры (первый
тормозной импульс используется для схода КЛА с опорной высокоэллипти¬
ческой орбиты) ;
h — время движения КЛА по опорной орбите;
tj — время движения КЛА между апоцентрами двух последующих про¬
межуточных орбит.
Анализ функционалов управления показывает, что Для рассматриваемой
схемы выведения КЛА решение сформулированных задач можно сущест¬
венно упростить. А именно с учетом последовательности операций ракето¬
динамического и аэродинамического способов торможения КЛА каждый
из функционалов управления (10.30) и (10.31) может быть представлен
в виде суммы двух функционалов:
/ = /1 + /2 = min ДУ* + пгнп(2ДУ1Т + ДУР),
/ = /1 + /2 = mint! +minStz.
(10.36)
(10.37)
Учитывая такое представление функционалов управления, решение каждой
задачи можно разделить на два этапа.
На первом этапе определяется минимум функционалов /lf а на втором
этапе решается задача минимизации функционалов /2. Затем осуществляет¬
ся сопряжение результатов решений.
Итак, на первом этапе требуется определить параметры опорной орбиты
(высоты апоцентра h&n и перицентра h%n), для которых достигается мини¬
мум функционала
2д ' J 2(i(R0+h°n)
Яо +Л™ V (2Ло+й°п+Л£п)(Ло+Л™)
(10.38)
при ограничении (10.32) или функционала
(10.39)
при ограничении (10.33).
338
Высота перицентра h„n определяется допускаемым конструкцией КЛА
газодинамическим нагревом и задается в качестве исходного параметра,
поэтому зависимости (10.38) и (10.39) являются функциями одной пере¬
менной
Анализ выражений (10.38) и (10.39) показывает, что функция ДУ* (h&n}
монотонно убывающая, а функция tr (h™) монотонно возрастающая. Сле¬
довательно, минимум величины ДУ* будет достигаться при высоте апо¬
центра А°п, соответствующей условию fj = fiдоп< а минимум времени
fi — при значении h^n, которое определяется условием ДУ/^ = ДУi ДОп-
На втором этапе решаются следующие вариационные задачи: для систе¬
мы дифференциальных уравнений (10.27) определяются законы управле¬
ния P(t) и Р (Г), доставляющие минимум функционалам
/2 =т1п(2ДУ/т + ДУР) (10.40)
и
/2 =minSfz (10.41)
при ограничениях (10.28), (10.29), начальных условиях в перицентре
орбиты
У(Г0) = И°п, 0(fo) = 0°п = 0, /7(f0) =Л°П, m(t0) = т™ (10.42)
и конечных условиях (10.35).
Решение вариационных задач проводится с использованием необходимых
условий оптимальности принципа максимума Понтрягина.
Введем в рассмотрение гамильтониан
(10-43)
где i/y
НИЯМИ
d'Pi
dt
(/ = 1, 2, 3, 4) — сопряженные переменные, определяемые уравне-
cxspV
т
'Pi +
f—
L r2v2
1
COS0 + — COS0
r
GJT
— COS0
V2
p
sin(p — 0)
mV2
( 3,25/4CtSyH
+ ^sin0+(
</^2 Гр ~ p 1
= — COS0 — GJTCOS0 sin(p — 0) 1//1 +
dt I r2 m
I д I/ ы2г ■ P ]
sin# +—sin0 + sin# + cos(p — #) Фг — Фз У cos#,
г V mV J
н v2,2s
r2V
mV
(10.44)
V
^2 +
1
■(
2д
-—-cos
r3V
2n
339
Г cxspV2
dt L 2л?2
P 1 P
+ —rcos(l>-0) k/j + ——sin(p —0)ф2
л? ] mV
при q(t) < 0 и £(Г) < 0.
Если q(t) = 0 или £ (Г) = 0, то система сопряженных переменных записыва¬
ется следующим образом:
где
-0,25
(10.45)
dq
=—=0,25(ео)
от
(Др°’5Г
-0,5
н
1/3,25
+ авр0,5гн I/3,2 )-0,75
X
X [0,5Д(ргн)-°’5\/3’25р + 3,254р0,5Гн 0,5У-2,25 V +
+ О,5авр_о,5гн V3’2p + 3,2aBp°'5rHV2,2V],
Л = ^~~~= [ OT-‘cos(p- 0)^1 + (л?У)_151п(р — 0)ф2 —
оу/оР
- (^уд0оз)’1^н][о.25(ео)_О’75"’_1Ргн_1^5,4со5(р-0)(3,25Д2У0’1 +
+ 6,45аД5г-°’5 У0’05 + 3,2а2В2гн)]"2
при g(t) = 0;
d% сх sp V
=— = ,—[ —pv2r3ms'\n0 —cxspV2r3 — 2gmsin0 +
dt рт*г
+ 2a>2r4msin0 + 2 V2r2msinO + 2Pcos(p — 6)r3],
A = Э7С/ЭР _ p[n?cos(p- 0)i//i + n?V~1sin(p- 0)^/2 - от2 (Руд^оз)-1ф4 ]
9<p/9P 2pVcxsr2cos(v — 0)
при £(t) = 0;
F; (t) = — (/ = 1,2, 3, 4) — выражения для правых частей системы
' Эх,
(10.44).
Сопряженные переменные в момент выхода КЛА на изотермический или
изоперегрузочный участок (гх или t2) скачком меняют свою величину:
* Эд Эд
^-ф,.(г) = М1^- + р2-^-,
ф Э£ 9£ (10.46)
Ф; (г? ) - Ф, (г) = Мз Т + Д4 -—,
' 7 Эх;- Эх;-
где Ди Д2 / Мз/ М4 — постоянные множители.
340
Необходимые и достаточные условия прохождения экстремали вдоль
ограничений имеют вид
^=0
(p = 0, 1,2,.
...n),
drp
(10.47)
9zg
“ o
(z = 0,1,2,...
Эг
где п и к — порядок производной функции q или £, которая содержит в яв¬
ном виде параметры управления. Для рассматриваемых задач п-к= 1. По¬
этому получаем следующие законы управления:
cxspV2 Г М 9
Pcos(p- 0) = + т\ у s’n^ “ corsin# +
+ (O,5/4p°’sr“0’5 l/4’2s0sin0 + О,Бавр°’5/Згн V4’2sin<9) X
X (3,25Ap0’Sr-°'5V2'2S + 3,2aBp0’SrHV'2’2)'1 j (10.48)
при движении КЛА по изотермическому участку и
Pcos(v — 0) = 0,5/ЗУ 2msin# + 0,5 cxspV 2 +
pm „ л?У2
+ —- sin# — со2 лиг sin# sin# (10.49)
r3 r
при его движении по изоперегрузочному участку.
Законы оптимального управления при q(t} < 0 и £(t) < 0 получаются из
условия максимума гамильтониана
[ cxspV2 р _ Р 1
К г sin# + o?rsin# +— cos(p — #)Ь/1 +
L 2m r3 m J
Г p V co2r P 1
+ — cos# + — cos# + 2gj + sin# + sin(p — #) \ф2 +
L r2V г V mV J
+ V^3sin0^ — (<7KOHB +а<7Рад - eoT*)-
Р
^уд^оз
и имеют вид
где
при
при
Ф(Г) =—cos(p — #) г//1
т
Ф(г)<0,
Ф(г) > 0,
+ _Z77sin(p- W2 ~
mV *уд#^оз
(10.50)
1
341
Рис. 10.40. Зависимости тор¬
мозного импульса AUj и вре¬
мени полета по опорной ор¬
бите г. от высоты апоцентра
- . оп
опорной орбиты па .
Видно, что величина тяги
двигательной установки Р
при оптимальном управле¬
нии КЛА внутри допусти¬
мой области фазовых коор¬
динат всегда имеет лишь
экстремальные значения.
Отметим также, что фун¬
кция Ф (г) определяет чис¬
ло прохождений КЛА
атмосферы планеты (А/), которое равно количеству интервалов времени,
на которых Ф (г) >0.
Из условия трансверсальности получаем
V
i//3(fK) и ^4(*Кне определены.
В результате определение оптимального управления сводится к решению
трехпараметрической краевой задачи для систем дифференциальных урав¬
нений (10.27), (10.44) и граничных условий (10.34), (1035), (10.42) и
(10.51) при ограничениях (10.28) и (10.29).
Приведем результаты решения задачи минимизации суммарных затрат
характеристической скорости, потребных на формирование орбиты искус¬
ственного спутника Венеры.
На рис. 10.40 представлены результаты расчетов ДУ{ и tlt проведенных
с использованием зависимостей (10.38) и (10.39) для различных значений
высоты апоцентра опорной орбиты /?°п. Высота перицентра опорной орбиты
принималась постоянной Л°п ~ 500 км. Видно, что при возрастании /?£п до
значения h°n « 600-^700 тыс. км происходит заметное уменьшение тормоз¬
ного импульса ДУ*. При дальнейшем увеличении h^n изменение ДУ{ несу¬
щественно. Так, например, возрастание /?°п от 60 тыс. км до 600 тыс. км
приводит к уменьшению импульса ДУ* от 1200 м/с до 800 м/с (примерно на
32%), но дальнейшее увеличение h°n до 1,5 млн. км вызывает изменение
ДУ[ лишь до 770 м/с (примерно на 4%) .
Видно также, что возрастание h^n ведет к значительному увеличению
времени движения по опорной орбите tr. Так, например, если при h™ =
= 60 тыс. км время tx — 0,8 сут, то при h°n » 600 тыс. км это время состав¬
ляет — 20 сут.,а при h^n = 1,5 млн. км время tj возрастает до 84 сут.
Таким образом, зависимости (10.38) и (10.39) позволяют однозначно
определить величину ДУ[ или при заданных ограничениях на параметры
движения. Так, для рассматриваемого примера (/?£п —500 км), если пред¬
положить, что время полета КЛА по опорной орбите ограничивается вели¬
чиной —20^-25 сут, легко определяется потребная минимальная величи-
342
на тормозного импульса ДУ? ~ 790-^800 м/с. Это соответствует высоте
апоцентра опорной орбиты h&n ~600^-700 тыс. км.
Приведем результаты решения задачи минимизации затрат характеристи¬
ческой скорости на втором этапе. Высота апоцентра формируемой орбиты
/7азад, максимально допустимая температура 7}jOn и приведенная нагрузка
на лобовую поверхность Рх варьировались в следующих пределах:
10 тыс. км < ha зад < 60 тыс. км, 800 °C < 7flOn < 900 °C,
100 кгс/м2 < Рх < 700 кгс/м2. (10.52)
Рассматривались три модели атмосферы: номинальная, максимальная и ми¬
нимальная. В качестве номинальных значений варьируемых параметров
использовались следующие:
зад 20 ТЫС. КМ» зад 500 КМ, ^доп ~ 840 С,
Рх = 300 кгс/м2 . (10.53)
Анализ результатов решения краевой задачи позволил выявить структу¬
ру оптимального управления тягой двигательной установки P(t} из усло¬
вия SAУ min . Во всем рассматриваемом диапазоне варьируемых парамет¬
ров ha зад, Тлоп и Рх и для всех моделей атмосферы управление тягой дви¬
гательной установки состоит в следующем: в апоцентре каждой промежу¬
точной эллиптической орбиты происходит однократное включение двига¬
тельной установки; величина потребного импульса характеристической
скорости выбирается- из условия обеспечения заданной величины допусти¬
мой температуры Гдоп или перегрузки лдоп; для всех включений» кроме
последнего, направление вектора тяги Р составляет угол v = 180° с векто¬
ром скорости К; в апоцентре промежуточного эллипса с ha — угол
р = 0, т.е. происходит разгон КЛА до заданной скорости.
В табл. 10.3 представлены результаты расчетов для каждого витка при
выведении КЛА с опорной на заданную орбиту искусственного спутника
Венеры [номинальный вариант исходных данных (10.53) ]. Здесь приведе¬
ны следующие параметры каждого витка входа КЛА в атмосферу:
— корректирующий апоцентрический импульс характеристической
скорости;
Таблица 10.3
Параметры траектории выведения КЛА на орбиту искусственного
спутника Венеры при многократном погружении в атмосферу
Номер
витка
д/,
м/с
Ц>,
км/с
град
nmax
км
fa, с
кДж/м2
Г, ч
км
0
—
—
—
—
—
-
-
2592
600 000
1
3,18
10,209
-1,95
0,05
113
84
1861
409
413 081
2
0,02
10,186
-1,96
0,06
112
84
1874
250
313 692
3
0,03
10,163
-1,99
0,07
111
85
1955
174
251 903
4
0,04
10,140
-2,20
0,09
110,5
97
2125
120
183 036
5
0,045
10,098
-2,24
0,12
110
98
2197
79
142 649
6
0,05
10,054
-2,35
0,13
109
107
2297
55
104 796
7
0,1
9,988
-2,58
0,25
107
120
2539
34
67 050
8
0,2
9,853
-2,84
0,59
103,5
141
2856
17
32 010
9
0,715
9,161
-2,93
1,9
98
319
3788
3,6
20 003
343
VQ — начальная скорость входа;
0q — начальный угол наклона траектории к местному горизонту;
nmax “ максимальная перегрузка;
^min ~ минимальная высота пролета над поверхностью планеты;
Га — время движения КЛА в атмосфере;
□s — интегральный тепловой поток;
t — время движения на внеатмосферном участке;
ha — высота апоцентра.
Исследования показали, что затраты характеристической скорости
AV* = ЕДУ ZT + ДУ р, потребные для перевода КЛА с опорной орбиты на
заданную, практически полностью определяются разгонным импульсом
ДУР, сообщаемым КЛА в апоцентре орбиты с ha = /?азад. Так, для рас¬
сматриваемого примера сумма тормозных импульсов равна приближенно
4,5 м/с, а ДУ р 65,5 м/с. При этом величины тормозных импульсов моно¬
тонно возрастают от ДУ2 = 0,02 м/с до ДУ 9 = 0,715 м/с (без учета им¬
пульса схода с опорной орбиты) .
Снижение высот апоцентра промежуточных эллиптических орбит проис¬
ходит с уменьшающейся интенсивностью. Так, если после первого витка
уменьшение высоты апоцентра /?^п - hxa %187 тыс, км, то после последнего
прохождения атмосферы Л® — Л9 % 12 тыс. км. Изменение высот апоцентра
приводит к тому, что при каждом входе в атмосферу меняются начальные
условия входа Уо и 0О. Так, скорость Уо постепенно уменьшается с V ъ
10,2 км/с до У 9 ^92 км/с, при этом угол 0О увеличивается по абсолют¬
ному значению с Oq = 1,95° до 0? = 2,93°.
Максимальная траекторная перегрузка лтах и минимальная высота про¬
лета над поверхностью планеты /?min достигаются во время последнего про-
Таблица 10.4
Изменение характеристической скорости, времени
и суммарного теплового потока при переводе КЛА
с опорной орбиты на заданную
. оп
"q- , ТЫС.КМ
^азад»
ТЫС.КМ
Рх, кгс/м2
т °р
'ДОП'
p(h)
л/
Тдоп)
ДИ'
ТдопИ
м/с
600
20
300
840
осн.
9
57
300
20
300
840
осн.
7
59
112, 667
20
300
840
осн.
4
68
66, 313
20
300
840
осн.
2
77
600
10
300
840
осн.
9
57
600
40
300
840
осн.
8
56
600
60
300
840
осн.
8
56
600
20
100
840
осн.
9
57
600
20
500
840
осн.
9
57
600
20
700
840
осн.
9
57
600
20
300
830
осн.
41
57
600
20
300
850
осн.
4
56
600
20
300
900
осн.
2
55
600
20
300
840
мин.
9
57
600
20
300
840
макс.
9
57
344
хождения КЛА атмосферы. Таким образом, определяющим с точки зрения
основных траекторных параметров является последний перед вылетом на
заданную орбиту вход КЛА в атмосферу.
Следует отметить, что при расчете траекторий движения КЛА в атмо¬
сфере при многократном ее прохождении во всем диапазоне варьируемых
параметров (10.53) величина максимальной траекторной перегрузки лтах
не превышает двух-трех единиц.
В табл. 10.4 приведены результаты, иллюстрирующие частное влияние ос¬
новных варьируемых параметров (/?£", ha зад, Рх, Тлоп) и моделей атмо¬
сферы на затраты характеристической скорости ДУ*, потребной для пере¬
вода КЛА с опорной на заданную орбиту искусственного спутника Венеры.
Видно, что импульс скорости уменьшается по мере увеличения высоты апо¬
центра опорной орбиты h°u, высоты апоцентра формируемой орбиты
/?азад и максимально допустимой температуры ТдОП. Изменение величины
приведенной нагрузки на лобовую поверхность PXf как и моделей атмо¬
сферы, не влияет на Д V'.
Число прохождений КЛА атмосферы /V, а следовательно, и число вклю¬
чений тяги двигательной установки также зависит от варьируемых пара¬
метров. Наиболее существенное влияние оказывает максимально допусти¬
мая температура Гдоп.
Анализ результатов решения вариационной задачи минимизации затрат
характеристической скорости показывает, что существует такое предельное
значение Таоп = 7"д*оп, при котором выведение КЛА на требуемую орбиту
осуществляется путем только однократного прохождения атмосферы. Это
значение Гд*оп в общем случае зависит от варьируемых параметров /?°п,
зад И Рх (РИС. 10.41) .
ди'
(Г — сво¬
бодно) , м/с
6ди', %
tv
(Г<
^7"доп) •
ч’
(Г — сво¬
бодно) ,ч
5tv, %
(^ Тдоп).
кДж/м1
Qr
(Т — сво¬
бодно),
кДж/м2
8ОГ.'
55
3,5
1420
510
64,2
3786
4289
13,3
58
1,7
550
250
55,5
3868
4255
10,0
66
3,0
150
50
66,7
3895
4126
5,9
75
2,6
34
26
23,5
3930
4065
3,4
55
3,5
1430
515
64,0
3875
4356
12,4
55
1,8
1400
500
64,3
3345
3945
17,9
55
1,8
1390
495
64,4
3112
3712
19,3
55
3,5
1400
510
63,6
3795
4296
13,2
55
3,5
1440
520
63,9
3781
4285
13,3
55
3,5
1450
530
63,4
3780
4280
13,2
—
-
8200
-
-
3665
—
—
—
-
720
-
-
3959
—
-
—
-
520
-
-
4287
—
55
3,5
1430
515
64,0
3780
4270
13,0
55
3,5
1410
505
64,2
3791
4293
13,3
345
Рис. 10.41. Зависимости температуры ГдОП от высоты апоцентра опорной и за¬
данной Лазад орбит и приведенной нагрузки на лобовую поверхность Р*.
Суммируя значения потребного импульса характеристической скорости,
найденные на первом и втором этапах решения задачи, получим, что сум¬
марные затраты характеристической скорости Д^^хар в основном опреде¬
ляются величиной импульса перевода КЛА на опорную орбиту Так,
при номинальных исходных данных » 70 м/с, а ДУ* ^810 м/с, т.е,
составляет около 88% от общих затрат характеристической скорости.
Рассмотрим задачу минимизации суммарного времени выведения КЛА
с опорной на заданную орбиту искусственного Спутника Венеры,
Используя необходимые условия оптимальности, ’ запишем систему
сопряженных уравнений при q(t) < 0 в виде
Р1//0 d\jj-
=0, - = F.(t) (/=1,2,3,4), (10.54)
dt dt
где i//0 — сопряженная переменная, полученная при введении в систему
(10.27) уравнения dt/dt = 1; Ff(t) — правые части системы (10.44).
При выходе на ограничение q(t) = 0 система сопряженных переменных
примет вид (10.45) .
Из условия трансверсальности получаем в конечной точке
i//o(U = -1- (10.55)
В результате решения краевой задачи определяется структура оптималь¬
ного управления: в апоцентрах промежуточных эллиптических орбит аппа¬
рату сообщаются тормозные импульсы (р = 180°), а в апоцентре последнего
эллипса производится его разгон (р = 0). При прохождениях атмосферы, в
моменты выхода на ограничения (10.29), производится включение двига¬
тельной установки с целью обеспечения изотермического или изоперегру-
зочного режима движения КЛА.
Данные, приведенные в табл. 10.3, показывают, что время выведения
КЛА на орбиту искусственного спутника Венеры t% = S(ta + t) практически
состоит только из времен полета на внеатмосферных участках. Суммарное
время движения КЛА в атмосфере Lta составляет 0,1% от времени t%-
Из всех промежуточных прохождений атмосферы наиболее длительным
является последнее, составляющее в рассматриваемом примере око¬
ло 5 мин.
Численны^ результаты решения задачи, представленные в табл. 10.4,
дают возможность оценить влияние всех варьируемых параметров на
346
величину Наиболее заметно суммарное время выведения зависит от
максимально допустимой температуры Тдоп. Крайне незначительное увели¬
чение Гдоп приводит к заметному сокращению t%. Это происходит вслед¬
ствие уменьшения количества прохождений КЛА в атмосфере. Сильное
влияние на оказывает также высота апоцентра опорной орбиты па .
Уменьшение h£n приводит к снижению
Влияние величины ha зад на время менее значительно. Приведенная
нагрузка на лобовую поверхность Рх и модели атмосферы практически
не влияют на величину f £. '
Необходимо отметить, что для задачи минимизации времени также*
существует некоторое предельное значение максимально допустимой
температуры ГдОп = при которой КЛА выводится на заданную орби¬
ту за одно прохождение атмосферы. Это приводит к весьма существенному
снижению
Глава 11
ИСПОЛЬЗОВАНИЕ КОРРЕКТИРУЮЩЕГО ИМПУЛЬСА В АТМОСФЕРЕ
ПРИ ВЫВЕДЕНИИ НА ОРБИТУ КОМБИНИРОВАННЫМ СПОСОБОМ
§ 11.1. Оптимальное управление при выведении
на орбиту с использованием корректирующего импульса
А
Задача оптимизации траекторий КЛА с ракетным двигателем в атмосфе¬
ре в последние годы привлекала внимание многих исследователей. С появ¬
лением КЛА, обладающих большим значением аэродинамического качества,
эта задача была достаточно подробно рассмотрена для аппаратов, маневри¬
рующих в атмосфере Земли (см., например, [32, 130]). В настоящее время
благодаря результатам, полученным рядом исследователей [23, 24], стало
возможным выявить наиболее общие результаты по оптимизации траекто¬
рий выведения на орбиту искусственного спутника любой планеты летатель¬
ного аппарата с ракетным двигателем, на который действуют аэродинами¬
ческие силы в обычном гравитационном поле.
Пусть текущее состояние КЛА в момент времени t определяется векто¬
ром положения г (Г), вектором скорости V(t) и величиной мгновенной
массы m(t) . Управление КЛА на траектории полета осуществляется путем
изменения вектора аэродинамической силы
Предполагается, что в любой момент време¬
ни t конец вектора аэродинамической силы
А находится на некоторой поверхности, изме¬
няющейся в функции, времени, а направ¬
ление силы тяги может быть произвольным,
однако ее величина ограничивается значе¬
ниями
0<Р<Ртах.
Иными словами, конец вектора тяги Р нахо¬
дится на сфере с центром в точке М (совпа¬
дающей с центром масс КЛА) и радиусом,
и вектора силы тяги Р.
Рис. 11.1. Пространство управления.
347
равным Pmax. Принято разлагать вектор аэродинамической силы А на силу
лобового сопротивления X, направленную против вектора скорости и подъ¬
емную силу У, ортогональную вектору скорости. Ограничение на величину
аэродинамической силы выражается в форме соотношения между аэродина¬
мической подъемной силой и силой лобового сопротивления
Х = Х(У, V, г).
Будем использовать обычное представление этих сил
Сх § « Су S
Х = pV2, У = — рУ2. (11.1)
2 2
Предполагается, что коэффициенты сх и су не зависят от числа Маха и числа
Рейнольдса. Считается также, что КЛА имеет плоскость симметрии, сила
тяги и аэродинамическая сила приложены в центре масс и в стационарном
режиме векторы аэродинамической силы и скорости лежат в плоскости
симметрии. Будем определять также обычным образом угол крена у как
угол между оскулирующей плоскостью г К и плоскостью AV летательного
аппарата (рис. 11.1).
Образуем правую ортогональную систему координат vyn, связанную с
центром масс М аппарата таким образом, что ось v направлена по вектору
скорости, ось у находится в оскулирующей плоскости, а ось п перпенди¬
кулярна к ней. Учитывая (11.1), соотношение между силой лобового
сопротивления и подъемной силой заменяется соотношением между аэро¬
динамическими коэффициентами
Сх ~ Сх (Су ) .
На величины коэффициента подъемной силы и угла крена накладываются
ограничения
0<су <сутах, (11.2)
0<7<Ттах- (11.3)
Предполагая, что КЛА рассматривается в виде точечной массы, совершаю¬
щей полет в обычном гравитационном поле под воздействием аэродинами¬
ческих сил и силы тяги, запишем уравнения движения КЛА в виде
dr dV 1 dm Р
— = К = — (P+A)+g, = ,
dt dt т dt с
где с — постоянная скорость истечения газа из сопла двигателя,g — вектор
ускорения силы тяжести.
Задача оптимального управления формулируется следующим образом.
Пусть в начальный моменд- времени t = 0 векторы г и V и скалярная ве¬
личина т имеют следующие значения:
г = ГО, V = Ко, т =т0.
В конечный момент времени t = tK имеем г =гк, т =тк, 0 =вк (высота
апоцентра ha формируемой орбиты задана). Задача состоит в том, чтобы
найти такие программы управления аэродинамической A(t) и силой тяги
P(t), которые обеспечивают минимум скалярной функции конечного
состояния ДУ = V& — Va, где V£ — конечная скорость, потребная для
формирования заданной орбиты ИСП. При этом направление вектора
скорости Va в пространстве ограничено условием выведения КЛА на задан¬
ную высоту апоцентра формируемой орбиты ha = ha3aa.
348
Чтобы воспользоваться необходимыми условиями оптимальности прин¬
ципа максимума Понтрягина введем векторы сопряженных переменных
—> —> —>
фг, и и сформируем гамильтониан
- фу - ф тР
JC=^rV+— [P + A} + ^vg-^~ . (11.4)
т с
—> —> —►
Сопряженные переменные i//r, фу и определяются уравнениями
d^r ЭК d^v _ ЭК d$m _ dJ€
dt dr ' dt dV ' dt dm
Оптимальными являются такие законы управления аэродинамической
силой Л(г) и силой тяги P{t), которые в своих ограниченных пространст¬
вах в каждый момент времени доставляют максимум гамильтониану
(11.4). Максимизация гамильтониана выполняется по двум управляющим
параметрам Р и А.
Учитывая, что управление космическим летательным аппаратом посред¬
ством тяги двигательной установки Р и аэродинамической силы А произ¬
водится независимо, для максимизации гамильтониана рассмотрим скаляр¬
ное произведение двух векторов фуР. Так как эти два вектора коллинеар¬
ны [ 146], т.е. сила тяги направлена вдоль вектора фу, получим
тж(фуР)~фуР. (11-5)
Определим аэродинамическую силу А таким образом, чтобы скалярное
произведение векторов ФуА приняло максимальное значение. Анализ
показывает [146], что максимум произведения фуА достигается при
выполнении условия
dX
tge
(11.6)
dY '
где e — угол между векторами V и ^у. Из изложенного ясно, что этот угол
равен углу между вектором скорости V и оптимальным направлением
силы тяги.
Таким образом, уравнение (11.6) задает закон оптимального управления
для аэродинамической подъемной силы. Предполагая, что подъемная сила Y
и сила лобового сопротивления X пропорциональны коэффициентам су и
сх, уравнение (11.6) можно заменить соотношением
tge=—. (П-7)
dcy
Анализ геометрической схемы определения оптимальной аэродинамической
силы показывает, что три вектора tyv, V \л А лежат в одной плоскости.
Это позволяет записать соотношение
(КХ^к)Л = 0, (11.8)
которое совместно с уравнением (11.6) определяет оптимальные програм¬
мы управления подъемной силой и креном, когда на управление аэродина¬
мической силой не накладываются ограничения.
Обозначим через х угол между касательной в точке максимальной
подъемной силы и направлением подъемной силы. Тогда, если величина
349
коэффициента подъемной силы су ограничена условием (11.2) и выполня¬
ется неравенство
X Хтах *
оптимальная программа управления подъемной силой определится со¬
отношением
опт _
су сутах-
Это соотношение действительно, если угол атаки не ограничен.
Определим оптимальное управление подъемной силой для случая, когда
выполняется ограничение (11.3) на величину угла крена, т.е. полет проте¬
каете 7 = 7тах- Пусть фу — проекция вектора фу на плоскость симмет¬
рии КЛА, определяемой векторами А и F, а фу — составляющая вектора
фу, перпендикулярная к плоскости, в которой находится вектор оптималь¬
ной аэродинамической силы А. Тогда будем иметь
Фу = Фу + ф"-
Отсюда получаем условие оптимального управления подъемной силой
при 7°пт=7тах:
, ЭХ
tg 6 = ,
ЭУ
где е‘ — угол между векторами V и фу.
Определим оптимальный закон управления вектором тяги двигательной
установки. Учитывая уравнение (11.5), перепишем гамильтониан (11.4)
в виде
= ФГУ + Фу[& + (1/т)А] + (Р/т) [фу - (тфт/с)].
Обозначая функцию переключения тяги через
получаем окончательно
-> Р
М = фгУ + фу[^ + (Мт)А] +к — . (11.9)
т
Анализ гамильтониана (11.9) показывает, что для его максимизации не¬
обходимо использовать следующий закон управления тягой:
Р ^тах
при
к >0
(участок разгона),
Р=0
при
к <0
(пассивный участок полета),
Р = var
при
к = 0
(участок маршевого полета)
Полученные результаты справедливы для произвольного гравитационно¬
го поля и при отсутствии ограничения на направление тяги двигательной
установки. Для практических приложений важным является случай полета
КЛА в атмосфере с малыми углами атаки при жестко связанном с корпу¬
сом КЛА сопле двигателя, т.е. когда направление вектора тяги незначитель¬
но отличается от направления вектора скорости. Рассмотрим этот случай
особо, предполагая, что вектор ускорения g инвариантен во времени, т.е.
g = const. Это допущение при движении КЛА в атмосферах планет Солнеч-
350
ной системы не оказывает заметного влияния на траекторию полета и
позволяет, вместе с тем, получить в явном виде параметры оптимальных
траекторий выведения КЛА на орбиту искусственного спутника пла¬
неты [145].
Запишем векторы скорости полета, аэродинамической силы и сопря¬
женных переменных в виде
И= (V,, У2/К3), 4 = (Д1,Д2,ДзЬ
Фу = (Ф1, Фг, ’hh Фг = (Ф^Фг.Фз)-
Выразим составляющие вектора скорости через угол наклона траектории
в и угол курса ф:
Vi = V cos 0 cos i//, V2 = Vcos 0 sin i//, l/3 = l/sin0. (11.10)
Для того чтобы обеспечивалось условие максимума гамильтониана (11.4),
должно выполняться условие
i/zjdUi + ф2д\/2 + \p3dV3 = 'I'vdV + фвс!0 + ф^с/ф.
Отсюда получается следующее линейное преобразование для составляющих
базиса-вектора [145] :
cos 0 cos ф cos 0 sin ф sin 0
'ФГ
Фу
— sin 0 cos ф — sin 0 sin ф cos 0
Ф2
=
•Фе/V
— cos 0 sin ф cos 0 cos ф 0
j/'a.
Фф/V.
Решая уравнение (11.11), получаем
(11.11)
(11.13)
На основании геометрических соотношений запишем выражения для
составляющих аэродинамической силы в виде
— X = (A, cos ф + A2sin ^Icos 0 + А3 sin 0,
— Y cos 7 = (A j cos ф + A2 sin ф) sin 0 — A3 cos 0,
— Y sin 7 = Aj sin ф — A2 cos ф.
Теперь можно получить следующие выражения для проекций аэродинами¬
ческой силы на оси декартовой системы координат:
Ai = — X cos ф cos 0 — X(cos 7 cos ф sin 0 + sin 7 sin ф),
A2 = — X sin ф cos 0 — X(cos 7 sin ф sin 0 — sin 7 cos ф), (11.14)
A3 = — X sin 0 + Y cos 7 cos 0.
Примем для простоты, что зависимость между коэффициентами силы
лобового сопротивления и подъемной силы описывается параболой
сх ~
(11.15)
351
где сх0 и у — постоянные. Будем определять параметр управления подъем¬
ной силой X соотношением
сх0
Тогда X = 1 означает, что полет КЛА в атмосфере планеты совершается с
максимальным аэродинамическим качеством. Учитывая формулу (11.7)
и соотношение (11.15), получаем следующий закон оптимального уп¬
равления аэродинамической силой:
tg е = 2ксу.
Из (11.8) и уравнений (11.10) и (11.12) для составляющих вектора ско¬
рости V и сопряженных переменных i//z, получим уравнение
(A j sin \jj — А 2 cos \jj) —
i// '
— —— [(A i cos ф + A2 sin i//)sin 0 — A3 cos 0] =0.
cos 0
Учитывая уравнения (11.14), найдем следующее выражение для оптималь¬
ного угла крена:
1//,
tgy = — . (11-16)
\рв cos О
Выразим теперь оптимальный закон управления аэродинамической
подъемной силой через сопряженные переменные. Поскольку фу =
= i/zl/cos е = можно записать
ф2 = £-• (11.17)
COS €
С другой стороны, из уравнений (11.10) и первого соотношения (11.13)
имеем
Фд tq у
= Фу + Фе +—• (11.18)
Приравнивая правые части уравнений (11.17) и (11.18), после несложных
преобразований будем иметь
Vi// v cos у
откуда получаем следующее выражение для оптимального закона управле¬
ния подъемной силой:
с =
у 2KV\jj rcosy
(11.19)
Одним из возможных режимов оптимального управления аэродинами¬
ческой силой является полет с постоянным максимальным значением
аэродинамического качества. Приведем результаты решения уравнений
оптимального движения КЛА для этого случая. Запишем уравнения дви¬
жения в проекциях на оси декартовой системы координат xix2x3 в сле-
352
дующем виде:
dxi
= V cos 9 cos i//,
dt
dV
dx2
= V cos 9 sin i//,
dt
dx3
= V sin 0,
dt
dt
с?ф
dt
(P-X)
g sin 9,
m
Y sin у
m V cos 9
dm
d9 Y cos у
dt mV
P
9
cos 9,
V
dt
c
где с — скорость истечения рабочего тела.
Запишем гамильтониан
К = (ф1 cos i// + i//2 sin i//) V cos в + i//3 sin в —
(11.20)
Фи — + g sin 0^ +
cos у g \ Y sin у P ( \
mV V / mV cos 9 m \ c /
Подставляя в гамильтониан К выражения (11.16) и (11.19) для опти¬
мального закона управления углом крена и коэффициентом подъемной
силы, получаем
К = (i//i cos i// + i//2 sin i//)l/cos 9 + i//3 V sin 9 - g sin 9 + cos 9 +
psi/2 P / m\b \
+ ~ (Kc2y ~сх0)фу +— .
2m y m\ c /
Если полет КЛА протекает с максимальным значением аэродинамичес¬
кого качества, то кс2 — сх0 = 0 и гамильтониан доказывается не зависящим
от составляющих вектора аэродинамической силы Л.
Функция переключения к, которая определяет режим работы двигателя
на оптимальной траектории, записывается следующим образом:
К = •
с
Сопряженные переменные на оптимальной траектории имеют вид
oty'i
= 0,
dt
dy^v 9Фв
—— = — (i//i cos i// + ф2 sin i//) cos 9 — i//3 sin 9
d^e
= (i// j cos i// + i//2 sin \p)V sin 9 — iI/3 V cos 9 +
dt
/ . n Фе Л Фф X sin у
+ 9 I фу cos 9 sin 9 ) — sin 9,
\ V / mVcos29
^Фф
dt
dt
23. Зак. 2069
d\p2
= 0,
dt
с/ф3 QpsV2
~a~ ' —
2m
= (i// x sin i// — i//2 cos ф) V cos 9,
psV2 0 Рфу
—<КСУ -Схо)Фу+—J-
2m2 m2
psVcx0
cos 9 +
(11.21)
m
353
Из рассмотрения системы уравнений (11.21) очевидны первые два ин¬
теграла [145] :
t//i =aj = const, i//2 = a2 = const. (11.22)
При свободных значениях продольной и боковой дальностей из условий
трансверсальности получаем
= ^2 = О,
а при полете с постоянным максимальным значением аэродинамического
качества
Фз = const.
Учитывая (11.22), запишем
d ., . d^
dt dt
откуда будем иметь
^1*2 - ^4*1 = Фф + Const.
При свободном значении боковой и продольной дальностей получаем для
сопряженной переменной следующий интеграл:
Фф =а6 = const.
Если в момент вылета КЛА из атмосферы (t = tK) величина угла крена
произвольна, то сопряженная переменная
=0.
Проведем анализ производной
d psV2 ~ Р / тфт \
— (тфт) = (к-Су-сх0)фу+ — [фу ). (11.23)
dt 2т т \ с /
Если движение КЛА осуществляется по оптимальной траектории с выклю¬
ченной двигательной установкой, то Р = 0, а если с включенной в стационар¬
ном режиме, то к = 0. При этом если в обоих случаях КЛА движетря с
постоянным максимальным значением аэродинамического качества, то
тфт = const.
При полете КЛА с переменной величиной подъемной силы на пассивном
участке или при равновесном полете из уравнения (11.23) найдем
d\p3 = (№(тфт).
Отсюда, интегрируя, будем иметь
Фз = РтФт + а3,
где а3 — постоянная интегрирования.
Проанализируем производную от произведения \/фу:
d / фв \ Р / ^Фт \
— (Уфу} = - JC - 2д ( фу sin е + у- cos 9 } + — ( 2фу 2- \.
Используя допущение о малости гравитационной силы по сравнению с аэро¬
динамической силой для пассивного участка полета (Р = 0), можно записать
354
(11.21) равен нулю и интеграл
после интегрирования последнего выражения
Уфу = — Kt+ а4,
гдеа4 — постоянная интегрирования. В случае, если время полета не закреп¬
лено, то гамильтониан системы
Фу =a4/V.
Пусть продольная и боковая
свободно. Тогда гамильтониан
писать в виде
PsV2
(КСу CXQ )ф у ~
дальности полета заданы, а время полета
(11.20) будет равен нулю и его можно пере-
2т
= — i//3 \Zsin 0 + д фу sin 0 +
4
(11.24)
Фе
— cos
V
Оставшаяся сопряженная переменная фв может быть найдена из (11.24),
если известна переменная 1//3, для которой из (11.24) имеем
= — (Зф3 V sin 0 + (3gl фу sin 0 + cos
eft \ У
Считая, что величина гравитационного ускорения существенно меньше
аэродинамического, получим следующее выражение [145] :
cfip3 dx3
= — (Зф3 Vsin 0 = — (Зф3
dt dt
4
(11.25)
Интегрируя (11.25), получаем
i//3 = const X р. (11.26)
Из изложенного выше видно, что оптимальные законы управления
(11.16) и (11.19) аэродинамической силой Л могут быть выражены в виде
аналитических зависимостей от текущих фазовых координат КЛА, если
использовать переменную р вместо х3. Будем предполагать, что плотность
атмосферы изменяется по экспоненциальному закону
р=рпе~0Хз.
Для того чтобы преобразование было каноническим и в то же время
обеспечивало сохранение гамильтониана (11.20), должно быть выполнено
условие
Фз^х3 = ^Pdp = — &рфpdx3,
т.е.
Фз = -&рфр-
Приравнивая правые части (11.26) и (11.27), увидим, что
фр = const.
Для свободных значений дальности и времени полета КЛА в атмосфере
найдем явные выражения для оптимальной величины подъемной силы и
угла крена.
Рассмотрим сначала участок пассивного полета
Фз =ь3р,
(11.27)
(11.28)
355
(11.29)
где b3 = const. Из уравнения (11.24) с учетом (11.28) имеем
2b3m sin 0
V^y = •
sfcxo - Ke],)
Выше было показано, что для незакрепленного времени полета произведе¬
ние \/фу = а4. Учитывая это, получаем из (11.29)
KCy 2b3m sin 0
CXQ ^4^x0
Отсюда, предполагая, что масса КЛА на пассивном участке полета не изме¬
няется, будем иметь следующее выражение для параметра подъемной силы:
X2 = 1 + a sin 0,
где а = const.
Оптимальный закон изменения угла крена запишется в виде
b
sin у = .
X cos 0
Постоянные значения коэффициентов а и b в оптимальных законах управ¬
ления величиной подъемной силы и углом крена определяются граничными
условиями на концах пассивного участка полета.
На участке с переменной величиной тяги имеем
= ^ +
2дФв
v
cos 0 +дфу sin 0.
Пренебрегая гравитационным ускорением в задаче со свободным временем
полета, получаем следующий простой закон управления величиной подъем¬
ной силы на участке равновесного полета:
V + с
V — с '
Рассмотрим участок полета с постоянным максимальным значением тяги
Я = Ртах (участок разгона) . Исключая время t из уравнений для изменения
скорости V и массы т, получаем
dV с с (X \
= + —+£sin0 . (11.30)
dm т Ятах \т /
Предполагая импульсную аппроксимацию тяги, уравнение (11.30) можно
проинтегрировать в явном виде:
где Ь2 = const.
Таким образом, в общем виде представлены оптимальные законы управ¬
ления аэродинамической силой и тягой двигательной установки для КЛА,
выводимого на орбиту ИСП. Найденные оптимальные законы управления
справедливы для всех рассматриваемых планет Солнечной системы, окру-
356
женных атмосферой, а также для любых аэродинамических форм КЛА и
различных способов управления ими. Для ряда частных (но важных в
практическом применении) случаев получены в явном виде интегралы
движения для оптимальных траекторий выведения КЛА на орбиту ИСП.
Ниже в качестве примера рассматривается задача оптимизации траекторий
выведения КЛА "скользящего" типа на орбиту искусственного спутника
Юпитера, Марса и Венеры с использованием корректирующего импульса в
атмосфере. Рассматриваются две взаимосвязанные задачи: о максимизации
коридора входа КЛА и о минимизации энергетических затрат на формиро¬
вание орбит.
§ 11.2. Максимизация коридора входа
11.2.1. Общие замечания
Задача максимизации коридора входа КЛА всегда находится в центре
внимания исследователей при изучении проблемы движения КЛА в атмо¬
сфере и переводе его с гиперболической траектории на орбиту ИСП ком¬
бинированным способом. Для выбранной схемы полета коридор входа
ДЛЯ зависит решающим образом от величины располагаемого значения
аэродинамического качества /Срасп, возрастая с увеличением последнего.
Для КЛА "скользящего" типа, управляемых изменением угла крена у,
верхняя граница коридора входа Ля определяется режимом движения с
^эфф = - ^тах (у = 180°) , а НИЖНЯЯ как правило, - С /<эфф=^тах
(у = 0). Однако максимизация ДЛЯ путем увеличения располагаемого
значения аэродинамического качества /Срасп во многих случаях неэффек¬
тивна, так как для аппарата "скользящего" типа достижение величины
располагаемого качества /Срасп 0,5-^0,6 сопряжено с большими принци¬
пиальными трудностями. Это заставляет искать другие пути максимиза¬
ции ДЛЯ.
В этом параграфе изучается возможность расширения коридора входа
путем проведения дополнительной коррекции траектории КЛА в атмосфе¬
ре1 . Термин "коррекция" означает, что включением двигательной установ¬
ки сообщается малое приращение скорости ДУа (Д1/а < V, где V — теку¬
щая скорость полета КЛА). Такая коррекция проводится обязательно на
атмосферном участке полета, ибо после входа КЛА в атмосферу появляет¬
ся дополнительная возможность по определению условий входа, что, естест¬
венно, позволяет судить о том, движется ли КЛА в расчетном коридоре
или нет.
Принципиальная возможность увеличения ДЛЯ при выведении КЛА на
орбиту ИСП путем проведения дополнительной коррекции в атмосфере вы¬
текает из следующих соображений. Если рассмотреть зависимость энерге¬
тических затрат Д\/, потребных на формирование орбит ИСП при реализа¬
ции комбинированного способа, от высоты условного перицентра подлет¬
ной траектории для любой планеты (см. главу 10) , то можно увидеть, что
вблизи нижней границы коридора входа Ля величина ДУ возрастает, а
скорость КЛА в момент вылета из атмосферы VK уменьшается,т.е. проис¬
ходит избыточное гашение скорости аппарата в атмосфере, и при входе с
< Ля КЛА не достигает заданного значения высоты апоцентра формируе¬
1 В дальнейшем для краткости вместо "коррекция траектории в атмосфере" будем
употреблять термин "атмосферная коррекция", а вместо "корректирующий импульс
в атмосфере" — термин "атмосферный импульс".
357
мой орбиты ha или вообще не вылетает из атмосферы. Своевременным при¬
ложением соответствующего разгонного импульса можно заставить КЛА
двигаться в более разреженных слоях атмосферы, т.е. уменьшить интенсив¬
ность его торможения. Однако в каждом конкретном случае следует сопо¬
ставить величину затрат на проведение коррекции Д1/а и возможность ее
проведения с трудностями реализации повышенного значения аэродинами¬
ческого качества Красп Для обеспечения требуемого коридора входа.
11.2.2. Постановка задачи
Итак, рассмотрим задачу максимизации коридора входа КЛА при фор¬
мировании орбиты искусственного спутника планеты комбинированным
способом при проведении дополнительной атмосферной коррекции. При
ее решении воспользуемся системой дифференциальных уравнений, запи¬
санной в скоростной системе координат с учетом уноса массы:
dV
dt
cxspV2
. P
g sin в + co г sin в + — cos v,
m
2m
de
cxspV „
9 n V n
w2r
p
— =
^эфф
cos в + — cos в + 2w +
cos
0 + sin p,
dt
2m ФФ
V r
V
mV
dh
dm
CjSyH
(ЭДрад + Qkohb
p (H.31
— =
v sin e,
-eoT^}-
_ ■ ■ ■ ■ z
dt
dt
pya9o3
где Р — тяга двигательной установки; Рул — удельная тяга; v — угол между
вектором скорости КЛА и направлением тяги двигательной установки,
отсчитываемый от вектора скорости против направления движения часовой
стрелки. Остальные обозначения аналогичны приведенным выше.
Управление движением КЛА осуществляется с помощью изменения ве¬
личин Р, v и эффективного аэродинамического качества /Сэфф. При этом
значения управляющих параметров могут изменяться в пределах
О P(t) ^тах» 0 ^4 2л, — /^бал = ^min ^эфф ^тах ~ + ^бал -
(11.32)
Поставленная задача может быть сформулирована следующим образом:
для системы дифференциальных уравнений (11.31), описывающей движе¬
ние КЛА в атмосфере, найти законы изменения P(t), v(t), КЭфф(Н • кото¬
рые реализуют максимум величины Д/?я при ограничениях (11.32) и гра¬
ничных условиях
^(го)=^ол Mto)=^o, m(to)=<no;
V(rK) = и <n(fK) = тк свободны, eK=f(VK), h(tK) = hK.
Задача максимизации коридора входа сводится к решению двух
не зависимых друг от друга вариационных задач о поиске минимума и
максимума высот условного перицентра (Л” = min, /7° = max) . Запишем
критерий оптимальности в виде
/ = min h* = min J
fl^cos20o 1
g(e + 1) Г Г
/ = max = max
Г ^yo2cos20Bo 1
I P(e + 1) Г
358
где е — эксцентриситет подлетной орбиты; д — гравитационный параметр
планеты; R — радиус планеты.
Как видно, минимум величины /?£ при заданных значениях VQ и /?0
однозначно определяется максимальным значением модуля угла наклона
траектории КЛА к местному горизонту | 0” | (соответственно, /?° дости¬
гает минимума при |0ol = max).
Используя замену переменных t = — т, трансформируем рассматривае¬
мую задачу в задачу Майера. В качестве начальной точки траектории будем
рассматривать момент вылета КЛА из плотных слоев атмосферы: твыл = т0-
Тогда граничные условия и функционал управления запишутся в виде
V{tq) и т(т0) свободны, 0(то) = 0То, Мго)=^т0,
V(tk)=VTk, А(тк) = hTK. т(тк) = тТк, (11.33)
/ = minA"(rK) или /=тахА®(тк).
Введем в рассмотрение гамильтониан
dV dO dh dm
JC = ф y + ф2 + — Фз + Ф4, (11.34)
dr dr dr dr
где ф/(7=1, 2, 3, 4) — сопряженные переменные, определяемые уравне¬
ниями
^1
dr
COS0
^2 +
г
ш2г P 3,28CiSyH . _ ,
+ —cos# + -i//2sinp — ф3sin# + aAr„ p0’11/2, 80д +
V mV2 rj
dty 2 9 Р
= 0ф 1 COS0 — GO гф 1 COS 0 Ф 1 .'4п V —
dr m
g V GO2r
ф251П0 + ф251П0 +
V г V
9
V
Р
\jj2s'\n0 + ф2 cosp — 1/фзcos0, (11.35)
mV
0^3
dr
cxspV2p 2psin0
+ Кзфф 2m
cxspV& 2/7COS0
V2 Vr3
V со2
+ — ф2СО50 — — ф2СО50 —
Ф2
Л
2т?
dipt cxspV2 P cxspV P
= +-т|/'1СО5Р + К'эфф—— ф2 + —y-ihsinp.
dr 2m2 m2 2m2 mlV
Из условия максимума гамильтониана (11.34) получим законы опти¬
мального управления эффективным качеством /Сэфф (т) • величиной Р (т )
359
и направлением р(т) тяги двигательной установки:
^эфф (т)
= sign ф2 (т).
р(т) = arctg
Ф2 (Т)
“Г Я,
0 при
l/(r)l//l (г)
(11.36)
(
Ф(т) < 0,
Р(т) =
I
/’max при
Ф(т) > 0,
где
1
1
|Д4
Ф(т) = —
- фхCOSP +—
- ф2 siпv —
у/ 1 uujj/ 1 у/2 bi 11 и .
т mV ^удЗЪз
Видно, что эффективное аэродинамическое качество /Сэфф и тяга дви-
гательной установки Р при оптимальном управлении всегда имеют лишь
экстремальные значения.
Из условия трансверсальности получаем
А(т0)
Ф1 (т0) = Фа (т0 ) = 0, ф2(го} = - Фз(то)- . (11.37)
0(то)
Итак, для определения оптимального управления требуется решить
трехпараметрическую краевую задачу с закрепленным левым концом
для систем дифференциальных уравнений (11.31) и (11.35) и граничных
условий (11.33) и (11.37).
11.2.3. Качественные результаты решения оптимальной задачи
Введем ряд обозначений, необходимых для дальнейшего изложения:
й" а , /7®a — соответственно нижняя и верхняя границы коридора входа,
реализованные с применением дополнительной атмосферной коррекции;
AV^ — суммарные энергетические затраты (в пересчете на характе¬
ристическую скорость), потребные на формирование орбиты ИСП, состо¬
ящие из затрат на коррекцию в атмосфере (АУа) и на сообщение импульса
скорости в апоцентре переходной орбиты (АУ), т.е. при проведении атмо¬
сферной коррекции для характеристики энергетических затрат будем ис¬
пользовать Av's = А +А1/, а без атмосферной коррекции — просто А У.
Приведем некоторые качественные результаты решения оптимальной
задачи перевода КЛА с гиперболической траектории на орбиту спутника
комбинированным способом с дополнительной атмосферной коррекцией
посредством включения двигательной установки.
1. Характер оптимального управления с использованием атмосферной
коррекции не зависит от проектно-баллистических характеристик КЛА
(здесь и далее рассматривается управление эффективным аэродинамичес¬
ким качеством), характеристик двигательной установки, параметров
формируемой орбиты, начальной скорости и параметров атмосферы и
состоит в следующем:
а) минимизация нижней границы коридора входа hn min; аппарат вхо¬
дит и движется на атмосферном участке с постоянным значением аэроди¬
намического качества /Сэфф = + Кбал; в момент достижения плотных
слоев атмосферы происходит однократное включение двигательной ус¬
тановки; вектор тяги направлен на кабрирование под углом к направле¬
нию вектора скорости, близким к 90°; в процессе работы двигательной
установки этот угол незначительно уменьшается (на 1 — 2°) ;
360
б) максимизация верхней границы коридора hятах; аппарат движется
в атмосфере с постоянным отрицательным значением аэродинамического
качества /Сэфф = “ двигательная установка начинает работать в
момент входа в плотные слои атмосферы; направление вектора тяги от-
носительно вектора скорости составляет около 90° (на пикирование);
за время работы угол изменяется на 1 — 2 .
2. Применение атмосферной коррекции позволяет существенно рас¬
ширить возможный коридор входа и тем больше, чем больше величина
корректирующего импульса. При этом основное увеличение коридора
входа происходит за счет смещения нижней границы Z^min- В среднем
можно ориентироваться на следующие цифры: увеличение коридора вхо¬
да в 1,5 раза требует затрат не более чем в 1,3 раза превышающих
потребные затраты для комбинированного способа, не предусматрива¬
ющего проведение атмосферной коррекции.
3. Величина характеристической скорости необходимой для фор¬
мирования орбиты ИСП комбинированным способом и с дополнительной
атмосферной коррекцией, всегда меньше, чем сумма импульса скорости
на выведение без использования атмосферной коррекции Д\/и скорости
на сообщение атмосферной коррекции ДУа: ДУ^<Д\/ + ДУа. Этот факт
объясняется эффектом снижения интенсивности атмосферного тормо¬
жения КЛА, вызванным проведением атмосферной коррекции, в ре¬
зультате чего скорость аппарата в апоцентре переходной орбиты нес¬
колько увеличивается и, следовательно, потребный разгонный апоцен-
трический импульс скорости уменьшается. При этом с ростом распола¬
гаемой величины аэродинамического качества эффективность уменьше¬
ния при использовании атмосферной коррекции несколько сни¬
жается. . „
4. В п. 1 отмечалось, что оптимальным местом проведения атмосфер¬
ной коррекции является момент входа в плотные слои атмосферы. Од¬
нако необходимость решения навигационной задачи на участке входа
выдвигает требование смещать коррекцию на более позднее время. В
ходе исследований был выявлен важный результат, состоящий в том,
что в каждом конкретном случае (для конкретных КЛА и планеты) мож¬
но подобрать время запаздывания проведения коррекции, достаточное
для решения навигационной задачи и очень незначительно (не более чем
на 1 - 2%) увеличивающее величину атмосферного импульса, компен¬
сирующего эту задержку.
5. При решении задачи максимизации коридора входа применение ат¬
мосферной коррекции целесообразно лишь при входе вблизи нижней гра¬
ницы коридора (для Марса — и вблизи верхней), где аэродинамических
подъемных сил недостаточно для достижения заданного значения высоты
апоцентра формируемой орбиты. Подача импульса в пределах всего кори¬
дора лишь увеличивает потребные энергетические затраты и затрудня¬
ет управление КЛА.
11.2.4. Максимизация коридора входа в атмосферу Юпитера
Численное решение проводилось для КЛА, выводимых на орбиту ис¬
кусственного спутника Юпитера комбинированным способом. При этом
скорость входа Vq, основные проектно-баллистические характеристики
КЛА Рх и /Стах, величины максимальной и удельной тяги двигателя
/’max и Руд, тягозооруженность Р, высота апоцентра формируемой ор¬
биты h а и величина атмосферного импульса ДУа варьировались
361
Таблица 11.1
Влияние основных варьируемых параметров на коридор входа в атмосферу Юпитера
(исходные параметры: Ио =60 км/с, Рх = 200 кгс/м2, = 0,5, Руд= 500 с,
Ла= 104 КМ, р = рном)
Варьируемые
параметры
АН
Л7Г '
КМ
ляа,
км
д'»*.
км
ДЛяа.
км
-1278
-1508
1147
1379
Vo = 55 км/с
-826
-943
691
812
Vo = 65 км/с
-2536
-3325
2407
3196
Рх = 100 кгс/м2
-1293
-1556
1162
1425
Рх = 300 кгс/м2
-1246
-1459
1115
1328
*бал = О-*
-907
-1057
776
926
*бал = 0.6
-1740
-2112
1609
1981
Руд = 200 с
1258
-1474
1127
1343
Руд = 1000 с
1292
-1540
1161
1409
ha = 5000 км
1553
-1852
1421
1722
ha = 2000 км
1227
-1435
1096
1303
Р = Рхол
-1129
—1351
998
1221
Р = Ртепл
-1471
-1709
1340
1579
в пределах:
50 км/с < VQ < 70 км/с, 100 кгс/м2 < Рх < 400 кгс/м2,
0,3<Ктах <0,6, 300 кгс<Ртах< 1200 кгс, 300 с < Руд < 1000 с,
0,05<Р<0,4, 2000 км < < 105 км, 0 < Д Уа < 1 км/с. (11.38)
Причем если ha < 104 км, то высота перицентра формируемой орбиты
принималась равной ha, в противном случае = 104 км. В качестве
номинальных значений варьируемых параметров использовались следу¬
ющие:
Уо = 60 км/с, Рх = 200 кгС/м2, /Стах = 0,5, Ртах = 900 кгс,
(11.39)
Руд = 800 с, Я = 0,1, ha = 104 км, ДУа =0,25 км/с.
Краевая задача решалась с использованием метода последовательных
приближений. Часть результатов представлена на рис. 11.2, 11.3 и в
табл. 11.1. Во всем рассматриваемом диапазоне изменения варьируемых
параметров и для всех моделей атмосферы оптимальное управление из
условия /?7rmin состоит в следующем: КЛА на атмосферном участке дви¬
жется к постоянным значением аэродинамического качества К’эфф =+ ^тах-
Происходит однократное включение двигательной установки в момент
достижения плотных слоев атмосферы. Вектор тяги направлен под углом
р ~ 80 + 89° к направлению вектора скорости полета на кабрирование.
В процессе работы двигательной установки угол у незначительно уменьшает¬
ся (на 1-2).
Оптимальным управлением, реализующим максимум высоты условно¬
го перицентра Л^тах» траектории входа является программа полета в
362
6ДЛ„
ДИ,
км/с
ДИ^,
км/с
6ДУ =
Д1/Б - ДИ
км
%
км/с
%
232
20,2
2,6
2,92
0,32
11,0
121
17,4
2,56
2,84
0,3
10,6
789
32,8
2,65
3,00
0,35
11,7
263
22,6
2,58
2,89
0,31
10,7
213
19,1
2,61
2,94
0,33
11,2
150
19,3
2,2
2,38
0,18
7,6
372
23,1
3,15
3,64
0,49
13,5
216
19,2
2,6
2,93
0,33
11,3
248
21,3
2,6
2,91
0,31
10,7
301
21,2
2,9
3,31
0,41
12,4
207
18,9
2,61
2,93
0,32
10,9
223
22,4
2,62
2,94
0,32
10,9
239
17,8
2,58
2,89
0,31
10,7
атмосфере с постоянным отрицательным значением аэродинамического
качества ^эфф = “^тах- Двигательная установка начинает работать в
момент входа КЛА в плотные слои атмосферы. Вектор тяги направлен
под углом и « — 85 -г — 90° на пикирование.
Из представленных результатов следует, что увеличение высоты /?®8
с использованием атмосферного импульса ДУа неэффективно. Так, для
изменения А® а всего лишь на 10 км требуется подача импульса ДУа
« 1,3 -г 1,5 км/с. Исходя из этого, в дальнейшем исследуется возможность
расширения коридора входа ДАяа только за счет смещения нижней границы
коридора А®а в сторону меньших значений высот условного перицентра Ая .
Результаты, приведенные в табл. 11.1, показывают частное влияние
варьируемых параметров Уо, Рх, K^nt Руд, ha и моделей атмосферы
на эффективность расширения коридора входа в атмосферу (6Д/7Я = ДАяа—
— ДАЯ) при использовании атмосферной коррекции (ДУа=0,5 км/с) с
учетом потребных энергетических затрат на формирование орбит искус¬
ственного спутника Юпитера при оптимальном управлении. Видно, что
коридор входа ДА^ расширяется по сравнению сДАя во всем рассматри¬
ваемом диапазоне изменения параметров Vo, Рх, /Сбал, Руд, ha, p{h). При
этом эффективность увеличения ДАяа за счет подачи импульса Диа несколь-
Рис. 11.2. Зависимость ширины ко¬
ридора входа Д/^тга и суммарного
импульса характеристической ско¬
рости от атмосферного им¬
пульса Д1/а при оптимальном управ¬
лении тягой двигательной установки
и эффективным аэродинамическим
качеством.
высоты условного перицентра /7Я при оптимальном управлении тягой двигательной
установки и эффективным аэродинамическим качеством.
ко возрастает с увеличением скорости входа 1/0, аэродинамического ка¬
чества /Сбал, удельной тяги двигателя Руд и с уменьшением приведенной
нагрузки на лобовую поверхность Рх и высоты апоцентра формируемой
орбиты Ьа. В среднем при реализации атмосферного импульса Д1/а =
=0,5 км/с коридор входа Д/?яа расширяется на 20%.
Увеличение атмосферного импульса Д1/а приводит к заметному расши¬
рению коридора входа Д/7яа. Так, при изменении Д1/а от 0 до 1 км/с зна¬
чение увеличивается от 998 до 1630 км, т.е. более чем в 1,5 раза.
Суммарные энергетические затраты Д1/2 при этом изменяются от 2,62 до
3,36 км/с, т.е. менее чем в 1,3 раза (К^ал =0,5).
Резюмируя изложенное, отметим достаточно высокую эффективность
максимизации коридора входа в атмосферу Д/?яа при выведении КЛА
"скользящего" типа (К^ал 0,4 -г 0,6) на орбиту искусственного спут¬
ника Юпитера с помощью атмосферной коррекции. При этом, если при¬
ращение коридора входа составляет 30 — 50%, то соответствующее уве¬
личение энергетических затрат не превышает 20 — 30%.
Из общих соображений ясно, что при входе КЛА с >/?£а величина
атмосферного импульса ДУа и соответствующие суммарные энергетичес
кие затраты ДУ^ должны уменьшаться до Д1/а=0 иД1/2=Д1/при =
= Более того, проведенные исследования позволяют отметить, что
подбором определенного значения Д1/а можно добиться существенного
снижения ДУ^. Это подтверждают данные рис. 11.6, где представлены
зависимости суммарных энергетических затрат ДУ^, потребных на фор¬
мирование круговой орбиты (Л = 104 км), от высоты условного пери¬
центра траектории входа для различных значений ДУа. Видно, что уп¬
равление КЛА при входе с /7я>/?“ане единственно, т.е. аппарат может
быть выведен на требуемую орбиту искусственного спутника Юпитера
с использованием атмосферных импульсов различной величины при раз¬
личных суммарных затратах Д1/2.
364
11.2.5. Максимизация коридора входа в атмосферу Марса
Численное решение проводилось для КЛА "скользящего" типа. При
этом скорость входа в атмосферу Vo и основные проектно-баллистичес¬
кие характеристкии КЛА варьировались в пределах
5 км/с < VQ < 8 км/с, /?£ < /?я < ,
200 кгс/м2 < Рх < 500 кгс/м2, 0,2 < Кбал 0»7;
высота апоцентра переходной орбиты ha и величина атмосферного импуль¬
са Д Va в пределах
300 км < ha < 20 000 км, 50 м/с < Д Va < 250 м/с.
В качестве номинальных значений брались:
У о = 6 км/с, Рх = 300 кгс/м2, К'бал =0,4,
Д1/а = 150 м/с, ha = 6000 км и ha = 500 км.
Рассматривались две модели атмосферы: зимняя минимальная и лет¬
няя максимальная. Величина тяги двигательной установки принималась
бесконечно большой, т.е. в расчетах предполагалось, что атмосферный
импульс прикладывается мгновенно (для получения качественных зави¬
симостей такое допущение является оправданным).
Численные результаты решения краевой задачи показывают, что во
всем рассматриваемом диапазоне варьируемых параметров VO,PX, Кбап,
Ьа,Д\/л и для всех моделей атмосферы оптимальное управление имеет
тот же вид, что и в случае движения в атмосфере Юпитера. Только вектор
тяги направлен под углом р = 80 4-85° при минимизации Л”а и под углом
и = — 80 + — 90° при максимизации /7®а.
Анализ численных результатов траектории выведения КЛА на орбиту
искусственного спутника Марса с использованием атмосферной коррек¬
ции, представленных на рис. 11.4 и в табл. 11.2, показывает следующее.
Эффект от приложения атмосферного импульса с точки зрения увеличения
коридора входа Д/?я представляется весьма значительным, особенно при
Рис. 11.4. Зависимости суммарного импульса скорости от высоты условного
перицентра подлетной орбиты hn (ha = 500 км, Кбал = 0А Рх = 300 кгс/м2, Vo =
= 6км/с, р0 = 0,0125 кг/м3, /3 =1,22 -10"4 м“‘).
365
Таблица 11.2
Основные характеристики траекторий движения КЛА в атмосфере Марса
(с проведением атмосферной коррекции) для уточненных моделей атмосферы
(исходные параметры: 1/0 = 6 км/с, Рх = 300 кгс/м2, Kgaji =0,4, ДИа = 150 м/с)
Модели
атмосферы
, В
/?яа, км
Л#а, км
км
/?Q —
6000 км
Р min зимы
46
-25
71
576
Ртах лети
61
-12
74
572
=
500 км
Pmin зимы
46
-51
97
138
Ртах лети
61
-42
103
124
выведении на высокие эллиптические орбиты. Так, в этом случае кори¬
дор входа расширяется с 35 км при ДУа = 0 до 72 км/с при ДУа = 150 м/с,
т.е. более чем в два раза. При выведении КЛА на низкие круговые орби¬
ты с высотой апоцентра = 500 км при той же величине атмосферного
импульса коридор входа расширяется примерно на 70% (Д/?я = 58 км при
Д\/а = 0 и ДЛуг = 98 км при ДУа= 150 м/с). При этом расширение коридо¬
ра входа в плотные слои атмосферы происходит почти в равной степени
как за счет увеличения так и уменьшения h™.
Таким образом, приложение разгонного импульса при движении КЛА
в атмосфере дает возможность осуществить выведение практически на
любые орбиты аппарата, обладающего величиной /Сбал 0,5 + 0,6, при
достижимой в настоящее время точности выведения КЛА в атмосферу
Марса на подлетном участке траектории. При этом величина разгонного
импульса не превышает ДУа % 100 -ь 150 м/с.
Рассмотрим более подробно влияние начальной скорости входа VQ ,
величины атмосферного импульса, проектно-баллистических характе¬
ристик КЛА и высоты апоцентра переходной орбиты ha на ширину кори¬
дора входа ДЛа. Соответствующие результаты приведены на рис. 11.5 —
11.12. Сравнение этих рисунков с рис. 10.14-10.17 показывает, что шири¬
на коридора входа ДЛяа при наличии атмосферной коррекции увеличи¬
вается по сравнению с Д/?я (когда атмосферная коррекция отсутствует)
во всем рассматриваемом диапазоне изменения параметров VQ, Рх, ,
ha и 1/а. При этом эффект увеличения ДЛяа за счет подачи атмосферного
импульса несколько возрастает с ростом начальной скорости входа Уо
и аэродинамического качества /Сбал- Особенно он заметен для случая
выведения КЛА на низкие круговые орбиты. При увеличении VQ и Кбал
расширение коридора входа происходит в основном за счет смещения
нижней границы коридора входа, которое становится весьма заметным
при /^бал 0,5. Изменение приведенной нагрузки на лобовую поверхность
практически не влияет на ширину коридора входа.
Заметное расширение коридора входа достигается при увеличении
атмосферного импульса А\/а. Например, для КЛА с приведенной нагруз¬
кой на лобовую поверхность Рх = 300 кгс/м2 и аэродинамическим ка¬
чеством /^бал = 0,4, выводимого на высокую эллиптическую орбиту ис-
366
, м/с
_в
п max
н
п max
^min» км
^min*
587
1
ha = 6000 км
3
I
33
23
585
1
2
47
36
263
1
ha = 500 км
5
32
18
268
1
4
46
28
Рис. 11.5. Зависимости суммарного импульса скорости и границ коридора входа в
атмосферу от проектно-баллистических характеристик КЛА, атмосферного импуль¬
са и начальной скорости входа (Ла=6000км, р0 =0,0125 кг/м3, 0=1,22-10" 4 м“И.
367
кусственного спутника Марса, изменение атмосферного импульса от
50 м/с до 250 м/с приводит к расширению коридора входа более чем в
два раза (от 21/7^=47 до Д/?яа = 96 км). Величина суммарного потреб¬
ного импульса ДУ2 при этом увеличивается в 1,2 раза (от 640 м/с до
740 м/с).
Как и в случае выведения на орбиту искусственного спутника Юпите¬
ра, величина суммарного потребного импульса скорости Д\/2 при опти¬
мальном управлении КЛА, выводимыми на орбиту искусственного спут¬
ника Марса, всегда меньше, чем сумма затрат скорости при выведении
КЛА на соответствующую орбиту комбинированным способом без ис¬
пользования атмосферной коррекции и энергетических затрат на сооб¬
щение корректирующего импульса Д1/а.
Рассмотрим влияние высоты апоцентра переходной орбиты ha на па¬
раметры траекторий выведения КЛА на орбиту искусственного спутни¬
ка Марса. Коридор входа при увеличении ha уменьшается, причем осо¬
бенно это заметно при ha < 103 км. В случае, когда ha > 1,5 • 103 км,
ширина коридора входа практически не изменяется. Уменьшение ДЛяа про¬
исходит только за счет смещения нижней границы. Отметим также, что
Рис. 11.6. Зависимости суммарного импульса скорости и границ коридора входа в
атмосферу от проектно-баллистических характеристик КЛА, атмосферного импульса
и начальной скорости входа (ha = 6000 км, р0 = 0,0106 кг/м3, /3 =0,84 • 10"4 м"1) .
км
• -80
50
Ф*бол)
h^(&va)у
О%(РХ)
Ws(Px)
CAJ
Л^бал
\
\ Д-
)
in
--40
^бал) /
hi(Px)
0,3
о,4
0,5
^бал
100
200\
150
500
200
400
AVa,M/C
PxiKZG/M2-
368
Рис. 11.7. Зависимости суммарного импульса скорости и границ коридора входа в
атмосферу от проектно-баллистических характеристик КЛА, атмосферного импульса
и начальной скорости входа (ha = 500 км, р0 = 0,0125 кг/м3, 0 = 1,22 -10~4 м"1).
ширина коридора входа для высоких эллиптических орбит (ha > 103 км)
составляет не более 90 км. Другой характер имеют зависимости .
Величина суммарного импульса при движении по верхней границе моно¬
тонно увеличивается с ростом ha. При входе КЛА в атмосферу по нижней
границе коридора = /?”а зависимость AVg(ha) имеет более явно выра¬
женный экстремум, соответствующий ha 650 км.
Приведенные материалы подтверждают высокую эффективность ат¬
мосферной коррекции с точки зрения расширения коридора входа при
выведении КЛА "скользящего" типа на орбиту искусственного спутника
Марса. Даже при подаче небольшого корректирующего импульса скорости
в атмосфере Д1/а—100 4- 150 м/с приращение ширины физического ко¬
ридора входа составляет около 80-90%. Ясно также, что при входе КЛА
в атмосферу внутри коридора входа с > Л” и последующим выведени¬
ем его на низкие круговые орбиты величина атмосферного импульса ДУа
24. Зак. 2069
369
Рис. 11.8. Зависимости суммарного импульса скорости и границ коридора входа в
атмосферу от проектно-баллистических характеристик КЛА, атмосферного импульса
и начальной скорости входа (ha = 500 км, р0 = 0,0106 кг/м3, /3 = 0,84 • Ю^м”1).
ЛУ^(ЛУа)
15Q ДУ^м/с
Рис. 11.9. Зависимости суммарного импульса скорости Д1/£ от атмосферного им¬
пульса Д1/а (р0 = 0,0125 кг/м3, /3 = 1,22 • 10"4 м"1) : a) ha = 6000 км; б) ha =
= 500 км.
Рис. 11.10. Зависимости суммарного импульса скорости ДИ^ от атмосферного им¬
пульса ДИа (р0 = 0,0106 кг/м3, /3 = 0,84 • 10"4 м~1 ) : a) ha = 6000 км; б) ha =
= 500 км.
Рис. 11.11. Зависимости суммарного импульса скорости Д1/^ и границ коридора вхо¬
да в атмосферу от высоты апоцентра заданной орбиты ha (Рх = 300 кгс/м2, Кдал =
= 0,4, 1/0 = 6 км/с, Д V а = 150 км/с; сплошные линии — р0 = 0,0125 кг/м3, /3 =
- 1,22 • 10"4 м-1 ; штриховые — р0 = 0,0106 кг/м3 , /3 = 0,84 • 10“4 м" 1 ) .
Рис. 11.12. Зависимости суммарного импульса скорости ДУ^ и границ коридора
входа в атмосферу от высоты апоцентра заданной орбиты ha (сплошные линии —
р0 = 0,0125 кг/м3, /3 = 1,22 • 10"4 м-1; штриховые — р0 = 0,0106 кг/м3, /3 =
= 0,84-10”4 м"1).
должна уменьшаться и в пределе достигнуть Д1/а = 0 при /?я = h*, так как
подача импульса при /?я = Л® приводит лишь к увеличению суммарных
энергетических затрат. Для высоких эллиптических орбит необходимо
приложение атмосферного импульса и в области Ля = Л® с целью расши¬
рения коридора входа. В этом случае следует выбирать оптимальную вели¬
чину атмосферного импульса. Отметим также, что управление КЛА при
входе с Ля >ЛЯ не единственно, т.е. КЛА может быть выведен на требуе¬
мую орбиту искусственного спутника Марса с использованием атмосфер¬
ных импульсов различной величины при различных суммарных затратах
скорости .
11.2.6. Максимизация коридора входа в атмосферу Венеры
Исследование оптимальной задачи выведения КЛА на орбиту искус¬
ственного спутника Венеры с использованием атмосферной коррекции
показало, что качественная картина остается той же самой, как и для
рассмотренных выше случаев выведения КЛА на орбиты искусственных
спутников Юпитера и Марса. Это касается и направления сообщения им¬
пульса Д1/а, увеличения коридора и уменьшения суммарных энергетичес¬
ких затрат. Некоторые результаты представлены на рис. 11.13 и 11.14.
Видно, что при одинаковых суммарных энергетических затратах на форми¬
рование заданной орбиты искусственного спутника Венеры исполь¬
зование атмосферной коррекции приводит к расширению коридора
входа.
Так, при подаче атмосферного импульса Д1/а= 100 м/с коридор входа
расширяется на 10% при одинаковой величине суммарного импульса Д1/2 =
= 450 м/с. Если допустить увеличение суммарного импульса по сравнению
с импульсом, потребным для реализации комбинированного способа, не
предполагающего использование атмосферной коррекции, то это приве¬
дет к дополнительному расширению коридора входа. Например, увеличе¬
ние суммарного импульса на 100 м/с приводит дополнительно к расшире¬
нию коридора входа на 3—4%.
Рис. 11.13. Зависимости суммарного импульса скорости от высоты условного
перицентра h п при выведении КЛА на орбиту искусственного спутника Венеры с ис¬
пользованием атмосферной коррекции (1/0 = 11 км/с, Рл = 500 кгс/м2, KgaT1 =0,5,
ha = 500 км; основная модель атмосферы) .
372
Рис. 11.14. Зависимости ширины коридора входа и суммарного импульса ско¬
рости ДI/£ от времени подачи атмосферного импульса ta (/^бал = 0,5, Рх =
= 500 кгс/м2, 1/0 = 11 км/с, Д 1/а = 1 00 м/с) .
Анализ зависимостей, представленных на рис. 11.14, показывает, что
ширина коридора зависит от времени подачи атмосферного импульса Га.
Как и следовало ожидать, с увеличением времени ta ширина коридора
входа сужается.
§ 11.3. Минимизация суммарных энергетических затрат
1L3.1. Постановка задачи оптимизации
Рассмотрим вариационную задачу об отыскании оптимального управ¬
ления, минимизирующего суммарные энергетические затраты Д1/2, по¬
требные для формирования орбиты ИСП с ha=ha32LJX и /?я = /?я зад при
использовании КЛА с заданным значением располагаемого аэродинамичес¬
кого качества /Срасп. При этом решение проводится в диапазоне измене¬
ния высот условного перицентра /?я от верхней границы коридора входа
/?я до нижней Ля, однозначно определяемых величиной /Срасп в случае
отсутствия атмосферной коррекции Д1/а.
Запишем функционал управления в виде
/ = ДУа+ДУ, (11.40)
где Д1/ — приращение скорости, сообщаемое КЛА в апоцентре переход¬
ной орбиты ИСП.
Сформулируем поставленную задачу: для системы дифференциальных
уравнений (11.31) требуется определить законы управления
P(t) и v(t), обеспечивающие минимум функционала (11.40) при ограни¬
чениях (11.32) и следующих граничных условиях:
t = t(): V(t0)=VQt 6(tQ) = 0, h(t0) = hQf m(t0}=m0;
(11.41)
t = tK: — заданы, mK — свободна.
Решение задачи будем проводить в два этапа. Прежде всего определим
минимум потребных энергетических затрат Д1/^ при Д\/а= const. В этом
случае критерий оптимальности можно записать в виде
/=УК. (11.42)
На втором этапе варьируется величина ДУа с целью получения экстре¬
мума не только функционала (11.42), но и функционала (11.40), что
будет соответствовать абсолютному минимуму потребных энергетических
затрат ДУ/^-
Воспользуемся найденными ранее выражениями (11.34) — (11.36)
для определения гамильтониана, сопряженных переменных и законов
оптимального управления. Из условия трансверсальности в конечной
точке траектории имеем
Ф1к = 1, 2 к = — — зк > Фак = 0. (11.43)
Как и в рассмотренном выше случае максимизации Д/7яа, поставленная
задача сводится к трехпараметрической краевой задаче для систем диф¬
ференциальных уравнений (11.31) и (11.35) и граничных условий (11.32)
и (11.33). Ее решение проводилось с использованием метода последова¬
тельных приближений.
11.3.2. Некоторые качественные резулътаты
Анализ результатов решения задачи для случая выведения на орбиты
планет выявил ряд общих закономерностей.
1. Оптимальное управление на атмосферном участке состоит в следу¬
ющем. Управление аэродинамическим качеством представляет собой одно¬
разовое переключение /Сэфф с Кт ах = + /Сбал на Kmin = - ^бал- Проис¬
ходит однократное включение двигателя в момент входа КЛА в атмо¬
сферу. Начальный угол направления тяги р0 существенно зависит от вели¬
чины /?я. Так, увеличение /?я от Ля до /?я приводит к изменению угла и 0
от 85 + 90 до — 90 . В процессе работы двигательной установки направ¬
ление импульса Д1/а меняется незначительно.
2. С уменьшением высоты условного перицентра от /?я до /?я величина
Д\/2 монотонно возрастает от Al/Smin при /?я = Ъя до ДУЕ тах при Ля =
= Лн
3. Коридор входа КЛА в атмосферу ДЛЯ = h* - h* целесообразно ус¬
ловно разделить на две характерные зоны по месту нахождения в кори¬
доре высоты условного перицентра Ля: Ля </?я < Л* и Л* <ЛЯ <ЛЯ. Прин¬
ципиальным отличием этих зон является то, что проведение атмосферной
коррекции при /?я G (h%, h*) приводит к значительному снижению (в
два-три раза) потребных энергетических затрат Д1/2 по сравнению со
случаем Д1/а=0, тогда как подача корректирующего импульса Д\/а при
входе КЛА с /?я Е (/?*, h*) не приводит к энергетическому выигрышу,
а наоборот несколько увеличивает (примерно на 1—1,5%) энергетические
затраты Д1/2.
Величина ДЛ* = h* — h* для всего практически важного диапазона варь¬
ируемых параметров составляет не более 25 — 35% от ширины коридора
входа ДЛЯ = Ля — /?я, достигая больших значений при увеличении аэро¬
динамического качества /Стах. Из этого следует, что для снижения сум¬
марных энергетических затрат. Д1/^ с учетом заданного коридора входа,
т.е. для достижения экстремума функционала (11.40), необходимо про¬
водить атмосферную коррекцию лишь для диапазона от /?* до /?я. При
^я ^я ^я подача импульса Д Va необязательна.
374
4. Для каждой планеты можно найти такую величину атмосферного
импульса ДУа, при которой достигается минимум функционала (11.40).
Будем называть ее оптимальной и обозначать через ДУ£ПТ. Интересно
отметить, что ДУа пт слабо зависит от конкретных значений варьируемых
параметров ( Уо , Рх, Km ах t Pm ах t Ру д, ha).
5. Результаты решения вариационной задачи минимизации суммарных
энергетических затрат, потребных при выведении КЛА "'скользящего"
типа (^бал % 0,4 4- 0,6) на орбиту любой планеты с использованием атмо¬
сферной коррекции (ДУа Ф 0), показали значительный энергетический
выигрыш (в два — три раза) по сравнению со случаем формирования ор¬
бит без подачи атмосферного импульса (ДУа = 0).
11.3.3. Некоторые численные результаты
для случаев выведения на орбиты
спутников Юпитера, Марса и Венеры
Приведенные в п. 11.3.2 данные подтверждаются численными результа¬
тами решения задачи выведения КЛА на орбиты спутников планеты ком¬
бинированным способом с использованием атмосферной коррекции.
1. Оптимальная величина атмосферного корректирующего импульса
составляет для номинальных значений варьируемых параметров 510 м/с,
150 м/с и 30 м/с соответственно для Юпитера, Венеры и Марса. Варьиро¬
вание параметров в практически важном диапазоне слабо влияет на ДУа.
Для Юпитера эта величина меняется от 500 м/с до 550 м/с, а для Венеры
и Марса — соответственно от 140 м/с до 160 м/с и от 25 м/с до 35 м/с.
Здесь следует сделать одно замечание. Если для Марса и Венеры ДУаопт
ищется достаточно строго, то для Юпитера эта величина берется минималь¬
ной из всех возможных значений при условии, что дальнейшее увеличение
ДУа не ведет к существенному уменьшению ДУ^ (в пределах 1 — 2%).
2. В случае выведения КЛА на орбиту искусственного спутника Юпите¬
ра при увеличении ha до некоторого значения h'a, существенно зависяще¬
го от величины навигационного коридора входа Д/?”ав, потребные энерге¬
тические затраты ДУ^ меняются очень слабо, однако дальнейшее измене¬
ние ha приводит к значительному возрастанию Д1А> Так, при увеличении
ha от 2 • 103 км до h'a = 10d км величина Достается практически посто¬
янной и равной 0,508 км/с; увеличение /?Q до 42 • 10* км вызывает воз¬
растание ДУ^ до 5,7 км/с (ДЛ»ав =1100 км). Нетрудно видеть, что умень¬
шение навигационного коридора входа Д/?вав приводит к существенному
снижению Ди дает возможность значительно увеличить высоту апоцент¬
ра формируемой орбиты при использовании комбинированного спо¬
соба выведения.
Исследования показали, что при выведении КЛА на орбиты искусствен¬
ных спутников Марса и Венеры качественно характер зависимости сум¬
марных энергетических затрат ДУ^ от высоты условного апоцентра h а
остается таким же, как и при выведении на орбиту искусственного спутни¬
ка Юпитера. Однако количественные результаты существенно отличаются:
величина ДУ^ ПРИ выведении на орбиту искусственного спутника Марса
составляет 200 — 300 м/с, а при выведении на орбиту искусственного
спутника Венеры ДУ^ = 250 ^-400 м/с.
3. Применение атмосферной коррекции приводит к существенному
снижению потребных суммарных энергетических затрат при выведении
на орбиту комбинированным способом в пределах коридора входа, рас¬
считанного для случая выведения без использования атмосферной кор¬
375
рекции. Суммарный выигрыш составляет почти в 2 раза для Юпитера и
Венеры и более 25% для Марса. Действительно, для КЛА с /Сбал = 0,5,
выводимых на орбиты:
Юпитера ДУ2 1,375 км/с (включая ДУа^ 0,5 км/с) вместо ДУа =
= 2,675 км/с;
Венеры ДУе = 0,275 км/с (ДУа~ 150 м/с) вместо ДУа = 0,475 км/с;
Марса Д = 200 м/с (Д Уа « 30м/с) вместо Д Va = 260 м/с.
Таким образом, приведенные в настоящем параграфе результаты реше¬
ния вариационной задачи позволили определить оптимальный закон управ¬
ления КЛА, выводимого на орбиту искусственного спутника планеты.
В качестве критерия оптимальности использовалось условие минимизации
суммарных энергетических затрат, потребных для формирования орбиты
искусственного спутника планеты с заданными значениями апоцентра
и перицентра.
Полученные качественные результаты подтверждаются численными
расчетами оптимальных траекторий выведения КЛА на орбиты искусст¬
венного спутника для трех планет Солнечной системы — Юпитера, Марса,
и Венеры,
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
А — коэффициент поглощательной спо¬
собности материала теплозащитного
покрытия;
С — теплоемкость;
/ — вектор эффективности; критерий
оптимальности;
/Х/ ^z /ху/ /xzz lyz — осевые и центро¬
бежные моменты инерции КЛА;
К — аэродинамическое качество;
L — дальность;
/WXz Му, Mz — моменты внешних и реак¬
тивных сил относительно соответ¬
ствующих осей координат;
М — число Маха;
Р— давление; тяга двигательной уста¬
новки;
приведенная нагрузка на лобовую
поверхность КЛА;
Q — тепловой поток;
Re — число Рейнольдса;
/?э — экваториальный радиус планеты;
Ry — расстояние от центра планеты до
ее поверхности;
/?0 — средний радиус планеты;
$ — площадь;
Т — сидерический период обращения;
температура;
Ts — синодический период обращения;
И — скорость полета;
Vyz ~ составляющие вектора ско¬
рости центра масс КЛА;
1/0 — начальная скорость входа КЛА в
_ атмосферу планеты;
1/ = 1/0/Икр— относительная начальная
скорость входа;
X — сила лобового сопротивления;
X, Y, Z — проекции равнодействующей
внешних сил и реактивной силы тяги
на оси инерциальной системы коор¬
динат;
Y — подъемная сила;
сх— коэффициент силы лобового сопро¬
тивления;
Су — коэффициент подъемной силы;
е — эксцентриситет;
д0 — ускорение силы тяжести на поверх¬
ности планеты;
h — высота полета;
ha — высота условного апоцентра ор¬
биты;
hn — высота условного перицентра
орбиты;
т — масса;
п — перегрузка;
q — удельный тепловой поток;
суммарный удельный тепловой
поток;
г = Ro + h — расстояние от центра плане¬
ты до центра масс КЛА;
гн— радиус затупления в критической
точке носовой части поверхнос¬
ти КЛА;
s — площадь миделева сечения; площадь
панели;
и — угол наклона вектора тяги к местно¬
му горизонту;
А— характеристическое число теплоизо¬
ляции;
а — угол атаки;
/3 — градиент плотности атмосферы;
7 — угол крена;
е — долгота; коэффициент излучатель¬
ной способности материала;
т? — безразмерная боковая дальность
полета;
^эфф” эффективная энтальпия;
в — угол наклона траектории к местно¬
му горизонту;
£ — истинная аномалия;
к — долгота; боковая угловая дальность
полета;
А. — теплоемкость;
377
д — гравитационный параметр; средний
молекулярный вес;
v — угол между продольной осью КЛА и
направлением вектора тяги двига¬
тельной установки;
% — безразмерная продольная дальность
полета;
р — плотность; удельный вес;
р0 — плотность атмосферы на уровне
моря;
о— продольная угловая дальность поле¬
та; постоянная Стефана — Больц¬
мана;
ах — баллистический параметр;
р — широта; угол отклонения вектора
тяги;
ф — угол курса;
ш — угловая скорость вращения плане¬
ты; безразмерная плотность атмо¬
сферы;
Верхние индексы
в — верхняя;
гр — граничное;
кр — критическая;
н — нижняя;
нав — навигационный;
оп — опорная;
опт — оптимальное;
пр — предельное; приближенное;
р — разгонный;
т — тормозной;
ч — численный.
Нижние индексы
а — атмосфера;
б — боковая;
бал — балансировочный;
в — вертикальная;
вн — внутренняя;
выл — вылет;
доп — допустимое;
зад — заданное;
зимн — зимняя;
из л — излучение;
к — конечное;
конв — конвективный;
кр — круговая;
л — левый;
летн — летняя;
н — носовая;
нагр — нагрев;
ном — номинальное;
отс — отсек;
ох л — охлаждение;
п — поверхность; правый; переклю¬
чение;
пл — планирование;
пр — прогреваемая; продольная;
п.г — полезный груз;
п.с — парашютная система;
р — разрушение; размерная; радиаль¬
ная;
равн — равноденствие;
рад — радиационный;
расп — располагаемый;
с — сублимирующий;
сх — сход;
сч — счет;
с.у — система управления;
т — топливо; тангенциальная;
тепл — теплая;
тз.п — теплозащитное покрытие;
уд — удельный;
ун — уносимая;
усл — условная;
хар — характеристическая;
хол — холодная;
э — экватор;
эфф — эффективная;
а — относящаяся к апоцентру;
я — относящаяся к перицентру;
О — начальное значение.
СПИСОК ЛИТЕРАТУРЫ
1. Алексеев К.Б., Бебенин Г. Г., Брошевский В.А. Маневрирование космических
аппаратов. — М.: Машиностроение, 1970.
2. Андреевский В.В. Динамика спуска космических аппаратов на Землю. — М.:
Машиностроение, 1970.
3. Аноров В.П. Принцип максимума для процессов с ограничениями общего вида. —
Автоматика и телемеханика, 1967, № 3,4.
А. Балакин В.Д., Белоконов В.М., Шершнев В.М. Комбинированный маневр пово¬
рота плоскости орбиты при наличии ограничений на режим движения.— Космичес¬
кие исследования, 1976, т. XIV, вып. 4.
5. Балакин В.Л., Белоконов В.М., Шершнев В.М. Об оптимальных режимах пово¬
рота плоскости орбиты спутника Земли с использованием аэродинамических
сил. — Космические исследования, 1974, т. XII, вып. 3.
6. Беллман Р. Динамическое программирование. — М.: Иностранная литерату¬
ра, 1960.
7. Боголепов В.Б., Елькин Ю.Г. Обтекание сферически затупленных конусов гипер¬
звуковым потоком невязкого излучающего газа. — Ученые записки ЦАГИ,
1971, т. II, №2.
8. Болтянский В.Г. Математические методы оптимального управления. — М.:
Наука, 1966.
9. Габасов Р., Кириллова Ф.М. Оптимальные управления с особыми участками. —
Автоматика и телемеханика, 1969, № 10.
10. Гамкрелидзе Р.В. О скользящих оптимальных режимах. — Доклады АН СССР,
1962, т. 143, №6.
11. Гершбейн Э.А., Суходольская Э.Я., Суходольский С.Л., Тирский Г.А. О движении
тел в атмосфере Юпитера с учетом изменения их массы и формы под действием
аэродинамического нагрева. — Космические исследования, 1978, т. XVI, вып. 3.
12. Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического полета с
малой тягой. — М.: Наука, 1966.
13. Гурман В.И. Метод кратных максимумов и условия относительной оптимальнос¬
ти вырожденных режимов. — Автоматика и телемеханика, 1967, № 12.
14. Гурман В.И., Салмин В.В., Шершнев В.М. Аналитическая оценка приближенно¬
оптимальных комбинированных разворотов. - Космические исследования, 1969,
т. VII, вып. 6.
15. Дикусар В.В., Шилов А.А. Оптимизация дальности полета аппарата в атмосфере
с учетом ограничения на полную перегрузку. Ученые записки ЦАГИ, 1970,
т. 1,№2.
16. Дикусар В.В., Шилов А.А. Нерегулярные оптимальные траектории аппарата при
полете в атмосфере. — Ученые записки ЦАГИ, 1970, т. I, № 4.
17. Жарков В.Н. Внутреннее строение Земли и планет. — М.: Наука, 1978.
18. Жарков В.Н., Трубицин В.П. Физика планетных недр. - М.: Наука, 1980.
19. Желнин Ю.Н. Исследование оптимальных траекторий входа в атмосферу гипер¬
звуковых летательных аппаратов, обладающих малым аэродинамическим качест¬
вом. — Труды ЦАГИ, 1976, вып. 1754.
20. Желнин Ю.Н., Шилов А.А. Траектории минимальной дальности при входе косми¬
ческого аппарата в атмосферу Земли со сверхкруговой скоростью. - Ученые
записки ЦАГИ, 1970, т. I, № 1.
21. Золотухина Н.И., Охоцимский Д.Е. Исследование движения космических аппа¬
ратов в атмосфере. — Космические исследования, 1965, т. Ill, вып. 4.
22. Иванов Н.М., Бочаров Л.А., Голуб И.Б. Алгоритм управления спуском аппара¬
тов, входящих в атмосферу Земли с гиперболическими скоростями. - Космичес¬
кие исследования, 1971, т. IX, вып. 2.
379
23. Иванов Н.М., Лысенко fl.И, Мартынов А.И. Методы теории систем в задачах
управления космическим аппаратом. — М.: Машиностроение, 1981 .
24. Иванов Н.М., Мартынов А.И. Управление движением космического аппарата в
атмосфере Марса. — М.: Наука, 1977.
25. Иванов Н.М., Мартынов А.И., Соколов Н.Л. Оптимальное управление КА в ат¬
мосфере Юпитера. — Космические исследования, 1980, т. XVIII, вып. 3.
26. Иванов Н.М., Мартынов А.И., Соколов Н.Л. Оптимальное управление КА при
выведении на орбиту искусственного спутника Юпитера комбинированным
способом. — Космические исследования, 1982, т. XX, вып. 2.
27. Иванов Н.М., Мартынов А.И., Соколов Н.Л. Приближенный аналитический метод
расчета траекторий движения летательного аппарата в атмосфере. — Прикладная
математика и механика, 1983, т. 47, № 2.
28. Иванов Н.М., Мартынов А.И., Соколов Н.Л. О максимизации коридора входа и
минимизации энергетических затрат при выведении КА на орбиту искусственного
спутника Юпитера комбинированным способом. — Космические исследования,
1982, т. XX, вып. 4.
29. Иванов Н.М., Мартынов А.И., Шилов А.А. О выведении космического аппарата
на орбиту искусственного спутника планеты с использованием аэродинамическо¬
го торможения в атмосфере. — Космические исследования, 1975, т. XIII,
вып. 4.
30. Иванов Н.М., Мартынов А.И., Шилов А.А. О переведении космического аппарата
с гиперболической траектории на орбиту искусственного спутника планеты с
использованием аэродинамического торможения в атмосфере. — Космические
исследования, 1975, т. XIII, вып. 4.
31. Ивашкин В.В. Классификация и анализ оптимальных импульсных переходов при
ограничениях на расстояние от притягивающего центра. — Космические иссле¬
дования, 1966, т. IV, вып. 6.
32. Ивашкин В.В. Оптимальные импульсные переходы внутри кольца на орбиты, не
пересекающие его границ. — Космические исследования, 1968, т. VI, вып 4.
33. Ивашкин В.В. Оптимизация космлческих маневров при ограничениях на расстоя¬
ния до планет. — М.: Наука, 1975.
34. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. — М.:
Физматгиз, 1962.
35. Кириллова Л. С., Пионковский А.А. Некорректные задачи в теории оптимального
управления. — Автоматика и телемеханика, 1968, № 10.
36. Кирилова Ф.М. Об одном направлении в теории оптимальных процессов — Авто¬
матика и телемеханика, 1967, № 11.
37. Кондратьев К.Я. "Викинги" на Марсе. — Л.: Гидрометеоиздат, 1977.
38. Кондратьев К.Я., Крупенио Н.Н. Новое о планете Венера. — М.: Знание, 1979.
39. Коняев В. Г. Оптимальное использование аэродинамических сил для маневра ле¬
тательного аппарата. — Космические исследования, 1967, т. V, вып. 2.
40. Коняев В.Г Дифференциальные уравнения изменения формы космического ле¬
тательного аппарата вследствие его обгара при движении в атмосфере на сверх-
круговых скоростях. - Труды ЦАГИ, 1973, вып. 1476.
41. Коняев В. Г. Энергетическая оценка потерь массы теплозащиты летательного ап¬
парата при торможении в атмосфере со сверхкруговой скоростью. — Ученые
записки ЦАГИ, 1973, т. IV, |\|° 6.
42. Коняев В. Г. Анализ возможностей комбинированного торможения космического
аппарата в атмосфере. — Космические исследования, 1977, т XV, вып 2
43. Копнин Ю.М. К задаче о повороте плоскости орбиты спутника. - Космические
исследования, 1965, т. Ill, вып. 4.
44. Красовский Н.Н. Теория оптимальных управляемых систем - В кн.: Механика
в СССР за 50 лет, т. 1 : Общая и прикладная механика. - М.: Наука, 1968.
45. Красовский Н.Н., Моисеев Н.Н. Теория оптимальных управляемых систем —
Изв. АН СССР. Техническая кибернетика, 1967, № 5.
46. Кротов В.Ф., Букреев В.З., Г урман В.И. Новые методы вариационного исчисле¬
ния в динамике полета. - М.: Машиностроение, 1969.
47. Кротов В.Ф., Гурман В.И. Оптимальное регулирование угла атаки крылатого ап¬
парата из условия минимума конечной скорости. — В кн : Исследования по ди¬
намике полета/Под ред. И.В. Остославского. - М.: Машиностроение, 1969
48. Кротов В.Ф., Г урман В.И. Методы и задачи оптимального управления. — М :
Наука, 1973.
49. Крупенио Н.Н. Радиофизические исследования Луны и планет. - М : Наука, 1976.
50. Крылов И.А., Черноусько Ф П Решение задачи оптимального управления ме¬
тодом локальных вариаций. - Журнал вычислительной математики и математи
ческой физики, 1966, т. 6, № 2.
380
51. Крылов И.А., Черноусько Ф.Л. О методе последовательных приближений для
решения задач оптимального управления. — Журнал вычислительной математики
и математической физики, 1972, т. 12, № 1.
52. Кузьмин А.Д., Маров М.Я. Физика планеты Венера. — М.: Наука, 1974.
53. Левантовский В.И. Механика космического полета. — М.: Наука, 1980.
54. Летов А.М. Динамика полета и управления. — М.: Наука, 1969.
55. Ли Р. Оптимальные оценки, определение характеристик и управление. — М.:
Наука, 1966.
56. Лиз Л. Ламинарный теплообмен на тупоносых телах при больших сверхзвуковых
скоростях. - В кн.: Научные проблемы искусственных спутников. - М.: Ино¬
странная литература, 1959.
57. Лох У. Динамика и термодинамика спуска в атмосфере планет. - М.: Мир, 1УЬЬ.
58. Маринеску А. Изопериметрическая формулировка некоторых задач оптимизации
входа в атмосферу. — Ракетная техника и космонавтика, 1973, т. XI, № 12.
59. Маров М.Я. Планеты Солнечной системы. — М.: Наука, 1981.
60. Маров. М.Я., Рябов О.Л. Модель атмосферы Венеры. — М.: Институт прикладной
математики АН СССР, 1972, препринт № 39.
61. Мельи И.О. Применение методов нелинейного программирования для оптимиза¬
ции динамических систем в функциональном пространстве. - Автоматика и те¬
лемеханика, 1968, №1.
62. Методы оптимизации с приложениями к механике космического полета/Под ред.
Дж. Лейтмана. — М.: Наука, 1965.
63. Мишин В.П., Осин М.И. Введение в машинное проектирование летательных ап¬
паратов. — М.: Машиностроение, 1978.
64. Моисеев Н.Н. Методы динамического программирования в теории оптимальных
управлений. — Журнал вычислительной математики и математической физики,
1964, т. 4, № 3; 1965, т. 5,№1.
65. Мороз В.И. Рабочая модель атмосферы Венеры. — М.: Институт космических ис¬
следований АН СССР, 1973, препринт № 162.
66. Мороз В.И. Физика планеты Марс. — М.: Наука, 1978.
67. Нейланд В.Я., Снигирев Ю.И. Тепловой режим летательного аппарата при скорос¬
тях входа в атмосферу Земли, близких к 15 км/сек.— Космические исследова¬
ния, 1967, т. V, вып. 2.
68 Охоцимский Д.Е., Голубев Ю.Ф., Вухаркина А.П., Филипович И.В., Шелухина В.К.
Выведение космического аппарата на орбиту искусственного спутника Марса с
помощью торможения в атмосфере планеты. — Космические исследования, 1977,
т. XV, вып. 3.
69. Пашинцев ВТ. Об одном способе построения приближенно-оптимальных траекто¬
рий гиперзвуковых аппаратов в атмосфере. — Ученые записки ЦАГИ,. 1973,
т. IV, № 1.
70. Пашинцев В.Т. Новый подход к проблеме приближенной аппроксимации опти¬
мального управления. — Труды ЦАГИ, 1976, вып. 1739.
71. Пашинцев В.Т. Оптимальное управление подъемной силой при планировании
гиперзвуковых аппаратов в атмосфере. — Труды ЦАГИ, 1977, вып. 1811 -
72. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема¬
тическая теория оптимальных процессов. — М.: Наука, 1961.
73. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математи¬
ческая теория оптимальных процессов. — М.: Наука, 1969.
74. Рабочая модель атмосферы и поверхности Марса, ч. Т Атмосфера/Под ред.
В.И Мороза. — М.: Институт космических исследований АН СССР, 1975, пре¬
принт № 240.
75. Рабочая модель атмосферы и поверхности Марса, ч. 2. Поверхность/Под ред.
В.И. Мороза. — М.: Институт космических исследований АН СССР, 1975, пре¬
принт № 241.
76. Рабочая модель атмосферы и околопланетного пространства Юпитера/Под ред.
В.И. Мороза. — М.: Институт космических исследований АН СССР, 1976,
препринт № 282.
77. Розоноэр Л.И. Принцип максимума Понтрягина Г1.С. в теории оптимальных
систем. — Автоматика и телемеханика, 1959, № 9 — 11.
78. Рощина А.А. Оптимизация траектории пассивного спуска летательного аппарата
в атмосфере Земли по критерию, связанному с весом хладагента внутренней
системы охлаждения. — В кн.: Исследования по динамике полета/Под ред.
И.В. Остославского. — М.: Машиностроение, 1969.
79. Рускол Е.Л. Спутники Марса. - Земля и Вселенная, 1978, N° 1.
80. Рускол Е.Л. Спутники Юпитера. — Земля и Вселенная, 1978, № 3.
81. Семенов В.В., Зотов В.Е., Крутов А.В. Исследование влияния неопределенности
параметров атмосферы на оптимальное управление аэродинамическим качеством
спускаемого аппарата. — Космические исследования, 1978, т. XVI, вып. 5.
82. Семенов В.В., Колокопьников А.В. Грибков И. Г. Траектории аэродинамическо¬
го торможения в атмосфере Марса, обеспечивающие минимум характеристичес¬
кой скорости на участке гравитационного разворота. — Космические исследова¬
ния, 1975, т. XIII, вып. 4.
83. Скипенко В.В. Траектории минимального нагрева и приближенный расчет тепло¬
защиты аппарата при сверхзвуковых скоростях полета в атмосфере. — Труды
ЦАГИ, 1973, вып. 1484.
84. Смольяков Э.Р. Оптимизация коридора входа в атмосферу. — Космические ис¬
следования, 1968, т. VI, вып. 1.
85. Спутники планет/Под ред. Дж. Бернса. — М.: Мир, 1980.
86. Стандартная атмосфера: параметры. — М.: ГОСТ 4410—73.
87. Тарасов Е.В. Алгоритмы оптимального проектирования летального аппарата. —
М.: Машиностроение, 1970.
88. Тейфель В.Г. Атмосфера планеты Юпитер. — М.: Наука, 1969.
89. Тейфель В. Г. Юпитер и Сатурн — гиганты Солнечной системы. — М.: Знание,
1976.
90. Тихонов А.Н. О некорректно поставленных задачах. — Вычислительные методы
и программирование, 1976, вып. 8.
91. Физические характеристики планет-гигантов/Под ред. В.Г.Тейфеля. — М.: Наука,
1971.
92. Филатьев А.С. Снижение с помощью малых управляющих воздействий максималь¬
ных динамических и тепловых нагрузок при пассивном движении гиперзвуковых
аппаратов. — Ученые записки ЦАГИ, 1978, т. IX, № 2.
93. Филатьев А.С. Приближенный аналитический синтез оптимального управления
гиперзвуковыми летательными аппаратами при движении в атмосфере с докру-
говой скоростью. — Ученые записки ЦАГИ, 1980, т. XI, №1,2.
94. Шаманский В.Е. Методы численного решения краевых задач на ЭЦВМ, ч. 11. —
Киев: Наукова думка, 1966.
95. Шаронова И.М. Достаточные условия относительного экстремума в задачах дина¬
мики полета. — В кн.: Исследования по динамике полета/Под ред. И.В. Остослав-
ского. — М.: Машиностроение, 1969.
96. Шатровский Л.И. Об одном численном методе решения задач оптимального уп¬
равления. — Журнал вычислительной математики и математической физики, 1962,
т. 2, № 3.
97. Шилов, А.А., Желнин Ю.Н. О минимуме максимальной перегрузки при торможе¬
нии аппарата в атмосфере. — Космические исследования, 1966, т. IV, вып. 4.
98. Шилов А.А. Об одном приближенном способе решения задачи минимума максималь¬
ного отклонения динамической системы. Автоматика и телемеханика, 1970, № 2.
99. Шкадов Л.М., Буханова Р.С., Илларионов В.Ф., Плохих В.П. Механика оптималь¬
ного пространственного движения летательных аппаратов в атмосфере. — М.:
Машиностроение, 1972.
100. Шкадов Л.М., Илларионов В.Ф., Балабанов О.В. Минимизация стандартной тем¬
пературы при спуске аппарата с орбиты. — Труды ЦАГИ, 1969, вып. 1148.
101. Эйсмонт Н.А. Оптимальное управление космическим аппаратом, переводимым
с гиперболической траектории на орбиту спутника планеты торможением в ат¬
мосфере. — Космические исследования, 1972, т X, вып. 2.
102. Эйсмонт Н.А. Использование аэродинамического торможения для перевода спут¬
ника планеты с орбиты с большим эксцентриситетом на почти круговую. —
Космические исследования, 1972, т. X, вып. 2.
103. Эйсмонт Н.А. Коридоры входа в атмосферу планет при проведении маневра
захвата космического аппарата аэродинамическим торможением. — В кн.: При¬
кладные задачи космической баллистики/Под ред. П.Е. Эльясберга. — М.: Наука,
1973.
104. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. —
М.: Наука, 1969.
105. Энеев Т.М. О применении градиентного метода в задачах теории оптимального,
управления. — Космические исследования, 1966, т. IV, вып. 5.
106. Юпитер/Под ред. Т. Герелса. — М.: Мир, 1978.
107. Ярошевский В.А. Приближенный расчет траекторий входа в атмосферу. — Косми¬
ческие исследования, 1964, т. II, вып. 4, 5.
108. A//en H.J., Eggers A.J. A study of the motion and aerodynamics heating of missile
entering the earth's atmosphere at hight supersonic speeds. - NASA Rept., 1958, No. 1381.
109. Bryson A. and oth. Determination of the lift or drag program that minimizes re-entry
with acceleration or range constraints using a steepest descent computation procedu¬
re. - IAS Paper, 1969, No 61 - 6.
110. Busemann A., Vinh N.X., Culp R.D. Optimum three-dimensional atmospheric entry. —
Acta Astronautica, 1975, v. 2, No. 7/8.
382
111. Busemann A., Vinh N.X., Kelley G.F. Optimum maneuvers of a skip vehicle with boun¬
ded lift constraints. — Journal of Optimization Theory and Applications, 1969, v. 3,
No. 4.
112. Campbell J.F., Brown C.A. Experimental ware frow properties of a Viking 75 entry
vehicle. — Journal of Spacecraft and Rockets, 1974, v. 11, No. 1.
113. Chapman D.R. An approximate analytical method for studying entry into planetary
atmospheres. — NASA Technical Report, 1959.
114. Colunga D., Tapley B.D. The computation of optimal control programmes using a
modified successive sweep method. — International Journal of Control, 1972, v. 15,
No. 3.
115. Fave /. Approche analytique du probleme domaine accessible a un planeur orbital. —
Recherche Aerospatiale, 1968, No. 124.
116. Finch I.W. Aerodynamic braking trajectories for Mars orbit attainment. — Journal
of Spacecraft and Rockets, 1965, v. 2, No 4.
T\7. Frastic F., Vinh N.X. Optimal aerodynamic control by matched asymptotic expansi¬
ons. — Acta Astronautica, 1976, v. 3, No. 5/6.
118. Garcia F., Fowler IV. Thermal protection optimization for the space shuttle. — AIAA
Paper, 1972, No. 977.
.Gottlieb R.G. Rapiol convergence to optimum solutuon using a min-H strategy. —
AIAA Journal, 1967, v. 5, No. 2.
120. Griffin J.W., Vinh N.X. Three dimensional optimal maneuvers of hypervelocity vehic¬
les. - AIAA Paper, 1971, No. 920.
121. H/7tz A.A.; Florense D.E., Low D.L. Selection, development and characterization of
a thermal protection system for a Mars entry vehicle. — AIAA Paper, 1968, No. 304.
122. Konig H. Lenkmethoden fur warmeoptimal dreidimensionale Abstiegsbahuen von
aerodynamischen Wiedereintrittskorpern. — Zeitschrift fur Flugwissenschaften, 1973,
B, 21. Nr. 1.
123. Konig H. Lenkmethoden fur wa’rmeoptimale ebehe Abstiegs-bahnen von aerodynami¬
schen Wiedereintrittskorpern. — Raumfahrtforscung, 1970, B. 14, Nr. 3.
124. Lau J. Implications of maneuvering-range constraints on lifting-vehicle design. — Journal
of Spacecraft and Rockets, 1967, v. 4, No. 4.
12Б. Leondes C.T., Niemann R.A. Optimization of aerospace re-entry vehicle trajectories
through independent control of lift and drag. — Journal of Spacecraft and Rockets,
1966, v. 3, No. 5.
126. Levine Ph. Analysis of planetary entry problem associated with manned space vehic¬
les. - IAS Paper, 1962, No. 162.
127. Levinsky E.S. Application of inequality constraints to variational problems of lifting
re-entry. — IAS Paper, 1961, No. 61—21.
128. Love E.S. Factors influencing configuration and performance of multipurpose manned
entry vehicles. — Journal of Spacecraft and Rockets, 1964, v. 1, No. 1.
129. Marshall E.J. Optimum re-entry via a variable control force. — Amer. Rocket Soc. Pre¬
prints, 1959, No. 956—59.
130. Matting F.W. Approximate bridging relations in the transitional regime between conti¬
nuum and free-molecule flows. — Journal of Spacecraft and Rockets, 1971, v. 8, No. 1.
131. Morrison D., Samz !. Voyage to Jupiter. — NASA SP-439,1980.
132. Okhotsimsky D.E., Golubiev I.F., Sikharulidze Y.G. Mars orbiter insertion by use of
atmospheric deceleration. — Acta Astronautica, 1978, v. 5, No. 9/10.
133. Pottsepp L., Shi Y.Y. Optima! lift control of a hypersonic glider. — AIAA Journal,
1968, v. 6, No. 6.
134. Schappe! R.T., Jonson R.G. Experimental and simulation study results on the selection
system. — AIAA Paper, 1972, No. 868.
135. Scoville C.L., Goruch P.O. Thermal protection for the space shuttle. - Raumfahrtfor-
schung, 1971, B. 15, No. 2.
136.Shi Yun-Yuan. Matched asymptotic solutions for optimum lift controlled atmospheric
entry. — AIAA Pap$r, 1971, No. 71—21.
137. Shi Yun-Yuan, Pottsepp L., Eckstein M.C. Optimal lift control of a hypersonic lifting
during atmospheric entry. — AIAA Journal, 1969, v. 7, No. 12.
138. South D.J. Real-time optimal guidance of lifting re-entry vehicles. — AIAA Paper, 1974,
No. 928.
139. Speyer J.I., Womble M.E. Approximate optimal atmospheric entry trajectories. — Jour¬
nal of Spacecraft and Rockets, 1971, v. 8, No. 11.
140. Speyer J.L, Womble M.E. Approximate optimal atmospheric entry trajectories. — AIAA
Paper, 1971, No. 919.
141. Stewart LD., Greenshields D.H. Entry vehicles for space programs. — Journal of Space¬
craft and Rockets, 1969, v. 6, No. 10.
142. Strauss E.L. Superlight ablative systems for Mars lauder thermal protection. — Journal of
Spacecraft and Rockets, 1967, v. 4, No. 10.
383
143. Sullivan H.C. Selected optimal shuttle entry computations. — AIAA Paper, 1974,
No. 818.
144. Sulton K. Radiative heating about outer planet entry probes. — AIAA Paper, 1975,
No. 183.
145. Vinh N.X. Integrals of the motion for optimal trajectories in atmospheric flight. —
AIAA Paper, 1972, No. 931.
146. Vinh N.X. General theory of optimal trajectory for rocket flight in a resisting medium. —
Journal of Optimization Theory and Applications, 1973, v. 11, No. 2.
147. Vinh N.X., Shieh C.l. Optimum coasting flight in a horizontal plane. — Journal of Opti¬
mization Theory and Applications, 1975, v. 17, No. 5/6.
148. Vojvodich N.S., Reynolds R.T., Grant T.L., Nachtshein P.R. Outer planet atmospheric
entry probes. An overview of technology readiness. — AIAA Paper, 1975, No. 1147.
149. Wingrove R.C. An analysis of minimum heat trajectories for entry at hyperbolic
speeds. — Journal of Spacecraft and Rockets,1967, v. 4, No. 8.
150. Zimni W.F., Hoffmann J.P., Ratz E.A. Die thermische Belastung eines aerodynamiscen
Wiedereintrittskorpers und die daraus resultierenden Optimierungs — und Auslegungs-
kriterien. — Raumfahrtforschung, 1970, B. 14, No. 2.