Г. Е. ШИЛОВ
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
ВТОРОЙ СПЕЦИАЛЬНЫЙ КУРС
\
Допущено Министерством
высшего и среднего специального образования РСФСР
в качестве учебного пособия
для государственных университетов
ИЗДАТЕЛЬСТВО «НАУКА>
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1965

517,
517.2 @75)
Ш 59
УДК 517. 0 @75.8)

ОГЛАВЛЕНИЕ
Предисловие. .• • .... 7
ЧАСТЬ 1
ОБОБЩЕННЫЕ ФУНКЦИИ
Глава I. Элементарная теория обобщенных функций . ... 9
§ 1. Задача о расширении совокупности обычных функций 9
§ 2. Основные функции одного переменного . . 12
§ 3. Обобщенные функции одного переменного 15
1. Определение и примеры обобщенных функций A5). 2. Обыч-
Обычные функции, как обобщенные A7). 3. Дальнейшие примеры
сингулярных обобщенных функций A8). 4. Обобщенные функ-
функции в комплексном пространстве B0). Задачи B1).
§ 4. Действия с обобщенными функциями одного переменного . . 23
1. Сложение и умножение на число и функцию B3). 2. Диф-
Дифференцирование B3). 3. Примеры B4). Задачи B7).
§ 5. Обыкновенные дифференциальные уравнения 28
1. Уравнение у' = 0 B8). 2. Система у' = Ау C0). 3. Суще-
Существование первообразной C1). 4. Система у' — Ay — f C2).
5. Решения, равные нулю на полуоси C3). 6. Граничная за-
задача C4). 7. Фундаментальная функция дифференциального
оператора C6). Задачи C7).
§ 6. Основные и обобщенные функции нескольких переменных . . 38
1. Определения C8). 2. Примеры D0). 3. Обобщенные функ-
функции в области D1). Задачи D2).
§ 7. Действия с обобщенными функциями нескольких переменных 43
1. Определения D3). 2. Примеры D3): /. Независимость
высших производных от порядка дифференцирования D3).
2. Производные по С. Л. Соболеву D4). 3. Производные функ-
функции 9 (х, хп) D4). 4. Дифференцирование обобщенной
функции / ((ю, х)) D4). 5. Функционал порядка сингуляр-
сингулярJ D6). 6. П й ф
фуци / ((, х)) D4) 5 Функционал орда сингуляр
ности <J/> D6). 6. Производные кусочно-непрерывной функ-
функции D6). 7. Истолкование формулы Грина D7). 8. Оператор
Лапласа и сферически симметричные функции D7). 9. Фунда-
Фундаментальная функция оператора Дт D9). 3. Однозначность
восстановления обобщенной функции по ее первым производ-
производным E1). 4. Обобщенная функция с непрерывными первыми
производными E3). Задачи E6).
I*

4 ОГЛАВЛЕНИЕ
Глава II. Специальные вопросы теории обобщенных функций . . 59
§ 8. Локальные свойства и носитель обобщенной функции .... 59
1. Обобщенная функция, равная нулю в области E9). 2. Со-
Сохранение локальных свойств при дифференцировании F1).
3. Основная функция, равная 1 на заданном множестве и О
вне его окрестности F2). 4. Разложение единицы F3).
5. Разложение основной функции F4). 6. Локальное равен-
равенство нулю обобщенной функции F4). Задачи F5).
§ 9. Предельный переход в пространстве обобщенных функций . . 66
1. Определение и простейшие свойства F6). 2. Дельта-об-
Дельта-образные последовательности F8). 3. Теорема о полноте про-
пространства К! F9). 4. Обобщенные функции, непрерывно зави-
зависящие от параметра G2). 5. Дифференцируемые функции
параметра G4). 6. Аналитические функции параметра G5).
7. Функции аргумента (ю, х) и их интегрирование по ш G6).
Задачи G9).
§ 10. Структура обобщенных функций .... 79
1. Формулировки результатов G9). 2. Лемма о порядке син-
сингулярности обобщенной функции в ограниченной области (80).
3. Обший вид функционала в ограниченной области (81).
4. Общий вид функционала в пространстве К (83). 5. Общий
вид финитного функционала (84). 6. Общий вид функционала,
сосредоточенного в одной точке (85). 7. Вопрос о гладкости
результата интегрирования функции от (<в, х) (87). Задачи (89).
§ 11. Некоторые специальные обобщенные функции 92
1. Обобщенная функция х\ (92). 2. Обобщенная функ-
функция х\ (94). 3. Обобщенные функции \х\к и \х^щпх (94).
4. Действия с обобщенными функциями х\ и прочими (96).
5. Обобщенная функция г*" (98). 6. Разложение rh на плоские
волны A00). Задачи A03).
§ 12. Свертка обобщенных функций 109
1. Свертка обычных функций A09). 2. Определение свертки
обобщенных функций (ПО). 3. Существование и основные
свойства свертки функционала с основной функцией A12).
4. Свойства свертки обобщенных функций A14). 5. Выраже-
Выражение свертки обобщенных функций через свертки обычных
функций A15). 6. Коммутативность свертки A18). 7. Носи-
Носитель свертки A19). 8. Предел и производная свертки A20).
9. Обобщение на случай нескольких переменных A20).
Задачи A22).
§ 13. Порядок сингулярности 123
1. Порядок сингулярности s (/) A23). 2. Порядок сингулярности
с(/) A24). 3. Теоремы о порядке сингулярности A25). 4. Ве-
Величина s (/) и свертка A26). 5. Связи между s (/) и с (/) A28).
6. Оценки s (/) и с (/) через s (Дт/) для финитных функцио-
функционалов A30). 7. Оценки для произвольных функционалов в огра-
ограниченной области A32). Задачи A33).
§ 14. Преобразование Фурье обобщенных функций 134
1. Преобразование Фурье обычной функции A34). 2. Про-
Пространство Z A36). 3. Функционалы на пространстве К и на
пространстве Z A38). 4. Преобраэование Фурье обобщенной
функции A41). 5. Примеры A44). Задачи A46).

ОГЛАВЛЕНИЕ 5
§ 15. Преобразование Фурье обобщенных функций (продолжение) . 147
1. Случай нескольких переменных A47). 2. Преобразование
Фурье и повороты A49). 3. Преобразование Фурье финит-
финитного функционала A50). 4. Бесселевы функции A52). 5. Пре-
Преобразование Фурье от 6 (г—а) A53). 6. Преобразование
Фурье и свертка A54). 7. Другие формы преобразования
Фурье A56). Задачи A56).
ЧАСТЬ 2
ПРОБЛЕМЫ ОБЩЕЙ ТЕОРИИ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Глава Ш. Фундаментальные функции дифференциальных опера-
операторов и локальные свойства решений 158
§ 16. Формула типа Пуассона 158
1. Свойства совокупности решений уравнения Р1-^—)« = 0
в К' A58). 2. Формула типа Пуассона A59). 3. Следствия, отно-
относящиеся к порядку сингулярности решения A62). 4. Формула
типа Пуассона для гипоэллиптического оператора A63).
5. Классы Жеврея A64). Задачи A67).
§ 17. Существование фундаментальной функции 169
1. Общие соображейия A69). 2. Запись многочлена Р в нор-
нормальной форме A70). 3. Лестница Хёрмандера A72). 4. Суще-
Существование фундаментальной функции A73). 5. Возможность
искривления лестницы A74). Задачи A75).
§ 18. Решение уравнения с правой частью 175
1. Разложение по системе лестниц Хёрмандера A75). 2. Суще-
Существование искомых лестниц A77). Задачи A79).
§ 19. Условие гипоэллиптичности по корням многочлена (необхо-
(необходимость) 180
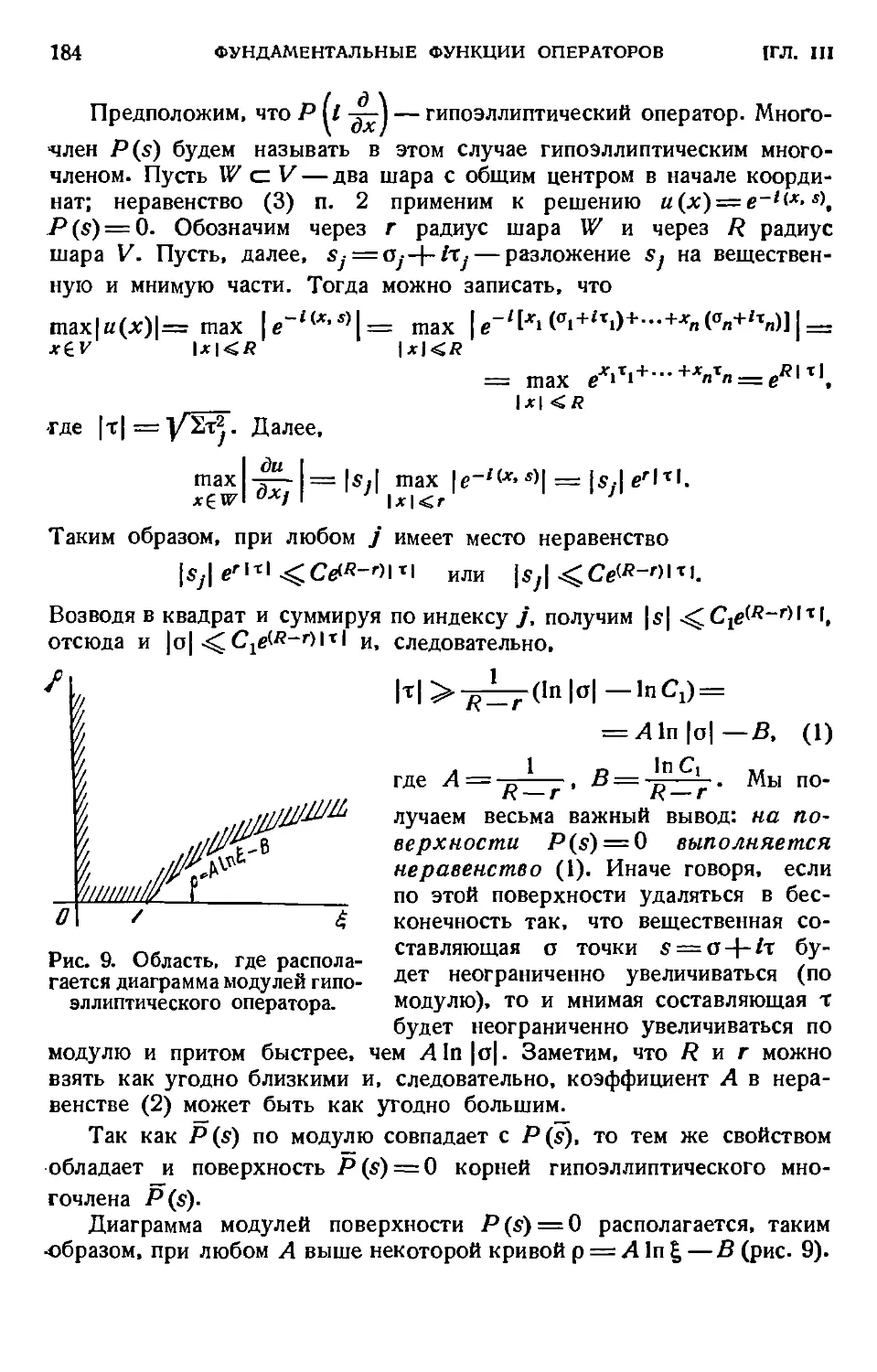
1. Диаграмма модулей дифференциального оператора A80).
2. Лемма о производных решения гипоэллиптического урав-
уравнения A82). 3. Характеристическое свойство поверхности
нулей гипоэллиптического многочлена A83). 4. Лемма о произ-
производных решения \-гипоэллиптического уравнения A85). 5. Ха-
Характеристическое свойство поверхности нулей v-гипоэллипти-
ческого уравнения A85) 6. Оценка нижней грани BqqQ®d~Q
A86). Задачи A87).
§ 20. Условие гипоэллиптичности по корням многочлена (доста-
(достаточность) 187
1. Лемма о модуле многочлена A88). 2. Доказательство основ-
основной теоремы A89). 3. Условие у-гипоэллиптичности A94).
4. Использование теоремы Зайденберга — Тарского A96).
Задачи A98).
§ 21. Условия гипоэллиптичности по поведению многочлена в веще-
вещественной области 199
1. Леммы Хёрмандера A99). 2. Эллиптические уравнения B02).
Задачи B04).
§ 22. Метод Радона 205
1. Общая схема метода B05). 2. Случай однородного эллипти-
эллиптического многочлена. B07). 3. Случай однородного неэллиптиче-
неэллиптического многочлена B08). 4. Расположение особенностей фунда-
фундаментальной функции B11). Задачи B13).

6 ОГЛАВЛЕНИЕ
Глава IV. Уравнения в полупространстве . 214
§ 23. Корректные краевые задачи для систем уравнений . 214
§ 24. Вспомогательные построения 219
1. Интерполяционный многочлен Ньютона B19). 2. Оценка
нормы матрицы etp через характеристические числа ма-
матрицы Р B22). 3. Обобщенные детерминанты Вандермонда B23).
4. Разделенные разности B27). 5. Двойные разделенные раз-
разности B28).
§ 25. Обыкновенные уравнения и системы 230
1. Простейшая корректная задача для системы B30). 2. Про-
Простейшая корректная задача для одного уравнения B32).
3. Общая корректная задача для системы B38). 4. Другие
условия на рост решения при t->co B39).
§ 26. Уравнения в частных производных . 239
1. Основная теорема для системы B39). 2. Основная теорема
для одного уравнения B43). 3. Необходимость условий кор-
корректности B46). 4. Общая краевая задача B46). 5. При-
Примеры B48). 6. Задачи с другими условиями на рост при
<->оо B50).
§ 27. Фундаментальные решения регулярных краевых задач .... 250
1. Свертка в пространстве &е B50). 2. Свойства свертки B52). *
3. Регулярные уравнения и системы B53). 4. Производные
фундаментального решения B54). 5. Выражение решения
с произвольными и0 @, х), ..., иг_\ @, х) через фундамен-
фундаментальное решение B57). 6. Фундаментальные решения класси-
классических краевых задач (п=1) B58). Задачи B60).
§ 28. Формулы фундаментальных решений регулярных уравнений
(п=1) ... .262
1. Выражение преобразования Фурье фундаментального ре-
решения однородного уравнения B62). 2. Случай гиперболиче-
гиперболического уравнения B65). 3. Случай регулярного уравнения B67).
Задачи B71).
§ 29. Фундаментальные решения регулярных уравнений (п > 1) . 272
1. Общая схема и классические примеры B72). 2. Общее ре-
регулярное уравнение B78). 3. Однородное гиперболическое
уравнение B81). 4. Регулярное однородное уравнение B84).
§ 30. Уравнения со свободным членом . . 287
1. Общая схема и формулировка основной теоремы B87).
2. Система обыкновенных уравнений B91). 3. Обыкновенное
уравнение порядка т B95). 4. Уравнение с частными произ-
производными C01).
§ 31. Смешанные задачи . - 303
1. Общая схема и формулировка основной теоремы C03).
2. Примеры C07). 3. Пространства Я^'и ^ q C11). 4. До-
Доказательство необходимости для системы C13). 5. Доказа-
Доказательство необходимости для уравнения m-го порядка C16).
6. Доказательство достаточности C18).
Краткие литературные указания 323
Алфавитныйуказатель .. 325

ПРЕДИСЛОВИЕ
Второй специальный курс математического анализа содержит
основы теории обобщенных функций и ее применения к общей теории
уравнений с частными производными. Под названием «Анализ-4»
этот курс несколько раз был прочитан автором на механико-мате-
механико-математическом факультете МГУ.
В первой части книги излагаются начала теории обобщенных
функций. За основу принято определение Соболева — Шварца (обоб-
(обобщенные функции = линейные непрерывные функционалы на про-
пространстве финитных бесконечно дифференцируемых функций).
Отбор фактов из теории обобщенных функций определялся в основном
требованиями второй части. Общая теория уравнений с частными
производными, которой посвящена вторая часть, насчитывает сейчас
уже большое количество серьезных результатов. Мы выбрали для
изложения в курсе два ее раздела: теорию фундаментальных функций
(и связанную с ней теорию гипоэллиптичности Л. Хёрмандера) и
вопросы корректных задач в полупространстве. Одним из сущест-
существенных оснований для выбора именно этих разделов была возмож-
возможность использования сравнительно элементарного аналитического
аппарата.
Вторым важным основанием было то, что эти разделы не получили
освещения в известной серии монографий «Обобщенные функции»
(И. М. Гельфанд и др.). Но самым главным, разумеется, является
тот факт, что на этих двух разделах весьма выпукло отразились
идеи общей теории уравнений с частными производными, не предъяв-
предъявляющей специальных требований к типу и порядку уравнений и тем
не менее позволяющей установить важные и глубокие закономерности.
Изложение, как и в первой книге, сопровождается рядом задач,
куда вынесены также и некоторые интересные, но не лежащие не-
непосредственно на пути вопросы теории (в частности, все. относя-
относящееся к пространству S' функций степенного роста и их производных).
От читателя требуется владение общим курсом математического
анализа и некоторое, впрочем небольшое, знакомство с книгой
«Математический анализ. Специальный курс» B-е изд., Физматгиз,
1961), которая в ссылках обозначается «Анализ III».

ЧАСТЬ 1
ОБОБЩЕННЫЕ ФУНКЦИИ
ГЛАВА I
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ
§ 1. Задача о расширении совокупности обычных функций
Проблемы математического анализа ставятся большей частью на
языке классической теории функций, сформировавшемся в начале
XIX века. Смотря по характеру задач, рассматриваются функции анали-
аналитические, дифференцируемые, непрерывные, интегрируемые (по Лебегу)
и пр. Несмотря на огромное богатство возможностей, которые предста-
представились в связи с глубокой разработкой различных разделов теории
функций, в наше время стало ясно, что классический аппарат
во многих случаях недостаточен и требует определенного расширения.
Чтобы пояснить это соображение, условимся называть обычной
функцией всякую функцию у ^/(х), определенную при —оо<л;<оо,
принимающую вещественные значения и интегрируемую (по Ле-
Лебегу) в каждом конечном промежутке а -^.х <^.Ь- Так, например,
всякая непрерывная функция, всякая ограниченная (измеримая) на
каждом конечном промежутке принадлежит к числу обычных функ-
функций. Как принято, мы будем считать, что /j (л:) и /2 (х) есть одна
и та же обычная функция, если почти всюду fl (x) = /2 (х).
Всю совокупность обычных функций мы обозначим через Е.
Обычные функции можно складывать и умножать на вещественные
числа, так что они образуют линейное вещественное пространство.
В пределах пространства Е можно выполнять также различные
операции предельного перехода. Например, если последовательность
обычных функций /j (х) /v (х), ... стремится почти всюду
к некоторой функции / (х) и при этом выполняется неравенство
где /0 (х) — фиксированная обычная функция, то, согласно известной
теореме Лебега, предельная функция f (х) будет интегрируемой
в каждом конечном промежутке, т. е. также обычной функцией.

Ю ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
С другой стороны, такую важную для анализа операцию, как
дифференцирование, можно применять далеко не ко всем обычным
функциям. Некоторые из обычных, даже непрерывных функций
вообще не имеют производных, как известная функция Вейерштрасса *);
у некоторых обычных функций производная хотя и имеется, но не
представляет собою обычной функции (например, у = - )• Иногда
производная у обычной непрерывной функции имеется (почти всюду)
и есть обычная функция, но она такова, что, интегрируя ее, мы
не возвращаемся к исходной функции (например, для канторовой
функции у = С(х)), так что эта производная не приносит пользы.
Известно **), что абсолютно непрерывные функции (и только они)
обладают такой обычной производной, что выполняется соотношение
/(*)=/(«)+/Г F)
(Функция Кантора С(х) непрерывна, но не абсолютно непрерывна.)
Наконец, из сходимости /v (лг) —> f (л;) далеко не всегда следует
сходимость производных fv(x)—>f (х), даже если они сущест-
существуют.
Имеется хорошо известный класс функций, в пределах которого
не встречаются указанные нежелательные явления — а именно класс
аналитических функций; но он слишком узок для приложений.
Желательно было бы сохранить для использования хотя бы все
обычные функции. Как это ни странно на первый взгляд, оказывается
возможным не сузить, а расширить класс обычных функций с тем,
чтобы устранить трудности с производными.
Мы расширим в этой главе совокупность Е до некоторой новой
совокупности, в пределах которой можно будет разумно определить
операцию дифференцирования, причем так, что эта операция будет
и непрерывной относительно предельного перехода.
Вначале отметим следующее. Пусть <р(лг) — ограниченная (изме-
(измеримая) финитная функция; последнее значит, что <р(лг) обращается
в нуль вне некоторого конечного промежутка а-^.х -^.Ь. Каждой
обычной функции мы можем сопоставить число
Ф)=
*) Или аналогичная функция Ван-дер-Вардена; см. Анализ III,
стр. 274 — 275.
**) Анализ III, гл. VI, §§ 2 и 3.

§ 1] РАСШИРЕНИЕ СОВОКУПНОСТИ ОБЫЧНЫХ ФУНКЦИИ Ц
причем фактически интеграл распространяется лишь по промежутку
[д, Ь\- Если функция f (х) абсолютно непрерывна и имеет обычную
производную /' (лг), то аналогично мы можем составить выражение
(/■ Ф) =
Предположим теперь, что <р (л:) также абсолютно непрерывна и имеет
ограниченную производную <р' (лг). Тогда в последнем интеграле мы
можем выполнить интегрирование по частям, которое приведет
к равенству
оо
f f(x)<p'(x)dx = ~ ff(x)y'(x)dx.
— CO —СО
Внеинтегральный член обращается в нуль, поскольку ф(лг) — финит-
финитная функция. Поэтому в рассматриваемом случае мы имеем
(/'. Ф) = —
—
Но если f (х) и не существует, выражение
wdx A)
все равно имеет смысл для каждой финитной ограниченной функции
<р(лг) с ограниченной производной ф'(лг). Таким образом, хотя у нас
и нет функции /' (х), как таковой, но если нам нужны только
результаты интегрирования произведений /' (х) с ограниченными
финитными функциями, обладающими ограниченными производными,
то такие результаты мы всегда можем найти, как если бы функция
f'(x) существовала: именно, следует взять интегралы A) с обрат-
обратным знаком.
Это наблюдение позволит нам подойти к надлежащему расшире-
расширению понятия функции. Раньше мы требовали от функции наличия
определенных значений в каждой (или почти в каждой) точке; теперь
мы будем интересоваться лишь значениями интегралов от произведе-
произведения данной функции с некоторыми «пробными» функциями; если для
данной функции известны только такие интегралы, будем говорить,
что у нас имеется обобщенная функция- Приведенное выше рас-
рассуждение показывает, что при должном выборе запаса пробных
функций всякая обобщенная «функция» будет обладать и производ-
производной— также обобщенной «функцией».
Но как же можно определить интеграл от произведения обоб-
обобщенной функции и пробной функции, не имея возможности дейст-

12 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. 1
вовать с значениями функции в отдельных точках? Ответ простой:
а данном случае не следует определять интеграл конструк-
конструктивно, а лишь аксиоматически, как это описывается в следую-
следующем пункте. Пробные функции можно выбирать по-разному и по-
получать тем самым различные классы обобщенных функций. Приве-
Приведенные рассуждения показывают, что для обеспечения существования
производной у каждой обобщенной функции производная (обычная) каж-
каждой пробной функции также должна быть пробной функцией; отсюда
вытекает, что пробные функции нужно брать бесконечно дифферен-
дифференцируемыми- С другой стороны, если мы желаем, чтобы любая обыч-
обычная функция / (х), как угодно быстро растущая при | х | —> оо,
попала в число обобщенных, т. е. чтобы интеграл
ff(x)<f(x)dx
существовал для любой обычной функции — необходимо считать*
что пробная функция <р(лг) сама финитна.
После этих наводящих соображений мы можем начать система-
систематическое изложение предмета.
§ 2. Основные функции одного переменного
Будем называть пробной или — что более укоренилось — основ-
основной функцией всякую вещественную функцию ф(лг), определенную-
при —оо < х < оо, непрерывную и имеющую производные (в обыч-
обычном смысле) любого порядка, и, кроме того, финитную, т. е. обра-
обращающуюся в нуль вне конечного промежутка.
В частности, если основная функция <р(х) обращается в нуль вне
промежутка [а, Ь\, то мы будем называть ее сосредоточенной на
промежутке [а, Ь\, а сам промежуток [а, Ь] будем называть но-
носителем функции <р (лг) (обозначение [a, ft] = supp <р).
Основные функции можно складывать друг с другом и умножать
на вещественные числа, так что они образуют линейное пространство;
мы обозначим всю совокупность основных функций через К-
В пространстве К определена также операция умножения основ-
основных функций <р(лг) на произвольную бесконечно дифференцируемую-
(любого роста на бесконечности) функцию g (х), дистрибутивная
со сложением.
Во многих вопросах бывает необходимо рассматривать в качестве
пробных (основных) функций также и комплекснозначные функции вида
<Pi (•"О+'ФгС*)' Где ЧНОО и ЧJ(лг) — определенные выше веществен-
вещественные основные функции. В пространстве комплекснозначных основных
функций (которые по-прежнему обозначаются через К) кроме указанных

$ 21 ОСНОВНЫЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО 13
операций возможно еще умножение на комплексные числа и на ком-
комплексные бесконечно дифференцируемые функции.
Введем в пространство К определение предельного перехода.
Мы будем говорить, что последовательность ф1 (л:) фл) (х), ...
основных функций сходится в пространстве К к нулю, если все
эти функции обращаются в нуль вне одного и того же ограниченного
промежутка [а, Ь] и равномерно сходятся к нулю, так же как и их
производные любого порядка.
Пример 1. Функция
f(x.a)
Ф(х; а)= " " "Р" 1*1<«- _
О при |лг|>с ^ -q
является основной (рис. 1). По-
, ч 1 Рис. 1.
следовательность qv (x) = — q> (л:, а)
стремится к нулю в пространстве К. Последовательность ф^л;) =
= — ф( —, а\ стремится к нулю равномерно на оси —со < х < со
вместе со всеми производными, но в пространстве К не стремится
к нулю, поскольку нет общего ограниченного промежутка, вне
которого все функции q>v (лг) обращались бы в нуль.
Будем далее говорить, что последовательность основных функ-
функций ф: (х) фг (х), ... сходится в К к функции ф (л:), если
ф(лг) входит в К и разность ф(лг) — Ф^С*0 стремится в К к нулю.
Операции сложения и умножения на число и бесконечно диф-
дифференцируемую функцию непрерывны относительно этой сходимости.
Иными словами, если q>v—>Ф в К, ifv->-^ в /(, то окр -f-fUl>v->
—> cup-f-Рф в К при любых вещественных а и р\ g (х) ф,^ (х) —>
—> g (x) <р (х) в К при любой бесконечно дифференцируемой
функции g(x).
Замечание. Пространство К не мет ризу емо; иными словами, в нем
нельзя ввести понятие расстояния р (ф, 1]з) с обычными свойствами *) так,
чтобы сходимость фл! к ф была бы равносильна выполнению соотношения
Р (ф, фу) -> 0.
Действительно, если в метрическом пространстве имеется система схо-
сходящихся последовательностей
*) См. Анализ 111, гл. 2.

14 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ |ГЛ I
и предельные элементы ф'1' ф'т\ ... сами сходятся к элементу ф, то
всегда возможно, выбрав должным образом по одному элементу из каждой
строки, получить последовательность,
фП)) фСл^
также сходящуюся к ф.
Но в пространстве К такая картина не имеет места. Пусть, например,
Ф^™' = — ф (х; т) (v = 1, 2, ...; т = 1, 2 ),
где ф (х; т) — функция из примера 1. При каждом фиксированном т по-
последовательность ф'^"' стремится в К к нулю, как в примере 1. Но никакая по-
последовательность вида ф^,т) не стремится к нулю в К, так как нет общего
т
отрезка, вне которого все функции ф'"*' обращаются в нуль.
ш
Таким образом, сходимость в К не может быть задана никакой
метрикой. Но она может быть задана некоторой топологией; см. задачу 7
к этому параграфу.
Задачи. 1. Показать, что пространство К полно относительно введен-
введенной сходимости. Полнота в данном случае означает следующее: если имеется
последовательность основных функций ф1 yv сосредоточенных
в одном и том же отрезке [а, Ь], и при каждом q = 0, 1, 2, ... последо-
последовательность производных ф*,9' (х) равномерно сходится к некоторому пределу
■ф (лг), то предельная функция г|>0 (x) = lim ф (х) является основной,
V->oo
tyq(x) = 1$\х) и последовательность <pv(x) сходится кфо(л:) в пространстве К.
2. Дана последовательность q>v (x), v=l, 2, .... основных функций,
обращающихся в нуль вие фиксированного отрезка [а, Ь]. Показать, что при
достаточно быстро стремящихся к 0 постоянных bv последовательность
оо
bv% (x) будет сходиться в К к нулю, а ряд 2 ^v^v (■*) будет в К сходиться.
v=i
Указание. Последовательность Ь~' должна стремиться в со быстрее,
чем любая последовательность mvp = max | ф(^' (х) | (при каждом фиксирован-
фиксированном р = 0, 1, 2, ...).
3. Пусть имеется семейство основных функций {ф(л; t)}, сосредоточен-
сосредоточенных на фиксированном отрезке [а, Ь\ и непрерывно зависящих от параметра t,
меняющегося в промежутке [с, d). Непрерывная зависимость от t означает
в данном случае следующее: если tv^>t, то
Ф (х; <%.) -> ф (х; t) в К-
Показать, что семейство {ф(лг; t)} можно проинтегрировать по параметру t,
причем интеграл, понимаемый как предел (в К) обычных интегральных
сумм
т
2
будет снова основной функцией, сосредотбченной на отрезке [в, Ь].
Указание. Использовать задачу 1. Функция ф (х\ t) равномерно не-
непрерывна по х и t, так же как и все ее производные по х.

§ 3] ОБОБЩЕННЫЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО 15
4. Рассмотрим линейное пространство Со всех финитных непрерывных
функций на оси —оо < х < оо. Введем в него топологию, задавая окрест-
окрестность нуля любой всюду положительной непрерывной функцией у (■*)■ как
совокупность всех <р£С0, для которых
I"PWI<YD
Показать, что сходимость, отвечающая этой топологии, следующая: по-
последовательность q>v (х) £ Со сходится в Со к нулю, если все q>v (х) обра-
обращаются в нуль вне одного и того же отрезка и при v -> со равномерно
стремятся к нулю.
У казание. Требуется доказать два факта: а) элементы q>v попадают
в любую окрестность нуля, начиная с некоторого номера; б) если функции
q>v(x) попадают в любую окрестность нуля, начиная с некоторого номера,
то они сходятся к нулю в указанном смысле (от противного).
5. Показать, что топология в задаче 4 неметризуема.
Указание. См. замечание на стр. 13.
6. Рассмотреть в Со счетное множество А элементов вида
т
где *=1, 2 т = 1, 2 ..., Фо @) ф 0, фт (х) = <р0 ^. *
Показать, что ф(л:)==0 принадлежит к замыканию множества А и тем
не менее не является пределом ни одной сходящейся к 0 последовательности
элементов из А (О. Г. Смолянов).
7. Зададим топологию в К следующим образом. Пусть дано любое т и
взяты т-\-\ положительных непрерывных функций уо(х) ут (х).
Окрестность нуля состоит из всех основных функций у(х), для которых
I Ф (■*) К Yo (х), .... | q?"° (х) | < ут (х).
Показать, что сходимость в К отвечает этой топологии.
Указание. Сравнить с задачей 4.
§ 3. Обобщенные функции одного переменного
1. Каждой обычной функции f (х) (§ 2) соответствует функционал
на пространстве К
(/. Ф)= / f(x)<[>(x)dx. A)
Этот функционал линеен, т е. для любых ф,, <р2 из К и любых
вещественных щ и а2
(/, а,ф, + а2ф2) = а, (/. ф,) -f- a2 (/, фг).
Кроме того, он непрерывен в следующем смысле: если последова-
последовательность основных функций фг .... фч, ... стремится к 0 в К, то
что вытекает из обычных свойств интеграла.

16 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
Таким образом, выражение A) является линейным непрерывным
функционалом на пространстве К.
Существуют и иные линейные непрерывные функционалы на
пространстве К, не приводящиеся к виду A).
Рассмотрим для примера функционал 6, который каждой основной
функции ф(х) ставит в соответствие число Ф@). Очевидно, этот
функционал линеен и непрерывен. С другой стороны, мы утверждаем,
что ни один из функционалов вида A) не может сопоставлять каждой
функции <р (аг) число ф@). Действительно, предположим, что для
некоторой обычной функции f (х) и любой основной функции
имеет место равенство
Пусть, в частности, ф(лг) = ф(лг; а) (§ 2, пример 1). Тогда мы
должны иметь
оо
а) = —. B)
Но при а —> 0 интеграл слева стремится к 0, что противоречит ра-
равенству B).
Мы будем называть обобщенной функцией любой линейный
непрерывный функционал на пространстве К, т. е. функционал /,
удовлетворяющий условиям
A) (/1а,ф1-|-а2ф2) = С11 (/, Ф1)Н-и2(/, ф2) для любых основных
функций ф1 и ф2 и любых вещественных чисел ах и о^;
B) если ФЛ,->0 в К, то (/, Фу)->0.
Если этот функционал представим в форме A), будем называть
его регулярным (или регулярной функцией), если же он не пред-
представим в форме A) — сингулярным функционалом (или сингуляр-
сингулярной функцией).
Только что рассмотренный функционал
F, <р) = ф(О)
сингулярен.
Каждой обычной функции соответствует по формуле A) обобщен-
обобщенная функция. Например, обычной функции /(л;) = С (постоянная)
отвечает обобщенная функция, задаваемая формулой
(f, ф) ^= (С, ф) ^s С
Естественно, что такую обобщенную функцию мы будем называть
постоянной С. В частности, обобщенная функция единица дей-

§ 3] ОБОБЩЕННЫЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО 17
ствует по формуле
A. ф)=
2. Две обобщенные функции f1 и /2 считаются равными, если
значения соответствующих функционалов совпадают на каждой
основной функции
(/.. ф) = (/2. Ф). (О
и различными, если есть хотя бы одна основная функция ф0, на ко-
которой эти значения различны:
(Л- Фо) Ф (/г- Фо)-
Покажем, что различным обычным функциям fi(x) и /2(х)
соответствуют и различные обобщенные функции. Допустим, что
две обычные функции fi(x) и f%(x) определяют по формуле A)
один и тот же функционал, т. е. что для любой q>(x)£K
оо оо
/ /i (*) Ф (х) dx= J /2 (л:) ф (л:) dx.
—оо —оо
Положим f (x) = fl(x) — /2(jc); функция f (x) также обычная, и мы
имеем
для любой функции <р (лг) £ К- Рассмотрим вначале только основные
функции Ф(х), сосредоточенные на фиксированном отрезке [а, Ь].
Для любой такой функции также
ь
Г / (л:) <р (л:) dx = 0. B)
а
х
Функция F(x)= I fCQdc, непрерывна; интегрируя B) по частям,
а
находим
ь
= 0. C)
По известной лемме вариационного исчисления отсюда вытекает,
что F(x) постоянна*). Так как F(a) = 0, то F(x)^0; но отсюда
*) Анализ III, гл. III, § 3, стр. 104.
2 Г. Е. Шилов

18 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ (ГЛ. I
и f (х), равная почти всюду производной от своего неопределенного
интеграла, почту всюду на [а, Ь\ равна нулю.
Так как отрезок [а, Ь\ произволен, то f (х) равна нулю почти
всюду на всей оси —оо < х < оо. Таким образом. fi(x) почти
всюду совпадает с f2(x), что и требовалось.
Приведем для полноты изложения доказательство упомянутой леммы
в применении к нашему случаю. Некоторые связанные с ней соображения
будут дальше использованы.
Допустим, что F (х) не постоянна, и, например, имеются точки xt и х2,
где F (х{) < F (х2). Покажем, что существует основная функция q> (x), для
которой равенство C) не выполняется. Возьмем произвольно число А между
значениями F (Xi) и F (х2). Так как F (х) — непрерывная функция, то най-
найдутся непересекающиеся интервалы Д|Э-*ь ДгЭ-*^. обладающие тем свой-
свойством, что для любых x'£hi, jt"£A2
F (xr) <A<F (x").
В качестве функции «р' (х) возьмем любую бесконечно дифференцируемую
функцию, равную нулю вне Д] и Д2, положительную на интервале Д[. отри-
отрицательную на интервале Д2 и такую, что
оо
Г ц' (х) dx=, С ф' (х) dx + Г ф' (х) dx «= 0.
—оо Ai Дз
Саму функцию ф (х) определим, естественно, формулой
X
очевидно, что ф (л:) принадлежит К. Далее, мы имеем
оо
J [F (х)-А] Ф' (х) dx = J -f J < 0,
—оо Д, Д3
поскольку оба слагаемых отрицательны. Но тогда и
со оо
Г F(x)(f'(x)dx= C[F(x) — A]<p'(x)dx+A
—оо —оо - -л:
так что при данной %' (х) равенство C) заведомо не выполняется. Для
дальнейшего заметим, что достаточно требовать выполнения равенства C)
не для всех ф£К, а лишь для некоторого счетного множества, например, для
каждой из счетного множества функций ф (х), построенных по указанному
правилу для каждой пары непересекающихся интервалов Д[, Д2 с рацио-
рациональными концами
3. Итак, всю совокупность обычных функций можно рассматри-
рассматривать как часть совокупности обобщенных функций. Совокупность
всех обобщенных функций мы обозначим через К'.

£ з] ОБОБЩЕННЫЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО 19
Приведем еще несколько примеров обобщенных функций, не
сводящихся к обычным функциям.
1. Сдвинутая дельта-функция 6(лг—а), которая ставит в соот-
соответствие каждой основной функции <р(х) число ср(#).
2. Функционал —. Функция — не является обычной (она не
является интегрируемой в окрестности начала координат). Тем не менее
для любой основной функции можно образовать выражение
где интеграл понимается как главное значение в смысле Коши, т. е. как
limi
e->0 I
Если произвести в первом слагаемом замену переменного х на —х,
то мы получим также
/1
оо оо
Г ф (— х) dx . Г
-J * +./
*dx\=
где интеграл сходится уже абсолютно. Легко проверить, что полу-
полученный функционал линеен и непрерывен.
3. Функционал порядка сингулярности •<!/?• Так называют
функционал вида
с/, ф)=2 / f«(x) ^ <*>dx=
*=0 -оо ft=0
где /0(лг) fp(x) — обычные функции.
В представлении A), в отличие от A) п. 1, функции fk{x) уже
не определяются однозначно (см. задачу 5 к § 4). Говорят, что
функционал / имеет порядок сингулярности ровно р, если он может
быть записан в форме A) с данным р и не может быть записан
в такой форме с меньшим р. Обычные функции имеют порядок
сингулярности 0.
2*

20 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
Функционал б имеет порядок сингулярности <^[ 1, поскольку можно
записать
сю со
(б, ср ) = ср @) = — J ср' (х) dx = J [— 6 (х)] ср' (х) dx.
0 —со
где в(х) — обычная функция, равная 1 при х > 0 и 0 при х < 0.
При этом, как было показано, Ь(х) не есть обычная функция, так
что ее порядок сингулярности равен точно 1.
Функционал /, который ставит в соответствие основной функ-
функции ср(х) число ф@)+ф'(ОН- ••• -гФ(А>(£)+ ••■> не имеет
конечного порядка сингулярности; мы будем говорить в таких слу-
случаях, что порядок сингулярности функционала / равен -f-oo.
4. Остановимся на вопросе о функционалах в комплексном про-
пространстве основных функций. Определение обобщенной функции как
линейного непрерывного функционала остается здесь прежним; доба-
добавляется лишь возможность принимать такому функционалу и ком-
комплексные значения. При этом функционалы могут быть первого рода,
т. е. при любом комплексном а удовлетворять условию
(/. аср) = а(/, ф),
или второго рода:
а(/. Ф).
где а есть комплексно-сопряженное к числу а.
Каждой обычной комплексной функции / (х) можно поставить в соот-
соответствие четыре линейных функционала:
со
(/. <P)i= ff(x)q(x)dx; A>
— СО
сю
(/. ФJ= fflx)<(>(x)dx; B)
Ф)з= (f(x)^)dx; C)
(/■ ФL= ffWvWd*- D)
— сю
Первые два из них — функционалы первого рода, последние два —
функционалы второго рода. Так как умножение функционала / на
число а всегда определяется формулой
(а/, ср) = а(/. ф),

§ 3] ОБОБЩЕННЫЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО 21
то в первом и третьем функционалах умножение на число а функ-
функции f (х) переходит в умножение соответствующего функционала
на это же число; во втором и четвертом умножение функции на
число а отвечает умножению функционала на комплексно сопряжен-
сопряженное число а. Таким образом, выбор того или иного из функцио-
функционалов A) — D) связан с различными способами вложения совокуп-
совокупности обычных функций в пространство обобщенных функций.
Если / (л!) — обычная функция и / (х) ее комплексно сопряжен-
сопряженная, то, как легко проверить, для любого j = 1, 2, 3, 4 выполняется
равенство
7Г
Это дает нам право определить функционал /, комплексно сопря-
сопряженный к данному функционалу /, по формуле
(/. Ф) = (/. Ф). E)
Очевидно, что функционал /, определенный равенством E), линеен
и непрерывен. Далее, переход от / к / для обычных функций f(x)
всегда отвечает переходу к комплексно сопряженной функции, неза-
независимо от того, каким из способов A) — D) совокупность обычных
функций вложена в пространство обобщенных функций.
Теоремы, доказанные для функционалов какого-нибудь одного
из типов A) — D), легко превращаются в теоремы для функционалов
любого другого типа наложением или снятием злаков комплексного
сопряжения. Пока, до § 14, мы для простоты в случае комплексного
пространства будем иметь в виду функционалы типа A).
Задачи. 1. Пусть основная функция <р(л:, t), зависящая от параметра t,
с <; t -^ d, непрерывна в К по t (§ 2, задача 3). Тогда, согласно задаче 3 § 2,
существует основная функция
d
<р (х) = J <р (х, t) dt. A)
с
Показать, что для любого f£K'
d \ d
J^) / t))dt.
Указание. Интеграл A) есть предел своих интегральных сумм
в смысле сходимости в пространстве К-
2. Показать, что функционал — (п.. 3, пример 2) сингулярен.
Указание. Допустив, что возможно представление I-—, <р) =
сю
= I / (•*) ф (х) dx, где / (л:) — обычная функция, и используя функции

22 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
<р£К, сосредоточенные вне начала координат, показать, что /(х) обязана
при х Ф 0 совпадать с —.
3. Показать, что функционал — имеет порядок сингулярности 1.
X
со
Указание. (—, ф) =— I 1п| х\ -ф' (х) dx.
4. Задача о регуляризации. Пусть /(х) — функция, локально
интегрируемая всюду, кроме точки х = 0, а в этой точке имеющая особен-
особенность не выше степенной, так что при некотором т и достаточно малых |л:|
г4
I -Ж" I
Показать, что существует функционал f^K', который на все основные
функции, равные 0 в окрестности точки х = О, действует по формуле
со
(/.Ф)= ff(x)<f(x)dx
—оо
Указание. Например,
</. q>)=
— ОО
где h (х) равна 1 при | х |< 1 и 0 при | х | > 1.
5. Показать, что для функции / (л:), допускающей при любом т = О,
1, 2, ... оценку
I/Wl> ТПйг (° <*<*»)• О)
1*1
задача 4 неразрешима (функция / (х) «не допускает регуляризации в К'»).
Указание. Пусть <р (л:) = ф (л:; а) из § 2; тогда функции ф.у (х) =
- e^IvIa: 1 1 при достаточно малых ev стремятся к 0 в К', пользуясь
условием A), числа ev можно подобрать при этом так. что
4>v) = / / (*> Фу (*) dx -> °°'

§ 4] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 2£
§ 4. Действия с обобщенными функциями
одного переменного
1. В совокупности обычных функций определены различные опе-
раиии (иногда частично — как дифференцирование). Мы ставим свое»
задачей перенести их на всю совокупность обобщенных функций.
Операции сложения и умножения на вещественные числа вводятся
по формуле
1 + 02/2. <9) = <hifv
Легко проверить, что определенный по этой формуле функционал
ai/i + a2/2 снова является линейным и непрерывным. Кроме того,
если fi и /2 — регулярные функционалы, соответствующие функ-
функциям /, (х) и /2 (х), то a,/j -f- a2/2 есть также регулярный функцио-
функционал, отвечающий функции a,/, (x) -f- a2/2 (х).
Можно, естественно, определить также произведение обобщенной
функции / на любую бесконечно дифференцируемую функцию а(х).
Действительно. если/(х) — обычная функция, то и а(х)/{х)—обыч-
а(х)/{х)—обычная и
(a(x)f(x). Ф)= fa(x)f(x)<p(x)dx= f f(x)a(x)y(x)dx= (/, aq>).
— сю — со
где a(x)q>(x) — опять основная функция. Если теперь / — любая
обобщенная функция, то произведение a(x)f можно определить-
по формуле
(a(x)f, ф) = (/\
Ясно, что функционал а(х) f линеен и непрерывен вместе с функ-
функционалом"/.
Если <х(л;) не бесконечно дифференцируема, в классе К' нельзя
разумно определить произведение функции <х(л;) на любую обобщен-
обобщенную функцию (см. задачу 3 к § 9).
2. Переходим к определению операции дифференцирования.
В соответствии со сказанным в § 1 для любой обобщенной функ-
функции / мы полагаем, по определению,
Поскольку ф'(лг) является основной функцией вместе с ф(лг), выра-
выражение справа определено. Полученный функционал, очевидно, линеен,
а также и непрерывен: если фv->0 в К. то и ф^->0 в К. а следо-
следовательно, и

24 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
Таким образом, каждая обобщенная функция обладает произ-
производной (которая также есть обобщенная функция). Поскольку процесс
дифференцирования можно продолжать, каждая обобщенная функ-
функция имеет производные любого порядка.
При этом
(Л ф) = (/'.- ф') = С/, ф").
аналогично при любом q,
(/«>, Ф)=(/. (_1)у«>)=(-пЧ/. <П (D
Легко видеть, что производная обладает обычными линейными
свойствами: если fx и /2-—обобщенные функции, щ и а? — постоян-
постоянные, то
((%/, +«2/2)'. Ф) = (а1/1 + <х2/2. -Ф') = а,(/,. _ф')+а2(/2. -фО =
= а, (/,'• Ф) + «2 (/2. Ф) = (а,/; + а2/2- ф).
откуда
' i
Далее, если а (х) — бесконечно дифференцируемая функция, то
((a(x)f)', Ф) = («/, — Ф') = (/. — «Ф') = (/. — (аф)') +
+ (/• «' ср) = (/', аср) + (a'f. <р) = (а/' + а'/. Ф)
и, следовательно,
(а/)' = а/'+ау.
Если обычная функция / (х) имеет обычную производную и вос-
восстанавливается по ней интегрированием (т. е. / (х) абсолютно непре-
непрерывна на каждом конечном промежутке), то, как мы видели в § 1,
производная от / (х), как от обобщенной функции, совпадает с /' (х).
Обратно, если f(x) обычная функция и ее производная /' в К'
также есть обычная функция, f' = f'(x), то f'(x) есть производная
от / (х) и в обычном смысле (почти всюду и даже всюду, если /' (х)
непрерывна; см. § 5, п. 1). Но в общем случае производная от
•обычной функции f (х) уже не есть обычная функция.
3. Рассмотрим несколько примеров, связанных с нахождением
производной.
/. Найдем производную от обычной функции
{1 при х > О,
О при х<0.
Согласно определению,
оо
F', ер) = F, — ер') = — J Ф' (х) dx = (? @) = F. ф).

§ «1
откуда
ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ
25
Аналогично при любом а
(Отметим, что производная от 6(лг) в обычном смысле равна 0 при
х ф 0, а при х — 0 не существует.)
2. Функция Q(x) есть простейшая разрывная функция. Рассмотрим
производную от кусочно абсолютно непрерывной функции " ч
Ряс. 2.
с кусочно непрерывной производной /'(х), точками разрыва xlt x2, ...
и соответствующими скачками hx, h2, - -. (рис. 2). Введем функцию
Л (*)=/(*) —
(*-**)•
Функция /, (х) абсолютно непрерывна и восстанавливается по своей
производной /J(Jf), совпадающей с f'(x) всюду, кроме точек раз-
разрыва f(x), где f (х) не существует. Поэтому f[(x) есть производ-
производная и обобщенной функции fx в К'•
С другой стороны, по доказанному в
примере 1,
где /' — производная обобщенной функ-
функции f(x). Из A) получаем
/' = /I (*) + 2 ЛА6 (х - xk), B) Рис. з.
т. е. производная обобщенной функции f(x) составляется из ее
обычной производной и суммы дельта-функций в точках разрыва
с соответствующими скачками в качестве коэффициентов.
В частности, если f{x) отлична от нуля лишь в отрезке [а, Ь\
и абсолютно непрерывна внутри этого отрезка (рис. 3), то
— а) — /ф —
— Ь).
C)

6 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
3. Найдем производную от обычной функции у = 1п|лг|. Заме-
Заметим, что производная в обычном смысле у' = — не есть обычная
■функция. Применяя общее правило, находим
со
< (In |*|)'. ф) = Aп|*|. —ф') = — f 1п|*|.ф'(*)</* =
—оо
1-е оо |
/ ln\x\y'(x)dx+ f\n\x\i[>'(x)dx\ =
-о г I
1-е оо |
1пеф(—е)— [ У^-йх — \пЕу{Е)— f y^dx\ =
J х J х I
-оо e \
e[(p(— в) — ф(еI— f 2±p-d
«Ига f
E->0
где функционал, определенный в примере 2 § 3, п. 3.
4. Производная от обобщенной функции 6(х) есть функционал
действующий по формуле
F', ф) = F. — ср') = — ф'@).
Аналогично при любом q
F<?\ ф) = F, (— I)" ф<?> (х)) = (—1)" ф<?) @). D)
5. Функционал порядка сингулярности ^ р (§ 3, п. 3, пример 3):
слф)=£.
используя A) п. 2, можно представить в форме
ft=0 \ft=0
т. е. в виде суммы производных порядка ^р от обычных функций;
и обратно, всякая такая сумма, очевидно, есть функционал порядка
сингулярности

4] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 27
Задачи. 1. Найти производные от функций
*~ при х > О,
а) У = ■*+ = .
( 0 при х < 0. — 1 < X < 0;
f In х при л: > 0,
б) у = пл:+ \
' ' I 0 при л: < 0.
О/ие.
со
а) (У', Ч>) = J Кя*~' [Ф (х) - Ф @)] rfx;
о
со
б) (у'. <р) = / ^ [ч> (*) - ф @) е A - х)] л*
6
2. Доказать формулу
а (х) 6(ft) (л:) = 2 (— l)y+*Cj(a(ft--') @) 6(У) (а:)
для любой бесконечно дифференцируемой функции а(л:).
3. Найти q-va производную от функции xk+ (ft = 0, 1, 2, ...).
Отв.
при
г ' (а:) при q > ft.
4. Что представляет собою производная от канторовой функции С(х}
(непрерывной на отрезке [0, 1], возрастающей от 0 до 1 и принимающей
постоянное значение в каждом смежном интервале к канторовому множеству)?
Отв.
(С (х), <р) = 2 cj I6 (* — «/) — 6 (* — Р./)].
j
где Су — значение функции С {х) на смежном интервале (ay, Py).
5. Если
J
для всякой основной функции <р (а:), то / (х) ^ 0 (§ 3). Какие выводы отно-
относительно обычных функций /0(л:), ..., fm(x) можно сделать, если известно,
что для любой основной функции ф (л:)
J
: = 0?
Отв. fk (х) имеет производные до порядка ft (ft = 0, 1, .... т) и
/о М-/!<*>+ ••- +(-l)m/

28 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
§ 5. Обыкновенные дифференциальные уравнения
Операции, которые установлены для обобщенных функций—диф-
функций—дифференцирование, умножение на функцию, сложение,—позволяют
строить дифференциальные выражения вида
ao(x)ym-\-al(x)ym-1-\- ... -\rci
где а0 (х) ат (х) — заданные бесконечно дифференцируемые
функции, а у и Ь{х) — обобщенные функции. Приравнивая такое
выражение нулю, мы получаем обыкновенное линейное дифференци-
дифференциальное уравнение т-то порядка относительно обобщенной функции у.
Возникает вопрос о том, как описывается совокупность всех реше-
решений такого уравнения.
1. Рассмотрим сначала простейшее уравнение
/ = 0. A)
Покажем, что в классе всех обобщенных функций это уравне-
уравнение имеет своим общим решением у = С (постоянную).
Уравнение A) эквивалентно уравнению
(/. Ф) = (У. — ф') = 0 B)
для любой основной функции ср. Но тем самым функционал у уже
задан на совокупности Ко тех основных функций, которые могут
быть представлены как производные от других основных функций.
Нам необходимо выяснить, какими способами функционал у может
быть распространен с совокупности Ко на всё основное простран-
пространство К-
Легко проверить, что основная функция сро(х) может быть пред-
представлена как производная от некоторой основной функции тогда и
только тогда, когда выполняется условие
сю
f
dx = O. C)
Действительно, если <р0 (х) = <р| (х), то
сю
J
с другой стороны, при выполнении условия C) мы полагаем

, 5] ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 29
и остается только проверить, что q)j (х) есть основная функция; но
это очевидно, поскольку (pi(x) вместе с сро(х) бесконечно дифферен-
дифференцируема и, в силу условия C), финитна.
Пусть теперь cpi(x) — фиксированная основная функция, обла-
обладающая свойством
со
Г cpj (x)dx = \.
—со
Для любой основной функции ср(х) можно написать равенство
со
ср(х) —ср^х). J cp(x)djc = cpo(jc).
— oo
где функция %(х), очевидно, удовлетворяет условию C). Отсюда
видно, что если задать значение искомого функционала у на основной
функции ср^х). то значение его на любой функции ср будет опреде-
определено однозначно:
со
(У. Ф) = (У- <Pi) • / V(x)dx. D)
— OO
Пусть, например, (у, ср^ = С1 — произвольное фиксированное
число. Тогда равенство D) дает
со со
(у, ф) = С, J cp (x)dx= J Ctf(x)dx,
— со —oo
т. е. обобщенная функция у есть постоянная Си что и утверждалось.
Как следствие, мы получаем: если для двух обобщенных функ-
функций f и ф мы имеем f' = g'. то f и g отличаются на по-
постоянную.
Пусть, например, относительно некоторого функционала / известно,
что /'' — /'' (х) есть обычная функция; покажем, что тогда и / есть
обычная функция, притом абсолютно непрерывная и ее производная
(в обычном смысле) совпадает с /' (х). В самом деле, построим
неопределенный интеграл
Функция g(x) определена везде и абсолютно непрерывна; ее про-
производная в обычном смысле почти всюду совпадает с /' (х), ее про-
производная в К' также есть f (х). Отсюда / = g{x)-\-C, что и
утверждалось.

30 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ I
2. Рассмотрим теперь произвольную однородную систему р урав-
уравнений с р неизвестными функциями *)
Уо + ■ ■ • + ао, р-х (*) Ур-
(О
,_,,о(*)у+ +vWV I
где ат(х), ..., вр-i, p_i (Jf) — бесконечно дифференцируемые функ-
функции. У этой системы имеется некоторое количество обычных (притом
бесконечно дифференцируемых) решений; мы покажем, что Она
в пространстве К' не имеет иных решений, кроме обычных. Как
известно, классические решения образуют р-мерное линейное про-
пространство, базисом которого является любая система р линейно неза-
независимых решений. Записывая составляющие отдельных решений по
столбцам, мы получаем матрицу базисной системы классических
решений
|«оо(*) ■ ■• «о, p-iW II
Vi,oW -■ Vi,;-iW I
Детерминант этой матрицы (детерминант Вронского) отличен от нуля.
Если записать систему A) в форме
/ = Лу. B)
где у есть /7-мерный неизвестный вектор в пространстве К'.
а А = || ajk (x) ||—матрица коэффициентов, то любой из столбцов
матрицы U, как вектор, будет ее решением; этот факт можно запи-
записать матричным равенством
U'=AU. C)
Положим у = Uz, где z — новый неизвестный вектор (в про-
пространстве К'}- Подставляя в B) и используя C), получим
U'z + Uz' = AUz == U'z.
откуда
Uz' = 0.
Умножая на U~ , приходим к системе распавшихся уравнений
По доказанному в п. 1, z = const, откуда y = Uz есть вектор,
являющийся линейной комбинацией векторов фундаментальной системы;
тем самым у оказывается классическим решением
*) Целесообразность нумерации от 0 до р — 1 (а не от 1 до р) станет
ясной из дальнейшего.

. 3] ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 31
3. Рассмотрим простейшее неоднородное уравнение
g' = f. ^ A)
где / — данная обобщенная функция, a g — искомая.
Покажем, что уравнение A) при любой правой части f имеет
решение в классе обобщенных функций. Естественно называть это
решение первообразной или неопределенным интегралом от
обобщенной функции /.
Уравнение A) эквивалентно уравнению
(g. — ф') = (£'. Ф) = (Л Ф)
для любой основной функции ф. Но тем самым функционал g уже
задан на любой основной функции ф0. являющейся производной
от какой-либо другой основной функции ф, т. е. он задан на
многообразии Ко- рассмотренном в п. 1. Мы должны продолжить
функционал g на все пространство К- Это можно осуществить,
например, так: как и в п. I, рассмотрим основную функцию ср.,
со
для которой I q>1(x)dx=l. и с ее помощью представим любую
—сю
основную функцию ф в форме
GO
ф (X) = ф! (X) ■ j ф (X) dX -J- ф0 (X),
— со
где фо принадлежит Ко- Тем самым каждой основной функции ф мы
сопоставили ее «проекцию» ф0 на подпространство Ко-
При этом если последовательность функций ф,, ф2, ... стремится
к 0 в К, то и последовательность их проекций ф10, ф20. ... стре-
стремится к 0 в К, поскольку
оо
f %
Полагаем теперь для функции
(go- Ф) = (g- Фо) = (/• J Фо (Ddl) •
Легко проверить, что построенный функционал g0 линеен и непре-
непрерывен. Общее решение уравнения A) получается прибавлением к най-
найденному частному решению общего решения однородного уравнения,
т- е., согласно п. 1, произвольной константы.

32 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
Итак, все решения уравнения A) описываются формулой
где функционал g0 задвн формулой B).
Если при этом / = /(лг) есть обычная функция, то ее обычный
неопределенный интеграл F(x) уже есть решение уравнения A),
а общее решение неоднородного уравнения A) получается из найден-
найденного частного решения F(x) и общего решения однородного уравне-
уравнения g^ = 0; это последнее опять-таки состоит из постоянных, и мы
получаем в качестве общего решения A) выражение F(x)-^-C.
Мы видим, что в рассматриваемом случае, когда / — обычная функ-
функция, все решения уравнения A) в пространстве К'—классические
решения.
4. Отыскание общего решения неоднородной системы
У'о — «со (■*) Уо — ■ • • — ао, Р-\ (■*> Vi = U
(О
где fj — обобщенные, a Ujk (лг) — обычные бесконечно дифференци-
дифференцируемые функции, сводится к решению уравнений вида A) п. 3.
Действительно, если выполнить уже применявшуюся выше под-
подстановку у =£/2, где U — матрица фундаментальных решений соот-
соответствующей однородной системы (/у- = 0), то мы получим Uz' = /
или z = U~ /. В этой системе неизвестные «разделились»: каждое
ее уравнение имеет вид (I) п. 3.
Наконец, неоднородное уравнение высшего порядка
У<*> — в,_, (х) у<*-» — ... — а0(х) у = /, B)
где dj{x) — бесконечно дифференцируемые функции, а/—произ-
а/—произвольная обобщенная функция, сводится к системе вида A) при
помощи подстановки уо = у, у1 = у\ .... у^_1 = у</'-1>. Следова-
Следовательно, отыскание общего решения уравнения вида B) также сво-
сводится к решению уравнений вида A) п- 3.
Во всех этих случаях, если правые части — обычные функции,
все решения в пространстве К' также оказываются обычными функ-
функциями — классическими решениями.
Замечание. Уравнения с особенностями в коэффициентах могут
вести себя сложнее; они могут иметь больше линейно независимых
решений, чем порядок уравнения (см. задачу 1), или меньше, чем
порядок (см. задачу 2, где уравнение первого порядка вовсе не имеет
ненулевых решений в пространстве К')~

S 5] ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 33
б. Будем говорить, что обобщенная функция / равна нулю при
х < О, если для любой основной функции ф, равной 0 при х^-0
(и отличной от нуля, возможно, только при х < 0), мы имеем
(/, ф) = 0. Этим свойством обладает любая обычная функция, равная 0
(в обычном смысле) при х < 0; далее, этим свойством обладает,
например, б(х), а также и ее производные.
Л е м м а. Если f£K' равна нулю при х < 0, то у нее
имеется и притом единственная первообразная g£K', также
равная нулю при х < 0.
Доказательство. Единственность первообразной, равной нулю
при х < 0, вытекает из того, что две первообразные отличаются на
постоянную; если постоянная равна 0 при х < 0, то она равна 0 и
тождественно. В качестве искомой первообразной g0 можно взять ту,
которая определяется формулой B) п. 3:
(во- Ф) = ЙГ. Фо).
где
и' ф, (л:) равна 0 при х > 0. Если при этом ф (х) = 0 при х > 0,
то и фо(х) = О при х > 0, а также и первообразная от ()
равна 0 при х > 0; поэтому
ф) = te- %)= (/• Г Фо (Б) аи = о,
что и требуется.
Рассмотрим систему уравнений (в векторной записи)
y>-Ay = f, A)
где обобщенная вектор-функция / равна 0 при х < 0.
Покажем, что у этой системы имеется и притом единственное
решение у = у(х), равное 0 при х < 0.
Действительно, как и ранее, подстановка у = Uz приводит си-
систему A) к виду
z' = U'1f, B)
где U~l f также, очевидно, равна 0 при х < 0. Применяя лемму,
находим у системы B) решение z, все координаты которого равны
нулю при х < 0. Отсюда и y = Uz равно 0 при х < 0, что и утвер-
утверждалось.
3 Г. Е. Шилов

34 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
6. Для системы линейных уравнений первого порядка с обычными
функциями /0(х) fp-i(x).
—аоо
решение у(х) = [у0(х) Ур-iC*)} однозначно определяется за-
заданием начального вектора у(О)={уо(О), .... yp^i@)}. Возникает
вопрос, как поставить соответствующую задачу в классе обобщенных
вектор-функций К=[К0 ^p-ib учитывая, что значения в от-
отдельных точках для обобщенных функций не имеют смысла.
Если / = {/0 (х) /p-i (х)} есть обычная вектор-функция, то, по
доказанному, всякое решение у(х) есть также обычная вектор-функ-
вектор-функция. Обозначим через У (х) обобщенную вектор-функцию, равную О
при х < 0 и искомому (обычному) решению у (х) при х > 0, и через
Уг(х) — обобщенную вектор-функцию, равную 0 при х<0 и у'(х)
при х > 0. Систему (I) можно теперь записать в форме
Y1—AY = F, B)
где А есть матрица из коэффициентов djk(j, k=0, I р—1),
a F — обобщенная вектор-функция, равная 0 при х < 0 и /(х)
при х > 0.
Вектор^функция К, не является, вообще говоря, производной
вектор-функции У в пространстве К'- Имеет место равенство, вы-
вытекающее из формулы B) п. 3 § 4:
Отсюда для вектор-функции К в пространстве К' получается
система уравнений
Y' — AY=F+y@)b{x). D)
Общее решение системы D) может быть получено из имеющегося
частного решения К добавлением общего решения однородной системы
Y' — АУ = 0.
которое, по доказанному, является классическим. Решение У вы-
выделяется однозначно из общего решения с помощью дополнительного
условия
У = 0 при х < 0. E)
Для обобщенной функции К, как мы уже говорили, условие E)
означает следующее: для любой основной функции ср(х), отличной

§5]
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
35
от нуля, возможно, только при х < 0, имеет место равенство
(К, ср) = О.
Итак, мы приходим к следующему результату:
Пусть дана система уравнений
Y' — A Y = F (х) + jr(O) 6 (лг),
где F— обобщенная вектор-функция, равная нулю при х < О,
у@) — заданный вектор.
У этой системы имеется решение Y£K', притом единст-
единственное, которое обращается в нуль при х < 0.
Если F(x) — обычная вектор-функция, то это решение
соответствует обычному решению у(х) системы
обращающемуся в у @) при л: = 0.
Сформулируем теперь соответствующий результат для уравнения
р-го порядка
Вводя новые неизвестные функции
мы записываем уравнение F) в форме системы
■Уо — У\
У[
Р-1 ар
—}
с
с матрицей А специального
А =
0
0
0
во
ар
h
ЧУ2
ар
вида
— 1
0
0
в,
ар
0 .
—1 .
0 .
в2
ар
0,
= 0,
аР_,Ут f(x)
ар ар
.. 0
.. 0
.. —1
вр-1
пр
и свободным членом @, 0, .... —/С*)].
V ар I
G)

36 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
В обобщенных функциях системе G) отвечает система
Ко ~уг =Уо(О)й(*).
у[ —У2 = Л @N (ж).
в0 а1 ао-\
Эта система в свою очередь эквивалентна уравнению р-ro порядка,
которое получается. когда исключают неизвестные функции
К, Уp-v Именно, мы имеем
У1=У'О — у0 @N (х),
Y2=Y[ — yi @) 6 (х) =Г'о—Уо @) 6' (х) — у, @) 6 (х).
и, следовательно,
У'Р-1 = УоР) — Уо @) б^» (х) — у, @) 6^) (х)- ... -У/,_а @) 6' (х) =
- ... -Ур_2@N(х))+
или, что то же,
S *> l^- S УуЮ^-'Ч*)] = FW- (8)
ft=0 [ y=0 J
В силу доказанного, мы получаем следующее:
Теорема. У уравнения (8) имеется решение Y£К' и притом
единственное, которое обращается в нуль при х < 0. Если
f (x) — обычная функция, то указанное решение соответст-
соответствует обычному решению уравнения F), определенному при х >-0
и при х = 0 удовлетворяющему условиям у @) = yY @), ...
.... у(т-1)(О) = у1Я(О).
7. Пусть дан линейный дифференциальный оператор
я[у]=2>*у<*>. О)
й=0

^ 5] ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 37
В некоторых вопросах существенную роль играет фундаментальная
функция оператора Р. По определению, фундаментальная функция
jf(x) есть решение уравнения
2/ D B)
Разумеется, уравнением B) фундаментальная функция не определена
однозначно, а лишь с точностью до слагаемого, являющегося реше-
решением однородного уравнения
Se/»W = o. C)
ft = 0
Можно определить фундаментальную функцию однозначно, если
потребовать дополнительно, чтобы она обращалась в нуль при х < 0.
Как видно из последней формулы п. 6, в этом случае фундамен-
фундаментальная функция £f (x) соответствует обычной функции, равной 0
при х < 0 и равной тому решению уравнения C) при х >■ 0, кото-
которое отвечает начальным значениям
Уо@)= ••• =У„-2@) = °- 3V-i@) = -^.
Прибавляя к такой обычной функции любое решение уравне-
уравнения C) на всей оси, получаем описание всех фундаментальных функ-
функций оператора A): всякая фундаментальная функция с? (х) есть
обычное решение уравнения C) при х < 0 и обычное решение
уравнения C) при х > 0, причем
Уо (+0) = Уо (-0) УР-2 (+0) =
Задачи. 1. Для уравнения g-го порядка
xky(Q) (j,-) = 0
построить ft+ 9 линейно независимых решений в пространстве К'-
Отв. При 1 2
2. Показать, что уравнение
— 2*3у' = у A)
не имеет ненулевого решения в пространстве К'.
Указание. Классическое решение уравнения A) есть .
Показать! что в пространстве К' на функцию ф (а:), равную 0 в ок-
окрестности точки х = 0, решение должно было бы действовать по

38 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
формуле
(У, <Р)= fCex\(x)dx.
— оо
Использовать задачу 5 к § 3.
3. Доказать, что уравнение
разрешимо при любой обобщенной функции /£(
Указание. Использовать метод п. 3. Основная функция ifi (х) может
быть представлена в форме (х<р)', у£К, тогда и только тогда, когда
fq(x)dx=0, (
4. Сформулировать в обобщенных функциях аналог классической гра-
граничной задачи
У («) = У а. У (Ь) = Уь
для уравнения
Отв. + Уа()уь() + уа(
+ [Y' + ya6(x — a) — ybb(x—b)] + q(x)V = F(x), где F(x) равна О
при х(£[а, Ь] и равна /(х) при х£[а, Ь\, а постоянные уа и уь опреде-
определяются из условий Y {х) = 0 вне отрезка [а, Ь].
§ 6. Основные и обобщенные функции
нескольких переменных
I. Определения предыдущих параграфов переносятся на случай
нескольких переменных без особых затруднений.
Обычные, основные и обобщенные функции будут определены
в «-мерном вещественном пространстве /?„, состоящем из точек
а: = (jCj х„). Обычная функция, по определению, есть функ-
функция, определенная почти везде в Rn и интегрируема (по Лебегу)
в каждом ограниченном брусе В= {х : al^^b ^^
<}
Каждая основная функция бесконечно дифференцируема и обра-
обращается в нуль вне достаточно большого бруса.
Брус или вообще любое множество, вне которого основная функ-
функция ф(х) равна нулю со всеми производными, называется носите-
носителем ф(лг) и обозначается через suppcp.
Линейное пространство всех основных функций в Rn обозначается
через К (или. К (/?„). или Кп, когда есть необходимость указать
число п). Последовательность q>v(x)£K, v=l, 2, ... называется

§ 6] ОБОБЩЕННЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 39
сходящейся к 0 в К, если все функции cpv (х) обращаются в нуль
вне одного и того же бруса и равномерно сходятся к 0, так же
как и их производные любого порядка.
Обобщенной функцией называется любой линейный непрерывный
функционал на пространстве К- Совокупность всех обобщенных
функций обозначается через К' (или К' (Rn), или /Сл)- Каждая обычная
функция f (х) определяет функционал на К по формуле
(/(х). ф(ж))= ff(x)<p(x)dx; A)
функционалы такого вида называются регулярными.
Как и в случае и=1, обычная функция f (x) определяется
по числам (/, ф) однозначно.
Достаточно показать, что из (/, ф) = 0 для любой (f^K вытекает, что
f (х) почти всюду равна нулю. Мы доказали это в § 3 для случая и = 1,
в общем случае докажем по индукции. В качестве основной функции ф (х)
возьмем произведение Ф1 (•*,) и ф„_1 {х2, .... хп_1), где ф[ и ф„_!—основ-
ф„_!—основные функции соответственно от одного и п — 1 независимых переменных.
По теореме Фубини
ICO
J/(*i хп) Ф1 (*i) dxl X
-со
причем внутренний интеграл представляет собою суммируемую функцию от
хг х„ на п — 1-мерном брусе, в котором сосредоточена функция фп-1-
Так как фл_1 — произвольная основная функция, то, по предположению
индукции,
со
I /0*i хп) (fi{xi)dx{ =0 B)
— со
на множестве Q полной меры значений хг, ..., хп.
Далее, фиксируя точку (хг, ..., xn)£Q, следовало бы применить резуль-
результат § 3, который и привел бы к выводу, что функция f (хи ..., хп) равна
нулю на множестве полной меры в Rn. Но положение осложнено тем, что
множество Q в данном случае может зависеть и от самой функции ф] (х{).
Поэтому для завершения доказательства мы воспользуемся фактом, заме-
замеченным в § 3; в одномерном случае достаточно выполнения равенства
иа некотором счетном множестве функций q> (x), чтобы сделать вывод о том,
что / (х) = 0 почти везде. Мы и возьмем в B) только это счетное

40 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. 1
множество функций. Для каждой из них найдется множество Q = Q (<р) полной
меры, где выполняется равенство B); для всех этих функций сразу равен-
равенство B) будет выполняться на пересечении указанных множеств полной
меры, которое также есть множество полной меры. А теперь в точках этого
последнего множества можно уже пользоваться результатом § 3, который
и приводит к выводу, что /(л:,,..., х„) почти всюду в Яп равна нулю.
Таким образом, совокупность обычных функций вложена в про-
пространство К' взаимно однозначным образом.
2. Кроме регулярных функционалов существуют еще и сингу-
сингулярные, которые не приводятся к виду A).
Вот несколько примеров обобщенных функций в /?„, не сводящихся,
вообще говоря, к обычным функциям:
1. Дельта-функция 6(х), действующая по формуле
или, более общим образом, сдвинутая дельта-функция, действую-
действующая по формуле
— а),
2. Функционал порядка сингулярности ^ р, по определению,
имеет вид
. Ф)= >J / А (*)Я*Ф (*)<**■ B)
где k — составной индекс: k = (k kn), D" =
т ъ—,
все fk(x)—обычные функции и суммирование проходит по индексам k,
для которых |£| = fti+ ••• -\-kn^.p.
Говорят, что порядок сингулярности функционала / равен ровно р.
если функционал / может быть записан в форме B) с данным р
и не может быть записан в такой форме с меньшим р.
Ниже будет показано, что функционал 6(лг), как и в случае я= 1.
имеет порядок сингулярности 1.
3. Функционал, сосредоточенный на поверхности L:
if- ф)= //(*)Ф(*)<«,.
где dlx — элемент поверхности L в точке х; более общим функ-
функционалом такого вида является, например,
га
С/. Ф)= J V/ft (*)Д*Ф (*)<«*■
причем fk{x) — обычные функции на поверхности L.

„ й ОБОБЩЕННЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 41
4. Обобщенные функции от аргумента (со, х).
Пусть (» = ((»! соп)— точка единичной сферы Q простран-
пространства /?,г* Поставим в соответствие каждой основной функции
i хп) функцию
Интеграл справа берется по гиперплоскости, ортогональной к вектору со
и находящейся на расстоянии (со знаком) £ от начала координат.
Если совершить поворот осей Ux = x'', при котором вектор со
перейдет в первый базисный вектор A, 0. .... 0), то можно написать
. *>) = / Ф1 «. *2 Х'„) dX2-'- dX'n'
где 1 р
Очевидно, что функция Ф(£; со) финитна вместе с ф(дг) и бесконечно
дифференцируема по £ при каждом фиксированном со. Таким обра-
образом, Ф (|; со) — основная функция (аргумента |). Каждой обобщенной
функции f £К\ мы можем теперь сопоставить функционал /ш ^ Кп>
зависящий от параметра со, по формуле
(/«.Ф(*1 л:„)) = (/. Ф(&;со)). A)
В частности,
! = F(£), Ф(£; co)) = Г ф (*)£?* =
(О), jt)=0
= Г ф^О, х' х'\dx'.. dx'\
= ir-Yf J —l-
К)
dx'2...dx'n.
4
Функционал /m мы будем обозначать также через /((со, х)).
3. Можно рассмотреть основные и обобщенные функции не во
всем пространстве Rn, а в некоторой области GcRn. Именно, про-
пространство К (О), по определению, образовано из всех основных функ-
функций ф (л:) £ К (Л„), которые сосредоточены строго внутри области О
(т. е. так, что замыкание множества [х : ф(л:)=£ 0} лежит внутри О).
Последовательность <pv(x)£K(G) называется сходящейся к нулю
в K(G), если все функции (pv(x) сосредоточены в одном и том же

42 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
множестве, находящемся строго внутри О. и при v->oo равномерно
сходятся к нулю со всеми производными. Линейный непрерывный
функционал на пространстве K(G) называется обобщенной функ-
функцией в области G. Большая часть результатов этого и следующих
параграфов непосредственно переносится на случай обобщенных функ-
функций в области.
Задачи. I. Обычная функция / (л:) называется сферически симмет-
симметричной, если /(Ux)—f (х), где U—любой поворот пространства /?„. Дать
определение обобщенной сферически симметричной функции.
Отв. (/, ф (Ux)) = (/, ф (х) ) для любой ф (х) £ К.
2. Сферически симметричная обобщенная функция / однозначно опре-
определяется на всем К по своим значениям на сферически симметричных основ-
основных функциях.
Указание. Для любой ф £ К сферическое среднее фср (л:) есть также
функция из К. которая является пределом средних арифметических поворо-
поворотов функции ф. Отсюда (/, ф) = (/. фср).
3. Обычная функция /(х) называется однородной степени р, если для
любого положительного t имеет место равенство / (tx) = tpf (x). Дать опре-
определение обобщенной однородной функции степени р.
Отв. (/. ф (tx) ) = t~P-tt (/, <р(х)) для любой <р£К.
4. Показать, что дельта-функция 6 (л:) однородна, и найти степень одно-
однородности.
Отв. р = — п.
5. Показать, что функционал, сосредоточенный на поверхности (при-
(пример 3), сингулярен.
Указание. Произвести построение, обобщающее доказательство син-
сингулярности дельта-функции из § 3,
6. Задача о регуляризации. Пусть / (х, хп) — функция, локально
интегрируемая всюду, кроме точки jc = O, а в окрестности этой точки удо-
удовлетворяющая неравенству
I/WK7H--
Показать, что существует функционал /£К'- который на все основные функ-
функции, равные 0 в окрестности точки л: = 0, действует по формуле
(/.ф)= ff(x)<f(x)dx.
Указание. Например.
г х х"п I ]
l\k\<m J J
где | k | = kx + ... + kn, h(x) равна 1 при |x|< 1 и 0 при | x\ > 1.
7. Показать, что для функции f (x), допускающей в некотором положи-
положительном телесном угле при любом »я = 0, 1. 2, ... оценку
задача 6 неразрешима (функция f (х) «не допускает регуляризации» в К')-
Указание. Обобщить конструкцию решения задачи 5 § 3.

. я ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 43
§ 7. Действия с обобщенными функциями
нескольких переменных
1. Мы можем здесь ограничиться простым перечислением этих
действий, имея в виду, что все, сказанное в § 4 в применении к слу-
чаЮ д=1, непосредственно переносится и на общий случай.
Итак, мы определяем следующие действия с обобщенными функ-
функциями:
1. Сложение и умножение на вещественные числа:
2, Ф) = а1(/,
2. Умножение на бесконечно дифференцируемую функцию а(х):
(а(*)/. Ф) = (/. а(*)«р).
3- Дифференцирование (по любой из координат):
(£■')—('•£)• о
Если f = f{x) есть обычная функция, абсолютно непрерывная
по х1 почти при всех х2. .... хп, с производной -J— в обычном
смысле (обычной функцией от xv x2 хп), то производная по х1
от функционала / в смысле обобщенных функций приводит к обыч-
обычной производной -^—.
Итерируя, получаем определение производной порядка \k\ =
*i+ ••• +*
( dX"'7h k'
2. Далее приводится несколько примеров на дифференцирование.
1. Для любой обобщенной функции /
dXj дхк dxk dxj '
иначе говоря, порядок дифференцирования по различным переменным
можно менять.
Для доказательства заметим, что аналогичное свойство в приме-
применении к основным функциям заведомо выполняется; поэтому
/ dff \_(f д2Ф \_(е d2g> \_( d*f \
[dxjdXb-Vj — V' dxjdxJ — V' dxkdxj)-{dxkdxj'4)'
что и требуется.

44 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. I
2. Производные в смысле С. Л. Соболева. Согласно С. Л. Собо-
Соболеву, (обычная) функция g {хх хп) есть обобщенная производ-
d*i+ ■■•+*«
ная вида —г г- от (обычной) функции fix, х„) в обла-
f)x l fix п
сти О, если для любой (бесконечно) дифференцируемой функции
Ф (JCp .... л:,,), сосредоточенной строго внутри области О, имеет
место равенство
(-О'* 'fg(*)Ф(*) dx = f f (x)Dftcp(x)их. A)
о о
Покажем, что g = Dkf в пространстве К'- Действительно, опреде-
определение A) можно записать в форме
(-!)'*'(«■. Ф) = (/. £>*Ф). B)
В то же время, согласно определению производной в К', мы имеем
(D"f, Ф) = (-l)ft(/, Ойф). C)
Сравнивая B) и C), находим, что g = Dkf, что и требовалось.
Таким образом, наличие у функции / некоторой производной по
Соболеву показывает, что эта производная функции / в К' приво-
приводится к обычной функции.
3. Пусть 8 = 8(л:1, .... х„) означает функцию, равную 1, когда
все координаты х1 хп положительны, и 0 в противном случае.
Найдем -з г—. Мы имеем
дх, ... дхп
со схэ
/ f
о о
откуда
4. Дифференцирование обобщенной функции /((w, x)) (§ 6, п. 2,
пример 4). Покажем, что обычная формула дифференцирования
df ((со. х)) ._ rf/ ((<о. х))
^ = d(ffl.jc) '&1 A)
применима и к случаю, когда / есть обобщенная функция. Для этого
выведем сначала формулу
/ -Щ** = Ъ-Щ f Vix)dx. B)
(to, jc)=6 (a, X)=E

g 7] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 45
справедливую для любой основной функции ср(лг)- Мы имеем
^[ f <p{x)dx- f
f
(tu, JC)=E
= ~k J №(ЛГ+иА^~ q>{x)]dx
Г С dm
(и, jc)=E la, jc)=E (a, x)=i
Разложим базисный вектор ej на составляющие по вектору со и
по вектору 6, лежащему в плоскости (со, jc) = |. При этом
Отсюда
(to, jt)=S la, jr)=J (a, j:)=£
£ (
(a, jc)=|
поскольку интеграл от -^-, очевидно, равен 0; итак, формула B)
доказана.
Переходим к выводу формулы A).
Мы имеем в этом случае
(/((со, х)), <р(*)) = (/(£). Ф(&; со)),
где Ф(|; со)== Г ф(д;)с?д;; отсюда, по основному правилу,
(a,jr)=6 .
\ (о, л:)=Е
с другой стороны,
и остается сослаться на формулу B).

46
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ
[ГЛ. I
5. Функционал порядка сингулярности
. Ф)= S /fk{x)D\{x)dx
есть сумма производных порядка
от обычных функций:
IftKp
= AйЕр(-1)ло*/*.Ф
Очевидно и обратное: обобщенная
функция, равная сумме производных
порядка <С/7 от обычных функций,
имеет порядок сингулярности -^ р.
Пример 3 показывает, что Ь(х)
имеет порядок сингулярности -^ п.
В действительности, как мы увидим
ниже, порядок сингулярности б(л:)
равен 1.
6. Найдем производную по xt от обычной функции f(x), непре-
непрерывной и имеющей непрерывные производные в замкнутой области О
с кусочно гладкой границей Г (рис. 4), а вне этой области равной 0.
По формуле A) п. 1
Рис. 4. Cj — проекция G на пло-
плоскость (х2 х„). п — нормаль-
нормальный вектор.
Мы видим, что искомая производная есть сумма двух функцио-
функционалов, первый из которых есть обычная функция, равная ~— в О
ОХ |
и 0 вне О, а второй—сингулярная функция, сосредоточенная на
поверхности Г. Это равенство является обобщением на «-мерный
случай формулы C) § 4, п. 3.

j 7] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 47
7. Классическая формула Грина (Д — оператор Лапласа, О — огра-
ограниченная область, Г — ее граница, -^ производная по внешней
нормали)
' /(*) ДФ(*)dx = f Д/(*).Mx)dx+f(f&-& Ф)
6 t
dl
с учетом равенства (Д/, ф) = (/, Дф) может быть источкована сле-
следующим образом: пусть f(x) есть обычная функция, имеющая в замк-
замкнутой области О непрерывные производные до второго порядка
(в обычном смысле), а вне О равная нулю; в пространстве К' опе-
оператор Лапласа переводит ее в сумму двух функционалов, один из
которых есть обычная функция, равная Д/(дг) (в обычном смысле)
внутри О, и нулю вне О, второй — сингулярный функционал, сосре-
сосредоточенный на границе Г области О.
Если написать аналогичное равенство для функции f (х), равной
нулю внутри О, и сложить с предыдущим, мы получим
*я
где fi и fe означают предельные значения функции f(x) соответ-
соответственно изнутри и снаружи области О; таким образом, функцио-
функционал Д/ выражается через обычную функцию Д/ и скачки / и —-
на границе области О.
8. Оператор Лапласа и сферически симметричные функции.
Найдем классическое выражение оператора Лапласа для дважды
дифференцируемой функции /(г) (зависящей только от радиуса). Мы
имеем
г
v2 .-2 „2
= /"(/-) 7Г+/40
)

48 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. II
Положим / (г) = гр; тогда мы получим
Агр = р(.р-\-п — 2) гр-К B)
Таким образом, оператор Лапласа понижает степень г на две еди-
единицы. Все это вычисление остается справедливым и в смысле диф-
дифференцирования в пространстве К', пока речь идет об обычных функ-
функциях. Так как функция гр интегрируема в окрестности начала коор-
координат при р > — п, то формула B) сохраняет смысл в К' при
р — 2> — п, /7>2 — п. Если же р = 2 — п, то при п > 2 правая
часть B) теряет смысл в К'- Известно, что г2~"— гармоническая
функция вне начала координат, т. е. Дг2~" = 0 при х Ф 0. Вычислим
выражение Аг2~п в пространстве К', считая п > 2.
Согласно определению,
К полученному интегралу применим формулу Грина (пример 7),
беря в качестве области О шаровой слой e<J><^a. где а настолько
велико, что вне шара г <^ а функция ф (л:) тождественно равна нулю.
Мы получим
г rn~l J дг г"
причем dl есть элемент сферы г—г. Мы имеем, далее,
/1
Г> Е
так как п2 вне шара г < е есть гармоническая функция;
г г11 е" l
т—е. г=е
где О„ есть поверхность единичной сферы в Rn, а 5Е [ф] — среднее
значение функции <${х) на сфере радиуса е. В пределе при е->0

§ 7] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 49
мы находим Se [ф]-> ф @), и следовательно.
-ТТ- ф)=Нт f -grrf* = —(n —2)О„Ф@) =
д г
Отсюда
Д-^_-г = -(/г-2H„б(д;). C)
В частности, при п — 3 мы имеем Qn = 4я и, следовательно,
д1 = — 4л6(лг).
Замечание. Полученный результат, в частности, показывает,
что порядок сингулярности обобщенной функции Ь{хх хп)
равен 1 независимо от числа п. Действительно, функция п_2 и ее
первые производные суть обычные функции и по доказанному
так что б(д;) есть сумма первых производных обычных функций.
9. Пусть дан линейный дифференциальный оператор P\~s-)^
= P[-g— -^—J, Обобщенная функция ^(х), удовлетворяю-
удовлетворяющая соотношению
щая соотношению
называется фундаментальной функцией оператора Pyg-)• На-
Например, функция
1 1__
(п-2)п„ гп~2
является фундаментальной функцией для оператора Лапласа Д при
л > 2 (пример 8).
Вообще говоря, фундаментальная функция ^"(л:) определяется не
однозначно, а с точностью до слагаемого и (х), являющегося реше-
решением уравнения
4 Г. Е. Шилов

50 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
Найдем фундаментальную функцию ^т (х) для итерированного
оператора Лапласа Дт в и-мерном пространстве. Если известна функ-
функция <И1<т~1), то функцию ^т можно найти, решая уравнение
Ввиду сферической симметрии оператора Лапласа естественно искать
%**пт в форме функции от г = Yx\ + • • • + х\ '> ПРИ этом можно
использовать формулу A) из примера 8:
Решение уравнения
B)
можно получить в общем виде, сведя заменой f'{r) = g{r) уравне-
уравнение B) к уравнению 1-го порядка. Решение имеет вид
Если h{r)=r\ кф—2, Хф—п, то
гК+2
что следует и из формулы B) примера 8). Если h(r)— г~2, то
/@1пг:
таким образом, в качестве фундаментальных функций у нас появятся
и логарифмические. Рассмотрим еще случай h(r) = rl\nr, кф—2,
к Ф ■— и; при этом
r).+n
rh+2\nr гк+2 ._ч
(о)
Формул C) — E) достаточно, чтобы найти искомые фундаментальные
функции. Нам известна функция g^ = cnr2~". Решая уравнения A)
при wi=2 (А, = 2 — п) и используя формулу C), находим
4 Г4'"
'" — С" 2D —и)

, 71 ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 51
Далее, аналогично
С каждым шагом показатель у г увеличивается на две единицы и соот-
соответствующие множители появляются в знаменателе. Если п нечетное,
т0 показатель 2 т— п никогда не становится равным —2, поэтому
при нечетном п для любого т справедлива формула
,2m-n
&n -c«2.4...Bm-2)Bm-n)...D-n)~C"'2'» • (J)
Если п четное, то формула F) справедлива лишь для небольших т,
именно, для 2т^и— 2. Если 2т~^-п, то последовательные пока-
показатели 2 — и, 4— п, ... на некотором шаге дойдут до значения —2.
после чего, согласно формулам D) и E), появятся функции, связан-
связанные с логарифмами:
е?п =сп,п-2г •
9 Сп п 2 Г2т~"\ПГ
6 п ——Z о"~ о /о™ «\ /« i О\ /о о\ ип*2т
П £. Z . . . У/.ТП П) • П \Т1 -\- £.)... \£.ТП Z) *
Слагаемые, содержащие степени г2 до r2m~2, здесь отброшены, так
как оператор Лапласа Дт переводит их в нуль. Итак, при п > 2 мы
получаем формулы
сп, 2т г2т~ "• если п нечетно, или п четно
и больше чем 2т; G)
ftn2mr2m-nln г, если п четно, п-^.2т.
При п — 2 легко проверить непосредственно, так же как и в при-
примере 8, что ei = — 2л In r; таким образом, формула G) сохраняется
для к = 2, т=\. Но тогда она сохраняется и для всех в^Г. по-
поскольку они выражаются указанным способом через е^2- Таким об-
образом, формулы G) справедливы и для и = 2.
3. Если f£Kr есть постоянная, то, очевидно, -^- = 0 при лю-
бом 7=1, .... п- Покажем, что верно и обратное.
Теорема 1. Из условий f £К''. -J—m — 0 для всех J, 1 <Гу-^и,
вытекает, что f есть постоянная.
Предварительно докажем две простые леммы.
4*

52 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
Лемма 1. Всякая основная функция ср (х1 хп) может
быть представлена как предел в пространстве К линейных
комбинаций основных функций вида ^>i{x{) ... ф„ (л;п), где
(Pj(Xj) — основная функция от'одного переменного.
Для доказательства, имея брус В= {х : | Xj |^£ aj}, внутри кото-
которого сосредоточена функция <р(х), найдем, пользуясь теоремой Вейер-
штрасса, при каждом v=l, 2, ... многочлен Pv^ xn), ко-
который в брусе В'=[х :\Xj\^2aj] отличается от ф(лг) меньше чем
на — вместе с производными до порядка v. Пусть, далее, е (хЛ —
основная функция, равная 1 при | Xj \ <^ й;- и 0 при | xf | ^> 2с Л
Тогда при v->oo функции Рч(х)е{х{) ... е(хп) стремятся к функ-
функции ф(л:) в пространстве К, что нам и требуется.
Лемма 2. Если -^-=0, то для любой основной функции
вида a (xj р (х2, .... л:,,)
со
a(x1)dxv
где щ (хг) произвольно фиксированная основная функция
Доказательство. Имея щ (хх), мы можем написать предста-
представление
ОО
где Г a0 (xl)dx1 = 0. Поэтому можно написать ао(хх) = уг (хх), где
— со
у(хг) — новая основная функция (§ 5, п. 1).
Отсюда
(/. of) = ( /■ U fa (Xl) dxx + у' p j = (/, ajj) f a (xj dxx +
(
/, f
поскольку
(f. v'P) = (/• i; OP)) = - (J^. M») = o;
лемма доказана.

j 7] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 53
Переходим к доказательству теоремы 1. Рассмотрим основную
функцию вида а (х{) E (х2) ... со (хп). Последовательно применяя
лемму 2, находим
СО
(/, ар ... со) = (/, аф ... со) • J а (хг) dx1 =
= (/, а^! ... со)
со
а (д:!)^! J p (x2) dx2 ...
—со — со
= J Сар ... u>dxr
где С = (/, OjPj ... «!). Таким образом, на функциях вида ар ... со
функционал / сводится к постоянной С. Для завершения доказатель-
доказательства достаточно воспользоваться леммой 1 и непрерывностью функ-
функционала /.
4. Теорема 2. Обобщенная функция /, у которой все
оизводные -^— = g}
представлена в виде
производные -^— = g} — непрерывные функции, может быть-
о
Хг
a(*i. h- 0
о
о
м является сама непрерывной и дифференцируемой функцией
с частными производными -J— = g, в обычном смысле.
Заметим, что функции g1 gn сами не предполагаются диф-
дифференцируемыми в обычном смысле. Тем не менее, если рассмотреть-

54 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
их производные в К', мы будем иметь при любых I и k
^LL = ^lL, B)
dxk dxj w
d2f d-'f
в силу равенства смешанных производных -т—^— и -^—^— .
Для доказательства теоремы рассмотрим функцию
п
• • • + J gn (xv x2
о
Мы покажем, что выполняются условия
dF дР
5'е
откуда следует по теореме 1, что функции F и / различаются на
постоянную:
C)
Полагая здесь д;==0, находим С = /@) и C) превращается в основ-
основную формулу A).
Выполнение равенства -т— —gn очевидно. Докажем, что
охп
■^ = ^-1' Для этого мы должны показать, что
ХП I
/ ёп (*l *я-1. U d£« = ffn-l (*l *„)•
о
или. что то же
-^5 g"n-i00 = — gn-i(xi хп~\' 0). D)
"хп— 1
где
хп
о
Дифференцировать интеграл E) формально (под знаком интеграла)
нельзя, так как функция gn может не иметь обычной производной

§ 7] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 55
по хп_х- Проверим вначале, что выражение слева в D) не зависит
от хп- Действительно, в силу условий B),
с) I dfn
oXn-xOXn dxn_x dxn_Y \dxn Sn) K/
поскольку последняя скобка, очевидно, равна нулю.
Теперь вычислим левую часть D). Возьмем основную функцию
ф(лг) в форме а(х1 xn-i) PC*n)- где а ИР — основные функции
своих аргументов. Согласно лемме 2 п. 3, можно написать
С другой стороны,
-1 [ J
и, следовательно,
С(а) = -
Так как С (а) не зависит от хп. можно положить хп = 0. Тогда
/„ (дГр .... xn_v 0) = 0, и мы получаем
С(а) = — / gn-i(xi xn-v 0)a(x)dx1 ... dxn_v
i ••• dxn.
Поскольку аир произвольны, мы получаем D).
Совершенно аналогично
±-\Г
ХП-2 \J g"~
Т х х |_
J I п~
0).

56 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ 11
Равенство G) позволит вычислить -т . Именно,
ОХ2
dF <j i / _ t n
* * 9/1 ~~2*
Г*П-2
— =Ж—\ Г g»-2(*l
П-2 0ХП-2 [_-'
ХП-\
+ J gn-l(Xl
0
хп
/ gnixl Хп-1- ln)
х
о
dF
■и т. д.; в результате равенства -^-—==gj оказываются доказанными
для любого у. что и требуется.
Итак, представление A) для функции / (х) получено. Из него
видно, что f(x) — непрерывная функция и -^~= g в обычном
охп
смысле. Но так как выбор порядка осей произволен, то равенство
A) справедливо и при любой иной последовательности координатных
осей; а тогда, выводя на последнее место у'-ю координату, получаем,
что и -J— =^ в обычном смысле.
Задачи. I. Найти &гк, где — п < Л < — п + 2.
Отв. (Дг\ ф) = 21 (К + п — 2) п„ J rK~2 [Sr (<р) — <р @)] dr. где Sr (<p)
о
есть среднее от функции <р (х) по сфере радиуса г с центром в начале коор-
координат.
2. Доказать, что уравнение , = g разрешимо для любой обобщенной
ОХ\
функции g(xt хп).
Указание. Функционал / определен однозначно на всякой функции
«Ро^/С. являющейся производной по xt. от некоторой основной функции 1|з.
Для любой основной функции ф можно написать
,. Х2 Xn)dl{+(f0(X Х„).
где ф! {ху) — фиксированная основная функция с интегралом 1. а на <р0 функ-

7] ДЕЙСТВИЯ С ОБОБЩЕННЫМИ ФУНКЦИЯМИ 67
ционал / известен по сказанному выше. Формула
(/о- Ф) = (#. *)■ где ^ = Фо>
дает одно из решений.
3. Доказать, что система уравнений ~- = gj (j=\ п) разрешима
при любых функционалах gj, удовлетворяющих условиям совместности
дхк ~~ dXj
Указание. Решение уравнения ~— = g{ можно взять в форме /0 +■
/n-i- r^e /n-i—любой функционал, не зависящий от хх. Второе уравне-
уравнение -^— — g2 теперь приводится к виду
dfn-x _f 0/0
дх2 дх2 '
При этом правая часть не зависит от xt. в силу условия совместности^
Можно найти решение в форме
/п-1 = fn-l "Т" /л-2>
где /п-2 — любой функционал, не зависящий от хх и х2, и т. д.
4. Доказать, что система уравнений в К'3
f0t
дх2 дх3
совместна, если div/?^0 и. например, D и R финитны.
5. Рассмотрим нелинейное уравнение с двумя переменными
ди , дФ(ц) _„
dt ~г дх ~Vl
где Ф (и) — заданная дифференцируемая функция. Будем рассматривать те ре-
решения и — и(х, t) этого уравнения в К', которые представляют собою обычные
кусочно непрерывные функции. Показать, что на линии разрыва решения вы-
выполняется соотношение
dx
и+—и
где м+ и и~ — предельные значения функции и справа и слева от точки
разрыва.
Указание. Использовать выражение производной кусочно гладкой
функции (пример 6).

58 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. I
6. Показать, что производная по Xj однородной обобщенной функции /
степени р есть обобщенная однородная функция степени р — 1 (§6, задача 3).
7. Показать, что однородные обобщенные функции различной степени
линейно независимы.
8. Найти фундаментальную функцию для оператора Д + к2 (к — постоян-
постоянная) в трехмерном пространстве.
Указание. Искомую функцию взять в форме / (г), использовать
выражение оператора Лапласа A) из примера 8 и найти классические решения
уравнения
f'
Применяя метод примера 8, найти Д/(г) в смысле обобщенных функций.
Отв. % (х) = или
е
-ikr
г г
9. Будем говорить, что обобщенная функция f ^К' стремится к 0 при
}л:|-*оо, если для любой основной функции (К)
lim (/, <р(* + й))=О. A)
|Й|->оо
Очевидно, что если f = f (х) есть обычная функция, стремящаяся к 0 на
бесконечности в обычном смысле, то определение A) выполняется. Опреде-
Определение A) может выполняться и для обычной функции f (х). не стремящейся
к 0 на бесконечности в обычном смысле Iпример: /(.*) = —j )■
Показать, что если / = /(.*) есть многочлен и выполнено условие A),
то f{x) ^0.
Указание. Если / (х) есть многочлен, то выражение (/. <р (х -\- Н))
есть многочлен от А.
Примечание. Теорема остается справедливой и в предположении
что / (л:) есть целая аналитическая функция порядка роста < I.

ГЛАВА II
СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ
ОБОБЩЕННЫХ ФУНКЦИЙ
От первоначального знакомства с обобщенными функциями, ко-
которому мы посвятили главу 1, мы должны перейти к более глубо-
глубокому и систематическому изучению их свойств, с тем, чтобы иметь
возможность активно применять обобщенные функции в проблемах
анализа и дифференциальных уравнений.
В ближайших параграфах мы получим выражения обобщенных
функций через производные от обычных функций. Мы введем и
изучим две новые операции — свертку и преобразование Фурье.
Весьма важную роль будут играть специальные обобщенные функ-
функции х^ и другие.
§ 8. Локальные свойства и носитель обобщенной функции
1. Мы знаем, что для обобщенных функций нет смысла говорить
о значениях в отдельных точках. Но высказыванию «обобщенная
функция / равна нулю в области О» можно придать вполне четкий
смысл: оно означает, что какую бы основную функцию, сосредо-
сосредоточенную строго внутри *) области О, мы ни взяли, всегда будет
(J, ф) = 0. Так, б(х1 лгп) равна нулю вне начала координат,
функционал, сосредоточенный на поверхности (§ 6, п. 2, пример 3),
равен нулю вне этой поверхности и т. д. Если / = /(#)— обычная
функция, то условие «/ равна 0 в области О» означает, что в обла-
области О почти всюду функция f(x) равна 0 в обычном смысле.
Далее, если h (x) — бесконечно дифференцируемая функция, рав-
равная 0 в области О, то для любой обобщенной функции / произ-
произведение hf есть обобщенная функция, равная нулю в О, действи-
действительно, если ф £ К сосредоточена строго внутри О, то
(Л/, Ф) = (/. ЛФ) = 0,
так как функция Л(д:)ф(д:) тождественно равна 0.
*) То есть так, что замыкание множества {л:: <р (л:) Ф 0} лежит внутри
области G.

60 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. II
Если обобщенная функция / равна нулю в области G. то допол-
дополнительное множество Rn — G называется носителем f и обозна-
обозначается supp/. Говорят также, что обобщенная функция / сосредо-
сосредоточена на множестве Rn — G. Так, у Ь(хх д:„) носителем
служит одна точка — начало координат; в этой точке и сосредото-
сосредоточена 6 (л;). Обобщенная функция с ограниченным носителем назы-
называется финитной.
Если основная функция (р(х) обращается в 0 на носителе
функционала /ив некоторой его окрестности, то (/, ф):=0,
поскольку в рассматриваемом случае ф сосредоточена строго внутри
области, где / равен нулю. Отсюда следует, что произвольное
изменение основной функции ф вне окрестности носителя
обобщенной функции f не влияет на значение величины (/, ф);
действительно, указанное изменение равносильно добавлению к основ-
основной функции ф другой основной функции я|), равной нулю в окрест-
окрестности носителя функционала /. поэтому (/, я|)) = 0, а следовательно,
С/, ф+*) = (/• ф)-
Пользуясь последним обстоятельством, мы можем в некоторых
случаях расширять область определения функционала /, включив
в нее кроме основных любую функцию ф(л;), совпадающую с какой-
либо основной функцией ф(л;) в окрестности носителя /. Именно,
можно положить
(/. Ф) = (А ф)-
Согласно сказанному выше, выражение справа не изменится, если
функцию ф заменить на другую основную функцию фг, также сов-
совпадающую с ф в окрестности носителя /; поэтому выражение (/, ф)
определяется только функцией ф.
Так, для финитного функционала / имеют точный смысл выра-
выражения (/, 1), (/, л;), .... (/, я|>), где ty(x)—любая бесконечно диф-
дифференцируемая функция (любого роста на бесконечности).
Если при этом имеется последовательность функций ij)v (л;), которая
в некоторой окрестности носителя функционала / равномерно
стремится к 0 вместе со всеми производными, то независимо от
поведения этой последовательности вне указанной окрестности мы
будем иметь (/, г^)->0.
Действительно, если умножить функцию ij)v на фиксированную
функцию h (х), равную 0 вне указанной окрестности носителя и 1
в некоторой меньшей окрестности носителя функционала /, то мы
будем иметь (f, ^v) = (/, Ail>v), в то же время произведение fttyv—> 0
в К, откуда и (/, /hl)vj->0.
Таким образом, финитный функционал обладает значительно более
сильными свойствами непрерывности, чем произвольный функцио-
функционал над К-

НОСИТЕЛЬ ОБОБЩЕННОЙ ФУНКЦИИ 61
§ 8]
2. Если обобщенная функция f равна О в области G. то
и любая ее производная -^— равна О в G. Действительно, если
для всех основных функций ф, сосредоточенных строго внутри G,
мы имеем
(/. ф) = 0.
то для этих эре функций и
,dxk ' v) V dxk
Вернемся к примеру на вычисление А п_2 (§ 7, п. 2, пример 8).
Вне начала координат функция д_2 бесконечно дифференцируема
и в обычном смысле А п_2 = 0; поэтому заранее можно сказать,
что обобщенная функция Д п_2 равна нулю вне начала координат
(и. следовательно, сосредоточена в одной точке — самом начале коор-
координат). Напомним, что вычисление в примере 8 привело к резуль-
результат А^=2
Если обобщенная функция f сосредоточена на множе-
множестве Е, то и все ее производные сосредоточены на этом же
множестве.
Действительно, на дополнении к Е обобщенная функция / равна 0;
по доказанному и все производные от / также на дополнении к Е
равны 0.
Две обобщенные функции fug. по определению, совпадают
в области G, если разность / — g равна нулю в О. В частности,
обобщенная функция / регулярна в области G, если она совпа-
совпадает в этой области с некоторой обычной функцией g(x). Так.
функция Ь(х) регулярна (и равна 0) вне начала координат.
Как следствие получаем: если обобщенные функции fug
совпадают в области G, то их производные , и ,° также
у dxk дхк
совпадают в этой области.
В частности, если в области G обобщенная функция / совпадает
с постоянной, то -J— равна 0 в G (k=l, 2 »). Обратно.
если в {связной) области G все производные первого порядка
обобщенной функции f равны 0, то f постоянна в этой
области. Если область G есть брус BcRn, то можно буквально
повторить доказательство, приведенное в п. 3, § 7, заменив в нем
пространство Rn на брус В. Любую же связную область можно
Получить как объединение сцепленной системы брусов.

62 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. ц
Всякая обобщенная функция в пространстве Rn есть, разумеется,
и обобщенная функция в любой области GczRn. Обратное неверно:
обобщенную функцию, заданную в области G, вообще говоря, нельзя
продолжить на все пространство /?„. Имеет место некоторый более
слабый факт: если дана обобщенная функция / в области G, то для
любой подобласти G', расположенной строго внутри G, можно ука-
указать обобщенную функцию fl £ К' (#„). которая совпадает с / на G'.
Для этого следует взять основную функцию а (х). сосредоточенную
строго внутри G и равную 1 на G', и положить (Д, ф) = (/,
3. В следующих пунктах мы рассмотрим некоторые дальнейшие
существенные свойства основных функций. В частности, метод «раз-
«разложения единицы» (п. 4) будет играть большую роль во многих
дальнейших рассмотрениях.
Лемма 1. Для любого ограниченного замкнутого мно-
множества F и содержащей его области G существует основная
функция п, равная 1 на F, нулю вне G и заключенная всюду
между 0 и 1.
Обозначим через Vf, 6-окрестность множества F, т. е. объеди-
объединение открытых шаров радиуса 6 с центрами в точках множества F.
Число 6 будем брать настолько малым, чтобы иметь V2uCzG.
Введем функцию
ф(;) | Г=\Х\<Ь.
( 0 при у = | лг | > 6,
где Сб = Г е v-'^dx, так что Г-ф(х; 6)dx = \.
\х\<ь Rn
Мы утверждаем, что функция
B)
удовлетворяет условию. Действительно, для всякого xfF интегри-
интегрирование в B) во всяком случае ведется по шару радиуса 6 с центром
в точке л; и в результате дает 1. Для всякого л;, не входящего
в G, подынтегральная функция в B) равна 0 на области Vt, и инте-
интеграл равен 0. В остальных точках, очевидно, значение функции h {x)
заключено между чистами 0 и 1. Наконец, вместе с функцией я]?(jc; 6)
и функция h (x) бесконечно дифференцируема, что и требуется.
Как следствие получаем: если f(x) — произвольная бесконечно
дифференцируемая функция, F—ограниченное замкнутое мно-
множество и G — содержащая его область, то существует основ-
основная функция <р(д:), совпадающая с f(x) на множестве F и

. gj НОСИТЕЛЬ ОБОБЩЕННОЙ ФУНКЦИИ 63
равная 0 вне G. Очевидно, можно положить ф(л;) = /(л;)Л(л;),
где h (х) — построенная выше основная функция, равная 1 на F
и 0 вне G.
4. Пусть имеется некоторое счетное покрытие «-мерного про-
пространства Rn открытыми ограниченными областями Ul LJm, . . .
и локально конечное—в том смысле, что у каждой точки л; имеется
окрестность W (л;), которая покрывается лишь конечным числом
множеств из совокупности {£/т}, а с остальными из этих множеств
не пересекается; мы желаем построить бесконечно дифференцируемые
функции ег (х) ет (л;), .. так, чтобы выполнялись следующие
условия:
а) 0 -От (х) -^ 1 при любом т — 1, 2, ...;
б) ет(х) = 0 вне области Um (m=l, 2, .. .);
в) «,(*)+ -. +*„(*)+ ...==1.
В последнем равенстве слева при каждом л; в силу б) отлично
от нуля лишь конечное число слагаемых. Совокупность функций (еЛ(л;)}
называется разложением единицы, точнее, разложением единицы,
соответствующим покрытию [Um\.
Вначале мы построим систему областей Vj Vm также
образующую локально конечное покрытие пространства /?„, и такую,
что замыкание Vm области Vm содержится в области Um (/и= 1,2, ...).
Для этого заметим, что дополнение к области £/2+ • ■ • + Um-\- ...
есть замкнутое множество F{, которое покрывается областью Ux;
в качестве Vj возьмем область, содержащую /*\ и содержащуюся
с замыканием в Uy
Далее, пусть области Vv .... Vm_1 уже построены так, что
VkcUk (ft=I т-l) и V, Vm_v Um, Um+l. ... есть
локально конечное покрытие пространства Rn. Дополнение к области
^1+ ... +^т_1+t/m+1-f- ... есть замкнутое множество Fm.
которое целиком покрывается областью Um. В качестве Vm можно
взять любую из открытых областей, содержащих Fm и содержа-
содержащихся в Um вместе со своим замыканием, и т. д.
Так как множество Vm ограничено, то, в силу результата п. 3,
существует бесконечно дифференцируемая функция hm(x), всюду
заключенная между 0 и 1, равная 1 в Vm и 0 вне Um. Положим
со
*(*)== Ца„D A)
т = 1
Эта функция существует при всех л; и заведомо не меньше 1.
Поскольку в окрестности W (х) точки л; в сумме A) отлично от нуля
лишь конечное число слагаемых, Л (л;) бесконечно дифференцируема.

64 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. II
Теперь остается положить
=ь 2.
очевидно, что функции ет(х) удовлетворяют поставленным тре-
требованиям.
Б. Лемма 2. Пусть имеется произвольная система обла-
областей Gv G2, ...; всякую основную функцию (р(х), сосредото-
сосредоточенную строго внутри объединения G = JjGv, можно предста-
V
вить в форме конечной суммы основных функций
Ф = Ф1+ ••■ +ФР. (О
причем q>k сосредоточена строго внутри области Gk
(А=1 /»)•
Прежде всего мы сразу можем ограничиться случаем, когда
система областей Gv G2, .. ■ конечна; действительно, в общем
случае замыкание множества Ф=[х : q>(x) ФО\ есть ограниченное
множество, покрытое объединением областей Glt G2, ...; но из
этого покрытия всегда можно выбрать конечное и затем все осталь-
остальные области отбросить.
Итак, мы можем предполагать, что область G есть объединение
конечной системы областей ОР .... Gp. _
Вместе с областью V, дополнительной к замыканию множества Ф,
эта система образует покрытие пространства Rn. Область Ф и области
Gl Gp, если они неограниченные, можно заменить (счетным)
объединением ограниченных областей, образующих в совокупности
локально конечное покрытие пространства Rn (п. 4). Рассмотрим
разложение единицы (ет(л:)), отвечающее построенным областям.
Для функции ф(лг) можно написать разложение
Сумма в правой части конечна, поскольку лишь конечное число
областей покрытия пересекается с носителем функции ф. В част-
частности, слагаемые, отвечающие частям области Ф, отсутствуют, так
как на них функция ф равна нулю. Объединяя слагаемые, отвечаю-
отвечающие частям областей Gv ..., Gp, получим искомое разложение.
Заметим, что если имеется последовательность основных функ-
иий ф.^ стремящаяся к нулю в пространстве К, то каждая из соста-
составляющих в разложении A) функции ф^, — если оно получено по
указанному правилу — также стремится к 0 в пространстве К-
6. Теорема- Если обобщенная функция f равна нулю
в каждой из областей Gx, G2 Gv, ..., то она равна нулю
и в их объединении G = [J Gv.

§ g] НОСИТЕЛЬ ОБОБЩЕННОЙ ФУНКЦИИ 65
Для доказательства, используя лемму п. 5, для заданной основной
функции ф, сосредоточенной в области G, построим разложение
где основная функция (fk сосредоточена строго внутри области Gk.
Применяя к этому разложению функционал / и используя условие
/ = 0 в Gk, получаем
что и требуется.
Как следствие получаем: обобщенная функция, равная нулю
в некоторой окрестности каждой точки пространства Rn,
есть нулевая обобщенная функция, т. е. (/, ф) = 0 для лю-
любой ф £ К.
Задачи. 1. Дано, что обобщенная функция / в окрестности U (лс0)
каждой точки х0 удовлетворяет условию g (х) / = О, где g (х) — бесконечно
дифференцируемая функция, отличная от нуля (зависящая от окрестности
U (х0)). Доказать, что / = 0.
Указание. Функция —г—— также бесконечно дифференцируема
в окрестности U (х0).
2. Условие задачи 1 выполнено всюду, кроме точек некоторого замкну-
замкнутого множества Ф. Показать, что обобщенная функция / сосредоточена на
множестве Ф.
Указание. Использовать теорему 1.
3. Построить основную функцию ц>(х), сосредоточенную в шаре ]л:|^а
и такую, что 1 представляется в виде ряда сдвигов функции ф {х):
DO
1= 2j"H* + £v). A)
v=0
Указание. Достаточно рассмотреть случай п = 1, поскольку в общем
случае можно перемножить равенства A), написанные для каждой из коорди-
координат. Для п = 1 можно взять любую бесконечно дифференцируемую функ-
функцию (f (х), равную 1 при 0 -< д: ■<-=-, 0 при х > —=- и доопределить ее при
о о
х < 0 по формуле ф (— х) = 1 — ф (— х + а).
4. Дана функция / (х). определенная и локально интегрируемая при х Ф 0.
и в окрестности начала координат имеющая особенность не выше степенной:
t4 A
Показать, что существует обобщенная функция f£K'n, совпадающая с f(x\
при х Ф 0.
У к а з ад и е. См. задачу 6 к § 6.
5 Г. Е. Шилов

66 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. Ц
§ 9. Предельный переход в пространстве обобщенных функций
1. Последовательность обобщенных функций fl / , ... назы-
называется сходящейся в К' к обобщенной функции /, если для любой
основной функции ф
(/, ф)= lim (/v. ф).
v-><x>
Из самого определения видно, что функционал / последователь-
последовательностью /v определен однозначно.
Аналогично ряд из обобщенных функций gt-\- ... +£fv+ -
называется сходящимся к обобщенной функции /, если частичные
суммы этого ряда
сходятся к обобщенной функции /.
Например, если /1 =/г(х) fv = fv(x), ... —обычные функ-
функции, сходящиеся почти всюду к функции f(x) и обладающие обыч-
обычной (т. е. локально интегрируемой) мажорантой F(x), так что
v=l, 2
то / сходятся к / и в смысле обобщенных функций. Более общим
образом, если fv(x) сходятся к f(x) по метрике, связанной с инте-
интегралом, так что
/|/v (*)-/(*) И*-> о
в
для каждого ограниченного бруса В, то также /v сходятся к / в К'-
Действительно, в этом случае
(/. Ф) —(A, <P) = (/-/V. Ф)= f(f — fv)<tdx.
в
где В тот брус, вне которого ф(л;) обращается в нуль; отсюда
|С/. <P)-(/v. Ф)|<шах|ф(дг)|. f\f{x) — fv{x)\dx-»0.
в
Всякая обобщенная функция f есть сумма ряда финитных
обобщенных функций. Действительно, возьмем произвольное локально
конечное покрытие пространства Rn (§ 8, п. 4) и соответствующее
разложение единицы {ет(х)\. Умножая ряд основных функций

§ 9] ПРЕДЕЛЬНЫЙ ПЕРЕХОД 67
на функционал /, получим его разложение
... +emf+ ... =/,-+■ ... +fm+ ... A)
в ряд по финитным обобщенным функциям. Очевидно, что ряд A)
является сходящимся, так как для любой основной функции в раз-
разложении
С/. <р) = (Д. <Р)+ ... +(fm.
лишь конечное число слагаемых отлично от нуля.
Операция предельного перехода линейна, т. е. если /v->/
в К'. gv—>gB К.'t а и р — вещественные числа, то
в К'-
Аналогично если а (л:) — бесконечно дифференцируемая функция, то
из /v->/ следует а (л;) Д -> а (л;) /. Действительно, для любой ф£/С
, ф).
В комплексном пространстве из /v->/ следует /v->/. поскольку
Несколько менее привычно то обстоятельство, что из сходи-
сходимости /v к / всегда следует сходимость . к -;—. В класси-
классическом анализе, как мы знаем, подобные факты требуют дополни-
дополнительных предположений. Для обобщенных функций доказательство
проводится просто:
дф \ / df
Пример 1. Функции /v (х) = — sin хх (— оо < х < оо) при v -> со
равномерно сходятся к 0 и, следовательно, сходятся к 0 в пространстве К'.
Их производные f'v (х) = cos хх не сходятся к нулю в обычнрм смысле, но
как обобщенные функции, они при v->oo стремятся к нулю в силу соотно-
соотношения
оо оо
(cos хх. ф) = / cos хх • ф (х) dx = / sin хх ■ ф (х) dx -> 0.
—оо —оо
Дальнейшие производные этой последовательности
/у = V Sin XX, /" = — V2 COS XX, . . .
также сходятся к нулю в пространстве К',

68
СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. ц
2. Последовательность обычных функций fv(x), сходящаяся в К?
к сингулярной функции 6(л;), называется дельта-образной после-
последовательностью. Такие последовательности часто встречаются в зада-
задачах, связанных с дифференциальными уравнениями. Мы приводим
ниже некоторые общие условия, достаточные, чтобы данная последо-
последовательность fх(х) была дельта-образной.
Лемма. Если для любого бруса Во числа
dx
, BczB0,
ограничены постоянной, не зависящей от В и v (а только
от BQ), и
О, если начало координат находится вне
/бруса В,
/v (x) dx = { ,
,_^„ v 1, если начало координат находится вну-
в три бруса В,
то
Iim / (х) = Ъ(х) в К'-
Для доказательства рассмотрим последовательность первообразных
функций
-1
-1
Эта последовательность равномерно ограничена в каждом ограничен-
ограниченном брусе; далее, если хотя бы одно из чисел xv .... хп меньше О,
она стремится к 0, а если все хк положительны — она стремится
к 1. Отсюда следует, что
Iim Fv(x) = Q(xl хп) в К'.
v-*oo
Дифференцируя это предельное соотношение, находим (ср. § 7, п. 2,
пример 3)
dnFv{x) d"Q{x)
Iim / (x)= Iim -3 3— = -3 з— = 6(jc) (в К'),
v OXi ... ОХ, "*"' riv \ / \ /
- Ц—
что и требовалось.
Заметим, что дельта-образная последовательность не обязана со-
состоять из знакоположительных функций (см. задачу 1).

9] ПРЕДЕЛЬНЫЙ ПЕРЕХОД
Пример 2. Пусть п=1 и
(см. рис. 5). Мы имеем
ь
= 1 [arctg A - arctg £-],
откуда легко следует выполнение условий леммы. Применяя ее,
получаем
Е-*0
Пример 3. Пусть п = 1, с > 0 и
Здесь при замене—— = у мы получим
ft bfcVT
[ft(x)dx = ^= f
a alcVt
Если a yi b разных знаков, полученный интеграл имеет пределом 1;
если же а и b одного и того же знака, то этот интеграл стремится
к нулю. Применяя лемму, получаем
Iim/,(*) =
3. Весьма важным является свойство полноты пространства К'
относительно введенной в нем сходимости:

70 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. II
Теорема- Пусть имеется последовательность линейных
непрерывных функционалов fv /2. • • - в пространстве К' такая,
что для каждой Ц>£К последовательность чисел (fv, ф\
является сходящейся при v—>-оо. Тогда функционал на К,
определяемый равенством
(/. Ф)= !im(/v. ф),
v>oo
v->oo
также является линейным и непрерывным.
Доказательство основано на важной лемме, имеющей и самостоя-
самостоятельные применения:
Лемма- Если последовательность функционалов fv£K'
(v—1, 2, ...) такова, что для каждой <р£К существует пре-
предел (/, ф) числовой последовательности (/v, ф), то для всякой
сходящейся в К последовательности основных функций q>v—>q>
существует также предел при v-*oo числовой последователь-
последовательности (/v, фч), который равен (/, ф).
Предполагая лемму доказанной, покажем, как доказывается тео-
теорема о полноте пространства К'-
Линейность предельного функционала /== lim /v доказывается
просто:
(/, а1ф,-Ьа2ф2)= lim (Д, а1ф1 + а2ф2)= lim [a,(/v. <p,)+a2(/v, Ф2I =
V->DO V->CO
= a, lim (/v, ф^+с^ lim (Д, Ф^^а^/, qj+a^f, Ф2).
V->CO V->DO
Докажем его непрерывность. Пусть ipv->0 в К; нам нужно доказать,
что (/, ф^->-0. В предположении противного и перейдя при необхо-
необходимости к подпоследовательности, мы можем принять, что для всех
v== 1, 2, ... выполняется неравенство
где а >0 — некоторая постоянная. Так как (/, Ф )= lim (/ , ф ).
то для каждого v = 1, 2, ... найдется номер ц = p. (v) такой, что
(f, <$v}\>a. Снова, переходя к подпоследовательности, можно считать,
что ji(v) = v. Таким образом, в рассматриваемом случае |(/v, ф^| > а>
v=l, 2, ... С другрй стороны, по лемме существует предел
lim (/ , ф) = (/, 0) = 0. Получившееся противоречие показывает,
что функционал / в действительности непрерывен, что и требовалось.
Остается доказать лемму. Без ограничения общности можно счи-
считать ф(л;) = 0; в противном случае мы заменим q>v на фЛ, — ф. Мы
должны доказать, что (fv, ф^->-0.

§ 9] ПРЕДЕЛЬНЫЙ ПЕРЕХОД 71
Допустим противное. Тогда, перейдя, если нужно, к подпоследо-
подпоследовательности, можем считать, что |(/v, <pv)|>-C>0. Сходимость
последовательности (pv к нулю в пространстве К означает, что все
функции q>v (x) равны 0 вне ограниченной области и стремятся к нулю
равномерно в /?„, так же как и их производные любого порядка.
Еше раз перейдя к подпоследовательности, можем полагать, что
^ = 0. I. 2. ...).
Положим tyv = 2vqy для функций tyv будем иметь неравенства
|04v(*)|<-^r (|*l<v=:0. 1, 2....).
которые показывают, что функции i|jv также стремятся к 0 в К; более
того, любой ряд вида
является в К сходящимся. В тоже время числа I (/v, tyv) I = 2V | (/v, <pv)>-
^. 2VC и тем самым стремятся в бесконечность.
Теперь будем строить некоторую подпоследовательность Д и
некоторую подпоследовательность tyv следующим образом.
Выберем сначала /v и ^v так, чтобы иметь |(/v. tyv)| > 1.
Пусть /v , \])v (y=l, 2 k—1) построены. Возьмем в каче-
качестве tyv элемент последовательности \J>v с настолько большим номе-
номером, что
и затем найдем /v так, чтобы иметь
Первое возможно, потому что функции \J>V стремятся к нулю
в пространстве К, и следовательно, для любой обобщенной функ-
функции /0 мы имеем (/0, \М—>(). Второе возможно потому, что
l(/ )| Д A /<*
Таким образом, построение \|) и / можно продолжить неогра-
k k
ннченно. Положим далее
со

72 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. Ц
По построению, ряд в правой части сходится в пространстве Д"
и, следовательно, его сумма я|) есть элемент К- Далее
J
Но в силу B) и того, что
получаем
т. е. при k—>oo также I(fv , т|ЛI —*■ оо. Но это противоречит соот-
соотношению lim (f , \])) = (/, я|>). Лемма доказана*).
V-ХхЛ V
4. Пусть каждому значению вещественного или комплексного
параметра К, пробегающего некоторую область Л, поставлена в соот-
соответствие обобщенная функция Д. В соответствии с определением,
данным в п. 1, обобщенная функция / называется пределом Д при
К -> h0, если при А. —> ^0 числовая функция (fh, cp\ стремится к (/, ф)
при любом ф. Функция /к называется непрерывной по К в области Л,
если при любом К0£А имеет место соотношение Д = lim Д.
Рассмотрим важный вопрос о доопределении обобщенной функ-
функции Д по непрерывности по параметру К. Представим себе,
что обобщенная функция Д определена и непрерывна на множе-
множестве Л, имеющем предельную точку ^0, в которой обобщенная функ-
функция Д заранее не задана. Спрашивается, возможно ли доопределить
обобщенную функцию Д в точке ^0 так, чтобы получилась обобщен-
обобщенная функция, непрерывная на множестве Л-|-^о.
Очевидно, что необходимым условием для возможности такого
доопределения является возможность доопределения по непрерывности
всех числовых функций (Д, ф) в точке ^0. Это условие является
и достаточным; действительно, если для любой основной функ-
функции ф и любой последовательности ^v—>^o- ^v€-^- существует пре-
предел последовательности чисел (Д , ф), то, согласно теореме о пол-
полноте пространства обобщенных функций существует обобщенная
функция / = Д, которая является пределом последовательности Д .
*) Это доказательство принадлежит М. Л. Бродскому.

$ 9] ПРЕДЕЛЬНЫЙ ПЕРЕХОД 73
Обычным путем доказывается, что эта обобщенная функция не зави-
зависит от выбора последовательности kv—>^o-
Заметим, далее, что производные (по xk) обобщенной функции /,,
непрерывно зависящей от параметра К, также непрерывно зависят от
параметра к. Действительно, как мы видели в п. 1, из fk —>/?
следует
бхь J К дхь J '•о
Непрерывные по параметру обобщенные функции fk можно инте-
интегрировать по этому параметру. Пусть, например, функционал fk не-
непрерывен по к на спрямляемой кривой Г. Составим интегральную
сумму
взяв разбиение кривой Г на /га частей точками деления Х.о, Кг кт
и выбрав произвольно точки kj на интервалах (X.y-_i, Xj)- При
max | Д^;-1 —> 0, в силу непрерывности выражения (fh, q>\ для любой
основной функции ф существует предел выражений
не зависящий от способа разбиения Г и выбора промежуточных
70чек л7-, равный интегралу от функции (fk, ф\. Этот предел опре-
определяет линейный непрерывный функционал на пространстве основных
функций; он называется интегралом от обобщенной функции fK
по кривой Г и обозначается обычным образом
J /k dX или J /k (x) dk.
г г
В силу непрерывности операции дифференцирования, мы имеем
так что интегрирование обобщенной функции по параметру к всегда
перестановочно с дифференцированием ее по координатам.
Разумеется, интегрировать можно не только по кривой, но и по
области любого числа измерений.

74 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. II
Б. Обобщенная функция g называется производной от обобщен-
обобщенной функции Д по параметру к при Х = Х0, если
g=
ад
Для существования производной —^— при А = А0 необходимо
и достаточно, чтобы все числовые функции (Д. ф) были диф-
дифференцируемы по X при А = А0. Необходимость этого условия оче-
очевидна; проверим его достаточность. По условию, для каждой ф и
любой последовательности A,v—>Xq существует предел отношения
A-AD
Но тогда, как было указано выше, обобщенная функция * ** ,
определенная при А Ф Ао, может быть доопределена по непрерывности
и при А = А0; иными словами, существует обобщенная функция,
Л —/,
являющаяся пределом отношения ° при А —> Ао, что и утвер-
утверждается.
Если Д имеет производную по А при любом X £ Л, то функ-
функция Д называется дифференцируемой по X в области Л.
Аналогично определяются высшие производные по параметру и
многократная дифференцируемость функций.
Легко проверить, что если функция Д дифференцируема по X
в области Л, то и все производные Д по л: дифференцируемы по X
и имеет место формула
[ д^ Л) = d^" ( dT А) •
Действительно, для любой основной функции ф числовая функция
\d-Kfc *•' ' \ *■' &хк I
дифференцируема по А и имеет производную
d/.
Это означает, что функционал -г— имеет производную по Я и спра-
справедлива формула A), что и утверждается.

§ 9] ПРЕДЕЛЬНЫЙ ПЕРЕХОД 75
6. Если к— комплексный параметр, пробегающий открытую об-
область Л, то дифференцируемая в области Л обобщенная функция Д
называется аналитической функцией от к. В этом случае все
числовые функции (Д, ц>) являются обычными аналитическими функ-
функциями от к в области Л. И обратно, если для обобщенной функ-
функции Д все числовые функции (Д, ф) являются аналитическими
функциями от к в области А, то и Д есть аналитическая
функция от к. В этом случае в каждой точке X области А
dfx d*f
существуют все производные-^,-^. ... ив окрестности
точки ко£А имеет место разложение в ряд Тейлора
... О)
Действительно, обобщенная функция ..г0 существует, так как, по
условию, при к = к0 существуют производные по к у всех числовых
функций (Д, ф); по такой же причине существуют и все высшие
d2fk
производные , ° .... Далее, для каждой основной функции ф
справедливо разложение Тейлора обычной аналитической функ-
функции (Д. ф):
^)(Л'ф) |+
откуда следует справедливость разложения A).
Две аналитические функции Д и gh, определенные в области Л
и совпадающие на множестве значений к, имеющем предельную
точку внутри Л, совпадают при всех значениях к £ Л. Действи-
Действительно, для любой основной функции ф выражения (Д, ф) и (gk, ф)
совпадают в области Л, в силу классической теоремы единствен-
единственности для аналитических функций.
На этом свойстве основан важный метод аналитического про-
продолжения функционала Д по параметру к. Допустим, что функ-
функционал Д аналитичен в области Л. Предположим, далее, что все
числовые функции (Д. ф) допускают аналитическое продолжение
в более широкую область Лх. Тогда мы можем утверждать, что

76 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. II
числа (fk. ф) при любом к£А1 также задают линейный непрерыв-
непрерывный функционал на пространстве К- Действительно, аналитическое
продолжение в любую точку области Аг, как известно, всегда мо-
может быть осуществлено при помощи конечного числа переразложе-
переразложений в ряд Тейлора. Но каждый ряд Тейлора
поскольку он сходится при любой основной функции ф и поскольку
радиус его круга сходимости определяется конфигурацией областей
Л и Лр не зависит от ф, имеет своей суммой в круге сходимости
снова линейный непрерывный функционал, что нам и требуется.
Очевидно, что производные (по л;) аналитической обобщенной
функции Д суть также аналитические обобщенные функции от X.
Если функционал ft k зависит непрерывно от параметра t в ог-
ограниченной замкнутой области Т и аналитически от параметра Я.
(при любом /) в области Л, то интеграл
остается аналитически зависящим от параметра к в области Л. Дей-
Действительно, для любой основной функции ф интеграл
,, w\dt
от аналитической функции (ft %, q>\ представляет снова аналитиче-
аналитическую функцию от к*) в области Л.
Если ft h при каждом t аналитически продолжается из области Л
в область Лр то и результат интегрирования gk аналитически про-
продолжается в ту же область; при этом аналитическое продолжение
интеграла (функции gA совпадает с интегралом от аналитического
продолжения (т. е. от функции /А в силу единственности анали-
аналитического продолжения.
7. Рассмотрим обобщенную функцию от аргумента ((О, л:) (§ 6,
п. 2, пример 4). Напомним ее построение. Если ю — фиксирован-
фиксированный единичный вектор, мы можем каждой основной функции
•) См.. например. В. И. Смирно в. Курс высшей математики, т. III»
ч. 2, п. 70, 1951. стр. 257.

ПРЕДЕЛЬНЫЙ ПЕРЕХОД 77
= Ф(-х;1 .... д:„) поставить в соответствие функцию
Ф(|: ©)=» / <t(x)dx.
(о, дг)=5
которая является основной функцией аргумента |, — оо < |< оо.
Любой обобщенной функции f(Q^K[ можно сопоставить функ-
функционал /а £ К'п. действующий по формуле
(/„• Ф) = (/©• Ф& «))•
Мы будем здесь изучать функционал /и в зависимости от пара-
параметра @, пробегающего всю единичную сферу Q. Функция Ф(£; со)
может быть рассмотрена как основная функция, зависящая от па-
параметра СО.
Эта функция сосредоточена на фиксированном отрезке оси | (не
зависящем от со) и, как интеграл от ц>{х1 л:п) по сечению
(со, х) = \, зависит от со непрерывным и бесконечно дифференци-
дифференцируемым образом (в силу равномерной непрерывности q>(xlt .... хп)
и каждой из ее производных).
Поэтому и функционал /ш на пространстве К„ непрерывным и
бесконечно дифференцируемым образом зависит от параметра со.
В частности, он может быть проинтегрирован по пара-
параметру со, пробегающему сферу Q.
Приведем вычисление соответствующего интеграла для обычной
функции /(|). Обозначим через Ц,(р) и Sn(p) поверхность сферы
и объем шара радиуса р в пространстве /?„. Между этими величи-
величинами имеется очевидная связь
Обозначим для краткости Qn(l) = &n, Sn(l)=Sn. По соображениям
размерности QB(p) = p"-ISl,(l) = PB~^- Sn(p) = pnSn(l) = p"Sn; no-
этому
Qn = np«-iSn(p) | =nSa.
p=i
В дальнейшем мы найдем выражения Q,, и Sn в явном виде. Мы
желаем вычислить интеграл
((*. co))tfco. A)
Вместо интеграла A) будем вычислять интеграл по шару 5„(р) ра-
радиуса р:

78 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. II
Функция f((x, у)) как функция аргумента у постоянна на плоско-
плоскостях, ортогональных к вектору л\ Если такая плоскость проходит
на расстоянии Л -^ р от начала координанат, то площадь ее сечения
шаром Sn (p) равна
Поэтому
1 / /'(rh) (р2 — Л2)" dh (г = \х\).
*'„№) -р
Чтобы получить интеграл по сфере Qn, мы должны полученное вы-
выражение продифференцировать по р и затем положить р= 1. Мы
получим
1 „-з
l- B)
В частности, если положить /(D=l, интеграл A) дает поверх-
поверхность Qn единичной сферы в Rn, и мы получим
1
-1
2)
Из этой формулы можно легко получить выражения чисел О„
при любом п.
Обозначим 2„Г I-^J = Ап; из формулы A) мы имеем
и так как Л2 = 2л, то при любом и > 1
Отсюда

s 10] СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИИ 79
Задачи. 1. Доказать, что при v -*■ со
1 sin хх . . . .,,
ял; ч ' 1
2. Построить последовательность обычных функций gv (x). сходящуюся
(в К') к обобщенной функции 6(*'(jc).
Указание. Положить gv (х) =/^ (х), где /v (х) -» 6 (х) (в К') —
последовательность бесконечно дифференцируемых функций.
3. Умножение на функцию р (лг). не являющуюся бесконечно дифферен-
дифференцируемой, не может быть «разумно» определено во всем К'. «Разумно» оз-
означает следующее: умножение на Р (лг) для обычных функций должно сов-
совпадать с обычным умножением, а для обобщенных должно во всяком
случае быть непрерывной операцией на К', т. е. такой, что из /v->/ в К'
следует P/V->P/.
Указание. Пусть k-я производная функции р (лг) имеет разрыв
при х = 0. Построить последовательность /v (лг) -*■ 6(*' (лг) и так, чтобы вы-
выражения (Р (лг) /v (x), ф (лг)) для некоторых ф не имели предела.
4. Если ряд
сходится в пространстве К[, то все коэффициенты ат, начиная с некото-
некоторого номера, равны О.
Указание. Использовать основную функцию <р(х). для которой
|/Ч||1|
5. Если <рк(х) — основная функция, дифференцируемая по параметру Я,
в пространстве /<, и Д — обобщенная функция, дифференцируемая по па-
параметру к в К', то (fk, <pjj есть дифференцируемая функция параметра Л и
Указание. Использовать лемму п. 3.
§ 10. Структура обобщенных функций
1. Пусть имеется последовательность обычных функций/j (л:), ...
.... fv(x), ... такая, что в любом брусе В= \х : ау<1 лгу-^р^.
7=1 п], начиная с некоторого номера \ = \(В), все они
равны нулю. Мы утверждаем, что ряд
fiPv(D)fv(x) A)
v=l
(с любыми дифференциальными операторами Pv(D)\ сходится в про-
пространстве К'. Действительно, для любой основной функции ф (л:) ряд.
S (v () /v () Ф {) = £ (/v (*)■ ^v (—
v=l v=l

80 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. Ц
содержит лишь конечное число слагаемых (поскольку (р(х) сосре-
сосредоточена в некотором брусе В). Поэтому сумма B) определена для
любой основной функции ср. Легко проверить, что эта сумма опре-
определяет линейный непрерывный функционал на пространстве К-
Мы покажем в этом параграфе, что любая обобщенная функ-
функция на пространстве К имеет вид (I). Если мы возьмем лишь ко-
конечное число обычных и притом финитных функций /, (х) fp (х),
то сумма
2р,(Д)Д,D C)
v=l
очевидно, является финитной обобщенной функцией; мы покажем,
что в форме C) может быть представлена любая финитная
обобщенная функция. Наконец, мы получим общую форму функ-
функционала /£ К', сосредоточенного в одной точке; если эта точка
есть начало координат, то / имеет вид
/= V akD4ix)i D»= *Ш D)
JftKp °xl ■■■°xn
2. Все эти результаты основаны на следующем свойстве обоб-
обобщенных функций:
Лемма 1. Для каждой обобщенной функции f и каждой
ограниченной области G существует число N = N(f, G) та-
такое, что для любой основной функции <р, сосредоточенной в
области G, имеет место неравенство
К/. Ф)|<С 2 max|D*<p(*)| E)
|*|<ЛГ £О
с постоянной C = C(f, G).
Доказательство. Допустим, что для некоторой обобщенной
функции / и области G требуемого числа N не существует; это зна-
значит, что для любого Л/=1, 2, ... найдется основная функция
ц> = ф^ (х). сосредоточенная в G, такая, что
тах|О*Флг(*)|. F)
Заменяя функцию <pN(x) любым ее кратным i]pN = CNq>N, мы не на-
нарушим неравенства F), т. е. при любых CN
Выберем CN так, чтобы иметь
V max|D4vWl=4r (N=1.2....).

Ю]
СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИИ
81
Последовательность функций tJj, (л:) ф^ (л:), ... стремится
к 0 в пространстве К. поскольку все они сосредоточены в ограни-
ограниченной области G и равномерно стремятся к 0 при N->oo, так
же как и их производные любого фиксированного порядка. Так как
функционал / непрерывен, то мы должны иметь (/, -ф^) —>0; с дру-
другой стороны, из G) следует, что |(/, tyN)\^> 1. Полученное проти-
противоречие доказывает справедливость утверждения.
Неравенство E) можно продолжить следующим образом (во вся-
всяком случае для области О достаточно простой конфигурации):
V
(8)
Действительно, при любом х £ G, по неравенству Коши-Буняков-
ского, мы имеем •
\D*<f>(x)\ =
i
дп £>ftq> (£)
dxt ... дхп
Го Г 1*кл
|*1<ЛЧ-л О
причем (flj, .... ал) — точка (возможно, вне области G), где функ-
функция <p(Jt) равна 0 со всеми производными.
3. Рассмотрим гильбертово пространство &€т, состоящее из ос-
основных функций, сосредоточенных в области G, со скалярным про-
произведением
(Ф- *)т = S
|ft|<m О
и, следовательно, с нормой
1ft |<m G
Как следует из (8), функционал / ограничен по норме простран-
пространства Wm при m = N~\-n и поэтому может быть продолжен,
как ограниченный функционал на пополнение пространства &6т.
6 Г. Е. Шилов

82 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ |ГЛ. Ir
Построим пополнение St?m пространства &6т. Если фг ..., <pv, —
фундаментальная последовательность в &6т, то
| *|<m О
> f\D\(x)—D\(x)fdx
а
при любом фиксированном k. \k\-^.m. Это означает, что каждая из
последовательностей D"<pv{x) фундаментальна в смысле сходимости
обычного пространства квадратично интегрируемых функций £.2(G)
и. следовательно, имеет пределом некоторую функцию ф'*' (л:) £ L2 (G);
индекс [ft] указывает на происхождение функции ф1*'(л:) из k-x про-
производных функций фv (дг) и не означает, вообще говоря, что ф'*1 (лг)
есть k-я производная от функции ф(лг). Итак, каждому элементу
пространства е$т отвечает система функций {ф^'С*))» |А|-Ст.
квадратично интегрируемых в области G, при этом, в силу непре-
непрерывности скалярного произведения,
(Ы"(х)}, Wk\x)))m= V f^\x)^{x)dx.
|ft|<rn С
Применим теперь теорему об общем виде линейного непрерыв-
непрерывного функционала в полном гильбертовом пространстве; эта теорема,
как известно, утверждает *). что всякий такой функционал есть
скалярное произведение с фиксированным элементом пространства.
В частности, и нашему функционалу / отвечает некоторая система
квадратично интегрируемых функций {/'*1(аг)], |ft|^m, такая, что
для любого'элемента {ф1*1 (х)} £ &в
(/, ф)= V ff™{X)<pW(x)dX.
|ft|<rn О
В частности, если ф(х) есть исходная бесконечно дифференци-
дифференцируемая функция, мы получаем
<Р)= 2 /
где fk(x) = f [{x) есть обычные (даже квадратично интегрируемые)
функции в области G. Итак, мы получили теорему:
Теорема 1. Для всякой обобщенной функции f и ограни-
ограниченной области G можно указать такое т и такие обычные
*) См. Анализ III. гл. V. § 2, п. 9.

,0| СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИИ 83
функции fk(x) (|A|<m), что для любой основной функции <р(лг).
сосредоточенной в области G, имеет место равенство
Используя определение производной, эту же формулу можно запи-
записать в форме
(/. ф) = ( 2 (—
или
где g"ft = (—II*1/* снова обычные функции. Итак, в ограни-
ограниченной области G каждая обобщенная функция действует,
как конечная сумма производных от обычных функций, со-
сосредоточенных в области G.
Заметим, что функции gk можно считать ограниченными в G,
непрерывными и даже имеющими любое заданное число непрерыв-
непрерывных производных, поскольку этого можно добиться, заменяя их
первообразными некоторого порядка.
Вспоминая определение лорядка сингулярности (§ 6, пример 2),
мы можем сформулировать этот результат так: всякая обобщенная
функция в ограниченной области G имеет конечный порядок
сингулярности.
4. Выясним теперь, как действует обобщенная функция / на
любую основную функцию ф {х) £ К. Для этого рассмотрим локально
конечное покрытие пространства Rn счетной системой ограниченных
областей Gx Gp, ... По теореме 1 для области Gp можно ука-
указать число т = т (р) и систему обычных функций /р1 fP,m {py
сосредоточенных в Go, такую, что для каждой основной функ-
функции ф(лг), сосредоточенной строго внутри Ор, имеет место пред-
представление
. ф)= 2 (/„*.
Далее, в силу результата п. 4 § 9, существует разложение
единицы
на бесконечно дифференцируемые слагаемые, причем ер (х) равна
нулю вне Gp. Для произвольной основной функции ф(лг) мы имеем
6*

84 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. Ц
1 |р .. и, следовательно,
(/. ф) = 2 (/■ *РФ) = 2 2 (fpk. D*ep<f>) =
Р Р 1*|<т(р)
Р Р
2 2 (/,*. 2
= 22B
B (-D
\|У 1<т(р)
р
= 22
= 2 2 (оЪд,. <р). (9)
Р |Л<т(р)
где £■,-„ = (—1)У 2 С1[в"~*е ■ f А снова есть обычная функ-
|ft|<m(p) P
ция, сосредоточенная в области Ор. Носители функций gjp при воз-
возрастающем р удаляются от начала координат, поэтому в сумме
(при фиксированном j по тем индексам />, для которых \J\
при всяком х лишь конечное число слагаемых может быть отличным
от нуля. Поэтому и сама сумма gj(x) существует при всяком х.
С увеличением |у| носитель функции gj(x) все дальше уходит от
начала координат. Изменив порядок суммирования в (9), приводим
эту формулу к виду
С/. ф) = 2(я'^(*). <р(*)).
откуда
/=2^/D (Ю)
/
Ряд A0) бесконечный, но в каждой конечной области отлично от
нуля лишь конечное число слагаемых-
Формула A0) дает общий вид функционала на пространстве К',
иными словами, любая обобщенная функция приводится к виду A0).
С другой стороны, и обратно, как мы заметили в начале этого
параграфа, при любых обычных функциях gj(x), носители которых
удаляются неограниченно от начала координат, ряд A0) сходится и
определяет некоторую обобщенную функцию.
б. Рассмотрим теперь случай финитной обобщенной функции /.
В этом случае области О,, G2 Gp, ... мы можем взять так,
чтобы в каждой из них, начиная с G2, функционал / был нулевым.
Поэтому все функции fpk при р^2 можно взять равными нулю,
и сумма (9) приводится к виду
(/• Ч>)= 2 (D'gji- Ф)-
<@

. ю] СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИЙ 85
Таким образом, имеет место представление
/= 2 D'gjix). m = m(l). A1)
1Л<
где gj(x)—обычные функции, равные 0 вне области Gv Так как
область Gi можно взять как угодно тесно облегающей носитель
функционала /, то к формуле A1) мы можем сделать существенное
дополнение: функции gj(x) всегда можно выбрать так, чтобы
их носители содержались в произвольно малой окрестности
носителя функционала /.
Как следствие, получаем: финитный функционал имеет конеч-
конечный порядок сингулярности во всем пространстве.
Если носитель функционала / есть замкнутая ограниченная область О0,
то в представлении A1) можно взять функции g, (х), сосредоточенные даже
в самой области О0 (не в ее окрестности). Этот результат, опирающийся на
теорему о продолжении гладких функций, приводится в задаче 2.
6. Рассмотрим, наконец, функционал /, сосредоточенный в одной
точке — для определенности, в начале координат 0. Любой брус В,
содержащий внутри себя точку 0, является носителем функционала /.
Фиксируем произвольно такой брус В и найдем представление
функционала / в форме A1)
(/. <Р)= S tej(x). D% A2)
\1\<т
где gj (x) — обычные функции, сосредоточенные в брусе В.
Покажем, что функционал f равен нулю на каждой основ-
основной функции ц>(х), равной нулю вместе с оизводными до
порядка т в точке 0. Достаточно убедиться, что существует после-
последовательность основных функций <pv (x), равных <р (х) (каждая в неко-
некоторой окрестности точки 0) и сходящаяся к 0 равномерно в брусе В
вместе с производными до порядка т. Действительно, если такая
последовательность <pv0>0 построена, то, во-первых, мы имеем
(/, ф) = (/, <pv) для каждого v—поскольку функционал / сосре-
сосредоточен в точке 0 — и, во-вторых, в силу формулы A2),
il{X) dx
М\<т В
откуда (/, ф) = 0, что и требуется.
Пусть теперь ф — произвольная основная функция. Ее можно
представить в форме
\j\<m

'86 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. 1Г
где hm+i(x) обращается в нуль в начале координат вместе с произ-
производными до порядка т. Слагаемые справа не являются основными
функциями, поэтому умножим равенство A3) на фиксированную
основную функцию е (х), равную 1 в окрестности точки 0; мы
получим
(*)«(*)■
■что дает разложение функции (ре уже на основные функции. При-
Применим функционал / к обеим частям равенства A4). Так как
Ф(х) совпадает с ц>(х)е(х) в окрестности точки 0, то (/, <ре) = (/, <р),
и мы получаем
Ф) = (/• ФО = 2 £>УФ @) (/,
\]\<т
Обозначим йу = (—1L/. х е} ]. Далее, мы имеем DAp(O) =
= ((—l)JDJf>. ф); наконец, поскольку основная функция hm+xe
обращается в нуль в начале координат со всеми производными до
порядка пи мы имеем (/, Am+le) = 0. В итоге для любой основной
функции ф
2 >Ъ ф)
и, следовательно,
2
/= 2 «у^У6- A5)
1У
В форме A5) записывается любая обобщенная функция, сосредоточен-
сосредоточенная в начале координат. Обобщенная функция, сосредоточенная
в любой другой точке х0, естественно, имеет вид
/= S
Нам осталось для всякой функции ф {х) £ К, равной 0 вместе с произ-
производными до порядка т при х = 0, построить последовательность
основных функций Ф^лг), равных ц>(х) в окрестности точки 0 и
сходящихся к 0 равномерно в брусе В вместе с производными
до порядка от. Для этого рассмотрим фиксированную основную
функцию Л (лг), равную 1 в некоторой шаровой окрестности точки 0.
положим, радиуса р, и равную 0 вне некоторой большей шаровой
•окрестности, положим, радиуса 2р.

§ 10] СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИИ 87'
Мы утверждаем,что последовательность функций
) (v=l. 2. ...) A6)
удовлетворяет требуемому условию.
Во-первых, функции <pv(Jt), определенные формулой E), действи-
действительно обращаются в Ф(х) каждая в некоторой окрестности точки 0.
Оценим, далее, производные функций фу(лг). По формуле Лейб-
Лейбница
O\W= 2 C{D*-^(*).^A(vjf).
Обозначим через М постоянную, превосходящую все значения | Dkh (х) |,.
\k\ ^m- Очевидно. \D!h(yx)\ ^\}M. Производные функции ц>(х) мы
должны оценить лишь при \х\ -^— . поскольку вне этого шара функ-
функция h(vx) равна 0. В указанной окрестности мы имеем max |Dm<p(Jt)| =
== о(I)(бесконечно малая величина вместе с —). Интегрируя это соот-
соотношение, получим max |Dm~1<p| = о I—J, .... тах|От~Лр | = о
Отсюда
max|D*<p (х)|< У С{ тах|С*~Уф(Аг)| • maxl D1 h{yx)\ <
В v I л^
I / I < *
т. е. стремится к 0 при v->oo, чем доказательство и завершается.
7. В качестве примера применения предыдущих теорем рассмотрим
интеграл по единичной сфере Q в л-мерном пространстве
J/((C0. X))d<0. (I)
Q
где /(£,) — обобщенная функция одномерного аргумента £, (§ 9, п. 7).
Нас интересует здесь вопрос о гладкости функции A), как функ-
функции от х. Более общим образом, поставим вопрос о гладкости
интеграла
/
Q
где g (ю) — бесконечно дифференцируемая функция на сфере Q.

88 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. Ц
Если /(£) сама бесконечно дифференцируема при всех |, то.
очевидно, интеграл B) есть бесконечно дифференцируемая функция
от х-
Рассмотрим случай, когда /(£)— обычная функция, бесконечно
дифференцируемая лишь при £, ф 0; покажем, что B) есть бесконечно
дифференцируемая функция при х ф 0.
Выберем на сфере систему координат (зависящую от х) так,
чтобы первой из них была величина £, = (ы, аг); совокупность осталь-
остальных обозначим через и'. При этом Ло = ./(£, о/. x)dh,d(ar, где
якобиан ./(£,, ь/, х) есть бесконечно дифференцируемая функция от £,,
о/ и х при условии, что хфО. Ъ,Ф \х\. Можно считать без огра-
ограничения общности, что функция /(£,) равна нулю в окрестности
точек |=±|л:|1 поскольку в противном случае мы всегда можем
написать /(£,) =/0 (£) +Л Ш. где /„(£,) удовлетворяет требуемому
условию, а /[ (£) всюду бесконечно дифференцируема.
Интегрирование в B) будем вести вначале по координатам и'.
Положим
co' = G(£,, л:);
функция G (|, Jt) также бесконечно дифференцируема по | и х при
л: =?t 0, %Ф ± [ лс |. Далее, мы имеем
]
= f
I
C)
и так как /D) в окрестности точек ±|л:| равна 0, интеграл C)
бесконечно дифференцируем по х при х Ф 0, что и утверждалось.
Пусть, наконец, /(£,) есть обобщенная функция, совпадающая
при |#0 с обычной бесконечно дифференцируемой функцией. Функ-
Функцию /(£,) можно считать финитной (отделив при необходимости
некоторое бесконечно дифференцируемое слагаемое). Тогда, в силу
теоремы п. 5, ее можно записать в форме
где /ft(|) — некоторые обычные функции. Заменяя их некоторыми
их первообразными, можно получить представление /(£,) в форме
где F (с) снова обычная функция. При £ ф 0 функция Z7 (£,) есть
решение обыкновенного дифференциального уравнения с обычной
функцией в правой части и по § 5, п. 4 является классическим

5 10] СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИИ 89
решением этого уравнения, в частности, является бесконечно диф-
дифференцируемой функцией вместе с /(£,). По доказанному,
есть бесконечно дифференцируемая функция от х при х Ф 0. Далее,
в силу § 9, п. 4 и § 7, п. 2.4 мы имеем
= ff (D ИГ г (о) rfo = /" / ((«, х)) g-
(о)
поэтому B) является бесконечно дифференцируемой функцией при
хфО вместе с Ф(аг), что и требовалось.
В частности, такие выражения, как
представляют собою бесконечно дифференцируемые функции от х
при х Ф 0; ниже, в § 11 мы укажем их значения.
Задачи. 1. Функционал /, сосредоточенный на замкнутом ограничен-
ограниченном множестве F, обращается в нуль на всякой основной функции ф (х),
равной нулю на F вместе со всеми производными.
Указание. Обобщить конструкцию п. 6, причем вместо функции h (vx)
рассмотреть е (х) * h (vx) = I ft (vg) e (x — £) dg. где е (х) равна 1 в некото-
некоторой окрестности множества F и нулю вне некоторой большей окрестности.
2. Согласно одной теореме Уитни*), всякая функция ф (лс,, ..., хп)
с непрерывными производными до порядка т на замкнутой ограниченной
области G (на самом деле у Уитни несколько более общий класс множеств)
может быть продолжена на все Rn с выполнением неравенств
max | £>*ф (х) I < Ст (G)-max | £>йф (х) | (| k | < т).
Пользуясь этой теоремой, показать, что функционал /, сосредоточенный,
в О. допускает представление
/= V D>fj(x).
\i\<m
где fj (x) — обычные функции, сосредоточенные в G.
Указание. Соответственно обобщить конструкцию пп. 2—3.
*) Доказательство можно найти в статье Л. Хёрмандера. О делении
обобщенных функций на полиномы. Сборник «Математика». № 5 A959),
стр. 117—130.

90 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. Ц
3. Дано, что функция / (х) при х ф 0 удовлетворяет линейному диффе-
дифференциальному уравнению Р (D) f (х) = 0 и в окрестности точки х = 0 имеет
особенность не выше степенной:
Пусть, далее, % (х) — фундаментальная функция оператора Р (£>) (§ 7, п. 2.
■ пример 9). Показать, что существует представление (при х Ф 0)
/(ж) = /?(£>) г (ж)+/„(*)•
где Р (D) /0 (х) = 0 всюду, R(D) — некоторый новый дифференциальный
оператор.
Указание. Существует обобщенная функция /, совпадающая с /(х)
при х Ф 0 (задача 4 к § 8). Выражение Р (£>) / равно нулю вне начала
координат и по п. 6 имеет вид R (D) 6 (х). Рассмотреть P(D) [f—R(D) t (x)].
4. Обозначим через S' совокупность всех обобщенных функций f£K',
представимых в форме конечных сумм
где fj(x)—обычные функции не более чем степенного роста при |лг|->оо,
Показать, что функционал / £ S' можно доопределить на функциях <р (х),
бесконечно дифференцируемых и удовлетворяющих условиям
xkDQ4,(x)\2dx<co (|ft|. |?|=0, 1.2....)
(пространство S). причем величина (/. q>) будет непрерывной на S в сле-
следующем смысле: если ||<PVL ->0 при v->cx> и любых фиксированных
к и q, то (/. Ф^->0.
Указание. Положить
(/. Ф> = Yi i~i)i S f>{x) D>y(x) dx- (l)
5. Показать, что обобщенная однородная функция f£K' любой сте-
степени А, (§ 6, задача 3) принадлежит пространству S'.
Указание. Если / действует на основную функцию ф, сосредоточен-
сосредоточенную в области 1 < | х I < 4, как т-я производная обычной функции / (х),
ограниченной числом М, то на основную функцию <|"Р- сосредоточенную
в области 2Р< |лг| < 2Р+2, она действует, как т-я производная функции,
ограниченной числом 2р(*+т)М Любая основная функция <р (х) предста-
представляется в форме суммы ряда функций вида фр.
6. Показать, что формула A) (задача 4) с обычными функциями fj(x),
возрастающими при | х \ -> оо не быстрее некоторой степени | х |, дает общий
вид линейного непрерывного функционала / на пространстве 6".
Указание. Показать, что существуют k и q, для которых функцио-
функционал / непрерывен по норме llqjfcj. Далее, повторить применительно к дан-
данному случаю рассуждения п. 3.

§ Ю|
СТРУКТУРА ОБОБЩЕННЫХ ФУНКЦИИ 9V
7. Известно, что обобщенная функция f£K' для любой основной функ-
функции ф(-*)- сосредоточенной в области |л|<;1, удовлетворяет неравенству
где С р и т — постоянные, а ||«р||т имеет тот же смысл, что и в п. 3.
Показать, что / продолжается с пространства К на пространство S.
как непрерывный линейный функционал.
Указание. Рассмотрим функцию г|> (х) £ К. сосредоточенную в шаре
| х К 1 и такую, что ее сдвиги в сумме дают I (§ 8, задача 3):
со
1 = 2 ф (-*+^v)-
v=0
Любую функцию <p£S можно представить в форме
V=0 v=0
где <pv (x) = q> (x — /tv) ty (х) сосредоточена в шаре | x | ■< 1. Показать, что-
|q>v||m при v->oo стремится к 0 быстрее любой отрицательной степени | ftv|.
Положить
со
(/•<Р)= 2 (/• «Pv(JC+*V»
v=0 %
8. Будем говорить, что обобщенная функция f £К' имеет при |jt|->oo
рост не выше степенного, если функция от h
растет при | Л | -> оо не быстрее некоторой степени | h |. какова бы ни была
основная функция <р£#. Показать, что в таком случае f£S'.
Указание. Вначале показать, что для функций <р с фиксированным
носителем те степени | Л I. которыми оценивается рост функции A), ограни-
ограничены. Для этого, предполагая противное и пользуясь тем, что указанные
степени не меняются при умножении <р на константу, построить основную-
функцию <р вида ^^v^vW (см- § 2- заДача 2)- Для которой функция A)
V
растет быстрее любой степени Л. Далее, имея неравенство
с фиксированным q. показать, что в качестве Сщ можно взять C||q>||m с не-
некоторым фиксированным т (тот же прием!). Тем самым задача сводится-
к задаче 7 (В. П. Паламодов).
9. Обозначим через Dm линейное пространство финитных функций <р (х),
имеющих непрерывные производные до порядка т. Сходимость в Dm опре-
определяется по правилу: <pv (х) -> 0 в £>,„, если все <pv (x) обращаются в нуль
вне одного и того же ограниченного множества и последовательность <pv (-v>
стремится к 0 равномерно вместе с производными до порядка т. Показать,
что Dm содержит К в качестве всюду плотного множества.
Указание. Использовать идею § 8. п. 3.
10. Показать, что всякий линейный непрерывный функционал f £К'
с порядком сингулярности s(/)<;m может быть распространен с К на

92 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [Гл. ц
все Dm как линейный непрерывный функционал; если же s(/):>m+l, то
такое распространение, вообще говоря, невозможно.
Указание. Использовать определение функционала с s (/) <J щ.
Функционал —, имеющий порядок сингулярности 1 (§ 3. задача 3). ие может
быть распространен с К на Da (пространство финитных непрерывных
функций).
11. Найти общий вид линейного непрерывного функционала на Dm.
Указание. При т = О из теоремы Рисса (Анализ III, гл. VI. § 7)
получить представление
(/■ Ф)= J <
где ц — мера Стилтьеса с (локально) ограниченным измерением.
В общем случае пространство Dm изоморфно пространству производных
m-го порядка функций <р ££>,„. являющемуся замкнутым подпространством
в прямой сумме пространств Do. Использовать теорему Хана-Банаха о про-
продолжении линейного функционала (Анализ 111, Дополнение).
Оте. (,.,)=
|ft!<m Rn ил1 ••• uxn
/
где ц. (x) меры ^ильтьеса с (локально) ограниченным изменением.
§ 11. Некоторые специальные обобщенные функции
В различных приложениях играют роль конкретные обобщенные
■функции х1^, х1^, гк и связанные с ними. Мы рассмотрим их свой-
свойства в этом параграфе.
1. Рассмотрим функцию х\. равную хк при х > 0 и 0 при х < 0.
Мы хотим построить и изучить отвечающую ей обобщенную функ-
функцию. При Re К > — 1 эта функция определяет регулярный функ-
функционал
со
X. A)
Числовая функция A), очевидно, аналитична по к; она имеет произ-
производную по 7-. равную
Г xKlnX(p(x)dx.
Это означает (ср. § 8, п. 6), что функционал д:^ аналитичен по Я.
при ReA,> — 1. Мы желаем продолжить его аналитически во всю

§ II] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 93
плоскость переменного X. Правую часть формулы A) перепишем
в виде
1
1
f
f [if, (x) - ф @)] dx + / *Чр {x) dx + |i^-. B)
0 I
Первое слагаемое определено для Re 7- > — 2, второе — для любых к,
третье — для к ф— 1. Следовательно, функционал A) аналитически
продолжается на область Re7,>—2, Кф— 1.
Аналогичным способом строится продолжение функционала х*^
на область Re^>—п—1, Хф— 1, —2 —п:
со
I Л
x =
k-l
И здесь правая часть дает регуляризованное значение интеграла,
стоящего слева. Тем самым обобщенная функция х1^ определяется
для всех К Ф — 1, — 2, ...
В полосе —п—l<Re^<—п формула C) может быть пре-
преобразована к более простому виду:
СО
= f х* [Ф (х) — Ф @) - *ф' @) - ... - (я^}1 ф(«-1) @)] dx, D)
о
в силу того, что в этом случае при 1 ^ k <Г п
со
Формула C) показывает, что (х1^, ф), как функция от к, имеет
полюсы 1-го порядка в точках 7- = —1, —2, —3, .... причем ее
„(ft-l) ,Q<.
вычет в точке Х = — k равен -у-—тгг-. Так как фС*-1)^)^
= (—1) ~ (б ~х\х), ф(х)), то, следовательно, сам функцио-
функционал х^ имеет при Х = — k полюс 1-го порядка с вычетом

94 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. [,
2. Рассмотрим теперь функцию х\, равную | jc |^ при х < 0 и о
при х > 0. Для Re А, > — 1 эта функция определяет регулярный
функционал
(**. ф)= / ИЧ{x)dx. A)
—со
Этот функционал можно продолжить в полуплоскость Re 7,^— 1
таким же образом, как х^. При этом проще всего, заменив х
на —х, представить (х\, ф) в виде
со
(ХК ф (X)) = J *1ф (— X) dX == (Х\, ф (- X)).
о
Это позволяет немедленно перенести все результаты, полученные
для функционала л:^, на функционал х\, заменив в соответствую-
соответствующих формулах функцию (р(х) на ф(—х). При этом фигурирующие
в формулах выражения ф(/)@) заменятся на (—1)^(-"@).
В частности, мы видим, что обобщенная функция д:^, так же
как и х^, существует и аналитична во всей плоскости К, за исклю-
исключением точек Х = —1, —2, ...; в точке Х = — k обобщенная
функция Jt^ имеет простой полюс с вычетом , ' .
Величину (д:^, ф) в полосе —п—1 <ReA,< — п можно вычи-
вычислить по формуле
СО
= / *fc [ф(~*)-Ф(О)+*Ф'@)- • ■ • -^п!1^'1
о
dx-
3. Обобщенная функция / называется четной, если
(f{x). Ф(*)) = -(/(*). Ф(-*)).
и нечетной, если
(J(x), <р (ж) ) = (/(*). ф(—*)).
Из выведенных в пп. 1—2 обобщенных функций составим следующие
четную и нечетную комбинации:
1*1*" = *^ + *^. A)
K x*t — xl. B)

^ И] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 95
Изучим особенности обобщенных функций | jc|^ и |х|*'sgn л\
Так как обобщенная функция д:^ имеет при %=■ — k полюс
с вычетом , .. Ъ(Ь~1\х), а функция хк—полюс с вычетом
(К 1I —
_—L--—-6tfe-1>(л:), то обобщенная функция |jc|** имеет полюсы только
прИ Я,=—1, —3. —5 — 2т — 1, ... Вычет \х\1 при
Я, = — 2т — 1 равен ^J^ 6B"° (х). В точках К = — 2т (т = 1, 2 )
обобщенная функция |jt| определена', при этих к мы, естественно,
будем вместо |Jt|~2m писать х~2т.
Аналогично обобщенная функция |д:| sgnx имеет полюсы в точ-
точках К = — 2, — 4 — 2т, ... с вычетом при К = — 2т,
равным ~ пт —1I б*2"*'(*)• При Х = — 2т— 1 (т = 0, 1, ...)
обобщенная функция |л:|*^пл: определена, и мы вместо |x|~2m~1sgnA:
будем писать х-2т~1. Таким образом, обобщенные функции х~"
определены у нас для всех га=1, 2, ...
Дадим непосредственные определения обобщенных функций \х\1'
и |jc|xsgn.x:. Для этого воспользуемся формулами D) п. 1 и B) п. 2;
в полосе — п — l<Re^< — п
{х\, Ф) =
— Ф@) — хф'(О)— ...
[, Ф) =
= / **■ [ф (— *) — Ф @) -4- *Ф' @) — ... — (~(яВ.Г1^"'1'ф<"-1» @)] их.
Заменяя здесь п на 2т, складывая и вычитая, находим
оо
A*1*. ф)=/**■{ ф (*)+<р (—*)—
о
- 2 [Ф@)+£ф*@) + ... ■+- B^!Г2)
ОО
, ф)=у л^|ф(л:) — ф(— л:) —
[

96 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. п
Первое разложение сходится при — 2от — 1 < Re % < — 2от — 1,
второе при —2т — 2 < Rek <—2т. В частности,
(— x) —
- 2 [ф @) + |i Ф" @) + ... + ~^ Ф<2-2> @)] } dx, E)
Например,
(х-2. ф) =
о
со
(л:, ф)= / ~ —— dx; (8)
6
последнее выражение совпадает с главным значением по Коши инте-
интеграла от (см. § 3, п. 3, пример 2):
J ~irdx-
—со е J
4. а) Умножение на функцию. Проверим справедливость
формулы (от — натуральное число)
v-rn . v^ у-т+К О, -j- 1 О  /1\
Л Х+ Х+ (A. =f= I, Z, ...) {I)
Формула требует доказательства, так как правая и левая части имеют
независимые определения. Доказательство простое: правая и левая
части аналитичны по К и совпадают при Re?. >—I, следовательно,
совпадают в их полной области аналитичности, т. е. во всяком слу-
случае при всех Кф — 1, —2. ... Но правая часть аналитична также
и при 7- = —1 —от, поэтому в этих точках и левая часть
сохраняет аналитичность; в частности, мы имеем
lim xmxh, =х™-ь (k=l, 2 от).

5 И] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 97
Таким образом, формула A) справедлива и при К = — 1 —щ,
если левую часть понимать как соответствующий предел. Аналогично
Xmx^--Xm + K.f_\уп (Кф — т— 1, — ОТ — 2, .. .), B>
xm\x\k=\x\m+k(sgnx)m '(Хф—т—1.—т — 2 ), C>
xm\x\Ksgnx=\x\m+K(sgnx)m+l (ХФ— от— 1, — от — 2, .. .)• D)
В частности, при любых натуральных k и от
хк • х-7" = хк-т. E)
Наконец, если fix) — любая бесконечно дифференцируемая функция,
имеющая при х = 0 корень кратности т, так что / (х) = xmg (x),
g @) Ф 0, мы можем написать
/ (х) x\=g (х) хтх\ = g (х) л;™+\
ft xm-ft. F)
б) Дифференцирование. При Re К > 0 мы имеем очепид-
dx
ное равенство +. = Я,х^~', т. е. (л:^, ф'(л:))^—(Ал:^-1, ф(л:)).
Так как обе части последнего равенства аналитически продолжаются
в плоскость (с выколотыми точками 0, —1, ...) то, в силу свойства
единственности, равенство будет справедливо и во всей плоскости.
Таким образом,
(кфО. —1. —2, ...)• (I)
Аналогично
dxK
__^ = _Я,л»-1 ф=И=0, — 1, —2). B)
dx - v ' ч 7
Если ^ = 0, то л:^ = 8(л:), хК_ — 6 (—х) и дифференцирование про-
проходит по уже известным формулам (§ 4, п. 3)
е'(лг)=6(л:), в'(—д;) = —6(лг). .
Далее,
^^+)^ =l\x\^ D)
AФ0, —1, ...)•
Правая и левая части равенства C) допускают аналитическое про-
продолжение на четные отрицательные значения Я,, правая и левая части
равенства D) — на нечетные отрицательные X.
7 Г. Е. Шилов

98 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. ц
В частности, при Я, = — п получаем
— (*-"):= — пх-"-1 (пфО). E)
Обращая формулы A)—E), получаем выражения неопределенных
интегралов от наших обобщенных функций. В частности, при любом
т ф 1 из E) мы получаем
/х-т+\
*-** = =й+Г + С- F)
Если /я=1, то формула F) не позволит найти соответствующую
первообразную. Но мы знаем (§ 4, п. 3), что соответствующей пер-
первообразной служит In Jjt|:
= ln\x\-\-C. G)
Б. Полагая r = "\fx2y-\- ... +-*v рассмотрим функционал г\
действующий по формуле
Jx, A)
которая имеет смысл при Re^> — п. В силу возможности формаль-
формального дифференцирования
ж(г\ ф)= J
функционал гк представляет собой аналитическую функцию от Я,
в области ReA,>—п. Для Re^^ — п функция гк локально неин-
тегрируема; мы определим функционал гк методом аналитического
продолжения.
Переходя в интеграле A) к сферическим координатам, приводим
его к виду
где d£ln(r) — элемент сферы радиуса г. Внутренний интеграл можно
представить в форме
0,@

5 11] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 99
где Qn означает поверхность единичной сферы в л-мерном простран-
пространстве, a Sr [ф] есть среднее из значений функции <р (х) на сфере ради-
радиуса г. Итак, мы приходим к формуле
со
(r\ q>) = О„ J>+«- 'S, [Ф] dr. B)
о
Установим некоторые свойства функции Sr [ф]. Мы утверждаем, что
функция Sr [ф] (определенная при г^Ь) финитна, бесконечно
дифференцируема и все ее производные нечетного порядка
обращаются в нуль при г = 0.
При достаточно большом г функция ф(х) обращается в нуль:
поэтому и ее среднее Sr [ф] обращается в нуль; таким образом,
Sr [ф] — финитная функция.
Очевидно также, что Sr [ф] бесконечно дифференцируема
при г > 0.
Чтобы убедиться в наличии всех производных у функции Sr [ф]
и при г = 0, разложим функцию <р(х) по формуле Тейлора с оста-
остаточным членом R2m+i порядка r2m+l. Тогда будем иметь
адм-
Ясно, что каждое слагаемое подынтегральной суммы (кроме оста-
остаточного члена), содержащее нечетное число множителей Xj, после
интегрирования обращается в нуль. Слагаемые подынтегральной
суммы, содержащие четное число, скажем 2k, множителей Xj,
после интегрирования и суммирования дадут член вида akr2k. Итак,
мы получаем
= Ф @) + агг2 -Ь а2/Ч + ... + атг*т + 0 (г2"^)- C)
Это выражение показывает, что при г = 0 функция Sr [ф] имеет
производные до порядка 2т, причем нечетные производные равны
нулю. Так как т можно взять произвольным, то Sr [ф] бесконечно
дифференцируема при г = 0 и все ее нечетные производные при г = 0
обращаются в нуль.
Отсюда следует, что функцию Sr [ф] можно рассматривать как
четную основную функцию переменного г. Интеграл B)^ в таком
случае можно понимать как результат применения функционала ЙД^
(\i = X-\-n—1) к основной функции 5£[ф]. Но мы хорошо знаем,
что функция %\ аналитическая при Re[A> —1 (т. е. Re>,> — п),
7*

100 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. ц
допускает аналитическое продолжение на всю плоскость ц, с исклю-
исключенными точками [*■ = — 1. — 2, ... (Я. = — п, — п-\- I, ...), в ко-
которых она имеет полюсы 1-го порядка; при этом вычет в полюсе
р, = — т (к = —п — т-\- 1) равен
(от —1)! " ~ *"■" (от—1)! t
Но так как нечетные производные функции S% [ф] обращаются в нуль
при | = 0, то полюсов, отвечающих четным значениям т, на самом
деле нет. Остается серия полюсов, отвечающих значениям т=\, 3.
5, ... или, что то же, Я.== — п, —п — 2, —п — 4, ...
Заметим, что вычет функции r\Sr[<p] при Я = —л — 2k (& = 0,
1, ...), как вытекает из вышесказанного, равен
BA)! BA)!
D)
В частности, в точке Я = — п функция (/■*•, Sr [ф]) имеет полюс
1-го порядка с вычетом 0л50[ф] =О„ф@). Это означает, что обоб-
обобщенная функция rh при Я. = — п имеет полюс 1-го порядка с выче-
вычетом 0„6(аг).
6. Пусть со = (сй1 соя) — точка единичной сферы Q в про-
пространстве Rn. Обозначим (со, х) = а1х1-{- ... -\-и>„хп. Рассмотрим
интеграл
Интеграл существует, как собственный, при Re Я, > 0 (и, как несоб-
стЬенный, при ReJi> — 1). Он представляет собою некоторую функ-
функцию от jc = (jc1, .... хп), которую мы пока обозначим F(x, Я). Эта
функция от х сферически симметрична: если h означает некоторый
поворот в пространстве /?„, то
F(hx, Я) = Г |(w, hx)\%da= Г |(Л'©, Ar)|^rfw= Г |(w', x)\hda/,
а а а
где ш' = а'и, и h' = h~l означает поворот, обратный к повороту h.
Таким образом. F(x. Я) есть функция от r = ~\fx\-\- ... +*„
и Я. Обозначим ее теперь F(r. Я). Заменяя х на cue, где а—поло-
а—положительное число, мы находим
F(ar. Я)= Г|(со, ax)\kdai = aK Г |(w, x)\hdaj = aKF(r, Я).
a q

s 11] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 101
Полагая здесь г = 1. получаем
F(a, k) = alF(l, к) = С(к)а\
Таким образом, F(r, к) пропорционально /•*-. Остается найти коэф-
коэффициент С (Я,). Мы имеем C(k) = F(e, к), где е—любой единичный
вектор. Положим е = @, 0 0, 1). Мы получим тогда
я
2
С (Я.) = / | со„ f*o = 2 J cos" е„_, sin" 6n_, &„_&„_»
а о
где 6„_1 — угол между е и со, Ц,_! — поверхность единичной сферы
в и — 1 -мерном пространстве. В результате
= 2Qn_l f
*
„_, г
поскольку по формуле C) п. 7 § 10 и по классической формуле
для В-функции *)
at
о
Запишем полученную формулу в следующем виде:
/
(СО, Х) \h , ГК n -5— /пч
Рассматривая правую и левую части как функционалы на про-
пространстве К, мы будем строить аналитическое продолжених их во всю
плоскость к.
Функция гК, как мы знаем, имеет аналитическое продолжение
во всю плоскость к с простыми полюсами в точках — п, — п — 2,
— п — 4. ... Известно, что гамма-функция Г(£) имеет простые по-
полюсы в точках 0, —1, —2, ...; следовательно, Г1—^~—J имеет
простые полюсы при к = — п, —п — 2. —п — 4, ... Мы видим,
Что числитель и знаменатель отношения ——г—■.—г- имеют простые
*) См., например, Г. М. Фихтенгольц, Курс дифференциального
и интегрального нсчислення, т. 11. 1962, стр. 769.

102
СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. Ц
полюсы в одних и тех же точках; следовательно, само это отно-
отношение есть целая аналитическая функция от А,. Найдем, в част-
частности, его значение при Я, = — п. Оно равно отношению вычетов
числителя и знаменателя; вычет числителя, как мы знаем, равен
Qn6(je), вычет знаменателя мы легко получим из функционального
уравнения для гамма-функции
Именно, полагая £ = —^—,
найдем
C)
при Я,—> — п
и следовательно, вычет ГI—^—J При Я, = — п равен 2Г A) = 2.
В
В итоге
\
D)
Рассмотрим теперь аналитическое продолжение левой части в фор-
формуле B). Аналитическое продолжение функционала 11 \1 имеет про-
простые полюсы А, =—1, —3, ... Но эти же простые полюсы имеет
и ГI—^—I. Найдем значение
,/_*+!
)
л=-!
т—1
«Bт) (|)
Вычет функции ||| при Я, = —1т—1 равен 2 . ■ (п. 3). Вы-
Вычет функции Г I—~-——I в этой же точке найдем из функционального
уравнения C), именно,
2 Г/Л + 3\ 2 2 г
К +
A-f 1
\ 2 )

. 11] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ ЮЗ
откуда
В итоге
l=-2m-I
При Я, = — 1т числитель и знаменатель не имеют особенностей.
В результате, в зависимости от четности или нечетности я, мы по-
получаем равенство
я-1
ji
о
. л;)) rf(O (я нечетное),
E)
I, x)~" da (я четное).
Эти равенства называются «формулами разложения дельта-функции
на плоские волны». В применении к основной функции ф они дают
решение «задачи Радона»: восстановить значение функции <р(х) при
х = 0, зная ее интегралы по гиперплоскостям (со, л;) = |.
Задачи. 1. Каноническая регуляризация. Каждой функции
f (х\
S (-*) = р/ \ • r^e / (■*) бесконечно дифференцируема, а Р (х) — многочлен.
f (X)
поставить в соответствие функционал g^Ki так, чтобы
а) сумме функций gi (x) -\- g2 {x) соответствовала сумма функционалов
б) произведению функции g (x) на бесконечно дифференцируемую функ-
функцию а (х) отвечало произведение а (х) ■ g в К'',
в) производной (в обычном смысле) g' (л:) отвечала производная g' в К'\
г) функции g{x) = f (х) (т. е. при Р (х) ^ 1) отвечал функционал
(/■ «0= Jf{x)ff{x)dx;
д) четной функции g (jc) отвечал четный функционал g. нечетной — не-
нечетный функционал.
Указание. Функция g (x) единственным образом представляется в виде
где Л (л:) бесконечно дифференцируема. Ajk — постоянные; поставить в соот-
соответствие функции g{x) функционал £= ^ А1*(х — xj)~k
2. Показать, что условиями а) —д) каноническая регуляризация опре-
определена однозначно.

104 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. ц
Указание. Пусть функции — отвечает функционал g; тогда фу нкции
х — = 1 отвечает функционал xg= 1; отсюда g = \- g0, где ga сосредо-
сосредоточен в точке х = 0. Используя теорему п. 6 в § 10, показать, что g0 = СЬ (х).
Так как g должен быть нечетным функционалом, С = 0. Для дальнейшей
проверки использовать в).
3. Показать, что функция ^^ (Re Л > — 1) продолжается во всю
плоскость переменного X, как целая аналитическая функция, и найти ее зна-
значения при X = —1, —2, ...
Отв.
>(*) (я = —1. -2. ...).
4. Доказать формулу
d я
Л
dx Г(>.+1) Т(К) "
Указание. Проверить при Re X > 0 и использовать аналитическое
продолжение.
5. Введем обобщенные функции х~" и xZ" по формулам
оо
;", ф) = f х-п [Ф(я) -<р@) - ... - {fZ\)\ «р^'
е с1 -Л>]dx-
— 1 ~~\
... —(—I)" *__ ф(п~'> @NA— х) \dx,
где 6 A — х) равна 0 при х > 1 и 1 при х < 1.
Показать, что функция х2" сосредоточена на полуоси ^>0н на любом
1
отрезке [а, *], 0 < а < Ь. совпадает с обычной функцией —; функция х_
сосредоточена на полуоси х ^ 0 и на любом отрезке [с. d], с < d < 0, сов-
совпадает с обычной функцией —„-. Далее, проверить формулы
„—2т | „ — 2т . „ — 2ш
—1т—1 — 2т — 1 . —2т—1
л+ х_ —Л ,
r~n— r~n+1
Х-Х+ Л+ ,
[Х+ ) - ПХ+ -+ п, О (.
(xZn)' = n^Z"-1 - -^р- 6(nJ (я).

j II] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 105
6. Показать, что функции х^ и х\ — однородные функции степени X
(при любом X Ф — 1, — 2. ...).
Указание. Обе части равенства (jc^, <p(rf. x) ^ = t~K~ l(x^_, <p (л:))
аналитически продолжаются по X из области Re X > — 1 на всю плоскость X
за вычетом особых точек X = —1. —2. ...
7. Показать, что любая обобщенная однородная функция /£/(| степени X
удовлетворяет уравнению
xf' = Xf.
Указание. Соотношение (/. <р {tx)) = tf"*- (/, <р (х) ) продифферен-
продифференцировать по t н затем положить t=\.
8. Показать, что А + от линейно независимых решений уравнения
xky(m) ^ = q
указанных в задаче 1 § 5. образуют полную систему линейно независимых
решений.
Указание. При х > 0 решение у {х) есть некоторый полином Р (л-+),
при х < 0 решение есть некоторый полином Q (х_); разность у — Р(х+) —
— Q (л:_) сосредоточена в точке 0 н согласно п. 6 представляется в форме
р . р
2 o,j 6(Л (*); подставить у = Р (х+) -\- Q (*_) -f- 2 ai biJ4x) B уравнение
и найти условия на коэффициенты.
9. Показать, что общее решение уравнения ху' = Ку имеет вид
при Хф — 1. — 2, ....
) (х) прн X = — п.
Указание. Решение у (х) при л: > 0 совпадает с Сх*^, при л: < 0
с С2л:'' (при X = — п последние выражения не являются решениями, но это
неважно). Разность у — Gxx+ — C2xh_ сосредоточена в точке х = 0 и в силу
р р
§ 10 имеет внд 2 aft6<ft) (■*)• Отсюда у = Схх\ + C2xh +. 2«ft6(ft'(jc). Под-
ft=0 ft=0
ставить в уравнение н найти условия на коэффициенты.
Замечание. Решение задачи 9 дает описание всех однородных обоб-
обобщенных функций в К\ (см. задачу 7).
10. Найтн интеграл
/(■*) = //((»■ x))d<s>.
а
если
а) 6(*>О
б)
в)
Указание. Использовать формулу B) п. 6; в случае в) дифференци-
дифференцировать по X.

106 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. Ц
Отв.
а)
О при k нечетном,
Cr"k~l при k-\- I < п. к четном, и при
k = и. и4-2, .... если и четно.
ft-n-i
СД 2 б (л:) при k-\-l^n. к четном, п нечетном;
О при k четном.
Cr~k при k < n, k нечетном и
= я+1. n-f-З если и четно.
к-п
СД 2 Ь{х) при А!>и, к нечетном, и нечетном;
б) / {х)
в) / (х) = dr* In r -f
11. Показать, что сферически симметрическая однородная функция
степени X есть Сгх {Хф—п. —п — 2, ...).
Указание. Пусть сначала Re X > — п. Функционалу /£К'„ поставим
в соответствие функционал g^K[ следующим образом. Пусть ф(£)(ЕЛТ| —
четная функция; тогда ф (г) принадлежит /С„. Положим (g-, ф (£)) = (/, ф (г)).
Для нечетных ф^АГ| положим {g. ф) = 0. Функционал g является четным
однородным функционалом степени п — X — 1 и (по задачам 7 и 9) имеет
вид С | х \"+t--1. Таким образом, для сферически симметричной функции ф (г)
(/. Ф (г)) = С f r"+J-V (r) dr) = С, f r\(r)dx.
0 *„
По задаче 2 § 6 (/, ф) = Сх (гк. ф) для любой ф ^ К„. Если Re X < — п. го
при некотором целом т будет ReA + 2/M>—п; поэтому r2mf=Cr2m+^.
Отсюда при х Ф0 f совпадает с Сг\ Если X Ф —и, —п — 2. .... то функ-
функционал / — Crh сосредоточен в 0 и есть линейная комбинация 6-функции
и ее производных; по задачам 6 и 7 § 7 / — 0^ = 0.
Примечание. Для Х = — п. —п — 2, ... см. § 15, задачу 4.
12. Пусть f(x) = f(xl .*:„).> О — однородная функция степени 1.
Рассмотреть функцию /* (jc), как аналитическую функцию от X. Она опре-
определяет функционал на пространстве Кп при Re X > — и; построить ее анали-
аналитическое продолжение в область Re X > — п — 1 и найти вычет при X = — п.
Указание. Пусть S — единичный шар и п — единичная сфера про-
пространства /?„; тогда при Re X > — и
(Л Ф) = J / \х) [ф {х) — ф @)] dx -f f fh (х) ф (х) dx + y @) J / W d*
S
Rn-S
Так как /*■(■*) — однородная функция степени X. то

§ II] НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОБОБЩЕННЫЕ ФУНКЦИИ 107
И
Отсюда по теореме Гаусса — Остроградского
Таким образом.
(Д ф) = f fx (х) [Ф (*) _ Ф @)] rfjc -Ь У* / (*) ф (х) dx +
D С
/
й
где все члены допускают аналитическое продолжение в область Re Л > — п—1.
Вычет функционала fh при Х = — п равен' j /~" (x)da-b(x).
а
13. Пусть f{x) = f(xx хп) — однородная функция степени —n-f-1-
Она локально интегрируема и определяет функционал / по формуле
(/■ Ф) = J / (■*) Ф (х) dx.
Показать, что производные функционала / можно определить по формулам
+ ф@) Jf(x)xkdo.*
I лг 1 = 1
Указание. В формуле

108 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. Ц
интегралы типа дивергенции преобразовать по формуле Гаусса — Остро-
Остроградского.
14. Проверить формулу Д (-^zy) = crfi(.x) прямым дифференцированием.
Указание. Первые производные вычислять непосредственно, вторые —
с использованием задачи 13.
15. Показать, что однородная функция / (х) степени — п удовлетворяет
соотношению
*=i * /
и найти с.
Указание. Использовать задачу 13.
Отв.
с= J / (х) da.
1*1=1
fix)
16. Возможно ли сопоставить каждой функции g (х) = т функцио-
функционал g£Kn так, чтобы выполнились условия
(х) + a2g2 (x) -* a,g, + a2£2 (a, н a2 — числа);
2) a{x) g (x) -*a(x) g (a (x) — бесконечно дифференцируемая функция);
4) если g (x) — обычная функция, то (g, <р) = Г g {х) <р (л:) dxi
Отв. Нет; наприм
гласно формуле Эйлера
п .
Отв. Нет; например, для g (х) = —^ мы должны были бы иметь со-
сов то время как по задаче 15 мы имеем
2 Ш; (Xkg) = f S(l)di-6(х) Ф0. (В. В. Грушин).
При п > 2 тот же вывод получается непосредственно из равенства
Д(/-2-") = с„6(*).
Примечание. Результат задачи 16 показывает, что для нескольких
переменных каноническая регуляризация (см. задачу 1) на совокупности
функций вида ■ д невозможна.

§ 12] СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИИ 109
§ 12, Свертка обобщенных функций
1. Пусть f {х) и g(x)— обычные функции переменного х.
— со < х < со. Образуем выражение
О)
которое называется сверткой функций f(x) и g{x).
Этот интеграл не всегда существует. Известно, например, что
если /6^-i(—°°> со)- £f€^i(—°°» °°)' то f*g существует почти
всюду на (— со, со) и также есть функция из Lx (— со, со) *). Мы
здесь рассмотрим другой случай существования свертки; именно,
предположим, что одна из функций f(x), g(x) финитна.
Пусть, например, финитна f(x), так что она обращается в 0
вне отрезка [а, Ь]. Покажем, что f*g существует почти для всех х
и представляет собою обычную функцию. Для доказательства возьмем
любой промежуток [с, d] и рассмотрим двойной интеграл
й Ь
f f\f(.l)\\g(x~l)\dldx. B)
с а
По теореме Фубини его можно вычислять в любом порядке
Сначала рассмотрим
— 1) I dx \ d\. C)
В фигурных скобках стоит ограниченная при а ^ | -< b функция
: — у | dx = Г
где О — первообразная от |g"(JC)|. Это доказывает существование
интеграла C), а с ним и B). Меняя порядок интегрирования, полу-
получаем существование почти всюду интеграла
D)
•) Анализ III, гл. VII. § 3.

ПО СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. [[
а с ним и интеграла A); кроме того, функция D) суммируема по х
в промежутке с -^.х <Cd, а вместе с тем суммируема в этом про-
промежутке и функция A).
Итак, в рассматриваемом случае (/ финитна) функция / * g сум-
суммируема в любом конечном промежутке и является, следовательно,
обычной функцией.
Пусть теперь g(x)— финитная функция, сосредоточенная, напри-
например, в отрезке [с, d\. Тогда интеграл A) также в действительности
берется в конечных пределах
х-с
f*g = / /©*(* —I) <*!■ E)
x-d
По доказанному, существует свертка
d
g*f — f g<n)f(x — i))dn- F)
с
Сдечаем в этом интеграле замену переменного х — Л —|; мы по-
получим
х-с х-с
g*f= / *(* —1)/(б)<*1= / fa)g(x—i)di=f*g.
x-d x-d
что доказывает существование интеграла E) и его совпадение
с интегралом F).
Итак, свертка / * g существует и представляет собою обычную
функцию, если хотя бы одна из функций /, g финитна.
Найдем еще носитель свертки /* g по известным носителям
функций /Kg. Если (/ * g) (x) ф 0, то это означает, что множества
supp/(|) и suppg-(jc — |) = JC — suppg-(|) пересекаются, напри-
например в точке |0; так как |о£л; — suppg\ то Ar£|0-f-suppg-c=supp/+
-J-suppg- (арифметическая сумма!*)). Итак,
supp (/ * g) «= supp / + supp g.
2. Мы будем переносить теперь определение свертки на обоб-
обобщенные функции. Чтобы найти нужное правило, применим фор-
формулу A) к основной функции (р(х) и, не заботясь о существовании
*) Арифметическая сумма (разность) множеств А к В состоит из всех
точек g вида а + р (соответственно а — Р). где а £ А. р £ В.

5 12] СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИЙ Ц1
интегралов, переменим порядок интегрирования:
со ( со
\
= //(I) f S(x~
G)
Равенство G) делает естественными следующие определения *).
Определение 1. Для любой обобщенной функции f£К'
функция от |
(8)
называется сверткой обобщенной функции g и основной функ-
функции (р.
Определение 2. Для любых обобщенных функций fug
функционал / * g, действующий по формуле
(f*g. <P) = (/(I). (£*Ф)A)). (9)
называется сверткой функционалов / и g.
Разумеется, свертка существует не всегда, как и для обычных
функций- Во всяком случае, учитывая вышеприведенные рассуждения,
мы видим, что если / и g — обычные функции и одна из них фи-
финитна, определение 2 приводит к обычной свертке функций / и g.
Далее, пусть, например, / — произвольный функционал, £=6(л:);
тогда для любой основной функции ф
(f*g. Ф) =
т. е. /*б=/. Аналогично для произвольного g
(b*g, ф) = F(|)
*) Точнее, делает естественными для случая вещественных функций.
В случае комплексных функций эти определения соответствуют только
функционалам первого из четырех типов, указанных в § 3, п. 4.
Определения для остальных трех типов следующие:
if*g- ф) = (/• g * ф)| = (/• g * ф>2 = (/• £*ФK = G- g * Ф>4-

112 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. п
т. е. 6 * g = g. Таким образом, свертка с дельта-функцией всегда
существует, и функционал 6 при свертке играет такую же роль, как
единица при умножении. Если g — 6'(x), то
(/*£• Ф) = (/(!)• — Ф'A))= (/'(!)■ Ф (!))•
т. е. /*6' = /'. Аналогично и Ь' *g = g', так что результат свертки
любого функционала с 6' есть его производная.
3. Далее мы будем рассматривать свертку функционалов / и g
в общем случае.
Естественно ожидать, что свертка двух обобщенных функций
будет существовать, если одна из этих обобщенных функций финитна.
Мы рассмотрим в этом пункте свертку функционала g и основ-
основной функции ф. Поскольку ф(аг-(-|) есть также основная функция,
выражение г]з(|) — {g(x), Ф (■£ + !)) определено при каждом |.
Легко проверить, что функция -ф (£) = (g (х), ф (a: -j-1)) непре-
непрерывна и имеет непрерывные производные всех порядков. Действи-
Действительно, если |v—»|0, то функции фГ^Ч-^) стремятся к ф(л; + |0)
равномерно по х вместе со всеми производными и остаются сосре-
сосредоточенными в одном и том же фиксированном промежутке; таким
образом, <р(х + |v) —> Ф(-к-|-£) в К. и так как функционал / не-
непрерывен, то
Это доказывает непрерывность г]з(у. Далее, отношение
Iv
ПРИ ^v"*"^ имеет пределом ф'С-^ + Ео) равномерно по х вместе со
всеми производными; поэтому
так что il>(i) имеет производную, причем
^ (D = <*(*)•
Так как, с другой стороны.
то мы получаем цепь равенств
(#*ф)' = #*ф' = — g'*<p- A°)

12] СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИЙ ПЗ
Повторяя процесс, мы видим, что функция гЩ) имеет производные
всех порядков, причем имеет место равенство
(g- * ф)С) = g* q><9> = (—I)9 g-<9> * ф.
В общем случае функция г1>(|) не финитна и потому не есть основ-
основная функция. Отметим один важный случай, когда ij)(|) финитна:
это будет иметь место, если финитна обобщенная функция g{x).
Мы можем даже описать в этом случае носитель функции i|)(s)-
Пусть, например, g(x) сосредоточена на промежутке Д^ оси х,
а основная функция ф(л:) — на промежутке Д,р той же оси. Тогда
функция cp(JC-f-l) будет сосредоточена на промежутке Д,р— £,.
Чтобы свертка г1) = £-*ф была отлична от нуля, нужно, чтобы про-
промежутки Дг и Дф — | пересекались. Пусть имеется общая точка
■»1£АгП(Аср — |); так как i)£\ — |, то т]-|-|£Д,р, |£Д,р —ть
а так как т] £ Д^, то | принадлежит к арифметической разности
ДФ —Дг-
Таким образом, имеет место включение
supp (g * ф) с: supp (р — supp g.
Но очевидно, что эта разность располагается в некотором ограни-
ограниченном промежутке Д; вне этого промежутка г]з(|) равна 0 и, сле-
следовательно, она финитна.
Теперь покажем, что свертка с финитной обобщенной функцией g
есть линейная и непрерывная операция в пространстве К- Иными
словами, если ф = а^ -f- а2(р2- то S * Ф = ai (S * 4>i) ~\~ а2 (£ * Фг)- и
если (pv—>0 в К. то g*(pv—>0 в К- Первое утверждение очевидно:
Проверим второе утверждение.
Пусть дана последовательность ф^ стремящаяся к 0 в простран-
пространстве К- По условию, функции ФЛ!(л) все сосредоточены в фиксиро-
фиксированном промежутке Д; но тогда и функции g * ф сосредоточены,
по доказанному, в фиксированном промежутке Д — Д^. Покажем,
далее, что функции (й'*ФЛ,)(|) равномерно стремятся к 0- Нам дано,
что функции cpv(je) равномерно стремятся к нулю в промежутке Д.
так же как и их производные любого порядка. Допустим, что
4'v (I) = (g * %) (I) не стремятся" равномерно к нулю; это означает,
что для некоторого е > 0 найдется последовательность точек |v
Такая, что
8 Г. Е. Шилов

114 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. II
Точки ^ образуют ограниченную последовательность (£Д—Д )ш
которую можно предполагать сходящейся к некоторому |q. Но тогда
функции <PV(* + IV) вместе с функциями <pv(x) стремятся к 0 в про-
пространстве К; отсюда
что противоречит A1). Итак, ^v (£) — (g-* ф^ (|) равномерно стре-
стремятся к 0. Аналогично ^ (|) == g * ф^. ^ (|) = g * ф", ... равно-
равномерно стремятся к нулю; таким образом, tpv(|)->0 в К, что и тре-
требовалось.
4. Продолжая считать g финитным функционалом, рассмотрим
свертку / * g, согласно определению 2. Так как (g * ф) (|) есть
основная функция вместе с (р, то выражение
(/ * g> ф) = <
определено. Очевидно, оно представляет собою линейный функцио-
функционал от ф, так как для любых (рр ф2 £ К и любых вещественных а,
и с^, по доказанному,
(f*g, а1<р1 + а2ф2) = (/. й-*(а1ф1 + а2ф2)) = (/, а[^*ф1 + а2^*ф2) =
= сц(/*£. 4>i)+(h(f*g- Ф2)-
Далее, этот функционал непрерывен: если <pv->0 в К. то, по
доказанному, также и g*tpv->0 в К, откуда, в силу непрерывности
функционала /, также (/ * g, q>\ = (f, g *ф^->0.
Итак, если g — финитный функционал, свертка f*g
является линейным и непрерывным функционалом в простран-
пространстве К. .
Рассмотрим случай, когда g — любой функционал, а / — финит-
финитный. В этом случае {g * ф) (|) не есть основная функция, хотя она
и [бесконечно дифференцируема. Ясно, что операция g * ф остается
линейной. Она также остается непрерывной в следующем смысле:
если ф.^—>0 в К, то g"*<pv = il'v равномерно стремится к 0 на
любом промежутке Д вместе со всеми производными. Для до-
доказательства заметим, что значение функции г]) (|) = (g (х). ф (# + !))
при данном | для своего определения не требует полной информации
о функционале g(x); требуется знать этот функционал только в про-
промежутке, где сосредоточена функция Ф(л;+|), т. е. на носителе
функции (р(х), сдвинутом влево на величину |. В частности, значения
функции il\,(|) определяются свойствами функционала g только на
множестве A,j,v—%, где А^ — тот промежуток, на котором сосредо-
сосредоточена функция tpv. Поэтому значения функций i])v(|) на проме-

j 12] СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИЙ 115
жутке Д определяются свойствами функционала g на арифметической
разности Av — Д сг Д — Д, где Д — тот промежуток, на котором со-
сосредоточены все функции cpv. Умножая g(x) на основную функцию
е(х), равную 1 на Д — Д, мы не изменим на промежутке Д ни
одной из функций ч1\,(|); в то же время функционал eg уже финит-
финитный- Применяя предыдущую теорему, получаем требуемое.
Теперь применим к выражению g * ф функционал /. Выражение
</• S * Ф) имеет смысл, поскольку функционал / финитный. Это вы-
выражение определяет линейный и непрерывный функционал на
пространстве К- Линейность его вытекает из линейности свертки
g * ф. Для доказательства непрерывности предположим, что ф —> О
в К: тогда g *<pv стремится равномерно к 0 вместе со всеми про-
производными на любом промежутке оси, в частности в окрестности
носителя функционала /; а тогда, как мы знаем, и (/, g * ф \ —> 0.
Б. Итак, у нас имеется корректное определение свертки / * g
в двух случаях: когда финитный функционал стоит на первом месте
и когда финитный функционал стоит на втором месте.
В этом пункте мы построим явное выражение свертки / * g
через свертки обычных функций; из этого выражения будет, в част-
частности, следовать равенство / * g = g * /. где, например, / — финит-
финитный функционал. Как мы знаем, произвольный функционал g можно
записать в форме
где gk(x)— обычные функции, носители которых удаляются от на-
начала координат с возрастанием k. Отсюда
(г*ф)О =
ft=O
со 6-|
V4. .ft Г
ft=O n-|
ft=0
где [a, b\ — отрезок, на котором сосредоточена функция ф(лт).
В сумме в действительности лишь конечное (зависящее от |) число

116 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. Ц
слагаемых, поскольку при каждом | функции gk (x — |) на отрезке
[а, Ь\ становятся равными нулю, начиная с некоторого номера.
Из предпоследнего из выражений A2) видно, что производные
бесконечно дифференцируемой функции (g * <р) (|) при любом щ
имеют вид
ос 6-|
=]2(—1)ft
fe=O
= S(~I)ft7'gk(x-D<P{k+m)Wdx. A3)
k
k=0
Рассмотрим теперь свертку f * g. предполагая, что функционал
/(I) финитен. Такой функционал, как мы знаем, имеет вид
где /т(|) — обычные и притом финитные функции, сосредоточен-
сосредоточенные, например, на отрезке [с, d]. Мы получим
т=0
= 51 (- 1Г / /m (I) (g *> Ф)(т) (I)
т=0
Применяя формулу A2), находим далее
(J*g, ср) =
р d ( со
т=0 г ( ft=O
Число слагаемых в сумме по k теперь можно считать фиксированным,
например N. поскольку величина | меняется в ограниченных преде-

§ 12] СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИИ 117
лах. Поэтому можно изменить порядок суммирования и интегрирова-
интегрирования и получить формулу
р N
2
ra=O ft=O
m=0 ft=0
где fm*gk — свертка обычных функций. Эту же формулу можно-
записать в форме
(f*g. ф) = ( 2 2 с/™ * gk)lk+m)- ф) .
\т=0 ft=O /
или даже
(р со \
2 2с/»***)(*+Ж). ф .
т = 0 ft=O /
поскольку, по построению, слагаемые в сумме по k, начиная с N -\- 1-го,
переводят данную функцию ф(аг) в 0. Таким образом, искомая фор-
формула, выражающая функционал / * g через обычные функции,
имеет вид .
р со
f*g= 2 2(/т*^)(*+т)- С14)-
т=0 ft=0
К аналогичному выражению функционала / * g мы придем, если
будем считать / произвольным, a g финитным функционалом. В этом
случае в формуле A2) будет с самого начала конечное число, по-
положим р, слагаемых, и функция g * ф станет не только бесконечно
дифференцируемой, но и финитной, сосредоточенной например, на
отрезке [с. d]. Зато функционал / будет представлен уже в форме
бесконечной суммы
/2
ft=0
причем носители обычных функций fk (x) удаляются от начала коор-
координат с возрастанием к. Поэтому в применении к финитной функции.

118 .СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. [I
g * ф используется только конечное число, положим, N слагаемых:
ft=O m=0
Отсюда, по тем же соображениям, что и выше.
со р
П»?/D A5)
ll=i) m=0
Формулы A4) и A5) можно было бы положить в основание теории
свертки. Разумеется, на этом пути необходимо было бы доказать
независимость сумм A4) и A5) от выбора обычных функций Д и gm.
участвующих в представлении функционалов fug. a
6. Из формул A4) и A5) вытекает для общего случая коммута-
коммутативность свертки обобщенных функций
f*g = g*f- A6)
Равенство A6) имеет следующий смысл. Свертка обобщенных функ-
функций, строго говоря, определялась нами различным образом, смотря
го тому, на первом или втором месте стоит финитный функционал.
Пусть, например, финитен функционал /; тогда f*g и g*f имеют
различные определения. Формула A6) утверждает, что результат
в обоих случаях один и тот же. Действительно, в силу формул A4)

§ 12] СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИЙ 119
р со
и A5), мы имеем: если /= 2/(Г'(^). ff = 2 gftft)(■*)• то
т=0 ft=O
р оо
/•er=S 2(/и
т=0 ft=O
со Р
*r*/=2 2teft
ft=Om=O
Но для обычных функций /т и g-ft, как мы видели, свертка комму-
коммутативна:
fm*ek = gk* fm-
Поэтому, меняя порядок суммирования (что возможно, так как
в применении к каждой основной функции <р(л:) в выражениях A7)
остается лишь конечное число ненулевых слагаемых), мы получаем A6),
что и требуется.
7. Выясним, где сосредоточен функционал / * g. Пусть (/ * g, <р) =
= (/, g * ф) Ф 0; отсюда следует, что имеется общая точка | у носи-
носителя функционала / и функции g * ф:
I (Е supp /, |€ supp (g* ф)сsupp ф — supp g.
Положим | = т] — £, где т^эиррф, C6SUPPS"- Отсюда т] = |-|-
-f-C6suPP f~\~ supp g- Иначе говоря, если основная функция ф со-
сосредоточена вне множества supp/-f-supp g, мы будем иметь-
О * £• ф) = 0. Отсюда следует, что
supp (/ * g)c:supp / + supp g.
Последняя формула бесполезна, если носитель функционала g занимает
всю ось. Но если мы интересуемся функционалом / * g не всюду,
а лишь в ограниченной области О, то нам не потребуется полная
информация о функционале g; нам достаточно будет знать его
в окрестности множества О — supp /. Действительно, рассмотрим
основную функцию е (х), равную 1 на множестве G — supp / и 0 вне
некоторой окрестности V этого множества. Функционал eg требует
для своего определения знания функционала g только на области V.
Для любой основной функции ф, сосредоточенной внутри области О-
мы имеем
(/*A— e)g. ф) = (A— e)g, /*ф) = 0,
так как supp (/ * ср) £ О — supp/, а A—е) g сосредоточена на допол-
дополнительном множестве. Следовательно, для указанных ф
(f*g. (p) = (f*eg. ф).
что и доказывает наше утверждение.

120 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. Ц
8. В этом пункте рассматриваются операции предельного перехода
и дифференцирования для свертки.
Теорема 1. (Теорема о непрерывности свертки). Если /v—>■/
в пространстве К', то
в следующих случаях:
(а) функционал g финитен;
(б) функционалы /v финитны и, более того, сосредоточены
в одном и том же промежутке [а, Ь\.
Доказательство. Для любой основной функции
поскольку: a) g * <р есть основная функция вместе с ср.
б) g * Ф можно заменить на основную функцию, не изменяя ее на
отрезке [а, Ь\, где сосредоточены все функционалы /v. Отсюда
fv*g—*'f*g' что и требуется.
В силу равенства A6) аналогичная теорема справедлива для
случая, когда зависит от v второй аргумент свертки.
Теорема 2. (Теорема о дифференцировании свертки). Если
один из функционалов /, g финитен, то
Доказательство. Согласно определению производной и
свертки
((/*£)'. Ф) = -(/*£• Ф')= — (/- g*4>')\
<j'*g, <p) = (/'. £*ф) = — (/.(£*ф)');
if*g'. ф) = (/. g'*4>).
последние три выражения имеют смысл, если один из функциона-
функционалов /, g финитен, и совпадают в силу формулы A0).
9. Определение и основные свойства свертки переносятся на
случай обобщенных функций нескольких переменных без труда.
Если /(*! xn) = f(x) и g(xx xn) = g(x)— обычные
функции, то их сверткой (/ * g) (x) называется функция
(f*g)(x)=
Функция (/ * g) (x) существует почти при каждом х £ /?„. и есть
снова обычная функция, если хотя бы одна из функций f (x), g(x)
финитна; в этом случае свертка коммутативна:

§ 121 СВЕРТКА ОБОБЩЕННЫХ ФУНКЦИЙ 121
Пусть / и g — две обобщенные функции. Выражение
есть бесконечно дифференцируемая функция от |, называемая сверт-
сверткой обобщенной функции g и основной функции <р. Функцио-
Функционал f * g. действующий по формуле
называется сверткой функционалов fug. Он определен на Кп
и непрерывен, если хотя бы один из функционалов /, g финитен.
В частности, для любых fug
Если /= 2 Dmfm(x), g=^Ei Dkgk(x) есть представление функ-
|m|<p ft
ционалов fug через обычные функции (/ финитен, fm(x) сосре-
сосредоточены в фиксированном брусе, носители gk (х) удаляются от
начала координат с возрастанием |/г|), то
A8)
есть представление свертки / * g через обычные функции. Используя
равенства типа A8), как и в п. 6, получаем, что свертка коммута-
коммутативна, т. е.
/ * g = g * f-
Функция g * <р сосредоточена на множестве
supp<p— suppg-,
функционал f * g сосредоточен на множестве
Свойства функционала / * g в области G определяются при финит-
финитном / свойствами g в произвольно малой окрестности множества
G — supp/.
Имеет место теорема о непрерывности свертки: предельное
соотношение /v * g—>f * g в К' имеет место в случаях:
а) функционалы fv—>f в К', функционал g финитен;
б) функционалы /v->/ в К' и их носители сосредоточены
в одном и том же ограниченном брусе.
Имеет место формула дифференцирования свертки:

122 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. ц
Задачи. 1. Пусть/! и /2— финитные функционалы, g — произволь-
произвольный функционал; показать, что /| * (/2 * g) = (/| * /2) * g (ассоциативность
свертки).
Указание. Исследовать выражение сверток через обычные функ-
функции (п. 5).
2. Показать, что «функционал типа меры»
(ц, <р) = J <р (л:) d\i (л:).'
где ц (х)— мера Стилтьеса. нмеет порядок сингулярности <1.
Указание. Можно считать, что \к фнннтна. Функция t * ц (% — фун-
фундаментальная функция оператора Лапласа) есть обычная функция с обыч-
обычными производными первого порядка (теорема Фубини). Использовать ра-
равенство Д (у * ц) = Д# * ц = ц.
3. Показать, что всякий линейный непрерывный функционал на про-
пространстве Dm финитных функций (р(х) с непрерывными производными до
порядка т (§ 10. задача 9), если его рассматривать только на функциях
<р(л:)£ К. представляет собою обобщенную функцию порядка сингулярности
.< т -f-1 (но, вообще говоря, не .< т).
Указание. Использовать задачу 2 н задачу 11 к § 10. Функционал
■6 (х) € Do и имеет порядок сингулярности 1.
4. Известно, что свертка функционала g£K' и любой основной функ-
функции хр (х) есть основная функция. Доказать, что g — финитный функционал.
Указание. (Е. А. Горин). Пусть g не финитен. Существует функция
q>i £ К. сосредоточенная в шаре | х К1, для которой при некотором
Xi (g * <Pi) (-^i) Ф 0. По условию, g * q>i сосредоточена в некотором шаре
|jc|<ri; найдем функцию <р2£К. сосредоточенную в шаре J-*]-^! так-
чтобы при некотором х2. \ х21 > rt -\- 1, иметь (g * q>2) (лс2) ф 0. Определим
функцию *|>2£К в форме -ф2 = Фй — '•'Pi так- чтобы иметь (g* ^2) (лс,) =
= (ё * Фг) (.xt) — Л (g * q>i) (xi) = 0. Продолжая так далее, найдем последова-
последовательность основных функций ^v (лс), сосредоточенных в шаре | х | <; 1, и
co, для которых (£ * ^v) (л:^) отлична от 0
лишь прн v = (i. Положим -ф (л:) = 2 Cft^fcC*); при достаточно малых c^^(jc)—
k=i
основная функция и g * ^ не финитна.
5. Показать, что определение и основные свойства свертки переносятся
на случай функционалов fug. сосредоточенных на полуоси х^>0, причем
результат оказывается также сосредоточенным на этой полуоси.
6. (Продолжение). Свертка функции / (л:), сосредоточенной на полуоси
xn-i
х > 0. с функцией ± равносильна п-кратному интегрированию функ-
(л —1I
ции f(x) в силу формулы Дирнхле
л-1I

,3] ПОРЯДОК СИНГУЛЯРНОСТИ 121
Естественно назвать поэтому выражение
„A.-1
Я-кратным неопределенным интегралом от /. Это определение действует
для любого функционала /, сосредоточенного на полуоси х~^0, и для
х\— 1
любого комплексного Л, поскольку обобщенная функция _£— определена
Г (Л)
при всех К (§ 11, задача 3). Показать, что выполняются следующие соот-
соотношении:
/-*/=/*>.
Указание. Использовать соотношение
X
/•
Г (к) Г
| &'" Ч-* —У" "Я6 =
о
7. (Продолжение). Показать, что интегральное уравнение Абеля
1 / _Л|М£_ j.
о
с известной (дифференцируемой) функцией g (x) имеет решение
/W~ r(a)J Сдс — ЕI-1 '
Указание. Записать уравнение A) в форме g = 1х_а/ и использовать
задачу 6.
§ 13. Порядок сингулярности
1. Порядок сингулярности обобщенной функции уже неодно-
неоднократно рассматривался нами в примерах. Мы уточним здесь era
определение и проанализируем более подробно.
Мы говорим, что обобщенная функция f имеет в области G
порядок сингулярности-^.р (и пишем s(f)-^.p или при необхо-
необходимости so (/) ^ р), если / допускает в этой области G пред-
представление
/= 2 *>*/*(*). (О
1*1
где fk(x) — обычные функции.

124 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. Ц
Если при этом представление в форме
/= 2 D*gk(x)
ift| <p-i
с обычными функциями gk(x) невозможно, мы говорим, что обоб-
обобщенная функция f имеет порядок сингулярности в области G
ровно p(s(f)=p или so(f) = p). Из результатов § 10 следует,
что каждая обобщенная функция / в ограниченной области G имеет
конечный порядок сингулярности, а финитная обобщенная функция
имеет конечный порядок сингулярности и во всем пространстве Rn.
По самому смыслу число р не отрицательно. Обобщенная функ-
функция /, для которой s(/) = 0. есть обычная функция. Распространим
теперь понятие порядка сингулярности и на отрицательные значе-
значения р. Именно, пусть р < 0 и g = — р > 0, мы говорим, что обоб-
обобщенная функция f в области G имеет порядок сингуляр-
сингулярности <^р, если / и все ее производные (в К') до порядка q
внутри области G суть обычные функции; далее, / имеет порядок
сингулярности в области G ровно р, если среди производных
функции / порядка q-\-\ имеются функционалы, не сводящиеся
в области G к обычным функциям.
Обобщенная функция f имеет в области G порядок син-
сингулярности равный—оо, если ее производные (в К') любого
порядка внутри области G суть обычные функции.
Подчеркнем, что речь идет здесь о производных в простран-
пространстве К'; вообще говоря, функция порядка сингулярности р < 0 не
обязана быть дифференцируемой в обычном смысле и даже может не
быть непрерывной. Только при достаточно большом \р\ можно
утверждать, что такая функция непрерывна (см. п. 6).
2. Определенный выше порядок сингулярности s(J) связывал
функционал / с обычными (локально суммируемыми) функциями.
Вместе с тем естественно ввести понятие порядка сингулярности и
по отношению к непрерывным функциям. Будем говорить, что обоб-
обобщенная функция f в области G имеет порядок с-сингуляр-
ности ^.р, и писать с (/)<!/? или cc(J)^p, если внутри этой
области справедливо представление
/= 2 *>*/»(*). B)
где Д (л:) — непрерывные функции. При этом порядок е-сингуляр-
ности функции / равен ровно р, (с (/) = р или со (/) = р), если
представление
/= 2 D*gk{x)
ftii
с непрерывными функциями gk (х) в области G невозможно.

^ 13] ПОРЯДОК СИНГУЛЯРНОСТИ 125
Распространим и это определение на отрицательные значения р.
Именно, если р<0 и д =—р > О, мы говорим, что функция
f = f(x) имеет порядок с-сингулярности ^ р в области G,
если f(x) внутри области G непрерывна и имеет непрерывные про-
производные до порядка q\ и при этом он равен ровно р, если среди
производных функции f(x) порядка 9+1 имеются функционалы,
не приводящиеся в области G к непрерывным функциям.
Очевидно, с (/) > s (/). Неравенство с (/) <! О во всяком случае
означает, что / (х) — обычная непрерывная функция. Равенство
с(/) = — со означает, что в области G функция непрерывна и имеет
непрерывные производные всех порядков.
Заметим, что наличие непрерывных производных в смысле про-
пространства К' обеспечивает уже тот факт, что эти производные су-
существуют и в обычном смысле (§ 7, п. 4).
3. Приведем несколько простых теорем, связанных с порядком
сингулярности s (/) или с (/). Все участвующие ниже обобщенные
функции рассматриваются в фиксированной области G.
1. При однократном дифференцировании порядок сингулярности
может увеличиться не более чем на 1; более общим образом, если
Р (-г-) есть дифференциальный оператор порядка т, то
. C)
Достаточно доказать первое утверждение. Если / = ^ Dk fk (x).
где fk (x) — обычные (непрерывные) функции, то —— =
= 2j -j—Dkfk(x), т. е. получается из обычных (непрерывных),
функций путем дифференцирования до порядка р-\-1; это и требуется.
2- s (/ + £■) ^тах Is (/)• s(g)] Для любых обобщенных функ-
функций fug.
Действительно, пусть для определенности max[s(/), s (§■)] =
== s (f) = р ~^. 0. Мы можем написать
Дописывая вместо недостающих функций gk (x) нули. Но тогда
е-

126 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [Гл. |,
что и требуется. Если же max[s(/), s(g)] = s(/) = р =—<7 < О,
то это означает, что и у / и у g производные до порядка q суть
обычные функции; но тогда и у f-}~g производные до порядка п
суть обычные функции, что и требуется.
Аналогично
(/). c(g)\.
3. Если обобщенная функция / имеет вид
7=1
где функционалы /n, fx /„ имеют порядок сингулярности (в любом
смысле) -s^m, то/, очевидно, имеет порядок сингулярности (в том
же смысле) -^м-}-!" Обратно, если f имеет порядок сингуляр-
сингулярности -^т+1, где /я ^> О, то его можно представить в форме
D), где функционалы /0, ..., /„ имеют порядок сингулярно-
сингулярности ^ т. Это представление получается непосредственно из формулы
A) выделением первых производных из операторов Dk.
4. Произведение функционала /, имеющего порядок сингу-
сингулярности (в любом смысле) <С/? на бесконечно дифференци-
дифференцируемую функцию а{х), имеет также порядок сингулярности
(в том же смысле) < р. Это утверждение очевидно для р^О; для
р > 0 будем рассуждать по индукции. Предположим, что утвержде-
утверждение верно для всех функционалов порядка сингулярности <^ р. Пред-
Представим данный функционал порядка сингулярности -^р-j-l в форме D),
где /0, fl /„ — функционалы порядка сингулярности -^ р.
Тогда мы будем иметь
да
откуда, используя предположение индукции, находим, что функцио-
функционал а/ имеет порядок "сингулярности -^ /? + 1, что и требуется.
4. Существенные соотношения между порядками сингулярности
получаются при свертке обобщенных функций. Пусть вначале обоб-
обобщенные функции fug рассматриваются во всем пространстве /?„
и одна из них финитна. Тогда
(g). E)
Действительно, если s(/) = /^>0, s(g) = m^-0 и, для определен-
определенности, функционал g финитен, то
/= 2

I3] ПОРЯДОК СИНГУЛЯРНОСТИ 127
с обычными функциями fj(x) и обычными финитными функциями
gk(x); отсюда
f*g = 2
где fj (x). gk (x) — снова обычные функции. Таким образом, / * g
имеет порядок сингулярности <^/-f-m. Предположим теперь, что
/ ^ 0, т < 0, так что функционал g имеет обычные производные
до порядка \т\. Тогда, если 1{^0
f*g= 2 /,() *() ^
\I\<1 \j\<l+m
где fj(x) * D~mg(x) — снова обычные функции. Таким образом,
(f)^^\ и в этом случае. Если же / -|- т < 0, то
f*g= 2 D'fj(x)*g(x)= ^ f.(x)*D>g(x)
\J\<1 U\<1
имеет обычные производные до порядка —т—I и, следовательно,
также имеет порядок сингулярности ^т-\-1.
Наконец, если числа I к т оба отрицательны, функция /(х)
имеет обычные производные до порядка |/|, функция g(x) имеет
обычные производные до порядка \т\. Тогда к свертке / * g можно
применять дифференцирование D1 l+'m| по правилу
результат представляет собою обычную функцию, и следовательно,
снова s(/*g-)<|/| + |m|-
В частности, свертка функции / (х), у которой s (/) = — со
(функция с обычными производными любого порядка), и любого
функционала g(x) конечного порядка сингулярности (в случае,
если она имеет смысл, т. е. / или g финитен) имеет снова порядок
сингулярности s (/) = — со.
Посмотрим, что можно сказать о порядке сингулярности функ-
функционала / * g в ограниченной области G. Поскольку здесь не тре-
требуется полной информации о функционалах fug, результат E)
возможно иногда улучшить. А именно, как мы знаем из § 12, п. 7,
если функционал / финитен, поведение свертки / * g в области G
°пределяется свойствами функционала g только в окрестности мно-
множества G — supp /; иначе говоря, в области G имеет место пред-
представление
(f*g. 4>) = (f*eg. ф).

128 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [ГЛ. ц
где е(х)— основная функция, равная 1 на множестве О — suppy
и 0 вне некоторой окрестности V этого множества. По доказанному
v(£). F)
что и представляет собой нужную формулу.
Б. Выясним теперь, в какой мере сохраняется при свертке непре-
непрерывность и дифференцируемость функции.
Рассмотрим вначале свертку обычных функций
причем одна из них, как и всегда, финитна. Предположим, что g(x)
непрерывна; покажем, что и f(x)*g(x) также непрерывна. Еои
финитна функция / (х), например сосредоточена в шаре | х |
то мы можем написать оценку
К/*£)(*„)-(/*£>(*i)К
1
< max \g(x0 — D — gix, — 0| Г \f(l)\dl.
откуда следует непрерывность функции (/ * g) (x) в точке х0. Если
финитна функция g (х) и сосредоточена, например, в шаре | х \
то аналогично
II/ * g)(xc)—(/
-1) | dc, —> 0 при
в силу интегральной непрерывности обычной функции / (л:) *).
По теореме о дифференцировании свертки мы имеем
поэтому если функция g не только непрерывна, но и имеет непре-
непрерывные производные до порядка, например, q, a / имеет обычные
производные до порядка р, то свертка имеет непрерывные произ-
производные до порядка p-\-q-
*) См. Анализ III, стр. 364. Очевидно, в последнем случае достаточно
требовать лишь ограниченности финитной функции g (x).

5 i3] порядок сингулярности 129
Полученный результат с помощью понятия порядка сингулярности
можно сформулировать так: если s (/) <[ 0. с (g) ^ 0, то
c{f*g)<sV)+c(g). G)
В действительности неравенство G) имеет место при любых
s (/) и с (g), а не только при неположительных.
Действительно, пусть, например, функционал / финитен, так что
/= 2 D'fj(x), s(f) = P>0.
ЧКр
где fj(x)—обычные финитные функции; пусть, далее.
g= 2 D"gk(x), c{g) = m>0.
|ft|<
где gk(x)— непрерывные функции. Тогда
2 2 Di+klfJ(x)*gk(x)]. (8)
1 <m
где f j * gk, по доказанному, непрерывны. Отсюда с (J * g) ^ p -\- т.
Для случая c(g)<C.O вместо равенства (8) мы напишем
f*g= ^ D'[fj*g].
\j\<p
откуда, по доказанному,
c{f*g)<P + c{f}*g)^p + c(g).
Если s (/) < 0, а с (gO = т ^- 0, то вместо (8) мы напишем
и, следовательно,
Во всех случаях неравенство G) оказывается справедливым.
Следствие 1. Свертка f*g — бесконечно дифференци-
дифференцируемая функция (в обычном смысле), если хотя бы один из функ-
функционалов /, g есть бесконечно дифференцируемая функция.
Доказательство. Будем предполагать, что / — финитный
функционал. Если g — g(x) — бесконечно дифференцируемая функ-
функция, то по формуле G)
c{f*g)<s(f) + c(g) = — оо,
поскольку s(/)<oo, c(g) = — оо. Если /:=/(лг) — бесконечно
дифференцируемая функция, то формула G) непосредственно не рабо-
работает*); представляя g(x) в виде предела финитных функционалов gv
*) Поскольку возможен случай с (g) = + оо.

130 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. ц
с носителями, удаляющимися от начала координат, мы получим
f*g=lim (f*gv). c(f*
и так как в любой ограниченной области функции / * gv, начиная
с некоторого номера, перестают изменяться, отсюда следует, что
/ * g есть бесконечно дифференцируемая функция всюду.
Следствие 2. Всякая обобщенная функция f может быть
представлена как предел (в К') последовательности обычных
функций fi(x), /2(-*0 притом бесконечно дифференци-
дифференцируемых и финитных.
Доказательство. Пусть /г,, Л2, ... —дельта-образная после-
последовательность бесконечно дифференцируемых функций, сосредото-
сосредоточенных в шаре |*|-<1 (§ 9, п. 2). Образуем функции gv—hv*f;
так как Лу->6 (в К'), то, в силу теоремы о непрерывности свертки
(§ 12. п. 8). мы имеем gv= hv*f->6*/ = /. В силу следствия 1,
функции gv(x) бесконечно дифференцируемы. Пусть, далее, ev(x)—
основная функция, равная 1 в шаре |jc|-^v (v=l, 2, ...). Положим
/v=evgr,;; функция fv(x) также бесконечно дифференцируема и
финитна. Наконец, для любой основной функции ф(л:) мы имеем
ф = еуф, начиная с достаточно большого v; поэтому
I'm (/v. ф)= Iim (eg ф)= lim (g e ф)= lim (g , ф) = (/, ф).
V-»uo V-»oo V->co ' V-Юо
T- e> fv~>f B f'» что и утверждалось.
Замечание. Если в условиях следствия 2 функционал / фи-
финитен и сосредоточен внутри ограниченной области G, то и функ-
функции / (х) можно взять сосредоточенными в той же области. Действи-
Действительно, пусть найдены какие-то функции gv g2, .... сходящиеся
к функционалу /. Умножая их на основную функцию е(х), равную 1
на множестве supp / и 0 вне G, мы получим последовательность
eSv е£ъ также сходящуюся к /; в то же время функции
egx, eg2, • •. сосредоточены в области G, что и требовалось.
6. Для дальнейшего напомним один результат из § 7 (п. 2, при-
пример 9). У уравнения
-«■
*-«■_.« (А-
мы нашли следующие решения:
(П Г2т-
ап. 2тГ
b rMi-
2/п-л ПрИ п нечетном или п четном и 2т < п;
'n.2mr2m~"lnr ПРИ " четном и

j 13] ПОРЯДОК СИНГУЛЯРНОСТИ 131
Очевидно, функция ^"(х) — обычная функция, имеющая обычные
производные до порядка 2т—1, так что
sW)=l-2ffl. (9)
Покажем, что
№т) . A0)
Если 2гп > п, то &1™ (х) непрерывна и имеет непрерывные произ-
производные, до порядка 2т — п—1, так что в этом случае c((fj") =
= 1 — 2т-\- п. Если 2т = и, то %*}, = а 1п г и уже не непрерывна при
х ■=■ 0; но она является суммой первых производных от непрерывных
функций (поскольку \х\г = аД (г2 In r)= с 2ja—(я—^'пп, а функ-
функции -д— г21п г непрерывны); поэтому с (^) = 1 = п — 2т-\- 1.
Наконец, при 2т < п функция ^т = сл2т~п может быть записана
в виде
п-2т + 1
а,Д 2 /■ при и нечетном,
п-1т
а2Д 2 г2 In r при и четном.
Во всех случаях мы также получаем
с (/-2"<-л) = 1 — 2т-I-п.
Дальнейшие теоремы имеют целью получение оценки порядка сингу-
сингулярности функционала через порядок сингулярности его производных.
Теорема 1. Если f — финитный функционал, то при
любом т
s(/)<s(Am/)-2m+l, A1)
с(/)<s(Д'7)- 2т + 1 + п. A2)
Действительно, применяя оценки E) и G) к равенству
calm a m х a mcalm , « г ,
мы получаем
используя (9) и A0), приходим к требуемым неравенствам A1) — A2).
Следствие 1. Для любого финитного функционала f
. A3)

132 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. ц
Этот результат получается из оценки A2) при замене s(Amf) на
не меньшую величину 5 (f)-\-2m.
Следствие 2. Если s(f) =— оо, то и с(/) = — оо; иными
словами, если все производные функционала f — обычные функ-
функции, то все они и непрерывны, и явлг.:о;исл обьп::ыми произ-
производными.
7. Далее мы получим аналогичные оценки для произвольных
(не финитных) функционалов, рассматривая их в ограниченной об-
области G. Как мы знаем, в ограниченной области G всякий функцио-
функционал / имеет конечный порядок сингулярности s(f). Пусть G'czG—.
область, содержащаяся в G вместе со своим замыканием, и е(х)—.
основная функция, сосредоточенная строго внутри G и равная 1
на G'. Тогда функционал ef финитен и, по доказанному,
с (*/)<s (efl + n+l.
В области G' мы имеем е/ —/; поэтому в G'
Таким образом, следствия 1 и 2 сохраняются и для произволь-
произвольного функционала / в любой области G', содержащейся строго
внутри G-
Что касается неравенств A1) — A2), то они, конечно, остаются
справедливыми для функционала ef, но сами по себе уже не пред-
представляют большого интереса, поскольку Дт (ef) выражается не только
через производные порядка 2т от функционала /, но и через проме-
промежуточные производные и саму функцию /. Все же и этот результат
полезен; сформулируем его в виде леммы:
Лемма 1. Если s(D7/Xft при всех \j\ ^2т, то
s(J)<k — 2m+l.
В самом деле, согласно неравенству A1),
< ft —
Так как для любой основной функции (р(х), сосредоточенной строго
внутри области G, при некоторой е (х) справедливо равенство
(/, ф) = (ef, ф). то и сам функционал / имеет в области G порядок
сингулярности -<С k — 2/и—f- 1, что и требуется.
Чтобы выразить s(f) только через величины s(D2mf), восполь-
воспользуемся следующей леммой:
Лемма 2. Если все производные 1-го порядка функцио-
функционала f в ограниченной области G имеют порядок сингуляр-
сингулярности s(/)<A, то и сам функционал f в этой области имеет
порядок сингулярности

§ 13] ПОРЯДОК СИНГУЛЯРНОСТИ 133
Доказательство. Во всяком случае, в области G порядок
сингулярности функционала / конечен, и мы можем написать для
некоторого т
/
Далее, по условию, s(D/)-<fc; отсюда s(D2f)<^.k-{~l, .... s(D2ra/)<;
^.k-\-2m—1- Мы видим, что порядок сингулярности / и его
производных до порядка 2т не превосходит k-\-2tn— 1. По лемме 1,
s(/)<^ft, что и требуется.
Теорема 2. Если в ограниченной области G все произ-
производные порядка 2т функционала f имеют порядок сингуляр-
сингулярности s(D2m/)^fc> m0
Доказательство. Последовательно применяя лемму 2, нахо-
находим s(D2m~1/)<^ s(O7/)<ft пРи всех |/| от 2т до 0;
остается сослаться на лемму 1.
Задачи. 1. Если c(-jhM<0 (ft= 1 п). то с(/)< —1.
Указание. См. теорему 2 § 7. п. 4.
2. Если с (тр-) <—и (*= 1 л), то с(/)< — т — 1.
Указание. Проанализировать структуру решения задачи 1.
Примечание. Существует функция /(лг|, х2). у которой
дх{
d2f d2f ,
—=^- непрерывны, а — = g {х1ш х2) не непрерывна (в одной точке обра-
d*2 дхг дх2
щается в бесконечность)*). Мы имеем
\dxj \ дх2 дх\ I \дх21 \ дхг дх\ )
в то время как с (g) > 0; таким образом, для отрицательных значений т
утверждение задачи 2 уже не справедливо.
3. Если s(-|^\=0 (ft=l п). то s(/)< —1.
V вх ^ I
Указание. См. лемму 2 п. 7 и определение s (/).
4. Если s 1-^р— )<—т (ft= 1 п). то s (/)< — т — \.
Т 3
d2f
—~^
Указание. То же, что и для задачи 3.
Примечание. Можно построить функцию /(лг|, х2). у которой ^
дх\
it —^- локально суммируемы, а — = g {xlt x2) не является локально
дх2 дх1 дх2
*) Б. С. М и т я г и н. О второй смешанной производной. ДАН СССР,
т. 123. № 4. A958). стр. 606—608.

134 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [гл. ц
суммируемой *). Тот же прием, что в примечании к задаче 2, показывает
что для отрицательных значений т утверждение задачи 4 уже не справедливо*
5. Можно ли представить обычную функцию / в форме
где s(/0)<—1 «(/„)<—1? (Иначе говоря, справедливо ли утвер-
утверждение п. 3 для случая т = — 1?)
Ответ неизвестен.
6. Можно ли представить непрерывную функцию / в форме
где с (/„)<— 1 £(/„)<— 1?
Ответ неизвестен.
§ 14. Преобразование Фурье обобщенных функций
1. Пусть (р(х) (—оо < х < оо) некоторая комплекснозначная
основная функция. Построим ее преобразование Фурье
оо
ф (о) = F [ф (*)] = Г ф (х) eiox dx. A)
Поскольку ф(-)с) — финитная функция, интеграл A) распространен
на конечную область, например —а«^х^.а; поэтому функция яр (о)
может быть определена и для комплексных значений s =
а а
= ftp(x)elsjcdx= f<p(x)etaxe-x*dx. B)
-а -а
Так как интеграл B) допускает дифференцирование по комплекс-
комплексному параметру s = oA-ix, то ty(o-\-it) — целая аналитическая функ-
функция. Дифференцирование функции (р(х) приводит к умножению il>)
на — Is; действительно,
а а а
Г ф' (х) elxs dx = q> (x) elxs I — Г isy (x) elxs dx = — tsty (s).
*) D. О r n s t e 1 n, A поп-Inequality for differential operators in the
/., — norm. Arch. Ration. Mech. and Analysis, т. 11, № 1, A962) стр. 40—49-

. 14] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 135
Продолжая дифференцирование, получим, далее, для любого
. = 0, 1. 2, ...
F [<pW (*)] = (— Is)" F [Ф (*I C)
и вообще
[jl)] D)
где Р — любой многочлен с постоянными коэффициентами. Вместе
с тем мы получаем оценку
и-
f ф№ (a;) eixs dx
Таким образом, преобразование Фурье ij)(s) каждой основной
функции у(х), обращающейся в нуль при \х\^а, есть целая
аналитическая функция переменного s = a-\-lx, удовлетворяю-
удовлетворяющая при каждом q = 0, 1, 2, ... неравенству
'4. E)
Мы утверждаем, что верно и обратное: всякая целая функ-
функция ty(s), удовлетворяющая при каждом g неравенству E),
есть преобразование Фурье некоторой бесконечно дифферен-
дифференцируемой функции ф(л:), обращающейся в нуль при \х\^.а.
Функцию ф(.к) мы, естественно, определим формулой обратного
преобразования Фурье
СО
i f F)
Поскольку функция ij) (о), как видно из неравенства E) при т = 0,
убывает при |о|—>оо быстрее любой отрицательной степени |о|, то
интеграл F) сходится абсолютно и равномерно по х. При формаль-
формальном дифференцировании под знаком интеграла он останется абсолютно
и равномерно сходящимся. Поэтому функция ф(-К) обладает первой
производной, а также и всеми последующими, при этом
со
Ф<<7) (а;) = -^ Г (_ la)" ij) (о) е~1«х da.
—оо
Чтобы убедиться в финитности функции ф(лг), заметим вначале,
что в ее выражении интегрирование по вещественной оси можно
заменить интегрированием по любой параллельной прямой
da. G)

136 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [гл. „
Действительно, по теореме Коши интеграл от аналитической функ.
ции -ф(s), s = a-\-t%, по прямоугольнику [—A; A; A~\-ix; —Л-f-fri
равен нулю; в силу оценки E), интеграл по вертикальным отрезкам
(Л; A-\-ix\ и [—А~\-1х; —Л] стремится к 0 при Л->оо, откуДа
и вытекает G). Далее, можно написать
оо
= -i- <?« J ij)(o+ ix) e-ia*
da.
Пусть | x | > а, зададим некоторое число / > О и найдем т из
условия jct = — t\x\. Используя неравенство E) при д — 0 и 9 = 2,
находим
ОО
-^еХХ f
Так как С не зависит от t, то, устремляя t к со, находим, что
ф(л;) = 0. Таким образом', при |jc|>a функция гр(х) обращается
в нуль. Итак, функция (р(х) удовлетворяет всем высказанным усло-
условиям. В силу известной теоремы об интеграле Фурье *), ее преобразо-
преобразование Фурье совпадает с функцией яр (о), что и требовалось.
2. Изучение преобразований Фурье функций из пространства К,
начатое в предыдущем пункте, естественно приводит к следующему
определению. Введем пространство Z всех целых функций ty(s),
удовлетворяющих неравенствам
М'Ж*)|<С,е-1" (9 = 0, 1, 2, ...) (I)
(где постоянные а и Cq зависят от функции яр), с очевидным опре-
определением основных линейных операций — сложения и умножения на
число.
Как показано в п. 1, преобразование Фурье устанавливает
между пространствами К и Z взаимно однозначное соответ-
соответствие. Очевидно, что это соответствие сохраняет указанные линейные
операции и является тем самым изоморфизмом.
В пространстве. Z допустимо также умножение на некоторые функ-
функции G(s), дистрибутивное со сложением. Функциями G(s), на которые
можно производить умножение в пределах класса Z, являются, на-
например, целые аналитические функции, удовлетворяющие оценке
(и никакие другие; см. задачу 5 к § 15).
*) См. Анализ Ш. гл. VII, § 2.

I4] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 137
Особую роль в пространстве Z играет операция инволюции,
„ереводящая функцию ty(s) в -ф* E)^=-ф (s).
Кроме того, можно переносить в пространство Z линейные опе-
операции из пространства К. пользуясь установленным изоморфизмом.
Каждой линейной операции, определенной в пространстве К,
отвечает некоторая «двойственная» линейная операция, определенная
в пространстве Z. Так, например, операции дифференцирования в про-
пространстве К соответствует, в силу формулы C) п. 1, операция умно-
умножения на —ts в пространстве Z. С другой стороны, формула
показывает, что операции умножения на 1х в пространстве К соот-
соответствует операция дифференцирования в пространстве Z; повторяя
эту операцию, приходим к формуле, справедливой при любом
9 = 0, 1, 2
C)
Из существования правой части следует существование левой;
поэтому в пространстве Z функции ^(s) можно неограниченно диф-
дифференцировать, не выходя за пределы этого пространства. Можно
написать и несколько более общую формулу:
где Р — любой многочлен с постоянными коэффициентами.
Операции отражения (р(х)—>ф(—jc) в пространстве К отвечает
операция отражения tJj(s)—>ty(—s) в пространстве Z, поскольку
оо оо
Г ф (— х) e'xs dx = J ф (х) e~ixs dx.
— ОО —ОО
Операции сдвига ср (х) -> ср (х — К) в пространстве К отвечает
операция умножения на etsh в пространстве Z; действительно.
оо
x — Л)]= J e'sx(f> (а; — Л) dx =
— ОО •
оо
— Г е'*(у+*)ф(у) dy = eishF [ф (х)\.

138 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [Гл. ц
Обратно, операции умножения на eixh (при любом, может быть и
комплексном, К) в пространстве К отвечает операция сдвига в про-
пространстве Z:
F[elJch(p(x)]= С eisxeihx(p (x) dx = С е'(*+А)*ф (JC) dx = ty (s-f-Л).
—оо —оо
В частности, мы видим, что в пределах пространства Z функции ty(s)
допускают всевозможные (вещественные и комплексные) сдвиги.
Можно перенести в пространство Z и операцию предельного
перехода, считая, что функции tyv(s) стремятся к нулю, если их
образы фу (х) стремятся к нулю в смысле, установленном для про-
пространства К. Впрочем, эту сходимость в Z можно описать и вну-
внутренним образом. Именно, последовательность i|)v (s) стремится к нулю
в Z, если, во-первых, выполняются неравенства
с постоянными Cq и а, не зависящими от v, и если, во-вторых, эти
функции стремятся к нулю равномерно на каждом интервале оси
(см. задачу 1).
Все приведенные выше операции — сложение, умножение на число
и на функцию, инволюция, сдвиг, производная — непрерывны в про-
пространстве Z относительно указанной сходимости.
Отметим, что разложение в ряд Тейлора .
9=0
с любым фиксированным (комплексным) h имеет место в смысле
указанной сходимости; это следует из справедливости двойственной
формулы
,7=0
в смысле сходимости в пространстве /С.
3. Вернемся на момент к функционалам на (комплексном) про-
пространстве К.
Обычной комплексной функции f(x) мы будем сопоставлять функ-
функционал / £ /£' по следующему правилу:
Ф)= f f(x)<p(x)dx.

^ l4] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 139
Этот выбор правила сопоставления объясняется тем. что в теории
преобразования Фурье существенную роль играет равенство Парсе-
валя, которое имеет следующую форму:
оо оо
f 77x)<P(x)dx = ^r J
где g (о) и яр (о) соответственно преобразования Фурье функций / (х)
и ф(-*0 (в предположении, например, что / (х) и (р(х) квадратично
интегрируемы)*).
На пространстве Z, как и на пространстве К, также можно строить
линейные непрерывные функционалы — обобщенные функции.
Всякая (комплексная) функция g (а), определенная при — оо < а <
< оо, локально интегрируемая и, кроме того, возрастающая на бес-
бесконечности не быстрее некоторой степени |о|, определяет функ-
функционал на Z по формуле **)
оо
(g. *)= fg~(o)q(<3)do. A)
—оо
Функционалы типа A) будем называть регулярными, остальные —
сингулярными. К числу сингулярных принадлежит дельта-функция
а также ее (даже комплексные) сдвиги
Совокупность всех обобщенных функций на пространстве Z обо-
обозначается через Z'. С обобщенными функциями на пространстве Z
можно производить операции, аналогичные операциям, введенным нами
для обобщенных функций на пространстве К. Ясно, что определения
линейных операций — сложения и умножения на число, а также пре-
предельного перехода не содержат ничего нового.
В частности, предельный переход в Z' определяется условием:
gv—*g в Z', если для любой основной функции
Умножение на функцию G(s), формально определяемое равенством
(G(s)g. i|>) = (g-. G*(s)il>). B)
*) См. Анализ III. гл. VII. § 6.
**) И здесь можно, конечно, сопоставить функции g(o) функционал по
любой из четырех формул, аналогичных формулам A) — D) § 3. п. 4.

140 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [Гл. ц
где G*(s) означает G(s), допустимо для целой функции, удовлетво-
удовлетворяющей неравенству B) п. 2.
Умножение на такую функцию G(s) дистрибутивно со сложением,
а также и непрерывно в том смысле, что из gv (s) —*■ g (s) в Z' сле-
следует G (s) gv (s) —> G (s) g (s) в Z'. Действительно,
(Ggv. Ц>) = (gv, G*i\>) -> (g, G*ty = (Gg, -ф). C)
Производная функционала g£Z' определяется формулой
Как и в пространстве К', дифференцирование непрерывно относи-
относительно сходимости Z': если gv^>g в Z', то для любой t])£Z
(g'v- <\>) = — (gv- tf)^ — (g. ■*') = (£'. -Ф)
и, следовательно, g'v —у g в Z'-
Так же как и в пространстве К', обобщенные функции
допускают неограниченное дифференцирование.
Но, в отличие от функционалов / £ К', обобщенные функции ^
не только бесконечно дифференцируемы, но и аналитичны; это
означает, что для каждой
^r D)
9=0
где ряд слева сходится в смысле сходимости в пространстве Z',
a g(s-\-h) — сдвиг обобщенной функции g(s) на число А, опреде-
определенный формулой
Действительно, для любой ty (s) £ Z
а ряд V -—-J- г)I9' (s) сходится в смысле сходимости в Z, как
мы уже отмечали, к функции -ф (s — А), таким образом,
что и требовалось.

н] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 14!
Отметим, в частности, разложение
справедливое при любом (комплексном) h.
4. Поскольку между пространствами К и Z существует взаимно
однозначное соответствие с сохранением линейных операций и схо-
сходимости, аналогичное соответствие можно установить и между линей-
линейными непрерывными функционалами на этих пространствах. Мы уста-
установим это соответствие так, чтобы на функционалах, отвечающих
абсолютно интегрируемым функциям, оно переходило бы в соответ-
соответствие между функцией и ее классическим преобразованием Фурье.
Пусть f (х) — абсолютно интегрируемая функция и g(p) — ее пре-
преобразование Фурье. Тогда для любой основной функции ф(л:) и ее
преобразования Фурье ty(a) имеет место соотношение
(ЛЧ>)=
= i f
do,
которое называют обычно равенством Парсеваля. Равенство Парсе-
Еаля показывает, что g(a) как обобщенная функция действует на
основную функцию я]) по формуле
(ff. Ю = 2я(/. Ф). A)
В этой форме оно может служить определением обобщенной
функции g на пространстве Z при любой заданной обобщенной функ-
функции / на пространстве К- Будем называть функционал g, определен-
определенный равенством A), преобразованием Фурье функционала f и
обозначать его символом F[f].
Подчеркнем, что функционал F[f] действует уже не в простран-
пространстве К. а в двойственном пространстве Z.
Оператор Фурье f [/]. переводящий пространство К' в простран-
пространство Z', является линейным непрерывным оператором. Действительно,

142 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. ц
для любых комплексных щ и сс2 и любых /р
= 2ла1(/1, Ф)+2ла2(/2, ф) = а1
далее, если /v—>/ в К', то
= 2л (Д, Ф) -у 2л(/. ф) = (F [/], F [ф]).
Для преобразования Фурье обобщенных функций сохраняются
формулы дифференцирования обычных преобразований Фурье
fl B)
F[p(-£)f\=P(--ls)Flf]- С3)
так что, в частности, умножению на 1х в пространстве К' соответ-
соответствует дифференцирование в пространстве Z' и дифференцированию
в пространстве К' отвечает умножение на — Is в пространстве Z'.
Для доказательства достаточно рассмотреть случай Pl-j—J^-j—.
Мы имеем в этом случае
(F[ixf\, F[<?])=2n(ixf, ф) = 2л(/,
что дает формулу B); аналогично устанавливается C).
Обратный оператор F~ определен на пространстве Z и перево-
переводит функционал g в функционал / по той же формуле A) (читаемой
справа налево), так что
/11 = /. ^l^ [^l] = ^.
D)
Отметим два простых и часто используемых правила.
1. Преобразование Фурье от /(— л:). Пусть имеется
функционал f(x)£K'', функционал /(— л:) определяется равенством
— *). Ф(*)) = (/(«)■ Ф( — *))• E)
Пусть F [/ (л:)] = g (о), F\f{ — л:)] = gl (о); мы имеем, согласно п. 2,
-*). Ф(*))=2я(/(*). ф(-х)) =
*( —о)) = (йГ( —о).

14) ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИИ 143
Отсюда gi(o) = g( — о); иными словами, отражению относительно
начала координат на оси х отвечает отражение относительно начала
координат на оси о.
Как следствие, получаем: четная обобщенная функция (/(—лг)г=
^f(x)) имеет четное преобразование Фурье, нечетная обобщен-
обобщенная функция (/(— ->0= —f (х)) имеет нечетное преобразование
Фурье.
2. Двойное преобразование Фурье. Если ф(л:) — основ-
основная функция, то, как мы знаем,
Но можно к функции \])=F((p) применить еще раз прямое пре-
преобразование Фурье; мы получим
поскольку операция F~ отличается от операции F коэффициентом ■=—
и знаком при независимом переменном.
Определим теперь двойное преобразование Фурье от функционала
/6К' (и прямое преобразование Фурье от функционала Ff = g£Z')
по формуле (аналогичной формуле A))
(FFf, FF<p) = {F(g). F№)) = 2.i(g, Ц>).
Установим связь между функционалами / и FFf. Подставляя в
полученное выражение g = F[f], ty=F[f], получаем
(FF[f], FF[<f]) = 2л(F[f\, F[q>]) = Bnf (/. Ф(*)).
Но слева вместо FF [ф] можно подставить 2лф (— л:). Сокращая
на 2л и заменяя л: на — л:, мы получаем
(FF[f], Ф(*)) = Bя/. Ф( —
т. е.
Аналогично
Например, пусть известно, что прямое преобразование Фурье функ-
функции /00 есть функция g(a); g(a)= F[f(x)]. Найдем обратное пре-
преобразование Фурье от / (х). Мы имеем
^g(-o). F)

144 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. ц
Аналогично если известно, что g (о) = F~l [f (х)], то
= 2ng( — а).
Б. Примеры. 7. Найдем F[b]. Согласно определению,
(F[61, /=>]) = 2лF, Ч)=2л<р@) =
—
откуда
F[b\=l. F-'HI^o- A)
2. Аналогично найдем F[\]:
= 2л Г ф (л:) е~ ш dx = 2лф @) = 2л F, ф).
— ОО
откуда
Н1] = 2л6, #-'№1 = ^. B)
Этот же результат получается и непосредственно из A) применением
формулы двойного преобразования Фурье E).
3. Преобразование Фурье от многочлена. Используя формулы
B) — C) п. 1, находим
F[P(x)\ = F[P (x) • 1] = 2лР (-/А.)бE). C)
fyb(x)]=P(-ls)F[b] = P(-is).l=P(-is). D)
В частности,
F[^m\x)]=(-irs2m 1
J
4. Преобразование Фурье от —ш- Обозначим F —1 = g (о); так
как нечетная обобщенная функция, то и g(a) — нечетная обоб-
обобщенная функция. Из равенства

М] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 145
следует, согласно B) и C),
Отсюда
Так как g(a) — нечетная функция, то С = ^ и. следовательно.
g (о) = л/ sgn a.
Далее, мы имеем
1 ( — цт-l dm-l ^
хт (т — 1)! dxm~l x
Отсюда
5. Преобразование Фурье от показательной функции еЬх. Восполь-
Воспользуемся тем, что ряд
оо
bkxk
fc=O
сходится в смысле сходимости в пространстве К'\ это позволит вы-
вычислить F[ebx\ путем почленного применения оператора F к этому
ряду. Мы получим (см. формулу E) п. 3)
ft=O ft=O
Формула F) позволяет легко получить преобразования Фурье
часто встречающихся функций s'mbx, cosbx, shbx, chbx:
Г е'Ьх_е-1Ьхл
F [sin bx\ = F ^ 1 = — /л [o (s -)- ft) — 6 (s — ft)],
F[sh bx] = F [ e"X~e "X ] = л [6(s — /ft) — 6(s + /ft)].
10 Г. Е. Шилов
/•'[chbx\ = F [ g Xj^e "X 1 = л[6(s — /ft) + 6(s + /ft)].

146 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. ц
6. Преобразование Фурье от сдвинутой дельта-функции. Найдем
F [6 (х — А)]. Согласно определению,
— A)], F[(p]) = 2nF(x —А), ф(л:))
СО
= J чр (о) е-'аЛ do = (е'ол, ц>).
—со
откуда
F[t>(x — h)] = ei<jh.
Далее, легко получаются формулы
Задачи. 1. Последовательности функций <pv (л:) £ /С, стремящейся к О
в К. отвечает последовательность функций -tyv (о) = F [cpv (а:)], обладающая
следующими свойствами:
| Л]^ (s) | <; Сде°' т' [а и Сд не зависят от v).
'"I'v (°) ~* ^ равномерно на каждом интервале ос и а и обратно.
Указание. Прямое утверждение следует из определения преобразова-
преобразования Фурье. Для доказательства обратного проверить, что все функции cpv (л:>
обращаются в нуль вне интервала |л:| < а и производные нх ограничены фик-
фиксированными постоянными; далее применить принцип компактности.
2. Найти преобразование Фурье обобщенной функции х^_ (§ 11).
Указание. При — 1 < Re Я < О
со
f
J
xhel<yxdx= lim
x-y+O
о
в последнем интеграле произвести замену isx = £. воспользоваться формулой
Коши и определением Г-функции. Далее использовать аналитическое продол-
продолжение по Я.
Отв. F\xhA = fc 2 Г(Я + 1) lim (a + i
1 +J т->+0
= /Г(Я+1)
Примечание. Функционал lim (о + h)K обозначают еще через
т->+0
3. Пусть Д (jc) = 2 hP /Л4-1 \' Показать- чт0
Г1)

. 15] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИИ 147
4. Найти преобразование Фурье функции 1пл:+.
Указание. Результат задачи 2 продифференцировать по Я н положить
я=о.
Отв.
где 1 п (а + *'О) = lim I n (о + «)■
т->+о
§ 15. Преобразование Фурье обобщенных функций
(продолжение)
1. Наши построения могут быть почти без изменений перенесены
на случай п независимых переменных. Преобразование Фурье основ-
основной функции ф(л:) = ф(л:1 хп) определяется по формуле
CO CO p
J J
—со —оо
или, короче.
г|) (о) = J ф (л:) е1 <*■ & dx, A)
где через (л:, о) обозначена величина х1а1-\- ... -\-хпап. Вследствие
финитности функции <р(х) функция г]) может быть распространена
и на комплексные значения аргумента s = (s1, ..., sn)=(o1-|-/T1, ...
...,а„ + /т„);
Ф (s) = Г ф (*) е1 <Л- $Ых. B)
Полученная функция 4>(s), определенная теперь в п-мерном ком-
комплексном пространстве С„, непрерывна и аналитична по каждому
из аргументов sx sn. Если функция ф(л:) обращается в нуль при
\хк\ 5* ak (Л = 1 п), то ее преобразование Фурье ij)(s) допускает
оценку
Обратно, всякая целая функция \])(sj sn), удовлетворяющая
неравенству C), является преобразованием Фурье основной функции
4>(х1 хп), обращающейся в нуль при \xk\ > ak. (k=l, .... re).
именно,
—оо —со
10*

148 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [гл. j.
Эта функция бесконечно дифференцируема по всем аргументам
Для доказательства ее финитности, например, по х1 следует по пере-
менному о, выйти в комплексную плоскость и далее провести рас-
рассуждение с теоремой Коши, как и в случае одного переменного.
Имеют место формулы, аналогичные формулам D) п. 1 и C) п. 2:
«) Ф (*)!■ D)
E)
где Р(-) — любой многочлен с постоянными коэффициентами.
Пространство всех целых функций i|)(s), удовлетворяющих нера-
неравенствам вида C), в котором естественным образом определены
линейные операции — сложение и умножение на число, по-прежнему,
будем обозначать через Z (или Zn). Преобразование Фурье устанав-
устанавливает между пространствами Кп и Zn взаимно однозначное соответ-
соответствие с сохранением линейных операций. Предельный переход в про-
пространстве Zn определяется следующим образом: последовательность
*l>v(s) (v=l, 2, ...) называется сходящейся к нулю, если после-
последовательность соответствующих основных функций фу (л:) стремится
к нулю в пространстве Кп- Внутренним образом эта сходимость
описывается так: выполняются неравенства
с постоянными Сд и a.j, не зависящими от v, и функции ijiv (о) стре-
стремятся равномерно к нулю на каждом ограниченном множестве вещест-
вещественного пространства Rn.
Преобразование Фурье функционала /, действующего на прост-
пространстве Кп, определяется как функционал g на пространстве Zn,
действующий по формуле
(g, г1)) = Bл)я(/, ф), F)
где \])=F[(p] есть преобразование Фурье функции ф(л:). Функцио-
Функционал g линеен и непрерывен, он обозначается через F [/]. Результаты
§ 14 переносятся на этот случай без особых изменений. Формулы
B) — C) п. 1 приобретают следующий вид: если Р — многочлен
от п переменных с постоянными коэффициентами, то
-k -£;)Flf]==FlPilXl iXn)fb G)

,5] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИИ 149
Обратный оператор F~ действу
его в пространство Кп по формуле
Обратный оператор F~ действует в пространстве Z'n и переводит
Если f(x)— функция, обладающая преобразованием Фурье в клас-
классическом смысле, то функционал F[f] есть регулярный функционал,,
соответствующий преобразованию Фурье функции /(х).
Из сингулярных функционалов простейшим является дельта-функ-
цня: для нее имеют место формулы
аналогичные формулам A) — B) п. 5 § 14.
Формула преобразования Фурье от многочлена получается'
комбинированием формул B) и E)
F[P(xv .... xn)] = F[P(Xl xn)-l] =
= B^P(-l-^-.....-l-^)ftW. (И)
2. Отметим формулу преобразования Фурье поворота обобщенной
функции. Пусть Ux = у есть некоторый поворот в пространстве Rn
(ортогональное преобразование с определителем 1). Каждая основная
функция ф(л:) в результате поворота переходит в основную функцию
(f(Ux). Преобразование Фурье фу (о) поворота основной функции
вычисляется по формуле
о) = J Ф (Ux) el {x- a)dx=:jq> (у) еЛи~Ч. о) dy =
A)
и оказывается равным соответствующему повороту преобразования
Фурье исходной функции.
Пусть f(x) — обычная функция и f{Ux) — ее поворот; функ-
функционал, отвечающий функции f(Ux), может быть записан в форме
(/ {Ux). <р (*)) = J
dx =
Это дает основание определить поворот любой обобщенной функ-
функции / по формуле
(/ (Ux). Ф (*)) = (/ (х), Ф (U-'x)). B>

150 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [гл. 1г
Найдем формулу преобразования Фурье поворота обобщенной
функции f(Ux). Пусть F [ср (л:)] = г|> (a), F [/ (х)] = g (о); мы имеем
(F [/ (Ux)]. г|> (о)) = Bя)я (/ (Ux). q> (*)) = Bл)п (/ (*). q> (tr'*))
= (F[f(x)]. F[
Мы получаем формулу
C)
которая показывает, что преобразование Фурье от поворота обоб-
обобщенной функции есть поворот преобразования Фурье от самой обоб-
обобщенной функции. Как следствие, получаем: преобразование Фурье
сферически симметричной обобщенной функции (f (Ux)^f(x)
при любом U) есть сферически симметричная обобщенная
функция.
3. Преобразование Фурье финитного функцио-
функционала- Пусть сначала финитный функционал / отвечает обычной
функции f (х), сосредоточенной в брусе В— [х : | Xj\ ^.dj}. Тогда
обычное преобразование Фурье функции / (х)
A)
может быть аналитически продолжено в комплексное пространство
s = a + /T = (Oi-l-ft1. .... an-\-ixn) по формуле
g(s)=
в
Функция g(s) допускает оценку
*aAxlf\dx = Ce*ajlxil. B)
Таким образом, g(s) есть целая функция не выше чем первого
порядка роста. Кроме того, при вещественных s = а функция g (о)
ограничена (и даже стремится к 0 при | сг[ —>сх>). в силу общих
свойств преобразования Фурье суммируемой функции.
Если /—произвольный финитный функционал, то мы можем
.представить его в форме
/= 2 *>*/*(*).
|ft|<m

. j5] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 151
где /* С*) — обычные функции, сосредоточенные на некотором брусе-
д, = [х: \х{ |< с, 4-е |лгя|<с;„ + е).
По доказанному,
|ft|<m
где gt(s) есть преобразование Фурье функции fk(л:). Таким образом,
g(s) = F[/] есть также целая функция первого порядка роста, но
уже, вообще говоря, со степенным ростом в вещественной области:
Степенной порядок роста функции g (о) определяется, очевидно,
порядком сингулярности функционала /.
Оценка C) в некоторых случаях, при специальных предположе-
предположениях относительно расположения носителя функционала /, может-
быть уточнена. Например, предположим, что носитель функционала /
и функций fь(х) лежит в пределах октанта {л:: л:, ^-а, > 0, ...
... л:я>ая>0}. Тогда при т, > 0 т„ > 0
мы имеем
и, следовательно, при указанных т
т. е. при Xj > 0. функция g(s) в действительности экспоненциально
убывает.
Равенство A) можно записать в форме
(f(x), *'<*>*>) E)
(разумеется, поскольку функция е'^-^не финитна, правую часть
равенства E) нужно понимать в этом случае так, как было указано
в п. I § 8).
Оказывается, что равенство E) имеет место не только для обыч-
обычной финитной функции f(x), но и для произвольного финитного
функционала /.
Действительно, поскольку финитный функционал есть сумма
производных от финитных функций, достаточно показать, что ра-
равенство E), если оно справедливо для некоторого финитного функ-
функционала /, остается справедливым и для любой его производной.

.152 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [гл.
-~-. Последнее следует из равенств
F [-Д-] = -iSjF [f] = —tsj (/. е1 С *>) = (/, —
чем утверждение и доказано.
4. В многомерных задачах, особенно связанных со сферической
симметрией, часто встречаются бесселевы функции. Приведем необхо-
необходимые нам определения и формулы.
Бесселева функция Jp(z) может быть определена равенством*)
л
, ,_ч 1
Vn
f e'zcos(isiP e <Ю- A)
5
При р. равном половине нечетного числа, этот интеграл может быть
выражен через элементарные функции. В частности,
т+—
B)
, = (_ 1)тгт4 A *Г i/T i!££. (з)
4 ' \z dzI V n z v/
Последняя формула допускает следующее обращение:
Для иллюстрации рассмотрим преобразование Фурье от обычной
интегрируемой сферически симметричной функции /(/"):
F [/(г)] = J7(r) «'<*•></*.
Преобразуем интеграл к сферическим координатам, направляя поляр-
полярную ось по вектору о. Если |о| = р, |л:| = г и 8 — угол между
векторами х и о, мы получаем
с» Г Л
= 4--,/ /
о Lo
eirPcoses\n"-2QdQ \ f(r)r"-ldr.
*) См.. например. Э. Т. У и т т е к е р и Дж. Н. В а т с о н. Курс совре-
современного анализа, ч. 2, гл. 17, Физматгиз. 1963.

,5] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИИ 15&
где ^я-1 = —/П 1 \ есть поверхность единичной сферы в п—1-
мерном пространстве. Поэтому, в силу A).
оо
= 2к~*~ (■£■) 2 J т~* / (г) 7 „ (rp) dr. E)
^ / 0 ~2
Для многих конкретных функций / (г) интегралы вида E) вычислены-
Например, при / (г) = e~iT известна формула *)
я п
I е~"Т 2 JJL_, (ГР) df = 2±Г
Таким образом, преобразование Фурье от функции е~и имеет вид.
п п ,
2
Б. Найдем преобразование Фурье от финитного функционала
t>(r — а), действующего по формуле
F (г — а), ф (л:) ) =
т. е. приводящего в соответствие основной функции ф (л:) ее интеграя
по сфере радиуса а с центром в начале координат.
По доказанному в п. 3
— а)\ = (б {г — а),
[хЫа
*) См., например, С. Б о х н е р. Лекции об интегралах Фурье, Физматгиз.
№62, стр. 266.

154 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИЙ [ГЛ. гг
Переходя к сферическим координатам (г = |лг| = с, р = |а|. 0 — угол
между векторами х и а), находим
F [6 (г — а)\ = С e'flPcos ec"-1 sin" QdQ Ло„_, =
я
= а"^-, J e'w™ esinn-2 6 dQ,
о
где da>n_i — элемент поверхности сферы в п—1-мерном подпро-
подпространстве, ортогональном к вектору р.
Полученный интеграл выражается через бесселеву функцию
_1
При п нечетном, п = 2т~\-Ъ, т^-О, бесселева функция выражается
через элементарные C), и мы получаем
sing I
p I *
z=ap
В частности, при п = 3, m = 0
6. Найдем преобразование Фурье от свертки f = fQ*fl, где,
для определенности, /0 есть финитный функционал. Пусть g, g0. gt
суть соответствующие преобразования Фурье. В частности, go = go(s)
есть целая функция первого (экспоненциального) порядка роста со
степенным ростом при вещественных s = о. Вначале рассмотрим
случай, когда оба функционала /0 и ft финитны и являются обыч-
обычными функциями. Тогда н свертка

15] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИЙ 155
еСть обычная финитная функция, и ее преобразование Фурье вычи-
вычисляется по классической формуле
«« Rn
J el «■ •) /o (I) d\ • JV U-e. 4/, (x -1) rf* = ft (s) • gl (s).
Таким образом, свертка функций fo(x) и fi(x) после преобразования
Фурье переходит в произведение образов Фурье этих функций.
Пусть теперь /0 и fx — произвольные финитные функционалы.
Тогда
ij\<m
где fOj(x) и /1й(л:) — обычные финитные функции, gOj(s) и glk(s) —
соответствующие преобразования Фурье. Поэтому
и
F [/о * /,1 = F \ S 2 £>>+* (/о; (*) * /
Liyi<m|ft|<p
2 2 ()
\j\<m |*|<p
Наконец, пусть /0 — финитный, а /х — произвольный функционал. Мы
знаем, что функционал f1 может быть представлен как предел (в К'У
финитных функционалов:
/, = "m U
V->oo
По теореме о непрерывности свертки
/o*/i= lim (/o*/v)-
V->oo
Пусть gv(s) — преобразование Фурье функционала /v и gi — пре-
преобразование Фурье функционала /[. Тогда, в силу непрерывности
оператора Фурье,
gi= Mm gv(s) (в Z')
V-»oo

156 СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ОБОБЩЕННЫХ ФУНКЦИИ [гл ц
и далее
F[fo*fd= I'm Flfo*fv]= I'm go(s)-gv(s) =
V->oo V->oo
== go (s) ''m gv (s) = go (s) ^( (rt
v->oo ''
что и требовалось.
7. Определение преобразования Фурье обобщенных функций отве-
отвечало тому случаю, когда обычной функции f(x) сопоставляется функ-
функционал над К по формуле
(/. q>)=
и аналогично, обычной функции g (о) сопоставляется функционал над Z
по формуле
Но легко можно написать определения преобразований Фурье и
в остальных случаях сопоставления /(*)—>/ (§ 3, п. 4). Имея в виду
имеющееся определение и равенство Парсеваля, мы можем написать
следующие определения:
(i. ФI=
(g, i])J = Bя)" (/, фJ. (принятое нами определение).
i ^ , ФK.
. ФL-
Задачи. 1. Функционалы вида /= 2 Dkfk(x). где /ft (л:) — обыч-
ная функция не более чем степенного роста при | х | -> оо (пространство 5^.
см. § 10, задачу 5), определены и в пространстве Кп. и в пространстве Zn-
Показать, что пространство Sn при преобразовании Фурье переходит в себя
самого.
У к а з а н и е. fk (х) = A + Г2)Р /oft (л:), где /oft (*) ^ L2 (/?„).
2. Показать, что преобразование Фурье обобщенной функции, однород-
однородной степени р (§ 6. задача 4) есть однородная обобщенная функция сте-
степени — п — р.
3. Показать, что преобразование Фурье функции г^(Кф — п. — п — 2, ...)
равно С^р"*'"", и найти С^.
Указание, г* есть сферически симметричная однородная функция сте-
степени Я. Использовать задачи 1, 2 и задачу 1 к § 11. Для вычисления С^ при-
применить функционал /•*• к функции e~l* £S.
Отв.
НУ

, 15] ПРЕОБРАЗОВАНИЕ ФУРЬЕ ОБОБЩЕННЫХ ФУНКЦИИ 157
4. Показать, что обобщенная однородная сферически симметричная функ-
функция /€^п степени —п — 2k имеет вид с ДЛ6 (л:).
Указание. Преобразование Фурье функции / есть обобщенная одно-
однородная сферически симметричная функция степени 2k. Использовать задачу 10
к § п-
5. Пусть умножение на функцию g (s) есть непрерывная операция в про-
пространстве Zn. Показать, что g (s) есть преобразование Фурье функционала
f£K'n. для которого определена и непрерывна операция свертки (/*<р) (л:) =
=-(/A). <Р(■* + £))•
Указание. Положить f=F г [g] и использовать формулу F [ф (•*-(-£)] =
i
e[t(l)]
Примечание. В силу результата задачи 4 к § 12. функционал /фини-
/финитен и. следовательно, функция g(s) — целая функция первого порядка и не
выше чем степенного роста при вещественных о.
6. Обозначим через Ат совокупность целых аналитических функций т]з (s).
для которых выполнены неравенства
Пусть, далее. Ст есть пространство финитных функций ср (х) с непре-
непрерывными производными до порядка т. Показать, что
F[Cm\czAm. r'l^lc^.^,

ЧАСТЬ 2
ПРОБЛЕМЫ ОБЩЕЙ ТЕОРИИ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
ГЛАВА 111
ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ДИФФЕРЕНЦИАЛЬНЫХ
ОПЕРАТОРОВ И ЛОКАЛЬНЫЕ СВОЙСТВА РЕШЕНИЙ
§ 16. Формула типа Пуассона
1. Рассмотрим дифференциальное уравнение в Кп
*,+ ...+*„<р 1 •••ох"
с постоянными коэффициентами аь. Если п=1, то, как мы видели
в § 5, все решения этого уравнения суть обычные функции — клас-
классические решения уравнения. Не так, вообще говоря, обстоит дело
при п > 1; здесь среди решений могут появиться и обобщенные функ-
функции, не сводящиеся к обычным. Например, при п = 2 уравнение
—— = 0 имеет в числе своих решений сингулярную функцию б(л:2).
ОХ j
определяемую формулой
со
(б(л:2), ф(лг„ л:2))= J ср(л: . 0)dxl.
—оо
Обозначим через L(P) всю совокупность решений уравнения A)
в пространстве Кп- Так как Р — линейный оператор, то L (Р) является
подпространством в пространстве К'- Укажем несколько более или
менее очевидных свойств подпространства L(P).
1. L(P) замкнуто в Кп-
Действительно, если Puv = 0 и uv—>u, то, в силу непрерывности
оператора Р на пространстве Кп, и Ри= Iim Puv = 0.
v->oo
2. Если u£L(P) и / — финитный функционал, то / * u
Действительно, если Ри = 0, то и

l6] ФОРМУЛА ТИПА ПУАССОНА 159
f i ,ns ди дЬ(х) _ . ,_
В частности, из и £ЦР) следует -т—- = , * u£L(P) и при
OXt ОХ I
любом векторе h£Rn также u(x-\-h) = t>(x-\-h)*u£L(P).
3. Каждое решение u£L{P) есть предел (в К') обычных, притом
даже бесконечно дифференцируемых решений — именно, решений вида
fv(x)*u, где fv(x) — дельта-образная последовательность (§ 9, п. 2)
финитных бесконечно дифференцируемых функций.
4. Каждое решение и £ L (Р) конечного порядка сингулярности
есть конечная сумма производных от обычных решений, имеющих
непрерывные производные до заданного порядка. Действительно, для
дельта-функции всегда можно написать представление
2
i*Kp
где @й(лг) обращаются в нуль при |х[^>е и имеют непрерывные
производные до заданного порядка q *). Поэтому любое решение
u£L(P) представляется в виде
и = и*Ь= 2 D"(и*wft).
Если порядок s-сингулярности обобщенной функции и равен т, то
порядок s-сингулярности свертки и * сой не превосходит т — q
(§ 13, п. 4) и при достаточно большом q меньше любого наперед
заданного числа, что и требуется.
Вообще говоря, среди решений могут существовать и реше-
решения бесконечного порядка сингулярности (например, u(xv x2) =
V№ (х2 — о) ди (хи Хэ)
- . . i———— для Уравнения ———— =
(/=0
для уравнения
дх% дх
2
2. Для изучения свойств решений уравнения большое значение
имеет фундаментальная функция оператора Р. Напомним, что фунда-
фундаментальной функцией называется (обобщенная) функция (f(x), удовле-
удовлетворяющая уравнению
*) Мы имеем, например, 6 = b.qt^ (x). где t% имеют непрерывные произ-
производные до порядка 2q — п+1 (§ 13. п. 6). Далее, если е{х) равна 1 при
\х\ <е и нулю при |*| >2е. мы имеем A'(et%) = б + е0(х). где е0 (*) от-
отлична от нуля только при е < | х\ < 2е и бесконечно дифференцируема; от-
отсюда Ь = Д9 (е^9) — е0 {х), т. е. получается 2д-кратным дифференцированием
из функций с непрерывными производными до порядка 2q — п + 1.

]60 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ_ ,.
Так. для оператора Лапласа Д в пространстве /?„(л>2) функцИя
&(*) Ir*~" B)
является фундаментальной (§ 7, п. 2, пример 8). В дальнейщем
(§ 17) мы покажем, что фундаментальная функция имеется у всякого
оператора Р \-^jA ■
Как известно, с помощью фундаментальной функции B) можно
построить интегральное представление любого решения уравнения
Аи = 0 внутри области G через его значения на границе области G
(формула Пуассона *)).
Оказывается, что аналогичное интегральное представление для
решений любого уравнения Р\-^— 1 и = 0 можно получить, используя
соответствующую фундаментальную функцию. Приведем это построение.
По определению, обобщенная функция и (х), заданная в области
GcRn (см. § 6, п. 3), является в этой области решением уравнения
Р [-*— I и = 0, если для любой основной функции ц>(х), сосредото-
сосредоточенной в области G, имеет место равенство **)
Ш- *)-(■• *(-£■)•)=<>■
Мы указывали в § 8, п. 2, что обобщенную функцию и, заданную
в области G, можно продолжить на все пространство /?„ так, что она
сохранится неизменной в заданной внутренней области VcG. Таким
образом, решение и в области G можно считать обобщенной функ-
функцией, определенной на всем пространстве Кп и являющейся решением
уравнения A) в области VaG. Заметим, что при этом в случае ограни-
ограниченной области G функционал и можно считать финитным, сосредо-
сосредоточенным в области G. умножив его в случае необходимости на
бесконечно дифференцируемую функцию Р(-к), равную 0 вне области О
и 1 в области V. Пусть cf(x) — фундаментальная функция уравне-
уравнения A). Пусть, далее, а(х) — бесконечно дифференцируемая функция,
равная нулю вне некоторой окрестности О начала координат про-
пространства Rn и равная 1 внутри некоторой меньшей окрестности
начала координат.
Обозначим через W область, обладающую тем свойством, что
арифметическая разность W — U содержится в V- При достаточно
малых размерах U область W заведомо не пуста.
*) См., например, Курант, Гильберт. Методы математической фи-
физики, т. 2, Гостехиздат, 1951. гл. 4, § 2, п. 1. _
**) Напомним, что если Р (|) = ^ aklk- т° Р<&)= 2 «*£*• причем ak
k k
есть число, комплексно сопряженное с числом ak.

, 16] ФОРМУЛА ТИПА ПУАССОНА 161
Лемма. В области W имеет место равенство
Доказательство- Пусть основная функция <р(лг) сосредото-
сосредоточена в области W; тогда мы имеем
(Р (■£) (о*) * и. Ф) = («ЙГ * Р (-£) и. V) =
где \J) = а^1 * <р есть бесконечно дифференцируемая функция, сосредо-
сосредоточенная в области W — UdV (§ 12, п. 3); так как в области V
функционал и(х) есть решение уравнения A), то результат равен
нулю. Поэтому для указанных функций ()
что и требовалось.
Формула C) и является искомым аналогом интегральной формулы
Пуассона. В самом деле, посмотрим, какие значения и(х) в левой
части участвуют при по-
построении и (х) в правой
части в области WoaW
(рис. 6). Функционал / =
^Z3^) К1-а) ^сосре-
^сосредоточен в области, где а(х)
отлична от 0 и от 1, т. е. в
области Ua U, примыкаю-
примыкающей к границе области U. По Рис. 6.
доказанному в § 12, чтобы по-
получить и (х) в области №0. нужно иметь и (х) в левой части B) в области
WQ — О. Эту область можно представить себе так: перенести начало
координат в любую точку области Wo и заметить результат переноса
области — О, я далее рассмотреть объединение всех этих результатов,
когда образ начала пробегает всю область №0. Если область Wo доста-
достаточно мала, a U отстоит от начала координат достаточно далеко, то Wo—О
будет областью, не пересекающейся с WQ, обходящей Wo со всех
сторон, и в то же время остающейся в пределах области V. где и {X)
есть еще решение уравнения A). Таким образом, значение функ-
функции и (х) в области Wo можно выразить через ее значения около
границы области V (Поскольку форма области U в нашей власти,
можно подойти к границе V сколь угодно близко.)
11 Г. Е. Шилов

162 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [Гл. „j
В частности, получается следующая теорема о единственности-
Теорема 1. Если два решения уравнения Р(-х—)и = 0 сов-
совпадают вблизи границы области V, то они совпадают всюду
в области V. Если решение уравнения Р(-т—}ц = 0 обращается
в нуль вблизи границы области V. то оно равно нулю тожде-
тождественно в области V.
3. Применяя к формуле C) неравенство G) § 13. п. 5, получаем
следующее соотношение между порядками сингулярности:
D)
Если порядок многочлена Р [-*—) есть т, то, далее, мы имеем
\q\<m-l \q\<m-l
где v.q(x) — бесконечно дифференцируемые функции. Отсюда
*„-.(«)<«— l + Si,(«O+<Vo_£(")- E)
Следствие 1. Если решение и{х) вблизи границы обла-
области V есть бесконечно дифференцируемая функция, то оно
является бесконечно дифференцируемой функцией и в любой
внутренней точке области V.
Следствие 2. Если оператор P\-g-) обладает фундамен-
фундаментальной функцией & (х), которая вне начала координат беско-
бесконечно дифференцируема, то всякое решение уравнения Р1-т-)и=0.
в любой области V, предполагаемое заранее лишь обобщенной
функцией, есть обычная бесконечно дифференцируемая функция.
Оба следствия вытекают из формулы E): условие первого след-
следствия означает, что cw_ly(u) = — со, условие второго — что
*/> (£") = — оо-
Следствие 3. Если оператор Р\-т—) обладает фундамен-
фундаментальной функцией ^(х), которая вне начала координат беско-
бесконечно дифференцируема, то всякая фундаментальная функция
«?, (х) этого оператора также бесконечно дифференцируема
вне начала координат.

j 16] ФОРМУЛА ТИПА ПУАССОНА 163
Действительно, вне начала координат #", (х) есть решение урав-
уравнения Р (-у—) cf i (х) = 0 и остается применить следствие 2.
Операторы Р I-r- ), для которых все решения уравнения Р (-j—) и =
=— О — бесконечно дифференцируемые функции, называются гипоэдлип-
тическими. У гипоэллиптического оператора всякая фундаменталь-
фундаментальная функция бесконечно дифференцируема вне начала координат.
Оператор Лапласа и его степени — гипоэллиптические операторы.
Замечание. УравнениеР 1-г—I и = О, все решения которого име-
имеют в области V порядок сингулярности, не превосходящий фиксирован-
фиксированного числа q, является в действительности также гипоэллиптическим.
Действительно, любая производная -j—, ^— и т. д. от реше-
решения (в смысле обобщенных функций) уравнения Р l-s— j и = 0, как
мы знаем (п.1), есть также решение этого уравнения. Если все ре-
решения уравнения Р\~д~]и = 0 в области V имеют порядок сингу-
сингулярности -^.q. то, в силу теоремы 1 § 13, п. 6, каждое решение
имеет порядок сингулярности ^.q—2m + 1 при любом т, т.е. яв-
является обычной бесконечно дифференцируемой функцией.
4. В случае гипоэллиптического уравнения (т. е. уравнения с
гнпоэллиптическим оператором Р 1-р 1 ) формулу C) можно преобра-
преобразовать к виду обычных формул типа Пуассона, дающих выражение
некоторой функции внутри области через граничные значения этой
функции и ее производных. С этой целью заметим, что равенство C)
в рассматриваемом случае есть равенство с обычными функциями
и может быть записано в форме интеграла
F)
„
Напомним, что это равенство справедливо в области W, обладающей
тем свойством, что результат арифметической разности области W и
области U, в которой сосредоточена функция а(|), лежит в преде-
пределах области V. в которой и(х) есть решение уравнения A).
Перейдем в этой формуле к пределу, устремляя функцию а(|)
к характеристической функции области U. Мы получим в пределе
Rn-U
G)
11*

164 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. 1ц
Как мы уже выяснили, функцию и (х) можно считать бесконечно
дифференцируемой вне области V и обращающейся в нуль вне
области О гэ V; но и (х), вообще говоря, уже не будет вне V реше-
решением уравнения A). Произведем в равенстве G) интегрирование по
частям, постепенно перебрасывая все производные с множителя и (х — £)
так как в /?„ — U мы имеем Р 1-^-1 §'(|) = 0, то останутся
лишь граничные члены
=/ 2 р* (~k) & ® •Q* (- ~k)и {х - D dl =*
(8)
/
Г
где Pk aQh — многочлены степени < т, сь (|) = Рк {-щЛ (? (I) и
Г — граница области U.
Эту же формулу можно записать в форме
ж-Г
Так как область U можно изменять вместе с х в большой мере
произвольно, то, фиксируя произвольно точку х0, можно заменить
границу х — Г на х0 — Г по крайней мере для небольших значений
разности х — х0. Мы получаем формулу
Формула (9), в частности, показывает, что решение гипоэллипти-
ческого уравнения порядка т однозначно определяется внутри об-
области по заданным значениям этого решения и его производных до
порядка т— 1 на границе области.
Для производных от функции и (х) мы получаем выражения вида
х,- Г ft
Эта формула позволит оценить и рост производных функции и (х)
через рост производных фундаментального решения ^"
Б. Описание роста производных функции можно удобно произ-
произвести с помощью понятия класса Жеврея.
Определение класса Жеврея дадим сначала для функций одного
переменного.

§ 16] ФОРМУЛА ТИПА ПУАССОНА 165
Фиксируем число р ^> 0; по определению, функция f (х) (a<^x -$^.b)
принадлежит классу Жеврея Gp (или, точнее, Gp[a, b\), если
она имеет на отрезке [а. Ь] производные всех порядков и выпол-
выполняются неравенства
|/М(*)|<СВ»0«е (9 = 0.1,2....)
с постоянными С к В (зависящими, возможно, от функции /).
Если Р-С 1. функция f (x) — аналитическая функция; дей-
действительно, если разность f(x-\- h) — f (x) разложить по формуле
Тейлора, мы получим равенство
где
Величины dm— С —— , — стремятся к нулю прит->схзи|Л|Ве< 1.
поскольку
Таким образом, при |Л| <^ -=— величина Rm стремится к нулю и,
следовательно, f(x-\-h) есть сумма своего ряда Тейлора, т.е. она
является аналитической функцией в каждой точке отрезка [а, Ь].
Обратно, если f(x) — аналитическая функция на отрезке [а, Ь],
она может быть продолжена аналитически в область V, содержащую
этот отрезок внутри себя. Можно написать формулу Коши
7 ^ ; 2т.I (С-
где замкнутый контур L проходит в области V на положительном
расстоянии р от точек отрезка [а, Ь\. Оценка по модулю дает
|/<>(*)| = <q\ jf max |/ Q\ = С (!
т. е. /£(Ма. Ь\, что и требовалось.
При р > 1 класс Go содержит и неаналитические функции; так,
функция е~1*1 принадлежит классу О i (см. задачу 3).
р

166
ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ
[ГЛ. ц,
хп определение класса Жеврея
В случае п переменных х1
Gp следующее: »
Классом Жеврея Gp—Gp(V) (P^-0) называется совокупность
всех функций u(xv .... хп) = и(х), определенных в замкнутой обла-
области V, непрерывных и имеющих производные всех порядков, которые
удовлетворяют неравенствам
Класс G, состоит из аналитических функций (по каждому из
переменных хх хп).
Очевидно, что в пределах класса п„ можно производить сложе-
сложение функций и умножение на числа. Покажем, что можно производить
также и дифференцирование. Пусть ul(x) = -^—ofO. Тогда
d4l+l+...+91
"U{X)
...dxqn
Последний множитель оценивается следующим образом:
Итак, мы получаем для левой части B) оценку A) с измененными
С и В,.
Предположим, что фундаментальная функция (f(x) оператора
Р|-т—) принадлежит классу О„ в любой ограниченной области, не
содержащей начала координат (ни внутри, ни на границе). Мы можем
тогда утверждать, что и любое решение уравнения
принадлежит классу G« в любой ограниченной области. Для этого
используем формулу (9) п. 4
Ь-Г ft

§ 16] ФОРМУЛА ТИПА ПУАССОНА 167
Здесь функции ck(x) суть некоторые производные от фундаменталь-
фундаментальной функции g'(x), взятые в области, не содержащей начала коор-
координат, и тем самым вместе с функцией ^(л:) принадлежащие классу
дч\"пи
С,, Поэтому для DP и = мы получаем оценки
1 Л
«о-Г ft
max
ft ° Х(,-Г
<C^ max \Dqck(x— ifl|.
к
откуда следует, что вместе с & (х) также и функция и (х) входит
в класс GB.
Справедливо, конечно, и обратное: если в любой ограниченной
области все решения уравнения
принадлежат классу Gp, то и фундаментальная функция ^(х) при-
принадлежит классу Gp в любой ограниченной области, не содержащей
начала координат (ни внутри, ни на границе); действительно, фунда-
фундаментальная функция в любой такой области является решением
уравнения C).
Так, при любом т=1. 2, ... все решения итерированного
уравнения Лапласа -
Дти=0
суть аналитические функции (принадлежат классу Gj), поскольку
таковым является фундаментальная функция оператора Дт (§ 7, п. 2,
пример 9) вне начала координат.
В дальнейшем уравнение P\-g— )и=0 (а также оператор Р i-g— ]
и многочлен Р) будем называть р-гипоэллиптическим, если все
решения уравнения Р(-~\и=0 локально принадлежат классу
Жеврея Gp.
Задачи. 1. Если оператор Р\-^ —) порядка т обладает фундамен-
фундаментальной функцией £ (л;), которая всюду вне начала координат имеет
обычные производные до порядка т (т. е. s(g)< — m), то оператор
Р — гипоэллиптический.

168 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. щ
Указание. Неравенство D) п. 3 в данном случае дает
Таким образом, порядок сингулярности решения и в области W меньше
чем у границы. Итерируя неравенство F). получить, что в любой вну.
тренней области порядок сингулярности решения и меньше любого целого
числа, т. е. равен —со.
Примечание. Более сильный результат дается в задаче 5 к § 20.
2. Дано, что всякое решение уравнения W-з— )« = 0 в области V.
имеющее обычные производные до порядка .Л/ (N фиксировано), является
бесконечно дифференцируемым. Показать, что оператор Р гипоэллиптичен.
Указание. Использовать свойство D) п. 1.
3. Да-но. что всякое решение уравнения Я(-т—)ы = 0 в области V,
имеющее порядок сингулярности s{u)^.p. имеет порядок сингулярности
s("XP— 1 (Р фиксировано). Доказать, что оператор Р[-т—) гипоэл-
гипоэллиптичен.
Указание. Все производные от решения и(х) имеют вместе с ним
порядок сингулярности <;/?. Использовать теорему 1 § 13, п. 6 и задачу 2.
4. Показать, что функция f (х) = £~1Ж1 р (р > 0) принадлежит классу
Жеврея- G ,.
1+—
р _i_
Указание. Функция / (z) = e гР аналитична при z = х -\- iy Ф 0.
По формуле Коши написать выражение /^ (х) через значения / (£) на
окружности с центром в точке х, касающейся прямых у = ± —, произвести
оценку по модулю и найти максимум по всем х.
5. Известно, что многочлен Я(а) = Я(а,, ...,а„)
а) не имеет вещественных нулей,
б) имеет единственный вещественный нуль при а = О,
в) имеет ограниченное множество вещественных нулей.
Показать, что всякое решение уравнения Р I i -^— J и (х) = 0. имеющее
при | х | -> со рост не выше степенного (более общим образом, принадле-
принадлежащее S', см. задачу 4 к § 10):
в случае а) есть тождественный нуль,
в случае б) есть многочлен от х.
в случае в) есть целая аналитическая функция от z = x + iy не выше
первого порядка роста.
Указание. По задаче 1 к § 15 преобразование Фурье v{а) решения
и (х) принадлежит S' (и, следовательно. К'). Найти его носитель (см. за-
задачу 2 к § 8). Использовать теорему п. 6 § 10 (для случая б) и теорему п. 3
§ 15 (для случая в)).
6. Показать. что всякое дифференцируемое решение уравнения
+ А2)ы = 0 (п = 3). удовлетворяющее «условиям Зоммерфельда»,
u(x) = o[—j, -£ — iku = o\^ при |лг|-»оо.
есть тождественный нуль.

§ 17] СУЩЕСТВОВАНИЕ ФУНДАМЕНТАЛЬНОЙ ФУНКЦИИ 169
Указание. Условиям Зоммерфельда удовлетворяет, в частности
elkr
фундаментальная функция, % (х) = оператора Д + *2 (§ 7. задача 8).
Пусть, далее, %R(х) = %(х) при |х|<R и 0 при \х\> Я Тогда по фор-
формуле Грина (§ 7, п. 2, пример 7)
Лди дЧо П
**йГ дГи\йх'
\x\=R
откуда
и, следовательно, и @) = 0. Так как за начало может быть взята любая
точка, то ы(л:)==0.
§ 17. Существование фундаментальной функции
1. В этом параграфе мы докажем, что уравнение
разрешимо в пространстве К', каков бы ни был многочлен Р ф 0.
В целях упрощения дальнейших выкладок мы будем писать уравне-
уравнение A) в форме
" (-^-) 84*) =6 (*)•). B)
Произведя формально преобразование Фурье, получим из B) урав-
уравнение в функционалах на пространстве Z
P(s)E(s)=l. C)
Если мы докажем существование линейного непрерывного функцио-
функционала E(s) в пространстве Z', удовлетворяющего уравнению C),
то, произведя обратное преобразование Фурье, мы получим одно-
одновременно и существование решения уравнения B) в пространстве К'-
Уравнение C) означает, что для любой функции ty(s)£Z
(P(s) E (s), ф (s)) = A, ф (s)) = J ф (a) do.
Если бы многочлен P(s) не имел корней при вещественных значе-
значениях s = a и при этом был ограничен снизу по модулю положи-
*) По определению,

170 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. щ
тельной постоянной, то можно было бы положить
Действительно, в этом случае формула D) определяет линейный
непрерывный функционал на Z и
(P(s)E(s), q(s)) =
что и требуется. В общем случае выражение D) не годится, так как
оно даже не определено для всех функций \|з (s) £ Z.
В случае п — 1 можно положить
интегрирование ведется по любой прямой, параллельной веществен-
вещественной оси и не проходящей через корни многочлена P(s). Мы имеем
здесь также
о
<P(s)E(s). $(s)) = (E(s), P(*)№))= f
последний переход может быть осуществлен с помощью теоремы
Коши, используя быстрое убывание функции я])(а+«т) при [а|->оо.
Таким образом, выход в комплексную область позволяет при и= 1
решить задачу. Естественно, что на таком пути мы будем ее решать
и в общем случае любого п. Оказывается, что и при любом п доста-
достаточно выходить в комплексную область только по одной координате.
2. Вначале мы покажем, что, совершив, если нужно, некоторый
поворот осей, данный многочлен Р (i -?—) степени т всегда можно
записать в нормальной форме
k=0
где а0 ф 0 — постоянная.
Если по формуле х' = Ux совершается поворот осей (матрица
U — i/1) в пространстве Rn, где заданы функции (р(х), то в про-

§ 17] СУЩЕСТВОВАНИЕ ФУНДАМЕНТАЛЬНОЙ ФУНКЦИИ 171
странстве, где заданы их преобразования Фурье, совершается ана-
аналогичный поворот a' = Ua (§ 15. п. 2).
Поэтому достаточно найти такой поворот в пространстве Rn,
после которого заданный многочлен Р(о) степени т примет вид
m-l
Sяо*О. F)
Если Р(а) не имеет с самого начала вида F), то мы произведем
линейное преобразование
с неопределенной пока действительной матрицей C = |[cyft[[. Много-
Многочлен Р(о) перейдет при этом в некоторый новый многочлен m-й сте-
степени относительно |j, .... %п. Коэффициент при |™ получается при
рассмотрении старших членов многочлена Р, именно, если
есть группа старших членов многочлена Р(а), то коэффициент
при |™ будет иметь вид
Как видим, он выражается только через элементы первого столбца
матрицы С. В качестве чисел Сц сп1 мы можем взять теперь
любую нормированную B ^j\ = 0 систему чисел, обеспечивающую
отличное от нуля значение P0(Ci): иными словами, любую точку
единичной сферы вещественного пространства, не лежащую на конусе
Р0(о) = 0. Остальные столбцы матрицы С можно выбрать произвольно
с тем, чтобы они были ортогональны и нормированы, как требуется
для матрицы поворота.
Таким образом,'для записи многочлена Р в форме F) достаточно
(и необходимо), чтобы первая ось системы координат (а: о„)
не была направлена по конусу Р0(о) = 0. Этот конус мы назовем
характеристическим конусом многочлена Р.
После того как многочлен Р(р) записан в форме F), аналогич-
аналогичный вид
т-\
P(s) = a0s?+%Pk(s2 sjs*
принимает и многочлен P(s) во всем комплексном пространстве Сп.
Имея в виду полученный результат и тот факт, что функцио-
функционал 6 инвариантен относительно поворотов, мы можем в дальней-
дальнейшем ограничиться рассмотрением многочленов в нормальной форме.

172
ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ
[ГЛ. Щ
3. Рассмотрим пространство п+ 1 (вещественных) измерений,
определяемых вещественными составляющими at о„ и мнимой
составляющей Т|. В этом пространстве мы построим разрывное много-
многообразие Н, которое будем называть «лестницей Хёрмандера».
Для этого разобьем (п — 1)-мерное вещественное пространство
о2 о„ на локально конечное
(т. е. конечное в каждом шаре)
множество частей А1 Дг, ...
(п — 2)-мерными гиперплоскостями,
параллельными координатным гипер-
гиперплоскостям, и части Ду сопоставим
некоторое значение х1=х^К Лес-
Лестницей Хёрмандера будем называть
множество всех точек (Oi о„,
т^), где —оо<0|<оо, и если
о„, .... о )£Д.. то х.=х\р (/ =
(=1.2. ...").
На рис. 7 показана лестница
для случая координат о,. о2. т,.
Ниже мы докажем, что для данного многочлена P(s) всегда можно
построить лестницу Н. на которой |P(s)[>C>0 и все |т(/>| огра-
ограничены одной и той же постоянной Со. Имея такую лестницу, положим
Рис. 7.
я
Этот интеграл существует вследствие того, что знаменатель по мо-
модулю превосходит С, а функция iK^ + rtpOj о„), как основная
в пространстве Z. равномерно по х1 (для ItJ-^Cq) стремится к нулю
быстрее любой степени -j—j-, когда |о|->оо, и, следовательно,
интегрируема. Очевидно также, что функционал G) непрерывен
в пространстве Z.
Покажем, что этот функционал переходит в 1 при умножении
на P(s)- Действительно, мы имеем
(P(s) E(s), i|)(s) ) = (E(s), P(s)$(s)) =
... don =
dan
В силу формулы Коши внутренний интеграл, который вычисляется
по прямой в плоскости s1 = o + /t1, параллельной вещественной оси
И
I

§ 17] СУЩЕСТВОВАНИЕ ФУНДАМЕНТАЛЬНОЙ ФУНКЦИИ 173
и проходящей на расстоянии |^/М от нее, можно заменить, не изме-
изменяя его величины, интегралом по самой вещественной оси. При
этом мы получаем
(P(s)E(s), i|>(s)) =
СО СО
/ •• / J"*(oi On)da* •••dan=
J A; -co
откуда следует, что
что и требовалось.
4. Покажем наконец, что лестница, на которой
существует для всякого многочлена в нормальной форме.
Рассмотрим многочлен
т-\
при произвольно фиксированных значениях S2 = a2, nn
На ^-плоскости он имеет не более чем т корней s^ s<m> и
допускает разложение
Р (s) = a(s — sW) (s — 42)) • • • (s — sfJ). (8)
В полосе ItJ-^m+l ширины 2m+2 всегда можно провести пря-
прямую xl = const, которая отстоит более чем на 1 от всех корней
многочлена; из разложения (8) видно, что на этой прямой заведомо
\P(s)\ > \a\.
Так как корни многочлена с постоянным старшим коэффициен-
коэффициентом непрерывно зависят от остальных коэффициентов, то для доста-
достаточно малой окрестности точки (о2 оя) соответствующие корни
s^h ..., s(jm> будут помещаться на Sj-плоскости в как угодно малых
кружках около их первоначальных положений. Поэтому вдоль найден-
найденной прямой Т] = const будет сохраняться неравенство
\P(s)\>a
и в некоторой окрестности взятой точки (о2 о„).
Итак, каждой точке в пространстве (о2, .... о„) мы можем со-
сопоставить некоторую ее окрестность по указанному правилу. Можно
считать, что эти окрестности ограничены гиперплоскостями, параллель-
параллельными координатным. Применяя лемму Гейне — Бореля, можно из всего
покрытия пространства (о2, .... о„) такими окрестностями выбрать
локально конечное покрытие А,, А2, .... Л;-, ...; заменяя, далее.

174 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. III
каждое Д, на Ду- = Ду— А] — ... —Ду_р получим непересекающиеся
участки, которые и определяют вместе с соответствующими значе-
значениями т<-') искомую лестницу.
Таким образом, доказано в общем случае существование функ-
функционала E(s) в пространстве Z'. удовлетворяющего уравнению
P(s)E(s)=l;
тем самым доказано и существование решения у уравнения
что и требовалось.
б. Наше построение допускает значительный произвол в выборе
лестницы Хёрмандера, которым можно пользоваться для уточнения
различных сведений о свойствах решений.
При фиксированных а,, ..., а„ соответствующее сечение лестницы
представляло собою прямую в плоскости s,, параллельную веще-
вещественной оси. Можно строить лестницу и с помощью кривых сече-
сечений, но не слишком быстро удаляющихся от вещественной оси.
Например, можно озять сечение L в форме *)
T, = (fl,ln+|oI|— a2f (fl,>0). A)
В полосе |с2|-^'п-г' 1 заведомо найдется кривая вида A), на которой
всюду |P(s)| ^-С >• 0. Покажем, что существует интеграл
со
Г
J
Действительно, мы имеем при любом k и больших |О|| на L и под L
и если взять k~^> Ьа1-\~ I. интеграл будет сходиться.
Далее, интеграл по вертикальному отрезку
а, 1п+ | O| l-ijj
f"i- о2 on)dxl
стремится к 0 с возрастанием |о,|, поскольку из неравенства A)
вытекает оценка
|о,|-о2
iKc^-Мт,, о2 ojdx,
*) Как обычно, /*■ (х) = max {/ (х), 0}.

§ 18] РЕШЕНИЕ УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 175
Поэтому, в силу теоремы Коши.
со со
J Ф (о, + "р о2 а„) ds1 = J ф (Ор о,. ... а„) dOj.
—со —с»
Отсюда следует, что функционал E(s), действующий по формуле
при умножении на P(s) переходит в 1; таким образом, и при
интегрировании по искривленной лестнице мы получаем некоторую
фундаментальную функцию. Кроме того, можно производить анало-
аналогичные выходы в комплексную область также и по другим перемен-
переменным, в том числе и по нескольким сразу.
Задачи. 1. Показать, что порядок сингулярности фундаментальной
функции любого дифференциального оператора порядка т не менее чем 1 — т.
Указание. Использовать § 13, п. 3,
2. Показать, что фундаментальная функция 5? (л:), построенная в п. 3,
имеет порядок сингулярности не выше п-\-2.
Указание. Функционал Е(s) может быть продолжен с сохранением
непрерывности на пространство An+i (§ 15, задача 6), следовательно,
функционал % (х)— на пространство Сп+Х (поскольку Cn+l cF~l {An+l) ).
Использовать задачу 3 к § 12.
3. Показать, что фундаментальная функция ч (х), построенная в п. 5
с помощью лестницы Хёрмандера. находящейся в области | т 1-^в] 1п+ | о |-f~a3>
имеет в области | лс | < Л порядок сингулярности не более п -j- bax -\- 4.
Указание. В доказательстве используется интегрируемость не только
самой функции г|з (s). но и ее произведения на некоторую степень s.
§ 18. Решение уравнения с правой частью
1. В этом параграфе мы покажем, что уравнение
имеет решение в пространстве К' при любой правой части / £ К'-
Если / — финитный функционал, то имеется решение
« = ?(*)./, B)
где ^(х) — фундаментальная функция оператора P\i-j-j. В общем
случае формула B) не действует, поскольку свертка двух нефинит-
нефинитных функционалов не определена.
Заметим, что в силу результата п. 2 § 17 мы можем ограни-
ограничиться рассмотрением многочлена в нормальной форме.
Если произвести преобразование Фурье, задача о решении урав-
уравнения A) перейдет в задачу о решении уравнения
P(s)v(s) = g C)

176 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. III
в пространстве Z'. Здесь g (s)—преобразование Фурье функционала/—■
некоторый функционал на пространстве Z. Финитному / отвечает
тот случай, когда g(s) есть целая функция 1-го экспоненциального
порядка роста в комплексной области и степенного роста в веще-
вещественной области. Формуле B) соответствует решение уравнения C),
имеющее вид C).
D)
где E(s)— функционал, определенный формулой
и
причем Н—подходящая лестница Хёрмандера.
При этом мы имеем
= (gE. ф) = (p. g*W = f «fl*M*. F)
н
Для перехода к решению общего уравнения A) мы заметим следую-
следующее. Допустим, что функционал / представлен в форме сходящегося
(в К') ряда финитных функционалов
/=:§/*• G)
Соответственно мы имеем
t
где gk(s) — целые функции указанного вида. Положим, далее,
где Ek — фундаментальная функция, определяемая по лестнице
Хёрмандера с номером k:
так что
(vk, я])) =
Если мы смогли при этом выбрать Ek (т. е. выбрать лестницы Hk)
так, что ряд
»=2о»*(«) (9)

5 18] РЕШЕНИЕ УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 177
сходится в Z', то мы можем утверждать, что функционал v есть
решение уравнения C). Действительно, умножая (9) на P{s), находим
СО
2)»* = 2 **(«) = *•
ft=0 ft=0
что и требуется. Таким образом, задача сводится к подбору разло-
разложения G) и фундаментальных функций (8) с тем, чтобы была обе-
обеспечена сходимость ряда (9). В свою очередь для сходимости ряда (9)
в пространстве Z' достаточно, чтобы при каждом iJ)£Z абсолютно
сходился числовой ряд
2 *
ft = 0
2. Переходим к реализации этого плана. Прежде всего мы
разобьем функционал / в сумму G) так, чтобы слагаемое /0 было
сосредоточено в некотором шаре с центром в точке 0. а носители
всех остальных финитных функционалов fk умещались бы после
некоторого поворота в пределах октанта Ок — [х: xf^.— ак]
(/=1, 2 п), причем числа ак > 0 стремятся в бесконечность
вместе с k. Считая, что k > 0 и что носитель функционала fk лежит
в указанном октанте, будем строить лестницу в пределах полосы
|т; — aftln+|o;||<m+l.
где ак > 0 — постоянные, которые мы укажем ниже.
Теперь оценим слагаемое
. ,. Г gk(s)$ (s)
<**• *)= ./ Я E) ds-
P(s)
Как преобразование Фурье финитного функционала, сосредоточенного
в октанте х} -^ — ак. функция gk (s) при т, < 0 допускает оценку
(§ 15. п. 3)
Соответственно аналогичную оценку имеет функция g*k(s)=gk(s)
при Ту > 0:
Функция ijp(s), как мы знаем, удовлетворяет неравенству
12 Г. Е. Шилов

178 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. ИГ
Многочлен P(s) на лестнице Хёрмандера ограничен снизу постоян-
постоянной | а |. В итоге мы получаем
и
Rn 7 = 1
2 1
Положим aft = рк -f- k " Mg -\-l. При любом фиксированном
мы имеем
при достаточно больших k; отсюда при указанных k
2 J
и, следовательно,
У = ■&
Пусть теперь носитель функционала fk попадает в октант Ок
только после некоторого поворота Uk, т. е.
Положим /ft(t/ft-^)==/ft(-^); по доказанному, для многочлена P(Uks)
существует лестница Хёрмандера Hk, для которой при любой ф £ Z
P(Uks) ^ к* ■
Здесь gk(s) есть преобразование Фурье функционала /ь(х) и по
формуле C) § 15, п. 2
Заменяя в интеграле по Нк переменное Uks на s', получим интеграл
по лестнице Щ^Нь. причем для достаточно большого k
г
J
c2

§ 18] РЕШЕНИЕ УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 179
Итак, для любого &>0 мы указали лестницу (Нк или и^1Нк), на
которой при любой i|> 6 Z для достаточно большого k > 0 выпол-
выполняется неравенство
!(«*■ *)!<-&■
с постоянной С2, зависящей от функции г|), но не зависящей от
номера k. Тем самым обеспечена абсолютная сходимость ряда из
(vk, ф).
Таким образом, существование решения уравнения A) при любой
правой части / £ К' доказано.
Задачи. 1. Доказать, что два решения уравнения Ру-ъ—)«=/■
совпадающие при | х | :> R (для некоторого R), совпадают всюду.
Указание. Использовать теорему единственности п. 2, § 16.
2. Если многочлен Р{а) не имеет вещественных нулей, то уравнение
Я|'-з—|и = / может иметь лишь единственное решение степенного роста
на бесконечности (более общим образом, принадлежащее S'. см. задачу 5
к § 16).
3. Если многочлен Р (а) имеет единственный вещественный нуль при
р = 0. то уравнение ^('-з—\u = f может иметь лишь единственное
\ ОХ [
решение, стремящееся к 0 на бесконечности (см. задачу 9 к § 7 и задачу 5
к § 16).
4. Показать, что уравнение Ди + k2u = / (я = 3) может иметь лишь
единственное решение в форме дифференцируемой функции, для которой
при | х | ->■ со
_«*«= о A
(условия Зоммерфельда).
Указание. Использовать задачу 6 к § 16j
5. Показать, что уравнение Р у-у-) " =/(■*)• где/(лг) — финитная бес-
бесконечно дифференцируемая функция, всегда обладает по крайней мере
одним бесконечно дифференцируемым решением.
Указание. См. п. 1.
6. (Продолжение.) Если всякое решение уравнения Р у -j— j и = / (х)
с финитной бесконечно дифференцируемой функцией f(x) само бесконечно
дифференцируемо, тоЯи-з—I—гипоэллиптический оператор.
Указание. Использовать связь общего и частного решений.
7. Если Р — гипоэллиптический оператор, / (х) — бесконечно дифферен-
дифференцируемая (не обязательно финитная) функция, то всякое решение уравнения
Pli-3—\u = f(x) — есть бесконечно дифференцируемая функция.
Указание. Использовать разложение единицы (§ 8, п. 4).
12*

180 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. Щ
§ 19. Условие гипоэллиптичности по корням многочлена
(необходимость)
1. Уравнение
имеет решения вида е~Цх' s)=e~l(xtst+"'+xnsn) с некоторыми ком-
комплексными Sj, .... sn. Выведем условия, которым должен удовлетво-
удовлетворять комплексный вектор s = (sl sn)£Cn, чтобы функция e~lix- s>
была решением уравнения A). Мы имеем
и чтобы последнее выражение обратилось в нуль, необходимо и
достаточно, чтобы s было корнем уравнения Р (s) = 0.
Геометрическое место всех точек s, удовлетворяющих уравнению
P(s)=rO, при п > 1 представляет собою гиперповерхность в я-мер-
ном комплексном Bл-мерном вещественном) пространстве, имеющую
(вещественную) размерность In— 2 (одно комплексное уравнение
равносильно двум вещественным).
Разумеется, наглядное представление о поверхности в я-мерном
пространстве затруднительно. Мы построим диаграмму модулей —
некоторый геометрический образ на плоскости, который поможет
судить об устройстве поверхности Р (s) = 0 в целом с интересующей
нас точки зрения.
Определение. Диаграммой модулей поверхности Р(s) = О
называется геометрическое место D всех точек на плоскости £, р.
= |о| = у SoJ. Р= М =
где 6=|о|= у 2^'Р=М = у £т2 иР(о+/т) = 0.
При п= 1 диаграмма модулей сводится к конечному числу точек. Для
иллюстрации различных возможностей, которые могут представиться
при и> 1, рассмотрим два примера. Пусть и = 2 и P(s) = s* — s%.
Условие P(s) = 0 приводит к равенствам аг= + а2, т, = + т2;
отсюда |= |о| = У2 |О]|, р= |т| = У~2 |тх|, и так как о, и тх не-
независимы ($] можно взять произвольно и определить по нему s2),
множество точек (£, р)^^ покрывает всю первую четверть
в плоскости (|, р).
Пусть снова п = 2 и Р (s) = sj -)- Sj- В этом случае условие
р ($) = 0 приводит к равенствам о, = ± т2, тх = ± о2, отсюда
= Уа\ -j-1\ = I Sj I и, следовательно, диаграмма модулей есть бис-
биссектриса р = | первой четверти в плоскости (£, р).

§ 19] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 181
В общем случае диаграмма модулей будет интересна нам только
со следующей точки зрения: может ли точка (£, p)£D при £—>оо
приближаться к оси £, или же эта точка обязана удаляться от оси £,
и если это так, то по какому закону; иначе говоря, какой функцией
вида р = р(£) ограничено множество D снизу.
С этой точки зрения рассмотрим произвольный многочлен Р (slf s2)
с двумя аргументами st и s2.
Приведя его, если необходимо, к нормальному виду путем веще-
вещественного поворота (§ 17, п. 2), можно считать, что уравнение
Р (s) = 0 имеет следующую форму:
т
р (sv s2) = of? + 2х <vr%*+Д v*i ~*s* = о C)
с явно выделенной главной частью.
Рассмотрим вначале случай Р@, s2) = 0, когда sx присутствует
фактически в каждом члене C). В этом случае любая точка о = @, о2)
и т = @, т2) лежит на поверхности нулей, и диаграмма модулей D
покрывает всю первую четверть плоскости (£, р). Пусть теперь
Р@, s2)^0. В этом случае в окрестности бесконечно удаленной
точки s2 все корни уравнения C) могут быть представлены в форме
s1 = As%E, АфО, D)
где y—вещественное число, Е имеет пределом (при |s2| —>оо)
единицу *).
Возьмем s2 = cr2 вещественным и положительным; мы получим
корень Sj=(oj, Tj), для которого при достаточно больших |сг2|
М = К|< К| < 2 H||o2|v<2 \A\\v\\
Таким образом, диаграмма модулей содержит кривую, на которой
Для вычисления показателя у подставим выражение D) в C);
мы получим тождество
Среди показателей у s2 в этом тождестве старший должен при-
присутствовать по крайней мере дважды; иначе, разделив на s2 в стар-
старшей степени и заставив s2 неограниченно возрастать, мы получили бы,
что А = 0. Диаграмма показателей п (у), как функций от у, имеет
вид, показанный на рис 8. Значения у, при которых имеются два
*) См., например. Н. Г. Чеботарев, Теория алгебраических функций..
Гостехиздат, гл. 6, 1948.

182
ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ
[ГЛ. ИГ
m
m-t
равных старших показателя, являются абсциссами угловых точек
ломаной ц (у) = max n {у).
Поскольку а0 ф 0, на диаграмме показателей заведомо присут-
присутствует прямая п{у) = ту. Кроме того, поскольку Р@, s2)^0,
имеется в C) слагаемое вида bpS2, р-^.т; таким образом, в составе
диаграммы показателей также имеется горизонтальная прямая п(у)= р.
Пересечением двух указанных прямых яв-
является точка с абсциссой V=—"С 1- Следо-
т
вательно, наименьший показатель у в
уравнении D) не превосходит 1, и есть
корень уравнения C), представляемый при
|s2| -> do выражением
sx=As\E, АФО, v<l-
Возьмем s2 = o2 вещественным и положитель-
положительным; мы получим корень s,—(о,, т,), для
которого при достаточно больших |о2|
М = Ы< Ы <2 H||o2|v<2H||o|v.
Итак, диаграмма модулей во всяком случае
содержит кривую вида р = C|v Е. где у ^ 1.
£->1.
Отметим один случай, когда можно заве-
заведомо утверждать, что диаграмма показате-
показателей содержит такую кривую с у < 1. Это
иметь место, если в уравнении C) отсутствует член ams™ (
т. е.
= 0); при этом, наверное, р < т
= — < 1-
2. Напомним, что дифференциальный оператор Р (-з—I называется
гипоэллиптическим, если все решения уравнения Р\-5—)и = 0
являются бесконечно дифференцируемыми функциями.
Гипоэллиптические операторы, как оказывается, могут быть пол-
полностью охарактеризованы в терминах, связанных с диаграммой моду-
модулей. А именно, диаграмма модулей гипоэллиптического оператора
с возрастанием £ удаляется от оси £; более точные формулировки
будут даны ниже.
Установим вначале лемму о производных от решения гипоэллип-
гипоэллиптического уравнения — лемму, имеющую большое самостоятельное
значение.
Лемма 1. Если решения uv(x) гипоэллиптического уравне-
уравнения равномерно ограничены в области V, то их частные

§ 19] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 183
duv (х)
производные —^ равномерно ограничены в любой под-
подобласти W, содержащейся в области V вместе со своим замы-
замыканием.
Доказательство. Из формулы C) п. 2 § 16 следует, что
в области W для любого решения и(х) имеет место соотношение
\-v)&\*u{x)=A{x)*u{x) = f A{x-l)u{Qdb (I)
о
где А (х) = Р (-3—) [A — a) <f] — бесконечно дифференцируемая функ-
функция; интегрирование ведется по ограниченной области СэК, вне
которой функция и(х) обращается в нуль. Равенство A) можно
продифференцировать по Xj, и мы получим
о
откуда
max -^-^ <Стах|и(д;)|, B)
где
Без ограничения общности можно заменить в B) тах|и(л:)| на
лг£О
тах|к(л:)|. Действительно, и(х) в области G получалась у нас
в результате умножения некоторого решения уравнения A) в об-
области G на бесконечно дифференцируемую функцию Р(л;), равную 1
в области V и 0 вне области G. Выбирая функцию р(д;) достаточно
быстро спадающей от значения 1 к 0, мы при любом е > 0 можем
получить для произведения неравенство
max | и (х)\ <^ max | и (х)\ -f- e;
x£G x£V
так как G не зависит от е, то в пределе при е—>0 мы получим
из неравенства B)
|^Ц C)
что и доказывает лемму.
3. Теперь мы можем получить характерное свойство поверхности
нулей гипоэллиптического оператора Pw-p) и ее диаграммы модулей.

184 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ (ГЛ. III
Предположим, что РI/ -х— I — гипоэллиптический оператор. Много-
Многочлен P(s) будем называть в этом случае гипоэллиптическим много-
многочленом. Пусть W с V — два шара с общим центром в начале коорди-
координат; неравенство C) п. 2 применим к решению и (х) = е~'<*•*>,
P(s) = 0. Обозначим через г радиус шара W и через R радиус
шара V. Пусть, далее, Sj = Gj-\-ttj— разложение Sj на веществен-
вещественную и мнимую части. Тогда можно записать, что
тах|и(*)|= max |«-'<*■->|= max |e-<[*i(°i+"i)+-+*n(en+4)]| =
£V 1|<Д |1<Д
= max
\x\<R
-где |т| = ySx2j. Далее,
I ди
max -з—
дх,
= \s}\ max
Таким образом, при любом j имеет место неравенство
->|T| или |^
Возводя в квадрат и суммируя по индексу /, получим \s\
отсюда и |о| ^С^я-ои! и, следовательно.
^ =A\u\o\—B, A)
где A = ■-, —, £» = p . Мы по-
^ 1/0^^^ лУчаем весьма важный вывод: на по-
///^t'^> верхности P(s) = 0 выполняется
'/ //гй*^ неравенство A). Иначе говоря, если
'////lllll/i/ \ по этой поверхности удаляться в бес-
/ <$ конечность так, что вещественная со-
п „ „, ставляющая о точки s = a-\-lx бу-
Рис. 9. Область, где распола- /
гается диаграмма модулей гипо- Дет неограниченно увеличиваться (по
эллиптического оператора. модулю), то и мнимая составляющая т
будет неограниченно увеличиваться по
модулю и притом быстрее, чем Л1п|о|. Заметим, что R и г можно
взять как угодно близкими и, следовательно, коэффициент А в нера-
неравенстве B) может быть как угодно большим.
Так как P(s) по модулю совпадает с P(s), то тем же свойством
обладает и поверхность P(s) = 0 корней гипоэллиптического мно-
многочлена P(s).
Диаграмма модулей поверхности P(s) = 0 располагается, таким
■образом, при любом А выше некоторой кривой р = А 1п £ —В (рис 9).

§ 19] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 185
4. Предположим теперь, что оператор Р It ^—J не только гипоэл-
липтичен. но и р-гипоэллиптичен, т. е. все решения уравнения
Ри-т—)и = 0 принадлежат локально к классу Жеврея Ор (§ 16»
п. 5), так что выполняются неравенства | D"u (х) \ -^ CEPq^. В этом
случае можно высказать более сильное утверждение о скорости
удаления диаграммы модулей от вещественной оси:
Теорема. Если Р(а) есть fi-гипоэллиптический многочлен,
то его диаграмма модулей располагается выше некоторой
кривой вида p = b£® — С.
Для доказательства используем следующее усиление леммы 1:
Лемма. 2. Для производных от решений $-гипоэллипти-
ческого уравнения в области V справедлива оценка
max I ЕР и {х) I < СВУР max I и (х) I
xew1 " xcv
в любой подобласти W, содержащейся в области V вместе
со своим замыканием.
Доказательство. В силу формулы A0) § 16, п. 4, при любом
* г
где Г — граница области W.
По доказанному выше, функция ск(х) вместе с фундаментальной
функцией ^(л;) принадлежит классу Од и, следовательно,
f | Lfck (x - т]) | *| = f | D"ck (I) | dl < CEPq®.
г г
С другой стороны, в силу результатов п. 2,
max
w
В результате мы получаем в области W оценку
w ^ 2 v
что и требовалось.
Б. Пусть снова WcV — два шара с общим центром в начале
координат.
В качестве решения и{х) рассмотрим функцию e~tlx-s|. где
Р(s) = 0. Как обычно, положим s =а-\-1т. Тогда
max |и(д;)| = еД1т1, max IDgu(x)\ = \sqi ... s9" \erlxl,
•л-КД \x\<r 'II "I

186 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ III
и следовательно, из A) п. 4 следует
■Отсюда, далее, следует, что
Переходя к нижней грани по всем qx qn, получаем (см. ниже п. 6):
'1*. О)
или, иными словами,
|т|>Е^|^Г-С2>&|^Г3-С2>&|о|1/р-С2.
что и требовалось.
6. Нам остается показать, что при любых В > О и d > О
Inf.^<&-Ml* «= 0,1.2....).
Считая временно # непрерывно меняющимся переменным, найдем минимум
■функции agqq^ = / (q) обычными средствами дифференциального исчисления.
.Логарифмируя, дифференцируя и приравнивая результат нулю, получаем
^^ а A)
где q0 — значение q, на котором реализуется искомый минимум. Из урав-
уравнения A) находим qo = —ш и, следовательно,
еа1Р
В —
= В^, min 9f(q) = в
еа "
Так как в действительности q меняется только по натуральным числам, то
f о. Мы
q ур
т\п f(q) на самом деле несколько выше найденного. Мы имеем
[In f(q)]"=j-
.Поэтому в целой точке qt, ближайшей справа к точке q0.
Поэтому

§ 20] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 187
откуда
W Ё_
mln,/<?)<« 2 -е
Ё£
Первый множитель при а<1 ограничен величиной е2. Если же а > 1. то
1 --8-
Итак, при любых а. 0 < а < со,
Р
что и требовалось.
Задачи. 1. Показать, что нижняя граница диаграммы модулей MHOro-
члена P(sv S2) = aosi""T- 2 aftsi*~*s2 ~Ь 21 a/W~*s2 содержит кривую
*i y<*
p = C^v с v < 0 тогда и только тогда, когда Р (sx, s2) содержит член вида
s\s%, где k превосходит степень многочлена Р@, s2), b Ф0.
Указание. Рассмотреть диаграмму показателей (п. 1).
2. Показать, что нижняя граница диаграммы модулей (в классе моно-
монотонных кривых р =/(!)). есть кривая р = 0 тогда и только тогда, когда
уравнение Р (at, a2) = 0 определяет кривую, уходящую в бесконечность.
3. Если диаграмма модулей многочлена Р(з) = Р(в} sn) целиком-
расположена в области р ;> \t (|). где t (|) -»• со при | -> со, то п=\ (т. е
Р есть многочлен от одной переменной и имеет лишь конечное число нулей)
§ 20. Условие гипоэллиптичности по корням многочлена
(достаточность)
В § 19 было показано, что координаты диаграммы модулей гипо-
эллиптического многочлена P(s) удовлетворяют неравенству вида
при любом А > 0. Если же многочлен Р (s) не только гипоэллипти-
ческий, но и р-гипоэллиптический, т. е. для любых решений уравнения
1г-т—|к =
рост производных ограничен условием
то координаты диаграммы модулей удовлетворяют более сильному
неравенству
|т|>Л2|о|1/р-А,- B>
Мы покажем здесь, что неравенства A) и B) являются не только
необходимыми, но и достаточными условиями гипоэллиптичности,
соответственно р-гипоэллиптичности, многочлена Р.

188
ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ
[ГЛ. III
1. Установим сначала следующую лемму:
Лемма 1. Если диаграмма модулей поверхности P(s) = 0
вся лежит в области р>/(£). где /(£)->оо при £->оо, а /'(£)
остается ограниченной, то в области p-^-j/d) при доста-
достаточно больших £ имеет место неравенство
\P(s)\>R
с произвольно заданной постоянной R.
Доказательство. Мы уже знаем, что многочлен P(s) всегда
.можно считать заданным в нормальной форме
Р (s) =
Pk (st sn) s*. a0 Ф 0.
Пусть Яу = Я,у(*2 sn) (J=l. 2 m) — корни (по st) мно-
многочлена P(s). Пусть, далее, Я,у = |у + /т]у — разложение корня Kj на
вещественную и мнимую составляющие. Тогда, по условию, при
любом у = 1 т
Рассмотрим значение многочлена
т. е. там, где
в области
... +О2).
Мы имеем
с0 П (Si -
y=i
п
У = 1
Мы покажем, что при достаточно больших |о| каждый из т мно-
множителей в правой части превосходит положительную постоянную.
Обозначим для краткости xl = t, х%~\- ... ~\-x2n = q2. a1 = Q,
<J^+ . • ■ -{-сРп = р2; r\.=i\, £-=£; мы должны из соотношений
C)
при заданной постоянной С^.0 получить, что при достаточно боль-
больших |сг|, каковы бы ни были pug,
D)

$ 20] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 189
Если |6 — \у^С—ясно, что неравенство D) выполняется;
поэтому достаточно ограничиться случаем 16 — \ | -^ С. Тогда и
I / iVW+J2) - f {V¥+T2) | < С max /' (и) < ВС.
Теперь из неравенств C) видно, что т] > t, когда | о | достаточно
велика Так как о2 = в2+ р2->оо. то /(^б2 + р2)-> оо и
{V) * °°- Поэтому
> f {VW+J2) -1 / (V&+J2)=
что даже больше, чем утверждалось.
2. Переходим теперь к доказательству основной теоремы:
Теорема 1. Если многообразие N(P) = [s :P(s) — 0} лежит
в области
|т|>С1п|о| —С, A)
i
при любом С, то фундаментальная функция У(х) оператора
P[t-fa) есть обычная бесконечно дифференцируемая функция
вне начала координат.
Доказательство. Пусть основная функция ф(х,, .... д;п)
сосредоточена в некоторой малой области G, не содержащей начала
координат. Мы покажем, что тогда выражение (с?(х), ф(д;)) можно
записать в виде интеграла по области G от произведения ф(л;) с не-
некоторой бесконечно дифференцируемой функцией.
Как мы уже знаем, оператор Р и -^—\ можно считать заданным
в нормальной форме *), так что
*) Заметим, что, используя теорему п. 2, § 21, можно показать, что
гипоэллиптический многочлен имеет нормальную форму относительно любого
переменного.

190 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. щ
Как мы видели в § 2, преобразование Фурье фундаментальной
функции есть функционал Е в пространстве Z. действующий по
формуле
<е. v-fiftg.. m
где Н — подходящая лестница Хёрмандера. Для простоты рассмотрим
случай п — 2, тогда лестница Хёрмандера есть многообразие, опре-
определяемое условиями
s, = о, -f- /Tlt — схэ < о, < оо, г, = I (o2) — кусочно постоянная
функция от сг2,
s2 = о2, — сю < о2 < сю.
Теперь используем неравенство A); оно поможет нам улучшить
поверхность интегрирования в формуле B).
В силу леммы I, в плоскости (av o2) при достаточно большом
|о| > а (зависящем только от постоянных С и Cj в неравенстве A))
выполняется неравенство
Поэтому все ступеньки лестницы Хёрмандера, проекции которых
на плоскость (о,, о2) оказываются целиком вне круга |о|<^о, можно
опустить на эту плоскость — т. е., можно считать, что кусочно по-
постоянная функция 1(а2) равна нулю при |о2|^-о. Таким образом,
на лестнице останется лишь конечное число ступенек, проекции ко-
которых пересекаются с кругом |оКо.
Рассмотрим любую из этих ступенек. Интегрирование по коор-
координате о, в пределах этой ступеньки производится по прямой
s, =о, -\- ixv т, — const. Но вне отрезка loj-^o можно заменить
участки этой прямой на вертикальные отрезки и участки оси ох-
Таким образом, мы сводим всю лестницу Хёрмандера в данном случае
к фигуре, поднимающейся над плоскостью (о,, о2) лишь в пределах
квадрата loj-^fl, |о2|-<;о, а вне него совпадающей с самой пло-
плоскостью (ор о2).
Интеграл B) мы разобьем теперь на две части: интеграл по части,
соответствующей квадрату Q, = (о: |'о, |-^ а, |о2|-<о} с присоеди-
присоединенной к нему совокупностью указанных вертикальных отрезков,
и по внешности Q этого квадрата. Рассмотрим вначале интеграл,
отвечающий квадрату Q,:
P(s) •

$ 201 УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 1Q1
Мы имеем
где
C)
есть, очевидно, бесконечно дифференцируемая (и даже аналитическая)
функция от х при всех х.
Для второго слагаемого
Яг
такое преобразование (с переменой порядка интегрирования) не может
быть проведено, так как область интегрирования уже не ограничена
и интеграл, аналогичный D), не сходится. Мы приведем это слагаемое
к виду C) с заменой плоских участков
лестницы Н на искривленные.
Будем изучать вначале фундаменталь-
фундаментальную функцию &(х) в окрестности V точ-
точки (л:,, х2), х1 > 0, х2 > 0, находящейся
на положительном расстоянии d от обеих
координатных осей, так что функция ф (х),
к которой применяется cf(x), сосредото-
сосредоточена в окрестности V. Разобьем область
интегрирования Q на 8 частей Q2, .... Qg,
как показано на рис. 10. Соответственно
напишем
*)■
Рис Ю.
Мы будем в соответствующих интегралах производить вначале
некоторую деформацию области интегрирования.
Рассмотрим функционал
(£2. 4,)= /"*№*>
Р(а)
В области интегрирования Q2 координата о2 остается ограниченной,
координата Oj изменяется от положительного значения а до -j~oo.

192
ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ
[ГЛ. Щ
Перейдем при фиксированном о2 в плоскости s, от интеграла по
полупрямой а <С о, < оо, тх = 0 к интегралу по линии а <^ о, < оо,
2т, =С1п+о1—С,, дополненной соответствующим отрезком на
прямой о, = а (рис. 11). Покажем, что интеграл по исходной полу-
полупрямой равен интегралу по этому контуру. Для этого достаточно
показать, что интеграл по вертикальному отрезку ААХ (А на оси
о,, Л, на указанной линии) стремится к нулю, когда этот огрезок
неограниченно удаляется вправо. Но, в силу леммы п. 1. величина
-р. остается на этом отрезке ограниченной; поэтому, используя
неравенство C) п. 1, § 15, находим
А,
, a2)ds,
<С0 max
s,t ЛА,
"• что при достаточно большом k стремится
к нулю.
Так как полученная оценка равномерна по всем о2, то двойной
интеграл
С
J
взятый по области Н2, определяемой условиями
s1 = al-\-txv 2xl=C\n+ ах—Си а
S2 = O2. |O2|<fl.
равен исходному двойному интегралу
оо.
-ob «■
Далее, мы имеем
(Е2, ф)=
\
Если произвести формальную перемену интегрирования по s и по X.
мы получим
/
й[

20] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 193
Для оправдания этой замены достаточно показать, что интеграл
pi U, s)
■7Ч5Г
сходится абсолютно и равномерно по х. Но мы имеем здесь, в силу
положительности тх на Н2,
| еЦх-s) | = е~(х'т) = e-'lXl < e~dx' = Be~d
и в соединении с ограниченностью D это приводит к абсолютной
и равномерной сходимости интеграла D). Из равенства C) следует,
что
что
-pw-ds-
>-/■
Формально дифференцируя §°2(*) п0 х\ и хр будем получать под
знаком интеграла добавочные множители S] и s2. Очевидно, что
сходимость интеграла не будет нарушаться при добавлении множи-
множителей s2 в любом числе и множителей st в таком числе, чтобы вы-
выражение
оставалось интегрируемым. Но по условию А можно брать как
угодно большим. Поэтому функция %>2(х) (не зависящая от специ-
специального выбора А) может быть продифференцирована любое число
раз и по х,. Таким образом, &2(х)—также бесконечно дифферен-
дифференцируемая функция.
Аналогичное рассуждение проводится для случая областей Q4 Q6
и Q8. Рассмотрим теперь случай области типа Q3, где а -^ а1 < оо.
а -«С о2 < оо. Здесь мы произведем последовательный переход от
первоначальной области интегрирования Q3 к области Н3, опреде-
определяемой условиями
o-<Oi<oo, 2Tj = Cln+Oj — Cv а-<о2<оо, T2=s0,
и затем к области Й3, определяемой условиями
fl-^°i<00' 2т1 = С1п+о1 — Сх,
а ^ о2 < оо, 2т2 = С 1п+ о2 — Сх.
Двойной интеграл
13 Г. Е. Шнло!

194 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. Щ
равен двойному интегралу
ds
■I P(s)
по тем же причинам, что и выше. Затем, заменяя ty(s) на ее выра-
выражение через функцию (р(х), мы приходим к выражению
с оценкой на Й3:
Эта оценка обеспечивает возможность неограниченного дифференци-
дифференцирования (?3(х) по xi и Х2- Аналогичное построение производится
для областей Q5, Q7 и Q9.
Таким образом, при х, > 0, х2 > 0 функция (f = (fl-\- ... +^9
оказывается бесконечно дифференцируемой. Отметим, что эта беско-
бесконечная дифференцируемость имеет место в смысле пространства К';
но из рассмотрений § 13 вытекает, что будет иметь место и беско-
бесконечная дифференцируемость в обычном смысле.
Рассмотрим теперь произвольную точку (х,, х2). Если xl^=0,
jc2 Ф 0, то некоторым поворотом (сводящимся к изменению знаков
у каких-то осей) можно перевести эти точки в положение, где хх > О,
х2 > 0. При этом повороте, разумеется, изменится многочлен P(s).
Но так как в неравенстве A) фигурируют только модули коорди-
координат Oj и Ту, то неравенство A) сохранится и для преобразованного
многочлена P(s). Так как размеры областей Q,, .... Qg зависят
только от постоянных С и С], то эти области не изменятся и не
изменится последующее рассуждение; оно основано только на пред-
предположении, что |P(s)| > R, а не на явном выражении этого много-
многочлена.
Если одна из координат х,, х2 равна нулю, то малым поворотом
можно ее сделать положительной и далее провести предыдущее
построение. При этом поворот не должен быть большим, чтобы
многочлен не потерял нормального вида.
В случае нескольких (более 2) переменных все рассуждения про-
проходят аналогично, с очевидными техническими усложнениями за счет
увеличения числа переменных.
Таким образом, теорему 1 можно считать полностью доказанной.
3. Теорема 2. Если многообразие N(P)={s :P(s) = 0]
лежит в области
М>С2|оГ-С,.

§ 20] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 195
то фундаментальная функция (?(х) многочлена P(s) принад-
принадлежит {вне любой окрестности начала координат) к классу
)Кеврея Ор:
Доказательство. Считая Xj > 0 и используя метод доказа-
доказательства предыдущей теоремы, мы представим выражение <f(x) в виде
суммы конечного числа (9 для п = 2) интегралов вида
Р J(x,s)
взятых по участкам, лестницы Хёрмандера, деформированных следую-
следующим образом: если одна из координат, например о,, изменяется
в проекции Qj участка Hj от а до -{-оо, то горизонтальный участок
пути интегрирования в плоскости s, заменяется на криволинейный
fl<Oi<oo, т, = А\па1 — Av
Рассмотрим для определенности участок Н2. Продеформируем
еще раз контур, заменив его на кривую
а < Oj < оо. 2т, = С2о\/Р — Су
Покажем, что интегралы A) будут существовать и на новом контуре
и будут иметь прежние значения. Достаточно проверить, что инте-
интегралы по вертикальным участкам
J
J
A In (Ti—Al
стремятся к 0 при о, —>схэ. Но мы имеем, как и ранее, \P(s)\~^\, a
| eix>s> I = c-*iTi < Ce~Ad In °i = Ca-Ad,
dsx
I
A In a,—A,
и так как А можно взять сколь угодно большим, полученное выра-
выражение стремится к 0 при Oj —> оо.
Далее, на самом контуре мы имеем
13*

196 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. 1Ц
„ dg2 (х)
откуда для производной мы получаем оценку
(х)
со
Интеграл легко вычисляется с помощью гамма-функции подстановкой
.а1о'/Р:=|1, и мы получаем
W
Оценки по различным переменным независимы друг от друга, поэтому
в результате мы получаем для любого /==1, .... 9
■что и утверждалось.
4. Мы сформулируем теперь одну алгебраическую лемму, которая
позволит сразу упростить и связать воедино полученные нами условия.
Лемма 2. Если диаграмма модулей многочлена P(s) лежит
яад некоторой кривой р = /(£)■ где /(I)-*00 пРи \-*-°°< то
■существует такой положительный показатель \ и коэффи-
коэффициент С, что эта диаграмма при достаточно больших £
лежит и над кривой р —C£v.
Применяя эту лемму к дифференциальному оператору ■'эи~з~) >
получаем теорему.
Теорема 3- Уравнение Pit -т—]и —0 является гипоэллипти-
ческим тогда и только тогда, когда из Р{а-\-гт) = О, |а|->оо,
следует |т|—>оо. При этом условии на поверхности нулей
многочлена P(s) для достаточно больших \а\ имеет место и
соотношение |t|^-C|o|v, откуда следует, что все' решения
гипоэллиптического уравнения принадлежат к некоторому
классу Жеврея.
Таким образом, всякое гипоэллиптическое уравнение является
р-гипоэллиптическим при некотором р > 0.
Доказательство леммы 2 не просто. Оно основано на применении
алгебраического «принципа исключения», который в последнее время
получил различные применения в вопросах анализа-
Пусть имеется некоторое количество вещественных многочленов
Р1 Рк от аргументов двух типов: основных аргументов х, хп
м параметров qx qm. Рассмотрим вопрос, при каких веществен-

$ 20] УСЛОВИЕ ГИПОЭЛЛИПТИЧНОСТИ ПО КОРНЯМ МНОГОЧЛЕНА 197
ных значениях параметров разрешима относительно хг
стема уравнений
o U=u 2 k). A)
Имеет место следующая теорема (Зайденберга — Тарского): Суще-
Существует конечная совокупность вещественных многочленов
Q(a°(?j Ят) (' = 1. 2 М; a=l, 2 а,-), обладающая
тем свойством, что система A) разрешима относительно
х1 хп тогда и только тогда, когда удовлетворяется
хотя бы одна из М систем неравенств
Q(a>, Ят)>0 (a=l a,-)
при некотором фиксированном i *).
Применим теорему Зайденберга — Тарского к рассматриваемому
случаю. Мы имеем систему уравнений:
^-2x5=0.
B)
Последнее уравнение, комплексное, можно заменить парой веществен-
вещественных уравнений с 2п вещественными аргументами о;- и Xj.
Примем в этих уравнениях О] и т,- за основные переменные, а |
и р за параметры. В силу теоремы Зайденберга — Тарского, суще-
существует конечная система многочленов от параметров Q$(&, p) такая,
что система B) разрешима относительно о7- и т;-, тогда и только тогда,
когда выполняется хотя бы одна из М систем неравенств
0%ЧЬ p)>0, a=l аг.
Обозначим через QW область в первой четверти плоскости (|, р),
где выполняется неравенство Ф^'ЧЕ- Р)^-0. Результат теоремы Зай-
Зайденберга— Тарского можно сформулировать так: чтобы система B)
была разрешима, необходимо и достаточно, чтобы точка (£, р) при-
принадлежала к множеству
М а1
ип
» = 1 а=1
*) Доказательство теоремы Зайденберга — Тарского см.. например, в ста-
статье Е. А. Горина. Асимптотические свойства многочленов и алгебраиче-
алгебраических функций. УМН. № 2, 1961.

198 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. Щ
По условию, диаграмма модулей многочлена P(s) лежит над некото-
некоторой кривой вида
Р = /(£). /(D->oo при 6-»оо. C)
С другой стороны, как известно из теории алгебраических кривых *)
контур каждой области Q^> имеет уравнение
где Е(£)— функция, имеющая при £->оо пределом 1. Поэтому и
область Q ограничена такими кривыми. Но так как она лежит над
кривой C), то она ограничена снизу некоторой кривой вида
р = А1чЕ. Л>0, y>0. £->l. D)
Следовательно, если Р — гипоэллиптический оператор, его диаграмма
модулей располагается не только выше логарифмической кривой A)
п. 1, но и выше некоторой степенной кривой D).
Точная верхняя грань значений ■у, для которых диаграмма моду-
модулей поверхности P(s) —0 лежит выше кривой D), называется показа-
показателем гипоэллиптичности многочлена Р. Существует формула для
его вычисления (см. задачу 6 к § 21)..
Задачи. 1. Доказать, что произведение многочленов
= Pl(s) ...Pr(s)
является гипоэллиптическим многочленом тогда и только тогда, когда гипо-
эллиптичен каждый множитель P/(s), /= 1 г.
Указание. Поверхность нулей многочлена Р есть объединение поверх-
поверхностей нулей многочленов Pj (s).
2. Известно, что оператор Р U-г-1 обладает фундаментальной функцией,
которая вне шара 17= [х: \ х \^ Я], Я фиксировано, бесконечно дифферен-
дифференцируема. Доказать, что Р гипоэллиптичен.
Указание. Лемма 1 § 19, п. 2, имеет место для оператора Р в при-
применении к такой подобласти W а V, для которой W — U а V. Отсюда
для точек поверхности Р (s) = 0 вывести неравенство
\%\>А\п\а\ — Ах
с некоторым фиксированным А. Использовать теорему 3.
3. Известно, что всякое решение уравнения Р /— в = 0 в любой
области V является бесконечно дифференцируемым в области W czV такой,
что W — L/dV, где {/= [х: | х\ <:/?}. Н фиксировано. Доказать, что
Р — гипоэллиптический оператор.
*) См.. например, Г. Е. Шилов. Особые точки алгебраических кривых
на плоскости. УМН, № 5, 1950, 180—192.

§ 21] УСЛОВИЯ ГИПОЭЛЛИПТИЧНОСТИ 199
Указание. Применяя условие к фундаментальной функции % (х) опе-
оператора P\i-£— J. показать, что она бесконечно дифференцируема вне неко-
некоторого шара с центром в начале координат. Использовать задачу 2.
4. Известно, что фундаментальная функция оператора бесконечно диф-
дифференцируема в окрестности некоторой замкнутой поверхности, внутри кото-
которой лежит начало координат. Показать, что Р гипоэллиптичен.
Указание. Используя формулу типа Пуассона (§ 1), показать, что
выполняется условие задачи 3.
5. Если фундаментальная функция оператора Р \-т—\ порядка т имеет
\ ох )
вне начала координат обычные производные до порядка т—1 включительно,
то оператор Р гипоэллиптичен (В. В. Грушин).
Указание. Формула C) § 16, п. 2 для решения и во всем пространстве
имеет место также во всем пространстве. Положить и(х) = е~1(х> *о), где
Р (s0) = 0, применить преобразование Фурье и из полученного равенства
вывести, что g(so) = \; далее, используя свойства преобразования Фурье
финитной суммируемой функции, показать, что поверхность Р (s) = 0 при
| s | -> со удаляется от вещественной гиперплоскости.
Примечание. Существуют негнпоэллиптические операторы Р (-г— I
порядка т с фундаментальной функцией, имеющей вне начала координат
обычные производные до порядка т — 2 (например, для уравнения струны,
см. § 27, п. 6, 2 и задачу 3 к нему).
6. Показать, что для многочлена Р (а), имеющего лишь ограниченное
множество вещественных нулей, справедлива оценка
|P(o)|>C|o|V
при достаточно большом \а\ и некоторых С > 0 и у (V может быть и отри-
отрицательным).
Указание. Применить к «диаграмме модулей» из точек £ = | а |.
р = | Р (а) | теорему Зайденберга — Тарского и рассуждения п. 4.
7. Показать, что оператор Р ('-г—) обладает фундаментальной функцией
£S', если Р (а) не имеет вещественных нулей.
Указание. В силу результата задачи 6 деление р. возможно в про-
пространстве S.
Примечание. В действительности любой оператор Р('-з—) обладает
фундаментальной функцией %(x)^S', но доказательство этого не элемен-
элементарно *).
§ 21. Условия гипоэллиптичности по поведению
многочлена в вещественной области
1. Условия гипоэллиптичности, выведенные в §§ 19—20, форму-
формулируются в терминах, связанных с многообразием комплексных
*) См. L. Н б г m a n d е г, On the division of distribution by polynomials,
Arkiv Mat. 3, № 6 A958), 555—568; русский перевод в сборнике «Матема-
«Математика», № 5 A959).

200 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. Щ
корней многочлена P(s), и поэтому их использование в конкретных
случаях затруднительно. Мы выведем в этом параграфе условия
гипоэллиптичности, использующие поведение самого многочлена P(s)
в действительной области.
Лемма 1. Если для любого с>0 существует такое А > 0,
что в области |т| < с, |о| > А нет корней у многочлена P(s),
то для любого вещественного вектора 6
>1 при |о|->оо.
Доказательство. Можно предположить, что 6 = A, 0 0).
Если |о|>Л + с и Я, — любая точка поверхности P(s) = 0, то
\а—К\ > с. Запишем многочлен Р(а) в виде
Отсюда
где
Очевидно, что при достаточно большом с эта величина становится
как угодно малой, чем наша лемма и доказана.
Лемма 2. Если при любом вещественном векторе 6 мы
имеем
/ио для любого оператора £У = — — с \q\=2qj>0
да]1... дапп
llm P(rt °-
|СТ|-».СО ^W
Доказательство. По формуле Тейлора, при 9 = (9lf .... 9„)
>0
причем сумма в правой части конечна. Далее,
_. . V1 Р"Р(о)
~~ ~г ^
Р (а) ~~ ~г ^ Р (а)
I 1>0

$ 21] УСЛОВИЯ ГИПОЭЛЛИПТИЧНОСТИ 201
и, по предположению, при |о| —>оо
Dip (о) 6«
Zi
P(o)
q
Так как одночлены —г- как функции от Qx 9„, линейно неза-
независимы, то р, I —> 0 при каждом <7=£0 и |о| —>оо. что и тре-
требуется.
Следствие. При выполнении условий леммы 2
Iim
1с|-»оо
Действительно, среди производных многочлена Р (о) имеется
постоянная, отличная от нуля; так как при любом <7=£0, по дока-
доказанному, ptV ~*°' то и р/о\ ~>°' откуда |Р(о)|->оо.
Лемма 3. Если при любом q ф 0
,. DQP(a) n
Iim -- р \ ■ == 0.
то соотношение
осуществляется равномерно по всем |9| < с {допускаются
и комплексные G).
Доказательство. Мы имеем
таким образом,
откуда и следует утверждение леммы.
Следствие. Если при любом q Ф 0
|СТ|-»-оо
mo для любого с > 0 можно найти такое А > 0, что в области
|т| < с. |о| > Л многочлен P(s) не имеет корней.
Действительно, пусть для некоторого с > 0 имеется последова-
последовательность kv = ov -f- /tv корней многочлена Р (s), удовлетворяющих
условию |tv| < с, |ov|—>оо. Шары радиуса с с центрами в точках

202 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. Щ
Я.1, .... Xv пересекают вещественное подпространство Rn по некото-
некоторым вещественным шарам. Многочлен P(s), отличный от тождест-
тождественного нуля, в каждом из этих шаров имеет точку о^, где
Р(а'^Ф0. Очевидно, Xv=o^+6v, где |6v|<c Мы имеем, далее.
что противоречит доказанному соотношению
Леммы 1, 2, 3 приводят к следующей теореме, дающей необхо-
необходимые и достаточные условия гипоэллиптичности многочлена P(s).
Теорема. Многочлен Р (s) гипоэллиптичен тогда и только
тогда, когда выполняется одно из двух (эквивалентных)
условий:
1) lim —Р7" -> 1 при любом векторе 9;
|СТ|->оо г (О)
2) lim-^ = 0 приафО.
|о|->.со Р(°)
Заметим при этом, что второе условие можно еще ослабить,
ограничившись рассмотрением только первых производных много-
многочлена Р(а):
Лемма. Если ■ р —>0 (ZI — символ любой из производ-
производных -ъ—), то многочлен P(s) гипоэллиптичен.
Доказательство. По формуле Лагранжа
ze,-
до.
полагая |о| —>оо (9 фиксировано), получаем, что In—p/l —*~Q>
Р (а + 6) ,
—р —> 1, что и требовалось.
2. Многочлен P(s) мы назвали эллиптическим, если все решения
уравнения РI/ -g—\ и = 0 — локально аналитические функции Мы
дадим здесь описание всех эллиптических многочленов по их коэф-
коэффициентам.

§ 21] УСЛОВИЯ ГИПОЭЛЛИПТИЧНОСТИ 203
Заметим, что локально аналитические функции — это функции
зкевреевского класса О, (§ 16, п. 5). Применяя результаты §§ 19—20.
получаем: необходимым и достаточным условием эллиптич-
эллиптичности многочлена P(s) является выполнение неравенства
\г\>С\а\-С1 A)
для всех точек s = a-\-ix нулевого многообразия N(P) много-
многочлена P(s). Мы выведем отсюда следующее явное определение:
Теорема. Многочлен P(s) эллиптичен тогда и только
тогда, когда главная его часть P0(s) (совокупность всех членов
максимальной степени) имеет единственный вещественный
корень в точке s = 0.
Доказательство. Пусть Ро(о) имеет единственный нуль при
о = 0. Покажем, что существует постоянная С>0 такая, что для
всех комплексных корней многочлена P(s) при достаточно больших |о|
выполняется неравенство
Действительно, предполагая противное, мы для каждого v= 1, 2, ...
найдем такой корень sv = ov+iTv> что |tv|< — |av|. причем
|av|—>оо. Далее, положим P(s) = P0(s)-\-Pl(s), где P0(s)—главная
часть многочлена P(s). Мы имеем
0 = Р (Ov + rtv) = Ро (ov + /tv) + Р, (о, + itv) =
0<|ft|<m |*l<m-l
Так как Pq(s) — однородный многочлен степени т, не обращаю-
обращающийся в нуль при вещественных s = а ф 0, то
|А,(оч,)|>Л|оч,|т.
где А > 0. С другой стороны,
В результате мы получаем, что
2 ^
0< |ft|<m
m1l*l1*1 М->оо.
что противоречит предположению P(av+rtv) = 0.

204 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. III
Итак, если Ро(°) имеет единственный корень 0 = 0. то много-
многочлен P(s) эллиптичен.
Предположим теперь, что Р0(а) имеет вещественный корень о Ф 0.
Так как Ро однороден, то множество его корней состоит из прямых
линий, проходящих через начало координат. Можно предположить,
что корнем многочлена Р0(о) является точка
A. 0 0)
и что точка
@, 1 0)
не является его корнем. Рассмотрим тогда многочлен Qis^ S2)s
^P(sv s2. 0 0). Запишем его в форме
т
Q(su s2)= 2 aks?-bS2-t- 2 akJs{'kS2 = Qo(Si. s2)+C?i(si. s2).
ft=0
При этом
<20(i, o)=co=o,
eo(O. 1)=атф0.
Но в таком случае, как мы видели еще в § 19, п. 1, нижний
контур границы диаграммы модулей многочлена Q (а следовательно,
и многочлена Р) имеет уравнение р—Л|УЕ, у < 1, так что много-
многочлен Р заведомо неэллиптический.
Задачи. 1. Построить негипоэллиптический многочлен Р (st, s2), для
которого
Iim | Р (ol <j2) I = со. A)
|<X|-»co
Указание. Поверхность нулей многочлена P(s,, s2) при |а|->со
не должна иметь пересечений с вещественной плоскостью, но и не должна
удаляться от нее. Для выполнения A) можно еще умножить на многочлен,
заведомо гипоэллиптический.
Отв. Например, P(sv s^ — (s2 — i)(s2—isl) = (sl — s1) — ls2
2. Построить негипоэллиптическнй многочлен Р (S|, s2)- для которого
Iim |P(ai-t-iTi, a2-t-t42) I = 00
|CT|->co
равномерно при | ti |<! С, | т21 .< С (С фиксировано).
Указание. Использовать конструкцию задачи 1.
Отв. Например. Р (s,, s2) = (s2 — 2Ci) (ss — ist).
3. Доказать, что уравнение первого порядка по t с одной пространствен-
пространственной координатой х *
ди
гнпоэллиптично тогда и только тогда, когда в разложении многочлена Q(a) =
= Qi (a) + 'Qi (a) на вещественную и мнимую части степень многочлена Q2
не выше степени многочлена Q,.

§ 22] МЕТОД РАДОНА 205
Указание. Применить лемму 4. Ее условия приводятся к виду
' ,0 B) ГСН'+даН' ,0
Если Q2 (а) имеет ббльшую степень, чем Q, (а), то на линии К = Q2 (я)
не выполняется B). Если степень Qi (а) равна я>1и степень Q2 (а) не пре-
превосходит т, то числитель в B) имеет степень •< 2 (т — 1), знаменатель
имеет степень (по а) !>2т.
4. Доказать, что уравнение любого порядка по t с одной пространствен-
пространственной переменной
т-\
дти _\ р (■ Л_\ д и
dtm ~ ^ "\ ~дх) dtk
гипоэллиптично тогда и только тогда, когда все старшие коэффициенты Aj
разложения на бесконечности
Xj= Ap'iE
любого корня уравнения
не являются чисто мнимыми числами.
Указание. Уравнение A) разложить на множители
ft
Д(Л-Л;-(а)>;=0
и воспользоваться методом задачи 3 и задачи 1 к § 20.
5. Уточнить для Р-гипоэллиптического многочлена Р (s) теорему п. 1 сле-
следующим образом:
2)
Указание. Соответственно уточнить рассуждения в леммах 1, 2,3.
6. Получить формулу для показателя гипоэллиптичности (В. П. Пала-
модов)
|gradP(a)| |
|<Х|-»со
In
\Р(°)\
lnla|
Указание. Использовать задачу 5.
§ 22. Метод Радона
1. Мы желаем теперь ознакомиться со структурой фундаменталь-
фундаментальной функции для негипоэллиптического оператора Р [-#-) • Можно
заранее сказать, что у таких фундаментальных функций имеются

06 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. ИГ
■особенности (в смысле потери бесконечной дифференцируемое™)
как угодно далеко от начала координат (§ 20, задача 4). Кроме
того, можно показать, что для любой области О существует решение
уравнения Р 1-х—) и = 0 с особенностью именно в этой области;
добавляя к фундаментальной функции, допустим, бесконечно диф-
дифференцируемой, такое решение, мы получим новое фундаментальное
решение, уже с особенностью в G. Таким образом, возможности
для построения «плохих» фундаментальных функций весьма велики;
нас будет интересовать вопрос о существовании фундаментальной
функции (?(х) с минимальным множеством особенностей. Мы покажем.
что для однородного многочлена Р(о, о„) с достаточно гладкой
поверхностью нулей всегда есть фундаментальная функция оператора
Р \-т—\ с особенностями, сосредоточенными в некотором конусе
размерности -^!«—1.
Средством для получения подобных результатов будет служить
метод представления фундаментальных функций, называемый мето-
методом Радона.
Пусть дан линейный дифференциальный оператор Р \-т—\ порядка т
с постоянными коэффициентами.
Мы хотим решить уравнение
^' *-> = *(*! *«)• (О
Представим дельта-функцию в правой части в виде сферического
интеграла (§ 11, п. 6)
J. x))da.
а
где
/ш
fan6(" П (I) ПРИ п нечетном.
при п четном.
Далее, вместо уравнения A) рассмотрим уравнение с пара-
параметром и:
B)
Естественно искать его решение в форме обобщенной функции с?ш(|),
зависящей только от аргумента (w, х) = | (см. § 6, п. 2, пример 4).
При этом заметим, что для функций /(((о, х)) справедлива обычная
формула дифференцирования
д d
*7

§ 221 МЕТОД РАДОНА 207
(§ 7, п. 2, пример 4); таким образом, уравнение B) для функции
приобретает форму
-^ о»-^)g>e (£)=/№)■ C)
Уравнение C) есть уже обыкновенное дифференциальное уравнение
с параметром ю. Допустим, что мы нашли его решение £ГИ(£). непре-
непрерывно зависящее от параметра w. Тогда можно утверждать, что
интеграл
?{x) = f&aG)da D)
Q —
дает решение поставленной задачи. Действительно, поскольку в обоб-
обобщенных функциях дифференцирование есть непрерывная операция,
мы имеем
что и требуется.
Итак, дело сводится к нахождению решения уравнения C), непре-
непрерывно зависящего от параметра @.
Пусть Ро (-3—) есть главная часть многочлена Р l-g—\. т. е. сово-
совокупность всех его членов размерности ровно т. Мы имеем Р = Р0-\-Р1,
где Рг — младшие члены, далее,
d д \ ,
Мы видим, что коэффициентом при старшей производной по | служит
Р0(ш). Если уравнение A) эллиптическое, то Р0(ы) не обращается
в нуль (§ 21, п. 2). В этом случае нетрудно найти решение cf,»(£)•
непрерывно зависящее от параметра о, используя методы § 5 (п. 3 и
далее). В общем случае положение более сложное; мы отложим его
рассмотрение до пункта 3.
2. Сейчас мы рассмотрим случай однородного эллиптического
многочлена Р степени т. В этом случае многочлен Р1 отсутствует,
и уравнение C) приводится к виду
dm4, Ш
Л) И ф = f (I). Л) («) Ф0. E)

208 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. III
Разберем два случая: четного и нечетного п. Если п нечетно,
то /(£) = сл0 (I) и уравнение E) легко интегрируется в явном
виде:
если
если
При п четном мы имеем f(%) = bn%~" и соответственно
"пт *—п+т
In |
при
при
Очевидно, что найденные решения непрерывно зависят от о. Поэтому,
в силу формулы D). мы можем написать
.(л-1-
при п нечетном, т-^п — 1,
/gm-я
р+ da при п нечетном, /и>«,
Q
•-/■
Q
u"mJ Р0(о)
t-n+m
F)
при п четном, т-^п — 1,
при п четном, т^-п.
Заметим, что полученные функции ^ (х) бесконечно дифференцируемы
по х при л: =^= 0; это, помимо общих соображений о свойствах эллип-
эллиптических уравнений, следует из рассуждений § 10, п. 7.
3. Рассмотрим случай неэллиптического, но однородного много-
многочлена Р^Р0. В этом случае выражение Р0(а) обращается в 0 в не-
некоторых точках сферы Q. Мы предположим, далее, что в тех
точках @0, где Ро (и) = 0, хотя бы одна из производных многочлена Р
уже не обращается в нуль. В таком случае в окрестности точки ю0
уравнение Ро (Ю1 wn)= 0 может быть разрешено относительно
соответствующей координаты. Поэтому в окрестности точки w0 можно
перейти к новой системе координат, одной из которых будет сама
величина

§ 22] МЕТОД РАДОНА 209
В качестве искомой фундаментальной функции мы снова рас-
рассмотрим интеграл вида F) п. 2, т. е.
Г
J
J
причем условимся понимать его в смысле Коши:
X). A)
Покажем прежде всего, что этот предел существует (в К')-
Напомним некоторые сведения об интеграле в смысле Коши для
обычных функций. Пусть имеется интеграл вида
g (to) da
где g (со) — бесконечно дифференцируемая функция, а Ро (со) удовле-
удовлетворяет указанным выше условиям.
Покажем, что выражение
g («) da
I
Ро («)
|Pol>e
B)
имеет предел при е—>0. Введем в области |/-*0С10)! -^^^ координаты
9 = Р0(@) и «/; тогда можно написать g (и) dm = G F, и') dQ du>'.
где О F, е»') — бесконечно дифференцируемая функция.
В частности, мы можем написать
0(8, w') = G@.
где Gj (9, ю') — ограниченная непрерывная функция. Далее.
=G@. со') / *. = 0.
/ = [ Gl(8, ^Л- / ol(e.
e<|ei<e<, e < 16^1 < со |в|<ео
откуда следует, что существует предел
,- С g<P)da ,. Г Г C(G, to')rfG
lim / = I'm / /
14 Г. Е. Шилов

2,0 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. III
который в сумме с интегралом по области 173,, (to) j ^- e0 и является
искомым интегралом в смысле Коши.
Применяя 1Ё(х) A) к основной функции <$(х), получаем
Функция от и, стоящая в числителе
(/(I). фМ) = (/((<». *)). ф(*)).
как мы видели в § 10, п. 7, бесконечно дифференцируема по w. По
сказанному выше, существует
(/(*).„)= Km
Предел A), в силу общей теоремы о пределе непрерывных функ-
функционалов, есть снова непрерывный функционал, что нам и требуется.
Покажем, что функционал
определенный, как выше, есть решение уравнения
Яо(-^-) ?(*) = *(*)■
Действительно, мы имеем
дх)" у"'— .1 Р„(ез)
откуда, по определению функционала /(|),
to = б (дг).

§ 22]
Итак, функционал
МЕТОД РАДОНА
211
есть искомое фундаментальное решение.
4. Покажем далее, что ^(х) есть бесконечно дифференцируемая
функция от х всюду, кроме некоторого конуса размерности < п.
Именно, будем считать направление х особым, если экватор
(со, х) = 0 касается (на сфере |со| = 1) в некоторой точке поверх-
поверхности Ро(со) = О, и обычным, если экватор (со, дг) = О или вовсе не
имеет общих точек с этой поверхностью, или каждая их общая точка
является точкой пересечения с различными
касательными плоскостями (размерности, есте-
естественно, п — 2).
Особые направления образуют конус, ко-
который можно построить следующим образом.
Возьмем любую точку соо на поверхности
Ро (а) = 0 и в этой точке проведем каса-
касательный большой круг к этой кривой; если
уравнение этого круга есть (ш, х0) = О," то
л:0—особое направление. Очевидно, что раз-
размерность конуса особых направлений равна
размерности конуса, определяемой кривой
Ро(со) = О. и тем самым меньше размерности
всего пространства.
Покажем, что вне конуса особых направлений функция
бесконечно дифференцируема.
Рассмотрим вначале интеграл в смысле Коши
Рис. 12. Особое напра-
направление.
где /(|)—бесконечно дифференцируемая функция при всех % ф О
и обычная функция для всех |. Мы можем написать разложение
«■(и) = йг1(и)-г-йг2(и) + ?з(ю)" гДе Si< gv #з — бесконечно диффе-
дифференцируемые функции такие, что
= 0
При этом
при |Я0(«I<|-.
при |Ро(со)|>е или |(со. х)\ <-|,
при |Р0(й))|>£, или |(со. лг)| > е.
=Fl(x) + F2 (*) -Ь F3 (*),
14*

212 ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ОПЕРАТОРОВ [ГЛ. Ill
где
/ ,ч _ /"Г
IPoKe
Функция /^(дг) бесконечно дифференцируема при д: =£ О в силу ре-
результатов § 10, п. 7.
Далее, в интеграле Коши
|£|>Е/2|Р0|<е
введем новые координаты, одной из которых будет 8 = Р0(@); со-
совокупность остальных обозначим через о/. Тогда /((со, дг))g2(со)da)
можно записать в форме g (8, а/, дг) d8 dco', где g F, w'. дг) —
бесконечно дифференцируемая функция от всех своих аргументов.
По определению интеграла Коши,
и' I e
= f
I
| в [ < е
причем й'^в, w', дг) снова является бесконечно дифференцируемой
функцией от своих аргументов. Но тогда и F2(x) бесконечно диф-
дифференцируема, что и требуется.
Остается рассмотреть интеграл
— J J
/ ((и, х) ) g3 (<о)
IPoKe, Ig |<e
Покажем, что F3(x) бесконечно дифференцируема при неособых х.
Фиксируем неособый вектор х ф 0. Используя предположение о том.
что х— не особый вектор, введем в области |/-*0(со)| < е, |£|<Се.
систему координат, одной из которых является | = (а, дг), другой
8=Р0(@), совокупность остальных обозначим через а/. Здесь мы
имеем
» = f ш О F.^.0;*)

§ 22] МЕТОД РАДОНА 213
где О(|, со', 6; х) — бесконечно дифференцируемая функция своих
аргументов. Согласно определению интеграла Коши,
Интегрируя по 8 и а/, получаем функцию
%)= f
в/
f J
|в/<е ш1
которая снова является бесконечно дифференцируемой функцией от
| и х. обращающейся в нуль при |||^>е. В итоге мы имеем
. в *=(/(& *(*. б» (о
и, следовательно, cf (х) является бесконечно дифференцируемой функ-
функцией от х. Далее, применяя тот же прием, что и в п. 7 § 10, мы
получаем, что выражение A) есть бесконечно дифференцируемая
функция от х (при х Ф 0) и в том случае, когда /(|) есть не просто
обычная функция, а интересующий нас функционал. Тем самым
теорема о бесконечной дифференцируемости фундаментальной функ-
функции (f(x) вне конуса особых направлений доказана полностью.
Задачи. 1. Получить по методу Радона фундаментальную функцию
итерированного оператора Лапласа Дт (§ 7, п. 2, пример 9).
Указание. P0(m) = 1; использовать задачу 10 к § П.
2. Получить по методу Радона фундаментальную функцию оператора
**5 (§ 7, задача 8) (л = 3).
Указание. Интеграл по Q от функции е1*(°>--*)+ можно вычислить
разложением в ряд, с использованием формул § 11, п. 6.
3. Если Р (а) — однородный многочлен степени т с гладкой поверх-
поверхностью нулей (как в п. 4), то решение и (х) уравнения Р 1-^—)и(л)=0,
бесконечно дифференцируемое в окрестности пересечения конуса особых
направлений с произвольно фиксированной замкнутой поверхностью, содер-
содержащей начало координат внутри себя, является бесконечно дифференцируе-
дифференцируемым и в окрестности начала координат.
Указание. Использовать формулу типа Пуассона из § 16.

ГЛАВА IV
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
§ 23. Корректные краевые задачи для систем уравнений
Мы будем рассматривать дифференциальные уравнения с выде-
выделенной координатой, обозначаемой через t и меняющейся (как пра-
правило) на полуоси 0<^.t < оо. В математической физике имеется ряд
классических задач, приводящих к уравнениям такого типа. Обычно
рассматривают уравнения, разрешенные относительно старшей про-
производной по t:
dmu(t, х) у / д \ d"u (t, х) __. . -j.
oi ft=o \ ox i 01
где pk 11 -г— I — некоторые многочлены от I -г— , ..., t -^— макси-
максимальной степени, например, р. К уравнению A) присоединяют на-
начальные условия, накладываемые, как правило, на функции и @, х),
диф, х) дт~1иф,х) D
-— — ■т_1 - . В некоторых случаях указывается жела-
желательное поведение решения u(t. x) при t—>oo. Все эти данные
образуют краевую задачу для уравнения A). Кроме того, указы-
указывается класс функций от х (может быть, обобщенных), кото-
которому должно принадлежать решение u(t, x) при каждом фиксиро-
фиксированном t.
Краевая задача считается корректно поставленной в некото-
некотором классе R, если при любой допустимой системе краевых данных
она имеет решение в этом классе, единственное в нем и непрерывно
зависящее от системы краевых данных; последнее условие требует,
чтобы класс R обладал некоторой топологией с тем, чтобы оператор,
переводящий допустимую начальную функцию и (х) в решение и (t, x),
был непрерывным в R.
Приведем несколько классических примеров корректных краевых
задач с одним пространственным переменным.

§23] КОРРЕКТНЫЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ СИСТЕМ УРАВНЕНИИ 215-
1. Для уравнения теплопроводности
ди (t, х) д2а (t, х)
dt ~ дх2
является корректной задача Коши: найти решение при заданной
функции и @, х). В качестве класса R можно взять, например, класс
ограниченных функций.
2. Для волнового уравнения
д!и (t, х) _ д2и (t. x)
дх>-
корректной является также задача Коши, которая в данном случае
требует задания и @, х) и ' х' . В качестве класса R можно-
взять все обобщенные функции.
3. Для уравнения Лапласа
d2u(t, х) д2и (t, х)
dt* ~ дх*
является корректной задача Дирихле (задана и@, х)) с дополни-
дополнительным условием u(t, x)=O(th) при ^^оо. В качестве класса R
можно при этом взять совокупность §€ квадратично интегрируемых
функций (по х) и их производных любого порядка (в К')-
Мы укажем корректные краевые задачи для любого уравнения
вида A)- При этом для всех уравнений A) можно взять один и тот
же класс R (хотя в различных случаях его можно и расширять) —
именно, совокупность £№ всех квадратично интегрируемых функций
f(x)^f(xv .... хп), определенных в л-мерном вещественном
евклидовом пространстве Rn = Rn (x). и их производных любого
порядка (в К')- Впрочем, как мы увидим ниже, окончательный ре-
результат можно сформулировать и в классических терминах, без обоб-
обобщенных функций; рйиение соответствующей краевой задачи будет
обычной функцией, если потребовать от начальных функций неко-
некоторой дополнительной гладкости.
Двойственным к пространству £№ в смысле преобразования Фурье
является пространство Н, состоящее из всех квадратично интегри-
интегрируемых функций g(a) = g(al, .... ап), определенных в «-мерном
вещественном евклидовом пространстве Rn = Rn (о), и их произве-
произведений на любые многочлены. В частности, пространство Н содержит
все функции g(o) не более чем степенного роста при |о|—>оо, по-
поскольку всякая такая функция, будучи разделена на некоторый мно-
многочлен достаточно большой степени, например вида
A +02+ . . . +02/ ИЛИ A + Й,Г •••(! + Л»„Г.

216 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
становится квадратично интегрируемой. Очевидно также, что в про-
пространстве Н допустимо умножение на всякую функцию, локально
ограниченную и не более чем степенного роста при \а\ —>оо.
Рост функций g{o) при |о| —>оо тесно связан с порядком син-
сингулярности соответствующих функций /(дг). Умножение g(a) на мно-
многочлен равносильно дифференцированию соответствующего порядка
функции f (x) = F~l [g\, отсюда, например, можно получить полез-
полезную формулу для порядка сингулярности
s [F~lPm (о) g (о)] < т + s [/="' \g (оI ] = т + s (/).
где Рт(о) — многочлен степени т. Если при этом gio)^!^, то и
f(x)£L2, так что s(/)^0. Поэтому если функция go(a) после
деления на многочлен Рт(о) степени т становится квадратично инте-
интегрируемой, то порядок сингулярности соответствующей функции /0 (дг)
не превосходит т.
Пространство е$ не замкнуто в К', поэтому в нем более есте-
естественна иная сходимость, относительно которой е$ полно. Удобнее
рассмотреть пространство Н. Это пространство можно представить
в форме объединения
где tr есть гильбертово пространство с метрикой
— С ^ @) g2 (g) d°
— J A+|0|2)в •
Будем говорить, что последовательность gv(o)£H сходится
в Н к нулю, если при некотором (следовательно, и при всех доста-
достаточно больших) q для элементов gv(o) определена норма
и 1^1,—>0 при v^oo. В соответствии с этим последовательность
/v (дг) ^ £№ сходится в е%? к нулю, если существует такое q, что
/v = (l— &)"fv. fv£L2 и /v(o) сходится к нулю в L2.
Линейный оператор В. действующий в Н (или е%?), называется
непрерывным, если из £v(o)->0 в #(ДДдг)->0 в ^в) следует
Bgv->0 в H (Bfv—>O в £%!\. Так, например, умножение на функ-
функцию G(a). удовлетворяющую неравенству

§ 23] КОРРЕКТНЫЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ СИСТЕМ УРАВНЕНИЙ 217*
есть непрерывный оператор в Н\ действительно, пусть при q^-q^
мы имеем
тогда при
что и требуется.
Последовательность gv(o)£H ограничена в Н. если все g (о)
принадлежат к одному и тому же HQ и ограничены по его норме.
Последовательность gv(o) возрастает в Н не быстрее неко-
некоторой {числовой) функции п(\), если последовательность —т-»# (о)
ограничена в Н.
Аналогичные определения естественно формулируются для случая
семейства gt(a) с непрерывно меняющимся параметром t. С помощью
обратного преобразования Фурье эти определения переносятся и в
пространство е№-
Рассмотрим теперь уравнение A), считая, что решения его разы-
разыскиваются в классе функций и(t. x), которые при каждом t^.0
принадлежат классу е%?, так же как и все производные иу х', .. .
дти It x)
... —-j^j—-. Наряду с уравнением A) рассмотрим алгебраиче-
алгебраическое уравнение, получающееся из A) заменой ^- на К и i ^— на о:
Это уравнение имеет (с учетом кратностей) т корней Я,о (о). .
.... Я,т_х(а). Нумерацию их при каждом о мы устанавливаем с тем
чтобы иметь
Re l0(о) < Re Кг (о) < ... < Re *.„,_! (о).
Обозначим через Aj множество точек о ^ /?я, для которых
(У=1,2 т);
очевидно, AqZdA^ ... ■^Ат_1. Все эти множества будем рассмат-
рассматривать с точностью до множеств меры 0. Следующая основная тео
рема указывает корректную аадачу для уравнения A):

218 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Основная теорема. Пусть на каждом из множеств Aj
задана функция Vj(a), продолжаемая на все пространство
Rn(a) до функции из пространства Н {будем писать Vj(a)£
£H(Aj)). Утверждается, что уравнение A) имеет решение
u(t, х), у которого преобразование Фурье функции "_ ' -
совпадает на множестве Aj_lcфункциейVj_l(o)(j=\, 2 т).
Это решение u(t, х) при каждом t^O принадлежит про-
пространству <Ш и при £—>оо возрастает в И не быстрее неко-
некоторой степени t вместе со всеми производными по t до по-
порядка /и—1. Оно единственно в классе всех решений уравне-
уравнения A), принадлежащих Ж. возрастающих в Н при t—>oo
вместе с производными по t до порядка т—1 не быстрее
степени t и удовлетворяющих тем ~же начальным условиям,
кроме того, оно непрерывно зависит в топологии £%? от за-
заданных функций Vj(o), если эти функции меняются непрерывно
в топологии пространства Н.
Доказательство этой теоремы будет дано в § 26. Здесь мы при-
приведем несколько примеров ее применения к конкретным уравнениям.
1. Уравнение теплопроводности
ди д2и
Здесь Я,о = — о2; множество Ао = {о: — о2 <J 0} совпадает со всей
осью о. Корректная задача состоит в задании vo(a) = F[u@, x)]
при всех о; но задать vo(a) при всех о в силу единственности пре-
преобразования Фурье все равно, что задать функцию «@, х). Итак,
корректная задача состоит в задании функции и @, х).
2. Волновое уравнение
~д*г== ~дх*'
здесь Я,2 =— о2, Ли1=±|о|, множества А0={о: ReX.0(o)^[0}
и Al = {o: Re Я,! (о)-<; 0] оба совпадают со всей осью о. Корректная
краевая задача состоит в задании v0 (а)=/7 [и @, х)] и vl (а)=/7 " '
при всех о, что равносильно заданию самих и @, х) и " j.' ^.
3. Уравнение Лапласа
Здесь Я,2 = о2, ^0|1=±|a|. Множество А0={а: —|о|-^0} совпа-
совпадает со всей осью о. множество А1 = {а: |о|-^0) состоит из одной
точки, иными словами, эквивалентно пустому множеству. Следует

§ 24] ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ 219
вадавать v0 (о) = F [и (О, х)] при всех о, что равносильно заданию
самой и (О, х); получаем задачу Дирихле.
Рассмотрим два неклассических уравнения.
4. Обратное уравнение теплопроводности -зт = j-^-. Здесь-
Я0 = о2 и Ло —@). В классе всех решений и (t, х)££№ имеется
единственное, возрастающее в е%? не быстрее степени t, именно,.
u(t, x) = 0.
5. Ультрагиперболическое уравнение
д2и д2и |^ д2и д2и
Здесь
при этом Re Я,о (о) неположительна всюду, a Re Xj (о) неположительна
в области ^j = |с^+°2^'(^]* Корректная задача состоит в зада-
задании v0 (о) всюду, т. е. в задании и @, х) £ <=%?, и vl (о) на области Лх»
т. е. в задании значений
при
Задача. 1. Указать корректные краевые задачи для уравнений
д*и д*и „ д*и д*и <ди д2и 2
_ „ . #л . йи @, х) ди @, jc) ,. ,„ .
Отв. Следует задавать: а) и @, х), ~z—-, 4^—-; б) и @, х),
со
ди ^ ^ ; в) Га @, х) elxa dx на множестве Аа = {а: | а | < k).
— со
§ 24. Вспомогательные построения
Для доказательства основной теоремы нам понадобятся некото-
некоторые сведения и оценки из теории интерполирования.
1. Пусть имеется функция /(Я,), аналитическая в выпуклой об-
области G и Я,о ^m-i — различные фиксированные точки в этоп
области. Построим многочлен R (Я.), принимающий в точках Я,о, ...
•••• ^m-i соответственно те же значения, что и функция f(k),
т. е. числа /0 = /(к0), .... /m_i = /(^m_i). Такой многочлен можно
построить по формуле Ньютона
R (Я,>= £0+ Ь, (к — Хо)+Ъ2 (Я, - Яо) (Я — Я,) + ...
1(Л-Я0)...(Я,-Л1В_а). A)

220
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ. IV
где т неизвестных коэффициентов b0 bm-i должны быть оп-
определены из т условий R(K0)=f0 /?(^-m— i) = /m— i- Подстав-
Подставляя в A) вместо А, поочередно значения Ко ^m-i» приходим к
системе уравнений
/я - Ьо+Ъх (Я, -
- а0) (Я, - Я,,),
B)
Эти уравнения позволяют последовательно получить значения Ьо, ...
.... t>m-\- Для построения простых и симметричных формул введем
обозначения
— я,й —Я,о '
[/otl [/oil
[/o...ft-l.ftl
Первое из уравнений B) дает bo = fo = [f0]. Второе дает b1 = l
= ,1 ^ [/oil- Проверим, что при любом k = 0, 1 /re
«ч — ло
мы будем иметь £ft = F/0I ftl. Допустим, что это справедливо
У<А. Тогда из А + 1-го уравнения B) мы находим
—1
при
k~
-К)~- ■ --[/
и ... к-
(Aft-A0)(Aft-A,)...(Aft-Aft_,)
[fox]
(Kk — A0)...(Aft — Aft_,) (Aft — A|)...(Aft — Aft_,)
Aft — Aft_!
(Aft — A,)... (Aft — Aft_,)
[/oift] [/012I
[/
oi
Aft — Aft_
ft-1]
Aft-Aft_,
— (Aft-A2)...(Aft-Aft_,) •••
Итак, многочлен Ньютона имеет вид
Я (Я,) = I/J + [/„,] (Я, — а0) + [/он] (Я, — а0) (Я, — Я,!) + ..
• • • + [/oi ... m-l] (Л - Ч) • • •
L/0I...ftJ-

■§ 24]
ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ
221
Можно дать для коэффициентов bk выражения через производные
функции /(Я,). Для этого рассмотрим числа
1 'ft
ft
«он = J /
— V + U (h — *i>l dh dti
О О
1'. 'ft
.. ftp
0 0 0
C)
Чтобы установить связь между числами Koi...ftp. произведем в вы-
выражении «01... ftp интегрирование по переменному tp. Мы получим
1 '. 'ft-.
о о
1 t
k-\
1 'ft
ft.
+tk(%p-Xk)\dtl... dtk-f ...f /*> [**+*! (*!-*«>+
0
f f
0 0
Так как ио = /
получаем «„ =
= [/о], то, применяя формулу D) для и01> и02
/„] «m...«-i = [/M ...m-J-

222 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Мы видим, что коэффициенты полинома Ньютона могут быть
вычислены и по формулам C), а именно,
** = [V..J = «m...» = J/■■• J /*4 + <i<*!-»«>+•••
0 0 0
... +tk{-kk--kk_l)]dtl...dtk. E)
Отсюда мы получим удобную оценку этих коэффициентов. Аргумент
функции f(k) в формуле E) можно записать в форме
сумма коэффициентов при Хо, ..., Хк здесь равна
поэтому число К из F), как центр тяжести неотрицательных масс
1 — tl% t1 —t2 /ft_j — tk, tk, расположенных в точках Ко, Х^. ...
.... Я,й_1» Xk, лежит в пределах наименьшего выпуклого многоуголь-
многоугольника Qk, содержащего точки Хо A,ft. Положим
Оценивая интеграл E) по модулю, получаем
.*|<nSf-. G)
2. Пусть имеется матрица m-го порядка P = ||jOyft||. Мы желаем
получить оценку нормы матрицы etp при t^-0.
Обозначим характеристические корни матрицы Р, т. е. корни
уравнения det||P — ЯУ||=О через А,о, T-i ^m-v ^ак известно,
в случае, если Хо ^т-\ различны, матрица etp может быть
представлена в виде R(P), где R(h) (любой) многочлен R(K), для
которого
Многочлен /?(?-) можно взять в форме Ньютона (п. 1)
причем
A)

§ 24]
ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ
223
Обозначим Ak = max [ReXo, .... ReA,ft}; тогда оценку G; п. 1 можно
записать в форме
Далее,
откуда для нормы матрицы etp получаем оценку
...\\P~K-2l\\)-
Поскольку каждое Xj есть собственное значение оператора Р, по-
получаемое на некотором собственном векторе ej, мы имеем
SUP II ^11 —11^*11 и> следовательно,
lll i
Таким образом.
+ 2/ЦРЩ-
Полученная оценка справедлива для всех операторов Р с различ-
различными собственными значениями. Так как любой оператор Р с про-
произвольными собственными значениями, возможно, кратными, есть
предел (по норме) операторов с различными собственными значе-
значениями, оценка B) справедлива и для любого оператора Р.
m~X
3. Пусть имеются т аналитических функции /°(Я,) f 0)
и т комплексных чисел Хо, kt ^m-i' обобщенным детерминан-
детерминантом Ван-дер-Монда называется детерминант
A)
/""'W Г
... Г
Преобразуем его следующим образом. Вычтем из /-го столбца (у > 0)
нулевой столбец и разделим на Я,у — Я,о; мы получим
f/oi] • • • |/o,m-l
,m-Il
J • • • [/™m-l]

224
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ IV
Далее, вычтем из ft-го столбца (k > 1) первый и разделим на Кк—Ху;
получим
[/о] [/м] [/012] . •• [/oi, m-i]
[/Я [/Oil Ш...\Ат-*\
\ fm-n \fm-l\ fwn-ll Г*-1 1
I/O J L/oi J 1/012 | ••• l/01,m-lJ
Продолжая таким образом далее, получаем
= П
0<7ft<
[/о] [/У
., m-lj
.. m-lj
B)
Положим, в частности. •/°= 1, /' = А, fm~ =кт~ ; тогда
^==А!. (/*)<*+1)==0 и по формуле E) п. 1
при j > k,
при у = й.
о о
{О
1
а при j < А эта величина есть однородный многочлен степени k — j
от Я,о, .... Kj. Мы получаем здесь значение детерминанта Ван-дер-
Монда
1 0 ... О
= П О-ц-Я-у)
0<y<ft<m
1 ... О
^7 <В</л
■#)•
. ... 1
Если же /°. f1 fm~X суть произвольные многочлены от к, то
мы получим
[Я] [/8J
иг1]
= Д &k — k,).R (lo Я,т_ 0. C)
где R(X0 hm-i) — многочлен от своих аргументов.

§ 24]
ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ
225
Дальнейшее преобразование формулы B) получим если запишем
ее в форме
W {/*
-li rfm-l ,
J • • • L/oi... m-lJ
и попробуем перейти к пределу при Xf—>Х0
формулы E) п. 1 следует, что
D)
А.,
Таким образом, существует предел правой части равенства D);
отсюда следует, что имеется предел и у левой части и он имеет
значение
lim
ПК) -^
~V0)
Преобразование детерминанта A) можно производить и несколько
более сложным образом, фиксировав в A) несколько групп столбцов,
например, с номерами от 0 до k—1; от k до /—1; .... от р до
т — 1 и производя вычитание и деление только в пределах каждой
группы. Мы получим аналогично
П
KJ
П
0<KJ<k
П
oj ■ • Ч'оь..*-
J---l/oi...ft-iJlVft J---L^ftft-ri.../-iJ---l-'p \---VJpp
Если здесь перейти к пределу при условии, что %
15 Г. Е. Шилов
J- • Ч-'Ol...ft-lJl-'ft J- • mlJ кк-i-l...l-ll" " V p \-"\.J pp+l...m-\

226 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
lim-
мы получим
TT fit —*-i)--- TT
,fn—1 I гл— 1 1 f m— 1 (ft — 1) - -ГЛ — 1 . I то— I (m —p)
1 (o)TT' "о)"(йГТI/ Kho)—' (V'"'(m-p)l/ (*7>
В случае детерминанта Ван-дер-Монда мы получаем формулу
пт —== ===
П frj—h) П (Л7„-Ч,)-
1 0 0...1 0 0...1 0 0...
11П 21П SilO
/\>Q I V/ ... /Vfc 1 \J . . . /V« 1 V/ ...
2 2 2
1 m—3 n m —I ,
В частности, если числа А.о, kk, ..., Хр различны, детерминант справа
отличен от нуля, поскольку в левой части после сокращения остаются
в числителе только разности вида Kj — А,,-, где А,,- и А,у принадлежат
к различным из выделенных групп; каждая такая разность имеет
пределом разность первых элементов соответствующих групп, т. е.
величину, отличную от нуля. Матрица
1-0 0 ... 1 О О
к0 1 0 ... 1р 1 О
2 2
Ар ^Л>о 1 ... Ар ^^р *
E)
называется обобщенной матрицей Ван-дер-Монда; она играет важную
роль в дальнейшем. Заметим, что не только ее детерминант отличен
от нуля, но и любой минор, построенный на первых s строках и
s столбцах, также отличен от нуля, поскольку он имеет такую же
структуру, как и весь детерминант.

§ 24] ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ 227
4. Мы приведем еще одно выражение для коэффициентов
b0 bm_x интерполяционного многочлена Ньютона, которое будет
использовано в дальнейшем (§ 30). Из уравнении B) п. 1 видно,
что коэффициент Ьк линейно выражается через /0, .... fk. Мы
утверждаем, что на самом деле имеет место следующее равенство:
где штрих у знака произведения означает, что множитель с t =
отсутствует. Для доказательства положим
Cn = un= ,
«=0, I, .... ft, I
и покажем, что величины справа в B) удовлетворяют тем же рекур-
рекуррентным соотношениям, что и величины [/0 t ft jj:
со,.... ft-i, i co ft-i, ft . /Оч
A), .... ft. f= , , ! (.О)
а так как
то равенство с0 ft = Г/о ft] = ftft окажется справедливым вместе
с C). Итак, докажем C). Мы имеем
о ft-i, /— со ft-i, ft _
j=o..1?k-i,i
^ft
|=аД!-1.|(Л/-а') ^°-:
1 1 \ i ^^ ft/ "/ — "
/ = 0,..., ft-If 1
^7 — ^ft
v /у
у
1
■i)
i = 0,.
.., ft-l, ft
1
15*

228 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
■ /, . __^_ Л !_ =
П' ih — Ч (h — bk) П' О-ь — h) h — Ьь
i = 0,..., ft-1, I '=0 ft-1, ft
что и требовалось.
Выражение
называется разделенной разностью для функции F(X,) в точках
Хо Я,г_1. При г = 0 разделенная разность совпадает с самим зна-
значением F(k0). При г > 0 для разделенной разности справедлива
формула C) п. 1
0 0 0
• • • + tr-Х (>-г-1 - К-7>\ dtf- dtr-V
из которой вытекает оценка G) п. 1:
VOH-TT-TTr max l^^
Б. Нам понадобится в дальнейшем оценка двойной разделенной
разности вида
Здесь функция F(X, С) аналитична по переменному £ в выпуклом
многоугольнике, натянутом на точки Хо, .... ^т_р и по перемен-
переменному К в выпуклом многоугольнике, натянутом наточки Хо V-r
Выражение F) может быть получено, как разделенная разность от
функции F(k, С), при фиксированном первом аргументе К по вто-
второму аргументу в точках к, %Т, .... А,т-1:
= Ф(Я,; Я,. Я,, lm^), G)

24]
ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ
229
от которой взята еще раз разделенная разность в точках
К = %0 A,,_i- По формуле E) п. 1.
| r-2
= f f ... f <lfr-ll
0 0 0
r-v (8)
Вычислим Ф(г~ (Я,), используя еще раз формулу E) п. 1:
1 <г
Ф(Я>)==// ■••
об
/
об о
(9)
Дифференцируя равенство полным ооразом по X. получим
0 0
^. A0)
Подставляя A0) в (8), находим
F(K0, .... Я,г_!; Я,г, .... A,m_i)
/
0 0
0 0 0
где "А, = Хо-\-^,(А,! — А,о)+ •■• +'r-i(
лом многоугольнике, натянутом на Хо
оценка
1-km_2)]dtl...dtm_1, A1)
i—1 — ^r-г) лежит в выпук-
выпукХг_1. Из A1) следует
1/7 (Я.,
A2)
где максимум берется по всем k-4^m — 1 и по всем точкам много-
многоугольника, натянутого на точки £ = А,, Яг, .... ^m_j. причем К —
любая точка многоугольника, натянутого на точки Я,о ^r-v

230 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
§ 25. Обыкновенные уравнения и системы
1. Рассмотрим систему обыкновенных уравнений
= P00V0 @ + • • • + А), т-
: ;A)
Vm =
где рад Pm-Um-i—некоторые (комплексные) числа. Как из-
известно, решение v(t)= {vo(t) vm-\(t)) определяется при £^>0
однозначно, если известно значение v(O)={vo(O) vm~i(.^))'
Назовем вектор v@) определяющим корректную начальную за-
задачу, если соответствующее решение v(f) возрастает при t—>oo
не быстрее некоторой степени от t:
м
Гт-\
* j=0 '
Поставим вопрос: каким условиям должен удовлетворять вектор
?>@). чтобы он определял корректную задачу.
Для ответа рассмотрим оператор Р, действующий в т-мерном
пространстве Q векторов £, = (Л0, ..., £m_i) по формулам
+ ••• +Po.m-ilm-V
-1 — Pm-i. 0&0+ ••• ~\-Рт-\, m-l&m-l*
Пусть Хо ^щ-1 — собственные значения оператора Р (среди
которых, возможно, имеются равные) и е0 ет-\ — базис про-
пространства Q из соответствующих собственных (и присоединенных,
в случае наличия кратности) векторов. Нумерацию чисел Kj мы уста-
установим в порядке возрастания вещественных частей
Определим число г соотношением
Re *,,_!<()< Re Я,,, B)
иными словами, г есть количество собственных значений оператора Р
(с учетом кратностей) с неположительной вещественной частью.
В частности, г = 0, если Re Xj > 0 для всех у, и г = т, если
ReA,y<0 для всех J.
Пространство Q можно разложить в прямую сумму подпространств
Q" и Q+, инвариантных относительно оператора Р, первое из кото-
которых порождается векторами е0 e#—i» a второе—векторами
е, Сщг-v Теперь мы формулируем теорему:

25]
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ И СИСТЕМЫ
231
Теорема 1. Вектор v@) определяет корректную задачу
для системы A) тогда и только тогда, когда он принадлежит
подпространству Q~.
Доказательство. Решение системы A) с начальным векто-
вектором v@), можно записать в форме
= etpv @).
Пусть v@) принадлежит подпространству Q~. Так как Q~ инва-
инвариантно относительно оператора Р. то оно инвариантно и относи-
относительно оператора etp. Мы можем, таким образом, ограни-
ограничиться подпространством Q~, в котором лежит решение v(f) при
всех 15> 0. Матрица оператора Р. приведенная в подпространстве Q~
к жордановой форме, квазидиагональна и по диагонали ее находятся
блоки вида
C)
h
0
0
1
h
0
0 .
1 .
X,.
.. 0
.. 0
.. 0
о о о ... %,
Как известно, зная жорданову форму матрицы Р, можно в том же
базисе сразу написать матрицу оператора f (JP). где /(Я,)—доста-
/(Я,)—достаточно гладкая функция. Именно*), /(Р) также квазидиагональна и
состоит из таких же блоков, как и матрица Р, но каждый блок C)
заменен на блок
1
О
О
0
В данном случае / (X) =
0 ... f(lj)
и соответствующий блок имеет вид
teaJ
etxi
• • • С J
*) См.. например, Ф. Р. Г а н т м а х е р. Теория матриц. Гостехиздат,
гл. 5. § 2, 1953, стр. 86—87.

232 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
Заметим, что числа е' I по модулю не превосходят 1, пвсквльку
в подпространстве Q~ мы имеем Re Xj ^ 0.
Мы видим, что каждый из базисных векторов е0, .... ег_х под-
подпространства QT под воздействием оператора е'р переходит в вектор
вида
где Cjk — фиксированные постоянные, среди которых заведома имеется
отличное от нуля (равное 1) число ckk.
Отсюда для любого вектора v @) = 2 \кек £ QT мы получаем
v @ = e">v @) = 2 Uetpek =
й *
и, следовательно,
Итак, если w@)^Q~, задача корректна. Пусть теперь v(%) имеет
ненулевую составляющую в подпространстве^ Q+. Иными словами,
rn-l
v@)= 2 \bek> причем среди чисел ^г \т-\ есть отличные от
нуля. Пусть Ъ,р— последняя отличная от нуля координата вектора ^@).
Как видно из предыдущего, вектор ер переводится оператором е'р
в вектор вида
причем на этот раз Re7,p>0. Предыдущие векторы es, s < p, пере-
переводятся оператором etp в аналогичные выражения, где, однако, фигу-
фигурируют слагаемые, не содержащие векторы ер. Таким образом, век-
вектор etPv@) имеет р-ю составляющую
которая с возрастанием t экспоненциально возрастает. Отсюда сле-
следует, что и норма самого вектора etpv@) экспоненциально возра-
возрастает, т. е. задача некорректна. Теорема доказана.
2. Рассмотрим теперь одно уравнение порядка т:
dmv(t) __ у d*v (t)
—^2рь—г о>
с комплексными коэффициентами pQ Pm-v Здесь решение v(t)

25]
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ И СИСТЕМЫ
233
определяется однозначно заданием значений г>@) v^m~^ @).
Задача называется корректной, если начальные данные таковы, что
им отвечает единственное решение v (t), которое возрастает при t —> оо
не быстрее некоторой степени от t, так же как и его производные
v'(t) vim~l*(t). Для решения вопроса об описании корректных
задач построим систему первого порядка, эквивалентную уравнению A)
dt
(t) _
dt
dvm-At)
dt
1 @ _
B)
Эта система получается при вводе неизвестных функций vQ (t) = v (f),
vx (t) = v' (t), .... vm_i (f) = v(m~l) (t). Системе B) отвечает матрица Р
специального вида
р =
О 1
О 0
0
1
.. О
.. О
О 0 0 ... 1
Ро Pi Р2
Рт-1
C)
Чтобы применить к данному случаю общую схему п. 1, найдем соб-
собственные векторы и собственные значения оператора Р в т-мерном
пространстве Q. На вектор £ = (!о- ii> •••».£m-i) оператор Р дей-
действует по формулам
+ P&2+ ••• +P,n-llm-\-
Если вектор | собственный, отвечающий собственному значению к,
то мы имеем Рс, = Xt, и, следовательно,

2A4
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ. IV
Положим £0=1 и тогда последовательно найдем
£о — 1 • h = л- 6г — л 6m-1 — л »
Таким образом, характеристические корни матрицы Р суть корни
уравнения
m-l
D)
а собственный вектор с собственным значением л коллинеарен
вектору
0i i^ im~l\
, #W, #V , а • • f *V J
и тем самым определен однозначно с точностью до коллинеарности;
(поэтому в случае, когда А — кратный корень, появляются только
присоединенные векторы).
Пусть, как и ранее, число г означает число собственных значе-
значений оператора Р (с учетом кратностей), действительные части которых
неположительны. Следующая теорема дает условия корректности
начальной задачи для уравнения A):
Теорема 2. Произвольное задание чисел v@), .... v^T~l) @)
определяет корректную задачу для уравнения A).
Для доказательства, имея в виду использование теоремы 1, мы
должны прежде всего найти базис подпространства Q~. Если все соб-
собственные значения Ао, .... "КТ_\ простые, базисная матрица имеет вид
1 1 ... 1
Кг-\
А Ш—1
Ао
/Л — 1 1 ТП— 1
Ai ... Ar_i
Если среди собственных значений а0, .... Аг_, имеются кратные,
базисная матрица будет иметь более сложный вид. Допустим, что
число Ао имеет кратность k. Тогда, как видно из жордановой формы
матрицы Р, базисные векторы е0, .... ek_l связаны соотношениями
Ре0 —
ek-2
E)

§ 25]
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ И СИСТЕМЫ
235
Векторы «1. ...» ek_i не определяются уравнениями E) однозначно;
но всякая система векторов е\ ek-i' удовлетворяющая уравне-
уравнениям E), может быть принята за базисную в соответствующем инва-
инвариантном подпространстве оператора Р (определяемом как совокупность
решений уравнения (Р — 7,0/)*£ = 0). Мы и построим сейчас одну
такую систему. Именно, рассмотрим первые k столбцов матрицы E)
§ 24. п. 3:
1
о
1
0
о
1
о
о
о
(m—
— ft— 1 \ ,m-ft
(m—k—l
"Л m-l
F)
Они определяют k векторов в пространстве Q. Обозначим их через
е0, в], .... eft_i и проверим, что для них выполняются равенства E).
Как мы знаем, матрица F) является пределом матрицы
[П]
oi... fc-i]
oi... ft-i]
Ivoi J • • • Ivoi... k-i
G)
i m—1
где /"=1, /*^Л /"" " — /,'■ ". Точнее, матрица F) полу-
получается ИЗ матрИЦЫ G) При УСЛОВИИ, ЧТО Я,! —>- Я,о ^<ft_l—>^о И
числа А,о, Я,! ^-ft-i различны. Обозначим через /01 .g вектор
с компонентами
,
.J, .... [Z^ s\- Мы
имеем Pfj =
G = 0, 1 k— 1) Далее.
п f р fs~~fo Pfs — Pfo Я,sfs — ^о/о
Wo* —И ls-K— ks-X0 — Xs-X0 —
Покажем, что справедлива формула
Phi... js = /oi... j + Kfm ... is (g > ■/)•
Допустим, что справедлива формула с меньшим числом индексов
^/oi... j-i, s = /oi... ;-i + ^i/oi... j-i,s" s ^ / 1-

236 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Тогда
р р /oi ... j-is — fp\...j-\,j Pfoi ... j-X, s~Pfo\ ... j-X, j
*/qi ... y-i~l~Aj/oi... j-xs—fox... }-\—^7/01... j-x, j
Aj — Ay
^sfoX ... j-X, s — Aj/pi ... j-X, j r JL \ f
В частности, мы имеем
* /m » —1 •• == /m * 1 1" "ifm i л i (■/== *■' /•
' Ul ... J — l, J ' Ul ... ] — 1 /•" Ul ... / —1, /
Переходя в этой формуле к пределу при Кг-*к0 Kk -> к0,
получаем
■
что и требовалось.
Итак, базисная матрица подпространства Q~ в общем случае имеет
вид обобщенной матрицы Ван-дер-Монда:
1 0 0 ... О
Я,о 1 0 ... О
п 2U 1 ... О
£• =
т-\ , ,ч,т-2 / ^ \,m-3 1 т — R — l\,m-ft
Теперь докажем лемму:
Лемма. Если оператор Р задается матрицей вида C), то,
каковы бы ни были числа £0 Ъ-v всегда можно — и при-
притом единственным образом — найти числа |г, .... \т_1'так,
что вектор £ = (£0 im-i) будет лежать в подпростран-
подпространстве Q~.
Доказательство. Мы должны доказать совместность системы
1 = Ес, (8)
где с = (с0, .... сг-1) — неизвестный вектор. Первые г уравнений
этой системы имеют определитель, построенный на первых г строках
матрицы Е. Согласно сказанному в конце § 24, п. 3, он отличен
от нуля. Поскольку числа |0, ..., Ъ,г_г известны, величины с0 сг_1
однозначно определяются. Из следующих т — г уравнений системы (8)
после этого однозначно определяются и Ьг, .... £„_!• что и тре-
требуется.

§ 25]
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ И СИСТЕМЫ
237
Для дальнейшего выведем формулы, выражающие |r £m-i
через £0 ir-i- Если корни Ко ^г-\ различны, то для
любого s^-r мы имеем
to
к
о
т-\
'О
s
1 ... 1
кх ... д.г_,
ч-1
1'
. . . Л
г-1
'г-1
1 s
\-1
= 0,
поскольку ранг расширенной матрицы системы (8) остается равным г.
Разлагая определитель слева по первому столбцу, получаем
где {/°, /! Л = |1Д Л', Is, %i+1 %r-l\. Коэф-
фициент при \j, как показано в § 24, п. 3, есть однородный много-
многочлен от Ха 7,г_! степени s — j. В итоге мы получаем: величины |s"
(s^-r) выражаются через |0 ^г-1 по формулам
г-1
;=о"
где
(9)
A0)
— однородный многочлен от Хо \-\ степени s — j.
Покажем, что эта же формула сохраняется и для случая кратных
корней.
Вынесем в числителе и знаменателе отношения A0) выражение
J\ (X, — ht)... J\ IX: — Я,,-' ) и сократим; мнегочлен Rjs
0<i</<* p<p<jp<m^ P PJ
не изменится. Далее, в правой части совершим предельный переход
Я-1, .... Xk_i—>Х0 и т. д.; в результате числители и знаменатели
обратятся в нужные нам миноры, дающие коэффициенты в разложе-
разложении |j по |0 ёг-1> левая же часть будет просто значением поли-
полинома Rsj при Хо= ... =Я,Й_1, Xk = kll+i= ... =)~i_i и т. д^ Таким
образом, формула (9) остается справедливой и для кратных корней.

238 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
3. Вернемся к системе A) п. 1
A)
и поставим следующую, более общую начальную задачу.
Имеется система уравнений
I
B)
ag, m-ilm-i = V j
Спрашивается, какова должна быть матрица Л = || Яу^ ||, чтобы при
любых числах b0 Ьд существовал и притом единственный век-
вектор v@), обеспечивающий корректную начальную задачу для си-
системы A) с координатами г>0 —lo vm-\==lm-i< удовлетворяю-
удовлетворяющими системе B). На этот ^вопрос теперь легко ответить.
Обозначим часть жордановой матрицы оператора Р, образованную
столбцами, соответствующими базисным векторам е0 ет_х под-
подпространства Q , через Е; эта матрица имеет г столбцов и тп строк.
Условие того, что некоторый вектор £ лежит в подпространстве Q~
или, что то же, является линейной комбинацией векторов е0, .... ег_\.
можно записать в форме
Ъ = Ес. C)
где с — вектор с координатами с0, сх, .... cr_v определяемый по £
единственным образом. С другой стороны, систему B) можно записать
в форме
А\ = Ь. D)
Если матрица А удовлетворяет поставленному условию, т. е. для
любого b имеется единственный вектор £, удовлетворяющий соотно-
соотношениям C) и D), то, как следствие, мы получаем однозначную раз-
разрешимость для любого b системы уравнений
АЕс = с. E)
Матрица АЕ имеет, очевидно, q-\- 1 строк и г столбцов. Из одно-
однозначной разрешимости системы E) следует, что q — г — 1 и квадрат-
квадратная матрица АЕ обратима, так что
F)
Покажем, что условие F) является не только необходимым, но и
достаточным условием существования единственности искомого вектора

§ 26] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 239
Z, = v@). Действительно, если условие F) выполнено, то по задан-
заданному b однозначно определяется
с = (АЕ)-1Ь. G)
а по с и вектор
1 (8)
из (8) следует, что А\ = Ь, т. е. что система B) удовлетворена.
Единственность вектора £ следует из (8) и единственности с. Итак,
мы получим теорему:
Теорема 3. Система уравнений B) определяет при любом
векторе b коррентную задачу для системы A) тогда и только
тогда, когда выполнено условие F).
4. Условие v(t) — O(th), фигурировавшее во всех результатах
этого параграфа, можно заменить другим условием роста:
if@ = o(/V). A)
где а — фиксированная вещественная постоянная.
Все результаты этого параграфа переносятся на случай A) в той же
общей формулировке, с той разницей, что число г должно быть опре-
определено не из соотношения B) п. 1, а из соотношения
Re^_,<a<Re?v B)
Доказательства в1 этом случае проходят точно по такому же пути,
как раньше. Но можно и непосредственно привести случай A) к преды-
предыдущему, а именно, ввести новую неизвестную (вектор)-функцию
va(t) = v(t) • e~at. Для этой функции, как легко проверить, соответ-
соответствующая система, полученная из A) п. 1, будет иметь характери-
характеристические корни Ко — a ^m-i — a- Д™ применения результатов
пп. 1—3 существенны будут условия ReA,y— a<T. О, которые обес-
обеспечат для va(f) рост не выше О(^); но это и означает, что условия
Re kj ^ a обеспечат для v (t) рост не выше О [theat\
§ 26. Уравнения в частных производных
1. Рассмотрим систему дифференциальных уравнений
м %pj*(l-£)u*v-х) и=0-1 т ~Х)- A)
ft = 0
где pi/, — многочлен от I-*— t-*— максимальной степени р.
Можно записать систему A) в векторной форме

240 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
где u(t, х) -* вектор-функция с компонентами uo(t. х), .... um_l{t. x).
Вектор-функция u(t, x) предполагается принадлежащей при каж-
каждом ^Ок пространству ©%? (это означает, что каждая составляю-
составляющая Uj(t, x) входит в е?<?).
Дифференцирование по t понимается как дифференцирование по
параметру и в смысле топологии £№.
К системе A) (или B)) предполагается присоединенным некоторое
начальное условие, налагаемое на вектор-функцию и @, л:), и условие
роста при t—>oo
и (Л x) = O(th).
Задача называется корректной, если существует и единственно реше-
решение системы A), удовлетворяющее всем поставленным условиям, не-
непрерывно зависящее от допустимой начальной вектор-функции и @, л:)
(в смысле сходимости в еЖ;)-
Мы укажем сейчас некоторую корректную задачу для уравне-
уравнения A). Для этого совершим преобразование Фурье по координа-
координатам х.
Двойственная система в пространстве Н имеет вид
dvj (t. a) V4
м = Zi ^*(о)«*С. о) G = 0. 1 т-\). C)
Система C) есть система обыкновенных дифференциальных урав-
уравнений с параметрОдМ о. При каждом фиксированном о система C)
есть система уравнений с постоянными коэффициентами, и мы можем
использовать для решения вопроса о корректной задаче результаты
§ 25, п. 1. В соответствии с этими результатами мы должны рас-
рассмотреть яг-мерное пространство Q, состоящее из векторов | =
— (£о im-i)- B котором действует оператор Р = Р(о) по фор-
формулам
Мы должны разложить пространство Q в прямую сумму подпро-
подпространств Q~ (о) и Q+ (о), инвариантных относительно оператора Р(а).
причем Q (о) порождается собственными и присоединенными векто-
векторами, отвечающими собственным значениям Я, (о) оператора Я (о)
с Re К (о) ^ 0, a Q+ (о) — собственными и присоединенными векто-
векторами этого оператора, отвечающими собственным значениям с Re Я, (о)>0.
Размерность /•==/• (а) подпространства Q~ (о) также,зависит ото. При

§ 26] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 241
фиксированном о корректная задача для системы C) состоит в усло-
условии v @, о) £ Q~ (о). Оказывается, что выполнение аналогичного усло-
условия при всех о (с точностью до множества меры 0) образует кор-
корректную задачу для системы C) в пространстве Н и тем самым и
корректную задачу для системы A) в пространстве £76:
Теорема 1. Если преобразование Фурье vo(a) вектор-функ-
вектор-функции ио(х)£<Ш почти при каждом а принадлежит соответ-
соответствующему подпространству Q~ (а), то система B) имеет
единственное решение и (t, х), принадлежащее простран-
пространству <Ш при каждом <>0к обращающееся в ио(х) при t = 0.
Это решение возрастает в W при rf—>оо не быстрее некото-
некоторой степени t. Если оке vo(a) не удовлетворяет поставленному
условию (т. е. на множестве положительной меры имеет не-
ненулевую составляющую в Q+ (о)), то решение системы B) при
начальной вектор-функции ио(х) если и существует в £76, то
во всяком случае возрастает в 36 при rf—>со быстрее любой
степени t.
Доказательство. Начнем с построения искомого решения.
Решение системы C) с начальным вектором vo(a) имеет вид
v(t, a) = etp<-akH(a).
Так как vo(a)£Q (о), то, по доказанному в § 25, п. 1, вектор
v(t, о) при фиксированном о возрастает при rf—>со не быстрее не-
некоторой степени t. Мы должны показать, что v(t, о), как элемент
пространства И, возрастает в И не быстрее степени t. Метод § 25,
п. 1, пригодный для фиксированного о, содержит в оценке постоян-
постоянные, зависимость которых от о трудно обозрима. Поэтому для оценки
нормы матрицы е'я<°) мы используем неравенство B) § 24, п. 2,
в котором зависимость постоянных от о легко учитывается. В дан-
данном случае это неравенство имеет вид
|е»'(о>|<в,А(о)[1+2*|/>(о)|+ ... + |^г|| Р (о) Г].
где Л(о) = max ReAy(o), причем корни ЯДа), естественно, следует
рассматривать лишь для инвариантного подпространства Q~ (о), кото-
которому принадлежит вектор v@, о). Таким образом, можно считать
Л(о)<^0, е'л<а><<;1. Далее, как известно*), квадрат нормы любой
матрицы в ортогональном базисе не превосходит суммы квадратов ее
элементов; поэтому
*) См. Г. Е. Шило в. Введение в теорию линейных пространств, § 53,
п. 4. стр. 149, Физматгиз, М., 1956.

242 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
откуда
|]Я(о)||<СA + |о|У.
Окончательно
||^я(о,||<1 + 2,СA+|о-|У+ ... +-^9тA + |о|)р(т-1>. D)
При достаточно большом t можно ограничиться старшим членом
|в'р@)|<С1Г-1A+|о|)р(|"-1). E)
Оценки D) — E) являются одновременно оценками для каждого
элемента матрицы etp (°). По условию, каждая компонента вектора
г; @, о) принадлежит пространству Н. Компоненты вектора v(t, о)
получаются как суммы произведений элементов матрицы е'р (°) и ком-
компонент вектора г» @, о); поэтому
\v{t. o)KC2*m-1(l + |o|)p(m-1)|«@. o)||. F)
Но в пространстве Н допустимо умножение на функции степенного
роста, поэтому v(t, o)£H при каждом фиксированном t. Далее,
оценка F) показывает, что m_l \\v(t, о)J ограничено в Н, поэтому в Н
v(t, o) = O(tm-1),
а следовательно, в Щ
u(t. x) = O{tm-1).
Единственность найденного решения v(t, о) вытекает из единствен-
единственности решения при каждом о; непрерывная зависимость v (t, о) от
г>@, о) — следовательно, и u(t, х) от и@, х) — видна из оценки F).
Замечание. В соответствии с замечанием 1 в § 1, п. 4 имеют
место следующие оценки для порядка сингулярности:
s(v(t, о))<р(те—l)+s(t»@, о)),
s(u(t, x))^p(m— l)+s(«@,
Поэтому, если и @, л:) — достаточно гладкая функция, так что
s(h@, ■*:))<; — р(т—1), решение u{t, x) является также обыч-
обычной функцией, если же s(m@, а:))> — р{т— 1), то решение u(tt x),
вообще говоря, уже не есть обычная функция. Фактически убедиться
в этом можно на примере волнового уравнения (§ 29, п. 1, пример 3).
Переходим к доказательству необходимости условия. Предположим,
что вектор-функция и0(о) на множестве G положительной меры имеет
ненулевую составляющую Vo (о) в подпространстве Q+ (о). Можно

§ 26] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 243
считать, что на этом множестве G положительной меры мы имеем
при некотором k
По доказанному в § 25, п. 1, при данном о имеем
lim e-ct\\v(t. o)|l =oo. G)
В силу теоремы Егорова, предельное соотношение G) имеет место
равномерно на множестве GocG положительной меры. Но тогда и
в любом пространстве // с q > -^ при достаточно большом t
так что соответствующее решение и (t, х) £ е%?, если и сущест-
существует, то при £—>со возрастает в £№ быстрее экспоненты. Теорема
доказана.
т-\
дти (t. х) у / д \ dku (t. х)
щг- 2 Р* \1 -Ш)
2. Рассмотрим теперь одно уравнение
/ д \
Считая, что решение u(t, х) вместе с производными ^
(й^О, 1 т) принадлежит пространству £$, произведем пре-
преобразование Фурье; мы получим обыкновенное уравнение
т-\
dmv(t. a)_ у d*v (t. a)
lP (°> B)
ft=0
й* и (t х\
^'
dtm - llP* (°> dtk B)
k = 0
с параметром о. При каждом фиксированном о уравнение B) есть
уравнение с постоянными коэффициентами и для построения коррект-
корректной задачи мы можем использовать результаты § 25, п. 2. А именно,
пусть г = г (о) — число корней уравнения
т-\
Г"(о)= 2
k=0
имеющих при данном о неположительную вещественную часть; тогда
корректная задача (опять-таки при данном о) состоит в указании
,„ . dv @, a) dr~x @. а)
величин v @, о), * ..... _ ■ .
dt dt

244 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
Оказывается, что аналогичное условие при всех о (с точностью
до множества меры 0) образует корректную задачу для уравнения B)
в пространстве Н — и следовательно, корректную задачу для урав-
уравнения A). (Заметим, что при этом само число г задаваемых началь-
начальных условий зависит от точки о.) Этот факт и составляет утвержде-
утверждение основной теоремы из § 1. Напомним ее формулировку:
Теорема 2. Пусть Gr есть множество точек o£Rn, в ко-
которых ровно г величин из числа ReA0(o) Це'кт_1(о) не
положительны. Пусть на каждом множестве Gr заданы функ-
функции г>0(о) vr_1(o), продолжаемые на все /?„(о) {например,
тождественным нулем) до функции из пространства И. Утвер-
Утверждается, что уравнение D) имеет решение u(t, x), у которого
преобразование Фурье функции ^^—- совпадает на каж-
каждом множестве Gr с функцией v^_1(p)(k = l, ..., г). Это реше-
решение u(t, х) при каждом f^-О принадлежит пространству Ж?
и при t—>oo возрастает в Ж не быстрее некоторой степени t
вместе со всеми производными по t до порядка т—1. Оно
единственно в классе всех решений уравнения D), принадле-
принадлежащих £№, возрастающих в Щ! при t^>oo вместе с произ-
производными по t до порядка т —■ 1 не быстрее степени t; кроме
того, оно непрерывно зависит в топологии J6 от заданных
функций vk(a), если эти функции меняются непрерывно в то-
топологии соответствующих пространств H{GT).
Доказательство. Уравнение B) эквивалентно системе
-dv* «■*).= v^t.a),
dt
dvy (t, a)
t, O),
dt
C)
dt m~lK
t, a)+ ...
В силу теоремы 1 (п. 1), начальный аектор
тогда и только тогда определяет корректную задачу для системы C),
когда он принадлежит почти при каждом о к соответствующему
пространству Q (о).

§ 26] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 245
Пусть нам заданы функции vf@, о), каждая на своем множестве
Gj(j = O, 1 т—1), продолжаемые (тождественным нулем) до
функций из пространства Н. По доказанному в § 25, п. 2, в каж-
каждой точке o£Gr величины vo(a) vr_1(a) можно дополнить вели-
величинами vr(o) vm-i(°) так> чт0 полученный вектор v(a) =
— (г>0(а) vm(a)) лежит в подпространстве Q (о). Покажем, что
этот вектор v(a), рассматриваемый как функция от о, принадлежит
пространству Н. В силу формулы (9) § 25, п. 2, величина v одно-
однозначно определяется по формуле
v, (о) = %vj (ayRJS(Я,о (о) А,,., (о)),
где Rjs — фиксированный однородный многочлен от Я,о (о) Xr_t (о)
степени s — j. Для всех характеристических корней Kj (о) имеет место
оценка (ср. § 24, п. 2)
Поэтому
I Rjs (К (о) К-1 (о)) | < С, A + | о | )"(*-Л <С, A + | о | f
Так как в пространстве И допустимо умножение на функции степен-
степенного роста, мы видим, что функции vs(o) вместе с функциями
г»;-(о)(У = 0, 1, ..., г—1) принадлежат пространству Н. Так как по
построению вектор v(o)£Q~(о), то, в силу теоремы 1, решение
v(t, о) принадлежит Н и удовлетворяет оценке v (t, o)= O(^m).
Единственность решения следует из единственности вектора v@, о)
по данным vo(O, о) vr_l@, о), непрерывная зависимость от
функций vo(O, о), .... wr_j@, о)—из непрерывной зависимости от
этих функций последующих функций г^@, о) и теоремы 1. Теорема
доказана.
Как следует из замечания к теореме 1, можно сделать опреде-
определенные выводы о существовании решения и в классических терминах.
т, . дки @, х)
Именно, можно утверждать, что если начальные функции ^—-
удовлетворяют условиям теоремы 2 и при этом являются обычными
функциями, имеющими квадратично интегрируемые производные до не-
некоторого фиксированного порядка q, то решение и (t, x) будет
обычной функцией. Число q определяется степенью по о многочленов
в правой части равенства D), т. е. величиной (т — 1) р с добавкой
еще (т—1)р. как было указано в замечании в теореме 1, таким
образом q=2(m—1)/>. Конечно, эта оценка необходимого числа
производных еще завышена.

246 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
3. Следующая теорема показывает, что приведенные в теореме 2
условия являются необходимыми и достаточными для корректной
постановки задачи с заданными значениями преобразований Фурье
начальных функций
. х),
на какой-либо системе вложенных друг в друга множеств л-мерного
пространства /?„(о).
Теорема 3. Если преобразования Фурье vJ_l(o) функций
и._[ х' (/= 1 т) заданы на множествах G'}, G'Q =>
гэ Gj гэ ... гэ G'm_l, не совпадающих с соответствующими мно-
множествами Gj (с точностью до множеств меры 0), то задача
становится некорректной. Точнее, если хотя бы для одного
j = jo мера разности G'. — G.G'. положительна, то решение,
вообще говоря, не существует; если все G'. содержатся в со-
соответствующих G. и хотя бы для одного j разность G — G'
имеет положительную меру, то решение не единственно.
Доказательство. Рассмотрим первый случай: мера разности
С — G.G'. положительна. Пусть a£G'. — G.G'.. Поскольку о не
входит в Gj, подпространство Q~ (о) имеет при данном о размер-
размерность <J, поэтому можно задать числа vo(d), •••• vj-i(a) TaKi
чтобы ни при каких значениях Vj(o), .... vm_1(o) вектор v(o) =
= (vo(a) vm-i(°)) He попадал в Q~ (о). Это построение можно
провести для всех a£G'. — G.G'. и притом так, чтобы функции г>Да)
@ <^ I <C j) были, например, финитными непрерывными функциями.
В силу теоремы 1, решение задачи с соответствующими начальными
данными, если и существует, то возрастает в £№ быстрее любой
степени t (может быть, и не сама функция u(t, x), а некоторая из
ее производных по t до порядка т— 1), так что задача некорректна.
Во втором случае, когда все G'. содержатся в соответствующих G.
и для некоторого j разность G. — G'. имеет положительную меру,
мы можем на этой разности задавать произвольно Vj_l(o) и за счет
этого получать различные решения задачи. Тем самым теорема пол-
полностью доказана.
4. Рассмотрим для системы
т—1
И/а"*)==2! Р1*[1-£х)и<!- *> С/=°-! m — V (О
ft=0
<юлее общую краевую задачу.

26] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 247
Имеется система уравнений
•• +aOim_1(p)vm_1(p) = bo(p). ]
B)
J
Спрашивается, какова должна быть матрица Л (о)= ||уА)||
чтобы при любом векторе Ъ (о) = (Ьо (о), ..., bq (о)) (с некоторыми
ограничениями на характер его зависимости от о, о которых будет
сказано ниже) существовало и было бы единственным решение и (t, х)
системы A), обращающееся при £ = 0 в вектор и@, л:), который
имеет своим преобразованием Фурье вектор г>(а)=(г>0 (а), .... vm_l(a)),
удовлетворяющий системе B).
При фиксированном о эта задача переходит в задачу п. 3 § 25,
и мы можем использовать соответствующий результат. Именно, пусть
Е — Е(о)— матрица из т строк и г столбцов, представляющая базис
подпространства Q~ (о); тогда при фиксированном о мы должны
иметь q = r(a)—l, и квадратная матрица r-го порядка А(о)Е(р}
должна иметь обратную матрицу. Если это условие выполнено, то ис-
искомый вектор v@. о) определяется равенством
v@, а) =
Вектор v@, о) принадлежит в каждой точке подпространству Q~ (о).
Чтобы он определял корректную задачу для системы B), нужно по-
потребовать еще, чтобы он входил в Н. Итак, мы получаем дополни-
дополнительное достаточное условие на Ь(р):
Е(АЕ)-1Ь(о)£Н.
Это и есть то дополнительное ограничение, которое нужно наложить
на вектор Ь(о) для обеспечения корректности задачи.
Мы доказали достаточность условий следующей теоремы:
Теорема 4. Система A) имеет единственное решение
u{t, x), принадлежащее пространству <Ш при каждом f^-0,
удовлетворяющее при t=0, после преобразования Фурье,
условиям B), возрастающее при t->oo не быстрее некоторой
степени t тогда и только тогда, когда матрица (АЕ)~Х су-
существует на каждом множестве Gr почти при каждом а и
Е(АЕ)-1Ь принадлежит^ (GT).
Для доказательства необходимости этих условий будем рассуждать,
следующим образом.
Пусть матрица АЕ вырождена на множестве положительной меры.
Мы сможем найти решение уравнения
АЕЬ(а) = 0
ненулевое и ограниченное на множестве положительной меры. Вектор-
функция v(a) = Eb(a) в каждой точке принадлежит пространству

248 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Q~ (о), а на всей оси принадлежит пространству И; таким образом,
по доказанному, имеется решение v(t, о) системы A), принадлежащее
пространству И при каждом t^>0 и возрастающее в Я не быстрее
некоторой степени t. При < = 0 выполняется условие
Av(a. 0) = Av (о) = 0.
Таким образом, если матрица АЕ вырождена на множестве положи-
положительной меры, то решение задачи A) — B) если и существует в Н,
то заведомо не единственное; следовательно, задача A) — B) не яв-
является корректной.
Если г постоянно (не зависит от а), то условия B) можно пере-
переформулировать в терминах функций «ДО, л:). Предположим допол-
дополнительно, что функции o,jk{o) суть многочлены от о, и пусть
(В0(х), .... Вг_1(х))— вектор, преобразование Фурье которого сов-
совпадает с вектором (Ь0(о) br_l(o)). Применяя к B) обратное
преобразование Фурье, получаем
«г-1. о (' ■£?) «о @. ( 4f)
C)
Условия подобного типа называются условиями «с косыми произ-
производными».
5. Рассмотрим некоторые примеры.
1. Уравнение Лапласа -^- = — Ди. Как мы уже знаем,
здесь т = 2, Я,01(о)= ± |о|, так что г=1, G0 = Rn. Gl=@); мат-
матрица Е имеет один столбец из двух элементов
Рассмотрим «вторую краевую задачу»: -гг- = щ (х), или, после пре-
преобразования Фурье, —тт- = г>1 (о). Соответствующая матрица А имеет
вид
Л=||0 1||.
Мы имеем

§ 26] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 249
так что (АЕ)-1 существует почти при всех о. Далее,
II II V (Q) II
Функция г»,(о), по условию, принадлежит пространству И; чтобы
задача была корректно разрешимой, нужно предположить, что также
■ £ И. Если предположить дополнительно, что vl (о) непрерывна
в окрестности нуля и л<^2, то мы должны будем вывести, что
t)j(O)=O (иначе -^\ не будет входить в И); это означает, что
;■
Итак, при п <^ 2, если заданная функция их (х) — " ' интегри-
интегрируема, то ее интеграл по всем х должен быть равен нулю. Это —
классический критерий корректности второй краевой задачи *).
2. Для того же уравнения рассмотрим начальную задачу «с косой
производной»
Л д v д
где ^у
7 = 1 '
После преобразования Фурье получаем
так что
Таким образом, данная задача корректна при условии, что . . (f H.
Это означает, в частности, что V(o) обращается в нуль при/ = (\>, а)=0;
для функции U (х) мы получаем необходимое условие
Г U {х) е1 (л- °> dx = 0 при (у, о) = 0. —
*) См., например. В. И. Смирнов. Курс высшей математики, т. IV,-
гл. IV, § 2, п. 202, стр. 608, Гостехиздат, М., 1953.

■250 уравнения в полупространстве [гл. iv
6. Условие и (t. х) = О (^) в ©%? можно заменить другим условием
u(t.x) = O(t"eat) в &в A)
с фиксированным вещественным а. Все результаты этого параграфа
переносятся на случай A) в той же общей формулировке, с той раз-
разницей, что число г должно быть определено не из соотношения
a), а из соотношения
Для доказательства достаточно воспользоваться заменой
ua(t. x) = e-atu(t. x)
и соображениями, высказанными в п. 4 § 25.
В связи с этим рассмотрим класс систем уравнений, называемых
корректными по Петровскому. Так называются системы вида A),
для которых вещественные части всех характеристических корней
ограничены при всех о:
В силу теоремы 1 п. 1, для системы, корректной по Петровскому.
задача Коши
в@, ж) = {во(О. х) ит_!@. х)\
■обладает решением и (t, х), которое принадлежит при каждом t ^> 0
пространству $в, возрастает в £%} при t—.>oo не быстрее thea' и
единственно в классе всех вектор-функций и (t, x), принадлежащих
к е?в при каждом t ^> 0, удовлетворяющих тому же условию роста
при t—>со, а при t = 0 обращающихся в вектор-функцию и@, х).
§ 27. Фундаментальные решения регулярных краевых задач
1. Мы знаем, что в пространстве И операция умножения на лю-
любую функцию V (о), локально ограниченную и не выше степенного
роста на бесконечности, определена и непрерывна. Найдем двойст-
двойственную операцию в пространстве $&• Если О (х) есть обратное пре-
преобразование Фурье функции V(a), то искомую операцию естественно
называть сверткой с функционалом О (л:). Отметим, что эта свертка
«сть нечто новое по сравнению с той сверткой, которую мы рас-
рассматривали в § 12. поскольку ни функционал G(x), ни обобщенная
функция / £ е%?, к которым применяется операция свертки, не явля-
являются финитными.
Функцию V (о) можно представить как результат умножения неко-
некоторой ограниченной интегрируемой функции V0(a) на некоторую,

§ 271 ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 251
например q-ю, степень многочлена 1-J- |о|2. Соответственно обрат-
обратное преобразование Фурье G(x) функции V(o) можно представить,
в виде
где G0(x) — некоторая непрерывная функция, стремящаяся к 0 при
|jc|->co. Далее, любая функция g(о)£ Н есть результат умножения
некоторого многочлена Q(o) на квадратично интегрируемую функцию
£0 (о), а соответствующая обобщенная функция / £ £$ есть результат
применения оператора Q и -^—J к квадратично интегрируемой функ-
функции fo(x) — F~* Ig0(o)]. Мы имеем
F~l IV (о) g (о)] = F~'[(l + o2y>Q (о) Vo (о) g0 (о)] =
= A - AfQ [t A.) f-1 [Vo (a) g0 (o)].
Таким образом, дело приводится к определению F г [V0(a)go(a)].
Этой операции, которую мы уже назвали сверткой G0(x) = F~1[V0(a)]
и /0(je)= F~X [go(p)\, мы должны дать явное определение. Свертка
в обычном смысле
в данном случае, вообще говоря, не существует. Но мы утверждаем,
что она существует в среднем квадратическом, т. е. как предел по
метрике L2(Rn) выражений
Так как G0(x) ограничена, a fo(x) на отрезке [—N. N] интегри-
интегрируема, то последнее выражение имеет смысл. Оно представляет собой
обычную свертку функции G0(x) с финитной квадратично интегриру-
интегрируемой функцией fo(x), равной fo(x) при |л:| <^N и 0 при |л:|>ЛЛ
Обозначим через gg(o) преобразование Фурье функции /$(х). По-
Поскольку при N —> со последовательность f*f (л:) сходится к /0 (л:) по
метрике LJR^, функции gff(o) также в метрике ^-2(/?п) СХ°ДЯТСЯ к
go(a). Так как V0(a) ограничена, то V0(a)g^(a) сходятся к Vo (о) go(a)
в метрике Z.2 (/?„). Отсюда следует! что функции [О0 * /o]w(-*:) =
= F'1 [Vo (о) go (о)] сходятся в метрике £2(#„) к F'^]

52 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
итак,
F-1 [Го(о) go(Р)] = "ш {F~l [Vo] * F'1 [gg]} = lim G0(x) * /^(je) =
/У->oo /V->oo
= lim Г G0(x — £)/0(i)rf|
в смысле сходимости в среднем.
Итак, для любого функционала О (л:), являющегося обратным пре-
преобразованием Фурье функции V (о), локально ограниченной и не выше
степенного роста при |о| ->оо. определена операция свертки О (л:)* f(x)
с любым функционалом / £ $в по правилу
4-) lim
Г
J
где (l—/S.fG0(x) = G(x) и Q ^ -^-j /„ (л:) = / (л:). Эта операция од-
однозначна (т. е. не зависит от выбора О0 и /0) и непрерывна в про-
пространстве £%?.
В дальнейшем обобщенные функции О (л:) указанного вида будем
называть свертывателями в <§$. Заметим еще, что для любых двух
свертывателей Gt и О2 свертка G^Gi есть снова свертыватель в $в,
причем для любой / (j gffl справедливо равенство О,*(О2*/) =
= (О,«О2)*/.
Последние два утверждения являются эквивалентом соответствую-
соответствующих свойств функций от о.
2. Покажем, что справедлива формула дифференцирования
д _ , dG . ~ df .
В самом деле, цепь равенств A) эквивалентна цепи равенств
to, (V (о) g (о)) = (to,V (о)) ^ (о) = V (о) (toyg (о)).
очевидно, справедливой.
Свертка G * /, как мы уже говорили, непрерывная операция в е?в,
т. е. из /v->/ в ©%? следует O*/V->O*/ в ©%?. Укажем теперь
условие сходимости GV-*G, из которого следует, что Ov* / —> О * /.
(В § 12 аналогичным условием служила равномерная финитность функ-
функционалов ОЛ Будем говорить, что последовательность свертывателей
Gv(x) правильно сходится к свертывателю О (л:), если соответст-
соответствующие преобразования Фурье Vv(a) имеют равномерно ограниченный
рост, т. е. справедлива оценка
д-де С и q не зависят от V, и, кроме того, функции V (о) равномерно

§ 27] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 253
сходятся к V(a) на каждом брусе пространства Rn. Покажем, что
если Gv(x) правильно сходятся к G(x), то Gv*f сходится к
G*f в пространстве Щ!.
Достаточно проверить, 4ToVv(o)g(o)^>V(o)g(o) в простран-
пространстве И. Мы имеем Vv (о) = A + a2)" vv (о), V (о) = A -\-ofv (о), g (о) =
= Q@)go(o). где ^О(оN^2(^п)- а vv(°) ограничены постоянной С
и сходятся к v(a) равномерно в каждом брусе.
Отсюда g0(o)vv(o)^-g0(o)v(o) в пространстве L2; а тогда
^v (о) g (о) = A + oTQ (о) ^0 (о) ^v (о) -> A + <?)«Q (о) ^0 (о) v (о) =
== ^ (°) fi1 (°) в ^- чт0 и требуется.
Аналогично можно определить правильную сходимость в случае,
когда v есть непрерывно изменяющийся параметр, например \ = t ~^>0;
в этом , случае также из правильной сходимости G(t)-+G следует
сходимость G(t)* f->G * f при любом / £ i№.
Функция G(t) называется правильно дифференцируемой, если
— А1 —^-при Д^->0 правильно сходится к некоторой функ-
функции G'(t), называемой производной от О по t. В этом случае мы
имеем точно таким же образом
V) *f->G'(t)*f в Ш\ или -
At
3. Уравнения и системы, рассмотренные в § 26, будем назы-
называть регулярными, если число г тех из характеристических корней
Я,0(о) ^m-i(°)> вещественные части которых неположительны
(или ограничены сверху), остается постоянным почти при всех о.
Для регулярных уравнений корректные задачи могут быть указаны
в терминах задания начальных функций ио(О, л:), .... иг_1@, х).
К числу регулярных уравнений относятся классические уравнения —
уравнения теплопроводности, волновое, уравнение Лапласа — и неко-
некоторые другие, как, например,
дАи д*и
~Ж = -д^ (« = 4. г = 3).
или
й4и д*и
дх*
= 4. г = 2).
Регулярное уравнение (система) с г = т называется корректным
по Петровскому (§ 26, п. 6); для таких уравнений корректная
задача есть задача Коши, в которой указываются т начальных функций
ио(О, х) «m-i@. x). Корректные краевые задачи для регуляр-
регулярных уравнений называются также регулярными краевыми задачами,
а соответствующее число г — показателем регулярности.

254
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
Рассмотрим регулярное уравнение
[ГЛ IV
I
7
A)
ft=0
с показателем регулярности г. Регулярная краевая задача, как мы
знаем, состоит в задании г начальных функций
и (О, je) = H0(je),
Специальное решение
д'^ЩО.х)
, л:), удовлетворяющее условиям
О @, л:) = 0.
B)
dG @. лг)
6t ~
0,
dt
,/•-2
= 0,
<3r-'G@. x)
C)
tr-l
называется фундаментальным решением, или функцией Грина
данной краевой задачи. Оно не только принадлежит пространству $&.
но и является свертывателем в <3№; и, как мы ниже увидим, зная
фундаментальное решение G(t, x), мы сможем написать и решение
общей краевой задачи B).
4. Вычислим значения последующих производных функций G (t, х)
при £ = 0. Обозначим через V (Л о) преобразование Фурье функции
G(t, x). Функция V(t, о) удовлетворяет уравнению
т-1
dmV(t, a)_ у dkV(t, a)
2иРъ W ..ь A)
1/@, о) = 0,
с начальными условиями
dr-W@, g) _^Qj
^-У@, g) _t

§ 27] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 255
Она называется разрешающей функцией для уравнения A). Согласно
общему построению §§ 25—26, последующие компоненты vs(a)(s'^-r)
начального вектора v0(o) корректной задачи выражаются через пре-
предыдущие Vj(a)(j < г) по формулам
v, (о) = S «у (о) «у, (К (о). • • • *■,-1 (о) )•
В нашем случае мы соответственно получаем
Как многочлен от характеристических корней, эта функция локально
ограничена и имеет на бесконечности рост не выше степенного. Далее,
в силу самого уравнения A) п. 3 и его производных
т-1
dmV@. а) _ VI ч dkV(Q. о)
Л™ — 2лРь W аТк "
тп-1
ft=O
и так далее; мы видим, что производные функции V(t. о) по t любого
порядка обращаются при < = 0 в функции, локально ограниченные,
и не выше чем степенного роста при |а|->-со.
Покажем, что функция G(t, х) и ее производные по t — пра-
правильно дифференцируемые свертыватели. Мы имеем (в векторной
записи)
W (t, о) = etp (°) W@, о).
о л, iv//п ч (т/,п ч dV(O.a) dm-1V(O. a))
Вектор-функция W@. о) —IV @, о), ^—- ^—^-1
имеет фиксированный (не выше, чем степенной) рост по о; а по до-
доказанному в § 26, п. 1
откуда следует, что составляющие вектора W (t. о) при ограниченном t
допускают равномерную степенную оценку по о. Поэтому G(t. x) —
свертыватель при любом фиксированном t. Очевидно, что на каждом
брусе пространства Rn функция W (t, о) непрерывно зависит от t;
точнее, из ^v—>^0 следует равномерная сходимость W(tv, о)к1^^0, а\
Учитывая равномерную степенную оценку W (t, о) по о, мы видим, что при

256 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
tv->t0 имеет место правильная сходимость Vft, о) к V(tQ, о) и
О(*„. х) к О(*„, х).
Для проверки правильной дифференцируемое™ функции V(£, о)
при t = 0 рассмотрим матрицу-функцию
JL[eTP(a)_/]f
имеющую прит->0 предел (в обычном смысле) — ' —P(o)\V@, a).
Чтобы показать правильную сходимость этой матрицы-функции
dW @, а)
к —t—-, мы должны проверить наличие у нее степенной оценки
по t, равномерной по о. Заменим — [ехР^ — /] соответствующим
интерполяционным многочленом. Согласно § 24, п. 1, для коэффи-
коэффициентов интерполяционного многочлена
функции f(X) справедливы оценки
где Qk — наименьший выпуклый многоугольник, содержащий точки
Я,о кк. В данном случае
о
поэтому для любого многоугольника Q
t
max|/(A.)|<
где Л = max Re К. Отсюда, как и в § 24, получаем
где A = max(Re/,0 ReA,m—1). Если оператор Р действует в под-
подпространстве Q~ (о), то etK <; 1 и B) дает искомую оценку. Далее,
производная по t от е'р(°> при любом t есть предел при т->0

§ 27) ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 257
выражения etp<-o) ; очевидно, что здесь также имеет место
правильная сходимость. Наконец, производная порядка k no t от etp (°)
имеет вид [Р(о)]* е1Р(а) и вместе с etp^o) правильно дифференци-
дифференцируема по t.
d"G (t x)
Таким образом, все обобщенные функции ^—- при k >■ г
dt"
являются свертывателями в Н, непрерывными и правильно
дифференци руемыми.
5. Покажем теперь, как с помошью фундаментального решения
G{t, x) найти решение общей задачи B) п. 3. Мы определим иско-
искомое решение u(t, x) формулой
u(t. x) = G(t. х)*/0(х)+да«;х)
... +-^Р=И" •/,-!(*). A)
где fo(x) fT-i(x)—некоторые, пока неизвестные функции из §6.
Покажем, прежде всего, что при любом выборе /0, .... fT_x
функция u(t, х) A) удовлетворяет уравнению A) п. 3. Достаточно
показать, что каждое слагаемое в D) удовлетворяет этому уравнению.
Мы имеем в силу свойств свертки
д™ Г dJG
dt"
dJG
так что для —г- *fj уравнение A) п. 3 удовлетворено. Далее, диф-
дифференцируя A) и подставляя / = 0, приходим к системе уравнений
относительно неизвестных функций
«(О, х)= /г.,D
17 Г. Е. Шилов

258 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ ГГЛ. IV
из которых последовательно могут быть найдены fr-x(x), fT^%(x), .. .
.... /„(*).
6. Для примера найдем фундаментальные решения для трех клас-
классических корректных задач математической физики при п=1 и вы-
выпишем соответствующие решения с заданными начальными функциями.
1. Уравнение теплопроводности
ди д2и ,_ .
-gf=-^r с заданной и (О, х).
После преобразования Фурье имеем
-jf=—о2г> с заданной г» @, о).
Разрешающая функция V(t, о) имеет вия
V(t, o) = e-to\
совершая обратное преобразование Фурье *), находим фундаменталь-
фундаментальное решение
1 £
G(t. х) = ^
Для решения и (/. х) с начальной функцией и @. х) £ £Ю полу-
получаем формулу
*< 41@. х),
которая в случае, когда и @. л:) — обычная функция, приводится
к виду классического интеграла Пуассона
"№ х)==тшг J е 4' в<°-в<*|.
тшг
—оо
2. Волновое уравнение
д2и д2и , ч гг. . , ^ ди @, лг)
-шг = -^ с заданными ио(д:) = «(О. д:) и а1(х) = —^—i.
После преобразования Фурье получим
-j^r = — o2v с заданными г»0 (о) = v @, о) и vt (о) = |м— -
*) См. Анализ III, гл. 7, п. 3.

$ 27| ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 25й
Разрешающая функция V(t, о) имеет вид
Так как V(t, о) удовлетворяет уравнению
aV(t, o) = sin to,
то G (t. jc) удовлетворяет уравнению
, д Off r\
Итак, O(f, jc) есть первообразная от функции -g-1^ (■* ~Ь')—&(х—01»
т- е. с точностью до постоянного слагаемого функция -^-1^ (-* + 0—
— Q(x — t)]. Эта последняя функция равна -g- при —t<.x<t и О
в остальных точках. Но постоянные не входят в пространство £№,
поэтому можно прямо написать
G(t. je) = l[6(je+ 0 — Q(x-~t)\.
Решение, отвечаюшее заданным начальным условиям, строим
в форме
и(*. x) = G(t. x)*fo(x)-+
При этом, очевидно.
Функции fo(x) и fi(x) определяются из системы уравнений
«<)(■*)= /iD
2G @, х) /
^^ * /
^ i (*)=/о (^);
таким образом.
Если «оС-^) и «Д-^) — обычные функции, мы получаем классическую
формулу Даламбера
x+t
u{t, x) = ~ f (t)dt +
x'-t
17*

260 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
3. Уравнение Лапласа
-тр- = — трг ПРИ заданной и0 (х) = и @, аг).
После преобразования Фурье находим
-—- = o2v при заданной г»0(о) = г»@, о). A)
Из общего решения уравнения A)
мы должны оставить только первое слагаемое, поскольку у нас есть
условие v(t, o) = 0(th). Учитывая начальное условие, находим разре-
разрешающую функцию
V(t, o)=e-'i°l.
Совершая обратное преобразование Фурье, получаем
о
I
q -' I сг \е - tax £q —
—со
1
2л
О оо j
Г eta-lax do-\- f e-'ae-iaxdo J =
-co 0 j
__LJ_1 I 1 1 1 *
~ 2n\ t — ix "•" t + ix i ~ n t* + x2 '
Решение u(t, x) уравнения Лапласа с начальной функцией ио(лг)£
получается по формуле
которая в случае обычной функции ио(х) переходит в классическую
формулу Пуассона
Задачи. 1. Пусть / (t, x) = / (t, xx хп) есть обобщенная функция
в пространстве Кп, непрерывно зависящая от /, как от параметра. Пусть
Ф (t, х) = ф (t, jt| хп) — основная функция в пространстве п -{- 1 перемен-
переменных t, хх хп. Положим
со
(/ (/. X). ф {t, X) ) = J (/ (t. X). ф (t, X) )х dt. A)

§ 27] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 261
где (• )х означает применение функционала / к основной функции ф по коор-
координатам х при фиксированном L Показать, что равенство A) определяет
обобщенную функцию в пространстве К'п+1.
2. Дано фундаментальное решение задачи Коши G (L х) для уравнения
ди {t, х) I д \ ч_0 ,
Построим с помощью G (t. x) обобщенную функцию % (t, x) в простран-
пространстве K'n+i, как указано в задаче 1. Показать, что эта обобщенная функция
удовлетворяет уравнению
т. е. является фундаментальной функцией оператора -^-т—^\'~лТ"
Указание. Подлежит доказательству равенство
' = Ф @. 0).
v l f» \ vx 1 j /ц
о
Использовать соотношение
о о
I. Дано фундаментальное решение задачи Коши G [t, x) для уравнения
т~1
Показать, что обобщенная функция %{t, x)£Kn+\ удовлетворяет уравнению
т-\
= b(t.x). A)
dt { дх
дт V^ dk I д \
т. е. является фундаментальной функцией оператора /, —-. Рц [» — )•
Qtm ■*" dtR \ дх I
18 Г. Е. Шилов

262 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
t
Указание. Записать уравнение A) в виде системы первого порядка
и повторить для вектор-функций рассуждение задачи 2.
4. Найти фундаментальное решение итерированного уравнения тепло-
теплопроводности (я=1)
д дг \т .
Ы"Ы ы=0-
X*
Отв. V (t, а) = —- е-'а\ G {L х) = — -4=- е 4'.
(т —1I (т —1I /2я*
5. Найти фундаментальное решение итерированного уравнения Лапласа
1)
т5
6. Найти фундаментальное решение уравнения
д д \т п
-ST-^—*в~д—J ~ ^ш веЩественН0)-
§ 28. Формулы фундаментальных решений
регулярных уравнений (я=1)
Удобные и обозримые формулы фундаментальных решений можно
получить для регулярных дифференциальных операторов, однородных
по всем аргументам. Мы рассмотрим в этом параграфе случай одного
пространственного переменного.
1. Дано уравнение
v m—k
• д">и (t, х) _ у / а у-* dku(t.x)
dtm —jLa*V^J dtk ■ V>
Совершая преобразование Фурье по х, получаем уравнение
v >
dtm и R dtk
ft = O
Уравнение характеристических корней имеет вид
т-\
2й/Л'(о). C)

§ 28] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИЙ 263
Полагая А, (о) = \х (о) о и сокращая на о™, получаем
2/о), D)
откуда видно, что \i(o) в действительности не зависит от о. Будем
предполагать, что корни \i0, \iv .... [im_, уравнения D) все различны.
Тогда общее решение уравнения B) можно записать в форме
v(t.a) = tGj(a)^f. E)
Нумерацию корней \\,j установим, как обычно, в порядке возра-
возрастания вещественных частей:
•. = Re (ir_! = 0 < Re ц, < ... < Re цт_,.
Здесь явно выделена группа' корней с нулевой ■ вещественной
частью- В решении E), растущем при ^—>оо не быстрее степени t,
при о>0 должны быть равны нулю постоянные СТ ^m-i-
а при о<0 — постоянные Со, ..., Ср-\- Пространство Q (о) при
о>0 имеет размерность г, а при о<0 — размерность р—1. Таким
образом, условие регулярности уравнения A) можно записать в форме
m — р = г.
Отметим два важных частных случая:
1) г — m, p = 0, иначе говоря.
Re 1^= ... =Rejim_,=O
(гиперболическое уравнение). К этому типу относится уравнение
струны, для которого уравнение D) имеет вид
2) г = р, т = 2р (эллиптическое уравнение). К этому типу отно-
относится уравнение Лапласа, где
18*

264
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ. IV
Рассмотрим общий случай. Искомую разрешающую функцию
V (t, о) мы должны подчинить условиям
F)
Записывая V((, о) в форме
V(t, o) =
j = 0
(o>0)
получаем для постоянных С,-(о) и Cs(o) системы уравнений
С0(о)+ •■•
G)
... +Си_1(о) = 0.
r-l .
,(о)+ ... +aim_io)/'~1cm_1(o)=
(о < 0).
(8)
Для упрощения положим при о >0 or~lCj(a) = Bj(o) и при о < 0
Pr~I^s(o) = ^s(o); тогда для величин Bj(p) и Л5(о) получатся
системы уравнений
(9)
(о > 0),
(О < 0).
(Ю)

§ 28] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИП 265
В частности, Bj(o) — Bj и As(a) = As не зависят в действитель-
действительности от о. Решения этих систем имеют вид
В: =
_ W[\ip (гд_1, \is+1
где W [...] означает детерминант Ван-дер-Монда от своих аргументов.
В итоге мы получаем
т-\
V(t. d) =
m-l
-^.Ха^' (о<0). A2)
\
где Bj и Л5 суть решения систем (9) и A0). .
2. В случае гиперболического уравнения формулы A1) — A2)
п. 1 приводятся к одной формуле
m-l
^f A)
Поскольку числитель и знаменатель имеют здесь при о = 0 нуль
одинакового порядка, отношение A) не имеет особенности при о =0.
Функция V(t. о) допускает аналитическое продолжение в плоскость
комплексного переменного s = a-\-ix в виде целой аналитической
функции
V(t. s) = ^rmyiBJefif'. B)
S j=0 о
Эта функция при больших |s| допускает оценку
\V(t. s)KCe'* i*i. M = max\\i£\.
т. е. является функцией первого порядка роста с типом -^ М. ква-
квадратично интегрируемой при /к > 1. В силу теоремы Палея — Винера *)
функция G{t, х) — обратное преобразование Фурье функции V(t. о),
есть финитная квадратично интегрируемая функция, сосредоточенная
на отрезке [—tM, (M]. Отсюда, при любой финитной (обобщенной)
*) Анализ III, гл. VII. § 6. п. 3.

266 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ (ГЛ. IV
начальной функции uQ(x), сосредоточенной, например, на отрезке
[с, Ь], мы получим, что соответствующее решение
u(t, x)=G(t, х)*ио(х)
сосредоточено на отрезке [с — (М, b-\~tM]; таким образом, носи-
носитель решения u(t, х) с течением времени расширяется со скоростью М.
Случай т= 1 легко рассмотреть отдельно. Исходное уравне-
уравнение A) п. 1 в этом случае есть уравнение первого порядка
ди ., ди
~dT~~W~d^'
преобразованное уравнение B) имеет вид
C)
а уравнение C) п. 1 сводится к равенству
Так как, по условию. Re \л = Re b = 0, положим ib = с, число а
уже вещественно. Таким образом, исходное уравнение A) имеет вид
ди ди
с вещественным а.
Решение V (t, о) уравнения A0) с начальным условием V@, o)= 1,
очевидно, следующее:
V(t, o) = e-ia<".
Функция Грина G(t, x)—обратное преобразование Фурье функции
V(t, о), согласно § 14, п. 5, имеет вид
G(t. x) = 6(x-\~at);
решение с любой начальной функцией ио(х) — вид
# и (t, х) — G (t, х) * и0 (л;) = и0 (х -\~ at).
Найдем теперь явный вид обратного преобразования Фурье функции
V (t, о) при /я> 1. Функция V (t, о) есть произведение обобщенной
функции —йгг-рбZ'czK' на бесконечно дифференцируемую функцию
m-l
'^jBjefj (cp- § 11, п- 4а, F)). В силу теоремы о свертке, мы
имеем
,-m-l

§ 28] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ 267
Мы знаем (§ 14, п. 5, пример 4), что
в силу правила F) п. 4 того же параграфа, мы получим
F-' [-£=г] = (- 1)""' 2 £22) | *т ~2 Sg" Х == Cm*m-
m-l
Обратное преобразование Фурье от 2 Bje^f равно
m-l
;=о J J '
В итоге
m-l
и (J, х) = Ст 2 Bj 6 (лг — @^) * лгт 2 sgn л; =
т-1
= ст 2 ^ / [* — ю/]т ~2 sgn [лг — aJ]. D)
/=0
Каждое из слагаемых представляет собою сдвиг на ю^ функции
xm~2sgnx, непрерывной и имеющей непрерывные производные до
порядка т — 3 (при т > 2); производная порядка т — 2 у этой
функции кусочно постоянна (равна (т — 2)! sgn л;); производная по-
порядка т — 1 есть дельта-функция. Отсюда следует, что и вся функ-
функция G (t, x) непрерывна и обладает непрерывными производными до
порядка т — 3 (при т > 2), производная порядка т — 2 кусочно
постоянна, производная порядка т —Nl есть линейная комбинация
дельта-функций. При х < щ£ все sgn(AT—v>jt) равны —1; рас-
раскрывая скобки и используя уравнения (9) п. 1, видим, что G(t, x) =0.
Аналогично G(t, лг) = О при Ar>(om_^. Между точками ю^ и ft>y+1f
функция G(t, х) есть многочлен степени т — 2 от лг.
3. Рассмотрим теперь общий случай регулярного уравнения.
Разрешающая функция V (t, о) задается формулами A1) —A2) п. 1:
г-1
"»• <*- 'Г
где Bj и As суть решения систем (9) и A0) п. 1.

268 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
Функция V(t. о), очевидно, бесконечно дифференцируема (и даже
аналитична) вне начала координат.
Поведение функции V(t, о) в окрестности (правой) точки о=0
мы выясним, разлагая числитель в ряд по степеням о:
г—\ г-\ со ь оо т—\
у=о j=o *=о ft=o y=o
Из формул (9) п. 1 следует, что лри о > 0 справедливо разложение
7=о 7=о
Аналогично в левой окрестности точки 0 = 0
m-1
5ji4X+I +... C)
Мы видим, что функция V (t, о) непрерывна при о = 0 (£>0) и,
если г ф гп, вообще говоря, имеет разрывную первую производную.
Поэтому функция G(t. x), вообще говоря, не есть финитная
функция; начальное возбуждение ио(аг) мгновенно передается на всю
ось х, так что если ио(лг) и финитна, решение u(t, x) отлично от
нуля при всех лг.
Вычислим функцию G(t, x). Обратное преобразование Фурье от
функции V(t, о), умноженное на 2л. есть сумма двух сходящихся
интегралов: *-
о 7=о
0 m-\
Заменяя во втором интеграле — о на о, получаем
2nG((. x) = f-±A \;
о l7=o s=P J
D)

28] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ 269
Мы видим, что дело сводится к вычислению интеграла вида
J_VC,c-<,4. Re a,:
6 7=о
/
где коэффициенты Cj обеспечивают наличие у числителя при | = 0
нуля порядка г—1. Такой интеграл при г>1 можно вычислить
следующим приемом. Рассмотрим интеграл с параметром К:
оо
= f
Re ay
Этот интеграл является сходящимся при — г < Re А, < 0 (а в случае,
если все Re ak > 0, на всей полуоси — г < Re X < оо) и аналити-
аналитически зависит от параметра "К. Если — 1 < Re К < 0, он может быть
вычислен путем почленного интегрирования
г-1
- Ч
7=о о
Интеграл под знаком суммы с помощью подстановки сД = Z при-
приводится к виду
zKe~zdz. E)
где Z-y- — луч z — Су|, 0 ^ £ < оо, идущий в правой полуплоскости.
По лемме Жордана, интеграл
Г zKe~z dz. F)
взятый по любой дуге на окружности радиуса R в правой полупло-
полуплоскости, стремится к 0 при R -> оо. Поэтому интеграл по лучу Lj
равен интегралу по положительной полуоси; а этот последний равен
Г 1). В итоге при — 1 < ЯеХ < О
7=0 о 7=о J l, j-o

270 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Правая часть аналитически продолжается в область Re л > — г и
мы можем найти ее значение при л =— г-\-\. Мы имеем
... (Л. + г — 1) *
г-1 г-1
Г-1
= —(А+Г— D^C^flTd+ninfl^O^ + r— 1).
Таким образом,
г-1
^
Применяя полученную формулу, выписываем значение интеграла D)
для г> 1
2я(г-2I L Яу(-
Ь=о
m-l
.(^—'*)'|п(^—'*)[■ G)
J
Если йу—комплексные, то In Cy = In|cy-| -j- latgaj имеет значение
в полосе |Im ^l-^-g-, поскольку arg ajt по условию, заключен в пре-
делах у g-, -y
Поскольку в первой сумме Re \Xj -^ 0, величина под знаком ло-
логарифма— в правой полуплоскости; во второй сумме Rep,y>-0 н
величина под знаком логарифма также в правой полуплоскости.
Случай г=\ мы должны рассмотреть особо. Поскольку р-^г,
мы должны иметь р = 0 или р = 1; так как т = р-\-г, то в пер-
первом случае т= 1, во втором т = 2. Если т=\, р = 0, то мы
имеем дело с гиперболическим уравнением первого порядка, разобран-
разобранным выше. Если р=1, т =2, то речь идет об эллиптическом
уравнении 2-го порядка.

§ 28] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ 271
Интеграл D) преобразуется к виду
со
G((, x) = -^- f [el
о
и вычисляется непосредственно:
da
*; ~ 2л [ пг — ц,* "Г" цг* — «л: J ~ 2я (/л: — ц,/) (цг* — lx) ' W
В простейшем случае оператора Лапласа мы имеем [i12 = ± 1,
и формула приводится к виду B) § 27, п. 6, 3.
Задачи. 1. Получить формулу фундаментального решения однород-
однородного гиперболического уравнения из общей формулы G) п. 3.
Указание. Если использовать принятое в тексте определение лога-
логарифма и А вещественно, то 1пМ — 1п(—/.4) = jisgnA
2. Найти фундаментальное решение для уравнений
Отв.
а) G(t, x) = ~^t\nV^+^t^
— \(t~л)!п \t — л| + -1[|* + л| + |/ — л|](С. А. Тимошкина),
б) G (/. х) = -1^ [arctg (l - ^?-) + arctg
(В. И. Авербух).
3. Построить фундаментальное решение уравнения
Указание. Для вычисления V(L о) использовать преобразование
Лапласа по t и обратное преобразование находить с помощью контурного
интеграла и вычетов *).
m1 \ " 1 flmii
(B- E- Кондратов).
(Я-1-Л1Л
У=о J
4. Написать выражение фундаментального решения для однородного
гиперболического уравнения в случае кратных корней.
Отв. G (t. х) -
й=1 ,=о 2i* Cfc — 2 — ■
*) См. Анализ III. гл. VII. § 4.

272 I УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
где гk — кратность корня ц^ = iak, а коэффициенты b^j удовлетворяют
уравнениям
ть m!n(rfe-l, s\ •
V V s-i(J\ /0. если 0<s<rfc-2,
2j 2u bkjH \s) = \ 1. если s = rk-l
(В. Е. Кондратов).
5. Написать выражение фундаментального решения для регулярного
однородного уравнения в случае кратных корней.-
U=l 7 = 0
ft=i 7=0
rk-2-J
Л
A
л=1
где ау= 2j —» a r* и **7 те же- чт0 в заДаче 4 (В. Е. Кондратов).
§ 29. Фундаментальные решения регулярных уравнений (я > 1)
1. Рассмотрим уравнение с несколькими пространственными пере-
переменными
гм-1
После преобразования Фурье оно переходит в уравнение
га-1
dmv if, а) V / \ d v ('•а) /
ft=0
Если уравнение A) регулярно, то среди корней алгебраического
уравнения
Ят(о)=2/>*(°Н*(о) C)
*=о
ровно г имеют (почти) при каждом о неотрицательную вещественную
часть. Если все они простые, то искомую разрешающую функцию
мы должны строить в виде
V{t, 0)=2С,Л((") D)
7о ;

§ 29] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИЙ 273
где коэффициенты Cj = Cj(o) удовлетворяют системе уравнений
^-о Со~\- ... -(- ^r_iCr_] = О,
™о Со~\~ • •• ~4"^r-iw-i = 1-
Найдя CQ Cr_j и подставив их в D), мы должны совершить
обратное преобразование Фурье. Эта процедура технически не всегда
выполнима, и в общем случае мы пойдем несколько иным путем.
Но в простых случаях этот путь приводит к цели, и мы рассмотрим
несколько классических примеров для иллюстрации.
1. Уравнение теплопроводности
Преобразованное уравнение имеет вид
(п
2 V 2
}=\ '.
с разрешающей функцией
V(t, o) = c-'p' =
Так как разрешающая функция есть произведение п множителей,
зависящих каждый только от одной координаты, мы можем произ-
произвести обратное преобразование Фурье по каждой координате в отдель-
отдельности и перемножить результаты. Поскольку (§ 27, п. 6, пример 1)
функция Грина уравнения A) имеет вид
~!Г I v-12 — V v2
п
BлОп/2
2. Уравнение Лапласа

274 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Преобразованное уравнение имеет вид
с разрешающей функцией
V(t, 0) = с-<р.
Функция Грина дается обратным преобразованием Фурье
По формуле F) § 15, п. 4 мы имеем
3. Волновое уравнение
д3и (t.
Преобразованное уравнение
имеет разрешающую функцию
p
Мы должны вычислить обратное преобразование Фурье от этой
функции.
Вспоминая формулу (8) § 15, п. 5, мы сразу можем написать
ответ в случае ге = 3:
Это означает, что при заданных начальных функциях
решение u(t, x) имеет вид
u{t, x)=G{t, x)
где 5, [и, (х)] означает среднее от начальной функции их (аг) по сфере
радиуса t с центром в точке аг.

§ 29] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ 275
Рассмотрим общий случай. Здесь по формуле G) § 15. п. 5
мы имеем
Flb(r-t)] = Bnyt'*~p~TJn (ф). A)
2 '
Используем формулу D) § 15. п. 4:
^1"- t2)
Заменим в формуле A) ф на 2. -^— 1 на m-f-j (т- е- п на 2^+ 3.
таким образом, дальнейшая выкладка идет при нечетном п ^> 3);
мы получим
-^i F [й(г -1)\ = Bя)^ *m+^m+i (г)-
Теперь применим B); мы придем к формуле
В подстановке z = tp безразлично, какую из величин справа
считать постоянной, какую зависящей от г; для удобства дальнейших
выкладок при дифференцировании по z будем считать постоянным р.
Тогда dz = p dt, zdz = ttfdt и
(
*[(ш) SJ^2 2 л
Отсюда
2
2 л 2
Для решения задачи Коши с заданной начальной функцией и, (лг) =
= —^—-мы получаем формулу
u{t, x) = G(t, x)*ul(x)= в+11|,_1 (т^/Г Ь(Г7*) *и1(х) =
2 2 л 2
О 2

276 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
где St[u}], как и выше, означает среднее от функции ч1(х) по сфере
\l-x\=t.
Заметим, что решение u(t, аг) волнового уравнения, поскольку
оно выражается путем /я-кратного дифференцирования начальной
функции, имеет, вообще говоря, на /к=—к— больший порядок
сингулярности, чем сама начальная функция.
Формула C) показывает, что в каждый данный момент времени
решение и (t, х) в точке аг определяется лишь значениями и, (аг)
в непосредственной окрестности сферы радиуса t с центром в точке аг.
Подчеркнем, что этот результат получен нами для нечетного п;
в действительности при п четном он не имеет места, и решение
и (t, at) при четном п зависит от значений и, (аг) в целом шаре
радиуса t.
Применяя несколько иной прием вычисления обратного преобра-
преобразования Фурье, можно получить формулу, справедливую при любом п,
четном или нечетном, хотя и не столь прозрачную. Заметим, что
классическая формула обратного преобразования Фурье для функции
не может быть использована вследствие расходимости получающе-
получающегося интеграла. Но если взять некоторую первообразную по t от
функции V(t, p), именно функцию
sin tp\
Р"-1
являющуюся первообразной от V (t, о) порядка п — 2, то соответ-
соответствующий обратный интеграл Фурье
1 • «»н. ,-Цо,х)ао
будет уже сходящимся, если произвести вначале интегрирование
по сфере радиуса р, а затем по р от 0 до оо. Действительно, послед-
последний интеграл в пределах от 0 до N имеет вид
Согласно формуле B) § 9, п. 7, мы имеем
-5-
J'е-/
—г

§ 29] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ 277
Поэтому
= {2л)Сп"гп-2 f(r2-t2iT~ /сО8ф • (COSpg-/sinpg) dp dl =
—г
г
п-3
— т
второе слагаемое при N—>co стремится к 0, а первое, в силу тео-
теоремы об обращении интеграла Фурье, имеет при N—>oo предел,
равный
f п-З
с (г2 — *2) 2 при t<r,
г [ О при t>r.
Аналогичный результат получается при замене cos ф на sin ф.
Отсюда
С ,< г). D)
L Р J й<"-2
О (t> r).
Для решения и (Л лг) задачи Коши £ заданными функциями
и @, лг) = О, ы ^' л) =: ы, (лг) получаем формулу
или, что то же,
П-З
! /2\ 2
При Kj(at)=1 мы должны иметь u{t, x)~.t; отсюда находим
с = . _ 2> ■ • Итак, искомая формула имеет вид

278 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ |ГЛ. IV
2. Рассмотрим теперь общий случай. Пусть дано уравнение
tS-SM'£)-&- x=ix *■>• A)
Предположим, что это уравнение регулярно, т. е. алгебраическое
уравнение
m-l
^m(o)=2pfc(o)^(o) B)
ft=O
имеет почти при всех о одно и то же фиксированное число г корней
с неположительной вещественной частью.
Фундаментальное решение G(t, х) удовлетворяет условиям
Обозначим через Gp(t, x) решение уравнения A), удовлетворяющее
условиям
дг~2прф. х) dr~1Gp@.x) 2p
где ^р(лг) — фундаментальная функция оператора Др (§ 7, п. 2, при-
пример 9):
2р ( српг2Р-п, если п нечетно или п четно и > 1р\
" ^ \ српг2Р~п In г, если п четно и -<2р.
Поскольку
мы можем получить интересующее нас фундаментальное решение
G(t, x) по формуле
О (Л х) = А"Ор<Л х). D)
В некоторых случаях при достаточно большом р оказывается
более легким построить обобщенное фундаментальное решение Gp{t, x),
а затем уже получить G(t, x) по формуле D).
Используем формулу разложения гк на плоские волны (§ 11, п. 6)
я\

§ 29] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ
и ее производную по X:
279
2я 2 ГГ~2~~)°
о, x)\d<s> +
!(<">. x)\*4to.
При значении % = 2р—п эти формулы дают разложение на плоские
волны функции <f2np(x):
с I |(@, л;) | р~" d(a
о
^ПР Г I («> ^) I2p~" ln I (w- Jf) I rf<° ПРИ ге четном, F)
о 2
при ге нечетном или E)
я > 2р.
В первом случае при п > 2р выражение |(@, лг)[2р " означает
6("~2р~1)((со, аг)) или ((ю, х))~2р+п, смотря по нечетности или чет-
четности п.
Слагаемое сп(к) Г|(ю, x)\2p~nd(o во втором случае (ге четно,
п •< 2р) отброшено, так как оператором Др оно переводится в нуль.
Формулы E), F) запишем в единой форме
^ (ж) = апр f &2р_п ((со, х) ) rfo.
G)
где ef2p-n(£) есть четная обобщенная функция аргумента \, опреде-
определяемая по формуле
|£|*. если k > 0 нечетно или А: < 0 четно,
Ь~ ~ (g), если А; < 0 нечетно,
£|*1п|Е|, если А:>-0 четно.
Нам понадобятся и первообразные
они имеют вид
q-то порядка от
**,© =
k+Q
akt£,k+Q< если * четно,
hgb~k~l+q©, если А: нечетно.
sSn Ъ если * нечетно,
. если k четно,

280 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ |ГЛ. IV
I
Имея в виду формулу G), мы вместо задачи A)—C) будем (при
фиксированном со) искать решение ир(со, t, x) уравнения A), удовле-
удовлетворяющее условиям
дг~2ир (со, 0, х)
ир(со, 0, х)= ... = ^2
(8)
dtr
Допустим, что найдено решение ир(со, /, х) этой задачи, завися-
зависящее непрерывно (в К') от со и те раз дифференцируемым образом
от t. Мы утверждаем, что функция
Оp[t, x) = anp Гир(со, t. x)da>
является решением поставленной задачи. Действительно, поскольку
в обобщенных функциях дифференцирование и предельный переход
перестановочны, мы имеем
i
,(*,*)
fc=0
Лт-l
дти (a,t,x) V / • d \ дки (со, t, x)
ft=0
dr~2Gp @, x)
}p@,x)
a
что и требуется.
Таким образом, отыскание фундаментального решения сводится
к решению задачи A) при условиях (8). Решение этой задачи будем
разыскивать в форме
Up (CO, t, X) == Ua (t, СО!*! + . . . + ®пХп) = U<* ('■ £)■ I — («>■ *)■ (9)
Поскольку для функции вида (9)
dxj dxj d| *' д\ '

§ 29] фундаментальные решения регулярных уравнений 281
подставляя в A), мы найдем
ttB
dt
Это уравнение уже с одним пространственным переменным £ (и па-
параметрами ш). Требуется найти его решение при условиях
Покажем, что уравнение A1) почти при всех ш регулярно с по-
показателем г. Мы должны для этого составить уравнение
т-\
К"Ъ «ух)*-* A3)
и найти число его корней с неположительной вещественной частью.
Но уравнение A3) получается из уравнения B) при замене а1 =
= (OjCt о„ = (о„а, т. е. при параметрах о, описывающих некото-
некоторую прямую в пространстве /?„. Так как уравнение A) регулярно
с показателем г, то почти при всех значениях ш и уравнение A1)
регулярно с тем же значением г. Следовательно, почти при всех ш
может быть однозначно решена и задача A1)—A2). Если ее реше-
решение зависит от (о непрерывно, то, как мы видели выше, интегриро-
интегрированием по (о мы получим решение и интересующей нас задачи.
3. Рассмотрим случай однородного гиперболического уравнения
У a *. i. > % A)
■■■+kn=m ot ох\ •••охп
Соответствующее алгебраическое уравнение имеет вид
*■■= ш 2 \...*<1---°№°- B)
Его корни Я,0(о), .... A,m_j(o) суть однородные функции 1-го по-
порядка по о. Если фиксировать луч, определяемый единичным векто-
вектором ш = ((о1, .... (о„), то на этом луче Oj = p(S)j, Я,А(о) = (лА(ш)р,
числа (лА и (о связаны уравнением
*nJS*' •••«*'I = o. • C)
Уравнение A) называется гиперболическим, если все числа й
чисто мнимы, и строго гиперболическим, если при этом все они раз-
различны. В этом случае фундаментальное решение задачи Коши для

282 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ - [ГЛ. IV
уравнения A) имеет вид (§ 28, п. 2, D))
m-l
\m~2
Ow(t, I) = С 2 Bj Ц — bj (со)t\m~2 sgn H — bj (со) /]. ibj (со) = Hj (со).
Искомое решение задачи Коши A1)—A2) п. 2 можно записать
в форме
m-l
Ua (t, I) = С 2 Я; [| — *у (со) tf'2 sgn [£ — ^ (со) t] * %2p_n (£). D)
Для упрощения свертки заметим, что
^Я - bj (со) /] = (и - 2)! 6 <£ - fty (со) /).
С другой стороны, если использовать первообразные от функции
^2p-/i(^)' можно написать, что
dm~1
&2Р-П (.1) = dt"»-l ^2p-n, m-1 (£)•
Перебрасывая —m_j со "второго множителя свертки D) на первый,
приходим к формуле
Ua(/. Б) = С -2 б/ [£ - Ь; (со) fl * ^2р_„, т_! (£) =
= С 2о
Отсюда
. х) = СрпАр f Up(t(«>,
m-l
2 вЛ-«. ffi_i [(со, х) — fty (со) fl rfco. E)
Оператор А может быть выражен здесь через оператор ^- в силу
равенств
■да-/((a. x)-bjt) = b)/'«<*, x)-bjt),
А/((со, *)-*у0 =
2^
п
= 2]/"((со, *)-ft/)co2=/"((co, x) — bjt).
справедливых для любой (даже обобщенной) функции /(£).

29] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИИ
Таким образом,
283
Я1-1
> х) - bi
. X)-bjt)d<S>. F)
/
Q /=0
Если уравнение A) сферически симметрично, т. е. дифференци-
дифференцирование по л: входит только в форме операторов Лапласа, то корни
йу(ш) на самом деле не зависят от ш. Мы можем тогда использовать
формулу B) § 9, п. 7, которая дает выражение интегралов по сфере
от функций аргумента (ш, х); согласно этой формуле,
О (/, х) =
гя-1
P-n, m-i
п-3
—А2Г5~
п-3 ""-'
;=0
-bjOdl G)
Число р пока еще произвольно; мы можем выбрать его так, чтобы
функция ^2р-п,т-\^> — fyO получила наиболее простой вид.
Пусть, например, речь идет об обычном волновом уравнении
Здесь
Если ге > 1 нечетно, мы положим 2р = п — 1 и получим
Х[_/,<]F) равна 1 при
и 0 при
^- Таким образом.
при
J (r2 —£2) 2 d% при

284 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
Произведя однократное дифференцирование, приходим к формуле
G(it х)==с д"~22 1 ^ 1 (/-2-яУ при r>t,
dtn~2 г"~2 | о при г < t,
совпадающей с формулой D) п. 1.
В общем случае в формуле фундаментального решения однород-
однородного гиперболического уравнения
т-\
можно совершить переход от интегрирования по сфере к интегриро-
интегрированию по поверхности
Соответствующая формула (один из вариантов формулы Херглотца —
Петровского) имеет вид
аи Х)-
где dHQ,) — элемент поверхности Я = 0 в точке |. Переход от (8)
к (9) проведен в ряде книг *).
4. Переходим к общему случаю, когда однородное уравнение
дти (<, х) _ у .*,+ ..■+*„ аиц(<.лс) п
dtm ~ ^ *!-*« «*»Л*« дЛ
регулярно. Это означает, что корни соответствующего алгебраиче-
алгебраического уравнения
удовлетворяют неравенствам
*) Ф. Й о н, Плоские волны и сферические средние, ИЛ, 1958; И. М. Г е л ь-
фанд и Г. Е. Шилов, Обобщенные функции и действия над нимн, Физ-
матгиз, 1958 и 1959.

5 29] ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ РЕГУЛЯРНЫХ УРАВНЕНИЙ 285
где q, г не зависят от ш и q-\-r=m. В качестве начальных функ-
._ . dr~lu(O,x) _
ций можно задавать и@, х), .... -Ч—-. Будем, кроме того,
дг
считать, что числа ц^ цт различны. В этом случае решение
уравнения A1) с начальными условиями A2) п. 1 принимает вид
г-1
. I) = С { 2 Bt (- lijt - it)r-2 In (- ц
m-1
B)
Заметим, что при 2/7 < n функция ^2р-и есть свертыватель в про-
пространстве 38 (равно как и Gm(t, с,)) и поэтому свертка B) опре-
определена.
Желая использовать тот же прием, который мы применили для
гиперболического уравнения, будем дифференцировать функцию Q(t, £).
Пользуясь формулой Лейбница, легко получить следующие формулы
многократного дифференцирования:
-' (/ > Я,).
Поэтому мы можем написать
m-l
+ (-1Г12л5(^-г6Г2
X [вг_Я, / Ш (М - /£)+ ft,-2. ll } * ?*Р-п, I (I). C)
причем постоянные ar_2>, обращаются в 0 при i > г — 2.
Числа р и I подчиним условию 2/7 + £ = п — 1.
При п нечетном м\л будем иметь ^р-я, z(D==^K£)> ПРИ й четном
, i (i) = а&~ ■ Следовательно, при и нечетном
= ftcr { Д в, (- и/4-
2p+rn1l D)
2

28b
Отсюда
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ. IV
г-1
>. x)fp+r-"-lX
m-1
причем ar_2i, = 0, если I > г — 2.
При п четном мы должны произвести свертку с а\~х. Свертку
любой обобщенной функции /(£) с а%~1 можно осуществить, напри-
например, так: найти преобразование Фурье g(a) функций /(£), умножить
его на -
и применить к результату обратное преобразование Фурье
/(s) * б"' = F~l [g (о) • па sgn о].
В нашем случае
т-\
О1"
при о-> О,
при о < 0.
s=q
Поэтому
ang (a) sgn о = алAаI
г-1
;=0
FH-1
при о>0.
при

§ 30] УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 287
Отсюда
£/«('■!) =
{ *°° г~1 ° m-1 1
2 By № - iy/-2 in (iE —
y=0
m-1 |
+ (- 1/ 5] AJ W - ®'~2 1П (^/ ~ ^ =
J
r-1
m-1
s=q )
Наконец, искомое фундаментальное решение G(t, x) получает вид
Gfx_CAPfi\B
J I ^J i i
X[er_2.i»n(—|i/ + *(a.
m-1
Здесь также постоянные ат_%, обращаются в нуль при I > г — 2.
Показатель /7 остается еще произвольным (при условии 2/7 < и) и
может быть использован для дальнейшего упрощения формул E) —
G) в различных возможных частных случаях.
§ 30. Уравнения со свободным членом
1. Мы рассмотрим здесь вопрос о существовании и форме кор-
корректных краевых задач для уравнений со свободным членом
m-1
dmu(t,x)
dtm
ft=0

288 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Как и раньше, наша задача — выяснить, какие начальные условия
определяют для уравнения A) корректную начальную задачу, т. е.
задачу, решение которой и (t, х) принадлежит при каждом t ^- О
пространству ■£№, при t—>оо возрастает в <з?в не быстрее степени t,
единственно в этом классе и непрерывно зависит от начальных усло-
условий и функции f[t, х). Естественно, будем предполагать, что функ-
функция f(t, x) сама удовлетворяет условиям, поставленным для решения,
т. е. принадлежит при каждом t ^ 0 пространству $6 и возрастает
в нем при t-+co не быстрее степени t; более точное условие будет
сформулировано ниже.
Переходя от A) к преобразованию Фурье по х, получаем уравне-
уравнение вида
где свободный член g(t, о) принадлежит пространству Н при каждом
£^>0, а при t~»-oo возрастает в Н не быстрее некоторой степени t.
Чтобы проиллюстрировать возникающие здесь возможности, отвле-
отвлечемся от параметра о, т. е. рассмотрим случай обыкновенного урав-
уравнения и притом для простоты первого порядка:
Решение этого уравнения при начальном условии v@) = v0 имеет
вид
v @ == еа\ + Г еа V-°>g (G) «Ю = eat \v0 + f e ~aeg (G) dG . D)
о L о J
Пусть вначале а^.0; покажем, что решение v(t) при /-»оо и
любом v0 возрастает не быстрее степени /. Действительно, в этом
случае
что и утверждалось.
Рассмотрим случай а > 0. Тогда интеграл
о
имеет конечное значение, и мы можем записать решение D) в форме
ОС
v @ = eat [v0 +/(g)\ — fea v-Vg (G) dQ. E)

§ 30] УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 289
Второе слагаемое имеет рост не выше степенного, поскольку
со со
J ea U-*g (G) dQ = fe ~"eg (G +1) dQ, F)
о
и следовательно,
I/
б
Если /v0'\-I{g)=hQ. то, очевидно, v(f) возрастает экспоненциально
при £-»оо; поэтому равенство vo-{-I(g) — O является необхо-
необходимым и достаточным условием существования решения сте-
степенного роста по t.
Таким образом, при а > 0 мы не можем наложить никаких доба-
добавочных условий на v0, поскольку эта величина однозначно опреде-
определяется по f(g).
Уравнение типа C), с параметром о, получается после преобразо-
преобразования Фурье уравнения A), имеющего' первый порядок по t:
да (t, х)
Роль коэффициента а играет многочлен р (о). Мы получаем здесь
следующий результат: в точках о,, где /?(а)^0, функция г;0(о)может
быть взята произвольно, в тех точках, где р (о) > 0, она не может
быть задана произвольно, а напротив, целиком определяется условием
со
^о (о) -Ь / e-PW*g ф. о) йШ = 0. G)
о
Решение v(t, о) при каждом фиксированном о имеет вид D), F):
t
e<PWv0(o)+fe(t-e)pMg(e,o)dQ при /7(о)<0; (8)
v{t. о) =
_ j" e-eP(°)g(t-{-B, o)dG при /?(о)>0. (9)
о
Выражение v(t, о) при р (о) -<[0 определяет функцию, принадле-
принадлежащую Н и возрастающую в Я не быстрее степени / вместе
с g(t, о); действительно, если
\g{t.

290 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
то при
При /?(о)>0 аналогичное утверждение требует дополнительных
предположений на g(t, о). Можно, например, потребовать, чтобы
функция g(t, о) достаточно быстро убывала в И при t —»oo, так,
чтобы выполнялась оценка
\g(t, о)|<СA + ^A+о2)Ч(о) с А< —
В этом случае при р (о) > 0
Более слабым условием является просто предположение, что
интеграл (9) при каждом t^-О принадлежит Н и возрастает в Н
не быстрее степени t.
Для общего уравнения A) мы докажем следующую теорему:
Теорема. Пусть Я,0(о), .... A,m_j(o) — корни уравнения
и множество Gr образовано из всех тех точек о£/?„, где
ровно г из корней Я,До) имеют неположительную веществен-
вещественную часть (г=0. 1, .... т—1).
Пусть, далее, функция f(t, x) принадлежит W при каждом
/>0 п возрастает в Ш не быстрее некоторой степени t и,
кроме того, на множестве Gr каждый из интегралов
со
J
. a)\dB (k = 0, I т — 2) A0)
принадлежит пространству И и возрастает в Н не быстрее
некоторой степени t.
Тогда для уравнения A) является корректной следующая на-
начальная задача: при t = 0 задано (и принадлежит простран-
пространству H{Gk_{) преобразование Фурье vk_x (о) функции "fc_J ■
почти всюду на множестве Gr (k — 1, 2 г; г — 0, ..., т — 1).

§ 30] УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 291
Доказательство будем проводить в предположении, что корни
Я,0(о) ^m-i(°) вСе различны почти всюду.
2. Рассмотрим линейную неоднородную систему обыкновенных
уравнений (т уравнений, т неизвестных функций vo(t) fm-i
с постоянными коэффициентами, имеющую в векторной форме вид
где
|^(/)|<СA+0Л- B)
Решение системы A) с начальным вектором v@) = v0 можно
записать в форме, аналогичной D) п. 1:
= eplv @)^ Г е('"е) Pg(Q)dB = ePt v@)+ Г е~^ёф) dQ . C)
о L о -I -
Предположим, что линейный оператор, заданный матрицей Р.
имеет г характеристических корней с неположительной вещественной
частью и т — г характеристических корней с положительной веще-
вещественной частью. Пространство Q, в котором действует оператор Р,
разлагается в прямую сумму инвариантных подпространств Q~ и Q+,
первое из которых порождается собственными (и присоединенными)
векторами, соответствующими собственным значениям первой группы,
а второе — собственными (и присоединенными) векторами, соответ-
соответствующими собственным значениям второй группы. Соответственно
разлагаются и векторы v (t), v0 и g (/):
Так как операторы Р и etp инвариантны в подпространствах Q~
и Q+, то
t
v' @ = etpvo + / е('-е) V F) dB. D)
о
/
о
/
v+ (/) = e'V + / e(') Pg+ F) dG. E)
о
Мы утверждаем, что вектор-функция v~ (f) возрастает в Q~ не
быстрее степени t. Для доказательства применим неравенство B)
§ 24, п. 2:
F)

292 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
где Л есть максимальная из вещественных частей собственных значе-
значений оператора Р. Обозначим собственные значения оператора Р
в подпространстве Q через Я,о, .... Я,,.^; можно написать
... <Re/,r_1<0.
Поэтому, в силу неравенства F), в подпространстве Q
||е'р||<^СA -\-t)m~*. G)
Следовательно,
j
о
t
о
что и утверждалось.
ур
Выражение функции v+ (t) запишем в виде
„+ (/) = е'Р \v+ + f e'epg+ (9) dB 1 (.8,
и покажем, что интеграл
со
J (9)
является сходящимся. Обозначим собственные значения оператора Р
в пространстве Q+ через \ ^m-i и предположим, что
по условию, Re Я,г > 0. Собственные значения оператора — Р в этом же
подпространстве суть —Я,г —Я,т-1 и при этом
Re(-*,„_,)< ...
Поэтому, в силу неравенства F) и оценки B), мы имеем
Гe-">g+ @)dG < Г
II ff II о

§ 30] УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 293
Очевидно, что вектор / принадлежит к подпространству Q+. Внося
его выражение в формулу (8), мы получим
В силу неравенства F) и оценки B), последний интеграл имеет в Q
норму
IOO II II ОО I
f е{'-в) V F) <*6 = / e-Wg + (9 +1) dQ
и, следовательно, возрастает в Q не быстрее степени t.
В то же время выражение
заведомо возрастает экспоненциально, если v£ + / ф 0; достаточно
заметить, что на каждый базисный вектор es оператора Р в под-
подпространстве Q^ оператор е действует, как множитель е *.
Отсюда следует, что необходимым условием существования реше-
решения системы A), возрастающего в Q не быстрее степени /, является
выполнение соотношения
При выполнении условия A0) система A) имеет решение
(t ОО 1
«0- + / e-f>pg- (G) dQ-f e-0Pg+ (Q)dQ \ ,
I о t j
возрастающее в Q при t—э-оо, как мы видели, не быстрее степени t.
Таким образом, условие A0) является не только необхо-
необходимым, но и достаточным для существования решения v(t),
которое возрастает в Q при t-*-co не быстрее степени t.
В частности, решение v(t) однозначно определяется по со-
составляющей Vq начального вектора vQ, которую можно взять
произвольно (в Q~); составляющая v+ определяется из A0)
по g{Q).

294 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
Пусть система A) получена из одного уравнения т-го порядка
обычной заменой v(t) — vo(t). -^- = vl(t), .... ~~^- =vm_1(t).
В этом случае можно утверждать, что искомое решение, возрастающее
при t—>oo не быстрее некоторой степени /, определяется однозначно
по (произвольно заданным) значениям v@) г-1 .
Действительно, пусть vo = v^ -+V+ и v+ =(^ 1Г_Х im_i).
Если заданы числа z;(O) = tio> .... "Д = i\r_lt то для вектора
Vq = vQ — v£ оказываются известными первые г составляющих
Ло—1о- •••• Лг — 1г- а тогДа- п0 доказанному в § 25, п. 2, этот
вектор v~ определяется и притом единственным образом.
В случае, когда система A) получена преобразованием Фурье
из системы с частными производными
A2)
она содержит вектор о в качестве параметра (в матрице Р и свобод-
свободном члене g = g(t, о)- Условие A0) принимает теперь вид
+ (9. о)«/е; = 0. A3)
Оно является по-прежнему необходимым и достаточным условием
корректной разрешимости системы A) в каждой точке о.
Рассматриваемое при всех о, соотношение A3) также является
необходимым для существования решения v(t, о) системы A2), воз-
возрастающего при каждом о не быстрее степени t. Но получаемое
при этом решение A1), как функция от о, a priori не обязано при-
принадлежать пространству Н. Мы покажем в дальнейшем, что для
системы A2), соответствующей одному уравнению
т-\
Ук\ )
dtm-\ ~*Ук\ дх) dt*
ft=0
=/(*. х). (И)
выполнение равенства A3) почти всюду по о является необхо-
необходимым и достаточным условием корректной разрешимости
задачи с начальным вектором wo(cQ.

5 30]
УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ
295
3. Для доказательства этого факта нам понадобится более тща-
тщательно проанализировать решение обыкновенной системы A) в случае,
отвечающем одному уравнению, и, в частности, выписать выражение
решения v(t) через начальные данные vQ vr-\-
Итак, рассмотрим снова одно уравнение порядка т:
гя-1
dmv (t)
dtm
Это уравнение эквивалентно системе
dv0
dkv (t)
dt"
=f@-
A)
dt
~w
— V,
0.
0,
dvm-\
dt
Оператор Р имеет матрицу
B)
О
О
1
О
о
о
1
0 0..
РО Pi ••• Pm-1
с собственными векторами
е; —(l, "к], kj, .... к?'1) (У=0, 1 т —
(см. § 25, п. 2), где Я,о ^m-i—корни уравнения
а/"-
2
ft=0
=о.
Как мы уже знаем, решение v(f) может быть однозначно выра-
выражено только через числа vo — v(O) vr_1 =
^
dtT~
Найдем
явное выражение v(t) через vQ, .... vr_v Для простоты будем пред-
предполагать, что корни 7,0, ..., ?-m_i различны.
Лб Q
р 0
Любой вектор 6=(s0
ным векторам е0, ех, .... ет_1:
можно разложить по базис-
-г- C)

296 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
В координатной форме равенство C) имеет вид системы:
в. <kf) I PI I [ f-W— 1
[ГЛ. IV
П~\
-Л1-1
D)
Разрешая эту систему относительно неизвестных £-, находим
1 ... L, ... 1
я—1
т—1
E)
Здесь W есть детерминант Ван-дер-Монда от величин Я^, .... /,m_j,
a W^y^ — его минор, полученный вычеркиванием у'-го столбца и
Л-й строки (у, ft = 0, 1 m — 1). В частности, для вектора
т-1
мы имеем
F)
Аналогично для вектора
получаем
т-1
/=0
G)
Проектируя равенство G) п. 2 на векторы ег ет_1 и учи-
учитывая, что оператор etp переводит вектор е, в е%^, мы можем
записать условие A0) п. 2 в эквивалентной форме:
= r т— 1).
(8)

$ 30] УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 297
Подставляя в (8) выражения F) и G), получаем после сокращений
-1Г "'/«"% (G)rfG = O. (9)
Условие (9) можно считать эквивалентным выражением (в исходной
координатной форме) основного условия A1) п. 2 корректной раз-
разрешимости рассматриваемой задачи. )
Положим
t СО
Aj = J e-ekIg (G) OB. Bj = f e-ekJg (G) OB.
A0)
Формула (8), эквивалентная равенству (9), определяет величины
vr vm~l через величины Сг, .... Ст_х:
b
Найдем величины v°, .... г»', для чего используем первые г урав»
нений системы D) для | = VQ:
Будем считать для простоты vo = vl= ... =vr_l*=0. Пере--
несем неизвестные в левую часть, а известные — в правую
V0 -\- V1 -\- ... -f- К' = — 2 ^.
s>r
Разрешая систему по правилу Крамера, получаем
t 1 ил»
20 Г. Е. Шилов

298 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
где Wr— детерминант Ван-дер-Монда от величин Ко ^r-i<
a Wf(Siy) получается из Wr заменой столбца из величин 1, Я,у Я,у~'
на столбец из величин 1, Xs, ..., Krs~ ; таким образом. Wr(Si ;) есть
детерминант Ван-дер-Монда от величин Я,о, .... Xj_v ks, Я,у+1, .... hr_v
Подставляя в последнее равенство известные значения A1) величин
V, ..., vm~l, находим:
Преобразуем коэффициент при Cs. По формулам для определи-
определителей Ван-дер-Монда
WT — rn-\ r-\
П о-ъ-ч
В числителе правой части в первом произведении не участвует 7.^,
а во втором произведении Xj заменено на Ks. Производя сокращения,
получаем
^■m-l Wr(StjI
W Wr ~~ (ks —
X
(Л, — А,)... (Л,- — Xj-riilj+i — Лу) ... (Лг_,—
JJ' (Л, - ЛА) Л' (Лу - Л,) (Л, - Лу)
ft=r t=l
Итак,
V'SmTI F# • 03)
k=l i=l
Вернемся к формуле A1) п. 2, дающей решение нашей задачи при
выполнении условия A0). Ее можно записать в форме
у=о
/=о

30]
УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ
299
Нас интересует основная компонента решения
г-1
i>(O=if0(')=Sw'(Q =
| I
A5)
|
Подставляя сюда найденные значения v' A3) и известные g1. gs G),
находим
j=0
г m-l
г-1
■+
-I Л^И
/•-1 fm-1
v
r-\
■4-
m-l
r-1
V
I m-l
fr-1
r-1
i /■ ,
m-l
l
+/ v;
Гг-1
П'^-^П'
ft=r
(-!)■
,j+m "^лт
w Ji
. A6)

300 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ (ГЛ IV
Фигурная скобка в первом интеграле приводится к виду
у 1 ГУ «У** , ш*г*1
^ т-1 Nj я-1 i m-l
>=°П' frj-м \s=r П'<**-**><*«-м П <**-*
1 = 0 k = r k = r
у
Аналогично вторая фигурная скобка в A6) преобразуется к виду
m-1 r r-1
V 1
т -J
=° JJ (Xj — %i) (Xs — Xj)
r-\
2
Выражение A7) ест^ двойная разделенная разность (см. § 24, п. 5)
вида F(l0 К-\\ Ьг ^m_i) Для функции F(z. Q = etz~^.
Поэтому, в силу оценки A2) п. 5 § 24, мы получаем
... К-и К *„_,)!<с/"1«'*-*•!. A9)
где z0— некоторая точка многоугольника, натянутого на точки
"Ко \-i< a So—некоторая точка многоугольника, натянутого
на точки z0, A., Д-m-i- Так как при этом все Rehj^O(j^r-l),
то Rez0<0, а так как Re7,s>0 при s>-r, то ReCo>Re^o. По-
Поэтому мы можем написать при 0 -< 8 <Г t
Re (tz0 —%)) = tRezo — Q Re£0 = (^—9) Re zo-\- 9 (Re го-
Окончательно для рассматриваемой двойной разделенной раз-
разности A7) мы получаем оценку
у 1 у
B0)
Выражение A8) есть двойная разделенная разность вида
F{\ lm-i, l0 Я.г_1) для функции F(z, Q = eK-&.
Поэтому, в силу той же оценки A2) п. 5 § 24,
\F(lr *,„,_,; 10 Яг_1)|<Свт-1|«'ь-в1ь|. B1)

§ 30] УРАВНЕНИЯ СО СВОБОДНЫМ ЧЛЕНОМ 301
где z0 — некоторая точка выпуклого многоугольника, натянутого на
точки %т ^m-i- a £о — некоторая точка выпуклого многоуголь-
многоугольника, натянутого на точки z0, Я-о K-v
Поскольку ReXs > 0 при s^-r, мы имеем Rez0^-ReЯ-г, а так как
<0 при j<r, то Re£o<Rezo. Поэтому при О</<;0
= (/—8)Re«0-|-/(Re£0—
Таким образом, вторая фигурная скобка в A6) по модулю не
сх
превосходит
В результате мы получаем неравенство
t оо
0 B2)
о t
с постоянными, зависящими только от г и т.
4. Теперь мы можем рассмотреть и уравнение
дти (t, х) \\ I д \ д"и (t, x)
т £-irK\ riy I jsj* j \-- —г- \Х)
dt
Для решения v(t, о) двойственного уравнения
т-\
с условиями
«@.,0= ...=, д0
мы можем написать оценку B2) п. 3, введя параметр о:
\v{t. o)
0. C)

302 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Тот факт, что g(t. о) принадлежит И и возрастает в Н не
быстрее некоторой степени t, можно записать неравенством
Ig(t. о)|<с0(t + \f (I + °УФ(о). Ф(оNL2. D)
Вставляя D) в C), получаем
т — \ со
/ f keReKW t, o)\dQ.
f
В силу условия A0) п. 1. результат представляет собою функцию,
принадлежащую при каждом t ^> 0 пространству Я и возрастающую
в Н при t—>oo не быстрее некоторой степени t, что и требовалось.
Рассмотрим теперь общий случай, когда начальные функции
г»0(о), .... vr_j(a) — произвольные функции, принадлежащие про-
пространству Н.
По доказанному в § 26, п. 2, существует решение w (t, a)
уравнения
dmw (t, о) V
Z
принадлежащее при каждом t~^-0 пространству Я, возрастающее
в Я не быстрее степени t и удовлетворяющее начальным условиям
At — lffrti /Л лЛ
Обозначим через V(t, о) решение уравнения A), построенное
нами выше и удовлетворяющее начальным условиям
V0@. а)= ... =IV,(O, о) = 0.
Функция
(t, о)
есть снова решение уравнения A), принадлежащее при каждом f^.0
пространству Н и возрастающее в Я не быстрее степени t. Оно
удовлетворяет начальным условиям
Таким образом, искомое решение существует, и наша теорема
доказана полностью.
Замечание. Как ив § 26, п. 5, условие задачи может быть
видоизменено: можно разыскивать решения в классе функций
и (t, х)£3в, растущих при t—>co не быстрее экспоненциально-

§ 31] СМЕШАННЫЕ ЗАДАЧИ 303
степенной функции вида theat с фиксированным а. Доказанная нами
теорема полностью сохраняется и для этого случая, с той разницей,
что число г ==г (о) нужно будет определять из условия
.. <ReA.r_I(o)<a<ReA.(.(q)< ••■
Рассмотрим, например, уравнение A), корректное по Петровскому
в обычном смысле; это означает, что вещественные части всех харак-
характеристических корней при всех о остаются ограниченными некоторой
фиксированной постоянной а. В силу нашей теоремы, задача Коши
для этого уравнения корректна при любых начальных функциях
ио(х) ит-\(.х) в том смысле, что решение существует в про-
пространстве J6, возрастает в Ш при t —> ;о не быстрее theat, является
в этом классе единственным решением и непрерывно зависит от на-
начальных функций.
§ 31. Смешанные задачи
1. В этом параграфе мы рассмотрим некоторые корректные сме-
смешанные задачи в области t ^> 0, х^-0 для уравнения вида
т-1
&и (t, x)
S?»
ft=0
Задача, корректность которой мы будем выяснять, состоит в рас-
расширении на обобщенные функции следующей классической задачи.
Требуется найти решение уравнения A) при заданных граничных
функциях
«b@=«(*. 0). «гМ-ЩУ- „,_1@=£^1 B)
и заданных начальных функциях
, , ,г. . , . ди@, х) , . дг~'и@, х) /ОЧ
ио(х) = и(О, х), «,(л:)=—^—L Uf_^X) — _L__i..C)
Число первых р есть порядок уравнения A) по -5—, число послед-
последних г будет указано ниже.
Граничные задачи для обыкновенных уравнений с обобщенными
функциями мы рассматривали в гл. 1, § 5, п. 6. Напомним резуль-
результат. Обыкновенному уравнению (в обычных функциях)
2
с граничными условиями

304 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ ЧГЛ IV
ставится в соответствие уравнение в обобщенных функциях
i = 0
Где F(x) равна f(x) при х > 0 и О при jc < О.
Всякое решение уравнения D) с условиями E), рассматриваемое
как обобщенная функция, равная 0 при х < 0, есть решение урав-
уравнения F). Обратно, всякое решение уравнения F), равное 0 при х < О,
есть обычная функция, являющаяся при л: > 0 решением уравнения
D) и удовлетворяющая условиям E).
В случае уравнения A), содержащего, кроме того, производные
по t, будем поступать аналогичным образом. Перепишем уравнение A)
в форме
т — \ р
дти (t, х) у /, д \ dku у .
fc=0 j=0
и затем каждую из производных по х в обычном смысле заменим
на производную по i в смысле пространства К' с исправляющим
слагаемым, составленным из 6-функций и их производных аналогично F).
В результате мы получаем уравнение
р i-i
дти (t, х) V /о / д \ Г д'и (*• х)
Решение этого уравнения, равное 0 при л: < 0, мы и будем называть
решением задачи A)—B).
В случае обыкновенного уравнения с обычной функцией мы уста-
установили, что всякое решение уравнения F) есть в действительности
обычная функция (с тем или иным скачком при л: = 0). Уравнение
в частных производных (8), вообще говоря, имеет решения и более
сложной природы. Тем не менее переход от A) — B) к (8) остается
естественным в том смысле, что если решение к (Л х) уравнения (8),
равное нулю при х < 0, есть обычная функция и при х~^-0 имею-
имеющая достаточное число непрерывных производных, то и (t, x) является
и 'решением задачи A) — B) в обычном смысле, и обратно.
Доказательство проведем для более общего случая: вместо урав'
нения A) рассмотрим систему уравнений 1-го порядка по л::
а вместо уравнения (8) — систему вида

§ 31] СМЕШАННЫЕ ЗАДАЧИ 305
В качестве к (Л х) возьмем обобщенную вектор-функцию, равную 0
при х < 0 и решению и (t, х) системы (9) при х > 0. Обозначим
через и, (Л х) обобщенную вектор-функцию, равную 0 при х < 0 и
■ ' *' при х > 0. Уравнение (9) можно записать в таком виде:
Функция ut(t, x) не есть производная (в К') функции u(t, x); так-
также как и в § 5 гл. 1, имеет место равенство
dui*'xx)=Ul(t. *)+«(*. 0MD A2)
Подставляя к, (Л Jf) из A2) в A1), получаем A0), что и требуется.
Рассуждая в обратном порядке, получим обратное утверждение.
Теперь уточним предположения относительно природы решения
и (t, х).
Искомая функция u(t. x) предполагается при каждом £^>0 при-
принадлежащей к пространству 36+ всех функций и (х), которые, бу-
будучи умножены на е~^, квадратично интегрируемы при лг^-О.
а также всех производных таких функций (в пространстве А").
Число р зависит от уравнения A) и будет указано ниже. Через Н%
обозначим совокупность всех преобразований Фурье функций прост-
пространства £/6%. В п. 3 будет показано, что класс /У^. состоит из
(обычных) функций v (s), аналитических в полуплоскости Im s > p и
после деления на некоторую степень s интегрируемых в квадрате го
каждой прямой Ims = T, причем интегралы
равномерно (для данной v(s)) ограничены по т. Заметим, что этот
класс обладает важным свойством монотонности; если vo(s)£H+ и
|Vj(s)\ <1C|t>0(s)|, причем vt(s) — аналитическая функция, то также
©!(s)G^+- Поэтому в классе Н% допустимо умножение на аналити-
аналитические функции степенного роста при |s|—>оо.
Как было сказано, искомое решение и (Л х) должно быть эле-
элементом пространства 36+• зависящим от t, как от параметра.
При t = 0 обобщенная функция и (t, x) и ее производные по t
до порядка г — 1 должны обращаться в заданные обобщенные же
функции ио(х) ur_i(x).
Укажем теперь допустимое поведение обобщенных функций и (t, x)
при t->co. Мы будем предполагать, что и (Л х) имеет в простран-

306 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
стве &%,% рост не выше степенного, т- е. что при некоторых q и h
выполняется неравенство
\\u{t,
Число р и число г, характеризующее количество начальных условий,
определяются из следующих соображений. Рассмотрим уравнение
Ьт=?£рк (s)lk. A4)
получающееся из уравнения A) заменой -^- на К, а t-т— Has. При
каждом комплексном s уравнение A4) имеет т. комплексных корней
ho(s) ^m-i(s)- Эти корни— аналитические функции от s, за
исключением конечного числа особых точек (точек ветвления алгеб-
алгебраической функции, определяемой уравнением A4)). Мы будем эти
корни рассматривать в полуплоскости Im s > р, где р выбрано так,
чтобы все особые точки корней лежали в полуплоскости Im s < p.
Будем предполагать также, что среди корней ho(s) A-m_j (s) нет
тождественно совпадающих, тогда р можно выбрать так, чтобы в по-
полуплоскости Im s > p все корни были бы всюду различны между со-
собой. Тем самым в указанной области функции Я,о (s), ... Am_, (s) являются
однозначными аналитическими функциями. Разобьем все эти корни
на две группы по следующему правилу, в первую группу входят
корни A.0(s), ..., A,r_, (s), у которых всюду в полуплоскости Ims^>p
вещественная часть остается неположительной, во вторую группу
Kr(s); ..., ^m-i(s) входят те корни,'которые хотя бы в одной точ-
точке полуплоскости Im s > p имеют положительную вещественную часть.
Этим определено число г.
Мы предположим далее, что функции
,.ч ,, -. ,,. du(t, 0) dP~lu(t. 0)
непрерывны, дифференцируемы по t т. — 1 раз (т. е. столько раз,
сколько требуется формулой (8)), и возрастают при t—>oo вместе
с соответствующими производными не быстрее, чем С№ с некото-
некоторым h. Составим функцию
р
8 if. s)= ^QJ(-±)[wJ_1(f) — iswJ_2(t)+ ... + (- is)*-* wo(t)].
A5)

§ 31] СМЕШАННЫЕ ЗАДАЧИ 307
В силу указанных условий на функции vOj(t), при каждом <: таКом,
что Im s > p, существуют интегралы
A6)
где ReA,?(s)>0. Мы будем предполагать, что всякая аналитическая
функция v(t, s), удовлетворяющая при Ims>p неравенству (хотя бы
для одного q и одного k)
\v(t, *)|<Ф4,в(*. s), A7)
принадлежит к классу #Р_ и возрастает в нем не быстрее степени U
Это условие, в конечном счете, есть условие на функции wo(f), ...
.... wp_i(t); оно выполняется, например, если предположить, что
существуют все интегралы
JQk\wf(Q)\dQ (£<m — 2, /<m— 1). A8)
о
Будет доказана следующая теорема:
Теорема 1. Пусть дано уравнение (I) с условиями B) — C),
причем числа р и г определены, как выше, и заданные функ-
функции wo(t) wp_1(t) удовлетворяют указанным выше усло-
условиям. Для существования (и единственности) решения задачи
A) — B) — C) в классе S@®+ необходимо и достаточно, чтобы
функции
оо
f (q = r m— 1), A9)
определенные первоначально в области Re^?(s)>0, Im s > p.
допускали аналитическое продолжение на всю полуплоскость
Im s > р до функций из класса Н^
2. Рассмотрим вначале несколько примеров.
а) Предположим, что все характеристические корни Я0E), ...
.... ^m-i(s) имеют в полуплоскости Im s > р неположительную вещест-
вещественную часть. Тогда г = т и корректная задача состоит в задании всех
функций ио(х) мт_,(лг), wo(t) wp_j(t). Простейшим при-
примером, в котором реализуется указанная возможность, служит урав-
уравнение
ди , ди п
+ 0 W

308 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
с общим решением u = f(t — х), линии уровня которого — прямые,
параллельные главной биссектрисе. Очевидно, что при произвольном
задании функций «@, л:) и w(t, 0) получается корректная задача.
В свете нашей теории имеем к = is, и область Re к < 0 совпадает
с полуплоскостью Im s > 0, так что k = is относится к первой группе
корней. Поэтому в корректной задаче фигурируют ио(х) = и(О, х) и
wo(O=«(f. 0).
Несколько более общий случай — однородное уравнение
т
д™и (L х)
а"д^дхт-к-0- B)
4=0
у которого все корни уравнения
т
2 abkk = 0 C)
вещественны и неотрицательны. Наконец в левой части уравнения
вида B) можно добавить произвольную группу младших членов.
б) Предположим, что характеристические корни ko(s), .... kr_l(s)
имеют в полуплоскости Im s > р неположительную вещественную
часть, а остальные корни kr(s) ^m-i(s) всюду в этой полу-
полуплоскости имеют положительную вещественную часть. Тогда условие
аналитической продолжимости интегралов A9) в условии теоремы
отпадает, и корректная задача состоит в задании функций ио(х), ...
.... Mr_,(jc), wo(t) ^m-iCO- В качестве примера рассмотрим
уравнение
ди ди _
~М ~дх~~
с общим решением и = f(t-\-x), линии уровня которого параллельны
побочной биссектрисе. Очевидно, что для задания решения достаточно
иметь только wo(t). В свете нашей теории имеем к = — Is, область
Re к < 0 совпадает с полуплоскостью Im s < 0, так что к = — Is
относится ко второй группе корней. Поэтому в корректной задаче
задаче фигурирует только wo(t).
Вторым примером является волновое уравнение
д2и д'и _ „
дР ~ дх* ~
Характеристические корни удовлетворяют уравнению Я,2 = — s2,
A,,2=±£S. Один из этих корней в полуплоскости Ims>0 имеет
отрицательную вещественную часть, другой — положительную. В силу
нашей общей теории корректная задача состоит в задании функций
Щ((), w1(t) и ио{х); это — классическая смешанная задача для вол-
волнового уравнения.

§ 31] СМЕШАННЫЕ ЗАДАЧИ 309
Вообще, если каждый из корней kj(s) сохраняет знак в полу-
полуплоскости Ims>-p, уравнение A) называется корректным по Петров-
Петровскому относительно -т—. Алгебраическая функция k = k(s) отобра-
отображает полуплоскость Ims>-P одними своими листами в полуплоскость
Re Я, >■ 0, другими — в полуплоскость Re к 4^. 0; но это означает, что
обратная функция s — s(k) всеми своими ветвями отображает прямую
ReA, = O в полуплоскость Ims-^p. Заменяя в уравнении A) -з— на
-гр, а -^т- на -тг-г и соответственно s на —ik', к на is', мы полу-
получаем условие корректности в более привычной форме (ср. § 26):
функция k' = k'(s') при Ims' = 0 принимает значения, вещественные
части которых Re А/(о) ограничены сверху (числом A). Уравнения
этого типа рассматривались С. Л. Соболевым. К ним относятся,
в частности, параболические и гиперболические уравнения, например,
однородное уравнение вида B), у которого все корни уравне-
уравнения C) вещественны.
в) Несколько более сложный характер имеют примеры, в которых
вещественные части корней kr(s) Я,т_,(s) не сохраняют знака
в полуплоскости Im s ^> p. Сюда относится обобщенное уравнение
Коши — Римана
ди . ди , „
dt дх
Очевидно, решением этого уравнения при а = 1 является функ-
функция и (t, х), аналитическая по аргументу t -f- lx. Задавать можно
wo(t) уже далеко не произвольно, а так, чтобы wo(t) аналитически
продолжалась в четверть плоскости t ^> 0, х ^> 0. В свете нашей
теории имеем к = s, область Re к > 0 есть полуплоскость Re s ■> 0.
Корректная задача получается при задании функции wo(t), удовлет-
удовлетворяющей условию: интеграл
J e-<sw0(t)dt
с полуплоскости Re s > 0, где он определен a priori, аналитически
продолжается в область Im s > 0 до функции класса Зв\.
При о=—1 получается уравнение антианалитических функций
ди ди
dt ~~ l дх'
Корректная задача состоит, в задании функции wo(t), для которой
интеграл .
со
fetswo(t)dt
о

310
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ IV
аналитически продолжается с полуплоскости Re s < 0, где он опреде-
определен a priori, в область Ims>0 до функции класса И%.
Рассмотрим, далее, уравнение Лапласа
д'и , д'и
W
- = 0.
Характеристические корни удовлетворяют уравнению А,2 = s2, К = ± s.
Корректная задача: заданы wo(t) и и», (t), причем должны быть удов-
удовлетворены следующие условия: интегралы
f e-'s[Wi(f)— tswo(t)]
dt.
tewb(Q]<tt
D)
должнь чналитически продолжаться со своей области определения
(Re s > в первом случае и Re s < 0 во втором) в полуплоскость
Ims>0 до функций пространства Н°+- Поскольку
Г e-tsw0 (t) dt— Г e~fsw'o (t) dt — w0 @),
о о
CO CO
s f etsw0 (t) dt = -f etsw'o (f) dt + w0 @),
о о
мы можем переписать интегралы D) в форме
E)
J е-" [w, @ - К Щ dt + tw0 @).
о
со
J ets [wl (t) + tw'o Щ dt — iw0 @)
F)
и в свете предыдущего примера высказать условие корректности
в следующей любопытной форме: функция wt (t) - iw'o{t) должна
продолжаться в область t > 0, х > 0, как аналитическая функция,
а функция wl(t)-±-lw'0{t) должна продолжаться в эту же область,
как антианалитическая функция.
Аналогично для любого однородного уравнения
dtm-kdxk
= 0

§ 31] СМЕШАННЫЕ ЗАДАЧИ 311
с характеристическими корнями Я,у- = \ijS, где [ij — не чисто мнимые
числа, мы получаем следующее условие корректности: интегралы
j[m) Кj ... - (-/s)'-1 w0 @)]
G)
должны аналитически продолжаться со своей области определения
(Reu.fes<CD в полуплоскость Im s > 0 до функций пространства Н%.
Интеграл G) можно переписать в форме
и высказать условие корректности следующим образом: функция
2 ^~^[ч-.@)- • • • —4т^-
должна продолжаться с полуоси (>0 в четверть плоскости t > О,
.£ > 0. как ^.^-аналитическая функция, т. е. как решение уравнения
ди , , ди _
3. Обозначим через р%"+° пространство всех (комплексных^ функ-
функций и (х), удовлетворяющих условию
I* | и (х) |2 е-"®* dx < оо. A)
о
Каждая функция и(х)£е%?%° обладает преобразованием Фурье
v(s)= f u(x)el*sdx, B)
6
существующим в смысле среднего квадратичного при всех комплекс-
комплексных s = o-j-/T с т^.р; при этом, по теореме Планшереля,
со
= ± f\u{x)fe-**dx. C)

312 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
Получающиеся функции v (s) допускают следующее внутреннее
описание: это те функции, аналитические при т^>р, для ко-
которых
оо
j\v(a-\-tx)\'2do
существует при каждом т и остается ограниченным во всей
области р <С т < оо (лемма Пэли и Винера). Необходимость
этого условия следует из равенства C), поскольку
со оо
J|и(х)|2е'2хх dx<cf\u(x)I2e-®*dx.
о о
Для доказательства достаточности рассмотрим интеграл
и(*)
представляющий собою обратное преобразование Фурье функции
v (a -f- ix) еТх. Мы имеем
со
и{х)е~г* = -^ J v(o-\-ix)e-ia*do.
— оо
i
и по теореме Планшереля
со %
f | и (х) |2 с-2" йх = JL v (a + /т)|2da. D)
—со
Мы утверждаем, что «(.£) = О почти всюду при х < 0. Действи-
Действительно если и(л;)=£0 при jc < 0 на множестве положительной меры,
мы получим, что при т->оо
о
что невозможно, поскольку правая часть равенства D) по условию
ограничена- Итак, и (х) = 0 при х < 0 и имеет место равенство

§ 31] СМЕШАННЫЕ ЗАДАЧИ 313
при всех т^>р; устремляя т к р, получаем
Таким образом, и (х) входит в класс S& + • Исходная функция v(s)
является преобразованием Фурье и (jc). в силу теоремы единствен-
единственности. Итак, лемма Пэли и Винера доказана.
Через e%?^.Q мы обозначим совокупность тех (обобщенных) функ-
функций и (jc), которые получаются применением к функциям из &в + °
дифференциальных операций порядка ^.q:
^^ «.weда*0.
Поскольку дифференцирование обобщенных функций переходит после
преобразования Фурье в умножение на — is, класс tfi+q преобразо-
преобразований Фурье функций k(jc)€ e%?^-4 состоит из функций v(s). полу-
получающихся из функций класса Н+ умножением на многочлены сте-
степени
со
Очевидно, что в класс Н+ = [J Н±9 входит любая аналитическая
■ ?=о
при Ims>p функция v(s), возрастающая при |s|->oo не быстрее
некоторой степени s, поскольку при делении такой функции на до-
достаточно большую степень s мы получим результат, заведомо при-
принадлежащий классу /У+°. Далее, ясно, что класс tfi+ обладает
указанным в п. 1 свойством монотонности: если г>о ($) £ Н + и ана-
аналитическая функция Vj(s) по модулю не превосходит |^o(s)|-
то также г», (s)£H^+. Отсюда следует, что в классе Я+ допустимо
умножение на аналитические функции, возрастающие при |s|->oo
не быстрее степени s.
4. В этом и следующем пунктах будет дано доказательство не-
необходимости условий теоремы 1. Здесь будет удобнее рассмотреть
вместо одного уравнения A п. 1) систему уравнений 1-го порядка
по t, в векторной записи имеющую вид
Здесь и(х, f) — /и-компонентная вектор-функция, ^U-s—) — квад-
квадратная тХ^-матрица, элементы которой — многочлены от оператора
/ -т— наибольшей степени р.
21 Г. Е.

314 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
К уравнению A) добавляется начальное (векторное) условие
и(х. 0) = щ(х) B)
и граничные (векторные) условия
U(o, о = wo(Q д"d"p(-i'°=wp-i(Q- C>
Для перехода к обобщенным функциям, как в п. 1, используем
формулы G) — (8) п. 1, где, однако, вместо скалярных выражений
будем понимать соответствующие /покомпонентные векторные выраже-
выражения. Запишем систему A) в форме
ЙМ *■ '• *'* ' - D)
где ak — числовые матрицы. Тогда, по формулам (8) п. 1, в обоб-
.щенных вектор-функциях система D) перейдет в систему:
dt
\k
..-wo(Q6(*-V)]-
Будем считать, что все рассматриваемые обобщенные функции,
как и выше, принадлежат к пространству £$\. После преобразова-
преобразования Фурье мы будем иметь
dv (s. t)
dt
. 0. E)
где вектор-функция g(s, t) определяется формулой
g(s, t) = 2 ["*wft_, @ - 'sw*_2@+ .••+(— is)"'* wo@1. F)
*0
а составляющие вектор-функции v(s, 0 входят в пространство tf+.
Начальное условие B) после применения преобразования Фурье пере-
переходит в начальное условие
v(s. O) = vo(s).
При данном s решение задачи E) — F) имеет вид
i
v(s, t) = etpls)\0(s)+ JeC-^Wgts, 0)d0. G)

§ 31] СМЕШАННЫЕ ЗАДАЧИ 315
Векторы v(s, t), xo(s), g(s, t) пр^и данном s определены
в /м-мерном комплексном пространстве R — Rs, в которое мы введем
обычным образом эвклидову метрику, так что для вектора
5 й 1
При данном s линейный оператор в пространстве Rs, заданный ма-
матрицей P(s), имеес некоторое число p = p(s) характеристических
корней с неположительной вещественной частью (О-^p-^ffi) и т — р
корней с положительной вещественной частью.
Соответственно, пространство Rs можно разложить в прямую
сумму инвариантных подпространств относительно оператора P(s),
которые мы обозначим R$ и RJ. Векторы v(s, t), v0, (s), g(s, t)
разлагаются на составляющие
v(s. t) = x~(s, O+v+(s, t) vo(s) = v-(s)+v+(s),
g(s. t) = g-(s, O + g+(s. 0-
Так как операторы P(s) и etp^ инвариантны в подпространствах
R7 и Rl' to мы имеем
V" (s, t) = e'P^v- (s)+ / e{t-e)P{s)g- (я, 0) d0,
v+(S, 0 =
о
/
0
Как и в § 30, легко проверить, что вектор-функция v"~ (s, 0 воз-
возрастает в RJ не быстрее некоторой степени t.
Выражение функции v+ (s, t) мы запишем так:
f Гс-ер(*)д+E, 0)de|. (8)
о j
Как и в § 30, проверяется, что интеграл
+(s, 0)d0
J
о
является сходящимся.
Очевидно, что он принадлежит подпространству Rf. Введя его
выражение в (8), мы получим
v+ (s. О = е*Р W [v+ (я)+1 (s)] - J c('-e)P(s) g+ (s. 0) rfO.

316
УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ
[ГЛ. IV
Как и в § 30, легко убедиться, что последний интеграл возрастает
в Rs не быстрее некоторой степени t. В то же время выражение
etp (J'fv+ (s)+I(s)l заведомо возрастает экспоненциально, если
Отсюда следует, что необходимым условием существования
решения задачи E) — F), возрастающего при данном s не
быстрее степени t, является выполнение соотношения:
со
= 0.
(9)
Б. Рассмотрим вид условия (9) п. 4 в интересующем нас случае
одного уравнения
Это уравнение эквивалентно системе
dU}
~дГ~~
М2,
B)
которая после преобразования Фурье переходит в систему
dt
dv,
Оператор P(s) соответствует матрице
0 1
0 0
0
0
P0(s) Я, (я) ... Pm.i(
Его собственные векторы имеют вид (§ 25, п. 2)
e;(s)=(l, Kj Я7)' СУ = О. 1 щ— 1).

§ 31] СМЕШАННЫЕ ЗАДАЧИ
где Я,о, Х,1, Я,2 ?-m_i—корни уравнения
317
т-1
2i
k=0
Любой вектор
векторам е0, е,
можно разложить по базисным
е;п_,:
В координатной форме это равенство принимает вид системы
га-1 1 ..Um —I
— Цт— 1
C)
Разрешая эту систему относительно неизвестных £у, мы находим
1 ... 1 60 1 ... 1
1 1 £ 1 '
о т-1
1
^0 • >ЛУ-1 Ь1
I га-1 ft т — ] ь
i т-1
Здесь IF (Я,) есть детерминант Вандермонда от величин Я,о, .... Кт_и
a Wjk — его минор, полученный вычеркиванием fe-го столбца и k-oR
строки (J, k — 0, 1, ..., т—1). т
га-1
В частности, для вектора v0(s) = (v0(s), .... ^m_i(s))= S7'''6;
7 = 0
мы имеем
ffJ/c4 — ( ^ Г^. /q\ 1W . >r. /оЛ IV/ I
m 1
Аналогично, для вектора g(s, 0 = @, 0 g(s, t))= 2 £*(?' 0e;
мы имеем
. О-
E)

31g УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ IV
Проектируя равенство (9) п. 4 на векторы ег, .... em jti вспоминая,
что оператор с'РE) переводит вектор ву в eaj{s)ej, мы можем за-
записать равенство (9) п. 4 в форме
со
(s) + J
vfV(s. 0)d6 = O (v = r m—l). F)
Подставляя в F) выражения D) и E) и сокращая на (—l)v, получаем
, m-1 ^v, rn-1 "Ч, m-1
= (—iy / e~vt-^s>g(s, 0)dO (v = r, .... m —1). G)
о
Это и есть интересующее нас соотношение. Коэффициенты ^ v'°—, ...
v, гя — 1
.... v-m~' — 1 представляют собою многочлены от величин
Я,о ^m-v степени не выше т—1. Сами корни — аналитические
функции от s в полуплоскости Im s > р, растущие при J s | -> оо
не быстрее \s\p. Функции v0 (s) wm_, (s) no условию, принадлежат
классу Н\. Поэтому левая часть равенства G) является аналитической
функцией от s при Im s > р, также принадлежащей классу Н\.
Каждая из величин
— l)m f e-ekv{s)g(s, 0)d0 = Gv(s) (v = r m—1), (8)
как функция от s определена a priori только в области, где
Re A,v (s) > 0, Im s > р и аналитична в этой области. Мы видим, что
необходимым условием разрешимости задачи A)—B)—C) п. 1
является условие аналитической продолжимости функции
Gv(s) с той. области, где она определена формулой (8), т. е.
в области Re A,v(s) > 0, Im s > р, на всю полуплоскость Im s > р,
причем полученная функция должна принадлежать классу Н\.
Необходимость условия теоремы 1, таким образом, доказана.
6. Переходим теперь к доказательству достаточности.
Пусть для уравнения A) и граничных условий B) п. 1 построена
функция g (s, t) по формуле A5) п. 1, и пусть известно, что все функции
Gv(s) = (—l)raJe~exv(s)g-(s, 0)d0 (v = r, .... m—l)

§ 31] СМЕШАННЫЕ ЗАДАЧИ 319
аналитически продолжаются в полуплоскость Im s > р до функций
класса Я+. Покажем, что задача A)—B)—C) п. 1 обладает реше-
решением, удовлетворяющим поставленным условиям.
Вначале убедимся, что уравнения G) п. 5, написанные в форме
A)
ЮА = Wv k/Wv ,„_,). позволяют однозначно определить в каждой
точке s значения vr(s), .... vm_l(s) через vo(s) vr_l(s) и Gv(s).
Прежде всего формула F) п. 5 определяет величины vr(s), ...
.... tf"-»(s) через О (А,,) QfrY
vv(s) = —f e~exv(s)r(s. 6) dQ =
о
Так как алгебраическая функция Qv m_1(s) имеет при |s|->oo рост
не выше степенного, то vv(s)£H®+ вместе с Gv(s).
Найдем величины v° vT~l. Для этого используем первые
г уравнений системы C) п. 5 для | = v^
Так как определитель этой системы при Im s > p отличен от нуля,
то величины v°, , vr~x определяются однозначно через v0, ...
.... vr_y и vT vm~l, т. е. в конечном счете, через v0, ...
.... vr_j и G(kr) G('km_1). Указанный определитель есть
алгебраическая функция от s; его обратная величина возрастает при
| s | —> оо не быстрее степени s и, следовательно, функции v°, ...
.... vr~x принадлежат к Я+ вместе с v0 vr-\- Искомые функ-
функции vr vm-i определяются через величины v0 vr-i< ^r(s)>
-... Om_! (s) по последним m — г уравнениям системы З п. 5, причем
снова ясно, что результаты принадлежат пространству н\.
Решение задачи, как мы знаем, при каждом s однозначно опре-
определяется через vo(s) vm-i(s) и #(s> 0 по формуле G) п. 4:
= е'Р W v0 (s) 4- /
v (s, t) = е'Р W v0 (s) 4- / с-ер W g (s, 0) dQ B)

320 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [Г Л IV
или с учетом (9) п. 4
v (s. t) = е'Р <*) v- (s) + J е-ер О £- (s. в) d6 —
ls, 6)d8. C)
Формула B) показывает, что v(s, t) при каждом f и каждом s
в полуплоскости Ims > Р есть аналитическая функция. Нужно показать,
что она принадлежит к классу Н% и возрастает в нем не быстрее Cth.
Мы воспользуемся при этом формулой C) и основным результатом
§ 30. Там было показано следующее: если имеется уравнение
*=о
и на области значений о, где вещественные части величин К0(а), ...
.... ^m-i(o) сохраняют знаки (так что, например, Re7,y(o)^0 при
/<!> — 1 и ReXv(o)>0 при v^-r) заданы квадратично интегри-
интегрируемые после деления на некоторую степень [ сг | —|— 1 начальные
удовлетворяющие соотношениям
то существует решение г; (а, t). удовлетворяющие поставленным
начальным условиям и неравенству:
t
\v(t, s
г-!
■"Skwi. E)
ft=O
где Kr (s) — корень с наименьшей положительной вещественной частью.
Поскольку вся полуплоскость Im s > p может быть представлена,
как конечное объединение областей, где вещественные части харак-

§ 31] СМЕШАННЫЕ ЗАДАЧИ 321
теристических корней не меняют знака, оценка вида E) справедлива
во всей полуплоскости Im s > р. Но в таком случае эта оценка,
по условию, приводит к тому,, что v(t, s) принадлежит к прост-
пространству Н\ и возрастает в нем не быстрее степени t, что и требовалось.
Замечание 1. Так же как в § 26, условие задачи может
быть видоизменено: можно разыскивать решения в классе функций
U(t, x)£H+. растущих при <->со не быстрее не степени t, а экспо-
экспоненциально-степенной функции вида Реш с фиксированным показате-
показателем а. При этом в определение числа г в условии теоремы нужно
будет ввести изменение; в полуплоскости Im s > р корни KQ (s), .. .
.... Xr^!(s) должны иметь всюду вещественную часть, не превосхо-
превосходящую а. В частности, это выполнено для уравнений, корректных
д ,
по Петровскому относительно -г— в обычном смысле, т. е. таких.
у которых Ims;(X) остается при Re^ = 0 ограниченной некоторой
постоянной. Обозначая эту постоянную через а. мы получаем, как
и выше в примере б) п. 2, что в полуплоскости Im s > 0 величины
ReX0(s), .... ReXr_!(s) не превосходят а. Таким образом, результаты
примера б) п. 2 распространяются с указанным изменением на этот
общий случай.
Замечание 2. Результаты, полученные для четверти плоскости,
могут быть применены для определения корректных задач в четверти
пространства: t >- 0, хг >- 0, —со < х2 < оо — оо < х„ < со,
для уравнений вида
дти V _ (, д , д \ дки
Это уравнение путем преобразования Фурье по х2, ..., хп приводится к
виду A) с параметрами о2 о„. Начальные функции и (О, Хх хп),
д"(°-х> *"> ef-»(O.^,.•■•■*„) преходят при этом в
dt dt
функции
и (У), хх, сг2, .... ап) -—j
Пусть, например, уравнение F) вполне корректно по Петровскому
относительно -з—. Это означает, что корни уравнения
0л |
т-Г
X" = 2pk(sv °2 °лН* G)
ft=0
при любых фиксированных о2( ..., оп в некоторой полуплоскости
Im Sj > p имеют всюду либо неположительную, либо положительную

322 УРАВНЕНИЯ В ПОЛУПРОСТРАНСТВЕ [ГЛ. IV
9
вещественную часть, причем число г корней с неположительной
вещественной частью не зависит от о2 о„. Тогда корректная
задача состоит в задании функций
и(, 0 , х ч y-'aff. О, хг хп)
и (t, и, х2 хп), .... ~
U(V. Хх, Х2 ХП)
удовлетворяющих условиям, аналогичным приведенным в примерах п. 2.
Условие, полной корректности по Петровскому относительно -—
имеет эквивалентную более привычную формулировку: если Re Я- = О,
то все корн» s1 = sI(X1, о2 а„) имеют неположительную вещест-
вещественную часть. Как и в замечании 1, могут быть рассмотрены и уравнения,
корректные по Петровскому, это означает, что при Re К — 0 вещест-
вещественные части корней S] (X,, а2 о„) ограничены фиксированной
постоянной а, и тогда рост искомых функций по t в корректных
задачах ограничивается экспоненциально-степенной функцией вида thea .

КРАТКИЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Хотя предпосылки для формирования теории обобщенных функций
складывались и в недрах классической математики, все же явно вводить и
использовать соответствующие понятия первыми стали физики [1]. Строгое
математическое оформление идея обобщенной функции как функционала
получила впервые в работах С. Л. Соболева [2]. Систематическое построе-
построение теории с многочисленными убедительными примерами было произведено
Л. Шварцем [3]. Весьма быстро после появления книг Шварца идеи обоб-
обобщенных функций распространились на большую часть анализа, где они
прояснили многие старые факты и позволили установить новые общие
закономерности. В серии книг И. М. Гельфанда и других авторов под общим
названием «Обобщенные функции» [4—8] теория обобщенных функций по-
получила дальнейшее развитие, которое кроме определенного вклада в клас-
классические области анализа включило в сферу своего действия новые области —
общую теорию меры в топологических линейных пространствах, теорию пред-
представлений классических групп, теорию случайных процессов.
С развитием теории обобщенных функций стало возможным построение
общей теории уравнений с частными производными, не налагающей каких-
либо условий на тип и порядок уравнения. Хотя роль фундаментальных
решений в классических задачах была известна во всяком случае еще
в прошлом веке, только теория обобщенных функций дала возможность
четко определить само понятие фундаментальной функции (фундаменталь-
(фундаментального решения) дифференциального оператора и поставить вопрос об ее
существовании. Для произвольного линейного дифференциального оператора
с постоянными коэффициентами существование фундаментальной функции
было доказано впервые Б. .Мальгранжем [9]. Класс гипоэллиптических урав-
уравнений был описан впервые Л. Хёрмандером [10]. Первое общее исследование
фундаментальных функций для негипоэллиптических операторов было прове-
проведено В. А. Боровиковым [11]. Метод Радона для построения фундаменталь-
фундаментальных решений эллиптических и гиперболических уравнений систематически
применял Ф. Йон [12]. Общая постановка проблемы об описании корректных
граничных задач в полупространстве и ее решение даны в работах Г. В. Дико-
полова, В. П. Паламодова, Г. Е. Шилова [13—16].
Мы описали в этой книге лишь весьма небольшую часть из всего мно-
многообразия идей, проблем, результатов, относящихся к общей теории уравне-
уравнений с частными производными. Читатели, желающие получить более полную
информацию о современном состоянии этой области, могут обратиться
к обзорному докладу М. И. Вишика и Г. Е. Шилова на IV Всесоюзном
математическом съезде [17]. где приведена и обширная библиография. Отме-
Отметим также две новые содержательные монографии — Л. Хёрмандера [18] и
Ф. Трева [19].
[1] П. А. Дирак. Принципы квантовой механики (перевод с четвертого
английского издания), Физмаггиз, 1960.

324 КРАТКИЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
[2] С. Л. Соболев, Methode nouvelle a resoudre le probleme de Cauchy
pour les equations llnealres hyperbollques normales, Математический сборник,
№ 1 D3) A936), 39—72.
[3] L. Schwartz, Theorle des distributions, I, II, Paris, 1950—1951.
[4] И. М. Г е л ь ф а н д и Г. Е. Ш и л о в, Обобщенные функции и дей-
действия над ними, 2-е изд., Физматгиз. 1959.
[5] И. М. Гельфанд и Г. Е. Шилов, Пространства основных и
обобщенных функций, Физматгиз, 1958.
[6] И. М. Г е л ь ф а н д и Г. Е. Шилов, Некоторые вопросы теории
дифференциальных уравнений, Физматгиз, 1958.
[7] И. М. Г е л ь ф а н д и Н. Я. В и л е н к и н. Некоторые применения
гармонического анализа. Оснащенные гильбертовы пространства, Физматгиз,
1961.
[8] И. М. Г е л ь ф а н д. Н. Я. В и л е н к и н, М. И. Г р а е в, Интеграль-
Интегральная геометрия и связанные с ней вопросы теории представлений, Физмат-
Физматгиз, 1962.
[9] В. Malgrange, Equations aux derlvees partlelles a coefficients
constants, I. Solution elementalre, С R. Acad. Scl., 237, № 25 A953), 1620—1622.
[10] L. Hormander, On the theory of general partial differential
operators, Acta Mathematlca, 94 A955), 161—248. (Русский перевод: Л. Хёр-
м а н д е р. К теории общих дифференциальных операторов в частных про-
производных, ИЛ, 1959.)
[11] В. А. Боровиков, Фундаментальные решения линейных уравне-
уравнений в частных производных с постоянными коэффициентами, Труды Москов~
ского Математического общества, т. 8 A959), 199—258.
[121 Ф. Йон. Плоские волны и сферические средние, ИЛ, 1958.
[13] Г. В. Дикополов и Г. Е. Шилов, О корректных краевых
задачах для уравнений в частных производных в полупространстве, ИАН,
сер. мат., т. 24 A960), 369—380.
[14] В. П. Паламодов, О корректных краевых задачах для уравне-
уравнений в частных производных в полупространстве, ИАН, сер. мат., т. 24
0960), 381—386.
[15] Г. В. Дикополов и Г. Е. Шилов, О корректных краевых
задачах в полупространстве для уравнений в частных производных с правой
частью, Сибирский матем. журнал, т. 2, № 1 (I960). 45—61.
[16] Г. Е. Шилов, О граничных задачах в четверти плоскости для
уравнений в частных производных с постоянными коэффициентами, Сибир-
Сибирский матем. журнал, т. 2, № 1 A961), 144—160.
[17] М. И. Вишик и Г. Е. Шилов, Общая теория уравнений с част-
частными производными и некоторые проблемы теории краевых задач, Труды
IV Всесоюзного математического съезда. Ленинград A961), т. I, Изд-во
АН СССР. Ленинград A963). стр. 55—85.
[18] L. Hormander, Linear differential operators, 1964. (Русский пере-
перевод: Л. Хёрмандер, Линейные дифференциальные операторы, «Мир», 1965.)
[19] F. Treves, Lectures on the theory of partial differential equations,
1963. (Русский перевод: Ф. Трев, Лекции по теории дифференциальных
уравнений в частных производных, «Мир», 1965.)

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абеля интегральное уравнение 123
Авербух В. И. 271
Антианалитические функции 309
Бесселевы функции 152
Бродский М. Л. 72
Гиперболическое уравнение 263
Гипоэллиптический оператор 163
Гипоэллиптическое уравнение 163
Горин Е. А. 122, 197
Граничная задача 34
Грушин В. В. 108, 199
б-образная последовательность 68
б-функция 16, 40
—, ее преобразование Фурье 144, 149
разложение на плоские волны
103
— сдвинутая 19, 40
, ее преобразование Фурье 146
Детерминант Ван-дер-Монда 224
— — обобщенный 223
Диаграмма модулей 180
Дифференцирование обобщенных
функций 23, 43
Задача Дирихле 215
— Коши 215
, ее фундаментальное решение
254
для системы, корректной по
Петровскому 250
для уравнения, корректного по
Петровскому 303
— Радона 103
Интегральное уравнение Абеля 123
Интерполяционный многочлен Ньюто-
Ньютона 219, 227
Каноническая регуляризация 103, 108
Класс Жеврея 164, 166
Кондратов В. Е. 271, 272
Краевая задача 214
корректная 214
Лемма Пэли и Винера 312
Лестница Хёрмандера 172
Локально конечное покрытие 63
Матрица Ван-дер-Монда обобщенная
226
Метод Радона 206
Митягин Б. С. 133
Неопределенный интеграл обобщен-
обобщенной функции 31
порядка Л 123
Носитель 12, 38, 60
Обобщенная производная по С. Л. Со-
Соболеву 44
— функция 16, 39
, аналитическая по параметру 75
, , ее аналитическое про-
продолжение 75
, , ее разложение в ряд
Тейлора 75
в комплексном пространстве 20
в области 42
, дифференцируемая по парамет-
параметру 74
.единица 16
, —, ее преобразование Фурье
143, 149
, ее интеграл по параметру 73
, ее неопределенный интеграл 31
, ее первообразная 31
, ее поворот 149
, ее преобразование Фурье 141,
147
, ее производная по параметру 74
, имеюшая рост не выше сте-
степенного 91

326
алфавитный указатель
Обобщенная функция, непрерывная
по параметру 72
нечетная 94
— — однородная 42
—, ее преобразование Фурье 156
— — от аргумента (о, х) 41
, ее интеграл по о
77, 87
— — постоянная 16
— —, равная нулю в области 59
при х<0 33
, сосредоточенная на множестве
60
— — ■ поверхности 40
, стремящаяся к нулю на беско-
бесконечности 58
сферически симметричная 42
типа меры 122
финитная 60
, ее преобразование Фурье 150
четная 94
6(х) 16, 40
— ■ , ее порядок сингулярности
20, 49
■—, ее преобразование Фурье
144, 149
6(х) 24, 44
--1 ,9
, ее преобразование Фурье
144
х\ 92
, ее преобразование Фурье
146
хк_ 94 .
\х\к 94 .
, ее преобразование Фурье
146
WSgnx 94
х\
) 104
хгт 95
, ее преобразование Фурье 144
х~п 104
xZn 104
, (c+t0)* 146
rx 98
t , ее преобразование Фурье
156
•— , ее разложение на плоские
волны 103
_ _ Ъ(г — а\ 153
Обобщенные функции, их дифферен-
дифференцирование 23, 43
, их свертка 111, 121, 280
, , ее преобразование Фурье
154
, их сложение 23, 43
,их сходимость 66
, их умножение 79
Обычная функция 9, 38
однородная 42
сферически симметричная 42
Объем шара 78
Оператор Р-гипоэллиптический 167
— гипоэллиптический 163
— Лапласа 47
— — итерированный 50
—■ , его фундаментальная функ-
функция 50
— эллиптический 202
однородный 207
Паламодов В. П. 91, 271, 323
Первообразная обобщенной функции
31
Петровский И. Г. 250, 284, 303, 321,
322
Поворот обобщенной функции 149
Показатель гипоэллиптичности 198,
205
— регулярности 253
Поверхность шара 78
Порядок сингулярности 19, 40
c(f) 124
s(f) 123
Правильная дифференцируемость 253
■— сходимость 252
Предел последовательности обобщен-
обобщенных функций 72
Преобразование Фурье обобщенной
функции 141, 147
двойное 143
—"— основной функции 134, 147
Пробная функция 12
Производная обобщенной функции 23
Пространство Ап 157
— С„ 157
— Dm 91
, свертыватели в нем 252
Я 215
305
305
q 313
313

алфавитный указатель
327
Пространство
— Н&° 313
— К 12, 38
, его неметризуемость 13
, его полнота 14
, сходимость в нем 13, 39
.топология в нем 15
— Кп 38
— K(G) 41
— К' 18
— Кп 39
■ , его полнота 69
— 5 90
— 5' 90
, его преобразование Фурье 156
— Z 136
— Z' 139
— Zn 148
— *'„ 148
Равенство обобщенных функций 16.
39
Разделенная разность 228
двойная 228
Разложение дельта-функции на пло-
плоские волны 103
— единицы 63
— функции гк на плоские волны 101
Разрешающая функция 255
Регуляризация 22, 42
— каноническая 103, 108
Регулярная краевая задача 253
.ее фундаментальное реше-
решение 254
— функция 16, 39
Регулярное уравнение 253
, его разрешающая функция 267
, его функция Грина 270, 287
Свертка обобщенных функций 111,
121, 250
—, ее преобразование Фурье 154
, сосредоточенных на полуоси
122
Свертка обычных функций 66
— основной и обобщенной функций
111
Сингулярная обобщенная функция
16, 40
Сложение обобщенных функций 43
Смолянов О. Г. 15
Соболев С. Л. 44, 309
Сходимость обобщенных функций 66
Теорема Зайденберга — Тарского 197
— Уитни 89
Тимошкина С. А. 271
Ультрагиперболическое уравнение 219
Уравнение Р-гипоэллиптическое 167
— волновое 215, 218, 258, 274, 308
—, вполне корректное по Петровскому
321
— гиперболическое 263
— гипоэллиптическое 163
—, корректное по Петровскому 250
— Лапласа 215. 218, 248. 260, 273,
310
— регулярное 253
— теплопроводности 215, 218, 258,
273
обратное 218
— ультрагиперболическое 219
— эллиптическое 263
Финитная обобщенная функция 60
, ее преобразование Фурье
150
— функция 10
Формула Грина 47
— Херглотца — Петровского 284
Фундаментальная функция 37, 49
, ее существование 169
оператора Лапласа 49
итерированного 50
Д+ft2 57
Функции Бесселя 152
Функция Грина 254
— обобщенная 16, 39
— обычная 9, 38
— основная 12, 38
— пробная 12
— регулярная 16, 39
— сингулярная 16, 40
— финитная 10
— фундаментальная 37, 49
Характеристический конус 171
Эллиптический оператор 202
однородный 207

35
О
з
Георгий Евгеньевич Ulu 106
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Второй специальный курс
М., 1965 г.. 328 стр. с нлл.
Редактор Е. А. Горин
Техн. редактор Л. А. Пыжова
Корректор 3. В. Автонеева
Сдано в набор 9/VI 1965 г. Подписано к печа-
печати 24/IX 1965 г. Бумага бОхЭО'/щ. Физ. печ. л. 20,5.
Условн. печ. л. 20,5. Уч.-изд. л. 19,78. Тираж 25 000 экз.
Т-10784. Цена книги 69 коп. Заказ J* 1569.
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № 2
имени Евгении Соколовой
Главполиграфпрома
Государственного комитета
Совета Министров СССР по печати.
Измайловский проспект, 29.
- i
1