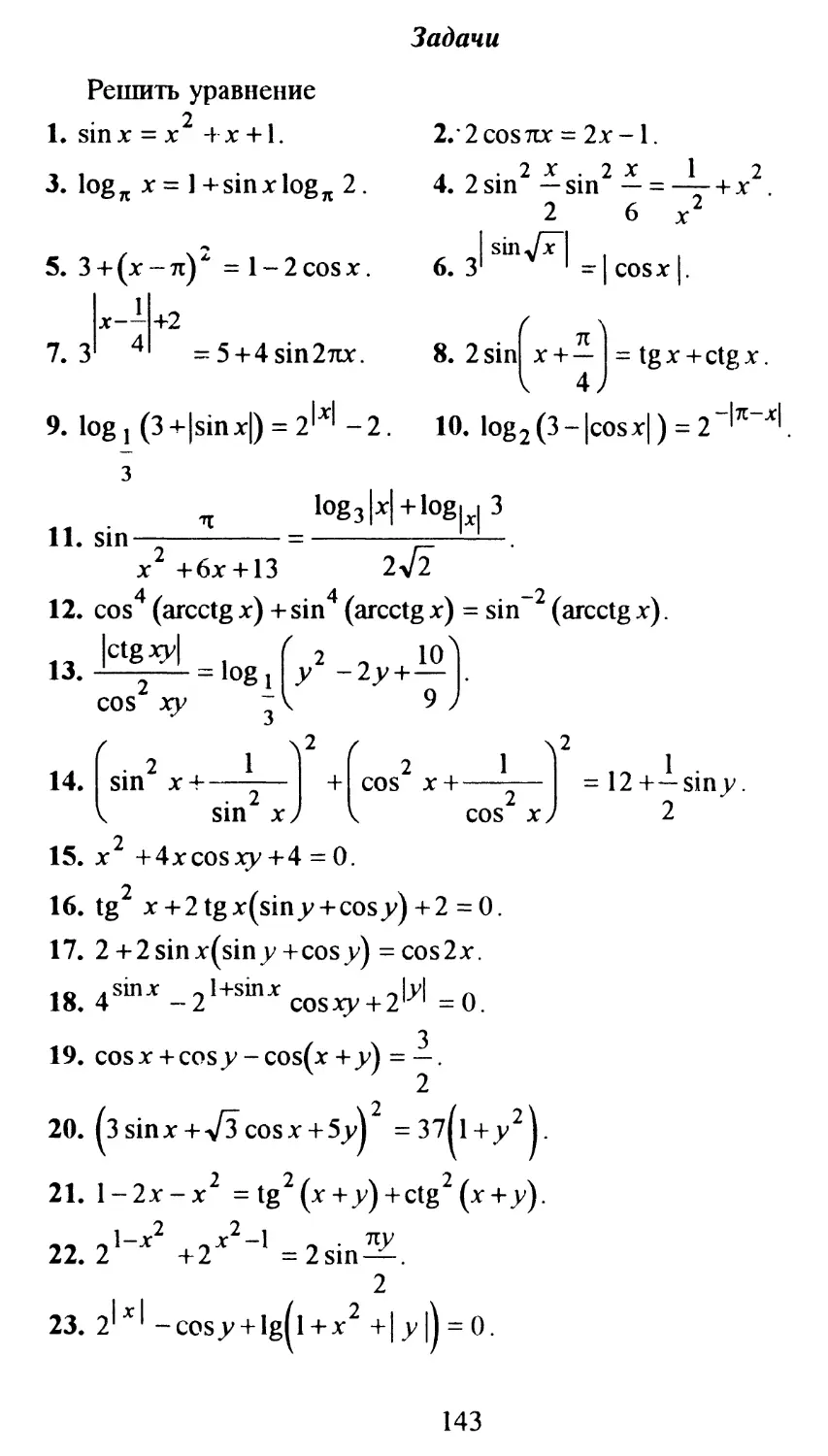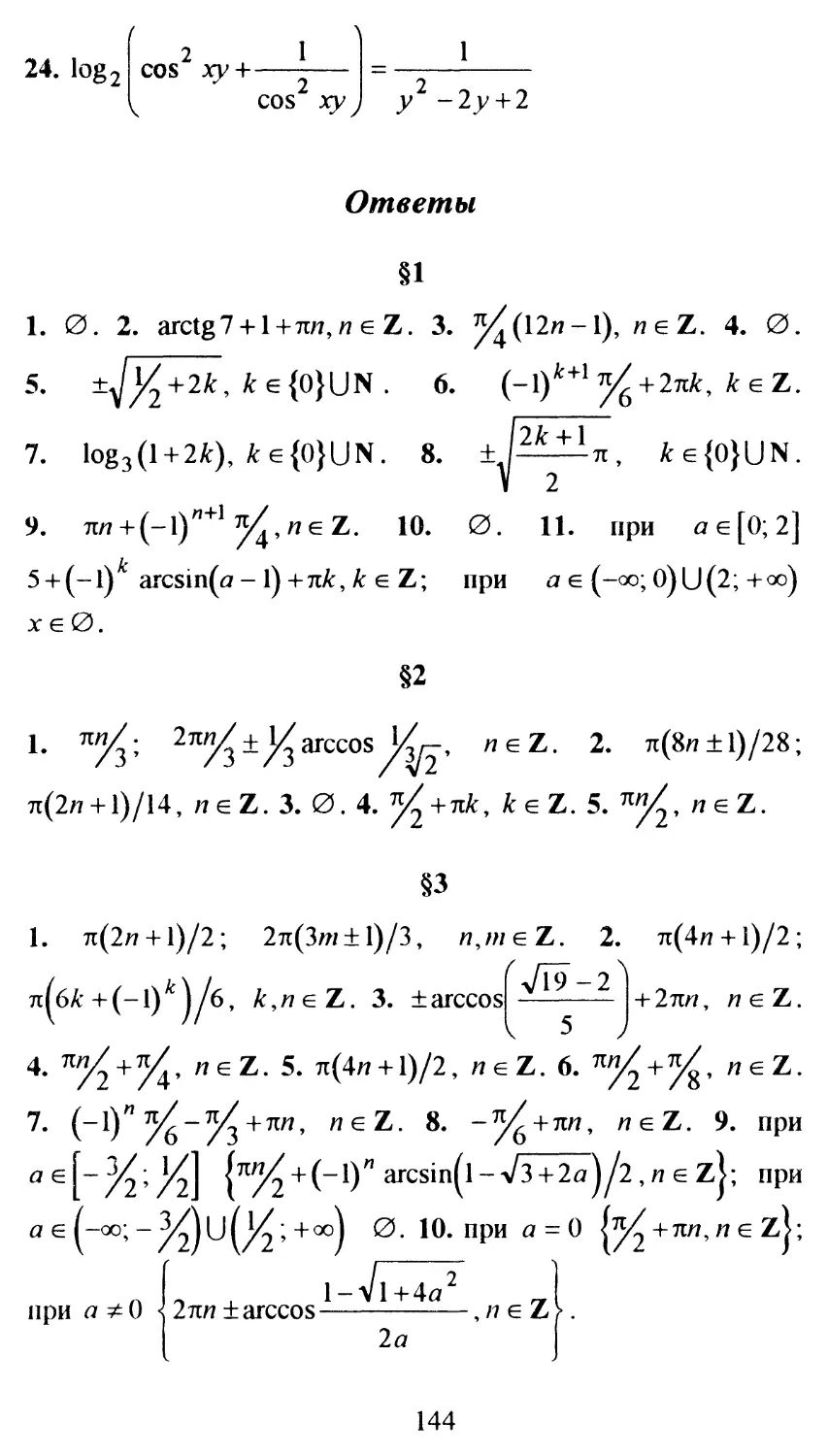Автор: Азаров А.И. Гладун О.М. Федосенко В.С.
Теги: геометрия топология математика тригонометрия механика издательство тривиум серия математика абитуриенту и школьнику
ISBN: 985-409-004-3
Год: 1994
А.И.Азаров, О.М.Гладун, В.С.Федосенко
Тригонометрические
уравнения
Пособие для абитуриентов и школьников
Минск
«Тривиум»
1994
ББК 22.151.0я721
А35
УДК 514.1(075.3)
Рекомендовано к изданию ученым советом механико-
математического факультета Белгосуниверситета
Азаров А.И. и др.
А35 Тригонометрические уравнения: Учеб, пособие
/ А.И.Азаров, О.М.Гладун, В.С.Федосенко/. —
ООО«Тривиум», 1994. — 160 с.
(Математика абитуриенту и школьнику).
ISBN 985-409-004-3
А 5140100000
ББК 22.151.0я721
ISBN 985-409-004-3
© ООО«Тривиум», 1994
Предлагаемое пособие по математике предназначено для
абитуриентов, желающих поступить в ВУЗы и техникумы, а
также школьникам, которые хотят научиться решать триго-
нометрические уравнения.
Основное содержание данной книга составляют методы
решения тригонометрических уравнений. Задачи распо-
ложены по уровню нарастания сложности, и для того, чтобы
решить задачи, расположенные в конце каждого параграфа,
а также в каждом последующем, нужно научиться решать
тригонометрические уравнения, начиная с простейших.
Подбор примеров, разбор методов решения тригоно-
метрических уравнений, достаточная полнота изложения, а
также отсутствие подобной литературы по тригоно-
метрическим уравнениям, позволит заинтересовать этой
книгой не только школьников и абитуриентов, желающих
научиться решать тригонометрические уравнения, но также
учителей математики и тех, кто уже в достаточной мере
умеет решать задачи.
Следует отметить, что данное учебное пособие является
первым из серии, указанной на обложке. Авторы планируют,
что серия «Математика абитуриенту и школьнику» будет
состоять из ряда учебных пособий, освещающих различные
разделы школьной математики.
Авторы
3
СОДЕРЖАНИЕ
§1 . Простейшие тригонометрические уравнения.....5
§2 . Решение тригонометрических уравнений
разложением на множители........................13
§3 . Решение тригонометрических уравнений,
сводящихся к квадратным уравнениям..............18
§4 . Решение однородных уравнений..............25
§5 . Решение уравнений преобразованием суммы
тригонометрических функций в произведение.......31
§6 . Решение уравнений с помощью введения
вспомогательно аргумента........................38
§7 . Решение уравнений преобразованием произведения
тригонометрических функций в сумму..............47
§8 . Решение уравнений с применением формул
понижения степени...............................53
§9 . Решение уравнений с применением формул
тройного аргумента..............................61
§10 . Решение уравнений домножением на некоторую
тригонометрическую функцию........................70
§11 . Уравнения вида P(sin х ±cos х, sin х • cos х) = 0,
где Р(у, z) - многочлен...........................76
§12 . Решение уравнений методом универсальной
подстановки.......................................83
§13 . Решение уравнений с помощью
подстановки у = tgx...............................89
§14 . Решение уравнений методом группировки......99
§15 . Решение тригонометрических уравнений,
содержащих знак модуля или знак корпя.............ПО
§16 . Использование ограниченности функций при
решении тригонометрических уравнений.............121
§17 . Функциональные методы решения тригонометри-
ческих и комбинированных уравнений...............128
Ответы...........................................144
4
§1. Простейшие тригонометрические уравнения
Напомним формулы для решения
метрических уравнений:
простейших тригоно-
sinx = а, х = (-1)” arcsina +лл, п е Z, |^1;
cosx = а, x = ±arccosa +2ли, п е Z, |а| < 1;
tgx = a, х = arctga + л/7, п е Z, a g R;
ctgx = а, х = arcctga +ли, п е Z, а е R.
Особо отметим некоторые частные случаи простейших
тригонометрических уравнений, когда решение может быть
записано без применения общих формул:
sinx = (), х = пку AeZ;
л
sinx=l, х- —+ 2лА, к g Z;
2
л
sinx = -l, х = -— + 2л£, к е Z;
2
л
cosx = 0, х = — + л&, к е Z;
2
cosx=l, х = 2л&, к g Z;
cosx = -l, х = л + 2л&, к е Z;
tgx = 0, х = 7ik, к el.
Каждая из функций arcsina и arccosa определена на
отрезке [-1; 1] и
л л г 1
< arcsine <у,
0<агссо8я<л, а е -1; 1.
Функция arcsina является нечетной, то есть
arcsin(-a) = -arcsina. Функция arccosa не является ни чет-
ной, ни нечетной: arccos(-a) = л-arccosa.
Функции arctga и arcctga определены на всей числовой
5
прямой и
л л
-y<arctgfl<y,
О < arcctg а < л,
a g R,
а е R.
Функция arctgtf является нечетной, то есть
arctg(-a) = -arctgtf Функция arcctgа не является ни четной,
ни нечетной: arcctg {-а) = л - arcctg а.
При решении тригонометрическою уравнения, не яв-
ляющегося простейшим, его сводят тем или иным способом
к одному или нескольким простейшим.
Пример 1. Решить уравнение
tg2x = 3. (1)
Решение. Исходное уравнение равносильно совокупности
tgx = ^
_tgx = -73.
Решением первого уравнения этой совокупности является
семейство х- у/^ + л/?, п g Z, а второго—семейство
х = -%+ли, и e Z. Объединение этих двух множеств и есть
решение уравнения (1). Эти решения можно для краткости
записать в виде х = ±^ч-л/7, п е Z.
Ответ: х = ± +лл, л е Z.
Пример 2. Решить уравнение
л
cosx = —.
3
(2)
Решение. Грубая ошибка, которую допускают при
решении этого уравнения состоит в следующем: абитуриенты
записывают решение х = ±arccos + 2пк, к eZ, однако
они не учитывают, что «1,04 > 1, следовательно, уравне-
ние (2) решений не имеет.
6
Ответ: х е 0.
Пример 3. Решить уравнение
БШЛд/х = -1.
(3)
Решение. Применив формулу решения простейшего
тригонометрического уравнения, получим
Г- л Г- 1
л Jx = - — + 2пк, к eloJx = -~i2k, к eZ. (4)
2 2
Далее многие абитуриенты для нахождения х возводят левую
и правую часть уравнения (4) в квадрат, не учитывая, что
у[х>0, а это влечет за собой -+ >0, I'eZ. Так как
последнему неравенству удовлетворяют только к е N, то
1
-+2к
2
, к е N.
( 1/ Y
Ответ: х = 1-^+2/: I
к е N.
Пример 4. Решить уравнение
sin х = 2 sin 47° sin 44°. (5)
Решение. Уравнение (5) также относится к классу простей-
ших. При этом мы должны исследовать правую часть уравне-
ния для выяснения того, в каких пределах находится ее зна-
чение. Так как функция j> = cosx на интервале ^0;
убывает, и, следовательно,
cos 44° > cos 45° <=> cos 44° >
а функция j>=sinx на интервале [О; возрастает, и,
следовательно,
sin47°> sin45°<=> sin47°>
7
то
2 sin 47° cos44° > *1^/^ ^/2 <=> 2 sin47°cos44°> 1.
Отсюда видно, что уравнение (5) решений не имеет.
Ответ: х е 0.
Пример 5. Решить уравнение
2
ИХ
sin-----=1. (6)
14-Х2
Решение. Имеем
2 2
7UC Л X 1
----— = —4-2л£, к g Z<=> — = — + 2к, к е Z. (7)
14-х2 2 14-х2 2
Ошибка, которую допускают многие абитуриенты, состоит в
том, что они начинают решать уравнение (7), предварительно
х2
не исследовав его. Так как 0<----------— <1, то должны
14-х2
выполняться неравенства 0 < 4- 2 к < 1. Этим неравенствам
удовлетворяет единственное к = 0. Следовательно, уравнение
(7) равносильно уравнению
х2 1
14-х2 2*
решением которого являются х = ±1.
Ответ: х = ±1.
Пример 6. Решить уравнение
f 5 1
sin I ~ ЛС05ЛХ 1 = —. (8)
) 2
Решение. Имеем
5 / \*71 (“О* 3
— лCOS71X-1-1) —4-л£, к е Z<=>costix =-------4- — к, £ g Z.
3 6 10 5
8
Так как | costix | < 1, то из всех к = 0; ±1; ±2;... можно взять
лишь £ = -1, к = 0, к = 1. При этих значениях к
соответственно получим
3
COS ЛХ — - —
5
7
- — <=> лх = 2 ли ± arccos
10
п 6 Z <=>
if 7
<=> х = 2п+— л-arccos—
Л I ю )
и g Z;
costix = — <=> лх = ±arccos----1-2 ли, п е Z <=>
10 10
1 1
<=> х = ± — arccos — 4-2и, и g Z;
л 10
3 11 л
COS7LX = — --= — <=> ЛХ = ± — + 2ЛИ, И G Z <=>
5 10 2 3
1
<=> х = ± — 4-2и, и g Z.
3
Ответ: х = 2и±—(л-arccos%)), /т g Z;
1 1/ 1/
x = ± —arccos4-2и, и g Z; x = ± /j4-2h, и g Z.
Пример 7. Решить уравнение
Решение. Уравнение (9) равносильно совокупности двух
уравнений
rz~ J2 Г- J2
sin2^ Х =-Хг, sin!'' х =-^—. (10)
2 2
Решением первого из уравнений (10) является множество
9
2yf~x =(-l)^+1— + nk, к gZ,
а второго
2^"* =(-l)k^ + 7tk’ к eZ
Объединяя их, получим
I—x Л
2V = ±- + л£; к g Z
4
Так как «J-х >0, то 2^~^ > 1. Значит к E N и
Ответ: x = -[ + I , к e N.
Пример 8. При каких значениях а уравнение
2sinx = а2 -2а (11)
имеет единственное решение на отрезке ^0; 2лj?
Решение. Рассмотрим графики функций у = 2 sin х и
у —а2—2а на отрезке ^0; 2тг| (см. рис. 1). Графиком
функции у-а2-2а является множество прямых,
параллельных оси ОХ, причем
10
у>-1 (т.к. а2-2а = а2-2а + 1-1 = (а-1)2-1 > 1).
Уравнение (11) имеет единственное решение, если графики
пересекаются в единственной точке, то есть при
а2-2а = 2 <=> а = 1±<^5.
Ответ: а = 1 ± ^5.
Пример 9. При всех значениях а решить уравнение
sin^x2 + 2xj- 2а. (12)
Решение. По условию задачи | 2а |< 1, то есть
а Дия этих а имеем
х2 + 2x = (-l)*arcsin2a + rc&, к е Z. (13)
Так как х2+2х = (х + 1)2 -1 >-1, то должно выполняться
неравенство
(-l)*arcsin2a+7i£ >-1, к е Z. (14)
Неравенству (14) удовлетворяют к е N при всех
а е[~//2’ а ПРИ ПОЛУЧИМ
1
arcsin2a > -1 <=>2а > -sinl <=> а > - —sinl,
2
то есть a e^-^sinl;
Уравнение (13) можно записать в виде
(х + 1)2 = 1+ (-!)* arcsin 2а+тг£,
откуда
хк = + + arcsin2a+Tt&;
11
х = хк, к е N, а е
1 1
—; sin 1
2 2
х = xk, к е {О} U N, a g sin 1; —
L 2 2_
х = -1±^1 + (-1)^ arcsin2a+rc&, к 6 N ;
при а е
х = -1±^1+(-1)^ arcsin2a+rc&, к е {0} U N;
при а е (~оо; U °0) х е 0-
Задачи
Решить уравнение
1. cosx = у[з .
3. ctg
7
5. SIIITIX = 1.
2. tg(x-l) = 7.
2 2
4. sin х =—.
2
6. sin^n sinxj = -1.
8. | sinx2 | = 1.
7з.
При всех значениях
1
10. sinx = а + —.
а
а решить уравнение
11. sin(x-5) = а-1.
12
§2. Решение тригонометрических уравнений
разложением на множители
Метод разложения на множители заключается в
следующем: если
то всякое решение уравнения
/М = 0 (1)
является решение совокупности уравнений
/1(х) = 0,/2(х) = 0, ... ,Д(х) = 0. (2)
Обратное утверждение, вообще говоря, неверно: не всякое
решение совокупности уравнений (2) является решением
уравнения (1). Это объясняется тем, что решения отдельных
уравнений (2) могут не входить в область определения
функции /(х).
Поэтому, если при решении тригонометрического урав-
нения методом разложения на множители, функции, вхо-
дящие в уравнение, определены не для всех значений
аргумента, после нахождения решения должна быть сделана
проверка, чтобы исключить лишние корни. Можно посту-
пать другим способом: находить область допустимых значе-
ний исходного уравнения и выбирать только те корни,
которые входят в найденную облать допустимых значений.
Пример 1. Решить уравнение
(2sinx-cosх)( 1 + cosх) = sin2 х. (3)
Решение. Используя основное тригонометрическое тож-
( . 2 2
дество 1 sin x + cos х = 1 I, уравнение представим в виде
(2sinx-cosx)(l + cosx) = 1-cos2 х<=>
<=> (2 sin х - cos х)( 1 + cos х) = (1 - cos х)( 1 + cosх). (4)
13
Грубой ошибкой, которую часто допускают абитуриенты,
является сокращение левой и правой части уравнения (4) на
1 + cosx, ибо при этом теряются корни. При правильном
подходе к решению данного уравнения следует перенести все
слагаемые в правую часть и вынести общий множитель за
скобки, получая равносильное уравнение
(l + cosx)( 2 sin x-cosx- 1 + cosx) = 0 <=>
1 + cosx = О,
2sinx-l = 0
cosx = -l, x = n + к g Z,
1 <-> / л
sinx = — x —(—1) — + nk,k g Z.
2 L 6
Ответ: x = л + 2л&, к g Z; x = (-1)* n/^+nk,k g Z.
Пример 2. Решить уравнение
1
-------1 = Ctg X - COS X.
sinx
(5)
Решение. Преобразуем правую часть уравнения (5) сле-
дующим образом
cosx 1
ctgx-cosx =-------COSX = COS XI---1 .
sinx ksinx J
Затем перенесем все слагаемые в левую часть и получим
(1-cosx) ------1 =0.
ksinx J
(6)
ОДЗ уравнения (6) являются все xg R, за исключением
х = лл, п g Z (sinx^o). На данной ОДЗ уравнение (6) рав-
носильно совокупности двух уравнений
1
l-cosx = 0 и ------1 = 0.
sinx
Первое уравнение имеет решение x = 2rc£,&GZ, а
14
второе x^y^ + litn.n е z(sinx = 1). Однако ОДЗ принад-
лежат лишь х = % + 2лл, hgZ, которые и являются
решением исходного уравнения (5).
Ответ: х= у^ + 2лл, и g Z.
Пример 3. Решить уравнение
f Зл / ч
cos I — + х 1= у/2 sin^x + л j cosx.
(7)
Решение. Используя формулы приведения, преобразуем
уравнение (7) к виду
sinx = -5/2 sinx cosx <=> sinxl 1 + -/2 cosxl = 0 <=>
sinx = 0,
1 «
COSX = -~7=г
y/2
x -nk ,k eZ,
3л
x = ± — + 2л£, к g Z.
4
Ответ: x = л£, £ g Z; x = ± + 2 nk ,keZ.
Пример 4. При всех значениях а решить уравнение
2 хх
sin a sin х = tg a sin — cos—. (8)
2 2
Решение. По условию задачи а ^у^+пк, к g Z (в этих
точках tgfl не существует). Домножим левую и правую часть
уравнения на 2. Затем воспользуемся формулой синуса
двойного угла, перенесем все слагаемые в левую часть и
вынесем общий множитель за скобки. В итоге получим
( 1
sina sinx 2sinx--- =0. (9)
V cosaj
Если sina = 0, то есть а = пк,к е Z, то xeR. Если
а^пк'к то уравнение (9) равносильно совокупности
15
двух уравнений
1
sinx = O, sinx =-------.
2 cos а
(10)
Решением первого уравнения являются x = 7tn,neZ, а
второе уравнение имеет решение, если
1/
/ (2cos<?)
< 1 или
COStf >у/2’ Т0 есть ПРИ - у'з+л/’< я < g Z (см.
рис. 2). (По определению cos а - это абсцисса точки
единичной окружноси, соответствующей дуге а. Отметим на
оружности точки, имеющие абсциссы равные и ~У1-
Тогда точки, абсциссы которых не меньше и не больше
- J/2 заполняют замкнутые дуги и ^^з]-)
Решением второго уравнения (10) при указанных условиях на
а являются
Ответ: при а = пк,к е Z х е. R;
16
при а е^-^ч-пк; nkj U ^4-лАг j, к е Z
1
ч 2 cos я ,
х = тот, и е Z,
х = (-1)™ arcsin
+iun,m е
Z;
при a e + y^ + nkj U (ч//2 + л^; Уз + л^/ e Z
x = л/?, n e Z.
Пример 5. При всех значениях а решить уравнение
. 2
a sin х
--------= tgx.
cosx
(И)
Решение, По условию задачи cosxО, то есть х*% + .
пк 9 к е Z. Воспользовавшись тем, что tg х = s*n /^os х,
получим уравнение
tgxl asinx- II = О,
которое на ОДЗ (х/^+лА;^ е Z) равносильно совокуп-
ности
tgx = O,
asinx = 1.
(12)
Первое уравнение (12) имеет решение х = пк9 к е1.
Рассмотрим второе. При а = 0 х е 0, при а Ф 0 имеем
1/ -г
sinx = yfl. Так как
sinx < 1, то
1/
/а
< 1. Следовательно,
а е I -оо; -1 |J 1; «I. При этих значениях а
х = (-1) т arcsin j/ +л/и, т е Z.
Здесь абитуриенты часто забывают сделать проверку на
принадлежность найденных решений ОДЗ исходного
уравнения (И). При а = ±1 решение второго уравнения (12)
не принадлежат ОДЗ исходного уравнения. Это решение
17
следует исключить.
Ответ: при а е(-оо; -1) U (1;
х = (-1)™ arcsin + ш?/, т g Z,x -пк.к е Z;
при а е -1; 1 x = h£,£gZ.
Задачи
Решить уравнение
1. tg3 3x-2sin3 3x = 0.
cosx
3. 1----— = 0.
l + cos2x
- • 4 , 4
5. sm х = 1 - cos х.
2. ^2 cos2 7x-cos7x = 0.
2
COS X + COSX
4.-----:------= 0.
sinx
При всех а решить уравнение
x
6. asin2x = cosx. 7. tga sinx=sina siny.
§3. Решение тригонометрических уравнений,
сводящихся к квадратным
При решении уравнений указанного типа в основном при-
меняются следующие тригонометрические тождества:
sin2 x + cos2 х = 1;
? 1 71
tg х + 1 =----—, х*~ + Т1п,п g Z;
cos2 х 2
2 1
Ctg X + 1 =----— , X * пп, п G Z .
sin2 х
Пример 1. Решить уравнение
6cos2 x4-5sinx-7 = 0. (1)
Решение. Используя основное тригонометрическое тож-
2 2
дество, осуществим замену cos x=l-sin х, тогда уравне-
ние (1) примет вид
18
2
6sin x-5sinx+l = 0.
Введем подстановку j>=sinx, тогда получим квадратное
уравнение
-5j> + l = 0.
Решая его, находим корни » У 2 = Уз • Затем
осуществляя обратную подстановку sinx = ^2 или sinx = ^,
получаем решение исходного уравнения
Ответ: х = (-1) % + л&, & g Z;
х = (-1)^ arcsin + к g Z.
Пример 2, Решить уравнение
4 4 3 2
sin x + cos х-2 sin2x+— sin 2х = 0. (2)
4
Решение. Так как
4 4/2 2 \2 2 2
sin x+cos x = lsin x+cos xl -2sin x cos x =
= 1-J/^sin2 2x,
то уравнение (2) примет вид
1 2 3 2
1- —sin 2x-2sin2x+—sin 2x = ()<=>
2 4
2
<=>sin 2x-8sin2x + 4 = 0.
Обозначая sin2x через у, получим
у1 -8^ + 4 = 0,
откуда У1 = 4-2 д/з, у^ = 4 + 2 у[з. Так как | у | < 1, то
корень у2 = 4 + 2 у[з следует исключить. Значит,
sin2x = 4-2>/7 <=> 2х = (-1)^ arcsin(4-2</з)к g Z<=>
19
Пример 3. Решить уравнение
1 3
—1+-------------4 = 0. (3)
sin х cos х sinx cosx
Решение. Введем подстановку тогда
/ yoiil Л vUo Л j
уравнение (3) примет вид
у1 -3 v-4 = o,
откуда У1 = 1,у2=-4. Так как /inxcosx = Xin2x и
2/
/sin2x
> 2, то корень = 1 не подходит. Следовательно,
2 1 / ч к+1 л Ttk
= -4 <=> sin2x = - — <=> х = (-1)-— + —, к е Z.
sin2x--------------------------------2 12 2
Ответ: х = (-1)^+^ //12 + Я//2 ’ * е
Пример 4. Решить уравнение
cos( 10 х +12j + 4«y^sin^5 х + б) = 4. (4)
2’
Решение. После применения формулы cos 2а = 1-2 sin а
уравнение (4) примет вид
1-2sin2 (5х4б)+4«/2 sin(5x + 6) = 4.
Обозначая у = sin(5x + 6), получим
2у2 -4^2 v + 3 = 0.
20
то корень У1 =
Следовательно,
а так как у < 1,
не подходит. В итоге имеем
sin(5x + 6) = -у- <=>5х + 6 = (-1) —+7Г&, к е Zo
6 / хк я пк
«х = --+(-1) -+-JeZ.
5 ' 7 20 5
Ответ: х =-^+(-1)^ + Д е Z.
Пример 5. Решить уравнение
2 3
2tgx+3 =------. (5)
cosx
Решение. Применяя формулу tg х+4= у 2 » преоб-
/ cos х
разуем уравнение (5) к виду
2 3
—+1= .
cos х cosx
Обозначая J?=//^osx, получим
ly1 -3>/+1 = 0.
Следовательно, ^=1, Jz2=//2- Так как
Xosx -1’ то
корень уследует исключить. В итоге имеем
cosx = 1 <=> х= 2л£, fceZ.
Ответ: х = 2л£, к е Ъ.
Пример 6. При всех значениях а решить уравнение
4 4
sin х + cos х = а . (6)
4 4 1/2
Решение, Так как sin x + cos х= 1- fysin 2х, то урав-
нение (6) равносильно уравнению
21
sin2 2х = 2(1-а). (7)
Если 2(1-а)<0 или 2(1-а)>1, то уравнение (7) реше-
ний не имеет I 0<sin 2х<11. Следовательно, при
а е ^-оо; ) U(Г, х е 0.
При а = 1
пк
sin2x = 0ox = —, к е Z.
2
При ° е [ /4»1)
sin2x
sin2x =
Л* _______
-—arcsin^ 2(1-а) +—, А: е Z;
2
Ответ: при а е
1; оо
х е 0;
лк
при а = 1 х = —, А: е Z;
(-1) ~г пк
х =--------arcsin^2(1-а) +—, AeZ.
22
Пример 7. Найти все значения а, для которых уравнение
cos2x + asinx = 2а-7 (8)
имеет решение.
Решение. Уравнение (8) равносильно уравнению
2
2sin x-asinx + 2a-8 = О,
которое равносильно системе
у- sinx, -1<у< 1,
2 (9)
2/-aj/ + 2a-8 = 0.
Система (9) имеет решение, если хотя бы один из корней
2
уравнения 2у -ау + 2а-8 = 0 принадлежит интервалу
-1; 1 . Рассмотрим два случая:
2
а) Квадратное уравнение 2у -а>/ + 2а-8 = 0 имеет два
корня, принадлежащих интервалу
Для этого должны выпол-
няться условия (см. рис. 3)
Ds0,/(-l)>0,
|/(1)>0,-1<-^-<1, (10)
где f(y) = 2у2 -ау + 2а-8.
Систему (10) решаем методом интервалов. Так как
D = а2 - 16а +64 = (а - 8)2, то неравенство D > 0 выпол-
няется для всех а е R;
/(-1) = 2 + а + 2а-8>0 <=> а > 2;
/(1) = 2-а+2а-8 > 0<=> а > 6;
23
-l£-b/2a = a/4^~4^4-
Находя пересечение полученных множеств, имеем а е 0.
2
б) Квадратное уравнение 2 у -aj/ + 2^-8 = 0 имеет
только один корень, принад- । А . ।
лежащий отрезку 1;1]. Для 1 \ / /
этого должно выполняться _________1 |_1 1 ।______I—>
условие \ -1 \ / 1 /
то есть (За-б)(а-б) > 0.
Рис. 4
Решая данное неравенство, на-
ходим а е ^2; ej.
Объединяя случаи а) и б), получаем a g ^2; б].
Ответ: a g 2; 6 .
Задачи
Решить уравнение
1. l + cosx + cos2x = 0. 2. cos2x + 3sinx = 2.
3. 2cos2 x + 4cosx = 3sin2 x. 4. 6sin2 x + 2sin2 2x = 5.
4 4 1
5. sin x+cos x = sin2x- —.
2
6. sin4 2x + cos4 2x = sin2x cos2x.
7. cos 2
+ 4 sin
2
8. 2 cos
- • 2
-3sin
5
2
При всех значениях а решить уравнение
2
9. a sin х 4- cos х = 0.
4 4
10. sin x + cos x + sin2x + a = 0.
24
§4. Решение однородных уравнений
Уравнения вида
. п . л-1 . л-2 2
sin ar+aiSin ax-cosaxsin ax-cos ax + ...+
01 , 2 (1)
л-1 л л
+ал_! sinax-cos ax+ancos ax = 0,
где a0, al, ... ,an - действительные числа, называются одно-
родными уравнениями степени п относительно функций
sinax и cosax.
К Квадратичным уравнениям вида (1) приводятся урав-
нения вида
2 2
Л sin ах + В sinax-cosax + С cos ax +
(2)
+Е sin2ax + 77’cos2ax + D = О,
при этом следует применить формулы синуса и косинуса
двойного угла
2 • 2
sin 2 ax = 2 sinax- cosax, cos2ax = cos ax-sin ax,
а также тождество
Г 2 2 1
Z) = DIsin ax + cos ax I.
Общий подход к решению однородных уравнений основан
на том, что корни уравнений sinax = 0 или cosax = 0 не
являются корнями уравнения (1), так как, если, например,
cosax = 0, то из уравнения (1) следует, что и sinax = 0, что
противоречит основному тригонометрическому тождеству
Г 2 2 а
I cos ax + sin ax= 11. Следовательно, левую и правую части
уравнения (1) можно разделить на cos'7 ax и ввести
подстановку у - tgax .
Пример 1. Решить уравнение
sinx-2cosx = 0. (3)
25
Решение. Уравнение (3) является однородным уравнением
первой степени. Разделив обе его части на cosx, получим
равносильное уравнение tgx = 2. Откуда находим семейство
х = arctg2 + 7t£ ,к е Z, представляющее собой решение исход-
ного уравнения (3).
Ответ : х = arctg2 + 7rfc,к е Z.
Пример 2. Решить уравнение
5sin2 x + sinx-cosx-3cos2 х = 2-sin2x. (4)
Решение. Уравнение (4) не является однородным, однако
оно может быть преобразовано к однородному, при этом
применяется тождество cos2 x + sin2 х = 1 и формула
sin2x = 2sinx cosx. В результате получим уравнение
3sin2 x + 3sinx-cosx-5cos2 х = 0,
которое равносильно квадратнму уравнению относительно
tgx
3tg2 x + 3tgx-5 = О,
откуда имеем
-3±Тб9
х = arctg------+7ifc, к е Z.
6
-3±Тб9
Ответ : х = arctg-----+ пк,к е Z.
6
Пример 3. Решить уравнение
sin3 х + 4 cos3 х = 0 (5)
Решение. Уравнение (5) равносильно кубическому урав-
нению
tg3 х = -4,
откуда х = -arctg^4 +тгл, п е Z.
Ответ : х = -arctg^4 +iui,neZ.
26
Пример 4. Решить уравнение
. 4 .3 .7 2
sin x + sin x-cosx + sin x-cos x +
3 4
+ sinxcos x+cos x= 1
Решение. Уравнение (6) не является однородным, однако
его можно преобразовать к однородному, если представить
единицу следующим образом
г Г • 2 2 ^2 -4 Л . 2 2 4
l = lsin x + cos xl =sin x + 2sm x-cos x + cos x.
Тогда уравнение (6) примет вид
sin3 x-cosx-sin2 x cos2 x + sinx-cos3 x = 0,
которое равносильно совокупности трех уравнений
sinx = 0, cosx = 0, tg2 x-tgx+l = 0.
Решая их, найдем х = ,nel.
Ответ : х = 6 Z.
Пример 5. Решить уравнение
sin2 x-sinx-cosx-2cos2 х = а. (7)
Решение. Заменив a = a(cos2 x + sin2 xj и разделив на
cos2 х обе части уравнения, получим равносильное урав-
нение
(l-a)tg2 x-tgx-(2 + a) = 0. (8)
При а = 1 уравнение (8) представляет собой линейное
уравнение относительно tgx, поэтому это значение
параметера является особым случаем и следует отдельно
рассматривать исходное уравнение при а = 1. В этом случае
имеем уравнение
-sinx-cosx-3cos2 х = О,
которое равносильно совокупности двух уравнений
27
cosx = 0, tgx = -3.
Откуда
Если исходить в данном случае (а = 1) из уравнения (8), то
будут потеряны корни х = ^/2 + ли, п е Z.
При а # 1 уравнение (8) является квадратным
относительно tgx, дискриминант которого зависит от а
следующим образом
£> = 1+4(2+о)(1-а) = 9-4о-4а2.
Если D <0, то есть.
то уравнение (8) не имеет корней.
Если D > 0, то есть
-1-J10
;1 и 1;
-1 + J10
-1 ±д/-4а2 -4а+ 9
откуда
х = arctg
-1±7~4а2 -4а + 9
+пк,к е Z.
-1-J10
-1+J10
Ответ: при а е -оо;
к
;+°°
х е 0;
28
-1-J10
при a e
-1+J10
;1 U 1;----—
2
2
x = arctg
4а2 -4а + 9
----г-----+пк,к е Z;
71
при а = 1 х = —+лл?, л е Z, х =-arctg3+7u?, л е Z.
2
Пример 6. При всех значениях а решить уравнение
Решение, Исходное уравнение равносильно уравнению
2 1 3 I 2 I 12 2 1
8а +1 sin х- 4а +1 sinx sin x + cos х +
з
+2 а cos х = 0,
или
2 3 12 1 2 3
4а sin х-14а +ljsinx-cos x + 2acos х = 0. (10)
При а 0 уравнение (10) является однородным, а случай
a = 0 нужно рассмотреть особо.
При a = 0 уравнение (10) принимает вид
2 А
sinxcos х = 0,
откуда х = >п 6 •
При a *0 уравнение (10) равносильно уравнению
4a2 tg3 x-l4a2 +l]tgx + 2a = 0 (11)
Умножим уравнение (11) на 2a и введем обозначение
у = 2 а tgx, тогда получим уравнение
у3 +(4а + 1) >> + 4а2 = 0<=>
29
. 2 л
+у-4а ) = 0.
Откуда
2atgx = 1,
4а2 tg2 x + 2atgx-4a2 =0
1
х = arctg—+itn, п е Z;
2а
-1±>/1 + 16а2
х = arctg-------------+тг/7,л 6 Z.
4а
Ответ: при а = 0 х = , л e Z; при а # 0
1 -1 + -Jl±16a2
х = arctg — + тги,и е Z, х = arctg---------------—+ ли, л е Z.
2а 4а
Задачи
Решить уравнение
1. 3sinx=2cosx. 2. 2sinx + cosx = 0.
2
3. sinxcosx-3cos х = 0.
2 2
4. sin x + sinxcosx-2cos x = 0:
2 2
5. sin x + 3cos x-2sin2x = 0.
2
6. 3 sin x + 2 sin x cos x = 2.
2 2
7. 2cos x-3sinxcosx + 5sin x=3.
o . 6 .4 2 .3 3 5
8. sin x + sin xcos x = sin xcos x+sinxcos X.
2 2 3 4
9. sin xcos x-10sinxcos x + 21cos x = 0.
При всех значениях а решить уравнение
2 2
10. 2cos 6x-9sin 6x + 4sin6xcos6x = a + 5.
30
§5. Решение уравнений преобразованием суммы
тригонометрических функций в произведение
При решении ряда уравнений применяются следующие
тригонометрические формулы:
. а + Р ос-р
sma + smp = 2 sm—у-cos-у-, (1)
а-p а+р
sina-sinp = 2 sin---cos----, (2)
2 2
а+р а-р
cosa + cosp = 2 cos-cos--, (3)
2 2
а-p а+р
cos a - cos P = -2 sin-; sin-
2 ’ 2
Пример 1. Решить уравнение
sin x +sin
= 0
(4)
(5)
Решение. Применив формулу (1), получим равносильное
уравнение
2 sin
л
cos—= 0,
8
ткуда
-^/g+ЛЛ, Л G Z.
X =
Ответ: х = -^ + л/?,л eZ.
Пример 2. Решить уравнение
cos3x + sin(9x + 2) = 0. (6)
Решение. В данном случае, прежде чем применять фор-
31
мулы (1) - (4), следует использовать формулу приведения
cos3x = sinl ЛЛ-Зх I. В итоге получим равносильное урав-
нение
л
л
2sin —4-3x4-! cos —-6x-l| = 0<z>
14
к 4
л
— 4-3x4-l = пк,к g Z;
4
л л
—-6х-1 = —4-ЛЛ,/76 Z
L4 2
Ответ: х =
зЛ е Z;
/ л/ , ля
6~/24+ /
Пример 3. Решить уравнение
1 л пк
— + , к G Zj
3 12 3
1 п Tin
— + , п
6 24 6
6 Z
2 [ 2 ]
81ПЛХ =8ШЛ X +2х .
(7)
Решение. Преобразуем уравнение (7)' к виду
I 2 1
2 cos л х 4-х IsinTtx = 0.
Уравнение sin лх = 0 имеет корни х = п, п e Z,
нение л^х2 +х^ = ^2+лЛ, Ле! имеет решение только при
к е {0}UN, так как
а урав-
2
2
1/_1/
/4 /4
V > V
-/4-/4’
-1±74* + 3
и его корнями являются х =-----------, к g Zo.
2
32
-l±74£ + 3
Ответ: x = g Z; x--------------9 k g Zo.
Пример 4. Решить уравнение
• 2 2 x
sm x-cos x = cos—. (8)
2
Решение. Уравнение (8) равносильно уравнению
х 5х Зх
-cos2x = cos— <=>2cos— cos— = 0,
2 4 4
откуда x = 2^ + 4ti^,/igZ; x = 2^ + 4k^,Z:gZ.
Ответ: x = + , n x= + д g Z.
Пример 5. Решить уравнение
л
sin
2л
х + — - COS I х + —
4j
(9)
л
Решение. Воспользовавшись формулой (2), уравнение (9)
преобразуем к виду
л
2cos х + —
I 4 У
5л
sin - —
I 6 J
। 71
= cos х+— <=>cos х + — =0,
4J
4J
л
откуда х = %+ли,л g Z.
Ответ: х = ^/д+лл,л g Z.
Пример 6. Решить уравнение
l + sin2x = (sin3x-cos
(Ю)
Решение. Возведя правую часть в квадрат и учтя основное
тригонометрическое тождество, получим
l + sin2x = l-sin6x. (11)
Уравнение (11) равносильно уравнению
33
2sin4x cos2x = 0,
откуда
лл л nk
x = —, л g Z; x = — + —, к g Z.
4 4 2
Ответ: x = ,neZ; x= ^4 + , к g Z.
Пример 7. Решить уравнение
cosx-cos3x = 2^/з sin2 х. (12)
Решение. В соответствии с формулой (4) преобразуем
уравнение (12) к виду
2 sinx sin2x = 2^/3 sin2 х.
Последнее равносильно совокупности уравнений
• 2 sm х = 0, yfi <=> cosx = — L 2 х = лл, л g Z; л х = ± —+ 2л&, к g Z. 6
Ответ: х = тт, п е Z;
х = ±у/б + 2л£, к g Z.
Пример 8. Решить уравнение
cos3x + sin2x-sin4x = 0. (13)
Решение. Применив формулу (2), получим
cos3x-2sinx cos3x = 0<=>
cos3x = 0,
l-2sinx = 0.
Следовательно,
х = ^+7Г%, к g Z; х = (-1)Л ^ + лл, л g Z,
при этом видно, что второе множество решений целиком
содержится в первом.
34
Ответ: х = //б + л%, Л е Z.
Пример 9. Решить уравнение
sin(л cos х) = cos( л sin х
(14)
Решение. Запишем исходное уравнение в виде
. / \ . л
sinl л cosxl-sm — -Л8шх =0.
Применив формулу (2), получим
2 sin
л
Л COSX —— + л sinx
2
2
л
лcosx- — + лsinx= 2пк,к е Z;
2
л
л cosx+—— л sinх = л + 2лл,/? е Z
2
sinx 4-cosx =
cosx-sinx =
4fc + l
2
4л + 1
2
к e Z;
n e Z.
(15)
Обратимся к первому уравнению совокупности (15). Так
как -VI<sinx4-cosx<^ то из всех к g Z следует взять
лишь к = 0. Тогда имеем
1
sin X + COS X =— <=> cos
2
л 1
4)242
1 л
<=>х = 2тип±arccos —;=+—, те L.
2^2 4
35
Решим второе уравнение совокупности (15). Аналогично
первому уравнению здесь подходит только п - 0. Поэтому
1
cos
<=>х = 2л^±агссо8
1
2^2
-JgZ.
4
Ответ: х = 2л/п±агссо8 ]/ f-±—, wgZ.
/2^2 4
Пример 10. При всех значениях а решить уравнение
sin(a + x) + sinx = cos—. (16)
Решение. Уравнение (16) равносильно уравнению
2 sin
а а а
cos— = cos— <=> cos—
2 2 2
г
2 sin
k
= 0.
Если cos% = 0, то есть а = п + 2пк,к последнее
уравнение примет вид
0-
2 sin
к
л
х + —+ л£
к 2 )
-1
J
= 0,
следовательно, х g R.
Если cos ^2 * 0» имеем
2 sin
-1 = 0 <=> sin
1
2
л
— + ЛЛ, И G Z.
6
Ответ: при а = л + 2л&, £gZ xgR;
при а*п + 2пк,ке% х =-^2+(-1)Л ^ + л/?, n g Z.
36
Пример 11. При всех значениях а решить уравнение
sin(x + fl) + cos(x + a) = sin(x-a) + cos(x-a). (17)
Решение. Запишем уравнение (17) в виде
(sin( х + а) - sin( х - a)j+(cos( х + а) - cos( х - а)) = 0.
Применив формулы (2) и (4), получим
2 sin a cos х - 2 sin a sin х = 0 <=> 2 sin а (cos х - sin х).
Если sina = 0, то есть а = пк, к g Z, то х & R.
При а * пк, к е Z имеем
л
cosx-sinx = 0<=>tgx = l<=>x = — + ли, и g Z.
4
Ответ: при а = пк, к tZ xgR;
при a^nk.k^Z х = ^/4+ли, п g Z.
Задачи
Решить уравнение
1. со5(Зх-4л) = 5ш(л-х). 2. cos5x + cos7x = cos^ + 6x)
з
3. sinx + sin3x + 4cos х = 0. 4. sinx + 2sin2x = -sin3x.
5. cos9x-cos7x + cos3x-cosx = 0.
6. cos5x-sin5x = sin7x-cos7x.
7. cos2x-sin3x-cos8x = sinl0x-cos5x.
8. sinx + sin2x + sin3x = l + cosx + cos2x.
При всех значениях а решить уравнение
9. sin(x-a) = sinx + sina.
10. sina + sin(x-a) + sin(2x + fl) = sin(x + a) + sin(2x-a).
37
§6. Решение уравнений с помощью введения
вспомогательного аргумента
Рассмотрим уравнение
2 2
asinx+£cosx = c, а л-Ь ^0. (1)
Разделим левую и правую часть уравнения (1)на J а2 л-Ь2 :
а b с
t=== sin х + —==== cos х = . ."т
/2,2 /2,2 /2,2
la л-b <da л-b л-b
Так как
то существует угол ср такой, что
а
coscp = ~f=
+ь2
при этом
а
Ф = arccos
Ja2+b2
b
или ф = arcsin-^ -- -- --
Ja2 л-Ь2
Тогда уравнение (1) примет вид
sinx СО8ф + СО8Х 8Шф =
С
V? +»2
откуда
38
х+ф = (-1) arcsin —р= ~ ~ • — + пк, keZo
/2,2
у а +£
<=> х - -arccos—f=-+ -1 arcsin-7= . +пк,к g Z.
/2.2 v 7 /2.2
ya +b ya +b
Отметим, что к выбору угла ср в задачах с параметрами
а
нужно относиться внимательно: выбор cp = arccos ..
yla2+b2
b
и выбор <p = arcsin -7== будут не всегда равносильны.
Ja2+b2
Пример 1. Решить уравнение
sinx+cosx = 1.
(2)
Решение. Разделим левую и правую часть уравнения на
у/1 . Тогда получим
11 1 71 71 1
-7^ sinX4-—7=COSX = ~7=г <=> COS— sin x + sin— COSX = —Т=Г<=>
72 T2 T2 4 4 y2
sin
7t 1 71 / П
X + “ =—=T<z>X = - — +1-1 — + 7t£, &gZ.
4; 72 4 v 7 4
Ответ можно записать в другом виде. Для этого положив
к = 2п, пе! и к = 2л + 1, п g Z, получим x = 2tu?,/?gZ;
х = ^/2 + 2лл, п g Z.
Ответ: х = 2пп,п g Z; х = ^2 + 2л/?, п g Z.
Пример 2. Решить уравнение
7з cosx-sinx = 2cos3x.
(3)
Решение. Разделим левую часть на 2 и положим
/2 = cos Y'l - sin /'б- Тогда уравнение (3) примет вид
39
cosу^cosx-sinу^ sinx = cos3x<=> cos!
cos3x = 0.
Применив формулу (4) из §5, получим
л
2 sin 2x+— sin x-
12;
л
откуда
л
2х +— = пк9 к
12
л
х- — - лл, п е L.
12
Следовательно,
л Ttk
x = -— + —, к e Z;
24 2
л
x = - — + лл, n e Z.
12
Ответ: *-~%4
Пример 3. Решить уравнение
<5 12
<5 12;
x 2л
= 2 sin — + —
\5 3 )
Зх л
-2 sin — + — .
I 5 6;
(4)
Решение. Разделив обе части
уравнения (4) на 2-^2,
л
перепишем его в виде
1
— cos
2
и 12;
V3
-— sin
2
x 2л
sin — + —
и з;
л
л
1
15
(5)
Зх л
-sin — + —
I 5 6 J
Учитывая, что = СО8Уз»
= sin %, применим к
40
левой части уравнения (5) формулу косинуса суммы двух
углов, а к правой части - формулу разности синусов двух
углов. Тогда уравнение (5) приводится к виду
cos
Л X Л 2
—-------- = -pr sin
5 12; V2
71 (2х 5л^
—COS ----+-
U 5J I 5 12?
или, поскольку
(Л
—
4
X (
X Л
— = cos —
5j t2
л
<4
к виду
cos
X 71^ 2
—+ — =-7=г cos
U 4? V2
cos
2х 5л
—+— <=>
I 5 12 J
5 я
<=>cos
2
1--7=т COS
V2
2х 5л
< 5 +12,
= 0<=>
cos
= 0,
2х 5л
cos — + —
I 5 12J
X л
—+ —
\5 4
Первое уравнение последней совокупности имеет серию
решений х = + 5л£, к е Z, а второе две серии решений
х = п е Z; х = - ^^ + 5лш, т е Z.
Ответ: х = 5^ + 5л£, £gZ;
х = -5л/^2 + 5лл,л е Z; х = -^^ + 5л?л,7л е Z.
Пример 4. Найти все решения уравнения
/— 2
2-^/3 cos2x + sin2x = 4cos Зх, (6)
41
удовлетворяющие неравенству cos ^2 х - J > 0.
Решение. Воспользовавшись тем, что
2
4cos 3x=2 + 2cos6x,
уравнение (6) запишем в виде
A/ycos2x-sin2x = -2 cos6x.
Разделив его на 2 и учитывая, что /2 =cos%>
^2 = sin получим уравнение равносильное уравнению (6)
cos 2х + — 4-cos6x = 0<=>2cos 4хч-— -cos 2х-—1 = 0.
I в) I 127 I 12j
Следовательно, исходное уравнение равносильно совокуп-
ности двух уравнений
cos 4x4-—1 = 0 и cos 2х-—1 = 0.
I 127 I 12>
< 12
Эти уравнения имеют соответственно решения
5л лк 7л лп
х-—4- — ,keZ и х =— 4-—,neZ.
48 4 24 2
Найденные серии решений составляют множество реше-
ний уравнения (6). Из них следует выбрать те, которые удов-
летворяют условию cos ^2 х - у^J > 0.
Пусть х = , Л € Z , тогда
cos ^2x-^^ = cos //24 + 7Г%)-
Условию задачи удовлетворяют следующие подмножества
данной серии исходного уравнения, получающиеся при
к = 4/л и к = 4/Л4-1, т е Z:
42
5л 4лт 5л 5л л(4/л + 1) 17л
х = —ч-------- —+ л/л, х = —+--------=---+ лш, m е Z.
48 4 48 48 4 48
Пусть х = 7^24+™У ’п е тогда
cos = cos ^/z3‘b7rw} =
= COSy^ COSЛ/7 — Sin 51ПЛЯ = (-1)” У^'
Условию задачи удовлетворяют решения, соответствующие
четным значения п = 2£:
х = ^у^+л^,f е Z,
Ответ: х = ^У^+лт,т е Z; х= ^У^^лп.п е Z;
х = 7^24+ л^, f е Z.
Пример 5. При всех значениях а решить уравнение
cosx —sinx = а.
(7)
Решение. Разделив уравнение (7) на и учтя, что
/^=cos%.
^/^ = sin^4 получим уравнение равно-
сильное исходному
л л а л
cos— cosx-sin— sinx = —— <^>cos x+-
4 4 J2 I 4
a
T= (8)
Если -1<
< 1, то есть при a e
нение (8), а значит и уравнение (7), имеет решения
х = - — ±arccos~7=+ 2л&,к е Z;
4 V2
при а е Ь-Л)и(^; ooj уравнение (8) решений не
имеет.
43
Ответ: при а е
-ул ±arccos
+ 2л£,к е Z;
при а е I -оо;
-7г) и (^2; оо)
х е 0.
Пример 6. При всех значениях а решить уравнение
sinx + cos (a + x)+cos (я-х) = 2. (9)
Решение. Воспользовавшись формулой суммы косинусов
двух углов, придем к уравнению типа (1)
sinx + 2cosa cosx = 2. (10)
Разделим левую и правую часть уравнения (10) на
-J1 + 4COS2 а. Условия, определяющие вспомогательный угол,
можно записать так:
1 2 cos а
sin<p = z^===, cos ср = -7=-• ----; -- , (11)
^/1 + 4cos2 a ^/1 + 4 cos2 а
тогда уравнение (10) приводится к виду
cos(x—<р)= . 2 (12)
1/1 + 4 cos а
Уравнение (12) имеет корни лишь в том случае, если
2
1 + 4 cos2 а
2 I 2
< 1о .... т - < 1<=>^1 + 4cos а >2,
д/1 + 4 cos2 а
2 ^3/
откуда cos а > . Следовательно,
”//6 + 7Г^ ~ а - е
(13)
Итак, уравнение (12), а вместе с ним и исходное урав-
нение, имеют решение только при значениях а, удовлетво-
ряющих условию (13).
44
Теперь нужно определить правильно угол ср. Помочь в
выборе выражения для вспомогательного угла ср может сле-
дующее соображение. Поскольку sin ср положителен (это
видно из первой формулы (11)), то сам угол ср можно выб-
рать либо в первой, либо во второй четвертях. Но именно в
этих четвертях лежат значения арккосинуса. Поэтому в
качестве вспомогательного угла можно взять
2 cos а
(р = arccos......
5/1 + 4 cosI 2 а
1
Если бы был взят угол ср = arcsin , =, то угол ср
^1 + 4 cos2 а
лежал бы в первой четверти и поэтому его косинус
принимал бы только положительные значения. Однако
вторая формула (11) показывает, что при cosa<0 косинус
вспомогательного угла отрицателен.
Ответ: при + +
2costf 2
х = arccos ,... =7±arccos . —=- + 2лал л e Z;
5/1 + 4 cos2 a 5/1 + 4 cos2 a
при a e +e Z xe0.
Пример 7. При каких значениях а уравнение
2 2
2sin x + 4sin2xcos2x + 5cos 2х = а (14)
имеет решение?
Решение. Воспользовавшись основным григонометричес-
ким тождеством, а также формулами синуса и косинуса
двойного угла, приведем уравнение (14) к виду
I 2 2 I / \ 2
2 sin 2x + cos 2х +2l2sin2x-cos2xl + 3cos 2x = a<=>
45
/
<=> 2 + 2sin4x + 3
cos4x + l
2
)
<=>4sin4x + 3cos4x = 2л-7.
(15)
Уравнение (15) решаем методом введения вспомога-
тельногог угла. Для чего разделим левую и правую часть
уравнения на ^/16 + 9 = 5 и получим
4 3 2л-5
— sin 4х-ь—cos 4х =--<=> cos (р sin 4х 4- sin (р cos 4х =
5 5 7
= ——-О COS (4х4-(р) = (16)
где coscp = ^, sincp=^.
Уравнение (16), а значит, и уравнение (14) имеют реше-
2л-5
ние, если -1 <----< 1. Следовательно, -1 < а < 6.
7
Ответ: а е -1; 6 .
Задачи
Решить уравнение
1. у[1 sinx4-cosx = у/1 .
2. sin5x = >/3(14-cos5x).
3. sin5x4-cos5x = cosl3x.
5. (sin2x4-cos2x) -5 = cos
4. 2sinx-3cosx = 3.
6. 3sinx-5sin
= 4cosx.
При всех значениях а решить уравнение
2
7. sinx4-cosx = а . 8. sin2x + 3cos2x = a.
9. (я - l)cosx4-(a + l)sinx = 2л.
При каких значениях р уравнение имеет решения?
10. j~p cosx-2sinx= ур2 4-^2-р.
46
§7. Решение уравнений преобразованием
произведения тригонометрических
функций в сумму
При решении ряда уравнений применяются следующие
формулы:
sina • cos Р = — ^sin(a + р) + sin(a - р)^, (1)
cosa • cos р = — ^cos(a + р) + cos(a - р)^, (2)
sina • sin p = —^cos(a - p) - cos(a + p)^. (3)
Пример 1. Решить уравнение
cos3x + sinxsin2x = 0. (4)
Решение. Применив формулу (3), получим
11 11
cos3x+— cosx-— cos3x = 0<=>— cos3x + — cosx = ()<=>
2 2 2 2
<=>cos2xcosx = 0<=>
71 Tlk
x = —+ — ,k g Z;
4 2
л
x = — + 7ГИ, n e Z.
2
Ответ: x = Д e Z ; x= у^ч-лл,n e Z.
Пример 2. Решить уравнение
cos3x cos6x = cos4x cos7x. (5)
Решение. Применив формулу (2), получим
47
—(cos9x + cos3x) = — (cosllx + cos3x) <=>
<=> cos 9x - cos 11 x = 0 <=> 2 sin lOx sin x = 0 о
sinl0x = 0, x = л%п,и e Z;
<=> . A « (0-
|_sinx = 0 |_x = 7t£,£eZ.
Учитывая, что решения первого уравнения (6) являются
решениями второго (л = 10&), получим ответ.
Ответ: х =л , п g Z.
Пример 3. Решить уравнение
tgx + tg2x- tg3x = 0. (7)
Решение. Имеем
sinx sin3x sin2x sinxcos3x-cosx-sin3x sin2x
_ _|_ — _|_
\cosx cos3xy cos2x cosx-cos3x cos2x
sin2x sin2x sin2x(cosx-cos3x-cos2x)
cosxcos3x cos2x cosx-cos2x-cos3x
sinxsin2x-sin3x
= --------------------------= 0.
cosx-cos2x-cos3x
Решая полученное уравнение, найдем
пт пк
х = тт,п е Z; х = — ,т е Z; х = — ,к е Z,
2 3
при этом найденные корни не должны обращять в ноль зна-
менатель.
Множества х = пн,и е Z; х = = 2р, peZ вхо-
дят в множество х =л^ при к = Зп и к = 3р. При
т = 2 р +1 корни х = , Р Е Z обращают в ноль знамена-
48
тель, то есть являются посторонними.
Ответ: х = ,k е Z.
Пример 4. Решить уравнение
sinxsinl х + 60° l-sinl х + 120° 1 = —. (8)
Решение. Применив формулу (3), получим
— sinx cos60°-cos 2х + 180о = —<=>
2 к к J) 4
1 1
о sinх • cos2x+—sinx = — <=>
2 2
1/ X 1 1
<=>— I sin 3x-sinx)+ — sinx = — <=>sin3x= 1 <=>
2 2 2
71 2тш
<=>x = —+-----,n e Z.
6 3
Ответ: x = 7^ + ^71^,wgZ.
Пример 5. Решить уравнение
1
3
tgl x-15° l-ctgl x + 15°
(9)
Решение. По смыслу задачи х* 15° +90° + 180°&Д g Z;
х*-15° +180° и, п g Z. Преобразуем уравнение (9), исполь-
зовав формулу (1),
sin х-15° -cos х + 15°
tgl х-15 l-ctgl х +15
cos х-15° -sin х + 15°
49
И 1
— sin 2х-sin 30 sin2x- — ,
2V=2 = 1
if .1 1 з
— sin 2x4-sin 30 sm2x+-
2k J 2
Откуда sin2x = 1, то есть x = 4-кк, keZ. Среди найден-
ного семейства решений посторонних корней нет.
Ответ: х = ^+тЛ, к е Z
Пример 6. При всех значениях а решить уравнение
Зх х
2 cos—-cos— = а. (10)
2 2
Решение. Уравнение (10) равносильно уравнению ( при-
меняем формулу (2))
2
cos2x4-cosx = а <=> 2cos x-14-cosx-a = 0.
Обозначив j^ = cosx, получим квадратное уравнение
2у2+у-1-а = 0 (11)
с ограничениями на корни -1<у<1. Здесь возможны
несколько случаев.
а) Два корня уравнения принадлежат отрезку [-Г, lj, при
этом исходное уравнение имеет два семейства решений.
Выпишем условия на коэффициенты уравнения (11),
обозначив /(у) = ly1 4-у-1-а = 0. Тогда получим следую-
щую систему неравенств
Z)>0, /(-1)>0, /(1)>0,
< b b
— >-1, — <1.
[ 2а 2а
Решаем полученную систему и определяем а. Каждое из
неравенств имеет соответственно решение а > - %, а < 0,
50
а <2, aeR, oeR Их пересечение дает а е
Тогда
-1-79 + 80 -1 + 79 + 8а
У1 =----:---> У2=-----;—
4
4
откуда
x = ±arccos
-1-79 + 8а
+ 2тг&, к е Z;
x = ±arccos
-1 + ^9 + 8а
4
+ 2пп, п eZ.
4
б) Больший корень принадлежит отрезку 1; 1], а мень-
ший нет. Условия на коэффициенты уравнения (11) выра-
жаются в виде следующей системы неравенств
р(-1)<0,
I /(1)^0.
откуда а>0 и а <2, то есть а е 10; 2 .Тогда
-l + V9 + 8a
и, следовательно,
x = ±arccos
-l + J9 + 8a'
----31--- +2nk,keZ.
в) Меньший корень уравнения (11) принадлежит отрезку
-1; 1 , а больший нет. Тогда
51
./(-i)so,
/(1)<о,
откуда а < 0 и а > 2. Следовательно, а е 0, то есть указан-
ный случай расположения корней не реализуется.
Ответ: при
Задачи
Решить уравнение
1. sin3xsin6x = sin8xsin5x.
2. cos4x cos2x = sin3x-sin5x.
3. sin5x cos3x = sin9x cos7x.
4. sin6x-cos2x = sin5x-cos3x-sin2x.
6. sin
f 71
•sin6x = sin 10x- —
I 4 J
7. cos2x + 2sinx-sin2x = 2cosx.
8. cos3x • tg 5x = sin 7x.
52
9. 4sinx sin
•sin
2л 1
X +--
I 3 J
+ cos3x = 1.
При каких значениях а уравнение имеет решения? Найти
эти решения
( ( пУ
10. 4 sin х+— -cos х—
\ 3) I б)
2 Г~
= а 4-^/3 sin2x-cos2x.
§8. Решение уравнений с применением формул
понижения степени
При решении широкого круга тригонометрических урав-
нений ключевую роль играют формулы понижения степени:
2 l-cos2oc
sin ос =---------------------------, (1)
2
2 l + cos2oc
cos а =---------. (2)
2
Пример 1. Решить уравнение
2 2 2 2
sin x + sin 2x-sin Зх-sin 4x = 0. (3)
Решение. Применив формулу (1), получим
l-cos2x l-cos4x 1-cos6x l-cos8x
4- - - = 0 <=>
2-----------------------------------2-2-2
<=> (cos8x-cos2x) +(cos6x-cos4x) = ()<=>
<=> -2 sin 3 x • sin 5x - 2 sin x • sin 5x = 0 <=>
<=> 2sin5x(sin3x + sinx) = 0 <=> 4sin5x sin2x sinx = 0.
Последнее уравнение равносильно совокупности трех
уравнений
sin5x = 0, sin2x = 0, cosx = 0,
53
которые имеют соответственно следующие множества
решений
лп лк
х =—х = —
5 2
л
х = —+ 71/И, т е Z.
2
Решения из множества x = 71^2,Z:gZ ПРИ £ = 2^eZ
содержаться в множестве х = ,п е Z (л = 5^), а при
к = 2^ + 1 в множестве х = у^+лл^л* е z(/n =
Ответ: х - ,п е Z; х = +тпи, т е Z.
Пример 2. Решить уравнение
sin2 (2 + 3x)+cos2 I ~ + 2х =
= cos2 (2-5x) + sin2
(4)
Решение. Применив формулы (1) и (2), приведем урав-
нение (4) к виду
1- cos(^
2
л
1 + cos - + 4х
l + cos(4
2
2
1 —cos
2
Далее осуществим ряд простых преобразований:
sin 12х - sin4x = cos(4 - 10х) + cos (4+6x) <=>
<=> 2 sin4x • cos8x = 2 cos(4 - 2x) • cos8x о
71
<=>2cos8x cos 4x-— -cos1
I 2
54
<=>-4cos8xsin| x + 2- —
I 4 J
/
sin 3x-2-
Последнее уравнение равносильно
нений
71
cos8x = 0, sin x + 2- — =0,
I 4 J
совокупности трех урав-
71
sin 3x-2-— 1 = 0.
I 4/
Решение первого из них есть х= е второго -
х = у^-2 + тги, и е Z, третьего - х = //^2 + //3 +ПГУз ’т 6
Решением исходного уравнения является объединение
полученных множеств.
Ответ:х=у^^ + л^Д eZ; x = ^-2 + 7tA7,A7eZ;
v _ 71/ 12/ 1717И/ с *7
х-/12 + /з + /3’/иеЛ-
Пример 3. Решить уравнение
4 4
sin x + cos x = sin2x-0,5.
(5)
Решение. Воспользовавшись формулами (1) и (2), полу-
чим равносильное уравнение
/ \2 / \2
l-cos2x l + cos2x
------- + ------------ = sin2x-0,5<=>
I 2 J I 2 J
2 2
<=> l-2cos2x + cos 2x +1 + 2 cos 2 x + cos 2x = 4sin2x-2 <=>
2 2
<=>cos 2x-2sin2x + 2 = 0<=> 1-sin 2x-2sin2x + 2 = ()<=>
2
<=> sin 2x + 2sin2x-3 = 0<=>
sin2x= 1,
sin2x = -3.
Решением первого уравнения является множество
х = у^ + тгА:, к е Z, а второе уравнение решений не имеет.
Ответ: x = ^ + ^JeZ.
55
Пример 4» Решить уравнение
10 10 29 д
sin x + cos х =— cos 2х. (6)
16
Решение. Применив формулы (1) и (2), получим равно-
сильное уравнение
/
l-cos2x
< 2
l + cos2x
29 4
= —cos 2х.
16
2
Возведя слагаемые в пятую степень ( (а±/>) = а5±5а4/> +
3 2 2 3 4 5
+10а b ±10а b +5аЬ ±Ь ) и приведя подобные члены,
имеем
4 2
24cos 2x-10cos 2х-1 = 0о
2 1
cos 2х = —,
2
2 1
cos 2х = -—
12
Первое уравнение дает два множества решений
x = ±^/g+7tfc,к е Z и х = ±Зл/^+л/7,п е Z, а второе реше-
нии не имеет.
Объединив найденные множества решений, получим
ответ.
Ответ: х=/4+^4^> ^eZ.
Пример 5. При всех значениях аи b решить уравнение
2х/ \ 2 х
a cos — -la + 2/>)sin — = acosx-й sinx. (7)
2 ' 2
Решение. Уравнение (7) равносильно уравнению
— (1+cosx)- — (a+2b) (1-cosx) = acosx-b sinx <=>
(cosx + sinx-1) = 0. (8)
56
При b = 0 уравнение (8) выполняется при любых
х е R, при 6 + 0 уравнение (8) равносильно уравнению
cosx + sinx = 1,
которое решаем с помощью введения вспомогательного угла.
Тогда получим
cos
71 1 71 71
х-~ =-7=г<=>х = — ±— + 2л£, к g Z<=>
I 4/ у/2 4 4
<=> х = — + 2пк, х = 2пк, к eZ.
2
Ответ: при а е R, b = 0 х е R;
при а е R, b *0 х=//2 + > х = 2пк, к eZ.
Пример 6. При всех значениях а решить уравнение
- 4 4
sin x + cos х = а. (9)
Решение. Применяя формулы (1) и (2), получим
. \2 / \2
l-cos2x l + cos2x
-------- + ---------
2 ) I 2 )
2
= a<=>cos 2x = 2a-l.
(10)
Если 2a-l<0 или 2a ~ 1 > 1, уравнение (10) решений не
имеет, следовательно, при а е (-оо; %) U (1; +«>) х е 0.
Если a g 1]» то уравнение (10) (а значит, и (9)) имеет
решения. Преобразуем его к виду
l + cos4x
------------ 2а- 1 <=>cos4x - 4а-3 <=>
2
1 , ч пк
<=>х = + — arccosl 4а-3) +—,
4 2
Ответ: при а е (h + 00) х е 0;
57
при а е
x = ±J/^arccos(4a-3)+7t^/2, к е Z.
Пример 7. При всех значениях а решить уравнение
4 4
sin x + cos x + sin2x + a.= 0. (11)
Решение. С помощью формул понижения степени полу-
чим равносильное уравнение
/, \2
l-cos2x
< 2 >
l + cos2x
+ sin2x + tf = 0<=>
<=>sin2 2x-2sin2x-2-2a = 0. (12)
Обозначив t = sin2x, получаем квадратное уравнение
t2-2t-2-2a = 0, (13)
причем с ограничениями на корни (-1 < t < 1). Учитывая, что
вершина параболы = t2 -2t-2-2a находится в точке
t- 1, рассмотрим следующие случаи принадлежности корней
уравнения (13) промежутку 1; 1|
a) D = 3 + 2а = 0, то есть а = - . Тогда корнем является
t - 1. Откуда sin2x= 1, следовательно, х = ^ + ti£, к е Z.
б) Меньший корень квадратного уравнения (13) принад-
лежит ин^рвалу |—1; 1). Это будет выполняться (рассмотри-
те чертеж), если
/(-1М
/(1)<0
1-2я > 0,
-3-2д <0,
откуда а е.
. Следовательно, при а е
имеем
sin2x = \-^3 + 2а,
58
откуда
1 / \п / I-------------\
х = — (-1) arcsin^l-^p + ltf J+—, п g Z.
При других значениях параметра а уравнение (12) реше-
ний не имеет.
Ответ: при ^ = -/4
х = /^(-l)” arcsin(l-73 + 2a) + 7l^2> и g Z;
при а е ;+оо^ хе0.
Пример 8, Найти все целые значения параметра к, при
каждом из которых уравнение
5-4sin2 x-8cos2 — = Зк (14)
2
имеет решения. Найти все эти решения.
Решение. Применяя формулы понижения степени, уравне-
ние (14) запишем в виде
2
<=>4cos x-4cosx-З-Зк = 0. (15)
Рассмотрим квадратное уравнение
4t2 -4Г-3-3* = О. (16)
Его дискриминант равен £) = 16(4 + 3& ). Если, D < 0 то
уравнение (16) не имеет действительных корней. Следова-
тельно, при целых к, для которых 4 + 3&<0, то есть при
к<-\, уравнение (16), а значит, и уравнение (15) решений
не имеют. Целых к, при которых £> = 0, не сущетвует. Сле-
довательно, при целых к>-\ уравнение (16) имеет’два
действительных корня:
59
1 + 74 + ЗЛ l-\]4 + 3k
Zj =----------- и t2 =---------------
2 2
Это значит, что уравнение (15) равносильно совокупности
COSX = /j,
cosx = /2-
(17)
Очевидно, что при любом целом к > 2 справедливы
неравенства > 1 и t2 <-1, а поэтому ни одно из уравнений
совокупности (17) решений не имеет. Остается рассмотреть
случаи к - -1, к =0, к = 1.
Если к = -1, то /j = 1, a t2 =0 и уравнения совокупности
(17) имеют соответственно решения
Л
x = 27U7,wgZ; х = — + пт,т g Z.
2
Следовательно, к = -1 удовлетворяет условию задачи.
Если & = 0, то t{ =%, z2 =“//2’ ПРИ этом пеРвое урав-
нение совокупности (17) решений не имеет, а решениями
второго являются
2л
х = ± — + 2л^, £ g Z.
3
Следовательно, к = 0 также удовлетворяет условию задачи.
Если к = 1, то
cosx =
или
cosx =
Первое из этих уравнений решений не имеет, а второе имеет
решение
x = ±arccos—-
2
+ 2лр, р g Z.
Итак, к = Г также удовлетворяет условию задачи.
Ответ: при к = -1 х = 2лл, п g Z и х = % +лш, т g Z;
60
при к = О
при к = 1
х = ±2^+2лМ е Z;
+ 2тгр, р е Z.
Задачи
Решить уравнение
1. sin4 x + cos4 х = sinx cosx. 2. sin2 x + sin2 2x + sin2 3x = ^2.
3. sin2 x + sin2 2x = cos2 Зх + cos2 4x.
л . A 4 3-cos6x
4. sin x + cos lx =------.
4
о © 41 in in 29
5. sin 2x + cos = 6. sin x + cos x = —.
При всех значениях а решить уравнение
7. sin6+cos6 =а 8. sin4 x-2cos2 x + a2 =0.
9. cos4 x-sin2 xcos2 x-3sin4 x= 2cos2x-2acos4x.
6* 6
10. cos x-sin x = —cos2x.
8
§9. Решение уравнений с применением формул
тройного аргумента
При решении ряда уравнений наряду с другими сущест-
венную роль играют формулы
sin3x = 3sinx-4sin3 х, (1)
cos3x = 4cos3 x-3cosx. (2)
Пример 1. Решить уравнение
cos3x = -2 cosx. (3)
Решение. Применив формулу (2), получим
I 2
cosx 4cos
ГР
х- 1 = 0<=>cosx cos2x + —
7 I 2)
= 0.
Последнее уравнение равносильно совокупности двух урав-
61
нений cosx = 0 и cos2x = -J^. Откуда x = ^+xt,weZ и
х = ±^з + л£Д е Z.
Ответ: х = ^2+тг&,и е Z; х = ±^/з + л&Д е Z.
Пример 2. Решить уравнение
cos4x = cos2 Зх. (4)
Решение. Применив формулы понижения степени, урав-
нение (4) приведем к виду:
2 l + cos6x
2cos 2х-1 =---------.
2
В соответствие с формулой (2), получаем равносильное урав-
нение
4cos2 2х-2 = 4cos3 2x-3cos2x + l <=>
<=>4cos3 2x-4cos2 2x-3cos2x + 3 = 0 <=>
<=> 4 cos2 2x(cos 2x -1) - 3(cos 2x -1) = 0 <=>
<=> (cos2x-1)^4cos2 2x-з) = 0 <=>
<=> (cos 2x -1)^2 cos 2x - V3^2 cos 2x + VJj = 0,
откуда имеем совокупность трех уравнений
д/З д/З
cos2x= 1, cos2x = —, cos2x =----.
2 2
Следовательно , х = ^, we Z; х = ±7У|2“Ь71^» * 6 2L;
x = ±^^2+7t^» е Z.
Объединив два последних множества решений , получим
X = ±2L + ’E* *ez.
12 2
Ответ: х = т ,п 6 Z; х = ±е
62
Пример 3. Решить уравнение
3 х
sin—х + 3 sinx = 3 sin—. (5)
2 2
Решение. Преобразуем уравнение (5) к виду
х л з х х х „ . х
3 sin —-4 sin —+ 6 sin—cos—= 3 sin— <=>
2 2 2 2 2
<=> sin—(-4 sin — + 6 cos—) = 0 <=>
2 2 2
<=>sin4 4cos2 —+ 6cos-“-4 =0,
2k 2 2 )
откуда sin^/2 = 0, cos^ - X ’ cos/^ = “2. Решением перво-
го уравнения является семейство x = 2tu7,/?gZ, второго -
х = ±^^-ь4т1^ Д е Z, а третье решений не имеет.
Ответ: х = 2тш,л е Z; х = ±^^-+-4тг^,к е Z.
Пример 4. Решить уравнение
. (71 Зх^ ~ • (Зтг х^
sin — +— = 2 sin — + — .
k4 2J <4 2J
Решение. Так как
. I Зтг X | . I Зтг X | . I 71 X |
sin — + — =sm л- —- — =sm —,
k 4 2) k 4 2) k4 2/
. | 71 3x| . I 71 3x| . | 3ti 3x| . (71 X|
Sin T + T' = Sin 71- — --— = sin — = Sin3 — -— ,
k4 2 ) k 4 2 ) k 4 2 J k4 2/
то подстановкой у = исходное уравнение сводится к
уравнению
sin3j/ = 2 sin j/.
Применяя формулу (1) и приводя подобные члены, полу-
чим
4sin3 —sinj/ = 0 <=>
<=>sin U 4sin2 y-lj = 0 <=>
63
<=>sinj/
= 0,
откуда имеем совокупность трех уравнений
sinj/ = 0, sin>, = y, sinj> = -
2
2
Следовательно,
j/ = 7t£,£eZ; ^ = (-1)” ^- + 7uiyn е Z;
/ лт+1 л _
•^ = \ 1/ ~ + 7w/,/weZ;
71 Л _ 71 / ,\и+1 71 _
х = — + 2тгЛД е Z; х = —+1-1) —+ 2тш, л е Z;
2 2 ' 7 3
Л / лт Л
х = —+1-1) — + 2тип,т е Z.
2 v 7 3
Объединяя два последних множества, получим
х = (-1)” ^+тот,/7 е Z.
Ответ: х = (-1)л у^ + 7ш,А? е Z, х= у/2 + 2тг&,к е Z.
Пример 5. Решить уравнение
3cosx + 3sinx + sin3x-cos3x = 0. (6)
Решение. Применив формулы (1) и (2) и приведя подоб-
ные члены, получим
3 3
6sinx+6cosx-4sin x-4cos x = 0c=>
(3 3 \
sin x+cos х)=0<=>
<=>6(sinx + cosx)-
-4(sinx+cosx)(sin2 x-sinxcosx + cos2 x) = 0c=>
<=>2(sinx+cosx)(3-2+2sinxcosx) = 0 <=>
<=> 2(sinx + cosx)(l + sin2x) = 0,
откуда sinx + cosx = 0 или sin2x = -l. Решением второго
64
уравнения является множество х =-%+тгАг, Ar g Z, а пер-
вое равносильно уравнению tgx = -l, которое имеет такое
же множество решений.
Ответ: х = , к е Z.
Пример 6. При всех значениях а решить уравнение
sin3x = asinx. (7)
Решение. Уравнение (7) равносильно уравнению
о • л • 3
3 sin х - 4 sm х = a sm х <=>
<=> sinx(4sin2 х-3+а) = 0 <=>
sinx = 0,
-1 -2 cos2x + а = 0.
Первое уравнение совокупности (8) имеет решение
х = тот , п е Z при любых а е R, а второе равносильно урав-
нению
а-\
cos2x =----,
2
которое имеет решение х = ±у arccos^yi+лАг, к е Z при
-1<-—1< 1, то есть при а е Г-1; 31.
2
Ответ: при а е(-оо, -1) U(3; +<ю) х = тот, п е Z;
при ае[-1;3] х = тот, x = ±J^arccos-—-+лАг ,к,п е Z.
Пример 7. При всех значениях а решить уравнение
2 2
a sin Зх = sin х. (9)
Решение. Перепишем уравнение (9) в виде
sin2 x-asin2 Зх = 0 (10)
и рассмотрим три случая.
а) а = 0. Тогда уравнение (10) равносильно уравнению
65
sin2 x = 0, и, следовательно, х = ли, и е Z.
б) а <0. Записав уравнение (10) в виде
2 2
sin x + (-a)sin 3x = 0,
получаем систему
( . 2 А
sin х = 0,
(-a) sin2 Зх = 0
f [x = 7U7,HeZ,
sm х = 0,
' ilk ,
sin3x = 0 х = —, £gZ,
I 3
так как сумма двух неотрицательных слагаемых равна нулю,
если каждое слагаемое равно нулю. Решением системы
является множество х = ли, п е Z.
в) а > 0. Тогда уравнение (10) равносильно уравнению
sinx
у/a sin Зх) = 0 <=>
sinx-Ja sin3x = 0,
sinx+Vtf sin 3x = 0.
(ID
Первое уравнение совокупности (11) равносильно урав-
нению
sinx - 0,
sin х(1 - Зу/а +4yfa sin2 х
Оо
cos2x =
(12)
Решениями первого уравнения совокупности (12) являются
х = ли , и е Z при любых а е R, а второе имеет решение
, 1 1-у^а „
х = ±—arccos--^-+ли,и е Z
2 2Ja
Рассмотрим второе уравнение совокупности (11). Оно
равносильно уравнению
66
sin x = О,
о 1+V д
cos2x =-----—
(13)
Первое уравнение совокупности (13) имеет
х = тот , и е Z при любых а е R , а решениями
решение
второго
являются
при a > 1
х = ±—arccos -
2 I
l±#sl .
1+V^
+тот, n e Z
Объединяя найденные множества решений, получаем
ответ.
Ответ: при а е
x = tot,/? eZ; '
при a e
. 1 / 1 — V л . , „
х = тот, х = ± 44arccos---—+лк, «,neZ;
при ае[1; +оо) х = тот, x = ±^arccos-—=^+л&,
I 1 +Vfl
arccos------—г-
+totj, k,n,meZ.
Пример 8. При всех значениях а решить уравнение
sin x+sin— = a sin—. (14)
2 2
Решение. Уравнение (14) равносильно уравнению
2sin — cos— + 3sin— -4sin3 —-asin— = 0 <=>
2 2 2 2 2
. x
<=> sin—
2
2cos—+ 3-a-4 1-cosI 2 — =0 <=>
I 2 I 2J)
67
sin — = О,
2
4cos2 — + 2cos— -l-a = 0.
2 2
(15)
Первое уравнение совокупности (15) имеет решение
х - 2тот, и е Z при любых а е R. Второе подстановкой
t = cos сводится к уравнению
4/2 + 2t - 1-а = 0, (16)
корни которого должны принадлежать отрезку [-1; 1].
Рассмотрим три случая.
а) Оба корня уравнения (16) принадлежат отрезку [-1; 1].
Для этого необходимо и достаточно выполнение условий
D = 4 +16 (1 + а) > 0, /(1) = 4 + 2 -1 - а > 0,
откуда aEj-fy lj, при этом корни уравнения (16) имеют
вид
-1 + 75 + 4а +
> t —
4 4
Тогда
-l + V5 + 4a
arccos---------------
( 4
*2
+ 4тг&, к е Z;
= ±2 arccos
-l-V5+4a
4
+4ти?, n e Z.
б) Больший корень уравнения (16) принадлежит отрезку
[-1; 1], а меньший нет. Для чего должны выполняться
68
условия
l/ow
то есть, а е (1; 5]. Тогда
х = ±2 arccos[ +| +4л£, к е Z.
I 4 J
в) Меньший корень уравнения (16) принадлежит отрезку
[-1; 1], а больший нет. Так как система
<
/(1)<о
решений не имеет, то указанный случай расположения кор-
ней не реализуется.
Объединяя найденные множества решений, получим
ответ.
Ответ: при а е
при а 1
(“°0’~%) U(5;+°о) х = 2лк,ке%;
1 . п f ~ 1 + >/5+4л
х = 2пк, х = ±2 arccos --------
+ 4ли,
х = ±2 arccos
-1-j5+4a
+4ши, k9m,neZ;
при де(1;5] х = 2пк,
х = ±2 arccos
"-1+75+40"
< 4
+ 4ТП7,
4
к,п eZ.
Задачи
Решить уравнение
1. 3sin— = sinx.
3
3. sin6x + 2 = 2cos4x.
5. cos3x-cos2x = sin3x.
2. cos9x-2cos6x = 2.
л .3 з>/з . _
4. sin3x + sm x =--sin2x.
4
6. sin3x-4sinxcos2x = 0.
69
(зх А
7. cos6x = 2sid— + 2х .
к 2 7
При всех значениях а решить уравнение
2 2 2
8. a sin 3x = sin х, а>0. 9. cos3x = acosx.
§10. Решение уравнений домножением на
некоторую тригонометрическую функцию
Рассмотрим суммы вида
Sj = sina + sin2a + sin3a+...+sinwa,
S2 = cosa + cos2a + cos3a+...+ cosMa.
Данные суммы можно преобразовать в произведения, домно-
жив и разделив их на sin^, тогда получим
. па . (« + 1)а : «а co<J" + 1)a
sin sin — Sin cos---------
g __2 2 g _________________2_______2
1 .a 2 .a
sin— sin—
2 2
Указанный прием может быть использован при решении
некоторых тригонометрических уравнений, однако следует
иметь в виду, что в результате возможно появление посто-
ронних корней.
Пример 1. Решить уравнение
sinx + sin2x + sin3x + sin4x = 0. (1)
Решение. Видно, что множество х = 2л/?,/? eZ является
решением уравнения (1). Поэтому умножение левой и правой
части уравнения на sin^ не приведет к появлению лишних
корней.
Имеем
XX XX
sin—sinx+sin—sin2x+sin—-sin3x+sin—sin4x = 0 <=>
2 2 2 2
70
11 x Зх Зх 5х 5х
— cos---COS +COS----cos—+COS----
2v 2 2 2 2 2
-cos—+cos-----cos— =0 <=>
2 2 2 )
<=> cos — - cos — = 0 <=> sin 2 x • sin — = 0,
2 2 2
откуда sin2x = 0 или sin^^2 = 0. Следовательно, Х = Я%>
ieZ; x = 2™/, nel.
Ответ: x = "%,к eZ; x = 2nn/ ,ne"L.
Пример 2. Решить уравнение
sinx + sin2x + sin3x = cosx + cos2x+cos3x. (2)
Решение. Домножив левую и правую части уравнения (2)
на sin ^2 и применив формулы преобразования произведения
тригонометрических функций в сумму, получим
I ( х Зх , Зх 5х 5х 7хА
— cos—cos—+cos--------cos—+cos------cos— =
2 \ 2 2 2 2 2 2 )
\/( . x , . 3x . 3x . . 5x • 5x , . 7xA
= -sin— + sin-----sin—+sin-----sin—+sin— <=>
/2k 2 2 2 2 2 2)
x lx lx x
<=> cos— - cos— = sm -— sin — <=>
2 2 2 2
<=>2sin—sin2x = 2sin—cos2x <=>,
2 2
<=>2sin-y-(sin2x--cos2x) =0. (3)
Уравнение (3) равносильно совокупности двух уравнений
sin3*^ = 0 и tg2x = l, откуда x = ^7ry/^,ZreZ и
тт/ пп/ _
х=/8+ /2,weZ.
71
Так как корни уравнения sin % = 0 не являются корнями
уравнения (2), то из полученных множеств решений следует
2л^ /
исключить х = 2лЛ UZ. Значит в множестве х= ,
к eZ нужно исключить к = 3£.
Ответ: х = к Ф 31, k,t^L\ х >п Е
Пример 3. Решить уравнение
cosxcos2xcos4xcos8x = —. (4)
16
Решение. Видно, что корни уравнения sinx = 0 не яв-
ляются конями уравнения (4). Домножив левую и правую
части уравнения (4) на sinx и последовательно четыре раза
воспользовавшись формулой синуса двойного угла, получим
sinl6x = sinx <=>2 sin^^cosi^- = 0,
2 2
2ттк / j г» <тт / 2tuti / г*
откуда х= yj^,ZreZ,x = ^7+ yj7,/weZ.
Из полученных множеств решений нужно исключить
2 л /
х = nn,n eZ. Сравнивая выражения и пп, найдем,
что они совпадают при к = 15^ и w = 2^,^eZ, следова-
тельно, из первого множества решений исключаем углы,
соответствующие £ = 15Л^eZ. Поступая аналогично, опре-
деляем, что из второго множества нужно исключить углы,
соответствующие т = 17^ +8,7 е Z.
Ответ: * = 2л%5, MeZ;
х = +2л/%7 , m * 17£ +8, т,£ е Z.
Пример 4. Решить уравнение
cosx cos 2х sin Зх = 0,25 sin 2х. (5)
Решение. Нетрудно проверить, что корни уравнения
sinx = 0 являются корнями уравнения (5). Поэтому умно-
жение уравнение (5) на sinx не приведет к появлению пос-
72
торонних корней.
Имеем
sin х cos х cos 2х sin Зх = sin 2x sin x <=>
<=> sin 2x cos 2x sin3x = sin 2x sin x <=>
<=> ^sin4xsin3x = J^sin2xsinx <=>
<=>sin4xsin 3x-sin2xsinx = 0 <=>
<=> (cos x - cos 7x) - y^ (cos x - cos 3x) = 0,
<=> cos 3x - cos 7x = 0 <=> 2 sin 2x sin5x = 0.
Последнее уравнение равносильно совокупности урав-
нений sin2x = 0 и sin5x = 0, откуда x = k^,^gZ;
х = л^,иеХ. В оба семейства решений входят углы
х = t е Z. Чтобы в ответе они не повторились, их следует
исключить, например, из первого семейства.
Ответ: х = +ък, £ g Z, х = , п g Z.
Пример 5. Решить уравнение
1 х
sinx + sin2x + sin3x = —ctg —. (6)
2 2
Решение. По условию задачи х *2пк,к eZ (в этих точ-
ках неопределен ctg^). Домножим левую и правую части
уравнения (6) на sin^, тогда получим
sin— sinx + sin— sin 2х + sin — sin Зх = — cos— <=>
2 2 2 2 2
<=> cos—-cos— = cos— <=> cos— = 0,
2 2 2 2
откуда x = + n G Z, при этом заметим, что углы
73
х = 2пк, к е Z не принадлежат найденному семейству
решений.
Ответ: х = ^ + 2лл// a?gZ.
Пример 6. Решить уравнение
cos2 xcos2x+cos4x+cos3xcosx+2cos4 х=—-—. (7)
2sin —
2
Решение. По условию задачи х*2пп, nel. Преобразуем
левую часть уравнения:
2 4
cos xcos2x+cos4x+cos3xcosx+2cos х =
= cos2 xcos2x+cos4x+cos3xcosx+cos2 x(l+cos2x) =
= cosx(2 cosxcos2x+cos3x+cosx)+cos4x =
= 2 cos x(cos 3x + cos x) + cos 4x =
2
= 2cosxcos3x + 2cos x+cos4x =
♦
= cos 4x + cos 2x +1 +cos 2x + cos 4x =
1 + 2(cos2x+cos4x) = l+4cos3xcosx.
Теперь исходное уравнение запишется в виде
l+4cos3xcosx = —-—. ' (8)
2sin —
2
Умножив обе части уравнения (8) на sinx, получим
л . о sinx
sin х+4 sin х cos x cos Зх =-,
2sin —
2
sin x + 2 sin 2x cos 3x = cos — <=>
2
<=> sinx +sin5x- sinx = cos— <=>
2
74
откуда lb/^-^ = nt,fceZ; 9^+^ = ^+m,«6Z.
4&+1 4& + 1
Следовательно, Xi =—л, x2 =—-—л, £,weZ
Заметим, что углы x = 2ли, n e Z не принадлежат найден-
ным семествам решений. Однако умножение уравнения на
sinx могло привести к появлению наряду с указанными
посторонних корней вида x = (2U1)MgZ. Сравнивая вы-
ражение (2M)MeZ с выражениями для Xj и х2, найдем,
что они совпадают при к = , ^ = 2p + l,peZ и
9^+4 0 ~ ~
и = —-—, £ = 2р, р е Z соотвественно.
Ответ:х = + * л, к £ = 2р4-1, к,реЪ\
11 2
4л 4-1 9£+4 0 - „
х = —-—л, nt—-—, £ = 2р, р,пе1.
Пример 7. При всех значениях а решить уравнение
. z ч COSfl
sin(x+fl) =------
sinx
(9)
Решение. По условию задачи х пк,к е Z. Домножив
левую и правую части уравнения на sinx, получим
sin(x 4- л) sin х = cos а <=> (cos а - cos(2x 4- а)) = cos а <=>
cosa4-cos(2x4-fl) = 0 <=> 2 cos(x4-a) cosx = 0.
Последнее уравнение равносильно совокупности двух
уравнений
cos(x4-tf) = 0 И cosx = 0,
откуда х = -а +% 4-л/л, т х = 4-лл, п е Z.
75
Из полученных семейств нужно исключить углы
x^Ttk.kt'L. Второе семейство их не содержит, а в первом
им соответствует параметр а = +к(т-к}, kjneZ.
Ответ: при а +тг(/и-к^к^п е Z х = ^+тгп,л eZ;
х = -а+^+тигц при я = +тг(м-А:), A\weZ
х = ^2 и g Z.
Задачи
3. sin х+sin 2х + sin Зх = 0.
Решить уравнение
х 5
1. cosx + cos2x+cos3x = -0,5. 2. 3tg — + ctgx =-.
2 sinx
4. cosx-cos2xcos4x = —
8
5. 4cosx-cos2x-cos3x = cos6x.
6. cosx-cos2x-cos4x-cos8x = -cos!5x.
8
При всех значениях а решить уравнение
7. 2cos(a-x) =
cosx
§11. Уравнения вида P(sinx±cosx,sinxcosx) = 0,
где P(y,Z) - многочлен.
Уравнения вида P(sinx±cosx,sinxcosx) = 0, где P(y.z) -
многочлен, решаются с помощью замен неизвестных
2 1
U “1 /IX
sinx + cosx = и => sinxcosx =-, (1)
2
1-V2
smx-cosx = v => sinxcosx =----. (2)
2
Пример 1. Решить уравнение
sin2x-12(sinx-cosx) + 12 =0. (3)
76
Решение. Сделав замену sinx-cosx = v и учитывая, что
sin2x = 2 sin х cos х, получим
l-v1 2 -l2v + 12=0,
откуда Vj = 1, v2=-13. Тогда уравнение (3) равносильно
совокупности уравнений sinx-cosx = l и sinx - cosх =-13.
Первое уравнение совокупности равносильно уравнению
cos(x » которое, имеет решения х = J^+lnk,
х = п(2к +1),к 6 Z, второе решений не имеет, так как
|sinx-cosx| < д/2 .
Ответ: х = + 2л&, х = тг(2к + 1), к е Z.
Пример 2. Решить уравнение
sin х+— =—^(1-sinxcosx). (4)
I 47 V2
Решение. Перепишем уравнение (4) в виде
л . п 1 z. ч
sinxcos— + cosxsm— = —— (1-sinxcosx)
4 4 y/2
1 1 1 z
——sinx+——cosx = ——(1-sinxcosx) <Z>
V2 y/2 V2
<=> sinx+cosx = 1-sinxcosx.
2 .
. W -1
Введя замену sinx+cosx = w, получим и = 1----------,
2
откуда Mj=l,м2=”3. Уравнение sinx+cosx = -3 решений
не имеет, а корнями уравнения sinx+cosx = 1 (решите мето-
дом вспомогательного угла) являются семейства
х = ^2+2лА:, х = 2пк,кeZ.
Ответ: х = ^+2тт&, х = 2пк, к е Z.
Пример 3. Решить уравнение
2 3
sinx+sin x+cos х=0. (5)
77
Решение. Приведем уравнение (5) к виду
sinx(l+sinx)+cosx|l-sin2 х| = 0<=>
(1+sin x)(sin х+cos х - sin х cos х) = 0. (6)
Уравнение (6) равносильно совокупности уравнений
sinx + l = 0 и sinx+cosx-sinxcosx = 0.
Первое уравнение совокупности имеет решение
х = - J^ + 2'Jik, keZ, а второе решаем с помощью замены
sinx+cosx = w, при этом получим и = 1+V2, и= 1-V2 .
Значение и = 1+^2 не подходит, так как |sinx+cosx| < у/1,
а уравнение sinx+cosx = I-V2 решаем методом введения
вспомогательного угла и найдем
х = (-1)л arcsin
1-V2 п
—=— I + пп , п е Z.
4
2
Ответ: х = -% +2пк, к eZ,
х = (-1)л arcsin *
I V2 )
71 г»
+7U? —, п е Z.
4
2(1-sinx-cosx)
Пример 4. Решить уравнение
/7)
Решение. По условию задачи х ф ,к eZ. Приведем
уравнение (7) к виду
2 . 2
cos x+sin X
+-------------= 0
sinx cosx
2
и введем замену и = sinx +cosx, тогда 2(1-w)+—-= 0,
и -1
1-V5 1+^5
откуда и = 0, и =---, и ------.
2 2
Решением уравнения sinx+cosx = 0 является семейство
78
х = - +7w, п е Z (уравнение однородное первого порядка),
71 , у/1 - V10 л „
семейство х = — ± arccos------+ 2тгс, £ е Z является
4 4
1-V5 z
решением уравнения sinx + cosx =---- (уравнение решаем
2
методом введения вспомогательного угла), а уравнение
1 + V5
sinx + cosx =----решении не имеет.
2
Заметим, что среди найденных решений углы х = 71%»
к е Z отсутствуют.
Ответ: х =-^+тот, л е Z;
х = —± arccos———^ + 27t^, ^eZ.
4 4
Пример 5. Решить уравнение
•5 5 1 1 /q\
sin x-cos х-------------. (8)
cosx sinx
Решение. По условию задачи х ,к е Z. Приведем
уравнение (8) к виду
/. 2 \ . з Л . 2 \ з sinx-cosx
11 —cos xlsin х —11-sin xlcos x =-----------о
\ \ ! cosxsinx
I . 3 3 \ . 2 2/. X
<=>|sin x-cos xl-sin xcos x(sinx-cosX)-
sinx-cosx _ q
sinxcosx
<=> (sin x-cos x)^l +sin xcos x-sin2 xcos2 x-
1 (9)
-----5---- =0.
sinxcosx?
Уравнение (9) на ОДЗ равносильно совокупности уравнений
79
sinx-cosx = 0,
sinxcosx + sin xcos x-sin xcos x-l = 0.
Первое уравнение совокупности имеет решение х = ^+л&,
к g Z, а второе преобразуем к виду
sin х cos х(1 + sin х cos х) - (1 + sin х cos х)(1 - sin х cos х +
2 2 \
+ sin xcos х) = 0<=>
<=> (1 + sin xcos х)(1-sinx cosx) 2 =0,
откуда sin x cos x = -1 или sin x cos x = 1. Оба уравнения
решений не имеют.
Ответ: х = ^+л&, к е Z.
Пример 6. При всех значениях b решить уравнение
sin2x-2>/2/>(sinx-cosx)+l-4/> =0. (10)
Решение. Приведем уравнение (10) к виду
2sinxcosx-2>/2/>(sinx-cosx) +1-46 = 0
и введем замену sinx-cosx = v. Тогда получим
V2 +2y/lbv+4b-2 = o, (11)
при этом корни уравнения (11) должны принадлежать
отрезку [-V2; д/г].
Находя корни уравнения (11), получим vx=-y/2,
v2 = -2>/2 b +V2. Первый корень Vj 6^-V2;V2j при любых
ZjgR, a v26^-V2;V2j при b е [0; 1]. Решая уравнение
sinx-cosx =-V2 при beR, a sinx-cosx =-2л/2/> + V2 при
b е [0; 1], найдем
х = - —+2л&, keZ, beR\
4
80
х = ±arccos(2Z> -1) - — + 2nk, к e Z, b e [0; 1].
4
Ответ: при g (-оо; 0) U(l; +<ю) х = -^ + 2л&, к g Z;
при b g [0; 1] x = -^ + 2л/г, к g Z,
x = ±arccos(2/?-l)-^+27t£, £gZ.
Пример 7. При всех значениях а решить уравнение
1
asinx + tgx + l =--. (12)
cosx
Решение, По условию задачи х * + 2пк, к g Z.
Умножив левую и правую часть уравнения (12) на cosx,
приведем его к виду
asinxcosx + sinx+cosx= 1.
Обозначив sinx + cosx = w, получим
и2 -1
а—-----+ w- 1 = 0 <=>аи2 +2w-2-а - 0, (13)
2
при этом корни уравнения (13) должны принадлежать
отрезку f~V2;V2j.
При я = 0 имеем sinx+cosx = l, откуда х = 2пк, keZ
(корень х = к g Z не подходит по условию задачи).
При а = -1, уравнение (13) примет вид (w-l)2=0,
откуда sinx+cosx = 1, х = 2пк, к eZ,
При уравнение (13) имеет корни =1,
и2=———Первый корень их е [-V2; V2j при всех
а е R(a Ф 0, а + -1). Тогда
х = 2пк , к eZ при а е (-оо; - 1)U(-1; 0)U(0; +оо).
Второй корень и2 принадлежит отрезку J-V2; V2j при
а е (-оо; -2(5/2 - 1hU|2(V2 - 11 +00I Решая уравнение
81
a g
при a g
угла, найдем
-2 ~ a
sinx+cosx =------- методом введения вспомогательного
о +2
± л - arccos —— + 2Tin,
< flv2 >
a +2
+ 2ли, k,n g Z.
ал/2
n g Z при
x = %± л-arccos
Ответ: при a g
x = Ink,к e Z;
Задачи.
Решить уравнение
1. 1 + tgx = 2\[1 sinx.
3. 3 + 2sin2x = tgx+ctgx.
2. sin——+cos—— = V2 sinvx.
2 2
л cos2x
4. cosx + sinx =----.
l-sin2x
1
. 1 1 л . f 5л)
5. +—-------------- - 4sm x+— .
sinx . f Зя) V 4 )
sm x-----------
I 4 )
, 3 3 . .
6. sin x-cos X = 1 + sinxcosx.
(3л
7. sinx + sin — + x = 1-O,5sin2x.
I 2 J
8. (1 - sin 2x)(cosx-sinx) = 1-2 sin2 x.
9. 2sin3x---— = 2cos3x+—-—.
sinx cosx
10. sec x+cosec x
При всех значениях а решить уравнение
<1’3 3 . I It I Л
11. sm x+cos x+tfsin x + — =0.
I 4 J
82
§12. Решение уравнений методом
универсальной подстановки
Тригонометрическое уравнение вида
/?(sin£x,cosnx,tgwx,ctg/x) = 0, (1)
где R - рациональная функция, k,n,m,l eZ, с помощью
тригонометрических формул двойного и тройного аргумента,
а также формул сложения можно свести к рациональному
уравнению относительно аргументов sinx, cosx, tgx, ctgx,
после чего уравнение (1) может быть сведено к
рациональному уравнению относительно t = tg^ с помощью
формул универсальной тригонометрической подстановки
п х 2 х
2tg— 1-tg -
2 2
sin X =----, COS X =---------— ,
1+tg2 * 1+tg2 *
2 2 (2)
2tg- 1-tg2-
2 2
fp X =------- CtP X =--------—
Следует отметить, что применение формул (2) может
приводить к сужению ОДЗ исходного уравнения, поскольку
tgне определен в точках х = л+2тг£, к е Z, поэтому в
таких случаях нужно проверять, являются ли углы
х = п +2л£, к е Z корнями исходного уравнения.
Пример 1. Решить уравнение
sinx + tg— = 0
2
(3)
Решение. По условию задачи х^л + 2л&, keZ. Приме-
нив формулы (2) и сделав замену tg % = /, получим
83
It
T+r = 0,
1+r2
откуда t = 0 и, следовательно, x = 2nk, к eZ.
Ответ: x = 2nk, к eZ.
Пример 2. Решить уравнение
15ctg~ + 130sinx = -у tgy. (4)
Решение, По условию задачи х *пк,к eZ. Используем
формулы (2) и заменим tg^ = t, тогда получим
15+260/= 53, 75+75? + 1300? = 53? +53?,
t 1+? 5
53/4 -1322?-75 = 0, t2 =25, ?=-^3>
откуда t = ±5. Следовательно, х = ±2arctg5 + 27U7, п е Z.
Заметим, что в данном случае применение подстановки
tg^ = t не сужает ОДЗ исходного уравнения.
Ответ: х = zt2 arctg 5+ 2 ли, hgZ.
Пример 3. Решить уравнение
2 ( Л | 2
2sin х— =2sin x-tgx. (5)
I 47
Решение. Применив формулы понижения степени, полу-
чим
I 71 |
1-cos 2х— = l-cos2x- tgx <=>cos2x + tgx-sin2x = 0.
k 2J
у
1 — tg x 2 tg x
Используем формулы cos 2 x =----—, sin 2 x =-----— и
1 + tg x l + tgx
введем замену Z = tgx, при этом ОДЗ исходного уравнения
не сужается. Тогда имеем
2
-^4-+/—= 0<=>? -t2 -/ + 1 = 0»
1+? 1+?
84
»z2(/-i)-(z-i) = o<=>p -ij(/-i) = o.
Значит, t = ±1 и поэтому tgx = ±l. Следовательно,
x = ±я^+пк, к 6 Z, при этом все эти значения принадлежат
ОДЗ исходного уравнения.
Ответ: х = +пк, к eZ.
Пример 4. Решить уравнение
sinx
1 + cosx
= 2 - ctg х.
(6)
Решение. По условию задачи х #лк, к g Z. Применив
sin х х
формулы (2) и формулу ------------= tg— и обозначив
1+cosx 2
Z = tg , не сужая при этом ОДЗ уравнения (6), получим
I-/2 2 г Г
t = t -4/+1 = 0, t} =2+V3,r2 =2-V3.
It
Следовательно, tg = 2 ± Vi, откуда x = 2 arctg^2 ± у[з j +
+2л&, к g Z.
Ответ: x =
2arctg^2±V3j
+2пк,к g Z.
Пример 5. Решить уравнение
5sinx-5tgx , ч Л
--------— +4(1 - cos х) = 0. (7)
sin х + tg х
Решение. Так как tgx не определен при x = 1y^+Tik,
к 6 Z, а
sinx + tgx = 0
при х = пк, £ g Z, то углы х = к g Z не входят в ОДЗ
уравнения (7).
Используем формулы (2) и обозначим t = tg^, при этом
по условию задачи t * 0; ± 1, тогда получим
85
5
2t It '
<1 + /2 1-Г2,
2t 2t
----2 +-----2
\+t2 1-r
f l-r2>
+ 4 1-------
I 1+f J
= 0.
(8)
Так как ±1, то уравнение (8) равносильно урав-
нению
? Qfl ~
-ЪГ +-^—- = 0<=>-5-5г +8 = 0,
1+/1 2
откуда t = +^^ • Следовательно, х = ±2 arctg + Ink,
keZ.
Ответ: x = ±2arctg+ 2nk, кeZ.
Пример 6. Решить уравнение
l-cos2x + tgx , . „
----------— = 1 + sin 2x (9)
1-tgx
Решение. По условию задачи х^^+л£, к g Z и
х*//4+л^’ Обозначим Z = tgx, тогда на ОДЗ
уравнения (9) имеем
. _ 2t 1-t2
sm2x =------ cos2x =----—,
1+r2 1+/2
1 1+/ t 2t
---------r +---= 1+ r-<=>
1-/ 1 + /-1-f---1 + /2
о (1 +t)2 (1 - 2/) = 0,
откуда tg x = -1 или tg x = . Следовательно, x = - + nk,
к e Z, x = arctg J^+tch, A:gZ.
Ответ: х = -^+л&, к g Z, x = arctg^+ли, &gZ.
86
Пример 7. Решить уравнение
tg-tgx + 1
—------------?------= 2Тз.
п . X 2 X <х t *
2tg —cos - tg —+ctgx
(Ю)
Решение, На ОДЗ исходное уравнение можно переписать
в виде
-----2--^------«
2 tg — cos2 — tg —tgx + Г
2 2 2
о-------—-tgx = 2-j3. (11)
2tg-
2
2tg^
Так как tgx =----—то уравнение(П) примет вид
—-----Igx = 2-Тз.
tgx
откуда tgх = -Л ±2, а х = arctg^-V3 ±2^ +лА; А е Z. Дан-
ные углы принадлежат ОДЗ исходного уравнения и, следо-
вательно, являются его корнями.
Ответ: х = arctg(-V3 ±2) +itk, А е Z.
Пример 8. Решить уравнение
(cosx-sinx) 2tg х +—!— + 2 = 0.
\ C0SX7
(12)
Решение, По условию задачи х*^+ли, /?cZ. Приме-
нив формулы (2) и обозначив t = tg , получим
87
откуда
и ‘2 = -у/[у Значит, tg^ = ±^/^,
а
х = ±^ + 2л&, к 6 Z
Заметим, корни уравнения cos^2 = 0 не являются кор-
нями уравнения (12), и, следовательно, потери корней не
произошло.
Ответ: х = ±^ + 2л&, к е Z.
Задачи.
Решить уравнение
2. 3 sin 4х = (cos 2х -1) tg х.
3. 1 + cosx + tgy = 0. 4. tg2x+ctgx = 4sin2x.
5. (l+cosx)^-2+sinx = 2cosx.
59 x x
6. — cosx+6 sinx tg у = 4 tgxctgy.
7. cos2 x-2cosx = 4sinx-sin2x.
8. sin2x - 2VI ~ 2x^ = 3.
9. cosx+cos— = 2----— .
2 i+ts2|
10. 1 - cos(n+x) += 0.
88
§13. Решение уравнений с помощью
подстановки у = tgx.
При решении ряда тригонометрических уравнений после
преобразовании можно применять методы, изложенные в §4
и §11, и их обобщения, а также использовать тригоно-
метрические формулы
I I |tgxl 71
sinx = • , х * —+ли, п е Z; (1)
Icos xl = —1 -, х — + ип, и 6 Z. (2)
2
Пример 1. Решить уравнение
1 + tgX ( • \2 /эх
-------= (sin X+COS X) . (3)
1-tgx
Решение. По условию задачи х +тш, п g Z и
+тш, и g Z. Запишем уравнение (3) в виде
1 + tgx _ sin2 x + 2sinxcosx+cos2 x
2 2
1-tgx sin x+cos x
Разделив числитель и знаменатель правой части данного
уравнения на cos х (область допустимых значении не
сужается) и обозначив tgx = y, получим
1+Д2 (1+J2)2
1-у у2+1
откуда у = -1, у = 0; tgх = -1, tgx = 0. Следовательно,
X =-^+7С&, X = 71&, £ G Z.
Ответ: x = -^+7tfc, x = Ttk,keZ.
89
Пример 2. Решить уравнение
tgxsinx-cosx =-----. (4)
2 cosx
Решение. Так как по условию задачи х ^y+iin.n eZ,
то разделив уравнение (4) на cosx и воспользовавшись
формулой tg2x + l = У 2 .получим
/ cos х
2 1/2 \ 2
tg X - 1 = — I tg X -F 11 <=> tg X = 3 .
2 \ )
Следовательно, tgx = ±V3 , откуда x = ±1У^лк, к e Z.
Ответ: x = +nk, keZ.
Пример 3. Решить уравнение
l+cos2x 1 + sin2 x
Решение. Запишем уравнение (5) в виде
.2 2 .2 2
sm x + cos х sin x+cos x 16 z,4
;—2——~=- • (6)
2 cos x + sin x 2 sin x + sin x 11
Так как углы x = ^+k/i,/?gZ не являются корнями
уравнения (5), то разделим в левой части уравнения (6) чис-
литель и знаменатель каждой дроби на cos2 х и обозначим
2
у = tg х, тогда получим
у + 1 t у + 1 _ 16
у+2 2у + 1 1Г
Откуда j/ = 7±4>/3. Следовательно, tg"! х = (2±Тз)2 или
tgx = ±^2 ±7з). Значит, х = ±arctg^2 ±7з) +лк, к е Z.
Ответ: х = ±arctg^2 ±) +л£, к g Z.
90
Пример 4. Решить уравнение
l±«!!2i+2l±JS£-3t0. (7)
l-sin2x 1-tgx
Решение. Запишем уравнение (7) в виде
2 2
COS X 4-2 sinx cosx -t-sin x 14-tgx
2 2 + ~
cos x-2sinxcosx-i-sin x 1-tgx
Так как по условию задачи хз^/^+пк, & е Z, х^у^+пк,
к то уравнение (7) равносильно уравнению
(1-tgx)* 1 2 1-tgx
1 4- tg X 2
Обозначив у =--------, получим у + 2 у - 3 = 0, откуда
1-tgx
-1±^=1,1±й±=_3. (8)
1-tgx 1-tgx
Решив совокупность (8), найдем tgx = 0 или tgx = 2. Следо-
вательно, х = пк, keZ,\ х = arctg2 +пк, к eL
Ответ: х = пк, х = arctg 2 4- пк, к е%.
Пример 5. Решить уравнение
(1-tgx)(14-sin2x) = 14-tgx, (9)
Решение. Представим уравнение (9) в виде
2 2
Sin X4-COS x4-2sinxcosx
1+tgX.
. 2 , 2
Sin X4-COS X
Так как по условию задачи х keZ, то данное
уравнение равносильно уравнению
91
( 1
I l + tg2x
-(1 + tgx) = 0 <=>
откуда tg x = -1, tg x = 0. Следовательно, x = - % + Ttk,
x = пк, keZ. Эти углы входят в ОДЗ исходного уравнения и
поэтому являются его корнями.
Ответ: х = ~^+лА,х = лА, к е Z.
Пример 6. Решить уравнение
• О 3,
sm3xcosx = — tgx.
(Ю)
Решение. Представим уравнение (11) в виде
^3sin3x-4sin3 xjcosx =-|tgx. (11)
Так как по условию задачи х^^+лА:, к е Z, то разделим
2
левую и правую части уравнения (11) на cos х. Тогда по-
лучим
/ 2 \ 3 1
(3-4sm х)tgx = — tgx----— <=>
’ ' 2 cos2 х
|tgx(tg2
1 — tg2 X
l+tg2x,
tgx =
о » 2
3 —tg x 1
1 + tg2 X
92
-3tgx4 -8tg2 x + 3
2(1 + tg2 xl
= 0,
2 1 / 2
откуда tgx = 0, tg x = , tg x = -3. Последнее уравнение
решений не имеет, а из первых двух найдем х-пк,
х = , keZ.
Ответ: х = пк, х = ±^+л&, keZ.
Пример 7. Решить уравнение:
tg(x2 - x)ctg6 = l.
(12)
Решение. Запишем уравнение (12) в виде
tg(x2 -x) = tg6.
Исходя из условия равенства тангенсов, получим
2
х -х = 6+пк, к е%.
Так как х2 -х = х2 то
уравнение имеет решение только при тех значениях к, идя
которых левая часть больше либо равна а именно, при
к = -1,0,1,Решив уравнение при этих значениях к,
найдем х =-------, к е |-1}UZ,O.
1±725+4лЛ ( П|1
Ответ: х =-------, к е |-1|UZO,
Пример 8. Решить уравнение
tg (л tg х) = ctg (л ctg х). (13)
Решение. Перепишем уравнение (13) в виде
tg(n tg х) = tg^ - л ctg xj.
93
Пользуясь условием равенства тангенсов, получим
л tgх = £л 4-^/- л ctgx <=>
tgx =
|7+Г]
i 2)
-ctgx, к e Z.
(14)
Решая уравнение (14), следует иметь в виду, что те корни,
при которых значения тангенса представляются в виде
2w + l 1 / г,\
----- или в виде — [т е Z), если они вообще существуют,
2----т
не могут являться корнями уравнения (13), поскольку при
. 2т +1
tgx =------- или ctgx = w теряют смысл левая или правая
2
часть данного уравнения. Такие корни уравнения (14) долж-
ны быть исключены.
Уравнение (14) на ОДЗ можно записать в виде
tg2 x-^Zr ч—Jtgx + l = 0.
(15)
2£ + l±J(2£+l)2 -16
Решая уравнение (15), найдем tgx =--------------------,
4
при этом должно выполняться условие (2к 4-1) 2 > 16 <=>
<=> | 2к +11 > 4. Следовательно, к * 0, ± 1, - 2. Кроме того
- . 4 2т 4-1
должны быть исключены те к, при которых tg х =----- или
2
tgx = ~,weZ. Для того чтобы тангенс имел указанные
т
значения необходимо, чтобы (2&4-1)2-16 было квадратом
целого числа, то есть чтобы (2к 4-1)2 - 16 = и2. Решая
уравнение в целых числах, найдем к =2 и к: - -3. В первом
. 5±3
случае tgx =-----, причем следует исключить только углы,
4
соответствующие tgx = ^, a tgx = 2 приводит к решению
94
х = arctg 2 + ли, n e Z. Во втором случае tgx =-. Здесь
4
исключаем tg x = - , a tg x = -2 дает решение
x = - arctg 2 + ли, и e Z.
Ответ: x = ±arctg2+ли,
2Jt+l±J(2A: + l)2 -16
x = arctg----------------+ли, к = 3, ±4, ±5,..., и e Z.
4
Пример 9. При каких значениях а уравнение
2 2 2
a sin х+а -2 z_,4
-----7- =------------• (16)
1-tg х cos2x
имеет решения? Найти эти решения.
Решение. Запишем уравнение (16) в виде
• 2 /2 Л( . 2 , 2 \
2 sin х + a -2||sin x+cos х
а _____\Д/
2 ~ 2 2
1-tg х cos x-sin х
Так как по условию задачи х^^+лДг, х ^//д+л^2» & е Z,
то разделив числитель и знаменатель правой части на cos2 х
и обозначив tg2 х = t, получим
Поскольку t * 1, то последнее уравнение равносильно урав-
нению
корни которого должны удовлетворять условиям t > 0 и t ф 1.
2
Уравнение (17) имеет решение Г = —------------ при
а2 -1
ае(-оо; -7з)U(--ч/з;-1)U(1; Л)и(>/3; +оо). Тогда при
этих же значениях а
95
.2 2 _i_ I 2
tg x = —,tgx = ±/—,
a -1 V a -1
I 2
откуда x = ± arctg —-+7C&, к e Z.
Na 2-l
Ответ: при ae(-oo; - VI) U VI, -1) U (1; VI)u(VI; +oo)
x = ±arctg^—^—+nk, keZ; при a e [-1; l]u|-VI, VI}
e0.
Пример 10. При всех значениях а решить уравнение
sinx tgx + cosx = —(18)
cosx
Решение. По условию задачи ОДЗ не содержит углов
х = + л&, к eZ. Разделив левую и правую части уравнения
на cosx, получим на ОДЗ равносильное уравнение
tg2 х + 1 = —<=>tg2 х +1 = aftg2 х +1) <=>
cos х ' '
(a-l)tg2 x= I—a. (19)
При a = l уравнению (19) удовлетворяют все x из ОДЗ
исходного уравнения. При получим tg2 х = -1, то есть
уравнение (19) решений не имеет.
Ответ: при а = 1 х е Rе ^}» ПРИ а * 1 х е 0.
Пример 11. При всех значениях а решить уравнение
sinatg2 x-2cosatgx + l = 0. (20)
Решение. По условию задачи х +лк, к е Z.
Если sina =0, уравнение (20) равносильно совокупности
tgx = —, а = 2ли, п е Z; tgx = - —, а = п + 2пп,п е Z. (21)
2 2
96
Следовательно, при а = 2пп, и е Z х = arctg^ 4-лли, т е Z,
при а = л4-2ли, wgZ х = - arctg +тип, meZ.
Если sin л* 0, то уравнение (20) представляет собой
квадратное уравнение относительно tgx. Оно имеет реше-
ние, если
2 2
£) = 4cos а-4 sin a > 0 <=> sin а 4-sin а - 1 < 0 <=>
(22)
Первое неравенство системы (22) выполняется всегда, а
—1 + л/5
правое с учетом, что sina^O при а е (2ли; arcsin----------+
+2ли) U л - arcsin —+ 2 ли; л 4- 2ли U (л 4- 2ли; 2л(и 4-1)),
\ 2 7
п е Z. Решая уравнение (20), найдем
. cos л ±v cos л-sinл
tgx =-------------------
sin а
откуда х = arctg
cos а ±у!cos2 а - sinZ
sin а
4 ли/, m е Z.
Ответ: при
а = 2ли, п е Z х
при
а = л 4- 2 ли, п е Z х =
4-ли/, и/е Z;
при
а е 2ли; arcsin-------
2
4-2 ЛИ и
U| л-arcsin—4-2ли,л4-2ли |и(л4-2ли, 2л(и4-1)), и е Z
. I 2
cosa±Vcos a-sina
sinx
4-лли, m е Z.
х = arctg
Пример 12. Сколько различных решений на отрезке
[-л; 0] имеет уравнение
97
tg2x = atgx
(23)
в зависимости от значений л, л *0?
Решение. Воспользовавшись формулой тангенса двойного
угла, уравнение (23) запишем в виде
2 6 ’
1-tg X
которое равносильно совокупности двух уравнений
7
tgx = 0, --= (24)
1-tg2 АГ
Первое уравнение совокупности (24) имеет на отрезке
[-л; 0] два корня х--п и х = 0 для любого а. Второе уравне-
ние запишем в виде
tg2 х = --- (л*0).
а
Это уравнение на отрезке [-л; 0] имеет корни отличные от
-л и 0 при условии -—- > 0, то есть при а е (-оо; 0) U
а
U(2;oo). При а = 2 получим tg х = 0, корни этого уравне-
ния совпадают с -л и 0.
Ответ: два корня при ае(0;2]; четыре корня при
а е (-оо; 0) U (2; оо).
Решить уравнение
1 _ 1 _ cos2x
tgx 1 + tgx
3. tgx+ctgx = 2.
5. sin2x + tgx = 2.
7. ——• (tg x — ctg x) = tg2 x
Задачи
2. 3ctgx-3tgx+4sin2x = 0.
4. tg (3x -1) ctg (x + 2) = 1.
2 3
6. 2tg x + 3 = ———.
cosx
+ ctg2 x-2.
98
8. sin2x(tg2 х+з) = 4(cos2x-l).
9. 3 cos2 x - sin2 x - sin 2x = 0.
При всех значениях а решить уравнение
10. tg2 х - 2 tg a tg x +1 = 0.
§14. Решение уравнений методом группировки
В этом параграфе рассматриваются тригонометрические
уравнения, решение которых построено на алгебраических
(возведение в степень, извлечение корня, выделение полного
квадрата, домножение на некоторый множитель, исполь-
зование формул сокращенного умножения, приведение
подобных слагаемых, разложение на множители и т.п.) и
тригонометрических (использование тригонометрических
формул) преобразованиях, позволяющих свести исходное
уравнение к простейшим.
Пример 1. Решить уравнение
32 cos6 x-cos6x = 1. (1)
2
Решение. Представив cos6x = 2cos Зх-1, уравнение (1)
можно преобразовать к виду
16 cos6 х - cos2 Зх = 0 <=>
<=>^4 cos3 x-cos3xj^4cos3 x+cos3x) =0<=>
4 cos3 x-cos3x = 0,
4 cos3 x+cos3x = 0.
Применяя формулу косинуса тройного угла, уравнения (2)
сводим к виду 3cosx = 0 и
cosx = 0 и
COSX = ±yIJ/^^.
з
8cos x-3cosx = 0, откуда
Следовательно, х = + лп,
99
Ответ:
nel, x = ±arccos
+ 2Tin, neZ.
x = +7Ш» и e Z;
x = ± arccos
2V2
+ 2ли,и e Z.
Пример 2» Решить уравнение
cos— = cos2 x. (3)
3
Решение. Запишем уравнение (3) в виде
1 - 2 sin2 — = 1 - sin2 х <=>
3
гт . 2х у гт . 2х . j „
2 sm----sm х v 2 sin— + sm х = 0.
з Д з )
Применяя формулы синуса двойного и тройного угла,
получим
~ ГТ . X X о • х ... з X Л
2у/2 sin —cos—3sin— +4sin — = О,
3 3 3 3 (4)
2V2 sin—cos— + 3sin--4sin3 — = 0.
L 3 3 3 3
Первое уравнение совокупности (4) равносильно
совокупности двух уравнений
sin—= 0 и 4| 1-cos2 — |+2>/2 cos—-3 = 0,
3 I 37 3
1±л/з
откуда х = Зл£, £ е Z; х = ±3arccos-—+ 6лА\ к е Z.
2V2
Второе уравнение совокупности (4) также равносильно
совокупности двух уравнений
sin—= 0 и -4| 1-cos2 — 1 + 2V2 cos—+3 = 0,
3 I 3J 3
100
откуда х = Зпк, keZ; х = ±3 arccos - +6л£, к е Z.
2V2
Объединяя найденные решения, получим ответ.
1 4-VI
Ответ: х = Зпк, к eZ, х = ±3 arccos +6пк, к cZ\
2V2
-1±7з
х = ±3arccos---т^—4-блА:, keZ.
2V2
Пример 3. Решить уравнение
sinx4-2cosx = cos2x-sin2x. (5)
Решение. Перенеся все слагаемые в левую часть, восполь-
зовавшись формулами двойного угла, отняв и добавив
единицу, уравнение (5) запишем в виде
(sinx + l)+2cosx(sinx + l)+2^sin2 x-lj = 0 о
<=> (sin х +1)(1 + 2 cos х + 2 sin х - 2) = 0 <=>
<=> (sin x 4-1)(2(sin x 4- cos x) -1) = 0 <=>
<=> (sinx 4-1) 2VI sin| x 4-— | -1 I = 0,
Л V 47 J
откуда sin x = -1 или sin(x 4- j = J/. Следовательно,
x = - 4-2 ля, «eZ; x = -n/A 4-(-M arcsin—\=+nk, к gZ.
/l /4 2VI
Ответ: x = 4-2лл, n g Z;
x = -n/A 4-(-l)* arcsin—\=+nk, к eZ.
/4 2VI
Пример 4. Решить уравнение
• 2 3
Sinx 4-SIH X 4-COS X=0. (6)
Решение. Исходное уравнение равносильно уравнению
sinx(14-sinx)4-cosx|l-sin2 xj = 0,
101
которое равносильно совокупности двух уравнений
l + sinx = 0 и sinx + cosx-sinxcosx = 0. (7)
Первое уравнение совокупности (7) имеет решение
х = + 2ли, п е Z, а второе равносильно уравнению
(sinx+cosx)2 -2(sinx+cosx)-l = 0,
откуда
sinx+cosx = 1 + ^2 или sinx+cosx = 1-V2.
Первое уравнение решений не имеет, так как
-V2 < sinx+cosx < V2 , а второе равносильно уравнению
. ( 7^ 1-V2
sin х+— =——
к 4> V2
~ 1 —V2 , , _
Следовательно, х = — +(-1) arcsin—-=- +пк, к eZ.
4 V2
Ответ: х = -+2тот, п е Z;
х = - —+(-lV arcsin—^-+лк, keZ.
4 V2
Пример 5. Решить уравнение
4sinx + 2cosx = 2 + 3tgx. (8)
Решение. По условию задачи neZ. Домно-
жим левую и правую части уравнения (8) на cosx, при этом
ОДЗ уравнения расширяется, так что в конце нужна провер-
ка на наличие посторонних корней. Тогда имеем
2
4sinxcosx+2cos x-2cosx-3sinx = 0 <=>
<=> 2cosx(2sinx-1) +^2cos2 x-3sinx) = 0 <=>
<=> 2cosx(2sinx-1) +^2 -3sinx-2sin2 x) = 0 <=>
<=> 2 cos x(2 sin x -1) - (2 sin x -1) (sin x + 2) = 0 <=>
102
<=> (2sinx-1)(2 cosx-sinx-2) = 0.
Последнее уравнение равносильно совокупности двух уравне-
ний
2sinx = 1 и 2cosx-sinx = 2. (9)
Первое уравнение совокупности (9) простейшее:
х = , к eZ, а второе решаем методом введения
вспомогательного угла:
cos
следовательно, х = 2пп, х = -2arccos у г + 2пп,п е Z.
Среди найденных множеств решений посторонних корней
нет.
Ответ: х
к /
у +пк, £ е Z; х = 2пп, п е Z;
/о
х = -2arccos уг- + 2лл, п е Z.
Пример 6. Решить уравнение
2
sin3x 4-sinх + 2cosх = sin2х+2cos x. (10)
Решение, Уравнение (10) преобразуем:
2
2sin2хcosx4-2cosx = 2sinxcosx4-2cos x <=>
<=> 2cosx(sin2x4-l) = 2cosx(sinx+cosx) <=>
<=> 2 cos x^sin2 x 4- 2 sin x cos x 4- cos2 xj = 2 cos x(cos x 4- sin x) <=>
<=> 2 cos x(cos x 4- sin x)(cos x 4- sin x -1) = 0.
Последнее
уравнений
уравнение равносильно совокупности трех
cosx = 0, tgx = -l, sin(x4-^j = У/-- Откуда
х = 4- пк, к е. Z; х = -^4-л/:, к е Z; х = “//4 +
+(-1)^ к е Z. Последнее множество решений можно
103
разбить на два множества ( к = 2///, к = 2т +1 ) : х - 1тип,
m^L\ х - +2тои т е Z.
Объединяя найденные множества, получим ответ.
Ответ: х = 4-лАг; х = - ^ 4- ; х = 2пк, кeZ.
Пример 7. Решить уравнение
6 tg х + 5 ctg Зх = tg2x. (11)
Решение. Уравнение (11) преобразуем:
5 (tg х + ctg Зх) = tg 2х - tg х,
51 sinxsinЗх4-cosxcos3x । _ sin2xcosx-cos2xsinx
I cosx sin 3x J cos 2x cosx
5 cos(3x-x) = sin(2x-x) 5COs2 2x - sin 3x sinx =
cosx sin 3x cosx cos 2x cosx sin 3x cos 2x
5cos 2x-3sin x4-4sin x _
cosx sin 3x cos 2x
Откуда имеем систему
2 2 / 2 \
5cos 2x-sin x|3-4sin x) = 0,.
cos x Ф 0, sin Зх 0, cos 2x Ф 0.
Решим уравнение
5cos2 2x-sin2 x^3-4sin2 xj =0. (12)
Понизив степень уравнения (12), получим
5 cos2 2х - * - cos (з - 2(1 - cos 2х)) = 0 <=>
<=> 12 cos2 2x-cos2x-1 = 0,
откуда cos 2х = или cos 2х = - , то есть
104
х = arccos^+л£, £gZ или х = ±^ arccos (-XW-
к е Z. Нетрудно убедится, что среди найденных решений нет
углов х = ^+л/?, х = х =//44’Л//2’ ^gZ (корней
уравнений cosx = 0, sin3x = 0, cos2x = 0).
Ответ: х = arccos^+л£, ZtgZ;
х = ±У^ arccos^-+ iik, keZ.
Пример 8. Решить уравнение
з з 3
sm xcos3x+cos xsin3x =—. (13)
8
Решение. Исходное уравнение равносильно уравнению
sinxcos3xsin2 х + cosxsinЗхcos2 х= - — <=>
8
<=> sin х cos Зх(1 - cos 2х) + cos х sin Зх(1+cos 2х) - - <=>
<=> (sin х cos Зх + cos х sin Зх) +
+cos 2x(sin Зх cosx- cos 3x sinx) = -—<=>
3 3 3
<=> sin4x + cos2xsin2x = -—<=> —sin4x = —.
4 2 4
Значит, sin4x = - откуда x = (~l)n+1 //24^Я/4’ 77 g Z.
Ответ: x = (-1V+1 +™/, neZ.
Пример 9. Решить уравнение
tgxctg3x = 4. (14)
Решение. Уравнение (14) преобразуем:
, > ~ о sinхcosЗх-cosxsinЗх _
tgxctg3x-l = 3, --------------------= 3,
cosx sin Зх
- sin 2x - 3cosx sinЗх
cosx sin Зх
- sin x cos x| 2 + 9 - 12 sin2 x j
------------'---------------'- = 0.
cosx sin 3x
105
Так как условию задачи х ^^4-лА', к е Z; х к е Z,
2
то smx^O, cosx^O. Значит, 11 - 12sin х = 0 <=>6cos2x +
+5 = 0<=> cos2x = - 5// <=> х = arccos^- + лА\ к е Z.
Ответ: х = arccos^-4-лА\ A'gZ.
Пример 10. Решить уравнение
7
2tg3x-3tg2x = tg 2xtg3x. (15)
Решение. ОДЗ уравнения (15) определяется условиями:
х^^+я^, х^^4л^, AeZ. Уравнение (15) равно-
сильно уравнению
2(tg Зх - tg 2х) = tg 2х(1 + tg Зх tg 2х) (16)
Найдем значения х, при которых 14-tg3xtg2x = 0. Последнее
Л Л гх
уравнение можно записать в виде ------------------= 0. Это
cos2xcos3x
уравнение решений не имеет, так как если cosx = 0, то и
cos3x = 0. Следовательно, уравнение (16) можно разделить
на l + tg3xtg2x, получая при этом равносильное уравнение
_ tg3x-tg2x
2 —---------= tg2x,
14-tg3xtg2x
которое на ОДЗ равносильно уравнению
2tgx =
2tgx
l-tg2x
или tgx = O, откуда х = лА\ к е Z. Найденные углы принад-
лежат ОДЗ уравнения (15) и, следовательно, являются его
корнями.
Ответ: х - лк, к е. Z.
Пример 11. При каких значениях b уравнение
/>cosx _ Z>4-sinx
2 cos 2х -1 ZCOs2 х - 3 sin2 x) tg x
106
имеет решения? Найти эти решения.
Решение. По условию задачи х * 4-, к е Z;
keZ (заметим, что 2cos2x-1 = cos2 x-3sin2 х).
На ОДЗ уравнение (17) равносильно уравнению
^cosxsinx = (b ч-sinx)cosx.
Так как cosx Ф0, то
b sinx = b + sinx <=> (b -1)sinx = b. (18)
При b = 1 уравнение (18) решений не имеет.
При Ь*\ имеем sinx = ——. Учитывая ОДЗ уравнения
Ь-\
(17), получим следующие ограничения на b :
-1< —<1, — *0, — *±-,
Ь-1 Ь-1 Ь-1 2
откуда b е (-оо; -1)U(-1; 0)U(о; U(%; Х)’
Ответ: при b е (-оо; -1) U (-1; 0) U (о; U
х = (-1)^ arcsin—^— 4-як, к eZ.
b-1
Пример 12. Решить уравнение
sinx4-2sin2x = 34-sin3x. (19)
Решение. Преобразуем уравнение (19) к виду
(sinx-sin3x) 4-2sin2x = 3 <=> 2sinxcos2x-2sin2x4-3 = 0.
Дополним имеющиеся удвоенные произведения 2 sin х cos 2 х
и 2sin2x до полных квадратов:
(sin2 х4-2sinxcos2x4-cos2 2x)4-(sin2 2x-2sin2x4-lj-
2/2 2 \
-sin x-lcos 2x-i-sin 2x1-14-3 = 0<=>
<=>(sinx4-cos2x)2 4-(sin2x-1)2 4-ll-sin2 x) = 0<=>
107
(sinx 4-cos 2 х) 2 +(sin2x-l)2 +cos2 x = (). (20)
Сумма неотрицательных слагаемых равна нулю тогда и
только тогда, когда каждое слагаемое равно нулю. Поэтому
уравнение (20) равносильно системе
sinx+cos2x = 0,
sin2x-l = (). (21)
cosx = 0.
Видно, что решения третьего уравнения х = ^4-л£, к е Z
не удовлетворяют второму уравнению. Следовательно, сис-
тема (21), а значит, и уравнение (19) решений не имеют.
Ответ: х е 0.
Пример 13. Решить уравнение
п 4-sinx _ а-гcosx
tfcosx + l tfsinx + l
Решение. Уравнение (22) равносильно системе
(tf+sinx)(a sinx+ 1) = (я 4-cos х)(я cosx 4-1),
< acosx4-1 ф0, (23)
asinx4-l ^0.
Решим первое уравнение системы (23). Преобразуем его к
виду
a2 (sinx-cosx) 4-а (sin2 x-cos2 xj 4-(sinx-cosx) = 0 <=>
<=>(sinx-cosx)(a2 4-14-a(sinx4-cosx)j = 0.
Последнее уравнение равносильно совокупности
sinx - cosx = 0,
/ • \ 2i (24)
a(sin x 4- cos x) = -a - 1.
Первое уравнение совокупности (24) имеет решение
108
x = %+7t&, к g Z при всех a g R.
Рассмотрим второе уравнение совокупности (24). При
а = 0 данное уравнение решений не имеет. При а * О
приведем его к виду
( С
smx + cosx = - я +— .
\ а)
(25)
Если а > 0, то -[а + “2; если а < 0, то -(я - 2, а
так как -V2 < sinx+cosx < д/2, то уравнение (25) решений
не имеет.
Рассмотрим теперь, при каких а углы х-^+лА, A g Z
являются решениями второго и третьего неравенств в (23).
Если х = + 2ти?, и g Z, то указанные неравенства удовлет-
воряются при а * -42. Следовательно, при а = -41 углы
х = ^ + 2ш7, п g Z нужно исключить из множества решений
уравнения (22). Если х = 5л^+2ют, wgZ, то неравенства в
(23) удовлетворяются при а*41. Следовательно, при
а = 41 нужно исключить из множества решений уравнения
(22) углы х = 5л,/ + 2ш?, п g Z
Ответ: при а = -41 х = + 2пк, к
при а = 41 х = 7у^+2пк, к g Z;
при a g (-оо; - V2)u(-V2; Л)и(Т2; +»)
х = + 2лА, к g Z.
Задачи
Решить уравнение
1. 16sinx-sin2x = l-cos2x. 2. 2cos2x + sin3x-2 = 0.
sinx+sin3x + sin5x ~ Л
3.-------------------+ 2tgx = 0.
cos х + cos Зх + cos 5x
4. sin8x - cos6x = л/з(sin6x +cos 8x).
3 3 41
5. cos xcos3x + sin xsin3x =—.
4
109
6. sinЗхcosx = 1,5tgx.
2
7. sinxcosxsin3x-cos3xsin x = 6ctgx.
8. 2cos4x+5cos2x-l = 2 sin2 x.
9. 2 +cos4x = 5cos2x +8sin6 x.
2
10. tg x+cos4x = 0. 11. tgx+ctgx-cos4x = 3.
12. 2sin3xsinx+ ^Зл/Т-1)cos2x = 3.
13. ctg x+ctg 15° +ctg(x + 25°) = ctg 15° ctgxctg*(x+ 25°).
При всех значениях а решить уравнение
. . a-sinx а-cosx
14.--------=--------.
а cosx-1 я sinx-1
§15. Решение тригонометрических уравнений,
содержащих знак модуля или знак корня
Специфика тригонометрических уравнений, содержащих
знак модуля или знак корня, состоит в том, что они сводятся
к смешанным системам, где кроме уравнений нужно решать
тригонометрические неравенства и из решений уравнений
выбирать лишь те, которые удовлетворяют неравенствам.
Пример 1. Решить уравнение
|х + 3| sin х = х + 3. (1)
Решение. Уравнение (1) равносильно совокупности двух
систем
{(x + 3)sinx = х + 3, j(-x-3)sinx = х + 3,
х+3>0, [х+3<0.
Уравнение (х + 3) sin х = х + 3 равносильно совокупности
двух уравнений х+3 = 0 и sinx = l, откуда х =-3 и
х = ^ + 2пп, п g Z. Промежутку [-3; +оо) принадлежат
х =-3 и х = ^/+2ла, п = 0,1,2,....
Уравнение -(х + 3)sinx = х + 3 равносильно совокупности
ПО
двух уравнений х + 3 = 0 и sinx = -l, откуда х = -3 и
х = - + 2тт, и с Z. Множеству (-оо; - 3) принадлежат
х = -^2+2ли, п = -1,-2,-3,....
Ответ: х = -3; х = ^+2ля, и = 0,1,2,..х = -^ + 2л£,
£ = -1,-2,-3,....
Пример 2. Решить уравнение
|cosx| = cosx-2 sinx.
(3)
Решение. Уравнение (3) равносильно совокупности двух
систем
cosx = cosx-2 sinx,
cosx> О,
-cosx = cosx-2 sinx,
(4)
cos x < 0.
Уравнение из первой системы совокупности (4) рав-
носильно уравнению sinx = 0, откуда х = пк, а
решением неравенства являются отрезки +2и; +2nj,
п е Z, в которые попадают точки х = 2пк, к е Z.
Во второй системе совокупности (4) уравнение равно-
сильно уравнению tg х = 1, откуда х = ^ + л&, к el.
Множеству ^2+2и;3^/+2и), weZ (решение неравенства
cos х < 0) принадлежат углы х = 5^/ +2л&, к с Z.
Ответ: х = 2пк, keZ,\ х = ^^+2лА:, fceZ.
Пример 3. Решить уравнение
. COSX п /сх
tgx+—=== = 2. (5)
Vl + sin2x
Решение. Преобразуем уравнение (5) к виду
, cosx ~ cosx ~ //СХ
tgx-ь-.—..........= 2 <=> tgx +—----- = 2. (6)
(sin х + cos х) 2 I sin x+cos x|
Так как sinx + cosx = V2sin(x+^j, то уравнение (6) на ОДЗ
111
равносильно совокупности двух систем
tgx +—-— = 2,
tgx + 1
sin(x+^j > О,
tgx----?— = 2.
tgx + 1
(7)
Уравнение из первой системы равносильно совокупности
двух уравнений tg х =------ и tg х =-------, а решением
2 2
неравенства является множество (- % +2л&; +2л&),
к е Z. Из решений х = arctg -
I 2
+л/?, и е Z указанному
+2л/?, п е Z.
решения х = arctg
множеству принадлежат х = arctg --
I 2
Во второй системе совокупности (7) уравнение имеет
^±713^ /
г -----j +т^, £ е z, множеству +
к е Z(penieHHe неравенства sin(x + %) <0)
принадлежат х = arctg
1-V13
~ 0 J 1+V13
+2л£, х = arctg ----
I 2
2
+2л^, £ е Z.
Ответ: х = arctg
+2ли, и е Z;
х = arctg
1-V13
+2л€, х = arctg
1+V13 л
------ +л+2л€,
2 )
^eZ.
2
2
Пример 4. Найти все решения уравнения
cosx = |sin(2x-1)|, (8)
удовлетворяющие условию |х| < 2л.
Решение. Искомые х есть те решения уравнения
sin2 (2х -1) = cos2 х, (9)
112
которые удовлетворяют условиям cosx > О и |х|<2л, то есть
принадлежат множеству
Решим уравнение (9). Понизив степень уравнения, полу-
чим
l-cos(4x-2) l+cos2x . ..
-------ь---__л --------<=> cos(4x- 2) -4-cos2х = 0 <=>
2 2
<=>2cos(x-l) cos(3x- 1) = 0.
Последнее уравнение, а следовательно, и уравнение (9)
равносильно совокупности двух уравнений cos(x-l)=0 и
cos(3x-l) = 0. Первое из этих уравнений имеет решение
п + 2 „ п + 2 пк , _ ..
х =-------+пп, neZ, а второе х =----------4-—, к е Z. Из
2 6 3
первой серии в множеству Л/ принадлежат числа, соот-
Зл + 2 -л + 2 ..
ветствующие п = ±1, то есть х =------- и х =------. Из
2 2
второй серии
в указанное множество попадают х =
±11л 4-2 -Зл-1-2 9л 4-2
X =---------, X =-------, X =-------.
6 6 6
„ Зл4-2 -л 4-2 ±Л4-2
Ответ: х =-------, х =--------, х-----------
2 2 6
-Зл + 2 9л + 2
X =-------, X ----------.
6 6
±11л4-2
х =--------;
6
Пример 5. Решить уравнение
sinх + 7з cosx = у2 4-cos2x4-V3 sin2x. (10)
Решение. Проведем равносильные преобразования:
J 1 . V3
2 — sinx-i-—cosx
<2 2
' 1 V3
2 4-2 — cos2x-i-—sin2x
12 2
113
<=>2 cosxcos— + sinx sin —
к 6 6
71 71 |
2+2 cos2xcos —+ sin2xsin— <=>
<3 3j
Искомые x есть те решения уравнения
2| Л^ 2( 71 |
COS X---= COS X----, (12)
I 67 I 67
которые удовлетворяют условию cos(x-^)>0. Так как
уравнению (12) удовлетворяют все xeR, то решением
исходной задачи будут те значения х, которые являются
решением неравенства cos(x-^0>O, а именно,
х е [-^/3+2ти?; +2тги], neZ.
Ответ: х+2лл;2^ + 2ли}, weZ.
Пример 6. Решить уравнение
Vsinx +^2 cosx = 0. (13)
Решение. Исходное уравнение равносильно системе
Г~ 2
sinx = v2 cos х,
cosx < 0.
/— 2 1—
Решая уравнение V2 sin x + sinx-V2=0, придем к
уравнению sinx = J/^-, откуда x = ^+2лт?, weZ и
х = ЗЛ//+2тот, weZ. Множеству [^ + 2ли;^^+2лл|, weZ
114
принадлежат только углы х = +2ли,
Ответ: х = weZ.
Пример 7. Решить уравнение
Vl+4sinxcosx = cos х - sin х. (14)
Решение. Уравнение (14) равносильно системе
1+4 sinxcosx = (cosx-sinx)2,
cosx-sinx> 0.
(15)
Из уравнения этой системы получаем совокупность двух
уравнений sinx = 0 и cosx = 0, то есть х = w е А не-
равенство системы (15) равносильно неравенству
cos(x+^j > 0, откуда xe[-3j/£+27tk;J/£+2nk], keZ. В
Полученные множества попадают только х = 2л£, £ е Z и
х = -^ + 2лЛ £eZ.
Ответ: х = 2л/?, ^eZ; х = -^ + 2л^, €eZ.
Пример 8. Решить уравнение
л ctg х
cosx ctgx+4 ----—
\ctgx-6
. 71
32 sin x + —
I 2
ctg x - 6
. (16)
Решение. Уравнение (16) равносильно совокупности двух
уравнений
cosx = 0,
< л ctgx 32
ctgx+4 I--------=-------
у Ctg X - 6 Ctg X - 6
Первое уравнение имеет решение х = ^+ли, /ieZ, а
второе равносильно совокупности двух систем
115
ctg x(ctg x - 6) + 4-Jctg x(ctg x - 6) -32 = 0,
[ctgx > 6,
ctg x(ctg x - 6) -4^ctgx(ctgx-6) -32 = 0,
[ctg x < 6.
Уравнение из системы (17) решаем с помощью замены
^ctgx(ctgx^6) = z, при этом получим z = -8 (не подходит,
так как z>0) и z = 4. Решая уравнение <Jctgx(ctgх-6) =4,
найдем ctg х = 8 и ctg х = -2 (не удовлетворяет условию
ctgx > 6). Следовательно, х = arctg84-ли, п g Z.
Уравнение из системы (18) решаем аналогично и получим
z = 8 и z = -4. Решая уравнение ^ctg x(ctg х - 6) = 8, найдем
ctg х = 3 - V?3 и ctg х = 3 + V73 (не подходит, так как
ctgх < 6). Следовательно, х = arcctg^3 - V73j 4-ли, и е Z.
Ответ: х = ^4-ли, neZ; х = arctg84-ли, neZ;
х = arcctg^3 -Ттз) 4-ли, и 6 Z.
Пример 9. Решить уравнение
! Л I / 2
2 sin 3x4-— = V14-8 sin2хcos 2х .
k 4J
Решение. Уравнение (19) равносильно системе
4 sin2 3x4-— = 14-8sin2x(l-sin2 2х),
к 47 V /
(19)
(20)
sin 3x4-— > 0.
к 4J
Решим уравнение из системы (20):
ль 1 I X Л I
2 1 — COS 6x4-—
к I 2J)
= l + 9sin2x-8sin3 2х <=>
116
<=> 2 + 2sin6x = 1 +8sin 2x -8sin 2x <=>
<=>2+2(3sin2x-4sin3 2x1 = 1 +8 sin 2x-8 sin3 2x <=>
o2sin2x= 1.
Откуда x = ^2 e Z и x~ 5/^2 +7Ш/ ’ m e z •
Подставим x = e Z в неравенство системы
(20). Тогда получим
sin Зх + — = sin —+ 3л^ +— = sin —+ 3л^ = cos3n^,
k 47 k4 47 k2 7
откуда cos3tl£ = 1 > 0 при € четном и cos3n€ = -1 < 0 при t
нечетном. Следовательно, решением системы (20) являются
х = ^2+2л&, к е Z.
Подставим теперь х^Я/^+л/л в неравенство
sin^3x 0, тогда получим
. л] . I 5л _ л
sin Зх+— = sin —+3ллл+—
к 47 к4 4,
Зл
— л-пт
2
-созЗл/и,
откуда - cos Зтип = -1 < 0 при четном m и - cos Зл/л = 1 > 0
при нечетном т. Поэтому в качестве решения системы (20)
следует взять х = -, А: е Z.
Ответ: х = ^2+2л£, ^eZ; х -, AeZ.
Пример 10. Решить уравнение
|cosx| = cos(x+tf).
(21)
Решение. Уравнение (21) равносильно совокупности двух
систем
cosx = cos(x+a),
cos х > 0,
(22)
117
-cosx = cos(x + a),
cos x < 0.
(23)
„ z- 67 . 2x4-67
Преобразуем уравнение в (22) к виду 2 sin —sin-----= 0,
2 2
откуда sin^^O или sin ^х + а - о. Если б? = 2ли, weZ, то
/2 2
х е [-к/1 +2'Ilk', +2л&], к е Z (решение неравенства
~ . 2x4-67 Л
cos х > 0). Решением уравнения sin---------= 0 являются
2
х = -^+л^, ^eZ. Подставим эти числа в неравенство
cos х > 0, тогда получим
67
cos — + л^
I 2
cos I > 0, £ = 2т, т е Z;
I 1)
- cos - — > 0, £ = 2т +1, т е Z.
I 2)
Решением неравенства cos^-^J^O является множество
[-л + 4ли; л 4- 4 ли], и с Z, а неравенства - cos(- > 0
множество [л + 4ли; Зл + 4ли], neZ. Следовательно, при
а 6 [-л +4ли; л +4ли], neZ х = -^+2ли/, hzgZ; при
а 6 [л +4ли; Зл +4ли], neZ х =4-л-ь2л/и, weZ.
Преобразуем уравнение в (23) к 2cos—cos - о,
2 2
67 ZA 2x4-67 /л г'* гг
откуда cos—= 0 или cos-------= 0. Если а = л + 2ли, neZ,
2 2
то х 6 +2л£; Зл,/ + 2л£ j, к g Z (решение неравенства
cos<0). Решением уравнения cos ^х^а. = о является
2
совокупность чисел х = -^-ь^4-л€, ^eZ. Подставим эти
числа в неравенство cosx<0, тогда получим
118
<4 z, I .14 л
cos------+л£ = sin----л£
<2 2 ) <2,
sin— < 0, = 2т, kZ;
2
-sin—<0, = 2zh + 1, £ е Z.
2
Решением неравенства sin^<0 является множество
[2л + 4ли; 4л + 4ли], neZ, а неравенства -sin^2<0 -
множество [4ли; 2л + 4ли], heZ. Следовательно, при
а е [2л +4ли; 4л +4ли], heZ х =-ь2л/л, zzzeZ;
при а е[4ли;2л+4ли], Z7eZ х =-^ ч-2л/>/, /weZ.
Объединяя найденные решения, получим ответ.
Ответ: при а = 2 ли х е [-^+2л£; ^+2л/ф и, &eZ;
при а = л + 2ли х e[^ + 2nk93^+2nkj, п, AzeZ;
при а е (4ли; л + 4 ли) х = - ,
х = -^+3^ + 2л/и, и, zheZ;
при а е (л + 4ли; 2л +4ли) х = -^+л+2л/и,
х = -Я//+3л^ + 2л/и, и, /hgZ;
при а е (2л +4ли; Зл +4ли) х = -^+^ + 2л/л,
х = -^2-ьл ч-2л/а/, и, zheZ;
при а е (Зл +4ли; 4л +4ли) х =+2л/н,
х = -^/+2ли/, и, zheZ.
Пример 11. Решить уравнение
sinx = yjacosx .
(24)
Решение. Уравнение (24) равносильно системе
sinx> 0,
acosx> 0,
(25)
sinx = a cosx. 9
Рассмотрим три случая.
119
а) При a = 0 уравнение (24) равносильно уравнению
sinх = 0. Следовательно, х=лт9 meZ.
б) При а > 0 неравенства в системе (25) выполняются при
х е[2лк9^ + 2лк], keZ, а решением уравнения системы
(25) является совокупность чисел х = arctg а + ли; п е Z. Так
как 0 < arctg а < эти числа будут попадать на отрезки
[2пк;'^2+2лк] при и = 2/и. Следовательно, х = arctga+2лли;
те Z.
в) При а < 0 неравенства в системе (25) выполняются для
хе[^+2л&;л + 2л&], keZ. Поскольку -^<arctga<0,
то решения х = arctg а + лп; п е Z уравнения sin х = a cos х
попадают на отрезки [^ + 2лк,л + 2лк] при и = 2и/ + 1.
Следовательно, х = л + arctg а 4- 2 лт, те Z,
Ответ: при а - 0 х=лт9 meZ\
при а > 0 х = arctg а + 2лт, т е Z;
при а <0 х = л +arctg я + 2л/и, т е Z.
Задачи
Решить уравнение
1. 2|x-6|cosx = х-6. 2. |ctgx| = ctgx+——.
sinx
3. \9-х2 (sin2x-3cosx) = 0. 4. V5-2sinx = 6sinx-l.
C ~ 2 1 + 3 tgX
5. \/3+2tgx-tg x =--------.
2
6. tgx+-ctgx = —-------1-1.
9 V cos2 x
7. Vcos2x +Vl + sin2x = 2>/sinx + cosx.
8. -^2 sin(x+2) - V? cos2 x = ^sin x(2 cos 2 - cosx) .
Jl + tgx
---— =sinx+cov-
1-tgx
120
10. 2V3sinr= 3 tgX-------Л.
2Vsinx -1
При всех значениях а решить уравнение
I Г Г
11. cosx— + cosx— =a.
N 2 N 3
12 1-л sinx I 1 + 2л sinx _
1+Л sinx V l-2flflsinx
§16. Использование ограниченности функций
при решении тригонометрических уравнений
При решении некоторых тригонометрических уравнений
часто используется свойство ограниченности функций
sinx и cosx, то есть следующие неравенства: |sinx|<l,
|cosx| < 1, |sinx±cosx| < Jl.
Пример 1. Решить уравнение
4 7
sin x+cos х = 1. (1)
Решение. Проведем равносильные преобразования:
• 4 7.4 7 -2,2
sin x+cos X = 1 <=> sin x+cos x = sin x+cos X <=>
2/2 \ 2/5 \
<=>sin I sin x-lj+cos xlcos x-lj = O. (2)
2 2 2 / 2 \
Так как sin x>0, a sin х-1<0, то sin xlsin x-l|<0;
2 5 2 / 5 \
так как cos x>0, a cos х-1<0, то cos xlcos x-l]<0.
Сумма двух неположительных слагаемых в (2) равна нулю
тогда и только тогда, когда каждое из слагаемых равно нулю.
Значит, уравнение (2) равносильно системе
[2 2
sin х = 0, sin х-1 = 0,
1г 2 (3)
cos х = 0, cos х -1 = 0.
121
Решением первой совокупности системы (3) являются углы
х~Л//2’ е а решением второй - х = ^+тп?;
х = 2пп, neZ. Общими являются углы х = neZ;
х = 2пп, п eZ.
Ответ: х = +тиг, п е Z; х = 2пп, п е Z.
Пример 2. Решить уравнение
• 1994
S1H
X 4- COS
1994
(4)
Решение. Используя прием, изложенный в примере 1, све-
дем уравнение (4) к равносильной системе
2
sin х = 0.
. 1992
sin
х-1 = 0
2 л
cos x = 0
(5)
1992 . n
cos x - 1 = 0.
Находя решение каждой совокупности системы (5), нетрудно
установить, что общими будут yi лы х = , п е Z.
Огвет: х = Л е Z,
Пример 3. Решить уравнение
2
tg 3x = cos2x-l. (6)
Решение. Запишем уравнение (6) в виде
tg2 Зх = -2 sin2 х. (7)
2 2
Так как tg Зх>0, а -2 sin х<0, то уравнение (7), а
значит, и уравнение (6) имеют решения тогда и только тогда,
когда
tg2 Зх = 0,
-2 sin2 х = 0.
(8)
Решением первого уравнения системы (8) являются числа
X = 1
122
Х = Л//3’ е а ВТОРОГО “ х~пп> neZ. Общими будут
числа x=Tin, w е Z.
Ответ: х=ти?, и g Z.
Пример 4. Решить уравнение
coskVx cosn>/x-4 = 1.
(9)
Решение. Уравнение (9) равносильно совокупности двух
систем
COSTtVx = 1, [cosnVx = -1,
---------- z____ (10-11)
COSKVX-4 = 1, [COS7t>/x-4 = -1.
Решением первого уравнения системы (10) с учетом, что
л<х>0, является множество чисел х = 4к , а
2 2 2
второго - х = 4 +4и , we Zo. Решая уравнение Ьк = 4 + 4л
в целых неотрицательных числах, находим к = 1, п = 0.
Следовательно, решением системы (10) является х = 4.
Решением первого уравнения системы (11) является
множество чисел х = (1+2&) , ZcgZ0, а второго -
х = 4+(1+2л)2, neZ0. Уравнение (1+ 2&)2 = 4+(1+2л)2 в
целых неотрицательных числах решений не имеет, а следо-
вательно, и система (11) решений не имеет.
Ответ: х = 4.
Пример 5. Решить уравнение
1 2
1+cos2xcos3x = — sin Зх. (12)
2
2 2
Решение. Заменив sin 3x = l-cos Зх и обозначив cos3x
через Г, получим квадратное уравнение относительно t
t2 + 2cos2x/+l = 0, (13)
2
дискриминант которого Z) = 4cos 2х-4<0. Следовательно,
уравнение (13), а значит, и уравнение (12) имеют решения
2
тогда и только тогда, когда D = 4cos 2х-4=0, то есть
123
cos2x = -1,
. i <14>
cos3x = 1.
Z = -cos2x. Таким образом, уравнение (12) равносильно
совокупности двух систем
cos2x = 1,
cos3x = -1,
В первой системе совокупности (14) уравнения имеют
соответственно решения х = пк, к eZ и х = ^3 + ’
п е Z. Пересечением данных множеств является множество
углов х = л +2л/и, т е Z.
Во второй системе совокупности уравнения имеют соот-
ветственно решения х = ^+7iA\ ^eZ и х = 2тгл//> a?gZ.
Общих решений нет.
Ответ: х = л+2л/л, meZ.
Пример 6. Решить уравнение
(sinx+V3 cosx)sin3x = 2.
(15)
Решение. Уравнение (15) равносильно уравнению
— sinx+-^— cosx sin3x = 1 <=>sin x+— sin3x = 1,
2 2) V ЗУ
которое равносильно совокупности двух систем
71 .
sin Х+ — = 1.
I з;
71 1
sin х+— = -1,
I з;
(16)
sin3x = 1,
sin3x = -1.
В первой системе совокупности
уравнений являются соответственно
x = 75/+2tiA:, к е Z и х = 7*/ + 2ли/
/6 /6 /3
общими будут углы х = + 2пк, к eZ.
(16) решениями
множества углов
п е Z, при этом
Во второй системе решениями уравнений являются соот-
ветственно углы х = - 5^/ 2 пк, к g Z и х = - ^ + »
п е Z. Пересечением является множество х = - + 2тгл?,
п е Z.
124
Объединяя найденные множества решений, получим
ответ.
Ответ: х = ^+ли, neZ.
Пример 7. Решить уравнение
V— 4
2 +sin 4х. (17)
Решение. Так как -Vl < sinx+cosx < у/1, a sin44x +
+V2 >5/2, то уравнение (17) имеет решение тогда и только
тогда, когда
sinx+cosx = V2,
sin4x = 0.
(18)
Решая первое уравнение системы (18) методом введения
вспомогательного аргумента, получим sin(x+^) = l, откуда
х = ^ + 2л/7, weZ; решением второго уравнения системы
(18) является множество чисел х = neZ. Следо-
вательно, решениями системы будут числа х = ^+2ли,
п е Z.
Ответ: х = ^ + 2ли, weZ.
Пример 8. Решить уравнение
sin3 х +\cos3 х = V2 .
(19)
Решение. Областью допустимых значений уравнения (19)
является множество отрезков ^2nZc;^ + 2nA:j, к е Z, причем
углы х = 2л£, £ е Z и х = ^ + 271/7, neZ не являются
решениями уравнения (19). На множестве (27tfc;^ + 27t&),
к El Z Vsin3 х < sin х и 7cos3 х < cos х, следовательно,
7sin3 х + Vcos3 х < sin х+cos x < y/l. Tаким образом, имеем
7 sin3 x + 7cos3 x < V2, значит, у уравнения (19) решений
нет.
Ответ: х е 0.
125
Пример 9. Решить уравнение
5 5 4
sin x+cos x = 2-sin х. (20)
п -5-2 5 2
Решение. Так как sin х < sin х, cos х < cos х, то
sin x+cos х< sin x+cos x = 1; a 2-sin х>1. Следова-
тельно, уравнение (20) имеет решение тогда и только тогда,
когда
. 5 5 ,
sin X+COS X = 1,
(21)
~ . 4 .
2 - sin х = 1.
Первое уравнение системы (21) решаем, используя
методику, изложенную в примере 1, при этом получим
х = ^2+2тсл, x = 2tu7, neZ. А второе уравнение имеет
решение х = ^+л^, ^eZ. Общими у обоих уравнений
являются углы х = + 2лл, п е Z.
Ответ: х = + 2лп, neZ.
Пример 10. При всех значениях а решить уравнение
2
1 + sin ах = cos х. (22)
2
Решение. Так как 1+sin ах>\, a cosx<l, то уравнение
(22) имеет решение тогда и только тогда, когда
2
1+sin дх=1,
cosx = 1.
Второе уравнение системы (23), имеет решение х = 2пк,
к g Z, а из первого получим ах=пп, neZ.
Если а - 0, то первое уравнение выполняется при всех
xgR, следовательно, решениями системы (23) будут числа
х = 2пк, к eZ.
Если а + 0, то решениями первого уравнения являются
числа x = neZ. Сравним выражения 2пк и
п,к g Z. Если а - иррациональное число то есть а е R\Q,
то данные выражения совпадают только при А=0, л = (),
126
следовательно, система (23) имеет единственное решение
х = 0. Если а е Q, при этом заметим, что всякое
рациональное число можно единственным образом
представить в виде а = е w е N, где - несокра-
тимая дробь (докажите), то решениями системы (23), а
следовательно, и уравнения (22) являются х = 2пт-к, к eZ.
Объединив найденные решения, получим ответ.
Ответ: при а=0 х = 2пк, к е Z;
при а*0, aeQ, а = х = 2лт-к, keZ;
при a g R \ Q х = 0.
Пример 11. При каких значениях а уравнение
cos2 ax+cosx = 2 (cos ах-ь cosx-1) (24)
имеет единственное решение?
Решение. Запишем уравнение (24) в виде
(cosax-1) 2 =cosx-l.
Так как (cosax-1) 2 >0, а cosx-l<0, то исходное уравне-
ние равносильно системе
Гcosax -1 = 0,
[cosx - 1 = 0.
При а = 0 решениями системы являются углы х = 2лк,
keZ.
При а Ф 0 получим
2ли rj
f = V”eZ; <25>
х = 2пк, к eZ.
Система (25) при любом а ф 0 имеет решение х = 0
( п = ОД = 0 ).
Если а = ~ рациональное число, (^eZ, weN), то
взяв п- Is, к = ms, 5 е Z, получим множество общих реше-
ний. Следовательно, при a е Q уравнение (24) имеет мно-
127
жество решений.
Если а - иррациональное число ( а * j, то при п * О
у Xj = множитель 2и/ . иррациональное число, а у
х2 = 2пк множитель 2к - целое число, следовательно, Xj и
х2 совпадать не могут.
Ответ: а е R\Q.
Задачи
2. sin- + 2cos —— = 3.
4 3
. 6 о 1-4
4. cos 2x.= l+sin x.
Решить уравнение
1. 3sin2 — +5sin2 x = 8.
3
2
3. sin 5x -bsin x = 2 +cos x.
2 12
5. sin x+—sin 3x = sinx+sin3x.
4
- _ . | 2 71- ( _ 71 I _
6. 2sin — x— -3cos 2x+— 1 = 5.
<3 6j I 3j
2
8. sin 18х +sin 10х +sin2x = 3 +cos 2x.
Г 3 2
9. cos2x 1 — sin 2x = 1.
I 4 J
10. 2 sin2 -
§17. Функциональные методы решения
тригонометрических и комбинированных
уравнений
Не всякое уравнение /(х) - g(x) в результате преобра-
зований может быть сведено к уравнению того или иного
стандартного вида, для которого существует определенный
метод решения. В таких случаях оказывается полезным
128
использовать такие свойства функций /(х) и g(x), как мо-
нотонность, ограниченность, четность, периодичность и
др. Так, если одна из функций убывает, а вторая возрастает
на промежутке X, то при наличии у уравнения /(х) = g(x)
корня на этом промежутке, этот корень единственный, и
тогда его, например, можно найти подбором. Если, далее,
функция /(х) на промежутке X О1раничена сверху, причем
шах/(х) = Л, а функция g(x) ограничена снизу, причем
хе А"
min/(х) - А, то уравнение /(х) = g(x) равносильно
хеХ
системе уравнений
g(*) = A.
Иногда для решения
уравнения /(х) = g(x) можно построить графики функции
у = /(х), y = g(x) и определить абсциссы точек пере-
сечения. В этом параграфе также рассматривается приме-
нение производной для исследования тригонометрических
уравнений.
Пример 1. Решить уравнение
2
cos тех ~ х -4х + 5.
(1)
Решение. Преобразуем уравнение (1) к виду
costix = (х-2)2 +1.
Так как costix <1, а (х-2)2 +1>1, то последнее уравнение
равносильно системе
costix = 1,
(х-2)2+1 = 1.
(2)
Второе уравнение системы (2) имеет единственный ко-
рень х = 2, подставляя его в первое уравнение, убеждаемся,
что он удовлетворяет ему. Следовательно, х = 2 - корень
системы (2), а значит, и уравнения (1).
Ответ: х = 2.
129
Пример 2. Решить уравнение
2 2
х -Зх+4,25-cos 7tx-2sin7ix. (3)
Решение. Воспользовавшись основным тригонометричес-
ким тождеством, запишем исходное уравнение в равносиль-
ном виде
2 2
х -3x+4,25+sm tlx+ 2sinлх - 1 = 0 <=>
<=>(х-1,5)2 +(sin7Lx + l)2 =0.
Последнее уравнение равносильно системе
1х-1,5 = 0,
[sinjtx + l = 0,
решением которой является х = 1,5.
Ответ: х = 1,5.
Пример 3. Решить уравнение
х +(l+x)sin— =-------------------. (4)
6 2
Решение. Преобразуем уравнение (4) к виду
2х +| 2 sin--1 x+2sin-----3 = 0
\6 ) 6
и решим его как квадратное относительно х. Тогда получим
. юс 3
х - -sin— +—,
6 2 (5)
х = -1.
Решим первое уравнение совокупности (5). Учтя ограни-
ченнось функции sin71^, приходим к выводу, что уравнение
может иметь корень только па отрезке На этом
промежутке функция у = х возрастает, а функция
у = - sin убывает. Следовательно, если уравнение
имеет корень, то этот корнь единственный. Подбором нахо
130
дим х = 1.
Ответ: х = ±1.
Пример 4. Решить уравнение
-iVSitsinx = |х4-л|4-|х-2л|. (6)
Решение. Рассмотрим уравнение (6) на трех промежутках,
а) Пусть х < —л. Тогда на этом множестве уравнение (6)
равносильно уравнению
-2-УЗл sinx - -2x4- л. (7)
На промежутке (-оо; - 2л] уравнение (7) решений не имеет,
так как -2-/Зл sin х < 2-/Зл, -2х+л>5л, а 2-УЗл<5л. На
промежутке (-2л; - л) уравнение (7) также корней не имеет,
так как -2>/Зл sinx < 0, а -2х+л > Зл.
б) Пусть -л < х < 2л. Тогда на этом множестве уравнение
(6) равносильно уравнению
-2л/3л5шх= Зл <=>sinx = '
корнями которого на промежутке [-л; 2л] являются числа
_2л/. _л/. 4л/. 5л/
/3’ /3’ /3’ /У
в) Пусть х>2л. Тогда на этом множестве уравнение (6)
равносильно уравнению
-2л/3л sinx = 2х- л. (8)
На промежутке (2л; Зл] уравнение (8) решений не имеет, так
как sinx < О, а 2х-л>3л. На промежутке (Зл; 4-оо)
уравнение (8) также решений не имеет, так как
-243пsinх < 2>/Зл, 2х-л>5л, а 2л/3л<5л.
Ответ: х~~1Уу х~^//3’ х = ^//3'
Пример 5. Решить уравнение
Ij-4x2I
5’ 1 ~ sinnx. (9)
131
I 21 |'-4x2|
Решение. Так как l-4x >0, 51 > 1, a 8шлх<1,
то уравнение (9) равносильно системе
И-4*2 *!
< 5' ' = 1,.
siniix = 1.
Решением первого уравнения являются числа х = ±у, при
этом второму удовлетворяет только х = .
Ответ: х =
Пример 6. Решить уравнение
log2 3+2х-х = tg —+ctg —. (10)
\ /44
Решение. Так как 3 + 2х-х2 = 4 -(1 -х)2 < 4, log2(3 +
2 \ 2 ЛХ 2 ТЕХ
+2х-х |<2, a tg —+ ctg —>2 (сумма двух положи-
/ 4 4
тельных взаимнообратных чисел больше либо равна 2), то
уравнение (10) равносильно системе
log2(3+2x-x2 j = 2,
(И)
t 2 их 2 ЛХ _
tg —+ ctg —= 2.
4 4
Решением первого уравнения системы (11) является число
х = 1, оно также удовлетворяет второму уравнению.
Ответ: х = 1.
Пример 7. Решить уравнение
16л 1
cos---------------= —------------—
7 2 2
16х -8х + 49 tg тгх + ctg лх
(12)
2 /21
Решение. Так как 16х -8х+49=(16х -8х +11+48 =
132
= (4х - l)2 + 48 > 4&, то 0 <-- -* 71-< —, и значит,
Ч6х-8х+49 3
1 16л . _ 4 2 . 4 2 ~
— < cos-------------<1. Так как tg лх+ctg лх>2, то
2 16х2-8х+49
0<— ------—-—<—. Следовательно, уравнение (12) рав-
tg тех + ctg лх 2
посильно системе
16х2-8х+49 2’
1 _ 1
2 2 —
tg лх+ctg лх 2
Решением первого уравнения является число х = I
которое также удовлетворяет и второму уравнению.
Ответ: х = у.
Пример 8. Решить уравнение
3
sinx- sin 15х cosx = —. (13)
2
Решение. Уравнение (13) решаем методом введения вспо-
могательного аргумента, для чего разделим левую и правую
части уравнения на 71 + sin215х. Обозначив
1 sinl5x
. = = cosy, -=== = sin у, получим
71 + sin2 15х \1 + sin2 15х
3 _
cosy sinx - sin у cosx = —-===== <=>
271+sin2 15x
<=> sin(x - y) = —y==== (14)
271 +sin2 15x
I : 2~ г~ зз
Так как \l + sinl5 x<V2, to —. — >—t=>1.
271+sin215x
Следовательно, уравнение (14), а значит, и (13) решений не
имеют.
133
Ответ: х е 0.
Пример 9. Решить уравнение
sin4 x+cos4 у+ 2 = 4sinxcosy. (15)
Решение. Выполним цепочку преобразований:
4 4
sin x+cos y + 2-4sinxcosy =
j • 4 п • 2 2 4 \ ,
= lsin x-2sin xcos y + cos y) +
(22 \
2sin xcos y-4 sinx cosy +2 j =
= (sin2 x-cos2 y} + 2(sinxcosy-1)2 = 0.
Так как (sin2 x-cos2 y} >0, (sin x cosy - l)2 > 0, to
сумма двух неотрицательных слагаемых равна нулю тогда и
только тогда, когда каждое из них равно нулю. Значит,
уравнение (15) равносильно системе двух тригономет-
рических уравнений
2 2
sin x-cos у = 0,
sin xcos у = 1.
Положив и = sinx, у = cosy, получим систему
f 2 2 п
и — у =0,
<
UV = 1,
откуда
. [м = 1, \и - -1,
[у = 1 [у = -1,
то есть
[sinx = 1, fsinx = -l,
< или < .
[cosy-1 [cosy = -l.
134
Из первой системы имеем
л
х = —к 2 пк, к eZ\
2
у = 2ли, п е Z,
а из второй
х = - — + 2л£, к е
2
у - Tt + lnn, и е Z.
Ответ; +2л£, 2ли), +2л£, л + 2лл), к,пе1.
Пример 10. Решить уравнение
2 2
cos x+cosxcosуч-cos у = 0, (16)
Решение. Рассмотрим уравнение (16) как квадратное
уравнение относительно cosx. Вычислим дискриминант
2
P = -3cos у<0. Следовательно, уравнение (16) равносиль-
но системе
Jcosy = 0,
[cosx - 0,
откуда У-^2 ’ к х = +ли, п е Z.
Ответ: (^+ли, ^+л/г^, к,пе1.
Пример 11. Решить уравнение
2^2 (sinx + cosx) cosy = 3+cos2y. (17)
Решение. Преобразуем уравнение (17) к равносильному
уравнению
cos2 у -41 (sinx+cos г)cosy + 1 = 0, (18)
которое рассмотрим как квадратное уравнение относительно
cosy. Вычислим дискриминант D = 2(sinx + cosx) -4. Так
как |sinx+cosx| < V2 , то £)<0. Следовательно, уравнение
135
(18) имеет решение тогда и только тогда, когда D = 0, и при
этом равносильно системе
|sinx+cosx| = VI,
л/2 (sinx + cosx)
cosy =-----------------
2
(19)
Первое уравнение системы (19) имеет два множества
решений х = ^+2лА:, к е Z и х = ^^/ + 2л£, к е Z; этим
множествам соответственно отвечают у = 2л/?, п е Z и
у = Л+2л/7, И G Z.
Ответ: (^+2л£, 2л/?^, &,/?eZ;
(5^/ + 2л£,л + 2л/?^, k,nEl.
Пример 12. Решить уравнение
cos(x-j/)~2sinx + 2sinу - 3. (20)
Решение. Проведем равносильные преобразования:
. п . 2 х-у . х — у х + у
1 — 2 sin----4sin---cos----—- — 3 = 0 <=>
2 2 2
«sin2^ + 2cos^sin^ + l = 0. (21)
2 2 2
Уравнение (21) рассматрим как квадратное относительно
sin——его дискриминант равен D = 4cos2 -4 < 0.
2 2
Следовательно, уравнение (21) имеет решение тогда и только
тогда, когда D = 0, и при этом равносильно системе
2 х+у ,
cos ----= 1,
2
. х — у х + у
sin--— = - cos—
2 2
Эта система равносильна совокупности двух систем
136
х+у .
cos—— - 1,
2
х+у 1
cos—— = -1,
2
sin----— = -1,
2
sin----— - 1.
2
Из первой системы получаем
2
—— = - — 4- Inn, A? 6 Z
2 2
Из второй получаем
-У- - л +2л£, к е Z;
2
—^- = —4-2ли, neZ
2 2
х =- —4-2л(£ 4-л),
у = — 4-2л(£-и), k,nel.
Зл / \
х =—+2л(£+и), к'П^Тл
у = —+2л(^ - и), LneZ.
Ответ: - —+ 2л(£ +и), — + 2л(£-и) , к,пе Z;
I 2 2 J
| — + 2л(& +и), —+ 2л(&-и)
\ 2 2 )
Пример 13. Решить уравнение
2 2X-y sin2(x-y) 34-2cos(x-y)
4-2x-x cos -—<-4--------=--------------b--±1. (22)
2 2
2
Решение. Воспользовавшись формулами косинуса и сину-
са двойного угла, сведем уравнение (22) к виду
2 2
COS
-У t п • 2 \Х~У) 2
-——-4-2 sin -----^cos
2 2
2
3
= — + COS
2
~У Cin2 Х~У
------sin
2
2
(23)
2 X-у
Положим t = cos ----, тогда уравнение (23) примет вид.
2
137
Так как /=0 не удовлетворяет последнему уравнению, то
разделив его на /, получим равносильное уравнение
>/з + 2х-х2 = 2t +—, (24)
2/
причем 0</<1. Так как \3+2х-х2 =^4-(1-х)2 <2, а
2t ~ 10 УРавнение (24) равносильно системе
т/з + 2х-х2 2.
2'+Х,=2'
откуда находим х = 1, t = 1, то есть
2 X — у <=><
cos ----= 1 |у = 1+2ли,и е Z
2
Ответ: (1,1+2ли), п е Z.
Пример 14. Решить уравнение
2 1 1
COS X -+ -—
cos х)
(25)
Решение. Так как
cos2 х + ——> 2, 1 + tg2 2у > 1, 3 + sin3z > 2,
cos х
то уравнение (25) равносильно системе
7 1
cos х +-------= 2,
< cos2 х
1+tg2 2у=1, 3 + sin3z = 2.
2 1
cos х — 1,
tg 2 у = 0, sin3z = -1.
Следовательно, х=л«, a?gZ; z ~ ~Уб
meZ.
Ответ:
I, k,n,meZ.
Пример 15. При каких значениях параметра а е
уравнение
2 Г
cos лхн-----+— = —
V 127 2 \27
(26)
имеет решения на отрезке [2; 3]?
/ \l+|sinax| 1
Решение. Так как 1 +1 sinaxl > 1, I —I <—, а
<27 2
21 5л ] 11
cos лх +—|+—>—, то уравнение (26) равносильно сис-
I 127 2 2
теме
1 + |sintfx| = 1,
f 5л
cos лх +— = 0.
I 127
(27)
Второе уравнение системы (27) на отрезке [2; 3] имеет
решение х = а из пеРВ0Г0 получим ах=пп, weZ или
A?eZ. Интервалу (1;5) принадлежат следующие
_____________-24л-----36л
числа: а =___, а = , а= .
25 25
24л 36л
я =----> q —----
25 25
12л
25
гч 12л
Ответ: а =----
25
Пример 16. При каких значениях а уравнение
1 1
COSX+—cos2x— cos3x - а
2 3
(28)
имеет решения?
Решение. Расмотрим функцию /(х) = cosxcosx-
- JZcos3x. Уравнение (28) имеет решения, если
139
min/(x) < a < max/(x), xeR.
Найдем производную функции f (x):
/'(x) = - sin x-sin 2x4-sin 3x
и решим уравнение
sin x 4- sin 2x - sin Зх = 0 <=>
<=> sinx 4-2 sinxcosx-3sinx+4 sin3 x = 0 <=>
<=>sinx(14-2cosx-34-4(l-cos2 x)| = 0 <=>
г
sinx = 0, cosx=l, <=> 1 cosx = — L 2 x = лк, к 6 Z; х = 2лп, n е Z; х = ±— 4-2л/и, т 6 Z. L з
Так как функция у- f(x) периодична и ее период равен
2л, то для нахождения минимального и максимального
значений функции достаточно вычислить значение функции
в экстремальных точках на промежутке [0; 2л). Имеем
/(«)=%. Л")=-Х- /(%)=-%• /(%)=-%
Следовательно, min /(х) = - 1, а тах /(*) = % и
уравнение (28) имеет решения, если -
Ответ: %].
Пример 17. При каких значениях а уравнение
sinx -i-Vcosx = а
(29)
имеет решения?
Решение. Областью определения исходного уравнения
является множесгво х е ^2л£; + 2лАф к е L. Рассмотрим
функцию у - Vcosx 4-Vsinx. Если найти область значений
этой функции, то тем самым фактически будут найдены те а,
при которых уравнение (29) имеет решения.
140
_ , cosx sinx ..
Вычислим у -—-==----------7 - Кориями уравнения
2vsinx 2vcosx
y-SX----S*n* = 0 являются числа x = ^ + л/7, n e Z.
2vsinx 2vcosx
Так как функция у - Vcos x + Vsinx периодична с периодом
7’ = 2л, то для нахождения наибольшего и наименьшего
значений функции достаточно вычислить значение функции
в точках Xj=O, х2 =^, х3=^. Получим j'(O) = 1,
“ V2V2 , “ 1 * Следовательно, 1 < Vcosx +
+Vsinx < V2V2 при всех х е ^2л&; + 2лА'], к е Z.
Таким образом, уравнение (29) имеет решен , если
Пример 18. При каких значениях а и b равенство
a sinx+/> = sin(dx+/>) (30)
верно при любых х е R?
Решение. Рассмотрим функцию /(х) = sin(«x +/>) - a sin х.
Вычислим
/'(х) = a cos(#x +b)-a cosx =
= -2а sin0,5((#+ 1)х+/>) sin0,5((«- 1)х+/>).
Равенство (30) будет выполняться при всех xeR, если
/'(х) = 0 при всех х е R и f(x) = b.
Рассмотрим случаи, когда /'(х) = 0 при всех хе R.
а) а-0. Равенство (30) примет вид sin/? -Ьч где |^|^1.
Учитывая, что |sinx| <|х| при 0 < |х| < , приходим к
заключению, что равенство sin/? - b возможно только при
b - 0. Итак, а = 0, b - 0.
б) sin05((tf + 1)х+/>) = 0. Тогда (а + 1)х+/> = 2лл, п е Z.
141
При а = -1 и b - 2itn, и е Z это равенство верно при любых
xeR. При этом (30) принимает вид - sinх + 2 ли - -sinx,
откуда и = 0, значит, b = 0. Итак, имеем а - -1, b = 0.
в) sin0,5((fl - 1)х +/>) = 0. Тогда (а - 1)х+/> = 2 ли, heZ,
то есть (а - 1)х = 2 ли -/?, heZ. Это равенство верно при
любых х е R, если а = 1 и b = 2 ли, и е Z. Подставив эти
числа в равенство (30), получим sinx +2ли = sin(x + 2ли),
что возможно для любых х е R при п - 0. Итак, а = 1, b = 0.
Ответ: (0,0), (-1,0), (1,0).
Пример 19. Найти все значения а, при которых уравнение
/'(х) = 0, где
г/ \ 1 а~ 1
f (х) = 1-COSX+-----X
а +1
имеет на отрезке [100л; 101л] не более одного корня.
Решение. Найдем призводную функции /(х):
\ Q 1
f (х) = sinx+----
и + 1
и приравняем ее к нулю:
sinx + -—- = 0. (31)
а +1
Функция У - f на промежутке [100л; 100,5л]
возрастает, причем ()<sinx<l, а на промежутке
(100,5л; 101л] убывает, причем 0<sinx<l Поэтому
уравнение (31) имеет одно решение либо не имеет решений
1-п .
если выполняется совокупность неравенств -------------> 1,
1 + а
1 -a n п
------<0. Решением первого неравенства служат значения
1 + а
а е (-1; 0], а второго - а е (-оо; - 1) U (1; +<*>).
Объединяя найденные решения, получим ответ.
Ответ: а е (-оо; - 1)U( - Г, 0] U(l; +<*>).
142
Задачи
Решить уравнение
1. sinx = х2 4х + 1.
3. logK х = 1 4-sinxlogn 2.
5. 3 + (х-л)х' = l-2cosx.
х-—1+2
7.3 41 =5+4sin27tx.
9. log j (3 +|sinx|) = - 2.
2/2 costix = 2x -1.
4. 2sin2 — sin2 — = 4- + x2
2 6 x2
I sinJFI
6. 3' - | cosx |.
8. 2 sin x + — = tgx+ctgx.
I 4 J
10. log2(3-|cosx|) = 2
з
n =in 71 log3|x|+log|x| 3
X1 +6x + 13 2V2
12. cos4 (arcctg x) + sin4 (arcctg x) = sin-2 (arcctg x).
n lCtg^ 1 „ f 2 1
13. ---= log ! у -2y + — .
cos xy 9 )
( \2 ( \2
12 1 I I 2 11 1
14. sin x +—-— + cos x +-----— = 12+—siny.
V sin x) v cos x) 2
2
15.x + 4xcosxy+4 = 0.
16. tg2 x+2tgx(sinj' + cosj') +2 = 0.
17. 2+2sinx(sinj'+cosj') =cos2x.
.sinx nl+smx Jyl
18. 4 -2 cosxy + 2lzl =0.
3
19. cosx + cosy-cos(x + J^) - —.
20. (3 sinx+V3 cosx+5^) =37^1+y2j.
21. l-2x-x2 - tg2 (x 4-j/) +ctg2 (x +y).
22. 21-Jf2 +2x2-1 =2sin — .
2
23. 2'- cos_y + lg(l +x2 +| у |j - 0.
143
24. log2
2
COS
1
cos xy J
/-2^ + 2
Ответы
§1
1. 0. 2. arctg?+ 1+Л/7, n e Z. 3. ^(12n -1), n e Z. 4. 0.
5. ±^У2+2к, fce{0}UN . 6. (~1/+1 + 2itk, к e Z.
I? fr 4-1
7. log3(l + 2fc), Are{0}UN. 8. ±p^—^л, fce{0}UN.
V 2
9. 10. 0. 11. при a g [0; 2]
5 + (-i)^ arcsin(fl - 1)+л£, £ g Z; при a g (-oo; 0)U(2; + oo)
x g 0.
§2
1. 2ли//±^/агсс05 nEz. 2. л(8и±1)/28;
л(2и + 1)/14, /7gZ. 3. 0. 4. ^+л&, к g Ъ. 5. 77
§3
1. л(2л + 1)/2; 2л(За//± l)/3, /?,//zgZ. 2. л(4и + 1)/2;
л(б£+(-1)^)/б, k,nel. 3. ±arccos^^—-^ + 2ля, wgZ.
4. 7l/7Z+7/, hgZ. 5. л(4и + 1)/2, hgZ. 6. hgZ.
/2/4 v z/ /2/o
(”0” ^6+7l/7’ neTj. 8. -у^+ли, /7gZ. 9. при
n arcsin (l-V3+2a)/2,«ez}; при
flG^-ooi-^juQ^+oo) 0. 10. при я = 0 ^y+7u?,nezj;
при а Ф 0 < 2лн ± arccos
1-71+4Д2
2a
, /7 G Z
144
§4
1. arctg 2//+ л A', ZreZ. 2. -arctg^+nZr, ZreZ. 3. ^+л£;
arctg 3 4-ли, k,nel. 4. ^+nZr; -arctg 2 4-ли, £,neZ.
5. 4-л&; arctg3+ли, к, n e Z. 6. arctg(-l ± д/з) 4-л£, к e Z.
7. arctg ~-^Z-+nk, keZ. 8. nk\ 7^/4-ли, k,n^l.
4 /4
9. + л^’> arctg74-ли; arctg3+лт, к, n, me Z.
§5
1. 7^+7l'7Z; Зл/+л£, k,neZ. 2. +™Z; ±2лХ+2л£,
k,neZ. 3. -^/4+ли; y^+iik, k,neZ. 4. л^, neZ.
5. Л^5’ /'б471^’ 6- ^4-ли; k,neZ.
7. (-1)” Л^о + 7Г%; %+7t^4; 3%+rot’ k,neZ.
8. (-1)” +ли; +lin’ —^^т, +2лп, п е Z. 9. при а = 2пк
xeR;npn а*2лк х = л4-2ли, х = а 4-л 4-2лаи, т, к, и е Z.
10. при а = лк xeR; при а *пк х = ± arccos 4-2 ли,
4
к, п е Z.
§6
1. 2ли +/^2’ 2ли4-2^2’ neZ. 2. -//5+^Л^5’
2^5 + 2Л%’ neZ* 3’ ~%2^nk/v %2+K%, k.neZ,
4. л4-2л£; 2arctg^4-2ли, k.neZ, 5. ^л/^^ли, neZ.
6. - JZarccos 3/-’Zz;+; Zarccos 3Z4-^7ZQ4-пп/л ,
/о /э / 5Ь /5 /© /э /4© /4
к,п<ЕЪ. 7. при ae[-^2;^2j х = ±arccos а/р4-л^4-2ли,
(-оо; -у/2)lj(V2; 4-оо) хе0. 8. при
arccos 4- ли,
и е Z; при
а е
и е Z; при
145
9. при я е (-qo;0)U(1;+°о) хе0; при ле[О; 1]
х = arcsin-^L--?-- +(-!)* arcsin——+л£, к е Z.
^2a2 + 2 ylla2 +2
10. [V5 -1; 2].
§7
1. ^+ли, к,пе%. 2. hgZ. 3. л%;
&,hgZ. 4. л%; ^Z+ли, k,nd, 5. и-VX
п + \/л, п eL. 6. п/~ + ™А\ Vfzc 4Л/Х» и g Z. 7. ±ЛХ + 2ли;
/4 /12 /о /16 /4 /5
Ул+™/>, wgZ. 8. ли; llAa+llk/^ 9. 7/ + 2л'Х;
/4 /2 / 2U / 1U /о /э
1 и2 -2
2л^Х, k,neZ. 10. при Ы < 2 х = ±—arccos--+л£,
/J 2 2
A gZ.
§8
1. neZ. 2. //8+Л//4’ ±^+л£, Z:,hgZ.
3. 7Х + Л/Х; л/п+л^ A:,weZ. 4. 7/п + л'Х> hgZ.
/4 /2 /1U /3 /Ю /3
5. ±/{2+Л%’ jteZ’ 6> %+Л%’ ke7j- 7’ Г1ри
а е (-°о;^/)и(1;+<») хей; при
«e(-oo;-VI)u(VI ; +ooj
XG0. 9. при
ае(’°°;“%]и[Х;+00)
х = ±—arccos-----+—,
4 16бг-1 2
п е Z;
при a g ( %;Х) хе0, 10, при а е (-ао; 6] U (8; + оо)
х = ^+л^, hgZ; при hg(6;8] х = //4+Л//2’
х = ±J^arccos(n -7) +л%, Zr, и е Z.
146
§9
1. Зли, neZ. 2. п/-+™А\ ±ln/Q+2™/i, nel. 3.
(_1)”+1л/ +яи/ „eZ. 4. ли/. ±л/+2лА-, i,neZ.
v f /12 /2 /2 /о
5. -я^+ли; -//24"2л^; +(-l)Z V2 arcsin^Кл/;
2л/и, kj,m,nel. 6. ли; ±я/^4~л/с, &,neZ. 7. у^4-71/^
-//б’|_л//2» ZreZ. 8. при а е ^0; х=ли, neZ;
г 1 \ . 1 1 п
при а е 11; + оо) х-ли, х = ±—arccos------+ ли,
2 2а
. 1 ( 1+л~ ГI/ А
х = ±—arccos]--+ ли, /ieZ; при яеН4;1) х=ли,
2 I 2а ) L/J 7
х = ±—arccos-——+ппу neZ. 9. при а е (-оо; -3)U(1; + °о)
2 2а
х = 7у2+71к, keZ,; при а е[-3; 1] х=па,
. 1 1+д „
х = ±—arccos-+ ли, neZ.
2 2а
§10
1. 2л"^, neZ, пФ1к. 2. 0. 3. пк/2\ ±2^/+2ли, k,neZ.
4. х = 2л^, k*7l, kJeZ; х = ^+2л^, и*9/+4,
n,ltZ. 5. //4+л//2» k,neZ. 6. к *14/,
k.l^Z, 7. при а = ^2*л(2и-^), k,neZ хе0; при
а +л(2и k,n^Z х - ^-b^(2Zr+ 1), к g Z.
§11
И^+4ли) , neZ0;
, meN.
1. ^ + 2ли; ^^2+2я/7’ -^^24-271,7’ weZ.2. ^^2*4ли
^4л/л-
3. (-1)^2+Л^2’ keZ' 4‘ 2лл; “/^4-71,7’ -^2^2л/7’
weZ. 5. -7Ь^+ли; (~0”+1 +л/4’ neZ.
/4 \ / / © / z
147
6. (“9” //4 + /z4+7U7’ neZ. 7. ^ч-2ли; лч-2ли, neZ.
8. ^2+2 ли; 2 ли; ^ч-ли, neZ. 9. ^+ли, neZ.
10. ^+2л£; //4+^Л//3’ А: е Z. 11. при
при а е
х = (-1)л arcsin(flV2 +2^/2 ч-71^,
_ л.
§12
1. arctg3/^+л£; лА-arctgJ^, kEZ. 2. пк\ ± arctg VI ч-л£;
±л/ч-лА:, к е Z. 3. -ll/„t+2iik, kEZ. 4. ±nX^-7tk\ ^/ч-лА',
/3 /2 /6 /2
к e Z. 5. ^2+2л&, к e Z. 6. ±2 arctg3 ч-2ли;
arctg^3 - 2 VI)
Ч-ЛИ,
2arctg^2 ±Vs)
+ 2ли,
и e Z.
8.
neZ. 9.
4я%, AeZ. 10. Tt + 2itk-
±4^/+4nA, A-eZ.
§13
1. ^+л£, kEZ. 2. ±^ч-лА', kEZ. 3. ^ч-л£, kEZ.
4. Л//2+//2» kEZ. 5. ту^+пк, kEZ. 6. 2ли, neZ.
7. л^2 +/^4 ’ Л//2 ~ ^6 ’ 77 e • 8. лА'; - + nk; - arctg 3 + Tik;
kEZ. 9. ^ч-л^; - arctg 3 ч- nk, к e Z. 10. при а = 1у^л-ип
xe0; при a e +ли; ^ч-ли) xe0; при п=л^ч-ли
х = ^ч-л^; при и^-^ч-ли х = -^ч-л£;
при
ч-л£, к.п е Z.
х = arctg
§14
1. х^пк, А: е Z. 2. х^лА:, (-1)* л/бч-л/г, к е Z. 3. х^пк,
148
± arctg +nk, kel. 4.
5. ± nZ + nk, к e Z. 6. nk;
/ о
к e Z. 8. +llZ'+Tik, £ e Z.
/о
+л^/; V^+лА', ^‘eZ.
/12 /6 /4
±л/ + nk
/ о
, ^eZ. 7. yC+nk,
9. %+Л^2; ?2+л^’
bZ.
10. ±— arccos—-—-+nk,
/4 /z 2 2
(-1)* V5-1
arcsin—-—keZ. 12.
2 2
keZ. 11. ^+л&;
±^/+л£, keZ.
/ о
13. 25°+90° и, weZ. 14. при a = 41 х = 5л/£+2л&,
keZ; при a =-Jl х = у^+2лк, keZ\ при
a e oo; — V2)u(-V2; V2)u(V2;+oo) x = y+nk, keZ.
§15
1. 6; 4^; 7^; ±^/+2лЛ, £ = 2,3,4...; ±2^+2лп,
и = 0,-1,-2.... 2. +у. 3. 2л£, £ е Z; 5^ + 2л£, к е Z.
4. (-l)^ 7Z+nk, keZ. 5. 7/+л£, к е Z.
6. -arctg^+n&; -arctg^+nfc, keZ. 7. 2л£; -^ + 2л&,
к е Z. 8. ^2+л£, к е Z. 9. 2л£; -^+л£, к е Z.
10. ^+2л£, keZ\ х = ^/9^/9 leZ. 11. при
/о /18/3 г
2V2+2V3
л/б
п е Z; при а
2V2+2V3
V6
при а ф 0 х=ли, п е Z.
х = ± arccos
4-2 ли,
х е 0. 12. при а=0 х е R;
§16
1. Зл^+3л£, k^Z. 2. 2л + 24л&, к е Z. 3. ^2+2л£, к е Z.
4. пк, keZ. 5. 7iky keZ. 6. 0. 7. 7^2+л£, к е Z.
8. 0. 9. лАг, keZ. 10. ^2+лАг; iarctg J^+лАг, к е Z.
149
§17
1. 0 2. 0,5. 3. л. 4. 0. 5. л. 6. 0. 7. 8. У+пк, keZ.
9. 0. 10. л. 11. -3. 12. 0. 13. х = У4+пку, keZ, у=1.
14. х = Т1У +пкА, keZ\ у = n/.+2nn, neZ. 15. (-2,пк)\
^2,^2+nZ:), ZreZ. 16. arctg 41 + ли, + 2л&);
^arctgV2+ли, ^^ + 2nZ:j, &,neZ. 17. ^(-l)^+l +л£,
^ + 2ли); ((-1)^ ^+лА:,^^ + 2ли^, Zr,neZ. 18. (л£,0)
^eZ. 19. (5^ + 2л(и+А:), -^ + 2л(и-£)); (^+2л(и+Аг),
+2л(и-Zr)); + 2л(и+&), ^+ 2л(и-£)) ; (-//з +
+2л(и+^),-^+2K(/?-Zr)j Zr,neZ. 20.
-,,'гу<,]- [у+л-5Уук^'2|- (-|-‘+/<+"‘Х)'
^eZ. 22. (1,1+4*); (-1,1+4Л), keZ. 23. (0,0). 24. (пк, 1),
keZ.
150