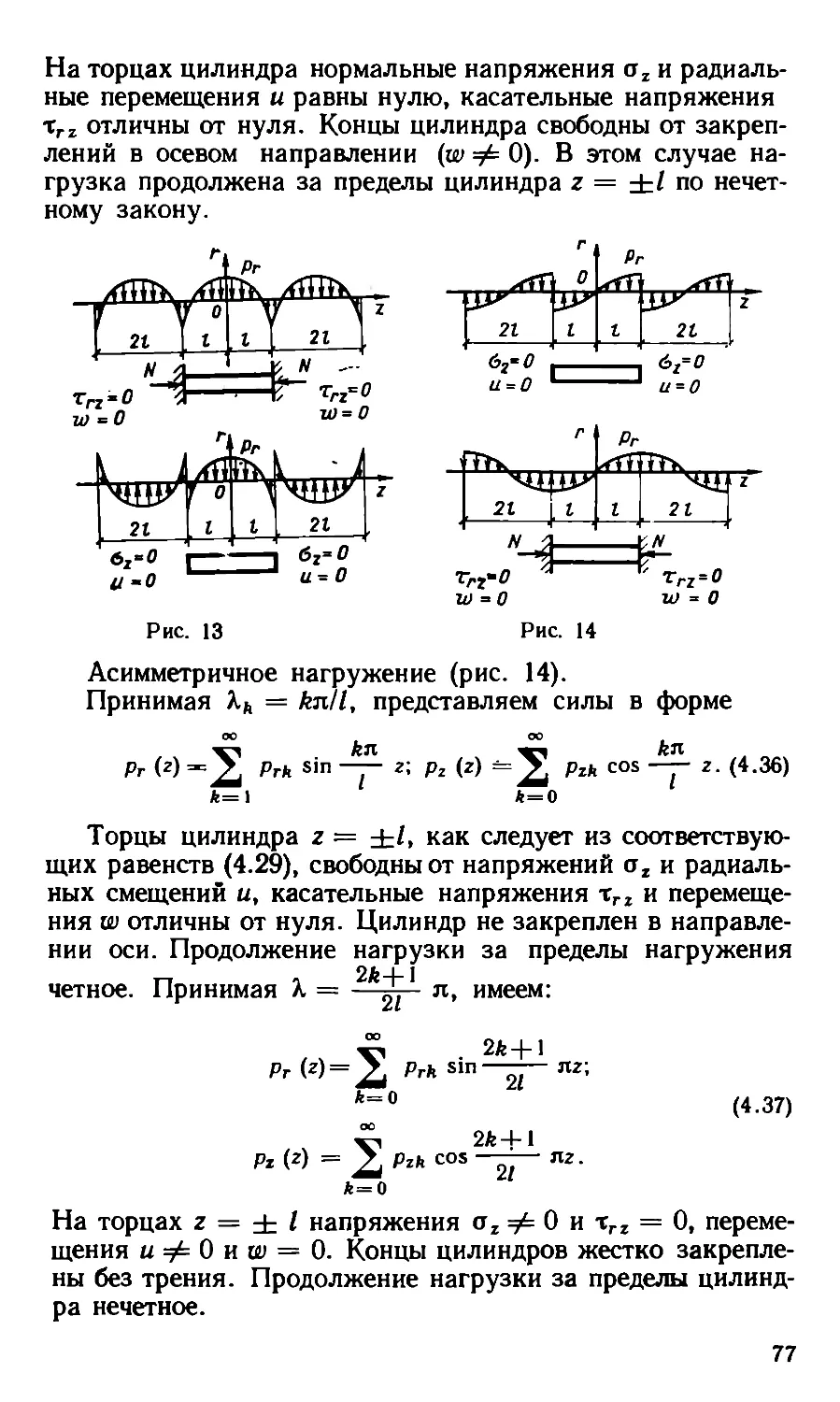
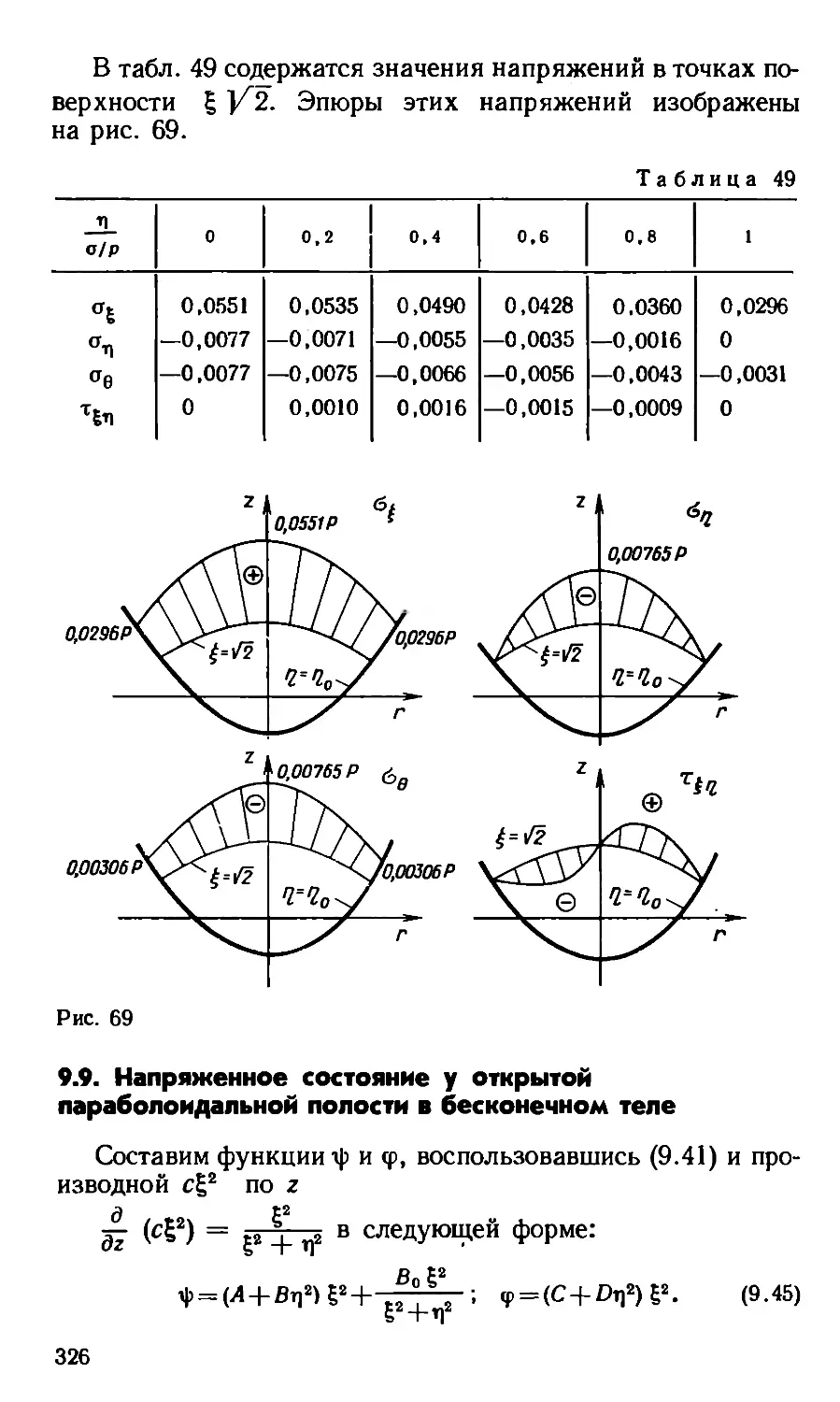
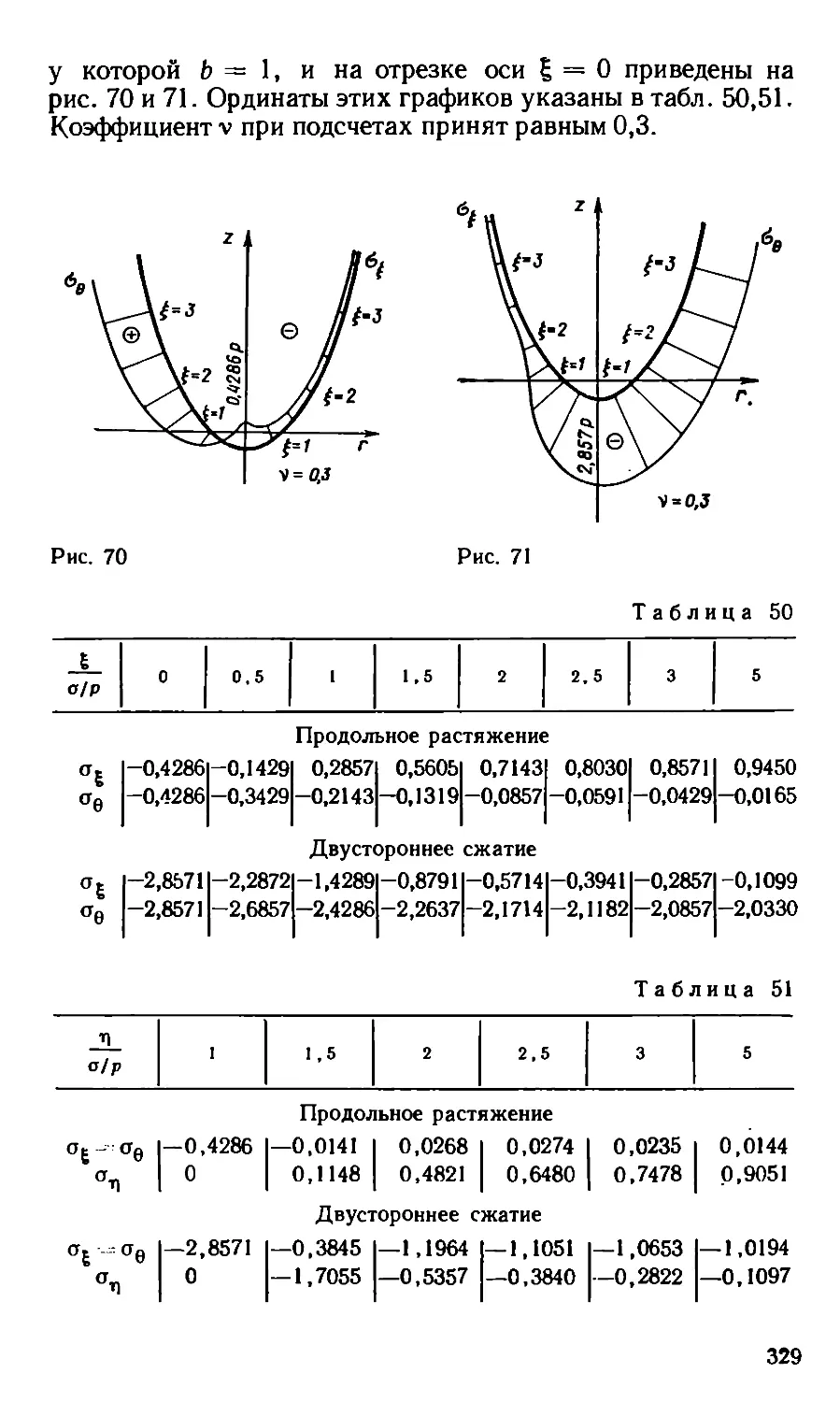
Текст
К. В. Соляник - Красса
ОСЕСИММЕТРИЧНАЯ
ЗАДАЧА
ТЕОРИИ УПРУГОСТИ
Москва Стройиздат
К. В. Соляник-Красса
ОСЕСИММЕТРИЧНАЯ
ЗАДАЧА
ТЕОРИИ УПРУГОСТИ
Москва
Стройиздат
1987
УДК 624.044.2 : 539.3
Соляник-Красса К. В. Осесимметричная задача теории уп-
ругости. — М..: Стройиздат, 1987. — 336 с.: ил.
Рассматривается осесимметричное напряженно-деформиро-
ванное состояние тел вращения. Приводятся решения о дефор-
мациях цилиндров, толстых плит, шаров, конусов, шаровых и
конических оболочек, тел, ограниченных эллиптическими и
параболическими поверхностями. Решения иллюстрированы
результатами подсчета численных значений напряжений и пе-
ремещений.
Для научных и инженерно-технических работников научно-
исследовательских и проектных организаций.
Табл. 51, ил. 71, список лит.: 120 назв.
Печатается по решению секции литературы по строитель-
ным конструкциям редакционного совета Стройиздата.
Рецензент д-р техн, наук, проф. В. 3. Васильев.
НАУЧНОЕ ИЗДАНИЕ
КОНСТАНТИН ВЛАДИМИРОВИЧ
СОЛЯНИК-КРАССА
ОСЕСИММЕТРИЧНАЯ
ЗАДАЧА
ТЕОРИИ УПРУГОСТИ
Редакция литературы по строительным материалам и конструкциям
Зав. редакцией И. X. Наназашвнли
Редактор 3. П. Злобина
Технический редактор Р. М. Вознесенская
Корректор Г. С. Беляева
ИБ № 4104
Сдано в набор 27.08.86. Подписано в печать 22.04.87.
Формат 84X108/32 Бумага кн.Журн. Гарнитура «Литературная».
Печать офсетная. Усл. печ. л. 17,64. Усл. кр.-отт. 17,85. Уч.-нзд. л. 15,68.
Тираж 2000 экз. Изд. № А VIII-1629. Зак. № 2045 Цена 2 р. 50 к.
Стройиздат, 101442, Москва' Каляевская, 23а
Московская типография № 4 Союзполнграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли.
129041, Москва, Б. Переяславская, 46
„ 3202000000—472
С --------------91—87
047(01)—87
© Стройиздат, 1987
ПРЕДИСЛОВИЕ
Элементы инженерных сооружений и машин нередко
имеют форму тел вращения. Выяснение значений напря-
жений и перемещений при деформации таких тел — важная
практическая задача, решение которой приводит к уточне-
нию расчетных формул для определения размеров частей
конструкции и, следовательно, к более рациональному
проектированию.
Напряженно деформированное состояние тел враще-
ния — одна из наиболее интересных областей пространст-
венной теории упругости.Исследования в этой области Ла-
ме, Кельвина, Сен-Венана, Похгальмера, Кри, Вангери-
на, Иериша, Шиффа, Стеклова внесли существенный вклад
в развитие общих представлений механики твердых дефор-
мируемых тел и ее теоретического аппарата.
Большое развитие получили исследования осесим-
метричного нагружения тел вращения или бесконечных про-
странства и полупространства. Изучение осесимметричного
поля напряжений является одной из наиболее развитых
областей теории упругости, уступающей по достигнутым
результатам только плоской задаче.
По разделению уравнений упругости в цилиндрических
координатах для нагружений, не зависящих от угловой
координаты, на две группы общая проблема изучения напря-
женного состояния делится на две независимые части —
определение тангенциального перемещения и двух связан-
ных с ним составляющих касательных напряжений и опре-
деление радиального и осевого перемещений и четырех со-
ставляющих тензора напряжений. Первая часть соответст-
вует обратно симметричному относительно оси распределе-
нию деформаций, т. е. кручению тел вращения, вторая —
симметричному распределению деформаций и поэтому может
быть названа осесимметричной задачей теории упругости.
Осесимметричная задача в отличие от плоской задачи
теории упругости решается с привлечением большого числа
форм функций напряжений. Если в плоской задаче, как
правило, применяются основные построения решений —
либо в форме Эри, либо в форме Колосова — Мусхелишви-
ли, основанной на применении аппарата теории функций
комплексного переменного,— то в области осесимметричной
задачи для получения результатов в частных случаях поль-
зуются решениями Лява, Мичела, Гродского — Папкови-
ча — Нейбера, а в последнее время и решением Положего.
При рассмотрении частных задач применение той или иной
3
формы функций напряжений обычно не обосновывается и
не всегда бывает удачным.
Цель работы — изложение с позиций одной из форм
решений осесимметричной задачи важных ее результатов.
В качестве основной формы принято решение, опублико-
ванное в ряде работ автора. Такой выбор оправдывается,
во-первых, сравнительно простой связью между напряже-
ниями и функциями напряжений — напряжения представ-
ляются первыми производными функций напряжений, в то
время как в решении Гродского—Папковича—Нейбера они
связаны с функциями напряжений через вторые производ-
ные, а в решениях Лява и Мичела — через третьи произ-
водные. Это обстоятельство приводит к значительному упро-
щению при получении результатов в частных задачах и осо-
бенно существенно, если решение производится в криволи-
нейных координатах. Во-вторых, для применяемых функций
напряжений могут быть указаны два простых условия на оси
вращения и два простых условия на контуре в осевом сече-
нии тела, позволяющие определить все постоянные, входя-
щие в решение, до подсчета напряжений. В частности, по-
стоянным значениям одной из функций напряжений соот-
ветствуют поверхности вращения, на которых отсутствуют
аксиально направленные нагрузки.
Большое насыщение монографии примерами решений
частных задач, доведенных до численных результатов, и
графиками распределения напряжений позволит читателю
ознакомиться не только с общей постановкой пробле-
мы изучения осесимметричных деформаций, но и с содер-
жанием ряда работ, посвященных этой проблеме. Разбро-
санность таких работ в журналах, библиографическая
редкость довольно большого их числа и отсутствие единой
методики в решениях — все это затрудняет ознакомление с
ними и как результат тормозит развитие проблемы в целом.
Обилие публикаций, посвященных осесимметричной за-
даче теории упругости, не позволяет привести их полный
перечень в списке литературы. Книга не охватывает все ти-
пы задач осесимметричной деформации тел вращения. Од-
нако, учитывая повышенный интерес к решению простран-
ственных задач теории упругости, можно предположить, что
предлагаемая вниманию читателей монография будет по-
лезна для изучения механики деформируемого тела.
Книгу посвящаю светлой памяти жены Анны Васильевны
Соляник-Красса, оказавшей большую помощь при подготов-
ке настоящего издания.
4
Глава 1. ОСНОВНЫЕ УРАВНЕНИЯ
1.1. Осесимметричное нагружение тел вращения
Отнесем тело вращения к цилиндрической системе коор-
динат OrOz, совместив ось Oz с осью тела (рис. 1). Обозна-
чим через и, v, w перемещения точек тела в направлении осей
г, 6 и z, через ег,ее, ez, yez, yzr компоненты тензора
деформадий в координатной системе OrOz и через ог,
<*б, 0Z, тгб, tOz, тгг компоненты тензора напряжений в той
же координатной системе.
Уравнения статики в перемещениях при отсутствии объ-
емных сил в цилиндрических координатах имеют следующую
форму1:
, « №
(Х+2И)^—
Or
, 1
(Х+адТ^ё
dcaz
~дё
(1-1)
, 00 Л 1
(Х+2^) —— — 2р.—
OZ г
Здесь О = ег + е© + ez — объемная деформация и сог,
<ое и (oz— компоненты вращения, связанные с перемеще-
ниями и, v, и w формулами:
ди и 1 dv dw
$= + до” "л ’
дг г г дб dz
1/1 dw dv \
г 2 \ г dQ dz )
1 ( ди dw \
(,2)
2 \ Oz Or /
1 I drv ди \
co, -=— -----—------ ,
2r \ dr dG ]
1 Впервые уравнения теории упругости в цилиндрических коор-
динатах были получены Ламе и Клапейроном в 1831 г. [99]. Они
приведены в курсах теории упругости [43], [48], [77] и др.
5
где X и |л — коэффициенты Ламе:
Ev
______________Е
~ (l+v)(l-2v) 1 2 (1 +v) ’
здесь v—коэффициент Пуассона, Е—модуль нормальной упругости.
Предположим, что нагрузка, действующая на тело вра-
распределена симметрично относительно оси Oz.
Тогда перемещения точек тела также
распределяются симметрично, т. е.
они не зависят от координаты 6: и =
щения,
Уравнения статики (1.1) при этом
значительно упрощаются и получают
вид:
д
дг
дЬ дш
(Х + 2И) —+ 2р— =0;
дг дг
1 drv
дг
дд
дг
(*+2н)
— 2 р.---------
дг
д2 v
£Г = °= (1.3)
агш =0,
дг
где объемная деформация
и вращение
ди
дг
dw
дг
(1.4)
и
1
о - (i)fi —-—
6 2
ди dw \
дг дг /
(1.5)
В полученных выражениях перемещения разделены:
перемещение v входит только во второе уравнение, а пере-
мещения и и w — только в первое и третье. Поэтому можно
отделить задачу определения перемещения v от задачи опре-
деления перемещений и и w. Первая задача соответствует
кручению стержней переменного сечения1, вторая — случаю
напряженного состояния тел вращения, называемому осе-
симметричной задачей.
Последняя задача и служит предметом настоящей книги.
1 Подробный список литературы по кручению валов переменно-
го сечения указан в [8] и [63].
6
1.2. Основные функции напряжений
Как показано ранее, решение осесимметричной задачи
сводится к интегрированию дифференциальных уравнений
равновесия
(Х+2И) — +2Н — = 0;
dr OZ
дЬ _ 1 дгы
(Н-2И)— ---— = 0
дг г дг
(1-6)
с последующим удовлетворением условий на поверхности
тела.
Решение может быть достигнуто различным образом. Во-
первых, можно найти для перемещений выражение и или
w путем решения уравнений1
------------4------— ---I и = 0;
дг2 г дг дг2 г2 /
/ д2 \ д d2 V
I -------------I- --- I £0 = 0
\ dr2 г dr dz2 /
г
в форме, соответствующей той или иной конкретной задаче
(например, в форме произведения функции координаты г
на функцию координаты z). Затем подобрать коэффициенты
этих выражений так, чтобы удовлетворялись уравнения
статики (1.6)2.
Таким образом, основные уравнения будут удовлетворе-
ны и полученные значения и и w дадут значение перемеще-
ний во всех точках тела вращения при осесимметричном за-
гружении.
Во-вторых, решение можно свести к отысканию некото-
рых вводимых определенным образом вспомогательных
функций — функций напряжений, выразив предваритель-
но перемещения и все компоненты тензора напряжений через
эти функции.
Такие функции, служащие решением осесимметричной за-
дачи, были введены Лявом и Мичелем, а также могут быть
получены из общих решений уравнений теории упругости
Галеркина и Буссинеска—Гродского—Нейбера—Папко-
1 См. курсы теории упругости А. Лява, [48], А. С. Лейбезона
[43] и др.
2 Такая последовательность решения принята, например, в ра-
боте А. П. Коробова [39]. См. также [92].
7
вича1. Для составления решений частных задач в настоящей
книге использована новая форма функций напряжений
[64], выгодность применения которой будет указана в даль-
нейшем. Представление напряжений и перемещений через
эти функции напряжений осуществляется в результате
нижеследующих преобразований.
Второе уравнение статики (1.6) выполняется, если поло-
жить
Л 2(1—v) 1 дф 1—v 1 дф
$ - - —----; й) =-------------------- , (1.7)
Х+2р. г dr ц, г дг
где Ф = ф (г, г) — некоторая функция переменных гиг.
Заменяя “О' и со в первом уравнении статики (1.6) их зна-
чениями (1.7) через производные функции <р, получим:
д / 1 дф \ д / 1 дф
дг \ г дг )' дг \ г дг
(1.8)
или в символической записи:
V2 <р = О, где V2 — опе-
ратор вида
д / 1 д
У2=Г-----------
дг \ г дг
д2
dz2
д2 1 д д2
дг2 г дг дг1
(1.9)
Следовательно, уравнения статики в перемещениях вы-
полняются, если задать -0 и со в форме (1.7) и если <р =
= <р (г, г) определяется как решение уравнения (1.8).
Имея в виду связь (1.4) между объемной деформацией Ф и
перемещениями и и w и связь (1.5) между вращением со и
перемещениями и и w, перепишем (1.7) в форме
1 дги dw 2(1 —у) 1 дф
г дг "1" дг X —|— 2р- г дг
ди dw 2(1—у) 1 дф
дг дг Н Г дг
(1.10)
Введем новую функцию Ф (г, z) условиями:
X дги . dw 1 дф
---—+(Х+2И)— =
г дг дг
г дг ’
дФ
дг
(1.11)
1 Основные формы функций напряжений приведены далее.
Функции Лява и Буссинеска — Гродского — Папковича — Ней-
бера широко используется в оригинальных работах, а также вошли
в учебную литературу (см., например, [51], [53], [77], [82] и т. д.).
8
Вычитая из первого уравнения (1.10) первое уравнение
(1.11), поделенное на X + 2р., и складывая второе уравне-
ние (1.10) со вторым уравнением (1.11), поделенным на р,,
получаем:
дги 1 д
дги 1 д
1ф + 2(1—v) <р].
дг 2р. дг
Отсюда следует первый фундаментальный результат —
связь между радиальными перемещениями и и функциями
напряжений <р и Ф:
и
------[ф + 2(1-у)ф].
2р г
(1.12)
Подставим в уравнение
( д2 1 д д2 1 \2
------4-----------+----------— и = 0
\ dr2 г dr dz2 г2 /
(1-13)
вместо и его значение (1.12)
f д2 1 д д2 1 V/ Ф+2(1— у)ф \
\ dr2 г dr + dz2 г2 ) I г /
Выполнив здесь дифференцирование и приняв во внима-
ние, что функция <р удовлетворяет уравнению (1.8), получим
основное дифференциальное уравнение,определяющее функ-
цию напряжений Ф:
д2 1 д д2 \2
—— —----------4------ Ф = 0
dr2 г dr dz2 /
(1.14)
или V4 Ф = 0, где V4 = V2 V2.
Заменив в (1.11) значение перемещения и через функции
Ф и <р, находим производные перемещения w по г и по г
dw 1 1 дФ lid л — о л 1Ф + 2(1 V) ф]; дг р г дг 2р г дг
dw dz 1 1 дФ X 1 д л л , х , — — [Ф 4-2(1 — v) ф] X-f-2p г дг (Х4-2р)2р г дг
или1
1 Здесь при преобразованиях принято во внимание, что
2р 1—2v X у
Х-|-2р 1—у ’ Х4-2р 1—у
9
(1.15)
dw lid
— ------— [Ф—2(1—v) Ф];
дг 2р, г дг
dw lid
—— =_—-------— ((D-j-2v<p).
дг 2ц г дг
По условию интегрируемости этих уравнений необхо-
димо выполнение равенства
dw
’дг’
д
dz
д
дг
dw
дг
Подставляя сюда значения производных (1.15) получим:
д2 Ф 1 дФ d2 Ф d2 ср
— +------= 2 —-
dr dz2 дг2
(Мб)
dr2
Этим равенством устанавливается связь между функциями
Ф и ф. Оно будет выполнено, если задавать функцию Ф в
форме
dip
ф=ф+г—V- (1.17)
дг
dtp
или Ф = ф—г----, (1-18)
дг
где ф — функция г и г, удовлетворяющая дифференциальному урав-
нению второго порядка
д2 ф 1 dip d2 ф
dr2 г дг + dr2
(1.19)
в символической записи ?2ф = 0.
1.3. Деформации и напряжения
Воспользовавшись выражениями, связывающими состав-
ляющие тензора деформации с перемещениями в цилиндри-
ческих координатах
ди 1
дг 6 г d0 г
do
ez = ~ ;
дг
(1.20)
1 ди dv v dv 1 dw
Vre = ~ ~d6~+ ~dr~~ 7вг= “d7 + ~ ~dQ~'
du dw
Yzr = —+ —.
дг dr
dv и
10
при принятых предположениях и = и (г, z), v = 0, w =
= w (rz) имеем:
ди и dw ди dw
8г=”л7"’ Ее== * ®г= “3 • Yrz = ~ + “т-;
дг ° г дг дг дг
Yre = Yez = °- (1-21)
Вводя в эти равенства вместо перемещений и и w функ-
ции Ф и ф в соответствии с выражениям^ 1.12) и (1.15), по-
лучим:
1 д Ф+2(1—v)<p
ег =------------------
2ц дг г
1 Ф+2(1— v) ф
Bfi =---------------.
®. 2ц г2
1 1
-------(Ф + 2Уф);
2ц г
1 1 дФ
ц г дг '
(1.22)
Применяя закон Гука в форме
ог = А.ф-|-2цег; ан = Х{Ц-2цей- <г2=Х{Н-2це2;
(1.23)
Tr0 = HYre; ^ez^HYez- br = HYzr.
1 —2v 1 dw
где 0 =----------—,
ц r dr
(1.24)
приходим к следующим выражениям для перемещений:
д Ф-}-2(1—у) ф 2v д<р
аг =~7 + ' “7 ; т/-е = о»
дг г г дг ™
Ф-f- 2 (1—у) ф 2у дф
= \---—+----------t6z = 0; (1.25)
г2 г dr v
1 дФ 1 дФ
CTz—— , ; Tzr— ..
г dr г дг
Для простоты записи введем обозначение
0„?+2<1-у)ф_ AJy , d.26)
г2 г дг
тогда для напряжений окончательно получим:
1 дФ 1 дФ
ог=-----— — й; ог = —---------—;
г дг г дг
(1.27)
2(14-v) дф 1 дф
Og— ~г О; тг2 —
г дг г дг
Напряженное состояние тела вращения при осесиммет-
ричном загружении характеризуется четырьмя составляю-
щими тензора напряжений — нормальными напряжениями
11
ar, oe, oz и касательным напряжением Trz.
Сумма напряжений ог и oz
иг + иг= —Q.
(1.28)
1.4. Граничные условия
На контуре осевого сечения тела вращения напряжения
связаны с радиальной рг и осевой рг составляющими внеш-
ней нагрузки (рис. 2) равенствами:
Рис. 2
or cos (л, г) 4-
+Trz cos (п, z) =рг;
Tr2C0S(n, r) +
+az cos (л, z) = pz.
Подставляя во второе
равенство
dz
COS (n, r) =----;
ds
dr
cos (л, z) = — ——
ds
и значения напряжений or и xrz через функцию напря-
жений Ф, получим:
1 дФ dz 1 дф dr
г dz ds г dr ds ?z
d(P
или ----= rpx
ds
на контуре осевого сечения (г = a (z)).
Произведем подстановку
dr dz
cos (п, г) =-; cos (nz) =---
dn dn
и напряжений (1.27) в первое уравнение (1.29):
1 / <ЭФ дг дФ dz \
— --------------Т~ —ficos (л« г) = Рг-
г \ dr on dz dn J
Отсюда
dФ
= г [й cos (л, г)+рг]
ап
на контуре осевого сечения (г = a (z)).
12
Итак, рассмотрение граничных условий на контуре осе-
вого сечения тела вращения определяет два равенства:
dO dG>
-j- = rpz; —— =r[Qcos (л, r)+pr], (1.30)
as an
связывающих функцию напряжений Ф с внешней нагрузкой,
приложенной к поверхности тела.
В том случае, когда поверхность тела свободна от внеш-
них сил, условия (1.30) упрощаются и получают вид
аФ
® = const; ---=rficos(n, г). (1-31)
dn
Из первого равенства (1.31) следует, что линии Ф =
= const в осевом сечении тела соответствуют поверхностям,
свободным от нагрузки, направленной вдоль оси вращения.
Кроме выполнения уравнений (1.29), сводящихся, как
показано, к условиям (1.30) и (1.31), функции напряжений
Ф и ф должны соответствовать некоторым условиям, нала-
гаемым на перемещения на оси вращения тела. В самом деле,
по симметричности задачи сдвиги и радиальные перемеще-
ния на оси вращения равны нулю. Первое требование в со-
ответствии с последним уравнением (1.22) приводит к ра-
венству Ф/г = 0 при г = 0.
На основании второго требования, т. е. по условию ра-
венства нулю перемещения и на оси вращения, 1Ф + 2 х
X (1 — v) ф] = 0 при г = 0.
Следовательно, функции напряжений Ф и ф при осесим-
метричном загружении сплошных тел вращений должны
быть взяты так, чтобы
—— Ф = |0; —— <р = 0 при г=0. (1-32)
г г
В приложениях иногда удобно, чтобы функция Ф была
равна нулю на контуре в осевом сечении тела и имела по-
стоянное значение Ф = С на оси вращения. Условия (1.32)
при этом получают форму
-у(Ф — С) = 0; -^-[Ф + 2(1—v) ф]=0 (1.33)
при г = 0.
Таким образом, задача отыскания перемещений и напря-
жений при осесимметричном их распределении сводится к
построению функций напряжений Ф и ф, удовлетворяющих
13
дифференциальным уравнениям (1.8), (1.14) и условиям
(1.30) и (1.32) или (1.33), связанным между собой равен-
ством (1.16).
Если тело вращения является полым, то условия (1.32)
теряют смысл, а условия (1.30) или (1.31) должны выпол-
няться как на внешней, так и на внутренней поверхностях.
1.5. Условия статической эквивалентности
В часто встречающихся случаях осесимметричного за-
гружения тел, весьма удлиненных вдоль оси вращения
(стержней), граничные условия (1.30), могут быть смягчены.
Для таких тел точного удовлетворе-
ния условий (1.30) нужно требовать
только на той части контура осевого
сечения, которая соответствует боковой
поверхности тела, и можно удовлетворять
условиям на торцах лишь в смысле
статической эквивалентности.
Если принять во внимание, что ?е2
= 0 и что напряжения т2Г и а2, возника-
ющие в поперечном сечении, момента
относительно оси вращения не дают
(рис. 3), то по условиям статической эк-
вивалентности напряжений внешним
силам, приложенным на торцах или на
части боковой поверхности, лежащей по
одну сторону от рассматриваемого поперечного сечения,
должны выполняться следующие интегралы:
( Trxcos0dF -0; f т,.2 sin QdF •=0; | azdF— N\
F F F
| a2 r sin 0dF-- 0; f o2 cos fidF 0,
F F
(1.34)
где F - na2 — площадь поперечного сечения, a N — нормальная
сила в рассматриваемом сечении.
После замены в первом интеграле dF через rdrdti и тг2
последним выражением (1.27) получим:
2л а 2л а
nd(& I С дФ
---cos 6drd6 = sin 0 I -dr=0.
dz I J dz
oo oo
14
Аналогичным образом нетрудно убедиться в равенстве
нулю второго интеграла. Вычисление четвертого интегра-
ла дает
2л а
г sin 0
дФ
дг
2л а
drdti = cos 6 J* г
о о
ЗФ
дг
dr = O.
К такому же результату приводит рассмотрение послед-
него условия статической эквивалентности.
Итак, при осессиметричном распределении напряжений
и перемещений из шести условий статической эквивалент-
ности пять выполняются тождественно при любом значении
функции напряжений Ф. Пользуясь третьим условием:
| ozd F.= N, можно связать функцию Ф с равнодействую-
щей внешней нагрузки, растягивающей стержень. Под-
ставляя в это равенство значение о2, получим:
2л а а
rdrdG= — 2лФ = —2лФ (аг) —/V
1 дФ
г дг
о о
о
для сплошного тела и
—2 л [Ф (a, z) — Ф (а0, z)] = N
для полого. Здесь через а и а0 обозначены соответственно
радиусы внешней и внутренней поверхностей тела вращения.
Следовательно, контурные значения функции Ф свя-
заны с величиной нормальной силы равенствами
N
Ф(а, г) = ———, (1.35)
2Л
если тело сплошное, и
/V
Ф(а,г)—Ф(а0, г)= —— , (1.36)
2л
если тело полое.
Когда боковые поверхности свободны от распределенных
сил осевого направления, то Ф (a, z) или разность Ф (а, г) —
— Ф (а0, г) постоянны и связаны с нагрузкой Р, приложен-
ной к торцам стержня,
Ф(а, z) = -4“ (1 37)
2Л
ИЛИ
р
Ф (а, г)—Ф(а0, z) = —--. (1.38)
2л
15
Этим условием определяется значение постоянной в (1.31).
Если осевая нагрузка pz равномерно распределена в
направлении оси z, то Ф (а, г) или Ф (az) — Ф (a0, z) должна
быть линейными функциями координаты z, при линейной
осевой нагрузке р2 — квадратичными функциями z и т. д.
Из всего вышеуказанного следует заключение: при ре-
шении осесимметричной задачи напряжения можно выра-
зить через первые производные двух функций, одна из ко-
торых (ф) является решением дифференциального уравнения
второго порядка, а вторая (Ф) представляет собой комбина-
цию первой с некоторой функцией (ф), отличающейся от
первой только значениями коэффициентов. В других же
известных формах решения задачи об осесиметричном за-
гружении тел вращения напряжения представлены вторыми
производными . (решения Буссинеска — Гродского — Пап-
ковича — Нейбера) или третьими производными (решение
Галеркина—Лява и решение Мичела) функций напряже-
ний, что значительно усложняет получение результатов
для частных задач, даже в простых случаях.
В отличие от других форм решения осесимметричной за-
дачи для введенных выше функций напряжений можно ука-
зать два простых условия на оси вращения и два простых
условия на контуре в осевом сечении тела, позволяющие
определять все коэффициенты, входящие в задаваемые функ-
ции, до подсчета напряжений. В частности, постоянным зна-
чениям одной из функций напряжений соответствуют поверх-
ности вращения, на которых отсутствует аксиально направ-
ленная нагрузка. В случаях осесимметричного загружения
удлиненных вдоль оси тел вращения (стержней) можно ука-
зать весьма простые условия статической эквивалентности,
связывающие одну из основных функций с внешней нагруз-
кой на торцах.
Указанные особенности рассмотренной формы решений
приводят к значительному упрощению вычислений и умень-
шению их объема, что особенно сказывается при применении
криволинейных координат.
1.6. Решение при нагружении объемными силами
Распространим приведенную форму решения осесиммет-
ричной задачи на случаи деформаций тел вращения под дей-
ствием осесимметрично распределенных объемных сил.
Уравнения равновесия в этих случаях записываются в виде
16
дЬ дш
(Х+2И) —+ 2ц—4
dr dz
2ц д гол
(Х-|-2р) ~ — -
дг г дг
(1.39)
гДе Sr — радиальная и gz — осевая составляющие объемной силы.
Уравнения (1.39) выполняются, если положить
2 (1—v) Г 1 д дф2 ]
V) I 1 д Зф2 ’
— —"Т" (ф+фг)—-г— .
[ г дг or
(1.40)
где ф—.общее решение однородной системы (1.06), а фг и ф2 —
частные решения неоднородной системы (1.39).
Фх-
Подстановка (1.40) в (1.39) приводит к следующим урав-
нениям, служащим для определения функций <рг и
д2 фг 1 дфг _ д1 фг 1
дг2 ~ ~г дГ + dz2 = ~ 2(1—v) 8г Г ’’
д2 ф2 1 дф2 д2 ф2______1
дг2 + г дг + дг2 ~ 2(1—v) 8z
или в сокращенной записи
-7йЬгг'г;
Дф2= ~ 2(1—v) 8z'
Вводя равенствами
1 дги . dw 1 дФ п дф2
----Т- +(^+2Н) -Z-= --------— - 2 (1 — V) -f-
г dr dz г dr dz
1 д ( ЗФ2 \
+-------г------- I;
г дг \ дг /
(ди dw \ 1 дФ Зф2 д2 Ф2
(1-42)
(1.43)
и
новые функции Ф и Ф2 и действуя так же, как в п. 1.2, полу-
чаем для перемещения и и производных перемещения w
следующие выражения:
1 1
ЭФИ
и =
2р г
дг
17
dw 1 ( 1 д
(1-44)
dw 1 f 1 d
~ =— {—------------— [<D-i-2v (фЧ-фг)|-;-
dz 2ц | г dr
d<pz 1 d ( дф,
t2(l-2v)-^-+-------— r—
dz r dr \ dr
По условию интегрируемости двух последних равенств
должны выполняться связи
d2 v dq>2
¥2Ф=2 (ф+фг)+-------grr. дф2_2-^-, (1.45)
на основании которых функции Ф и Ф2 должны быть взяты
в форме
d
Ф = ,Ф-Т^г —2v<pr-h?(ф-Ьфг); Фг+'Фг-Нфг. (1-46)
OZ
rz dgr gr z
где V^-0. (1.47)
Воспользовавшись второй связью (1.45) между функциями
Ф2 и ф2, перемещение w можно представить в виде
дФ2
a»=air+4 (1—v) ф2 ———, (1.48)
OZ
где wr определяется после интегрирования равенств:
da/r lid,
—=----------— ]Ф—2(1—v) (q>+<pr)]: (1.49)
dr 2р г dz
dwr lid ft ,
——= _ ----------— [Ф + 2? (<р +<pr)].
dz 2ц г dr
Вычисляя по значениям (1.44) компоненты деформации
и пользуясь законом Гука, получаем для напряжений сле-
дующие формулы:
1 дФ д2 Ф2 d(f>z
°г=--------— й— ——— +2v—— ;
г dr dr2 dz
2 (1+v)
®e- r
d 1 d<Dx dq>2
— (Ф+Фг +Q---------77f+2v—? ;
dr r dr dz
1 дФ , J d
r dr r dr
(1.50)
18
где
дф
dz
д2Фг
drdz
+ 2(l-v)
дф2
dr
1 , 2 d
Й=-Г [Ф + 2 (I—V) (ф + фг)] —---------------— (ф-ГФг).
г1- г dr
(1-51)
Подстановка напряжений в контурные условия (1.29)
и преобразования, аналогичные преобразованиям в п.1.4,
дают
дф
ds
= rpz
d(Dz
dr
dz /
(1-52)
dO
dn
Q—2
-2(l-v)r-^-Z;
dn
d
cos (nr)-I——
dn
на контуре осевого сечения.
Таким образом, при решении осесимметричной задачи с
учетом массовых сил в первую очередь надлежит определить
частные решения уравнений (1.41), и (1.47), т. е. значения
функций фг, <pz, фг иф2. В конкретных случаях нагружения
вид этих частных решений устанавливается достаточно
просто. После этого определяется форма контурных условий
(1.52), и задача сводится к отысканию функций ф и <р, им со-
ответствующих. Задача о нагружении массовыми силами фор-
мально сводится к задаче о нагружении тела вращения по-
верхностными силами, вид которых определяется частными
решениями (1.41) и (1.47), т. е. заданием нагрузок gr и gz
1.7. Функции перемещений
Нетрудно установить связь между введенными функ-
циями <р иФи функциями напряжений Буссинеска—Брод-
ского—Нейбера—Папковича, Галеркина—Лява и Мичела
[66]. С этой целью введем в рассмотрение новые функции
f и F условиями
д/ dF
w—r --- ; ф=г ---
т dr dr
(1.53)
Подставляя эти значения в (1.8) и (1.14), получаем урав-
нения, которым должны удовлетворять функции F и f
Iff1 1 d d2 \ / d2 Id d2 \2
+ !- -l/~0; 4- +- F — 0,
\ dr2--------------------------------------------r dr-dz2 / \ dr2-r dr-dz2 /
(1.54)
19
или, если ввести операторы Лапласа
д2 1 д д , / д2 1 д д2 V2
dr2 г dr dz2 \ dr2 г dr dz2 /
более компактно: А/ = О, A2F = 0.
Функции F и f не являются независимыми. Действитель-
но, подставляя (1.53) в равенство (1.16), после некоторых
преобразований получим:
д2 f
bF = 2—±-, (1.55)
dz2
откуда следует, что функция F должна быть задана в форме
df
F = r+z-±-, (1.56)
дг
где g — некоторая функция гиг, удовлетворяющая уравнению
Ag-O. (1.57)
Заменим в производных перемещения w (1.15) функции
ф и Ф функциями f и F
dw 1 д2 dw
--------------[F —2 (1 —v) /1; - =
дг 2ц drdz 1 ' дг
1 1 д Г dF л df 1
= —-----------г------|-2vr-- .
2ц г dr [ dr dr J
Из второго уравнения (1.54) и условия (1.55) следует,
что
1 d / df \ d2/ 1 d / dF \ 2 д2 f д2 F
г дг \ дг / dz2 'г dr \ dr ) dz2 дг2
поэтому последнее равенство преобразовывается к виду
dw 1 д2
— = — — (F-2(l -v) /1.
дг 2ц дг2
Таким образом, введение функции F и / позволяет вы-
разить перемещения и и w через частные производные этих
двух функций. Воспользовавшись (1.12) и (1.53) и последни-
ми выражениями производных перемещения w по г и по z,
найдем:
id id
« =— — [F+2(l-v)/J; u- — — [F—2 (1 —v) f\. (1.58)
2ц dr 1 2ц dz
Далее, пользуясь законом Гука или заменяя в (1.25) ф
и Ф функциями f и F, для напряжений получим:
20
2v df
d1 2 „ лл , 2v df Id
or = (^+2/)+ oz----
dr2 r dr r dr
Id t d2 f
oe =----— (f+2/)F2v —
° r dr dr2
f dF
r-----
dr
d2 F
drdz
(1.59)
; Tr2 =
Здесь напряжения связаны вторыми производными с функ-
циями F и /.
Функции f и F, производными которых определяются пе-
ремещения и и w, можно назвать функциями перемещений.
Введение их принадлежит Веберу [120].
С решением Вебера тесно связаны решения, предложен-
ные Буссинеском и Тимпе, в которых перемещения пред-
ставлены также первыми производными двух функций.
Положив в (1.58)
F+2(l-v)/ = B(r, г)~-Р(г, г),
OZ
получаем выражения для перемещений в форме, указанной
Буссинеском [881,
1 dB I
и =----------; w ----
2р dr 2р
дВ
—-_4 (1 — v) р .
dz
(1-60)
Здесь В (г, z) — бигармоническая и р (г, г) — гармони-
ческая функции; по введению этих функций в соответствии
с равенством (1.55), получаем:
др
АВ—2—^—. (1.61)
OZ
Если в (1.58) положить
df 1
£ — 2 (1 — v) fг------------=---------ib».
v dr 2(1—2v)
то перемещения и и w представляются в форме Тимпе [1181:
1 [ d [ 1 \ 2(1—v) 1 1
1 d : 1 \
2ц dz 2(1—2v) >
Функции и ф2 связаны с объемной деформацией О и
вращением w равенствами
1 1 1 —2v
-7— — Фа-—-------г Г(о О-63)
2ц 2ц 2(1 —v)
и определяются как решения однородных уравнений
Аф, =0; ф, = 0. (1-64)
21
Составление выражений для напряжений в решениях
Буссинеска и Тимпе не представляет труда после соответ-
ствующих замен в формулах (1.59) функций / и F функциями
Р и В или хр! и ф2-
1.8. Решение в форме
Буссинеска — Гродского — Папковича — Нейбера
Представив функцию F в виде
F=fo—г— +2
дг
df2
dz
[см. (1.56)1 для перемещений и и w по (1.58), получим:
1 д Г . dfi df*
« =—— /o + 2(l-v) (A+f2)-r^- + z^- ;
2р. дг [ dr . dz
1 д d/j df2 1
w = — — [/о -2 (1 - v) (/, 4-/.J -г _|_2 -22-1
2р dz dr dz |
Введем следующие обозначения:
/о+2 (I—v) (/2-/.)^ И <р0:
2(1 —V)
d/i = И ( . д!г Н (
дг 2 (I—v) Ф” dz ' 2(1 —V)
(1.65)
Как нетрудно убедиться простыми вычислениями, функ-
ции <р0, Ф1 и ф2 должны определяться уравнениями
Л<р0 —()4 Л — — « । 0; Лсра =0. (1.66)
i г- /
Тогда
I д
и;—Т~ <Г<Р» +г,1’2 4-<ро); (I -67)
4(1 — v) дг
I д
----Г — (''‘Pi 4 2ф2 4 <Ро)-
4 (1 — v) dz
Эти выражения для перемещений совпадают с выраже-
ниями для перемещений, получаемыми из общего решения
уравнений теории упругости Буссинеска—Гродского—Пап-
ковича—Нейбера в частном случае осесимметричной дефор-
мации1.
1 Указываемое общее решение уравнений теории упругости не-
зависимо друг от друга получено почти одновременно П. Ф. Папко-
вичем [521, Г. Нейбером [107] и Г. Д. Гродским [29], [30]; элементы
этого решения были известны и М. Буссинеску [88]. Применение
этой формы к осесимметричной задаче содержится, в частности, в
[49] [55]. [47] и др.
21
При построении решений в частных случаях осесиммет-
ричного нагружения одна из функций <pj или ф2 может быть
отброшена.
Напряжения связаны с функциями ф0, <pj и ф2 равенст-
вами
Г
Ф1__ дф2 1 / д2
г dz 2 (1—v) \ dz2
дф1 дф2 1 ( &
~~ ~д7~ дг + 2 (I—v) k’dz2’ +
d2 \ 1
+ ТТ Нг<Р1+2(*)2 '
дг* /
I дф2 дф! ф! । 1 / д2
rL дг дг г 2(1—v) \ дг2
1 д \ I
+ Т-1 (ГФ1 Н~2ф2 + ф0) ;
г dr I I
(1.68)
Г дф2 дф! Id2, 1
тм = и — + ---Г (гФ1 + 2Ф2+фо)
[ дг дг 2(1—v) drdz J
Решение в рассматриваемой форме, несмотря на слож-
ность представлений напряжений через функции ф0, Ф1
ф2, что особенно сказывается при применении криволиней-
ных координат, широко используется для получения ре-
зультатов в частных задачах.
1.9. Решение в форме Галеркина — Лява
Положим, в равенствах (1.58)
F+2(l-v)f О-69)
дг
где % — некоторая би гармоническая функция координат гиг,
Д2Х = 0. (1.70)
Перемещения и и w при этом получают следующие зна-
чения:
и
1 1 Г d2 X
=--------------; ц) =------ -------
2р drdz 2р. [ dz2
df_
дг
По условию (1.55)
д2 F
дг2
1 dF
г дг +
д2 F_______д_
дг2 дг
, 1 дх а»х]
дг2 г дг дг3]
Л
дг2
23
поэтому
Ax = 2
df
dz
(1.71)
и, следовательно,
1 d2 X If I д 7 дх VI
u=-----w = — — (1—2v)Ax+—— (<“ • (1-72)
2ц drdz 2ц r dr \ dr /
Этот результат совпадает с известным решением осесим-
метричной задачи теории упругости в форме, предложенной
А. Лявом [48] и следующей из общего решения Б. Г. Га-
леркина [21], [22].
Подставляя в формулы (1.59) функцию % для напря-
жений, найдем:
d / 1 dr \ d Г d2 х 1
-----vAx) ; тгг = — —--------------------(1 — v) Ах . (1.73)
dz \ г dr / dr | dz2 |
Здесь напряжения связаны с функцией напряжений че-
рез третьи производные.
Форма решения осесимметричной задачи Галеркина—
Лява предложена одной из первых и с большим успехом при-
менена к вычислению значений перемещений и напряжений
при нагружениях цилиндров и шаров.
1.10. Решение в форме Мичела
(1-74)
Если положить в равенствах (1.58)
1 d4
F—2(1—v)/——
г dr
то перемещения и и w выразятся через функцию ¥ равенст-
вами
1 I д2 V
2ц г drdz
1_ дЧ_
г dr
1 d
и —-------
2ц dr
Пользуясь первым уравнением (1.31), нетрудно пока-
зать, что функция ¥ должна удовлетворять уравнению
/ д2 1 d d2 \2
I —г—-------+ —г У=0-
\ dr2 г dr dz2 J
По условию
(1.75)
AF=i.LJL=2±l
г dr dz2
24
устанавливается связь между функциями Y и /
df
V2 —2г —— .
дг
Таким образом, перемещения и и w получают следующие
окончательные выражения:
1
2И
и --
д
дг
1__дУ
г дг
— 2 (I—v) —у2 V ;
I 1 d2 Т
2р. г дгдг
(1.76)
Для напряжений после подстановки функции V в равен-
ства (1.59) получим:
ае =
d
dr
d
or——
dr
\ V d i 1 dW\ I
= — ---------1—2 (I—v) — V-V
r | dr \ r dr
d
dr
d
dz
Gz =
dr
-2 (1 — v) —
v
V2 T — — V2 V;
д I I \
— v— —V2V ;
dr ' r J
d ।
dr ’
d
dr
dW
dr
ay
dr
_(1— V)W ;
I —v
V2 V .
Выражения (1.75) для перемещений и (1.77) для напря-
жений даны Д. Мичелом [105]. Связь напряжений с функ-
цией напряжений в этом решении, так же как и в решении
Галеркина—Лява, осуществляется через третьи производ-
ные, однако по форме они более сложны и поэтому приме-
нения не получили.
Ограничимся указанными выше формами решения урав-
нений осесимметричной задачи, хотя они не охватывают всех
предложенных форм, применяемых в частных случаях. Не
исключена также возможность составления новых форм,
однако с обязательным обоснованием их необходимости и
рациональности,—форм, приводящих к существенным упро-
щениям процесса вычисления, и в первую очередь к упроще-
нию краевых условий. Следует подчеркнуть, что любая фор-
ма решений может быть сведена к вышеприведенным или
получена их преобразованием1. В качестве подтверждений
составим новое решение, основываясь на представлении
перемещений в форме Вебера.
1 К примеру, выражения для напряжений, применяемые в [38]
(см. также [37]) простой заменой обозначений, сводятся к (1.27).
25
Положив в (1.58)
df 1 dip, df I dip, dg 1 dip2 dg 1 dip2
dr r dz ' dz r dr ’ dr r dz ' dz r dr
после некоторых преобразований, получаем:
I I d
и - -------— [Ф*4-2 (1— v) ip,]; w =
2pi r dz
I I d
- ---------— ]Ф*-(1 — 2v) ipr], (1.78)
2р. r dr
где Ф* — ip2 + z и функции ipt и ip2 определяются как реше-
dz
ния уравнений:
Л2 ip, -О, Д2 ip2-~0.
Представление перемещений в форме (1.78) неизвестно
в литературе, но никаких преимуществ по сравнению с пред-
ставлениями Вебера, Буссинеска и Тимпе не имеет. Оно
указано здесь для пояснения утверждения, высказанного
автором.
В заключении обзора общих решений осесимметричной
задачи остановимся весьма кратко на методах, основанных
на применении к пространственным задачам теории упруго-
сти аппарата теории функций комплексного переменного,
весьма эффективного и распространенного при решении плос-
кой задачи-. Аналогия между плоской и осесимметричной
задачами отмечалась неоднократно, однако только в после-
военные годы А. Я. Александровым и Г. Н. Положим было
положено начало разработки указанного аппарата, привед-
шей к законченным методам. Составляющие пространст-
венного деформированного и напряженного состояния выра-
жены интегралами, содержащими аналитические функции
комплексной переменной (метод интегральных положений
Александрова), производными обобщенных аналитических
функций (метод обобщенных аналитических функций Алек-
сандрова) и производными p-аналитических функций (ме-
тод p-аналитических функций Г. Н. Положего). В мно-
гочисленных работах А. Я. Александрова и Г. Н. Положего
и их учеников и последователей методы аналитических
функций получили обширное освещение и реализацию
в применениях к конкретным осесимметричным задачам1.
1 Здесь невозможно перечисление всех работ, посвященных при-
менению аналитических функций, достаточно полная библиография
содержится в [7] и [55]. См. также [1].
26
Глава 2. РЕШЕНИЕ ОСЕСИММЕТРИЧНОЙ ЗАДАЧИ
В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
2.1. Криволинейные ортогональные
изотермические координаты
Для получения решений в довольно большом числе
случаев осесимметричного загружения тел вращения рацио-
нальным является введение криволинейных ортогональных
изотермических координат — сферических, эллиптических,
параболических и т. д. Если контур в осевом сечении тела
вращения совпадает с одной из координатных линий, то
запись граничных условий упрощается, что значительно
облегчает выбор приводящих к решению функций напряже-
ний, определенных в той же системе координат. Здесь будут
получены общие выражения в криволинейных координатах
основных уравнений и формул для напряжений, деформаций
и перемещений, а в последующих главах даны их частные
применения.
Пусть £ и т] — некоторые криволинейные ортогональ-
ные изотермические координаты в плоскости осевого сече-
ния тела вращения: £ = £ (г, г); т] = т] (г, г). Пределы изме-
нения значений | и т] определены условиями однозначности
обратных зависимостей: г = г (£, т]); z = г (£, т]).
По свойству изотермических координат
d£ dn . dl dn
дг дг ’ dz dr
dt, dn d£ _ dt]
dr dz ' dz dr ’
(2.1)
(2.2)
что зависит от выбора направления возрастания координат
I И Т].
В силу указанного свойства
d2 £ d2£ л d2 n d2 n л
---—4- —- -0; --------L-4------1 0.
dr2 dz2 dr2 dz2
(2-3)
£ (r, z) и T| (r, z) являются гармоническими функциями.
Нетрудно также указать на целый ряд других связей
между производными £ и 1]. Например, после умножений
27
первого равенства (2.1) или (2.2) на и второго на и сло-
жения
dl dr] <% di] _ о
dr dr dz dz
(2.4)
После возведения каждого из равенств (2.1)
в квадрат и сложения
f — f+ I — Y = f У i ( d1] У 1
\ dr J \ dz / \ dr / \ дг / H '
что тождественно следующей записи:
или (2.2)
(2.5)
(2.6)
Н = Н (£, 1]) является параметром координатной си-
стемы £, т] и называется параметром или коэффициентом
Ламе. Для выяснения его геометрического смысла составим
сумму квадратов дифференциалов и di]:
где ds — длина элемента дуги,
(ds)*=-H [(^)2+(dT])2|- (2-7)
Следовательно, параметр Ламе И характеризует изме-
нение линейных размеров при переходе от метрики г, z
к метрике т).
Связь между производными £, т] по г, z и производными
г, г по т] устанавливается после применения следующих
формальных равенств:
dr dz dr] дт] дг дт] дг
^~дг~ + ~дг~д^ "дГ"" + ~дг д^~°'
из которых
di] д£
дг дг ________дг______
~д^= д1 дт] _ д^ f дП2 | f дГУ
dr дг дг dr \ dr ) \ дг )
dr ' dz
28
Производные г и z пот] получаются подобным образом. Итак,
dr д£, dr 0n dz 0£ dz 0п
----=Н—— \---------— Н—L ; — = L. (2.8)
0£ dr 0т] дг 0£ дг 0т) дг
Заменяя в (2.5) и (2.6) по этим формулам производные £ и т]
по г и z производными г и z по £ и т), приходим к следующим
формам записи параметра Ламе:
(2.9)
В заключение составим формулы для косинусов углов
между осями .г и 2 и направлениями нормалей £ и т] к соот-
ветствующим координатам:
dr
cos (rl) = —
ds
дг дг
"Ч" d71
/я |(^)2 + (di])j2
При перемещении по нормали £ координаты т] не меняют-
ся (dx] = 0), следовательно,
cos (г£) =
1__0Г
УТГ di
дг
Аналогично составляются выражения и для других косину-
сов указанных углов. По удобству применения результаты
сведены в нижеследующую таблицу, которая дополнена
значениями косинусов углов между | и т] и тангенциальным
направлением 6.
29
2.2. Дифференциальные уравнения осесимметричной
задачи в криволинейных координатах
Приступим к составлению дифференциальных уравне-
ний осесимметричной задачи и формул для напряжений и
перемещений в системе криволинейных ортогональных изо-
термических координат | и т). Произведем в первую очередь
преобразование к этим координатам дифференциального
оператора:
d2 1 д д1
V2 ---------—---------4-------
дг- г дг дг1
Последовательное вычисление производных дает:
д д д£ д th) д д di, д di]
dr д1- дг К dp dr ' дг di, dz дг] дг ’
д2___д2 / di, V d2 dl dn d2 / dp \2
dr1 d£2 \ dr ) d£dr) dr dr dr)2 \ дг /
d d2 £ d d2 р
+-------— I---------L;
di, dr2 dp dr2
d2 d2 / d^ \2 2——
dz2 d£2 \ dz J dgdp dz dz
d2 / dp \ 2 ±21 d
dp2 \ dz / П d£ dz2 ' dr) dz2
После подстановки производных в оператор V2 и неко-
торых преобразований с использованием равенств (2.3),
(2.4) получаем:
2 I / d2 i d2 | 1 I д d| д dp \
Н \ d£2 1 dp ' г ( d£ dr dp dr j
d£ dp
и окончательно, заменив производные и согласно
/о о\ дг дг
(2.8) производными и
V»
д2 д2
____ I ______
dg1 "И dp2
I д дг д
k~dr~dF+ "dp
dr
— (2.10)
dp /J
1
н
г
или в более компактной форме
г
Н
V» =
д / 1 d \ d / J д_
d| \ г d£/~*~dp\r dp
(2.11)
30
Таким образом, основные функции осесимметричной за-
дачи ф (£, т]) и (р (I, т]) определяются как решения дифферен-
циальных уравнений:
д / 1 дф \ д / 1 дф \ о д / 1 дф \ .
d£ \ г d£ dq \ г дт] ) ’ д£ \ г д£ J
д [ \ dtp \
+ — — Ь °- (2.12)
ОТ] \ Г ОТ] /
Функция Ф, входящая в выражения для напряжений и
перемещений и в краевые условия, связанная с ф и <р
одним из равенств (1.17) или (1.18)
dtp да>
ф= -ф+г---- или ф- ф—г--------,
dz дг
получающая в криволинейных координатах форму
z / dtp дг да> дг \
н т н \ д£ г dr] dr] )
г I dw дг д<р дг \
Ф — — —Т-----------------I. (2-13)
Н \ д£ dg dq dr] /
является квазибигармонической, удовлетворяющей уравне-
нию
Г д I 1 д \ д / 1 д \1 | г Г д / 1 дф \
[ д£ \ г д£ /"*" дт] \ г di] / J I И I dg I г dg /
д ( 1 дФ VI) Л
+ Т Г0’ (2 ,4)
Л] \ г dq JJJ
В дальнейшем при решениях частных задач будем вы-
бирать систему координат g и т] так, чтобы контур в осевом
сечении тела вращения совпадал с одной из координатных
линий £ = g() или т] = т]0. При этом контурные условия
(1.30) будут:
дф /— дФ I дг ./ \
—-^rVHpz-, —Q—(2.15)
dq dg \ /
при £ = |0, если боковая поверхность определяется значе-
нием |0, и
дФ /-- дф / дг /---------------\
= -rV Н рг\ —-=r fi —- +ИН рг (2.16)
Ofc ОТ] \ ОТ] /
при т] = т]0, если боковая поверхность определяется значе-
нием Т]о.
Равенства (12.15) и (2.16) соответствуют координатной
системе, для которой справедливы зависимости между про-
изводными (2.1). В тех случаях, когда по каким-либо при-
31
чинам (чаще всего по удобству записей) приняты криволи-
нейные координаты со связью (2.2) между производными,
в (2.15) и (2.16) знаки в правых частях первых равенств
должны быть изменены на обратные.
Через й в приведенных формулах обозначена комбина-
ция (1.26) функций фиФ
1 2 дф
Q-=— ГФ--1-2 (1 — v) ф]_—
г* г rir
или в криволинейных координатах
I 2 / дф dr dtp дг \
П = —[Ф + 2(1-у)ф]—— —- . (2.17)
г2 nr \ dfc dg дц дт) /
Для полых тел вращения условия (2.15) или (2.16) долж-
ны выполняться как на внешнем, так и на внутреннем кон-
турах в осевом сечении.
Вместо первых равенств в (2.15) и (2.16) можно (и во
многих случаях весьма эффективно) пользоваться связью
(1.35)
между контурным значением функции Ф (при £ = |0 или
т] = Tjo) и нормальной силой в поперечном сечении тела вра-
щения. Знак силы N при этом должен быть связан с приня-
той системой криволинейных координат. Для полых тел
следует применять равенство (1.36), т. е. заменить левую
часть в (1.35) разностью функций напряжений на внешнем
и на внутреннем контурах осевого сечения.
В случаях, когда боковая поверхность свободна от внеш-
ней нагрузки, условия (2.15) и (2.16) упрощаются:
ф = —— 2л дФ дг ' ль ~rQ ль при £о. (2.18) ofe О£
Ф-— ; 2л дф дг л л —— rQ при «]-По. (2.19) дт) дт)
Условия на оси вращения сохраняют прежнюю форму (1.32).
2.3. Выражения для напряжений и перемещений
Обозначим составляющие тензора напряжений в криво-
линейных координатах £, 6, tj через стЕ, ст0, стп, тЕ0, т0п,
Для получения их выражений в функциях Ф и ф вос-
пользуемся формулами преобразования компонентов напря-
жений при повороте координатных осей:
32
oj = ur cos2 (5, r)4-oz cos2 (£, z)4-2Trz cos (£, r) cos (£, z);
on=or cos2 (q, r)4-oz cos2 (q, z) + 2Trz cos (q, r) cos (q, z);
T£n = ar cos cos r) + az cos <5. H cos (q, z) +
4-Trz [cos (5, r) cos (q, z)4-cos (£, Z) cos (q, r)J,
которые при указанных выше значениях косинусов углов
имеют вид
1 / dr \2 1 / dz \2 1 dr dz
°l = °r Н k d£ J Ь°г H \ d£ / +2Тгг Н dl д£ ’
о = or — I I 4-oz I I 4-2Trz -------------- —
71 H \ dq ) H \ di} ) H dr\ dq
I dr dr 1 dz dz
^~°r~H d£ ~dq”+Oz 7Г~дГ~дц +
1 / dr dz dz dr \
~h (IF + ) •
Подставляем сюда значения (1.27) напряжений оГ, ст2 и
Trz
1 f 1 do / дг \2 / dr \2 1 дФ ( dz V
о. —----<--------I--) — Q I-----I —--------1------) 4-
« Н ( г д£ \ д£ ) \ д£ ) г дг \ )
2 d<D dr dz )
r dz d£ d£ J ’
1 f 1 d<P / dr \2 / dr \2 1 d<P / dz \2
W [ r di] \ dr] / \ dq / r dr \ dr] J
1
2 d(P dr dz i
+ r dz dr) dq J ’
1 d® dr dr dr dr
-------------- — Q —
r dr d£ dq-d£ dq
1 d<P dz dz 1 d<P / dr dz dz dr
г dr d£ dq r dz \ d£ dq d£ dq
После некоторых преобразований, имеющих характер
нижеследующего
d<P , dr \2 d(P / dz \2 d<P dr dz l дФ dr
dr \ dl ) dr \ dl ) dz d£ d£ \ dr d£
d<P dz \ dr / d<P dz d<D dr \ dz
dz d£ ) dt, ~ dr d£ ~ dz d£ J d£ ”
d<P dr I дф dr дф dz \ dr d<P dr
d£ d£ \ dr dq + dz dq J dq d£ d£
d<P dr
dq dq
33
где использованы зависимости (2.1) и (2.8), получаем окончательные
выражения для напряжений в криволинейных ортогональных изо-
гермических координатах:
dr \*
1
ое =
дФ дг
Ь1= H
Г к д£
1 / дф дг
г \ dq дт)
2(l+v) / дф
Hr
1 ( дФ дг
. г \ д£ дт(
дФ
dl
dr
dl +
дф
дт) д^
TE0=" t0t) "°’
дг \
---I__<
d£ J
дф дг
(2.20)
Применяя эти выражения к точкам поверхности тела вра-
щения, при заданных силах р% и рл можно граничные усло-
вия записать в форме, отличной от указанных раньше [см.
(2.15) и (2.16)1. Если поверхность тела определена значением
координаты £ = £0, то по равенству <% = Pt и = рп
при £ = получаем:
дФ дг дФ дг
д£ д£ дт] dq
дФ дг дф дг
дГ ~д7+ дт) dg =
(2.21)
Аналогично, если поверхности тела соответствует по-
стоянное значение координаты т] = tj0, то в силу равенств
= рп и тЕт) = рЕ при т] = т]0 должно быть:
-----'----—--------- r Q I ---------1 + Нр-п
dT] дт) д£ д£ \ дт] /
дФ дг дФ dr I dr дг
д£ дт] дт] д£ Г д£ дт] Р^
(2.22)
По равенству суммы нормальных напряжений и стп
функции — й
о^-|- = — Q (2.23)
в точках поверхности £ = |0 имеем ст,) — —й — рЕ, и в част-
ности, если рЕ = 0, напряжение о,) = —й. Аналогично в
точках поверхности tj = т]0 напряжения стЕ = —й — ръ
и, если рл = 0, то аЕ = —й.
Таким образом, на участках контура осевого сечения |=
= £0 (или т] = т]0), свободных от нагружения, нормальные
напряжения стп (или о£) полностью определяются значением
функции й.
34
Поскольку радиальные перемещения связаны с функция-
ми <р и Ф простым равенством (1.12) и = -у [Ф + 2 (1 +
+ v) ср], получение их в криволинейных координатах не при-
водит ни к каким дополнительным трудностям. Определение
осевых перемещений w требует интегрирования зависимостей
(115)
dw
дг
dw
dz
1 1 д
|O_2(l-v) ф1;
2ц г-dz
1 1 д
= -----— (<DH-2v(p),
2ц г дг
что нетрудно выполнить, если ср и Ф, найденные в криволи-
нейных координатах, имеют простую форму записи в декар-
товых (г, z). В тех случаях, когда переход от криволиней-
ных координат к декартовым приводит к сложной записи
правых частей равенств (1.15), более просто составить выра-
жения производных до по £ и т) через функции <р и Ф и про-
о dw
извести их интегрирование. Заменив в производных и
dw dw dw ,, .
производными и (1.15), получим:
dw dw dr dw dz
~d^ ~dr~ dl dz d£
d 2 f dq> dz dq> dz \ dz '
(Ф4 2v<p)- -77
n \ d£ d£ or] dr] / dq
dw dr dw dz
- -j- --
dr dq dz dq
2 [ dtp dz dtp dz \
™ H\dldl dq dq J
1
2цг J dq
dw
dq
(2.24)
1
2цг
Здесь верхний знак соответствует координатной системе,
при которой выполняются связи (2.1), а нижний — системе
при выполнении связей (2.2). z
Перемещения и un в криво-
линейных координатах при из-
вестных значениях и и w опре-
деляются равенствами
Ug=UCOS(£, г) 4- W COS (£, z);
0^ = 0 cos (q, г) -j- w cos (q, z)
(рис. 4). Заменив в них косинусы
углов их значениями, взятыми р
из таблицы косинусов, получим: Рис. 4
35
1 I dr dz \ 1 / dr dz \
“i “ yiF (" 7 A ’= К+" ^P2 25'
Частные формы криволинейных координат — сферичес-
кие, эллиптические и параболические, и их применение к
решению пространственных осесимметричных задач теории
упругости будут изложены в п. 2.5 и в последующих главах.
2.4. Решение осесимметричной задачи
в криволинейных координатах
при нагружениях объемными силами
Решение задач о напряженно-деформированном состоя-
нии упругих осесимметричных тел при наличии объемных
сил согласно методу, изложенному в п.1.6, осуществляется
введением в выражение перемещений, напряжений и кон-
турных условий частных решений фг, ф2, <рг и <рг дифферен-
циальных уравнений (1.45), (1.47)
ф'='• Афг=-ТлЬггг:
Vs = о <7 ; “Т- '• А*1 =;||1 > е‘ г-
2(1—v) dr 2(1—v)
В большом числе частных задач достаточно найти фГ,
(рг и фг в декартовых координатах, а затем преобразо-
вать их к криволинейным. Можно значения этих функций
определять непосредственно из уравнений, получаемых пре-
образованием уравнений (1.45) и (1.47) к координатам | и
Л
d / 1 d<pr \ d /1 д<рг \ Hgr
\ г у”1" дт] \ г дт\ ) 2 (1—v)
д / 1 дфг \ д / 1 дфг \ Hz dgr
dl \ г Г \ г di] / 2(1—v) dz ’ (2.26)
d I dq>z 1 d ( dq>z \ Hr
--- I f - + ---- I f - I - —------- Jfzl
J dr] I ch] / 2(1—V) 6Z’
V J <*] V dq ) ‘ 2(1—v) gz‘
Выражения для напряжений, деформаций и перемещений
усложняются включением в них функций фг, фг, <рги (рг.
Опуская выкладки повторяющихся вычислений в п. 2.3,
приведем сводку основных формул осесимметричной задачи
теории упругости в криволинейных координатах при на-
личии объемных сил.
Радиальные и и осевые w перемещения определяются ра-
венствами
36
и =
1
2pr
O + 2(l-v) (<р + фг)- г
дФг '
дг
(2.27)
дФг
w — u/r + 4(l—v) <pz———
dz
В последнем значение wr находится интегрированием
производных
dwr 1 | д 2 1 д(ф + фг) дг
~ ± "о ]~Г" 1ф + 2у (ф+<₽г 1- и TZ 7Г" +
d£ 2рг I dp Н L d£ d£
д(фтфг' дг 1 дг I
dp dp J dp )’
(2.28)
dwr 1 | д _
^=т^гЬг|Ф+2',(’,+фг)|~
2 1’д(ф-|-фг; дг д(ф4~фг) dz 1 дг 1
~7r[ dj df + d^ d71~di”j’
По вычисленным значениям и и w перемещения uj и в
криволинейных координатах нетрудно составить, обратив-
шись к формулам (2.27).
Обобщая формулы (2.20), для напряжений имеем:
п - —
6 Н
дФ
1 дф d d<Dz \ dr
“dT/lf
f dq>z dz
I d£
fi-2-^
dz
г d£ д£
dr
— + 2(1—v)
dr j dn
dg
dr
"dj
1 d /
r dp \
dфг dz
dq dp
(2.29)
d<D3
~Г dr J dl '
-ffi-2^
\ dz
d<D d dOz \ dr
dp dp dr / dp
dфг dz dфг dz \
dp dp d£ d% )
dr \21
дг
— 4-2(1-v)
dn
1 Г 1 ( d dr
"e = [— [2 (I +v) (Ф+Фг)-Ф.1
d dr )
+ — [2(l+v) (Ф4-Фг) — Фг1— 1 +
dp dp J
1 d
r dg
«1
37
1 д
г дт]
(dtp, дг dtp, дг \1
—7х —н- ——--------------H-fi
д£ дт) /]
____1 17 1 ^Ф д дфг \ дг
Н г о£ dr J дт]
дФ? \ д,
Ф — г---- —
дг ) д£
dq>z \ дг дг '
Q — 2—— |----------
дг / <Эт)
1 д
+ г д^
/ дФ, \ <
Ф — г--- ]-
\ дг)
(а
Л) dj ) \
dz dtpz дг \
дт] ' дт) д£ J
д_ дФг \ дг
г <Эт] <Эт] дг ) д£
'г дг
; 0Т]
dr dr 1
df
v)
д<рг
дФ
Я [
дг
— -4-2 (1—v)
ОТ]
!-2-^
дг
Введение функций фг» <Рг» Фг и срг в контурные условия
приводит их к виду
дФ Г _ ,— 1 д дФг Л да>г 1
— =г Ч=Ун р. г — — г-~ ± 2 <1 —v) -S2- ;
[ г дг дт] J
(2.30)
дФ
дт)
д<рг \ д
Q—2—) —
дг J д
п х d<₽z
дФг
дг
' д^
на контурной линии т) = т]0 или
дФ
дФг
дФ
д»)
dtpz \ дг д
рГ 4 [Q —2 J— 4-—^ дг
±2(l-v)
ОТ]
дФ
г дт) дг
(2-31)
^<Pz
dl J
д
на контурной линии £ £0.
2.5. Функции напряжений в сферических координатах
Предположим, что £ и т] являются полярными координа-
тами в плоскости rOz, связанными с координатами г и z за-
висимостями (рис. 5).
r = ce^sinq; z=ce^ cost] (2.32)
и обратно
£ = 1п l/f24 z2I T] = arctg—.
38
В этой системе линии
const представляют собой
семейство окружностей с цент-
рами в начале координат, а
линии т] = const — пучок пря-
мых, проходящих через нача-
ло координат. В пространстве
первым соответствует семей-
ство сферических поверхнос-
тей, а вторым — конических;
координаты £, т), 6 образуют
сферическую систему.
Параметр Ламе Н этой сис-
темы [см. (2.9)1 имеет значе-
ние:
Рис. 5
Найдем решение уравнения (2.12)
d f 1 дФ \ , д / 1 дф\__0
\ г ) дт) \ г дт] /
в виде произведения двух функций, из которых одна/! (|) —
функция только координаты а вторая /2 (т]) — только
координаты т): <р = /г (£) /2 (tj). Подстановка функции ф в
таком виде в уравнение (2.12) дает
'2 +/1 Jt]2 f \h +/1 dri drf )
или после замены г его значением (2.32)
d2 fi d2f2 1 / df. t df2 t \
/2 -77- 4 /1 -7-7 — —E-:--1 /2 -7Г- sin t] -j-fi -f- ce* cos p 1=0.
dtf dr]2 ce6sini] \ d^ at] J
Группируя члены, содержащие функцию /ъ и члены,
содержащие функцию /2
1 (dMi df. х 1 / (Pf2 df2\
— -----г- — ~~ -И — I-------— ctg n--- =0,
fi k <*2 d^ I Г f2\ drf 1 dr])
получим два уравнения:
d2 fi df.
(2.34)
d2 fi df2
-ctg т) -7- + * (Л+1) f2 =0,
arf dr]
где к — некоторое постоянное число (форма постоянного множителя
при /j и ft здесь принята по удобству записи окончательного резуль-
тата).
39
Положив в первом из этих уравнений Д (£) = ет$, имеем:
т2— т—k 1) = 0
откуда т =— [1 ±(2^4-1)]
и, следовательно,
/1(6) =--/1ле(Л+,)Ч (2.35)
Решение второго уравнения (2.34) ищем в виде
/2 О]) =sin т|У (cos п) = V1 — У2 У (у).
где у = cost]. После подстановки в уравнение получим:
d Г dy 11
+ *(*+1)-------г у = 0-
dy dy 1 — у2
(2.36)
Это уравнение Лежандра (см., например [41, 42] и др.). Ре-
шение его:
/---/ dPb dQb \
у = У1-!/2 Ck-^+Dk-^- . (2.37)
\ dy dy /
где Ph (у) и Qh (у) — сферические функции Лежандра соответствен-
но первого и второго рода; Ch, Dh — постоянные.
При k целом Pk (у) является полиномом Лежандра /г-ого
порядка и определяется равенством
Pk (у) =
1-3-5 ... (2fe—1)
1-2-3 ... k
k(k-\) t
У 2 (2k — 1) У
k (k—\) (k — 2) (k—3)
--------------------uR
2-4 (2k — 1) (2k—3)
(2.38)
Ниже выписаны значения полиномов Лежандра при k =
= 0, 1,2, .... 6:
Р* (к)=1;
Pi (У) = У,
Рг(у) =
^s(!/)=4"(5!/3_3!z): (2-39)
Р4 (!/)=4"(351/4-30^ + 3);
Рь (У) = -7Т (126у^-140у2+15у);
1D
Ре (У) (231^-315^+105^-5).
40
Сферическая функция Лежандра второго рода определя-
ется равенством
1 14- у
Qk(y)=—Pk(y) In -r^--Rk(y), (2.40)
2 1— у
где
Rh (у) = Rk-L (У) + Д*~5П Ph-3 (!/) + ... (2.41)
1 .ft .5 (к — 1)
Итак, для функции /2 (rj) имеем:
/ dPh dOk \
/2 (Ф = Ch + Dh sin21). (2.42)
\ dy dy j
Этим решением не охватывается случай k = 0. При таком
значении k второе уравнение (2.33) получает вид
d2f2 df2
-ГТ—ctg 114^=0. (2.43)
di]2 ат.
Решение его:
f2 = С(, cos Т| -f- Do. (2.44)
Вид функций напряжений ф и <р в сферических коорди-
натах установлен:
Фо = MJ et-i-B'o) Со cost]-|-Dq);
?“+ »«+а;«-«, (С; р;+d; едл;
фо -- (^о 4’ ®о) (Со cos 1] -f- Do);
(2-45)
фь = (A h e<k +1 > 4 Bh e “ (Ck P'k + Dh (ty s in2 q;
P'k (у) =
dPh (У)
dy
Q'k (!/) =
dQk (У)
dy
k^=l, 2, 3 ...
Функции Фл и Qh, соответствующие значениям и
<рл, составляются без затруднений по формулам (2.7) и (2.11).
Они будут приведены дальше в формах, удобных для задач
различного типа.
Решение в сферических координатах имеет обширную
область применения при изучении напряжения деформи-
рованного состояния цилиндров, конусов, шаров, полупро-
странства и пространства, ослабленного шаровой полостью.
Рассмотрению задач о деформациях этих тел с использо-
ванием функций (2.45) посвящены частично гл. 4. и 5 и пол-
ностью гл. 7 и 8. Там же указаны и некоторые другие формы
решений уравнений (2.5) в сферических кооординатах.
41
Практическую реализацию получили также решения в
эллиптических и параболических координатах, выражения
функций напряжений в которых и их применение к частным
задачам приведены в главе 9.
Глава 3. ДЕФОРМАЦИИ ЦИЛИНДРОВ.
РЕШЕНИЕ В ПОЛИНОМАХ
3.1. Граничные условия. Функции напряжений
Изучению напряженного состояния упругих круглых
цилиндров посвящено большое число исследований. Начало
им положено «Ламе и Клапейроном [99]. Рассмотрение равно-
весия цилиндров в общем случае нагружения составляет со-
держание фундаментальных работ «Л. Похгаммера, К. Кри,
В. А. Стеклова, Б. Г. Галеркина. Решения осесимметричных
задач приведены в работах К. Кри, Л. Файлона, Ф. Персе-
ра, А. и Л. Феппль, А. П. Коробова, Г. С. Шапиро, Б. Л. Аб-
рамяна, А. Ф. Улитко, В. Т. Гринченко, Г. М. Валова,
В. 3. Васильева и др. Большое число результатов в частных
случаях нагружения сплошных и полых цилиндров приве-
дено в [37]. Специальные приемы предложены М. А. Шиф-
фом [112], А. И. Лурье [44—46], Г. Н. Бухариновым [11,
121, В. К. Прокоповым [56—601, Г. Н. Положим [55],
А. Я. Александровым и Ю. И. Соловьевым [7]. Решения в
области задач о равновесии анизотропных цилиндров и в об-
ласти термоупругости приведены в книгах С. Г. Лехниц-
кого, В. Новацкого [50].
Для цилиндрических стержней в силу того, что направ-
ление нормали к боковой поверхности цилиндра совпадает
с направлением координатной оси г, а направление образую-
щей — с направлением координатной оси z, граничные ус-
ловия (1.30) получают более простую форму. На боковой по-
верхности цилиндра при г — а, где а — радиус цилиндра
дФ дФ
-r~^rpz-, ——г (Q-|-рг). (3.1)
dz dr
Первое условие можно заменить связью (1.36) функции
с нормальной силой N (z) в поперечных сечениях, определе-
ние которой не представляет обычно затруднений
42
Для полых цилиндров указанные условия (3.1) должны
выполняться как на внешней цилиндрической поверхности,
так и на внутренней с соответствующей корректировкой
знака производной по г. На торцах цилиндра, принимая во
внимание направление нормали и касательной к соответст-
вующей части контура осевого сечения, из (1.30), имеем:
дФ дФ
— = —rpz ; — = грг.
dr dz
(3.2)
Так же, как и на цилиндрической поверхности, функ-
ция Ф на торцах связана с нормальной нагрузкой на
площади круга (или кольца — в случае полого цилиндра)
простым равенством
Ф-—(3.3)
Действительно, интегрируя первое условие (3.2) по г
в пределах от 0 до г, имеем
г 2л г
f 1 Г С N (г)
Ф = — I rpzdr = ——- | 1 pz rdrdG—- — —-.
J 2л J J 2л
о oo
Рассмотрение осесимметричных напряженно деформи-
рованных состояний упругих цилиндров начнем с наиболее
простых случаев, соответствующих нагружению их радиаль-
ными и осевыми силами, распределенными на поверхности
вдоль длины цилиндров по степенным законам1. Очевидно,
что при таком характере нагрузки нормальные силы N в по-
перечных сечениях являются степенными функциями осевой
координаты z, поэтому на основании зависимости (1.36) не-
трудно заключить, что функция Ф (г, z) должна иметь
форму полинома переменной z. Такая форма определена ре-
шениями основных уравнений осесимметричной задачи в
сферических координатах, т. е. равенствами (2.45). Положив
в них постоянные Bh = Dh = 0 и изменив значения по-
стоянных A k и Ch соответственно на Ak ck+' и Ch ck+', по-
лучим следующую систему функций
4>o= Ao cos П = Ао z;
(се^)2 sin2 т) Л j г2; (3.4)
ф2 = А2 (се^)3 sin2 т] cos т, = А2 г2 z;
= ?|8 (се^)4 (5 cos2 т]— 1) sin2 т] — /13 (4z2—г2) г2;
1 Эти решения аналогичны решениям Менаже плоской задачи
в целых полиномах.
43
г]?4= А4 (се^)ь (7 cos2 т]— 3) sin2 т] cos т] = Л4 (4z2—3r2) г2 z;
фБ = Л5 (се^)6 (42 cos2 г]—28 cos21] 4-1) sin2 т] = ЛБ (15z4—
—26r2z24-r4) г2 (3.4)
и аналогичные выражения для <pft(r, z) после замены постоян-
ных Ah и Ck.
3.2. Первая простейшая форма функций напряжений
Функции ipi и <рь взятые из числа (3.4) при k = 1
ф = Аг2, <р = Сг2,
зависящие только от координаты г, соответствуют однород-
ному напряженному состоянию среды, и в частности цилинд-
ров. При осевом растяжении или сжатии равномерно распре-
деленной по торцам нагрузкой Pz = Р выполнение условий
(3.1) на контуре осевого сечения приводит к следующим зна-
чениям постоянных А и С:
л=с=_____________р____
2па2 ’ 4n(l-^v)a2
где а — радиус цилиндра; Р — растягивающая сила.
Функции напряжений имеют вид1
Р / г \2 Р / г \2
ф == —---I----I ; ф —-----------I-- I ;
2л \ a J 4ji(l-f-v) \ а /
г \2 Л Р
— I; Й = —.
а ] па2
(3.5)
Подстановка их в формулы (1.27), (1.12) и (1.15) приводит
к значениям напряжений и перемещений, известным по
элементарному решению,
Р Pvr
ar=ae = xrz=0; a2 = —u = — ——;
ла2 лсд2
Pz
w = ——+w0, (3.6)
пса2
где постоянная о»0 определяется условиями закрепления стержня.
В случаях нагружения боковой поверхности цилиндра
равномерно распределенными сжимающими силами рг =
1 Приведенные здесь функции напряжений для элементарных
форм нагружения необходимы для составления функций напряже-
ний в более сложных случаях деформаций цилиндров.
44
= —р (равномерное поперечное обжатие цилиндра) по-
стоянные А = О, С = — 2 » функции напряжений
р
ф = Ф = 0; ф^ —--------г2; Q = p, (3.7)
напряжения и перемещения, как и следовало ожидать,
1 —V
(Уг=—Р, (Ге —Р, Рг = тг2^0, и=— —-—рг,
Решения при осевом растяжении или равномерном попереч-
ном обжатии полых цилиндров составляются аналогично
выше приведенным после присоединения к функциям 44 и
<рх (3.4) постоянных В и D
ty = Ar2-}-B; <p = Cr2+D. (3.9)
Соответствующие функции Ф и й имеют вид
ф^Лг2 + В; Й = Д — 2 (1 + v) С4-— [B4~2(l — v)D]. (3.10)
г2
Используя эту форму функций, легко получить решение
известной задачи Ламе о загружении внешней и внутренней
боковых поверхностей полых цилиндров или кольцевых
плит равномерно распределенными радиальными силами.
Обозначим через р и р0
нагрузки, приходящиеся на
единицу площади соответ-
ственно внешней и внутренней
цилиндрических поверхнос-
тей, через а — радиус внеш-
него и а0 — радиус внутрен-
него контуров поперечного
сечения (рис. 6).
Выполняя на внешней и
внутренней поверхностях ус-
ловия (3.1) при рг = 0; Ф = 0;
дФ
---=—г (£2 + рг), получим;
Рис. 6
Ла24-е = 0, 2Л=Л—2(1 4-v)C+ —[В4-2(1—v)D]—p;
а2
Ла24-В = О, 2Д=—44-2(14-v)C—— [В4-2(1—v)D]—Ро-
°?
45
Отсюда /1 = 6= 0;
Ро Др —Р°2
2 (1 +v) (a2-a§) '
D _ (Po—P) (ДЯо)2
2 (1 — v) (a2—a§)
и, следовательно,
m Pofl?— pa2 2t (Po—P)(flflo)2 ,q ...
2 (1 4-v) (a2 —aj) 2(1—v) (a2-a§)
Выполнение условий (3.2) на торцах цилиндра обеспечи-
вается равенством нулю функции Ф.
Применяя формулы (1.27) для напряжений, найдем:
°т=--~ * , [Poflg (д2-г2)+рд2(г2-д?)1. Oz = 0;
(a2 — ag) г2
(3.12)
ae == Vi---V ao (Д2 + r2) — pa2 (r2 -j- a?)]; xrz = 0 .
(a1 —ag) r2
Перемещения после подстановки (3.11) в формулы (1.12)
и (1.15) и интегрирования последних определяются равенст-
вами
и = W------Г— В1 — v) (Ро °0 — рд2) г‘2 4- (1 4- v) (Ро—р) (ддо)21;
t (a* — ag) г
(3.13)
2v
™= — —v Ох»a’—рд2)2+“'° ’
Е (a2—ag)
где a»o — постоянная интегрирования.
В частном случае, когда р = 0, т. е. при нагружении
только внутренней поверхности, формулы (3.12) принимают
вид
а2—г2 / ао \2 а2-]-г2 / а0 \2
° Г ~ -Р° в I- I ’ I ’ СТв — Ро 2 I I ’
а2—aj \ г / а2—а§ \ г J
из которого следует, что напряжения ог всюду сжимающие,
а напряжения Ое — растягивающие. Наибольшие значения
последних
д24-д2
получаются в точках внутренней поверхности при г = а0.
В другом частном случае при р0 = 0, т. е. в случае, ког-
да нагружена только внешняя боковая поверхность ци-
линдра,
г1—д? / Д \2 г2 4-д§ / Д \2
= Р 9 9 I I » ^6= Р о 2 I / ’
a2—aj \ г ) ° a2 —ag \ г J
46
Напряжения ог и ое сжимающие. Наибольшие значения
Ое получают также в точках внутренней поверхности
2ра2
Если радиус а значительно больше радиуса а0, то на-
пряжения ое = —2р по абсолютной величине в два раза
превышают напряжения ое = ог = —Р при двустороннем
сжатии (или растяжении). Коэффициент концентрации
у круглого цилиндрического отверстия, ось которого перпен-
ликулярна плоскости действия сил, в этом напряженном
состоянии равен двум.
При увеличении отношения а/а„ максимальные напряже-
ния о© как при нагружении внутренней, так и внешней
поверхности цилиндра вначале изменяются весьма быстро,
а затем асимптотически приближаются к р0 в первом слу-
чае или к 2р во втором. Так как напряжения лимитируются
допускаемыми значениями, то и давления р и р0 должны
быть ограниченными. Таким образом, при больших отноше-
ниях а/а0 увеличение толщины стенок (а— а0) полого цилинд-
ра не приводит к заметному увеличению его прочности. Ес-
ли давления р и р0 велики, то обеспечение прочности может
быть достигнуто иными средствами, а именно, применением
цилиндров, составленных из нескольких частей, обжимаю-
щих одна другую. Наличие такого начального обжатия при-
водит к уменьшению напряжений в наиболее нагруженных
точках внутренней поверхности, что позволяет значительно
увеличить приложенную к цилиндру радиальную нагрузку.
3.3. Вторая простейшая форма решения
Второй простейшей формой функций напряжений назо-
вем произведение функций радиальной координаты г на осе-
вую координату z. Она просто составляется при использова-
нии значений (3.4) для k = 0 и k 2 и записывается в виде
ф (Дг2-|-б) г\ ф - (Сг- i-D) z. (3.14)
Соответствующие функции Фий (см. (1.17) и 1.26))
Ф = [(Д j-C) г2 B-I-DJ z;
Применение рассматриваемой формы приводит к значе-
ниям напряжений и перемещений при некоторых частных
деформациях цилиндров, а именно: при растяжении или
47
сжатии осевыми силами, равномерно распределенными
по цилиндрической поверхности, при чистом изгибе круг-
лых плит, при растяжении цилиндра под действием
собственного веса.
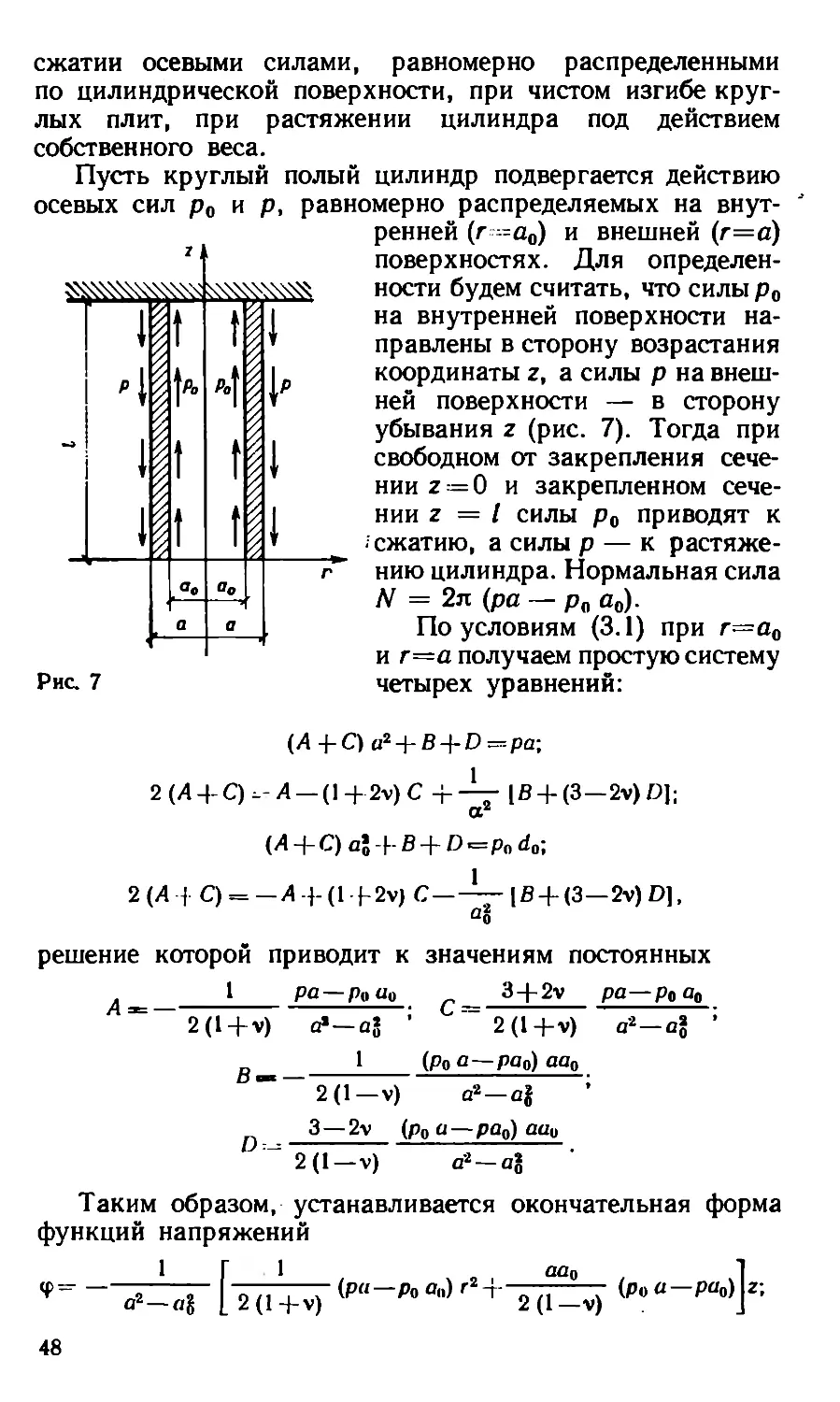
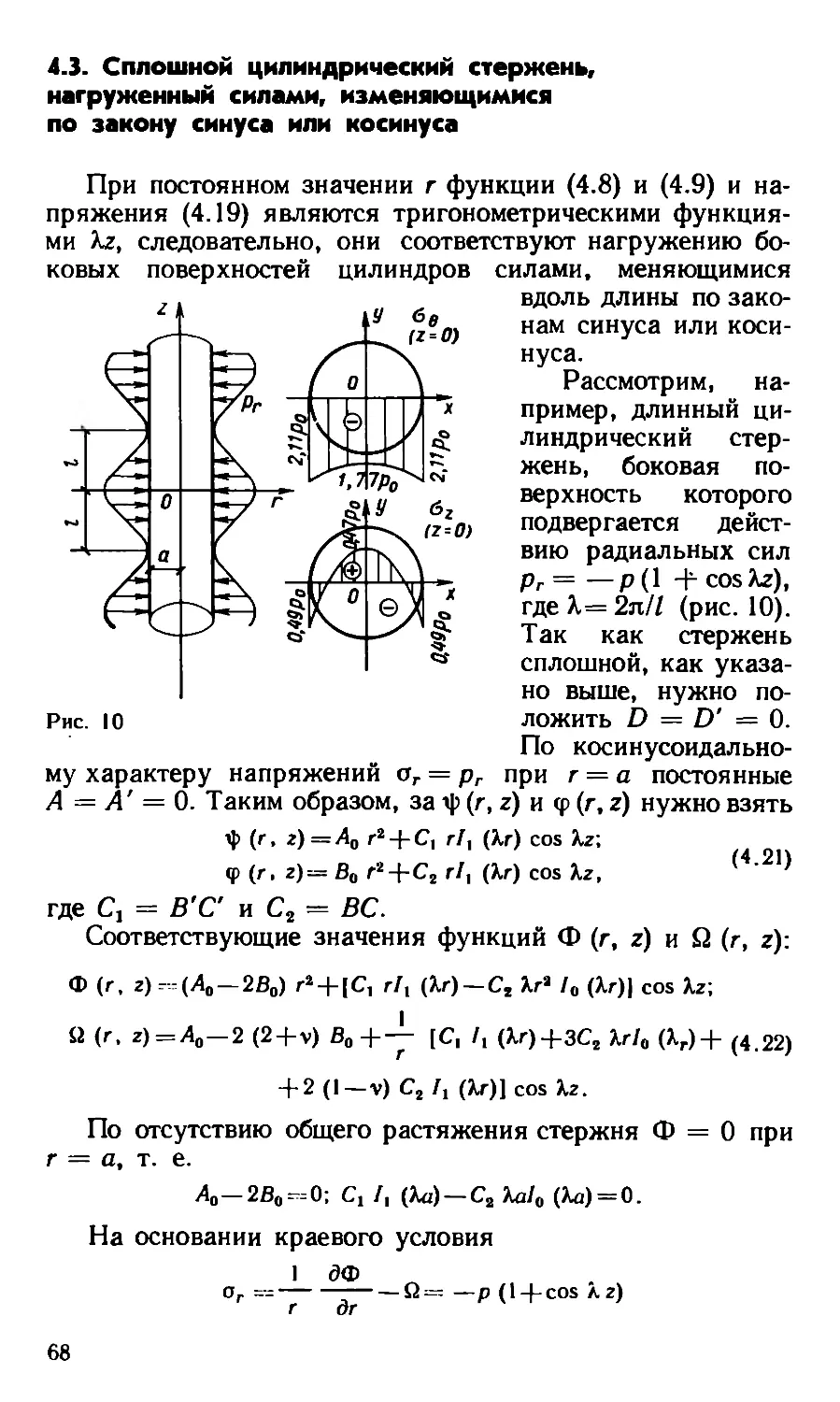
Пусть круглый полый цилиндр подвергается действию
осевых сил р0 и р, равномерно распределяемых на внут-
Рис. 7
ренней (г =а0) и внешней (г=а)
поверхностях. Для определен-
ности будем считать, что силы р0
на внутренней поверхности на-
правлены в сторону возрастания
координаты z, а силы р на внеш-
ней поверхности — в сторону
убывания z (рис. 7). Тогда при
свободном от закрепления сече-
нии z — 0 и закрепленном сече-
нии z = I силы р0 приводят к
- сжатию, а силы р — к растяже-
нию цилиндра. Нормальная сила
N = 2п (ра — р0 а0).
По условиям (3.1) при г—а0
и г=а получаем простую систему
четырех уравнений:
(А -|- С) а2 4- В 4- D — ра;
2 (А 4- С) - А - (1 4- 2v) С 4- 4- (3—2v) DJ;
а2
(Л 4-С) a2|-fi4-D = Po d0;
2(Д4. С) = -Л4-(1 -f-2v) С—[fi4-(3-2v)D],
ао
решение которой приводит к значениям постоянных
А __ 1 ра — раа0 с 34-2у ра—роао
2(l4-v) а’-а? : ~2(l4-v) а2-а? '
в~_ 1 (Po a—pao) аа0
“ 2(1—v) a2 — ’
D 3~2v (Po a~Pap) aa*>
2(1—v) a2—
Таким образом, устанавливается окончательная форма
функций напряжений
1 Г 1 _ аао
<₽= —г-----Т- о/) , . (р«—Рр ар) г -----Г (Po a—pap) Z;
а—«б 2 (1 4-у) 2(1—у)
48
Ф=—:-----— 1(ра—Ро а0) r2 + (Ро а—ра0) аа0] z ;
a2—flo
2
Й = —----— (ра—ро а0) z (3.16)
а2—а§
и после применения формул (1.27), (1.12), (1.15) значения
напряжений и перемещений
CTrr_oe = 0; az
pa—PqOq
„2 2
a2—iin
I
a2-ag
(pa — p0 а01 r 4- (Po n—p<i0)
и
2v
771----— (pa— Po a0) rz-,
E (a2 —al)
(3.17)
4-2 (1 4-v) (pa0—Po a) aa0 In
w(); (Wq~ const).
В случае сплошного цилиндра
р г2 г г
ф!=--------- г2 2\ Ф — — р----; У — 2р —;
2(14-v)a а а
2 Г
ar=at. = G\ az = 2p—; xrz = — р—; (3.18)
а а
и = —— rz; d) = — (г2—z2) 4-Юо-
Еа Еа
Как следует из выражений для напряжений, решение
справедливо для всего объема цилиндрического стержня
только тогда, когда на его торцах приложены касательные
силы, меняющиеся вдоль радиуса по линейному закону, се-
чение z = 0 свободно от нормальных сил, в сечении z = I
нормальные силы распределены равномерно. Если хотя бы
одно из таких условий не выполняется, то в соответствии с
принципом Сен-Венана решение можно считать пригодным
только для средней части цилиндра, достаточно отдаленной
от концов. Рассмотрение приемов, приводящих к более со-
вершенным решениям — с выполнением краевых условий
на всей поверхности цилиндра, — произведено в гл. 6.
В качестве второго примера применения решения в форме
(3.14) рассмотрим нагружение цилиндра радиальными сила-
49
ми, распределенными по внутренней (г = а0) и наружной
боковой поверхности по линейному закону
Z Z
РгО~ — Ро ~Г~ > Рг ~~ —Р~Г »
п h
где h — постоянная.
По равенству нормальной силы нулю функция Ф равна
нулю при г = а0 и г = а, т. е. Л + С = О, В + D = О
и значит А = —С, В = —D.
На основании второго условия (3.1)
2(1 —v) D р
2 (1 -i-v) С—1 ---= —~
а2 п
2 (1 —v) D р0
2(l+v)C-—
«о л
откуда - - Po aS — pa2 D (Po — p) (aa„)2
с — 2(14 v)(a2 — a?) h ’ 2(1—v) (a2 — ag) h
Функции напряжений:
1 Г 1
Ч> ---------77" Т7—(Ро “ pfl2) г'2 н
2 (а2 — а§) [ 1 Ф v
1 1 г
4- ----(Ро—Р) (<шо)2 —;
1 —V J п
1 Г 14 2V
—-----------I-------(Ро аЯ— ра2)—
2 (а2 —а2) [ l-4-v 0 ’
3 — 2v / ado VI z
— ~------(Ро — Р) -- —,
1—V \ г J J п
(3.19)
напряжения и перемещения:
о г = — — - [ра2 (г2 — а?) 4- Ро а2 (а2 — г2) 1 ; а2-0;
а2— aj hr2
ае=—Т-Ц-1раг(гг + «§)-Роа§(а2 + г2)]-^-2, тг2--=0; (3.20)
<г—ag лг
и “ ~ [(1 — v) (Р«2 — Ро а§) г +
с \ал — aj) L
(<z<z0)2 1 z
+ (l+v) (P-Po) -r;
r J л
w =-оЁТг----ZvjT i (pa2--Po a’o) 1(1 —v) r242vz2] 4
2E(a2 — a%) h I
r )
+ 2 (1 4-v) (p—Po) (aao)2 1"-14-Wo-
50
По равенству о2 = тГ2 = 0 во всем объеме стержня реше-
ние является точным, когда торцевые поверхности свобод-
ны от внешних сил. При загружении только внутренней
поверхности (р = 0)
Роа2 , . Z
----!--(а2 — Г2)--; ов-=
a2—al v ' hr2 ’ е
Po al ~ z
и = ~„----------1(1 —v) r -|- (1 4- v) a2] —;— ;
E (a2 —al) 1 hr
w —
4- “’<>•
Po a2
2E (a2 — a§) h
2vz2 + (1—v) r24-2(1 4-v) a2 In —
a
При загружении только внешней поверхности
Если а0 а, то при г ап величина тангенциальных на-
пряжений оа в два раза превышает величину нагрузки р
(при фиксированном z — h).
Функциями (3.14) определяется напряженно-деформиро-
ванное состояние при чистом изгибе круглых сплошных и
кольцевых плит, ограниченных плоскостями z — ± Л, по-
2 В 9
гонными моментами Mr^^ph2 и Л4" = р Л2, прило-
о
женными соответственно к внешнему и внутреннему конту-
рам. Выражения для напряжений и перемещений через Мг
3 м
И М? получить просто, ПОЛОЖИВ В (3.20) р=ъ-г£ и Ро =
_ 3 м*
~~ 2 /I2 •
3.4. Растяжение цилиндрического стержня
собственным весом
В пп. 3.4 и 3.5 формы (3.4) и (3.14) функций напряжений
применяются к двум простейшим нагружениям тел враще-
ния массовыми силами — растяжению цилиндрического
стержня собственным весом и к определению напряжений
и перемещений при равномерном вращении цилиндра.
Граничные условия (1.52) на цилиндрической поверхно-
сти (г = а) получают следующую запись:
51
дф д2Ф
— =rpz+r——
дг дгдг
2(l-v)r-^-;
дг
дф
дг ~Г
—2v
dq>z
дг
(3-21)
В первом случае рассматриваемого нагружения — при
растяжении цилиндра собственным весом — массовые силы,
приходящиеся на единицу объема gr = 0 и gz = —у:
дФ 1 дФ
=——у а2 ', -= ай при г=а. (3.22)
дг--------------------------------------2 дг
Этим контурным условиям можно удовлетворить, если,
воспользовавшись решениями (3.14) уравнений (1.8) (1.19),
положить:
ty=Ar2z-, (р — Сг2г.
После подстановки в (1.52) для постоянных А и С по-
лучим значения
4 34-2v „ у
А = —-------у; С =--------- •
4(1-Н) 4(l-f-v)
Следовательно, в рассматриваемом случае функции ср,
Ф и й имеют вид
<р=--------г2 г\ ф=——yr2 z\ Q=—yz. (3.23)
v 4(14-v) 2 r r
Подставляя их в равенства (1.50), находим напряжения
ог = Ое = тГ2 = 0; о2 = yz и в равенства (1.44) — пере-
мещения
v у
и = ———yrz\ w = —— z2-4-ui(l,
Е r 2Е
что совпадает с элементарным решением.
3.5. Равномерное вращение цилиндра
вокруг собственной оси
При равномерном вращении цилиндра вокруг собствен-
ной оси gr = jr\ gz = 0, где / ~ т(р2/а\ со — угловая ско-
рость вращения; т — масса материала цилидра.
По равенству составляющей gz нулю ф2 = 0 и <р2 = 0.
Частным решением уравнения V2 <рг = — 2~(\Г— q)
является функция
/г4
Ф^-7777—г- (3-24)
16 ( 1 —V)
52
По независимости gr от координаты z производная
dgT!dz = 0 и функция фг = 0.
Подставляя эти значения в контурные условия (1.52),
получим:
дф дф
=0; —— = гй, при г = а. (3.25)
дг-----------------------------------дг
Задаем функции ф и <р в форме ф = Аг1 2 3; <р = Сг2.
Тогда [см. (1.46)1 Ф = Лг2Н-——г*.
8 (1 —v)
По независимости Ф от z первое условие (3.25) выполня-
ется при любом А. Значение этой постоянной определяется
условием отсутствия общего растяжения цилиндра, по кото-
рому функция Ф должна быть равна нулю при г = а. Поэто-
му
и окончательно
V/
Ф = —---------(а2 — г2) г2.
8(1—v)
(3.26)
По формуле (1.51) находим функцию Q
V/ 3+v
я = - а/, ч (о2-г2) + —----- /г2-2(1 + V)
8(1—v) 8(1—v)
Вторым контурным условием (3.25)
v id1 3 -Т V
-----L---= Г-------/а2 —2 (1 +v) С
4(1—V) 8(1—v)
3 — V . о
определяется постоянная С: С = 16 _ v2) /g •
Окончательные значения функций <р и Q таковы:
3—v /'
(Г ==-------— i (аг)2; й = —--------(За2 — (3 + 2v) г2|. (3.27)
Y 16(1—v)2 8(1—v)
Для напряжений в рассматриваемом случае нагружения
получаем:1
1 Решение подобной задачи в условиях плоского напряженного
состояния приводит к напряжениям:
or = Ч- j (а2 — г2); ое - -. -1- I (3 + v) а2 —(14- 3v) г2];
О о
в условиях плоского деформированного состояния —
3 — 2v /
°’ = 17ГД71 ’о “ l(3“2v) “ +2v) r’’ •
См. С. П. Тимошенко. Теория упругости. 1937, с. 31 или А. Ляв.
(Математическая теория упругости. 1935, с. 157).
53
3 — 2v vi
--------j (a2 — r2); oz =--------(a2 — 2r2);
8(1—v) 4(1—v)
(3.28)
a6 = fl/1- —Г IO -2v) a2—(1 +2v) r2]; xrz - 0.
8(1—v)
Соответствующие перемещения [см. (1.44)1
« "8Е(1-Г)I(3-5v) fl2“( 1 +v)(1 -2v) f2l r:
vj
w= — ——
2E
(3.29)
В случае равномерного вращения полого цилиндра форма
частного решения (3.24) не изменяется. Контурные условия
(3.25) должны быть выполнены как на внешнем контуре
меридиального сечения (при г = а), так и на внутреннем
(при г = ап). Этого можно достигнуть, положив
<p —Cr2-f-D; Ф^Лг2 + — г4. (3.30)
Первое условие (3.25) при таком задании функции Ф
удовлетворяется и на одном и на другом контурах при лю-
бом значении постоянной А. По равенству растягивающей
силы нулю разность контурных значений функции Ф долж-
на быть равна нулю: Ф (а) — Ф (а0) — 0. Этим определяет-
ся значение постоянной А
vi
А= —---------(a24-a2).
8(1—v) k °'
Поэтому
Ф = — ——-—- (а2 4-0? — г2) г1.
8(1—v)
Функция Q [см. (1.51)1 имеет вид
(3.31)
2(1—V)
— 2(l+v)C4-—-1——- D.
г-
По второму условию (3.25)
v/ . v/ , , 3+v .
— — (a- — ag)- ——------ ag + —--“ /«" —
4(1—v) 8(1—v) 8(1—v)
2(1—v)
-2(l+v)C+ 2 D;
a2
54
vi . , V/ о , 3+v . ,
2(1— v)
-2(l+v)CH---
«о
После решения этих двух уравнений определяются
значения постоянных
3—v
16 (1 —V2)
3—2v
f (a2 — ag); D- ——----— /(aa0)s
16 (1 —v)2
Функции ф и Q получают следующую окончательную
форму:
3—<р 3—2v
Ф iTTi---»Г"* ("2+"о) r2+_J77;—/ (а«о)2;
16(1—V2) 16(1—v)2
Q--—7 Гз (a-2 + a2)_(3 + 2v) г2-
8(1—v) L
—(3 — 2v)f-—(3.32)
\ r J J
Напряжения:
3—2v . ' / aa0 Л
CTr = —--Г 7 a-+ag —r2— -- ;
8(1—v) k Г J J
o,~ , (a^+og—2r»>;
4 (1 —v)
(3.33)
ae^T7T----[(3-2v)(a2+ag)-(H-2v)r2 +
8(1—v) L
+(3~2v)[ —] 1; TrZ--=0.
\ r / J
Перемещения:
---ч((3—5v)(a2—4)-(l+v)(l-2v) r2 +
8£ (1 —v) I
/ аал \21
+(3-2v)(l +v) —M r; (3.34)
\ r } \
0)= — (a2-t «о) z+tt>0.
Наибольшую величину радиальные напряжения полу-
чают при г = Уаа0:
(Ог)шах = 8ц_v)’ ’
55
а наибольшую величину окружные напряжения ое —
в точках внутренней поверхности цилиндра (г = а0):
°е = 4(/_v) 1(3 - 2v) «2+(1 - 2v) og ].
Если ап значительно меньше а, то напряжения Ое при
г --- а0 будут: oe = _ v)/fl2.
Они в два раза превышают напряжения ое на оси при рав-
номерном вращении сплошного цилиндра (см. равенства
(3.28)). Напряжения oz в точках внешней и внутренней по-
верхностей равны между собой по величине, но различны
по знаку:
V/
/ (с*2 —og).
4 (1 —v)
Внешние волокна цилиндра сжаты в осевом направлении,
а внутренние растянуты. При г = )/0,5 (а2 + напряже-
ния о2 обращаются в нуль.
Торцы цилиндра не свободны от внешних сил, величины
которых сравнимы с внутренними напряжениями, поэтому
полученные результаты следует считать первым приближе-
нием к решению рассматриваемой задачи.
3.6. Растяжение сплошного цилиндра силами,
равномерно распределенными
вдоль длины по линейному закону
Рассмотрим задачу о растяжении заделанного в сечении
z = 0 цилиндра силами, распределенными по боковой по-
верхности, по линейному закону pz = pz/a (р — интенсив-
ность нагрузки при г = а, а — радиус цилиндра, / — дли-
на). Опорная реакция равна л р I2, нормальная сила в се-
чении z : N = я р 12 — и р z2.
Первому члену соответствуют напряжения и переме-
щения при осевом растяжении стержня. Задача, следова-
тельно, заключается в определении напряженно-деформи-
рованного состояния цилиндра, соответствующего второму
члену. По пропорциональности его второй степени коорди-
наты z функции напряжений, как указано выше, должны
содержать также эту степень z, т. е. из числа (3.4) нужно
взять
= (аг)2 + Л3(4г2—г2) г2; ф (аг)2 + С3 (4г2 — г2) г2. (3.35)
56
При этом
ф = 4 (А3+2С3) (rz)2 - А3 г* + At (аг)2;
Й = 4(Л3 —2vC3)z2-Mia2—Л3г2 + 2(3-Н)С3г2—2(l+v)Cia2.
По условию (1.36) получаем два равенства:
4 (Л3 + 2С3) а2 = ^-р; Лз-Л^О,
из которых А3 = Лх; А3 + 2С3 = g^.
По второму контурному условию [см. (3.1)] имеем:
Л3 2vB3 = р; Л3-(- (3 -J-v) С3 =(14~v) .
4аг
Решение полученных уравнений приводит к значениям
л _ (2т+-у)р . с _ р . с ___ р
1 8(l+v)a2 ’ 1 16(1 +v)a2 ’ 3 16(l+v)a2
и окончательной форме функций напряжений в рассматри-
ваемой задаче
Вычисление напряжений сводится к формальной под-
становке найденных функций в формулы (1-27). После ее
выполнения
prz
где в oz включены напряжения от растяжения цилиндра силой лрР.
Распределение напряжений, соответствующих второму
члену npz2 нормальной силы N, вдоль радиуса цилиндра при
z = а иллюстрируется графиками (рис. 8) (v взято равным
0,3).
Для перемещений, после подстановки функций напря-
жений в формулы (1.12) и (1.15), выполнения интегриро-
57
вания и присоединения значений от силы яр/2, нетрудно
получить следующие выражения:
Р ( Г / \2 I z VI ( г VI
«=—------------ - — -3-H1+2V) --------- г; (3.38)
ос ( l\ а / \ а / J \ а / J
Перемещение w = 0 при z — 0; следовательно, это се-
чение при деформации остается плоским. Остальные сече-
ния искривляются, образуя поверхности параболоидов вра-
щения, причем искривление увеличивается с увеличением
координаты z.
Рис. 8
Удлинение продольных волокон различно. Разница меж-
ду удлинениями волокон, лежащих на поверхности г = а,
и осевого волокна составляет pl/2E.
Функции напряжений ф и ф в использованной здесь фор-
ме при ином выборе постоянных интегрирования приводят
к значениям напряжений и перемещений при нагружении
боковой поверхности цилиндра радиальными силами, рас-
пределенными вдоль длины по закону квадратной пара-
болы.
Решения в целых полиномах несовершенны — краевые
условия выполняются точно только на боковой поверхно-
сти цилиндра, а на торцах лишь в соответствии с принципом
Сен-Венана интегрально. В приведенной задаче ненагру-
женное торцевое сечение z = I не свободно ни от нор-
мальных, ни от касательных сил (естественно, уравнове-
шенных). Влияние их имеет местный характер, следователь-
но, нужно предполагать, что длина цилиндра / достаточно
велика по сравнению с радиусом а. Уточнение результатов
требует значительного усложнения формы функций ф
и <р (см. гл. 6).
58
3.7. Нагружение полых цилиндров
полиномиальными силами
Переходя к исследованию напряженно-деформированно-
го состояния полых цилиндров силами, распределенными
по боковой поверхности по степенному закону, дополним
систему функций (3.4) решениями уравнения V2ip = О,
взятыми в форме
Vn = zn+fni (г) гп~ 2 +fn?. (г) zn—4 + ...
при п = 2, 3, ... [значения п = 0 и п = 1 входят в систему
(3.4)]. Выполнив подстановку, получим:
L(n-l)+r -7- — -^2-|гп-2 + [(л-2)(л-3)М1 +
[ dr г dr | [
। • 1 dfn2 1 п_.л , Г
+ г ~ ~ г + (я—4)(п—5)/П2-[-
dr г dr [
+ г — -^-1гп-6+...=0.
dr г dr J
Приравнивая каждую квадратную скобку нулю и ограни-
чиваясь только частными решениями получаемых урав-
нений, последовательно находим значения функций:
, Г2 I 1 \
fni(r)=— п(п— 1) — I In г—— I;
г* ( 1 \
fni(r) = n(n— 1)(л—2)(л—3)—— I In г — 1— —
X * 1» \ Ж f
и в общей форме
2А
U(r) = (-l)An(n-l)...(n-2ft+l)—— ---------- X
22«—1 1)! fe!
/ *-l j , \
X I Inr— — —------ I; k= 1,2, 3,...
I tn 2k I
\ rn= 1 /
Таким образом, искомое решение представляется ра-
венствами
— В2
(3.39)
чр3 = В3 Г г2 —Зг2 f In г —-Ml z;
59
В качестве примера рассмотрим следующую задачу.
Полый цилиндр длины 21 с внешним радиусом а и внутрен-
ним а0 нагружен по внешней поверхности радиальными си-
лами по параболическому закону (рис. 9). Помещая
начало координат в
центре среднего сечения, имеем: рг—
Как и в предыдущем примере,
задача разделяется на две — задачу
Ламе о нагружении полого цилиндра
равномерно распределенными силами
рг — —р и задачу о нагружении по-
лого цилиндра силами рг = рг2И2. Ре-
шение первой задачи приведено в
п. 3.2, здесь составим решение для
второй. За функции напряжений
принимаем полиномы второй сте-
пени:
ф= А г’ + Л3 (4z2—г2) r’ + Bj
2z2—г2 12 In — — 1
\ а
<Р = С04-С1 г24-Сз(4г2—г2) г24-Di
2z2 —r2|21n —— 1
\ а
(3.40)
Функции Ф ий [см. (1.17) и (1.29)] получают вид
Ф = [4(А,+2С3) r«+2(B1+2D1)] z2—А, г’-
— Bi г21 2 In —— 1
\ а
+Аг2;
fi= 4(Hs-2vC3) r2 + 2[B1+2(l-v)D1] — -
I J \ r /
- Из-2 (14-V) C3] r2—2 [/?!-2(1 +v) DJ In—+
a
+H1-2(l+v)C1+B1+2(l-v)D1 + 20~V) Co-
По равенству нулю нормальной силы в сечениях цилинд-
ра разность значений функции Ф на внешней и внутренней
поверхностях цилиндра должна быть равна нулю, Ф (а) —
60
— Ф (а0) — 0, что дает следующую связь между постоян-
ными:
(2а! ап \
1 + - ", 1п—-Л1==0.
а2—ag а /
Выполнение условий (3.1) при г = а0 и г = а приводит
к системе уравнений:
/ а \2
4(l+v)aM3—2(1—v^+pl—I =0;
4(l+v)aJ As-2(1-v) В1=0;
[(5+2v)as-aJM3+ l+v-F
a2—aj
ap
a
2(1—v)
-2(l+v)C1+ V Co = 0;
a1
[(5+2v) a2-a2] A, + [(l+v)[l-21n—П
L \ a J
+ ,2Q\ In——~1
a2—a’ a J
B1-2(l+v)C1
2(1—v)
«о
Co = 0.
После решения этой системы получаем значения всех
постоянных:
ра
Ая= — 2С3=— . ,
3 3 4 (1 +v) (a2 —aj) Р
В1= -2D1 = ------;
1 1 2(1—v)(a2—aj)/2
(a2 + a2) Л3—( 1 + , \ In
\ cr—aj a /
5 + 2v
2(l+v)
(a’+aj) As—
2ag
a2—aj
в,;
(1 - v) C0 = (3+v) (aa0)s A,+ V^aa°}' Bl In — •
a1—ag a
Выполнив подстановку функций напряжений при най-
денных значениях постоянных в формулы (1.27), (1.12) и
(1.15), составляем выражения для напряжений и перемеще-
ний: тгг = О
61
_____pa2_____
4Е(а» —al) I2
(3.41)
4v(l+v)ag
+ 1—v
-73— ](a2+o3)+vr’-2(3+v)(^-),+
14-v / \ r /
a2—al
pc?
2E(a2—al)l2
(3-42)
3v \f
(a’+4)+2( +v)o«* X
Z(I +V) / \
(2—v)ag , a0 7)
-------Z----Z~ *n ) z.
(1—v)(a*—aj) a JJ
Постоянная интегрирования принята равной нулю.
Для получения окончательных значений напряжений и
перемещений в рассматриваемом случае нагружения полого
цилиндра нужно к приведенным выражениям присоединить
значения (3.12) и (3.13).
62
Глава 4. ДЕФОРМАЦИИ ЦИЛИНДРОВ.
РЕШЕНИЕ В ЦИЛИНДРИЧЕСКИХ ФУНКЦИЯХ
4.1. Функции напряжений
Применение функций ф (г, z) и <р (г, z) в форме целых по-
линомов (3.4) и (3.39) к задачам осесимметричного нагруже-
ния цилиндров ограничено только случаями нагружения
их боковых поверхностей силами, распределенными по дли-
не по степенному закону. Значительно более эффективно
применение другой формы, которую по числу достигнутых
результатов следует считать основной.
Следуя методу Фурье, найдем решение уравнения (1.8)
д2 ф 1 Эф д2 ф
dr2 г dr + дг2
в виде произведения функции R переменной г на функцию Z
переменной z: <р = R (г) Z (z).
После подстановки
„ / d2 R 1 dR \ „ d2 z п
Z I о ' I “Ь R о О
\ dr2 г dr ) dz2
приходим
НИЯМ для
к разделению переменных, т. е. к двум уравне-
определения функции R (г) и Z (z):
d2R I dR d2Z
— -------— ±X2/?=0; — W = 0, (4.1)
dr2 r dr dz2
где X — некоторый параметр.
Первое из них — уравнение Бесселя, его
R=CrJl(kr)+DrYl(kr)
решение
(4.2)
при верхнем знаке перед X2 или
R = CrIl(kr)+DrKl(Kr)
(4.3)
при нижнем знаке.
Jr (Xr); Yt (Xr); (Хг); (Хг) — функции Бесселя первого
и второго рода первого порядка соответственно действи-
тельного и мнимого аргумента1.
Соответствующие решения второго уравнения (4.1):
Z=AeKz+Be~tz, (4.4)
1 Здесь приняты такие же обозначения, как в [25], [41].
63
если перед вторым членом равенства знак минус и
Z = HsinXz-|- В cosXz. (4.5)
если перед ним знак плюс.
Таким образом, функция напряжений <р (г, z), а следо-
вательно и ф (г, г), может быть записана в одной из следую-
щих форм: в функциях Бесселя действительного аргумента
Ф(г, z) = (A^z+Be~Kz) [CJi (W+DYi (Xr)] г;
(4.6)
ф(г, z) = (A' <fz+B' e~Kz) [C JitKry+D'
или после замены показательных функций гиперболиче-
скими
Ф (г, z) = (A sh kz-f-B ch Xz) [CJj (Хг)+ЛУ\ (Xr)] r;
(4.7)
ф(г, z) = (A' sh Xz-f-B' ch Xz) ]C' (Xr)-f-D' Kj (Xr)] r;
в функциях Бесселя мнимого аргумента
ф (г, z) = (A sin Xz4~B cos Xz) [C/j (XrJ+DKj (Xr)] r;
(4.8)
ф (r, z) = (A' sin kz+B' cos Xz( [C' /i(Xr)4-D' Kx(Xr)]r.
Переходя к составлению функций Ф (г, z) и Q (г, z), со-
ответствующих ф и <р в указанных формах, напомним фор-
мулы, связывающие функции Бесселя с их производными.
Функции Бесселя действительного аргумента:
d d
— Jo (х) = -л (X), — Уо (х)= -Y. (х);
dx dx
-j-хп Jn(x) = xn Jn-i(x), -y~'xnYn(x) = xnYn-1(x);
dx dx (4.9)
d d
— x nJn(x)=—x nJn+l(x), ——X nYn(x)=— x nYn+1(x).
dx dx
Функции Бесселя мнимого аргумента:
d d
— 19(х) = 11(хУ, — K0(x) = -K1(xy,
dx dx
-^xnIn(x) = xnln-1(x)-, xnKn(x)=-xnKn-1(x); (4.10)
dx dx
x~n In(x) = x~n In+i(x)\ -j— x~n Kn(x)= — x~n Kn+i(x).
dx dx
Значения Ф (r, z) и fi (r, z) при ф и <p, определенных ра-
венствами (4.6) и (4.7), составим по формулам (1.17) и (1.26):
дю 1 2 дф
Ф=ф+г-^-; [Ф + 2(1—v)T]—
г* Г ОГ
64
Получаем:
ф(г, z) = {[C' Zj(kz)+CkzZ' (М1Л(И+
+ [D' Zj (Xz)+DXzZ' (Xz)] (Ml r;
(4.П)
Q(rz)= — {[Cz ZUXzJ-J-CXzZ' (Xz) + 2(1—v)CZ(Xz)] J,(Xr) +
r
+ [D' Z^XzJ+DXzZ' (Xz) + 2(l—v)DZ(lz)]F1(Xr) —
—2VZ(Az)[CJo(br)+DVo(V)]).
Здесь в целях сокращения записи сохранены обозна-
чения (4.4) и (4.5)
Z(Kz) = A^z + Be~Kz-, Z1(Kz) = A' ^Z+B' e~kz;
(4.12)
Z' (kz)=Aekz — Be~Kz; ZJ (Xz) = 4z eKz—B' e~Kz
ДЛЯ (4.6);
Z(Xz) = i4 shlz + fi ch Xz; Zt = A' sh Xz-j-B' chXz;
(4.13)
Z' (Xz) = 4 ch Iz-j-Bsh Xz; Z' = A' ch Xz-f-B' sh Xz
для (4.7).
Составление функции Ф (г, z) и Q (г, z) для решений
в форме (4.8) выполним, применяя формулы (1.18) и (1.26)
dw I 2 дф
ф='*’-г л : 12 ~~ [Ф+2(1-у)ф1------------
дг г2 г дг
заметив попутно, что последнюю удобно представлять
в виде
Й = -^-[ЗФ—2ф+2(1—у)ф], (4.14)
приводящем к упрощению вычислений. После подстановок,
дифференцирования и группировок имеем:
Ф = (Л' sin Xz4~B' cos Xz) (Xr)—(Л sin Xz-|-B cos Xz) Xr₽z (Xr),
(4.15)
Q = —7- {(A' sin Xz-f-B' cos Xz) Rx (Хг)+(Л sin Xz-j-B cos Xz) X
r1
X [3Xr₽' (Xr)+2(1—v)₽(Xr)l),
где J?(Xr)=Cr/1(Xr)4-DrK1(Xr); J?i(Xr)=C' r/j (XrJ+D'rKj(Xr);
(4.16)
/?'(Xr) = Cr/0(Xr)—DrKo(Xr), ₽;(Xr)=C' r/0(Xr)—D’rK0(br).
65
Приведенные формы функций Ф (г, z) и Q (г, z) могут
быть дополнены еще двумя, получаемыми после составления
Ф (г, z) по формуле (1.17) при значении (4.8) для функции
Ф (г, г) и после составления Ф (г, z) по формуле (1.26) при
Ф (г, z), определяемой равенствами (4.6) и (4.7). Однако эти
формы обычно не применяются.
4.2. Выражения для напряжений и перемещений
в цилиндрических функциях
Формулы для напряжений и перемещений, соответст-
вующие форме решения осесимметричной задачи предыду-
щего параграфа, без труда составляются формальной под-
становкой значений функций (4.6), (4.7), (4.11) или (4.8),
(4.15), в равенства (1.27) и (1.12). Ниже приведена сводка
результатов подстановки.
Первая форма, содержащая функции Бесселя действи-
тельного аргумента:
ог = —— {[С' Zj (Xz)+ CXzZ' (Xz) +
+2(1 — v)CZ(Xz)] A (Xr) + [D' Zt(Xz) +
+DkzZ'(Xz) + 2 (1 — v) DZ (Xz)] У, (Xr) —
—Xr [C' Zx (Xz)+CXzZ' (Xz)+2CZ (Xz)] Jb(Xr)-
—Xr [C' Zx (Xz)+DXzZ' (Xz)+2DZ (Xz)] Уо (Xr)};
oe =-- ЦС' Zx (Xz) + CXzZ' (Xz) +
+ 2(1—v) CZ (Xz)] JjfXrJ + fD' Zt(Xz) +
+DXzZ' (Xz)+2(1 — v)DZ(Xz)] Fj(Xr) +
+ 2vXrZ (Xz) [CJ0 (Xr)+DF0 (Xr)]};
uz=— X{fC' ZJXzJ + CXzZ' (Xz)] J0(Xr)+[D' Zj(Xz) +
+DXzZ' (Xz)] У0(Хг)};
тг2 = Х {[C' ZJ (Xz) + CZ' (Xz)+CXzZ(Xz)] Л (Xr) +
+ [D' Z\ (Xz)+DZ' (Xz)+DXzZ(Xz)] Vj (Xr)}; (4.17)
1
2ц
ЦС' Zj(Xz) + CXzZ' (Xz)+2(1—v)CZ(Xz)]Л(Хг) +
(4.18)
+ [D' Zj(Xz)+DXzZ' (Xz)+2(1—v)DZ(Xz)] У^Хг)};
w= —~ ЦС' ZJ(Xz)+CXzZ(Xz)—(1— 2v)CZ' (Xz)] J0(Xr) +
2ц
+Р' z; (Xz)+DXzZ(Xz)—(1—2v)DZ' (Xz)] УоM} + const.
66
Здесь Z (Xz) и Zr (Xz) определены равенствами (4.12) или
(4.13).
Вторая форма, содержащая функции Бесселя мнимого
аргумента:
ог =±“ {(А' sin Xz-f-B' cos Xz) [Xr/?: (Xr)—Ri (Xr)] +
r2
4-(Д sin Xz + B cos Xz) [Xr/?' (Xr)—(Xr)2 /?(Xr)—2(1 —v) /?(Xr)]};
o0 = -^- {(Д' sin Xz4~B' cos Xz) /?j (Xr) +
+(4 sin Xz4~B cos Xz) [2(1 —v) /?(Xr)—(1 —2v) Xr/?' (Xr)};
(4.19)
X
иг — —----{(Д' sin Xz4~B' cos Xz) /?{(Xr) —
— (Д sin Xz4-B cos Xz) [2/?' (Xr)4-Xr/?(Xr)]};
X
тг2 =---{(Д' cosXz—B' sin Xz) /?! (Xr) —
r
—(Д cos Xz — В sin Xz) Xr/?' (Xr)};
u =------ {(Д'sin Xz + B'cos Xz)/?j (Xr) —
2gr
—(Д sin Xz + B cos Xz) [Xr/?' (Xr) —
-2 (1 -v) R (Xr)]};
(4.20)
w =-----
2gr
{Д' cos Xz—B' sin Xz) /?{(Xr) —
—(Д cos Xz —В sin Xz) [2(1 —v) /?' (Xr)+
4 - Xr/? (Xr)]} 4- const.
Значения R (“кг) и R' (кг) даны формулами (4.16).
Функции Бесселя Ro (кг) и (кг) имеют бесконеч-
но большие значения при г = 0. Поэтому при рас-
смотрении деформаций сплошных цилиндров по условиям
<р = 0иФч=0на оси вращения они должны быть исклю-
чены из приведенных выше выражений, т. е. постоянные Du
D' должны быть приняты равными нулю. При рассмотре-
нии задач о напряженном состоянии у цилиндрических
полостей в бесконечно большой среде, наоборот, в равенст-
вах ((4.19) и (4.20) следует отбросить функции Бесселя пер-
вого рода /0 (V) и 1г (кг), т. е. положить С и С' равными
нулю, так как эти функции возрастают до бесконечно боль-
шой величины при г->оо.
67
4.3. Сплошной цилиндрический стержень,
нагруженный силами, изменяющимися
по закону синуса или косинуса
При постоянном значении г функции (4.8) и (4.9) и на-
пряжения (4.19) являются тригонометрическими функция-
ми Xz, следовательно, они соответствуют нагружению бо-
ковых поверхностей цилиндров силами, меняющимися
Рис. ю
вдоль длины по зако-
нам синуса или коси-
нуса.
Рассмотрим, на-
пример, длинный ци-
линдрический стер-
жень, боковая по-
верхность которого
подвергается дейст-
вию радиальных сил
Рг = — Р (1 + cosXz),
где Х= 2л// (рис. 10).
Так как стержень
сплошной, как указа-
но выше, нужно по-
ложить D = D' = 0.
По косинусоидально-
му характеру напряжений аг = рг при г = а постоянные
А = А' = 0. Таким образом, за ф (г, z) и <р (г, z) нужно взять
ф (г, z) = 40 г2 + С| г!। (Xr) cos Xz;
ф (г, г) — Во г'2 —|—С2 r/| (Xr) cos Xz,
(4.21)
где Cj = В'С и С2 = ВС.
Соответствующие значения функций Ф (г, z) и Q (г, z):
Ф (г, z) (4 — 2В0) г2 + [С, гЦ (кг) — Сг Хг2 /0 (Xr)] cos Xz;
Й (г, z) = 40—2 (24-v) Во+у [С, /, (Xr)+3C2 Xr/0 (Хг)+ (4.22)
+ 2 (1—v) С2 (Хг)] cos Xz.
По
г = а.
На
отсутствию общего растяжения стержня Ф = 0 при
т. е.
Aq—2Во--0; Cj /| (Хи) — С2 Хй/g (Хо) = 0.
основании краевого условия
1 дФ
дг
о
68
должно быть: Ао — 2 (2 + X) Вп = —р;
С, [Ха /0 (Ха) — Л (М1 + С, [Wo (Ха) —(Ха)2 Л (Ха)—
—2 (1—v) Л (Ха)] = — р.
Совместное решение полученных равенств приводит к зна-
чениям всех постоянных:
Л о = 2В0 - [ | ©♦" > С2= [j* (Ха)•
где знаменатель
О* —(Ха)2 /g (Xa)-[(Xa)*+2 (I — v)] /? (Xa). (4.23)
В табл. 1 приведены численные значения k~2 D* при k =
= Ха от 0 до 10.
Напряжения и перемещения определяются формулами
(4.19) и (4.20) после подстановки в них найденных постоян-
ных. Они меняются по длине стержня по периодическим за-
конам; нормальные напряжения пропорциональны cos Xz
и имеют наибольшую абсолютную величину при г = а в
поперечных сечениях z = ±2/г/, гдетг2 = 0; касательные на-
пряжения тг2 пропорциональны sin Xz, их наибольшая ве-
личина получается в сечениях z = (2k + 1) I, где a2 = 0.
В табл. 2 содержатся результаты подсчета напряжений при
/ = -у ла, v = 0,3. Графики распределения напряжений
ffe и в поперечном сечении z = 0 изображены на рис. 10.
На оси z при г = О1
рХа
аг — р— [Wfl (Xa) + 2v/, (Ха)| cos Xz;
£•1 J
рУм
ai [Xa/0 (Xa) —2/, (Xa)[ cos Xz, тг2=0.
Таблица 1
k k о- а> Л 7Г (Л)
0 0,65 3,5 1,152406-10 7 3,38012-103
0,5 0,692035 4 2,415213-10 7.5 8,06927-1О3
1 0,836351 4,5 5,238990-10 8 1,94138-104
1,5 1,148414 5 1,166226-102 8.5 4,70544-104
2 1,780838 5,5 2,649153-102 9 1.147947-105
2,5 3,079398 6 6,112371 -10® 9,5 2,81571-10®
3 5,761120 6,5 1,429553-103 10 6,94046-105
1 Здесь принято во внимание, что [/0 (Xr)]r=0 1;
[(Xr)-i /х(Хг)1г=0 =
69
о
Таблица 2
r/a z/a 0 0,2 0,4 0,6 0,8 1
Нагружение силами рг =-р( 1+cos Xz)
or/p 0 -1,7740 — 1,7881 -1,8286 — 1,8892 -1,9547 -2
л —0,2260 —0,2119 -0,1714 -0,1109 —0,0453 0
1 0 — 1,7740 - 1,7849 -1,8225 -1,8854 — 1,9792 -2,1081
OQIP Л —0,2260 -0,2151 -0,1775 -0,1146 -0,0208 +0,1081
Oz/p 0 +0,4697 0,3661 0,2966 0,1562 -0,0981 -0,4942
XrzlP л/2 0 -0,0753 -0,1373 -0,1679 -0,1382 0
°r/P 0 Harpy» —0,4079 ,ение силами -0,4023 pz=psin Xz -0,3800 —0,3275 —0,2169 0
06/p 0 —0,4079 —0,4120 —0,4274 -0,4521 —0,4875 -0,5340
<h/P 0 —0,2677 -0,3125 -0,4566 —0,7305 -1,1918 -1,9943
Тр 2 / p л/2 0 +0,0579 0.1441 0,2926 0,5531 1
В точках боковой поверхности
2р/. (Ха)
ог --- — Р (1 + cos Xz); ае = — р —-—— [vXa/0 (Аа) +
+ (1 —v) /> (Ха)] cos Xz;
рХа
— у* [Аа/§ (Ха)—270 (Ха) Ц (Ха) —Аа/? (Ха)] cos Az, xrZ = 0.
Решение задачи о нагружении цилиндрических стержней
синусоидальной нагрузкой осевого направления pz —
= psin Az определяется теми же функциями (4.21) и
(4.22), которые были применены в предыдущем случае
(Ло = Во = 0).
Условиями для определения постоянных служат равен-
ства Ф = —Л72л и аг = 0 при г = а, где
7V =
2л
т
ра cos Xz
— нормальная сила в поперечных сечениях стержня (пред-
полагается, что стержень не подвержен равномерному рас-
тяжению силами, приложенными на торцах).
Применяя указанные условия, получаем:
Ci /j (Ха) — Сг Ха/0 (Ха) = -^- р\
Q [Ха/0 (М-Л (М1+Са [Ха/0 (Ха)—(Ха)2 Л (Ха)-
— 2 (1 — v) Л (Ха)] = 0.
Отсюда:
С’ (М~(М2 Л (М-2 (1 -v) /, (Ха)];
АД-'
С2= [Ха /о (М-Л (ML
KU
где D* имеет значение (4.23).
Напряжения определены формулами (4.19). Значения их
при I = у- ла и v = 0,3 приведены в табл. 2. Характер из-
менения вдоль радиусов в сечениях z = 0 и Az = л/2 изо-
бражен на рис. 11.
На оси цилиндра (г = 0)
ar = ое [Xa (1— 2v) /0 (М~(М2 Л (Аа)—
—2 (1 — 2v) /0 (Ха)] cos Xz;
oz= —[ЗАа/0 (М—(М2 Л (М—2 (2—v) Л (Ml cos Az,
тгх—0.
71
В точках боковой поверхности
р
аг = 0; ае =-^-[(l-2v) Ха/| (2^) —(1 — 2v) /0 (Ха) Л (Ха) -
и
— Ха1\ (Ха)] cos Xz;
~[3W° (M-2 (2-v) /о (Ха) /, (Ха) -
— Ха/f (Ха)] cos Xz; тг2 = р sin Xz.
Рис. 11
4.4. Решение в рядах
Во всех рассмотренных выше частных задачах предпола-
галось, что силы рг и рг на боковой поверхности цилинд-
ров — непрерывные функции координаты z. В случаях,
когда эти функции кусочно непрерывные, решения можно
получать, составляя функции напряжений ф (г, z) и <р (г, z),
а следовательно, и Ф (г, г) и Й (г, z) в виде бесконечной сум-
мы значений (4.8) и (4.15). Приведем запись этих сумм и
соответствующих им напряжений и перемещений.
Если силы рГ (г) и рг (z) определены рядами
оо оо
Рт (*) =Pro + У, Prh cos Xft z, pz (z)= 2 Pzk sin Xfc z, (4.24)
k=1 k=1
где Xft равно либо fail l, либо (2k + 1) л/2/, I — длина ци-
линдра1, то за функции напряжений нужно взять:
1 Строго говоря — длина, определяющая периодичность измене-
ния нагружения.
72
OO
ф (r, z) = Ао r2 + r 2 Ak Л (h r) cos kh z;
k= 1
oo
<p (r, z) — Вог2-^-г У Bh fl (kh r) cos kh z;
k= 1
OO
ф (r, z) = (A0-2B0) r2 + r 2 И* Л r)-
k= 1
(4.25)
— Bh Xft rl0 (Xfcr)] cos kh z;
Q (r, z)=A0
k== 1
— Bh [3Xfc-r/0 (kh r) — 2 (1—v) /i (Xfc r)]) cos khz.
Соответствующие выражения для напряжений и-переме-
щений:
<Jr = -^o + 2vBo+_^_ г/о f) —
k= 1
— Л (К r)J —Bk I (A* r)2+l—2v] /j (Xfc r)) cos Xfc z;
1
Oy-Ao + 2vB0+—2 {[ЛЛ 4-2(1— v) BAh&krj-fl-
k= i
— 2v) Bh kh rl0 (Xfc r)) cos Xft z;
ог— —2 (Ло—2B0) 2 K^fc—2B&) l0 (Xfc r) —
h= 1
— Bh A* r/i (Xfc r)] cos kh z;
OO
Trz 2 f) —Sfc К rlo (Xfc r)l sin Xfc z:
k= i
и =— (Ло—2vB0) r +— 7, {[лл4-2(1—v) Bfc] Ii(khr)—
2(1 2ц —
— Bk kh rlo (kh r)| cos Xft z;
1 00
»= --i-[40-2(l-v)B„]z-— У {|A*—
2»* *= l
—2 (1—v) fifc] /0 (Xfc r) — Bh Xh гЦ (ХЛ r)) sin Xfc z-j-w0,
где w0 — постоянная интегрирования.
(4.27)
73
Будем также пользоваться следующей краткой записью
этих формул:
оо
<b- = 4o-r-2vBo У («Мл COS z\ az- — 2 (Ло—2В0) +
А= 1
2; (°zh cos z;
Л = 1
(4.28)
оо со
oe=^0 + 2vB0+ У, (oe)fc cos Xfc z; тг2 — 2 (Trz) sin Xh z;
k= 1 k-=\
CO
(Ло—2vB0) f+2
*= 1
(uh) cos Xfc z
2Л0 -
oo
— 4 (1 —v) fi0 -J- У (w)k sin z
A—1
Если силы определены рядами
оо оо
Рг (z) 2 Prh sin Хл z: рг (z) -. У ptfl cos z, (4.29)
A= 1 k^.\
то выражения для функций напряжения, перемещений и
напряжений имеют форму, подобную выше приведенной, с
соответствующей перестановкой тригонометрических функ-
ций sinXfcZ и cos Xfcz, изменением первых членов и некоторой
корректировкой знаков. Приведем только краткую запись:
со оо
ПГ= 2 (°r)h sin z; az = У (oz)fc sin z;
k=\ A=1
OO oo
ае = У (ae)h sin 2: T« = 2 (Trz)fc cos z; (4.30)
A=1 A=1
co oo
« = У («fc^sin Xfc z; w = 2 (“»)* cos 2 +^0-
*=i k=i
Переходим к выполнению граничных условий.
В случае симметричного нагружения по равенству
°г — Рг (^), тгг = pz (z) на цилиндрической поверхности
(г = а), приравнивая коэффициенты при индексах k выра-
жений аг и Trz (4.26) и сил pr (z) и pz (г) (4.24), получаем сис-
тему уравнений:
74
/0 + 2vB0 = pr0; Ak a/0 (^k a)—/x (Xfc a)] +
+ ВЛ [Xft alo (kfc a) —(Xft a)2 /, (Xfc a) —2 (1 —v) (Xfc a)]==
~Prk a»
Ak h (^fc a) — Bh X* a/0 (Xfc a) — — •
Aft
k = l, 2, 3, ...
Решением этой системы определяются значения всех посто-
янных:
Ah =------г lPrh (^Л и)2 !о (kfc a) — Pzk Щ al о (ХЛ a) —
XfcDfc
-(** а)2 Л (Xfc a) —2 (1 -v) /, (Xfc a)]}; (4 32)
1
&h = Г-' (Prh а!г (Хд u) +
Xfc Dk
“ЬРхЛ [Xft alo (Xfc a) — Ji (Xfc o)}.
Знаменатель был указан выше,
D*k = (Xfc a)2 /02 (X* a)2 + 2 (1 — v)] I2 (Xfc a) (4.23)
Дополнительным для получения постоянных Ао и Во слу-
жит условие Ф= —Л72л (2.36), которым определяется влия-
ние на напряженное состояние цилиндра сил, приложенных
к торцам. По этому условию:
л Л N N 1
° 0 2па2 2F 2 Иг0
где pz0 — равномерно распределенные силы на торцах.
Присоединив сюда первое равенство (4.31), имеем:
^Pro+'vPio 2prt — pz0
Л 0 =----------; Во =------------ (4.33)
2 (1+v) 4 (1+v)
В случае асимметричного нагружения цилиндра выпол-
нение граничных условиях ur = pr (z) и xrz = pz (z) при-
водит к формулам для постоянных Ак и Вк, отличающимся
от (4.32) только знаком перед pzh.
Таким образом, задача сводится к разложению функ-
ций рг (г) и pz (z) в ряды Фурье, осуществимому, если зако-
ны задания сил рг (z) и pz (z) удовлетворяют условиям Ди-
рихле. Такое построение решения, строго говоря, соответ-
ствует нагружению цилиндров бесконечной длины уравно-
вешенными периодическими силами. При рассмотрении ци-
линдров конечной длины (только такие задачи имеют прак-
75
тический смысл) выделяется один из участников периодич-
ности длиной 21 (рис .12). Пользуясь произвольностью про-
должения закона распределения сил за пределы выделен-
ного участка, можно частично распорядиться напряжени-
ями на торцах цилиндра — освободить их от нормальных
или касательных сил.
Рис. 12
Как известно, любое нагружение цилиндра может быть
расчленено на два частных нагружения— симметричное й
асимметричное по отношению к среднему поперечному сече-
нию. Такое расчленение приводит к упрощению процесса
решения и поэтому широко практикуется. Приведем формы
представлений разложений в ряд сил в каждом из этих двух
частных случаев при различных условиях на торцах цилинд-
ра.
Симметричное нагружение (рис. 13).
Положив = kn/l по (4.25), получаем:
оо оо
2ftn kn
Prh cos— z; pz (z) Pzk Sin — z. (4.34)
k=o 1 k=\
При таком выборе касательные напряжения xrz и осе-
вые смещения w на торцах цилиндра (z = ±/) обращаются
в нуль, а нормальные напряжения oz отличны от нуля. Ци-
линдр находится в условиях жесткого закрепления концов
в осевом направлении. Этот случай соответствует четному
продолжению нагрузки за пределы цилиндра.
п . 2Л-Н
Положив — л, имеем:
2ft-|-1 2ft -|-1
Рг = Prh COS 21 ~ nz'' Pz = Pzh Sin 2/~ Я2‘ <4*35
76
На торцах цилиндра нормальные напряжения oz и радиаль-
ные перемещения и равны нулю, касательные напряжения
xrz отличны от нуля. Концы цилиндра свободны от закреп-
лений в осевом направлении (ш У= 0). В этом случае на-
грузка продолжена за пределы цилиндра z = ±/ по нечет-
ному закону.
Рг
21 | Г t 21
6Z‘O |-------1 бг=0
ц.О и = °
Рис. 13
Асимметричное нагружение (рис. 14).
Принимая = knll, представляем силы в форме
оо оо
2Лл Лл
Prk sin —— г; рг (z) = Pzk cos — z. (4.36)
k=\ k=o
Торцы цилиндра z - ±/, как следует из соответствую-
щих равенств (4.29), свободны от напряжений uz и радиаль-
ных смещений и, касательные напряжения xrz и перемеще-
ния w отличны от нуля. Цилиндр не закреплен в направле-
нии оси. Продолжение нагрузки за пределы нагружения
четное. Принимая X = -k+1 л, имеем:
л* L
2Л+1
Pr(z) = 2i Prh s»n nz
Л=о
2Л4-1
Pz (z) = cos 21 ’ Пг'
k=o
(4.37)
На торцах z = ± I напряжения ozy= 0 и trz = 0, переме-
щения и Ф 0 и w = 0. Концы цилиндров жестко закрепле-
ны без трения. Продолжение нагрузки за пределы цилинд-
ра нечетное.
77
Во всех приведенных случаях нагружения стержней
условия закрепления левого и правого торцевых сечений
предполагались одинаковыми. Возможно выполнение раз-
личных условий на разных концах цилиндра: на одном —
равенство нулю касательных напряжений тгг и осевых пе-
ремещений w, на другом — равенство нулю нормальных
напряжений az и радиальных перемещений и. Такое реше-
ние можно получить, воспользовавшись представлениями
сил равенствами (4.35) или (4.37) и.считая, что цилиндр
ограничен сечениями z = 0 и z = I.
Итак, при построении решения в форме рядов Фурье
достигается только частичное выполнение граничных ус-
ловий на торцах цилиндра при точном выполнении их на
боковой поверхности. Поэтому, применяя эту форму, не-
обходимо предполагать, что длина цилиндра превышает в
несколько раз его диаметр (21 > 2a). Отличие заданного
распределения сил на торцах от получаемых в результате
решения приводит к местному перераспределению на-
пряжений у концов цилиндра и, согласно принципу Сен-
Венана, не влияет на деформации и напряжения в большей
части его объема. Значение имеет только суммарная вели-
чина указанных сил, при осесимметричном нагружении они
могут вызывать либо общее продольное растяжение, либо
сжатие стержня. Если на каждом торце силы взаимно урав-
новешены, то напряженно-деформированное состояние ци-
линдра полностью определяется силами, приложенными
к боковой поверхности, за исключением небольших участ-
ков у торцов1.
Применяя решения (4.28) и (4.30) будем считать, не ого-
варивая каждый раз, условие достаточной величины отно-
шения l/а выполненным, иногда подчеркивая это обстоя-
тельство термином «длинный» цилиндр.
Следует также иметь в виду, что точность получаемого
решения для данных цилиндров зависит от места располо-
жения нагрузки по отношению к торцам цилиндра. Дей-
ствительно, для выравнивания напряженного деформиро-
ванного состояния, согласно принципу Сен-Венана, не-
обходимо, чтобы внешние силы были приложены в доста-
точном отдалении от торцов. Если это выполняется, то зна-
чения напряжений на торцах, как правило, невелики.
Противоположными в смысле выполнения краевых усло-
вий задачам о деформациях длинных цилиндров являются
задачи о деформациях коротких цилиндров — плит, длина
1 Сказанное подтверждается решением, приведенным в п. 6.6.
78
образующих которых значительно меньше длины диаметра
(2 I <z 2а). Напряжения и деформации в плитах опреде-
ляются в основном характером распределения сил на тор-
цах — основаниях плит. Краевые условия на них должны
быть выполнены точно. Выполнение же условий на боковых
цилиндрических поверхностях в большинстве случаев ока-
зывается возможным по равенствам статической эквива-
лентности. Форма функций напряжений, приводящая к та-
ким решениям, и примеры нагружений круглых толстых
плит приведены в гл. 5.
Наибольшие трудности представляют решения задач о
напряженно-деформированном состоянии цилиндров «сред-
ней» длины, когда отношение На близко к единице. Необ-
ходимость точного удовлетворения условий на торцах и
боковой поверхности цилиндра одновременно значительно
усложняет процесс получения числовых результатов. Спо-
собам исследования деформаций цилиндров средней длины
посвящена гл. 6.
4.5. Асимптотические выражения
для напряжений и перемещений
Практическое осуществление расчетов напряжений и пе-
ремещений по формулам (4.28) и (4.30) в конкретных зада-
чах является длительным и сложным вычислительным про-
цессом. Ряды, входящие в выражения того или иного на-
пряжения или перемещения, часто плохо сходятся. Это
приводит к необходимости удержания большого числа их
членов и подсчетов с большим числом значащих цифр.
Обычно ухудшение сходимости рядов, составляющих
выражения (4.28) и (4.30),имеет место на поверхности и в
области, близкой к поверхности цилиндров, т. е. при г
достаточно больших. Приемом, предлагаемым ниже, можно
значительно улучшать сходимость рядов в этих областях.
Воспользовавшись асимптотическими представления-
ми Бесселя
/о (М=
V 2пкг
eVL 1 , 1 ‘° 1 ‘° ’°
1 'Г 1! 81г 2! (8Хг)2 *" 3! (8Хг)3 ‘
Л (М= ev fl ——- 1 118V 15 315 ( 2! (8Хг)2 3! (8Хг)з *”)
(4.38)
79
составим асимптотические формулы для коэффициентов A k и
Bh [см. (4.32^]. Будем обозначать их Ак и Bh. После под-
становок и преобразований имеем:
15—16у 201—736у+512у2
8Xfe а 2 (8Х* о2)
3—16v , 81—608v-|-512 v2
8X/t a
~Kha
Ak = a ~\^2лХь о e
Bh = -7— V2nXfe a e
A*
2 (8Xfc я)2
-16v «1— 608v + 512v2
; (4.39)
Асимптотическое
РгЛ[1~ 8Хла ~ 2(8Xfefl)2 'r'*'
7—16y 25—480y 4~512v2 Ц
8Xh a + 2 (8Xfe a)2 + ‘ Jr
представление функции напряжений
Ф (r, z) = — ~^Pzo r2 — a
oo
V ~ 4 («— r)
ar e *
k= 1
Pzh
Kh a
Prh 1 + T7
L oAft a \
16v—3
(4.40)
+ Pzh 1 +—--- 7-16V-3
8Хд fl \
При r = a
Ф («, z)
OO
V1 Pzh
a2
N
ЪГ- <441>
\ ft= 1 /
Подстановка постоянных Ah и Bh в (4.28) приводит к асимп-
тотическим формулам для напряжений в случае нагруже-
ния, симметричного относительно среднего поперечного
сечения цилиндра. При удержании двух членов A h и Bh они
имеют вид:
(<Мл
3
2
eh
02
°©2 \
« I Pzh >
^h a )
(4.42)
a
eh U^zi— ^Z2 °) Prh~\~(Dzl — Dz2 Хд fl) Pzftli
a
eh [(^rzi ^-tz2 ^h °) Prh ~i~ (^rzi BrZ2 Хд u) Pzhl'
— I a
(°e)fc = ( —
2
ХЛ fl
cos Xfc z.
cos X/, z
80
Здесь eh = е Xfe(a г) и через Сг1, Сг2, ... , Drz2 обозначены
следующие функции г и коэффициента Пуассона v:
_ 1 / а \ / г \
Сп=1 +—- 11 —16v—7— 1 —— ;
8 \ г }\ и }
1 / а \ / г \
Dn 7-16V-7— 1 — ;
8 \ г / \ а /
СГ2 — — ^Z2 ~—Dzz —Crz2 — Drzz
г
a
CQx=Dqx=-\-(\-2v}~-,
1 Г a r 1
Cy2 - — 30 (1—V)—3 — — (1 —2v) (11 — 16v) — ;
® I r «J
cxl=i~4’(,,-,6v+—)(i L <4-43>
8 \ t }\ a J
DQ2 =4- |б (3-5v)-3——(1—2v) (7—16v) —1,
8[ r a j
D21 = 2 M7-I6V + —U1 );
8 \ r ) \ a /
1 I a \ ( r \
Crzi= 11-16V-3— 1 — ,
8 \ r J\ a J
Drzl=l-^-(7-16v-3—}(l Y
8 \ r / \ a )
В сокращенной записи
oo 00
Gr= у (or)h COS z; o2= У (а2)Л cos z;
k=o k=o
00 00
У (ае)Л cos ** z' — У (Trzh sin X* z.
fc=0 Л=1
(4.44)
Введем следующие обозначения
г 1 л г 1
[Pjls = >, Pjhe * sin Xfe z; fpjc =
k= 1
= 2 Pjh e~^h (a~r> cos ХЛ z, (4.45)
k= 1
где j либо г, либо z.
81
Имея в виду, что
k= 1
(4.46)
d ~
1рЛс=" — У PJk bh eh sin Xh z;
л= i
cos Xj, z;
co
J lP/]c d«=2 pjk sin Xh z
(если аддитивную постоянную при интегрировании прини-
мать равной нулю), можно напряжения представить в такой
асимптотической форме:
где СтгП и Dm,n (m = г, в, г, п = 1, 2) — функции г!а и
коэффициента Пуассона v, определенные формулами (4.43).
82
Используя приведенные асимптотические представле-
ния, вычисление напряжений в областях, близких к поверх-
ности цилиндра, рационально осуществлять следующим
образом. Прибавим к правой части выражений для напря-
жений (4.28), вычтем из нее соответствующие им асимпто-
тические представления и получаем:
Если для рассматриваемого нагружения можно указать
значения сумм (4.45) и (4.46), то основная цель приведенного
преобразования — улучшение сходимости и рядов выраже-
ний (4.26) — достигнута. Действительно, по свойству асим-
птотических представлений разности в квадратных скоб-
ках полученных равенств при возрастании индекса сумми-
рования обычно быстро уменьшаются. Следовательно, вы-
полнение расчетов не требует удержания большого числа
членов рядов, что существенно сокращает объем вычисли-
тельной работы.
При г = а коэффициенты Cfn и Dfn имеют значения:
СГ] = Сц = Drzl — I, Dr । — Cr2 = Dr2 — CZ2 = DZ2 — Cr21 =
=Crzs = Drzz = 0;
(4.49)
= C02=2+v—4v2, Dq2 = ~^~ (5—8v2), Dzi =2.
83
Напряжение в точках цилиндрической поверхности:
Ог — Рг. *trz—pz\
оо оо
а0-Рго+ 2 [(сте)Л— ( °©)л] cos z + 2
Л=1
Prh 2v +
+ —(2 + 4v —v2)]+ plh 2v +-7-— (I — 4v2)l] cos ХЛ г; (4.50)
h-k J A'k a J J
OO OO Г [
<h Pzo + у 1(о2)л —(az)A] cos XA z 4- У prh 11 +
л=1 h=iL \
1—2v\ / 1 — 2v VI
+ -T----j+Pzfe ( 2 4— --- cos Xh z,
Xh и / \ Xfc a /J
где при составлении (u2)h удержан третий член асимптотического
представления.
Отметим следующее важное для приложений свойство
одной из сумм, входящих в выражения о2 и Ое, по (4.41),
она может быть заменена нормальной силой, просто вычис-
ляемой в любой задаче. Действительно
ft *»а
cos Xh z
N
2паг
1
2 Pz0‘
(4.51)
Распространим изложенный прием на вычисление пере-
мещений в области, близкой к боковой поверхности цилинд-
ра. Асимптотические представления (и)Л и (со)Л имеют сле-
дующую форму:
(г \
1 — ) +
я /
(Cu Prh4“^u Pzfc)] ’«
- a
(to)h= ——
2p
(4.52)
a I
---eh I (Prh 4- Pzh)
. (J--w Prh Dw Pzh) •
Xh fl J
где
a
8—3—4-(l 1 — 16v)
r
1 Г о г
Cw-- ~ 2 4— —(11 — 16v) —
8 [ r a
1 Г a r
Du, =—10 — 4-(7-16v) —
8 I r a
(4.53)
84
Расчетные формулы при введении обозначений (4.45)
и (4.46):
1
U = —((1—v) Pro—VPzol r +
оо
2 [(“)* —Йл1 cos * +
k= 1
(4.54)
OO
(2vprl — pz0) z + V [(ьу)л — Й1 sin X* z —
k= 1
где и>0 — постоянная интегрирования.
На поверхности цилиндра
“ =-£- [(1 —V) Pro—vPzo] “ + 2 К«)а — (“)/<] cos Z +
k= 1
+ ~ V [2 (1—v) Prh + (1— 2v) pzh] cos ЛЛ z; (4.55)
оо
1 хт
ЬУ= — —-(2vpr0—pz0) Z + > (Ил—Мл1 Sin Kh z +
ь= 1
+ — 7, ~ [(1 —2v) ргл +2 (1 — v) pzh] sin z +ti)0.
При асимметричном нагружении цилиндров асимптотичес-
кие формулы для напряжений и перемещений имеют форму,
аналогичную приведенным; как уже указывалось, в них
нужно заменить cos Xz на sin Xz в выражениях ar, ое, oz и
и, sin Xz на —cos Xz в выражениях %rz и со. • В равенствах
(4.44) и (4.45) следует поменять знаки перед некоторыми чле-
нами.
85
Для напряжений имеем:
оо
’г = 2 [(Ог)л — (0>)л 1 sin Xh Z +
k=i
СГ1 IPris
^Г2 а . [Рг]с4-^Г1 [Pzis ^Г2 а . [Pzlc
dz dz
3
оо
°е= 2 [(ае)л~ (^е)л] sin х* 2 +
Л= 1
4“ ^02 а j* lPr]c rfz + D01 |pz]s 4'^02 u [Pzlc » (4-56)
oo /~
°z = I(CTz)& (CTz)h) sin X/t Z 4“!/ |czl [PrL 4-
fc=l r r I
„ d d I
4“^'Z2 U j IPrlc4-Ozi [Pzls 4~^Z2 a . [Pzjcf i
dz dz J
°°1 1 (
^rz I(^rz)ft (’’rzJh] COS Хд z |Crzi [pr]c —
Л=1 r I
d d 1
CrZ2a , (Pr]s4-^rzi [Pz]c Drz-z a ~~ [Pz]sp
dz dz I
Для перемещений:
oo
= У, [(“л) — (“)d sin ХЛ z 4--^
»-1 2Н
и
В точках поверхности цилиндра напряжения и переме-
щения представляются соответственно равенствами (4.50) и
(4.55) после указанной выше перестановки тригонометри-
ческих функций cos и sin изменения знака у тгг и to
и изменения свободных членов.
Преобразованием полученных выражений можно соста-
вить простые приближенные формулы для вычисления на-
86
пряжений и перемещений, представляющие некоторое обоб-
щение формул сопротивления материалов. Идея преобразо-
вания заключается в замене функций Бесселя суммой ко-
нечного числа членов определяющих их рядов:
/ Ха V 1 / Ха \4 1 / Ха \8
7° ( 2 / + (2!)2 О,' + (З!)2 ( 2 J +
Ха 1 / Ха \2 1 / Ха \4
[1+ЛГ2ГЧТ /+“2'3!"ГГ / + (4-58)
1 / Ха у
+ 3! 4! + “
Предполагается, естественно, что отношение На мало. Сте-
пень приближения зависит от числа удержанных членов, а
также от характера приложенной нагрузки.
После подстановки (4.58) в равенства (4.32) для постоян-
ных, которые отметим индексом «О» сверху, найдем:
Ло________2-
1. 1
Prh
1
** a
2
а* Д у
2 )
/ Хьа
13+7v I
72(14-v) V
(2+v)2
+ 6(l+v) \ 2
I _Pzh_
J ХЛ a
9— lOv—7v2 / Xfe a \6
(4.59)
v—---
2
2 /
2
в°к =------—
k (l+v)X*
17—7v / X^aX6
Prh
XfeQ V
2 J
Pzh
v
6(J+v)
1 ,
'+t!
2
ha .
I 2 j
xftQy
2 )
Напряжения при этих значениях постоянных, если со-
хранить только два первых члена, будут:
^1 j-j-zv / Г V
a“=Pro+ 7, (Prh—Qzl , . Pzh M 1—1 — I )cosX*z;
Al 8(14-v) L
°8 = Pro + V jPrh--o/- " Pzh ^-h a 3+2v — (4.60)
h=il 8(1+v) L
— (1 -~2v)(~) ||cosXfe z;
87
г
a
2-f-v l г VI)
7<77^М'~2(т)]/с“’‘ьг
k~-1
Pzh sin ^h z •
Перемещения:
1
1(1—V) Pro—vp20| r H-
oo
+~^~ 2 к*—v>₽r*
k=i l
2v
Pzh
cos X/i z;
(4-61)
1 2 X? 1 / 1 \
— (2vpr0—Pzo) г — — > — vprh -------------Pzh sin z.
Ь E k^\ KhQ' ** a /
Заменив в (4.60) и (4.61) суммы их значениями (4.45) и
(4.46), получим окончательную запись приближенных фор-
мул для напряжений и перемещений:
1 Г vN 1 1
*7" К1—v)Pr—— П аР=- —
Е I г Е
Prdz
Как не трудно видеть, область их применения ограничена
значениями pt (z), имеющими конечную непрерывную про-
изводную по z. Формулы, аналогичные (4.62), могут быть
составлены, естественно, и для асимметричного нагружения.
4.6. Решение Файлона
К настоящему времени решено большое число задач о
частных осесимметричных нагружениях сплошных и полых
цилиндров с представлением результатов в форме рядов.
88
Приведем одно из первых реше-
ний Л. Файлона [94] — задачу о
растяжении цилиндра силами р
осевого направления, равномер-
но распределенными на кольце-
вых участках боковой цилиндри-
ческой поверхности, симметрич-
но расположенных по отноше-
нию к среднему сечению (рис. 15).
При выборе начала координат
в центре тяжести этого сечения
Рис. 15
нагружение определяется следующими равенствами: при
г = а радиальные силы рг — 0, осевые силы
где Zj иг2 — координаты границы участков нагружения.
Представим pz в форме (4.35). При таком выборе разло-
жения нагрузки в ряд, как было указано, торцы свободны
от нормальных сил. Значения коэффициентов ряда:
I *1
2 Г 2*4-1 2р Г 2*4-1
р,ъ =---- 1 р, (г) sin--nzdz ------ I sin------Jtzdz =
кгя z j fz v / 2/ z J 2/
0 z,
4p Г 2*4-1 2*-}-l I
=------------I COS------Л21 — cos------nz21 •
(2*4-l)n L 2Z 2/ 2 J
Следовательно,
4p 1 ( 2*4-1 2*4-1 \ 2*4-1
Pz =---- z ------1 cos -----nz, —cos ---- nz2 I sin---- nz.
я -^2*4-11 2/ 1 21 J 21
k = 1
Подставляя рг}1 в формулы (4.32), нетрудно определить по-
стоянные Ah и Bh (prh = 0) и затем по формулам (4.26) и
(4.27) — напряжения и перемещения. Не будем приводить
эти выражения по их частному характеру и сложности.
Таким образом, для составления решения в общем виде
достаточно разложить внешние силы в ряд Фурье.
Ряды, представляющие напряжения, довольно хорошо
сходятся при небольших отношениях г/а (не превышающих
0,75, как было установлено при расчете). В области г, близ-
кой к а, для получения численных результатов рационально
применить прием, изложенный в п.4.5, — воспользовать-
ся асимптотическими представлениями и составить выраже-
ния напряжений и перемещений по схеме формул (4.48).
89
Входящие в них функции [рг]8 и [рг]с равны нулю по харак-
теру нагружения (рг = 0), а функции [pz]8 и [pz]c и их
производные можно представить конечными выражениями.
Действительно, в нашем случае
, 4р ^62*+1Г 2*4-1 2*4-1 1 2*4-1
1₽Л=— 2 £тт с“—Я2--СО5—"45i"—Я2:
k= о
4р ^62*+*Г 2*4-1 2*4-1 1 2*4-1
[Pzlc =- Z --- COS nz, —COS Л2о cos--- nz
ifzjc n 2*4-l I 2/ 2/ 21 2/
k=0
при обозначении b = exp (——).
Заменим в каждом члене этих рядов произведения триго-
нометрических функций их суммами и, воспользовавшись
формулами1
b2k+1 1 2b sin т]
2 £77sin (2*+ ”4=Т arctg_T^“;
k= 1 1
~ 62Л+1 1 14-26 cos п 4~Ь2
/ ------cos (2* 4~ 1) П = — in --—---г;
^02*4-1 4 1—26 cost] 4-62
для [рг]8 и [pzlc получим:
[PzL—
4
Vi .I 26 sin а
2<-‘>
Z=1
i = 1
1 4-26cosai4-&2
1—26 cos а, 4~^2
если считать
ai = -^y-(z—zO, O2 = -^-(z—z2), а3=-^-(г4-г1);
л
а4 = — U4-*9).
Дифференцируя по z, имеем:
d г _£_ь/А2 П V (—l/cosaj .
dz lPzle I 6‘—262cos2ai4-l ’
d _______P_ ...2 n V ( — I)1 sina,
dz lPz c I 6‘ — 262cos2af4-l
1 Cm. (31) и (32), c. 278 в (61].
90
Итак, необходимые для применения формул (4.48)
значения сумм [рz]8 и [pz]c определены.
В точках цилиндрической поверхности b — 1 и стг = 0;
^rz = Pz,
__ ~ 2k +1
ае= У [(ao)ft— (ae)ft]cos -nz +
k=0
N 2vp X’’ i ai
+(l-4v’)—-^2 (-D'lnctg—;
i= 1
OO
az= ? [(az)ft— (az)ft]cos —— nz +
k^o
4
Л/ 2p x^ i. ttf
+0-2v)^--
i= 1
где F — площадь поперечного сечения; N — нормальная сила;
N = 0 при | г | > z2, N = 2пра (z2 — zj при | z | < zx.
Как следует из последних выражений, напряжения ае и
az имеют бесконечно большие значения при z= ±Zj и z —
= ±z2 на границах участка нагружения.
В статье Файлона приведен пример расчета напряжений и
перемещений в цилиндре, длина 21 и радиус а которого свя-
заны равенством ла =21 с участками нагружения определяе-
мыми значениями zr = 1/3 и z2 = 21/3. Коэффициент
Пуассона принят равным 0,25. Такой цилиндр не относится
к категории «длинных>. Границы участков распределения
сил близки к торцам, расстояние внешней границы от
концов цилиндра составляет 0,212 длины диаметра. След-
ствием указываемого является большая величина касатель-
ных напряжений (по условиям задачи равным нулю) на
торцах по сравнению с интенсивностью сил р. Распределе-
ние напряжений az в сечении z = 0 значительно отличается
от равномерного.
Значения напряжений и перемещений приведены в
табл. 3. За и0 приняты равномерно распределенные напря-
жения при растяжении стержня силами N = у pl2 =
=4- р (ла)2, т. е.
о
N л л
а0 = —=—р; и>о = -Т7Г pz и u0 = — va>0
г о ОС
— перемещения при растяжении указанной силой N.
91
t£>
to
2// r/a 0 0,1 0,2 0,3 0,4 0,5
or/a0
0 0,2299 0,2260 0,2082 0,1706 0,1069 0,0270
0,2 0,2198 0,2186 0,2084 0,1749 0,1093 0,0224
0,4 0,1859 0,1924 0,2023 0,1875 0,1218 0,0153
0,6 0,1179 0,1354 0,1810 0,2126 0,1505 0,0070
1 0 0 0 0 0 0
)/°o
0 0,2299 0,2260 0,2082 0,1706 0,1069 0,0270
0,2 0,2292 0,2263 0,2121 0,1748 0,1086 0,0241
0,4 0,2257 0,2262 0,2199 0,1883 0,1181 0,0205
0,6 0,2140 0,2215 0,2336 0,2185 0,1416 0,0150
1,0 0,1236 0,1536 0,2216 0,4290 0,2554 0,0016
a z/^o
o. 0,6891 0,6727 0,6312 0,5820 0,5394 0,5030
0,2 0,7190 0,7001 0,6517 0,5940 0,5450 0,5050
0,4 0,8105 0,7859 0,7198 0,6366 0,5645 0,5083
0,6 0,9616 0,9370 0,8592 0,7371 0,6169 0,5081
1 1,1172 1,1633 1,3440 2,0225 1,3680 -0,4786
Таблица 3
0,6 0,7 0,8 0,9
—0,0456 —0,0906 —0,0889 -0,0543 0
-0,0575 —0,1019 —0,0995 —0,0594 0
—0,0861 —0,1360 -0,1222 —0,0683 0
—0,1343 —0,1876 —0,1404 -0,0663 0
0 0 0 0 0
—0,0456
—0,0531
—0,0702
-0,1056
—0,2487
—0,0906
—0,0970
-0,1192
-0,1635
-0,4116
-0,0889
—0,0965
—0,1140
—0,1444
—0,1829
-0,0534
-0,0584
-0,0671
—0,0798
-0,0788
О
О
О
О
О
0,4571 0,3841 0,2780 0,1453 0
0,4566 0,3806 0,2720 0,1408 0
0,4474 0,3596 0,2444 0,1206 0
0,3996 0,2781 0,1520 0,0604 0
—0,4087 — 1,0555 -0,3575 -0,1345 0
Продолжение табл. 3
г// г/а 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Т rz!
0 0 0 0 0 0 0 0 0 0 0 0
0,2 0 0,0215 0,0335 0,0326 0,0257 0,0250 0,0372 0,0562 0,0775 0,0889 0,0923
0,4 0 0,0513 0,0820 0,0812 0,0626 0,0570 0,0808 0,1226 0,1560 0,1647 0,1721
0,6 0 0,0888 0,1555 0,1652 0,1360 0,1190 0,1488 0,2053 0,2311 0,2192 0,2099
1,0 0 0 0 0 0,9549 0,9549 0,9549 0 0 0 Q
u/u0
0 0 0 0 0 0 0 0 0 0 0 0
0,2 0,0449 0,0388 0,0262 0,0202 0,0314 0,0575 0,0838 0,0934 0,0790 0,0446 0
0,4 0,0375 0,0294 0,0170 0,0284 0,0856 0,1767 0,2569 0,2803 0,2313 0,1283 0
0,6 0,1341 0,1120 0,0635 0,0454 0,1206 0,2731 0,4127 0,4466 0,3535 0,1880 0
1,0 0,5789 0,5488 0,4578 0,1847 0,3709 0,4963 0,5861 0,5907 0,3741 0,1807 0
w/w0
0 0 0,0569 0,1113 0,1624 0,2113 0,2601 0,3089 0,3549 0,3930 0,4181 0,4263
0,2 0 0,0600 0,1169 0,1695 0,2192 0,2683 0,3174 0,3636 0,4016 0,4265 0,4351
0,4 0 0,0699 0,1349 0,1926 0,2446 0,2947 0,3442 0,3903 0,4270 0,4500 0,4577
0,6 0 0,0868 0,1675 0,2368 0,2949 0,3471 0,3954 0,4372 0,4668 0,4825 0,4872
со СО 1 ,0 0 0,1097 0,2290 0,3825 0,5929 0,6715 0,6681 0,5742 0,5176 0,4972 0,4920
Кроме приведенного примера нагружения, в статье Фай-
лона рассмотрено сжатие цилиндра силами, распределен-
ными по торцам при условии равенства нулю радиальных пе-
ремещений по контуру торцов. С целью обоснования ха-
рактера разрушения хрупких материалов при сжатии про-
изведено подробное исследование распределения напряже-
ний. Определены значения главных напряжений и положе-
ние их траекторий. Теоретические результаты хорошо согла-
суются с экспериментальными. Направление траекторий
главных растягивающих напряжений совпадают с направле-
ниями развития трещин в материале образцов.
4.7. Напряженное состояние среды
с цилиндрической полостью
К решению внешних осесимметричных задач в рядах для
бесконечной среды, имеющей цилиндрическую полость,
поверхность которой нагружена некоторой системой сил,
приводят, как было указано, функции напряжений (4.8) при
сохранении только функций Макдональда К-t. (V).
Положив в (4.8) постоянные С и С' равными нулю, имеем
<p(r, z) = (A sin kz-f-B cos Xz) гКг (Xr),
i|)(r, z) = (A' sin Xz+B’ cos 7^z)rKi (Xr) (4.63)
и соответствующие им Ф и fi
Ф = (4' sin Xz + B' cos Xz) rKi (Xr)+(4 sin kz-f-B cos Xz) XrK0(Xr);
(4.64)
й = — [(4' sin Xz+B' cosXz)K^kr) —
—(4 sin Xz + В cos Xz) [3XrK0 (Xr)—2(1—v)^ (Xr)].
Составляющие напряжений и перемещений, как следует
из (4.18) и (4.19), получают следующую запись:
аг= —— {(4' sin Xz+B'cos Xz) [XrK0(^r)+^i(Xr)] +
r
+(4 sin XzВ cos Xz) [XrK0(Xr)+(Xr)*Ki (Xr)+2(1 —v)Kj (Xr)]};
oe = —— {(4' sin Xz + B' cosXz)Kx(Xr) +
+(4 sin Xz+B cos Xz) [(1 —2v) XrK0 (V)+2 (1 — v) Kx (Xr)]};
(4.65)
<jz = X {(41 sinXz+B' cosXz)Ko(Xr)—
—(4 sin Xz + B cos Xz) [2K0 —krKi (Xr)];
Trz = X {(4' cosXz—B' sin Xz)Kj(Xr)+
+ (4cosXz—BsinXz) XrK0(Xr)};
94
и = ~-— {(Л' sin Xz-|-B cos Xz) Кг (Xr) +
2р.
+ (Д sin Xz-|-B cos Xz) [XrK0(Xr)-]-2 (1 — v) Ki (Xr)]);
(4.66)
w = —-----{(.4' cos Xz — B' sin Xz) Ko (Xr)—
2ц
—(Д cos Xz —В sin Xz) [2(1 —v) A'0(Xr)—ХгКг (Xr)]}
Ограничимся симметричным распределением нагрузки
относительно плоскости z = О, В этом случае [см. (4.28)]
k= 1
а0 — а0о + 2 (°о)к COS Z'
k = 1
1 °°
“=“o+-T~ Л (u)hCOsXhz;
2>*
°z = ^zo + 2a
k= 1
OO
°rZ= (Tp;
Д= 1
1
W = Wo + ~—
(4.67)
где, как следует из (4.66),
(ar)h~ г {(Дл + fife) lXfc rKo (Xfe r) + Ki Xfc r)] +
+ Bfe [(Xh r)2+ 1 -2v] K(Xh r));
(ao)fe = ~ (4r)+(l-2v)Bfc[XJkr^o(X*r)+^(Xfcr)]};
(az)h =Xft [(Ah -2Bft) K0(Xft r) + Bh Xft гКг (Xft r)];
(Trz)fe = Xfc [Д& Ki (Xft r) + Bft Xft rK0(Xft r)];
(u)ft = Ah Кг (Xh r) + Bft [Xft rK0 (Xfc r)+2 (1 -v) (Xft r)];
(uOfe = Ak Ko (Xh r)— Bft [2 (1 - v) Ko (Xft r)-Xft rKt (Xft r)].
Представляя внешние силы рг и pz в форме разложения
в ряды
оо оо
Pr = Pro“l_ Prk cos Xfc z; Pz~ Pzh г»
*=1 fe=i
по условиям (or)h = ргК и (Trz)fe = prh при r = a (a — ра-
диус полости) нетрудно получить для постоянных Ah и
Bk следующие выражения:
Ak= —, n. {Prh (bfe а)2 Ко (^ a)4-Pzk Rfe аКо (Xh а) +
+ (Xft а)2 Kt (Xft а) +2 (1 -v) Кг (Xft а)]};
(4.68)
Bfe = -—— {prk Xh аКг (Xh a)-f-Pzk [Xfea K0(Xfta) + Ki (Xfc а)]},
Xh
95
где
DJ = (Xh а)*К% (Xft а)-[(Xft а)2+2 (1 -v)] К® (Xft а). (4.69)
Значения D*K приведены в табл. 4.
Таблица 4
k ~Dk k ~Dk k
0,5 4,31363 4,5 2,55249-10-* 8,5 7,49759- IO-8
1 6,92240-IO-1 5 9,12697-10-5 9 2,73574-10-8
1.5 1,77992-10-* 5,5 3,28054-10-5 9,5 9,99106-10-’
2 5,37500-10-’ 6 1,183107-10-5 10 3,65150-10-’
2,5 1,74728-10-’ 6,5 4,28467-IO"6 10,5 1,33529-10-’
3 5,90891-Ю"3 7 1,55448-Ю-7 11 4,88635-10-*°
3,5 2,04573-10-3 7,5 5,65080-Ю-7 11,5 1,78883-10-*°
4 7,18963-10-* 8 2,05694 IO-7 12 6,55136-10-**
В случаях плохой сходимости рядов, входящих в (4.67),
в области, близкой к поверхности полости, в целях облег-
чения вычислительного процесса рационально прибегнуть к
приему, изложенному в п. 4.7. Воспользовавшись асимпто-
тическими представлениями функций Макдональда
, . / я” _лгГ 1 1-9
°< 2кг е 1 — l!8kr + 2! (8кг)2
1925
~ 3! (8V)3 +
(4-70)
/Л 1г
2кг
Г 3 3-5 5-7-9 j
Х[1+ 1!8V~ 2! (8кг)2 + 3!(8кг)з —•••]•
составим асимптотические формы для напряжений и пере-
мещений. При удержании двух членов Ло (кг) и (кг) они
имеют вид:
(°r)k = ek I^rl-----^Г® Prk Фп &Г2 kf, a) Pzkli
\°z)h I/ eh [^zi4~^z2 кь a) prk—(DZ1 + D22 kftz a) Pzkl't (4-71)
r r
96
(u)k =
2ц
eh [Crzi 4"CfZ2 °) Prk —(Prz~l~Drz2 a) Pzkl’
(и>)к =
a
2ц
(Cu prh Du Pzh)t
(Prk Pzh)
1
^ka
(r \
1 j
a /
(Cw Prh + ^w Pzfe)L
(4-72)
k \ 1
a / Xfe a
Здесь ek = e~Kk {r~an и функции Сг1, Сг2, Dw оп-
ределены выражениями (4.43) и (4.53).
Расчетные формулы подобны (4.45) и (4.54), отличие
только в форме свободных членов и в знаках перед некото-
рыми слагаемыми:
97
В=—(l+v)-^z—+ У к«)»—(«)»)«»***+
Ег к-1
В приведенных формулах суммы [prlc, (рг18, (рг]с и
[pz]8 и их производные и интегралы имеют значения (4.47)
и (4.48) при eh e~Kft {г~а}.
4.8. Нагружение поверхности цилиндрической
полости радиальными силами
Приведем некоторые результаты расчета напряжений в
бесконечной среде с цилиндрической полостью, на конеч-
ных участках поверхности которой приложены радиальные
равномерно распределенные силы (рис. 16):
О при —e<z<— z0
— Р ъ — Zq<Z Z <Z Zq
О » Zo < г < е
(pz = 0). После вычисления коэффициентов Фурье
i Zo
1 С . Р С . р?о
Pro — j I Prdz — I dz — ,
o o
z z.
! f fen 2p C fen
-,lprcos—-—zdz =—— 1 cos —-—zdz=
о о
2p fen
= ——— sin—— z0
fen I
98
имеем следующее представление заданной нагрузки в форме
ряда
( z0 2 1 kn kn \
Pr=— Р —— - —-Sin—— Z0cos—— г •
I I л k I II
\ k= 1 /
По формулам (4.68) для постоянных Ak и Bk получаем:
2ра 2р
Ak=-^-^o(^ka)sinkkzo, Bk=——— KiCXfeaJsinXfeZ,
где Xfe = knit.
Рис. 16
Напряжения Oo и oz в точках поверхности полости, если
выделить из бесконечных сумм асимптотические приближе-
ния (ае)ь = 2vlk и (az)fe — 1/Л, определяются равенствами
0е = Чрг+р (1 +2v)—
2р 1
2а ~Т l(ae)ft-(ao)fe] sin ** z°cos z-
п л=1 й
Oz = Pr+p—T- —---- 7, [(o2)fe—(02)fe]sinz0cos z.
I Л
k= 1
Значения этих напряжений приведены в табл. 5 при
ла = I и v = 0,3 в случаях z0 = 0,2Z; 0,4Z; 0,6Z; 0,8Z.
По мере сближений участков нагружения прослежива-
ется увеличение напряжений в областях z = ±Z; ±3Z;
±5Z и т. д., т. е. эффект, аналогичный концентрации на-
пряжений при приложении сосредоточенных сил.
Подсчет напряжений в области, близкой к поверхности
полости в случае z0 = 0,2Z выполнен по формулам (4.73)
после замены
2sinXfc z0cosXfc z = sinXfc(z-|-z0)—sin Xfc (z—z0);
2 sin Xfc z0 sin Xfc z =cos Xft (z—z0)—cos (z-j-z0)
99
Т аблица 5
гЦ г»/! 0 0.2 0,4 0,6 0,8 1
0,2 0,4669 0,3932 ое/р 0,2033 0,1004 0,0629 0,0528
0,4 0,7468 0,6703 0,4698 0,2665 0,1529 0,1256
0,6 0,8744 0,8471 0,7335 0,5302 0,3297 0,2532
0,8 0,9472 0,9371 0,8996 0,7967 0,6267 0,5331
0,2 —0,6610 —0,2178 <Jzfp 0,1638 0,1571 0,1298 0,1205
0,4 —0,4346 —0,4602 —0,0602 0,3306 0,2775 0,2595
0,6 —0,2595 —0,2775 —0,3307 0,0602 0,4602 0,4346
0,8 —0,1205 —0,1298 -0,1571 —0,1638 0,2173 0,6610
и введения обозначений b = ехр [— у (г — а)], =
= * (z + z0) и а2 = у (z — z0), для грузовых функций
(рг]с и [pr]s и их производных получено:
Р I
— — arctg
л
2₽ V ьк • i 1
---- У ---- Sin Aft Zo COS Aft z =
Л k
k= 1
bsincij 6sina2
------------—arctg-----------
1 —b cos a.
b cos а2
2p v1
[рЛ=~ —
k= 1
bk P
— sin Aft z0 sin Aft z = —
R ZJl
1—2b cos аг4-Ь2
1—26cosa24-fe2
d r _ _2p
. [Prlc — .
dz l
OO
2 bk sin At sin Aft z =
1
d
dz
costij — b cosa2 — b
1—2fecosa14-62 1 — 26cosa24-b2
2' w
[Prls= — —— V bk sin At z0 cos Aft z =
k= 1
sinoq
1 — 2b cos ttj -j- б2
_____sin Oj
1 — 26cosa24-&2
Результаты подсчета сведены в табл. 6.
100
Таблица 6
гЦ г/а 0 0.2 0,4 0,6 0,8 1
1,25 —0,7223 —0,3263 ог/р 0,0330 0,0215 0,0156 0,0111
1,5 —0,5231 —0,2557 0,0209 0,0254 0,0184 0,0160
1,75 0,3703 —0,1980 0,0003 0,0248 0,0216 0,0198
2 —0,2649 —0,1569 —0,0177 0,0205 0,0234 0,0299
1,25 0,2768 0,2300 °q!p 0,1303 0,0768 0,0476 0,0399
1,5 0,1810 0,1497 0,0942 0,0559 0,0383 0,0334
1,75 0,1231 0,1048 0,0700 0,0445 0,0318 0,0280
2 0,0877 0,0763 0,0540 0,0365 0,0272 0,0243
1,25 —0,2041 —0,0698 ог/р 0,0533 0,0623 0,0604 0,0517
1,5 —0,0467 —0.0438 0,0081 0,0286 0,0316 0,0304
1,75 —0,0003 —0,0221 -0,0243 0,0105 0,0242 0,0271
2 0,0185 —0,0078 —0,0220 —0,0008 0,0128 0,0116
1,25 0 —0,2058 тгг/р 0,0015 0,0080 0,0038 0
1.5 0 —1,1501 —0,0284 0,0029 0,0037 0
1,75 0 —0,1096 —0,0447 —0,0047 0,0014 0
2 0 —0,0798 —0,0484 —0,0123 -0,0018 0
В заключение отметим, что решения осесимметричных
задач, составленные для цилиндрической полости в беско-
нечной среде, могут быть приемлемы как приближенные
при осесимметричном нагружении полупространства с по-
лостью и бесконечного слоя с цилиндрическим отверстием,
с выполнением краевых условий на плоских границах в
интегральном смысле. Точность результатов в каждом кон-
кретном случае различна и может быть практически вполне
приемлемой для области, достаточно удаленной от плоских
границ, где очевидно, получаемые значения напряжений
и перемещений должны быть близки к точным.
4.9. Решение в интегральной форме
Применение функций напряжений в рядах, строго гово-
ря, приводит к решениям осесимметричных задач при нагру-
жениях поверхности бесконечно длинных цилиндров или ци-
линдрических полостей в бесконечной среде силами, изме-
101
няющимися по периодическому закону по осевой координа-
те z. Если силы приложены только на некотором конечном
участке поверхности при свободной остальной ее части, по-
лучение решений осуществимо при применении функций на-
пряжений в интегральной форме. Перемещения и напряже-
ния представляют интегралами переменной X. Выражения
для них следуют из соответствующих представлений в форме
сумм (см. п. 4.4). Приведем эти выражения, сохраняя, как
и прежде, в целях упрощения записей, только функции
Бесселя первого рода и разложения нормальных напряже-
ний по косинусам координаты г и касательных по синусам.
Считая Ak и Bh в равенствах (4.25) функциями парамет-
ра X, непрерывно°заданного от 0 до оо, и заменяя знак сум-
мирования знаком интегрирования, получаем следующую
запись формул для функции напряжений:
оо оо
яр = г J А (X)/0 (Xr) cos XzdX, ф = г J В (X) /г (Xr) cos XzdX;
о о
оо
<D = rj [Л (X) (Xr) — fi(X)Xr/0(Xr)]cosXzdX; (4.75)
О
оо
Q = -y- § (А(Х)/1(Xr) + B(X)^ЗXr/o(Xr)-Ь
0
4-2(1—v) /1 (Xr)]} cosXrdX,
для напряжений
оо
°r = — j {[A (Х)4-В (X)] [Хг/0(Хг)-/1 (Хг)] —
о
— В (X) [(Хг)® 4-1 —2v] (Xr)} cos XzdX;
OO
ae = j {[A (X)4- В (X)] /r (Xr) -(1 —2v) В (X) X
0
X [Xr/0Xr) — li (Xr)]) cosXzdX;
(4-76)
OO
oz= — [ X {[A (X)—2B (X)] 70 (Xr) — В (X) Xr/j (Xr)} cos XzdX;
о
OO
Trz= —J X [A (X) li (Xr)—В (X) Xr/o (Xr)] sin XzdX
о
102
и перемещений:
оо
((Л(Х)+2(1-у)В(Х)НнМ-
2И J
—В(Х)Хг/0(Хг)} cosXz; (4.77)
ОО
№=--{[Л (X)-2 (1- V) В (X)] /0(М-
о
—В (X) Xr/j (Xr)) sin XzdX4-a>0,
где tw0 = const.
На оси цилиндра (г = 0)
оо
ar = oe=—1 Х[Л (X)+2vB(X)] cosXzdX;
о
oz=—J Х[Л(Х)—2В (X)] cos XzdX, тгг = 0; (4.78)
о
ОО
u=0, w=—f [Л (X)—2(1—v) В (X)] sin XzdX.
2,1 <!
При заданных на боковой поверхности цилиндра на-
грузках pr = pr (z) И Pz = Pz (z) ПО условиям Or = рг
и Trz = Pz при г = а получаем два неравенства для опреде-
ления функций А (X) и В (X):
оо
о
{[Л(Х) + В(Х)][Ха/0(Ха)-/1 (Xa)]-B (X) [(Ха)Ч +
+ 1—2v] /i (Xa)} cos XzdX = pr;
(4.79)
ОО
j* X [Л (X) (Ха)—В (X) Ха/0 (Ха)] sinXzdX = —pz.
о
Отсюда в соответствии с преобразованием Фурье имеем:
Л (X) [Ха/0 (Ха) — Л (Ха)] + В (X) [Ха/0 (Ха)—(Ха)2 /, (Ха)—
ОО
2а С
—2(1—v)/!(Xa)]=------I prcosXzdz; (4.80)
л J
о
оо
2 Г
Л (X) /1(Ха)—В(Х)Ха/0(Ха)=——— I pzsinXzdz.
лХ J
о
103
и, следовательно1,
Д(Х) =
2
jiD* (X)
Ха2 /0 (М
ОО
J pr cos kzdz—
О
— v l^'o (М —(М2 li (М—
Л
2
nD* (X)
all (Ха)
(4.81)
В(Х) =
ОО
—/1 (Ха)] j* рг sin Xzdz ;
b
D* (X) = (Xa)2 /§ (M-[(M2 + 2 (1 -v)J /2 (Xa).
Эти формулы в точности повторяют формулы (4.32) и
(4.23) для коэффициентов Ak и Bh при решении задачи в
рядах после замены prh и pzh интегралами правой части
равенств (4.80) и отбрасывания индекса k у параметра X.
Такое же повторение с указанной корректировкой и заменой
знака суммирования знаком интегрирования будет и во всех
остальных формулах общего характера. Так же, как и при
решениях в рядах, для функций напряжений, перемеще-
ний и напряжений можно получить асимптотические пред-
ставления и воспользоваться ими для вычислений в точках
поверхности цилиндра и близких к ней. Расчетные формулы
совпадают по форме с соответствующими выражениями,
приведенными в п. 4.5, в которых нужно считать
оо
[Pj]s = _^“ J Pj e~^a~r^ sin XzdX;
о
(4.82)
ОО
[Р/1с=г‘—I Pj е~^а~r> cos Kzdk,
л J
о
где / равен г или z.
1 В случаях нечетных нагружений нужно поменять местами
cos Xz и sin Xz и перед вторым членом в скобках правой части изме-
нить знак на обратный.
104
Возможны случаи, когда вместо граничного условия
Trz=Pz удобно применять условие, связывающее функцию
напряжений Ф с нормальной силой 7V: Ф = —NI2n (г = а).
Второе равенство (4.80) при этом получает форму
оо
А (X) (Ха)—В (X) Ха/0 (Ха) = — —J— f N cos XzdX. (4.83)
л2 a j
о
Общая форма равенств для напряжений и перемещений
при этом не изменяется. Функции А (X) и В (X) определяют-
со
1 с
ся формулами (4.81) с заменой в них интеграла ? J pz sin \zdz
X- о
1 00
интегралом J N cos X zdz.
4.10. Растяжение цилиндра силами,
равномерно распределенными по периметру
начального сечения
В качестве примера решения осесимметричной задачи в
интегральной форме рассмотрим нагружение бесконечно
длинного цилиндра силами осевого направления, распреде-
ленными вдоль окружности некоторого сечения (рис. 17)
Расположим начало координат в центре этого сечения и
предположим, что в бесконечности нагрузка уравновеши-
вается силами^ Р = nqa. При таких условиях нормальная
сила 7V = — Р, если z <Z 0, и N = Р, если z > 0. Ле-
е. 1 п
вая полубесконечная часть стержня сжата силами Р, пра-
вая растянута. Напряженное
состояние цилиндра имеет
асимметричный характер, сле-
довательно, нормальные на-
пряжения должны быть пред-
ставлены разложениями по
sin Xz, а касательные по cos Xz.
Предположим, что нагру-
жение осуществлено силами
q равномерно распределенными
участка, длина которого 2е,
—е < z< е и <7 = 0 при —с
Рис. 17
по поверхности кольцевого
q Р
т. е. qz = к- = л--- при
л 2е 4л ае г
о <С z <С—е и e<z<Coo.
105
Тогда
oo ft e
C . . f q . . q sinXz I tysinXe
I qz cos Kzdz = I --cos kzdz = —---------I =---------
J J 2e 2e X | 2eX
0 0 0
Уменьшая e до нуля в пределе, получаем:
qz cos Xzdz =
0
1 Р
— q =------
2 4ла
1 _ Р
2 4ла
Подстановка этого интеграла в (4.81) приводит к значе-
ниям функций А (X) и В (к):
р 2(1—v)
А (М = ± 2п2£>,(Х) [/о (Ха)—Xa/j (Ха)- IL (Ха)];
Напряжения и перемещения определяются равенствами
(4.76) и (4.77).
Постоянная м>0 может быть определена по условию w =
= 0 при г = 0 и z — 0, тогда
оо
= 4^ f [(3-2v) мм-w, (М-
о
4 (1 —V) I
—4------Л(Ха) dX.
Ха J
На оси цилиндра в соответствии с формулами (4.78)
оо
ar=°e = 1^7 .f -5^" К1 —[Лл/о(Ха)—2/r (Xa)J —
о
—(Ха)2 li (Ха)} sin XzdX;
ОО
— -7— (* —7—[ЗХа/0(Ха) — (Ха)2 Л(Ха) —
4л2 a J D* (X)
0
—2(2 —v) /j (Ха)] sin XzdX;
ОО
W=— ——-----f —7T—[(1— 2v) /о (Ха)—ХаЛ (Ха)—
4л2 р. J D* (X) [
0
Л (Ха) cos XzdX-]- u»0.
106
По приведенным формулам подсчеты просто осуществля-
ются при небольших отношениях г /а, т. к. интегралы доста-
точно быстро сходятся. По мере приближения к поверхности
сходимость ухудшается, для получения результатов в этой
части цилиндра рационально обратиться к асимптотичес-
ким представлениям и выполнить расчеты по схеме, наме-
ченной в п. 4.9.
Применяем равенства (4.48) и (4.54), заменив в них знак
суммирования знаком интегрирования и подставляя зна-
чения Drl, Dr2t .... Dw по формулам (4.43), и (4.53), имеем:
7— 16v —
+-£ Н f+<7~ ,в»> (2 “ 4г)И[₽Jc
оо
С 1—v с
и>= 1 [(10) —(u>)] cos kzdk—-I [pz]s dz •+ 10O.
J H J
0
107
В приведенных равенствах
2„2 а J
О
г
е (а r)sinXzdX = ,
2л2 а (а—r)2+z2
[Pzlc— о о I
2л2 а J
о
е * (а r) cos XzdX= —-—
2л2 а
а — г
(а—г)2Н
d Р (
. iPzls— о , I
dz 2л2 а J
1
Хе (а г) cosXzdX = ———
2л2 а
(а—г)2 — z2
ОО
——[Pzlc=--------Т— (*Хе—х,(я—г) sin XzdX =
dz 1 Jc 2л2 а J
о
Р 2 (а—г) г
2л2 а [(а—r)2-|-z2]2
ОО
[PzL dz ------—у— f -J- е {a~r) cos XzdX=
2л2 a J X
о
Р 17 г \2 ( г \21
= ——т~ 1г»(1 — — 4-— ;
4л2 а [\ a J \ a j J
оо
[ [Pz]c^ = о a f 4" е Х (а~Г} sin XzdX=
J 2л2 а J X
о
Р z
=--------arctg--------.
2л2 а а—г
При г = а в точках боковой поверхности цилиндра аг =
= 0; xrz = 0;
оо
°е = J [(<М-(?е)] - 4v!)
о
оо
az = f l(oz)—(oz )] sin XzdX+ — 4- (1 — 2v) ~-P~\
J n2 az 4ло2
о
u
sin XzdX+(l — 2v)
P
8лра ’
OO
u>=| [(co) —(u>)] cos XzdX-|--^——In-—,
J 2лр.а a
o
108
за исключением сечения z = О, где напряжения имеют бес-
конечно большое значение.
В табл. 7 приведены значения отношений напряжений
иг к равномерно распределенным по сечению напряжениям
и0 = Р/2ла2 при z = 0,25а; 0,5а; 0,75а и а (v = 0,3). Как
и следовало ожидать, выравнивание напряжений проис-
ходит достаточно быстро.
Таблица 7
г/а z/a 0 0,25 0.5 0,75 1
0,25 0,1242 0,1410 0,2282 0,7547 2,8329
0,5 0,3872 0,4377 0,6416 1,1489 1,6015
0,75 0,6743 0,7391 0,8922 1,0948 1,2791
1 0,8958 0,8996 0,9687 1,0274 1,1837
4.11. Деформация полых цилиндров
Решение осесимметричной задачи о нагружениях полых
цилиндров выполняется в той же последовательности, что и
цилиндров сплошных и цилиндрических полостей в беско-
нечной среде, однако сильно усложняется громоздкостью
записи выражений для функций напряжения и в связи с
этим сложностью выкладок и окончательных формул для
напряжений и перемещений. Составление решений требует
удержания в функциях напряжений как функций Бесселя,
так и функций Макдональда, т. е. записи их в форме (4.8) и
напряжений и перемещений в формах (4.19) и (4.20). Число
постоянных, подлежащих определению, удваивается. В си-
лу указанной громоздкости процесса вычислений воздер-
жимся от его подробного изложения, связанного с каким-
либо частным нагружением поверхностей цилиндра. Огра-
ничимся лишь приведением результатов статьи Г. С. Ша-
пиро [8311.
В этой статье рассматривается нагружение бесконечно
длинного цилиндра радиальными силами р, равномерно рас-
пределенными по некоторому конечному участку внешней
1 Решения в интегральной форме применены В. 3. Васильевым
[16] к нагружению цилиндров силами, линейно распределенными на
конечном участке боковой поверхности. В статье содержатся резуль-
таты подсчета напряжений и графики их распределения по толщине
цилиндра.
109
боковой поверхности —z0< z< z0 (рис. 18) и, как пре-
дельный случай, силами q, распределенными по окруж-
ности сечения z = 0. Такое нагружение обычно называют
радиальным обжатием цилиндра по кольцу. Постоянные,
входящие в функции напряжений, определяются из четырех
Рис. 18
уравнений, следующих из
граничных условий задачи:
на внутренней поверхности
(г = а) иг = 0 и %rz = 0; на
внешней (г = b) %rz = 0,
сгг = 0при —oo<z<—Zo
HZ0<Z< оо и ог =—р при
—Zo < Z < z0.
Окончательные выраже-
ния для напряжений сге и
gz и перемещений и в случае распределения сил q по окруж-
ности сечения z = 0 получены в нижеприводимых формах:
в точках внутренней поверхности
ае=
2q С 1 Г . 1—v
-- I -- v — А —-----
л J D* } а ка
о
cos XzdX;
2<‘-vnDl
(Мг ) J
(Ха)2-J-2 (1—у)
Ха
cos XzdX;
2 (1 —у2) q
и = —----------
лЕ
1 I Ъ \
----IB—С — I cos Xzdz;
W* I a I
в точках внешней поверхности
а Г 1 ( 2(1 — у) Г
ае= — I — 2уХа(ЛВ-СР) - —----------- 2yCD +
л J D* ( Хо [
о
+ Х6 (B2_D2)__L_ (2D2-J- 1) 1 cos XzdX;
Ха J
ПО
oo
trz =± —- Р-[(Ш2(Л2-В2-С2 + £>2) +
л J D* { b
о
b Г /
+ 2XZ>(4B-CD)4-1] + — 2(1— v) D2 —C2—
a \
2 \ 1 11
—-----CD + —-—— ? cos XzdX;
Kb (Kb)2 JJ
2 (1 —v2) q
U==~ ЙЁ
KaB2 —
2(1—v) 1 1 1
Ka 4-------- D~ — ——} cos KzaK.
Ka Ka I
Здесь введены следующие обозначения:
А = 7(, (Ха) Ко (КЬ) — Ко (Ка\ 10 (М>);
С = Л (Ка) Ко (КЬ) 4- Кг (Ka) Io (КЬ);
В=10 (Ка) Кг (КЬ) 4- Ко (М Ц (КЬ);
D = Iy (Ка) Кг (КЬ) — Кг (Ка) Ц (W>);
2(1—v) Г
D* — abK2(A2—В2—С24-О2) 4-—*---------- а2(В2 + О2) —
ab I.
1 1 / Ь \2
-fe2(C2-D2) + —- (О24-2) +14- — •
X2 J а /
В случаях нагружения силами, распределенными по
кольцу шириной 2z0, в приведенных формулах следует вели-
чину q заменить через 2р sin Xz0.
В сечении z = 0 при г = а для нагружения силами q
по внешнему контуру этого сечения и при г = а и г = b для
нагружения силами р, распределенными по кольцу шириной
2z0, произведено исследование величины напряжений az и
перемещений и в зависимости от отношения радиусов а/Ь
и отношения половины длины загружения к внешнему ра-
диусу z0/b. Подсчеты произведены при коэффициенте Пуас-
сона v = 0,3. При выполнении подсчетов интегралы разде-
лены на две части, соответствующие значениям 0< W>< 16
и 16сХдСоо. К первым частям применено численное
интегрирование по формуле Симпсона; во вторых частях ци-
линдрические функции заменены их асимптотическими пред-
ставлениями, что позволило выразить интегралы через табу-
лированные функции.
Результаты подсчета приведены в табл. 8 и 9. Табл. 8
содержит указанные выше значения напряжений az и пере-
111
to
b a z, = 0 i 2. =-7- (b—a) 4
b Q E -^-oz(a) P — oz(b) p — «(a) pb
0,5 2,549 -1,443 0,590 —1,077 -0,351
0,6 3,768 —2,169 0,703 -1,175 -0,425
0,7 6,079 -3,529 0,863 —1,292 —0,520
(b/a) = 0,5 (b/a) = 0,6
zp — «(a) — u(b) Zp — U(a)
b Pb pb b Pb
0,125 -0,351 -0,495 0,1 —0,425
0,25 —0,651 —0,779 0,2 —0,803
0,5 — 1,022 -1,082 0,5 — 1,481
0,8 -1,145 -1,170 0,8 —1,630
00 — 1,333 —1,367 oo -1,875
Таблица У
2, = — (Ь—а) 2
— и(Ь) Pb — а Ла) Р — <у2(Ь) Р — и(а) pb — и(Ь) pb
-0,495 -0,531 -0,591 0,953 1,177 1,486 —0,968 — 1,197 -1,518 -0,651 —0,803 — 1,000 -0,779 -0,882 —1,038
Таблица 9
(Ь/а) =0,7
— и(Ь) 29 — и(а) — и(Ь)
Pb ь Pb Pb
—0,531 0,125 —0,820 -0,591
—0,882 0,25 -1,000 — 1,038
-1,465 0,5 —2,279 -2,176
-1,583 0,8 —2,424 —2,312
— 1,875 оо —2,745 -2,622
мещении и в двух случаях распределения сил по контуру
сечения z = 0 и по поверхности кольца при z0 = (Ь — а)
и z0 = 1 (b — а) для отношений радиусов 0,5; 0,6 и 0,7.
В табл. 9 при тех же отношениях радиусов приведены ве-
личины перемещений в сечении z — 0 в зависимости от дли-
ны загружения кольцевого участка. Перемещения при z0 =
— оо соответствуют решению задачи Ламе. Автор статьи
указывает, что при малых длинах участка загружения (мень-
ше толщины цилиндра) распределение напряжений заметно
отличается от вычисляемых по теории тонких оболочек.
Если отношение длины загруженного участка к толщине ци-
линдра равно половине, то напряжения oz на внешней по-
верхности цилиндра примерно в 1,5 раза превышают по ве-
личине напряжения на внутренней поверхности.
Глава 5. ДЕФОРМАЦИИ КРУГЛЫХ ПЛИТ
5.1. Изгиб круглых плит
В гл. 4 рассматривалось напряженно-деформированное
состояние цилиндров, длина которых значительно больше
радиуса. Точно выполнялись условия на боковой цилиндри-
ческой поверхности и приближенно (в смысле статической
эквивалентности) на торцах, так как гТри достаточно боль-
шой длине цилиндра по сравнению с радиусом характер рас-
пределения сил на концах, согласно принципу Сен-Венана,
не влияет на напряженное состояние в средней части.
Обратимся к изучению деформаций цилиндров, длина
образующих которых меньше радиуса, — толстых круглых и
и кольцевых плит. Как и в гл. 4, ограничимся частичным точ-
ным выполнением граничных условий — только на плоских
поверхностях плиты. Статические условия на цилиндричес-
кой поверхности будем выполнять в интегральном смысле,
кинематические — задавая перемещения точек, расположен-
ных на некоторых окружностях этой поверхности. Такая по-
становка задачи часто вполне справедливо критикуется, но
практически приемлема, так как при отношении диаметра
плиты к ее высоте больше трех значения наибольших напря-
жений получаются достаточно точными (что будет подтверж-
113
дено некоторыми результатами вычислений). Кроме того,
уточнение краевых условий на опорах плиты в первую
очередь требует выяснения характера конструктивного вы-
полнения опорных устройств и их упругих свойств1. Изло-
жению методов решения осесимметричной задачи для ци-
линдрических тел с точным выполнением граничных усло-
вий на всей поверхности посвящена гл. 6* *.
Отнесем плиту к цилиндрической системе координат с
началом в центре срединной плоскости и с осью Oz, перпенди-
кулярной этой плоскости. Радиус плиты обозначим через а,
а высоту—через 2h (рис. 19).
Поскольку напряжения oz и тГ2 определены как первые
производные функции Ф (г, z) по г и z, соответственно [см.
(1.27) и (3.2)1 условия на плоских границах плиты имеют
вид
дФ дФ
—— Гр+. =гр+ прИ Z=/l;
дг дг
(5-1)
дФ
дг
дФ
— rPz : “Т- ^гРг > 7 - ' ~Л’
дг Г
где р+ и — силы, приложенные к верхней плоскости плиты;
р~ и р~ — силы, приложенные к нижней плоскости плиты.
Принято считать положительными внешние силы р£ и
Pz , если они направлены в сторону возрастания координат
z и г, и силы Pz и р7, если они направлены в сторону убы-
вания координат (см. рис. 19).
По устройству опорных креплений плиты различают три
случая их технического осуществления — шарнирно подвиж-
1 Проблема точного выполнения контурных условий на опорах
актуальна в одинаковой степени и для толстых и для тонких плит,
поскольку распределение напряжений у краев плиты имеет местный
характер, как и распределение напряжений на концах длинных
стержней.
* К настоящему времени в области исследования напряженно-
деформнрованного состояния толстых плит опубликовано большое
число работ. Начало им положено Сен-Венаном в приложениях к
переводу на французский язык книги Клебша «Теория упругости
твердых тел» [91]. Теория толстых плит получила развитие в после-
дующих работах Мичелла [105] и Лява [48]. Обширные указания
на литературу, содержащую решения задач о равновесии круглых
плит, можно найти в [1], [44].
114
ное, шарнирно неподвижное и жестко заделанное. Во всех
случаях, если это не оговорено, будем предполагать, что
опоры расположены на уровне нижней плоскости плиты,
т. е. перемещения w = 0 при г = а и z = —h (рис. 20)1.
Шарнирно подвижная опора не препятствует свободным
перемещениям в радиальном направлении и повороту обра-
зующей цилиндрической поверхности, ограничивающей
Рис. 19
z
.Pz
Рг *
Pz
♦ Pr
( I *
P* a
p
Рис. 20
о *
плиту. При точном решении задачи она должна быть осво-
бождена от сил радиального направления, при приближен-
ном они должны быть уравновешенными. По условиям
равенства нулю суммы и момента указанных сил при г = а
h h
| pdz -0-, j* pzdz~0.
~ Л - h
(5.2)
Здесь p = or + p' + p" z/h, p' — равномерная и p"zlh —
линейно распределенная нагрузки по цилиндрической по-
верхности, интегрально уравновешивающие напряжения
ог, получаемые после решения задачи с выполнением крае-
вых условий только на плоских поверхностях [т. е. условий
(5.1)]. Напряжения и перемещения, соответствующие на-
грузкам р' и p"zlh, имеют значения (3.8),(3.12), (3.20); для
сплошных плит они просты:
1 Отходим здесь от предположения, принятого в теории тонких
плит, что опорным служит контур средней плоскости плиты. Выбор
его положения не влияет на величину напряжений и радиальных
перемещений от изгиба и сжатия, а при небольшой величине отно-
шения толщины к диаметру — и на значение прогиба. В толстых
плитах поперечные перемещения от сжатия сравнимы с перемеще-
ниями от изгиба, ими не следует пренебрегать. Это приводит к не-
обходимости при построении решений считаться с фактическим
расположением опор, обычным по контуру нижней плоскости.
115
, г
а'^а^р-\-р"-— ffz = Trz = O;
r h
1—v / z \
и —-— р' 4- р” г; (5.3)
Ь \ Л ]
w = — -Jrtavp' z+~- [(1 — V) r2 + 2vz2]).
с. [ 2Л J
Подставляя р в (5.2), получаем:
h h
1 с 3 f
р'= —— J Ordz; р* = _J <jrzdz. (5.4)
— h — h
При шарнирно неподвижном закреплении плиты, огра-
ничиваясь приближенным выполнением краевых условий на
цилиндрической поверхности, требуется равенство нулю
моментов сил и радиальных перемещений и на некоторой за-
данной окружности:
h
з f
р" = ——- I arzdz\ uO6m==u-i W j-u" = 0, (5.5)
J
— Л
где и и и" — перемещения при нагружении цилиндричес-
кой поверхности радиальными силами соответственно равно-
мерными р' и линейно распределенными p"zlh. В частности,
если считать, что перемещения на контуре средней плоско-
сти равны нулю (схема осуществления такого закрепления
плиты указана на рис. 22), то и = *~v р' а\ и" = 0.
Отсюда
где и — радиальное перемещение, полученное только при выполне-
нии условий (5.1).
Наконец, при жесткой заделке цилиндрической по-
верхности, как и в теории тонких плит, можно выполнять
равенство нулю радиальных перемещений и = 0 и производ-
ной = 0 или = 0 при г = а и z = 0. Первое условие
du _
= 0 соответствует отсутствию поворота малого эле-
мента образующей криволинейной поверхности плиты при
z = 0, второе — отсутствию поворота концов радиусов в
средней плоскости при г = а. Применение того или иного ус-
ловия зависит от конструктивного осуществления опоры.
116
Для толстых плит применима и третья форма записи ус-
ловий на заделанной опоре, пожалуй, более точно отражаю-
щая действительное закрепление края плиты. По этому ва-
рианту радиальные перемещения принимаются равными
нулю на контурах верхней и нижней плоскости плиты:
«обт~« + “' + «* —О ПРИ г=а и z~ ±h. (5.7)
Смысл и, и ни" указан ранее. Связь их с силами р' и р”
получена ранее (см. (3.8), (3.20)] при рассмотрении первой и
второй простейших форм решения осесимметричной Задачи.
Для сплошной плиты
1 —V 1 —V
и' -— р’ я; и" = ± —~— р" а. (5.8)
С с
Возможны и иные предположения, моделирующие опор-
ные закрепления толстых плит. Однако различие в результа-
тах, соответствующих той или иной форме жесткого закреп-
ления, незначительно при размерах плит, допускающих вы-
полнение краевых условий в интегральном смысле, и умень-
шается по мере возрастания отношения радиуса к высоте
плиты1.
5.2. Плита, свободно опертая по контуру
К значениям напряжений и перемещений при осесиммет-
ричном нагружении плит силами, приложенными к плоским
поверхностям по степенному закону кординаты г, приводит
применение функций напряжений, взятых в форме (3.4) и
(3.9), т. е. в форме решения осесимметричной задачи в сфери-
ческих координатах 2.
Рассмотрим ряд задач об изгибе круглых сплошных и
кольцевых плит силами, равномерно распределенными по
верхней плоскости и под действием собственного веса. По-
лучение решений при других полиномиальных нагрузках
достигается аналогично при применении функций (3.5) и
(3.9) более высоких степеней, чем использованные ниже.
1 Подчеркнем еще раз несовершенство постановки задачи изги-
ба толстых плит, основанной на применении решения в целых поли-
номах, заключающееся в принципиальной невозможности оценки
перераспределения напряжений у опор. Поэтому частные результа-
ты, полученные в такой постановке, нужно относить только к обла-
сти плиты, достаточно отдаленной от опор.
2 Первое подробное исследование о напряжении деформирован-
ного состояния толстых плит при полиномиальных нагрузках при-
надлежит А. П. Коробову, получившему ряд практически важных
результатов.
117
В первую очередь рассмотрим изгиб круглой сплошной
плиты, размеры которой указаны на рис. 20, силами р,
приложенными равномерно по верхней плоскости. Согласно
условиям (5.1), функция Ф = 0 при z = —h (нижняя плос-
кость) и
дФ дФ
при z = h (верхняя плоскость).
За функции ф и <р принимаем выражения
ф = г2 + Д2 f2 z-f-A4 (4а2—Зг2) г2 а;
<р= В4 (4а2—Зг2) г2 а,
отдельные члены которых взяты из числа (3.5) при k = 1,
2 и 4. Соответствующая им функция Ф имеет вид:
Ф = |Д,4-Л2а-3 (Д4 + в4) г2а + 4 (Л4+ЗВ4) а»] г2.
Положив здесь z = —h, получаем:
A2h—4(Д4 + 3fi4)h® -0, Д4+В4=0.
По условиям (5.9)
2А, Н- 2А2 h -|- 8 (Л* ЗВ4) Л® = р;
Л2+12(Д4-|-ЗЯ4)Л2 - 0.
Решение этих уравнений приводит к следующим значе-
ниям постоянных:
Таким образом, форма функций напряжений <р, Ф и £2
установлена:
ф(3r2—4z2) г‘2
о4Ла
р / а а3 \
Ф=4-2'-3—-— г2; (5.10)
о \ Л Ла у
р । Г / г \2 /а \21 z j
|2~3(3 Hv) т +4v v hr •
[_ \ Л у у Л у J Л у
Подставляя эти функции в формулы (1.27) и (1.12), со-
ставляем выражения для напряжений и перемещений:
р ( Г Л / r V / a VI а )
я'= ld8+l,2+3(3+v)br) -4 (2+v>(t) J т];
Р ( Г / г \2 / z \21 а ]
°в= ад 8+ 12+3o+3v) -г- ~4<2-iv)hr hr ;
oZ ( |_ \ Л / \ л у J Л )
118
Однако эти выражения не являются окончательными, их
нужно дополнить значениями, соответствующими силам р'
и pnzlh, зависящими от характера закрепления цилиндричес-
кой поверхности плиты. В случае шарнирно подвижных
опор р' и р” определены равенствами (5.4). После подстанов-
ки в них аг при г = а и интегрирования
р Зр
р' = -~ р"^—-^-l5(3 + v)^ + 4(3-v)h2].
4 160л2
Присоединяя к (5.11) напряжения и перемещения (5.3),
вычисленные при этих значениях р' и р", получаем окон-
чательную форму записи напряженияй огиое и перемеще-
ний и и w в рассматриваемом случае изгиба плиты:
Зр
32/13
(З-f-v) (а2 —г2)— 4 (2-|-v)
Зр
32Л3
(3-+- v) а2—(l+3v)r2 —4(2+v)
vp Зр {
1(3+v> °2-(l+’> -
- 4- (2+9V-V’) hs+4“ (I + v)
О о
(2—v) z2} rz\
(5.12)
P 3p /(
— (h + z) — Ц( 1 — v)[(5+ v) а2 —(1+v) r2-|-
-j-12,8A2] ia2—r2) -i 4 (v [(3-b v) a2—2 (1 -J-v) r2] —
4 2
— (5+2v + v2) h2+— (1 -j- v)2 (h2 + z2)
О О
(h2-z2)
Выражения для напряжений oz и xrz не приведены, так
как приложение сил р' и p”z!h не изменяет их значения. По-
стоянная и>0 найдена по вышеуказанному условию — w = О
при г = а и z = —h, соответствующему опиранию плиты не
основание по контуру нижней плоскости.
119
При z = 0 напряжения ог и о© обращаются в нуль, сле-
довательно, средняя плоскость плиты, как принято гово-
рить, нейтральная. Относительно этой плоскости ог и о©
распределяются асимметрично (в равноотстоящих по разные
стороны от средней плоскости точках они равны по величине
и обратны по знаку), абсолютная величина их не зависит
Р
Рис. 21
___1
^040.972
—10,846
—10.784
-40648
Ч 0.5
У 0.352
1 0.216
0.104
0,028
О
от того, какая плоскость пли-
ты нагружена — верхняя или
нижняя.
При приближенности ре-
шения цилиндрическая по-
верхность плиты не свободна
от напряжений касательных
тГ2, распределенных по высоте
по параболическому закону
с максимальным значением
(^rz)max = Spafoh, и нормаль-
ных (рис. 21)
наибольшая абсолютная величина которых не превышает
0,125р независимо от отношения hla. Эта величина мала по
сравнению с наибольшими напряжениями (ог)наиб ПРИ г =
= 0; если a = 3h и v = 0,3, она составляет 3,93 % (<тг)наиб-
Уравнение средней поверхности изогнутой плиты
ph
Ц)= —---—
2Е
(5-f-v) а2—(1 4-v) г2 —
Зр
128ЕЛ3
v (1 —v) а2 —
Максимальный прогиб
I И' Imax—
Ph
2Е
P
128Ehs
3(1—v) (5 + v) a* +
3 (16 + 7v—3v2) a2—2 (25+2v4-v2) h2 h2
Сравним полученные результаты с результатами решения
теории тонких плит для рассматриваемого случая изгиба
свободно опертой плиты. По этой теории
120
°? = - (3+v) г;
л Зр
““^7 l(3+v) a2-(l-3v) г2] г;
Зр
т° = —— (h2—z2).
гг 8h3 ' '
Выражения для касательных напряжений совпадают.
Напряжениями о2, т. е. сжатием по толщине плиты, в теории
тонких плит пренебрегают. Разность между напряжениями
ог, ое и oj, ое не зависит от г:
п п Р Г 3 / z \21 г
or-o0=oe-o»=-— (2-J-v> —- — —
о \ Л ] Л
2 (2 + у)Р
+ 20
и, следовательно, различие между ними возрастает по мере
удаления от оси z, т. е. в области, где напряжения малы.
Наибольшие напряжения
л Зр / а \2
«и»=(°e)„a»6=;
Зр /а
°наиб = (^г)наиб : (°е)наиб = ~32~ <3+v)
близки друг к другу. Поправка к теории тонких плит харак-
теризуется вторым членом отношения
Онаиб = j . 8(2+v) / _h_\2
®нанб 15 (З + v) \ а )
и не превышает 4,23% при а 3h.
По теории тонких плит уравнение изогнутой средней
плоскости
3 (1 —v) р
& = -----128£/t3 l(5 + v) а2 —(1 +v) г2] (а2—г2)
и максимальный прогиб
Зра4
------- (1—v) (5-|-v).
128Ehs ’ v ’
I Imax —
Сравнение максимальных прогибов в толстых и тонких пли-
тах при малом a/h приводит к значительной разнице между
ними, — следствие влияния нормальных и перерезыва-
ющих сил и сжатия по толщине плиты. Представление о
величине этой разницы можно получить по значениям в
табл. 10, подсчитанным при а = 5Л и v = 0,3.
121
КЗ
КЗ
Таблица 10
О 00 1
г/а
0
0.2
0,4
Тонкие плиты (свободно опертые)
z = h —7,734 —7,425 —6,497 —4,950 —2,784 0
z = h —7,734 -7,554 —7,020 —6,619 —4,883 —3,280
W, 2 = 0 —54,35 —51,66 (заде —43,85 данные) —31,71 — 16,86 0
<ь-; z = h —3,046 —2,737 —1,809 —0,862 — 1,902 4,689
z = h —3,046 —2,868 -2,334 — 1,443 —0,197 1,406
W\ 2 = 0 — 13,13 Tc — 12,28 )лстые плиты —9,406 (ширнирно ПОДВ1 —5,460 <жные опоры) -3,071 0
СТГ> z = h —7,849 —7,540 —6,612 —5,065 -2,899 —0,115
z = h —7,849 —7,671 —7,137 —6,246 —4,999 —3,396
о»; 2 ’ = 0 —62,88 —59,88 (шарнирно неп —51,14 одвижные опоры —37,42 ) —20,00 —0,671
л J 2 = ft —8,064 —7,754 —6,826 —5,279 —3,114 —0,329
иг 1 2= — ft —7,635 7,326 6,398 4,851 2,685 0,099
Пл 2 = ft —8,064 -7,806 -7,351 —6,461 —5,214 —3,611
О0 2= — ft 7,635 7,457 6,923 6,032 4,786 3,182
ш; 2 = 0 -62,75 -59,75 (задела —51,01 иные края) —37,29 —19,87 —0,542
/т 2 = ft —3,475 -3,166 —2,238 —0,691 1,475 4,259
ог 2 = —ft 3,047 2,738 1,809 0,262 —1,903 —4,687
[ 2 = ft -3,475 —3,297 —2,763 — 1,872 —0,625 0,978
ст0 | 2= —ft 3,047 2,869 2,334 1,444 0,197 —1,406
z = 0 —21,19 — 19,78 —15,81 -10,05 —3,78 1,21
Примечание. Приведены значения отношений напряжений or н 0^ к нагрузке р и прогибов w к ра/Е.
5.3. Плита, закрепленная по контуру
Для плиты с шарнирно неподвижным закреплением
(верхняя схема на рис. 22), изгибаемой силами, равномерно
распределенными по верхней плоскости, выражения для на-
пряжений и перемещений нетрудно составить, присоединяя
к (5.11) значения (5.3), где р' и р" определены равенствами
(5.5). Напряжения о2 и тГ2 при этом не изменяются, а ог и
ое и перемещения и и w получают следующие значения:
ур _ Зр
2(1—v) 32h3
(34-V) (а2 —г2) —
-4(2 + v)(4-ft2- “J"*2
\ э 3
vp Зр
On — — —
6 2(1—v) 32h2
(3-|-v) а2— (1 +3v) г2—
-4(2+v)
Зр ('
и= ~ 0-v) K3 + v> o2-(1+v) г2] -
- (2+9v-v2) h2+^- (1 +v) (2—v) z2
o a
w =
(5-13)
(l+v)(l-2v) 3p
2E(1— v) P +Z) 128ЕЛЗ
(5+v) a2—
(h2—z2)—8v (I + v> 1(аЛ)2 — (rz)2]
2
+ — (14-v)2 (h2+z2)
О
Постоянная интегрирования, входящая в w, определена по
условию w = 0 при г = а и z = —h.
В средней плоскости плиты радиальные перемещения
и = 0, а напряжения ог и ое отличны от нуля. Выражения
для этих напряжений отличаются от полученных для плит
с подвижным шарнирным опиранием наличием членов—
pv/[2 (1 — v)j, соответствующих общему радиальному сжа-
тию плиты. Асимметричное распределение напряжений на-
рушается — сжимающие напряжения несколько увеличи-
123
ваются, а растягивающие уменьшаются. Наибольшие по
абсолютной величине напряжения получаются в точке г =
= 0 и z = h:
I ° 1наиб — I °г 1наиб — | |наиб —
р
8
Г 3 / а \2
T(3 + V) V +
L 4 \ п /
2 (2-|-2v—v2)
5(1—v)
Сравнение их с наибольшими напряжениями, подсчитан-
ными по приближенной теории тонких плит, приводят к та-
ким же поправкам, как и
в случае плиты, свободно
опертой по краям, если
считать, что тонкая пли-
та сжата в радиальном
направлении силами
pv/[2 (1 —v)].
Перейдем к случаю, ког-
да цилиндрическая поверх-
ность закреплена непо-
движно— заделанная опо-
ра (нижняя схема на рис.
22). По условиям (5.07)
получаем два простых уравнения для определения сил
р' и р” z/h:
р ( Г 3 fa \2]] 1—v 1—v
2 h+v+--(l-v) — + р' +—-Р" = О;
16 р. (|_ 4 \ Л / JJ Е с
р ( Г 3 /а VI)
-£-2- l+v+ —(1-V) — +
lop, ( 4 \ л / JJ
1—v
— Р
1—у
Е
р" = 0,
из которых
рО+у)
4(1—у) :
рО+у)
8(1—у)
После составления выражений для напряжений и пере-
мещений по формулам (5.3) и присоединения их к (5.11)
получаем:
ур р ( 2—5у—у2
2(1—v) + 8 ( 1—у
/ г VI / z V) z
-(3+v)(t)]-(2+v4t))t:
124
“ = ~ (32Eft3P 13 (1 “V) (a2-f2)“4 <2-v> <Л2-г2)1 гг=
u> = —---------(h4-z) —-----------
2E ' 128Ehs
16 г
+ — (2—v) ft2 (a2—r2) + 4 v (a2—2r2) —
<J I
.6(1—v)
-L (i+v) (h2 + z2)] (h2-z2)l. (5.14)
<J 1 J
В середине пролета (г = 0) напряжения имеют значения
(аг)г=о — (ae)r=o-----Р
ГЗ(1+у)
L 32
при z = h;
dp [ay
(ar)r=0 =(ae)r=o =-32" (1 + v) при z = “h’
на защемленной цилиндрической поверхности
Зр / 4vh2 \ 3vp ( „ 4vft2 \
г =----г- °2— -------I: =------— I а2— ------I при z = п;
т 16Я2 \ 1—v/’ е 16А2 \ 1— v)
Зр [ а \2 3vp I а \2
аг =--- — : ай= ------ — при z=—п.
16 h J ’ е 16 \ h J F
Уравнение срединной поверхности изогнутой плиты
(14-v) ра
и> = —----------—
2Е
3(1+?)Р
128Eh3
(l-v)(a2-r2)4-
8 1 Г I (I -bv)2 \ 1.1
+ — (4+v) h2 ] (a2—r2)—4 lva2+4^1— 6(1_^ p2]*2]
Максимальный прогиб
(t^lmax —
(1 4-v) ph
2E
3(l+v)P
128ЕЛ8
(1 —v) a4+
Г 1 ( d+v)2 \ 1
+4 — (8-v)a2-4/l- U2P2
L з \ 6 (i •=—v) j j
125
При изгибе тонкой круглой заделанной плиты равномер-
но распределенными силами напряжения и перемещения
средней плоскости имеют следующие значения:
Зр
°’ = 32/Р 1(1 + V) (3 + V) Z;
T° =--------- (ft2 — Z2) r;
rz 8h3 1 ’
1(1 + v) a2-(l+3v) r2] z;
oZn?
W® =
3(1—v2) p
128£h3
(a2—r2)2.
Различие между ними и напряжениями и перемещениями
в (5.14) более значительно, чем для шарнирно опертых плит,
что связано с увеличением влияния на деформацию плит
перерезывающих сил. Для максимальных напряжений и
прогибов поправки, учитывающие это влияние, определяют-
ся вторыми членами отношений:
Например, если а = 5/ihv = 0,3, то напряжения |ог|наиб =
= 1,141 |о®|иаиб и перемещения к|тах = 1,824 к°|тах,
а для шарнирно опертых плит при тех же размерах
I °г 1наиб—1,015 | о® |наиб И 1и,1н*иб—1,157 | и>°/наиб-
Сказанное подтверждается и сравнением значений напря-
жений ог и ое при z = и прогибов w средней плоскости,
приведенных в табл. 10, при изгибе равномерно распреде-
ленной нагрузкой тонких и толстых плит, свободно опертых
и заделанных по краям. При подсчетах принято а = 5h и
v = 0,3.
5.4. Кольцевая плита,
нагруженная по боковым поверхностям
Рассмотрение осесимметричных деформаций круглых
кольцевых плит начнем с изгиба силами q и qQ осевого на-
правления, равномерно распределенными вдоль контура
соответственно на внешней (г = а) и внутренней (г = а0) бо-
126
ковых цилиндрических поверхностях (рис. 23). Верхняя
(z = h) и нижняя (z = —h) плоскости плиты свободны от
нагружения. Выполнение этих условий приводит к решению
в целых полиномах в форме, которая определяется характе-
ром распределения внешних сил вдоль образующих цилинд-
рических поверхностей, суммарно равных q и q0.
По условию равновесия между q и qQ должна выполнять-
ся следующая связь: qQ =—q.
ао
Как и ранее, будем считать, что опоры расположены на
внешнем или внутреннем контуре нижней плоскости плиты,
т. е. при вычислении перемещений w полагать w = 0 при
z = —h, г = а или г = —а0. Пользуясь решениями осесим-
метричной задачи в целых полиномах (3.04) и (3.39), для
функций ф и ф принимаем:
ф = До z-i-Di (z2—3r2 In—- )z; q> = C1 (z2—3r2 In ) z.
\ ° J \ a /
Составляем функцию Ф:
Ф= Aoz + Dx (z2—3r2 In — z2— r2 In—)z.
\ a I V a ]
Требуя выполнение равенств (5.01) на свободных от на-
гружения плоскостях плиты z = ±А, имеем Ао = —бС^2;
D± — —Clt и функция Ф получает вид: Ф = —2СГ (ЗА2 —
— z2) z. Функция й, соответствующая ф и Ф:
Г2_ЗЯ2_|_(2—v) Z2 — .
J г
Применяя формулы (1.27) и (1.12), для напряжений и
перемещений находим:
(5.15)
Z
Т2"'
6СХ а
oz = 0; тгг ——^-(h2 —z2); (5.15)
ог =
3 l + (14-v) In—I г2—ЗЛ2-|~ (2—v) z2
а
oe= —2CJ3 v-Hl + v) In — г2—3h2—(2—v) z2
I I a
(1 — v) r2—2vz2 —2 [(1 —v» r2-|-
_|_ 2vz2—2Л2] In i + wo
a J
127
Равенство суммы касательных напряжений на каждой
из цилиндрических поверхностей плиты внешним силам q
и qQ
h h
f 6С. С 8С,
q = | irZ dz = —---- | (h2—z2) dz = —----hs
J a J о
—h -h
приводит к значению постоянной .
По форме выражений (5.15) нетрудно сделать следущие
заключения. Касательные напряжения тГ2 не зависят от ха-
рактера закрепления плиты, они распределены по толщине
плиты по параболическому закону с максимумом при z =
= 0. По асимметрии распределения нормальных напряже-
ний ог и о© и радиальных перемещений и относительно сред-
ней плоскости нормальные силы вдоль радиусов равны ну-
лю. Следовательно, плита не подвергается общему радиаль-
ному растяжению или сжатию — на цилиндрической грани-
це отсутствуют равномерно распределенные нагрузки ра-
диального направления. В случаях свободной от закрепле-
ния боковой поверхности и шарнирно подвижной опоры
первое
На
плиту,
условие (5.4) выполняется автоматически.
цилиндрических поверхностях, ограничивающих
отличны от нуля и не уравновешены
ог=—2СХ [3 (а2—h2)4-(2—v) z2]~v при г = а;
а2
ог= —2Cj (3 1 + (1 4-v) In
Др
а
al-3h* +
+ (2—v)z2 при г=а0,
J Др
что приводит к чистому изгибу плиты, дополнительному к
изгибу силами q и q0. Для его исключения, выполняя гра-
ничные условия в среднем, напряжения ог нужно уравнове-
сить линейно распределенными силами р" zlh (внешний край)
и ро zlh (внутренний край), определяемыми равенствами
(5.4). После подстановки в них ог и интегрирования имеем:
Г 1 I h
р^бСД! —-(34-v) — h;
I 5 \ а / J
h.
Присоединяя к значениям (5.15) значения (3.20), полу-
чаем полные выражения для напряжений и перемещений в
кольцевой плите, опертой по внешнему контуру нижней
Г а0 1 / h
Ро = 6Cj 1 + (1 + v) In-- - — (3+v) —
I а 5 \ do
128
плоскости, при изгибе силами q0, распределенными по внут-
ренней поверхности:
3</о а0
°Гг= ~ 4ft3
a2—ag
+ (a0r)2ln-- +(2-v)
Qo J
3?o Oo f.. . ,
°*=—ir p-v)'!-
(aa0)2 In — (ar)2 In — +
a a
T”
z
~г^’'
14-v , 1О, а0
—------ (аа0)21п---
а2—ag а
4-(ar)2 In — — (a0r)2ln------ — (2—v) — ft2—-— z2
о а
z
w
u
а
З^о а0
4Ehs
«0 J
.2 ’
a
r2— (14-v) (2—v)
(14-v)(aa0)2 a0
--------------In ----
a
л2__2
a 0
ag , а0
—------ In -—
а2—ag а
-г'
Z
(5.16)
3</о а0
16Ehs
a2—ag
Qq
а
v—-------
a2 —ag
2
5
, 2(l-f-v) , 1О, a0 , г
4- —-----— (aa0)2 In--- In —
a2 — ag a J a J
Если плита шарнирно оперта по внутреннему контуру
нижней плоскости и изгибается силами, приложенными к
внешней цилиндрической поверхности (нижняя схема на
рис. 23), выражения для напряжений и радиальных пере-
z
%Й^Й8^йИ1ИИ1ИЙЙЙЙйт
’Л
7Я/////Л
Рис. 24
Рис. 23
129
мещений не меняются, а для осевых перемещений записы-
ваются в несколько иной форме1:
3qa
w —-------
16Eh»
2 (1 +v) a2
(r2—al) —
Л Г, 2 (1 H-v) a2 , a0 1 Г 2
—2v 1 -v- у ' in - 2 (1 + v) — (8+
L a —a6 a J I о
4-v) h2—~~~~ (oflo)2 In -^- — (1 — v) t2 — 2vz2l In — 1.
а2—a J a0J
Обратимся к случаю изгиба кольцеобразных плит, в
которых один из краев, скажем, внешний, (верхняя схе-
ма на рис. 24), заделан. Внутреннюю поверхность освободим
от распределенных моментов, выполнив, как и прежде,
второе равенство (5.4), что приводит к значениям
Ро =6G [1 + (1 + V) In — - 4- (3 +V) (—П Л.
L о. 5 \ По / J
По равенству радиальных перемещений и = 0 при г = а
и z — ±/i
= - 2(1+V-1C1 [ЗЛ2_(2_v) h2] h +
Еа
+ - К1-v) а*~Р° а* + (1 + v)(^-РП (««о)2]=О
Е (a2 —ng) а
определяется дополнительная нагрузка, обеспечивающая в
среднем заделку внешней цилиндрической поверхности,
2[(1+у)»С1(а2-аЗ)Л>+рИ<Юо)*1
Р [(1-v)a2 + (l+v)a§]a2
Напряжения и перемещения теперь нетрудно получить,
суммируя значения (5.15) и (3.20) при найденных р” и ро-
Запись их в общем виде весьма громоздка и поэтому не
приводится.
1 Напряжения и перемещения в рассматриваемом случае изги-
ба кольцевой плиты, вычисленные по теории тонких плит, нетрудно
получить из (5.16) после исключения членов, содержащих Л2 и z2.
130
Если заделан внутренний край (нижняя схема на
рис. 24), то аналогичные рассуждения приводят к следую-
щим значениям р" и ро*
Г I / h VI.
Р*=6С1| 1-—(3+v) ----- h;
I. 5 \ a0 / J
Op
a
al)h-p”(aa0)*
Po —
В качестве числовых иллюстраций произведены подсчеты
напряжений ог и Ое при г = h и прогибов средней плоско-
сти в рассматриваемом случае нагружения плиты, когда
а0 = 2h и а = 8Л. Коэффициент Пуассона принят равным
0,3. Результаты указаны в табл. 11.
5.5. Изгиб кольцевых плит
равномерно распределенной нагрузкой
Выяснение напряженно деформированного состояния
круглых кольцевых плит при изгибе равномерно распреде-
ленной на плоской поверхности нагрузкой не требует
введения новых форм функций напряжения, отличных от
использованных в п. 5.1—5.4. Построение решений в каж-
дом частном случае опорных закреплений сводится к ком-
бинации уже полученных результатов и выполнению задан-
ных граничных условий. Во избежание повторения формул
и громоздкости записей будем приводить их только в исклю-
чительных случаях.
Составляющие напряжений и перемещений запишем в
форме сумм четырех членов:
4 4 4 4
Ог~ 2 aQ~ 2 °6k'* °г= °zh> хгг= TrzhJ
fe=l k= 1 fe==l k= 1
4 4
U= У Uh\ w= 2 wh, (5.17)
fe=i
где члены с индексом «1» определены формулами (5.11), с
индексом «2» — формулами (5.15), с индексом «3» — фор-
мулами (3.30) и с индексом «4» — формулами решения за-
дачи Ламе для полого цилиндра (3.12) и (3.13).
Подробно произведем выкладки для случая изгиба пли-
ты с шарнирно подвижными опорами, расположенными на
131
со
ю
Т аблица 11
г 2 3 4 5 6 7 8
ог/<7о; z = h 0,040 Плита, с —0,794 тертая по вн —0,801 ешнему краю —0,629 —0,416 —0,192 0,0025
°е/Чо'< z — h —6,812 —4,442 —3,313 —2,614 —2,116 -1,729 — 1,413
“»о Е/Яо‘, z = 0 —77,14 -62,95 -49,72 -36,89 —24,34 — 12,09 —0,212
<Jr/<io; z = h 0,040 Плита, 3aj 0,216 желанная по е 0,562 шешнему кра 0,898 ю 1,200 1,467 1,707
ае/Яо', z — h —3,034 —1,629 —0,853 —0,318 —0,091 0,425 0,706
о»о £/<?о; 2 = 0 —26,15 —19,97 — 14,28 —9,23 —5,00 — 1,78 0,251
внешнем контуре нижней плоскости (рис. 25). В первую
очередь освободим внутреннюю цилиндрическую поверх-
ность плиты от касательных напряжений, т. е. положим
T-rz = Ъ-Zl + ^rz2 + 'Сггз + ^rz4 = 0 ПрИ Г = а0. ПОДСТЗВ-
ляя сюда значения тгг1 (5.11) и тгг2 (5.15) и имея в виду,
что тгг3 = тгг4 = 0 во всей области плиты, имеем:
Зр 3<7п
(Л2_22)ао+_^.(Л2_22) = О.
он 4/1
Отсюда определяется значение
уравновешивающей нагрузки
pan
qn - ~ 2 •
Требуя равенство нулю нор-
мальной силы на цилиндричес-
ких поверхностях
h
j (CTrl+<Tr4)dz = O,
— h
где слагаемые иг2 и ог 3 исключе-
ны как нечетные функции z, мы
Рис. 25
возвращаемся к первому усло-
вию (5.4), по которому р' = ро = — р.
Наконец, равенство нулю моментов сил на цилиндричес-
ких поверхностях г = а и г — а0
h
f (^п+сггг+агз) zdz = Q
приводит ко второму условию (5.4) и после подстановки в
него иг1, иг2 и огз и интегрирования к следующему резуль-
тату:
Зр f 4
р"= —77“ (3+v)a2-4fl2+—[(3-v)O2 +
32л2 [ 5
I Л \21
+(3 + v)og] — ;
\ а / I
Зр I 24 а0 1
Ро = {(1 - V) - — Л2 + 4 (1 +М In j.
Дальнейшее заключается в составлении сумм (5.17) при
найденных значениях q0, р', ро, р" и ро- Выполнив все под-
становки и группировки, получаем:
133
— (14-3v) г2
(aa0)2 In —— +(<w)2 In — —
a a
= [2А3+(ЗЛ2-г2)2]; тгг=—(г2-а§)(Л2_22).
4nd ой3 r
vp 3p (
“=^" r~"3^l(|-v)
(34-v)a2—(1—v) a§ —
(5-18)
-(1 +v) r2+-^- (3—v) й21—4 (1 +v)
b I
A2-y(2-v)z2
+(14-v)f 4 (1+v) (aa0)2 In v)(ar)2ln — —
I cr—ag [a a
— (1—v) (a0r)2 In —~—] 4-(34-v)a2 +
°o J
+ 4(2-v)
(1—v) p Зр / ( Г
w = — 4-~: - (h + z) —Ц( 1 -v) |^(54-v) a2-2 (3+v) -
-(1+v) '2+-^- (3^)Л2+8(21+^ °o In —1 (a2-r2) +
5 a£—a§ a
+4^(3+v)a2+(l+3v) a2_2(i+v)r2+-£(3_v)A2 +
4(1 +v) an 1 2 )
; a*0 In- (14-v)[(5~v)h2-(14-v)?2] | (Л2—r2)—
ar—ag a J 3 J
134
Соответствующее решение по теории тонких плит полу-
чается отсюда после исключения членов, содержащих мно-
жители h и г. Для кольцевых плит с размерами а0 = 2/i и
а = 8h и коэффициентом v = 0,3 в табл. 12 приведены зна-
чения напряжений иг и Ое при z = -±Ji и прогибов w0 сред-
ней плоскости (z = 0) в двух случаях изгиба плит — свобод-
но опертых [подсчитаны по формулам (5.18)] и заданных по
краю г =а. Во втором случае силы р' и р" определены по
условиям (5.7), а силы рб и ро—по интегральным усло-
виям (5.4), соответствующим отсутствию на свободной
поверхности г — а0 нормальных сил и моментов. Равен-
ство нулю касательных напряжений на этой поверхности,
как и прежде, выполняется выбором величины q0:
Приведем значения указанных сил:
= _ Рво. . ,___Р[(1+у) о2+(1—у) flg] . ,___[
2 ’Р ~ 4[(l-v)a2+(l+v)a§] ’ Ро ~ 4
__________J________ГЗ(1+у)рГ /
(1-v)a2+(l+v)a§ [32 (ah)2 *4
+ ~"'(а24-а§)Л2] (а8—а§)—2р;
О J
Зр ([ 1 Go 1 6 1
pS Т (1-у)+(1+у)1п— ag-— Л2 .
оп£ IL 4 a J 5 J
Если опорным является не внешний, а внутренний кон-
тур плиты, выражения для сил q, р', р'о, р" и ро мало отли-
чаются от приведенных. Так, при шарнирном опирании (см.
рис. 23) они записываются в виде:
„ 3Р
р" =.----
п„____Зр
Р° W
1 » 6 1
(l-v)g8-—Л2 ;
4 О J
1
Т(3-
Qq
а
при заделке (см. рис. 24):
1
д=—— ра; р
1 Зр
— р; р" =---------
4 И И 8/l2
_L(l_v)a2_
4
Ро =
135
Таблица 12
2 3 4 Л 5 6 7 8
Плита, опертая по внешнему краю
аг/р; 2 = Я —0,200 —8,795 — 10,463 -9,628 —7,404 -4,305 —0,120
ае/р; z = h —33,34 —23,89 -19,13 — 17,25 -14,82 -12,31 -9,57
wE/p; z = 0 -198,2 -198,0 -177,3 —142,9 -98,9 -50,9 — 1,10
Плита, 3aj деланная no e жешнему кра ю
z — h —0,387 —2,097 -1,354 0.556 3,427 7,015 11,311
P z= —h 0,387 1,883 1,066 —0,878 -3,768 -7,368 -11,671
% z = h —10,763 —7,771 —5,890 —3,935 — 1,780 0,656 3,408
P z= —h 9,995 7,417 5,410 3,490 1,353 -1,072 —3,801
wE/p; z = 0 -85,72 -66,31 —46,97 —28,35 — 12,230 -1,155 1,706
„ __________I______ (3(l+v)pr 1
P° (l+v)a2+(l-v)«§ l 8/i2 [4 <1-v)aS-
। / A
—(1—v)a2ln —— — (1+v) (a2—ag)(—) (a2—a2)+2p" a2
a 3 \ a ] I
При наличии опор как на внешнем, так и на внутреннем
краях плиты реализация процесса решения по приведенной
схеме весьма усложняется1. Системы в этих случаях отно-
сятся к внешне статически неопределимым. При их расчете
следует прибегнуть к общеизвестному приему метода сил
строительной механики. А именно, отбросив лишние связи,
получить некоторую геометрически неизменяемую статичес-
ки определимую систему, которую принято именовать «ос-
новной», и рассмотреть ее нагружение заданными силами
(«грузовое») и единичными силами, заменяющими реакции
отброшенных связей — лишние неизвестные в уравнениях
статики. Условие равенства нулю перемещений, соответст-
вующих отброшенным связям, при полном нагружении ос-
новной системы, эквивалентном нагружению статически
неопределимой, приводит к канонической системе линейных
алгебраических уравнений для определения лишних неиз-
вестных. После ее решения напряжения и перемещения со-
ставляются суммированием напряжений и перемещений в
грузовом состоянии основной
системы и в каждом нагружении
ее единичными силами, умножен-
ными на величину соответствую-
щей опорной реакции.
Поясним сказанное примером
расчета кольцевой плиты с шар-
нирными опорами на внешнем
и внутреннем контурах нижней
плоскости (рис.26). За основную
систему принимаем плиту, опер-
тую только по внешнему конту-
ру. Лишней неизвестной явля-
ется сила X, заменяющая реак-
цию опоры внутреннего контура.
По эквивалентности деформиро-
Рис. 26
вания полного нагружения ос-
новной системы и рассматриваемой статически неопредели-
мой перемещения w = 0 при г = а0. Расчленяем нагружение
основной системы на грузовое (см. на рис. 26 0) и на
1 Это в равной мере относится и к круглым плитам без отверстия,
имеющим дополнительные опоры в пролете, в частности в центре.
137
нагружение единичной силой (см. на рис. 26 /). Переме-
щения и направления в первом случае обозначим верхним
индексом «о», а во втором —штрихом. Тогда перемещения
w при полном нагружении будут
t»=w°+a,/
и по равенству нулю при г = а0
(а’0)г=ао+(“',)г=а.х=°-
Это и есть каноническое уравнение задачи.
Искомое значение опорной реакции X = — —-.
В рассматриваемом примере перемещения и напряжения
в состоянии О определены равенствами (5.18), а в состоянии
/ равенствами (5.15) при q0 = —1. Следовательно, без осо-
бых затруднений могут быть получены (и/))г_ав и (о>')г=а.»
—ао»
а затем и составляющие перемещений и напряжений, сумми-
рованием значений (5.18) и (5.15) после замены в последних
q0 на X. В табл. 13 приведены результаты для плиты с раз-
мерами а0 = 2/i и а = 8h (v = 0,3).
Таблица 13
Г h 2 3 4 5 6 7 8
м N N н II II О > » -0,30 -16,15 -3,57 -6,79 -12,68 -39,17 -8,44 -10,77 -51,85 -8,04 -10,65 -49,82 -6,35 -9,48 -37,49 -3,82 -7,95 -20,40 -0,126 -6,00 -1,63
5.6. Изгиб круглых плит
под действием собственного веса
Перейдем к задачам изгиба осесимметрично нагруженных
плит под действием массовых сил. Рассмотрим изгиб круглой
сплошной плиты, опертой некоторым образом, под дейст-
вием сил собственного веса, т. е. под действием сил g, рав-
номерно распределенных по объему и направленных пер-
пендикулярно средней плоскости. Высоту плиты обозна-
чим по-прежнему через 2Л, радиус — через а. По равенству
gr = 0 и gz = —g в соответствии с первыми формулами
138
(1.43) и (1.47) должно бытьфг = 0 и <рг = 0, а по вторым фор-
мулам нетрудно установить, что1
фг = —---—----г2 г; ®г =--—---г2
8(1—v) Y 8(1—v)
г4.
Поэтому [см. (1.46)] Фг = О И Ф = Ф + 2 |у-.
По контурным условиям (1.52) в данном частном случае
на плоских поверхностях плиты должны выполняться ра-
венства:
дФ дфг 1
Ф = 0; —— =— 2(1— v)r——=— —-gr2 приг = ±Л. (5.19)
dz or 2
За функции напряжений ф и <р принимаем те же самые
значения, что и при изгибе плиты, равномерно распределен-
ной по ее верхней плоскости нагрузкой (см. п. 5.2). Тогда
Ф = [Л14-Л2 г—3 (Л4+В4) г2 г+4 (Л4+ЗВ4) z’J г* -
Выполнение условий (5.19) приводит к трем уравнениям:
^4-Л2 Л—3 (Л44-В4) г2 Л4-4 (Л44-ЗВ4) ЛЗ = 0;
At — А2 Л4-3 (4- в<) г2 h—4 (Л4-ЗВ4) h2 =0;
А,-3 (At 4- г24-12 (Л4-ЗВ,) h2 = —у g;
^2 4 St B4 32Л2 •
решение которых Аг = 0;
Следовательно, функции <p, Ф и Q имеют следующую фор-
му:
(4z2—3r2)r2z; Ф = —(h2—z2) r2z;
32Л2 4h2
(5.20)
g g
Q (h2—z2)z —[3 (3 4-v) r2—4 (14-v) z2] z.
Ml* 10/1*
После подстановки этих функций в формулы (1.50), (1.44)
и (1.48) для напряжений и перемещений получаем:
[3 (3 4-v) г2 4- 4Л« - 4 (2 4- v) z2] z;
16л4
Ge = -^T-l3(1+3v)r8 + 4/i2-4(24-v)z2] z;
1иЛ4
a 3g
°Z= (Л2 — z2)z. Trz = —— (Л2—z2)r\
2h2 K ' rz 4h2 '
1 Напомним, что фг, фг, фг и ф2 — частные решения уравнений
(1.42) и (1.47) (см. п. 1.6).
139
(1 +v)g
u= 1L/2 [3(l-v)r2 + 4h2-4(2-v)z2]rz;
16c №
(1 +v)g
w= ~ Jf/,2 <3 * К1-*) '2 + 8А21 r2 +
t)4£/lz
+ 8 [3vr2 + 2Й2—(1 +v)z2] z2} -|~u>0; u>0=const. (5.21)
Форма напряжений oz и xrz установлена окончательно.
В отличие от ог и о© и перемещений и и w эти напряжения не
зависят от характера закрепления плиты. Составление окон-
чательных выражений ог и о©, и и w требует выполнения
условий закрепления на цилиндрических границах плиты.
Как и выше удовлетворим этим условиям в соответствии с
принципом Сен-Венана в интегральном смысле. В случае
шарнирно подвижного опирания края плиты к (5.21)
должны быть добавлены напряжения и перемещения (5.3)
при р' и р", определенных по формулам (5.4). После подста-
новки в последние ог и интегрирования имеем:
р'=0; р" =
g
16Л
3 (34-V) а2—4- (1 +3v) h2
5
Присоединение к (5.21) значений (5.3) приводит к следую-
щим, теперь уже окончательным выражениям для напряже-
ний и перемещений в плите с шарнирно подвижной опорой
на крае:
ог=— [(3+v)(a2— г2}—4(2+v)M- h2—z;
16л2 [ \ 5 3 / J
3g Г
ae = —(3 + v)a2-(l+3v)r2-
ion* l
z;
«= —dbi-fac1-*) K3+v)a2-(1 +v)r2]-
—(6+7v — 3v2) h2 + 4 (1 + v) (2—v) z21 rz\
5 J
(5.22)
w = If3 (1 ~v> K5+v) a2-(1 +v>f2] -
64ch2 \(
32 If
—---(8+1 lv+v2)h2 (a2—r2)+4l3v [(3+v)a2—2 (1 +v) r2] —
5 JI
2 ) \
——(5 + 2v+v2)h2+2(l+v)2z2Hh2—z2) •
5 J /
140
Напряжения ог и о® при g — p/2h полностью совпадают
с напряжениями ог и о® решения (5.12). Таким образом, на-
пряженные состояния толстых плит при изгибе собственным
весом и при изгибе внешними силами, равномерно распре-
деленными по верхней плоскости, различаются только ха-
рактером распределения напряжений о z и незначительно —
перемещений и и w.
В случае заделанной опоры силы р' и р", распределенные
по цилиндрической поверхности плиты, определяются ус-
ловием и = 0 при г = а и z = ±Л 1см. (5.7) и (5.8)1.
Их значения таковы:
, Л п 0+V)& 2
Р =0; р =———-—(За2—4Л2).
Суммируя (5.21) и (5.3), составленные при этих силах,
приходим к следующим выражениям для напряжений и
перемещений:
°г=—{3[(l+v)a2-(3+v)r2J-4(2+v)(h2-z2)} z;
16nz
Ое=----{3[(1 +v)o’-(l+3v)r>)-4(2-НМЛ*-z»)) Z-, 23)
(1 +v)g
“ = - - iaf/,2 <3 (1 (a2-H-4 (2-v) (Л2—z2)} rz;
locnz
w= - a3(1 (a2—Г2) — 16(2+v)h2](a2—r2) +
+4 [3v (a2—2r2)—2 (1 + v) (h2+z2)] (h2—z2)}.
Перемещения и в этом случае изгиба (при g = p/2h) сов-
падают с перемещениями и в плите, изгибаемой равномерно
распределенной по верхней плоскости нагрузкой (5.14).
По форме полученных выражений нетрудно видеть, что на-
пряжения ог и о® при z = ± h имеют такие же значения, как
и в теории изгиба тонких плит.
В круглой кольцевой плите, изгибаемой собственным ве-
сом, выражения для напряжений и перемещений составить
просто, соединяя ранее указанные решения (5.21), (5.15),
и (2.35),аналогично тому как это было сделано в п. 5.5 при
изгибе ее нагрузкой, равномерно распределенной по пло-
щади верхней плоскости [см. (5.17)1. При этом, как и рань-
ше, силы q и 70 определяются по условию равенства нулю
касательных напряжений на свободной от закрепления ци-
линдрической поверхности плиты (при г — а0 или г = а), а
значения сил р' и р" в зависимости от характера опор —
либо по равенству нулю моментов на цилиндрической по-
141
верхности плиты (шарнирная опора или свободный край),
либо по равенству нулю перемещений при г = ±h и г= а
или г — а0 (заделанный край).
В любом случае осуществления опор напряжения1
g Зе
°г = xrz= ..2 (о2—/-2)(ft2 —z2).
2 л2 4л2 г
Напряжения о, и Ое совпадают со значениями напряже-
ний в кольцевых плитах, изгибаемых равномерно распре-
деленными по верхней плоскости плиты силами р = 2g/i.
Различие в выражениях перемещений и и w при изгибе внеш-
ними силами р = 2g и собственным весом незначительно.
5.7. Решение в рядах
Решение осесимметричной задачи в целых полиномах в
практическом отношении имеет ограниченную область при-
менения, в задачах о деформациях толстых плит, — пожа-
луй, только при изгибе равномерно распределенными по
плоской поверхности силами (не считая тривиальных слу-
чаев — равномерного и линейного нагружения по цилиндри-
ческой поверхности). Иного вида нагружения силами, из-
меняющимися по степенному закону вдоль радиуса, практи-
чески маловероятны. Значения соответствующих им напря-
жений и перемещений можно найти, действуя по плану при-
веденных выше задач, при надлежащем выборе функций
напряжений из числа (3.4). Выполнение контурных условий
на цилиндрической поверхности плиты возможно лишь в
интегральном виде.
Если распределение внешних сил не является степенным
(по г), выяснение напряженности деформированного состоя-
ния в плитах достигается применением формы решения осе-
симметричной задачи в цилиндрических функциях (см.
п. 4.1)2. Последовательность вычисления при этом повторяет
последовательность решения в рядах для длинных цилинд-
ров, приведенную в гл. 4, различие заключается в замене
формы решения (4.8), применяемой для длинных цилиндров,
формой (4.6) или (4.7), что как следствие требует представ-
ления закона приложения внешней нагрузки не тригономет-
рическими рядами, а разложениями в ряды Фурье-Бесселя.
Построение решения с использованием обеих форм (4.8) и
1 Если опорным является внутренний край плиты, перед выра-
жением тгг нужно изменить знак и радиус а заменить радиусом а0.
2 Первые решения задач о равновесии цилиндров с применением
цилиндрических функций содержатся в [89], [108], [ПО],
142
(4.6) или (4.7) позволяет точно удовлетворить краевым усло-
виям на всей поверхности плиты (как на плоских частях
ее, так и на цилиндрической). Однако в этой главе ограни*
чимся их точным выполнением только на плоских поверх-
ностях. Это ограничение оправдывается, с одной стороны,
значительным упрощением математического аппарата и
окончательных выражений для напряжений и перемещений
и, с другой стороны, достаточной точностью результатов
для практических целей в довольно большом числе задач.
С единственной целью упрощения записей рассмотрим
нагружения только круглых плит без центрального отвер-
стия и бесконечного слоя, ослабленного круговым отвер-
стием. Исследование напряженного состояния плит с отвер-
стием не встречает принципиальных затруднений, но при-
водит к весьма значительному усложнению вычислительного
процесса.
По условию конечности функции напряжений Ф (г, z) при
г = 0 в выражениях функций (4.7) и (4.11), напряжений
(4.17) и перемещений (4.18) должны быть исключены члены,
содержащие функции Вебера Y (г, z). Тогда представление
функций напряжений в рядах получает форму
1 оо 1
ip (г, г) = —Г Por2+r V ——(4n sh Xn z 4-ch Xnz) Л (Хп г);
п— 1
2 °°
ф(г, z)= Ро' + г V —-(Сп shX„ Z 4- Dn ch кп z) (Xn r);
4(l+v)
(5.24)
Ф(г, Z) = —— p0r2+r У —— [4n shXn z + Bn ch knz +
* Лп
+ ^n z (Cn ch Xn z-]-Dn sh Xn z)J Jj (Xn r);
+ Xn z (Cn ch Xn z -J- Dn sh Xn z)] J1 (Xn r) 4~ (Cn sh Xn z-j”
4~£>n ch Xn z) [2 (I —v) Jj (Xn r)—2Xn rJ 0 (Xn r)l} •
где p0 — равномерное растяжение по толщине плиты.
Как правило, при решениях задач о напряженно-дефор-
мированном состоянии толстых плит в частных случаях на-
гружения прибегают к обычному в строительной механике
143
приему преобразования нагружения на симметричное и
асимметричное (рис. 27). Таким приемом задача общего
нагружения разделяется на две более простые — растяже-
ние или сжатие плиты (pz и р+) и изгиб ее (рГ и р7)- Первой
задаче соответствует четная по z часть функций напряжений
(Лп = Сп = 0), второй — нечетная (Вп = Dn = 0). В силу
, 0.5Р, ♦ Q5P,
0.5Р2 | IOJP3 \Q5Py
iSSSSSSSSSSSSSSSSSSSSSSi
0.5 Ру I 0.5Pj (одр, I 0,5Pt\0.5Pj f^SPy
05Py ♦ °.?pj |G5P’ 0,SPl I °'5P3 f 0,5
^msssssssssss^sssssssssss
u^ssssss^sssssssss^
0.5Рг I Q5/> \a5Pt I °fpi I 0.5P3 f
этого разложение в ряды наг-
рузок Pz.Pr И Рг, р7 доста-
точно выполнить на одной из
плоских границ плиты— верх-
ней или нижней. Выправление
знака в случае асимметрич-
ного нагружения осуществля-
ется автоматически.
По граничным условиям
при г = ± h для обоих типов
нагружения az = pz и xrz=pr.
Напомним, что pz и рг нужно
считать положительными на
верхней плоскости (z = Л),
если они направлены в сторо-
ну возрастания координат z и
г, а на нижней (z — — h), если
они направлены в сторону
Рис 27 убывания гиг.
По связи напряжений oz
и xrz с функцией Ф (r,z) на плоских границах плиты при
симметричном и асимметричном нагружениях должны быть
выполнены равенства (см. (5.1)]:
дФ
дг
—гРг.
дф
~^~=ГРг,
дг
(5.25)
по которым могут быть найдены постоянные Ап, Вп, Сп и
Dn до составления выражений для напряжений.
Предположим, что плита нагружена только нормальны-
ми силами pz = р (рг = 0). Расчленив нагружение на
симметричные р+ и асимметричные р~ части, представим
закон их изменения в форме разложения в ряды Фурье-
Бесселя:
оо оо
р+=Ро + S Р^/о(Хпг); р-= 2 P7Jo&nr). (5.26)
п—1 п=1
Такое разложение, может быть выполнено при трех сле-
дующих различных выборах значений Хп, а именно*
Хп — корни уравнения Jo (Ха) = 0; Хп — корни уравне-
144
ния Jq (ка) = —Jr (ка) = 0 и кп — корни уравнения
ка Jq (Ха) + AJ0 (ка) = 0, где А — постоянная. Будем при-
менять второй вариант, при котором функция Ф (г, z), а сле-
довательно, и касательные напряжения xrz на цилиндричес-
кой поверхности обращаются в нуль, а радиальные переме-
щения и имеют постоянные значения. Это соответствует
уравновешенному нагружению плиты с шарнирными опора-
ми или с закреплением по цилиндрической поверхности,
допускающим свободное скольжение по толщине1.
По первому равенству (5.25), приравнивая при z = h
члены с одинаковыми индексами производной
d<D Vi
-т-= — Рог+г Л (finchin z+DnXnzshXnz +
or -1
-|-’Лп sh Xn z-|-Cn Xn z ch Xn z) J о (In f) (5.27)
и соответствующих разложений (5.25), получаем:
fin ch Xn h+Dn XnhshXnh = —p+;
An sh Xn k-±-Cn Xn h ch Xn h=—p~. (5.28)
По второму условию (5.25) при pr = 0, так как
[(fin +£>n) sh Xn z-j-Dn Xn 2 ch Xn z-j-
+ (ЛП +Cn) ch Xn z-^-Cn Xn z sh Xn z[ J1 (Xn f), (5.29)
должны выполняться равенства:
(fin -Dn) sh Xn Л ~l~Dn Xn h ch Xn h = 0j
(Л n~[— Cn) ch Xn h —|-Cji Xn к sh Xn Л ==0.
(5.30)
p0 — сводный член разложения (5.26), соответствующий
равномерному сжатию плиты при симметричном нагружении.
После решения полученных уравнений (5.28) и (5.30)
определяются общие выражения для постоянных:
2р+ (sh Хп h + Хп к ch Хп h) 2р+ sh Хп h
Вп = — — ---------------------; Dn =---------------;
sh2Xnh + 2Xnh sh2Xnk+2Xnk
(5.31)
2p (ch Xn h ~т~Хп к sh Xn k) ^Pn ch In к
д — ---------------------:— . q =----.
n sh2Xnk—2Xnk ’ n sh2Xnk—2Xnk
1 В первом случае, естественно, необходимо снять напряжения
ог на цилиндрической поверхности, а во втором — добавить равно-
мерное сжатие в радиальном направлении.
145
Подобным образом устанавливаются значения постоян-
ных при наличии на плоских основаниях плит касательных
сил pz. Однако такое нагружение не представляет практичес-
кого интереса. Приведем выражения в рядах для напряже-
ний и перемещений.
Напряжения:
оо
1 ’’t'l 1
ог=— Д —7 {[(^n + 2Cn) sh кп z-|-(fin -|-2Dn) ch Xn z-Ь
Г
n= 1
-b^n z (Cn ch Xn z-f-Dn sh Xn z)] [Jj (Xn r)—Xn. rJ й (Xn /)] —
—2v (Cn sh Xn z-|- D-ц ch Xn z) Jk (Xn /)} I
OO
°0= “7 {[(i4n +2Cn)sh Xnz-|-(Bn + 2Dn)ch Xnz-|-
r n=\
~b Xn z (Cn ch Xn z-f- Dn sh Xn z)] Jj (Xn r)—2v (Cn sh Xn z-4-
Dn ch Xn z) [Ji (Xn f) — Xn rJо (Xn r)]};
(5.32)
OO
Qz — Po— [^n sh Xn z-|-fin ch Xn z-|-Xn z (Cn ch Xn z-|-
n= 1
-f-Dn sh Xn z)] J о (Xn r)~,
Trz= । [(^n+Cn)ch Xn z-|-(fin +Cn) sh Xn z-j-
n= 1
4~Xn z (Cn sh Xn z-f-Dn ch Xn z)] Jl (Xn f).
Перемещения:
“= — “TTPo r+“^— V "T—{[^n + 2(l—v)Cn]sh Xn z-b
С Лп
• n= 1
“b[fin4~2(1 —v)Dn] ch Xz z-1-Xn z (Cnch Xn z-|-
-|-Dn sh Xn z)} Jj (Xn r):
(5.33)
1 1 00 1
w = —poz——— V — ([Лп—(1 —2v) Cn] Ch Xnz+
E 2|i Xn
n= 1
-|-[fin — (1 —2v) On] sh Xn Z “f-Xn Z (Cn sh Xn z-|~Dn Ch Xn z)} +и>0;
И)о = const.
Напряжения и перемещения, вычисляемые по этим фор-
мулам, должны быть дополнены напряжениями и перемеще-
ниями, определяемыми условиями закрепления плиты по
146
краю. В случае шарнирного опирания плиты при прибли-
женном суммарном выполнении этих условий по (5.4) долж-
но быть:
h h
1 Г 3 Г
р' = —------ I ardr\ р" ——----------- I urzdz;(r = a).
И 2h J 2ft2 J г
— h —h
После подстановки сюда значений ог при г — а и вы-
полнения интегрирования имеем:
Р' — . . [(fin + Dn) sh h
Л An
n= 1
Dn “kn h ch Xn Л] J0 (Xn a) =0;
(5-34)
3 'V' 1 .
p" = — , [^n (Xn Л ch Xn Л—shXnft) +
h2 Xn
n— 1
4~ (Xn Л)2 Cn sh (Xn ft) Jq (Xn a)].
В случае заделанной опоры по условию и = 0 при г —
= а, получаем значения распределенных по цилиндрической
поверхности сил:
, v
Р =“----------Ро-
1 — V
(5.35)
При отсутствии поворотов образующей р” = 0. Предпо-
лагается, что опора не препятствует свободному смещению
вдоль образующей.
5.8. Изгиб плиты силами, распределенными
по кольцевой области
Начнем рассмотрение конкретных решений в рядах за-
дач об осесимметричном нагружении плит с достаточно об-
щего случая — изгиба силами, равномерно распределенны-
ми по кольцевым областям в верхней и нижней плоскостях
(рис. 28). Случая общего в том смысле, что пользуясь его
результатами без труда, как частные могут быть получены
147
решения задач об изгибе плит силами, распределенными по
площади круга, силой, сосредоточенной в центре, й также
путем наложения решений для множества других типов на-
гружения (например, по двум кольцевым областям, по коль-
цевой области и сосредоточенной силой в центре и т. д.).
Итак, круглая толстая плита радиуса а и толщины 2h
нагружена на верхней плоскости силами рг = —р, распре-
деленными по кольцевой области, определяемой радиуса-
ми а2 >» а1. Плита свободно оперта по кольцу а3 <2 г <2
2
<С а4 нижней плоскости. Пред-
положим, что силы реакции
Pj распределены по площади
контакта равномерно. По ус-
ловию равновесия
Pi =
а®—а?
al— Оз
Р-
(5.36)
0.5р, 0.5р 0,5р 0,5р,
Расчленив нагружение на
симметричную и асимметрич-
ную части (см. рис. 28), на
поверхности z = ±h имеем:
Рис, 28
р+=0; р~ = 0 при 0<r<aj;
Ог <2 г <2 Пз • а4 <2 f <2 о;
р + = — 0,5р; р~ = Т0,5р при
О] <2 г < а2\
Р% = — O-Spji p- = ±0,5pj
при a3</’<a4
(5.37)
(верхний знак относится к плоскости z = +/i, нижний —
к плоскости z = —h). Применяя формулу для коэффициен-
тов рядов Фурье-Бесселя,
а
2 Г
Р” 7 , /1—77 I ГР(Л) J°(Хн r) dr
[aJ0(Kn a)]2 J
о
(5.38)
где, как было сказано, кпа— корни функции J j (Ха), вы-
числяем коэффициенты рп сумм (5.26)1:
1 Здесь использовано табличное значение интеграла
dr= —— rZj (Xn г).
148
аг
₽" = ~ Гп/ (L f rJ° (Хп Л) ЛГ~
[см о (Хп о)р J
а»
а«
Р1 С 1
г г /1 М2 1 r^o(^nr)dr= — — {pla^Ji^n а2) —
[а/о (Хп а)] J Xn [а«/о (Хп а)12
as
— Qi Jj (Х„ Qj)] -|- Pi [а^ Ji (Хп at)— а3 Jj (Xn а3)J); (5.39)
Рп —— « - г ti м2 {₽ [^2-/j (Xn а2) aj Ji (Хп й])]
Хп [<iJo(Xn а)]2
— Pj [°4 J 1 (^п а«)—п3 Jj (Хп а3)]}.
Равномерно распределенная по плоским поверхностям на-
грузка, сжимающая плиту по толщине,
р Pi
Ро=—(5.40)
а2 ст
Завершение задачи заключается в выполнении чисто
формальных подстановок. По формулам (5.31) при значе-
ниях Рп и рп (5.39) составляются выражения для постоян-
ных Ап, Вп, Сп и Dn, которыми определяются напряжения
и перемещения; основные по формулам (5.32) и (5.33) и до-
полнительные, связанные с выполнением контурных усло-
вий на цилиндрической поверхности плиты, по формулам
(5.5) при значениях р' и р” (5.34) или (5.35)1.
В областях, близких к плоским поверхностям плиты,
значения напряжений ог и сге представляются плохо сходя-
щимися рядами. Вычисление их требует применения специ-
альных приемов улучшения сходимости. В точках поверх-
ности плиты можно указать простой путь, приводящий к
значительному упрощению процесса подсчета напряжений
ог и ое, заключающийся в нижеследующем преобразовании
их выражений. Воспользуемся равенствами (1.25):
а
1 дФ 1 2
----—- —[O + 2(l-v)<p] + —
Г дг Г2 г
о
да 1
— [ФН-2( 1 — V) <р] —
дг г2
2 д<р
г дг
1 Выражения для напряжений и перемещений в каждом частном
случае не приводятся из-за их сложности.
149
При z = ±h здесь Ф = — и -J- = —az = —pz, еле-
J l> t \)e
довательно,
_ (N)z=±h , 2 00 2nr2 ' r2 дф (1—v)q>+vr dr
Подставляя значение <p (5.24), имеем:
°г— 2лг2 ^«=±Л“^»=±й+ 2 Ро~
/, . (± Сп sh Xn h -|- Dn ch h) [(I—v)Jj(Xnf)—
n=i n
—Xn rJ о (Xn f)]:
aQ = ~~^{N}*=±h + ~2 Po +
2 xci 1
+ ~7 (± Cn sh Xn A-f-^n ch Xn h) X
Г Kn
X [(1 — v) Л (Xn r) + vXn rJ0 (Xn r)].
Заменив здесь Cn и Dn значениями (5.31) в результате
преобразования
2р~ sh Xn h ch Xn h
zb Cn sh Xn АЦ- Dn ch Xn A = ± ~ ~ ~ -|-
sh 2Xn A—2Xn A
2p+ sh Xn A ch Xn A
+ sh 2Xn A-f-2Xn A
Г 2Xn A 1
+ P" I ’ ~sh 2Xn A-|-2Xn a] = P” ± P" hpn (± h}-
при обозначении
pn{± )-8Ь2ХпА-|-2ХпАТ5Ь2ХпЛ —2XnA
2Xn A
1+------------
sh 2Xn A — 2Xn A
150
приходим к следующим выражениям для <тг и сге:
п= 1
—2Л У, Рп (± Л) [(I—v) Jl (Хп г) -|-vXn. rJ0 (Xnf)] •
n— 1
Однако no (5.26)
У, J0 (hnr) = p+— p0-, У P~ J0(lnr) = p-'
n=l n=l
Таким образом, для напряжений ог и Og в точках плос-
ких поверхностей плиты получаем:
1—2v 1
°Г= —^-(^=±h+(Pz),= ±h—(1+2V) р0 +
+— 2Рп (± Л) 1(1 ~v) Ji (Xn r)-Xn rJ°(Xn r)1; (5,42)
n= 1
1—2v 1
°e=±*+2 v ±h“ V U +2v> P»~
oo
— Pn (± Л) [(1—v) Jj (Xn r)4-vXn fJofyn f)]«
n= 1
151
Верхний знак соответствует плоскости z = +/i, ниж-
ний z — —h.
По наличию в членах сумм знаменателей, быстро возра-
стающих с увеличением а, ряды в равенствах (5.42) хо-
рошо сходятся — цель преобразования выполнена.
По полученным формулам произведен подсчет напряже-
ний ог и de для плиты, нагруженной по кольцевым областям
а, = 0,3а и а2 = 0,5а по верхней плоскости, а3 = 0,7а и
а4 = 0,9а — по нижней (рис. 28). Толщина плиты — 2h =
= 0,4а. В этом случае р0 = —0,16р и рг 0,5 р. Условия
на цилиндрической поверхности выполнены в интегральном
смысле: р' = 0 и р" = —0,6050 р. Результаты подсчета на-
пряжений приведены в табл. 14 (v — 0,3).
5.9. Изгиб круглой плиты нагрузкой,
распределенной по площади круга,
и сосредоточенной силой в центре
Приведем результаты решения задач об изгибе круглых
сплошных толстых плит в двух частных случаях приложе-
ния внешних сил — равномерно распределенных сил р по
области круга с центром,
совпадающим с центром
верхней плоскости . (верх-
няя схема на рис 29), и си-
лой р, приложенной в цен-
тре верхней плоскости
Рис. 29
Р,
(нижняя схема на рис. 29).
Как и раньше, будем пред-
полагать, что плита оперта
по кольцевому основанию
на нижней плоскости и что
силы реакции опоры равно-
мерно распределены по ее
площади. При этих предпо-
ложениях для симметрич-
ной р+ и асимметричной
р~ составляющих нагруже-
ния при z = должны
быть выполнены условия:
р"*" = —0,5/г, р~ = ±0,5р при 0 < г < а2;
р"*” =0; р~ =0 при а2 < r<z а3 иа4< г <а;
р+ = —0,5р1; р~ = ± 0,5 pj при а3 < г < а4.
152
Таблица 14
г/а 0 0.2 0,4 0,6 0.8 1
Нагружение по кольцевой области
°г z---h — 1,129 -1,069 — 1,644 —0,294 +0,037 +0,031
Р . г — —h + 1,295 + 1,368 + 1,291 +0,621 —2.262 +0,199
°0 z — h -1,129 — 1,094 — 1,667 —0,808 -0,554 —0,366
Р z— —h + 1,295 + 1,335 + 1,328 + 1,017 +0,222 +0,531
Нагружение по круговой области
— 1 z-h -3,143 —2,971 —2,392 —0,647 -0,153 —0,164
Р । г -- —h +3,063 +2,708 + 1,968 + 1,064 -0,218 +0,532
qe [ z = A -3,143 —3,040 —2,718 — 1,567 -1,338 —0,814
р z = — А +3,063 +2,920 +2,476 + 1,871 +0,942 + 1,096
Нагружение сосредоточенной силой
<?г z—h. — -5,313 —3,629 -1,619 —0,808 +0,030
Р z — — A + 16,488 +9.117 +3,485 + 1,337 -0,101 +0,947
qe z A 1 —9,162 —5,878 —4,122 —3,147 — 1,086
Р i Z —A + 16,488 + 11,864 +6,553 +4,407 +2,928 +2,651
Значения коэффициентов р„ и рп сумм (5.26) следуют
из (5.39) при ах = 0:
, 1
Рп ~~ 1 г I ч12 •'l (^П °2) “Ь Р1 [°* Л (^’» а«) -
Ml (GJ о \”П *J)J
—аз JI (^-п аз)]}I
Рп = ~2 , , 712 {Pai i (^» °г) —
An [aJ0 (hn a)]2
—Pi [a« Ji (^n a4) a3 Jj (Xn аз)]}.
Для плиты при а2 = 0,5 а; а3 = 0,7 а; а4 = 0,9 а и h —
= 0,2 а по формулам (5.42) приведен расчет напряжений
ог и Ое в точках верхней и нижней плоскостей. По условиям
равновесия силы реакции в этом случае
(0,5a)2
pt 1------------р = 0,78125р.
'* (0,9a)2—(0,7a)2 Р
Силы равномерно сжимающие плиту по толщине, р0 =
•- —0,25 р, а силы, определяемые равенством нулю сжатия
в радиальном направлении и моментов на цилиндрической
поверхности плиты, р' = 0, р" = —1,2282. Подсчитанные
значения напряжений указаны в соответствующих строках
табл. 14.
Переход от рассмотренного случая к изгибу плиты со-
средоточенной силой, приложенной в центре, совершается
без труда после уменьшения до нуля радиуса а2 при условии,
что (па% р)а,_^ = Р. Тогда
Pat , ,, ч ] Ра2 а4 ] Р
— (Ап а4) — . о ~ о
An Jat-*0 хЛ
и, следовательно, при прежних предположениях о характере
опирания плиты
р+ — — . . 72 + "Т la4 Ji (Ъ-п а4) —а3 Jt (Хп а3)]| ;
п [а/0 (^t а)]2 ( 2л Хп J
Р^ = — . . мй — а*> ~аз J1
[ало (лп о)]2 I 2л Лп J
Если а3 = 0,7 а и а4 = 0,9 а, силы реакции опоры
р Р Р
п л(а|—а2) 0,32ла2 а2
_ Р
Равномерное сжатие плиты по толщине р0 = — =
Р
— —0,3183-2- и силы на цилиндрической поверхности
р' = 0; р” = —3,2729 Р/а2.
154
Как и в первых двух случаях, вычисленные значения на-
пряжений аг и ао при z = ±Л приведены в табл. 14. Как и
следовало ожидать (по приближенному выполнению гранич-
ных условий), на цилиндрической поверхности плиты напря-
жения аг наиболее отличны от нуля в точках контура ниж-
ней плоскости. Это связано с влиянием опоры, близко рас-
положенной у контура, и весьма существенно зависит от
размеров площади контакта и характера распределения сил
на ней (в произведенных расчетах оно принято равномер-
ным). В точках контура верхней плоскости, достаточно отда-
ленных от опоры, значения напряжений ог малы по срав-
нению с максимальными.
5.10. Осесимметричное нагружение слоя
Слоем называют бесконечную упругую среду, ограничен-
ную двумя параллельными плоскостями. Понятие условное,
подобно тому, как условно понятие «бесконечно длинный
цилиндр». Слоем, по существу, является тонкая плита, т. е.
плита, толщина которой значительно меньше ее других раз-
меров, нагруженная на конечном малом участке ( чаще все-
го уравновешенными силами), достаточно отдаленном от
ограничивающего плиту контура. Решение задач об упру-
годеформированном состоянии в таких случаях нагружения
преследует цель выяснения величины и характера распреде-
ления напряжений в области расположения сил и поэтому
имеет не только познавательное теоретическое значение , но
и представляется интересным в практическом отношении1.
Получение решений при осесимметричных нагружениях
слоя достигается после перехода к интегральной форме
записи функций напряжений и применения аппарата ин-
тегральных преобразований Ганкеля. Считая параметр
X непрерывным и заменяя в (5.24) суммирование интегриро-
ванием, для функций напряжений, принятых здесь, полу-
чаем следующие выражения:
Ф = rj [С (X) sh Xz-f-D (X) ch Xz] (Xr) dX;
о
1 Задача о равновесии упругого слоя рассмотрена во многих
f*a6oTax, некоторые из них указаны в списке литературы. См. [6],
28], [84], [111], [114]. А. И. Лурье предложен символический при-
ем решения уравнений теории упругости для слоя, изложенный
155
Ф =r j {Л (X) sh Xz + B (X) ch Xz-f-Xz [С (X) ch Xz +
o
+ D (X) sh Xz]} Jj (Xr) dX; (5.43)
OO
Й = — Ф+— f [C (X) sh Xz+D (X) ch Xz] [2(1—v) J, (Xr) —
о
— 2XrJ0 (Xr)] dX.
Подобные выражения без труда могут быть составлены
для напряжений, радиальных перемещений и и производ-
ных перемещений w по г и по 2 после использования равенств
(5.32).
Функции А (X), В (X), С (X) и D (X), входящие в равенства
(5.43), находятся после выполнения граничных условий
(5.25), что сводится к приравниванию подинтегрального вы-
ражения левой части (5.25) трансформанте Ганкеля заданой
нагрузки. Ограничимся как и раньше, нагружениями толь-
ко нормальными к поверхности слоя силами pz = —р
(рг = 0) и обозначим трансформанты Ганкеля при симмет-
ричном нагружении через р+ (X) и при асимметричном через
р- (X). Выполнив подстановку в (5.25) и несложные преоб-
разования, получаем:
Л (X)
_ 2р+(X) (sh XA + XAchXA) __ 2р+ (X) sh Xh
( sh 2ХЛ + 2ХА ’ ~ sh 2ХЛ4-2ХЛ ’
(5.44)
2р~ (X) (ch ХА 4-ХА sh Xh) с ^у (X)ch ХА
sh 2ХА — 2ХА
sh 2ХА— 2ХА
Таким образом, принципиальная сторона построения ре-
шения в рассматриваемой форме выяснена, остальное отно-
сится к технике вычислений — определению трансформант
р+ (X) и р~ (X), составлению выражений для напряжений и
подсчету их величин. Один из частных случаев нагружения
бесконечного слоя изложен в п. 5.11.
5.11. Нагружение слоя силами,
распределенными по окружности
Для сил интенсивности р, равномерно распределенных по
площади кольца а0 < г < а, трансформанта имеет зна-
чение
Р (Х) = р
а
f rJ0 (Xr) dr =-у
•J ”
Oo
[а/г (Xa)— a0 Ji (Xa0)l-
156
Отсюда после предельного перехода при а0 а и
пр (а2 — ао) -► 2nqa следует значение трансформанты для
случая нагрузки q, равномерно распределенной вдоль ок-
ружности радиуса а,
q (k)=qaJ0 (ка). (5.45)
В табл. 15 приведены напряжения аг и сге в случае нагру-
жения слоя взаимно уравновешенными силами q, приложен-
ными к верхней плоскости по окружности г = а, и'^ =
= aq/aA, приложенными к нижней плоскости по окружности
г = аг. В этом случае, разделяя силы на симметричную и
асимметричную составляющие, в соответствии с (5.44) имеем:
I 1 WU
q н (М = —— [qaJn (М+91 «1 Jo (М)1 = — Ро(М+А(М)Г.
А ~
q (к)— Ро (ка) А (М)1-
Таблица 15
rfll 0 2 4 6 8 10
arh z--h -1,325 -0,599 -0,145 -0,092 -0,076 -0,066
q L z— —h 2,261 1,296 0,441 0,192 0,178 0,143
aQh ( z^-h -1,325 -1,119 -0,520 -0,332 -0,255 -0,206
q 1 z= — h 2,261 1,780 0,979 0,660 0,490 0,398
Подсчет произведен в точках верхней и нижней плос-
костей слоя (z = ±Л) по преобразованным формулам, ана-
логичным формулам (5.42):
1—2v 4h С Г q+ (к)
о L
д~ (к)
sh 2kh—2kh
[(1 — v) (Xr)4-vXr Jo (Xr)l dk',
1—2v 4Л f
°* = ~2nr^~ (N}z= ±h+ 2V (₽z)*= ±h “ ~ J
o
q+(k)
sh 2ХА + 2ХЛ
q~ (X)
+ sh 2kh—2kh
1(1 —v) A (Xr) + vXrJo (Xr)] dk.
157
Коэффициент Пуассона v =0,3, толщина слоя 2Л, радиу-
сы а = h и Qj = З/i.
С возрастанием X подинтегральные выражения быстро
убывают по наличию гиперболических синусов 2ХЛ в знаме-
нателях слагаемых в первой квадратной скобке. На нижнем
пределе X = 0 подинтегральное выражение имеет значение
—(1 4-v) qar/Sh при z = h и (1 4-v) qar/Ah при z = —h,
что нетрудно показать, удерживая при малых X в выра-
жениях Jo (кг), J! (кг) и sh 2ХЛ два первых члена представ-
лений в рядах.
Глава 6. ДЕФОРМАЦИИ ЦИЛИНДРОВ
СРЕДНЕЙ ДЛИНЫ
6.1. Симметричное нагружение цилиндров
относительно среднего сечения
Применение к решению задач о нагружениях цилиндров
функций напряжений в форме (4.1) или в форме (4.2) позво-
ляет точно выполнить краевые условия только на части бо-
ковой поверхности тела либо на цилиндрической, либо на
торцах. Поэтому напряжения и перемещения, полученные в
результате решения, являются приближенными.
Они тем более отличаются от точных, чем ближе к
единице отношение диаметра цилиндра к образующей. Ес-
ли это отношение мало (длинные цилиндры), применение
функций (4.2) приводит к точным значениям напряжений и
перемещений в средней части цилиндра, так как согласно
принципу Сен-Венана характер распределения внешних сил
на торцах не влияет на напряженное состояние этой части.
Если диаметр значительно превышает образующую (плиты)
в области, достаточно отдаленной от цилиндрической поверх-
ности, напряжения и перемещения, полученные при приме-
нении функций (4.1), мало отличаются от точных.
Таким образом, уточнения требуются для цилиндров,
диаметр 2а и образующая I которых близки по величине
(ориентировочно < у < 3), и для оценки напряженного
состояния у торцов длинных цилиндров или у цилиндричес-
кой поверхности плит. Получить решение в этих случаях,
158
можно, применяя одновременно обе формы функций на-
пряжений — (4.1) и (4.2).
Для упрощения рассуждений и записей мы ограничимся
рассмотрением деформаций сплошных цилиндров и крае-
выми условиями, заданными в напряжениях. Расположив
начало координат в центре тяжести среднего сечения и обо-
значив через а радиус и I половину длины образующей ци-
линдра, на цилиндрической и торцевых поверхностях со-
ответственно имеем:
°г=Рг (*); T„ = pz (z) при г— а,
Trz= ± Р° (Г); ог = р° (г) при z = ± I
в случаях симметричного нагружения по отношению к сред-
ней плоскости и
аг = р'(z), xrz = p' при г = а,
01 01 (6-2)
Ъ-z = Рг (г)' = ± Рг >фИ 2 = ± I
в случаях асимметричного нагружения.
В первом случае за функции <р (г, z) и Ф (г, z) принимаем
суммы соответствующих значений (4.2), (4.9) и (4.1),
(4.4), четных относительно переменной z (обозначения по-
стоянных изменены):
ф = б0 г2 + аг У fift /(| (ХЛ г) cos z +
k= 1
4-or У Dh Jt (gfe r) ch z; (6.3)
ft=l
Ф = ЛО r2+ar У /1 (Xfe r)~Bh rl0 (XA /)] cos z +
k= 1
OO
+«Г У (Cfe ch Hk z + Dfe Pfe z sh pA z) J, (рЛ r).
1
Напряжения при таких значениях функций <р (г, z) и
Ф (г, z) определяются формулами:
оо
аг=-.-Л0+2 (1 + v) fio+y- 2 {(Лл + йл) 1^ (Ur)~
Г k = 1
— Л (*fc Hl— Bfc r)24-l—2v] /| (Xfe /)) cos Xfe z +
OO
+ — 2 U(Cfc + 2Dfc) ch Hfc Z + Dh Pk z Sh Pfe z] x
r k= 1
X [Pfe rJ0 (Pfe г)—Л (Pfe r)l+2vDfe Ji (Pfe r) ch Pfe z}; (6.4)
159
ое= До4~2 (1+v) В0+-7 2 «Л* + 2 G-v) х
Л=1
оо
X h (Xfc Г)—(1—2v) Bh Xft r/0 (Xft r)} cos Xh z-\- — Ucft +
r k= 1
4-2 (1—v) Dft) ch pft гЧ-Dfc pfc z sh pfc z] А (pft r)-|-
4-2vDft Цй rJ0 (pft r) ch pft z}; (6.4)
OO
Oz~ 2Д0 2 Xh a [ (Дд 2Вд) /0 (Хд г) Bk Хд г/i (Хд r)[ X
Л=1
оо
X cos Xft z — 2 a (Ch ch pft z+Dh pft z sh pft г) Jo (Рл r)l
k= 1
OO
тГ2= 2 Xh a Mfc zi (** H — Bh Xft r/0 (Xh r)J sin Xft г-ь
k= 1
OO
+ S НЛ ° [(Ch + D*) sh Hh г +Dh Нл г ch Uh z]J| (ць r).
k= 1
Перемещения:
oo
« -^l44-2(I-v)B.]r+£ У Ц^л—2 (1—V) Bft] x
k= 1
OO
x 11 (Xfe r) — Bh Xft r/0 (Xft r)} cos Xft ?4-~- V ![Cft4-
20
1
4-2 (I—v) DftJ ch Ph ?4-Dh Нл г sh Ил г! Л (Нл r)> (6.5)
1 00
— (40-]-2vB0) z 2 iMfc—2 (>—v) £h[ /0 (>-h r) —
О 20
Л=1
oo
Bh Xh (Xh 0} Xh Z [ [Ch
kr= 1
— (I—2v) Dft] sh gh *4-Dh рь г ch ph z\ Ja(Hh r)^-w0,
где G — модуль сдвига, м>0 — постоянная интегрирования.
Принимая Xh = kn/l и за рь** корни функций Бесселя
J) (ра), в случае симметричного нагружения по (6.1), полу-
чим:
160
при z =
оо
2Л0 + 2 (“0* ^a[(Ah-2Bh)I9(Khr)-BhKh Пг (Xfc г)]+
Л= 1
оо
+ 2 НА а 1СА ch НА l-\-Dk На I sh (ift /] Jo (Ha r)= ~ P°z (r)- (6-6)
ft= 1
OO
2 Hao [(Cft + Dft) sh /+Cft Ha I ch (Afc I] (р-л O = P“ (0
k= 1
и при г = a
2 XA a Mb Z1 Ma a)— B* a/o Ma a)l sin *a z= Pz (z);
k= 1
A>+2 (1+v) Bo+ 2 (Mfc+^b) Ma a/o Ma а)“Л Ma a)] —
k= i
-Bh [(Xft a)2+l—2v] Ц (Xft a)} cos z + 2 HA a [(Cft+
k = i
+ 2Dft) ch z+Dft |Aft z sh (ih z] Jo ((ift a) = pr (*)• (6-7)
Умножая первое равенство (6.6) на rJ0 (pn г), второе
на г Jx (jw), и интегрируя в пределах от нуля до а,
приходим к следующей группе зависимостей, связывающих
постоянные Ah, Bh с постоянными Cnt Dn:
2 у (-1)* Xfe
7o(Hna) *а+Нл
Ah It Ма а)~^л
Хда/ 0(кьа) +
(6.8)
12 , 2 Ma а)]
Ч + Нп
— —р?п—(Ап а (Сп ch (An l-\-Dn (in / sh (Ап /);
(6-9)
(An a [(C^+^n) sh (in l+Dn (in / ch (in l] = P?n-
Здесь n = 1, 2, 3, ...:
zn [aJ0 ((An a)]2
a
J rPz O’) Jo (Hn r) dr,
o
(6.Ю)
0
rn
a
2 r
[a/o ((An a)J2 J
0
fPr M) 70 (Hn r) dr
P
161
и использованы интегралы
а а
Г а2 (* а2
I rJ% (Цп г) dr = —J2 (|ап a); I rJ2 (цп г) dr =— J2 (цп а);
aJ ~ v
о о
С ,г / х г /1 xj Хд а/0 (Цп a) /j (Xfc а)
I rJ0 (|Ап г) /0 (Xft r)dr=--------------—— -----------------; (6.11)
а
J Г2 Jo (Нп г) 1г (Xft г) dr =
о
aJ о (Hn а)
al о (ХЛ а) —
Л О*а)
Связь между постоянными Cht Dh и постоянными Ап,
Вп устанавливается по тому же плану. Умножаем первое
равенство (6.7) на sin Xnz и второе на cos Xn z и, интегри-
руя в пределах (—Z, Z), имеем:
Хп а /1 (Хп а)—Вп Хп а/0 (Хп а)]—Pzn» (6.12)
2а у Hfc
' ft.
(Cfc-f-Dfc) sh p.fc Z-f-Dfc p-fc I ch p,fc I +
(6.13)
2Х2 sh ца /
J о (Hh a) = (-1)" Pm- (-1)" {(4+
4~-®n) [Xn a/0 (Xn a)—/i (Xn a)] — Bn [(Xn fl)24~l 2v] /j (Xn g)J »
где n = 1, 2, 3,
i i
Pm =-f' J Pz (z) sin Xn zdz\ prn = —^ J pr (z) cos Xn zdz,
— I — l
(6-14)
и приняты во внимание значения
С 2 (—1)"
I ch p.fc z cos Xn zdz = —j sh p.ft Г,
J, An+
— /
z sh p,fc z cos Xn zdz =
2 (—l)n
Hfc I ch J4fc I +
sh ць I
+
(6.15)
162
Воспользовавшись равенствами (6.9) и (6.12), выразим по-
стоянные Сп и Ап соответственно через Dn и Вп:
р°
Сп =-----------— Dn (1 4-Цп I cth рп
a sh Цп I
Pzn ^>П о!О (Xn fl)
^•п al 1 (Хп с) Л (Хп о)
и заменим их в равенствах (6.10) и (6.13). После выполнения
всех преобразований и группировок получим:
(6.16)
Л 71 —
4Нп (-1)* Ха „ , „ v г. Нпа
. , Ч / , 2 I 2\2 1 — Dn , X
Jo (p-n а) (^а + Ри)2 sh Hn I
X(sh |An I ch pn /+|An o+p“n+p?n cth Un Z4- (6.17)
. _____2 yi (— 1)* К/,
aJotHna) Х£ + И2 Pzh'
I
4X2 а
Ha sh Ha 1
(^+h2)2
Da Jo (НА а) = D* X
X (Xn a) -j-(—l)n Prn — (—1)л Pzn
Io (Xn o)
. Л (Xn a)
Ha Pr°, a r
1 1
Xn a J
(6.18)
при обозначении
D* (Xn a) = (Xn a)2 /2 (xn a)-[(Xn a)2 + 2 (1 —v)J /? (Xn a) (6.19)
n = l, 2, 3, ...
Таким образом, точное выполнение граничных усло-
вий на цилиндрической и торцевой поверхностях цилиндра
привело к совокупности двух бесконечных систем алгебра-
ических уравнений, которые в дальнейшем будут сведены в
одну систему (см. п. 6.2). Решение последней приведет к оп-
ределению значений групп постоянных Aht Bh, Ck и Dh
(к= 1,2, 3, ...).
Постоянные Ло и Во нетрудно найти из равенств
>
Ло=-4-Р“о; Ло + 2 (1 +v) Во = Рго. (6.20)
л»
163
соответствующих растяжению или сжатию цилиндра равно-
мерно распределенными силами р“о на торцах и рг0 на ци-
линдрической поверхности:
а I
2 с 1 с
PzO=~£ J PzW rdr' Pro=-^- ] Pr (z) dz. (6.21>
0 — I
Расчет по изложенному здесь плану осуществляется ли-
бо укорочением бесконечной системы, либо последователь-
ным поэтапным приближением к значениям напряжений и
перемещений, заданным на поверхностях цилиндра. Приме-
нение этих процессов возможно, если бесконечные системы
(6.17) и (6.18) удовлетворяют определенным условиям, вы-
полнение которых приводит к сходящимся результатам при
реализации подсчетов. При поэтапном решении на каждом
последующем этапе должно быть обеспечено более близкое
приближение к граничным условиям, чем на предыдущем.
Исследование систем (6.17), (6.18) в этом отношении произ-
ведено в п. 6. 2.
6.2. Исследование решения
Бесконечная система алгебраических уравнений
оо
Xi = У Ois Xs + 6f,
s= 1
i — 1, 2, 3 ..., называется регулярной, если сумма модулей
коэффициентов в каждом уравнении меньше единицы
оо
2 I Qfsl < 1.
z= 1
и вполне регулярной, если эта сумма не превосходит неко-
торого постоянного числа 1 — е <Z 1.
Доказано, что вполне регулярная система имеет ограни-
ченное решение, которое может быть найдено методом после-
довательных приближений, если свободные члены ее огра-
ничены | bi | < т, а регулярная — если |6J<m(l —
оо
— | Aid)» где т — некоторое постоянное положительное
k= 1
число.
Приступая к исследованию регулярности систем (6.17),
(6.18), установим в первую очередь необходимые для дока-
зательства зависимости х.
1 В изложении использованы работы [2], [3] и [26].
164
Интегралы [см. (6.11)1.
а
2 С
7-7-7-----~ 1 rJ0 (pin г) /0 (Xft г) dr
[0/0 (Мп a)]i 2 J
о
2Xft Л (^k о)__
а(Хл+Нп) Jo(HnQ)
р,0 = О, п = 1, 2, 3, ..., представляют собой коэффициенты
разложения функции /0 (Xftr) в ряд Фурье-Дини по функци-
ям Jo (рпа), если (рпа) = 0, поэтому
2/^ а)
lo&h г) =-:---
а
При г = а — 0 имеем:
оо
У——
Ч+г
п=
•fo (Нп Г)
q/q (Xfc а) 1
О'-h °)
Продифференцируем эту сумму по Xft:
(bfe + НЙ)2 2[Xh Ix (ХЛ a)]2 IXft а/‘ (X* a)
2.
— all (Xh a)] H- —,
следовательно,
oo 1
2 “rW = |D' a)-2 (1 +v)0)' •
(6.22)
D* (M) [cm. (6.19)].
Коэффициенты разложения ch pnz в ряд no cos X.ft z име-
ют значения
i
J ch Цп z cos Xfc zdz =
— 1
[см. (6.15)], поэтому
ch |An z =
( —1)* 2цп sh I
l (Ц + НЙ)
sh цп I
Цп I
165
Положив здесь z = I — 0, получаем:
________1______________Z ch |iw / 1
Я_1 2|1П sh рп I 2р.2
и после дифференцирования по рп
k=
2рп 1
1-------------------й----(нп 1 sh2 Рп 1~
-1- Рп) 2 (Нп sh Нп О2
— sh (An I ch jin I—pn / ch2 pn /)+—-г
Hn
или окончательно
у-----!--
" (Ч+нЭ*
sh p.n I ch |АП I
4р2 sh2 рп I
2 sh2 рп /
Рп I
Обращаясь к системам (6.17), (6.18), положим
Xfc
(6.23)
Dh =
(Ph а) Jo (Ph а) sh Ph 1
Л=1, 2. 3, . . .
Тогда из системы равенств (6.18) для постоянных Вп по-
лучим:
(6.24)
Вп= -(-1)л
4Х2 (Хп а) “
a/D* (Хп а) 2
К=
Xh_____
4- n.2\2
/1 (Хп а)
D*(Kna)
10 №n a)
Prn --Pzn
/1 (Хп с) ^п а
(6.25)
/
2( —1)п
70 (Ph а) .
k=
Подставив эти значения Вп в (6.17), приходим к следующей
бесконечной системе уравнений:
16р» sh2 рп I “ Ц (Xfe а)
I (shpn I ch рп I+рп I) (Xjg+p2)2De (Xft а) Х
ОО
Х(?1'(Ч+н?)>=Л'‘_₽- (626)
166
где через рп обозначена следующая комбинация внешних
приложенных к цилиндру сил:
Рп —
Рп aJp (м-n a) sh2 Нп *
sh pn I ch рп / + рп 1
(Pzn+ Р°т cth Нп I-
2 у (-О*
aJ0(nna) X£+p8 Pzh J о ([in a)
” (-1)M 71 a)
X 2i ^ + p2)«D*(Xfta)
k= 1
Prh Pzh
' h (Xfe a)
. Л (^h Q)
2_y P°rl H
1 tx
70 (Pifl)
(6-27)
Оценивая сумму абсолютных значений каждого уравне-
ния системы (6.26), при использовании (6.23) и (6.24) име-
ем:
16И3 sh2 Ип / « Ц /2 (Xft q)
/ (sh pn I ch pn / + цп О (Х^ + р8)2 D* (** а) Х
у 1 = sh2 Ип f « j
Х k~\ (Ха + Н2)2 I (sh рр I ch рп Z+pn I) (^+ р8)2 Х
2(1+у) Ц (1ft а) 1 4Нл sh2 Нп 1
D* (^л а) J < I (sh рп I ch рп Z + рп О
_________2 sh8 рп I__________
Рр I (sh рп I ch рп /-|~рп О
где 0 < е < 1.
Система (6.26) вполне регулярна, что и требовалось пока-
зать.
Итак, решение первой основной задачи теории упруго-
сти для цилиндров с точным выполнением краевых условий
на всей поверхности сводится к вполне регулярной системе
(6.26). Решение ее при ограничении некоторым конечным
числом уравнений, зависящим от желаемой точности резуль-
татов, приводит к значениям Хп, а затем по (6.24) и (6.25)
к значениям постоянных Dn и Вп и по (6.16) к значениям Сп и
Лп. Вычисление напряжений и перемещений [см. (6.4) и
(6.5)1 является чисто формальным процессом.
167
6.3. Асимметричное нагружение цилиндров
относительно средхЗго сечения
В случае асимметричного нагружения цилиндров общие
выражения для напряжений и перемещений нетрудно полу-
чить из (6.4) и (6.5) после замены в равенствах для нормаль-
ных напряжений ог, ое и oz и перемещений и в радиальном
направлении cos Xftz, ch pftz и pftz sh pftz соответственно на
sin z, sh pi* z и phz ch z и в равенствах для касательных
напряжений тгг и перемещений w в осевом направлении
sin Xftz, sh и рь z ch рь/ на — cos X.fc z, ch pfcz и
pftz sh pfcz. Выражения для составляющих напряжений и
перемещений после указанных замен приводить не будем.
Процесс решения задачи при асимметричном нагруже-
нии цилиндров с точным выполнением граничных условий
как на цилиндрических, так и на торцевых поверхностях
повторяет подробно изложенный процесс решения при сим-
метричном нагружении. Различие заключается в заменах
одних тригонометрических и гиперболических функций дру-
гими и в знаках некоторых членов равенств. Поэтому огра-
ничимся только приведением окончательных формул, нуж-
ных для осуществления расчетов в частных задачах.
Принимая kha = —------л и равными корням функ-
ции Бесселя (рАа) — 0. приходим к бесконечной системе
алгебраических уравнений, аналогичной (6.26):
16p* ch* pn I ^1 °)
I (sh pn /сЛрп / —pp /) (4 + Pn)2 D* a)
i=
2 —ХП— Рп *
(6.28)
где
Рп а/о (рп a) ch2 рп I
sh рЛ I ch рп I—рп I
Pzn ~ Prn th рп / +
'Л
aJo(pna)
у (-l)*^'f(Xha)
2(-D* y
I
4р£
Jo (рп а)
Г /» (Xh Q) ____ t
| ly (Xft a) Xh a
—------- Jo (pi а)
(6.29)
2
1
168
После решения этой системы уравнений значения постоян-
ных Dnt Сп, Вп и Ап определяются следующей группой фор-
мул:
(|АП a)2 Jo (|Ы °) ch Цп I
Р°т
Сп = “ ~ —Dn (I “ЬЦп 7 th цп /);
Цп а сп |An I
(— 1)л 4Хп 71 (Хп а) _____________Xh_____
г= alD* (Хп а) (X2+pft2)2
. Л (Хп о)
+ Р*(Хпа)
Prn Pzn
7о (Xn а) 1
71 (Xn a) Xn Q
Pzn | _ Xn q70 (Xn tl)
Xn a7i (Xn a) 7i (Xn a)
(6.30)
Постоянные Ло и Bo при асимметричном нагружении рав-
ны нулю. В случае смешанных граничных условий преобра-
зованиями, мало отличными от ранее выполненных, реше-
ние задачи сводится также к регулярной бесконечной сис-
теме типа (6.26) или (6.29). Основные равенства, соответст-
вующие этому типу условий, можно найти в [26], [17].
6.4. Сжатие цилиндра силами, распределенными
по окружности среднего сечения
Поясним процесс расчета по изложенной схеме на при-
мере определений напряжений в коротком цилиндре, длина
образующей 2/ которого равна диаметру 2а при сжатии си-
лами qt равномерно распределенными по контуру среднего
сечения (рис. 30) *.
Деформация цилиндра симметрична. Силы рг = р° =
= pz = 0. Граничные условия записываются в форме
<Ъ- = Рг'. Trz = 0 при r = a; — а < z < at
(о .ol)
az=0; Trz = 0 при z=±a;0<r<a.
* Решения задач об осесимметричной деформации цилиндров
сточным выполнением краевых условий на всей поверхности — тор-
цевой и цилиндрической — изложены в [5]. [17—19], [54], [97],
[98].
169
причем pr = 0, если z =/= О, и рг = оо, если z = О по харак-
теру приложения нагрузки д. Представление рг в форме ря-
да осуществляется по установившейся схеме, предполагая,
что силы рг = — р распределены равномерно на поверхно-
сти цилиндра по кольцу — z0 < z < z0 у среднего сечения,
как указано в п. 5.1, имеем:
(принято во внимание, что I = а).
Уменьшая до нуля ширину кольца и считая, что
(2pzo)2.=o = д, получаем для рг следующее значение:
При такой форме задания внешней нагрузки вычисление
напряжений на поверхности цилиндра и в области, близкой
к ней, затруднено крайне плохой сходимостью их выраже-
ний. Рационально перед сведением задачи к бесконечной
Рис. 30
системе (6.26) решить задачу
для бесконечного цилиндра с
выполнением условий (6.31)
только на цилиндрической
поверхности и, пользуясь
асимптотическими представ-
лениями напряжений, выде-
лить расходящуюся часть,
как это сделано в п. 4.5.
Решение этой задачи осу-
ществляется в рядах при ис-
пользовании формы (4.21).
Приравнивая ог = рг итгг=0,
находим постоянные Во, Ah
и Bfc:
4 (1 -|- v) а
lo (^k а) . о _ дЦ (Xft а)
D*(Xha) ’ k~ aD*(Kha) ’
где Xha = kn\ D* (Х^а) — значение (6.19), постоянная Ао = 0 по
равенству нулю нормальной силы в поперечных сечениях цилиндра.
Результаты расчета напряжений по формулам (4.26)
приведены в табл. 16 (о? = о© и о® при г = 0, о§ ио® при
170
г = а) и табл. 17 (ое и о® при z = 0). В точках поверхности
цилиндра (г = а) напряжения подсчитаны по формулам [см.
(4.56)1:
Л (1— 2v)g q
Ч=- о + о (2+v-4v«) In [2 (1 -cos z)l +
2a 2ла
1
---- (2-|-v—4v2) J cos Xh z;
kn J
q (1 — 2v) q Г
CTz° = -V + —9 In [2 (1-cos Xfc z)l- V (О2)Л +
Za Zita [
a \
cos Xfcz,
при составлении которых использовано значение ряда
cos kx — —1п [2(1 —cos х)].
Вернемся теперь к короткому цилиндру, ограниченно-
му плоскостями z = ± а. Условия (6.31) для него будут
выполнены, если к найденным напряжениям присоединить
напряжения, соответствующие нагружению короткого ци-
линдра силами:
PS 2 |,х‘ (Х‘ а)~
-2/, (X* а)] /0 (Xfc г)-Кк гЦ (X* а) /Л (Xfc г)).
Задача должна быть решена при следующих граничных
условиях:
or = 0; тгг = 0 при r = a; —а < z < a;
^z=Pz (r)* 'trz = ^ при z = ± a; 0 < r < a.
p*zn>
Разрешающая система уравнений имеет вид (6.26) при
Рг = Pz = Рг = 0 и
Hn aJo (ЦП a) sh8 рп а
Рп — “ г :
sh |in a ch рп а + рп а
где по (6.10) р2. = 0;
2
a
₽2п a8 (рп a) J
о
у (-1)* bk II (Xfea)
Jo (Нп а) 2- (Х£+ p8)2D* (Xh а)
171
Таблица 16
z/a 0 0.2 0.4 0.6 0,8 1
r=0
О ® _ og —1,0061 —0,8811 —0,6000 —0,3237 —0,1482 —0,0903
<1 0,4402 0,3210 0,0615 —0,1624 —0,2810 —0,3211
°г = ае —1,0686 —0,9392 —0,6301 —0,3074 —0,0350 0,2108
Oz 0,5720 0,4657 0,2459 0,0380 0,0149 —0,0038
г=а
°? — 0 0 0 0 0
сте — —0,3882 —0,0653 0,0498 0,0903 0,1007
о» — 0,6695 0,5621 0,4557 0,3645 0,3327
ог — 0,0031 0,0037 0,0031 0,0010 —
сте — —0,4380 —0,1158 0,0005 0,0526 0,1329
Ог — 0,6998 0,4936 0,2696 0,0804 0,0035
Расчет выполнен при удержании двенадцати уравнений
системы (6.26). Значения напряжений (ог, ае, ог)
приведены в табл. 16 и 17. Точность результатов опреде-
ляется точностью выполнения граничных условий.
Напряжения ог на цилиндрической и uz на торцевых
поверхностях составляют тысячные и десятитысячные доли
единицы. В силу этого можно считать верными две первые
цифры после запятой во всех приведенных значениях.
Особенно резкое изменение напряжений по сравнению с
напряжениями в бесконечно длинном цилиндре наблюдает-
ся у торцов.
Таблица 17
г/а 0 0.2 0,4 0,6 0,8 1
Z = a
О N О —0,0903 —0,0800 —0,0490 —0,0320 —0,0121 0
сте —0,0903 —0,0790 —0,0471 0,0011 0,0542 0,1007
”. —0,3211 —0,3020 —0,2428 0,1152 0,1223 0,3327
Ог 0,2108 0,1977 0,1777 0,1228 0,0520 —
°е 0,2108 0,2098 0,2062 0,1940 0,1683 0,1329
Oz —0,0038 —0,0006 —0,0032 —0,0017 0,0016 0,0035
Прим е ч а и и е. Здесь приведены отношения Cj К ч/а (j=r , © , Z).
172
6.5. Изгиб толстой плиты, жестко закрепленной
по цилиндрической поверхности
Изгиб толстых плит — предмет многих публикаций 1.
Воспользовавшись результатами [4], приведем значения
перемещений и напряжений для плиты, заделанной по ци-
линдрической поверхности, при нагружении верхней пло-
скости силами р, равномерно распределенными по площади
круга радиуса а0. Расчеты выполнены при следующих гра-
ничных условиях: на цилиндрической поверхности (г = а)
Зра2
Trz=--------(Л2—z2); и = 0 при —h <_ z < h
8а/3
и w=Q при z — О,
на верхней плоскости (z = h) oz = — р при 0 < г < а0;
ог = 0 при а0 < г < а; тгг = О при 0 г < а, на нижней
плоскости ог = 0; тгг = 0 при 0 < г < а.
Здесь, как и раньше, через а и 2h обозначены радиус и вы-
сота плиты (см. п. 5.1), начало координат расположено в
центре серединной плоскости (см. рис. 19). В табл. 18 со-
держатся значения напряжений ог в долях о0 = р (а0/а)2,
а в табл. 19 — перемещений в долях = 2pa*l/a2G. Слу-
чай (а0/а) = 0 соответствует приложению сосредоточенной
силы Р в центре верхней плоскости.
Таблица 18
г Ов а a=2h a = 6h
— h 0 h — h 0 h
1 0,760 —0,214 —3,589 3,504 —0,214 —3,589'
0,5 1,602 0,449 —3,727 13,730 0,459 —12,859
0,25 2,105 1,327 —13,392 24,783 3,532 —29,524
0,10 2,290 1,865 —80,614 28,105 13,555 —99,698
0,05 2,319 1,964 —320,620 37,178 18,830 —340,200
0 2,389 1,999 — 38,024 21,379 —
1 Осесимметричным деформациям толстых плит с выполне-
нием граничных условий на плоских и цилиндрической поверхно-
стях посвящены [4], [20], [28], [33], [75].
173
Таблица 19
г U9 а а= 2h a = 6h
—h 0 h —h 0 h
r=0
1 I -0.324 I —0,387 I —0,467 I —6,996 I —7,918 1 —8,425
0,2 | —0.582 | —0,787 | —1,242 | —19,388| —19,450| —21,172
r=a
1 —0.033 — —0,176 0,327 — —1,102
0.2 —0.085 — —0,294 0,106 — - 1,149
6.6. Растяжение цилиндра сосредоточенной силой,
приложенной в центре торцевого сечения
Ранее были приведены решения задач о нагружении ко-
ротких цилиндров, полученные при непосредственном ис-
пользовании бесконечной системы уравнений (6.26). Однако
решение может быть найдено в результате процесса по-
следовательных приближений, при которых поочередно вы-
полняются краевые условия сначала на цилиндрической по-
верхности (или на торцах) цилиндра, а затем на торцах (или
на цилиндрической поверхности). Возможность выполне-
ния такого процесса определяется наличием двух различных
форм решения осесимметричной задачи в цилиндрических
координатах (4.6) и (4.8), позволяющих точно выполнить,
как указывалось, граничные условия на цилиндрической
поверхности либо на торцах. Сходимость процесса для пер-
вой краевой задачи теории упругости обеспечивается регу-
лярностью бесконечной системы (6.26) или (6.28). На пер-
вом и на каждом нечетном этапе расчета рассматривается
нагружение по боковой поверхности бесконечного цилиндра
заданными силами или силами, полученными на предыдущем
четном этапе 1, на втором и на каждом четном этапе — на-
гружение слоя заданными силами или силами, полученными
на предыдущем нечетном этапе. Результирующие напряже-
ния составляются суммированием частных значений =
оо
= 2 (—О* • (°j)k (j = f, 6, z или rz). Вычисления имеют
циклический характер, что важно для составления про-
1 В зависимости от условий задачи осуществляется четное или
нечетное продолжение за пределы промежутка, определяемого раз-
мерами короткого цилиндра.
174
граммы расчета на ЭВМ. Достоинством его является возмож-
ность оценки на каждом этапе отклонений граничных усло-
вий от заданных. Отпадает необходимость решения системы
алгебраических уравнений со многими неизвестными.
Указываемый путь предложен и широко применяется
в работах В. 3. Васильева *. Поскольку на каждом этапе
вычислений граничные условия выполняются частично,- со-
ответствующие им решения могут быть названы «неполны-
ми», а последовательность всего процесса «методом непол-
ных решений».
Проследим порядок построения решения на примере за-
дачи о растяжении цилиндрического стержня вдоль его
оси сосредоточенной силой Р. В соот-
ветствии с принципом Сен-Венана нап-
ряженное состояние отлично от элемен- г -г
тарного ог0 = Р/F только в ограниченной \_____
области у торца цилиндра, поэтому мож- г
но пренебречь влиянием характера при- [
ложения внешних сил на одном из I
концов на другой и цилиндр можно счи- 1
тать полубесконечным (рис. 31). Целью >
расчета является выяснение распределе-
ния напряжений у места приложения , 2
силы и оценка величины зоны отклоне-
ний напряжений от Рис. 31
^ZO (Of - Тгг —0).
Граничные условия записываются в виде
oz = p (г). Trz=0 при 2 = 0; 0 < г < (Г,
л л л (6.32)
ar = 0, xrz=0 при г = а; 0 < z < оо.
В любом поперечном сечении нормальная сила имеет по-
стоянное значение N = Р, что выполняется, если за функ-
цию напряжений, воспользовавшись решением (4.11),- при-
нять
оо
Ф=Л0 г2-1-г У (Ch —Dh p.fc z) e ZJ1 (pfe r),
A=1
1 В [22] и [23] процесс последовательного решения применен
к исследованию напряженного состояния полупространства, ослаб-
ленного цилиндрическим отверстием, и полупространства с жестким
цилиндрическим включением. См. также. В. 3. Васильев. Концент-
рация напряжений в полупространстве вблизи цилиндрического вы-
ступа при осесимметричном нагружении //Изв. АН СССР. Сер. мех.
тверд, тел.— 1974.— № 4.— С. 46—58.
175
где pha—корни функции (phr)- По связи Ф = — NI2n
при г = а имеем значение постоянной Ло = — Р12па.
Составляя аг и тгг по формулам (4.17), на основании пер-
вых равенств (6.32), получаем:
оо
2 Pfc а (Cfc+^fc) Л (Pfc 0=0;
Л= I
ОО
У Ph aCk Jn (Ph r) = —p (r).
h=l
Отсюда Dh
разложения
Л (Pfc г)
— — Ch = ph/pha, где ph — коэффициенты
нагрузки p (г) в ряд по функциям Бесселя
ав
2 С . . , , ч j 2ра0 (р.£ а0)
Ph = ТТ~,-------1 rP J° (Н* О Jr =-------------7~Г~,------77,
[aJ0 (Ра «)]2 J Ph [а/о (Ph а)Р
о
при нагружении силами р (г) = р, равномерно распределен-
Р
ными по площади круга радиуса а0, и pft = (p,fea)]2
при нагружении сосредоточенной силой в центре торцевого
сечения.
На этом первый этап приближения закончен. Граничные
условия на торцах выполнены точно, а на цилиндрической
поверхности — частично, а именно: касательные напряже-
ния тг2 — 0, а нормальные
оо
ог = — 2 Pfc «(*—Pfc z)€ Z^o(ph «) = Р1 (z)
h = 1
отличны от нуля.
По равенству нулю касательных напряжений тгг и ра-
диальных перемещений и при г = а результат этого этапа
можно трактовать как окончательный для полубесконечного
цилиндра, находящегося в жесткой цилиндрической обой-
ме, допускающей свободные смещения вдоль образующей.
Во втором приближении производится решение задачи
для полубесконечного цилиндра при условиях
or = Pi(z); тгг=0 при г =а, 0 < г < оо.
176
Решение составляется в интегральной форме (см. п. 4.9).
Выполнение граничных условий приводит к равенствам:
Ло + 2(1+у) Во+У {И(1) + В(Х)][Ха/о(М-/1(М1-
b
— В (X) [(Ха)2 + I —2v] li (Ха)} cos Xzdz = pj (z);
f Ха [A (X) /j (Ха) — В (X) Ха/0 (Ха)] sin XzdX =0,
о
из которых, выполнив интегральное косинус-преобразова-
ние, для функций А (X) и В (X), получаем следующие зна-
чения:
л/у гП у Л (Ха) о,- к
D* (Ха) £>* (Ха)
где D* = (Xa)2 702 (Ха) —[(Ха)2 + 2(1—v)]7?(Xa) и
ОО
2 Г
S (Ха) = — | Pi (z) cos Xzdz =
л J
о
2P хл 1 Г —h. z
= —------— У ---------- I (I—u.fez)e h cosXzdz =
(ла)2 Jo(Hho) J И
«= i o
4PX2 Lih
= ~77V Z 7 2-L1242 7 /--------[Л + 2(1-Н)Во = 0].
(ла)2 (ц2_|_х2)2 J0(Hh fi)
Соединение первого и второго приближений приводит к
точному удовлетворению условий (6.32) на цилиндрической
поверхности. На торце равенство тгг = 0 сохраняется (по
пропорциональности этих напряжений sin Xz), а к нормаль-
ным напряжениям присоединяется член
р XaS(Xa)
= - * / {Ха/о (Ха) /0 (Хг) — /х (Ха) [2/0 (Хг) —
j L/ (ЛХ2)
о
—Хг/j (Хг)]} cos XzdX = p8(r).
В следующем, третьем приближении решается задача по
плану первого этапа с заменой р (г) на р2 (г). Затем выпол-
няется следующее, четвертое приближение, и процесс пов-
торяется до тех пор, пока не будут удовлетворены гранич-
ные условия с желательной степенью точности.
В табл. 20 приведены значения отношений напряжений
ог к равномерно распределенным напряжениям ог0 = PIF
в сечениях, близких к нагруженному торцу. Выполнено
177
Таблица 20
г/а z/a 0 0.2 0.4 0,6 0,8 1.0
0,4 9,970 5,892 1,980 0,592 0,102
0,8 2,916 2,546 1,666 1,004 0,576 0,312
1,2 1,553 1,472 1,268 1,017 0,848 0,809
1,6 1,141 1,121 1,066 1,002 0,958 0,967
2 1,025 1,021 1,007 0,996 0,993 0,984
семь приближений. Коэффициент Пуассона принят равным
0,3. В поперечном сечении, отстоящем от торца на расстоя-
нии, равном диаметру, напряжения отличаются от равно-
мерных не более чем на 2,5 %. Здесь имеется еще одно под-
тверждение принципа Сен-Венана.
6.7. Метод однородных решений
К принципиально отличной от рассмотренной приводит
схема решения осесимметричной задачи для коротких ци-
линдров, основанная на применении метода однородных
решений. Впервые эта форма указана М. А. Шиффом при ис-
следовании осесимметричной деформации сплошных цилинд-
ров [112]. Развитию метода и применению его к частным слу-
чаям деформаций тел посвящено много публикаций *. По-
мимо решений для цилиндров, он широко использовался
при построении решений задач о напряженно-деформиро-
ванном состоянии толстых и тонких плит, полых сфер, ко-
нусов, а также в плоской задаче. Здесь, в изложении, мы
следуем содержанию [58].
Пусть на первой стадии расчета выполнены граничные
условия на цилиндрической поверхности (т. е. задача реше-
на для бесконечно длинного цилиндра). Очевидно, они не
будут нарушены, если к ним присоединить решения, соот-
ветствующие равенству напряжений аг итг2 нулю при г =а.
Такие решения называют однородными. Записывая ог и
тгг в форме (4.17) и приравнивая их нулю, для определения
постоянных А и В получаем два равенства:
(Л + В) [Ха/0 (Ха)—Л (Ха)]—В [(Ха)8 +1 — 2v] (Ха) =0;
Л/JXa)— ВХа/о(Ха) = 0 (6.33)
независимо от того, симметрично или асимметрично распре-
делены силы по координате z.
1 Достаточно полные сведения об исследованиях и применении
метода однородных решений содержатся в [461. См. также [56—60].
178
Система однородных уравнений (6.33) имеет решение, от-
личное от нуля, если определитель, составленный из коэф-
фициентов при А и В, равен нулю. Это требование приводит
к равенству
D* (Ха) = (Ха)2 П (М—КМ8 + 2 (I—V)] 7? (Ха) = 0, (6.34}
которое по ее первой публикации может быть названо урав-
нением Шиффа. Корни его находят после преобразования к
форме ординарного ряда
оо
d*(M=(M82
Л=0
(1—v)(2fe+l) | (2fe)! / Ха \2fe
(* + 1)(Л4-2) )(Л+1)!(Л!)«\ 2 )
(6.35)
получаемого после применения формулы для произведения
функций Бесселя (см., например, с. 322 в [61]):
J т (х) Jп (*) =
у ______( —l)fer(m + n4-2fe + l)__f^\m+n + 2*
fe! Г(т+/г+1)Г(т+п + /г + 1)Г(п+/г+1)к 2 )
R= U
Уравнение (6.35) не имеет ни действительных, ни чисто
мнимых корней (кроме двукратного корня ка = 0, соответ-
ствующего элементарному решению — равномерному про-
дольному растяжению цилиндра). Все корни этого уравне-
ния комплексные, они группируются по четыре с равными
модулями, так как если х + iy — корень уравнения (6.35),
то его корнями являются х — iy и соответственно — (х +
+ iy), — (х — iy). Значения первых десяти групп вычисле-
ны при v = 0,25 и приведены в табл. 21.
При весьма больших по модулю корнях уравнения (6.35)
они определяются формулой
Хь а ~ ± 1п 4Ал ± kni,
полученной после замены в (6.34) функции Бесселя асимпто-
тическими представлениями. После определения корней
Таблица 21
k ±x±iy k ±x±iy
1 ±1,37±2,707 6 ±2,16± 18,797
2 ±1,56±6,067 7 ±2,24±21,947
3 ±1,82±9,32’7 8 ±2,31 ±25,097
4 ±1,96±12,497 9 ±2,36 ±28,037
5 ±2,07± 15,647 10 ±2,42±31,387
179
а для постоянных Ah в Bh с точностью до произвольного
комплексного множителя bh имеем:
Ak = bh alo a), bfc Л a). (6.36)
k= 1, 2, 3,...
Напряжения и перемещения представляются формула-
ми (4.17) при указанных значениях постоянных (6.36).
Соединение напряжений, составленных по методу одно-
родных решений, и напряжений, найденных на первом эта-
пе, удовлетворяет условиям на боковой поверхности ци-
линдра при любых значениях постоянных Таким об-
разом, можно, не прибегая к бесконечной системе, удов-
летворить краевым условиям на торцах точно либо для нор-
мальных напряжений, либо для касательных, либо для од-
ного из перемещений (а для другого лишь при некотором
фиксированном значении радиуса г). Задача сводится к раз-
ложению заданной нагрузки в ряд по неортогональным
функциям, зависящим от корней \ка трансцендентного
уравнения (6.34). По равенству коэффициентов этого разло-
жения коэффициентам соответствующего напряжения оп-
ределяются значения Ьк.
Как указано, корни kka составляются группами сопря-
женных значений, поэтому и постоянные bh должны быть
взяты сопряженными. При таком выборе ряды в выраже-
ниях напряжений будут действительными величинами.
Практическая реализация метода затруднена сложно-
стью проблемы разложения заданной функции в ряд по не-
ортогональным функциям комплексного переменного. По-
этому, ограничиваясь конечным числом членов рядов, кон-
турные условия выполняют только в точках конечного чис-
ла окружностей на торцах или же по условиям минимума
квадратичного отклонения напряжений от заданных сил.
Метод распространен и на полые валы [56] [59].
Глава 7. ДЕФОРМАЦИИ КОНУСОВ
7.1. Сжатие конического стержня
Решение основных уравнений в сферических координа-
тах (см. п. 2.5) позволяет сравнительно просто получать
значения напряжений и перемещений при осесимметричном
нагружении тел вращения, имеющих форму конуса или ша-
180
ра. Контур в осевом сечении этих тел определяется постоян-
ным значением одной из сферических координат (т] = т]0
для конусов и £ — £0 для шаров). В силу этого запись кон-
турных условий значительно упрощается, что позволяет без
особого труда выбирать из функций (2.45) те, которые при-
водят к решению той или иной частной задачи.
При выяснении напряженно-деформированного состоя-
ния осесимметрично нагруженных конусов ограничимся
традиционной постановкой задачи, выполняя точно контур-
ные условия на боковых конических поверхностях и только
в смысле статической эквивалентности на торцах [106], [85],
[32]. Такая постановка предполагает достаточную длину
конуса — «бесконечный конус». Точное выполнение контур-
ных условий на всей поверхности конуса — конической и
торцевой — возможно, но оно приводит к весьма громозд-
кому процессу вычислений. Построение решений для корот-
ких конусов достигается теми же методами, которые бы-
ли применены к задачам осесимметрично нагруженных ци-
линдров средней длины.
Значения функций напряжений в сферических коорди-
натах указаны в п. 2.5*:
Фо = (^6 «6 + ^б) (Со COST] + £>о);
th = е(Л+ 1)6 +*; [С; P'k (y) + D'k Q'k (у)] sin*т];
фо = (Ло е6-J- Во) (Со cos т] £>0); (2.45)
Фь = (Ah е<Л+ ‘>4 Bh е~к^ [Cfe P'k (y)+Dfe Q; (у)] sin« т].
Здесь у = cos т], P'k (у) и Q'k (у) — первые производные
функции Лежандра Ph (у) и Qfe (у) по у:
На оси вращения (т] = 0) для сплошных конусов нужно тре-
бовать выполнения равенства <р — 0 и Ф = 0ина кониче-
ской поверхности, определяемой координатой т] — т]0, ус-
ловий (2.16), получающих в сферических координатах фор-
му
= (ce^)a(Ocosi] + pr)sinT], (7.1)
* Напомним принятые связи между цилиндрическими координа-
тами гиги сферическими £ и ц: г = се^ sin ц; г = се^ cos т] и обратно
£ = In — Д/г» + г*-, т] = arctg —.
181
— где рг и pz — радиальная и осевая составляющие по-
верхностных сил, а Ф (£, т]) и Q (£, т]) связаны с функциями
ф (£, т]) и <р (£, т]) равенствами (1.17) и (1.26)
дф 1 2 дф
Ф = ф+г-^-; Q = —[Ф+2(1-у)Ф]---------
дг гг г дг
Первое контурное условие (7.1) может быть заменено равен-
ством (1.35)
N
Ф«. 4.)=-^.
где N = N (г) — нормальная сила в поперечном сечении конуса.
Рассмотрение частных задач об осесимметричной дефор-
мации конусов начнем со случая сжатия конуса силой, при-
ложенной в вершине по направлению оси (рис. 32*). По
постановке задачи — сосредоточенная сила приложена к
острию — все характеристики деформации в области вер-
шины, естественно, должны быть бесконечны. Это резуль-
тат физической нереальности понятия «сосредоточенная» си-
ла и практической невозможности приложения ее к острию.
Затруднение обычное в подобного рода задачах (например,
в задаче о нагружении клина сосредоточенной силой в вер-
шине). Оно преодолевается исключением части области у
вершины (усеченный конус).
В силу постоянства нормальной силы N = — Р функция
не должна зависеть от 5, что будет выполнено, если за функ-
ции ф и <р взять значения ф0 и <р0, положив в них А о = А 0 = О,
Bq = Во — 1, Со = A, Dq = В, Со = С, Dq = D, т. е.
задать ф и <р в форме
ф = Л cosi]-{-B; <p = Ccosi]-|-D. (7.2)
Подставляя эти значения в (1.17), составляем функцию
Ф = Л cosт]ВС sin*т] cost]. (7-3)
По условиям <р = 0 и Ф = 0 на оси конуса (т) = 0) следу-
ет положить С = — D и А = — В. Число подлежащих оп-
ределению постоянных сокращается до двух, функции <р и
Ф получают вид
ф = Р(1 — cosi]); Ф = В(1—cosi]) — Dsin8t] cost].
Воспользовавшись равенством (1.35), связывающим контур-
ное значение Ф с нормальной силой N = — Р, имеем:
B(]-b)-D(\-b*)b=-?- ,
2л
где b = cos т]0, т)0 — координата, определяющая поверхность кону-
са.
* Первое решение этой задачи принадлежит Д. Мичелу {106].
182
Функция Q в соответствии с формулой (1.26) имеет зна-
чение:
Q = — [Л cost] +В+ЗСsin8t] cost] 4-2 (1 —v)(Ccost] +D)], (7.4)
г8
а при C — .— D и A = — В
Q = -- - - 1---[B—3D (1 4-cos Tj) cos T]+2 (1 — v) D].
(ce6)2(l -|-cost])
Подставляя ее и производную функции Ф по т) во второе
граничное условие (7.1), получим второе уравнение, связы-
вающие постоянные В и D:
В (14-Ь)—2D(l+b) b8+D(l + ba)(l—Ь8) =
= Bb —3D(l-f-b)b8-f-2(l— v) Db,
по которому В = — [1—(1 — 2v) dl D.
Используя указанную выше связь между В, D и силой Р,
без труда находим:
Р Р
В=(1—b4-2vfc)— ; Р* = 2л(1—b)(l-]-2vb—62).
Таким образом, окончательный вид функций напряжений
установлен:
Р Р
ф=—тт(1—cost]); Ф=— (1— cosт])[1 — (1— 2v)6-|-
и и
4-(14-cost]) cost]];
Р L (l-2v)(14-b) 1
Q =----3 cos П —-------ГТ-------- •
D* (се6)2 [ 14-cos т]
Выражения для напряжений (2.20) в сферических коорди-
натах имеют следующую запись:
(се*)2
дф дф , »
-— ctg т] — Q (се6 sin тй2 ;
дт]
дФ
дф / t
_ ctgT] — -——Q (се6COST])
(се*)2 L
2(l+v)
°е= -
(7.5)
1
Т£т) -
(се*)2 .
дф дф \ л
даctgT1 +й;
дб От] /
дФ дФ ,
—й(сс6) sin т] cos т]
% =
183
В рассматриваемом случае сжатия конуса силой, прило-
женной в вершине, после подстановки сюда найденных зна-
чений ф, Ф и Q получаем:
a6=-^rzrt2(2-v)COSTi-(1-2vH1+^:
* и* к*
(1 —2v) P(b—cosт))cost]
a_ - - —----------------------;
11 D* R2 1-|-cost]
(1 —2v)P/ 1+Ь X (7.6)
0 D* R2 \14-COST] 7
(I —2v) P (b—cos T]) sin T]
T£n D* R2 14-cost]
где R = ce^ — расстояния от точки, в которой находятся напряже-
ния, до вершины конуса.
По форме выражений (7.6) следует, что напряжения по
мере удаления от точки приложения силы убывают; величи-
ны их обратно пропорциональны квадратам расстояний от
вершины конуса. Характер распределения напряжений в
каждом из сечений R = const не зависит от расстояния R.
Составляющие напряжений в цилиндрических коорди-
натах представляются следующими равенствами [см. (1.27)]:
(1 —2v) P/(l-|-fe) R _z_\ _ ______Р 3z
~ D* R2 \ R + z ~ R J XrZ D* R3 . R
Для конуса с углом раствора 2т]0 = 60° произведен под-
счет напряжений. Результаты подсчета приведены в табл.,22.
Таблица 22
ч 0* 5° 10е 15° 20° 25° 30°
R2<j£ /Р -1,389 -1,383 -1,362 -1,329 -1,283 -1,223 -1,151
-0,0138 -0,0136 -0,0124 -0,0103 -0,0065 -0,0040 0
R2 uQ/P -0,0138 -0,0129 -0,0094 -0,0035 -0,0058 -0,0152 -0,0280
^ТЕч/Р 0 -0,0012 -0,0022 -0,0028 -0,0024 -0,0019 0
184
На рис. 33 изображены эпюры напряжений вдоль дуги 7? =
— const. Коэффициент Пуассона v принят равным 0,3. По-
стоянная D* = — 0,5235.
Рис. 32
Рис. 33
Приведем выражения для перемещений.
Радиальные перемещения [см. (1.12)1:
Р 1 / 1—COST]
и== —Ё 1/ ТТ---------L((I-2v)(1+6)-(1-}-cost])cost]]. (7.8)
2pD* се* у l+cos?]
Производные осевых перемещений [см. (2.24]:
dw Р
— = ~9 пж TtU-gvHl-^+l-l-co^T]];
2р£>* се*
dw Р
—— = —-----------— sin т] cos т].
p,D* сес
После интегрирования этих равенств
Р
------ [(j _2v) (I -Ь)+1 +cos8 т]] + се0. (7.9)
2pD* ce*
185
Далее, пользуясь формулами (2.25), для перемещений
и вдоль осей криволинейных координат получим:
Р
Ut = —-------~[(1 —2v)(l+b—2cost])—2cost]j-|-u/ocos т];
2pD* ее*
(7.10)
P 1+6
------ 3—2v—(1 — 2v)—----- — w0
2p.D* ce* 1+cost] j
sin?).
В равенствах (7.9) и (7.10) t^0 — постоянная интегрирова-
ния.
7.2. Сосредоточенная сила, приложенная к плоскости,
ограничивающей полубесконечное тело
Пользуясь результатами предыдущего параграфа, не-
трудно получить решение задачи о нагружении полупро-
странства сосредоточенной силой, приложенной к некото-
рой точке, ограничивающей его плоскости Ч Действитель-
но, если предположить, что угол т)0, определяющий по-
верхность конуса, прямой:
т)о = 0,5л, то коническая по-
верхность превращается в
плоскость, а область кону-
са— в полупространство (рис.
34). Значения функций напря-
жений и значения напряже-
ний и перемещений при этом
следуют из выражений, най-
денных в п. 7.1, достаточно
положить в них т]о=0,5л,т. е.
b = 0. Произведя подстанов-
ку, имеем для функций нап-
ряжений:
Р
ф= —— (1— cost]); Ф=—(1—cos’t])
и для напряжений:
1 Такое решение, как известно, найдено впервые Буссииеском
наложением напряжений от сосредоточенной силы в точке тела
бесконечных размеров и напряжений от центров сжатия, равномерно
распределенных по оси z от z = 0 до z — — оо [881.
186
в сферических координатах
<4 = ~~2^ 12 (2“ v) cos n “1 + 2v]:
(1—2v) P cos8T]
0,1 2nR2 1-j-cosT]
(7.U)
(1—2v)Psin2T]—cost] (1—2v)P sinT]cosi]
® 2л/?2 1+cost]. ’ 2л/?2 1-|-cost]
в цилиндрических координатах
_ P 3r*z (1—v)P] _ ЗРг2
°г = —2лР2 рз — J’ а2 = ~2лР«’
(7.12)
_ (1—2v)P/ R z \ _ 3Prz
a0“~ 2л/?2 \ R+z ~ R )' Тг2-~ 2л/?4 ’
где R — по-прежнему расстояние между рассматриваемой точкой и
точкой приложения силы Р.
Как и в случае сжатия конуса сосредоточенной силой в
вершине, напряжения о$, сгп, ое и в полупространстве,
нагруженном сосредоточенной силой, обратно пропорцио-
нальны квадратам расстояний от точки приложения силы.
Как нетрудно усмотреть из формул (7.12), отношение
напряжений <т2 и тГ2 равно отношению координат z и
г: (uz/xrz) = (z/r). Эго означает, что направление равнодей-
ствующего напряжения о на любой площадке, перпендику-
лярной оси z (см. рис. 34), проходит через точку приложе-
ния силы Р. Величина о определяется как геометрическая
сумма напряжений о2 и тГ2:
----- ЗР гг ЗР cos2T]
IT
Равенство R = d cos т) представляет собой уравнение
сферической поверхности, проходящей через начало отсчета,
с центром, лежащим на оси z, и диаметром d. В точках такой
поверхности о = 3P/(2nd2), т. е. полное напряжение на
горизонтальных площадках имеет постоянное значение.
В силу этого определение значения и сводится к определе-
нию диаметра d. Графически это осуществляется просто
(см. рис. 34): чтобы найти напряжение о в точке М, нужно
через эту точку провести прямую, перпендикулярную пря-
мой ОМ, до пересечения с осью z в точке /V; отрезок ON и
будет искомым диаметром.
187
Выражения для перемещений ut wt и следуют из
соответствующих формул (7.8)—(7.10) при b = 0:
(1—2v)P] Р
Г', W—
/?4~г------------4лр./?
z
z2
u =
-l-tt’o;
4n^R2 [ R
uE =-----[4(1 —v) cos T] — 1 4- 2vJ 4-cos ti;
5 4np.R
P 2(1—v)4-(3 — 4v)cost]
= — -----—--------—-------------sin t] 4-w0 sin n ,
n 4л|л7? 14-cos т]
(7-13)
где ш0 — аддитивная постоянная.
7.3. Сжатие полого конуса
Для получения значений напряжений и перемещений
при сжатии полого конуса силой, приложенной к его верши-
не, можно воспользоваться теми же функциями (7.2)
ф = A cos т] 4~ <р — С cost] 4-D,
которые применялись при решении подобной задачи для
сплошного конуса (п. 7.1). Нужно лишь иным образом вы-
брать значение постоянных, входящих в эти функции. Для
полого конуса условия (7.1) должны быть выполнены как
на внешней т[ = т[0, так и на внутренней т] = поверхно-
стях, а последнее условие записано в виде (1.36).
Ф(£. По)-Ф(5;П1) = —£-•
Подставим сюда значение функции (7.3)
4 (Ь—ft,) 4-С [(1 -ft2) ft—( 1 -ft2) ft,] = Р/(2л),
где b = cos ц0 и bi = cos
Поскольку функция Ф определяется с точностью до не-
которой постоянной, положим в (7.3) В — 0. Контурное ус-
ловие (7.1)
——Й sinn cost]
dr)
после подстановки функций Ф и й [см. (7.3) и (7.4)] при т)=
— “По и Л = “Hi и некоторых преобразований приводит к сле-
дующим двум уравнениям:
Л 4-С (1 — ft2)4-2 (1 — v)(Cft4-D)ft=0;
4+C(l-ft2) + 2(l-v)(Cft1+D)ft1 = 0.
188
Отсюда и из указанной выше зависимости между посто-
янными А и С и силой Р имеем:
р р (1_2v) Р
А=-С=— ; P=-2(I_V)D< (*+»>•
где знаменатель D* = 2л (bt — Ь) (Ь2 4- 2vdbj 4- b2)
Подставив функции <р, Ф, Q при найденных значениях
постоянных в формулы (7.5), для напряжений получаем
(R = а*):
°1= — г^вг I2 (2—v) cost] —(1—2v)(b4-bj)];
* D* К.
(1___2v)P
u« = —----------[bb. —(b4-bi—costi) cosn] cos n;
Л D»r2 1 1 v 1 1 ” ,J i (7.14)
(]__2v) P
f2— [b-4-bj — (1 4-Wi+sin8T])cost]];
(1—2v)P
•c6T)=— D,r2 [frfei—(fr + frt—cost]) cosn] sin Т].
Выпуская промежуточные выкладки, приведем выражения
для радиальных и осевых перемещений
Р
2pD*r
и =
{sin8 т] cos т]—(1 —2v) [b + —(1 4~ bb2) cos лШ
(7.15)
P
2ц D* R
w —
[ 1 4-cos8 t] +(1 — 2v) (1 — bbt)] + tt>0
и для перемещений в криволинейной системе координат £ и т]
Р
ut »=-------
« 2pD* R
[4(1 —v) cos т] —(1 — 2v) (b 4- bi)]+“^0 cos t) ;
P L, л J + . (i—b)(i—b>)
u =---------< (1 — 2v) I-----4--------------
n 2p.D* R ( [1+cost] sin8T]
—3 -]-4v i sin T) —w0 sin t] ,
где w0 — постоянная интегрирования.
Распределение напряжений в полых конусах при нагру-
жении сосредоточенной силой в вершине проиллюстрируем
несколькими частными примерами.
Для конуса, поверхности которого определены углами
»]х = 15° и т]о = 30°, значения напряжений приведены
в табл. 23. Подсчеты произведены, как и в остальных слу-
чаях, при v = 0,3. По результатам подсчета нетрудно ви-
деть, что напряжения erg во много раз больше напряжений
1в9
Таблица 23
ч 15* 18е 21® 24® 27® 30®
R* а6/Р — 1,8654 —0,8284 — 1,7850 —1,7352 —1,6792 —1,6171
R'<\/P 0 0,0034 0,0045 0,0039 0,0028 0
R*o6/P 0,0252 0,0176 0,0060 —0,0044 —0,0164 —0,0285
0 0,0011 0,0017 0,0017 0,0014 0
оп, ое и Т|П. Поэтому последние не оказывают существен-
ного влияния на напряженное состояние конуса, которое
близко к линейному.
В качестве второго примера рассмотрим тело, одна из по-
верхностей которого определена значением т)0 = 0,5 л,
т. е. бесконечную область, ограниченную плоскостью и ко-
нической поверхностью (рис. 35). Так как в этом случае
b = 0, то постоянные А, С и D будут:
Р Р 1—2v Р
А= —------; С =------ ; D=—--------------;
2л5» 2л6» 2(1—v) лЬ*
напряжения:
a|= 12 (2“V) C°S 11 -(1 -2v) &11:
(1—2v)P
°Ч = 2лЬ» г» (Ь1 “C0S Л) C°S Л;
(1—2v)P
°е= Owfca а К1 +sin* П) cos П —*11;
(1—2v)P .
Si = 2лЬ»г* (*i -cos т]) s»n П cos т].
190
перемещения:
Р
2цО* г
[sin2т] cost]—(1—2v)(6!—cosi)j];
Р
2y.D* R
[2 (1 — v)+cos21 +
P
ut —----------
6 2p,D* R
[4(1—v)cost]—(1—2v) 6J+ wo cost];
4 4цD* R [ [4-cost] sin2!]
—3-|-4v> sin t]—w0 sin T] .
В табл. 24 приведены значения напряжений в теле рас-
сматриваемого вида при т)г = 60°.
При т)! = 180° — т)0 полый конус вырождается в область,
представляющую собой внешность двух соосных конусов
с общей вершиной и с одинаковым углом раствора (рис. 36).
Рис. 36
Постоянные задачи напряжения и перемещения в этом слу-
чае представляются равенствами:
Л = —^f[l+(l-2v)b2]; С=-^"’ 0=0; D*=8n(l-v)b»;
2(2—v)P (1 —2v)P
а5==—БГ£Г" costl; % = - D*r2 (cos2t]-62)cost];
(1—2v)P
a® =~D>'r2 (1 “+sin’ COS11 ’
(1— 2v)P
- D*r2 <cos n - *?)sin n;
191
ID
КЗ
n во* 65’
— 1.9099 — 1,5749
/?’ <Jn/P 0 0,0086
/?’ Qe/ P 0,2546 0,1673
0 0,0184
n 60’ 120° 65’ 115’
/?2а6/Р ±0,7730 ±0,6534
R*<Jn/P 0 ±0,0067
R^/P ±0,1819 ±0,1471
№rSn/P 0 +0,0143
Таблица 24
70° 75’ 80’ 85’ 90’
-1,2259 —0,8658 —0,4971 —0,0312 +0,2546
0,0107 —0,0098 0,0099 0,0016 0
0,0831 0,0002 —0,0771 -0,1675 —0,2546
0,0293 0,0329 0,0293 0,0184 0
Таблица 25
70’ 110° 75’ 105’ 80’ 100’ 85’ 95° 90е
±0,5288 ±0,4002 ±0,2685 ±0,1348 0
±0,0094 ±0,0092 ±0,0072 ±0,0039 0
±0,1150 ±0,0849 ±0,0560 ±0,0278 0
+0,0258 +0,0345 +0,0406 +0,0443 +0,0455
р
2pD*r
[sin21] +(1 —2v) (1 —b*) cos T)] cos t];
w =-------
2[lD*R
“5 =
-----------h^o cos n;
2jiD* R °] 1
“n
1-6?
П
3-4v-(1-2v)
sin2
sini).
Значения напряжений, подсчитанных в том случае, ког-
да углы Th = 60° и т) = 120°, указаны в табл. 25.
7.4. Нагружение конусов равномерно
распределенными поверхностными силами
В пп. 7.4.—7.5 рассматриваются деформация конусов
под действием сил, распределенных по их боковым поверх-
ностям, причем в п. 7.4— в случае равномерно распределен-
ной нагрузки, в п. 7.5 — при линейно распределенной.
Предположим, что конус полый. Внешняя и внутренняя
поверхности его загружены некоторыми различными по ве-
личине равномерно распределенными силами. Если нормаль-
ная сила в поперечных сечениях отлична от нуля, то, оче-
видно, при равномерно распределенной нагрузке она долж-
на быть пропорциональна квадрату расстояния поперечно-
го сечения от вершины конуса. Отсюда следует, что контур-
ные значения функции Ф должны быть пропорциональны
квадрату е%. Это будет выполнено, если выбрать из числа
(2.45) функции Ф и <р в формуле
Ф = [А + BQ; (</)] г2; ф = [С+DQ [ (у)] г*, (7.16)
где у = cos т).
Соответствующие им значения функций Фи й:
Ф = M+BQIG/)
2D
sin2T)
cos г2;
(7.17)
COS Т)
q=x+bq;(i/)+6D — 1 -2(i+v)[C+dq;(</)].
Sin2T)
При составлении этих функций принято во внимание, что
_ 9
« = -аетг-
193
Остановимся на двух случаях нагружения, сочетанием
которых можно получать любые другие,— на сжатии кону-
са силами радиального направления и на сжатии осевыми
силами.
В первом случае рг = — р0; pz = О при т] = т]0; Рг =
=— Р',Рг = 0 ПрИТ] = Т^.
Нормальная сила равна нулю в любом поперечном сече-
нии поэтому Ф = О при т) = т)0 и Л — “Hi (как и в п.7.3 т)0—
— координата, определяющая внешнюю поверхность кону-
са» Л1 — внутренню; далее cos т)0 = b и cos = bj.
Указанное условие и второе контурное условие (7.1) при
т) = т]0 и т] = приводят к системе четырех уравнений для
определения постоянных А, В, С и D. Выполнив соответст-
вующие подстановки и решение этой системы, имеем:
А = До; С = —[р0 (1 -62) Bi (bj-p (6)1;
(7.18)
В = -^-Во; D = -^-(l-v)(l-6®)(l-6?)(p061-p6).
Здесь для простоты записи приняты следующие значе-
ния:
А=2 1( 1 -ь*) bQ; (6Х)—(1 —ьъ) ь, Q; (6)];
B0=-2[i-6?)6-(i-62)61];
В, (6) = (l+v)(I-6®)6Q;(6)-B0-(l+36)2;
А (Ь1)=(1 +v) (1-6?) ь, q; (Вг)—в0—(I +36?);
(7.19)
в* =(1 -6«) (1 -6?) [Q; (6)—q ; (6i)];
D* = (1 + V) [(1 -6«) 6, Bi (61)-(1-6?) 6Bi (6)].
Напряжения после вычислений по формулам (2.20) и неко-
торых преобразований определяются равенствами:
а£= {[3<D + 2(l+v)(p]sin8ti-2<D} +
cost]
+ 2 [В —D(1 —3 cos* т])] - -L;
sin® Т)
°ч= {[ЗФ+2(1+v)qp] cos®t]—2Ф}—
COS t]
-21B+D0 + 3COS’,)]—; (?20)
1 COS T]
°0= 7ri<I>+2<1+v)<P1“4vD‘^rr:
194
T6n=—— [ЗФ-|-2 (1-|-v) tp] sinr) cost] +
2
+ -------+[B + D(1 +3cos2 t])l.
Sin T]
По форме полученных выражений следует, что напряже-
ния не зависят от расстояний точек до вершины конуса. На
любой конической поверхности т) = const они имеют по-
стоянные значения. В частности, в точках внешней и внут-
ренней поверхностей:
1-6«
Ph~7 +
6 °k
Ph 2
°е = —— {В+D [ 1 +(3-2v)frft]};
Ofc bh(\ — &£)
здесь нужно считать bk = b и pk = р0 при т) = т)0 и bk =
= bj nph = р при Т] = Т]1.
В цилиндрических координатах составляющие напряже-
ний имеют следующие значения:
°е =— [Ф + 2(1-Н)ф—4vD/?z].
(7.21)
2 ( Г / г* XI ]
°2==— Г I®—+ 1 )1 ^21 ’
г2 V L \ Я2 J] J
2 Г ( г*
Trz=— B+D 1 + — Я-
г L \ Я1 /J
Произведя подстановку <р и Ф в формулы (1.12) и (2.31),
преобразования и интегрирование, для перемещений и и
w находим:
“ = ^-b+BQ;(!/)+2D-^- + 2(l-v)[C + DQ1'(i/)]]r;
2р. [ sin’t] J
w= — ([A+BQ; (i/)]cost] + 2v[C4-DQ; (i/)] cost]+ (7.22)
B+2vD
sin21]
Я+и»о.
где w0 = const.
♦ Значение b = 0 или = 0 в приведенных равенствах исклю-
чаются. Эти особые случаи требуют специального рассмотрения.
195
В случае сплошного конуса В = D = 0. По равенству
нормальной силы нулю постоянная А = 0. Задача приво-
дит к равномерному двустороннему сжатию в каждой точке
области конуса (см. п. 3.1). Такое же напряженное состоя-
ние имеет место, если между силами, приложенными к по-
верхностям полого конуса, выполняется связь р0Ь± = pb.
Второй случай нагружения. Внешняя (т) = т]0) и внут-
ренняя (т] = Th) поверхности конуса подвергаются дейст-
вию сил, имеющих осевое направление: pz = р0, рг = 0
при т) = т)0 и pz = р; рг = 0 при т) = т)г
Выполнив контурные условия (7.1), получаем следую-
щие выражения для постоянных:
А_________J_______/ Ро Qi (^i) pQt (6) \ . в д
~ ” УГ=6? / °:
1 / Ро Р \ D
В = —-------------| —— — -------) 4- Во,
с = —[ в J (М Р (Ь)-В1 (6) Р (601;
D= [(1 -6«) bt Р (6)-( 1 -62) ЬР (601, (7.23)
где введены обозначения
4
+ J/ Ро _ Р \.
«tow-oic»)) \ уг^я /'
Р№)=-ГР»1У1^ +
4
1 / Ро Р \
+ -------------- ; (7.24)
2[q;(60-q;(6)1 \ Vi-*2 Vi-6?/
Ло, Во, Вх (b), В± (bj), В* и D* имеют значения (7.19).
Напряжения и перемещения определяются формулами
(7.21) и (7.22). В точках поверхности конуса
Pkbf 2
<ч= -ут^+ |B+D (1+6?>'
°ч=-₽>.Уг+»1;
2
{a+P['+(3-2vHl};
т6п = Ph bh ’
196
где bh — b и ph = p0 на внешней поверхности т) = т]о и
bk = Ьг и рк = р — на внутренней т] = т)1-
Соответствующее решение для сплошного конуса нетруд-
но составить, положив Th и постоянные В и D равными нулю
(bi — 1). Напряжения при этом ог = сте = xrz = О, oz =
= —pj]f 1 — Ь2, т. е. сплошной конус при нагружении
по боковой поверхности равномерно распределенными си-
лами осевого направления находится в условиях простого
сжатия.
Было указано, что при нагружении сплошных или по-
лых конусов силами, приложенными к вершине, одно из со-
ставляющих напряжения, а именно о$, значительно превы-
шает по величине другие. При распределенных нагрузках
дело обстоит иначе: например, в случае равномерно распре-
деленных сил -все составляющие имеют близкие между со-
бой численные значения. В табл. 26 приведены значения
напряжений а2, оо и xrz в сечениях конической трубы при
равномерном нагружении внешней поверхности нормальны-
ми к ней силами для различных значений углов т)о и т]1-
Все напряжения существенно зависят от величины этих уг-
лов т)0 и Иг Они увеличиваются с уменьшением толщины
стенок трубы (т. е. разности т)х — т]о) и с увеличением на-
Таблица 26
п а2/Р C0/P Xrz/P п az/P а0/р xrz,'P
По = 45° Hi —30° По = 30° Hi = 20°
45° 0,492 1,861 0,589
40° 0,448 2,159 0,588 30° 0,648 1,816 0,378
35° 0,512 2,571 0,714 25° 0,658 2,265 0,470
30° 0,526 3,186 0,878 20° 0,668 3,084 0,608
По = 45° П! = 35° По = 30° Hi = 25°
45° 0,938 3,636 0,942
40° 0,953 4,221 1,139 30° 1,873 5,293 1,083
35° 0,978 5,040 1,389 25° 1,894 6,619 1,351
По = 45° П1 = 40° По = 15° Hi —5°
45° 2,358 9,266 2,356
40° 2,404 10,701 2,854 15° 0,118 1,445 0,0317
По = 30 ° П1=15° 10° 5° 0,119 0,120 1,812 3,021 0,0482 0,0976
30° 25° 0,267 0,269 0,694 0,856 0,156 0,194 По=15° Hi = 10°
20° 0,273 1,150 0,251 15° 0,762 1,646 0,204
15° 0,279 1,773 0,343 10° 0,766 2,617 0,311
197
клона внешних поверхностей (подсчет произведен при v =
= 1/3).
В частном случае, когда граничная координата т)0 =
= 0,5 л, внешняя боковая поверхность представляет со-
бой проходящую через вершину конуса плоскость, перпен-
дикулярную к оси вращения, область конуса вырождается
в полупространство с коническим вырезом (см. рис. 35).
Значения напряжений и перемещений в таком теле при на-
гружении поверхности его силами радиального и осевого на-
правлений определяются формулами (7.21) и (7.22), в кото-
рых постоянные А, В, С и D получают более простые выра-
жения, так как b = 0 и Q[ (Ь) = 0, при нагружении ради-
альными силами (рг)
Л=0; В = —-------1----
(l-62)Q;(b)
РрВ1(61)
(1-ь?) b, вльу
D =-—— ,
2В, (Ь)
причем Вг (b) = 1 —
равенством (7.19).
26i
(1 -6») Qi (6,)
и Bi (М определено
7.5. Нагружение конусов линейно распределенными
поверхностными силами
При линейном распределении осесимметричных внеш-
них сил на поверхности конуса нормальная сила является
функцией третьей степени осевой координаты z. На основа-
нии этого нетрудно заключить, что к решению задачи для на-
груженного конуса, таким образом, приведут функции на-
пряжений, содержащие третью степень е*, т. е. взятые в ви-
де
ф = [Л cos t] H-BQi (v)] (ce6)3 sin21] = [Az + Bce*Q’t (i/)] r2;
(7-25)
Ф = [C cos T] + DQi (i/)] (ce6)3 sin21] = [Cz-j-Dce^ Qi (i/)] r2
(cm. (2.451. Подставляя эти функции в равенства (1.17) и
(1.26) для Фи Q, после преобразований, при которых ис-
пользованы следующие связи между функциями Лежандра
(l-«/')Q;(!/) = 2f/Q;(y)-6Q,(!/); 2Qt(y)=yQi{y)-Q’l (у).
198
получаем:
Ф= {[Л+ C+3DQ; (i/)] cos^+BQi (</))) (се6)3 si
(7.26)
Q = {[А -(1 + 2v) С] cos т) + В2 Qi (y)-D [2 (2+v) Qi (y)-
—3Q; (y) cos q]} ce*.
Процесс построения решения при нагружении поверх-
ностей полого конуса линейно распределенными силами по-
вторяет процесс, реализованный в п. 7.4, поэтому огра-
ничимся только приведением его результатов-выраже-
ний для постоянных Л, В, С и D, напряжений и перемеще-
ний. В случае нагружения радиальными силами рг =
= — р^/а при т]= т)0 и pr = — pz/a при г] = (pz= 0),
где а — некоторое значение z,
А Аь-С- [р0Ь2 В2 (bj-pb* В2 0)];
(7.27}
D 2(14-v)
В = — Во; D = (р0 b. - pb) (bbtf.
В случае нагружения осевыми силами рг = p^z/a при
т) = т)0 и р2 = pz/a при т] = т]1 (рг = 0)
А =Ра + -£ Ло-С; С = —1- [В2 00 Р (Ь)-В2 0) Р 00];
о’ aD*
D 2(l+v)
В =Рь + — Во; D = - Z. 1 [Р (b) bf -Р 00 63J. (7.28}
В* aD*
Здесь введены следующие обозначения:
ло= -3 [6Q i (6) Qi 00 Q{ 00 Qi 0)];
B0=366j [Qi 0)-Qi 001;
2(B04-56«)
B2 0) = 2 (1+V) 63 Qi 0) - ;
В*=^0О-б!С;0); (7.29)
B2 (60-2 (I +v) bl QI (Ц- ,21»; ;
D> =2 (1 +v) (W Bt (6,)-bl B, (6)];
_ 1 j PobQ2 0Q pbi Qj 0) \
Pa ~ 3B0 ( Уь^ /’
199
Pb =
ььг
зв~0
Ро _ Р
УТ^ь* 1/T^df
Р.Ь(1-2^)
31/1—д2
2Pb
1—62 ’
рЬ1 (1—2Ьр
31/1—д2
2рь
1-д2 •
Р (Ь? =
Вычисление напряжений по формулам (7.5) приводит к
следующим выражениям
а6=- — {2Ф —[5ФЧ-2 (1 Ч-v) <p] Sin2 Т)} +
+ (2—5 cos1 2 tj)];
Sin2 Т]
1
<г_= — — {4Ф — [5Ф + 2 (1 +v) ф] cos2 т]} —
1 f2
— —Г~г— (В +5D cos2 т]);
Sin2 Т]
1 4vDce*
°е= Т1Ф+2(1+?) ф] — — — ;
Г2 Sin 2 Т]
£т1=--{Ф — [5Ф + 2 (1 4-V) ф] cos2T]} tgTj —
(7.30)
—------------ (В 4- 5D cos2 Ti).
sin Т] COST]
Напряжения возрастают по мере удаления сечения | =
= const от вершины по линейному закону.
Подставляя функции напряжений (7.25) и (7.26) в фор-
мулы (1.12), (2.24) и интегрируя, для перемещений полу-
чим:
и {[Л 4 (3—2v) С] cos Т] + В Q'(у) 4- D [2 (1 - v) (у) +
2р
+ 3Q( (у) cos Т]] (се*)2 sin tj; (7.31)
w=-----{— [i4-|-(l+2v) С] (1—3cos2T])4-2Csin2i]4-
4р
+6fiQ2 у) Ч- 6D [(14 2v) Q2 (у) 4 (у) s in2 т]1} (се*)2+w0 •
1 При преобразованиях использовано равенство
2
Qz (у) 3yQi (у)= . 2 •
1— у
200
В случае сплошного конуса В = D = 0. При нагруже-
нии радиальными силами С = — А = р0/2 (1 -f-v) ab,
р
при нагружении осевыми силами А-}-С=-----. - С =
За V1 — Ъ1 2
Ро (1 — 2d2)
=-------—----решение сводится к применению
6 (1 + v) аб2 Д/l-b2 г к
второй элементарной формы функций напряжений (см.
п. 3.3). Выражения для напряжений и перемещений после
перехода к цилиндрическим координатам составляются по
формулам (1.12), (1.15), (1.27).
Наложением приведенных решений для полых конусов
можно составлять выражения для напряжений и перемеще-
ний при нагружении равномерно и линейно распределен-
ными силами конических оболочек и плит переменной тол-
щины типа, изображенного на рис. 35 и 36. Как и во всех
случаях деформаций конусов, условия на краях оболочек
и плит, определяемых значениями | = |0 и | выпол-
няются в интегральном смысле.
7.6. Осесимметричная деформация сплошного конуса
под действием собственного веса
Перейдем к рассмотрению задач о деформациях кону-
сов под действием объемных сил. В первую очередь выяс-
ним характер распределения напряжений и перемещений в
сплошном конусе, вызываемых собственным весом. Будем
считать, что силы веса уравновешены силами, приложен-
ными в достаточном удалении от вершины конуса. Здесь,
как и в предыдущих примерах, рассматривается область, до-
статочно близкая к вершине конуса.
К осесимметричному напряженному состоянию силы веса
приводят только в том случае, когда они направлены парал-
лельно оси вращения, т. е. когда g = 0 и gz = g. Соответст-
вующие таким силам частные решения неоднородных урав-
нений (1-42) и (1.47)
1 1
Л фг = — ----Г gz; АФг = ----Г gz г
2 (1 —v) 2 (1 —v)
определяются равенствами
g g
tz =----------г3 * * *; Фг = —---z2 (7.32)
У 12(1—v) ’ Y 4(1—v) К 7
201
и, следовательно, функция Ф2 — равенством
Ф2 = 'К 4- z<pz = - 6(1g_v) 23 • (7 • 33)
Функции ф и ф принимаем в форме
ф = Ar2 z = A (cety3 sin2 q cos q; <p = Cr2 z = C (ce^)3 sin2 q cos q.
По формулам (1.46) и (1.49), имея в виду, чтофг = фг =
= 0, составляем функции Ф и й:
Ф = (Л + С) г2 z = (.4 -|- С) (се6)3 sin2 т] cos q;
(7.34)
О = [Л — (1 4-2v) С] z = [A— (1 -f-2v) С] се^ sinr).
Контурные условия (2.30), так как рг = pz = 0 и Ф2 не
зависит от г, после выбора знаков, соответствующих рассмат-
риваемой системе координат, получают следующую форму:
дФ
дФ Л д<рг
---= — 2(1 — V)/"—
' 5q dq
дг
dq
—g(ce6)3ft(l — Ь2);
Подстановка сюда производных ф2 по | и по q приводит
к окончательным выражениям:
_дФ
дЬ
— = Iq+ —bee11 (се6)2 b V1—6а .
dq L 1 —v
Пользуясь ими, находим значения постоянных задачи:
Л-ЬС=— — g; С=——-
3 е 6(1 +
(7 35)
(7.:%)
b = cos т]о, т)о — координата, определяющая поверхность
конуса.
Таким образом, функции напряжений получают вид
(1 — ——— Ы2} г2 z;
6(14-v)5a \ 1—v /
1 . 1/1 1 \
ф=-Т«г г: Q=TS(^-
(7.37)
Решение ограничено условием т]0 < у» так как при
b = 0 уравнения (7.35) несовместны (это легко проверяет-
ся).
202
Выражения для напряжений и перемещений нетрудно
составить, подставляя функции (7.34) в соответствующие
формулы. В цилиндрических координатах по формулам
(1.27) будем иметь:
1— ft2 1—b2 1
°г = —----Z— —--------------— gz; о2 = —— gz:
3b2 e 3b2 3
1
в сферических координатах по формулам (2.27) —
= ~ ~ +sin2 Ti)cos n; CTTi = (fe2 —cos2 ’i)cos Ti;
Ot/ Ou
(7.38)
gce^ gce^
a6 = ~ ^b2 1 ~C°S П’ Tfcn = "з^г V*~cos2 П) sin q.
В результате решения получена довольно своеобразная
картина распределения напряжений в объеме конуса. Нор-
мальные напряжения ог, оо и о2 не меняют величины при
г = const, — распределены равномерно, а касательные на-
пряжения не зависят от z и в любом поперечном сечении рас-
пределены линейно. Нормальные напряжения о2 точно сов-
падают со значениями, подсчитанными элементарно, — де-
лением веса объема конуса, находящегося над рассматрива-
емым сечением, на площадь сечения.
Перемещения и и w находятся после подстановки функ-
ции (7.34) в равенства (1.50) и интегрирования:
(7.39)
а г / 2v \ / I — v \ 1
—— I ( 1 —2v — —]z2+i3-h2v — )r2H-a>0.
6с о2 ] \ b2 ] J
Приведем решения еще двух задач о напряженно-дефор-
мированном состоянии тяжелых конусов, которые просто
получить, основываясь на той же форме (7.34) функций на-
пряжений. Рассмотрим деформацию конусов, находящихся
в обойме с абсолютно жесткими стенками. В первой задаче
предположим равенство нулю на поверхности конуса каса-
тельных сил и перемещений, нормальных к поверхности
т. е. т£л = 0 и = 0 при т] = т]0. Первое условие означа-
ет возможность скольжения вдоль образующей (т. е. нера-
венство нулю перемещений и* при т] = т]0)-
203
Пользуясь формулами (2.25) и (2.27), составляем общие
выражения для тЕл и После некоторых преобразований
2 (1+v) С cos2 т] —
«I
1— 2v 1 .
—-----g cos2 t] ce6 sin T];
sin Т).
u = —— Д — (1 —
1—2v
+ 1—V
Положив здесь т] = т)0 (cos т]0 = Ь) и приравнивая каждое
равенство нулю, получаем два уравнения:
„ 1—2v gb2 Л
А=-------------; С=0.
1—V 1— 5Ь2 ’
Вычисление напряжений приводит к значениям в ци-
линдрических координатах:
(l+3v)b2-v g Г
аг—сто—т; 775 £г* 02 —,
(1—v) (1—5b2) 1—v
(1—2v)gb2r
Тг2“ (1 — v) (1 — 5b2) ’
в сферических координатах
g
2(1—2v)b2
1—5b2
z;
1—V
g
сте= "5-
w 1 —v
z;
z;
g
аП- !_v
(l+3v)b2—v t E.
(1 — v) (1 — 5b2) e
3b2—cos2 ti
<'-2v>-fz^2L-v
(1—2v)b2 1
1— 5b2 J
. „ sin2n—b2
(I-2*) . '
L 1 —bo
g (1 —2y) (b2—cos2 tj)
T&T1 = ~ (1—v) (1—5b2)
На контуре осевого сечения
(2+v)b2— v .
CTE= ------771--gbce ’ CT0
6 (1 — v) (1 — 5b2)
(2 + v)b2—1—v .
a_ =---------------gbce^, — 0.
n (1 — v) (1 — 5Ь2) * 6tl
Напряжения ол определяют давление на поверхность обой-
мы. Как и в случае деформации сплошного конуса, решение
ограничено условием Ь2 >.0,2. При Ь2 = 0,2 выполнение
204
равенств т$п = 0 и = 0 на контуре осевого сечения т) =
= т)о приводит к требованию g = О
При малом угле т]0, считая b 1, имеем
l+2v i+2v
а= ая = — --------gz\ orz = —------gz:
6 4(1— v) * 2(1—v) к
1—2v
*rz= — —-----~gr.
4(1—v)
Во второй задаче деформации тяжелого конуса в жесткой
обойме предположим равенство нулю нормальных и каса-
тельных перемещений на поверхности конуса: =0
при т] = т]0 (жесткая заделка поверхности). Постоянные
А + С и С в этом случае имеют значения:
1 — 2v 1—2v
А + С =------ gb2-, С= —---------gb2
D* ® 2(1—v)D*s
при обозначении знаменателя D* = 2 [1 — v — (2—3v)b2].
Решение справедливо только при Ь2 > 2 —3v ’
Напряжения:
е (2 (1—2v) 1
= ----I----------[(1 —2v) b2— (1 —v) cos2 T)] — v > z;
6 1—v I D* I
g r 2(1— 2v) o )
%=---j------[vft2 —(1 —v) sin2 rj] +vj z;
2(1 —2v)d2
---~1 z;
D*
_ _yg
CT0—- — ,
1 —V
(1 —2v) g
= - • -D*' № - 2 c°s2 n)r
В точках поверхности конуса:
vg Г 2 (1 —2v) b2
CTs=ae=-7^7 +
-n = -—
n i—v
2(1—2v)
D*
(d2—l-j-v)+v
in = ° D?v) V1 ~b2 ce*-
Перемещения в направлении оси z:
g
2ц
w =
1— 2v n /
-----b2 | r2
D* (
1—2v
1—v
2(l-v) J
+ tt»o.
а радиальные и = 0 во всем объеме конуса.
1 Этот результат принадлежит А. А. Ильюшину [35].
205
7.7. Осесимметричная деформация полого конуса
под действием собственного веса
Решение задачи о напряженно-деформированном состо-
янии полого конуса, нагруженного силами собственного ве-
са в направлении оси вращения Oz, осуществляется по пла-
ну, примененному в п. 7.6 при решении аналогичной зада-
чи для сплошного конуса с некоторым усложнением записей.
Условия (2.30) на внешнем (tj = т]0) и внутреннем конту-
рах осевого сечения можно выполнить, если к функциям
(7.34) присоединить члены, содержащие производные функ-
ции Лежандра второго порядка, т. е. задать их в форме
(7.25) и (7.26), примененной в п. 7.5 при рассмотрении на-
пряженно-деформированного состояния полых конусов,
нагруженных силами, распределенными на поверхностях
по линейному закону от координаты z. Подстановка указан-
ных функций в равенства (2.28) и некоторые преобразова-
ния приводят к системе четырех уравнений:
(Л + С) b + BQ'2 (b) + 3DQ! (Ь) ь = -4- gb-
о
(Л+С) bt + BQ' (bj +3DQ{ (bj b1 = -4-gdn
О
J? / 24-v \
2 (1 + v) Cb* + B2 (b) D = - -f- i - —b* b;
3 \ 1—v /
g I 24-v \
2(l+v)Cb3 + B2 (b1)D= —Ml —-3— bf b,.
o \ 1 — V /
Решение этой системы:
1 D D
A+C-- 3 g+ B' A,; B- B. B,,-.
2(l-j-v) h2\hh
D=—— (ft? —ft2) ftftj;
c=——
3D*
1 —V
(7.40)
Здесь b = cos t)0 и bx = cos T]lt обозначения Ao, Bo
B2 (b), B2 (bx), B*tD* применялись в п. 7.5, и они определе-
ны равенствами (7.29).
206
Напряжения и перемещения можно представить в сле-
дующем виде (см. (2.27)—(2.29)]:
[v + (1 — 2v) cos2 tj ) ce^ cos П +
i-
vg ,
J _v cel cos n + ae;
1—2v
------COS2 T)
cos t) 4- or^;
(7.41)
1—2v ►
TEn ‘ = j_v &ce cos2 П sin n-Ь
, 1—2v / t x2
u=u ; w=—----------- (ce6cosTi) -Pur
4р. (1 — v)
где oj, o^. oe, Tgn, u', w' имеют запись (7.30) и (7.31) при зна-
чениях постоянных (7.40).
В точках поверхности конуса
В
T+3D
в
—- + (5-2v)D
bk
G6=
CTe I 36
g ____________
36ft r 1-^
2
-ь‘)+^г
ce\ a^- = 0;
ce\ = о»
2
причем на внешней поверхности нужно считать bh =
b — cos т]0, а на внутренней bh = = cos
В частности, для бесконечного тела вращения, ограни-
ченного двумя коническими поверхностями b = — Ь} (см.
рис. 36), постоянные В = D ~ О, а 4 и С совпадают со зна-
чениями (7.36). Напряжения определены равенствами
(7.38). В сечениях г = const нормальные напряжения сг2
распределены по линейному закону, а касательные тГ2 —
— равномерно.
7.8. Деформация сплошного конуса
при равномерном вращении
При равномерном вращении сплошного конуса вокруг
оси объемные силы имеют значения gr = jr и gz = 0, где
J =/пей’. Таким силам соответствуют частные решения
уравнений (1.42) и (1.47)
„ rz dgr „ 1
взятые в форме фг = 0; <рг =
16(1—V) ’
207
(ф2 = <pz = 0 по равенству объемной силы gz нулю).
Контурное значение функции фг(т) = т)0 = const) про-
порционально (се^)4. Очевидно, что условия (3.33) могут
быть удовлетворены только тогда, когда функции ф и ф
будут также пропорциональны (се^)4. Выбирая из числа
(2.45) соответствующие функции (а именно при к = 3) и имея
в виду требование равенства нулю функций ф и Ф на оси
вращения, принимаем:
ф = А (1 — 5 cos2 т]) (се^)4 sin2 т);
(7.42)
Ф= С (1 —5 cos2 т]) (се^)4 sin2 q
или при записи в цилиндрических координатах:
ф = Л(г2—4z2) г2, ф--С(г2—4z2) г2.
По формулам (1.46) и (1.50) при этих значениях функций
ф и ф находим:
jvr2
8(1—v)
= & —y- + A (1 — 5 cos2 T])—8C cos2 t] | (ce^)4 sin2
q=J!±*L
8(l-v)
Ф=
4z2)—8Cz2 r2 =
sin-4 Т];
— 4z2) — 2С [(3 + v) г2 — 4vz2] =
——------- j sin2 т] 4- A (1 — 5 cos2 t]) —
I. 8(1—v)
—2С [3-|-v — (3-|-5v) cos2
(7.43)
Нормальная сила в любом поперечном сечении вращаю-
щегося конуса равна нулю, поэтому должно выполняться
равенство Ф = 0 при т] = т)0, т. е.
iv
А (1—5Л2)—8С624- _ (1—fe2)—0,
(b — cos т]0).
После подстановки функций Ф и Q во второе контурное
дф х-s дг
условие = гЯ
и соответствующих преобразований приходим к равенству:
3—v
5Л (1 -6») -|-С [ 11 + v-5 (3 + v) 62] = —-- / (1 -б2).
,16(1—v)
208
Совместное решение двух полученных уравнений дает
следующие значения постоянных А и С:
Н1—ь2)
А =_T7i—к12+1 lv ч-5v)d2-v о1+v)i;
8 (1 —v)D*
j (1— b2)
C = ^77-77T[3(l+3v)-5(3+v)62], (7.44)
16 (1 —v) D*
где знаменатель D* = 114-v — 10 (34-v) b2 + 5 (7+5v)b4.
Дальнейшее заключается в вычислениях напряжений
по формулам (2.27) и перемещений по формулам (2.-30).
После выполнения всех подсчетов и преобразований будем
иметь:
для напряжений
а6 = (в(Л+2С)-{-^
[4v43 (1—2v) sin2 т)] +
+ 5Л (1 +7cos2 т])4-2С [5—v4 5 (74v) cos2 tj] 1 sin2t) ) (ce^)2',
a_ = —(4 [A+ 2 (24 v) C] + [--/- -- [4v+3 (1 -2v) cos2 n] —
\ l о (I —V)
—35Д cos2 T]—2C (4 (24 v)-|-5 (7-|-v) cos2 tj]j sin2(ce^)2J (7.45)
<ye = -pn+2(2+v)t]4-
— 2C (9 + 7V)
f „ Г 3(1— 2v)
= -[4 [5Д + 2 (6 4- v) C] 4 /-
—35Л — 10 (74 v) СI sin2 T] 1 (сЛ)2 sin T] cos q;
для перемещений
u ="7“ [— A. 2v. + л (r2—4z2)4
2(1 [ 8 (1 — v)
42C [(1 — v) r2—4 (2—v) z2lj r;
2
w=— — {Л (3r2—2z2)42C [3vr2—2 (14v) z2]} z + ®o. (7.46)
209
Напряжения на контуре осевого сечения могут быть вы-
ражены через одну постоянную. Они имеют вид:
f 34- v 1
аЕ= 8 (1-V) ' ° “62) ~2С l3 + v-(7-5v) ft2] j (ce6)2; % =0.
ae= -[g\t3Vx / (1 —62)—2C [1-f-3v—(5 4- 7v) ft2]!^)2;
I 8 (1—v) J
TSn=°-
На оси вращения
ап=сге== ~4 И+2 (2+v) CJ (се*)2',
о^ = 8(Л4-2С)(^)2; т5т1=0.
Из полученных выражений следует, что в рассматривае-
мом случае напряжения возрастают пропорционально
квадрату расстояния точек от вершины конуса.
Пользуясь выражениями функций напряжений в ци-
линдрических координатах гиги применяя формулы (1.30),
для напряжений получим:
3—2v
ог = ---Г/Г2 + Д (Зг2—4z2)-J-2C [(3 + v) г2—4 (2-f-v) z2];
8 I1 —
°Q= ~ 8(t-V ir2 + A <r2~4z^ + 2C l<1 -b3v> r2~4 (2+v> z2b
az = ~ 2(1—v) /r2~4 [Л (r2-2z2)-4Cz2l:
Тгг = — 8(Л4-2С) rz. (7.47)
Характер распределения этих напряжений в поперечном
сечении z = с|/3/2 изображен на рис. 37. Значения ординат
графиков приведены в табл. 27. Подсчет произведен при
v = 0,3 и т]0 = 30°.
Таблица 27
г/с 0 0,1 0,2 0,3 0,4 0,5
Oz/ja1 0,08877 0,08462 0,07219 0,05401 0,02244 -0,014191
0,08877 0,08568 0,07661 0,06143 0,04015 0,01279
Gz/ja? 0,04484 0,0*116 0,03044 0,01252 —0,01252 —0,04476
^rz/ja1 0 —0,00517 —0,01034 —0,01551 —0,02068 —0,02584
К распределению напряжений и перемещений при вра-
щении полого конуса вокруг собственной оси с постоянной
210
угловой скоростью приводят те же самые частные решения
уравнений (1.42) и (1.47) и функции напряжений (7.42),
которые были использованы при рассмотрении вращения
сплошного конуса при условии, однако, включения в ф и
и <р производной полиномов Лежандра второго рода фз (у)
в соответствии с общей формой решения основного диффе-
ренциального уравнения в сферических координатах (см.
(2.45)].
7.9. Вторая форма решения осесимметричной
задачи в сферических координатах
Решение осесимметричной задачи в сферических коорди-
натах в форме (2.44) позволяет с той или иной степенью слож-
ности выкладок получать значения напряжений и перемеще-
нии при нагружениях конусов
боковым поверхностям (внеш-
ней и внутренней) по степен-
ному закону от координаты г,
а также при осесимметричном
нагружении объемными сила-
ми. Такие нагружения рас-
смотрены ранее. Если силы,
вызывающие деформацию ко-
нуса, распределены по его по-
верхности по закону, отлич-
ному от степенного, занимают
не всю поверхность, а только
ее часть или несколько ее
частей, отдельных одна от
другой, иными словами, при-
ложены кусочно-непрерывно,
то для выяснения соответ-
ствующих им деформаций
требуется применение иной
формы решения уравнений
(2.12) (см. (701):
силами, распределенными по
Рис. 37
д I 1 дф \ д / 1 дф \
д£ к г д£ дт] \ г дп /
д / 1 дф \ д / 1
к г д£ /+ к г
дт] /
Приступим к ее составлению. По-прежнему будем искать
значения функций ф и <р в форме произведения функции пере-
211
менной | на функцию переменной т], где | и т) — сфериче-
ские координаты, связанные с цилиндрическими гиг ра-
венствами г = се* sin т], z = се^ cos т].
Подстановка ф = А (I) /2 Сп) в первое уравнение (2.12)
приводит к разделению переменных и двум уравнениям для
определения А (Е) и А Сп)2
d2 fi df i d2 f2 df,
----—— — + m2f1=0; —— ctg T] ——— m2f2 = 0. (7.48)
d£2 d^1 di]2 e 1 dr) '2 v 1
При мнимом значении т = itc возвращаемся к решению
(2.44.). Считая т действительным, преобразуем первое урав-
Lg
нение (7.48), положив в нем fx (|) = е2 / (£). Тогда
d2f / , 1
dt,2 V 4 Г
следовательно,
1
f (£) = Л sin cos где №=-т2 +—.
4
Решение второго уравнения (7.47) в форме / (tj) =
= (1 — 1/2)2" Y (у), если, как и раньше, обозначить у =
= cos Т] и положить
уравнению
— х (х + 1), приводит к
I-!/2
0.
Его решение имеет вид:
1
у (») = (1 -s2) 2 [CKl (y)+DK* (-»)].
dKH (у) dKK (-»)
Здесь К (у) = —------; К' (— у) =----------
dt/ ay
Км (у) и Км (—у) — конические функции Мелера первого
и второго рода или функции Лежандра комплексного индек-
са х =-----g 4- определяемые гипергеометрическими
рядами (см. [24]):
(У) = 1 + -4-Х22+1 sin2 -у п
, (4А2+1) (4А2+3) 1
+--------;—;------sin4 —-пн-
22-42 2
„ 4А2-Н e 1
(-!/) =1 + ~2------cos V Л +
(4А2+1) (4Х2 + 3) 1
+-----------------cos V ’I+• • •
2Z 4Z 2
212
Итак
Мч) = [с*х W+DK* (-!/)].
Вид функции ф, а следовательно и ф, установлен:
4- Б
ф = (Л sin 4- В cos А,£) [СК* (y)+DKn (~у)] е 2 sin2i);
(7.49)
<р = (Л' sinX^ + B' cosXg) [С' K^(t/)+D' К^(—у)] е 2 5sin2т).
Ограничимся рассмотрением только сплошных конусов.
По условиям на оси вращения (1.32) для них постоянные D
и D' должны быть приняты равными нулю, поскольку функ-
ция Ки (— у) имеет бесконечное значение при т) = 0. По-
ложив С — С ' = 1 и изменив обозначения постоянных
функций ф, получаем:
ф = (Л sin 4- В cos Х£) К* (у) е 2 sin2 т);
4"5
<р= (С sin X£4-£)cos А£) (у) е 2 sin2T).
(7.50)
После подстановки ф и ф в равенства (2.13) и (2.17) функции
Ф и Я запишем в следующем виде:
Ф = (Fi sin Х£4'7‘2 cos Х£) е sin2 т];
(7.51)
1 —— Б
Й = — [(ЗЛ -F3) sin Ц4- (3F-Ft) cos е 2
при обозначениях функций
Л
COS2 Т]
я* (!/)+(Х2 + "у) C^v. (у) cos п;
=[в+("7 £>+*'C)cos2t/| К'к (у)+(^2+ "7"]D^x(f/) C0S1i;
L \ J J \ • /
F3 = [2Д -(1 —2v) C-2W] К; (у)-
(7.52)
F. = [2B-(1 -2v) D4-2XC] К; (у).
213
Укажем значения производных функций Fx (т]) и F2 (tj),
входящие в выражения для напряжений,
F[ =—(fi 4-[д + (-^“С—W^cos2,q
(у) cost] —
— |д - [(ь2+ -7) C-wj cos2 т] j к; (у) ) tg т);
(7.53)
F't = ~(Х+ [^+[-|-D+Xc]cos2t]]k" (£,) cos т) —
Г Г/ 3 \ 1 ) \
— В— Х2+ р + ХС I cos2 т) к: (у) tgij.
I I \ 4 / J J 1
Подставляя (7.51) в формулы (7.5) для напряжений, пос-
ле выполнения ряда преобразований и группировок, полу-
чим:
_ 1
[(2FJ-I-FI sin2 t]4-F{ sin "q cos-q) sin X£4~
4- (2F24~ F2 sin2 T) 4- F2 sin Л cos q) cos X£;
1
11 R VcR
[(Fj—F3—F* sin2 -q — F{ sin r) cos tj) sin X£4~
4-(F2—Ft—F2 sin2-q—F2 sin-q cost]) cos X£];
(7.54)
°e=7V^{[(1-2v)fl-fa+
4- (1 4-v) (2Д 4-C-2W) К; (1/)] sin Ц4- [(1 —2v) F2-F44-
4- (1 +v) (2B4-O + 2XC) K; (y)] cos X£];
t£ti = “ D-I/-P f<Fi ~Fi *8 П) sin 4+
ъ 1 R V CR
4- (F;—F; tg T]) cos X£1 sin T] cos T],
где R=c^\
Fi* =4" Fi + XF2-F8, F-2=4- F2-XF1-F4. (7.55)
Л» Л»
214
На оси вращения (т] = 0); тСп = 0
а«= rVTr (х’+ т)[(л-Тc-w) sinч+
/з
4- I В—cos Ц||;
’п=’е=-5ет Н Т){[Л+Т<1+4У>С-
— wjsin А£4-р4--£- (1 +4v) D4-Xc] cos XfcJ, (7.56)
где принято во внимание, что Км (1) = 1 и Км (1) =
=—-fxa+— Y
2 к 4 I
Подстановка <р и Ф в выражения для перемещения и
и производных перемещения w по 5, по т) и интегрирование
последних приводят к следующему результату:
“ = 211'VcT {IF1+2 ° ~V) CK*(!/)I 5‘П 4 +
+ [^2+2(1 — V) D K* (!/)] cos A£} sin tj;
w= 4u Up ({[2F1 —(2Л + C—2X0) к; (y)] cost]—
Ц (7.57)
—[Л—2XB—(1—2v) (C—2XD)] (y)} sin
+ {[2F2-(2B4-D4-2XC) K; (i/)J cos n-
-[fi + 2M-(l-2v) (D + 2XC)] KK (*/)}cosX£) +ш0;
(tt>o = const).
7.10. Решение в рядах
Практическая реализация решения (7.50) осесимметрич-
ной задачи в сферических координатах сводится к осуществ-
лению решения в рядах для конусов конечной длины и в ин-
тегральной форме для бесконечных конусов. В первом слу-
чае функции Ф и Й записываются в виде
Ф=Л{
sin2 Т] cos ЬтЛ);
п= О
(7.58)
О— з [(3Fin—F8n) s*n 54“(З/Чп ^2n)cosXn£],
j.T1 п=°
215
где Xn = п л/|0, —| и £0 — координаты, определяющие тор-
цы конуса.
Заданные на поверхности конуса i] = т]0 силы рг и pz
также представляются разложениями в ряды:
—— S 00
Рг = е 2 2 (Г™ sin £ + Prn cos £),
п=0
—— S 00
Pz = e 2 2 (PznsinXnS + Pzncos^nl), (7.59)
n=0
коэффициенты которых
So
р'л=
имеют значения рг0 = pz0 = 0;
Рг е d^.
-So
So з »
(* 25
| pr e sin Xn £d
-So
5° з
C 25
I pre cos Xn^dS:
-E.
So _3_f
Г 2 s
p*= IT J p“
—io
So _3_£
J Pze 2 sinxnljd£;
-So
So
C 2 s
1 Pz e cos Xn .
V
-So
л=1, 2, 3...
Составляем производные функции Ф по S и по т)
дФ 4-S
----= е z
Pm—
So
1
Prn ’ t
So
Pzn —
60
Pzn t
So
(7.60)
sin2’’ 2[(t
n= 0
Fin—4 F2n
in 4“ Pin I COS Xn £ I;
ЭФ
di] e
2 sin2r) 2 [(2Лп cos T]-f-F{n sin tj) sin Xn S +
n= 0
-I- (2Ftn cos T] + F'2n sin tj) cos Xn £]
(7.61)
216
и по контурным условиям (7.1)
^Ф / дф t t\2
—— = (cee) Pz sin 1]; —— = (се6» [Q cos q-|- pr] sin q
ot, dq
где q =т)о'> приравнивая коэффициенты при одинаковых зна-
чениях sin Хп£ и cos слева и справа, получаем группу
уравнений:
2 Fin ^п F%n j s*n Ло — Pzn о2;
— (fin—Fan) cos По + F{n sinq0 = prn с2;
(7.62)
1
2 F2nH-A,n Fin) sin т]о = Р2пс2;
— (F2n —F4n) cosq04-F2rt sinT]o = p'nc2,
для определения постоянных A„, Bn, Cn и D (n =
”=0,1,2,...).
В результате решения частных задач по приведенному
плану условия на боковой конической поверхности выпол-
няются точно, а на торцах — только в смысле статистиче-
ской эквивалентности приложенным силам. Если считать
торцевые поверхности сферическими и использовать первую
(2.45) и вторую (7.49) формы решений, то можно удовлетво-
рить точно условиям на всей поверхности конуса. Процесс
решения усложняется, число постоянных удваивается, оп-
ределение их величины требует исследования и решения бес-
конечной системы уравнений.
В случаях деформаций бесконечно длинных конусов
функции напряжений представляются в интегральной фор-
ме. Две задачи в этой форме рассмотрены далее.
7.11. Сжатие конуса радиальными силами,
равномерно распределенными по контуру
поперечного сечения
Рассмотрим следующую задачу.
Бесконечно длинный конус нагружен радиальными си-
лами, равномерно распределенными по окружности некото-
рого поперечного сечения (рис. 38). Выбирая параметр с,
совместим начало отсчета координаты | с местом приложе-
ния нагрузки.
Предполагая, что силы q распределены по полоске —
—е < | < е поверхности конуса, и уменьшая ширину этой
217
полоски до нуля, получим выражение для нагрузки р
в форме несобственного интеграла:
(7.63)
g (
Fr — з I
2 ’ J
лее о
Функции напряжений <p, Ф и й запишем также в форме
несобственных интегралов:
-L £ °°
Ф = А0 е 2 sin2 q J D (X) К* (у) cos XgdX;
1 °°
Ф = Аое 2 sin2 q j* [Fj (X, q) sin X£-f-F2 (X, q) cos Xg] dX;
о
(7-64)
n)]sinX!j4-
cLe ~ о
-H3F2(X, q) —F4(X, q)]cosX£} dX.
Здесь (X, г]) (к = 1, 2, 3, 4) — функции X и tj, определяе-
мые равенствами (7.52) при С = 0; А (X), В (X) и D (X)
— функции X, подлежащие определению.
По равенству нормальной силы нулю в
рассматриваемой задаче функция Ф должна
быть равна нулю на поверхности конуса,
т. е. Fv (X, т]) = О, F2 (Хт)) = 0 при q = т]0.
Этим условиям нетрудно удовлетворить
соответствующим выбором функций А (X) и
В (X), именно положив
A (X) = XD(X)62; fi(X) =
(Ь)
^(0
Рис. Зв
D(X),
где b = cos т]0.
По второму контурному условию (7.1)
Л, sin т]о f [F{ (Ь, По) sin Xg+F£ (X, По) cos Х£] dX =
О
p ас Г
= — Ло I [Fi (X, т]0) sin X£+F« (X, q) cos X£] dX— J
о о
216
получаем значение постоянной Ао = — и два уравнения:
Л
F3(X, ЛоН + Ff (X, Т|о) sin 0;
^i(X, По) 6+^2 (А-. По) sint]o= ~ 1.
первое из которых приводит к уже установленной связи
А (X) = XD (X) Ь2, а из второго, при обозначении
D* = 2 (1 -v) ЬК^ (б)+( Х»+-Ц М +62) (Ь) +
4-6(1—б2) К; (Л)
Кх(Ь)*х(Ь) 1
к; (6)
(7.65)
следуют значение функции D (X) и окончательные выраже-
ния функции А (X) и В (X):
~ , 1 Х£2
D(X) = ——; Л(Х) = —— ;
В(Х) = -
1
2D*
1 \ ькк (Ь) -
4 ) К^(Ь)
(7.66)
Задача в принципе решена. Остальное заключается в
формальном составлении по формулам (7.52), (7.57), (7.54)
функций Fh (X, т]) (k = 1,2, 3, 4), перемещений и напряже-
ний, соответствующих рассматриваемому нагружению кону-
са, и в выполнении подсчетов. Общие записи сложны, по-
этому ограничимся приведением наиболее просто записы-
ваемых результатов.
Представим напряжения в таком сокращенном виде:
n л° f
e R VcR J
__ ^0 (
°'’- rV^r J
i sin Xg + (an)2 cos Xg] dX;
A
°e=Ti
7=" I sin4+(ae)2cos^l
J
(7.67)
A f*
*1-----O1/-D I Sin Ч+(Т8ч)* COS 41 Л-
RycR J
219
Здесь через и (сг/)2 обозначены коэффициенты соот-
ветственно перед sin XI- и cos равенств (7.54), не зависящие
от Подсчет напряжений в зоне, достаточно отдаленной от
поверхности конуса, выполняется по приведенным формулам
без особых затруднений. В частности, на оси вращения
2ЬКк (Ь)
Ч (Ь)
dk
cos ХЕ ---- ;
ь D*
00 = 0^; =0 (b =cost]o)- Перемещения и=0;
ЬКк(Ь) 1
—-------- sin ХЕ
к; (Ь) |
ЬК„(Ь) 1 dx
^r]cosXi(^-
оо
Др / 1 \
ш = —i X 1—2v-|-624- х2+—
2ИУсК J \ 4 /
В точках боковой поверхности конуса (т) = т]0) напряже-
ния и перемещения представляются расходящимися интегра-
лами. Поэтому в области, близкой к поверхности, не говоря
уже о самой поверхности, подсчет напряжений и перемеще-
ний по полученным формулам практически невозможен.
Для улучшения сходимости в этой области воспользуемся
приемом, который был применен в гл. 4 при рассмотрении
аналогичных нагружений цилиндров. Заменим подинте-
гральные выражения в формулах (7.67) их асимптоти-
ческими представлениями (с^),-.
Запишем затем каждый компонент напряжений в форме
Ло
RVcR
1(^)1—(ai)J sin 4+ l(ai)2—(<y i)z] cos XHdX+
220
Разности в квадратных скобках подинтегрального выра-
жения первого интеграла при увеличении 1 убывают по ха-
рактеру их построения. Численное вычисление этих инте-
гралов оказывается практически осуществимым. Вычисли-
тельные трудности, связанные с плохой сходимостью выра-
жений для напряжений, переносятся во второй и третий
слагаемые последнего равенства, связанные с асимптоти-
ческим представлением подинтегральной функции. Вы-
кладки приводят для них к известным интегралам:
е ^esinX£dX.=
е ке cos X£dX, = е
ь е24Ча
О о
где е = т)0 — т) — малая величина при т), близком к т)0-
Удерживая только первые члены асимптотических пред-
ставлений функций Меллера и их производных [24]
еХт) /
Kx(cost])=
у2лЛ51ПТ] \
К; (cosт]) = —------
sinT] [/2лк sinт]
(cos т]) =------
sin2T] 1/2nXsinT]
COST] \
8Х sin т] у
1 3 cos т] \
8Х sin т] у
15cost] \
8XsinT] /
после выполнения всех довольно длительных преобразова-
ний получим для напряжений в области, близкой к поверх-
ности конуса, следующие выражения:
Ао sin2 т]
о» =-------1
6 R^/cR
sin т]
о
+ [(о^)2—(1 — V) S cos т]е“Хе
1 Г
~ 2_Lt2 8(1-
е2+£ L sin т]
] cos X£>dX—
Ao cos T]
aT1 RVcR
J 1 (°n)icos П sin *£ + [(°т))2 cos n -
о
—(14-cos2 T]V sin2 T]) Se Ze] cos Ц} dX4— --
X (14-cos2 t] 4“ V sin2 T]) S
221
oe =
о©)!—2vsini]Se
^]ЛЧ + |(„Л +
+2v cos T]Se Xe] cos X£} dX 4
2v \
—— (£ sin t] — ecosi])S ;
(7.68)
j40sinr) ( С
Т6Ч = Н {(T6n) COS ч sin U-I
—(1+cos2 i)+Vsin2»]) Se~^е1 cos Л£} dZ-f*
е
Здесь
S =
sinTjo
sin i]
В точках поверхности конуса (т) = т)0, е = 0)
1
V ~ о . ------(462— 156 sin n0 ctg т] 4-3 cos2 п).
8sin2T] *
а.
(
«Т/cR
, 2 ,____
4- [(1 — Л2) (o6\2- fr] cos X£) dX- у У1 -б2
(7.69)
(ОС
f ([(0^-2* УГ^2] sin 4 +
J
+ |(a6)-2 + 2vfrl COSXM dK
<уп = т6я=0, если ^0и on:^т£т1--оо если $=0.
В табл. 28 приведены значения напряжений на оси на
поверхности конуса, подсчитанные в точках, достаточно
близких к месту приложения нагрузки. При расчетах при-
няты ц0 = 15°, коэффициент Пуассона v = 0,3.
222
Таблица 28
Е л 12 л 18 л 36 0 л 36 л 18 л 12
e^ = R/c 0,770 0,840 0,916 0 1,091 1,191 । 1,307
1)=-.= 0
а£/ qc —0,45 0,15 1,45 1,58 —0,02 —0,83 -0,62
uQ/qc — ,,44 —1,71 —3,73 —3,82 —2,30 —0,54 0,01
o£/gc
ae/gc
0,29
—0,72—1,07 —2,63 —оо
0,35-0,22 —сю
—3,02—1,26—0,46
—0,21 0,02 0,09
7.12. Сжатие конуса в направлении оси вращения
силами, равномерно распределенными по контуру
поперечного сечения
о.
Рис. 39
Для получения значений напряжений и перемещений
при нагружении конуса осевыми силами qz = q, равно-
мерно распределенными по окружности поперечного сечения
5 = 0 (рис. 39), воспользуемся функ-
циями напряжений (7.64), дополнив
подинтегральное выражение функции
Ф членом С (X, т|) Кх (у) sin Х£.
По характеру нагружения нормаль-
ная сила N равна нулю в части конуса
от вершины до места приложения сил q
и имеет значение 2V =— 2jt^csin>]0 в
остальной части. Следовательно, функ-
ции Ft (X, h) и F2 (Хгт)) должны быть взя-
ты такими, чтобы их контурные значения
определяли такой же характер измене-
ния функции Ф, связанной с 2V равен-
ством (1.36). Это будет выполнено, если
положить
^(Х, т]о)=---’ F»(X’ 1 1 < • <7 70>
Ха+— 21Х24-—)
4 \ 4 /
223
Действительно
— g
Ф = Ао е 2 sin2 т)о
Xsin cosX$
------------dX=
V+T
f 0 при £ = 0
( i40nsin2T]() при £>О,
л N
где постоянная я0=———---------------•
2л2 sin21] о
Подставляя в (7.70) значения (7.52), получим два равен-
ства, из которых нетрудно выразить функции А (X) и В (X)
через функции С (X) и D (X):
По второму контурному условию (7.1) для С (X) и D (X)
находим:
X 1
с=---------; D=—---------------—- . (7.71)
(x2+~)d* 2(X2+-^-Jd*
к; (6) г
где D*=---------------—-------- 2(l-v)WC;(b) +
6K;(6)+k2+-y-Ux(6) 1
(1+Ь2)Кх(Ь) +
-м>(1-62)
[K;(fr)]2-Kx(fe)^(fr) ъ
к;<») If
(7.72)
224
Функции А (X) и В (X) получают окончательные значения:
X Г 4 '
к; (6) [ 4Х2+1 + D*
В(Х) =
1
2*; (ft)
4 2ft2+ft/(x(ft)'
4Х2+1 + D*
(7.73)
Напряжения определяются формулами (7.67) при Ло =
= Л7(2л2 sin2!]). На оси вращения
— [8к; (ft)+(4X2+1) ькя (ft)] j sin 4+
[ 1 +-7^- [8К; (ft) - 2 (4Х2+1) (1 - 62) (6)+
£ I Ls
+(4X24-l)ftKx(ft)] > cos Х£
dX
2K;(ft) :
J H1 lSvK* <',>-<4V+» bK* <«J}sin«+
"o'
+V ( 1 —77T [8vKx (b)+2 (4X2+1) (1 -ft2) (ft)-
1 \ dX
- (4X2+1) bK„ (ft)] cosXfc)—— ;
J / 2/\x(o)
w =---
2И
1—ft2
sinX£ +
К; (ft) 2D*
о
ft*x (ft)
+ (4X24-1)—-------
2K; (ft)
cos X£ I dX;
°e=%; TEn=0; u=°-
В области конуса, близкой к поверхности, для подсчета
напряжений следует (как сделано в п. 7.11) выделить рас-
ходящуюся часть интегралов, представляющих напряже-
ния, прибегая к асимптотическим представлениям подинте-
225
гральных выражений. В результате такого выделения на-
пряжения в точках поверхности конуса записываются в
следующем виде:
Ло(1-И
аЕ=----7=^
6 RVcR
2b
_______sinX£ +
У1-62
о
+ [(at)2—Ч cosiqdH
2Ь
л0
ай= —---;—
rVFr
14-2v6 Vl—62]sin +
o
+[(°б)2+2v(1 cos ^1<&—V'b Vi-ь21;
оп=т£т) = 0 если £=#=0 и оп = т£т) = оо если £ = 0.
Напряжения на оси и на поверхности конуса, подсчи-
танные для конуса с боковой поверхностью, определяемой
значением углат)0 = 15°, в точках, близких нагруженному
сечению, приведены в табл. 29. Там же приведены напряже-
ния при сжатии конуса сосредоточенной силой, приложен-
ной в вершине, подсчитанные по (7.6).
Таблица 29
&
л Л л л 36 л 18
12 18 36
л
12
т)=0
qc oQlqc — 1,68 0,50 —2,03 0,75 —2,36 0,52 —2,57 —0,86 —3,10 —0,51 —3,11 —0,21
G^/qc cQlqc —0,94 0,28 —0,13 —0,55 Т] = Т]о —2,26 1,54 —6,16 — 1,08 —3,89 —0,27 —3,09 —0,10
а6/qc °^bc —0,820 0,021 Сила в —6,885 0,018 вершине т)=0 —5.791 0,015 конуса —4,074 0,011 —3,425 0,009 —2,844 0,007
а£/ qc aQ/qc —10,593 —0,043 —8,850 —0,036 Т) = Т)О —7,442 -0,03 —5,287 —0,021 —4,402 —0,018 —3,655 —0,015
226
Глава 8. ДЕФОРМАЦИИ ШАРОВ
И СФЕРИЧЕСКИХ ОБОЛОЧЕК
8.1. Сжатие открытой сферической оболочки
Рассмотрим некоторые осесимметричные задачи о де-
формациях шаров и шаровых оболочек при нагружении их
поверхностными или объемными силами. Изучение напря-
женно-деформированного состояния шара, в частности, важ-
но для геофизики, что послужило причиной особого внима-
ния исследователей к этой проблеме. Работами Ламе и
Кельвина было положено начало теории напряженного со-
стояния Земли. Ими указаны формы решений уравнений те-
ории упругости в сферических координатах и получены не-
которые частные результаты. Также большое практическое
значение имеют задачи определения напряжений и деформа-
ций при нагружении сферических оболочек и определения
концентрации напряжений у шаровых полостей или включе-
ний инородного материала в нагруженном теле.
В настоящее время имеется обширная литература, по-
священная изучению деформаций шаров и сферических обо-
лочек, указания на которую можно
найти в [46], [48] и др.
Приведем в первую очередь про-
сто составляемое решение задачи о
сжатии открытой сферической обо-
лочки вдоль оси вращения (рис. 40).
Открытой сферической оболоч-
кой (термин введен Б. Г. Галерки-
ным [23]) принято называть оболоч-
ку, которая имеет два выреза с ко-
ническими поверхностями, общей
осью и вершинами в центре сферы.
Такими оболочками являются, в
частности, купола, снабженные в Рис. 40
верхней части фонарями. Давление
от фонарей (собственный вес и равномерная нагрузка на
перекрытие) распределяется равномерно по длине окруж-
ности кольцевого верхнего выреза и эквивалентно силе,
сжимающей оболочку по оси. Распределение деформаций
и перемещений при этом симметрично х.
1 Влияние ветра и неравномерное нагружение фонаря куполь-
ного перекрытия приводят к чистому изгибу оболочки и к изгибу си-
лой, направленной перпендикулярно оси. Значение напряжений и
перемещений в этих случаях нагружения оболочки см. [67].
227
Обозначим через и £0 координаты, определяющие соот-
ветственно внутреннюю и внешнюю сферические поверхно-
сти оболочки. Используя значения (2.45) при к = 0, за
функции ф и <р принимаем: ф = A -j- Bet; <р = С + De*.
По формуле (1.17) Ф = ф + z составляем функцию Ф
Ф = А + Ве^ + De^ cos21].
Контурное условие (1.38) для функции Ф
N
2л
где а — радиус внешней и аг — радиус внутренней поверх-
ности тела вращения, при сферических поверхностях, сво-
бодных от сил, направленных вдоль оси z, запишем в форме
N N
Ф(а)=——— ; O(ai)=——,
4л 4л
что приводит к более симметричной записи окончательных
результатов. Тогда на внутреннем и внешнем контурах осе-
вого сечения
р р
A=Bbi=—-------- ; А-\-ВЬ= -, где Ь=е^° и bi = e^1,
4л 4л
я Р
нормальная сила N = —Р. Отсюда А=—---------—,
4л Ь — Ьг
Р
В=-----------,
2л (Ь — bj)
Функция Ф получает следующий вид:
Р 64-6, —2е£
ф = —------—-------.
4л 6—Ь±
Составляем функцию Q [см. формулу (1.26)]
Q = — —
г2
Р b + fei-
4л 6 — 6
2(1—v)C
и применяем второе контурное условие (2.15) при £ = £0
и 5 = ^:
Pb Р
intb — bi) 4 л
дф дг
——;
Pbi
— v)C;----
7 2л(6—60
4-2(l-v)C.
4л
228
Оба равенства выполняются, если
с_ P(b+bt)
8л (1—v)(6—by)
Окончательное значение функции Q:
Р
й =--------------
2л (Ь — by) г2
Напряжения, соответствующие полученным функциям,
следующие:
Р
си — т»_ =0; О-= — = —------------------(8.1)
* £т) п 6 2л (b—by) г2 v '
или, если обозначить через R0 = cb и Ry = cbx радиусы, оп-
ределяющие поверхности оболочки, а через R = рас-
стояние от точки, в которой определяются напряжения,
до центра оболочки:
R
°е- 2я (Ro_Ri}r2 •
Таким образом, в рассматриваемом случае нагруже-
ния открытой сферической оболочки напряженное состоя-
ние соответствует чистому сдвигу Ч
Подстановка найденных функций напряжений в равенст-
ва (1.12) и интегрирование их приводят к следующим выра-
жениям для перемещений:
Р R Р 1 (. 1-f-cosn \
и =----------------: w = —--------------In---------4- Dn I.
2лр. (Ro — Ry) г 2лр. Ro—Ry \ sin i] /
(8.2)
где Do— постоянная интегрирования, определяемая усло-
виями закрепления оболочки. Если положение опорного
кольца соответствует координате т] = >]0, то =
, 1 cos п
— 1п —Ц------1, и поэтому окончательно
sin Т)о J
Р , (1-|-cos т]о) sin 1]
W = —----------- In ------------- •
2лр.(Я0— Ry) sinT]0(14-cos ц)
1 Заключение справедливо для всего объема оболочки только в
том случае, когда приложение силы Р по конической поверхности
осуществлено по такому закону, по которому определены напряже-
ния (У^ и т^. В противном случае напряженное состояние у краев
оболочки должно быть уточнено.
229
8.2. Деформация шаровой оболочки
при нагружении ее поверхностей
равномерно распределенными нормальными силами
Рассмотрим решение задачи Ламе о полом шаре, находя-
щемся под внешним и внутренним давлением. Обозначим
через р и рг равномерно распределенные радиальные си-
лы, приложенные соответственно к внешней и внутренней
поверхностям сферической оболочки. Нормальная сила в
некотором сечении, определяемом координатой т], имеет
значение
ч ч
N = —J 2npr cos т]се*в dr\ + J 2nprr cos цсе*1 dr\ =
о о
= —л (pR2—p! R2) sin2 т].
Здесь £0 и — координаты, соответствующие внешней
и внутренней поверхностям оболочки, R = се^> = cb и
= се^1 = сЬг — радиусы этих поверхностей.
N
По условию Ф (£0, Т]) — Ф (£lt п) = — 2л > следует, что
функция Ф (£, т]) на каждом из контуров в осевом сече-
нии должна быть пропорциональна sin2 т), т. е. из числа зна-
чений ф и ф в сферических координатах [см. (2.45)] для по-
лучения решения нужно взять
ф=с2 (Ае2£-}-Ве~sin2 т], <р = с2 (Ce2^-j-De~sin2 т],
при которых
ф =с2 (Ae2^-j-Be~—3De~cos2 т]) sin2 т).
По сказанному ранее, постоянная D = 0. По условию
(2.15)
дФ
“7— = — ryHpz, при £=£о и
дт)
имеем:
AtP+Bb-i=-^-pb2-, Ль2+вь7«=-^Р1ь2,
£ £
так как рг = — р cos т) на внешнем контуре и рх =
= — Pi cos т) на внутреннем. Из последних равенств
А = pb3—p! fr? в = _ (p—pJ (bbJ3
2(Ь3 —ft3) ’ 2(Ь3—Ь3)
230
Составив функцию й [см. (1.26)]
Q = A—2(l+v)C + Be~3E
и применив второе контурное условие (2.15)
+ "]А/рг , где Pr = — psinr] при £=£0
и рг = — hsinij при $ = $!,
находим постоянную С:
с_ 3(р&3-Р1Ь?)
4(14-v)(ft3-b3)
Итак, в рассматриваемом случае нагружения полого ша-
ра
Ф='9/М1 азч \pb3—Pib9i—(P—Pi} ] e26sin2T];
2 (d3—o’) L \ е* / J
(8.3}
Л 1 г / ьь. \31
Q=L2 {рЬЗ-р> *?)+('-*) hr) J •
После подстановки этих значений в формулы для напря-
жений (2.20) имеем:
а6=------------— [рЬз (езЕ_ьз)+р1 Ьз
5 (&з—ЬЗ)еЗЕ
(8-4}
°т) = аб = ------?(2*3*+&?)-Р1 Ь? (2е3^ 4-Ь»)];
л 2(Ьз_ьз)ез$
Ъ. = °-
Соответствующие перемещения:
ut =
2(l-2v)(pb3-P1ft3) +
се^
2Е(Ь*—Ь*)
и =0
ч
(8.5}
В частном случае, когда внешняя поверхность оболочки
не нагружена (р = 0)
Pi f Pi ь,
аЕ=-------------тг (Ь3 —edfe); о_ =ое =----------—
6 (Ь3_&з)е3£ л ° 2(&з_ьз)еЗЕ
(2е3^+6з),
напряжения <тЕ — сжимающие, а <тп и ст© — растягиваю-
щие во всей области оболочки. При Ь = 2ЬХ графики этих
напряжений представлены на рис. 41.
231
Если радиус внешней поверхности значительно больше
радиуса внутренней (b > bj), то <т6 = — рх (bYe~^) 3,
о,) = ое = pj (b£)3.
Эти значения соответствуют напряжениям в бесконеч-
ном пространстве, вызванным центром равностороннего дав-
ления в точке, принятой за начало координат. В другом ча-
стном случае, если от нагружения свободна внутренняя по-
верхность полой сферы (pj = 0)
Pft3 , ot pb3 . Ot х
оЕ=—-----------— (e3£-ft3;; о —oe= —--------------— (2e3*+ft3),
6 (fe3_ь3)е3* Л 2 (ft3— ft3)e3«
напряжения сжимающие. Наибольшие значения по абсо-
лютной величине оч и (Те имеют в точках внутреннего конту-
ра
3pft3
<4 нанб — 2 (ft3 —ft3)
Считая b blt получим значения напряжений в беско-
нечной среде, имеющей сферическую полость радиуса
= cbx. Наибольшая абсолютная величина напряжений
оп и сте при этом |<тл| = ]сге| = 1,5 р превышает в полтора
раза напряжения в среде,
Рис. 41
не имеющей полости, — коэффи-
циент концентрации напряжений
равен 1,5.
Используя полученные ре-
зультаты, нетрудно получить
значения напряжений и переме-
щений в слоистом полом шаре,
составленном из вложенных одна
в другую сферических оболочек
с общим центром. Ограничимся
рассмотрением простого слу-
чая — сферической оболочкой с
полостью, заполненной упругим
веществом. Модуль упругости
последнего обозначим через Ег.
Напряжения и перемещения
при равномерном обжатии шара силами р имеют значения
(8.4) и (8.5) при Ьх=О. По условию равенства перемещений
по поверхности контакта (£ = £х)
сЬг
2 (1 —2v) (pft3—Pi ft ?)+(1 + v) (P-P1) ft3 =
2E(ft3—ft3)
1—2v
"Т----Pi cbi
232
для контактного давления рх получаем следующее значение:
________________*3(1— у) __________________
Р1~ 2(1— 2v)(E —Ejfb3 — Ь’)+3(1— Р'
В частном случае, если ядро абсолютно жесткое (Е1 -= оо),
3(1—v) ьз
Pi=------------------------------р •
(1+у)Ь3 + 2(1—2у)Ь3
При b bi (равномерно сжатое бесконечное пространство
с жестким ядром) ру = 3 р и напряжения
з
оЕ=-р
2(1—2v) / b
1—2у
1—-----
31
%=°е=-Р
е*
Л
В точках поверхности контакта о6 = — plf
у
1 —v ^1‘
(Гц — 00
8.3. Концентрация напряжений
у мелких шаровых полостей
Решение уравнений осесимметричной задачи в сфериче-
ских координатах позволяет довольно просто получить
приближенные значения напряжений и перемещений в об-
ласти шаровой полости при осесимметричном нагружении
среды, тем ближе к точным, чем меньше радиус полости по
сравнению с размерами тела. Задача эта привлекала вни-
мание многих исследователей. Первое решение ее для кон-
центрации напряжений у шаровой полости в растянутом
стержне принадлежит Р. Саусвеллу [113], оно повторено
в работах Дж. Гудьера [96], К. Мар герра [103], Г. Ней-
бера [49] и др. В п. 8.2 уже получены значения напряже-
ний у шаровой полости и у шарообразного включения в
среде, находящейся в условиях равномерного трехсторон-
него сжатия. Здесь и в пп. 8.4—8.5 рассмотрим напряжен-
ные состояния у шаровой полости в растянутом стержне и
в сжатой и изогнутой толстой плите, пользуясь формулой
(2.45) функций напряжений.
Воспользовавшись значениями этих функций при к =1
и к — 3, составим выражения ф и <р в следующей форме:
ф = [Л14-В1 е~3^4-Езе(5cos2T] —1)1 г2;
^-(CH-D^-36)/-2. (8-6)
233
Соответствующие им функции Ф и й имеют вид:
ф = [А 4-В! е-36 — В3 е~56 + (5В3 е~56 — 3D, е“3*) cos2 т]] г2;
(8.7)
Q =— Ф—2 (1 4-v) (С, 4-Dx е ~3*) +6D, е“3* sin2 т].
г2
Функции ф и Ф, как нетрудно заключить, удовлетворяют
условиям (1.32) при любых значениях входящих в них по-
стоянных (за исключением начала координат). При боль-
ших значениях аргумента £ члены с коэффициентами Вг,
В3 и D3 в функциях (8.6) и (8.7) малы по сравнению с чле-
нами с коэффициентами и Cv Поэтому при £ достаточно
большом в <р, Ф и й можно сохранять только последние
члены. Тогда
ф- Cjr2; Ф = Д,г2; й =А — 2(1 -f-v) С. (8.8)
Если положить здесь постоянные А± = — р/2, С± =
= р/[4 (1 + v)], получим решение задачи растяжения ци-
линдрического стержня силой р = рпа2, приведенной в
п. 3.2. Если считать = 0; С± = 2 то (8.8) сов-
падают с решением задачи сжатия сплошной круглой пли-
ты радиальными силами (см. п. 3.2).
Для сплошных цилиндров и плит постоянные В1г В3, и
должны быть приравнены нулю. Если же внутри обла-
сти, занимаемой цилиндром или плитой, имеется небольшая
сферическая полость, то, распоряжаясь соответствующим
образом значениями этих постоянных, можно освободить
поверхность полости от напряжений и тем самым получить
решение задач растяжения стержня и радиального сжатия
плиты, имеющих сферические полости. Совмещая начало от-
счета с центром полости и требуя выполнения условий (2.15)
Ф = 0 и = г при е* = еЪ = Ь, где — координата,
определяющая поверхность полости, для постоянных Вь
В3 и Dt получим следующие значения:
ь3
51 = -о/'? I5<1 л 1 —6 (1 +v)С11;
Z I / —DVJ
зм
В.=9,, .. [ЗЛ,+2(1+у) C.J;
D^=HV=^j|ЗЛ,+2<1+v)c,1•
234
В частных случаях стержня, растянутого силой Р =
— рла2,
4—5v 3 5
fli =-------pb3', Ba = —-------pb6', D, = —--------pb9
2(7 — 5v) 2(7—5v) 1 2(7—5v) P
и плиты, сжатой радиальной нагрузкой р,
3 3 5
Bi = —------— pb3', В3 = —------— pb6', D, = —-----pb3.
1 2(7 — 5v) 3 2(7—5v) 1 2(7—5v)F
Подставляя выражения функций (8.6), (8.7) в формулы
(7.5) при частных значениях постоянных, получим значения
напряжений в имеющих сферическую полость областях, на-
пряженное состояние которых на бесконечности определя-
ется функциями (8.8). Приведем эти значения и проиллюст-
рируем распределение напряжений соответствующими гра-
фиками.
При растяжении стержня
3—5v—4
(8.9)
Зр
2(7—5v)
На контуре полости при £ = £0
Зр
<’1-=',6Ч=0: % = - 2(7—5v) ।1 +Sv~10si"»41;
235
Зр
2(7 —5v)
На оси вращения (т] = 0)
[ 1 4-5v— lOv sin* T] ].
Зр
П о г 2(7—5v)
T6n=0-
3—5v—4
cb \3
Z J
В поперечном сечении стержня, проходящем через центр
полости (т) = 90°),
бр
о, = иг =--------------
6 г 7—5v
2
ТЬ1=°-
На рис. 42 и 43 представлены эпюры напряжений на
контуре полости и вдоль осей гиг. Ординаты этих графи-
Рис. 42
ков содержатся в табл. 30—32. Подсчеты произведены при
значении коэффициента Пуассона v = 0,3.
236
Напряжения в плите с полостью при нагружении ци-
линдрической поверхности равномерно распределенными ра-
диальными силами:
На контуре полости (£ = £0)
Зр
°{=’и=0; %=-^zS7<4-5sin’^
Зр
ae=-V-TT(4-5sin«n).
/ —DV
237
Таблица 30
238
0 1Б’ 30’ 45е 60е 75е 90’
% —0,682 Полос —0,499 гь в растянут 0 ом стержне 0,682 1,364 1,854 2,045
ае —0,682 -0,621 -0,477 —0,273 —0,068 -0,081 0,136
Полость в сжатой плите
% —2,182 —2,000 — 1,500 —0,818 -0,136 —0,363 0,545
*0 -2,182 —2,128 -1,977 — 1,773 -1,568 -1,419 —1,364
o^h/cb -1,835 Поле -1,565 сть в изогну! —0,894 ой плите —0,162 0,287 0,275 0
c^hjcb — 1,835 — 1,779 —1,380 -0,950 —0,556 —0,240 0
Таблица 31
239
г/св о/Р 1 1.2 1,4 1,6 1,8 2 2,5 3 ОО
°5 0 0,037 Полосп 0,245 в растянуто 0,412 м стержне 0,569 0,670 0,818 0,895 1
ф о II D₽ -0,682 -0,202 -0.054 -0,007 0,012 0,017 0,016 0,011 0
°Е 0 0,385 Пол( 0,390 эсть в сжато# 0,323 плите 0,259 0,205 0,117 —0,072 0
°i) = °e —2,182 -1,491 — 1,236 — 1,104 — 1,072 -1,046 -1,017 — 1,008 1
a^h/cb 0 0,269 Полос 0,234 ть в изогнуто 0,176 й плите 0,121 0,084 0,039 0,020 0
u^h/cb -1,855 — 1,484 — 1,500 — 1,642 - 1,820 —2,009 -2,502 -3,000 —
240
Таблица 32
r/cb о/Р 1 1,2 1.4 |.б 1.8 2 2,Б 3 ОО
Полость в растянутом стержне
0 0,204 0,195 0,162 0,140 0,102 0,059 0,036 0
% 2,045 1,460 1,236 1,132 1,082 1,053 1.223 1,012 1
°9 0,136 0.031 0,002 —0,022 —0,014 —0,009 -0,006 -0,004 0
Полость в сжатой плите
0 -0,230 —0,436 —0,596 —0,698 -0,773 —0,877 -0,927 -1
% 0,545 0,171 0,053 0,012 —0,004 —0,009 —0,008 -0,007 0
ст9 -1,364 -1,258 — 1,182 — 1,127 -1,094 — 1,071 —1,039 —1,022 —1
На оси вращения (А = 0)
В точках плоскости z = 0 (т] = 90°).
Значения этих напряжений при v = 0,3 приведены в
табл. 30—32, а их эпюры на рис. 44 и 45.
Функциями (8.6) определены следующие значения пере-
мещений:
« = ^{41 + 2(l-v)C1+[Bi+2(l-v)D1]e-3*-B1e-5t +
2И
+(5Bt е~—3Dy е~3^) cos2 т]} г;
№=--5-{2(41+2vC1)-(B1+2vD1)e-36+3B1e-56-
2И
—(5В3е~—3Dx е-3^) cos2 т)} (o»0 = const). (831)
В случае полости в растянутом стержне
241
при условии, что центр полости неподвижен (w0 = 0).
На контуре полости
р v 3—5v 1 р Г 1 13—15v '
и = —•-- -----—---------I г; и> =- -----+--------- z
2ц 1+v 2(7—5v)J 2ц | 1+v 2(7—5v)J
Рис. 44
В случае полости в сжатой плите
р / 1—v 1
2ц\ 1+v + 2(7—5v)
13 —10v—3
— 15
(8.13)
р / 2v 1
U) = -- I -----— ---------
2ц 1+v 2(7—5v)
3 + 10v—9
На контуре полости
p Г1—v 5(1—v) 1 p Г 2v , 3—5v "I
— T— I------+----------Ir'> “’=-------------------I 2.
2ц L 1+v 7—5v J 2ц [ 1+v 7—5v J
242
Следуя последовательности вышеприведенного решения,
нетрудно получить значения напряжений и перемещений у
малой шаровой полости с центром, расположенным в нейт-
ральной полости плиты, находящейся в условиях чистого
изгиба \ К значениям напряжений и перемещений в этом
случае приводят функции напряжений взятые из числа
(2.45) при к = 2 и к = 4.
Составим функции напряжений ф и ср в виде
ф= [Л2 + В2 е5^ + В4 е~7^ (3 — 7 cos2 т])] г2 г;
<P = (C2+D2e“56)r2z. (8.14)
Им соответствуют функции
ф = [Д2+С2+(В2 + Ра)е-5*+ЗВ4е-7*-
—(7Вле~ 7^+5D4 е~5&) cos1 2 т)| г2 г;
(8.15)
» = (2(l+v) (C2 + £)2e~56/— 10D2e-56 sin2T]1 z.
При достаточно больших £ функции (8.14) и (8.15) стре-
мятся к значениям
ф = Л2г2г; <p = C2r2z; Ф = (Лг-тС2) г2 z; Q = [42—(l+2v)C2Jz,
1 В [65] дано решение для случая, когда шаровая полость сме-
щена по отношению к нейтральной плоскости, а также для случаев
шаровой полости в плите, изгибаемой равномерно распределенными
силами.
243
которые при
Az-р/[2(1 +v) Л]; C2 = p/[2(l+v)Л]
представляют собой решение задачи чистого изгиба круглой
плиты. Силы р связаны с погонным изгибающим моментом
М равенством 2ph2 = 32И.
Предполагая, что центр полости находится в нейтраль-
ной плоскости, определим постоянные В2, Вл и D2 по усло-
виям отсутствия напряжений на поверхности полости, т. е.
по условиям (2.15). После выполнения вычислений
(l+v)65 4
— (7Л2+15С2) =--------
2 13—7v ' ’ 13—7v
5Ь7 t 5 pb'
Bt = — ---------[542+(7 + 2v) С21= — —------------—
* 2(13—7v) 1 v 2(13—7v) h
7b* 1 pb*
= —---------[5Дб+(7 + 2v) C21 = —-------- —---•
2 2(13—7v) 1 2(13—7v) h
Таким образом, решение задачи достигнуто.
Подставляя функции (8.14) и (8.15) в формулы (2.20) и
(1.12) при найденных значениях постоянных, получаем вы-
ражения для напряжений и перемещений:
(10+13 sin2 ij)
pz iГ Ib \5 5
CT_ =-- I 1 — I--- I cos2 n——---------- 2(3—7cos2n) —
h \L '• e6 / J 2(13—7v) ' "
CTe =
{10 (4—7v sin2 ij) +
(8.16)
244
— 21
Р I 1—V
2p,/t I 1-J-v
(3—7 cos2 ij)
1
2(13—7v)
1
2(13—7v)
14(l-v) +
l + 14v —9
(2—3 sin2 ij)—
(2—5 sin2 ij) cos2 ij
(r24-z2)+a»0;
(8.17)
[0O = const. Если считать перемещения в центре полости
равными нулю, ш0 = 0.
На контуре полости (£ = Ео)
5pz
а». = т,_ = 0; ст_ =----(4—7 sin2 п),
6 tn П (13—7v)h '
afi =---------(4—7v sin2 л);
6 (13—7v)h "
_ (1—v)p
Eh
7(l+v)
Ф 13—7v
(3—7cos2ij) rz;
P
w—----
6Eh
- 12 ~3 sin* 4)] <ra+2*)-
13—7v J |
Рис. 46
245
На оси вращения
В табл. 30 и 31 приведены значения напряжений на кон-
туре полости и на оси вращений при v = 0,3, эпюры даны
на рис. 46 и 47.
8.4. Концентрация напряжений
у жестких сферических включений
Решение задачи о напряженном состоянии у малого жест-
кого шарового включения в бесконечной среде составляется
аналогично решению задачи в п. 8.3. Функции напряжений
принимаются в форме (8.5). Значения постоянных Ах и Сг
определяются нагружением на бесконечности. Постоянные
Blt В3 и Dj связываются с Аг и С\ условиями отсутствия
перемещений на шаровой поверхности включения.
Приравнивая нулю перемещения и и w [см. (8.11)1 при
Е — Во» где Ео— координата, определяющая поверхность
полости, и обозначая е6* = Ь, приходим к трем уравнени-
ям:
4x+2(l-v) D,] =
2 +2vC!)—(Bj + 2vDi) Ь~я +ЗВ3 b~°=0:
246
5В, Ь-в—3Dj 6-s=0.
Решая эту систему относительно постоянных Blt В9 и D
получаем:
1 [5(1 —2v) Дх-6(3-1 lv+ 10v2) CJ6»;
4(4 — 5v)
Bi=—
2 4 (4—5v)
5
= -л/. +2 <1 +v> •
4 (4 — DV)
В случае растяжения среды в направлении оси г, т. е.
в случае растяжения стержня, размеры поперечного сече-
ния которого во много раз превышают радиус включения,
Аг = — р/2; Ci =——;В1 = —7~ 19v+1_Ov—
4(l+v) 4(l+v)(4—5v)
3 5
В3 =--------pft6; D, =--------pb3.
8 4(4 —5v) 1 4(4—5v)
Перемещения (w = 0)
b
Р
и = — —
ST
1 —
V
2
Э
4- —----— (4—5 sin2 tj)
4(4—5v) "
1 —
э
Ь
Р
е
2
*"77;—— (2—5sin2t])
4 (4—5v)
b_ V
/
Ь
е'
г. (8.18)
Напряжения имеют значения р
о,=р cos2
П —
p
2(1+v)(4-5v)
6 5—v—2 (1+v)
b
2
( ь
-(1+v) 5(5—v)—18 —
\
2П
sin2 ij
s
; (8.19)
b
247
(Г / L \2
/ и \
12 1—2v— (1+v) I- I
\ Л /
— (1+v) 5(1— 2v)—21
(8.19)
'.=--------*—
6 4 (1+v) (4—5v)
1 Г / b \2]/ b V)
F?T^7)[5(2-v)-3^J ) sin Y) cosy).
1
На контуре включения
0 __ 30—V)P
6 2 (1+v) (4—5v)
[6 — 5 (1 +v) sin2 tj];
°* = °" =2'(F+v)(4-5v) 16~5 <'+ V) Sin’ ”1:
15 (1 —v) p
^=—l(4-5v) “"’’««’I.
На оси z (y] = 0),
В точках плоскости z = 0 (i) = 90°)
Зр Г I cb \21 / cb \s
o.=ar = — ----------— 1 +8v—5v2— 2 (1 +v) ---I I-----I ;
6 2 (l-b-v) (4—5v) L 4 r r )'
P г
%=^ = P-4-(7Tv)(4^^v) [(|-2V> <7-5V>+
3p f cb \21 / cb \s
6 = ,,,, . . (l-2v)(l+5v)-(l+v) ---- ------ ;
♦ (l+v)(4—»v)L \ r I i\ r )
ъ>-°-
248
В случае равномерного сжатия среды в направлении,
перпендикулярном оси z, т. е. в случае радиального сжатия
круглой плиты, толщина которой значительно превышает
радиус включения, постоянные Ах = 0; Сг =—р/[2 (1+v)];
3(3— llv+10v2) 3 5
Bi =----------------pb3; Вя =--------pb6; D, =-------pb3.
1 4(l+v)(4—5v) 3 4(4—5v) 1 4(4—5v)
Перемещения
3(i+v)
4 (4—5v)
(4—5 sin2 т]) X
(8.20)
(2—5 sin T])
3(l + v)
4(4 —5v)
Соответствующие напряжения
ст = —p sin2 т] + f..—— (б (1 + 8v—5v2)—
6 2 (1+v) (4 —5v) (
-12 (1+v)
5(5—v) —
P I
о = — p c°s2 T] + — —— 4 (1 - 7v + 10v2) +
1 4(1 +v) (4 —5v) |
+ 12(l+v)
5(1—2vl—21
(8.21)
p
<>Q=-P+ . 4 (1 -7v+ 10v2) +
4 (1+v) (4 — 5v)
249
5(2—v) —
₽i1+2(4—5v)
Ha контуре включения (£ = £0)
3 (1 —v) p
°* В * * *= -2n+v)(4-5v)12
3vp
%=’•= -2(| + v)(4-.5v)12 ('-5v)+fH'+’)’in’4b
15(1—v)
Tt_ = ——------p sin Ti cos Ti.
tT1 2(4—5v) 1 1
На оси z (т) = 0)
3p „ / cb \2’ / cb \3
at=oz = —————— 1+8v—5v2—2(1+v) I-------- (--);
6 (1+v) (4—5v) \ г / .1 \ z /
P
o_ = On = Or = — p 4
n e r F-г (1_|_v)(4_5v)
in-0-
В плоскости z = 0 (т) = 90°)
P
at = a = — p—-----------
* r 2(l+v)(4—5v)
19—28v+25v2—
% = oz =
3p
3—llv+10v2 —
19—43v+10v2—
P+ 4(1+v) (4—5v)
-3(1-v)
=0.
В табл. 33—35 приведены значения напряжений на кон-
туре включения, на оси z и в сечении z = 0. Подсчеты выпол-
нены при v = 0,3. По результатам подсчетов нетрудно за-
ключить, что на расстояниях, превышающих радиус вклю-
чения в три раза, влияние включения на напряженное со-
стояние среды мало.
250
Таблица 33
п а/р 0 15е 30е 45е 60е 75° 90"
Жесткое включение в растянутом стержне
Q Q J Л» II Q а> 1,938 0,831 1,798 0,771 1,413 0,606 0,888 0,381 0,363 0,156 0,001 0,001 —0,162 —0,069
Жесткое включение в сжатой плите
Q Q II Q а> 0,323 0,138 0,181 0,080 —0,202 —0,067 —0,727 —0,316 — 1,252 —0,537 — 1,614 —0,692 — 1,777 —0,762
Таблица 34
z/a о/Р 1 1Д 1.4 1.6 1,8 2 2,5 3 ОО
Жесткое включение в растянутом стержне
Or
Oz
I 0,831
| 1,938
0,269
1,852
0,089 I 0,024 I 0 I —0,009
1,625 | 1,440 | 1,307 | 1,217
—0,011
1,087
—0,009 I 0
1,040 | 1
Жесткое включение в сжатой плите
Or
Oz
I 0,138
| 0,323
—0,551
0,772
—0,779
0,546
—0,901
0,436
—0,985
0,340
—0,997
0,265
—0,999
0,150
| 0,091
Таблица 35
г/а ~Г 1 1,2 1.4 1,6 1,8 2 2.5 3 сю о/Р
Жесткое включение в растянутом стержне
Ог -0,162 -0,386 -0,273 -0,218 -0,170 -0,133 -0,075 -0,045 0
Ог -0,069 0,451 0,771 0,873 0,923 0,951 0,980 0,990 1
ае -0,069 0,013 0,028 0,028 0,024 0,019 0,012 0,007 0
Жесткое включение в сжатой плите
От -1,777 -1,662 -1,496 -1,3681-1,275 -1,210 -1,114 -1,068 -1
ог -0,762 -0,487 -0,321 -0,213-0,139 -0,087 -0,006 -0,004 0
-0,762 -0,809 -0,860 -0,897-0,925 -0,942 -0,969 -0,981 -1
Не будем приводить решение задачи о концентрации на-
правлений у жесткого сферического включения в нейтраль-
ной плоскости изгибаемой плиты. Оно может быть состав-
лено так, как было сделано в п. 8.3. для шаровой полости,
при использовании той же формы (8.14) функций напряже-
ний. Граничные условия, естественно, должны быть измене-
ны: вместо равенства нулю напряжений на поверхности по-
лости нужно требовать равенство нулю перемещений на по-
верхности контакта среды с жестким включением.
8.5. Концентрация напряжений у сферических
полостей при несимметричном нагружении среды
Выйдем за рамки рассматриваемой области задач теории
упругости, соответствующих осесимметричному деформиро-
ванному состоянию тел вращения. Пользуясь полученными
результатами [см. (8.9) и (8.11)] по совершенной симметрии
шара, т. е. симметрии относительно любой оси, проходящей
через центр, можно просто составить выражения для напря-
жений и перемещений у шаровой полости или шарового ино-
родного включения в теле достаточно больших размеров по
сравнению с диаметром полости при однородном трехсторон-
нем растяжении или сжатии различными силами — следо-
вательно, в любом однородном напряженном состоянии сре-
ды. Указываемые выражения являются суммами напряже-
ний и перемещений, вызванных силами с интенсивностями
Pi» Рг» Рз> направленными соответственно вдоль осей х, у, z
декартовых координат. В последнем случае для среды с по-
лостью напряжения определены равенствами (8.9). Их сле-
252
дует преобразовать к декартовой системе, что осуществляет-
ся просто, но приводит к громоздким выражениям, поэтому
ограничимся приведением значений напряжений только в
точках поверхности полости (£ = £0). Обозначая радиус
полости через а, имеем:
(г2~?+ L 2К*2+3^) а2“5 &+у*> г211;
2а2 ( (7—5v)a2 J
Зрч ( 2 1
г2-х2 + --- • [(г2+Зх2)а2— 5 (г2 + х2) г2] ;
2а2 [ (7—5v)a2 J
(8.22)
Зрз
2а2
2
(7—5v) а2
Зр, Г 2
т.., - — —— 1 +------------(а2 — 5z2) иг;
yz 2а2 [ (7—5v)a2 * 'J* ’
Зр» Г 2 7
тгх= —yf- 1+ ' (a2—5z2) zx.
2а2 (7—5v)a2 J
При растяжении среды в направлении оси х выражения
для напряжений в точках поверхности полости не трудно
составить по (8.22) после замены р3 на plt z на х, х на у и у
на z, а при растяжении в направлении оси у — после заме-
ны р3 на р2, z на у, х на z и у на х1 2.
Получение напряжений при трехстороннем нагружении
силами рх, р2, и р3 сводится к суммированию значений (8.22),
соответствующих частным нагружениям каждой из сил рх,-
р2 и р3 в отдельности, после внесения в них указанных кор-
ректур. В частном случае, равных по величине и обратных
по знаку сил, действующих в двух взаимно перпендикуляр-
ных направлениях по осям z и х, р3 = — рх = р, т. е.
в случае чистого сдвига на бесконечности, напряжения в
точках поверхности полости имеют значения 2:
Зр г 1 1
ох = —г у2- Л с \ 2 I2 (‘Ч')2+5 (У2 + 2‘) (*2 -у2» Г
а2 ( (7—5v) a2 J
°" = V- {' ~ (7-1)* 12°*+5<г,+**)]}
1 Необходимо прибегнуть в (8.22) к круговой перестановке букв
и индексов в соответствии с порядком следования координат в пра-
вой системе.
2 Решение этой задачи было получено впервые Дж. Лармором
[100].
253
Зр f 1 )
Ог=~Г Vs- Z7 l2(Q//)2 + 5(x2 + //2) (г2-//2)] ; (8.23)
Зр f 1 )
Т-=-И' - (7—5v)oa
Зр ( 1 1
T»’= {' - (7—5v)o* (2°’-5 ^-г2)|)
15р (г2—х2) zx
Тгх“ (7—5v) а4 ‘
В сферических координатах в точках поверхности поло-
сти os = гЕт) = 0 в сечении х = О
а =3р 11 — 1 (24-5 cos2t]) 1;
L • — J
ое — —3p|^sin2 т)———~ (2—7 cos2 т]) |,
в сечении у = О
15p 15vp
о_ = —-------cos2 Т1, ой = —------cos2 Т).
” 7—5v е 7—5v
Графики этих напряжений изображены на рис. 48.
8.6. Напряжено-деформированное состояние
вращающегося шара
Первые решения задачи о распределении напряжений и
перемещений в равномерно вращающемся шаре и сфериче-
ской оболочке принадлежит Кри. Получим это решение,
следуя процессу вычислений, указанному в п. 1.6.
254
При равномерном вращении шара с угловой скоростью
<о массовые силы распределены симметрично относительно
оси вращения г и имеют значения gr = jr и gz = 0, где / =
= та)1 2 * — центробежная сила на расстоянии от оси z, рав-
ном единице, т — масса материала шара.
Частные решения грг, гр 2, <рг, <р2 уравнений (1.42) и (1.47) в
этом случае приведены в (3.24):
фг=ф2=фг=О;
Л4 . 4
ф, = —--------= —Аг*,
Т 16 (1 — v)
где для простоты дальнейших записей будем считать А =
= //[16 (1 -v)].
В соответствии с равенством (1.46) функция Ф получает
форму
д vj д<р
Ф = гргрг — 2vфr + г — (ф + фг) = - - - г4 + гр + г —-
OZ О (1 + V) OZ
или O = 2i4v (се^ sin тг)4-4-ip-j-г--------.
dz
Функция Ф2 = 0.
Очевидно, что краевые условия (2.15), в данном случае
имеющие вид
дФ дф Л дг
= 0; —— = ,
дт]------------------д£ д£
(рГ = pz = 0), можно удовлетворить только тогда, когда в
функции гр и <р будут включены четвертые степени sin т). Эти
функции нужно составить, принимая из (2.45) решения, со-
ответствующие к = 1 и к = 3 (отбрасывая те их части, ко-
торые не удовлетворяют условиям (1-32) на оси вращения).
Таким образом
ip = C4 [Лд— А2 е2^ -1~5А2е2% cos2 т)1 е2^ sin2 т),
(8.24)
ф = С* [Сг— С2е2* + 5С2е2* cos2 iq] e2^sin2T].
Составление функции Ф по вышеуказанной формуле и
функции Q по формуле (1.51)
1 2 д
Й = —[Ф+2(1—v) (ф+фг)1 —------—- (ф + фг)
г2 г дг
255
приводит к значениям:
Ф = с4 [Лх + (2vd — Л2)е2б + (—2vA + 5Л,+
+ 8С2) е2^ cos2 т]] (e^sin т])2;
Й= ~+2с2{ —(1+v) Сг +е2* [(3 + v) (Д + С2)-
г£
— (3 + v) A cos2 т] — (7 + 5v) С2 cos2 т)] }.
По равенству нулю производной Ф по q при £ = £0,
где £0 — контурное значение координаты
4j + (2v4 — 42)fe2 = 0; — 2v4 + 542 + 8C2 = 0;
(b = e^*).
По второму натурному условию
Л1 + 2 (2vA - А2) Ь2 = - (1 + v) С, + (3+v) (Д + С2) Ь2-,
— (3+v) A — (7 + 5v) С2 = 0.
После решений приведенных уравнений имеем:
4 (3—v)
Сг =—п------ АЬ\
v —
л=2
4 (З + v) \ я
-------- А -,
7 + 5v J
Окончательная форма функций
4(3—v) ie 3+v ,
----- fe2 + —-— (1 -
С2 —
<р, Ф и й
А.
Ф =
5
8 /
ф= —— Ac41 v —
5 \
3+v
8 Г /
й = — Ас2 2 I v —
5 I V
3 + 2v l(3±i)
[4—5 (1 —v) cos2 т]] 1 (b2
v
Подставляем эти значения в формулы (2.20) для напря-
жений. После соответствующих группировок получаем:
/с2
°* 5(1—v)
= /с2
0x1 5(1—v)
(З+v) (б2 — 2е2*') —
256
ic2 ( 1
’e= {(3-2-) Ь2 + <5 +3v) — [(3+v)
—8e2^ —15(1+ v) (3 + v) e2^ cos2 T] j;
• о 3+-2v . ~
T. = /с2 (b2 —e ъ) sin T] cos 7].
1 1 + bv
В точках поверхности шара (£ = £0; = а)
л /я2 f 1
аб = °; сте = “Г7Г77-Г 8+v—7ТТ- l5~v+ (1 +v) (3+
6 10(1 — v) [ 7 + 5v
+ v) cos2 T)] j;
ja2 / 3+v \
0_ = .-------I v— -------- : Tt„ = 0.
4 5(1—v) \ 7 + 5v /
Ha оси вращения (tj = 0)
Ot = 0Z = — ------(v— ———(a2—z2); TtT1 =0;
6 5(1—v) \ 7 + 5v / tn ’
1 Г/
0_ = ой=ог = —------- v—4
11 e 5(1—v) |_\
В полюсах
Л l'a*
Ot = 0; о =стй= —------------
6 n 6 5(1 —v)
В экватериальной плоскости (т] = л/2)
ae =
/
10(1—v)
/
Ot = ur = — ------
6 5(1—v)
4(3 + 2v)\
7 + 5v )
(a2—r2);
tn — 0;
(a2 —2r2);
4(3 + 2v)
7 + 5v
0^ = 0,=
Вдоль диаметров, совпадающих с осями гиг, напряже-
ния распределены по параболическому закону (рис. 49 *).
Напряжения в центре сферы
/а2 / 4(3+2v) \ ja2 / 3 + 2v \
5(1—v) \ 7 + 5v J 5(1—v) \ 7 + 5v /
* В связи с большой разницей значений cr, 0Z и ое эпюры на-
пряжений построены в различных масштабах.
257
заключены в пределах 0,383 ja2<C <Jr <С 0,474 /а2, 0,086 ja2<Z
< l°zl < 0,412 /а2, соответствующих v = 0 и v = 0,5. На-
ибольшую величину напряжения Ое имеют в точках контура
экваториального сечения (г = a, z = 0):
ia2 ( 5—v \
ой =--------- 18 4- v —-------I;
6 10(1—v) \ 7 + 5v /
их значения о© = 0,72857 /а2 при v = 0; Ое = 1,56526 /а2
при v = 0,5.
Рис. 49
После подстановки функций <р и Ф в формулы для пере-
мещений получаем:
+------------------- (Ь2 — е cos2 т]) I е 2^ cos т]-|-и’о-
4(1—v)(7 + 5v) "j 1
258
Радиальные перемещения и на экваторе сферы и осевые
перемещения w в полюсах имеют значения:
/а3 8—v—5v2 2ja3 l + 8v + 5v2
=------------; w=—-------------
5E 7+5v 5E 7+5v
Эти выражения были использованы для подсчета моду-
ля сдвига Земли: G = 2,6- 10Б кг/см2 при v = 1/3.
Последовательность решения задачи о напряженно-де-
формированном состоянии равномерно вращающейся толсто-
стенной шаровой оболочки совпадает с последовательно-
стью решения для шара. Не повторяя вычислений, приведем
значения напряжений и перемещений в этом случае деформа-
ции оболочки. Функции напряжений ф и ср усложняются
присоединением членов, содержащих и е~3Ъ
ф=с4[Д1е2^ + В1в—^ + (Д2е4^ + В2е —(5 cos2 т) — 1)1 sin2 т);
ф = с4 [Cj е—^ + С2 е4^ (5 cos2 т]—1)1 sin2 т].
Значения входящих в них постоянных, определяемых по
краевым условиям на внешней £ = £0 и внутренней £ =
= £i поверхностях оболочки, таковы:
А
8 л „ b*—bl
— (yA + CJ J ;
5 b3—bl
6 2
(l~2v) A (7 + v)C2;
Ob I
1 (A л . (fc6 — fel)2
ь3—ы ~
B1 b3—b3
2
- -TT- l(3+29v) Д + 5 (7+v) C2] (6’-b’) ;
ob J
2 (fee—bl) (bbi)3
S = —7Z- 1(3+V) A + (7 + 5v) C2]
35 o2—bl
4 3 — v b3—bl
Q _---------Д ______L_ .
1 5 14-v b3—b3 ’
2 b'-bl
—- [(3+v) A +(7+5v) C2] » ;
21 o2—bl
c2=-L
2 D*
2(3—4v)(b3— Ц)(Ы>1)®+
+ TF(1+V) (7-5v)(&3-fe2)(fe7-4)M;
1 I
D* = 6 (fe2—Е2)2 (bbi)3— — (49—25v2) (&3— bf) (b'—bl),
где b = , b, = e^‘, A = ---------------
16(1 —v)
259
Общие выражения для напряжений и перемещений:
а5 = а2 (—2£ (^) + |ЗЛ1 + 2 (1 + v) ^ + [5^4-2 (5—v) С2-
—2 (3—2v) Л] е2* —2 (5—v) £>, е~3* + 12В2 е~56} sin2 т));
ап = а2 (£ (^) + 2 (1 + v) (Сг-|- 4С2 е2’ +DX е "3*) -{ЗДХ +
+ 2 (14-v) G + 8 [(24-v) С24^Л] е26-
— (1 — 2v) Dj е~ 35 4- 7В2 е~ 5*} sin2 т]);
ае = а2 (£ (У 4- 2 (14- v) 4- 4С2 e2t 4- £>i е“ 3t) -
— {[5Д2 + 2 (94-7v) С2— 3(14-v) Д]е26 —
— 3(1 —2v) Dre~4-5В2 е~5^} sin2 т])’,
т5т)= а2 {3^4-2 (14-v) G4-4 [5Л24-2 (64-v) С2] е2’ +
4-2 (1 -}-v) Dy е 3^—8В2е 5^} sin т) cos tj;
а2
u =— (£ (£) 4-2(1-v) (С14-4Са^4-Die-3^)-{[5Л24-
4-2(9—5v) С2-|-2Л] е2^—8Dye 3^4-5В2е 5^}sin2T])r;
а2
2ц
w =
2^i4-4vCi4-““- (Л2 4- 2C2)e26 + (3-2v)Die--3^-
О
-2В2е“56—(4- [5Л24-2(2 4- 5v) С2] е^-ЬЗЯ, е~п —
I о
— 5В2е 5^j sin2 tjJ z-j-w0.
Здесь введено обозначение группы членов
Е (£) = Ах 4-4 (Л24-2С2) е*4- (Вх-ЗЯХ) е~3* 4-4В2 е~ 5Ч
обращающейся в нуль на поверхностях оболочки.
В случае оболочки, радиус внутренней поверхности ко-
торой равен 0,8 радиуса внешней поверхности (ах = 0,8а),
постоянные имеют следующие значения: Лх = 0,185553; Вх=
= 0,030484 /; Сх = 0,204385 /; Dx = 0,135590 /; Л2 =
= 0,226996 /; В2 =- 0,044295 /; С2 = 0,110962 j.
Напряжения в точках поверхностей на оси вращения:
оп = ое = 0,4814 /а2 при £ = т] = 0;
ап = 0е = --0,2701 /а2 при £ = 0, т] = 0;
(а6 = т6ч = 0) — в точках экваториальных окружностей
внутренней (£ = £х) и внешней (£ = 0) поверхностей обо-
лочки;
оп = — 0,5549 /а2, оч = 1,2019 /а2 при £ = £lt
I) = 0,5 л;
ап = 0,2135 /а2, ое = 1,3562 /а2 при £ = 0, ц = 0,5 л.
260
Различие в значениях напряжений на внутренней и
внешней поверхности не только по величине, но и по знаку
указывает на наличие значительных изгибающих моментов
в сечениях оболочки.
8.7. Гравитационные напряжения
Рассмотрим напряженное состояние шара, возникающее
под действием гравитационных сил, т. е. направленных к
центру шара объемных сил, пропорциональных расстоянию
до центра g = — yR/a, где R = p^r2 + г2, а — радиус ша-
ра, у — объемная сила на поверхности шара. Составляющие
силы g в цилиндрических координатах gr = — yr/а\ gz=
=—yz la. После подстановки gr и gz в уравнения (1.42) и
1.47) получаем следующие частные решения:
фг = 0; фг=ЗДг4; ф2 =—2Дг4; фг = 4Дг3
при обозначении А = -----------.
48 (1 —V) а
Соответствующая функция
Ф2 = Фг + гф2=2Дг4.
За функции ф и<р принимаем те же выражения, что и при
решении задачи о равномерном вращении шара (см. (8.24)].
Для функций Ф и й получаем:
Ф = Ф+ФГ — 2^фг + 2 (ф+фг) =с4 {Д1 62 + [4Д24-2С2), —
OZ
— (6v4 + 5Л2 + 8С2) s in2 Т)] е 2Ь} (еЬ sin Т])2;
Л 1 2(1 —v) ч 2 д 1
й=-^-ф+—~2—(ф+Фг)— — — (ф+фг) = —ф—
- с2 {2 (1 + v) С, 62+8 (1 +v) С2 Л+ 2 [3 (3+v) А —
— (7+5v) C2](e6sin т])2}.
Выполнение контурных условий (2.31)
dO Г-i/тт . „ дфг \ дг д дФ2 d<pz 1
— =r V// Рг + й-2-^- —+ — —^-2(l-v)^- ;
dg L \ dz / d£ dfe dr drj J
дФ
дт] ~Г
--Pz +
1 d
r dt)
)Ф2 dф2 1
dr d£ J
261
приводит к следующим значениям постоянных:
12 6
Л1 = —(2-v)4; Д2 - (1 —2v) Д;
О и
с=_.J8
1 5
3—v
----Д; С2 = 0.
Напряжения и перемещения в рассматриваемом случае
деформации шара определяются равенствами:
аЕ = —Дс1 2 (3—v) (б2—е2»); т6л = 0;
* о
<4=ае = - ПГ Ас21(1+3v) (б2 -е26)+2 (1 — 2v) б2];
1 о
12 Г, ₽\2 3—v 1 ►
а. = —— (1 — 2v) Д I (се*)2——-а2 се*', и = 0.
* 5ц L 14-v J
На поверхности шара
1—2v
a. = т._ = 0; а_ = ай = —----уа,
6 6ч ’ п 6 5(1—v) Г
в центре
(3-v)
а^ат = ае=____Yfl.
8.8. Решение в рядах
В первой части этой главы приведены решения осесиммет-
ричной задачи в случаях простого распределения сил на по-
верхности шара или сферической оболочки. Результаты
были получены при использовании только первых значений
функций напряжений (2.45), соответствующих индексу к =
= 0,1, 2 и 3. Напряжения и перемещения при этом пред-
ставляются достаточно простыми формулами, удобными для
практических применений. Определение напряжений и пере-
мещений в общем случае распределения поверхностных сил,
например по кусочно-непрерывному закону, требует приме-
нения всего спектра значений фЛ и <pft, т. е. построения реше-
ний осесимметричной задачи в сферических координатах в
рядах х.
Значения функцийф и <р в рядах без труда составляются
суммированием выражений (2.45) по индексу к. Отбрасывая
1 Решение в рядах при осесимметричном нагружении сфериче-
ских оболочек см. [46] с ссылками на соответствующую литературу.
262
члены, содержащие производные функции «Лежандра второ-
го рода, нужные только при рассмотрении деформаций от-
крытых сферических оболочек, имеем:
= cost) + 2 (Л£е(*+,) е-*1 )Р£ (у) sin9 Т);
k= 1
ф=С'Л+D'cost) + 2 {Ckeik+X^+Dke~k^)pk(y) sin2T).
k= 1
(8.25)
Составление соответствующих этим функциям выраже-
ний для напряжений и перемещений после выполнения всех
формальных преобразований, связанных с подстановкой в-
формулы (2.20) и некоторой перегруппировкой членов, при-
водит к следующим равенствам:
для напряжений
<4= 2 {[(^-l)Mfe+(^ + l) (£2-£-2'-2v)Cfte24e(*-2)* +
k=0
+ U* + 1) (k + 2)Bh-k(k^3k-2v)Dhe^]e-{k+3^}Ph(y)-
%=- £ {l^2 4'(^4~ 1) (^24_4£4_ 2 4~ 2v) e2M 2) 4-
k=o
(8.26)
+ l(£+l)9Bh-H*2-2*-l +2v)Dfee24e-(A+3)4Pfc(‘/) +
+ 2 {[^ + (* + 5-4v)Cfee24e(*~2)t-b ’
k=l
+ [Bh-(k - 4 + 4v) Dk Л] e~ <A+3) 6) P’k (y) cos tj;
«6= 2 {[^h + (ft+l)[(l-4v)fe-2(l +v)]Cfte24e(A-2)b-
*=o
— [(£ + 1)Bft — k(k — 4v£ + 3—2v)Dhe2k]e~(k + 3> Ph (y) —
- 2 {Ufc + (*+5- 4v) Che2t] e(k “2) * +
&= 1
+[Bfc— (k—4+ 4v) Dfcfi24 e~(*+3) &} P' (y) cos t) ;
т6п = - 2 {[(*-lMft + (^ + 2£-l +2v)Cfee2*b<A-2>*-
k= 1
-[(*4-2) Bft-(^-24-2v) Dh e21] e~ <*+3) ^}P'k (y) sin t);
263
для перемещений
оо
«6= V" y <[^ft + (H-l)(^-2+4v)Cke2»! е^-’Н-
Л= о
-[(*+ 1) Bn-k (fc-f- 3-4v) Dh е2Ч е -(*+2) Ч Ph (у)-, (8.27)
ОО
и -----У <Us + (A + 5 -4т)Сле2Че,4-',6 +
2Н
4-[Bfc—(k—4+ 4v)Dfte24 е (Л+2) Ч Р'k (у) sin т]
(и% — перемещение вдоль радиуса шара, un — перемещение
в осевом сечении в перпендикулярном направлении к радиу-
су). Здесь для упрощения записи введены новые постоянные
ДЛ, Bh, Ck, и Dh, связанные с A'kl B'k, C'k, Dk ра-
венствами,
», _ д' IM-J)2-2(l-v)
c Дь+i — — ДЛ
2Л + 1
£2—2(1— v)
c2 Bfc-i = — BL +----------
h 1 k 2Jfe-H
^k\ c2 Ch
c2 Dh+i— —
2fc-M k'
Il «’
(8.28)
czD0 = C'-, c2D1=Dq-, До=Д1 = 0*.
Члены равенств (8.26) и (8.27), содержащие постоянные
Ah и Ch. соответствуют внутренней задаче — нагружению
шаров, а члены, содержащие постоянные Bh и Dh, — внеш-
ней — нагружению бесконечного пространства с шаровой
полостью.
Построение решения сводится к обычной процедуре раз-
ложения в ряд по полиномам Лежандра Ph (у) или по их
производным Рк (у) sin т] нагрузки и заданной на
шаровой поверхности, и приравнивания коэффициентов
разложения соответствующим коэффициентам представле-
ний в ряд напряжений о« или согласно равенствам на по-
верхности шара = ръ', Т£П = рт), т- е.
оо оо
а6= 2 Glkph(y)= S P\kPh(y)\
k=Q k=0
00 00
= 2 T6n*PHf/)sinT)= 2j Pi\ pk (y) sin n- (8 29)
k--= 1 k= 1
* Постоянные До и Alt как нетрудно проследить, исключаются
из выражений для напряжений, так как соответствуют жестким
смещениям тела.
264
По условиям ортогональности ПОЛИНОМОВ Ph (у) И P'k (у)
— i
1 1
f Ph(y)Pn(y)dy = O-, J P'k(y)P^y)sm^dy=O (8.30)
— 1
при к =/= fl
1
С 2 (£+1)!
I fPb (У) s*n ’ll2 dy =---:--------
J L few И у 26+ 1 (k— 1)!
— 1
(8.31)
Таким образом, коэффициенты разложений (8.29) пред-
ставляются равенствами:
1
2й + 1 с
— ] P^Pk(y)dy,
— 1
1
(2Л-Н) (k — 1)! C
Pnfe = 9/b_|_ni----- Pnpk(y)smrldy. (8.32)
Z -j- 1 J ! J
— 1
Равномерно распределенные по поверхности шара нормаль-
ные силы определены членом к = 0 ряда для pi (8.29). По
центральной симметрии они уравновешены при любом зна-
чении р|0 на любой шаровой поверхности £ = const. Напря-
жения и перемещения имеют значения:
= — 2 (1 + V) Со + 2В0 е ~ 36; an = ae = — 2 (1 + v) Со — Во е ~ 35
«g = — [2(1 —2v) СЛ 4-Вое—2Ч; т1п = 0, un = 0. (8.33)
Члены pi и рт) при к = 1 соответствуют силам р^ cos ц и
рП1 sin т], нормальным и касательным к шаровой поверхности.
Составляя для них условие равновесия — равенство нулю
суммы проекций всех сил на ось Ог1 — получим:
2a л
d0 j* (Pgi cos2 т) — pnl sin2 tj) a* sin =
b
I
C 4
= 2na2 | [(P6i +Pni)!/2-Pni}^= yna2^i~2pni)= °-
— 1
1 Остальные уравнения равновесия по симметричности нагру-
жения выполняют тождественно.
265
Равенство нулю реализуется при -= 2р1}1 либо при
Рь = рт), = 0 одновременно.
В случае внутренней задачи из (8.26) и (8.24) при к =--1
а^=—4 (1 +v) С} cos т); аТ) = ае=—' ® (1 +v) cos 1);
Т£П = —2 (1 4-v) sinr); (8.34)
= —---(1 —4v) Сге2^ cos п; ип =——— (3—2v) Cj е2^ sin 1].
’ И Н
По равенству коэффициентов рядов (8.29) о^, =Ръ и Т£т),=
=рП1 соотношение р^ = 2p1h выполняется и для
и Чп1» т- е- неравное нулю значение Сх приводит к нагру-
жению шаровой поверхности при любом фиксированном зна-
чении £ взаимно уравновешенными силами. При свободной
от сил поверхности необходимо положить CL = 0.
В случае внешней задачи Сх = 0, и поэтому
а^—2[ЗВ1е“— (2—v) Dj е~ cos т);
T6n=[3Bj е~ 2*4-(1 —2v) Djl е — 2^ sin tj; (8.35)
ая = ае=;—[SBje-2^ — (1 — 2v) Dj е ” 2^ cos т];
£
и. = —— [В, е~2^ — 2 (1 —v) Dj ] е cos тк
6 И
ия=—— [Bje 2Ь4-(3 — 4v)Dje 6sini].
Неравенство нулю постоянной Вх (DY =0) соответствует
нагружению поверхности шаровой полости взаимноурав-
новешенными силами p^ = о^, и рП1 = т$П1, так как
ai, = 2т|П1. Если постоянная Dx 0, то силы на поверхно-
сти полости не уравновешены. Равнодействующая их на-
правлена вдоль оси и имеет значение
2л л
Р CD
В. — — 1 df) I —7- 12 (2—v) cos2 т) — (1 —2v) sin2 vj] sin2 т]Л) =
J J Qo
о 0
1
2nD, С . 8л (14-v) _
= —------— I [(5—4v) j/2—(1 — 2v)] dy= — —— -------Di
J dao
— 1
(a0 = c&* — радиус полости).
266
Отсюда при заданной силе Pz постоянная Dx определя-
ется равенством (1+?)'
Считая в (8.35) обе постоянные неравными нулю и опреде-
ляя связь между ними условием = 0 или = 0, не-
трудно получить случаи нагружения поверхности полости
неуравновешенными только нормальными или только каса-
тельными силами. Нагрузки, соответствующие членам раз-
ложения в ряд сил pi и Рт), при к > 2 уравновешены на
любой шаровой поверхности независимо от соотношения
между pih и рт)Л. Действительно, составляя уравнения
равновесия для каждой из них, имеем :
2л л
I* de J [Plk Pk (у) COS 1] — pnk P 'k (y) sin2 q] sin TjcfT] -
b о
1 1
=2na9 pik f yPk(y)dy — pnk f Р*(у) sin2 qdy =0.
— 1 —i
так как по свойству полиномов «Лежандра (8.30) при к > 2
1 1
J yPk(y)dy=- J Рг (y)Pkdy-0\
1 1 1
f p'k(y) ^—у)2 dy = Pk(y) 0— У2) I +2 f yPk(y)dy = O.
— 1 -1 — 1
В общем случае деформации сферических оболочек урав-
нения равновесия содержат силы, приложенные к внешней
и внутренней поверхностям. В зависимости от постановки
задачи они могут быть уравновешены и не уравновешены в
отдельности на каждой из указанных поверхностей. Как по-
казано выше, составляющие напряжений и с индек-
сами к = 0 и к = 2 уравновешены на любой шаровой по-
верхности | = const, в силу этого равновесие определяется
только связью между силами рП1 cos q; р^, sin q на внешней
поверхности (се^ = а) и силами р£» cos q; p^t sin q на внут-
ренней (се% = a0). После подстановки в равенство1
2л л 2л л
J d0 | (р^ cos q — р^ sin q) a2 sin q dq— J d0 [ (pjcos q —
o o oo
— pi) sin q)a§ sin qdq~0
значений p6 и p^ (8.29) и аналогичных значений pl и p^ по-
лучаем:
1 Внешняя нормаль к внутренней поверхности облочки направ-
лена к центру шара, поэтому положительные направления сил р|
и р° противоположны положительным направлениям р^ и р^.
267
Л oo oo
2llo8f 5 plk Ph (y) cosi} — 2pu*P*^)sin2n sin T) dn —
о[л=о
n
—2ла2 J
о
k
sin t] di) =-
— 2л. a2
2 pb Ph cos n — 2 pnk pk (y) sin2 n
k=0 fe=l
2 ры j уръ (y) dy— 2 pnk Г pk(y)sin2 —
_Л=0 —1 fe=l —1
—2na§ 2 plk f yPh(y)dy— 2 P^k f pk (У)sin2 Vdy
_k=0 —1 fe=l —i
= 0.
Здесь все интегралы при обращаются в нуль, и,
следовательно, приведенное равенство получает вид:
— а§
1 1
о2 pll J УР1(У) dy — Рц, f pi (У) О— У2) dy —
— 1 —1
1 1
р11 f yPi dy ~ pTit I (У> ~У^ dy] = °-
— 1 —1
Выполнив интегрирование, имеем:
а2(р5.-^т>.)-а§ Н.-2О = °- <8-36)
Присоединив к этой связи два условия, определяемые ха-
рактером приложения внешней силы на поверхностях обо-
лочки (например: рП1 = = 0 при нагружении только
нормальными силами р^, и р^,), получаем систему трех
уравнений для определения постоянных Сх, Вт и Dx.
8.9. Осесимметричное нагружение шаровых оболочек
кусочно распределенными силами,
нормальными к поверхности
Ограничимся рассмотрением деформаций сферических
оболочек под действием только нормальных к их поверх-
ности сил. Предоставив напряжения и силы в форме рядов
(8.29) и приравняв коэффициенты с одинаковыми индекса-
ми, получим уравнения, служащие для нахождения постоян-
ных Ah, Bh, Ch, Dh*-
Будем определять внешнюю поверхность оболочки коор-
динатой £ = 0 (т. е. положим с = а — радиусу этой по-
верхности) и внутреннюю — координатой |0. Введем обо- 1
1 В дальнейшем индекс £ у сил отброшен из-за ненадобности.
268
значение & = b = а0/а, где a0 — радиус внутренней по-
верхности. В случае к = 0 имеем:
— 2 (1 -|- v) С0-|-2В0 = р0: —2 (1 -f-v) Со+2Во Ь~8 =Ро.
Отсюда
„ (Ро—Ро)Ь3 „ Ро—РоЬ3
2(1—ft3) ’ ° 2 (1-f-v) (1 — ft3)
В случае k = 1
4 (1 4-V) ^+65,-2 (2—v) D1 = pi;
— 4(1 4-v) Ci 6 + 6Bj ft-4 —2 (2—v) Di ft-2= p°;
2(1 4-v) Ci — 3Bi — (1— 2v)D1=0;
2 (1 4-v) Ci b — 3Bi ft-4—(1 —2v) Di ft-2 = 0.
(8.37)
Принимая во внимание связь (8.36) между силами на
внешней и внутренней поверхности рх = р® Ь2, приходим
к системе трех уравнений, решение которых
в = !-2v Pj(l—fe3)fe2 с l-2v Pi(l-b2)
1 18(1—v) 1—ft® ’ 1 12(1—v2) 1 —ft8 ’
В случаях k >2
(Л-l) Mft4-(^4-l)(^-Jfe-2-2v)Cft + (ft4-l)(^4-2)Bft-
-k (ft24-3ft-2v) Dft = pft;
(k — l)Mftft*-24-(Jfe4-l) (k2—k — 2—2v)Cftftfe4-
4-(Л4- 1) (Jfe4-2)Bftft -(fe+3)—ft(A24-3Jfe—2v) Dftft-(fe+1)=p»;
(£-1) 4ft4-(£24-2*-14-2v)Cft-(*4-2) Bft4-(ft2-24-2v) Dft = 0;
(ft—1) ДЛft*-24-(ft24-2ft— 14-2v) Cbb*—
— (ft4-2) Bftft“(*+3)4-(ft2—24-2v) Dftft-(*+,) = 0.
Решение этой системы запишем в виде
л‘=- (it_|)(L^+.) (1-^+’)с,+
+ (^-2+ 2v) (I -6») Dn|; (8.39)
e‘= - (t+2)(L^)' 1<Л2+2*-1+2v) ° ‘s‘+i С‘“
— (*2—2+2v) (1—б24-1) Ь2Оц];
с»=4- [-л(аЦ+О+р!(Чь-‘+2+«;»*+>)];
D»= 4" (w’*+ Ni)-Pi (Ni »~*+г+И1 ‘‘+’)L
269
где введены обозначения:
№k = 2 (Л2 + Л + 2kv + 1 + v) (1—62Л+з); N'k^k(2kl + 3k — 2) (1— ft2);
^ = (Л+1)(2Л2 + Л-3) (1 - ft2);
N^ — —2(/г2+Л — 2/fevH-1 — v) (1 — b~ik+l).
(8.40)
В случае нагружения сплошного шара
——Ро
°' 2 (1+v)
С] — 0;
Ph
2 (1+v)
k— 1
(8.41)
Cfc= —D; = 2 (F+*+2*v+ 1 +v),
k = 2, 3, 4, ...
При нагружениях поверхности шаровой полости нор-
мальными силами (внешняя задача), если напряжения на
бесконечности равны нулю,
D.
2 (1+v)
(8.42)
с; = 2 (Л2+Л—2Ztv— 1 +v),
к = 2, 3, 4,..., значение b принято равным единице, т.е. по-
верхность полости определена координатой £ = £0 = 0.
8.10. Деформация оболочки под действием сил,
равномерно распределенных на участках
поверхности
Рассмотрим осесимметричное нагружение сфериче-
ской оболочки силами р и р', нормальными к внешней по-
верхности и равномерно распределенными на участках, оп-
ределяемых координатами т)! и т]2 для сил р и т]3 и т]4 для
сил р' (рис. 50). Внутренняя поверхность свободна от сил.
По условию равновесия должно выполняться равенство
нулю суммы проекций всех сил на ось вращения:
2л T)s 2л Т)«
J d6 f Р cos т]-а2 sin T]dr)+J dQ J p' cos ip a2 sin т]Л] =0;
0 T)t 0 i)»
p (cos 2i]2—cos Stjj) + Po (cos 2i)4 —cos 2tj3) = 0,
270
и, следовательно,
cos 2г)! — cos 2r)2
cos 2Т|4—cos 2Т)з
(8.43)
В зависимости от величины углов т)я, т)2, Яз и силы р
и р' могут быть направлены либо в одну сторону по отноше-
нию к внешней нормали (как на рис. 51), либо в разные.
По характеру рассматриваемого
нагружения на внутреннем контуре
осевого сечения (г = а0\ = Ь)
= =0» на внешнем контуре
(г = а\ е* = 1) (% = т^т = 0 при
0<y] <т]1;т)2<т)<т]з; y]4< т]<л;
<4 = — р; Чп = 0 при т)!<т)<т)2;
<4 = —р'; тЬтг= 0 ПРИ 11з<т1< П4-
Положив <%= У, ph Ph (у) и
А=0
умножив правую и левую части
этого равенства на Ph (у) после
интегрирования в пределах от — 1
до +1, по ортогональности полиномов Лежандра [см.
(8.31)1, получаем:
1
Pfe = Y(2*+,) j aipk(y)dy=
— i
= 4-(2* + D
- Уя У*
P J Ph (y) dy\~ p’ J Pk (y) dy
- Уя Уя
где yi = cos tj; i = 1, 2, 3, 4.
Воспользовавшись зависимостью
Ph = o/i l₽ k+1 (у)“ pk -1 (у) I,
I 1
выполняем интегрирование:
Уя Уя i
f Pk (у) dy — С —— [P' + 1 (y)—P’k_A (у)] dy =
V </ l" 1
Уя Уя
Уя
1 1
= 9. /Т l^fe+1 (y) — Ph-1 (y)l = 9 ~ . [Pfe+1 (y2) —
Уя
—Ph+1 (У1)—Ph—1 (y2)+Pfe—1 (!/i)b
27]
Итак, искомый коэффициент ряда, представляющего крае-
вое напряжение имеет значение
Ph =-£-р [Pfe+i (у2) — Ph+i (У1)—Ph-i (yz)+Ph-i
+ “ р' lpfc+i (У<) — Ph+1 (Уз) —Ph-1 (У*)~ Ph-1 (Уз)1 (8.44)
при к > 2. По условиям равновесия = 0 (см. вы-
ше). Если к = 0, то
. Ул Ул
If If 1
Ро = | рйуА-— I p°dy = — [р(у2—У1) + р' (У4—Уз)]. (8.45)
У1 У»
Приведем значения коэффициентов ph в двух частных
случаях симметричного относительно плоскости г = 0 на-
гружения шаровой поверхности: когда силы распределены
у полюсов (рис. 51, слева) и когда силы распределены по
поверхности шарового пояса у диаметра г = 0 (рис. 51, спра-
ва).
Рис. 51
В первом случае: р' = р, yY = 1 (тц = 0), у3 =
= —|/2(т1з = л — Лг)» Уь~ — 1 614 = л). Принимая во вни-
мание, что при k = 2п 4- 1 нечетном полиномы Рп2 (—у2)=
= Р2п(^2). а при k = 2п четном Р2п+1( — у2) =
= — Р2п+1 (у2), получаем:
Ро— Р (1 Уг); Рга—Р[Рзп+1(Уз)—Ргп — 1 (Уг)]- (8-46)
Этот результат можно записать в иной форме, если вос-
пользоваться следующей зависимостью:
(2Л+1) (1 -у2) P'k (у) =k (* + 1) [РА_Х (y)-Ph+1 (у)],
272
тогда
(4n-|-l) р
Ро = -Р(1-№); Рап = - о Лп ^-У1)р1п(У^- (8-47)
2п(2п + 1)
Во втором случае: р' = р, у2 = Уз = 0 (т1а = Лз =
= л/2), у4 = — yt (т]4 = л — тн). Выражения для р2п
(8.44) после использования связей между полиномами
Лежандра с четными и нечетными индексами Р2п (— У1)=
= Ргп (У1) и P2n+1 (—yj = — Р2п+1 (t/J получают
вид
Ро= РУГ Ръп = P[Pin+i(yi) Pzn—i tei)] (8.48)
и если заменить выражение в квадратных скобках производ-
ной полинома Р2п (у) с соответствующим коэффициентом, то:
(4пЧ-1)р
Ро = — РУГ, Pin = . (1 -!/?) P2n tel)• (8-49)
При кусочно распределенной нагрузке ряды, представ-
ляющие собой напряжения, в точках поверхности (се* = а)
расходятся. Однако вычисление их значений удается осу-
ществить, прибегая к специальным приемам. Изложение по-
следовательности суммирования расходящихся рядов при-
менительно к рассматриваемым здесь задачам содержится в
[46]. В частных задачах напряжения оп и ое вычисляются
посредством использования значений и тЬт) на поверхно-
сти. Во внутренних точках шара или оболочки сходимость
рядов улучшается по наличию в их членах множителей
а < о).
В частности, в центре сплошного шара (£ = — оо) по
равенству = 0 в рядах (8.32) в нуль не обращаются
только члены с коэффициентами Со и А2:
„ Ро л 7 + 2v
С п--- • /in = к рп,
2 (1+v)’ 2(7+5v)F2
Соответствующие напряжения
7+2v 7 + 2v
^ = PO~??T^P2(,-3COS T,); CTe=P°- 2 (7 + 5v) Р2:
(8.50)
7+2v п о 7+2v . л
о_ = Ро +-------Ра (2—3cos2ri); т-- = -------ptsin2n.
11 2(7+5v) 21 ” 4(7+5v)
Следовательно, в центре шара при любом характере рас-
пределения сил на поверхности напряжения определяются
значениями только двух составляющих внешних сил р0 и
Ра-
273
8.11. Сжатие шара силами, приложенными
в полюсах
Сжатие шара или шаровой оболочки сосредоточенными
силами, направленными вдоль диаметра, является частным
случаем нагружения силами, распределенными по участкам
О < т] < т]2 и л — т|2 < т] Оу полюсов внешней шаро-
вой поверхности, — случаем, когда размеры участков на-
гружений, определяемые углом tj2 = е, бесконечно малы, а
суммарная сила Р = л (ел)2р сохраняет постоянное значе-
ние. Выражения для составляющих разложения нагрузки
в ряд следуют из формул (8.47), в которых нужно положить
р = р/[л (ел)2]; sin2T)2 = е2 и у2 = cos т]2 = 1 — е2 /2.
После выполнения подстановок
Р Р 4п+1
Ро 2ла2 ’ р2П = ~ 2па2 п (2n +1) Р^п
и замены производной полиномов Лежандра при у = 1 зна-
чением Р^п (1) = п (2 л + О получаем:
Р (4и + 1)Р
Р°-- 2ж? ’’ Р"'~~ 2па‘
(8.51)
Итак, рассматриваемая нагрузка представляется расходя-
щимся рядом
сю оо
2р2пР2п (!/)=--У (4л+1)Р2п(у), (8.52)
п=0 п=0
что, однако, не служит препятствием для вычисления на-
пряжений и перемещений в области, занимаемой шаром или
оболочкой, включая их поверхности, за исключением полю-
сов.
После подстановки значений (8.51) в формулы (8.37) и
(8.39) получаем постоянные Л2П, В2П, С2п и D2n, а затем по
формулам (8.26) и (8.27) — напряжения и перемещения.
В случае шара B2n = D2n = 0 [ см. ( 8. 41)]
> ^2П
Со =
4па2 D2n
2n—1
Csn=------Г“<4л+1); D*=4n + 2n+4nv+ 1+v. (8.53)
4ло2 D2n
Напряжения представляются рядами, члены которых
имеют порядок л2. Ряды плохо сходятся даже при малых
<1, а в точках поверхности шара (е6 = 1) расходятся.
274
Следуя общему приему, можно, выделив плохо сходящиеся
части рядов, представить каждый ряд в форме сумм четырех
рядов с членами порядка п.2, п, п° и и-1 и ряда, содержаще-
го члены порядка п~2 и ниже. Последний ряд сходится при
любом е* <1, а для сумм первых четырех можно указать
значения в конечной форме.
Поясним сказанное на примере преобразования выраже-
ния для напряжений о6, которое при значениях постоянных
(8.53) и обозначении е* = р имеет вид:
Р
4 ла2
(2л (4л24- 4л — 1 4- 2v) — (2п4- 1)
Х(4л2 —2л—2—2v) р2] р2 1 ^Р2П (£/) =
Р X-
—— У(4п4-1) 2 4-
4л(Ор)2
I 1 1
4- —— [4л2—2л —2 (1+v)] (1-р2) р2п Р2„ (у). (8.54)
»2п I
Преобразуем коэффициент перед скобкой (1 — р2) по ниже
следующему:
2л+ 1 1
(4п+1) —— [4л2 — 2п — 2 (1+v)] =(32л* + 8пэ —8(3 + 2v) X
D2n D2n
X л2—2 (74-6v) л—2 (l+v)]==8n4—2 (l+4v) л— (7—8v2) +
1 +v
-t —[2 (I +12v —16v2) л+5 —8v2].
&2n
Присоединим к полученному и вычтем из него член, пропор-
циональный (2п + I)-1, получим:
8л2—2 (l + 4v) л —(7—8v2) (1 + 12v-16v2)+
где (аг)2п=~^~ [5-8V2 — (l + 12v— 16v2) 6]; 6^2v+ 2n {
(8.55)
Слагаемое (<Jt)2n имеет порядок п~2 и ниже.
После несложной группировки коэффициентов напряже-
ния удобно записать в форме
а1 = ~ 4Мар)4(4 С^—0+2 *v> n-(7-8v») +
275
1 -J-v 1
+ (l + 12v-l6v‘)^T+(ae)„j
(1-р’)+8л+2 р2пР!П (у).
Тогда, обозначив
оо
У] р2л Р2П (У) = Slt
л=0
(8.56)
а также первую и вторую производные по р через S'i и
S*, составим окончательное выражение для
°{‘=- Т Г~7Г if Р2+ с - 4v> s: ₽~<7- 8v2> S1 +
в 4л (ар)2 [[ 1 1
+(1 +v) (14- 12v— 16v2) — fSj dp 4-
P J
OO
+ 2 (CT02n
n= 0
p2nP,n^ (1-P2)4-4S;p4-2S,
(8.57)
В результате произведенных операций вычисление напря-
жений ng сведено к суммированию рядов, соответствующих
каждому слагаемому в (8.57), т. е. к вычислению суммы Slt
ао
ее производных и интеграла. Ряд У, (Ufc)2n р2п Р2п (у) сходится
л=0
при любом р < 1.
Аналогичным образом составляются выражения для ос-
тальных компонентов напряжений:
Р
СТт1 4л (ар)2
[2S;p24-(и - V) S; р4-2 (3-6v4-4v2) SJ (1 -р2)-
ОО
- 4S; р-2 (3-4v) Sj + f Sj dp 4- 2 (а^2п Р2пр^ (У)~а
Р J л=0
Р
4 л (ар)2
[2 (l-4v) S; р-(34- 12v- 16v2) SA] (1 -р2) 4-
4-8vS' р4-8 (1—v) (14-2v) 4-— Pi dp 4-
1 P J
OO
+ 2 (ae)2nP2n₽2n (!/)-<r ;
л=0
(8.58)
P (1- P2)
4л (ар)2
2S; p24-(3-4v) S2 p-
276
— (5—8v2) -j- C S2 dp + 2 (T£n)2n P2n P2n (У)
H n = 0
sin т].
Здесь приняты следующие обозначения:
(%)2n = —ТГ- (2 (»+^) [2 (1 -v) (1—2v)(l—р2) —
D2n
-54-4VH-V, 6—26.1; 6i--o0+^ ;
2n— 1
!(!+*) (04- 12v~ >6v2) (1-P2)-8v (1 -v)l -
D2n
-vJ6+261);
-(TEn)2n =—7“ [4—3v —4v2—(5—8v2) 6j;
D2n
s, = 2 p2,1-1 p*n (8.59)
n = 1
V1=—(1—v) (5+4v —16v2) (1 — p2)+2 (3 + 4v—8v2);
v2=—2 (1—4v) (2+v —4v2) (1— p2) + 2 (2—9v—4v2 + 16v3);
о = 2S2 p (1 — p2) +13 (3—4v) (1—p2) —4 (1-
1 Г °°
—2v) I Si pdp — 2 (a)2n P2” Р2л (У)
P J n=l
(ahn=-4- (3 [1—2v —(3 —4v) 6] (1 -p8) +2 [1 +
D2n
+4v+2(l-2v) 6+6J}.
Воспользовавшись формулами (8.27) и выполняя преоб-
разования по тому же плану, приходим к следующим выраже-
ниям для перемещений (постоянная интегрирования опу-
щена):
Р
= — -о---
6 8лрор
[2S; р —(3—4v) Si-(4-
1 f
— 13 v+8v2) — I S. dp
P J
(l-p2)+8(l-v)S1 +
+ 4(1—2v)2 J.
P
OO
s, dp + 2 (*4)« ₽2"
n=0
(8.60)
277
и —- ——
4 4лр,ар
2S2 p i-3 (3 —4v) — fs2pdp
P J
(l-Р8) ~
Si pdp + 2 (%)2n P1 2 3 *" P2n (У) sin n;
n— 1
при обозначениях
(“t)2n=-7“ {[l + 3v-4v2+(4-13v + 8v2) 6] (1 -p2) +
^2n
+ 2 [2v (I -|-4v) — 2 (1— 2v)2 6+ 6j]};
(“n)2n = —T- !3 [l-2v-(3-4v) 6] (l-p«) +
D2n
4-2 fl i 4v + 2 (1—2v) 64-6J}. (8.61)
Укажем значения сумм S, и S2 и их производных и интегра-
лов.
Воспользовавшись значениями образующих функций по-
линомов Лежандра
оо
1 --- V Рп Рп (у)\ ----
V 1+р2—2ру л=0 I 1 +р2 + ?р|/
ОО
(-р)" рп(у).
п = 0
на основании формального равенства
2 р2п м V i рл (у)+ 2 (-р)п р» с*/)
л=0 2 |_п—. О л —О
получаем:
оо I
Si 2 р2п р*" (у) +*)> <8-62)
п=0 2
__1_ ________________1_
где S1=(l-|-p2—2ру) 2 ;sz(l+p2+2py) 2. (8.63)
Далее, дифференцируя (8.62) дважды по р, имеем:
s; = V2np2"-1 Р9П(у) = - -^-[(р-у) s’ +
п— 0 2
+ (Р+!/) *31= —T-lsi + ^-G-P2) (s»+sl)I; (8.64)
S' - 2 (2"-П2пр2"-2Р2П(у)==-4-[«?+^-
п=0 2
— 3 (р—у)2 s|—3 (р+у)2 s‘J = —jsf+s’ —
3 1
- [«i+s.-2 (1 -р2) (s«+s’) + (l-p2)2 (sj +s{)]j.
278
Интегрируя равенство (8.62) по р в пределах от 0 до р, на-
ходим:
(8.65)
Производная Sj (см. (8.62)1 по у, поделенная на р, опреде-
ляет значение суммы
«2 = 2 ₽2"“ ' P'ln <0 = 4" (4 “4>- <8 66)
л=0 *
После дифференцирования этого равенства по р
s; = S (2«-‘) ₽2"“2 —|- !(₽-«) «5-(₽+») 41 =
л=0 Z
3
= -— [sf-sl-n-P2) (s?-^)] (8.67)
4р
и после умножения на р и интегрирования
Js2₽dp=Д -frrr ₽’" <*> =^7) К'-р») s> +
+ (1 + ру) s2]= -Т775-—Z [S- 1 - V1 +(!-Р2) (*!-%)]• (8-68)
4 0— у)
Таким образом, все суммы, входящие в выражения для
напряжений и перемещений, определены.
В точках поверхности шара (р = 1) напряжения =
= Т|т) — 0, исключая полюсы (у = ± 1):
_____Р_
СТт1= 4ла2
2 (1—2v) &+«,)-
sr‘+1-^
-<3+4v-8v») In - 2 <Р>+°
2 " Л=0
6 4ЛО2
2 (2+v—4v2) (s1 + s2) + (2—9v—4v2 +
+ I6v3) in (aehn Р2П (у) — о
2 П=0
[12 °°
YZ^(sr1— sr’) +2 <abnP2n(y)
n=0
COSI),
(8.69)
279
перемещения:
Р з—1 +1—у
= —7— 4 (1 — v) (S1 +se)+2 (1-2v)« in -i---- +
* олца s—i —1—у
(ul)in P*n W
$— 1 —s— 1
(1- 2v) ----*-
1— yl
(Ui\hn P2n (У)
(8.70)
P
U =------
1 4лра
Здесь
__
si =[2(1- 6)] 2
1
2 sin — n
2 1
_______________
s,=[2(I+!/)) 2
2 cos — n
2 1
— 1
; 1 — t/® = sin2T).
В ПЛОСКОСТИ Z = 0 (у = COS T] = 0) Sjl = s2
= (I + p’) 2. Соответствующие напряжения:
oo
+2 2<оЛ"₽2"р’"(0)
n=0
280
4?
р
4л (ар)2
1— р2
(1-4?)—^-4 o+2v-4v2)+
1+р2
4 (2+v—4v2)
(8.71)
ОО
+ 2 (о^2п р2п р’" <°>
п= О
(2л—1)1!
₽•<»)=': ^»(»>=Ар^Г
На оси z, вдоль которой направлены силы Р, полиномы
Р2п (у) = Pzn (0=1 ПРИ любом п, а их производные воз-
растают с увеличением индекса п: Pzn (1) = п (2п + 1).
Поэтому при у = 1 в целях улучшения вычислительного
процесса рационально выделить из ряда, содержащего про-
изводные полиномов Р2П (см. о в (8.59)], плохо сходящиеся
части. Действуя подобно тому, как при составлении общего
выражения а^, получим:
р а. = — е 4л (ар)2 24 8 (4+v)
(1 -f-v) (1 + 12?— 16?2) In
_ Р 8 (1—2?) 8 (2—3?—2?2)
аП - a0 = 8л (Qp)S (l-p2)2 “ 1—p2
1—p
1
2p
n= 0
(8.72)
В центре шара, как нетрудно получить из (8.50) или пре-
дельным переходом при р -> 0 из соответствующих формул
для напряжений:
Р Г 5(7+2?) , 1 21Р
°t = — 4ла» [ ~ 7+5v * °в-4яо» (7 4-5v) '
4 4ла2 7+5?
5 (7+2v) Р
Тет,“ 8 (7+5v) ла2
sin 2 т).
281
В цилиндрических координатах:
_ 21Р _ ЗР (14+5у)
аг=а0 = 4яа2 (7+5v) . <Tz-— 2ла» (7+5v)
В табл. 36 и 37 приведены значения напряжений в долях
р = Р/(па2) в точках поверхности шара (сА = а), оси Oz и
плоскости z = 0. Подсчеты произведены при v = 0,3.
Таблица 36
П 15° 30° 4 5° 60° 75° 90°
с/р
а1 —0,799 —0,593 —0,416 —0,310 —0,259 —0,243
ап = ае —1.101 —0,120 0,423 0,442 0,439 0,435
Таблица 37
р с/р 0 0,2 0,4 0,6 0,8 1
г = 0
—2,7353 —3,1303 -4,7137 —9,8471 —68,004 —
%=ао 0,6176 0,6431 0,7422 1,0509 2,7421 —
7 = 0
0,6176 0,5003 0,2573 0,0652 0,0044 0
% ] 2,7353 —2,4815 — 1,7826 —1,0923 —0,5725 —0,2428
ае 0,6176 0,6340 0,5565 0,5090 0,4668 0,4353
8.12. Напряженное состояние цилиндра
с шаровой полостью конечных размеров
Ранее было приведено решение задачи о концентрации
напряжений у шаровой полости в бесконечной среде. Было
отмечено, что возмущения в основном напряженном состоя-
нии среды, вызванные наличием полости, быстро убывают
по мере удаления от полости, следовательно, полученные
результаты можно применять как приближенные и в тех
случаях, когда внешние размеры тела сравнимы с диамет-
ром полости, однако превышают его не менее чем в 3—4
раза (см. п. 8. 4). Погрешности в величинах напряжений
и коэффициентов концентрации при этом невелики.
282
Указанные решения подкупают своей простотой. Полу-
чение решений о распределении напряжений в осесиммет-
рично нагруженном цилиндре, имеющем шаровую полость
на оси вращения, с точным выполнением граничных ус-
ловий на поверхности цилиндра и на
вой полости, представляет более слож-
ную задачу. Случай осевого растяже-
ния в такой постановке рассмотрен
Лингом в [101]. Решение задачи при
любом нагружении цилиндрической
поверхности доложено автором этой
книги в 1967 г. на Всесоюзной кон-
ференции цо теории упругости и
пластичности. Приведем это решение.
Расположим начало координат в
центре полости (рис. 52). Положение
точек в области цилиндра будем оп-
ределять безразмерными цилиндри-
ческими координатами р = г 1с и £= zlc
и сферическими координатами £ и т].
Связь между ними:
р = sin т>; £ = cos т]. Контур
полости определим значением £ = 0.
Отношение радиуса а цилиндра к
радиусу полости обозначим через 6;
по смыслу задачи b = > 1.
поверхности шаро-
В соответствии с краевыми условиями (1.30) для функций
напряжений Ф и Q должны выполняться равенства
дФ дФ
'-^Г=а2р2; ——=Q4-a2pr (8.73)
д£ др
при р = Ь (г = а) на боковой поверхности цилиндра и ра-
венства
дФ до
Ф=0;—— = pQ------= й sin2 т) (8.74)
05 05
при £ = 0 на поверхности сферической полости. Здесь
дф 1 2 д<р
ф ; Й = —[Ф+2 (1 -V) ф]—--;
д£ р2 р др
рг и pz — соответственно радиальная и осевая составляющие
нагрузки на поверхности цилиндра.
283
Запишем функции Ф и й в форме рядов
Ф=Ф* + 2 ф2П; Й=Й*+ 2 fi2H. (8.75)
п= 0 п=0
в которых Ф* ий* — решение задачи о нагружении ци-
линдра без полости силами рг и pz, распределенными по бо-
ковой поверхности, а также как частный случай растягива-
ющими или сжимающими силами, приложенными к торцам,
удаленным в бесконечность. Значения Ф* и fi* приведены
в гл. 3 и 4 и могут быть составлены на основании получен-
ных решений задач о различных нагружениях цилиндров.
Функции Ф2п и Й2П, входящие в ряды (8.75), служат для
выполнения граничных условий (8.74) и условий (8.73) на по-
верхности цилиндра, нарушающихся при наличии полости.
В силу того что функции Ф* и й* соответствуют приложен-
ным к цилиндрической поверхности силам рг и рх, для всех
членов рядов (8.75), как следует из (8.73), при р = b долж-
но быть
ЗФяп
ф2П=0;----— = рЙ.п, л =0, 1, 2, ... (8.76)
др
Используя решение осесимметричной задачи в цилиндри-
ческих (4.08) и сферических координатах (2.45), составим
функции <р2п, Ф2п и Й2П в виде
<f>zn=Bne {2л+,) 6 P'n+i (у) s>n2 i) +
п °°
+ (~?. р f *2n D" (М Л (М cos (8-77)
I J
0
Ф2п = [лп Р'2п + 1 (у) +ВпР’2п+2 (у) sin® Т)] er <2n+1) * sin® т) +
+ Р f X2n [Сп (X) Ц (kp)-Dn (к) Хр/0 (Хр)] cos X£dX;
(лП)1 j
о
й2п = ~ Ф2п—^Вп [(1 -j-v) P2ni 1 (У) —
Р
ОО
- ^„+2 to) »!•>• Ч] е-<2»+3> V f Dn (X) X
о
X [(1—v) (Хр)—Хр/0 (Хр)] cos XJ4X,
где y = cos т).
284
Заметим, что эта форма функций напряжений может быть
применена к случаям нагружений цилиндров силами, рас-
пределенными симметрично относительно плоскости £ =0,
которыми мы и ограничимся с единственной целью упроще-
ния дальнейших записей. Переход к нагрузкам, асиммет-
ричным по отношению к плоскости £ = 0, не представляет
принципиальных трудностей и требует только повышения
на единицу порядка полиномов Лежандра Рп (cos -q), исполь-
зованных при составлении первых членов функций (8.77), и
замены в подинтегральных выражениях во вторых членах
cos X-q на sin Х-q.
Переходим к выполнению контурных условий (8.76), на
цилиндрической поверхности р = Ь. Составляем производ-
ную Ф2П по р:
— = [2ЛП ^2п+1 (У)— (^п — 4Bn) ^2n4-2 G/) S*n’ Ч
~Вп р2п+з (у) sin< п] е {2п+1) 6 sinq-p ( р X
оо
X J X2n {Cn (X) /0 (Хр) — Dn (X) [2/0 (XpJ + Xp/j (Хр)]} cos X£dX.
о
(8.78)
Заменив sin -q значением sin -q = b№ и подставляя (8.77)
и (8.78) в равенства (8.76), после группировки членов полу-
чаем:
^п^2п4-1 0/)“Ь Вп
Р2п + 2 (У)
Ьав-(2п+3)6 +
ОО
b С Х2п [Cn (X) Л (Х6) —Dn (X) Шо (ХЬ)1 cosX£dX=0;
(2л)1 J
0
[ , I Ъ \
\2 [Лп-|-(1 -f-v) Вп] В2л+1 (у)—(^n4-2Bn) I Г" I X
I \ е* /
\ е* / Л
оо
X $ x2n {Сп (X) XW0 (Xd) — Dn (X) [ (Х6)» + 2 (1—v) л (Xft)} cos X£dX=O.
о
(8.79)
285
Эти равенства служат для определения функций Сп (X) и
Dn (X) через постоянные Ап и Вп. По правилам косинус-пре-
образования Фурье имеем:
Cn (X) Л (Xfr)-Dn (Х)Ш0 (Xd) —(2on)1 х
лХ2п
ь \г .
t ) ^2п + 2 (у)
ее /
e-(2n + 3) ScosX£d£.
(8.80)
Сп (X) /0 (Xfe)-D,, (X) [(Xd)»+2 (1 — v)] /х (Xft) =
„-,.2?(2п)! CL
лХ2п J |
о
b
е*
(Ап —2Вп)
2
^2п+2 (У) —
-вп(-т') ₽г„+з<4<,_'2"+3,1сга^-
\ ей /
Значения интегралов, входящих в правые части полу-
ченных равенств, можно вычислить интегрированием по час-
тям. Действительно, применяя формулу
2т (У)
д^2п e(2m+l)t < е(2п+2т+1)Ъ ’
получим:
С W+m (У) „„______1_ С d2n ч
J e(2n+2m+l)l C°S (2л)1 J ^2п
о о
(8.81)
(у)
е(2ги4-1) t
1
(2л)1
а2—1 Г рУ’(у)
д^2п~1 е<2т+1)6
д2п-1
ас2"-1
р^1 to)
e(2m4-l) 6
sin XCdC
cos Xfcdfc =
j. Pg+M-.to> Г x f a2"-1
2n .(2л+2т>6 “S 4 + (2/1)1 J ar2"-1
о о
f*,”11 to)
e(2m + l)J
sin X^.
286
Первый член этой суммы равен нулю, так как при С =
= 0 обращается в нуль производная полинома Лежандра,
и при £ оо знаменатель е<2п+2,п) 6-> оо. Повторное
интегрирование по частям:
X Г
(2л)! J
о
д2п~ 1
ЙС2"-'
W (у)
e(2m+D{
sin X£d£ =
(2л)!
д2п~2
д£2п~2
(у)
c(2m+ 1) £
sin Х£
к ~
о
—к
f* д2п~2
J д£2л~2
о ь
С (У)
e(2m+l)fc
cos X£d£ =
^Р2п + т-2 (У)_____
2п (2 л —1) е<2п + 2,п-,)6
X» Г д2п~2 Г рУ(у)
(2л)! J ас2"-2 е(2т+1)Е
Здесь также первый член полученной суммы обращается
в нуль при £ =0 и при £—>- оо, так как sin Л£ = 0 и
€-(2n+2m-i)fc Q После повторения этого процесса
2п раз приходим к интегралу
(0
e(2m+D S
= (-l)n
(2/n — 1)!!
(2л)!
cos X£d£ =
k2n
C cos X£
l --------~ at,
J e(2m+D6
0
значение которого известно [см., например, в [36] формулу
(7.19)],
7 COS X£d£ f к Km (kb)
I -------------— у л I------I ------------=
1 m -L 1 \ 26 / [ 1 \
J * + 9 P I Л1+— I
0 (b’ + p) 2 k 2 j
( к \m Km (kb)
\b J (2m —1)!!
где Km (M) — функция Макдональда.
287
Таким образом, для интегралов, входящих в (8.79), при т =
= 1,23 получаем:
У~п J е(2п+3)Е . ь
О
_gn)! Г
у2п J е(2п + 5) £ b b V
О
_да . .
Р2п + з(У> п1
--------- COS Atdt = (—)
g(2n + 7)l b Ъ V / |
1 \а
Г) К, (М); (8.82)
О /
(2 л)!
12n I
О
Воспользовавшись связью между функциями Макдо-
нальда
2m
^+1 W = — (X).
заменим в полученных выражениях К2 (Kb) и Ks (Kb) через
К о (М) и Кг (КЬ):
КЬК2 (Kb)=2Kt (КЬ) + КЬК0 (ЛЬ);
(Ь6)=4К2 (М)+Ж (КЬ) = (кь +-£-)(КЬ) +4КЬК0 (КЬ).
\ Ло /
Подставляя значения интегралов (принимая во внимание
указываемые замены) в правые части уравнений (8.80),
получаем их окончательную запись:
2К
Сп (К) Л (Kb)—Dn (К) Шо (КЬ) = - — [(ЛП+2ВП) Кг (КЬ) +
4-Вп КЬК0 (ХЬ)];
Сп (К) Io (Kb) — Dn (К) [(Х6)’ + 2 (1 —v)] Л (КЬ) =
= — {(Ап-[-2Вп) КЬК0 (КЬ) + Вп [(М)2+2 (1 — v)] Kt (КЬ)}. (8.83 )
л
Решение этих уравнений может быть записано в виде 1
2К
Сп (^)= (Ип+2Вп) D0 (*6) + Вп [(Х6)« +2 (1 —V)l);
пи* (Л, О)
С*п (К) = J2* Мп + 2Вп +Вл Z)° (М)] (8.84)
ПО* (№)
при следующих обозначениях:
D* (КЬ) = (КЬ)* II (КЬ)-[(КЬ)* + 2 (1 — v)l /» (КЬ);
D° (КЬ)=(КЬУ /0 (Kb) Ко (КЬ) +[(ХЬ)2+2 (1 — v)] /, (Kb) Кг (КЬ). (8.85)
1 При преобразованиях использована формула
КЬ [/0 (Kb) Kt (КЬ) + /, (АЛ) Ко (М>)] = 1 •
288
Для выполнения условий (8.74) на контуре полости в
осевом сечении преобразуем подинтегральные выражения
функций Ф2П и й2п, заменив в соответствии с формулами
[104]
1, (Ар) cos 4= Л (- О* ' Ргк (/):
».о (2*>'
~ (Xe^2fe-1
Л (М cos Ч=У (— 1)*-------—-------sinт] p'2k_i (у) (8.86)
^*1 w
произведения функций Бесселя /0 (Хр) и Ц (Хр) на cos Х£
бесконечными суммами полиномов Лежандра или их про-
изводных.
Применив формулу
Pik (у) =. 4jL I . 1^2*+1 (у)-P2k — 1 (fr)] ’
сгруппируем члены Ф и Q с одинаковыми производными
Ргл-1 (у)- После перемены порядка интегрирования и сум-
мирования получаем:
_ . 'V I Гл , (2Л +1) (2Л-+-2) п
Ф = Ф*4-51пат) У лл-1+---------——------- Bk_i-
4Л + 1
(2k - 3) (2k —2) 4k—3 — 1 g У — (2fc)! v ’ n=0 -0 2* ~ . . a Dn (X) -В4_2е2ф-<2‘-'>« + Jv"+2<’' C-(X)- 0 ИВ,(1)]Д1,;(_1М; (8.87)
4R О 4R-f-l 1 Й = Й*+-- > Ф2л-1- K k=i (2fe+l) (2fe+2) 4Л+1 , (2fe-3) (2k-2) + 4Л-3 Bk- е(2Л-2)£ oo (2fc)t 2 (2 n=0 V (2fe—1) 2k (Xe* )2 ' 4k — 3 4Л-Н 2 2 |[(>+v- k=l )^_1 + 2e2fcj e-(2fe+Dt_ IZL f X2n+2fe-l [l_v_ «)! J 0 Dn (X) P2k— 1 (У)’
289
Представим известные функции Ф* и Q* также в форме
разложений в ряды по первым производным полиномов Ле-
жандра
Ф*— sin2 Т] 2 ®2А — 1 ^2А—1 (у)' Q*— 2 ®2Л— 1 ^2А—1
А=1 А=1
(8.88)
Очевидно, условия (8.74) для функций Ф и й при £ = О
будут удовлетворены, если они выполняются для каждого
члена рядов (8.87). Приравнивая нулю эти члены, заменив в
них Сп (X) и Dn (1) значениями (8.84), приходим к беско-
нечной системе алгебраических уравнений для определе-
ния постоянных Ап и Вп (вторая группа уравнений (8.89)
является результатом преобразований, сводящихся к иск-
лючению постоянных в части членов, не входящих в
бесконечную систему).
2k 2k—2
₽‘-'+х‘-'+«+1 Z‘-2 +
2 °°
+(-•)*-' n2 (“-»-• x"+₽«*-! r")=0; (в-89»
' n=0
Г (2* + 1)(2*+2) 1 У>-!
6‘-' + 2l tt + l —I—*J 2k_l ~
OO
' ' n = 0
£ = 1,2,3, ...
Здесь приняты следующие обозначения:
Дп+2ВП —Xni Bn —
п
n
anft-1
X» (n+A)
J D* (X6)
о
(2k—1)2 k
4k—3
X2
— dk.
РпА-1 (2п-|-1)!
n p ^2 (n + A)
J D* (XB)
о
(2fe —1) 2k
4k—3
Do (X Ь) dX;
(8.90)
290
Tnfe-1 =
(—1)" (4fe —1) Г X2 (n+*>
(2n)! J D* (Kb)
о
D° (Kb)—2 (1—v) —
(2k-\)2k X2 I
4k— 1 4ft+lJd
6 _(-!)" (4fe —1)
nft-’ (2n + l)!
12 (n+A) r
Тчм r>2+2
(dk-1) 2k+2 (1-v) » \ 1
- ( zrs------------- -STi) ( Ч
* • 1 •
Pfe _ i = ф*_ i; — i =2ЛФа _ j ч — — Qk_ i.
Строгое доказательство регулярности бесконечной сис-
темы (8.89) затрудняется сложностью выражений коэффи-
циентов anft_lt Pnfe-!, Vnh-i и 6nft-i. Однако, воспользо-
вавшись асимптотическими представлениями функций Бес-
селя, можно численно обосновать регулярность для доста-
точно больших отношений радиусов полости и цилиндра
b = da.
8.13. Исследование решения
Подставляя в D* (КЬ) и D° (Kb) асимптотические выраже-,
ния (4.38) функций 10 (КЬ) и Ii(Kb), после некоторых фор-
мальных преобразований имеем:
D* (КЬ)
2л
е2ХЬ
7—8у
4ХЬ
41 — 176v-|-128v2
2 (4ХЬ)2
(8.91)
D° (Kb) 2лКЬ Г 7—8у 69—208у+128у2
D*(Xfe) " е2Хь + ш + 2 (4ХЬ)2 + • • •
Составим соответствующие асимптотические представления
сумм абсолютных значений коэффициентов (8.90):
2 °° ~ 2 °°
1: ₽‘-‘=Т^г2 |fu-,|;
v п=0 п=0
(8.92)
^*-,= л (2ft)l lVnA-1 I’ л(2Л)! 2
' п=0 п=0
10*
291
Для первой из них, переставляя порядок суммирования
и интегрирования
2 n f v Х2(п+А) / 7—8v \
аь 1=----------2л 1 z --------:— ХЬ| 1 4-------I —
я(2k)! J (2n)t е2ХЬ (, Ш> I
(2ft — 1) 2ft X2 / 7—8v\| .
— 4ft —3 “4ft 4-1 \ + 4ХЬ )гХ
и принимая во внимание, что
Х2п
(2л)!
получаем:
аА-1 =
1
е(2Ь-1) X
о
7—8v (2fe—1) 2ft
4 ~ 4ft—3
1
е(2Ь+1) X
X2*
хь +
(4ft 4-1) Ь2
(Х6)2 +
7
4
dX.
„ , (* X»*dX
Далее, применяя формулу J —
о е
чения b-x = (2Ь — I)-1 и Ьг =
(2Ае)! л
= и вводя обозна-
mk+1
(2b 4- I)-1, окончатель-
но имеем:
— 9b_L I ( 1 Г (2^----1) 2ft 1
“‘-=2 <2*+‘> 2 ь‘ + Ь+гТТгК «-3 -
i
- яТТГ +vi6-,lb Ъ=7-Г-’ (8-93>
4ft 4-1 J 4
где i = — 1 и i = 1.
Подобным образом устанавливаются значения и осталь-
ных сумм:
292
v4_,=2 (2*4-1) (4*-1)2»5*+,Ц+-57'
i ( 2Л -
(2*-1) 2*4-2 (1—v) ] bj
4ft — 1 ]~ 4 A 4-1
[(2*4-2) bi 4-Vi 6-1]
*k-
(2k —I) 2*4-2 (1—v)
4ft— 1
1
2k (2*4-1)
1
г (1_v)_ i_
I 4ft — 1
[(2*4-2) W>? +*,!< + * 1|,
L (zft 4-1) о Jj
va=(68 — 208v +128v2).
02
(8.94)
Положим в (8.89) Yn = v.Zn. Условиями регулярности
так преобразованной системы требуется выполнение нера-
венств
2ftx
4ft 4-1
2 (ft —1) х
4ft—3
“a— i + Pa—i—
ak— 1. A — 1
< 1;
(8.95)
,, + ^A—1 — ®A— 1, A — 1
в которых
“a — i — i+®ft *’* —
2
2ft — 1
(2fe4-l)(2fe + 2)
4ft 4-1
— 6A-1,A-1'
(8.96)
и параметр x определяется требованием одновременного вы-
полнения неравенств (8.95) — выравниванием сумм Si и
S2 (т. е. исключением значений Si<; 1, а22>1 или нао-
борот).
Асимптотические выражения и h-i со-
ставляются подобно тому, как было составлено выражение
afe_lt после замены \/D* (Хд) и D° (hb)/D* (ХЬ) в afc_i, h-i
и 6 Л-!, (8.90) асимптотическими представлениями (8.91)
293
и после интегрирования полученных равенств. В результате
указываемых операций
2(2fe—1) (4fe —1)11 г 2 / (fe—l)2fe \
(4At)I! fe4**-1 L+4A— IV1 4k —3 /
2fe+vi
(4/fe-J- 1) fc2
&k— 1. k— 1
(4fe—1) (4fe —1)1!
(4k — 2)!! б4*”1
(2fe —l)2fe+2(l—v)
4k— 1
2 (1—v) —
(2fe-1) 2fe + 2 (1 -v) 1_ 1 Г 2vt va 1 j
4k— 1 V1J 2ft2 [ +4й+1 + (4k +l)fc]j
По форме выражений (8.93) и (8.94) нетрудно заключить,
что с увеличением к суммы Рл-i, и 6Л-! умень-
шаются, и тем более быстро, чем больше отношение b =с/а.
Следовательно, 2Х возрастает от некоторого значения при
к = 1 до х, а 22 уменьшается от некоторого значения при
k = 1 до нуля; параметр х должен быть меньше единицы.
Поэтому при заданном b для установления регулярности
системы (8.89) достаточно произвести проверку неравенств
(8.95) при нескольких первых значениях к.
В случае b = 2 (для которого ниже выполнено вычис-
ление напряжений) четыре первых значений «h-i,
Tfe-i. fife-i и сумм 2Х и 22 приведены в табл. 38. Параметр
х принят по условию равенства суммы 2Х при к-»- оо сумме
2 2 при к = 1. После соответствующего подсчета х =
= 0,53866.
Таблица 38
k ₽fe-1 Vfe-1 Xi Si
1 0,05987 0,04062 0,41346 0,63646 0,26452 0,53866
2 0,01358 0,01819 0,12518 0,21727 0,46883 0,29497
3 0,00175 0,00238 0,02394 0,03816 0,49028 0,06289
4 0,00022 0,00043 0,00402 0,00283 0,50232 0,00666
294
8.14. Напряжения у шаровой полости
в деформированных цилиндрах
- Здесь приведены некоторые результаты вычислений на-
пряжений в цилиндрических стержнях, имеющих шаровую
полость конечных размеров, в частных случаях — растяже-
ния силами, приложенными на торцах, достаточно удален-
ных от полости, и сжатия силами, равномерно распределен-
ными на цилиндрической поверхности. Свободные члены.
Рл и 6ft уравнений (8.89) в этих случаях нагружения имеют
следующие значения. При растяжении стержня вдоль оси
силами Р = ла1 2 р
Р „ Р
•ф* = —-----р2; ср* =---------- р2;
v 2л к т 4 (1+v) л к
Р Р
Ф* = —------Р2; Q* =-------
2л л
поэтому р0 = — = — у ра2, б0 = 0;
(см. п. 3.2), и
Рь = бь = 0;
к=1,2, 3, 4, ...
При равномерном обжатии цилиндра радиальными сила-
ми р0
= 0; <р*= ф* = 0; а* = р„
(см. п. 2.1), следовательно, 60 = — р0; р0 = 0;
Рл = бь = 0; № 1,2, 3, ...
После подстановки функций Ф и й (8.90) в формулы
(1.27) для напряжений, получаем :
1 / 1 дФ* \ 1 .
— —~7------О* +— У X
о2 \ р ор ] а2, 41
х Р2л+1 («/) —Ип—4Bn) Sin2 лР2п+2 (у) —
- В„ sin< „Р”+3 (р>) f X
оо
X J X2" (or)ncos X£dk);
о
295
1 Г 1 (ЭФ* 1 I V L .
°e=.rf 2(1+',) р др +й|+ <? 2ДИ4”-
— (1 —2v) Вп] P'2n+i (z/) + (l—2v) Вп sin2 т] Р"2п+ 2 (у)) X
ОО
х e-<2n+3>6 +-tlp -L J X2"(ae)„ cos j .
0 '
1 дф* 1
az = --TT-~Z--— Z l^+O (2n+2) [Mn~
a2 p dp a2
—3Bn) P2n+2 (i/)+ Bn sin2 т\Р2п+2 (г/)] x
X e-(2n+3) 6 + < 0 C X2n+ i (CTz)n cos .
№n)! J
0
1 °°
— 2 pm-o зв„)₽;„+2 и +
1 ЭФ*
a* p d£
n= 0
+ Bn sin2T)P£n + 3(
(2n + 3) 6 sjn j] _|_
OO
+ * f Х2п+’ (тгг)п sin X£dX
(2 л)! J
о
(8.97)
при обозначениях, которые уже применялись (см. п. 4.4):
(Рг)п = Сп (X) [Хр/0 (Хр)—1г (Хр)]-|-Dn (X) {Хр/0 (Хр) —
-[(XP)2+2(i-v)]/1(M};
(ae)n = cn (X) Л (Xp) + Dn (X) [2 (1 — V) /j (Хр) —(1 —2v) Хр/0 (Хр)];
(Pz)n—Сп (X) /0 (Хр) — Dn (X) [2/0 (XpJ-f-Xp/i (Хр)];
(trzin — Сп (X) /i (Хр) — Dn (X) Xp/g (Хр);
Сп (X) и Dn (X) определены равенствами (8.84).
Укажем значения напряжений в поперечном (ослаблен-
ном) сечении £ = 0 и на оси вращения р = 0. В первом слу-
чае, так как у = cos т] = 0, для полиномов Лежандра и их
производных справедливы равенства:
^а(0)= (—1)а
(2fe— 1)!!
(2/г)!!
Р&т} (0)=(-1)А-"1
(2fe4-2m—1)!!
(2k—2m)!!
(0) =0;
₽2» + l (0) =0;₽<2Д>,(0) =0; РВД'» (0) =
= ,_n*-l <2*+2т>!1
1 7 (2k—2m— 1)!!
296
Используя эти равенства, имеем:
1 дФ* \ 1
— Q* 1+ — 7
Р др--/а2
л=0
— (1 — 2v) Вп-(2л+3) (Лп-4Вп)-
(2n +1)11
(2л)!! ( n
Qr= —
tr
-(2л+3) (2n + 5) Bn]p~(2n+3) + (2n), p j
о
X2" (ог)п dX > ;
ofi = —-
6 а2
d<p*
(2п+1)ПгЛ
(2л)1! 1 п
— (1 —2v) Bn + (l-2v) (2n + 3) Bn] p-(2n+3) +
Р др
п=0
,п
1 (
(2n)!p J
о
X2n (CTe)n dX ;
1 дФ*
а2 р др
(2п+1).Ч/А
(2 л)!! ( п
ОО
- ЗВ„) ₽-<2"+з> ++— [ V"+' (о,)» А
(2п)1 J
О
(8.98)
На оси вращения р = е£ sin т], подставляя в (8.97) производ-
ные Ргп+i (У) при cos т] = 1: Pzn+1 (1) = (2п + 1) X
X (2п + 2), получаем:
0Г а
6 а2
1 дФ* л
-------— Q*
Р др
2а2
п=0
(2л +1) (2л+ 2) (Л„-
ОО
— (1 —2v) Вп] £-(2п+3)+(-;-Г7Г f *2n+1 [Сп (Х) +
И*)! J
О
+ 2v Dn (X)]cos X^dX
(8.99)
-ЗВп) £-<2п+3) +
1 дФ*
а2 р др
п= о
(2л +1) (2п+2) (Лп —
(- 0п
(2л)!
ОО
С х2п+1
О
[Сп (X) — 2Dn (X)] cos X£dX
297
298
Таблица 39
Ь=а/с г/а а/Р 0,25 0,375 0,5 0,625 0,75 0,875 1
Продольное растяжение
Or 0 0,1796 0,1022 0,0698 0,0359 0,0234 0,0160
оо °6 0,1361 —0,0045 —0,0085 -0,0059 —0,0039 —0,0027 —0,0018
Oz 2,0454 1,1751 1,0530 1,0229 1,0118 1,0069 1,0044
Or 0 0,1914 0,1026 0,0514 0,0238 0,0084 0
4 °6 0,1335 —0,0172 -0,0213 —0,0198 -0,0201 —0,0221 —0,0253
Oz 2,1632 1,2022 1,0708 1,0367 1,0213 1,0079 0,9906
Or — — 0 0,2454 0,1591 0,0677 0
2 — — 0,0986 —0,1002 —0,1550 -0,1878 —0,2209
Oz — — 2,8443 1,6834 1,3457 1,1511 0,9847
По перечное сжатие
Or 0 -0,5242 —0,7727 —0,8774 -0,9270 —0,9533 —0,9839
П0 — 1,3636 —1,1526 -1,0710 — 1,0379 — 1,0224 — 1,0143 -1,0097
Oz 0,5455 0,0269 -0,0085 —0,0091 -0,0067 —0,0048 —0,0035
Or 0 —0,5108 —0,7802 —0,8968 —0,9538 —0,9848 — 1
4 °6 — 1,3932 — 1,1887 -1,1035 -1,0705 -1,0575 -1,0541 — 1,0505
Oz 0,6971 —0,0480 —0,0009 -0,0067 —0,0129 —0,0288 -0,0585
Or — — 0 —0,2703 -0,6233 -0,8568 — 1
2 — — — 1,5836 — 1,5549 — 1,5049 — 1,4964 — 1,5242
Oz — — 1,3790 0,3817 0,1258 —0,1508 —0,3939
В табл. 39 приведены отношения напряжений к напряжени-
ям в сплошном цилиндре в точках ослабленного сечения.
Значения коэффициентов концентрации, т. е. отношений
напряжений к силам, приходящимся на единицу площади
ослабленного сечения Fnetto = л (а2 — с2), суть следую-
щие: для напряжений о2 в случае продольного растяжения
2,029 и 2,133, для напряжений ое в случае радиального
сжатия 1,306 и 1,188, где первое значение соответствует
а/с = 4, второе а/с = 2.
Глава 9. РЕШЕНИЯ В ЭЛЛИПТИЧЕСКИХ
И ПАРАБОЛИЧЕСКИХ КООРДИНАТАХ
9.1. Решение в эллиптических координатах
при расположении полюсов на оси вращения
Обратимся к решению осесимметричной задачи в двух
формах криволинейных координат — эллиптических и па-
раболических. Применение их приводит к обогащению об-
щих представлений о напряженно-деформированном состоя-
нии среды и позволяет в достаточно простой форме получать
решения в практически интересных случаях нагружений
тел, ограниченных эллиптическими, гиперболическими и
параболическими поверхностями вращения. Частные слу-
чаи деформаций эллипсоидов вращения рассматривались
Кельвином, Максвеллом, Кри. В 30-е годы нашего столетия
Маргерром и Нейбером положено начало серии исследова-
ний в области применения эллиптических и параболических
координат к решению задач теории упругости. Весьма
эффективным для построения решений задач в кри-
волинейных координатах оказалось применение общего ре-
шения осесимметричной задачи в форме, предложенной [641.
Для нижеследующего изложения использованы [68—731.
Система ортогональных изотермических эллиптических
координат в плоскости Orz определяется следующей связью
с координатами г и z:
r = csh£sinT]; z=cch£cosT]. (9.1)
Линии £ = const в этой системе представляют собой се-
мейство софокусных эллипсов, межфокусное расстояние
которых равно 2 с, и большая ось совпадает с осью Oz
299
(рис. 53). Линии т) = const — семейство гипербол, ортого-
нальных эллипсам В = const, вещественная ось которых —
— ось Oz, а мнимая ось — Or.
Система (9.1) «двулистная», поэтому пределы изменения
£ и т] могут быть выбраны двояким образом. Если считать £
положительным, то для соответствия знаков г, z и |, т] коор-
динату т) нужно принимать
положительной справа от оси
Oz и отрицательной слева от
нее, т. е. для одной и той же
гиперболы правая часть име-
ет один знак, а левая-другой.
Все гиперболы как бы рассе-
чены на отрезке оси Oz между
фокусами (где £ = 0), по
представлениям одвулистнос-
ти переходят на другой
лист значений | и т) (где |<;0).
На рассматриваемой плоскос-
ти пределы изменения £ от 0
до оо, т) от — л до л. Знаки
Рис. 53
на рис. 53 соответствуют такому предположению.
Можно, наоборот, согласование знаков координат полу-
чить, меняя знак координаты считать | справа от оси Oz
положительным и слева отрицательным. Переход на нижний
лист осуществляется вдоль частей оси Oz — оо <z z<Z — с
и с < z < оо. Пределы изменения координат — оо < z <
<Z —с и 0 < Tj < л. Первая альтернатива применяется при
рассмотрении внешних задач для эллиптической области,
вторая — при рассмотрении внутренних задач.
Для рассматриваемой эллиптической системы коорди-
нат [см. (2.09)]
/ дг \2 l dz \2
Н = (— ) 4- I —— ) = с2 (ch2 —cos2 т)) = с2 (sh2 £+sin2 т)) .
\ ОТ) / \ ОТ) J
(9.2)
Перейдем к определению формы функций ф и <р. Реше-
ние уравнения (2.12)
д / 1 дф \ д / 1 дф \
\ г д£ / дт] к г дт) /
в виде произведения двух функций (|) и /2 (tj), из которых
одна функция только координаты В, а другая — только ко-
300
ординаты tj: Ф (£т]) = (£) f2 (tj), приводит к разделению
переменных
—cth £ -k (Л+1) Л =0;
dg2 at,
d? fi s
-ГТ~-^W-T^ + k (*+ I) fa=0. (9.3)
dr] ат)
Второе из этих уравнений совершенно тождественно вто-
рому уравнению (2.34), поэтому если под Tj понимать коорди-
нату, определяемую зависимостями (9.1), то за функцию
/2 (tj) можно принять любое решение второго уравнения
(2.34), т. е. значения (2.42) и (2.44).
После подстановки
fi ф=$Ь 5 X (ch 5) = У^=_1 X (х),
где х = ch I, первое уравнение (9.3) сводится к уравнению
Лежандра:
d2X dX г 11
(1-х2)——2х—+ Л(Л + 1)-- — Х = 0, (9.4)
dx£ dx I 1 —х“ J
которое отличается от (2.36) только заменой у и х. Следо-
вательно, за решение первого уравнения (9.3) можно при-
нять решение второго уравнения (2.34) с заменой перемен-
ной т] на переменную В и тригонометрических функций ги-
перболическими.
На основании сказанного решения уравнений (9.3) за-
писываются в следующем виде:
при k = 0;
. /1 = Л ch 5 +В; f2 = CcosT)-j-D
h = [AkP’k (x)+BfeQ* (x)]sh4;
(9.5)
(9.6)
/г = [Cfc P'k (у) +Dh Q'k ((/)] sin2 T)
при любом другом целом k. Злрсь
p'kM
dPh (X)
dx
dQk (x) .
dx
dPk (у) .
dy
Qk (y) =
dQk (y) .
dy
Qk W =
W=
Pk (*); Qk (X) и Ph (y); Qk (у) — сферические функции Ле-
жандра соответственно первого и второго рода от х =
= ch | и у = cos т).
301
Таким образом, в эллиптических координатах (9.1) функ-
ции ф и ф (которая составляется подобно ф и отличается от
нее только значениями постоянных) имеют следующие зна-
чения:
ф0 = (A ch £4-В0) (C0COST]4-D0);
Фл = [А P’k (X) + Вк Q’k (X)] [Ch P'k (y) + Db Q'k (у)] (sh g sin t])2; (9.7)
<Po = (A ch £ + Bo) (Co cost] + Do);
<Ph = [A P’k (x) + Bh Q'k (x)] [Cft P‘k (y) + Dh Q’k (y)] (sh g sin t])2.
Можно получить и другие формы решений уравнений (2.12)
в эллиптических координатах. Например, имея в виду, что
если некоторая функция ф есть решение уравнения (2.12),
то любая производная ф по z должна быть решением этого
уравнения, после дифференцирования функций (9.7) по
z получим новые решения рассматриваемого уравнения.
Укажем два из них:
д с2
с —— (cos т]) = — ch £ sin2 гр
ог п
с (ch £) = sh2 £ cosrj, (9.8)
Ог п
которые будут использованы в частных задачах.
9.2. Сжатие эллипсоида вращения
Наиболее простым решением осесимметричной задачи в
эллиптических координатах является решение для сжатия
(или растяжения) продолговатого эллипсоида вращения си-
Рис. 54
лами, приложенными в вершинах в нап-
равлении большой оси (рис. 54). Функции
ф и <р определяются равенствами:
ф = ЛсЬ£ + В+ sh2 £ ch £;
п
<p = Cch£ + D, (9.9).
два первых члена которых взяты из (9.7)
при k = 0, а последний член функции ф
представляет собой комбинацию ch £ и ре-
шения (9.8) в первой форме
д с2 „
ch£ —-с—— (cos т]) = —- sh2 £ ch £.
ог п
Функция Ф получает значение
с£
Ф = А ch £ + В + ~ (B04-Ccos2T)) sh2£ch£.
н
302
По равенству функции Ф и <р нулю на оси вращения (В =0)
должно быть В = — А и D = — С. По постоянному зна-
чению нормальной силы N = — Р во всех поперечных сече-
ниях контурное значение функций Ф должно быть посто-
янным. Обозначив через b = ch Ео, где Ео — координата,
определяющая поверхность эллипсоида, и положив Во =
= — СЬ1 2 * * * 6, получим при £ = Ео:
ф = Д (6—1) —С(62—1)6 = Р/2л.
Составив по формуле (1.26) функцию Q
0= , ' » !TTZ7 И +2 “v>с|-
(с Sint])2 (ch Е + 1
с2 ch Е 1
— ——— (62—cos2 т) +2 sin2 т]) С|,
Г7 )
по второму условию (2.15)
дф / дг \
~^Г = Г ; (Рг = 0)
ое \ »Е /
после подстановок и некоторых преобразовании имеем:
А = 1(1 — 2v) b—НС. Таким образом, значения постоян-
ных А и С устанавливаются:
1 —(1—2v)6 Р с_ _______________1_________р_
(b— 1) (62+1+-2у6) 2л ’ (6—1) (62+1+2у6) 2л *
Окончательный вид функций Ф и Й таков:
62 — COS2T1 _ )
- , _.----— sh2 Е ch Е |;
ch2 Е—cos2T) )
(9.10)
(l_2v)(6+l) с2 ch Е 2
ch 1+1------ — }•
Ф = С [6(1 — 2v) —11 (ch£ — 1)
С
Й=---------
(с sint])2
Напряжения [см. (2.20]) в рассматриваемой задаче пред-
ставляются следующими выражениями:
CchE Г 9 6—ch Е ch2 Е—62 I
Н V chE+1 "I” ch2 Е—cos2T) j
о = —[(1 —2v) (6+ 1) (ch Е-1) ctg2 т) -
Jj I
62 —1 ch2E — 62
sin2 т) ch2 Е —cos2 т]
ch Е
С Г (1 —2у) 0+1) _ 1 62-1 V
с2 | (ch Е+1) sin2 т) ch2 Е—cos2i] \ V sin2 т) /
_ С sh Е ctg т) Г _ 6—chE _ ch2 Е—62 *
Н V ch Е + 1 ch2E—cos2T)
(9.И)
303
Составляя функции напряжений ф и <р в форме сумм зна-
чений (9.7), можно получать решения при нагружениях про-
долговатых эллипсоидов вращения силами, распределенны-
ми по поверхности по полиноминальным или кусочно непре-
рывным законам. Выполнение таких решений примерно сле-
дует плану составления решений в рядах для цилиндров,
конусов, шаров. Однако выражения, полученные в про-
цессе выкладок и в их результате, значительно более гро-
моздки. Поскольку эллипсоид, мягко говоря, довольно
необычная форма сооружений, интерес к построению
подобных решений неоправдан. Теоретическое и практи-
ческое значение, пожалуй, может иметь исследование
напряженно-деформированного состояния полых эллип-
соидов вращения (эллипсоидальных оболочек как замкну-
тых, так и открытых).
9.3. Концентрация напряжений у продольных
эллипсоидальных полостей
Применение эллиптических координат позволило с
достаточной простотой составить решения задач о рас-
пределении напряжений у эллипсоидальных полостей в
бесконечной среде. Первый результат в этой области — кон-
центрация напряжений у малой эллипсоидальной полости в
растянутом стержне — принадлежит Г. Нейберу Г49].
Рассмотрим напряженное состояние у малой полости в
форме эллипсоида вращения, вытянутого вдоль оси Oz
(продольная полость), в сплошной среде в трех случаях на-
гружения ее на бесконечности: растяжения вдоль оси Oz,
двустороннего сжатия и двустороннего изгиба в направле-
нии, перпендикулярном оси Oz. Указываемым условиям и
условиям на контуре полости | = |0 можно удовлетворить,
принимая за функции ф и <р следующие выражения из чис-'
ла (9.7) и (9.8):
f 2D. ( be \2 Г
+ (х)—~7Г~ "тт) ch£+c p2ch£4-B2Q2(x) —
I Н \ sn § / [
2D2 / be \21 1 Л Л
——coslllr; (9-12)
n \ sn / J J
<P = {C1 + D1Q; (x)+c[C2ch £+D2Q2 (x)]cost)} r2,
где b = ch £0- Им соответствуют функции Ф и Q
304
Ф = Mi + BiQ; (x)-2D1
(b2—cos2T])ch£
(ch2 £—cos2 T]) sh2 5
+c [(Л2+С2) ch ^ + (B2+d2) Q2 (x)) cost) —
2D2(fc2—cos2T]) 1
(ch2 —cos2 rj) sh2 £j
(9.13)
q = 4-<d-2(i+v) [G+DjQ; toj-
4Dj ch £ sin2 t]
(ch2 £—cos2 T]) sha £
-c 2(l+v)[C2ch£+D2Q; (x)]
4D2 sin2T]
(ch2 £—cos2 T]) sh2 £
COST] .
Функции ф и Ф, как нетрудно проследить, удовлетворя-
ют при г=0, за исключением отрезка оси Oz, заключенного
между фокусами (отрезка, находящегося вне рассматривае-
мой области), условиям <р = 0 и Ф = 0 при любых значени-
ях входящих в них постоянных.
При больших значениях координаты члены с коэффици-
ентами Bt nDi(i= 1,2) в равенствах (9.12) и (9.13) малы по
сравнению с членами с коэффициентами Ai и Ct. Поэтому
при £, достаточно большом в <р, Ф и Q, можно сохранить
только последние члены. Тогда
<р = С1Г2 + Схг2г; Ф = Лг г2 + (Л2 + С2) г2 г;
(9.14)
Й = Лд-2 (1 +v) СЖЛ,-(1 +2v) CJ г.
Это простейшая форма функций напряжений (см. пп. 3.2
и 3.3), из которой выбором значений постоянных Л2,
Ct и С2 можно получать решения при однородном напря-
женном состоянии. Так, если положить Ах = — р/2; Cj=
= р/[4 (1 + v)]; Л2=С2 = 0, то функции (9.14) обращаются
в решение задачи о растяжении стержня силами Р = рла2
в направлении оси Oz. Если
C2=-p/[2(l+v)], Л1 = Л2 = С2=0,
то (9.14) совпадают с решением задачи о двустороннем сжа-
тии среды нагрузкой р. Если
Ла= -р/[2 (1 -Н) h\\ С2 = р/[2 (1 +v) hl; Л1=С1=0,
то из (9.14) следует решение задачи чистого изгиба круглой
плиты, высота которой 2h и закон нагружения боковых по-
верхностей р = z/h.
Для сплошных цилиндров и плит постоянные Bi и Di
должны быть приравнены нулю. При наличии внутри обла-
305
сти малой эллиптической полости значения этих постоян-
ных находятся по условиям на поверхности полости
дф дг
Ф=0; — = гй — (9.15)
os 05
при | = £0. После выполнения всех подстановок и преобра-
зований имеем (b = ch |0):
= jjr Mi-0 +v) b (b2~ В
(9-16)
b2— If. Г bQ"2 (b) 1 J
D> = (Лг + С2) (62- 1) 1- +2 (1 +v) C2 62 ;
^2 1. (0) J )
1 ( . 2b \ Г 2 1
B,=—------( A.—------D,), B2 = —-----------— 1 D2.
Q;(b) ( 1 62—i 7’ (62-i)Q2 (b)
Здесь приняты следующие обозначения:
26
d; =——+[1+з62 + (i +v) b (b2_ i) Q; (6)1 Q; (6).
6z— i
6Q2 (6)
d;=26+(i+v) 6(62-i) Q' (6)+ у;; . (9.i7>
4 2 (0*
Общие выражения для напряжений весьма сложны ( их
можно найти в [68]), поэтому ограничимся приведением их
частных записей.
Продольное растяжение и двустороннее сжатие среды.
Напряжения на контуре полости:
<Ч=Чч=0;
2 (
% =“й------2— О+V) IC1+D1 Qi' (*)] (fc2-’)cos2n-
1 62—COS2 T] (
[6 sin2 t] )
B, + D, (362— 1)----1 >;
it м ) f)2_l j. (9,18)
4vDb sin2 Ti
oe=2 (1 + v) [Cj+DjQJ (6)]+ •
(62— 1) (62—COS2T])
Напряжения в ослабленном сечении (z = 0) при обозна-
чении р = г/с:
62D
Рг (Ьр)2
fl
(9.19)
306
<ye = A + 2 (1+v) C1 + [B1+2(l+v) DJQlCl/l+p»)-
2(^-2v)D1
—----/ ; TEn = °-
₽2Vi+₽2 ”
Напряжения на оси вращения (г = 0) при обозначении
£ = z/c:
2Di (У-IK
(£2-1)2
ot=-2 A + ^QKO
an=ae = ?,i+2(1+v) ^ + [^ + 2(1 -+ v) DJ Q; (0-
2D, (fe2-lK
К2—I)2
(9.20)
Напряжения на контуре полости при чистом изгибе пли-
ты:
°Е=т{ч=0;
an=2c[(l+v)[C26+Di<2;(6)l+— ^‘и2'1 2 ,)смЧ; (9.21)
’ I (О2—1) (О2— COS2T])J
Г 2v D si Т) 1
°е = 2с I (1 +v) [С2 Ь +О2 Qi (fc) | +——-J cos n.
Для полости, контур которой определен значением £0=
= 0,5, подсчитаны напряжения при продольном растяже-
нии среды в направлении оси вращения (продольное растя-
жение), сжатии и изгибе в направлении, перпендикуляр-
ном оси Oz (соответственно двустороннее сжатие и чистый
изгиб). Результаты приведены в таблицах: в точках контура
(табл. 40), плоскости z = 0 (табл. 41) и оси г==0 (табл. 42).
Графики распределения напряжений изображены на
рис. 55. 56 (продольное растяжение), рис. 57, 58 (двусто-
роннее сжатие) и рис. 59 (чистый изгиб). При подсчетах при-
нято: v = 0,3.
Характер распределения напряжений и величины макси-
мальных напряжений существенно зависит от отношения
к = z0/r0, где г0 — меньший и z0 — больший полудиамет-
ры полости. На рис. 60 изображены графики напряжений
оп и оо при т] = 0 ит] = 90° (т. е. на оси вращения и в
плоскости, перпендикулярной этой оси и проходящей че-
рез центр полости) при изменении к от /, что соответствует
сферической полости, до к = оо, когда полость превраща-
ется в трещину, ориентированную вдоль оси вращения. В по-
следнем случае 6=1, и величина напряжений в вершине
полости без труда находится из соответствующих выраже-
ний для оя и Ое. Для полости в растянутом стержне оп =
= Ое = —vp/(l — v). Эти напряжения меняются от
0 до — р при изменении v от 0 до 0,5. При v = 0,3 оп =
307
Таблица 40
n а/p 0 15е 30’ 45’ 60’ 75’ 90’
% —0,5819 —0,084 Продольное р 0,625 астяжение 1,049 1,266 1,368 1,3975
сте —0,5819 -0,432 —0,220 —0,093 —0,028 0,003 0,0119
% —2,5683 — 1,846 Двусторонне —0,820 е сжатие —0,205 0,109 0,262 0,3010
ст0 —2,5683 —2,353 —2,045 — 1,859 — 1,765 — 1,719 —1,7076
% 2,5909 L679 Чистый 0,155 изгиб —0,119 —0,286 —0,193 0
ст0 2,5909 2,265 1,707 1,240 0,821 0,411 0
Таблица 41
Г/с а//> 0,5211 0,6 0.8 1 1,5 2 2,5
0 0,038 Продольное р -0,066 астяжение 0,044 0,038 0,021 0,013
% 1,3969 1,304 1,158 1,087 1.025 1,009 1,004
°0 0,0118 -0,003 —0,013 —0,011 -0,007 —0,004 —0,002
°C 0 -0,191 Двусторонне —0,512 >е сжатие -0,675 -0,861 -0,928 —0,961
% 0,3010 0,200 0,088 0,034 —0,018 —0,007 —0,001
го 05 . —1,7076 —1,518 -1,270 -1,158 —1,056 — 1,026 — 1,014
Таблица 42
Z/C D/P 1,1276 1,5 1,75 2 2.5 3 3,5 4 5
0 0,652 г 0,813 [родольное рг 0,886 1стяжение 0,948 0,971 0,982 0,988 0,994
°т) = <70 —0,5819 0,018 0,015 0,011 0,009 0,005 0,003 0,001 0,001
0 -0,296 —0,166 Двустороннее -0,103 г сжатие —0,048 —0,027 -0,016 —0,011 —0,005
W °Т| — °0 —2,5683 — 1,078 -1,031 —1,016 — 1,006 — 1,003 —1,002 -1,001 -1,000
= a© = — ЗрП. Для полости в сжатой или изогнутой пли-
те напряжения в вершине определяются равенством ол =
= о© = — 2р /(1 — v) и находятся в пределах от —2р до
— 4 р. Если v = 0,3, то оп = о0 = — 20 рП. В ослаблен-
ном сечении (т) = л/2) ст,) = р; о© = 0 для полости в рас-
тянутом стержне и оч = 0; о© = —2 р для полости в сжа-
той плите.
Значения коэффициентов концентрации напряжений к
приведены в табл. 43.
зю
311
— полость В растянутом стержне
—----полость в сжатой плите
6д (fl-SO’)
Таблица 43
k Продольное растяжение Двустороннее растяжение Чистый изгиб
Т)-=0 Т) = 90° Т)= 0 П = 90° Т) = 0
ае стт) —сте % стп —ае
1 0,682 2,045 0,136 2,182 0,546 1,364 1,835
1,2 0,657 1,836 0,091 2,283 0,482 1,453 0,943
1,4 0.639 1,690 0,062 2,371 0,436 1,528 2,036
1.6 0.622 1,587 0,041 2,438 0,394 1,588 2,119
1,8 0,606 1,501 0,026 2,492 0,357 1,638 2,192
2 0,592 1,440 0,018 2,535 0,326 1,677 2,268
2,5 0,563 1,328 0,004 2,619 0,261 1,755 2,377
3 0,542 1,256 — 2,674 0,216 1,807 2,468
4 0,516 1,175 — 2,744 0,156 1,874 2,588
5 0,493 1,125 — 2,776 0,119 1,907 2,656
оо 0,429 1,000 — 2,857 0,000 2,000 2,857
312
9.4. Решение в эллиптических координатах
при расположении полюсов на оси,
перпендикулярной оси вращения
Переменив роль г и z в выражениях (9.1), т. е. положив
г — с ch cost]'. г =с sh £ sin г], (9.22)
мы получим систему эллиптических координат в плоскости
Orz, в которой постоянными значениями £ = const определе-
на система эллипсов с большой осью, расположенной на оси
Or, и малой — на оси вращения Oz, постоянными значения-
ми 1] = const — система гипербол с вещественной осью Or.
Двулистный характер координат предполагает разрез либо
между полюсами (Е > 0; — л < т] < л), либо вдоль
частей — оо <Z г <Z — с и с < г < оо оси Or.
Решение уравнений (2.12) для функцийф и <р в виде про-
изведения ф (|, т]) == /, (|)/2 (т]) в координатах (9.22) при-
водит к двум уравнениям:
4* А
№
dl
(k
Dfi- 0;
(9.23)
d2 f. df2
—Y4-tgT]-^--+ H*4 i)f2 0.
dry di}
При k --=0
d2fy
dl2
-thg-^
dl
0;
d2ft
drf
dft
dr]
rtg »|
0
откуда /,(£)•“40shg4-В , f2 (rj) -Co sin rj j-D0.
(9.24)
При k — 1, 2, 3, .... после подстановки в (9.23)
fl (5) -ch (i sh I) X (X);
f2 in) cos n) (sin n) V1 — y2 Y (y) •
где x i sh | и у — sin т], получаем два уравнения Ле-
жандра:
( 1 — А2)
d- X dX
---------------- 2х
dx2-----------dx
k (k-])-
(9.25)
(I -у2)
d-Y
dir
k (k
отличные от (9.4) и (2.36) только значениями х и у. Следова-
тельно, функции и /2 имеют форму, аналогичную (9.6):
/1 |А P'k(x)~BkQk (x)|ch4:
ft |Cfc P'k (у) тгЬк Qk (y)| cos21],
313
где Pk (х); Qk (х); P’k (у) и Qk (у) — первые производные сфе-
рических функций «Лежандра переменных х = i sh Е и
у = sin tj.
Итак, искомая форма функций ф и <р установлена:
фо - (А„ sh £ + б„) (С„ sin т] -l-Do);
Ф*=[А P'k М -|-Bh Q'k (х)] |СЛ Р; (у) -\-Dk Q'k («/)] (ch cost])2;
(9.26)
<р,)=-(Я(; sh 5-J-fio') (Co sin T]+Do):
Фл = [л* p'k (x) + B'k Q'k (x)] [C; P’k {y)+D'k Qk (У) 1 (ch £ COST1)2-
Составляя производные sin т] и sh | no z, получаем следую-
щие значения функций ф и <р:
д с2 д с2
с-г- (sin ?])=-—sh£ cos2 tj; с—— (sh |) ch2 £ sin i], (9.27)
oz п oz п
используемые при составлении решений в частных задачах.
Дифференциальный параметр криволинейных коорди-
нат имеет прежнее значение (9.2).
9.5. Сжатие гиперболоида вращения
Используяформу функций (9.26), можно получить реше-
ние для сжатия (или растяжения) однополостного гипербо-
лоида вращения
Рис. 61
вдоль оси (рис. 61) подобно тому, как в п.
9.2 была решена задача о сжатии эл-
липсоида вращения. За функции ф и <р
нужно принять
В„ с2
ф — Л sin г] + fi + —~— sin т] cos21];
«р =- С sin ?] 4- D, (9.28)
где первые два члена решения (9.26) при
к — 0 с изменением обозначений постоянных
и последний член функции ф —комбинация
вида [см. (9.27)]:
д с2
с----(sh §)— sin т] — —— sin т] cos- rj.
dz п
Функция:
с2
Ф ----- A sin т] + В -j- — (fi04- С sh2 £) sin г] cos2 tj .
Если положить А = — В и С = — D, то функции ф и Ф
будут равны нулю на оси Oz (при т] = л/2), т. е. будут удов-
летворены основные условия (1.32) для сплошных тел.
314
Положив далее Во = СЬ2, где b = sin т]0 и т]0 — коорди-
ната, определяющая контур осевого сечения, для функции
Ф получим постоянное значение при т] = т]0 по условию
(1.36), равное сжимающей силе, поделенной на 2 л:
Ф = б (1— 6) 4-Сб(1 — ь2) = Р 2л.
Функция й имеет вид
Q--=••• ' (ттА-------[В-2 (1 — v) CJ +
(cch g)2 I 1 4-sin т]
c2 sin n 1
+ —-Ч/>2-1+ЗсЬ2£]С •
п I
По второму условию (2.19) получаем В = [1 —
— 6(1— 2v)J С.
Присоединяя сюда связь между постоянными В и С и
силой Р, находим
1 Р 1— (1— 2v)b Р
С =-----------------------; В=~------------------------.
(1— b) (fe2+2vft-bl) 2л (1— b) (624-2v64-l) 2л
После этого устанавливается окончательный вид функций
Ф и й:
sh2 £ -4- 62
Ф = С [1 —(1 —2v) Л] (1 — sin 71) 4----------si п 71 cos2 ti ;
sh2 g + sin21]
(9.29)
C ( (1 —2v) (14-6) c2 sin n , |
fi= —------— I -------' v —-------------L (b2 — I 4-3ch2 £) •
(cch£)2 [ 14-sin 7] H I
Напряжения:
1(1-2v) (14-6) (1 —sint]) th2 [з—(1—2v) 6 —
n ( L
1—62 62—Sin2 7] . I
“ch25 + sh214-sin2 7] S,nT
(9.30)
C sin ti ' sin ti—6 62 — sin2 ti
о =--------L (1—2v)------!-----1-----------— ;
11 fi ’ 14-sin 7] sh2 4-sin2 7]
_ С Г (l-2v)(14-6) _ 1 fi -2v I 1 Yl
с2 (1 4-sin 7]) ch2 I sh2^4-sin2 7] ' ch2 £ ’
C th cos 7] sin 7]—6 62—sin2i)
H 14-sin 7] sh2 £4-sin21]
Приведенное решение Нейбер [49] использовал для оп-
ределения коэффициента концентрации напряжений в глу-
бокой кольцевой выточке на поверхности цилиндра (реше-
315
ние приближенное — без выполнения граничных условий
на цилиндрической поверхности). Значения коэффициента
концентрации поставлены в связь со значением радиуса за-
кругления в углублении выточки.
9.6. Концентрация напряжений у сплюснутых
эллипсоидальных полостей
Построение решения для определения концентрации на-
пряжений у сплюснутых полостей, т. е. полостей, у которых
меньший диаметр совпадает с осью вращения, в симметрич-
но нагруженной среде производится совершенно аналогично
построению решений для случая продольных полостей.
Функции ф и <р и числа (9.26) принимаются в форме
( . (Ъс)2 sh Е
ф = М,-|-В1 iQ't (х)—2D, 4-c[42sh E + 62Q2 (x)|sin ц-;
I H clr §
2D, / be V)
-I----- ----- r2;
H \chE/l (9.31)
(I' JC, ; D, Ip; (x)H c[C2sh E + D2Q; (x)J sin r2,
где b ~ shE, Eo — координата, определяющая контур полости в осе-
вом сечении.
Соответствующие функции:
ф
Л. + Bj/Q; W-2D,
(fe2-f-sin2 т]) sh Е
(sh2 E + sin2 т]) ch2 E
-R (A2+C2)shE + (B2tD9)Q;(x)
2D2 (b2 + sin2 7]) ~ . 1
11 s 1П Tl '
(sh2 E + sin2 tj) ch2 E I
(9.32)
1 4D, sh E cos2 7i
O = — Ф —2(1 +v [CRD, iQ\(x)l+ . 2 . * -
r2 (sh2 E+sin2 tj) ch2 E
{_ 4D»cos2ti |
2 (i + v) (C2 sh E +d2 q; (x)J+. . 2 t , . 2 4—П sin П•
(sh2 E+sm2 7]) cn2 El
Легко заключить, что введенные таким образом функции
<р и Ф равны нулю на оси вращения вне полости. При £ до-
статочно большом они принимают форму (9.14). Следова-
тельно, в области достаточно больших Е функции (9.31) и
(9.32) при определенном выборе постоянных (см. п. 9.3) сов-
падают с соответстввющими значениями функций <р, Ф и Q
для растянутого стержня, для сжатой радиальной нагрузки
по боковой поверхности плиты и для чистого изгиба плиты.
Предполагая в одном из указываемых видов осесиммет-
ричного нагружения среды наличие полости, имеющей вид
316
сплюснутого эллипсоида вращения, так распорядимся по-
стоянными Bit Dlt В2, D2, чтобы освободить от напряжений
поверхность полости Выполнив условия (9.15), получаем:
Mj + (1+v) fe(ft2+i)iQ; (ib)]-t
LJ 1
W^l(4' + C!,(‘!+I) '~'’oQ№)>]+2('+V)Cifc2|:(9 33)
1 / 2b X Г 2
), —----------Mi —-------D, ; В , •--= —------------hl D2.
iQ’t(ib) k 62+l l) L (62+l)Q;0'6)
В этих выражениях b = sh £0:
D* +v) hiQ'< <ib>] iQ*
tr 1
6iQ2 (<b)
d; -2b-(14-v) b (b*+1) Q; - ?2\ / •
Qa (lb)
Приведем значения напряжений в точках контура полости
ослабленного сечения (z = 0) и на оси вращения. В случае
продольного растяжения и двустороннего сжатия среды:
на контуре полости
2 (
% = А2 • 2 (’ +V) lCJ + Dl ‘Ci (/fc)l (fc2+ ’) sin2 n +
1 bl 4- sin2 t) I
fecosn 1 ___
+ lfl1-D1(l+362)] ; (9.34)
о г I •
Л 4vD. b cos2 n
ofi =2 (1 +v) [C. + D) iQ'. (ib)] —----1!;
e v -г /I it i л (62_|_1)(62+sin2T1)
в ослабленном сечении
<Ъ = ЛтЬ2 (1+v) Cj + lBj+2 (1+v) DJ/QlOVp-2-!)-
D. fe2 I 1
—2 В)— 2 (b2— l)Di — —! -------- ;
L p2 — 1 J p2 Vp2— 1
= -2IA+в, iQ; (I VF=T*1 -
_ B _ (frp)2 1 .
p2—1 p2 Vp2—i ’
oe=A+2(1 +v) Cj-H^+2 (1 -v) DJ iQ; (i Vp’— i )-
_2Di (fe2+2v)
p» Vp*—i
(9.35)
317
на оси вращения при г -- О (С = z /с)
= —2
ЛН-BhQ; (Ф-
2Ц (ft*+l)CT
(1ЧЧ2)2 Г
<\1 -*0 Л 4 2 (1 Ч- v) С, +[В, + 2 (1 + v) DjHQ, (ф -
2D, (fe2-H)£
ОЧЧ2)2
(9.36)
В случае чистого изгиба плиты на контуре полости
( 2D2cos2r ]
о = 2с {(1 Ч" v) [С2 ft -j- D2 Q2 (lb)] Ч"-------------— г sin n;
11 | V / I 2 I 2 X2 V n-Г (b2 + 1) (ft2_|_sin2n)f 1 (9.37)
| 2D,v cos2 ti )
oe -2c (1 4-v) ]C2 b4-D2 Qi O'fo)l4- - -- . 2 - sin »].
I. (b24-l) (b24-sin2T])J
В табл. 44—46 даны значения напряжений, подсчитан-
ных для полости при = 0,5 в трех случаях нагружения
среды на бесконечности — продольном растяжении, дву-
стороннем сжатии и чистом изгибе, причем в табл. 44 —в
точках контура (| = £0), в табл. 45 — в точках плоскости
ослабленного сечения (z — 0) и в табл. 46 — в точках оси
(г = 0). Эпюры распределения напряжений изображены:
на рис. 62—63 — продольное растяжение, на рис. 64, 65 —
Рис. 62
Рис. 63
318
Таблица 44
n а/Р 0 15° ;ю 45° 60" 75° 90'
Продольное р астяжение
% 3,5216 2,443 0,916 —0,001 —0,469 -0,689 —0,7531
0,5293 0,207 —0,252 —0,528 —0,668 —0.734 —0,7531
Двусторонне е сжатие
CTn 0,7591 0,132 —0,758 -1,290 — 1,564 -1,692 -1,7294
сте —0,9828 — 1,171 -1,438 — 1.599 - 1,680 — 1,718 — 1,7294
Чистый изгиб
% 0 -0,208 —0,027 0,278 0,540 0,704 0.7603
сте 0 0,076 0,258 0,460 0,623 0,725 0,7603
320
г/с о/Р 1.1276 1.25 1.5
%
°н
0
3,5216
0.5293
0,502
1,815
0,262
0,393
1,175
О',036
0 —0,168 -0,570
% 0,7591 0,119 —0,001
пн —0,9828 — 1,088 — 1,083
о/Р 0.5211 0,6
ПБ
Пп ‘ пе
о
-0,7531
О
—0,7294
- 0,022
—0,57(
- 0,13(
— 1,584
Таблица 45
1,75 2 2.5 3 3.5 4
Продольное растяжение
0,243 0,146 0,071 0,039 0,025 0,017
1,085 1,051 1,022 1,012 1,008 1,005
0,021 0.010 0,002 —0.001 — —
Двусторонн ее сжатие
-0,734 —0,837 -0,921 -0,955 —0.972 -0,981
—0,018 —0.010 -0,006 —0,004 -0,003 —0,002
— 1,045 -1,039 — 1,021 — 1,012 -1,007 -1,005
Таблица 46
0.8 1 1.5 2 2,5
Продольное растяжение
0,025 0,167 0,513 0,727 0,837
—0,261 -0,109 -0,011
Двустороннее сжатие
—0,243 -0.258 -0,183 —0,105 —0,074
— 1,325 -1,185 -1,048 -1,016 -1,006
двустороннее сжатие и на рис. 66 — чистый изгиб. Как и
раньше, v = 0,3. На рис. 67 представлены графики напряже-
ний оп и Ое в точках контура при z = 0 (плоскость ослаблен-
ного сечения) и т] = 90° (ось вращения) в зависимости от
отношения к = r0/z0 большого полудиаметра г0 полости к ма-
лому z0, а в табл. 47 содержатся значения этих напряжений.
Случай k = 1 соответствует сферической полости. В случае
к = оо (Ь = 0) эллипсоидальная полость превращается в
круглую трещину, расположенную в плоскости z = 0.
Рис. 64
Рис. 65
В заключение заметим, что распределение напряжений у
эллиптической полости (как продолговатой, так и сплюс-
нутой) в случае трехстороннего растяжения или сжатия сре-
ды, очевидно, нетрудно получить наложением приведенных
решений при продольном нагружении вдоль оси вращения
Ог и поперечном двустороннем, перпендикулярном этой оси.
Исследование напряженного состояния у жестких эл-
липсоидальных включений в осесимметрично деформирован-
ной среде содержится в [93].
321
Таблица 47
k Продольное растяжение Поперечное сжатие Чистый изгиб
Т) = 90° Т) = 0 Т] = 90° | т) = 0 Т]=90°
стТ) = СТе % сте СТТ] = СТе сте
1 0,682 2,045 0,136 2,182 0,546 1,364 1,835
1.2 0,697 2,289 0,199 2,076 0,586 1,278 1,706
1.4 0,713 2,549 0,264 1,975 0,641 1,190 1,648
1.6 0,730 2,802 0,330 1,899 0,684 1,124 1,592
1.8 0,740 3,059 0,399 1,832 0,717 1,068 1,532
2 0,748 3,113 0,470 1,773 0,742 1,019 1,482
2.5 0,762 3,949 0,652 1,655 0,790 0,921 1,398
3 0,770 4,590 0,838 1,566 0,824 0,849 1,309
4 0,782 5,871 1,214 1,447 0,873 0,751 1,260
5 0,786 7,138 2,591 1,367 0,892 0,689 1,211
ОО 0,800 ОО ОО 1,000 1,000 0,400 1,000
9.7. Решение в параболических координатах
Ортогональная изотермическая система параболиче-
ских координат L т] в плоскости Orz определена следующей
зависимостью с цилиндрическими координатами гиг:
r=2c^; z = c(£2—if), (9.38)
где с — некоторый параметр, имеющий размерность длины.
322
Линии £ = const и т] = const образуют два семейства
взаимно перпендикулярных парабол (рис. 68). Значениям
£ = 0 и т] = 0 соответствуют части оси Oz: — оо <z z <Z О
постоянное число.
Полученные уравнения являются уравнениями Бесселя.
Решения их при к = 1,2, 3, ...:
fi (6)=А^1да+вл£г1да; Mn) = c*
Здесь (к£) и — функции Бесселя первого и
второго рода первого порядка от действительного аргумента
Л (кт)) и Ki (ят]) — функции Бесселя первого и второго
рода первого порядка мнимого аргумента /cq.
При к = 0 значения и /2 устанавливаются без труда:
f2(x\) = c0+D0tf.
Составляя функции ф и <р как произведения h и /2 име-
ем:
Фо = (Ао + Во £2) (Со + Do Т]2); <р0 = (^о + £2) (С^ + D'o т];
Ф* = [ЛЛ (^)+Bft (*£)] [Cft Ц (kvi)+Dk (Ь])] ЬГ. (9.41)
фл = [ЛPi + В; Л (££)] [C'k 1г да + D'k Кг да] •
Далее приведем два примера применения этих функций—
к определению напряжений в растянутом параболоиде вра-
щения и в бесконечной среде с параболоидальной полостью
при осесимметричном нагружении. Решение осесимметрич-
ной задачи в параболических координатах содержится в
[69], [79], [87].
323
9.8. Растяжение параболоида вращения
К решению задачи о растяжении параболоида вращения
сосредоточенной силой Р, приложенной в вершине, приво-
дят функции ф и <р, взятые в виде
D
Ф=(с+од1)’+—£4
52+Л
где последний член функции ф
eq2 noz:
<р = (А + В12) т)2, (9.42)
получен как производная
-^W) =
п2
£2 + +
Составляем функции Ф по формуле (1.17)
2
(9.43)
и по условию Ф = — Р/2л на контуре т] = т)0 = Ь в осевом
сечении параболоида получаем:
D—0; Do=—2Ab2', C — A = ———•
211b2
По формуле (1.26) составляем функцию Q:
С —A 4-2(1 -v) (Л +B£2) -
1
Й =--------—
(2с£)2
- B-F
£2+т)2
А
(9.44)
Выполнив условия (2.15)
дФ дг
-------------------=гй----
дт)
дт]
при т] = Ь, находим:
Л]==------—
1 Л — /1 I
В = 0:
4л (1 +v) b2
Таким образом, окончательные значения функций <р, Ф и
Q таковы:
( £2 1 & \
<р=Лт)2; Ф=—2Л v + Ь]2;
\ § +л /
Г 1 / Ь2—Г)2 \ 1
- А ------I 2v 4-------!— I +------------
[2(^)2^ £2+т12^ С2(£2+Т)2)
2
324
После подстановки их в формулы (2.20) и некоторых преоб-
разований для напряжений имеем:
А 2(^ + 6») £2+(Ь2—т)2)т]2
о, =-------- v Ч-------------------------
5 («Ч2 2(^+т)2)
_ A (fr2 —т]2)
— 2с2 (£2 +т)2) ’
А (Ь2—т]2) т)
2с2 ^(^+т)2)
Для параболоида, ограниченного поверхностью т]0 =
= b = 1, произведен подсчет напряжений (размерный пара-
метр принят равным 1 см, v = 0,3). В табл. 48 приведены их
значения в точках контура (rq = b) и оси вращения (т] = 0).
Часть области параболоида, соответствующая участку £ =0
оси Oz, должна быть исключена по равенству о£ и бес-
конечным значениям. Это результат условности понятия
«сосредоточенная» сила. Нужно считать, что сила, растяги-
вающая параболоид, распределена по некоторой поверхно-
сти, определяемой либо значением £ = £0, близким к нулю,
либо плоскостью z = 0, либо любой другой поверхностью,
симметричной относительно оси Oz. Распределение силы на
такой поверхности определено решением (9.44) или задается
произвольно (однако осесимметричным и суммарно эквива-
лентным продольной силе Р). В последнем случае в неболь-
шой части объема параболоида у вершины происходит пе-
рераспределение напряжений, имеющее местный характер.
Таблица 48
JL О/Р 0,5 1 1.5 2 2,5 3 5
МА Ф to to 0,1224 -0,0588 0,0491 -0,0092 rj = b 0,0270 -0,0023 0,0168 -0,0009 0,0113 -0,0004 0,0081 -0,0002 0,0031
II Q I1 ow to <s 1,2857 -0,4897 0,1408 -0,0306 T) - C 0,0475 -0,0061 0,0236 -0,0019 0,0143 -0,0008 0,0096 -0,0004 0,0033
325
В табл. 49 содержатся значения напряжений в точках по-
верхности £ )^2. Эпюры этих напряжений изображены
на рис. 69.
Таблица 49
Т) о/р 0 0,2 0.4 0,6 0,8 1
а1 0,0551 0,0535 0,0490 0,0428 0,0360 0,0296
—0,0077 —0,0071 —0,0055 —0,0035 —0,0016 0
—0,0077 —0,0075 —0,0066 —0,0056 —0,0043 —0,0031
Т£т> 0 0,0010 0,0016 —0,0015 —0,0009 0
Рис. 69
9.9. Напряженное состояние у открытой
параболоидальной полости в бесконечном теле
Составим функцииф и <р, воспользовавшись (9.41) и про-
изводной с£2 по z
д , I2 v ж
а? Н ) = 41 в следующей форме:
Ф = (Л + ВП2) £2+ ; Ф = (С + Dtj2) ¥. (9.45)
326
Соответствующее значение функции Ф будет:
ф= Л+Вт)2 +
С(^2-т)2) + Во
£2+112
£2.
(9.46)
Функции <р и Ф обращаются в нуль на отрицательной час-
ти оси Oz (при £ = 0) и отличны от нуля — на положитель-
ной. Чтобы функция Ф была равна нулю на некоторой по-
верхности т] = Ь, образованной вращением параболы, оче-
видно, нужно положить Во = 2СЬ2-, А = — С + ВЬ2, тог-
да
Ф =р-ТГГГ (П2-*2)£2;
\ S2 + n J
+ (C+*V)]-
-(D+V^r)- <»«>
По условию (2.15) при т] = b выражаем постоянную С через
постоянные В и D: (1 — v) С = [(1 + v)D + В] Ь2.
Нетрудно проследить, что если т] b и £2 + т]2 велико,
то функции i|), <р, Ф и й получают форму
тр=в(Ы)2; п=£>(£п)2; ф = в(^)2; [В-2 (i-f-v) я]
и представляют собой записанные в параболических коорди-
натах решения (3.5), соответствующие растяжению стержня,
радиус которого а, если постоянные В и D имеют значения
п __ Р __ Р Г)___ ? __ Р
° ~ 2ла2 — 2 * и — 4 (1 + V) ла2 — 4 (1 + v) ’ ИЛИ
обжатию плиты радиальной нагрузкой р, приложенной к
боковой поверхности, если В = 0; D = — р/2 (1 + v).
При таком выборе постоянных функции (9.45) и (9.47) яв-
ляются решением задач о концентрации напряжений у до-
статочно узкой, ориентированной вдоль оси вращения пара-
болической полости в цилиндре, растягиваемом продоль-
ными силами (продольное растяжение) или обжатом ради-
альной нагрузкой по боковой поверхности (двустороннее
сжатие среды). Напряжения в первом случае:
2Р
6 ла2 И
2Р (rf—b2)
ла2 Н
Ь2
2(£2-Н2) —:---
1—v
1 /
2—----- 1-
1—v \
2_ 112-Ь2
£2+n2 /Г
т]2 \( b у
Б2+П2 Д П /.
327
° ЛС12(1— v) И . \ Т) / J’
2Р1 (т]2-Ь2) Г fe2 7
'' ла* Ят) L 2 + (1 - v) (£2 + T]2) J ’ (9 ’48)
H = 4 (£2+ t]2). При £ = oo, как нетрудно видеть, oE =
= Р /па2, оп = ое = тЕл = 0, при т] = оо оп = р/па2\
og = сге = т^т) = 0, как и должно быть при растяжении
цилиндра силой Р. В месте пересечения полости с осью
вращения
V Р
* 6 1 —v ла2
напряжения не зависят от координаты т]0» определяющей
контур, и величина их заключена в пределах от 0 до Р/па2.
Во втором частном случае для параболической полости в
среде, обжатой радиальной нагрузкой р:
4р( ь* 2Ь* )
i = — "7Г 1 — 7,--- t2. 2Ч (п2—*2) +“------ :
Н 1. (1 — v) (ё2+т)2) J 1 — v J
?Р(п2-ь2) Г Ь2 / n2 V.
11 Ят]2 |1 — v V £24-1]2 /]’
(9.49)
(1 — 2у) Т)2 —Ь2
£2+i]2
4р^(т)2-й2) Ь*
Нт? . +(l-v)a2 + r)2)
Положив здесь tj == оо, получим: on = Tgn = 0; Og -- а© =
~ — р, т. е. значения напряжений при обжатии сплошно-
го цилиндра радиальной нагрузкой р. При £ = оо
что совпадает с известным решением Ламе (см. п. 32) для об-
жатого по внешней поверхности полого цилиндра при ма-
лом отношении внутреннего диаметра к внешнему.
На контуре полости наибольшие напряжения в вершине
(£ = 0) имеют значение оЕ = ое = — т-2р - и изменяют-
' ' • 1 — v
ся в зависимости от v в пределах от —2р до —4р. Эпюры
напряжений и на контуре осевого сечения полости,
328
у которой b = 1, и на отрезке оси £ = 0 приведены на
рис. 70 и 71. Ординаты этих графиков указаны в табл. 50,51.
Коэффициент v при подсчетах принят равным 0,3.
Рис. 70
Таблица 50
JL с/р 0 0,5 1 1.5 2 2.5 3 5
0,9450
Продольное растяжение
-0,4286 -0,1429 0,2857 0,5605 0,7143 0,8030 0,8571
-0,4286 -0,3429 -0,2143 -0,1319 -0,0857 -0,0591 -0,0429 -0,0165
<4
сте
Двустороннее сжатие
-2,8571 -2,2872 -1,4289 -0,8791 -0,5714 -0,3941 -0,2857 -0,1099
-2,8571 -2,6857 -2,4286 -2,2637 -2,1714 -2,1182 -2,0857 -2,0330
Таблица 51
Т) с/р 1 1,5 2 2.5 3 5
Продольное растяжение
Ot ~ о0 -0,4286 —0,0141 0,0268 0,0274 0,0235 0,0144
0 0,1148 0,4821 0,6480 0,7478 0,9051
Двустороннее сжатие
О, о0 —2,8571 —0,3845 —1,1964 — 1,1051 —1,0653 — 1,0194
% 0 — 1,7055 —0,5357 —0,3840 —0,2822 —0,1097
329
СПИСОК ЛИТЕРАТУРЫ
1. Абрамян Б. Л. Александров А. Я. Осесимметричные задачи
теории упругости// Тр. 2 Всесоюз. съезд по теорет. и прикл. ме-
ханике 1964. г. — М.: Наука, 1966.— № 3. — С. 7—37.
2. Абрамян Б. Л. К задаче осесимметричной деформации круглого
цилиндра // Докл. АН Арм. ССР. — 1954.— Т. 19.— № 3.—
— С. 3—12.
3. Абрамян Б. Л. Некоторые задачи равновесия круглого цилинд-
ра // Докл. АН Арм. ССР. — 1958.— Т. 26.— № 2.— С. 65—72.
4. Абрамян Б. Л., Баблоян А. А. К изгибу толстых круглых плит
осесимметричной нагрузкой// Изв. АН Арм. ССР. Сер. физ.-мат.
наук. — 1958.— Т.Н,—№ 4,—С.95—106.
5. Абрамян Б. Л., Баблоян А. А. Об одной задаче осесимметричной
деформации полого цилиндра конечной длины //Изв. АН Арм.
ССР. Сер. физ.-мат. наук.— 1968.— Т.15.— № 2.— С.87—99.
6. Айзенберг Д. Ю., Шапиро Г. С. О распределении напряжений в
неограниченном слое //Инж. сб.— 1950.— Т.7.—С. 65—78.
7. Александров А. Я., Соловьев Ю. И. Пространственные задачи
теории упругости.— М.: Наука, 1978.—462 с.
8. Арутюнян Н. X., Абрамян Б. Л. Кручение упругих тел.— М.
Физматиздат, 1963.— 686 с.
9. Бейтмен Г., Эрдейн А. Высшие трансцендентные функции. Ги-
пергеометрическая функция. Функция Лежандра.— М.: Нау-
ка, 1965,— 294 с.
10. Блох В. И. К общей теории упругих толстых плит//Инж. сб.—
Т. 18,— М.: 1954. — С. 31—49.
11. Бухаринов Г. Н. К задаче о равновесии упругого круглого ци-
линдра//Вести. Лен. гос. университета.— Сер. мат., физ. и хим.
1952,— Т.2.— С. 3—23.
12. Бухаринов Г. Н. Осесимметричная деформация цилиндра ко-
нечной длины//Вести. Лен. гос. университета. Сер мат. и хим.—
1956,— Т.7.—С.77—86.
13. Валов Г. М. Об одной задаче о деформации упругого кругового
цилиндра //Тр. Сибирск. метал, ин-та. Сер. прикл. математика
и механика.— 1957.— № 4А. — С. 29—32.
14. Валов Г. М. Осесимметричная задача о сжатии упругого круг-
лого цилиндра, покоящегося на гладком жестком основании //
Изв. АН СССР. Отд. техн, наук, механика и машиностр.— 1961.
— Т.6.—С. 151 — 154.
15. Валов Г. М. Об осесимметричной деформации сплошного круго-
вого цилиндра конечной длины// Прикл. математика и механика.
— 1962.— Т. 26.— № 4,— С. 650—667.
16. Васильев В. 3. Сжатие бесконечного полого кругового цилинд-
ра линейной нагрузкой, приложенной на участке боковой по-
верхности // Расчет простр. констр. — М.: Стройиздат, 1965.—
— Вып. 10. — С. 93—100.
17. Васильев В. 3. Осесимметричная деформация упругого изот-
ропного полупространства с бесконечной цилиндрической вы-
330
емкой // Инж. жур. Механ. твер. тела.— 1968.— Т. 5.—С.
124—129.
18. Васильев В. 3. Осесимметричная деформация полупространства
с жестким полубесконечным цилиндрическим включением //Изв.
выс. учеб, завед. Сер. стр-во и архитектура.— 1969.— № 6. —
С. 25—28.
19. Васильев В. 3. Концентрация напряжений около торца полубес-
конечного кругового цилиндра при осесимметричном нагруже-
нии // Изв. высш. учеб, завед. — М.: Машиностроение, 1972.—
— № 12. — С. 29—31.
20. Васильев В. 3., Самодуров А. А. Напряженное состояние сп-
лошного короткого цилиндра, стоящего на кольцевой опоре и
нагруженного сосредоточенной силой // Межвуз. темат. сбор./
Тр. ЛИСИ — 1982. — Вып. 14. — С. 14—22.
21. Галеркин Б. Г. К вопросу об исследовании напряжений и де-
формаций в упругом изотропном теле// Докл. АН СССР. — 1930.
— С. 353—358.
22. Галеркин Б. Г. Общее решение уравнений теории упругости для
изотропного тела и некотрые применения этого решения к част-
ным случаям// Вести, механики и прикл. математики.— 1931. —
— Т. 2.—С. 6—11.
23. Галеркин Б. Г. Равновесие упругой сферической оболочки //
Прикл. математика и механика.— 1942.— Т. 6.— № 6.— С.
487—496.
24. Гобсон Е. В. Теория сферических и эллипсоидальных функций.
— М.: ИЛ, 1952.—475 с.
25. Грей Э., Мэтьюз Г. Б. Функции Бесселя и их применение к фи-
зике и механике.— М.: ИЛ, 1953.— 372 с.
26. Гринченко В. Т., Улитко А. Ф. О точном решении осесиммет-
ричной задачи теории упругости для круглой жестко защемлен-
ной плиты // Изв. АН Арм. ССР. Сер. физ.-матем. наук.—
1963.--------Т. 16. — № 5. — С. 125—132.
27. Гринченко В. Т. Напряженное состояние круглого толстого дис-
ка в поле центробежных сил // Теория оболочек и пластин. АН
Арм ССР.— Ереван, 1964. —С. 423—429.
28. Гринченко В. Т., Улитко А. Ф. Точное решение задачи о распре-
делении напряжений около кругового отверстия в упругом
слое// Прикл. механика. — 1968.— Т. 4.— № 10. — С. 38—45.
29. Гродский Г. Д. Интегрирование уравнений равновесия упругого
тела вращения при симметричном относительно его оси распреде-
лении «объемных» и повер-хностных сил // Изв. АН СССР . Отд.
матем. и ест. наук. — 1934.— Т. 7. — № 10. — С. 1536—1550.
30. Гродский Г. Д. Интегрирование общих уравнений равновесия
изотропного упругого тела при помощи ньютоновских потенци-
алов и гармонических функций // Изв. АН СССР. Отд. матем. и
ест. наук — 1935,— Т.7.— № 4. — С. 587—614.
31. Гутман С. Г. Общее решение задачи теории упругости в обобщен-
ных цилиндрических координатах //Докл. АН СССР.— 1947.—
— Т. 58. — № 6.— С. 993—996.
32. Гутман С. Г. Расчет толстых упругих плит под непрерывным рас-
пределенным давлением //Изв. НИИ гидротехн.— 1940.— №28.
— С. 212.
33. Деев В. М., Нечепоренко Н. А. К точному решению пространст-
венной задачи теории упругости для толстой круглой плиты при
осесимметричном деформировании // Тепл, сварка в машиностр.
— 1968.— С. 81—89.
331
34. Джанелидзе Г. Ю. Обзор работ по теории изгиба толстых и тон-
ких плит, опубликованных в СССР // Прикл. матем., и мех. —
— 1948.— Т. 12,— № 1. — С. 109—128.
35. Диткин В. А., Прудников А. П. Интегральные преобразования
и операционное исчисление.— М.: Физматиздат, 1961.— 524 с.
36. Ильюшин А. А. К теории малых упруго-пластических деформа-
ций // Прикл. матем. и мех. — 1946.— Т. 10.— № 3.— С. 13—
— 19.
37. Колтунов М. А., Васильев Ю. Н., Черных В. А. Упругость и
прочность цилиндрических тел. — М.: Высшая школа, 1975.—
— 526 с.
38. Корниенко В. Т., Бобырь И.С. Электрическое моделирование
осесимметричной задачи теории упругости // Тепл, напряж. в
элем, констр. — Киев., Изд-во АН УССР, 1963.— № 3.—
— С. 85—98.
39. Коробов А. П. Деформации, имеющие ось симметрии // Изв./
Киев. Политех, ин-т, 1913.—С. 267—338.
40. Круг Е. М. К теории изгиба толстых круглых плит// Науч. тр.
зап. Черновиц. ун-та.— 1955.— Т. 12.— С.25—43.
41. Кузьмин Р. О. Бесселевы функции.— М.: 1935.—244 с.
42. Лебедев Н. Н. Специальные функции и их приложения.— М.:
Физматиздат, 1963.—358 с.
43. Лейбензон Л. С. Курс теории упругости. — М.: Гостехиздат,
1947. — 464 с.
44. Лурье А. И. К теории толстых плит // Прикл. матем. и мех. —
— 1942.— Т.6. Вып. 2—3. — С. 151—168.
45. Лурье А. И. Напряженное состояние в круглом упругом цилинд-
ре, нагруженном по боковой поверхности // Инж. сбор. — 1953.
— Т. 17. — С. 43—58.
46. Лурье А. И. Пространственные задачи теории упругости.— М.:
Гостехиздат, 1955. — 492 с.
47. Лурье А. И. Теория упругости. — М.: Физматиздат, 1970. —
— 940 с.
48. Ляв А. Математическая теория упругости. — М.: 1935.— 676 с.
49. Нейбер Г. Концентрация напряжений.— М.: Гостехизадт, 1947.
— 204 с.
50. Новацкий В. Теория упругости.— М. : Мир, 1975. — 872 с.
51. Новожилов В. В. Теория упругости. — Л.: Судопромгиз, 1958.
372 с.
52. Папкович П. Ф. Выражение общего интеграла уравнений тео-
рии упругости через гармонические функции // Изв. АН СССР.
Сер. физ.-мат. — 1932. — Т. 6.—С. 1426—1435.
53. Папкович П. Ф. Теория упругости.— М.: Оборонгиз, 1934.—
640 с.
54. Плиев С. Б. О равновесии упругого цилиндра конечных разме-
ров // Докл. Ан Азерб. ССР.— 1957. — Т. 13. — №8. — С.
832—842.
55. Положий’Г. Н. Теория и применение p-аналитических и (р, q)-
-аналитических функций.— 2-е изд. — Киев: Наукова думка,
1973. — 424 с.
56. Прокопов В. К. Равновесие упругого осесимметрично нагружен-
ного толстостенного цилиндра // Прикл. матем. и мех. 1949.—
— Т. 13.— № 2. — С. 134—144.
57. Прокопов В. К. Изгиб круглой плиты осесимметричной нагруз-
кой//Прикл. матем и мех. — Т. 14, № 5,— 1950.— С. 527—536.
332
58. Прокопов В. К. Осесимметричная задача теории упругости для
изотропного цилиндра// Тр./Ленингр. политехи, ин-т.— 1950.—
№ 2. С. 286—303.
59. Прокопов В. К. О равновесии полого цилиндра конечной дли-
ны, нагруженного осесимметричной нагрузкой // Тр. /Ленингр.
политехи, ин-т. —1958.— № 192.— С. 43—59.
60. Прокопов В. К- Изгиб тяжелой круглой плиты // Тр./Ленингр.
политехи, ин-т. — 1963.— № 226. — С. 103—108.
61. Рыжик И. М. Таблицы интегралов, сумм, рядов и произведе-
ний.— М.: Гостехиздат, 1948. — 398 с.
62. Снеддон И. Н., Берри Д. С. Классическая теория упругости.—
М.: Физматиздат, 1961.—220 с.
63. Соляник-Красса К. В. Кручение валов переменного сечения.—
М.: Гостехиздат, 1949.— 166 с.
64. Соляник-Красса К- В. К решению осесимметричной задачи тео-
рии упругости // Докл. АН СССР.— 1952.— Т. 86.— № 3.—
С. 481—484.
65. Соляник-Красса К. В. Решение осесимметричной задачи теории
упругости в сферических координатах//Тр./Ленингр. политехи,
ин-т. — 1955. — № 178.— С. 133—148.
66. Соляник-Красса К. В. Функции напряжений осесимметричной
задачи теории упругости // Прикл. матем. и мех. — 1957. —
Т. 21. — № 2. — С. 285—286.
67. Соляник-Красса К. В. Сжатие и изгиб открытых сферических
оболочек // Тр./Ленингр. политехи, ин-т.— 1958.— № 192.—
— С. 71—80.
68. Соляник-Красса К- В. Решение осесимметричной задачи теории
упругости в эллиптических координатах //Тр. /Ленингр. поли-
техи. ин-т. — 1958.— № 196. — С. 5—25.
69. Соляник-Красса К. В. К вопросу о концентрации напряжений
у открытых полостей // Тр./Ленингр. политехи, ин-т.—1958.—
— № 196. — С. 26—45.
70. Соляник-Красса К. В. Осесимметричная деформация конусов //
Инж. журн.— 1962.— Т. 2.— № 3. — С. 74—87.
71. Соляник-Красса К. В. Осесимметричное нагружение гипербо-
лических оболочек вращения // Расчет пространственных кон-
струкций. — М.: Стройиздат, 1964.— Вып. 9. — С. 5—18.
72. Соляник-Красса К. В. Сжатие и изгиб гиперболических оболо-
чек// Тр. IV Всесоюз. конф, по теории оболочек и пластин.—
Ереван. — 1964. — С. 904—910.
73. Соляник-Красса К. В. К расчету оболочек вращения перемен-
ной толщины // Расчет пространственных конструкций — М.:
Стройиздат, 1969.— Вып. 12. — С. 41—50.
74. Соляник-Красса К. В. Осесимметричная деформация конусов
под действием объемных сил//Межвуз. темат. сб./Тр. ЛИСИ.—
1977. — Вып. 10. — С. 5—18.
75. Терегулов И. Г. Круглая плита при осесимметричном попереч-
ном нагружении //Прикл. математика и механика.— 1961.—
— Т. 25. — С. 927—930.
76. Тимошенко С. П. Курс теории упругости. — Киев: Наукова
думка. — 1972.— 508 с.
77. Тимошенко С. П., Гудьер Дж. Теория упругости.— М.: Наука,
1979,— 560 с.
78. Улитко А. Ф. Общая задача равновесия конуса // Прикл. меха-
ника. — 1960.— Т.6.—№ 3. — С. 302—310 (на укр. яз.).
333
79. Улитко А. Ф. Осесимметричная деформация упругого парабо-
лоида вращения // Докл. АН УССР. — 1968. — Т. 12.— Сер.
А.— С. 1129—1132 (на укр. яз.).
80. Улитко А. Ф. Напряженное состояние полой сферы, нагружен-
ной сосредоточенными силами// Прикл. мех. — 1968.— Т.4.—
№ 5. — С. 38—45.
81. Фёппль А., Фёппль Л. Сила и деформация: Пер. с нем. Т. 2 —
— М.: 1936. —480 с.
82. Филоненко-Бородич М. М. Теория упругости.— М.: Физматгиз,
1959,— 364 с.
83. Шапиро Г. С. О сжатии бесконечного полого кругового цилинд-
ра давлением, приложенным на участке боковой поверхности //
Прикл. матем. и мех. — 1943.— Т. 7.— № 5.— С. 379—382.
84. Шапиро Г. С. О распределении напряжений в неограниченном
слое // Прикл. матем. и мех. — 1944.— Т. 8.— № 2. — С. 167—
176.
85. Шапиро Г. С. О равновесии конуса и конической оболочки //
Прикл. матем. и мех.— 1944.—Т. 8.— №4.— С. 1309—1312.
86. Шапиро Г. С. Осесимметричная деформация эллипсоида враще-
ния //Докл. АН СССР.— 1947.— Т. 58.—№7. — С. 1308— 1312.
87. Шапиро Г. С. Упругое равновесие параболоида вращения //
// Прикл. матем. и мех. — 1950, —Т. 14.—№ 6.—С. 672—673.
88. Boussinesq J. Applications des potentiels a I’etude de 1’equilibre
et du mouvent des solides elastiques. Gautier-Villars, Paris, 1885.
89. Chree C. The equations of an isotropic elastic solid in polar and
cylindrical co-ordinates, their solution and application. Trans.
Cambridge phil. Soc., 1889, 14, 250—369.
90. Chree C. The stresses and strains in isotropic solid ellipsoids in
equilibrium under bodily forces derivable from a potential of the
second degree. Proc. Roy. Soc. London, 1895, 58, 39—59.
91. Clebsch A. Theorie de Г elasticite des corps solides. Traduite par
MM. Barre de Saint — Yenant et Flamant. Avec des notes etendues
de M. de Saint — Venant. Paris., 1881, 932.
92. Clemmow C. A. Flexure of thick circular plates. Proc. Roy. Soc.
of London, ser. A, 1926, 112, N 762, 559—598.
93. Eshelby J. D. The elastic field outside an ellipsoidal inclusion.
Pros. Roy. Soc., 1959, A 252, N 1271, 561—569.
94. Filon L. N. G. On the elastic equilibrium of circular cylinders
under certain practical systems. Phil. Trans. Roy. Soc. London,
1902, ser. A, v. 198, 147—292.
95. Green A. F. Three dimensional strees systems in isotropic plates.
Phil. Trans, of the Roy. Soc. London, 1948, ser. A, 825, 561—597.
96. Goodier J. N. Trans. Am. soc. mech. ing., 1933. 55, 39.
97. Horvay G., Mirabal J. A. The end problem of cylinders. Paper
Amer. Soc. Mech. Engrs., A—24, 1958, Journ. Appl. Mech.,
1958, 25, N 4, 561—570.
98. Iyengar К. T. S. R., Yogananda С. V. The end problem of hallow
cylinders. Trans. ASME, 1966, E33, N 3, 685—686.
99. Lame G., Clapeyron В. P. E. Memoire sur 1’equilibre interieur
des corps solides homogenes. Jour, fur die reine und angew. Mat-
hem., 1831, 7, H. 2, N.19, 145—169. 1831. Memoires presen-
tes par divers Sowans, 1833, 4, 465—562.
100. Larmor J. The influens of flaws and air cavites on the strength
of materials. Phil. Mag., 1892, ser. 5, 33, 70—78. Leon A. Std-
rungen der Spannungsverteilung. Wien, 1908.
334
101. Ling Chin-Bing. Stresses in a circular cylinder having a spheri-
cal cavity under tension. Quart, appl. math., 1956, 13, N. 4 38
— 391.
102. Marguerre K. Spannungswerteilung und Wellenausbreitung in
der kontinuierlich gestiitsten Platte. Ing. Arch., 1933. 4, 332—
— 353.
103. Marguerre K- Ansatze zur Losung der Grundgleichungen der
Elastizitatstheorie. ZAMM, *1955, 35, N. 6/7, 242—263.
104. Mac Robert T. M. Spherical harmonics. 2-nded., 1947, 562.
105. Michell J. H. On the direct determination of stress in om elastic
solid, with application to the theory of plates. Proc. London Math.
Soc., 1900, v. 31, 100—124.
106. Michell J. H. Some elementary distributions of stress in three
dimensions. Proc. Math. Soc. London, 1900, v. 32, 23—35.
107.
108.
109.
110.
111.
Neuber H. Ein neuer Ansatz zur Losung raumlicher Probleme
der Elastizitatstheorie. ZAMM, 1934, 14, N. 4, 203—212.
Pochhammer L. Beitrag zur Theorie der Biegung des Kreis-
cyliriders. Crelle’s Journ. Berlin, 1876, Bd. 81, 33—61.
Poschl. Th. Zur Theorie des Druckversuchs fur zylindrische Kor-
per. ZAMM, 1927, Bd. 7, N. 6., 424—425.
3urser F. Some applications of Bessel’s functions to Physics.
5roc. Roy. Irish. Academy. Dublin, 1906—1907. v. 26, 25—41.
^eiss E. L. Extension of an infinite plate with a circular hole.
Journ. of the soc. for indust, and appl. math., 1963, v. 11, N. 4,
23—34.
112. Schiff M. Sur I’equibre d’un cylindre e’lastique. Journ. de Math,
pures et appliq., 1883, ser. 3, 9, 407—419.
113. Southwell R. V. On the concentration of stress in the neighbor-
hood of a small spherical flow. Phil. mag. 1926, ser. 7, v. 1, 71—84.
114. Sternberg E., Sadowsky M. Three dimensional solution for the
stress concentration around circular hole in a plate of arbitrary
thickness. Journ. of applied, mech., 1949, 16, N 1, 28—38.
115. Sternberg E., Rosenthal F. The elastic sphere under concentra-
ted loads. Journ, of appl. mech., 1952, 10, N 4, 413—421.
116. Sternberg E., Eubanks R. A., Sadowsky M. On the axisym —
— metric problem of elasticity for a region bounded by two con-
centric spheres. Congr. appl. mech., Proc. 1st. USA, 1953, 27—34.
117. Szabo I. Beitrage zur Theorie der achsensymmetrisch belas-
tienten schweren dicken Kreisplatte. ZAMM, 1952, 32, N 11/12,
359—371.
118. Timpe A. Achsensymmetricsche Deformation von Umdrehungs-
korpern. ZAMM, 1924, 4, N 5, 361—376.
119. Timpe A. Spannungsfunktion achsensymmetrischer Deforma-
tion in Zylinderkoordinaten. ZAMM, 1951, 31, № 4, 45—57.
120. Weber C. Achsensymmetrische Deformation von Umdreh.ungs-
korpern. ZaMM, 1925, 5, N. 6, 466—468.
ОГЛАВЛЕНИЕ
Предисловие
3
Глава 1. Основные уравнения ....................................
1.1. Осесимметричное нагружение тел вращения....................
1.2. Основные функции напряжений........................
1.3. Деформации и напряжения....................................
1.4. Граничные условия..........................................
1.5. Условия статической эквивалентности .......................
1.6 Решение при нагружении объемными силами....................
1.7. Функции перемещений........................................
1.8. Решение в форме Буссинеска— Гродского—Папковича — Нейбера
1.9. Решение в форме Галеркина — Лява...........................
1.10. Решение в форме Мичела....................................
Глава 2. Решение осесимметричной задачи в криволинейных коор-
динатах ........................................................
2.1. Криволинейные ортогональные изотермические координаты .
2.2. Дифференциальные, уравнения осесимметричной задачи в криво-
линейных координатах ...........................................
2.3. Выражения для напряжений и перемещений.....................
2.4. Решение осесимметричной задачи в криволинейных координатах
при нагружениях объемными силами................................
2.5. Функции напряжений в сферических координатах . . . .
Глава 3. Деформации цилиндров. Решение в полиномах
3.1. Граничные условия. Функции напряжений......................
3.2. Первая простейшая форма функций напряжений . .
3.3. Вторая простейшая форма решения............................
3.4. Растяжение цилиндрического стержня собственным весом
3.5. Равномерное вращение цилиндра вокруг собственной оси
3.6. Растяжение сплошного цилиндра силами, равномерно распреде-
ленными вдоль длины по линейному закону ........................
3.7. Нагружение полых, цилиндров полиномиальными силами
Глава 4. Деформации цилиндров. Решение в цилиндрических функциях
4.1. Функции напряжений.........................................
4.2. Выражения для напряжений и перемещений в цилиндрических
функциях ' .....................................................
4.3. Сплошной цилиндрический стержень, нагруженный силами, изме-
няющимися по закону синуса или косинуса ........................
4.4. Решение в рядах............................................
4.5. Асимптотические выражения для напряжений и перемещений
4.6. Решение Файлоиа............................................
4.7. Напряженное состояние среды с цилиндрической полостью .
4.8. Нагружение поверхности цилиндрической полости радиальными
силами .........................................................
4.9. Решение в интегральной форме...............................
4.10. Растяжение цилиндра силами, равномерно распределенными по
периметру начального сечения ...................................
4.11. Деформация полых цилиндров................................
Глава 5. Деформации круглых плит................................
5.1. Изгиб круглых плит.........................................
5.2. Плита, свободно опертая по контуру.........................
5.3. Плита, закрепленная по контуру.............................
5.4. Кольцевая плита, нагруженная по боковым поверхностям
5.5. Изгиб кольцевых плит равномерно распределенной нагрузкой
5.6. Изгиб круглых плит под действием собственного веса
5.7. Решение в рядах............................................
5.8. Изгиб плиты силами, распределенными по кольцевой области
5.9. Изгиб круглой плиты нагрузкой, распределенной по площади
круга, и сосредоточенной силой в центре ....................
5.10. Осесимметричное нагружение слоя...........................
5.11. Нагружение слоя силами, распределенными по окружности
Глава 6. Деформации цилиндров средней длины.....................
6.1. Симметричное нагружение цилиндров относительно среднего
сечения ........................................................
6.2. Исследование решения.......................................
6.3. Асимметричное нагружение цилиндров относительно среднего
сечения ........................................................
6.4. Сжатие цилиндра силами, распределенными по окружности сред-
него сечения ...................................................
6.5. Изгиб толстой плиты, жестко закрепленной по цилиндрической
поверхности ....................................................
6.6. Растяжение цилиндра сосредоточенной силой, приложенной
в центре торцевого сечения .....................................
6.7. Метод однородных решений...................................
5
5
7
10
12
14
16
19
22
23
24
27
27
30
32
36
38
42
42
44
47
51
52
56
59
63
63
66
68
72
79
88
94
98
101
105
109
117
123
126
131
138
142
147
152
155
156
158
158
164
168
169
173
174
178
Глава 7. Деформации конусов........................................180
7.1. Сжатие конического стержня....................................180
7.2. Сосредоточенная сила, приложенная к плоскости, ограничиваю-
щей полубескоиечное тело...........................................186
7.3. Сжатие полого конуса..........................................188
7.4. Нагружение конусов равномерно распределенными поверхностны-
ми силами .........................................................193
7.5. Нагружение конусов линейно распределенными поверхностными
силами.........................................................198
7.6. Осесимметричная деформация сплошного конуса под действием
собственного веса..............................................201
7.7. Осесимметричная деформация полого конуса под действием соб-
ственного веса.....................................................206
7.8. Деформация сплошного конуса при равномерном вращении . 207
7.9. Вторая форма решения осесимметричной задач в сферических
координатах....................................................211
7.10. Решение в рядах..............................................215
7.11. Сжатие конуса радиальными силами, равномерно распределен-
ными по контуру поперечного сечения ........................ 217
7.12. Сжатие конуса в направлении оси вращения силами, равномерно
распределенными по контуру поперечного сечения .... 223
Глава 8- Деформации шаров и сферических оболочек 227
8.1. Сжатие открытой сферической оболочки..........................227
8.2. Деформация шаровой оболочки при нагружении ее поверхностей
равномерно распределенными нормальными силами .... 230
8.3. Концентрация напряжений у мелких шаровых полостей 233
8.4. Концентрация напряжений у жестких сферических включений 246
8.5. Концентрация напряжений у сферических полостей при несим-
метричном нагружении среды.........................................252
8.6. Напряжеиио-деформнрованиое состояние вращающегося шара 254
8.7. Гравитационные напряжения.....................................261
8.8. Решение в рядах...............................................262
8.9. Осесимметричное нагружение шаровых оболочек кусочно распре-
деленными силами, нормальными к поверхности .... 268
8.10. Деформация оболочки под действием сил, равномерно распреде-
ленных на участках поверхности ................................... 270
8.11. Сжатие шара силами, приложенными в полюсах .... 274
8.12. Напряженное состояние цилиндра с шаровой полостью конечных
размеров.........................................282
8.13. Исследование решения...........................291
8.14. Напряжения у шаровой полости в деформированных цилиндрах 295
Глава 9. Решения в эллиптических и параболических координатах . 299
9.1. Решение в эллиптических координатах при расположении полюсов
на оси вращения 299
9.2. Сжатие эллипсоида вращения......................302
9.3. Концентрация напряжений у продольных эллипсоидальных по-
лостей ........................................................304
9.4. Решение в эллиптических координатах при расположении полю-
сов на оси, перпендикулярной оси вращения...........................313
9.5. Сжатие гиперболоида вращения...................................314
9.6. Концентрация напряжений у сплюснутых эллипсоидальных поло-
стей ...............................................................«16
9.7. Решение в параболических координатах...........................322
9.8. Растяжение параболоида вращения................................324
9.9. Напряженное состояние у открытой параболоидальной полости
в бесконечном теле .......................................«26
Список литературы ................................................. 33J