УДК ooU.l	ff	Издание осуществлено при поддержке
ББК 22.31	г dip и: Российского фонда фундаментальных
g 31	* *	исследований по проекту 05-02-30049д
Вергелес С. Н. Лекции по квантовой электродинамике. —
М.: ФИЗМАТЛИТ, 2005. - 248 с. - ISBN 5-9221-0634-1.
В книге излагаются основы квантовой электродинамики. В первой
части на простейших примерах формулируются метод функционально-
функционального интегрирования и основные понятия квантовой теории поля. Вторая
часть содержит семь лекций непосредственно по квантовой электро-
электродинамике, в которых, в частности, проводятся строгие вычисления
в однопетлевом приближении для некоторых наблюдаемых эффектов.
Третья часть может рассматриваться как необязательное дополнение
к семестровому курсу лекций. В книге содержится около пятидесяти
задач и упражнений, существенно дополняющих основной текст.
Книга предназначена для студентов и аспирантов, изучающих тео-
теоретическую физику, а также для преподавателей, читающих лекции и
ведущих семинарские занятия по основам квантовой теории поля.
© ФИЗМАТЛИТ, 2005
ISBN 5-9221-0634-1	© С. Н. Вергелес, 2005

ОГЛАВЛЕНИЕ
Предисловие .
Обозначения .
I. Общие принципы квантования полей
Лекция 1. Континуальный интеграл для конечномерных систем. . .	10
1.1.	Одномерный случай		10
1.2.	Хронологические средние		14
1.3.	Доопределение операторов при вычислении гауссовых функцио-
функциональных интегралов в квантовой механике		15
1.4.	Теорема Вика		18
1.5.	Поворот Вика		19
Лекция 2. Голоморфное представление континуального интеграла,
^-матрица и скалярная теория поля		22
2.1.	Операторы рождения и уничтожения		22
2.2.	Операторы общего вида		24
2.3.	Функциональный интеграл в голоморфном представлении		25
2.4.	Определение б'-матрицы		28
2.5.	б'-матрица в скалярной теории поля		29
2.6.	б'-матрица в теории поля со взаимодействием		35
Лекция 3. Диаграммная техника Фейнмана		39
3.1.	Разложение по константе связи		39
3.2.	Диаграммы Фейнмана и правила Фейнмана 		43
3.3.	Производящий функционал гриновских функций		49
3.4.	О физической интерпретации пропагаторов и проблема причинно-
причинности в квантовой теории поля		51
Лекция 4. Ультрафиолетовые расходимости и регуляризация		55
4.1. Размерностная регуляризация расходимостей		55

Оглавление
4.2.	Индекс расходимости диаграмм		58
4.3.	Диаграмма с четырьмя внешними линиями		59
4.4.	Устранение расходимостей		61
4.5.	Инвариантные переменные Мандельстама		62
Лекция 5. Общая схема перенормировок		66
5.1.	Спектральное представление Челлена-Лемана двухточечной функ-
функции 		66
5.2.	Перенормировки		71
5.3.	Условие унитарности		75
Лекция 6. Ренормализационная группа		78
6.1.	Подход Вильсона к теории перенормировок		78
6.2.	Уравнение Каллана-Симанчика		85
6.3.	Эволюция бегущей константы связи		87
II. Квантовая электродинамика
Лекция 7. Квантование электромагнитного поля		90
7.1.	Континуальный интеграл для вырожденных систем		90
7.2.	Электромагнитное поле как динамическая система		93
7.3.	Ковариантные правила квантования и трюк Фаддеева-Попова. ...	99
Лекция 8. Уравнение Дирака. Каноническое квантование дираков-
ского поля		104
8.1.	Уравнение Дирака		104
8.2.	Нерелятивистский предел		107
8.3.	Квантование дираковского поля		109
8.4.	Алгебра матриц Дирака		115
8.5.	Дискретные симметрии уравнения Дирака		116
8.6.	Уравнение Вейля		118
8.7.	Точное решение уравнения Дирака в кулоновом потенциале		119
Лекция 9. Квантование фермионов при помощи функционального
интеграла. S-матрица и правила Фейнмана в КЭД		126
9.1.	Фермионный осциллятор		126
9.2.	Представление фермионных амплитуд при помощи функциональ-
функциональных интегралов		127
9.3.	Функциональный интеграл в теории Дирака		133

Оглавление
9.4.	Общая формула для S-матрицы в КЭД и простейшие амплитуды. .	136
9.5.	Правила Фейнмана для КЭД		140
Лекция 10. Теорема Фарри, тождества Уорда-Такахаши и условия
перенормировки в электродинамике		144
10.1.	Теорема Фарри		144
10.2.	Тождество Уорда-Такахаши		145
10.3.	Индекс расходимости диаграмм		147
10.4.	Условия перенормировки		151
Лекция 11. I. Однопетлевая структура КЭД. Электронный и фотон-
фотонный пропагаторы		157
11.1.	Массовый оператор		157
11.2.	Поляризационный оператор		162
11.3.	Радиационные поправки к закону Кулона		166
Лекция 12. П. Однопетлевая структура КЭД. Вершинный оператор
и аномальный магнитный момент электрона		169
12.1.	Формфакторы электрона		169
12.2.	Аналитические свойства формфакторов		171
12.3.	Вычисление мнимых частей по интегралу Фейнмана		173
12.4.	Аномальный магнитный момент электрона		180
Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней . .	182
13.1.	Массивное векторное поле		182
13.2.	Излучение мягких фотонов		183
13.3.	Сокращение инфракрасных расходимостей 		189
13.4.	Лэмбовский сдвиг уровней		191
III. Дополнительные вопросы
Лекция 14. Квантовые аномалии		200
14.1.	Введение		200
14.2.	Диаграммный метод вычисления аксиальной аномалии		204
14.3.	Неинвариантность функциональной меры как источник аномалии	209
Лекция 15. Спонтанное нарушение симметрии		216
15.1.	Спонтанное нарушение симметрии в классической теории		216
15.2.	Теорема Голдстоуна		218

Оглавление
15.3. Эффективное действие		220
Приложение А. Выражение вероятностей процессов через амплиту-
амплитуды		228
Приложение Б. Спиновые матрицы плотности		233
Приложение В. Тензор энергии-импульса		237
Предметный указатель		242
Список литературы		244

Предисловие
Предлагаемый семестровый курс лекций автор читает студентам
старших курсов Московского физико-технического института, изуча-
изучающих теоретическую физику под руководством специалистов из Ин-
Института теоретической физики им. Л.Д. Ландау РАН. Этот курс са-
самодостаточен и весьма компактен. Изложение ведётся при помощи ап-
аппарата функционального интегрирования, применяется размерностный
метод ультрафиолетовой регуляризации. Все вычисления проводятся
подробно и до конца. Курс начинается с квантования скалярного по-
поля и заканчивается вычислением однопетлевых поправок, лэмбовского
сдвига уровней и квантовых аномалий. Основной текст существенно
дополняется упражнениями и задачами, приведенными в конце каж-
каждой лекции. Большинство задач достаточно просты, но часть из них,
отмеченных звездочкой, потребуют при решении ощутимых усилий по
причине либо технических трудностей, либо необходимости достаточно
ясного понимания идеологии предмета и овладения его аппаратом. Для
полноценного и минимального изучения квантовой электродинамики
представляется необходимым самостоятельное решение большинства
приведенных задач.
Конечно, предлагаемый курс лекций является лишь введением в
круг проблем, изучаемых релятивистской квантовой теорией поля. Для
углубленного овладения этой наукой необходимо систематическое и
длительное изучение так называемых «толстых» учебников, немалый
список которых недавно пополнился выдающейся книгой С. Вайнберга
«Квантовая теория поля».
Я благодарен М.Ю. Лашкевичу, любезно предоставившему мне
конспект своих лекций по квантовой электродинамике, которые
он читал ранее студентам МФТИ тех же специальностей. Я
позаимствовал из лекций Лашкевича общую структуру, а также
несколько задач.
2005 г.	Сергей Вергелес

Обозначения
Латинские индексы г, j, к и т.д. пробегают три значения 1, 2, 3, со-
соответствующие трём пространственным координатам. В общем случае
^-мерного пространства-времени г, j, к = 1, 2, ... , (d — 1).
Греческие индексы /i, z/ и т.д. пробегают четыре значения 0, 1,2, 3,
соответствующие четырём пространственно-временным координатам. В
общем случаен-мерного пространства-времени /i, z/, ... = 0, 1, ... , (d —
Пространственно-временная метрика rj^ диагональна. Соответству-
Соответствующие ненулевые элементы: 7700 — 1> Ш\ — ^22 — ••• — Ш-ы-i — ~1-
?ijfc — абсолютно антисимметричный трёхмерный тензор, ?123 = 1-
?/xz^Ap _ абсолютно антисимметричный тензор в 4-мерном простран-
пространстве МИНКОВСКОГО, ?0123 = —?q123 — 1-
Комплексное сопряжение, транспонирование и эрмитово сопря-
сопряжение числа, вектора или матрицы А обозначается соответственно
А*, Ат, А^. Черта над дираковским спинором и обозначает величину
п = г^7° •
Символ е обозначает заряд электрона, так что е < 0 и постоянная
тонкой структуры равна а = е2/(Тьс) « 1/137.
Т = Т — операция хронологического упорядочения.
Нижний символ Т указывает на операцию обращения времени.
Dc(...) — причинная гриновская функция.
Л — ультрафиолетовый импульс обрезания.
$ (х) — ступенчатая функция Хевисайда, равная нулю, при отрица-
отрицательных х, и единице, при положительных х.
аг — матрицы Паули.
7м — матрицы Дирака.

Часть I
ОБЩИЕ ПРИНЦИПЫ
КВАНТОВАНИЯ ПОЛЕЙ

Лекция 1
КОНТИНУАЛЬНЫЙ ИНТЕГРАЛ ДЛЯ
КОНЕЧНОМЕРНЫХ СИСТЕМ
1.1. Одномерный случай
Пусть H(p,q) — функция Гамильтона некоей одномерной системы.
Классические скобки Пуассона (СП) имеют вид
{q,q} = 0, {p,p} = 0, {q,p}=\.
Каноническая процедура квантования заключается в том, что перемен-
переменным q, p ставятся в соответствие эрмитовы операторы Q, Р, причём
скобкам Пуассона ставятся в соответствие перестановочные соотноше-
соотношения:
{q,P} = \ — [Q,P] = i (П=1).
В сложных случаях возникает проблема упорядочения операторов в
гамильтониане. Решим её следующим образом. Пусть в представлении
Шредингера | q) является собственным вектором оператора координаты
Q'	Q\q)=q\q), W\q) = 6(q-q').	A.1)
Так как для вещественного s имеем [Q, elsP] = —selsP, то
eisP\q) = \q-s).	A.2)
Рассмотрим унитарный оператор
u(s,t) =exp(iPs + iQt) =u\-s,-t),	A.3)
где s и t — вещественные числа. Воспользуемся формулой Хаусдорфа,
еА+в = е"A/2)[ЛБ]еАеБ,
которая справедлива, если [А, [А, В]] = [В, [А, В]] = 0. Полагая А =
= UQ, В = isP, находим
u(s, t) = eW" j** eisP,	A.4)
а также

1.1. Одномерный случай	11
u(s, t)\qf) = exp (i?-^t\ 5(q" - qf + s).	A.5)
Пусть
H(s,t)= I H(p, q)e~isp-itq dpdq = H*(s, -t)
— Фурье-образ гамильтониана. Согласно Вейлю проблема упорядоче-
упорядочения операторов в гамильтониане решается при помощи формулы
' Q) = 7^9 [wE' *)u(s> t)dsdt = H\P, Q). A.6)
При помощи формул A.1)-A.6) получаем
Если (t" — tf) —> 0, то оператор эволюции U(t", ?') = exp[—i(t" —
\- i(t" - t') H. Поэтому
( q" | е-**""*')й | ^ ) = [ 11 - i{t" - tf) П (p, ^
d p
xexp(ip(q"-q')) — =
2тг"
Если интервал {t" — tr) конечен, то его разбивают на N равных
частей так, чтобы At = ti+\ — U = (tn — t')/N —> 0. Пусть tr = to <
< t\ < ... < tjsf = t" и q(U) = ^, p(t^) = pi. Имеем
U(t", tr) = U(tN, tN-i)U(tN-U tN_2)...U(tu t0).	A.8)
Вычислим матричные элементы произведения A.8) при помощи фор-
формулы A.7):
(q" | U(t", tf) | qf) = f exp \i [pN{qN - qN-i) + ...+pi(q\- qo)} -
dpi
Перейдём к пределу N ^ oo, At -^ 0. Число переменных инте-
интегрирования стремится к бесконечности, и считается, что в пределе
интегрирование происходит по p(t), q(t) при всех t' < t < t". При этом
q(t') = q', q(t")=q".	A.10)

12 Лекция 1. Континуальный интеграл для конечномерных систем
Тогда показатель экспоненты стремится к
t"
S(t",t') = j{p(t)q(t)-n(p(t),q(t))}dt,	A.11)
V
причём все пути в A.11) имеют граничные условия A.10). Мера в
континуальном (или функциональном) интеграле A.9) записывается в
ВИД6	dj/'
n
При t" —> +оо можно опустить интеграл по dp". Тогда
<U2>
Здесь восстановлена правильная размерность.
Замечание. На первый взгляд формула A.12) решает проблему
упорядочения операторов в гамильтониане. Однако это не так, по-
поскольку функциональный интеграл A.12) не определён во внутренних
терминах. Он нуждается в доопределении. ?
Обобщение полученных формул на случай системы со многими
степенями свободы очевидно. Пусть q = {qa}, р = {ра}, а — 1,2,...
и набор переменных {ра, qa} образует совокупность канонических
переменных. Если обозначить
a	t	t a
то амплитуда перехода для такой системы записывается в виде A.12).
Мы неоднократно будем использовать следующую формулу для
гауссова интеграла:
\ exp i ?-pT M~lp + i?Tp\ dp = B7ri)N/2(detM)
Здесь p = (pi,... ,pn), M — невырожденная N x N матрица и dp =
= dpi ...dpN- Везде верхний индекс Т означает транспонирование, так
что t;Tp = Y^a=\ iaVa- Существует простое правило для вычисления
гауссовых интегралов: гауссов интеграл равен (с точностью до число-
числового множителя, который обычно включается в общую нормировочную
константу) подынтегральному выражению, вычисленному в точке экс-
экстремума показателя экспоненты, делённому на корень из определителя
матрицы квадратичной формы в экспоненте.

/./. Одномерный случай	13
Действительно, вычислим n-мерный интеграл:
U(rj)= [dn xexp(-^xTAx + r]Tx\ , Ат = А.
При помощи подстановки
x = x + A~xr], dnx = dnx
этот интеграл переписывается как
и(т])=ехр(^г]тА-хЛ ^Апхещ>(-Х-хтАх\ =
Здесь N — некий числовой множитель, не зависящий ни от переменной
г], ни от матрицы А. С другой стороны, экстремум показателя экспо-
экспоненты находится в точке xq = А~х rj, и значение показателя экспоненты
в этой точке равно
А.	/17	/17	\	\_	/17	1
	гу*-*- Л /-у»- I />О О^л I 	 	 fYl /л	fYl
Xq SIXQ ~\- I/ XQ I — // I\ I/.
При помощи формулы A.13) определим значение гауссова функци-
функционального интеграла:
ехр I - d(n) х d{n)yp(x)M-x(x, y)p(y) + i d(n) x?(x)p(x)
x
П
= const (det M)xl2- exp \-%- fd(n) x d(n) y?(x)M(x, y) ?(y)\. A.14)
ч	J	)
Здесь ]\Л и М~х — взаимно обратные линейные операторы, действую-
действующие на интегрируемые функции в n-мерном пространстве и константа
в A.14) не зависит ни от поля ?(#), ни от оператора Л4. Неопределён-
Неопределённость, которая может возникнуть при вычислении величин det Ai и
Mrx, обычно устраняется, исходя из требований конкретной задачи.
Предположим, что лагранжиан имеет вид
C = ^qTMq + lTq-V(q),	A.15)
где Л4 и / не зависят от q. Тогда р = Л4 q + /, и соответствующее
действие, записанное в форме A.11), имеет вид
t"
{\TX	T Ty A.16)

14 Лекция 1. Континуальный интеграл для конечномерных систем
Интеграл по p(t) в A.12) вычисляется как функциональный гауссов:
if/ i*'i \
(q"\U(t",tf)\q') = - exp- \cdt\Y\(detM(t)y^dq(t).
J V I J *
Здесь С — лагранжиан A.15), a N — нормировочная константа, не за-
зависящая от q', q"'. Пусть det M(t) не зависит от q(t). Тогда
можно включить в константу N. В этом случае
t"
(q//\U(t//,t/)\q/}=^- I I exp ^ \ С dt I Dq, Dq = 1 I dq(t). A.17)
Представление амплитуды перехода в форме A.17) называется
функциональным интегралом Фейнмана.
1.2. Хронологические средние
Пусть | А} — вектор-состояние при t = 0 в представлении Шре-
Шредингера, \A,t) — зависящее от времени состояние в представлении
Шредингера, а | А}* — вектор-состояние в представлении Гейзенберга,
так что
\А}* = \А) =еип\А, t).
Операторы в представлениях Гейзенберга и Шредингера связаны фор-
формулой	^	^
О* {t) = eitn О e~im.
Пусть t" > tn > tn-\ > ... > t\ > t'. Вычислим следующий матрич-
матричный элемент:
*(^|g*(tn)g*(tn_1)...g*(t1)|E)* =
= {Aitn\e-it"H{eitnHQe-itnH) ... (eiun Q e~iun) eit>n \ B, tr) =
= (A, t'le-W-^KQe-^"-*"- ^n Q ... Qe"*-*'^ | B, tf).
Так как Q = jdq-q\q)(q\, то
*(A\Q*(tn)Q*(tn-i) ...Q*(*i)|B}* =
f f f	/ г ? \
= ^ dq" dqf Dqy*A(q", t") q(tx) ... q(tn) exp - \ С dt I x
хФб(^, ?).	A.18)
Здесь Ф (g, t) — волновая функция в представлении Шредингера, зави-
зависящая от времени. Введём операцию хронологического упорядочения
Т. В произведении гейзенберговых операторов под знаком хроноло-

1.3. Доопределение гауссовых функциональных интегралов	15
гического упорядочения эти операторы располагаются таким образом,
что по мере движения справа налево временные аргументы операторов
монотонно растут. Например, TQ*(t\) Q*(t2) = Q*(h) Q*(t\), если ?2 >
> t\. Мы видим, что среднее от координат, вычисленное при помощи
функционального интеграла, автоматически даёт среднее от хроноло-
хронологически упорядоченного произведения {хронологического произведе-
произведения) операторов в представлении Гейзенберга. Далее для обозначения
хронологического среднего A.18) используется стандартная формула
(индекс * для обозначения гейзенберговых величин как правило опус-
опускается)
{A\TQ{U) ...Q{tn)\B).
Заметим также, что формула A.18) по сути остаётся справедливой,
если в ней координатные переменные Q* заменены полностью или
частично импульсными переменными Р*. Однако в этом, более общем,
случае вместо A.18), например, имеем
*{A\Q*{tn)P*{tn-{)...Q*{U)\B)* =
= 1 | dq" J dq' ^DqDpWA(q", *")e(*i) ¦¦¦ P(*n-i)?(*n) x
Для вывода последней формулы следует учесть, что матричный эле-
элемент (q" | PU(t", tf) | qf) отличается от A.9) введением под интеграл
в правой части A.9) множителя pN. Аналогично устанавливается тот
факт, что любое среднее различных величин, вычисленных при помо-
помощи функционального интеграла, автоматически является средним от
соответствующих хронологически упорядоченных операторов в гейзен-
берговом представлении.
1.3. Доопределение операторов при вычислении
гауссовых функциональных интегралов в квантовой
механике
Изучим гармонический осциллятор с внешним источником (внеш-
(внешней силой). Действие такой системы
A.19)

16 Лекция 1. Континуальный интеграл для конечномерных систем
Вычислим амплитуду перехода A.17). При этом удобно сдвинуть пере-
переменную интегрирования следующим образом:
q(t) = q(t) + 5q(t) , q(t) = qo(t) + f dt, D(t,
f + uJ q = Г), % + uJ q0 = 0,
qo(t')=q', qo(t")=q", 6 q(t') = 5 q{t") = 0.	A.20)
Функциональное интегрирование идёт по переменной 5q(t) с нулевыми
граничными условиями. Из A.20) следует, что гриновская функция
удовлетворяет следующим уравнениям:
/ i2	\
и;2) D(t,ti) = 5(t-ti), D(t", U) = D(tf, U) =0. A.21)
Vй2 ,
Условия A.21) однозначно определяют гриновскую функцию (Т = t" —
-t'):
, t2) = DC{U - t2) - . l „ \Dc(t" - t2) sin (ш (h - t')) +
Sill U! 1
+Dc(t'-t2) sin(и:A"-Щ,	A.22)
(L23)
Функция A.23) называется причинной гриновской функцией. Она
удовлетворяет первому из уравнений A.21). Легко находится решение
для q0:
Перепишем действие A.19) при помощи введенных функций:
t"
2
i'
; 	 /2 , .//2а
2 sin ujT lv
t"
So = ^—- [(q12 + q) cos coT - 2q'q"} + Sir,),
Z Sill Lul
S(ri)= \dtri(t)qo(t) + ^
A.24)
Поскольку cSo не зависит от 5q и 5 q{tf) = 5 q(t/f) = 0, то функциональ-
функциональное интегрирование в A.17) приводит лишь к появлению множителя,

1.3. Доопределение гауссовых функциональных интегралов	17
зависящего от Т, но не от q', q/f, r\. Этот временной множитель не
будет использоваться, однако приведём точный ответ:
A.25)
где {фп{у)} — полный ортонормированный набор собственных функ-
функций гамильтониана свободного осциллятора.
До сих пор в этом пункте рассматривался гармонический осцил-
осциллятор, или свободная (без взаимодействия) теория. Теория с взаимо-
взаимодействием отличается от свободной теории тем, что лагранжиан такой
теории не является квадратичной формой (возможно, неоднородной)
относительно канонических переменных. Например, в случае осцил-
осциллятора дополнительное слагаемое вида \qA делает теорию с взаимо-
взаимодействием. Далее мы увидим, что такого вида слагаемое даёт взаи-
взаимодействие между элементарными возбуждениями в скалярной теории
поля. Как правило, в квантовой теории поля принимается гипотеза,
что а) при t —> ±00, взаимодействие адиабатически выключается и
теория превращается в свободную и б) основное состояние при t —>
—> +00 отличается от основного состояния при t —> —оо не более чем
фазовым множителем. Это — очень сильная гипотеза. В техническом
отношении эта гипотеза реализуется автоматически, если считать, что
в случае осциллятора частота ио содержит бесконечно малую отрица-
отрицательную мнимую часть. Иными словами, для этого необходимо во всех
формулах сделать замену
u^{\-ie)u, ?^+0.	A.26)
Действительно, в результате такой замены, после выключения взаимо-
взаимодействия все слагаемые в волновой функции, отличные от основного
состояния свободной теории, «вымирают» (то есть стремятся к нулю)
относительно основного состояния при t" = Т/2 —> оо, вследствие
содержания ими дополнительного множителя ехр(—ent/f), n > 0. Кроме
того, в рамках этой гипотезы нелинейности (или взаимодействие) учи-
учитываются при помощи теории возмущений (ТВ). В следующих лекциях
будет показано, что в ТВ-разложении участвуют причинные гриновские
функции Dc(ti — tj), где ti, tj, и т.д. — временные аргументы опера-
операторов взаимодействия. Так как Dc(ti — tj) —> 0 при | ti — tj | —> оо, то
всё взаимодействие «скучивается» по времени в неком ограниченном
временном интервале, т.е. при 111 —> оо взаимодействие выключается.
При замене A.26), знаменатель в подынтегральном выражении в
A.23) может быть взят просто как (—к2 + оо1) и Dc(±T/2) —> 0 при
Т —> оо. Поэтому согласно A.22), при Т —> оо, гриновская функция

18 Лекция 1. Континуальный интеграл для конечномерных систем
D (t\, ?2) —> Dc (t\ — ?2) и в S(rj) вместо D (t\, ?2) следует использовать
причинную (или фейнмановскую) гриновскую функцию Dc(t\ —?2).
Замечание. Если отсутствует требование симметрии теории от-
относительно операции инверсии времени, то вместо причинной гринов-
ской функции A.23) можно использовать какую либо иную гриновскую
функцию. Например, это могла бы быть запаздывающая гриновская
функция
которая получается при помощи интеграла A.23), если оба полюса
подынтегрального выражения смещены вниз от вещественной оси на
бесконечно малую величину г > О (в то время как в случае причин-
причинной гриновской функции левый полюс находится выше, а правый —
ниже вещественной оси (см. рис. 1)). Действительно, в случае Т —> оо
функция DTet(t, t\) удовлетворяет граничным условиям A.21) и потому
в этом пределе, так же как и функция Dc(t, t\), может использоваться
вместо D(t, t\). Однако в теориях, обратимых по времени, эта возмож-
возможность исключается, т.к. DTet(—t) ^ DTet(t). ?
1.4. Теорема Вика
В результате замены A.26) в пределе t" = — t1 = Т/2 —> оо в сумме
A.25) «выживает» лишь основное состояние. Выпишем в этом случае
амплитуду перехода из основного состояния в основное состояние за
бесконечное время в присутствии источника r](t), отличного от нуля
лишь при конечных t:
^^\	A.27)
Слагаемое в S(rj), пропорциональное до, вымирает в рассматриваемом
случае. Это следует из того, что Imcj = — г —> —0, гТ —> оо. Согласно
A.17), A.18) и A.21),
Ъ \ п 1	Лп 7
A.28)
jj=O
ij Z 6V(U) ...6V(tn)
Например, при п = 2,
(О\Тд(и)д(г2)\О}=(^) ?>c(t,-t2) = Ае-Ч*.-Ч (i.29)
При t\ = ?2 получаем известный результат: @ | q2 | 0) = Ь/2ио. Очевид-
Очевидно, при нечётном п коррелятор A.28) равен нулю. Введём обозначение
A.30)

1.5. Поворот Вика
19
Из формулы A.28) находим при п = 4:
. A.31)
Теперь нетрудно сообразить, что справедлива
Теорема Вика. Хронологически упорядоченное среднее от-
относительно основного состояния от п гейзенберговых коорди-
координат (или полей, играющих роль координатных переменных) с
квадратичным действием равно сумме произведений всех хроноло-
хронологически упорядоченных парных средних (спариваний).
1.5. Поворот Вика
На рис. 1 изображена комплексная плоскость переменной к, по
которой идёт интегрирование в A.23) вдоль вещественной оси; обход
полюсов указан на рисунке.
®
®
Рис. 1
Рис. 2
Очевидно, обход полюсов допускает «гладкий» поворот контура
интегрирования согласно правилу
• ei(pk,
т,
0
7Г.
При (р = О имеем исходный контур, а при (р = тг/2 интеграл идёт по
мнимой оси так, как показано на рис. 2.
При этом t = — ir, где переменная г — вещественная, называемая
«мнимым временем». Описанный поворот контура интегрирования на-
называется поворотом Вика. При этом повороте
(q"\e
-аи
*„(?") KW)=
A.32)

20 Лекция 1. Континуальный интеграл для конечномерных систем
Имеем
Dc(t)=iDE(r), DB(r)=f^if^T = ^-e-M,
\ 2тг kz + ljz 2uo
--5(т).	A.33)
При достаточно большом мнимом времени г правая часть в A.32)
переходит (сравни с A.27)) в сумму
+ ОО
ZE{r)}~ \Dqexp{-^ \ dr
— СЮ
+ СЮ
о
UJ
^2
A.34)
Величина A.34) называется (классической) статистической суммой, а
правая часть равенства A.32) — квантовой матрицей плотности.
Задачи
1.	Докажите теорему Вика в следующих редакциях.
а)	Хронологически упорядоченное вакуумное среднее в теории с
квадратичным действием от п гейзенберговых координат равно сумме
произведений всех спариваний (парных средних).
б)	Среднее по вакууму от произведения любого числа бозонных
лестничных операторов (рождения и уничтожения) а^, а равно сумме
произведений всех возможных попарных средних (или свёрток) этих
операторов. При этом в каждой свёртке множители должны стоять в
той же последовательности, что и в первоначальном произведении.
2.	а) Пусть ТС(р, q) — оператор Гамильтона. Представьте квантовую
статистическую сумму
Z(/3) = tre-?n
в виде функционального интеграла.
б) Вычислите статистическую сумму гармонического осциллятора
(с точностью до множителя, зависящего лишь от температуры) в
присутствии внешнего источника. Используя эту статистическую
сумму, найдите парный хронологический коррелятор переменной
q(r) в представлении Мацубары. Согласно определению, оператор
в представлении Мацубары имеет вид (ср. с представлением
Гейзенберга) О(т) = (ехр тН) О (ехр— тН), где г — мнимое время.

1.5. Поворот Вика	21
Парный хронологический коррелятор в представлении Мацубары
определяется как
Указание: Действовать аналогично тому, как действовали при
получении формулы A.25), но в мнимом времени т. Учесть, что в
данном случае гриновская функция De(t\, t^) периодична:
DE@, т2) = DE(f3, т2).
Вычислите эту гриновскую функцию в виде ряда Фурье и отсуммируй-
те этот ряд. ?

Лекция 2
ГОЛОМОРФНОЕ ПРЕДСТАВЛЕНИЕ
КОНТИНУАЛЬНОГО ИНТЕГРАЛА, ^-МАТРИЦА И
СКАЛЯРНАЯ ТЕОРИЯ ПОЛЯ
2.1. Операторы рождения и уничтожения
Далее полагаем Тг = с = 1.
Действие осциллятора A.19) в случае нулевого источника приводит
к следующему гамильтониану:
П(р, q) = \v2 + \п2-	B.1)
Введём комплексные взаимно сопряжённые переменные а, а*:
В квантовой теории формулы B.2) сохраняются для операторов и
коммутационные соотношения
[Q, Q] = [Р, Р] = О, [Q, Р] = i	B.3)
И
[а, а] = [af, af] = 0, [a, af] = 1	B.4)
эквивалентны.
Перестановочные соотношения B.4) имеют представление в про-
пространстве аналитических и, более того, голоморфных функций /(а*)
со скалярным произведением
(/i|/2)= |(/i(a*))*/2(a*)e~a*a a a .	B.5)
Пояснение. Можно считать, что
а = х + гу , (а)* = а* = х — iy , а*а = х + у .
Тогда

2.1. Операторы рождения и уничтожения
23
<9а*	<9а*
дх	ду
да	да
дх	ду
1 -г
= 2г.
Поэтому
da* da Ax Ay рАрАср
B.6)
2тгг	тг	тг
где (р, ф) — полярные координаты в плоскости (х, у). ?
Произведение B.5) положительно определено. Действительно, про-
произвольная голоморфная функция /(а*) является линейной комбинаци-
комбинацией одночленов фп(а*) = (а*)п/л/^Т, n ^ 0. Имеем
г>/ -а-\<m 	n*nQ^ ua
п\ га!
2тгг
п\ га!
B.7)
Поэтому множество функций {фп}, п = 0, 1, ... образует полный ор-
тонормированный базис (ОНБ).
По определению, операторы а^ и а действуют согласно правилу
at /(a*) = а*/(а*), а /(а*) = -^/(а*).
B.8)
Заметим, что
(
da ~ 2 Vdx %dy) '
_d_ _ j. /_9_ ._9_
d^ ~ 2 1^? + г^У '
a* = 1,
da*
da*
a = 0. B.9)
Согласно определениям скалярного произведения B.5) и операторов
at, a B.8), эти операторы взаимно сопряжены. Действительно,
da
da
/(«*)= 0,
и потому
< /. I a)f2) = |(/. (а*))* а*Ыа*) е~а'а ^^ = - J(/, (a*))* /2(a*) x

24 Лекция 2. Голоморфное представление континуального интеграла ...
<1.е_в.Л do^da = Г Г d	I e_e.e da* da
da ; 2тгг J [da w'v " JAy '\	2m
2.2. Операторы общего вида
В голоморфном представлении операторы общего вида описываются
при помощи ядра. Пусть А — некий оператор и
Атп = (фт | А | фп )	B.10)
— матрица этого оператора относительно введенного выше ОНБ.
Ядром оператора А называется следующая функция:
А(а\ а) = ^Апт^=--= = ^УАпт\фп){фт\.	B.11)
Основываясь на условии полноты, J2n \фп)(Фп | = 1, получаем следу-
следующие очевидные формулы:
(Af)(a*) =^А(а\ а) /(а*) е^** %^>
(AiA2)(a*, а) = \ А{(а\ а) А2(а*, а) е~а*а d°[ da.	B.12)
J	l^i
Теперь представим оператор А в виде нормально упорядочен-
упорядоченного ряда относительно операторов рождения и уничтожения: А =
= Хт т-К-пт {о))п ат. Функция операторов рождения и уничтожения
называется нормально упорядоченной, если в этой функции все опе-
операторы рождения расположены левее всех операторов уничтожения.
Оператору А поставим в соответствие функцию
которая называется нормальным символом этого оператора.
Докажем, что
А(а*, а) = еа*аК(а\ а).	B.13)
Достаточно проверить B.13) в частном случае А = (а^)к а1. Имеем
Апп = -J= @\an (at)fea1 {o))m \ 0).
\/п\ т\

2.3. Функциональный интеграл в голоморфном представлении 25
Это выражение отлично от нуля лишь при m^lnn^knm — I = n —
— к. Обозначим
1, если га ^ I
{ О, если га < I.
При 171^1
a/(at)m|0)=m(m- 1) ... (га - I + 1) (a*)™ | 0).
Поэтому
Апт = 6m-iin-k&(m ^ Z)#(n ^ к)х
л^т • (т - 1) ... (га - / + 1) • п • (п - 1) ... (п - к + I)
Х	у/(т - 1I (п ^Щ
x@|an-/c(at)m-/|0) =
= у/т • (га - 1) ... (га - I + 1) • \Jn • (п - 1) ... (п - к+ 1) х
Теперь имеем
v^
Ашп
(а*)паш
п\ утл
7	I	Г
\ утл
/(n_kV(m_lv 2
— (п*\к+пп1+п -
Тем самым формула B.13) доказана.
2.3. Функциональный интеграл в голоморфном
представлении
Пусть функция /г (а*, а) является нормальным символом оператора
Гамильтона TL(a), а). Тогда ядро оператора эволюции,
U =
согласно сказанному выше, представляется как
U(a*, a; At) = exp{a*a -ih(a*, a) At} .	B.14)
Для произвольного интервала времени, t" — t' = N At,
U (а*, а; ?/х, ?х) = exp {[a^ajv-i — ^дг-1^лг-1 + ••• — a^ai +a^ao] —
jv-i

26 Лекция 2. Голоморфное представление континуального интеграла ...
Мы обозначили а^ = a, a*N = а*. Теперь перейдём к пределу N —
-> оо, At -> 0:
U (а*, а; ?", ?') = f e**W')o.tt") exp J f dt [-a*a - г h (а*, а)
^.	BЛ5)
Граничные условия таковы:
а*(?")=а\ a(tx)=a;	B.16)
причём по переменным a{t") и a*(tx) идёт интегрирование. С учётом
того, что
t"	t"
V	V
имеем для ядра оператора эволюции:
U (а\ a; t", tf) = [exp ji [a*(t/x) a(t") + a*(tx) a(tf)] X x
xexpJ г Г dt |"^(a* a - a* a) - h(a*, a)]
Обратим внимание на то, что здесь интеграл по времени во второй
экспоненте есть действие системы.
В случае гармонического осциллятора интеграл B.15) как гауссов
функциональный интеграл легко вычисляется. Так как
V ( *\
у/2п
то, при наличии источника, гамильтониан гармонического осциллятора
h (а\ а)=си(а*а+ 1/2) - -jL= (a + а*).	B.17)
Из B.16) имеем
5a*(t") = 5a(t')=O.	B.18)
Поэтому для вариации показателя экспоненты в континуальном инте-
интеграле B.15) находим
t"
6{a*(if')a(t")+ \dt\-c
/2 ио

2.3. Функциональный интеграл в голоморфном представлении 27
= a*(t"Na(t") +
*Г Г
- At \-а*5а
+ d ? -а 5а + 5а -ги а -\	т= ) - 5а [ а + гиа -
/2а; 7	V	V2u
V Г Л .	г 77 \	Л
= At \5а а* — ги;а* Н	;	 — 5а* а -\- iuia —
Отсюда следует, что точка экстремума показателя экспоненты 0 есть
решение уравнений движения:
a = —icua-\—	,	a*=icua*	.	B.19)
Здесь для дальнейшего удобства сделана замена (г]/\/2п)(а + а*) ^
-^ A/л/2а; )(гу*а + гуа*), хотя в рассматриваемом случае ту* = ту.
Заметим, что в интересных здесь задачах решения уравнений B.19)
не являются взаимно комплексно сопряженными. Дело в том, что в
представлении а = х + iy, а* = х — iy переменные х и у на массовой
поверхности с заданными граничными условиями не являются веще-
вещественными величинами. В этом смысле переменные интегрирования
а* и а в интеграле B.15) могут рассматриваться как независимые
переменные.
Рассмотрим случай т\ = 0, когда уравнения B.19) с граничными
условиями B.16) решаются тривиально:
a (t) = e-iuj^-^a(tf), a*(t) = e^^'V^").	B.20)
Далее вместо a(t') и a*(t") пишем а и а*, соответственно. Находим
экстремальное значение показателя экспоненты в интеграле B.15):
а*а ехр(—iuo(t" — ?')). Таким образом,
U0(a*, a; t" - t') = ехр {а* ae^t*""*')} .	B.21)
Вследствие унитарности оператора B.21) нормировочный множитель
X/N равен единице. Если /(а*) — произвольная функция, то
= f
a*ae--*} /(a*) е-** ^^ = / (a* е~ш) .
B.22)
(Проверьте эту формулу для /(а*) = (а*)п).
Функция B.21) является ядром оператора е~г^°, где Но — га-
гамильтониан свободного осциллятора.
1) Такая экстремаль в теории поля называется массовой поверхностью.

28 Лекция 2. Голоморфное представление континуального интеграла ...
Замечание. Здесь мы выбросили «нулевую» энергию из гамиль-
гамильтониана. В противном случае имели бы
(а*, а; t) = exp < а*
а
Пусть А — оператор с ядром А (а*, а). Нам понадобится обобщение
формулы B.22), то есть ядро оператора еи п° Ае~и п°:
[U0(-t") AU0(tf)](a\ a)=A (a* eiujt\ ae~iujt') .	B.23)
2.4. Определение ^-матрицы
Пусть Н — гамильтониан теории, Но — свободный гамильтониан и
U (tf/, tf) — оператор эволюции взаимодействующей теории, ^-матрица
определяется при помощи следующей формулы:
5 = lim
Обкладки е
?/(*", tf)e
-lt'n\
+oo, t' -+ -oo. B.24)
lt
... e
lt
в B.24) приводят к исключению свободного
движения, которое не представляет интереса. Действительно, если TL =
= TYo, то ^-матрица B.24) равна единичному оператору.
Вычислим ^-матрицу гармонического осциллятора при наличии
внешнего источника. Согласно определению B.24) и формуле B.23),
теперь граничные условия B.16) должны быть заменены на следую-
следующие:
а* (?") = а* eiujt , а (?') = a e~iujt .	B.25)
Легко находим решения уравнений B.19) с граничными условиями
B.25):
t"
a* (t) = е1
•I
ds-
a + г I ds-
v
s/2uo
*ri(s)
B.26)
Подставим решение B.26) в показатель экспоненты в B.15) и раздви-
раздвинем пределы интегрирования (tr —> —oo, t" -^ +оо). Таким образом мы
получим ядро ^-матрицы для гармонического осциллятора в присут-
присутствии внешнего источника:
+ОО

2.5. S-матрица в скалярной теории поля	29
+оо	t	.
г	e—iuj(t—s)
dt dsr?{t)i	i]{s)\ .	B.27)
— oo — oo
При помощи A.23) выражение B.27) переписывается как
{+ОО
{
а*а
{
-oo
+оо +оо	Л
М I dtdsV*(t)Dc(t-s)V(s)\. B.
Подчеркнём, что в B.28) используется именно причинная гринов-
ская функция, так как уже в определении ^-матрицы B.24) сделано
предположение, что при 111 —> оо взаимодействие выключается адиаба-
адиабатически и система описывается свободным гамильтонианом Но.
В дальнейшем нам понадобится формула B.26), записанная в
несколько изменённом виде:
2co L
v
t"
dsDc(t - s)rj(s). B.26х)
2.5. ^-матрица в скалярной теории поля
Рассмотрим скалярную теорию поля в ^-мерном пространстве-
времени. В свободном случае в присутствии внешнего источника дей-
действие такой теории имеет вид
y	B.29)
Отсюда получаем лагранжиан
С = Jd^-1' х Ш2 - I (V фJ - \т2 ф2 -У(ф) + г)ф\ , B.30)
где ф = d(j)(t, x)/dt. Варьируя лагранжиан B.30) относительно поля
ф, находим обобщённый импульс поля ф:
> п = ф.	B.31)

30 Лекция 2. Голоморфное представление континуального интеграла ...
Теперь путём канонической процедуры получаем гамильтониан теории:
П= \&{d~X) хиф-С —>
B.32)
Выпишем лишь ненулевые одновременные коммутационные соотноше-
соотношения (КС):
[{1, х),тг(*, у)]=г^-1)(х-у).	B.33)
Как правило, реализация КС B.33) осуществляется согласно следу-
следующей схеме:
Ф (*. х) = J ^-^ ^= (ak(t) е- + ai(t) e"
B.34)
Разложение B.34) является естественным в случае свободной теории,
когда У(ф) = 0. Действительно, если
ик = л/k2 + т2,	B.35)
то гамильтониан B.32) распадается на сумму гамильтонианов гармо-
гармонических осцилляторов (мы здесь полагаем г] = 0):
2j
gj B7r)
d-i
где Bтг)с^~1 5^~^ @) = Jd^ ~ ' x = V — объём пространства. Второе
слагаемое в правой части последнего равенства является энергией
нулевых колебаний осцилляторов. Хотя плотность этой энергии беско-
бесконечна, она, как правило, не играет роли и потому в обычной квантовой
теории поля вычёркивается. Энергия нулевых колебаний (или энергия
вакуума) является серьёзной проблемой в квантовой теории гравита-
гравитации, однако эта тема лежит за рамками нашего курса лекций. Отметим
лишь, что рассматриваемый далее эффект Казимира существует вслед-
вследствие реальности энергии вакуума.

2.5. S-матрица в скалярной теории поля	31
Сделаем замечание об используемой здесь нормировке. Везде инте-
интегрирование в координатном пространстве осуществляется по правилу
j S ' х, в то время как интегрирование в импульсном пространстве
— по правилу JcT 'k/{2ii)d. Это правило согласовано с правилами
коммутации B.33) и B.34). Иными словами, единичный оператор в
линейном пространстве функций в координатном представлении есть
§(d) (^х _^ав импульсном представлении — Bn)d5^ (к — р).
Основное состояние или вакуум в теории B.32)-B.35) обозначает-
обозначается | 0) и определяется условиями
ак|0)=0, @|0) = 1.	B.36)
Очевидно, что
Wo|O)=O.	B.37)
Возбуждённые состояния строятся при помощи операторов рожде-
рождения а^. Например, одночастичное состояние имеет вид
B.38)
Вследствие B.34) и B.36) скалярное произведение двух одночастичных
состояний имеет вид
(к | р) = 2сок Bir)d-1 a^) (к - р).	B.39)
Можно показать (см. задачи), что правая часть B.39) лоренц-
инвариантна. Нормировка состояний B.38) оправдывается именно
лоренц-инвариантностью скалярных произведений одночастичных
состояний. Заметим также, что лоренц-инвариантная мера в
пространстве одночастичных состояний равна
Мера B.40) согласована со скалярным произведением B.39), то есть
k)(k| = l,	B.41)
где единица в правой части равенства B.40) обозначает единичный
оператор в пространстве одночастичных состояний.
Энергия состояния B.38) легко вычисляется при помощи равенства
B.37) и КС B.34):
Н0\к)=и;к\к).
Оператор импульса в скалярной теории поля имеет вид (см. Прило-
Приложение В)
'Р — — Н^) г тг(т) V сЬ (г)	(9 А9)

32 Лекция 2. Голоморфное представление континуального интеграла ...
что оправдывается значениями следующих коммутаторов:
[ф(х), V] = -гУ^(ж), [тт(ж), V] = -гУтг(ж),
и так далее. Подставляя разложение B.34) в B.42), получаем
Легко найти, что
Таким образом, состояние |к) имеет определённый импульс к.
Пусть {к^}, г = 1, ... , п — такой набор импульсов, что попарно
к^ ф kj. Тогда многочастичное состояние представляется в виде
п
| ki, к2, ... , кп ) = ТТ (д/2 uok i ^k) I 0)-	B.43)
г=1
Имеем:
Н0|к,,к2, ...,к„> = B^wfcl I |кьк2, ...,к„>,
V;' /	B.44)
Р|кьк2)...,к„>= (УкЛ |кьк2, ... .кп),
\»=1 /
а также
(рь р2, ... ,р„|кь к2, ... ,к„) =
г=1
х	>	S^-'Hki -ph) ... S^-'HK-pi ). B.45)
все перестановки pi
Естественно, существуют также состояния вида (a^k)n|0) (n ча-
частиц в одном состоянии), однако в теории ^-матрицы эти состояния
интереса не представляют.
Пространство состояний, построенное описанным способом, назы-
называется фоковским пространством состояний.
Пусть
7?k (t) = j d**) x V (t, x) e-kx = <k.	B.46)
Для гамильтониана B.32) имеем
П
BГ47)
Отсюда видно, что в данном случае гамильтониан является суммой
гамильтонианов вида B.17) и потому ядро ^-матрицы системы B.29)

2.5. S-матрица в скалярной теории поля
33
получается непосредственно из ядра ^-матрицы B.27). Первое слагае-
слагаемое в экспоненте в B.27) будет иметь вид
второе —
]xrj(x) фо(х), фо(х) = f2l{y-\ /2^~
а третье —
+ ОО	t
« j d« I d.J.
— oo —oo
ГЪ t/y 	 IX) JL>	jPk. -*»-ч
'fc _., Г.е-«ш*(*-8)
— ikx\
B.48)
ZT»?*k(*) \i-
где
= г
m2) L>c (ж) =
B.49)
Из правой части равенства B.49) очевидны лоренц-инвариантность
причинной гриновской функции Dc (х) и то, что везде Im Uk = —?, ? —>
-^> +0. Для ядра ^-матрицы имеем
S (а*, а) = 1 exp J J dg^ _fc, a*k ak + i J d(d) ж?? (x) ф0 (х) +
+ l-\ld{d)xd{d)yV(x)Dc(x-y)i1(y)\.	B.50)
Теперь перейдём от ядра к нормальному символу ^-матрицы:
1	(Г
S(a*, а) = — exp U \ d(d) xr] (х) ф0 (ж) +
+| |jd(d) xd(d) у ?] (ж) Dc {х-у)г, {у)\ = So (фо; 11). B.51)
Поле B.48) удовлетворяет свободному уравнению
(д^ + т2) фо = 0,
которое называется уравнением Клейна-Гордона-Фока.
2 С.Н. Вергелес

34 Лекция 2. Голоморфное представление континуального интеграла ...
Укажем, что нормальный символ ^-матрицы представляется также
как функциональный интеграл:
S(a*, а) = -^ [ехр |г [dt \d{d~l) хтгф - Н~\ 1
n(x), Вф = Цйф(х),
= 1
Г
=J
k 1
akin = cik, akout = aL kx = k°x° -kx, k° = uk. B.52)
Действие S в B.52) может быть как свободным действием B.29), так
и включающим взаимодействие (см. ниже B.54)).
В справедливости представления B.52) нетрудно убедиться следу-
следующим образом. В случае свободной теории с внешним источником,
описывающейся действием B.29), функциональный интеграл B.52) как
гауссов вычисляется точно. В этом случае действие в экспоненте функ-
функционального интеграла экстремально при условии (д^д^ + т2) ф = г\.
Решение последнего уравнения с необходимыми граничными условия-
условиями типа B.25) есть (сравни с одномерным случаем B.26х)
ф (х) = ф0 (х) + | d(d) у Dc (x - у) ц (у).	B.53)
Подстановка B.53) в экспоненту функционального интеграла приводит
к выражению B.51) 0. Очевидно, полученный результат не случа-
случаен, поскольку, согласно лекции 1, амплитуда перехода вообще, и S-
матрица в частности, представляется в виде функционального интегра-
интеграла B.52). Поэтому единственный остающийся вопрос при вычислении
нормального символа ^-матрицы — это вопрос о граничных условиях
динамического поля при \t\ —> оо. Важность голоморфного представ-
представления функционального интеграла заключается именно в том, что это
представление даёт ответ на вопрос, каковы должны быть граничные
условия при вычислении нормального символа ^-матрицы: положи-
положительно частотные волны в ф^ и отрицательно частотные волны в фоиъ
совпадают с соответствующими волнами в фо B.48). Здесь уместно
ещё раз подчеркнуть, что такие граничные условия и сама теория
1) Следует обратить внимание на следующую тонкость, возникающую
при проведении этого простого вычисления: неопределенность интеграла
Jd^ хфо(х)(дцд^ + m2) Jd^ у Dc(x — у)т](у) решается в пользу равенства
нулю этого интеграла. Действительно, поле фо принадлежит ядру оператора
(<9М<9М + ш2). Поэтому оператор (<9М<9М + m2)Dc является проектором, обраща-
обращающим в нуль упомянутое ядро.

2.6. S-матрица в теории поля со взаимодействием	35
^-матрицы существуют лишь при справедливости предположения об
адиабатическом выключении взаимодействия при \t\ —> оо.
2.6. ^-матрица в теории поля со взаимодействием
Рассмотрим теорию скалярного поля с самодействием, описываю-
описывающуюся действием
S = ^ х \^-{д^фJ -Х-т1ф2 -V {ф) + г1ф\.	B.54)
Наибольший интерес для нас представляет случай
-^\оф*.	B.55)
Размерность полей и констант определяется, исходя из того, что
действие имеет размерность постоянной Планка, а в случае ft = 1 —
безразмерно. Например, из безразмерности действия B.54) имеем:
[т] = см, [ф] = см^/2), [Л] = см d~\
Теперь континуальный интеграл не может быть вычислен точно,
но существует вычислительная техника, основанная на теории возму-
возмущений (ТВ). Идея заключается в разложении ^-матрицы по потен-
потенциалу взаимодействия (JcT ' xV (ф)\. Тогда в нулевом приближении
мы имеем точный результат B.51), а при разложении по потенциалу
взаимодействия fjcr^ ж V (</>)) возникают интегралы от гауссовых
средних вида @\Тф\ ... фп |0), где фг = ф(хг).
Замечание. Рассмотрим интеграл
+ ОО
d х ехр ( — - х2 — Л хА
I (X) = Ах ехр (
2
Очевидно, что функция / (Л) при Л = 0 не аналитична, она имеет
особенность. Тем не менее при Л <С 1 имеет смысл разложение
хж4е"A/2)жЧ ....	B.56)
Это разложение имеет смысл лишь до тех пор, пока следующий
член разложения меньше предыдущего. Интегралы вида
J-n = dxx e	(z.o/j
вычисляются при помощи следующих формул:
хпе-(\/2)х2 = й c-(\/2)x2+rix
dr]n
77=0

36 Лекция 2. Голоморфное представление континуального интеграла ...
\ Ах e
In= \dx
o-(\/2)x2+r)x
drjn
77=0
dn
dr]n
dr]n
так что
?
Если Ф (х) — произвольная функция, то
'1 (
•<*> =
1Г)Х
Это равенство позволяет свести вычисление негауссова интеграла к
следующей формуле:
d х exp <J г [ - х2 — V (х) ) \ =
ТУТ: ) \ И ж ехр {г ( -;
B.60)
77=0
Интеграл в правой части B.60) гауссов и потому легко вычисляется.
После этого мы можем развить ТВ, разлагая правую часть B.60)
относительно V и пользуясь теоремой Вика.
В теории поля действуем аналогично. Имеем
(хп) = -
1
Г Г
-— ехр < г \ ф (х) г] (х) d x
п)	{ J
i 5г)(х\) г 5г] (х.
Для любого функционала Ф{ф(х)}
ехр <i (/> (х) г] (х) d x
г]=0
B.61)
77=0
и, в частности,
ехр ^-г У(ф) dx\ =
= ехр <j — г I V ( —
г 5rj(x)
dx> exp < г
ф (х) г] (х) dx
B.62)
77=0
Теперь, прямолинейно обобщая одномерную формулу B.60) на случай
теории поля и пользуясь формулой B.51) для значения функциональ-

2.6. S-матрица в теории поля со взаимодействием	37
ного гауссова интеграла в задаче об ^-матрице, выпишем нормальный
символ ^-матрицы в скалярной теории поля со взаимодействием:
х exp 1 г d х г] (х) фо(х) + %- d х d у г] (х) Dc(x -у)г)(у)\\ . B.63)
I J	Z JJ	J 1т7=0
т7=0
Здесь и далее Dc(x) задаётся согласно B.49).
Разложим функционал B.63) по фо и перейдём от нормального
символа оператора ^-матрицы к самому оператору ^-матрицы:
\ Sn(x\, ... , хп) : фъ(х\) ... фо (хп) : dx\ ... dxn,
п '
— \ Sn(x\, ... , хп) : фъ(х\) ... фо (хп) :
ikx +aleihx), k° =ujk.
B.64)
Функции Sn (x\, ... , xn) являются коэффициентами при степенях
поля фо(х) в разложении функционала B.63) по степеням этого
поля и они называются коэффициентными функциями ^-матрицы,
а S (фо) — производящим функционалом для функций Sn. Поле фо
в B.64) является свободным квантованным полем в представлении
Гейзенберга. Согласно определению, размещение любого оператора,
являющегося функцией операторов рождения и уничтожения, между
двумя двоеточиями означает применение оператора нормального
упорядочения или приведение оператора к нормальному виду, причём
в процессе этого приведения все операторы рождения и уничтожения
считаются коммутативными. Например, : а^а := а^а, : аа^ : =
= ata, :am(at)n := (at)nam, : ad a: = a^a2, и т.д.
Задачи
1.	Проверьте в скалярной теории поля, что уравнения Гейзенберга
г О = [О, ТС] совпадают по форме с лагранжевыми уравнениями.
2.	Рассмотрите теорию комплексного скалярного поля с действием
S= Id4 х(д^ф*д»ф-т2ф*ф).
Изучите эту теорию, рассматривая в качестве базисных динамических
переменных ф(х) и ф* (х), а не вещественную и мнимую части поля
ф(х).

38 Лекция 2. Голоморфное представление континуального интеграла ...
а)	Выпишите канонически сопряжённые импульсы к ф (х) и ф* (х)
и канонические коммутационные соотношения. Покажите, что гамиль-
гамильтониан	Р
-j	га
Выпишите уравнение Гейзенберга для ф (х) и покажите, что оно сов-
совпадает с уравнением Клейна-Гордона-Фока.
б)	Диагонализуйте гамильтониан, вводя операторы рождения и уни-
уничтожения. Покажите, что теория содержит два типа частиц с массой
га.
в)	Докажите, что заряд,
сохраняется, и перепишите его в терминах операторов рождения и
уничтожения и вычислите заряд частиц каждого типа.
3. а) Докажите, что величина
/ + к2
лоренц-инвариантна.
б) Докажите, что мера
лоренц-инвариантна.
4. а) Пусть Н(а\ а) — оператор Гамильтона. Представьте квантовую
статистическую сумму
У У У
в виде функционального интеграла в голоморфном представлении.
б) Вычислите статистическую сумму гармонического осциллятора
(с точностью до множителя, зависящего лишь от температуры) в голо-
голоморфном представлении в присутствии внешнего источника. Исполь-
Используя эту статистическую сумму, найдите хронологический коррелятор
(ТТ аУ (т\)а(т2)) в представлении Мацубары. При помощи полученной
формулы найдите также статистические средние
Г+г (&~Р 1~L п^ п\~\ I +г (/э~C7~(-\ лл Г+г (&~Р 7~L п г»1Л1 / i г (/э~ C 7~L\
Lllo	U/U/I/Lllo	I И LI 1С	U/U/I/Lllo	I.

Лекция 3
ДИАГРАММНАЯ ТЕХНИКА ФЕЙНМАНА
3.1. Разложение по константе связи
Рассмотрим очень интересный случай, когда потенциал самодей-
самодействия задаётся согласно B.55), и разложим первую экспоненту в B.63)
в ряд по потенциалу V. Члены этого ряда содержат произведения четы-
четырёхкратных дифференцирований по г] (xi) с последующим интегрирова-
интегрированием по Х{. Кратное применение операторов 5/5rj(xi) к Sq (фо', rj) (см.
B.51)) и последующее обращение в нуль поля г] приводит к появлению
в ^-матрице множителей Фо(хг) и Dc(xi — Xj), причём последняя
функция соответствует дифференциальному оператору второго поряд-
порядка (—iM2/5rj(xiMrj(xj). Изобразим графически каждый член этого
разложения. Эти графики называются диаграммами Фейнмана. Члену
разложения n-го порядка, содержащему дифференциальный оператор
...dxnV[-T—_)...y(I_* ), C.1)
n\ J	\i Srj(xi)J	\i Srj(xn)
ставится в соответствие диаграмма, состоящая из п вершин в точ-
точках Xi, г = 1, ... , п, находящихся под n-кратным интегралом по
пространству-времени. В рассматриваемом случае B.55) из каждой
вершины выходит 4 линии (в теории с потенциалом Хфв из каждой
вершины выходит s линий). Эти линии могут либо замыкаться, со-
соединяя пару вершин (такие линии называются внутренними), либо
выходить из диаграммы, соответствуя полю фо (х^ (такие линии —
внешние). Каждой внутренней линии, соединяющей точки Xi и Xj,
ставится в соответствие функция Dc (xi — Xj). Каждой внешней линии,
выходящей из точки Xi, ставится в соответствие поле фо(х^. По всем
точкам {хг} производится пространственно-временное интегрирование.
Полное выражение для S (фо) B.63) получается суммированием по
всем диаграммам.

40	Лекция 3. Диаграммная техника Фейнмана
Приступим к конкретным вычислениям. Представим ^-матрицу в
виде
5=1+гТ.	C.2)
Пусть начальное и конечное состояния имеют вид B.43); обозначим
через |г) и |/) начальное и конечное состояния, соответственно:
|г) = |кьк2, ...), |/} = |pi,P2, ...}.	C.3)
Вследствие общей трансляционной инвариантности теории справедли-
справедлива формула
гТ|кь к2, ...) = Bir)d 6W (Pf - Pi) i Mfi. C.4)
Здесь Pi = k\ + &2 + ... — суммарный начальный и Pf = p\ -\-p2 -\- ...
—	суммарный конечный 4-импульсы. Введенная при помощи равенства
C.4) величина Mfi называется амплитудой рассеяния. Информация о
взаимодействии содержится в операторе Т в C.2) и в амплитуде Mfi,
через которую выражаются сечения рассеяния, вероятности распадов
частиц, и т.п. (в зависимости от постановки задачи). Из общих прин-
принципов квантовой механики следует, что эти величины квадратичны по
Вычислим ^-матрицу B.64) с точностью до второго порядка по Ао
и четвёртого по фо. Будем пользоваться формулами B.51) и формулой
-	я , ч #0 (Фо; rj) = \ \фо (xi) +\dyDc(xi-y)ri (у) So (ф0; г,) : =
г or)yxi)	[_	J	J
= : [Xi ] So (фо', rj) :, C.5 а)
1 Л
—г ис ухг — Хп).	уо.о о)
г Sriixj)
В первом порядке по Ао находим (нормировочную константу X/N
можно опускать, так как она всегда сокращается в окончательном
результате) величину
= -i^Jcb : {-3 ?2@)-6iDc@) $(*) + $(*)}:. C.6)
Во втором порядке следует вычислить величину

3.1. Разложение по константе связи
41
77=0
Далее целесообразно использовать формулу кратного дифференциро-
дифференцирования,
U 9)"" = Г 9 + 4 /'" д' + 6f"g" + 4f'g'" + fg"",
подразумевая под / фигурную скобку в последнем равенстве, а под д
— оператор So (фо', rj). Таким образом, находим искомую величину:
1	/АЛ2
2	\4\)
+24Dc(x\ — х2)] — iDc(x\ — Х2) [96 Dl(x\ — Х2) + 144^@)] х
хфо(х1)фо(х2) -iDc@) [72D2c(x{-x2) + \8D2c@)] (ф20(х{) + ф20(х2)) +
+ [72D2c(Xl -х2) + 36В2с(О)]ф2о(х1)ф2о(х2)+48Вс(О)Вс(х1 -х2)х
х[фо(х\)ФоЫ) +Фо(х\)ФоЫ)] +3D^@) [фо(х\) + Фо(х2)]\ : . C.7)
При помощи теоремы Вика (см. задачу 1 к лекции 1), а также разло-
разложения для фо B.64) и определения векторов состояния B.43) находим
следующие значения для элементов S-матрицы в случае перехода од-
ночастичного состояния |к) в одночастичное состояние |р) (заметим,
что все частоты о;к, содержащиеся в формулах, определяющих вектора-
состояния (см. B.38) и 2.43)), и в лоренц-инвариантной мере B.40),
взаимно сокращаются):
В нулевом приближении по
(нет взаимодействия).
В первом порядке по
C.8)
¦')(k-
p)J
Bn)
Во втором порядке по Ао,
.71) о [к р) а
C.9)
(d)
х2
D2c(Xl - x2) -

42	Лекция 3. Диаграммная техника Фейнмана
\2
Согласно B.49),
В частности,
|>)
'ж, d(d)x2I?c@)JD2(;
J
( h»\ p Ъ К X T~\ f h»\
v\ ~х2)ег
d^x2DUo;
i
)X\— ikx2 _
)e«(P-fc)-,.
\-ie
C.10)
(З.П)
B7Г)" ^^¦
Преобразуем некоторые интегралы при помощи C.11):
(ЗЛЮ
C.12а)
C.12 6)
- p) J ^ | ^
C.12 c)
) ал d{d)x2Dc(xi -x2)eipXl-ikX2 = {2it)d5(d\k -p)Dc(k), C.12d)
ж, did) x2 e«(P-*)*i Д2(Ж1 _ Ж2) =
Г d(d) A-
= Bir)d 6W(k - p) -—Dc(k)Dc(-k), C.12 e)
J {^)
Теперь при помощи выписанных формул вычислим вклад в амплитуду
перехода |к) —> |р), содержащийся в сумме членов C.8)—C.10), с

3.2. Диаграммы Фейнмана и правила Фейнмана
43
точностью O(Aq):
2\.
-А?
d(d)
а) h	\ Г (\^а) а
I DM-
C.13)
3.2. Диаграммы Фейнмана и правила Фейнмана
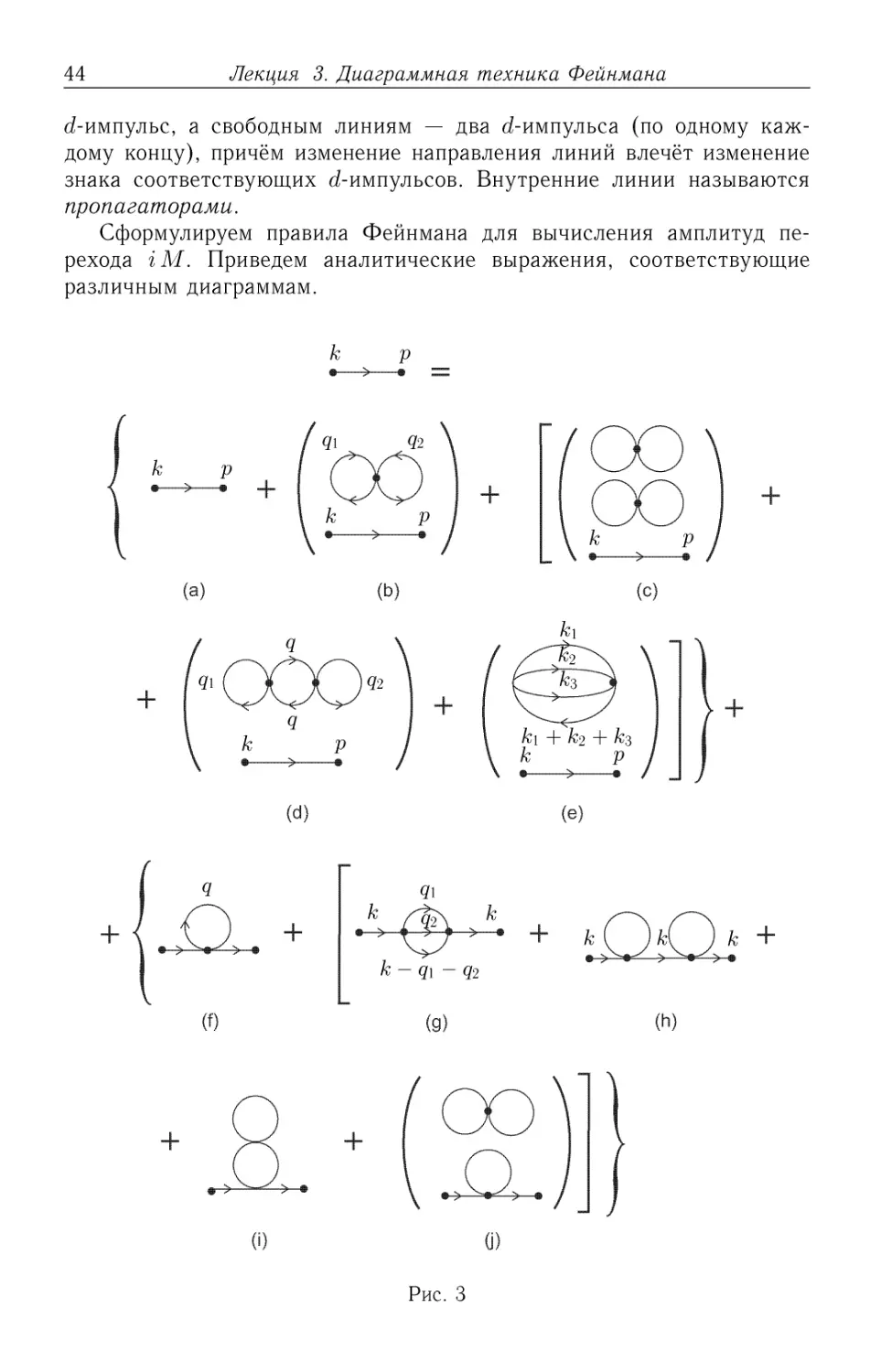
Аналитическому выражению C.13) соответствует следующая сумма
диаграмм Фейнмана (см. рис. 3; диаграммы выписаны в том же поряд-
порядке, в котором расположены слагаемые в C.13)).
На этом этапе уместно сформулировать правила Фейнмана приме-
применительно к рассматриваемой модели. При помощи правил Фейнмана
каждой амплитуде в каждом порядке теории возмущений ставится в
соответствие конечный набор диаграмм Фейнмана. Каждая диаграмма
Фейнмана имеет однозначное аналитическое выражение. Амплитуда
перехода (в данном порядке теории возмущений) является суммой этих
аналитических выражений. Каждая диаграмма состоит из вершин и
линий, соединяющих эти вершины (внутренние линии), отрезков, лишь
один конец которых заканчивается (или начинается) в вершине (внеш-
(внешние линии) и отдельных отрезков (свободные линии). Каждая линия
имеет направление. Внутренним и внешним линиям приписывается

44
Лекция 3. Диаграммная техника Фейнмана
d-импульс, а свободным линиям — два d-импульса (по одному каж-
каждому концу), причём изменение направления линий влечёт изменение
знака соответствующих d-импульсов. Внутренние линии называются
пропагаторами.
Сформулируем правила Фейнмана для вычисления амплитуд пе-
перехода гМ. Приведем аналитические выражения, соответствующие
различным диаграммам.
(d)
(е)
к — q\ — qi
(g)
к +
(h)
(i)
(i)
Рис. 3

3.2. Диаграммы Фейнмана и правила Фейнмана	45
1. Для каждого свободного отрезка (см. рис. За)
B)^1^
где к и р — d-импульсы концов отрезка.
2.	Каждой внутренней линии ставится в соответствие пропагатор
>	= —iDc(k), где к — d-импульс пропагатора.
3.	Для каждой вершины
= -г А.
4.	Для каждой внешней входящей линии
^ ^	 	 I
для каждой внешней выходящей линии
5.	Потребовать выполнения закона сохранения d-импульса в каж-
каждой вершине.
6.	Проинтегрировать по каждому не зафиксированному законом
rd<*>p
сохранения импульсу:	.
7.	Разделить на множитель Dn — порядок группы симметрии диа-
диаграммы.
8.	Каждый связный вакуумный пузырёк (как «восьмёрка» на
рис. 3 (Ь)) содержит множитель ( сГ ' х 1.
Так как практически всегда очевидно, когда конец какой-либо ли-
линии свободен, то точки на свободных концах линий диаграмм далее не
ставятся.
Все интегрирования интерпретируются как следствие принципа су-
суперпозиции, согласно которому амплитуды суммируются.
Правило 1 имеет значение лишь для тривиальной части амплитуды
рассеяния. Важная для физики частиц амплитуда М (см. C.4)) содер-
содержится во второй фигурной скобке в C.13), а также во второй фигурной
скобке на рис. 3. Правило 8 имеет значение, как мы увидим, лишь для
амплитуды перехода из вакуума в вакуум.
Укажем порядки групп симметрии Dn диаграмм на рис. 3:
(b)	Dn = 8 — по две перестановки каждого из концов двух пропа-
гаторов и две перестановки самих пропагаторов B-2-2 = 8);
(c)	Dn =2-8-8 = 27;
(d)	Dn = 2 • 2 • 2 • 2 = 24;

46	Лекция 3. Диаграммная техника Фейнмана
(e)	Dn = 2-4! — две перестановки вершин и 4! перестановки
пропагаторов вакуумного пузырька;
(f)	Dn = 2 — перестановка концов пропагатора;
(g)	Dn = 3! — число перестановок пропагаторов;
(h) Dn = 2 • 2 = 4;
(i) Dn = 2-2 = 4 — две перестановки пропагаторов в нижней петле
и две перестановки концов пропагатора в верхней петле;
(j) Dn = 8 • 2 = D'n • 2 = 16 — D'n = 8 для вакуумного пузырька и
две перестановки концов пропагатора.
В случае сомнения при вычислении Dn следует непосредственно
вычислить коэффициент при диаграмме.
Нетрудно понять происхождение правил Фейнмана. Действительно,
каждой вершине соответствует множитель сг ' х(—гЛ/4!) и в случае
n-вершинной диаграммы имеется общий множитель A/п!) из ряда
Тейлора. Но множитель 1/п! всегда сокращается множителем п! от
перестановок вершин. Кроме того, каждая вершина имеет 4 линии,
приходящие из четырёх различных мест. Перестановки относительно
этих мест (что делается автоматически при вычислении {5/г5г]{х)^ )
дают множитель 4!, сокращающий знаменатель в (—гЛ/4!). Поэтому
каждой вершине соответствует множитель сг ' ж(—гХ). Если
имеем, например, вакуумный пузырёк с двумя вершинами такой, как
на рис.З(е), то из двух исходных множителей 1/4! один остаётся.
Не сокращается также общий множитель A/2). Но в данном случае
как раз Dn = 2 • 4!. Действительно, при действии дифференциального
оператора U5/i5r](x)) U5/i5r](y)) на величину 5Ь@о; V) та квад-
квадратная скобка, которая действует первая, не даёт множителя 4!.
Легко сообразить, что, например, при вычислении диаграммы на
рис. 4,
же мы
n
Рис. 4.
множитель A/п!) в дифференциальном операторе C.1) не сокраща-
сокращается: каждый множитель — с1жЛ — -z—-,—г ) даёт в амплитуде
4!	V % о т)(х¦) /
множитель, соответствующий одной диаграмме-восьмёрке. Таким
образом, в случае диаграммы на рис. 4, порядок группы симметрии

3.2. Диаграммы Фейнмана и правила Фейнмана
47
Dn = п\ (8)п. Аналогично, если мы имеем несвязную вакуумную
диаграмму вида
п	т
Рис. 5.
то она равна
n! га!
Рис. 6.
Подчеркнём исключительно важное и нетривиальное свойство диа-
диаграмм Фейнмана: общий числовой коэффициент в диаграмме не зави-
зависит от её порядка.
Поясним физический смысл диаграмм на рис. 3.
Сумма первых пяти диаграмм равна произведению амплитуды пе-
перехода | к) —> | р) в нулевом приближении на сумму первых пяти
вакуумных пузырьков (начиная от тривиального, равного единице).
Обозначим через Vi какой-либо из вакуумных пузырьков:
Из сказанного видно, что любая диаграмма, не содержащая несвязных
вакуумных компонент, умножается на ряд
ГТ Vi = ехР
C.14)
Таким образом, сумма всех диаграмм с заданным числом внешних
линий равна сумме всех связных диаграмм с этими же внешними
линиями, умноженной на экспоненту от суммы всех разных несвязных
диаграмм без внешних линий (вакуумных пузырьков). Эта экспонен-
экспонента интерпретируется как фаза, набегающая при переходе вакуума в
вакуум за бесконечное время. Заметим, что каждая диаграмма Vi
содержит множитель (Jd^x). Эта вакуумная фаза не представляет

48	Лекция 3. Диаграммная техника Фейнмана
интереса, поскольку сокращается в физических величинах. Поэтому её
не учитывают.
Во второй фигурной скобке на рис. 3 диаграммы (f), (g), (h), (i)
дают поправки к амплитуде распространения одной частицы в вакууме.
Все эти поправки могут лишь привести к изменению (перенормиров-
(перенормировке) тех параметров частицы, которые могут изменяться непрерывно.
Например, это может быть масса. Эти поправки далее рассматрива-
рассматриваются в меру необходимости. Здесь лишь заметим, что буквальный
учёт диаграмм типа рис. 3 (f)-(i) затруднителен, поскольку, например,
диаграммы (f) и (g) квадратично расходятся, диаграмма (h) содержит
множитель
rv П^ О
Однако, к2 = ttIq, и потому Dc(k) = ^ = oo. Мы видим, что поправки
к внешним линиям, 4-импульсы которых кг удовлетворяют условию
к2 = т2, где т — наблюдаемая (или физическая) масса, требуют от-
отдельного рассмотрения. Такое рассмотрение далее проводится в более
изящной теории поля — квантовой электродинамике. В скалярной тео-
теории поля квантовые поправки к внешним линиям здесь не изучаются.
(Говорят, что если импульс частицы удовлетворяет условию к2 = т2,
то её импульс находится на массовой поверхности; в этой ситуации
говорят также, что частица находится на массовой поверхности.) Таким
образом, из двух диаграмм
левая будет учитываться, а правая — нет. Будем говорить, что у
диаграммы ноги на массовой поверхности «ампутированы», если её
нельзя рассечь на две несвязных диаграммы, разрезая одну внутрен-
внутреннюю линию, и при этом одна из двух диаграмм имеет две внешних
линии на массовой поверхности.
Таким образом, при проведении вычислений по ТВ сле-
следует нарисовать все диаграммы процесса, имеющие фи-
физический смысл, с заданным числом вершим, определяе-
определяемым степенью необходимой точности вычисления, сопоста-
сопоставить диаграммам аналитические выражения согласно правилам
Фейнмана и вычислить их.
Например, рассмотрим взаимное рассеяние двух начальных частиц
с импульсами ki и k2, в результате чего при t —> оо имеем две частицы
с импульсами р{ и р2. Этот процесс с точностью О (Aq) описывается
следующими диаграммами (см. рис. 7).

3.3. Производящий функционал гриновских функций	49
р2
кх q	Pi	кх >^х > рх	кх >
^	\ р	q+k2-px
fc/ kx+k2-ct p2	k2 \шУ у р2	к2 \
Рис. 7.
Аналитическое выражение этих диаграмм таково:
Г 1 Г d^о	Г
г М = -гЛ0 + { 2 Ло j Щ? Dc{q) Гс(
Dc(k2 -pl+q)\\. C.15)
Амплитуду C.15) легко также получить непосредственно при помощи
выражений C.6) и C.7).
Диаграммы вида
и т.п. по указанным выше причинам не рассматриваются.
3.3. Производящий функционал гриновских функций
Если в B.63) не полагать т\ = 0, то полученный функционал обо-
обозначим #((/>о; г\)\ он является нормальным символом ^-матрицы для
рассеяния взаимодействующих частиц в присутствии источника rj(x).
Рассмотрим также функционал
г Г	1
rj(x)Dc(x-y)rj(y) Ax &у\, C.16)
имеющий смысл амплитуды перехода из вакуума в вакуум в присут-
присутствии внешнего источника. Коэффициентные функции Gn(x\,... ,хп) в
разложении функционала C.16) в ряд по rj(x),
\G()()()&	d	C.17)
n

50	Лекция 3. Диаграммная техника Фейнмана
определяют функции Грина, то есть вакуумные средние от хроно-
хронологических произведений гейзенберговых операторов поля (см. конец
лекции 1). Поэтому функционал C.16) называется производящим
функционалом.
Функционал Z{rj) содержит в себе больше информации, чем функ-
функционал S((/)o) B.63): зная Z(rj), можно восстановить S((/)o). Чтобы полу-
получить явные формулы, введём расширенный функционал 3(ф), заменив
в B.63) поле фо(х) произвольной функцией четырёх переменных ф(х).
Коэффициентные расширенные функции Sn (см. B.64)) суть вариа-
вариационные производные (под расширенными функциями мы понимаем
коэффициентные функции для
Sn(xl9...,xn) = (i
г 5ф{х\
ф=0
x exp I - ф) Dc(x - y) r)(y) dxdy\. C.18)
Пусть
ф) =\dy Dc(x - y) rj(y) -> ф) = (d^ + ra2) rj(x),
— if) ЯМ _i_ m2)	И 1 Q^
5ф) *	5ф)
Очевидно
г 5rj(x)J	\ J \i Srj(z)J j
x exp <^ - rj(y) D(y - z) ф) dydz\,
гу C.20)
и т.д. Применение оператора
\ 5 \ П 5
г 5ф\)) '" у г

ЗА. О физической интерпретации пропагаторов и причинность 51
к функционалу C.16) даёт функционал того же вида, что в правой
части C.20), где квадратная скобка заменяется на величину
причём
фо(х\)... фо(хп)к(хи... ,хп) dx\ ...dxn = 0.	C.21)
Теперь при помощи C.18)—C.21) находим
I
Ахх ... Ахпф^хх)... фо(хп)
ф=0
C.22)
г 5rj(x\)J '" \i 5rj(xn)
Таким образом, для вычисления нормального символа ^-матрицы нуж-
нужно вычислить вариационные производные
C.23)
т.е. функции Грина Gn(x\,... ,хп), подействовать на эти функции диф-
дифференциальным оператором
'(д^г+т2),	C.24)
умножить результат на произведение
1
проинтегрировать по всем xi и просуммировать по п.
3.4. О физической интерпретации пропагаторов и
проблема причинности в квантовой теории поля
Пусть в нерелятивистской квантовой механике |х) и |к) обо-
обозначают нормированные собственные состояния операторов координа-
координаты и импульса частицы, соответственно, с собственными значениями
операторов, указанными в обозначениях этих состояний. Тогда, как
известно, (х|к) = егкх. Аналогичная формула в квантовой теории
поля получается при помощи формул B.38) и B.64):
C.25)
Из этой формулы мы делаем вывод, что состояние
x
)	C.26)

52	Лекция 3. Диаграммная техника Фейнмана
есть состояние в свободной релятивистской квантовой теории поля, в
котором частица полностью локализована в точке х в момент времени
х° = 0.
Рассмотрим хронологическое среднее от гейзенбергова поля B.64):
-{Ос(х-у).	C.27)
Равенство C.27) легко проверяется непосредственно. Так как величина
C.27) зависит лишь от разности координат, то при х° > у0 её можно
интерпретировать как амплитуду, описывающую распространение ча-
частицы, локализованной в точке у в момент времени у0, в точку
х за промежуток времени (х° — у0). Действительно, величина C.27)
может быть представлена также как (х | е~г (ж ~у ) п° | у) (см. лекцию
1). Если же х° < у0, то точки х и у меняются местами. Эта
интерпретация пропагатора C.27) находится в полном соответствии с
правилами Фейнмана.
Нетрудно убедиться, что
-Wc(x - у)\х	ф ,
J B7Г) 2/2 + к2	C.28)
-iDc(x - у)\хо=уо ~ e~m|x~y|1 если m |х - у| > 1.
Не следует ли из C.28) вывод, что в построенной нами релятивист-
релятивистской квантовой теории поля нарушен принцип причинности? Действи-
Действительно, на первый взгляд из C.28) следует, что частица, рождённая
в одной точке пространства, мгновенно распространяется до других
точек пространства. Однако, при правильной интерпретации принципа
причинности в релятивистской квантовой теории поля, каких либо про-
противоречий не возникает. Действительно, в нашем случае необходимым
требованием является условие
[ фо(х), фо(у) ] = 0, если (х - уJ < 0.	C.29)
Равенство C.29) означает, что если точки х и у разделены простран-
ственноподобным интервалом, то никакие измерения в этих точках
не скоррелированы между собою. Иными словами, в релятивистской
квантовой теории поля информация не передаётся со скоростью, пре-
превышающей скорость света.
Оценка C.28) интерпретируется следующим образом. Имеет место
принцип неопределенности At • As ^ Ti, где At — время измерения
энергии и Аг — неопределенность измеренной энергии, заключенной в
тестируемом участке пространства размером г (для наглядности здесь
восстановлена правильная размерность). Если тестируемая частица с
массой m покоится, то по смыслу введенных величин me2 ^ Аг, от-
откуда At ^ Ь/тс2 и размер тестируемой области г ~ cAt ^ Ь/тс. Из
приведенных оценок следует вывод, что в релятивистской квантовой

ЗА. О физической интерпретации пропагаторов и причинность 53
теории частица с массой т не может быть локализована в объеме про-
пространства с размером меньше чем Тг/тс. Величина Тг/тс называется
комптоновской длиной волны соответствующей частицы.
Для гейзенберговых полей во взаимодействующей теории равенство
C.29) также имеет место и при этом оно является весьма содержа-
содержательным, определяя аналитические свойства различных корреляторов
(см., например, [1]).
Задачи
1.	Вычислите среднее число частиц и среднюю энергию, рождённых
внешним источником, в свободной теории Клейна-Гордона при t —> оо.
Считать, что при t —> —оо система находится в основном состоянии.
Указание. Решить сначала эту задачу в случае одномерного
осциллятора. ?
2.	Рассмотрите скалярную теорию, описываемую лагранжианом
? = \ (ад2 - \т\& + \ (d^f -Х-т2ф2-яФф2.
Последнее слагаемое описывает взаимодействие, позволяющее Ф-
частице распадаться на две 0-частицы, если гпа > 2т. Вычислите
время жизни Ф-частицы в наинизшем порядке.
Указание. Воспользоваться формулой (А.9) из приложения А. ?
3.	Рассмотрим линейную сигма-модель, описываемую гамильтонианом
п = Jd3х | l-(^f + х-
г=1
Примените диаграммную технику для этой модели. Покажите, что
она совпадает с диаграммной техникой скалярной теории, если в неё
внесены следующие поправки:
а)	пропагатор
i	j
б)	вершина
Ч х
= -2i\ Eij5kl + 8il8kj + 8ik8jl).
I

54	Лекция 3. Диаграммная техника Фейнмана
Везде г, j, ... — сорта частиц. Таким образом начальное и конечное
состояния несут наборы этих индексов.
4.	Докажите прямым вычислением формулу C.29).
5.	Выпишите все диаграммы для амплитуды рассеяния двух частиц в
две частицы с точностью О (Aq) как графически, так и аналитически.
Сделайте то же самое для рассеяния двух частиц в четыре частицы.

Лекция 4
УЛЬТРАФИОЛЕТОВЫЕ РАСХОДИМОСТИ И
РЕГУЛЯРИЗАЦИЯ
4.1. Размерностная регуляризация расходимостей
Попробуем вычислить простейшую диаграмму (/) на рис. 3
q
Соответствующий вклад в iM, обозначаемый — гХ, равен
4* (d)	1
С dw к
Здесь [i — константа, имеющая размерность массы, так что Ао —
безразмерная константа.
При интегрировании по fe° сделаем поворот Вика (см. рис. 1, 2 в
лекции 1) к0 = ikd:
Di)
Обозначение J^ d^ fc указывает на то, что интегрирование идёт по
^-мерному евклидову пространству, в котором к2 = (к1J + ... + (kdJ.
Интеграл D.1) при d ^ 2 расходится, при d < 2 — сходится. Мы
видим, что сходимость диаграмм Фейнмана существенно зависит от
размерности d пространства-времени. С другой стороны, большинство
симметрии теории поля не зависят от d. Важнейшими из таких
симметрии являются лоренц- и калибровочная инвариантности. Поэто-
Поэтому возникла идея (Ж. 'тХоофт, М. Вельтман) вычислять диаграммы

56
Лекция 4. Ультрафиолетовые расходимости и регуляризация
Фейнмана при произвольной комплексной размерности пространства,
устремляя в конце вычислений параметр d к нужному значению.
Для дальнейших вычислений нам понадобятся следующие формулы
и интегралы.
Пусть Vft ' = S^Rd — объём шара радиусом R в ^-мерном ев-
евклидовом пространстве. Вычислим S^ — объём единичного шара в
^-мерном пространстве. Имеем
7Г ' =
оо
fdWa.e-(*!+-+4)= f,
J	J
Таким образом,
S(d) =
7Г'
d/2
Td/2
d\ (d
D.2)
2 \2
Везде Г (z) — гамма-функция. При с > 0 и а > d/2 имеем
оо , .	. .	оо
d
(к2 + с)'
„d/2-a
rifir
Г (a)
Теперь при помощи D.2) получаем
г d{dh d/2
J (fc2 + с)а-Ж (
Г (a)
D.3)
Интеграл D.3) был вычислен при условии d < 2а. Однако, правая
часть в D.3) является аналитической функцией всех параметров. По-
Поэтому при произвольных комплексных значениях параметров d, а и с
будем считать правую часть уравнения D.3) определением интеграла,
стоящего в левой части равенства D.3).
При помощи D.3) вычисляем интеграл D.1):
D.4)

4.1. Размерностная регуляризация расходимостей	57
Нас интересует значение d = 4 или значения d, близкие к числу 4.
Поэтому введём обозначения:
d = 4-e, ln- = -, ?^+0.	D.5)
II е
Как будет видно из дальнейших вычислений, параметр Л —> оо играет
в теории роль максимально допустимого импульса — импульса (пара-
(параметра) обрезания. Перепишем D.4) в новых обозначениях:
При помощи формул
T(z) = Г(^+1), ГA) = 1	D.7)
находим, что величина D.6)
П™~	-const,	D.8)
где const — конечная величина при г —> 0.
Теперь займёмся вычислением однопетлевых диаграмм на рис. 7
(n-петлевой диаграммой называется такая диаграмма, у которой имеет-
имеется п нефиксированных импульсов, по которым идёт интегрирование).
Каждая из этих трёх диаграмм представляется интегралом:
^| DM Dc(p - q).	D.9)
Сначала оценим интеграл D.9) непосредственно в 4-мерном
пространстве-времени. Рассмотрим этот интеграл в ультрафиолетовой
области (q —> оо). Так как внешние импульсы и масса фиксированы,
то ими можно пренебречь при вычислении расходящейся части.
Это можно сделать не всегда, но в данном случае, когда степень
расходимости интеграла не выше логарифмической, внешними
импульсами и массами можно пренебречь: учёт поправок к интегралу
D.9), пропорциональных тир, приводит к сходящимся интегралам.
Сделаем поворот Вика. Тогда расходящаяся часть суммы трёх ин-
интегралов в C.15) равна
dD)(/ ЗгД U
Здесь Л — промежуточный импульс обрезания, /i — нижний предел
интегрирования, имеющий порядок физической массы частицы или
внешних импульсов, который называется точкой (масштабом) нор-
нормировки.

58	Лекция 4. Ультрафиолетовые расходимости и регуляризация
Мы опять видим, что амплитуды перехода в квантовой теории поля
содержат расходящиеся вклады.
Приведём ещё один пример.
Диаграмма (д) на рис. 3 даёт вклад в амплитуду перехода частицы
в эту же частицу, аналогично диаграмме (/) на рис. 3:
^^ Dc(qi) Dc(q2) Dc(k - qi -ft). D.11)
Интеграл D.11), так же как и интеграл D.1), при d = 4 расходится
квадратично.
4.2. Индекс расходимости диаграмм
Вычислим индекс расходимости или просто индекс произволь-
произвольной диаграммы. Для этого сделаем масштабное преобразование всех
импульсов в диаграмме, а также массы частицы: ki, pf, q, m —>
—> aki, apf, aq, am. При таком преобразовании подынтегральное
выражение умножается на аш, где ио и есть индекс диаграммы.
Очевидно, что все внутренние линии дают вклад в число ио, равный
(—2 Lin). Легко увидеть, что число ^-мерных дифференциалов от внут-
внутренних независимых импульсов равно L = [Lin — (п — 1)], где п —
число вершин диаграммы. Действительно, независимых внутренних
импульсов в диаграмме с п вершинами имеется на (п — 1) меньше,
чем внутренних линий, так как в каждой из п вершин имеет место
закон сохранения d-импульса. Однако совокупность п законов сохра-
сохранения содержит в себе один закон сохранения совокупности внешних
входящих и выходящих d-импульсов. Этим объясняется уменьшение
независимых d-импульсов не на п, а на (п — 1). Поэтому для числа uj
получаем
w = d(LIn-n+l)-2Lin.	D.12)
Обозначим через Lex суммарное число внешних линий. Имеем
iex + 2Lin=4n.	D.13)
Действительно, к каждой вершине подходит 4 линии, но каждая внут-
внутренняя линия подходит к двум вершинам. Исключим из D.12) число
п при помощи равенства D.13):
(IfY	D.14)
Диаграмма является формально сходящейся, если ио < 0.
Мы рассмотрели расходимости диаграмм / и g на рис. 3 с Lex = 2
и однопетлевые диаграммы на рис. 7 с Lex = 4 при d = 4. Согласно
D.14), при d = 4, диаграммы с двумя внешними линиями расходятся
квадратично, однако в них содержатся также и логарифмические расхо-
расходимости. Это будет показано ниже. Диаграммы с четырьмя внешними

4.3. Диаграмма с четырьмя внешними линиями	59
линиями расходятся лишь логарифмически, что и было выяснено на
примере однопетлевых диаграмм на рис. 7. Подчеркнём, что в рас-
рассматриваемой модели при d = 4 степень расходимости диаграммы
зависит не от её числа петель, а от числа внешних линий. Фак-
Фактически это свойство является следствием безразмерности константы
связи Ао, по которой идёт разложение. Действительно, лишь при d =
= 4 константа Ао безразмерна. При d > 4 её размерность такова, что
степень расходимости диаграммы возрастает по мере её усложнения
(см. D.14)). Такие теории называются неперенормируемыми. При d<
< 4 теория ф4 относится к так называемым сверхперенормируемым,
поскольку в теории содержится лишь конечное число расходящихся
диаграмм.
4.3. Диаграмма с четырьмя внешними линиями
Теперь займёмся вычислением интеграла D.9) при произвольном
комплексном значении параметра d. Причинные гриновские функции
допускают следующее представление:
сю
г
Dc(q) = i exp[ia(q2 — ml + is)] da.	D.15)
о
Делая поворот Вика и используя D.15), переписываем D.9) в виде
\2 lf2D-d) °Г °Г
1= ~1 2{^уГ J d« j d/3
О	О	Е
Здесь интеграл по q является гауссовым и вычисляется при помощи
формулы A.13), где следует сделать замены: N —> d, M —> — [2(а +
+ /^)]-1' С "^ 2/Зр. После вычисления этого интеграла возвращаемся в
пространство Минковского:
сю сю
- _1 \2M2D-d) (л^Л-б./Ч
da d/3—-
J J (a-
o о
' . D.16)
Перепишем интеграл D.16) в новых переменных интегрирования а
= At, /3 = A - А)?, 0 < А < 1, 0<?<оо:
l-d/2)x

60 Лекция 4. Ультрафиолетовые расходимости и регуляризация
х ехр{-?[-гАA - \)р2 + im20 + е}\ . D.17)
Внутренний интеграл в D.17) вычисляется при помощи формулы
ttz-le~kt = k~zT(z), Rek>0.	D.18)
В нашем случае z = 2 — d/2, k = г[т^ — A(l — А)р2] + е. Поэтому
имеем
B - !)	/2_2
2D7г)}/2
D.19)
Разложим (с учётом D.7)) правую часть D.19) в ряд Лорана вблизи
точки d = 4:
I _ i\20 +гА2[^A)
^4-d DтгJD-^)	8BтгJ
1
1 о I л л i^ шо v )Р	л/,/лл _ i^ т/^л м 20)
8BтгJ J		/i2	' ^y~da
о
Отсюда мы видим, что расходящаяся часть в Ш'2' равна
-Ц.	D.21)
Сравнивая D.21) и D.10), мы оправдываем соотношение D.5):
= -=1п-.	D.22)
A-d e
Укажем на следующее важное обстоятельство: метод размерност-
ной регуляризации учитывает лишь логарифмические расходимости.
Действительно, если d > 2а, то полагая с = 0 в D.3), получаем
-^2^ = 0, при d > 2а.	D.23)
Е
Равенство D.23) означает, что в методе размерностной регуляризации
при d > 2а интеграл D.23) определён и он равен нулю. Отсюда
следует автоматическое устранение расходимостей степени выше лога-
логарифмической. Это же видно, в частности, из формулы D.8).

4.4. Устранение расходимостей	61
4.4. Устранение расходимостей
Предположим, что в теории возмущений, описываемой рядом диа-
диаграмм Фейнмана, содержатся расходимости в диаграммах с ограни-
ограниченным числом внешних линий. Таким примером является рассматри-
рассматриваемая теория ф4 при d = 4. Более того, в этой теории расходятся
лишь диаграммы с двумя и четырьмя внешними линиями, а действие
содержит слагаемые, пропорциональные ф2 и ф4. В такой ситуации
для устранения расходимостей вводится промежуточная регуляриза-
регуляризация, смысл которой заключается в обрезании петлевых интегралов
по нефиксированным импульсам неким параметром Л, стремящимся
к бесконечности, Это обрезание проводится таким образом, чтобы
была сохранена лоренц-инвариантность, а также, по возможности, все
прочие симметрии, имеющиеся в теории. Размерностная регуляриза-
регуляризация является наиболее используемым методом такой регуляризации.
Оказывается, что в некоторых случаях (как в теории ф4 при d =
= 4) исходные параметры теории (затравочные константы) можно
выбрать такими функциями параметра обрезания Л, что при Л —>
—> оо все расходимости в теории сокращаются. В рассматриваемой
нами скалярной теории поля способ действий таков: если в неком
порядке теории возмущений расходимости уже устранены, то в сле-
следующем порядке ТВ расходятся диаграммы с двумя и с четырьмя
внешними линиями. В первом случае расходимость устраняется пере-
переделкой (перенормировкой) затравочной массы , а во втором случае
— перенормировкой затравочной константы связи. При этом может
оказаться, что затравочные константы не имеют конечного предела при
устремлении промежуточного импульса обрезания к бесконечности.
Но в процедуре перенормировки наблюдаемые (или физические, или
перенормированные) величины (массы частиц, константы взаимодей-
взаимодействия физических частиц, амплитуды перехода) должны стремиться
к определённому пределу при устремлении промежуточного импульса
обрезания к бесконечности. Затравочные константы теории разлагают-
разлагаются в ряд по перенормированным константам, причём коэффициенты в
этом разложении являются функциями параметра обрезания.
Теории, допускающие подобную процедуру перенормировки, назы-
называются перенормируемыми теориями.
Продемонстрируем сказанное на примере перенормировки констант
в теории ф4 в четырёхмерном пространстве-времени. Мы увидим, что
эта теория является перенормируемой. Пусть затравочная константа
связи Ао, входящая в исходное (затравочное) действие, разлагается в
ряд по физической константе связи А. Далее мы увидим, что физи-
физическая константа связи может быть определена через значение ампли-
амплитуды перехода двух частиц в две частицы при некоторых значениях

62	Лекция 4. Ультрафиолетовые расходимости и регуляризация
импульсов частиц. Пусть во втором порядке
о д2	д
Ао = А + —-rln-, А^ =
lO7Tz	\1
D.24)
Тогда, согласно D.10) и D.24), в сумме диаграмм на рис. 7 расходи-
расходимости сокращаются по крайней мере с точностью О(А3) и амплитуда
2^2 является конечным выражением, зависящим от физической
безразмерной константы Л.
4.5. Инвариантные переменные Мандельстама
В заключение лекции дадим определение лоренц-инвариантных пе-
переменных, при помощи которых удобнее всего описывать амплитуды
перехода двух частиц в две частицы.
Прежде всего заметим, что построенная ТВ явно лоренц-
инвариантна. Это значит, что все амплитуды перехода как функции
внешних 4-импульсов являются лоренц-инвариантами, то есть они
зависят лишь от лоренц-инвариантов, построенных из внешних 4-
импульсов. Это замечание остаётся в силе для диаграмм Фейнмана,
внешние импульсы которых не находятся на массовой поверхности.
Пусть в реакции участвует всего 4 частицы с массами
т\, ТП2, шз, т\, причём при t —> —оо имелось 2 частицы и при
t —> +00 имеется также 2 частицы. Обобщённый закон сохранения
4-импульса запишем в виде
fci + к2 + к3 + к4 = 0.	D.25)
При этом предполагается, что, если, например, идёт реакция 1 + 2 —>
~"	' Т°	к°{ > О, к°2 > О к°3 < О, к\< 0,	D.26)
и т.д.
Из четырёх 4-импульсов, находящихся на массовой поверхности и
удовлетворяющих уравнению D.25), можно составить всего 2 независи-
независимых инвариантных переменных. Действительно, в силу D.25) всего три
импульса независимы, например, fci, k2, к%. Из них можно составить
всего 6 инвариантов: к\ = т\, к\ = т\, Щ = т\, к\к2, к\к%, к2к%.
Лишь последние 3 из них являются переменными. Кроме того, так как
(fci + &2 + &зJ = к\ = ml, то независимых переменных остаётся 2.
Удобно ввести три лоренц-инвариантных переменных Мандельстама:
и = (к{+к4J = (к2 + к3J.	D.27)
Легко проверить, что
s +1 + г^ = т\ + Ш2 + га2 + ш2.	D.28)

4.5. Инвариантные переменные Мандельстама	63
Теперь рассмотрим самый простой случай, т\ = m^ = m^ = m\ =
= га, и реакцию
1+2—>3 + 4,	D.29)
для которой переменные мандельстама принимают значения в следую-
следующих областях:
s > 4m2, t < О, гх < 0.	D.30)
О реакции D.29) говорят, что это — s-канальная реакция. Амплитуда
реакции в t-канале,
1 +3 —> 2 + 4,	D.31)
получается аналитическим продолжением амплитуды в s-канале в об-
область переменных
?>4га2, 5^0, г^^О.	D.32)
Это возможно, так как в теории ^-матрицы амплитуды являются
аналитическими функциями инвариантных переменных.
Введём обозначение
г MW(s) = \\1 | ^ Dc(q) Dc{kx + k2 - q).	D.33)
Тогда амплитуда в C.15) представляется симметричным образом:
= г \М^ (s) + M^ (t) + М^ (и)] .	D.34)
Укажем ещё один удобный способ параметризации петлевых инте-
интегралов, отличный от параметризации D.14)—D.15).
Очевидно, имеем
= Г
J
1
\ = Г	Ах	= Г Ах dy5(x + y- 1)
]	J
0
' }
AB J [xA + {l -x)B}2
О	х,у^О
Дифференцируя D.35) по В, получаем
—	г=	Ах Ау5(х + у — 1) -—	т^г-	D.36)
Задачи
1. Докажите по индукции, что
А1А2...Ап
Xi^ О
D.37)

64	Лекция 4. Ультрафиолетовые расходимости и регуляризация
Переменные {xi} в этом интеграле называются фейнмановскими
параметрами.
Указание. Использовать равенства D.35) и D.36). ?
2. Вычислите s-канальную однопетлевую диаграмму
при помощи параметризации Фейнмана. Укажите, при каких значениях
s эта диаграмма вещественна.
Ответ:
2 2;
о
М вещественна при s ^ 4 т2.
3. Эффект Казимира.
Рассмотрим свободное безмассовое скалярное поле ф(х) на отрезке
длиной L с граничными условиями ф@) = ф(а) = ф(а + /) = 0A/) =
= 0, где а ~ A/2)L, / <C L (см. рисунок).
О	а о+/	L
Вычислите силу (—д?о/д1), где ^о — энергия нулевых колебаний
вакуума.
Замечание. Рассмотренная ситуация даёт одномерную модель
взаимодействия двух близко расположенных параллельных проводя-
проводящих пластин, устанавливающих соответствующие граничные условия
для электромагнитного поля. ?
Указание. Для решения задачи необходимо пройти следующие
этапы:
а) на отрезке [а, а + /] проквантовать скалярное поле с лагранжи-
лагранжианом
о
и граничными условиями ф@) = ф{1)\
б) выразить гамильтониан через бозонные операторы рождения и
уничтожения и вычислить энергию вакуума ?q;

4.5. Инвариантные переменные Мандельстама	65
в) регуляризовать энергию вакуума двумя методами:
(ii) при помощи дзета-функции Римана,
П=1
формально полагая, что
оо	1
i2
сравнить оба метода;
г) вычислить регуляризованную энергию системы ?o(reg)> опреде-
определённой на рис. 1, и вычислить силу
= д ?р (reg)
7	9/ *
3 С.Н. Вергелес

Лекция 5
ОБЩАЯ СХЕМА ПЕРЕНОРМИРОВОК
5.1. Спектральное представление
Челлена-Лемана двухточечной функции
Согласно C.27) фурье-образ вакуумного среднего (О | Т ф(х)ф@) | 0)
для свободного квантованного поля ф имеет вид
<\хе>кх{0\Тф(х)ф@) |0} =	%-т— = -iDc(k). E.1)
к1 — uIq + ге
Теперь попробуем вычислить это же среднее в теории с взаимо-
взаимодействием. Мы будем опираться только на общие принципы теории
относительности и квантовой механики; при этом вид взаимодействия,
специфика ряда ТВ и другие детали не существенны. Предполагается
лишь, что имеются частицы с определённой массой (и, возможно, дру-
другими квантовыми числами), динамика которых лоренц-инвариантна и
описывается согласно законам квантовой механики. Поэтому результа-
результаты, полученные в этой лекции, справедливы для очень широкого класса
квантовых теорий поля. Предполагается также, что ультрафиолето-
ультрафиолетовые расходимости устранены путем введения комплексной размерности
пространства-времени. Заметим, что эта регуляризация сохраняет как
трансляционную, так и лоренцеву инвариантности.
Обозначим через Т^ оператор d-импулъса теории, так что V0 =
= ТС — гамильтониан теории, а V1, г = 1, ..., (d — 1), — компонен-
компоненты импульса (см. приложение В). Согласно самому определению d-
импульса, для любого локального поля ф{х) имеем
ф(х) = eiVx ф@) e~iVx.	E.2)
По определению основного состояния,
7^|0)=0.	E.3)

5.1. Спектральное представление Челлена-Лемана	67
Согласно алгебре Пуанкаре (см. приложение а также [2]) все
компоненты d-импульса взаимно коммутируют. Поэтому можно счи-
считать, что каждое состояние имеет определённое значение d-импульса.
Обозначим через | Ак) какое либо из таких состояний, так что
Р|Лк)=к|Ак>.	E.4)
Вследствие лоренц-инвариантности
Я + к^ > 0,	E.5)
где т\ — энергия состояния в той системе отсчёта, в которой сум-
суммарный пространственный импульс равен нулю. Неравенство в E.5)
означает, что энергия вакуума является наименьшей энергией в тео-
теории, которая согласно E.3) равна нулю. Мы часто будем выделять
из совокупности состояний {|Ак)} одночастичные состояния {|к)}.
Тогда | Ак) обозначает многочастичное состояние. Состояние | к) име-
имеет импульс к и энергию u;k = \/m2 + к2 . Подчеркнём, что в случае
одночастичного состояния импульс к полностью определяет энергию
состояния, в то время как энергия неодночастичного состояния |Ак)
не определяется параметром к. Предположим, что все возбуждённые
состояния принадлежат линейной оболочке одно-, двух- и т.д. ча-
частичных состояний, то есть состояния с определённым числом частиц
образуют базис пространства состояний. Если в теории имеется всего
один сорт частиц с массой га, то для n-частичного состояния
E.6)
причём т\ — непрерывный параметр. Мы предполагаем также, что со-
состояния | Ак) нормированы лоренц-инвариантным образом (см. B.43),
B.45)), так что разложение единичного оператора имеет вид
где суммирование идёт по всем многочастичным состояниям с нулевым
суммарным импульсом | Л о } - Справедливость формулы E.7) очевидна,
если заметить, что в одночастичном секторе, согласно B.38), B.39),
одночастичная
]к 1
k)(k|.	E.8)
Будем считать, что х° > у0, и вставим разложение единицы E.7)
между полями в среднее @ | ф(х)ф(у) \ 0). Пренебрежём постоянной
величиной @ | ф(х)\ 0) @ | ф(у) | 0), которая в большинстве случаев

68
Лекция 5. Общая схема перенормировок
равна нулю. Таким образом, получаем, что
E.9)
Преобразуем матричные элементы в E.9) при помощи формул
E.10)
(О\ф(х)\Хк) = (О\ег1
= @ | ф@) | Лк) e~ikx	= @ | ф@) | Ло ) e~ikx
к°=Еь(\)
Последнее равенство является следствием следующих соотношений:
|Ак) = С/|А0),	и~1ф@)и =
где унитарный оператор U генерирует соответствующее преобразова-
преобразование Лоренца. Такие операторы называются бустами. Подставим E.10)
в E.9):
(О\ф(х)ф(у)\О) =
Ао
Так как xq > г/о, то можно воспользоваться формулой A.23). Таким
образом, получаем
В случае х° < у0 имеет место аналогичная формула. Обе формулы
объединяются в следующем выражении:
Dc(x
Г
; М2) =
J J
E.11)
е~гкх
Bir)d -к2 + М2 -is
где р(М2) — положительная спектральная плотность,
р(М2) = ?Bтг) 5(М2 - т2х) |@1 0@) | Ао>|2.
Л
График спектральной плотности р(М2) для типичной теории поля
показан на рис. 8.
E.12)

5.1. Спектральное представление Челлена-Лемана
69
р(М2)
одночас-
тичные
состояния
связанные
, состояния
двухчастичные
состояния
BтJ
(МJ
Рис. 8.
Одночастичные состояния вносят в спектральную плотность вклад
в виде изолированных (^-функций:
p(M2)=2irZ5(M2-m2) +
+ (ничего другого вплоть до М2 > BтJ), E.13)
где
2	E.14)
Константа Z называется константой перенормировки поля ф. Вели-
Величина т есть физически наблюдаемая масса элементарных возбужде-
возбуждений поля ф, а то в B.53) является затравочной или «голой» массой,
причём т ф ^о- Непосредственно наблюдаемой является физическая
масса т, а не затравочная масса.
С помощью E.11) и E.13) находим в теории с взаимодействием
фурье-образ хронологического парного среднего, являющегося анало-
аналогом величины E.1) в теории свободного поля:
iZ
к2 - m2
оо
dM2
2тг
k2-M2
E.15)
Аналитическая структура этой функции в комплексной &2-плоскости
показана на рис. 9.
BтJ
t t
изолированный
полюс
полюса
связанных
состояний
разрез
Рис. 9.

70	Лекция 5. Общая схема перенормировок
Первое слагаемое в E.15) соответствует изолированному полюсу
при к2 = т2, а второе — разрезу, начинающемуся в точке 4 т2. Если
существуют двухчастичные связанные состояния, то в E.15) возника-
возникают дополнительные полюса.
Сравнивая E.1) и E.15) мы видим, что взаимодействующее поле,
в отличие от свободного, рождает из вакуума не только одночастич-
ное, но и многочастичные состояния. Кроме того, в первом полюсном
слагаемом содержится константа перенормировки поля E.14), то есть
вероятность того, что ф @) родит данное одночастичное состояние из
вакуума.
Проводя вычисления, аналогичные приведенным выше, легко полу-
получаем также, что
оо
Н Д/f2	Г Н^) h
{О\[ф(х),ф(у)}\О)= I ^/>(М2) ?—^х
о
E.16)
Здесь х° т^ У°, и введена перестановочная функция Паули-Йордана,
d~x) k e~ikx -eikx
D(x;M) =i
Aid)
o—i к x 	 г к х\
с-	I
которая лоренц-инвариантна, равна нулю вне светового конуса 0 и
удовлетворяет однородному уравнению Клейна-Гордона,
(d^ + M2)D(x; M)=0,
а также соотношению
1) Действительно, если хмжм < 0, то существует система отсчета, в которой
хм = @, х1). В этой системе отсчета обращение в нуль функции Паули-
Йордана очевидно. Этот результат имеет большое значение, так как отсюда
вытекает причинность релятивистской квантовой теории поля (см. конец лек-
лекции 3).

5.2. Перенормировки	71
Поэтому из E.16) находим, что
сю
@\[ф(х), ф(у)]\О}\хО=уО = J ^Р{М2) И3) (х-у)].
О
С другой стороны, левая часть этого равенства по определению равна
[г(Г3)(х — у)], и потому
\^p(M2) = \^0<Z<\.	E.17)
о
Последние неравенства получаются при учёте представления E.13).
5.2. Перенормировки
Теперь опишем индуктивную процедуру, при помощи которой из
расходящихся диаграмм выделяются различные физические величины,
остающиеся конечными в пределе Л —> оо. Будем пользоваться раз-
мерностной регуляризацией, которая выделяет лишь логарифмические
расходимости. Кроме того, вакуумные пузырьки, как ненаблюдаемые
поправки, мы не рассматриваем. Таким образом, расходящимися явля-
являются лишь два типа диаграмм:
\ат
конечные слагаемые,
E.18)
G) In Л + конечные слагаемые.
Здесь а, /3, 7 ~ безразмерные ряды по Л. Мы не предполагаем, что
импульсы внешних концов диаграмм лежат на массовой поверхности.
Очевидно, степень расходимости диаграмм не зависит от значений
внешних импульсов.
Рассмотрим сначала n-точечную корреляционную функцию
С(жь ... , хп) = {0\Тф(Х]) ... ф(хп)\0).	E.19)
Любая диаграмма, дающая вклад в коррелятор E.19), содержит рас-
расходящиеся поддиаграммы указанных двух типов. Для устранения рас-
ходимостей действуют последовательно; этот процесс начинается с
однопетлевых диаграмм. Так, согласно D.8) в Е^1) имеется расходя-

72	Лекция 5. Общая схема перенормировок
щаяся часть. Она устраняется путём введения в затравочную массу
соответствующей добавки:
т20 = т2 + 5т, 5т + ?^ = 0.	E.20)
Здесь ml — квадрат затравочной массы в однопетлевом приближении.
Легче всего это установить следующим образом.
Назовём диаграмму сильно связной, если её нельзя разделить на
две отдельные диаграммы путём разрезания всего лишь одной внут-
внутренней линии. Обозначим через
k = -i J2(k2)	E.21)
сумму всех сильно связных вставок в двухточечную корреляционную
функцию E.13) или сумму всех сильно связных диаграмм с двумя
внешними линиями и «ампутированными ногами». Тогда полная
функция E.13) определяется геометрической прогрессией:
E.22)
В первом порядке по Л величина X задаётся согласно D.6). Поэтому,
с учётом E.20), в этом приближении
E.23)
к2 — т2 + г е
и полюс корреляционной функции E.13) находится при к2 = т2, то
есть там, где и должен быть.
Устранение логарифмической расходимости в однопетлевом прибли-
приближении из четырёхточечного коррелятора было проведено в предыдущей
лекции (см. D.24)).
Предположим, что во всех s-петлевых диаграммах при описанном
способе действий устранены ультрафиолетовые расходимости. Пока-
Покажем, что действуя так же, можно устранить расходимости в (s + 1)-
петлевых диаграммах. Действительно, по предположению в любой (s +
+ 1)-петлевой диаграмме все s-петлевые поддиаграммы уже конечны.
Поэтому (s + 1)-петлевые диаграммы с двумя и четырьмя внешними
линиями расходятся лишь в той области интегрирования, где все
(s+1) промежуточных импульсов стремятся к бесконечности. Эти
новые расходимости можно устранить и сделать диаграммы конечны-
конечными путём соответствующего подбора величин 5т (A), Aq (А) и
константы перенормировки поля Z(S+1)(A), являющихся полиномами

5.2. Перенормировки	73
5 (
относительно физической константы связи Л. Очевидно, что 5т (А)
^+1)	{\ A^s)
ф	д,	т
), Z(S+1)(A)) отличается от 5{т\\) (A^s)(A), Z^S\X)) лишь
более высокими степенями константы А, чем степень полинома 5т (А)
(Aq (A), Z(s\\)). Действительно, диаграммы с четырьмя внешними
концами расходятся лишь логарифмически и притом (s + 1)-петлевые
расходимости набегают в области, где все импульсы интегрирования
стремятся к бесконечности. Поэтому расходящиеся части таких диа-
диаграмм являются числами, не зависящими от внешних импульсов и их
можно поглотить за счёт подбора Aq (А). Аналогично (см. первую
диаграмму в E.18)), для устранения (s + 1)-петлевых расходимостей
диаграмм с двумя внешними концами достаточно подобрать соответ-
соответствующим образом константы гп^(Х) и Z(X) в нужном порядке по фи-
физической константе связи, причём второе слагаемое в первой диаграмме
в E.18) вносит вклад в константу перенормировки поля. Оказывается,
что n-точечный коррелятор полей E.19) равен Znl2 x (конечная часть)
(см. ниже). Таким образом устраняются расходимости во всех (s + 1)-
петлевых диаграммах.
Замечание. Если бы оказалось, что в теории ф4 имеются расхо-
расходящиеся диаграммы, например, с шестью внешними линиями, то такие
расходимости было бы невозможно устранить путём переопределения
массы и константы связи. Для устранения таких расходимостей потре-
потребовалось бы введение в теорию членов нового типа, пропорциональных
ф6. Это означало бы, что теория неперенормируема. ?
Можно показать, что имеет место соотношение
i=\J	j = T
i\[Z
ij — m2 + i г
E.24)
Здесь в обеих частях равенства Щ, р® -^ Uk, oop (ook — л/^2 + к2),
Z — константа перенормировки поля. Знак ^ в E.24) означает, что
обе части равенства ведут себя одинаково вблизи полюсов. Форму-
Формула E.24) называется редукционной формулой Лемана-Симанчика-
Циммермана.
Описанную процедуру перенормировки можно технически упро-
упростить и работать непосредственно с перенормированными физическими
величинами. Начнём рассуждение с записи затравочного лагранжиа-
лагранжиана:	1	1	Л
?=2 (9,фJ--т20ф2-^ф\	E.25)
Устраним множитель Z в значении вычета в полюсе хронологического
парного среднего поля ф (см. E.17)). Для этого введём перенормиро-

74	Лекция 5. Общая схема перенормировок
ванное поле фг согласно равенству
ф = y/z фг.	E.26)
Корреляторы, построенные из полей фг, содержат столько дополни-
дополнительных (по сравнению с аналогичными корреляторами полей ф) мно-
множителей Z/2, сколько полей стоит под знаком коррелятора. Теперь
лагранжиан E.25) принимает вид
..V{J ~ rr - —- Z фг.	E.27)
Определим константы:
5z = Z — I, 5т = m0 Z — т , $а = Ло ^ — А,	E.28)
где т и Л — физические константы. При помощи введенных констант
лагранжиан переписывается следующим образом:
2 гг 4! г | 12 ^	2 г
E.^9)
Первая квадратная скобка в правой части E.29) теперь выглядит как
стандартный лагранжиан в теории ф4, но записанный через перенор-
перенормированные величины и поля. Слагаемые во второй квадратной скобке
называются контрчленами, они поглощают расходимости в ТВ. Всё
что было сделано — это проведено разбиение затравочного действия
E.25) так, чтобы было удобно проводить дальнейшие вычисления. Мы
имеем следующие условия перенормировки:
= ^хегкх@\Тфг(х)фг@)\0}= к2_т2г_
	Ь (слагаемые, регулярные при к2 = тп2).
к2 — гп2 -\-ге
Последнее равенство означает, что
=т2 =0, -^2 Е (к2)	= 0.	E.30 а)
m	d к	k2=m2
Индекс г на диаграммах указывает на то, что эти величины — пере-
перенормированные. Однако, этот факт далее, как правило, не отмечается,
что не ведёт к недоразумениям. Условия E.30 а) означают, что на каж-
каждом следующем шаге индуктивной вычислительной процедуры следует
сделать замену (провести вычитание):
Имеет место также условие, фиксирующее константу связи:

5.3. Условие унитарности
75
= -гЛ
«ампутированная»
при s = Am2, t = u =
E.306)
Описываемая процедура перенормировки называется перенормировкой
на ходу.
Продемонстрируем эту процедуру перенормировки при вычислении
^2К Согласно D.20), D.31) и D.34), без учёта контрчленов в E.29),
г М^ > (s, t, и) = const —г
А2
32 тг2
|л т2 — х(\ — х) s — ге
Ах Цп	—ту-1-	+
1
Л т2 — х(\ — х) t — is , m2 — х(\ — х) и — ге\
1п	v o J	+ ln	^—^	!>. E.31)
Здесь const — расходящаяся константа, не зависящая от переменных
Мандельстама. Для выполнения условия нормировки C06) следует
провести одно вычитание:
iM^2\s, t,u)=i [MB)(s, t, и) - Ш2\Ат2, 0, 0)] =
Л2 Г . (. т2 — х(\ — х) s — ге
= -г х^^т I а х {In	+
32^
' т2 [1 — Ах A — х) — ге]
. т2 — х(\ — х) t — ie л т2 — х(\ — х) и — ге\
1п	^—тг1	+ 1п	тг1	\- E.32)
mz
5.3. Условие унитарности
Согласно C.2), ^-матрица представляется как S= 1+гТ. Из
условия унитарности, S^S = 1, следуют важные соотношения для
амплитуд. Имеем
(Т-Т*) =iT^T.	E.33)
Пусть бра-вектор (/1 — конечное, а кет-вектор | г) — начальное
состояние. Поместим равенство E.33) в обкладки (/|... |г), и между
операторами Т^ и Т в правой части E.33) вставим единичный опера-
оператор в форме E.7). Кроме того, перейдём к амплитуде Mfi, согласно
C.4). Таким образом, получим:
¦S^(Pf-k)M*XkfMXki. E.34)

76	Лекция 5. Общая схема перенормировок
Множитель (г '(Pf — Pi) в обеих частях равенства E.34) сокра-
сокращается.
Равенство E.34) полезно переписать также в виде
М/г-М*/ = B^L^
п s ^ а=\ V {^7Г)° ^^kj )
п \
~	E.34х)
где п — число частиц в состоянии | Ак), ка — 4-импульс, ш^ = кРа
— частота частицы с номером a, J2S — сумма по спинам проме-
промежуточных частиц и D — множитель, учитывающий тождественность
частиц. Например, если промежуточное состояние содержит всего две
тождественные частицы, то D = 2.
Рассмотрим важный частный случай, когда промежуточное состоя-
состояние является одночастичным с массой М. Тогда суммирование J^A в
E.34) ограничивается суммой по спинам промежуточной частицы J^s,
М2, и
н3 ь
= tf (k°) 5 (к^ - М2) d4 к.	E.35)
2?к(А)
Подставляя E.35) в E.34) и интегрируя по d4 к, находим:
Mfi -Mtf = 2т 5(р2 - М2) J2 ЩР8)! Щрф,	E.36)
S
где | ps) — состояние частицы с массой М, спином s и импульсом
Предположим, что теория Т- и Р-инвариантна. Тогда Mif = Mf>i>,
где штрихованные состояния могут отличаться от соответствующих
нештрихованных не более чем ориентацией спина. Если начальное и
конечное состояния усреднены по спину, то Mif = Mfi, и равенство
E.36) означает, что
Im Mfi = тг S(p2 - М2) Y, M{ps)f M(ps)i.	E.37)
2 М2)
S
Отсюда следует, что при р2 —> М2
^ -ЩЩ±фI.	E.38)
J	р1 - М2 + ге
В этом случае говорят, что при переходе из состояния | г) в состояние
| /) процесс идёт через промежуточную виртуальную частицу с массой
М.

5.3. Условие унитарности	77
Задачи
1. Вычислите в безмассовой теории ф4 при d —> 4 оператор собствен-
собственной энергии — гХ(&2) E.21) в двухпетлевом приближении.
Указание. В безмассовом случае (т2 =0) вместо условий нор-
нормировки E.30 а), E.30 6) при к2 =0, которые оказываются бессмыс-
бессмысленными, используют следующие нормировочные условия:
= 0 (отсутствие массы), ——^ ?
Применить параметризацию Фейнмана. П
= 0.
2. Вычислите при помощи условия унитарности мнимую часть ампли-
амплитуды рассеяния 2^2 при s > Am2 в однопетлевом приближении.

Лекция 6
РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
6.1. Подход Вильсона к теории перенормировок
Метод Вильсона основан на описании теории поля с помощью
функционального интеграла, в котором степени свободы квантового
поля являются переменными интегрирования. При этом подходе про-
происходит разделение переменных интегрирования на длинноволновые
и коротковолновые. Предполагается, что длинноволновые флуктуации
описывают реальные физические процессы, а учёт коротковолновых
флуктуации (то есть интегрирование по коротковолновым степеням
свободы) даёт эффективное действие для описания длинноволновой
физики.
Такая идеология возникла из понятия перенормируемости в кван-
квантовой теории поля. Мы видели, что суть перенормируемой квантовой
теории в том, что в ней на процессы с энергией ~ М степени свободы
с энергией ~ Л ^> М влияют лишь косвенно: через перенормировку
констант теории. В канонической квантовой теории поля импульс об-
обрезания Л является конечным лишь в промежуточных вычислениях,
и в конце вычислений он устремляется к бесконечности. Вильсо-
новский анализ основан на противоположной точке зрения, согласно
которой любая квантовая теория на фундаментальном уровне опреде-
определена с обрезанием Л, которое имеет некоторое физическое значение.
В приложениях к статистической механике этот масштаб импульсов
равен обратному межатомному расстоянию. В КЭД и других фунда-
фундаментальных квантовых теориях поля обрезание может быть связано
с фундаментальной зернистостью пространства-времени, природа ко-
которой, по-видимому, может быть изучена лишь вместе с построением
квантовой теории гравитации. Во всяком случае этот элементарный
масштаб очень далёк от масштабов, экспериментально достижимых в
настоящее время.
Продемонстрируем вильсоновский подход на примере теории ф4 в
евклидовом ^-мерном пространстве, поскольку в пространстве Мин-

6.1. Подход Вильсона к теории перенормировок
79
ковского ограниченное значение квадрата d-импульса не означает огра-
ограниченности его компонент, если d-импульс изотропен, что внесло бы
дополнительные усложнения.
Разложим вещественное скалярное поле в интеграл Фурье:
Равенство
(х) =
х фх (х) ф2(х) =
Ф\ (к) ф2 (к)
F.1)
F.2)
показывает, что преобразование Фурье является унитарным в про-
пространстве полей с метрикой F.2). Поэтому функциональные меры
Y\x d ф (х) и Ylk d ф (к) можно считать равными. Это даёт возмож-
возможность определения регуляризованной функциональной меры:
\ф (к).	F.3)
\к\<А
Регуляризованная статистическая сумма скалярного поля (сравни с
A.34)) представляется интегралом
Z=
1
т
X
F.4)
Здесь мы положили внешний источник равным нулю. В F.4) т и Л
являются голыми параметрами или параметрами на масштабе Л.
Разделим в F.4) переменные интегрирования на две группы. Пусть
0< Ъ< 1 и
ф(к) =
ф(к) =
ф(к),	для	ЬА < |fc| < Л,
О,	для	|fc| < ЬА,
О,	для	ЬА < |fc| < Л,
ф (к),	для	|fc| < ЬА.
F.5)
Тогда в F.4) следует заменить ф (к) на (ф (к)-\-ф (к)):

2
Z =
exp|-
= (
X
D ф ехр < —
1
4!(
F.6)

80	Лекция 6. Ренормализационная группа
В F.6) лагранжиан С(ф) зависит лишь от поля ф и он имеет тот же
вид, что и в F.4). Квадратичные слагаемые вида 00 ^исчезают в F.6)
вследствие равенства F.2) и определения полей ф и ф, согласно F.5).
Проинтегрируем F.6) по полю ф:
f()j	F.7)
Здесь ?ef@) содержит только те фурье-компоненты ф(к), для которых
|fc| < ЬА. Если вычислять интеграл по ф при помощи ТВ, разлагая
по константе Л, то окажется, что ?ef@) отличается от С @) на
поправки, пропорциональные степеням Л и ф и их производным. Эти
поправочные члены компенсируют отсутствующие фурье-компоненты
ф.
Поправки в ?ef могут быть представлены в диаграммной форме.
Все слагаемые в F.6), пропорциональные степеням Л, рассматрива-
рассматриваются как возмущение. Поскольку предполагается, что т2 <С Л2, то
слагаемое A/2)га202 также считается возмущением. Тогда слагаемое
старшего порядка в последней экспоненте в F.6) имеет вид
j щ*	F.8)
ЪА<\к\<А
Это слагаемое приводит к пропагатору
(Ф(к)ф(Р)} =
1, если ЬА < \к\ < Л,
' '	F.9)
0, если |fc| < о Л.
Оставшиеся в F.6) 0-слагаемые рассматриваются как возмущения, и
их учёт осуществляется путём разложения и использования теоремы
Вика (см. конец лекции 1). При этом правильная нормировка достига-
достигается, когда интеграл по полю ф в F.6) заменяется на
1 + поправки.	F.10)
Разложим сначала F.6) относительно ф2 ф2 и учтём, что
к pik(x~y)
FП)
j
ЪА<\к\<А

6.1. Подход Вильсона к теории перенормировок
81
При помощи F.11) легко находим эту поправку:
х <?{#) = -^5т
х<?,
5т2 = ^
1
XAd-2
F.12)
F.13)
2 J B7r)d к2 Dn)d/2T{d/2) d-2 '
ЬА<\к\<А
Представим пропагатор F.9) двойной линией. Поля ф представим как
одинарные внешние линии.
Тогда вклад F.12) изображается следующей диаграммой:
Рис.10
Второй порядок относительно ф2 ф2
двум диаграммам на рис. 11
дает вклад, соответствующий
Рис.11
Первое слагаемое на рис. 11 равно A/2) х (величина F.12)J, при-
причём множитель A/2) — комбинаторного происхождения. Если учесть
все степени величины F.12), возникающие во всех порядках, то ока-
окажется, что все эти слагаемые соберутся в экспоненту. Аналогичное
утверждение справедливо в отношении любой связной диаграммы.
Поэтому имеем следующий результат:
1	т2	Л
^ef— 9 (д/^ФJ Н—^~ 02 + ту 04 + (сумма связных диаграмм). F.14)
Вычислим вторую диаграмму на рис. 11. При помощи теоремы Вика
находим результат:
16
Введём новые переменные,
eik(x,-x2)
Bтг)«
ф\х2). F.15)
Х2 = X - -,
F.16)

82
Лекция 6. Ренормализационная группа
в которых F.15) принимает вид
eiky
bA<|fc|<A
{2ir)
-2(x-|). F.17)
Рассмотрим предельный случай, когда импульсы, переносимые полем
ф, исчезающе малы по сравнению с (ЬЛ). Тогда F.17) переходит в
if
F.18)
ДА = -4!
\2
16
J
ЪА<\к\<А
Bтг
ЗА2У
к
)d
1
(*2J "
Я \2	1
ЗЛ ^1 F.19)
Описанная диаграммная теория возмущений генерирует не только
вклады в ?ef, пропорциональные ф2 и ф4, но и вклады высших сте-
степеней 0, а также вклады от производных поля ф. Например, в F.17)
содержится слагаемое, пропорциональное
F.20)
6, получается из диаграммы
/А\2 Г
Вклад, пропорциональный ( — I
Вообще говоря, вильсоновская процедура генерирует все возмож-
возможные взаимодействия поля ф и их производных.
При помощи формулы F.6) легко увидеть, что поправки с точно-
точностью О (А) дают, при d = 4,
(тJ
А
^2	2 АA-62)Л2
W=W+
F.21)
Здесь Am2 задаётся согласно F.13). (Последнее равенство в F.21)
сравните с D.24).)
\ ЗА2 . 1
= А- -^—у In-.
16	о

6.1. Подход Вильсона к теории перенормировок
83
Для более детального сравнения нового интеграла F.7) с исходным
интегралом F.4) изменим в F.7) масштаб расстояний и импульсов по
следующему правилу:
x' = bx, &' = т> \k'\<A.	F.22)
о
Теперь импульсы в F.7) изменяются в тех же пределах, что и в F.4).
Имеем (сравните с E.29)):
d(d) x?ef =
х \^(\+Аг)(д^фJ + -(т2 + Ат2)ф2-
--(Л + АА),
= l
L + АС/ + ...|
F.23)
Чтобы в новом функциональном интеграле пропагатор сохранил преж-
прежний вид F.9), изменим масштаб поля ф по правилу
ф1 = \b2-d(l + AZ)Y/2 ф,	F.24)
после чего эффективное действие приобретает первоначальную форму,
\/ J/4 i о/ /Я/ J,/\4
В' (д^
...\, F.25)
с новыми параметрами:
т'2 = (m2 + Am2)(l
В' =
F.26)
и т.д. Заметим, что в исходном лагранжиане В = С = 0, но если бы
эти константы отличались от нуля, то мы имели бы формулы F.26).
Теперь повторим ещё и ещё раз описанную процедуру интегрирова-
интегрирования по коротковолновым флуктуациям с последующими масштабными
преобразованиями F.22)-F.26). Получаемые таким образом преоб-
преобразования лагранжиана называются преобразованиями под действием
ренормализационной группы (сокращённо — ренормгруппы). Это не
есть группа в математическом смысле, поскольку при усреднении по

84	Лекция 6. Ренормализационная группа
коротковолновым флуктуациям теряется информация, эта процедура
необратима.
Рассмотрим сначала с этой точки зрения простейший пример сво-
свободной теории, когда в затравочном лагранжиане т2 = А = В = С =
= ... = 0 и все возмущения исчезают. Тогда на всех этапах описанной
рекурсионной процедуры Вильсона эффективный лагранжиан остаётся
свободным. Поэтому говорят, что свободный лагранжиан
?о = о (д^ФJ	F-27)
2
является фиксированной точкой преобразований ренормгруппы.
Если мы находимся в непосредственной близости фиксированной
точки, то можно отбросить в итерационных формулах Am2, AA, и т.д.
Тогда при помощи F.26) получаем:
f = Bbd, Cf = Cb2d~\ F.28)
и т.д. Так как Ъ < 1, то параметры, которые умножаются на отри-
отрицательные степени Ь, растут, и наоборот. Если лагранжиан содержит
растущие коэффициенты, они уводят его от точки ?q.
Отдельные слагаемые в квадратной скобке в F.25) называются
локальными операторами. Операторы, коэффициенты которых растут
(вымирают) при рекурсионной процедуре, называются существенными
(несущественными). Если коэффициент оператора умножается на Ь°
(например, оператор ф4 при d = 4), мы называем его маргинальным.
Для выяснения того, растёт ли или уменьшается его коэффициент,
требуется вычисление высших поправок.
Из F.26) и F.28) видно, что массовый оператор ф2 является
существенным, а два последних слагаемых в F.25) при d = 4 явля-
являются несущественными операторами. Этим и объясняется, что теория
ф4 является перенормируемой при d = 4, так как фактически и при
вильсоновской процедуре перенормировок эта теория восстанавливает
свой исходный вид. Это же утверждение справедливо в отношении
любой перенормируемой теории.
Так как в порядке О (Л) AZ = 0, то при помощи F.26) и F.21)
находим, что с точностью О (А2), при d = 4,
Q Л 2	1
А-АШ-.	F.29)
Отсюда видно, что коэффициент при маргинальном операторе ф4
уменьшается, то есть константа связи уменьшается по логарифми-
логарифмическому закону. Соотношение F.29) является аналогом соотношения
D.24), разница лишь в том, что в F.29) и D.24) представлены взаимно
обратные функции. Из сказанного следует, что при d = 4 теория ф4
в результате вильсоновской процедуры перенормировок стремится к
свободной теории. Эта картина справедлива, конечно, лишь до тех пор,
пока массовый оператор не становится преобладающим.

6.2. Уравнение Каллана-Симанчика	85
6.2. Уравнение Каллана-Симанчика
На языке Вильсона перенормируемая квантовая теория поля с про-
произвольно большим обрезанием отвечает эффективной теории, испытав-
испытавшей большое число ренормгрупповых операций Вильсона и которая
проэволюционировала до большой величины массового параметра. Та-
Такая траектория должна пройти произвольно близко от фиксированной
точки. В результате этой эволюции несущественные операторы в пер-
первоначальном лагранжиане вымирают и остаются только существенные
и маргинальные операторы. Коэффициенты при оставшихся операто-
операторах находятся во взаимно однозначном соответствии с наблюдаемыми
параметрами, а информация об эволюции несущественных операторов
утрачивается полностью в перенормируемой теории поля. Информацию
же об эволюции параметров при существенных и маргинальных опера-
операторах можно восстановить, изучая их зависимость от нормировочного
масштаба.
Для конкретности рассмотрим теорию ф4 в четырёхмерном про-
пространстве Минковского, изученную нами, и ограничимся случаем
т2 = 0. Поскольку физический размерностный оператор отсутству-
отсутствует, то для проведения программы перенормировок необходимо ввести
размерностный параметр /j2 > 0. Поскольку условия перенормировки
E.30а, 5.30 6) приводят к сингулярностям при т2 —> 0 (см. E.32)), то
наложим эти же условия перенормировки, но при пространственнопо-
добных значениях импульсов р2 = —/i2:
= 0,
= -i A. F 30)
«ампутированная»	v 7
(fci + k2J = (fci + hJ = (fci + k4J = -fi2
Заметим, что в F.30) импульсы ka не предполагаются находящимися
на массовой поверхности и потому условия F.30) совместны. Таким
образом, теория определена на масштабе /А
Обозначим через фо(х) и ф(х) — затравочное и перенормирован-
перенормированное поля, соответственно, и пусть Gq (х\, ... , хп) — связная корре-
корреляционная функция (хронологическое среднее) неперенормированных
полей, определяемая согласно E.19), а
G{n\xu ... , хп) = @\Тф(Х1) ... ф(хп)\0)	F.31)
— связный коррелятор перенормированных полей (для удобства мы

86	Лекция 6. Ренормализационная группа
сменили обозначения, сделав замены ф —> фо, фг —> ф). Так как соглас-
согласно E.26) фо = VZ ф, то
Zn/2G^(xu ... , хп- /х, А(/х)) = G^ (xlt ... , хп).	F.32)
Обозначение G^(xi, ... , хп; /л, A(/i)) подчёркивает, что этот корре-
коррелятор зависит от точки нормировки \± и перенормированной константы
связи A(/i).
Теперь изменим точку нормировки /i —> //, константу связи А и
константу перенормировки Z, но оставим неизменными импульс об-
обрезания Л, а также затравочные константы. Это означает, что мы
продвинулись вдоль траектории ренормгруппы. Ясно, что при этом
«голые» (неперенормированные) гриновские функции F.32) остаются
неизменными, поскольку они зависят лишь от затравочных параметров
и импульса обрезания Л. Поэтому производная по параметру /i от
обоих частей равенства F.32) равна нулю:
+ /3(A)+n7 (A)l G ({хг}; /z, А) = 0.	F.33)
Здесь	1 я
m = *w iw^-,-z. F.34)
Функции /3 (А) и 7 W ~ ОДНИ и т^ ж^ для всех корреляторов в
теории и они не могут зависеть от импульса обрезания, поскольку
перенормированные корреляторы не зависят от обрезания. Следова-
Следовательно, по размерным соображениям, они не могут зависеть и от /i.
Поэтому функции F.34) могут зависеть лишь от перенормированной
константы связи А. Уравнение F.33) называется уравнением Каллана-
Симанчика.
Вычислим функцию C в наинизшем неисчезающем приближении
при d = 4. Так как Z = 1 + О (А2), то с точностью О (А2) перенорми-
перенормированный четырёхточечный коррелятор в импульсном представлении
(см. рис. 7 и D.20)) равен
+ 1п-Ц-*?+]п-^?>I [fi F.35)
Так как 7 = 0(A2), то в порядке О(А2) функция 7 выпадает из
уравнения Каллана-Симанчика. Поэтому, подставляя F.35) в F.33),
получаем
ЗД2 —ч\	C6)

6.3. Эволюция бегущей константы связи	87
6.3. Эволюция бегущей константы связи
Сопоставим уравнения F.34) и F.34):
^	F.36)
16тг2
Здесь первое равенство является точным по определению, а второе —
приближённое. Проинтегрируем явно второе равенство в F.36):
F.37)
ОД 1 III)	LL
1	' ' In —
\bnz га
Будем считать, что га — некий масштаб порядка физической массы.
Тогда следует считать, что \± ^> га, так что на масштабах ~ \± теория
фактически безмассовая и уравнения F.34)-F.36) справедливы. Тогда
уравнение F.37) показывает, что эффективная константа связи растёт
при возрастании импульса согласно формуле F.37). При этом А (га) —
константа связи при импульсах, стремящихся к нулю.
Мы видим, что квантовая теория поля приводит к новому понятию:
бегущей константе связи. При этом в теории ф4, при d = 4, бегущая
(эффективная) константа связи уменьшается, если нас интересуют всё
меньшие и меньшие энергии взаимодействия (вплоть до масштаба
физической массы частиц). Мы увидим, что константа взаимодействия
в электродинамике (электрический заряд) также уменьшается при по-
понижении энергии взаимодействия. Такие теории называются нульза-
рядными и в них /3-функции положительны. Однако существуют такие
теории (например, теория Янга-Миллса и построенная на её основе
теория сильного взаимодействия — квантовая хромодинамика), в ко-
которых эффективная константа связи растёт при уменьшении энергии
взаимодействующих частиц. Такие теории называются асимптотически
свободными, /3-функции в этих теориях отрицательны.
/3-функция в уравнениях F.33), F.34) называется функцией Гелл-
Манна и Лоу.
Напоследок сделаем следующую оценку. Рассмотрим двухточечный
коррелятор при высоких энергиях, когда можно пренебречь массой.
Согласно сказанному выше, имеем
F.38)
К"
Но при помощи F.34) находим, что
т1 )

Лекция 6. Ренормализационная группа
если 7 (^2) изменяется медленно. Комбинируя F.38) и D0), получаем
GW	F40)
откуда
\
Таким образом, функции 7 ответственны за появление аномальных
размерностей полей.
Задачи
1. Покажите, что при d < А в теории фА имеется фиксированная точка
ренормгруппы с ненулевой константой связи Ло и найдите это значение
константы связи в однопетлевом приближении.
vA °J
A_d
2. Используя уравнение Каллана-Симанчика, вычислите в безмассовой
теории ф4, при d = 4, функцию 7(^) в наинизшем приближении.
3. Вычислите /3-функцию в первом неисчезающем порядке в теории с
лагранжианом (см. задачу 3 к лекции 3)

Часть II
КВАНТОВАЯ
ЭЛЕКТРОДИНАМИКА

Лекция 7
КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
7.1. Континуальный интеграл для вырожденных
систем
Рассмотрим многомерную динамическую систему, гамильтониан
которой зависит от п пар канонически сопряжённых переменных
{Pa, Qa} и в которой имеется т < п связей первого рода (fi(p, q), a
связи второго рода отсутствуют. Связи первого рода — это такие связи
между динамическими переменными
<Рг(Р> (?) = 0, г = 1, ... , га,	G.1)
что
[<Рй<Рз]=^<рк, [<РпН]=Ь1<Рз.	G.2)
В этом пункте [...,...] обозначает классическую скобку Пуассона
(СП), а ТС, как и везде, — гамильтониан. При вычислении всех СП
связи игнорируются. В рассматриваемом случае полный гамильтониан
системы, ТСт = ТС -\- Y^ZLi vi(fi^ зависит от га произвольных функций
времени г^. Действительно, уравнения Гамильтона для связей,
—j = [(fi, ТСт] = 0 (mod (fj),
показывают, что при любых значениях множителей Лагранжа {г^}
равенства G.1) совместны с динамикой системы.
Рассмотрим динамическое изменение какой либо величины F(p, q)
за бесконечно малый промежуток времени 5t в двух случаях, отлича-
отличающихся значениями коэффициентов Vi, и найдём разность этих изме-
изменений. Так как динамическое изменение 5F = [F, TCr]5t, то искомая
разность изменений величины F в этих двух случаях
A5F = [F, ipi] Avi • 5t.

7.1. Континуальный интеграл для вырожденных систем	91
Величины {F + 5F) и (F + 5F + A5F) являются физически эквива-
эквивалентными, а сама разность Д№ называется калибровочным преобра-
преобразованием величины F. Калибровочно инвариантной называется такая
величина, которая удовлетворяет условиям [F, (fi\ = 0. В такого рода
теориях экспериментально могут наблюдаться лишь калибровочно ин-
инвариантные величины.
Обозначим через Г2п фазовое 2п-мерное пространство с координа-
координатами {ра, qa}.
На классическом уровне рассматриваемая обобщённая гамильтоно-
ва система эквивалентна обычной гамильтоновой системе с (п — га)
степенями свободы. Фазовое пространство Г*2(п-т) последней систе-
системы реализуем следующим образом. Рассмотрим га дополнительных
условий,
XJ(P^)=O,	G.3)
фиксирующих калибровку, для которых выполняются требования
det \\lvi, Xj}\\ ^ 0, [x\xj}=0.	G.4)
Фиксация калибровки означает определённый выбор набора функций
{vi} (см. ниже G.11)). Подпространство в Г2п, определяемое равен-
равенствами
Хг(р, q) = 0, <р{(р, q)=0, г = 1, ... , га,	G.5)
является пространством Y*2(n~m\ Вследствие G.4) можно выбрать в
Г2п канонические переменные так, чтобы первые га координатных
переменных ql, ... , qm совпали с величинами х1, ... , хт:
Ч = {х\-,Хт,Ч*}-	G-6)
Здесь q* — остальные (п — га) координатных переменных. Записывая
лагранжиан в переменных G.6), находим соответствующие канониче-
канонически сопряжённые импульсные переменные. Обозначим их через
В новых переменных условия G.4) принимают вид
det
0.	G.8)
Отсюда следует, что уравнения связей G.1) можно разрешить отно-
относительно pi с г = 1, ... , га. Эти решения обозначим Pi(p*, q*). В
результате подпространство Г*2(п-т) задаётся уравнениями
Хг = Чг = 0, Рг = Рг(р*, д*), г = 1, ... , га.	G.9)
Переменные {р*, q*} являются каноническими, и гамильтонианом си-
системы является функция
)l=Ox=o.	G.10)

92	Лекция 7. Квантование электромагнитного поля
Обозначим исходную систему с гамильтонианом ТСт и фазовым
пространством Г2п и новую систему с гамильтонианом ТС* и фазовым
пространством Г*2(п-т) через Г и Г*, соответственно.
Системы Г и Г* эквивалентны, и эквивалентность означает сле-
следующее.
Выберем в ТСт лагранжевы множители V{ так, чтобы выполнялись
равенства
¦з г з v 1 &П ^ dipt	.
qj = \-yJ, ТСт\ —	h / ^г	 — 0, 7 = 1,..., 7тг. G.11)
opj *—^ opj
Вследствие G.4), эта задача имеет однозначное решение. При этом
уравнения Гамильтона д = [д, ТСт] и связей G.1), G.9) совпадают с
уравнениями Гамильтона для системы Г*.
Докажем этот факт в координатах G.6). При помощи равенств
G.11) получаем следующие соотношения:
ОП О Pi \ 	 y л^ | ^у^жл^у^ w j^j .
dpi dа* I ^-^ \ да* ^-^ dpj да*
G.12)
m
%=\ \ ~r	~ гь ~ r /	^_j	\~ r	/J._1 ^ /^J ^ /^
Последние равенства в G.12) вытекают из того, что имеются тождества
Vi(p(p*> 4*),P*, q*) =0, i= I, ... , m.
Из G.12) следует, что уравнения
dq
дТС dPi
совпадают (соответствующие уравнения для переменных q* не выпи-
выписываются). Таким образом, утверждение об эквивалентности систем Г
и Г* доказано.
Система Г может быть проквантована в переменных {р*, q*}, в
которых она является невырожденной. В этих переменных квантовый
оператор эволюции задаётся континуальным интегралом (см. A.12))
С)
G.13,

7.2. Электромагнитное поле как динамическая система	93
Чаще всего (как в электродинамике и многих других калибровочных
теориях) нецелесообразно разрешать связи явно. Напротив, оператор
эволюции полезно представить непосредственно в терминах перемен-
переменных обобщённой системы Г. Покажем, что континуальный интеграл
t"
explil [pq- (H(p, q)JrViLpi(p, q))} At \ x
t г	сх
совпадает с интегралом G.13). Для этого проинтегрируем G.14) по
лагранжеву множителю v, в результате чего он принимает вид
t"
q — Н(р, q)} dt f TT TT 5(хг) ^(^Рг) det |
t i
Мера в интеграле G.15) инвариантна относительно канонических пре-
преобразований переменных интегрирования. Будем считать, что он вы-
вычисляется в переменных G.6), G.7), в которых
П П <*(*') *to) det II [^' ^ II = П П
t i
Теперь очевидно, что после интегрирования по переменным {pi, q1} с
г = 1, ... , т интеграл G.15) сводится к G.13).
Заметим, что выражение в круглой скобке в экспоненте в G.14)
является полным гамильтонианом ТСт-
7.2. Электромагнитное поле как динамическая
система
Свободное электромагнитное поле описывается действием
|dD)
Электрическое и магнитное поля равны, соответственно,
Ег = ргО = _д.А0 _ ^<1	Hi = _}_?i

94	Лекция 7. Квантование электромагнитного поля
Выпишем лагранжиан системы:
f J |>>*i*.	G.18)
J
О7Г J
Ш7Г
Проварьируем лагранжиан G.18) относительно А^\
)хЕ{бА\	G.19)
5АС ^ \dxFSA ^
4тг J	4тг
Отсюда видно, что если поле А^ рассматривается как совокупность
координатных переменных, то соответствующие импульсные перемен-
переменные тгм равны
щ{х) = -^-Е\х),	G.20)
тго(х)=О.	G.21)
При помощи формул G.17)—G.21) находим гамильтониан:
ПТ= \<1®хщА'-?= [d^(Eo+H--J-A°VEl. G.22)
отг	4тг
Канонические одновременные СП имеют вид (выписаны лишь ненуле-
ненулевые СП)
[Д*(х), АЧу)]=47г^<3>(х-у),
G.23)
Мы имеем множество первичных связей G.21). Вычислим их СП с
гамильтонианом:	,
[тг°(х), П} = — VE(x).	G.24)
4тг
Чтобы связи G.21) сохранялись, необходимо наложить множество но-
новых связей:
<р(х) = VE(x) =0.	G.25)
При помощи G.23) находим
Г •	1 Г *
\Аг(х), — d3yA°(y)VE(y)\ = <Ми(х).	G.26)
Таким образом, связи G.25) генерируют калибровочные преобразова-
преобразования. Нетрудно проверить, что положительная часть гамильтониана
G.27)
8^
калибровочно инвариантна:
[VE(x),H] =0.	G.28)
Кроме того, все взаимные СП связей G.21), G.25) обращаются в ноль.
Поэтому все связи — первого рода и поле А0 играет роль лагранжевого

7.2. Электромагнитное поле как динамическая система	95
множителя, принимающего произвольные значения и гамильтониан
G.22)	является полным гамильтонианом.
Равенство G.26) показывает, что естественными дополнительными
условиями, аналогичными G.3), в рассматриваемом случае являются
условия, фиксирующие калибровку:
Х(х) = VA(ai) =0.	G.29)
Вычислим одновременные СП связей G.25) и G.29). При помощи СП
G.23)	находим, что
= [VE(x), VA(y)] = -47rV2^3)(x-y). G.30)
Таким образом, det ||[</?(х), х(у)]|| = const, то есть этот определитель
является величиной, не зависящей от динамических переменных, кото-
которая включается в общий нормировочный множитель. (В более сложных
калибровочных теориях, как теория Янга-Миллса, аналог оператора
G.30) зависит от полей и соответствующий определитель должен быть
явно учтён.)
Обозначим через А1- (х) поперечное векторнозначное поле, удовле-
удовлетворяющее условию
VAx=0.	G.31)
В нашем случае система Г описывается переменными {Е, тг°, А^1},
а система Г* — переменными {Е-1, А-1}. Однако удобнее взять в
качестве исходной системы Г несколько сокращённую систему с фа-
фазовым пространством, точками которого являются поля {Е, А}, свя-
связями G.25) и условиями G.29), фиксирующими калибровку. При таком
подходе роль лагранжевых множителей {vi} из предыдущего пункта
берёт на себя поле, обозначаемое А0.
При квантовании переменные системы Г* удовлетворяют следую-
следующим одновременным КС (сравни с G.23)):
^) **(х-у). G.32)
Последние КС реализуются, если полевые переменные разлагаются
следующим образом (сравни с B.34)):
а=1,2

96	Лекция 7. Квантование электромагнитного поля
р), а, /3=1,2,
а=1,2
Если в G.27) подставить переменные G.33), то мы получим гамильто-
гамильтониан Г*-системы:
Фотонный вакуум определяется условиями
скск|0)=0.	G.35)
Однофотонное состояние с импульсом к и поляризацией а в
релятивистской нормировке представляется как (сравни с B.38))
Двух- и т.д. фотонные состояния строятся из вакуумного очевидным
образом при помощи операторов рождения с^ка. Приведём гамильтони-
гамильтониан G.34) к нормальному виду (далее индекс *, отмечающую принад-
принадлежность к Г*-системе, не выписываем):
Г А C) 7х»
Ж	Л I (Л	гь	4-
п/	\	I	HIT	\ С	A ОГ7\
/10= 2_^ \ То—Y3 II СкскСкск +^0,	\i-Ji)
Здесь V — объём пространства. Величина G.38) является энергией
нулевых колебаний или энергией вакуума. Также как и в скалярной
теории, в электродинамике она положительна и её плотность бесконеч-
бесконечна. Существуют экспериментальные методы «тестирования» энергии
вакуума (эффект Казимира, см. задачу к этой лекции).
Как известно, оператор импульса электромагнитного поля (см. При-
Приложение В) равен A/4 тг) [Е, Н]. Поэтому оператор импульса электро-
электромагнитного поля (сравни с B.42))
4^Г ~L~'"J в^2П2т)
Из данных определений следует, что (энергия вакуума вычеркнута из
гамильтониана)
П\0)=Г\0)=0, П\к,а) = |k||k, a), V\k, a)=k\k,a).

7.2. Электромагнитное поле как динамическая система	97
Таким образом, фотон является безмассовой частицей, распространяю-
распространяющейся со скоростью света.
Теперь при помощи формул из предыдущего пункта и лекции 2 мы
можем, минуя детальные вычисления, выписать нормальный символ S-
матрицы в фотодинамике в терминах переменных исходной Г-системы
(сравни с B.52)):
х П Пs (v А(ж))d Ei^d Ai^d
x i=\
Граничные условия в интеграле G.39) таковы:
__l_ _ Ъ К X | „*	«-L * рЪ К X
kaoutekae	"Г ckQ_outekae
Ckcin = ckcK, 4aout = 4а, А;ж = к°х°- кх, ^° = |к|. G.40)
Обратим внимание на то, что граничные условия G.40) имеют ме-
место лишь для физических степеней свободы, описываемых поперечной
частью поля А-1 (ж) G.31). Проинтегрируем в G.39) по импульсным
переменным Е (х) и введём в теорию внешний источник. Это интегри-
интегрирование проводится однозначно при помощи правила вычисления функ-
функциональных гауссовых интегралов, поскольку проблема граничных
условий при этом интегрировании отсутствует. С учётом G.16)—G.18)
получаем
Sj(c*. с) = 1 [exp |i [dD) x f-
dA^(x).	G.41)
X	X \1
Интеграл G.41) вычисляется с граничными условиями G.40).
Из континуального интеграла G.41) видно, что интегрирование
идёт не по всем полям, а лишь по поперечным физическим полям А-1.
Для вычисления пропагатора электромагнитного поля преобразуем
интеграл G.41) следующим образом:
16тг
M + Л diAi
Y[dX(x)DAll. G.42)
4 С.Н. Вергелес

98	Лекция 7. Квантование электромагнитного поля
Гауссов интеграл вычисляется нахождением экстремума показателя
экспоненты в G.42) относительно переменных {Л, А^}. Этот экстре-
экстремум находится при помощи системы уравнений:
дгАг = 0, AA° = 4ttJ°,
г	г	G-43)
Естественно считать, что источник удовлетворяет условию поперечности:
diJ* = 0.	G.44)
Вычисляя дивергенцию последнего из уравнений G.43) и учитывая
первые два, находим, что
AA = 90J°.	G.45)
В результате система уравнений G.43)-G.44) сводится к уравнению
G.45), а также уравнениям
AA° = 4 7rJ°, <9м<^Ах =-4ttJx.	G.46)
Теперь, аналогично B.53), мы можем представить электромагнитное
поле, для которого действие в G.42) экстремально:
А^(х) = А$(х) + [ dD) у Dj^(x - у) Jv(y),
А°0 = 0, k° = \k\;
е~гкх
Dg(x) = -4 7rj
е
BтгL k2 + ie V	к2
G.48)
-ikx
e
BтгL к2 '
Явное выражение для D^'(x) показывает, что распространяются во
времени только трёхмерно поперечные составляющие поля А^.
Преимуществом изложенного подхода является очевидная унитар-
унитарность полученного выражения для ^-матрицы, поскольку формула для
б'-матрицы была получена путём перехода к невырожденной дина-
динамической системе. Недостатком диаграммной техники, развитой при
помощи пропагатора G.48), является отсутствие явной релятивистской
инвариантности.

7.3. Ковариантные правила квантования и трюк Фаддеева-Попова 99
7.3. Ковариантные правила квантования и трюк
Фаддеева-Попова
Чтобы восстановить явную релятивистскую инвариантность, посту-
поступим следующим образом. Обозначим через а (х) некое скалярное поле
и через А^ — калибровочно преобразованное электромагнитное поле:
А%=А1Л + д1Лш.	G.49)
Определим величину А^ при помощи равенства
[d»A4-a(x)]du}(x) = \.	G.50)
Очевидно, Al не зависит от полей А^ и а(х): Al = det д2.
Теперь вставим левую часть G.50) в интеграл G.41), что не изменит
его значения:
ЬАс , с) - N
х~[[5{дгА\х))Аь5[д»А%-а{х)} Au)(x)DAil.	G.51)
X
Теперь в интеграле G.51) сделаем калибровочное преобразование,
обратное к G.49), и учтём, что мера D А^ и плотность действия
F2^ при этом не изменяются, являясь калибровочными инвариантами.
В результате интеграл G.51) принимает вид
Sj(c*, с) = — ехр \ г d^ x -^т~ *'lu,*'h"' + J^An - J^c)u,uj
N ] у J	[ штг
х JJ S(diAf~\x))ALS[d^ Ац-а(х)] Auo(x)DA^.
X
За слагаемым вида J^d^uo в экспоненте нет смысла следить, потому
что асимптотическое поле G.47) определено с точностью до слагаемого
д^ии, где поле ш, так же как и в рассматриваемых функциональных
интегралах — произвольное, удовлетворяющее уравнению дхАламбера
(см. ниже ур. G.57)). Так как интеграл
Г т—г	-1
\\ 5 [di Af (x)] d и (х) = det
также не зависит от от вектор-потенциала, то его можно выбросить.
Таким образом,

100	Лекция 7. Квантование электромагнитного поля
Sj{c\ c) = l
1О7Г
X
Поскольку здесь левая часть не зависит от поля а(х), мы можем
проинтегрировать последнее выражение с весом
ехр
8тга
что влияет лишь на нормировочный множитель:
Sj(c\ c) = — J ехр | г
G.52)
Находя пропагатор таким же образом, как это было сделано выше,
находим, что континуальный интеграл G.52) приводит к ковариантному
пропагатору:
ryMZ, = diag(l, -1, -1, -1).
Калибровка, в которой пропагатор имеет вид G.53), называется а-
калибровкой. Частный случай этой калибровки, а = 1, называется
калибровкой Фейнмана, а частный случай, а = 0, — калибровкой
Ландау.
Правильность задания обхода полюсов в G.53) легче всего уста-
устанавливается следующим образом. Пропагатор G.48), конечно, как про-
пропагатор, описывающий распространение реальных частиц в рамках
теории ^-матрицы, позволяет сделать поворот Вика в евклидово про-
пространство. Иными словами, при вычислении ^-матрицы можно ис-
использовать интеграл вида G.41) в евклидовом пространстве, и лишь
после вывода правил Фейнмана перейти в пространство Минковского.
В евклидовом пространстве можно перейти к а-калибровке G.52) при
помощи описанного трюка Фаддеева-Попова и получить соответству-
соответствующий евклидовский пропагатор. После этого обратный поворот Вика в
пространство Минковского приводит к пропагатору G.53) с указанным
обходом полюсов.
Теперь мы можем выписать нормальный символ ^-матрицы для
свободного электромагнитного поля при наличии внешнего источника

7.3. Ковариантные правила квантования и трюк Фаддеева-Попова 101
(сравни с B.51). Значение экстремального значения электромагнитного
поля задаётся формулой (см. G.47))
А"(ж) = А$(х) + dWyDa ^(x - у) J,(y),
а нормальный символ ^-матрицы имеет вид
Sj(c*, с) = 1 exp Si \ dD)
N
AD> yJ»(x) D;v(x - у) Г(у)\ . G.54)
Поскольку выписанное выражение для ^-матрицы получено пу-
путём тождественных преобразований из выражения для унитарной S-
матрицы, то это выражение также является унитарным.
Последнее замечание касается вопроса об однозначности определе-
определения векторов поляризации фотонов е^а. Введём 4-вектор поляризации
фотона е^.а = @, е-^а). Если k^ = (|k|, к) — 4-импульс фотона, то
согласно G.33),
*/ко = 0, г,»* е^ а е"к*р = Sap-	G.55)
Очевидно, что оба свойства G.55) сохраняются, если сделать преобра-
преобразование вектора поляризации, согласно правилу
4«-4a + /(k)fc<\	G.56)
где /(к) — любая функция. Поэтому вектор поляризации фотона
определён неоднозначно с точностью до преобразования G.56), изме-
изменяющего четырёхмерно продольную часть фотона. Поэтому и асимпто-
асимптотическое поле G.47) определено с точностью до произвольного калиб-
калибровочного преобразования вида
А>м -^ 4)М + д^со, д^и = 0.	G.57)
В то же время, как мы увидим ниже, все физические величины
инвариантны относительно преобразований G.56). Эта инвариантность
является следствием калибровочной инвариантности теории.
Задачи
1. Трёхмерный эффект Казимира1).
а) В трёхмерном пространстве на расстоянии / друг от друга рас-
расположены две бесконечные плоские параллельные металлические пла-
пластины. Считая, что на пластинах обращаются в ноль тангенциальные
*) Последние экспериментальные данные подтверждают эффект Казимира с
точностью ~ 10%.

102	Лекция 7. Квантование электромагнитного поля
компоненты электрического поля Е и разность потенциалов между
пластинами равна нулю, проквантуйте фотонное поле и выразите его
гамильтониан через лестничные операторы.
б) Вычислите силу на единицу площади пластин, с которой взаи-
взаимодействуют эти пластины вследствие искажений нулевых колебаний
фотонного поля и сдвига энергии вакуума.
Указание. При регуляризации интеграла типа G.38), формально
задающего энергию вакуума, использовать формулу размерностной ре-
регуляризации D.3), а при регуляризации расходящихся сумм степеней
целых чисел использовать аналитическое продолжение ("-функции Ри-
мана. ?
2. Вычислите явно в координатном представлении в четырёхмерном
пространстве фотонный пропагатор в а-калибровке.
3* 0. Сделаем замену геА^ —> А^ и определим оператор ковариантной
производной VM = <9М + А^. Очевидно А* = — А^ и напряженность
Fpv — [VM, \7y\ = д^Ау — дуА^ отличается от стандартного значения
G.16) лишь множителем ге. Поэтому в данном случае действие элек-
электромагнитного поля имеет вид
1
Oj J. jJ^y-L
Обобщим это действие на неабелев случай.
Пусть ta = — (ta) , a = 1, ... , N — образующие некой алгебры Ли
в матричном представлении, причём
I	±а±Ъ 	 _ габ	\+а j-b] 	 ? ±с
II	L L — су ° '	L6'6J — J abc L >
и структурные константы fabc вещественны. Определим неабелево ка-
калибровочное вещественное многокомпонентное поле А^, или неабелево
калибровочное антиэрмитово поле А^ = Аа^Ьа = —Aj^. Ковариантная
производная имеет прежний вид VM = д^ + А^, а напряжённость поля
и его действие
Fny(A) = [Vu, V^] = дпАу — дуАп + [An, Ay].
Определим калибровочное преобразование как
1) Эта задача может быть решена лишь при использовании техники, изло-
изложенной в лекции 9.

7.3. Ковариантные правила квантования и трюк Фаддеева-Попова 103
где	,
AI	Л
Определённая таким образом теория называется теорией Янга-
Миллса.
а) Проверьте, что
Таким образом, действие Янга-Миллса калибровочно инвариантно.
б) Проквантуйте теорию Янга-Миллса и выпишите выражение для
производящего функционала cS-матрицы в этой теории.
Ответ:
- с д» VMc - 2 J^ Ац]} D A^Dc Dc.
Здесь с = cata и с = cata — поля духов, независимые друг от друга и
антикоммутирующие как между собой, так и с прочими фермионными
полями (см. следующие лекции).

Лекция 8
УРАВНЕНИЕ ДИРАКА. КАНОНИЧЕСКОЕ
КВАНТОВАНИЕ ДИРАКОВСКОГО ПОЛЯ
8.1. Уравнение Дирака
В этой лекции рассмотрение идёт в четырёхмерном пространстве
Минковского, /i, z/, ... = 0, 1,2, 3, г, j, ... = 1,2, 3.
Рассмотрим операторы
•Г = -г?у*а^ + ^<Л	(8.1)
где
— сигма-матрицы Паули. Легко проверить, что
[J\ji]=ieijkJk.	(8.3)
Таким образом, оператор J является оператором полного момента
импульса, включая спин частицы, который в рассмотренном случае
равен A/2). Как известно, операторы полного момента J являют-
являются генераторами вращений в 3-мерном пространстве, что выражается
следующими формулами:
A +го;Л)хA -го;Л) =х+ [о;, х],
A + г uj J) а A - г и J) = а + [о;, а],
(l+iu>J)d(liu>J) d+[u>d]	( '
где lo — бесконечно малый вектор угла поворота и <т = («г1, сг2, сг3).
Задача заключается в обобщении формул (8.1)—(8.4) на случай
четырёхмерного пространства Минковского. На этом пути строится
релятивистская теория частиц со спином A/2).

8.1. Уравнение Дирака	105
Введём четыре комплексные матрицы 7м четвёртого порядка
со следующими свойствами (сравни с соотношениями <tVj + а^аг =
Чаще всего используются:
а) спинорное представление Gм = G°> 7г))>
б) стандартное представление,
1 0 \	, / 0 а
О -1 У 7 V -о1 О
Из E)-G) вытекает, что
G°)t=7°, G«)t = -y, 7oGi)t7o = 7i. (88)
Последние соотношения имеют место в любом представлении, по-
поскольку 7~матРиЦы в разных представлениях различаются унитарным
преобразованием.
Введенные матрицы (8.5) называются ^-матрицами Дирака.
Пусть 75 = —i7°717273- И3 этого определения имеем:
G5)t=75> 757м + 7м75=0, G5J=1;	(8.9)
5 ( ~Х °\
7=1 п ) — спинорное представление;
75 = (	п ) — стандартное представление.
Введём набор из шести матриц:
а^ = ^ [7м, Y] = -°V[l'	(8.Ю)
Вследствие (8),
7°(cr^)t7° = -^У •	(8.П)
Используя лишь алгебру (8.5), находим
\al±v Ai _ v\ и _ и\ у
\\	МЛ vp	v\ ^р	(8Л2)
Генераторы четырёхмерных вращений 1^у = х^ду — ху д^ удовле-
удовлетворяют тем же перестановочным соотношениям, что и матрицы а^у.
Поэтому для J^y = l^y + a^y имеем
['Jfivi J\p\ == Vp^p ^у\ Vvp ^[i\ 7?A/,A Jyp -\- Tfy\ Jjj,p>	yo.io)

106	Лекция 8. Уравнение Дирака
Мы видим, что матрицы а^и являются обобщением нерелятивистских
спиновых матриц A/2) аг на релятивистский случай.
Пусть поле
' ф\ (х) \
<Ж=1 %$ \=(ZU)	(8Л4)
Фа{х)
является матрицей-столбцом, состоящим из четырёх комплексных по-
полей фа, а = 1, 2, 3, 4, и
ф (х) = ф* (ж) 7	(8.15)
— матрица-строка. Поля (р и \ в (8.14) являются двухрядными
матрицами-столбцами, задающими верхнюю и нижнюю половины поля
(8.14), соответственно. Поля ф и ф в (8.14) и (8.15) взаимно сопря-
сопряжены (в смысле Дирака).
Уравнение Дирака во внешнем электромагнитном поле имеет вид
(гП^ VM - тс) ф (х) = 0, VM = -?- + г ^- Ам (ж). (8.16)
Далее, как обычно, полагаем Ь = с = 1.
Прежде всего установим факт лоренц-инвариантности уравнения
Дирака. Пуст и^ = — ujV[1 — шесть вещественных параметров преоб-
преобразования Лоренца и
^	(8.17)
Путём прямого вычисления находим:
х!Л = к-{х*1К = {пшУ1/хи,	(8.18 а)
^' ^	(8.186)
А-[ГАш = (пшГ„^.	(8.18 в)
Равенство (8.18 а) коротко можно записать в виде х = ?1шх. Из
(8.18 6) и (8.18 в) следует, что
Аш1»д^А^=Гд».	(8.19)
Определим лоренц-преобразованное дираковское поле как
ф(х) = Ашф{х) = (ехр Х-ш^а^\ ф^х).	(8.20)
Здесь второе равенство получено при помощи (8.18 а). Комбинируя
(8.19) и (8.20), находим
г^д^ф(х)=гА^\Аш^д^А^1)(Ашф(х))=А^1[г^д1Лф(х)]. (8.21)

8.2. Нерелятивистский предел	107
Поэтому	_
(){	^[{д^-т)^(х)},	(8.22)
откуда следует лоренц-инвариантность свободного уравнения Дирака.
Уравнение Дирака во внешнем калибровочном поле также лоренц-
инвариантно, поскольку наряду с (8.19) имеет место равенство
А* 7м VM Л = 7м VM = 7М(9М + геЛД	(8.23)
если оператор лоренц-преобразования Л^ преобразует электромагнит-
электромагнитное поле согласно формуле (8.18 6), так что А^(х) = (пиу^ Аи(п~1х).
Умножим тождество (8.20) на оператор Л и сделаем затем дира-
ково сопряжение:
^(х) = ^(жOОGоЛ-^7°).	(8.24)
Поскольку, вследствие (8.11),
7°Л-^7° = ЛШ,	(8.25)
то (8.24) означает, что	_
ф{х) = ф{х)Аш.	(8.26)
Уравнение Дирака A6) может быть получено путём вариации фер-
мионного действия
|'D)^	(8.27)
в котором комплексные поля ф, ф следует рассматривать как незави-
независимые динамические переменные. При помощи формул (8.22) и (8.26)
устанавливается, что действие (8.27) лоренц-инвариантно. Веществен-
Вещественность действия (8.27) устанавливается при помощи равенств (8.8) и
(8.15).
По определению, вариация действия материи относительно элек-
электромагнитного поля даёт электромагнитный ток материи JM. В нашем
случае имеем
5А S^ = -е [ dD) х J^ 5 Ац, JM = ф ^ ф.
8.2. Нерелятивистский предел
Перейдём к нерелятивистскому пределу в уравнении Дирака (8.16).
Для этого подействуем на уравнение (8.16) оператором (i7MVM + m)
и учтём, что согласно уравнениям (8.5) и (8.10) 7мlv — V^ + 2<7Mzy.
Таким образом, получим
{VM Vх + а^ [VM, V,] + m2} ф = 0.
Но [VM, Vzy] =ieF^. При переходе к нерелятивистскому пределу

108	Лекция 8. Уравнение Дирака
следует сделать замену:
ф^е~шгф, Vo = — + ieA0^ —+ieA0-im,
(V0J -> -m2 -2im (—+ieA0
Членами, не содержащими т (точнее — тс2), мы вправе пренебречь
в нерелятивистском пределе. С учётом этого, последнее уравнение для
дираковского поля принимает вид
Здесь учтено, что согласно определению электрическое Е и магнитное
Н поля связаны с тензором электромагнитного поля следующими
формулами: Ег = Fl°, Fij = —е^Як. Далее работаем в стандартном
представлении (8.7), в котором
Рассмотрим плоскую волну
Фк = e~imt~lkxuk, uk = const.
Для покоящейся частицы (к^ = 0) свободное уравнение Дирака при-
принимает вид
то есть х = 0 (см. (8.14)). Нетрудно проследить, что при малых к,
вследствие уравнения Дирака, имеет место оценка \к ~ (|к|/га) (/?&,
и потому в нерелятивистском пределе \ следует положить равным
нулю. Поэтому из (8.28) для верхней компоненты (р следует уравнение
Паули:
?Ь^?(!)Ь (830)
Так как оператор спина электрона s = A/2) а (см. задачу 2. в),
то уравнение Паули показывает, что в рассмотренном приближении
магнитный момент электрона
/x=-s.	(8.31)
т

8.3. Квантование дираковского поля	109
8.3. Квантование дираковского поля
Пусть ф = (d/di)i/j. Определим стандартным образом обобщённый
импульс дираковского поля:
Отсюда и из (8.27) имеем	_
тгф = г^7° = гф]-	(8.32)
(8.33)
Дираковский гамильтониан имеет вид
Щ = [dC) хифф- С= [dC) ж^(-га*Уг
J	J
а*=7°7*> («')* = «'•
Оператор в круглых скобках в (8.33), который назовём оператором
Гамильтона-Дирака, — эрмитовский. Поэтому имеет смысл задача о
собственных функциях этого оператора. Рассмотрим эту задачу для
случая свободного дираковского поля, когда А^ = 0, что предполага-
предполагается до конца этого параграфа.
Уравнение для собственных функций оператора Гамильтона-
Дирака в свободной теории имеет вид
(-1а*д{ + т'у0)фк = еъфк.	(8.34)
Решение этого уравнения ищется в виде бегущих волн, фь(х) =
= г^квгкх, амплитуды которых удовлетворяют уравнениям
(а к + т 7° - ?к) ^к = 0.	(8.35)
Умножая последнее уравнение на (ак + ш7° + ?к) и учитывая, что
7° ol + а 7° = 0, о? aj + aj a1 = 2 5ij,	(8.36)
получаем
D-ш2-к2)пк = 0.
Отсюда видно, что при е^ = ±л/^г2 + к2 уравнение (8.35) имеет ре-
решение. Если г^к удовлетворяет уравнению (8.35), то йк = 7°75'ик
удовлетворяет уравнению
(ак + т7° + ?к)йк = 0.	(8.37)
Поэтому имеется два независимых решения уравнения (8.35) с ?к =
= л/m2 + к2 = uok и два независимых решения с ?к = —\/тп2 + к2 = —
—сс;^. Эти решения называются положительно и отрицательно частот-
частотными. Далее положительно частотные решения с амплитудой г^к обо-
обозначаются Uk, а отрицательно частотные решения с амплитудой г?(_к)
обозначаются u-k. Для любого 4-вектора рм введём обозначение

ПО	Лекция 8. Уравнение Дирака
7м р^ =ф. Тогда уравнение (8.35) для положительно и отрицательно
частотных мод записывается как
(ft-m)uk=0,	(8.38 а)
(}к + т)и-к = 0,	(8.38 6)
где к^ = (о;&, к). Заметим, что если ф\ и гр2 — дираковские спиноры,
то Ф1Ф2 есть лоренц-инвариант, a V^T^V^ — 4-вектор. Поэтому мы
примем лоренц-инвариантные условия нормировки:
ukUk = 2m, u-kU-k = —2m.	(8.39)
При этом предполагается, что спиноры и±к получаются (с точностью
до фазового множителя) из спиноров в системе покоя частицы при
помощи соответствующего преобразования Лоренца. Равенства (8.39)
согласованы с равенствами
пк 7м ик = п_к 7м и_к = 2 №.	(8.40)
Для проверки равенств (8.39)-(8.40) заметим, что в системе покоя
частицы, где к^ = (т, 0), уравнения (8.38 а, 8.38 6) принимают вид
7°?/^ = ±u±k, из которых непосредственно вытекают следующие со-
соотношения:
= ±^±ь 7°7 и±к = Т7 и±к-
Умножая скалярно соответственно левые и правые части последних
уравнений, получаем
п±к7и±к = ~п±к7и±к = 0.
Таким образом в системе покоя частицы
п±к^и±к = (и]±ки±к, 0, 0, 0).
Так как u\_ku±k > 0, то примем нормировку u\_ku±k = 2m. Тогда
равенства (8.40) в любой системе отсчёта получаются путём преобра-
преобразования Лоренца. Теперь умножим равенства (8.38а, 8.38 6) на п±к,
соответственно, и учтём (8.40):
тп±ки±к = ±u±kjtJ"u±kkfJb = ±2m2.
Полученные равенства равносильны равенствам (8.39).
При помощи явных вычислений легко найти, что в стандартном
представлении (8.7) решения уравнений (8.38 а, 8.38 6) имеют вид
Uk =
\ л/dJu — m, (n rr) ?/; /	\ л/dJu 4- m, ?/;'	/
(8.41)
t	1	/t / 1
n = ^—, гу'г1;=1, гу'г/; = 1.

8.3. Квантование дираковского поля	111
В системе покоя (ujk = га) имеем
ик = У2^ (WA, u_fc = V2^ Г °Л ;	(8.42)
то есть w (wf) представляет собой тот двухкомпонентный спинор в
трёхмерном пространстве, к которому сводится в нерелятивистском
пределе амплитуда волны. Сопрягая (8.41), получаем
(8.43)
При помощи формул (8.41) и (8.43) равенства (8.39) и (8.40) полу-
получаются непосредственно. Ортонормированный базис в спинорном про-
пространстве {г^} ({w'}) состоит из двух элементов, которые выбираются
ортонормированными:
wa = V asw^b a =1,2,
/ j \s)
s=l,2
(8.44)
Yl W(s)W(s>) =Sss>,	Yl W(s)W(s) = 5^'
a=l,2	s=l,2
Везде a, /3,... — спинорные индексы, а индексы s, sf,... нумеруют
спиноры. Аналогичные формулы имеют место для штрихованных спи-
спиноров. Обозначим через u±ks, 5=1,2 дираковские спиноры (8.41), в
которых сделаны подстановки w —> w^, w1 —> wi у Тогда при помощи
(8.40) и (8.41) получаем
s,
(8.45)
u[su-pSt = 0, если р = —k.
Последнее равенство в (8.45) является следствием того, что u\s и
U-ps> при р = —к являются собственными векторами эрмитовой мат-
матрицы (8.35) с разными собственными значениями.
Теперь мы можем выписать квантованное дираковское поле:
(8.46)
Далее мы покажем, что величины из множества {a^s, b\^s, a^s, b^s}
являются фермиевскими операторами уничтожения и рождения. При

112	Лекция 8. Уравнение Дирака
помощи соотношений (8.38 а, 8.38 6) и (8.45) вычисляем значение сво-
свободного гамильтониана (8.33) на полях (8.46):
ED64)	(8.47)
(8.48)
'	s=l,2
Находим также оператор электрического заряда:
Г
= e \
s=l,2
—-з
Обратим внимание на то, что условия квантования, определяющие
фермионный вакуум, должны иметь вид
aks|0>=0, 6ks|0)=0.	(8.49)
Действительно, пусть х° > у0 и рассмотрим величину
@\ф(х)ф(у)\0),	(8.50)
где ф (х) и ф (у) — дираковские поля в представлении Гейзенберга.
Гейзенберговские поля представляются согласно (8.46) с той лишь
поправкой, что в (8.46) производятся замены ехр (±гкх) —> ехр (=р
^ikx), где к х = ujk %° — кх. Действительно, вследствие (8.38 а, 8.38 б)
в результате этой замены экспонент поля (8.46) удовлетворяют сво-
свободному уравнению Дирака. Поэтому величина (8.50) равна, как и в
скалярной теории, амплитуде распространения частицы, рождённой в
точке у и распространяющейся в точку х. Вследствие условий (8.49)
эта амплитуда является суперпозицией амплитуд с импульсом к,
содержащих множитель ехр [—гUk (x° — у0)], то есть суперпозицией
положительночастотных волн. Такая зависимость от времени означает,
что распространяется частица с положительной энергией. Амплитуда
распространения скалярной частицы из точки у в точку х (см. лекцию
2) (О\ф(х)ф(у)\О) содержит такую же зависимость от времени.
Условия квантования, отличные от (8.49), нарушили бы эту закономер-
закономерность. Проведенное рассмотрение подтверждает правильность условий
квантования (8.49).
Так как тг^ =гф\ то одновременные перестановочные соотношения
дираковских полей должны иметь вид либо
-у),	(8.51)
либо
Ш*), Ф1(У)} = Фа(х)ф\(у) + Ф1(у)фа(х) = 5аЬ5^(*-у). (8.52)
Вариант (8.51) реализуется, если (выписываются лишь ненулевые (ан-
(антикоммутаторы),
К*, а\,в,] = [bls, bps,} = Bтг)Ч88,5^(к-р),	(8.53)

8.3. Квантование дираковского поля	113
а вариант (8.52) — если
{aks, aps,} = {bks, bps,} = BтгK555/5C)(к-р).	(8.54)
Действительно, для (8.51), при помощи (8.53), и для (8.52), при помо-
помощи (8.54), получаем
1 ^г^ Г ,- к (х_у) икзщз _^_е-г к (х-у) и_к - "I 0^
BтгK 2о,к Д2
Теперь учтём, что
=ft±m.	(8.56)
s=l,2
Соотношения (8.56) следуют из равенств
S'=±2ra5Ss>, uks u_ks, = 0,	(8.57)
уточняющих условия нормировки (8.39), и уравнений (8.38а), (8.38 6).
Последнее из равенств (8.57) легко проверяется в системе отсчёта,
в которой к = 0. При помощи (8.38 а), (8.38 6) и (8.57) немедленно
устанавливается, что все матричные элементы вида u±ks' ••• u±ks" 4 х
х 4 матриц в левых и правых частях равенств (8.56) совпадают. При
помощи (8.56) выражение (8.55) преобразуется к виду
BтгK 2Wfc ^2
е-гк(х-у) (
что и требовалось.
Теперь покажем, что коммутационные соотношения (8.53) непри-
неприемлемы с физической точки зрения. Действительно, с учётом условий
квантования (8.49) КС (8.53) приводят к индефинитной метрике в про-
пространстве состояний. Например, если \ks) = b^s | 0), то (ks|k,s)<0.
Поэтому остаётся единственная возможность (8.52), (8.54). Выпишем
дополняющие (8.52), (8.54) одновременные антикоммутационные соот-
соотношения:
= {^ks, ^PS'} = De, a^s,} =	(8.58)
= {«ks, bps'} = {aks, 6pS/} = 0.

114
Лекция 8. Уравнение Дирака
Приведём оператор Гамильтона-Дирака (8.47) к нормальному виду при
помощи (8.54) (сравни с G.38)):
(8.59)
s=1'2
где V — объём пространства. Аналогично для электрического заряда
(8.48) получаем
к ^ ( +	,+ , \ п
= е
10-
(8.60)
Из (8.59) и (8.60) мы видим, что плотность энергии и заряда в теории
Дирака равны (—оо) (поскольку е < 0). Если эти постоянные значения
Sod и Qod вычеркнуть, то энергия любого фермионного состояния (за
исключением вакуумного с нулевой энергией) положительна, а заряд
равен е х (число частиц — число античастиц). Считается, что части-
частицы порождаются операторами а), а античастицы — операторами Ъ^.
Первые называются электронами, а вторые — позитронами. Например,
одноэлектронное состояние
а однопозитронное состояние
Оператор импульса дираковского поля (см. приложение В)
НC) к
Имеем
s=l2
up\ps),
P |ps),
=pp|(+)ps)
Таким образом, операторы рождения порождают состояния с теми
импульсами, которые содержатся в обозначениях этих операторов. Из
(8.58) следует, что (a^sJ = (b^sJ = 0. Последние равенства означают,
что в фермионной системе в одном состоянии не может находиться

8.4. Алгебра матриц Дирака	115
более одной частицы. Таким образом, имеется фундаментальное раз-
различие между бозонными и фермионными системами.
Описанная ситуация в теории Дирака интерпретируется следующим
образом. В теории имеется равное число состояний с положительной и
отрицательной энергией. Вакуумное состояние — это такое состояние,
в котором все состояния с отрицательной энергией заполнены, а все
состояния с положительной энергией — пустые. Электронные состоя-
состояния получаются путём заполнения уровней с положительной энергией,
а позитронные — путём освобождения (создания дырок) некоторых
заселённых отрицательночастотных состояний. При этом энергия и
заряд относительно основного состояния возрастают (помните, что е <
< 0). Поэтому энергия и заряд позитронов положительны. Заметим,
что антикоммутационные соотношения симметричны относительно пе-
перестановок операторов рождения и уничтожения. Таким образом, ответ
на вопрос, какие операторы являются операторами рождения, а какие
— операторами уничтожения, а также как заполняется вакуум, опре-
определяется общим знаком перед гамильтонианом.
Обозначим через |/;0) ложный вакуум, то есть такое со-
состояние, в котором и положительно- и отрицательночастотные
состояния не заполнены. Такое состояние удовлетворяет условиям
aks | f\ 0) — 0, ^ks | f\ 0) — 0. Это — действительно не заполненное
состояние, поскольку оно обращает в нуль операторы Гамильтона (8.47)
и заряда (8.48). Кроме того, ф | /; 0) = 0. В теории с таким вакуумом
следовало бы сделать переобозначение b^ks <—> b\^s. Мы видим,
что с физической точки зрения такая теория неудовлетворительна,
поскольку в ней существуют и распространяются во времени состояния
с отрицательной энергией.
8.4. Алгебра матриц Дирака
Из соотношений (8.5) вытекает ряд соотношений между 7~
матрицами, необходимыми при конкретных вычислениях. Напрмер,
WV = 7m7m=4,	(8.61)
где 7м = t)\Lvlv• Далее:
7д7^7м =-2 -у", 7д7 V7M = 4 г]Хи, 7д7 V7P7M =-2 7P7V>
(8.62)
Az'7p7cj7m = 2 (t^VtV + 7P7Z'7V)-
Введём обозначение:
Очевидно, что
^	M = 0,	(8>64)

116	Лекция 8. Уравнение Дирака
так как из (8.18 в) следует, что tr7M = (О^)^ ir^". Из (8.5) находим,
что
Т^ = rfv	(8.65)
(след единичной 4 х 4-матрицы равен 4). Протаскивая в Tx^vp матри-
матрицу 7Л П°Д знаком следа слева направо и пользуясь при этом (8.5) и
(8.65), получаем
Отсюда следует, что
tr 75 = 0.	(8.67)
Имеем также:	«
- tr 757 VtV = i ех^Р.	(8.68)
Отметим, что след от любого нечётного числа 7-матриц равен нулю.
8.5. Дискретные симметрии уравнения Дирака
А. Пространственная инверсия (Р-чётностъ)
В результате этой инверсии пространственные компоненты 4-
векторов изменяют знак, а временные компоненты остаются неизмен-
неизменными. Пусть штрих сверху отмечает преобразованные величины. Тогда
х'° = х°, х^-х,
J' °(х°, х) = J°(x°, -х), У(х°, х) = -J (х°, -х).
Кроме того мы потребуем, чтобы преобразованное дираковское поле
так же, как и исходное поле, удовлетворяло уравнению Дирака.
Легко проверить, что если
Ф' (ж0, х) = фР(х°, х) = 7V (ж0, -х),	(8.70)
то все перечисленные требования удовлетворяются.
Действительно, для J1^ (x) = ф' (х)^^ ф' (х) имеем соотношения
(8.69) вследствие свойств 7~матРиД (8.5) и (8.8). Кроме того, из урав-
уравнения Дирака вытекает уравнение
(i^V^-m)^P(x°, x)=0,	(8.71)
Наоборот, из последнего уравнения следует уравнение Дирака для
поля ф(х). Аналогично можно показать, что
(фф)'(х\^) = (фф)(х\ -х),
то есть величина (фф) является скалярной относительно преобразо-
преобразования чётности.
Повторное применение преобразования чётности приводит к тожде-
тождественному преобразованию.

8.5. Дискретные симметрии уравнения Дирака	117
Б. Обращение времени (Т-чётностъ)
При обращении времени имеем
х1 ° =-х°,	Xх =х,
J/0(x°, x) =J°(-x°, x),	Jx(x°, x) = -J(-x°, х), (8.72)
А/0(х°, х) =Л°(-ж°, х),	Ах(х°, х) =-А(-ж°, х).
Уравнение Дирака может сохранять свой вид лишь если дираков-
ское поле сопрягается комплексно, что следует из уравнения Паули, в
которое переходит уравнение Дирака в нерелятивистском пределе. О
необходимости в данном случае эрмитовского сопряжения состояний
и операторов говорит также тот факт, что при обращении времени
начальное и конечное состояния меняются местами, но в амплиту-
амплитуды перехода первые входят в бра-представлении, а вторые — в кет-
представлении.
Всем этим требованиям удовлетворяет преобразование дираковско-
го поля вида
ф'(х°, х) =фТ(х°, х) = итфт(-х°, х),
_	(8.73)
фт(х°, х) = -фт(-х°, х)С/т,
где в спинорном и стандартном представлениях
^т = 73717°, С4 = -1-	(8-74)
Имеем
Поскольку при обращении времени переставляются начальное и
конечное состояния, то формулы преобразования (8.72)-(8.75) должны
быть дополнены правилом, согласно которому всякое произведение
операторов преобразуется в произведение преобразованных операторов
в обратном порядке. При помощи формул (8.73)-(8.75) устанавливаем,
что поле фт удовлетворяет уравнению Дирака, если поле ф удовле-
удовлетворяет сопряжённому уравнению Дирака, и наоборот. Кроме того,
согласно (8.73)-(8.75) и указанному правилу,
(ф^ф)т(х0, х) = -(фтит^итфт)т\-х°, х) =
(8.76)
ТТТТ^	(-х°, х).
Здесь отсутствует суммирование по индексу /i.
В. Зарядовое сопряжение (С-чётностъ)
Из (8.46) и (8.49) видно, что поля ф и ф уничтожают частицу
и античастицу, соответственно, которые имеют взаимно противопо-
противоположные заряды. Поэтому операция зарядового сопряжения должна

118	Лекция 8. Уравнение Дирака
сопровождаться операцией дираковского сопряжения полей. При этом
векторный ток должен менять знак:
J'Hx) = Jc(x) = -J^x).	(8.77)
Следует также считать, что при зарядовом сопряжении изменяет знак
либо электрический заряд, либо 4-потенциал. Кроме того, исходные
и зарядово-сопряжённые поля должны одновременно удовлетворять
уравнению Дирака.
Все указанные требования выполнены, если
ф'(х) = фс(х) = исфт(х), фс = -фт(х) Uc\	(8.78)
причём в спинорном и стандартном представлениях
Uc =^727°>	U^l^Uc = -^т,
(8.79)
= 75Т,	Ucla^Uc =-a^T.
При помощи (8.79) легко проверить, что после преобразования (8.78)
и изменения знака 4-потенциала уравнение Дирака переходит в урав-
уравнение Дирака для зарядово сопряжённого поля. Кроме того,
Отсюда и из свойства антикоммутативности (8.52) следует равенство
(8.77).
Повторное применение операции зарядового сопряжения приводят
к тождественному преобразованию.
Сформулируем понятие «вещественности» дираковского поля. «Ве-
«Вещественное» дираковское поле называется майорановским полем.
Определение. Дираковское поле называется майорановским, если
операция зарядового сопряжения (8.78) не изменяет это поле, то есть
если
ф(х) = исфТ{х) =г^ф^т(х).	(8.80)
Формула (8.80) имеет смысл в спинорном и стандартном представ-
представлениях.
Так как уравнение Дирака инвариантно относительно зарядового
сопряжения, то майорановское поле может быть решением уравнения
Дирака: если поле ф удовлетворяет уравнению Дирака, то и поле
11сфт также удовлетворяет уравнению Дирака. Поэтому и майоранов-
майорановское поле (ф + 11сфт) удовлетворяет уравнению Дирака.
8.6. Уравнение Вейля
Пусть поле ф удовлетворяет уравнению Дирака с нулевой массой
[ш = 0). Тогда этому же уравнению удовлетворяет и поле ^ф, а также
поля	1
Ф± = ^AТ15)Ф-	(8.81)

8.7. Точное решение уравнения Дирака в кулоновом потенциале
119
Два поля (8.81) называются правым и левым вейлевскими полями,
соответственно.
В спинорном представлении (8.6)
и
:
и уравнения Дирака для вейлевских полей имеют вид
(8.82)
(8.83)
Уравнения (8.83) называются уравнениями Вейля.
Так как генераторы преобразования Лоренца о~^и (8.10) коммути-
коммутируют с проекционными операторами A/2)A ±75)> то уравнения Вейля
лоренц-инвариантны.
8.7. Точное решение уравнения Дирака в кулоновом
потенциале
Рассмотрим стационарное уравнение Гамильтона-Дирака в кулоно-
кулоновом потенциале (см. (8.33), (8.34)):
—г а. д
Za
a =
(8.84)
Безразмерная величина а называется постоянной тонкой структу-
структуры.
Для решения уравнения Дирака (8.84) в центрально симметрич-
симметричном поле следует пользоваться нерелятивистскими двухкомпонентны-
ми спинорными состояниями QjiM> имеющими определённые значе-
значения квадрата орбитального момента 1^ = —ге^х^д^, квадрата полного
момента (8.1) и его проекции М. Из нерелятивистской квантовой
механики известно, что
4 + 1/2,1,M
4-\/2,l,M
lj + i+м
2j + 2 У'-м+1/2 i
(8.85)
о = 5
j j>
5мм'-

120	Лекция 8. Уравнение Дирака
Так как
[j , (а 8)} = [j , (an)} =0, n = x/r,	(8.86)
то спиноры
(8.87)
имеют прежние значения чисел j и М. Однако числа орбитальных
моментов спиноров (8.87) изменяются, поскольку чётности спинора
fljiM и спиноров (8.87) относительно преобразования х^ —х про-
противоположны. Так как при заданном значении j для / имеется всего
две возможности I = j ± A/2), то ясно, что спиноры (8.87) пропорци-
пропорциональны друг другу:
-1A+1) ~1
-{ап)плм- (8.88)
г
Коэффициент в равенстве (8.88) проверяется путём умножения этого
равенства слева на (<тп).
Будем решать уравнение (8.84) в стандартном представлении (8.7)
при помощи подстановки
/ /(гЩш(#,Ф) \
ф =	.	(8.89)
\ (){)п{$Ф) )
Спинор (8.89) имеет определённую чётность относительно операции
пространственного сопряжения: согласно (8.7), (8.69) и (8.70) имеем
для спинора (8.89) фр = (—1)^. Так как оператор Гамильтона-Дирака
в левой части уравнения (8.84) коммутирует с оператором Р-чётности
(см. (8.70)), то диагонализовать следует одновременно эти два опе-
оператора. Подставляя (8.89) в уравнение (8.84), пользуясь равенством
(8.88), в результате несложных преобразований приходим к следующей
системе уравнений:
'	(8.90)
{ -{j + 1/2) = -(I + 1), если j = l + 1/2
x=\ U ' ' V ;	.	(8.91)
\ (j+l/2) = l,	если j = 1-1/2
Штрих сверху означает производную по г.
Исследуем поведение решений системы уравнений (8.90) при г —> 0
и г —> оо.

8.7. Точное решение уравнения Дирака в кулоновом потенциале 121
При г —> 0 система (8.90) переходит в систему
(rf' + (l+x)f-Zag = O.
{ rg' + (l-x)g + Zaf = O,
решение которой ищется в виде / = аог7, д = Ъ^г1. Подстановка
такого вида / и д в (8.92) приводит к уравнению
Za 7+1-
Для существования ненулевого и нормируемого решения уравнения
(8.93) необходимо и достаточно, чтобы
-(^о02.	(8.94)
Соответствующее ненулевое решение с точностью до общего множите-
множителя имеет вид
ry	7	/ , / 0 ( ry \0 \	/О ПС\
При г ^ оо система (8.90) переходит в систему
f /' - (га + е) д = О,
\ , _	(8-96)
Мы будем интересоваться лишь дискретными уровнями, для кото-
которых га2 — е2 > 0. Тогда система уравнений (8.96) приводит к следую-
следующему поведению / и д нормируемых состояний при г —> оо:
f ~ е~Хг	п ~ е~Хг	Л — л/га2 — е2	(8 97)
Из проведенного рассмотрения видно, что решение системы урав-
уравнений (8.90) в случае дискретных уровней энергии следует искать в
виде
/ = e~Xr ^]asr7+s, ^ = е-Лг ^6sr7+s.	(8.98)
s=0	s=0
В (8.98) константы j и X задаются согласно (8.94) и (8.97), соответ-
соответственно, а коэффициенты clq и bo — согласно (8.95).
Подставим анзац (8.98) в систему (8.90) и приравняем нулю по
отдельности коэффициенты при одинаковых степенях г. Таким образом
получается следующая система рекурсионных уравнений:
Za
Asus+\=Bus, 5 = 0,1,..., us=

122	Лекция 8. Уравнение Дирака
x2-(ZaJ +s + x -Za
А8=\ V	,		| , (8.99)
Za	\ + a x2-(ZaJ+s-x
В =
\m-e A /
Заметим, что самое первое соотношение при степени г~\ связывающее
лишь значения ао и Lq между собой, удовлетворяется автоматически,
вследствие специального выбора щ в соответствии с (8.95).
Так как
det As = (I + s) (I + s + 2^х2 - (ZaJ) ^ 0,	(8.100)
то уравнение (8.99) переписывается в виде
us+\ = А~х • В -us, Ajl = (detAs)~lx
\+Jx2-(ZaJ+s-x	Za
x | V			| . (8.101)
-Za	l+A x2-(Za)
Собственные значения матрицы В равны нулю и 2 Л, и пусть v\
и v2 обозначают соответствующие собственные векторы:
В v{ =0,	Bv2 =2Xv2,
(8.102)
Согласно (8.100) и (8.101), при s -^ оо,
А~х -^ -.	(8.103)
s
Поэтому, если при достаточно больших s
us = pv\ +qv2, q^0,	(8.104)
где р и q — некие числа, то согласно (8.98), (8.102) и (8.103), при г —>
—> оо функции / и д ведут себя как еЛг. Волновые функции с таким
поведением ненормируемы и потому неприемлемы. Чтобы избежать
этой ситуации, для некоего s мы должны иметь
A~xv2 = tvx.	(8.105)
Здесь t — некое число. Действительно, для вектора общего вида
(8.104) Bus = 2\qv2. Если имеет место равенство (8.105) для некоего
числа t, то вследствие (8.102) us+2 = 0, рекурсионная цепочка об-
обрывается и волновая функция оказывается нормируемой. При помощи
(8.102) уравнение (8.105) переписывается как

8.7. Точное решение уравнения Дирака в кулоновом потенциале
123
В-А~1
=0,
5 = 0, 1, ... .
(8.106)
Ещё одна возможность обрыва рекурсионной цепочки (8.101), не
учтённая в (8.106), реализуется при к < 0 в случае щ = tv\ для
некоего числа t. Действительно, при к < 0, компоненты вектора щ
разного знака (при к > 0 — одного знака) и уравнение щ = tv\
может быть реализовано соответствующим подбором параметров г и
t. Следовательно, уравнение
Вщ=0 при ж 0	(8.107)
также является условием квантования энергии.
Поскольку В — вырожденная матрица 2 х 2, то каждое из уравне-
уравнений (8.106) и (8.107) содержит лишь одно независимое алгебраическое
уравнение, решение совокупности которых приводит к следующим зна-
значениям уровней энергии связанных состояний:
П-1/2
е = тс
1
(Zaf
nr
(8.108)
Пг =
, если j = l+ 1/2
, если j = l- 1/2
При получении формулы (8.108) было использовано соотношение
(8.91). Энергия основного состояния получается из формулы (8.108),
если в ней положить / = 0, j = 1/2, пг = 0:
г0 =
-(Za
(8.109)
Формулы (8.108), (8.109) являются точными и они остаются спра-
справедливыми при всех значениях заряда ядра, удовлетворяющих условию
(Zа) < 1. Поскольку |х| = j + 1/2, то согласно (8.108) имеет место
двукратное вырождение (не считая вырождения относительно прекции
полного момента М) уровней: энергии при I = j ± 1/2 совпадают, что
является точным результатом.
При малых зарядах ядра, когда (Z а) <С 1, представляет инте-
интерес разложение формулы (8.108) относительно (Zа). Поскольку а =
= е2/Tic, то это разложение можно трактовать как учёт релятивистских
поправок. Имеем:
(Za)Wf, , (Zaf Г 1	3]\ ,.o((ZaN)f
= тс: —
2п2
j+1/2
1
nr+j + - = I, 2, ... .
(8.110)

124	Лекция 8. Уравнение Дирака
Учёт поправок порядка O((ZaN) не имеет смысла, поскольку они
перекрываются радиационными поправками, имеющими порядок
O(a(ZaL) (см. лекцию 13). Формула (8.110) может быть также
получена при помощи ТВ в рамках нерелятивистской квантовой
механики, когда спин-орбитальное взаимодействие и релятивистская
поправка к кинетической энергии электрона воспринимаются как
возмущение (см. задачу (8.5)).
Задачи
1.	Выпишите уравнение Дирака для сопряжённого поля ф.
2.	а) Покажите, что векторный ток JM = ф^ф сохраняется в си-
силу уравнения Дирака (во внешнем электромагнитном поле), то есть
д^ = 0.
б) Докажите, что аксиально-векторный ток J5/x = ф^^ф веще-
веществен и в силу уравнения Дирака
Это означает, что в безмассовой теории сохраняется также и
аксиально-векторный ток (в классической теории),
в) Покажите, что полный 4-момент
= и
'ф
сохраняется, если поле ф удовлетворяет свободному уравнению Дира-
Дирака. Проверьте, что в стандартном представлении
е
где J1 совпадает с оператором полного 3-момента (8.1), если в (8.1)
сделать замену
* 0
Таким образом, в нерелятивистском пределе оператор s = A/2)<т
является оператором спина электрона.
3.	Используя закон преобразования дираковских полей при лоренц-
преобразованиях покажите, что векторный и аксиально-векторный
токи являются 4-векторами.
4.	Покажите, что уравнение Дирака инвариантно относительно калиб-
калибровочных преобразований:

8.7. Точное решение уравнения Дирака в кулоновом потенциале 125
где а (х) — произвольная вещественная функция.
5. Продолжите разложение уравнения Дирака до членов ~ 1/с2
и получите соответствующий гамильтониан для шредингеровской
двухкомпонентной волновой функции. Считать, что имеется только
электрическое центрально-симметричное внешнее поле (А = 0, еАо =
= Ф(г)). Получите выражение для спин-орбитальной связи в случае
атома водорода.
Ответ:
тт
6. а) Докажите, что при преобразовании Р-чётности
)'{рр, х) = -(ф*уЬ<фУ(х°, -х).
Здесь нет суммирования по индексу /i.
б)	Покажите, что при Т- и С-преобразованиях уравнение Дирака
сохраняет свой вид.
в)	Пусть ферт обозначает поле, возникающее из дираковского по-
поля ф при последовательном проведении операций обращения времени,
затем пространственной инверсии и, наконец, зарядового сопряжения.
Выразите ферт через ф.
г)	Покажите, что векторный ток майорановского поля тождественно
равен нулю.
7. Покажите, что уравнения Вейля инвариантны относительно обраще-
обращения времени и комбинированного СР-преобразования. Существуют ли
вейлевско-майорановские (т.е. одновременно вейлевские и майоранов-
ские) поля?

Лекция 9
КВАНТОВАНИЕ ФЕРМИОНОВ ПРИ ПОМОЩИ
ФУНКЦИОНАЛЬНОГО ИНТЕГРАЛА. S-МАТРИЦА
И ПРАВИЛА ФЕЙНМАНА В КЭД
9.1. Фермионный осциллятор
Рассмотрим гармонический фермионный осциллятор, динамика ко-
которого описывается гамильтонианом
H = uata,	(9.1)
где а^ и а — взаимно сопряжённые фермионные операторы рождения
и уничтожения:
{a, af}=l, a2 = 0, (afJ = 0.	(9.2)
Основное состояние |0) определяется условиями
а | 0) = 0, < 0 | 0 > = 1.	(9.3)
Очевидно, что в теории имеется ещё лишь одно состояние, ортогональ-
ортогональное к основному:
| 1)=а+|0), A|0) = @|а|0)=0,
A|1) = @|а^|0) = @|0) = 1.
Кроме того, в силу (9.1)—(9.3),
Н\0)=0, Н\1)=и\1).	(9.5)
Простейшая фермионная система (9.1)—(9.5) интересна тем, что ди-
раковская система (8.59) является суммой простейших ферми-систем.
Обратим внимание на следующий факт. Если бы гамильтониан был
равен ТС = —ио а) а, где фермионные операторы а) и а удовлетво-
удовлетворяют соотношениям (9.2), а основное состояние |/; 0) удовлетворяет
условию а |/; 0) =0 и |/; 1) = at |/; 0), то H\f\ 0) = 0, H\f\ 1) =
В этом случае энергия возбуждённого состояния меньше энергии
основного. Однако путём переопределения а = а\ а^ = а, |0) =

I
m
0
—m
9.2. Фермионный функциональный интеграл	127
= |/; 1), | 1) = |/; 0) мы приходим к ситуации, описанной формулами
(9.1)—(9.5) с той лишь разницей, что TL = и а) а — и. Здесь последнее
слагаемое в гамильтониане соответствует энергии вакуума Sq (8.59).
Таким образом, после переопределения новое основное состояние сов-
совпадает с исходным возбуждённым или заполненным состоянием.
Описанная процедура переопределе-
ния называется операцией заполнения
состояний с отрицательной энергией.
В результате, хотя основное состоя-
состояние имеет отрицательную энергию, все
возбуждённые состояния имеют энер-
энергию большую, чем энергия основного
состояния. Мы видели, что в кванто-
квантовой теории Дирака все состояния с от-
отрицательной энергией заполнены. На
рис. 12 изображено основное состоя-
состояние в теории Дирака. Заштрихованная
область спектра с энергиями меньше (—га) полностью заполнена.
9.2. Представление фермионных амплитуд
при помощи функциональных интегралов
Для решения этой задачи необходимо использование основ матема-
математического анализа над грассмановой алгеброй.
Пусть {аа, а^} — образующие алгебры Грассмана над комплекс-
комплексными числами, а = 1, 2, ... , п, причём
(oQ)* = а*, Ю* = аа.	(9.6)
а*раа= 0,
где с — комплексное число. Других соотношений, кроме (9.7), между
образующими грассмановой алгебры нет. Из (9.7) следует, что
а\ = а\ = ... = а\ = КJ = КJ = ¦¦¦ = (О2 = 0.	(9.8)
Отсюда видно, что общий элемент грассмановой алгебры представля-
представляется в виде
/(а, а*) = / = /О|О+
По
определению,
&(x &j3 ~т~
араа
= an
<%-
c,
с a*
= aa a
= a*c,
где коэффициенты /O|o, /ai|o и т. д. — комплексные числа.

128	Лекция 9. Функциональный интеграл и правила Фейнмана
Определим производные на грассмановой алгебре при помощи сле-
следующих формул:
д -я	д * -
о -р -ар,	г, -р- -ар,
о	о	(9Л°)
о #	а
9 аа	9 а*^
Представим элемент (9.9) в двух следующих видах:
/ = /о + aafa = /0 + а*/а ,	(9.11)
где /о и /а не зависят от аа, a /0 и /а не зависят от а*.
(В (9.11)_нет_суммирования по а.) Вследствие (9.7) коэффициенты
/о, /а> /о» /а определены однозначно элементом (9.9). Согласно
определению (9.10),
—/ = /а,	—/=7а-	(9-12)
9аа	' ^^а	а
Из сказанного следует, что
99	99	99	99
даа дар дар даа' да^ да^ да** даа'
о о	о о	(9.13)
до	до
даа да% да% даа'
Интегрирование на алгебре Грассмана определяется с помощью правил
<f = 7a-	(9-14)
Кратный интеграл понимается как повторный. Например,
da* daf3f= da* ( dapf) = da* fp.	(9.15)
Введенное правило интегрирования оправдывается тем, что интеграл
от полной производной равен нулю:
г	/ я \
= 0.	(9.16)
Из данных определений видно, что дифференциалы грассмановых об-
образующих антиперестановочны:
daa dар = — dар daa, da^ da^ = — da^ da^,
d aa d a*p = — da^ daa.
Обозначим через
da* da = Aa\ &a*2 ... da* dan dan_i ... da\.	(9.18)

9.2. Фермионный функциональный интеграл	129
Имеем
da* da /(a, a*) = fn...n\n{n-\)... l-
(9.19)
Пусть полное множество образующих грассмановой алгебры состо-
состоит из двух множеств {аа, а*а} и {г]а, г]а}. Будем называть чётными
(нечётными) элементами грассмановой алгебры те элементы, которые
разлагаются по чётным (нечётным) суммарным степеням образующих
грассмановой алгебры. Суммарная степень (или просто степень) произ-
произведения образующих алгебры Грассмана называется чётной (нечётной),
если произведение составлено из чётного (нечётного) числа образую-
образующих. Таким образом, все образующие грассмановой алгебры являются
нечётными элементами.
Пусть
aa = aa + qa, а* = а* + р*а,	(9.20)
где qa, р^ — нечётные элементы, разлагающиеся лишь по образующим
{г]а, г]а}. Согласно данным определениям (сравни с (9.19))
da* da/ (a, a*) =/i2...n|n(n-i)... 1 = da* da/(a, a*), (9.21)
то есть сдвиг переменных интегрирования согласно равенствам (9.20)
не изменяет значения интеграла.
Сделаем линейную однородную замену образующих грассмановой
алгебры:
аа = Uapbp, aa = U^pb*j,	(9.22)
или, сокращённо,
a = Ub, a*t = 6*t/7t.	(9.22х)
Для интеграла (9.19) имеем
/i2...n|n(n-i)... I = da* da/(a, a*) = da* da/ (Ub, V
= da* daf\2...n\n{n-\)...\(U\aibai) ... (UnOLnban)(U*pnb*pn) ...
••• (^1%%) = /i2...n|n(n-i)... l I det U\2 da* dab\ ... bn 6* ... 6*,
J
то есть
Hdet ?/|2da* dafri ... bn 6* ... b\ = 1.
Отсюда следует заключение, что (обратите внимание!)
| det U\2da* da = db* db.	(9.23)
Подчеркнём, что при замене переменных (9.22) в случае коммутирую-
коммутирующих переменных мы имели бы da* da = | det U\2 db* db.
5 C.H. Вергелес

130	Лекция 9. Функциональный интеграл и правила Фейнмана
Рассмотрим гауссов интеграл
7= [da* da ехр (a* Aapap).	(9.24)
Будем считать, что все элементы Аар — чётные. Имеем
ехр(а^Аарар) = 1 +...+ — (а* Аарар)п.
Нас интересует лишь последнее слагаемое, которое равно
(а*ахАа1рхарх) ... (а*апАапрпарп) = n!(detA)a* ... a* an ... ах =
= (-l)nn!(detA)ai ... апа*п ... a*. (9.25)
Поэтому в соответствии с (9.19) (общий знак здесь нас не интересует)
I=(detA).	(9.26)
Рассмотрим теперь интеграл
/ (ту, rj*) = Ida* da ехр (а*аАарар + г г]*ааа + г а* т^),	(9.27)
где {г]а, т?*} — образующие алгебры Грассмана, независимые от обра-
образующих {аа, а^}. Если сдвинуть переменные интегрирования в (9.27),
согласно (9.20), с qa = —iA~prjp, p* = —irj^A^ то интеграл (9.27)
переписывается как
1(г], rj*)=\da* da exp(a^Aapap) ехр(г/*А~^г//з).
С учётом (9.26) окончательно получаем
г
7 (г], г]*) = d a* d a ехр (а*аАарар + г г]^аа + г а* г]а) =
= (detA) ехр(г/*А~^г//з). (9.28)
Далее мы будем использовать тот факт, что показатель экспоненты
в правой части (9.28) равен экстремуму показателя экспоненты в
левой части (9.28) относительно переменных интегрирования {аа, а^},
рассматриваемых как независимые переменные. Действительно, диф-
дифференцируя показатель экспоненты в левой части (9.28) и приравнивая
результат нулю, находим экстремальные значения переменных:
п(с1) 	 _ • Д — \т„	л* (с0 	 —о <п* Л ~1	(О 9Ch
OL 		(У.0 /Р '	OL			//3'3d.'	\Zj.AiZJ)
Подставляя значения (9.29) в показатель экспоненты в левой части
(9.28) мы получаем показатель экспоненты в правой части (9.28). В
этом отношении фермионные гауссовы интегралы аналогичны бозон-
ным.
Теперь разработаем аппарат для фермионных операторов и фер-
мионных фоковских пространств в голоморфном представлении. Для

9.2. Фермионный функциональный интеграл	131
простоты ограничимся одной степенью свободы. Обобщение на много-
многомерный случай очевидно.
Голоморфными функциями назовём элементы грассмановой алгеб-
алгебры, зависящие только от а*:
f(a*) = fo + fia*.	(9.30)
Множество таких функций образует двумерное пространство, и
мы используем их для представления векторов состояний системы
(9.1)-(9.5). Скалярное произведение в пространстве голоморфных
функций определяется формулой
(f\g) = ^da*da(f(a*)yg(a*)e-a*a, (/(а*))* = /о* + /Г а. (9.31)
Легко проверить, что
(/Is) = /o
Таким образом, комплексное линейное пространство функций (9.30)
образует двумерное комплексное евклидово (или эрмитово) простран-
пространство с ортонормированным базисом (^о =1, Ф\ = &*). Согласно (9.32),
Операторы а) и а действуют в пространстве (9.30) следующим обра-
образом:	d
at / (a*) = a* / (a*), a f (a*) = — / (a*).	(9.33)
Если введенный базис представить базисными векторами в двумерном
эрмитовом пространстве как
(?) (?)	(9-34)
то операторы а) и а в этом базисе представляются матрицами
откуда очевидна их взаимная сопряжённость, а также правила анти-
антикоммутации (9.2).
Опишем способы задания операторов в голоморфном представле-
представлении. Запишем оператор общего вида
А = Коо + Кю af +Koia + Kn о)а.	(9.36)
Оператору (9.36) поставим в соответствие его нормальный символ
К (а*, а) = Кт + Кю а* + К01 а + Кхх а* а	(9.37)
и ядро
А (а*, а) = Д)о + Аюа* + Дм « + Ап а* а.	(9.38)

132	Лекция 9. Функциональный интеграл и правила Фейнмана
По определению действие оператора (9.36) задаётся в голоморфном
представлении, согласно правилу (сравни с B.10))
(Af)(a*)= \A(a*, a) f (a*) e~a ada*da.	(9.39)
Отсюда находим:
Афо = Аоофо + Аюфх, Аф\ = А0\ фо + Ап фи
откуда видно, что матрица ядра и матрица оператора,
Атп = (т\А\п), т,п = 0,1,	(9.40)
совпадают (сравни с B.11) и B.12)). Произведение операторов в голо-
голоморфном представлении задаётся формулой
(AiA2)(a*, a)=\Ai (a*, а)А2(а\ a) e~a*a da* da.	(9.41)
Для записи (9.39) и (9.41) необходимо было ввести две новые образу-
образующие грассмановой алгебры (а*, а), которые и далее будут вводиться
по мере необходимости.
Подставляя оператор (9.36) в (9.40), находим
Отсюда видно, что связь между ядром оператора и его нормальным
символом такова (сравни с B.13)):
А (а*, а) = еа*а К (а*, а).	(9.42)
Поскольку ядро ^-матрицы для одномерного бозонного осциллято-
осциллятора B.28) было получено при помощи лишь двух формул B.12) и B.13),
аналоги которых в фермионном случае (9.41) и (9.42) имеют точно
такой же вид, то выражение для ^-матрицы фермионного гармониче-
гармонического осциллятора с внешним антикоммутирующим источником г] и
гамильтонианом,
h = ua*a- -rL=- G7* а + а* г]),	(9.43)
V2
может быть выписано при помощи справедливых также и в фермион-
фермионном случае формул B.15) и B.26). Однако в фермионном случае следу-
следует учитывать антикоммутативность образующих грассмановой алгебры
и правило вычисления гауссовых функциональных интегралов (9.28).

9.3. Функциональный интеграл в теории Дирака	133
В результате в фермионном случае мы получим следующее выражение
для оператора ^-матрицы:
Sv(a\ а) = 1 : ехр |-^ | d t [ry*(t) а е^*+
W V (t) егшг] + Л [ d?ds 77*(t) 'e ^J * r/ (s) I: . (9.44)
Выражение (9.44) формально совпадает с оператором ^-матрицы, сле-
следующим из формулы B.27).
Заметим, что в фермиевском случае операция нормального упорядо-
упорядочения : ... : приводит произведение фермиевских операторов к нормаль-
нормальному виду с учётом их антикоммутативности. Например, : а\а\а^ := —
9.3. Функциональный интеграл в теории Дирака
В теории Дирака аналогом одночастичного гамильтониана (9.43)
является гамильтониан (см. (8.33))
Щ= [dC) х {ф (-if di + т) ф - (фг) + т?^)}>	(9-45)
в котором дираковские поля представляются согласно (8.46) и ферми-
евские операторы рождения и уничтожения удовлетворяют антикомму-
антикоммутационным соотношениям (8.54), (8.58); поля r\ [x) rj(x) — антиком-
мутирующие. Согласно (8.59), выражение (9.45) переписывается в виде
Г
= J
s=l,2
1
l±ks(t) = rj±b(t) U±ks ,	S±ks(t) = U±ksr]±k(t),
(9.46)
Jkx
Представление (9.46) показывает, что дираковский гамильтониан (9.45)
распадается на сумму одночастичных гамильтонианов вида (9.43). По-
Поэтому оператор ^-матрицы равен
^ (af, a) = — : exp \ i\
i\ dD) x (rj^o

134	Лекция 9. Функциональный интеграл и правила Фейнмана
dtd\
S<t	S=1'2	J
(9.47)
При помощи формул (8.56) преобразуем суммы в экспоненте следую-
следующим образом:
Y^ Jks(t) 5ks(s) =Y]k(t) (ft + m)rjk(s),
s=l,2
s=l,2
где k = (cjfc, k). Последние равенства позволяют преобразовать второе
слагаемое в экспоненте в (9.47) сначала к виду
и затем к виду
где Dc(x — у)	определена согласно B.49). Определим дираковский
пропагатор как
Sc(x — у) =	—(г 7М(9/х + m) Dc(x — у) =
Г №к	U + ™ Г №к
—		^ ^ р-гк (х-у) _ ^	[^_ q (ъ.\ -гк (х-у)
~ \ BттL к2-т2+ ip	~ \ BтгL с[)
I \ Zj \ ) гь	//о \^ о с I \ ?i /I / ,ъ а г^\
Таким образом,
^iaK Ъ\а,Ъ) = — :exp i dD)
-i^dD)xdW уr](x)Sc(x-y)r](y)
s=l,2

9.3. Функциональный интеграл в теории Дирака	135
4"'
гр0 (X) -
где к = (а;&, к).
Укажем, что правая часть уравнения (9.50) может быть получена
также при помощи формулы (9.28) путём прямого вычисления ферми-
онного функционального интеграла (сравни с G.44)),
D ф D ф ехр < г \ d^ х [ф (г 7^<9Д — га) ф -\-т\ф + фг}]>, (9.51)
J	I J	J
с граничными условиями, фиксирующими, при t —> —оо,
положительночастотные составляющие полей ф^ \х) и ф^ (х), и
при t —> +00, — отрицательночастотные составляющие полей ^q \x)
и i/jq'(x), согласно (9.50). В (9.51) дираковская функциональная мера
= const- ]Jl[l[da*ks(t)daks(t)db*ks(t)dbks(t). (9.52)
t k
Это утверждение легко проверяется, если учесть, что экстремальное
значение показателя экспоненты в (9.51) при указанных граничных
условиях достигается на полях (сравни с B.53))
ф(С1)(х) = фо(х) - d{4)ySc(x-y)r](y),
Ф{с1)\х) = Уо\х) ¦
Подстановка полей (9.53) в экспоненту в (9.51) опять приводит к (9.50).
Второе равенство в (9.52) легко получается из соотношения для
интегралов от квадратичных форм дифференциалов фермионных пере-
переменных:
). (9.54)
При выводе (9.54) фермионные операторы {aks, bks, a^ks, b^ks} в выра-
выражениях для дираковских полей (8.46) заменяются на соответствующие
грассмановы переменные и используются формулы (8.57).

136	Лекция 9. Функциональный интеграл и правила Фейнмана
9.4. Общая формула для S-матрицы в КЭД и
простейшие амплитуды
Мы можем, наконец, собрать все формулы вместе и выписать общее
выражение для S-матрицы в КЭД при помощи континуального инте-
интеграла по бозонным и фермионным полям:
16тг
_ "П _
+ ф (i7MVM — га) ф + JMAM + ту ^ + ^ ^ г ^Л^ ^ Ф Еф. (9.55)
Граничные условия для полей при \t\ -^ оо указаны в лекции 7 и
предыдущем пункте. Как обычно, для развития ТВ действие в экспо-
экспоненте в (9.55) разбивается на квадратичную (линейную) и нелинейную
части. Последняя описывает взаимодействие:
S = S0{A, ф, ф; J, % r)}+Sint, iSint = -ie \d{d)xA^ фа^аЬфь- (9.56)
Представим Sint в виде дифференциального оператора
(9.57)
который может находиться как под знаком функционального интегра-
интеграла, так и вне его. Это позволяет переписать выражение (9.55) в виде
'л\	О	О	I,	О
X5J»(x) 5г]а{хIаЪ Srjb(x)
:ехр|г [dD) x (-J Ao + rj ф0 + ф0 rj) + i fdD)xdD)y
1
— x
2
»{x - у) Г(у) - rj(x) Sc(x - y) ri(y)
, (9.58)
J,rJ,r]=O
где пропагаторы D^v и Sc задаются формулами G.53) и (9.49),
соответственно. Асимптотические поля Ао, ф0, фо разлагаются,

9.4. Общая формула для S-матрицы в КЭД и простейшие амплитуды 137
(см. G.47) и (8.46)):
	 г ^C) и I о
Л / \	\~^	/	/	—ikx f * г/сж\
^о(ж) = [ ^^ -^ ^ (aks^se-^ + bisii-kseikx), (9.59)
r
=
J
Здесь вектора поляризации фотонов вка удовлетворяют условиям
G.55), а спиноры г^, г^-^з — уравнениям (8.38а, 8.38 6) и условиям
(8.57). Коммутационные или антикоммутационные соотношения опе-
операторов рождения и уничтожения имеют вид G.33) и (8.54), (8.58).
Вакуумное состояние определяется условиями
aks|O)=6ks|O)=ckcK|O)=O,
а, например, состояние электрона с импульсом р и спином s и
позитрона с импульсом q и спином sf и фотона с импульсом к и
поляризацией а имеет вид
|ps, qsx, ka) = yj2up2uq2\k\ 4s^s,4a|0),
и т.д.
Из выражения (9.58) получаем также амплитуду перехода из ваку-
вакуума в вакуум в присутствии внешних источников:
Z(J,r?,77) = lexp(-e[d^ * *
1
'(9.60)
Укажем здесь, что, при комплексном значении параметра размер-
размерности пространства d, базовое соотношение для матриц Дирака (8.5)
остаётся в силе, в то время как ряд других принимают следующий вид:
Поэтому если в (8.63) определить
то все формулы для этой величины, полученные в лекции 8, сохра-
сохраняются. Парадоксы возникают при комплексном d лишь при работе

138	Лекция 9. Функциональный интеграл и правила Фейнмана
с 75~матРиЦей, однако с этим парадоксом нам придётся столкнуться
лишь в лекции, посвященной аксиальной аномалии.
При комплексном значении размерности пространства d, выра-
выражения для ^-матрицы (9.58) и производящего функционала (9.60)
регуляризованы. При этом сохранена калибровочная инвариантность
теории, поскольку эта симметрия имеет место при любом d.
Рассмотрим простейший процесс рассеяния двух электронов в два
электрона. Для этого следует выражение для оператора ^-матрицы
(9.58) поместить в обкладки между бра-состоянием @1 су^ ap>2S>2
и кет-состоянием ctp2S2 aplSl |0)- Здесь рь sj и р[, s[, г = 1, 2 —
p22 pll
импульсы и спины начальных и конечных электронов. Чтобы сократить
запись формул, мы будем писать щ вместо uPlSl и п2 вместо %>^>
и_\ вместо u-PlSl, и т.д. Наинизший порядок, в котором амплитуда
этого процесса отличается от нуля, получается при разложении первой
экспоненты в (9.58) до второго порядка, что даёт вклад в ^-матрицу:
(9.62)
Поскольку поле фо удовлетворяет уравнению Дирака, то
<9М [фо(х)"у^фо(х)] = 0, и потому продольная часть фотонного
пропагатора в (9.62) выпадает; в качестве фотонного пропагатора
можно взять D1^ ~ ц^у. Мы видим, что физические величины не
зависят от калибровки. Это утверждение имеет место во всех порядках
теории возмущений. Помещая выражение (9.62) в указанные выше
обкладки, в результате простых вычислений получаем для амплитуды
гМ:
гМ = 4те2 (- (п'2^щ) {п\^^их) - - (п'2^их) (п[-/^и2)\ , (9.63)
[t	и	J
где используются введенные согласно D.27) инварианты
s = (pi +p2J, t = {pi -р[J, и = (pi -р'2J,
(9.64)
Формула для сечения рассеяния а двух частиц в две частицы в
системе центра инерции содержится в Приложении (см. (А 19)). Пусть
? — Р°\ + р1 ~ полная энергия, р{ = —р2 = р и р^ = — р2 = рх —
начальный и конечный импульсы. Тогда в нашем случае
da= 1М1 dox,	(9.65)
64тг2?2
где Ао1 — дифференциал телесного угла конечного импульса рх.

9.4. Общая формула для S-матрицы в КЭД и простейшие амплитуды 139
В системе центра инерции
/	/ \ 9	л 9 • 9 ^	а 9	9 ^
t = "(Pi - Pi) = - 4р2 sm2 -, u = -4p2 cos2 - ,
2	D2	(9-66)
2	= — do',
7Г
где i? — угол рассеяния.
Рассмотрим это сечение в нерелятивистском пределе, когда, соглас-
согласно (8.42),
uf^u = 2mw^w5g.	(9.67)
Подставим (9.63) с учётом (9.67) в (9.65) и усредним по начальным
спинам электронов (то есть заменим везде waw^ —> \5аC для началь-
начальных частиц):
Теперь просуммируем независимо по спинам конечных частиц. В ре-
результате получим, что
А
tz uz tu
¦
У Shi*! COS4f Sin f C0S 2/
где v = 2p/m — относительная скорость электронов. Сечение (9.69)
совпадает с известным результатом в нерелятивистской теории.
Графически амплитуда (9.63) представляется в виде суммы двух
следующих диаграмм Фейнмана (рис. 13).
Р\ —>	^	^ Р\	Р\
2
(а)	(б)
Рис.13
Вычислим теперь в наинизшем порядке упругую амплитуду рассея-
рассеяния электрона на позитроне. Для этого следует вычислить выражение
(9.62) в обкладках @ | ap;s; bp/s/ и Ь^^ а^51 | 0):
гМ = 4тгге2 J -(п^^^г) (u_27m^i) - т(^-27м^-2) (^i7^i) [» (9-70)
Is	г	)
где 5, t и и задаются согласно (9.64). Амплитуда (9.70) представля-
представляется двумя диаграммами (рис. 14).

140	Лекция 9. Функциональный интеграл и правила Фейнмана
-pf2	-P2 < <	<- ~pf2
(a)	F)
Рис. 14
Легко увидеть, что амплитуда (9.70) получается из амплитуды (9.63)
(и наоборот) путём замены р^ —> — р2, Р2 ~^ ~Р2, При этом происходят
замены t <-> t, и ^ s; диаграмма (а) на рис. 13 переходит в диаграмму
(б) на рис. 14, диаграмма (б) на рис. 13 переходит в диаграмму (а) на
рис. 14.
9.5. Правила Фейнмана для КЭД
Рассмотренные два примера для амплитуд (9.63) и (9.70) помогают
понять правила Фейнмана для диаграммной техники при вычислении
амплитуды рассеяния гМ (в импульсном представлении). Эти правила
выводятся при помощи выражения для ^-матрицы (9.58).
1.	Приближению n-го порядка ТВ отвечают диаграммы с п верши-
вершинами, в каждой из которых сходятся одна входящая и одна выходящая
электронные (сплошные) и одна фотонная (волнистая) линии. В ампли-
амплитуду процесса рассеяния входят все диаграммы, имеющие свободные
концы (внешние линии) в количестве, равном числу начальных и
конечных частиц.
2.	Каждой внешней входящей сплошной линии соответствует ам-
амплитуда начального электрона ир или конечного позитрона u-v (р
— 4-импульс частицы). Каждой выходящей сплошной линии ставится
в соответствие амплитуда конечного электрона пр или начального
позитрона п-р.
3.	Каждой вершине ставится в соответствие 4-вектор (—ге^).
4.	Каждой внешней входящей волнистой линии соответствует ам-
амплитуда начального фотона л/4тг ем, а выходящей линии — амплитуда
л/4тг е* конечного фотона (е — 4-вектор поляризации фотона). Вектор-
Векторный индекс \i совпадает с индексом матрицы 7м в соответствующей
вершине (так что возникает скалярное произведение 7мем или 7^ер-
5.	Каждой внутренней сплошной линии ставится в соответствие
множитель iSc(p) = г (j/— m + ie)~\ а внутренней волнистой линии —
множитель
ге
ге

9.5. Правила Фейнмана для КЭД	141
Тензорные индексы fi, v совпадают с индексами матриц 7М> 1и в
вершинах, соединяемых волнистой линией.
6.	Вдоль каждой непрерывной последовательности электронных ли-
линий стрелки имеют неизменное направление, а расположение биспи-
норных индексов вдоль них соответствует записи матриц слева направо
при движении против стрелок. Замкнутой электронной петле отвечает
след произведения расположенных вдоль неё матриц.
7.	В каждой вершине 4-импульсы пересекающихся в ней линий
удовлетворяют закону сохранения, то есть сумма импульсов входящих
линий равна сумме импульсов выходящих линий. Импульсы свобод-
свободных концов — заданные (с соблюдением общего закона сохранения
4-импульса) величины, причём позитронной линии приписывается 4-
импульс (—р). По импульсам внутренних линий, остающимся нефик-
нефиксированными после учёта законов сохранения во всех вершинах, про-
производится интегрирование (по сг ^р/BтгL).
8.	Входящему свободному концу, отвечающему внешнему электро-
электромагнитному полю, ставится в соответствие множитель
4-вектор q связан с 4-импульсами сплошных электрон-позитронных
линий в этой же вершине законом сохранения. Если поле не зависит
от времени, свободному концу ставится в соответствие множитель
а по остающимся нефиксированными трёхмерным импульсам внутрен-
внутренних линий производится интегрирование по сг ^р/BтгK.
9. Дополнительный множитель (—1) привносится в выражение для
гМ каждой замкнутой электронной петлёй и каждой парой пози-
тронных внешних концов, если эти концы — начало и конец одной
последовательности сплощных линий. Если среди начальных или сре-
среди конечных частиц имеется несколько электронов или позитронов,
то относительный знак диаграмм, различающихся нечётным числом
перестановок пар тождественных частиц (т. е. соответствующих им
внешних концов), должен быть противоположным.
Последнее правило означает, в частности, что одинаковыми знаками
должны обладать диаграммы с одинаковыми сплошными линиями, т. е.
диаграммы, которые оказались бы тождественными после снятия с них
всех фотонных линий. Укажем также, что при наличии тождественных
фермионов общий знак амплитуды условен. Однонаправленность стре-
стрелок вдоль фермионных линий (правило 6) очевидна из того, что любая
фермионная линия даёт в диаграмму множитель вида
... -fSc(x - у) YSc(y - z) 7A Sc(z - и) ...

142	Лекция 9. Функциональный интеграл и правила Фейнмана
Если определить направление стрелки фермионногой линии совпада-
совпадающим с направлением распространения электрона, то в пропагаторе
г Sc(x — у) стрелка направлена от точки у к точке х. Действительно,
согласно задаче 1.в) при х° > у0, величина iSc(x — y) является
амплитудой распространения электрона из точки у к точке х и при
х° < у0 — амплитудой распространения позитрона от точки х к точке
у. Так как направление стрелки пропагатора не зависит от значения
его аргументов, то мы видим, что вдоль стрелок электрон-позитронной
линии распространяется электрон, а против стрелок —позитрон.
Задачи
1. Определим хронологически упорядоченное произведение от любого
числа дираковских полей в представлении Гейзенберга,
как произведение всех этих операторов, расположенных справа налево
в порядке возрастания их временных аргументов, причём знак этого
произведения определяется чётностью перестановки, которую нужно
произвести, чтобы получить этот порядок из порядка, указанного под
знаком Т-произведения.
а)	Покажите, что
@\(Тфа1(Х1) ...фа1(Х1)фа1
у( Y\m-l	S	S	и	Z
б)	Покажите, что этот коррелятор не равен нулю лишь если m =
= 21.
Указание. В функциональном интеграле (9.55) (под знаком ко-
которого имеются усредняемые поля) сделать глобальное преобразование
полей:
и учесть, что при этом мера D ф Иф инвариантна. ?
в)	Покажите, что в свободной теории
2. Сформулируйте и докажите теорему Вика для фермиевских
операторов рождения и уничтожения.
3*. Вычислите сечение рассеяния фотона на электроне (эффект Комп-
тона) в наинизшем приближении, считая начальные частицы непо-

9.5. Правила Фейнмана для КЭД	143
ляризованными и не фиксируя спины конечных частиц. Используя
формулу (А.22), выпишите ответ через инвариантные переменные Ман-
дельстама и затем перейдите в систему отсчёта покоя электрона. Рас-
Рассмотрите случай uj <С т (здесь и — энергия начального фотона, т —
энергия покоя электрона) и сравните ответ с классической нереляти-
нерелятивистской формулой Томсона.
Ответ:
dcr = 87Г ( — ) -	Ш{ ( 	2+ 	2 + 	2 +
\тJ (s — mz)z [ \s — mz и — ml J \s — ml
m2 \ 1 / s — m2 и — m2
и — ml J 4 у и — ml s — ml
4.	Используя ответ предыдущей задачи, получите ответ для диффе-
дифференциального сечения процесса аннигиляции электрон-позитронной
пары в два фотона. Считайте начальные частицы неполяризованными
и спины конечных частиц нефиксированными.
5.	а) Пусть ТС(а\ а) — оператор Гамильтона фермионной системы.
Представьте квантовую статистическую сумму
в виде функционального интеграла в голоморфном представлении.
б) Вычислите статистическую сумму гармонического осциллято-
осциллятора (с точностью до множителя, зависящего лишь от температу-
температуры) в голоморфном представлении в присутствии внешнего источ-
источника. Используя эту статистическую сумму, найдите хронологиче-
хронологический коррелятор (Тт а)(т\)а(т2)) в представлении Мацубары. При по-
помощи полученной формулы найдите также статистические средние
[tr(e"'3wata)]/tr(e-'3w) и [tr (e^^W)] /tr (e"'3*).

Лекция 10
ТЕОРЕМА ФАРРИ, ТОЖДЕСТВА
УОРДА-ТАКАХАШИ И УСЛОВИЯ
ПЕРЕНОРМИРОВКИ В ЭЛЕКТРОДИНАМИКЕ
В этой лекции предполагается, что функциональный интеграл
(9.55) вычисляется при d = 4 — г и, таким образом, является регуля-
ризованным.
10.1. Теорема Фарри
Докажем теорему Фарри, утверждающую, что диаграммы, содер-
содержащие хотя бы один нечётный замкнутый спинорный цикл (петлю),
взаимно аннулируются. Рассмотрим некую фермионную петлю, изоб-
изображённую на рис. 15.
Рис.15
Пусть при обходе петли в направлении стрелок индекс j следует
за индексом г и kji есть 4-импульс линии, соединяющей вершины
г и j и направленный от вершины г к вершине j. Кроме петли на
рис. 15, содержащейся в некой диаграмме, обозначаемой L+, имеется
диаграмма L-, отличающаяся от L+ лишь тем, что она содержит
такую же петлю с обращенными стрелками. Сумма этих двух диаграмм
(а точнее — самих петель) равна нулю при нечётном числе п вершин
этих петель.
Множитель в диаграмме L+, соответствующий петле на рис. 15 (до
проведения интегрирования по импульсам), равен
fcin)].	A0.1)

10.2. Тождество Уорда-Такахаши	145
Воспользуемся тем, что ни один результат теории Дирака не изменя-
изменяется при замене (см. (8.79))
7м -> -7Mt = U^l^Uc.	(Ю.2)
Действительно, при замене A0.2) остаются инвариантными как фун-
фундаментальные соотношения 7"матРиД (8.5), так и вся алгебра матриц
Дирака, включая значения следов произведения матриц Дирака. По-
Поэтому в результате замены A0.2) находим:
г+ = -(-1)п^[7*^(*:(п-1)п)---7*^(*12O*^(*п1)] =
= -(-l)n ir[iSc(knx)iSc(kX2) ..-ISc(k(n_x)n)] = (-l)n/-,
где /_ — соответствующая петля в диаграмме L_. Отсюда видно,
что при нечётном п /+ + /_= 0 —> L+ + L_ = 0, что и требовалось
доказать.
10.2. Тождество Уорда-Такахаши
Сделаем в функциональном интеграле (9.55) замену переменных,
пи(гуЛ — pia(x) iff \	^h(rp\ —^Г, '(rp\ p — iol{x)	(AO'W
и будем считать поле а(х) бесконечно малым. Учитывая вклад в
интеграл лишь первого порядка относительно поля а и тот факт, что
Вф Вф = Вф 'Вф1 0, получаем следующее равенство:
xa
Здесь J3{A, ф', ф ; J,rj,rj} — действие в экспоненте в интеграле (9.55),
Jxm = ф '<у^ф\ а нормировочный множитель N — такой же функци-
функциональный интеграл, как в A0.4), но с нулевыми источниками. Срав-
Сравнивая обе части последнего равенства, мы видим, что равна нулю та
величина, которая пропорциональна полю а(х). Так как поле а(х) —
произвольно, то мы имеем в каждой точке х следующее равенство:
J^ J»(x) > = -щ{х)(ф{х)) + 1(ф(х)) V(x).	A0.5)
— \(ехр18{А,ф,ф] J^^BAB^ Вф =
^f,^f; J, г], г]}) 11 + г l
+ г (т)фг - ф fr])] | В А Вф ' Вф'. A0.4)
*) Вопрос об инвариантности дираковской функциональной меры в регуля-
ризованной теории обсуждается также в лекции 14.

146	Лекция 10. Тождества У орда и условия перенормировки
Теперь вычислим повторные функциональные производные
E/5г](х\))E/5г](х2)) от равенства A0.5), затем положим источники
равными нулю. При этом следует учесть, что обе части равенства
A0.5) являются рядами по источникам, коэффициентные функции
при степенях которых есть хронологически упорядоченные средние, и
операторы частных производных д/дх^1, 5/5г](х\), 5/5г)(х2) взаимно
(анти)коммутируют. В результате находим
0}.	A0.6)
Заметим, что вследствие трансляционной инвариантности все корреля-
корреляторы зависят лишь от разностей координат. Поэтому
y2[i6(xi -2/i)]r"B/i - x, x - y2) [isB/2 - x2)], A0.7)
где
6(x-y) = -i@ | Tф(х) ф(у) | 0)	A0.8)
—	точный электрон-позитронный пропагатор, а Г^(у\ — х,х — у2)
—	вершинный оператор (в координатном пространстве).
Приведём все диаграммы вершинного оператора с точностью до
величин пятого порядка.
--г А
У2 / \ у1
Рис. 16
Из определения вершинного оператора A0.7) видно, что первое сла-
слагаемое справа на рис. 16 равно —ге^5^\у\ — х) 5^d\x — у2). Таким
образом, вершинный оператор есть сумма всех диаграмм с двумя фер-
мионными и одной фотонной внешними ампутированными линиями.
Выразим обе части уравнения A0.6) при помощи формул A0.7) и
A0.8) и затем проинтегрируем с весом Jcr ' х\ сг ' х^ ехр[г(р + к)х\ —
] С учётом того, что

10.3. Индекс расходимости диаграмм	147
&(k)= \d{d)xe(x)eikx,
!	d	(Ю.9)
_ j
(так что в наинизшем порядке T^(q,p) = 7м) находим соотношение
&{р) - &{р + к) = &(р + к) [к^(р + /с, р)] б(р),
откуда получается равенство, называемое тождеством Уорда-
Такахаши :
При fc^O из A0.10) получаем также, что
.).	(io.il)
10.3. Индекс расходимости диаграмм
Для произвольной диаграммы введём следующие обозначения:
Le — число внешних электронных линий;
L7 — число внешних фотонных линий;
Ne — число внутренних электронных линий;
7V7 — число внутренних фотонных линий;
п — число вершин;
/ — число петель.
Тогда индекс расходимости диаграммы
uj = dl-Ne-2N1.	A0.12)
Для числа петель имеем
/ = ЛГе + ЛГ7-п+ 1,	A0.13)
так как каждому пропагатору соответствует интегрирование (по своему
d-импульсу), но каждая верщина содержит (^-функцию по входящим
импульсам, однако одна (^-функция даёт общий закон сохранения. Для
числа вершин имеем
п = L1 + 2N1 = -(Le + 27Ve).	A0.14)
Теперь подставим / из A0.13) в A0.12) и при помощи уравнений
A0.14) исключим JV7 и Ne. Таким образом получим, что
и = - (d-4) +d	^Le	^Ь7-	A0.15)
Отсюда видно, что при d > 4 теория заведомо неперенормируема, а
при d = 4,
u; = 4-L7-^Le,	A0.16)

148
Лекция 10. Тождества У орда и условия перенормировки
то есть формальная расходимость диаграммы зависит лишь от числа
внешних концов. Диаграмма расходится при ио > 0. Подчеркнём, что
импульсы внешних концов диаграмм не предполагаются находящимися
на массовой поверхности.
Укажем сразу, что суммы диаграмм при фиксированном порядке
по е с нечётным числом L7 и Le = 0, согласно теореме Фарри,
равны нулю. Действительно, в таких диаграммах полное число вершин
нечётно (см. A0.14)), и потому имеется хотя бы одна фермионная
петля с нечётным числом вершин. Вакуумные пузырьки (L7 = Le = 0)
нет смысла рассматривать, так как они дают ненаблюдаемый сдвиг
энергии вакуумного состояния. Поэтому имеется всего 4 расходящихся
диаграммы:
(б)
= 3
Рис. 17
Покажем, что диаграмма (г) на рис. 17 конечна.
Прежде всего заметим, что имеют место равенства
= 0.
A0.17)
Действительно, если бы мы рассмотрели вместо интеграла (9.55)
этот же интеграл со вставкой под функциональный интеграл выраже-
выражения (JMl(xi)... J^n(xn)) и проделали бы манипуляции, приводящие
к A0.5), то мы получили бы вместо A0.5) равенство, отличающееся
лишь вставкой во все средние выражения (^J^l(x\)... J^n(xn)). Таким
образом после зануления внешних источников получается равенство
A0.17). В импульсном пространстве равенство A0.17) означает, что
к»
= 0.

10.3. Индекс расходимости диаграмм	149
Равенство, изображённое на рис. 18, возможно, лишь если диаграм-
диаграмма в круглых скобках на рис. 18 пропорциональна структуре вида
(t^mmi fcM2 _ ^мм2^аы)ш Аналогичные множители содержатся в остальных
трёх вершинах. Каждый из указанных множителей линеен и одноро-
однороден относительно импульсов, которые «вытягиваются» из пропагаторов
внутренних линий. Поэтому некоторым внутренним линиям соответ-
соответствуют множители, убывающие быстрее при возрастании импульсов,
чем при формальном подсчёте. В результате оказывается, что степень
расходимости диаграммы (г) на рис. 17 и = —4 и она конечна.
Подчеркнём, что внешние импульсы входят в расходящиеся ча-
части диаграмм лишь в неотрицательных степенях, поскольку по их
отношениям к большим промежуточным импульсам интегрирования
производится разложение.
Рассмотрим диаграммы вида (а) на рис. 17. Обозначим через
гР^У4тг сумму всех сильно связанных диаграмм вида (а) на рис. 17.
Функция V^v(k) называется поляризационным оператором. Рассуж-
Рассуждения, аналогичные применённым при рассмотрении диаграмм вида (г)
на рис. 17, показывают, что
4тг	4тг
где оператор V(k2) расходится лишь логарифмически. Обозначим точ-
точный фотонный пропагатор
2V (х - у) = г @ | ТА^(х)А„(у) | 0)	A0.19)
жирной волнистой линией. Тогда на диаграммном языке имеем
а аналитически (в импульсном пространстве)
При помощи формул G.53) и A0.18) эта геометрическая прогрессия
легко суммируется:
W • (ю-20)

150	Лекция 10. Тождества Уорда и условия перенормировки
Обозначим через (—i^K) сумму всех сильно связанных диаграмм
вида (б) на рис. 17 и назовём эту функцию массовым оператором.
Для точного фермионного пропагатора A0.8) имеет место разложение,
аналогичное разложению точного фотонного пропагатора:
&(к) = Sc(k) + Sc(k) JK{k) Sc(k) +... =
y^, A0.21)
где mo — затравочная масса.
Общий вид массового оператора таков:
J{(k) = aomo + ai Ц+т{к),	A0.22)
где т(к) — конечная функция. Из размерностных соображений оче-
очевидно, что константы ао и а\ расходятся логарифмически. Важно,
что в правой части A0.22) не может быть слагаемого с&2, не обращаю-
обращающегося в нуль при то = 0 и к^ = 0 и потому расходящегося линейно.
Согласно A0.21), такое слагаемое а^ давало бы ненулевую массу
фермионам даже в случае то = 0 и потому нарушало бы глобальную
75-симметрию:
ф^е^ф, ф^фе^\ а = const.	A0.23)
При то = 0 имеет место глобальная 75"симметРия A0.23) и она не
может быть нарушена квантовыми поправками, т.е. точный фермион-
ный пропагатор антикоммутирует с 75;
в(к) 75 = 0 <—> j5^(k) + JK(k) 75 = 0.
Действительно, любая диаграмма, дающая вклад в точный пропагатор,
представляется как одна сплошная фермионная линия с внешними
концами и некоторое количество фермионных петель, соединённых
между собою фотонными пропагаторами. Так как каждая фермионная
петля находится под знаком спинорного следа, то спинорная структура
всей диаграммы определяется произведением свободных пропагаторов
Sc и 7~матРиЦ вдоль единственной фермионной линии с внешними
концами. Очевидно, что спинорная структура этой линии определяется
произведением
ЗД^'ЯсЫ] ¦¦¦ b^SciPn)] [7МЗД]. п = 1, 2, ...,
которое антикоммутирует с 75 в случае то = 0. Отсюда видно, что
в случае то = 0, упомянутое слагаемое а^ не может появиться при
учёте квантовых поправок.
Мы видим, что в квантовой электродинамике имеются лишь ло-
логарифмические расходимости, которые, как мы покажем, могут быть
устранены при помощи перенормировки полей и затравочных констант

10.4. Условия перенормировки	151
то и во. Таким образом, квантовая электродинамика в четырехмерном
пространстве-времени является перенормируемой теорией.
Пусть исходный (затравочный) лагранжиан КЭД равен
>- то)ф - еофГФА^.	A0.24)
Вычислим с помощью этого лагранжиана в размерности d = 4 — г
точные электронный A0.8) и фотонный A0.19) пропагаторы, которые
вблизи полюсов ведут себя как
-Jz^ + s(k),	A0.25)
d^(k).	(Ю.26)
В A0.25) и A0.26) операторы s(k) и dlllJ{k) конечны при стремлении
к2 —> т2 и к2 —> 0, соответственно.
10.4. Условия перенормировки
Займёмся перенормировкой внешних линий. Рассмотрим выходя-
выходящую внешнюю линию электрона с импульсом р и спиновым состо-
состоянием s. Пусть эта линия является единственной выходящей линией
амплитуды M^ps^, изображённой на рис. 20. Здесь все входящие и
выходящие линии — жирные, кото-
которым соответствуют точные величины
с учётом всех радиационных попра-
поправок. В КЭД все 4-импульсы входящих ps
линий в амплитуде на рис. 20 не мо-
могут находиться на массовой поверхно-
поверхности, если выходящий электрон — ре-
реальный с р2 = т2, поскольку законы	^ис- 20
сохранения 4-импульса и заряда не допускают этого. Однако именно
случай р2 = т2 нас интересует, поэтому входящие линии амплитуды
M(ps^ не соответствуют, вообще говоря, реальным частицам. Такая
ситуация может быть получена путём аналитического продолжения
некоторой амплитуды с массовой поверхности в нужную область её
переменных. Множитель в M(ps^, соответствующий выходящему элек-
электрону и обозначаемый Црз, получается так же, как точный электрон-
электронный пропагатор с той лишь разницей, что в разложении A0.21) во всех
слагаемых самый левый пропагатор Sc заменяется на биспинор пр,
который содержится в разложении затравочного дираковского поля в
A0.24) и удовлетворяет условиям нормировки (8.20), (8.56) и (8.57):
A0.27)

152
Лекция 10. Тождества У орда и условия перенормировки
Таким образом, имеем
Щрз) i - -
A0.28)
где M'pi является дираковским спинором — 4-рядной матрицей-
столбцом. Сопрягая комплексно равенство A0.28) и заменяя состояние
г) на | /), получаем
4ps)f
= Mpf tips •
A0.29)
Теперь воспользуемся формулой E.38) для значения амплитуды
Mfi при Р2 = Pj = р2 —> га2, которая была получена из общего
требования унитарности теории:
г Mfi = -M
p2 — m2 + is
A0.30)
Амплитуда A0.30) является аналитическим выражением процесса,
изображённого на рис. 21.
pf
Рис. 21
В силу лоренц-инвариантности для биспиноров tips имеют место
те же соотношения, что и для затравочных биспиноров ups, кроме
нормировки. Следовательно (сравни с (8.56)),
x—^ —
и потому при р2
т
p2 _
A0.31)
С другой стороны, вычисление этой же амплитуды непосредственно по
диаграмме на рис. 21 даёт (учтём, что в рассматриваемой области пере-
переменных у амплитуды Mf(ps^ нет реальных промежуточных состояний,
и потому согласно E.36) имеем Mf(ps^ = Mf w = Mpf tips', следо-
следовательно, левой части амплитуды на рис.21 соответствует амплитуда
(гMpf), пропагатору — (г &(р)), а правой части — (iM'pi))
iMfl=(iM'vf)(i&(p))iMrvl.
A0.32)

10.4. Условия перенормировки
153
Сопоставляя формулы A0.31), A0.32) и A0.25), находим Z' = Z2.
Поэтому
ilps = V %2 ups,	A0.33)
где ups — дираковский биспинор, удовлетворяющий всем соотношени-
соотношениям, приведенным в лекции 8.
Аналогичные вычисления показывают, что точный вектор поляри-
поляризации фотона <#ка связан с нормированным согласно G.55) вектором
поляризации е\^а формулой
~~	A0.34)
Теперь введём перенормированные поля при помощи формул
A0.35)
Константа т в A0.25) является физической массой. Пусть е обознача-
обозначает физический заряд, измеряемый на больших расстояниях. Определим
масштабный множитель Z\ как
В результате этой замены лагранжиан принимает вид
С = —^ Z3(F?VJ + Z2 Vv(i ф -mo) фг -e0Z2^/Z3
еО^2л/^з =eZx.
Теперь разобьём лагранжиан A0.36) на две части:
^ (FD2 + VY(i 9 ~т) фг-ефг
-5т)фг -
= Z2 — 1, 5т = Z2 то — т,
A0.37)
A0.38)
= Z% — 1,
Здесь первое слагаемое в лагранжиане даёт правила Фейнмана, опи-
описанные в лекции 9, а слагаемое в квадратной скобке — контрчлены.
Перепишем равенство A0.7) для перенормированных полей:
~x,x-y2)[i вг(У2-х2)},
где &г(х) — точный перенормированный фермионный пропагатор, по-
построенный из перенормированных ферми-полей при помощи формулы
A0.8), a F?f — перенормированный вершинный оператор. Так как

154
Лекция 10. Тождества У орда и условия перенормировки
%2&г — б> то из сравнения последнего равенства с равенством A0.7)
мы видим, что F?f = Гм.
Теперь точный электронный A0.8) и точный фотонный A0.19)
пропагаторы вблизи полюсов ведут себя как
1
1
f—га'
4тг
k2
4тг
W
Vr{k2 = 0) = 0.
A0.39)
Отсюда вытекают следующие условия нормировки:
A0.40 а)
A0.406)
При помощи A0.39), A0.40а), A0.406) и (8.38 а) получаем, что
д
1Р. A0.41)
Обратим внимание на то что требование, наложенное на вид массового
оператора A0.40а), является минимальным для того чтобы имело
место равенство A0.41). Равенство A0.41) заменяет собою условие
поведения дираковского пропагатора вблизи полюса. Именно равенство
A0.41) используется ниже при получении условий нормировки.
Так как тождество Уорда A0.11) имеет место для неперенормиро-
ванных величин, то при помощи A0.41) находим тождество Уорда для
перенормированных величин:
, р)ир
= Z2
A0.42)
Р2
Р\
Рис. 22
Рассмотрим диаграмму на рис. 22, опи-
описывающую рассеяние электрона во внеш-
внешнем поле Л(ув\к) (в первом порядке по
полю) с учётом всех радиационных попра-
поправок. В пределе к —> 0, Р2 ^ Р\ = Р, этой
диаграмме соответствует амплитуда

10.4. Условия перенормировки	155
iMfl = -ie0Upr^p, р) \р2=т2 йР Ale\k -+ 0) =
p2=m2 upA^(k^0)= A0.43)
= -iZxZ~x еп
Переписывая амплитуду A0.43) в терминах перенормированных ве-
величин, мы воспользовались определением A0.37) и тождеством Уор-
да A0.42). Подчеркнём, что формула A0.43) возникла как результат
вычислений в рассматриваемой модели квантовой электродинамики.
С другой стороны, естественно определить физически наблюдаемый
заряд е на больших масштабах так чтобы эта же амплитуда имела вид
iMfi = -ieup^UpA^k -> 0).	A0.44)
Таким образом, равенство A0.44) является тем звеном в условиях
нормировки, которое связывает экспериментально наблюдаемый заряд
в процессе рассеяния реального электрона в слабом медленно меня-
меняющемся классическом электромагнитном поле с формулами кванто-
квантовой теории поля. Заметим, что вид формулы A0.44) вытекает лишь
из общих требований лоренц-инвариантности и определения экспери-
экспериментально наблюдаемого электрического заряда. Сравнивая формулы
A0.43) и A0.44), находим
Zi=Z2, e=^Z3e0.	A0.45)
Воспользуемся неопределённостью, возникающей из-за расходимо-
стей, содержащихся в Г, и потребуем, чтобы имело место равенство
Г'Чр, р) |у=т= 7м,	(Ю.46)
то есть Z\ = Z2 = 1. Подразумевается, что равенство A0.46) имеет
место в обкладках пр...ир, когда ф = га. Удобство этого определения
состоит в том, что отпадает необходимость введения поправок во
внешние электронные линии, так как теперь (см. A0.33)) Hps = ups,
и перенормированный фермионный пропагатор совпадает с неперенор-
мированным. Кроме того, в силу A0.34) и A0.45), ее^а = eo<?ka> а
также [е2?)ГАШ] = е^ ^^ (здесь справа стоят неперенормированные
величины). Поэтому, хотя в неперенормированной теории используется
затравочный заряд ео, внешней фотонной линии соответствует вектор
поляризации 4а, а в качестве точного фотонного пропагатора ис-
используется функция Tifiu, вместо них можно использовать физический
заряд е, стандартные вектора поляризации (см. лекцию 7) е^а и
перенормированные пропагаторы :ЭГАШ. В результате такой замены
значения амплитуд не изменяются.
Таким образом, если в диаграммной технике используются фи-
физический заряд, физическая масса и перенормированные величины с

156	Лекция 10. Тождества Уорда и условия перенормировки
условиями нормировки A0.40а), A0.40 6), A0.46), то внешним ли-
линиям сопоставляются стандартные биспиноры u±ps, u±ps и вектора
поляризации л/4тг е\^а, удовлетворяющие естественным условиям нор-
нормировки, данным в лекциях 7 и 8. Указанное правило предполагает,
что если какая либо внешняя линия диаграммы находится на массо-
массовой поверхности, то соответствующая «нога» ампутирована (поскольку
все радиационные поправки уже учтены). Асимптотические состояния
нормированы обычным способом. Например, для одноэлектронного со-
состояния |ps) имеем (qsf \ ps) = BтгKcjp5ss>5C\q — р).
Далее индекс г у перенормированных величин опускается.
Задачи
1. а) Сформулируйте теорию дираковских спиноров в двумерном
пространстве-времени Минковского.
Указание. Исходите из необходимости реализации алгебры
Дирака 7М7^ + 7^7М = 2 7^ в двумерном пространстве Минковского.
?
б) Рассмотрите в двумерном пространстве Минковского модель
Тирринга с действием
Г B) Г		Q
S = сг ' х < фуь^дц — т)ф	уф ^^ф) уф 7/i^
Здесь g — константа связи. Сформулируйте правила диаграммной
техники Фейнмана для модели Тирринга. Исследуйте модель на
предмет перенормируемости.
2. Докажите, что

Лекция 11
I. ОДНОПЕТЛЕВАЯ СТРУКТУРА КЭД.
ЭЛЕКТРОННЫЙ И ФОТОННЫЙ ПРОПАГАТОРЫ
11.1. Массовый оператор
В наинизшем приближении массовый оператор —г.Ж{р) определя-
определяется диаграммой
р — к
аналитическое выражение которой даётся выражением
= НеJ j
Bтг)«
Проще всего вычисление проводится в калибровке Фейнмана, а = 1,
в которой
—iJt(v) = —4тге2
Мы ввели массу фотона Л2 <С т2, необходимую (см. ниже) для удо-
удовлетворения условий нормировки. Разумеется, масса фотона выпадает
из физически наблюдаемых величин (см. лекцию 13). Пусть d = 4 — е.
Тогда 7м i>l[i = —B — s) ф, 7м7м = d = 4 — е, и
4тгге2 Г
Bтгр J

158	Лекция 11. I. Однопетлевая структура КЭД.
Воспользуемся формулой D.35), положив А = (р — кJ — т2, В = к2 —
-А2:
4тпе2
[(k-xpf-a^ '
О
а2 = —х{\ — х)р2 + хт2 + A — х) А2.
После сдвига переменной интегрирования, к —> /с + жр, интеграл пере-
переписывается как
4тгге2
F - а2J
а2J
о
причём линейное относительно Ц слагаемое в числителе теперь может
быть опущено, так как интегрирование по углам обращает его в нуль.
Интеграл в импульсном пространстве берётся при помощи поворота
Вика и формулы D.3):
е2Т(е12) Г
JZ{p) =	K-LJ- \&x[(A-s)m-B-s)(\-x)$\x
DтгI-/2 J
г /1 \ 2 i 2 i /i \\ 2i— f/2
Последнее выражение разложим по ? с точностью О(?°):
9	9 г 1
е ,.	/ч el
+ I -m + ^
2тг I 2
2тг
[A
)—m x
о
Обратим внимание на то, что в точках нормировки оператор Ж
используется в обкладках пр^ир, причём р2 = тп2 и фир = тпир,
пр ф = тг^р (см. A0.41) и A0.42)). Поэтому для приведения оператора
JZ к виду A0.40 а) следует, во первых, сделать вычитание:
^„^ (*-"»)•"'(*).	A1-2)

//./. Массовый оператор
159
Затем операцию вычитания следует повторить для величины Ж' 0.
В результате двух таких вычитаний первые два слагаемых в A1.1)
исчезают. Последнее слагаемое в A1.1) переписываем как
dx(\-x) In[m2(l - р)(х - хх)(х - ж2)], A1.3)
2
-^ dx(l+x) In[m2(l
о
X2) ,
где введены параметры
О	О
m — р
13 = —2,
т1
т1
P-PY AP
\-р
A1.4)
Вычисления проводятся в предположении
р>0,—> ххл <0.	A1.5)
Напомним, что т2 имеет бесконечно малую отрицательную мнимую
часть. Поэтому
lim X] 9 = X] 9 = х/3 =;
Проведём одно вычитание A1.2) для ^2-
1
- Х) 111 	;	—
ezm Г
2тг J
о
е2т
1
X — Х\ X — Х2 X — Х\ X — Х2
При преобразовании интеграла A1.7) было учтено, что
A1.7)
Последний интеграл вычисляется при помощи формулы
х1 + аж
ж — ж?-
+ а)
X-Xi
A1.8)
О Заметим, что согласно данным определениям 1 — JZ'($)\р2=ш2^=ш =

160
Лекция 11.1. Однопетлевая структура КЭД.
Имеем
.. е2т 1	| 1 - /3 1
^2 = "^' о(-Р)
2тг 2V
\-р
г=1,2
¦ 2) In -
In-
Так как
то
1
m2
A1.9)
A1.10)
i + 2) In
1 — Xj
i +2) In
l-Xi
A1.11)
Для приведения вклада в Ж от ^^ к окончательному виду следует
вместо j^^f) использовать величину
- Bт)
Заметим, что в пределе Л2 —> 0, р > 0,
. A1.12)
= #2 = 0,
= o,
>-„¦
1
A1.13)
'"'^' 2ir2m(l-p)
Поэтому первое слагаемое в A1.12) определено корректно в пределе
нулевой массы фотона. Для вычисления второго слагаемого в A1.12)
следует вычислить ./^"(О), для чего необходимо в A1.11) перейти к
пределу р —> 0 при фиксированном значении 0 < А2 « т2. В резуль-
результате несложных вычислений находим
AМ4)
В A1.14) все коэффициенты, зависящие от /3, берутся в точке /3 = 0,
поскольку при этом не возникает неопределённостей и расходимостей.
Собирая формулы A1.2), A1.12), A1.13) и A1.14), получаем для Л^-

//./. Массовый оператор
161
2тгга
1
2A -
1
B - Зр)
2 in A
т
тр [\-р A-рJ
Действуя аналогично и делая вычитание A1.2) для
е
2^
- < const + Y^ :
[	г=1,2 L
находим
г. _|_ г.(г- _ 9") In
1
1 — 0^
2ттг
m 2A - р)
1 -
. A1.15)
, A1.16)
A1.17)
Складывая A1.15) и A1.17), окончательно получаем
о2	Г	1
Л =
\2
тр
2тгт
1
2A -Р)
1
1 -
1
+ 4р - 4
lnp
In —
m
2A-/9) V	Р
Оператор A1.18) вычислен в предположении р > 0, р > Х/т. При
аналитическом продолжении в область р < 0 следует помнить, что
точка ветвления р = 0 обходится снизу, так как ш2 содержит отрица-
отрицательную бесконечно малую мнимую часть. Поэтому, при р < О,
1пр = 1п|р| -гтт, р<0.	A1.19)
Из A1.18) видно, что при нулевой массе фотона массовый оператор
не определён, если используются условия нормировки A0.40 а).
2 2
р
При р2
т2
из A1.18) получаем следующую оценку:
2
A1.20)
Так как A1.20) есть поправка к ф (см. A0.39)), то для того чтобы ТВ
была справедливой, должно быть
о	о
^«1.	A1.21)
4^
Поскольку е2 = 1/137, то условие A1.21) нарушается лишь при чрез-
чрезвычайно больших импульсах.
Заметим, что массовый оператор калибровочно не инвариантен.
В этом нет противоречий, поскольку массовый оператор не является
непосредственно наблюдаемой величиной. В частности, в калибровке
б С.Н. Вергелес

162	Лекция 11. I. Однопетлевая структура КЭД.
а = 3 удовлетворение условиям нормировки A0.40 а) не требует вве-
введения массы фотона.
11.2. Поляризационный оператор
Можно существенно облегчить вычисления, если сначала найти
мнимую часть диаграммы и затем восстановить всю диаграмму при
помощи дисперсионного соотношения. Продемонстрируем этот метод
на примере вычисления поляризационного оператора. В первом при-
приближении ТВ он даётся петлёй в диаграмме.
Здесь внешняя линия виртуального фотона формально рассматрива-
рассматривается как отвечающая реальной частице — векторному бозону с массой
М2 = к2, взаимодействующему с электрон-позитронным полем по тому
же закону, что и фотон. При этом все соотношения условия унитарно-
унитарности остаются справедливыми. Диаграмма представляет диагональный
элемент амплитуды гМц, дающей переход бозона самого в себя через
распад на электрон-позитронную пару. Крестики на диаграмме пока-
показывают, по каким линиям она должна быть рассечена на две части
так, чтобы дать реальное промежуточное состояние, фигурирующее
при применении соотношения унитарности. Это состояние содержит
электрон и позитрон с 4-импульсами р_ = р и р+ = (к — р), соответ-
соответственно.
Для вычисления мнимой части Мц при помощи условия унитарно-
унитарности в соотношении E.34х) в данном случае следует использовать меру
причём далее J^A означает сумму лишь по поляризациям промежуточ-
промежуточных частиц, р2_ = р\ = т2, и в сумме по промежуточным состояниям
3-вектора р_ и р+ считаются независимыми. Имеем
A1.22)
где амплитуда M\i даётся частью диаграммы на рис. 24 правее кре-
крестиков:
гМХг =пр_ (-ге7м) и_р+ л/4тг ем.	A1.23)

11.2. Поляризационный оператор
163
Введём параметр
t = к2 = (р_ + р+J = 2 (р_р+ + т2).
В процессе вычисления будем предполагать, что t > Am2. Так как
интеграл в A1.22) лоренц-инвариантен, то вычислим его в системе
отсчёта, где к = 0, к0 = лД. Сначала проинтегрируем по р+:
|p|2d|p|
5 (Vi-2p0) \МХ
Так как | р| d | р| = р° dp0, то
2 Im Ma =
1
DтгJ
don
A1.24)
В A1.24) p° = A/2) уД, |р| = (l/2)Vt-4m2, dop - дифференциал
телесного угла, внутри которого находится вектор р = р_. С учётом
A1.23)
/ и ^vn и	(]] 2М
В A1.25) ^2Х означает независимое суммирование по поляризациям
электрона и позитрона. Поэтому при помощи (8.56) находим
Е
А
MXi
ее^
_ + ш
. A1.26)
Здесь второе равенство получено при помощи формул (8.65) и (8.66).
Так как /с = р_ + р+, и
= О,
ТО
rj^ \ =4 тг а
A1.27)
Коэффициент а в A1.27) находится путём вычисления свёртки по
векторным индексам в A1.27):
а = — -
С другой стороны,
гМц = л/4тт е* л/4тг
4тг
A1.28)
A1.29)

164	Лекция 11. I. Однопетлевая структура КЭД.
Если считать вектора поляризации бозона вещественными, то сопо-
сопоставляя формулы A1.24) и A1.26)—A1.29), получаем
2 e,ev Im
Теперь можно отбросить вектора поляризации бозона и использовать
определение A0.18). Окончательно находим
Очевидно, Im V (t) = 0 при t < 4 m2. Поэтому по мнимой части A1.30)
при помощи дисперсионного соотношения восстанавливается вся
функция:
Am2
Этот интеграл является представлением Челлена-Лемана (см. E.15)).
Величина A1.30) является значением мнимой части поляризационного
оператора на верхнем берегу разреза. Окончательное выражение для
поляризационного оператора получается при учёте условия нормиров-
нормировки A0.40 6), согласно которому необходимо сделать замену V (t) —>
Am2
Будем считать, что t < 0. Тогда интеграл A1.32) берётся при
помощи подстановки t'/Am2 =1/A —х2), 0 < х < 1:
A1.33)
Мы выразили V через переменную
t/ru2 = -(l-O2/C	(П-34)
Значение V (t) в предельном случае малых t легче всего ищется
непосредственно из выражения A1.32). Для этого следует положить
под интегралом t = 0:
е2 t
V (t) = -—	х, 111 <C 4 m2.	A1.35)
1о7г mz

11.2. Поляризационный оператор	165
Из соотношения A1.34) видно, что при стремлении переменной ?
к единице снизу, t стремится к нулю. Чтобы продвинуться далее от
t = 0 до t = 4 га2, следует положить ? = ег(р. Тогда, согласно A1.34),
? = 4ra2sin2|, 0<(^<тг.	A1.36)
В области ? > 4 га2 переменная ? заключена в интервале —1 < ? < 0.
Из соотношения A1.36) следует, что в этом интервале 1п? = 1п|?| +
+ гтг. Из A1.34) получаем также, что при больших \t\
?? = -га2, |?|>4ra2.	A1.37)
Поэтому из выражения A1.33) получаем асимптотику при больших
t\:
P(t) =
е2 Л \t\	л 9
-— In—?,	если —?>4raz
Зтг га/
-— (In—о— гтг), если t>4ra2.
Зтг
A1.38)
Мнимые части V(t), полученные при помощи соотношений A1.30) и
A1.38), совпадают. Это подтверждает равенство 1п? = 1п|?| +гтг при
По смыслу ТВ полученные формулы справедливы до тех пор пока
\V\ <С 1 (см. A0.20)). Поэтому ТВ справедлива до тех пор, пока
е2 , \t\ л
з^1п^ <<L
<J /I	III
Мы опять пришли к ограничению A1.21).
Константа перенормировки Z3 получается, если в выражение
A0.20) подставить неперенормированный оператор A1.31) и устремить
t к нулю. Обрезая интеграл в A1.31) масштабом Л —> оо, находим с
точностью О(е2):
1	2е2 Л
Z~\K) = 1 -V(t = O; Л) « 1 + —- In—.	A1.39)
Зтг га
Теперь в соотношении A0.45) е^ (Л) = Z^x (Л) е2 сделаем подста-
подстановку Л —> М, вд (Л) ^ е2 (М), где М — масштаб нормировки, М ^>
> га, а е2 (М) — бегущая константа связи. Таким образом,
+ ^ь
[ Зтг
Отсюда с точностью О (е3) получаем, что
.	A1.40)
отг

166	Лекция 11. I. Однопетлевая структура КЭД.
Решая это дифференциальное уравнение, находим
е2(М) =	4~^И-
1
In
1 ^ In s
Зтг га2
Формула A1.41) показывает, что эффективная константа связи растёт
при продвижении в ультрафиолетовую область. Это свойство является
общим для скалярной теории и КЭД.
11.3. Радиационные поправки к закону Кулона
Рассмотрим квантовые поправки к кулоновскому полю неподвиж-
неподвижного сверхмассивного точечного заряда е\, потенциал которого (без
учёта поправок)
ро(г) = 4е)(г) = 7' А(е) =°-	О1-42)
В импульсном пространстве
А 7Г Рл
A1.43)
kz
С учётом квантовых поправок потенциал A1.42) заменяется на
p = A{oe)+Vo^AieK	A1.44)
Получим первую поправку. Для этого возьмём поляризационный
оператор A1.32) и заменим точный фотонный пропагатор на свобод-
свободный. С учётом того, что к0 = 0, получаем
A1.45)
Отсюда видно, что возмущение потенциала есть
6<р(к) = ^Р(-к2) = ^Р-РН,2) ЕЕ б<р(-у*)9
A1.46)
1 Г
^2 I
о
Так как подынтегральное выражение четно, то
+ ОО
1 J 5<p(-y2)eiryydy.	A1.47)
— СЮ

11.3. Радиационные поправки к закону Кулона
167
Теперь сместим контур интегрирования с вещественной оси пе-
переменной у в верхнюю полуплоскость так, как показано на рис. 25.
G)
2im
Рис. 25
На рис. 25 Im V на левом берегу разреза задаётся при помощи A1.30).
Положим у = гх. Тогда соотношение A1.47) переписывается как
6(p(r) = —
г
- Ах
2га
Теперь выпишем потенциал A1.45):
.A1.48)
Оценим ip (r) в двух предельных случаях.
1. тг ^> 1.
Интеграл A1.48) легко оценивается при помощи подстановки ? =
е\
emr
г > —.
т
2. mr <C 1.
Опуская вычисления, приводим ответ (см. [3, § 114]):
Зтг
6
1
г <С —,
m
A1.49)
A1.50)
где С = 0, 577 ... — постоянная Эйлера.
Мы видим, что поляризация вакуума искажает кулоново поле то-
точечного заряда в области г < 1/га (= Ti/mc), где m — масса электрона.
Заметим, что формулы A1.41) и A1.50), конечно, взаимно согласованы,
так как приводят к одинаковому искажению кулонова потенциала.

168	Лекция 11. I. Однопетлевая структура КЭД.
Вне этой области искажение поля убывает по экспоненциальному
закону.
Задачи
1. Вычислите в однопетлевом приближении константу перенормировки
дираковского поля Z^.
2*. Установите путём прямого вычисления, что в калибровке а =
= 3 для удовлетворения массовым оператором условий нормировки
A0.40 а) не требуется введение массы фотона.

Лекция 12
II. ОДНОПЕТЛЕВАЯ СТРУКТУРА КЭД.
ВЕРШИННЫЙ ОПЕРАТОР И АНОМАЛЬНЫЙ
МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
12.1. Формфакторы электрона
Рассмотрим вершинный оператор Гм(р2, Pi) в случае, когда две
электронные линии являются внешними, а фотонная — внутренней с
4-импульсом к = р2 — р\ (если рассматривать её как входящую).
к = Р2 ~ Р\
Электронным внешним линиям отвечают множители щ = иРх и Й2 =
= пР2, так что Г входит в выражение для диаграмм в виде J^ =
= U2T^u\. Амплитуда перехода, описывающая рассеяние электрона во
внешнем поле в первом порядке по этому полю, представляется как
Mfi = -eJ%A^(k),	A2.1)
где Ар — эффективное (с учётом поляризации вакуума) внешнее
поле. Однопетлевой вклад в эффективное внешнее поле задаётся диа-
диаграммой (с) на рис. 26. Поскольку эта амплитуда является скаляром
(а не псевдоскаляром), а Дд — вектором, то величина j? является
вектором во всех приближениях и она может быть выражена лишь че-
через истинные векторы, которые могут быть составлены из имеющихся

170	Лекция 12. II. Однопетлевая структура КЭД.
в нашем распоряжении 4-векторов р\ и р2 (к = Р2 ~ Р\) и биспиноров
щ и щ. Всего имеется три таких вектора:
Щ^щ, (Щщ)Р^, (Щщ)^,	A2.2)
где Р^ = р^ + р%. Вследствие тождества Уорда A0.10), формул A0.39),
A0.40 а) и равенства (8.38 а) имеем
М/г=°-	О2-3)
Так как 4-импульсы р\ и р^ находятся на массовой поверхности, то
к^Р^ = 0, но к^ ^ 0. Кроме того, вследствие (8.38 а), к^Щ^щ = 0.
Поэтому
J% = /i ¦ («2 щ)Р^ + /2- (U27"«i),	A2.4)
где /i и /2 — инварианты, которые называются электромагнитными
формфакторами электрона. Из двух векторов р\ и р% (jp\ = р\ =
= т2) можно составить лишь одну инвариантную величину, в качестве
которой возьмём к2. Формфакторы являются функциями лишь к2.
При помощи формул (8.5), (8.10) и (8.38 а), (8.38 6) получаем
(Ща^щ) kv = -т {Щ^щ) + Х- (п2щ) Р».	A2.5)
Поэтому представление A2.4) может быть переписано как
2	^2,щ)К,	A2.6)
где / и д — другие формфакторы.
Член в амплитуде рассеяния A2.1), пропорциональный д(к2), имеет
вид
SMfi = —д(к2)(п2а^щ)киЛ1е).	A2.7)
Рассмотрим чисто магнитное поле Л^0^ = @, А) и пусть № = @, к),
к —> 0. Это значит, что поле не зависит от времени и оно медленно
изменяется в пространстве 0. Перепишем A2.7) с учётом того, что
в данном случае имеются лишь пространственно-пространственные
компоненты тензора электромагнитного поля и Нг(к) = iSijkkjA^(к):
SMfi = ^
1) В этом случае в A2.7) можно заменить «одетое» поле Л^ на «го-
«голое» поле Ajj^K Действительно, в конце лекции 11 было показано, что (в
однопетлевом приближении) слабое медленно меняющееся «одетое» кулоново
поле фактически совпадает с «голым». Это же утверждение во всех порядках
ТВ имеет место в отношении любого слабого и медленно изменяющегося
электромагнитного поля.

12.2. Аналитические свойства формфакторов	171
Такой же вклад в амплитуду даст добавка к гамильтониану
\d{3)x^ \-—g@)sU\ ср. A2.8)
J	V m	J
Последнее выражение в A2.8) получается из предыдущего в нереляти-
нерелятивистском пределе в стандартном представлении. Сравнение выражения
A2.8) с уравнениями (8.28) и (8.30) показывает, что радиационные
поправки дают дополнительный вклад в магнитный момент электрона,
так что его полный магнитный момент (в обычных единицах)
A
Очевидно, что первое слагаемое в A2.6) не может дать вклад в
аномальный магнитный момент. Действительно, при к —> 0 для перво-
первого слагаемого в представлении A2.6) имеем f(k2)(u2l^u\) —> 2/@)рм,
где р^ — импульс электрона.
12.2. Аналитические свойства формфакторов
Амплитуда A2.1) описывает два канала реакции. В канале рассея-
рассеяния переменная
t = k2 = (Р2-Р\J <0.	A2.10)
Путём замены р^ —>р~, Р\ —> —р+ мы приходим к аннигиляционно-
му каналу, отвечающему рождению электрон-позитронной пары с 4-
импульсами р_ и р+. В этом канале
t = (p-+p+J >4ra2.	A2.11)
Область значений 0 < t < 4 m2 — нефизическая.
Применим условие унитарности E.34). В канале рассеяния (t < 0)
нет физических промежуточных состояний: один свободный электрон
не может изменить свой импульс или родить какие либо другие реаль-
реальные (не виртуальные) частицы; в нефизической области их также нет.
Поэтому при t < 4 т2 правая сторона равенства E.34) отсутствует,
так что
Mfi = M*f.	A2.12)
Равенство A2.12) справедливо, конечно, во всех приближениях. Пе-
Перестановка начального и конечного состояний означает перестановку
р\ и р2, а тем самым замену к —> —к. Из соотношения A2.12) для
выражения A2.1) вытекает, что

172	Лекция 12. II. Однопетлевая структура КЭД.
Но вследствие вещественности электромагнитного поля А^ (к) =
= Л^ (—к), и потому
J? = Jf/, t<Am\	A2.13)
Легко проверить, что (см. (8.8) и (8.11))
Поэтому /*j отличается от /^ лишь заменой функций / (?) и g (t)
их комплексно сопряжёнными. Тогда из равенства A2.13) следует, что
Imf(t)=Img(t)=O, ?<4га2.	A2.14)
Из диаграмм (б) и (в) на рис. 26 видно, что в аннигиляционном канале
(t > Am2) уже в однопетлевом приближении существуют реальные про-
промежуточные частицы. Поэтому правая часть условия унитарности для
амплитуды A2.1) отлична от нуля и формфакторы / и g комплексны.
Аналитические свойства функций / (?) и g (t) аналогичны свойствам
функций V(t). Эти функции аналитичны в комплексной плоскости
переменной t, разрезанной вдоль положительной вещественной оси t >
> 4 m2, причём
/•(*) = /(*'). g*(t) = g(t*).	A2.15)
Условие перенормировки A0.46), применённое к выражению A2.6),
даёт условие
/@) 1.	A2.16)
Это условие учитывается автоматически, если в дисперсионном соот-
соотношении использовать не /(?), а (/ (?) — 1)/?. Таким образом,
Am2
Для формфактора g (t) условие перенормировки A0.46) не даёт огра-
ограничений, так что аналогичная формула имеет вид
Am2
В A2.17), A2.18) мнимые части функций, как и обычно, берутся на
верхних берегах разреза.
Рассмотрение, проведенное до сих пор, справедливо во всех поряд-
порядках ТВ.

12.3. Вычисление мнимых частей по интегралу Фейнмана	173
12.3. Вычисление мнимых частей по интегралу
Фейнмана
Выпишем амплитуду, соответствующую диаграмме (б) на рис. 26 в
аннигиляционном канале (р2 —> Р-, Р\ —> — Р+, Q —> Р — Р-, к = р- -\-
+ р+):
Г dD) v
xSc(p-k)jxu_p+DUp-P-)- A2.19)
Далее обкладки пр_ ... и_р+ во всех формулах опускаются для сокра-
сокращения записи, но равенства пр_ ф_ = тпр_ и ф+ U-p+ = —mu-p+
используются в вычислениях. В калибровке Фейнмана, а = 1, имеем
f{^-Lg{k*)a^=\ ^(Ар)^Р 21, A2.20)
где	о
?>"(/. Р) = -i4 ¦	г/ То л 1	•	A2-21)
4 7Г13	^(Р — р_)^ — Xz\
Здесь опять введена бесконечно малая масса фотона А в фотонный
пропагатор.
Разрез проходит в t-плоскости при t > Am2. При таких значениях
t = к2 существует система отсчёта Kq, в которой к = (к0, 0). В
системе Ко
| ГУЛ 	 I/* J		 | ГУЛ		 I/*	J		 Т"\	/V^		 /V^		 	 I/*
,	2	2 ' A2.22)
I /
Р- = -Р+,	|Р- =
Введём обозначение о; = +J |р|2 + ш2 . Тогда
d4p= |p|o; dp° Auj dop.	A2.23)
В системе отсчёта Kq знаменатель в интеграле A2.20) имеет полюса
по р° в точках
а)	ро = со — ie,	af) po = —ио + ге,
A2.24)
б)	ро = ^о — ^ + ^,	Ъ') ро = ко +ои — ie.
Для определённости считаем к0 > 0, что отвечает процессу рождения
пары (ответ не зависит от этого предположения, поскольку является
функцией (к0J). Ясно, что лишь полюса а) и Ь) могут совпасть при
интегрировании в выражении A2.20), что происходит при ио = A/2) к0

174
Лекция 12. II. Однопетлевая структура КЭД.
(это возможно лишь при к0 > 2т). На рис. 27 показано расположе-
расположение полюсов в комплексной плоскости р° 0. При замене в интеграле
A2.20) к2 —> к2 — i5, 5 —> +0, интеграл изменяется скачкообразно,
Рис. 27
поскольку при такой замене мы попадаем на нижний берег разреза.
Однако из рис. 27 видно, что если полюса а и Ь не совпадают, то
при указанной замене параметра скачка быть не может, поскольку
контур интегрирования может быть плавно изменён (на рис. 27 новый
контур интегрирования изображён пунктиром). Поэтому бесконечно
малое смещение полюсов не переводит их на другую сторону кон-
контура интегрирования. Отсюда видно, что мнимая часть (или скачок
интеграла) появляется лишь при условии совпадения полюсов а и Ъ.
Такое совпадение происходит лишь при одновременном обращении в
нуль обоих сомножителей в знаменателе интеграла A2.20). Это значит,
что для нахождения скачка в интеграле A2.20) следует вставить под
интеграл вместо знаменателя множитель 5(р2 — т2) 5[(р — кJ — т2].
Для вычисления коэффициента при этом множителе заменим исходный
контур интегрирования С на два других С и С" так, как показано
на рис. 28.
о!	Ъ
Рис. 28
Интеграл по контуру С уводится от полюсов а и Ъ и потому не даёт
скачка. Интеграл по контуру С" легко вычисляется взятием вычета,
х) Совпадение полюсов внутренних фотонной и одной из фермионных линий
невозможно, поскольку, вследствие сохранения 4-импульса, электрон не может
излучить частицу.

12.3. Вычисление мнимых частей по интегралу Фейнмана	175
что эквивалентно следующей замене под интегралом A2.20):
1
р2 — т2
(-2mM(pz -mz).	A2.25)
Знак «—» в A2.25) имеет место вследствие отрицательной ориентации
контура С". Теперь очевидно, что разность значений интеграла A2.20)
на верхнем и нижнем берегах разреза даётся величиной
°,p) \-2ш'5(р2 -т2)]
Ро>О
1	1
{р - кJ - т2 + iS {р- кJ -m2-iS_
p°,p) \-2т5(р2-т2)\ \-2т5((р-кJ -т2)]. A2.26)
Po>O
Можно доказать общее правило Каткосского для отыскания скач-
скачка диаграмм:
1)	разобьём диаграмму на две всеми возможными способами путём
разрезания её пропагаторов;
2)	для каждого разрезанного пропагатора частицы массой т де-
делаем замену (р2 — т2 + ге)~х —> (—2тгг) 5(р2 — т2), затем вычисляем
петлевые интегралы;
3)	суммируем вклады от всех возможных разрезаний.
В результате интегрирования в системе Ко (^-функции в A2.26)
легко снимаются. При помощи формул A2.22), A2.23) и A2.26) нахо-
находим для скачка интеграла A2.20):
Disc -г-р	оутт	ТТ9	от = |р|о; dp° do; Aорг^х
J (p2-m2)[(p-kf-m2} J
Po>O
x [-2тгг 5 {pi - u;2)] [-2m 5 ((p0 - k0J - uj2
= -*уА/—^ Idop^(^-.P). A2-27)
A2.28)
Вычислим интеграл в A2.27) в системе центра инерции Kq, в
которой

176
Лекция 12. II. Однопетлевая структура КЭД.
р= 1-^,
A2.29)
(sin $ cos 0, sin $ sin 0, cos
При помощи формул (8.62), A2.22), A2.28) и A2.29) величина A2.21)
переписывается в виде
- 2т
р = (?-4га2)A -
Введём обозначения
= don
P
A2.30)
A2.31)
Приведём ненулевые значения компонент этих величин:
тг
лД
' t-Am2
In
oo
c =
t-Am2
A2 '
tt?	t—Am2
2(t-Am2) ~^~'
t-4m21
-2+In
t-4m2
-2+ln
A2
t-Am2'
A2
X =2
-2 + In ¦
A2
a, /3= 1,2.
A2.32)
Далее в этом пункте обозначаем символом « те равенства, кото-
которые имеют место лишь в обкладках пр_ ...и-р+. Например, формула
A2.5) в аннигиляционном канале имеет вид
A2.33)
Теперь вычислим скачок на разрезе равенства A2.20) и, в первом
случае, свернём его с вектором Р^, а во втором случае рассмотрим
скачок этого векторного равенства с индексами \± = а = 1, 2 (напом-
(напомним, что равенство A2.20) рассматривается в обкладках пр_ ...и-р+).
Таким образом, мы получим два независимых уравнения, при помощи
которых найдём мнимые части формфакторов.
В первом случае, учитывая равенство A2.33), находим скачок левой
части уравнения A2.20):
2mlmf(t) + —lmg(t)
A2.34)

12.3. Вычисление мнимых частей по интегралу Фейнмана	177
Скачок же правой части этого равенства в данном случае равен
гл (тгт Т> mMi,	^	/19 Qt^4
Op \ир--1ц,(Р U—р. ) .	yiZ.oO)
Согласно уравнению A2.30),
Проведём простые преобразования:
= — 2 ^_ ^+ ^+2(р_р+) ф « —2ш
= — 4т (р+р) + 2т j^j^+ +2(р_р+) ф «
Согласно уравнению A2.29),
и потому
Up_ ф U-p+ = m cos i? (up_ U-p+) —
Таким образом,
. A2.36)
A2.37)
— m2) ф— Am (p+p).
, 0),	A2.38)
pau_p+) . A2.39)
так как
cos^=
A2.40)
A2.41)
v — 4m2
В правой части A2.40) слагаемые вида р3ра, а = 1,2 не выписаны,
так как, согласно A2.32), под интегралом в A2.35) они обращаются в
нуль.
Комбинируя уравнения A2.34), A2.35) и A2.40), получаем
2m Im f(t) + -^— Im g(t) =
е2т It — Am2 f do]
2тг
t
2(P3J-
. A2.42)

178
Лекция 12. II. Однопетлевая структура КЭД.
Во втором случае скачок равенства A2.20) принимает вид
(Im f(t) + Im g(t))up_<yau-p+ =
е2 It - Am2 f d Or,_
2ttV t
Здесь было учтено, что
1
_р+. A2.43)
-=0, ка=0, а =1,2.
J Р Р
Легко устанавливается следующее равенство:
]-пр_ ft<ya $u_p+ = -{v+V)uP-Tu_pjr.	A2.44)
z
Уравнение A2.43) переписывается при помощи равенства A2.44) как
lmf{t)+lmg{t) =
A2.45)
Уравнения A2.42) и A2.45) позволяют найти мнимые части обоих
формфакторов по отдельности:
о
2 2	л j
тг Jt(t - Am2) J P
Теперь при помощи формул A2.32) приводим равенства A2.46) к
окончательному виду:
9 9
е т
Ьп/(*) =
lmg(t) =
-3t+8m2+2(t-2m2) In
t-4m2
A2.47)
Инфракрасная расходимость имеется только в /(?).

12.3. Вычисление мнимых частей по интегралу Фейнмана	179
Формфакторы могут быть вычислены точно по их мнимым частям
при помощи уже использовавшейся подстановки t1 = 4m2/(l — х2)
(см. [3, § 117]). Однако мы ограничимся их асимптотическими значе-
значениями.
Согласно формулам A2.18) и A2.47),
2 2 7	dt	2
д@) = е-^-	.	= ^—.	A2.48)
W тг J ty/t(t - 4m2) 2^
4 m2
При 111 <C 4m2 можно пренебречь параметром t под знаком инте-
интеграла в A2.17):
2+ \ [-1-2 2	2Н 4х2
J
о
1 VA ' " у^ А2 | "З^ш2
Поэтому
бЧ Л m П	'- ^ ¦¦¦ =С4Ш2. A2.49)
При t'»4m2 из A2.47) получаем, что 1т/(?') = (е2/2) ln(t7A2).
Оценим сначала / (?) при —t>4m2. Делая соответствующие прене-
пренебрежения, сводим интеграл в A2.17) к интегралу
4 /'(*'+1*1)'
который легко оценивается при помощи подстановки tr = 4m2ex,
О < х < оо:
00 ' ж + In —2~ ) d ж
Знаменатель в подынтегральном выражении почти равен |?|, при
х < хо, и быстро падает при х > хо, где хо = ln[|t|/4m2]. Поэтому,
при —t > 4 m2,

180
Лекция 12. II. Однопетлевая структура КЭД.
При больших положительных 1t \ этот формфактор приобретает мни-
мнимую часть, а вещественная остаётся прежней. Легко сделать аналогич-
аналогичную оценку для g(t). Таким образом,
0,
^, если t»4ra2,
0,	если — ?>4га2,
2 2
^L, если t»4m2,
если -
9
12.4. Аномальный магнитный момент электрона
Согласно формулам A2.9) и A2.48), в однопетлевом приближении
магнитный момент электрона
2тс
Эта формула впервые была получена Ю. Швингером в 1949 году.
Задачи
1. а) Оцените качественно вклад в магнитный момент электрона
#пол@)> происходящий от поляризации вакуума мюонной петлёй 0.
Иными словами, оценить вклад в #L\@) от последней диаграммы
на рис. 16 в том случае, когда по вакуумной петле распространяется
виртуальная мюонная пара.
б) Сделайте то же самое, взаимно заменяя электроны и мюоны.
Указание. Согласно A0.20) вклад в формфакторы от нужной
диаграммы получается путём замены
1) Считать мюон элементарной частицей, отличающейся от электрона лишь
массой: тм = 206, 8те. В остальном динамика мюонов и их взаимодействие с
электромагнитным полем не отличаются от динамики электронов и их взаимо-
взаимодействия с фотонами.

12.4. Аномальный магнитный момент электрона	181
Так как q2 = —р, то учёт нужной диаграммы означает замену
в выражении для Im g(t) в правой части уравнения A2.46). В случае
а) поляризационный оператор зависит от массы мюона тм, в то время
как в интеграле A2.46) (за исключением поляризационного опертора)
используется электронная масса те. В случае б) делается взаимная
замена т^ <—> те. ?
Ответ:

Лекция 13
ИНФРАКРАСНАЯ ПРОБЛЕМА. ЛЭМБОВСКИЙ
СДВИГ УРОВНЕЙ
Мы видели, что некоторые величины в КЭД вследствие инфра-
инфракрасных расходимостей не могут быть вычислены без конечной массы
фотона. В этой лекции будет показано, что в физически наблюдаемых
величинах (в отличие от ненаблюдаемых величин) нефизическая масса
фотона может быть устремлена к нулю и при этом наблюдаемые вели-
величины имеют конечный предел.
13.1. Массивное векторное поле
Поскольку массивное векторное поле имеет (для каждого импульса)
три физических степени свободы (а не две — как в случае фотонного
поля), то для корректного обращения с массивным векторным полем
следует внести исправления в некоторые формулы.
Действие массивного векторного поля имеет вид
Мы выбрали нормировку, совпадающую с нормировкой электромагнит-
электромагнитного поля (сравни с G.16)) для облегчения дальнейшего предельного
перехода. Действие A3.1) приводит к следующему уравнению движе-
движения:
Х2А^ = 0.	A3.2)
Из уравнения A3.2) следует условие
8^ = 0.	A3.3)
В результате уравнение движения A3.2) упрощается:
{дуду + Л2) А» = 0.	A3.4)

13.2. Излучение мягких фотонов
183
При помощи уравнения движения A3.2) находим пропагатор (сравни с
G.53))
^L^#V	A3.5)
Сумма по поляризациям векторной частицы даёт правило (сравни с
G.33)):
OL=\
Л2
A3.6)
Эта формула вытекает из равенств к^е^ = О и к2 = Л2.
Взаимодействие векторного поля с электрон-позитронным полем
описывается тем же действием Sint = —е d^ xA^J^, что и в случае
фотонного поля. Поэтому вследствие калибровочной инвариантности,
то есть независимости физических величин от продольной части пропа-
гатора, мы можем опустить в A3.5) продольную часть и пользоваться
пропагатором
4 7Г
A3.7)
Именно пропагатор A3.7) использовался в предыдущих лекциях.
13.2. Излучение мягких фотонов
Для определённости рассмотрим процесс рассеяния электрона
внешним электромагнитным полем. Например, это может быть
неподвижное массивное ядро. На рис. 29 (а) изображена диаграмма
упругого процесса рассеяния электрона, в результате которого
электрон переходит из состояния с импульсом р в состояние с
импульсом р1. Диаграммы на рис. 29 (б), (в) изображают процесс
неупругого рассеяния, отличающийся от упругого процесса испуска-
испусканием дополнительного мягкого фотона (к —> 0).
р — к
Р	р'	к	р

184 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
Диаграмма на рис. 29 (а) аналитически представляется в виде
M/fS) =пр>Мир.	A3.8)
Рассмотрим амплитуду, изображённую на рис. 29 (в). Эта ампли-
амплитуда получается из амплитуды, изображённой на рис. 29 (а), путём
замены
/4тг
(р- кJ - т2
Здесь было учтено, что к2 = Л2 и к —> 0. Так как
ф f = 2ре*- f ф, ф ир = тир,
то A3.9) переписывается как
?^е*	A3.10)
Аналогичное рассмотрение показывает, что диаграмма, изображённая
на рис. 29 (б), получается из диаграммы, изображённой на рис. 29 (а),
путём замены
Таким образом, сумма амплитуд (б) и (в) на рис. 29
)!	,,,.12)
а соответствующее неупругое сечение
р' е	ре
Г/о ' (Отг\зо,.и '
A3.13)
р'к + Л2/2 р/с - Л2/2
Из формулы A3.13) видна причина, по которой следует учитывать
лишь фотоны, излучённые внешними электронными линиями, но не
учитывать мягкие фотоны, излучённые внутренними линиями: внеш-
внешние электронные линии дают в амплитуде дополнительный множитель
— электронный пропагатор, импульс которого при к —> 0 находится
очень близко к массовой поверхности. Такой пропагатор находится
вблизи своего полюса и он численно велик. Поэтому при к —> 0
дифференциальное сечение A3.13) стремится к бесконечности. Если
же мягкий фотон излучается внутренней линией, то численно большой

13.2. Излучение мягких фотонов	185
множитель не появляется, так как по импульсу виртуального электрона
происходит интегрирование и потому можно считать, что он находится
вдали от массовой поверхности.
Просуммируем в A3.13) по поляризациям векторной частицы при
помощи A3.6). Легко увидеть, что второе слагаемое в A3.6) даёт
относительный вклад в сечение ~ О(Х2). Так как А2 —> 0, то вклад в
сечение от второго слагаемого в A3.6) можно опустить. По этой же
причине может быть опущено слагаемое А2 в знаменателях под знаком
модуля в A3.13). В результате получаем
4	) ^ daK	A3.14)
p'k pkj Anluo
Пусть n = k/cjfc, a v и Vх — начальная и конечная скорости
электрона. Тогда в случае А = 0 выражение A3.14) в трёхмерных
обозначениях принимает вид О
dai = e2 (^Щ - p^L) ¦ dJ1^"- da^>.	A3.15)
у 1 — ПУ' 1 — ПУ J	4 7YZ Uk
Точно к такому же выражению для сечения мы придём, если в A3.13)
с А = 0 просуммировать по двум поляризациям безмассовых фотонов
при помощи правила G.33), справедливого для реальных безмассовых
фотонов. Мы видим, что формула A3.14) для неупругого сечения
справедлива как в случае излучения реальных безмассовых мягких
*) Действительно, р = р°A, v), и так как при Л = 0 иок — |к|, то рк =
= р°|к| A — nv), рр' = рор'оA — vv'), и потому
' р' рУ_	т2	т2	2A-уу;)
Кр'к рк)	(pjJ(l-nv'J p2(l-nv02 (l-nv)(l-nv') ~
2vv;
A-nvO2 A-nvJ (l-nv)(l-nv;)
1	1	2
-nv'J A-nvJ A -nv)(l -nv;)
С другой стороны,
p/ pY_( у'2	v2
(*)
р'к рк) \{\-nw'f A-nvJ (I -nv)(l -nv')
(nvQ2	(nvJ	(пу)(пуО
A - nv;J A - nvJ A - nv)(l - nv;)
Простое вычисление показывает, что квадратные скобки в (*) и (**) равны
одному и тому же значению (n, v — v;) [(I — nvJ(l — nv'J]. Отсюда
следует равенство выражений A3.14) и A3.15) в случае нулевой массы фотона.

186 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
фотонов, так и в случае излучения мягких векторных частиц с беско-
бесконечно малой, но ненулевой массой, и тремя поляризациями.
Обратим внимание на то, что в случае реальных фотонов (Л = 0)
амплитуда A3.12) калибровочно инвариантна, т.е. она не изменяется
при преобразовании вектора поляризации согласно G.56). Таким обра-
образом, в случае реальных фотонов можно суммировать в сечении A3.13)
по трём поляризациям фотона, включая продольную поляризацию.
Это не изменит результат вследствие калибровочной инвариантности
амплитуды и сечения. Но это означает, что при суммировании по
поляризациям реального фотона можно пользоваться формулой A3.6)
с последующим переходом к пределу Л —> 0. Именно такой подход и
был использован при получении формулы A3.14). Приведенное рас-
рассуждение объясняет переход формулы A3.14) в формулу A3.15) при
Л —> 0. Сама же формула A3.15) легче всего получается из формулы
A3.13) при Л = 0 при помощи правила G.33).
Множитель, стоящий перед d<j(elas) в A3.15), совпадает с (делён-
(делённой на Uk) классической интенсивностью d/ тормозного излучения
малых частот (см. [4, § 69]). Таким образом, излучение длинноволно-
длинноволновых фотонов является, по сути, классическим процессом.
Полученные формулы применимы, конечно, при условии
u;-|k|<Cp°.	A3.16)
Необходимо также, чтобы передача импульса q = рх — р рассеива-
рассеивающему центру (ядру) была велика по сравнению с изменением этой
величины вследствие испускания мягкого фотона. Так как
то имеем ограничение
wfc/|q|t;«l.	A3.17)
Полученный результат легко обобщается на случай испускания
нескольких фотонов. Например, в случае испускания двух мягких
фотонов с импульсами и векторами поляризации, нумеруемыми индек-
индексами 1 и 2, амплитуда A3.12) содержала бы вместо одного множителя
в квадратной скобке два аналогичных множителя:
^?)^е(^-^П1.	A3.18)
pfkx pkx)	\pfk2 pk2j\
В этом нетрудно убедиться прямым вычислением. Действительно, рас-
рассмотрим диаграмму, отличающуюся от диаграммы на рис. 29 (с) тем,
что входящий электрон с импульсом р излучает сначала мягкий фотон
с импульсом к\ и затем мягкий фотон с импульсом к2. Будем считать
фотоны безмассовыми. Вычисление, аналогичное тому, которое приве-
привело к формуле A3.10), теперь показывает, что в данном случае вклад в

13.2. Излучение мягких фотонов
187
амплитуду получается из амплитуды на рис. 29 (а), если в ней сделать
замену (учитываются лишь главные вклады по fci и fc2)
Up^Up	(pkl+pk2){pkl)
Если с правой частью этого равенства сложить такую же величину с
перестановкой k\ <-> к2, то мы получим
/4тг е(ре*)
рк\
/4тг
рк2
Теперь очевидно, что если учесть все возможности излучения двух
мягких фотонов внешними электронными линиями, то в результате
амплитуда получит множитель A3.18), поскольку этот множитель ка-
либровочно инвариантен.
В случае испускания п мягких фотонов, для каждого фотона
имеется свой множитель в амплитуде. Поэтому сечение процесса с
испусканием п мягких фотонов представляется в виде
dan =
... dwn,
A3.19)
где dwi (г = 1 ... п) — вероятность отдельного испускания фотона
Поэтому полное неупругое сечение представляется в виде
A3.20)
n=0
Здесь u;max — некое значение частоты, удовлетворяющее условиям
A3.16), A3.17). Под знаком суммы в A3.20) множитель 1/п! учиты-
учитывает тождественность фотонов.
Как было указано,
dwu, = —,	A3.21)
где d/ — классическая интенсивность излучения мягких фотонов. По-
Поэтому величина A3.21) может интерпретироваться как среднее число
излучённых фотонов dn в заданном интервале частот. Тогда среднее
число излучённых фотонов
п =
[-= [
= d wu
e2ln-
A3.22)

188 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
Последняя оценка получена при помощи A3.15). Хотя cjmax <C p°, при
А^О с логарифмической точностью имеем оценку
п = е2\пР-.	A3.23)
Если п ^ 1, то ТВ оказывается неприменимой, т.к. первая поправка
A3.15) оказывается того же порядка, что и d<j(elas). Однако сама
формула A3.15) тем точнее, чем меньше энергия мягкого фотона.
Выход из этой противоречивой ситуации таков.
При Л —> 0 среднее число излучённых фотонов п —> оо. Мягкие
фотоны излучаются статистически независимо. Этот факт подтвержда-
подтверждается всеми порядками ТВ. Поэтому к процессу множественного излу-
излучения фотонов можно применить формулу Пуассона: вероятность wn
излучения п фотонов выражается через их среднее число п формулой
пп -
wn = —e-n.	A3.24)
п\
Теперь формулу A3.20) можно модернизировать следующим образом:
in.	A3.25)
n=0
Так как J2nwn = 1, то согласно A3.25),
da = d^elas).	A3.26)
При этом, конечно, упругое сечение в формулах A3.25), A3.26) отли-
отличается от упругого сечения в A3.20) множителем:
e-nd5:(elas) =d(J(elas)>	^3^7)
Таким образом мы видим, что сечение чисто упругого рассеяния
равно нулю при Л —> 0 (или п —> оо), что видно из формулы A3.27).
Вместе с этим обращается в нуль сечение рассеяния с излучением
любого конечного числа мягких фотонов. Тем не менее те сечения,
которые вычисляются при помощи ТВ, конечны во всех порядках по
константе связи, если учесть также и излучение мягких фотонов.
Более того, в каждом порядке по константе связи существует конечный
предел для сечений при устремлении массы фотона к нулю, хотя в
каждом порядке по константе связи может быть излучено лишь конеч-
конечное число мягких фотонов. Этот факт демонстрируется в следующем
пункте. Таким образом, сечение рассеяния в борновском (без учёта
радиационных поправок) приближении может интерпретироваться как
полное сечение рассеяния с учётом излучения любого числа мягких
фотонов, но в наинизшем приближении по константе связи (F. Bloch,
A. Nordsieck, 1937 [5]).

13.3. Сокращение инфракрасных расходимостей	189
13.3. Сокращение инфракрасных расходимостей
Для подтверждения сделанного в конце предыдущего пункта утвер-
утверждения и проверки формулы A3.26) проследим за сокращением инфра-
инфракрасной расходимости в низшем порядке ТВ.
Сначала продолжим вычисление сечения A3.14). Имеем
_ ( р' p \ m<1 m<1
Воспользуемся равенством
-2рр' = -
при помощи которого находим, что
.2	г	„ {р_р1J
К =
w И2+{р>кJ ~2 {рк){р'к)]
тЦ(р'-р)к}2 (p'-pf
{рк){р'кУ У '
В нерелятивистском пределе величина A3.28)
ХИЖГЖГ q = p'"p- A3-29)
Подставим A3.29) в A3.14) и выполним тривиальное интегрирование
по углам:
d o\ = d erg ¦
7ГШ2 J
0
1 -
k2 + A2
3/2'
A3.30)
где d<Jo — упругое сечение рассеяния в неком порядке по теории
возмущений. В предположении иотж/\ > 1, интеграл в A3.30) легко
берётся:
2е2 q2 / 2u;max 5\	2	2	/1ОО1Ч
^ lq2<Cm2.	13.31
^	2 ln^
Зтг m^ у A
Все сечения dcrn являются рядами относительно е2:
a^,	A3.32)
так что величина dan пропорциональна е2г.
Согласно формулам A3.1), A3.6) и A3.49) лекции 13, в однопетле-
вом приближении

190 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
iMfi = (-ie2ff2
9 9 /	o\	(lo.oo)
Л
Нас интересуют лишь инфракрасно расходящиеся вклады. Поэтому мы
не учитываем вклад в iMfi от формфактора д, а также вклад от
амплитуды (в) на рис.26. В нашем приближении в A3.31) следует
B}
использовать d <Tq . Это сечение строится по амплитуде первого при-
приближения г My) = —ieA^up'j^Up. Согласно A3.33),
При помощи A3.31) и A3.34) находим
^ ^)] 03.35)
Теперь в A3.35) можно перейти к пределу Л —> 0. Однако появляется
зависимость сечения от u;max. Эта зависимость является следствием
того, что величина иотж входит в определение рассеяния как процес-
процесса, в котором может быть испущено любое число мягких фотонов с
энергиями меньше оотж. Сечение такого процесса будет тем меньше,
чем меньше оотж. Из формулы A3.35) видно также, что радиационные
поправки к сечению малы, если частота иотж соизмерима с энергией
покоя электрона.
Сравнение A3.35) и A3.34) показывает, что в нерелятивистском
пределе инфракрасно регуляризованный формфактор
Замечание. Полученный результат означает следующее: в вели-
величине A3.35) взаимно сокращаются вклады виртуальных и реальных
испущенных фотонов с энергиями, меньшими штж. Поэтому регуля-
регуляризованный формфактор A3.36) содержит лишь вклады тех промежу-
промежуточных виртуальных фотонов, энергии которых больше cjmax. Таким
образом, формфактор A3.36) описывает упругий процесс рассеяния, в
котором не учитываются мягкие виртуальные фотоны. ?
Доказательство сокращения инфракрасных расходимостей в сече-
сечениях, в четвёртом порядке относительно константы связи, при любых
энергиях, проводится аналогично, но при помощи более трудоёмких
вычислений. Эти вычисления содержатся в работе [3].
Имеет место следующее утверждение: в суммах A3.20) и A3.25)
инфракрасные расходимости сокращаются во всех порядках относи-
относительно константы связи.

13.4. Лэмбовский сдвиг уровней	191
13.4. Лэмбовский сдвиг уровней
Рассмотрим многоуровневую нерелятивистскую систему, взаимо-
взаимодействующую с электромагнитным полем. Мы будем иметь ввиду во-
дородоподобный атом с зарядом ядра Z е, причём
Ze2«l.	A3.37)
Эта система имеет ряд дискретных одноэлектронных уровней. Элек-
Электрон взаимодействует с квантованным фотонным полем, и вследствие
этого дискретные уровни сдвигаются. В этом пункте вычисляется сдвиг
дискретных уровней, обусловленный этим взаимодействием.
Согласно (8.30) нерелятивистский гамильтониан электрона имеет
вид (в рассматриваемой задаче релятивистскими поправками к гамиль-
гамильтониану можно пренебречь)
е	d2
ТС = ТС0	рА\	По = у— + Ф(г),
т	2га ^	A3.38)
р = —id,	Ф(г) =	.
Здесь А1- (х) — квантованное фотонное поле G.33). Спиновую состав-
составляющую гамильтониана взаимодействия с фотонным полем (см. га-
гамильтониан Паули (8.30)) здесь можно опустить ввиду относительной
малости (~ | к | а ~ а, где а — боровский радиус, а а — постоянная
тонкой структуры) соответствующей поправки. Обозначим через \N)
электронный уровень невозмущённого гамильтониана:
H0\N)=EN\N).	A3.39)
При помощи G.36) находим матричный элемент фотонного поля между
фотонным вакуумом и однофотонным состоянием:
(к, а | Ах (х) | 0) = >/4тге?* e~ikx « >/4тге?*.	A3.40)
Последнее приближённое равенство означает, что задача решается в
дипольном приближении, которое в данном случае является удовле-
удовлетворительным. Воспринимая второе слагаемое в ТС как возмущение,
выпишем первую неисчезающую поправку к уровням:
5ЕМ =
адз2|к|
" г wF |РУ|2 .иг A3-41)
N- о
При переходе ко второму равенству в A3.41) мы воспользовались
правилом суммирования по векторам поляризации G.33) и затем про-

192 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
интегрировали по углам виртуального фотона. Интеграл по энергии
виртуального фотона |к| в A3.41) расходится линейно. Необходимо
выделить логарифмическую расходимость на фоне линейной. Для этого
воспользуемся тождеством
|k|	EN - EN,
EN - EN, - |k| EN - EN, -
Таким образом,
- 1.
2e2 ^ Г \pNN,\2(EN-E
N>
En — Ejs[> — |k|
Предположим, что мы рассмотрели бы эту же задачу для сво-
свободного электрона с гамильтонианом Но = р2/2т. В этом случае,
если состояния \N) — плоские волны, то Рдгдг/ ^ ^лглг' и второе
слагаемое в правой части A3.42) обращается в нуль. Первое, линейно
расходящееся слагаемое, устраняется путём перенормировки массы 0.
Действительно, пусть затравочный гамильтониан
п_,	Р2	Р2	Р2	5т 2	П<3/1<^
где то — затравочная масса. В свободной теории A3.43) имеются
лишь непрерывне уровни \N) — плоские волны. Подберём 5т в
A3.43) так, чтобы линейные расходимости всех уровней энергии со-
сокращались. Согласно A3.42) и A3.43), имеем
Так как к гамильтониану A3.38) должно быть добавлено второе слага-
слагаемое из правой части A3.43), то мы видим, что с точностью О(е2) ли-
линейно расходящиеся поправки ко всем уровням энергии сокращаются.
1) В предыдущих лекциях мы выяснили, что в дираковской теории поправ-
поправки к массе электрона расходятся логарифмически. Однако, изучаемый здесь
гамильтониан нерелятивистской заряженной частицы в равной степени может
описывать как фермиевскую, так и бозевскую частицу. Поэтому линейная
расходимость перенормировки её массы, вследствие взаимодействия с электро-
электромагнитным полем, не противоречит полученным результатам.

13.4. Лэмбовский сдвиг уровней	193
Поэтому сдвиг дискретного уровня энергии вследствие взаимодействия
с фотонным полем определяется вторым слагаемым в A3.42), в котором
вычислим интеграл по фотонной энергии от нуля до cjmax. Так как
наше вычисление — нерелятивистское, то неизвестная частота cjmax
должна удовлетворять следующим неравенствам:
(Z е2J т <С u;max <C га.	A3.44)
Здесь первое неравенство означает, что учитываемые энергии фотонов
в A3.42) много больше разности энергий дискретных уровней: \En —
— Е^'\ <С штах. Таким образом,
^	A3.45)
Вследствие первого неравенства A3.44) аргумент логарифма возможно
заменить на [иотж/\Ех> — EN\]. Перепишем A3.45) в виде
N'
о
p^ -—»	~	m
. A3.46)
N,	2\EN,-EN[
Для дальнейших преобразований воспользуемся следующими соотно-
соотношениями:
pNN,(EN< -EN) = [р, H0}nn' = -i(d<$>)NN<,	A3.47)
TV'	N'
pNN, [(EN-EN')pN,N]} = ^^{-(9Ф)дгЛг/рдГ/дГ+ A3.48)
N'
i	1
Рлглг' = -im[r, Ho]nn> = -imrNN>(EN> - EN).	A3.49)
Ещё раз перепишем первое и второе слагаемые в A3.46) при помощи
A3.48) и A3.49), соответственно:
7 С.Н. Вергелес

194 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
Здесь верхний индекс (I) указывает на то, что соответствующий вклад
получен от фотонов с частотами ио < иотж.
Зависимость сдвига уровней A3.50) от нефизического параметра
^тах указывает на то, что формула A3.50) учитывает лишь часть
сдвига: в дополнение к A3.50) следует учесть вклад от жёстких
фотонов, который содержится в диаграмме (б) на рис. 26, а также
вклад от поправки потенциала Ф, описываемый диаграммой (в) на
рис. 26. Диаграмма (б) на рис. 26 даёт квантовые поправки к движению
электрона, которые можно рассматривать как поправки вследствие
изменения эффективного электронного гамильтониана. Вклад в эф-
эффективный гамильтониан от диаграммы (б) на рис. 26 следует учесть,
используя инфракрасно регуляризованный формфактор / A3.36). При
этом частота иотж в A3.50) и A3.36) — одна и та же. Действительно, в
регуляризованном формфакторе A3.36) фактически учитывается лишь
вклад от виртуальных фотонов с частотами и > иотж (см. замечание
после A3.36)). Вклад в сдвиг уровней именно от такого формфактора и
следует добавить к A3.50), поскольку в A3.50) уже учтён вклад от фо-
фотонов с частотами и < итж. Формфактор g задаётся согласно A2.49)
и он не содержит нефизических параметров, поскольку не требует
инфракрасной регуляризации. Таким образом добавка к амплитуде,
описываемая диаграммой (б) на рис. 26, имеет вид
т
'A3.51)
Здесь q — 4-импульс, приносимый потенциалом Ф, причём q = @, q).
Добавка к амплитуде, вытекающая из радиационных поправок к по-
потенциалу и описываемая диаграммой (с) на рис.26, согласно A1.45),
равна
5{c)Mfl(q) = -Г(-ч2)(пП°иг) Ф(о).	A3.52)
Представим сумму амплитуд A3.51) и A3.52) в виде
5 Mfi = 5(b)Mfi + 6(c)Mfi = -v)fA Ф щ,
А =
Величина 5Н^ = ЛФ должна восприниматься как высокочастотная
радиационная поправка к одноэлектронному гамильтониану. При помо-
помощи A3.53), A3.36), A1.35) и A2.49) находим значение этой поправки
в импульсном представлении:

13.4. Лэмбовский сдвиг уровней	195
Функция, соответствующая A3.54) в координатном представлении,
имеет вид
24 Ь) v J Anm
A3.55)
Соответствующее смещение уровней получается усреднением операто-
оператора A3.55) по волновой функции невозмущённого состояния электрона
в атоме:
° f in ii i \
In	h ^т - = х
^ In	h ^г =
Зтгш2 у 2иитах 24 5
е2
х (ЛГ|АФ|ЛГ)-г-	(ЛГ|7аФ|ЛГ). A3.56)
Замечание. Хотя формфакторы / и д были получены для
электронов на массовой поверхности, их использование в A3.56)
является законным, хотя усреднение идёт по связанным состояниям.
Действительно, формфакторы в A3.56) получены от вклада вирту-
виртуальных фотонов с энергиями и > итж. С другой стороны, так как
энергия связанных состояний (включая энергию покоя) [1 — (Ze2J]m
почти совпадает с энергией покоя электрона и вследствие первого
неравенства A3.44), использование формфакторов /Штах и д в A3.53)
законно. ?
В первом слагаемом в A3.56) можно пользоваться непосредственно
нерелятивистскими волновыми функциями электрона. Так как диаго-
диагональные матричные элементы от спиновых операторов равны нулю, то
во втором слагаемом в A3.56) необходимо использовать в качестве
невозмущённых собственных функций \N) собственные функции га-
гамильтониана Дирака (см. (8.33)) Но = — г a. d + т 7° + Ф(г). Тогда при
помощи уравнения A3.39), в котором En включает энергию покоя
электрона, в стандартном представлении выражаем спинор \ через
спинор ф. Пренебрегая энергией связи и потенциалом Ф (их учёт был
бы превышением точности), находим
¦дф.	A3.57)
Спинор ф в A3.57) следует рассматривать как нерелятивистскую
волновую функцию. Подставляя A3.57) в A3.56), после несложных
вычислений получаем
с- ^(п) е2 Д т 19\ . _, А ^ , _х е2
9 I	Г)	' ОЛ
-mz \ 2сотях 30,
1 н съ
). A3.58)

196 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
В A3.58) и далее \N) — уже нерелятивистский вектор состояния
электрона в центральном потенциале Ф(г) и / — оператор орбиталь-
орбитального момента.
Складывая формулы A3.50) и A3.58), находим полный сдвиг уров-
уровней:
2е2
- ENY In
т
N'
19
30 Зтгш2
(ЛГ|ДФ|ЛГ)+
Ант2
г dr
A3.59)
В A3.59) сокращается промежуточная частота и;тах, что являет-
является необходимым условием корректности вычисления. Все матричные
элементы в A3.59) берутся по отношению к нерелятивистским вол-
волновым функциям электрона в атоме. Для водородоподобного атома
эти функции зависят только от четырёх квантовых чисел: главного
квантового числа п, орбитального момента I, полного момента j и
его проекции М, так что | N) = \nljM). Это состояние может быть
представлено как двухкомпонентный спинор (см. (8.74)) \nljM) =
j
Второе слагаемое в формуле A3.59) вычисляется при помощи урав-
уравнений
ДФ(х) =
= 4irZez
Полезно ввести обозначение
(п^'М|ДФ|п^М) =
2 = 4m3(Ze2Ln-35/0.
A3.60)
О2\2
A3.61)
Поскольку невозмущённые уровни энергии пропорциональны (Ze2J,
а характерный размер атома пропорционален {Z е2), то величины
Ln/ A3.61) не зависят от Z и они могут быть найдены численно для
атома водорода. При помощи обозначения A3.61) перепишем первое
слагаемое в A3.59) как
4mZ4e10
Зтгп3
In-
1
2m(Ze2L ^ (Z e2)
2J
¦N N'
\EN,-ENf
N'
Ещё раз используя A3.48) и A3.49), преобразуем второе слагаемое в
квадратной скобке в A3.62) к виду
nljM\A<$> nljM) =ln
{Ze
A3.63)

13.4. Лэмбовский сдвиг уровней
197
Последнее равенство здесь получается при помощи A3.60). Используя
A3.60), A3.62) и A3.63), переписываем лэмбовский сдвиг в оконча-
окончательном виде:
4mZV°
(Ze2J
19
30
4 тг га2
1 d Ф
)-• I— \nljM). A3.64)
r dr
Необходимо по отдельности рассмотреть случаи / = 0 и / ф 0.
При / = 0 последнее слагаемое в A3.64) исчезает, и мы имеем (в
обычных единицах)
Amc2ZAab
In
1	19
uxfi + 30
A3.65)
Приведём числовые значения нескольких величин Ьп^\
п = \	2	3	4	оо
Ьп0 = -2,984 -2,812 -2,768 -2,750 -2,721 '
Так как невозмущённые уровни Еп = — mc2(ZaJ/Bn2), то
5Еп0
1
A3.66)
При / ф 0 исчезает второе слагаемое в A3.64). Так как
= Ze2/r3 и
¦>-!•
1)'
ТО
Lnl+ о
-3/4
A3.67)
. A3.68)
Согласно соотношению (8.110) релятивистская поправка к энергии
водородоподобных атомов — энергия тонкой структуры:
5EnljM = -
mc2(ZaL
1
A3.69)
2n3 [j + 1/2 Ап\
Из сравнения формул A3.68) и A3.69) видно, что квантовая теория

198 Лекция 13. Инфракрасная проблема. Лэмбовский сдвиг уровней
поля даёт вклад в сдвиг уровней по порядку величины в а раз
меньше чем вклад от релятивистских поправок в одноэлектронной
задаче. Однако радиационный сдвиг A3.68) снимает последнее
вырождение, сохраняющееся в формуле A3.69): вырождение уровней
с одинаковыми значениями п и j, но разными / = j ± 1/2. Именно
поэтому лэмбовский сдвиг уровней легко отделить и потому измерить.
Задачи
1. Вычислите радиационный сдвиг уровней заряженного простран-
пространственного осциллятора.
Указание. Поскольку гармонический потенциал есть некая иде-
идеализация, то можно считать, что рассматривается движение нереля-
нерелятивистского электрона в глубокой, но конечной потенциальной яме с
потенциалом Ф(г) = тел2 г2/2, г < L, Ф(г) = тел2 L2/2, г > L.
Считайте, что %ш <С muj2 L2/2 <С гас2. В этом случае при вычислении
радиационных поправок к нижним уровням учёт высокочастотного
вклада при помощи формфакторов A3.51) является оправданным.

Часть III
ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ

Лекция 14
КВАНТОВЫЕ АНОМАЛИИ
14.1. Введение
В этой лекции мы рассматриваем безмассовую электродинамику
(га = 0). В безмассовом случае имеются две глобальные симметрии:
дираковское действие инвариантно относительно двух непрерывных
глобальных преобразований:
ф = е{аф;, ф = ф'е-{а,	A4.1)
ф = е1C1ъф', ф = ф'ег^\	A4.2)
Здесь а, C — вещественные числа.
Если (в пункте 2 лекции 10) д^а = 0, то преобразование A0.3)
сводится к преобразованию A4.1). Согласно теореме Нётер, в классиче-
классической теории поля каждой непрерывной симметрии соответствует сохра-
сохраняющийся ток. Таким образом, в безмассовой классической электро-
электродинамике имеется два сохраняющихся тока: векторный и аксиально-
векторный:	_
д^=0, 3^ = ф^ф,	A4.3)
<9MJ5^ = 0, ^^ = ф^>у5ф.	A4.4)
В квантовой теории поля теорема Нётер не может оставаться ав-
автоматически справедливой вследствие расходимостей. Действительно,
рассмотрим амплитуду перехода Z из вакуума в вакуум. Для получе-
получения, например, закона сохранения A4.3), в континуальном интеграле
для Z следует сделать бесконечно близкую к тождественной замену
переменных вида A0.3) и провести все те манипуляции, которые при-
привели к равенству A0.5). Если затем положить r\ = fj = 0, то из A0.5)
следует закон сохранения
)=0.	A4.5)

14.1. Введение	201
Чрезвычайно важно, что равенство A4.5) получается не в четырёх-
четырёхмерном, а в комплексном ^-мерном пространстве, в котором ампли-
амплитуда перехода регуляризованна и все те свойства теории, на которых
основывается получение равенства A4.5), остаются справедливыми
при комплексной размерности пространства. Поэтому после получения
равенства A4.5) мы можем перейти к пределу d —> 4 и провести
перенормировку. Тем самым закон сохранения A4.5) остаётся справед-
справедливым в уже перенормированной теории.
Аналогичный подход для получения закона сохранения аксиально-
векторного тока оказывается несостоятельным. Это видно, в частности,
из того, что в предположении аналитичности относительно размерно-
размерности пространства d и справедливости формул (9.61) имеем
tr^V1 ••• 7М2гг) =0	A4.6)
для всех п. Это входит в противоречие с (8.68). Равенство A4.6) озна-
означает, что размерная регуляризация неудовлетворительна, когда иссле-
исследуются аксиальные преобразования A4.2). Более того, не существует
такой регуляризации в рамках теории ^-матрицы, которая сохраняет
аксиальную инвариантность (инвариантность относительно преобра-
преобразования A4.2)). Поэтому аксиально-векторный ток не сохраняется в
квантовой безмассовой электродинамике, что далее показывается.
Для доказательства равенства A4.6) вставим под знак следа тож-
тождество 7м7м — d, затем «протащим» по циклу одну из матриц 7м П°Д
знаком следа, используя правила антикоммутации (8.5). В результате
получим
(d-2n) tr^V1 ...7М2гг)+ ... = 0.	A4.7)
Здесь многоточие означает сумму таких же следов с B п — 2) ди-
раковскими матрицами. В частности, для п = 0 имеем 6ЙГ7 = 0,
т.е. tr75 = 0. Теперь равенство A4.6) следует из равенства A4.7) по
индукции.
Покажем, что если бы не было ультрафиолетовых расходимостей, то
аксиальная аномалия (несохранение аксиально-векторного тока) также
отсутствовала бы. Для наших целей достаточно рассмотреть распро-
распространение квантованного дираковского поля на фоне неквантованного,
но произвольного электромагнитного поля. На языке функционально-
функционального интеграла такая ситуация реализуется, если сначала вычисляется
функциональный интеграл по дираковскому полю, и лишь после этого
вычисляется интеграл по электромагнитному полю. Тогда внутренний
фермионный интеграл, который обозначим Z{A}, и описывает ампли-
амплитуду перехода дираковского поля в заданном электромагнитном поле.
Заметим, что согласно (9.26),
A4.8)

202	Лекция 14. Квантовые аномалии
Формула A4.8) верна, если внешние источники равны нулю. В против-
противном случае эта формула должна быть исправлена за счёт соответству-
соответствующей экспоненты.
Рассмотрим эту же задачу на операторном языке.
Пусть {i/jN(t, x)} образует в каждый момент времени t полный
ортонормированный набор дираковских мод, т.е.
d{s)x^M(t, x)il>N(t, x) = 5M^N <—>
A4.9)
Для упрощения записи мы ввели дискретный индекс N, нумерующий
моды. Кроме того предполагается, что эти моды являются решениями
уравнения Дирака в заданном электромагнитном поле:
il^ii^N = 0' ^ VM ^лг 7м = 0-	A4.10)
Удобно считать, что в момент времени ? = to набор мод {^лг} является
полным ортонормированным набором следующего эрмитового опера-
оператора:
' ' '	A4.11)
Уравнение Дирака A4.10) может быть записано в виде
§	Щ = -1аг\7г + еА0.	A4.12)
Так как оператор ТСф является эрмитовым (сравни с (8.33)), то
условия A4.9)—A4.11) совместны. Если в A4.11) eN > 0 (eN < 0),
то соответствующая мода называется положительно-(отрицательно-)
частотной и обозначается ф^ (^дГ )• Имеется взаимно однозначное
соответствие между положительно- и отрицательно-частотными мо-
модами, так как преобразование фн ^7°75/0лг меняет их местами.
Поэтому будем считать, что индекс N нумерует лишь положительно-
частотные моды. Представим квантованное дираковское поле в виде
(сравни с (8.46))
A4.13)
N
Чтобы дираковские поля удовлетворяли каноническому антикоммута-
антикоммутационному соотношению (8.52), должны выполняться следующие анти-
антикоммутационные соотношения (как обычно, выписываются лишь нену-
ненулевые соотношения):
{ам, ajv} = {Ъм, 4} = 5M^N.	A4.14)

14.1. Введение	203
Подчеркнём, что операторы рождения и уничтожения в разложениях
A4.13) не зависят от времени. Поэтому квантованные дираковские
поля удовлетворяют уравнению Дирака:
i^V^ = 0, iVM^7M = 0,	A4.15)
и, таким образом, они являются гейзенберговыми операторами во
внешнем электромагнитном поле. Вакуумное состояние естественно
определить как
aN\0)=bN\0)=0.	A4.16)
Составим из квантованных полей векторный, J^ = ф^ф, и
аксиально-векторный, J5/x = ф^^ъф, токи. Формально, в силу урав-
уравнений Дирака-Гейзенберга A4.15), оба эти тока сохраняются, т.е. они
удовлетворяют уравнениям A4.3) и A4.4), соответственно. Однако в
данном случае мы имеем дело с неопределённостями, которые требуют
тщательного рассмотрения. Выпишем вакуумные средние рассматрива-
рассматриваемых токов:
@| J^(x)\O) = -i tr S(x, x+e)^, ?» = (?,0,0,0), ?^+0, A4.17)
= -i trS(x, x + ^V,	A4.18)
S(x, у) = -1@\Тф(х)ф(у)\0),
= / Ф^ Л^Фы (у)-
N
Из A4.19) видно, что средние A4.17), A4.18) сингулярны. Поэтому
непосредственное вычисление дивергенций правых частей в A4.17),
A4.18) невозможно до проведения регуляризации. Регуляризация, в
свою очередь, должна быть согласована с условиями квантования тео-
теории. В КЭД регуляризация должна:
(i) сохранять возможность поворота Вика в евклидово простран-
пространство;
(ii) сохранять калибровочную инвариантность.
Мы видели, что условие (i) означает, что за бесконечное время
вакуум переходит в вакуум и вакуумы при t —> ±оо различаются
не более чем фазовым множителем. Нарушение условия (ii) означало
бы нарушение свойства перенормируемости КЭД, поскольку свойство
перенормируемости основывается, в частности, на тождествах Уорда,
отражающих калибровочную инвариантность.
Например, регуляризация по энергиям, заключающаяся в отбрасы-
отбрасывании высокочастотных мод с такими N, для которых |?^| > Л —>
—> оо, удовлетворяет условию (ii), но не удовлетворяет условию (i).
Действительно, оператор Дирака в евклидовом пространстве относит-
относится к операторам эллиптического типа первого порядка. Поэтому все

204	Лекция 14. Квантовые аномалии
решения уравнения Дирака A4.10) в евклидовом пространстве растут
на пространственной бесконечности. Так как, при регуляризации по
энергии после поворота Вика, уравнения Дирака в евклидовом про-
пространстве для регуляризованных полей по прежнему имеют место, то
мы видим, что в данном случае поворот Вика приводит к неприем-
неприемлемым с физической точки зрения решениям. Поэтому поворот Вика
несовместен с регуляризацией по энергии. Стоит, однако, заметить, что
при регуляризации по энергии оба закона сохранения, A4.3) и A4.4),
выполняются.
Размерностная регуляризация сохраняет оба требования (i) и (ii).
Однако, вследствие парадокса A4.6), использовать этот метод для
вычисления дивергенции аксиально-векторного тока затруднительно.
Поэтому мы будем использовать другие подходы.
14.2. Диаграммный метод вычисления аксиальной
аномалии
Легко увидеть, что пропагатор A4.19) удовлетворяет уравнению
i^V^Six, у) = 5{А)(х-у). A4.20)
Действительно, если х° ф у0, то в силу уравнения A4.15) имеем
Sr = 0. При х° = у0 пропагатор испытывает разрыв:
[S(x + e, y)-S(x-e, У)]\?^о = ~г{ф(х\ х), ф (х\ у)} =
-у). A4.21)
Поэтому производная д/дх° в A4.20) даёт дополнительный вклад,
равный г 7°5 (х° — у0) х (разрыв пропагатора). Таким образом уравнение
A4.20) проверено.
Заметим, что пропагатор свободного безмассового дираковского по-
поля удовлетворяет уравнению (ср. с (9.49))
^	-y).	A4.22)
Поэтому
S(x, у) = (г7"^ - е^А„)~\х, у) = Sc(x - у) + [dD) z{ Sc(x - z,)x
- y) + [dD) z, dD) z2 Sc(x - z,)x
u(z2))Sc(z2-y)+ .... A4.23)
Далее мы изучаем среднее от аксиально-векторного тока A4.18).
Так как tr 757М7^ = 0, то первое слагаемое в правой части A4.23) не
даёт вклада в A4.18). Второе слагаемое в правой части A4.23) также

14.2. Диаграммный метод вычисления аксиальной аномалии
205
не даёт вклада в A4.18), поскольку оно, согласно (8.68) и (9.49), про-
пропорционально г^\р(х — z\)x(x — z\)p = 0. Поэтому начнём с изучения
третьего слагаемого в правой части A4.23), которое перепишем через
фурье-образы соответствующих величин:
) Г сг ^ р d
я
B7ГLЛ"
Подставим A4.24) в A4.18):
Sc(r
Sc(r)>yxSc(r-q). A4.24)
— е
х < ге
Sc(r + g) 7Л
A4.25)
В правой части множитель 1/2 перед интегралом появился вследствие
бозе-симметризации квадратной скобки в A4.25): лишь симметричная
часть квадратной скобки в A4.25) относительно перестановки (р, v) <—
<—> (q, Л) даёт вклад в интеграл. Далее будем изучать выражение в
фигурной скобке в A4.25), которое изображается суммой двух диа-
диаграмм на рис. 30.
г +_р
г — р
Р
Рис. 30
Крестик в вершинах диаграмм означает, что в этих вершинах вме-
вместо множителя (—ге7м) имеется множитель G57М)- В A4.25) можно
положить г = 0 ещё до вычисления интеграла, так как это не влияет
на результат (те величины, которые зависят от порядка устремления г
к нулю, не дают вклада в изучаемое среднее).
Обозначим через T^x(p,q) величину в фигурной скобке в A4.25)
x	x^	A4.26)

206	Лекция 14. Квантовые аномалии
где T^x(p,q) и T^Xu(q,p) изображаются первой и второй диаграмма-
диаграммами на рис. 30, соответственно.
Диаграммы на рис. 30 расходятся линейно. Поэтому сдвиг перемен-
переменной интегрирования изменяет эти диаграммы. При изучении диаграмм,
встречавшихся в предыдущих лекциях, такого рода неопределённости
устранялись условиями нормировки. В настоящем же случае никаких
условий, кроме условия (ii), мы не имеем (условие (i) выполнено авто-
автоматически, так как используются фейнмановские пропагаторы). Таким
образом, мы должны рассмотреть семейство величин rMzyA(p, q | а),
зависящих от сдвигового параметра 4-вектора ам:
, q\a) = Г^л(р, q) + А^л(р, q | а),	A4.27)
r
Vc(rOA^c(r-g), A4.28)
Г d{4)r
——
x {Sc(r + a +p) 7^ Sc(r + а) 7Л Sc(r -\- a — q) —
-Sc(r +p)l"Sc(rIx Sc(r - q)} . A4.29)
Для прояснения ситуации рассмотрим одномерный интеграл
+ ОО
A(a)= f dx[f(x + a)-f(x)].	A4.30)
— сю
Если / (х) — интегрируемая функция на всей прямой, то при помощи
сдвига переменной интегрирования устанавливается, что А (а) = 0.
Теперь разложим подынтегральное выражение:
+ СЮ
А (а) = Ах
— сю
= а [/ (+оо) - / (-оо)] + j [/(+оо) - /(-оо)] + ....
Отсюда видно, что если / (х) стремится к разным пределам при х —>
—> +00 И X —> —00, ТО
А (а) = а [/ (+оо) - / (-оо)] ф 0.	A4.31)
Аналогично вычисляется в задаче 1 величина A4.29):
- 2
x) = ^s^xPapy ap = {a + b)pp + bqp. A4.32)
O7TZ

14.2. Диаграммный метод вычисления аксиальной аномалии	207
Мы ограничили класс векторов ар тем требованием, чтобы вектор ар
зависел лишь от векторов р, q, уже имеющихся в задаче. В A4.32)
а и Ъ — некие числа. Тогда наиболее общий вид величины A4.26)
таков:
(?x^^^^-qp). A4.33)
Комбинируя A4.25) и A4.26) и вычисляя дивергенцию, находим
d P d q r
x^(p)AA(g) [(p + g)MT^A(p,g)] + .... A4.34)
При помощи явной формулы A4.28) получаем
riD)r
^r tr75 [(/ + j()Se
¦tr75 [7^с(гOЛ5с(г-^) + 5с(г + рO^с(гOЛ] =0.
A4.35)
Здесь в последнем интеграле каждое из слагаемых является двухин-
дексным псевдотензором в 4-мерном пространстве, составленным при
помощи одного единственного вектора (q или р), что невозможно.
Отсюда следует обращение в нуль величины A4.35). Поэтому, согласно
A4.33) и A4.35),
(р + д)„Т^(р, q) = -a l^?^PPliqp.	A4.36)
[ и
Далее следует учесть, что калибровочная инвариантность не нару-
нарушена. Очевидно, что оба изучаемых тока A4.17) и A4.18) инвариантны
относительно калибровочных преобразований. Поэтому так же, как в
лекции 10 при выводе тождества Уорда, находим тождество
из которого в наинизшем приближении следует равенство
pvT»vX(p,q)=0.	A4.37)
Из A4.28) находим
dD)

208	Лекция 14. Квантовые аномалии
х [5с(гOЛ Sc(r -q)- Sc(r + рOЛ Sc(r - q)}.	A4.38)
Первый интеграл в правой части A4.38) исчезает, так как невозможно
построить псевдотензор с двумя индексами из одного единственного
4-вектора. Аналогичное вычисление даёт
D) r
5	xSc(r-p). A4.39)
Нам нужна сумма интегралов A4.38) и A4.39):
Г dD) r
, q) = г е2 j ^4 tr W х
х [Sc(r+p+a) 7Л Sc(r-q+a)-Sc(r+p) 7Л Sc(r-q)], a = q-p. A4.40)
В задаче 2 эта величина вычислена:
2
Xqp.	A4.41)
' 4тг2	'"*"
При помощи A4.26), A4.27), A4.32) и A4.41) находим
\ + - j .	A4.42)
Отсюда видно, что для выполнения калибровочной инвариантности
теории необходимо, чтобы
a = -2.	A4.43)
Согласно A4.36) такое значение параметра а означает несохранение
аксиально-векторного тока. С другой стороны, если потребовать сохра-
сохранение аксиально-векторного тока, для чего необходимо положить а =
= 0, то нарушается калибровочная инвариантность и векторный ток не
сохраняется. Поэтому теория самосогласована лишь при выполнении
равенства A4.43).
Важно, что многоточие в A4.34) может быть опущено, так как все
слагаемые, обозначенные многоточием, не содержат ультрафиолетовых
расходимостей и потому, как это было указано во введении, не могут
дать вклад в аномальную дивергенцию каких либо величин. Этот
факт даёт возможность переписать с учётом равенств A4.36) и A4.43)
соотношение A4.34) как точное равенство вида
е
х [РцАи(р) - риА^(р)] [q\Ap(q) - qpAx(q)} = -r^ e^Xf>F^(x) FXp(x).
Ж	A4.44)

14.3. Неинвариантность функциональной меры	209
Равенство A4.44) было получено Ю. Швингером A951) и затем ещё
раз открыто С. Л. Адлером A969) и Ю. С. Беллом и Р. Джекивом
A969) [6].
14.3. Неинвариантность функциональной меры как
источник аномалии
Рассмотрим задачу об аксиальной аномалии непосредственно в ев-
евклидовом пространстве. Тем самым условие (i) автоматически выпол-
выполнено.
Формулировка фотодинамики в евклидовом пространстве очевидна.
Поэтому мы лишь прокомментируем формулировку теории Дирака в
евклидовом пространстве размерностью d.
Пусть {7м }, /i = 1, ... ,d — набор эрмитовых матриц Дирака таких,
что
7*V +7V = 25^, т5 = tVtV = G5)f (d = 4), A4.45)
где 5^и — символ Кронекера. Дираковское действие в безмассовом
случае имеет вид
а)	^e^.	A4.46)
Здесь поля ф и ф взаимно эрмитовски сопряжены, и поэтому действие
A4.46) эрмитово. Рассмотрим фермионный функциональный интеграл
(аналог величины A4.8))
I	A4.47)
В функциональном интеграле A4.47) переменные {ф,ф} рассматри-
рассматриваются как независимые.
Определим математически строго функциональную меру в инте-
интеграле A4.47) следующим образом. Предположим, во-первых, что х-
пространство является компактным множеством (например, это может
быть тор, на котором для полей заданы периодические граничные усло-
условия). Пусть { фн } — полный ортонормированный набор собственных
функций оператора Дирака:
Н^^фм=е1Чф1Ч.	A4.48)
Заметим, что (гу^^м) ~~ эрмитов оператор и индекс N, вследствие
компактности ж-пространства, пробегает счётное неограниченное мно-
множество. Разложим фермионные поля по этому полному набору функ-
функций:
Ф(х) = Y^ ^мФм^)' Ф(х) = Y Vn Фм(х)>	A4.49)
N	N

210	Лекция 14. Квантовые аномалии
где {г],г]} — множество независимых грассмановых переменных и
переменные rjN, rjN взаимно комплексно сопряжены. В разложениях
A4.49) штрих над знаком суммы означает, что суммирование ограни-
ограничено теми значениями N, для которых
?дг|<Л^оо,	A4.50)
где Л — импульс обрезания. Таким образом, фермионные поля ока-
оказываются регуляризованными и при этом они разложены по конечному
числу мод.
Обычно подразумевается, что континуальная фермионная мера в
интеграле A4.47) представляется в виде
= ]\drj
jN &VN-	A4-51)
N
Здесь все равенства являются формальными, поскольку произведение
континуального или счётного бесконечного числа дифференциалов не
является корректно и однозначно определённой величиной. Поэтому
определим регуляризованную фермионную меру при помощи следую-
следующей формулы:
drjNdriN.	A4.52)
N	\sN\<A
Определение A4.52) является вторым моментом в определении регуля-
ризованной дираковской континуальной меры. Мера A4.52) является
калибровочно инвариантной. Действительно, при калибровочных пре-
преобразованиях
собственные значения en, & также грассмановы переменные {rj,rj}
остаются инвариантными.
Далее мы используем регуляризованную меру A4.52), которая опре-
определена математически строго. Таким образом, условие квантования (ii)
также выполнено.
Совершим бесконечно малое аксиальное преобразование фермион-
ных полей:	_
ф(х) -^ ф(х) = ф(х) + га{х) ^^(х),
A4.53)
ф(х) -^ ф(х) = ф(х) + га(х) ф(х) 75-
В терминах переменных rjN и rjN преобразование A4.53) переписы-
переписывается следующим образом:

14.3. Неинвариантность функциональной меры	211
A4.54)
м
Преобразование A4.54) изменяет меру A4.52) в первом порядке по а
(см. (9.23)) 0:
drjN drjN= I 1 +2г dl } xa \ ^мТТм N drjNdrjN.
N	V	М	/ N
A4.55)
Используя в выражении A4.47) регуляризованную и калибровочно
инвариантную фермионную меру A4.52), произведём в этом функци-
функциональном интеграле замену переменных согласно формулам A4.53),
A4.54):
d rjN d rjN e s* = Y[ drlN drlN e
-J AT
N	J N
2г
A4.56)
M
Здесь J5/x = i ф 7^75/0 — эрмитов аксиальный ток. Все функции или
функционалы, над которыми стоит волна, выражены через переменные
с волной по обычным правилам. Полагая в A4.56) а(х) ~ 5^d\x — у),
получаем
(<V5^) = -2 ^'^attVat.	A4.57)
N
В уравнении A4.57) (...) означает усреднение по фермионному ваку-
вакууму. Правая часть в уравнении A4.57) возникла вследствие неинва-
неинвариантности регуляризованной фермионной меры A4.52) относительно
преобразований A4.54). Правая часть в A4.57) легко вычисляется,
если обрезание в сумме сделать «мягким», то есть вместо обрезанной
суммы YI'n использовать регуляризованную сумму Х^лгехР(~г?лг)'
г —> +0. Таким образом, перепишем равенство A4.57) в виде
)) = -2tvj5K(x,x\r), т^+0,	A4.58)
х) Бесконечно малое калибровочное преобразование дираковских полей
приводит к формулам преобразования переменных rjN и rjN, отличающимся от
A4.54) лишь отсутствием матрицы 75 и противоположным значением знаков
перед суммами в этих формулах. Поэтому соответствующий якобиан тожде-
тождественно равен единице.

212
Лекция 14. Квантовые аномалии
К(х,у\т) = $(т) 2_^е
N
= #(т) {ехр \-т (i7MVMJl ) . A4.59)
L L	J J xy
Для оператора К имеем уравнение
К(х, у\т) = 6(т) S^d\x - у).	A4.60)
Воспользуемся равенством
и запишем оператор
в виде
Теперь уравнение A4.60) принимает вид
A4.61)
A4.62)
Будем вычислять оператор К(х, у\т) в пределе г —> +0 при помо-
помощи ТВ. В нулевом приближении оператор
уравнению
и он равен, при d = 4,
г) удовлетворяет
A4.63)
A4.64)
4г
Это выражение проще всего получить, переходя в импульсное пред-
представление, в котором
Tc(Q)(k I т) — ?9(V^ р~тк К^(т — а т\ —
Таким образом, имеем
dr,
о
D)
dn dr2 | d^
о о
xK^\y-z\TX-T2) [iecrxPFXp(z)
r - r,)
(z - x \ r2)
A4.65)

14.3. Неинвариантность функциональной меры	213
Невыписанные здесь слагаемые, обозначенные многоточием, либо ис-
исчезают под знаком следа в A4.58), либо исчезают в пределе г —> +0.
Так как
tr75 = 0, tr7W = 0, tr7W7A7p = 4?^Ч A4.66)
то вклад в A4.58) даёт лишь третье слагаемое в A4.65). Из A4.64)
видно, что при г —> +0 интегралы по у и z насыщаются при у —>
—> ж, z —> ж и потому гладкие величины F^v(y) и F\p(z) могут быть
вынесены из под знака интеграла и взяты в точке х. После этого
все свёртки между функциями К^ следует вычислять при помощи
тривиальной формулы
wzK(°\x -z\t- n) K(°\z - у | п) = К^\х - у | г)
Таким образом, находим, что третье слагаемое в A4.65) равно
r, . . . <Ы-	A4-67)
О О
Из проведенного вычисления видно, что если бы мы учли более вы-
высокие члены разложения в A4.65), то они были бы пропорциональны,
например (в следующем порядке)
Т2
d т2 d т3 = - -> 0.
J	6
0 0 0
Все такие слагаемые стремятся к нулю в пределе г —> +0. Поэтому,
подставляя A4.67) в A4.58) и используя A4.66), окончательно находим
A4.68)
Замечание 1. Строго говоря, преобразованные поля A4.53)
должны быть спроектированы на регуляризованное пространство фер-
мионных полей A4.49) с базисом мод {^лг}, |?jv| < Л. Иными словами,
для преобразованных полей также должны иметь место разложения
A4.49):
Ф(х) = J2^n ^n(x)> Ф(х) = J2 ^n ^n(x)-	A4.69)
N	N
В противном случае действие
в A4.56) как функция переменных {fjM, rjM} оказалось бы отличным
от действия S в A4.47) как функции переменных {г]м, г]м}, и из

214	Лекция 14. Квантовые аномалии
A4.56) не следовало бы соотношение A4.57). Однако вследствие того,
что моды в разложениях A4.49) и A4.69) являются собственными для
оператора Дирака ij^V^, мы имеем
\eN\<K	\eN\>A
Здесь второе слагаемое имеет порядок О (а2) и потому не играет
роли в приведенном выше вычислении. Мы видим, что в фермионном
действии проектирование преобразованных фермионных полей на регу-
ляризованное фермионное подпространство происходит автоматически.
Подчеркнём, что этот факт является следствием использования соб-
собственных функций оператора Дирака для регуляризации фермионных
полей. Поэтому корректность перехода от равенства A4.56) между
регуляризованными фермионными интегралами к соотношению A4.57)
очевидна. ?
Замечание 2. Операторы A4.23) и A4.65) зависят лишь от ве-
величин (ет4м7м) и (eF^a^, соответственно. Согласно A0.35) и A0.45)
эти величины не изменяются при одновременном переходе от затра-
затравочных значений константы ео и поля А^ к их перенормированным
(физическим) значениям е и А^^. Очевидно, в пункте 2 используются
перенормированные величины, а в пункте 3 — затравочные. Таким
образом, полученные ответы для дивергенции аксиально-векторного
тока A4.44) и A4.68) численно совпадают. ?
Вычисление аномальной расходимости аксиально-векторного тока
путём учёта неинвариантности фермионной меры впервые было проде-
проделано С. Н. Вергелесом [7]].
Вывод: Не все сохраняющиеся величины в классической теории
поля остаются сохраняющимися в квантовой теории. Этому
препятствуют квантовые аномалии. В частности, в безмассовой
КЭД векторный ток сохраняется, а аксиально-векторный ток не
сохраняется вследствие квантовой аномалии.
Задачи
1. Вычислите интеграл A4.29).
Ответ:	. 2
\Ци\(	I \ _ l e
/л [р, q | а) —
2
2. Вычислите интеграл A4.40).
Ответ:

14.3. Неинвариантность функциональной меры	215
3. Сформулируйте и выпишите действие для двумерной электро-
электродинамики (электромагнитное + дираковское поля). В безмассовом
случае решите задачу также и в евклидовом пространстве. Вычислите
аномалию в дивергенции аксиально-векторного тока в безмассовой
евклидовой теории.
4*. Вычислите в двумерной безмассовой электродинамике (модель
Швингера) величину In Z {А}.
Указание. Действовать в евклидовом пространстве и принять во
внимание следующие факты:
а)	г
5А In Z {А} = -е dB) xSA^{ J* ),
где JM = ф 7Mi/> ~~ векторный ток;
б)	кинематическое соотношение
^v,	^,	= г ф'у^
в) равенства 9M{J^)=0 и 0„( J5"> = -^s^F^. D

Лекция 15
СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
15.1. Спонтанное нарушение симметрии
в классической теории
Рассмотрим теорию скалярного вещественного поля с лагранжиа-
лагранжианом	2
С = - (д^фJ + —- ф2 - — ф4.	A5.1)
Гамильтониан такой теории
-^V + ^гИ.	A5.2)
2	4!
В теории A5.1)—A5.2) имеется дискретная симметрия ф —> —ф.
Энергия классической системы A5.2) принимает минимальное зна-
значение в том случае, когда ф = const и потенциал
у @) =	ф -|— 0	A5.3)
минимален, что имеет место при
фо = ±17 = ±у — /1 ^ 0.	A5.4)
Константа i; называется вакуумным средним поля ф.
Предположим, что система находится вблизи одного из минимумов
потенциала, совершая вблизи него малые колебания. Поэтому есте-
естественно разложить поле ф вблизи вакуумного среднего:
ф = 0q -|- (j.	A5.5)
Подставим A5.5) в лагранжиан A5.1):

15.1. Спонтанное нарушение симметрии в классической теории 217
Мы учли, что линейное слагаемое относительно а автоматически
исчезает в A5.6), и опустили С(фо) = const. Лагранжиан A5.6) опи-
описывает скалярное поле а с массой т = л/2 /i. Симметрия ф —> —ф
теперь проявляется лишь в соотношении между тремя коэффициентми
теории с лагранжианом A5.6).
Теперь рассмотрим линейную сигма-модель (см. задачу 3 к лекции
3) с лагранжианом
A5.7)
Лагранжиан A5.7) инвариантен относительно преобразований
<Р^О)<Р, ООг=\.	A5.8)
Таким образом О — элемент ортогональной группы вращений 71-
мерного евклидового пространства.
Также, как и в вышеприведенном случае, классическая конфигура-
конфигурация с минимальной энергией есть постоянное поле фг0, минимизирую-
минимизирующее потенциал
2
Этот минимум достигается, если
($J = т-	A5Л0)
А
Условие A5.10) определяет лишь длину вектора фг0, но не его направ-
направление. Для удобства будем считать, что
ФЬ = (О,...,у), « = -д-	A5.11)
Аналогично A5.5), теперь имеем
ф1 = (itk(x), v + a(x)), k= 1, ... , п- 1.	A5.12)
Перепишем лагранжиан A5.7) в терминах новых полей:
С = i (Vf + \ (VJ - \ BМ2) *2 ~ VX ^ - VX /i (nk)\-
Лагранжиан A5.13) описывает динамику массивного поля а и (п —
— 1) безмассовых полей тг^. Исходная О (п) симметрия оказывается
нарушенной, от неё остаётся подгруппа О (п — 1) вращений полей тг

218	Лекция 15. Спонтанное нарушение симметрии
в своём пространстве. Колебания поля а происходят вдоль длины век-
вектора фг, изменяя эту длину. Поэтому вторая производная лагранжиана
по а отлична от нуля и масса этого поля не равна нулю. Масса тг-
частиц равна нулю, так как тг-частицы деформируют поле фг в (п— 1)
направлениях, ортогональных вакуумному среднему.
15.2. Теорема Голдстоуна
Заметим, что группа симметрии исходного лагранжиана A5.7) ин-
инвариантна относительно группы Ли О(п), размерность которой п(п—
—	1)/2 (число различных двумерных плоскостей, в которых можно
делать независимые друг от друга повороты). Когда исходная симмет-
симметрия нарушена до симметрии, содержащейся в лагранжиане A5.13),
остаточная симметрия описывается группой О (п — 1) с (п — \)(п—
—	2)/2 независимыми преобразованиями. Таким образом, утрачены
п(п-\) (п-\)(п-2)
—2	2	= (n}
преобразований симметрии и вместе с тем появились (п— 1) безмас-
безмассовые частицы, которые называются голдстоуновскими бозонами.
Теорема Голдстоуна утверждает, что для каждой спонтанно на-
нарушенной непрерывной симметрии в теории содержится безмассовая
частица.
Доказательство теоремы Голдстоуна проведём в самом общем случае.
Рассмотрим теорию, содержащую несколько полей фг с лагранжи-
лагранжианом
С = (члены с производными) — V (ф).	A5.14)
Пусть фг0 — постоянное поле, минимизирующее V:
= 0.	A5.15)
Разложим V в окрестности этого минимума:
Коэффициент при квадратичном слагаемом,
является симметричной матрицей, собственные значения которой дают
массы полей. Они неотрицательны, так как V минимален при ф = ф$.
Для доказательства теоремы Голдстоуна необходимо показать,

15.2. Теорема Голдстоуна
219
что всякая непрерывная симметрия лагранжиана A5.14), не являю-
являющаяся симметрией (т.е. изменяющая поле фо), приводит к нулевому
собственному значению матрицы A5.17).
Произвольное преобразование непрерывной симметрии имеет вид
ф{ —> ф{ + аА{(ф), а^О,	A5.18)
где Аг(ф) — некие функции поля ф, определяющие данное пре-
преобразование симметрии. Достаточно рассмотреть поля, постоянные в
пространстве-времени. Тогда потенциал V инвариантен сам по себе
относительно преобразования A5.18):
V
аАг(ф))
г\
д
dv
Вследствие условия A5.15),
%АЦфо)=О.	A5.19)
= 0, то фг0 + Аг (фо) = фг0. Это означает,
Заметим, что если Аг (фо)
что вакуумное среднее инвариантно относительно рассматриваемого
преобразования. Наоборот, если Аг (фо) ф 0, то мы имеем преобра-
преобразование, изменяющее фг0. Соответствующая симметрия отсутствует в
лагранжиане вида A5.13). Но равенство A5.19) означает, что такому
преобразованию соответствует нулевая масса. Тем самым теорема Гол-
дстоуна доказана.
Вернёмся к линейной сг-модели с лагранжианом A5.13) и построим
соответствующую квантовую теорию поля. Обозначим пропагаторы а-
и тг-частиц, соответственно, двойной и одинарной линиями. Тогда
элементы диаграммной техники Фейнмана будут иметь вид, представ-
представленный на рис. 31.
Очевидно, что теория с указанной на рис. 31 диаграммной техни-
техникой перенормируема, так как перенормируема теория с лагранжианом
A5.7), а ультрафиолетовые расходимости не могут зависеть от того,
как «растасованы» и обозначены отдельные поля теории. Однако имеют
место гораздо более сильные утверждения.
1.	Для устранения ультрафиолетовых расходимостей в теории
A5.13) с диаграммной техникой, представленной на рис. 31, достаточно
введение контрчленов того же вида, что и в лагранжиане A5.13).
2.	Теорема Голдстоуна остаётся справедливой с учётом квантовых
поправок.

220
Лекция 15. Спонтанное нарушение симметрии
а
k2 - 2/i2
= —i6Xv ,
Xv,
= -гбЛ,
к	/
= -12 5v ,
^	J
Рис. 31
Ввиду громоздкости мы не доказываем здесь этих утверждений.
Укажем лишь удобные условия перенормировки, фиксирующие все
константы теории:
= 0;
= 0;
/с2=0
A5.20)
= —гбЛ при s = 4m2, t = u = 0.
«ампутированная»
15.3. Эффективное действие
Рассмотрим для некоторой скалярной теории поля с лагранжианом
С (ф) производящий функционал (см. C.16))
e-iE(V) =Z(r)) =
i j*d(d) х (С(ф) + г]фЦ .
j	j
A5.21)

15.3. Эффективное действие	221
Имеем
5 „, ч . 5
XliZ=-—r-
A5.22)
Здесь правая часть — среднее по вакууму в присутствии внешнего
источника rj(x). Определим классическое поле,
фс\(х) = (ф(х))Г],	A5.23)
и эффективное действие:
Г (фс\) = —E{rj) — сг ' ут){у) Фс\(у) •	A5.24)
Тот факт, что эффективное действие зависит лишь от классического
поля, но не от внешнего источника, устанавливается вычислением
полной вариации величины A5.24):
6 г=~ I шаS71{v) d(d) у ~ Iфс1 {у) s v{-y) d(d) y ~ \v{s) 6 фсх {у) d(d)y'
С учётом A5.22) здесь первые два слагаемых взаимно сокращаются.
Поэтому
*Г^>-= _„(*).	A5.25)
Если внешний источник обратить в нуль, то из A5.25) получаем
Решения последнего уравнения являются значениями (ф{х)} в
стабильных квантовых состояниях теории. Для трансляционно-
инвариантного вакуума фс\ также не зависит от х. Именно такой
случай далее мы будем рассматривать. Заметим лишь, что в случае
трансляционно- и лоренц-инвариантного вакуума иногда могут
быть дополнительные решения уравнения A5.26), нарушающие
симметрию вакуума и соответствующие локализованным сгусткам
поля, удерживаемым за счёт самодействия и топологических факторов.
В случае, когда действие таких сгустков конечно, они называются
инстантонами, а если конечен гамильтониан, то они называются
солитонами. Солитоны являются частицами, которые отсутствуют
при наивном изучении теории с помощью теории возмущений.
Если фс\ = const, то поскольку Т(фс\) есть экстенсивная величина
— она пропорциональна объёму пространства-времени — мы имеем
Г(фс1) = -(УТ)У^фс1).	A5.27)
Здесь Т — временная протяжённость пространства-времени, а V —
объём. V^f@ci) в A5.27) называется эффективным потенциалом.

222
Лекция 15. Спонтанное нарушение симметрии
В терминах эффективного потенциала уравнение A5.26) записывается
как	г,у ,, ч
^Р^=0.	A5.28)
Так как Г = — Е при г] = 0, то потенциал Vef, вычисленный в точке
A5.28), является плотностью энергии в этом состоянии.
Будем вычислять Vef при помощи ТВ. Разобьём лагранжиан, как
обычно, на слагаемое, зависящее от перенормированных параметров, и
слагаемое, содержащее лишь контрчлены:
? = ?х+5?.	A5.29)
Наша цель — вычисление функции Г(фс\), в то время как Z(rj) зависит
от фс\ косвенно через источник г]. Попробуем найти, хотя бы неявно,
связь между г] и фс\. В наинизшем порядке ТВ эта связь задаётся
уравнением (см. A5.25))
5ф(х)
Тогда уравнение
= —г](х) (в низшем порядке).
6ф(х)
определяет «перенормированный» источник rj\(x), так что
rj(x) = г/1 (ж) +5г](х).
A5.30)
A5.31)
A5.32)
«Контрчлен» 5г](х) определяется последовательно при помощи ТВ
и уравнений A5.23), A5.31), A5.32). Перепишем формулу A5.21)
следующим образом:
o-iE{ri) =
ехр г
&{d)
ехр
A5.33)
В первой экспоненте справа разложим показатель вблизи фс\ : ф(х) =
= фс\(х) + р(х). Имеем
d{d)x {Сх{ф)
d{d)xp(x
5?{

15.3. Эффективное действие	223
A5.34)
Вследствие A5.30), линейное по р слагаемое в A5.34) исчезает. Та-
Таким образом, следует вычислить функциональный гауссов интеграл
по полю р, а нелинейности учесть при помощи ТВ в соответствии с
разработанной схемой.
В низшем приближении вторая экспонента справа в A5.33) не даёт
вклада, а первая экспонента даёт функциональный гауссов интеграл:
Dp exp
= ехр i (?,(&,) + »?,&,) ¦ det -7777	¦ A5.35)
Отсюда видно, что при дальнейшем учёте квантовых поправок воз-
возникают фейнмановские диаграммы, в которых в качестве пропагатора
используется оператор
(У	A5-36)
а вершинами являются третья и т.д. функциональные производные С\.
Вторая экспонента в A5.33) также разлагается вблизи фс\ по полю
р и даёт контрчлены. Как обычно в аналогичных вычислениях (см.
F.14)), получаем
- \ In det (-
+ (связные диаграммы
) + г d(d) х FС(фс\) + 5г] • фс\). A5.37)
Здесь последнее слагаемое является нулевым приближением при раз-
разложении по р показателя второй экспоненты в A5.33). Сопоставляя
A5.24) и A5.37), находим
Т(фс1) =^^хС{(фс1) ^'-Ы det (-
— г (связные диаграммы) + d^ х5С(фс\). A5.38)
Здесь все слагаемые зависят явно от фс\. Важно также то, что каждая
связная диаграмма в A5.38) не имеет внешних линий и потому яв-
является не ниже чем двухпетлевой. Таким образом однопетлевой вклад
содержится во втором слагаемом в A5.38).
Отметим, что контрчлен 5 rj определяется из того требования,
чтобы во всех порядках было (ф) = фс\: если в процессе вычислений

224	Лекция 15. Спонтанное нарушение симметрии
возникает ненулевой вклад в (р), то его «убивают», добавляя соответ-
соответствующий вклад в 5 г].
Вычислим эффективное действие A5.38) для линейной сигма-
модели в однопетлевом приближении, т.е. учитывая в A5.38) лишь
первые два слагаемых. При помощи A5.7) мы находим
= 8* (-д2 + /х2) - А [(<^J^ + 2ф1{ ^]. A5.39)
фс1
Предположим, что фгс1 = const и
<^ = @, 0, ...,0, фс1).	A5.40)
Тогда оператор A5.39) совпадает с диагональной матрицей п х п,
на диагонали которой находятся операторы Клейна-Гордона-Фока
(-д2 - га2), где
Г Л021—/i2, при действии на р1, ... , рп~1,
т\ = <	A5.41)
у 3A02j — /i2, при действии на рп.
Поэтому детерминант в A5.38) равен произведению детерминантов
этих операторов:
A5.42)
Воспользуемся известной формулой
lndet A = trln A,
где А — линейный оператор. Имеем
In det (<92 + га2) = tr In (<92 + га2).	A5.43)
Сделаем поворот Вика в евклидово пространство. При помощи A5.7),
A5.38), A5.42), A5.43) получаем
2
г=\
A5-44)
Здесь набор масс rrii задаётся согласно A5.41), д2 = X]^=i(^J' a
два последних слагаемых — возможные контрчлены. Задача свелась к
вычислению величины tr In (—д2 + га2). В ортонормированном базисе
{егкх} матричные элементы оператора 1п(—92 + га2) равны
(р\ ln(-<92 + ra2)|&) = l{)

15.3. Эффективное действие	225
Поэтому
tr In (-д2 + т2) = (VT) ^ф In D + m2).	A5.45)
E
Ho
я г hW h 1
In(k%+m2) = -^\f—t 2 *
	 (m2)d/2~a r(a-d/2I
9q! ["' D7r)d/2 ' ГA+а) J
a=0
D7r)d/2
A5.46)
Теперь, при помощи A5.41), A5.42), A5.44), A5.46), получаем
кш - -1 ,'й + \ (й) -' ¦ Щ$ {<« - о
^^i + ^a(^,J.	A5.47)
Здесь (?!J| = (</>*iJ. Эффективное действие A5.47), конечно, О(п)-
инвариантно. Выражение A5.47) конечно при d —> 4 (т.е. конечны
коэффициенты при степенях фс\), если
дп = —л ii (п + 2) —^——г^—^ + конечные члены;
DтгJ
A5.48)
л2/ очгB^/2)
Ол = А [п + 8) ———г^	h конечные члены.
D 7TJZ
Конечные члены в A5.48) регулируются условиями нормировки. Под-
Подберём их так, чтобы
We) = ~\ ^ФЪ + \ fa)* + ^ {(« - 1) х
A5.49)
Здесь М — точка нормировки. На рис. 32 пунктирной линией изоб-
изображён график классического эффективного потенциала, а сплошной
линией — потенциала с квантовой поправкой A5.49). Сплошная линия
рвётся там, где поправка не определена. Из A5.49) видно, что при
/j2 > 0 симметрия спонтанно нарушена, при /j2 = — т2 = — М2 < О
имеется один тривиальный минимум потенциала при фс\ = 0.
8 С.Н. Вергелес

226
Лекция 15. Спонтанное нарушение симметрии
\
\
\
1 /
I /
1 /
1 /
Рис. 32.
Рассмотрим V^f A5.49) в случае /i2 = 0:
4
D*0
A5.50)
Интересен вопрос: имеет ли потенциал A5.50) нетривиальный мини-
минимум? Легко найти, что d V^f/d^ = 0, при
D 7Г)
(п + 8) Л
A5.51)
Однако при таком значении ф^{ второе слагаемое в фигурной скобке
в A5.50) почти сокращает первое слагаемое, т.е. поправки имеют тот
же порядок, что и нулевое приближение. Это означает, что что для
решения поставленной задачи ТВ непригодна.
Задачи
1. Нарисуйте все однопетлевые диаграммы, определяющие поправки
к вершине j\ > дающей амплитуду рассеяния двух сг-частиц в
линейной сигма-модели.
Ответ:
/кроссканальные \
I диаграммы )
/кроссканальные \
I диаграммы J
(кроссканальные
диаграммы

15.3. Эффективное действие	227
2. Имеет место равенство
- ФЫ >сс,	A5.52)
где индекс ее означает, что этот коррелятор сильно связан и его ноги
ампутированы.
а) Докажите, что
1-1
где
= -1(Тф(х)ф(у))сшз.
Индекс «связ» означает, что коррелятор является связным. Если ваку-
вакуум трансляционно инвариантен, то согласно E.13) и E.22),
p-ik{x-y)
где Е(/с2) — сумма сильно связных диаграмм с двумя концами,
б) Докажите формулу A5.52) для п = 3.

Приложение А
ВЫРАЖЕНИЕ ВЕРОЯТНОСТЕЙ ПРОЦЕССОВ
ЧЕРЕЗ АМПЛИТУДЫ
Рассмотрим вопрос о выражении сечений рассеяния и вероятностей
распадов частиц через инвариантные амплитуды рассеяния в трёхмер-
трёхмерном пространстве.
Сначала проясним вопрос о нормировке r-частичных состояний.
Согласно B.39),
(к\к)=2и;кB7гK5^@).	(АЛ)
Так как объём пространства представляется как
р=к
то (АЛ) означает, что принятая нами лоренц-инвариантная нормировка
состояний B.38) такова, что в единице объёма содержится
(А.2)
частиц.
Построим r-частичное нормированное состояние. Пусть G — малая
область в импульсном пространстве частиц вблизи значений импульсов
(р1? ... , рг), так что объём G равен
(А.З)
G
Состояние
J
dO),
Pi, .. ,Pr

Прил. А. Выражение вероятностей процессов через амплитуды 229
имеет норму
Pr Pb
-n
#),
G
При получении (А.4) была использована формула B.45), а также тот
факт, что импульсы р^- и р^ почти совпадают при всех j, в то время как
импульсы Pj и р^ при г ф j принадлежат непересекающимся областям
Apj и Api. Следует заметить, что (А.4) есть лоренц-инвариант. Таким
образом состояние
П-1/2
п
J=l
(А.5)
нормировано, причём это свойство лоренц-инвариантно.
Пусть |г) — n-частичное состояние B.43) и |/) — состояние (А.5).
Тогда для недиагональных матричных элементов (см. C.2)-C.4))
(f\S\i) = (f\iT
г =
п
J=1
-1/2
г г
п
рь ... ,Pr|iT|kb ... ,к„>. (А.6)
Согласно вышесказанному, выражение (А.6) лоренц-инвариантно. Пе-
Перепишем (А.6) при помощи амплитуды Mft (см. C.4) и вычислим
вероятность перехода из состояния |i) в состояние |/). Так как |/)
— нормированное состояние, то согласно общим правилам квантовой
механики эта вероятность
d0)
Pi
(А.7)
i=lGltZ7V>
При получении последней формулы была учтена малость объёма G, а
также равенство
П
dC)
Pi
= 1.

230 Прил. А. Выражение вероятностей процессов через амплитуды
В выражении (А.7)
Pi = ki+ ... +кп, Р/=р\+ ...
Положим
где V — объём пространства, а Т — полный промежуток времени,
в течение которого рассматривается процесс. Таким образом, деля
выражение (А.7) на 4-объём VT, мы получаем вероятность перехода в
единице пространства в единицу времени:
г	,C)
dwfl = B«)W>(Pf - Pt) |М/г|2 П /
В выражении (А.8) опущен знак интеграла по импульсам конечных
частиц. Поэтому вероятность перехода (А.8) является дифференциаль-
дифференциальной вероятностью перехода в бесконечно малый элемент импульсного
пространства конечных состояний.
Ещё раз подчеркнём, что выражение (А.8) лоренц-инвариантно и
в случае применимости ТВ амплитуда Mfi вычисляется при помощи
диаграммной техники Фейнмана согласно вышеизложенным правилам.
Теперь рассмотрим частные случаи.
1. Процессы распада
В этом процессе в начальном состоянии имеется одна частица с
массой М. Чтобы получить вероятность распада одной частицы, следу-
следует разделить (А.8) на плотность начальных частиц Пк = 2уМ2 + к2 =
= 2u)k. Таким образом, вероятность распада частицы в единицу
времени равна
2. Взаимное рассеяние двух частиц
В системе отсчёта, в которой одна из рассеивающихся частиц поко-
покоится, вероятность (А.8) представляется в виде
dwfi = da • v0THп\П2,	(АЛО)
где п\ и П2 — плотности частиц сортов 1 и 2, соответственно, v0TH — от-
относительная скорость частиц и da — лоренц-инвариантное дифферен-
дифференциальное сечение рассеяния. Из определения (АЛО) видно, что сечение
имеет размерность площади, если щ и п^ в (АЛО) нормируются так же,

Прил. А. Выражение вероятностей процессов через амплитуды 231
как и начальные состояния при вычислении амплитуды рассеяния, т.е.
согласно (А.2).
Для проведения лоренц-инвариантных вычислений при нахождении
сечений введём инвариантную величину, которую можно назвать ин-
инвариантной плотностью потока:
k2J-m2lml.	(AM)
В системе отсчёта, в которой частица 2 покоится,
mim2v0TH 1
3 = ,л	= т^отнП1П2,	(А. 12)
12	4
где
П\ =
Если же налетающая частица 1 является безмассовой, то выражение
для j при помощи правой части (А. 12) остаётся справедливым, если
положить v0TH = 1- Таким образом лоренц-инвариантное дифференци-
дифференциальное сечение рассеяния представляется как
Легко проверить следующую формулу:
2? = J[s - (m, + m2J] [s - (m, - m2J], s = (fc, + fc2J. (A.14)
В системе центра инерции частиц
fci = (cj\, k), &2 = (и;2, —
и плотность потока
(A. 15)
Рассмотрим подробнее формулу (А. 13) в системе центра инерции в
том случае, когда в конечном состоянии имеется также две частицы с
массами гп[ и тп^. Имеем
p\ = {cj[, p), Р2 = Н, -р), и[2-т[2=и'22-т22 = \р\2. (А. 16)
Отсюда
ио[Аио[ =uof2&uof2 = |p|d|p| -^ d(w[ + и>'2) = (lj[ + u>'2) ^f ^ . (A.17)
При помощи обозначений

232 Прил. А. Выражение вероятностей процессов через амплитуды
формулы (А. 15) и (А. 17) переписываются как
j = |k|o;, |p|d |p| = ^du/,	(A
что позволяет представить сечение (А. 13) в виде
64тг21 к | и;2
(А.1Щ
Здесь А о' — элемент телесного угла, в котором заключён импульс
рассеянной частицы:
do' = sintf dtfd0,	(A.20)
так что # есть угол между векторами к и р, а угол ф является
азимутальным углом вектора р относительно некого фиксированного
ортогонального репера, третья ось которого совпадает с к. Таким
образом
t = (fci -piJ =m? + m/12-2u;u/
Поэтому при фиксированной энергии ио
costf) = ^[Г) ,
z|k||p|
так что
\Mfi\4t Аф \Mfj\4t &±
64тг|к|2|о;2 ' 2тг 64ttj2 " 2тг'	У '
Так как в физически интересных случаях амплитуда не зависит от угла
ф, то, интегрируя (А.21) по этому углу, находим, что
(А.22)
Поскольку в последнем равенстве инвариантное дифференциальное
сечение представлено через инвариантные же величины, то этим ра-
равенством можно пользоваться в любой системе отсчёта.

Приложение Б
СПИНОВЫЕ МАТРИЦЫ ПЛОТНОСТИ
Выпишем некоторые формулы, относящиеся к спиновым матрицам
плотности. Спиновые матрицы плотности необходимы при вычислении
сечений и вероятностей распадов, т.к. в процессе таких вычислений
приходится делать замены выражений, билинейных относительно спи-
спиновых волновых функций начальных и конечных частиц, согласно
правилу
где p^v(k) — спиновая матрица плотности фотона, р^ (к) (р^ъ (к)) —
спиновая матрица плотности электрона (позитрона), причём импульс
всех этих частиц равен к.
1. Фотонные спиновые матрицы плотности
Для неполяризованного фотона в трёхмерно-поперечной калибровке
(см. G.33))
1
Pij = g
Структура матрицы плотности неполяризованного фотона (Б.2) очевид-
очевидна, а общий коэффициент определяется требованием того, что сумма
вероятностей нахождения спина фотона во всех состояниях равна
минус единице:
РЛ = -1.	(Б.З)
Преобразуем выражение (Б.2) к более удобному для использова-
использования виду, воспользовавшись свойством калибровочной инвариантности
теории. В отношении фотонной матрицы плотности последнее свойство
означает, что с физической точки зрения матрица плотности не изме-
изменяется при замене (сравни с G.56))
р1лЛк) —> /V(&) + (xjxfci/ + хДД	(Б-4)

234	Прил. Б. Спиновые матрицы плотности
где Хд(&) — произвольный 4-вектор. Действительно, каждый из векто-
векторов к^ в круглых скобках в (Б.4) сворачивается по векторному индексу
с хронологическими корреляторами токов, из которых строятся все
амплитуды. При этом импульс фотона № есть входящий (или выхо-
выходящий) импульс в соответствующую вершину. Вследствие равенств
A0.17), описанные слагаемые обращаются в нуль и потому слагаемое в
круглых скобках в (Б.4) несущественно. При помощи преобразования
(Б.4) матрица плотности (Б.2) приводится к виду
В общем случае матрица плотности представляется в виде
2
а, C=1
Здесь (eiM, в2м) — базис векторов поляризации фотона. Эрмитовость
матрицы (Б.6) обеспечивается эрмитовостью матрицы ра@:
р^ = р^а*.	(Б.7)
Очевидно, в рассмотренном случае неполяризованного фотона
раC = A/2)^.	(Б.8)
Из (Б.8) находим, что
detpaf3 = 1/4.	(Б.9)
В случае полностью поляризованного фотона матрица (Б.6) должна
представляться как тензорное произведение двух взаимно сопряжён-
сопряжённых 4-векторов. Это возможно лишь в том случае когда
paC = vavC\	(Б. 10)
Очевидно, что в этом случае
detpaC=0.	(Б. 11)
В общем случае матрица paf3 подчиняется условию (Б.7), условию
2
у р =1,	(b.lz)
а=\
вытекающему из (Б.З), а также условию
O^detpaf3 < 1/4.	(Б. 13)

Прил. Б. Спиновые матрицы плотности	235
Общий вид матрицы ранга 2, удовлетворяющий условиям (Б.7) и
(Б. 12), таков:
Здесь <т = (а1, а2, <т3) — матрицы Паули. Имеем
л \х	SI	SZ	ScJ/*	v~.^/
Из условия (Б. 13) следует, что
Из сказанного выше вытекает, что в неполяризованном случае
?2 = 0,	(Б. 17)
а в полностью поляризованном случае
?2=1>	(Б.18)
2. Спинорные матрицы плотности
Из определения (Б.1) и (8.39) находим, что
trp(±)(&) = ±2m.	(Б. 19)
Спинорные матрицы плотности удовлетворяют уравнениям (ср. с
(8.38 а), (8.38 а))
(Ц^т)р{±\к) =p^(k)()iTm) =0.	(Б.20)
При заданной матрице плотности среднее значение спина вычисляет-
вычисляется при помощи формулы (определение спинового оператора X см. в
(8.111))
/ \	1 , / (-\-Л П<^\	1	' ' ч "
Матрица плотности для неполяризованного состояния получается
при помощи суммы (8.56), делённой на 2. Действительно, в неполя-
неполяризованном состоянии обе проекции спина имеют одинаковую вероят-
вероятность A/2). Таким образом, в неполяризованном состоянии
р^\к) = {\/2){Ц±т).	(Б.22)
Матрица плотности (Б.22) удовлетворяет условиям (Б. 19) и (Б.20).
В общем случае спинорные матрицы плотности представляются в
виде
№)	75?0>	(Б.23)

236	Прил. Б. Спиновые матрицы плотности
где ам есть 4-вектор, характеризующий поляризацию и удовлетворяю-
удовлетворяющий условию
к^ = 0<—> ^#+#^ = 0.	(Б.24)
Непосредственно проверяется, что при условии выполнения равенств
(Б.24) матрица (Б.23) также удовлетворяет условиям (Б. 19) и (Б.20).
Имеем также	,
tV^V)-	(Б.25)
Сравнение формулы (Б.21), (Б.24) и (Б.25) показывает, что в системе
покоя частицы
а" = @, ±2(s».	(Б.26)
Поскольку
0^{sJ<l/4,
то 4-вектор ам удовлетворяет ограничению
-1<а2<0.	(Б.27)
Напоследок укажем, что в случае рассеяния неполяризованных
частиц, без фиксации поляризации рассеянных частиц, каждой началь-
начальной и конечной частице в сечении рассеяния соответствуют матрицы
(Б.5) либо (Б.22) (в зависимости от сорта частиц), причём в сечение
рассеяния следует внести дополнительный множитель 2Г, где г —
суммарное число электронов, позитронов и фотонов в конечном состо-
состоянии. Этот множитель означает учёт обоих состояний спина каждой
конечной частицы.

Приложение В
ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА
Пусть ф, Ац и ф — скалярное, электромагнитное и спинорное поля,
соответственно, и 5х^(х) — d произвольных бесконечно малых функ-
функций координат. Рассмотрим следующие вариации полей:
(_/ A/ \ JU ) — (_/ JU \ JU ) kJ ij A/ \ JU ) •
\1	[I	[IV	,	(В. 1)
UlfJyXI — UX \Jj \Uy П^ \UnUXy\X))(J	ljJ\X).
I	2	\
Преобразования (В.1) имеют следующее обоснование. В случае
= LU j.X ,	UJпУ = —Ldyn = COIlSt,
правая часть последнего уравнения в (В.1) совпадает с разностью
5ф(х) = ф(х) — ф(х), вычисленной согласно (8.20) для бесконечно ма-
малого преобразования Лоренца. Знак перед вторым слагаемым в форму-
формуле преобразования векторного поля в (В.1) определяется тем требова-
требованием, чтобы величина ф^у^фА^ преобразовывалась как скалярное поле
в (В.1).
Пусть лагранжиан С состоит из трех слагаемых:
с1(д,ф)
1	(В.2)
16тг р
А = п Ф («7м VM - m) ф + э.с.
Таким образом, рассматривается полный лагранжиан системы
Максвелла-Дирака и нейтрального скалярного поля.

238	Прил. В. Тензор энергии-импульса
Вычислим вариации этих лагранжианов при вариациях полей (В.1):
1
(B.3)
Собирая последние формулы, находим с точностью до поверхностного
члена:
5S = d(d) х 5С =
э.с.1 -
(В.4)
Величина
t^ = t^	(B.5)
называется тензором энергии-импульса материи.
Перепишем правую часть (В.4) в виде
5S = - ld{d)x (dvt^Mx^.	(B.6)
Теперь применим такой же прием, какой был применен в пункте
3 лекции 14 при выводе аксиальной аномалии: в амплитуде перехо-
перехода, представленной в форме функционального интеграла, произведем
бесконечно малую вариацию переменных вида (В.1). Поскольку эти
преобразования переменных имеют смысл в пространствах любой раз-
размерности, то размерность пространства будем считать аналитической.
Важно также, что якобиан функциональной меры при преобразовани-
преобразованиях переменных интегрирования (В.1) равен единице при комплексной
размерности пространства-времени 0. Поэтому, в отличие от случая,
рассмотренного в лекции 14, в данном случае получаем
dJAlt^ B)=0,
1) Поскольку вариации (В.1) не только бесконечно малы, но и линейны
относительно переменных интегрирования, то соответствующий якобиан от-
отличается от единицы следом линейных операторов, действующих на поля
в (В.1). Этот след равен нулю. Действительно, так как след оператора не
зависит от базиса, в котором он вычисляется, то возьмем в качестве базиса
плоские волны Ф&(ж) ~ expikx. Нужный нам след пропорционален величине
J d^ к J d^ жехр(—гкх) ... ехр(г/сж), где вместо многоточия находится опера-
оператор из (В.1). После интегрирования по переменной х след оказывается про-
пропорциональным величине J к d^ к, которая равна нулю вследствие симметрии
базиса относительно инверсии к —»> —к.

Прил. В. Тензор энергии-импульса	239
где \ А) и \В) — произвольные состояния. Последнее равенство экви-
эквивалентно операторному равенству
dvtv» = 0.	(В.7)
Из (В.7) следует, что сохраняются d операторов d-импульса (далее
«шляпки» над операторами не пишем):
= [
.	(B.8)
Действительно, вследствие равенств (В.7),
если на пространственной бесконечности ^г/х —> 0. Из (В.5) и (В.7)
следует, что сохраняются также d(d— l)/2 операторов ^-момента,
)	(В.9)
поскольку
^ X	x = 0.	(В. 10)
Обозначим через Ф(х) любое из полей ф(х), А^(х), ф(х) в пред-
представлении Гейзенберга и вычислим матричный элемент (А\Ф(х)\В).
Представим этот матричный элемент в форме функционального инте-
интеграла (см. пункт 2 лекции 1) и проведем в нем вариацию переменных
интегрирования (В.1). В результате этого вычисления сумма слагаемых
первого порядка относительно 5xv должна быть приравнена нулю.
Одно из этих слагаемых есть (А\5Ф(х) \В), а второе происходит от
вариации действия, которую возьмем в виде (В.4), но не в виде (В.6).
Это удобнее, поскольку при рассмотрении коррелятора
(А\ТФ(х)д0Ь°»(у)\В)
при х° = гр требуется особенная тщательность. В противном случае
может быть потеряно слагаемое вида [tOu(x°, у), Ф(х)]. При использо-
использовании вариации действия в виде (В.4) это слагаемое легко учитывает-
учитывается. Таким образом, имеем
(А\6Ф(х)\В) +ifd(d) у(д^х„(у))(А\ТФ(х)^(у)\В) =0. (В. 11)
Теперь перебросим оператор д/ду^ на хронологический коррелятор в
(В. 11) и учтем, что коррелятор
[А\ТФ(х)^(у)\В
имеет разрыв при х° = у0:

240
Прил. В. Тензор энергии-импульса
Поэтому равенство (В. 11) после опускания обкладок переписывается
следующим образом:
5Ф(х) = г
,{уM{у*-х*)[^{х\у),
(В.12)
При переходе от (В.11) к (В.12) было учтено уравнение (В.7).
Поскольку вариации 5хи(у) независимы в разных точках у, то
интегральное равенство (В.12) распадается на семейство равенств в
каждой точке у. Выпишем их в случае дираковского поля:
- Х)
Свернем равенство (В. 13) с величиной (ev + uov\yx^ и затем проинте-
проинтегрируем по переменной у.
= г
Если в уравнении (В.1) положить 5xv = ev
(В.14)
то правая часть
этого уравнения совпадет с
образом, операторы Vv и
левой частью уравнения (В.14). Таким
являются генераторами ^-трансляций и
0
р	рр	рр	р
^-поворотов в ^-мерном пространстве Минковского. В частности, V0 =
= ТС есть гамильтониан, а V1 — оператор импульса системы. При
помощи формул (В.2), (В.4), (В.8) и (В.9) находим
V0 =
1 ;о
т
Л
V1 =
8тг
х{ -¦
1
4^
(В.15)
(В.16)
Правые части в (В.15) и (В.16) должны быть выражены через гейзен-
берговы поля.
Мы видим, что правые части в (В.15) и (В.16) совпадают с опера-
операторами Гамильтона и импульса соответствующих полей, уже использо-
использовавшихся в лекциях.

Прил. В. Тензор энергии-импульса	241
Очевидно, что любой тензорный оператор преобразуется аналогично
(В. 14). Поэтому для тензора энергии-импульса имеем
=i sxV
(B.17)
Интегрируя равенство (В.17) по переменной х по (d — 1)-мерной гипер-
гиперповерхности х° = const с соответствующими весами, находим следую-
следующие коммутационные соотношения:
[P^,V"}=0,	(В. 18)
[J^, Vх] = г (r)vXV^ - rfxTv) ,	(В. 19)
^, Jxp] = i (г]^ JvX - rfp J^x - т^Л Jvp + rfx jw) . (B.20)
(Сравните последние два равенства с равенствами (8.12), (8.13).) Ко-
Конечно, коммутационные соотношения (В. 14), (В.17)-(В.2О) могут быть
установлены также и путем прямого вычисления.
Согласно определению, линейная оболочка совокупности эрмитовых
операторов (V^, Jxp), удовлетворяющих коммутационным соотноше-
соотношениям (В.18)-(В.2О), называется алгеброй Пуанкаре.
При помощи формулы (В. 14) немедленно получаем
= Ф(х).	(В.21)
Унитарные операторы
U = exp (ieiJOi)	(B.22)
называются бустами. Эти операторы генерируют преобразования Ло-
Лоренца.

Предметный указатель
Алгебра Грассмана, 127-132
Алгебра Пуанкаре, 67
Амплитуда рассеяния, 40, 45, 62, 63,
75, 77, 136, 138-140, 162, 169,
170, 184, 226, 228, 231, 234
Бегущая константа связи, 87, 165
Буст, 68, 241
Вероятность распада частицы, 230
Вика поворот, 19, 55, 57, 59, 100,
158, 203, 204, 224
Вика теорема, 18-20, 36, 41, 80, 81,
142
Гауссов интеграл, 12, 36, 59, 130
Гауссов функциональный интеграл,
13-15, 26, 34, 37, 97, 98, 132,
223
Голдстоуновские бозоны, 218
Гриновская функция, 16, 18, 21, 49
—	запаздывающая, 18
-	причинная, 16-18, 29, 33, 59, 86
Двухфотонная аннигиляция
электрон-позитронной пары, 143
Диаграммы Фейнмана, 39
Дифференциальное сечение рассея-
рассеяния, 231, 232
Духи, 103
Затравочная константа связи, 61
Затравочная масса, 61, 69, 72, 150,
192
Затравочное действие, 61, 74
Затравочное поле, 85, 151
Затравочные константы, 61, 86, 150
Затравочный гамильтониан, 192
Затравочный заряд, 155
Затравочный лагранжиан, 73, 84,
151
Импульс (параметр) обрезания, 57,
61, 78, 86, 210
Индекс расходимости диаграммы,
58, 147
Калибровка, 91, 95, 138, 162, 168,
233
—	а-калибровка, 100, 102
—	Ландау, 100
—	Фейнмана, 100, 157, 173
Клейна-Гордона-Фока уравнение
—	операторы, 224
Комптоновская длина волны, 53
Константа перенормировки поля, 69,
70, 72, 73, 86
Контрчлены, 74, 75, 153, 219,
222-224
Массовая поверхность, 27
Матрицы
-Дирака, 105, 115, 137, 145, 201,
209
—	Паули, 104
Модель
—	Тирринга, 156
—	Швингера, 215
Нормально упорядоченный ряд, 24
Нормальный символ оператора, 24,
25, 131, 132
—	^-матрицы, 33, 34, 37, 49, 51, 97,
100, 101
Оператор
—	d-импульса, 66, 96
—	электрического заряда, 118
—	Гамильтона-Дирака, 109, 114,
120, 202
—	вершинный, 146, 153, 169
—	локальный, 84
—	маргинальный, 84, 85
—	массовый, 84, 150, 157, 158, 161,
168
—	несущественный, 84, 85
—	нормального упорядочения, 37,
133
—	полного момента импульса, 104
—	поляризационный, 149, 162, 164

Предметный указатель
243
—	поляризационным, 166
—	спиновый, 235
—	существенный, 84
—	эволюции, 11, 25, 26, 28, 92
—	электрического заряда, 112, 114
Операция
—	зарядового сопряжения, 117, 118
—	инверсии времени, 18
—	обращения времени, 117, 125
—	пространственной инверсии, 116,
120
—	хронологического упорядочения,
14, 15, 19
Перенормировка на ходу, 75
Поле
—	вейлевское, 119, 125
—	майорановское, 118, 125
Постоянная тонкой структуры, 119,
191
Правило Каткосского, 175
Представление
—	Гейзенберга, 14, 15, 20, 37, 112,
142, 239
—	Мацубары, 20, 38, 143
—	Челлена-Лемана, 164
—	Шредингера, 10, 14
Пропагатор, 44, 45, 51, 53, 80, 81,
83, 97, 98, 100, 102, 134, 136,
138, 142, 147, 149, 150, 157, 173,
175, 183, 184, 204, 206, 219, 223
—	точный фотонный, 149, 151, 154,
155, 166
—	точный электрон-позитронный,
146, 150-153, 155
Редукционная формула
Лемана-Симанчика-Циммермана,
73
Ренормализационная группа, 83-86,
88
Сильно связная диаграмма, 72
Спектральная плотность, 68, 69
Теорема Фарри, 144, 148
Теория
—	Янга-Миллса, 103
—	неперенормируемая, 59, 147
—	перенормируемая, 61, 78, 84, 85,
156, 203, 219
—	сверхперенормируемая, 59
Тождество Уорда-Такахаши, 144,
145, 147, 154, 170, 203, 207
Точка нормировки, 57, 86, 158, 165,
225
Уравнение
—	Каллана-Симанчика, 85, 86, 88
—	Клейна-Гордона-Фока, 33, 38, 70
—	Паули, 108
Фейнмановские параметры, 64
Функция
—	Паули-Йордана, 70
Функция Гелл-Манна и Лоу, 87
Хронологическое произведение, 15,
50, 142
Хронологическое среднее, 14, 15,
19, 52, 69, 73, 85, 146, 234
Электромагнитные формфакторы
электрона, 170
Энергия тонкой структуры, 197
Эффект Казимира, 30, 64, 96, 101
Эффект Комптона, 142
Эффективный потенциал, 221
Ядро оператора, 24, 25, 27, 28, 131,
132
—	^-матрицы, 28, 32, 132

Список литературы
1.	Грибов В.И. Квантовая электродинамика. — Новосибирск, 2000. — 291 с.
2.	Швингер Ю. Частицы, Источники, Поля: В 2 т. / Пер. с англ. под ред.
Бродского A.M. - М.: Мир, Т. 1, 1973. - 504 с. Т. 2, 1976. - 575 с.
3.	Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 т. Т. 4: Бере-
стецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая электродина-
электродинамика. — 3-е изд., исправленное. — М.: Наука, 1989. — 725 с.
4.	Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 т. Т. 2: Теория по-
поля. — 7-е изд., исправленное. — М.: Наука, Гл. ред. физ. мат. лит., 1988. —
512 с.
5.	Block F., Nordsieck А. // Phys. Rev. 1937. Vol. 37. P. 54.
6.	Schwinger J. // Phys. Rev. 1951. V. 82. P. 664;
Bell J.S., Jackiw R. // Nuovo Cimento, 1969. 60A. P47;
Adler S. H Phys.Rev. 1969. V. 177. P 2426.
7.	Вергелес СИ. Некоторые вопросы квантовой теории калибровочных полей:
Автореф. Дис. на соискание степени канд. физ.-мат. наук.— Черноголовка,
1979; См. также в Migdal A.A. Effective low energy lagrangian for QCD //
Physics Letters. 1979. V. 81B, P. 37.
8.	Ахиезер А.И. Введение в релятивистскую квантовую теорию поля — М.:
Наука, 1969. - 623 с.
9.	Боголюбов И.И., Ширков Д.В.. Введение в теорию квантованных полей. —
М.: Наука, 1976. - 480 с.
10.	Бьёркен Дж.Д., Дрелл С. Д. Релятивистская квантовая теория: В 2 т. /
Пер. с англ. под ред. Берестецкого В.Б. — М.: Наука, 1978. — Bт. 407 с)
11.	Вайнберг С. Квантовая теория поля. В 2 т. / Пер. с англ. под ред.
Жуковского В.Ч. - М.: Физматлит, 2003. 1 т. - 648 с, 2 т. - 528 с.
12.	Дирак П.A.M. Лекции по квантовой теории поля. / Пер. с англ. под ред.
Соколова А.А. - М.: Мир, 1971. - 243 с.
13.	Пескин М., Шредер Д. Введение в квантовую теорию поля / Пер. с англ.
под ред. Белавина А.А. и Беркова А.В. — Москва-Ижевск: НИЦ «Регу-
«Регулярная и хаотическая динамика», 2001.
14.	Славное А. А., Фаддеев Л.Д. Введение в квантовую теорию калибровочных
полей. - М.: Наука, 1988. - 269 с.
15.	Швебер С. Введение в релятивистскую квантовую теорию поля / Пер. с
англ. под ред. Смородинского Я.А. — М.: ИНЛ, 1963. — 842 с.

ВЕРГЕЛЕС Сергей Никитович
ЛЕКЦИИ ПО КВАНТОВОЙ ЭЛЕКТРОДИНАМИКЕ
Редактор М.Б. Козинцова
Оригинал-макет: Т.Н. Савицкая
Оформление переплета: А.Ю. Алехина
Подписано в печать 16.09.05. Формат 60x90/16.
Бумага офсетная. Печать офсетная. Усл. печ. л. 15,5.
Уч.-изд. л. 15,5. Тираж 300 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ФГУП «Производственно-издательский комбинат ВИНИТИ»
140010, г. Люберцы, Московская обл., Октябрьский пр-т, 403