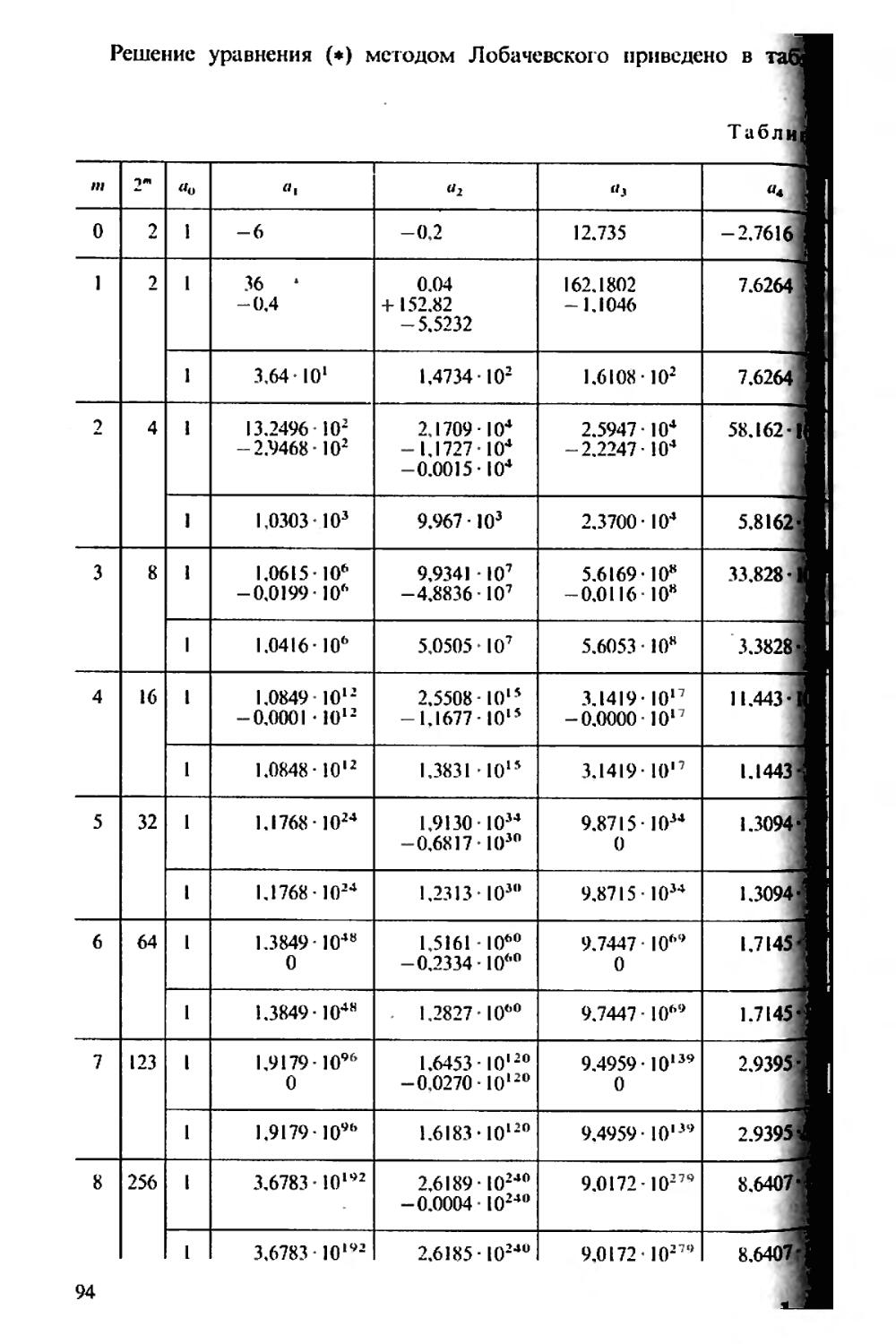
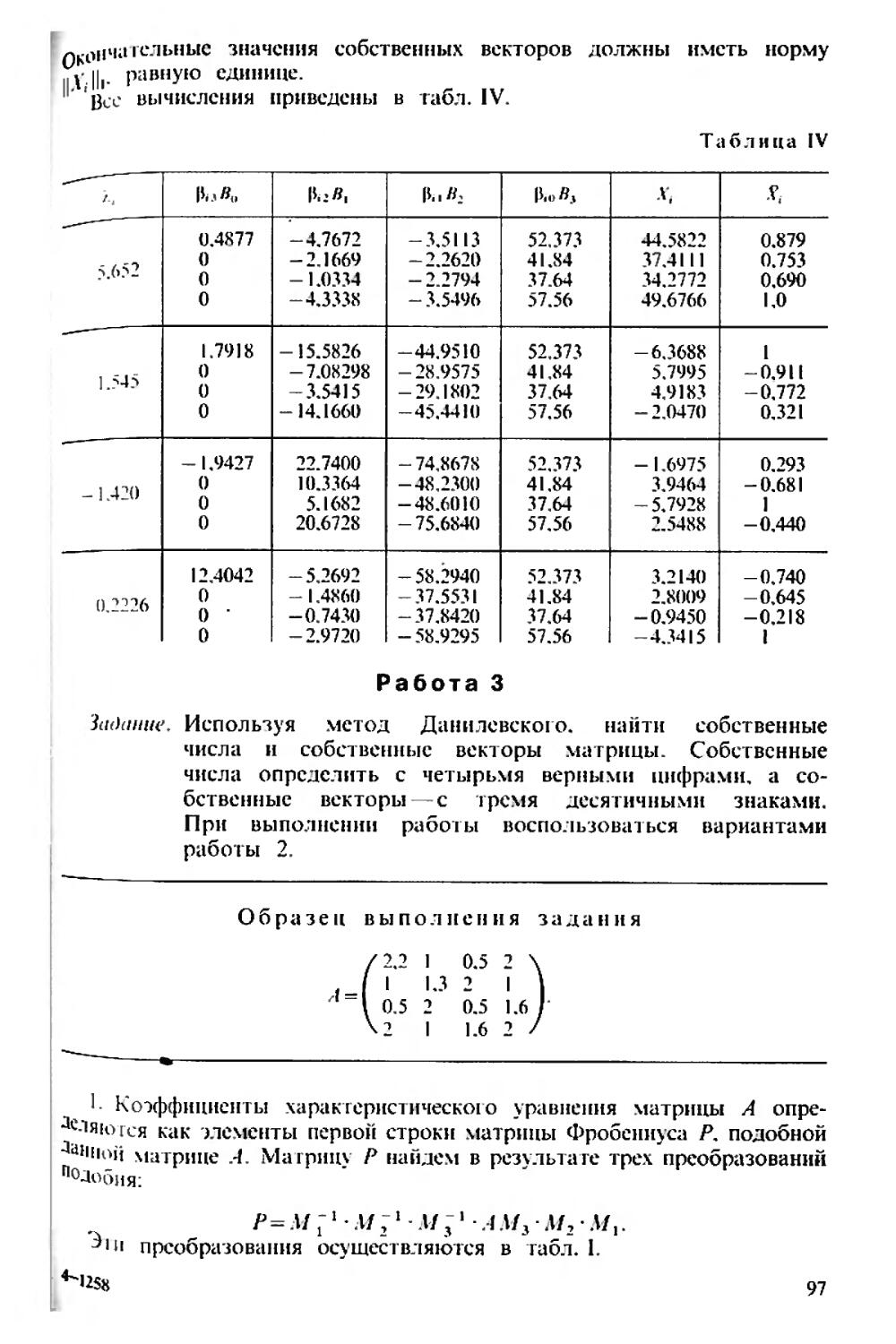
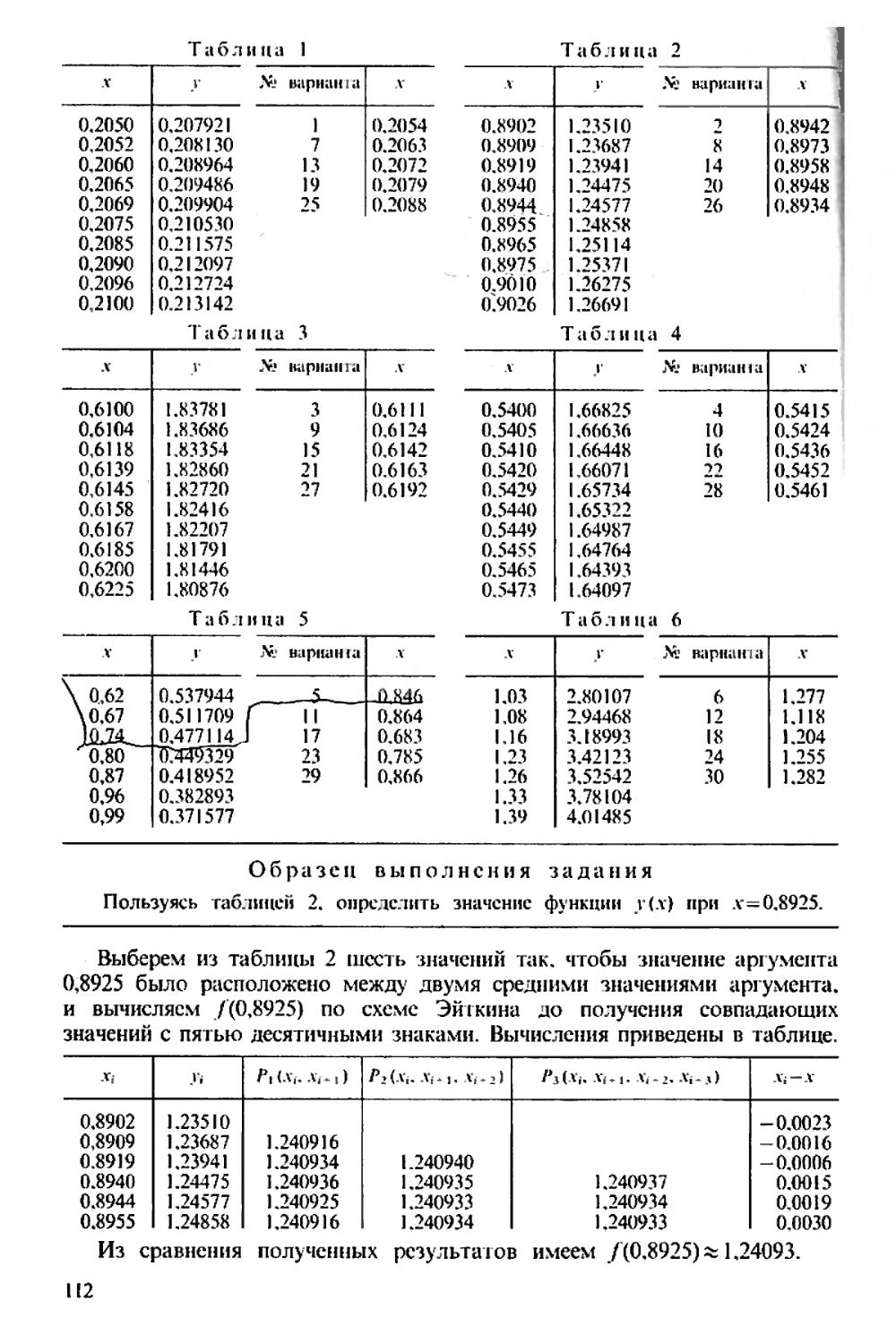
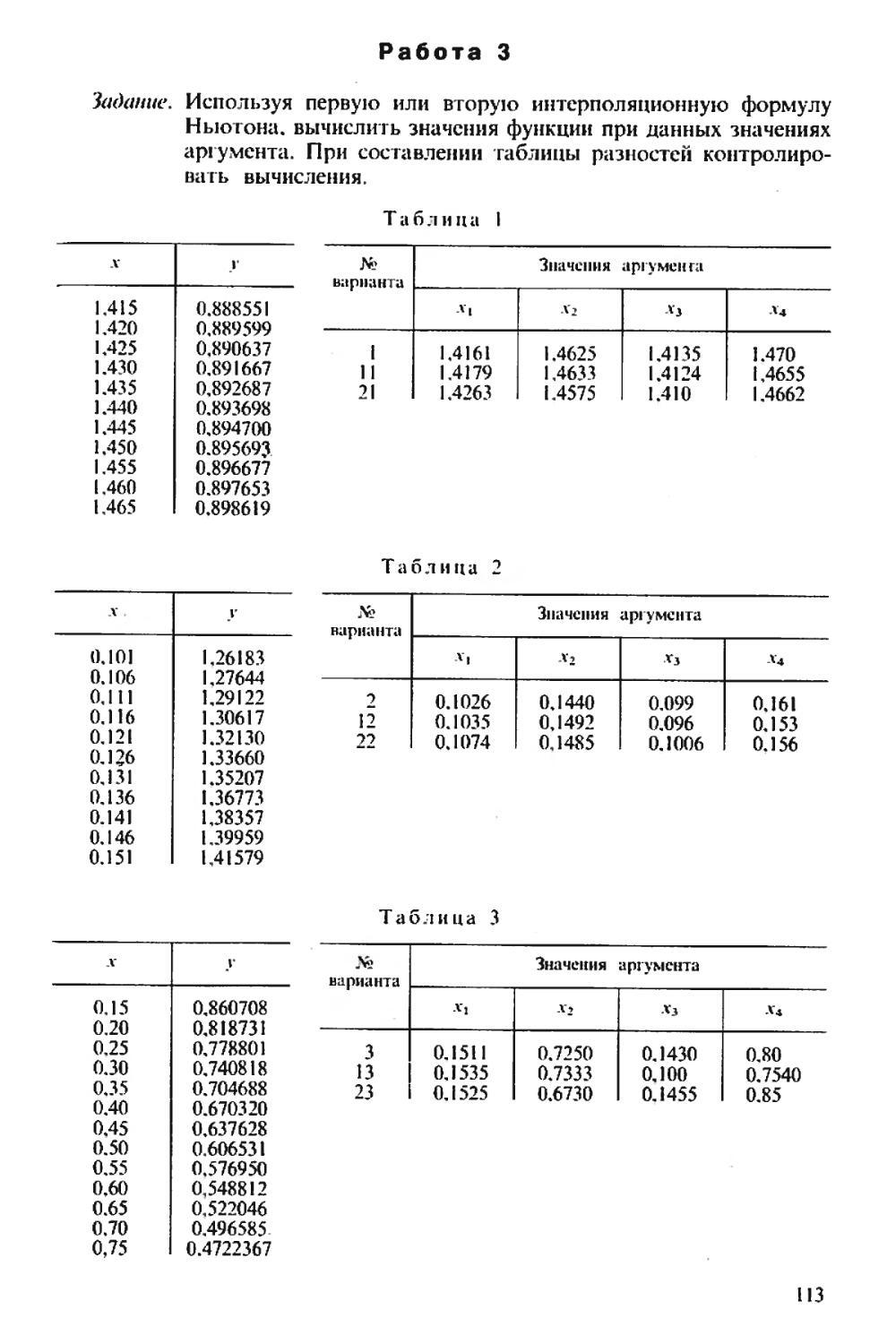
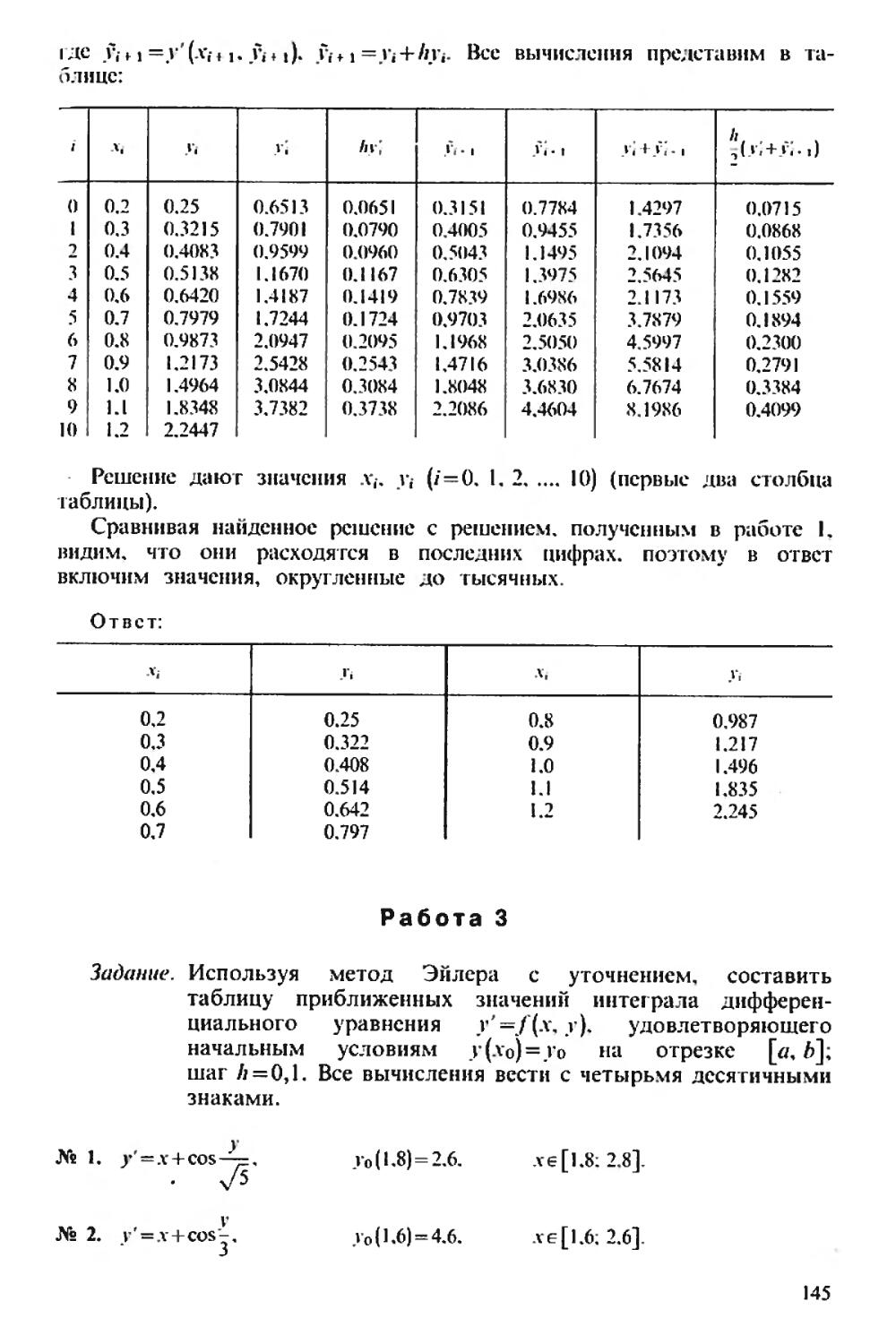
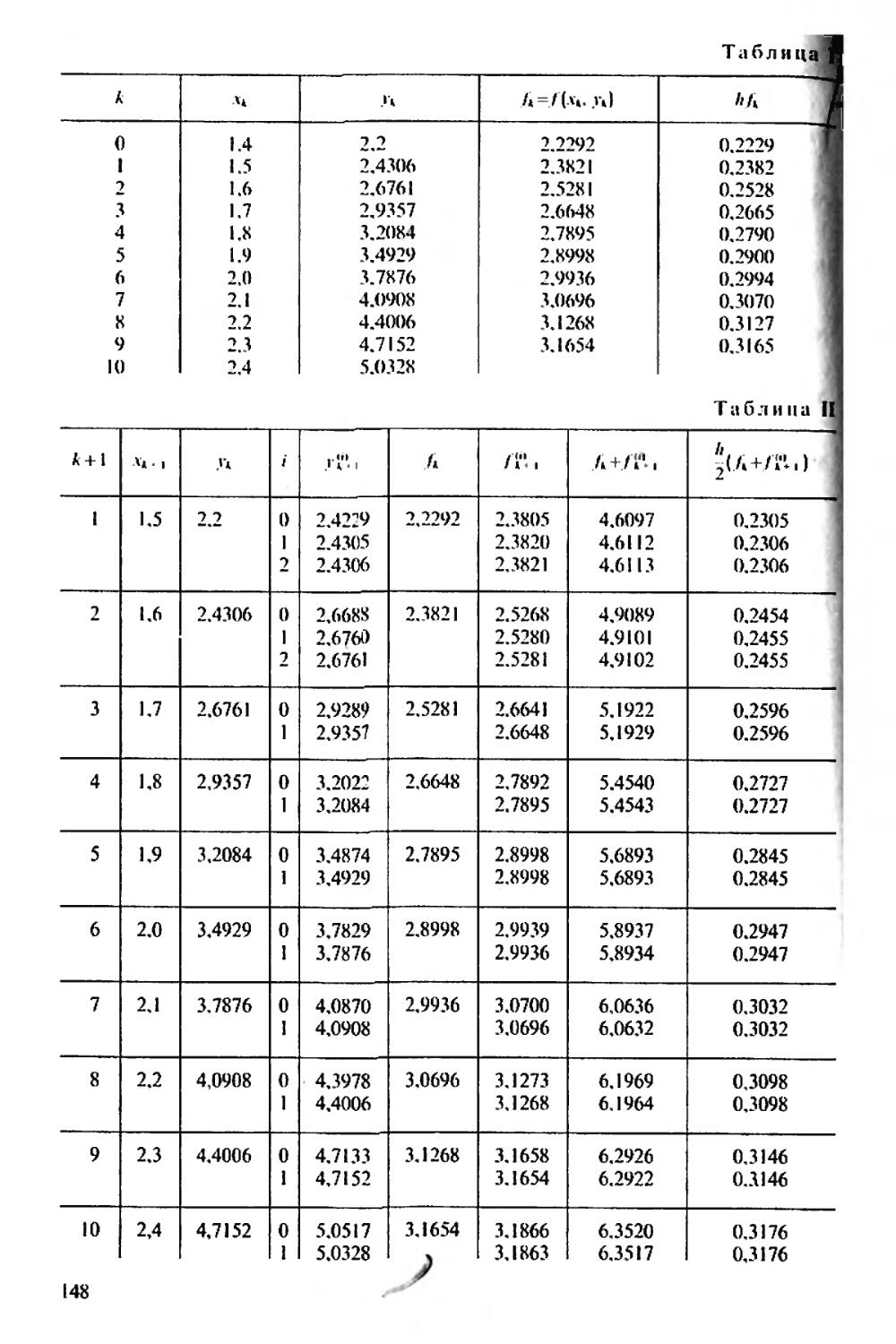
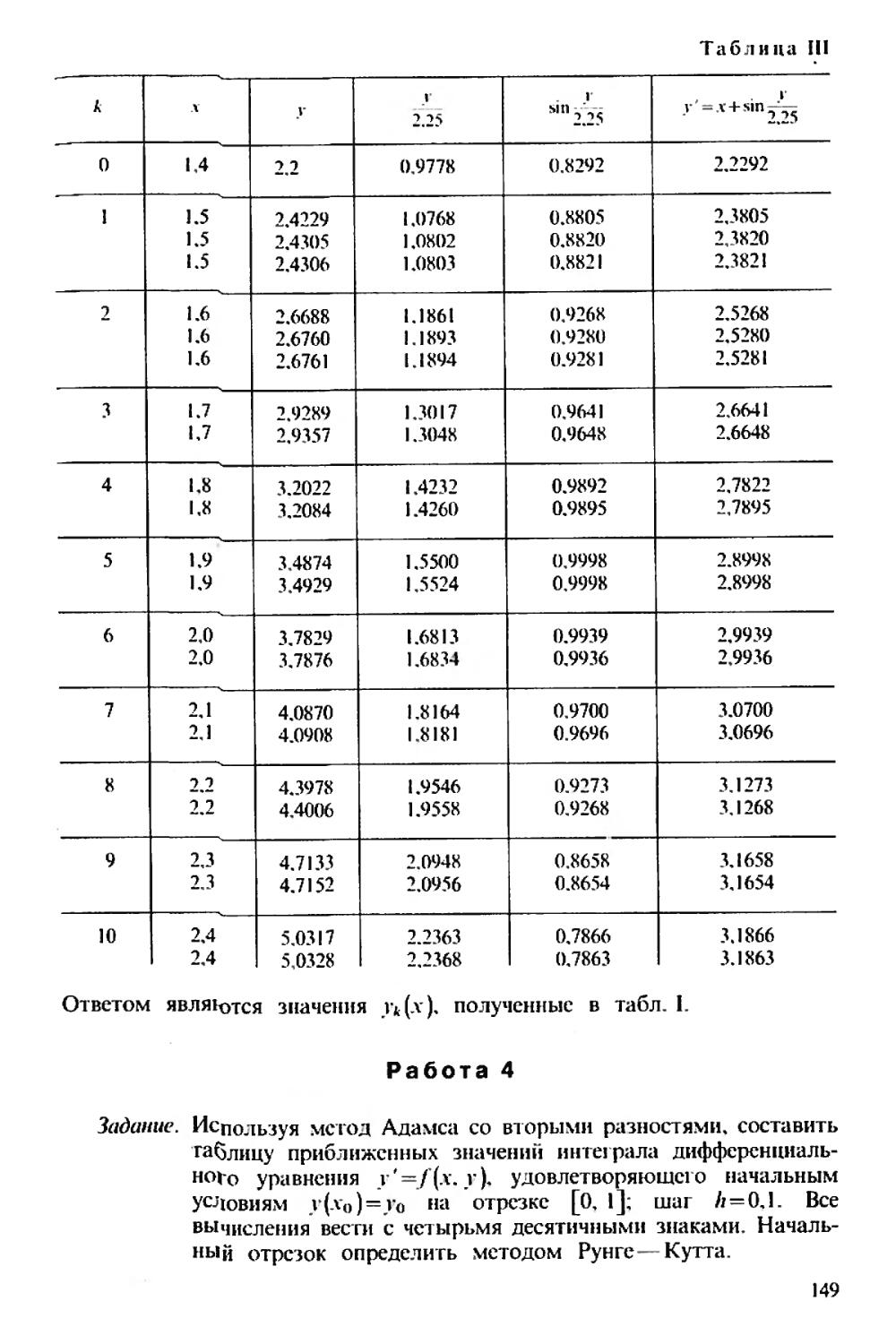
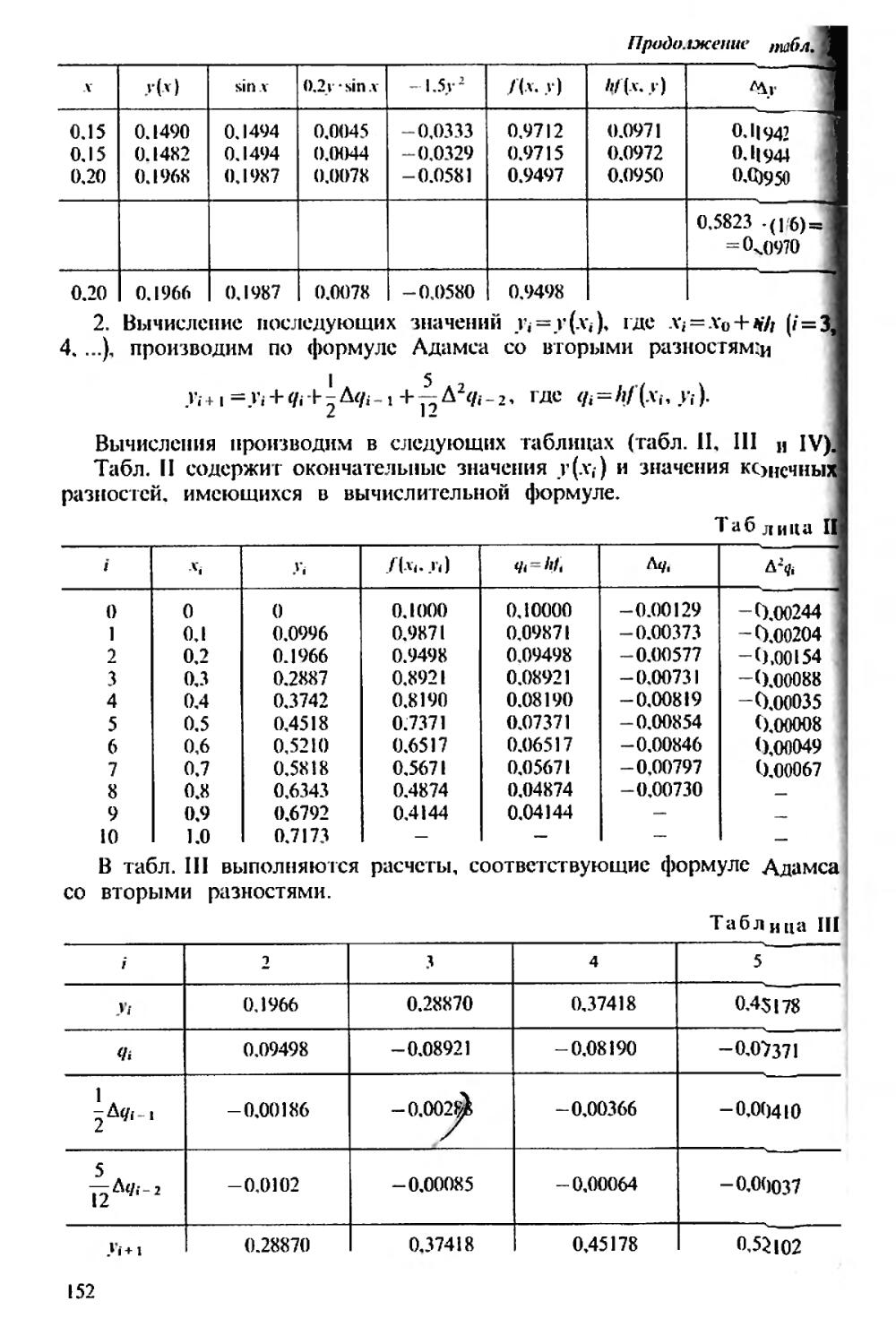
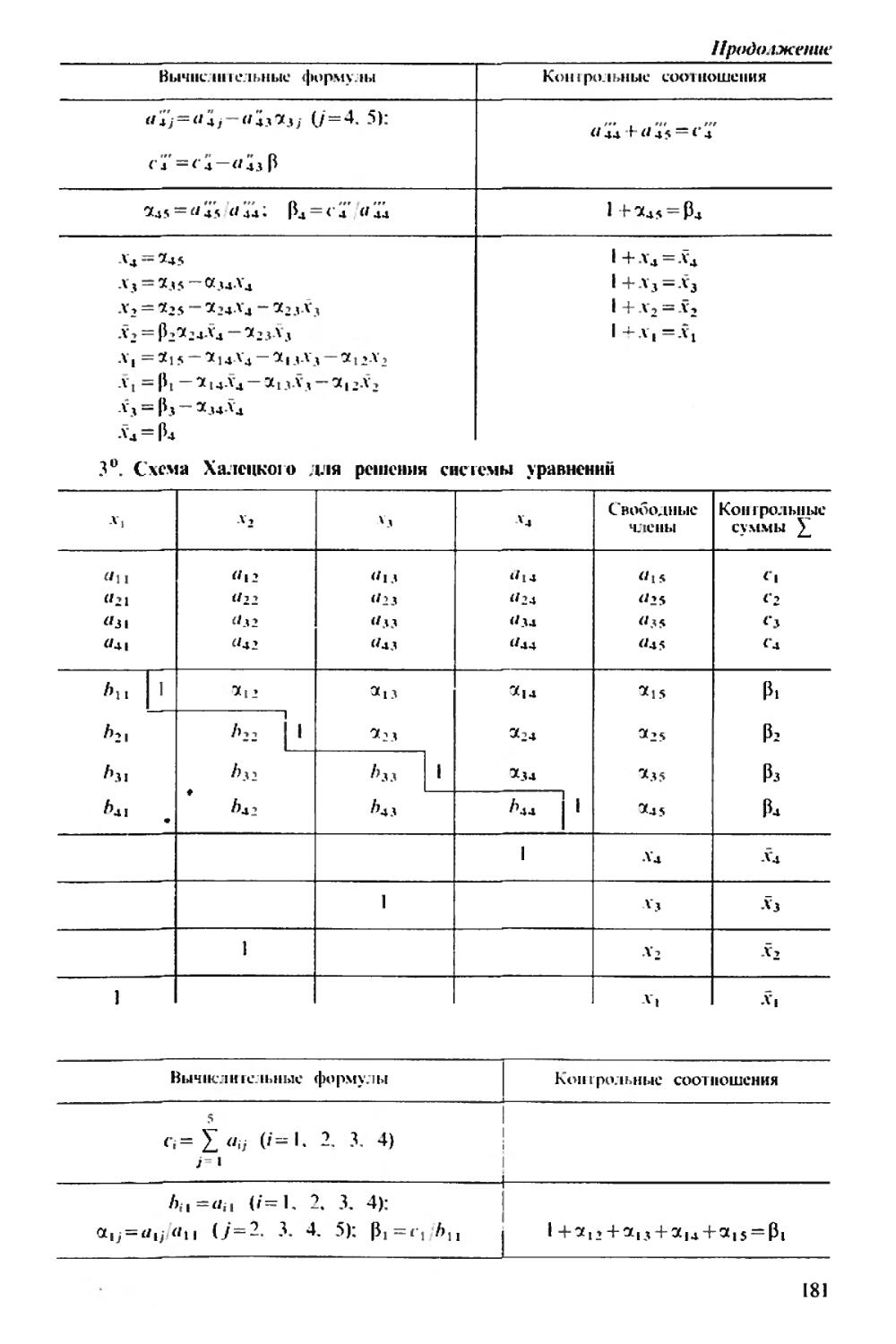
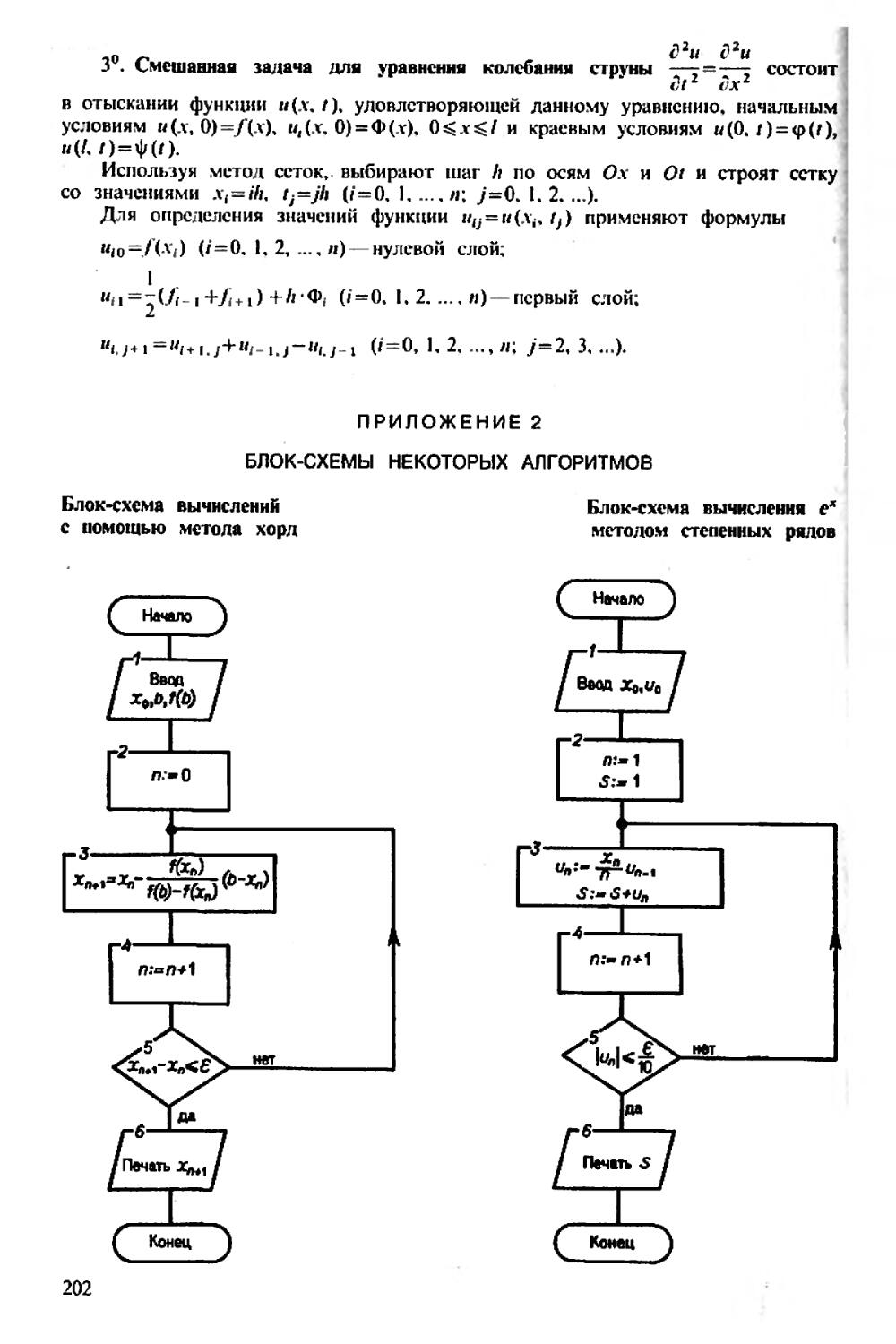
Текст
Г. Н. ВОРОБЬЕВА, А. Н. ДАНИЛОВА
ПРАКТИКУМ
по
ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКЕ
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего и среднего специального образования РСФСР в качестве учебного пособия для учащихся средних специальных учебных заведений
* Ч. " -iOTEKA
МОСКВА «ВЫСШАЯ ШКОЛА» 1990
ББК 22.19 В 75
УДК 518(075)
Рецензенты: канд. фнз.-мат. наук В. В. Клюев (НИИ вычислительной математики и процессов управления Ленишрадского Государственного университета); прсп. Скворцова О. М. (Московский приборос гроитсльный техникум)
Воробьева Г. Н., Данилова А. Н.
В 75 Практикум по вычислительной математике: Учеб, пособие для техникумов.— 2-е изд., перераб. и доп.— М.: Высш школа, 1990.— 208 с.: ил.
ISBN 5-06-001544-0
Пособие представляет собой руководство к выполнению лабораторно-практических работ но курсу «Вычислительная математика». Материал разбит на главы, в которых дастся набор работ по темам в соответствии с программой. Каждая работа начинается с задания, общего для любою из имеющихся 30 вариантов. В копие работы приводится образец ее выполнения и оформления. В основу пособия положена книга тех же авторов «Практикум по численным методам» (1979).
в 1602120000(4308000000)—484
001(01)—90 94—90
ББК 22.19
518
ISBN 5-06-001544-0
© Г. Н. Воробьева, А. Н. Данилова, 1990
ПРЕДИСЛОВИЕ
Современная вычислительная техника требует от инженеров и техников знаний основ вычислительной математики и применения этих знаний к решению различных практических задач.
Вычислительная математика является одной из основных дисциплин, необходимых для подготовки специалистов, работающих в различных областях народного хозяйства.
Настоящее пособие представляет собой руководство к выполнению лабораторно-практических работ по вычислительной математике. Книга составлена в соответствии с программой для учащихся техникумов, обучающихся по специальности 1735 «Программировали’' чая быстродействующих математических машин», но может быть использована для подготовки техников и инженеров других специальностей, имеющих в своих учебных планах вычислительную математику.
Пособие позволяет преподавателю выдать индивидуальное задание каждому учащемуся из группы в 30 человек. Все задания имеют одинаковую степень сложности. Весь материал разбит на главы, в которых дается набор работ по соответствующей теме. Каждая работа начинается с задания, которое одинаково для любого из 30 вариантов. В конце работы приводится образец ее выполнения и оформления.
В пособие также включены работы, выходящие за рамки действующей программы и предназначенные для наиболее подготовленных учащихся.
В Приложении 1 содержатся все соотношения и формулы, необходимые для выполнения работ. В Приложении 2 приводятся блок-схемы, с помощью которых можно выполнить некоторые работы, а в Приложении 3 — примеры программ некоторых расчетов на микрокалькуляторе «Электроника БЗ-34».
Лабораторно-практические работы должны выполняться на микрокалькуляторах. Для выполнения работ группу следует делить на подгруппы.
Первое издание книги вышло под названием «Практикум по численным методам». Настоящее издание переработано, дополнено и значительно отличается от предыдущего.
Авторы выражают искреннюю признательность рецензентам канд. физ.-мат. наук В. В. Клюеву и препод. О. М. Скворцовой за ценные замечания, способствовавшие улучшению данного пособия.
Авторы
Глава I
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ
Работа 1
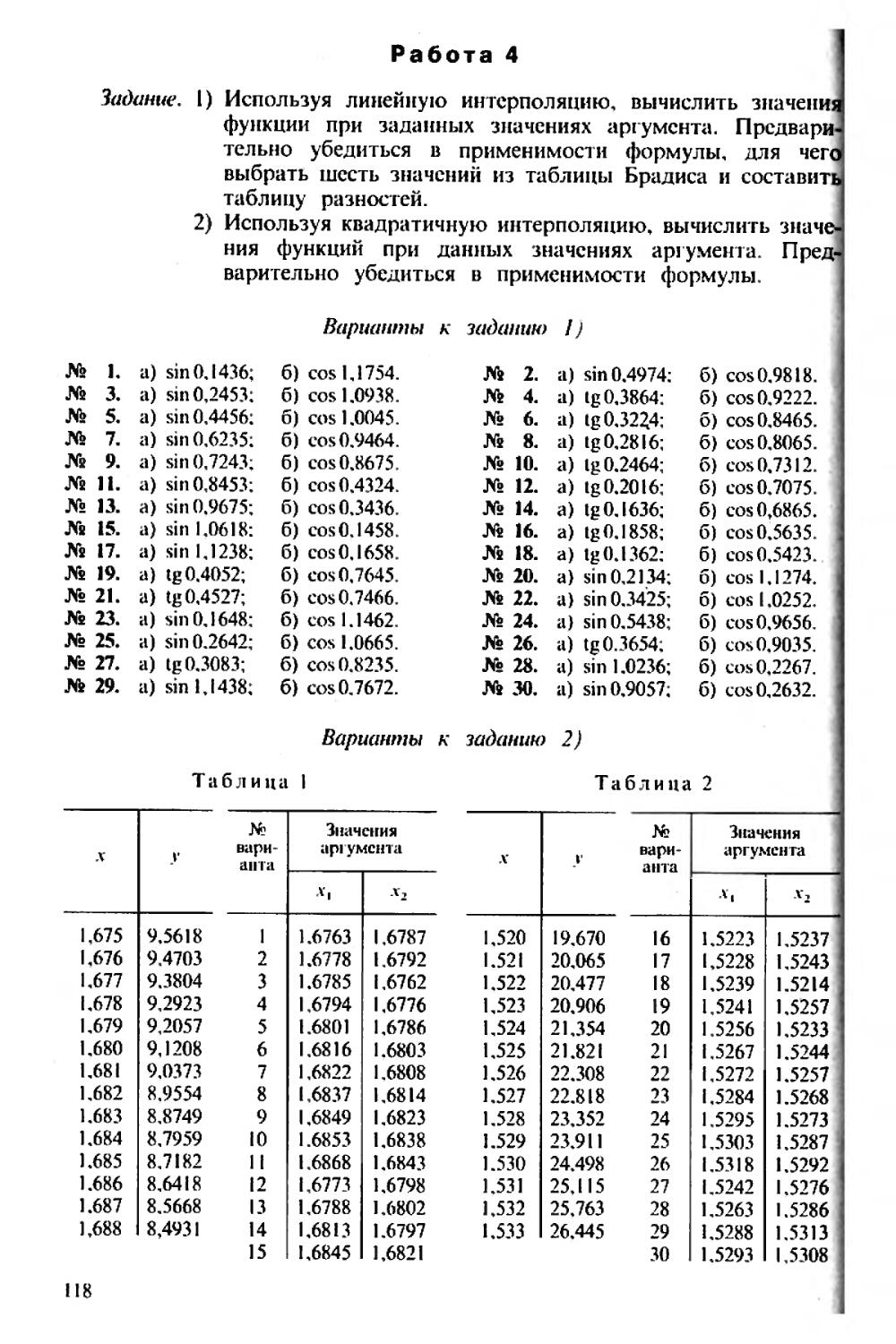
Задание. I) Определить, какое равенство точнее.
2) Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.
3) Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.
№ 1. 1) ч/44 = 6.63; 19/41=0.463.
2) а) 22.553 (±0,016):
6) 2.8546; 5=0,3%.
3) а) 0,2387; б) 42,884. № 3. 1) /153=3.24: 4/17=0.235.
2) а) 34,834; 6=0.1%;
б) 0.5748 (±0,0034).
3) а) 11.445; б) 2.043.
№ 5. I) 6/7 = 0.857; /0 = 2,19.
2) а) 5.435 (±0.0028);
б) 10,8441; 5=0.5%.
3) а) 8,345; б) 0.288.
Кг 7. 1) 2/21=0,095; ,/22 = 4,69.
2) а) 2.4543 (±0.0032);
б) 24,5643; 5=0,1 %.
3) а) 0,374; б) 4.348.
№ 9. 1) 6/11=0.545; ч/83 = 9,11.
2) а) 21,68563. 6=0.3%;
б) 3,7834 (±0,0041).
3) а) 41.72; б) 0,678.
№ 11. I) 21/29=0.723; ч/44 = 6,63.
2) а) 0.3567; 6=0.042%;
б) 13.6253 (±0.0021).
3) а) 18.357; б) 2,16.
№ 13. I) 13/17=0,764. /зТ=5.56.
2) а) 3,6878 (±0.0013);
б) 15.873; 6 = 0.42%.
3) а) 14,862; б) 8,73.
№2. I) 7/15 = 0.467; /30 = 5.48.
2) а) 17.2834; 6=0,3%.
б) 6.4257 (±0,0024).
3) а) 3,751; б) 0,537.
№4. 1) 15/7=2.14; /10 = 3.16.
2) а) 2.3485 (±0.0042);
б) 0.34484: 5 = 0.4%.
3) а) 2.3445: б) 0,745. №6. 1) 12/11 = 1,091; /бЗ=2.61.
2) а) 8,24163: 6 = 0.2%: б) 0.12356 (±0,00036).
3) а) 12.45: б) 3,4453.
№ 8. 1) 23/15=1.53; /0 = 3,13.
2) а) 23,574: 6 = 0,2%:
б) 8,3445 (±0,0022).
3) а) 20,43: б) 0,576.
№ 10. I) 17/19=0.895; /52 = 7.21.
<2) а) 13.537 (±0.0026);
б) 7.521; 6=0.12%.
3) а) 5.634: б) 0,0748. № 12. 1) 50/19 = 2.63: /27 = 5.19.
2) а) 1.784 (±0,0063):
б) 0.85637: 6 = 0.21%.
3) а) 0.5746: б) 236.58.
№ 14. 1) 7/22 = 0,318: /13 = 3.60.
2) а) 27,1548 (±0,0016):
б) 0.3945: 6=0.16%.
3) а) 0.3648: б) 21.7.
4
№ 15. 1) 17/11 = 1.545: /18 = 4.24.
2) а) 0.8647 (±0.0013):
б) 24,3618; 5=0.22%.
3) а) 2.4516: б) 0,863.
№ 17. I) 49/13 = 3.77; /14=3.74.
2) а) 83.736; 5=0.085%: б) 5.6483 (±0.0017).
3) а) 5.6432; б) 0.00858.
№ 19. I) 19/12=1.58: ч 12 = 3.46.
2) а) 4.88445 (±0.00052);
б) 0,096835; 5 = 0.32%.
3) а) 12.688; б) 4.636.
№21. 1) 18/7 = 2,57; /22 = 4,69.
2) а) 0.39642 (±0.00022);
б) 46.453: 5 = 0.15%.
3) а) 15.644: б) 6.125.
№ 23. 1) 16/7 = 2.28; /п=3,32.
2) а) 24,3872; 5=0,34%, б) 0,75244 (±0.00013).
3) а) 16,383; б) 5.734.
№ 25. I) 12/7=1.71; v 47 = 6.86
2) а) 72.354; 5=0.24%;
б) 0.38725 (±0.00112).
3) а) 18.275: 6) 0.00644.
№ 27. 1) 23/9 = 2.56: /87=9.33.
2) а) 23.7564: 5 = 0.44%;
б) 4.57633 (±0,00042).
3) а) 3.75; б) 6.8343.
№ 29. 1) 7/3 = 2.33: ч 58 = 7.61.
2) а) 3.87683; 5 = 0.33%: б) 13.5726 (±0.0072).
3) а) 26.3; б) 4.8556.
№ 16. I) 5/3=1,667; /38 = 6.16
2) а) 3.7542; 5 = 0.32%;
б) 0.98351 (±0.00042).
3) а) 62.74; б) 0.389.
№ 18. I) 13 7=1.857: /7 = 2,64.
2) а) 2.8867; 5=0.43%:
б) 32.7486 (±0.0012).
3) а) 0.0384; б) 63.745.
№ 20. 1) 51/11=4.64; /35 = 5.91.
2) а) 38.4258 (±0.0014);
б) 0.66385; 5 = 0.34%.
3) а) 6.743; б) 0.543.
№ 22. 1) 19/9 = 2.11; /17=4.12.
2) а) 5.8425: 5 = 0.23%.
б) 0,66385 (±0,00042).
3) а) 0.3825; б) 24,6.
№ 24. 1) 20/13=1.54: /63 = 7.94.
2) а) 2,3684 (±0,0017):
б) 45,7832; 5=0,18%.
3) а) 0.573; б) 3.6761.
№ 26. 1) 6/7=0.857; /41 = 6.40.
2) а) 0.36127 (±0.00034);
б) 46.7843; 5 = 0.32%.
3) а) 3.425; б) 7.38.
№ 28. 1) 27/31=0.872; /42 = 6.48.
2) а) 15.8372 (±0.0026);
б) 0.088748; 5 = 0.56%.
3) а) 3.643; б) 72,385. № 30. 1) 14/17=0.823: /53 = 7,28.
2) а) 0,66835 (±0.00115);
б) 23.3748; 5=0.27%.
3) а) 43.813; б) 0.645.
Образец выполнения задания
1)9/11=0.818: /18=4.24; 2) а) 72.353 (±0,026); б) 2.3544: 5 = 0,2%; 3) а) 0 4357; б) 12.384
1) Находим значения данных выражений с большим числом десятичных знаков: «1=9/11=0.81818..., «2 =/18=4.2426... . Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:
= 10.81818 - 0,8181 0,00019, _ = |4,2426 - 4,241 0,0027.
Предельные относительные погрешности составляют
«I
0.00019
0.81 Г
= 0.00024 = 0,024%:
а 0 0077
5и = 0,00064 = 0.064%.
а2 4,24
5
Так как то равенство 9/11=0,818 является более точным.
2) а) Пусть 72,353 (±0,026) = а. Согласно условию, погрешность ай = 0,026 < 0,05; это означает, что в числе 72,353 верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдем приближенное значение числа, сохранив десятые доли:
а, = 72,4; оц = + Дожр = 0,026 + 0,047 = 0,073.
Полученная погрешность больше 0,05; значит, нужно уменьшить число цифр в приближенном числе до двух:
и2 = 72; adt=аа+Дожр=0,026 4- 0,353 = 0,379.
Так как а(,, <0,5, то обе оставшиеся цифры верны в узком смысле.
б) Пусть « = 2,3544; 6d=0,2%; тогда ая = «-6и=0.00471. В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры*
«, =2,35; оц =0,0044 + 0,00471 =0,00911 <0,01.
Значит, и в округленном числе 2,35 все три цифры верны в широком смысле.
3) а) Так как все четыре числа « = 0,4357 верны в узком смысле, то абсолютная погрешность ad = 0.00005, а относительная погрешность 8d= 1/(2,-4-103) = 0,000125=0,0125%.
б) Так как все пять цифр числа «=12,384 верны в широком смысле, то ая = 0,001; 5Я= 1/(1 104) = 0.0001 =0,01%.
Работа 2
Задание. 1) Вычислить и определить погрешности результата. 2) Вычислить и определить погрешности результата. 3) Вычислить, пользуясь правилами подсчета цифр.
№ 1. I)
а б в
а 3 85 (±0,01) 4,16 (±0 005) 7,27 (±0,01)
b 2,0435 (±0,0004) 12,163 (±0,002) 5.205 (±0.002)
с 962,6 (±0,1) 55.18 (±0.01) 87,32 (±0.03)
2) У= (а + Ь)с 2
т — п
а б в
а 4,3 (±0.05) 5,2 (±0,04) . 2,13 (±0.01)
b 17,21 (±0,02) 15,32 (±0.01) 22,16 (±0.03)
с 8,2 (±0,05) 7,5 (±0,05) 6.3 (±0,04)
т 12.417 (±0,003) 21,823 (±0,002) 16,825 (±0.004)
п 8.37 (±0.005) 7,56 (±0,003) 8,13 (±0.002)
6
a2 + 4ab + b2 (a + b)2
a 6 в
(l 1,141 2.234 5.813
b 3,156 4.518 1,315
h 1,14 4,48 2.56
№ 2.
a 6 в
a 228.6 (±0.06) 315.6 (±0.05) 186.7 (±0.04)
b 86.4 (±0.02) 72,5 (±0.03) 66.6 (±0.02)
c 68,7 (±0.05) 53.8 (±0,04) 72,3 (±0.03)
i 2) A'=- H *(« + £)
c—d
a 6 к
a 13,5 (±0,02) 18.5 (±0.03) 11.8 ( + 0.02)
b 3,7 (±0.02) 5,6 (±0.02) 7.4 (±0.03)
nt 4,22 (±0,004) 3,42 (±0,003) 5.82 (+ 0.005)
< 34,5 (±0.02) 26,3 (±0,01) 26,7 ( + 0.03)
d 23.725 (±0,005) 14,782 (±0,006) 11.234 (+0.004)
3) A/ = [u + b)h3 (a+b)h
4 ‘ 12
a 6 l:
a 8,53 6,44 9.05
b 6,271 5,323 3.244
h 12.48 15.44 20.18
^fab
№ 3. ) X=^—
c
a 6 в
a 3.845 (±0,004) 4.632 (+0.003, '.312 i -0.0u4)
h 16.2 (±0,05) 23.3 (±0,04) 18.4 ( r0,03)
c 10.8 (±0.1) 11.3 (±0.06) 20.2 (±0.08)
7
(<—<Z)2
a 6 в
a 2,754 (±0,001) 3.236 (±0,002) 4.523 (±0.003)
b 11.7 (±0.04) 15.8 (±0,03) 10.8 (±0.02)
m 0,56 (±0,005) 0,64 (±0,004) 0.85 (±0,003)
c 10,536 (±0,002) 12.415 (±0.003) 9.318 (±0,002)
d 6,32 (±0,008) 7.18 (±0,006) 4,17 (±0.004)
3) ±+fr|2 («2+*2M
2Л 5
a 6 в
a 0.562 0.834 0.445
b 0,2518 0.3523 0,4834
h 0,68 0.74 0.87
a2b
№ 4. 1) JT=—
c
a 6 в
a 3,456 (±0,002) 1.245 (±0.001) 0.327 (±0,005)
b 0,642 (±0.0005) 0.121 (±0,0002) 3.147 (±0,0001)
c 7,12 (±0.004) 2.34 (±0,003) 1.78 (±0.001)
a+b)m
2) ±=-
yjc—d
a 6 в
a 23,16 (±0.02) 17,41 (±0.01) 32,37 (±0,03)
b 8 23 (±0,005) 1,27 (±0,002) 2,35 (±0.001)
c 145,5 (±0,08) 342,3 (±0,04) 128,7 (±0,02)
d 28,6 (±0.1) 11,7 (±0.1) 27,3 (±0,04)
m 0,28 (±0.006) 0,71 (±0.003) 0,93 (±0.001)
h ( а аг\
3) r= -S 1+-+—
3 \ A Ay
a о в
a 8,51 5.71 7.28
A 23,42 32.17 11.71
S 45,8 51,7 21,8
h 3,81 2,42 5,31
8
ah3 № 5. 1) Л'=— c
a 6 в
a 0.643 (±0.0005) 0.142 (±0.0003) 0,258 (±0.0002)
b 2.17 (±0.002) 1.71 (±0.002) 3.45 (±0.001)
c 5.843 (±0.001) 3.727 (±0.001) 7.221 (±0.003)
2) *=•
a 6 в
a 27.16 (±0.006) 15.71 (±0.005) 12,31 (±0.004)
b 5.03 (±0.01) 3.28 (±0.02) 1.73 (±0,03)
e 3.6 (±0.02) 7.2 (±0.01) 3.7 (±0,02)
m 12.375 (+0.004) 13.752 (±0.001) 17.428 (±0.003)
n 86.2 (±6.05) 33.7 (±0.03) 41.7 (±0,01)
i2 a2 + 4ab + b2
8 (</+Л)2
a 6 в
Л 21.1 17.8 32,5
a 22.08 32.47 27,51
b 31.11 11.42 21,78
ab
№ 6. 1) X = ~
a 6 в
a 0.3575 (±0.0002) 0.1756 (±0.0001) 0.2731 (±0,0003)
b 2.63 (±0.01) 3.71 (±0.03) 5.12 (±0.02)
c 0.854 (±0.0005) 0.285 (±0.0002) 0,374 (±0.0001)
a+b
2) .¥ = -
a 6 в
a 16.342 (±0.001) 12.751 (±0,001) 31.456 (±0.002)
b 2.5 (±0.03) 3.7 (±0.02) 7,3 (±0.01)
c 38.17 (±0.002) 23.76 (±0.003) 33,28 (±0,003)
d 9.14 (±0.005) 8.12 (±0.004) 6.7! (±0.001)
in 3.6 (±0.04) 1.7 (±0.01) 5,8 (±0.02)
9
3) rJ •пЛ(3«2±Л2)
a 6 в
a h № 7. 1 2,456 1.76 я2 , ) r=-w2 4 7,751 3.35 5.441 6.17
a 6 в
я D d 2> 4=6 3.14 54 (±0,5) 8,235 (±0,001) i-Jtx/D4-rf4 >4 3,14 72 (±0.3) 3.274 (±0,002) 3.14 31 (±0.01) 7,345 (±0.001)
a 6 в
D d n 3) a — c 36,5 (±0.1) 26.35 (±0.005) 3,14 \ 1 c~ / 41.4 (±0.2) 31.75 (±0.003) 3,14 52,6 (±0,01) 48.39 (±0.001) 3.14
a 6 в
c P Y № 8. 1 2.435 0,15 1.27 m zn ’r- ,3 7,834 0,21 3,71 4,539 0.34 5.93 l •
a 6 в
/Н w r 1.6531 (±0.0003) 3,78 (±0,002) 0.158 (±0,0005) 2.348 (±0,002) 4,37 (±0,004) 0.235 (±0,0003) .. 3,804 (±0.003) 4,05 (±0,003) 0,318 (±0.0002) )
т Ja—b 2) х= V { c + d
а 6 в
а b 10 9.542 (±0.001) 3,128 (±0.002) 8.357 (±0,003) 2,48 (±0,004) 4.218 (±0.001) 1,57 (±0.006)
Продолжение
а б в
nt 2.8 (±0.03) 3.17 (±0.01) 2.32 (±0,02)
с 0.172 (±0.001) 1.315 (±0.0004) 2.418 (±0.004)
d 5.4 (±0.02) 2.4 (±0.02) 1.8 (±0,01)
3) 1=- ^n/t(2D2 + Dd+0.75d2)
а 6 в
л 84.2 76 45
D 28.3 17,2 48.3
<! 42,08 9.344 32,14
№ 9. 1 ' ‘-Л •
а б в
с 0.7568 (±0.0002) 0.8345 (±0.0004) 0.6384 (±0,0002)
(1 21.7 (±0.02) 13.8 (±0,03) 32.7 (±0,04)
b 2,65 (±0.01) 1.84 (±0,006) 4,88 (±0,03)
3/а-Ь
2) г=-
т{п—а)
а б в
а 10,82 (±0.03) 9.37 (±0.004) 11,45 (±0.01)
h 2.786 (±0.0006) 3.108 (±0.0003) 4,431 (±0.002)
т 0.28 (±0,006) 0.46 (±0.002) 0.75 (±0,003)
п 14,7 (±0.06) 15.2 (±0.04) 16,7 (±0,05)
3) Л’=, /р(р-а)(р-Ь)(р-с}. где р=(а+Ь+с}/2 -
а б в
а 46.3 10,5 2.48
h 29.72 34.18 5,344
с 37,654 27.327 6.0218
№ 10. . Qe3 1) / = —
. ’ 48 Л'
а б в
Q 54.8 (±0.02) 38,5 (±0.01) 17.3 (±0,0“)
е 2,45 (±0,01) 3.35 (±0,02) 5,73 (±0,01)
Е 0,863 (±0.004) 0,734 (±0.001) 0,956 (±0,004)
11
(2,-1)г(л+у)
Л —Г
a б 1
« 2.0435 (±0.0001) 1.1753 (±0,0002) 4,5681 (±0.0001)
.V 4.2 (±0.05) 5.8 (±0.01) 6.3 (±0.02)
г 0.82 (±0.01) 0.65 (±0.02) 0.42 (±0.03)
-0«)
h1 2 h2 (Л+Р)
a б в
а 5.27 7.31 3.28
Р 0,0562 0.0761 0.0545
а 158.35 234.36 341.17
b 61,21 81.26 52,34
Образец выполнения задания
2 3 т
I) Х=——. где т = 28.3 (±0.02), « = 7.45 (±0.01). А =0.678 (±0.003);
„ (л—!)(?« + «)
2) t п \ где « = 3,0567 (±0,0001). ш = 5.72 (±0.02);
('«-«Г
3) F=n/r( Я--|, где Л=11.8; R=23.67.
\ 3/
1) Находим т2 = 800.9; л3 *=413,5: у/к = 0,8234;
у=^^Уг?=402200=4’02’105-
Далее, имеем Sm = 0.02/28,3 = 0,00071; 5И = 0,01/7,45 = 0,00135; 5* = = 0,003/0,678 = 0,00443, откуда
Ъх = 26т + 35„±0,55* = 0,00142 + 0,00405 ± 0,00222 = 0,00769 = 0.77%;
«л =4,02 105 0,0077 = 3,1 • Ю3.
О т в с г: X=4.02 105 (± 3.1 103); 5Х = 0.77%.
2) Имеем п-1 =2,0567 (±0,0001); m±w=3,057 (±0,0004)±5J2 (±0,02) = = 8,777 (±0,0204); ш-»=5,72 (±0,02)-3,057(±0,0004) = 2,663 (±0,0204);
2.0567-8.777 2.0567-8.777 _ _л _ _ „
/у=---------—=-----------------= 2,545 2,55;
2,663 2
7.092
0.0001
2,0567
0 0э04 0 0204
+2 =0,000049 ± 0,00233 ± 2 0.00766 =
8.777 2,663
= 0,00238 ± 0,01532 = 0,0177 = 1,77 %; aN = 2,55 • 0.0-177=0,046.
Ответ W%2,55 (±0,046); 5V=1.77%.
3) Находим
Г=3,142 -11.82 (23,67 - 3,933) = 3,142 11,82 • 19.737 = = 3.142 • 139,2 -19,737 = 437,37 • 19,737 = 8630^8,63 103.
Ответ: И^8,63 103.
12
Глава II
АЛГЕБРА МАТРИЦ
Работа 1
Задание. Обратить матрицу методом
разбиения ее на клетки.
/1 1 1 1\
V» 7 J-/1 4 2 3 1
№ 2. Л — I ( |0 3 6 I.
\6 10 1 4/
/-2 2 1 0\
\ —5 4 -1 2/
/3 -2 2 0\
(1
°
I
(2
I
/-!
№ 14. Я = 1
\-1
/3 1
/ 7 7
Jte 16. Л- - -
\1 I
4 -3 0\
4 1 2 |
2 4 I I’ 0—15/
1 2 0\
-3 3-11
3-8 1 г
- I 2 -1 /
3 3 2\
2 2 11
1 2 О Г
3 3 3/
3 3\
1 31
2 О Г
1 3/
/2 ! 0 1\
№ 17. .4= 2 3 2 0 |
I О I 2 О I
\1 0 -2 1/
(-2 -2
7 1
3 2
4 3
-1 3\
О -I ]
1 ~3 г
2 -4/
(I 1 2 3\
3 -1 —1 —2 1
2 3-1-1
1 2 3 -1/
(I 2
з 2 -3
3 _7
-1
2
13
/1 2 3 4’\ /2 1 2 3i № 21. 4 = i i 7 н . 1 J М 1 X Г \4 3 2 1/ /1 2 -1 1\ №23. Л=Н "] J J1- \| -1 1 з/ /2 1 -3 0\ v / 1 5 12 № 25. Л-1 3 6 4]1- \0 -1 -1 5/ /2 -1 3 2\ /3 3 3 21 №27. 2. \з -1 3-1/ /2 1 1 -1\ / 9 - 1 0 —3 1 №2’--'=3 0-1 I- \2 2 -2 5/ /1 ! -3 0\ Е /25121 < №22-Л= 0 6 41- I \6 -1 -1 5/ ( /2 5 -3 2\ J № 74 4-Р ~4 5 “2 1 ! № 24. J-I j 3 _8 j 1. | \1 -1 2 -|/ I /1 2 3 4\ j № 26. А= “ * “ | \4 3 2 1/ /I 2 3 4\ / 7 3 4 1 \ №23.4= к 4 , 2 . 1 \4 1 2 3/ /2 1 -3 4\ v ™ А- 1 0 “2 3 1 ! Na 30. А —13^ q 5 г 1 \4 3 -5 о/ !
Образец выпол / 1 1 1 -1 0 нения 3 4\ 3 -2 ’ задания )
О — 1 2 1 \ 1 2 2 .-3 \ -1 1 /
А В\ (К L\
Пусть *> = ( — — ); тогда S = ( — — \С DJ \М N}
где ,V = (D -СЛ"1#)"1, M=-NCA~', К=А~'-А
Матрица А 1 находится легче, чем D~l.
Последовательно находим:
'ВМ
14
6. N=( до —5/ ’ A—-100; —Л12—10; /12i=9; /122 = 2;
1/20 -9/100\ — 1/10 -1/50 )'
1/20 —9/100\_Z 7/20 — 23/100\
-1/10 -1/50 /Д-1/10 29/50 /
„ 1/20 -9/100W1 -1\/13 100 14/100\
S. Al- ika 10 _1/50 д2 7/50 _4/50 j,
. x-i Л-1ОА, f° /-3 2\/13/100 14/100\
9’ K=A ~A BM = [1 1Д 6 2Д 7/50 -4/50 Г
/0 —1\_/ —11/100 —58/100\_/ 11/100* -42/100Y
\l IJ \ 106/100 68/100 J \-6/100 32/100/
/ 11/100 -42/100 7/20 —23/100 \ t
c-i-l -б'ЮО 32/100 — 1/10 29/50 \
IU’ d “I 13/100 14/100 1/20 -9/100 Г
\ 7/50 -4/50 - 1/10 -1/50 /
Проверка:
/11 3 4\ / 11/100
/—10 3—21/ -6/100
2 1 2 -3 fl 13/100
\ 12-1 1/ \ 7/50
-42/100 7/20 —23/100 4 /1 0 0 0\
32/100 -1/10 29/50 JO I 0 0
14/100 1/20 -9/100 ПО 0 1 0
-4/50 -1/10 -1/50 / \0 0 0 1/
Работа 2
Задание. Обратить матрицу методом окаймления. При выполнении работы воспользоваться вариантами работы 1.
Образец выполнения задания
1 1 3 4
Л = [ -1 2 0 1 3 2 2 -3
1 2 -1 1
Пусть следующей . f Ап— 1 схеме: А л-1 <4 к ^ии / 13„ аждый этап процесса выполняется по
ив ^пл
I де %,=««„+(- УПА п-\ ) Un
15
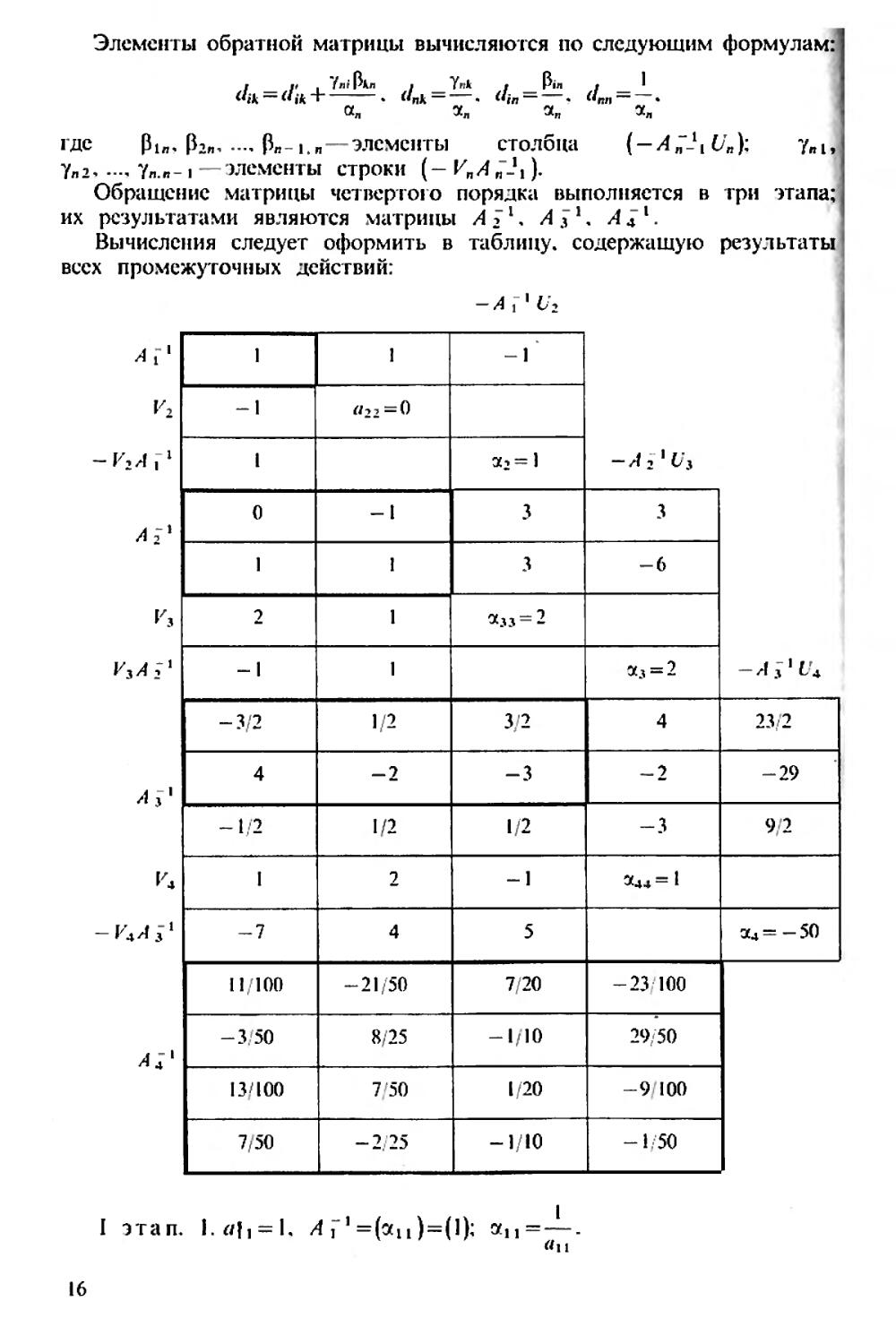
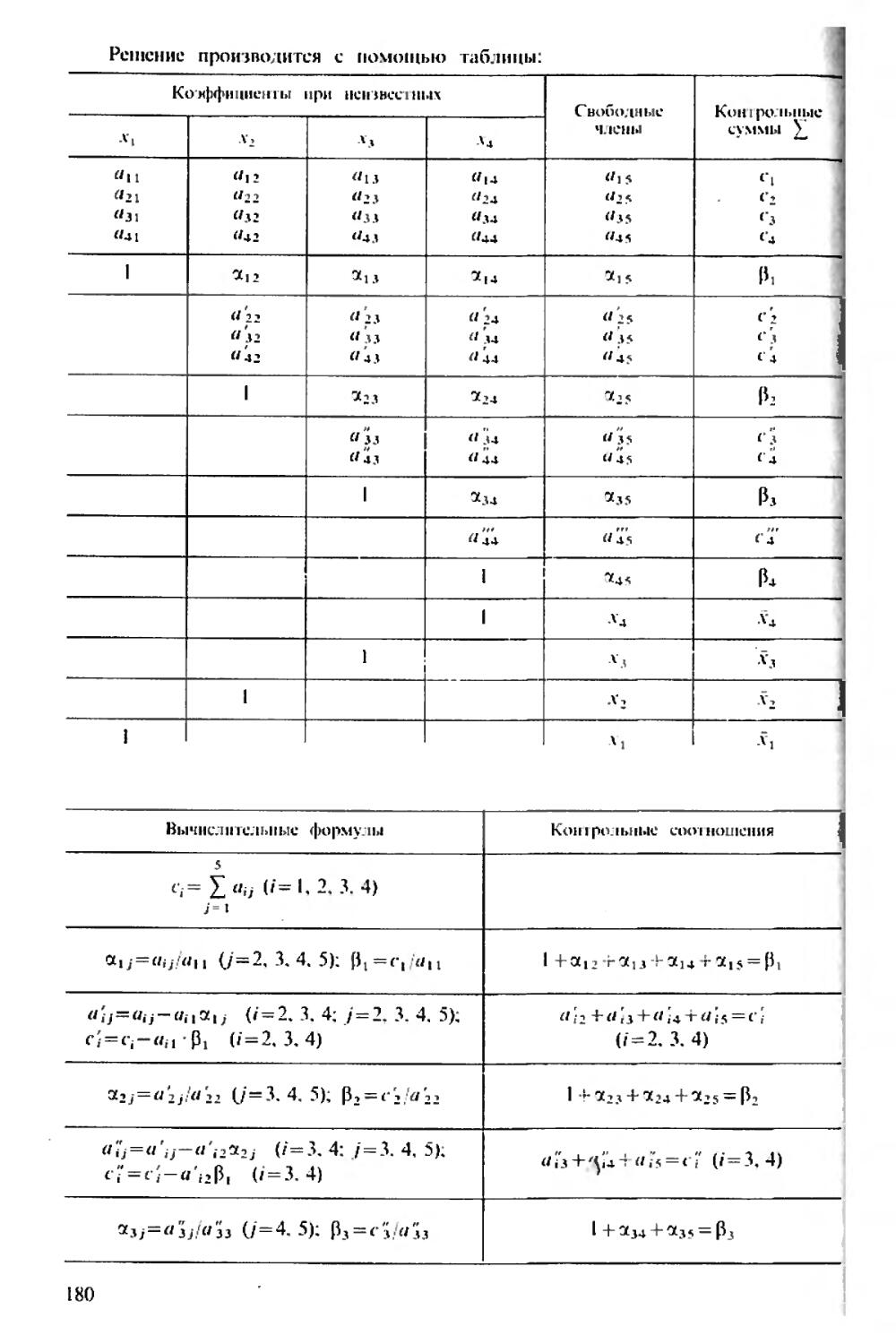
Элементы обратной матрицы вычисляются по следующим формулам:
Г II . /лгркл 1 Ynl f Р|Л f
"ik ™ik "I • “nk • "in • "пл • «л «я «„ «я
где p i„. p2„..p„ _ i. „—элементы столбца (- A “J( U„): y„ t,
Y«2...y„.„_ i - элементы строки (-ИПЛ „Л).
Обращение матрицы четвертого порядка выполняется в три этапа;
их результатами являются матрицы /1 71. Л.?1. Л4-1.
Вычисления следует оформить в таблицу, содержащую результаты всех промежуточных действий:
— А Г' U2
1 1 -1
— 1 Й22 ~ 0
1 а2 = 1 — А 2 1 С’з
0 — 1 3 3
1 1 3 -6
2 1 «зз = 2
— 1 1 аз = 2 -А 5-'Г4
-3/2 1/2 3'2 4 23/2
4 — 2 -3 — 2 -29
-1/2 1/2 1/2 -3 9 2
I 2 -1 «44= 1
-7 4 5 я4=—50
11 100 -21/50 7 20 -23 100
-3.50 8/25 -1/10 29/50
13/100 7 50 1/20 -9 100
7/50 -2.25 -1/10 -1/50
I этап. = А г’ = (яи)=(1); яп =—. «п
16
рядом с матрицей ЯГ1 запишем окаймляющие ее значения И2, U2, , взятые из данной матрицы.
-ЯГ1Г2=-(1)(1) = (-‘) = (Р1з).
1 -Г2ЛГ1 = -(-»)(П = (1) = (Т21).
4. 'х2 = «22 + (-Г2ЛГ,^) = 0 + (1)(1)=1.
S По приведенным выше формулам найдем элементы матрицы J7*=WJ: -
Jn = 14-——-=0; ~ 1’ ^2i=j= G ^22 = у=1.
]1 этап. 1. Рядом с найденной матрицей А 7* выписываем из данной матрицы Я окаймляющие значения U3, И3, а33.
4. 7.3 = «33 + (— Ид Я 2 1 t/3 ).
Произведение -И3Я£1С/3 найдем двумя способами, что можно использовать для проверки правильности вычислений:
Таким образом, а3 = 2 + 0 = 2.
5. Найдем матрицу Я 71 =(</,,):
Значит, /—3/2 1/2 3/2 \
Я7’= 4 -2 -3 )
у —1/2 1/2 1/2 /
При выполнении вычислений вручную их правильность можно проверить с помощью равенства Я3Я/ = Е3:
/ 1 1 з\/—3'2 1/2 3/2 \ /1 0 0\ -103 4 -2 -3 =010 .
\ 2 1 2/ \ —1/2 1/2 1/27 \0 0 1/
17
двух
III этап. Все вычисления аналогичны проведенным на этапах.
Выписываем окаймляющие значения t/4, lz4, а^.
-3/2 1/2 3/2
4
-1/2 1/2 1/2
-3/2
-2
-1/2
-3
5. Найдем матрицу А
9
— 58—-=—51;
)(:9-(Э-(0
1/2 3/2 \
1/2 1/2
— 28 —8—15=—51;
3 ( —7)(23/2)_ 11 . 1 1 4(23/2)^ 21
2 + -50 100’ ‘12 2+ -50 ’ 50’
3 5(23/2) 7 2+ -50 20’
3 ~50'
7
-л;‘1/4=-
4(-29) 8 . . , 5(-29)_ 1 .
-50 25’ 23 -50 10’
^31 1 (~7)9/2_ 2 -50 >3 . . 100’ d32~ J 4 9/3_ 14 _ 2+ -50 100 7 50’
d -'+5<9'2) dsi 2+ -50 . 1 . _ -7-20’ 41 -50 7 :; “42— 50 4 -_2. / -50 25' '43 5 -50 1 10’
, 1 «44 — — — -50 1 . 23/2 50 14 -50 31. ,/ 100’ 24 -29 29 — 50 50’ ^34 9/2 -50 9 100'
Итак, / 0,11 -0,42 0,35 -0,23 \
./ -0,06 А = 0,13 0,32 - 0,14 0,1 0,58 | 0,05 -0,09 Г
\ 0,14 -0,08 - 0,1 —0,02/
Этот результат совпадает с матрицей, найденной в работе.
18
Работа 3
Задание. Обратить матрицу методом разбиения ее на произведение двух треугольных матриц. При выполнении работы воспользоваться вариантами работы L
Образец выполнения задания
/ 1 1 3 4\ .1-10 3-2 1
2 2 2 — 3 |
12-1 I /
Решение состоит из следующих этапов:
I. Представление матрицы А в виде произведения Л = Г1Т2, где 7'1 и Л — треугольное матрицы.
II. Обращение матриц 7\ и Г2. т. е. нахождение матриц Tf1
III. Нахождение искомой матрицы А найденных матриц: А ~1 = 7" 71 Т Г1.
I. Для отыскания матриц Т\ и Т2 используют схему
и Т2-‘.
"1 с помощью умножения
Элементы матриц
«11 [ «12 «13 «14 <‘|
«21 «22 «23 «24 4'2
«31 «32 «33 «34 4'3
«41 «42 «43 «44 С4
1 /и 1 * П2 ИЗ Г13 <‘1
/21 /22 1 Г23 Г24 <-2
/31 /32 /33 * Г34 с'з
/41 /42 /43 /44 | 1 <4
Столбец Z является контрольным; числа с2. с3, с4—строчные ? суммы.
Элементы схемы находят в следующем порядке:
I- /ц=Лц; /21=<72Ь hl=tt31« ^41=«41-
«12 «13 «14 , <’1
—; Г1з— -—; г14—-—* <1——.
/| 1 ‘II ‘II 'II
Контрольное соотношение: = 1+г12 + г13 + Г]4.
3. /?? =«22 —/21 Г22 J ^32 = «32 —Ъ1Г12^ ^42 =«42 ~’ U1 г12 •
«|4 .
э
19
«23 ~ Ь|г13 «24 ~l21 Г14 ,
____________• r - « — -----—-----— * f' ----------
Контрольное соотношение: c\ — I Ч-гзз + гц-5. /33=«33“ blr13 — /32r23i U3 = </43 — /41/'13 —U2r23-
Контрольное соотношение: с'з=1+гз4.
7. /44 = «44 —/41 Г14 — ^42 ^*24 —^43^*34»
Контрольное соотношение: ci=L
Из найденных элементов составляют матрицы
В данном случае имеем
Элементы матриц 1
1 1 3 4 9
-1 0 3 — 2 0
4^ 1 9 А» -3 2
1 2 -1 1 3
1 1 1 3 4 9
— 1 1 1 6 2 9
2 — 1 2 1 —4.5 -3,5
I 1 -10 -50 1
/22 = 0-(-1)-1 = 1; /32=1-2-1 = -!; /42 = 2-1-1 = 1,
(контрольное соотношение: 1 + 6 + 2 = 9 = с'2 );
1+(-4,5)= —3,5=c’j);
(контрольное соотношение:
20
z44= I — 1 -4—1 -2—{—10)-(-4.5)=-50;
, 3-1 9-1-9-(-IO)(-3.5) (. * 4 =------------------= I
-50
(кон i-рольное соотношение -<-д = 1 выполняется). Таким образом.
В соответствии с этим равенством получим систему уравнений
С Лц = 1. Л'22 + 2л'32=0,
I л 1 1 T-V? 1 = О, Д*22— Юл'з2 ”Ь 50л*Д2 =0,
л 2л'! j — л'21+2л'з1 =0. 2л'зз=1,
I Л 11 + Л'21 — 10л*з 1 — 50л'д 1=0. — Юл’зз — 5ОЛ'43 = 0.
Л'22 = 1 ’ — 50Лдд = 1 •
Отсюда находим
1/2; Л'д1 —7/50; л'22 — 1; х*з2= 1/2; 2; _\4з= — I/Ю; .v44=-l/50.
С Л*14+-'*24+ЗЛ'з4+4 = 0,
. л Л'24 ”Ь 6л*34 + 2 = 0, ( л-34 — 4.5 = 0,
3; л*з4 = 4,5; л-24=—29; л-14=11,5. Значит,
21
/1—1 3 Il,5\
T-i_ О 1 -6 —29 |
2 IO О 1 4,5 I
\O 0 0,1/
ill. Используя равенство /1-I = 7'7I Tf’, находим
/1-1 3 11.5 \ / 1 0 0 0\
А -I = 0 I -6 -29 || 1 1 0 ° \
О 0 1 4,5 II -1/2 1/2 1/2 0 |“
\О 0 0 1 /\ 7/50 -2/25 -1/10 — 1/5о/
/ 11/100 -21/50 7/20 -23/100\
_ -6/100 8/25 -1/10 29/50 |
I 13/100 7/50 1/20 -9/100 I
\ 7/50 -2/25 -1/10 — 1/50./
Эта матрица совпадает с матрицей, полученной в работах 1 и
Глава 111 МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Работа 1
Задание. I) Решить систему по формулам Крамера.
2) Решить систему с помощью обратной матрицы.
3) Выполнить действия над матрицами.
4) Решить уравнение
2) 15д + 8г—z= —7; < д + 2г + 3г=1; l2.v-3r+2- = 9.
3) 2 (Л + В)(2В—А).
/23 -l\ /-I 0 5\
где Л=( 4 5 2 I, Л=( 0 I 3 ).
\ — I 0 7/ \ 2 -2 4/
/ 2 3 1\ /27 I3X
4) -I 2 4 ) -I 0 5 ].
\ 5 3 0/ \ 5 13 21/
№2. 1) Г А’!+2лч4-Зд'3 —2д*4 = 6; 2) Г д + 2г+г —4;
I л1-л-2-2л-3-Зл4 = 8; <За-5г + Зг= I;
|3л*| +2.Vj—л‘3 + 2д'4=4; (,2л'+7_г—z = 8.
[2д' । — 3.V т, + 2.V 3 + Ад = — 8.
3) ЗЛ-(Л + 2й)Я,
/4 5
где А = I 3 — 1
\4 2
_ 2\
0 ’
7/
/2 1 —1\
В=I0 I 3
\5 7 3/
22
(-\ -2 3\ /4 II 3\
4) -V 2 3 5 =( I 6 1 .
\ I 4 — I/ \2 2 16/
3) 2(4-Я)(Л2 + й).
/ 5 I 7\ /2 4 1\
где .4=1 - 10 -2 1 ), Я=| 3 10.
\ 0 12/ V 2 I/
/4 -2 0\ /0 -2 6\
4) I 12 ) У=| 2 4 3.
\3 -2 О/ \0 -3 4/
№ 4. I) Г л 2 - Злл + 4л-4 = - 5; 2^ [ \, + 2х2 + 4л 3 = 31;
I ' 1 2л'з + Зл'д = 4; \ 5л*। + хч + 2л"з = 29;
|3л! +2л*2 — 5л’4— 12; (3 vt — л*2 + лч= 10.
(4л1+Зл-2-5л-3 = 5.
3) (.42-Я-)(.4 + В).
23
( х । + 4as — 7 ,vj + 6.v4 = 0.
3) 2(Л — 0.5tf)+ AB.
24
3) (2Л-/?)(ЗЛ + В)-2ЯЯ.
/ 1 ° 3\ / 7 5 2\
где Л= -2 О 1 ), Я=| О I 2 1.
\-1 3 I/ \-3 -I -1/
25
= 7;
= 0;
= 2.
= 20;
<5 = 3:
Lv, = -8.
= 1;
= 11.
л'з = 7;
сз=4;
4л'з=11.
26
3) 2Л-ЛЯ(Л-Л)+5, /3 2 —1\ /О 3 -1\
где /1=0 -1 2 к й= 2-1 2 1.
\5 7 I/ \-3 I 4/
/3 2 — 5\ /-1 2 4\
4) Л - 4 2 0 = 0 3 2.
\1 I 2/ \-1 -3 4/
№20. I) f 2л-|-л-3-2л-4= - I: 2) f 11л + 3г-с = 2:
I л2 + 2л-3—л4 = 2; л 2л + 5у— 5г = 0;
] Л| — л2 —л4 = — I: I л + г+г = 2.
(—л'|+3л'2 —2л’з=0.
3) Л2—(/1+ /?)(/! —3/?).
/ 4 5 6\ /0 -1 2\
где Я= -I О 3 ). £=( I 0 -2 ).
\—I 2 — I/ \3 1 2/
/1 2 1\ /42 1\
4) 3-5 3 Х= I -5 3 .
\2 7-1/ \8 7—1/
№21. 1) Г-л-14-л-2+л-з + л-4=4: 2) (7.v+5r+2r= 18;
I 2.vt +.v2 + 2a-3 + 3.v4 = 1; < л —r-r = 3;
1 Зл1+2л'2+л-з + 2л-4=1: I л + г+2.-=-2.
[ 4л‘ [ + Зл’2 + 2л'з + лж4 = — 5.
3) В(Л + 2В)—ЗАВ.
/7 -3 0\ /-4 2 1\
где /1=1 I -1 0 1, Я=( 10 1).
\2 0 3/ \ 3 2 1/
/-1 2 0\ / 5 -I 3\
4) X♦( -3 21= 4 2 1.
\ 1 2 3/ \-1 0 2/
№ 22. I) Г5л-, + Зл-2 - 7л*з + Зл4 = 1; 2) Г 2.v+3 г+г = I;
) -V2 — Зл'з + 4л’4=—5; \ л_ + г=О;
| л-i -2л-3-Зл‘4= -4; (. л-г-г = 2.
[4л* । + Зл'2 — 5л'з = 5.
3) 3(Л + 5)-(Л-5)А
2 3\ / 4 2 1\
где /1 = 1 0 —2 3 . 5= -12 О ).
\1 11/ \ 23 -1/
/1 1 -1\ /7 0 -5\
4) 4 -3 1 Х= 4 11 2 .
\0 21/ \1 3 I/
№ 23. 1) г Л1+Л-2_Л-3_Л-4 = О. 2) (л—2г-2- = 3;
1 л-1+2л-з-2л-4=1; <v+}’-2z=0;
j Xj— л2-л’4= — 1; Lv — г — -=l.
1-л1 + Зл-2-2л-з=0.
27
3) /1 (Л-Я) + 2Я(Л + В).
= 15:
= 9:
= 1:
= 0.
5;
I*
3.
28
Образец выполнения задания
I) (2л-! + as — 2л з+л'д = 1:
13.v j + 4л2 + л з—Злд = — 7;
}4л" 1 — 2л'2 + Зл’з —4л'д = 3» 12л1+2л2-Зл-з-л-4=-]].
29
3) (3/1 + В)(2Л - й).
f
9
в=
10 1.
3 ), 2/
13 —4 6 2 -4 2 1.
-2 5 5/
о
2
-2
О
О
_9
4
-2 =—(105+16 + 56 —98ч-10 + 96)= — 185;
8
— 2
4
9 м
О
4
4
-2
9
8
-9
4
_ 9
9
— 2
О
Ах
Д
-11
-13
9
4
2
4
-2
9
9 — 7
-2
-4
3
-13
4
-2
2
О
9
О
_9
О
4
7
-7
0
-13
9
-25
О
10
-13
9
4
— 7 = -(360-91 -700 + 36-700 + 910)= 185;
10
Д
2
3
2
4
— 2
2
-7
-4
0
-5
8
— 2
5
-13
_9
О
О
4
2
8
-2 -13 -3
5 -2 =-(75-44+728-70+ 130-264)=-555;
2
— 2
О
Д
2
О
4
4
4
— 2
2
3
8
— 2
9
0
-11
5
-13
4 -11
8
-2 -1 -13
5 =-(455-40+88-154+416-25)=-740;
30
_А'._-37О_П. . _АЧ_ 185
A —I85~*"* Л2-д“-^85“
_Ati_-555_ _A,._- 740
3-A--185- ' Л4-Т--185
3
2
4
= 24-24- 15-27+16 + 20= -6;
3 ()-(
4) Имеем
AX—В, откуда X=A lB. Находим
Д= 0
-2 0
I — 1
-2
0
Л12----
О
1
31
Работа 2
Задание. Используя схему Tayi ностью до 0,001.
№ 1.
{4,4Л | — 2,5л,4- 19.2л3 — 10,8л4=4.3. 5.5л, —9.3л, — 14.2л34- 13.2л4 = 6,8, 7.1л, -11.5л, + 5,Зл3-6.7л4 =-1.8. 14.2л , + 23.4л, - 8,8л з + 5.3л4 = 7,2.
№ 3.
{5.7л 1 - 7.8л, - 5.6лэ-8.3л-4 = 2.7, 6.6л ,4-13,1 л, - 6.3л3 + 4.3л-4 = - 5,5, 14,7л, -2,8\, + 5.6лл- 12,1л4 = 8.6, 8,5л, + 12,7л-, - 23.7.V, + 5,7 л4 = 14,7.
№ 5.
{15,7л, + 6.6л, — 5,7л'з + 11,5л'4 = — 2.4, 8,8л, - 6.7л, + 5,5л*з - 4.5л4 = 5.6.
6,3л। - 5.7л, - 23.4л3 + 6.6л4 = 7.7.
14.3л, + 8.7л, - 15.7лз -5.8л4 = 23.4.
№ 7.
{14,4л, - 5.3л, + 14.3л, -1 2,7л4 = -14.4. 23,4л, - 14.2л , - 5.4л ,4-2.1 л4 = 6.6.
6.3л, -13.2л, - 6.5л з 4- 14.3л4=9.4.
5.6л, 4- 8.8л, - 6.7лз - 23.8л4 = 7.3.
, решить систему уравнений с точ
№ 2.
{8.2л, - 3.2л, 4-14.2л3 4-14.8 \4 = - 8.4.
5,6л, — 12л, 4-15л3 — 6,4л4 = 4.5.
5.7л-, 4- 3,6.v, - 12,4л3 -2.3л4 = 3.3.
6.8л, 4-13.2л, -6,Зл3 - 8.7л4 = 14.3.
№ 4.
[3.8 V, 4-14,2л, + 6.3лз - 15.5л4 = 2.8.
18.3л, -6.6л,4-5.8лз4- 12.2л4= -4.7.
) 6.4л, - 8.5л, - 4.3л з 4- 8.8л4 = 7.7.
117,1 ч -8.3л, 4- 14.4лз- 7,2л4 = 13.5.
№ 6.
4.3л, - 12.1л, + 23,2лз - 14,1 л4 = 15.5.
2.4л, - 4.4л, 4- 3.5л 3 4- 5,5л4 = 2.5.
’ 5.4л, 4- 8,3л, - 7.4л з - 12.7л4 = 8.6.
,6.3л, - 7.6л, 4-1,34л3 4- 3.7л4 = 12,1.
№ 10,
32
Хе И-
7э 1 д, -3.1*, + 4,2л'з-5.1*4 = 6.01. । з у, + 2.2*, — 1.4л'з 4-1.5*4 = 10.
< 2 v 1 — 7.4*, + 8.5* з — 9.6*4 =1.1.
। п v । + 1 .3*, + 1 .4*з + 4,5л* д = 1.6.
№ 13.
I *1 4- 1.7*2 + 37.5*3 — 2.8*д = 7,5, i’siv,+21.1*2-!.1л-з-1.2л-д= 11,1. < -21.1*1 + 31.7*,+l.2*3—1.5*4 = 2,1. 31.7* । + 18.1 *2 - 31.7*з + 2,2*4 = 0,5.
№ 12.
'35,8л! + 2.1 л_, - 34.5л* 3 - 11.8*4 = 0.5, 27.1 л, - 7,5*2 + 11 ’7*з - 23,5*4 = 12.8.
‘ 11.7*1 + 1.8*2 - 6.5*з + 7.1*4 = 1,7.
6.3*! + 10*2 + 7.1* з + 3.4*4 = 20.8.
№ 14.
{1.1*! 4-11,2*2+ Н.1*з- 13.1*4= 1.3, - 3.3* 1 + 1,1 as + 30.1 л з - 20.1 *4 = 1 -1. 7.5*! + 1.3*2 + I. I *3 + 10*4 = 20.
1.7*! + 7.5*2 - 1.8*3 + 2.1 *4 = I, I.
№ 15.
г7.5*1 + 1.8*2— 2,1*з— 7.7*4= 1.1.
- 1 Од 1 + 1.3*2 - 20*з - 1.4*4 =1.5, Ъ 8V1 - 1.7*,+ 3,9*з+4,8*4= 1.2. [|0*,+ 31.4*2-2.1*3- 10*4= -1.1.
№ 16.
{30. l*i-l .4*2 + 10*з - 1. 5*4 = 10.
- 17.5*j + 11.1 *2 + 1,3*з - 7.5*4 =1.3.
1.7*! -21.1*,+ 7J.V,- 17,1л'4= Ю.
2.1*! + 2.1*, + 3.5*з + 3.3*4=!.7.
№ 17.
г 7.3.V [ — 8.1*,+ 12.7*з — 6.7*4 = 8.8.
111.5*, + 6.2*2 - 8.3*з+9.2*4 = 21.5.
) 8.2*, - 5.4л, + 4,3*з - 2.5*4 = 6,2. [2.4*| + 11.5*2 — 3,3*з + 14,2*4= —6.2.
№ 19.
[6.4л-, 4- 7.2*2 - 8.3*з + 42*4 = 2.23.
15.8*, - 8.3*, + 14,3*з - 6,2*4 = 17,1.
) 8.6л j + 7.7*, - 18.3*, + 8.8*4 = - 5.4.
[ 13.2 л! - 5.2*, - 6.5*з + 12.2*4 = 6,5.
№ 18.
{4.8*! + 12.5*2 - 6,3*з - 9.7*4=3,5. 22* । - 31,7*2 + 12,4*з - 8.7*4=4.6, 15л* । +21.1 *, —4,5*з + 14.4л*4 — 15, 8.6*! - 14,4*2 + 6.2*3 + 2.8*4 = - 1,2-
№ 20.
{14.2*1 + 3.2*2 -4.2*з + 8.5*4 = 13,2.
6.3*| —4.3*2 + 12.7*з — 5,8*4 = —4.4.
8,4*। - 22.3*2 - 5.2*з + 4.7*4 = 6.4.
2.7* । + 13.7*, + 6,4*з — 12,7*4 = 8,5.
№ 21.
7.3*, + 12.4*2 - 3.8*з -14.3*4 = 5.8.
10.7*! - 7,7*, + 12.5*з + 6.6*4 = - 6.6. < 15.6л, + 6.6*, + 14.4*з - 8.7*4 = 12.4.
7.5*! + 12.2*, —8.3*з+ 3,7*4 = 9.2.
№ 22.
' 13.2* । - 8.3*2 -4.4*з + 6,2*4 = 6.8.
8.3*! + 4.2*2 - 5.6*з + 7.7*4 = 12.4,
< 5.8*! - 3.7*2 + 12.4*з - 6.2*4 = 8,7, 3.5*1+6.6*2-13.8*3-9.3*4= -10,8.
№ 23.
[8.1 *! + 1,2л, - 9.1 *3 + 1.7*4 = 10, 11.1 * 1 - 1.7л, + 7.2*з - 3,4*4 =1.7, | 1.7*! - | ,8л , + 10*з + 2.3*4 = 2,1, 11 ’Зл j + | ,7л 2 - 9,9*з + 3.5*4 = 27.1
№ 24.
3.3* 1 - 2.2л, - 10*3 + 1,7*4 =1.1.
1,8* j + 21.1 *2 + 1,3*з - 2,2*4 = 2.2 — 10*1 + 1.1*2 + 20*3—4,5*4= 10.
70*i - । ’7*2 - 2.2*з + 3.3*4 = 2.1.
№ 25.
[1 -7*, + 9,9*, - 20*з - 17*4 =1’7. ) 20*! + 0.5л, - 30.1 *з -1.1 *4 = 2.1.
10* । - 20*, + 30,2*з + 0.5*4 = 1.8. и.Зл! - 0.7*2 + 3.3*з + 20*4 =-1,7.
Ле 27.
’ l-v। + 11,3*2 -1.7*з + 1,8*4 = 10.
1 ,3л-! - 11,7л-, + | <8л-з + J 4Лд = | з ‘ ~ 1 °’5*2 -1.7*з - 1.5*4 = 1.1, 11 -5.Vi - 0.5*, + 1,8*з - 1,1 л-4 = 10.
№ 26.
' 1.7*! - 1,3*2 - 1, 1*3 - 1.2*4 = 2.2. 10*, — 10*, — 1,3*з + 1.3*4 =1.1. 3.5*1 +3.3*, + 1,2*з + 1.3*4= 1.2. 1.3*4 + 1, 1*, - 1,3*з - 1. 1*4 = 10.
№ 28.
{1.4*! + 2.1*, - 3,3*з + 1. 1*4 = 10.
10*! - 1.7л, + 1, 1*з -1.5*4 = 1.7.
2,2*1 + 34,4*, - 1. 1*з - 1.2*4 = 20.
1,1л*। + 1,3л*2 + 1,2л* з + 1,4*4 = 1,3.
2'1258
33
№ 29. 1,3л-1 -1 ,7л2 + 3,3л'з + 1 ,7л4 =1.1. I Ол j + 5,5л2 - 1 .Зл-3 + 3.4л 4 = 1.3. ’ 1,1 xj + 1 ,8л-2 - 2.2л з - 1, 1х4 = Ю. 1,3л! - 1 .2л2 + 2,1 лз + 2,2л4 = 1,8. J < Уя 30. ' 1,2л! + 1 ,8л2 - 2.2л 3 - 4.1 л4 = 10лj - 5,1 л2 + 1,2л3 + 5.5л4 = 2.2л! - 30.1л2 + 3.1лз + 5.8л4 Юл, + 2.4л2 - 30.5л з - 2,2л4 = 1.3. = 1.2, = 10. = 34.1.
Образец выполнения задания
(0,68х! + 0.0 5л2 - 0.11 л з+0.08л-4 = 2,15, 10,21 л-, - 0.1 Зл2 + 0.27лз - 0,8л4=0,44. ] - 0.11 л i - 0.84л2 + 0.28лз + 0.06л4 = - 0.83. 1 - 0,08л! + 0.1 5л2 - 0,5л з - 0,12л4 = 1,16.
Вычисления производим по схеме единственного деления:
Коэффициенты при неизвестных Свободные члены <онтрольные суммы Строчные суммы
Л1 *2 *3 Л'4 Е I'
0.68 0,21 -0,11 -0,08 0.05 -0,13 -0,84 0,15 -0,11 0,27 0,28 -0,5 0,08 -0.8 0.06 -0.12 2,15 0,44 -0,83 1.16 2.85 -0,01 -1.44 0.61 2,85 -0,01 -1.44 , 0,61
1 0,0735 -0,1618 0,1176 3,1618 4,1912 4.1912
-0,1454 -0,8319 0,1559 0.30398 0,2622 -0.5129 -0.8247 0.0729 -0.1106 -0,22398 -0,4822 1.4129 -0.89015 -0.97897 0,9453 -0,8901 — 0,9789( 0,9453 •
1 -2.0906 5,6719 1.5404 6,1221 6.1217
-1.47697 -0,18697 4.79139 -0.9948 0.7992 1,1723 4,1140 -0,00913 4.1136 —0.0095
1 -3,2441 -0.5411 -2.7854 -2,7851
-1.6013 1,0711 -0.5299 -0.5302
1 -0.6689 0.3309 0,3311
2,8264 -0.3337 -2,7110 -0.6689
3,8263 0,6664 -1,7119 0,3309
Ответ : Л! =2,826; л2=-0,334; лз = - -2,711; л4=-0,669.
34
Работа 3
Задание. 1) Обратить матрицу по схеме единственного деления. Все расчеты вести с четырьмя десятичными знаками. Ответ
округлить до трех десятичных знаков.
2) Вычислить определитель до 0,0001.
по схеме Гаусса с точностью
№ !• Xs 2. 1) | 1) 1 / 1.00 0.42 -0.25 0.54 / 0,15 -0,52 0,35 0,74 0.47 -0,11 0.55 1,00 0,35 0.17 0.67 1.00 0.36 -0,32 - 0,74 1.00 0.23 0,12 0.44 0.35 0,21 -0,72 0.42 0,38 -0,63 -0,25 0.37 0,55 j 2) 1.00 0.42 0.54 0.66 0.42 1.00 0,32 0.44 0.54 0,32 1.00 0.22 0.66 0,44 0,22 1.00 1,00 0,17 -0.25 0.54 -0,32 -0.74 1.00
0.47 1.00 -0.11 0,35 0.55 0.43 0.67 1.00’ 0.36
№ 3. / 0.75 0,16 0,27 0.83 \ 8,2 1.4 - 2.3 0,2
' 0,55 0.22 -0,12 0.32 V -1,6 5.4 - 7,7 3,1
1) 1 1.00 0.42 0,35 0.18 Г 0,7 1,9 - 8.5 4.8 ‘
\ -0,37 0,23 0,15 0,28/ 5.3 -5.9 2.7 - -7.9
Xs 4. / 1.5 2,7 -1,3 5.2 \ 0.42 1.00 0.32 0,44
2,7 -3.4 1.8 2,2 1.00 0.42 0.54 0.66
1) -1,3 0.16 0.82 1.05 0.66 0.44 0.22 1.00
\ 5,2 2,2 1.05 3,4 У 0.54 0.32 1,00 0,22
J с 6 . '7 < > > <) — -. (
№ 5. /1.17 2 .13 0.32 0.56 \ 0.47 1.00 0.67 -0.32
1 \ 1 2.13 0.82 -0.72 1,10 ЭХ 1.00 0.17 - 0.25 0.54
1) 0.32 0.25 -0.42 0,16 Г 0,55 0.43 0.36 1.00
\0.56 1 .10 -0.25 -0,44/ -0,11 0.35 1,00 -0.74
№ 6. / ’’2 3.2 -1.5 2,7 \ -1,6 5.4 - 7.7 3,1
1 ъ i f -5,3 4,1 3.8 1.7 \ 8.2 1,4 - 2,3 0.2
1) 0,3 1,5 -1.6 4,2 Г 5,3 -5.9 2.7 - -7.9
\ 1,6 4.5 6.3 — 1.2/ 0,7 1,9 - 8.5 4.8
№ 7. / 0,62 0.73 - -0,43 -0.23 \ 0.42 1.00 0.32 0.44
1 х 1 0,73 1.00 0,25 0,64 1 2) 1.00 0.42 0.54 0.66
' 1 -0,41 0.62 0,21 0.44 Г 0.66 0.44 0,22 1.00
\ 0.84 0.32 0.18 -0.47 / 0,54 0,32 1,00 0,22
№ 8. / 1.13 2,15 0.83 0.77 \ -1,6 5.4 -7.7 3.1
f 0.64 -0,43 0.62 -0,32 | 2) 8,2 1.4 -2,3 0.2
2.32 1.15 1,84 0.68 ’ 5.3 -5.9 2,7 - -7.9 *
\ - 0.72 0.53 0.64 — 0.57/ 0,7 1.9 -8.5 4.8
№ 9. /0.42 0.26 0,33 -0,22 \ 0.47 1.00 0,67 -0,32
|\ 0.74 - -0.55 0.28 -0.65 | ЭХ 1.00 0.17 -0,25 0.54
0.88 0.42 - -0,33 0.75 Г 0,55 0.43 0.36 1.00
\ 0.92 0.82 - -0,62 0.75/ -0,11 0,35 1.00 -0.74
№ 10. / 0.75 0.18 0,63 -0,32 \ 1.00 0.42 0.54 0,66
1) f 0,92 . 0,63 0.38 -0.42 -0.14 0.56 | 0,18 0,37 Г 2) 0.42 1,00 0.32 0.44 0.54 0.32 1.00 0,22 -
\ -0,65 0.52 0.47 0.27 / 0.66 0.44 0.22 1,00
35
№ 11. 1) | /—2.41 7,55 0.82 0.33 \ 0.28 -3.44 0.75 0.23 | 0.17 0.28 0.05 3,48 Г ^-1.00 0.23 2,00 7.00 / 2) 1.13 0.15 0.26 0.45 0,62 -0.80 0,62 -1,12 0,64 -0.13 0,73 0.16 -0,43 0.74 0.78 -0,36
№ 12. 1) /—1.09 7.56 3,45 0,78 \ 3,33 4,45 -0,21 3,44 1 2.33 -4.45 0,17 2.21 Г \ 4.03 1.00 3,05 0.11/ 2) 0.84 1.32 0.48 1.16 -0.46 0.64 0,44 0.83 -1.12 0,16 0.32 0.08 -1.13 -0.13 0.44 -0.57 •
№ 13. 1) | / 4,5 4.8 -3.7 2.1 \ 4.5 -3.7 5.6 3.3 I 4.8 7.5 8.3 9.2 Г \—1.5 2.3 4,8 3.1 / 2) 0.52 0,83 -1.2 0.32 0,63 -0,42 0,57 1,15 0,44 0,52 0.44 0.18 0,62 - 0.12 0.08 0.42 •
№ 14. ’) | / 5.5 3.7 -8,3 9,1 \ -4.5 6.8 7,2 3.4 I 7.5 -4,9 3,5 7.1 Г \ 5.6 -4,8 7,3 5.3 / 2) 1,5 0,84 0.63 0.15 0,36 -0.16 -0,27 0.45 0.64 0.41 -0.83 0.62 -0.18 0.88 -0.38 0.27
№ Л5> D 1 / 1,8 1,02 1,03 1.05 \ 7.03 8,04 9.05 6.08 \ 1,11 -2,02 2.03 -3.04 F \- 3.41 4,52 7.28 5.51 / •i) 0.8 1,3 -0,12 -1,2 0.18 0.72 1.6 0.2 0.12 - 1.4 0.15 -0.83 0.25 0,13 -0,11 0,41 •
№ 16. о 1 / 1.71 3.56 -0.33 0.17 \ 2.81 3.45 0.17 -0.22 \ -0.34 0,75 0.33 0,22 ' \ 7.03 -3.45 0.32 0.17/ 2) 2.5 0.35 0.4 0,2 -1,5 0,61 0,16 -0,42 0,57 0.23 0,15 -0,08 -0.8 2,3 0,63 3.1 -
№ 17. I) 1 / 0.17 -0,13 0,45 0.66 \ f 0.18 0,22 -0.11 0.71 ] 0,82 0,33 0.18 -0,63 Г \ - 0,28 0,41 0.28 0.33 / 2) 0.42 1.00 0.32 0,44 1,00 0,42 0,54 0.66 0,66 0.44 0.22 1.00 0.54 0.32 1.00 0.22 •
№ 18. I) 1 /1.41 2.42 3.53 4.48 \ Г 1.28 -3.04 1.09 1,05 1 7,01 8,03 9.01 7,04 Г \3,15 4,18 -8,11 7,12/ 2) 1.00 0,17 -0,25 0,47 1,00 0,67 -0,11 0,35 1.00 0.55 0,43 0,36 0,54 -0,32 -0.74 1,00
№ 19. 1) / 0.28 0,33 0.42 0,51 \ ' 0.17 0.88 0.19 0.22 \ -0.23 0,18 0.11 -0.13 * \ 0.51 0.15 0.72 -0.14/ 2) 8,2 1,4 -2,3 -1,6 5,4 -7,7 0,7 1,9 -8,5 5.3 -5.9 2.7 - 0,2 3.1 4.8 -7,9
№ 20. 1) /1,17 4,12 1.08 3,05 \ 2,01 -1,02 1.03 1,00 | . 1.00 2.00 1.00 3.00 г \ 7,05 8.03 -4.04 5,55/ 2) 1.6 5.4 -7.7 -3.1 8.2 1.4 -2.3 0,2 5.3 -5.9 2.7 -7.9 0,7 1.9 -8.5 4.8 -
№ 21. 1) /1,00 0,42 0,54 0,66 \ ' 0.42 1,00 0.32 0.44 \ । 0,54 0,32 1,00 0,22 Г \0,66 0,44 0,22 1,00 / 2) 0,47 1,00 0,67 1.00 0,17 -0,25 0.55 0.43 0,36 -0.11 0,35 1.00 -0,32 0.54 1,00 -0,74 •
36
f
jVs 22. 1) I /2.11 3.01 4.02 0,22 \ 0.18 3.41 0.15 1.43 V 2.14 0.17 0.26 0.18 Г ^1.28-0.42 0.54 1.00/ 2) 1,00 0.42 0.54 0.66 0.42 1.00 0.32 0.44 0.54 0.32 1.00 0.22 0.66 0.44 0.22 1.00
№ 23. 1) / 7.13 8,21 4.47 — 2.11 \ ' 3.25 1.54 2.91 5.43 I -6.34 -8.17 -10.2 3.93 ’ 4.52 6,73 1.37 — 9.89/ 2) 0.2 -7.7 3.1 -1.6 0.7 1.4 -8.5 4,8 8.2 -2.3 0.3 -7.9 0.55 1.00 0.32 0.4
№ 24. 1) /—2.00 3.01 0.12 —0.11 \ 2.92 -0.17 0.11 0.22 ] 0.66 0.52 3.17 2,11 ' [ 3.01 0.42 -0.27 — 0.15/ 2) 0.25 0.16 0.35 1.2 -0.8 0.62 0.83 0.48 -0.18 0.43 0.57 0.62 - 0,18 0.34 0,72 -0,13 -
№ 25. 1) /3.41 -0.18 2,34 7.08 \ 0.21 0.17 -0,51 -0.44 1 0.33 3.42 -5,17 0.66 ' \0.77 3.68 0.22 —0.19/ 2) 1.0 2.14 0.42 0.23 0.42 -1.5 0.34 -0.12 0.18 0.83 -0.17 0.62 -1.13 0.16 0.57 -0.83
As 26. 1) /4.20 0,32 0.11 0.13 \ f 0.17 0.25 0.48 0.52 0.12 0.08 0,72 0.61 Г \0.54 0.13 0.81 0.17/ 2) 0.92 0,16 -0.23 0.16 0.12 0.15 -0.23 0.15 0.88 0.8 0,72 -0.13 0.8 0.72 0.16 0.72 -
№ 27. 1) /2.00 0.17 3.02 0.11 \ ' 0.28 0,13 0.54 3.12 | . 0.54 0.18 2.11 3.08 1* \ 2.33 0.11 0.22 2.22/ 2) 1,00 0.13 0.25 -0.15 0.27 Q.35 -0,83 0.11 0.72 -0.94 0.08 0.32 0.82 0.44 0.32 0.12
As 28. 1) /0.54 0,32 1.00 0,22 \ 1 0.66 0.44 0.22 1.00 1 I 1.00 0.42 0.54 0.66 ' \0,42 1,00 0.32 0.44/ 2) 1.03 0.88 0.64 0,12 0,12 0.62 -0.13 0.32 0,18 0 25 0.42 0.82 0.32 0.43 0.85 0.93
As 29. 1) / — 0,33 0.42 0.51 — 0,11 \ 2.71 -0.92 -2.17 0.81 1 0,75 0,68 0.33 0.17 ' \ 0.28 -3,71 2.17 0.16/ 2) 1,00 0,27 0.64 0.27 0.35 -0.81 0.64 -0.81 -0.14 0.83 -0.14 0.25 0.83 0.16 0.15 0.37
As 30. 1) / 0.72 3.54 7.28 0.33 \ / —0.28 -0,72 3.04 0.22 1.00 0.35 -0,78 1,00 Г \ 7.03 -5.04 -3.75 3,41 / 2) 0.52 0.42 0.36 0.42 0.56 0.83 - 0,36 0,83 -0.13 0,84 0,24 -0.38 0.84 0.73 0.28 0.49
Образец выполнения задания
032
0.44
-1.06
0.96
0,52 -0.42 0.23 \ 0.32 0.54 0.67 -0.82
-0,25 0.74 0,36 -0.83 -0’51 ->) A= 0.48 ' a 0.84 1.02 0.88 0.32 -0.35 0.48 0.71 0.57
0.82 0.55 0.36/ -0.18 0.64 -0,24 0.43
37
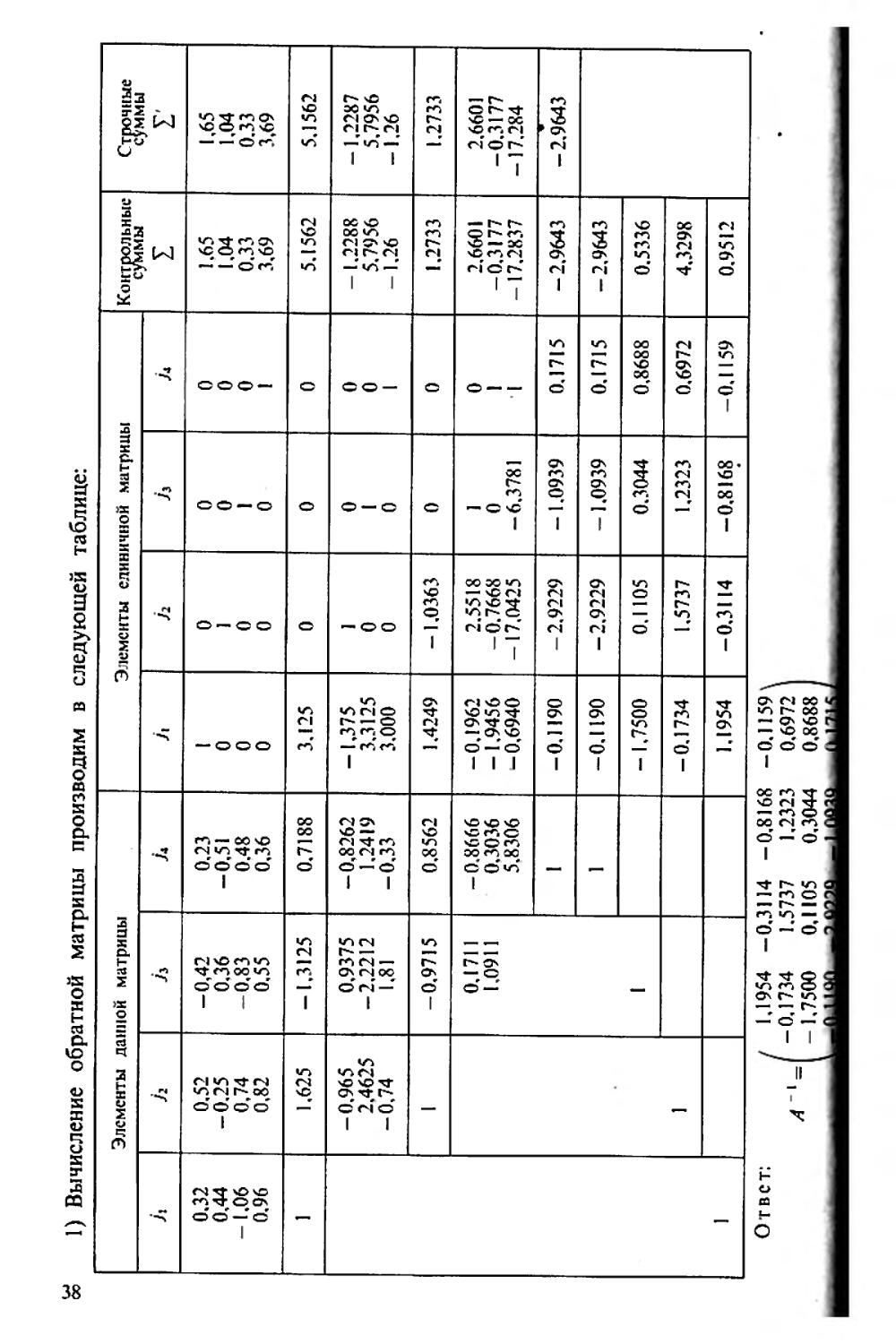
« 1) Вычисление обратной матрицы производим в следующей таблице:
Элементы данной матрицы Элементы единичной матрицы Контрольные суммы Е Строчные суммы Е'
Л Л Л Л h J2 Ji Л
0.32 0,52 -0,42 0,23 1 0 0 0 1.65 1,65
0,44 -0,25 0,36 -0,51 0 1 0 0 1,04 1,04
-1,06 0,74 -0,83 0,48 0 0 1 0 0,33 0.33
0,96 0,82 0,55 0,36 0 0 0 1 3,69 3,69
1 1,625 -1,3125 0,7188 3.125 0 0 0 5.1562 5,1562
-0,965 0,9375 -0,8262 -1,375 1 0 0 -1.2288 -1,2287
2,4625 -2,2212 1.2419 3,3125 0 1 0 5.7956 5.7956
-0,74 1,81 -0.33 3,000 0 0 1 -1.26 -1,26
1 -0,9715 0,8562 1.4249 -1.0363 0 0 1.2733 1.2733
0,1711 -0,8666 -0.1962 2.5518 1 0 2,6601 2,6601
1,0911 0,3036 -1,9456 -0.7668 0 1 -0.3177 -0,3177
5.8306 -0,6940 -17.0425 -6,3781 1 - 17.2837 -17,284
1 -0,1190 - 2,9229 -1,0939 0.1715 -2.9643 — 2,9643
1 -0,1190 — 2,9229 -1.0939 0,1715 -2,9643
1 -1,7500 0,1105 0.3044 0,8688 0.5336
1 -0,1734 1,5737 1,2323 0,6972 4,3298
1 1,1954 -0,3114 -0,8168 « -0.1159 0,9512
2) Вычисление определителя производим в таблице:
Элементы определителя Контрольные СУММЫ Z
0.32 0.54 0.88 0.32 0.64 0.67 -0.35 0.48 -0,24 -0.82 0.71 0.57 0.43 0.71 2,08 2.39 0.65
0.84 1.02 -0.18
1 1.6875 2.09375 -2.5625 2.21875
-0,5375 -2.10875 -1.65562 0.13688 2.8625 3.18375 -0.03125 0.21625 0.12688 1.04938
-1.40125 0.94375
1 3.92326 -5,32558 -0.40232
• 3.84184 -4.27872 4.99477 -0.43687 1.42907
-3.56570
1 -1.11372 -0.11371
1.02358 1.0236
0.32 -0.5375 3.84184 1.02358
Д = 0,32 (—0,5375)-3,84184-1,02358= -0,676378.
Ответ: Дчг—0,6764.
Работа 4
Задание. Решить систему линейных уравнений элементов с точностью до 0,001.
методом главных
№ 1. f 0,34.Vj + 0.71л-2+0,63л3 = 2,08;
-j 0.71л,- 0.65л2 - 0.18л‘3 = 0.17; 11,17.VJ - 2.35л2 + 0,75л'з = 1,28.
№ 3. Г 0,21 л, - 0,18л, + 0,75л*з = 0.11; < 0.13л, + 0.75л,—0,11л*з = 2,00: ( 3,01 л, - 0.33л, + 0,11 л*з=0,13.
№ 5. Г 3,01 л ,-0.14л, - 0.15л3 = 1,00; 5 1.11л-1 + 0.1 Зл, - 0,75лз = 0.13; 10,17л-!-2,11л,+0.71л3 =0.17.
№ 2. ( 3.75л i - 0.28л, + 0.17л3 = 0.75: < 2.11л, - 0.11л, - 0.12лз = 1.11; 10.22л] - 3.17л, + 1.81 л'з = 0.05.
№ 4. f 0.13л-! —0.14л,— 2,00л3 = 0,15;
< 0.75л! + 0.18л, - 0.77л'з = 0.11:
10.28л t - 0.17л, +0.39лз=0.12.
№ 6. Г0,92л! -0.83л,+0.62л3 = 2.15: < 0.24л। — 0.54л,+0.43л'з= 0,62; 10,73л j - 0.81 л, - 0.67лз = 0.88.
39
№ 7. ' 1.24л-, - 0.87л 2 - 3.17л з = 0.46; 2.11 л, — 0.45 л- , + 1.44л‘3 = 1.50; . 0.48л-, + 1.25л, -О.бЗл-з =0.35. № 8. । 0.64л, —0.83л, + 4.2л з = 2.23; 0.58л, -0.83л, + 1,43л\з = 1.71; 0.86л, + 0.77л, + О.88лз = -0.54.
№ 9. ' 0.32л-, - 0.42л, + 0.85л-з = 1.32; 0.63л, - 1.43л, -0.58л з = -0.44: ь 0.84л-, - 2.23л, -0.52л з = 0.64. № 10. ' 0.73л, + 1.24л, -0.38 у, =0.58; 1.25л, + 0.66л, -0.78л, = 0.66; . 0.75л, + 1.22л, -0.83л.,=0.92.
№ II. Г 0.62л, -0.44л,-0.86л 3 = 0.68; < 0.83л-, + 0.42л, — 0.56л-3= 1.24; { 0,58.x, - 0.37л, - 0.62л з = 0,87. № 12. 1 ' 1.26л,-2.34 л,+ 1,17л з = 3.14; 0.75л, + 1,24л, - 0.48хз =-1.17 3.44л, - 1.85л , + 1.16л-з = 1.83.
№ 13. f 0.46 v, + 1.72л, + 2.53.x, = 2.44; < 1.53л-, - 2.32л, - 1.83л-з = 2.83; ( 0,75л-, + 0.86 л, + 3,72 х3 = 1.06 № 14. ' 2.47л, + 0.65 х, - 1.88л з = 1.24; 1.34л, + 1.17.x, + 2.54х, = 2.35: . 0.86л, - 1,73л, - 1.08л-з = 3.15.
№ 15. [ 4.24л-, + 2.73х2 - 1.55л-з = 1,87; < 2.34л-1 + 1 ,27л-2 + 3.15л-з = 2,16; ( 3.05л-, - 1,05л 2 - О.бЗл-з = - 1,25. № 16. 1 0.43л, + 1.24л,-0.58x3 = 2.71; 0.74х, + 0.83х, + 1.17х з = ! .26; 11.43л, - 1.58х, + 0.83л з= 1.03.
№ 17. Г 0,43л-, + 0,63л, + 1,44л з = 2.18; < 1.64л-, - 0.83л-, —2.45л-з = 1 -84. ( 0.58л, + 1,55х, + 3.18л ,з = 0.74. № 18. ' 1.24х, + 0.62х, - 0.95 х, = 1.43; 2.15л । - 1.18х, + 0,57л , = 2.43; . 1.72л, -0.83.x, + 1.57х3 = 3.88.
№ 19. Г 0.62л, + 0.56л-, - 0.43л з =1.16; < 1.32л-, - 0.88л-, + 1.76л-з = 2.07; (. 0.73л-, + 1,42л, - 0.34л-3 = 2.18. № 20. ' 1.06х, + 0,34х, + 1.26л з = 1.17: 2.54л, - 1.16л, +0.55хз = 2.23; к 1,34 х, - 0.47л, - 0.83лз = 3.26.
№ 21. f 3.15.x, - 1.72х, - 1.23л 3 = 2.15; < 0,72л-, + 0.67л, + 1,18л 3= 1.43; ( 2,57 v, - 1.34л,-0.68л з= 1.03. № 22. ' 1.73л, -0.83х, + 1.82x3 = 0.36; 0.27 х । + 0.53л, - 0.64 х, = 1.23; к 0.56л, -0.48л, + 1.95лд = -0.76
№ 23. f 0.95л, + 0.72л-, - 1.14л-3 = 2.15; < 0.63л-, + 0.24л, + 0,38лз = 0.74; 11.23л-, - 1.08л-2- 1.16л-з = 0.97, № 24. ' 2.18х, + 1.72х, - 0.93л л = 1.06; 1,42 л, + 0.18л, + 1.12л3 = 2.07; ш 0.92л, - 1.14л, - 2,53лз = -0.45,
№ 25. ( 2,23 х, - 0.73л-, + 1,27л з = 2.43: < 2.15л, + 3.17л,- 1.43хз = -0.73: (. 0,83 х, + 0.72х2 + 2,12 х3 = 1.42. № 26. ' 0.65 л, - 0.93л, + 0.45лз = - 0.72; 1.15х । + 0.43л, - 0.72лз = 1.24; , 0.56 л ,-0.18л, + 1.03 хз = 2.15.
№ 27. f 1.16.x, - 0.28л-, + 2,16л‘з = 1.16; 4 0.65х, + 0.76л, -1.18л-з = 0.28; L 0.53л, + 1.07л, - О.бЗл-з = 1,27. № 28. ' 2.16л, - 2.83л, + 1.15хз = 2.32; 1.71 л, + 2.17х, - 0.83л-з = 1,25: . 0.35 л, - 0.72х, + 1,03хз = 0.82.
№ 29. ( 1.02л-, + 0,72л, - 0.65 х3 = 1,27; 0,74л, - 1.24х,- 1.73хз = 0.77; (. 1.78 х, + 2.32х, + 0.74л'з =1,16. № 30. । 1.53л, - 1,63х, - 0.76хз = 2.18; 0.86л-, + 1.17х, + 1.84л-з= 1.95; . 0.32л, -0.65х, + 1.11 хч = - 0.47.
Образец выполнения задания
2.74х, —1.18х2 + 3.17хз=2.18;
1.12х, + 0.83х, - 2.1 6.x3 = - I. I
40
Вычисления производим по следующей схеме:
Кои|к])ициен гы при игизвес! пых Свободные члены Z'
л. X,
-1 2.74 -1,18 3.17 2.18 6.91 6.91
0.6814 1.12 0.83 -2.16 -1.15 -1.36 -1.36
-0.2397 0.18 1.27 0.76 3.23 5,44 5.44
-1 2.9870 0,0259 — 0.3355 3.3485 3.3484
0.1596 -0.4768 1.5528 2.7075 3.7837 3.7835
— 1,5569 —- 2.7601 4,3181 4,3170
0.0970 1.7728 1.2638
1,0970 2,7735 2.2638
2,7602 1П,П() _ 4,3181
------=1,7728: х,=---------= 2,7735;
1,5569 " 1.5569
О.В55-О.О259-1.7728 = ао97О: = 3.3485 - 0 0259-2.7735 =
2.9870
2,9870
2.18 —2.74 0.0970+1.18 1,7728 , ___ = 1.2638;
3,17
6.91 - 2.74 -1,0970 +1.18- 2.7735 --------------——----------------= 2,2638.
Ответ: х, *0.097; л, *1,773; х3* 1.264.
Работа 5
Задание. Решить систему линейных уравнений методом квадратных корней с точностью до 0,001.
№ 1.
f 3.14.v, - 2.1 2х2 +1.17х3 = 1,27;
] - 2.12х, + | ,32х2 - 2,45л'3 = 2,13;
I 1. 17х, - 2.45л-, + 1.18д-3 = 3.14.
№ 3.
Г 1.65л- j - 2.27л, + 0,18л‘3 = 2,25;
- 2,27л- , + 1.73л, - 0.46л-3 = 0,93;
I 0.18л- j - 0.46л, + 2.16л з = 1.33.
№ 5.
J 0.93л-, + 1,42л, - 2.55x3 = 2,48;
) I Л2л, - 2,87л, + 2,36л з = -0,75;
I -2.55л, + 2.36л, -1,44хз = 1,83.
№ 2.
Г 2.45л, + 1,75л, - 3,24л з = 1.23;
< 1,75л'1 -1.16л2 + 2.18лз = 3,43;
I - 3.24x1 + 2,18л, -1,85лз = - 0,16.
№ 4.
f 3.23х, + 1 ,62л2 + 0,65лз = 1,28;
< 1,62л, - 2,33л2 -1,43л3=0,87;
(. 0.65л, - 1,43х, + 2,18хз = - 2.87.
№ 6.
( 1,42л, - 2.15х, + 1,07л‘з = 2.48; <-2,15л*! + 0,76л2 - 2,18л з = 1.15; (. 1,07л ] - 2,1 8х2 + 1,23лз = 0,88.
41
№ 7.
f 2.23.V, —0,71x2+0.63x» = 1.28;
< - 0.7I x, + I ,45x2 - 1.34лч = 0.64;
l 0.63л-1 - 1,34л-, + 0.77л*з = - 0.87.
0.78л-! + I.08.V1- l.35x3=0.57;
1.08л! - 1 ,28x2 + 0.37х3 = 1.27; - 1.35л-! + 0.37х2 + 2.86хз = 0.47.
№ 11.
( 2,74л-1 - 1,1 8х2 + 1.23хз = 0.16;
< - 1.18х, + 1.71 х, - 0.52xj = 1.81;
I 1.23л-! -0.52л-,+0.62хз= - 1.25.
№ 13.
{1,48х । + 0.75х, - 1,23х3 = 0.83;
0.75л-1 - 0.96х, + 1.64хз = - 1. 12;
- 1,23л-| + 1.64х, - 0.55хз = 0.47.
№ 15.
f 0.63х, - 1.72х2 + 3,37хз = -0.75;
< - 1,72х । - 2.27х2 + 1.62хз = 1.27;
I 3.27х! + 1.62х, - ОДЗхз = 2.74.
№ 17.
Г 2.32х । + 1.17х2 - 0.28хз = 1,43;
< 1.17х । - 1.43X1 + 0.88хз = - 0,47;
I - 0.28л-! + 0.88х2 -1,45л*з = 1,09.
№ 19.
f 1.18х, + 2,32х2 - 0,67л"з = 1,83;
< 2,32х । + 1,87х, +1,35хз = - 0.73;
( — 0,67л'| + 1,35х2 -0,88хз=0,68.
№ 21.
( 1,17x1 - 0,65х, + 1,54л"з = - 1.43;
< -0.65л-! + 1.16х2 - 1.73хз=0,68;
I 1.54л-) - 1,73X1 + 2.15х3 = 1,87.
№ 23.
Г 1.17х, + 2,23х2 - 0.77хз = J J1;
< 2.23Х| - 0,81х2 + 1,72х3 = 1,88;
I - 0.77xj + 1.72х,-0.65хз=0,57.
№ 25.
f 0,64х । + 1 ,05х2 - 2,93хз = 1.18;
< 1,05х, - 1.41х2 + 0.1 бл'з = -0.27;
(. - 2.93х, + 0.16х, - 1.51 л'з = 0.72.
№ 27.
[ 2.44л-, -1,16х, + 0,83х3 = 0,65;
< - 1.16х, - 3.45х, + 0,57хз = 1,88;
I 0.83х, + 0.57х, - 1.7 Ьз = 0.74.
№ 29.
f 0.53х, - 0,75х2 + 1,83х3=0,68;
< —0.75х, +0,68x1-1,19x3 = 0,95;
I 1.83л-! - 1,19X1 + 2,15хз = 1,27.
№ 8.
f 1,63xj + I ,27х2 - 0,84хз =1.51;
< 1,27x j + 0.65х2 + 1,27хз = - 0.63;
I - 0.84X1 +1.27x2 - L21 л‘з = 2,15.
№ 10.
f 0.83x1 + 2.18х,- 1.73x3=0.28:
< 2.18х 1 -1,41 х, + I.ОЗл'з = -1.18;
I - 1.73X1 + 1,03л-2 + 2.27хз =0.72.
№ 12.
f 1.35X1 - 0,72х2 + 1,38хз=0.88;
< -0,72л-! + 1.45x1 - 2,18x3 = 1.72;
(. 1,38х। - 2.1 8х2 + 0,93хз = -0.72.
№ 14.
f 2.16х, - 3.1 8х2 + 1,26хз = 1.83;
< -3,18л-! + 0,63х2 - 2.73хз =0.54;
I 1,26х! - 2,73х2 + 3,15х3 =1,72.
№ 16.
f 1,36х 1 + 0.92X1 - 1,87хз = 2.15;
< 0.92л-1 - 2,24хэ + 0.77хз = - 2.06;
( - 1.87х, +0,77x2-1,16x3=0.17.
№ 18.
f О.75х, - I ,24х2 + 1.56хз=0.49;
< - 1.24х ,+0,18X1-1.72хз = - 0*57;
I 1.56х, - I .72х2 + 0.79хз = 1.03.
№ 20.
( 0,78х i + l.l Зх2 + 1.87хз=0.83;
< 1.1 Зх । - 0.68x2 + 2.1 бхз = - 0.27;
(. 1,87х । + 2.16х2 - 2.63хз = 1.37.
№ 22.
f 0.87х, + I ,35х2 - 0.44хз =1.51;
< 1.35xi - । -22x1 + 2,32хз =0,71;
I -0.44л-, +2.32х2-3.73х3 =0.53.
№ 24.
f 2.16х, + I .45х2 - 0.89хз=0.61;
1,45х, - 2.44x2 + 1.18х3 = 1.05;
I - 0.89x1 + 1.1 8л-2 - 2.07хз = - 0.83,
№ 26.
( 1.54х, — 0,75х2 + 1,36х3=2.45;
< -0.75л-! + 0,87x2 -0,79х3 = 1.07;
I 1,36х t - 0.79л-2 + О.64хз = 0.54.
№ 28.
f 2.56х, +0,67x2 - 1,78лз = 1.14;
< 0,67X1 - 2.67x2 + 1.35хз = 0.66;
( - 1.78X1 + 1.35x1-0.55x3= 1,72.
№ 30.
f 1.65X1 - 1 ,?6х2 + 0.77х3 = 2,15;
< -1.76X1 + 1.04x2 - 2,61 л'з = 0.82;
( 0.77л-! - 2.61X2 - 3,18х3 = -0,73.
42
Образец выполнения задания
4.25 v, - 1.48л, + 0.73л, = 1.44:
- 1,48л-, + 1.73/ - 1,85л-3 = 2.73: 0.73л, - 1.85л, + 1.93лч = -0,64.
Вычисления производим по следующей схеме:
Ко м|>фи11ис1и ы при неизвестных Свободные члены Z Z'
*| V, Ъ
4.25 -1,48 0.73 1,44 4,94 4.94
-1.48 1,73 -1,85 2.73 1.13 1.13
0.73 / -1.85 1.93 -0.64 0.17 0.17
2.0616 -0,7179 0.3541 0.6985 2.3962 2.3963
1.1021 -1,4480 2.9323 2.5862 2.5864
0.5405/ -6.2141/ — 5.6731/ — 5.6736/
-2.0200 -12.4446 -11.4969
- 1.0199 -11.4436 - 10.4960
6,2141/
0,5405/
-11,4969;
5.6731/
0.5405/
= -10,4960;
2.9323 -1.4480 11.4969
-12.4446;
2.5862-1.4480 -10.4960
1.1021
-11.4436;
0,6985 + 0.3541 • 11,4469 - 0.7179-12.4446 _ ?
2,0616 ” ’
2.3962+0.3541 10,4960 —0.7179 -11.4436
2.0616
= -1.0199.
Отпет: л,=е-2.020: л,*- 12.445: л3*-11.497.
Работа 6
Задание. Решить систему уравнений по схеме Халецкого с точностью до 0.0001.
1 - 0.63л-, + 1,00л, + 0.71л3 + 0.34л-4 = 2.08;
1.17х। + 0.18л, - 0.65л3 + 0,71л4 = 0.17; ' 2.71л, —0.75л, + 1.17л3 — 2,35л'4 = 1.28; . 3,58л-1 + 0.21 л, - З.45л3 -1.18л4 = 0.05.
43
№
2.
3.5I л, + О, I 7л, + 3,75x3 - 0.28л4 = 0.75:
4.52л-1 + 2.11 л, - 0.11 л-j - 0.12л4 = 1.11;
- 2.11л1 + 3.17л-, + 0.12x3 - 0.1 5л4 = 0.21;
3.17л- ,4-1,8! x, - 3.17л 3 + 0.22л-4 = 0.05.
№
3.
’ 0.17л-1 + 0.75л, - 0.18л3 + 0.21 x4 = 0,11: 0,75л-1 + 0.1 Зл, + 0.11 л, + 1.00л-4 = 2.00; - 0.33л-(+ 0.11 л, + 3.01 л-3 - 2.01 л-4 = 0,11; 0.11л, + 1.12л-, + 1.11л'з - 1.31л-4 = 0.13.
№ 4. ( -1.00л-,ч-0,1 Зл, - 2.00л-з - 0.14л4 = 0.15:
I 0.75л-, + 0,18л-, - 0.21 л'з - 0.77л4 = 0.11:
1 0.28л-1 - 0.17л-, 4- 0,39л-, + 0.48л4=0.12:
( 1.00л-1 + 3,14л-, - 0,21 Л'з - 1.00л’4 = - 0.11.
№ 5. ( 3.01л,—0.14л, + 1.00л , — 0.15х4= 1.00:
I -1,75л, +1.11 л, + 0.1 Зл'з - 0.75л-4=0.13:
1 0.17л-, - 2,11л, + 0.71л-з - 1.71л-4 = 1.00:
( 0,21л, +0,21л, + 0.35л-з + 0.33л-4=0.17.
№
6.
' 1.15л- j + 0.62л-, - 0.83х3 + 0.92л-4 = 2.15; 0,82л-1 - 0.54л-2 + 0.43л-з - 0.25х4 = 0.62; 0.24л-, + 1.15л,-0.33л-з+ 1,42л-4= -0.62; 0,73л-1 - 0,81 л, + 1.27л-з - 0,67х4 = 0.88.
№ 7.
2,2 л, — 3.17л, + 1.24л-з—0.87л'4=0.46;
1,5 л-, + 2,11 л2 -0.45лз + 1 .44л'4 =1.50;
0,86л-, - 1,44л,+0.62лз + 0.28л4 =-0.12;
0,48л-, 4-1.25л, -0.63лз -0,97х4 = 0,35.
№
8.
' 0.64л । + 0.72л, - 0.83лз + 4.2 л4 = 2,23; 0.58л, —0.83л, + 1.43л, -0.62л-4 = 1.71;
* 0.86л 14- 0.77л, - 1.83л3 + 0.88х4 = - 0,54;
1,32л। -0.52л, -0.65лз 4-1.22л4 = 0.65.
№
9.
' 1.42л । + 0.32л, - 0.42л з + 0.85л4 =1.32;
0.63л-1 — 0.43л, + 1.27л з-0,58л4= -0,44;
' 0.84л । - 2.23л, - 0.52лз + 0.47л4=0.64;
0,27л । + 1,37л, + 0,64л з - 1.27л4=0,85.
№ 10. [ 0,73л j + 1,24л-, - 0,38л*з -1,43л4=0.58:
I 1.07л j - 0,77л, + 1.25л3 + 0.66л4 = - 0.66:
) 1,56л j + 0,66л, + 1.44л*з - 0.87л4 = 1.24; [0.75л-! + 1.22л,-0.83лз + 0.37л4=0.92.
№ 11. ( 1,32л, - 0.83л2 - 0.44лз + 0.62л4=0.68;
I 0.83л, + 0.42л,-0,56лз + 0.77л4= 1.24;
1 0.58л, -0.37л, + 1.24л-з-0,62л4=0.87;
[ 0.35л, +0.66л, - 1,38л‘з - 0,93л4 = - 1,08.
№ 12. (0,11Л4-0.17л-, +0,72л-з-0,34л-4=0.17;
I 0.81 лI + 0.12л-,-0.91 л*з + 0.17л4 = 1.00;
] 0,17л, - 0,18л, + 1 .ООлз + 0.23л4 = 0.21;
( 0.1 Зл, + 0.17л, -0.99лз + 0.35л4 = 2.71.
№ 13. ( 0.18л, +2.11л-, + 0.1 Зл-л-0.22л-4 = 0.22; I 0,33X1 ~ 0.22л, - 1 .000 з + 0.17х4 = 0.11; 1 - 1.00л-! +0.11 л, + 2.00лз - 0.45л4 = 1,00; [ 7.00л-! — 0.17л,—0.22л-з + 0.33л-4 = 0,21.
44
Vo 14. Г 2.00л, + 0.05л, —3.01 л3 —0.1 lx4 ' 1.00л-, - 2.00л’2 4- З.О2л3 + 0.05.v4
] 0.17x, + 0.99л, - 2.00л’з - 0.17л4 | О.ЗЗл-i - 0,07л2 + О,ЗЗх3 + 2.00x4
,Vo 15. f 0. i 7x, - 0.1 Зх2 - 0.11 л’з - 0.1 2x4 I 1.00л-, — 1,00x, — 0.1 Зл’з + 0.1Зх4 ) O.35x। + О.ЗЗх, + 0,12x я + 0.1 Зл*4 (0.1 Зл-, + 0.11 л, - 0.1 Зл з - 0.11 х4
\ь |6. Г 0.1 l.v, + 1.13л*,—0,17л*з + 0.1 8л*4 I 0.1 Зл-1-1,1 7х, + 0.18л*з + 0.1 4л-4 ] 0.11 л-1 - I ,05х, - 0,17л-3 - 0.1 5л-4 10.15х1 - 0.05х2 + 0.18л’з - 0,11 х4
уо 17.fi .(Юл ,-0.17л-2 + 0,11 л-j - 0,1 5л4 I 0.14л, • 0.21 х, - О.ЗЗл’з + 0.11 л*4 1 0.22л । + 3.44х, -0.11 л з + 0.12х4 ( 0.11 л-1 + 0.1 Зл, + 0.12л з + 0.1 4л4
№ 18. Г 1.00л-,+0.55л 2-0.13л з + 0.34л-4 I 0.1 Зл-, - 0.17л-2 + О.ЗЗл-з + 0.17л4 1 0,1 l.v, +0.18л-2-0.22л з-0.11л4 (0.1 Зл- ,-0.12л- 2+0.21 л j + 0.22л-4
№ 19. f 1.00л,-0.51л-2+0.12лз+0.55л-4 I 0.12л-, + 0.1 8л, -0.22л з - 0,41 л4 1 0.22л-, - 3.01л, +0.31лл +0.58л4 11.00л-, + 0.24х, - 3.05лз - 0.22х4
№ 20. Г 0.1 Зх, + О.22х, -0.14х3 + 0.15х4 I 0.22л-, - 0.31л, + 0.42л, - 5.1 х4 ] 0.62.V, - 0,74х2 + 0.85л-, - 0.96х4 10.12х, + 0.1 Зх, + 0.14л’з + 0.45х4
№ 21. Г0.18л,+0.19л’2+0.20л’з-0.21л’4 I 0.5 lx, -0.50л, + 0.49л-3 -0.48х4 ) 0.61 л , + 0.62л, - 0.63л-з + 0.64л-4 10.11 л, - 0.15х, + 0.22л- з - 0.38л’4
№ 22. Г 0.17л-, - 0.1 8х2 + 0.19л3 - 5.74х4 I 0.11 л, - 0.43л-, + 0,15х3 - 0.1 7л-4 ) 0.12л-, + 0.14л, + 0.16л'з + 0.1 8л-4 (. 0.71 л-, - 0.1 Зл-2 - 0.41 л-з + 0.52л-4
0.21;
0.18;
0,17;
0.17.
0.22;
0.11;
0.12;
1.00.
1.00;
0.13;
0.11;
1.00.
0,17;
1.00;
2.00;
0.13.
0.13;
0.11:
1.00:
0.18.
0.12:
0.13:
1.00:
3.41.
1.00;
6.01:
0.11:
0.16.
0.22;
0.47:
0.65;
0,42.
1.00:
1.9;
2.00:
1.00.
0.18;
0.19;
0.21;
0.31.
0.66;
-1.44;
0.94:
0,73.
1.21;
0.86:
0.25:
1.55.
№ 23. ' 1.00л-, — 2,01 л’2 + 2.04л’з +0.17л-4 0,33л-, - 0,77л-, + 0.44л-3 - 0,51 л4
4 0.31 л-, + 0,17л-, - 0.21 л-з + 0,54л-4 0.17л-, + 1.00л,—0.1 Зл*з +0.21 л*4
№ 24. Г 2.34л, - 1,42л, -0.54л-з + 0.21л4
I 1.44л, -0.53л-, + 1.43л'з - 1.27л4 | 0,63л-, - 1.32л,— 0.65л з + 1.43х4 10,56л-, +0.88л, -0,67х3 - 2.38х4
№ 25. ' 0.63л, - 0.76л, + 1,34л’з+0.37л4
0.54л, + 0.83л, —0.74л’з— 1.27л4
0.24л-, —0.44л, + О,35л+ +0.55х4
. 0,43л, -1.21 л, + 2,32л з - 1.41 л4
45
№ 26. f 1.43x, + 0.87л, - 1.57х3 -0.58х4 = 2.34: 1 0.63л, - 0.57л-, — 2.34х3 + 0.66х4 =0,77: ] 1,57л-, + 0,66л-2 -0,57л‘з +1.15х4 = - 0.24; 10.88л-, - 0.67л, + 0.55л3 - 0.45х4=0.56. № 27. (1.71л,-0.83л, + 1.44х3 -0.72х4 = 1.35: 0,64л-1 - 0,85л-, - 0.43х3 + 0.88х4=0.77: ’ 0.38л-, + 1,42л-, + 0.63л-, - 1 ,55л4=0.28: . 0.83л-1 - 0.66л, + 0.58л-3 + 1 .22л-4 = -0.47. № 28. ( 0.85л-1 + 1,27х, - 2.37x3 + 0,57х4 = 1.47; 1 1.47л-, - 0.28л-2 + 0.56л‘з -1.21 л4 = 0.86; j 0.66л, + 1.31 л, — 0,63л*з + 0.43л4 = —0.55; ( 0.57л, - 0.78х2 - 0.56хз - 0.83х4 = 0.27. № 29. 0.68х, + 1,32л, - 0.63х3 -0,87х4 = 1,43: 0.57л, + 0.36л, - 1.24хз - 0.23х4 = 0.33: ' 0.82л, -0.32x2 + 1.42хз+ 1.48х4= -0.84; . 0.56л, - 1,20л, + 1.50хз - 0.64х4 = 0,45. № 30. ( 1.42л, + 2.34л, -0.88х3+0.53х4 = 0,72; 1 0.71 х। - 1.15х, + 0.53лз - 0.67х4 = - 0.18; ) О.55х, -0.93x2- 1.42л'з+ 1.32х4=0.68: 10.44л, - 0.25л, + 1.92хз -1.08х4 =0.43.
Образец выполнения задания ' 1,35х । - 1 ,72л-2 - 0.62х, + 0.48х4 = 0.93: 1.08л, +0,64х,- 0.95л’з+ 1.54х4 = 1.64; < 0.88л-, -0.72x2 + 1.36x3-0.68x4= -0.85: 0.64х, + 1.48x2 + 0.82x3- 1.58х4= - 1,32.
Вычисления производим по следующей схеме:
Л| х. Л'Л -*4 С вободпый член
1,35 1,08 0,88 0.64 -1.72 0,64 -0,72 1,48 -0.62 -0.95 1.36 0,82 0.48 1,54 -0,68 -1.58 0.93 1,64 -0.85 -1.32 0.42 3,95 -0,01 0.04
1.35 1 -1.27410 -0,45926 -0.22520 0.35555 0.57341 —0.65945 0.68888 0.44444 -0.88138 0,65598 0.31111 < 1.79263 -0.54085 1.65596
1.08 0.88 0.64 2.01603 1
0.40121 2.29542 1.85450 1
1,63086 -2.04830 1
1 Ответ: л 46 1 г, =0.2078; х, г, = 1.2078; х. 1 = -0.0328; хз = 0.9672: хз = ' 1 = -0,4488; х. 0,5512; х4=1. 0.65598 -0.44879 -0.03277 0,20778 1 = 0,6560; 6569. 1.65596 0.55117 0,96721 1.20778
Работа 7
Задание. Используя компактную схему Халецкого, обратить матрицу и уточнить ее элементы до 10 “5.
Ks 1. / 1.22 0,83 0.54^ < № 2. / ' 0,64 -0.35 O.28X
0.66 -0.32 0,47 1 . -1.43 -0.84 0.52 I.
\ —0,83 0,25 0,63/ k 0.77 0.54 —0.64/
.Vs 3. / ' 0,42 0.36 0,21 № 4. / '1,72 -0,88 0.72X
1.43 -0.84 0,92 I I. 0.76 -1,04 0.38 ).
,—0,85 0,45 —0,62 >/ .0,64 0.35 0.57/
.Vs / ' 3.56 1.23 0.85\ № 6. / '0,63 0.57 -0.83X
-1,21 0,64 0,88 ) 1,24 0,87 -0.54 ).
, — 0,83 0,47 -0,36/ J ,32 -0.44 0.63/
jYs 7. / ' 1.45 —0.55 0.72\ № 8. / ' 0.84 -0.34 0.27\
-0.73 0,62 0.48 ) • -0.68 -0.56 0,32 I.
, 0,84 -0.48 0,23/ , 0.27 -0,34 0.78/
№ 9. / ' 0.36 0.25 0.44\ № 10. /1.32 1,22 0.64\
0.84 -0.72 0,57 0.57 -0,48 0.24 .
.-1,33 0.28 1.05/ \0,38 -1,23 —0.21/
.Vs 11. /0.54 0.38 -0,48> i № 12. / 0.64 -1,04 0.53X
1,45 0,84 0,92 1 -1,44 0.68 0.87 J
\l.23 -0,43 0,65/ \ 0.35 0.27 —0,44/
№ 13. /1.83 -0,64 0.34> l № 14. /0.64 0.54 -0.33X
0.63 -0,25 -0.57 1 « 0.84 -0.92 0.43 ).
\0.77 0.36 0.68; \0.24 1.03 —0.41/
As 15. /0,18 0.18 0.17X № 16. /0.5 1,77 0.39\
0,54 1.24 0,95 . 0.81 1.79 0.95 ).
\0.t5 0.83 0,51/ \0,64 0.33 0,04/
№ 17. /2.17 0,79 O.32X № 18. /0.94 0.33 O,75\
0.88 0,45 0.37 . 0.68 3.15 0,81 1.
\0,88 0,01 2.41/ \0.2l 0,64 0,57/
№ 19. /0,89 0.85 0,79\ № 20. /0.19 0.51 0.86\
0.75 0,77 0,85 . 0.87 0.32 0.85 1.
\0.89 0,68 0,65/ \0.66 0.67 0,84/
As 21. /0,28 0.69 0.29\ № 22. /0.73 0,56 0.56\
0.56 0.98 0,42 ). 1.74 1,98 0.31 1.
\0,88 0.35 0.85/ \0,15 0.17 0.18/
As 23. /0.12 0,79 0.48\ № 24. /1.75 0,89 0,57\
0.18 0.89 0.08 . 0,27 0.98 0,69 .
\0.76 0.48 0.12/ \0.65 0,27 0,55/
As 25. /0,45 0.87 0.31\ № 26. /0.25 0,47 0.67X
0,78 0,27 0,79 1. 0,93 0,17 0.46 1.
\1,32 0.88 0.45/ \0.77 0.71 0.13/
As 27. /0,47 0.45 0.49\ № 28. /0,61 0.17 0,85\
0,59 0,74 0.36 . 0.43 0.76 0.47 I.
\O,35 0.61 0.17/ <0.86 0.32 0.56/
47
№ 29. /0,15 0.68 0.22 I 0.78 0.36 0.83 \0.37 0.94 0.52
№ 30. /0.12 0.13 0.74
I 0.47 0.14 0.29 \0.16 0.17 0.56
Образец выполнения задания
/1.16 0.83 - 0.664
А = 0.45 -0.54 0.83 .
\0.32 0.28 1.06/
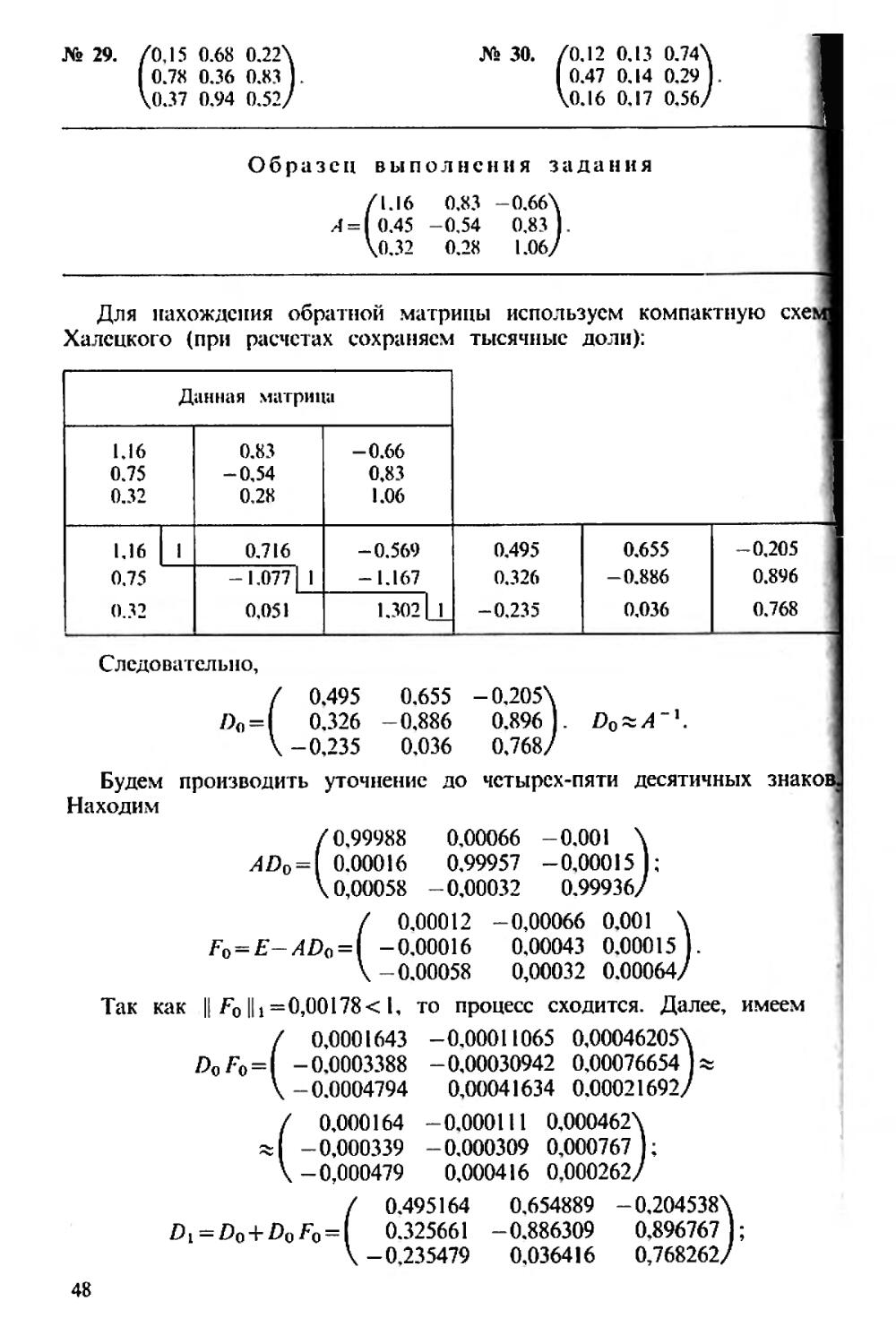
Для нахождения обратной матрицы используем компактную схе Халецкого (при расчетах сохраняем тысячные доли):
Данная матрица
1.16 0.75 0.32 0.83 -0,54 0.28 -0.66 0,83 1.06
1,16 1 0,716 -0.569 -1.167
0.75 0.32 -1.077 1
0.051 1,302 1
0,495 0.655 -0,205
0.326 -0.886 0.896
-0.235 0,036 0.768
Следовательно,
0,495
0.326 -0.886
-0,235 0,036
Будем производить уточнение Находим
0.655 -0,2054 0.896 . 0,768/
A-1.
до четырех-пяти десятичных знаков
Л£)о =
0,00066 -0.001 4
0,99957 -0,00015 ;
0.99936/
F0 = E-AD0 =
0,00043 0,00015 .
0,00032 0.00064/
Do =
Так как || Fo ||i =0,00178< 1,
0,0001643 -0,0003388
-0.0004794
0,000164
-0,000339
-0,000479
DqFq —
0.99988
0.00016
0,00058 -0,00032
0,00012 -0.00066 0,001
-0.00016
-0.00058
то процесс сходится. Далее, имеем -0,00011065 0,000462054 -0,00030942 0,00076654 U 0,00041634 0.00021692/
-0,000111 0,0004624
-0.000309 0,000767 );
0,000416 0,000262/
0.495164
0.325661 -0.886309
-0,235479
0,654889 — 0,2045384
0.896767 ;
0,768262/
0,036416
48
/ 1,00010501 - 0,00000021 - 0,00000039\ AD. = [ 0,00006849 0,99999889 -0,00000022 ;
\ 0,00002982 - 0,00000108 1,00000032/
l\ = E-AD.=
-0,00010501
-0.00006849
-0,00002982
0.00000021 0.00000111 0.00000108
0.00000039\
0.00000022 :
— 0,00000032/
/—0,000091 0,000001 0\
D.F.=\ 0 0,000001 0 ;
\-0,000001 0,000001 0/
d2=d. + d.f.=
0.495073
0,325661
-0,235480
0,654890 — 0.204538X
-0,886308 0.896767 .
0.036417 0.768262/
/ 0.49507 0.65489 -0.20454\
Ответ: /Г1* 0.32566 -0.88631 0.89677 .
\ -0.23548 0.03642 0.76826/
Работа 8
Задание. Методом итераций решить систему линейных уравнений с точностью до 0.001, предварительно оценив число необходимых для этого шагов.
№ 1.
ЛI = 0.23.V j - 0.04л-, + 0.21 v3 - 0.1 8х4 + 1.24; х, = 0,45л , -0.23л, + 0.06х3 -0.88;
v, = 0,26л*, + 0.34л-, - 0.11 л з + 0.62;
v4 = 0.05x, -0.26л,+ 0.34л3-0.12х4- 1.17.
Л® 2.
X-, = 0,21 Л-, + 0.12л-, - 0.34л-з - 0.16л4 - 0.64; v, = 0.34л-, - 0.08л-, + 0.17л з - 0.18х4 + 1.42; \3 = 0.16х, + 0.34л, + 0.15х3 - 0.31 л 4 - 0.42; х4 = 0.12х, - 0.26л-, - 0.08л3 + 0.25х4 + 0.83
№ 3. гл, = о.32х,-0.18х, + 0,02х3+0.21 х4 + 1.83;
I х, = 0.16х ,+0.12х, - 0,14л,+0.27х4 - 0.65;
I л з = 0.37л, + 0.27л, - 0,02л3 - 0.24л4 + 2.23; |л4 =0.12х, + 0.21 л, - 0.18л‘3 + 0,25л4 -1.13.
№ 4.
v, = 0.42 х, - 0.32л, + О.ОЗхз + 0.44;
v, = 0.11 х, - 0.26х, - О.Збл-з + 1.42;
х3 = 0.12л, + 0,08л ,-0.14хз - 0.24х4 - 0.83.
v4 = 0.15л, - 0,35л, - 0.18х3 - 1.42.
№ 5.
v, =0. Т8л, — 0,34л2 — 0,12л3 + 0.15л4 — 1.33; v, = 0.11 х, + 0.23х, - 0,15л-3 + 0.32х4 + 0.84; v3 = 0.05.x, - 0.12х, + 0.14х3 - 0.18л4 - 1,16; v4 = 0.12л", + 0,08л, + 0.06 х3 + 0.57.
л« 6. 'Сх|=о.13л,+0,23х2-0.44х3-0.05х4+2,13;
I л, = 0,24х, - 0.31х3 + 0.15х4 - 0.18;
| л-3 = О.Обх, + 0,15х, - 0,23х4 + 1.44; [х4 == 0,72х, - 0.08х, - 0.05х3 + 2.42.
49
№ 9.
№ 10.
№ 11.
№ 12.
№ 13.
№ 14.
№ 15.
№ 16.
№ 17.
№ 18.
№ 7.
№ 8.
0.17л-, 4- 031 л*j - 0.18х3 + 0.22x4 - 1,71;
- 0,21 л, + O.33x3 + 0.22x4 4-0.62;
032.V , - О, I8x, 4- 0.05.V, -0.19x4 - 0,89;
0.12x, 4- 0.28л 2 - 0.14л-j 4- 0.94.
0.13x , 4- 0.27л 2 - 6.22л з - 0.18x4 4-1.21;
— 0,21 х, — 0.45л-з 4- 0,18х4 — 0.33;
0,12л-1 4- 0,1 Зх, - 0.ЗЗл-з 4- 0.1 8х4 - 0.48;
О.ЗЗх! - 0,05х, 4- O.O6.V3 - 0,28х4 -0,17.
0.19л-1 - 0,07л-2 + 0.38л з - 0,21 х4 - 0,81;
\-2 = - 0.22л-, 4- 0.08л-, 4- 0.11 лз 4- 0.33х4 - 0,64;
\з = 0.51л-!- 0.07л-, + 0.09л’з - 0.11 х4 4-1.71;
д4 = 0.33л-, —0,41 л,— 1.21.
л, = 0,22л-, - 0.11 <з 4- 031 х4 4- 2.7;
х, = 0,38л-1 - 0.12лз 4- 0.22л4 - 1.5;
’ л-3 = 0,11 л , 4- 0.23л-2 - 0.51 л4 4-1,2;
,х4 = 0,17л, - 0.2I х, 4- 0.31 л-з -0,17.
{л, =0.07х, -0.08л-, 4-0.11л3-0.18л4-0.51;
л-з = 0,18л, 4-0.52л-, 4-0,21х4 4-1.17;
л-з = 0,1 Зх, 4-0.31 х, -0,21 х4 - I.02;
\4 = 0.08л-, - 0. ЗЗл-з + 0.28 х4 - 0.28.
Гх, = 0.05х, —О.Обх, —0,12х3 4-0.14х4 —2.17; I х2=0.04х । - 0,12 г2 4- 0,08х3 + 0.11 х4 4-1.4;
] л з = 0.34л- f 4- 0.08 х2 - О.Обхз 4- 0.14х4 -2.1; |х4 = 0. И л-1 4- 0,12х, - О.ОЗл-4 - 0.8.
л, = 0.08л-, - 0.03л, - 0,04х4 - 1.2;
л, = 0.31 х2 4- 0.27л з - 0,08х4 4- 0.81;
" Лз = О.ЗЗх, -0.07Хз 4-0.21х4-0.92;
Х4 = 0,11 х, 4- О.ОЗхз 4- 0.58х4 4-0.17.
[х, =0,12X1 - 0.23 v, 4-0.25хз-0,16х4 4-1.24;
I л-2 = 0,14л 1 + 0.34 \- 0.18x3 4- 0,24х4 - 0.89;
) л-3 = О.ЗЗх 1 4- О.ОЗл-2 4- 0.16л з - 0,32х4 4-1.15; (х4 = 0.12x1 -0.05.V2 4-0.15х4 -0,57.
{Xi = 0.23х,—0,1 4х2 4- 0,06хз - 0.12х4 4-1.21; л-2 = 0.12х! 4- 0,32х з - 0,1 8х4 - 0.72;
л"з = 0.08х 1-0,1 2х2 4- 0,23хз + 0,32х4 - 0,58; х4=0.25х, 4-0,22х, 4-0.14хз 4-1,56.
{х, = 0,14х। 4- 0,23л з 4- 0.18x3 4- 0.17х4 - 1,42; х2 = 0, I2х । - 0.14л, 4- 0,08л 3 4- 0,09х4 - 0.83; Хз = 0,16 л, 4- 0.24X2 - 0.35х4 4-1.21;
х4 =0.23Х| -0.08х, 4-0,05хз 4-0.25х44-0,65.
{х, = 0.24л-1 4- 0,21 х2 4- 0.06x3 -0.34х4 4-1.42;
х, = 0.05х । 4- 0,32хз 4- 0.12х4 -0.57; л-з=0,35л-, — 0.27 v, — 0.05х4 4-0.68; х4 = 0.12х । - 0,43 v, 4- 0.04хз - 0,21 х4 -2,14
{х । = 0.17х! 4- 0.27л, - 0,1 Зх3 - 0.11 х4 - 1,42; х2 = 0.1 Зх। - 0.12х, 4- 0,09х3 -0.06х4 4- 0,48; хз = 0.11л1 4- 0.05х2 - 0.02хз + 0,12х4 -2,34; л4 = 0,1 Зх, 4- 0.18х, 4- 0,24хз 4- 0,43х4 4- 0,72.
50
№ I*
№ 20-
№ 21.
№ 22.
№ 23.
№ 24.
№ 25.
№ 26.
№ 27.
№ 28.
As 29.
№ 30.
f vt = 0J 5л-1 + 0.05x, - 0.08x3 + 0.14x4 - 0.48: v, = 0.32лj - 0,1 Зх2 - 0.12x3 4-0.11 x4 + 1.24: ’ v‘,=0.17 xj + 0.06 v2 - 0.08x3 + 0.12x4 +1.15: л j = 0.21 x, - 0.16 x 2 + О.Збл-з - 0.88.
v, = 0.28x, - 0.17л- л+0.06х4 + 0.21:
v, = 0.52л-,+0.12х3 +0.17х4 -1.17;
х д 3 = 0.17л , - 0.18 v2 + 0.21 Л'з - 0,81; л4 = 0.11х, + 0.22л 2 + 0.03л з + 0.05х4 + 0.72.
г.х-, = 0.52л, + 0.08л- з + 0.1 Зх4 - 0.22:
л , = 0.07л-| -0.38л,-0.05.V3 + 0.41 л-4+ 1.8: ) л* = 0,04 х-1 + 0,42 х, + 0.11 л 3 - 0.07х4 -1,3, |л-4 = 0.17х ,+0.1 8л-2 - 0.1 Зл-з + 0.19х4 + 0.33
Гл-, = 0.01 х, + 0,02л-2 - 0.62л-3 + 0.08х4 -1.3: л, = 0.03л, + 0.28л-, + О.ЗЗл-з - 0.07х4 +1.1: ' л3 = 0.09л-, + 0,13 v2 + 0.42Л-3 + 0.28л4 - 1.7: х4 = 0.19х, - 0.23л-, + 0.08-х-з +0.37х4 +1.5
Гл ,=0.17х, - О,33л-з + 0.1 8л-4 - 1.2:
I л, = 0.18х, + 0.43л3 - 0.08л4+0,33;
) л з = 0.22л-, + 0,18 х-2 + 0.21 л 3 + 0,07.v4 + 0.48: (x4 = 0.08x, + 0.07х2 + 0.21лз+0,04л-4- 1.2.
Гл, = 0.03л-, - 0.05л*, + 0.22л-з - 0.33х4+0.43;
I л= 0.22л-, + 0,55л-2 - 0.08л-з + 0,07.v4 -1.8: ] д з = 0.33л, + 0,13 V, - 0.08x3 - 0.05х4 - 0.8: |_х4 = 0,08х, + 0.17 х, + 0.29 х'з + 0,33л*4 + 1.7.
(л, = 0.1 Зл, +0.22.V, -О.ЗЗлз + 0.07х4 + 0.11; 1 х, = 0.45л-, - 0.23л-3+0.07х4 - 0.33:
] л з = 0,11 л, - 0.08 Х-/+ 0.1 8л-4+0.85: [x4 = 0 08 v, + 0.09 х, + 0,33л*з + 0.21 х4 — 1.7.
(л, = 0,32л- ,-0.16л-, - 0.08л-з + 0,15х4 + 2.42; л, = 0.16л-, - 0.23л-, + 0.11 лз - 0,21 х4 + 1.43; л з = 0,05х, - 0.08х2 + 0.34х4 - 0,16;
хч = 0,12л, + 0,14л 2 - 0.18х3+0.06х4 + 1.62.
л, = 0.08х, - 0,23хз + 0.32х4 + 1.34;
х, = 0.16х, - 0.23 х 2 + 0.18х3 + 0.16х4 - 2.33; 4 хз = 0.15х, + 0.12х, + 0.32хз - 0.18х4 + 0.34;
х4=0,25х, + 0.21 х2—0,16х3 + 0,03х4 + 0,63-
[ л, = О.Обх, + 0.18л, + О.ЗЗхз + 0.16х4 + 2,43;
I х, = 0.32x1 + 0,23хз - 0.05х4 -1,12;
) хз = О 16х, - 0.08 V, - 0.12х4 + 0,43; 1-х4 = 0.09х, + 0,22х2 - 0.1 Зхз + 0,83.
{л 1 = 0,34х,+0.23х3 - О.Обл-4 + 1.42:
л, = 0,11 х, - 0,23л, - 0.18хз + 0.36л4 - 0.66; лз = 0.23х, -0.12х, + 0.16л*з -0.35х4 + 1.08; х4=0,12х ,+0.12х, - 0.47л-3 + 0.18х4 + 1.72.
л, =0.32х, -О.23х, +0,11хз - 0.06х4 + 0,67;
л, = 0,18х ,+0.12 х, - О.ЗЗхз - 0.88: ’ л-з = 0,12х, + 0.32 v, -0,05л з + 0.07х4 -0.18, л-4 = 0,05х, - 0.11 х, + 0.09х 1-0,12х4 + 1.44.
51
Образец выполнения задания
{л-1 = 0.32.V । - 0.05.V, + 0.11 л- < - 0.08л-4 + 2.15; л, =0.11л-, +0.16л-2-0.28л,-О.Обл-4-0.83; л*з = 0.08л-! - 0.15х2 + 0.12л-д +1.16;
л-4 = - 0.21 л-1 + 0.1 Зл-, - 0.27л-, + 0.44.
Число шагов, дающих наверняка ответ с точностью до 0, определим с помощью соотношения
и л и * f
Здесь || А || ! = max {0,56; 0.61; 0.35; 0,61] <1; значит, итерационный про; сходится; || F || j = 2.15. Имеем
^^-•2.15<0.001; 0.61д,|<(МЮ1,039;
0.39 2.15
(А + 1) -lgO.61 < -3 + 1g0.39 — lg2.15;
, , -3+1,5911-0,3324 3,7413 г
1,7853 0.2147
Вычисления располагаем в таблице:
к Л"| *2 Л'Л Л'д
0 2.15 -0,83 1,16 0.44
1 2.9719 -1,0775 1.5093 -0.4326
2 2.3555 -1.0721 1.5075 -0.7317
3 3.5017 -1.0106 1.5015 -0.81 II
4 3.5511 -0.9277 1.4944 , -0.8321
5 3,5637 -0.9563 1.4834 -0.8298
6 3,5678 -0.9566 1.4890 -0.8332
7 3,5700 -0.9575 1.4889 -0,8356
8 3,5709 -0.9573 1.4890 -0.8362
9 3.5712 -0.9571 1.4889 -0.8364
10 3.5713 -0,9570 1.4890 -0.8364
Сходимость в тысячных долях имеет место уже на 10-м шаге.
-0.836.
Ответ: % 3,571; л, ~ — 0,957; л'3
Работа 9
№
Задание. Методом Зейделя решить с точностью 0.001 систему лиц ных уравнений, приведя ее к виду, удобному для итеращ
1. Г2.7х,+3.3х,+ 1.3х3=2.1; №2. (1.7л,+2.8л,+1.9х,= 0.7;
3.
1.7.r3=0.8.
з = 5.6.
№
<2.1л1+3.4л-2+1.8л-3 = 1.1;
(,4.2л-! - 1.7л,+ 1.3л-3 = 2,8.
№ 4. С9,1л*j + 5.6л-, + 7.8л ,=9.8;
3.8.V, + 5.hv,+ 2.8л'3 = 6.7
52
З.Зх,+2.1л'2 + 2.8л3 = 0.8; 4.1л'| + 3.7л, + 4,8л з = 5.7: 2.7л । + 1.8л,+ 1.1 л'з = 3,2. № 6. । 7.6л, 4-5.8л,+4.7лз=10.1: 3.8л, + 4.1л,+ 2.7л3 = 9.7; 2.9л, +2.1л'2 4-3,843 = 7.8.
^is 3.2л 1 — 2.5л 2 + 3.7л3 = 6.5: 0.5л, +0.34л, + 1.7л3 = —0.24: 1,6л । + 2,3л2 — 1,5л3 = 4,3 № 8. । 5.4л, - 2.3л, 4- 3.4л 3 = - 3.5; 4.2л, + 1.7л,-2,3л 3 = 2.7; 3.4л,+2.44-2 +7.4л з=1.9.
№ 9- । 3.6л, + 1.8л, — 4.7л'з = 3.8; 2.7 л,—3.6л, + 1.9л з = 0.4: 1.5л, + 4.5л2 + З.Зл3= —1.6. № 10. (5.6л, + 2.7л, —1.7л3 = 1.9; 3.4л, - 3.6л, - 6.7лз = -2.4; (0.8л,+ 1.3л, + 3.7л3 = 1.2.
№ 11. (2.7л, + 0.9л,-1,5л3 = 3.5. < 4.5л 1 — 2.8л, + 6,7л з = 2.6: (5.1 л 1 + 3.7л, - 1.4л 3 =-0.14. № 12. [4.5л, - 3.5л, + 7.4л, = 2.5; 3.1л, - 0.6л, — 2.3л"з= -1.5: (0.8л, + 7.4л, - 0.5л 3 = 6,4.
№ 13. (3.8л ,+ 6.7л, -1.2.4'3 = 5.2; 6.4л, + 1.3л2-2,7лз = 3.8; (2.4л, -4.5л, + 3.5лз = -0.6. № 14. [5.4л, - 6.2л2 - 0.5 4'з = 0.52; 3.4л, + 2.3л2 + 0.8v3 = -0.8; [2.4л, — 1.1л,+ З,8л3 = 1.8.
№ 15. (7.8л, + 5.3л, +4.8л3 = 1.8. 3.3л, + 1.1л, + 1.8л3 = 2,3: (4.5л 14* 3.3л, 4" 2.8л'з = 3,4. № 16. [ 3.8л,+4.1л,-2.3лз=4.8: - 2.1л, + 3.9л, - 5.8лз = 3,3; [ 1.8л, + 1,1л2 —2,1л3 = 5.8.
№ 17. (1.7л,—2.2л,+ З.Ол3= 1.8; 2.1л, !-1,9л2 — 2.3л-3 = 2.8; (4.2л ,4- 3,9л, -3.1 лз = 5.1. № 18. [,2.8л, + 3.8л, - 3.2л з =4,5; 2.5л,—2,8л,+ З.Зл3 = 7,1; [,6.5л, -7.1л, +4.8 гз = 6,3.
№ 19. (3.3л,+3.7л,+4.2л3 = 5.8: 2.7л, + 2.3л,— 2,9л3 = 6.1: [,4.1л,+4.8л2 — 5.0л3 = 7,0. № 20. [7.1л, + 6.8л, +6.1 л3 = 7,0; , 5.0л, + 4.8л, + 5,3л з = 6.1; (8.2л, + 7.8л,+ 7.1л'з = 5.8.
№ 21. ( 3.7л,+3.1л, + 4.0л'з = 5.0; 4.1л, + 4.5л,—4.8л3 =4.9; ( — 2.1л,—3.7л, + 1.8л3 = 2,7. № 22. [4.1л, + 5.2л,-5.8л3 = 7.0; 3.8л,-3.1л,+4.0л3 = 5.3; 7.8л, +5.3.4,-6.343 = 5.8.
№ 23. [3.7л,-2.3л, 4-4,5л з = 2.4; 2.5л, + 4.7л, —7.8л3 = 3.5; [1.6л, + 5.3л, + 1.3л3=—2,4. № 24. [6.3л, + 5.2л, —0.6л 3=1.5; 3.4л,-2.3 л,+ 3.4л'з = 2.7: ,0.8л, + 1,4л2 +З.5л3= -2.3.
№ 25. [1.5л,+ 2,3л2 —З.7л3 = 4,5: 12.8л। 4* 3.4л, 4" 5,8л 3 = — 3.2; [1.2л, + 7.3л, — 2.3л'з = 5.6. № 26. [0.9л,+2.7л,-3.8 4'з = 2.4; 2.5л,+ 5.8л2-0.5л3 = 3.5; 14.5л,-2.1л, + 3.2л3=-1.2.
№ 27. [2.4л,+2,5л2 — 2,9л3= 4.5; ,0.84,4-3.5.4-,-1,4 л з = 3.2: [ 1.5л j - 2,3л, + 8,6лз = - 5,5. № 28. [5.4л,-2,4л2 + 3.8л3 = 5.5; 2.5л, + 6.8л,-1.1л3= 4,3; 7.7л, —0,6л2+1,5л3 = -3.5.
-Vs 29. [2.4 л,+ 3.7л2 — 8.3л3 = 2,3: . 1.8л,+4,3л2+1.2л3= — 1.2; (3.4л, — 2.3л24-5.2л'з = 3.5. № 30. 3.2л, — 1 1.5л2 + 3,8лз = 2.8: 0.8л, + 1.3л2 -6,4л3 = -6,5; ,2.4л 1 +7.2.4,- 1.2л з = 4.5.
Образец выполнения задания
(4.5л,-1.8л, <3.1л, + 2.3л2 (1,8л, 4* 2,5л*, + З.6л3= —1.7; — 1,2л3 = 3.6; 4-4.6л з = 2,2. (0 (II) (III)
Приведем систему к виду, в котором элементы главной диагонали Ревосходили бы остальные элементы строк:
53
( 7,6xi+0,5x2 + 2,4x3 = 1,9; (I + II)
< 2,2xi+9,1x2+ 4,4хз= 9,7; (2III + II —I)
I - 1.3л, +0,2x2 + 5,8x3 =-1,4; (III - II)
f 10xt = 2.4xi -0.5x2-2,4хз + 1,9;
\ 10x2 = - 2,2xi + 0,9x2 — 4,4хз + 9.7;
110хз= 1.3xi—0,2x2—4,2хз— 1,4.
f xi = 0.24.V! -0.05x2-0.24x3+0,19;
< X2 = - 0,22x1 + 0.09x2 - 0.44x3+0,97;
l хз = 0,13x i - 0.02x2 + 0,42x3 - 0,14.
Норма || A || t матрицы, состоящей из коэффициентов при неизвест в правых частях уравнений, равна (0,53; 0,77; 0,57} =0,77 < 1; зна процесс Зейделя сходится.
Вычисления располагаем в таблице:
А' Х| х> Хз Л Xi х2 х31
0 0.19 0,97 -0,14 5 0.2467 1.1138 —0,22,
1 0.2207 1.0703 -0.1915 6 0.2472 1.1143 - 0,22-
2 0.2354 1,0988 -0,2118 7 0.2474 1,1145 -0,22-
3 4 О 0.2424 0.2454 твет: х, 1,1088 1.1124 ,248; х2*1. -0.2196 -0.2226 115; х3^- 8 0,224. 0.2475 1,1145 -0,22
Глава IV
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Работа 1
Задание. Используя схему Горнера, составить таблицу значе: многочлена на отрезке [0.5; 2,0]; шаг Л = 0,25. Вычисли выполнять с точностью до 0,0001, ответ округлить до тысячи № 1. 1.723х5 + 0.137х4 - 0.814х3 + 2.364х2 -1,176х+3.962.
№ 2. 1,654х5 + 0.21 Зх4 - 0,744х 3 4- 1,283х2 - 2.151 х 4- 4.134.
№ 3. 1.514х5—0,124х4 —0,548х34-3,214х2 — 1.124x4-2.258.
№ 4. 0,372х5—0.612х4 4-0,532х3 4-1,134х2—1.247х—1,624.
№ 5. 0.853х5 - 1.514х4 - 0.143х 3 4-1.217х2 - 2.243х 4- 2.415.
№ 6. 0,623х5 4- 1,275х4 - 0,217х 3 4-1.315х2 - 3,174х - 1,862.
№ 7. 1,273х 5 4- 0.116х4 - 0.343х 3 4- 3,115х 2 - 1.262х 4- 0,375.
№ 8. 0,375х5 -1,21 Зх4 4-1,108х3 4- 0,742х2 - 3.115х 4- 2,724.
№ 9. 1.116х54-0.127х4 —0.316х3 + 1,164х2-2.273х-1,123.
№ 10. 0,764х5 - 0.312х4 4-1.216х 3 - 2.458х 2 4- 1,273х 4- 0,834.
№ 11. 0,374х5 4- 0.242х4 - 1.41 Зх3 4- 0.746х2 4- 3.183х -0.678.
№ 12. 1,073х5 - 0,143х4 4- 0,568х 3 4-1,215х 2 - 3.146х 4-1.618.
№ 13. 0.513х5 —0,837х44-1.215х34-2,453х2— 1,783х—0.847.
№ 14. 1,087х5 - 1,243л 4 + 0.656.x3 - 0,783х 2 + 2.574х 4- 0.564.
№ 15. 0,683х5+1.143х4—0.562х3+1.844х2 —2.154х+1.472.
№ 16. 1,21 Зх5 - 0,216х4 4-1.316х 3 - 2,758х2 4- 3,612х - 0,388.
№ 17. 1,316х5 -0,144х4 -0.572л-3 4-1,854х2 - 2,71 Зх4-1,625.
№ 18. 1,172х5 - 0.534л 4 - 0.316х 3 4-1.283х 2 4-1,615х - 2.652.
№ 19. 0,61 Зх 5 4-0,318х4-1.216л-3 4-2.517л-2-3,712x4-0,454.
№ 20. 0,278л-5 - 0.763л4 4-1.072х 3 4-1.61 Зх 2 - 2,312х -1,418.
54
21 0.475л5-0.612л4 + 1.314л3 + 1.183л2-3.154л+ 0.844. {? г{ 0.683л5+ 0,514л4—0.817л3 + 2.432л2 + 1,072л—0.833. {? 23 । .028л5 - 0.71 Зл4 - 1.072л 3 + 1.625л 2 - 3.184л - 1,546. {? 24 0.243л5 - 1.065л4 - 0.364л3 + 2.445л2 - 1.265л + 0.318. 5 2Ч- 0.831 л5 -0.722л4 + 1.157л3 + 1.615л2 - 2.844л - 0.685. № 26 0.354л5 + 0.583л4- 1.072л3+ 1.548л2-2.436л-0.367. м, 27. 1.273л5 + 0.172л4 - 0.788л3 + 1.453л2 - 2.81 Зл + 3.154.
28. 0.421 л5 - 0.544л4 - 1.21 Зл 3 + 0.683л2 + 3J 45л - 0.185. чъ 29. 1.342л5 -0.254л4 + 0.872л3 + 1.273л2 - 1,483л + 0.584.
30. 1.418л5- 1,547л4 + 0.418л3 + 1.783л2-2.517л+2.434.
Образец выполнения задания
Р (л)=0.883л5 - 1.217л4 + 1.452л3 + 0.572л2 - 2.343л +1.158.
Для вычислений по схеме Горнера составим таблицу, содержащую все промежуточные результаты и значения искомого многочлена:
0.883 -1.217 1,452 0.572 -2.343 1,158
0.50 0.883 — 0.7755 1.06425 1.1041 -1.7909 0.2625
0.75 0.883 -0.5547 1.0359 1.3490 -1.3313 0.1595
1.00 0.883 -0.3340 1.1180 1.6900 -0.6530 0.5050
1.25 0.883 -0.1132 1.3104 2.2100 0.9721 2.3731
1.50 0.883 0.1075 1.6132 2.9919 2.1448 4.3752
1.75 0.883 0.3282 2.0264 4.1183 4.8640 9.6699
2.00 0,883 0.5490 2.550 5.6720 9.0010 19.1600
В верхней строке таблицы запишем коэффициенты л, данного многочлена, в первом столбце—значения аргумента .v. Остальные строки содержат значения которые в схеме Горнера находятся по единой формуле: bi = bi-iх+«i (/ = 1. 2. 3. 4. 5); bG=а0-
В последнем столбце таблицы получаются значения многочлена />(.г). Округляя их до тысячных долей, получим ответ:
Xi
0.5 0.263
0,75 0.160
1,00 0.505
1.25 2.373
1.50 4.375
1.75 9,670
2.00 19.160
55
Работа 2
Задание. Вычислить значения функций при заданных значениях гумента методом разложения в ряд с точностью до 1
I) >=<>Л при а) л, =0.716 +0.043л; б) л2 = 2.834-0.028л;
2) у = In (I + л) при л" = 0.122 + 0.018л;
3) у = sin л* и у=cos л при a) xj =0.232+0.012л; 6) л'2 = 0,747—0.014л.
Здесь л=1. 2. 3...30. т. с. соответствует номеру варианта.
Образец выполнения задания
I) г=ех при: a) л'| =0,826: б) л2 = 2.417;
2) у=In (I + .г) при л*=0.437;
3) у=sin л" и у=cos Л' при: а) л= 0.476; б) л*=0.684.
1) Воспользуемся разложением
е*=Мо + М1 +М2+ ... +
где «о=1, м,=^«/-1 0=1, 2, 3,...). i
Вычисление отдельных слагаемых продолжаем до тех пор. пока будет выполнено неравенство |«;|<е, где е=10-6.
Составим таблицу значения отдельных слагаемых.
а) л* = 0,826
1 «г । Mi
0 1 6 0.0004411
1 0.826 7 0.0000520
2 0.341138 8 0.0000053'
3 0.09392666 9 0,0000004
4 0.01939586 10 0.0000000
5 0,003200420
Искомое значение представляет собой следующую сумму: ю
fo.826% £ W/ = 2.28416378 % 2.284164.
i=0
б) х=2.417
। Mi i
0 1 9
1 2,417 10
2 2,9209445 II
3 2.3533076 12
4 1,4219861 13
5 0,68738808 14
6 0.27690283 15
7 0.09561059
8 0,02888635
0.0077575'
0.00187501 0.00041199 0.00008298 0.00001543 0.0000026 о.оооооо4:
56
16
с2’417* £ М1= 11.2121722* 11,212172.
i —О
ч) Воспользуемся равенством
1П ( 1 + Л") = Wj +Н2 + М3 + ... + И, + ....
где »,=.< (г=1. 2. 3. ...).
Значения слагаемых занесем в таблицу
i и. / Ui
1 0.437 9 0,00006458
О -0.0954845 10 -0.00002540
1 0,02781782 II 0,00001009
4 -0,00911729 12 -0,00000404
S 0.003187440 13 0.00000163
6 -0.00116075 14 -0.00000066
7 0.00043478 15 0.00000027
X -0,00016625 16 -0.00000011
17 0.00000005
17
In 1,437 * £ щ *0,36255762 *0.362558.
i = 1
3) Будем использовать равенства
Sin .V = Ho + Ml + Мз + ... +Mj+ ....
V"
где m0=.v. М,= -——— М;-1 (/=1, 2. 3,...);
21(2/4-1)
COSA' = Го + l’i + Ст + ... +Г/+ ....
2
где ГО=1. g= Л Г.-1 (1=1, 2. 3. ...).
2'0-1)
Составим таблицу значений слагаемых вида м, и г,, а) л =0.476
Значит,
/ Ui
0 0.476 1
1 -0.01797503 -0.113288
2 0.00020364 0,00213903
3 -0,00000110 -0.00001615
4 0,000000003 0.00000007
з
sin 0.476* £ in = 0.45822751*0.458228;
1 = 0
cos 0,476* £ ^=0,88883495 *0,888835.
n ,=0
JT1* контроля правильности вычислений найдем сумму квадратов ОлУЧенных значений:
57
sin 2 0,476+cos2 0,476 = 0,2099729+0,79002766= 1,0000006^ 1.
Близость суммы к 1 свидетельствует о правильности вычислений, б) л-= 0,684.
i Wi
0 0,684 1
1 — 0,05333558 -0.233928
2 0.00124767 0.00912038
3 -0,00001390 -0,00014223
4 0,00000009 0.00000119
5 -0,00000001
4
sin 0,684 % £ 0,63189828 ^0,631898,
i = o
5
cos 0,684* X ^*0,7750513 % 0,775051; i = O
sin2 0,684+cos2 0,684 = 0,39929508 + 0,60070405 = 0,99999913*1.
Работа 3
Задание. Вычислить значения функций при заданных значениях гумента методом итераций с шестью верными значащ цифрами. Для определения начальных значений использо метод прикидки. Выполнить проверку результата.
1) у= ^/.v при а) л j = 7,86 + 1,27л; б) .v2 = 0.017 + 0,012л;
1
2)1’=—= при a) Aj = 12.55+ 0,213л; б) .v2 = 0.247 + О.О22л;
ч/л-
3) у = Vх ПРИ а) Л1 = 18352 + 0,343л; б) л-2 = 0.037 + 0.024л.
Здесь л=1. 2, 3, ..., 30, т. е. соответствует номеру варианта.
Образец выполнения задания
1) у=^/л при а) .1^ = 14.76; б) л2=0.142;
1
2) у=—= при а) л, = 17,32; б) л2 = 0,464; ч/л-
3) у=3^х при а) л'] =26.15; б) л2 = 0.078.
‘ Для решения задачи методом итераций составляем последовать ность приближенных значений искомой функции _у0, у^ у2, _у3, ...» ..., сходящуюся к точному значению у(х). Вычисления продолжаем сходимости с заданной точностью.
58
1) При вычислении значений функций r(.v) = x/.v члены последовательней определяем по формуле
(' = 0, 1. 2. 3, ...),
2\
где г(> подбираем прикидкой с одной или двумя верными цифрами.
а) При .v= 14,76 имеем г,-+1=-( г,+пусть г0 = 3,8. Составим
2 \ i-j /
таблиц} значений членов последовательности:
1 То
0 1 2 3 3,8 3.842105 3.841874 3.841874
Искомым значением является х/14,76 % г3 % 3,84187.
Для проверки найдем квадрат полученного числа: 3.841872= 14.759965% 14,76.
1/ 0.142 \
б) При л*=0,142 имеем rl + 1=-|rtH-------|; пусть го = 0,4. Значения
2\ Я /
членов последовательности приведены в таблице:
i
0 0,4
1 0.3775
2 0.3768295
3 0.3768289
4 0.3768289
Искомое значение есть ^/0,142 % 0,376829.
Проверка: 0,3768292 = 0,1420001 %0.142.
2) При вычислении значений функции у=-Д= члены последователь-\/Л"
ностн определяем по формуле
г1 + 1=^(3-.п7) (f=0, 1. 2, 3, ...)
а) ' = 17,32; >„=0,24; jit,=^(3- 17.32г,2).
Составим таблицу значений членов последовательности:
f г.
0 0,24
1 0,2402842
2 0.2402846
3 0.2402847
59
Искомым значением является % 0,240285. Для проверки вост У17.32
зуемся равенством .vi'2=l: имеем 17,32-0,2402852 = 1.0000028s: 1.
6) .v=0,464: ,i„=1.5; у,-, । =^(3 - 0.464)-,2).
А*
Составим таблицу:
I л
0 1 2 3 Искомое значение есть — ./о 1.5 1.464 1.468049 1.468051 = % 1,46805. .464
Проверка: 0,464 • 1,468052 = 0,99999925% 1.
3) Для вычисления значений функции у=Лу/.х члены послсдоват ности определяем по формуле
а) л = 26.15; г = 3; ri+1 =|(.2г,+ —)• 3\ УГ /
Составим таблицу значений членов последовательности:
/ У1
0 3
1 2,968518
2 2,968182
3 2.968182
Искомым значением является Зч/26,15 % 2,96818.
Для проверки воспользуемся равенством 2,968183 = 26,14994 % 26,15.
1/ 0,078 \
б) л*=0,078, уо = 0,4, Г|Ч. 1 =-( 2у + —— ).
3\ УГ /
Составим таблицу
и;
i л
0 0,4
1 0.4291667
2 0.4272743
3 0,4272659
4 0,4272659
Искомое значение есть 3ч/0,078 % 0,427266. Проверка: 0,4272663 = 0,07800007%0,078.
60
ГЛАВА V
МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Работа 1
Задание. О Отделить корни аналитически.
2) Отделить корни аналитически и уточнить один из них методом проб с точностью до 0,01.
3) Отделить корни графически.
4) Отделить корни графически и уточнить один из них метолом проб с точностью до 0,01.
й 1. 1) 2' • 3-и.
ч ъ-ч 4л-'-5 ^0;
3) 0.5'+1 =(л —2)2;
4) (л-3)cos.v= I. —2пО$2п.
№ 3. I) 5' + Зл = 0;
2) л4-л- I =0;
3) л2 —2+0.5х = 0;
4) (л - I)2 lg(.<+ 11)= 1.
№5. 1) 3'1-2-л = О;
2) Зл-4 + 8л’3+6л'2—10 = 0:
3) (л-4)2 logo<5(.v-3)= -1:
4) 5чпл = г.
№ 7. I) с "2л — 2л +I =0.
2) л4! 4л-3 —8л2—17=0;
3) 0.5'-1=(л + 2)2;
4) a2cos2a= —1.
Л'» 9. I) arete (л — 1) + 2х = 0;
2) Зл4 + 4л-3-12л-2+1=0:
3) (л —2)22х = I;
4) v2 — 20 sin ,v = 0.
№ 13. ]) 3' +2л —5 = 0;
2) л4-4л3 —8л2+I =0:
3) л2-3 + 0.5х=0;
4) (л-2)21е(л + 11)=1.
№2. 1) arctg.v------ = 0;
Зл4
2) 2л*3 —9л2 —60л-+ 1=0;
3) [log,(-.v)]*(.v+2)=-l:
/
4) чп( л + - 1 — 0.5л =0.
№ 4. 1) 2<А=5л
2) 2л-4-а-2-10 = 0;
3) A -log3(v+ 1) = 1;
4) cos (л-+0.5)=л 3.
№6. 1) 2 arete л*---г = 0;
2л-3
2) л-4-18л-2+ 6 = 0;
3) л-2 -2л=1;
4) lg л*=л* + 1 — я/2 л < п/ 2
№ 8. 1) 5х-6л-3=0:
2) л-4-л-3-2л-2 + Зл—3=0;
3) 2л2 —0.5 х —3=0;
4) .vlg(.V + l) = 1.
№ 10. 1) 2 arcclg л-— л-+ 3 = 0;
2) Зл-4-8л3-18л-2 + 2 = 0;
(п\
л + - | = 0.5л‘_— I;
3 J
4) 2lgx-^ + l=0.
№ 12. I) 2 arete л —Зл +2 = 0:
2) 2л4 + 8л-3 + 8№-1=0;
3) [log2 (л-+ 2)] (л-— 1) = 1;
4) sin (л — 0.5) — л*+ 0,8 = 0
№ 14. 1) 2ех+Зл + 1=0;
2) Зл4 + 4л-3-12л-2-5=0;
3) vlogj(A + l)=2:
4) cos (л-+0,3)=л2.
И. 1) 3'-'_4-л=0;
2) 2лл-9л-2-60л+1=0:
3) (л - З)2 logo>s I* - 2) = - ।;
4) 5 sin л = л — 1.
Ле 16. 1) arctg \ - 0. Зл-3
2) л4-л—1=0; 3) (л-1)22х=1; 4) tg3A' = A —1, ri "к у/ V/ сч 1
61
№•17. 1) ех+х+1=0;
2) 2.v4—л2—10=0;
3) 0,5х-3=(л + 2)2;
4) № cos 2л = — 1, — 2п <л-< 2п.
№ 19. 1) arctg(x—1)+3л —2=0;
2) л4- 18л-2 + 6 = 0:
3) (л-2)22х = 1;
4) л 2 —20 sin л*=0.
№ 21. 1) 2х —Зх —2=0;
2) л-4-л-3-2л-2 + Зл—3=0;
3) (0,5)х+1 =(л —2)2;
4) (л - 3) cos л = 1, — 2п л- < 2п.
№ 23. i) Зх + 2л-3=О;
2) Зл4-8л3-18л-2+ 2=0;
3) л-2-4 + 0,5*=0;
4) (л—2)2lg(x+11)= 1.
№ 25. 1) Зх+2 + л=О;
2) 2x3—9х2 —60х+I =0;
3) (x—4)2log0 5(х —3)= — 1;
4) 5 sin л-=л —0,5.
№ 27. 1) е-2х —2л +I =0;
2) 2х4 —х2 —10=0;
3) 0.5х —3= — (х+I)2;
4) л 2 cos 2л = — 1.
№ 29. 1) arclg (л- - 1) + 2х=0;
2) л-4-18л-2+ 6=0;
3) (л—2)22х=1;
4) л*2—10 sin л-=0.
№ 18. 1) 3х—2х+5=О;
2) Зх4 + 8х3 + 6х2 — 10 = 0; 3) 2л-2-0,5х-2 = 0; 4) xlg(x + 1) = 1.
№ 20. 1) 2 arccig л — л+ 3 = 0; 2) х4+4х3 —8х2—17 = 0; ( У 3) 2sinl х + - |=х2—0,5; \ 3/ 4) 21gv—^ + 1=0.
№ 22. 1) arcclgx+2x-1 =0; 2) Зх4 + 4х3-12х2+1=0; 3) (x+2)log2(x)= 1; 4) sin(x+l)=0.5x.
№ 24. 1) 2ех—2х —3=0; 2) 3x4 + 4x3-1Zv2-5 = 0; 3) xlog3(x+l)=l; 4) cos(x+0,5)=x3.
№ 26. 1) arcctg (л - 1) + 2л- - 3=0; 2) л4-х-1=0; 3) (л-1)22х=1; 4) lg3A=x+l, -я/2^л-^
№ 28. 1) Зх-2л-5 = О; 2) Зл-4 + 8л-3 + 6х2-10 = 0; 3) 2л-2-0,5х-3=0; 4) xlg(x+l)=l.
№ 30. 1) Зх + 5л-2 = 0: 2) Зх4+4л-3-12л-2+1=0; 3) 0,5х+1=(х-2)2; 4) (x+3)cosx= 1.
— 2п<х<2л.
Образец выполнения задания
I) 5х—6х —3=0; 2) х4—х3 —2х2 + 3х—3 = 0;
3) 2cos| л+ - ] +х2 = 3х —2; 4) x2log0 5(х+ 1)= 1.
1) Обозначим /(л) = 5х — 6л —3. Находим производную f (х) = 5х In 5 Вычислим корень производной:
5*lg5-6=0; 5’=Д; .vlg5 = lg6-lg(ln5);
In Ъ
_ 1g 6 - 1g (In 5) _ 0,7782 - 0,2065 _ 0,5717 lg5 ” 0.6990 ~ 0,6990^ ’
Составим таблицу знаков функции /(х), полагая х равным: а) кри ческим значениям функции (корням производной) или близким к fl
62
.П1НИЧНЫМ значениям (исходя из области допустимых значении б) 1 ” \
'..шестого).
sign / (л)
— X i + X
+ — +
так как происходят две перемены знака функции, то уравнение имеет два действительных корня. Чтобы завершить операцию отделения корней, следует уменьшить промежутки, содержащие корни, так чтобы их длина была не больше 1. Для этого составим новую таблицу знаков функции /(.v):
Л’ -1 0 1 2
sign/(л) + — — +
Отсюда видно, что корни заключены в следующих промежутках: .v,e [- 1. 0]; л-,е [1, 2].
2) Полагая /(л) = л'4 —Л'3 —2л*24-Зл* —3. имеем /'(x)=4.v3 —Зл2—4л + 3. Найдем корни производной:
4л'3-Зл-2-4л + 3=0; 4л(.г2- 1) —3(л2— 1) = 0: (л*2-1)(4.г-3)=0; .¥, = -1;
л'2=1: л-з = 3/4.
Составим таблицу знаков функций /(л):
V — X 1 3/4 1 + X
sign/(.v) + 1 — — +
Из таблицы видно, что уравнение имеет два действительных корня: vie]-x. -1): л,б[1, + х [.
Уменьшим промежутки, в которых находятся корни:
.V -1 1 2
sign/(.v) + — — +
леДователыю, е [ — 2: — 1 ]; a,g [1, 2].
Уточним один из корней, например л,е[ —2. — 1], методом проб 0 сотых долей. Все вычисления удобно производить, используя ЛеДующую таблицу:
63
п Ия К Ч'+Ья Ля- 2 Ля4 -Ля3 -2л-2 Зл, /(J
0 -2 -1 -1.5 5.0625 3.375 -4.5 -4,5 -3.J
1 _э -1,5 -1,75 9.3789 5.3594 -6.125 -5,25 0,3
2 -1,75 -1.5 -1.63 7.0591 4.3307 -5.3138 -4.89 —1,8|
3 -1,75 -1.63 -1.69 8.1573 4.8268 -5.7122 -5,07 -0,7
4 -1.75 -1.69 -1.72 8.7521 5.0884 -5.9168 -5.16 -0,2
5 -1,75 -1,72 -1.73 8.9575 5.1777 - 5,9858 -5.19 -0,0
6 -1,75 -1.73 -1.74 9,1664 5.2680 -6.0552 -5.22 0,1
7 -1,74 -1.73
я \
6/’
v1 = 2cos( л*4* - ), \ 0/
(рис. 1).
Из графика
л-2%2,9.
4) Перепишем
Ответ: л 15; —1,73.
уравнение в виде 2cos[ л*+ - )= — л'24-3л—2. Обозна) \ 6/
Г2 = — .V2 4- Зл — 2, построим графики этих фу ню видно, что уравнение имеет два корня: л, уравнение в виде logo< 5 (л* 4-1) = 1 /х2. Обозна
г, =log0,5(.v4-1), r2=l/x2, построим графики этих функций (рис. 2). графика видно, что уравнение имеет один корень 0,8.
Для уточнения этого корня методом проб выберем промежуток, концах которого функция 7'(.v) = .v2logo 5(л +1) — 1 имеет разные зна Составим таблицу:
л -0,5 -0.8
sign /(л) — 4-
Для удобства расчетов перейдем к десятичным логарифмам:
64
Дальнейшие вычисления производим в таблице:
п К ля- 2 л» lg(v.+ l) /(-*)
о -0.8 -0,5 -0.65 0.4225 -0.4559 -0.360
-0.8 -0,65 -0,73 0,5329 -0.5686 0.0067
-> -0.73 -0.65 -0.69 0,4761 -0.5086 -0.196
-0.73 -0,69 -0.71 0.5041 -0.5376 -0,099
4 -0.73 -0,71 -0.72 0.5184 -0.5528 -0,048
4 -0.73 -0,72
О гнет: х %—0.73.
Работа 2
Задание. 1) Отделить корни уравнения графически и уточнить один из них методом хорд с точностью до 0.001.
2) Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до 0,001.
№ №
№ №
№
№ № Л» № Ле Ле № № №
1. I) 2. I) 3. I) 4. I)
5. I)
6. I) 7. I) 8. 1) 9. 1) 10. 1 11. 1
12. I 13. 1 14. 1
х —sin х=0.25; tg(0,58x4-0.1) = x2; vx -cos(0,387л)=0; tg (0.4x4-0,4)=х ,
ig (0.5x4-0,2)=х2;
Зх—cosx— 1 =0; л 4-1g х=0,5; lg(0.5x4-0,l)=x2;
) x“4-4sinx=0; ) ctg 1,05х—х2 = 0;
) tg (0,4x4-0,3)=x2;
) xlgx- 1,2 = 0; ) l,8x2 —sin 10x=0;
2) х3 —Зх24-9х—8=0.
2) х3 —6х —8 = 0.
2) х3 —Зх24-6х4-3=0.
2) х3 —0.1х24-0,4х— 1,5 = 0.
2) х3—Зх24-9х+2=0.____
2) х34-х—5 = 0.
2) х34-0,2х24-0,5х—1,2 = 0.
2) х34-3x4-1=0.
2) х34-0,2х24-0,5х—2 = 0.
2) х3 —Зх24-12х—9 = 0.
2) х 3 - 0,2х2 4- О.Зх -1.2 = 0.
2) х3 —Зх24-6х—2 = 0.
2) х3 —0,1х24-0.4х— 1.5=0.
2) х34-Зх24-6х—1 =0.
Ле 15.
Ле 16.
Ле 17.
Лё 18.
Лв 19,
Лё 20.
Лё 21.
Лё 22.
№ 23.
Лй 24.
) ctgx--=0;
4
) lg (0,3x4-0,4)=х2;
) х2 —20sinx=0;
) ctgx--=0;
3
) tg (0.47x4-0.2)=х2;
) x24-4sinx=0;
) ctgx—-=0;
) 2x-lgx—7=0;
) tg (0,44x4-0,3) = х2;
) Зх-cosx-1=0;
25. 1) ctgx—— = 0;
10
2) х34-0,1х24-0,4х— 1.2 = 0.
2) х34-4х—6=0.
2) х34-0,2х24-0,5х4-0,8 = 0.
2) х3—Зх24-12х—12 = 0.
2) х3 —0,2х24-0,Зх4-1.2 = 0.
2) х3 —2х4-4=0.
2) х3 —0,2х24-0.5х—1.4=0.
2) х3 —Зх24-6х—5 = 0.
2) х3 —0,1х24-0.4л+1.2 = 0.
2) л3-0.2х24-0,5х— 1 =0.
2) х34-3х24- 12x4-3=0.
^1258
65
№26. 1) x2+ 4sin л=0; №27. 1) tg (0,36л+0.4)=л2; № 28. 1) л + IgA-=0.5;
№29. I) clgx—-=0;
№ 30. I) 2lgx-- + 1=0: 9
2) л3-0,1л2 + 0.4л+2 = 0.
2) л3 —0.2л 2+0.4л —1,4=0.
2) л 3 + 0.4л-2 + 0.6л- -1.6=0.
2) л3 + л-3 = 0.
2) л 3 - 0.2л 2 + 0.5л+1.4=0.
Образец выполнения задания
I) lg(0,55A+0.1)=xI) 2; 2) л3-0,2л2 + 0.5л +1.5=0.
I) Отделим корень графически. Построим графики функций =tg (0,55л- + + 0,1) и у2=л'2 (рис. 3), составив таблицы значений этих функций:
V 0 0.2 0,4 0,6 0,8 1
г2 = л2 0 0,04 0.16 0.36 0,64 1
0.55л- 0 0,11 0.22 0.33 0,44 0,55
3'1 0,1 0,21 0,33 0,46 0,60 0,76
Таким образом, положительный корень уравнения заключен в промел ке [0,6; 0,8].
Чтобы уточнить корень методом хорд, определим знаки функ /(x) = tg(O,55x+O,l) — х2 на концах промежутка [0,6; 0,8] и знак второй производной в этом промежутке:
/(0,6) = tg 0,43 - 0,36 = 0,4586 - 0,36 = 0,0986; /(0,8) = tg 0,54 - 0,64 =
= 0,5994 - 0,64= -0,0406;
cos2 (0,55x+0,l)
/" (х)=0,55 2 cos3 (0,55х+0,1) sin (O,55x + 0,1) 0,55 - 2 =
0,605 sin (0.55л + 0,1) cos3 (0,55x + 0,1)
при ле [0,6; 0,8].
Для вычислений применяем формулу
'я+1”Ли"/(6)-/(хр ЛяЬ где 6 = 0,8; хо = 0,6.
66
Вычисления удобно располагать в таблице:
я Ля 0.8-х. О.55ля+0.1 ig(O.55x„+O.l)
0 0.6 0.2 0.43 0,4586
0.742 0.058 0.5081 0.5570
э 0.750 0.50 0.5125 0.5627
з 0,7502 0.0498 0.5126 0,5628
«——” я V ДМ /(0.8) -/(л„) /{0.8) —Дл’и) х
х(Л-Ля)
0 0,36 0,0986 -0.1392 -0,142
1 0,5506 0,0064 -0.0470 -0.008
2 0,5625 0,0002 -0,0408 -0.0002
3 0.5628 0
Ответ: л*=0,750.
2) Отделим корни аналитически. Находим
/(л)=л-3-0,2т2+0,5л-+ 1,5; /'(л) = 3т2-0,4л+0.5; D=0,16-6<0.
Составим таблицу знаков функции /(л):
.V — со -1 0 + X
sign/(л) — — + 4-
Уравнение имеет один действительный корень, лежащий в промежутке [-1.0].
Чтобы уточнить корень, находим вторую производную/"(.v) = 6.v—0.4;
в промежутке [-1,0] выполняется неравенство/"(.v)< б.
Для вычислений применяем формулу
где «=-1; ,го = 0; /(</)=/’(—1)= — 1—0.2 —0.54-1.5=—0,2.
Вычисления располагаем в таблице:
п Л’я л,3 Ля 0.2ля- 0.5.v„
0 0 0 0 0 0
1 -0.882 -0.6861 0.7779 0,1556 -0,441
2 -0,943 -0.8386 0.8892 0,1778 -0,4715
3 -0,946 -0.8466 0,8949 0.1790 -0.473
4 -0.946
з*
67
ТЙТ:
п /К) ./(vJ+0.2 v„ —н /('J Да)
0 1,5 1,7 1 -0.118
1 0.2173 0.4173 0.118 -0.057
2 0.0121 0.2121 0.057 -0.054
3 0.0014 0.2014 0.054 -0.054
Ответ: л — 0.946.
3
Задание. I) Отделить корни уравнения графически и
уточнить о, ~ из них методом касательных с точностью до 0,001.
2) Отделить корни уравнения аналитически и уточнить о, из них с точностью до 0,001 методом касательных. Воспользоваться вариантами работы 2.
Образец выполнения задания
1) tg (0,55л + 0,1)=л 2; 2) л 3 - 0.2 л2 + 0.5л 4-1,5 = 0.
1) Выше (см. с. 00) мы отделили один из корней этого уравнеш и установили, чго он заключен в промежутке [0,6; 0,8]. Уточним этс корень методом касательных. Так как /(0,6) >0: /(0,8) <0 и /"(л*)< то за начальное приближение примем ло=0.8.
Вычисления производим
по формуле
•^п + 1 Л'л
Предварительно найдем 0,55
/'(0,8)= ----v
' ' cos2 (0,44+ 0,1)
2.0.8=_2^__l.6=J^ 0 85772 0.7356
= 0,7477-1,6=-0,8523.
Составим таблицу:
и л; 0,55л.+0,1 tg (0.55 л.+0.1) /(V.) ./U)
-0,8523 (
0 0,8 0.64 0.54 0,5994 -0,0406 0.0476
1 0,7524 0.5661 0.5138 0,5643 -0,0018 0,0021
2 0.7503 0,5630 0,5127 0,5630 -0.0000 0
мы установили, что
уравнение имеет дей
Ответ: л % 0,750.
2) Выше (см. с. 00) вительный корень, принадлежащий промежутку [—1,0]. Уточним эт<
68
-орень методом касательных. Так как /(—!)<О, /(0)>0 и /"(.г)<0, 0 за начальное приближение принимаем л*о = — 1.
для вычислений применяем формулу
Яу»)
/иг
Находим /(л*) = л*3 —0.2х2+0,5л*+1,5: /'(л*) = 3л*2—0.4л*+ 0.5. Для вычислений используем таблицу:
п х„ х2 х3 /(М /U) А=ли /'(-<-)
0 - 1 1 — 1 -0,2 3.9 -0.051
1 -0.949 0.9006 - 1,8547 -0,0093 3,5814 -0.0026
-0,9464 0,8957 -0,8477 -0,0004 3.5657 -0.00001
О г в е т: л — 0.946.
Работа 4
Задание. Комбинированным методом хорд и касательных решить уравнение третьей степени, вычислив корни с точностью до 0.001.
№ 1. 2х3 —Зл*2—12х—5=0. № 2. х3 —Зл*2 —24х —3=0.
№ 3. х3 —Зл*2 + 3=0. № 4. х3—12л*+6 = 0.
№ 5. х3 + Зх2 —24х—10 = 0. № 6. 2х3 —Зх2—12х+10=0
№ 7. 2х3 + 9л*2 —21 =0. № 8. х3-Зх2 + 2.5 = 0.
№ 9. х3 + Зх2 —2 = 0. № 10. х3 + Зх2 —3,5 = 0.
№ 11. х3 + Зх2 —24х+10 = 0. № 12. х3 —Зх2 —24х—8 = 0.
№ 13. 2х3 + 9х2—10 = 0. № 14. л*3—12л*+10 = 0.
№ 15. х3 + Зх2 —3 = 0. № 16. Г ы 1 + и ©
№ 17. х3 —Зл*2 —24л —5=0. № 18. х3— 4х2 + 2 = 0.
№ 19. х3—12л —5=0. № 20. х3 + Зх2 —24х+1 =0.
№ 21. 2х3 — Зх2- 12х + 12 = 0. № 22. 2л*3 + 9х2 —6 = 0.
№ 23. х3 — Зх2+1.5 = 0. № 24. х3 —Зл*2 —24х+10=0.
№ 25. х3 + Зл*2 — 24х - 3=0. № 26. х3-12х-10=0.
№ 27. 2х3 + 9х2— 4=0. № 28. Zv3 —Зл*2—12х + 8=0.
№ 29. х3 + Зл*2—1=0. № 30. х3 —Зх2 + 3,5 = 0.
Образец выполнения задания х3 —2х2—4х+7 = 0.
Отделим корни аналитически. Находим
/(л*)=.г 3 — 2л* 2—4.V+7. /' (х) = Зл*2 — 4л*—4:
69
Составим таблицу знаков функций /(.т):
Д' — со -2/3 2 + х
Sign /(л) — + — +
Итак, уравнение имеет три действительных корня: л^б] —х, — 2/3* х2е[ —2/3, 2]; д-3е[2, +со[.
Уменьшим промежутки, содержащие корпи, до длины, pai ной I:
Д' — 1 0 1 2 3
sign у (л ) — + + + — +
Значит, лче[-2, -1]; д-2е[1, 2]; д'3е[2. 3].
Уточним корни комбинированным методом хорд и касател]
1. л,6[-2. - 1];/(-2)<0;/(—1)>0;/"(л)=6л—4. При -2«:.v=g-имеем /"(д)<0. Для расчетов применяем формулы
V — V f(X") . С- f(Xn) _ \ /
где дл и лп — значения корня соответственно по недостатку и избытк; Полагаем л0 = — 2; л0 = — 1.
Все вычисления производим в таблице, обозначив f _/(Л'п) . г /(Л~п) /- \
1И 2п (Лп Лл)*
N 'и <я-л„ Ля2 л.3 /и.) Л|Я 1
Ли -V2 /и-) Лзн 1
0 -2 1 4 -8 1 16 9 -0.06
-1 1 -1 8 -0.11
1 -1.94 0.05 3,7636 -7.3014 -0,0686 15,0508 0.7331 -0.0045
-1.89 3.5721 -6.7513 0.6645 -0.0047
2 -1.9355 0.0002 3.7462 -7.2507 -0.0011 — — —
-1.9353 3,7454 -7.2484 0,0020 —
Ответ: д-|л — 1,935.
2. д-2е[1, 2]; /(1)>0; /(2)<0; /"(л)>0 при ЮС Для расчето) применяем те же формулы (*), полагая Ло=1, х0==2.
70
Вычисления производим в таблице:
и Л« V» xi л; л3 V3 У(л-) /(•М Ai. А2.
0 1 1 1 1 2 -5 -3 -0.4
-> 4 8 -1 -0.7
1 1.4 0.3 1.96 2,744 0.224 -3.72 -0.891 -0,060
1.7 2.89 4.913 -0.667 -0.075
э 1.46 0,015 2,1316 3.1121 0.0089 -3,4452 -0.0511 -0.0025
1.475 2,1756 3.2090 -0.0422 -0.0026
3 1.4625 0,0001 2.1389 3.1282 0.0004
1.4626 2.1392 3.1288 0
Ответ: 1.463.
3. .v3e[2, 3]; /(2)<2; /(3)>0; /"(л )>0 при 2^д%3. Для расчетов применяем формулы
где л'о = 2, х0 = 3.
Вычисления производим в таблице, обозначив
‘-Н1 /W- >(•'•" Л"); А J v'n J 1 pF
п -V» Л'а ” х„ л; Л3 /Ы /(.{.) -/(.г.) /'(<-) Ala
Л'« V3 Л'-) Л2(,
0 7 1 4 8 — 1 5 И -0.20
9 27 4 0,36
1 2.2 0.44 4,84 10.648 -0,832 1.7325 6.3488 -0.126
2.64 6.9696 18.3997 -0,9005 0.142
2 2.326 0.172 5.4103 12.8430 -0.2816 0,3971 4,728 -0.122
2.498 6.2400 15,5875) 0.1155 0,024
3 4 2.448 2.474 2.4728 0,026 1 0 5.9927 6.1207 14,6701 15,1426 -0.1073 0.0052 0.1125 4.4661 -0,0248 0.0012
2.4728
Ответ: .г3аг2,473.
71
Работа 5
Задание. 1) Отделить корни уравнения графически и уточнить о, из них методом итераций с точностью до 0,001.
2) Отделить корни уравнения аналитически и уточнить о, из них методом итераций с точностью до 0,001.
№ 1. 1) 1пл-+(л'+ 1)3=0; 2) х3 4- 2л-1 2 4- 2=0.
№ 2. 1) х-2л = 1; 2) х3 —Зх24-9л— 10 = 0.
№ 3. о 7Тй=1; 2) л-3-2л-4-2 = 0.
№ 4. 1) л— cos х—0; 2) х3 + Зл— 1=0.
№ 5. 1) 3x4-cosx4-1 =0; 2) л-3 4-л— 3 = 0.
№ 6. 1) х+In х = 0.5; /71 -V 5 + 0,4.v2 4- 0.6л- - 1.6 = 0.
№ 7. 1) 2-л = 1пх; 2) л 3-0.2л-2 4-0.4л—1.4 = 0.
№ 8. 2) Л'3-0.1 л-24-0.4л-4-2 = 0.
№ 9. 1) (2—х)ед = 0,5; 2) х34 Зх2 4- 12x4-3 = 0.
№ 10. 1) 2,2л—2д = 0; 2) л-3-0,2х2 4-0,5л— 1=0.
№ 11. 1) x24-4sinx = 0; 2) х3 —0.1х2 4-0,4х4-1.2 = 0.
№ 12. 1) 2л—lgx=7; 2) х3 —Зх2 4-6л—5 = 0.
№ 13. 1) 5л— 81пх=8; 2) х3—О.2х2 4- 0,5л—1,4 = 0.
№ 14. |) Зл—<'д = 0; 2) х3 4-2x4-4 = 0.
№ 15. 1) л(л + 1)2=1; 2) х3 —Зх24- 12л— 12 = 0.
№ 16. 1) х=(х4-1)3; 2) х3 4- 0.2х 2 4- 0,5х 4- 0.8 = 0.
№ 17. 1) л’2 = sin л" 2) х34-4л—6 = 0.
№ 18. 1) x3 = sinx; 2) х34-0,1х24 0.4л—1.2 = 0.
№ 19. 1) x = >/lg(x4-2); 2) х34-Зх2 + 6х- 1 =0.
№ 20. 1) х2 = 1п(х4- 1); 2) х3—0,1 х 2 4-0,4л—1,5 = 0.
№ 21. 1) 2л-4- 1gл = -0,5; 2) х3 —Зх24-6л—2 = 0.
№ 22. 1) 2x4-cosx=0,5; 2) х3—0.2х2 4-0.3х—1.2 = 0.
№ 23. 1) sin 0,5л* 4-1 = х2; л- > 0; 2) х3-Зх24- 12л—9 = 0.
№ 24. 1) 0,5x4-lg(x-l) = 0.5; 2) х3 4-0.2х2 4-0,5х — 2 = 0.
№ 25. 1) sin (0.5 4-х) = 2л—0.5; 2) х3 4-3x4-1=0.
№ 26. 1) lg(24-x)4-2x = 3; 2) х34-0.2х24-0,5л—1,2=0.
№ 27. 1) lg(l 4-2х)=2 —х; 2) х3 —Зх2 4-9x4-2 = 0.
№ 28. 1) 2 sin (.v—0,6) = 1.5 - л-; 2) х3-0.1л-2 4-0.4л—1.5 = 0.
№ 29. 1) .r+lg(l+л)= 1.5; 2) х3-Зх24-6x4-3=0.
№ 30. 1) x4-cosx=l; 2) х3-0,1х24-0.3л— 0,6 = 0.
Образец выполнения задания
1) 2x4-lg(2x4-3)=l: 2) х3-2х24-7х 4-3 = 0.
1) Найдем приближенные значения корней графически; для этот уравнение удобно представить в виде lg(2x + 3)= 1 — 2х (рис. 4). графика видно, что уравнение имеет один корень, лежащий в промежу
[0; 0,5]. Для уточнения его методом итераций приведем уравне] к виду x=ip(.v).
72
Функцию ф(л ) будем искать из / X /(л) соотношения ф(л )=л-——. считая. ЧТО | А-1>£?/2, где 0 = тах|/'(л)|; число А' имеет тот же знак, что н / (v) в промежутке [0; 0.5].
Находим
Рис. 4
Q= max /'(л) = 2 + в'—6 2.2895; /'(.?)>0 при О^л ^О.5.
[0:0.5]’ 2-t+3
Примем к = 2. тогда
( х ./(<) lg(2.v+3) . 1 I 1.
<р(лНл—---------------------+_=._-lg(2.v+3).
За начальное приближение возьмем .vo=0, все остальные приближения будем определять из равенства
i=i-^g(2.vn + 3).
Вычисления удобно располагать в таблице:
я Л» 2л.+3 ls(lv.+3) |lg(lv.+3)
0 0 3 0.4771 0.2386
1 0.2614 3.5228 0.5469 0.2734
2 0.2266 3.4532 0.5382 0.2691
3 0.2309 3.4618 0.5394 0.2697
4 0.2303 3.4606 0.5392 0,2696
5 0.2304
Ответ: д-%0,230.
2. Отделяем корни аналитически. Находим ./(.v)=.v3-2.v2 + 7a-+3; f (,v) = 3.v2-4.v + 7; £ = 4-21-4<0.
Составим таблицу:
л- — сс -1 0 + X
sign / (л) — — + +
Уравнение имеет действительный корень, лежащий в промежутке [—1,0].
Приведем уравнение к виду л = ф(л) так, чтобы |ф'(л)|<1 при ~1<л^0. Так как Q= max |/'(-v)|=/'(—1) = 3+4+7= 14. то можно взять А-=<10. Тогда l"k°]
73
<р(л)=л- Пусть х0 = = х - 0.1 л 3+0.2х 2 - 0.7х - 0,3 = - 0.1 х 3 +0.2х2 + 0,Зх - 0,3. | Л 0. тогда хл+|=<р(хя). Вычисления располагаем в таблице:!
п X, х2 Ля фК)
0 1 2 3 4 5 От вст: ЗаданиеУ 0 -0.3 -0,3693 -0.3785 -0,3795 -0,3796 v* - 0.380. fl) Используя уравнений с 2J Используя уравнений с 0 0.09 0.1364 0.1433 0.1440 Работа С метод итераций : точностью дс метод Ньютона : точностью дс 0 -0,027 -0,0504 -0,0542 -0.0546 к , решить систе > 0,001. 1, решить систе > 0,001. -0.3 -0,3693 -0,3785 -0.3795 -0.3796 му нелинейны му нелинейны
№ 1. ° ] ' sin (х 4-1) — у = 1.2; [2x4-cosy = 2.
№ 2. 1) ] cos (х—1) 4-у = 0,5; [ х—cos у=3.
№ 3. 1) ] [ sin х 4- 2 г = 2; [cos( у— 1) 4-х = 0.7.
№ А 1 \ ] । cosx4-У= 1,5;
4* 1) j [2х—sin ( у—0,5) = 1.
№ 5. 1) 1 । sin (х + 0.'5) — у = 1; [cos(y—2)4-х=0.
№ 6. D J । cos (х 4- 0.5) 4-у = 0,8; [sin г—2х= 1,6.
№ 7. 1) ] [ sin(x—1)= 1,3— г; [х—sin(j-4-1)=0,8.
№ 8. ° j [2г—cos(x4-1)=0; [ \ + sin г= —0,4.
№ 9. 1) [cos (х 4- 0,5)—у = 2; [sin у —2х= 1.
№ 10. 1) 1 [ sin(x4-2)-y= 1,5; [x4-cos(y-2)=0,5.
№ 11. ° 4- ' о о 4-у п Т 1ч) II *
№ 12. 1) ] [cos{ г— 1)4-х=0,5; [ у—cos л = 3.
№ 13. 1) ’ [ sin у4-2х = 2; (cos(x—1)4-у=0,7.
74
2)
2)
2)
2)
2)
2)
2)
2)
2)
2)
2)
2)
2)
tg(xy4-0.4)=x2:
0.6л 2 + 2 г 2 = 1, х > О, у > О. sin(v+ г)— 1.6х=0;
х24-у2 = 1. х>0. г>0. tg(xy + 0,l)=x2;
х24-2у2=1.
sin (.г + у) — 1,2х = 0,2; х24-у2 = 1.
tg(xy4-0.3)=x2; 0,9х24-2у2 = 1.
sin(x4-y)— 1.3х=0;
х2+у2=1.
tgxy=x2;
0,8л-2 4- 2г 2 =1. ' sin (х 4-у) — 1,5х=0.1;
л24-у2= 1.
tgxy=x2;
0.7л-2+ 2/2 =1.
sin (л 4- у) — 1,2х=0.1;
л'2 4- г 2 = 1.
lg (ху 4- 0,2)=Л'2; 0,6х24-2г2=1.
sin (х 4- г) = 1,5х—0,1; х2Ч-у2 = 1.
tg(xy4-0,4)=x2; 0,8х2 + 2у2 = 1.
Xs 14. I)
Xs 1**'
Xs 16. 0
№ 17. I)
X» 18- О
>*s 19- 1)
Xs 20. I)
cos г+л = 1,5: 2y-sin (л—0.5)= 1.
sin (у+0.5)—л = 1: cos (л -2)+з =0.
cos (у + 0.5) + .v = 0.8: sin л —2y= 1.6.
sin ( y— l) + .v = 1,3: y—sin(.v+ I)=0.8.
2.v—cos(y+ l)=0: у + sin.v = —0.4.
cos (y+ 0,5) — ,v = 2;
sin.v—2i = I.
sin(y + 2)-.v= 1.5: у+cos (л -2)=0.5.
[sin(v4?l)-y = 1; (2.v+cos г=2.
№ 21. 1) <
Xs 22. 1) < [ cosf.v— l)+y=0,8;
[ л — cos у=2.
Xs 23. [sin.v+2r= 1.6:
1) < [cos(y- l)+.v= 1. f COSA+y= 1.2:
Xs 24.
1) J
12л- - sin ( y—0,5)=2.
Xs 25. D [sin(.v+0.5)-y= 1,2: [cos(y-2)+.v=0.
Xs 26. 1) J [cos(.v+0,5)+y= 1;
[ sin у — 2л*=2.
Xs 27. D J [sin (л*— l)+y= 1.5; l л —sin(y+ 1)= 1.
Xs 28. 1) ] [sin(y+ 1)-л = 1;
[2y+cosA=2.
Xs 29. 1) | [cos( y— l)+.v=0,8;
। y—cosa = 2.
№ 30. n J i cos(.v- l)+y= I; Xiny+2.v= 1.6.
— 1
Образец выполнения задания
(sin (л-0,6)-у =1,6: 1Зл —cos у=0,9.
J sin (2л-—у) — 1,2.v=0.4.
10.8.V 2 + 1,5у 2 =1.
1) Перепишем данную систему в виде
г=sin (л—0,6) —1.6: .г=- cos у 4-0,3.
75
Отделение корней произво, графически (рис. 5). Из гра ка видим, что система им одно решение, заключен в области D: 0<х<1
ТГ-
y^Sl/)(^Q6)-f,6
Рис. 5
Убедимся в том, что мет< итераций применим для уз чнения решения системы, д чего запишем ее в следуют виде:
д = ф j (л\ у) = |cos у+0,3;
у = ф2 (д’, у) = sin (,v—0,6) — 1,
т <Ф1 л <’Ф.
Так как - = 0. —
cos (.v—0,1
^•=--sinv, ^=0, то в области D су 3 * су
имеем
f Ф
= | cos (,v - 0,6) | cos 0,3=0,2955 < 1;
ь<Р1 Л»
cep
cy
Таким образом, условия сходимости выполняются. Вычисления производим по формулам
С 1
I д-и+1 =-cosy„ + 0,3:
( у„ + j = sin (д-„ - 0,6) -1,6.
За начальные приближения принимаем ло = 0,15, у0=—2.
п 0.6 sin (v„- 0.6) cosr„ 1 3COS>- J
0 0,15 -2 -0,45 -0,4350 -0.4161 -0.1384 I
1 0,1616 -2.035 -0.4384 -0.4245 -0.4477 -0,1492
2 0,1508 -2,0245 -0.4492 -0.4342 -0.4382 -0.1461
3 0,1539 -2,0342. -0.4461 -0.4313 -0.4470 -0.1490
4 0,1510 -2.0313 -0,4490 -0,4341 -0.4444 -0,1481
5 0,1519 -2.0341 -0.4481 -0.4333 -0,4469 -0,1490
6 0.1510 -2,0333 -0,449 -0.4341 -0.4462 -0,1487
7 0.1513 -2.0341 -0,4487 -0.4340 -0.4469 -0.1490
8 0.1510 -2.0340
Ответ: л«0.151; у^-2.034.
2) Отделение корней производим графически (рис. 6). Для построения графиков функций составим таблицу значений функций yt и у2, входящих в первое и второе уравнения (табл. I).
76
Рис. 6
Таблица I
л -1,1 -1 -0.8 -0,6 -0.2 -0.4 0 0.2 0,4 0.5
Л * 1.21 1 0.64 0.36 0,04 0,16 0 0.04 0,16 0.25
0.8л2 0,97 0.8 0,51 0.29 0,032 0.13 0 0,032 0,13 0.2
1 -0.8л2 0,03 0.2 0,49 0.71 0.97 0.87 1 0.97 0.87 0,8
1-0.8л 2 1.5 0.02 0.13 0.33 0.47 0.65 0.58 0.67 0.65 0.58 0.53
г2 ±0,14 ±0,36 ±0,57 ±0.69 ±0.81 ±0,76 ±0.82 ±0.81 ±0,76 ±0.73
1.2 л -1,32 -1.2 -0,96 -0,72 -0,24 -0.48 0 0.24 0,48 0,6
0.4 4-1.2л- -0.92 -0.8 -0.56 -0,32 0.16 -0.08 0,4 0,64 0.88 1
2л —г -1.17 -0,93 -0,59 -0,33 0,16 -0.08 0,41 0,69 2.06 1,08 1.57
У1 -1.03 -1.07 -1.01 -0.87 -0,56 -0.72 -0,41 -0,29 -1.26 -1,28 -0,57
Значения для ,v можно брать исходя из следующих условий: из первого уравнения — 1 1,2.у4-0,41. т. е. —1.16^ а*< 0.5; из второго Уравнения - ^/1,25 1,25, т. с. — 1 J2<x< 1,12. Таким образом,
~L12o^0.5.
Система имеет два решения. Уточним одно из них, принадлежащее области D: 0,4<.v<0,5; -0,76<у< —0,73. За начальное приближение примем ло = 0,4; у0=—0,75. Имеем
F(.v, у)=sin (2.v - у) - 1,2л-—0,4;
<7(л,у) = 0,8л-2+1,5у2-1;
77
эо
Таблица II
п Ал 0,8Ля 2.x, - у* sin(2.v„—г,) F(.Va. у„) F х (л'я. Гл ) А. Л*, Ля
Ул 1.5г; cos (2.v„ - у„) G(.v..y.) У„) гя) Л‘. Ля
0 0.4 0.128 0.55 0,9988 0.1198 -1.1584 -0,0208 2.6197 0,2701 0.10
0,75 0.8438 0.0208 -0.0282 0.64 -2.25 0.0440 0,017
1 0.50 0.2 0.733 0.9869 -0.0131 -1.523 0.1615 3,2199 -0,0193 -0,0060
-0.733 0.8059 -0.1615 0.059 0.8 -2,199 0.0794 0.0247
2 0.4940 0.1952 1.6963 0.9921 -0.0007 -1.4502 0.1251 2,9827 -0,0080 -0,0027
-0,7083 0.7525 -0,1251 -0.0523 0.7904 -2,1249 -0,0764 -0,0256
3 0,4913 0,1931 1.7165 0,9894 -0,0002 -1,4904 0.1452 3.1673 -0.0003 -0.0001
-0,7339 , 0,8079 -0.1452 0.0010 0.7861 -2,2017 0.0013 0.0004
4 0,4912
-0,7335
Ответ: 0,491; г %—0,734.
уточнение корней проводим методом Ньютона:
Все вычисления производим в табл. II.
Работа 7
Задание. Используя метод Горнера, найти один из корней уравнения с шестью значащими цифрами.
№ 1. л3—15л+25 = 0. № 2. л3 + 21х2 + ЗО = О.
№ 3. л-3 + 25х+19=0. № 4. л3-18л2+ 50=0.
№ 5. л*3 —23л —42=0. № 6. х3 + 35х2 — 12 = 0.
№ 7. л3 + 20л—41 =0. № 8. л*3-24л2-27 = 0.
№ 9. л3-23л+47=0. № 10. л-3 + 31л-2 + 26 = 0.
№ 11. х3 + 34л+23 = 0. № 12. л3 - 19л-2+ 56 = 0.
№ 13. л3 —21л —37=0. № 14. х3 +27л2 —35 = 0.
№ 15. л-3 + 23л--42=0. № 16. л-3-27л*2+ 36 = 0.
№ 17. л-3-18л-+ 33=0. Ks 18. л-3 + 23л-2 + 32 = 0.
№ 19. л-3 + ЗЗл + 21=0. № 20. л-3-21л-2+43 = 0.
№ 21. л-3-37л -52 = 0. № 22. л-3 +39л-2-24=0.
№ 23. л*3 + 25л- -37 = 0. № о II •л + <ч СП 1 г, 3
№ 25. х3 —26х+43 = 0. № 26. л-3 +34л-2+ 27=0.
№ 27. х3 +29л+34=0. № 28. л3 —21х2 + 55 = 0.
29. л3 - 30л-41 =0. № 30. л 3 +28л-2-47=0.
Образец выполнения задания л-3- 25л+52=0.
(1)
1. Для отделения корней воспользуемся аналитическим способом:
,/(л)=.г’-25л+52; /'(x)=3x2-25; 3.v2-25=0; л-,.2= ±ч/25/3%+2.9.
Составим таблицу знаков функции /(л):
X — со — 6 -5 -3 3 + ОС
sign/(л) — — + + + +
79
Из таблицы видно, что это уравнение имеет один действительна (отрицательный) корень, причем ле[—6, —5].
2. Для уточнения корня по методу Горнера следует предварителы преобразовать уравнение с помощью подстановки л*= — у. В результа* получим уравнение
ф(у)=у3 —25у—52 = 0. (
Искомый корень этою уравнения уе[5, 6]. Отсюда следует, что пер» цифра корня уравнения (2) есть Со = 5.
3. Составим уравнение, с помощью которого определяется следующ; цифра корня, для чего выполним деление по схеме Горнера:
1 0 -25 -52 1
1 5 0 |-52 | j
1 10 50
1 15
В результате получим уравнение
Ф t (у)=у 3 +150у 2 + 5000г - 52 000 = 0. (
Определим значения многочлена <pi(v) при некоторых значени уе[0, 10] по схеме Горнера:
У 1 150 5000 -52000
8 1 158 6264 -1888
9 1 159 6431 5879
Так как <pi(8)<0, tpi(9)>0, то ye [8, 9]. Отсюда следует, что Ci=8. |
4. Для определения следующей цифры составим уравнение, коэффициенты которого можно определить из таблицы деления по схеме Горнера:
1 150 5000 -52000
1 158 6264 -1888
1 166 7592 а
1 174
Следовательно,
ср 2 (у) = у 3 +1 740у2+ 759 200у -1 888 000=0.
(4)
80
Определим значения многочлена ср2( 10] по схеме Горнера: у) при некоторых значениях
г 1 1740 759 200 - 1 888000
1 762 684 762 684 -362632
з 1 1743 764429 405 287
Так как <р2(2) = 0, ср3(3)>0, то уе[2, 3]. Отсюда следует, что С2 = 2.
5 Составим уравнение для определения последующих цифр, коэффициенты которого можно найти из таблицы деления по схеме Горнера:
С2=-
1 1740 759200 -1 888000
1 1742 762684 -362632
1 1744 [766 172
1 1746
Таким образо.м.
Фз (у)=У 3 +17 460г2 + 76 617 200j - 362 632 000 = 0. » (5)
Разделив теперь модуль свободного члена на коэффициент при у, получим следующие три цифры искомого числа:
362 632 000/76 617 200 % 4,73.
В результате находим корень данного уравнения: -5,82473.
Работа 8
Задание. Используя метод Лобачевского, решить уравнение с точностью до 0,001.
ЛЬ 1- л-4 + 6х3+1 lx2 —2.v—28=0. № 2. л-4 + 5л-3 + 9л2 + 5л-1=0.
ЛЬ 3. л4 + Зх3 + Зл-2 —2=0. № 4. л-4 + л-3-7л2 + 8л-6=0.
Ль 5. л4-10л3+16л + 5=0. № 6. л4 —Зл3—4л2 —л —3=0.
Ль 7. л4 + 4л3 + 4л-2 + 4л-1=0 № 8. л4 + 6л-3+ 13л-2+ Юл + 1 =0.
Л» 9- л-4 + л3-4л’2+16л-8=0 № 10. л*4—л3 —4х2—11л —3=0.
Ла И- л4—бх2—12л —8 = 0. № 12. л-4 + 4л3 + 4х2-4=0.
Лй 13. л-4 + л-3 + 2х+ 1 =0. № 14. х4 + 2л 3 + л2 +2л+ 1=0.
Л'й 15. л4 + 3л'2—4л—1 =0. № 16. л-4 + Зл-3 + 8л-2-5=0
Ль 17. л4 —6х3+11х2 + 2л —28 = 0. № 18. л 4-5 л3+ 9 v2-5л-1=0.
л» 19. л4 —Зх3 + Зл*2 —2 = 0. № 20. л4-л3-7л-2-8л-6=0.
ль 21. л4-Юл2- 16л + 5=0. № 22. л4 + Зл3 + 4л-2 + л-3=0.
Лй Xi* 23. л 4 - 4 v 3 - 4л2 - 4л- - 1 = 0 № 24. л4+2х3 + Зх2 + 2х—2 = 0.
Jib Хп 25. л4 —6л 3+13х2—10.v+1 =0. № 26. л4-Зл-2 + 4л-3 = 0.
ль Хр 27. л-4-6л 2 + 12л-8=0. № 28. х4—4х3+4х2—4=0.
ль 29. л4-х3-2л+ 1=0. № 30. л 4 - 2л 3 + х 2 - 2х + 1 = 0.
81
Образец выполнения задания a4 —2.v?+ .v—1,5=0 Вычисления помещаем в таблице:
т 2т «о «1 «2 "л «4
0 1 1 -2 0 1 -1.5 Я
1 2 1 4 1 1 2.25 Я
2 4 ] 14 -2,5 -3.5 5.0625И
3 8 1 1.96 102 0,05 10 2,01 • 102 6.25 98 10.125 114.375 12.25 25.3125 37,5625 25.629 В
] 2,01 I02 1.1438 -102 3,7562-10 2.5629 • 10 Я
4 16 1 4,0401 • 104 -0,0229 -104 1.30828 -104 -1,50999-104 +0.00513 -104 1.4109 -103 -5.86629 -103 6 5685 1021
4,0172 -104 -4.4520-103
-0.19658 -104
1 4.0172 -104 -1.9656 -103 -4.4520 -103 6.5685 Ю21
5 32 1 1,6138 -109 0 3.8644 -106 35.7691 107 0-10’ 1,98203 -107 0.25825 107 4,3145 -1051
1 1,6138 -109 3,6155 -108 2.2403-107 4.3145-105 1
6 64 1 2.6044-1018 13,0718- Ю16 -7,2308 -10*6 0-1016 5.0189-1014 — 3.1198- Ю*4 1.8615- ЮпII
1 2,6044-1018 5,8410 Ю16 1.8991 • 1014 1.8615-10*«1
7 128 1 6.7829 1036 3.4117 -1033 -0.9892 -1033 3.6066 • 1028 -2.1746-1028 3,4652 1022 Я
1 6.7829 -1036 2.4225 -1033 1.4320-1028 3.4652 -1022’]
8 256 1 4,6008-1073 5,8685 -1066 -0.1943 -1066 2.05062 • 1056 — 1.67899 -1056 1,2008- 104|
1 4.6008-1073 5,6742 • 10м’ 3.7173 -105 5 1.2008 -1045|
J
82
Предо. iMceaue
1» 9 «1 «2 «3
512 1 2.1167 - Ю147 3.2197 - Ю133 -0,0003 -10*33 1,3818- 101И -13.6272 -10111 1,4419 -Ю90
1 2.1167-Ю147 3,2194 -10*33 — 1.2245 • 10'12 1.4419 - Ю90
10 1024 1 4.4804 -10294 1,0365 10267 0 1.4994 -10224 -0,9284 -10224 2.0791 -10,8°
1 4,4804 -10294 1.0365 -10267 0.5710-10224 2,0791 • 10*80
1. 1g| л-j | = -J- • 1g2,1167 IO147 = — -147.3257 = 0.2877.
|.v, |=1,939; .v, = 1,939.
1 3'’194-10133 I
’ 1еЬг2|=^-,627ЙГ^=^'-,4 + 0-5077 -03257Ь
= - (- 13,8180) = - 0,02699 = T,97301.
|л*21=0,9397; ,v2 =-0,9397.
3. л'1 +-V2 + V3 + -V4 —2; Xj=u+iv; Xt^u—iv; .v3+.v4 = 2-1,939 + 0,9397=1; 2и=1; u=0,5; и2 + г2 = г2.
0,1590 - 0,5077)=
=^ * (- 43,3487) = - 0,08467 = T,91533;
r2 = 0,8228; v 2 = r2 - и2 = 0,8228 - 0,25 = 0,5728;
v— 0,7568; л-3.4 = 0,5 ±0,7568-/.
Ответ: .v, ъ 1,939; л2% -0,940; л 34 2= 0.5 ±0.757/.
Работа 9
Задание. Используя метод выделения квадратного множителя (метод Хичкока), решить уравнение с точностью до 0,001.
1. 2л-4 + 0,2л3+1,4л2 + № 2. л4 + 0,77л3-1,002л2 + 6,164л-
+ 2.3л-1.5 = 0. -1.6=0.
3. л4 + х3 + 2л-+ 1=0. № 4. л 4 + 1,4л3 -2,26л2 + 0.5л-
v -3.5 = 0.
Л5 5- л-4 + 2л 3 + л 2 + 2л +1=0. №6. л-4 + 2,5л 3 - 0,4л2 + 2,6л+
+7,2 = 0.
7. л4 + 4л3 + 4л- + 4л-1=0. № 8. л4 + 2л3-0,4л2+ 1.6л +
w +0,64=0.
83
Хе 9. л-4 + 4л-3 + 2,2л'2 + 6.4л + № 10. л4 —8л3 —5л2-12л + 2,25=Я
+ 2.56=0.
№ 11, л4+10л3+1.8л2 —31л + № 12. л 4 - 6л3 - 1,2л2 - 14.4л- +
+ 9,61 =0. + 5J
№ 13. л 4 + 8л 3 - 16 v 2 + 24.492л - Xs 14. л4 —6л3 —7л2—18л—1 =0.
-1=0.
№ 15. л4-2л3-5л2-10л-1=0. Ха 16. л4 + 6л3 —5л2 + 24л+2 = 0.
№ 17. л4-8л3- 10л2-40л + 7 = 0. Ха 18. л4 + Юл3 —Зл2 +36л+2=0.
Xs 19. л4 + 6л3 —16л2 + 24л —2=0. Ха 20. л 4-8л’-5л2-42л+ 6 = 0.
№ 21. л4 - 2л3 + 2.2л-2 + 2л -4 = 0. Хе 22. л4 + 4л3 + 7.2л2 + 4л-1=0. •
№ 23. л4-4л 3 +5.2л 2-4 = 0. Хе 24. л4 + 2л 3 + 6,2л 2 + 10л + 4=0.
№ 25. л 4 - 2 v3 + 4.2л2 - 8л - 1 = 0. Хе 26. л4-4л-3 1 л2-Юл-0.8=0.
№ 27. л4 —4л3—19л2 —26л+1 =0. Хе 28. л 4 - 4л3 + 4.2л2 - 10л - 4=0,
№ 29. л-4 + 4 л3 - 19л2 - 10л- + 1=0. Хе 30. л 4 + 4л3 - 2л2 + 14л + 3,1= 0.
Образец в ы п о л н с н и я зад а и и я \-4 + 4л3+4.8л2 + 16л-1=0.
Отделим какие-нибудь два корня уравнения; для этого опред знаки функции /’(х) = л'4 + 4л'3 + 4.8л'2 +16v-1 при некоторых знамени
л -4 —эд -3 _2 — 1 0 1 11
sign f + — — — — 4-1
Итак, один корень принадлежит промежутку [0, 1]. а другой — npoMi ку [ 4. -3].
Примем Л'^0,5; л'2%—3.5; тогда за начальное приближение
ратного трехчлена — делителя данного многочлена — можно взять
т/о(л) = л-2 + (-0,5 + 3,5) л-- 3,5 • 0.5=л 2 + Зл - 1.75,
1де ро = 3. </о=-1,75.
Уточнение коэффициентов делителя производим по формулам
, . Д„ Д„
А +1 —Рк+Ль; hk ——
Д* Дх
где
Значения производных находятся по формулам
84
P'p(p^ 4k)=PkRk-Sk: P'q(Pk.(ik)= -R^
Q'p(p^ Як)=Як^к: Qч(/4. Як) = -Sk.
Величины Р(рк< Як) и Q(pk. Як) определяются из тождества
/М = Як М ‘ Lk (л ) + Рк (рк, Як) v + Qk (Рк- Як)-
а величины Rk и Sk — из тождества
Lk ( v) = Як (-'*) L 1к (л-) + Rk л' 4- Sfc.
Все расчеты можно оформить в виде двух вычислительных таб-пии. одна из которых (табл. I) служит для двукратною деления на ^(л) по схеме Горнера, а другая (табл. II)—для вычисления поправок Л* и 1к-
Таблица I
к 1 4 А8 16 1
0 II II II II II II 1 1 Ch м? 1 1 ,1 L- L “ । । О -3 1.75 3.55 1.75 5.30 = 5» -10.65 1.75 7.1 =Го 6.2125 5.2125 = Со
1 -3.9 0.15 -3.9 0.15 1 1 -3.9 0.1 -3.9 -3.8 = Я, -0.39 0.15 4.56 0.15 4.71=5, -17.784 0.015 -1.769 = Р, 0.684 -0.316 = 0,
2 -3.79 0,23 - 3.79 0.23 1 1 -3.79 0.21 -3.79 -3.58 = /?, -0.7959 0.23 4.2341 0.23 4.4641 = 5, -16.0472 0.0483 0.0011 = Р, 0.9738 -0,0262 = 2г
3 . _ — 3.7889 0.2361 — 3.7889 0.2361 I 1 -3.7889 0.2111 -3,7889 -3,5778 -0.79984 0.2361 4.23626 0.2361 4.47236 -16.05077 0.04984 -0.00093 1.00018 0.00018
4 -3.78885 0.23607 1 -3.78885 0,21115 -0.800016 0,23607 4.236054 -16.04977 0.049846 0.000076 1.000005 0.000005
85
Табл
к Рк Л* Рк Р'Др* Чк) Р'ч(Рк'. Чк) Ад Ал
Чк Sk Qk Q'APk* Чк) Q'4(Pk‘ Чк)
0 3 -2 7.1 -11.3 2 52,89 48.055
-1.75 5,3 5.2125 3.5 -5,3 83.751 и
I 3,9 3.8 -1,769 -19.53 3.8 89,82 -9,533 -0,
-0,15 4.71 -0.316 0.57 -4.71 -7.180 -оз
2 3,79 -3.58 0.0011 -18.0323 3.58 77.55 -0.0889 -0,1
-0,23 4.4641 -0.0262 0.8234 -4.4641 -0.4715 -0,1
3 3,7889 -3.5778 -0,0093 -18.0283 3,5778 77.607 -0,00352 -0j
-0.2361 4.47236 0,00018 0.8447 -4.47236 0,00246 0j
4 3,78885 -0,23607
Итак,
/'(л*)%(л'2 + 3,78885л —0,23607)(л*2+0,21 11 5л+4.23605)=0. j
Для определения корней остается решить два квадратных уравя л-2 + 3,78885л-0,23607 = 0; л1>2= - 1,894425 ± У3,588846 +0,23607 = — 1,894425+1,955739; %-3,8502; х2^0,0613;
л2+ 0,21115л*+4,23605 = 0; л3.4 = -0,105575±х/0,01115-4,23605= = —0,105575 + 2,0555/; .v3.4* -0.1056 ±2,0555/.
О т в с т: д-j * - 3,850; л*, % 0.0613; лУ4 * - 0,106 + 2,055/.
Глава VI
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЧИСЕЛ И СОБСТВЕННЫ ВЕКТОРОВ МАТРИЦ
Работа 1
Задание. Найти собственные числа и собственные векторы мат методом непосредственного развертывания с точностью до
86
/1 — 1 2\ / -1 1
14-1 21 j* ' ' \2 о з) 1 • № 2. A = 1 4 4 1 2 NJ 1
3 1 l\ 3 2
я-1 А = ( 1 2 3 )• № 4. A = 2 4 1 1 *
-2 5- 2/ -1 0 — 2)
5 2 5' 6 3 8A
я 5- |= ( -2 -1 2 -3 — 8 _? 1 № 6. A = 3 2 -1 0 3 -4; 1 -
1 4 1 2 3'>
7 | — -1 1 3 )’ № 8. A = ( 7 -1 5 1 .
/ft/*1 1 1 2 - 1/ 2 3 -3/
1 -1 — I / 1 1 - -4
Кв 9. J == 0 6 -6 -3 2 — 2 1 № 10. A = | 1 -3 1 2 I. 4/
'25- -6\ /3 1
Jft П- Л ~ 1 4 3 - -1 • № 12. /1= I [ 2 — 1 3 )
4-l 2 -2/ \4 1 1/
<21- /-2 4 3\
№ 13. .4 = 1 1 2 1 * № 14. A = I 5 1 1 -
4-1 2 о J \ 2 -4 -1 1/
f-2 1 -l> / 2 3 2\
.Vs 15. .4 = 0 4 2 1 . № 16. A = I 4 — 6 -4 ).
k-1 2 3> \-l 4 1J
<-5 -4 4> /-1 3 - l\
№ 17. .4 = 2 3 1 1 1 . № 18. A = 1 4 — 2 1 1
к 5 f > o; \ 3 — 2 V
( 3 1 o> / 6 -3 < 5\
.Vs 19. .4 = 1 4 2 3 № 20. A = 1 3 । 5
k-4 2 -1; \ —2 4 -37
I 1 —2 2> / i 1 -- 4\
№ 21. .4 = -2 1 1 1 № 22. .4 = 1 — 2 4 1
\ 3-1 1 2y \-3 0 3/
№ 23. I = ) / I 2 -Г /-I 3
-2 4 — 6 № 24. A = 7 2 4
\-l 0 — 2/ \ 5 1 2)
/-3 1 O' /-4 1 —
№ 25. j = 4 - 1 3 № 26. A = 1 2 — 2 3 •
\ 6 2 3, \ 3 1 3/
27. = / 3 1 -5' / 2 1 —
-3 ! 1 № 28. .4 = ( —2 3 6 1 *
\-4 3 -4, \ 1 1 - 2>
* 29. j = /0 3 7 1 4\ 4 ). № 30. .4 = /1 ( 9 2 1> 1 2
\2 1 - 2/ \2 - -1 0;
87
Образец выполнения задания
/ 2 — 1 3\
Д= -2 4 5 ).
\ 3 2—1/
1. Составим характеристическое уравнение матрицы, корнями рого являются собственные числа матрицы:
_э
= 0.
Непосредственно развернув определитель третьего порядка, по.
(2 — Х)(4 — X) (— 1 -X)- 15-12-9(4-1)- 10 (2 — А) — 2 (— 1 -Х)=0,
откуда после раскрытия скобок, приведения подобных членов и ножения обеих частей уравнения на — 1 имеем
X3-5Х2 - 19X4-89 = 0. 1
Полученное уравнение решим с помощью метода Ныотона| уточнения
корней, предварительно отделив корни. Находим ,/(Х) = X3 — 5Х2 — 19Х + 89; f (X) = ЗХ2 - 10Х - 19;
Составим
4.2 ? 3 ’ М
таблицу знаков функции /‘(X):
4.7
4- оо
sign/(X)
Из таблицы знаков видим, что уравнение имеет три_ действии корня: Xig] —х уточнения один из них. например Х2.
Уменьшим промежуток [-1,2; 4,7]. i
Для этого вычислим значения функции /(X) в промежутка: ./(2) = 39 > 0; /(3) = 14 > 0; /(4) = - 3 Х2 содержится внутри промежутка [3. 4].
Уточнение корня производим по формуле
— 1.2]: Х2 е [ — I.2: 4.7]; Х3 е [4.7; 4- х [. Выберем;
в котором находится этот некоторых D. Итак,
KI
к<
X
3
2
'п I !
в*л
•w м
Для выбора начального приближения Хо определим знак 1 производной (X) в промежутке [3,4]; имеем /"(Х) = 6Х—10; f при З^Х<4; значит, Хо = 3.
Для вычисления значений функций и ее производной будем в зовать схему Горнера. Корень определим с четырьмя верными тичными знаками.
88
рсс вычисления располагаем в трех таблицах. В табл. I вычисляем ,иия функции /(X). в табл. II—значения производной /'(Z). з*13 габ |. ill производим уточнение X. а ® тс, Т а о л и ц а 1
п к 1 -5 -10 89
0 3 3 - 6 -75
1 — 2 -25 14
1 3.63 3.63 4,9731 -87.0224
1 -1.37 -23.9731 1.9776
3.75 3.75 - 4.6875 -88.8281
1 -1.25 -23.6875 0.1719
3 3.762 3.762 - 4.6574 -88.9991
1 -1.238 -23.6574 0.0009
4 3.7621 3.7621 - 4.65710 -89.0004
1 - 1.2379 -23.65710 - 0.0004 Таблица II
н 3 -10 -19
О 3 9 - 3
3 — 1 — 22
1 3.63 10.89 3.2307
3 0.89 -15.7693
2 3.75 11.25 4.6875
3 * 1.25 -14.3125
3 1 3,762 11.286 4.8379
3 1.286 -14.1621 89
Таблица
н /'(М
0 3 14 -22 -0.63
1 3.63 1.9776 -15,7693 -0.12
2 3,75 0,1719 -14.3125 -0.012
3 3.762 0,0009 -14.1621 -0.00006
4 3.7621
Итак, Х2 % 3,7621.
Для определения двух других собственных чисел решим квадрат уравнение, полученное при делении многочлена /(X) на X-3.7621:
X2— 1,2379Х —23,6571 =0; X,. 3 = 0,61895 + ^/673831 + 23,6571 = 0,61895
+ 7^4,0402 = 0,61895 ±4,90302; X, =4,2841; Х3 = 5,5220.
2. Для определения собственных векторов, соответствующих найде ным числам, воспользуемся системами линейных уравнений, полученньп из равенства (Л —Х£’)^=0.
При Х, = — 4,2841 получим систему
6,2841л,- х2 + Зх3 = 0,
-2v, + 8.2841x2 + 5x3 = 0, Зх,+2х2 +3.2841х3 = 0.
Эта система линейных однородных уравнений является неопределенно так как ее главный определитель равен нулю. •
Решение можно найти, используя любые два уравнения систе: например второе и третье:
Л'| _ Л'2
8.2841 5 ~ = ~5 ^2
2 3.2841 3,2841 3
•Уз
-2 8.2841
3 2
или
17,2058 21,5622 -28.8523
Для того чтобы норма j| У, || вектора была равна единице, раздел все его координаты на наибольшую из них по абсолютной величи; тогда получим У, = С(-0,597; -0,746; 1).
Аналогично определяются два других собственных вектора.
При Х2 = 3,7621 имеем:
— l,7621xi—х2 + Зх3 = 0, -2л,+0,2379х2 + 5хз=0, Зх,+2х2—4.7621х3 = 0;
90
0.2379 4
2 -4.7621
AS
—5 2 ~ ~—2
-4,7621 3 3
0.2379
-11,13229 5.4758 -4.7137
X2 = C (1; -0.492; 0,423).
9
При ^з = 5.5220 имеем:
- 3.522л-l-.v2 + 3.vJ =0, -2л-1-1.522л-2 + 5л-з = 0, Зл1+2л-,-6.522л-3=0:
Л'|
-0.0735
1.956 8.566
С(- 0.00858;
0.228;
О т в е г:
'"(2 Л.3
-4,284 -0.597 -0.746 1
3,762 1 -0.492 0.423
5,522 -0.00858 0.228 1
Работа 2
Задание. Используя метод Крылова, найти собственные числа и собственные векторы матрицы. Собственные числа определить с четырьмя верными цифрами, а собственные векторы — с тремя десятичными знаками.
/1 1,5 2 5 3,5\
№ 1. л = f 1.5 2.5 1 2 2 1 1,6 ] 1,7 Г
^3.5 1.6 1.7 I /
/1 1.2 2 0,5\
3. А=1 ' 1.2 1 0.5 1 1
ft 1 2 0,5 2 1,5 Г
^0.5 1 1.5 0.5/
/2 1 1.4 0.5\
Л'п /4 = 1 1 1 0.5 1 1’
1.4 0,5 2 1.2 Г
^0.5 1 1.2 0.5/
/2 1,5 3,5 4,5\
Л® 7. А — \ 1.5 2 2 1.61
3,5 2 2 1,7 Г
U.5 1.6 1,7 2 /
/1 1.2 2 0.5\
1 1 № 2. .4= 1 0.4 0.4 2 12 1 1.5 Г
\0,5 1.2 1.5 1 /
/ 2,5 1
№ * —0.5 1.2
\ 2 0.4
-0,5
1,2
-1
1,5
' 1 0.5 1,2
0.5 2 -0,5 0 1
№ 8. Л = | 1.2 -0.5 -1 1,4 ’
-1 0 1,4
91
1.2 0.5 2 1 /0,5 1,2 1 0,9\
№ 9. /4=( 0.5 1 0,8 2] 2 0.8 1 1 ' № 10. - :-2 2 0.5 0.5 1 1.2] 1 Г
1 2 1 I 2/ \0,5 1.2 1 2.2/
/1.2 0,5 2 1\ /9 1.5 4.5 5,5\
№ И. [ 0,5 2 1 0.6 0.6 1 2 ] 1 / № 12. 4= h5 1 4.5 3 2 2 3 1,6] 1.7 ’
\5,5 1,6 1.7 3 /
/1.6 1 1.4 1 \ /2.4 0.5 2 1 \
№ 13. Я = | / 1 1.4 1 0.5 0,5 2 1.21 • № 14. Л 1 0,5 Л= 2 1 0,8 0,8 1 2 ] 0,5 Г
\1 2 |,2 0.5/ \1 2 0,5 1,2/
/0.5 1,2 2 1 \ /1.8 1.6 1,7 1,8\
№ 15. /1 = 1 к2 1 э 2 0.5 0.5 1 1.2] 0.5 № 16. А- Е6 1 1,7 2.8 1.5 1,5 3.8 1.3] 1.4 '
\! 1.2 0,5 1.6/ \ 1.8 1.3 1.4 4,8/
/1 1,5 1.2 0.5\ / 1 0.5 -0.5 1 Ш
№ 17. А = / 1.5 1.2 2 0.4 0.4 1.5 2 ] 1.41 * № 18. . 0.5 - Я= -0,5 -1 2 7 1 0 (1
\0.5 2 1,4 1,3/ \ 1 0 -1,5 2 /
/1 1.5 0,4 2 \ /1.9 1,6 1,7 1.8\
№ 19. А = | 1,5 1 0,4 -1,2 1 1 2 0.5] 1.2 Г № 20. 1-1 к6 Л-1 1.7 2,9 1.6 1,6 3,9 1,3] 1,4 Г
\2 -0,5 1,2 2.5/ \1,8 1.3 1.4 4,9/
/1.5 1.6 1.7 1,8\ /0.5 1 1.2 2 \ i
№ 21. А — / 1.6 1.7 2.5 1.2 1.2 3,5 1.3] 1,4 № 22. Л = 1 1.2 1.2 - -0.5 -0,5 1 - 0,6] I 1 Г 111
\1.8 1.3 1.4 4.5/ \з 0,6 - -1 L2/ |
/1.6 1,6 1,7 1,8\ /2 1.6 1,7 1,8\'
№ 23. А = 1 1,7 2.6 1.3 1.3 3,6 1.3 1.4 • № 24. А= к6 I 1,7 3 1,7 1.7 4 1.3] 1,4 Г
\ 1,8 1.3 1.4 4.6/ \ 1.8 1,3 1,4 5 /
/0.5 1,4 2 1 \ /1 1,2 0.3 2 \
№ 25. А = 1 1.4 1 2 1 0 0 2.5 1,5 2 - № 26. /4=1 1,2 1 0.3 0.5 1 1 0,7 ’ -0.4 1
\1 1.5 2 1 / \2 0,7 1 1.5/
/1.7 1,6 1,7 1,8\ /2 1,7 1,6 4.5\
№ 27. А — / 1.6 1.7 2,7 1,4 1,4 3,7 1.31 1.4 । 1 ’ № 28. '-7 1,6 2 2 2 1 3.5] 1.5 ’
\ 1,8 1,3 1,4 4.7? \4.5 3.5 1,5 1 /
/1,6 0.4 1 2 \ /3 1,7 1,6 5,5\
№ 29. /4 = / 0.4 1 1 0.5 0.5 0 1 ' 0.2 • № 30. И-Р’7 1 2 2 3 4,5 ] 1,5 Г
\2 1 0,2 0.5/ \5,5 4,5 1,5 1 /
Образец выполнения задания
/2.2 1 0,5 2 \
А = j 1 1 0.5 1,3 2 2 0,5 1 ] 1,6 Г
\- 1 1,6 2 /
92
IT 1 Для определения коэффициентов характеристического уравнения X4 — Pi V — р,Х2 — р3Х — р4 = О
рОнм последовательность векторов: произвольный вектор; Bt = AB{i: В2 = А В{; Bi = AB2: B4 — ABS. рИц векторы Во, В{, В2. В$ окажутся линейно независимыми, то 0)ффиипеиты рь р2. рз, р4 определяются из решения системы линейных ^равнений. соответствующей равенству В4=р\В$+р2В2 +Р3В1 -ip^Bo. Систему линейных уравнений будем решать с помощью схемы Халецкого. Все вычисления располагаем в таблице. Т а б л и и а !
.1 я. fi2 в}
2.2 1 0.5 2 2.2 10.09 52.373 291.0006 356.6636
1 1.3 2 1 0 1 6.5 41.84 239.605 288.945
0.5 э 0.5 1.6 0 0,5 6.55 37.64 220.7825 265.4725
2 1 1.6 2 0 2 10,20 57.56 321.930 391.69
Таким образе . ' Опредслени Ценного хар; х Ранее мето; 1 1 7 7 10.00 52.373 291.0006 356.6636
0 1 1 6.5 41.84 239.605 288.945
0 0.5 3.3 1 5.066667 30.6 36.666667
0 2 -2.8 - 11 933333 1 6.00000 7.00000
1 6 7
1 0.2 1.2
1 - 12.735 - 11.735
1 )М, с с 1кте[ 1ОВ. каракте -6Р-обстве! эистиче ристичес 0.2??+1. ных чи ского ур кое уравнение 2,735л —2.7616 сел матрицы авнения каких 2.7616 матрицы = 0. состоит 4-ЛИбО ИЗ [ 3.7616 имеет вид (*) в решении >ассмотрен-
93
Решение уравнения (*) методом Лобачевского приведено в
Табли
HI 2я "о «1 «2 "л «4
0 9 ! — 6 -0.2 12.735 -2,761а
1 2 1 36 ‘ -0,4 0.04 + 152.82 -5.5232 162.1802 -1.1046 7.6264
1 3,64-101 1.4734-102 1.6108 -102 7,6264]
2 4 1 13.2496-1 О2 -2.9468 -102 2,1709 -104 - 1,1727-104 -0.0015 -104 2.5947 -104 -2.2247-104 58.162-1
1 1.0303-103 9.967 I03 2.3700 -104 5.81621
3 8 1 1,0615- 10е —0,0199 -10" 9,9341 I07 —4,8836-107 5.6169-108 -0.0116 -108 33,828-
1 1.0416 -106 5,0505 -107 5.6053 -108 3.38281
4 16 1 1.0849 -1012 -0,0001 • 1012 2,5508 -10*5 — 1.1677 - Ю15 3.1419-1017 -0.0000-10*7 11.443-1
1 1.0848 1012 1,3831 -10*5 3.1419- 1017 1.1443
5 32 1 1.1768 -1024 1,9130 • 1034 — 0,6817-1О30 9.8715 -1034 0 1.3094’
1 1.1768 Ю24 1,2313 - Ю30 9.8715 -1034 1.30944
6 64 1 1.3849 -1048 0 1,516! - IOft0 —0,2334-1060 9.7447 • I069 0 1,71451
1 1.3849 -1048 1.2827-10**° 9.7447-1069 1.71451
7 123 1 1,9179-1096 0 1.6453 -1 О'20 -0,0270 -10*20 9.4959-10*39 0 2.93954
1 1,9179-109ь 1.6183-1О120 9.4959- 10'39 2.9395j
8 256 1 3.6783-10192 2.6189 -10240 -0.0004 -10240 9.0172-10279 8.64071
94 1 3,6783 Ю192 2.6185 - Ю240 9.0172 -102 79 8,64071
Цмесм
|ц |л, 1=2- 1g 3.6735 • 10’92 = 4- 192,5657=0.7522; |Х, | = 5,652;
256 256
I ? 61ЗХ • I О240 I
lg|X,|= -Igil— =— (48 + 0.4180-0.5657) =
" 256 3.6783 10 92 256 v '
= Йб’47,8523 = °'1869; lX2l=L538;
1 9 0172 IO279 1
,«|X2l = ^lel6i8F^ = 256 <39 + 0-9550-°-4,8<,) =
= 2^ 39.537 = °,! 544; l^^1’427-
|^х^^|8^^4(-167+о-9366-°-9550>=
=2- (- 167.0184) = - 0,6524 = 1,3476; |Х4|=0,2226.
256
Непосредственной подстановкой найденных корней в уравнение определяем знаки корней; получим
>4 = 5,652; Х2 = 1.538; Х3=- 1.427; = 0,2226.
Уточним последние цифры найденных значений корней, используя для вычислений схему Горнера (см. табл. III).
Табл и па III
1 -6 -0.2 12.735 -2,7616
5.652 5.652 -1.9669 -12.24752 2,7584
1 -0,348 -2,1669 0.48768 -0.0052
5.653 5,653 -1.96159 -12.21947 2.9143
1.538 1 -0,347 -2.16159 0.51553 0.1527
1.538 -6.86256 -10.86222 2.8808
1 -4.462 -7.06256 1.87278 0,118
1.540 1,540 -6.8684 -10,8853 2.8485
1 -4.46 -7,0684 1,8497 0.0869
1.544 1.544 -6.88006 -10.9316 2,7844
1 -4.456 -7.08006 1,8034 0,0228
95
Продолжение
1 -6 -0.2 12,735 -2,1
1.545 1.545 -6.88298 -10.9432 2,4
1 -4,455 -7.08298 1.7918 0,(J
1,546 1,546 -6,88588 -10.95477 2,1
1 -4.454 -7.08588 1.78023 -0,0|
- 1,427 -1,427 10,59833 -14,83842 з,о!
1 -7.427 10.39833 -2,10342 oJ
-1.425 -1.425 10.58062 -14.79239 2,9;
1 -7.425 10.38062 -2,05739 0,1|
-1.421 -1.421 10.54524 -14,70059 2.J
! -7.421 10.34524 -1,96555 0.J
-1.420 -1.420 10.5364 -14,6777 2 Л
1 -7,420 10.3364 -1,9427 - о,о]
0,2226 0.2226 -1.28605 -0,33079 2,1
1 -5.7774 -1.48605 + 12.40421 -o,oj
0.2227 0.2227 -1.286605 -0.33107 2,7
1 -5,7773 -1.486605 12.40393 o,oj
Следовательно, собственные числа матрицы таковы:
X, = 5,652; Х2= 1,545; Х3=-1,420; Х4 = 0,2226.
3. Собственный вектор Д',-. соответствующий собственному чи< определяется по формуле
3’
где коэффициенты при ранее найденных векторах /?0, В> находятся из равенства
£Р4 = В р
Х-л; P/0?v
96
лконча гельныс значения собственных векторов должны иметь норму nV.Hr равную единице.
Все вычисления приведены в табл. IV.
Таблица IV
Ы, ft. А ft<A -V,
0.4877 -4.7672 -3.5113 52.373 44.5822 0.879
- /S') 0 -2.1669 -2.2620 41.84 37.4111 0.753
0 -1.0334 -2.2794 37.64 34.2772 0,690
0 -4.3338 - 3.5496 57.56 49.6766 1,0
1.7918 -15.5826 -44.9510 52.373 -6.3688 1
0 -7.08298 -28.9575 41.84 5.7995 -0.9U
1 .?*? 0 -3.5415 -29.1802 37.64 4.9183 -0.772
0 -14.1660 -45.4410 57.56 -2.0470 0.321
-1.9427 22.7400 - 74.8678 52.373 -1.6975 0.293
0 10.3364 -48.2300 41.84 3.9464 -0.681
— 1и 0 5.1682 -48.6010 37.64 -5.7928 1
0 20.6728 -75.6840 57.56 2.5488 -0,440
12.4042 -5.2692 — 58.2940 52.373 3.2140 -0.740
П '’’’'V» 0 - 1.4860 — 37.5531 41.84 2.8009 -0,645
0 ’ -0.7430 -37.8420 37.64 -0.9450 -0,218
0 -2.9720 — 58.9295 57.56 -4.3415 1
Работа 3
Задание. Используя метод Данилевского, найти собственные числа и собственные векторы матрицы. Собственные числа определить с четырьмя верными цифрами, а собственные векторы — с тремя десятичными знаками. Прн выполнении работы воспользоваться вариантами работы 2.
Образец выполнения задания
1- Коэффициенты характеристическою уравнения матрицы А опре-Дс1Я!отся как элементы первой строки матрицы Фробениуса А подобной Данной матрице А. Матрицу Р найдем в результате трех преобразований п°Добия:
р-м ;1 • л/;1 - л/;1 а л/з л/2 • л/,.
преобразования осуществляются в табл. 1.
^1258
97
Табли
Строки \ л/ АГ Элементы матриц 1 а 1
1 -> 7 1 0,5 2 5.7
2 1 1.3 2 1 5.3
3 0.5 2 0,5 1.6 4.6
4 2 1 1,6 2 6.6
1 \ И) -1.25 -0,625 0.625-1 21.25 -4.125
5 2 1.575 0,6875 0.3125 1,375 3,95 3.6
6 1 -1.5 0,05 1,25 1.5 -1,7 -2,
7 1.6 -0,125 1,6875 0.3125 0.975 2.85 2,
8 2 0 0 1 0 1 0
Т 1.45 4,125 4.375 2.81 12.76
II Л/, АЛ'\. -0,351515 0.242424-1 - 1.060606 -0,681212 -0.093333
9 1.45 1,333333 0.166667 -0,416667 0,906667 1,990000 1.ОД
10 4,125 -1,517575 0.012121 1.196970 -1.534061 -1.842546 -1, 1 i
11 4,375 0 1 0 0 1 0
12 2,81 0 0 1 0 1 1
10' -4,326668 4.666666 7.143334 -5.013335 2,469998
III Х. М, -0.231125-1 1,078582 1.651001 -1.158706 0,570878
13 -4,326668 0.308167 1.604776 1,784667 -0.638274 2.443002 2.71
14 4,666666 1 0 0 0 1 0 1
15 7.143334 0 1 0 0 1 1
16 -5,013335 0 0 1 0 1 1 ]
13' 6.000002 0,200001 -12.734997 2.761600 -3.773394
98
Округляя значения
коэффициентов до четырех десятичных
знаков.
цоЛУчиМ
уравнение
X4 - 6Х 3 - 0.2 X 2 + 12,735k - 2,7616 = 0.
Это
уравнение было решено выше (см. с. 93); его корни
Х1 = 5,652; Х2= 1.545; Х3=-1,420; Х4=0.2226.
2 Собственный вектор Xt, соответстветствующий числу X,-, определяется равенством
Л?
А', = Л/3 Л/, Л/1У„ где \ 1'
При этом отдельные координаты вектора X'f = (.vli .v2; л3( v41) находятся по формулам
Л*1 i — nil А / +12^-1“ + III I з\ 4- Ш14. Л‘2 j = Ш2 1A 1 i + Mb 2k ? + Ш2зХ,- + 1П24,
А‘з, — П1$ i A* 11 4- /»32 V 2i 4* W33?v( +M34,
Вычисление собственных векторов приведено в табл. Н.
Табл и на 11
Л/, -V,
-0.231125 -0.351515 -1.25 180.5537 0.8977 0.898
5 65"> 1.078582 0,242424 -0.625 31.9451 0.7529 0.753
•1.651001 -1,060606 0.625 5,652 0.6898 0,690
1.158706 -0,681212 -1.25 1 I 1
-0.231125 -0.351515 -1.25 3.6880 3.1143 1
1 5JS 1.078582 0.242424 -0.625 2.3870 -2.8359 -0.911
1.651001 -1.060606 0.625 1.545 -2,4048 -0.772
—___ -1,158706 -0.681212 -1.25 1 1 -0.440
-0.231125 —0.351515 -1.25 0.01103 -0.7403 -0.740
0.2 1.078582 0.242424 -0.625 0.4955 -0.6451 -0.645
1.651001 -1.060606 0.625 0,2226 0.2177 0.218
-1.158706 -0.681212 -1.25 1 1 1
-0.231125 — 0.351515 -1.25 -2.8633 -0 6665 0 293
"1.420 1,078582 0.242424 -0.625 2.0164 1 5480 -0.681
1,651001 -1.060606 0,625 - 1.420 -2.2719 1
-1,158706 -0.681212 -1.25 1 1 -0.440
99
Работа 4
Задание. Используя метод Леверрье— Фаддеева, найти собе ные числа и собственные векторы матрицы. Собе ные числа определить с четырьмя верными щ ми, а собственные векторы — с тремя десятич! знаками.
При выполнении работы воспользоваться вариантами боты 2.
Образец выполнения задания
2.2 2 0.5 2
1 1,3 2 I
0.5 2 0,5 1,6
2 ! 1.6 2
1. Коэффициенты характеристического уравнения X4——р2 р3к—р4=0 определяются при помощи последовательности ма построенной следующим образом:
л, = л: Р1=8рЛр
Л2 = ЛВ1; 1^* j />2 — —• /?2 = Л2 />2Е;
Л3 = ЛЯ2; Рз * Б3 Л3 />3Е,
Л4 = ЛЯ3: _Sp/l4 Р*~ 4 ’
Эти вычисления удобно располагать в таблице (см. табл. I). В результате получим уравнение
Х4-6Х3-0.2Х2 + 12,7351 — 2,7616=0, корнями которого, как это было установлено выше, служат X, =5,652; Х2= 1,545: Х3=- 1.420: Х4=0,2226.
2. Собственный вектор Х^ соответствующий числ^ Xf. опреде. по формуле
X; = X 3 в+X f b ] + Л2 + Я3,
где ё—какой-либо единичный вектор, Ь2, Ь3 — одноименные с ё торы матриц В2, В3.
Последовательно вычисляем векторы
йо/ = ё; Wii = X(-Woi'4-^ W2i = X(-Wi(- + />2; йтц = Х- = ^й21-}~b3.
Эти вычисления приведены в таблице (см. табл. II).
100
Таблица I
" Я, я,
1 (15 Л 1 1.3 7 1 0.5 т 6.5 1.6 2 7 Т.б 2 -3.8 1 0.5 2 1 -4.7 2 Т 0.5 2 — 5.5 1.6 2 Т 1.6 -4
Pl =6
''"Sjl —“ -0.11 4.06 -0.44 -3.31 0.5 3.55 -1.8 0.5 -0.31 -6.3 2.5 3.55 -6.3 3.86 -2.6 -1.8 2.5 -2.6 -0,64
/,,=0.4:2=0.2
-8.607 -10.003 — 13.055 -6.54 4.128 2.64 -1.76 -4.04 2,64 2.732 0.48 -4,39 -1,76 0.48 -0.32 1.776 -4,04 -4.39 1.776 6,195
рЛ= -38.205:3 = -12.735
2.7616 2.7616 2.7616 2.7616
/>4 = 2.7616
Таблица II
й<Н Й’1
1 1,852 7.1575 45.5892 0.897
0 1 6,152 37,4111 0,763
5.652 0 0.5 6.3760 34,2772 0,690
•——— 0 2 9.504 49,6766 1
1 -2.255 -6.7940 -6.3687 1
0 1 2.045 5.7995 -0,911
1.545 0 0.5 4.3225 4.9183 -0,772
0 7 1,290 -2.0470 0.321
0 1 —0.92 3.9464 0.293
1 -6.12 8,3804 -9.1682 -0,681
-1.420 0 2 -9.14 13.4588 1
0 I 1.08 -5.9236 -0,440
0 1 0,7226 2.8009 -0.740
1 -4.4774 -1,3067 2.4411 -0,645
0.2226 0 2 - 5.8548 -0.8233 0,218
0 1 2.7226 -3.7839 1
101
Работа 5
Задание. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю) с пятью-шестью верными цифрами. Зачем найти соответствующий ему собственный вектор, имеющий первую норму, равную 1 (координаты вектора вычислить с тремя десятичными знаками).
2.1 1 l.lX
Л 1. .4 = 1 1 2.6 1.1 . 1.1 1.1 3.1/ 1.3 0.4 0.5 X
ЛЗ. .4 = 1 0.4 1.3 0.3 . 0,5 0.3 1,3/ 2.2 1 I.2X
Л 5. 4 = 1 1 2.7 1.2 . 1,2 1.2 3.2/ 1,4 0.5 0,6 X
Л 7. .4 = 1 0.5 1.4 0.3 . ,0,6 0.3 1.4/ ’ 2.3 1 1.3 X
А9. ,4 = 1 1 2.8 1.3 J.3 1.3 3.3/ /3.5 1 2.5 X
Д11. 4 = 1 4 2.5 ). \2.5 2.5 4.5/ /1.5 0,6 0,7 X
Л 13. 4 = 0,6 1.5 0,3 . \0,7 0.3 1.5/ / 1.4 1.2 -1.3\
Л15. 4 = ( 1.2 0.9 0.4 . \-1,3 0.4 0.8/ /2,8 1 1.8 X
Л17. 4 = 1 3,3 1.8 . \ 1.8 1.8 ^.8/ / 1.6 1.2 -1,1 X
Л19. 4 = ( 1,2 1.1 0,6 . \-l.l 0.6 0.8/ /2,9 1 1.9\
№21. 4 = 1 3.4 1.9 \ 1,9 1.9 3.9/ / 1,8 1.2 —0.9\
№23. .4 = I 1,2 1.3 0.8 ). \ — 0,9 0.8 0.8/ /3.1 1 2.1 X
№1$, 4 = 1 3.6 2.1 \2,1 2,1 4,1 /
'2.4 1 1,4Х
№ 2. 4 = [ 1 2.9 1.4 .
< L4 1.4 3.4 /
' 1,6 0.7 0.8 X
№ 4. 4=1 0.7 1.6 0.3 .
<0.8 0.3 1,6/
'2.5 1 1,5\
№ 6. 4 = 1 1 3 1.5 .
<1.5 1,5 3.5/
'1.7 0.8 0.9 X
№ 8. 4 = 0.8 0.7 0.3 .
<0.9 0.3 1,7/
/2.6 1 1,6\
№ 10. 4 = 1 3.1 1.6
\ 1.6 1.6 3.6 /
/ 1,8 0.9 1 X
№ 12. 4 = 0,9 1.8 0.3
\ 1 0.3 1.8/
/2.7 1 1,7\
№ 14. 4 = 1 3,2 1.7
\ L7 1.7 3.7/
(3,2 1 2,2 \
I 3.7 2,2 ).
2,2 2.2 4,2 /
/ 2.4 1.2 -0.3 \
№ 18. /1 = 1 1,2 1.9 1.4 .
\-0.3 1.4 0,8/
/ 3.3 1 2,3 \
№ 20. 4 = 1 I 3.8 2,3 .
\ 2.3 2.3 4,3 /
/ 2.6 1.2 -0.1 X № 22. 4 = 1.2 2.1 1.6 .
\-0,1 1.6 0.8/
/ 3.4 1 2,4 X
№ 24. 4=1 I 3.9 2,4 .
\2,4 2.4 4,4/
/2.8 1.2 0.1 X № 26. 4 = 1 1,2 2,3 1.8 .
\0,1 1.8 0.8/
102
/ 2 1.2 -0.7 \
№ 27. J= 1.2 1,5 I ).
\ — 0,7 1 0.8/
/ 2,2 1,2 -0.5 \ .№ 29. J=( 1,2 1,7 1.2 .
\ - 0.5 1.2 0.8/
/ 1.6 2.3 - 0.5 \
№ 28. J= 2,3 2 1.2 .
\ —0.5 1.2 0.6/
/2.4 1.2 2.5 \ № 30. .4=1 1.2 3.5 1.4 .
\2.5 1.4 4.2/
Образец выполнения задания
/1.6 2.3 1.2 \ .4 = 1 2.3 0.6 1.5 .
\ 1.2 1.5 3.8/
1. Строим последовательность векторов К,-= Л Г,. где
) 0 — произвольный вектор; тогда X, л г}* * где
г-О1) и yjk>— одноименные координаты двух последовательных векторов.
Все вычисления приведены в таблице.
А 1,6 2.3 1.2 ,.<* * i> i r'.4’ i A‘- •» VF-
2.3 0.6 1.5
1.2 1.5 3.8
/о 1 1 1
г. 5.1 4.4 6.5 5.11 5.48 5.76
У2 26.08 24.12 37.42 5.45 5.41 5.60
Уз 142.108 130.586 209.672 5.484 5.511 5.548
>'д 7,79327-102 7.19708 102 1.16316- IO3 5.5151 5.5148 5,5321
Г5 42,9804-103 3,96902-103 6.43476 IO3 5.5205 5.5225 5.5267
)'б 2,37273 104 2.19190 104 3,55633 104 5.5233 5.5235 5.5251
г7 1.31053-105 1,21069 10s 1.96492 - 10s 5.5240 5.5241 5.5246
г» 7.23934 -105 6,68801 J05 10.85537 -105 5.5242 5.5243 5.5244
Уч 3,99918-10* 3.69463 106 5.99696 10” 5.5243 5.5243 5.5244
110 2.20927 • 107 2.04103 - IO7 2.31294 -107 5.5243 5.5243 5.5243
Гц 1,22047 -108 1.12753 - 10s 1.830184-108
Итак, Xi = 5,5243.
2. Собственный вектор X, определяется из равенства Сле-
довательно, Уп = (1,22047-10s; 1,12753-Ю8; 1,830184-108).
103
Чтобы первая норма вектора была равна I, разделим координаты вектора на наибольшую из них по абсолютной величине; тогда окончательно получим =(0.667; 0,616; 1).
Работа 6
Задание. Используя метод итераций, определить второе собственное
число матрицы Х2 с тремя верными цифрами. Затем найти соответствующий ему собственный вектор, имеющий первую норму, равную 1 (координаты вектора вычислить с тремя десятичными знаками). При выполнении работы воспользоваться вариантами работы 5.
Образец выполнения задания
1.6 2.3 1.2
J= 2.3 0.6 1,5
\ 1.2 1,5 3.8
1. Выше (см. с. 103) была построена последовательность векторов где Уо — произвольный вектор Второе собственное число определяем из соотношения
Ч Л1.» i
где у|к+1) — одноименные координаты трех последовательных
векторов; Xj—первое собственное число.
Предварительно найдем Xt с большей точностью, для чего продолжим вычисления, выполненные на с. 103;
Л1 1.22047- Ю8 1.127535-108 1,830185-108 X, X! Х1
К|2 6.7423100-108 6,2288875-108 10,1105731 108 5.524342 5.524342 5.524342
Пз 3,7246825 • 109 3,4410505-10° 5,5854281 109 5.524343 5.524243 5,524343
Хы 2.057642 -10'0 1.9009542-1010 3.0855822 1010
Отсюда Xi = 5,524343. Для вычисления Х2 выберем векторы У8, У9, У1о; будем использовать различные координаты этих векторов. Все расчеты заносим в таблицу.
Л| 1^10 — Ко х,г« Kq — х2
2,2092689-107 2,2092842-107 -153 3,9991813 Ю6 3.9992597 • I06 -78,4 1.95
2,0410332 -107 2.0410403 • 107 -71 3.6946338 I06 3.6946861 106 -52,3 1.36
3,3129409-107 3.3129264 -107 145 5,9969621 -106 5.9968787-106 83,4 1.74
104
Принимаем X,ft (1.95 + 1,36+ l,74)/3= 1,68.
2. Собственный вектор Х2 определяется из равенства .¥,ft УЛ +, — Xj Yk. Таким образом. X2ft У10-Х, У9 = (-153; -71: 145). Разделив координаты вектора па наибольшую из них по абсолютной величине, т. е. на —153, получим Х2ML 0,464; — 0.948).
Работа 7
Задание. Вычислить собственные числа X, и Х2 матрицы и соответствующие им собственные векторы ¥, и Х2, имеющие первую норму, равную единице. Для улучшения сходимости итерационного процесса воспользоваться возведением мат-
рицы в степень (ограничиться 8-й или 16-й степенью).
1.2 0.3 1 X 0,6 1.2 1 X
№ 1. Л = ( 0.3 0.5 1,2 ) № 2. Я = [ 1.2 0.3 1.2 |
J 1.2 0,8/ . 1 1.2 1.5/
'1.3 0,4 2 X 1.4 0.6 1.3 X
№ 3. /1 = 1 0,4 0.3 0.5 ) № 4. А=1 0.6 0.8 1 )
,2 0.5 1,5/ .1.3 1 0.5/
'0,8 1.4 1,3 X 0.8 1.3 0.2 X
№ 5. /1=1 1.4 1 1.2 № 6. Я=( 1.3 1.5 2 )
J.3 1,2 0,5/ .0.2 2 0.6/
'1.4 0,5 1 X 0.5 2 1.3Х
№ 7, Я = 1 0.5 2 0.4 № 8. Я = 1 2 1.2 0.7 с,
J 0,4 1.5/ .1.3 0.7 1 /
'1,6 0.3 0.5 X /1 1.3 1.2 >
№ 9. /1=1 0.3 1,2 1 № 10. Л = 1.3 0.6 1.5 1
ч0,5 1 0.4/ \ 1.2 1.5 0.8/
/0 6 1 2.2" /2.3 0.3 0.5'
№ И. А = 1 1.4 0.5 ). № 12. .4 = 1 0.3 1.2 0.6 1 .
\2,2 0.5 1 > \0,5 0,6 1 /
/1,2 1.5 0.3" /1.3 0.6 0.8"
№ 13. А = 1,5 0,4 2 ). № 14. Л = 0.6 1 1.2 1 .
\0,3 2 1.2, \0,8 1.2 1.5/
/1.6 1.2 0.4" /0.6 1,3 2.4"
№ 15. А = 1.2 0.5 1 1. № 16. А = 1.3 1.5 0,7 1 .
\0.4 1 0.8, \2.4 0.7 2 ,
/1 1.3 0.6" / 1,2 0.4 2.5"
№ 17. А = ( 1.3 2.4 0,7 ). № 18. Я = ( 0.4 1,4 0.6 I =
\0.6 0,7 1.5, \2.5 0.6 0.7 >
/0.6 0.8 2.5" /0.7 0,8 1.3"
№ 19. /1 0.8 1.4 0.3 1. № 20. А = 0.8 2.6 1.3 1 .
\2.5 0.3 1.2, \ 1.3 1,3 0.8,
/2.3 2 1,2" /1.2 2 0.5"
№ 21. Я = ( 2 0.5 0.7 ). № 22. А = 2 1,4 1,7 1 .
\ 1.2 0.7 0.4, \0,5 1.7 0.3,
105
< 1.5 0.7 1.3 X /0.8 0.6 1.3 X
№ 23. Я = ( 0.7 9 ? 1 |. № 24. /1 = 0.6 2 1.5 ).
< 1.3 1 0.6 / <1.3 1.5 1 /
f 1.8 0.6 1.5 X / 2 1.3 1 X
№ 25. ,1=( 0.6 0.2 1.4 № 26. /1 = 1 1.3 0.5 0.7 .
< 1.5 1.4 0.7 ) к 1 0.7 0.8 /
f 1.7 0.5 0.4 X Л /0.6 2 1.2Х
№ 27. /1=1 0,5 1.3 1 1. № 28. /1=1 2 1,2 0.5 .
<0.4 1 9 -7 J 11.3 0.5 0.8/
<2.3 0.5 0,4 > /0.7 0.9 1.5 \
№ 29. Л=1 0.5 1.2 0.8 1. № 30. .4=^ 0.9 1.4 1 1-
<0.4 0.8 1.3/ <1.5 1 0.8 /
Образец выполнения задания
/0,8 1.2 2.3 X /1=1 1.2 0.4 0.6 I.
\ 2.3 0.6 1.5/
1. Составляем последовательность четных степеней матрицы А:
/0.8 1,2 2,3 \ / 0,8 1.2 2.3 \ /7.37 2.82 6.01 \
Л2 = 1.2 0.4 0.6 )•( 1.2 0.4 0,6 = 2,82 1,96 3.90 ,
\2.3 0.6 1.5/ \ 2,3 0,6 1,5/ \6.01 3.90 7.90/
/7,37 2.82 6,01 \ /7.37 2.82 6.01 \ / 98,3894 49,7496 102,7077 \
= 2.82 1.96 3.90 • 2.82 1,96 3.90 = 1 49,7496 27.0040 55,4022 ;
\6ЛН 3,(Л) 7.90/ \6,01 3,90 7,90/ \ 102,7707 55.4022 113,7401 /
/ 2.2717314 -104 1,1931994 • 104 2,4556934 -104 \
/18 = Л4Л4= 1.1931994 104 0,6273642-104 1.2910334-104 .
\2.4556934• IО4 1.2910334- Ю4 2.6568131 • 104/
Возьмем три последовательных вектора Уо = ( 1:0:0), У1=^48У0 и У2 = ЛУ1. Тогда X) г-3,/г-и: А^У,. Эти вычисления заносим в таблицу.
1 о .г.
1 2.2717314 -104 8.8973192 -104 3.9165 0.925
0 1.1931994- 104 4,6767735 104 3,9195 0.486
0 2.4556934•I04 9,6244420 -104 3.9192 1
Для определения более точного значения Xt найдем первый столбец матрицы А16, а затем составим векторы Уо(1: 0: 0), У! =И,6У0 и Y'2 = A Y{ и вычислим более точное значение Эти вычисления также заносим в таблицу.
106
Уо У|' = /1И,Го М г,
1 12.614914 -104 49.42736 -104 3.91817 0.925
0 6.629578 104 25.975798 I04 3.91817 0.486
0 13.643450 -104 53.457224 I04 3.91816 1
Итак, 1^3,91817; Л\ =(0.925; 0,486; 1).
2. Для вычисления второго собственного числа составим последовательность векторов У,. У2. Уд, где У, и У2 уже вычислены, грГ_х г!2>
а УД = ЛУ2. Тогда % У, —Л, У,. Эти вычисления
.»•; -Mi
располагаем в таблице.
Г,-/.,}', >-2 А*2
8.8973192 -104 8.9010298104 -37.106 34.866200-104 34.861208 I04 49.92 -1.35 1
4.6767735-1О4 4.6751581-104 16.154 18.322158-104 18.324396-104 -22.38 -1.38 -0.448
9.6244420-I04 9.6218242-104 26.178 37.706561 -104 37.710200-104 -36.39 - 1.39 -0.729
Итак, Х2%-1,37; Х2«(1; -0,448; -0,729).
Работа 8
Задание. Используя метод скалярных произведений, определить первое собственное число матрицы с пятью верными цифрами.
/1.7 2.8 0.3 1 /1,7 0.4 2.8 \
№ 1. /4 = 1 2.8 1.2 0.6 № 2. ,4=( 0,4 3.2 1.2 ).
к о.з 0.6 1.5/ \ 2.8 1.2 0.5/
/2.3 1.4 0.6 \ /2.3 3.5 1.4\
№ 3. /4=1 1.4 1,7 0,5 №4. /4=13.5 0.4 0.6 .
к 0,6 0,5 1.3 ) \ 1.4 0.6 1,3/
/0,6 1.3 1.7 \ , / 3.7 0.3 1,2\
№ 5. /4 = 1 1,3 2.5 0.8 №6. А =| 0.3 2.4 0,8 .
к L7 0.8 1.4/ \ 1.2 0.8 1.5/
/3.2 0.5 1.2\ /4.1 0.4 1,3 \
№ 7. /4 = 1 0.5 1.4 2.3 №8. /4=1 0.4 2.2 1.7 ).
к 1.2 2.3 0,6 > \ 1.3 1*7 0.5/
<2.3 0.7 0.6 \ /1,5 0.8 2,9 \
№ 9. /4 = 0.7 3.4 1.2 № 10. /4= 0.8 3.4 2.2 ).
к 0.6 1.2 1.7/ \2.9 э ? 0.4/
107
/1.8 2.4 0.5 X /0.7 1.5 3.2 X
№ 11. А = | 2.4 1.3 0.7 № 12. /1 = | 0.7 2.3 1.3 )
к 0.5 0.7 1.6? <3.2 1.3 0.4/
/2.4 3.5 0.7 X /2.3 1.7 0.8 X
№ 13. А = | 3.5 1.2 0.4 |. № 14. /1 = | 1.7 0.5 1.2 )
к 0.7 0.4 1.3? <0.8 1.2 1.9/
/2.4 1.3 0.5 X /1.5 2.3 0.4 X
№ 15. Я = | 1.3 0.8 2.4 |. № 16. /1 = | 2.3 1.4 2,5
к 0.5 2.4 3.3? <0.4 2.5 0,8/
/3.4 1.3 2.3 X /2.5 1.2 0.8 X
№ 17. /1 = | 1,3 0.6 1.2 |. № 18. /1 = | 1.2 3,4 0.5 )
<2,3 1.2 0.5) <0.8 0,5 1.2/
/2.6 1.4 0.7 X /3.6 0.5 1.2 X
№ 19. /1 = | 1.4 0.9 1.5 № 20. /1 = 1 0.5 0.8 2.3 )
<0.7 1.5 0.3? <1.2 2.3 1.6/
/1.4 0.3 1.7Х /0.8 1.3 3.2 X
№ 21. А = | 0.3 2.4 1.3 |. № 22. .4 = | 1.3 4,2 0.5 |
<1.7 1.3 0.5? <3.2 0.5 0.7/
/2.5 1.3 0.5 X /0.7 1,5 2.7 X
№ 23. /1 = | 1.3 0,6 0.7 1. № 24. А = 1 1.5 2.4 1.3
<0.5 0.7 2.3? <2.7 1,3 0.5/
/1.6 2.7 0.9 X /1.3 2.7 0.5 X
№ 25. /1 = | 2,7 3.4 0.5 |. № 26. J = | 2.7 3.2 4.1 )
<0,9 0.5 1.3? <0.5 4.1 0.4/
/2.4 0,5 2.6 X /2.3 1.5 0,6 X
№ 27. А = | 0.5 1.4 0.6 |. № 28. Л = | 1.5 2.4 0.8
<2.6 0.6 1.3? <0.6 0.8 1.7/
/2.3 0.5 I.4X /2.4 2.5 0.7 X
№ 29. /1=| 0.5 3.3 0.8 . № 30. Я = 1 2.5 1.2 0,3 )
<1.4 0.8 1.2? <0.7 0,3 3.5/
Образец выполнения задания
2.4 0.8 3.3 X
0.8 1.4 1.7 ).
3.3 1.7 0.6/
Строим последовательность векторов Ук f (=Л }\, где Уо — произвольный вектор. Вычисление производим по формуле
108
,.а> (П Ш (h-rh)
0 I 1 1 —
I 6.5 3.9 5.6 88.82 16.0 5.5512
7 37,20 20.18 31.44 2779.5460 496.566 5.5975
3 209.176 111.460 175.930 3.712930 -104 1.55618 -104 5.5989
4 11.717594- Ю2 6.224658 I02 9.853208 102 2.731341 -10* 4.87831 • 10s 5.5989
Ответ: л, *5.5989.
Глава VII
ИНТЕРПОЛИРОВАНИЕ И ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
Работа 1
Задание. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана: I) в неравноотстоящих узлах таблицы: 2) в равноотстоящих узлах таблицы.
Варианты к заданию /)
Таблица I
л г № варианта X
0,43 1.63597 1 0.702
0.48 1,73234 7 0.512
0.55 1,87686 13 0.645
0,62 2.03345 19 0.736
0,70 2.22846 25 0.608
0,75 2.35973
Таблица 2
.V г № вариант X
0.02 1.02316 2 0.102
0.08 1.09590 8 0.114.‘
0,12 1.14725 14 0.125
0.17 1.21483 20 0.203
0.23 1.30120 26 0.154
0.30 1.40976
Таблица 3
.V г № варианта д-
0.35 2.73951 3 0.526
0.41 2.30080 9 0.453
0.47 1.96864 15 0.482
0.51 1,78776 21 0.552
0,56 1.59502 27 0.436
0,64 1.34310
Т а б л ина 4
л г № варианта X
0.41 2.57418 4 0.616
0.46 2.32513 10 0.478
0.52 2.09336 16 0.665
0.60 1.86203 97 0,537
0.65 1.74926 28 0.673
0.72 1:62098
109
Та6.1 и на 5
X v № вариант х
0.68 0.80866 5 0.896
0.73 0.89492 11 0.812
0.80 1.02964 17 0.774
0.88 1.20966 23 0.955
0.93 1.34087 29 0.715
0.99 1.52368
Варианты к
Т а б л и и а 1
Л у № вариант а
1.375 5.04192 1 1,3832
1.380 5.17744 7 1.3926
1.385 5.32016 13 1.3862
1.390 5,47069 19 1.3934
1.395 5.62968 25 1.3866
1.400 5.79788
Т а 6 л и п а 3
.V у № вариант х
0.150 6.61659 3 0,1521
0.155 6,39989 9 0.1611
0,160 6.19658 15 0,1662
0,165 6.00551 21 0,1542
0.170 5.82558 27 0.1625
0.175 5,65583
Таблнца 5
X г - № варианта л*
0.210 4,83170 5 0.2121
0,215 4,72261 II 0,2165
0.220 4.61855 17 0,2232
0.225 4,51919 23 0.2263
0.230 4,42422 29 0.2244
0,235 4.33337
Т а б л и и а 6
X г № варианта х
0.11 9.05421 6 0.314
TU5 6.61659 12 0,235
0.21 4,69170 18 0.332
0.29 3.35106 24 0.275
0.35 2.73951 30 ^0.186
0.40 2.36522
задании! 2 )
Т абл и ца
.V у № вариант х
0.115 8,65729 2 0.1264
0,120 8.29329 8 0.1315
0,125 7.95829 14 0.1232
0.130 7.64893 20 0.1334
0,135 7.36235 26 0.1285
0,140 7.09613
Табл и ца 4
X у № вариант х
0.180 5.61543 4 0.1838
0.185 5,46693 10 0.1875
0,190 5,32634 16 0,1944
0.195 5.19304 22 0.1976
0.200 5.06649 28 0,2038
0.205 4,94619
Таблица 6
Л' у № вариант х
1.415 0.888551 6 1,4179
1.420 0.889599 12 1.4258
1.425 0.890637 18 1.4396
1,430 0.891667 24 1,4236
1.435 0.892687 30 1,4315
1.440 0.893698
Образец выполнения задания
1) 2)
X у X у
0.05 0.10 0.17 0.25 0,30 0.36 0.050042 0.100335 0.171657 0,255342 0.309336 0,376403 0.101 0.106 0.1 II 0.116 0,121 0,126 1,26183 1,27644 1,29122 1.30617 1.32130 1,32660
Вычислить значение функции ./ (•' )= г (л ) при х=0,263. Определить значение функции г(х) при х=0,1157.
НО
1) Воспользуемся формулой
/(.'•)«= Пл<1
i-0 где
п„+, =(л-л0)(л-л-, )... (л—л„),
О,=(л-, - л0) (л; - л ,) ... (л-| - Л-, _ , ) (л- - .V,) (.V, - ,) ... (.V; -Л-„).
Вычисления приведены в таблице.
/ Разности /Л удЪ
0 0.213 — 0.05 -0,12 -0.20 -0.25 -0.31 — 0.19809 10'4 -2526.2
1 0,05 0.163 -0.07 -0.15 -0.20 -0.26 0.44499 10’5 25547.7
9 0.12 0,07 0.093 -0.08 -0.13 -0.19 -0.154365 10"5 -111202.0
3 0.20 0,15 0,08 0,013 -0.05 -0.11 0.1716*10 ° 1488007.0
4 0.25 0.20 0.13 0.05 -0.037 -0.06 0,7215 -10'6 428740.0
5 0.31 0.26 0.19 0.11 0 06 -0,097 -0.980402-10'ь -38392.7
Итак, П5 + 1 =0,1506492 106, £ (г,./Ц.)= 1790173.8. Следовательно, i = O 5
/(0.263)^n5i! • X (У. D,) = 0,1506492 * 10-6 • 1790173,8 = 0,269678. 1 = 0
2) Для вычислений используем формулу ” V.
где
Пл+1(0 = '('-,)-('-"): '=(Л‘-Л'о)/А: Л=л*,м-л-,-;
С; = (-1)"“; •'!•("-')!
Здесь / = (0,1157 —0,101 )/0,005 = 2,94. Вычисления располагаем в таблице.
i -v< i; t-i c. (f-i)Ci J. (t-i> a
0 0.101 1.26183 2.94 -120 -352,8 -0.0035766
I 0.106 1.27644 1.94 24 46.56 0.0274149
2 0,11 Г J 1.29122 0.94 -12 -11.28 -0.1144691
3 0,116 1.30617 -0.06 12 -0.72 -1.8141250
4 0.121 1,32130 -1.06 -24 25.44 0.0519379
5 0.126 1,33660 -2.06 4 120 -247.2 -0.0054069
Итак, П5+1| (t) = — 0,7024271: У ——— = - 1,858225. Следовательно, i = o (z~/)
/(0,1157)^ 1,30527.
Работа 2
Задание. Используя схему Эйткина, вычислить приближенное значение функции, заданной таблично, при данном значении ар-I у мента.
111
Таблица 1 Таблица 2
Л" г № варнаша V .V г № варианта V
0.2050 0.207921 1 0.2054 0.8902 1.23510 2 0.8942
0,2052 0.208130 7 0.2063 0.8909 1.23687 8 0.8973
0,2060 0.208964 13 0.2072 0.8919 1.23941 14 0.8958
0.2065 0.209486 19 0.2079 0.8940 1.24475 20 0,8948
0.2069 0.209904 7S 0.2088 0.8944 1.24577 26 0.8934
0,2075 0,210530 0.8955 1.24858
0.2085 0.211575 0.8965 1.25114
0.2090 0.212097 0.8975 1.25371
0.2096 0.212724 0.9010 1.26275
0,2100 0.213142 0'9026 1.26691
Табл и на 3 Табл и на 4
.V г № варианта Д' А’ .с № варнак । а Л'
0,6100 1.83781 3 0.6111 0.5400 1.66825 4 0.5415
0.6104 1.83686 9 0.6124 0.5405 1.66636 10 0.5424
0,6118 1.83354 15 0.6142 0.5410 1.66448 16 0.5436
0,6139 1.82860 21 0.6163 0.5420 1.66071 22 0.5452
0,6145 1.82720 27 0.6192 0.5429 1.65734 28 0.5461
0,6158 1.82416 0.5440 1.65322
0,6167 1.82207 0.5449 1.64987
0,6185 1.81791 0.5455 1.64764
0,6200 1.81446 0.5465 1.64393
0,6225 1.80876 0.5473 1.64097
Табл и на 5 Т а б л и ц а 6
.V г № Варнаи га Л" Л г № варианта Л"
\ 0,62 0.537944 . V. -0 846 1.03 2.80107 6 1.277
\o.67 0.511709 [ II 0.864 1,08 2.94468 12 1.118
0.477114J 17 0.683 1.16 3.18993 18 1.204
'0^80л ТШ5329 23 0.785 1.23 3.42123 24 1.255
0,87 0.418952 29 0.866 1.26 3.52542 30 1.282
0,96 0.382893 1.33 3.78104
0,99 0.371577 1.39 4.01485
Образец выполнения задания
Пользуясь таблицей 2. определить значение функции г(.т) при л*=0.8925.
Выберем из таблицы 2 шесть значений так. чтобы значение аргумента 0,8925 было расположено между двумя средними значениями аргумента, и вычисляем /’(0,8925) по схеме Эйткина до получения совпадающих значений с пятью десятичными знаками. Вычисления приведены в таблице.
Л л Pl < Л- Л * t ) PltVi. A’;-, j. .V,. 2 ) ЛПл. Л-Ь л-л-й Л;-А
0.8902 1.23510 -0.0023
0,8909 1.23687 1.240916 -0.0016
0.8919 1,23941 1.240934 1.240940 -0.0006
0.8940 1.24475 1.240936 1.240935 1.240937 0,0015
0.8944 1.24577 1.240925 1.240933 1.240934 0.0019
0.8955 1,24858 1,240916 1.240934 1.240933 0.0030
Из сравнения полученных результатов имеем /(0.8925) % 1,24093.
112
Работа 3
Задание. Используя первую или вторую интерполяционную формулу Ньютона, вычислить значения функции при данных значениях аргумента. При составлении таблицы разностей контролировать вычисления.
.V г
1.415 0.888551
1.420 0,889599
1.425 0,890637
1.430 0.891667
1.435 0,892687
1.440 0.893698
1.445 0.894700
1.450 0.89569?
1.455 0.896677
1.460 0.897653
1.465 0.898619
Таблица I
№ варианта Значения аргумента
Ч Л'2 Ъ Л'4
1 1.4161 1.4625 1.4135 1.470
11 1.4179 1,4633 1.4124 1.4655
21 1.4263 1.4575 1.410 1.4662
V г
0.101 1,26183
0.106 1,27644
0.111 1,29122
0.116 1.306П
0.121 1.32130
0,126 1.33660
0,131 1.35207
0.136 1.36773
0.141 1,38357
0.146 1.39959
0.151 1,41579
Таблица 2
№ варианта Значения аргумента
'| Д, Ч ч
2 0.1026 0.1440 0.099 0,161
12 0.1035 0,1492 0,096 0,153
22 0.1074 0,1485 0.1006 0.156
Д' г
0.15 0,860708
0.20 0,818731
0.25 0.778801
0.30 0.740818
0.35 0.704688
0.40 0.670320
0.45 0.637628
0.50 0.606531
0.55 0.576950
0,60 0,548812
0.65 0,522046
0.70 0.496585
0.75 0.4722367
Таблица 3
№ варианта Значения аргумента
V1 д> •ъ д4
3 0.15! 1 0.7250 0.1430 0.80
13 0.1535 0.7333 0,100 0.7540
23 0,1525 0.6730 0,1455 0.85
ИЗ
Таблица 4
Л У № Значения аргумента
варианта
0.180 5.61543 Л’| л- л’л х*
0 1X5 5 4ЛА0Ч 1
5/« К хУ Л Л,ЧОО л Л
0.190 5.32634 4 0.1817 0,2275 0.175 0.2375
0.195 5,19304 |4 0.1827 0.2292 0.1776 0,240
0.200 5,06649 24 0.1873 0.2326 0.1783 0,245
0.205 4,94619
0,210 4,83170
0.215 4.72261
0.220 4.61855
0,225 4.51919
0,230 4.42422
0.235 4.33337
Таблица 5
Л _у № Значения аргумента
варианта _
3.50 33,1154 л, л, лл л-4
3 « 1Л V 1 12
Л « Л Л ЛЧ,О 1 ЛЛ
3.60 36.5982 5 3.522 4,176 3,475 4.25
3.65 38.4747 15 3.543 4,184 3.488 4,30
3,70 40.4473 25 3.575 4,142 3.45 4,204
3.75 42,5211
3.80 44,7012
3.85 46,9931
3.90 49.4024
3.95 51.9354
4.00 54.5982
4,05 57.3975
4,10 60.3403
4.15 63.4340
4,20 66.6863
Таблица 6 .
.V у № Значения аргумента
варианта
0.115 8.65729 лл л-д
П 1 7П R7G17Q
I хи
0.125 7.95829 6 0.1217 0.1736 0.1141 0.185
0.130 7.64893 |б 0.1168 0.1745 0.110 0.1825
0.135 7,36235 26 0.1175 0.1773 0.1134 0.190
0.140 7.09613
0.145 6.84815
0.150 6.61659
0.155 6,39986
0.160 6,19658
0.165 6.00551
0,170 5.82558
0.175 5.65583
0.180 5.49543
114
.г г
1,340 4.25562
1.345 4.35325
1,350 4.45522
1.355 4.56184
1.360 4.67344
1.365 4.79038
1.370 4.91306
1.375 5.04192
1.380 5.17744
1.385 5.32016
1.390 5.47069
1.395 5.62968
Таблица 7
№ варнаша Значения api умен га
•V| '2 •V.1 v4
7 1.3617 1.3921 1.3359 1.400
17 1.3463 1.3868 1.335 1.3990
27 1.3432 1.3936 1.3365 1,3975
.V г
0,01 0.991824
0,06 0.951935
0,11 0.913650
0,16 0.87690?
0,21 0.841638
0.26 0.807789
0.31 0.775301
0.36 0.744120
0.41 0,714193
0,46 0,685470
0.51 0.657902
0,56 0.631442
Т а б л и и а 8
№ вари* анта Значения ар) умен га
•'1 Л’ 'з *4
8 0.027 0.525 0.008 0,61
18 0.1243 0.492 0.0094 0.66
28 0.083 0.5454 0.0075 0.573
Л' г
0,15 4.4817
0,16 4,9530
0,17 5.4739
0,18 6,0496
0.19 6.6859
0.20 7.3891
0.21 8.1662
0.22 9,0250
0,23 9.9742
0,24 11,0232
0,25 12.1825
0,26 13,4637
Табл и ц а 9
№ вари-анта Значения аргумента
•V) Л2 *3 *4
9 0.1539 0.2569 0.14 0.2665
19 0.1732 0,2444 0.1415 0,27
29 0.1648 0.2550 0.1387 0.28
115
Л‘ г
0.45 20.1946
0.46 19.6133
0.47 18.9425
0.48 18.1746
0.49 17.3010
0.50 16.3123
0.51 15.1984
0.52 13.9484
0.53 12.5508
0.54 10.9937
0.55 9.2647
0.56 7.3510
Таблица К)
№ вари- Значения api умен га
aura Л", № л. 1
10 0.455 0.5575 0.44 0.5674
20 0.4732 0.5568 0.445 0.57
30 0.4675 0,5511 0.4423 0.58
Образец выполнения задания
А' Определить значения функции г(л) кнцих значениях аргумента: при следу-
1,215 1,220 0,106044 0.113276 1) № = 1.2273; 3) №=1.253; 2) №=1.210; 4) №=1.2638.
1.225 0,119671
1,230 0.125324
1,235 0,130328
1.240 0.134776
1,245 0.138759
1.250 0.142367
1,255 0.145688
1,260 0.148809
Составим таблицу конечных разностей. Для контроля вычислений добавим к ней две строки: в строке £ запишем суммы элементов столбцов конечных разностей, а в строке Р—разности крайних значений столбцов.
A'i У, Л2 Г; ^у.
1.215 0.106044 0.007232 -0.000837 0.000095
1.220 0,1(3276 0,006395 -0.000742 0.000093
1.225 0,119671 0.005653 -0,000649 0.000093
1,230 0,125324 0.005004 -0.000556 0.000091
1.235 0,130328 0.004448 -0,000465 0.000090
1.240 0.134776 0.003983 -0,000375 0.000088
1.245 0.138759 0.003608 -0.000287 0.000087
1,250 0.142367 0.003321 -0.000200 1
1.255 0,145688 0,003121 —.
1.260 0,148809 — — —
Z — 0,042765 -0.004111 . 0.000637
р 0,042765 -0,004111 0,000637
116
При составлении таблицы разностей ограничиваемся разностями третьего порядка, так как они практически постоянны. Для вычисления значений функции при л* =1.2273 и л = 1.210 воспользуемся формулой Ньютона для интерполирования вперед:
>1
д2.. . </(4-1)(4-3)
/1 Jo I---
А3 г0.
I
где <7 = (л —д-()
1) Если л* =1.2273, то примем л*0= 1.225; тогда
1.2273-1.225
<7 =-----------= 0,46.
1 0.005
г(1,2273) а 0.119671 + 0.46 • 0,005653+°-461~0-54)(_0,000649)+
f-°— °’54)( L54) 0*000093=0.119671+- 0,0026004+0,0000806 + 0,0000059 =
6
= 0,1223579 * 0,122358.
2) Если л = 1,210, то примем .г0= 1.215; тогда
1.210-1.215
Ч~ 0.005 ” ” ’
^—^(—0,000837)4
X
6
х 0,000095=0.097880.
Для вычисления значений функции при л = 1.253 и пользуемся формулой Ньютона для интерполирования
.г = 1.2638 вос-назад:
/т'л2,. . Ч \Ч г
) и - ----------- 2!-------------------------’ 3!
AJr„. .3.
где q = (x—xn/h.
3) Если х =1.253, то примем ли= 1,255: тогда
1.253- 1.255 (1~ 0005 ’
г (1.253) * 0.145688 + (- 0.4) 0,003321 + Ь0.^0:6
(—0,000287)1-6 х 6
X 0,000088 = 0,145688 - 0,0013284 + 0.0000344 - 0.0000056 = 0.1443884
*0,144388.
4) Если л = 1,2638. то примем _v„= 1,260; тогда
1.2638-0.260 _
7 =----------= 0,76,
1 0,005
г (1.2638) * 0,148809+0,76 ♦ 0,003121+ в’76^'76 (_ 0.000200) + °^'LJ6-76
х 0,000087 = 0,148809 + 0.0023720 - 0.0001338 + 0.0000535 = = 0.1511007*0.151101.
117
Работа 4
Задание. I) Используя линейную интерполяцию, вычислить значение функции при заданных значениях аргумента. Предварительно убедиться в применимости формулы, для чего выбрать шесть значений из таблицы Брадиса и составить таблицу разностей.
2) Используя квадратичную интерполяцию, вычислить значения функций при данных значениях аргумента. Предварительно убедиться в применимости формулы.
Варианты к заданию I)
№ 1. а) sin 0,1436; 6) cos 1,1754. № 2. a) sin 0.4974; 6) cos 0.9818.
№ 3. а) sin 0,2453; 6) cos 1,0938. № 4. a) tg 0.3864; 6) cos 0.9222.
№ 5. а) sin 0,4456; 6) cos 1,0045. № 6. a) tg 0.3224; 6) cos 0.8465
№ 7. а) sin 0,6235; 6) cos 0.9464. № 8. a) tg 0,2816; 6) cos 0.8065.
№ 9. а) sin 0,7243; 6) cos 0.8675. № 10. a) tg 0.2464; 6) cos 0.7312.
Ла 11. а) sin 0,8453; 6) cos 0.4324. № 12. a) tg 0.2016; 6) cos 0.7075.
№ 13. а) sin 0.9675; 6) cos 0.3436 № 14. a) tg 0.1636; 6) cos 0,6865.
№ 15. а) sin 1,0618; 6) cos0,1458. № 16. a) tg 0.1858; 6) cos 0.5635
№ 17. а) sin 1,1238; 6) cos 0.1658. № 18. a) tg 0.1362; 6) cos0.5423.
№ 19. а) tg 0,4052; 6) cos 0,7645. № 20. a) sin 0,2134; 6) cos 1.1274.
№ 21. а) tg 0,4527; 6) cos 0.7466. № 22. a) sin 0.3425; 6) cos 1.0252.
№ 23. а) sin 0,1648; 6) cos 1.1462. № 24. a) sin 0,5438; 6) cos 0.9656.
№ 25. а) sin 0.2642; 6) cos 1.0665. № 26. a) tg 0.3654; 6) cos 0.9035.
№ 27. а) tg 0,3083; 6) cos 0.8235. № 28. a) sin 1.0236; 6) cos 0,2267.
№ 29. а) sin 1,1438; 6) cos 0,7672. № 30. a) sin 0,9057; 6) cos 0,2632.
Варианты к заданию 2)
T аблица 1 Та блица 2
№ Значения № Значения
v вари- аргумента 1» вари- аргумен га
анта анта
А| -X, А, А 2
1,675 9.5618 1 1.6763 1,6787 1,520 19.670 16 1.5223 1.5237
1,676 9.4703 2 1.6778 1.6792 1.521 20,065 17 1.5228 1,5243
1,677 9,3804 3 1.6785 1.6762 1.522 20.477 18 1.5239 1.5214
1.678 9,2923 4 1,6794 1,6776 1,523 20.906 19 1,5241 1.5257
1,679 9,2057 5 1.6801 1,6786 1,524 21.354 20 1.5256 1.5233
1,680 9,1208 6 1,6816 1.6803 1.525 21.821 21 1,5267 1.5244
1.681 9,0373 7 1,6822 1.6808 1.526 22.308 22 1,5272 1.5257
1.682 8.9554 8 1,6837 1.6814 1.527 22.818 23 1.5284 1.5268
1.683 8,8749 9 1.6849 1.6823 1.528 23.352 24 1.5295 1.5273
1.684 8.7959 10 1.6853 1.6838 1.529 23.911 25 1,5303 1.5287
1.685 8.7182 11 1,6868 1.6843 1.530 24.498 26 1.5318 1.5292
1.686 8.6418 12 1,6773 1.6798 1.531 25,115 27 1.5242 1.5276
1.687 8.5668 13 1.6788 1.6802 1,532 25.763 28 1.5263 1.5286
1,688 8,4931 14 1.6813 1.6797 1,533 26.445 29 1.5288 1.5313
15 1,6845 1,6821 30 1.5293 1,5308
118
Образец выполнения задания 4
I) Определить sin 0.6682 и cos0.3033.
2) Пользуясь таблицей 2. определить значения функции г(л) при л'1 = 1.5306 н л-2= 1.5282.
1) Выберем из таблицы синусов несколько значений и составим таблицу разностей первого и второго порядков:
.V sin л- А.П Д21\
0.63 0.5891 0,0081 -0.0001
0,64 0,5972 0,0080 -0.0001
0,65 0.6052 0.0079 0.0000
0.66 0.6131 0.0079 -0.0001
0,67 0.6210 0,0078 —
0.68 0.6288 — —
На возможность использования линейной интерполяции указывает тот факт, что разности первого порядка практически постоянны, а также выполнение соотношения | max | Д2 г, | < 10 “ 4; действительно,
8 i
- 0,0001 <0,0001. 8
При вычислении пользуемся формулой
./'(л)=/(л-о)+47-Д/(ло).
где q=(x—л‘о)/Л, а л"о— ближайшее значение в таблице, меньшее чем 0,6682. Имеем ло=0.66; г/=(0.6682—0,66)/0,01 =0,82;
sin 0,6682 *0,6131 +0,82-0,0079 = 0,6131 +0,0065 = 0,6196.
Выберем теперь из таблицы косинусов несколько значений и составим таблицу разностей первого и второго порядков:
.V COS Л" А\г,
0.28 0.9611 -0.0029 0
0,29 0.9582 -0,0029 -0.001
0,30 0.9553 -0,0030 -0.001
0,31 0.9523 -0,0031 —
0.32 0.9492 — —
Разности первого порядка практически постоянны, а также справед-
ливо соотношение -тах| Д2г(-|< 10 “4 (так как 0,0001 <0.0001), что 8 , * 8
указывает на возможность применения линейной интерполяции.
Полагаем .vo=0,30; тогда 47=(0,3033 — 0,30)/0,01 =0,33: значит.
cos 0,3033 * 0,9553+0,33 - (- 0,0030) = 0,9553 - 0,0010=0,9543.
119
2) Выберем из таблицы 2 несколько значений и составим таблиц^ разностей первого, второго и третьего порядков:
V, Л Ai; Ап, Л'г,
1.527 22,818 0,534 0.025 0.003
1.528 23,352 0.559 0.028 0.002
1.529 23.911 0.587 0.030 0.001
1.530 24.498 0.617 0.031 —
1.531 25.115 0.648 — —
1.532 25.763 — — —
В этой таблице разности
практически
кроме того, справедливо соотношение
второго порядка
1 max | А3г,-1 < 10“3
постоянны, (так как
— 0.003 <0,001: 0,0002 <0,001). Все это указывает на возможность применения квадратичной интерполяции.
Для вычислений воспользуемся формулой
’/ л2
5—Л го.
Если л-= 1,5306. то л0= 1.530: </=(1.5306- 1,53О)/0,001 =0,6;
/(1.5303) = 24.498 + 0,6 • 0,617 + аб<~0’4) - 0.031 = 24,498+0,3702 - 0,0037 =
= 24,8645.
Принимаем /'(1,5306)^24,864.
Если л = 1,5282, то л0= 1,528: </=(1,5282-|,528)/0,001 =0.2;
/(1,5282)=23,352+0,2 0,559 +°-2(~0-8). 0.028 = 23.352+0.1118 -0.0022 =
= 23,4616.
Принимаем /(1,5282)^23.462.
Работа 5
Задание. Используя интерполяционные формулы Гаусса, Стирлинга
и
Бесселя, вычислить приближенные значения функции r(.v) при данных значениях аргумента: 1) л* = 1,60 4- 0,006/;: 2) л = 1,725 + +0.002//: 3)л = 1.83+0.003//; 4) л = 2-0.013// (//=1, 2. 3.30).
Функция г (л ) задана таблицей:
Л" Ф) .V Ф)
1.50 15.132 1.85 43,189
1.55 17.422 1.90 48.689
1.60 20.393 1.95 54,225
120
Продолжение
.V .Ф) .V ,Ф)
1.65 23.994 2.00 59.653
1.70 28,160 2.05 64.817
1.75 32.812 2.10 69.550
1.80 37.857
Образец выполнения задания
Л ,Ф) .V Ф) Найти значения функции г-- /'(а ) при следующих значениях аргумента:
0,12 6.278 0.20 6.436 1)л=0.168: 2) а =0.192; 3)л=0.204;
0,14 6.405 - 0.22 6.259 4) л = 0.175.
0,16 0,18 6.487 6.505 0,24 5,954
Составим диагональную таблицу конечных разностей функции /(л):
.ФЛ Ду, А2 у,
а-з = 0.12 л_ 2 =0.14 А-.=0,16 _г_ з = 6.278 г_2=6.404 г-1=6.487 126 83 -43 -65 — 22
18 -69 21
Ао=0.18 Уо —6,505 -87
AJ =0.20 а, =0.22 ад = 0.24 г.., =6.436 г-2 = 6.259 ,г_з = 5,954 -108 -128
-177 -305 -20
Таблица заканчивается разностями третьего порядка, так как они являются практически постоянными.
1) Для определения значения г(0.168) примем ло = 0.16; тогда f=(х - А’О) / Л=(0,168 -0.16) /0,02 = 0,4.
Воспользуемся первой формулой Гаусса:
. . . ф-1),-» и+1)Ф-1)*Ч
r(.v)% р(л-) = Го +1Аг0+А" г-, 4---—----- А\г-1 -
Находим
>• (0,168)« 6.487 + 0,4 0,018 +(l~4*~0,6* • (- 0.065)+ '•4'0-4(~0-6> х
х (- 0,022) а 6.487 + 0,0072 + 0.0078 + 0.0012 = 6.5032 % 6.503.
2) Для определения г (0,192) примем ло=0,18; тогда t=(0.192—0.18) /0,02 = 0,6.
Воспользуемся формулой Бесселя:
121
Находим
г (0,192) % — °j±6436+(0.6 - 0,5)(- 0,069)+°,6'(~°,4) х
-0.087-0.108 (0.6-0.5) 0.6 (-0.4) , х-----------+1-------i (- 0.021) %
% 6,4705-0,0069+0.0117 + 0.0001 = 6.4754^6,475.
3) Для определения г (0.204) примем ло=0,20; тогда / = (0,204 — 0.20)
/0.02 = 0.2.
Воспользуемся формулой Стирлинга:
Hv)= .о+г • д2.р- ,
Находим
(0,204)^6,436 + 0.2--()Q69-OJ77+^(-0,l08)+
+0А(0.04- ). -0^.-0.020^ 6436_0 0246_00022 +000()7= 6 2
= 6,4099 % 6,410.
4) Для определения г (0,175) примем Л‘о = 0,18; тогда / = (0,175 — 0.18)
/0,02 =-0,25.
Воспользуемся второй формулой Гаусса.
Находим
г (0,175)=6,505 +(- 0,25) • 0,018 +°-75 (~0-25). (_ 0,087)+
+0-7?(-0-25Н-'-25) •(_ 0,022)» 6,505 - 0,0045 +0,0082 - 0,0009 = 6
= 6,5078 % 6,508.
Работа 6
Задание. Вычислить значения функции при заданных значениях аргумента, используя интерполяционную формулу Ньютона для неравноотстоящих узлов. При вычислениях учитывать только разделенные разности первого и второго порядков. Вычисления провести дважды используя, если это возможно, различные узлы
122
Таблица I
Таблица 2
А" (1 № ва- рианта <1 Л» А № варианта 'I хч
0.298 0.303 0.310 0,317 0.323 0.330 0.339 3.25578 1 3,17639 7 3.12180 13 3.04819 19 2.98755 25 2,91950 2.83598 Таблица 0.308 0.314 0.325 0.312 0,321 3 0.335 0.593 0.337 0,598 0.303 0,605 0.304 0.613 0,336 0.619 0.627 0.632 0.532050 2 0.535625 8 0.540598 14 0.546235 20 0.550431 26 0.555983 0,559428 Табли на 0.608 0.615 0.622 0.603 0.610 4 0.630 0.594 0.596 0.631 0.628
Л‘ v № ва- рианта V1 АЧ -V г № ва- рианта *1 АЧ
0.698 0.706 0.714 0,727 0.736 0.747 0,760 0.769 0.782 2.22336 3 2,24382 9 2.26446 15 2.29841 21 2,32221 27 2’35?64 2.38690 2.41162 2.44777 Таблица 0.720 0.740 0.750 0,765 0.755 5 0.775 0.100 0.705 0,108 0.777 0.119 0.700 0,127 0.704 0.135 0.146 0.157 0.169 1.12128 4 1.13160 10 1.14594 16 1,15648 22 1,16712 28 1.18191 1.19689 1,21344 Таблица 0,115 0,124 0.130 0.140 0,150 6 0.160 0.162 0,164 0.104 0.102
.V г № ва- рианта *1 АЧ А r № ва- рианта Л| *2
0.235 0.240 0.250 0,255 0,265 0,280 0,295 0.300 0,305 1,20800 5 1,21256 11 1,22169 17 1.22628 23 1,23547 29 1.24933 1.26328 1.26795 1.27263 0.238 0.261 0.244 0,275 0.268 0.257 0,095 0.298 0,102 0.272 0.104 0.303 0,107 0,292 0.110 0,112 0.116 0.120 1,09131 6 1.23490 12 1.27994 18 1.35142 26 1.42815 30 1,48256 1.60033 1,73205 0,105 0.103 0,109 0,108 0.111 0,114 0.117 0.115 0,100 0.118
Образец выполнения задания
Л г
0,103 2,01284
0.108 2.03342
0,115 2.06070
0.120 2.07918
0,128 2.10721
0,136 2,13354
0,141 2,14922
0,150 2,17609
Определить значения функции _г(л) при следующих значениях аргумента: 1) .4^=0.112; 2) .г2=0,133.
123
Вычисления производим по формуле
где.
Предварительно вычислим необходимые значения разделенных ра ностей.
V, г» /(д,. л;. t) /(Л,. Ai - 1. V, , 2)
о. юз 2.01284 4.116 -18.238166
0.108* 2.03342 3.896142 - 16.761833
0.Н5 2.06070 3.696 -14.788461
0,120 2.079 IS 3.503750 -13.281250
0,128 2.10721 3.291250 -11.942307
0,136 2.13354 3.136 —
0,141 2,14922
взяв за
Ло
сначала
1) Найдем значение /(0,112) двумя способами, 0,103, а затем 0,108:
/(0,112)^2.01284 + 4,116 (0.112-0,103) + (-18.238166)-(0,112-0,103)х х(0,112-0,106)^2,01284 1-0.037044-0.000657 = 2,04923;
J (0,112)% 2,03342 + 3,897142 (0.112 - 0,108) и - (- 16.761833) (0.112 - 0,108) х
х (0,112 - 0,115) = 2,03342 + 0,0155S9 4- 0,000201 = 2.04921.
Принимаем /’(0.112) 2,04922.
2) Значение /(0.133) также определим двумя способами, л0 сначала 0.120, а затем 0.128:
взяв за
/(0,133) % 2,07918 + 3.50375 • (0,133 - 0,120) + (- 13,28125) (0,133 - 0,120) х
х (0,133 - 0,128) = 2,07918 + 0,045549 - 0,000863 = 2,12387;
/(0,133) % 2.10721 + 3,29125 (0.133 - 0,128) + (- 11,942307) • (0,133 - 0,128) х х (0,133 - 0,136) = 2,10721 + 0,016456 + 0,000179 = 2,12385.
Принимаем /(0,133) % 2,12386.
Глава VIII
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Работа 1
Задание.
С помощью Стирлинга и производных
заданной таблично.
интерполяционных формул Ньютона, Гаусса
Бесселя найти значение первой и второй при данных значениях аргумента для функции
124
Таблица I
.V г(л) Д’ г (д)
2,4 3.526 3.6 4.222 1) л-=2.4+0.05я:
2.6 3.782 3.8 4.33Т 2) л=3.12+0.03я;
2.8 - 3.945 4.0 4.507 3) л-=4.5-0.06/,:
3.0 4.043 4.2 4.775 4) л-=4.04 — 0.04»
3,2 4.104 4.4 5.159 (w = 1. 3. 5. 7 29).
3.4 4.155 4.6 5.683
Таблица 2
.V .Г(Л) .V г (г)
А
1.5 10,517 4.5 8.442 1) л* =1.6 + 0.08»:
2.0 10.193 5,0 8.482 2) л = 3.27 + 0.11»:
2,5 9.807 5.5 8.862 3) л-= 6.3-0.12»:
3.0 9.387 6.0 9.701 4) А’= 5,85—0.09/,
3.5 8.977 6,5 11.132 (« = 2. 4, 6. 8 30).
4,0 8.637 7.0 13.302
’Образен выполнения задания
.V Г (.V) .V У (а ) Найти значения первой и второй производных дан-
0.8 1,2 1.6 2.857 3.946 4,938 2.4 2,8 3.2 6.503 7.010 7.288 ных функций при: 1) л , = 1.2: 2) as = 2.23: 3) .v3 = 2,76; 4) Л-4 = ЗЛ.
2.0 5.801 3.6 7,301
Составим диагональную таблицу конечных разностей данной функции:
-V г (л) Лг, л2.п А5г,
0,8 2.857 1.089 0.992 0.863 0.702 0.507 0,278 0.013
1.2 1,6 2.0 2,4 2.8 з’б 3.946 4.938 5.801 6.503 7,010 7,288 7,301 -0.097 -0.129 .-0.161 -0.195 -0,229 -0.265 -0.032 -0.032 -0,034 -0,034 -0.036
1) Положим л0 = 1.2; тогда / = (л*—л0 ) й = (1,2—1,2)/0.4 = 0.
Восполь-
зуемся для вычислений формулами, . \ 1/ 1 , 1 .
;• дУо-;дл„+ -Д.г0 + й\ 2 3
/г
получающимися из первой интерполяционной формулы Ньютона.
125
Находим
у (1,2) х (о,992 + 0.129 - ‘0.032^ = 2.5 • (0.992+0,0645 - 0.0107)=2.614;
г" (1.2) х (- 0. 1J9 + 0.032)=0.606.
2) Положим ло = 2.0; тогда / = (2,23-2.0)/0.4=0,575. Воспользуемся для вычислений формулами
получающимися из формулы Бесселя.
Находим
1 1Л5-1 -0.161-0,195 0,992—1,725 + 0.5 ,
J (2,23) * од ‘ V’ 02 + Т"'-----Г~~ + ---------6------ ‘(' °’034)=
= 2,5 (0,702 - 0.0134+0.0013) = 1.725.
-0.161-0.195 1.15-1 . Л
-----2-----+ -у- * (- 0,034) J =
= 6.25 (-0,178-0,0026)= - 1,129.
3) Положим л'0 = 2,8; тогда / = (2,76-2.8)/0.4=—0,1. Воспользуемся формулами
Дг^ + Дго Л2 3,2-1 Дэг_2+Д3г_1
+1 * Д Г — 1 Н--"
2 6 2
0.03-1 -0.034-0.036
~6 Г~
получающимися из формулы Стирлинга.
Находим
1 /0.507 + 0.207 Л1 у (2,76)% —(-----------+0,1 0,229 +
' ' ' 0.4 \ 6
= 2,5 • (0.3925 + 0.0229+0.0057) = 1,053,
г" (2,76) а0,229 - 0,1 ~ 0-034 ~0-036) = 6,25 (-0,229 + 0'0035)= -1,409.
4) Положим л0 = 2,8, тогда / = (3</-2,8)/0,4=0,75. Воспользуемся формулами
г (л>1(ду.1+/д^- +
126
получающимися из первой формулы Гаусса.
Находим
у' (3.1)*^- (о,278 + Ц1!. (_ о,229) + L68Zlz2. (_ 0,036) = = 2,5 • (0.278 - 0.0572 - 0,0041) = 0,542:
г" (3.1) * - 0,229 + 0,75 • (- 0,036) = - 1.600.
Работа 2
Задание. 1) Вычислить интеграл по формулам левых и правых прямоугольников при //=10. оценивая точность с помощью сравнения полученных результатов.
2) Вычислить интеграл по формуле средних прямоугольников, используя для оценки точности двойной просчет при z/^8: п2 — Ю.
1
2.
3.
4.
5.
1 0. 1 * о. 1 .4 0 ” 7-v2 + 5rfx 2) . 2.v+y.v2 + 0,5 J 6 о. ' 70,5л + 2</л 2) 72л2+1+0.8 J 4 0. .8 ’ 1 ' v/0,8a2+IJ.v 2) 8 * sin (2x + 0.5) dx 2+cos(x2 + I) 2 ' cos (0.8л + 1.2)</x 1.5 + sin(x2 + 0.6) 3 .0 sin (л + 1.4) dx
0. 2 1. 2 1 2 1 1 1 л+71,5л2 + 2 J 8 O. .2 1 ' v/1.5.v + 0.6f/A- 2) 1.6+J0,8a-2 + 2 J 0 0. ’ 4/2.v2+1.6Ja- 2) 2v + у/ 0,5 x ~ + 3 . 2 O. .5 0 ’ 7-v2+0.6//a 2) 1.4 +70,8л-2+1.3 J з о .6 i * 70,4л+i. 7 jx 2) । 1.5а + 7л‘2 +1’3 2 0 .6 1 ' 70,3л-2 + 2,3 dx 2) 0.8 + cos (2л-2 + 0,5) 4 0 ' cos (0,6л2 + 0.4) dx 1,4 +sin2 (л+ 0,7) h .3 ’ sin (0,5л + 0.4) dx 1.2 +cos (л2+ 0.4) 5 .8 cos (л 2+ 0.6) t/л 0.7 +sin (0.8л + I) 4 * sin (0.3л + 1.2) «/л 1 1.3 +cos2 (0.5л + 1) 3 8 cos (a 2 + 0,6) dx
О 1,8 + 72-'+ Г6 8 0 1,2+sin (0,7л+ 0.2) 5
127
№
9. 1)
№
10.
о.#
1.2
2) f cos (л2 4- 0.8) dx J 1.5 4-sin (0.6л 4-0.5)
0.4
2.8
№
11.
1.2
№
12.
0.6
№
13.
0.7
№
14.
о.и
1.3
f sin (0.7x4- 0.4) dx
J 2.24-cos(0.3x24-0.7)
0.5
1.4
f cos(0.8x24- \)dx
J 1,4 4-sin (0.3x4-0.5)
0.4
I
j* sin(0,8x24-0.3)dx
J 0.7 4-cos (1,2x4-0,3)
0.2
*
1.1
f cos (0.3x 4- 0.5) dx
J 1.8 4-sin (x2 4-0.8)
O.3
2.6
№
15.
1.9
i.i
f sin (0,6x2 4- 0.3)dx
J 2.4 4-cos (x 4-0.5)
0.3
№ 16.
I)
1.9
’ ч/0,7л-2 + 2.3</г J 3.2 + ./0.8л 4-1.4'
0.5
1.2
0.4
2.6
№
17.
1.8
2) f sin (0.2x2 4-0.7) dx
№ 18.
I)
2.1
' у1»7.У2 + 0.5^л-J 1,4 4-ч/1.2x4-1.3
0.7
i
' cos (0,3x4- 0.8) dx
0.9 4-2 sin (0.4x 4-0.3)
O.2
№ 19. i) f \/1.5x4-ldx'
J 1.2x4-v/-v2 + 1.8
0,6
2)
1.1
sin (0.8x4- 0.3) dx
J 1.2 4-cos (л2 4-0.4)
0.3
3 _________
* ч 2x2-rO.7dx
, 1.54" 0.8х 4" 1
2)
1.3
cos(x24-0.2)dx
1,3 4-sin (2л-0.4) o'. 5
128
№ 21.
№ 26.
№ 30.
\s 22.
№ 23.
,Vt 24.
№ 25.
№ 27.
№ 28.
№ 29.
2 О 1 1 1) 0 I 1) О. 1 1) * 0 2 1) * 2 1) I. 1) ъ I. 1) fa I. 1 1) 0. 1) *\ w 1. .7 1 ’ У1.3л2 + 0,8г/л 2) 1. 7л- + У 2л-+0.5 J 3 0 .4 0 ’ Ул2 + 0.5</л 2) .2 ' sin (0.6л + 0.5) (Lx 1.5+cos (л2+ 0.4) 4 .8 COS (л 2 + 1)</Л' 2+sin (2л*+0.5)’ 2 .9 sin (л2 + 0,6) d.x
2л + Ул2+ 2,5 J 6 0. .2 0 ’ У2л2+1г/л 2)
0.8л+У0,5л+2 J 4Х 0. ' У|.5л: + 2</л- 2) Л-+У о.8л-2+1 J к о. *_У°.8л-2 + 2</л- 2) 1.5 +cos (0.8л-+1.2)’ 3 i ' cos (2л2 +0.5)rfx 0.8 + sin (л* + 1.4)’ 4 1 sin (л+0.7) d.x
1,6 + У'1.5л+0.6 J о. .0 1 * yo.5.v2 + 3rf.v 2) 1.4+cos (0.6л + 0.4)’ 6 .3 cos (л2+0.4)</л
2л + У2л-2+1.6 J 2 0. .5 0 ' У0.8.у2+1.3</.у 2) 1.4+./л-2+ 0.6 J 3 0. .6 1 Ул-2+1,3</л- 2) 1,2 +sin (0.5л+0.4)’ 5 .» sin (0,8л + 1)</л 0.7+cos(x2 + 0.6) 4 .5 cos (0,5л2 + l)(/.y
1,5.у+У0.4л-+1.7 J 2 0. .6 ' 1 72.r+1.6rf.r . 2) 1.3 + sin (0.3л + 1.2)' 3 ' cos (0,7л + 0.2) d.x 1,2 +sin (л2+ 0.6) 5 2 cos (0.4л2 + 1) d.x 2,3 + sin(1.5x+0.3)’ 4
1.8 + Jo.3x2 + 2.3 J 8 0. 2 I ' уо.7л-2 + 1 </л- 2)
2,1 л- + У 0,6л- +1.7 J 2 0.
Образец выполнения задания
5—1258
129
I) Для вычислений по формулам левых и правых прямоугольнике! при п =10 разобьем отрезок интегрирования на 10 частей с шаток* /> = —= 2J~L5 = 0.08.
п 10
Составим таблицу значений подынтегральной функции в точках деления отрезка:
i Л » 0,3л; t 1.2 7.у;Ю.5 1.6л; + ч/л* + 0.5
/О.Зл-, + 1,2
0 1.5 • 1.65 1,2845 1.6583 4.0583 0.3165
1 1.58 1.674 1.2938 1.7310 4.2590 0.3037
2 1,66 1.698 1.3031 1.8043 4,4603 0.2922
3 1,74 1.722 1,3122 1.8782 4,6622 O,28?5
4 1,82 1.746 1,3214 1.9525 4,8545 0.2716
5 1,90 1.77 1.3304 2.0273 5,0673 0,2626
6 1.98 1.794 1.3394 2.1025 5.2705 0,2541
7 2.06 1.818 1.3483 2,1780 5.4740 0.2463
8 2.14 1.842 1,3572 2.2538 5.6778 0,2390
9 2.22 1.866 1.3660 2.3299 5,8819 0.2322
10 2,30 1.89 1.3748 2.4062 6,0862 0,2259
£. =2.6997
£, = 2.6091
9 10
В таблице найдены значения сумм: £t = £j/ = 2,6997; £,= £ .г, = 2,6091.* 1^0 <=1
Найдем приближенные значения интеграла. По формуле левых прямоугольников получим
9
Л=/г £ Г; = 0,08-2,6997=0,2158.
По формуле правых прямоугольников находим ю
/2 = Л £ г, = 0,08 • 2,6091 = 0,2087. t— 1
Эти результаты отличаются уже в сотых долях. За окончательное значение примем полусумму найденных значений, округлив результат •до тысячных:
/=LtZx = o,212.
7
2) Для решения воспользуемся формулой средних прямоугольников: ь
f(x)dx*h £y(-v1 + ; ).
J i -- О \ - /
a
130
Вычисления выполним дважды при /^=8 и я2~Ю и соответственно при Л, =(/>-«)/«, = (1,2 —0,4)/8 = 0,1 и h2 = (b-a)/n2=( 1.2-0,4)/10 = 0,08. Результаты вычислений приведены в таблицах I и II.
Таблица 1
1 Л Л, + 2 sin (0.6.v+0.3) l.7 + cos(.v2+ 1.2) / й\ /I v4+- )
0 0.4 0.45 0.53963» 1,86750 0,28896
1 0,5 0.55 0.58914 1,76824 0.33318
? 0.6 0.65 0,63654 1.64832 0.38618
3 0.7 0.75 0,68164 1,50947 0,45158
4 0.8 0.85 0,72429 1.35550 0.53433
5 0.9 0.95 0,76433 1.19300 0.64068
6 1.0 1,05 0.80162 1.03186 0.77687
7 1.1 1.15 0.83603 0.88559 0.94404
£, =4,35582
Таблица II
г Л -Vi+ 5 sin(0.6.v+0.3) 1.7+cos(№ + 1.2) 'V<+V
0 0.4 0.44 0.53457 1.87627 0,28491
1 0.48 0.52 0.57451 1.80022 0,31913
2 0.56 0.60 0.61312 1.71080 0,35838
3 0,64 0,68 0,65032 1,60852 0.40430
4 0,72 0,76 0,68602 1.49467 0.45898
5 0,80 0.84 0.72014 1,37142 0.52511
6 0,88 0,92 0,75260 1.24212 0,60590
7 0.96 1.00 0,78333 1.11150 0,70475
8 1.04 1.08 0.81225 0.98571 0.82403
9 1.12 1,16 0,83930 0.87241 0,96205
£, = 5.44754
Найдем приближенные значения интеграла
А =/71 £, =0,1 -4,35582 = 0,43558;
4 = Л2 D = 0’08 5,44754=0,43580.
Значения различаются в десятичных долях, но второе значение точнее первого, поэтому принимаем 0,4358.
Работа 3
Задание. 1) Вычислить интеграл по формуле трапеций с тремя десятичными знаками.
2) Вычислить интеграл по формуле Симпсона при л = 8; оценить погрешность результата, составив таблицу конечных разностей.
5
131
№ I.
№ 2.
№ 3.
№ 4.
№ 5.
№ 6.
№ 7.
№ 8.
№ 9.
№ 10.
№ 11.
№ 12.
132
1.2
'sin (2л)
----з—dx.
Л“
0.H
№ 13.
Л» 14.
Л“ 15.
№ 16.
№ 17.
№ 18.
Л» 19.
№ 20.
№ 21.
Л» 22.
№ 23.
№ 24.
з
2) j jrlg.vt/x.
1.4
1.2
cos(.v’) .
---------dx.
л + 1
0.4
1.6
2) J (№ + I) sin (л— 0.5)f/.v.
O.K
1.4
2) J .v2cos ,v dx.
0.6
3.3
f lg(.v2 + 0.8) t -------------dx.
л-1
133
№ 25.
1.4
dx
J уПл-Чол’ o.<>
2.К
V
1.2
№ 26.
0.72
0.6
Ke 27.
1.2
№ 2«.
№ 29.
O.K
2.K
O.H
3.2
№ 30.
1.6
Образец выполнения задания
1)
i.6
dx.
1.2
1) Для достижения заданной степени точности необходимо определить значение н так. чтобы
+++/,<0.0005. (*)
12м
Здесь «=0.7; Л =1.3; Л/2> max |/"(v)|, где / (л)= 1 /У2л'2 + 0.3. Находим 10.7; 1.3]
|Л\/(2л-24-0.3)'’ 7 1 \/(2л2 + 0.3)5’
шах | f" (.г) | < l. L3i~JLL_ % 6.98.
(О.7: 1.3] ‘ ч/(2 0.72#4-0,3)5
Положим М2 = 7, тогда неравенство (*) примет вид /<0,0005, откуда п2 > 252, т. е. н > 16; возьмем л = 20.
134
Вычисление интеграла производим по формуле
/ Л I -----Fl'i +.1'2 + — +.1’19 j'
где Л=(Л-а)/Л=0,6/20 =0.003; r,= r(.v,)= l/>/lr?+0.3; л, = 0,7 + й (i=0, I. 2...20).
Все расчеты приведены в табл. 1.
Таблица I
i Vi л; lvr+0.3 У«>. У’о .1’1. Ул Уш- У г»
0 0.7 0.49 1.28 1.1314 0.88386
1 0.73 0.5329 1.3658 1,1686 0,85572
э 0.76 0.5776 1.4552 1.2063 0.82898
3 0.79 0.6241 1.5482 1.2443 0.80366
4 0.82 0.6724 1.6448 1.2825 0.77973
5 0.85 0,7225 1.7450 1,3210 0,75700
6 0.88 0.7744 1.8488 1.3597 0.73546
7 0.91 0.8281 1.9562 1,3986 0,71501
8 0.94 0.8836 2.0672 1.4378 0.69551
9 0.97 0.9409 2.1818 1.4771 0.67700
10 1.00 1.0000 2.3000 1,5166 0.65937
II 1.03 1.0609 2.4218 1,5562 0.64259
12 1.06 1.1236 2.5472 1.5960 0.62657
13 1.09 1.1881 2.6762 1.6356 0.61140
14 1.12 1.2544 2.8088 1.6759 0.59669
15 1.15 1.3225 2.9450 1.7161 0.58272
16 1.18 1.3924 3.0848 1.7564 0.56935
17 1.21 1.4641 3,2282 1.7967 0,55658
18 1.24 1.5376 3.3752 1.8372 0.54431
19 1.27 1.6129 3,5258 1,8777 0.53253
20 1,30 1,6900 3,6800 1.9187 0,52129
Е 1.40515 12.77022
Таким образом,
/=0,0з( l,40?Sb+ 12.77022^=0.40418 4:0.404.
2) Согласно условию л = 8, поэтому h=(b—а)/п — (1,6— 1,2)/8=0,05. Вычислительная формула имеет вид
7—- (/о+4 г j 4- 21'2+4г.з + 2,Гд + 4,1’5 + - Гб+4 г? + г»),
«л
где г, = г (л,)=s>n^‘ -1). л-. = ] ,2 + ih (/=0, 1.8).
лг+1
Вычисление значений функции, а также сложение значений функции, имеющих одинаковые коэффициенты в формуле, производим в табл. II.
135
Таблица I]
/ V, sin (2л,-2,1) Л‘7 + 1 Уо. У в Ун Ул* Ул* У? У2* У*»* Уь
0 1.20 0.30 0,29552 2,44 0.1211
1 1.25 0.40 0.38942 2.5625 0,1520
2 1.30 0.50 0.4794 2.69 0.1782
3 1.35 0.60 0.5646 2.8225 0,2000
4 1.40 0.70 0,6442 2.96 0.2176
5 1.45 0.80 0.7174 3.1024 0,2312
6 1.50 0.90 0.7833 3,25 0.2410
7 1.55 1.00 0.8415 3.4025 0,2473
8 1.60 1.10 0.8912 3,56 0,2503
Е 0.3713 0.8305 0.6368
Следовательно,
/ = (0.3714 + 4 - 0.8305 + 2 0,6368)=• 4,9670 а 0,88278.
Для оценки точности полученного результата составим таблицу конечных разное!ей функций до разностей четвертого порядка (табл. III)
Таблица III
/ у, Ду,- Л2»’/ Д3п Л4у,
0 0.1211 0,0309 -0.0047 0,0003 -0.0001
1 0.1520 0.0262 -0,0044 0,0002 0,0000
2 0,1782 0.0218 -0,0042 0,0002 0,0000
3 0,2000 0,0176 -0,0040 0.0002 0,0001
4 0,2176 0,0136 -0,0038 0,0003 -0,0001
5 0.2312 0,0098 -0,0035 0,0002
6 0.2410 0.0063 -0,0033
7 0.2473 0,0030
8 0.2503
Так как max [А4 г;| = 0,0001, то остаточный член формулы
(Л—«Ьтах 1 A4v.l 0.4 0.0001
/\nei ' ' — -л 0,0000003.
,к' 180 180
Вычисления производились с четырьмя значащими цифрами, а потому
величина остаточного члена на погрешность не влияет.
Погрешность вычислений можно оценить из соотношения
А/=(/?-«) Ду <0,4 0,0001 <0.00005.
Значит, полученные четыре десятичных знака верны.
Работа 4
Задание. Найти приближенное значение интеграла по формуле «трех восьмых», используя для контроля точности вычислений ДВОЙНОЙ просчет при Hl—9 и «2—12.
136
2.4
2.64
№
1.
№
2.
№
№
№
№
№
№
5.
7.
9.
0.6
2.96
0.8
2.74
1.3
2.5
0.7
3.16
1
2.84
11.
13.
15.
17.
19.
21.
23.
№
№
4.
6.
№ 8.
№
№
1.4
2.64
№
1.2
2.3
№
0.5
2.64
№
2.6
№
0.8
2.66
0.5
2.34
0.9
2.9
i.i
1.2
2.6 Г
0.8 +
0.8
2.66
0.5
2.34
10.
12.
0.9
14.
16.
18.
20.
№ 22.
№ 24.
№ 26.
2.2.v2 ‘ 0.5
1.1
2.5b
0.4
1.3
2.4
0.6
2.96
о.н
2.74
1.3
(14-0.5л-'М<
0.7
3.1 6
f (l+0.8.v2)J.v
1
2.84
(I +0.8л-2)</л
137
2.56
2.64
№ 27.
№ 29.
f (1+0,5\2)г/л
J 1.2 +Jo.6a2+I,5 0.4
3.46
(I + 1.2л2) dx J 2,3 + ч/0.4л2 + 3.2 1.3
№ 28.
№ 30.
Г (1+0.3л-2)гЛ-
J 0.9 +J1.2л2+ 0.5
1.2
2.3
* (1+0,6л2)г/л
J 2.5 + . 0.3л"+1.6 0.5
Образец выполнения задания
3.36
Г {1+0.4л2)(/л
J 2 + ч/О.5л2+ 1.3
Воспользуемся формулой «трех восьмых», выражающей данный интеграл через суммы значений подынтегральной функции:
h
f /’(.V) </лу (А, + 3£2 + 2£ А
I л \ /
а
где Л =-----; У1=.Го + гп; Уз= П +3'2 +.Г4 + Г5 + •••; £з=Уз+.Гб +Гд+
л
число разбиений п должно быть кратным трем.
I. н,=9:
3.36-1.2
= 0.24.
Вычисления запишем в следующей таблице:
i •Vi 1 +0.4л 2 2+ч/О.5л-,2 + 1.3 Го.ч .1’1.2.4.5. Т.Н — Уз.ь
0 1.2 1.576 3.42127 0.46065
1 1,44 1.82944 3.52866 0.51845
2 1,68 2,12896 3.64657 0.58383
3 1.92 2,47456 3.77291 0.65588
4 2,16 2,86624 3.90599 0,73381
5 2.40 3,304 4.04450 0,81691
6 2.64 3.78784 4,18742 0.90458
7 2.88 4.31776 4,33392 0,99627
8 3.12 4.89376 4.48338 1.09153
9 3,36 5.51584 4.63530 1,18996
1,65061 4.74080 1.56046
X. Б
3-0 ^4
h = —— (1.65061 + 3 4,74080 + 21,56046) = 1,709453.
8
138
И. «2 = 12; />|=3'36 L2=O.I8.
12
Составим таблицу
i 1+ОДгг 2 + v 0.5л f+ 1,3 Jo. 1 2 Jl.2.4.5.".H.1O.i 1 J.*.»'.4*
0 1.2 1.576 3.42127 0.46065
1 1.38 1.76176 3.50073 0.50325
2 1.56 1.97344 3.58644 0.55025
3 1.74 2.21104 3.67744 0.60124
4 1.92 2,47456 3.77299 0.65588
5 2.10 2.764 3.87216 0,71381
6 2.28 3.07936 3.97464 0,77475
7 2.46 3,42064 4.07986 . 0.83842
8 2.64 3,78784 4.18742 0.90458
9 2.82 4.18096 4.29700 0.97300
10 3,00 4,6000 4.40832 1.04348
II 3.18 5.04496 4.52115 1.11586
12 3,36 5,51584 4.63530 1.18996
1.65061 6.32553 2.34899
L M b
А=—z-— (1,65061 + 3 6.32553 + 2 • 2,34899) = 1.709450. Полученные резуль-о
таты совпадают с точностью до стотысячных, поэтому принимаем 1,70945.
Работа 5
Задание. 1) Применяя экстраполяцию по Ричардсону, вычислить ин-и + З
теграл J y/x2+hdx по формуле трапеций при /^=3.
п2 = 6 и найти его уточненное значение; «=0.1А. Л = 4 —O.IA, к = 1. 2, 3.30 (к — номер варианта).
2) Применяя экстраполяцию по Ричардсону, вычислить ин-с + 4
теграл J lg(.v2 + 2)</.v по формуле Симпсона при /^=2, п2 = 4 и найти его уточненное значение; <=3 — 0,1 А. А=1, 2, 3, ...» 30.
Образец выполнения задания
.1.5
I) /= J У2л-2 + 3</л\
U.S
с
2) /=fln(.v2 + 3,5)dv.
139
1) Если Л2 = (Л—а)/п «1=3, то / 2=(3,5-0,5)/6 = ii=(h-a)/Hi=(: =0,5. Составив J,5 — 0.5)/3= 1; если н2 = 6, т<1 таблицу значений подынтегв
ральной функции г(л) = ^ (/ = 0, 1. 2 6). '2.v2 + 3 с шагом Л2=0,5, причем л\ = 0,5 + м
/ А/ 2.vf То. _>'б »3. У: Ъ
0 0.5 0.5 1,871
1 1.0 2.0 1,236
2 1.5 4,5 2,739
3 2.0 8.0 3.317
4 2,5 12,5 3,937
5 3.0 18.0 4,583
6 3.5 24.5 5.244
7,115 16.812
Используя формулу трапеций, получим:
при п — 3:
/1 г /З’о+Л . = "1 —^—+1’2 \ 2 j f7JI5 4/— \ ~ + 2,739 + 3,937^ = 10.234:
при «2 = 6:
г i Л'о+-Г‘ . /2=«21 — Ь 5 \ /7 115 \ L .г, =0,5 ( --^+16.8121=10,185. i = 1 / X 2 /
Найдем уточненное значение интеграла по формуле
/ м II мэ 1 -3 -э
Так как для формулы трапеций т = 2, то
/|.2=10,185+-Л-;(10.185-10,234)=
6* —
= 10.185+|(—0,049)= 10,185-0,016= 10,169.
Ответ: /а 10.169.
2) Если П{=2, то ftj st (Л — a)/Hi =(6 — 2)/2 = 2; если «2 = 4, то /ь = (/) —л)/и2=(6-2)/4= 1. Составим таблицу значений подынтегральной функции r(.v) = lg(.v2 + 3,5) с шагом Л2=1, причем л*1 = 2 + /Л (/=0, 1, 2, 3, 4).
140
f vf v/ + 35 Igh; i 3.5)
0 . 9 7,5 0.875!
1 3 12.5 1.0969
2 4 19,5 1.2900
3 5 28.5 1.4548
4 6 39.5 1.5966
Используя формулу Симпсона, получим: при /ь=2:
h, 7
Л *у(.1Ъ + 4у2+у4) = -(0,8751 +4-1,29004-1.5966) = 5.0878,
при п2=4:
Л ~ j (До+41'1 + 2г2 + 4гд +у4) =
Ц(0.8751 +4-1.0969 + 2-1,2900+4-1.4548+ 1,5966) = 5.0862.
Найдем уточненное значение интеграла, считая ш=4: /,.2 = 5.0862+тг7я ’ (5.0862 - 5.0878) =
= 5,0862 + -^ (- 0,0! 6) = 5,0862 - 0,001 = 5.0861.
Ответ: /%5,0861.
Работа 6
Задание. Вычислить интеграл по формуле оценки точности двойной пересчет
Гаусса, применяя для (при /?1=4 и л2 = 5).
№ 2.
№ 5.
№ 8.
14!
№ 13. 2 Л‘ f/.V № 14 3 .2 x2dx № Л 15. 2 л-+ 0.5 f . dx. v -v2+l
к 0. 1 Н ' .5 f > . -к /л‘ + 2 2 / . п ‘ 4Ч,а + 2 .5 o. >
№ 16. -^±l_,/v. № 17. Xs Xs Xs 18. 21 л dx
№ 19. 0. 5 7 ' .4 /л'2 + 1 xdx Xs № 20. 23. о. 1 л* + 2 2 .6 —' dx • 1 4 1 v л2+ 2.5 xdx
№ 22. 1 4а. 2 ’ I.H /л'2+1 № + 2 dx. 0. ,/.Г2 + 1 4 • л 2 <6 24. 2 •• .8 Jx2+\X 5 Л'2 dx
-0.4 1.1 1 ч/л‘ * 4-1 « 0. 1 /г2+ 2 ft N 1.6 l.H x/x + 1.2
№ № 25. * y.v2+l dx. № № 26. 29. ' х2 dx № № b 27 л2 + 1.4 —, dx. v л-2+ 0.2 л-+ 2.2 — dx. /v2+i
28. 0 2 2 .8 2л+2,5 1 —лр/.г 0. 1 /v+1.7 ft ' xdx 30. o. 1 4 .7
2 2 /л-2+1 1). Ул-2+ 2.4 8 o. 4
Образец выполнения задания
/= ' л-+0.8 , —, dx. J ,/№+1.2
Формула Гаусса имеет вид ь |Av)dv»^[C1/(.v1)+CV(.V2)+ ... +С„Дхп)' а Ь+и Ь—а гдс *<=— + — ft (/=1.2 я). „ 2.7+1.6 2.7-1.6 В данном примере л*,-=— 1 —/, = 2.15+0,55/, G и /; берем из таблицы квадратурных коэффициентов Вычисления удобно располагать в таблице. При п = < I- , а значения) ! имеем:
V, ЛГ+1.2 /(-V.) СДл.)
0.34785 0.65215 0.65215 0.34785 -0,86114 -0.33998 0.33998 0.86114 1.6764 1.9630 2,3370 2,6236 4.0103 5.0534 6,6616 8,0833 2,0026 2.22480 2,5810 2,8431 1.2366 1.2291 1.2154 1.2042 0.43015 0.80155 0.79264 0.41887
142 £ = 2,44321
Следовательно, /0,55 • 2.44321 = 1,3438.
При л = 5 имеем:
с. V, vf+ 1.2 /(',)
/'Г+ 1.2
0,23693 -0,90618 1.6516 3.9278 1.9819 1.2370 0.2903
0.47863 -0.538469 1,8538 4,6366 2.1533 1.2324 0.58988
0.56889 0 2.1500 5.8225 2.4130 1.2225 0.69549
0.47863 0.538469 2.4462 7.1839 2.6803 1.2111 0.57968
0.23693 0.90618 2.6484 8.2140 2.8660 1.2032 0.28508
£ = 2.44321
Значит, /%0,55 -2,44321 — 1,3438. Совпадение результатов свидетельствует о правилыгости вычислений.
Глава IX ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Работа 1
Задание. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка усовершенствованным методом ломаных на отрезке [0,2: 1,2] с шагом = 0,1 при начальном условии г (0,2) = 0,25. Все вычисления выполнять с четырьмя десятичными знаками.
№ 1. У=O.I33| [л-2 + sin 2л) + 0.872г.
№ 2. г'=О,215| л-2 + cos 1.5л-) + 1.283 г.
№ 3. г'=0,158| л-2 + sin 0.8л) +1.164у.
№ 4. г'=0,!73| [л-2 + cos 0,7л-)+0.754у.
№ 5. г'= 0.2211 Lv2 + sin 1.2л-)+0.452г.
№ 6. г'=0,163| л2 + cos 0.4.v)+0.635г.
№ 7. г' = 0.218( л 2 + sin 1,6.v) + 0,718 г.
№ 8. г'= 0.1451 л2 + cos0.5.v)+0,842г.
№ 9. г' = 0,213| Lv2 + sin 1,8л) + 0.368г.
№ 10. г'= 0.1271 л 2 + cos 0.6л) + 0.573 г.
№ И. у'= 0,2321 (л*2 + si п 1.4л) + 1.453 г.
№ 12. г' = 0,417| (л*2+cos 0.8х) + 0,972 г.
№ 13. г'= 0,3241 Lv2 + sin 1.5л) + 1,612г.
№ 14. г'= 0.2631 л-2+cos 1.2л-) + 0,453у.
№ 15. г'= 0.3721 Lv 2 + sin 0.7л)+0.758г.
№ 16. г'=0.3431 [л2 + cos 0.4х) + 1.315 г.
№ 17. г'= 0.2761 v2 + sin 1.6л)+ 0.988 г.
№ 18. г'= 0.1731 л-2 + cos 0,6л-) + 1,534г.
№ 19. г'= 0,2581 [л2 + sin 0,4л)+0.724г.
№ 20. г' = 0.317 (л-2 + cos 1,4.v) + 1,344г.
№ 21. г' = 0.166| (л*2 + sin 1,1 л) + 0.883 г.
№ 22. г'= 0.215| 1л 2 + cos 0,9л) + 1,21 Зг.
№ 23. у'= 0.1881 [л 2 + sin 1,5л)+0,885г.
143
№ 24. Кв 25. № 26. № 27. № 28. № 29. № 30. "w* II II II II II II II р р о р р р о t j — г j — w л — ос Л -J —• — t'J Л t-п О ос л (л 2 + cos 0.6л‘)+0.772v (л2 + sin 1.2л) + 1.344г. 1л‘2 + cos 1,3л) + 0,687г (л 2 4- sin 0,8 л) + 1,247 г. (л2 + cos 0.4л) + 1 >452г 1л2 + sin 0.6л) + 0.747 г. (л2 + cos 1,2л) + 1,544г
Образец выполнения задания ж
0.185 (.V 2 + cos 0.7.V) + 1.843г. !
Используем формулу г' 1 = »’ । +, гн 1=п+лг;1.1,глс / Л \ 2 ’ 4 2/ ’ h =y‘ + 2yi'
Bet ' вычисления представим в таблице (учитывая, что Л/2 = 0,05):
i Vi л r'i Л . ,'У1 Л Vi + 2
0 1 2 3 4 5 6 7 8 9 10 0,2 0.3 0.4 0.5 0.6 0.7 0,8 0,9 1.0 1.1 1,2 0,25 0,3215 0.4083 0.5137 0,6419 0.7977 0.9870 1,2169 1,4959 1.8341 2.2438 0.6513 0.7901 0,9599 1.1668 1.4185 1,7240 2,0942 2,5421 3,0834 3,7369 0.0326 0.0395 0.0480 0.0583 0.0709 0.0862 0.1047 0,1271 0.1542 0.1868 0,25 0,35 0.45 0.55 0,65 0.75 0.85 0.95 1.05 1,15 0,2826 0,3610 0,4563 0.5720 0,7128 0.8839 1,0917 1.3440 1.6501 2.0209 0.7145 0,8675 1.0543 1.2816 1.5581 1.8932 2.2989 2,7895 3.3823 4.0974 0,0715 0.0868 0.1054 0.1282 0.1558 0.1893 0.2299 0.2790 0.3382 0,4097
Решение дает значения Л (' = 0, 1, 2, ... 10), полученные в процессе
вычислений (первые два столбца таблицы).
Работа 2
Задание. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка методом Эйлера— Коши. Воспользоваться вариантами работы 1. Вычисления выполнять с четырьмя десятичными знаками. В ответ включить цифры, совпавшие при решении в работах 1 и 2.
Образец выполнения задания
г'=О J 85 (л-2 + cos 0,7л) +1,843 г.
Используем формулу
V/+1
ht , , _ , Vi+y. + i),
144
где Л и =г'(л',ч i. _П+1). r, f i = .п+Лг,. Ike вычисления представим в таблице:
! V/ J7 г! /в-; j*<.1 Ji • • i<- rj". । Л. . э (»,+ »,. i)
0 0.2 0.25 0.6513 0.0651 0.3151 0.7784 1.4297 0.0715
1 0.3 0.3215 0.7901 0.0790 0.4005 0.9455 1.7356 0.0868
2 0.4 0.4083 0.9599 0.0960 0.5043 1.1495 2.1094 0.1055
3 0.5 0.5138 1.1670 0.1167 0.6305 1.3975 2.5645 0.1282
4 0.6 0.6420 1.4187 0.1419 0.7839 1.6986 2.1173 0.1559
5 0.7 0.7979 1.7244 0.1724 0.9703 2.0635 3.7879 0,1894
6 0.8 0.9873 2.0947 0.2095 1.1968 2.5050 4.5997 0.2300
7 0.9 1.2173 2.5428 0.2543 1.4716 3.0386 5.5814 0.2791
8 1.0 1.4964 3.0844 0.3084 1.8048 3.6830 6.7674 0.3384
9 1.1 1.8348 3.7382 0.3738 2.2086 4.4604 8.1986 0.4099
10 1.2 2.2447
Решение дают значения л*,-. г,- (/=0. 1. 2. 10) (первые два столбца
таблицы).
Сравнивая найденное решение с решением, полученным в работе I. видим, что они расходятся в последних цифрах, поэтому в ответ включим значения, округленные до тысячных.
Ответ:
A'i j* A. J‘i
0,2 0.25 0.8 0,987
0,3 0.322 0.9 1.217
0,4 0.408 1.0 1.496
0.5 0.514 1.1 1.835
0,6 0.642 1.2 2.245
0,7 0.797
Работа 3
Задание. Используя метод Эйлера с уточнением, составить таблицу приближенных значений интеграла дифференциального уравнения г'=/(л\ г). удовлетворяющего начальным условиям r(.v0)= Го на отрезке [а, />]; шаг Л = 0,1. Все вычисления вести с четырьмя десятичными знаками.
№ 1
.v + cos—— л
№ 2. v'=.v+cos'x 3
r0(L8) = 2.6. хе [1.8: 2.8].
г0(1,6) = 4.6. л е [1.6; 2.6].
145
№ 3. r' = .v + cos—5=. 4/io г0 (0.6)=0.8. ле [0.6; 1.6].
№ 4. , г г = л:+cos . V7 го (0.5)=0.6. ле [0.5; 1.5]
№ J 5. , г г =.r+cos-. я ,го(1.7) = 5.3. л е [1.7; 2.7],
№ 6. , г г =.v+cos——. э ?5 >•„(1,4)= 2.2 л е [1.4; 2.4].
№ 7. , г Г =.v + cos'“, е у„(1.4)=2.5. л е [1.4; 2.4].
№ 8. , г г =.r + cos——. Го (0.8)= 1.4. ле [0.8; 1.8].
№ 9. , г Г = .V + COS—tz, Уз ,г„(1.2) = 2.1. ф t'j • • к)
10. , г Г = Л~ 4- COS ~ , УГГ у„(2.1) = 2.5. ,ге[2.1: 3,1].
№ 11. , г Г =Л’4-51П-^, ч/5 ,1„(1.8)=2.6. л е[1.8; 2.8].
№ 12. , . г „г =.v+sm~. .|„(1.6)=4.6. . ле [1.6; 2,6].
№ 13. г =.v + sin— yio Го (0,6) = 0,8. ле [0.6; 1.6].
№ 14. , г г =л + »т-^—, •Л Го (0.5) = 0.6, ле [0.5; 1.5].
№ 15. , - V г = .v + sin —, я .го (1.7) = 5,3, л е [1.7; 2,7].
№ 16. Г = .V-ь sin \ , ч/2Л Го (1.4) = 2.2. л-с [1,4; 2.4].
№ 17. , г Г = л-4-sin'-, е Л„(1,4) = 2.5. л-с [1,4; 2,4].
№ 18. , Г Г = Л" + S1И —. ч/2 Го (0,8)= 1,3. ле [0,8; 1.8].
№ 19. , г Г = л* 4- sin———, ч/З ?„(!.!)= 1.5, хе[1.1; 2.1].
№ 20. Г = Л' + Sin—-— ч/п Го (0.6)= 1,2, ле [0,6: 1.6].
№ 21. , г г = .v + sin ——. 1.25 .г„(0,5)= 1,8. ле [0,5; 1,5].
146
№ 22. ув г0 (0.2) =1,1 ле [0.2; 1.2].
.Ye 23. г г'= Л-4-Sin ' 1 э >„(0.1) = 0.8. ле[0.1: 1.1].
ч/1.3
.Ye 24. , • Г Г = .V -4- Sin , Уо.з Го (0.5) = 0.6. ле [0.5; 1.5].
№ 25. г 1 - =Л + МП 0.7 Го (1.2) =1.4. ле[1.2; 2.2].
Ле 26. •,,= V+<;OSi25- Го (0,4) = 0.8. хе [0.4: 1.4].
№ 27. , г Г =A' + COS ' L. V1.5 .Го (0.3) = 0.9. ле [0.3; 1.3].
№ 28. , г V = Л' + COS . уп >„(!.2)= 1.8. л е[1,2; 2.2].
№ 29. , г г = л -4- cos —, >03 ,>„(0.7)=2.1. ле [0.7; 1.7].
№ 30. , г >• =.v к cos у/бЗ ><>(0.9)= 1.7. ле [0.9; 1,9].
Образец выполнения задания
г' = л+sin ; Го (1.4) = 2.2. .vе [ 1.4; 2.4].
Метод Эйлера с уточнением заключается в том, что каждое значение Ук +1 = У (л +1), где у (л ) — искомая функция, a х*ц = х0 4- Л {к + 1), к = 0. 1, 2, определяется следующим образом:
за начальное приближение берется
у1°+1 = л + kf(xk, ук), где /(х, г)=г' (х, г);
найденное значение г1% уточняется по формуле
У t+1 = л4-~ [/(л, Л) +/(Л +1, г!' +!**)] 0'= U “•
А*
Уточнение продолжают до тех пор, пока в пределах требуемой точности два рослсдовательных приближения не совпадут.
Все описанные вычисления удобно производить, составив следующие таблицы:
основную таблицу, в которой записывается ответ примера (табл. I);
таблицу, в которой выполняется процесс последовательных приближений (табл. II);
вспомогательную таблицу, в которой вычисляются значения функции /(л, л) (табл. III).
147
Таблица
А л* Уд ./* — ./ (.<л. Ул) l,fk 1
0 1.4 7 7 2.2292 0.2229
1.5 2.4306 2.3821 0.2382
2 1.6 2.6761 2.5281 0.2528
3 1.7 2.9357 2.6648 0.2665
4 1.8 3.2084 2.7895 0.2790
5 1.9 3.4929 2.8998 0.2900
6 2,0 3.7876 2.9936 0.2994
7 2.1 4.0908 3.0696 0.3070
8 ”> 9 4.4006 3.1268 0.3127
9 2.3 4.7152 3.1654 0.3165
К ) 2.4 5.0328
Табл и на II
А + 1 л*. । Ул / Уд* i Л /-о» / Д < 1 ^(./л + /д"*|)
1 1.5 7 7 0 2.4229 2,2292 2.3805 4.6097 0,2305
1 2.4305 2.3820 4.6112 0,2306
2 2.4306 2.3821 4.6113 0.2306
2 1.6 2.4306 0 2.6688 2.3821 2.5268 4,9089 0.2454
1 2.6760 2.5280 4.9101 0,2455
2 2.6761 2.5281 4,9102 0.2455
3 1.7 2.6761 0 2.9289 2.5281 2.6641 5.1922 0.2596
1 2.9357 2.6648 5,1929 0.2596
4 1.8 2.9357 0 3.2022 2.6648 2.7892 5.4540 0.2727
1 3.2084 2.7895 5.4543 0.2727
5 1,9 3.2084 0 3.4874 2.7895 2.8998 5,6893 0.2845
1 3,4929 2.8998 5,6893 0.2845
6 2.0 3.4929 0 3,7829 2.8998 2.9939 5,8937 0.2947
1 3.7876 2.9936 5,8934 0.2947
7 2.1 3.7876 0 4,0870 2,9936 3.0700 6,0636 0.3032
1 4,0908 3.0696 6.0632 0.3032
8 2.2 4,0908 0 4.3978 3.0696 3.1273 6.1969 0,3098
1 4,4006 3.1268 6.1964 0,3098
9 2.3 4.4006 0 4.7133 3,1268 3.1658 6.2926 0.3146
1 4,7152 3.1654 6.2922 0.3146
10 2,4 4,7152 0 5.0517 3,1654 3.1866 6.3520 0,3176
1 5,0328 ж 3.1863 6,3517 0,3176
148
Таблица III
А Л г 2 25 v=Y+sin225
0 1,4 2.2 0,9778 0.8292 2.2292
1 1.5 2.4229 1,0768 0.8805 2,3805
1,5 2.4305 1.0802 0.8820 2,3820
1.5 2,4306 1.0803 0.8821 2.3821
2 1.6 2.6688 1.1861 0.9268 2.5268
1.6 2.6760 1.1893 0.9280 2.5280
1.6 2.6761 1.1894 0.9281 2.5281
3 1.7 2.9289 1.3017 0.9641 2.6641
1.7 2.9357 1.3048 0,9648 2.6648
4 1.8 3.2022 1.4232 0.9892 2,7822
1.8 3.2084 1.4260 0.9895 2,7895
5 1.9 3.4874 1.5500 0.9998 2.8998
1.9 3.4929 1.5524 0.9998 2.8998
6 2,0 3.7829 1.6813 0.9939 2,9939
2,0 3.7876 1.6834 0.9936 2,9936
7 2.1 4.0870 1.8164 0.9700 3.0700
2,1 4.0908 1.8181 0.9696 3.0696
8 2.2 4.3978 1.9546 0.9273 3.1273
э 7 4.4006 1.9558 0.9268 3.1268
9 2,3 4.7133 2.0948 0.8658 3.1658
2.3 4.7152 2.0956 0.8654 3,1654
10 2.4 5.0317 2.2363 0.7866 3,1866
2.4 5,0328 2.2368 0.7863 3.1863
Ответом является значения г* (л). полученные в табл. I.
Работа 4
Задание. Используя метод Адамса со вторыми разностями, составить гардину приближенных значений интеграла дифференциального уравнения г'=/’(.¥. г), удовлетворяющего начальным условиям г(л*о)=го на отрезке [О, 1]; шаг Л = 0,1. Все вычисления вести с четырьмя десятичными знаками. Начальный отрезок определить методом Рунге—Кутта.
149
№ 1. у' = I + 0,2 г sin л- -г2. г (0)=0.
№ 2. r'=cos(.v+r)+0.5(.v—г). г(0) = 0.
cos Л' , ,
№ 3. г’ =--------0.5г2. г 0 =0.
д + 1
№ 4. г' = (I — г2) cos л + 0.6 г. г(0) = 0.
№ 5. г' = 1 + 0,4 г sin л — 1.5 г2, г(0)=0.
cos г , , .
№ 6. г' = —7 + О.Зг2. г(0) = 0.
’ ’ .V + 2
№ 7. .г' = со$(1.5д+.г) + {д —г). _г(0) = 0.
. / 1 0.5г . .
№ «. г = I —sm(.v + r)+—г(0)=0.
д* + 2
№ 9. г' = -^- + 0.1г2, г(0)=0.
1.5 + д'
№ 10. г' = 0,6sin д- - 1,25г2 + 1, г(0) = 0.
№ 11. r'=cos(2x + _г)+ 1.5(д — г). г(0) = 0.
0,1г . t . , 4
№ 12. г'= I------sin(2.v+r). г(0)=0.
л' + 2
cos г , . .
№ 13. г' = — -------0.1г2. г 0 =0-
1.2:> + д' ' '
№ 14. г' = 1 + 0.8г sin л- - 2г 2. .г (0)=0.
№ 15. r'=cos(l.5.v+г)+1.5(л —г). г(0)=0.
№ 16. г'=1-ып(2д + г) + ^, г(0) = 0.
COS V’
№ 17. г' = —-=------0.5г2. j(0)=0.
1.75 + д-
№ 18. _г' = I +(1 — д')sin.г—(2 + д).г. _г(0) = 0.
№ 19. г'=(0.8-г2)со$д+0,3г. г(0)=0.
№ 20. г'= 1 + 2.2sinд +1.5г2. г(0)=0.
№ 21. r' = cos(.v + r)+0,75(.v—.г). г(0)=0. . . 0.5г , .
№ 22. г'= l-sin(l.25.r+v) + -~. г(0)=0.
№ 23. г' = —i-О.Зг2. г(0) = 0.
д'+2
№ 24. г' = 1 — sin (1,75л' + г) Ч—. г(0) = 0.
cos г , . .
№ 25. г'-——---------0.5г2. г(0) = 0.
150
№ 26. y'=cos(1.5.v+y)—2.25(л+y), y(0) = 0.
№ 27. r'=-^L-1.25r2. i(0)=0.
1.5+л
№ 28. y'= 1 —(л —l)siny+2(.v+y). y(0)=0.
№ 29. у' = 1 — sin (0.75.v - у)+(0)=0.
1.251-
№ 30. r'=cos(.v—r. r(0) = 0.
l.5+.v
Образец выполнения задания
у' = I + 0,2у sin л- - 1.5у2 =/(.v. у): у (0)=0. л е [0. ! ]. Л=0.!.
1. Определим значения yi = r(0. 1). у2=у(0.2) (начальный отрезок) методом Рунге — Кутта. При этом значения г, h! = y(.vl + i), где л;- ♦ i =л',-+Л. находятся по формулам
.Пн =я+ДГ|>
Аг,=g (А-1;’++ 2А-з'+*41 )•
где
Af=Ш> гД
2 = A/l A*| + - . Г/ + “7 L
,61 , г/ Л
А'(з°=А/(л-1+-, г.ч-у-к
А'^=Л/(х.+Л, г.+А'П
Все вычисления будем располагать в таблице (см. табл. I).
Таблица I
.V -Ф) sin .v 0.2v sin .v - 1.5у2 /(л.у) Лф.у) Ду
0 0 0 0 0 1 0.1 0.1000
0,05 0.05 0.10 0.05 0.0498 0.0997 0.0500 0.0500 0.0998 0,0005 0,0005 0.0020 -0.0038 -0.0037 -0.0149 0.9967 0.9968 0.9871 0.0997 0.0997 0.0987 0.1994 0.1994 0,0987
• 0.5979 (1,6) = =0.0996
0,10 0.0996 0,0998 0.0020 -0.0149 0.9871 0.0987 0.0987
151
Продолжение табл.
Л' у(<) sin А* 0.2г • sin .v -1.5г2 л Л. г) Л/(л. у) 'Чг
0.15 0.15 0.20 0.1490 0.1482 0.1968 0.1494 0.1494 0.1987 0.0045 ().(Ю44 0.0078 -0,0333 -0.0329 -0.0581 0,9712 0.9715 0.9497 0.0971 0.0972 0.0950 0.1194? 0.11944 0.0)950
0,5823 .(|'6)==1 = 0^)970
0.20 0.1966 0.1987 0.0078 -0.0580 0.9498
2. Вычисление последующих значений г, = г(л;), где л7=.г0+ДгЛ (/ = 31
4. ...), производим по формуле Адамса со вторыми разностям^
г. +1 = ,П + Vi Ь Аг/, -1 + — д2Ф - 2, где г/, = /?/’(.¥,, г,-). |
Вычисления производим в следующих таблицах (табл. II, III и IV).
Табл. II содержит окончательные значения .г(а',-) и значения ксэнечныл разностей, имеющихся в вычислительной формуле.
1 а б л и ца II
i •Ч У. /(Д7..17) 4i = hfi Л</, д-ф
0 1 2 3 4 5 6 7 8 9 10 В та( со втор1 0 0,1 0,2 0,3 0.4 0.5 0,6 0.7 0.8 0.9 1.0 )Л. III ВЬ лми раз 0 0.0996 0.1966 0.2887 0.3742 0,4518 0,5210 0.5818 0,6343 0.6792 0.7173 шолняются костями. 0.1000 0.9871 0.9498 0.8921 0.8190 0.7371 0.6517 0.5671 0.4874 0.4144 расчеты, с 0.10000 0.09871 0.09498 0.08921 0.08190 0.07371 0.06517 0.05671 0.04874 0.04144 соответствуя -0.00129 -0.00373 -0.00577 -0.00731 -0.00819 -0.00854 -0.00846 -0,00797 -0,00730 эщис форм; 7 - 0.00244 - П.00204 - 0,00154 - 0.00088 -0,00035 0.00008 0,00049 0,00067 — ] уле Адамса аблииа П1
/ 2 3 4 5
37 0.1966 0.28870 0,37418 0.45178
Vi 0.09498 -0.08921 -0.08190 -0.07371
2 A Vi-, — 0,00186 - 0.002^ -0,00366 -0,0()4Ю
2 — 0.0102 -0.00085 -0,00064 -0,00037
*7+1 0.28870 0.37418 0,45178 0.52Ю2
152
Продолжение табл. Ill
i 6 7 X 9
Vi 0.52102 0.58177 0,63428 0.67924
Ч< 0.6517 0.05671 0,04874 0.04144
1 ^Д^-i -0.00427 -0.00423 -0.00398 -0.00365
if/, _ > 12 1 -0.00015 0.00003 0.00020 0,00028
У1 * । В табл. 0.58177 IV производит 0.63428 ся вычисление f, rj= 1+0.2r.si 0.67924 значений функт пл; - 1,5г?. 0.71731 ШИ
Таблица IV
•V, 0.2 sin ,v4 0.2г, sin л. -1,5.17 J (л-,, л)
0,3 0.2887 0.0591 0.0171 -0,1250 0.8921
0,4 0,3742 0,0779 0.0292 -0,2102 0.8190
0,5 0,4518 0,0959 0.0433 -0,3062 0.7371
0,6 0.5210 0.1129 0.0588 -0,4071 0,6517
0,7 0.5818 0.1288 0.0749 -0,5078 0.5671
0,8 0,6343 0,1435 0.0910 -0,6036 0.4874
0.9 0.6792 0,1567 0.1064 -0,6920 0.4144
Ответом являются значения функции r(.vf), полученные в табл. II.
Работа 5
Задание. Используя метод Милна, составить таблицу приближенных значений интеграла дифференциального уравнения г=/(л\ .г), удовлетворяющего начальным условиям г(л'о) = Го на отрезке [О, 1 ]; шаг Л=0,1; все вычисления вести с четырьмя десятичными знаками. Начальный отрезок определить методом
Рунге—Кутта.
№ 1. г' = л + г2, г(0)=0.5.
№ 3. г' = 2л + г2. г(0)=0.3.
№ 5. г'=0,2л + г2, г(0)=0.1.
№ 7./=л2 + 2г. г(0)=0.1.
№ 9./ = л 2 + г2, г(0)=0.7.
№ 11. г'= 0.3л + г2, г(0)=0,4.
№ 13. г'=л+0.3г2, г (О)=0,3. № 15. г' = 0,1л2 + 2лг. г(0)=0.8. № 17. г' = Зл2 + 0.1лг, г(0) = 0,2. № 19. г'=л-2+ 0,1 г2, г(0) = 0,7. № 21. ? = 0,2.ч-2 + г2, г (0)=0,8.
№ 2. г' = 2л+0.1_г2. г(0) = 0.2.
№ 4. г' = л*2+лт. г (6) = 0.2.
№ 6. г' = л2 + г, г(0)=0.4.
№ 8. г' = лг+г2, г(0)=0,6.
№ 10. г' = л2 + 0.2г2. г(0) = 0.2.
№ 12. г' = 0.1л+0.2г2. г(0)=0.3.
№ 14. г' = 2л2 + лт. г(0)=0.5.
№ 16. г' = л2+ 0,2лт. г (0)=0.6.
№ 18. г' = л2 + 3лг. г(0)=0.3.
№ 20. г' = 2л2 + 3г2. г(0)=0.2.
№ 22. г* = 0,3л-2 + 0.1 г2. г(0)=0,3.
153
№23. г' = хг+0.1Н. r(0) = 0.5. № 25. г' = 0.1хг+0.3г2. г(0)=0.2. № 27. v' = xr + 0.2r2. г(б) = 0,7. № 29. ? = Зх + О.й-2, г(0)=0.4.
№24. г'=0.2л1 +г2. г(0)=0.4. №26. г'= 0.3л-1 +г2, г (0)=0.6. № 28. г'=0,1 х24-2г2. г(0)=0.2 № 30. г' = 0.2х + Зг2. г(0)=0.2.
Образец выполнения задания
г' = 1.6л-+0.5 г2=/(х. г): г(0) = 0.3.
1. Определение начального отрезка уо. Гь г?. Уз произведем по формуле Рунге — Кутта
l•,+1 = l^+2(A<;'+2A-Ч,+2Л,Jl+A•!;,) (г=0. 1, 2),
6
где
Все необходимые расчеты осуществляем с помощью табл. I, в которой
Ду,=2 +2* +2к •»+к'»).
и
Таблица I
/ Л' г 1.6л 0,5у2 /(л'.г) А ДП
0 0 0.05 0.05 0.1 0,3 0.3022 0.3063 0,3127 0 0,08 0,08 0,16 0,045 0,0457 0,0469 0,0489 0,0450 0,1257 0,1269 0,2089 0.00450 0.01257 0.01269 0,02089 0.00450 0,02514 0.025318 0,02089
0,07591 (1/6) = = 0,0127
1 0,1 0.15 0.15 0,20 0,3127 0,3231 0,3273 0,3421 0,16 0,240 0.240 0.32 0.0489 0.0522 0,0536 0,0585 0.2089 0.2922 0J936 0.3785 0.02089 0.02922 0.01936 0.03785 0,02099 0,05844 0.05872 0.03785
0,17590 (1/6) = =0.0293
154
Продолжение табл. 1
/ .V 1.6 л 0.5г2 /(«..>•) к Л.1<
2 0,2 0,25 0.25 0,30 0,3420 0.3609 0.3653 0.3887 0.32 0.40 0.40 0.48 0,0585 0,0651 0.0667 0,0755 0,3785 0,4651 0,4667 0,5555 0.03785 0.04651 0.04667 0.05555 0.03785 0.09302 0.09334 0.05555
0.27976 (1/6) = = 0.0466
3 0,30 0.3886 0,48 0,0755 0,5555
2. Последующие значения функции 3’1 +1 = г(л'1+1) (/=3. 4.9) будем
определять методом Милна. Согласно этому методу, по ходу вычислений следует составить таблицу, содержащую значения г,- и /(.г,, г,) (табл. II).
Таблица II
/ Л/ л 1.6л, 0,5 г 2 /(•Vi. .ГJ
0 0 0.3 0 0,0450 0.0450
1 0,1 0.3127 0.16 0,0489 0.2089
2 0,2 0.3420 0,32 0.0585 0.3785
3 0,3 0.3886 0,48 0,0755 0.5555
4 0,4 0,4534 0,64 0.1028 0,7428
5 0,5 0.5376 0,80 0.1445 0,9445
6 0.6 0,6430 0.96 0.2067 0,1667
7 0.7 0,7719 1.12 0.2979 0.4179
8 0,8 0,9280 1.28 0,4306 1.7105
9 0.9 1,1160 - 1,44 0,6227 2.0627
10 1,0 1.3434 — — —
На каждом шаге вычисление ведется в два этапа. Сначала по первой формуле Милна находим
а затем по второй формуле Милна находим окончательное значение
г, — v — г, - 2 + - (f - 2 -Т 4ft _ 1 +f\1 1),
где г}1»).
I • >• 4 ’ =.>'«+у (2/1 -Л+2/з)=0,3+у (2 • 0,2089 - 0,3785 + 2 • 0,5555)= =0.4534; Д1’=0.64 +0,1028 = 0,7428:
>' 4 ’ =3'2+^ (Л+4/з +. / V ’)=0.3420+у (0,3785 + 4 0,5555 +0.7428)= =0,4534.
Из сравнения и J’i2* имеем j4 = 0,4534.
155
2. у (5‘ > = п + у (2/, -fr + 2/4) = 0.3127+-у (2.03785 - 0.5555+2 • 0.7428) =
= 0,5376; Дп = 0,80+ 0.1445 = 0,9445;
у <52> =у3+fl (fi+4/4+/V ’) = 0,3886 + у (0,5555 + 4 0,7428 + 0,9445)=0,5376.
Из сравнения у(5п и у(52’ имеем у$ = 0,5376.
3. г <J > - у,+у (2/д - /4 4- 2/s) = 0,3420 4- у (2 0.5555 - 0,7428 4- 2 • 0.9445) = =0.6430; J" ’ = 0.96 4- 0,2067 =1.1667;
у <* >=у4 4- * (./4 4- 4Д 4-./’ ’) = 0,4534 4- • (0,7428 4- 4 • 0,9445 4-1.1667) =
= 0.6430.
4. у 7’ =у3 4- ~ (2/4 -/5 + 2/ь) = 0.3886 + ^ (2 • 0,7428 - 0.9445 4- 2 1,1667)= = 0,7719; г У ‘ = 1. 12 4- 0.2979 = 1,4179;
у у >=у 5 4- (/5 4- 4/6 4-./ У ’) = 0,5376 4- у (0.9445 4- 4 • 1,1667 4-1,4179)=0,7719.
5. гУ’ = .Г4+у(2/5-/б + 2/7)==0.45344-^(2 0.9445-1,1667)+2 х
х 1,4179) = 0,9278; Д" = 1.284-0,4304= 1,7104;
у у >=у6 +'- (/6 + 4/'7 +Д* >)=0.6430 4- y (1,1667+4 • 1,4179 4-1,7104)=0,9280.
6. у 1/ » =у5 4- у (2/6 -/7 + 2/«) = 0.5376 +^ (2 1.1667 - 1,4179 + 2 • 1,7106)= = 1.1158; Д1 > = 1,44 + 0,6225 = 2,0625;
уУ’=у7+^(/7+4/8+Д1,) = 0.7719+^(1,4149+4 1,7106 + 2,0625)= 1,1160.
7. Гн!--.г<.4-у(2Л-/»4-2/9) = 0,64304-у(2-1,4179- 1,7106 + 2-2,0627) = = 1,3431; /Й =1,6+0,9020 = 2,5020;
г j2о = г«+^ (Л + 3/9 + / У’)=0,9280+(1,7106+4 2,0627 + 2,5020) = 1,3434. 3 3
Ответом являются значения функции, приведенные в табл. II.
Работа 6
Задание. Используя метод конечных разностей, составить решение краевой задачи для обыкновенного дифференциального уравнения с точностью е = 10 " Л; шаг Л = 0,1.
№ 1. г" + — + 2r=.v.
.V
(у(0,7) = 0,5
{2у(1) + 3у'(1)=1,2.
№ 2. у"-лу' + 2у = л-+1.
у(0.9)-0.5у'(0.9) = 2.
\г(1.2)=1.
156
№ 3. у" + лу'+у = л + I.
у(О.5)+2у'(О.5) = 1. у'(0.8) = 1.2.
5s 5. у" + 2у' —лу=л 2.
г'(0.6)=0,7.
,г (0,9)— 0.5 г' (0,9)= I.
№ 7. г"—3r' + -= 1, .V
у (0,4) = 2.
у (0.7) + 2г' (0.7)=0,7.
у(1) + 2у'(1)=0.6, \у(1,3)=1.
№ II. г" + 2лт'-у=0.4.
(2у(О,3)+у'(0.3)= 1. (у'(0,6) = 2. 2г'
Ай 13. г" + -----Зг = 2.
Л'
у'(0,8) =1.5.
2у(1,1)+у'(1.|) = 3.
№ |5. у"—Злу' + 2у= 1.5,
(г'(0,7)= 1.3. (0,5у(1)+у'(1) = 2.
Ай 17. г" +——0.4г = 2л\ л*
Гу(0,6)—0,3 г'(0.6) = 0.6.
(у'(0,9)= 1,7.
№ 19. у"—у+лу=2,
(г (0,8) =1,6,
I Зу(1,1)—0,5у '(1.1)= I.
№ 21. г" + 2г'—
Л .V
[0.5у(0,9)+у'(0.9)=1, (у(1,2)=0,8.
№ 4. г" + 2г'-- = 3. л
(у(0,2) = 2,
(0,5 г (0.5)-у (0.5) = I.
2 г
№ 6. г " — г' + — = л* -I- 0.4. л*
(у(1,1)-О.5г'(1.1)=2, Ъ<1.4)=4.
№ 8. i "+3.i '-i=.r+I.
[2r(l.5)-.r'(l.5) = 0.5.
№ 10. г" + 1.5 г'—лт=0.5.
f2r(l.3)-.r'(l.3)=l.
1.г(1.6)=3.
№ 12. у" — 0.5лу'+у=2.
(у (0.4)= 1.2.
( г (0.7) + 2у'(0.7)= 1.4.
№ 14. у" + 2л‘"г'4-у=л\
(2у(0.5)-у'(0,5)=1.
(г(О.8) = 3.
№ 16. у''4-2лу'-2г = 0.6.
f.r'P)=L
(О.4у(2.3)-у'(2.3)=1.
№ 18. г"- —+ 0.8г = л\ 2л-
(г(1.7)+1.2у'(1.7) = 2.
Ъ'(2)=1.
№ 20. у" + 0.8у'-лу=1.4,
Г у( 1.8) = 0,5.
(2у(2.1)+у'(21)=1,7.
„ г' 2г л
№ 22. г
4 л 2
( 1.5у(1.3)-у'(1.3) = 0.6.
(2у(1.6)=0.3.
157
2
№ 23. г"-0,5у' + 0.5лт = 2л-.
P'(i) = 0.5 (2r(l,3)-r'(l.3)=2.
№ 25. j" + 2.\t'—1.5=.v.
f 1.4r(l.l) + 0.5r'(l.l) = 2.
(r'(l.4) = 2.5.
№ 27. r" + 0,6.vj' —2.r= I.
(r(1.5)=0.6.
(2y(l,8)-0,8p'(l,8) = 3.
№ 29. r"-0,5л-2 г'+2y = .v2.
( r(l,6)+0.7j'(l.6)=2,
b(i.9)=0,8.
№ 24. у" + 2г'-1,5лгг=-.
(г'(0.8)=1.
(г(1.1) + 2.г'(1,1)= I.
№ 26. г"-—+0,5г = 2л\ 2
( 0.4г (0.2) -г' (0,2) =1,5.
(0.5)=0,4.
№ 28. г"4~-г = -,
2л- ' л-
Ь (0,6) =1.3,
(0,5г(0.9)-1,2/(0,9)=1.
№ 30. у"-лу' + 2.п=0.8.
J г(1,2)-0,5г'(1,2)= I.
Ь’'(1,5)=2.
Образец выполнения задания г" + лт'—0,5^= I, Ь(2)+2г'(2)=1.
[г (2,3)=2,15.
Разбив отрезок [2; 2,3] на части с шагом Л = 0,1 (рис. 7), получив четыре узловые точки с абсциссами л0 = 2; xt=2,l; х2 = 2,2; л*3 = 2,3 Две точки х0 = 2 и л*3 = 2,3 являются конечными, а две другие —
----1---1---1---1—
& 2,1 2,2 Z3
Рис. 7
внутренними. Данное уравнение во внутренних точках заменим конечноразностным уравнением
.Пм-гл+л-, + Vj..П..-Л-1_0>5.л = 1 (i = 1. 2). й “ 2Л л*1
Из краевых условий составим конечно-разностные уравнения в конечных точках:
Гу,+2~>,<,+^'~^ = 1 (г=0).
J 2Л
(гз = 2,15 (f=3).
Данная задача сводится к решению системы уравнений
158
-y2+4Fi-3v0
Ta ~ 2 г । 4-Гр , । . 3’2~3о _ q 5.3'| _ j
0.01 0.2 ’ 2.1“
n-2.12+1, 2 2 .n-.n 0 5.21= I 0,01 0.2 2.2
.3’3 = 2,15.
Выполнив преобразования, имеем
— 2,9 Го 4" 4 г 1 — 3’2 — 0,1, 375,9з’0 - 841 п + 464,I34 = 4,2, 391,6з’ i - 881з’2+488,4у=4,4, r3 = 2.I5.
Подставив значение з*3 в третье уравнение, получим для определения остальных неизвестных систему
— 2,9jo+4j’i — Ji = 0.1, 375.9ГО-8413Ч +464,1з’2=4,2, 391,634—881г2= — 1045,66.
Для решения полученной системы воспользуемся, например, схемой «главных элементов».
Зо 3’1 У: Свободные члены Е
-0,00113507 0,526788 -1 -2.9 375.9 0 4 -841 391.6 — 1 464,1 [-881 0,1 4,2 -1045,66 0,2 3,2 — 1535,06
0.00560179 -1 -2.9 375.9 3,55551 1-643.70981 — 1.28690 -546.6411 1,94240 -805,4511
-1 -0,79429 — — -1.77527 — 2.56957
2.2350 3.2351 2.1849 3.1849 2.1580 3.1580
Ответ:
.V у Л' г
2,0 2.235 2,2 2,158
2,1 2.185 2.3 2,150
Работа 7
Задание. Используя метод прогонки, составить решение краевой задачи для обыкновенного дифференциального уравнения с точностью е=10“3; шаг Л = 0,05. Воспользоваться вариантами работы 6.
159
ОбразЧ‘И
в ы п о л II сн и я з а д а н и я
2 + 0,05/: коэффициенты д-
В данной краевой заы.1че а = ] узловые row,, имеют ;1бсш1“сы ч.= -0.5/л,; 1 (i=o. ii7 6)
Метод прсэрнки состс^ коэффициенты, ^ит из <<прямого хода>>’ в котором определяю'
2Л2</(-4 _ .
fb = -—Ti г.= GU-1 э
а также
"а, ' »/f
” Q _ , <lt _ j (/=1,2.н - 1).
После выползня «прям*, Л /* чого хода» переходят к выполнению «обратного хода», когорт состоит ~ v формулам В определенни значении искомой функции пс Po/»+l\k Hlj’ Л = </(4-»’Н1) (/=//-!. //-2 |, 0). Здесь 0.0025 4 + /»;=^ Л» .. 2—0.05л;
2 +0,05л; /•'- 2 1 (!— 1 0 2 +0.05л; * 5). 0-05 л z, , = = 0.0: 2 таблице.
Все е (ЫЧИСсдиНИЯ 2+0.05л; 2 = 0^-=-L02564: буде^ располагать в >5.
/ Л, 1гГ< л
0 1 2 3 4 5 6 2,00 2.05 2.10 2,15 2,20 2,25 2,30 1 1 1 1 1 56 6tf<5f && \С чо чо ОО 4л ОС О О t-j гл ос О — w О -J VzJ LA L»J -J 0’9Qj497 0’9C)(p™ 0,89)Й° W734 0.002378 0.002375 0.002372 0.002370 0,002367 -1.02564 -1.02308 -1.02063 -1.01830 -1.01611 -1,01406 О.О25()0О 0.095S19 0.025878 0,026()90 0.026167 0.026ИЗ 2.2490 2.2178 2,1933 2.1748 2.1618 2.1537 2,15
160
Ответ:
X .V
• 2,00 2,249 2,20 2.162
2,05 2,218 2.25 2.154
2,10 2.193 2.30 2.150
2,15 2.175
Глава X
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Работа 1
Задание. Используя метод сеток, составить приближенное решение
задачи Дирихле для уравнения Лапласа —- + —-=0 в квад-дх~ сЧ-
рате ABCD с вершинами А (0; 0), Я(0; I), С(1; 1), £>(1; 0): шаг й=0,2. При решении задачи использовать итерационный процесс усреднения Либмана до получения ответа с точностью до 0,01.
В таблице вариантов приведены формулы, задающие искомую функцию на сторонах квадрата A BCD.
Номер варианта ы1лв «1вс UlcD «1,<О
1 ЗОу 30(1-х2) 0 0
2 20у ял- 30 cos—-2 яг 30 cos — 2 20х2
3 50/(1 ~З’2) 0 0 50sinnx
4 20у 20 20 г 2 50х(1—х)
5 0 50л (1 -х) 50/(1 -у2) 50х(1—х)
6 30 sin л у 20х 20у 30х(1—х)
7 30(1-/) 20/Г 20у 30(1-х)
8 50 sin п у 30 7* ЗОу2 50 sin пх
9 40у 2 40 40 лх 40 sin — 2
6-1258
161
Продолжен
Номер варианта «lee U|CD “Ld
10 50/ 50(1-х) 0 60х(1 —х2)
11 20/ 20 20/ 10х(1-х)
12 40 Уу 40(1-х) 20Я1 -я 0 1
13 лу 20 cos л» 30х(1 — л) 30/(1-/) 20(1-х2)
14 30/(1—/) 50sin лх 0 10х2(1 —х)
15 20/ 20(1—х2) зо^/7(1-л) 0
16 30(1-/) 30х 30 30
17 30 COS 2 30/ 30/ ТЕХ 30 cos— 2
18 0 50 sin ял' 50у (1 -/) 0
19 20^7 20 20/2 40х(! —х)
20 50>’(1 -у) 20х2(1—х) 0 40х(1 —х2)
21 20 sin п}’ ЗОх 30/ 20х(1 - х)
22 40(1->•) 30 у? 30/ 40(1-х)
23 20 sin п/ 50^7 50/ 20 sin пх
24 40 40 • 40/2 40 sin ^(1 — х)
25 30/ 30(1-х) 0 40х2(1 —х)
26 25/ 25 25/ 20х(1—х)
27 15 yjy 15(l-.v) 30у(1—Д’) 0
162
Продолжение
Номер варианта «1вс «1со °1ло
28 30 cos — 2 20х(1—х) 25г(1 — г2) 30(1-х2)
29 •О.г2(1—>’) 30 sin пх 0 15х(1—х2)
30 25г 25(1—х2) зоч/Г (!->) 0
Образец выполнения задания
М1 лв
ПЛ
=45г(1-г). н|вс = 25л; m|cd = 25; ы|ло=25х5ту.
Процесс решения разобьем на несколько этапов.
I. Построим область решения, покроем ее сеткой с шагом Л=0,2; вычислим значения искомой функции м(х, у) в граничных точках области (рис. 8).
Рис. 8
Рис. 9
1. Значения функции w(x, у) на стороне АВ найдем по формуле и (х, >’)=45у (1 — г); имеем и (0; 0)=0; и (0; 0,2) = 7,2; и (0; 0,4) =10,8; и (0; 0,6)= 10,8; н(0; 0,8)=7,2; н(0; 1)=0.
2. На стороне ВС: и(х, у) — 25х: ы(0,2; 1) = 5: и (0,4; d) =10; «(0,6; 1)=I5; м(0,8; 1)=20; w(l; 1)=25.
3. На стороне CD: «(х, у) = 25; м(1; 0,8) = «(1; 0,6) = и(1; 0,4) = =w(l;0,2)=w(l;0)=25.
4. На стороне AD: и(х, y)=25xsin—; м(0,2; 0)= 1,545; и(0,4; 0) = 5,878; «(0,6; 0)= 12,135; м(0,8; 0)= 19,021.
6*
163
II. Для определения значений функции во внутренних точках области методом сеток заданное уравнение Лапласа в каждой точке заменим конечно-разностным уравнением по формуле
М0 = н(х,-, = u + wi+ u + Uij- I I )
Используя эту формулу, составим уравнение для каждой внутренней точки. Предварительно пронумеруем искомые значения функции, изобразив их на рис. 9, соответствующем построенной выше сеточной области; на этом рисунке отметим также найденные граничные значения. В результате получаем систему уравнений
«! = - (7,2 + 1,545 + м2 + и5); и2 = (5,878 + иi + w3 + w6);
u3=-(12,1354-u2 + u4+h7); m4 = ^(I9,021 +25 + w34-u8);
w5 = I-(10,8+и, + w6 4-w9); m6 (u2 + u5 4- u7 4- w10);
= -(«3 + «6 + »8 + JO j); w8 = i(25 4- u4 4- w7 4- 2);
h9 = 2(10.84-w54-u104-«13); w10=2(w64-W9 4-Wh4-«i4):
Мц=-("7 + «ю + «12 + М15): Wi2=^(254-w84-M11+u16);
Wi3=^(7,24-54-w9 + h14); М14=^(Ю4-м1О4-м134-м15);
Wi5=^(154-m114-Ui44-m16); м16=^(20 + 254:ы12 + м15).
Решение этой системы выполним итерационным способом типа Зейделя. Для каждого значения составим последовательность w,(0), мр\ м}2), ..., которую строим до сходимости в сотых долях Запишем
соотношения, с помощью которых будем находить элементы всех последовательностей:
м<*’=1(8,7454-и?-1)4-нГи); «?,=^(5,8784-«(1*с) + н?-1,4-|4к-1));
i4k)=-(12,I354-«2[)4"w4 ~ l,4-w?"n); ulk)=-(44,0214-u3k)4-wjk“l>);
= ^(10,84- w(k)4-Ub~ n4-Ug~ u); «6 ’=-(w?) + M5k) + u7~ n + «Io U)’
и<м=1(м(М + н(М + ма- 1> + м<Д-1>); w<k»=l(254-H?> + ^,4-W(1k2-1));
164
4 4
U«'=-K'+<+«& ’): ’);
4 4
и1‘>5(12Д+<+И&-*’): «Й^^Ю-иЙ+ий+ий'1’);
«й=;(15 - «ft>+«ft+«’,V1»Й=;(45+«ft+«ft). 4 4
Для вычислений по этим формулам нужно определить начальные значения которые могут быть найдены каким-либо способом.
111. Чтобы получить начальное приближенное решение задачи, будем считать, что функция и(х, г) по горизонталям области распределена равномерно.
Сначала рассмотрим горизонталь с граничными точками (0; 0,2) и (1; 0,2) (рис. 10). Обозначим искомые значения функции во внутренних
«г Ug Ug 25 tij u* u7 Ug 25
1 в 1 1 >
! 1
(OiO,2) (fiD,2) (MW
Рис. 10 Рис. 11
точках через wJ0). mJ0’, wjo\ м10>- Так как отрезок разбит на 5 частей, то шаг измерения функции Кх = (25-7,2)/5 = 3,56. Тогда получим
i?1O) = 7,2+K'l =7,2 + 3,56= 10,76; w^W^ + Kj = 10,76 + 3,56= 14,32;
И|<»=ГД<»+К'1 = 14,32 + 3,56= 17,88; 40) = u<°> + К, = 17,88 + 3,56 = 21.44.
Аналогично найдем значения функции во внутренних точках других горизонталей. Для горизонтали с граничными точками (0; 0,4) и (I; 0,04) (рис. 11) имеем tf2=(25-10,8)/5=2,84 и, значит,
fOS и№ и„ а„ 25
---1—4-------1—1------> ; 1
(о; о,6) (а о,6)
Рис. 12
7,2 и1Л ufS иа 25 ----j----1------1----j-----1 1------ (OiO,8)--(f;0t8)
Рис. 13
<40> = 10,8 + 2,84 = 13,64; wJ0) = 13,64 + 2,84 = 16,48;
wi0)= 16,48 + 2.84= 19,32; mJ0)= 19,32 + 2,84 = 22.16.
Значения в граничных точках третьей горизонтали (рис. 12) такие же, как и для второй горизонтали; следовательно, Ug0) = M50)= 13,64; w‘°J« 16,48; <= 19,32; w‘°2’ = 22,16.
Наконец, значения в граничных точках четвертой горизонтали (рис. 13) те же, что и для первой горизонтали; поэтому 10,76; «}?= 14,32;
»й = 17,88; «Й=21,44.
Все полученные значения представим в следующей таблице, которая называется нулевым шаблоном'.
165
1 0 ‘ 5 10 15 20 u 25
0,8 7,2 10,76 14,32 17,88 21,44 25
0,6 10,8 13,64 16,48 19,32 22,16 25
0,4 10,8 13,64 16,48 19,32 22,16 25
0,2 7,2 10,76 14,32 17,88 21,44 25
0 0 1,545 5,878 12,135 19,021 25
Уу/ 0 0,2 0,4 0,6 0,8 1
IV. Для каждого нового приближенного решения задачи будем составлять таблицу, содержащую только внутренние значения, которые изменяются в процессе вычислений. Эти таблицы называются шаблонами. В результате получим следующую последовательность шаблонов:
№ 1 № 2
9,790 13,258 17,027 20,904 9,346 12,708 16,561 20,679
12,641 15,363 18,411 21,589 11,927 14,460 17,630 21.153
12,524 15,170 18,241 21,506 11,754 14,243 17,443 21,079
9,176 12,354 16,312 20,623 8,406 11,442 15,610 20,384 ;
№ 3 ЛЬ 4
9,092 12,371 16,287 20,544 * 8,930 12,158 16,116 20.458
11,461 13,829 17,100 20,887 11,150 13,414 16,761 20,718
11,239 13,518 16,856 20,771 10,877 13,036 16,454 20,567
7,985 10,929 15,189 20,074 7,728 10,581 14,911 19,926
Лё 5 № 6
8,826 12,021 16,005 20,403 8,758 11.933 15,934 20,368
10,945 13,144 16,542 20,608 10,811 12,968 16,399 20,537
10,634 12,712 16,189 20,433 10,472 12,497 16,014 20.345
। 7,551 10,344 14,715 19,826 7,431 10,184 14,583 19,759
166
№ 7
ЛЬ 8
8,714 11,875 15,887 20,344 8,685 1*1,837 15,851 20,327
10,723 12,853 «6,306 20,490 10,665 12,777 16,221 20,457
10,365 12,365 15,899 20,288 10,294 12,263 15,875 20,263
7,350 10,077 14,496 19,716 7,297 10,007 14,439 19,687
№9 Л? 10
8,666 11,811 15,835 20,319 8,654 11,796 15,823 20,313
10,628 12,725 16,203 20,439 10,603 12,695 16,178 20,427
10,248 12,215 15,778 20,228 10,220 12,165 15,744 20,210
7,262 9,960 14,414 19,675 7,238 9,936 14,381 19,658
М 11 № 12
8,646 11,786 15,815 20,308 8,640 11,779 15,809 20,306
10,587 12,674 16,162 20,418 10,576 12,661 16,150 20,413
10,198 12,137 15,722 20,199 10,184 12,120 15,708 20.192
7,225 9,912 14,362 19,648 7,214 9,898 14,351 19.643
№ 13 ЛЬ 14
8,637 11,774 15,806 20,304 8,635 11,772 15,803 20,303
10,569 12,652 16,143 20,409 10,565 12,646 16,138 20,407
10,176 12,108 15,699 20,188 10,170 12,101 15,693 20.185
7,207 9,889 14,344 19,639 7,202 9,883 14,339 19,637
№ 15
8,634 11,770 15,802 20,302
10,562 12,642 16,135 20,405
10,167 12,096 15,689 20,183
7,200 9,879 14,336 19,636
167
Шаблоны № 14 и №15 содержат значения, отличающиеся друг от друга меньше, чем на 0,01 (заданная точность); поэтому вычисления прекращаем. Последние значения округляем до сотых долей и получаем ответ:
1 0 5 10 15 20 25
0.8 7.2 8,63 11.77 15,80 20,30 25
0.6 10.8 10.56 12.64 16.14 20,40 25
0,4 10.8 10,17 12,10 15.69 20.18 25
0.2 7,2 7,20 9,88 14,34 19,64 25
0 0 1.54 5.88 12.14 19.02 25
xXi 0 0.2 0,4 0.6 0.8 1
Задание. Используя метод сеток, составить решение диффере-
_ с2 и .
нциального уравнения Лапласа —-4------; = 0 с заданным»
дх ду~
начальными условиями; шаг Л=1. Уточнение решения производить до Либмана.
сотых долей с помощью процесса
Л'2 V2
№ 1. — + —=1 (Г),
9 16
№ 2. (|х 1+2)(Ь>|+2)
№ 3. |у| =4—х2
>(Г),
хе [-2- 2]J
№ 4. хг 4-у -16 (Г),
X2 г2
№ 5. — + —=1 (Г).
16 9
№ 6. | х| =4—у2 ।
хе [-4.4]J ЦП,
Ха 7. (|х I+2)(|J'I + 2)=
2 2
X V
№ 8. — + -=1 (Г),
9 16
..2 ..2
X V
№ 9. — 16 + — =1 (Г), 25
№ 10. |у|=4-х2
12 (Г),
ИГ),
168
№ 11. х2+у2*=16 .2 2 (Г). (Г), «(х./)|г=0,5|х| + |^|. «(x.j)|r=|x|+0.5Jy|.
хл у~ № 12. — + — =1 16 9
№ 13. |х|=4—у2’ *>
хб[—4, 4] ► (Г). «(-V. v)|r=|x| + у.
№ 14. (|х|+2)(|/| + 2)= 12 (О. u(x. y)|r=2|x|+0.5|y|.
№ 15. х2/25 + у2/9 = 1 (Г). м(х. г)1г = |х| + |у|.
№ 16. х2/9+у2/16 = 1 (Г). «U jjlr=2|-v| + 0.5 |у|.
№ 17. |у|=9-х2’ X х 1
хе[ —3, 3]: ►,(Г). ф. }jlr=l*l + -|.H-
7
№ 18. х2+у2=16(Г), 1 «к З’)1г = -И +2|у|.
№ 19. х2/16+у2/9 = 1 (Г), ф. у)|г=0.5|х| + |у|.
№ 20. |х|=9—у2 К к >’)1г=0.5|х| + 1 г|.
хе [—9. 9] (ГК
№ 21. х2/9+у2/25 = 1 (Г), и(х. у)|г=0,5|х|+2|у|.
'№ 22. х2/25+у2/16=1 (Г), ф.у)1г=0.5|х|-|у|.
№ 23. (|х| +3)-(|>'| +2)= 18 (Г). Ф 3?)1г = 1х| +0.51 у|.
№ 24. |у|=9—№1 w(x. у)|г = 2|х| +0,51 у |.
хе [-3.3]. ► (Г),
№ 25. х2+у2= 16 (Г). w(x. у)|г=0.5(|х| + |у|).
№ 26. х2/16+у2/25 = 1 (Г). и(х У)1г=~И + 1 г|.
№ 27. |х|=4-у2’ 4v»>’)lr=M +0.5|у|.
хе [—4, 4] ► (Г).
№ 28. (|х|+2)(|>’| +3)=18 (Г). и(х. у)|г=2|х| +0.5 |у|.
№ 29. х2/9+>-2/25=1 (Г). «{х,у)|г = |х|+0.5|у|.
№ 30. (|х| + 5)(|» |+5)=45 (Г), "(х г)1г = |л-| +0.51 у |.
Образец выполнения задания
х2 у2
- + 7-=1 (О; «(х,..)|г=0.5(|х| + Ь1).
1о У
1. Исп >1ьзуя симметрию заданных начальных условий, построим
решение только в I четверти (рис. 14). Возьмем шаг Л=1 и составим таблицу значений х и у:
X 0 1 2 3 4
3 2,90 2,60 1,98 0
109
На рисунке крестиками помечены граничные узлы, а кружочками — внутренние.
Вычислим значения функции и(х, у) на границе:
/1(0; 3); м(Л) = 0,5(0 + 3)= 1,5,
5(1; 2,90); м (5)=0,5(1+2,9)= 1,95, С(2; 2,60); и (С) = 0,5 (2 + 2,6) = 2,3, D(3; 1,98); м(Д)=0,5(3 +1,98) = 2,49, /Г(3,77; 1); м(Е) =0,5(3,77 +1)=2,39, 5(4; 0); «(Г) =0,5(4+0)=2.
Для определения начальных значений функций и (х, у) во внутренних гонках составим систему уравнений, содержащих эти значения. Каждое уравнение получается приравниванием значения функции во внутренней точке среднему арифметическому четырех значений функции в соседних точках:
u2=^(l,95 + м1+н3 + м5), m3=^(4,79+u2+m6), 1/4 = ^(m1+U8 + 2«5), М5=^(н2 + К4 + Ыб + Ы<Д W6 = ^(W3 + W5 + «7 + «1о)> m7=^(4,88+m6+wh), ы8=^(4м5), m9 = ^(u8 + u10 + 2m5), Mio=“(w9 + wn+2w6), Mu =1(4,78 + 2u6).
Решая эту систему, получим ы1 = 1„91, м2=:2,05, м3=2,10, м4 = 2,05, м5 = 2, w6 = 2,18, w7 = 2,34, h8 = 2,1I, u9 = 2,13, м1О = 2,19, ми=2,28.
Найденные значения функции u(x, j) позволяют составить шаблон № I, в котором внутренние значения соответствуют найденным, а граничные получаются в результате уточнения предыдущих граничных значений по формуле линейной интерполяции
«И»)="И) +8------ГТ!—’
Л I +о
170
где Ah—узловая граничная точка; А — ближайшая к А,, точка, лежащая на границе; Вл—ближайшая к Ah узловая точка, лежащая внутри области; 5 — расстояние между точками А и Ah. взятое со знаком плюс, если точка Ah лежит внутри области, и со знаком минус, если она лежит вне области.
В данном примере имеем:
2 05- 1 95 и(Л)=«(Л)=1,5; 8В=2,90-3=-0,1; и(В„)= 1,95-0,1 -—= 1,94;
I _Э 1
5С=2,60 - 3 = 3 - 0,4; и (СА) = 2,3 - 0,4 -—— = 2,43;
0.6
"> 34 —2 49
5О = 1,98 — 2 = 0,02; и (Dh) = 2,49 - 0,02 -—=2,49;
° ' 0.98
8е=3,77-4= -0,23; и{Е„)=2.39-0,23^~~^=2.40; u(F„)=u(F)=2.
№ 1.
1,5 1,94 2,43
1,91 2,05 2,10 2,49
‘ 2.05 2.11 2,18 2,34 2,40
2,11 2,13 2,19 2,28 2
2. Процесс Либмана заключается в уточнении значений, входящих в шаблон № 1. Каждый следующий шаблон Получается из предыдущего так: значения функции во внутренних точках равны среднему арифметическому четырех соседних значений предыдущего шаблона, а значения функции в граничных точках находятся по формуле линейной интерполяции, уже использованной при получении шаблона № I. Это уточнение производится до тех пор, пока два последовательных шаблона не совпадут с заданной степенью точности. В результате вычислений получим следующую последовательность шаблонов:
ль 2.
1,5 1.94 2,31
1,91 2,02 2,29 2,49
2,06 2,10 2,18 2.34 2,40
2.09 2,13 2,19 2,22 9 л*
Л° 3.
1,5 1,94 2,33
1.90 3,06 2,25 2.49
2,05 3,10 2,23 2.32 2.41
2,10 * 12 2,18 2,22 2
171
№ 4. № 5.
1,5 1,94 2,31 1,5 1,94 2,33 i
1,92 2,05 2,28 2,49 1,91 2,06 2,26 2,49
2,05 2,12 2,21 2,34 2,40 2,06 2,11 2,23 2,33 2,41
2,09 2,12 2,20 2,20 2 2,09 2,14 2,19 2,22 2
№ 6. № 7.
1,5 1,94 2,31 1,5 1,94 2,32
1,92 2,06 2,28 2,49 1,92 2,06 2,27 2,49
2,062 2,12 2,22 2,34 2,40 2,06 2,12 2,23 2,33 2,41
2,10 2МЗ 2,20 2,21 9 4Ы 2,10 2,20 2,22 2,22 2
Лр я.
1,5 1,94 2,32
1,92 2,06 2,27 2,49
2,06 2,12 2,23 2,33 2,41
2,10 2,13 2,20 2,22 2
Шаблон № 8 является ответом.
Работа 3
Задание. Используя метод сеток, составить решение смешанной задачи для дифференциального уравнения параболического типа rw д2и , .
—=—- (уравнения теплопроводности) при заданных началь-
dt дх2
ных условиях н(х, 0)=/(х), м(0, f) = <p(f), и (0,6, /) = ф(О, где хе [0; 0,6]. Решение выполнить при //=0,1 для /е [0; 0,01] с четырьмя десятичными знаками, считая о =1/6.
№ 1. «(х, 0) = cos2x, ы(0, /)=1 — 6t, и(0,6; /)—0,3624.
№ 2. м(х, 0]=х(х+1), м(0, /)=0, «(0,6; 0 = 2/4-0,96.
№ 3. м(х, 0)= 1,2 4-1g (х 4-0,4), «(0, /)=0,8-Н, «(0,6;/)= 1,2.
№ 4. м(х, 0)=sin2x, «(0, t)=2tf и(0,6; /)=0,932.
№ 5. м(х, 0)=Зх(2 —х), «(0, /)=0, «(0,6; /)=/4-2,52.
№6. м(х, 0)=l-lg(x4-0,^, м(0,/)=1,4, г 50.6; /) = /4-1.
№7. м(х, 0 = sin (0,55x4-0,03), м(0,/)=/4-0,03, и (0,6; /)=0,354.
№8. « х,0)=2х(1-х) 4-0,2, ы(0, /)=0,2, ы(0,6;/)=/4-0,68.
№9. м(х, 0)=sinx4-0,08, м(0,/)=0,084-2/, и(0,6; /)=0,6446.
172
№ № № № № № № № № №
11.
12. 13. 14. 15. 16. 17. 18. 19.
№ 20. № 21. № 22. № 23. № 24. № 25. № 26. № 27. № 28. № 29. № 30.
10. м(х, 0)=cos(2x+0,19), «(О, г)=0,932, «(0.6; г)=0,1798. и (х, 0)=2х (х+0,2) + 0,4, и (0, t)=2t+0,4, ы (0,6; t) =1.36. wlx, 0) = lg(x+0,26) + 1, м(0, г)=0,415 + г, м(0,6; г)=0,9345. и х, 0) = sin (х+0,45), м(0, г)=0.435 — 2г, «(0,6; г)=0,8674. и lx, 0)=0,3+х (х+0,4), и (0. t)=0,3, и (0,6; t)=6г+0.9. «IX, м(х. MIX. м(х, «(х< w(x, м(х, 0)= 1,5 -х (1 -х), и(0, г )=3 (0,5 - г), «(0,6; г )= 1,26. «(х, 0)=cos(х+0,845). м(0, г)=6(г+0,11), «(0,6; г)=0,1205. и । х, 0)=1g (2,42+х). «(0, г) =0,3838. и (0.6; г)=6 (0,08 - г). и । х, 0)=0,6+х (0,8—х), «(0. г)=0,6, и (0,6; г)=3 (0,24+г). «|х, 0)=cos(х+0,66). «10. г)=Зг+0,79, «(0,6; г)=0,3058.
0)=(х-0Д)(х+1)+0Д; м(0, г)=6г; «(0,6;/)=0.84. sin (х+0,48). и (0, /1=0,4618, «(0,6; t)=3t+0.882.
0)=cos (л+0,48), ы(0. г')=6г+0.887, и(0,6; г)=0,4713.
0)=х(0,3 + 2х), и(0, г)=0, «(0,6; г) = 6г+0,9.
0)=Г ' .....
0) = sin (х+0,02). м(0, г) = Зг + 0,02, и(0,6; t)=0,581. I
О)=1g(2,63—л). «(О', г)=3(0.14—г), «(0,6; г)=0,3075.
и и и «(х, О’
х, 0)=1g(1,95 + х), «(0, t)=0,29 - 6/, «(0,6; г)=0,4065.
х, 0)=2cos(x+0,55), м(0./)= 1.705, «(0,6; г)=0,817 + Зг.
Образец выполнения задания и(х, 0)=Зх(1 —х)+0,12, м(0, г)=2(г+0.06), м(0.6; г)=0,84.
Параболическое уравнение решается методом сеток постепенным переходом от значений функции u(xf, /,) к значениям «(.v^ rj+1); причем r5'+1 = r;+Jt, где /с=Л2/6=0,01/6=0,0017.
Вычисления производятся по формуле
=7(“.-+i.j+4wy+M«-i.j) 0’=Ь 2» 4» 5» Ь /=1’ 2» 4» 5» 6)-
6
Все расчеты приведены в таблице:
J i 0 1 3 4 5 6
0 0.1 0,2 0,3 0,4 0,5 0,6
0 0 0,12 0,39 0,60 0,75 0,84 0,87 0,84
1 0,0017 0,1233 0,3800 0,5900 0,7400 0,8300 0,8600 0.84
2 0,0033 0,1267 0,6372 0.5800 0,7300 0,8200 0,8517 0,84
3 0,0050 0,1300 0,3659 0,5704 0,7200 0,8103 0,8445 0.84
4 0.0067 0,1333 0,3607 0.5612 0,7101 0.8010 0,8380 0,84
5 0,0083 0,1367 0,3562 0,5526 0,7004 0,7920 0,8322 0,84
6 0,01 0,1400 0,3524 0,5445 0,6910 0,7834 0,8268 0,84
173
Работа 4
Задание. Используя метод сеток, составить решение смешанной зада* <?2м д2и
для уравнения колебания струны —г=—- с начальныь dr 8х
условиями м(л-, 0) =/(.v), ut(x, 0)=Ф(х) (0^х< 1) и краевьв условиями w(0,/)=ф(/), и(1,/) = ф(/). Решение выполни* с шагом Л = 0,1, определяя значения функции и(х, /) с четыр мя десятичными знаками, причем 0^/<0,5.
№ 1.у(х)=х(х+1), Ф(х)=СО8Х, ф(/)=0, ф(/)=2(/+1).
. , ПЛ'
№ 3. У (л )=cos—,
Ф(х) = Л'2, ф(/) = 1 +2/, ф (/ )=0.
№ 2. /(х) = xcos пх, Ф[х)=х(2-х), фп)=2/, ф(/)= -1.
№ 4. У(х)=(х+0,5)(х-1).
Ф(х)=5т(х+0,2), фи)=/—0,5, <|ф)=3л
№ 5. Дх)=2х(х+ I) +0,3. Ф(л') = 281ПХ, фШ=0,3, ф(/)=4,3 + /.
№ 7. у(х)=л' sin пх, Ф(х)=(х+1)2. ф(/) = 2л <|ф)=0.
№ 9. /(л)=л'(2л--0,5), Ф(х) = СО$2х, <р ')='2-ф(г)=1.5.
№ 6. У(л)=(л-+0,2)sin —, Ф(х)= 1 +л'2, ф /)=0, ф(/)= 1,2(/+1).
№ 8. У(л)=Зл (I -х), Ф (х)=cos (х+0,5), ф(/)=2/, ij/(r)=O.
№ 10. У(х)=(х + 1) sin пх. Ф(л-)=х2 + х. ф(/1=0, ф(/)=0,5/.
№ ll.y(x)=(l-x)cos-y,
Ф(х) = 2х+1, Ф (/)=2/+ I, ф(0=0.
№ 12. У(х)=0,5х(х+1),
Ф(х) = ХСО5Х, Й|:Г
№ 13. У(х)=0,5(х2+1),
O(x)=xsin 2х, ф(/)=О.5 + 3/, ^(/) = 1.
№ 15. У(л)=х2 cos пх, Ф(х)=х2(х + I), ф(/)=0,5/, ф(0 = /-1.
№ 17. у(х)=(х+0,5)2, Ф(х)=(х + l)sinx. ф(/)=О,5(О,5 + /), х|/(/)=2,25.
№14. У(х)=(х + 1) sin—,
Ф(х)= 1 —х2, ф(/)=0,5/, ф(/)=2.
№ 16. f(x)=(l — x2)cosnx, Ф(х)=2х+0,6, ф(/)= 1 +0.4/, ф(/)=0.
№ 18. У(х)= 1,2х—х2, Ф (х) = (х+0,6) sin х. ф(/)=0, 4ф)=О,2+О,5л
1/4
№ 19./(х)=(х+0,5)(х+1), Ф (x)=cos (x+0,3), фк)=0,5, Ф(/)=3-2/.
№ 21./(x)=(x+0,4)sin лх, Ф(х)»(х+1)*, ф(/1=0,5/, ф(/)=0.
. . лх № 23. /(x)=xcos—,
Ф(х)=2х2, ф(/)=0, ф(/) = /2.
№ 25. /(х)=(1-х2)+х, Ф (х)=2 sin (х+0,4), ф(/)= I, ф(/)=(/+1)2.
№ 27. /(х)=(х 2 +0,5) cos лх, Ф(х)=(х+0,7)2, ф(/)=0,5, ф(/)=2/-1,5.
№ 20. /(х)=0,5(х+ I)2.
Ф (х)=(х+0.5) cos лх. ф(/)=0.5.
ф(/)=2 —3/.
№ 22./(х)=(2 —x)sin лх, Ф(х)=(х+0.6)2. Ф(/1=0,5/, Ф(О=о.
№ 24./(x)=(x+0.4)cos—, Ф(х)=0.3(х2+I). ф(/)=0,4, хр(/)=1.2/.
№ 26. /(х)=0,4(х+0,5)2. ф 1 у)=х sin (х+0.6), ф(/)=0.1 +0.5/. ф(/)=0.9.
№ 28./(х)=(х + 2)(0,5х+1). (л\ х+ - 1,
ф(/) = 2.
ф(/) =4.5-3/.
№ 29. /(х)=(х2+1)(1-х).
Ф(х)= I — sinx, ф(П= I, ф(/)=0,5/.
№ 30. /(х)=(х + 0.2) sin—, Ф(х)=1+х2. 2
Ф (/)=0.6/.
Ф(')=1.2.
Образец выполнения задания
/(х) = 2х(1 —х2), Ф(х)=(х+0,4)со5(х+0.3), ф(/)=0,5/2. х|/(/)=0.
Для решения воспользуемся соотношением
М|. J+ 1 =Mi+ 1. j+ Ui~ 1. j~ 1’
где /=1, 2, ...; y=l, 2, 3, ....
При этом Uio=fi4 а для определения ми можно использовать один из возможных приемов, например,
причем
(/=0, 1, 2..//),. //=-—-= 10.
h
lj=O+jh (j=0, I, 2, 3,4, 5).
Кроме того, Ыо;=ф(/;); ил7 = ф(/;).
Решения по указанным формулам удобно выполнять в таблице, которая и является решением данной задачи.
175
Порядок заполнения таблицы:
1. Вычисляем значения ui0^f(xi)=2xl(l-xl2) при х,=0,1/ и записываем их в первую строку (она соответствует значению /о=0).
2. Вычисляем значения ио,=ф(0=О’5// при /,=0,1 и записываем их в первый столбец таблицы (°н соответствует значению ло=0).
h 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0 0 0,198 0,384 0,546 0.672 0,750 0,768 0,714 0,576 0,342 0
0J 0,005 0,2381 0,4247 0,5858 0.7092 0,7677 0,7942 0,7315 0,5825 0,3354 0
0.2 0,02 0,2317 0,4399 0,5879 0.6815 0,7534 0,7312 0,6627 0,4909 0,2405 0
0,3 0,045 0,2218 0,3949 0,5356 0.6321 0,6450 0,6219 0,4906 0,3207 0,1555 0
0,4 0,08 0,2082 0,3175 0,4391 0.4991 0,5006 0,4044 0,2799 0,1552 0,0802 0
0.5 0.125 0,1757 0,2524 0,2810 0.3076 0,2585 0,1586 0,6090 0.0394 -0,0003 0
3. Заносим значения в послеД«ий столбец таблицы
(он соответствует значению хю = Ь0)-
4. Вычисляем значения wfl по формуле ып =-(/f+1 +/i-i) +ЛФ(, где /i+i n/i-i берутся из первой строки таблицы, а Ф| = (^ + 0,4)со8(л'£+0,3); л,=0,1/ (/= 1, 2,..., 9); А=0,1. результаты записываем во вторую строку таблицы.
5. Вычисляем значения иц в последующих строках по формуле И;,j+1 =ty+1,j-!-w,-itj—где значения ц + 1,р ty-i.j* м/, y-i берутся из двух предыдущих строк таблицы.
ПРИЛОЖЕНИЕ 1
СПРАВОЧНЫЙ МАТЕРИАЛ ПО ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКЕ
Элементарная теория погрешностей
I . Формулы точною подсчета hoi решност ей
«6и 1
о (</ + />) =-. —: 7 (« ± А ) -
«± А
б («А) = 6„ + 7 (ah } = ab(c>a - ) = Aau + а^:
A74J
<ou + M = —
1 «">?. h2
6 («'") = ш6„: 7. (</'”) - т ат 1 7„: т рациональное число.
Здесь 7 абсолютная пот рентное ть приближенною числа: 5 относительная нот рентное! ь приближенною числа.
2 . Таблица относительных пот рентное гей чисел, имеющих п верных знаков н узком смысле (в %)
«т н 1 ** 3 4 5 6
1 50 5 0.5 0.05 0.005 0.0005
Э 25 2_5 0.25 0.025 0.0025 0.00025
3 17 L7 0.17 0.0)7 0.0017 0.00017
4 13 1.3 0.13 0.013 0.0013 0.00013
10 1.0 0.1 0.0) 0.001 0,0001
6 8.4 0.84 0.084 0.0084 0.00084 0.000084
7 7.2 0.72 0.0072 0.0072 0.00072 0.000072
8 6.3 0.63 0.063 0.0063 0.00063 0.000063
9 5.6 0.56 0.056 0.0056 0.00056 0.000056
Здесь ат
первая значащая цифра приближенною числа, считая слева направо.
А л1 с б р а матриц
1 . Определители. Oiipetk'.iwne.ib второго порядка
«II «'12
«2! «22
= «11«22~«21«12-
Опреде.штсяь третьего порядка
«п «12 «13
«21 «22 «23
«31 «32 «33
— «I 1«22«3 I Т «1 2«23«31 «I3«2!«32 — «I 3«22«31 — «I 2«2 1«33 — «11«J3«32-
2 . Нормы матрицы
f'«il «12 «13 «1п
<*21 <*22 <*2Л <*2п
\ ^тп 1 <*лг 2 <*m 3 ’ - - <*Л1Л
п
Пернач норма |j.-l ||( = max \
7-1258
177
Л1
Вторая норма ||Л ||ц = тах £ |«ц|. J i
Третья норма IM ||1и = %/£«.>
3 . Обратная матрица А для данной квадратной неособенной матрицы А находится по формуле
где Д определитель матрицы А: А1}- алгебраические дополнения соответствующих элементов матрицы А.
4°. Формулы для обращения клеточной матрицы
/Л | Я\
U1 4
Обратная матрица ищется в виде клеточной матрицы
\Л/ | JV/
а) Если легко определяется матрица Л-1, то К=Л-1 —Л ’ЯЛ/. L = A~lBM. M=—NCA~l, N=(D — CA~lBy
б) Если легко определяется матрица D”’. то K=(A — BD~lC)~1, L— —KBD~l. M=-D~lCK, N=D~l-D lCL.
5°. Обращение матриц методом окаймления. Пусть
где U„ столбец. строка. </ял число. Обратная матрица Л„ ’ ищется в виде
где
,z «-ir-._____ Lf-t
. ^Л-’1//лГпЛй_’1
Лп-1 +--------------
Каждый этап обращения осуществляется по схеме
л,-', -.4^1
Уя «лл
-УлА-а-\ 1
178
6°. Обращение матрицы с помощью разбиения се на произведение двух треугольных матриц. Пусть
(/11 0 0 ... О \ /1 12 G з 1"\
f21 ^22 В ...0 ].тг | 0 l ^23 • • • ?2n I
I’ “ = l f
C.1 '„2 ini ... tnJ \o 0 0 ... 1 /
Обратная матрица ищется в виде А ~1 = Т£1 Т f1.
7°. Исправление элеменгов приближенной обратной матрицы. Пусть для матрицы А найдена приближенная обратная матрица Do, причем ||£— .4£>0||<1. Строят последовательность матриц Do. £>t....D„;
По.
D i — Dq + DqI" o.
D, = Dl + £\.
F0 = E-ADv. F^E-AD^F'-F2 = E-AD, = F\.
Dm = Dm_1 + Dm_lFm_1. Fm = £-/1Dm = ^_l.
Вычисления продолжают до тех пор. пока с заданной степенью точности все элементы матриц D„-x и Dm не совпадут.
Методы решения систем линейных уравнений
1°. Формулы Крамера. Пусть дана система н уравнений с неизвестными:
</i1.r14-ni2.r2+ ... +«|„ЛВ=Л1.
«2|Л'1 + «22-V2 + +«2лАв = Л2.
«п i<i +лл2л-2+ ... +г/ляли=Ля.
Если определитель системы отличен от нуля, то се решения находятся по формулам
Дг Дх Д. Д-
Л1 л2 дз ’‘п
л,=—. .v, = —. л,=—...........л= —
где
«11 «12 «1л
«21 «22 «2л
7^0 определитель
системы.
«Я| «Я2 «j
<li2 ... «1Я «и bi ... «1п «11 «12 • . Л|
д..= />2 6/22 . . . <i2n ’ Д- = «21 Ь2 ... <ЬЯ «21 «22 -- Ь2
Ьп ^п2 • - «я1 Ьп ... йяя «Я1 «я2 - - Ь„
дополнительные определители для Ар л2......л„.
8 . Схема единственного деления (схема Гаусса) для решения системы уравнении (на примере системы четырех уравнений)
«11 Л*1 + «12Л2 + «I3-Vj + «14.V.| =«|5-«21 4"«22-^2 ^"«23-'’з "Ь«24-'"4 ~«25-
«31 Л1 +«32-V2 +«33Л‘з +«34-'4 = «35> «41 -'’j +«42Л"2 4 «43-^3 +«44Л4 = «45-
7
179
Решение производится с помощью таблицы:
Коэффициенты при неизвестных Свободные члены Конiрольные СУММЫ У *
•<» AS Л3 Л 4
«и «21 «31 «41 «12 ^22 «32 «42 «13 «23 «33 «43 «14 «24 «34 «44 «is «35 «45 ‘‘1 (’2 ‘3 «4
1 «12 «13 «14 «15 Pl
«22 « 32 «42 «23 «33 « 4 3 « 24 «34 « 44 «25 «35 «45 с 2 i 3 I 4
1 «23 «24 «25 Р2
« 33 « 43 « 34 « 44 «35 «45 <’3 С 4
1 «34 «35 Рз
«44 «45 ( 4
«45 Р4
<4 *4
1 Л'з <3
1 ЛЧ
1 'i *1
Вычислительные формулы Контрольные соотношения
<;= Z "о ('= 1. 2. 3. 4) j= 1
= (/=2, 3.4. 5): Р1=с| «н 1 +«12-г«1з + а14 + «15 = Р1
«/ j=«и - «11 а и 0=2. 3. 4; J=2. 3. 4. 5); с- = с\-ац Pi (/=2.3.4) « i 2 4 « г 3 4"« i 4 4 И i 5 ( f 0 = 2.3. 4)
«2j = « ’>/« 22 t/ = 3. 4. 5); Р2 = <*’/« 22 1 r0t23 + «24+«25 = P2
a'ij = a'ij—a'i2^2j 0=3. 4: / = 3. 4, 5); < ” = t (/ = 3.4) « i3 + z^4 4 « i5 = < i' 0 = 3.4)
«з/=«з;/«зз О'=4. 5); р3 = г';.-'«Зз 1+Зз44а35 = рз
180
I
Продолжение
Вычисли тельные формулы Кон грольные соотношения
и л] = И 4 j ~ « 43 (7=4. 5): (’4 =<’д— «43 Р <1 44 ь « 45 = Г* 4
*45 =«45 «44» 1(1 = <4 «44 1 Ь*45 = р4
— Г| ’> > •*. **"< 1 « '< L, ,? L, 1^ i 4 ' 4 'l 1 '< "• Г| 1 — Ч ч t> К |> м - ~-II Д । * ” L L. r< L 1 1 Ч ц м — - и-, -) Я К frf CS. Ъ 5S. гс. 52. II II II II II II II II '< '< И Г< '< '< 'И1'? Г4 1> »> 1> <> II II !1 II •J <ч — + + + -+’
3°. Схема Халеикого для решения сне гемм уравнений
-V| Лэ Л’4 Свободные члены Кон грольные суммы У
«11 «12 «13 «14 «15
«21 «22 (/ > X «24 <2
«Л «3 2 «33 «34 «35 <3
«41 «42 «43 «44 «45
Ли 1 *12 *13 *14 * 1 5 р.
^21 М: ' 1 *2 3 *24 *25 Р2
^31 7’32 /’зз 1 *34 * Рз
^41 /’4 2 /’43 /’44 । *4 5 Р4
•
Л д Л д
1 Л'з Л'з
1 ь AS
] -V1 Д' ।
ВычислиГС.1Ы1ЫС формулы Кон грольные соотношения
н II Л w 1 ||_
Л,,=«н {/=1. 2. 3. 4): *и = «и «11 (>=- 4- 5К Р1=п /’п 1 + * ! 2 + «13 + *14 + *1 5 = Pl
181
Продолжение
Вычисли гельные формулы Контрольные соотношения
Р к/ А гГ 3? II "i г? со ,? 1 ,J - -L 1 Р и" 1 Ъ- :: е. со Г" I! - '— !О II ' <мЛ * * I 4" «23 4- 0(24 + 0(25 = 02
/>(з = «1з—/>» i«i з —/>12«23 (/=3. 4); «з; = («зу-/>з1«и“/>з2«2з)//>зз (./=4, 5); 03 =(<'з—/>31 01 “/>3202)//>33 1 +0(34 + 0(35 = 03
/>44 = «44 —/>4 1 0t|4 — />42«24 — />43«34 (/ = 4)l «45 = 7“ («45 “ Л41 «1 5 “ />42 «25 “/>43 «35 ) ( J = 5)1 «44 04 “7—(<4 “/>41 01 “/>42 02 “/>43 03 ) />44 1 + 0(45 = 04
Значения неизвестных определяются по формулам единственного деления.
4°. Обращение матрицы с помощью схемы Халецкого. Пусть матрица А с помощью схемы Халецкого разложена на произведение двух треугольных матриц: А —ВС. Обратная матрица ищется в виде А -1 = £) = [а,;]:
«11 «12 «13 «14
«21 «22 «23 «24
«31 «32 «33 «34
«41 «42 «43 «44
/>1 1 ] <12 <13 <14 «II 0<|2 «13 «14
/>21 />22 ] <23 <24 0t2l 0<22 «23 «24
/>31 />32 />зз 1 <34 0(31 Я32 «33 «34
/>41 />42 />43 />44 1 «41 0(42 «43 «44
Элементы обратной матрицы вычисляются по формулам, вытекающим из соотношений:
/ =
«М />1 | +0t;2^21 + «1з/>31 + а»4^41 —
«1г/>22 4“ «1з/>32 4" «ы/>42 ~
Я1зЛзз+Я|'4^43 =
«14^44 =
7
4
о о о
0
0
4
0
0
0
0
0
0
0
Вычисления следует производить, начиная со значения /=4, затем 7=4 и т. д.
182
5°. Метод главных элементов для решения системы уравнении
{«11*1 + «12*2 + «13 *3 = «14, «21*1 + «22*2 + «23*3=fl24» «31*1 + «32*2+ «33*3 = «34-
На каждом этапе исключения неизвестного выбирают главный элемент наибольший по модулю коэффициент при неизвестных, затем находят значения т(, равные частному от деления элементов столбца, содержащих главный элемент, на главный элемент, взятый с противоположным знаком.
Для получения элементов следующего этапа прибавляют главную строку (строку, содержащую главный элемент) к остальным строкам, умножая ее на соответствующее значение п?4.
Олин из возможных вариантов схемы главных элементов приводится ниже.
т. Коэффициенты при неизвестных Свободные члены Контрольные суммы S
*i *2 *3
Mi «и «12 «13 «14 «15
-1 «21 «22 «23 «24 «25
«31 «32 «33 «34 «35
— 1 «11 «12 — «14 «15
т'з «31 «32 — «34 «35
— «32 — «34 «35
*1 *2 *3
*1 *2 *3
В приведенной схеме |fl23l = maxl«ijl» ГЛС ,= 1» 2, 3; /=!• 2. 3; |о'ц | = тах|п};|, j <• j
где /=1, 3, j=\, 2.
Вычисления выполняют по формулам:
«И = —«!з/«гз» «»з= —«зз/«2з»
o'ij=Oij+'«i«2j (/=1,2,4, 5); tf'3j=«3j+/W3«2j (j=l, 2,4, 5); т'3= -«'3i/«'n » аз,=а’3;+т’3а'и (j=2, 4. 5).
Неизвестные находят из соотношений:
*2—«34М32;
*i=(«i4-«i2*2)/«'n;
*3= («24 "“«21*1 ~«22*г)/«23 »
*2 = «3s/«32 ;
*1 =(« 15 “« 12*г)/«11 :
Л'з = («25 — «21*1 — «22*г)/«23 •
Контроль вычислений осуществляют так же, как и в схеме единственного деления.
6°. Метод квадратных корней для решения системы уравнений
{«11*1 + «1 2*2 + «13*3 + «14*4 =«1 5» «21*1 + «22*2 + «23*3 + «24*4 = «25» «31* I + «32*2 + «33*3 + «34*4 = «35» «41*1 +«42*2+ «43*3 + «44*4 = «45»
коэффициенты которой симметричны относительно главной диагонали, т. е. «у=«л (>=1, 2, 3, 4; у=1, 2, 3, 4).
183
Решение производят во схеме:
Коэффициенты при неизвестных Свобо шые Кон 1 рольные
V1 <2 Лд ч. 1СНЫ с) ммы L
«и «12 «22 «13 «23 «33 «14 «24 «34 «44 «15 «35 «45 «16 «26 «36 «46
' 11 '12 '22 '13 '23 'зз '24 '34 II II II II '16 '26 'зь '46
А| *2 Л'д д
*1 *2 Д" । -Я
Вычислительпые формулы:
r,, = v^ '«=—= |С- Х'Г. (>=2- *• 5- * '=2- 4>-
'и v *= ।
г 1
^ij У', ’ К]
fii =--5-?------ (/</; / = 2. 3. 4; /=3. 4. 5, 6):
Gi
<4 —'45/'44 I *4— '4b?'44 •
*3=('35“ /34 *4)//.».%- * 3 = ('36 ~ '34-'4) 'зз -
Vj = ('2S - '24*4 - '’3*з)/'22 : *2 =('2ь - '24*4 - /2з*з) '22 •
*| =('l5 ~ '|4*4 — ' 13*3 — '12*2) '| 1 *1 =('|б~ ' 14*4 — '13*3 ~ 'l2-'z) '11
В схеме осуществляют строчный контроль, подобно тому, как это производят в схеме единственного деления.
7°. Метод последовательных приближений для решения системы уравнений (метод простой итерации). Систему следует привести к виду А" =.4 А' I /'. С троят пос гслователь-ность векторов: А'о — произвольный век гор; Л’| = .4А'О г А\ = .4 А1 + F: Л 3 = .4Ал; + Л;
A„=/LVn> !+/•’. Процесс сходится, если || .4 ]|< I для какой-либо нормы матрицы.
Отдельные координаты вычисляют но формулам:
Л !'=/.. .г!м=Ё «.Л'У" + /. ('=1- 2......")
j I
Точность вычислений можно оцепить из соотношения
I - '! -4 II
если АЛ0 = F. I о
II 4 I * * 1 II
...........
где А'* точное решение.
184
8. Метод Зейделя для решения системы уравнении. Систему следует привести к виду X=AX+F. Строят последовательность векторов А'о. AS........А\....где
А'о произвольный вектор.
Координаты вектора А\ опре <сляют но формуле
vI4' = X аи.\ ~1 ’ +.I] (/=1.2.и).
7^1 j-i
Условия сходимости и точности вычислений можно определить так же. как и в методе простой итерации.
Методы решения нелинейных уравнений
1°. Метод хорд.
а) Если /(A)-/"(.v)>0 на [«./>]. то
л»
.Я») М-ГЫ
1 = А и
(при ЭТОМ А’о = «).
6) Если Да)! "(л )>0
на [«. Л], то
(при этом АО = Л).
2°. Метод Ньютона (метод касательных):
л ♦ 1
причем л(| = «. если /'(«)•/"(л)>0; хо = /’. если /(/>) /"(а)>° на [«.*]• Видоизмененная формула
Ля.1 лл .
./ (-*«)
3°. Комбинированный метод хорд и касательных. Пусть и л„+| приближенные значения корня по недостатку и но избытку.
а) Если Да}-/" (а ) > 0 на [«. Л], то
ЯЛ. /('„)
А‘п< I — А'л ~ . .. А„+। — Л‘п ч ДЛ„ X„f
f (-*«) ./(л„)-/(л-я)
(при ЭТОМ Ли=</. Аи = />)-
б) Если /(/»)_/" (а} > 0 на [«./>]. то
Ял) , Ял)
Лл^ Ли .Я„)-/(АнГЛп Ля” Лл лл)
(при ЭТОМ Л'о=ТЬ Л'о = />).
4°. Метод итераций. Уравнение /(л)=0 следует привести к виду д-=(р(л). например, по формуле
t 1 z Я)
ф(л) = .¥---—.
К
причем к следует выбрать так. чтобы |А |>0 2. где 0 = max| Л*)1 11 знак [а- Ь]
А- совпадал бы со знаком /'(а) на [«./>]. Итерационный процесс сходится при условии 1ф'(а)|<1 на [«-/»].
185
Уточнение корня производится по формуле л-л+1=ф(л„), н=0. 1, 2,..., л'о - значение, взятое из промежутка [«, Л].
Точное!ь вычисления можно оценить из соотношения
Л/" l-v -ля|^7—- Ixj-.vol, 1 — м
где л*— точное значение корня, а Л/= max | ф'(.v) |. к. м
5°. Метод итерации для решения системы уравнении вида (л=ф(\. г), [з-Фк Л
Пусть одно из решений системы принадлежит области D: c^y^d.
Для уточнения решения используют формулы
Л*я+1=ф(Лл, у„). ги+1=ф(л-я. у„). где значения л0 и у0 принадлежат области D. Процесс сходится, если в области D выполняются соотношения
6°. Метод Ньютона для решения системы уравнении
/•'(х, у)=0, G(.v,y)=O.
Значения д0 и уо определяют графически. Для нахождения последующих приближений используют соотношения
Г -V |
где
Д «(-'Я’ Зп) у(-^л» Ул)
уя) с;(л„, ул) ’
д _ (•'«• Зл) у(-'л* Зл) д __________ (*^Л< Зл) х(-^Л< Зл)
Хп~~ G{x„.yn) с;.(л-п,уп): G(.v„.yn) G'x(.vr.y„)
7°. Метод Лобачевского для решения уравнения
ПоЛ'" +Д1Л"-1 + ... +ай = 0.
Предварительно выполняют процесс квадрирования корней. При квадрирова-нии корней каждый коэффициент преобразованного уравнения разен квадрату прежнего коэффициента, минус удвоенное произведение соседних с ним коэф-фицисн гов в порядке близости к исходному коэффициенту и т. д., причем если нужный коэффициент отсутствует, то он считается равным нулю.
а) Случай действительных различных корней. Процесс квадрирования следует прекратить, если коэффициенты некоторого преобразованного уравнения в пределах точности вычислений равны квадратам соответствующих коэффициентов предыдущего преобразованного уравнения.
186
В результате получится уравнение Aoz"4 Л)?"-1 ♦ ...+Лп=0. корни коюрого находят по формуле
|v‘l=2'/r?- <* = ’- 2.">•
У "4 I
где р число квадрирований.
Знаки корней определяют грубой прикидкой или на основании соот ношений между корнями и коэффициентами.
б) Случай пары комплексных корней. Сначала находят дсйсгви гельные корни. Действительные части комплексных корней определяют из соотношений
«г 1
«=~5—L
~а° “t/uHm+l
где найденные действительные корни. Квадрат модуля комплексных корней
2 » l^m + I
Г = 2 /---.
У Ьт- I
где Ьм коэффициент с продолжающими оказывать влияние удвоенными коэффициентами. Коэффициент мнимой части v = >Jr2 -и2. Тогда । =u±iv.
8°. Схема Горнера для деления многочлена
/эя(л)=«ол*"+«1Л"“‘ + ... +«„
на двучлен \—р:
«п «1 а2 ... «»-1
р bop htp ... Ьп2Р Ь„-1Р
^0 ®= Л<> hi =«i УЬор b2 = a2+bxp ... bn-i=an-i+b„_2p R = a„ + bn-ip
В результате получается соотношение
/’flCv)=(/?oVn-1 +61.гя-2 + ... +ЛП_ ,)(.v-p)+tf.
где />, \""1 + ... 4-Лп_! — частное, a R — остаток.
9°. Схема Горнера для деления многочлена
Ри(л)=лох"+а1л-я"1+ ... 4-а„
на квадратный трехчлен x2+px+q:
ао «г a2 «3 ... a„
-Р -bop -biP -b2p — bn-2q —
-ч — ~boq ~b\q ... — bn-$q ~b„-2q
bf> — Qq h\~a\ - Z>o =, П 1 tri II i-" •C; ... “CL । гч 1 й 1 -5 II < I О 1 1 w 1 53 I II < c 1
187
В результате получас гея соотношение
P„(.v) = (/>o-v" ~+hlx" J4- ... b/>n-2)Cv"+/M.' + </} + (<o.V + <'|).
где box"”24-А1л"-л + ... 4 bn 2 частное, a <(>л +С| остаток.
10°. Метод Хичкока (метод выделения квадратного множителя) для решения уравнения
д' ” + a j л" 1 4- ... 4- ап ! л 4 а„ = 0.
Предварительно определяют ipyooc приближение квадратного множителя левой части уравнения <7(,(.v)=.v2 4-/>ол+</о.
Для уточнения коэффициентов квадратного множителя q'k* = x2 + pkx + qk применяют двукратное деление левой части />п(л ) = л"4-О|Д>л *4-... 4-«„ на имеющийся множитель. Первое деление:
^.{v) = (.v24-/v4-(/J+ хР(рк. 7i)4-(?(a« ед).
Второе деление:
(л‘) = (.V 2 4- ркх 4- <д) LK 4- л R (рк. (fk) 4- S (qk. рк).
Тогда рк. 1 = рк 4- A. <д . 1 — <д 4- &^к. i дс
Л -- Р'ч(Рк. 7fc) 7г) I’lPk* 7 J 2(А- 7г) A — - /’(a. 71) <?(A - 7i) /*p(A- 7i) Cp(/4. 7i)
Р'ЛР^ 7к) Q'AP^ elk) P'APk- 71) 2Ua- <b) P'APk-7i) СИ A- 7i) ^w(A- 7i) Ci(A’ 7i)
PplPk* 7i)=/4«(/4- 7i)-S(A- 71): СИ А- 7i)=7i«(A- 7i):
П(а. 7i)= ~^(Л- 71): СИ А- 7i) = -S(A- 71)-
11 °. Метод Горнсра для уточнения корня уравнения
/ (.<) = -Vя 4- </| Л'л 1 4"f/2.Vn “4- ... 4-(/„ — 0.
а) Если корень имеет вид аСо 10т4 • 10™"1 4- ... . то следует
предварительно сделать подстановку л = 1()'яг при л>0 или л= —10”’г при лсО.
В результате получается уравнение, соответственный корень которого принадлежит о’трезку [0. 10].
б) Если искомый корень данного уравнения принадлежит отрезку [0. 10]. то для определения цифры Сп пользуются непосредственным подсчетом значений /’(д') при д'=0, J. 2. 10 по схеме Горнера. Затем производят две подстановки
т=.г —Со и с=10г. используя для первой из них схему Горнера. С помощью полученного уравнения определяют цифру С,. Все последующие цифры корня определяют аналогично.
Нахождение собственных чисел н собственных векторов матрицы 1°. Метод Крылова. Собственные числа матрицы А определяют путем решения характеристического уравнения, приведенного к виду
/?(/.)=(-Ifp-r/!/."-1 ... -</и) = 0.
Значения //!, t[2.7л являются решениями системы, полученной из векторного
равенства
^о7л + ^17л 1 + 4 - л 71 = л,
где Со начальный вектор (произвольный). Ci = /fCi 1 (/=1. 2. 3......п). Решая
эту систему, например при помощи схемы Гаусса, находят </|. г/2- 7з......7л-
188
Собственные векторы матрицы J определяют из соотношения
v.= I м; (/=i.2.........4
i «>
где р,, коэффициенты частного, полученного при делении (—!)"/)(/.) на X—л, (ио схеме Горнера).
2°. Метод Данилевского. Для определения коэффициентов характеристического уравнения матрицу .-1 с помощью //—I преобразований подобия заменяют подобной ей матрицей
На первом этане находят:
(I 0-0 0
0 1 0 0
.....................
'«л 1.1 »/« 1.2 «'п 1.л 1 «»л I.» 0 0 0 I
где тп к» ,=----------. т„ Kj= —
^П. Л I «Л. л 1
(1 о ••• о о
0 1- 0 о
.....................
«л I <<л2 ’" «я п 1 «пл 0 0-0 1
С=Л/п-,1 В=Мп\АМ„^, (матрица С подобна матрице А):
/<н <12 < 1л 1 <!п
/ <21 < 22 - • • <2л 1 <'2л
\ 1'п 1. 1 \о <‘л- 2. 2 0 ’ • - <л- 1. л - 1 1 < л - 1. л 0
где (ц=Ьи (/=1.2....//). £ и'А/’Ч (7=1...«)•
к I
Все эти вычисления одного этана оформляют в следующей схеме (на примере матрицы четвертою порядка):
189
Номер строки л/-‘ С голбцы ма грицы L'
1 2 3 4
1 «II «12 «13 «14
2 «21 «22 «23 «24 4/2
3 «31 «32 «33 «34
4 «41 «42 «43 «44 </4
\ м3
1 «31 «зг «33 ~ 1 «34 «1
5 «41 1 Л12 ^13 Z>)4 Р1 Yi
6 О 42 /?i 1 />22 ^23 1)24. р2 Y2
7 «43 ^31 ^32 /Ъз />34 Рз Уз
8 «44 0 0 0 0 1 1
7' <*31 <32 <’зз <34 Рз
В этой схеме столбцы Е и I' вводят для выполнения построчного контроля производимых вычислений, причем
"г/ "
<4 = X «.> ОС! =-у^с/. + а.за, (/= I, 2, 3); Р,= £
j=l «43 j=|
Контрольные соотношения:
Л
oti =ш31+/к32 + (—1)+ш34, pi = Yi+Aj3 (/= L 2. 3), р3= £ c3j.
i= i
В результате всех преобразований получается уравнение
(-1)пП(Х) = ??-р1Г“1-/ь1я“2- ... -аЛ = о.
корнями которого являются собственные числа матрицы А.
Собственные векторы определяют из соотношения
А?-1\
/*ГЧ
Х^М^М^-ММ, где У(= ........... (/=1,2,...).
/
\] /
Каждое умножение в правой части этого равенства, начиная с Y,, позволяет определить одну из координат вектора X-,.
3°. Метод Леверрье—Фаддеева.
а) Метод Леверрье для определения коэффициентов характеристического уравнения матрицы А. Вычисляют степени матрицы А:
А^А'-'-А (А- =1,2..«).
Находят след для каждой из матриц Л*:
Л
Sp/1* = M + V2+ ... +х*= £ Л*=М>].
i= 1
190
Коэффициенты характеристического уравнения определяют по формуле kpk = Sp Ак — pi Sp/l*"1 — ... — рк-1 Sp/l.
В результате получается характеристическое уравнение матрицы А: (- 1)"О(Х) = Х"-р1>."-1 -р2Х"-2- ... -р„=0.
б) Видоизменение метода доватсльность матриц: Леверрье. предложенное Фаддеевым. Строят послс-
Л1 = Л; Sp^t=pi; Bi =At —pi
А2 = АВХ; -SpJ2=p2: B2 = A2^p2p;:
Ап-1 — Л- 2' , Sp Ап_ j —рп_ 1, Вп- । — Апj — р-~ i Е',
Ля = Л5л_1. — 5рЛп = рп, Вп — Ап—рпЕ.
В результате получается уравнение
Г-р,Х'’-1-рДй2-...-/?я=0.
При этом контролем служит соотношение В„=0. Кроме того, метод даст возможность найти А ~1 = В„ _ i /р„.
Собственные векторы находят по формулам
Х0=ё; Х^ = ккХ\к\+ЬГ (i=1.2.......I),
где ё — столбец единичной матрицы, Ьк- одноименный столбец матрицы Вк. Собственный вектор ATj,*21 соответствует А*.
4°. Метод итерации для определения первого и второго собственных чисел матрицы и их векторов. Строят последовательность векторов: Уо произвольный вектор, У| = /1У1_1 (/=1,2,...). Тогда
где г|“ и г}*4 одноименные координаты двух последовательных векторов; r!fc+,’-MrP
где у}‘+1), г|“. у!•*“" —одноименные координаты трех последовательных векторов При этом zVi^n, X2=Yk>i-)^Yk.
5°. Способы улучшения сходимости итерационного процесса.
а) Способ возведения матрицы в степень. Строят последовательность матриц
А, А2, А4..... А2\ затем находят Ym = AmY0; Y„^t = AYm, где /н=2‘. Тогда
б) Способ скалярных произведении. Строят две последовательности векторов: r0; у,=лу0; Г2=ЛГ,: ... У*=луА_,
Уо» У>Л'У0; y'2 = A'Y\. ... Y'k = A'Yk^,
где А и А'—соответственно данная и транспонированная матрицы. Тогда
191
если матрица .4 симметрическая, то .4 = Я' и
- _
Л* и; .•>;)•
Интерполирование и экстраполирование функции
1°. Интерполяционная формула Лагранжа:
При вычислении коэффициентов Лагранжа разности удобно расположить следующим образом:
л-АО Ло-Л1 Л‘() “Л э А'(» —Ли
Л* 1 — Л'о A-A t А| “Лэ А| “Ап
Л'2 —-Тр Л2 “Al Л — Лэ Аэ — Л„
*
Ап “АО АИ-Л| АИ-Лэ л-л„
Если обозначить произведение элементов строк через D: (/ = 0,1 и), а произведение элементов главной диагонали через (|„+1 (.г), то получится формула
В случае равноотстоящих узлов интерполяционная формула Лагранжа принимает вид
Л(л)=||(01 Зр(— р-
где /=(л—л‘0)/Л. = !-.V; (/ = 0, 1.2 «).
Для оценки погрешности интерполяционной формулы Лагранжа можно использовать соотношение
где
(//+1)! ь.б|
2°. Интерполяционные формулы Ныоюна.
а) Первая интерпол.чционна.ч фюрмула Ньютона:
где <7={л— л'0)//л Л = л;+1—л, (/ = (). I./г). А‘г0 конечная разность /-го порядка,
причем Д'у0 = Др ‘j| — Д'" \г0 (/ = I. 2.//).
192
Если «=1. то получае гея (формула линейной интерполяции Pi(.v) = ro + </Ar0-
Если п — 2. то получается формула квадратичной интерполяции
</(«/—I) , Р2 к)=Уо +</ Д.’ о -----Л~ 1'о-
6) Вторая интерполяционная (формула Ньютона:
где (/ = (л -л„) It.
в) Интерполяционная формула Ньютона для неравноотетояи/их точений аргумента:
/’п(•')=./(-'о) + (л—Ло)./(л<). .Vj) + (a-AoJIa- vJ/I.v,,. а,. а2) + ...
... + (A -Au)(a--A,)(a -A:) ...(А -Л„ 1 )/(ЛО. A j.л„).
/(<]. л2....U - /Ъ’о- -'1.....Ч 1)
где /(л0. А-j...v,) =--------------------------------- разделенная разность /-го
А]— А"п порядка.
3“. Интерполяционная схема Эйткина:
вычислений определяют путем сравнения Поспелова тельных значе-
Конец ний Р(х}.
4°. Интерполяционные формулы Гаусса.
Л2г !
------------------A*v
(<7 + 2)((/+ !)</(*/— !)(// —2) (//-и-
+ -----------------------------------Д’ г > -Г ... ч-----------------------------
где г/=(а-л0)7/.
193
Вторая формула Гаусса: . . (</+ 0</ ,
Р (л) = ro + </ А .1 ., + ——— Д ‘г
3!
+
4!
Д4г
Д2"“'г-П
А2"г-В.
где
5°. Интерполяционная формула Стирлинга:
<Г .2 &3У
— А г_ । +--------
2 3!
_ j -г I
=Ус + Ч——~
i-------Д V
41
.‘о
э
2
+
</2(<Г-1)(</2-22) </(</2-l)(v2-22) <[</2-(«-О2]
+------------------Д г_ з + ... +-------------------------------- х
6! ' (2м-1)!
Д2я" 1 г_п +Д2"“ 'г_ (и_ „ (г/2- 1)(г-22)... [г/2- («- О2] А,„
х-----------------------+ ---------------7—Г---------------Д Г_г
где г/= (,v — л‘о )/Л. Обычно эту формулу используюг при | |^О,25 6°. Интерполяционная формула Бесселя:
Д6г з + Д6г_2 ц(ц-!)(</+ ]}((/-2)(// + 2)...(</ — п)(д+п-I) х----------------+ ... ч----------------------—------------------------х
2 (2«)!
Д2”г_п + Д2пг_я + 1 х--------------------+
j-----------------------------------------------------Л Г
(2н+1)!
где </ = (.v—л0)/Л. Обычно эту формулу используют при 0,25 <<у^0.75.
Численное дифференцирование и интегрирование
1°. Формулы численною дифференцирования
а) основанные на первой интерполяционной формуле Ньютона:
2ц— Г , ^1у2 —6г/ + 2 2</3 — 9t/2+ 11<у~3 .
А.го + Д2 Го + ———— Д3гп + —--------------------— А4
2 “ 6 Л'Г» +
5ц 4 - 40г/3 + 105г/ 2 - 100г/ + 24
Л
120
194
где ?=(л-л0)/Л. Л=л,+ 1-л< (/=0.1.2....);
б) основанные на первой формуле Гаусса: , v I/ 2//-1 , 3//2-1 .
г' (л) % - ( Д г0 + -^7- Д' г _, + -- Д" г _ ,
Д4г
Д4г
2i 1 h2
в) основанные на второй формуле Гаусса:
г+1 З/?2—I 2</' + 3<r-f/-l
---Д‘ г _, +-----Д3 г _ -, +----------Д г
2 6 12
1 / , , 6</2 —6//—1 \
-{ Д"г_!+^Д3з’_2+-----------Д г_2 + ):
Л
г
г) основанные на формуле Стирлинга:
д) основанные на формуле Бесселя:
и/ v 1/A2r_j+A2ro 2q-1 , 6<72-6//-l Д4г_2 + Д4г_, \
r(.v)~— -----------ч--------Д r_ j ч---------------------+ ... I.
' ' /r\ 2 2 12 2 J
2°. Формулы численного интегрирования.
а) Пусть отрезок интегрирования [«, b ] разбит на и частей с шагом h-{b-a)!n. Тогда:
Ь п~ 1
Х/(Л*/) (Ф°РЛ1У‘1а гевых прямоугольников): а i = 0
h n
jf(x)(L\^h (формула правых прямоугольников):
a is 1
ь, / А
jf(x)dx^h Е.Л л|+-о / = О \ 2
где xf=a + ih (/=0, 1. 2..л).
(формула средних прямоугольников).
195
Остаточные члены них форму.! соответственно равны
где
б) Формула Ньютона Котсса:
ь л
и АО
।, (С л, = л\, I /Л (/ = 0.1.2.н). л-(, = « h = (h-a) п.
Коэффициенты Ck = Hk„INn определяю! заранее и ия них составлены таблицы:
п /Ль //1л н2„ //Лл //4л //<„ н,.п У,
1 1 1
2 1 4 1 6
3 1 3 3 1 8
4 7 32 12 32 7 90
5 19 75 50 50 75 19 288
6 41 216 27 ">7"’ 27 216 41 840
в) Форму io трапеции:
ь
а
где (/=(). 1. 2...и). причем
(/’—</)' Л„(./)=-----— г/"(4 о^.^Ь.
12/г
г) Формула Симпсона (число п обязательно четное): h
_/(л)т/л -[т0+ Г„ + 2( Г2 + Т„ + т64- ... + 4( 1 ! 4 г, 4- ... +у„ | )].
л
причем
д) Формула Гаусса:
Л
а
by a h—a где л-(. = —+ (,= 1.2..........................н).
196
Значения i, и С, берутся из таблицы:
п С,
! /,=0 Ci=2
2 G ,= ±0.577350 (,=6’2=1
3 г, х= ±0-774597 /.=() С, =(’,=- = 0.555556 9 8 С. =- = 0.888889 ‘ 9
4 G 4 = ±0.К61136 //д= ±0.339981 С, =(’4 = 0.347855 С2 = Сл = 0.652|45
е) Экстрапол.чцн.ч по Ричардсону. Пусть /„ и /л два приближенных значения ь
найденных но одной и гой же формуле при и, и п2 (л> >*/!). Тогда
CJ более точное значение згою unici рала можно найти по формуле
= 4 +~—-(4-4.Г
где т порядок остаточного члена выбранной формулы (например- Для формулы трапеций /// = 2. для формулы Симпсона т = 4).
Приближенные методы решения обыкновенных ли ФФ е р е нии а л ь н ы х уравнений
Г’. Решение задачи Коши для дифференциальною уравнения л-т о порядка г<я' = /(л. г. г'....................г<я П)
заключается в отыскании функции г(л). удовлетворяющей згому уравнению и начальным условиям ,г(ло)=_го. ...г1п и(л'о)=Го и. гас л(). г0. ...
...Го-1’ заданные числа.
Для решения поставленной задачи применяются следующие методы.
а) Метод степенных рядов. Решение ищут в виде суммы ряда г(л)= г(ло) т .г0) -г- —— (л -ло) -г ... 4---—(л - л(|)" ... -
I! 2! п'
Приближенное решение задачи лает частичная сумма этою ряда.
б) Метод Jii.tepa О.т.ч уравнепи.ч y=f(x. i) с начальным условием г(л0)=г0-Составляют таблицу значений гк=г(л\). тле л\=л0 + АА (А ==0, 1. 2 н). //=(/>—«)«, [«./>) отрезок. на котором ищется решение. Значения yk „1 определяются по формуле
Л • 1 = А + А/’(а\. ) (А = 0. 1. 2.п - 1).
Погрешность вычислений на каждом шаге составляет Я4=0.5/гг"(е). где
в) Усовершенствованный истод ломаных. Сначала вычисляют промежуточные значения
197
Л * 1.2 - 2• Л + 1’2- Л + ~/(-<* Л).
а затем находят ц . t =л + А/(ц. ,/2. i\+,,2). Метол имеет несколько большую точность, чем метод Эйлера.
г) Усовершенствованный метод Эйлера — Коши. Сначала вычисляют «грубое» значение
J*+’ 1 =Л + А/ (л, 1\), которое затем уточняют по формуле 1 г , Лм=Л+-Л[/(л4. л)+/‘(л+р Л+,)].
Погрешность метода на каждом шаге имеет порядок Л3.
л) Усовершенствованный метод Эйлера с уточнением. Сначала вычисляют уГ?1=л+а/(-л-л).
а затем это значение уточняют по формуле
i«> =.п+^[/КЛ) +г(ч.i-l';,1’)] 0=1.2, ...у
Итерации продолжают до тех пор. пока в пределах требуемой точности два последовательных приближения нс совпадут. Погрешность метода на каждом I этапе имеет порядок Л3.
с) Метод Рунге — Кутта. Па каждом шаге вычисления выполняю! по формуле
Л+1=Л+ЧАГ, + 2АГ + 2А‘‘‘ + А«’). о
где
А Г’—А/( л л)’ А':"—Л/ /л*( + у. + -2-
причем л\ = л0 + /Л (г=0, 1.2...., я). Погрешность метода на каждом шаге имеет порядок Л5.
ж) Метод Адамса. Формула с первыми разностями:
]
Л+i =Л + 'А + ~&Чк-1- </к=А/(л\. r4) (А= 1. 2. ...).
Значение у, находят другим способом. Погрешность на каждом шаге имеет порядок /г.
Формула со вторыми разностями:
• 5 ,
Л +1 - Л + Як + ~&к-1 + ~ - 2 (А = 2, 3. ...).
1а.
198
Значения yi и уа находят другим способом. Погрешность на каждом шаге имеет порядок Л3.
з) Метод Милна. Пусть для уравнения у' =/(.v. у). кроме начального условия У(-*о)=Уо’ найден «начальный отрезок», т. с. значения искомой функции y(.vj)=yf в точках л; = л0 + /А (/=1.2.3).
Последующие значения rf при / = 4, 5, ... определяют на каждом шаге следующим образом. Для предсказания используют первую формулу Милна
Г"1"'’
=.>1-4+ у(2/(-Э-Л-2 + ?Л-.)-
Используя у"рсл, находят/•ир'л=/(л1. у "рм) и производят уточнения (коррекцию) значения yf по второй формуле Милна
Абсолютная погрешность е, значения у“ор приближенно определяется по формуле
Если точность результата достаточна, то полагают у^у‘ор-
2°. Решение краевой задачи для уравнения y"+p(.v)y' + 9(.v)y=/(.v) состоит в определении значений функции у(л). удовлетворяющей данному уравнению и краевым условиям
аоу(«) +а1у'(й)=Л. РоУ(Л)+₽,/(*)==*
где |а01 + 1^11^0, IPol + IPil^O-
Разбив отрезок («./>] на п равных частей с шагом h = (b—а), и. получают точки .¥, = //+th (/=0.1.2....//). в которых требуется найти искомые значения
У/ »У (•*/)•
а) Метод конечных разностей. Производные заменяют конечно-разностными отношениями; тогда для внутренних точек, т. с. при / = 1. 2....п — I. выполняются
равенства
г, +1 — г, _ j „ \'i +1 — 2у,+у,- - j
•Г'= 2Л ’ Л “ А2
а для краевых точек л0 = « и х„=Ь — равенства
У1 У о , 3* ?л-1 __----- .. _----------
или
199
В результате получается система уравнений с неизвестными го. г,.. г„. Решив
эту систему, получают таблицу приближенных значений искомой функции.
б) Метод прогонки. Предварительно определяют коэффициенты уравнений вида
,г( • t Ьт,г, + А, г,_x=h4'i (L 2.н- 1).
где
h
h h h
' + ~Pi 1 + l +
Затем находя) элементы «прямого хода»:
ос. Ah I
Gj = ;------• <4»=—• <,=------------: 4 = । (/=1.2......н-1).
— 71 ос, m, Ar,- j
Наконец, выполняется «обратный ход»: находя г
J (/ = «-
_ + Pi<„-i<4 1
Г""0оЛ + р1(<л-1 + 1): '
Вычисления удобно выполнять в следующей таблице:
А; Oli А/ л-л, г/. Г.
АО — /г/-, <о //о Го
А1 /»1 А1 <1 с/1 »1
АЧ «ь А;2 /г/-; с2 с/2 П
"'п-1 А’я - 1 frf-'n ! <п- 1 /4 । J п 1
--- J п
Приближенные методы решения дифференциальных уравнений в частных производи ы х
,П ( ~и < ‘и
1 . у равнение Лапласа —— ч--------- = 0.
( Г“ f г*
схема для замены уравнения Лапласа конечно-разностным уравнением:
4
II
схема для замены уравнения Лап.ласа конечно-разное!ным уравнением:
4
200
а) Задача Mitpu.x.ie д.с.ч уравнения Лап.шеа заключается в нахождении функции w=w(.v.r). удовлетворяющей данному уравнению внутри некоторой области G. а на границе пой области Г условию и, =<p(.v. г), где <p(.v. г) — заданная непрерывная функция.
Метод сеток состоит в том. что выбирают шаг h и строят сетку л; = л0 + /Л. .П=.'<>+./Л (/=0. I. 2. ...: /=0._|. 2. ...). покрывающую данную область G.
Выделив граничные и вну грсннис узлы, заменяют данное уравнение во внутренних точках конечно-разностным уравнением, используя I или II схему, а в граничных точках значения функции w(.v. г) находят из дополнительного условия. Решив полученную систему, составляют таблицу значений искомой функции.
б) Процесс усреднения Липмана применяется при решении задачи Дирихле для уравнения Лапласа. При лом используют формулы:
,тля внутренних точек
(t = i. 2.
где ич начальные значения внутренних точек, найденные из решения системы или взятые произвольно:
для граничных точек
«°(Л)=Н(.4)=Ф(.4).
где w°(.4h) начальное значение функции в точке .4fc. w(.4) значение функции в точке .4. лежащей на границе:
Л + о
где 6 расстояние между точками .4 и .4А. взятое со знаком плюс, если Ah -внутренняя точка области G. и со знаком минус, если .4fc внешняя точка.
э(> <» <”«
2 . Смешанная задача для уравнения теплопроводности — = -— состоит
Г/ GV2
в определении функции и (л. f). удовлетворяющей данному уравнению, начальному условию м(л. ()) = /(л) ()<а^/ и краевым условиям u(0. i ) = <р(/). н(/./) = ф(/).
Используя метод сеток, выбирают шаг Л по оси О.х и вычисляют шаг Л=а/г по оси Ol а затем строят сетку со значениями л\=/л. (/=0. 1. 2...п;
/=0. 1.2....А).
Значения wi7=m(.v17.вычисляют по формулам:
м,о = и (л,. 0) = / (л; ) — из начального условия.
Но, = <₽(</)• из краевых условий.
Для определения значений во внутренних точках применяют формулы
1 + -i.j
при о=- м,.у-1=-----——•
I I
ПрИ 6 = - «i./+l=7(W(t|.j + 4Mi-+ttf , ).
6 о
201
3°. Смешанная задача для уравнения колебания струны —--—- состоит с?/2 сх
в отыскании функции н(л, /). удовлетворяющей данному уравнению, начальным условиям w(.v, 0)=/(л), и,(х, 0) = Ф(л). 0<х</ и краевым условиям м(0./) = <р(г), «(А /) = ф(/).
Используя метод сеток, выбирают шаг Л по осям От и Ot и строят сетку со значениями xt=ih, t—jh (/=0,1.л; j=Q. 1,2,...).
Для определения значений функции ни = и(л1, tj) применяют формулы
«Оо =/(-*/) (/=0, 1. 2, , л) — нулевой слой;
I
и{ 1= (h -1 +Л +1) + Л ‘ Ф 0=0, 1.2.л) — первый слой;
«<.Н1=М/+(' = 0. Ь 2...........«; 7=2, 3. ...).
ПРИЛОЖЕНИЕ 2 БЛОК-СХЕМЫ НЕКОТОРЫХ АЛГОРИТМОВ
Блок-схема вычислений Блок-схема вычисления ех
с помощью метода хорд методом степенных рядов
202
Блок-схема вычисления интеграла ио формуле Симпсона
Блок-схема решения задачи Коши методом
ПРОГРАММЫ НЕКОТОРЫХ РАСЧЕТОВ НА МИКРОКАЛЬКУЛЯТОРЕ «ЭЛЕКТРОНИКА БЗ-34»
1°. Метод итераций для системы линейных уравнений. При решении системы четырех линейных уравнений методом итераций выполняют вычисления вида
а}*’—a j л'*i ~ *1 + а2 т? ’11+аз х~11+ад-Гд ” п+а$
Значения данных величин заносят в регистры памяти: я2-*П2;
о3->ПЗ: «4->П4; н5-П5; л(1*'"-*ПА; л?"1,-ПС: а?" 1)->ПД.
При вычислении лл*) используют программу: ЙП1; ИПЛ; х; f; ИП2;
t; ИПВ: х; + ; Т: ИПЗ; f; ИПС; х; +; f; ИП4; f; ИПД; х; +; J; ИП5; +; с/п.
Меняя содержимое регистров памяти, можно находить значения других переменных.
2°. Метод хорд для уточнения корня нелинейного уравнения с постоянным концом. Для вычислений применяют формулу
203
послсдователыюсть значений вида гг|. t
2v„4-
JM „ .
л"‘1 = л"“7Гк\" гГ\*' “л"* Ли = а-
Вычисления выполняют, используя критерий л„.|—а„^е. где е заданная точность. Информацию распределяют по pci неграм намят: />-»ПЛ. /(/>)-»ПВ; л„-»П1: /(а)-»П2.
Программа вычислений: ИП2; J; ИПВ; ИП2; —: J; ИПЛ. J; ИП1:
—; х; /—/; ИП1; ч-; П1: с/п; во.
3°. Вычисление значений функции сл методом степенных рядов. Здесь нрименя-" л
ют формулу е'ь У Ся. где н0=1. (и--1. 2...).
<ТЙ п
Вычисления выполняют, используя |Г'„|^е/1(). где с заданная точность.
Регистры памяти содержат: л-»П1: л-»П2: (Я-»ПЗ, У-»П4. Первоначально в ли регистры заносят л-»П1; 0-+П2; 1-»ПЗ: 1-»П4.
Программа вычислений: ИП2; 1: 4-; П2: ИП1: ИП2; 4-: ИПЗ; х; ПЗ; с п; ИП4; 4 •; П4: с. и: во;
Программа предусматривает фиксирование отдельных слагаемых и сумм.
4°. Вычисление значений функции r=V-v методом те раций. Составляют а \
— ). где го определяется прикид-
Зл /
кой. Вычисления продолжают до выполнения условия |г„— гя t|<E 2, где с заданная точность. Регистры памяти содержат: а-»ПЛ; г-»П1. Первоначально в эти регистры заносят \-»ПЛ: го-»П1
Программа вычислений: ИПЛ: ]: ИГП; /*л2: —: ИГП. 2: х; 4-: |; 3; 4-; П1; с/п
5* Мигрирование но формуле Симпсона. Эта формула имеет вид
h
' h
/ (а ) d.\ * - ( г0 4- 4г, + 2 г2 4- ... 4-_г„).
а
Здесь н = 2А. t.—ZIaJ. х, —/7/ (/=0. 1. 2....). Л=(/> — «)/л.
Рассматривают программу вычислений по формуле с фиксированием номера функции в процессе вычислений. Значения a, b, п. Л. а\. /(а.) заносят в регистры памяти: «-Г1Л; Л-ПВ; и-» ПС; Л-»ПД: х-->ГП; ,/(л1)->П2: /->114.
Программа вычислении: ИПВ; |; ИПЛ; « —»; ИПС: ПД; ИП1; ...: ИП2;
ПЗ; с/п: ИП4; f; I; +; П4: с/п; ИГП; |; ИПД; 4-. П1: с п; ИП1. ...: ИП2; j; 4; л-; ИПЗ; +; ПЗ; ИП4: f; 1; Ч-: П4; с/п; ...: ИП2; |; 2; х; ИПЗ; +: ПЗ; ...; ИПЗ; J; 3; ИПД. а; с н.
Программа предусматривает наличие подпрограммы для вычисления значений функции /(л*,), а также повторение отдельных ее фрагментов, зависящих от номера /.
6°. Приближенное решение дифференциального уравнения r' = /(v. i) методом Эйлера — Коши. Этот меюд предусматривает наличие условия г(«) = г0: тага Л, отрезка [«. />J; применение формулы
< Л. к
.» <+ I —З г+ -( ./; Ч- /;. 1 ),
где I -/ (л\. I. г,- > t ). г, > I = Г; Ч hf .
Регистры памяти содержат: а,-»ПЛ. г,—»ПВ; /(а,, г,)-»ПС: Л—*11Д; /;.!-»П1.
Программа вычислений: ИПЛ; |. ИПД; 4-; ПЛ; с/п; ИПС; |; ИП1; ч ИПД; х. 2; -; ИПВ; 4-: ПВ. с/п.
Приведенную программу следует пополнить программой вычисления значений .*7+| и .Fi + i-
ЛИТЕРАТУРА
1. Воробьева Г Н.. Данилова Л II Практикум но численным методам. Мл Высш школа. 1979.
2. Данилина II. И.. Дубровска я II. С.. КвашаО.П.. Смирнов Г. Л. Вычислительная математика. М.: Высш, школа. 19X5.
3. Демидович Б. Г!.. Марон И. А. Основы вычислительной математики. М.: Паука. 1970.
4. Демидович Б II.. Марой И. А.. Шувалова 3.3. Численные методы анализа. М.: Паука. I96S.
5. Дьяконов В П. Справочник по расчетам на микрокалькуляторах.— М.: Наука. 19X6.
6. К о пч с нова II В.. Марон И А Вычислительная математика в примерах и задачах. М.: Наука, 1972.
7. Пу х паче в Ю. В.. Да и илов И. Д. Микрокалькуляторы для всех. М.: Знание. 19X6.
СОДЕРЖАНИЕ
Предисловие ......................................................... 3
Глава I. Элементарная 1еория погрешностей
Работа I. Определение абсолютной и относительной погрешностей приближенного числа. Верные цифры числа ................................ 4
Работа 2. Действия нал приближенными числами. Оценка погрешностей результата .......................................................... 6
Глава II. Алгебра матриц
Работа 1. Обращение матрицы методом разбиения се на клетки ......... 13
Работа 2. Обращение матрицы методом окаймления ..................... 15
Работа 3. Обращение матрицы методом разбиения ее в произведение двух треугольных матриц ................................................. 19
Глава III. Методы решения систем линейных уравнений
Работа 1. Решение систем линейных уравнений по формулам Крамера и с помощью обратной матрицы ....................................... 22
Работа 2. Решение систем линейных уравнений по схеме Гаусса ........ 32
Работа 3. Обращение матрицы и вычисление определителя по схеме
Работа 4. Решение системы линейных уравнений методом главных элементов ................................................................... 39
Работа 5. Решение системы линейных уравнений методом квадратных корней ................................................................ 41
Работа 6. Решение системы линейных уравнений по схеме Халецкого...... 43
Работа 7. Обращение матрицы по схеме Халецкого с уточнением се элементов ............................................................. 47
Работа 8. Решение системы линейных уравнений методом итераций ......... 49
Работа 9. Решение системы линейных уравнений методом Зсйделя .......... 52
Глава IV. Вычисление значений элементарных функции
Работа 1. Вычисление значений многочлена по схеме Горнера ............. 54
Работа 2. Вычисление значений функции методом разложения в ряд .... 56
Работа 3. Вычисление значений функций методом итераций ................ 58
Глава V. Методы решений нелинейных уравнений
Работа 1. Графическое и аналитическое отделение корней нелинейного уравнения. Уточнение корней методом половинного деления.............. 61
Работа 2. Уточнение корней уравнения методом хорд ..................... 65
Работа 3. Уточнение корней уравнения методом касательных .............. 68
Работа 4. Уточнение корней уравнения комбинированным методом хорд и касательных ......................................................... 69
Работа 5. Решение уравнения методом итераций .......................... 72
Работа 6. Решение систем нелинейных уравнений методом итераций и методом Ньютона ......................................................... 74
Работа 7. Решение алгебраических уравнений методом Горнера ............ 79
Работа 8. Решение алгебраических уравнений метолом Лобачевского 81
Работа 9. Решение алгебраических уравнений методом выделения квадратного множителя ........................................................ 83
206
Глава VI. Нахождение собственных чисел и собовенных векторов матриц
Работа 1. Определение собственных чисел и векторов матрицы методом непосредственного развертывания ...................................... §6
Работа 2 Определение собственных чисел и векторов матрицы метолом Крылова .............................................................. 91
Работа 3. Определение собственных чисел и собственных векторов матрицы методом Данилевского ................................................. 97
Работа 4. Определение собственных чисел и собственных векторов матрицы методом Л еверрье—Фаддеева ............................................ 100
Работа 5. Нахождение первою собственного числа и первого собственного вектора матрицы методом итераций .......................... 102
Работа 6. Нахождение второго собственного числа и второго собственною вектора матрицы методом итераций .......................... 104
Работа 7. Вычисление первого и второго собственных чисел и соответствующих им собственных векторов матрицы с использованием возведения матрицы в степень для улучшения сходимости итерационного процесса .............................................. 105
Работа 8. Определение первого собственного числа матрицы методом скалярных произведений .............................................. 107
Глава VII. Интерполирование н экстраполирование функций
Работа I. Нахождение значений функции с помощью интерполяционного многочлена Лагранжа ................................................. 109
Работа 2. Вычисление значений функций но схеме Эйткина ............. 111
Работа 3. Вычисление значений функции по первой и второй интерполяционным формулам Ньютона .............................................. 113
Работа 4 Вычисление значений функции с помощью линейной и квадратичной интерполяции ............................................... 118
Работа ?• Вычисление значений функции с использованием интерполяционных формул Гаусса. Стирлинга, Бесселя ............................... 120
Работа 6. Вычисления значений функции с использованием интерполяционной формулы Ньютона для неравноотстоящих узлов ...................... 122
Глава VIII. Численное дифференцирование и интегрирование
Работа 1. Нахождение первой и второй производной функции с помощью формул, построенных на интерполяционных формулах Ньютона. Гаусса. Стирлинга. Бесселя .......................................... 124
Работа 2. Вычисление определенных интегра юв по формулам прямоугольников ............................................................... 127
Работа 3. Вычисление определенных интегралов по формулам трапеций и Симпсона .......................................................... 131
Работа 4. Вычисление определенных интегралов по формуле «трех восьмых» ................................................................ 13б
Работа 5. Определение уточненных значений интегралов с помощью экстраполяции по Ричардсону ............................................ 139
Работа 6. Вычисление определенных интегралов по формулам Гаусса .. 141
Глава IX. Приближенные методы решения обыкновенных дифференциальных уравнений
Работа /. Приближенное решение дифференциального уравнения усовершенствованным методом ломаных ....................................... 143
Работа 2. Приближенное решение дифференциального уравнения методом Эйлера —Коши ...................................................... 144
Работа 3. Приближенное решение дифференциального уравнения методом Эйлера с уточнением ................................................. 145
Работа 4. Приближенное решение дифференциального уравнения методом Рунге —Кутта и Адамса ............................................... 149
Работа 5 Приближенное решение дифференциального уравнения методом Милна ............................................................... 153
207
Работа 6. Решение краевой задачи для обыкновенною дифференциального уравнения методом конечных разностей ............................. 156
Работа 7. Решение краевой задачи для обыкновенною дифференциальною уравнения методом прогонки ....................................... 159
Глава X. Приближенные методы решения дифференциальных уравнений с частными производными
Работа /. Приближенное решение задачи Дирихле для уравнения Лапласа ... 161
Работа 2. Приближенное решение уравнения Лапласа для криволинейной границы .......................................................... 168
Работа 3. Приближенное решение уравнения юплопроводносги методом сеток ............................................................ 172
Работа 4 Приближенное решение уравнения колебания с груша методом 4сеюк ...............................................'............ 174
Приложение I. Справочный материал по вычислительной ма гема гике .... 177
Приложение 2 Блок-схемы некоторых алгоритмов ..................... 202
Приложение 3. Программы некоторых расчетов на микрокалькуляторе «Электроника БЗ-34» .............................................. 203
Литература ........................................................ 205
Учебное издание
Воробьева Галина Николаевна
Данилова Александра Николаевна
ПРАК ГИКУ М
ПО ВЫЧИС 11! ИЛЬНОЙ МАТЕМАТИКЕ
Зав. редакцией Г. I Гридасова Редактор А. М. ( холскнй Мл рслакюр НИ Майкова Хуложсс! венный редактор В. И. Пономаренко Технический рсдакюр \ К Нестерова
И Б № «567
Изд. ЛГ« ФМ-06. Сдано в набор 25.01.90. Поли, в ncnaib 14.08.90. Формат 60 X 90’Ав.
Бум. кн.-журн. Гарнитура 1аймс. Печать офсетная. Объем 13,0 уел. неч. л. 13,25 уел. кр.-отт. 12,38 уч -изд. л. Тираж 90 000 экз. Зак № 1258. Цена 35 коп.
Итдательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная у г, д. 29/14
Набрано в ордена Октябрьской Революции и ордена Трудового Красного Знамени МПО «Первая Образцовая типография» Государственного комитета СССР по печати. 113054, Москва. Валовая, 28. Отпечатано в Ярославском полиграфкомбинатс Госкомпечати СССР. 150049, Ярославль, ул. Свободы, 97.