Текст
APPLIED MATHEMATICS AND COMPUTATION
A Series of Graduate Textbooks, Monographs, Reference Works
Series Editor: Robert Kalaba, University of Southern
California
PATTERN RECOGNITION PRINCIPLES
Julius T. Tou
Center for Information Research
University of Florida. Gainesviile
Rafael С Gonzalez
Department of Electrical Engineering
University of Tennessee, Knoxvllle
Addison-Wesley Publishing Company
Advanced Book Program
Reading, Massachusetts
London-Amsterdam-Don Mills, Ontario-Sydney-Tokyo
1974
Дж. Ту, Р. Гонсалес
Принципы распознавания
образов
Перевод с английского И. Б. Гуревича
под редакцией Ю. И. Журавлева
Издательство «Мир» Москва 1978
УДК 519.92
В книге представлены методы построения распознающих си-
систем и систем обработки больших информационных массивов.
Рассматриваются основные постановки задач и важнейшие мо-
модели алгоритмов (комбинаторно-логические, статистические и
лингвистические). Изложение ведется на достаточно высоком
уровне математической строгости.
Особенность книги состоит в том, что рассматриваемые про-
проблемы авторы трактуют в тесной связи с задачами эффективной
обработки информации, причем теория распознавания выступает
как самостоятельное направление прикладной математики со
своими задачами, аппаратом и методологией.
Книга может быть использована в качестве учебного посо-
пособия по математическим методам обработки информации, а также
как справочное пособие для теоретиков и для тех, кто в своей
практической работе сталкивается с задачами обработки инфор-
информации.
Редакция литературы по математическим наукам
апппл поо © 1974 by Addison-Wesley Publishing Company. Inc.
T 2Q-78
041 @l)-78 " © Перевод на русский язык, «Мир», 1978
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Предлагаемая вниманию читателя книга известных амери-
американских ученых Дж. Ту и Р. Гонсалеса содержит в форме, до-
доступной для широкого круга специалистов, некоторые из основ-
основных идей и методов математической теории распознавания и
классификации. Эта теория, включая ее применения к разнооб-
разнообразным прикладным задачам, является одной из наиболее
активно развивающихся областей прикладной математики и
математической кибернетики. В рамках указанной теории сло-
сложилось несколько весьма общих нацравлений. Они описаны
здесь с достаточной для математика степенью строгости и в то
же время сопровождаются большим числом примеров и обшир-
обширных комментариев, что позволяет специалисту-прикладнику при-
применять описываемые методы, не изучая во всех тонкостях мате-
математический аппарат.
Большая часть монографии посвящена описанию «классиче-
«классической» задачи распознавания. При ее постановке предполагается
следующее: объекты .распознавания заданы набором признаков,
известно некоторое число эталонных объектов, и их описания
составляют исходную (обучающую) информацию. На основе
этой информации синтезируется алгоритм, определяющий для
вновь поступивших объектов, к какому (или к каким) из конеч-
конечного числа классов они принадлежат. Авторы подробно описы-
описывают статистический подход к задачам распознавания, основан-
основанный на хорошо известных результатах о выборе из конечного
числа конкурирующих гипотез, и детерминистские методы распо-
распознавания— методы потенциальных функций. Вне внимания
авторов остаются логические и алгебраические методы. Впро-
Впрочем, в книге приведены описания отдельных алгоритмов.
Большое внимание уделено отбору признаков, используемых
для описания объектов. Хорошо известно, что удачный выбор
признаков во многом определяет успешность решения задач
распознавания. В монографии освещена большая часть матема-
математических методов реализации такого выбора.
В конце книги дано краткое описание сравнительно новых
методов — структурных, или формально-лингвистических. По-
Появление этих методов обусловлено тем обстоятельством, что
во многих случаях информацию о классах нецелесообразно
6 Предисловие редактора перевода
задавать перечислением известных объектов класса. В таких об-
областях, как алгебра, математическая логика и теория множеств,
хорошо известен и давно применяется другой способ: задаются
базисные элементы и правила порождения новых элементов.
Именно так задается каждый из классов, рассматриваемых в
задаче распознавания. При появлении нового объекта требуется
установить, может ли он быть сконструирован из заданных
базисных элементов при помощи заданных операций. Возникаю-
Возникающие при этом методы и алгоритмы являются, по существу,
переложениями соответствующих методов дискретной матема-
математики. По нашему мнению, для глубокого изучения структурных
методов распознавания и особенно для подготовки к самостоя-
самостоятельной работе необходимо освоить предварительно хотя бы
основы математической логики, теории формальных систем,
современной алгебры. К сожалению, в настоящее время струк-
структурные методы развиваются в основном для решения конкретных
задач. Более или менее общие методы в данном направлении
пока не созданы, и их создание вряд ли возможно без при-
привлечения к этой работе специалистов по дискретной матема-
математике. В настоящей монографии отмечаются трудности, которые
надо преодолеть для создания таких методов, и отдельные воз-
возможные пути развития теории.
В заключение следует отметить, что читатели в целом по-
получат интересную книгу. Она полезна студентам и аспирантам,
специализирующимся по прикладной математике и математиче-
математической кибернетике, а также инженерам, биологам, химикам, ме-
медикам, геологам, социологам и другим лицам, интересующимся
задачами классификации, распознавания и прогнозирования.
Ю. И. Журавлев
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
«ПРИКЛАДНАЯ МАТЕМАТИКА И ВЫЧИСЛИТЕЛЬНЫЕ
ПРОЦЕССЫ»
Команды современных ЭВМ выполняются в течение наносе-
наносекунд. Это позволяет быстро и точно решать системы, составлен-
составленные из нескольких сотен обыкновенных дифференциальных
уравнений. Как, однако, эти поразительные возможности ЭВМ
могут повлиять на решение тех научных, технических, экономи-
экономических и социальных проблем, с которыми сталкивается чело-
человечество? Для ответа на этот вопрос несомненно требуются
значительные усилия.
В некоторых областях человеческой деятельности мы еще
не в состоянии составлять уравнения, достаточно точно описы-
описывающие изучаемый процесс. В таких случаях вычислительную
машину можно использовать просто для получения модели про-
процесса и, возможно, оценки эффективности различных систем
управления. Есть области, в которых математическое описание
не составляет проблемы, но численное решение соответствующих.
уравнений оказывается затруднительным. В подобных случаях
следует попытаться честно преодолеть возникшие сложности;
если же эти попытки не приведут к успеху, то надо постараться
отыскать описание, в большей степени соответствующее возмож-
возможностям вычислительных машин. Математика предоставляет
почву для применения такой стратегии и в свою очередь пи-
питается ее плодами.
Каждый раз, когда быстродействие и размер памяти вы-
вычислительных машин увеличиваются на порядок, необходимо
производить переоценку вычислительных методов и классов
задач, входящих в категорию поддающихся решению. В книгах,
включенных в данную серию, представлена современная точка
зрения на постановку, анализ с использованием математического
аппарата и машинное решение соответствующих задач.
Задачи распознавания образов возникают во многих обла-
областях— в качестве примеров можно назвать медицинскую диагно-
диагностику, перевод и статистику. Настоящая книга вводит читателя
в круг основных идей и методов распознавания образов и спо-
способствует дальнейшему развитию этого направления приклад-
прикладной математики, переживающего пору расцвета.
Роберт Калаба
Посвящается нашим женам
Лизе Ту и Конни Гонсалес
ПРЕДИСЛОВИЕ
Эта книга написана с целью снабдить инженеров, исследо-
исследователей и студентов, занимающихся проблемами анализа дан-
данных и обработки информации, исчерпывающим, упорядоченным
и современным руководством, излагающим основные принципы
и практические методы анализа и распознавания образов, а
также синтеза соответствующих систем.
Первые попытки изучения возможностей автоматизации про-
процесса распознавания образов относятся к началу 50-х годов,
когда цифровые вычислительные машины постепенно стали
общедоступным средством обработки информации. Часть этих
первоначальных работ в области распознавания образов была
посвящена разработке программ автоматического принятия реше-
решений и созданию специализированной аппаратуры, предназначен-
предназначенной для автоматического «чтения» образов типа печатных бук-
буквенно-цифровых знаков. В конце 50-х годов Розенблатт предло-
предложил перцептронный алгоритм, который представлял собой одну
из первых моделей процессов запоминания и организации ин-
информации, реализуемых мозгом. В этот период ведущие подходы
к решению задач распознавания были основаны на идеях теории
статистических решений и пороговой логики. Исследования в
области синтеза систем распознавания набирали темп на протя-
протяжении 60-х годов по мере того, как расширялось использование
вычислительных машин и становилась очевидной потребность
в более быстрой и эффективной связи человека с ЭВМ. Для того
чтобы при решении некоторых типов задач распознавания зри-
зрительных образов можно было пользоваться результатами теории
машинных языков и соответствующими возможностями обра-
обработки информации, был предложен синтаксический подход как
дополнение к аналитическим методам.
Основные концепции теории распознавания приобретают все
большее признание в качестве фактора, существенного для по-
построения современных информационных систем, реализованных
на основе вычислительных машин. Интерес к этому направлению
продолжает быстро расти — соответствующие задачи являются
объектами междисциплинарных исследований, проводимых в
рамках столь различных областей, как техника, вычислительная
математика и кибернетика, теория информации, статистика,
Предисловие
физика, химия, лингвистика, психология, биология, физиология
и медицина. В каждой из них основное внимание уделяется
какому-то конкретному аспекту задачи распознавания — от мо-
моделирования физиологических процессов до развития аналити-
аналитических методов автоматического принятия решений. Колоссаль-
Колоссальный материал, связанный с теорией распознавания образов и ее
приложениями, рассеян по всевозможным техническим журна-
журналам, трудам конференций, монографиям, излагающим резуль-
результаты последних исследований, и отдельным учебникам, трактую-
трактующим лишь некоторые частные подходы к решению задач распо-
распознавания. Поэтому не так уж просто,, особенно новичку в этой
дисциплине, расположенной на «стыке» других областей, усвоить
широкий спектр принципов, лежащих в ее основе. При написа-
написании данного руководства мы попытались собрать в его рамках
основные аналитические методы и фундаментальные принципы,
изложив их в определенной логической последовательности и с
единых позиций. В результате получилась книга, которую можно
использовать и как учебник, и как справочник. Для тех, кто
собирается изучать предмет, она позволяет последовательно
ознакомиться с основными теориями и важнейшими методами.
Для инженеров и исследователей — это удобный источник систе-
систематически организованного справочного материала.
Предполагается, что читатель обладает соответствующей
подготовкой в области программирования, статистики, теории
матриц и математического анализа. При изложении материала
основное внимание уделяется получению фундаментальных ре-
результатов, опирающихся на основные концепции теории. В текст
включен разбор многочисленных примеров, а в конце каждой
главы приводятся упражнения, имеющие самый различный ха-
характер и сложность. Часть этих задач предназначена для того,
чтобы читатель в процессе их решения мог лучше уяснить от-
отдельные обсуждавшиеся положения, другие служат дополнением
или продолжением материала основного текста.
Настоящая книга основана непосредственно на конспектах
лекционных курсов, прочитанных авторами в Университете
штата Флорида и Университете штата Теннесси. Первый ва-
вариант этих конспектов появился в 1962 г., когда читался трехме-
трехмесячный курс в Северо-западном университете; позднее тот же
материал был прочитан в Университете штата Огайо. Различные
варианты этого курса были «опробованы» на студентах, специа-
специализирующихся в области вычислительной математики и кибер-
кибернетики и электротехники, что позволило тщательно отобрать
материал. Советы и критика, высказанные студентами на лек-
лекциях, привели к существенному изменению исходной рукописи.
Мы выражаем признательность целому ряду лиц, непосред-
непосредственно или косвенно содействовавших подготовке книги.
10 'Предисловие
В частности, мы хотели бы поблагодарить профессоров
У. X. Чжэня, Дж. М. Гуджа, Дж. Ф. Пирса, М. Дж. Томасона,
К. К. Ли, К. С. Фу, д-ра Р. К. Крайтера, д-ра П. X. Суэйна,
К. У. Суонгера, д-ра Нила Вальда и Г. К. Геррана. Мы хотели
бы также поблагодарить Мэри Бэрден, Грейс Серл, Дебру Дил-
лингхам, весь секретарский состав Университета штата Флорида
и Университета штата Теннесси за перепечатку многочисленных
вариантов рукописи. Кроме того, мы выражаем свою призна-
признательность за финансирование наших исследований в области
обработки информации и распознавания образов Управлению
научно-исследовательских работ ВМС США, Научно-исследова-
Научно-исследовательскому управлению сухопутных войск США, Национальному
управлению по аэронавтике и исследованию космического про-
пространства США, Окриджской национальной лаборатории и На-
Национальному научному фонду США.
Джулиус Т. Ту
Рафаэл К. Гонсалес
Глава 1
ВВЕДЕНИЕ
Несколько лет назад в воскресном выпуске газеты «Нью-
Йорк тайме» был задан следующий вопрос: «Облегчит ли поло-
положение маклерских фирм, все служебные помещения которых пе-
переполнены документами, сокращенный рабочий день?» Далее
сообщалось: «Профессор психологии Гарвардского университета
предупреждает, что к 2000 году возможности человеческого
мозга воспринимать информацию могут оказаться исчерпан-
исчерпанными. „Быть может, наименее способные из нас в каком-то
смысле уже близки к этому пределу, — заявил он, — потребность
же в тех, кто все еще в состоянии справляться с современным
уровнем сложности, все время увеличивается"». Впрочем, теку-
текущую прессу мало заботит информационный взрыв.
В последнее время в нашем весьма сложном технологически
ориентированном обществе создалось такое положение, при ко-
котором все большее количество людей и организаций занимаются
обработкой информации и все меньшее — обработкой мате-
материальных объектов. Ощутимой стала потребность в более совер-
совершенных информационных системах, поскольку информация —
ключевой элемент процесса принятия решений, а количество
разнохарактерной и разной степени сложности информации,
которую порождает наш мир, растет. Одной из важнейших за-
задач, возникающих в связи с созданием современных информа-
информационных систем, является автоматизация процесса распознава-
распознавания образов. Именно этой проблеме и посвящена наша книга.
1.1. ПРОБЛЕМА ОБРАБОТКИ ИНФОРМАЦИИ
Прогресс «технологической» цивилизации и развитие науки
породили информационную проблему, с которой столкнулось сей-
сейчас человеческое общество. У первобытных людей такой про-
проблемы не было. В самом деле, уровень развития общества
можно оценить количеством генерируемой им информации и
знания. Без информации цивилизация, как мы ее понимаем, су-
существовать не может. Решение современных социальных проб-
проблем также зависит от разрешения информационной проблемы.
Информационный взрыв — один из наиболее драматических вы-
12 Гл. 1. Введение
зовов, угрожающих нашему обществу в 1970-х и 1980-х годах,
причем темп роста этой угрозы будет продолжать увели-
увеличиваться.
Проблему информационного взрыва хорошо иллюстрирует
следующая статистика. В 1830 г. выходило около 300 техниче-
технических и научных журналов. Сегодня во всем мире на более чем
50 языках в год выходит свыше 60 000 журналов, содержащих
около 2,5 миллиона статей. Ежегодно во всем мире выпускается
в свет около 80 000 новых названий книг. Ежегодно через банки
проходит около 20 миллиардов чеков, причем каждый обраба-
обрабатывается 4—5 раз. Ведущие банки выполняют в день около
25 миллионов операций. Министерство почт Соединенных Шта-
Штатов очень серьезно озабочено проблемой почтовой корреспонден-
корреспонденции. В настоящее время в почтовых отделениях США за одну
секунду обрабатывается около 27 000 единиц почтовых отправ-
отправлений; это соответствует 84 миллиардам в год, а к 1980 г. ожи-
ожидается увеличение этой цифры до 116 миллиардов. Главный
почтмейстер заявил несколько лет назад в подкомитете конгрес-
конгресса: «Откровенно говоря, наше министерство состязается в ско-
скорости с надвигающейся катастрофой».
В архивах федеральных служб Соединенных Штатов в на-
настоящее время хранится более 200 миллионов отпечатков паль-
пальцев и около 150 миллионов счетов по выплатам в рамках
системы социального обеспечения. В 1940 г. было зарегистриро-
зарегистрировано всего 15 миллионов налоговых деклараций — в 1973 г.
Налоговое управление обработало уже свыше 100 миллионов
налоговых деклараций и 360 миллионов единиц соответствую-
соответствующих документов. Налоговое управление ожидает, что к 1980 г.
число налоговых деклараций достигнет 137 миллионов. Про-
Проблема объема операций осложняется еще и тем обстоятель-
обстоятельством, что налоговая система в Соединенных Штатах регули-
регулируется довольно сложным законодательством и отражает по-
постоянно увеличивающееся разнообразие финансовых сделок.
Проблемы, встающие перед медициной в связи с информа-
информационным взрывом, аналогичны тем, которые сегодня возникают
и в других направлениях деятельности общества. Врачи начи-
начинают ощущать, что они не в силах эффективно справляться с чу-
чудовищными информационными потоками, поступающими к ним
при медицинском обслуживании населения и при исследова-
исследовательской работе. Для того чтобы поставить правильный диагноз
и назначить соответствующее лечение, врач должен опросить
и обследовать пациента, провести лабораторные и другие иссле-
исследования и зарегистрировать собранную информацию. Он должен
отобрать, проверить и сопоставить полученные данные с соб-
собственным опытом и на этой основе поставить диагноз, идентифи-
идентифицирующий заболевание. Как при диагностике, так и при лечении
/./. Проблема обработки информации 13
врач постоянно занят анализом и обработкой информации, что
и позволяет^ ему достичь соответствующие медицинские цели.
Если бы в процессе повседневной работы он мог без чрезмерных
сложностей использовать медицинскую информационную си-
систему для выборки и хранения клинических данных, аналитиче-
аналитические возможности и быстродействие такой системы способство-
способствовали бы расширению профессиональных возможностей врача.
Применительно к обслуживанию пациентов медицинский работ-
работник смог бы молниеносно восстановить всю необходимую меди-
медицинскую информацию и информацию о способах лечения в
форме, максимально удобной для эффективного использования.
Сталкиваясь с нестандартным заболеванием, врач может захо-
захотеть получить таблицу статистических данных, содержащую
сотни или тысячи наборов признаков, симптомов или результа-
результатов лабораторных анализов, характеризующих больных, кото-
которым был поставлен этот же диагноз. Клинические лаборатории
нуждаются в автоматизированных системах, предназначенных
для расшифровки рентгеновских снимков, идентификации кле-
клеточных препаратов, обработки кардиограмм при массовых кар-
кардиологических обследованиях и диагностики. Больницам нужны
автоматизированные информационные системы, включающие
информационно-поисковые подсистемы для историй болезни,
подсистемы назначения процедур и подсистемы управления
больницей. Медицинские информационные системы явятся для
медиков средством, способствующим обострению их интуиции
и расширению профессиональных возможностей.
Промышленность сталкивается с насущной необходимостью
улучшить информационные связи между предприятиями. Адми-
Административный персонал и руководство компаний нуждаются в
большем количестве информации о положении внутри компа-
компаний, результатах собственной деятельности и рынке, на который
компания работает, причем информация нужна им своевремен-
своевременно— так, чтобы они могли найти наилучшее решение в условиях
быстро меняющейся конъюнктуры. Информационные системы
играют важную роль в процессах принятия решений, как на
правительственном, так и на «деловом» уровне. Окончательная
оценка таких решений всегда будет производиться человеком,
однако появившиеся концепции и методы, предусматривающие
использование вычислительных машин, обеспечивают выдвиже-
выдвижение и оценку такого количества вариантов, какое ни один руко-
руководитель не мог осмыслить. Возможность использовать, кроме
того, методы анализа риска позволяет руководителю оценивать
потенциальную опасность, связанную с каждой из множества
изучаемых стратегий. Информационные системы обеспечат ру-
руководителю возможность более ясно представлять результаты
принимаемых им решений.
14 Гл. 1. Введение
Наше счастье, что цифровые вычислительные машины —одно
из важнейших технических достижений XX в.— начинают за-
заполнять все расширяющуюся информационную «брешь». Вычис-
Вычислительная машина, отметившая только что свой тридцатый день
рождения, достигла совершеннолетия, пройдя за/ короткий срок
путь от научного курьеза до существенного элемента человеческо-
человеческого существования. История человечества не знает технического
достижения, которое в большей степени оказало бы непосред-
непосредственное влияние на человека и его образ жизни. Вычислитель-
Вычислительные машины во многих отношениях изменили представление
о времени, сместили общепринятые пределы и связи, регулирую-
регулирующие нашу жизнь и деятельность организаций, в рамках которых
она протекает, ускорили темп перемен. Только представьте, что
бы произошло, если бы разом были исключены все вычисли-
вычислительные машины из нашей жизни. Воздушное сообщение было
бы повергнуто в хаос, банки оказались бы завалены необрабо-
необработанными документами, промышленное производство распалось
бы и многое в нашей жизни из того, что мы привыкли считать
само собой разумеющимся, вдруг неожиданно испарилось бы.
Банковское дело претерпело много перемен со времени «бан-
«банковских каникул» 1933 г.1) Эти перемены привели к так назы-
называемой «банковской революции». Электронная цифровая вычис-
вычислительная машина хотя и не являлась ее причиной, но оказалась
инструментом, использованным для ее ускорения. «Банковская
революция» заключалась в признании банками существования
розничного рынка — потребностей отдельных лиц — в отличие
от приоритета, стандартно предоставлявшегося нуждам, связан-
связанным с деловой активностью, деятельностью крупных корпора-
корпораций и отдельных бизнесменов. Эта «революция» привела к росту
внимания, уделяемого индивидуальным счетам, взносам по бан-
банковским ссудам, кредитным карточкам и различным способам
привлечения сбережения с соответственно различными процент-
процентными ставками. «Революция» породила и проблему «бумаж-
«бумажного» взрыва. За последние 30 лет количество чеков, обработан-
обработанных банками, возросло более чем в 15 раз. К концу 1950-х
годов количество использовавшихся финансовых документов
и подлежащих обработке чеков увеличилось в такой степени, что
') Одним из следствий международного экономического кризиса 1929—
1933 гг. было массовое и паническое изъятие вкладчиками своих сбережений
и капиталов из банков; этот процесс в свою очередь приводил к еще боль-
большему хаосу финансовой системы. В качестве одной из мер борьбы с этим
явлением использовалось введение банковских нерабочих дней и даже недель.
6 марта 1933 г. новоизбранный президент США Франклин Делано Рузвельт,
сразу же по вступлении в должность, воспользовавшись законом военного
времени, закрыл банки, чтобы впредь до того, как конгресс сможет принять
необходимое законодательство, приостановить массовое изъятие вкладов.—
Прим. перев.
/./. Проблема обработки информации 15 .
грозило зйдушить банковскую систему Соединенных Штатов.
В этот момент на помощь пришли цифровые вычислительные
машины. ОнЦ позволили банкам быстро и с приемлемыми затра-
затратами обрабатывать огромное количество финансовых докумен-
документов, обеспечивая, таким образом, банкам возможность продолже-
продолжения роста. Кроме того, вычислительные машины использовались
в качестве мощного инструмента управления. Рост и уско-
ускорение оборота капиталов заставлял банки постоянно искать
новые рынки и новых клиентов, что приводило к еще большему
ускорению роста. Таким образом, появление вычислительных
машин действительно обеспечило увеличение темпа «банковской
революции». Именно информационная система сделала эту «ре-
«революцию» необходимой.
Проблемы, связанные со взысканием налогов, относятся к
наиболее серьезным из вызванных бумажной бурей. Налоговое
управление с нетерпением ждет появления вычислительных
машин и систем, обладающих большим быстродействием, луч-
лучшими возможностями накопления и поиска информации и наде-
наделенных способностью эффективно распознавать символы. Необ-
Необходима хорошая налоговая информационная система, которая
не только обеспечивает возможность работы в естественном мас-
масштабе времени и произвольной выборки информации, но также
благодаря наличию сети терминалов, снабженных дисплеями,
позволяет любому местному отделению получать любую необхо-
необходимую информацию буквально нажатием кнопки. Это не только
даст возможность местным отделениям своевременно отвечать
на вопросы налогоплательщиков, но и приведет к уменьшению
количества запросов налогоплательщикам, касающихся уже
предоставлявшейся ими информации.
Судя по всему, мы вступаем в эпоху, когда человек, приоб-
приобретя в качестве нового партнера созданные им информационные
системы, окажется в состоянии решать много более сложные,
чем когда бы то ни было, задачи. Этот новый вид «сотрудниче-
«сотрудничества» сделает общество более совершенным, а жизнь людей —
лучшей. Одной из важнейших проблем, возникающих в связи с
созданием современных полностью автоматизированных инфор-
информационных систем, является автоматизация процесса распозна-
распознавания образов — область, изучением которой занято множество
исследовательских групп. В их состав входят инженеры, специа-
специалисты в области вычислительной математики, кибернетики и
теории информации, физики, статистики, психологи, биологи,
физиологи, медики и лингвисты. Каждая из таких групп посвя-
посвящает свою работу какому-тЬ определенному аспекту общей
проблемы распознавания. Haiiia книга представляет собой по-
попытку обсудить фундаментальные принципы, лежащие в основе
разработки автоматических систем распознавания образов.
16 Гл. 1. Введение
1.2. ОСНОВНЫЕ ПОНЯТИЯ РАСПОЗНАВАНИЯ ОБРАЗрВ
Способность «распознавать» считается основным свойством
человеческих существ, как, впрочем, и других живых организ-
организмов. Образ представляет собой описание объекта. В каждое
мгновение нашего бодрствования мы совершаем ^кты распозна-
распознавания. Мы опознаем окружающие нас объекты и в соответствии
с этим перемещаемся и совершаем определенные действия. Мы
можем заметить в толпе друга и понять, что он говорит, можем
узнать голос знакомого, прочесть рукопись и идентифицировать
отпечатки пальцев, можем отличить улыбку от злобной гримасы.
Человеческое существо представляет собой очень сложную ин-
информационную систему — в определенной степени это опре-
определяется чрезвычайно развитыми у человека способностями
распознавать образы.
В соответствии с характером распознаваемых образов акты
распознавания можно разделить на два основных типа: распо-
распознавание конкретных объектов и распознавание абстрактных
объектов. Мы распознаем символы, рисунки, музыку и объекты,
нас окружающие. Процесс, включающий распознавание зритель-
зрительных и слуховых образов, можно определить как «сенсорное»
распознавание. Процессы этого типа обеспечивают идентифика-
идентификацию и классификацию пространственных и временных образов.
С другой стороны, мы в состоянии с закрытыми ушами и гла-
глазами опознать старый довод или найти решение задачи. Подоб-
Подобные процессы обеспечивают распознавание абстрактных объек-
объектов и их можно определить как «понятийное» распознавание в
отличие от зрительного или слухового распознавания. В данной
книге мы будем иметь дело с распознаванием первого типа.
Примерами пространственных образов служат символы, отпе-
отпечатки пальцев, синоптические карты, физические объекты и
рисунки. В разряд временных образов входят речь, переменные
сигналы, электрокардиограммы, характеристики цели и времен-
временные ряды.
Распознавание человеком конкретных образов можно рас-
рассматривать как психофизиологическую задачу, связанную с про-
процессом взаимодействия индивида с определенным физическим
раздражителем. Когда индивид воспринимает образ, он реали-
реализует процесс индуктивного вывода и устанавливает ассоциатив-
ассоциативную связь между своим восприятием и определенными обобщен-
обобщенными понятиями или «ориентирами», установленными им на
основании прошлого опыта. В сущности распознавание челове-
человеком образов можно свести к вопросу оценки относительных
шансов на то, что исходные данные соответствуют тому или
иному из известных множеств статистических совокупностей,
определяющихся прошлым опытом человека и предоставляющих
1.2. Основные понятия распознавания образов 17
ориентиры и \хприорную информацию для распознавания. Таким
образом, задачу распознавания образов можно рассматривать
как задачу установления различий между исходными данными,
причем не посредством отождествления с отдельными образами,
но с их совокупностями; последнее осуществляется при помощи
поиска признаков (инвариантных свойств) на множестве объек-
объектов, образующих определенную совокупность.
В задачах распознавания образов можно выделить два
основных направления.
1. Изучение способностей к распознаванию, которыми обла-
обладают человеческие существа и другие живые организмы.
2. Развитие теории и методов построения устройств, пред-
предназначенных для решения отдельных задач распознавания обра-
образов в определенных прикладных областях.
Первое направление связано с такими дисциплинами, как
психология, физиология и биология, второе же имеет дело в
первую очередь с техникой, вычислительными машинами и ин-
информатикой. В нашей книге речь будет идти о вычислительных
машинах, информатике и технических аспектах построения
автоматических систем распознавания образов.
Проще говоря, распознавание образов можно определить как
отнесение исходных данных к определенному классу с помощью
выделения существенных признаков или свойств, характеризую-
характеризующих эти данные, из общей массы несущественных деталей. Про-
Прогноз погоды можно интерпретировать как задачу распознавания
образов. Исходные данные в этом случае принимают вид синоп-
синоптических карт. Система интерпретирует их, выделяя существен-
существенные признаки и формируя на их основе прогноз. Постановку
медицинского диагноза также можно рассматривать как задачу
распознавания образов. Симптомы служат исходными данными
для распознающей системы, которая на основе их анализа иден-
идентифицирует заболевание. Система распознавания символов
представляет собой систему распознавания образов, в которую
в качестве исходных данных вводятся оптические сигналы и
которая индентифицирует названия символов. В системе распо-
распознавания речи произнесенное слово идентифицируется посред-
посредством анализа воспринятого системой звукового сигнала.
В табл. 1.1 перечислен ряд задач классификации, а также соот-
соответствующие исходные данные и ответы, выдаваемые системой.
Предмет распознавания образов объединяет ряд научных
дисциплин; их связывает поиск решения общей задачи — выде-
выделить элементы, принадлежащие конкретному классу, среди мно-
множества размытых элементов, относящихся к нескольким клас-
классам. Под классом, о.бдазов понимается некоторая категория, опре-
определяющаяся ррдом^свойет^^щих для всех ее элементов.
18
Гл. /. Введение
Таблица 1.1
Содержательный характер
задачи классификации
Вид исходных данных
Вид ответа системы
распознавания
Распознавание символов
Распознавание речи
Идентификация говоря-
говорящего человека
Прогноз погоды
Установление медицинско-
медицинского диагноза
Прогноз состояния фон-
фондовой биржи
Оптические : сигналы
или элементы раз-
развертки
Акустические сигналы
Голос
Синоптические карты
Симптомы заболевания
Финансовые новости и
сводки
Название символа
«Имя» слова
Имя говорящего чело-
человека
Прогноз погоды
Вид заболевания
Прогноз повышения
или понижения цен
на рынке
Образ — это описание любого элемента как представителя соот-
соответствующего класса образов. В случае когда множество обра-
образов разделяется на непересекающиеся классы, желательно
использовать для отнесения этих образов к соответствующим
классам какое-либо автоматическое устройство. Считывание и
обработка погашенных банковских чеков являются примером
задачи распознавания образов. Подобные задачи могут вы-
выполняться и людьми; машина, однако, справляется с ними много
быстрее. С другой стороны, некоторые задачи распознавания
таковы, что человек едва ли в состоянии решать их. Примером
задач такого рода служит выделение из множества морских
сигналов и шумов тона подводной лодки посредством анализа
подводных звуковых сигналов.
Очевидное, но совсем уж «бесхитростное» решение задачи
распознавания заключается в применении к отдельным предъяв-
предъявленным образам ряда простых тестов для выделения признаков
каждого класса. Совокупность этих тестов должна различать
все допустимые образы из разных классов. Рассмотрим, напри-
например, следующие четыре китайских иероглифа:
Эти простые символы можно распознать с помощью тестов, про-
проверяющих наличие вертикальной черточки, горизонтальной чер-
черточки, отдельной точки, открытой верхней части, открытой ниж-
нижней части и последовательности точек, подсчитав затем коли-
количества и последовательности черточек. В качестве второго
примера рассмотрим следующие пять английских букв:
COINS
1.2. Основные понятия распознавания образов
19
Эти буквы можно классифицировать, применив тесты на нали-
наличие таких признаков, как замкнутая кривая, изгиб, двойной из-
изгиб, вертикальный отрезок, короткий отрезок. На рис. 1.1 приве-
приведена функциональная блок-схема, иллюстрирующая описанный
подход к распознаванию образов.
Вход
Нет
Нет
Имеются ли
сдвоенные горизонтальные
черточки ?
Да
Имеются ли
вертикальные
черточки ?
Да
Имеется ли
последовательность
точек ?
Имеется ли
открытая
верхняя
часть ?
Рис. l.l. Блок-схема простой логической (вопросно-ответной) процедуры клас-
классификации символов.
Если следовать такому интуитивному подходу, то построение
автоматической системы распознавания образов может пока-
показаться довольно простой задачей. Не существует, однако, общей
теории, позволяющей определить, какие из всего множества
мыслимых тестов следует применить к предъявленным образам.
Очень ограниченное количество или небрежный выбор тестов не
дадут возможности получить характеристики предъявленных
20
Гл. / Введение
для распознавания образов, достаточные для отнесения их к со-
соответствующим классам.Слишком много тестов, с другой сто-
стороны, необоснованно усложнят вычисления, осуществляемые в
процессе дальнейшего анализа. Отсутствует какое-либо общее
правило для получения неких ориентиров, способствующих
определению набора таких тестов. Подобный подход чрезмерно
зависит от опыта и технической интуиции разработчика и по-
поэтому часто не дает удовлетворительного решения задач распо-
распознавания образов, встречающихся в практической деятельности.
Символы
букбет-щщя-
бые симболы
Буквы
английского
...
\
Арабские
цирры
•
Китайские
иероглифы
/
Дребние
• • •
Современные
Печатные\ \ Рукописные \Прописные\ Строчные[ |Печатные[ рукописные]
Рис. 1.2. Иерархия отношений между образами и классами образов.
Тщательное изучение задач, возникающих в процессе распозна-
распознавания образов, позволяет прийти к более эффективным подхо-
подходам. Именно эти задачи рассматриваются и анализируются в
нашей книге.
Между образами и классами образов существует некое
иерархическое упорядочение. Так, на схеме, приведенной на
рис. 1.2, буквенно-цифровые символы и китайские иероглифы
являются образами, а символы соответствуют классу образов.
Буквы алфавитов и цифры являются образами, если буквенно-
цифровые символы рассматриваются как класс образов. Печат-
Печатные и рукописные изображения, например, буквы А являются
образами буквы английского алфавита А, которая представляет
в этом случае класс образов. Многие информационные системы
нуждаются в устройстве для распознавания печатных букв и
цифр, набранных различными шрифтами, и рукописных букв и
цифр, написанных различными почерками. Это означает, что
имеется 62 класса образов, представляющие 26 прописных букв,
26 строчных букв и 10 цифр 1). Разнообразие наборных шрифтов
') Имеются в виду 26 букв английского алфавита. — Прим. перев.
1.3. Основные задачи, возникающие при разработке систем 21
и способов написания определенной буквы или цифры порож-
порождает образы, принадлежащие к определяющему данный символ
классу.
Остановимся на задаче распознавания письменных знаков.
Конкретная буква или цифра вне зависимости от того, как она
напечатана или написана, обладает рядом общих признаков,
которые используются в качестве средств ее идентификации.
Буквы и цифры идентифицируются и классифицируются со-
согласно отмеченным у них таким признакам. Следовательно,
основные функции системы распознавания образов заключаются
в обнаружении и выделении общих признаков образов, описы-
описывающих объекты, принадлежащие к одному и тому же классу
образов, узнавании этого образа в любой другой обстановке и
отнесении его к одному из заданных классов.
^ОСНОВНЫЕ ЗАДАЧИ, ВОЗНИКАЮЩИЕ
ПРИ РАЗРАБОТКЕ СИСТЕМ РАСПОЗНАВАНИЯ
ОБРАЗОВ
Задачи, возникающие при построении автоматической систе-
системы распознавания образов, можно обычно отнести к нескольким
основным областям. Первая из них связана с представлением.
исходных данных, полученных как результаты измерений для
"подлежащего распознаванию объекта. Это проблема чувстви-
чувствительности. Каждая измеренная величина является некоторой
"характеристикой образа или объекта. Допустим, например, что
образами являются буквенно-цифровые символы. В таком слу-
случае в датчике может быть успешно использована измерительная
сетчатка, подобно приведенной на рис. 1.3, а. Если сетчатка
состоит из п элементов, то результаты измерений можно пред-
представить в виде вектора измерений или вектора образа
х=
х2
A.3.1)
где каждый элемент *,• принимает, например, значение 1, если
через /-Ю ячейку сетчатки проходит изображение символа, и
значение 0 в противном случае. В последующем изложении бу-
будем называть векторы образов просто образами в тех случаях,
когда это не приводит к изменению смысла.
Второй пример проиллюстрирован на рис. 1.3,6. В этом слу-
случае образами служат непрерывные функции (типа звуковых
22
Гл. 1 Введение
сигналов) переменной t. Если измерение значений функций про-
производится в дискретных точках t\, t2, ..., tn, вектор образа
можно сформировать, приняв xi = f(ti), x% =f(t2), ..., х„ =
= f(tn).
Векторы образов будут обозначаться строчными буквами,
выделенными жирным шрифтом, например х, у и г. Условимся,
fit)
U U
U
: \, Х{'0until
Рис. 1.3. Две простые схемы порождения вектора образа.
что эти векторы везде будут вектор-столбцами, как в уравнении
A.3.1). Эквивалентная запись х = (*i, x2, ..., хп)', где штрих
обозначает транспонирование, будет также использоваться в
тексте.
Векторы образов содержат всю поддающуюся измерению
информацию об образах. Процесс измерения, которому подвер-
подвергаются объекты определенного класса образов, можно рассмат-
рассматривать как процесс кодирования, заключающийся в присвоении
каждой характеристике образа символа из множества элементов
алфавита {*,¦}. Когда измерения приводят к информации, пред-
представленной действительными числами, часто оказывается полез-
полезным рассматривать векторы образов в качестве точек п-мерного
евклидова пространства. Множество образов, принадлежащих
одному классу, соответствует совокупности точек, рассеянных
в некоторой области пространства измерений. Соответствующий
простой пример приведен на рис. 1.4 для случая двух классов,
обозначенных coi и ©г. В этом примере предполагается, что
1.3. Основные задачи, возникающие при разработке систем
23
классы <Di и «г представляют соответственно группы футболи-
футболистов-профессионалов и жокеев. Каждый «образ» характери-
характеризуется результатами двух измерений: ростом и весом. Векторы
образов имеют, следовательно, вид x = (a:i, х^)', где параметр
х\ — рост, а параметр л:2— вес. Каждый вектор образа можно
считать точкой двумерного пространства. К^^сд.едхехи[3_2исЛ^4,
эти два класса образуют непересекающиеся множеагвд^что
oбъяcняeJXЯ-^aдaктegOl^L и^^?Р_я5Щ.М??_Да-?9Мб1Е°й: В практи-
ч"ёскй"х~ситуациях, однако, далёко не всегда удается выбрать
. о а, -
- корост
¦ А
Рис. 1.4. Два непересекающихся класса образов.
измеряемые параметры так, чтобы получить строго непересекаю-
непересекающиеся множества. В частности, если в качестве критериев раз-
разбиения выбран рост и вес, может наблюдаться существенное,
пересеч^ниа__кддсход^,представляющих профессиональных фут-
футболистов и баскетболистов ').
Вторая задача распознавания образов связана с выделением
характерных признаков или свойств из полученных исходных
данных и снижением размерности векторов образов. Эту за-
задачу часто определяют как задачу предварительной обработки
и выбора признаков. При распознавании речи, например, можно
отличать гласные и полугласные звуки от фрикативных и неко-
некоторых других консонант, измеряя частотное распределение энер-
энергии в спектрах. Шире всего при распознавании речи исполь-
используются такие признаки, как длительность звука, отношения
величин энергии в различных диапазонах частот, расположение
пиков спектров (или формант) и их смещение во времени.
Признаки класса образов представляют собой характерные
свойства, общие для всех образов данного класса. Признаки,
характеризующие различия между отдельными классами, можно
) Авторы имеют в виду американский футбол, в котором игроки отли-
отличаются значительным ростом и весом. — Прим. перев.
24 Гл. 1. Введение
интерпретировать как межклассовые признаки. Внутриклассо-
Внутриклассовые признаки, общие для всех рассматриваемых классов, не
несут полезной информации с точки зрения распознавания и
могут не приниматься во внимание. Выбор признакоа.хчи2а§1ся
одной из важных задач, связанных с "построением распознающих,
QjjCXgM. Если результаты измерений позволяют получить полный
набор различительных признаков для всех классов, собственно
распознавание и классификация образов не вызовут особых за-
затруднений. Автоматическое распознавание тогда сведется к
процессу простого сопоставления или процедурам типа про-
просмотра таблиц. В большинстве практических задач распознава-
распознавания, однако, определение полного набора различительных при-
признаков оказывается делом исключительно трудным, если вообще
не невозможным. К счастью, из исходных данных обычно
удается извлечь, некоторые из различительных признаков и ис-
использовать их для упрощения процесса автоматического распо-
распознавания образов. В частности, размерность векторов измерений
можно снизить с помощью преобразований, обеспечивающих
минимизацию потери информации; этот метод обсуждается
в гл. 7.
Третья задача, связанная с построением систем распознава-
распознавания образов, состоит в отыскании оптимальных решающих про-
процедур, необходимых при идентификации и классификации. После
того как данные, собранные о подлежащих распознаванию об-
образах, представлены точками или векторами измерений в
пространстве образов, предоставим машине выяснить, какому
классу образов эти данные соответствуют. Пусть машина пред-
предназначена для различения М классов, обозначенных ац, сог, ...
..., сом- В таком случае пространство образов можно считать
состоящим из М областей, каждая из которых содержит точки,
соответствующие образам из одного класса. При этом задача
распознавания может рассматриваться как построение границ
областей решений, разделяющих М классов, исходя из зареги-
зарегистрированных векторов измерений. Пусть эти границы опреде-
определены, например, решающими функциями di(x), d2(\), ...
..., йм(х). Эти функции, называемые также дискриминантными
функциями, представляют собой скалярные и однозначные функ-
функции образа х. Если d*(x)>d/(x) для всех i, }= 1, 2, ..., М,
/ Ф i, то образ х принадлежит классу со,-. Другими словами, если
i-я решающая функция d,(x) имеет наибольшее значение, то
х е ю». Содержательной иллюстрацией подобной схемы автома-
автоматической классификации, основанной на реализации процесса
принятия решения, служит приведенная на рис. 1.5 блок-схема
(на схеме ГРФ означает «генератор решающих функций»).
Решающие функции можно получать целым рядом способов.
В тех случаях, когда о распознаваемых образах имеются полные
/ 3 Основные задачи, возникающие при разработке систем
25
априорные сведения, решающие функции могут быть определены
точно на основе этой информации. Если относительно образов
имеются лишь качественные сведения, могут быть выдвинуты
разумные допущения о виде решающих функций. В последнем
случае границы областей решений могут существенно откло-
отклоняться от истинных, и поэтому необходимо создавать систему,
способную приходить к удовлетворительному результату посред-
посредством ряда последовательных корректировок. Но, как правило,
ГРФ
Г РФ
-ч
ГРФ
dkW
ГРФ
ПРОЦЕСС
ПРИНЯТИЯ
РЕШЕНИЯ
хщ,
если djixl
Рис. 1.5. Блок-схема системы классификации образов.
мы обладаем лишь немногочисленными (если они вообще
имеются!) априорными сведениями о распознаваемых образах.
В этих условиях при построении распознающей системы лучше
всего использовать обучающую процедуру. На первом этапе
выбираются произвольные решающие функции и затем в про-
процессе выполнения итеративных шагов обучения эти решающие
функции доводятся до оптимального либо приемлемого вида.
Классификацию объектов с помощью решающих функций можно
осуществлять самыми различными способами. В данной книге
мы изучим несколько детерминистских и статистических алго-
алгоритмов нахождения решающих функций.
Решение задачи предварительной обработки и выделения
признаков и задачи получения оптимального решения и класси-
классификации обычно связано с необходимостью оценки и оптимиза-
оптимизации ряда параметров. Это приводит к задаче оценки параметров.
Кроме того, понятно, что и процесс выделения признаков, и
процесс принятия решений могут быть существенно усовершен-
усовершенствованы за счет использования информации, заключенной в
26 Гл. 1. Введете
контексте образов. Информация, содержащаяся в контексте,
может быть измерена с помощью условных вероятностей, линг-
лингвистических статистик и близких вариантов. В некоторых при-
приложениях просто необходимо использовать контекстуальную
информацию для точного распознавания. В частности, полная
автоматизация распознавания речи возможна только при нали-
наличии контекстуальной и лингвистической информации, дополняю-
дополняющей информацию, содержащуюся в записи звуковых сигналов
речи. По аналогичным причинам крайне желательно привлече-
привлечение контекстуальной информации при распознавании скорописи
и классификации отпечатков пальцев. Пытаясь построить рас-
распознающую систему, устойчивую по отношению к помехам, спо-
способную справиться с существенными отклонениями распозна-
распознаваемых объектов и обладающую способностью к самонастройке,
мы встречаемся с задачей адаптации.
Проведенное выше беглое обсуждение основных задач при-
приводит к помещенной на рис. 1.6 функциональной блок-схеме,
содержательно иллюстрирующей адаптивную систему распозна-
распознавания образов. Эта блок-схема показывает, как можно наибо-
наиболее естественно и разумно разделить функции, которые должна
выполнять распознающая система. Функциональные блоки вы-
выделены для удобства анализа, что отнюдь не означает их изо-
изоляцию и отсутствие межблочного взаимодействия. Хотя разли-
различия между получением оптимального решения и предваритель-
предварительной обработкой или выделением признаков несущественны, идея
функционального разделения создает четкую картину, поясняю-
поясняющую задачу распознавания образов.
Объекты (образы), подлежащие распознаванию и классифи-
классификации с помощью автоматической системы распознавания обра-
образов, должны обладать набором измеримых характеристик. Когда
для целой группы образов результаты соответствующих измере-
измерений оказываются аналогичными, считается, что эти объекты
принадлежат одному классу. Цель работы системы распознава-
распознавания образов заключается в том, чтобы на основе собранной
информации определить класс объектов с характеристиками,
аналогичными измеренным у распознаваемых объектов. Пра-
Правильность распознавания зависит от объема различающей ин-
информации, содержащейся в измеряемых характеристиках, и
эффективности использования этой информации. Если бы мы
были в состоянии измерить все возможные характеристики и
обладали неограниченным временем для обработки собранной
информации, то можно было бы достичь вполне адекватного
уровня распознавания, используя самые примитивные ме-
методы. В обычной практике, однако, ограничения по времени,
пространству и затратам требуют развития реалистических
подходов.
Объекты
ВОСПРИЯТИЕ
Результаты
измерении
АНАЛИЗ
С УЧЕТОМ
КОНТЕКСТА
ПРЕДВАРИТЕЛЬНАЯ
ОБРАБОТКА
И ВЫБОР
ПРИЗНАКОВ
Векторы признаков
или непрошбодные элементы
КЛАССИФИКАЦИЯ
Классы
образов
ОЦЕНКА,
АДАПТАЦИЯ,
ОБУЧЕНИЕ
Рис. 1.6. Функциональная блок-схема адаптивной системы распознавания образов.
28 Гл. 1. Введение
1.4. КРАТКОЕ ОПИСАНИЕ КОНЦЕПЦИЙ
И МЕТОДОЛОГИИ
В основе идеи синтеза систем автоматического
^ с помощью которых описываются и разде-
разделяются классы образов. Опираясь на наш опыт, мы предлагаем
рассмотреть несколько основных вариантов. Когда класс харак-
характеризуется перечнем входящих в него членов, построение си-
системы распознавания образов может быть основано на принципе
принадлежности к этому перечню. Когда класс характеризуется
некоторыми общими свойствами, присущими всем его членам,
построение системы распознавания может основываться на прин-
принципе общности свойств. Когда при рассмотрении класса обна-
обнаруживается тенденция к образованию кластеров в простран-
пространстве образов, построение системы распознавания может
основываться на принципе кластеризации1). Эти три основных
принципа построения систем распознавания образов обсуж-
обсуждаются ниже.
1. Принцип перечисления членов класса
Задание класса перечислением образов, входящих в его
состав, предполагает реализацию процесса автоматического
распознавания образов посредством сравнения с эталоном. Мно-
Множество образов, принадлежащих одному классу, запоминается
системой распознавания. При предъявлении системе незнакомых
(новых) образов она последовательно сравнивает их с храня-
хранящимися в ее памяти. Система распознавания образов относит
новый образ к тому классу, к которому принадлежал находя-
находящийся в памяти системы образ, совпавший с новым. Так, напри-
например, если в память системы распознавания введены литеры
различных наборных шрифтов, то подход, основанный на пере-
перечислении членов класса, позволяет распознавать соответствую-
соответствующие буквы, но только в тех случаях, когда их изображения не
искажены шумом, связанным с размазыванием или плохим на-
нанесением краски, пористостью бумаги и т. п. Несомненно, это
') Под кластером понимают обычно группу объектов (образов), обра-
образующих в пространстве описания компактную в некотором смысле область.
Понятие «кластеризация» стало использоваться в последнее время незави-
независимо от понятия «таксономия», хотя и тот, и другой методы разбиения осно-
основаны на принципе геометрической «близости» объектов на данном иерархи-
иерархическом уровне рассмотрения, и понятия «кластер» и «таксон» в сущности
идентичны. Более подробные сведения по поводу особенностей этой группы
методов распознавания можно найти в монографиях Н. Г. Загоруйко «Ме-
«Методы распознавания и их применение», «Советское Радио», М, 1972, и Б. Дю-
рана и П. Оделла «Кластерный анализ», «Статистика», М., 1977. — Прим.
перев.
1.4. Краткое описание концепций и методологии 29
несложный метод, однако он позволяет строить недорогие си-
системы распознавания, которые в отдельных прикладных обла-
областях вполне справляются со своими задачами. Метод перечис-
перечисления членов класса работает удовлетворительно, если выборка
образов близка к идеальной ').
2. Принцип общности свойств
Задание класса с помощью свойств, общих для всех входя-
входящих в его состав членов, предусматривает реализацию процесса
автоматического распознавания путем выделения подобных при-
признаков и работы с ними. Основное допущение в этом методе
заключается в том, что образы, принадлежащие одному и тому
же классу, обладают рядом общих свойств или признаков, отра-
отражающих подобие таких образов. Эти общие свойства можно,
в частности, ввести в память системы распознавания. Когда
системе предъявляется неклассифицированный образ, то выде-
выделяется набор описывающих его признаков, причем последние
иногда кодируются, и затем они сравниваются с признаками,
заложенными в память системы распознавания. В таком случае
последняя зачислит предъявленный для распознавания образ в
класс, характеризующийся системой признаков, подобных при-
признакам этого образа. Итак, при использовании данного метода
основная задача заключается в выделении ряда общих свойств
по конечной выборке образов, принадлежность которых иско-
искомому классу известна.
Очевидно, что эта концепция распознавания во многих отно-
отношениях превосходит распознавание по принципу перечисления
членов класса. Для запоминания признаков класса требуется
значительно меньше памяти, чем для хранения всех объектов,
входящих в класс. Поскольку признаки, характеризующие класс
Bjjejjpjvi, обладают инвариантностью, ^^^цип^сшюст^вления^
ПЕИзнак?в_до_пускает_^адиайи1о^„х^д^гщщс^и"к^ отд^л ьн ы Xjo6p_a -
зов...Процедура сопоставления с эталоном, с другой стороны, не
допускает существенных вариаций характеристик отдельных
') Авторы имеют в виду, что идея пириципа перечисления элементов клас-
класса достаточно проста. В тех случаях, когда классы состоят из большого чис-
числа элементов и каждый элемент описывается значениями большого числа
признаков, реализация этого принципа является весьма нетривиальной и при-
приводит к необходимости решать трудные математические задачи. Существуют
специальные разделы прикладной математики, исследующие такие задачи.
В качестве примера можно указать на теорию тестов (И. А. Чегис, С. В. Яб-
Яблонский, Логические способы контроля электрических схем, Труды Мат. ин-та
им. В. А. Стеклова, 51, 1958), активно применяемую в последние годы к ре-
решению задач распознавания. Обзор таких применений можно найти в статье
Ю. И. Журавлева «Непараметрнческне задачи распознавания образов» (Ки-
(Кибернетика, № 6, 1976 г.). —Прим. ред.
30 Гл. 1 Введение
образов. Если все признаки, определяющие класс, можно найти
по имеющейся выборке ^образов, то процесс распознавания сво-
сводится просто к сопоставлению по признакам. Исключительно
трудно, однако, если не невозможно вообще, как уже упоми-
упоминалось выше, найти для некоторого класса полный набор раз-
различающих признаков. Следовательно, обращение к этому прин-
принципу распознавания часто связано с необходимостью развития
методов выбора признаков, являющихся в некотором смысле
оптимальными. В гл. 7 рассмотрено несколько методов выбора
признаков. Кроме того, как мы убедимся ниже, принцип общ-
общности свойств лежит в основе процессов распознавания, реали-
реализуемых методами теории формальных языков.
3. Принцип кластеризации
Когда образы некоторого класса представляют собой век-
векторы, компонентами которых являются действительные числа,
этот класс можно рассматривать как кластер и выделять только
его свойства в пространстве образов кластера. Построение си-
систем распознавания, основанных на реализации данного прин-
принципа, определяется взаимным пространственным расположением
отдельных кластеров. Если кластеры, соответствующие различ-
различным классам, разнесены достаточно далеко друг от друга, то с
успехом можно воспользоваться сравнительно простыми схе-
схемами распознавания, например такими, как классификация по
принципу минимального расстояния, рассмотренная в гл. 3.
Если же кластеры перекрываются, приходится обращаться к
более сложным методам разбиения пространства образов, по-
подобно, например, рассмотренным в гл. 4—6. Перекрытие класте-
кластеров является результатом неполноценности доступной информа-
информации и шумовых искажений результатов измерения. Поэтому
степень перекрытия часто удается уменьшить, увеличивая коли-
количество и качество измерений, выполняемых над образами не-
некоторого класса.
.Для реализации рассмотренных выше основных принципов
построения автоматических систем распознавания образов суще-
существуют три основных типа методологии: эвристическая, матема-
математическая и лингвистическая (синтаксическая). Нередко системы
распознавания создаются на основе комбинации этих методов.
1. Эвристические методы
За основу эвристического подхода взяты интуиция и опыт
человека; в нем используются принципы перечисления членов
класса и общности свойств. Обычно системы, построенные та-
1.4. Краткое описание концепций и методологии 31
ними методами, включают набор специфических процедур, раз-
разработанных применительно к конкретным задачам распознава-
распознавания. В § 1.2 приведен пример подобного подхода в связи с
задачей распознавания символов, в которой классификация
образа (символа) производилась на основе выделения опреде-
определенных признаков, в частности таких, как количество и после-
последовательность расположения специфических штрихов (черто-
(черточек). Хотя эвристический подход играет большую роль в по-
построении систем распознавания образов, не много может быть
скаэа-но относительно общих принципов синтеза, так как реше-
решение, каждой конкретной задачи требует использования специфи-
специфических приемов разработки системы. Это означает, следова-
следовательно, что структура и качество эвристической системы в зна-
значительной степени определяются одаренностью и опытом
разработчиков.
2. Математические методы
" В основу математического подхода положены правила клас-
классификации, которые формулируются и выводятся в рамках опре-
определенного математического формализма с помощью принципов
общности свойств и кластеризации. Этим данный подход отли-
отличается от эвристического, в котором решения определяются с
помощью правил, тесно связанных с характером решаемой за-
задачи. Математические методы построения систем распознавания
можно разделить на два класса: детерминистские и статисти-
статистические.
"Детерминистский подход базируется на математическом ап-
аппарате, не использующем в явном виде статистические свойства
изучаемых классов образов. Примером детерминистского под-
подхода могут служить рассматриваемые в гл. 5 итеративные алго-
алгоритмы обучения.
Статистический подход основывается на математических пра-
правилах классификации, которые формулируются и выводятся в
терминах математической статистики. Как мы увидим ниже
в гл. 4 и 6, построение статистического классиф^укатода^Т^д^
сАу«1ае_ предполагает использование баиесова5о_го__классифика-
ционного правила и его разновидностейГНтсГправило'оо'ёспечи-
вает получение оптимального классйГфйкатора в тех случаях,
когда известны плотности распределения для всех совокупностей
образов и вероятности появления образов для каждого класса.
3. Лингвистические (синтаксические) методы
Если описание образов производится с помощью непроиз-
непроизводных элементов (подобразов) и их отношений, то для по-
построения автоматических систем распознавания применяется
32 Гл. I. Введение
лингвистический или синтаксический подход с использованием
принципа общности свойств. Образ можно описать с помощью
иерархической структуры подобразов, аналогичной синтаксиче-
синтаксической структуре языка. Это обстоятельство позволяет применять
при решении задач распознавания образов теорию формальных
языков. Предполагается, что грамматика образов содержит ко-
конечные множества элементов, называемых переменными, непро-
непроизводными элементами и правилами подстановки. Характер пра-
правил подстановки определяет тип грамматики. Среди наиболее
изученных грамматик можно отметить регулярные, бесконтекст-
бесконтекстные и грамматики непосредственно составляющих. Ключевыми
моментами данного подхода являются выбор непроизводных
элементов образа, объединение этих элементов и связывающих
их отношении в грамматики образов и, наконец, реализация в
соответствующем языке процессов анализа и распознавания.
Такой подход (он обсуждается в гл. 8) особенно полезен при
работе с образами, которые либо не могут быть описаны число-
числовыми измерениями, либо столь сложны, что их локальные при-
признаки идентифицировать не удается и приходится обращаться к
глобальным свойствам объектов.
В нашей книге основное внимание будет уделено второму
и третьему подходам. Хотя, как отмечалось выше, эвристический
подход весьма важен, в целом о нем можно сказать очень не-
немного1). Следует, однако, заметить, что глубокое понимание
других методов является прочной гарантией построения систем
распознавания на основании интуитивного подхода.
Выбор метода синтеза системы еще не решает до конца проб-
проблему составления конкретной программы и проблемы реализа-
реализации. В большинстве случаев у нас в распоряжении имеются
репрезентативные образы, представляющие каждый из рассмат-
рассматриваемых классов. В таких ситуациях можно воспользоваться
методами распознавания, называющимися обучением с учите-
учителем. В схеме обучения с учителем система «обучается» распозна-
распознавать образы с помощью разного рода адаптивных схем. Клю-
Ключевыми элементами такого подхода являются обучающие мно-
') После выхода в свет монографии Ту и Гонсалеса появились работы,
в которых исследовались модели эвристических алгоритмов. Оказалось, что
эвристические методы принципиально мало отличаются от методов, которые
авторы называют математическими. Оказалось также, что если модели эври-
эвристических алгоритмов удовлетворяют простым, сравнительно несложно про-
проверяемым условиям, то нетрудно построить специальную алгебру над такими
алгоритмами. Элементы этой алгебры сами являются алгоритмами, и, кроме
того, оперируя с алгоритмами из алгебры, можно не только доказать теоремы
существования безошибочных алгоритмов распознавания, но и получить яв-
явные формулы для реализации таких алгоритмов (Ю. И. Журавлев, Коррект-
Корректные алгебры над множествами некорректных (эвристических) алгоритмов I,
И, III, Кибернетика, № 4, 6, 1977, № 2, 1978). — Прим.. ред.
IS. Примеры автоматических систем распознавания образов 33
жества образов, классификация которых известна, и реализация
соответствующей процедуры обучения.
В некоторых прикладных задачах принадлежность к опреде-
определенным классам элементов обучающего множества неизвестна.
В таких случаях можно обратиться к методам распознавания
образов, называющимся распознаванием без учителя. Как ука-
указывалось ранее, распознавание по схеме «обучение с учителем»
характеризуется тем, что известна правильная классификация
каждого обучающего образа. В случае «обучения без учителя»
требуется, однако, конкретно изучить классы образов, которые
имеются в данной информации. Эта задача довольно подробно
рассматривается в гл. :3.
Важно ясно представлять себе, что обучение происходит
только на этапе построения (или коррекции в связи с поступле-
поступлением новой информации) системы распознавания. Как только
система, работая с обучающим множеством образов, добивается
приемлемых результатов, ей предлагается реальная задача рас-
распознавания пробных объектов, взятых из той среды, в которой
системе предстоит работать. Естественно, качество распознава-
распознавания будет в существенной степени определяться тем, насколько
хорошо обучающие образы представляют реальные данные, с
которыми система будет сталкиваться в процессе нормальной
эксплуатации.
1.5. ПРИМЕРЫ АВТОМАТИЧЕСКИХ СИСТЕМ
РАСПОЗНАВАНИЯ ОБРАЗОВ
В последнее десятилетие возник значительный интерес к
исследованию и построению систем автоматического распозна-
распознавания образов и машинного обучения. Мы стали свидетелями
быстрого прогресса в этой области. Примеры автоматических
систем распознавания образов имеются в изобилии. Были пред-
предприняты успешные попытки создавать устройства и программы
чтения наборных и напечатанных на машинке символов, обра-
обработки электрокардиограмм и. электроэнцеф_ал.ограм_м, распозна-
распознавания^ произнесенных слов, идентификации отпечатков пальцев
и интерпретации фотоснимков. В качестве других приложений
можно указать распознавание символов и слов, написанных от
руки, постановку медицинского диагноза, классификацию сейсми-
сейсмических волн, обнаружение объектов противника, прогноз погоды,
идентификацию отказов и неисправностей отдельных механиз-
механизмов и целых производственных процессов. В данном параграфе
рассмотрим несколько иллюстративных примеров, относящихся
к тем областям, в которых принципы распознавания образов
нашли удачное применение.
2 За к. 594
34
Гл. I. Введение
Распознавание символов
Примером практического использования автоматической
классификации образов являются оптические устройства распо-
распознавания символов, в частности машины для считывания кодо-
кодовых символов с обычных банковских чеков. На большинстве
J
A
4
I
/
\
\
\
1
4i
IV
1*
/
L
V
т
\
\
г
i
1
1
U
у
i
\
1
\
f
I
\
1
\
\
\
\
j
1
\
1
/L,
Д
Рис. 1.7. Комплект шрифта Е-13В Американской банковской ассоаиации (Ame-
(American Bankers Association) и формы сигнала, соответствующие отдельным
символам набора.
чеков, имеющих хождение в настоящее время в Соединенных
Штатах, в качестве стилизованных символов используется стан-
стандартный комплект шрифта Е-13В Американской банковской ас-
ассоциации (American Bankers Association). Как следует из
рис. 1.7, этот комплект включает 14 символов, специально адап-
адаптированных к сетчатке, содержащей 9X7 участков, с тем что-
чтобы упростить процесс считывания. Эти символы обычно нано-
наносятся особой типографской краской, которая содержит очень
1.5. Примеры автоматических систем распознавания образов 35
тонко измельченный магнитный материал. Если символы счи-
тываются с помощью магнитного устройства, краску предвари-
предварительно намагничивают, для того чтобы выделить символы из
фона и способствовать, таким образом, реализации процесса
считывания.
Обычно символы просматриваются по горизонтали с по-
помощью считывающей головки, снабженной одной прорезью, ко-
которая уже и выше, чем один символ. При пересечении символа
головка вырабатывает электрический сигнал, величина которого
пропорциональна скорости увеличения занимаемого символом
пространства под сканирующей головкой. Рассмотрим в качестве
примера сигнал, соответствующий цифре «О» (рис. 1.7). По
мере перемещения считывающей головки слева направо площадь
символа, которую видит головка, начинает увеличиваться, что
приводит к положительной производной. Когда головка начи-
начинает покидать левую «стойку» нуля, площадь цифры, находя-
находящаяся в зоне видимости головки, начинает уменьшаться, что
дает отрицательную производную. Когда головка находится
в средней зоне символа, площадь остается постоянной и произ-
производная соответственно равна нулю. Эта закономерность повто-
повторяется, когда головка достигает правой стойки цифры, как это
показано на рисунке. Мы видим, что форма символов выбрана
таким образом, чтобы сигналы, соответствующие разным сим-
символам, явно отличались друг от друга. Следует отметить, что
экстремальные точки и нули каждого сигнала появляются почти
точно на вертикальных образующих сетки, используемой в ка-
качестве фона для изображения сигналов. Форма символов
шрифта Е-13В была подобрана таким образом, чтобы выборки
значений сигналов только в этих точках было достаточно для их
правильной классификации. В память считывающего устройства
для каждого из 14 символов шрифта введены значения, соответ-
соответствующие только этим точкам. Когда символ поступает на клас-
классификацию, система сопоставляет соответствующий ему сигнал
с эталонами-сигналами, заранее введенными в память, и при-
причисляет его к классу наиболее сходного с ним эталона. При та-
такой схеме классификации должен использоваться либо принцип
перечисления членов класса, либо принцип общности свойств.
Подобным образом действует большинство современных
устройств, предназначенных для считывания стилизованных
шрифтов.
Существуют также коммерческие варианты устройств для
считывания шрифтов разных типов. Так, например, система
«Input 80» (рис. 1.8), разработанная компанией Recognition
Equipment Incorporated, может считывать информацию, пред-
представленную в машинописном, типографском и рукописном виде.
непосредственно с оригиналов документов со скоростью до
2
36
Гл. 1. Введение
3600 символов в секунду. Словарь системы построен по модуль-
модульному принципу, и его можно перестраивать, исходя из требова-
требований конкретной прикладной задачи. Одношрифтовая система
способна считывать символы одного из множества известных
комплектов шрифта, а многошрифтовая система позволяет ра-
работать «одновременно» с рядом типов шрифта, выбранных поль-
пользователем из множества допустимых. Одно устройство может
Рис. 1.8. Система распознавания символов «REI Input 80 Model А» компании
Recognition Equipment Incorporated, Даллас, штат Техас. На рисунке пред-
представлены следующие компоненты системы (по часовой стрелке): блок рас-
распознавания, контроллер с программным управлением, печатающее устройство
для ввода/вывода данных, построчно-печатающее устройство, блок распозна-
распознавания, блок магнитной ленты и страничный процессор. Фотография любезно
предоставлена Recognition Equipment Incorporated.
распознавать вплоть до 360 различных символов. Система может
быть настроена и таким образом, чтобы она считывала машино-
машинописные числа, отбирала машинописные буквы и символы и счи-
считывала данные, напечатанные типографским способом.
Основные особенности работы системы «Input 80» REI за-
заключаются в следующем. Страницы с помощью системы разре-
разреженных участков и воздушных эжекторов попадают на ленточ-
ленточный конвейер, который подает их в считывающее устройство.
Здесь зеркальце, совершающее высокочастотные колебания,
фокусирует луч света высокой интенсивности на символах, под-
подлежащих считыванию; луч пересекает строку печатных симво-
символов со скоростью около 7,62 м/с. Второе, синхронизирующее,
зеркальце воспринимает световые изображения, представляю-
15. Примеры автоматических систем распознавания образов 37
щие различные части символа, и проектирует их на «инте-
«интегральную ретину» — считывающее устройство, выполненное на
.интегральной схеме; оно состоит из 96 фотодиодов, размещен-
размещенных в одной кремниевой пластине длиной около 38,1 мм. Это
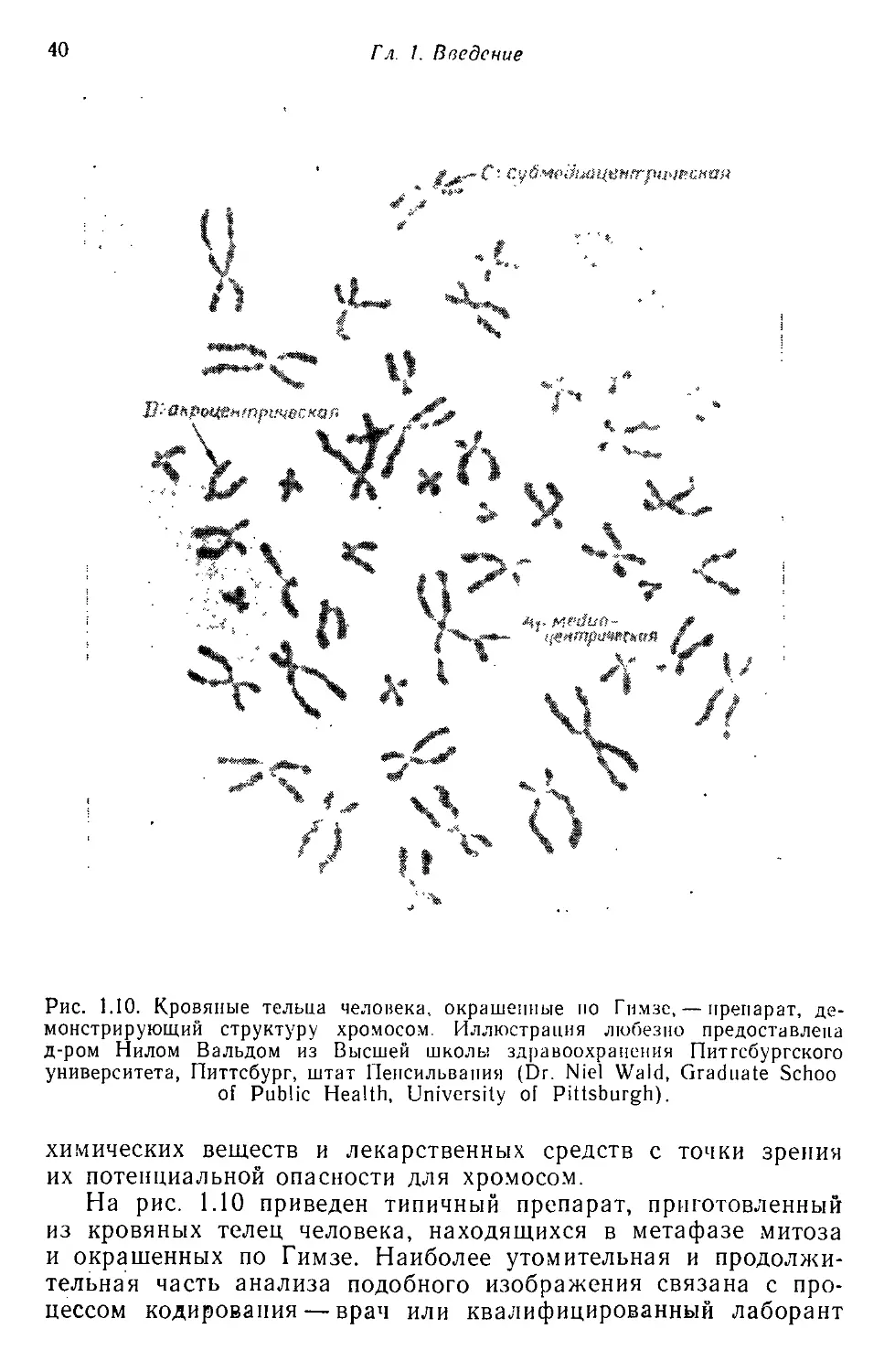
устройство является «глазом» системы. Интегральная ретина
кодирует каждый символ, представляя его с помощью матрицы
16X12 ячеек, стандартизует символы, производит коррекцию
в соответствии с вариациями их размера, действуя со скоростью
до 3600 символов в секунду. Интегральная ретина, кроме того,
классифицирует каждую ячейку представления каждого сим-
символа в соответствии с принадлежностью к одному из 16 уровней
зачерненности.
Данные с выхода считывающего устройства передаются
в блок распознавания, в котором уровни зачерненности всех
ячеек изображения символа сравниваются с уровнями зачернен-
зачерненности 24 соседних ячеек; для этого используется соответствую-
соответствующая схема усиления видеосигнала. Полученные в результате
этой операции данные подвергаются квантованию, что приводит
к получению однобитового черно-белого изображения. Этот про-
процесс позволяет сгладить изображение символа, насытить мало-
малозаметные штрихи, устранить пятна и повысить контрастность
при зашумленном фоне. Система распознает символы, набранные
-типографским способом, отыскивая наименьшее рассогласова-
рассогласование между прочитанным символом и символами, включенными
в словарь блока распознавания. Система также удостоверяется
в том, что найденное минимальное рассогласование отличается
на достаточную величину от наиболее близкого к нему рассо-
рассогласования с другим символом словаря. Соответствующий ме-
метод осуществления классификации будет рассмотрен в гл. 3.
Распознавание машинописных символов производится с по-
помощью логической процедуры иного типа. Машинописные сим-
символы не сопоставляются с образами, заранее введенными
в память, а анализируются с точки зрения наличия определен-
определенных общих признаков, таких, как искривленные, горизонтальные
и вертикальные линии, углы и пересечения. В этом случае клас-
классификация символа проводится на основе обнаружения у него
определенных признаков, а также их взаимосвязей. Блоки си-
системы распознавания символов представлены на рис. 1.8, их
названия даны в подписи под рисунком.
Автоматическая классификация данных,
полученных дистанционно
Сравнительно недавно возникший в Соединенных Штатах
интерес к качеству окружающей среды и состоянию природные
ресурсов вызвал к жизни множество приложений методов
38 Гл. /. Введение
распознавания образов. Наибольшее внимание среди них при-
привлекает автоматическая классификация данных, полученных
дистанционно. Поскольку объем данных, получаемых от много-
многодиапазонных спектральных развертывающих устройств, уста-
установленных на самолетах, спутниках и космических стан-
станциях, чрезвычайно велик, возникла необходимость обратиться
к автоматическим средствам обработки и анализа этой инфор-
информации. Дистанционный сбор данных используется при решении
различных задач. Среди областей, вызывающих интерес в на-
настоящее время, можно отметить землепользование, оценку уро-
урожая, выявление заболеваний сельскохозяйственных культур, ле-
лесоводство, контроль качества воздуха и воды, геологические
и географические исследования, прогноз погоды и массу других
задач, связанных с охраной окружающей среды.
В качестве примера автоматической классификации резуль-
результатов спектрального исследования рассмотрим рис. 1.9, а, па
котором приведена цветная фотография земной поверхности,
сделанная с самолета. Изображение представляет небольшой
участок по маршруту полета (несколько миль), расположенный
в центральном районе штата Индиана. Цель заключается
в сборе данных, достаточных для обучения машины автоматиче-
автоматическому опознаванию различных типов напочвенного покрова
(классов), например светлый или темный почвенный слой, реч-
речная или прудовая вода, и стадии созревания зеленой расти-
растительности.
Многодиапазонное развертывающее устройство реагирует на
свет с определенными полосами длин волн. Развертывающее
устройство, использованное в упоминавшемся полете, работает
в полосах длин волн 0,40—0,44, 0,58—0,62, 0,66—0,72 и 0,80—
1,00 микрон A0~6 метра). Эти диапазоны относятся к фиолето-
фиолетовой, зеленой, красной и инфракрасной областям соответственно.
Использование такого метода приводит к получению для одного
участка земной поверхности четырех изображений — по одному
на каждую цветовую область. Следовательно, каждая точка
участка характеризуется четырьмя компонентами, представляю-
представляющими цвет. Информацию по каждой точке можно представить
четырехмерным вектором образа х = (дгьхг, х3, х4)', где х\ — от-
оттенок фиолетового цвета, хг — оттенок зеленого и т. д. Набор
образов, относящихся к определенному классу почвенного слоя,
составляет обучающее множество для этого класса. Эти обучаю-
обучающие образы можно затем использовать при построении класси-
классифицирующего устройства.
На основе спектральных данных, полученных во время
рассматриваемого полета, построен байесовский классификатор
для образов, подчиняющихся нормальному распределению
(см. § 4.3). На рис. 1.9,6 приведена машинная выдача резуль-
Ilill
illllli!
I
ijiilljHImm,
Рис. 1-9. а —цветная фотографин района, сделанная с самолета; 6— распечатка результатов машинно» классификации. Иллюстра-
Иллюстрации любезно предоставлены Лабораторией прикладного листлициоплого распознавания Университета Псрдыо. Лафайстт, штат I lii-
диана (Laboratory of Application of Remote, Sensing, Purdue University.). ISBN 0-201-C7586-5.
t.5. Примеры автоматических систем распознавания образов 39
татов применения такого классификатора для автоматической
классификации миогодиапазонных спектральных данных, соот-
соответствующих небольшому участку земной поверхности, пред-
представленному на рис. 1.9, а. Стрелками отмечены некоторые
признаки, представляющие специальный интерес. Стрелка 1
помещена в углу поля зеленой растительности, стрелка 2 обо-
обозначает реку. Стрелкой 3 отмечена небольшая живая изгородь,
разделяющая два участка обнаженной почвы; эти объекты точно
идентифицированы на распечатке. Приток, который также пра-
правильно идентифицирован, отмечен стрелкой 4. Стрелка 5 ука-
указывает на очень маленький пруд, который на цветной фотогра-
фотографии почти неразличим. При сопоставлении исходного изо-
изображения с результатами машинной классификации становится
очевидно, что последние весьма точно соответствуют тем выво-
выводам, к которым пришел бы человек, интерпретируя исходную
фотографию визуально.
^/ Биомедицинские приложения
Как отмечалось в § 1.1, медицина в настоящее время стал-
сталкивается с серьезными проблемами, связанными с обработкой
информации. Методы распознавания образов с переменным
успехом применялись для автоматической обработки данных,
полученных с помощью различных технических средств, при-
применяемых в медицинской диагностике, например, таких, как
рентгенограммы, электрокардиограммы, электроэнцефалограм-
электроэнцефалограммы, и анализа и интерпретации вопросников, заполняемых па-
пациентами. Одной из задач, которым уделялось много внимания,
является автоматизация анализа и классификации хромосом.
Интерес к автоматизации анализа хромосом вызван тем об-
обстоятельством, что автоматизация цитогенетического анализа
расширит возможности использования хромосомных исследова-
исследований в клинической диагностике. Кроме того, это сделает воз-
возможным проведение крупномасштабных профилактических по-
пуляционных исследований с тем, чтобы оценить патологическое
влияние ряда небольших вариаций хромосомного портрета, воз-
воздействие которых в настоящее время неизвестно. К тому же
возможность обследовать большие группы населения позволит
провести и ряд других ценных медицинских исследований, на-
например поголовное цитогенетическое обследование плода до
рождения и новорожденных с целью определения необходимости
профилактического или лечебного воздействия, скрининг отдель
ных групп людей, выделенных по факторам профессиональной
принадлежности или проживания в определенном районе и от-
отличающихся повышенной хромосомной аберрацией, вызван-
вызванной каким-либо вредным воздействием, или проверка новых
40 Гл. 1. Введение
Рис. 1.10. Кровяные тельца человека, окрашенные по Гимзс, — препарат, де-
демонстрирующий структуру хромосом. Иллюстрация любезно предоставлена
д-ром Нилом Вальдом из Высшей школы здравоохранения Питгсбургского
университета, Питтсбург, штат Пенсильвания (Dr. Niel Wald, Graduate Schoo
of Public Health, University of Pittsburgh).
химических веществ и лекарственных средств с точки зрения
их потенциальной опасности для хромосом.
На рис. 1.10 приведен типичный препарат, приготовленный
из кровяных телец человека, находящихся в метафазе митоза
и окрашенных по Гимзе. Наиболее утомительная и продолжи-
продолжительная часть анализа подобного изображения связана с про-
процессом кодирования — врач или квалифицированный лаборант
/ 5 Примеры автоматических систем распознавания образов 41
должен классифицировать каждую хромосому отдельно. На
рисунке представлены объекты, относящиеся к некоторым ти-
типичным классификационным группам,
Для машинной классификации хромосом предложено мно-
множество методов. Один из подходов, который оказался эффек-
эффективным при классификации хромосом типов, представленных на
рис. 1.10, основан на принципе синтаксического распознавания
образов, обсуждаемом в гл. 8. Суть этого подхода заключается
в следующем. Выделяются непроизводные элементы образа типа
длинных дуг, коротких дуг и полупрямых отрезков, обозначаю-
обозначающих границы хромосомы. Объединение таких иепроизводных
элементов приводит к цепочкам или предложениям, составлен-
составленным из некоторых символов; последние могут быть поставлены
в соответствие так называемой грамматике образов. Каждому
типу (классу) хромосом соответствует своя грамматика. Для
того чтобы опознать конкретную хромосому, вычислительная
машина прослеживает ее границы и порождает цепочку, состав-
составленную из непроизводпых элементов. Основой алгоритма слеже-
слежения обычно является эвристическая процедура, позволяющая
разрешить трудности, связанные с смежностью и перекрытием
хромосом. Полученная таким образом цепочка вводится в рас-
распознающую систему, которая определяет, представляет ли она
собой правильное предложение, составленное из символов со-
согласно правилам некоторой грамматики. Если этот процесс при-
приводит к указанию одной определенной грамматики, хромосома
зачисляется в класс, соответствующий этой грамматике. Если
подобный процесс не позволяет получить однозначное толкова-
толкование либо вообще заканчивается неудачей, работа системы с
данной хромосомой прекращается и дальнейший анализ выпол-
выполняется оператором.
Хотя решение задачи автоматического распознавания хромо-
хромосом в общем виде найдено не было, современные распознающие
системы, использующие синтаксический подход, представляют
собой важный шаг в нужном направлении. В § 8.5 мы вернемся
к этой схеме распознавания и подробно рассмотрим соответ-
соответствующую хромосомную грамматику.
Распознавание отпечатков пальцев
Как мы отмечали в § 1.1, правительственные агентства рас-
располагают архивами, в которых хранятся свыше 200 миллионов
отпечатков пальцев. Отдел идентификации (The Identification
Division) Федерального Бюро Расследований располагает, в ча-
частности, самым большим в мире архивом отпечатков пальцев —
свыше 160 миллионов. Ежедневно в отдел поступает до 30 тысяч
запросов. Для того чтобы справиться с таким объемом работы,
42
Гл. I. Введение
2. Indexing
около 1400 технических специалистов и чиновников должны
тщательно классифицировать новые отпечатки и затем педан-
педантично искать совпадения.
В течение ряда лет ФБР проявляло интерес к разработке
автоматической системы идентификации отпечатков пальцев.
Примером усилий, предпринятых в этом направлении, служит
система-прототип FINDER, разрабо-
разработанная компанией Calspan Corporation
по заданию ФБР. Эта система авто-
автоматически обнаруживает и локализует
признаки, характерные для отпечатка.
Признаки, которые обнаруживает си-
система,— это не крупные структурные
элементы типа дуг, контуров или за-
завитков, используемых в процессе пер-
первичной классификации отпечатков, —
это скорее мелкие детали — концы и
разветвления бороздок, аналогичные
изображенным на рис. 1.11.
На рис. 1.12 приведена блок-схема
системы. Вкратце действие системы
FINDER можно описать следующим
образом. Оператор вводит стандарт-
стандартный бланк отпечатка в автоматиче-
Рис. 1.11. Фрагменты —коп- ское входное устройство, которое до-
доставляет отпечаток к «глазу» систе-
системы— развертывающему устройству и
точно размещает под ним отпечаток.
Каждый отпечаток подвергается кван-
Фотография любезно предо- тованию и представляется матрицей
ставлена мистером К. У. Су- содержащей 750X750 точек, причем
каждая точка кодируется одним из
16 возможных уровней зачерненно-
сти. Процесс сканирования осуще-
осуществляется под управлением универсальной вычислительной ма-
машины. На рис. 1.13 приведен пример, показывающий, какой вид
принимает отпечаток, пройдя развертывающее устройство.
Данные, полученные на выходе развертывающего устройства,
вводятся в фильтр бороздок-желобков, который реализуется
С помощью быстродействующего алгоритма параллельной об-
обработки двумерных объектов; этот алгоритм последовательно
осматривает все точки матрицы 750X750. На выходе фильтра
воспроизводится усиленное бинарное изображение типа приве-
приведенного на рис. 1.14. Этот же алгоритм фиксирует направление
бороздок в каждой точке отпечатка; данняя информация ис-
пользуется в процессе дальнейшей обработки.
*'¦" - - "J
цы бороздок (квадраты) и
разветвления (окружно-
(окружности) , — используемые систе-
системой FINDER при идентифи-
идентификации отпечатков пальцеа.
онгером из Calspan Corpo-
Corporation, Буффало, штат Нью-
Йорк.
Отпечатки
пальцев
подающее
УСТРОЙСТВО
СКАНИРУЮЩЕЕ
УСТРОЙСТвО-
ПРЕ0ВРА308АНИЕ
ОТПЕЧАТКОВ
В ЭЛЕКТРОННЫЕ
ИЗОБШЕНИЯ
6Л0К
ПРЕДВАРИТЕЛЬНОГО
РШКТИЮШИЯ-
УСТРАНЕНИЕ РАЗМЫТЫХ
И МАЛОЮНТРАСТНЫХ
УЧАСТКОВ
ЁЛОК
ИЗМЕРЕНИЯ
НАПРАВЛЕНИЯ
вОРОЗДОК
К0е-<РОРМИР08АЖ ЬИ-
ПАРНОГО ИЗОБРАЖЕНИЯ,
УСТРАНЕНИЕ
НЕ60ЛЫ1/ИХ
РАЗРЫВЫ
УНИВЕРСАЛЬНАЯ
звм-
УПРАВЛЕНИЕ
СИСТЕМОЙ,
шибРоекА
блок
6ЫИЕПЕНИЯ ЧЧИГМЕНШ
выделение шгмтов,
ОПРЕДЕЛЕНИЕ
ИХ ПОЛОЖЕНИЯ
И ОРИЕНТАЦИИ
елок окончательного
РЕДАКТИРОВАНИЯ-
УСТРАНЕНИЕ
ВЗАИМОИСКЛЮЧАЮЩИХ
И ШбПИРУЩИХ
ДЕТАЛЕЙ
1
АЛГОРИТМЫ
ПОИСКА ВМАССШ
Рис. 1.12. Блок-схема системы, распознавания отпечатков пальцев FINDER. Фотография любезно предоставлена
мистером К. У. Суонгером из Caispan Corporation, Буффало, штат Нью-Йорк.
44
Гл. I Введение
При обработке большинства отпечатков в некоторых зонах
не удается выделить достаточно четкую структуру бороздок,
обеспечивающую возможность надежного выявления фрагмен-
фрагментов. Устройство предварительного редактирования исключает
такие участки из дальнейшего анализа в качестве источников
ft • -
0 4-
1 M
1С
I 2
1 i
1 <•
1 &
4
л;
11 *
<-l
¦м.
10 I
1 11
m
111
111
i »i
i * i
10
.11 -1
11
1 1
1 I
1'.
1 \
4'
11'
n
1I1 ¦J I ".
1 / '1 1 ' *l
I'lll
111
I ) •> I
11 11
T 1 1
1 U / Ч Л I I
T P il
* i Я 4 *. /Ц
J't
я r •
6 *. «,
6 * '
| r
1 I
/ \
м
M
r i
i/i
i ) i
1Л I
1 11
1 t
I'-
I'.
и
11
11 * •¦
lll?l
DIM
1 II II
I U И
1 ПН
lilt
MO
i )
и?
) I 1
H 1
'•
'.
'¦
1
J
г
>
t
01 4 1
11 *• I 1
4 M 1
l > i /
111 4 1 1 «• f
I 1, 1 7 't Л / *.
11 (j J '
n ^ d /
•> si i
i
?
1
1
;
» 1 J > *> M / I'. I
; r i г i *i t m
1 T S •> ^
t Ь 1 S 1
? л h •> -.lilt * * '.
no ¦> ^ щ n / ь
l t
* <• S ^ 4 л l
Г ^ / I Milt
i.
111! 1 ^
111 4 '¦
1 t I U \
1
-.
)
i
11
* 1
»I
1 t
у 1 ¦,
I >
\\\t\?\
U1?H1
1 H 11 '• 1
ihii;
1 M M И
|||/ T
I I ¦! 5
\> 4 S |
1U 10
) Л J ',
0 I » л
r f r f
111 J '
1
-
i •>
* мл
i
¦;
1
11
it
MIIU
nimi
i ¦• t '¦ i <* i
I '• I I 10
I <* ' 1
'. I / I ^
T Ь ^
Ъ 6 -
/l Л*
1WH
U i* 1 U
Mi 4
Jl I ¦)
Рис. 1.13. Распечатка участка, полученного на выходе сканирующего устрой-
устройства. На этом цифровом изображении черные элементы представлены циф-
цифрой «О», а белые —«15». Иллюстрация любезно предоставлена мистером
К. У. Суонгером из Calspan Corporation, Буффало, штат Нью-Йорк.
достоверной информации. Чтобы обеспечить надежное обнару-
обнаружение фрагментов, используются тесты на белизну, черноту, не-
недостаточность структуры бороздок или контрастности.
Следующий этап обработки отпечатков посвящен практиче-
практическому выделению фрагментов. Этот процесс реализуется с по-
помощью алгоритма, синхронизированного с выходом фильтра
бороздок-желобков. Он выделяет фрагменты, предположительно
являющиеся характерными признаками, и регистрирует их по-
положение и величины соответствующих углов.
Результаты работы блока выделения фрагментов вводятся
в блок окончательного редактирования. В первую очередь пло-
площадь и периметр выбранного фрагмента сопоставляются с по-
пороговыми значениями, соответствующими истинным признакам,
Что позволяет исключить заведомо неверные данные. Далее
исключаются признаки-дубликаты. Если какой-либо частный
фрагмент обнаружен несколько раз, то сохраняется только об-
1.5. Примеры автоматических систем распознавания образов
45
наруженпе наибольшей длины. Использование цепной про-
процедуры, при которой объектом поиска являются только фраг-
фрагменты, соседние с выделенными, существенно сокращает время
обработки. Далее производится удаление взаимоисключающих
фрагментов и фрагментов, появление которых связано с разры-
разрывами в структуре бороздок. После этого список признаков сво-
свободен от фрагментов, форма и качество которых лежат ниже
1
I г
1 )
1 i
1
1 г
г 1 i
i 1
1 1 1
1 I I
1 I
I I I
1 I 1
I I I
i i ;
I I
7 г 7 ?
7 I I i г
> 1 1 1 г
1 i г 1 1
> 1 I 2 I
г i г i
i i
г i
i i i i
t i i i i
i i i i i
i i
i
t
l j
i i i i
III!
I I I I
'III
1111
I
1 1
1 1
1 1 t
I I 1
г г
i i
г г
t t i
i i t
г г
г
i
i
i i
i i
i i i i i i
i i i i i i
i i г i i
iiii
i г i
i i
iii i
iii i
г г ii
i iiii
i •' i
iiii
l i
: ; j i
iiii
i t i i
ii >ii
i l i t i i г l
г ill
i i
i i
i i
l i
i i
i i
i i
i i i
i i
i i
i
i
i
;
i
t
i
i i
i
i i
г i
iiii
i i i
г i
1 2
i ;
i i >
г i г i
Рис. 1.14. Результаты пропуска данных, представленных па рис. 1.13, через
фильтр бороздок-желобков. В данном случае черные точки представлены сим-
символами «г». Иллюстрация любезно предоставлена мистером К. У. Суопгеро.ч
из Calspan Corporation, Буффало, штат Нью-Йорк.
определенного порога. На последнем этапе процесса оконча-
окончательного редактирования определяется, относится ли признак
к кластеру признаков либо соответствующий угол существенно
отличается от локальной ориентации структуры бороздок. Клас-
Кластерный тест исключает из рассмотрения группы признаков та-
такого типа, как, например, появившиеся из-за шрама на пальце.
Если рядом с анализируемым признаком обнаруживаются при-
признаки, число которых превышает определенную величину, данный
признак как ложный из дальнейшего анализа исключается. Если
признак проходит последний тест, то логическая часть системы
переходит к реализации теста на аномальность угла, используя
набор данных (матрицу) о направлении бороздок, собранных
46 Гл. 1. Введение
в процессе предварительной обработки. В зависимости от ве-
величины отклонения от среднего угла бороздки признак остав-
оставляется, отвергается или, если отклонение невелико, угол кор-
корректируется в соответствии со средним значением углов сосед-
соседних бороздок.
Окончательно около 2500 битов данных, представляющих
признаки, которые выдержали все тесты, предусмотренные бло-
блоком окончательного редактирования, записываются на магнит-
магнитную ленту с тем, чтобы можно было приступить к их сопостав-
сопоставлению с признаками отпечатков, находящихся в архиве.
Применение методов распознавания образов в техническом
надзоре за состоянием узлов ядерного реактора
Этот последний пример относится к сравнительно новой об-
области применения принципов распознавания образов. В схемы
энергетических ядерных установок включаются многочисленные
датчики, обеспечивающие контроль за целостностью работы
установки. В частности, в сфере контрольно-измерительной тех-
техники широкое распространение получил нейтронный регистра-
регистратор. Прибор этот, предназначенный для измерения плотности
нейтронов, генерирует сигнал, зависящий также и от механиче-
механических колебаний, которые происходят в реакторе. Одна из ос-
основных целей применения этого регистратора в ядерном реак-
реакторе заключается в обнаружении на возможно более ранней
стадии любых режимов внутренних колебаний, не характерных
для нормальных эксплуатационных условий реактора.
В настоящее время в области анализа шумов (нейтронных,
акустических, тепловых и т. п.) наибольший интерес вызывает
создание таких систем.технического контроля, которые обеспе-
обеспечивают слежение за режимом работы установки в целом, по
меньшей мере частично автоматизированы и обладают возмож-
возможностями адаптироваться к изменениям режима, не связанным
с отклонением от нормы. Системы управления воспроизводят
информацию в огромных объемах, которая, для того чтобы ею
можно было воспользоваться, должна обрабатываться с по-
помощью каких-либо систематических процедур. Хотя в данное
время это обстоятельство не приводит к возникновению каких-
либо реальных сложностей, поскольку к моменту написания
книги в Соединенных Штатах действовало не более 50 энерге-
энергетических ядерных установок, по оценкам Комиссии по атомной
энергии к 2000 году количество таких установок только в Со-
Соединенных Штатах превысит 1000. Естественно, придется соз-
создать методы автоматической обработки информации, воспроиз-
воспроизводимой многочисленными системами управления, которые бу-
будут входить в состав подобных ядерных энергетических
1.5. Примеры автоматических систем разпознавания образов
47
установок. Хотя распознавание в этой области только начинает
делать первые шаги, его потенциальные возможности уже пол-
полностью определились. Ниже мы кратко опишем основные ре-
результаты, полученные в этом направлении.
На рис. 1.15 приведены основные компоненты автоматиче-
автоматической системы управления. Представляющие шум сигналы, по-
поступающие от датчиков, которые установлены в энергетиче-
энергетической ядерной установке, нормируются, подвергаются предвари-
предварительной обработке и вводятся в систему распознавания
образов. На выходе этой системы воспроизводится решение, ха-
характеризующее текущее состояние установки. В нашем случае
ЭНЕРГЕТИЧЕСКАЯ
ЯДЕРНАЯ
УСТАНОВКА
Результаты
измерения шума
БЛОК
ПРЕДВАРИТЕЛЬНОЙ
ОБРАБОТКИ
СИСТЕМА
РАСПОЗНАВАНИЯ*
ОбРАЗОВ
Рис. 1.15 Основные компоненты автоматической системы анализа шума.
речь идет о ядерном реакторе с большой плотностью нейтрон-
нейтронного потока, предназначенном для производства изотопов: реак-
реактор установлен в Окриджской национальной лаборатории (Oak
Ridge National Laboratory). В качестве исходных данных для
контроля за режимом этого реактора используются результаты
измерений нейтронного шума, которые проводятся в среднем
трижды в день. Топливный цикл (промежуток времени между
перезарядкой топливных элементов) составляет обычно при ра-
работе с полной мощностью 22 дня. Блок предварительной обра-
обработки на основании этих данных определяет спектральную плот-
плотность мощности в диапазоне частот от 0 до 31 Гц с интервалом
в 1 Гц. Следовательно, результаты каждого измерения можно
представить 32-мерным вектором образа х = {х\, Хг,..., Хзг)',
где Х\ — амплитуда спектральной плотности мощности излуче-
излучения на частоте 0 Гц, хг—амплитуда на частоте 1 Гц и т. д. За-
Задача в таком случае сводится к построению системы распозна-
распознавания образов, способной автоматически анализировать
подобные образы.
Данные для двух топливных циклов изотопного реактора
с большой плотностью нейтронного потока приведены в трех-
трехмерной системе координат на рис. 1.16, а и б. Ось х характери-
характеризует время топливного цикла, ось у представляет 32 компоненты
48
Гл. I Введение
каждого образа, а ось г — нормированную амплитуду спект-
спектральной плотности мощности. Приведенные данные соответ-
соответствуют нормальному режиму работы. Отметим, что обе группы
данных в общем весьма сходны.
Система распознавания, предназначенная для контроля ре-
режима изотопного реактора с высокой плотностью нейтронного
Рис. 1.16. Типичные спектральные плотности мощности нейтронного излучения,
соответствующие нормальному режиму ядерного реактора с большой плот-
плотностью нейтронного потока, предназначенного для производства изотопов.
Наибольшим пикам на каждом из графиков соответствует значение 1. Истин-
Истинные значения спектральной плотности можно получить, умножив значения,
полученные из графика, на соответствующие масштабные коэффициенты. Они
равны: а— 1,831-Ю-4; б — 2,881-Ю-4. Графики заимствованы из статьи Гопса-
леса, Фрая и Крайтера, IEEE Trans. Nucl. Sri., 21, No. 1, February 1974
(R. С Gonzales, D. N. Fry, R. С Kryter, Results in the Application of Pattern
Recognition Methods to Nuclear Reactor Core Component Surveillance).
потока, выделяет признаки, характерные для нормального ре-
режима работы, из записей нейтронного шума, подвергнутых со-
соответствующей обработке. Эта процедура в основном сводится
к отысканию кластеров векторов образов при помощи последо-
последовательного применения алгоритма кластеризации (соответ-
(соответствующие методы обсуждаются в гл. 3). Данные, характеризую-
характеризующие положение центров кластеров, а также соответствующие
описательные статистики типа рассеяния для отдельных класте-
кластеров можно затем использовать в качестве эталонов для сравне-
сравнения в любой заданный момент времени с результатами измере-
измерений для того, чтобы идентифициропать текущее состояние уста-
установки. Существенные отклонения от заданных характеристик
I.в Простая модель распознавания образов
49
нормального режима работы служат индикаторами возникно-
возникновения аномального процесса. На рис. 1.17, а и б, например,
приведен образ поведения реактора, который можно легко клас-
классифицировать как резко отличающийся от нормального рабочего
режима. Приведенные данные соответствуют случаю поломки
направляющего подшипника одного из механических узлов,
Рис. 1.17. Спектральные плотности, соответствующие аномальному поведению
ядерного реактора с большой плотностью нейтронного потока, предназначен-
предназначенного для производства изотопов. Масштабные коэффициенты в данном слу-
случае равны: а — 5,555-10~4; б — 2,832-10—4. Графики заимствованы из статьи
Гонсалеса, Фрая и Крайтера, IEEE Trans. Nucl. Set, 21, No. 1, February 1974
(R. С Gonzalez, D. N. Fry, R. С Kryter, Results in the Application of Pattern
Recognition Methods to Nuclear Reactor Core Component Surveillance).
расположенных вблизи активной зоны реактора. Хотя выявлен-
выявленные отклонения и не создают ситуации, представляющей непо-
непосредственную опасность, подобные результаты демонстрируют
потенциальную важность использования методов распознавания
образов в качестве составной части системы мероприятий, обе-
обеспечивающих технический надзор за состоянием энергетической
ядерной установки. Дополнительные детали, относящиеся
к этой проблеме, можно почерпнуть из статьи Гонсалеса, Фрая
и Крайтера [1974].
1.6. ПРОСТАЯ МОДЕЛЬ РАСПОЗНАВАНИЯ ОБРАЗОВ
Завершим эту вводную главу описанием простой математи-
математической модели автоматического распознавания образов, иллю-
иллюстрирующей ряд основных понятий. Простая схема распознава-
распознавания содержит два основных блока: датчик и классификатор.
50 Гл. /. Введение
Датчик^ представ.ляет собой, устройство, преобразующее физиче-
CKne_ja:pjjKT?pjiciiiKH--. объекта, подлежащего распознаванию,
в набор признаков х = {х\. ..х„)', которые характеризуют дан-
данный объект. Классификатор представляет собой'устроиство, от-
относящее каждый поступающий на его вход допустимый набор
значений к одному из конечного числа классов (категорий),
вычислив множество значений решающих функций.
Считается, что система распознавания допускает ошибку
в том случае, если она относит к классу со/ объект, на самом
деле принадлежащий отличному от соу классу. Считается, что
система распознавания /?i лучше системы распознавания #2,
если вероятность совершить ошибку для системы R\ меньше,
чем для системы #2- Датчик выдает информацию в виде вектора
x = {xi,X2,...,Xn)r, где п — число измеренных характеристик
каждого физического объекта. Предполагается, что вектор из-
измерений х принадлежит одному из М классов образов coi,
со2, ¦ ¦ •, сом.
Мы принимаем допущение о том, что априорные вероятности
появления объектов каждого класса одинаковы, т. е. вектор х
может с равной вероятностью относиться как к одному, так
и к другому классу. Пусть р(х|ю,-) = р,-(х) есть плотность рас-
распределения для вектора х при условии, что он принадлежит
классу юг. В таком случае вероятность того, что на самом деле
вектор х принадлежит классу со/, определяется выражением
Вероятность того, что вектор х не принадлежит классу со;, опре-
определяется выражением
р (х
1 — Я/ = 1 л?
задающим вероятность ошибки.
Решающая функция представляет собой функцию d(x), от-
относящую х точно к одному из М заданных классов. Оптималь
ной считается решающая функция d°(x), которая дает наимень
шую вероятность ошибки при всех допустимых значениях х.
Значение /, при котором величина 1—р\ будет наименьшей,
совпадает с тем значением /, которому соответствует наибольшее
значение вероятности р(х|со/). Итак, оптимальная решающая
1.6. Простая модель распознавания образов 51
функция d°(x) относит набор х к классу со, в том и только том
случае, если выполняются неравенства
р (х ! щ) > р (х | со/) у]ф1
или
При р(х|со,)= р(х|соа) и р(х|й),)>р(х|со/), /=1, 2, .... М,
/ Ф i Ф k, оптимальная решающая функция d°(x) может отне-
отнести вектор х как к классу аи, так и к классу со*. Для заданного
значения х классификатор определяет оптимальную решающую
функцию.
Допустим, наконец, что измеренные значения распределены
нормально и соответствующие ковариационные матрицы имеют
вид
/ С11 С12 ' " " с\п
\ сп1 сп4 ' ' ' Спп
где Сц — ковариация t-й и /-й компонент вектора измерений х,
а Си — дисперсия г-й компоненты вектора измерений х. По-
Поскольку в случае нормального распределения имеем
рЫ\щ) =
где т, — вектор математического ожидания, отношение двух
плотностей р(х|со,) и р(х|соу) определяется выражением
р (х | ш,-)
= ехр{— у[(х — т()'С '(х-т,-) —
(X |
Так как ковариационная матрица симметрична, данное отно-
отношение условных вероятностей сводится к следующему:
Введем величину
тогда получим выражения для разделяющей функции
rit (х) = х' С" (oii - ш/) - у (т, + ш/)' С (oii - m;).
52
Гл. 1. Введение
Для определения оптимальной разделяющей функции следует
вычислить М (М — 1) значений функций г,/(х) для всех t, /, 1ф],
и выбрать наибольшее из полученных значений. Если окажется,
что этот максимум равен rk-h то относим х к классу со*. Схема
оптимального распознавания, воспроизводящая описанный ме-
метод, приведена на рис. 1.18.
ВЫЧИСЛЕНИЕ
КОВАРИАЦИОННОЙ
ШТРИЦЫ
ДЛЯ КАЖДОГО
КЛАССА
O5PAU
МАП
1ЕНИЕ
ЩЫ
ВЫЧИСЛЕНИЕ
ВЕКТОРА
СРЕДНЕГО
ДЛЯ КАЖДОГО
КЛАССА
ВЫЧИСЛЕНИЕ
гц
,
ВЫ60Р
МАКСИМАЛЬНОГО
ЗНАЧЕНИЯ
ИЗМЕРЕНИЕ
ЗНАЧЕНИЯ
X
I Решение
Рис. 1.18. Пример простой схемы распознавания образов.
Отметим, что уравнение
гц (х) = х'С ' (щ, - ш/) - \ (т, + т/)'С-' (тг - та,) = О
описывает гиперплоскость, проведенную в n-мерном простран-
пространстве и разделяющую его в случае наличия двух классов на
две части:
Гц > 0 для х е шь
Тц < О ДЛЯ X е Шу.
Следовательно, уравнение щ = 0 определяет разделяющую по-
поверхность для i-ro и /-го классов образов. В следующей главе
проводится исчерпывающее рассмотрение решающих функций
и разделяющих поверхностей.
Глава 2
РЕШАЮЩИЕ ФУНКЦИИ
2.1. ВВЕДЕНИЕ
Основным назначением системы распознавания образов яв-
является отыскание решений о принадлежности предъявляемых
ей образов некоторому классу. Для того чтобы справиться с та-
такой задачей, необходимо ввести ряд правил, на которых иско-
искомые решения будут основываться. Один из важных подходов
к задаче предполагает использование решающих функций. Про-
Проиллюстрируем этот довольно простой метод с помощью рис. 2.1,
на котором представлены образы, предположительно принад-
принадлежащие двум классам. Из рисунка видно, что две совокупно-
совокупности образов удобно разделить прямой.
Пусть d (х) = W\K\ + w2x2 + w3 = 0 — уравнение разделяю-
разделяющей прямой, где wi—параметры, а Х\ и х2— переменные. Из
рисунка очевидно, что подстановка в d(x) любого образа х,
принадлежащего классу соь даст положительное значение. От-
Отрицательное значение функция d(x) примет при подстановке
образа, относящегося к классу сог. Таким образом, функцию
d(x) можно использовать в качестве решающей (или дискри-
минантной) функции, поскольку, рассматривая образ х, класси-
классификация которого неизвестна, можно утверждать, что образ х
принадлежит классу coi, если d(x)>0, и классу со2, если
сКх)<0. Если образ лежит на разделяющей границе, имеет
место случай, соответствующий условию неопределенности
d(x) = 0. Как будет видно из дальнейшего, этот метод справед-
справедлив и для числа классов, большего 2. Его нетрудно распростра-
распространить на более общий случай нелинейных границ в любом ко-
конечномерном евклидовом пространстве.
Успех применения описанной схемы распознавания образов
зависит от двух факторов: 1) вида функции d(x) и 2) практи-
практической возможности определения ее коэффициентов. Первый из
них непосредственно связан с геометрическими свойствами рас-
рассматриваемых классов. Нетрудно представить ситуацию, в ко-
которой для разделения заданных совокупностей образов могут
потребоваться границы, значительно более сложные, чем в об-
обсуждавшемся случае линейной разделимости. Если размерность
образов оказывается больше трех, то зрительное воображение
перестает быть нашим помощником при определении границ.
54
Гл. 2. Решающие функции
В этом случае единственно разумный выход — обратиться к су-
сугубо аналитическим процедурам. К сожалению, при отсутствии
какой-либо априорной информации оценить эффективность вы-
выбранной решающей функции можно только эмпирически.
Как только определенная функция (или функции, если про-
проводится разбиение более чем на два класса^ выбрана, возникает
задача определения коэффициентов. В следующих главах будет
показано, что для ее решения можно использовать несколько
Рис. 2.1. Пример простой решающей функции для случая разделения образов
на два класса.
адаптивных схем или процедур обучения. Мы увидим, что если
рассматриваемые классы разделяются некоторыми решающими
функциями, то для отыскания их коэффициентов можно исполь-
использовать заданную выборку образов.
2.2. ЛИНЕЙНЫЕ РЕШАЮЩИЕ ФУНКЦИИ
Простой вариант двумерной линейной решающей функции,
введенной в § 2.1, можно легко обобщить на л-мерный случай.
Общий вид линейной решающей функции задается формулой
d (х) = а;,*, + w2x2 + ...+ wnxn
w
n+,
= w'x + w
n+v
B.2.1)
где вектор v/a = (w\,w2,.. .,wn)' называется весовым или па-
параметрическим.
Общепринято во все векторы образов вводить после послед-
последней компоненты 1 и представлять соотношение B.2.1) в виде
d(x) = w'x, B.2.2)
2.2. Линейные решающие функции 55
где х = (xi,x2,..., An, 1)' и w = (w\, w2, ¦ . ., wn, wn+\)' — попол-
пополненные векторы образов и весов соответственно. Поскольку
одна и та же величина вводится в описания всех образов, ос-
основные геометрические свойства соответствующих классов не
затрагиваются. Обычно из контекста можно определить, был
или не был пополнен вектор образов или весовой вектор. В даль-
дальнейшем мы, как правило, будем называть х и w, входящие
в формулу B.2.2), просто вектором образа и весовым вектором
соответственно.
Предполагается, что в случае разбиения на два класса ре-
решающая функция d(x) обладает следующим свойством:
( > 0, если х е со,,
d(x) = w'x| ^Л B.2.3)
' (. < 0, если х е ш2.
Рассмотрим случаи разбиения на несколько классов
coi, (о2, ..., им, т. е. предполагается, что объекты принадлежат
более чем двум классам.
Случай 1. Каждый класс отделяется от всех остальных одной
разделяющей поверхностью. В этом случае существует М ре-
решающих функций, обладающих свойством
{> 0, если х е ю,-, )
. n . \, i=l, 2 М, B.2.4)
< 0, если хф®[ )
где v/i = {wn, wi2, ..., Win, Wi,n+\)' — весовой вектор, соответ-
соответствующий t-й решающей функции.
Пример. Простой пример, иллюстрирующий случай 1, приве-
приведен на рис. 2.2, а. Отметим, что каждый класс можно отделить
от всех остальных с помощью одной разделяющей границы. Так,
например, если некоторый образ х принадлежит классу eoi, из
рис. 2.2, а на основании чисто геометрических соображений за-
заключаем, что di(\)~> 0, a d2(x)< 0 и d3(x.)< 0. Граница, отде-
отделяющая класс (Oi от остальных, определяется значениями х, при
которых d\ (х) = 0.
Приведем численную иллюстрацию; пусть решающие функ-
функции, соответствующие рис. 2.2, а, имеют вид
di (х) = — хх + хъ d2 (х) = х, + х2 — 5, d3 (х) = — хг + 1.
Следовательно, три разделяющие границы определяются урав-
уравнениями
— хх + х2 = О, Х\ + х2 — 5 = 0, — х2 + 1 = 0.
Итак, любой образ, для которого выполняются условия
tfi(x)>0, йг(х)<0 и d3(x)<0, автоматически зачисляется
Хг
Область -—.j—j.
решения, s=s=
Ф&- Пушил классу gg^
?;=!= й(х)<ш
0HP-Шесть непринятия решения
Рис. 2.2, Иллюстрация к случаю 1 разделения на несколько классо!
2.2 Линейные решающие функции 57
в класс (Оь Следовательно, область, соответствующая классу юь
включает область с той стороны от прямой d\ (х) =====—ati + х2 = О,
где d\(x) положительна, и область отрицательных значений
функций а?г(х) и а?з(х), ограниченную прямыми d2(x.) = *i+
+ Х2 — 5 = 0 и о!з(х) =—Х2 + 1 == 0. Эта область отмечена на
рис. 2.2,6, и сопоставление его с рис. 2.2, с показывает, что хотя
класс coi занимает сравнительно небольшой участок, в действи-
действительности область, соответствующая решению об отнесении
объекта к данному классу, безгранична. Аналогичные сообра-
соображения справедливы и для двух других классов.
Интересно отметить, что если функция d,(x) больше нуля
при более чем одном значении i, рассматриваемая схема клас-
классификации не позволяет найти решение. Это справедливо также
и при d;(x)<0 для всех i. Как видно из рис. 2.2,6, в данном
примере существуют четыре области неопределенности, соответ-
соответствующие одной из этих ситуаций.
Отнесение неклассифицированного объекта к одному из трех
классов, определяемых рассмотренными решающими функ-
функциями, производится самым непосредственным образом. Пусть,
например, необходимо классифицировать образ х == F, 5)'. Под-
Подстановка его характеристик в три наши решающие функции
дает следующее:
d,(x) = -l, d2(x) = 6, d3(x)=-4.
Так как с(г(х)>0 при di(x)<0 и й?3(х)<0, образ зачисляется
в класс со2.
Случай 2. Каждый класс отделяется от любого другого взя-
взятого в отдельности класса «индивидуальной» разделяющей по-
поверхностью, т. е. классы попарно разделимы. В этом случае-
существует М(М— 1)/2 (число сочетаний из М классов по два)
разделяющих поверхностей. Решающие функции имеют вид
dr(x)=w^xH обладают тем свойством, что если образ х при-
принадлежит классу (о,-, то
d;, (х)>0 для всех \Ф1; B.2.5)
кроме того, d,7(x) = —d,i(x).
Не так уж редки задачи, представляющие собой комбинацию
случаев 1 и 2. Для их решения требуется менее М(М—1)/2
разделяющих поверхностей, совершенно необходимых в той си-
ситуации, когда все классы разделимы только попарно. ¦
Пример. На рис. 2.3, а представлены три класса образов,
разделимых согласно случаю 2. Очевидно, что ни один класс
нельзя отделить от всех остальных с помощью единственной
разделяющей поверхности. Каждая из приведенных на рисунке
Рис. 2.З. Иллюстрация к случаю 2 разделения на несколько классо
2.2. Линейные решающие функции 59
границ обеспечивает разделение точно двух классов. Так, на-
например, хотя граница di2(x) = 0 проходит через класс ю3, она
дает эффективное разделение лишь для классов (Oi и ю2.
Пусть решающие функции имеют следующий вид:
di2 (х) == — *i — х2 + 5, d13(x) = —х,+ 3, dn (x) = — *, + х2.
Разделяющие границы снова получим, приравнивая решающие
функции нулю. Области решений, однако, теперь могут содер-
содержать несколько зон, где соответствующие функции положи-
положительны. В частности, область, отвечающая классу coi, опреде-
определяется значениями образа х, при которых uf]2(x)>0
и б?1з(х)> 0. Значение решающей функции й?2з(х) в этой области
не существенно, поскольку эта решающая функция никак не
связана с классом соь
Области, определяемые тремя указанными решающими
функциями, представлены на рис. 2.3,6, причем для выделения
областей, соответствующих разным классам, использовано ус-
условие di, (х) = —<2/i(x). Так, поскольку di2(x) = —х\—5
d2\ (х) = х\ + Х2~ 5, то зона положительности функции )
совпадает с зоной отрицательности функции dn (x). Как и в слу-
случае 1, оказывается, что области решения безграничны и суще-
существуют области неопределенности, в которых условия случая 2
не выполняются.
Рассмотрим классификацию объекта, заданного вектором
х = D, 3)'. Подстановка его элементов в выбранные решающие
функции лает
Отсюда автоматически следует, что d2t(x) = 2, d3i(x)=l,
^з2(х)= 1. Так как
d3y(x)>0 для /=1, 2
и в область неопределенности мы не попали, то рассматривае-
рассматриваемый образ зачисляем в класс аз-
Случай 3. Существует М решающих функций dk (х) = wk\y
k= I, 2, ..., М, таких, что если образ х принадлежит классу
@„ ТО
di(x)>dj(x) для всех )Фп B.2.6)
Эта ситуация является разновидностью случая 2, поскольку
можно положить
dц (х) = dt (x) - dt (x) = (w, - w;)' x = w;;x, B.2.7)
60 Г л 2 Решающие функции
где w,v = Wi — w;. Легко убедиться и юм, что если d,(x)>
> dj(\) для всех / Ф i, то di,(\) > 0 для всех / Ф i, т. е. если
классы разделимы, как в случае 3, то они автоматически раз-
разделимы и как в случае 2. Обратное, сообще говоря, не верно. ¦
Пример. Прежде чем приводить иллюстрацию случая 3, от-
отметим, что граница между классами со,- и со,- определяется теми
значениями вектора х, при которых имеет место равенство
di(\) = dj{\), или (что то же самое) di(x) — d,(x) = 0. Таким
образом, при выводе уравнения разделяющей границы для
классов со,- и ю,- значения решающих функций d,;(x) и dj(\) ис-
используются совместно.
Простой пример случая 3 при М = 3 приведен на рис. 2.4, а.
Для образов, принадлежащих классу a>i, должны выполняться
условия di(x)> d2(x) и di (х) > d3(x). Это эквивалентно тре-
требованию того, чтобы входящие в данный класс образы распо-
располагались в положительных зонах поверхностей d\ (х)—d2(x) = 0
и d,(x) —rfa(x) = 0.
В общем случае требуется, чтобы входящие в класс со, об-
образы располагались в положительных зонах поверхностей
di(x) — dj(x) = 0, /= 1, 2, ..., М, j ф i. Как и выше, положи-
положительная зона границы d,(x)—dj(x) — 0 совпадает с отрицатель-
отрицательной зоной границы dj(x)—di(x) = 0.
Пусть в качестве решающих функций выбраны следующие:
di (х) = — х{ + хп, d2(\) = x] + x,— \, d3(х) = — Хп.
Разделяющие границы для трех классов выглядят при этом
так:
rf,(x)-d2(x)=-2.v,+ 1=0,
rf, (x) - d3 (x) = - xi + 2x2 = 0,
d2 (х) - d3 (х) = х, + 2х2 - 1 = 0.
Для того чтобы определить область решений, соответствующую
классу Ш[, необходимо выделить область, в которой выпол-
выполняются неравенства d[(x) > с/2(х) и d\ (x) > d3{\). Эта область,
как видно на рис. 2.4,6, совпадает с положительными зонами
для прямых —2*1 + 1 = 0 и —х\ + 2*2 = 0. Область принятия
решения о принадлежности образа классу а»2 совпадает с поло-
положительными зонами для прямых 2х\ — 1 = 0 и Ху -f- 2х2— 1 = 0
Область, отвечающая классу а>з, наконец, определяется положи-
положительными зонами для прямых х\ — 2х2 = 0 и —х\ — 2лг2 +1=0.
Интересно отметить, что в случае 3 области неопределенности
как таковые отсутствуют, за исключением собственно разделяю-
разделяющих границ.
d,[*)'d3w--0
Область решения, !|
соотВетсшбующая
массу
Рис. 2.4. Иллюстрация к случаю 3 разделения на несколько классо
62 Га. 2 Решающие функции
В качестве примера классификации рассмотрим обработку
образа х = A, 1)'. Подстановка компонент этого вектора в вы-
выбранные решающие функции дает
Поскольку
d2(\)> dj(\) для /= 1, 3,
образ относится к классу со2- ¦
Если какой-либо из рассмотренных выше вариантов линей-
линейной решающей функции обеспечивает классификацию в некото-
некоторой заданной ситуации, то соответствующие классы называются
линейно разделимыми. Читателю следует четко уяснить, что
основная проблема, возникающая после определения набора
решающих функций (линейных либо каких-то иных), заклю-
заключается в отыскании коэффициентов. Как уже указывалось выше,
для определения этих коэффициентов обычно используется до-
доступная выборка образов. После того как коэффициенты осех
решающих функций определены, можно приступать к построе-
построению системы распознавания, как это описано в гл. 1.
2.3. ОБОБЩЕННЫЕ РЕШАЮЩИЕ ФУНКЦИИ
Нетрудно показать, что для классов, в состав которых не
бходят идентичные векторы образов, можно всегда найти раз-
разделяющие границы. Сложность таких границ колеблется от ли-
линейных до сугубо нелинейных, для описания которых требуется
очень большое количество членов. В прикладных задачах часто
оказывается, что из-за экономических или технических затруд-
затруднений классы в истинном смысле не разделимы и желательно
найти приближения решающих функций. Один из удобных спо-
способов обобщить понятие линейной решающей функции состоит
во введении решающих функций вида
к+\
d (х) = wj 1 (х) + w2f2 (х) + ... + wKfK (х) + wK+] = 2 wJi (x),
г=1
B.3.1)
где {f,(x)}; i=\, 2, ..., К, — действительные однозначные
функции образа х, f/c+i(x)= I, a /(+1 —число членов разло-
разложения. Соотношение B.3.1) представляет бесконечное множе-
множество решающих функций, вид которых зависит от выбора функ-
функций (fj(x)} и количества членов, использованных в разложении.
Несмотря на то обстоятельство, что формула B.3.1) может
задавать очень сложные решающие функции, применение соот-
соответствующего преобразования позволит работать с ними как
2.3 Обобщенные решающие функции
63
с линейными. Продемонстрируем этот прием, определив век-
вектор х*, компонентами которого являются функции f/(x):
X =
Ых)
f2(x)
B.3.2)
1
Используя B.3.2), можно записать B.3.1) как
d (x) = w V,
B.3.3)
где. w = (шь w2,..., wK, wK+i)'.
Функции (f;(x)} после того, как их значения вычислены,
представляют собой просто набор чисел, а вектор х* — обычный
/(-мерный вектор, пополненный единицей, как это было описано
в § 2.2. Итак, по отношению к новому представлению образов х*
выражение B.3.3) является линейной функцией. Очевидно, что
преобразование всех исходных образов х в образы х* посред-
посредством вычисления всех х значений функций {/;(х)} эффективно
превращает нашу задачу в линейную. Смысл всего этого заклю-
заключается в том, что все дальнейшее обсуждение можно без потери
общности ограничить линейными решающими функциями. Лю-
Любую решающую функцию вида B.3.1) можно, воспользовавшись
преобразованиями B.3.2) и B.3.3), превратить в линейную.
Все эти манипуляции имеют исключительно математический
смысл. Никаких реальных изменений, как можно убедиться, со-
сопоставив уравнения B.3.1) — B.3.3), не произошло. Если об-
образы х были n-мерными, то преобразованные образы х* стали
/(-мерными (не считая приписанной 1), причем К может ока-
оказаться существенно больше п. Таким образом, хотя в /(-мерном
пространстве решающие функции можно считать линейными,
в n-мерном пространстве исходных образов они полностью со-
сохраняют свой принципиально нелинейный характер.
Представление функций {f-(x)} в виде многочленов — один
из наиболее часто используемых способов задания обобщенных
решающих функций. В простейшем случае эти функции линей-
линейные, т. е. если х = (х\,х2,.. ¦ ,хп)', то /;(х) = х; при К = п,
и тогда решающая функция имеет вид d{\) = w'x + wn+\.
Следующий уровень сложности соответствует функциям вто-
второго порядка (квадратичным). Если образы двумерные (х =
~{xi, *2)')> a решающие функции представляются в виде
d (x) = wnx\
-f w1xl + w2x2
B.3.4)
64 Гл. 2. Решающие функции
то линейное представление d(x*)= w'x* можно получить, задав
Х* = (*2, Х{Х2, Х\, Хх,\.., 1)' И W = {Wn,Ww, W22, Wi,W2,W3)'.
Общий случай квадратичной функции получается аналогич-
аналогичным образом, т. е. посредством построения всех комбинаций
компонент вектора х, образующих члены не выше второй сте-
степени; для n-мерных образов имеем
п га —1 п п
d(х) = Z wjjX) + ? ^ ™ikx.,xk + E w,Xl + wn+l. B.3.5)
Первая из находящихся в правой части этого равенства функ-
функций насчитывает п членов, вторая п(п—1)/2 и третья п. Сле-
Следовательно, общее число членов равно (п -\- 1) (п + 2)/2, что
равно общему числу параметров (весов). Сопоставление соотно-
соотношения B.3.5) с общей формой задания B.3.1) показывает, что
псе члены /,(х), из которых составляется решающая функция,
имеют вид
f{(x) = xspxtQ, p,q=l,2 л; s, f = 0, 1. B.3.6)
Формула B.3.6) подсказывает общую схему построения поли-
полиномиальных решающих функций конечного порядка. Для того
чтобы получить полиномиальную функцию порядка г, следует
задать функции
1 2 г B.3.7)
ру, р2, ..., Рг=1, 2, ..., п; sit s2, ..., sr = 0, 1.
Поскольку эти функции представляют все степени, не пре-
превышающие г, полиномиальную решающую функцию можно за-
задать рекуррентным соотношением
B.3.8)
где г указывает степень нелинейности и rf°(x)= wn+\. Это соот-
соотношение дает удобный способ формирования решающих функ-
функций произвольного конечного порядка.
Пример. В качестве простой иллюстрации применим B.3.8)
для получения квадратичной решающей функции, определяе-
определяемой соотношением B.3.4). В данном случае г = 2 и п = 2, по-
поэтому
2.3. Обобщенные решающие функции
где dl (х) есть линейная решающая функция:
2
' E °(х) = а;,*!
65
Pi ='
х
Выполнив суммирование, получим
d2 (х) = адпд* + wl2xlx2 + ау22^ + с?1 (x) =
что совпадает с B.3.4). Функции высших порядков строятся
точно таким же образом. |
Как можно было бы предположить, число членов, необходи-
необходимое для представления полиномиальной решающей функции,
быстро растет как функция от порядка г и размерности п. Не-
Нетрудно показать, что в «-мерном случае число коэффициентов
для функции порядка г определяется по формуле
Nw = Crn+r = ^0-, B.3.9)
где Сп+г— число сочетаний из п-\-г по г.
В табл. 2.1 приведены величины Nw для различных значений
порядка г решающей функции и размерности п. Следует отме-
отметить, что хотя Nw быстро растет по мере увеличения г и п, нет
Таблица 2.1
Количество Nw членов разложения решающей функции
в зависимости от ее порядка г и размерности д
X
I
2
3
4
б
6
7
8
9
10
1
2
3
4
5
в
7
8
9
10
11
2
3
в
10
15
21
28
36
45
55
<!в
3
4
10
20
35
66
84
120
1С5
220
280
4
5
15
35
70
120
210
330
495
715
1 001
5
К
21
5«
12R
252
402
792
1 287
2 002
3 003
6
7
28
84
210
462
924
1 716
3 003
5 005
8 008
1
3
6
11
19
7
8
30
120
330
792
710
432
435
440
448
!
3
6
12
24
43
8
9
45
165
495
287
003
435
870
310
758
9
10
55
220
715
2 002
5 005
II 440
24 310
48 620
92 378
1
• 3
8
19
43
92
184
10
11
66
286
001
003
ООН
44S
758
378
756
необходимости всегда использовать все члены, определяющие
общий вид разложения B.3.8). Так, при построении решающей
-функции второго порядка можно отказаться от всех членов, ли-
линейных относительно компонент образа х.
' 3 Зак, 694,
<>6
Гл. 2. Решающие функции
Задав
/=1, 2 п,
/, k=\, 2, .... п,
/=1, 2, ..., п,
можно представить соотношение B.3.5) в более компактном
виде:
d (х) = х'Ах + х'Ь + с, B.3.10)
где
A = (a/jk) B.3.11)
и
B.3.12)
Свойства матрицы А определяют форму разделяющей границы.
Если А —единичная матрица, решающая функция представляет
собой гиперсферу. Если А — положительно определенная мат-
матрица, решающая функция представляет собой гиперэллипсоид,
направление осей которого определяется собственными векто-
векторами матрицы А. Если А — положительно полуопределенная
матрица, разделяющая граница представляет собой гиперэллип-
гиперэллипсоидальный цилиндр, поперечными сечениями которого яв-
являются гиперэллипсоиды низших порядков, причем направление
их осей определяется собственными векторами матрицы А, соот-
соответствующими ненулевым характеристическим значениям.
Если А —отрицательно определенная матрица, разделяющая
граница представляет собой гипергиперболоид.
Существуют, естественно, и другие методы порождения ре-
решающих функций. Более подробно теоретические основы функ-
функций многих переменных и методы их построения будут рассмот-
рассмотрены в § 2.7.
2.4. ПРОСТРАНСТВО ОБРАЗОВ И ПРОСТРАНСТВО ВЕСОВ
Выше было отмечено, что решающая функция в случае раз-
разбиения на два класса должна обладать следующим свойством:
для всех образов одного класса должно выполняться неравен-
неравенство с?(х)>0 и для всех образов второго класса — неравенство
rf(x) <Z 0. Допустим, что в каждый класс входят по два двумер-
двумерных образа, {х[, х'} и (х^, х|}, где верхние индексы обозна*
чают классы an и со2 соответственно. Если классы линейно раз-
2.4. Пространство образов и пространство весов 67
делимы, задача сводится к отысканию вектора w = (w\, wz, \
для которого справедливы следующие неравенства:
w{x\{ + w2x\2 + w3>Q,
wtxl21 + wx\2 + о?, > О,
о I 2 I /Л С2'4'1)
Другими словами, вектор w является решением системы линей-
линейных неравенств, определяемой всеми образами, входящими
в состав обоих классов.
Умножив пополненные образы, принадлежащие одному из
классов, на —1, систему неравенств B.4.1) можно переписать
в виде
2 2 ^П B-4-2)
-o>,4 - w2x222-w3>0
(на —1 умножены образы, принадлежащие классу со2). В этом
случае задача сводится к отысканию вектора w, обеспечиваю-
обеспечивающего положительность всех неравенств. Очевидно, что системы
B.4.1) и B.4.2) идентичны, поскольку один и тот же вектор w
будет удовлетворять обеим системам. Ниже мы будем исполь-
использовать обе формы записи.
Неравенства B.4.1) и B.4.2) требуют только, чтобы компо-
компоненты вектора w определяли разделяющую границу для клас-
классов Ш| и ш2. Для того чтобы получить более полное представле-
представление о геометрических свойствах вектора решения w, целесо-
целесообразно обсудить различия между понятиями пространства
образов и пространства весов.
Пространство образов представляет собой n-мерное евкли-
евклидово пространство, содержащее векторы образов, как это пока-
показано на рис. 2.5, а для гипотетического примера, соответствую-
соответствующего системе неравенств B.4.1). Координатные переменные
обозначены через х\, хч, ..., хп- В данном пространстве вектор w
представляется набором коэффициентов, определяющим разде-
разделяющую поверхность.
Пространство весов представляет собой (п+1)-мерное ев-
евклидово пространство, где w\, w2, ..., wn+\ — координатные пе-
переменные. В этом пространстве каждое неравенство соответ-
соответствует положительной или отрицательной зоне гиперплоскости.
проходящей через начало координат. В этом можно убедиться
68
Г л 2 Решающие функции
А
* wrx, * w2x2+w3=О
Рис. 2.5. Геометрическая интерпретация понятий пространства образов и про-
пространства весов, а — пространство образов: б — пространство весов, соответ-
соответствующее системе неравенств B.4.1)- в — пространство весов, соответствую-
соответствующее системе неравенств B.4.2). Заштрихованные области обозначают положи-
положительные стороны плоскостей.
непосредственно, проанализировав систему неравенств B.4.1).
Так, например, приравнивая первое неравенство нулю, приходим
к уравнению а;,*}, + w2x\.,-\- а»3 = 0, которое, как известно, пред-
представляет собой уравнение плоскости, проходящей через начало
координат пространства весов. Решением сйстемь? неравенств.
B.4.1) является всякий вектор w, расположенный в положи-
положительных зонах всех плоскостей, соответствующих классу обргн
2.5. Геометрические свойства 60
зов <0|, и в отрицательных 30Fiax всех плоскостей, соответствую-
соответствующих классу образов <»2. Решением системы неравенств B.4.2)
служит всякий вектор w, расположенный в положительных зо-
зонах всех плоскостей, поскольку пополненные образы класса щ
были умножены на —1. Оба случая представлены на рис. 2.5,6
и в, где заключенными в окружности цифрами обозначены об-
образы и соответствующие им плоскости, находящиеся в простран-
пространстве весов. Отметим, что в обоих случаях вектор решения один
и тот же, причем область решения ограничена конической по-
поверхностью. В общем случае поверхность границы представляет
собой выпуклый многогранный конус. Как будет показано
в п. 2.5.2, общее число конусов зависит от числа образов и их
размерности.
Из проведенного обсуждения заключаем, что общая задача,
возникающая в связи с использованием линейных решающих
функций, сводится к решению системы линейных неравенств,
каждое из которых определяется отдельным вектором образа.
В пятой и шестой главах рассматривается несколько подходов
к решению этой задачи.
2.5. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА
В данном параграфе обсуждается ряд важных геометриче-
геометрических свойств линейных решающих функций. Отталкиваясь ог
свойств гиперплоскостей, мы вводим понятие дихотомии обра-
образов как простой меры разделяющей мощности решающих функ-
функций. Далее это понятие используется в качестве определения
дихотомизационной мощности.
2.5.1. Свойства гиперплоскостей
В задаче разделения на два класса, так же, как и на нег
сколько классов (случаи 1 и 2, рассмотренные в § 2.2), по-
поверхности, разделяющие эти классы, получаются в результате
приравнивания решающих функций нулю. Другими словами,
при рассмотрении двух классов разделяющая поверхность за-
задается уравнением
d{x) = w1xi + w2x2+ ... +wnxn + wn+[ = 0. B.5.1)
В случае 1 граница, отделяющая класс ю, от всех остальных
классов, определяется уравнением
di(x) = wnxl + wi2x2 + ... +winxn + Wt,n+l = 0. B.5.2)
Подобным же образом граница, разделяющая классы со,
И (В/ в случае 2, определяется уравнением
d( ... +Wi!nxn + wi!,n_?[ = 0. B.5.3)
70 ' Гл. 2. Решающие функции
В случае 3 из § 2.2 приравнивание нулю решающих функций
по отдельности не позволяет получить разделяющую поверх-
поверхность. Уравнение поверхности, обеспечивающей разделение
классов о», и о»/, в общем виде задается так:
dit (х) = dt (х) — d, (х) = (wn — о)ц) х\ + (wi2 — wn) хг + ...
• •. + (Win — wln) xn + (ад,, п+1 — ад;, п+1) = 0. B.5.4)
Уравнения B.5.1) —B.5.4) показывают, что соответствую-
соответствующие границы идентичны, отличаясь друг от друга лишь значе-
значениями 'оэффициентов. Поэтому в дальнейшем обсуждении нам
Начало координат х\
Рис. 2.6. Представление некоторых геометрических свойств гиперплоскостей
удобно будет временно отказаться от нижних индексов и запи-
записывать уравнения разделяющих границ такого рода в общем
виде:
d (х) = ад,*! + w2x2 + ... +wnXn + wn+i =
= \<х-г-ад„+1=0, B.5.5)
где wo = (w\,W2,... ,wn)'. Отметим, что вектор х не был попол-
пополнен, поскольку, как мы убедимся ниже, коэффициенту wn+\
принадлежит важная роль в геометрической интерпретации
уравнения B.5.5).
Известно, что уравнение B.5.5) представляет прямую при
п = 2 и плоскость при п = 3; при п > 3 уравнение B.5.5)
определяет гиперплоскость. Поскольку в настоящей главе
2.5 Геометрические сппйства 71
(и в последующих) линейные разделяющие границы находятся
в центре внимания, важно добиться полного понимания геомет-
геометрических свойств гиперплоскостей.
Рассмотрим рис. 2.6, на котором «гиперплоскость» представ-
представлена схематически. Пусть и — единичная положительно ориен-
ориентированная нормаль, т. е. единичный вектор, нормальный к ги-
гиперплоскости в некоторой точке р и направленный в сторону
положительной зоны гиперплоскости. Из чисто геометрических
соображений уравнение гиперплоскости можно записать в виде
и'(х-р) = 0 B.5.6а)
или
u'x = u'p. B.5.66)
Деление уравнения B.5.5) на ||w 11= */wz_)_w2-\-... _)_w* при-
приводит к уравнению
VX W~" . B.5.7)
-llwjl || wo.
Сопоставив уравнения B.5.66) и B.5.7), заключаем, что еди-
единичная нормаль к гиперплоскости задается как
B.5.8)
Кроме того,
B.5.9)
Сопоставление рис. 2.6 и соотношения B.5.9) позволяет обна-
обнаружить, что абсолютное значение произведения и'р характери-
характеризует расстояние по нормали от начала координат до гиперпло-
гиперплоскости. Обозначив это расстояние через Du, получим
B.5.10)
Из рис. 2.6 видно также, что расстояние Dx по нормали от ги-
гиперплоскости до произвольной точки х определяется уравнением
W,
п+х — ° ¦ "TI B.5.11)
Нормальный единичный вектор и характеризует ориентацию
гиперплоскости. Если какая-либо из компонент вектора равна
нулю, то гиперплоскость параллельна координатной оси, соот-
соответствующей этой компоненте. Итак, поскольку и = wo/|| w» ||,
72
Г1 1 Решающие функции
по вектору wo можно нудить, параллельна ли данная гиперпло-
гиперплоскость какой-либо из координатных осей. Из соотношения
B.5.10) видно также, что при ayn+i = 0 гиперплоскость проходит
через начало координат.
2.5.2. Дихотомии
Одной из характеристик разделяющей мощности решающей
функции является число способов классификации заданного
множества объектов, осуществимых с ее помощью. Обратимся,
в частности, к рис. 2.7, на котором представлен набор, состоя-
состоящий из четырех двумерных образов \и х2, х3, Х4. Каждая прямая
з
,2
Рис. 2.7. Линейная дихотомия для четырех «хорошо» разметенных образов
в двумерном случае.
на рисунке соответствует определенному варианту разбиения
образов на два класса. Прямая 1, например, выделяет две
группы: образ Xi и образы х2, х3, х4. Поскольку образ Xi можно
отнести как к классу соь так и к классу сог, прямая 1 определяет
две возможные классификации. В данном случае общее число
разбиений на два класса или дихотомий равно 14. Интересно
сопоставить эту оценку с общим числом возможных способов
распределения четырех объектов по двум классам B4). Оче-
Очевидно, что 2 из этих 16 дихотомий линейно реализовать нельзя.
-Количество линейных дихотомий N точек в n-мерном евкли-
евклидовом пространстве равно удвоенному числу способов разделе-
разделения этих точек (п — 1)-мерной гиперплоскостью. Можно
2.5 Геометрические свойстпа 73
показать, что при «хорошем» размещении точек число линейных
дихотомий для N образов размерности п определяется следую-
следующим выражением:
!п
2loCL., N>n, B5Л2).
2", jV<«,
где Cjv_i = (jV—l)!/(Af—1 — k){ k\. Множество, состоящее из
N точек n-мерного пространства, называют хорошо размещен-
размещенным^), если ни одно из его подмножеств, состоящее из п+1
точек, не лежит на (п—1)-мерной гиперплоскости. Так, напри-,
мер, N двумерных точек хорошо размещены, если никакие три
точки не лежат на одной прямой (одномерной гиперплоскости).
Величины 2)(N,n) для различных вариантов сочетаний
числа точек N и размерности п приведены в табл. 2.2. Обра-,
тите внимание на чрезвычайно бурный рост числа линейных,
дихотомий &(N,n) при сравнительно умеренном увеличения
значений Л' и п.
Таблица 2.2 ¦
Оценка числа линейных дихотомий 2) (N, п) в зависимости
от числа образов N и их размерности п
N\
1
2
3
4
5
6
7
9
10
25
50
100
200
1
2
в
К
10
12
14
16
18
20
50
100
200
400
о
о
4
8
14
22
32
44
;>8
74
92
602
2 4Г>2
9 902
39 802
3
2
4
8
16
30
Г>2
84
128
180
2(>0
4 050
39 300
323 000
2 027200
4
2
4
S
16
32
02
114
198
326
512
15 662
463 052
7 8Г>2 352
129 40» 702
5
2
4
8
16
32
64
126
240
438
764
100 670
4 276 820
150 898 640
5 073 927 280
6
2
4
8
It!
32
64
128
254
494
932
379 862
32 244 452
Z 391 957 152
164 946 602 302
Интересно установить связь оценки B.5.12) с числом выпуклых
многогранных конусов, обсуждавшихся при рассмотрении про-
пространства весов в § 2.4 Обратимся снова к рис. 2.5,в Любой
') В литературе довольно часто встречается и термин «размещение общего
Типа» (in general position)
74 Гл. 2 Решающие функции
вектор w, расположенный внутри одного из выпуклых конусов,
соответствует определенному варианту классификации заданной
совокупности образов Поскольку число линейных дихотомий
определяется оценкой ?D(N.n) (при условии правильного раз-
размещения образов), следует сделать вывод, что в пространстве
весов, соответствующем N образам размерности п, должно раз-
размещаться такое же количество выпуклых многогранных
конусов.
Результаты проведенного анализа легко продолжить на слу-
случай обобщенных решающих функций, рассмотренных в § 2.3.
Поскольку введение этих функций приводит к образам новой
размерности, следует просто заменить п размерностью получен-
полученных образов. Пусть, например, задано 10 двумерных образов
и эта выборка хорошо размещена. Тогда общее количество воз-
возможных дихотомий равно <Z>A0,2) = 92. При использовании
полиномиальной решающей функции второго порядка размер-
размерность новых образов равна n — Nw—\=5, что приводит
к <Z)A0,5) = 764 потенциально возможным дихотомиям.
Так как число дихотомий используется в качестве меры клас-
классификационной мощности, должно быть очевидным, что чем
больше дихотомий для заданных N образов может быть реали-
реализовано, тем более вероятно, что мы найдем решение заданных
неравенств. Это обстоятельство, естественно, согласуется с тем
фактом, что вероятность успешного разделения двух групп об-
образов с помощью дихотомической процедуры увеличивается по
мере того, как растет степень нелинейности испытываемых раз-
разделяющих границ.
2.5.3. Дихотомизационная мощность обобщенных решающих
функций
Рассмотрим обобщенные решающие функции в виде B.3.1),
определяемые /С —J— 1 регулируемыми весами (параметрами).
При задании N преобразованных образов с хорошим размеще-
размещением существует 2N дихотомий, 3)(N, К) из которых линейно
реализуемы относительно полученного /С-мерного пространства
образов Вероятность /?,v, к того, что вариант дихотомии, выбран-
выбранный случайным образом, окажется линейно реализуемым, опре-
определяется формулой
J^-"tcU ыж,
1, ,?</<.
Иначе говоря, если число образов меньше или равно К, мы
утверждаем, что независимо от способа группировки заданных
2.5. Геометрические свойства
75
образов они будут линейно разделимы в /(-мерном пространстве
образов.
Вероятность рц, к линейной реализуемости обладает еще
рядом интересных свойств. При обсуждении последних удобно
положить N = К(К + 1) и построить график зависимости рн,к
от параметра %. Очевидно, % всегда можно выбрать так, чтобы
независимо от размерности Л' пространства образов Х(К-\-I)
было равно количеству образов N. График зависимости рик+\),к
РЬ {К*1),К
Рис. 2.8. Зависимость вероятности линейной реализуемости случайным обра-
образом выбранной дихотомии р?(Л+1), * от параметра X при различных значениях
размерности пространства преобразованных обра ;o:i К.
от параметра % приведен на рис. 2.8. Обратите внимание на воз-
возникновение порогового эффекта при А, = 2 для больших значе-
значений К. Следует также отметить, что />2</гм),л = '/2 для всех зна-
значений размерности К пространства образов.
Внимательное изучение порогового эффекта при % = 2 пока-
показывает, что при больших значениях К возможность полной
классификации N — 2(K-{-\) хорошо размещенных образов
с помощью обобщенной решающей функции, характеризующейся
К + 1 параметрами, практически гарантирована. С другой сто-
стороны, если число образов N больше 2(/С+1), очевидно, что
вероятность реализации дихотомического разбиения резко па-
падает для больших значений размерности К-
Проведенный анализ подводит нас к определению дихотоми-
зационной мощности обобщенной решающей функции в виде
Ck = 2(K+\). B.5.14)
Мы видим, что так определенная мощность равна удвоенному
числу степеней свободы (регулируемых параметров) обобщен-
обобщенных решающих функций B.3.1). Это понятие будет снова
76 Гл. 2. Решающие функции
использовано в гл. 5 в связи с обсуждением свойств ряда важ-
важных детерминистских алгоритмов.
Приведем для сравнения значения дихотомизационной мощ-
мощности некоторых решающих функций при разделении п-мерных
образов.
Тип разделяющей границы Дихотомизационная
мощность
Гиперплоскость 2(и+1)
Гиперсфера 2(п + 2)
Поверхность второго порядка (n-f-1) (гс + 2)
Полиномиальная поверхность 2Сп+г
порядка г
2.6. РЕАЛИЗАЦИЯ РЕШАЮЩИХ ФУНКЦИЙ
Возникают два вполне правомерных вопроса: 1) Как именно
следует определять решающие функции? 2) Как следует эти
функции реализовывать с тем, чтобы построить классификатор,
обеспечивающий искомое разбиение образов? Ответ на первый
вопрос охватывает большую часть материала книги. К счастью,
достаточно полный ответ на второй вопрос можно дать в пре-
пределах этого параграфа.
Этап реализации классификатора, основанного на рассмот-
рассмотренных выше решающих функциях, состоит просто в выборе
подходящего метода «материализации» этих функций. Во мно-
многих приложениях система распознавания образов полностью
реализуется на вычислительной машине. В других случаях, когда
вычислительная машина применима только на стадии разра-
разработки системы или когда выдвигаются какие-либо специальные
требования, например высокое быстродействие, возможно, при-
придется воспользоваться для этой цели специализированным
устройством.
На рис. 2.9 приведена принципиальная схема классифика-
классификатора, построенного на основе обобщенных решающих функций
и обеспечивающего разбиение объектов на несколько классов.
Для простоты здесь будет рассмотрена ситуация разделения на
несколько классов, соответствующая случаю 3 из § 2.2. Два дру-
других случая можно реализовать с помощью аналогичных систем.
Блок предварительной обработки в этой системе просто воспро-
воспроизводит уравнение B.3.2). Блок, следующий за блоком предва-
предварительной обработки, вычисляет значения решающих функций
cl{(х*) = w^x*, /=1, 2, 3, ..., М, где М — общее число клас-
классов. Последний блок — селектор максимума, обеспечивающий
выбор наибольшего скалярного произведения векторов и отне-
отнесение классифицируемого образа к соответствующему классу.
1.6 Реализация решающих функций
77
На рис. 2.10 приведена очень недорогая и весьма эффектив-
эффективная в вычислительном смысле схема, реализующая метод ли-
линейных решающих функций. На схеме указано, что полная
БЛОК
ПРЕДВАРИТЕЛЬНОЙ
ОБРАБОТКИ
•
*
•
W1
w,x
wjx* ^
wkx*
СЕЛЕКТОР
МАпЬпМупА
Решение
Рис. 2.9. Принципиальная схема классификатора, обеспечивающего разделе-
разделение образов на несколько классов.
проводимость каждого резистора выбирается равной весу ре-
решающей функции. Если считать, что компоненты вектора соот-
соответствуют напряжениям, то величина тока в /-м резисторе г-й
xz
nti*1
Y-w
h
Yu-Wi2
hz
\
Yin
hn
ли
(
Win
' селектору
максимума
Рис. 2.10. Реализация операции произведения векторов wjx. В схеме преду-
предусмотрено М батарей резисторов, по одной на каждый класс.
батареи определяется выражением 1ц = wijXj. В схеме пре-
предусмотрено по одной батарее резисторов на каждый класс обра-
образов. Поскольку, как это показано на рисунке, узел является
точкой суммирования токов резисторов, величина тока на
78
Гл. 2 Решающие функции
выходе i-и батареи равна скалярному произведению w^x. Вели-
Величины, воспроизводимые на выходе всех резисторных батарей,
вводятся в селектор максимума, в котором выбирается наиболь-
наибольшее значение решающей функции и осуществляется соответ-
соответствующая классификация.
При разбиении на два класса комбинация «резпсторная ба-
батарея/селектор максимума» принимает форму, широко извест-
известную под названием порогового устройства. Принципиальная
схема порогового устройства приведена на рис. 2.11. На выходе
Рис. 2.11. Принципиальная схема порогового устройства.
такого устройства могут воспроизводиться величины только двух
типов. Одна из них соответствует выполнению условия w'x > Т,
а вторая — выполнению условия w'x ^ Т, где Т—неотрицатель-
Т—неотрицательная пороговая величина. Эти две выходные величины (возмож-
(возможные реакции порогового устройства) обычно обозначаются как
1 и —1 соответственно. Так как здесь речь идет о разделении
на два класса, требуется только один набор коэффициентов. Не-
Нетрудно заметить, что в сущности пороговое устройство представ-
представляет собой классификатор, обеспечивающий разделение образов
на два класса, поскольку он отвечает всем требованиям, предъ-
предъявляемым к классифицирующим системам, за исключением воз-
возможности осуществлять предварительную обработку образов.
Пороговые устройства выпускаются целым рядом фирм, про-
производящих электронные компоненты. Пороговые устройства,
помимо того, что они являются устройством, полезным с точки
зрения построения систем распознавания, обладают свойствами,
делающими их весьма привлекательными в глазах разработчи-
разработчиков цифровых вычислительных машин. Читателю, интересую-
интересующемуся этой проблемой, можно рекомендовать обратиться к
соответствующей литературе, где она рассмотрена сямым под-
подробным образом (см., в частности, Уиндер [1962, .1963, 1968].).
2.7 Функции многих переменных 79
2.7. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Функции многих переменных играют важнейшую роль в изу-
изучении и построении систем распознавания образов. Задача этого
параграфа — дать краткие теоретические сведения об этих функ-
функциях и их построении. Дальнейшее обсуждение на первом этапе
ограничивается функциями одной переменной, а затем получен-
полученные результаты распространяются на случай многих пере-
переменных.
2.7.1. Определения
Скалярное произведение двух функций f(x) n g(x) в интер-
интервале [а, Ь] = а ^ х ^ Ъ определяется как
ь
(/, g)=\f(x)g(x)dx. B.7.1)
а
Скалярное произведение функции f(x) на себя, называемое
нормой функции }{х), вводится как
ь
(f, f) = \f(x)dx. B.7.2)
а
Функция, норма которой равна единице, называется нормиро-
нормированной. Нормировка легко достигается делением функции hj
квадратный корень ее нормы.
Две функции f(x) и g(x) ортогональны относительно весовой
функции и(х) в интервале [а,Ь], если
г>
\u(x)f(x)g(x)dx=O. B.7.3)
а
Несколько примеров ортогональных функций будет приведено
в п. 2.7.3.
Система функций Ф\(х), <f>2(x) каждая пара которых
ортогональна в интервале [а,Ь], называется ортогональной си-
системой. Для этой системы функций имеют место обычные уело
вия ортогональности:
h
dx = Atfitl, B.7 A)
a
где
1, если i = j,
' .' B.7.5)
О, если t Ф /;
80 Г л 2. Решающие функции
Aij — коэффициент, зависящий от параметров / и /. Поскольку
правая часть уравнения B.7.4) всегда равна нулю, за исключе-
исключением случая i = /, коэффициент A,j записывают просто в виде
А, или А/. При Л, = 1 для всех значений i система функций
называется ортонормированной системой, а соответствующие
условия ортонормированности задаются следующим образом:
ь
и (х) ф1 (х) ф, (х) dx = ЬИ. B.7.6а)
При работе с ортонормированными функциями принято исполь-
использовать форму записи, при которой весовая функция и(х) входит
в ортонормированные; при этом условии B.7.6а) можно пред-
представить в виде
1(х)ф,(х)йх = Ь1,. B.7.66)
Функции ф1 (х) иф)(х) в B.7.66) представляют собой выражения
V" (х) ft (x) и -y/ujx) ф / (х) из B.7.6а) соответственно. При ис-
использовании записи B.7.66) следует следить за тем, чтобы квад-
квадратный корень от весовой функции был введен в каждую орто-
нормированную функцию. Очевидно, что соотношения B.7.4)
также можно записать в таком упрощением виде, введя весовую
функцию и ( v) в ортогональные.
Если система функций Ф\(х), ф'.2(х), ... ортогональна в ин-
интервале [а,Ь\, то для получения в этом же интервале ортонор-
ортонормированной системы функций можно воспользоваться соотно-
соотношением
Ф, (х) = д/"^Г ^ (х)' B7-7)
где коэффициент Л; определяется из B.7 4) при / = /, т. е.
ь
А^\и{х)ф]Нх)йх. B.7.8)
а
Нетрудно показать, что функции {ф,(х)} ортонормированны,
так как
Ь
ф1 (х) ф, (х) dx = 4~ \ и (х) Ф] W Ф]
±-
= б*/;
последнее преобразование определяется гем обстоятельством,
что функции \ф\ (х)) ортогональны.
2.7. Функции многих переменных 81
Множество функций {/i(x), }2(х), ••-, Ы(х)} называется ли-
линейно независимым, если не существует коэффициентов с\, с2, ...
..., ст, не всех равных нулю и таких, что уравнение
cxf, (х) + c2f2 (х) + ... + с Jm (х) = О B.7.9)
справедливо для всех х. Все функции, образующие ортогональ-
ортогональную систему, линейно независимы.
И наконец, система функций называется полной, если любую
кусочно-непрерывную функцию можно в среднем сколь угодно
точно аппроксимировать с помощью линейной комбинации функ-
функций, входящих в данную систему. Этому условию удовлетво-
удовлетворяют все функции, рассматриваемые нами ниже.
2.7.2. Построение функций многих переменных
Пусть нам задана полная система ортонормированных функ-
функций одной переменной ф\(х), ф2(х), ... на интервале а ^ х ^ Ь.
В таком случае полную систему ортонормированных функций
двух переменных Х\ и х2 можно построить следующим образом
(Курант и Гильберт [1955]):
<Pi(*i. х2) = </>, (*,) ф1 (х2),
х2) = ФЛх1)ФЛх.2), B.7.10)
х2) = ф2 (хх) ф2 (х2),
Легко показать, что функции <р|, ф2, ... ортонормировании
в квадрате а ^ Х\ ^ Ь, а ^ х2 ^ Ь, т. е.
(fi(xu х2)ц>,(хи x2)dx]dx2=bii. B.7.11)
Отметим, что использованное выше правило построения сво-
сводится просто к выбору пар функций из множества функций од-
одной переменной и перемножению их после соответствующей под-
подстановки переменных х\ и х2. Порядок выбора функций одной
переменной не имеет значения до тех пор, пока сохраняется
порядок переменных, указанный в соотношениях B.7.10).
При работе с функциями многих переменных удобно запи-
записывать условие ортонормированности в векторной форме:
(x)q>i(x)q>/(x)dx = e//, B.7.12)
82 Г л 2. Решающие функции
где функции и(х) и ф, (х) от п переменных расшифровываются
как и(\) = и(хи х% .. ., хп), ф,(х) = ф,(хь х2, ..., хп), а знак
\ обозначает кратный интеграл
X
S 5- \
Способ распространения описанной процедуры на обший
случай п переменных очевиден. Здесь требуется только со-
составлять группы произведений из п функций одной переменной,
подставляя соответственно переменные х\, х2, ..., хп. Если
исходные функции ортонормированны в интервале а ^ х ^ Ь,
то полученные в результате реализации этой процедуры функции
п переменных фЬ ф2, ... ортонормированны на гиперкубе
а ^ Xj ^ b, j = 1, 2, ..., п. В частности, множество функций п
переменных при л = 4 строится следующим образом:
ф1 (х) = фх (Х]) фх (х,) ф{ (х3) фх (х4),
Ф, (х) = </-, (х,) ф, (х2) ф2 (*3) ф{ (хА), B.7.13)
ф4 (Х) = ф{ (Xi) ф\ (Х2) ф2 (X,) ф2 (ХА),
Фз М = Ф\ {Х\) фч (х-,) ф{ (лгз) ^i (х4),
где, как и выше, ф,(х)= ф,(лг|, х2, х3, х4). В следующем пункте
мы рассмотрим некоторые системы ортонормированных функ-
функций, представляющие интерес для распознавания образов.
2.7.3. Ортогональные и ортонормированные системы функций
В этом пункте обратимся к полиномиальным ортогональным
и ортонормированным функциям. Использование в распознава-
распознавании таких функций объясняется двумя причинами. Во-первых,
их легко воспроизводить. Во-вторых, они удовлетворяют усло-
условиям теоремы Вейсрштрасса о приближении, которая утверж-
утверждает, что любую функцию, непрерывную в замкнутом интерпале
а ^ х ^ Ь, можно равномерно аппроксимировать на этом ин-
интервале с любой заданной точностью некоторым многочленом.
Многочлены Лежандра
Ортогональные полиномиальные функции Лежандра Р0(х),
Р\(х), Ръ{х), ... можно получить, воспользовавшись следующим
рекуррентным соотношением:
(k + \)Pk+i(x)-Bk+\)xPk(x) + kPk_l(x) = 0, k^[, B.7.И)
2.7. Функции многих переменных 83
где Р0(х)= 1 и Р\{х) = х. Эти функции ортогональны в интер-
интервале — 1 г?: х ^ 1.
Приведем несколько первых многочленов Лежандра:
Ро(х)=1, Р,(х) = х, Р2(х)=±х*-±,
Рз(х) = -?х Jx' pdx) = -g-x"-—x- + Y,
где функции Рц{х) и Р\(х) заданы, а функции Р2(.\), Р$(х) и
Pi(x) получены по формуле B.7.14). Эти функции ортогональны
относительно весовой функции и(х)= 1. Для того чтобы полу-
получить ортонормированную систему, воспользуемся уравнением
B.7.8) в следующем виде:
i
Ak = \ Р\ (х) их.
\
Можно показать с помощью ряда алгебраических преобразова-
преобразований (см. Курант и Гильберт [1951]), что
"* 2k + 1 '
Следовательно, задавая Ф\(х) = Рk (x) и используя B.7.7),
можно получать ортонормироваиные многочлены Лежандра:
~'Pti{x), k = 0, 1, 2, ...
B.7.15)
Многочлены Лагерра
Для получения многочленов Лагерра можно воспользоваться
рекуррентным соотношением
Lk+l(x)-Bk+l-x)Lk(x) + k2Lk-.1(x) = 0, &>1, B.7.16)
где Lo(x)= 1 и L\{x) = —х-\- 1. Эти многочлены ортогональны
относительно весовой функции и(х) = е~х в интервале
Приведем несколько первых многочленов Лагерра:
L4 (л;) = х* - 1 бх3 + 72л;2 - 96л: + 24,
где функции LoM и L\(x) заданы, а остальные получены по
формуле B.7.16).
84 Г л ? Решающие функции
Определив коэффициент Ак согласно B.7.8) и подставив его
в соотношение B.7.7) при <fk (x) = Lk (х), можно показать, что
ортонормированные многочлены Лагерра определяются следую-
следующим соотношением:
ехр (— л/2) L. (х)
Ы*)= kl * ¦ * = 0, 1, 2 B.7.17)
Многочлены Эрмита
Для получения многочленов Эрмита используется рекуррент-
рекуррентное соотношение
Hk+x(x)-2xHk(x) + 2kHk_x(x) = 0, Л>1, B.7.18)
где Н0(х)= 1 и Н\(х)= 2х. Эти функции ортогональны относи-
относительно весовой функции и(л:) = ехр(—х2), причем интервал
ортогональности составляет —оо << х < оо; это обстоятельство
делает использование таких функций чрезвычайно удобным, по-
поскольку освобождает нас от забот относительно диапазона из-
изменения переменных.
Приведем несколько первых многочленов Эрмита:
Но (х) = 1; Я, (х) = 2х, Н2 (х) = 4х2 - 2,
Н6 (х) = 8ЛГ3 - 12*, Я4 (х) = 16л:4 - 48Х2 + 12,
где функции По(х) и Hi(x) заданы, а остальные определяются
по формуле B.7.18).
Определив коэффициент Ak согласно B.7.8) и подставив его
в соотношение B.7.7), можно показать, что ортонормированные
многочлены Эрмита определяются следующим соотношением:
ехр (— х2/2) Н. (х)
Ы)^. А = 0, 1, 2 B.7.19)
Пример. Построение функций многих переменных с помощью
рассмотренных выше многочленов не вызывает каких-либо за-
затруднений. Пусть, например, требуется сформировать пять орто-
ортогональных функций Лежандра от трех переменных. На основа
изложенного в п. 2.7.2 имеем:
(х3) = 1,
= ^i (хх) Фх {х2) ф2 (х6) = х3,
Фз (X) = ф\ (Xi) ф2 {Х2) фХ (JCj) = Х2,
Ф4 (X) = ф2 (Хд ф1 (Х2) фХ (Х3) = ХЬ
Ф5 (X) = </>! (Х{) ф2 {Х2) ф2 (Хг) = Х2Х3,
2.7 Функции многих переменных 85
где <pi(x) = Р0(х) и <}>2{х) = Р\(х). Естественно, что для по-
построения этих пяти функций можно было бы выбрать множе-
множество иных комбинаций. |
Рассмотренные выше системы функций часто будут использо-
использоваться в качестве основы для обобщения решающих функций,
подобно описанному в § 2.3. Если задано множество, состоящее
из т ортонормированных функций ф((х), фг(х) фт(х), то
множество решающих функций d\(\), d2(\), ..., dM(x) можно
представить в виде линейной комбинации функций ф(х) с неиз-
неизвестными коэффициентами, т. е.
di(x)=Zwi,<f>,(x). B.7.20)
Каждая ортонормированная функция ф;(х) связана с соответ-
соответствующей ортогональной функцией ф^ (х) весовой функцией
и(х) и коэффициентами Ak, определяемыми соотношением B.7.7)
для случая одной переменной. Пусть, в частности, функция
ф[(х) образуется из ортонормированных функций одной пере-
переменной следующим образом:
ф| (X) = j>! (*,) 0, (Х2) ... ф[ (Хп).
Воспользовавшись формулой B.7.7), приходим к следующему
выражению для ф*(х):
где и(к) = u(xi)u(x2) ¦ ¦. и(хп). Изучение этого выражения по-
показывает, что член \J^и (х) присутствует во всех функциях
Ф*(х). Если записать B.7.20) с помощью ортогональных функ-
функций, то из проведенного анализа следует, что
7^T?Cl/<P/(x)' Bl7-2I)
/ — i
причем коэффициенты Л1 вошли в коэффициенты сц. Так как
коэффициент \/<у/и(х) положителен и он присутствует в выра-
жениях для всех решающих функций dt(x), его можно исклю-
исключить, что никак не отразится на принципиальных классифика-
классификационных качествах этих решающих функций. В таком случае
имеем
m
^(х)=1с,/Ф/(х). B.7.22)
86 Гл. 2 Решающие функции
Сопоставление выражений B.7.20) и B.7.22) показывает, что
различие, вызванное использованием ортонормированных или
ортогональных функций для разложения решающих функций,
отражено в коэффициентах. Поскольку, однако, эти коэффи-
коэффициенты неизвестны и должны определяться из условий конкрет-
конкретной задачи, во многих случаях можно пользоваться ортогональ-
ортогональными и ортонормироваиными функциями «попеременно» без
ьсякого вреда для качества классификации. При решении чис-
численных задач мы будем пользоваться ортогональными функ-
функциями, поскольку их проще вычислять. Читатель должен хорошо
сознавать, что проведенный анализ относится только к функ-
функциям, используемым для принятия решения. Фундаментальные
различия, существующие между этими двумя типами функ-
функций, должны четко прослеживаться в теоретических исследо-
исследованиях.
2.8. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Главная задача этой главы заключалась в обсуждении
свойств решающих функций и их применения к распознаванию
образов. В рамках этой задачи были введены и проиллюстриро-
проиллюстрированы существенные элементы, необходимые для математиче-
математического и геометрического осмысления соответствующих подходов.
Решающие функции сыграли важнейшую роль в развитии
теории распознавания образов, что станет вполне очевидным
при чтении следующих глав. Их роль определяется не только
тем обстоятельством, что они являются действенным и осмыс-
осмысленным средством, но также и тем, что обычно их можно по-
построить, опираясь на репрезентативные образы, представляющие
все изучаемые классы. Эта «обучаемость» становится существен-
существеннейшим качеством, когда мы начинаем интерпретировать распо-
распознавание образов как один из важных разделов искусственного
интеллекта.
Четыре следующие главы тем или иным образом связаны
с задачей определения решающих функций. Хотя главы эти во
многих отношениях будут существенно отличаться в связи с
различиями в используемых подходах, основная задача остается
неизменной — развитие методов, пригодных для построения по
обучающей выборке образов функций, которые могут явиться
основой автоматизации процесса принятия решений.
Библиография
Первые упоминания о линейных решающих функциях можно обнаружить
в диссертации Хаилимана [1962], статье Уидроу [1962] и монографии Ниль-
сопа [1967]. Довольно подробный обзор по решающим функциям составлен
Хо и Агравала [1968]. Дополнительный материал по обобщенным решающим
Задачи
87
функциям можно найти в отчете Ковера [1964]. монографии Нильсоиа [1967]
и статье Смекта [1967].
Понятие дихотомии и его использование для определения дихотомиза-
нионнон мощности изучалось Кофордом [1962], Брауном [1963] и Уипдером
[1962, 1963, 1968]. При написании § 2.7 нспользопана монография Куранта
и Гильберта [1951].
Задачи
2.1. (а) Определите решающую функцию, обеспечивающую правильную
классификацию образов, изображенных на помещенном ниже ри-
рисунке.
(б) Изобразите зависимость решающей функции d(x) от xi и х2 при
*i 3= 0 и х2 ^ 0.
Докажите, что условия d(x) > 0 при хеш| и d(x) < 0 при х е и>2 не-
непосредственно следуют из условий rfi(x) > d2(x) при х е «>i и rfi(x) <
< d2(\) при х е wo.
Пусть в задаче распознавания образов, предусматривающей разбиение
на десять классов, три класса соответствуют случаю 1, я остальные
классы — случаю 2 (см. § 2.2). Чему равно минимальное число решаю-
решающих функций, необходимых для решения этой задачи?
2.4 Для задачи разделения па три класса заданы следующие решающие
функции:
2.2
2.3
— — xi, d2 (x) =
х2 — 1,
(х) = *, — хг — 1.
(а) При условии, что эти функции определены для случая 1 разделения
на несколько классов, начертите разделяющие границы и области,
соответствующие каждому классу образои.
(б) Начертите разделяющие границы и соответствующие области для
случая 2 разбиения на несколько классов при следующих условиях:
с?,2(х) = d,(x), d|3(x) = d2(x) и d2S(x) = d3(x).
(в) Начертите разделяющие границы и соответствующие области для
каждого класса исходя из условия что решающие функции d,(x),
d-i(x) и ds(\) определялись для случая 3.
2.5 Построите полиномиальную решающую функцию многочлена третьего
порядка, носпользонаншпсь'соотношением B.3.8) и взяв в качестве ис-
исходной (Г(х)= с1.?: п ¦-- ').
88 Гл 2 Решающие функции
2.6. Рис. 2.5, в построен для четырех двумерных образов, являющихся ли-
линейно разделимыми.
(а) Сделайте соответствующий рисунок для четырех линейно раздели-
разделимых одномерных образов.
(б) Как изменится рисунок, построенный в п. (а), если вместо условия
линейной разделимости d(\) > 0 будет введено условие d(\) > Т,
где Т— неотрицательная пороговая величина?
2.7. Обратитесь к рис. 2.7 и найдите две дихотомии, которые нельзя линейно
реализовать.
2.8. Предложите доказательство, подтверждающее, что при отсутствии у
двух классов общих членов всегда можно построить разделяющую по-
поверхность, правильно дихотомизирующую эти классы, независимо от ха-
характера размещения образов.
2.9. Заданы два класса, каждый из которых содержит по пять различных
трехмерных образов, причем эти образы характеризуются хорошим раз-
метением. Необходимо построить полиномиальную решающую функцию,
обеспечивающую разделение двух классов независимо от геометрии
взаимного расположения образов, но при условии их хорошего разме-
размещения. Каково минимальное количество коэффициентов, требующееся
для реализации такой функции1
2 10. Какова в обшем случае вероятность линейной разделимости на два
класса набора, состоящего из пяти двумерных образов, обладающих
хорошим размещением?
Глава 3
КЛАССИФИКАЦИЯ ОБРАЗОВ С ПОМОЩЬЮ
ФУНКЦИЙ РАССТОЯНИЯ
3.1. ВВЕДЕНИЕ
В этой главе мы приступаем к изучению систем классифи-
классификации образов, опираясь на один из простейших и наиболее
эвристических подходов — использование для классификации
образов функций расстояния. Выбор функций расстояния в ка-
качестве инструмента классификации является естественным след-
следствием того обстоятельства, что наиболее очевидный способ
Рис. 3.1. Образы, поддающиеся классификации с помощью понятия близости.
введения меры сходства для векторов образов, интерпрети-
интерпретируемых нами также как точки в евклидовом пространстве,—
определение их близости. В частности, изучая рис. 3.1, можно
прийти к интуитивному выводу о принадлежности вектора х
классу (Ot исключительно из тех соображений, что этот вектор
находится ближе к векторам образов класса со,-.
Можно рассчитывать на получение удовлетворительных прак-
практических результатов при классификации образов с помощью
функций расстояния только в тех случаях, когда классы образов
обнаруживают тенденцию к проявлению кластеризационных
свойств. Это обстоятельство можно оценить, сопоставив рис. 3.1
и 3.2. Изучение первого рисунка показывает, что отнесение об-
образа х к классу аи не вызовет сомнений в связи с его близостью
к этому классу, как уже отмечалось выше. Что касается ситуа-
ситуации, представленной на рис. 3.2, то довольно трудно найти осно-
основание для зачисления образа х в один из классов, исходя из
90
Гл. 3. Классификация пбразпк с помощью функции расстояния
оценки его близости образам соответствующего класса, хотя
классы и не пересекаются.
В следующих параграфах этим идеям придается общая фор-
форма и они развиваются на уровне соответствующей математиче-
математической строгости. Поскольку близость классифицируемого образа
к образам некоторого класса будет использоваться в качестве
критерия для его классификации, назовем такой подход класси-
классификацией образов по критерию минимума расстояния. Так как
Рис. 3.2. Образы, классификация кото-
которых с помощью понятия близости вы-
вызывает затру цнения.
кластеризационные свойства весьма существенно влияют на ра-
работу классификаторов, основанных на концепции расстоянии, з
настоящей главе будет предложено несколько алгоритмов оты-
отыскания кластеров.
3.2. КЛАССИФИКАЦИЯ ОБРАЗОВ ПО КРИТЕРИЮ
МИНИМУМА РАССТОЯНИЯ
Классификация образов с помощью функций расстояния —
одна из первых идей автоматического распознавания образов.
Этот простой метод классификации оказывается весьма эффек-
эффективным инструментом при решении таких задач, в которых
классы характеризуются степенью изменчивости, ограниченной
в разумных пределах. В данном параграфе подробно рассмат-
рассматриваются свойства и способы реализации классификаторов, ра-
работающих на основе критерия минимума расстояния. Мы начнем
с рассмотрения классов, которые можно характеризовать, вы-
выбрав по одному эталонному образу из класса. Затем полученные
для этого случая результаты распространяются па случай не-
нескольких эталонов. И, наконец, рассматриваются общие свой-
свойства этого метода классификации и определяются границы его
классификационных возможностей.
3.2. Классификация образов по минимуму расстояния 91
3.2.1. Случай единственности эталона
В некоторых случаях образы любого из рассматриваемых
классов проявляют тенденцию к тесной группировке вокруг
некоторого образа, являющегося типичным или репрезентатив-
репрезентативным для соответствующего класса. Подобные ситуации возни-
возникают, если изменчивость образов невелика, а помехи легко
поддаются учету. Типичным примером этого служит задача счи-
считывания банковских чеков с помощью ЭВМ. Символы, помещае-
помещаемые на чеках, сильно стилизованы и обычно наносятся магнит-
магнитной печатной краской с тем, чтобы упростить процесс снятия
показаний. В ситуациях, подобных этой, векторы измерений
(образы) в каждом классе будут почти идентичны, поскольку
одинаковые символы на всех практически используемых чеках
идентичны. В таких условиях классификаторы, действующие по
принципу минимального расстояния, могут оказаться чрезвы-
чрезвычайно эффективным средством решения задачи классификации.
Рассмотрим М классов; пусть эти классы допускают пред-
представление с помощью эталонных образов z,, z2, .... zM. Евкли-
Евклидово расстояние между произвольным вектором образа х и г-м
эталоном бпределяется следующим выражением:
Dt = || х - z, I! = У(* - z{)' (x - z,). C.2.1)
Классификатор, построенный по принципу минимума расстоя-
расстояния, вычисляет расстояние, отделяющее неклассифицированный
образ х от эталона каждого класса, и зачисляет этот образ в
класс, оказавшийся ближайшим к нему. Другими словами, об-
образ х приписывается к классу cot-, если условие Di < D,- выпол-
выполняется для всех / ф I. Случаи равенства расстояний разре-
разрешаются произвольным образом.
Формуле C.2.1) можно придать более удобный вид. Возве-
Возведение всех членов в квадрат дает
= х х - 2x'z; + г'.г1 = х'х - 2 (x'z. -1 zjz,). C.2.2)
Выбор минимального значения /)? эквивалентен выбору ми-
минимального Di, поскольку все расстояния — величины неотрица-
неотрицательные. Формула C.2.2), однако, показывает, что выбор мини-
минимального значения o2t эквивалентен выбору максимального
значения разности Ix z.—-^г^Л, поскольку при вычислении
любых Ь\, г = 1, 2, ..., М, член х'х не зависит от значения L
Следовательно, решающие функции можно определять как
dt (х) = x'z, - С/2) zjz,, i=l,2 М, C.2.3)
92
Г л 3. Классификация образов с помощью функций расстояния
где образ х относится к классу со,, если условие rf,(x) > d;(x)
справедливо для всех / ф i.
Отметим, что rf,(x) — линейная решающая функция, т. е. если
г,/, /= 1, 2 л, —компоненты вектора z,, причем
wil = zih /=1,2,..., л,
Х =
*•)
1
ТО C.2.3) можно представить в обычной линейной форме
dt(x) = w/ix, i=l, 2 Л/. C.2.5)
где W/ = (oy/b i?.',2 ffi'*.n+i)'.
На рис. 3.3 изображена разделяющая граница для примера
с двумя классами, каждый из которых задавался единственным
Эталон масса
Разделяющая граница
Рис. 3.3. Граница, разделяющая два класса, каждый из которых определяется
одним эталоном.
эталоном. В конце данной главы в качестве одного из упражне-
упражнений предлагается показать, что линейная разделяющая поверх-
поверхность, обеспечивающая разделение всех пар эталонных точек
z; и z/, является гиперплоскостью, которая представляет собой
геометрическое место точек, равноудаленных от этих двух эта-
эталонных точек. Мы убедились, таким образом, что классифика-
S 7 Классификация образов по минимуму расстояния 9Эг
торы, основанные на принципе минимального расстояния, пред-
представляют собой частный случай линейного классификатора, раз-
разделяющие границы которого должны обладать указанным
свойством. Поскольку классификатор, основанный на принципе
минимального расстояния, классифицирует образы, исходя из
наиболее полного совпадения образа с эталонами соответствую-
соответствующих классов, этот подход называют также корреляцией или
сопоставлением с кластером.
3.2.2. Множественность эталонов
Допустим, что каждый класс можно охарактеризовать не
единственным, а несколькими эталонными образами, т. е. любой
образ, принадлежащий классу со,-, проявляет тенденцию к груп-
группировке вокруг одного из эталонов z{, z?, .. ., z^/( где /V,-—ко-
/V,-—количество эталонных образов, определяющих i-й класс. В этом
случае можно воспользоваться классификатором, подобным рас-
рассмотренному в предыдущем пункте. Запишем функцию, опре-
определяющую расстояние между произвольным образом х и клас-
классом со,-, в виде
?>. = гшп||л: — г'Л, /= 1, 2, ...,#,-; C.2.6)
это означает, что Д-— наименьшее из расстояний от образа х
до каждого эталона класса со;. Как и раньше, вычисляются зна-
значения расстояний Д-, r=l, 2 М, и классифицируемый
образ зачисляется в класс со,-, если условие D, < D, справедливо
для всех / Ф i. В случае равенства расстояний решение прини-
принимается произвольным образом.
Следуя процедуре, рассмотренной в п. 3.2.1, получаем ре-
решающие функции
dt (х) = max {(x'z<) - (•/„) (z{)' z<}, / = 1, 2, ..., ЛЛ, C.2.7)
й, как и раньше, образ х зачисляется в класс со,-, если условие
rf,(x)>d/(x) справедливо для всех \Ф L
На рис. 3.4 представлены разделяющие границы для случая
двух классов, когда каждый класс имеет два эталона. Обратите
внимание на то обстоятельство, что границы, разделяющие
классы со, и со/, являются кусочно-линейными^ Этот случай
можно было бы интерпретировать как задачу о разбиении на
четыре класса, каждый из которых обладает единственным эта-
эталоном, тогда участки границ представляют собой геометрические
места точек, равноудаленных от прямых, соединяющих эталоны
различных классов. Это утверждение согласуется со свойствами
94
Гл. 3. Классификация образов с помощью функций расстояния
разделяющих границ классификаторов для случая единственно-
единственности эталонов, являющегося частным случаем соотношений
C.2.6) и C.2.7).
Точно так же, как выражение C.2.3) представляло частный
случай линейного классификатора, выражение C.2.7) является
Эталон
класса
Разделяющая граница
Рис. 3.4. Кусочно-линейные границы, разделяющие два класса, каждый из
которых определяется двумя эталонами.
частным случаем классификаторов более общего вида — кусочно-
линейных. Решающие функции таких классификаторов имеют
следующий вид:
^(х) = тах{^.(х)}, /=1, 2 М, /= 1, 2 ЛЛ, C.2.8)
где функция d\ (х) определяется выражением
d\ (х) =
w'2x2
w
\nXn
= (w{)' x. C.2.9)
В огличие от решающих функций, определяемых формулой
C.2.7), от этих решающих функций не требуется соответствия
форме, представленной на рис. 3.4.
Читатель должен вспомнить, что, как указывалось в гл. 2,
одной из основных проблем синтеза классификаторов- образов-
является задача определения параметров решающей функции.
3.2 Классификация образов по минимуму расстояния §5
Выше отмечалось, что известны универсальные итеративные
алгоритмы, которые можно использовать для определения пара-
параметров линейной решающей функции (они рассматриваются в
гл. 5 и 6). К сожалению, до сих пор не известен действительно
общий алгоритм для кусочно-линейного случая C.2.8), C.2.9).
Заметим, однако, что частные случаи C.2.6) и C.2.7) реали-
реализуются легко, если классы обладают относительно небольшим
числом эталонов.
3.2.3. Обобщение принципов классификации по минимуму
расстояния
Хотя идеи работы с небольшим количеством эталонов и
евклидовыми расстояниями обладают геометрической привлека-
привлекательностью, подход, основанный на классификации но критерию
минимума расстояния, ими не исчерпывается. Для того чтобы
продолжить исследование общих свойств этой схемы классифи-
классификации, рассмотрим выборку образов с известной классифика-
классификацией {s\, s2, ..., sN}, причем предполагается, что каждый образ
выборки входит в один из классов Wj, «г, •¦-, <*>м. Можно опре-
определить правило классификации, основанное на принципе бли-
ближайшего соседа (БС-правило); это правило относит классифи-
классифицируемый образ к классу, к которому принадлежит его ближай-
ближайший сосед, причем образ S;e{si, s2, ..., sw} называется бли-
ближайшим соседом образа х, если
D(s(, x) = min{D(sb x)}, l=\, 2, ..., N, C.2.10)
где D — любое расстояние, определение которого допустимо на
пространстве образов.
Эту процедуру классификации можно назвать 1-БС-прави-
лом, так как при ее применении учитывается принадлежность
некоторому классу только одного ближайшего соседа образа х.
Нет, однако, причин, которые могли бы воспрепятствовать вве-
введению <7-БС-правила, предусматривающего определение q бли-
ближайших к х образов и зачисление его в тот класс, к которому
относится наибольшее число образов, входящих в эту группу.
Сопоставление соотношений C.2.10) и C.2.6) показывает, что
1-БС-правило есть не что иное, как рассмотренный в предыду-
предыдущем разделе случай множественности эталонов, если в качестве
D выбирается евклидово расстояние.
Интересный результат, относящийся к сравнению 1-БС- и
д-БС-правил, можно получить, обратившись к рис. 3.5. Допу-
Допустим, что вероятность появления образов обоих представленных
классов одинакова и, как показано на рисунке, образы классов
ш, и о)/ равномерно распределены в пределах соответствующих
96 Га 3. Классификация образов с помощью функций расстояний.
кругов Ri и Rj. В таком случае для выборки объема N вероят-
вероятность того, что точно а выбранных образов принадлежит классу
со,-, определяется выражением
Pi = -p-C%, C.2.11)
где Cn = ЛП/а! (N — а)!—число способов, которыми выборку
объема N можно разделить на два класса, содержащих а и
N— а элементов соответственно; 2W определяет общее число
способов разбиения N элементов на два класса. Очевидно, что
вероятность /?, принадлежности а из N элементов выборки клас-
классу со/ равна вероятности /?,-.
h>2l
Рис. 3.5. Два класса, покрывающие идентичные области, в которых образы
распределены равномерно.
Допустим, что классифицируемый образ х принадлежит
классу со,-. При этом применение 1-БС-правила приведет к ошиб-
ошибке только в том случае, если ближайший сосед образа х входит
в класс со/ и, следовательно, расположен в круге R/. С другой
стороны, если образ х принадлежит классу со,-, а его ближайший
сосед находится в круге Rj, то в этом круге должны быть распо-
расположены все образы, что абсолютно очевидно из рис. 3.5. Это
означает, что вероятность ошибки при применении 1-БС-правила
равна в этом случае вероятности принадлежности всех образов
классу со/, которую можно определить, положив а = N ъ выра-
выражении C.2.11), т. е.
Ре, = ^Г- C-2.12)
Подобным же образом можно определить вероятность совер-
совершить ошибку при использовании <7-БС-правила. Это правило
зачисляет классифицируемый образ в класс, к которому при-
принадлежит большинство его q ближайших соседей. Поскольку
рассматривается случай разделения на два класса, в качестве
q можно выбрать нечетное целое число, и следовательно, прин-
принцип большинства всегда будет работать.
Допустим, что образ х принадлежит классу со, и он, следова-
следовательно, расположен в круге Ri. В таком случае применение
3.2. Классификация образов по минимуму расстояния 97
9-БС-правила приведет к неправильной классификации только
при условии, что в круге Rt находится (q—1)/2 или меньшее
количество образов. При этом нельзя располагать большин-
большинством, превышающим {q—1)/2 ближайших соседей из круга
Ri, необходимым для подтверждения правильности зачисления
образа х в класс ьц. Соответствующая вероятность, являющаяся,
по существу, вероятностью ошибки при использовании q-bC-npa-
вила, равна сумме вероятностей вхождения 0, 1, 2, ..., (q— 1)/2
элементов выборки в круг R{. Следовательно, воспользовавшись
уравнением C.2.11), получаем выражение для вероятности
ошибки дри использовании <7-БС-правила:
C9-D/2
Сопоставление вероятностей ошибки классификации рв{ и ре
показывает, что в данном случае 1-БС-правило характеризуется
строго меньшей вероятностью ошибки, чем любое ^-БС-правило
От этого примера можно прийти к общему случаю, указав,
что при задании М классов 1-БС-правило работает лучше, чем
^-БС-правило (<7=5^=1), если все расстояния, разделяющие об-
образы одного класса, меньше всех расстояний между образами,
принадлежащими различным классам.
Можно также показать, что в случае выборок большого
объема (N—*-oo) и при выполнении некоторых благоприятных
условий вероятность ошибки 1-БС-правила заключена в сле-
следующих пределах:
где рв—байесовская вероятность ошибки. Как будет показано
в следующей главе, байесовская вероятность ошибки — наи-
наименьшая вероятность ошибки, достижимая в среднем.
Неравенство C.2.14) показывает, что вероятность ошибки
для 1-БС-правила превышает вероятность ошибки для правила
Байеса не более чем в два раза. Это выражение устанавливает
теоретические верхний и нижний пределы качества классифика-
классификации с помощью 1-БС-правила. Практическим препятствием,
однако, является то обстоятельство, что для достижения указан-
указанных границ необходимо сохранять в памяти большое число об-
образов, о которых известна принадлежность их некоторому клас-
классу. Кроме того, при осуществлении классификации необходимо
вычислять расстояния между каждым классифицируемым об-
образом и всеми образами, хранящимися в памяти системы. При
больших объемах обучающих выборок это обстоятельство вызы-
вызывает Серьезные вычислительные трудности.
4 Зак. 591
98 Гл. 3 Классификация образов с помощью функций расстояния
3.2.4. Синтез системы распознавания. Пример
Классификация образов по критерию минимума расстояния
широко используется в специализированных устройствах, пред-
предназначенных для распознавания символов, в частности в устрой-
устройствах для считывания кодовых символов с банковских чеков,
описанных в гл. 1. Данный пример приводится для того, чтобы
достаточно подробно обсудить принципы работы подобных
устройств и использовать их для иллюстрации этапов построе-
построения несложной системы распознавания, основанной на рассмот-
рассмотренных методах.
Основным принципом распознавания символов комплекта
стилизованного шрифта является сопоставление но признакам,
упомянутое в § 1.5. Реализовать процесс сопоставления можно по-
посредством классификатора, использующего критерий минимума
расстояния. В связи с высокой степенью стилизации и хорошим
качеством символов мы, в сущности, имеем дело с задачей раз-
разбиения на четырнадцать классов, каждый из которых пред-
представляется единственным эталоном. Форма символов гаранти-
гарантирует необходимую степень разделения эталонов. Обозначим
векторами z,-, i= I, 2, ..., 14, точки, соответствующие запоми-
запоминаемым значениям сигнала, представляющего каждый символ,
а вектором х — аналогичные точки сигнала от подаваемого на
вход системы распознавания символа. Если рассматривать зна-
значения сигнала лишь на девяти внутренних вертикальных обра-
образующих сетки (см. рис. 1.7), то каждый образ будет представ-
представлен девятимерным вектором. Вполне естественно при этом отно-
относить образ х, классификация которого неизвестна, к тому классу,
эталон которого является для этого образа х ближайшим.
Реализация процедуры использует принцип минимума рас-
расстояния.
Как было показано в C.2.4) и C.2.5), задача с единственным
эталоном допускает представление с помощью линейных решаю-
решающих функций. Это обстоятельство было использовано практи-
практически, когда соответствующие решающие функции реализовы-
вались с помощью несложной матрицы резисторов (см. рис. 2.10),
что позволило увеличить скорость классификации в устройствах
считывания стилизованного шрифта.
Хотя большинство современных коммерческих устройств,
предназначенных для считывания стилизованного шрифта, осно-
основаны на рассмотренных выше принципах, полезно еще раз
проанализировать эту задачу и синтезировать несложную си-
систему распознавания символов, ориентированную на машинную
реализацию. Наша цель в этом случае состоит не в обсуждении
подробностей и вариантов разработки системы, а заключается
скорее в том, чтобы на примере известной задачи системати-
3.2 Классификация образов по минимуму расстояния 99
чески проиллюстрировать общепринятую методику построения
системы распознавания образов.
Первым этапом разработки системы является выбор измери-
измерительного устройства, которое должно обеспечить преобразование
каждого символа в образ, представленный количественными
параметрами. Хотя рассмотренная выше схема, вероятно, реали-
реализует наиболее эффективный метод измерения, рассмотрим аль-
альтернативный вариант, изображенный на рис. 3.6, а. Этот метод,
который часто используется в более сложных устройствах, пред-
предназначенных для считывания различных наборов шрифта, в
частности символов, используемых в печатающих устройствах,
сводится к следующему. Символ освещается и его изображение
с помощью системы линз (на рисунке показана лишь одна из
них) проектируется на матрицу фотоэлементов. Каждый фото-
фотоэлемент, входящий в матрицу, срабатывает только при доста-
достаточно интенсивном освещении его поверхности. Обозначив вы-
выходную величину возбужденного элемента как 0, а невозбуж-
невозбужденного— как 1, можно считать, что в результате подобной
процедуры измерения для каждого символа получается соответ-
соответствующая двоичная матрица. Эта матрица, в сущности, дает
двоичное изображение символа, в котором нулями представлены
белые участки спроектированного изображения, а единицами —
черные.
Если матрица фотоэлементов идентична сетчатке, представ-
представленной на рис. 1.7 для каждого символа, очевидно, что каждый
символ преобразуется в двоичную матрицу размера 9X7. По-
Последнюю в свою очередь можно трансформировать в 63-мерный
вектор, считая, скажем, первую строку семью первыми компо-
компонентами вектора, вторую строку — семью следующими и т. д.
Эта операция, естественно, совершенно не обязательна, однако
ради единообразия системы обозначений будем полагать, что
все матрицы образов представлены в векторной форме.
Следующий стандартный этап построения системы распозна-
распознавания связан с выбором набора признаков, характеризующих
изучаемые объекты. В данном случае можно опустить этот этап,
так как решается простая задача, в которой каждый класс пред-
представляется единственным эталоном. Методы выбора признаков,
пригодные для решения обширного набора более сложных задач,
будут рассмотрены в гл. 7.
И, наконец, следует заняться синтезом собственно класси-
классификатора. В данном случае этот этап сводится просто к разра-
разработке устройства, обеспечивающего вычисление расстояний от
заданного образа до всех эталонов и выбор минимального рас-
расстояния для классификации этого образа.
Укрупненная блок-схема реализации на ЭВМ классифика-
классификатора, действующего по принципу минимума расстояния, приве-
Источник \
света
Перемещение бумаги
СЧИТЫВАЮЩЕЕ
УСТРОЙСТВО
ВХОДНОЕ
ЗАПОМИНАЮЩЕ
УСТРОЙСТВО
ПАМЯТЬ,
СОДЕРЖАЩАЯ ДАННЫЕ
Об ЭТАЛОНАХ
И ПРОГРАММУ ОПРЕДЕЛЕ-
ОПРЕДЕЛЕНИЯ МИНИМАЛЬНОГО
РАССТОЯНИЯ
ЦИФРОВАЯ
ВЫЧИСЛИТЕЛЬНАЯ
МАШИНА
ПАМЯТЬ
ДЛЯ ТЕКУЩЕЙ
ИНФОРМАЦИИ
ЗАГРУЗКА ЭТАЛОНОВ
СЧИТЫВАНИЕ ОЬРАЗА X
ИЗ ВХОДНОГО
ЗАПОМИНАЮЩЕГО
УСТРОЙСТВА
¦
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ
и,2,"-,М
ЗАЧИСЛЕНИЕ ОЬРАЗА X
В КЛАСС Ц, ЕСЛИ
Л[ < Dj ДЛЯ
Решение
Нет ^пАССИВ^\
—-^ЗАКОНЧИЛСЯ/*
)Ма
( ОСТАНОВ )
В память для
*¦ текущей
информации
Рис. 3.6. Система, распознавания стилизованных символов: а — оптическое читающее устройство;
б — вычислительная система; в — блок-схема основного программного обеспечения.
3.3. Выявление кластеров 101
дена на рис. 3.6, б. Блок считывания, как отмечалось выше,
обеспечивает получение вектора образа для каждого считывае-
считываемого символа. Отмеченное на схеме входное запоминающее
устройство представляет собой просто буфер; как правило, это
магнитная лента или магнитный диск, используемый для хране-
хранения результатов, полученных на этапе считывания; последние
затем поступают в машину для обработки. Эталоны и программы
определения минимального расстояния обычно хранятся во
внешнем запоминающем устройстве на магнитном диске, маг-
магнитной ленте, перфокартах или других подходящих носителях.
Блок-схема программы приведена на рис. 3.6, в. Эта программа
вводится в машину только в тех случаях, когда она необходима
для обработки символов. На заключительном этапе работы
системы полученные результаты запоминаются с тем, чтобы их
можно было использовать впоследствии, например, для выписы-
выписывания и ведения счетов, а также осуществления различных опе-
операций по взаимным расчетам между отдельными банками.
Система, представленная на рис. 3.6, может быть реализо-
реализована на любой снабженной соответствующим периферийным
оборудованием универсальной вычислительной машине, по-
поскольку требования, предъявляемые системой и к памяти, и к
возможностям обработки, явно не очень суровы. Реальные
системы распознавания символов обычно выпускаются в виде
специализированного вычислительного устройства с тем, чтобы
увеличить скорость обработки символов.
3.3. ВЫЯВЛЕНИЕ КЛАСТЕРОВ
Из сказанного в предыдущих разделах следует, что умение
находить в заданном наборе данных эталоны или центры кла-
кластеров играет главную роль в построении классификаторов об-
образов по принципу минимума расстояния. В данном параграфе
будут достаточно подробно рассмотрены методы выявления кла-
кластеров. Эти методы являются как бы поперечным разрезом мно-
множества типичных подходов к решению задачи выявления кла-
кластеров. С самого начала стоит заметить, что выявление класте-
кластеров во многих отношениях является «искусством» весьма
эмпирическим, так как качество работы определенного алго-
алгоритма зависит не только от характера анализируемых данных,
но также в значительной степени определяется выбранной мерой
подобия образов и методом, используемым для идентификации
кластеров в системе данных. Соответствующие понятия, рас-
рассматриваемые ниже, обеспечивают также основу для построе-
построения систем распознавания без учителя (эта тема обсуждается
в§ 3.4).
102 Га 3. Классификация образов с помощью функций расстояния
3.3.1. Меры сходства
До сих пор идея кластеризации данных обсуждалась на
довольно неформальном уровне. Для того чтобы определить на
множестве данных кластер, необходимо в первую очередь ввести
меру сходства (подобия), которая может быть положена в
основу правила отнесения образов к области,, характеризуемой
некоторым центром кластера. Ранее рассматривалось евклидово
расстояние между образами х и z:
?> = ||x-z||; C.3.1)
эта характеристика использовалась в качестве меры сходства
соответствующих образов: чем меньше расстояние между ними,
тем больше сходство. На этом понятии основаны все алгоритмы,
рассматриваемые в данной главе. Существуют, однако, и другие
состоятельные расстояния, которые в ряде случаев оказываются
полезны. Так, например, расстояние Махаланобиса, определяе-
определяемое для образов хит как
О = (х-т)'С-*(х-т), C.3.2)
является полезной мерой сходства в тех случаях, когда статисти-
статистические характеристики образов присутствуют в явном виде.
В формуле C.3.2) С — ковариационная матрица совокупности
образов, m — вектор средних значений, а х представляет образ
с переменными характеристиками. Соответствующие методы
подробно рассматриваются в следующей главе.
Меры сходства не исчерпываются расстояниями. В качестве
примера можно привести неметрическую функцию сходства
представляющую собой косинус угла, образованного векторами
х и z, и достигающую максимума, когда их направления совпа-
совпадают. Этой мерой сходства удобно пользоваться в тех случаях,
когда кластеры обнаруживают тенденцию располагаться вдоль
главных осей, как это показано на рис. 3.7. Этот рисунок, в част-
частности, показывает, что образ z\ обладает большим сходством
с образом х, чем образ Z2, поскольку значение функции s(x, z\)
больше значения s(x, z2). Следует, однако, отметить, что исполь-
использование данной меры сходства связано определенными ограни-
ограничениями, например такими, как достаточное отстояние класте-
кластеров друг от друга и от начала координат.
Когда рассматриваются двоичные образы и их элементы при-
принимают значения из множества {0, 1}, функции сходства C.3.3)
можно дать интересную негеометрическую интерпретацию. Если
3.3. Выявление кластеров ' ЮЗ
Xi = 1, считается, что двоичный образ х обладает /-м признаком.
В таком случае член x'z в C.3.3) просто характеризует число
общих для образов х и z признаков, a ||xj|||z ||= V(x'x)(z'z) —
среднее геометрическое числа признаков, которыми обладает'
образ х, и числа признаков, которыми обладает образ z. По-
Понятно, что функция s(x, z) есть мера наличия общих признаков
у двоичных векторов х и z.
Двоичным вариантом формулы C.3.3), который нашел широ-
широкое распространен^ в информационном поиске, нозологии
Начало координат
x'l,
тщ
Рис. 3.7. Иллюстрация понятия меры сходства.
(классификации болезней) и таксономии (классификации видов
животных и растенийI), является так называемая мера Тани-
мото, определяемая как
Предоставляем читателю в качестве упражнения дать интерпре-
интерпретацию этой меры.
Рассмотренные меры сходства ни в коем случае не следует
считать единственными — это просто типичные меры. Как уже
указывалось, дальнейшее обсуждение будет проходить на основе
') Мы уже отмечали, что в отечественной литературе по распознаванию
образов до последнего времени не было принято разделение терминов «таксо-
«таксономия» и «кластер-анализ», причем для обозначения соответствующего метода
в основном применяется т^рвый из них (см. прим. на стр. 28) Биологическая
«окраска» таксономии отражает традиции англоязычной литературы по клас-
классификациям.— Прим. перев.
104 Гл. 3. Классификация образов с помощью функций расстояния
использования евклидовой меры подобия C.3.1) в связи с про-
простотой ее интерпретации в рамках известной концепции близо-
близости. Кроме того, эта мера совместима с методами классифика-
классификации образов, обсуждавшимися в § 3.2.
3.3.2. Критерии кластеризации
Проблема определения процедуры разбиения анализируемых
данных на кластеры остается открытой и после выбора меры
сходства образов. Критерий кластеризации может либо воспро-
воспроизводить некие эвристические соображения, либо основываться
на минимизации (или максимизации) какого-нибудь показателя
качества.
При эвристическом подходе решающую роль играют интуи-
интуиция и опыт. Он предусматривает задание набора правил, кото-
которые обеспечивают использование выбранной меры сходства для
отнесения образов к одному из кластеров. Евклидово расстоя-
расстояние C.3.1) хорошо приспособлено для подобного подхода, что
связано с естественностью его интерпретации как меры близо-
близости. Поскольку, однако, близость двух образов является относи-
относительной мерой их подобия, обычно приходится вводить порог,
чтобы установить приемлемые степени сходства для процесса
отыскания кластеров. Алгоритмы, рассматриваемые в следую-
следующих двух пунктах, служат для этого хорошей иллюстрацией.
Подход к кластеризации, предусматривающий использование
показателя качества, связан с разработкой процедур, которые
обеспечат минимизацию или максимизацию выбранного пока-
показателя качества. Одним из наиболее популярных показателей
является сумма квадратов ошибки
"с
v tn II2 «4 11
где Nc — число кластеров, 5/ — множество образов, относящихся
к /-му кластеру, а
m^~17 L x ^iCS-^
— вектор выборочных средних значений для множества 5у; Nj
характеризует количество образов, входящих во множество Sj.
Показатель качества C.3.5) определяет общую сумму квадра-
квадратов отклонений характеристик всех образов, входящих в неко-
некоторый кластер, от соответствующих средних значений по кла-
кластеру. Алгоритм, основанный на этом показателе качества, рас-
рассматривается в п. 3.3.5.
3.3. Выявление кластеров 105
Естественно, существует масса показателей качества помимо
рассмотренного. Вот некоторые широко распространенные пока-
показатели: среднее квадратов расстояний между образами в кла-
кластере; среднее квадратов расстояний между образами, входя-
входящими в разные кластеры; показатели, основанные на понятии
матрицы рассеяния; минимум и максимум дисперсии, а также
еще дюжина показателей качества, использовавшихся прежде.
Нередко применяются алгоритмы отыскания кластеров, осно-
основанные на совместном использовании эвристического подхода и
показателя качества. Подобной комбинацией является алгоритм
ИСОМАД1), рассматриваемый в п. 3.3.6. В свете наших преды-
предыдущих замечаний о состоянии дел в области кластеризации это
обстоятельство нельзя назвать неожиданным, так как качество
отдельных алгоритмов отыскания кластеров в значительной сте-у
пени определяется способностями его авторов по части извле-
извлечения полезной информации из анализируемых данных. '
3.3.3. Простой алгоритм выявления кластеров
Пусть задано множество N образов {хь х2, ..., xjv}. Пусть
также центр первого кластера zi совпадает с любым из заданных
образов и определена произвольная неотрицательная пороговая
величина Т; для удобства можно считать, что zj = xj. После
этого вычисляется расстояние D2i между образом х2 и центром
кластера zi по формуле C.2.1). Если это расстояние больше
значения пороговой величины Т, то учреждается новый центр
кластера z2 = x2. В противном случае образ х2 включается в
кластер, центром которого является z\. Пусть условие Dzi > Т
выполнено, т. е. z2 — центр нового кластера. На следующем шаге
вычисляются расстояния D3i и D32 от образа хз до центров кла-
кластеров zi и z2. Если оба расстояния оказываются больше порога
Т, то учреждается новый центр кластера z3 = хз. В противном
случае образ Хз зачисляется в тот кластер, чей центр к нему
ближе. Подобным же образом расстояния от каждого нового
образа до каждого известного центра кластера вычисляются и
сравниваются с пороговой величиной — если все эти расстояния
превосходят значение порога Т, учреждается новый центр кла-
кластера. В противном случае образ зачисляется в кластер с самым
близким к нему центром.
Результаты описанной процедуры определяются выбором
первого центра кластера, порядком осмотра образов, значением
пороговой величины Т и, конечно, геометрическими характери-
характеристиками данных. Эти влияния иллюстрируются рис. 3.8, на кото-
котором представлены три различных варианта выбора центров
') См. прим. на стр. 112. — Прим, перев.
106
Гл. 3. Классификация образов с ппмпшью функций расстояния
кластеров для одни\ и ге\ же- данных, возникшие в результате
изменения только значения порога Т и исходной точки кластери-
кластеризации.
Хотя эгот алгоритм обладает рядом очевидных недостатков,
он позволяет просто и быстро получить приблизительные оценки
Рнс. 3.8. Иллюстрация влияния выбора величины порога и исходных точек
в простой схеме кластеризации.
основных характеристик заданного набора данных. Кроме того,
этот алгоритм привлекателен с вычислительной точки зрения,
так как для выявления центров кластеров, соответствующих
определенному значению порога Г, ему требуется только одно-
однократный просмотр выборки. Практически же, для того чтобы
хорошо понять геометрию распределения образов с помощью
такой процедуры, приходится проводить многочисленные экспе-
эксперименты с различными значениями порога и различными исход-
исходными точками кластеризации. Поскольку изучаемые образы
обычно имеют высокую размерность, визуальная интерпретация
результатов исключается; поэтому необходимая информация
добывается в основном при. помощи сопоставления после каж-
3.3 Выявление кластеров 107
дого цикла просмотра данных расстояний, разделяющих центры
кластеров, и количества образов, вошедших в различные кла-
кластеры. Полезными характеристиками являются также ближай-
ближайшая и наиболее удаленная от центра точки кластера и различие
размеров отдельных кластеров. Информацию, полученную таким
образом после каждого цикла обработки данных, можно исполь-
использовать для коррекции выбора нового значения порога Т и новой
исходной точки кластеризации в следующем цикле. Можно рас-
рассчитывать на получение с помощью подобной процедуры полез-
полезных результатов в тех случаях, когда в данных имеются харак-
характерные «гнезда», которые достаточно хорошо разделяются при
соответствующем выборе значения порога.
3.3.4. Алгоритм максиминного расстояния
Алгоритм, основанный на принципе максиминного (макси-
(максимально-минимального) расстояния, представляет собой еще
одну простую эвристическую процедуру, использующую евкли-
евклидово расстояние. Этот алгоритм в принципе аналогичен схеме
из п. 3.3.3, за исключением того обстоятельства, что в первую
очередь он выявляет наиболее удаленные кластеры. Соответ-
Соответствующую процедуру удобнее всего рассмотреть на конкретном
примере.
Возьмем выборку, состоящую из десяти двумерных образов
(рис. 3.9,а). Для того чтобы получить представление о количе-
количестве кластеров, выделяющихся в этих данных, целесообразно
воспользоваться алгоритмом, основанным на максиминном рас-
расстоянии. Описание алгоритма упрощают таблицы, приведенные
на рис. 3.9,6. Одна из них содержит выборочные образы, дру-
другая— список центров кластеров, установленных алгоритмом; до
начала работы алгоритма эта таблица пустая. На первом шаге
алгоритма один из объектов, например xi, произвольным обра-
образом назначается центром первого кластера (на рис. 3.9,6 этог
центр обозначен zi). Цифры, расположенные на этом рисунке
над стрелками, обозначают порядковый номер шага, на котором
производится выделение соответствующего центра кластера.
Затем отыскивается образ, отстоящий от образа xi на наи-
наибольшее расстояние; в данном случае это образ хе, который и
назначается центром кластера z2. На третьем шаге алгоритма
производится вычисление расстояний между всеми остальными
образами выборки и центрами кластеров zi и z2. В каждой паре
этих расстояний выделяется минимальное. После этого вы-
деляется максимальное из этих минимальных расстояний. Если
последнее составляет значительную часть расстояния между
центрами кластеров zi и z2 (скажем, по меньшей мере половину
этого расстояния), соответствующий образ назначается центром
*t
_L
_L
_L
1 2 3 h 5 6 7
a
/2
/3
X4
X6 /
/7
Хю
ID
/13)/
—*-?i
h
Рис. 3.9. a — выборка образов, использованная для иллюстрации работы ал-
алгоритма максиминного расстояния; б — таблицы, содержащие выборочные об-
образы и классы соответственно.
3.3. Выявление кластеров 109
кластера z3. В противном случае выполнение алгоритма прекра-
прекращается. Если воспользоваться таким критерием в приведенном
примере, легко убедиться в том, что центром кластера z3 стано-
становится образ Х7.
На следующем шаге алгоритма вычисляется расстояние меж-
между тремя выделенными центрами кластеров и всеми остальными
выборочными образами; в каждой группе из трех расстояний
выбирается минимальное. После этого, как и на предыдущем
шаге, находится максимальное из этих минимальных расстоя-
расстояний. Если последнее составляет значительную часть «типичных»
предыдущих максимальных расстояний, то соответствующий
образ назначается центром кластера z4. В противном случае
выполнение алгоритма прекращается. Хорошей мерой для
оценки типичных предыдущих расстояний является их среднее
значение. Если воспользоваться этим критерием в данном при-
примере и потребовать, чтобы новое максимальное расстояние со-
составляло по меньшей мере половину среднего, то из рис. 3.9, а
следует, что очередное максимальное расстояние, которым ока-
оказалось расстояние между образами xi и хз, не удовлетворяет
такому условию. Поэтому на данном шаге работа алгоритма
прерывается. В общем случае описанная процедура повторяется
до тех пор, пока на каком-либо шаге не будет получено макси-
максимальное расстояние, для которого условие, определяющее вы-
выделение нового кластера, не выполняется.
В этом простом примере были выделены три кластерных
центра xi, хе и Х7. При отнесении остальных выборочных образов
к одному из учрежденных кластеров используется критерий,
предусматривающий введение классифицируемого образа в тот
кластер, центр которого для него ближайший. В таком случае
из рис. 3.9, а заключаем, что получены три кластера: {хь х3, х4},
{хг, Хб} и {х5, х7, х8, х9, хю}. Результаты соответствуют нашим
интуитивным представлениям об этих данных. Можно более
точно определить центры кластеров, вычислив для каждого
набора выборочное среднее по формуле C.3.6). Эти средние
можно считать новыми центрами кластеров.
3.3.5. Алгоритм К внутригрупповых средних
Несложные алгоритмы, рассмотренные в пп. 3.3.3 и 3.3.4,
являются в сущности эвристическими процедурами. С другой
стороны, алгоритм, представленный ниже, минимизирует пока-
показатель качества, определенный как сумма квадратов расстояний
всех точек, входящих в кластерную область, до центра кластера.
Эта процедура, которую' часто называют алгоритмом, основан-
основанным на вычислении К внутригрупповых средних, состоит из сле-
следующих шагов.
110 Гл. 3. Классификация образов с помощью функций расстояния
Шаг 1. Выбираются К исходных центров кластеров zi(l),
z2(l), ..., z*(l). Этот выбор производится произвольно, и обыч-
обычно в качестве исходных центров используются первые К резуль-
результатов выборки из заданного множества образов.
Шаг 2. На k-м шаге итерации заданное множество образов
{х} распределяется но К кластерам по следующему правилу:
х е S, (*), если || х - z, (k) ||< || х - zt (k) || C.3.7)
для всех /= 1, 2 К, i?*j, где Sj(k) — множество образов,
входящих в кластер с центром Zj(k). В случае равенства в
C.3.7) решение принимается произвольным образом.
Шаг 3. На основе результатов шага 2 определяются новые
центры кластеров z,(& + 1), /= 1, 2, ..., К, исходя из условия,
что сумма квадратов расстояний между всеми образами, при-
принадлежащими множеству Sj(k), и новым центром кластера
должна быть минимальной. Другими словами, новые центры
кластеров z;(& + 1) выбираются таким образом, чтобы миними-
минимизировать показатель качества
'/ = I \\x-z,(k + l)\f, /=1,2 К. C.3.8)
S(ft)
Центр z/(&+!)> обеспечивающий минимизацию показателя ка-
качества, является, в сущности, выборочным средним, определен-
определенным по множеству Sj(k). Следовательно, новые центры класте-
кластеров определяются как
Zj(k + l) = ^j ? х, /=1,2, .... К, C.3.9)
где Nj — число выборочных образов, входящих в множество
Sj{k). Очевидно, что название алгоритма «/( внутригрупповых
средних» определяется способом, принятым для последователь-
последовательной коррекции назначения центров кластеров.
Шаг 4. Равенство Zj(k-\- 1) = Zj{k) при /=1, 2, ..., К яв-
ляетгя условием сходимости алгоритма, и при его достижении
выполнение алгоритма заканчивается. В противном случае алго-
алгоритм повторяется от шага 2.
Качество работы алгоритмов, основанных на вычислении К
внутригрупповых средних, зависит от числа выбираемых цент-
центров кластеров, от выбора исходных центров кластеров, от после-
последовательности осмотра образов и, естественно, от геометриче-
геометрических особенностей данных. Хотя для этого алгоритма общее до-
доказательство сходимости не известно, получения приемлемых
результатов можно ожидать в тех случаях, когда данные обра-
образуют характерные гроздья, отстоящие друг от друга достаточно
3.3 Выявление кластеров
II!
далеко. В большинстве случаев практическое применение этого
алгоритма потребует проведения экспериментов, связанных с
выбором различных значений параметра К и исходного распо-
расположения центров кластеров.
J L_L
7 8
1С
Рис. 3.10. Выборка образов, использованная для иллюстрации работы алго-
алгоритма выборочных средних по К центрам кластеризации.
Пример. В качестве простой численной иллюстрации алго-
алгоритма К внутригрупповых средних рассмотрим образы, пред-
представленные на рис. 3.10. Процедура протекает следующим
образом:
Шаг 1. Задается К = 2 и выбирается Zi(l) = Xi =@, 0)',
l) (l0)'
Шаг 2. Так как ||xi —z,(l)|| < Rx, —z,(l)|| и ||хз —zi(l)|| <
< ||х3 — Zi(l)||, i = 2, то Si(l) = {xi, хз}. Аналогично устанав-
устанавливается, что остальные образы расположены ближе к центру
кластера z2(l), и поэтому S2(l)= {х2, Х4, xs. .... х2о}.
Шаг 3. Коррекция назначения центров кластеров:
... +X20) =
112 Гл. 3. Классификация образов с помощью функций расстояния
Шаг 4. Так как z/B) Ф z/(l), / = 1, 2, то возврат к шагу 2.
Шаг 2. Выбор новых центров кластеров приводит к нера-
неравенству || х/ — zi B) || < || xi — z2B) || для / = 1, 2 8 и нера-
неравенству ||x;-z2B)|| < ||х/ —ziB)|| для / = 9, Ю, ..., 20. Сле-
Следовательно, Si B)= {Xi, Х2, ..., Х8} И S2B)= {Xg, Хю Х2о}.
Шаг 3. Коррекция назначения центров кластеров:
_ 1 у _ 1 _/7.(
2 seS,B) ''
Шаг 4. Так как z,C)=/=z/B), /= 1, 2, то возврат к шагу 2.
Шаг 2. Получаем те же результаты, что и на предыдущей
итерации: ZiD) = ZiC) и z2D) = z2C).
Шаг 3. Также получаем идентичные результаты.
Шаг 4. Так как z,D) = z/C), / = 1, 2, алгоритм сошелся и в
результате получены следующие центры кластеров:
1,25 \ /7,67"
Эти результаты согласуются с тем, что можно было бы ожи-
ожидать, ознакомившись с заданными образами.
3.3.6. Алгоритм ИСОМАД
Алгоритм ИСОМАД (Isodata) ') в принципе аналогичен про-
процедуре, предусматривающей вычисление К внутригрупповых
средних, поскольку и в этом алгоритме центрами кластеров слу-
служат выборочные средние, определяемые итеративно. Однако в
отличие от предыдущего алгоритма ИСОМАД обладает обшир-
обширным набором вспомогательных эвристических процедур, встроен-
встроенных в схему итерации. Это определение «эвристические» сле-
следует постоянно иметь в виду, следя за нашим изложением, по-
поскольку целый ряд описываемых ниже этапов вошел в алгоритм
в результате осмысления эмпирического опыта его использо-
использования.
До выполнения алгоритма следует задать набор Nc исходных
центров кластеров z\, z2 z . Этот набор, число элементов
•) Isodata — Iterative Self-Organizing Data Analysis Techniques
(ИСОМАД — Итеративный СамоОрганивуюшийся Метод Анализа Данных);
второе «а» введено в английскую аббревиатуру для благозвучия.
113
3.3 Выявление кластеров
которого не обязательно должно быть равно предписанному ко-
количеству кластеров, может быть получен выборкой образов из
заданного множества данных.
При работе с набором {xi, x2 \N}, составленным из N
элементов, алгоритм ИСОМАД выполняет следующие основные
шаги.
Шаг 1. Задаются параметры, определяющие процесс класте-
кластеризации:
К — необходимое число кластеров;
QN—параметр, с которым сравнивается количество выбо-
выборочных образов, вошедших в кластер;
6s—параметр, характеризующий среднеквадратичное от-
отклонение;
0с — параметр, характеризующий компактность;
L — максимальное количество пар центров кластеров, кото-
которые можно объединить;
/ — допустимое число циклов итерации.
Шаг 2. Заданные N образов распределяются по кластерам,
соответствующим выбранным исходным центрам, по правилу
xeS/, если || х — Z/IKHx — zt\\, /=1, 2, ..., Nc; 1ф\,
применяемому ко всем образам х, вошедшим в выборку; через
Sj обозначено подмножество образов выборки, включенных в
кластер с центром z/.
Шаг 3. Ликвидируются подмножества образов, в состав ко-
которых входит менее QN элементов, т. е. если для некоторого j
выполняется условие N/ < Вы, то подмножество 5/ исключается
из рассмотрения и значение Nc уменьшается на 1.
Шаг 4. Каждый центр кластера Z/, /=1, 2, ..., Nc, лока-
локализуется и корректируется посредством приравнивания его вы-
выборочному среднему, найденному по соответствующему подмно-
подмножеству S/, т. е.
Л х /12Ne,
где Nj — число объектов, вошедших в подмножество 5/.
Шаг 5. Вычисляется среднее расстояние D/ между объек-
объектами, входящими в подмножество S/, и соответствующим цент-
центром кластера по формуле
S Hx~z/li' /=1, 2, ..., tfe.
114 Гл. 3. Классификация образов с помощью функций расстояния
Шаг 6. Вычисляется обобщенное среднее расстонпн-. между
объектами, находящимися в отдельных кластерах, и соответ-
соответствующими центрами кластеров по формуле
Шаг 7. (а) Если текущий цикл итерации — последний, то
задается 0С = 0; переход к шагу 11. (б) Если условие Nc^ К/2
выполняется, то переход к шагу 8. (в) Если текущий цикл ите-
итерации имеет четный порядковый номер или выполняется условие
NC^2K, то переход к шагу 11; в противном случае процесс
итерации продолжается.
Шаг 8. Для каждого подмножества выборочных образов с
помощью соотношения
V
-щ Yj (Xik — Zi/J' t=l, 2, .... л; /=1,2 Nc
вычисляется вектор среднеквадратичного отклонения а/ =
= (оц, ст2/, ..., On/)', где п есть размерность образа, хц, есть
i-я компонента fe-ro объекта в подмножестве S/, Zy есть i-я ком-
компонента вектора, представляющего центр кластера Z/, и N/ — ко-
количество выборочных образов, включенных в подмножество S/.
Каждая компонента вектора среднеквадратичного отклонения
О] характеризует среднеквадратичное отклонение образа, вхо-
входящего в подмножество S,-, по одной из главных осей координат.
Шаг 9. В каждом векторе среднеквадратичного отклонения
а], /=1, 2, ..., Nc, отыскивается максимальная компонента
Су max-
Шаг 10. Если для любого ojmax, /= 1, 2 #<;, выпол-
выполняются УСЛОВИЯ СГ/ max > 6S «
а) Dj>D и JVy > 2(ew + 1)
или
б) ЛГс</С/2,
то кластер с центром zs расщепляется на два новых кластера
с центрами z+ и г~ соответственно, кластер с центром Z/ ликви-
ликвидируется, а значение Nc увеличивается на 1. Для определенич
центра кластера г^ к компоненте вектора z/, соответствующей
максимальной компоненте вектора а;, прибавляется заданная
величина -у,-: центр кластера г~ определяется вычитанием этой
же величины у/ из той же самой компоненты вектора Z/. В ка-
3.3 Выявление кластеров 115
честве величины у/ можно выбрать некоторую долю значения
максимальной среднеквадратичной компоненты ст/max, т. е. по-
положить у/ = kat max, где 0<fe^l. При выборе у/ следует
руководствоваться в основном тем, чтобы ее величина была до-
достаточно большой для различения разницы в расстояниях от
произвольного образа до новых двух центров кластеров, но до-
достаточно малой, чтобы общая структура кластеризации суще-
существенно не изменилась.
Если расщепление происходит на этом шаге, надо перейти к
шагу 2, в противном случае продолжать выполнение алгоритма.
Шаг 11. Вычисляются расстояния D,7 между всеми парами
центров кластеров:
Dt, = ^z,-z,l 1 = 1,2 Ne-l; j = i+\, ..., Nc.
Шаг 12. Расстояния Dq сравниваются с параметром 6С. Те
L расстояний, которые оказались меньше 6с, ранжируются в по-
порядке возрастания:
причем Dixtx < Di2i2 < ... <.DiLjL a L — максимальное число
пар центров кластеров, которые можно объединить. Следующий
шаг осуществляет процесс слияния кластеров.
Шаг 13. Каждое расстояние Dt[jl вычислено для определен-
определенной пары кластеров с центрами zt и z.. К этим парам в по-
последовательности, соответствующей увеличению расстояния
между центрами, применяется процедура слияния, осуществляе-
осуществляемая на основе следующего правила.
Кластеры с центрами г. и z/, 1=1, 2, .... L, объеди-
объединяются (при условии, что в текущем цикле итерации процедура
слияния не применялась ни к тому, ни к другому кластеру), при-
причем новый центр кластера определяется по формуле
Центры кластеров zt и z^ ликвидируются и значение Nc
уменьшается на 1.
Отметим, что допускается только попарное слияние класте-
кластеров и центр полученного в результате кластера рассчитывается,
исходя из позиций, занимаемых центрами объединяемых класте-
кластеров и взятых с весами, определяемыми количеством выборочных
образов в соответствующем кластере. Опыт свидетельствует
о том, что использование более сложных процедур объединения
кластеров может привести к получению неудовлетворительных
116 Гл. 3. Классификация образов с помощью функций расстояния
результатов. Описанная процедура обеспечивает выбор в каче-
качестве центра объединенного кластера точки, представляющей
истинное среднее сливаемых подмножеств образов. Важно
также иметь в виду, что, поскольку к каждому центру кластера
Рис. 3.11. Выборка образов, использованная для иллюстрации работы алго-
алгоритма ИСОМАД.
процедуру слияния можно применить только один раз, реализа-
реализация данного шага ни при каких обстоятельствах не может при-
привести к получению L объединенных кластеров.
Шаг 14. Если текущий цикл итерации — последний, то вы-
выполнение алгоритма прекращается. В противном случае следует
возвратиться либо к шагу 1, если но предписанию пользователя
меняется какой-либо из параметров, определяющих процесс
кластеризации, либо к шагу 2, если в очередном цикле итерации
параметры процесса должны остаться неизменными. Заверше-
Завершением цикла итерации считается каждый переход к шагам 1
или 2.
Пример. Хотя алгоритм ИСОМАД не очень подходит для
ручных вычислений, принцип его работы можно проиллюстри-
проиллюстрировать на простом примере. Рассмотрим выборку, образы кото-
которой размещены так, как это изображено на рис. 3.11.
3.3. Выявление кластеров 117
В данном случае N = 8 и п = 2. В качестве начальных
условий задаем Nc = 1, Zi = @, 0)' и следующие значения па-
параметров процесса кластеризации:
Шаг 1.
К = 2, QN=l, es=l, 6С = 4, L = 0, / = 4.
Если всякая априорная информация об анализируемых дан-
данных отсутствует, эти параметры выбираются произвольным об-
образом и затем корректируются от итерации к итерации.
Шаг 2. Так как задан только один центр кластера, то
и yVi = 8.
Шаг 3. Поскольку N\ > 6#, ни одно подмножество не лик-
ликвидируется.
Шаг 4. Корректируется положение центра кластера:
3,38
Шаг 5. Вычисляется расстояние ?>,-:
S IIх-2,11 = 2,26.
Шаг 6. Вычисляется расстояние D:
Шаг 7. Поскольку данный цикл итерации — не последний
и Nc = К/2, осуществляется переход к шагу 8.
Шаг 8. Для подмножества Si вычисляется вектор средне-
среднеквадратичного отклонения:
1,99'
Шаг 9. Максимальная компонента вектора <п равна 1,99, сле-
следовательно, 0! max = 1,99.
Шаг 10. Поскольку а\ max > 6S и Nc = К/2, кластер с цент-
центром zi расщепляется на два новых кластера. Следуя процедуре,
предусмотренной шагом 10, выбираем vy = 0,5a/ max » 1,0. При
этом
•4,38'
+ _/4,38\
Ei ~\2,75J'
118 Г л 3. Классификация образов с помощью функций расстояния
Для удобства записи будем называть центры этих кластеров Ъ\
и z2 соответственно. Значение Nc увеличивается на 1; переход
к шагу 2.
Шаг 2. Подмножества образов имеют теперь следующий вид:
5, = {х4, х5, х6> х7, xj, S2={xu x2, x3}
и yv, = 5, УУ2 = 3.
Шаг 3. Поскольку обе величины — и УУь и N2 — больше Q»,
ни одно подмножество не ликвидируется.
Шаг 4. Корректируется положение центров кластеров:
1 v D'80\ ' V -(['00
Шаг 5. Вычисляется расстояние Djt /=1,2:
D^-щ 2 llx-z,|| = 0,80,
Шаг 6. Вычисляется расстояние D:
Шаг 7. Поскольку данная итерация имеет четный порядко-
порядковый номер, условие (в) шага 7 выполняется. Поэтому следует
перейти к шагу 11.
Шаг 11. Вычисление расстояний между парами центров кла-
кластеров:
Шаг 12. Величина расстояния Di2 сопоставляется с парамет-
параметром 6С. В данном случае D12 > 6С.
Шаг 13. Результаты шага 12 показывают, что объединение
кластеров невозможно.
Шаг 14. Поскольку данный цикл итерации — не последний,
необходимо принять решение: вносить или не вносить изменения
в параметры процесса кластеризации. Так как в данном (про-
(простом) случае 1) число выделенных кластеров соответствует за-
заданному, 2) расстояние между ними больше среднего разброса,
3..? Выявление кластеров 119"
характеризуемого среднеквадратичными отклонениями, и 3) каж-
каждый кластер содержит существенную часть общего количества
выборочных образов, то делается вывод о том, что локализация
центров кластеров правильно отражает специфику анализируе-
анализируемых данных. Следовательно, переходим к шагу 2.
Шаги 2—6 дают те же результаты, что и в предыдущем
цикле итерации.
Шаг 7. Ни одно из условий, проверяемых при реализации
данного шага, не выполняется. Поэтому переходим к шагу 8.
Шаг 8. Для множеств St = {х4, х5, х6, х7, х8} и S2 = {хи х2). х3}
0,75 \ ( 0,82
Шаг 9. В данном случае а\ max = 0,75 и а2тах = 0,82.
Шаг 10. Условия расщепления кластеров не выполняются.
Следовательно, переходим к шагу 11.
Шаг 11. Полученный результат идентичен результату по-
последнего цикла итерации
Шаг 12. Полученный результат идентичен результату послед-
последнего цикла итерации.
Шаг 13. Полученный результат идентичен результату по-
последнего цикла итерации.
Шаг 14. На данном цикле итерации не были получены новые
результаты, за исключением изменения векторов среднеквадра-
среднеквадратичного отклонения. Поэтому переходим к шагу 2.
Шаги 2—6 дают те же результаты, что и в предыдущем
цикле итерации.
Шаг 7. Поскольку данный цикл итерации — последний, за-
задаем 0с = 0 и переходим к шагу 11.
Шаг 11. Как и раньше,
Шаг 12. Полученный результат идентичен результату послед-
последнего цикла итерации.
Шаг 13. Результаты шага 12 показывают, что объединение
кластеров невозможно.
120 Гл. 3. Классификация образов с помощью функций расстояния
Шаг 14. Поскольку данный цикл итерации —последний, вы*
полнение алгоритма заканчивается.
Даже из этого простого примера должно быть ясно, что при-
применение алгоритма ИСОМАД к набору данных умеренной
сложности в принципе позволяет получить интересные резуль-
результаты только после проведения обширных экспериментов. Выяв-
Выявление структуры данных может быть, однако, существенно
ускорено благодаря эффективному использованию информации,
получаемой после каждого цикла итерационного процесса. Эту
информацию, как будет показано ниже, можно использовать
для коррекции параметров процесса кластеризации непосред-
непосредственно при реализации алгоритма.
3.3.7. Оценка результатов процесса кластеризации
Принципиальная трудность оценки результатов алгоритмов
кластеризации связана с тем, что мы не в состоянии зрительно
представить геометрические особенности многомерного прост-
пространства. Хотя в предыдущих примерах число измерений было
ограничено двумя с тем, чтобы облегчить изложение основ ме-
метода, читатель должен иметь в виду, что в большинстве задач
распознавания образов размерность много выше. Поэтому, для
того чтобы иметь возможность должным образом интерпрети-
интерпретировать результаты процедуры отыскания кластеров, нам следует
обратиться к схемам, которые обеспечивают по крайней мере
некоторое представление о геометрических свойствах получен-
полученных кластеров. Ниже описывается несколько методов интерпре-
интерпретации результатов кластеризации.
При интерпретации очень полезно использовать расстояние
между центрами кластеров. Лучше всего информацию подобного
рода представлять с помощью таблиц типа табл. 3.1, составлен-
составленной для модельного численного примера; из нее можно почерп-
Таблица 3.1
Пример таблицы расстояний для интерпретации
результатов
центры
кластеров
Ч
ч
ч
ч
ч
ч
0,0
кластеризации
Ч
4,8
0,0
ч
14,7
21,1
0,0
ч
2.1
б,(
15,0
0,0
'¦з
50,6
48,3
30,7
49,3
0,0
3.3. Выявление кластеров 121
нуть ряд важных сведений. Наиболее важным является то
обстоятельство, что центр кластера z5 существенно смещен от-
относительно четырех других центров кластеров. Кроме того, рас-
расстояния между центрами кластеров zi и z2, как, впрочем, между
zi и Z4, относительно одинаковы, если разделять только близко
и далеко расположенные центры кластеров.
Таблица расстояний не является, естественно, достаточной
основой для получения содержательных выводов. При интерпре-
интерпретации таблицы расстояний обычно используют в качестве вспо-
вспомогательного средства количество образов классифицируемой
выборки, вошедшее в каждый кластер. Так, например, из
табл. 3.1 следует, что центр кластера z5 далеко отстоит о г
центров остальных кластеров. Если известно, что в этот кластер
входит много образов, его следует принять в качестве элемента
истинного описания данных. Если же, с другой стороны, в кла-
кластер входит только один или два образа, можно после соответ-
соответствующего анализа устранить этот центр кластера, заключив,
что данные образы являются шумом. Может, естественно, ока-
оказаться, что образ, сильно отличающийся от всех других,
представляет существенное событие, но установить это позволит
лишь скрупулезный анализ представленных данных.
Информацию об образах, содержащихся в кластерах, можно
также использовать при проведении объединения кластеров.
Если центры двух кластеров расположены сравнительно близко
друг от друга и в одном из соответствующих кластеров содер-
содержится намного больше образов, чем в другом, то часто удается
слить эти кластеры в один.
Рассеяние характеристик кластера относительно средних
значений можно использовать для получения представления об
относительном расположении образов внутри кластера. Эту
информацию также легко оформить в виде таблицы, на этот раз
таблицы дисперсий типа табл. 3.2, построенной для модельного
Таблица 3.2
Пример таблицы дисперсий для интерпретации
результатов кластеризации
st
s2
s3
si
«i
1,2
2,0
3,7
0,3
4,2
Дисперсии
*2
0,9
1,3
4,8
0,8
5,4
0,7
1,5
7,3
0,7
18,3
1,0
0,9
10,4
1,1
3,3
122 Гл. 3. Классификация образов с помощью функций расстояния
примера (для простоты принято, что образы четырехмерные).
Как и раньше, Si обозначает t-й кластер. Мы считаем, что
каждая компонента дисперсии представляет отклонение по од-
одной из координатных осей. На основании этой таблицы можно
установить некоторые свойства классифицируемой выборки об-
образов. Так, поскольку кластер S\ характеризуется примерно
одинаковыми дисперсиями по всем осям координат, можно
предположить, что его форма близка к сферической. С другой
стороны, кластер S5 отличается значительной протяженностью
вдоль третьей оси координат. Подобным же образом можно про-
проанализировать и остальные кластеры. Эта информация в соче-
сочетании с таблицей расстояний и списком образов, входящих
в каждый из выделенных кластеров, может оказаться весьма
ценным подспорьем при интерпретации результатов класте-
кластеризации.
Естественно, существует множество других количественных
оценок кластерной структуры. Полезно, например, иметь сведе-
сведения о ближайшей и наиболее удаленной от центра кластера
точках для всех кластеров. Помимо информации, содержащейся
в таблице расстояний, можно учитывать среднюю величину
расстояния между центрами кластеров. Ковариационная мат-
матрица, построенная для множества образов каждого кластера,
также представляет значительный интерес, хотя в задачах вы-
высокой размерности ее непросто интерпретировать, а вычисление
может вызвать затруднения при реализации итеративного
алгоритма.
При использовании оценок качества кластеризации типа при-
приведенных выше информацию следует представлять в таком
виде, чтобы соответствующая интерпретация не вызывала за-
затруднений. Поскольку эта информация часто используется для
коррекции выбора параметров в процессе выполнения итератив-
итеративного алгоритма (например, алгоритма ИСОМАД), принято
встраивать в соответствующие процедуры операции, связанные
с вычислением и воспроизведением выбранного набора оценок
качества кластеризации. Характер алгоритмов отыскания кла-
кластеров показывает, что наилучший способ их реализации — ре-
режим диалога, когда результаты каждого цикла итерации пред-
представляются пользователю в таком виде, чтобы он, выбирая
нужные параметры, мог управлять процессом выполнения ал-
алгоритма.
3.3.8. Кластеризация, основанная на теории графов
Алгоритмы построения кластеров, рассмотренные в преды-
предыдущих разделах, используют меры сходства, в основу которых
положено понятие расстояния. Эти алгоритмы оказались полез-
3.4. Распознавание образов без учителя 123
ными при задании классифицируемых образов в виде числовых
векторов. Кластеры при этом выбираются так, чтобы расстояния
между отдельными образами в каждом кластере минимизирова-
минимизировались, а расстояния между образами, относящимися к двум
различным классам, были как можно больше. В основе всех
процедур лежит именно эта идея.
Другой возможный подход к отысканию кластеров связан
с использованием ряда фундаментальных понятий теории гра-
графов. Этот подход предусматривает построение в первую очередь
графа образов по заданной выборке. Образы, вошедшие
в предъявленную для классификации выборку, представляются
вершинами графа, причем вершины / и к связываются ребром,
если соответствующие им образы сходны или между ними су-
существует некоторое отношение. Считается, что образы х;- и х*
сходны, если значение соответствующей меры сходства
s(xj, Xk) оказывается больше величины заданного порога Т.
Меру сходства можно использовать для построения матрицы
сходства S, элементами которой являются 0 и 1. Матрица сход-
сходства обеспечивает возможность применять при построении
графа образа систематическую процедуру. Поскольку клики
графа образа соответствуют кластерам, для отыскания послед-
последних можно воспользоваться процедурой выделения клик графа
образов. В литературе описано несколько алгоритмов и про-
программ поиска клик графа. Читателю можно рекомендовать об-
обратиться к работам Боннера [1969], Джардина и Сибсона
[1968], Харари [1973], Огастсона и Минкера [1970], Зана
[1971] и Остина и Ту [1973]. Данный теоретико-графовый под-
подход можно использовать и для выделения кластеров в тех слу-
случаях, когда классифицируемые образы характеризуются не чис-
числовыми оценками, а отношениями, что позволяет сделать вывод
о его применимости для решения широкого спектра задач
кластеризации.
3.4. РАСПОЗНАВАНИЕ ОБРАЗОВ БЕЗ УЧИТЕЛЯ
Построение кластеров можно рассматривать как задачу рас-
распознавания образов без учителя. Пусть для заданного множе-
множества образов отсутствует всякая информация, касающаяся
числа классов, на которые разбивается выборка. Задачу обуче-
обучения без учителя можно сформулировать как задачу идентифи-
идентификации классов в заданном множестве образов. Если мы хотим
в качестве средства представления использовать центры класте-
кластеров, то одним из естественных способов описания заданного
множества данных является идентификация кластеров.
В принципе применение алгоритмов кластеризации для ре-
решения задачи обучения без учителя не вызывает никаких
124 Гл. 3. Классификация образов с помощью функций расстояния
затруднений. Пусть задано множество образов {xi, хг,..., xN},
классификация которых неизвестна. К ним можно применить
один из рассмотренных алгоритмов с тем, чтобы попытаться
идентифицировать репрезентативные центры кластеров. Полу-
Полученные в результате кластеры можно считать классами образов.
После того как «классы» определены таким способом, их можно
использовать для получения решающих функций с помощью
одного или нескольких алгоритмов обучения, которые будут
описаны в гл. 5 и 6. С другой стороны, центры кластеров, выде-
выделенные в процессе реализации этапа обучения без учителя,
можно использовать как основу для построения классификатора,
действующего по принципу минимума расстояния.
Из приведенных в этом параграфе замечаний следует, что
в принципе синтез системы, реализующей схему распознавания
без учителя, в значительной степени опирается на интуицию
разработчика и соответствующие эксперименты. Это, есте-
естественно, связано с собственно природой задачи выделения кла-
кластеров во множестве данных с неизвестными характеристиками.
3.5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Материал, содержащийся в этой главе, иллюстрирует основ-
основные концепции, составляющие идеологию классификации обра-
образов на основе критерия расстояния. Изучена схема классифика-
классификаторов, действующих по принципу минимального расстояния,
в варианте с одним эталоном. Эта схема обобщена таким
образом, что при обеспечении возможности запоминать значи-
значительное количество образов с известной классификацией она
может достигать качества классификации, соответствующего
теоретическому оптимуму байесовского классификатора.
При построении классификаторов по принципу минимума
расстояния отыскание кластеров и задание эталонов являются
вопросами первостепенной важности. Приведенные в § 3.3 алго-
алгоритмы показывают, как выделяются репрезентативные кластеры
в заданном множестве данных. При построении таких алгорит-
алгоритмов используются два подхода. Один из них — эвристический,
и в его основе лежат интуиция и опыт. Второй подход преду-
предусматривает минимизацию или максимизацию соответственно
выбранного показателя качества. Этот подход в принципе более
изящен и хорошо подходит для реализации с помощью итера-
итеративных процедур. Примеры, использующие оба подхода, были
приведены в § 3.3. Все алгоритмы, представленные в настоящей
главе, основаны на оценке сходства образов с помощью евкли-
евклидова расстояния. Этот выбор хорошо согласуется с общеприня-
общепринятой концепцией близости, а также и с подходом к классифика-
классификации, развитым в § 3.2.
Задачи 125
Когда принадлежность некоторому классу заданной выборки
образов не известна, возникает задача обучения без учителя.
Применение алгоритмов кластеризации для решения задачи
обучения без учителя является естественным следствием того
обстоятельства, что наиболее прямым способом решения задачи
идентификации групп сходных образов в анализируемом мно-
множестве данных служит выделение в этих данных кластеров об-
образов. Будучи определены, эти кластеры могут рассматриваться
в качестве классов образов и использоваться при построении
классификаторов образов с помощью методов, изложенных
в этой и следующих главах.
Библиография
Первые упоминания о классификаторах, действующих по принципу ми-
минимума расстояния, можно найти в монографиях Нильсона [1967] и Ту
[1969а]. Сведения о классификации с помощью кусочно-линейных разделяю-
разделяющих границ содержатся, помимо монографии Нильсона [1967], в статье Дуды
и Фоссама [1966]. Обобщение, полученное в п. 3.2.2, основывается на работе
Ковера и Харта [1967].
Задача отыскания кластеров обсуждалась множеством авторов с самых
различных сторон. Целый ряд не упомянутых нами мер сходства образов
и критериев кластеризации можно найти в монографии Дуды и Харта [1976],V
в которой приведено также несколько алгоритмов построения кластеров, и в
статье Роджерса и Танимото [I960]. Алгоритм из п. 3.3.4, действующий по
принципу максиминпого расстояния, базируется на алгоритме, предложенном
Батчилором и Уилкипсом [1969]. Алгоритм, основанный на вычислении К
внутригрупповых средних, был подробно исследован Маккуином [1967].
Представленный в п. 3.3.6 алгоритм ИСОМАД основан на работах Болла и
Холла [1965а, 19656]. Интересный пример применения алгоритма ИСОМАД
для организации технического надзора за состоянием компонентов ядерного
реактора можно найти в статье Гонсалеса, Фрая и Крайтера [1974] .^Допол-
.^Дополнительными источниками сведений об алгоритмах кластеризации могут слу-
служить монографии Патрика [1972] и Фукупаги [1972]. Последние источники
особенно интересны с точки зрения статистического подхода к построению
кластеров. Прекрасный набор процедур, ориентированных на обработку
двоичных образов, можно найти в статье Боннера [1969].
Дополнительные сведения о задаче обучения без учителя можно найти
в уже упомянутых монографиях Дуды и Харта и Фукунаги, а также в статьях
Спрейгинса [1966], Д. Купера и П. Купера [1965] и Ковера [1969].
Задачи
3.1. Покажите, что при использовании метода классификации, основанного на
критерии минимума расстояния, для разбиения па два класса, каждый
из которых характеризуется одним эталоном — Zi = (zn, zn, ..., гы)' и
Z2 = B21, Z22, ..., 2гп)' соответственно, разделяющей границей служит
гиперплоскость, представляющая собой геометрическое место точек, рав-
равноудаленных от эталонов Zj и z2.
3.2. Рассмотрите три непересекающиеся класса в двумерном евклидовом про-
пространстве. Определите границы, разделяющие эти классы, с помощью
классификатора, действующего по принципу минимума расстояния.
3.3. Дайте интерпретацию меры сходства Танимото, определяемой формулой
C.3.4). •
126 Гл. 3. Классификация образов с помощью функций расстояния
3.4. Покажите для множества образов S = {xi, хг х*}, что центр кла«
стера z, обеспечивающий минимизацию суммы квадратов расстояния от
каждого образа, входяшего в множество S, до центра кластера г
[см. C.3.8)], представляет собой выборочное среднее
3.5. Примените алгоритм отыскания кластеров, изложенный в п. 3.3.3, к спе-
дуюшему множеству данных: {0, 0)', @, 1)', E, 4)', E, 5)', D, 5)',
A, 0)'}.
3.6. Примените к задаче 3.5 алгоритм, действующий по принципу максимин-
ного расстояния.
3.7. Примените к задаче 3.5 алгоритм, основанный на вычислении К. внутри-
групповых средних.
3.8. Примените к задаче 3.5 алгоритм ИСОМАД. Начните процедуру с вари-
варианта, предусматривающего выделение одного центра кластера.
ГлаваМ
КЛАССИФИКАЦИЯ ОБРАЗОВ С ПОМОЩЬЮ
ФУНКЦИИ ПРАВДОПОДОБИЯ
4.1. ВВЕДЕНИЕ
В этой главе мы приступаем к рассмотрению статистического
подхода к распознаванию образов. Как явствует из названия,
этот подход предусматривает построение классификации, исходя
из статистических свойств классов образов.
Как и в других областях, связанных с регистрацией и интер-
интерпретацией физических явлений, статистический анализ начинает
играть важную роль в распознавании в тех случаях, когда слу-
случайные факторы оказывают влияние на порождение образов,
относящихся к различным классам. Рассмотрим, например, за-
задачу разделения электрокардиограмм (ЭКГ) на два класса —
нормальные и анормальные. Выборки образов, представляющие
эти два класса, формируются из ЭКГ, квалифицированных вра-
врачом как нормальные и анормальные. Очевидно, что соответ-
соответствующие выборки будут характеризоваться некоторым стати-
статистическим распределением, так как, в частности, ЭКГ, отнесен-
отнесенные к группе нормальных, будут отличаться существенной
изменчивостью (случайностью). Последняя вызывается разли-
различием физических данных отдельных пациентов, электрическими
помехами, влияющими на работу записывающих устройств,
и дюжиной других переменных факторов, всегда присутствую-
присутствующих в биологических экспериментах.
Эта глава знакомит читателя с постановкой задач распозна-
распознавания образов в рамках статистической теории. При помощи
статистического анализа представляется возможным построить
классификационное правило, являющееся оптимальным в том
смысле, что его использование обеспечивает в среднем наимень-
наименьшую вероятность совершения ошибки классификации. Это
классификационное правило, оптимальное в статистическом
смысле, обычно принимается в качестве стандартов, с которым
часто сравнивается качество других алгоритмов классификации.
4.2. КЛАССИФИКАЦИЯ ОБРАЗОВ КАК ЗАДАЧА
ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
Процесс принятия решений в распознавании образов можно
рассматривать как игру статистического характера, которую
классификационный механизм системы распознавания образов
128 Гл. 4. Классификация образов с помощью функций правдоподобия
ведет с природой. Этот процесс аналогичен игре двух лиц с ну-
нулевой суммой, в которой игроком А является природа, а игро-
игроком В — классификационный механизм системы распознавания.
Игрой с нулевой суммой называется такая игра, в которой
выигрыш одного участника точно равен по величине проигрышу
другого участника. В играх такого типа используются различ-
различные стратегии, в частности байесовская стратегия, минимаксная
стратегия и стратегия Неймана — Пирсона. Задача классифика-
классификационного механизма заключается в том, чтобы определить такое
оптимальное решение, которое обеспечит минимизацию среднего
риска или стоимости потерь.
Игра характеризуется определенным набором правил, обла-
обладающих специфической формальной структурой и определяю-
определяющих поведение отдельных лиц или групп, выступающих под
именем игроков. Игра G в нормальной форме задается набором
из трех элементов (Y,Z,L), где У и Z—пространства произ-
произвольной природы, a L — ограниченная числовая функция, опре-
определенная на пространстве прямых произведений Yy,Z пар
(у,z), t/e У и 2GZ. Элементы у и z называются стратегиями
игроков А и В соответственно, а функция L интерпретируется
как функция выигрыша или функция потерь. Игра G протекает
следующим образом. Игрок А выбирает стратегию j/бУ, и иг-
игрок В выбирает стратегию zeZ. Если игрок А проигрывает, то
он выплачивает игроку В свой проигрыш, равный L(y,z). Если
игрок А выигрывает, то он приобретает «сумму» L{y,z).
Игра
О = (У, Z, L) D.2.1)
называется конечной, если оба множества стратегий У и Z со-
содержат конечное число элементов. Если конечная игра G распо-
располагает следующими множествами стратегий:
У = (Уь У2, ..., Ум) D.2.2а)
и
Z = (zu гъ ..., zN), D.2.26)
то пространство Yy,Z представляет собой множество пар
У X Z = [(*/,, Zi), {уь z2), .... (уь zN), ...
• ¦ •, (Ум, zi), (Ум, z2), .... (ум, zN)]. D.2.3)
Матрица L = (/.//) размера Л1ХА/с элементами
Lt, = L(yt, z^ D.2.4)
называется матрицей выигрышей или матрицей потерь игры G.
Каждый элемент этой матрицы определяет потери, соответствую-
соответствующие некоторой паре действий, предпринятых игроками, т. е. эле-
элемент матрицы Lij определяет потери для случая, когда игрок В
4.2. Классификация как задача теории статистических решений 129
использует стратегию z/, а игрок А — стратегию уи Принято счи-
считать, что положительное значение потерь представляет истинные
потери, а нулевое и отрицательное значение потерь — выигрыш.
В настоящем параграфе приводятся основные сведения из
элементарной теории статистических решений, являющиеся обоб-
обобщением результатов теории игр двух лиц с нулевой суммой. Как
отмечалось выше, процесс принятия решений в распознавании
образов можно рассматривать как игру против природы — по-
последнюю можно считать игроком А, а классификатор — игро-
игроком В. Стратегии, используемые игроком А, называются состоя-
состояниями природы и обозначаются через ю,-. Состояния природы
соответствуют классам образов. Стратегии, используемые клас-
классификатором, представляют собой решения, относящиеся к со-
состояниям природы. Множество У, следовательно, содержит до-
допустимые классы образов, а множество Z — допустимые реше-
решения, находящиеся в распоряжении классификатора при
реализации конкретной игры. Ниже мы будем считать, что
число решений равно числу допустимых классов.
При каждой реализации игры природа выбирает стратегию
u>i в соответствии с вероятностью р(со,), называющейся априор-
априорной вероятностью появления класса чц. Эта величина просто
характеризует вероятность встретить класс ю*. В результате
хода, реализованного природой, появляется выборочный об-
образ х. Другими словами, нам не известно, какой именно класс
предпочла природа в данном случае. Вся информация, имею-
имеющаяся в нашем распоряжении, ограничивается самим обра-
образом х. Задача классифицирующего механизма — определить,
опираясь на эту информацию, к какому классу принадлежит
образ х. Ход классификатора, следовательно, представляет со-
собой некоторое решение, определяющее класс, который, «по мне-
мнению» классификатора, выбрала природа.
Игру классифицирующего механизма против природы отли-
отличают от обычной игры два основных фактора. Игры рассматри-
рассматриваемого нами типа часто называют статистическими. Во-первых,
природа не является «разумным противником», который
способен сознательно выбирать свои стратегии таким образом,
чтобы добиться максимизации наших потерь. Можно допустить,
что природа выбирает стратегии, основываясь на вероятностях
р(ю(), t=l, 2, ..., М, и придерживается их, несмотря на их
возможную иеоптимальность с точки зрения постулатов теории
игр. Во-вторых, существует возможность «шпионить» за приро-
природой. Мы можем осуществлять эксперименты с тем, чтобы улуч-
улучшить наше понимание методов, используемых природой при вы-
выборе стратегий. Результатом подобного эксперимента является
множество образов, которое можно использовать при построе-
130 Гл. 4. Классификация образов с помощью
Пусть при реализации игры между природой и классифика-
классификатором природа выбирает класс со,- и воспроизводит образ х.
Вероятность принадлежности образа х классу со,- обозначается
как р(со,|х). Если классификатор принимает решение о том, что
образ х принадлежит классу со/, когда на самом деле он при-
принадлежит классу со,-, то классификатор терпит убытки, рав-
равные Li/. Так как образ х может принадлежать любому из М
рассматриваемых классов, то математическое ожидание потерь,
связанных с отнесением образа х к классу со/, определяется
следующим выражением:
О (х) =? 1„р (со, |х); D.2.5)
в теории статистических решений эту величину часто называют
условным средним риском или условными средними потерями.
При распознавании каждого образа, предъявляемого приро-
природой, классификатор может отнести его к одной из М возможных
категорий. Если для каждого образа х вычисляются значения
условных средних потерь п(х), г2(х), ..., гм(х) и классифика-
классификатор причисляет его к классу, которому соответствуют наимень-
наименьшие условные потери, то очевидно, что и математическое ожи-
ожидание полных потерь на множестве всех решений также будет
минимизировано. Классификатор, минимизирующий математи-
математическое ожидание общих потерь, называется байесовским клас-
классификатором. Со статистической точки зрения байесовский
классификатор соответствует оптимальному качеству класси-
классификации.
Воспользовавшись формулой Байеса
D.2.6)
выражение D.2.5) можно представить в следующем виде:
м
где р(х|со,) называется функцией правдоподобия для класса со;.
Поскольку выражение 1/р(х) входит во все формулы вычисле-
вычисления условных средних потерь г,(х), / = 1, 2, ..., М, в качестве
общего множителя, его можно устранить из соотношения D.2.7).
В таком случае выражение для средних потерь сводится к сле-
следующему:
г, (х) =? 1„р (х | со,-) Р(ю<). D.2.8)
4.2 Классификация как задача теории статистических решений 131
При М = 2 и выборе стратегии 1 средние потери для предъ-
предъявленного образа х равны
г, (х) = Lup (х | со,) р (©,) + L2lp (x | ш2) р (со2), D.2.9)
а при выборе стратегии 2 —
г2 (х) = Li2p (х |<в,) р (со,) + L22p (х |со2) Р (<*>)• D.2.10)
Как уже отмечалось выше, байесовский классификатор обеспе-
обеспечивает отнесение образа х к классу с наименьшим значением
средних потерь г. Поэтому образ х зачисляется в класс <ш, если
выполняется условие ri(x)<r2(x); это должно означать, что
(х | со,) р (ю,) + L2ip (х | со2) р (со2) <
< L12p (х |<в,) р @,) + Ь22р (х| со2) р @2), D.2.11)
или, что то же самое,
.(/.21 - /-и) р (х | со2) Р Ы < (/-12 - Ln) Р (х | со,) р (o»i). D.2.12)
Обычно считается, что Ьц > Ьц. При этом допущении выраже-
выражение D.2.12) приводит к получению условий
p(*|e>i) -^ Р (ч>г) (Lti — LM) . 0 .
Р(х|со2) ^ р (со,) (LIf - L,,) ' **-г-1*>
выполнение которых определяет зачисление образа х в класс соь
Левую часть неравенства D.2.13) часто называют отношением
правдоподобия:
(оно является отношением двух функций правдоподобия). Итак,
для случая М = 2 байесовское решающее правило формули-
формулируется следующим образом:
1) образ х зачисляется в класс coi, если выполняется усло-
условие /i2(x) > 9i2;
2) образ х зачисляется в класс со2, если выполняется усло-
условие /i2(x)<9i2;
3) решение выбирается произвольным образом, если имеет
место равенство /i2(x) = 9i2.
Величину 9i2 часто называют пороговым значением и исполь-
используют для ее определения следующее выражение:
о Р (<йг) (^-21 — Lu) /и о 1К\
012 -*>(«>,) (i»-?.„)• D'2Л5)
Пример. Рассмотрим простую схему классификации, обесцве-
обесцвечивающую разделение сигналов, представленных в виде единиц
и нулей на выходе, канала с шумом, как это показзЦр на
132 Гл. 4. Классификация образов с помощью функции правдоподобия
рис. 4.1. Каждый входной сигнал представляет собой 0 или 1,
и в результате каждого эксперимента на выходе канала вос-
воспроизводится величина х, на которую налагается гауссовский
шум с нулевым средним значением и дисперсией а2. Требуется
найти оптимальное решающее правило.
Пусть coi представляет гипотезу, состоящую в том, что пере-
передан символ 0, а о>2 — гипотезу, состоящую в том, что передан
символ 1. На основе наблюдения значений х необходимо произ-
произвести выбор между гипотезами иц и «2- Интуиция нам подска-
подсказывает, что решающее правило должно быть таким, чтобы при
выполнении условия х < 0,5 образу х присваивалось значение О,
Шум
сигналы
ИНФОРМАЦИОН-
ИНФОРМАЦИОННЫЙ КАНАЛ
КЛАССИФИКАТОР
Решение
Рис. 4.1. Пример простой задачи классификации.
а при выполнении условия л: > 0,5 — значение 1. Проверим,
соответствуют ли наши предположения правильному ответу.
Пусть р@) и рA)—априорные вероятности того, что пере-
переданными символами были 0 и 1 соответственно. Пусть матрица
потерь имеет вид
й\ а2
0 1,2
L2I 0
где fli и а2 — решения, утверждающие, что был передан сим-
символ 0 и 1 соответственно, Li2 — потери при выборе решения а2,
когда истинный класс — он, L2i — потери при выборе решения а\,
когда истинный класс — ю2. Из этой матрицы следует, что пра-
правильным решениям соответствуют нулевые потери. Применение
байесовского решающего правила приводит к решению о пере-
передаче символа 0 при выполнении условия 1\2{\)> $ц, где поро-
пороговое значение 0i2 определяется как в12 = Z-2ip(l)/Z-i2p@). Так
как шум характеризуется нулевым средним значением и дис-
дисперсией а2, плотность вероятности принятого сигнала опреде-
определяется при условии передачи символа 0 выражением
4.2 Классификация как задача теории статистических пешенип 133
а плотность вероятности принятого сигнала при условии пере-
передачи символа 1 — выражением
Итак, отношение правдоподобия имеет вид
и, следовательно, принимается решение о принадлежности
классу (Oi, если выполнены условия
/ 1 — 2* \ . Q .1 о.п
ехр I—2^2—) > 2 или ^<-2—<тЧп612.
Другими словами, применение байесовского решающего правила
приводит к выводу о передаче символа 0, если выполнено
условие
Эти результаты совпадают с интуитивными предположениями
только в тех случаях, когда а2 = 0 или 9i2 = 1. ¦
В общем случае разделения на несколько классов образ х
причисляется к классу (о/, если условие г»(х)< г/(х) справед-
справедливо при у = 1, 2, ..., М, j ф i; другими словами, образ х при-
причисляется к классу 0», если справедливо условие
,), D.2.16)
/=1,2, ..., M; ]фи
Неравенство D.2.16) можно с помощью приемов, аналогичных
использованным при разделении на два класса, перевести на
язык отношений правдоподобия и соответствующих пороговых
величин1). В принципе для представления общего случая раз-
разделения на несколько классов лучше всего использовать функ-
функцию потерь специального вида. В большинстве задач распозна-
распознавания образов при принятии правильного решения потери равны
нулю и одинаковы при принятии любого неправильного реше-
решения. Поэтому функцию потерь можно представить как
L,,= l-6it, D.2.17)
') Читатель при желании может самостоятельно убедиться в том, что в об-
шем виде отношение правдоподобия определяет как ///(х) = р(х|(о,)/р(х|о)/)
и. что соответствующая пороговая величина для всех пар значений индексов
(I, j) определяется как &/ в р@/) {L,t — Ln)/p(<j)t) (Ц — La).
134 Гл. 4. Классификация образов с помощью функций правдоподобия
где б*/ = 1 при i = / и б*/ = 0 при i ф /. Это соотношение уста-
устанавливает нормированную величину потерь, равную единице
при неправильной классификации, и отсутствие потерь в случае
правильной классификации образа. Подстановка выражения
D.2.17) в D.2.8) приводит к выражению
м
г, (х) = ? A - б,7) р (х | со,) р (со,) = р (х) - р (х | ш,) р (ш;). D.2.18)
Байесовский классификатор обеспечивает отнесение образа х
к классу (О(, если выполняется условие
р (х) - р (х | ш,) р (со,) < р (х) - р (х | ш,) р @;), D.2.19)
или условие
р (х 10,) р @,) > р (х 10/) р @У), / = 1, 2, ..., М, \ф1. D.2.20)
Необходимо отметить, что из проведенного в гл. 2 обсужде-
обсуждения свойств решающих функций следует эквивалентность байе-
байесовского решающего правила, представленного соотношением
D.2.20), решающим функциям вида
ё<(х) = р(х\щ)р(щ), /=1,2, ..., М, D.2.21)
причем образ х зачисляется в класс со,-, если для него выпол-
выполняется условие di(x) > dj(x) при всех / Ф L Это соответствует
случаю 3 разбиения на несколько классов, рассмотренному
в § 2.2.
Выражение, эквивалентное D.2.21), но не требующее знания
в явном виде вероятностей p(x|coj) или р(со,), получается в ре-
результате подстановки соотношения D.2.6) в D.2.21). Эта опе-
операция дает формулу
d, (х) = р @с | х) р (х), / = 1, 2, ..., М. D.2.22)
Поскольку, однако, вероятность р(х) не зависит от /, ее можно
исключить, что приводит к следующему выражению для ре-
решающих функций:
ф(х) = р@,|х). D.2.23)
Формулы D.2.21) и D.2.23) выражают два различных, хотя
и эквивалентных подхода к решению одной и той же задачи.
Поскольку оценка априорной вероятности классов р(со,), /= 1,
2, ..., М, обычно не вызывает затруднений1), основное разли-
различие этих двух постановок заключается в том, что в первом
случае используется функция правдоподобия р(х|со,), а во вто-
втором— вероятность р(со,|х) принадлежности образа х классу ая.
') При использовании схемы распознавания образов с учителем наличие
информации о рассматриваемых классах упрощает задачу назначения вероят-
вероятности появления для каждого класса.
4.2 Классификация как задача теории статистических решений 135
Остальная часть данной главы посвящена проблемам, связан-
связанным с описанием и оценкой плостностей распределения р(х|0,).
Большая часть шестой главы отведена задачам оценки
плотностей распределения р(ю,|х); в ней же обсуждаются со-
соответствующие достоинства и недостатки этих двух подходов.
Проведенное обсуждение позволяет реализовать схему рас-
распознавания в виде, представленном на рис. 4.2. Это частный
случай байесовского классификатора, в котором правильной
ОЦЕНКА
плотностей
РАСПРЕДЕЛЕНИЯ
Н,г,-,м
РШ
СЕЛЕКТОР
МАКСИМУМА
Решение
Рис. 4.2. Принципиальная схема байесовского классификатора.
классификации соответствуют нулевые потери, а при любых
правильных классификациях потери одинаковы, причем опти-
оптимальное решение минимизирует вероятность ошибки классифи-
классификации. Благодаря этому важному свойству, а также весьма
разумному назначению потерь, такая схема классификации
часто используется как постановка задачи распознавания. При
отсутствии специальных оговорок все, что в нашей книге гово-
говорится о байесовских классификаторах, относится именно к этому
его варианту.
Синтез байесовского классификатора на основе решающих
функций D.2.21) требует знания априорных вероятностей
и плотностей распределения для каждого класса образов,
а также и стоимостей принятия соответствующих решений. Оп-
Оптимальность (в статистическом смысле) решений все еще может
быть достигнута и при отсутствии этих сведений. Если априор-
априорные вероятности не известны или не поддаются непосредствен-
непосредственной оценке, то существует другая возможность решения этой
задачи — использовать минимаксный критерий. Идея, лежащая ^
в основе минимаксного критерия, заключается в выборе такого
136 Гл. 4. Классификация образов с помощью функций правдоподобия
решающего правила, которое минимизирует средние потери
при наихудших возможных условиях. В этом случае можно быть
уверенным в том, что нейтрализуются любые неблагоприятные
случайности, связанные с недостатком информации об априор~
ных вероятностях. Если же не известны ни априорные вероят-
вероятности, ни значения потерь, то можно обратиться к критерию
Неймана — Пирсона.
Хотя все три упомянутые выше критерия явно различны, по-
построение минимаксного решающего правила и решающего пра-
правила по Нейману—Пирсону показывает, что все они основы-
основываются на том же отношении правдоподобия. Единственный
фактор, который изменяется при переходе от одного критерия
принятия решения к другому, — это вид пороговой величины.
Несмотря на то что и минимаксный критерий, и критерий Ней-
Неймана — Пирсона были тщательно изучены в связи с решением
многих прикладных задач, в распознавании образов значи-
значительно большее распространение получил критерий Байеса. Это
определяется тем обстоятельством, что в большинстве задач
распознавания образов оказывается возможным задать априор-
априорные вероятности и потери. В следующем параграфе подробно
рассматривается один из вариантов байесовского класси-
классификатора.
4.3. БАЙЕСОВСКИЙ КЛАССИФИКАТОР В СЛУЧАЕ
ОБРАЗОВ, ХАРАКТЕРИЗУЮЩИХСЯ НОРМАЛЬНЫМ
РАСПРЕДЕЛЕНИЕМ
Если известно или с достаточными основаниями можно счи-
считать, что плотности распределения функций правдоподобия
p(x|(D,) суть многомерные нормальные (гауссовские), то при-
применение синтезированного в предыдущем параграфе байесов-
байесовского классификатора приводит к получению ряда интересных
и хорошо известных решающих функций. Многомерная нор-
нормальная плотность распределения является объектом усиленного
внимания в связи с удобством ее аналитической обработки.
Кроме того, она представляет собой подходящую модель для
множества важных прикладных задач. Для начала мы обра-
обратимся к одномерной плотности нормального распределения од-
одной случайной переменной х:
\1(ЛЛ)*] D.3.1)
которая полностью определяется двумя параметрами — средним
значением m и дисперсией а2. Эти параметры в свою очередь
4.3 Байесовский классификатор при нормальном распределении 137
определяются как
«в
m = E{x}= J xp(x)dx D.3.2)
и
оо
а2 = Е {{х - mJ} = J (* - тJ /7 (*) d* D.3.3)
—оо
соответственно, где символ Е{-} обозначает математическое
ожидание. Так как плотность нормального распределения опре-
определяется двумя этими параметрами, то ее часто для простоты
записывают как р(х) ~ N (т, а2). Образы, характеризующиеся
нормальным распределением, проявляют тенденцию к группи-
группировке вокруг среднего значения, а их рассеяние пропорцио-
пропорционально среднеквадратичному отклонению а. Около 95% объек-
объектов, извлеченных из совокупности с нормальным распределе-
распределением, попадут в интервал, равный 2а, и имеющий в качестве
центра среднее значение.
Итак, рассмотрим М классов образов, описываемых много-
многомерными плотностями нормального распределения
р (х |юЛ = -J» п-ехр Г (х — m.V СГ1 (х — тЛ 1,
^ iJ Bп)п/21 Ci | '* L 2 ^ iJ l к ''} D.3.4)
/=1,2, .... М,
где каждая плотность распределения полностью определяется
вектором средних значений т* и ковариационной матрицей С;,
заданных соответственно как
mi^Ei{x} D.3.5)
Cf = Et {(x - mt) (x - m<)'}, D.3.6)
где Et{-} обозначает оператор математического ожидания, опре-
определенный на образах класса ац. Символ п обозначает в D.3.4)
размерность векторов образов, а запись |С(| — определитель
ковариационной матрицы С;.
Ковариационная матрица Сг является симметрической и по-
положительно полуопределенной. Ее диагональный элемент Ckk
есть дисперсия &-го элемента вектора образов. Элемент С/а, не
стоящий на диагонали матрицы, представляет собой ковариа-
цию случайных переменных х\ и хи. Если переменные х/ и Xk
статистически независимы, то элемент с/а = 0. Многомерная
плотность нормального распределения сводится к произведению
одномерных плотностей нормальных распределений, если все
недиагональные элементы ковариационной матрицы — нули.
138 Гл. 4. Классификация образов с помощью функций правдоподобия
Многомерная плотность нормального распределения пол-
полностью определяется п +Gг)я(я + 1) параметрами, которыми
служат компоненты вектора средних значений и независимые
элементы ковариационной матрицы. Образы, выбранные из со-
совокупности с нормальным распределением, проявляют тенден-
тенденцию к образованию одного кластера, центр которого опреде-
определяется вектором средних значений, а форма — ковариационной
матрицей. Из D.3.4) следует, что геометрическими местами то-
точек с постоянной плотностью распределения служат гиперэл-
гиперэллипсоиды, направление главных осей которых определяется
собственными векторами ковариационной матрицы, а длина
этих осей — ее собственными значениями.
Согласно соотношению D.2.21), решающую функцию для
класса он можно выбрать в виде d, (x) = р(х|а>;)р(а>/). В связи
с тем, однако, что плотность нормального распределения выра-
выражается экспонентой, удобнее работать с натуральным логариф-
логарифмом от этой решающей функции. Другими словами, решаю-
решающую функцию можно представить в виде
d, (х) = In [р (х | щ) р (щ)] = In р (х | ш,) + In p (ш(), D.3.7)
что полностью эквивалентно представлению D.2.21) с точки
зрения качества классификации, поскольку натуральный лога-
логарифм— монотонно возрастающая функция.
Подстановка выражения D.3.4) в D.3.7) приводит к
/=12 М
D-3-8)
Поскольку член (л/2Iп2я не зависит от i, его можно исклю-
исключить; при этом решающая функция d,(x) примет вид
dt (х) = In р @,) - ~ In | С, | - у [(х - т,)' СГ1 (х - ш,)].
/-12 М D-3-9>
Выражения D.3.8) и D.3.9) представляют байесовские ре-
решающие функции для нормально распределенных образов. Чи-
Читателю необходимо помнить, что эти решающие функции выво-
выводились для случая нулевых потерь при правильной класси-
классификации и равенства потерь при всех видах неправильной
классификации.
Решающие функции, определяемые формулами D.3.8)
и D.3.9), являются гиперквадриками, поскольку видно, что ни
один член выше второго порядка, составленный из компонент
образа х, в эти соотношения не входит. В таком случае оче-
4.3. Байесовский классификатор при нормальном распределении 139
видно, что наилучшим результатом применения байесовского
классификатора к нормально распределенным образам служит
построение обобщенных разделяющих поверхностей второго по-
порядка для всех пар классов. Если, однако, совокупность образов
действительно распределена нормально, то в среднем никакие
поверхности другого типа не обеспечат получение лучших ре-
результатов.
Если для всех /=1, 2, ..., М ковариационные матрицы
одинаковы, т. е. С; = С, то легко можно показать, что удаление
из соотношения D.3.9) членов, не зависящих от значения, при-
принимаемого индексом г, приводит к
di(x) = \np{<ui) + х'С""'пц — ym|C~'m,, i—\, 2, .... Af;
D.3.10)
это выражение представляет множество линейных решающих
функций.
Если к тому же С = I, где I — единичная матрица, и вероят-
вероятность появления класса аи есть р((о,) = 1/Af, i = 1, 2, ..., Af, то
выражение для решающей функции принимает вид
dt(х) = х'т. — ym^m., t = l, 2, ..., Af. D.3.11)
Читатель должен узнать в D.3.11) решающие функции класси-
классификатора, действующего по критерию минимума расстояния,
для случая единственного эталона класса, причем в роли этого
эталона выступает вектор средних значений образов, входящих
в соответствующий класс. Из уравнения D.3.10) следует, что
разделяющая граница для классов ю,- и юу определяется как
dt (х) — dj (х) = In р (юО — In р (со,) + х'СГ1 (т, — т/) —
i = 0- D.3.12)
Из предшествующего обсуждения очевидно, что при равен-
равенстве ковариационных матриц определяемая формулой D.3.12)
разделяющая поверхность линейна относительно переменных,
описывающих гиперплоскость. В тех случаях, когда ковариа-
ковариационные матрицы различны, разделяющая поверхность пред-
представляется суммой линейных и квадратичных членов, описы-
описывающих гиперквадрику. Можно показать, что линейные
и квадратичные решающие функции обеспечивают при соот-
соответствующем выборе коэффициентов достижение теоретического
оптимума не только при работе с плотностью нормального рас-
распределения, но и для ряда распределений других типов. Интерес
140 Гл. 4. Классификация образов с помощью функций правдоподобия
к линейным и квадратичным дискриминантным функциям воз-
возникает также в связи с использованием их в качестве аппрокси-
аппроксимаций первого и второго порядка произвольных отношений
правдоподобия, поскольку при решении целого ряда приклад-
прикладных задач эти функции являются практическим решением, ко-
@,1,1)
(W)
Рис. 4.3. Образы, использованные в иллюстрирующем примере; границы, их
разделяющие, получены с помощью байесовской процедуры.
торое может быть без особых проблем реализовано в виде
специализированного устройства или машинной программы.
Пример. Рассмотрим образы, изображенные на рис. 4.3.
В § 4.6 будет показано, что векторы средних значений и кова-
ковариационные матрицы можно оценивать, используя следующие
соотношения:
хих'и
где через Ni обозначено количество образов, вошедшее в класс
ш„ а вектор х,-у представляет /-й образ г-го класса.
4$ Байесовский классификатор при нормальном распределении 141
Применение этих выражений к образам, представленным на
рис. 4.3, позволяет установить, что
Так как ковариационные матрицы равны, байесовские решаю-
решающие функции для данного примера определяются из D.3.10).
Допустив, что p((Oi) =/?((ог)= 1/2, член уравнения In/? (юг)
можно опустить, перейдя к следующему выражению:
di (х) = х'с'т, — ^ miC"'m(,
где
Выполнив разложения, приходим к следующим выражениям для
решающих функций:
d, (х) = 4лг, — у
и
d2(х) == — 4лг1 -}- 8л:2-f 8*3 — -g-.
Искомая разделяющая поверхность определяется уравнением
di (х) — d2 (х) = 8л:, — 8х2 — 8х3 + 4 = 0.
Часть этой поверхности изображена на рис. 4.3. Обратите вни-
внимание на то, что она эффективно осуществляет дихотомию
двух классов.
Следует заметить, что хотя в данном случае метод привел
к получению очень хороших результатов, байесовское класси-
классификационное правило, будучи статистической концепцией, не
должно в принципе приводить к получению оптимальных ре-
результатов на малых выборках.
142 Гл. 4. Классификация образов с помощью функций правдоподобия
4.4. ВЕРОЯТНОСТИ ОШИБОК
Обсудив байесовский классификатор, предназначенный для
работы с нормально распределенными образами, перейдем
к анализу вероятности ошибки, совершаемой при использовании
такой схемы классификации. Рассмотрим два класса со; и со/,
в которых векторы образов характеризуются следующими плот-
плотностями многомерного нормального распределения:
Р (Х ' Щ) = Bя)"/2|С1'/,еХР [" 7 (Х ~ т'У С"' (Х
И
Р (х I со/) = Bя)Я/11 c [Vi ехр [-1 (х - т,)' (Г1 (х - mf)], D.4.2)
причем их ковариационные матрицы равны. Поскольку плотно-
плотности распределения представлены в экспоненциальной форме,
анализ можно упростить, воспользовавшись логарифмом отно-
отношения правдоподобия. Пусть
ии = In 1Ц (х) = 1п р (х | сог) — In p (х | со/). D.4.3)
В таком случае из D.4.1) и D.4.2) следует, что
иИ (х) = х'С (т. - my) - у (т, + т;)' С-'(т. - т^. D.4.4)
При выборе двоичной функции потерь @ — правильное реше-
решение, 1 — ошибка) условие, определяющее принадлежность об-
образа х классу со; по критерию минимизации вероятности ошибки
классификации, принимает вид
иц (х) > а, D.4.5)
где параметр а равен логарифму пороговой величины
Вероятность неправильной классификации образа, принадлежа-
принадлежащего классу со/, есть р(м,-/ > ос | со/) и вероятность неправильной
классификации образа, принадлежащего классу о*, есть
р (иц < а | со,).
Так как логарифм отношения правдоподобия иц(\) является
линейной комбинацией компонент образа х, подчиняющихся
нормальному распределению, то иц также описывается нор-
нормальным распределением. Поэтому на основании соотношения
D.4.4) математическое ожидание логарифма отношения прав-
правдоподобия иц для класса с>; можно записать как
Е. {иц} = т,С-'(т, - т/) - j(mi + т^'С (т, - т,); D.4.7)
4.4 Вероятности ошибок 143
это выражение можно свести к
?*{"*/} =й// = у г«' D.4.8)
где
гц — (mt - m/)'c~' (mi - m/> D-4-9)
Последнее часто называют расстоянием Махаланобиса между
плотностями распределений р(х|(о,) и р(х|ш;). Если С—еди-
С—единичная матрица, то расстояние Махаланобиса Гц представляет
собой квадрат расстояния между средними значениями величин
/?(х|©(-) и р(х|©/).
Поскольку дисперсия логарифма отношения правдоподобия
иц определяется как
D, {uti) = Et {(ut! -utif), D.4.10)
то из D.4.4) и D.4.8) следует, что
Di Ы = Ei i(mi - m/)'c"' (x - md (x ~ mt)'c"' (mi - mi)}'
D.4.11)
последнее выражение можно упростить до вида
Dt{uu}=*rti. D.4.12)
Итак, при хем, логарифм отношения правдоподобия иц под-
подчиняется закону нормального распределения Ы{гц12,гц). По-
Подобным же образом при х е а>, соответствующий логарифм
отношения правдоподобия иц подчиняется нормальному распре-
распределению /V(—гц/2,Гц). Следовательно,
У^г> D-4ЛЗ)
и
р (щ, < a I со;) =
1.1 4W. ¦ S.f . ,
[- 'У 2 ' 'У J duu =
где функция Ф определена как
Ф@= \ -~exp(-y^/2)dy. D.4.15)
144 Гл. 4. Классификация образов с помощью функций правдоподобия
Вероятность ошибки определяется по формуле
р(е) = р (со,) р (щ, < а | ©,) + р (со,) р (щ, > а | еэ,). D.4.16)
Воспользовавшись уравнениями D.4.13) и D.4.14), приходим
к следующему:
-l- ')\. D.4.17)
В тех случаях, когда априорные вероятности появления со-
соответствующих классов равны, т. е.
р ((а{) = р (со,),
пороговая величина Э равна единице, а ее логарифм а соответ-
соответственно равен нулю. В таком случае вероятность ошибки опре-
определяется как
= D.4.18)
1 С ]_ схр (
2 J л/Чл
оо
= S ^ехрН
D>4-19)
Итак, функция, связывающая расстояние Махаланобиса с ве-
вероятностью ошибки, является плотностью одномерного нормаль-
нормального распределения с нулевым средним и единичной дисперсией.
График зависимости вероятности ошибки классификации р(е)
от величины расстояния Махаланобиса Гц приведен на рис. 4.4.
Очевидно, что вероятность ошибки р(е) представляет собой
монотонно убывающую функцию расстояния Махаланобиса гц.
При г,7=П вероятность ошибки классификации меньше 5%.
Проведенный анализ можно распространить на случай
оценки вероятности ошибки классификации, связанной с ис-
использованием рассмотренных в гл. 2 линейных решающих функ-
функций при нормальном распределении образов в каждом из двух
заданных классов. Линейный классификатор относит образ х
к классу to,-, если выполняется условие w'x >6, и к классу о/
4.4. Вероятности ошибок
145
в противном случае. Поскольку образ х выбран из совокупности,
характеризующейся многомерным нормальным распределением,
и w'x —линейная функция вектора образа х, то последняя опи-
описывается плотностью одномерного нормального распределения,
среднее значение и дисперсия которого задаются следующим
образом.
40
35
30
25
20
15
10
5
1 Pie), %
\
Л
-\
- \
- \
I 1 ^ ' Г
5"
10
15
Рис. 4.4. Зависимость вероятности ошибки от величины расстояния Махала-
нобиса.
Среднее значение решающей функции w'x определяется как
?{w'x} = w'?{x}. D.4.20)
Дисперсия решающей функции w'x по определению равна
a2=?(w'x-w'?{x}J; D.4.21)
последнее выражение можно записать как
о2 = Е {w' (х - Е {х}) (х - Е {х})' w} = w'Cw, D.4.22)
где С—ковариационная матрица. Таким образом, при хеа,
решающая функция w'x подчиняется нормальному распределе-
распределению N(vf'nii, w'C,w); при хео)| эта функция подчиняется нор-
нормальному распределению jV(w'm;-, w'Cyw). Поэтому вероятность
ошибки определяется как
Р{е) = р (»() Р (w'x < 01 щ) + р (Ш/) р (w'x > Э | ©,), D.4.23)
146 Гл. 4 Классификация образов с помощью функций правдоподобия
где
V2nw'C,w L 2w'CjW
= ф(-^=^Л D.4.24)
и
p (w'x > e i Ш/) =
Г ' г (w'x-w'm/Jb, м
= \ - exp d (w x) =
J V2nw'C/w L 2w'C/w J
• 0 - w'm/ \
,-y—l )¦ D.4.25)
/w'C/w /
Эти формулы аналогичны D.4.13) и D.4.14). Используя соот-
соответствующую подстановку, получаем для вероятности ошибки
следующее выражение:
@ —w'ni(\ Г /0 — w'm/ \1
,-т—- +РЮ 1 -Ф ,^—-i ) ; D.4.26)
Vw C;w / L \ V* C/w /J
последнее аналогично соотношению D.4.17), определяющему
вероятность ошибки для байесовского классификатора.
Исходя из проведенного анализа вероятности ошибки клас-
классификации, можно на основе минимаксного критерия определить
вектор весов для дихотомического разделения. При допущении
о равенстве априорных вероятностей, т. е. p{<ai) = р(ш/) = '/г.
вероятность ошибки классификации, определяемую формулой
D.4.26), можно представить следующим образом:
/?(е) = у[1 — <&(yi)] + -j[l — Ф 0//)], D.4.27)
где
9 - w'm,
у, = -===+. D.4.29)
Vw C/w
C/w
В D.4.27) использовано соотношение
ф(е-м^шА , _ ф/ м^еч D 4 30)
4.4. Вероятности ошибок 147
Из формулы D.4.27) следует, что вероятность ошибки р(е)
минимизируется при максимизации функций Ф(</<) и Ф(г//). По-
Поскольку интеграл вероятности ошибки Ф{у) является однознач-
однозначной и монотонно возрастающей функцией, то вероятность
ошибки р(е) минимизируется при максимизации у,- и у,-. Отме-
Отметим, что связь величин г/, и у\ определяется выбором вектора
весов w и пороговой величины 0. Оптимизационную задачу
в этом случае можно сформулировать как задачу максимизации
у,- при фиксированном значении у,.
Из формул D.4.28) и D.4.29) можно получить
D.4.31)
-. D.4.32)
Поскольку у\ есть функция вектора весов w, максимальному
значению у\ соответствует равенство нулю производной dyj/dv/.
Более строгое обоснование, в том числе доказательство доста-
достаточности, можно найти в статье Андерсона и Бахадура [1962].
Дифференцирование выражения D.4.32) по вектору весов w
приводит к
?*L = _ [w' (m, - m,) + y{ (w'Cfw)^ (w'C/Wr
- (w'C/W)-1'1-^- [v/ (m, - m,) + y, (w'C,-w)'A]. D.4.33)
Можно легко показать, что
-^ [W (m, - m,)] = (my - m()'(
-j^-bi (w'CiW)'/2] = yt (w'CiW)-'/2 v/'Ct.
В таком случае уравнение D.4.33) принимает вид
^L = W (m, - m,) + yt (w'C.wO2] (w'C/W)-3/- w'C; -
- (w'C/W)-1/! [(m, - m,)' + yt (w'CiW)-1/2 w'C,]. D.4.34)
Итак, при использовании минимаксного критерия в случае
равенства априорных вероятностей равновероятными оказы-
оказываются оба вида ошибок. Это эквивалентно утверждению о том,
что yi = у/. При использовании данного условия из D.4.32)
следует, что
w' (my - mt) = - уi [(w'C,w)'/2 + (w'Cw)*]. D.4.35)
148 Гл. 4. Классификация образов с помощью функций правдоподобия
Подставив выражение D.4.35) в уравнение D.4.34), произведя
упрощения и приравняв полученный результат нулю, получим
следующее выражение:
yi (w'C/w)-1 w'C, + (w'C/w)-'/2[(m/ - m,) + y{ (w'CiW)'/s w'C,] = 0,
из которого в свою очередь получим
Ц'Г'ст, —т,). D.4.36)
w = — Г п\ Цт
У{ |_ (у/CjW)'1 ^ (w'C,w)'/2
Уравнение D.4.36) можно записать как i
1 Г (w'C/w)'/2 (w'CiwI'2 I r(w'C/wI/2Cf + (w'Qw)'/2c;1
W ~~ ~~ ~t L (yCjwI'1 + (w'C^w)'/' J L (w'CyW)''1 + (w'C,w)'/a J
X (m, - in,). D.4.37)
Отметим, что вектор весов w можно заменить вектором sw,
где s — произвольная положительная скалярная постоянная, что
не нарушит справедливости соотношения. Постоянная s выби-
выбирается таким образом, чтобы выполнялось условие
у. L(w'C/w)/2 + (w'Ciw)Aj
Итак, искомый вектор весов можно найти из следующего урав-
уравнения, заданного в неявной форме:
Г (w'C/wI* С? + (w'C;w)'/* С/1
w= г, -,—L I (шг — ni/). D.4.39)
Воспользовавшись соотношениями D.4.28) и D.4.38), получим
выражение для пороговой величины
(w'C/w)* (w'C,w)
6 = w'nii г, ; тг- D.4.40)
(w'C/w)/2 + (w'C;w) 'A v
Формулы D.4.39) и D.4.40) позволяют найти вектор весов и
пороговую величину для линейной решающей функции, обеспе-
обеспечивающей осуществление дихотомизации с минимальной ве-
вероятностью ошибки.
4.5. ВАЖНОЕ СЕМЕЙСТВО ПЛОТНОСТЕЙ
РАСПРЕДЕЛЕНИЯ
Рассмотрим важное семейство плотностей распределения,
задаваемое в общем виде соотношением
р (х) = Кп I W |'/2 / [(х - m)' W (х - т)], D.5.1)
где Кп — нормировочная постоянная, W — действительная сим-
симметрическая и положительно определенная матрица весов, m —
4.5. Важное семейство плотностей распределения 149
вектор средних значений и п — размерность образа х1). Эта
плотность распределения интегрируема в пространстве образов
х. Она обладает эллипсоидальной симметрией, так как контуры
постоянной вероятности являются гиперэллипсоидами. Если
матрица весов есть W= [al]2, где a — скалярная величина, а
I — единичная матрица, то р(х)—плотность распределения со
сферической симметрией, которая определяется как
р (х) = Ы К (х - т)' (х - т)]. D.5.2)
Плотность нормального распределения
Р (Х) = B,)*|С|* 6ХР [- ? (Х - Ш)' С" (Х -
принадлежит классу плотностей распределения D.5.1). Сопо-
Сопоставление соответствующих выражений позволяет установить,
что
г 1 ,т
= ехр[-|(х-ш)'С-1(х-т)].
D-5.4)
Плотность распределения второго пирсоновского типа является
симметрической функцией и определяется как
h (x) в области R,
л « п D-5.5)
О вне области R, v '
где
ЬЫ=*Т Jtovtbll IW|'/2[l-(x-m)'W(x-m)rft, D.5.6)
причем /? обозначает внутреннюю область гиперэллипсоида,
(x-m)'W(x-m)=l D.5.7)
и Г — гамма-функция.
Матрица весов, входящая в D.5.6), определяется формулой
где С—ковариационная матрица. Параметр k определяет фор-
форму плотности распределения. При k = 0 плотность распределе-
распределения второго пирсоновского типа превращается в равномерную
') Для того чтобы упростить запись, из формулы удалено обозначение при-
принадлежности некоторому классу. В противном случае D.5.1) имело бы вид
Р (* I «•>,) = *» I wi I''' / К* ~ mi)' W, (x - m J].
150 Гл. 4. Классификация образов с помощью функций правдоподобия
плотность распределения, при k = 1/2 она представляется обра-
обращенным гиперполуэллипсоидом, а при k = 1—обращенным
гиперпараболоидом. При k, стремящемся к бесконечности,
плотность распределения второго пирсоновского типа прибли-
приближается к плотности нормального распределения.
Плотность распределения седьмого пирсоновского типа так-
также относится к классу функций, описываемых выражением
D.5.1). Эта плотность имеет вид
;р(х) =
| W |'/г [ 1 + (х - m)' W (х - т)
-ft
Матрица весов определяется по формуле
1
2k - (я + 2)
k > (л/2 + 1).
D.5.9)
D.5.10)
(гауссодо)
В пределе при /г, стремящемся к бесконечности, эта функция
также обращается в плотность нормального распределения. На
рис. 4.5 для сравнения приведены плотности одномерных нор-
нормальною и пирсоновских
второго и седьмого типов
распределений. Представ-
Представленные на рисунке плотно-
плотности нормированы с тем, что-
чтобы обеспечить равенство
максимальных значений.
Если плотности распре-
распределений образов, относя-
относящихся к двум классам, яв-
являются симметрическими
многомерными и монотонно
убывающими, можно по-
показать, что байесовская гра-
граница, разделяющая эти
два класса, является либо
Рис. 4.5. Симметрические одномерные гиперплоскостью, либо ГИ-
плотности распределения. перквадрикой в зависимости
от характера матрицы ве-
весов. Этот факт был продемонстрирован для плотностей нор-
нормального распределения . в § 4.3. Напомним, что там было
показано, что ковариационная матрица определяет, является
.ли разделяющая граница для двух нормальных совокупностей
типерквадрикой или гиперплоскостью. В следующем примере
показано, как эти два типа разделяющих границ строятся в
¦случае образов, характеризующихся пирсоновской плотностью
распределения седьмого типа.
4.5. Важное семейство плотностей распределения 151
Пример. П>сть образы, принадлежащие классам «i и а>2,
имеют пирсоновские плотности распределения седьмое©, типа с
равными значениями параметра k, т. е.
р (х | со,) = V/k) . | W, |'А [1 + (х - m,)' W, (х - пг,ЯГ*и
р (х | ш2) = T/k) . | W2 |'/г [ 1 + (х - m2)' W2 (x - m2)]-fe..
«'2 (!)
Требуется построить байесовскую разделяющую границу для
этих двух классов.
Из D.2.21) следует, что
dx (х) = р (х | со,) р (со,), d2 (х) = р (х | ш2) р (ш2).
Уравнение, определяющее разделяющую границу, имеет вид
d,(x)-d2(x) = 0,
откуда следует, что на границе должно выполняться условие
р (х | ом) р {а{) = р{х\(о2)р (ш2).
Допустив, что вероятности появления классов одинаковы,
=/?(ш2), и подставив выражения, определяющие пирсо>-
новские плотности распределения седьмого типа, в значения
вероятности принадлежности образа х соответствующим клас-
классам /з(х|a>i) и р(х|ш2), приходим к следующему соотношению^;
| W, Г' [1 + (х - m,)' W, (х - тОГ* =
= IW21'/2 [ 1 + (х - т2)' W2 (x - т2)] ~*;
или
2k
VTwTl [I + (х - т2)' W2 (х - т2)] =
2k
= VTCI [1 + (х - т,)' W, (х - т,)]..
2k 2ft
Положив для простоты Ki = Vl wi I и %2 = Vl W21. получаем
уравнение разделяющей границы
Ki (x - m2)' W2 (x - m2) - K2 (x - mO' W! (x - my) + (/C1-/C2) = 0;
очевидно, что эта разделяющая граница выражается квадра-
квадратичной функцией.
Матрицы весов Wi и W2 пропорциональны ковариационным
матрицам d и С2 соответственно, что следует из D.5.10). Если
152 Гл. 4. Классификация образов с помощью функций правдоподобия
ковариационные матрицы равны, то Wi = W2 = W и К\ = К%.
В данном случае
(х - m2)' W (х - т2) - (х - тО' W (х - т,) = 0.
Однако, поскольку входящий в уравнение член x'Wx не зависит
от номера класса, его можно исключить из процесса принятия
решения. При этом разделяющая граница примет более про-
простой вид:
2x'W (m, - m2) + т^т2 - т^т, = 0,
т. е. мы пришли к уравнению гиперплоскости. Как и в случае
нормальных распределений образов, ковариационная матрица
играет центральную роль в определении разделяющих границ
при классификации образов, распределенных согласно седь-
седьмому пирсоновскому типу.
4.6. ОЦЕНКА ФУНКЦИЙ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
Из сказанного в предыдущих разделах следует, что оценка
плотностей распределения р(х\ац) является важнейшей зада-
задачей, возникающей при реализации байесовского классифика-
классификатора образов. В данном параграфе обратимся к нескольким
основным подходам, при помощи которых можно получить
оценки подобных плотностей распределения, исходя из задан-
заданной выборки образов.
4.6.1. Вид плотности распределения
Прежде чем приступать к изложению методов оценки плот-
плотностей распределения, целесообразно остановиться на мотивах
выбора плотности распределения определенного вида. Понятие
энтропии является хорошей основой для подобного обсуждения.
Принцип максимума энтропии утверждает, что если плотность
распределения некоторой случайной величины неизвестна, то
из логических соображений следует выбрать такую плотность
распределения, которая обеспечивает максимизацию энтропии
случайной величины при учете всех известных ограничений.
Применение этого критерия приводит к решению, отличаю-
отличающемуся минимальным смещением, так как плотность распреде-
распределения любого другого вида будет обладать большим смещением
«в сторону» информации, содержащейся в известном наборе
данных. Плотность распределения, обеспечивающую максимум
энтропии, особенно легко определять в тех случаях, когда все
известные ограничения представлены в форме средних оценок,
таких, например, как математические ожидания и дисперсии
плотности распределения,
4.6 Оценка функций плотности распределения 153
Энтропия совокупности образов с плотностью распределения
р{х) определяется как
H = -\p{x)\np(x)dx. D.6.1)
х
Для упрощения формы записи мы снова опускаем указание
о принадлежности образа определенному классу, т. е., как и
выше, плотность распределения р(\) — это плотность распреде-
распределения р(х\ац). Пусть априорная информация о случайной ве-
величине х задается в виде
\(x)dx=l {4.6.2а)
\bk(x)p(x)dx = ak, 6 = 1,2 Q. D.6.26)
X
Наша цель заключается в таком задании плотности распреде-
распределения р(х), чтобы величина энтропии при выполнении ограни-
ограничений D.6.2а) и D.6.26) была максимальной. Использование
множителей Лагранжа Яо, Яг, ..., Kq позволяет построить функ-
функцию
Г Q "I Q
Я, = - \р (х) In р (х) - ? КЪъ (х) \dx-J] hak, D.6.3)
где ao = 1 и bo(x)= 1 для всех образов х.
Взяв частные производные от функции Hi по плотности рас-
распределения р(х), имеем
= - И In р(х) - ? Яййй (х) + 11 rfx. D.6.4)
х IL fe=o ' J
dp(x)
Приравняв подынтегральное выражение нулю и выразив из
этого уравнения р(х), получим
D.6.5)
р (х) = ехр [ Е Kbk (х) - 11.
Здесь Q+1 параметров Яо, Я Яс? следует выбирать так,
чтобы они соответствовали априорной информации об образах
х, содержащейся в соотношениях D.6.2а) и D.6.26).
Исходя из D.6.5), легко показать, что, когда известно, что
случайная величина отлична от нуля только в конечном интер-
интервале, следует выбирать равномерное распределение. Если
случайная величина может принимать любое действительное
T54 Гл. 4. Классификация образов с помощью функций правдоподобия
значение, а единственными разумными характеристиками счи-
считаются математическое ожидание и дисперсия, то следует
выбирать нормальное распределение. Выбрав плотность рас-
распределения, необходимо заняться оценкой параметров выбран-
выбранной функции. Проведенный анализ показывает, что при следо-
следовании энтропийной концепции выбор нормального распределения
является вполне приемлемым допущением, если единствен-
единственными известными характеристиками образов х являются мате-
математическое ожидание и дисперсия. Поскольку с практической
точки зрения эта задача весьма важна, в следующих двух пунк-
пунктах основное внимание уделяется методам оценки вектора сред-
средних значений и ковариационной матрицы выборки образов.
Пример. Рассмотрим в качестве иллюстрации случай, когда
априорная информация о случайной величине х заключается
р(х) dx= I. Тогда из D.6.5) следует,
0 г в
что р{х) = ехр(Я0 — 1). Так как \аехр(А0 — Y)dx= 1, то
ехр(Я0 — 1)=1/(Р —а) и
ПРИ а < * < Р'
в противном случае;
р(х)
последнее выражение характеризует равномерную плотность
распределения в заданном интервале.
Пусть теперь априорная информация о случайной величине
p(x)dx=l и \ xp(x)dx = m.
В таком случае из формулы D.6.5) следует, что р(х)=.
«= ехр(А,о— 1 -\-b-ix). Поскольку решение уравнений
от
\ ехр (Яо — 1
— 1
J *ехр(Я0-
относительно множителей Яо и ki приводит к
то
f "ш*ехР(~"*^') ПРИ
О в противном случае.
4.6 Оценка функций плотности распределения 155
И если, наконец, априорная информация о случайной пере-
переменной х заключается в том, что
— оо < х < оо, \ р(х) dx=l, J хр (х) dx — tn, ^ x?p(x)dx=<r2t
—оо —оо —оо
то из D.6.5) заключаем, что
р (*) == ехр (Яо — 1 + Ь\Х + Я2х2),
а использование заданной априорной информации позволяет
получить следующее:
ехр(Я0- 1+ Xix + M2)dx*= 1,
л;ехр(Я0 — 1 + Яь*: + К2х2) dx = m,
о
х2 ехр (Яо - 1 + Кх + Кх2) dx = а2.
Решение этих уравнений относительно множителей Яо, Я1 и Я2
дает
1 Г - (* - mJ "I
^ J'
т. е. получена плотность нормального распределения.
4.6.2. Оценка вектора средних значений
и ковариационной матрицы
В § 4.5 было показано, что ряд представляющих опреде-
определенный интерес плотностей распределений, к которым, в част-
частности, относится плотность нормального распределения, пол-
ностью определяются своими векторами средних значений и
ковариационными матрицами. Если тип плотности распределе-
распределения определяется набором параметров, то соответствующую
задачу оценки называют параметрической оценкой. В статисти-
статистической литературе этой теме уделяется очень много внимания,
поэтому здесь мы коснемся ее только в той мере, насколько это
необходимо для рассмотрения методов оценки вектора средних
значений и ковариационной матрицы, характеризующих неко-.
торую совокупность образов.
156 Гл. 4. Классификация образов с помощью функций
Пусть совокупность образов описывается плотностью рас-
распределения р(х). Вектор средних значений для этой совокуп-
совокупности определяется как
m = Е {х} = J xp (х) dx, D.6.6)
X
i, Xi, ..., Хп) и m = (mi, tti2, • • •» mn) •
Если аппроксимировать математическое ожидание выбороч-
выборочным средним значением, то вектор средних значений можно
записать как
N
т = ?{х}«у^х,, D.6.7)
где N — объем выборки.
Соответствующая ковариационная матрица определяется
как
с12 ••• с1п'
С= | С") С'2 '" Т |, D.6.8)
сп? ' ' ' С!Р
где элементы $щ матрицы С заданы следующим образом:
clk ¦= Е {(xi — mi) (Хк — "h)} =
, xk) dx, dxk, D.6.9)
— оо —с»
где Xi, Xk и mi, rrik суть 1-е и k-e компоненты векторов образов х
и средних значений m соответственно. Матрицу ковариацин
можно представить в векторной форме
С = Е {(х — ш) (х - ш)'} = Е {хх'-гхт'+тт'} = Е {хх'} - mm'.
D.6.10)
Аппроксимировав снова математическое ожидание выборочным
средним значением, получаем
N
D.6.11)
Известно (Андерсон [1963]), что при N > п \\ выборке из
совокупности нормально распределенных образов оценка мат-
матрицы С, определяемая D.6.11), с вероятностью 1 обладает об-
обратной матрицей С~'\
Оценки вектора средних значений и ковариационной матри-
матрицы можно задать рекуррентными соотношениями. Допустим,
4 6 Оценка функций плотности распределения 157
что необходимо скорректировать оценку вектора средних зна-
значений, вычисленную по выборке объема N, с учетом появления
еще одного объекта. Обозначив новую оценку через m (Л^ + 1),
записываем
ЛГ+1 / N
m(N -4-1) =
1JT D.6.12)
где m(N)—оценка, полученная по N выборочным объектам.
На начальном шаге процедуры m(l) = Xi. Полученное рекур-
рекуррентное соотношение можно использовать как для вычисления,
так и для коррекции значений вектора средних.
Аналогичное выражение можно получить и для ковариа-
ковариационной матрицы. Пусть C(N) представляет собой оценку ко-
ковариационной матрицы, вычисленную по N выборочным объ-
объектам:
N
Xlx'i-mWm'(N). D.6.13)
Пополнение выборки одним объектом приводит к следующему;
х/х/~
D-6>14)
Это выражение обеспечивает удобный способ оценки и кор-
коррекции ковариационной матрицы, причем на первом шаге
C(l) = x,xj — m (l)m'(l) и тA)=хь Анализ этого условия
показывает, что СA) = 0, т. е. это нулевая матрица.
4.6.3. Оценка вектора средних значений и ковариационной
матрицы с помощью байесовской обучающей процедуры
Если бы мы были в состоянии при неизвестных векторах
средних значений и ковариационных матрицах соответствую-
соответствующим образом задавать плотности распределений, то можно
была.бы построить итеративную процедуру вычисления оценок,
158 Гл. 4 Классификация образов с помощью функций правдоподобия
основанную на использовании обучающей выборки образов.
Ниже будем полагать, что плотность распределения р(х|<о<)
соответствует нормальному распределению с вектором средних
значений п\{ и ковариационной матрицей С,-. Допустим, что
ковариационная матрица С,- задана, а вектор средних значений
пи рассматривается как некоторый неизвестный параметр в,
подчиняющийся нормальному распределению с начальным век-
вектором средних значений т,@) и начальной ковариационной
матрицей К@). В таком случае
p(Q\<ot)~N[mt(f)), K@)]. D.6.15)
Наличие неопределенности относительно значения вектора
средних приводит к увеличению ковариационной матрицы, ха-
характеризующей образы х, со значения С/ до значения С; +
-f-K(O). Начальное значение ковариационной матрицы К@)
представляет собой меру неопределенности. Итак, начальная
плотность распределения для образов х имеет вид
р (х | (оь в) ~ N [щ, @), С, + К @)]. D.6.16)
Использование формулы Байеса
Xi ХН) —
р (xN | (о,., в, х,. х2 Xyv_,) р @ | со,., х,, х2 х„_,
1' хг
D.6.17)
позволяет вычислить для параметра 9 апостериорную плот-
плотность распределения на основе априорной плотности распреде-
распределения и информации, содержащейся в обучающей выборке
образов.
После предъявления первого из входящих в обучающую вы-
выборку образов Xi можно записать апостериорную плотность рас-
распределения для вектора средних значений как
р(х. 1@,, в)р(в|й)Л
*>= [5 • <4бл8>
это выражение определяет плотность нормального распределе-
распределения, так как произведение плотностей распределений p(xi\a>i,Q)
и р(9|(о,) образует плотность нормального распределения. Под-
Подстановка в D.6.18) выражений D.6.15) и D.6.16) дает
р@\щ, x,)~tf[m,(l), КО)], D.6.19)
где
mi A) = К @) [К @) + С,] Х1 + С, [К @) + С,] шг @) D.6.20)
И
,Г1С1. D.6.21)
4 6. Оценка функций плотности распределения 159
Плотность распределения для образов х при условии, что образ
Xi задан, является нормальной и определяется как
р(х|»,, 6, x,)~tf[m,(l), С, + К@], D-б-22>
так как сумма двух статистически независимых нормально рас-
распределенных векторов также подчиняется нормальному распре-
распределению, причем среднее суммы равно сумме средних, а кова-
ковариационная матрица суммы равна сумме ковариационных мат-
матриц слагаемых.
После предъявления второго образа х2 из обучающей вы-
выборки апостериорную плотность распределения для вектора
средних значений можно записать как
р (8 | щ, х„ х2) =
После подстановки в D.6.23) выражений D.6.19) и D.6.22)
данная плотность распределения принимает вид
p(Q\at, х,, x2)~N[m{B), КB)], D.6.24)
где
т, B) = К A) [К A) + С,-] х2 + Ct [К A) + С,-] т, A) D.6.25)
и
КB) = КA)[КA) + СгГ'С,- D.6.26)
представляют соответственно новые значения вектора средних
и ковариационной матрицы для неизвестного параметра в.
Плотность распределения образов х при заданных образах Xi
и х2 все еще остается нормальной; в таком случае
р(х\щ, 8, х„ x2)~W[mfB), d + KB)]. D.6.27)
После предъявления N образов обучающей выборки Xi,
х2, ..., хк апостериорную плотность распределения для век-
вектора средних значений можно на основе формулы D.6.17)
записать как
p(Q\ah х,, х2, .... xN)~N[mi(N), K(N)], D.6.28)
где
m, (N) = К (N - 1) [К (N - 1) + С,] xN +
-1 m{ (N-l) =
Г' Я + СЛЛ^К(О) + С]
= NK @) [NK @) + С<Г' Я + СЛЛ^К(О) + С;] тКО) D.6.29)
( rt С,] С,.
D.6.30)
160 Гл. 4. Классификация образов с помощью функций правдоподобия
Величина т,, входящая в D.6.29), представляет собой вектор
выборочных средних для класса со; и определяется как
N
i- D-6-31)
Из D.6.29) следует, что оценка вектора средних значений, по-
полученная в результате использования байесовской процедуры,
равна сумме априорного значения вектора средних и вектора
выборочных средних, взятых с соответствующими весами.
Плотность распределения образов х при заданных образах
Xi, x2 Xn имеет следующий вид:
р(х|<о„ в, хь х2 xN)~N[mi(N), С< + К(Л0]. D.6.32)
Принцип восстановления распределения упрощает получение
оценки вектора средних значений с помощью реализации обу-
обучающей процедуры на заданной выборке образов.
Легко показать, что в случае, когда размерность образа х
равна единице, введение параметра ос = /(@)/С,- приводит по-
полученные с помощью байесовской процедуры оценки математи-
математического ожидания и дисперсии к виду
™Мл + т<о) <4633>
<4-6-34>
Проведенное обсуждение позволяет сделать ряд замечаний.
Если начальное значение ковариации для неизвестного сред-
среднего значения велико, то в байесовскую оценку математиче-
математического ожидания nti(N) начальное значение среднего входит с
малым весом, а выборочное среднее — с большим. При больших
значения параметра а априорные оценки математического
ожидания и ковариации влияют на результат сравнительно
мало и параметры распределения определяются почти исклю-
исключительно по образам, входящим в обучающую выборку. Если
начальное значение ковариации для неизвестного среднего зна-
значения мало, байесовская оценка математического ожидания
обнаруживает тенденцию к медленной коррекции начального
среднего значения, причем даже в тех случаях, когда вектор
выборочных средних существенно отличается от начального
вектора средних значений. Из этих двух замечаний следует, что
константу а можно рассматривать как меру нашего доверия
к начальному значению среднего т,@).
Если ковариационная матрица неизвестна, то мы бы хотели,
чтобы система распознавания образов определила ее посред-
4.6 Оценка функций плотности распределения 161
ством реализации процесса обучения. Плотность распределения
вектора образов х для класса со,- при допущении о равенстве
нулю среднего значения определяется выражением
р (х | в,) = Bяр/21 С, Г'А ехр (- 4х'СГ'х) , D.6.35)
где С,- — случайная функция.
Ниже нам будет удобнее иметь дело с обратной матрицей
ковариаций Р;= СГ • В таком случае плотность распределения
принимает вид
р (х | в,) = Bя)-"/21 Р, |'/2 ехр (-1 х'Р,х) . D.6.36)
Применяя формулу Байеса
^1^^-. D.6.37)
в качестве восстанавливаемой априорной плотности распреде-
распределения для нормального распределения р(х|0,-, со,) с неизвестной
ковариационной матрицей С; выбираем плотность распределе-
распределения Уишарта:
|("№|P,p-||-JWexp[-4tr(v0O0Pl)] на S,
вне S,
D.6.38)
где S —область евклидова пространства размерности п (га+1) /2,
Р; — положительно определенная и симметрическая матрица
' Рп Рхг •" Pin\
\, D.6.39)
*Рп1 -Рп2 ¦" Рпч I
pa — pji't нормирующая константа определяется выражением
D.6.40)
Симметрическая матрица Р, имеет л(п + 1)/2 различных эле-
элементов.
Приняв, что априорная плотность распределения Р,- пред-
представляет собой распределение Уишарта, мы обеспечили фено-
феномен восстановления. Матрица Фо, входящая в D.6.38), является
положительно определенной и представляет исходные сведения
6 Заказ 594
162 Гл. 4. Классификация образов с помощью функций правдоподобия
о Р,, vo — действительное число, большее п, оно характеризует
достоверность начальной оценки матрицы Фо-
Рассматриваемая модель плотности распределения
p(xN\Qi, со,) предусматривает, что образы каждого класса под-
подчиняются нормальному распределению с нулевым вектором
математического ожидания и ковариационной матрицей С,-, по
одной на каждый класс.
Пусть определена плотность распределения
р@, |хь ..., Хл_ь со,),
после чего предъявлен еще один образ \N из обучающей вы-
выборки; требуется определить новое значение плотности распре-
распределения
р@( |хь ..., \N\ щ),
имеющей такое же параметрическое описание, как и выше.
Структура классификатора при восстановлении априорной
плотности распределения р@<) остается неизменной — с изме-
изменением величины JV будут изменяться только параметры, свя-
связанные с вычислением функции правдоподобия:
p(xN\xu . .., х^_ь со*)-
Поскольку
р (х | Р,) = Bя)-"/21 Р( |'А ехр (- \ х'Р,х)
и результаты измерений характеристик образов хь ..., х# не-
независимы, то
N
р(хь ....
._ »г/л я г т Г 1
. D.6.41)
где
а также использован тот факт, что
Здесь хх' обозначает внешнее произведение матриц, результа-
результатом которого является симметрическая матрица ранга 1.
Поскольку
4.6. Оценка функций плотности распределения 163
из D.6.38) и D.6.42) следует, что
vo<l>o
(vo-l)/2
i(vo-n-2)/2
\
P(Pj1*i. •••- хлг)=^ l-».v. 2
X exp [- 4" tr (voOoP,)] } { Bn)-"v/21 P, Iv/2 exp [- 1 tr (JVP,xx')] } ,
D.6.43)
где К—константа.
Роль знаменателя в D.6.42) сводится исключительно к нор-
нормированию плотности распределения, являющейся функцией
Р;. Собрав вместе все члены, представляющие функцию Р;, не-
нетрудно убедиться в том, что апостериорная плотность распре-
распределения также есть распределение Уишарта:
р(Р? |х! xA,)=^|Pil(v-v~"~2)/2exp[— Ytr(vJv<DtfPi)]. D.6.44)
где
Vjv = v0 + ЛГ D.6.45)
и
В выражение для апостериорной вероятности входит пара-
параметр Флг, характеризующий веса, которые присвоены начальной
оценке матрицы Фо и внешнему произведению матриц хх'; вве-
введение весов осуществляется при помощи вычисления взвешен-
взвешенной суммы с коэффициентами vo и N соответственно. Параметр
Флг представляет взвешенное среднее априорной информации о
матрицах Р,- и Фо и обучающей информации, заключенной в
произведении хх'.
4.6.4. Аппроксимация плотностей распределения функциями
В пп. 4.6.2 и 4.6.3 были рассмотрены частные случаи оценки
параметров плотности распределения — предполагалось, что
тип распределения известен. Часто, однако, это допущение не-
неприемлемо и возникает необходимость оценивать плотность
распределения непосредственно.
Пусть р(х) — оценка плотности распределения р{\), при-
причем, как и раньше, под р(х) подразумевается р(х\ац). Мы пы-
пытаемся найти такую оценку, которая обеспечила бы минимиза-
минимизацию среднеквадратичной ошибки (интегрального квадратичного
показателя качества), определяемой как
R=\u(x)[p(x)-p(x)fdx, D.6.47)
164 Гл. 4. Классификация образов с помощью функций правдоподобия
где и(х)—весовая функция. Воспользуемся разложением оцен-
оценки р(х) в ряд
т
f> (х) = Е с/Ф/ (х), D.6.48)
где с; — коэффициенты, подлежащие определению, а (срДх)} —
множество заданных базисных функций. В § 2.7 обсуждался
способ построения таких функций. Известное разложение в ряд
Фурье является частным случаем разложения D.6.48)— он воз-
возникает, если базисные функции имеют синусоидальный ха-
характер.
Подстановка D.6.48) в соотношение D.6.47) дает
[т -Л
Р (х) - ? с/Ф/ (х) dx. D.6.49)
/-1 J
Требуется найти такие коэффициенты с,, которые обеспечат
минимизацию интеграла вероятности ошибки R. Необходимое
условие минимальности интеграла вероятности ошибки R за-
заключается в том, что
.М- = 0, /г=1, 2, .... т. D.6.50)
ack
Взяв частную производную, получим
/-1 X X
Взглянув на правую часть уравнения D.6.51), нетрудно убе-
убедиться в том, что она по определению равна математическому
ожиданию функции и(х)ф«(х). В соответствии с нашим преды-
предыдущим анализом математическое ожидание можно аппрокси-
аппроксимировать выборочным средним, т. е.
N
J и (х) ф, (х) р (х) dx « y J] и (х() q>k (xi). D.6.52)
Подстановка этой аппроксимирующей оценки в уравнение
D.6.51) дает
N
l\u W Ф/ (х^ Ч>* (х)rfx = "F Е "(Х;) ф* ^'^ D-6-53)
/=1 X ( = 1
Если базисные функции {ф(х)} выбраны таким образом, что
они ортогональны весовой функции «(х), то из определения
4.6 Оценка функций плотности распределения 165
ортогональности [см. B.7.4)] следует
= ( Ak< если i==k> D.6.54)
\ 0, если / Ф k.
Подстановка D.6.54) в уравнение D.6.53) приводит к следую-
следующему соотношению, позволяющему вычислить искомые коэф-
коэффициенты:
N
fe = l, 2, .... от. D.6.55)
Если базисные функции {ср&(х)} ортонормированны, то Ak = 1
для всех k. Кроме того, поскольку члены и(х,) не зависят от k
и, следовательно, для всех коэффициентов одинаковы, то их
можно исключить из аппроксимирующего выражения без вся-
всякого ущерба для классификационной мощности коэффициентов.
В таком случае
N
^ ^), ft=l, 2 m. D.6.56)
После того как коэффициенты определены, с помощью форму-
формулы D.6.48) формируется оценка плотности распределения ^(х).
Использование процедуры, рассмотренной в п. 4.6.2, позво-
позволяет представить выражение D.6.56) в более удобной рекур-
рекуррентной форме. Если Ck(N) представляет коэффициент, опреде-
определенный по выборке объема N, то выражение для коэффициента
при увеличении выборки на один объект имеет следующий вид:
D.6.57)
где Cfe(l) = <pk(x\). При использовании этой формулы для опре-
определения новых коэффициентов необходимы только уже извест-
известные коэффициенты Ck{N), что существенно упрощает вычисли-
вычислительную процедуру.
Для того чтобы применение выражений D.6.48) и D.6.55)
или D.6.56) приводило к успеху, необходимо иметь в виду два
существенных обстоятельства. Во-первых, следует полностью
отдавать себе отчет в том, что качество аппроксимации с по-
помощью выбранной системы базисных функций зависит от
числа m членов разложения. Поскольку, по всей вероятности,
вид плотности распределения р(х) нам не известен, оценить
качество аппроксимации р(\) при помощи непосредственного
сравнения невозможно. С другой стороны, так как оценка /5(х)
166 Гл. 4. Классификация образов с помощью функций правдоподобия
отыскивается для того, чтобы построить байесовский классифи-
классификатор, то заботиться следует только о качестве распознавания,
доступном этому классификатору. Последнее можно установить
непосредственно в эксперименте с обучающей выборкой. Если
при некоторой оценке /3(х) качество классификации оказы-
оказывается неудовлетворительным, следует попробовать увеличить
число базисных функций и посмотреть, приводит ли улучшение
качества оценки р(х) к улучшению качества классификатора.
Эту процедуру можно продолжать вплоть до наступления «на-
«насыщения» (когда введение дополнительных членов не произво-
производит никакого либо очень малый эффект) или до тех пор, пока
число членов не начнет превосходить допустимую величину.
Вторым важным моментом является выбор базисных функ-
функций. Так, например, если плотность распределения р(х) имеет
синусоидальный характер, а для разложения оценки р(х) ис-
использован степенной ряд, то очевидно, что число членов будет
значительно больше, чем при выборе синусоидальных базисных
функций. Естественно, при отсутствии априорных сведений о
характере плотности распределения р(х) базисные функции в
первую очередь должны выбираться исходя из простоты реали-
реализации. Все, что можно было бы сказать об общих правилах
выбора базисных функций, сводится к тому, что при выполне-
выполнении условия линейной независимости и некоторых других не
очень жестких ограничений на вид плотности распределения
р(х) можно доказать сходимость р(х)->р(х) при т—*оо и
JV->oo. Отметим, что ортогональность является частным слу-
случаем линейной независимости.
Пример. Рассмотрим классы, приведенные на рис. 4.6. Для
этих классов требуется сформировать байесовский классифи-
классификатор, воспользовавшись плотностями распределений, получен-
полученными непосредственной оценкой по обучающим выборкам. Эти
плотности можно аппроксимировать, применив выражения вида
D.6.48):
в котором первый индекс коэффициента указывает класс (со,).
Как следует из D.6.54), базисные функции {ср;(х)} счи-
считаются ортогональными в области определения образов. Осо-
Особенно удобны для применения многочлены Эрмита, рассмотрен-
рассмотренные в § 2.7, поскольку областью их ортогональности является
интервал (—оо, оо). В одномерном случае эти функции опре-
определяются рекуррентным соотношением
Н1+1 (х) - 2xHt (je) + 2lHl_l (x) = О
4.6. Оценка функций плотности распределения
167
[см. B.7.18)]. Первые члены функции Н(х) имеют следующий
вид:
Но (х) = 1, Я, (х) = 2х, Н2 {х) = 4х2 - 2,
Я3 (х) = 8а:3 - \2х, Н4 (х) = 16х4 — 48х2 + 12.
Все эти функции ортогональны. Как показано в п. 2.7.3, орто-
-6 -5 -4 -3 -2 -¦
1 2
I I I
5 В
r
Рис. 4.6. Определение границы, разделяющей классы, методом Байеса с ис-
использованием аппроксимации плотностей распределения функциями.
нормированные функции определяются следующим выра-
выражением:
в котором множитель при Hi(x) представляет собой ортонорми-
рующий коэффициент. В иллюстративных целях с ортогональ-
ортогональными функциями мы будем обращаться так, как если бы они
были ортонормирсжаиными. Обычно этот прием работает хо-
хорошо и позволяет избежать вычислительных трудностей в
168 Гл. 4. Классификация образов с помощью функций правдоподобия
D.6.55) при больших значениях k. В частности, при k = 50 для
многочленов Эрмита Ak « 6,07 X Ю79.
Множество ортогональных функций для двумерного случая
легко получить, формируя произвольные попарные комбинации
одномерных функций. Пусть т = 4'). Четыре члена низшего
порядка двумерного ортогонального множества выглядят сле-
следующим образом:
Ф, (х) = ф, (хи х2) = Яо (xi) Яо (х2) = 1,
Ф2 (х) = ф2 (хи х2) = Н{ (xi) Но (х2) = 2хь
Фз (х) — Фз (xi, х2) — Но (х{) Нх (х2) = 2х2,
ф4 (х) = ф4 (хи х2) = Hi (xi) Hi {x2) = 4лг,л;2.
Должно быть очевидно, что порядок формирования этих функ-
функций не единственный. Для получения любой функции ф(х)
можно использовать произвольную парную комбинацию функ-
функций одной переменной. Любой иной выбор Я/(х) просто приве-
приведет к получению более сложных членов.
Теперь задача заключается в определении коэффициентов
сц разложения р(х|со,). Используя допущение об ортонорми-
рованности функций, эти коэффициенты можно вычислить по-
посредством D.6.56). Для класса coi
N,
J = I
где Ni — число образов, входящих в класс coi, k изменяется в
диапазоне от 1 до т. Для образов класса соь представленного
на рис. 4.6, применение данной процедуры дает
где первый индекс образа указывает, какому классу он принад-
принадлежит (в данном случае coi). Так как ф1(х)= 1, то
Следующий коэффициент определяется выражением
[
') Это значение выбрано произвольным образом и имеет смысл только в
качестве иллюстрации. В принципе правильное значение т следует определять
экспериментально.
4.6 Оценка фцнкиий плотности распределения 16q
и так как реализация функции ф2(х) эквивалентна удвоению
первой компоненты образа х, то
Аналогично получим
С13==у[фз(Хп) + Фз(Х12) + Фз(Х13)+ ... +ф3(Х17)] =
[ф(Х) +
у
••• +Ф4(х17)] =
Применение этой же процедуры к образам класса со2 приво-
приводит к следующим коэффициентам:
c2i=l, с22 = —6, с23=—6,7, с24 = 40.
Следовательно, согласно D.6.48), аппроксимация плотности
распределения р(х|со,) такова:
j6 (X | СО,) = С,,ф, (X) + С12ф2 (X) + С13Фз (X) -Ь С14ф4 (X) =
= 1 + 12*1 + 12*2 + 148,4*,*2;
р (х | со2) = с21ф, (х) + с22ф2 (х) + с23фз (х) + с24Ф4 (х) =
= 1 — 12*, — 13,4х2 + 160х,*2.
В таком случае искомые решающие функции имеют вид
d, (х) = р (х | со,) р (со,),
d2 (х) = р (х | со2) р (со2).
Если предположить, что p(coi) =¦ р(со2)= 1/2, то
d\ (х) = '/г + 6х, + 6х2 + 74,2*^2,
d2 (х) = '/2 — 6*i — 6,7*2 + 80х,*2.
В таком случае уравнением разделяющей границы будет
d, (х) — d2 (х) = 12*, + 12,7*2 — 5,8*1*2 = 0.
Соответствующая граница показана на рис. 4.6. Поскольку
данная задача требует разделения образов на два класса, раз-
разность решающих функций d\(х)—d2(x) представляет класси-
классификационную решающую функцию. Следует отметить также,
что в данном случае с равным успехом можно было воспользо-
воспользоваться линейной аппроксимацией плотностей распределения
р(х|со,) и р(х|со2). В этом можно убедиться, приравняв нулю
нелинейный член последнего выражения. Хотя мы для того,
чтобы проиллюстрировать процедуры во всех подробностях, с
самого начала работали с нелинейной решающей функцией.
170 Гл. 4. Классификация образов с помощью функций правдоподобия
должно быть очевидно, что в большинстве задач в первую оче-
очередь используется линейная аппроксимация. Только получение
неприемлемых результатов заставляет увеличивать сложность
аппроксимации. |
Важный частный случай аппроксимации посредством функ-
функций возникает при оценке плотностей распределения для двоич-
двоичных образов. Если имеется образ \ = (хи х2, ..., xk, ..., хп)'
и каждая его компонента хк принимает значения 1 или 0, то
общее число возможных различных образов равно 2", причем
каждому из них соответствует «своя» вершина единичного
«-мерного куба. В таком случае нам нужно определять не
плотность непрерывного распределения, а плотность дискрет-
дискретного распределения р(х = х/), где индекс / пробегает значения
от 1 до 2"; другими словами, нас интересует вероятность появ-
появления каждого из 2" возможных векторов образов. Результаты
настоящего раздела нетрудно использовать для решения данной
задачи посредством соответствующего выбора базисных функ-
функций (ф(х)}. В качестве последних можно использовать полино-
полиномиальные функции Радемахера — Уолша, которые часто при-
применяются при разложении дискретных функций. Искомое мно-
множество содержит 2" членов, полученных перемножением раз-
различных членов вида Bхь—1) в количестве пуля, одного, двух,
трех н т. д. — вплоть до п. Эта процедура проиллюстрирована
в табл. 4.1.
Эти дискретные полиномиальные функции ортогональны
относительно весовой функции и(\) = 1 (см. п. 2.7.1), так как
если / = k,
D.6.58)
где суммирование проводится по всем 2" значениям двоичных
векторов х.
Если в разложении используется только т базисных функ-
функций, то приближенное значение плотности дискретного распре-
распределения р(\) имеет, согласно D.6.48), следующий вид:
m
Р W = ? С/ф/ (Х),
где коэффициенты определяются из D.6.55) при Ak = 2" и
и(\) = 1, т. е.
1 = 1
4.6. Оценка функций плотности распределения 171
Соответствующие коэффициенты для ортонормированных функ-
функций задаются соотношением D.6.56).
Таблица 4.1
Формирование полиномиальных функций Радемахера — Уолш!
j
1
2
8
« + 1
» + 2
и + 3
n + 2 + я -
я + 3 + я -
к + 4 + п -
» + 2 + »(« -
и + 3 + я(п -
» + 3 + »(» — 1)/2 + п(п
1
1
1
!)/¦
D/2
- 1)(» - 21/в
1
2Xl- 1
\ 1 / \ 3
Bл-2 — 1)Bл-4
B*n_j — 1)Bл
- 1)
-1)
- 1)
-1)
-1)
¦»- J)
.(•ж, - 1)
Поскольку в данном случае полное множество базисных
функций состоит из 2п элементов, сходимость аппроксимиро-
аппроксимированной плотности распределения р(х) к истинной плотности
распределения р(х) обеспечивается при m = 2п и N — 2" (об-
(общее число различных двоичных образов).
Пример. В качестве примера аппроксимации посредством
дискретных функций рассмотрим снова образы, представленные
на рис. 4.3. Образы принадлежат двум классам: шг. {(О, 0, 0)',
A,0,1)', A,0,0)', A,1,0)'}, и со2: {@,0,1)', @,1,1)', @,1,0)',
AЛ,1)'}.
Решив воспользоваться линейной аппроксимацией плотности
распределения р(х), из табл. 4.1 получаем
Ф,(х) = 1, (p2(x) = 2xi — 1, ф3(х) = 2*2—1, ф4(х) = 2лг3—1.
где все xi принимают значения 0 или 1.
172 Гл. 4. Классификация образов с помощью функций правдоподобия
Коэффициенты для класса ом, согласно D.6.59), суть
где iVi представляет количество образов, входящих в класс щ,
и п = 3. Проведя суммирование по образам класса сем, по-
получим
4
С|1= -32" ^ ф! (хи) = -^ A + 1 + 1 + 1)=4";
==15"^~ 1 + 1 + 1 + 1) = -^-;
: 32" (—1 + 1 — 1 — 1)== — -^-.
Применение такой же процедуры к классу ©2 дает
_ 1 _ 1 _ 1 _ 1
С21— 8 ' С22~~ 16"' С23 ~~ Тб"' °2i ~ ~Ш •
В таком случае аппроксимации плотностей распределения вы-
выглядят следующим образом:
J» (X | Юз) = J] С2/ф/ (X) =
= 1 - -i-Bдг, - 1) + -1 Bх2- 1) + -jL Bx3 - 1).
Приняв, что p(coi) = р(со2)= 1/2, получим следующие решаю-
решающие функции:
d, (х) = р (х | ш,) р (ш,) =
^B«D +
4.7 Заключительные замечания 173
Одну решающую функцию, обеспечивающую разделение обоих
классов, можно получить, положив d(x) = di(\)—d2(x). Таким
образом,
d (х) = -^ B*, - 1) - -^ B*2 - 1) - -jj Bx3 - 1);
после умножения на 16 эта функция принимает вид
d (х) = Bх! - 1) - Bх2 - 1) - Bх3 - 1).
Легко убедиться в том, что d(x)>0 для всех образов класса
аи, и d(x)< 0 для всех образов класса ©2- Использование орто-
нормированных функций дает такие же результаты.
Следует отметить, что решающая функция d{x) имеет смысл
только для двоичных образов х. Следовательно, в данном
случае понятие разделяющей поверхности в том виде, как оно
вводилось выше, перестает работать. Функция d(x) имеет только
восемь значений — по одному на каждый из восьми различных
двоичных образов, которые могут существовать в трехмерном
пространстве. |
4.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Основным результатом данной главы является построение
байесовского классификационного правила на основе элемен-
элементарной теории статистических решений. С точки зрения теории
распознавания образов частный случай, соответствующий допу-
допущению о двоичной (принимающей значения 0 или 1) функции
потерь, устанавливает верхнюю границу качества, которое в
среднем может обеспечить любой классификатор, построенный
на основе концепции решающей функции. Этот важный теоре-
теоретический результат относится, следовательно, ко всем схемам
классификации, рассмотренным в гл. 3—6.
Так как реализация байесовского классификатора предпо-
предполагает знание плотности распределения для каждого класса, то
становится совершенно очевидным, что оценка плотностей —
основная проблема применения такой схемы классификации.
Воспользовавшись принципом максимума энтропии, мы пока-
показали, что в тех случаях, когда единственными известными пара-
параметрами являются математическое ожидание и дисперсия, це-
целесообразно пользоваться плотностью нормального распределе-
распределения. Так как эта задача имеет и практическую, и теоретическую
ценность, для развития методов оценки параметров были затра-
затрачены существенные усилия. Если параметрическая оценка не
174 Гл. 4. Классификация образов с помощью функций правдоподобия
приносит желаемого успеха, можно обратиться к методам
непосредственной аппроксимации плотностей распределения с
помощью функций. Как указывалось в предыдущем разделе,
истинную плотность распределения можно с произвольной сте-
степенью точности аппроксимировать путем увеличения числа
включенных в разложение членов, так же как и числа образов,
использованных при определении коэффициентов.
В гл. 6 мы вернемся к задаче аппроксимации плотностей
распределений посредством функций, рассмотрев ее с иных
позиций. Стоит заметить, что несмотря на то, что предметом
обсуждения служили статистические решающие функции, эти
функции вполне укладываются в общую схему, сформулиро-
сформулированную в гл. 2. Соответствующие свидетельства были получены
при построении байесовского классификатора для нормально
распределенных образов, а также для образов, характеризую-
характеризующихся плотностью распределения седьмого пирсоновского типа.
Это же справедливо и для более общего метода аппроксимации
посредством функций, описанного в п. 4.6.4. Очевидно, что после
аппроксимации плотности распределения в виде разложения
по системе базисных функций (например, полиномиальных
функций) формы статистических решающих функций и решаю-
решающих функций того же типа, полученных детерминистскими сред-
средствами, отличаться не будут. Качество соответствующих ре-
решающих функций несомненно зависит от метода, выбранного
для вычисления.
Библиография
Статистические игры и теория решений имеют обширную литературу.
Отличным источником, в частности, может служить монография Блекуэлла и
Гиршнка [1958]. К результатам, приведенным в § 4.2, можно прийти с пози-
позиций теории связи. Технические аспекты построения байесовского классифика-
классификационного правила рассматриваются в монографиях Реза [19611, Ван Триса
[19721 п Хелстрома [1963].
Классификация нормально распределенных образов с помощью байесов-
байесовских процедур— также хорошо представленная в литературе тема. Дополни-
Дополнительные сведения по этому поводу можно найти в работах П. Купера [1967],
Андерсона и Бахадура [1962]. монографиях Фукупаги [1972]. Патрика [1972],
работах Ту [1969а|. Кэнэла и Рандла [1964], монографиях Нильсона [1967],
Дуды и Харта [1976], Фу [1977] и Майзела [1972].
Первые упоминания о применении байесовского обучения для определе-
определения вектора математического ожидания и ковариационной матрицы можно
найти в статьях Абрамсона и Бравермана [1962] и Кипа [1965]. Кроме того,
эта проблема г разной степенью подробности рассматривается почти во всех
книгах по статистическому распознаванию образов. Монографии Патрика,
Фукупаги и Дуды и Харта посвящены статистическим методам распознава-
распознавания образов и поэтому являются отличным дополнением к материалу, изло-
изложенному в этой главе. Дополнительный материал по проблеме аппроксима-
аппроксимации посредством функций можно найти в работах Ту [1969а, 19696] и моно-
монографин Майзела [1972].
Задача
175
Задачи
4.1. Рассмотрите задачу разделения одномерных образов на М классов, каж-
каждый из которых определяется плотностью распределения Рэлея:
ехр
{
( 0,
х<0.
Построите соответствующие решающие функции при условии, что функ-
функция потерь принимает значения 0 и 1. Положите р(ин) = 1/М.
4.2. (а) Решите задачу 4.1 для плотности распределения
= —=—exp
/2
(б) Постройте плотности распределения для задачи разделения на дна
класса при ai = аг = 2, nti = 0, и т2 =• 2. Определите расположе-
расположение разделяющем границы.
4.3. Распределение одномерных образов для двух классов характеризуется
представленными па рисунке плотностями распределений:
(а) Постройте соответствующие решающие функции при условии, что
функция потерь принимает значения 0 и 1 и что априорные вероят-
вероятности равны.
(б) Определите расположение разделяющей границы.
4.4. Заданы классы, характеризующиеся нормальными плотностями распреде-
распределений, со,: {0,0)', B,0)', B,2)', @,2'} и со2: {D,4)', F,4)*, F,6)',
D,6)'}.
(а) Найдите уравнение байесовской разделяющей границы для этих клас-
классов при условии p(toi) = p(a>2) = *k-
(б) Постройте эту границу.
4.5. Решите задачу 4.4 для классов ы,: {(—1,0)', @,-1)', A,0)', @,1)'} и
со2: {(—2,0)', @,-2)', B,0)', @,2)'}. Обратите внимание на то, что эгн
классы не являются линейно разделимыми.
4.6. (а) Найдите уравнение байесовской разделяющей границы для двух клас-
классов, характеризующихся пнреоновскимн плотностями распределений
второго типа с равными k.
(б) Проанализируйте свойства разделяющей границы, построенной в
и. (а) при условии равенства и неравенства весовых матриц.
4.7. (а) Воспользуйтесь методом аппроксимации посредством функций для
получения оценок плотностей распределения p(x|toi) и р"(х|м2), ха-
характеризующих классы со2: {(—5.-5)', (—5,-4)', (—4,-5)', (—5,
176 Гл. 4. Классификация образов с помощью функций правдоподобия
—6)', (—6,-5)'} и со2: {E,5)', E,6)', F,5)', E,4)', D,5)'}. Исполь-
Используйте четыре первые ортогональные полиномиальные функции двух
переменных Эрмита, а коэффициенты определите с помощью фор-
формулы D.6.55). Обратите внимание на то, что из B.7.7) и B.7.19)
следует Л/. = 2*61 л/л .
(б) Повторите решение задачи 4.7(а), используя ортогональные функции
и вычисляя коэффициенты по формуле D.6.56).
(в) Постройте байесовские решающие функции для задач 4.7(а) и (б)
при условии p(toi)= р(сог) = 1/2.
(г) Проведите разделяющие границы, найденные в п. (в).
(д) Повторите решение задач 4.7F) — (г), используя ортонормированные
многочлены Эрмита, и сравните результаты.
4.8. Решающие функции d,(x) = p(x|co,)p(w,) получены при условии, что
функции потерь принимают значения 0 и 1. Докажите, что эти решающие
функции минимизируют вероятность ошибки. Указание. Вероятность
ошибки р(е) равна 1— р(с), где р(с)— вероятность принять правильное
решение. Для заданного образа х, принадлежащего классу ю<, имеет
место р(с\х) = р(со,-|х). Используйте эту информацию для определения
вероятности правильной классификации р(с) и покажите, что эта вероят-
вероятность максимальна (вероятность ошибки р(е) минимальна) при макси-
максимальном значении р(х|со,)р(со,).
Глава 5
ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ ОБРАЗОВ.
ДЕТЕРМИНИСТСКИЙ ПОДХОД
5.1. ВВЕДЕНИЕ
Подходы к построению классификаторов образов, изучав-
изучавшиеся нами до сих пор, основаны на непосредственных вычис-
вычислениях, т. е. разделяющие границы, полученные в результате
реализации этих подходов, определяются заданной выборкой
образов, по которой путем непосредственных вычислений оты-
отыскиваются соответствующие коэффициенты. Примеры такого
рода мы встречали в третьей главе, когда требовалось опреде-
определять центры кластеров или «стандартные» образы до построения
классификаторов, и в четвертой главе, когда структура байесов-
байесовского классификатора для нормально распределенных образов
полностью определялась вектором математического ожидания и
ковариационной матрицей каждого класса.
В настоящей главе мы приступаем к изучению классифика-
классификаторов, решающие функции которых строятся по заданной вы-
выборке образов с помощью итеративных, «обучающих» алгорит-
алгоритмов. Как отмечалось в гл. 2, когда тип решающей функции вы-
выбран, задача заключается в определении коэффициентов. Алго-
Алгоритмы, представленные в этой главе, позволяют определять
коэффициенты искомого решения посредством обучения по за-
заданным множествам образов при условии, что эти обучаю-
обучающие множества разделяются выбранными решающими функ-
функциями.
В § 2.4 было показано, что решение задачи о разделении
на два класса эквивалентно решению системы линейных нера-
неравенств. Таким образом, если заданы два множества образов,
принадлежащих соответственно классам coi и ю2, то решение
ищется в виде вектора весов w, обладающего тем свойством,
что для всех образов класса coi выполняется условие w'x > О
и для всех образов класса (о2 — условие w'x < 0. Если образы
класса ю2 умножить на —1, то эквивалентное условие w'x > 0
становится общим для всех образов. Обозначив через N общее
количество пополненных выборочных образов (см. гл. 2) обоих
классов, нашу задачу можно свести к отысканию вектора весов
178 Га. 5. Детерминистский подход
w, обеспечивающего справедливость системы неравенств
Xw>0, E.1.1)
где
х2
х'„
E.1.2)
w = (Ш], и>2, .... wn, Wn+\)' и 0 — нулевой вектор. Если образы
обладают хорошим размещением в том смысле, как это было
введено в гл. 2, матрица X удовлетворяет условию Хаара, т. е.
всякая подматрица (п+ 1)Х(«+ 1)-матрицы X имеет ранг
п.-}- 1 (Чини [1966]).
Если вектор весов w, удовлетворяющий условию E.1.1),
существует, то неравенства называются совместными; в против-
противном случае они несовместны. На языке распознавания образов
мы говорим, что классы соответственно разделимы или нераз-
неразделимы. Читателю следует иметь в виду, что формулировка
условия E.1.1) предполагает, что все образы одного из классов
умножены на —1 и, кроме того, все образы пополнены в соот-
соответствии с процедурой, описанной в гл. 2.
В принципе для решения E.1.1) можно воспользоваться
и детерминистским, и статистическим подходами. Детерминист-
Детерминистский подход служит основой алгоритмов, рассматриваемых в
данной главе. Как и следует из названия, эти алгоритмы кон-
конструируются независимо от каких-либо предположений о стати-
статистических свойствах классов образов. Статистические алго-
алгоритмы, представляемые в гл. 6, отражают, с другой стороны,
попытку найти аппроксимацию плотностей распределения
р(со, | х) и использовать их затем в качестве байесовских решаю-
решающих функций в соответствии с соотношением D.2.23). Однако,
завершив изучение обоих подходов, мы заметим поразительное
сходство между статистическими и детерминистскими алго-
алгоритмами.
5.2. ПЕРЦЕПТРОННЫЙ ПОДХОД
Происхождение алгоритмов классификации образов, пред-
представляемых в настоящем параграфе, можно проследить вплоть
до первых экспериментов в области бионики (область науки,
посвященная приложению биологических концепций к электрон-
электронным устройствам), которые были связаны с проблемами, воз-
5.2. Перцептронный подход 179
никающими при обучении животных и машин1). В середине
50-х и начале 60-х годов многие исследователи считали, что
класс устройств, предложенных Розспблаттом [1957] и назы-
называемых обычно перцептронами, представляет естественную л
обладающую большими возможностями модель процесса обу-
обучения машины. Хотя в настоящее время в общем все согласны
с тем, что надежды и ожидания, связанные со свойствами пер-
цептронов, оказались чрезмерно оптимистическими, математи-
математические результаты, к которым привело развитие перцептрон-
ного подхода, продолжают играть центральную роль в теории
распознавания образов2).
Основная модель перцептрона, обеспечивающая отнесение
образа к одному из двух заданных классов, приведена на
рис. 5.1. Устройство состоит из сетчатки 5 сенсорных элементов,
которые случайным образом соединены с ассоциативными эле-
элементами второй сетчатки А. Каждый из элементов второй сет-
сетчатки воспроизводит выходной сигнал только в том случае, если
достаточное число сенсорных элементов, соединенных с его
входом, находится в возбужденном состоянии. Сенсорные эле-
элементы можно рассматривать в качестве устройств, с помощью
которых вся система воспринимает из внешней среды стимулы,
т. е. как некие измерительные устройства, а ассоциативные эле-
элементы— как входную часть системы.
Реакция всей системы пропорциональна сумме взятых с
определенными весами реакций элементов ассоциативной сет-
сетчатки; таким образом, обозначив через Xi реакцию г-го ассо-
ассоциативного элемента и через Wi — соответствующий вес, реак-
реакцию системы можно записать как
га+1
? w'x. E.2.1)
') Это не совсем точно. Как указывает Норберт Винер (Кибернетика или
управление и связь в животном и машине. «Советское Радио», М., 1968,
стр. 70—71), впервые соответствующая задача была поставлена У. С. Мак-
Каллохом в связи с созданием аппарата, дающего слепому возможность вос-
воспринимать печатный текст на слух (весна 1947 г.). — Прим. перев.
2) В настоящее время это уже не совсем так. Хотя перцептронная модель
сыграла в распознавании, да и вообще в кибернетике, существенную роль и
продолжает занимать определенное место и сейчас, в последнее время в рас-
распознавании нее большее значение приобретают попытки построить общую
теорию распознавания па основе так называемого алгебраического подхода
(см. по этому поводу, например, монографию У. Грепапдера «Лекции по тео-
теории образов», т. I (Мир, М., 1979) и работу Ю. И. Журавлева «Об алгебраи-
алгебраическом походе к решению задач распознавания или классификации», Проб-
Проблемы кибернетики, 33, 1978. пр. 1—68), а также возможности, связанные с
использованием методов теории формальных грамматик — последняя тема
отражена в гл. 8 настоящей книги. — Прим. перев.
180
Гл. 5. Детерминистский подход
Если R > 0, значит предъявленный системе образ принадлежит
классу шь если R <. 0, то образ относится к классу ш2. Описа-
Описание этой процедуры классификации вполне соответствует вве-
введенным нами раньше принципам классификации, и. судя по
Сетчатка S
Сетчатка А
Сетчатка R
Рис. 5.1. Основной вариант модели перцептрона.
всему, основная перцептронная модель представляет собой, за
исключением сенсорной сетчатки, не что иное, как реализацию
линейной решающей функции.
Схему, приведенную на рис. 5.1, легко распространить на
случай разделения на несколько классов посредством увеличе-
увеличения числа реагирующих элементов в /?-сетчатке. Так, например,
разделение на несколько классов, сответствующее случаю 3
(§ 2.2), можно реализовать, добавив М элементов в ^-сетчатку,
где М — число классов. Классификация проводится обычным
способом: рассматриваются значения реакций R\, R2, .,,, Rm и
5.2 Перцептронный подход 181
образ причисляется к классу а>,, если Ri > /?/ для всех / ф L
Основную модель можно также легко распространить на слу-
случай нелинейных решающих функций введением соответствую-
соответствующих нелинейных преобразователей между сетчатками А и R.
Из обсуждения, проведенного в § 2.3, читатель должен, однако,
помнить, что анализ можно без всякой потери общности пол-
полностью ограничить линейными решающими функциями, так
как нелинейные решающие функции можно рассматривать как
линейные функции в пополненном пространстве.
5.2.1. Принцип подкрепления — наказания
Обучающий алгоритм для перцептрона, приведенного на
рис. 5.1, сводится к простой схеме итеративного определения
вектора весов w. Дадим краткое описание этой схемы, которую
обычно называют алгоритмом перцептрона.
Заданы два обучающих множества, представляющие классы
(?>\ и (о2 соответственно; пусть w(l)—начальный вектор весов,
который выбирается произвольно. В таком случае k-и шаг
обучения выглядит следующим образом.
Если хD)ей| и w'(k)x(k) ^ 0, то вектор весов w(k) за-
заменяется вектором
vf(k + \) = w(k) + cx(k), E.2.2)
где с — корректирующее приращение.
Если х(?)ею2 и w' (k) x (k) ^ 0, то w{k) заменяется век-
вектором
w(&+1) = w(/j) — cx(k). E.2.3)
В противном случае w(&) не изменяется, т. е.
w (k + 1) = w (k). E.2.4)
Короче говоря, алгоритм вносит изменения в вектор весов w
в том и только том случае, если образ, предъявленный на
k-м шаге обучения, был при выполнении этого шага непра-
неправильно классифицирован с помощью соответствующего вектора
весов. Корректирующее приращение должно быть положитель-
положительным, и в данном случае предполагается, что оно постоянно.
Очевидно, что алгоритм перцептрона является процедурой
типа «подкрепление — наказание», причем, надо признаться,
подкреплением за правильную классификацию образа, в сущ-
сущности, служит отсутствие наказания. Иными словами, если
образ классифицирован правильно, то система подкрепляется
182
Гл. S. Детерминистский подход
тем, что в вектор весов w не вносится никаких изменений.
С другой стороны, если образ классифицируется неправильно и
произведение w'(k)x(k) оказывается меньше нуля, когда оно
должно бы быть больше нуля, система «наказывается» увели-
увеличением значения вектора весов w(k) на величину, пропорцио-
пропорциональную x(k). Точно так же, если произведение w'(k)x(k) ока-
оказывается больше нуля, когда оно должно быть меньше нуля,
система наказывается противоположным образом.
Сходимость алгоритма наступает при правильной класси-
классификации всех образов с помощью некоторого вектора весов.
В следующем разделе показано, что алгоритм перцептрона схо-
сходится за конечное число итераций, если заданные классы ли-
линейно разделимы. Прежде чем приступить к доказательству,
будет полезно подробно рассмотреть простой численный
пример.
Пример. Рассмотрим образы, представленные на рис. 5.2, а.
Следует применить к этим образам алгоритм перцептрона с
тем, чтобы с его помощью определить весовой вектор решения.
d(x)=-2x,+1-0
1 п
хг
0
о
1
ш,
Рис. IJ.2. Иллюстрация принципа действия алгоритма перцептронного типа.
а — образы, принадлежащие двум классам; б — разделяющая граница, полу-
полученная с помощью реализации процесса обучения.
Осмотр образов показывает, что два заданных класса линейно
разделимы и, следовательно, применение алгоритма окажется
успешным.
До качала применения алгоритма пополним все образы. При
этом рассматриваемые классы обратятся в иг. {@,0,1)'
@, 1, 1) } и и2: {A, 0, 1)', A, 1, 1)'}. Задав с= 1 и w(l) = 0 и
5.2. Перцептронный подход 183
предъявив образы в указанном выше порядке, получим (по
шагам):
w'(l)x(l) = @,0,0)l 0 1 = 0,
w'B) х B) = @,0, 1)| 1 1=1,
wC) = wB) = | 0 I,
w'C)xC) = @,0,1I 0 =1,
wD) = wC)-xC) = | О],
\ 0/
w' D) x D) = (-1,0, 0)| 1 |=-1,
wE) = wD)= 0 .
Коррекция вектора весов проводилась на первом и третьем
шагах в соответствии с формулами E.2.2) и E.2.3) в связи с
ошибками классификации. Так как получаемый результат
можно считать искомым решением только в том случае, когда
алгоритм осуществит без ошибок полный цикл итерации по
всем образам, обучающее множество следует предъявить еще
раз. Процесс обучения системы продолжается при хE) =хA),
184 Гл. 5. Детерминистский подход
хF) = хB), хG) = хC) и х(8)=хD). Второй цикл итерации
приводит к следующим результатам:
w' E) х E) = О,
wF) = wE).+ xE) = l О I,
w'F)xF)=l,
wG) = wF) = ( О I,
w'G)xG) = 0,
w(8) = wG)-xG) = 0 ,
V 0/
w'(8)x(8) = -2,
(~2\
w(9) = w(8)= 0 .
V 0/
Поскольку в данном цикле итерации совершено две ошибки,
все образы предъявляются еще раз:
w' (9) х (9) = 0,
-2-
= l 0 |,
w'A0)xA0)=l,
-2Ч
= wA0) = [ 0 ,
wA2) = w(ll) = l 0 ,
w'A2)xA2) = -l,
(~2)
wA3) = wA2)= 0 .
5.2 Перцептронный подход 185
Нетрудно убедиться в том, что в следующем итеративном цикле
все образы классифицируются правильно. Итак, вектор реше-
решения имеет вид w = (—2,0,1)'. Соответствующей решающей
функцией будет d(\) = —2х\-\-\\ приравнивание этой функции
нулю дает уравнение разделяющей границы, приведенной на
рис. 5.2, б. щ
В соответствии с анализом, проведенным в § 5.1, алгоритм
перцептрона можно представить в другой, эквивалентной фор-
форме, умножив пополненные образы одного из классов на —1. Та-
Таким образом, умножив все образы, например класса со2, на —1,
алгоритм перцептрона можно записать как
(*)« если W(*)x(*)>0,
(k) + cx(k), если w'(k)x(k)<0, l°-" '
где с — положительное корректирующее приращение. В данной
главе будем пользоваться именно этим эквивалентным пред-
представлением алгоритма перцептрона.
5.2.2. Доказательство сходимости
В настоящем разделе будет показано, что в случае линейной
разделимости рассматриваемых классов алгоритм, описанный
выше, обеспечивает получение весового вектора решения за
конечное число шагов. Прежде чем приступать к доказатель-
доказательству, представим нашу задачу с помощью обозначений, кото-
которые упростят изложение доказательства.
Пусть xi, x2, ..., xN представляют обучающее множество
образов, относящихся к двум заданным классам, причем все
образы, принадлежащие классу са2, умножены на —1. Постули-
Постулируется, что в случае линейной разделимости классов алгоритм
обучения E.2.5) обеспечивает определение весового вектора
решения w*, отличающегося тем, что
w"x?>0, /=l, 2, .... N. E.2.6)
Выражение E.2.6) можно представить в несколько более об-
общем виде, введя неотрицательную пороговую величину Т, та-
такую, что при линейной разделимости классов
w"xt>7\ »=1, 2, ..., N. E.2.7)
При этих условиях алгоритм E.2.5) принимает следующий вид:
(*>' еСЛИ W(*)x((*)>7\
{k) + xt{k), если ^(*)х,(*)<Г, (Ь '
причем вектор w(l) выбирается произвольным образом. Пусть
для простоты с=1. Это допущение не нарушает общности
186 Гл. 5. Детерминистский подход
рассуждений, так как любое другое значение с может быть
введено в векторы образов в качестве нормирующей константы.
Из проведенного в § 2.4 геометрического анализа и из рис. 2.5
следует, что пороговая величина Т создает с обеих сторон ги-
гиперплоскости w'(k)x(k) = 0 буферные области. Всякий образ,
попадающий в эти области, классифицируется неправильно.
Обращаясь к рис. 2.5, в, следует отметить, что непосредствен-
непосредственным результатом увеличения пороговой величины Т является
уменьшение объема конуса решений.
Предполагая возможность предъявления каждого образа
необходимое количество раз, мы утверждаем, что при линейной
разделимости заданных классов алгоритм, представленный вы-
выражением E.2.8), приведет за конечное число шагов к получе-
получению искомого результата. Доказательство существенно упро-
упростится, если помимо применения введенных выше обозначений
принимать во внимание только те индексы k, при которых в
процессе обучения имела место коррекция. Иначе говоря, если
исключить те значения индекса k, которым соответствует пра-
правильная классификация образов, то, изменив снова запись ин-
индексов, можно прийти к выражению
w(*+l) = w(*) + x,(*), E.2.9)
w'(*) х, (*) < Г E.2.10)
для всех значений индекса k в обучающей последовательности,
при которых происходила коррекция. Сходимость алгоритма
на самом деле означает, что после некоторого конечного значе-
значения индекса km имеет место равенство
После введения этих упрощений доказательство сходимости
алгоритма состоит в следующем. Из E.2.9) получаем
w(* + l) = w(l) + x,(l) + xlB)+ ••• +х,(*). E.2.11)
Скалярное произведение вектора w* с обеими частями уравне-
уравнения E.2.11) дает
w'(A:+l)w* = w'(l)w* + x;(l)w*+ ... +x't(k)w*. E.2.12)
Так как из условия E.2.7) следует, что каждый член
x'.(j)vf*, 7=1 k, больше пороговой величины Т, то
w'(k + l)w*>w'(l)w' + *7'. E.2.13)
Неравенство Коши — Шварца (||a||2||b||2 ^ (a'bJ) приводит к
выражению
[w' (k + 1) w*]2 < |1 w (* + 1) f || w* IP, E.2.14)
5.2. Перцептронный подход 18 7
где ||а||2 обозначает квадрат модуля вектсра а. Неравенство
E.2.14) можно переписать в виде
Iw'(* + 1f)w'1>. E.2.15)
После подстановки неравенства E.2.13) в E.2.15) получим не-
неравенство
Другая ветвь рассуждений приводит к противоречию, касаю-
касающемуся величины ||w(&+l)H2- Из E.2.9) заключаем, что
II w (/ + 1) ||2 = || w (/) ||2 + 2w' (j) xt (!) + || xt (}) ||2 E.2.17)
или
II w (j + 1) ||2 - || w (!) ||2 = 2w' (j) Xi (/) + || xt (j) ||2. E.2.18)
Используя неравенство E.2.10) и полагая Q = max ||хг (j) |p,
придем к '
l|w(/ + l)H2-||w(/)||2<2r + Q. E.2.19)
Суммируя эти неравенства по всем /= 1, 2, ..., k, получим
Q)?. E.2.20)
Сопоставление неравенств E.2.16) и E.2.20) показывает,
что при достаточно больших значениях k границы, устанавли-
устанавливаемые для величины ||w(?+l)H2 соответствующими неравен-
неравенствами, противоречат друг другу. В самом деле, индекс k не
может принимать значений, больших значения km, удовлетво-
удовлетворяющего уравнению
= 'Iw @ 'I2 + BГ + Q) km- E-2.21)
Согласно E.2.21), km—конечная величина, из чего следует
сходимость алгоритма перцептрона за конечное число шагов
при условии линейной разделимости заданных классов. Это
завершает доказательство сходимости алгоритма перцептрона.
Замечания. Частный случай при Т = 0 доказывается не-
несколько иначе. Неравенство E.2.13) принимает вид
w' (k -f 1) w* > w' A) w* + ka, E.2.22)
где
a = min[x;(/)w*]. E.2.23)
Так как согласно нашей гипотезе w* — вектор решения, то
а ~> 0. Кроме того, поскольку w' (j) x,- (/) ^ 0, неравенство
E.2.19) превращается в
II w (j + 1) |р - || w (j) IP < || xt (j) 1|2 < Q. E.2.24)
188 Гл. S. Детерминистский подход
Остальная часть доказательства остается неизменной. Число
шагов алгоритма, необходимое для его сходимости при Т = О,
задается решением уравнения
lw (I) W -f- КщД] и /1 \ ц2 I qи /g 2 25)
Обратите внимание на то обстоятельство, что, хотя уравне-
уравнения E.2.21) и E.2.25) определяют границу значений km, их
нельзя использовать для вычисления числа шагов, необходимых
для сходимости алгоритма, поскольку последнее предполагает
знание вектора решения w*. Отметим также, что значение ин-
индекса km зависит и от начального вектора весов w(l). Сходи-
Сходимость алгоритма перцептрона можно доказывать целым рядом
способов. Доказательство, приведенное выше, является, однако,
одним из наиболее четких.
5.2.3. Разновидности перцептронного подхода
Варьируя способ выбора корректирующего приращения с,
можно получить несколько модификаций алгоритма перцеп-
перцептрона. К наиболее распространенным алгоритмам обучения от-
относятся алгоритм фиксированного приращения, алгоритм кор-
коррекции абсолютной величины и алгоритм дробной коррекции.
В алгоритме фиксированного приращения корректирующее при-
приращение с является константой, большей нуля. Пример приме-
применения этого алгоритма был приведен в п. 5.2.1 для с= 1.
В алгоритме коррекции абсолютной величины с выбирается
достаточно большим, для того чтобы гарантировать правиль-
правильную классификацию образа после коррекции весов. Другими
словами, если w'(k)x(k) ^ 0, то коэффициент с выбирается
таким образом, чтобы
w'{k+l)x(k) = [w(k) + ex(k)]f x(k) > 0. E.2.26)
Отметим, что, согласно определению алгоритма перцептрона
E.2.5) .ошибка совершается только в том случае, когда произ-
произведение w'(k)x(k) меньше или равно нулю. Один из способов,
обеспечивающих справедливость E.2.26), состоит в выборе в
качестве с наименьшего целого числа, превышающего
\vr'(k)x(k)\/x'(k)x(k).
В алгоритме дробной коррекции с выбирается таким обра-
образом, чтобы величина \w'(k)x(k)l—w'(k + l)x(k) \ была поло-
положительной и составляла некоторую долю % от величины
\w'(k)x(k)\, т. е.
| w' (*) х (*) - w' (* + 1) х (*) | = % I w' (*) x (k) |. E.2.27)
5.3. Построение алгоритмов классификации образов 189
Подстановка w(k+l)~ w(k)+cx(k) в E.2.27) дает
с = % 'l-^wfeI • E.2.28)
Этот алгоритм, очевидно, требует, чтобы начальный вектор ве-
весов отличался от 0. Из геометрической интерпретации, данной
в п. 2.5.1, следует, что дробная величина К представляет собой
отношение расстояния, разделяющего прежний вектор весов
vt(k) и новый вектор весов w(k-\- 1), к нормальному евклидову
расстоянию от вектора весов w(?) до гиперплоскости образов
в пространстве весов. Если Я,>1, то образ классифицируется
правильно после каждой коррекции весов. Можно показать,
что при 0 < "К < 2 этот алгоритм сходится.
5.3. ПОСТРОЕНИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ
ОБРАЗОВ
В § 5.2 отмечалось, что первые алгоритмы перцептронов
были построены на основе применения метода адаптации по-
посредством подкрепления и наказания. В данном параграфе
воспользуемся более общим подходом к задаче построения ал-
алгоритмов классификации образов. Покажем, что алгоритм пер-
цептрона является просто одним из представителей семейства
итеративных процедур, которые можно легко строить с помо-
помощью хорошо известного метода градиента.
5.3.1. Метод градиента
В принципе градиентные схемы являются средством отыска-
отыскания минимума функции. Напомним читателю, что в курсе век-
векторного анализа градиент функции f (у) по вектору у =
— (Уи Уг, • ••> Уп)' определяется как
Of
di/,
dj
дуг
д!
E.3.1)
Из этого соотношения следует, что градиент скалярной функции
векторного аргумента есть вектор и что каждая компонента
градиента характеризует скорость изменения этой функции в
направлении данной компоненты.
190
Гл. !). Детерминистский подход
Одно из важнейших свойств вектора градиента заключается
в том, что его направление указывает направление наискорей-
наискорейшего роста функции / при увеличении ее аргументов. Отрица-
Отрицательный градиент в свою очередь указывает направление наи-
наискорейшего уменьшения функции /. Используя это свойство,
Тангенс=-2
ноЛ1=-2,если w*0,
dw
=0, если w>0.
-w(k), если w>0,
Рис. 5.З. Геометрическая интерпретация алгоритма градиентного спуска.
можно строить итеративные схемы отыскания минимума функ-
функции. Ниже будем рассматривать функции, имеющие только
один минимум. Если функция задана так, что она достигает
минимального значения при выполнении условия w'x,- > 0, где
х, есть i-я строка матрицы X размера N Х(^+ 1) системы не-
неравенств E.1.1), то отыскание минимума функции для всех i,
t=l, 2, ..., N, эквивалентно решению этой системы линей-
линейных неравенств. Рассмотрим, например, функцию критерия
/(w, x) = (|w'x|-w'x), E.3.2)
где |w'x|—абсолютное значение w'x. Очевидно, что минимум
этой функции есть 7(w, х) = 0 и достигается он при w'x > 0.
Мы, естественно, опускаем тривиальный случай w = 0.
5.3. Построение алгоритмов классификации образов 191
Используемый нами ниже метод состоит в увеличении зна-
значений w в направлении отрицательного градиента функции
J(w, x) с тем, чтобы найти минимум этой функции. Другими
словами, если w(?) представляет значение вектора w на 6-м
шаге, то в общем виде алгоритм градиентного спуска можно
записать как
{a/()} ' , E.3.3)
где w(?-j-l) представляет новое значение вектора w, а вели-
величина с > 0 определяет размер коррекции. Отмстим, что при
(dJ/dw) = О, т. е. при достижении минимума, значение вектора
w никак не корректируется.
Геометрическую интерпретацию уравнения E.3.3) даст
рис. 5.3. В этом простом примере при отрицательности гра-
градиента скалярной функции (dJ/dw) на k-м шаге значение w
увеличивается в направлении минимума функции /. Из рисунка
видно, что эта схема спуска по градиенту приводит в конечном
счете к положительному значению w и, следовательно, к мини-
минимальному значению функции /. Заметим также, что на рис. 5.3
представлен график функции E.3.2) при х= 1. Очевидно, что
число кривых соответствует числу образов в задаче.
Если неравенства совместны и функция 7(w, х) задана
надлежащим образом, то алгоритм E.3.3) обеспечит получение
решения. В противном случае он зациклится и будет работать
в таком режиме до тех пор, пока процедуру не остановят. В сле-
следующем пункте рассматривается несколько частных алгоритмов,
которые получаются подстановкой ряда различных функций
критерия 7(w, x) в уравнение E.3.3), определяющее метод спу-
спуска в общем виде.
5.3.2. Алгоритм перцептрона
Алгоритм перцептрона был введен в п. 5.2.1 в виде итератив-
итеративной схемы, действующей по принципу подкрепления и наказа-
наказания. Здесь будет показано, что этот алгоритм можно получить
из уравнения E.3.3) при соответствующем выборе функции
/(w, х). Пусть эта функция критерия имеет вид
/ (w, х) = y (I Wx I - w'x). E.3.4)
Частная производная функции / по w определяется как
-J?- = y[xsgn(w'x)-x], E.3.5)
где, по определению,
( 1, если w'x > О,
sgn(w'x) = < , , ,п E.3.6)
(. — 1, если wx^.0, V '
1 92 Гл. 5. Детерминистский подход
Отмстим, что в E.3.6) условия w'x = 0 и w'x <C 0 объединены.
Это, естественно, отражает то обстоятельство, что, согласно
формулировке алгоритма перцептрона E.2.5), вектор w весов
корректируется во всех тех случаях, когда w'x ^ 0.
Подстановка выражения для частной производной E.3.5)
в уравнение E.3.3) приводит к
w {k + 1) = w (k) + ± {х (k) - х (A) sgn [w' (k) x (?)]}, E.3.7)
где \(k) представляет образ из обучающей выборки, предъяв-
предъявляемый на 6-м шаге итерации.
Подстановка выражения E.3.6) в E.3.7) дает формулу для
алгоритма:
, если w'(k)x(k)>0,
№I если w-D)xW<0, <5'3-8»
где значения с > 0 и w(l) — произвольные. Очевидно, что дан-
данный алгоритм удовлетворяет формулировке алгоритма перцеп-
перцептрона E.2.5).
Модификации алгоритма перцептрона п. 5.2.3 легко выво-
выводятся из общей схемы алгоритма E.3.3). Рассмотрим, в част-
частности, следующую функцию критерия:
/ (w, х) = -^ (| w'x |2 - | w'x | w'x). E.3.9)
Частная производная функции У по вектору w определяется как
W'X ' X Sgn ^W'X^ ~~ ' W'X 'Х "" ^W'X^X Sgn
где sgn (w'x) определяется формулой E.3.6). Нетрудно пока-
показать, что последнее выражение можно представить в эквива-
эквивалентной форме
-J^ - ^ [ I w'x | х sgn (w'x) - | w'x | x]. E.3.10)
Подстановка E.3.10) в общее определение алгоритма
E.3.3) приводит к алгоритму
X
w(A+l) = w(ft)+ 2x'(*)x(ft)
X{x(k)-x(k)sgn[wf(k)x(k)}}, E-3.11)
где корректирующее приращение с, входящее в уравнение
E.3.3), временно обозначено через X с тем, чтобы избежать
путаницы при сравнении, которое будет проводиться ниже.
5.3. Построение алгоритмов классификации образов 193
Используя выражения E.3.6), получаем следующее:
Mw'(*)x(fe)| ГО, если w'(?)x(?)>0,
A+l) w(A)+ |
E.3.12)
Сопоставив уравнения E.3.12) и E.2.28), убеждаемся, что по-
получен алгоритм дробной коррекции. В следующем разделе мы
снова воспользуемся этими основными приемами для получения
алгоритма, обладающего очень важными свойствами.
5.3.3. Алгоритм, основанный на минимизации
среднеквадратичной ошибки
Алгоритм перцептрона и его модификация сходятся в тех
случаях, когда заданные классы можно разделить поверхностью
выбранного типа. В тех ситуациях, когда разделимость отсут-
отсутствует, эти алгоритмы зацикливаются и работают в таком ре-
режиме до тех пор, пока их выполнение не прерывается извне.
Поскольку при наличии разделимости невозможно заранее
рассчитать число шагов, необходимое для сходимости алго-
алгоритма, редко можно с абсолютной уверенностью судить о том,
означает или нет наличие длинной обучающей последователь-
последовательности отсутствие линейной разделимости заданных классов.
Алгоритмы, рассматриваемые здесь, кроме того, что они
сходятся при наличии разделимости классов, указывают также
в процессе их выполнения на отсутствие такой разделимости,
если рассматриваемые классы действительно не разделимы. Это
уникальное качество делает данный алгоритм ценным инстру-
инструментом построения систем классификации образов.
В следующем ниже выводе используется постановка задачи,
определяемая соотношением E.1.1). Однако вместо того, чтобы
рассматривать ее как задачу отыскания вектора w, обеспечи-
обеспечивающего выполнение условия Xw > 0, будем пытаться нахо-
находить векторы w и Ь, обеспечивающие выполнение равенства
Xw = b, E.3.13)
где все компоненты вектора b = F1,62,.. • ,?>«)' положительны.
Очевидно, что обе эти формулировки эквивалентны.
Рассмотрим функцию критерия
N
J (w, х, Ь) = 1 ? (w'X/ - b,f = 11| Xw - b|p, E.3.14)
/-1
где || Xw — b || обозначает модуль вектора (Xw — b). Функция
7(w, x, b) достигает своего минимального значения при выпол-
выполнении условия E.3.13). Поскольку эта функция зависит от век-
7 Зик. KQ4
194 Гл. 5. Детерминистский подход
торов w и Ь, ничто не мешает использовать при минимизации
обе переменные, увеличив тем самым число степеней свободы.
Такой способ может привести к увеличению скорости сходимо-
сходимости алгоритма. Обратите внимание на то обстоятельство, что
член (w'x/ — b,J или || Xw — b ||2 представляет квадратичную
ошибку, т. е. квадрат разности величин, входящих в аргумент
функции. Так как сумма этих ошибок пропорциональна сред-
среднему значению или математическому ожиданию и так как мы
пытаемся эту сумму минимизировать, то соответствующий ал-
алгоритм называется алгоритмом наименьшей среднеквадратич-
среднеквадратичной ошибки (НСКО-алгоритм). Иногда эту процедуру назы-
называют алгоритмом Хо — Кашьяпа.
В связи с тем что функция / минимизируется по обеим
переменным w и Ь, метод минимизации неизбежно должен не-
несколько отличаться от общего алгоритма E.3.3). Градиентами
в нашей задаче будут
J? b) • E.3.15)
и
|Z- = - (Xw - b). E.3.16)
Поскольку на вектор весов w не налагается никаких ограни-
ограничений, можно положить dj/dw = 0, что приводит к
w = (X'Xr1X'b = X*b, E.3.17)
где X*—объект, который часто называют обобщенным обра-
обращением матрицы X. Так как все компоненты вектора b должны
быть положительными, его следует изменять только таким об-
образом, чтобы это условие не нарушалось. Последнее можно
обеспечить, положив
b(fc + l) = b(fc) + 6b(fc), E.3.18)
где
2с [Xw (k) - Ь (k)]t, если [Xw (k) - b {k)]t > О
л rv ,,. . ,, Ч1 ^ п (э.3.19)
0, если [Xw(fe) — b(fe)]<0 '
/
В формулах E.3.18) и E.3.19) k обозначает индекс итерацион-
итерационной процедуры, i — индекс компонент вектора и с—положи-
с—положительное корректирующее приращение, которое будет опреде-
определено ниже.
Уравнение E.3.19) можно представить в векторной форме:
6b (k) = с [Xw (k) - Ь (ft) +1 Xw (ft) - b (ft) | ], E.3.20)
5.3. Построение алгоритмов классификации образов 195
где выражение |Xw(&)— b(k)\ определяет абсолютную вели-
величину каждой компоненты вектора \\w{k) — b(k)]. Из E.3.17)
и E.3.18) следует, что
w(k+ l) = \*b(k+ 1) = Х*[Ь(Л) + бЬ(Л)] =
= Xlfb {k) + Х!^ 6b (It) = w [k) + X* 6b (k). E.3.21)
Положив
)-b(fc), E.3.22)
приходим к следующему алгоритму:
w(l) = X*b(l), bt{\)>0,
в остальных случаях произвольно,
t(k) = \w(k)-b(k), E.3.23)
w (k + 1) = w (k) + cX* [e (k) + | e (k) \ ],
В соотношениях E.3.23) через |е(&)| обозначен вектор, компо-
компонентами которого являются абсолютные значения компонент
вектора еF). Отметим, что значение вектора w(/fe-f-l) также
можно определить, используя соотношение w(^+l) =
= Х#Ь(А+1).
Если неравенства Xw > 0 имеют решение, данный алгоритм
сходится при 0<с^ 1. Более того, если на любом шаге ите-
итерации все компоненты вектора е(&) становятся неположитель-
неположительными (но не все — равными нулю), это означает, что заданные
классы нельзя разделить с помощью границы выбранного типа.
Естественно, в тех случаях, когда е(&) = 0, вектор w(k) яв-
является решением, так как из этого следует, что Xw(?)=b(?)
и b{k)—положительный вектор. Как отмечалось выше, наличие
критерия разделимости — заметное достоинство этого алго-
алгоритма.
Пример, (а) Рассмотрим снова класс «ь содержащий об-
образы {@,0)', @,1)}, и класс сй2, содержащий образы {A,0)',
A, 1)'}. Путем пополнения образов и умножения всех образов,
входящих в класс cd2, на —1 получим матрицу
0
0
-1
- ]
0
1
0
-1
1
1
- 1
- 1
196 Гл. /> Детерминистский подход
Обобщенная обратная матрица \ц — (Х'Х)~'Х' равна
I i -i J
Положив b(l) = (l, 1,1,1)' и с=1 и применив алгоритм
E.3.23), получим
w(l) = X*b(l) = | 0 |.
Так как
Xw(l)="
из E.3.13) следует, что вектор w(l) есть решение. Подтверж-
Подтверждением этого служит и тот факт, что вектор ошибки еA) равен
нулю. Практически обычно считается, что алгоритм определил
вектор решения w(fe), если Xw(?)>0. Это условие сходимости
алгоритма обычно выполняется раньше, чем достигается равен-
равенство E.3.13).
(б) Рассмотрим теперь классы cof. {@,0)', A,1)'} и «2:
{@, 1)', A,0)'}; эти классы не обладают линейном раздели-
разделимостью. Положив с = 1 и ЬA) = A, 1, 1, 1)', получим
0
X
5.3. Построение алгоритмов классификации образов 197
То, что вектор еA) — отрицательный, означает отсутствие ре-
решения у неравенства Xw > 0 |
Скорость сходимости, отличающая НСКО-алгоритм, объяс-
объясняется тем, что 1) изменение обоих векторов w и b произво-
производится на каждом шаге и 2) процедура является адаптивной
схемой, учитывающей на каждом шаге итерации информацию
о всех образах обоих классов.
Единственный явный недостаток применения НСКО-алго-
ритма связан с обращением матрицы (Х'Х). Если, однако, раз-
размерность образов не очень велика, этот недостаток не вызывает
особых проблем, так как при решении каждой задачи матрицу
приходится обращать только один раз. К тому же обратную
матрицу (Х'Х)" можно рекуррентно модифицировать при по-
появлении новых строк (т. е. образов) в матрице X (Бодевиг
[1956]).
Мы допускали, что (Х'Х) обладает обратной матрицей —
это условие выполняется, когда ранг матрицы X равен «-f 1.
Поскольку эта матрица сформирована из пополненных обра-
образов, очевидно, что не только набор заданных образов, но и
выбор решающей функции определяют, является матрица
(Х'Х) вырожденной или нет. Отметим, что если по крайней
мере п + 1 образов из использованных при формировании мат-
матрицы X обладают хорошим размещением в смысле гл. 2, то
матрица X непременно имеет ранг п-\- 1.
Помимо приведенных выше существуют и другие алго-
алгоритмы. Действительно, количество алгоритмов, которые можно
получить с помощью метода градиента, ограничено только ко-
количеством разумных функций критерия, которые мы в состоя-
состоянии предложить. Многие из этих алгоритмов, отличаясь по
форме, тем не менее мало отличаются по мощности. Это обна-
обнаружилось, в частности, при построении двух вариантов алго-
алгоритма перцептрона, соответствующих двум различным функ-
функциям критерия.
Два основных алгоритма, построенных в данной главе, по-
покрывают весь спектр алгоритмов, получаемых с помощью гра-
градиентного метода. Интерес они, однако, вызывают по разным
причинам. Алгоритм перцептрона привлекает сравнительной
простотой реализации и, как будет показано в § 5.4, возмож-
возможностью непосредственного обобщения на случай разбиения на
несколько классов. НСКО-алгоритм, с другой стороны, обла-
обладает критерием разделимости для случая двух классов. Есте-
Естественно, за это качество алгоритма приходится платить его
усложнением.
Хотя скорость сходимости и является важной характеристи-
характеристикой, но на ее основе трудно сформировать показатель качества
1&8 Гл. 5. Детврминиетекий подход
алгоритма. Так, например, в общем случае НСКО-алгоритм
сходится к решению за меньшее число итераций, чем алгоритм
перцептрона, однако следует принять во внимание, что первый
из них является процедурой более сложной, в нем на одну ите-
итерацию приходится больше операций и, кроме того, он преду-
предусматривает обращение матрицы. Более того, то обстоятельство,
что эти вычислительные схемы существенно зависят от геомет-
геометрических свойств задачи и начальных значений векторов веса,
делает формулировку критериев прямого сравнения алгоритмов
почти невыполнимой задачей.
5.3.4. Доказательство сходимости НСКО-алгоритма
В данном разделе доказывается сходимость НСКО-алго-
НСКО-алгоритма при линейной разделимости заданных классов и коррек-
корректирующем приращении, удовлетворяющем условию 0<Сс<=;1.
Ключевым моментом обоснования сходимости является дока-
доказательство того факта, что вектор ошибки e(ft)=Xw(?)— b(k)
в пределе обращается в 0. Поскольку из определения алгоритма
E.3.23) следует, что у начального вектора b(k) все компоненты
положительны и значения этих компонент не уменьшаются, то
очевидно, что если при некотором значении k имеет место
e(ft) = 0, то Xw(ft) = b(k) > 0, т. е. получено решение урав-
уравнения E.3.13).
На основании соотношений E.3.23) записываем
e(/e) = Xw(/e)-b(/e).
Поскольку, однако, w(fc) = X*b(ft), последнее уравнение можно
переписать как
е (k) = (XX* — I) b (k). E.3.24)
Отсюда следует, что
e(/e + l) = (XX*-l)b(fe+ 1). E.3.25)
Используя соотношения b(fe + l) = b (k) + с [e(k) -f| e(k) ] ], по-
получаем
e(ft+l) = (XX*-l){b (ft)+ c[e(fe) + l «(*)!]} =
= e (k) + с (XX* - I) [e (k) +1 e (k) | ]. E.3.26)
Из последнего в свою очередь получаем
+1 с (XX* - I) [e (ft) +1 е (k) | ] f. E.3.27)
Запись E.3.27) можно упростить, введя обозначение
е*(*) = е(*) + |е(*)|. E.3.28)
5.3. Построение алгоритмов классификации образов 199
В таком случае E.3.27) принимает вид
II е (ft + 1) ||2 = || е (k) |р + 2се' (k) (XX* - i) e* (k) +
+ |c(XX*-l)e'(A)f. E.3.29)
Это уравнение можно существенно упростить. Обратим, прежде
всего, внимание на то, что (ХХ*)' (XX*) = XX* и w (ft) = X*b(ft).
Следовательно,
XX* е (ft) = XX* [Xw (ft) - b (k)] = XX* [XX*b (ft) - b (ft)] = 0.
Матрица XXfr симметрическая, значит, е'(?)ХХ =0. Следова-
Следовательно, E.3.29) принимает вид
|| е (ft + 1) IP = || е (ft) ||2 - 2се' (ft) e* (k) +1 с (XX* - i) e* (ft) f. E.3.30)
Так как, однако, e' (ft) e* (ft) = -^ || e* (ft) ||2, то
E.3.31)
Поскольку матрица XX* симметрическая и (ХХ*)'(ХХ*) = XX*,
последний член в E.3.31) можно представить как
| с (XX* - I) e* (k) if = cV (ft) (XX* - I)' (XX* -l)t'{k) =
¦ =c2\\ e* (ft) ||2 - сV (k) XX*e* (ft).
Подстановка этого соотношения в E.3.31) дает следующее:
||e(ft)|p-||e(ft+l)lP =
= с A - с) || е* (k) f + с2 е" (ft) XX*e* (k). E.3.32)
Это уравнение позволяет доказать сходимость алгоритма
при наличии разделимости заданных классов. Прежде всего,
отмечая, что матрица XX* — положительно полуопределенная,
получаем с2е*' {k) XX* е* (ft) > 0. Следовательно, при 0 < с ^ 1
правая часть уравнения E.3.32) больше или равна нулю.
Значит,
||e(?)|]2>||e(ft+l)||2, E.3.33)
причем последовательность ||еA)||2, || е B) ||2, ...— монотонно
убывающая. Без особых затруднений можно понять, что един-
единственный способ обеспечить выполнение равенства ||e(ft-|-
+ 1) ||2 = || e(k) II2 для всех значений k после некоторого эле-
элемента последовательности заключается в том, чтобы обеспечить
отрицательность или равенство нулю всех компонент вектора
ошибок. Если при некотором k получено e(ft) = 0, это означает,
что найдено решение, так как компоненты вектора b(k) всегда
положительны и e(ft) = Xw(ft) — b(ft). Если e(ft) = 0, то ясно,
что алгоритм прекратит вводить коррекции. Это же произойдет,
200 Гл. 5. Детерминистский подход
если все компоненты вектора е(/е) станут неположительными.
Остается, следовательно, показать, что при наличии раздели-
разделимости такая ситуация возникнуть не может. Это нетрудно сде-
сделать доказательством от противного. Если заданные классы
линейно разделимы, то существуют векторы w и b >0, такие,
что Xw = b. Если допустить существование вектора ошибки
е(&), у которого все компоненты неположительны, то
е'(*)Ь<0, E.3.34)
так как все компоненты вектора b положительны. Итак,
Х'е (k) = X' [Xw (k) - b (k)} = X' (XX* - I) b (k) =
= (X' - X') b (k) = 0,
где обоснованием последнего преобразования является тот
факт, что Х'ХХ*= Х/Х(Х/Х)-'Х/ = Х/, если (Х'Х)-' суще-
существует. Условия, при которых такая обратная матрица суще-
существует, были рассмотрены в п. 5.3.3.
Если Х^е(/г) = 0, то (X'w)'e(/j) = w'X'e(yfe) = 0. Поскольку,
однако, Xw = b, должно также выполняться и равенство
Ь'е(/г) = е'(/г)Ь — 0. Последнее противоречит условию E.3.34).
Следовательно, вектор ошибки е(&) при наличии разделимости
классов не может быть таким, что все его компоненты неполо-
неположительны. Это означает, что появление неположительного век-
вектора ошибок является ясным указанием невозможности линей-
линейного разделения заданных классов.
Возвращаясь теперь к монотонно убывающей последова-
последовательности ||еA)||2, || е B) ||2, ..., отмечаем, исходя из проведен-
проведенного анализа, что в случае разделимости классов выполнение
алгоритма не прекратится до тех пор, пока вектор ошибки e(k)
не станет равен 0. Из теоремы Ляпунова, определяющей устей-
чивость дискретных систем, известно, что
Iim || е (As) IP = 0. E.3.35)
Это, следовательно, является доказательством сходимости алго-
алгоритма при наличии разделимости для бесконечного k. Для
доказательства сходимости при конечном k замечаем, что
\w(k) = b(&) + е(/г). Поскольку вектор Ь(/г) не уменьшается,
очевидно, что если вектор ошибок е(/г) сходится к 0 при бес-
бесконечном k, то при конечном k он должен войти в гиперсферу
|| е(/г) || = fcmiHl при этом выполняется условие Xw(/j)>0
(здесь fcmin обозначает минимальную компоненту вектора ЬA)).
На этом доказательство сходимости завершается.
Проведенное доказательство не определяет точное число ша-
шагов, необходимых для получения решения. Следовательно, при
5.4. Классификация для случая нескольких классов 201
реализации алгоритма приходится контролировать процедуру
с тем, чтобы обнаружить получение решения. Один из способов
такого контроля заключается в проверке значения Xw(/j) и век-
вектора ошибки после каждой итерации. Если выполняется усло-
условие Xw(/j)>0 или вектор ошибки е(/г) обращается в 0, это
означает, что решение найдено. Если же, с другой стороны,
вектор ошибки е(/г) становится неположительным, это озна-
означает, что рассматриваемые классы линейно не разделимы и вы-
выполнение алгоритма прекращается. Отметим, что число шагов,
необходимое для обнаружения неразделимости заданных
классов, неограниченно.
5.4. КЛАССИФИКАЦИЯ ДЛЯ СЛУЧАЯ НЕСКОЛЬКИХ
КЛАССОВ
В § 2.2 были рассмотрены три случая разделения на не-
несколько классов. В первом случае каждый из М классов отде-
отделялся ото всех остальных единственной разделяющей поверх-
поверхностью. Очевидно, все М решающих функций, необходимых для
решения этой задачи, можно найти с помощью любого из рас-
рассмотренных в данной главе алгоритмов обучения. Так, напри-
например, чтобы построить решающую функцию для г-ro класса, до-
достаточно рассмотреть задачу о разделении на два класса аи
и со,-, где со; обозначает совокупность всех классов, за исключе-
исключением класса со,-.
Во втором случае каждый класс отделим от любого другого
класса. Задача при этом заключается в построении М(М—1)/2
решающих функций. Эти функции можно найти, применяя лю-
любой из описанных алгоритмов ко всем парам заданных
классов.
В третьем случае допускается существование М решающих
функций, обладающих тем свойством, что при xefflj
dt (х) > d,- (х) для всех / ф i. E.4.1)
В настоящем параграфе представлен алгоритм, который
можно применить для непосредственного определения решаю-
решающих функций в случае 3. Этот алгоритм, обобщающий алго-
алгоритм перцептрона, можно описать следующим образом.
Рассмотрим М классов a>i, AJ, •••, w.w- Пусть на /г-м шаге
итерации процедуры обучения системе предъявляется образ
х(/г), принадлежащий классу со,-. Вычисляются значения М ре-
решающих функций
dj\\(k)] = w^(/j) х(/г), /==1, 2, ..., М. Затем если выполняются
условия
dt[x(k)]>d,[x(k)], /=1, 2, ..., М- !Ф1, E.4.2)
202 Га. а. Детерминистский подход
то векторы весов не изменяются, т. е.
vr,(k + l) = w,(k), /=1, 2, ..., М. E.4.3)
Допустим, с другой стороны, что для некоторого I
d,[x(*)]<d/[x(*)]. E.4.4)
В этом случае производятся следующие коррекции весов:
w,(*+l) = w,(*) + cx(*),
w, (k+ l) = w, (&) — cx(k), E.4.5)
j=l, 2, ..., M; <?=i, \Ф1,
где с — положительная константа. 1:сли при рассмотрении слу-
случая 3 классы разделимы, то можно показать, что этот алгоритм
сходится за конечное число итераций при произвольных на-
начальных векторах веса w,(l), ( = 1, 2, ..., М. Проиллюстри-
Проиллюстрируем эту процедуру на примере.
Пример. Рассмотрим следующие классы, причем каждый из
них содержит один образ: ац: {@,0)'}, w2: {A,1)'} и w3:
{(—1,1)'}. Прежде чем применить обобщенный алгоритм пер-
цептрона к этим классам, образы следует пополнить: @, 0,1)',
A,1,1)' и (—1,1,1)'. Отметим, что ни один из образов не
умножается на —1. Выберем в качестве начальных векторов
весов Wi A) = w2(l) = w3(l) = @, 0, 0)', положим с=1 и,
предъявляя образы в указанном порядке, придем к следующей
последовательности шагов:
Так как x(l)eu)i и cf2[x(l)] = d3[x(l)] = d\ [x(l)], первый
весовой вектор увеличивается, а два других уменьшаются в со-
соответствии с соотношениями E.4.5), т. е.
О'
5.4. Классификация для случая нескольких классов 203
Следующий предъявленный образ хB) —A, 1, 1)' принад-
принадлежит классу «г; для него получаем
W;B)xB)=l,
Поскольку все произведения больше либо равны w^B)xB),
вводятся коррекции
WlC) = w,B)-xB)= -1 .
\ О/
1
о.
= w3B)-xB) = | -1 I.
Следующий предъявленный образ хC) = (—1,1,1)' принад-
принадлежит классу соз; для него имеем
w[ C) х C) = 0,
Все эти произведения снова «неверны», поэтому вводятся кор-
коррекции
( °\
w,D) = w,C) — xC)= —2 ,
= w2C)-xC) = | 0 |,
-1
—2:
= 1 о |.
204 . Гл. 5. Детерминистский подход
Поскольку в данном цикле итерации присутствовали
ошибки, следует провести новый цикл. Положив хD)=хA),
хE)=хB) и хF) = хC), получим
w;D)xD)=-l,
w;,D)xD) = — 1,
w;D)xD) = -l.
Так как образ хD) принадлежит классу wb то все произведе-
произведения «неверны». Поэтому
О'
= w2D)-xD)=
Следующий предъявляемый образ хE) = A, 1, 1)' принад-
принадлежит классу (й2. Соответствующие скалярные произведения
равны
уг|E)хE) = -2,
w;E)xE) = 0,
Отмечаем, что образ хE) классифицирован правильно. Поэтому
' = 1 -2 1
О/
*\
W2F)==w2E) = | 0 ,
W3F) = W3E) = | Oj.
5.4 Классификация для случая нескольких классов 205
Следующий образ хF) = (—1, 1, 1)' принадлежит класс} шу,
для него получаем
W;F)xF) = -2,
W;;F)xF) = o.
Этот образ также классифицирован правильно, так что ника-
никакие коррекции не нужны, т. е.
°\
w,G) = w,F) = | -2 ,
О/
т
i = w2F) = | 0 |,
-2'
w3G) = w3F) = | 0 |.
Продолжим процедуру обучения, рассматривая образ
хG) = @,0, 1)', принадлежащий классу wr, для этого образа
получаем
w;G)xG) = 0,
W;G)xG) = -2.
На этом шаге вектор весов w,G) ведет себя удовлетворительно,
поэтому он не изменяется:
w,(8) = w,G) = | -2 I,
2n
206 Гл. 5. Детерминистский подход
Легко проверить, что в следующем полном цикле итерации ни-
никакие коррекции не производятся. Итак, искомые решающие
функции имеют следующий вид:
d, (х) = 0 • х{ - 2х2 + 0 = —2х2,
d2 (х) = 2лг, + 0 • х2 — 2 = 2дг, — 2,
d3 (х) = — 2лг, + 0 • х2 — 2 = — 2л:, — 2. |
5.5. ОБУЧЕНИЕ И ОБОБЩЕНИЕ
Все алгоритмы, описанные в этой главе, используют задан-
заданную выборку образов для определения коэффициентов решаю-
решающих функций. Как отмечалось выше, использование таких ал-
алгоритмов при построении классификатора образов называется
этапом обучения. Способность классификатора к обобщению
проверяется при предъявлении ему данных, с которыми на
этапе обучения он не встречался. Очевидно, что хороший клас-
классификатор можно построить только на основе данных, доста-
достаточно репрезентативных по отношению к «полевым» данным.
Остается обсудить еще один важный вопрос: сколько обра-
образов необходимо включить в обучающую выборку для того, чтобы
выработать у классификатора хорошие способности к обобще-
обобщению? Казалось бы, ответить на него не трудно: пользуйтесь
как можно большей выборкой. Практически, однако, экономи-
экономические соображения обычно требуют ограничения числа обу-
обучающих образов, так же как \\ количества машинного времени,
отводимого на этап обучения.
Известно очень немного аналитических результатов, пригод-
пригодных для использования при выборе образов. Ковер [1965], од-
однако, показал, что при полном отсутствии информации вероят-
вероятностного характера общее количество образов, отбираемых для
решения задачи разбиения на два класса с помощью алгорит-
алгоритмов типа рассмотренных в данной главе, необходимое для по-
получения удовлетворительных способностей к обобщению,
должно быть по крайней мере равно удвоенной размерности
векторов образов. Это положение согласуется с понятием ди-
хотомизационной мощности, С к — 2 (К + 1), определенной фор-
формулой B.5.14), где К+ 1 —число весов, входящих в решающую
функцию.
Понятие дихотомизационной мощности сводится, в сущно-
сущности, к тому, что при числе N обучающих образов, обладающих
хорошим размещением, меньшем Ск, вероятность правильной
дихотомизации обучающей выборки является низкой. Если, од-
однако, N > Ск и обучающее множество классифицируется пра-
правильно, то к полученному решению (классификатору) и соот-
а.в Подход, использующий потенциальные функции 207
ветств^енио его способности к обобщению можно относиться
с большим доверием. Практически хорошим эмпирическим пра-
правилом служит выбор числа образов N порядка десяти зна-
значений Ctf,
В тех случаях, когда заданные классы нельзя разделить
с помощью выбранной разделяющей поверхности, интересно
определить максимальное количество образов, которые удается
разделить с помощью этой поверхности. Если известна плот-
плотность распределения каждой совокупности образов, то можно
обратиться к рассмотренному в § 4.2 байесовскому классифи-
классификатору, что обеспечит наименьшую вероятность совершения
ошибки в среднем. Для детерминистского случая получен
алгоритм минимума ошибки, использование которого гаранти-
гарантирует построение оптимального классификатора (Уормак и Гон-
салес [1972, 1973]). Эта процедура обладает рядом важных
свойств, которые стоит упомянуть в связи с предметом нашего
обсуждения. Если образы обладают хорошим размещением, то
алгоритм обеспечивает получение всех оптимальных решений1).
Если классы разделимы, естественно, существует единственное
решение. Если же классы неразделимы, то получение более чем
одного оптимального решения означает, что либо обучающее
множество не является репрезентативным для истинной сово-
совокупности образов, либо сложность выбранных решающих функ-
функций неадекватна, либо и то и другое одновременно. Это объяс-
объясняется тем обстоятельством, что, согласно байесовскому пра-
правилу классификации, оптимальный классификатор должен быть
единственным. Хотя сам алгоритм детерминистский, это никак
не меняет того факта, что абсолютный предел качества класси-
классификации определяется байесовским классификационным пра-
правилом. Следовательно, данный алгоритм является средством
построения подходящего оптимального классификатора в тех
случаях, когда классы неразделимы.
5.6. ПОДХОД, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ
ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
Обсуждение, проведенное в предыдущих параграфах, пока-
показывает, что при построении систем классификации образов
аналитическими методами первоочередной задачей является
определение решающих функций, которые порождают в про-
пространстве образов границы, отделяющие образы, принадлежа-
принадлежащие различным классам. Было рассмотрено несколько основ-
основных подходов к классификации образов и построению алгорит-
') В нашем обсуждении два решения считаются различными только в том
случае, когда они соответствуют различным образам.
208 Гл. 5. Петерминистский подход
мов обучения для определения решающих функций. Обсуждены
свойства нескольких алгоритмов обучения, обеспечивающих
коррекцию весов и представляющих удобное средство построе-
построения разделяющих границ на основе выборки образов, для ко-
которой известна принадлежность входящих в нее образов к М
допустимым классам. В настоящем параграфе рассматривается
подход к определению решающих функций и разделяющих
границ, основанный на использовании понятия потенциальной
функции.
Допустим, что необходимо разделить два класса wi и ©2-
Выборочные образы, принадлежащие обоим классам, представ-
представлены векторами или точками в n-мерном пространстве обра-
образов. Если ввести аналогию между точками, представляющими
выборочные образы, и некоторым источником энергии, то в лю-
любой из этих точек потенциал достигает максимального значения
и быстро уменьшается при переходе во всякую точку, отстоя-
отстоящую от точки, представляющей выборочный образ х*. На ос-
основе этой аналогии можно допустить существование эквипотен-
эквипотенциальных контуров, которые описываются потенциальной функ-
функцией /С(х, х*). Можно считать, что кластер, образованный вы-
выборочными образами, принадлежащими классу а>|, образует
«плато», причем выборочные образы размещаются на вершинах
некоторой группы холмов. Подобную геометрическую интер-
интерпретацию можно ввести и для образов класса ю2- Эти два
«плато» разделены «долиной», в которой, как считается, по-
потенциал падает до нуля. На основе таких интуитивных дово-
доводов создан метод потенциальных функций, позволяющий при
проведении классификации определять решающие функции.
5.6.1. Получение решающих функций )
Решающие функции для классификации образов можно по-
получить из потенциальных функций для векторов, представляю-
представляющих выборочные образы х*, k=\, 2, 3, ..., в пространстве
образов. Потенциальную функцию для любой точки х*, соот-
соответствующей выборочному образу, можно представить выра-
выражением
оо
К(х, х*) = ? Я,?ф,(х)Ф,(х*)' E.6.1)
где функции ф;(х), /= 1, 2, ..., полагаются для удобства орто-
иормнрованными, а действительные числа Xi, /=1, 2, ..., от-
отличные от нуля, выбраны таким образом, чтобы потенциальная
') Настоящий пункт написан по материалам четвертой главы сборника
«Advances in Information Systems Science», Vol. 1, Plenum Press.
5.6. Подход, использующий потенциальные функции 209
функция К(х, Хк) для образов х*. е ©i U W2 была ограничена. За-
Задача \выбора соответствующей потенциальной функции рассмат-
рассматривается в следующем пункте.
Решающую функцию d(x) можно построить, исходя из по-
последовательности потенциальных функций Л"(х, Х[), /С(х, х2), ...
..., соответствующей последовательности образов обучающей
выборки Х[, х2 предъявляемых системе в процессе обуче-
обучения. Решающую функцию d(\), связанную с потенциальными
функциями /((х, \к) множеством ортонормированных функций
ф,(х), можно представить в виде ряда
оо
<*(х)=1с/ф1(х). E.6.2)
<¦=!
Коэффициенты Ci, i=\, 2, ..., входящие в E.6.2), неизвестны
и могут быть определены по обучающей выборке образов с по-
помощью итеративной процедуры. Решающая функция d(x) яв-
является относительно гладкой функцией, и в малой области
число ее экстремумов невелико; значения d(x) в близко рас-
расположенных точках мало отличаются.
Ниже будет показано, что решающая функция, определяе-
определяемая формулой E.6.2), связана с потенциальной функцией
E.6.1) рекуррентным соотношением
rf*+.(x) = rf*(x) + rft+1/C(x, xft+1), E.6.3)
где k — номер шага итерации, a rk+i — коэффициент, смысл ко-
которого прояснится ниже. Важный момент, который следует
иметь в виду, состоит в том, что решающую функцию d(x)
можно непосредственно получить из потенциальных функций.
Поэтому дальнейшее обсуждение будет посвящено в первую
очередь определению потенциальных функций.
На этапе обучения выборочные образы предъявляются си-
системе, которая последовательно вычисляет значения соответ-
соответствующих потенциальных функций. Кумулятивный потенциал
на /е-м шаге итерации определяется совокупностью значений
отдельных потенциальных функций. Этот кумулятивный потен-
потенциал, который мы будем обозначать через /С*(х), определен
таким образом, чтобы при неправильной классификации образа
обучающей выборки хк+] производилась коррекция значения
кумулятивного потенциала. Если же этот образ классифици-
классифицируется правильно, то на данном шаге итерации значение куму-
кумулятивного потенциала не изменяется. Кумулятивный потенциал
вводится следующим образом.
В начале этапа обучения исходное значение кумулятивного
потенциала Л'о(х) полагается для удобства записи равным
нулю. При предъявлении первого образа Xi из обучающей вы-
210 Гл. .5. Детерминистский подход
борки значение кумулятивного потенциала корректируется со-
согласно следующему соотношению:
( К0(х) + К(х, xi), если х, <= со,,
1 (Х) ~ I Ко (х) - К (х, х,), если х, е= со2. ' E'Ь-4)
Поскольку, однако, До(х)=О, результат первого вычисления
значения кумулятивного потенциала можно представить как
К(х, Xt), если х, ecoi,
В этом случае кумулятивный потенциал просто равен значению
потенциальной функции для выборочного образа Хь Потенциал
предполагается положительным для образов, принадлежащих
классу соь и отрицательным для образов, принадлежащих
классу «2. В этом случае кумулятивный потенциал Ki(\) пред-
представляет начальный вариант разделяющей границы.
При предъявлении второго образа х2 обучающей выборки
значение кумулятивного потенциала определяется следующим
образом:
1. Если х2 е «1 и Ki(x2)>0 или х2 е со2 и /Ci(x2)<;0, то
/С2(х) = /С,(х). E.6.6)
Последнее означает, что кумулятивный потенциал не изме-
изменяется, если точка, представляющая выборочный образ, лежит
с «правильной» стороны разделяющей границы, определенной
кумулятивным потенциалом Ki(x).
2. Если Хо е со, и К\ (х2) <; 0, то
К2 (х) = К, (х) + К (х, х2) = ± К (х, х,) + К (х, х2). E.6.7)
3. Если Хо е ш_> и /(](х2)^0, то
К2 (х) = К, (х) - К (х, х2) = ±К(х, х,) - К (х, х2). E.6.8)
Возникновение этих двух ситуаций означает, что при располо-
расположении точки, представляющей выборочный образ х2, с «непра-
«неправильной» стороны разделяющей границы, определенной куму-
кумулятивным потенциалом /Ci (x), значение кумулятивного потен-
потенциала увеличивается на величину К(х,х2) для образа x2scoi
и уменьшается на величину К(х,х2) для образа х2 е со2.
При предъявлении третьего образа х3 обучающей выборки
кумулятивный потенциал определяется аналогично.
1. Если xs^coi и /B(х3)>0 или х3 е со2 и /С2(хз)<0, то
/Сз(х) = К2(х). E.6.9)
Другими словами, в тех случаях, когда разделяющая граница,
определенная кумулятивным потенциалом К2(х), обеспечивает
5.6. Подход, использующий потенциальные функции 211
правильную классификацию, кумулятивный потенциал не из-
изменяется.
2. ЕСЛИ Х3^(й1 И Л2(Хз)^0, ТО
x,)±tf(x, x2) + tf(x, х3).
E.6.10)
3. Если х3 ^ щ и /С2(х3)^0, то
/С3(х) = ^2(х)-^(х, хя) = ±/С(х, х,)±К(х, х2)-/С(х, х3). E.6.11)
Другими словами, в тех случаях, когда разделяющая граница,
определенная кумулятивным потенциалом Лг(х)> не обеспечи-
обеспечивает правильной классификации, значение кумулятивного по-
потенциала увеличивается или уменьшается на величину К(х, х3)
в зависимости от принадлежности образа х3 классу coj или со2.
Член К(х, х2), входящий в уравнения E.6.10) и E.6.11), будет,
естественно, отсутствовать, если образ х2 классифицируется
правильно.
Пусть, наконец, Kk(\) — значение кумулятивного потен-
потенциала, полученное после предъявления k образов обучающей
выборки хь х2, ..., х*. Кумулятивный потенциал Kk+i(x), воз-
возникающий после предъявления (й+1)-го выборочного образа,
определяется так:
1. Если xft+i«=©i H#fe(xft+i)> 0илих*+1есо2 и Kk(xk+i) <0,то
Kk+i(*) = Kk(x). E.6.12)
2. Если хА+, <=ю, и /СА(хА+,Х0, то
Kk+i (x) = Kk (x) + К (х, х*+1). E.6.13)
3. Если xs+ieffl2 и /(ft(xft+i)^0, то
Kk+x (х) = /(* (х) - К (х, х*+1). E.6.14)
Уравнения E.6.12) — E.6.14) определяют алгоритм итератив-
итеративного вычисления кумулятивного потенциала. Этот алгоритм
можно записать как
К*+1(х) = #*(х) + гл+1*Г(х, х*+1), E.6.15)
где коэффициенты r^+i при корректирующем члене опреде-
определяются соотношениями
E-ЬЛЬ)
Если алгоритм дает правильную классификацию, то коэффи-
коэффициент rk+\ = 0. Если же алгоритм классифицирует образ не-
неправильно, то коэффициент rk+\ = -(-1 или (—1) в зависимости
0
0
1
-1
при
при
при
при
Х*+1
Xfc+1
Xft+l
xk+i
е «! И
е (о2 и
е «! И
е (о2 и
д*
а:*
кк
(x*+i)
(Xft+i)
(Xft+l)
(Xfe+l)
>
<
<
0,
0,
0,
0.
212 Гл. 5. Детерминистский подход
от принадлежности соответствующего образа классу ©[ или
классу ш2.
Исключив из заданной обучающей последовательности
{Х[,х2,... ,х*,...} те образы, при классификации которых зна-
значения кумулятивных потенциалов не подвергаются изменению,
т. е. образы, для которых выполняются условия Kj(xl+i)> Q
при х/+1 е (Oi или Kj(xj+i) <i 0 при х^емг, можно сформиро-
сформировать последовательность {xi,x2 ху,...}. Элементами этой
редуцированной обучающей последовательности являются вы-
выборочные образы, обеспечивающие исправление ошибок. В та-
таком случае рекуррентные уравнения E.6.13) и E.6.14) дают
следующее выражение для определения значения кумулятив-
кумулятивного потенциала Kk+\ (x) после предъявления обучающей вы-
выборки:
Kk+i(x)=Za,K(x, xi), E.6.17)
где
при х/ею,,
f+1
"'-{-1
E.6.18)
При X; е @2.
Коэффициент а,- называют показателем класса, поскольку
он указывает, к какому классу принадлежит выборочный об-
образ X/. Из E.6.17) и E.6.18) следует, что кумулятивный потен-
потенциал, вызванный последовательностью k + 1 выборочного об-
образа, равен разности между полным потенциалом, вызванным
исправляющими ошибки выборочными образами, принадлежа-
принадлежащими классу ©1, и полным потенциалом, вызванным исправ-
исправляющими ошибки выборочными образами, принадлежащими
классу (о2.
Из описания алгоритма метода потенциальных функций оче-
очевидно, что кумулятивный потенциал выполняет роль решающей
функции. Другими словами, в тех случаях, когда значение ку-
кумулятивного потенциала Кь(хц+\) больше нуля, если Xk+i при-
принадлежит классу (oi, либо меньше нуля, если x^+i принадлежит
классу (о2, значение кумулятивного потенциала не корректи-
корректируется. С другой стороны, неправильная классификация образа
в процессе обучения приводит к изменению потенциальной
функции. Следовательно, алгоритм метода потенциальных
функций представляет собой итеративную процедуру, обеспе-
обеспечивающую непосредственное определение решающей функции
для разделения классов ©) и ©2; таким образом, положив
d(x)=K(x), из уравнения E.6.15) получаем
E.6.19)
что полностью соответствует формулировке E.6.3).
5.6. Подход, использующий потенциильныр фцнкиии 213
Способ вычисления коэффициента rk+\ формулируется в ком-
компактном виде так:
E.6.20)
где показатель a.k+\ определяется выражением E.6.18) и функ-
функция sgn [rfft(Xfe+i)] имеет в данном частном случае вид
sgn [rf(xft+i)j = 1 или —1 в зависимости от того, больше нуля
значение функции dk{x-k+\) или оно меньше или равно нулю соот-
соответственно. Если решающая функция dfe(x) классифицирует об-
образ \k+\ правильно, то гк = 0 и в результате значение кумуля-
кумулятивного потенциала не изменяется. Нетрудно убедиться в том,
что уравнение E.6.20) покрывает все остальные условия клас-
классификации.
Исходя из E.6.2), уравнение E.6.19) можно представить
в другой рекуррентной форме:
оо
<**+1(х)=1М*+0<Мх), E.6.21)
где коэффициенты c,(k-\-l) зависят от числа итераций, выпол-
выполненных в процессе обучения. Из этого уравнения, а также про-
проведенного выше анализа заключаем, что кумулятивный потен-
потенциал также имеет вид
по
Кш (х) = I ci (k + 1) Ф( (х). E.6.22)
Объединив уравнения E.6.19) и E.6.21) и E.6.1), получим
формулу
ct (k + l) = ct (k) + rk+tf<p{ (x*+I), E.6.23)
которую можно использовать для итеративного вычисления
коэффициентов разложения.
5.6.2. Выбор потенциальных функций
Общий вид потенциальной функции /C(x,xs) определен фор-
формулой E.6.1). Хотя при обсуждении математических свойств
алгоритмов метода потенциальных функций часто используется
разложение в бесконечный ряд, очевидно, что с практической
точки зрения это бесполезно. Обычно при реальном построении
потенциальных функций пользуются двумя основными ме-
методами.
Первый заключается в применении усеченных рядов
m
К (х, х,) = ? <р, (х) Ф, (х*), E.6.24)
211 Гл. 5. Детерминистский подход
где (ф,(х)}—ортонормированные функции на множестве об-
образов. Это допущение не вызывает практических затруднений,
так как ортонормированные функции легко строятся, как было
продемонстрировано в § 2.7. Коэффициенты X,-, входящие в об-
общее выражение потенциальной функции E.6.1), связаны
Рис. 5.4. Примеры одномерных потенциальных функций: а — график, соот-
соответствующий уравнению E.6.25); б — график, соответствующий уравнению
E.6.26); «— график, соответствующий уравнению E.6.27). Во всех трех слу-
случаях а = 1 и х„ = 0.
с ограниченностью потенциальных функций и для того типа
функций, который будет рассматриваться, могут быть опущены.
Функции, получаемые согласно E.6.24), называются потенци-
потенциальными функциями типа 1.
Второй метод использует некую симметрическую функцию
двух переменных х и х& в качестве потенциальной функции.
Условие симметричности формулируется так, чтобы полученные
в результате потенциальные функции соответствовали их об-
общему определению E.6.1). Из этого соотношения, в сущности,
следует, что К(х, xk) = K(xk,x). Кроме того, требуется, чтобы
выбранные функции допускали разложение в бесконечный ряд.
Это условие также соответствует общему определению потен-
потенциальной функции E.6.1). Функции, удовлетворяющие этим
двум условиям, будем называть потенциальными функциями
5.6. Подход, использующий потенциальные функции 21!>
типа 2. Отметим, что наиболее употребительны такие потен-
потенциальные функции типа 2:
К (х, к,) - ехр {-а || х — х* ||2}, E.6.25)
К(х, xk) =
а || х — \k f
E.6.27)
где а — положительная константа, а || х — х& || — норма вектора
(х — Xfe). Следует отметить, что эти функции обратно пропор-
пропорциональны квадрату расстояния D2 = || х — х* ||2, которое слу-
служит, в частности, характеристикой силы в потенциальном поле
тяготения. Функции этого вида представлены на рис. 5.4 для
случая одномерных образов и на рис. 5.5 для случая двумер-
двумерных образов.
Пример 1. Рассмотрим применение метода потенциальных
функций к образам рис. 5.6, причем воспользуемся потенциаль-
потенциальными функциями типа 1. Прежде всего следует выбрать подхо-
подходящее множество ортонормированных функций {ф((х)}. Удобно,
в частности, использовать полиномиальные функции Эрмита,.
рассмотренные в § 2.7, так как они ортонормировании в интер-
интервале (—оо,оо). В одномерном случае эти функции опреде-
определяются формулой
где выражение при функции Ht(x) является ортонормирующим
множителем. Выпишем несколько первых членов функ-
функции Hi (x):
Н0(х)=1 НЛх) = 2х,
Н2 (х) = 4х2 - 2, Я3 (х) = 8х3 - 12х,
12.
Для наглядности воспользуемся ортогональными функциями
вместо их ортонормированных аналогов, более сложных
с точки зрения вычислений. В § 2.7 было показано, что исполь-
использование ортогональных функций часто позволяет получить эк-
эквивалентные результаты для ортонормированных функций. Вы-
Выбрав в качестве первого приближения m = 4 и следуя изло-
изложенному в § 2.7 методу формирования ортогональных функций
K(x)
К(х)
Рис. 5.5. Двумерные потенциальные функции: а —график, соответствующей
уравнению E.6.25); б—график, соответствующий уравнению E.6.26); в —
график, соответствующий уравнению E.6.27). Во всех трех случаях значения
координат образа х =(х\,хг)' изменяются в диапазоне от —3 до 3, а = 1
и \к = 0.
5.6. Подход, использующий потенциальные функции
217
многих переменных из множества ортогональных функций од-
одной переменной, получаем
Ф, (х) = cpi (хи х2) == //0 (х,) Яо (х2) = 1,
Фг (х) = Ф2 (хи х2) = Я, (х,) Яо (х.) = 2хи
Фз (х) = ф.) (xi, х2) = Яо (х,) Я, (х2) = 2х2,
Ф4 (х) = ф4 (хи х2) = Hi (дс,) Я, (х2) — 4xiX2.
Воспользовавшись соотношением E.6.24), можно сформировать
потенциальную функцию
К (х, xft) =
(х) Ф,- (хА) =
где Xk\ и дглг2 суть компоненты вектора х&. В класс coi входя г
образы {A,0)', @,—1)'} и в класс ш2 — образы {(—1,0)',
1
-2
/
-1
/
/
X
2
и
/
-2
2
-
/
а
/
1
/
2
Рис. 5.6. Образы, использованные для иллюстрации принципа действия алго-
алгоритма метода потенциальных функции.
@,1)'}. Применение алгоритма обучения по методу потенци-
потенциальных функций [уравнение E.6.15)] дает следующую после-
последовательность шагов.
Пусть Xi = A,0)'—первый предъявленный образ. Поскольку
он принадлежит классу coi, значение кумулятивного потенциала
определяется как
Я,(х) = К(х, х,)= 1 +4.v,AL-4jc2@)+ 16х,х2A)@)= 1+4х„
218 Гл. 5. Детерминистский подход
Образ х2 = @,—1)' принадлежит классу соь Вычислим
*1(хг)=1+4@)=1.
Так как К\ (х2) > 0 и х2 е щ, то
Следующий предъявленный образ х3 = (—1,0)' принадле-
принадлежит классу со2, и, поскольку
/С2(х3)= 1 + 4(—1)==—3,
т. е. /B(х3) меньше нуля, можно считать, что
Четвертый предъявленный образ х4 = @, 1)' принадлежит
классу (о2, и, поскольку
т. е. /(з(х4) больше нуля, следует провести коррекцию:
К, (х) = К3 (х) - К (х, х4) = 1 + 4дс, - A + 4*2) = 4х, - Ах2.
Очередной цикл итерации по всем образам дает
х5= \п)=»и Кь{х)=КЛх) = 4х1
xfi-l , ,^-»„ - — =/С5(х)==4х,-4х2,
^7 (х) = К6 (х) = 4х, - 4х2,
_ ^7 (х8) = -4,
х„ — I , I е со2, ^ (х) = ^ (х) = 4jfi _ 4л.2
Так как в данном цикле итерации при просмотре всех образов
не совершено ни одной ошибки, это означает, что алгоритм
сошелся и выдал решающую функцию
Разделяющая граница, заданная этой функцией, приведена
на рис. 5.6. |
Пример 2. Проиллюстрируем применение потенциальных
функций типа 2 на примере образов рис. 5.7, а. Воспользуемся
в данном примере экспоненциальной функцией E.6.25) при
d(x) < 0 бэтой o5nacwus
о с
с U)g
Рис. 5.7. Образы, использованные для иллюстрации принципа действия алго-
алгоритма метода потенциальных функций, а —образы и разделяющая поверх-
поверхность; б —график потенциальной функции d(\) в диапазоне —1 < xi ^ 3 и
—2 а? хг < 2.
220 Гл. !>. Петррминистский подход
а=1, что приводит в рассматриваемом двумерном случае к
К (х, \k) = ехр {—|| х — \k ||2} = ехр {— [(*, — xk[f + (х2 — xk2f]}.
В класс (oi входят образы {@,0)', B,0)'} и в класс ю2—
образы {A,1)'. A. — !)'}¦ Отметим, что эти классы линейно не
разделимы. Применение к этим образам алгоритма потенциаль-
потенциальных функций сводится к следующим шагам.
Пусть Xi=@,0)' — образ обучающей выборки, предъявляе-
предъявляемый первым. Поскольку он принадлежит классу оси, имеем
К, (х) = К (х, х,) = ехр {- [(*, - ОJ + (х2 - ОJ]} =
= ехр {-О2+ 4)}.
Элемент обучающей выборки х2 = B, 0)' принадлежит клас-
классу со;. Вычислим /d(x2):
/С, (х2) = е-<«+°> = в >0.
Поэтому имеем
К2 (х) = /С, (х) = ехр {- (х\ + х2)}.
Теперь предъявим хз = A,1)', принадлежащий классу
и вычислим /B(хз)- Получим
Поскольку значение кумулятивного потенциала /С2(х3) должно
быть меньше нуля, производится следующая коррекция:
/Сз(х) = /С2(х)-/С(х, х3) =
= ехр {- (х\ + хЩ - ехр {- [(*, - 1 f + (х2 - 1 J]}.
Образ х4 = A,—1)', предъявляемый следующим, принадле-
принадлежит классу со2. Подстановка характеристик Х4 в /Сз(х) дает
., (х4) = е~ A+|» — е~ <°+4' = е~2 — е~4 > 0.
Так как значение Кз(х^) должно быть меньше пуля, кумуля-
кумулятивный потенциал подвергается коррекции:
= ехр {- (*? + л-0) - ехр {- [(х, - \f + (х.2 -
Легко убедиться в том, что эта функция не обеспечивает без-
безошибочной классификации всех образов, входящих в обучаю-
5.6. Подход, использующий потенциальные функции 221
щую выборку. Следовательно, необходим еще один итерацион-
итерационный цикл:
- @>) GE Л'" (Х5) = е~° "~ ^ ~~ в~2 > 0>
- о-
/СГх, х6) =
Кй (х7) = е-'2 - <?° - е~* + е-'1 < О,
х7 =
^ К7(х8) = е-2-е-2-е° + е~2<0,
- Q
Sl0= (о)'
:С0"
Поскольку получен цикл итерации, в котором ошибки от-
отсутствовали, это означает, что алгоритм сошелся и выдал ре-
решающую функцию
й (х) = /Сю (х) = ехр [- (x'f + 4)] - ехр{- [(дс, - 1 J +
[(^.- 1)'2 + (^+ 02]} +
Разделяющая граница, определяемая уравнением d(x) = 0,
показана па рис. 5.7, а. График потенциальной функции d(x) =
=/Сю(х) для —1 ^ Xi ^ 3 и —2^л:2^2 приведен на
рис. 5.7,6. |
Полезно сопоставить два рассмотренных примера. Из пер-
первого примера очевидно, что при выборе потенциальной функции
типа 1 полученный алгоритм весьма напоминает алгоритм пер-
цептрона в том отношении, что заранее предопределен вид ре-
решающей функции. В нервом примере была выбрана квадратич-
квадратичная решающая функция. Ее коэффициенты определялись
в процессе реализации обучающей процедуры.
222
Гл. 5. Детерминистский подход
Если выбирается потенциальная функция типа 2, то из вто-
второго примера следует, что вид решающей функции зависит от
числа коррекций кумулятивного потенциала. Причиной этого
является, естественно, то обстоятельство, что при проведении
каждой коррекции в связи с появлением нового образа в выра-
выражение потенциальной функции добавляется очередной член.
Вполне возможно, что полученная в результате решающая
функция будет содержать число членов, равное числу разных
образов, присутствующих в обучающем множестве, как это
имело место в примере 2. В принципе при больших обучающих
множествах выбор потенциальных функций типа 2 приводит
к трудностям, связанным с памятью ЭВМ, так как в этих слу-
случаях необходимо запоминать значительное количество членов.
Естественно, при этом не следует пренебрегать тем обстоятель-
обстоятельством, что введение в процессе обучения новых членов суще-
существенно увеличивает классификационную мощность метода.
5.6.3. Геометрическая интерпретация коррекции весов ')
В этом разделе дается геометрическая интерпретация ме-
метода потенциальных функций и построения решающих функций
при помощи коррекции вектора весов. Положив
E.6.28)
E.6.29)
где i=l, 2, ..., т, а переменная у представляет выборочные
образы, предъявляемые в процессе обучения, получим потен-
потенциальную функцию E.6.24) в виде
К(х, y) = z'u. E.6.30)
Векторы z и и, входящие в E.6.30), суть /n-мерные векторы
Zt = А;ф; (X)
Щ = КЧЧ (У).
Zn
E.6.31)
') Данный раздел написан по материалам четвертой главы сборника «Ad-
«Advances in Infermation Systems Science», Vol. 1, Plenum Press.
5.5. Подход, использующий потенциальные функции
223
«1
щ
E.6.32)
В таком случае решающая функция rf*(x), определенная на
шаге k, представляется выражением
(k) Zi = z'w (k),
E.6.33)
где
Щ
E.6.34)
вектор весов, компоненты wt(k) которого суть
... „л_М*>
E.6.35)
Переход от области X к области Z, осуществляемый в соответ-
соответствии с E.6.28), приводит к линеаризации решающей функции.
Разделяющая граница принимает в области Z вид гиперпло-
гиперплоскости
z'w(?) = 0 E.6.36)
с нормальным вектором w, проходящей через начало координат,
как показано на рис. 5.8. В таком случае при xemi выпол-
выполняется условие z'w(?)>0, а при х е ш2 — условие z'w(&)<0.
Пусть известно, что две группы образов, входящих в обу-
обучающую выборку, Fi еш; и Т2 е ш2, лежат с противоположных
сторон разделяющей гиперплоскости, как это показано на
рис. 5.8. Задача в данном случае сводится к построению алго-
алгоритма, позволяющего в процессе последовательного осмотра
224
Гл. '> Детерминистский подход
образов обучающей выборки найти такой весовой вектор w(&),
что для всех образов, принадлежащих обучающему множеству
Т\, выполняется условие
z'w (k) > О, E.6.37)
и для всех образов, принадлежащих обучающему множеству Т2,
выполняется условие
z'w (k) < 0. E.6.38)
Образовав множество Г2 при помощи симметричного относи-
относительно начала координат отражения обучающего множества
Рис. 5.8. Непересекающиеся классы.
Г2, можно сформулировать условие разделимости множеств Т\
и Т'2 гиперплоскостью с нормальным вектором w(k) просто как
z'w F) > 0 для геГ,иг;
E.6.39)
Другими словами, обучающие множества Т\ и Т2 разделяются
этой гиперплоскостью, если все точки, представляющие входя-
входящие в обучающую выборку образы, лежат по одну сторону ог
этой гиперплоскости, как показано на рис. 5.9.
Пусть задано обучающее множество {zi, z2, ..., Z/, ...} и
Zi, z2, ..., z,-, ... — последовательность образов, корректирую-
корректирующих ошибку. Кумулятивный потенциал в области 2 определяется
на k-м шаге как
" " " E.6.40)
5.6 Подход использующий потенциальные функции
225
В начале этана обучения кумулятивный потенциал /Co(z) при-
принимается равным нулю и начальная разделяющая граница
имеет вид
Ko(z) = z'w(O) = O. E.6.41)
При предъявлении первого образа обучающей выборки Zi зна-
значение кумулятивного потенциала равно
/C,(z) = /((z>z1) = z/z1. E.6.42)
Соответствующая разделяющая граница определяется как
z'w(l) = 0. E.6.43)
Вектор весов w(l) определен таким образом, что вектор выбо-
выборочного образа zi перпендикулярен гиперплоскости, заданной
Рис. 5.9. Классы, отраженные относительно начала координат.
уравнением E.6.43). Следовательно,
w(l)=-z,. E.6.44)
Отметим, что на разделяющей границе значение потенциала
падает до нуля. Это условие также приводит к E.6.44).
Если при предъявлении второго образа обучающей выборки
z2 выполняется условие Ki (z2) = zazi > °> то кумулятивный по-
потенциал равен
K2(z) = Ki(z) = z%, E.6.45)
если же Кх (z2) = z?z, < 0, то значение кумулятивного потен-
потенциала увеличивается:
К2 (z) = Ki (г) + К (z, z2) = г' (z, + z2). E.6.46)
226 Га. в. Детерминистский подход
Разделяющая граница при этом задается уравнением
z'w B) = 0. E.6.47)
Вектор весов wB) определен таким образом, что результирую-
результирующая векторов выборочных образов zi и z2 перпендикулярна ги-
гиперплоскости E.6.47). Имеем
wB) = z1 + z2 = w(l) + z2. E.6.48)
Если при предъявлении третьего образа обучающей выборки
гз выполняется условие /B(гз)> 0, то кумулятивный потенциал
равен
К3{г) = К2{г), E.6.49)
если же /B(гз)<0, то значение кумулятивного потенциала уве-
увеличивается:
К3 (z) = K2 (z) + К (г, 2з) = г' (z, + z2 + z3). E.6.50)
В таком случае вектор весов определяется выражением
wC) = ?,+?2 + z:3 = wB) + Z3. E.6.51)
Построение последовательных вариантов разделяющих гра-
границ проиллюстрировано на рис. 5.10. Если вектор выборочного
образа гз расположен в положительной зоне гиперплоскости
z'w B) = 0, то разделяющая граница не изменяется и вектор
wC) определяется как wC) = wB) = zi + z2. Если вектор об-
образа z3 расположен в отрицательной зоне гиперплоскости
z'wB) = 0, то разделяющей границей становится гиперпло-
гиперплоскость z'wC) = 0 и wC) = zi + z2 + z3.
Обозначим через Kn(z) значение кумулятивного потенциала,
полученное после предъявления k образов обучающей выборки
Zi, z2 z*. Если при этом Kk{zk+\) > 0, то кумулятивный по-
потенциал Kk+i{z) после предъявления выборочного образа
принимает значение
, E.6.52)
а при выполнении условия /С^ (zft+i) < 0 его значение увеличи-
увеличивается до
Kk+1 (z) = Кк B) + К B, zft+I) = z' ( Z Zi). E.6.53)
Вектор весов w(fe + l) определяется в виде
k
w (* + 1) = Z 2, = w (*н ik+l, E.6.54)
5.6. Подход, использующий потенциальные функции
227
где zk+l e Г, U Т\. Воспользовавшись формулой E.6.28), полу-
получим рекуррентное соотношение для определения весов Wi(k-{- 1):
Щ (k+l) = w, (k) + A,,q>, (xft+I). E.6.55)
Уравнения E.6.54) и E.6.55) представляют алгоритмы обуче-
обучения системы распознавания образов посредством итеративной
Рис. 5.10. Порождение разделяющих границ.
коррекции весов при предъявлении выборочных образов, кор-
корректирующих ошибку. Читателю следует обратить внимание
на сходство алгоритма E.6.55) и алгоритма перцептрона.
5.6.4. Сходимость алгоритмов обучения
В настоящем пункте приводится несколько полезных тео-
теорем, которые касаются алгоритмов обучения, из пп. 5.6.1 и
5.6.2. Рассматриваются теоремы о сходимости, о скорости схо-
сходимости и об условиях, при которых алгоритм прекращает свою
работу. Эти теоремы играют фундаментальную роль в класси-
классификации методом потенциальных функций.
Теорема 1. (О свойствах сходимости алгоритма.) Пусть век-
векторы образов х удовлетворяют в пространстве образов следую-
следующим условиям.
1. Потенциальная функция
К(х, х/)=
ограничена для х е Т\ (J Т2.
E.6.56)
228 Гл. 5. Детерминистский подход
2. Существует решающая функция, представимая в виде
Ех), E.6.57)
«=¦1
такая, что
С > е, если х е аУ|,
d(x)< ' E.6.58)
(. < — е, если хеш2|
где е > 0.
3. Обучающая выборка образов обладает следующими ста-
статистическими свойствами: (а) в обучающей последовательности
выборочные образы появляются независимо; (б) если на k-м
шаге алгоритма обучения решающая функция dk{\) не обеспе-
обеспечивает правильной классификации всех образов xi, хг, .... х*,
то с положительной вероятностью будет предъявлен образ
Xft+i, корректирующий ошибку.
Тогда с вероятностью 1 можно определить конечное число
шагов R, таких, что кумулятивный потенциал
> 0 при х е Wi,
E659)
Другими словами, последовательная аппроксимация решаю-
решающей функции dk(x) с вероятностью 1 сходится к решающей
функции d(\) за конечное число предъявлений образов обучаю-
обучающей выборки. Это означает, что разделение классов coi и ciJ
осуществляется за конечное число шагов с вероятностью 1.
Теорема 2. (О скорости сходимости алгоритма.) Пусть
S,-={x,, x2 х„, ...} E.6.60)
— бесконечная последовательность обучающих образов, выбран-
выбранных из обучающего множества Т = Т\[) Т2, причем Тх е a>i и
Т2 е ос»2- Допустим, что потенциальная функция К(х,х/) огра-
ограничена при х е 7i (J Т2 и существует решающая функция, пред-
представимая разложением E.6.57) и удовлетворяющая условиям
E.6.58). Тогда существует целое число
up К(х, х
не зависящее от выбора обучающей последовательности 5, и
такое, что при использовании алгоритмов из пп. 5.6.1 и 5.6.2
число коррекций не превышает величины R.
Приведем доказательство этой теоремы с тем, чтобы проил-
проиллюстрировать типичную методику, используемую при доказа-
доказательстве теорем этого пункта.
S.6. Подход, использующий потенциальные функции 229
Доказательство. Прежде всего с помощью уравнения
E.6.28) преобразуем область X в Z. Обучающее множество Тг
отразится симметрично относительно начала координат, образо-
образовав множество т'2- Пусть, наконец,
а= inf —r E.6.62)
Р= sup ||z||. E.6.63)
7
Величина а положительна и с геометрической точки зрения
представляет собой минимальное расстояние между гиперпло-
гиперплоскостью z'w = 0 и обучающим множеством Г, U Г*, а величина
Р — расстояние от начала координат до наиболее удаленной
точки множества Г, U Т*2. Исходя из того факта, что нормальное
евклидово расстояние от гиперплоскости до произвольной точки
z равно z'w/||w||, величина а — минимальное нормальное рас-
расстояние. Так как, по определению, модуль вектора ||z|| есть рас-
расстояние от начала координат до множества Tz = Tl [}T*2, вели-
величина р является соответствующим максимальным расстоянием.
Для любого образа zi^T\\}T2, согласно E.6.62), имеем
z;w>a||w||. E.6.64)
Из условия E.6.63) следует, что
||z,.||<|3. E.6.65)
Мы хотим показать, что для числа шагов k существует верхняя
граница, при которой вектор весов w(&) не будет изменяться в
результате предъявления образа из обучающей выборки. После
предъявления системе k образов обучающей выборки, входящих
в последовательность образов, корректирующих ошибки,
S-={zltz2, ...,zt, ...}, E.6.66)
вектор весов принимает вид
к
w (*)=?**¦ E.6.67)
Этот вектор нормален гиперплоскости z'w(fe) = 0, полученной
после реализации k шагов. Теорему можно доказать, продемон-
продемонстрировав, что последовательность образов S-, корректирующих
ошибки, является конечной.
Из соотношений E.6.64) и E.6.67) получаем, что
w' (k) w > ak |i w i|. E.6.68)
230 Гл. 5. Детерминистский подход
Применение неравенства Коши — Шварца дает
|w'(*)w|<||wOfe)||||w||. E.6.69)
Согласно E.6.68) и E.6.69),
!|w()fe)||>a*. E.6.70)
Принимая во внимание неравенство E.6.64), приходим к соот-
соотношению
||w(*)|P = ||w(*-l)||! + 2i;w(*-l) + ||zJk!p. E.6.71)
Так как ||z*|| ^f и существует вектор zk, удовлетворяющий
условию z&w(&—1)<0, формулу E.6.71) можно записать
в виде
|iw(fc-l)f + p2. E.6.72)
Приняв, что w@) = 0, при помощи итерации получим
II w (k) IP < ktf. E.6.73)
Объединив E.6.70) и E.6.73), имеем
*<К = |!-. E-6.74)
т. е. верхняя граница значений параметра k — длины последо-
последовательности S-, составленной из корректирующих ошибки обра-
образов, равна р2/а2 и- следовательно, конечна.
В области X значения аир следующие:
inf
s
1-1
inf
х<=Г
« =-r-= T7— = TF^ ЧПГ- E.6.75)
[<х>
i, x,). E.6.76)
xe'T
Таким образом, выражение E.6.61) для верхней границы k по-
получено. Поскольку потенциальная функция Л (х, х,) ограниченна
и |d(x)| не равно нулю, константа к конечна, если выполняется
условие
-jj-Ч < оо. E.6.77)
Известно, что этот ряд сходится, если при / > т все коэффи-
коэффициенты с, равны нулю. ¦
5.6 Подход, использующий потенциальные функции 231
Из проведенного анализа следует, что значение R меньше,
если минимум решающей функции d\x) больше при неизмен-
неизменных остальных условиях. Поскольку R обратно пропорциональ-
пропорционально величине infx<=iuB(x), размер обучающей последовательно-
последовательности, корректирующей ошибки, можно уменьшать, увеличивая
минимум |of(x)|. Это означает, что размер последовательности,
корректирующей ошибки, уменьшается по мере удаления обра-
образов обучающей выборки Т U Г* от разделяющей границы
d(x) = О, т. е. по мере удаления их друг от друга. Этот резуль-
результат соответствует интуитивным предположениям.
Теорема 3. (Условия прекращения выполнения алгоритма.)
Пусть процесс обучения прекращается, если после осуществле-
осуществления k коррекций неправильной классификации при предъявле-
предъявлении Lo следующих выборочных образов никакие коррекции
больше не производятся. Другими словами, процесс обучения
прекращается после предъявления Lk выборочных образов, где
Lk определяется выражением
Lk = L0 + k. E.6.78)
Таким образом, общее число предъявлений образов, необходи-
необходимое для прекращения работы алгоритма, увеличивается на 1
после каждой коррекции неправильной классификации. Задача
заключается в определении числа контрольных выборочных об-
разов Lo, необходимых для обеспечения заданного качества
процедуры обучения. Обозначим через р. (е) вероятность со-
k
вершения ошибки после предъявления системе Lk выборочных
образов. Тогда для любых е > 0 и б > 0 вероятность того, что
pL (е) < е, будет больше, чем 1 — б, если
j Ioge6 ,,. R _o.
La> log A-е) • E-6J9>
Отметим, что выбор числа контрольных выборочных образов
зависит, согласно этому неравенству, только от заданных зна-
значений е и б, характеризующих качество обучающей процедуры.
Выбор величины Lq не зависит от свойств классов щ, и ш2 и ста-
статистических характеристик образов.
5.6.5. Обобщение на случай нескольких классов
Алгоритм метода потенциальных функций, как и алгоритм
перцептрона, легко обобщается на любой из трех случаев раз-
разделения на несколько классов, рассмотренных в § 2.2. В пер-
первых двух случаях можно, естественно, воспользоваться после-
последовательным применением рассмотренного выше алгоритма,
232 Гл. 5 Петерминистскип подход
обеспечивающего разделение двух классов. В случае 3 алгоритм
метода потенциальных функций использует при разделении
нескольких классов непосредственное обобщение, примененное
для перцептронной процедуры в § 5.4. Итак, алгоритм метода
потенциальных функций E.6.12) — E.6.14) может быть обобщен
следующим образом.
Для удобства записи будем считать, что значения кумуля-
кумулятивных потенциалов Ко\х), /Сп2) (х), ..., КоМ) (х) в начале
процесса обучения равны нулю. Верхние индексы здесь указы-
указывают принадлежность образа соответствующему классу. Пусть
на F 4-1)-м шаге итерации предъявляется выборочный образ
Xk+i, принадлежащий классу ы«. Если для всех / Ф i выпол-
выполняется условие
< 4"
то значения кумулятивных потенциалов изменению не подвер-
подвергаются, т. е.
<+, (х) = Kf (х), * = 1, 2, ..., М. E.6.81)
Если же, однако, xfe+1 е ш( и для некоторого I
то производятся следующие коррекции:
С(х) = <(х) + ^(х, х,+1),
Kf+l (x) = Kf (x) - К (х, хА+1), E.6.83)
<'+, (х) = К{1] (х), /=1,2 М; ]ф1,1ф1.
Поскольку решающие функции d(i) (x) равны кумулятивным
потенциалам /C(i)(x). эквивалентный алгоритм, заданный урав-
уравнением E.6.21), можно обобщить на случай разделения не-
нескольких классов простой заменой кумулятивных потенциалов
K(i){\) решающими функциями d(i)(\) в формулах E.6.80) —
E.6.83).
5.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В данной главе рассмотрено несколько важнейших концеп-
концепций, лежащих в основе классификации образов при помощи
детерминистских алгоритмов обучения. Использовав в качестве
отправной точки стандартную градиентную методику, мы по-
построили алгоритмы трех различных типов. Как отмечалось, эти
алгоритмы, не исчерпывая все варианты, дают все-таки пред-
представление о спектре возможных вычислительных схем. Прове-
5.7. Заключительные замечания 233
ден также сравнительный анализ основных свойств алгоритма
перцептрона и алгоритма наименьшей среднеквадратичной
ошибки.
Основная задача, возникающая при применении алгоритмов
этих трех типов, заключается в выборе подходящего множества
решающих функций. Эта задача решается, в сущности, мето-
методом проб и ошибок, поскольку единственным способом оценить
качество выбранной системы решающих функций является пря-
прямая проверка. В тех случаях, когда рассматриваемые классы
не содержат одинаковых образов, всегда можно отыскать мно-
множество решающих функций, которые обеспечат правильную
классификацию всех образов, входящих в обучающее множе-
множество, хотя сами функции могут оказаться весьма сложными.
При решении большинства практических задач следует, однако,
учитывая экономические и вычислительные возможности, счи-
считать, что некоторое количество неверных классификаций допу-
допустимо. Если решено определенный процент ошибок считать
допустимым, это необходимо учитывать при построении класси-
классификатора. Во многих случаях предписанный процент обеспе-
обеспечить невозможно, не нарушив ограничений по сложности, нало-
наложенных на классификатор. В таких случаях необходимо либо
увеличить допустимый процент неправильных классификаций,
либо повысить сложность классификатора, либо обратиться к
иному методу классификации.
Завершает главу обсуждение классификации образов с по-
помощью потенциальных функций, когда обучение классифика-
классификатора обеспечивается не посредством итеративной коррекции ве-
весового вектора, а последовательным изменением значений куму-
кумулятивного потенциала. Приведены два метода построения
потенциальных функций. В первом методе вид решающей функ-
функции заранее фиксирован, в то время как во втором допускается
увеличение классификационной мощности решающих функций
в процессе обучения. Первый метод не очень сильно отличается
от процедуры обучения, осуществляемой с помощью алгоритма
перцептрона, что становится очевидным из примеров, рассмот-
рассмотренных в п. 5.6.2. Из этих примеров следует также, что приме-
применение второго метода в общем случае приведет к вычислитель-
вычислительным трудностям при работе со сравнительно большими множе-
множествами образов.
Следующая глава посвящена в основном статистическому
подходу к классификации. Как мы увидим, понятие решающей
функции сохраняет смысл и в статистическом случае, за исклю-
исключением, естественно, того обстоятельства, что построение этих
функций связано с использованием вероятностных, а не детер-
детерминистских концепций. Завершая эту главу, стоит все же за-
заметить, что помимо приведенных здесь алгоритмов существуют
234 Гл. 5. Детерминистский подход
и другие подходы к решению систем линейных неравенств вида
E.1.1). Уже достаточно давно для решения линейных нера-
неравенств используются методы линейного программирования
(Саймоннард [1966]). Распознаванию образов, однако, линей-
линейное программирование может предложить не много, поскольку
более простые алгоритмы, типа приведенных в данной главе, не-
несомненно обладают равными возможностями.
Библиография
Первые результаты, связанные с перцептронами, содержатся в несколь-
нескольких работах Розенблатта [1957, 1960, 1965]. Первые результаты по линейным
классификаторам имеются также в диссертации Хайлимана [1962] и статье
Блока [1962]. Простое доказательство сходимости алгоритма перцептрона,
приведенное в этой глапе, принадлежит Новикову [1963]; другие варианты
доказательства предложены Розенблаттом [1960], Блоком [1962], Джозефом
[1960], Синглтоном [1962] и Чарпсом [1964].
Усилия, связанные с применением градиентного подхода к построению
алгоритмов классификации образов, нашли отражение в отчете Блейдона
[1967], статьях Девятерикова, Пропоя и Цыпкииа [1967], Хо и Кашьяпа
1965], а также в ряде других работ. Алгоритм, приведенный в п. 5.3.3, пред-
предложен Хо и Кашьяпом [1965]. Доказательство сходимости алгоритма из § 5.4
можно найти в монографии Нильсона [1967].
Большая часть ранних работ по потенциальным функциям приходится на
советскую литературу. Фундаментальный вклад в эту область сделан Айзер-
маном, Браверманом и Розопоэром [1964а, 19646, 1965]. Некоторая часть
материала, содержащегося в § 5.6, взята из работы Ту [1969а].
Задачи
5.1. Используйте алгоритм коррекции абсолютной величины для классифи-
классификации образов из примера, приведенного в п. 5.2.1.
5.2. Решите задачу 5.1, воспользовавшись алгоритмом дробной коррекции.
5.3. Покажите, что результаты решения примера из п. 5.2.1 согласуются
с E.2.25).
5.4. Воспользуйтесь формулой E.3.3) и функцией критерия
/ (w, х, Ь) = ¦
где Ь > 0, для построения алгоритма разбиения образов на два класса.
5.5. (а) Используйте алгоритм, полученный при решении задачи 5.4, для
классификации образов из задачи 5.1 при условии, что с = Ъ = 1.
(б) Рассмотрите влияние увеличения значения параметра Ь на сходи-
сходимость алгоритма в случае линейно разделимых классов. Указание:
обратитесь к § 2.4.
5.6. Докажите, что алгоритм, построенный при решении задачи 5.4, сходится
в случае разделимости классов при 0 < с < 2.
5.7. Примените алгоритм перцептрона к классам coi: {@,0,0)', A,0,0)',
A,0,1)', A,1,0)'} и со2: {@,0,1)', @,1,1)', @,1,0)', A,1,1)'}. Пусть
w(l) = (—1, —2, —2, 0)'.
5.8. Изобразите разделяющую поверхность, найденную при решении зада-
задачи 5.7. Укажите расположение образов и положительную зону разде-
разделяющей поверхности.
Задачи 235
5.9. (а) Задайте подходящую решающие функцию для разделения классов,
содержащих одномерные образы coi: {0,2} и ад {1,3}; воспользуй-
воспользуйтесь для определения решающей функции алгоритмом перцентрона.
Обратите внимание на то, что эти классы линейно не разделимы.
(Здесь предполагается использование ЭВМ.)
(б) Постройте график решающей функции d(x) от х.
5.10. Воспользуйтесь НСКО-алгоритмом при с= 1 и ЬA) = A,1)' для опре-
определения границы, разделяющей два простых класса одномерных образов
Wi: {1} и ад {0}.
5.11. Решите задачу 5.7, воспользовавшись НСКО-алгоритмом.
5.12 Проверьте с помощью НСКО-алгоритма линейную разделимость следую-
следующих классов: со,: {(—1,-1)', @,0)', A,1)'} и со2: {(—1,1)', A, —1)'}.
5.13. Примените алгоритм метода потенциальных функций к классам coi:
{@, 1)', @, —1)'} и со2: {A, 0)', (—1, 0)'}. Используйте решающую
функцию второго порядка в виде E.6.24).
5.14. Решите задачу 5.13, воспользовавшись потенциальной функцией типа
E.6.25).
5.15. Примените алгоритм перцептрона, обеспечивающий разделение несколь-
нескольких классов, к классам coi: {(—1, —1)'}, сог: {@, О)'} и соз: {A,1I.
5.16. Решите задачу 5.15, воспользовавшись потенциальной функцией типа 1,
содержащей только линейные члены.
Глава 6
ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ ОБРАЗОВ.
СТАТИСТИЧЕСКИЙ ПОДХОД
6.1. ВВЕДЕНИЕ
Алгоритмы классификации образов, развитые в гл. 5, харак-
характеризуют детерминистский подход, поскольку статистические
свойства классов образов не играют никакой роли ни при опре-
определении, ни при построении этих алгоритмов. Все алгоритмы
настоящей главы, напротив, являются результатом статистиче-
статистического анализа.
Так как байесовское правило классификации устанавливает
стандарт оптимальной классификации, вполне логично основы-
основывать на нем статистическое определение алгоритмов класси-
классификации образов. В гл. 4 было показано, что байесовские ре-
решающие функции
<Мх) = р(х|ш,)р(в>«), /=1, 2 М, F.1.1)
минимизируют среднюю стоимость неправильной классифика-
классификации и вероятность ошибки.
При использовании соотношения р (х | со,) = р (со,-1 х) р (х) /р (со,)
выражение F.1.1) принимает вид di{\) = p(a>i\\)p(\). Посколь-
Поскольку, однако, член р(\) не зависит от i, его можно опустить, что
дает эквивалентное выражение для байесовских решающих
функций:
d,(x) = p(a>,|x), /=1, 2 М. F.1.2)
Для двух классов разделяющая граница определяется уравне-
уравнением di(x) — йг(х) = 0. В таком случае можно получить соот-
соответствующее эквивалентное выражение для разделяющей гра-
границы
d (х) = rf, (х) - d2 (х) = р (со, | х) - р (со21 х) =
х)- 1. F.1.3)
При использовании последней формулировки образы класси-
классифицируются согласно следующему правилу: xeoi, если
dr(x)>0, и х е AJ, если d(x)<0. Это правило с учетом F.1.3)
можно сформулировать так:
если p(coi|x)> 1/2, то образ х относится к a>i;
если р(со,|х)< 1/2, то образ х относится к со2.
6.2 Методы стохастической аппроксимации 237
Глава 4 была посвящена рассмотрению решающих функций
F.1.1). Здесь же наше внимание будет сосредоточено на ре-
решающих функциях F.1.2). Прежде, однако, чем приступать
к обсуждению их свойств, необходимо получить четкое пред-,
ставленис о различии между этими двумя подходами.
Ключевой проблемой при реализации функций вида F.1.1)
является оценка плотности распределения для каждого класса
p(\\(Oi). Как было отмечено в гл. 4, при оценке плотности рас-
распределения р(х|(о,) рассматриваются только образы, принадле-
принадлежащие классу со,-. Поэтому никакого обучения в смысле гл. 5
не происходит, так как образы, принадлежащие другим клас-
классам, на процесс получения оценки плотности распределения для
данного класса не влияют.
Как будет показано ниже, оценку плотностей распределений
р(со, | х) в связи с реализацией решающих функций F.1.2)
можно сформулировать как задачу обучения, решаемую в диа-
диалоговом режиме. В результате принятия такой постановки бу-
будут построены алгоритмы обучения, с формальной точки зрения
очень похожие на алгоритмы, рассмотренные в гл. 5.
6.2. МЕТОДЫ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ
Прежде чем переходить к изучению статистических алго-
алгоритмов классификации образов, необходимо ввести несколько
концепций, которые позволят должным образом описывать по-
построение этих алгоритмов. Методы, используемые в этой главе,
весьма сходны с градиентными методами, рассматривавшимися
в гл. 5. Вместо детерминистских функций критерия мы сталки-
сталкиваемся теперь со статистическими функциями, которые стати-
статистики обычно называют функциями регрессии. Для определения
корней функции регрессии воспользуемся методами так назы-
называемой стохастической аппроксимации. Если функция регрессии
представляет производную от должным образом заданной функ-
функции критерия, то определение корня этой производной обеспе-
обеспечивает отыскание минимума функции критерия. При помощи
соответствующего выбора функций критерия можно построить
итеративные алгоритмы обучения, аппроксимирующие в некото-
некотором смысле байесовский классификатор. Для того чтобы упро-
упростить изложение, в начале мы сосредоточим внимание на одно-
одномерных задачах. Затем обобщим полученные результаты на
многомерный случай.
6.2.1. Алгоритм Роббинса — Монро
Рассмотрим функцию g(w) переменной w, имеющую един-
единственный корень w, такой, что g(w) — 0. Пусть функция g(w)
отрицательна при всех значениях переменной ш, меньших $, и
238
Гл. 6. Статистический подход
положительна при всех значениях до, больших до. Это допуще-
допущение лишь незначительно нарушит общность, так как большин-
большинство функций, имеющих один корень и не удовлетворяющих
этому условию, можно привести в соответствие с ним, умножив
функцию на —1.
Допустим, что вместо непосредственного наблюдения функ-
функции g(w) мы имеем дело с зашумлечными значениями g(w).
', h(w)
hfw(k)J
g№*)J
•
Функция \
регрессии д (w)
Г
Ошибка
_L_ -
V w(k)
Корень w
W
Рис. 6.1. Функция регрессии, искаженная шумом.
Эти случайные значения функции g(w) обозначим через ft (до).
Ошибка, характеризующая разницу между истинным и получен-
полученным при наблюдении зашумленным значениями, определяется
в любой точке до, как показано на рис. 6.1, выражением
g(w) — h(w).
Два необременительных допущения следует ввести для слу-
случайных величин h(w). Во-первых, будем считать их несмещен-
несмещенными, т. е.
E{h(w)) = g(w). F.2.1)
Это означает только то, что для ряда наблюдений, полученных
при фиксированном значении переменной до, их среднее, обозна-
обозначаемое буквой Е, будет приближаться по мере увеличения объ-
объема выборки к значению функции g(w) в этой точке.
Во-вторых, допустим, что среднеквадратичное отклонение
значений наблюдений h (до) от истинного значения функции
6.2 Методы стохастической аппроксимации 239
g(w) конечно для всех значений переменной w. Другими сло-
словами, для дисперсии
должно выполняться неравенство
a2 (w) < L F.2.3)
при всех значениях переменной w, где L < оо — положитель-
положительная константа. Это допущение исключает возможность исполь-
использования наблюдений, отличающихся от истинных значений функ-
функции g(w) столь сильно, что процедура отыскания корня ни в
коем случае не приведет к получению искомого результата.
В физическом смысле это означает, что наблюдения должны
быть зашумлены в разумных пределах..
Если слабые условия F.2.1) и F.2.2) выполняются, то
алгоритм, предложенный Роббинсом и Монро, можно применить
для итеративного определения корня w функции g(w). Обо-
Обозначив через w(\) произвольную начальную оценку корня w и
через w(k) оценку этого корня, полученную на k-u шаге итера-
итерации, процедуру коррекции оценки с помощью алгоритма Роб-
бинса — Монро выразим в виде соотношения
и- (k+l) = w (k) — akh [w (k)}, F.2.4)
где a.k — элемент последовательности положительных чисел,
удовлетворяющей следующим условиям:
lim ctft = O, F.2.5а)
оо
Z «* = <», F.2.56)
оо
Z «| < оо. F.2.5в)
Примером последовательности, удовлетворяющей этим усло-
условиям, служит гармонический ряд {1/6} = {1, '/г, 7я, •¦¦}•
Отметим, что коррекции оценок, вводимые алгоритмом
Роббинса — Монро, пропорциональны значению предыдущего
наблюдения h[w{k)\. Чтобы предотвратить введение чрезмер-
чрезмерных коррекций, предполагается, что значения функции g(w)
ограничены прямыми в областях значений переменной, больших
и меньших значения корня w, как это показано на рис. 6.2.
Выбор такой ограничивающей функции обусловлен ее просто-
простотой; ограничение при этом задается неравенством
| g И |< А | w — w | + В < оо, F.2.6)
240
Гл. 6. Статистический подход
где А—тангенс угла наклона прямых и +В — значения функ-
функции g(w) непосредственно справа и слева от корня w соответ-
соответственно. Это допущение не является столь жестким ограниче-
ограничением, как это может показаться, поскольку для доказательства
справедливости алгоритма знания значений Л и В не требуется.
Из рис. 6.2 очевидно также, что, если значение корня заключено
g(w), h(w)
Ограничивающая прямая
*-w
Рис. 6.2. Граничные условия для алгоритма Роббинса — Монро.
в некотором конечном интервале, всегда можно считать, что су-
существуют такие А я В, при которых неравенство F.2.6) вы-
выполняется.
Роббинс и Монро [1951] показали, что при выполнении
условий F.2.1), F.2.3), F.2.5) и F.2.6) алгоритм, представ-
представленный уравнением F.2.4), сходится к значению корня й> в
среднеквадратичном смысле, т. е.
lim {E [(w (k) - даJ]} = 0.
F.2.7)
Проще говоря, это означает, что по мере приближения числа
итераций к бесконечности дисперсия оценок w(k) относительно
истинного значения корня w будет стремиться к нулю.
Вскоре после появления алгоритма Роббинса — Монро Блюм
[1954а] установил еще более сильный вид сходимости, который
предусматривает при тех же условиях достижение оценкой
w(k) истинного значения корня w с вероятностью 1 при ?—><»,
т. е.
Prob{Hma>(Jfe)=d>}=l. F.2.8)
6.2 Методы стохастической аппроксимации
241
Это отношение указывает, что в пределе оценка w(k) гаран-
гарантированно равна истинному значению корня w.
Интересно отметить, что доказательства, предложенные Роб-
бинсом — Монро и Блюмом, являются частными случаями тео-
теоремы, установленной позже Дворецки [1956]. Ему удалось по-
показать, что оба критерия сходимости F.2.7) и F.2.8) выпол-
выполняются для любой процедуры стохастической аппроксимации,
удовлетворяющей условиям его теоремы. Рассмотрение условий
Рис. 6.3. Иллюстрация использования алгоритма Роббинса — Монро.
Дворецки и их связи с алгоритмом Роббинса — Монро выходит
за пределы нашего обсуждения, однако читатель, обратившись
к статье Дворецки, несомненно найдет ее интересной и инфор-
информативной.
Пример. Рассмотрим простой пример алгоритма Роббинса —
Монро. Требуется применить этот алгоритм для определения
корня функции g(w) = th(oi>), изображенной на рис. 6.3. Наблю-
Наблюдаются, однако, не истинные значения функции, а только за-
шумленные, которые обозначены через h(w). Будем считать,
что шум представлен, например, появляющимися случайным
образом значениями ±0,1, которые с равной вероятностью
наложены на функцию g(w).
Выполнение алгоритма начинается с выбора первой произ-
произвольной оценки значения корня и соответствующей последова-
последовательности {а*}- Пусть соA) = 1,0 и аи = 1/&. Допустим, что
шумовая компонента первого наблюдения равна —0,1. В таком
случае h[w{\)] = g[w(l)]~0,1 = thA) — 0,1 = 0,662. Восполь-
Воспользовавшись алгоритмом Роббинса — Монро, корректируем оценку
242 Г л в Статистический подход
корня:
w B) = -V A) - <х,А [и> A)] = 1,000 - 0,662 = 0,338.
Скорректированная оценка приведена на рис. 6.3. Если этому
новому значению соответствует шумовая компонента, равная
+0,1, то h[wB)] = g[wB)] + 0,\ =0,426. Следовательно,
w C) = wB) - a2h [w B)] = 0,338 - 0,426/2 = 0,125.
Это значение явно ближе к истинному значению корня
w = 0,0. В приведенной ниже таблице помещены значения по-
последовательных оценок вплоть до k = 50, где через x\k обозна-
обозначена шумовая компонента на k-м шаге.
k
1
2
3
4
5
10
20
30
40
50
w(h)
1,000
0,338
0,125
0.117
0,003
0,039
0,029
0,020
0,014
0,015
g[w(k)]
0,715-2
0,321!
0,125
0,117
0,0<>3
0,039
0,029
0,02E
0,014
0,015
<**
1,000
0,500
0,333
0,250
0,200
0,100
0,050
0,033
0,025
((,020
Vk
- 0,100
¦4- 0,100
- 0,100
+ 0,100
- 0,100
- 0,100
- О.100
-L 0,100
- 0,100
+ 0,100
h[w(h)]
0,662
0,426
0,025
0,217
- 0,037
- 0,001
- 0,071
0,126
- 0,086
0,115
w(h + 1)
0,338
0,125
0,117
0,063
0,070
0,045
0,033
0,022
0,016
0,013
Отметим, что в течение нескольких первых итераций оценка
быстро приближается к значению корня, а затем эта скорость
уменьшается с увеличением k. Во-первых, при увеличении k
коэффициент ам теряет корректирующую мощность, так как
ak = l/k. Во-вторых, очевидно, что шум оказывает сильное
влияние на значения функции g(w), соответствующие близким
к корню значениям переменной w. В связи с этим, обстоятель-
обстоятельством приближение к значению корня в этой области в большой
степени зависит от случайной природы шума. |
6.2.2. Скорость сходимости
Хотя в предыдущем примере алгоритм Роббинса — Монро
обеспечил достаточно быстрое приближение к значению корня,
подобная картина наблюдается не всегда. Уменьшение значений
корректирующего коэффициента а* при увеличении k приводит
к уменьшению величины коррекций в последовательных итера-
итерациях. Поскольку всякая последовательность {а*}, удовлетво-
удовлетворяющая условиям F.2.5), должна уменьшаться с ростом k,
6.2. Методы стохастической аппроксимации 243
алгоритм Роббинса — Монро, так же как и другие подобные
схемы стохастической аппроксимации, обычно обнаруживает
медленную сходимость.
Очень эффективный метод ускорения сходимости алгоритма
Роббинса — Монро состоит в сохранении постоянного значения
а* на тех шагах, где значения h[w(k)\ имеют одинаковый
знак. Этот прием основывается на том факте, что обычно изме-
изменения знака h[w(k)\ происходят в окрестности корня w.
В точках, удаленных от корня, желательны значительные кор-
коррекции, и в то же время по мере приближения к корню коррек-
коррекции должны становиться все меньше и меньше. Этот метод
для аи = 1/& проиллюстрирован в табл. 6.1.
Таблица 6.1
Иллюстрация метода ускорения сходимости для последовательности
корректирующих коэффициентов a,, =\/k
k:
Знак h[w(k)] :
Обычный кощнрициент <xk:
ak,t/CK0pmi4ui! сходимость :
1
+
1
1
2
+
1
3
+
\
1
4
—
\
\
5
—
i
+
i
7
—
7
1
I
8
+
*
i
9
-
10
i
6.2.3. Обобщение на многомерный случай
Алгоритм Роббинса — Монро допускает непосредственное
обобщение на многомерный случай. Задача принимает вид
отыскания корня функции регрессии g(w) по результатам за-
шумленных измерений h(w), где w = (w\, Wi,..., wn, wn+\)' со-
согласно принятым обозначениям. Другими словами, алгоритм
Роббинса — Монро обеспечивает в многомерном случае кор-
коррекцию оценки w(?) корня w, полученной на шаге итерации k
при начальной (произвольной) оценке w(l), с помощью соот-
соотношения
F.2.9)
где a.k — элемент последовательности положительных чисел,
удовлетворяющей условиям F.2.5). Если к тому же справед-
справедливы векторные аналоги допущений F.2.1), F.2.3) и F.2.6), то
сходимость алгоритма Роббинса — Монро в многомерном слу-
случае гарантируется как в среднеквадратичном, так и по вероят-
вероятности 1. Это означает, что при несмещенности результатов
зашумленных измерений, конечности их дисперсии относительно
функции регрессии g(w) и ограниченности самой этой функции
можно доказать сходимость алгоритма F.2.9), если последо-
последовательность корректирующих коэффициентов {а*} подчиняется
244 Гл. 6. Статистический подход
условиям F.2.5), т. е. показать, что
lim ?{||w(?)-w||2} = 0 F.2.10)
и
Prob{lim W(?) = w}=l, F.2.11)
k-?<x>
где ||w(?)— w ||2 — квадрат модуля вектора \w(k)— w).
Правила ускорения сходимости для многомерного случая
сформулировать очень трудно. Хотя для ускорения сходимости
и предполагались специфические комбинации стохастической
аппроксимации с другими известными методами оптимизации,
алгоритмы, получаемые в результате, как правило, в силу своей
сложности не оправдывали предпринятых чрезвычайных мер.
Поэтому мы сосредоточимся на алгоритме Роббинса — Монро
в его первозданном виде F.2.9). Следует иметь в виду, что
медленная сходимость этого алгоритма типична для всех алго-
алгоритмов стохастической аппроксимации.
6.3. ПОСТРОЕНИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ
ОБРАЗОВ
Этот параграф воспроизводит структуру § 5.3, в котором
описывалось построение детерминистских алгоритмов. В п. 6.3.1
метод стохастической аппроксимации вводится как общий под-
подход к построению статистических алгоритмов классификации
образов. Строится общий алгоритм, аналогичный градиентному
алгоритму, определенному уравнением E.3.3), и затем прово-
проводится сопоставление двух этих алгоритмов.
На основе полученных в п. 6.3.1 результатов в п. 6.3.2
строится статистический алгоритм, напоминающий алгоритм
перцептрона. Подобным же образом в п 6.3.3 выводится ста-
статистический алгоритм, обеспечивающий наименьшую средне-
среднеквадратичную ошибку. Как и в гл. 5, построение статистических
алгоритмов на основе развитых ниже общих методов ограни-
ограничивается исключительно возможностью задать разумные функ-
функции критерия.
6.3.1. Оценка оптимума решающих функций методами
стохастической аппроксимации
Как указывалось в § 6.1, ведущей темой данной главы яв-
является оценка на основе обучающей выборки образов плотно-
плотностей распределения р(со,|х) для получения байесовских решаю-
решающих функций di{\) = р(со/|х), /=1, 2 М. Воспользуемся
б.З. Построение алгоритмов классификации образов 245
разложением этих функций по множеству известных базисных
функций согласно формуле
d, (х) = р (со, | х) « ? ш4/фу (х) = Wj<p (х), F.3.1)
где w^ —(о>П, а»<2, ..., ш(.^, да, ^+0'— вектор весов /-го класса
образов и (р(х) = [cpi(x),cp2(x), ..., срк(х), 1]'. Это разложение
идентично использованному при определении обобщенных ре-
решающих функций (формула B.3.1)). Таким образом, на основе
представлений, развитых в § 2.3, можно без потери общности
дальнейшее обсуждение посвятить линейным аппроксимациям
вида
р(со,|х)«ту;х, F.3.2)
где vl = (wil, wi2, ..., win, Щ.п+\У и х = (*ь х2, ..., х„, 1)'.
В качестве идеальной ситуации хотелось бы наблюдать зна-
значения плотностей распределения р((о,-|х) в процессе обучения
или оценки. К сожалению, эта плотность распределения не
поддается ни наблюдениям, ни измерениям. Единственная ин-
информация, которая доступна в процессе обучения, — это при-
принадлежность каждого вектора образа определенному классу.
Для того чтобы, учитывая это обстоятельство, сформулировать
задачу в виде, пригодном для использования методов из § 6.2,
воспользуемся неким искусственным преобразованием. Опреде-
Определим для каждого класса случайную переменную классификации
г,-(х), обладающую следующим свойством:
( 1, если х е аь,
г,(х) = < . F.3.3)
' ; (,0 в противном случае. v
Значения 1 и 0 для переменной г,(х) выбраны произвольно.
Можно использовать и другие значения, но обязательно раз-
различающиеся.
Хотя в процессе обучения нельзя наблюдать значения плот-
плотностей распределения р(ю,-|х), значения переменной классифи-
классификации г<(х) при реализации этого этапа нам известны, так как
известно, какому классу принадлежит каждый образ. Следо-
Следовательно, поскольку знание плотностей распределения р(ац\х)
нам было необходимо исключительно для осуществления клас-
классификации, переменную классификации г,(х) будем считать
зашумленным результатом наблюдения значения плотности
распределения р(оо,-|х), т. е.
гг(х) = р@г|х) + т], F.3.4)
где т) — шум, математическое ожидание которого предпола-
предполагается равным нулю, и, следовательно, Е{п(х)} = Е{р(ац\х)},
246 Гл. 6 Статистический подход
Это допущение нельзя считать необоснованным, так как в про-
противном случае шум легко привести к соответствию этому усло-
условию обычной нормировкой. При другой интерпретации случайной
переменной классификации г,(х) она рассматривается в каче-
качестве аппроксимации плотности распределения р(со«|х) в том
смысле, что р[г,-(х)= 1|х] «p(o)ijx) и р[г,(х) = 0|х] »
« р(ш/|х), где символ 6э, обозначает «не класс ы,». Мы на-
намереваемся найти аппроксимацию плотности распределения
p((Oi|x) в виде w^x на основе наблюдения значений случайной
переменной классификации г,(х).
В гл. 5 использовались детерминистские функции критерия,
которые подставлялись в общее выражение градиентного алго-
алгоритма с тем, чтобы получить алгоритмы классификации. Здесь
мы пойдем по тому же пути, за исключением того, что функции
критерия — статистические, а универсальный алгоритм — алго-
алгоритм Роббинса — Монро. Прежде чем перейти к делу, рассмот-
рассмотрим функцию критерия /(w^, х) = ?'{|/\ (х) — w^xU. Минимум
этой функции равен нулю, он достигается при W;X = /\ (x). Ми-
Минимум функции критерия, другими словами, соответствует пра-
правильной классификации образа х. Последнее следует из того
факта, что значения переменной классификации г,(х) известны
на этапе обучения. Следовательно, если для всех образов обу-
обучающего множества справедливо равенство w^x = rt (x), то век-
вектор весов w,- обеспечивает правильную классификацию всех
этих образов.
V Поскольку считается, что ?{г,(х)} = ?{р(ы,|х)}, функцию
критерия можно представить также как J (w(-, х) = ?{1р((й.) х) —
— w'x|}. Это соотношение ясно указывает, что отыскание
минимума функции критерия /(w,-, x) эквивалентно средней ап-
аппроксимации плотности распределения р(со,|х). Другими сло-
словами, аппроксимация такова, что математическое ожидание
абсолютной величины разности плотности распределения и ее
аппроксимации равно нулю.
Для того чтобы определить минимум функции, надо найти
корень ее производной. В данном случае нас интересует мини-
минимум функции критерия /(w, х)— математического ожидания не-
некоторой другой функции f(w, х), т. е.
/(w, x) = ?{/(w, x)}. F.3.5)
Взяв частную производную от функции критерия /(w, х) по век-
вектору весов w, получим
•_, х) _ с I dj (w, х) 1 F36)
dw
6.3 Построение алгоритмов классификации образов 247
Воспользовавшись алгоритмом Роббинса — Монро, можно те-
теперь получить последовательность оценок корня производной
d/(w, x)/dw, положив
Использование соотношения F.2.9) дает
x) } , F.3.8)
где начальный вектор w(l) выбирается произвольно.
Интересно сравнить полученный результат с записью детер-
детерминистского градиентного алгоритма в общем виде:
E.3.3)
Эти два уравнения имеют несколько явных отличий. Они свя-
связаны с характером корректирующих коэффициентов а* и с
и с видом частных производных. Отметим, что в детермини-
детерминистском алгоритме функция критерия /(w,x) присутствует нет
посредственно. Это объясняется тем обстоятельством, что в де-
детерминистском случае функция критерия /(w, х) поддается
непосредственному наблюдению. Поскольку в статистическом
случае функцию критерия /(w,х) явно наблюдать нельзя, в ал-
алгоритме F.3.8) используется наблюдаемая реально функция
f(w, х). Другое существенное отличие определяется тем фактом,
что статистический алгоритм будет искать аппроксимацию байе-
байесовского классификатора, в то время как его детерминистский
аналог не обладает этой возможностью. Стоит также подчерк-
подчеркнуть, что статистический алгоритм сходится к аппроксимации
независимо от наличия или отсутствия строгой разделимости
классов, в то время как детерминистский алгоритм в случае
неразделимости просто зацикливается. Ценой, которую прихо-
приходится платить за гарантированную сходимость статистического
алгоритма, является, несомненно, медлительность, проявляемая
им обычно в процессе достижения этой сходимости.
Оставшуюся часть главы посвятим использованию алго-
алгоритма F.3.8) для построения алгоритмов классификации обра-
образов. Читателю рекомендуется тщательно сопоставить этот ма-
материал с соответствующим анализом в гл. 5.
6.3.2. Алгоритм корректирующих приращений
Алгоритм, подобный алгоритму перцептрона, можно по-
построить с помощью введенной в предыдущем разделе функции
критерия
/(w(, x) = ?{|r((x)-w;x|}, F.3.9)
248 Гл. 6. Статистический подход
где, как и раньше,
если х е со,-,
в противном случае.
Как указывалось выше, минимум функции критерия /(w*,x) по
w,- соответствует правильной классификации всех образов.
Следует определить частную производную функции крите-
критерия J(wi, x) по вектору весов w<:
-, (х) - w;xi}, F.3.10)
где функция sgn(-) равна +1 или —1 в зависимости от знака
ее аргумента.
Положив ^(w;) = — х sgn [r. (х) — WjX] и подставив эту
функцию в общее выражение алгоритма F.3.8), получим
w.(& + 1) = w,. (k) + akx(k) sgn {r, [x (k)] - w;(*)x(*)}, F.3.11)
где начальное значение вектора весов w,(l) выбирается произ-
произвольно. Воспользовавшись приведенным выше определением
функции sgn, уравнение F.3.11) можно представить в эквива-
эквивалентной форме
w((k)+akx(k), если wj (*) х (А)<г, [х (*)],
W| (*)-<х4х (*), если w't(k)x(k)^rt[x(k)]. F'ЗЛ2)
Интересно отметить, что этот алгоритм корректирует значение
вектора весов на каждом шаге. Указанное свойство отличает
его от алгоритма перцептрона, который осуществляет коррек-
коррекцию только в случае неправильной классификации образа. На-
Название алгоритма, представленного выражениями F.3.11) или
F.3.12), определяется тем обстоятельством, что величина кор-
коррекции пропорциональна приращению а*.
Считается, что итеративная процедура, определяемая выра-
выражениями F.3.11) или F.3.12), сошлась к точному (свободному
от ошибок) решению, если все образы обучающей выборки,
принадлежащие классу со/, i = 1, 2, ..., М, классифицированы
правильно. Более строго это означает, что w^x = rt (x), т. е.
w?x = l, если хеш., и w?x = 0b противном случае. Для пра-
правильного распознавания, однако, достаточно потребовать, чтобы
для всех образов из класса со,- выполнялось условие
dt(x)>d,(x) при всех \Ф1, F.3.13)
где dt (х) = w^x и d. (х) = w^x. Эта ситуация представляет слу-
случай 3 разделения нескольких классов, рассмотренный в § 2.2.
в.З Построение алгоритмоп классификации образов 249
Следует отметить, что алгоритм разделения нескольких классов
был построен непосредственно как таковой в отличие от ме-
метода, использованного в гл. 5, где сначала был рассмотрен слу-
случай разделения двух классов.
Когда рассматриваемые классы не поддаются точному раз-
разделению с помощью выбранной решающей функции, есть га-
гарантия, что в пределе решение сойдется в смысле минимизации
абсолютной величины его расхождения с р(со;|х) в соответ-
соответствии с функцией критерия F.3.9). Поскольку байесовские ре-
решающие функции тождественно равны этим плотностям рас-
распределения, то, следовательно, аппроксимация байесовского
классификатора по минимуму абсолютных величин гаран-
гарантирована.
При разделении двух классов вектор весов разделяющей по-
поверхности можно определить непосредственно. В этом случае
F.3.11) принимает вид
w (k + 1) = w (k) + akx (k) sgn {r [x (k)] - w' (k) x (k)}, F.3.14)
где начальный вектор весов w(l) выбирается произвольно. При
использовании уравнения F.3.14) предполагается, что w — век-
вектор весов класса ©i; поэтому r[x(k)]= 1, если образ x(k) при-
принадлежит классу со;, и r[x(k)] = 0, если образ x(k) принадле-
принадлежит классу со2. В таком случае по аналогии с F.1.4) можно
сформулировать следующее решающее правило:
если р (со, | х) = w'x > %, образ х относится к со^
если р (со, | х) = w'x < '/г. образ х относится к со2.
так как произведение w'x есть некая аппроксимация плотности
распределения р(со;|х). Алгоритм, представленный уравнением
F.3.14), легко выразить в форме F.3.12).
Из выражения для решающего правила F.3.15) следует, что
алгоритм разделения двух классов сходится к точному реше-
решению, когда w'x > 7г для всех образов класса ©i и w'x < l/2
для всех образов класса со2. Вполне оправданно в этом случае
и использование алгоритма разделения нескольких классов, что
приводит к получению двух решающих функций: g?i(x) = w'xh
d2(x) — w'2x. Как отмечалось выше, единственную решающую
функцию в этом случае можно получить в виде d(x) = di(x) —
d()
Пример. В гл. 4 для образов, представленных на рис. 6.4,
были определены байесовские решающие функции di(x) =
= р(х|со,)р((О;). Интересно при таком же задании классов вос-
воспользоваться построенным в этом разделе алгоритмом коррек-
корректирующих приращений для определения решающих функции
250
Гл. 6. Статистический подход
в форме di{x) = р(@(|х). Операция пополнения образов приво-
приводит к классам ©ь {@,0,0,1)', A,0,0,1)', A,0,1,1)', A,1,0,1)'}
и <о2: {@,0,1,1)', @,1,0,1)', @,1,1,1)', A,1,1,1)'}. Отметим,
что ни в одном из классов образы не умножались на —1, как
это делалось в гл. 5 для случая разделения двух классов.
@,1,1)
а о,1)
Рис. 6.4. Разделяющая граница, найденная с помощью алгоритма корректи-
корректирующих приращений.
Положив w(l)=0, ak=Mk и хA) = @,0,0, 1)' и восполь-
воспользовавшись алгоритмом корректирующих приращений, получим
0
На следующем шаге предъявляется образ хB) = A,0,0, 1)',
а2 = 1/2, и, так как образ хB) также принадлежит классу a>i,
имеем г[хB)]= 1. Следовательно,
w C) = w B) + а2х B) sgn {г [х B)] - w' B) х B)} =
sgn{0}:
о
о
6.3 Построение алгоритмов классификации образов
251
На следующем шаге x(,3j = A, О, 1, 1)', а3 = 1/3 и г[хC)]=1,
так что
jxC)sgn{l} =
Продолжая эту процедуру и проверяя после каждого шага ите-
итерации правильность классификации новым вектором весов всех
образов, мы обнаружим при k = 15, что алгоритм сошелся
и выдал следующий вектор весов:
1
2
0
0
1
+
1
3
0
1
3
1
3
-
1
6
0
1
3
5
6
Чтобы найти уравнение, определяющее разделяющую гра-
границу, следует учитывать, что решения принимаются на основе
правил w'x > 0,5 или w'x < 0,5. Итак, разделяющая граница
определяется уравнениями w'x = 0,5 или w'x — 0,5 = 0, что
с учетом значения вектора весов дает
0,233х, — 0,239x2 — 0,216хз + 0,119 = 0.
Эта разделяющая граница показана на рис. 6.4. |
6.3.3. Алгоритм наименьшей среднеквадратичной ошибки
Алгоритм, построенный в п. 6.3.2, аппроксимирует плотность
распределения p(w,|x) в смысле минимизации абсолютной ве-
величины расхождения. С тем же успехом для построения алго-
алгоритма обучения можно воспользоваться аппроксимацией по
критерию наименьшей среднеквадратичной ошибки (НСКО).
Рассмотрим функцию критерия
F.3.16)
Эта функция также, как и требуется, достигает минимума при
правильной классификации всех образов.
252 Гл. б Статистический подход
Взяв частную производную функции критерия J по вектору
весов W;, получим
Д- = ?{-х[/-г(х)-1<х]}, F.3.17)
Положив ft(w,) = — х[гг(х) — w^x] и подставив эту функцию
в общее выражение F.3.8) для алгоритма, получим
w, (k + 1) = w, (k) + aAx (k) {rt [x (k)] - w; (k) x Щ, F.3.18)
где начальное значение весового вектора w«(l) выбирается
произвольным образом, a r,[x(fe)] равно 1 или 0 в зависимости
от того, входит образ x(k) в класс со; или нет. Отметим, что этот
алгоритм также на каждом шаге итерации корректирует значе-
значения вектора весов W;, но величины этих коррекций отличаются
от коррекций, вводимых алгоритмом из п. 6.3.2, множителями
г {[х (&)] — W; (k) х (k)j. НСКО-алгоритм сходится к решению,
минимизирующему функцию критерия F.3.16), при выполнении
следующих условий (Блейдон [1967]):
1) элементы последовательности а*, удовлетворяют усло-
условиям F.2.5);
2) математические ожидания ?{хх'} и ?{(хх'J} существуют
и положительно определены;
3) математические ожидания ?{хр(ю,-|х)} и ?{xx'xp(w<|x)}
существуют.
При разделении двух классов уравнение F.3.18) принимает вид
F.3.19)
где начальное значение вектора весов w(l) произвольно. Сле-
Следует иметь в виду, что формулировка алгоритма предполагает,
что решения принимаются на основе правила w'x > У2 и
w'x < V2» сформулированного в F.3.15).
Пример. Решим тот же пример из п. 6.3.2, воспользовавшись
НСКО-алгоритмом. Пополненные образы образуют классы ац:
{@,0,0,1/, A,0,0,1)', A,0,1,1)', A,1,0,1)'} и со2: {@,0,1,1)',
@,1,0,1)', @,1,1,1)', A,1,1,1)'}.
Положим w(l) = 0, а/, = l/k и хA) = @,0,0, 1)' и применим
алгоритм F.3.19); получим
6.3. Построение алгоритмов классификации образов
253
На следующем шаге х B) = A,0, О, 1)', а2=1/2 и г[хB)]=1.
Поэтому
А *СА (:
wC)=wB)+a2xB)[l-w'B)xB)]=| Q +11 Q =1 Q
Легко убедиться в том, что wE) = wD) = wC). На следую-
следующем шаге хE) = @,0,1, 1)', as =1/5 и г[хE)] = 0, поскольку
@,W
40,1)
A,1,0)
• «UJ,
о ьиг
Рис. 6.5. Разделяющая граница, найденная с помощью метода наименьшей
среднеквадратичной ошибки.
образ хE) принадлежит классу ац; так что
0
wF)=wE)+a5xE)[0-w' E)xE)]=
о
о
Продолжая эту процедуру и проверяя после каждого шага
итерации правильность классификации всех образов с помощью
254 Г л 6. Статистический подход
нового вектора весов, мы обнаруживаем, что НСКО-алгоритм
сходится при k = 19, определив вектор весов
0,135
- 0,238
-0,305
0,721
Как и в предыдущем примере, разделяющая граница опреде-
определяется уравнением w'x — 0,5 = 0, т. е.
0,135*t — 0,238x2 — 0,305*;, + 0,221 = 0.
Образы, использованные в этом примере, и соответствующие
разделяющие поверхности приведены на рис. 6.5. Щ
6.4. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
Подход, основанный на использовании потенциальных функ-
функций, был введен в § 5.6. При этом предполагалось, что образы,
принадлежащие разным классам, образуют в обучающей вы-
выборке непересекающиеся множества. Результаты наблюдений
могут относиться к любому из классов со, и ш/, но не к обоим
классам одновременно. Исходя из этого допущения, можно по-
построить границы, разделяющие отдельные классы. Основная
проблема, возникающая при классификации образов, заклю-
заключается в построении разделяющих границ на основе информа-
информации о выборочных образах, принадлежащих определенному
классу.
Во многих практических случаях указанное допущение ока-
оказывается неправомерным. Соответствующие примеры имеются
в избытке. В системе радиолокационного обнаружения образ,
наблюдаемый на экране индикатора радиолокационной стан-
станции, может соответствовать как наличию, так и отсутствию
объекта поиска. В медицине при постановке диагноза имею-
имеющиеся клинические данные обычно не позволяют однозначно
распознать заболевание. В связи с наличием шума и неполно-
неполнотой информации, содержащейся в полученных при помощи из-
измерений векторах образов, результаты наблюдений, сделанные
в одни моменты времени, могут быть отнесены к классу иц,
а в другие — к классу й,-, где й,-обозначает совокупность обра-
образов, не принадлежащих классу со,-. Другими словами, выбороч-
выборочные образы, относящиеся к. различным классам, не образуют
непересекающихся множеств. Следовательно, нельзя построить
границы, гарантирующие полное разделение классов. Для каж-
каждого наблюдаемого образа можно определить лишь вероятность
в 4 Метод потенциальных функций 255
зачисления его в класс со, или со,-. Это те вероятности, с кото-
которыми образы порождаются классами со, и со*. Задача вероятно-
вероятностной классификации образов заключается в обучении машины
правильно определять вероятность того, что новые образы при-
принадлежат некоторому классу, на основе отдельных наблюде-
наблюдений, выполненных в процессе обучения, причем связь выбороч-
выборочных образов с соответствующими классами задается априори.
В вероятностном случае классификация новых образов про-
проводится с помощью набора условных вероятностей р(со;|х),
i = 1, 2, ..., М, исполняющих, в сущности, роль распознающих
функций. Если для всех \ф[ выполняется условие р(со,|х)>
>р(со/|х), то новый образ х зачисляется в класс со*. Оценить
распознающую функцию р(со«|х) можно итеративно, применив
метод потенциальных функций к обучающей выборке. Пусть
распознающая функция р(со,|х) аппроксимируется функцией
ffc(x). Эта функция, значения которой лежат в диапазоне между
нулем и единицей, определяется следующим образом:
О, если — оо <fft(x)< О,
f*(x), если 0<f*(x)<l, F.4.1)
О, если 1 < fk (x) < оо,
где функцию fk (x) можно представить в виде
х). F.4.2)
Функции ф/(х), входящие в это разложение, заданы, a Cj(k) —
неизвестные коэффициенты. Напомним выражение E.6.24),
определяющее потенциальную функцию для точки, представ-
представляющей произвольный образ х*:
К(х, ха)=1л2Ф/(х)Ф/(х,). F.4.3)
Рекуррентный алгоритм, предназначенный для определения
аппроксимирующей функции /*(х), можно сформулировать сле-
следующим образом. В качестве начального значения аппроксими-
аппроксимирующей функции принимается /0(х)=0, затем системе предъ-
предъявляется выборочный образ Xj, причем потенциальная функция
для образа xi равна К(х,х\). Здесь могут возникнуть три
ситуации.
1. Если либо XiSco; и /0(xi)>0, либо х^ш,- и /o(xi)<O,
то fi(x) = fo(x). Другими словами, если система классифици-
классифицирует образ xi правильно, то аппроксимирующая функция /о(х)'
не изменяется.
256 Гл. 6. Статистический подход
2. Если x(ec0i и fo(xi)<O, то f\{x) = fo(x) + y{K(x,xx).
Другими словами, если система неправильно классифицирует
образ xj, принадлежащий, как известно, классу сог, то аппрок-
аппроксимирующая функция fi(x) равна функции fo(x), увеличенной
на Yi^(x,xi).
3. Если х\фин и fo(xi)>O, то fi(x) = fo(x) — y\K(x,xi).
Другими словами, если система неправильно классифицирует
образ xi, который, как известно, не принадлежит классу со,, то
аппроксимирующая функция f\(x) равна fo(x), уменьшенной
на величину yi/C(x, xt).
Множитель yi представляет собой корректирующий коэффи-
коэффициент; его свойства будут рассмотрены ниже.
Когда предъявляется второй выборочный образ x2, соответ-
соответствующая потенциальная функция равна К{х, х2). Если либо
х2ео>,- и f 1 (х2) > 0, либо х2^соЛ и f 1 (х2) < 0, то f2 (х) = f 1 (х).
Если х2есо(- и f i (х2) < 0, то f2 (x) = f t (x) -f \2K (x, х2). Если
X2^(Oj И fl(x2)>0, ТО ^2(x) = fj(x)— \2К(Х, Х2).
После предъявления системе выборочного образа xk+{ потен-
потенциальная функция для образа хк+1 равна К (х, хк+1). Если
либо хк+1фщ и f*(xft+,)>0, либо xk+l<?e>i и fft(xft+,)<0, то
fft+i(x) = fft(x). F.4.4)
Если xk+i <= со,- и ffe (xft+1) < 0, то
fk+\(x) = fk(x) + 4k+iK(x, xk+l). F.4.5)
ЕСЛИ ХА+1^@; И fft(xft+1)>0, ТО
/ k+i (х) = f к (х) — ya+i^\ (х, Х?+1). F.4.6)
Коэффициенты y*> fe = l,2 образуют последовательность
положительных чисел, удовлетворяющую условиям
lim Yft = 0, F.4.7)
oo
Iyj=~ F.4.8)
Z Y| < «>. F.4.9)
Гармонический ряд {1/&} = {1, '/г. '/з, • • •} удовлетворяет этим
условиям и может быть использован для задания значений ко-
коэффициентов yk-
Поскольку построение аппроксимирующей функции />(х)
связано с использованием образов обучающей выборки х^, ко-
6.4. Метод потенциальных функций 257
торые появляются случайным образом и, следовательно, при-
принадлежность предъявляемого образа классу со* или любому
другому из рассматриваемых классов — также случайная вели-
величина, значит аппроксимирующая функция fk(x) является слу-
случайной функцией. Аппроксимирующая функция ft(x) в диапа-
диапазоне от нуля до единицы при увеличении k сходится к распо-
распознающей функции р(ю,|х). Можно показать, что описанный
алгоритм обеспечивает сходимость аппроксимирующей функ-
функции f(x), определенной соотношением F.4.1), к распознающей
функции р(сО(|х) в среднем, т. е.
lira \i[fk(x)-p(ayi\x)]2p(x)dx = 0. F.4.10)
Рассмотренный вариант алгоритма предполагает запомина-
запоминание значений функции fk+\(x), k=l, 2, ..., во всей области X.
Это затруднение можно обойти, воспользовавшись кумулятив-
кумулятивным потенциалом. Из F.4.5) и F.4.6) с помощью итеративной
процедуры получаем
fft+i (х) = ? уаК(х,ха) — ? уьК(х,х.ь), F.4.11)
где наблюдаемые выборочные образы принадлежат обучающей
последовательности, корректирующей ошибки. Следовательно,
в памяти системы достаточно хранить всего лишь две последо-
последовательности чисел. Ими являются обучающая последователь-
последовательность корректирующих ошибки образов хь Хг, ..., Xk+i и после-
последовательность соответствующих коэффициентов у(, уг, •••, Y*+i-
При предъявлении нового образа х* система вычисляет функцию
fb+\(x*) по формуле F.4.11), что позволяет получить оценку
распознающей функции р(со«|х*). Распознающие функции для
других классов можно определить аналогично.
Другой вариант алгоритма можно построить, воспользовав-
воспользовавшись F.4.2) и F.4.3). Из соотношений F.4.5), F.4.6) и F.4.3)
следует, что
m
ffc+i W = f* (*) ± Yft+1 ? Щ (x*+l) Ф, (x). F.4.12)
Подстановка выражения F.4.2) в уравнение F.4.12) дает
jn m
(х) = ? [С/ (fe) ± ушЩ (xft+I)] Ф/ (х). F.4.13)
Следовательно, при правильной классификации системой выбо-
выборочного образа Х/г+\
c,{k+l) = c,{k). F.4.14)
258 Гл. б Статистический подход
Если система неправильно классифицирует выборочный образ
Xfc-н, то при xft+1e@; имеем
с, (k+l) = с, (k) + ушЩ (хш), F.4.15)
а при xfe+I^@(
xk+l). F.4.16)
При реализации этого алгоритма нет необходимости запоми-
запоминать образы X/, /= 1, 2, ..., входящие в обучающую выборку.
На /-М шаге итерации система запоминает последовательность
C\(i), сг(/), ..., cm{i) ¦ На (г-)-1)-м шаге итерации система
определяет коэффициенты с помощью приведенного выше алго-
алгоритма c,(i + 1), / = 1, 2, ..., т. После этого значения коэффи-
коэффициентов Cj(i-\-\) занимают в памяти место коэффициентов
c,-(i). По окончании этапа обучения по формулам F.4.1)
и F.4.2) определяются оценки распознающих функций р(со,|х)
для всех классов.
6.5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В настоящей главе были изложены основные концепции,
позволяющие применять для классификации образов статисти-
статистические алгоритмы обучения. Как и в гл. 5, исходя из общей
итеративной схемы при соответствующем задании различных
функций критерия было выведено несколько алгоритмов. Кроме
рассмотренных здесь, нетрудно построить и ряд других алго-
алгоритмов. Приведенные алгоритмы, однако, дают представление
о диапазоне возможных схем.
Качество решающих функций, полученных статистическими
методами, что справедливо и при использовании детерминист-
ских подходов, в принципе существенно зависит от сложности
функций, выбранных для аппроксимации соответствующих ре-
решающих функций. В отличие, однако, от своих детерминистских
аналогов статистические алгоритмы этой главы сходятся в пре-
пределе к некоторой аппроксимации байесовского классификатора.
Следует в то же время отметить, что медленная сходимость,
свойственная статистическим классификаторам, в общем пере-
перевешивает их потенциальную способность обеспечивать опти-
оптимальное качество. Поэтому алгоритмы, построенные в гл. 5,
вполне могут конкурировать со схемами классификации, рас-
рассматривавшимися здесь.
Материал этой главы завершает изучение классификации
образов с помощью решающих функций. Мы начали его с кон-
концепций классификации по минимуму расстояния, использующей
функции правдоподобия, и довели до алгоритмов обучения,
рассмотренных в данной и предыдущей главах. Интересно еще
Задачи 259
раз сопоставить разнообразие подходов, заключенных в этих
методах. Если просмотреть гл. 3—5, то можно заметить, что
методы, изложенные в гл. 3 и 4, не базируются на итеративных
схемах обучения, которые были введены в гл. 5 и данной. Оче-
нидно также, что методы, рассмотренные в этих главах, вполне
определенно опирались либо на детерминистские, либо на ве-
вероятностные концепции. Эффективность определенного метода
существенно зависит как от исходных данных, так и от постав-
поставленной цели. Тем не менее рассмотренные методы классифика-
классификации образов представляют собой разнообразный и мощный
набор средств для решения широкого круга практических за-
задач. В следующей главе мы займемся изучением методов вы-
выбора и выделения признаков. Как мы увидим, эти методы чрез-
чрезвычайно полезны для организации этапов предварительной
обработки данных системами распознавания образов.
Библиография
Метод стохастической аппроксимации, рассмотренный в § 6.2, предложен
Роббинсом и Монро [1951]. Алгоритм Роббинса — Монро был обобщен на
многомерный случай Блюмом [19546]. Свойства сходимости алгоритма стоха-
стохастической аппроксимации в общем виде были изучены Дворецки [1956]. Мо-
Монография Уайлда [1964] содержит очень доступное введение в методы стоха-
стохастической аппроксимации.
Истоки применения методов стохастической аппроксимации в распозна-
распознавании образов относятся к началу 60-х годов. Интересно, что очень много
ранних работ в этой области посвящено методам потенциальных функций и
стохастической аппроксимации. Серия статей Айзермана, Бравермана и Розо-
ноэра [1964а, 19646, 1965] описывает метод потенциальных функций и стоха-
стохастическую аппроксимацию; там же содержится большая часть фундаменталь-
фундаментальных теоретических результатов, связанных с приложением этих методов в
распознавании образов. Кроме того, результаты, относящиеся к этой теме,
имеются в статьях Бравермана [1965], отчете Блейдона [1967], статье Хо и
Лгравалы [1968]. а также в монографиях Фу [1971], Ту [1969а], Фукунаги
[1972], Патрика [1972], Майзела [1972] и Дуды и Харта [19761.
Задачи
6.1. Используйте алгоритм Роббинса—Монро для определения корня функ-
функции регрессии
. . Aw
выбрав в качестве начального значения а>A) = 1 и положив а* = \/k.
Для того чтобы промоделировать ошибку эксперимента, подбрасывайте
на каждом шаге итерации монету и считайте, что
h[w(k)]=g[w (k)] + r\k.
где
{О, 1. если выпадает „герб",
— 0, 1, если выпадает „решетка".
Выполняйте алгоритм вплоть до k = 10.
260 Гл. 6 Статистический подход
6.2. Повторите решение задачи 6.1 с последовательностью, обеспечивающей
ускорение сходимости (описанной в § 6.2), и сопоставьте результаты.
6.3. Позволит ли алгоритм Роббинса — Монро отыскать корень функции
g(w)=wa + w при h[w(k)]= g[w(k)]+ r\k, где Т|* определено в за-
задаче 6.1, и произвольном начальном значении о>A)? Приведите необхо-
необходимые пояснения.
6.4. Задайте разумную функцию критерия и воспользуйтесь методами § 6.3
для построения алгоритма классификации образов. Учтите, что функция
критерия должна иметь один минимум, который должен соответствовать
правильной классификации всех образов.
6.5. Используйте алгоритм из задачи 6.4 для разделения классов coi: {@,0)',
A,0H и ю,: {@,1)', A,1H-
6.6. Используйте алгоритм корректирующих приращений для разделения клас-
классов из задачи 6.5.
6.7. Используйте НСКО-алгоритм для разделения классов из задачи 6.5.
6.8. Выберите подходящую потенциальную функцию (см. п. 5.6.2) и приме-
примените алгоритм метода потенциальных функций для разделения классов
из задачи 6.5.
6.9. Решите задачу 6.8 для классов cot: {@,0)', B,0)'} и ш2. {A—1)',
A, 1H- Обратите внимание на то, что эти классы линейно не разде-
разделимы.
Глава 7
ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ОБРАЗОВ
И ВЫБОР ПРИЗНАКОВ
7.1. ВВЕДЕНИЕ
До сих пор мы изучали различные методы классификации
образов. Однако прежде чем приступать к синтезу искомой си-
системы распознавания образов, необходимо решить задачи вы-
выделения признаков и сжатия данных. Хотя этими задачами
следует заниматься до начала синтеза классификатора, наш
опыт свидетельствует о том, что материал лучше восприни-
воспринимается и должным образом оценивается при изложении этих
двух тем в обратной последовательности, как и сделано в на-
нашей книге.
Любой объект или образ, подлежащий распознаванию
и классификации, обладает рядом различительных качеств или
признаков. Первым шагом всякого процесса распознавания,
реализуется он вычислительной машиной или человеком, яв-
является анализ задачи выбора различительных признаков
и определения способа их выделения (измерения). Очевидно,
что количество признаков, необходимое для успешного решения
некоторой задачи распознавания, зависит от разделяющих ка-
качеств выбранных признаков. Задача выбора признаков услож-
усложняется обычно тем обстоятельством, что наиболее важные при-
признаки не всегда легко измерить либо, как оказывается во
многих случаях, соответствующие возможности измерения сдер-
сдерживаются экономическими факторами.
Обратимся, в частности, к задаче распознавания рукопис-
рукописных символов, обсуждавшейся в гл. 1. Самыми важными раз-
различительными признаками в этом случае являются последова-
последовательность, в которой отдельные штрихи следуют друг за
другом, ориентация штрихов, комплексы, образованные соеди-
соединением отдельных штрихов, и отношения между отдельными
штрихами, которые обычно не легко измерить с помощью обыч-
обычных измерительных устройств. С другой стороны, посредством
сканирующего устройства легко преобразовать символ в мат-
матрицу из нулей и единиц или эквивалентный п-мерный вектор
измерений. Результаты измерения, однако, не обязательно со-
содержат много «различительной» информации. Подобные дан-
данные, полученные в результате измерений, могут даже привести
262 Г л 7 Предварительная обработка образов
к усложнению схемы соответствующей классификации из-за
того, что они не несут достаточного количества различительной
информации. При возникновении такой ситуации, мы, есте-
естественно, стараемся выделить из векторов измерений более су-
существенные признаки с тем, чтобы создать более эффективную
и точную систему классификации образов. Эту процедуру часто
называют предварительной обработкой с целью выделения при-
признаков.
В качестве второго примера рассмотрим задачу разведки
нефтяных месторождений, которую можно трактовать как за-
задачу распознавания с двумя классами. В этом случае тре-
требуется определить, имеется в определенной географической зоне
представляющее интерес количество нефти или нет. Очевидно,
можно попытаться отнести соответствующую зону к одному из
этих двух классов, буря в ней одну за другой нефтяные сква-
скважины до тех пор, пока не будет обнаружена нефть, либо число
«сухих» или «почти сухих» скважин не достигнет величины,
позволяющей считать эту зону с практической точки зрения
действительно лишенной нефти. Такие измерения при решении
задачи и дадут значения наиболее существенных признаков.
Как, однако, подтвердит любой нефтяник, при использовании
такого способа фирме пришлось бы не долго ждать своего бан-
банкротства. Из-за высокой стоимости бурения ученые и инжене-
инженеры-нефтяники вынуждены довольствоваться признаками, кото-
которые хотя и менее информативны, зато обходятся дешевле. Эти
признаки обычно имеют вид сейсмических характеристик, опре-
определенных по длинным отраженным волнам, которые обра-
образуются, например, при взрыве динамита, направленном в глубь
поверхности земли, в нескольких точках исследуемой зоны.
В результате строится локальная карта земной коры, на основе
которой зона может классифицироваться как обладающая или
не обладающая в принципе возможностью иметь нефть. Итак,
вынужденный компромисс при выборе признаков приводит
в этой задаче к процессу классификации, который существенно
отличается от оптимального. К сожалению, такое ограничение,
вызванное компромиссом между набором признаков и каче-
качеством классификации, присутствует в большинстве практиче-
практических задач распознавания образов.
Из сказанного очевидно, что выбор и выделение признаков
играют в распознавании образов центральную роль. Действи-
Действительно, выбор адекватного множества признаков, учитывающий
трудности, которые связаны с реализацией процессов выделения
или выбора признаков, и обеспечивающий в то же время необ-
необходимое качество классификации, представляет собой одну из
наиболее трудных задач построения распознающих систем. Для
того чтобы облегчить анализ этой задачи, разделим признаки
7.1. Введение 263
на три категории: 1) «физические», 2) структурные и 3) мате-
математические.
Физические и структурные признаки обычно используются
людьми при распознавании образов, поскольку такие признаки
легко обнаружить на ощупь, визуально и с помощью других
органов чувств. Отличая апельсины от бананов, мы обычно
пользуемся такими признаками, как цвет и форма. При разли-
различении лимонов и бананов цвет, однако, перестает быть эффек-
эффективным признаком. При отделении флоридских апельсинов от
калифорнийских ни цвет, ни форма уже не являются полезными
признаками; вместо них следует использовать другие признаки,
например аромат и структуру кожуры. Цвет и аромат служат
примерами физических признаков. Форма, структура и другие
геометрические свойства образов считаются структурными при-
признаками. Хотя структурные признаки также можно было бы
отнести к физическим, читатель должен учитывать, что разде-
разделение признаков на отдельные группы введено нами исключи-
исключительно для удобства и группы эти выбраны в определенном
смысле произвольно.
Поскольку органы чувств обучены распознаванию физиче-
физических и структурных признаков, человек, естественно, пользуется
в основном такими признаками при классификации и распозна-
распознавании. В случае же построения вычислительной системы распо-
распознавания образов эффективность таких признаков с точки зре-
зрения организации процесса распознавания может существенно
снижаться, так как, вообще говоря, в большинстве практиче-
практических ситуаций довольно сложно имитировать возможности ор-
органов чувств человека. С другой стороны, можно создать си-
систему, обеспечивающую выделение математических признаков
образов, что может оказаться затруднительным для человека
при отсутствии «механической» помощи. Примерами признаков
этого типа являются статистические средние, коэффициенты
корреляции, характеристические числа и собственные векторы
ковариационных матриц и прочие инвариантные свойства
объектов.
При автоматическом распознавании образов физические
и структурные признаки используются в основном в области
обработки изображений. Эти признаки являются сугубо проб-
проблемно-ориентированными в том смысле, что их использование
связано с созданием специализированных алгоритмов, предна-
предназначенных для решения поставленной конкретной задачи. Если,
например, требуется оценить урожай с помощью аэрофото-
аэрофотосъемки, то использование физических признаков (скажем, цвета)
будет вполне оправданно. С другой стороны, идентификация
таких объектов, как грузовые автомобили, здания и автострады,
Уй4 Гл. 7. Предварительная обработка образов
должна основываться на анализе структурных признаков. Сле-
Следует иметь в виду одно важное положение, которое состоит
в том, что практически невозможно сформулировать общие
принципы выбора физических и структурных признаков.
В этой книге мы будем иметь дело только со структурными
и математическими признаками. Структурные признаки играют
важную роль в проблемах, которые рассматриваются в следую-
следующей главе. В данной главе наше внимание сосредоточено на
методах выбора и выделения математических признаков по об-
образам обучающей выборки. Эти признаки обладают двумя
принципиальными преимуществами перед структурными: 1) они
более общие по своей природе и 2) они легко поддаются ма-
машинной реализации.
В математическом подходе к предварительной обработке
и сжатию данных задача выделения признаков занимает цент-
центральное место. Будет показано, что эта задача заключается
в определении ряда инвариантных свойств рассматриваемых
классов. Затем эти свойства используются, например, для по-
понижения размерности векторов образов при помощи линейного
преобразования. После установления набора этих свойств про-
процесс выделения признаков сводится к непосредственному выде-
выделению таких свойств у заданных образов. В последующих раз-
разделах вводится множество процедур, связанных с выбором
и выделением математических признаков. Хотя большая часть
этих методов пригодна для решения широкого класса задач,
важно иметь в виду, что приоритет любой процедуры полностью
определяется конкретной задачей.
Предварительная обработка образов обычно включает ре-
решение двух основных задач: преобразование кластеризации
и выбор признаков. Основной задачей распознавания образов
является построение решающих функций, исходя из конечных
множеств заданных образов, представляющих некоторые
классы. Эти функции должны обеспечивать разделение про-
пространства измерений на области, каждая из которых содержит
точки, представляющие образы только одного из рассматри-
рассматриваемых классов. Данное положение приводит к идее преобра-
преобразования кластеризации, реализуемого в пространстве измере-
измерений, для того чтобы обеспечить группировку точек, представ-
представляющих выборочные образы одного класса. В результате такого
преобразования максимизируются расстояния между множе-
множествами и минимизируются внутримножественные расстояния.
Расстояния между множествами определяются как среднеквад-
среднеквадратичное расстояние между точками, представляющими образы
двух различных классов. Внутримножественное расстояние —
это среднеквадратичное расстояние между точками, представ-
представляющими образы одного класса.
7.2 Расстояния 265
Выбор наиболее эффективных признаков позволяет снизить
размерность вектора измерений. Выбор признаков можно осу-
осуществлять вне связи с качеством схемы классификации. Опти-
Оптимальный выбор признаков при этом определяется максимиза-
максимизацией или минимизацией некоторой функции критерия. Такой
подход можно считать выбором признаков без учета ограни-
ограничений. Другой подход связывает выбор признаков с качеством
классификации: эффективность выбранных признаков непо-
непосредственно связана с качеством классифицирующей системы,
причем обычно эта связь выражается в терминах вероятности
правильного распознавания. Если распределение признаков из-
известно для всех классов, то можно использовать понятия ди-
дивергенции и энтропии при осуществлении выбора признаков.
Если распределения признаков для каждого класса неизвестны,
можно воспользоваться непараметрическими методами выбора
признаков, основанными на прямой оценке вероятности ошибки.
7.2. РАССТОЯНИЯ
Расстояния играют фундаментальную роль при обработке
информации, заключенной в образе. Данный параграф посвя-
посвящен обсуждению расстояний, используемых при предваритель-
предварительной обработке и выделении признаков. Рассмотрение начи-
начинается с расстояний, разделяющих отдельные точки, а затем
путем обобщения соответствующих понятий вводятся расстоя-
расстояния между точкой и множеством и расстояния между мно-
множествами.
(а) Расстояние между точками
В n-мерном евклидовом пространстве расстояние между
двумя точками а и b определяется как
D(a, b) = ||a-b[| = V(a-b)'(a-b) = Л/t (ak-bkf,
G.2.1)
где а и b суть п-мериые векторы, k-e компоненты которых равны
пк и bk соответственно.
(б) Расстояние между точкой и множеством
Расстояние между точкой, соответствующей образу х, и мно-
множеством точек, соответствующих образам {а'}, представляю-
представляющих класс К образов, определяется как среднеквадратичное
расстояние между х и К элементами множества {а'}. Квадрат
266 Гл. 7 Предварительная обработка образов
расстояния между точками х и а' равен
D2 (х, а') = (х - а')' (х - а') = ? (xk - a[)\ G.2.2)
В таком случае среднеквадратичное расстояние определяется
как
г=1 k=\
(в) Внутримножественное расстояние
Расстояние внутри множества точек, соответствующих об-
образам {a1, i = 1,2,..., К], определяется как
D2({a'}, {аг}), i, /=1,2, .... К - U i ф \. G.2.4)
Из G.2.2) имеем
П
?>2(а>, a<)=Z (ai-а'Л2. G.2.5)
Частное среднее для фиксированной точки а' и точек а', соот-
соответствующих всем К—1 оставшимся точкам множества {а1},
определяется по формуле G.2.3) подстановкой вместо х точки а1.
Следовательно,
К п
, {а'}) = -^ X ? К - 4J. G.2.6)
Отметим, что при i = / соответствующее слагаемое равно нулю
и его можно безболезненно исключить. Выражение содержит
К членов, однако только К— 1 из них отличны от нуля.
Аналогично определяем среднее по всем Л" точкам множе-
множества {а7}, что позволяет представить внутримножественное рас-
расстояние как
D2
, {а'}) = ^ t f ^ t t К - <f] =
/=i j«.i k=\
Внутримножественное расстояние можно выразить также че-
через дисперсии значений компонент точек, представляющих об-
7.2 Расстояния 267
разы. После перегруппировки членов выражение G.2.7) при-
примет вид:
/-U-I / = l i = l J
Последний шаг следует из того факта, что (#?J = (aJ02. ПО"
скольку мы имеем дело с одним и тем же выборочным множе-
множеством. Отметим также, что
Так как
есть смещенная выборочная дисперсия k-й компоненты для
К точек множества {а'}, то внутримножествениое расстояние
определяется выражением
Поскольку смещенная дисперсия определяется выражением
а несмещенная дисперсия — выражением
то из этих двух соотношении получаем
/_ V2 К
G.2.13)
268 Гл. 7. Предварительная обработка образов
Следовательно, используя несмещенную оценку выборочной
дисперсии, получаем выражение для внутримножественного
расстояния
^ G.2.14)
Это расстояние будет использоваться в следующих разделах
при изучении преобразования кластеризации и упорядочения
признаков.
(г) Расстояние между множествами
Расстояние между множествами {а'} и {Ь1}, состоящих из
Ка и Кь выборочных образов соответственно, определяется как
?>2({а'}, {Ь'}), /=1, 2, .... Ка, } = \, 2, ..-, Кь- G.2.15)
Это выражение, однако, не так уж легко свести к простому
замкнутому виду, используя статистические характеристики.
Другой способ измерения расстояний между множествами свя-
связан с использованием расстояния между центроидами двух
рассматриваемых множеств или расстояния Махаланобнса,
о котором шла речь в гл. 4.
7.3. ПРЕОБРАЗОВАНИЯ КЛАСТЕРИЗАЦИИ
И УПОРЯДОЧЕНИЕ ПРИЗНАКОВ
Не все измерения характеристик образа, соответствующие
отдельным координатным осям Xk, в равной степени важны для
определения класса, которому принадлежат сходные образы.
При сопоставлении двух образов последовательным сравнением
признаков измерениям с меньшей значимостью следует припи-
приписать меньшие веса. Назначение весов признаков можно осуще-
осуществить посредством линейного преобразования, которое обеспе-
обеспечит более благоприятную группировку точек, представляющих
образы, в новом пространстве.
Рассмотрим векторы образов а и Ь, которые после примене-
применения к ним преобразования W перешли в векторы а* и Ь*. В та-
таком случае
* W и b* =
где
f w12
причем элементы wkl суть весовые коэффициенты.
7.3. Преобразования кластеризации 269
Итак,
а
dk — b'k=Yj ww (aj — bt).
Каждый элемент преобразованного вектора образа пред-
представляет собой линейную комбинацию элементов исходного
вектора образа. В новом пространстве евклидово расстояние
между векторами а* и Ь* определяется как
D (а*, V) = aJ^ (al - Kf = aJ ^ [t wki (a, - b,)]- G.3.1)
В тех случаях, когда линейное преобразование сводится
к изменению масштабных коэффициентов координатных осей,
матрица W является диагональной, т. е. ее ненулевые элементы
расположены только на главной диагонали. В таком случае
выражение для евклидова расстояния сводится к
G.3.2)
где элементы Wkk представляют весовые коэффициенты при
признаках. Задача преобразования кластеризации заключается
в том, чтобы определить весовые коэффициенты признаков wnk,
минимизирующие расстояние между {a', i = 1,2, ...,/С} и {а',
/ = 1, 2,..., К} с учетом определенных ограничений, наложен-
наложенных на коэффициенты Wkk-
Из материала предыдущего параграфа следует, что в новом
пространстве внутреннее расстояние для множества точек,
представляющих образы, определяется как
&= 2 t («ttOtf, G-3.3)
где cr| — несмещенная оценка выборочной дисперсии компо-
компонент, соответствующих координатной оси хн. При осуществле-
осуществлении процедуры минимизации будем рассматривать два случая.
п
Случай 1. Ограничение ? wkk—l.
Минимизация D2 при таком ограничении эквивалентна мини-
минимизации величины
5, = 2
- р, (t Wkk ~ 0 • G-3-4)
270 Гл. 7. /7редварительная обработка образов
Возьмем частную производную от G.3.4) но весовому коэффи-
коэффициенту Wkk и приравняем ее нулю. После проведения соответ-
соответствующих упрощений получим
= ТТ G35)
где р! — множитель Лагранжа, определяемый выражением
G-3.6)
ч2
Итак, весовой коэффициент признака равен
^ . G.3.7)
Из G.3.5) заключаем, что значения коэффициента ш>^ малы,
если дисперсия а\ велика. Это означает, что при измерении
расстояния малые веса следует приписывать признакам, кото-
которым свойственна значительная изменчивость. Если же, с другой
стороны, дисперсия а\ мала, то соответствующему признаку
должен быть приписан существенный вес.
В данном случае преобразование кластеризации было осу-
осуществлено посредством «взвешивания» признаков. Интуитивно
понятно, что малая дисперсия ai определяет большую надеж-
надежность &-го измерения, а большая дисперсия а\ меньшую на-
надежность й-го измерения. Результатам более надежных измере-
измерений присваиваются большие веса.
Случай 2. Ограничение JJ.wkk=
=l.
Минимизация D2 при таком ограничении эквивалентна ми-
минимизации выражения
П
Взяв частную производную от G.3.8) по весовому коэффи-
коэффициенту Wkk и приравняв ее нулю, получим
где р2 — множитель Лагранжа, определяемый выражением
, G.3.10)
7.3. Преобразования кластеризации 271
Таким образом, весовой коэффициент признака определяется
выражением
значение этого коэффициента обратно пропорционально средне-
среднеквадратичному отклонению &-го измерения.
Формулы G.3.7) и G.3.11) определяют матрицу преобразо-
преобразования W с учетом введенных выше ограничений. Если векторы
образов переводятся из пространства X в пространство X* с по-
помощью преобразования
x* = Wx, G.3.12)
то внутреннее расстояние множества в пространстве X* мини-
минимизируется. Теперь требуется провести второе преобразование
х** = Ах*
для того, чтобы выделить компоненты, имеющие малую (или
большую) дисперсию, обеспечив таким образом возможность
провести упорядочение и выбор признаков. Это преобразование
превратит ковариационную матрицу точек, представляющих об-
образы в пространстве X**, в диагональную. Более того, матрица
преобразования А должна быть ортонормированной для того,
чтобы расстояния оставались неизменными.
Задача заключается в выражении матрицы А посредством
собственных векторов известной ковариационной матрицы.
Пусть С — ковариационная матрица для точек, представляю-
представляющих образы в пространстве X, а С* и С** — аналогичные кова-
ковариационные матрицы в пространствах X* и X** соответственно.
Пусть m — вектор математического ожидания точек, отвечаю-
отвечающих образам в пространстве X, и ш* и ш** — векторы матема-
математического ожидания в пространствах X* и X** соответственно.
В таком случае
m' = Wm G.3.13)
и
x*-m* = W(x-m) = Wz, G.3.14)
где
m" = Е {х*} и z = х — т.
В этом выражении Е— оператор математического ожидания.
Ковариационная матрица в пространстве X* определяется как
С* = Е{(х* - т*) (х* - т*)'} = Е {Wzz'W} = WCW, G.3.15)
поскольку C = ?{zz'}.
272 Гл. 7. Предварительная обработка образов
Подобным же образом можно легко показать, что
С** = АС*А' = AWCWA'. G.3.16)
Так как матрица А — ортонормированная, то
АА' = I и А' = А.
В таком случае мы приходим к
. G.3.17)
это выражение представляет преобразование подобия.
Хорошо известно, что преобразование подобия дает диаго-
диагональную матрицу С**, если в качестве матрицы А-1 выбирается
модальная матрица матрицы С*, т. е. столбцами матрицы А
являются собственные векторы матрицы С* либо строками мат-
матрицы А являются собственные векторы матрицы С*. Итак, стро-
строками матрицы А являются собственные векторы матрицы
С* = WCW. Это преобразование, которое является скорее
конгруэнтным, нежели преобразованием подобия, не позво-
позволяет легко выразить собственные векторы матрицы WCW че-
через собственные векторы матрицы С.
Пусть е*, k = 1, 2, ..., п, — нормированные собственные век-
векторы матрицы С* и %и, k=\, 2, ..., n, — соответствующие
характеристические числа. Тогда
G.3.18)
). G.3.19)
Матрица А выбирается так, чтобы
А-' =(е!е2... е„),
и так как собственные векторы образуют ортонормированное
множество, то АА' = I. В таком случае
7.3. Преобразования кластеризации 273
Воспользовавшись уравнением G.3.18), можно записать
Я2е/е2 • • • Я^'е^
_ - _ Я2е2'е2 • • • Я„е2'е„
С** =
G.3.20)
так как e'kek=l и е^е;=0 при кф]. Можно показать, что
Л* = ог?. G.3.21)
Матрица А преобразует ковариационную матрицу С* в диаго-
диагональную, элементами которой являются несмещенные оценки
выборочной дисперсии. Результаты измерений, которым соот-
соответствуют малые дисперсии, более надежны и могут считаться
более существенными признаками.
Описанная процедура исследования ковариационной мат-
матрицы не позволяет связать простой зависимостью собственные
векторы матрицы WCW с собственными векторами исходной
ковариационной матрицы С. Можно, однако, найти простое
выражение, связывающее строки матрицы А с элементами ис-
исходной ковариационной матрицы, если обратить последователь-
последовательность операций (W,А). Выбирается ортонормированная мат-
матрица А, строки которой являются собственными векторами ко-
ковариационной матрицы С. Матрица А преобразует матрицу С
в диагональную матрицу С*. Затем от матрицы преобразова-
преобразования W требуется, чтобы она была диагональной и минимизиро-
минимизировала внутримножественное расстояние в пространстве X
с учетом заданного ограничения. Если выбрано ограничение
**
ТО
ч 1/1
П Wkk=\,
Шч 1/1
о Л -L, G.3.22)
274 Гл. 7 Предварительная обработка образов
где о\ — элементы ковариационной матрицы С*, приведенной
к диагональному виду:
Ковариационная матрица после преобразования кластери-
кластеризации будет иметь вид
C** = WC*W' = WACAW. G.3.23)
Так как все матрицы W, С* и W — диагональные, а произведе-
произведением диагональных матриц всегда будет диагональная мат-
матрица, то очевидно, что, как и требовалось, матрица С** — диа-
диагональная.
Соотношения среднеквадратичного расстояния и отношения
правдоподобия
Здесь устанавливается связь между отношением правдопо-
правдоподобия, рассмотренным в гл. 4, и среднеквадратичным расстоя-
расстоянием; для этого используются преобразования, описанные
выше. Рассмотрим плотность нормального распределения
где С — ковариационная матрица, m — вектор математического
ожидания для класса образов в пространстве X. Отметим, что
кривые равной вероятности соответствуют тем значениям х,
при которых значение аргумента —у(х — т)'С~'(х— т)
показательной функции остается постоянным.
Для исследования ковариационной матрицы осуществляется
ортонормирующее преобразование
х*=Ах, G.3.25)
где строками матрицы А служат нормированные собственные
векторы ковариационной матрицы С. Это преобразование об-
облегчает установление связи между отношением правдоподобия
и среднеквадратичным расстоянием. После преобразования век-
вектор математического ожидания и ковариационная матрица
определяются как
m* = Am G.3.26)
С* = АСА' G.3.27)
соответственно.
7.3. Преобразпвания кластеризации 275
Пусть tk — собственные векторы матрицы С и "Kk — соответ-
соответствующие характеристические числа. В таком случае, согласно
G.3.27), имеем
С* = ( . . . . . | = А. G.3.28)
\0 О
На основе формул G.3.27) и G.3.28) получаем
С = А'ЛА G.3.29)
С-' = А'Л~'А. G.3.30)
Итак, плотность распределения в пространстве X* определяется
выражением
Р(х')= Bn)J|A|v, ехр[-1(х*-тТА-'(х*-т')]. G.3.31)
Это выражение для плотности распределения показывает, что
кривыми равной вероятности являются эллипсоиды с центрами
в точке т*. Направления главных осей совпадают с собствен-
собственными векторами ковариационной матрицы, а диаметры пропор-
пропорциональны квадратному корню от соответствующих характери-
характеристических чисел или среднеквадратичных отклонений, поскольку
д/А^ = ak. Это становится более очевидным после разложения
показательной функции:
^Ь^1, G.3.32)
где х\ — координата вектора х*, соответствующая &-му соб-
собственному вектору, a m*k — среднее всех значений координат,
соответствующих этому собственному вектору
Среднеквадратичное расстояние, отделяющее точку — произ-
произвольный образ х — от множества точек (образов) {ghj=\,
2,...,N}, определяется как
D2 (х, {g,}) = (x - g,Y (x - g/). G.3.33)
Усреднение проводится по всем N точкам, входящим в заданное
множество. В первую очередь осуществляется преобразование
оргонормировки, причем собственные векторы ковариационной
276 Гл. 7. Предварительная обработка образов
матрицы становятся строками матрицы А:
= (х - g,)' А'А (х - g,) = (х - g,)' (x - g,), G.3.34)
поскольку А — ортонормированная матрица и А'А = 1. Рас-
Расстояние при выполнении этого преобразования остается не-
неизменным.
При выполнении преобразования кластеризации
хм = Wx* G.3.35)
среднеквадратичное расстояние принимает вид
= (x*-g;)'ww(X*-g;). G.3.36)
Выбранная матрица W является диагональной, и ее элементы
равны величинам, обратным среднеквадратичным отклонениям
координат образов множества {g^, /=1, 2, ...,М\, соответ-
соответствующих отдельным собственным векторам. Было показано,
что преобразование такого вида минимизирует внутреннее рас-
расстояние множества образов.
Матрица W'W —диагональная, и ее элементы равны вели-
величинам, обратным дисперсиям координат образов множества
{gj,} = 1,2,... ,N}. Так как эти дисперсии суть соответствую-
соответствующие характеристические числа, т. е. o2k = Xk, получаем
W'W = A-'. G.3.37)
Следовательно, среднеквадратичное расстояние определяется
выражением
D2(хм, {g;}) = (х* - g*y Л-i (х- - g}), G.3.38)
которое после выполнения соответствующих операций можно
представить в виде
~ 7 ~
G.з.39)
Поскольку усреднение проводится по всем N точкам множества
образов, оно не зависит от процесса суммирования. Поэтому
7.3. Преобразования кластеризации 277
G.3.39) можно привести к
fc=l
f * *\
1—1 Л.
G.3.41)
где m^= g}ft по всем /== 1, 2, ..., АЛ Так как
то формула G.3.40) превращается в
(**-m*J +д. G.3.42)
В таком случае, если опустить константу п, среднеквадратичное
расстояние для класса a>i определяется выражением
Ц = (х* - га*)' Л (х* - т!) G.3.43)
и, аналогичным образом, среднеквадратичное расстояние для
класса ©/ — выражением
DJ = (х* - го*/)' А,-1 (х* - т)). G.3.44)
Исходя из принципа расстояния, решающее правило можно
сформулировать в таком виде: х е ©«¦ в том и только том слу-
случае, если
Щ — Dj>Q, где 9 —пороговая величина.
Для образов, подчиняющихся нормальному распределению,
плотность распределения или функция правдоподобия для
класса а>г определяется как
р (х | щ) = Bя)"п/21 С, Г4" ехр [-1 (х - ш,)' СГ> (х - ш,)]. G.3.45)
После осуществления ортонормирующего преобразования вы-
выражение G.3.45) принимает вид
р (х') | со,) = BпГп/21 Л, Г% ехр [- i- (х* - ш^' АГ' (х* - т!)].
G.3.46)
Точно так же для класса ©у находим плотность распреде-
распределения
р (х* | со,) = Bя)-"/21 At Г'/гехр [-1 (х* - m])f Af (х* - т))].
G.3.47)
278 Гл. 7. Предварительная обработка образов
Если мы прологарифмируем и опустим постоянные члены, то
получим решающие функции
dt = (х* - т'у Л-' (х* - т\) G.3.48)
dt = (х* - т*)' Л/-1 (х* - т*). G.3.49)
В таком случае решающее правило, основанное на этих двух
функциях, гласит, что х е со,- тогда и только тогда, когда
dj — di > 9, где 9 — пороговая величина.
На основе проведенного анализа можно сделать вывод
о том, что аппроксимация заданных выборок наблюдений для
классов образов плотностями нормального распределения экви-
эквивалентна нахождению среднеквадратичных расстояний для
соответствующих классов после осуществления преобразования
кластеризации над пространством измерений.
7.4. РОЛЬ КЛАСТЕРИЗАЦИИ В ВЫБОРЕ ПРИЗНАКОВ
Выбор признаков, основанный на использовании понятия
внутреннего расстояния множества, можно рассматривать как
задачу кластеризации. Линейное преобразование применяется
для группировки точек образов, принадлежащих одному классу,
и понижения размерности пространства измерений. В настоя-
настоящем параграфе при помощи преобразования кластеризации
устанавливается набор оптимальных признаков. Эти векторы
признаков используются затем для формирования ортогональ-
ортогональной матрицы преобразования.
Рассмотрим класс образов, представленный многомерной со-
совокупностью. Один из его нормированных членов, например zi,
выбирается в качестве точки отсчета для формирования после-
последовательности расстояний до всех соседних нормированных век-
векторов образов z. Предполагается, что выбор вектора образа i\
не зависит от выбора остальных векторов образов z. Итак,
р(г, z,) = p(z)p(z,). G.4.1)
Обозначив вероятности p(z) через р и p(zi) через ри опреде-
определяем внутреннее расстояние для многомерной совокупности
в виде
D^Ep^llz-z.U2}; G-4.2)
это выражение можно переписать как
Упростим последнюю формулу
б5 = Е.„ {z'z} + Epi {z;z,} = 2?р (z'z). G.4.4)
7.4. Роль кластеризации в выборе признаков 279
Воспользовавшись матрицей ковариации
Cz = ?p{zz'}, G.4.5)
выражение G.4.4) можно записать как
ZT2 = 2?p{trzz'} = 2trCz. G.4.6)
Преобразования, реализуемые ортогональной матрицей А
и диагональной матрицей W, приводят к ковариационной мат-
матрице для преобразованного пространства
C" = WACzA'W. G.4.7)
В таком случае внутреннее расстояние множества в преобра-
преобразованном пространстве определяется выражением
D = 2tr(WACzA'W). G.4.8)
Пусть еь ег, ..., еп — собственные векторы ковариационной
матрицы Cz и А,ь ^2, •••, Яя — соответствующие характеристи-
характеристические числа. Тогда
С«е* = Я,*е*. G.4.9)
Элементы ортогональной матрицы преобразования А выби-
выбираются так, что в преобразованном пространстве ковариацион-
ковариационная матрица становится диагональной. Этого можно достичь,
используя тип транспонированных собственных векторов ко-
ковариационной матрицы Cz в качестве строк ортогональной
матрицы А, т. е.
: !
G.4.10)
Размерность преобразованного пространства понижена до т.
Согласно G.4.9) и G.4.10),
С,А' = (Х,е,Л2е2...Лтет). G.4.11)
Матрица ACZA' в силу ее ортонормированности имеет диаго-
диагональный вид
;<> •¦• о
ACZ.V= ( Д" ° | =Л.
\0 О
280 Гл. 7. Предварительная обработка обраяов
Поэтому внутреннее расстояние множества можно записать как
Zf2 = 2 tr (WAW) = G.4.13а)
m
G.4.136)
Теперь необходимо так определить матрицу весов W, чтобы
расстояние D2 принимало при выполнении заданного ограниче-
ограничения экстремальное значение. Будут рассмотрены два случая.
m
Рассмотрим в первую очередь ограничение Ц nyfeft=l. Для
fe=i
того чтобы исключить тривиальное решение W = 0, ограни-
ограничение можно представить в виде |W|—1=0. Минимизация
внутреннего расстояния D2 с учетом этого ограничения экви-
эквивалентна минимизации величины
m S m \
S = 2 Z Kkw\k - Y (Д »tt - 1) • G-4.14)
Взяв частную производную от G.4.14) по весовому коэффи-
коэффициенту Wkk, приравняв ее нулю и упростив, получим
^ G.4.15)
2 Vх*
где множитель Лагранжа у определяется выражением
(• m \2/m
nV^T) • G.4.16)
Подстановка выражения G.4.16) в G.4.15) дает
1/пг
¦ <7Л17)
Итак, матрица весов W определяется следующим образом:
А/2 о ••• о
\1/2т / А З/- • А
) ¦:;
о о
Подстановка выражения G.4.17) в G.4.13) приводит к формуле
для минимального внутреннего расстояния множества
Шч I'm
A.J • G.4.19)
7.5. Минимизация энтропии 281
Из этого сотношения очевидно, что расстояние D2 является гло-
глобальным минимумом, если используются m наименьших ха-
характеристических чисел. Таким образом, если мы хотим мини-
минимизировать внутреннее расстояние множества, то в качестве
векторов признаков следует выбирать собственные векторы,
соответствующие наименьшим характеристическим числам ко-
ковариационной матрицы Cz
С другой стороны, можно показать, что при ограничении
m
2 wkk = 1 весовыми коэффициентами будут
<7-420)
а минимальное внутреннее расстояние множества определяется
выражением
—1
G.4.21)
Таким образом, мы считаем, что значение внутреннего расстоя-
расстояния множества достигнет глобального минимума, если в ка-
качестве характеристических чисел А./ выбраны m наименьших
из п характеристических чисел ковариационной матрицы Cz
и матрица преобразования А составлена из m соответствующих
собственных векторов.
7.5. ВЫБОР ПРИЗНАКОВ ПРИ ПОМОЩИ МИНИМИЗАЦИИ
ЭНТРОПИИ
Энтропия представляет собой статистическую меру неопре-
неопределенности. Хорошей мерой внутреннего разнообразия для за-
заданного семейства векторов образов служит энтропия совокуп-
совокупности, определяемая как
Н = -Ер{\пр}, G.5.1)
где р — плотность вероятности совокупности образов, а Ер —
оператор математического ожидания плотности р. Понятие
энтропии удобно использовать в качестве критерия при органи-
организации оптимального выбора признаков. Признаки, уменьшаю-
уменьшающие неопределенность заданной ситуации, считаются более ин-
информативными, чем те, которые приводят к противоположном.
282 Гл. 7. Предварительная обработка образов
результату. Таким образом, если считать энтропию мерой не-
неопределенности, то разумным правилом является выбор при-
признаков, обеспечивающих минимизацию энтропии рассматривае-
рассматриваемых классов. Поскольку это правило эквивалентно минимиза-
минимизации дисперсии в различных совокупностях образов, то вполне
можно ожидать, что соответствующая процедура будет обла-
обладать кластеризационными свойствами.
Рассмотрим М классов, соответствующие совокупности об-
образов которых характеризуются плотностями распределения
p(x|a)i), р(х|оJ), ..., р(х|а)м). В силу G.5.1) энтропия /-й со-
совокупности образов определяется как
G.5.2)
где интегрирование осуществляется по пространству образов.
Очевидно, что при /?(х|о),-) = 1, т. е. при отсутствии неопреде-
неопределенности, имеем Hi = О в полном соответствии с данной выше
интерпретацией понятия энтропии.
Далее будет предполагаться, что каждая из М совокупно-
совокупностей образов характеризуется плотностью нормального распре-
распределения /?(x|o)i) ~ Af(nij, С/), где т,- и С,- — соответственно век-
вектор математического ожидания и ковариационная матрица t-н
совокупности образов (см. гл. 4). Кроме того, будет предпола-
предполагаться, что ковариационные матрицы, описывающие статисти-
статистические характеристики всех М классов, идентичны. Этот случай
возникает, если каждый образ, принадлежащий некоторому
классу, является случайным вектором, полученным в резуль-
результате наложения случайного вектора на неслучайный. Наложен-
Наложенные случайные векторы, что характерно для многих приложе-
приложений, выбираются из одной и той же нормально распределенной
совокупности.
Основная идея, лежащая в основе рассматриваемых в дан-
данном параграфе методов, с учетом введенных допущений заклю-
заключается в определении матрицы линейного преобразования А,
переводящей заданные векторы образов в новые векторы мень-
меньшей размерности — изображения. Это преобразование можно
представить как
у = Ах, G.5.3)
причем матрица преобразования отыскивается при помощи ми-
минимизации энтропии совокупностей образов, входящих в рас-
рассматриваемые классы. Здесь х — вектор размерности я, у —
отображенный вектор, имеющий размерность m, m < я и А —
матрица размерности пгУ^п. Строками матрицы А служат га
выбранных векторов признаков а[, &'2, ...,&[, .. ., &'т, представ-
7.5 Минимизация энтропии 283
ляющих собой вектор-строки. Таким образом, матрица А имеет
вид
А=
а
G.5.4)
Задача состоит в определении такого способа выбора m векто-
векторов признаков, чтобы вектор х преобразовывался в изображе-
изображение у и одновременно минимизировалась величина энтропии,
определяемой формулой G.5.2).
Многомерное нормальное распределение полностью опреде-
определяется вектором математического ожидания и ковариационной
матрицей. Эта матрица в свою очередь определяется характе-
характеристическими числами и собственными векторами. Последние
можно рассматривать как векторы, представляющие свойства
рассматриваемых образов. Часть из этих векторов свойств со-
содержит меньше информации, ценной для распознавания, чем
другие векторы, и поэтому ими можно пренебречь. Это явление
приводит к процедуре выбора признаков, предусматривающей
использование наиболее важных векторов свойств в качестве
векторов-признаков. Такие векторы-признаки можно затем ис-
использовать для формирования матрицы преобразования А. Один
из подходов к выбору векторов-признаков, использующий прин-
принцип минимума энтропии, состоит в следующем.
В силу предположения о равенстве всех ковариационных
матриц положим Ci = С2 = ... = См = С и получим следую-
следующее выражение для плотности нормального распределения обра-
образов г-го класса:
1 exp[-'/2(x-mtyC-'(x-m,-)l. G 5 5)
Вектор математического ожидания для изображений у, обозна-
обозначенный через т*, определяется, согласно G.5.3), как
m* = Amr G.5.6)
Положив z = x —Ш/, из G.5.6) получаем, что
y-m*-A(x-m;) = Az. G.5.7)
В таком случае ковариационная матрица для изображений
равна
C*=?{(y-m;)(y-mt)'}= G.5.8)
= А? {zz'} A' = АСА', G.5.9)
так как Е {zz'} = Е {(х — ш,-) (х — т,)'} = С.
284 Гл. 7. Предварительная обработка образов
Плотность распределения для изображений определяется,
исходя из G.5.6) и G.5.9), как
Хехр[- 1(у - mtf (АСА') (у - т^]. G.5.10)
Энтропия изображений равна
Щ=-\р(у\щ)\пр(у\щ)с1у. G.5.11)
Подстановка выражения для плотности распределения G.5.10)
в выражение для энтропии G.5.11) и минимизация относи-
относительно собственных векторов ковариационной матрицы С по-
позволяют сформулировать следующий результат1):
Функция энтропии Я* принимает минимальное значение,
если матрица преобразования А составлена из m нормирован-
нормированных собственных векторов, соответствующих наименьшим ха-
характеристическим числам ковариационной матрицы С.
Применяя этот результат, надо иметь в виду, что число век-
векторов, используемых для формирования матрицы А, должно быть
достаточно большим, чтобы изображения несли достаточное
количество различительной информации.
Следует четко представлять себе разницу между выбором и
выделением признаков. В данном параграфе процедура выбора
признаков сводится к выбору в качестве признаков m собствен-
собственных векторов ковариационной матрицы С, удовлетворяющих
сформулированным выше условиям. Процедура выделения
признаков состоит в определении характеристических чисел и
собственных векторов ковариационной матрицы С по обучаю-
обучающей выборке.
Пример. Проиллюстрируем описанную процедуру простым
примером. Допустим, что требуется понизить размерность обра-
образов, представленных на рис. 7.1, а, с помощью преобразования,
') Доказательство этого результата занимает несколько страниц довольно
сложных алгебраических выкладок. Будучи уверены в том, что, опустив это
доказательство, мы ни в коей мере не затруднили читателю понимание основ-
основных принципов распознавания образов, рекомендуем тем, кто интересуется
подробным доказательством этого результата, обратиться к работе Ту и Хей-
дориа [1967].
@,1,1)
Кластер,
^содержащий
i r аба образа
¦Мастер,
содержащ
о 2
содержащий——о /
два образа
i [ i
i i
12
J I
-4-3-2-1
Кластеры,
содержащие
три образа
i i i
12
Рис. .7.1. Иллюстрация концепции мииимальной энтропии, а — исходные о5-
разы; б—результаты, полученные после первого преобразования; в—резуль-
в—результаты, полученные после второго преобразования.
286 Гл. 7 Предварительная обработка образов
минимизирующего энтропию. Заданные образы имеют следую-
следующий вид (рассматриваются два класса):
Г
Х21 =- I О
Х22 =
Х23 =
Ход —
где первая цифра в индексе кодирует либо класс аи, либо ©2.
Напомним оценки для вектора математического ожидания и
ковариационной матрицы, полученные в § 4.6:
m; =
1 /-1
где Ni — число образов класса ©,-, входящих в обучающую вы-
выборку. Из этих двух соотношений получаем
7.5 Минимизация энтропии 287
Характеристические числа ковариационной матрицы С равны
Я.] = -jg-, Я.2 = А3 = -j.
Поскольку ковариационная матрица — симметрическая, то всег-
всегда можно определить набор действительных ортогональных соб-
собственных векторов независимо от кратности характеристических
чисел. Нормированные собственные векторы, соответствующие
этим характеристическим числам, имеют вид
e2~'W
где собственные векторы ei, е2 и е3 соответствуют характери-
характеристическим числам %\, 12 и 1з в указанной последовательности.
Выбор собственных векторов ei и е2 приводит к матрице пре-
преобразования
_/е1\_/1/Уз -1/V3 ' ЛЩ
~ W/ " \2/У« 1/Ув l/Уб
Выбор собственных векторов ei и е3 столь же оправдан, так как
собственные векторы ег и е3 соответствуют одинаковым харак-
характеристическим числам.
Изображения, полученные в результате преобразования
у = Ах, имеют следующий вид:
°
_ /1/Кз\
y""\2/Vo/ У22"
v -I
о \ /— i/V-3\
зТб/ >24 \ 4/V'6/
Образы с пониженной размерностью представлены на рис. 7.1,6.
Интересно отметить эффект кластеризации, полученный после
этого преобразования. Читатель может без труда убедиться
288 Гл. 7. Предварительная обработка образов
в том, что при перестановке собственных векторов ei и е2 в мат-
матрице А мы придем к тому же результату. Единственным отли-
отличием будет соответствующая перестановка компонент вектора у.
Дальнейшего понижения размерности можно добиться, ис-
используя для матрицы А только собственный вектор еь
Применение этого преобразования к исходным образам приво-
приводит к новым изображениям:
Уп=О у21 - -
Уп = 1/V3 у22 1/V5"
Уп = 0 . y%z = - 2/Уз
Ун = 0 У24 = - 1/Уз
Образы пониженной размерности представлены на рис. 7.1, в.
На этом рисунке снова отчетливо виден эффект кластеризации,
возникающий в результате преобразования, минимизирующего
энтропию. |
7.6. ВЫБОР ПРИЗНАКОВ ПРИ ПОМОЩИ РАЗЛОЖЕНИЙ
ПО СИСТЕМЕ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
Концепция минимальной энтропии, развитая в предыдущем
параграфе, основывается на предположении о нормальности
распределения образов, составляющих заданные классы. Если
это условие не выполняется, то следует воспользоваться другим
подходом к решению задачи выбора признаков — методом раз-
разложения по системе ортогональных функций. Мы будем при-
применять разложение Карунена — Лоэва. Основное преимущество
этого разложения состоит в том, что оно позволяет обойтись
без знания плотностей распределения образов, входящих в от-
отдельные классы. Кроме того, как мы увидим ниже, разложение
Карунена — Лоэва обладает двумя оптимальными свойствами,
позволяющими ему служить полезным критерием при выборке
признаков.
Прежде чем перейти к рассмотрению разложения Каруне-
Карунена— Лоэва, дадим краткий обзор процедуры разложения в ряд
7.6. Разложение по системе ортогональных функций 289
Фурье с тем, чтобы подчеркнуть некоторую аналогию между
этими разложениями. Разложение Карунена — Лоэва вво-
вводится для случая непрерывных образов, а затем распростра-
распространяется на более важный с практической точки зрения дискрет-
дискретный случай. Последнему уделяется основное внимание, что объ-
объясняется важностью этого случая с точки зрения вычислений
на ЭВМ и распознавания образов.
7.6.1. Разложение в ряд Фурье. Обзор
Стационарный периодический случайный процесс с перио-
периодом Т можно представить рядом Фурье
оо
x{t) = S *„ехр(/шооО, G.6.1)'
л= — оо
где (О0 = 2я/Г — угловая частота, а случайные величины
г
1 Г
хп = у \ х @ ехр (— упад dt G.6.2)
о
суть коэффициенты Фурье. Для различных реализаций формула
G.6.2) в принципе дает различные значения коэффициентов
Фурье хп. При рассмотрении некоторого множества выборочных
функций соотношение G.6.2) определяет коэффициенты хп как
случайные величины. Интеграл в G.6.2) существует с вероят-
вероятностью 1. Можно показать, что
N
/ N \
= Hm I 2 лс* exp (j&ffloO) •
N-*<x>\ k--N /
Выполнение условия периодичности случайного процесса
гарантирует взаимную независимость коэффициентов хп и хп
при пфт. Используя выражение G.6.2), получаем
т т >
' {xnxm} =-ftE\\\x(t)x(s) exp (— /па>оО exp (jmaQs) ds dt \ =
= jj 3 }R (t - s) exp [/«во (ms — nt)] ds dt, G.6.3)
о о
где x обозначает величину, комплексно сопряженную х, а
— s) = E{x{t)x{s)}
290 Гл. 7. Предварительная обработка образов
— корреляционную функцию. Поскольку корреляционная функ-
функция R (т) (т = / — s) периодическая, запишем
p G-6.4)
Из G.6.3) и G.6.4) следует, что
Iff °°
Е {хпхт} = 72 J J /С 6ft ехр 1/&с0° ^ ~~ s^ exp f/c0° ^ms ~ nt^ ds dt =
О 0 ft=~oo
ос Г Г
1
f
= \
) exP f^00 (m ~ *) sl ds ) exP t^
ft=-oo 0 0
6„, если п = т,
0, если пфт.
Формула G.6.5) свидетельствует не только о взаимной незави-
независимости коэффициентов Фурье х„ и хт при пф т, но также и
о том, что п-й коэффициент Фурье корреляционной функции
R(x) равен дисперсии п-го случайного коэффициента Фурье
функции x(t). Это аналогично ситуации, имеющей место в де-
детерминистском случае: для периодической функции x(t) n-k
коэффициент Фурье корреляционной функции равен квадрату
я-го коэффициента Фурье функции x(t).
Если стационарный процесс является периодическим, то
случайные значения коэффициентов Фурье хп и хт при пФ т
взаимно независимы. Можно показать и обратное: для того
чтобы коэффициенты были взаимно независимы, необходима
периодичность процесса. Если заданный случайный процесс не
является периодическим, то соответствующая корреляционная
функция не допускает подобного простого представления через
дисперсии коэффициентов Фурье функции x(t).
7.6.2. Разложение Карунена — Лоэва
Непериодический случайный процесс нельзя представить в
виде ряда Фурье с взаимно независимыми коэффициентами, яв-
являющимися случайными величинами, но его можно разложить
в ряд по системе ортогональных функций <j>n{t) с взаимно не-
независимыми коэффициентами. Эту процедуру часто называют
разложением Карунена — Лоэва.
Непериодический случайный процесс x(t) в интервале [а, Ь\
можно разложить в ряд
оо
х @ = ? УпХпФп @, а < / < Ь, G.6.6)
1
7.6. Разложение по системе ортогональных функций 291
где
b
1,
о,
I,
о,
если
если
если
если
т
т
т
т.
=
Ф
=
Ф
п,
п,
п,
f 1, если пг = п,
E{xnxm} = \ n , G.6.8^
1 " "" [0, если тфп, v
причем коэффициенты Y"— действительные или комплексные
числа. Эти выражения представляют так называемое ортого-
ортогональное разложение случайного процесса в заданном интер-
интервале. Если процесс является стационарным периодическим, то
это разложение задается при <f>n(t) = (\/T)exp(jne>ot) и коэф-
коэффициентах упхп, равных соответствующим случайным значениям
коэффициентов Фурье. Если условие периодичности отбросить,
то условие G.6.8) нарушится и при <j>n(t) = A/7)ехр(/лсооО-
Ортогональные функции <j>n(t) и числа уп определяются сле-
следующим образом. Пусть соотношения G.6.6) — G.6.8) справед-
справедливы для некоторого множества функций <f>n{t), некоторого
множества чисел уп и некоторого множества случайных пере-
переменных хп. В таком случае корреляционная функция R (t,s)
определяется как
R (t, s) = E{x (t) x is)} = E \ ? упхпфп (t) ? yxkj>k (s) ) =
= Z\Vn?4>n(t)$n(b, G.6.9)
n
где t и s принадлежат интервалу [a, b]. Отметим, что, поскольку
случайный процесс предполагается непериодическим, корреля-
корреляционную функцию больше нельзя представлять в виде R(t — s).
Из G.6.9) получаем
ь ь
\ R (t, s) фк (s) ds = ? | уп |2 </>„ (/) \ фк (s) фп (s) ds. G.6.10)
а па
Использование G.6.7) дает
k{s)ds = \ykfфk{t). G.6.11)
\R(t,
На языке теории интегральных уравнений числа JyaI2 пред-
представляют собой собственные значения, а функции fk(t) — соб-
собственные функции известного интегрального уравнения, записы-
записываемого в общем виде как
\ G.6.12)
292 Гл. 7. Предварительная обработка образов
где а ^ t ^Z Ь. Определение уп и <j>n{t) сводится к решению этого
интегрального уравнения. С другой стороны, можно построить
ортогональное разложение, справедливое в любом заданном
интервале а ^ / ^ Ь, для случайного процесса с непрерывной
корреляционной функцией, используя в формулах G.6.6) —
G.6.8) в качестве коэффициентов у и функций ^>(/) положитель-
положительные значения квадратного корня от собственных значений и
собственные функции уравнения G.6.12) соответственно.
Применим введенные понятия к теории распознавания. Рас-
Рассмотрим М классов ©1, 02. •••, <им, образы которых представ-
представлены непрерывными случайными функциями действительной
переменной; пусть xi(t), T\^t^T2,i=l,2,..., M, — наблю-
наблюдения, относящиеся к одному из классов М. Тогда можно полу-
получить разложение Xi(t) в виде линейной комбинации заданных
базисных функций <j>j{t):
оо
х, (t) = ? Citf, (t), 7, < t < Тъ i = 1, 2, ..., M, G.6.13)
где сц — случайные коэффициенты, удовлетворяющие условию
Е{сц} = 0. Практические следствия этого допущения будут рас-
рассмотрены несколько позже. Будем считать также, что в качестве
базисных функций <f>j{t) используется множество детерминиро-
детерминированных ортонормированных функций, заданных на интервале
Т\ ^ t ^ Т2.
Автокорреляционная функция для М распознаваемых клас-
классов определяется выражением
R (t, s) = Е р (щ) Е {Xi (t) Xi (s)}. G.6.14)
где p((oi) — априорная вероятность появления i-ro класса, а
E{xi(t)xt(s)}—оператор математического ожидания, вычисляе-
вычисляемого по всем наблюдениям, относящимся к этому классу. По-
Поскольку очевидно, что выражение E{xi(t)xi(s)} есть не что
иное, как стандартное определение автокорреляционной функ-
функции, из этого следует, что G.6.14) определяет «усредненную»
автокорреляционную функцию, исходя из возможности порож-
порождения случайных функций Xj(t) более чем одним источником,
т. е. из того, что существует М источников или классов, порож-
порождающих эту функцию. Известно, что оба определения автокор-
автокорреляционной функции приводят к одним и тем же оптимальным
свойствам разложения Карунена — Лоэва (которые рассматри-
рассматриваются ниже). С точки зрения теории распознавания лишь
определение G.6.14) имеет смысл, так как оно учитывает суще-
существование более чем одного класса, в то время как выражение
7.6. Разложение по системе ортогональных функций 293
E{xi(t)Xi(s)} применимо для распознавания лишь к случайным
функциям «одного происхождения».
Подстановка выражения G.6.13) в G.6.14) приводит к
R(t,s)=ZpЫЕ Z ctli>, (О S с1кфк (s) \. G.6.15)
i=i l/=i fe=i )
Отметим, что в разложении функции x,(s) изменен индекс. По-
Поскольку базисные функции детерминированны, соотношение
G.6.15) можно записать как
R(t,s)=tp К) Z If (t) Фк (s) E {сИс1к} =
г1 yi fei
= lb, @ фк (s) E P (<»i) E {cifcik}. G.6.16)
/=1 ft=l i=l
Допустим, что случайные коэффициенты статистически незави-
независимы в том смысле, что
м
рЫЕ{с,,с1к) = \ ' G.6.17)
l=x I 0, если /^=fe,
где Xj > 0 — константа. При выполнении этих условий формула
G.6.16) принимает следующий вид:
R(t>s)=Zli<l>l(t)<l>l(s). G.6.18)
'¦=i
Умножение обеих частей G.6 18) на фь(и) и интегрирование по
интервалу [Т\, Т2], где фк ортонормированны, дает
Тг Т. оо
Я (/, s) фк (s) ds = \Y, ^}Ф1 (О Ф1 (s) Фк (s) ds. G.6.19)
Г, Г, /=1
Поменяв порядок выполнения суммирования и интегрирования,
получим
Г, оо Г,
J Я (t, s) фк (s) ds^Y, Wi @ S ^/ (s) fk (s) ds. G.6.20)
Г, /-1 T,
В силу предположения об ортонормировацности базисных функ-
функций уравнение G.6.20) сводится к интегральному уравнению
ds = lkфk(t). G.6.21)
294 Гл. 7. Предварительная обработка образов
Разложение, определяемое формулой G.6.13), базисные
функции которого отыскиваются с помощью уравнения G.6.20)
или G.6.21) и автокорреляционная функция вычисляется со-
согласно G.6.14), называют обобщенным разложением Кару-
нена — Лоэва. Термин «обобщенное» добавляется для того,
чтобы подчеркнуть определение корреляционной функции по
формуле G.6.14), а не с помощью выражения E{xi(f)xi(s)},
представляющего стандартное определение автокорреляционной
функции.
Разложение Карунена — Лоэва обладает следующими опти-
оптимальными свойствами: 1) оно минимизирует среднеквадратич-
среднеквадратичную ошибку при использовании лишь конечного числа базис-
базисных функций в разложении G.6.13), и 2) оно минимизирует
функцию энтропии, выраженную через дисперсии коэффициен-
коэффициентов разложения. Важность первого свойства заключается в
том, что оно гарантирует невозможность получения меньшей в
среднеквадратичном смысле ошибки аппроксимации с помощью
другого разложения. Важность второго свойства заключается
в том, что оно связывает с коэффициентами разложения оценку
минимальной энтропии или дисперсии. Как будет показано
ниже, эти коэффициенты играют роль составляющих векторов
изображений. Они подобны у-векторам, полученным в резуль-
результате преобразования у = Ах из § 7.5. Следовательно, поскольку
разложение Карунена — Лоэва обладает свойством минимиза-
минимизации энтропии, можно рассчитывать, что разложение Каруне-
Карунена— Лоэва имеет также свойства, типичные для преобразова-
преобразования кластеризации.
Дискретный случай
Если в интервале Т\ ^Lt ^ Г2 через равные промежутки вре-
времени произвести выборку значений Xt(t), то результат можно
представить в следующем векторном виде:
f */('¦) I
X; =
G.6.22)
X*
где п — количество наблюдений для функции Xi(f), осущест-
осуществленных в интервале [Т\,Т2\. Выражение G.6.13) принимает
в этом случае вид конечной суммы
G.6.23)
7.6. Разложение по системе ортогональных функций
295
причем относительно коэффициентов предпола1ас1ся, что они
удовлетворяют условию ?{с,у} = 0 и ^ — вектор:
G.6.24)
ф,(и)
/ (*„)
Если коэффициенты представлены в векторной форме
С12
сч
Сщ.
где ?{с,} = 0, то G.6.23) можно представить в более удобной
матричной записи:
х,- = Фс?, G.6.26)
где Ф — матрица:
@# ... Фп). G.6.27)
G.6.25)
Дискретным аналогом автокорреляционной функции G.6.14)
служит автокорреляционная матрица, определяемая как
м
R=b((oj)?{?;}. G.6.28)
Подстановка в это соотношение выражения G.6.26) для х,- дает
м / м \
R = Z Р (со,) Е {Фс,.с;Ф'} = Ф [ Z р (со,.) Е {сг<} J Ф' G.6.
29)
Здесь второй шаг следует из детерминистской природы мат-
матрицы Ф.
Введя условие
?
G.6.30)
296 Г л 7 Предварительная обработка образов
где D^ — диагональная матрица:
ах о
о д2
G.6.31)
/
\0 О ••• Я,
формулу G.6.29) можно привести к виду
Ц = ФОЯ,Ф'. G.6.32)
Если базисные векторы ф\ предполагаются ортонормирован-
ными, то обычным умножением G.6.32) на матрицу Ф получим
Цф = ф^Ф'Ф = Ф&ъ, G.6.33)
так как Ф'Ф = I в силу ортонормированности базисных векто-
векторов, составляющих матрицу Ф.
Из G.6.33) следует, что
Г(ф1 = Х1ф!; G.6.34)
это уравнение является дискретным аналогом уравнения
G.6.21).
Из уравнения G.6.34) и определения характеристических
чисел и собственных векторов очевидно, что /-Й базисный век-
вектор, входящий в разложение G.6.23), является собственным
вектором корреляционной матрицы, соответствующим /-му ха-
характеристическому числу. Поскольку базисные векторы пред-
представляют собой собственные векторы действительной симмет-
симметрической матрицы, то они взаимно ортогональны. Если, кроме
того, они ортонормированны, то
если / = k,
... G.6.35)
если ]?= k;
последнее условие позволило получить G.6.33). Исходя из этого
свойства, определим коэффициенты разложения:
Фс, = хь Ф'Фс, = Ф'хь сг = Ф'х,. G.6.36)
С помощью прямой подстановки можно проверить, что эти
коэффициенты удовлетворяют условию G.6.30). Кроме того, из
формул G.6.36) следует, что условие ?{с,} = 0 допускает еще
одну интерпретацию:
Е {с,} = Е {Ф'х,} = Ф'? {xj = 0, G.6.37)
7.6. Разложение по системе ортогональных функций 297
т. е. предположение Е {d} = 0 выполняется автоматически, если
различные совокупности образов характеризуются нулевыми
математическими ожиданиями.
Дискретный вариант обобщенного разложения Карунена —
Лоэва представляется формулами G.6.23) или G.6.26), где
базисными векторами служат ортонормированные собственные
векторы корреляционной матрицы G.6.28). Коэффициенты этого
разложения определяются по формулам G.6.36). Ниже рас-
рассматривается применение этих понятий при выборе признаков.
Применение дискретного разложения Карунена —Лоэва
при выборе признаков
Основанием применения дискретного разложения Каруне-
Карунена—Лоэва в качестве средства выбора признаков является
наличие у него отмеченных выше оптимальных свойств. В ди-
дискретном случае принцип минимизации среднеквадратичной
ошибки предполагает, что разложение Карунена — Лоэва ми-
минимизирует ошибку аппроксимации при использовании в разло-
разложении G.6.23) или G.6.26) числа базисных векторов, меньшего
п1). Принцип минимизации энтропии обеспечивает искомые эф-
эффекты кластеризации, которыми обладает метод из § 7.5.
Применение дискретного разложения Карунена — Лоэва при
выборе признаков можно рассматривать как линейное преоб-
преобразование. Если
Ф = (Ф\фо ¦ ¦ ¦ фт), т<п G.6.38)
—матрица преобразования, то, согласно G.6.36), преобразован-
преобразованные образы (изображения) являются коэффициентами разложе-
разложения Карунена — Лоэва, т. е. для любого образа х,-, принадлежа-
принадлежащего классу со,, в силу G.3.36) выполняется
с, = Ф'хг.
Поскольку Ф'— матрица размера тХя и х — «-мерный век-
вектор, то очевидно, что с,- при пг < п представляют собой изобра-
изображения, имеющие размерность, меньшую п.
Можно показать, что условия оптимальности разложения
Карунена — Лоэва выполняются, если в качестве столбцов мат-
матрицы преобразования Ф выбраны пг нормированных собствен-
') Эта ошибка определяется выражением
е=*i -
где, вообще говоря, m < п. Из G.6.23) следует, что при пг = п эта ошибка
рапна нулю.
298 Гл. 7. Предварительная обработка образов
ных векторов, соответствующих наибольшим характеристиче-
характеристическим числам корреляцонной матрицы R.
Этот результат можно представить в той же форме, что
была предложена в § 7.5, с помощью матрицы
Ф'Л
Ф'
G.6.39)
где строками матрицы А служат нормированные собственные
векторы, соответствующие наибольшим характеристическим чис-
числам корреляционной матрицы R. Если положить у = с, то, как
и ранее, для любого вектора х его изображения меньшей раз-
размерности определяются как
у = Ах.
Резюмируем описанные выше результаты.
1. По образам, входящим в обучающую выборку, при по-
помощи соотношения G.6.28) вычисляется корреляционная мат-
матрица R.
2. Определяются характеристические числа и соответствую-
соответствующие собственные векторы корреляционной матрицы R. Прово-
Проводится нормировка собственных векторов.
3. Из m собственных векторов, соответствующих наибольшим
характеристическим числам корреляционной матрицы R, по
формуле G.6.38) формируется матрица преобразования Ф.
4. По формулам G.6.36) вычисляются коэффициенты разло-
разложения. Эти коэффициенты задают изображения с меньшей раз-
размерностью описания.
Для того чтобы применение разложения Карунена — Лоэва
приводило к получению оптимальных результатов, необходимо
выполнение условия ?{с:}=0 или равносильного условия
Е{х;} = 0. Как отмечалось выше, последнее выполняется авто-
автоматически, если отдельные классы характеризуются пулевыми
математическими ожиданиями. На первый взгляд может пока-
показаться, что проблему можно решить, центрируя образы отдель-
отдельных классов относительно соответствующих математических
ожиданий. Однако читатель должен иметь в виду, что при ре-
решении задач распознавания отсутствуют сведения о принадлеж-
принадлежности образа определенному классу (за исключением, вообще
говоря, этапа обучения). Хотя образы обучающей выборки, дей-
действительно, можно центрировать, прежде чем они будут исполь-
использованы для оценки корреляционной матрицы, этот прием ока-
7.6. Разложение по системе ортогональных функций 299
жется бесполезным, так как он предусматривает изменение ха-
характеристик рассматриваемых классов. Естественно, затрудне-
затруднения.не возникнут в одном частном случае, когда математические
ожидания всех классов равны. В этом случае все образы неза-
независимо от их принадлежности классам будут центрироваться
относительно одного и того же математического ожидания как
в процессе обучения, так и в процессе распознавания.
Хотя предположение об идентичности математических ожи-
ожиданий всех совокупностей образов ограничивает возможности
применения разложения Карунена — Лоэва, не следует считать,
что этот подход к выбору признаков не имеет достоинств. Допу-
Допущения такого типа характерны для большинства статистических
методов анализа. Успех применения любого метода зависит
только от того, насколько хорошо анализируемые данные соот-
соответствуют основным предположениям, принятым при разра-
разработке соответствующего статистического метода.
Пример. В качестве простой иллюстрации применения ди-
дискретного разложения Карунена — Лоэва рассмотрим обработ-
обработку образов, представленных на рис. 7.2.
Здесь первый индекс указывает номер класса, которому при-
принадлежит образ, а второй — номер соответствующего образа.
Допустив, что р(и1) = р(ш2)= '/г, получим
2
*=I р Ы Е М=т Е М + т
1=1
*? @,1,1)
A,0,1)
ш,
(a)
I I I I I
- o"
i
о
Кластер, содеон<ащип д!а образа
1 2 3 U 5
• Кластер, содержащий
дда образа
Кластеры, содержащие яри образа,
принадлежащие к разным классам
I I I I I
О 1 2
Рис. 7.2. Иллюстрация применения разложения Карунена — Лоэва. а—игход
ные образы; б — образы, сжатые до двумерного варианта; в — образы, ежа
тые до одномерного варианта.
7.6. Разложение по системе ортогональных функций 301
где ?{х,х(} и ?{х2х2} обозначают математические ожидания,
вычисляемые по всем образам классов ©i и (о2 соответственно.
Выполнение этих операций по методу из § 4.6 дает следующее:
Характеристические числа и соответствующие им нормирован-
нормированные собственные векторы корреляционой матрицы R равны:
• • e2 ~ Л17Г
Выбрав собственные векторы ei и ег, соответствующие наиболь-
наибольшим характеристическим числам, получим матрицу преобра-
преобразования
302 Гл. 7. Предварительная обработка образов
Воспользовавшись преобразованием с = Ф'х, получаем изобра-
изображения:
с
U
c14 =
уа
= Д/з1/2
Уел (i
Эти изображения представлены на рис. 7.2,6. Обратите внима-
внимание на эффект кластеризации, а также на то обстоятельство,
что линейная разделимость образов сохранилась.
Рассмотрим матрицу преобразования
1
1
собственный вектор которой соответствует наибольшему ха-
характеристическому числу. Это преобразование переводит образы
в точки:
°*1 ft>2
еи =0 с21 = Уз"
Чг - ^3 с22 = Уз
•„ - гУэ с23 - 2F3*
«к - 2Уз с24 = зУз"
Соответствующие образы представлены на рис. 7.2, в, из кото-
которого видно, что образы, принадлежащие различным классам,
перекрываются, — поэтому последнее преобразование нежела-
нежелательно.
Интересно отметить, что преобразование, минимизирующее
энтропию, привело в этом случае к получению существенно
7.7. Аппроксимация функциями 303
лучших результатов, чем преобразование, основанное на разло-
разложении Карунена — Лоэва. Это обстоятельство снова подчерки-
подчеркивает тот важный факт, что достоинства определенного метода
выбора признаков зависят от того, к какой задаче он при-
применяется. ¦
7.7. ВЫБОР ПРИЗНАКОВ ПОСРЕДСТВОМ
АППРОКСИМАЦИИ ФУНКЦИЯМИ
Если признаки образов, составляющих некоторый класс,
можно охарактеризовать с помощью функции /(х), определяе-
определяемой на основе результатов наблюдений, то процесс выбора
признаков можно рассматривать как задачу аппроксимации
некоторой функцией. В процессе обучения известны значения
функции признаков Дх) в точках, соответствующих выбороч-
выборочным образам xi, х2, ..., х#. Необходимо найти такую аппрок-
аппроксимацию f(x) функции /(х), чтобы обеспечивалась оптимизация
по некоторому критерию качества. Существуют различные ме-
методы определения аппроксимирующих функций. В данном раз-
разделе мы рассмотрим метод разложения по системе функций,
метод стохастической аппроксимации и метод аппроксимации с
помощью ядер применительно к задаче аппроксимации функций
признаков.
7.7.1 Разложение по системе функций
Пусть задано М классов и /,(х) представляет функцию при-
признаков i-ro класса. При определении аппроксимирующей функ-
функции f,(x) целесообразно в качестве критерия качества исполь-
использовать минимум суммы взвешенных квадратов ошибок в выбо-
выборочных точках. Этот критерий точности можно записать в виде
et = Z{ {Щ (х«) [fi (xik) - f, (xik)]2}, G.7.1)
где Xik есть k-й образ /-го класса, Ni — количество образов, вхо-
входящих в этот класс, и ы,(х,*) —некоторые положительные весо-
весовые коэффициенты, поставленные в соответствие векторам об-
образов xik. Теперь задача сводится к определению для каждого
класса аппроксимирующей функции fi(x), минимизирующей
функцию ошибок G.7.1), /= 1, 2, ..., М.
Аппроксимирующую функцию /,(х) можно представить в
виде линейной комбинации базисных функций:
fi(x)=?ciJ4>u(x) = cfa(x). G.7.2)
1
304 Гл. 7 Предварительная обработка образов
В этом соотношении
Фп (х)
Фь (х)=
(х)
G.7.3)
Сц
G.7.4)
где mi — число членов, использованных для аппроксимации i-n
функции признаков, и {^-/(х)} —линейно независимые функции,
определенные на множестве дискретных наблюдений хп, х,-2, ...
..., \шг Из G.7.2) заключаем, что значение аппроксимирую-
аппроксимирующего функционала /,(х,*) зависит от коэффициентов с,-/, / =
= 1, 2, ..., mi, причем nii<LNi. Если выбрать т, равным Nu
то ошибка станет нулевой, однако число членов разложения
окажется равным количеству образов, входящих в класс со/.
Минимум е,- можно определить, взяв частную производную по
сц. Условие минимальности
= 0, /=1, 2,
Af, /=1, 2, ..., mh G.7.5)
порождает систему алгебраических уравнений для вычисления
коэффициентов разложения. Если базисные функции ^,/(х) вы-
выбраны и коэффициенты разложения вычислены, то аппроксима-
аппроксимация функции признаков /,(х) определяется из G.7.1).
Подставив выражения G.7.2) в G.7.1) и взяв частную про-
производную, получим
(xtk)
{xi
)
ik) .
G.7.6)
7.7, Аппроксимация функциями 305
Приравняв частную производную нулю и упростив выражение,
получим
fc=» I L /=• I J
= I Щ (x«) ^/ (xifc) /, (x«), /=1,2 M. G.7.7)
Запись G.7.7) в матричном виде приводит к следующему усло-
условию минимальности:
В,с, = у„ G.7.8)
где В,- — положительно определенная симметрическая матрица
размера гщ X пи с элементами
biq =Lut (xik) фи (\ik) ф1ч {xlk), G.7.9)
k=\
а уi — mj-мерный вектор с компонентами
Ni
¦o-a = E u, (xik) фп (x,k) ft (xik). G.7.10)
fei
Так как предполагалось, что базисные функции фц(х) на обра-
образах класса со,- линейно независимы, то нетрудно показать, что
матрица В,- имеет обратную матрицу. Поэтому коэффициенты
разложения можно определять как
с, = ВГ'у,, 1 = 1, 2, ..., Af. G.7.11)
Вычисление этих коэффициентов упрощается, если базисные
функции фц-(х) выбрать так, чтобы они были ортогональны
весовым коэффициентам м,-(х,-*). В этом случае базисные функ-
функции удовлетворяют условию
E «; (x«) ^,7 (x«) фц (xlk) = 0, /,4=^, G.7.12)
и матрица В,- становится, следовательно, диагональной, что су-
существенно упрощает определение обратной матрицы В. При
306 Гл. 7. Предварительная обработка образов
выполнении условия G.7.12) коэффициенты разложения при-
принимают вид
Ni
Z ui Ы) *ц (xik) f Ы)
сч = ^4г, G-7.13)
или, в векторной форме,
С/ = ВГЛь G.7.14)
где В,д— диагональная матрица с элементами
ьи = — " ¦ G-7-15)
? «i Ы) *?« Ы)
Если, кроме того, функции фц(\) выбраны так, что они орто-
нормированны относительно весовых коэффициентов, то
?//:==L 2^ U-t (х/&) фп {Xik) f i (Х(^), G.7.1Ь)
и так как при выполнении этого условия В = I, то из G.7.11)
следует
C< = IV/ = V/. G.7.17)
Описанный подход к выбору признаков основывается на тео-
теореме Вейерштрасса о приближении, которая, как указывалось
в п. 2.7.3, утверждает, что любую функцию, непрерывную в
замкнутом интервале, можно с любой заданной точностью рав-
равномерно приблизить в этом интервале некоторым многочленом.
В данном случае признаки каждого класса оказываются просто
векторами коэффициентов с,-, /=1,2, ..., М. Процесс выбора
признаков заключается в выборе достаточного числа коэффи-
коэффициентов с тем, чтобы ошибки G.7.1) были достаточно малыми.
Обращение к формулам G.7.13) или G.7.16) позволяет устано-
установить, что коэффициенты не зависят от размерности векторов
#,-(х). Следовательно, если сумма квадратов ошибок в точках,
соответствующих наблюдаемым образам, оказывается недоста-
недостаточно малой, то можно обратиться к аппроксимации высшего
порядка, введя дополнительный член cLm.+$i, т. + \(х), где
^j,m+i(x) —другая ортогональная или ортонормированная
функция. Более того, все коэффициенты Сц, Сц, ..., cim.'Опре-.
деленные ранее, остаются неизменными. Мы просто добавляем
новый член в аппроксимирующее выражение.
7.7. Аппроксимация функциями 307
Пример. Рассмотрим следующие наблюдения функций приз-
признаков двух классов, соответствующие указанным точкам выбо-
выборочных образов
I / t\ \ - — 9
2/' '-1 -1' ~ z
¦A
\3/
-4\
o] • /з(х2з) = — 1
Требуется с помощью описанных здесь методов найти аппрокси-
аппроксимации fi(x) и f2(x) функций признаков.
Первый шаг решения этой задачи состоит в выборе подхо-
подходящего множества базисных функций. Нетрудно убедиться, что
базисные функции
^п (х) = </>2i (х) = Xi и fi2 (х) = ф22 (х) = х2
ортогональны относительно весовых коэффициентов ы,(х,а)=1
при всех значениях k во всех классах (здесь через х\ и х2 обо-
обозначены первая и вторая компоненты вектора х = (лп, х2)').
Отметим, что в данном случае базисные функции каждого из
классов идентичны, а также равно их число. Как следует из
предыдущего, такая ситуация не обязательно будет иметь место
в общем случае. Использованные здесь базисные функции
имеют чисто иллюстративное значение.
Коэффициенты разложения определяются по формуле
G.7.13), поскольку ортогонализация базисных функций не про-
проводилась. Подставив в это соотношение весовые коэффициен-
коэффициенты Uj(xift)=l, получим следующие коэффициенты разложения!
ft=l 1
сп з 6 '
? Ф\1 ()
10 „ 9
-^g" > C21 = U, C22 = yf,
где, в частности, величина ^п(хп), согласно определению этой
базисной функции, равна значению первой компоненты век-
вектора Хц.
308 Гл. 7. Предварительная обработка образов
Аппроксимирующие функции для функций признаков нахо-
находим по формуле G.7.2):
U (X) = Сцфц (х) + С12ф12 (X) = -g-Х, — -|§- ХЪ
U (х) = спфп (х) + с^фя (х) = — -jy х2.
Отметим, что эти функции все еще обладают тем свойством, что
аппроксимирующая функция Д(х) неотрицательна при подста-
подстановке любого образа класса ©i и f2(x) отрицательна при подста-
подстановке любого образа класса ©2-
Ошибку, возникающую при использовании менее трех ба-
базисных функций для каждого класса, можно вычислить по фор-
формуле G.7.1). Следует, однако, отметить, что ошибка аппрокси-
аппроксимации не может непосредственно служить критерием качества
полученных функций признаков. Во многих случаях оказы-
оказываются приемлемыми достаточно большие ошибки аппроксима-
аппроксимации, поскольку они не ухудшают качества системы распознава-
распознавания образов. g
7.7.2. Метод стохастической аппроксимации
Если наблюдаемые в выбранных точках хщ, k=l, 2, ...
.,., ni, значения функции признаков f,(x) являются случайными
величинами, описываемыми плотностями распределения /?,(х) =
= p(x\o)i), то получение аппроксимирующей функции f/(x)
нельзя основывать на критерии, определяемом формулой
G.7.1). В этом случае удобно в качестве соответствующего кри-
критерия выбрать математическое ожидание некоторой выпуклой
функции отклонения аппроксимирующей функции /,(х) от ап-
аппроксимируемой функции fi(x). Подобный критерий ошибки
можно представить в виде
Gl[fl(x)-fl(x)]p(x\a>i)dx, i=\,2,...,M, G.7.18)
где Gi[fi(x) — f;(x)] — выпуклые функции типа |f/(x) — f;(x) |
и [fi(x) — fi(x)]2. Задача выделения признаков сводится к оты-
отысканию наилучшей аппроксимирующей функции f;(x), миними-
минимизирующей ошибки G.7.18).
При представлении функции признаков /,(х) в виде линей-
линейной комбинации базисных функций подстановка выражения
G.7.2) в G.7.18) приводит к
G|[/l(x)-c^(x)]p(x|©l)dx, / = 1,2, ...,Af. G.7.19)
7.7. Аппроксимация функциями 309
Реализация процедуры минимизации относительно коэффициен-
коэффициентов приводит к соотношению
Ж~ = \ §i Ui« - <*i Щ Фц « Р (х I ад dx = °- GJ-2°)
/=1, 2 М; /=1, 2, ..., ть
где
g. [/, (х) - <#, (х)] = -^Gt [ft (x) - cfo (х)].
Для каждого значения i формула G.7.20) определяет систему
mi уравнений для определения коэффициентов сц. Поскольку в
G.7.20) входит неизвестная плотность распределения, решение
можно найти методом стохастической аппроксимации (см. гл.6).
Воспользовавшись этим методом, получаем решение уравне-
уравнения G.7.20) в виде рекуррентной формулы
/=12 М- i = 1 2 т-
где Cij(k) — значение коэффициента сц на k-u шаге итерации,
d(k) — вектор коэффициентов на k-м шаге итерации и а* —
элемент последовательности {а*, /г= 1, 2, ...}, такой, что
оо оо ,
ak > 0, Е «ft = °°. Z «I < °° G.7.22)
(см. F.2.5)). Алгоритм G.7.21) обеспечивает выполнение некой
процедуры последовательных приближений, т. е. коэффициенты
сходятся по вероятности к решению уравнения G.7.20) при
стремлении числа итераций к бесконечности. Другими словами,
lim {? \си (k) - с* Г] = 0 G.7.23)
и
Prob{lim c.} (k) = c'u}= I, G.7.24)
где с*ц, i = 1, 2, ..., М; \ — 1, 2, ..., пгг —коэффициенты
решения. Начальные знамения коэффициентов, используемые в
рекуррентном алгоритме, выбираются произвольно.
Рассмотрим частный случай алгоритма G.7.21), когда в ка-
качестве функции d выбирается абсолютная величина отклонении
аппроксимирующей функции f,(x) от функции признаков f;(x),
т. е.
Gi Ui w - U Щ=I fi« - c#i (x) I- G-7-25)
310 Гл. 7- П редварительная обработка образов
В таком случае, поскольку
д
дс„
Gt [f, (х) - с#; (х)] = sgn [/((х„) - с; (Л) ф{ (х„)], G.7.26)
рекуррентный алгоритм принимает вид
ci/(A! + l) = C,./(A:) + aftsgn[c;(fe)^.(xi.ft)-/i.(xt.ft)]^,.(x>.ft). G.7.27)
Если в качестве функции G, выбирается квадрат отклонения
аппроксимирующей функции /,(х) от /,- (х), то
G, [/, (х) - f ((х)] == [/, (х) - с^(. (х)]2, G.7.28)
тл рекуррентный алгоритм принимает вид
сц (k + 1) = сц (k) + 2aft [/, (х/Л) - < (k) ф, (xrt)] ^4/ (xit). G.7.29)
Эти рекуррентные алгоритмы являются удобной схемой для
определения приближенных статистических функций признаков
по предъявленной обучающей выборке.
7.7.3. Ядерная аппроксимация
Статистические функции признаков можно определить по
предьявленной выборке образов с помощью аппроксимации яд-
ядром. Можно показать, что аппроксимирующая функция f(-(x)
для статистической функции признаков /, (х) определяется вы-
выражением
f*(x)= \ Kin(x,y)f(y)dy, G.7.30)
где /Cin(x. у) — известное ядро, которое удовлетворяет следую-
следующим условиям:
ь
ь
J/C,«(x, y)dy=l,
<б) lim /Сг„(х, у) = б(х, у) (дельта-функция),
<в) /С,-„(х, у)>0,
(г) /С,„(х, у) = /С,„(У, х). G.7.31)
К ядрам, удовлетворяющим этим условиям, относятся ядро
Фейера, ядро Джексона и ядро Вейерштрасса. На основании
усиленного закона больших чисел аппроксимирующую функцию
f,(x) можно оценить, используя независимо выбранные образы,
выражением
»(x, x,), G.7.32)
7.8. Концепция дивергенции 311
причем fik(x) сходится к /,-(х) с вероятностью 1 при 4->оо и
f,(x) сходится к fi(\) равномерно при п->оо.
Качество аппроксимации по формуле G.7.30) зависит от
свойств ядер Ki/i(x, у). Для обеспечения аппроксимации высо-
высокого качества ядро /w«(x> у) следует «настраивать» на значения
fi(y) ПРИ у = х- Три упомянутых ядра позволяют делать это.
7.7.4. Использование функций признаков при классификации
Аппроксимирующие функции f;(x), t=l, 2, ..., М, полу-
полученные любым из рассмотренных методов, могут быть положены
в основу процесса классификации и распознавания. После того
как по обучающей информации определены функции призна-
признаков, простую схему классификации можно реализовать следую-
следующим образом: для образа с неизвестной классификацией х*
вычисляются значения функций f,(x*), i= 1, 2, .... М, и предъ-
предъявленный образ относят к тому классу, функция признаков
которого принимает наибольшее значение. Успешность приме-
применения этой схемы зависит от «взаимоотношений» свойств от-
отдельных классов и, конечно, от числа членов, использованных
при аппроксимации функций признаков.
7.8. КОНЦЕПЦИЯ ДИВЕРГЕНЦИИ
Дивергенция') представляет собой меру «расстояния» или
несходства между двумя классами. Его можно использовать
для ранжировки признаков и оценки эффективности разделения
классов. В данном параграфе мы вводим понятие дивергенции
и обсуждаем возможности его использования для определения
эффективности выбора и упорядочения признаков.
Пусть вероятность появления образа х при условии его при-
принадлежности классу ы,- есть р,(х) = р(х|со,) и вероятность появ-
появления образа х при условии его принадлежности классу ю/ есть
р;-(х)= р(х|ю/). Тогда различающую информацию для ац по
отношению к со/ можно измерить логарифмом отношения правдо-
правдоподобия:
Mi/ = lnAg. G.8.1)
Средняя различающая информация для класса со,- определяется
выражением
\i(x)\n^dx. G.8.2)
') Помимо термина «дивергенция» в литературе встречается также термин.
«расхождение» — Прим. перев.
312 • Гл. 7. Прсдварительная обработка образов
Информацию, отличающую класс ы, от класса со,, можно
измерить логарифмом отношения правдоподобия
"/<=1п7тЙ- G-8-3)
Средняя различающая информация для класса со/ определяется
выражением
I(j,i)=\pj(x)\n^Ldx. G.8.4)
Полную среднюю информацию для различения классов со,- и со/
часто называют дивергенцией и задают как
/*/ = / d, /) + / (/, i) = \ [Pi (x) - р, (х)] In ^~ dx. G.8.5)
X '
Допустим, что заданы два класса, характеризуемые двумя
n-мерными нормально распределенными совокупностями
N(m,,Ct) и ЛГ(шу, С,),
где т, и т/ — векторы математического ожидания и С,- и С,—
ковариационные матрицы размера п~Х.п. Плотности распреде-
распределения совокупностей определяются выражениями
Pi (х) = ряу'ЧсГ''ехр [~ 7(х ~ mY сг'(х ~ т)] G-8'6)
p.(x) = ~ - ехр Г- - (x - m,)' C/ (x - my)l, G.8.7)
Ht {2л)пи | С/Г'2 L 2 ' J
а логарифм отношения правдоподобия
- -1 tr [СГ1 (х - tn«) (x - m,)'] +
_i ' r A— if 1~ /y in Л ^v tr\ \*~\ C7 Я, Я,\
Средняя различающая информация для этих двух классов равна
/ (г, /) == ^ pi (хи х2, ..., хп) In ' '' х2' "" " dxx dx2 ... dxn =
1 tr [СГ1 (tn/ - my) (m, - tn,-)']. G.8.9)
7.8. Концепция дивергенции 313
Следовательно, дивергенция для этих двух классов есть
hi — \ [Pi (*i> х*> •¦•' хп) — Pi (хп *2 хп)] X
Х2 хп)
+ 1 tr [(СГ1 + CTl)(mt - tny) (mt - m,)']. G.8.10)
Особый интерес представляют два частных случая.
Случай 1. Равенство ковариационных матриц: С; = Су= С.
Из G.8.9) заключаем, что
/ (/, }) = у tr [С (ш, - шу) (ш, - ш/)'] =
= Ytr(C~'SS')=yS'C-1S, G.8.11)
hi = tr [С (m,- - tny) (tn, - tn;)'] = S'C-'S, G.8.12)
где 6 = rtii — ttij. Отметим, что произведение 6'C~'S представ-
представляет собой обобщенное расстояние Махаланобиса.
Для одномерной нормально распределенной совокупности,
где (Xj и ni — математические ожидания и а2 — дисперсия.
Случай 2. Равенство математических ожиданий совокупно-
совокупностей: т, = ту, 6 = 0.
Средняя различающая информация и дивергенция опреде-
определяются выражениями
соответственно.
r1]-n
G.8.14)
314 . Гл. 7. Предварительная обработка образов
Дивергенция обладает следующими полезными свойствами:
1) 1ц > 0 при i ф /;
2) Jij = О при i = j;
з) /,7 = //<;
4) при независимых измерениях дивергенция /,-/ аддитивна:
m
hi {Х\, х2, ..., xm) = 2j hi (XkY>
5) добавление результата нового измерения никогда не при-
приводит к уменьшению дивергенции:
hi(x\, x<i, ..., хт) ^ hi(xu %2, ¦¦•, хт, хт+\).
Аддитивность дивергенций означает, что при независимости
измерений дивергенция, определенная по результатам т изме-
измерений, равна сумме т дивергенций, определенных по результа-
результатам каждого отдельного измерения. Это свойство можно ис-
использовать для оценки относительной важности каждого из
выбираемых признаков. Признаки, которым соответствуют
большие значения дивергенции, более важны, так как они несут
больше различающей информации. Таким образом, ранг важно-
важности каждого признака можно установить, исходя из значения
соответствующей ему дивергенции. Всяким признаком, вклад
которого в общую дивергенцию невелик, можно пренебречь.
Концепция дивергенции предоставляет в наше распоряжение
удобный способ упорядочения и выбора признаков.
Ниже будем использовать понятие дивергенции для изучения
влияния выбора признаков на качество системы распознавания.
Начнем с установления связи между вероятностью ошибки и
дивергенцией, а затем построим рекуррентные соотношения,
обеспечивающие выбор признаков, исходя из условия мини-
минимальности дивергенции при заданной вероятности ошибки.
В гл. 4 было показано, что при выборе функции потерь, при-
принимающей значения 0 или 1, принадлежность образа х классу со,-
по критерию минимальной вероятности классификационной
ошибки определяется условием
р(со,)р(х\щ)>р (©;) р (х |©/) G.8.15)
для всех /ф i. В случае равной априорной вероятности появле-
появления образов обоих классов разделяющая граница определяется
уравнением
p,(x) = P/(x). G.8.16)
Для нормально распределенных совокупностей с равными кова-
ковариационными матрицами уравнение G.8.8) дает следующую
разделяющую границу:
иц = х'СГ1 (tnt - mj) - | (m,- + т/)' (Г1 (т, - ту) = 0. G.8.17)
7.8 Концепция дивергенции 315
Решающее правило таково: х е со*, если иц > 0, и хеш/, если
иц < 0.
Вероятность ошибки выражается как
et! = yP(Uij > О Iоэу) + ^Р(и'1 < u |ю^). (/.8.lo)
В гл. 4 было показано также, что
—^=ехр(— —"Wr/, G.8.19)
A/2) лЛ7/
где
гц = (т. _ т/)' с~' (mt - т,) = 8'С~'§ G.8.20) •
обозначает расстояние Махаланобиса между плотностями рас-
распределения р,(х) и р/(х). Сопоставив формулы G.8.12) и'
G.8.20), для равных ковариационных матриц получаем
r,, = Jth G.8.21)
т. е. дивергенцию классов w,- и ы,-. Итак, дивергенция является
подходящей мерой расстояния для пар нормальных распреде-
распределений и может служить оценкой сложности разделения двух
классов. Если ковариационная матрица С — единичная, то ди-
дивергенция /;/ характеризует квадратичное расстояние между
математическими ожиданиями р, (х) и Ру(х). Из G.8.19) сле-
следует, что вероятность ошибки е-ц есть монотонно убывающая
функция расстояния Махалаиобиса гц и что функция, связы-
связывающая гц с вероятностью ошибки ец, есть одномерная плот-
плотность нормального распределения с нулевым математическим
ожиданием и единичной дисперсией.
При выборе т признаков их эффективность можно оценить
через rij(m). При введении дополнительного признака мера эф-
эффективности определяется как п,(т-\- 1). В таком случае при-
прирост эффективности от введения некоторого признака опре-
определяется выражением
гц(т+ \) — гц{т).
Пусть xm+i — переменная, представляющая введенный дополни-
дополнительно признак и имеющая математическое ожидание ц,- или ц/
и дисперсию а2; пусть также v — вектор ковариаций случайной
величины xm+i и компонент вектора х. Новыми векторами мате-
316 Г л 7 П редварительная обработка образов
математического ожидания и новой ковариационной матрицей
в таком случае будут
/ m, \
G.8.22)
G.8.23)
¦ч /
/С v \
Cv=(v, ff2J. G.8.24)
Обратная матрица для Cv есть
, /сг' + ре-'р' -ре~'\
, /сг + рр ре
где
Новой оценкой эффективности системы признаков является
П, (т + 1) = (т? - т?)' С71 (т/ - mj) =
с ч-рв~'р' -ре~'
что после проведения упрощений сводится к
г„ (ш + 1) = rl} (m) + ]• [fa - ix,) - (т{ - т/)'р]2. G.8.27)
Следовательно, прирост эффективности определяется как
Г(ц, — ц,) — (ш, — ш,)' C~'v"l2
Г1,(т+1)-г„(т)= 1[ ' [ ' '* L. G.8.28)
о - v С v
Если дополнительно введенный признак хт+\ не зависит от
остальных признаков х\, лг2, • ••. хт, то v = 0 и, следовательно,
G.8.29)
В предыдущих разделах число признаков т предполагалось
известным. Проведенный анализ позволяет следующим образом
построить рекуррентное соотношение для определения значения
7Я Концепция дивергенции
317
т, удовлетворяющего требованиям к вероятности ошибки. Мат-
Матрица преобразования А имеет вид
где в], ег, ..., ет — ортогональные собственные векторы, соот-
соответствующие т наименьшим характеристическим числам А,ь
ta, •••, hm Ковариационной матрицы С. Было показано, что
m* = Am,
С* = АСА' =
,0 0 ... А
Таким образом,
тц (т) = (т; - т)) (С) (т* - mj) =
, G.8.30)
k=i
где mik и т*1к — компоненты преобразованных векторов матема-
математических ожиданий mt и rnji соответственно. Из G.8.30) сле-
следует, что
G.8.31)
Так как
mi (m+l) =
TO
Итак, искомое рекуррентное соотношение имеет вид
.. . е„ . ,65 е.
ет+1
причем
e' e
G.8.33)
G.8.34)
318 Гл. 7 Предварительная обработка образов
где ei — собственный вектор, соответствующий наименьшему
характеристическому числу ковариационной матрицы С. Ис-
Используя в качестве отправной точки оценку эффективности наи-
наиболее значимого признака, оценки эффективности дополнитель-
дополнительных признаков, удовлетворяющих требованиям к вероятности
ошибки, можно получить, используя рекуррентное соотношение
G.8.33). При определении оценок эффективности мы воспользо-
воспользовались кривой, приведенной на рис. 4.4; она представляет связь
вероятности ошибки с расстоянием.
7.9. ВЫБОР ПРИЗНАКОВ НА ОСНОВЕ
МАКСИМИЗАЦИИ ДИВЕРГЕНЦИИ ')
Соответствующий подход к выделению признаков заклю-
заключается в порождении множества признаков, свойства которых
позволяют максимизировать меру различия между классами.
Если выделено множество признаков, которое после примене-
применения с помощью соответствующего преобразования к двум или
нескольким совокупностям образов обеспечит получение мно-
множества преобразованных образов, отличающееся более замет-
заметным разделением совокупностей образов различных классов, то
такие признаки можно рассматривать как характеристики, вы-
выявляющие различия совокупностей. Эта задача рассмотрена с
точки зрения использования матричного преобразования для
получения таких преобразованных образов, которые обеспечи-
обеспечивают максимизацию расстояния между множествами при сохра-
сохранении постоянства внутримножественного расстояния или соот-
соответственно суммы расстояний между множествами и внутримно-
жественных расстояний. Разделение классов, однако, можно
оценивать не евклидовым расстоянием, а иными величинами.
Более общим понятием расстояния является рассмотренная в
§ 7.8 дивергенция.
Рассмотрим две совокупности образов он и сог, характери-
характеризующиеся плотностями распределения р\ (x) = p(x|coi) и
рг(х) = р(х|о)г) соответственно. Дивергенция между этими
двумя классами определяется как
Pi(x)-Mx)]ln-j??Idx. G.9.1)
Дивергенция должна быть использована в качестве функции
критерия при порождении оптимального множества признаков.
Как и в § 7.5, нам требуется матрица преобразования А, при-
') Данный раздел написан по материалам сборника «Computer and Infor-
Information Sciences» — II, J. Т. Той, ed. Academic Press, New York, 1967.
7.9. Максимизация дивергенции 319
водящая к преобразованным образам меньшей размерности.
Эти преобразованные образы определяются уравнением
У = Ах, G.9.2)
где у есть m-мерный вектор, х есть n-мерный вектор и А — мат-
матрица размера иХ". строками которой являются линейно неза-
независимые векторы &k, k=l, 2, ..., т < п. Дивергенция преоб-
преобразованных образов определяется выражением
Допустим, что образы классов «i и сог подчиняются нормальным
распределениям N(mu С\) и N(m2, Сг) соответственно. Из
G.5.6) и G.5.9) следует, что векторы математического ожида-
ожидания после преобразования определяются формулами
m* = Am,, т* = Ат2, G.9.4)
а ковариационные матрицы —
q = АС1А/, С; = АС2А'. G.9.5)
В таком случае дивергенция преобразованных совокупностей
определяется как
7 G-9.6)
где
S* = AS = A(m1-m2) = m;-m;. G.9.7)
Так как след матрицы равен сумме ее характеристических чи-
чисел, то
т
7'2=т Z (lk + Л* ^ ~ т + т Km+l + т %т+ь G-9-8)
ft-1
где ^ — характеристические числа матрицы (Cj) (С*), Хт+1 —
характеристические числа матрицы (С*) S*(S*)' и Ат+2 —харак-
—характеристические числа матрицы (С2)"' 8* (8*)'.
Дифференциал от G.9.8) есть
т
Y A * ') dX + dl + 4 dX G.9.9)
320 . Гл. 7. Предварительная обработка образов
Поскольку Xk — характеристические числа матрицы (С*) (С*),
то они удовлетворяют соотношению
(АС2А')(АС,А')еА = ЯАеА G.9.10)
или
(АС1А')еА = й,*(АС2А/)е*, G.9.11)
где ek — собственный вектор матрицы ((^"'(С*), соответствую-
соответствующий характеристическому числу Xk. Дифференциал от G.9.11)
равен
(dA) (С,А' - ЯАС2А') eft + (АС, - Я,АС2) (dA') h =
= - (АСА' - АААС2А') dek + (dkk) АС2А'еА. G.9.12)
Так как матрицы С* и С*; — симметрические, то собственные
векторы взаимно ортогональны относительно С*г Можно опре-
определить полное множество собственных векторов и записать
дифференциал dtk как
m
de*=Zc/te,, G.9.13)
где собственные векторы е;. нормированны относительно С*,
т. е. еу'С*е;= 1.
Подстановка выражения G.9.13) в G.9.12) дает
(dA) (dA' - AftC2A') ek + (AC, - AAAC2) (dA') tk =
m
= Z cik {X, - K) AC2A'ey + AC2A'eft {dXk). G.9.14)
/=-1
Умножив G.9.14) на tk и использовав условия
e'fcAC2A'eft=l, e^AC2A'efe = 0, j Ф ft, G.9.15)
получим
d\ = t'k (dA) (C,A' - AftC2A') efc + t'k (ACL - Я,АС2) (dAO e, =
= 2e'k (dA) (C,A' - A,C2A') ek. G.9.16)
Дифференциалы dkm+i и d'Km+2 можно определить анало-
аналогично. Так как Xm+\ — характеристическое число матрицы
(С)"' 5* (8*)'» то оно Удовлетворяет соотношению
(ASS'A') em+1 = Xm+1 (AC,A') em+I. G.9.17)
Дифференциал от G.9.17) равен
(dA) (SS'A' - Am+1C,A') em+1 + (ASS' - ^m+IAC,) (dA') em+1 =
= - {ASS'A' - *m+1ACiA') dem+I + AC,A'em+1 (dXm+l). G.9.18)
7.9. Максимизация дивергенции 32!
Так как матрицы С[ и [S* (8*)'] — симметрические, то все соб-
собственные векторы взаимно ортогональны относительно С*. От-
Отметим, однако, что ранг матрицы [8* (8*)'] равен 1 и, следова-
следовательно, ранг матрицы (С*) [8* (8*)'] также равен 1. Можно
найти полное множество собственных векторов em+i, Y21. ¦¦¦> Y*n
матрицы (С*)"' [8* (8*)']. Эти собственные векторы ортогональны
относительно С*, так что
= 1, / = 2, 3, .... от. G'9Л9)
Характеристические числа матрицы (С*) [8* (8*)'], соответ-
соответствующие пополненным собственным векторам 7*1, k = 2, 3, ...
..., от, равны нулю. Итак, дифференциал dem+i можно пред-
представить как
m
Л~ r ~ _L.V/>m C7Q 9flY
4=2
Подставив G.9.20) в G.9.18) и упростив полученное выражение,
(получим
d\) (85'А' - Am+1C,A') em+, + (ASS' - A,m+IAC,) (dA') em+l =
AC,A'em+1 (dAm+1). G.9.21)
При выводе последней формулы мы воспользовались G.9.17) и
тем фактом, что характеристические числа, соответствующие
собственным векторам ykl, равны нулю. Умножение G.9.21) на
em+i и использование G.9.19) приводит к
(88'А' - Ят+,С, А') ет+, +
= 2ет+| (dA) (88'А' - Ят+1С,А') ет+1. G.9.22)
Аналогичным образом находим
dK+2 = 2<,+2 (^А) (88'А' - Ят+2С2А') ет+2. G.9.23)
322 • Г л 7 П рсдаарительная обработка образоп
После подстановки выражений G.9.16), G.9.22) и G.9.23J
в G.9.9) получаем
m
dfvi = Е A - ^k2) e'* (dA) (С,А' - Я*С2А') efe +
+ e'm+,(dA)ES'A'-Am+1C1A')em+1 =
= С, (dA) (88'A' - Ят+2С2А') ет+2. G.9.24)
Использование понятия следа матрицы позволяет преобразовать
последнее выражение к виду
G.9.25)
где
m
= E (l -A,iT2)(C1A/-A*C2A/)e*ei +
ft=i
+ (88'A' - Xm+1C, A') em+1e;+1 + (88'A' -
G.9.26)
Поскольку значение d\ произвольно, необходимое условие
экстремальности /*,, состоит в равенстве матрицы G нулю. По-
Полученные результаты можно кратко сформулировать так.
Если две совокупности образов coi и со2 подчиняются нор-
нормальным распределениям N{n\\, Ci) и N (т2, С2) соответственно
и если эти образы с помощью преобразования у = Ах отобра-
отображаются в пространство меньшей размерности, где у есть т-мер-
ный вектор, х есть n-мерный вектор, т < п и А — матрица раз-
размера т X п, строками которой являются линейно независимые
векторы признаков а*, то необходимое условие достижения ди-
дивергенцией ]\2 экстремального значения состоит в выполнении
для матрицы А соотношения
Z 0 - A-*2) (CiA' - Й,*С2А') е*е* +
+ (88'A'-A,m+1C1A') em+[e;+1 + E5'А' - Ят+2С2А') ет+2е'т+2 = О,
где "Kk и Ск — характеристические числа и собственные векторы
матрицы (AC2A')-'(ACiA'); %m+u em+i и Хт+2, еш+2 — характе-
характеристические числа и собственные векторы матриц (С*)~1 (А88'А')
и (С*) (А88'А') соответственно; 8 = Ш| — т2.
7.9. Максимизация дивергенции 323
Ниже обсуждаются три частных случая.
Случай 1. Ci = С2 = С и ni] Ф т2.
При равенстве ковариационных матриц Ct и Сг уравнение
G.9.11) принимает вид
1-М)е* = 0, G.9.27)
откуда следует, что >.«. = 0. В таком случае G.9.26) сводится к
G = 2 (88'А' - Я,т+1СА') е„+,е;+1. G.9.28)
Положив т = 1 и А'= а, вектор е,„и можно свести к скаляр-
скалярной величине <?; выражение G.9.28) при этом примет вид
G = 2(88'a- Аш+1Са)<?2. G.9.29)
С учетом формулы G.9.17) можно показать, что
*т+. = -а5^г- G-9.30)
Следовательно,
G.9.31)
ii необходимое условие экстремальности дивергенции принимает
вид
(?) Са G-9-32>
или
(-И (^), G.9.33)
откуда следует, что а — собственный вектор матрицы O'fifi' и
соответствующее характеристическое число равно (а'66'а)/
/(а'Са). Следовательно, для экстремальности дивергенции за-
задаем А' равным а — собственному вектору матрицы С~'66'. Со-
Соответствующая дивергенция равна
hi = \ tr (СГ'С2 + С2"'С,) - п + 4 (СГ' + С2"') 55' = tr (C-'88'),
G.9.34)
т. е. ненулевому характеристическому числу матриц С~'66'.
С учетом G.9.6) получаем для преобразованных образов
4 = Ят+1, G.9.35)
т. е. согласно G.9.30) эта величина равна ненулевому харак-
характеристическому числу матрицы О'бб'. Следовательно, в данном
частном случае переход от векторов х к векторам у не приво-
приводит к потере информации, так как Jl2 = l\r
324
Гл. 7. Предварительная обработка образов
Случай 2. Ci ф С2 и mi = tn2.
Если векторы математического ожидания равны, то 6 = 0 и
%т+] = %т+2 = 0. Таким образом, соотношение G.9.26) приво-
приводится к
т
G = ? A - ЯГ2) (С,А' - А*С2А') е*е*.
G.9.36)
Если строками матрицы преобразования А служат собственные
векторы матрицы С^'Сь нормированные относительно Сг, то
можно показать, что
0
G.9.37)
АС2А' = I,
G.9.38)
где а&, ft = 1, 2, ..., m, — т характеристических чисел мат-
матрицы С2~'Сг При этом G.9.11) принимает вид
G.9.39)
Следовательно,
и, кроме того,
О
О
G.9.40)
G.9.41)
7.9. Максимизация дивергенции 325
причем 1 появляется в k-м элементе. Это свойство собственного
вектора е* приводит к
А'е* = аь G.9.42)
где а* есть k-ц столбец матрицы А'. Поэтому G.9.36) прини-
принимает вид
т
G = Е 0 - Xk2) (С,а* - ЪкС2ък) е*. G.9.43)
4 = 1
Так как Я,* = а*, и вектор а* удовлетворяет соотношению
Cia* = >.ftC2aft, то очевидно, что G — нулевая матрица и условие
экстремальности выполняется. Из G.9.8) следует, что диверген-
дивергенция /*2 принимает максимальное значение, если собственные
векторы матрицы C^'Cj, соответствующие характеристическим
числам а/г, для которых выполняется условие
(а* + aiT1)>(<*/ +а/"'). /=1. 2, .... я; * = 1, 2, .... т, /#=?,
G.9.44)
использованы в качестве строк матрицы преобразования А.
Случай 3. С] ф С2 и mi Ф т2.
В общем случае решение уравнения G = 0 вызывает суще-
существенно большие трудности. Воспользовавшись G.9.25), по-
получаем
d/;2 = tr[(rfA)G] =
. G.9.45)
Таким образом, вектор (g[, g'2 g-^) есть градиент дивер-
дивергенции /*2 относительно векторов признаков a*, k= \, ..., т.
Если, следовательно, увеличить А на GG, где G — некоторый мно-
множитель, обеспечивающий сходимость, то дивергенция /*., уве-
увеличится. Можно воспользоваться методом наискорейшего подъ-
подъема и решать следующую систему разностных уравнений:
A(s+l) = A(s) + 8G(s), G.9.46)
где s — порядковый номер шага итерации.
Пример. В качестве простой иллюстрации применения ре-
результатов этого раздела рассмотрим образы, представленные
326 Гл. 7 Предварительная обработка образов
на рис. 7.1. Так как для этих образов выполняются условия
Ci = С2 = С и mi=?bm2, то воспользуемся результатами слу-
случая 1.
В § 7.5 было показано, что
3'
1
следовательно,.
Ковариационная матрица равна
1 V
3 -1
1-1 3/
а ее обратная матрица
В таком случае матрица С~'6б' есть
Нейулевое характеристическое число и соответствующий соб-
собственный вектор матрицы C~'66' равны
Этот собственный вектор используется для формирования мат-
матрицы преобразования:
А = (-1 1 1).
7.10 Выбор двоичных признаков 327
Применение преобразования у = Ах к заданным образам при-
приводит к следующим одномерным изображениям:
У12 - ~ 1 )'22 = 1
Уп = 0 у23 = 2
У,4 = 0 у24 = ]
Эти образы отличают те же кластеризационные свойства, кото-
которые были обнаружены в § 7.5. Кроме того, очевидно, что пре-
преобразование не приводит к перекрытию любых двух образов,
принадлежащих разным классам. |
7.10. ВЫБОР ДВОИЧНЫХ ПРИЗНАКОВ
Признаки, определяемые при помощи методов выбора, раз-
развитых в предыдущих разделах, являются величинами, прини-
принимающими в принципе любое действительное значение. В этом
параграфе рассматривается задача выделения и выбора двоич-
двоичных признаков но предъявленной выборке образов.
Наиболее важные аспекты выбора двоичных признаков в
отличие от рассмотренных выше методов не связаны с пониже-
понижением размерности. Наоборот, основная задача заключается в
выборе минимального набора двоичных признаков той же, что
и образы, размерности, который окажется достаточным для вос-
восстановления исходных образов с минимально возможным коли-
количеством ошибок. Хотя в общем виде эта задача до сих пор не
решена, приведенные ниже алгоритмы представляют разумный
(хотя и не всегда приводящий к полному успеху) подход к по-
порождению хороших двоичных признаков. Как будет показано
ниже, эти алгоритмы предназначены для определения минималь-
минимального набора признаков, общего для некоторой группы образов.
7.10.1. Последовательный алгоритм
Рассматриваемый здесь алгоритм обеспечивает порождение
одного двоичного признака в каждом цикле итерации по предъ-
предъявленным образам. Процедура в основном сводится к заданию
переменной пороговой величины и изменению порожденного
признака, как только значение порога будет превышено. Алго-
Алгоритм вводится разбором на частном примере.
328
Гл. 7. Предварительная обработка обращая
Рассмотрим три двоичных образа, представленных нз
рис. 7.3, а: пезаштрихованные квадраты соответствуют 0, а за-
заштрихованные 1. Этот способ представления выбран исключи-
исключительно для удобства объяснений. При необходимости образы
f,@)
ш
ш
ж
Щ
W,
Ж.
ш
щ
ш
1
щ
щ
щ
81
1
ш
щ
m
ш
ж
ш
ш
а1
Рг
62
f,B)=f,H)nP2
ш
ш
1
щ
ж
ш
щ
62
ш
щ
аг
щ
53
1
р
и.
83
щ
1
аЗ 6U 64
/ ¦•.". а 6 в
Рис. ?<3. Иллюстрация принципа действия последовательного алгоритма.
можно представить в векторной форме, выбрав соответствую-
соответствующим образом элементы двоичных матриц. Поскольку ниже эти
образы будут интерпретироваться как множества, то для их
обозначения будут использоваться символы Р,- вместо привыч-
привычной векторной записи х,-.
Процедура начинается с произвольного выбора пороговой
величины 0, рассматриваемой ниже, и признаков, состоящих,
как это видно из рис. 7.3, бив, исключительно из единиц..
Признак /i порождается на 1-й итерации по предъявленным об-
образам, признак f2 — на 2-й итерации, признак /* — на k-н итера-
итерации и т. д.
Порождение первого признака происходит так. Пусть f, @) —
исходное значение признака fu a || /i @) П Р\ II — „расстояние"
между f 1 @) и Р[, определяемое как число единиц в пересечении
7.10 Выбор двоичных признаков 329
f 1 @) и образа Р\. В таком случае при II/i @)f| ^i II 5s в прини-
принимается /i(l) = /i@)fl Pi', в противном случае /i(l) = /i@). Вы-
Выбрав в данном случае 0 = 3, с помощью рис. 7.3, al и 61, уста-
устанавливаем, что || /i @)П Р) || = 6 > 0. Поэтому, как показано на
рис. 7.3,62, принимаем f\ A) = /i @)fl Pi. Так как пересечение
/i(l) и образа Р2 равно II/i A)П ^2II = 3 = G, то, как показано
на рис. 7.3,63, принимаем /i B) = Ы1)П Рг- Очевидно, что на
следующем шаге итерации || /iB)f] Рз| = 0 < 0; поэтому признак
не изменяется, т. е. /iC) = /[B), как показано на рис. 7.3,64.
Этот рисунок представляет окончательное значение признака /ь
так как к этому моменту просмотрены уже все предъявленные
образы.
Для определения принака f2 процедура полностью повто-
повторяется, за исключением того, что перед каждым сравнением ве-
величина порога вычисляется заново. Первое новое значение по-
порога определяется выражением 6* = 0 + НМЗ)П [Ы0)П Pi] II.
где fiC) представляет окончательное значение признака /ь
В таком случае при !l/2@)f) PJI 5= 0* принимаем /2A) = /2@)П
Г)Рь в противном случае f2 A) = /2@). В нашем случае 0* =
= 3 + 3 = 6; так как ||/2@)П ЛИ = 6 = 9*, то принимаем
Ы0 =/г(О)П ^1, как показано на рис. 7.3, в2. В основе подоб-
подобного увеличения порога лежит желание избежать дублирования
признаков. Перед выполнением очередного сравнения следует
вычислить новое значение порога. Воспользовавшись скоррек-
скорректированным значением признака /2, определяем новое значение
пороговой величины: 0* = 0 + || f, C)f| [МОП РЛ II = 3 + 3 = 6.
Поскольку || f2(l)f) Р2II = 3 < 9*, то, как показано на рис. 7.3, вЗ,
принимаем /2B) = f2(l). И, наконец, 0* = 0 + || /, C)П [/гB)П
П Р3] || = 3 + 0 = 3; теперь, поскольку || f2 B) П Р3II = 3 = 0*,
принимаем /гC) =/2B)П Рз, как показано на рис. 7.3, в4. Вни-
Внимательно изучив образы, можно убедиться в том, что признаки
1\ и /г, найденные в процессе реализации описанной процедуры,
представляют собой минимальный набор признаков, необходи-
необходимый для безошибочного восстановления заданных образов.
Последовательный алгоритм допускает следующее формаль-
формальное представление. Признак на г-м шаге k-w. итерации по мно-
множеству ./V двоичных образов Pi, P2, ..., Рл/ определяется так:
/а = ( fk {i ~ ° П Р" 6СЛ" |! h {l ~ l) П Pi l! > G*' G
I fk(i— О В противном случае,
/=1, 2, ..., Л',
где
ll- G-10.2)
330 Гл. 7. Предварительная обработка образов
Остались открытыми два вопроса, связанные с этим алго-
алгоритмом.
1) Каким образом выбирается значение пороговой вели-
величины 0?
2) Сколько признаков должно быть порождено? К сожале-
сожалению, к настоящему времени ответ ни на один из этих вопросов
в общем случае неизвестен. Поскольку, однако, при решении
реальных задач проблема заключается в выборе значения по-
порога 0, то часто оказывается полезным повторить описанную
процедуру с несколькими значениями порога 0 и выбрать зна-
значение, приводящее к наилучшим результатам.
7.10.2. Параллельный алгоритм
Вместо того чтобы в каждой итерации определять один
признак, можно одновременно определять с помощью парал-
параллельной процедуры несколько признаков. Как и предыдущий, •
рассматриваемый ниже параллельный алгоритм начинает рабо-
работать с одним признаком, однако, как только возникает необхо-
необходимость использовать новые признаки для восстановления объ-
объекта, предъявленного на данном шаге итерации, они немедленно
вводятся. После предъявления образа и внесения изменений
в признаки проводится проверка достаточности объединения
новых признаков для восстановления рассматриваемого образа.
Если результат проверки положительный, то предъявляется сле-
следующий образ. Если же нет, то порождается новый признак,
тождественно равный рассматриваемому образу, после чего
предъявляется следующий образ. Поскольку параллельный ал-
алгоритм— процедура более сложная, чем его последовательный
аналог, целесообразно вначале описать его в общем виде, а за-
затем проиллюстрировать механизм его действия на примере.
Рассмотрим Л' двоичных образов Рь Рг, ..., Ры и допустим,
что па /-м шаге итерационного процесса работа ведется с / при-
признаками МО. Ы0. ¦••> МО- При предъявлении образа Pi+1
новые признаки определяются так:
1. Mi+1) = МОП^/+ь если НМ0ПРм11>0. В против-
противном случае М' + 1) = М0-
2.'Ы/+1) = Ы/)ПЛ--м, если || МОП/V, || ^0 + 02. В про-
противном случае f2(i' + 1) = Ы0- Значение параметра О2 опреде-
определяется как 02= IIM/+ 1I1, если а) || МОП Р-'-и II ^ б » б) при-
признак fi(i-\-l) поглощается признаком ^@, т. е. fi(i'-j-l)^
г/2@- В противном случае 02 = 0.
3. В общем случае f/(i"+1) = МОП Р<ч-1. есл" II МОП
П Pi+i II 5= 0 + 0/. В противном случае /;('-(- 1) = МО- Значение
7.10. Выбор двоичных признаков 331
параметра 0( определяется из выражения
е,= ? II/*('+ 1I!
k
(при &</), где член ||/*(( + 1I| учитывается при суммирова-
суммировании только в тех случаях, когда а) || /*(/)Л Pi+i II ^ 6 + 9*
иб) /*(»+1) = МО.
После определения значений у новых образов формируется
объединение образов, подвергавшихся изменению. Если это
объединение дает образ P,-+i, то предъявляется следующий
образ. В противном случае порождается новый образ />н = P'+i
и затем предъявляется новый признак.
Для иллюстрации работы параллельного алгоритма вос-
воспользуемся образами, представленными на рис. 7.4, а. Примем,
что 0 равно 3, и выберем в качестве начального признака
/,(!) = Р,. После этого предъявляется признак Р2. Так как
|| /i A)П Рг II = 6 ~> 8, то, как показано на рис. 7.4,6.2, полагаем
f] B) = /i A)Л Рг- Поскольку этот признак позволяет восстано-
восстановить образ Р2. предъявляется очередной образ. Так как
||fiB)nP3ll = 4 > 0, то, как показано на рис. 7.4,63, полагаем
/iC) = f\ B)П Р3. Образ Р3, однако, не удается восстановить
с помощью одного признака fiC), поэтому порождается новый
признак /2C) = Р3, как показано на рис. 7.4, el. Далее, обнару-
обнаружив, что ||/,CH^4 II = 3 = 6, полагаем frD) = fiC)fl Р4. Так
как ||/iC)n ^4II =6 и /iD)s/2C), то для признака /2 значение
пороговой величины увеличивается до 0 + 02 = 0 + || f\ D) || =
= 3 + 3 = 6. Как видно из рис. 7.4, эта операция позволяет
избежать равенства признака /2D) признаку fiD). Поскольку
||/2C)ПР4 11 = 3<@ + е2), то /2D) = /2C). Единственным при-
признаком, изменившимся на этом шаге, является признак /iD).
Так как образ Р4 нельзя восстановить с помощью только этого
признака, то порождается новый признак /3D)=Р4. При
предъявлении образа Р5 обнаруживается, что fi E) =/| D), по-
поскольку || /i D)П Рь II < 0- В результате значение порога для
признака /2 не изменяется. С другой стороны, ||/2D)f]P5ll < 9,
поэтому /2E) = f2D). Эти два обстоятельства означают, что
пороговое значение для признака f3 также не изменяется. По-
Поэтому, так как || ЬD)П Рь II = 3 = 0, полагаем /3E) = /3D)f] Ръ-
Признак /3E) позволяет восстановить образ РE) (единствен-
(единственный признак, подвергавшийся изменению); следовательно, на
этом шаге не нужно порождать новый признак. Признаки, по-
полученные в результате осуществления следующего шага, пред-
представлены на рис. 7.4. Поскольку, однако, эти признаки не поз-
позволяют восстановить все шесть заданных образов, необходимо
выполнить новый цикл итерации.
ш
ш,
щ
ш
ж
1
а1
Рг
щ
1
Ш
Ж
ш
i
ii
ш
аЗ
щ
щ
1
ш
ш
ш
ш
а5
Рб
щ
ш
ш
ш
Ш
аб
ш
1
щ
щ
Щ,
Ш
1
а!
'В.
щ
ш
ш
ш
ш
щ
Щ
В.
щ
i
ш
ш
f,CH,B)nP3 f2C)'P3
ш
Щ
63
f,M=f,C)C\Pll
т.
ы
т
55
ш
ш
1
66
ш
ш
ш
67
ш
ш
ш
Ж
01
щ
ш
ш
ш
ш
ш
1
У/А
'Ш
62
И
63
щ
ш
ш
Z2
f,F)-f,E) f2f6J=f?f5jnP6 f3F)-f3[5)
ш
ш
ш
щ
W,
щ
гз
ш
ш
щ
щ
ш
щ
35
ш
щ
ш
W
ж
ш
68
б-
66
a8
a.- •,
Рис. УА. Иллюстрация принципа действия параллельного алгоритма.
г5
г
m
Щ
щ
ш
д1
м
ш.
ш
ш
щ
62
1
ш
ш
щ
дЗ
д
7.11. Заключительные замечания 333
При новом предъявлении образа Р\ обнаруживается, что
II/i F) Л Я, || = 3 = 6, поэтому /,G) = /,F)ЛР1. Так как при-
признак /iG) не поглощается признаком f2F), значение пороговой
величины для признака f2 не увеличивается. Следовательно,
f2G) = /2F)f]Pi, так как || f2F)f| P, || = 3 = 6. Остальные при-
признаки определяются аналогично. На очередном шаге реализат
ция процедуры прекращается, поскольку, как можно убедиться
с помощью рис. 7.4, полученных в результате признаков доста-
достаточно для восстановления шести рассматриваемых образов.
Так, например, образ Р\ определяется пересечением признаков
/i П /2 П ft, образ Pi — пересечением признаков \\ П \\, образ Р3 —
пересечением признаков f 1 Л h и т. д.
Параллельный алгоритм часто позволяет получить множе-
множество признаков за меньшее число итераций, чем последователь-
последовательный алгоритм. Скорость процедуры повышается за счет порож-
порождения новых признаков, без полного определения старых. Этот
прием, однако, усложняет механизм увеличения пороговой ве-
величины и часто приводит к получению большего, чем нужно
для восстановления заданных образов, числа признаков. Как
и в случае последовательного алгоритма, в принципе един-
единственный способ определения искомого множества признаков
заключается в реализации алгоритма с различными значениями
пороговой величины 0 и выборе лучших из полученных ре-
результатов.
7.11 ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В данной главе достаточно подробно представлен ряд мате-
математических методов, предназначенных для упорядочения, вы-
выбора и выделения признаков. Дан вывод выражений, связы-
связывающих расстояние между множествами с дисперсиями, и про-
проиллюстрирована их роль в изучении преобразования кластери-
кластеризации и упорядочения признаков, осуществляемых посредством
минимизации внутримножественного расстояния и приведения
ковариационной матрицы к диагональному виду. Измерения,
соответствующие малым дисперсиям, более надежны и могут
рассматриваться в качестве более важных признаков. Восполь-
Воспользовавшись преобразованием кластеризации, мы показали, что
аппроксимация обучающих выборок, представляющих рассмат-
рассматриваемые классы, плотностями нормального распределения
эквивалентна измерению среднеквадратичных расстояний для
класса после осуществления преобразования кластеризации над
пространством измерений. Затем принцип преобразования кла-
кластеризации распространяется на задачу понижения размерно-
размерности пространства измерений и задачу порождения оптимального
множества признаков. Эти векторы признаков используются
334 Гл. 7. Предварительная обработка образов
в ортогональных преобразованиях, осуществляемых с целью
понижения размерности векторов образов.
Понятие энтропии используется в качестве альтернативного
способа определения преобразования, обеспечивающего умень-
уменьшение размерности векторов образов. Вывод этого преобразо-
преобразования основывается па допущении о нормальности распределе-
распределения всех классов и равенстве их ковариационных матриц.
В тех случаях, когда это допущение неприемлемо, предлагается
дискретный вариант обобщенного разложения Карунена —
Лоэва в качестве другого подхода к отбору признаков. Разло-
Разложение Карунена — Лоэва выведено в предположении о нулевых
или идентичных математических ожиданиях всех классов. Как
показано в § 7.6, эти условия играют важную роль в приложе-
приложениях разложения Карунепа — Лоэва.
Если признаки, характеризующие класс, можно задать не-
некоторой функцией, определяемой но результатам наблюдений,
применимы методы аппроксимации функциями из § 7.7. В этом
параграфе представлены три основных метода. При работе
с детерминистскими данными годится метод разложения по си-
системе функций. В статистическом случае появляются методы
стохастической и ядерной аппроксимации.
В качестве удобной меры «расстояния» для пар распределе-
распределений произвольного вида и меры сложности разделения двух
совокупностей предложена концепция дивергенции. В случае
двух нормальных распределений с равными ковариацпями ди-
дивергенция равна расстоянию Махалапобиса между этими рас-
распределениями. Понятие дивергенции используется при упорядо-
упорядочении признаков и определении количества измерений, приво-
приводящих к требуемой вероятности ошибки. Описан критерий
выбора признаков по расстоянию между множествами, осно-
основанный на максимизации величины дивергенции. Эта процедура
ограничена случаем разделения на два класса, хотя подобный
подход, основанный на введении «средней» дивергенции, ис-
использовался для случая разделения на несколько классов.
И наконец, рассмотрена задача выбора двоичных признаков.
Хотя общее решение этой задачи не получено, алгоритмы из
§ 7.10 отражают, вероятно, наиболее серьезные попытки, пред-
предпринимаемые в этой области.
Библиография
Дополнительный материал к § 7.2 можно пайти в книге С.ебестиана
[1962] и работах Купера [1964] и Бабу [1973]. Дополнительными истоши-
ками материала § 7,3 и 7.4 служат следующие работы Себестпаи [1962],
Ту A9686, 1969а, 1970], Фу [1971], Болевиг [1956], Ковалевский [1970] и
Ватаиабе [1970]. Подход к выбору признаков по минимуму энтропии, рас-
рассмотренный в § 7.5, предложен Ту и Хейдорном [1967]. Некоторые резуль-
Задачи ЗЗГ>
таты, касающиеся приложения этого метода к случаю дпопчных образов,
можно найти в статье Гонсалеса и Ту [1968].
Впервые разложение Каруиена — Лоэва, описанное и § 7,6, было рассмо-
рассмотрено в статье Каруиена [1947]. Впоследствии Ватанабе применил эту кон-
концепцию в распознавании образов [1969]. Обобщенное разложение Карунена —
Лоэва предложено Цзяием и Фу [1967]. Источники материала § 7.7 следую-
следующие: Логинов [1966], Райе [1964] и Ту [1969а]. Дополнительной литературой
к § 7.8 и 7.9 служат книги Кульбака [1967], Резы [19611 и работа Ту и Хей-
дорпа [1967]. Алгоритмы выбора двоичных признаков, представленные в
§ 7.10, описаны Блоком, Нильсоном и Дудой [1964].
Задачи
7.1. Выведите соотношение G.3.21).
7.2. Выведите формулу G.4.20).
7.3. Рассмотрите два класса (О[ и a>z, Ri — автокорреляционная матрица для
класса (О| и Rz— автокорреляционная матрица для класса (Ог. Опреде-
Определите матрицу преобразования А, у = Ах, такую, что
A(R, + R2)A' = I.
Подобное преобразование полезно при выборе признаков, разделяющих
множества.
7.4. При помощи рассмотренного в § 7.5 преобразования, минимизирующего
энтропию, сведите образы он: {(—5,-5)', (—5,—4)', (—4,-5)',
(—5,-6)', (—6,-5)'} и со2: {E,5)', E,6)', F,5)', E,4)', D,5)'} к од-
одномерным.
7.5. Решите задачу 7.4, воспользовавшись преобразованием, основанным на
разложении Карунена — Лоэва.
7.6. Проведите сраннительпый анализ методов уменьшения размерности век-
векторов образов, основанных па преобразовании кластеризации и миними-
минимизации энтропии.
7.7. Покажите, что функция энтропии //!_ определенная соотношением
G.5.11), минимизируется, если матрица преобразования А состоит из т
ортогональных собственных вектороп, соответствующих наименьшим ха-
характеристическим числам ковариационной матрицы 1-й совокупности (см.
Ту и Хейдорн [1967]).
7.8. Получите уравнение G.7.21) методами стохастической аппроксимации.
7.9. Решите задачу 7.4, воспользовавшись рассмотренным в § 7.9 преобразо-
преобразованием, основанным ни понятии дивергенции.
7.10. Примените к образам рис. 7.4 последовательный алгоритм выбора двоич-
двоичных признаком.
7.11. Примените к образам, представленным па рис. 7.3, параллельный алго-
алгоритм выбора двоичных признаков.
Глава 8
СИНТАКСИЧЕСКОЕ РАСПОЗНАВАНИЕ
ОБРАЗОВ)
8.1. ВВЕДЕНИЕ
Предыдущие главы были посвящены математическому под-
подходу к распознаванию образов. В настоящей главе мы иссле-
исследуем относительно новый и многообещающий подход, исполь-
использующий понятия теории формальных языков. Этот подход часто
называют синтаксическим распознаванием образов, хотя в ли-
литературе часто встречаются и другие названия, например: линг-
лингвистическое распознавание, структурное распознавание, распо-
распознавание методами теории формальных грамматик.
Основным отличием синтаксического распознавания образов
от всех рассмотренных ранее является непосредственное ис-
использование структуры образов в процессе распознавания. Все
аналитические методы, с другой стороны, отличаются строго
количественным подходом к образам, почти полностью игнори-
игнорирующим взаимосвязи между компонентами образа. Несомненно,
существование распознаваемой «структуры» необходимо для
успешного применения синтаксических методов в распознава-
распознавании. Именно поэтому исследования в области синтаксического
распознавания образов до сих пор в основном сводились к рас-
распознаванию изображений, характеризующихся хорошо разли-
различимыми формами, в частности символов, хромосом, фотосним-
фотоснимков столкновений частиц.
Интерес к синтаксическому распознаванию образов заро-
зародился в начале 60-х годов, хотя исследования в этой области
не набрали силы вплоть до конца этого десятилетия. Даже
сегодня многие вопросы, связанные с синтезом синтаксических
систем распознавания образов, решены лишь частично. До сих
пор, например, не построены универсальные алгоритмы обуче-
обучения для синтаксических систем.
После введения некоторых понятий теории формальных язы-
языков внимание в последующих параграфах будет сосредоточено
на основных проблемах, возникающих в процессе применения
таких понятий в синтаксическом распознавании образов. Боль-
Большинство современных исследований в данной области имеет
дело именно с этими проблемами.
') Глава 8 переведена Н. Г. Гуревич.—Прим. ред.
8.2. Понятия теории формальных языков 337
8.2. ПОНЯТИЯ ТЕОРИИ ФОРМАЛЬНЫХ ЯЗЫКОВ
Возникновение теории формальных языков в середине 50-х
годов связано с разработкой Ноамом Хомским математических
моделей грамматик при исследовании естественных языков. Од-
Одной из первоначальных задач лингвистов, работающих в данной
области, было создание «вычислительных» грамматик, способ-
способных описывать естественные языки, например английский. Была
надежда на то, что если замысел удастся, не составит большого
труда научить машину «понимать» естественные языки в целях
машинного перевода и решения задач. И хотя, по всеобщему
мнению, надежды пока не оправдались, побочные результаты
этих исследований оказали важное влияние в других областях,
например при разработке компиляторов, в языках программи-
программирования, теории автоматов и, совсем недавно, в распознавании
образов. В этом разделе мы прослеживаем развитие основных
идей теории формальных языков в связи с проблемами синтак-
синтаксического распознавания образов и обучения ЭВМ.
8.2.1. Определения
Понятия, определяемые ниже, играют центральную роль в
теории формальных языков. И хотя некоторые из этих понятий
легко отождествляются с понятиями, применяемыми при изуче-
изучении естественных языков, мы предостерегаем читателя от про-
проведения слишком глубоких аналогий.
Алфавит — любое конечное множество символов.
Предложение в некотором алфавите — произвольная цепочка
конечной длины, состоящая из символов этого алфавита. На-
Например, для алфавита {0, 1} допустимыми являются следующие
предложения: {0, 1, 00, 01, 10, ...}. Обычно для обозначения
предложения используют также термины цепочка и слово.
Предложение, не содержащее ни одного символа, называется
пустым предложением. В дальнейшем пустое предложение будет
обозначаться so- Для произвольного алфавита V знак V* будет
использоваться для обозначения множества всех предложений,
составленных из символов алфавита V, включая пустое пред-
предложение. Символ V+ будет обозначать множество предложений
V* — so. Если, например, задан алфавит V = {а, Ь}, то V* —
= {s0, a, b, aa, ab, Ьа, ...} и V+ = {a, b, aat ab, Ьа, . ..}.
Язык— произвольное множество (не обязательно конечное)
предложений в некотором алфавите.
Так же как и в естественных языках, серьезное изучение
теории формальных языков должно концентрироваться на грам-
грамматиках и их свойствах. Грамматикой мы называем четверку
G = (VN,VT,P,S), (8.2.1)
338
Гл. 8. Синтаксическое распознавание пбрапоа
где
VN — множество нетерминальных символов (переменных);
VT — множество терминальных символов (констант);
Р — множество грамматических правил или правил
подстановки;
5 — начальный или корневой символ.
Предполагается, что S принадлежит множеству Vn и что Vn и
Vt— непересекающиеся множества. Алфавит V является объ-
объединением алфавитов Vn и Vt.
<предложение>
<именная составляющая >
< глагольная составляющая}
<артинльу
^непереходный глагол>
runs
<предлвтение> —*- <именнпя спста8пяющая><глагапышя состабпяютя)
<иминная составляющая? *~<вргг:мъ> (.существительное)
(глагольная составляющая} —•-<непереходный ?лашь
<артикль> —•-1 h e
ЩщестВительноеУ -— boy
<нелереходнып глаголу —»- runs
Риг. 8.1. Правила подстановки, использованные при порождении предложения
«The boy runs» и соответствующего семантического дерева.
В данном случае будет полезно сравнить приведенное выше
определение формальной грамматики со стандартными поня-
понятиями грамматики английского языка. Это поможет читателю
лучше понять обозначения и терминологию. Рассмотрим простое
предложение The boy runs (мальчик бежит). На рис. 8.1 по-
показана запись этого предложения в виде дерева. Порождение
8.2. Понятия теории формальных языков 339
данного предложения происходит следующим образом. Мы на-
начинаем с абстрактного понятия, которое называем (предложе-
(предложение). На этом этапе (предложение) — не более чем синтаксиче-
синтаксическое понятие, представляющее все правильные предложения
английского языка. Затем мы заменяем (предложение) на
(именная составляющая) плюс (глагольная составляющая).
В теории формальных языков мы всегда начинаем с описанного
выше символа S. Правила подстановки грамматики G вида
(8.2.1) соответствуют в английском языке следующему, напри-
например, замещению: (предложение) заменяется на (именная со-
составляющая) и (глагольная составляющая). Как видно из
рис. 8.1, в результате дальнейшего применения грамматических
правил или правил подстановки (именная составляющая > сво-
сводится к (артикль) плюс (существительное), а (глагольная со-
составляющая) к (непереходный глагол). Наконец, применение
правил подстановки, отображающих (артикль) в «the», (суще-
(существительное) в «boy», а (непереходный глагол) в «runs», при-
приводит к искомому предложению. Нетерминальные символы
грамматики G сответствуют синтаксическим категориям (имен-
(именная составляющая), (глагольная составляющая), (артикль),
(существительное > и т д., тогда как терминальные символы
соответствуют словам естественного языка «the», «boy», «runs».
Другими словами, нетерминальные символы играют роль пере-
переменных, терминальные — констант.
Язык, порождаемый грамматикой G и обозначенный L(G),—
это множество цепочек, удовлетворяющих двум условиям:
1) каждая цепочка составлена только из терминальных сим-
символов (т. е. является терминальным предложением), 2) каждая
цепочка может быть выведена из S путем соответствующего
применения правил подстановки из множества Р.
В этой главе используются следующие обозначения. Нетер-
Нетерминальные символы обозначаются прописными буквами S, А,
В, С, ... . Строчные буквы из первой половины латинского ал-
алфавита о, Ь, с, ... используются для терминальных символов.
Цепочки терминальных символов обозначаются строчными бук-
буквами из конца латинского алфавита v, до, х Смешанные
цепочки терминальных и нетерминальных символов представ-
представлены строчными буквами греческого алфавита ос, [3, у, б, ... .
Множество Р правил подстановки состоит из выражений
вида а->|3, где а—цепочка в словаре V+ и |3 — цепочка в сло-
словаре V*. Иначе говоря, символ —*¦ означает замещение цепочкг:
ос цепочкой [3. Символ =4- будет использован для обозначения
операций вида Ya8=?-Y|36 в грамматике G, т. е. => указывает
о а
на замещение ос па C в результате применения правила подста-
подстановки ос->р\ при этом y и бостаются неизменными. В тех слу-
340 Гл. 8. Синтаксическое распознавание образов
чаях, когда ясно, о какой грамматике идет речь, G опускается
и используется символ =»-.
Пример. Рассмотрим грамматику G = (Vn, Vt, Р, S), где
Vw={5}, VT={a,b} и Р= {S-+aSb, S-+ab). Применяя
первое правило пг— 1 раз, получаем
S=>aSb=s*aaSbb=>a3Sb3=> ...=*> a^'Sfe7".
Применение второго правила приводит к цепочке
a bb =>-a о .
Язык, порождаемый этой грамматикой, состоит, как мы видим,
исключительно из цепочек подобного вида, причем длина кон-
конкретной цепочки зависит от т. Язык L(G) можно представить
в виде L(G) = {ambm\m ^ 1}. Стоит отметить, что простая
грамматика, описанная в этом примере, обладает способностью
порождать язык с бесконечным числом цепочек или предложе-
предложений. В следующих разделах будет видно, как это свойство
создает трудности при использовании этих понятий в распозна-
распознавании образов. g
8.2.2. Типы грамматик
В этом пункте рассмотрим грамматики, являющиеся част-
частным случаем (8.2.1). Все эти грамматики идоеют форму G =
= (Vn, Vt, P, S) и различаются лишь по типу правил подста-
подстановки, допустимых в каждой из них1).
Неограниченная грамматика характеризуется правилами
подстановки вида а-*р\ где а — цепочка алфавита V+, ар —
цепочка алфавита V*.
Грамматика непосредственно составляющих характеризуется
правилами подстановки вида aiy4a2->aipa2, где cti и а2 — эле-
элементы алфавита V*, р принадлежит V+, а А принадлежит Vn.
Эта грамматика допускает замещение нетерминального символа
А цепочкой р только в том случае, если А появляется в контек-
контексте а.\Аа.2, составленном из цепочек ai и осг-
') Наряду с приведенными ниже в отечественной литературе встречаются
также следующие термины:
а) неограниченная грамматика — обобщенная грамматика;
б) грамматика непосредственно составляющих — грамматика состапляю-
щих, НС-грамматика, грамматика контекстная;
в) бесконтекстная грамматика — контекстно-свободная грамматика. К.С-
грамматнка;
г) регулярная (автоматная) грамматика—грамматика конечно-автомат-
конечно-автоматная, грамматика с конечным числом состояний. Английские эквиваленты этих
терминов приведены в предметном указателе в конце книги. — Прим. перев.
8.2. Понятия теории формальных языков 341
Бесконтекстная грамматика характеризуется правилами под-
подстановки вида Л->р, где А принадлежит множеству Vn и р при-
принадлежит множеству V+. Само название «бесконтекстная» ука-
указывает на то, что переменная А может замещаться цепочкой Р
независимо от контекста, в котором появляется А.
Наконец, регулярная (или автоматная) грамматика — это
грамматика с правилами подстановки вида А—*аВ или А—*а,
где А и В— переменные из Vn, a — терминальный символ из
Иг. Альтернативными допустимыми правилами подстановки яв-
являются А—*Ва и Л-»а, Выбор одного из этих двух типов пра-
правил исключает, однако, применение правил другого типа.
Эти грамматики называют иногда грамматиками типа О, 1,
2 и 3 соответственно. Кроме того, их часто обозначают как
грамматики структуры составляющих.
Если каждое правило подстановки бесконтекстной грамма-
грамматики имеет вид A-^-xBw или A-*-w, где А и В — нетерминаль-
нетерминальные символы, а х и w— терминальные цепочки, то грамматика
считается линейной.
Интересно отметить, что все регулярные грамматики бескон-
бесконтекстны, все бесконтекстные грамматики являются граммати-
грамматиками непосредственно составляющих, а все грамматики непо-
непосредственно составляющих — неограниченны.
Пример. Способы функционирования обсуждаемых грамма-
грамматик показаны на следующих простых примерах грамматик,
(а) Неограниченная грамматика
G = (VN,VT,P,S)
при
К*, = {S, А, В], VT = {a,b,c)
Р: S-+aAbc
АЪ'—ЪА
Ac
ЪВ
аВ
аВ
-'¦ВЬсс
^ВЬ
-* ааА
-* S,
порождает предложения вида х = апЬп+2сп+2, где п^О озна-
означает длину цепочки символов. Например, для порождения це-
цепочки х = а°Ь2с2 = ЬЬсс мы применяем первые четыре правила
342 Г л S Синтаксическое распознавание образов
и затем последнее, т. с.
S =»¦ a Abe => abAc => аЪВЬсс => аВЬЬсс =>¦ ЬЪсс.
Заметим, что последнее правило допустимо лишь в неог[
пых грамматиках.
(б) Грамматика непосредственно составляющих
G = (VN, VT,P,S)
при
VN = {S, А, В}, VT = {a,b,c}
Р: S — abc
S -*аЛЬс
АЬ -* ЬА
Ас
аВ -> яя
порождает предложения вида х = anbncn, где /г
(в) Бесконтекстная грамматика
G = (l\, VT,P,S)
при
V« = {S}, V'r = {a, 6},
Р: S-^-ab,
порождает цепочки вида х = а"Ь", где п ^ 1.
(г) Регулярная грамматика
G = (VNl Гг, Я, S)
при
V.v = {S}. VT = {a,b),
Р: S->a,
S-+b,
S -> aS,
S-+bS
лооождает цепочки, состоящие из символов а и b.
8.3. Постановка задачи синтаксического распознавания 343
Как и предполагалось, неограниченные грамматики обла-
обладают значительно большей мощностью, чем грамматики трех
остальных типов. Однако степень общности этих грамматик
создает ряд серьезных трудностей в их теоретических и прак-
практических приложениях. Это утверждение верно и для грамматик
непосредственно составляющих. |
Хотя в литературе часто встречаются и другие грамматиче-
грамматические структуры, грамматики, представленные здесь, составляют
основу для большей части исследований в этой области. В сле-
следующих разделах речь будет идти о расширении этих понятий
и их приложении к распознаванию образов.
8.3. ПОСТАНОВКА ЗАДАЧИ СИНТАКСИЧЕСКОГО
РАСПОЗНАВАНИЯ ОБРАЗОВ
Понятия, описанные в § 8.2, могут быть связаны с распозна-
распознаванием следующим образом. Предположим, у нас имеются два
класса образов coi и сог и пусть образы этих классов могут быть
построены из признаков, принадлежащих некоторому конечному
множеству. Назовем эти признаки треминалами и обозначим
множество терминалов символом Vr в соответствии с системой
обозначений, введенной в § 8.2. В синтаксическом распознава-
распознавании образов терминалы называются также непроизводными
символами (элементами). Каждый образ может рассматри-
рассматриваться как цепочка или предложение, поскольку он составлен
из терминалов множества VT. Допустим, что существует грам-
грамматика G, такая, что порождаемый ею язык состоит из предло-
предложений (образов), принадлежащих исключительно одному из
классов, скажем щ. Очевидно, что эта грамматика может быть
использована в целях классификации образов, так как задан-
заданный образ неизвестной природы может быть отнесен к соь если
он является предложением языка L(G). В противном случае
образ приписывается классу ©2. Например, бесконтекстная
грамматика G = (Vn, Vr, P, S) при Vn= {S}, Vr = {a, b) и
множестве правил подстановки Р= {S-+aaSb, S-^aab} обла-
обладает способностью порождать лишь предложения, содержащие
вдвое больше символов а, чем Ь. Если мы сформулируем гипо-
гипотетическую задачу разбиения образов на два класса, причем
объекты класса coi — это цепочки вида aab, aaaabb и т. д., а
объекты класса со2 содержат одинаковое число символов а и Ь
(т. е. ab, aabb и т. д.), то очевидно, что классификация задан-
заданной цепочки производится простым определением того, может
ли данная цепочка порождаться грамматикой G. рассмотрен-
рассмотренной выше. Если может, то объект принадлежит ©i. если нет —
он автоматически приписывается классу оъ. Процедура, ис-
используемая для определения, является или не является цепочка
344 Гл. 8. Синтаксическое распознавание образов
предложением, грамматически правильным для данного языка,
называется грамматическим разбором. На способах граммати-
грамматического разбора мы остановимся несколько позже.
По приведенной выше схеме классификации образ попадает
в класс «г исключительно потому, что он не принадлежит клас-
классу (Di. Если обнаружится, что образ не является правильным
для G предложением, предполагается, что он должен принад-
принадлежать «г- Тем не менее не исключено, что образ не принадле-
принадлежит и классу «г. Он может представлять собой зашумленную
или искаженную цепочку, которую лучше всего изъять из
распознавания. Для того чтобы обеспечить возможность изъ-
изъятия, необходимо задать две грамматики G\ и G2, порождающие
языки L(G\) и L(Gi) соответственно. Образ зачисляется в
класс, язык которого позволяет считать этот образ граммати-
грамматически правильным предложением. Если обнаружится, что образ
может принадлежать обоим классам, е'го произвольно зачисляют
в любой из этих классов. Если он не является предложением
ни L{G\), ни /.(Ог), образ изымается.
В случае М классов мы рассматриваем М грамматик и свя-
связанных с ними языков L(Gi), i— I, 2, ..., М. Распознаваемый
объект относится к классу со,- в том и только том случае, если
он является предложением языка L(Gi). Если объект является
предложением более чем одного языка или не принадлежит ни
одному из них, он может быть изъят из рассмотрения или про-
произвольно отнесен к одному из классов неопределенных объектов.
В связи с изложенным выше подходом к распознаванию воз-
возникает ряд существенных вопросов. 1) Как наилучшим образом
описывать объекты для их классификации подобным способом?
2) Как выбираются грамматики распознавания? 3) Любая
задача, имеющая практическое значение, обычно искажается
случайными переменными, например шумами измерения; каким
образом в синтаксическом подходе можно использовать стати-
статистический аппарат с тем, чтобы учесть эти случайные перемен-
переменные? 4) Одной из наиболее важных особенностей рассмотренных
ранее подходов к распознаванию образов является способность
строить решающие функции посредством итеративных проце-
процедур обучения; можно ли распространить концепцию обучающей
выборки на синтаксическое распознавание? Каждому из этих
вопросов соответствует отдельный параграф.
8.4. СИНТАКСИЧЕСКОЕ ОПИСАНИЕ ОБРАЗОВ
До сих пор в этой главе рассматривались образы — цепочки
символов. Если мы хотим получить реальную пользу от струк-
структурных свойств объекта в процессе синтаксического распозна-
распознавания, понятие цепочки должно быть обобщено на двумерный
8.4 Синтаксическое описание образов 345
случай. Как отмечалось в § 8.1, в этой главе мы в основном за-
занимаемся двумерными объектами.
Правила подстановки в грамматиках цепочек заключаются
в простом соединении1) цепочек с целью формирования новых.
Соединение двумерных структур не является, однако, простым
вопросом. Читатель может лично в этом убедиться, рассмотрев
разнообразные двумерные структуры, получающиеся в резуль-
результате соединения простых непроизводных символов | и —. Непо-
Непосредственное решение этого вопроса связано с заданием поло-
положения двумерных объектов достаточно общим образом. Рас-
Рассмотрим, например, позиционный дескриптор НАД (а,Ь), обо-
обозначающий, что структура, представленная символом а, распо-
расположена над структурой, представленной Ь, и позиционный де-
дескриптор СЛЕВА (а, Ь), означающий, что а находится слева от
Ь. Квадратная структура D, составленная из непроизводных
элементов | и —-, описывается при помощи этих дискрипторов
предложением НАД (—, НАД (СЛЕВА (|, |), —)). Основная
трудность при подобном подходе заключается в определении
содержания дескрипторов НАД и СЛЕВА. Так, например, пре-
предыдущему описанию квадрата удовлетворяет также и структура
| |~. Можно считать этот образ допустимым или нет, зависит
от конкретной ситуации. Очевидно, однако, что обобщенные
позиционные дескрипторы с трудом поддаются точному опре-
определению. Чаще всего в таких случаях на взаимоотношения
структур налагаются ограничения. В частности, разумным огра-
ограничением для дескриптора НАД (а, Ь) является требование,
чтобы хотя бы часть элемента а находилась над элементом Ь.
В таком случае структура | |~ не будет считаться допустимой,
так как элемент — не находится над элементом | | и элемент
| | не находится над элементом —
Можно пойти еще на один шаг дальше по пути ограничения
правил соединения и провести значительные упрощения, веду-
ведущие к введению грамматических формализмов, необходимых
для описания и распознавания объектов. В наиболее удачных
работах по синтаксическому распознаванию образов применя-
') Часто применяется также термин конкатенация. Между этими двумя
терминами есть, однако, разница. Соединение двух объектов означает простое
расположение этих объектов рядом при полном сохранении индивидуальных
особенностей каждого. Конкатенация в свою очередь предполагает как про-
пространственную переструктуризацию, так и потерю некоторых существенных
особенностей объектов. Важное различие при этом заключается в том, что
всякая конкатенация объектов является также объектом, тогда как соедине-
соединение объектов может (хотя и необязательно) быть рассмотрено как единый
объект. Так как при описании образов способность сохранять индивидуаль-
индивидуальность зачастую играет решающую роль, в этой главе мы будем пользоваться
термином соединение. Читатель тем не менее должен иметь в виду, что в ли-
литературе эти два термина используются на равных началах.
346
Гл. 8. Синтаксическое распознавание образов
лась простая схема, заключающаяся в соединении структур
только в особых точках. Одним из способов достижения этого
является требование, чтобы каждая структура имела две выде-
выделенные точки. Более того, соединение структур должно происхо-
происходить только в этих точках. Позднее мы рассмотрим систему
синтаксического распознавания образов, использующую этот
Рис. 8.2. Сведение задачи соединения объектов к одномерному случаю по-
посредством обобщенного представления объектов ориентированными отрезка-
отрезками прямых, а — выборочные образы; б — характерные действенные правила
соединения обобщенных образов.
способ. Как показано на рис. 8.2, о, две выделенные точки в этой
системе интерпретируются как «головной» и «хвостовой» концы
стрелы. Типичные допустимые правила соединения для данной
системы показаны на рис. 8.2,6. Совершенно очевидно, что
такой подход эффективно сводит задачу двумерного соединения
к эквивалентной задаче действий с цепочками, поддающейся
решению с помощью обыкновенной цепочечной грамматики,
рассмотренной выше.
Для описания двумерных отношений используется и другая
полезная методика, основывающаяся на древовидных струк-
структурах. Дерево — это конечное множество Т, состоящее из одного
или более узлов, таких, что 1) существует один выделенный
узел, называемый корнем дерева, и 2) остальные узлы (исклю-
(исключая корень) разделены на m ^ 0 непересекающихся множеств
7'ь Г2, ..., Тт, каждое из которых в свою очередь является дере-
8 4. Синтаксическое описание образов
347
вом. Деревья Т\, Т2, ..., Тт называются поддеревьями корня.
Число поддеревьев узла называется степенью этого узла. Узел
с нулевой степенью называется листом, а узел с наиболее вы-
высокой степенью—узлом ветви. Наконец, представление образа
в виде дерева называется деревом образа
а
b d в
6
9 с
9
Рис. 8.3. Представление образов в зпде деревьев.
Использование деревьев для описания многомерных струк-
структур— довольно простая процедура. В сущности, любая иерархи-
иерархически упорядоченная схема ведет к представлению объекта в
виде дерева. Два примера, иллюстрирующие это обстоятельство,
приведены на рис. 8.3. На рис. 8.3, а упорядочение состоит в
группировке областей, причем область b находится в области а,
в свою очередь находящейся в области г. Обозначив корень
дерева символом г, получаем древовидную структуру
(рис. 8.3,6), естественно вытекающую из схемы упорядочения,
приведенной выше. Второй пример показан на рис. 8.3, е. В этом
случае получившийся двумерный объект определяется связями
между различными компонентами схемы. На рис. 8.3, г изобра-
изображено соответствующее дерево. Отметим, что каждый узел де-
348 Гл 8. Синтаксическое распознавание образов
рева представляет узел схемы и что корень дерева образа про-
произвольно определяется как крайний левый верхний узел образа.
8.5. ГРАММАТИКИ, ИСПОЛЬЗУЕМЫЕ
В РАСПОЗНАВАНИИ ОБРАЗОВ
В этом параграфе рассматривается распознавание образов
при помощи синтаксического подхода. В п. 8.5.1 обсуждается спо-
способ определения потенциальной возможности порождения неко-
некоторого образа определенной грамматикой. Пункт 8.5.2 посвя-
посвящен распознаванию двумерных объектов, которые могут сво-
сводится к эквивалентному представлению в виде цепочки. Это
упрощение играет важную роль в создании синтаксических
систем распознавания, так как позволяет использовать стан-
стандартные понятия из теории грамматик цепочек. Наконец, в
п. 8.5.3 мы рассматриваем распознавание образов, допускаю-
допускающих представление древовидной структурой. Эти структуры не-
непосредственно связаны с грамматиками деревьев, являющимися
расширением результатов, о которых до сих пор шла речь в
данной главе.
8.5.1. Синтаксически ориентированное распознавание
В § 8.3 было отмечено, что формальные грамматики можно
использовать в распознавании образов, определяя, является ли
данных объект терминальным предложением какой-либо из со-
соответствующих рассматриваемой задаче грамматик. Основным
вопросом, после того как определены грамматики, является раз-
разработка процедуры, устанавливающей, является или нет данный
объект допустимым предложением. Процедура, применяемая
для этого в теории формальных языков, называется граммати-
грамматическим разбором. Мы рассматриваем в основном два типа грам-
грамматического разбора: сверху вниз и снизу вверх. Эти названия
становятся более осмысленными, если обратиться к семантиче-
семантическому дереву, такому, например, как представленное на рис. 8.1.
Вершина или корень (инвертированного) дерева — это началь-
начальный символ S. Терминальные предложения (образы) пред-
представляют нижнюю часть или листья дерева. Процедура разбора
сверху вниз начинается с корневого символа S и заключается
в попытках посредством повторяющегося применения граммати-
грамматических правил получить заданное терминальное предложение.
С другой стороны, процедура разбора снизу вверх начинается
с конкретного предложения и заключается в попытках дойти до
символа S с помощью инверсии правил подстановки. В каждом
из этих случаев при неудачном исходе грамматического разбора
if! 5 Грамматики, используемые я распознавании образов 349
заданный образ отклоняется как представляющий неправиль-
неправильное предложение.
Совершенно очевидно, что описанные выше схемы граммати-
грамматического разбора принципиально неэффективны, так "как тре-
требуют полного перебора при применении грамматических правил.
Зачастую нет необходимости применять последовательность
грамматических правил от начала до конца, поскольку суще-
стзует возможность проверять на соответствие поставленным
целям промежуточные результаты и определять тем самым, спо-
способна ли данная последовательность правил обеспечивать
успешный грамматический разбор.
Дальнейшее усовершенствование процесса грамматического
разбора связано с применением правил синтаксиса грамматики.
Синтаксис определяется как соединение и конкатенация объек-
объектов. Синтаксическое правило устанавливает некоторые допусти-
допустимые (или запрещенные) отношения между объектами. Напри-
Например, соединение qqq никогда не встречается в английском языке.
В этой терминологии грамматика является не более чем множе-
множеством синтаксических правил, определяющих допустимые или
желательные отношения между объектами. Синтаксически ори-
ориентированный грамматический анализатор, таким образом,
включает в процесс грамматического разбора синтаксис грам-
грамматики. Следующий пример позволит нам внести большую
ясность в эти понятия.
Пример. Вернемся к структурам типа квадрат, использован-
использованным для иллюстрации содержания предыдущего параграфа.
Непроизводными элементами, как показано на рис. 8.4, а, слу-
служат горизонтальный и вертикальный отрезки определенной
длины, обозначенные а\ и аг соответственно. Бесконтекстная
грамматика G, способная порождать квадраты, задается набо-
набором G = {VN, Vt. P, S) при
VT = {aua2}, VN = {S,Ol,O2};
Р: S^A(au O2),
02->Л@,, а,),
Ox-+L(a2, а2),
где А (х, у) и L(x,y) читаются соответственно «х расположен
над у» и «се расположен слева от у». Важно еще раз указать, что
для того, чтобы обрабатывать изображения, мы должны уметь
обобщать грамматические правила так, чтобы они могли при-
применяться к двумерным соединениям. В этом простом примере
мы считаем позиционный дескриптор А (х, у) допустимым только
в том случае, если часть у находится непосредственно над х,
а дескриптор L(x,y) допустим только тогда, когда часть у на-
находится непосредственно справа от х.
350
Гл S. Синтаксическое распознавание образов
Структуры, напоминающие квадраты, изображенные на
рис. 8.4, б, порождаются последовательностью грамматических
правил
S->A(au О о).
Это правило заменяет начальный символ непроизводным эле-
элементом а\, расположенным над некоторым пока еще не опреде-
определенным объектом О2. Правило
02->Л@ь d)
заменяет не определенный объект О2 другим объектом О\, еще
не определенным, расположенным над горизонтальным отрез-
а,:
а,-.
Рис. 8.4. Образы, использованные для иллюстрации синтаксически-ориентиро-
синтаксически-ориентированного грамматического разбора, а—непроизводпые элементы образов;
б — образы, поддающиеся разбору с помощью описанной схемы; в — образы,
не поддающиеся разбору с помощью описанной схемы.
ком а.\. Наконец, О\ заменяется на два вертикальных непроиз-
непроизводных элемента посредством применения правила
О{-*L (а2, а2).
Короче говоря, построение этих структур начинается с горизон-
горизонтального отрезка, затем следует другой горизонтальный отре-
8.5 Грамматики, используемые в распознавании образов 351
зок под ним, и завершается все помещением между ними двух
вертикальных отрезков. Изменчивостью структур можно управ-
управлять, налагая ограничения на позиционные дескрипторы А(х, у)
и L{x,y). Стоит также отметить, что приведенная выше грам-
грамматика способна порождать лишь структуры типа квадратоз
и что только приведенная выше последовательность правил счи-
считается допустимой.
Грамматический разбор, проведенный в этой простой си-
системе, представляет собой тривиальную процедуру, поскольку
используется только одна последовательность правил подста-
подстановки. Предположим, например, что требуется установить, при-
принадлежит или не принадлежит данная структура к классу объ-
объектов, порождаемых описанной выше грамматикой. Синтакси-
Синтаксически ориентированный разбор сверху вниз будет произво-
производиться следующим образом. Первое правило подстановки начи-
начинается с S и предполагает поиск некоторого объекта О2 ниже
непроизводного элемента а.\. Если ниже некоторого а,\ не най-
найдено ни одного объекта, грамматический разбор прерывается и
образ отклоняется. Если же это правило применено успешно, на
следующем шаге отыскивается некоторый объект О\ над дру-
другим непроизводным элементом а.\. Первый элемент а\ не счи-
считается частью О\. Если О\ обнаружен, грамматический разбор
продолжается, в противном случае образ отклоняется. Наконец,
объект О[, обнаруженный на предыдущем шаге, должен для
принятия образа разделиться на два непроизводных элемента
а2 по условию L(a2, а2). Этой схеме грамматического разбора
удовлетворяют структуры, изображенные на рис. 8.4, б, и не
удовлетворяют структуры, изображенные на рис. 8.4,6.
Синтаксически ориентированный грамматический разбор
снизу вверх, заключающийся в применении правил подстановки
в обратном порядке, происходит следующим образом. Сначала
мы пытаемся обнаружить объект О\, определяя, содержит ли
данный объект непроизводпый элемент а2 слева от непроизвод-
непроизводного элемента а2. Если поиск оказался удачным, процедура
продолжается; в противном случае образ отклоняется. Заметим,
что, поскольку процедура разбора снизу вверх начинается с
терминального предложения, сначала должны рассматриваться
те правила подстановки, применение которых приводит исклю-
исключительно к терминальным символам. Для продолжения грам-
грамматического разбора необходимо на следующем шаге получить
объект О2, который состоит из объекта Ои расположенного над
непроизводным элементом а.\. Если этот шаг оказался успеш-
успешным, мы пытаемся вывести начальный символ S, отыскивая
непроизводпый элемент а\, расположенный над О2. Если S
может быть выведен, то образ принимается, в противном случае
на этом шаге он отклоняется. Объекты, изображенные на
352
Гл. 8. Синтаксическое распознавание образов
рис. 8.4,6, поддаются грамматическому разбору, тогда как
объекты, изображенные на рис. 8.4, в, будут отклонены на од-
одном из этапов грамматического разбора. I
8.5.2. Распознавание образов, представленных графами
Хотя предыдущий пример, несомненно, иллюстрирует основ-
основные положения синтаксического подхода, мы признаем, что он
в значительной мере идеализирован, особенно если учесть, что
грамматика позволяет реализовать только одну последователь-
последовательность грамматических правил. При рассмотрении этого при-
примера возникает, однако, один важный вопрос. Должно быть
ГолоВчая
точка
Обобщенный
непроизводный
элемент
Об~оо~щеннь'й
непроиу'зЗныи
элемент
Хвостодая
течка
ХВостоВая
точка
Хвостовая
точка
Рис. 8.5. Обобщенное представление структур образа с помощью ориентиро-
ориентированных отрезков прямых, связанное с использованием языка PDL.
ясно, что поиск непроизводных элементов или подструктур,
представляющих интерес с точки зрения анализа двумерных
объектов, может оказаться для вычислительной машины почти
неразрешимой задачей. И хотя этот вопрос обсуждался в пре-
предыдущем разделе, стоит упомянуть о нем еще раз, поскольку
он является одним из основных препятствий на пути создания
истинно универсальной системы синтаксического распознавания
образов. К настоящему времени наиболее успешные исследова-
исследования в данной области связаны с объектами, сводимыми к струк-
структурам типа графов. В данном разделе мы обсуждаем некоторые
из этих подходов с целью иллюстрации основных понятий, вво-
вводимых при синтаксическом распознавании объектов, представ-
представленных графами.
Интересным приложением лингвистических понятий в распо-
распознавании образов является язык PDL (Picture Description Lan-
Language)— язык описания изображений, предложенный Шоу
A970). Непроизводным элементом в PDL служит любая «-мер-
«-мерная структура с двумя выделенными точками — хвостовой и
головной, как это показано на рис. 8.5 для двумерных структур.
Заметим, что практически любая структура может обобщенно
рассматриваться как ориентированный отрезок прямой, так как
определение вводит только две точки.
8.5. Грамматики, используемые в распознавании образов 353
Непроизводный элемент может примыкать к другим непро-
непроизводным элементам только в своей хвостовой и/или головной
точке. На основании этой допу-
допустимой формы соединения, а так-
также вследствие того, что каждый а + b
непроизводный элемент обоб-
обобщается до ориентированного от-
отрезка прямой, очевидно, что струк-
структуры языка PDL представляют
собой ориентированные графы и
для обработки этих структур
можно использовать грамматики °
цепочек.
Основные правила соединения
обобщенных непроизводных эле-
элементов приведены на рис. 8.6. а~Ь
Важно отметить, что пустые не-
непроизводные элементы могут быть
использованы для порождения
внешне разъединенных структур,
подчиняющихся при этом прави-
правилам связности. Иногда полезно
также рассмотрение нулевой точ- а*Ь
ки — ненроизводного элемента с
идентичными головной и хвосто- ь
вой точками. „ „с л
п , „ - Рис. 8.6. Правила соединения, ис-
ПриНЦИПЫ действия языка пользуемые в языке PDL.
PDL лучше всего проиллюстри-
проиллюстрировать на примере. Рассмотрим следующую простую грамматику
языка PDL:
где
G = {VN,
-IS.AU<
--= {a/>, b\
P: S -
A,-.
A2 -~
42. A
, C-*
d +
с -f
P.S),
ls.At,.
¦ <W
Аг
*A,
At
354
Гл 8 Синтаксическое распознавание образов
причем (~d) означает перемену мест головной и хвостовой
точек непроизводного элемента d.
Применение первого правила подстановки приводит к полу-
получению непроизводного элемента d, сопровождаемого еще не
определенной переменной. На этом этапе мы знаем только, что
хвостовая точка структуры, представленной символом А\, будет
h
d
t-
d* (c+(~d
a+b
(а+Ь)«с
ld+(c+(~d)))*((a*b)*c)
Рис. 8.7. Шаги построения структуры в языке PDL. Обратите внимание на
головные и хвостовые точки составных подструктур,
связана с головной точкой элемента d, потому что этот непро-
непроизводный элемент сопровождается оператором «-)-». Перемен-
Переменная А\ разлагается на с + А2, причем А2 пока не определена.
Аналогичным образом А2 разлагается на ~d*A%. Результаты
применения первых трех правил подстановки приведены на
рис. 8.7, а, б и в. Из определения оператора «*» мы знаем, что
при разложении элемента Лз происходит его соединение с со-
составной структурой, показанной на рис. 8.7, в путем присоеди-
присоединения хвостовых точек к хвостовым, а головных к головным.
Конечный результат, полученный после применения всех пра-
правил подстановки, показан на рис. 8.7, е.
Грамматика языка PDL, описанная выше, способна порож-
порождать только одну структуру. Можно, однако, расширить число
структур, порождаемых этой грамматикой, введением в правила
подстановки рекурсивности — способности переменной заме-
замещаться этой же переменной. Предположим, например, что мы
8.5. Грамматики, используемые в распознавании образоп 355
определяем правила подстановки следующим образом;
S -*d + A,.
А ! -> С + А х
Ь * А
Результатом применения этих правил в указанном порядке
является структура, изображенная на рис. 8.7, е. Между тем это
новое множество правил допускает, например, возможность за
первым правилом подстановки применять третье, опуская вто-
второе. Применяя в указанном порядке оставшиеся правила под-
подстановки, мы получили бы треугольную структуру. Более того,
эти правила позволяют порождать бесконечные структуры по-
посредством многократного замещения переменной этой же пере-
переменной. Многообразие структур, порождаемых приведенной
выше грамматикой, может быть еще более расширено, если
положить, что А\ и А2 равны S. При этом возможности грамма-
грамматики возрастут до максимума. Нужно отметить, однако, что
подобное увеличение порождающей способности грамматики
может иногда оказаться- нежелательным. Особенно верно это
замечание для тех прикладных исследований в области синтак-
синтаксического распознавания образов, где требуется более чем одна
грамматика. В этом случае чрезмерное многообразие приводит
к уменьшению различающей мощности применяемых грам-
грамматик.
Грамматический разбор структур при помощи предложен-
предложенной грамматики в принципе несложен. Предположим, напри-
например, что объектом, представленным на распознавание, служит
изображение на рис. 8.7, е, причем используется второе множе-
множество правил подстановки. Грамматический разбор сверху вниз
будет происходить в следующей последовательности. Предполо-
Предположим, что интересующий нас объект сканируется с целью полу-
получения соответствующего терминального представления
(d + (с + (~d)))*(\a + Ь)*с). Как отмечалось ранее, процесс
сканирования, вообще говоря, не является тривиальной проце-
процедурой. Грамматический анализатор, работающий по принципу
«сверху вниз», начинает с корневого символа S и пытается по-
получить интересующий нас объект, применяя правила подста-
подстановки данной грамматики. В настоящем случае 5 заменяется на
356 Г л 8 Синтаксическое распознавание образов
d-\-А\. Терминальный символ d, сопровождаемый знаком «+»,
обнаружен, поэтому происходит грамматический разбор эле-
элемента А\. Здесь имеются две возможности, поскольку А\ может
заменяться при помощи как второго, так и третьего правила.
Применение второго правила приводит к успеху, так как пер-
первый «+» образа сопровождается символом с. Третье правило
этому условию не соответствует. Для того чтобы разложить
элемент А\, следующий за «-{-» после символа с, необходимо
найти правило подстановки вида A\—*-~d, сопровождающееся
«*». Этому условию отвечает третье правило. Продолжая эту
процедуру, устанавливаем, что данный образ поддается грам-
грамматическому разбору. При наличии двух или более грамматик
анализ производится для каждой из них до тех пор, пока образ
не идентифицируется либо пока не исчерпаются возможности
грамматики; в последнем случае образ отклоняется.
Другим интересным приложением синтаксического распозна-
распознавания образов является работа Ледли [1964, 1965] по автомати-
автоматической классификации хромосом. Бесконтекстная грамматика,
способная классифицировать V-образные и телоцентрические
хромосомы, задается следующим образом:
VT={a, Ъ, с, d, е},
VN = { S, Т, Основание, Сторона, Пара плеч, Правая часть,
Левая часть, Плечо},
Р: S-+ Пара плеч • Пара плеч,
Т —у Основание • Пара плеч,
Пара плеч-*Сторона • Пара плеч,
Пара плеч —> Пара плеч • Сторона,
Пара плеч —> Плечо • Правая часть,
Пара плеч -*¦ Левая часть • Плечо,
Левая часть -> Плечо • с,
Правая часть ~* с • Плечо,
Основание -> Ъ • Основание,
Основание -> Основание ¦ Ъ,
Основание -*¦ е,
Сторона -у Ъ • Сторона,
Сторона —> Сторона • Ъ,
Сторона —у Ъ,
Сторона -> d,
Плечо —> Ъ - Плечо,
Плечо -*¦ Плечо • Ь,
Плечо -*¦ а.
Я 5 Грамматики, использиемые в распознавании образов
357
На рис. 8.8, а изображены непроизводные элементы {а,Ь,с,
d,e}, на рис. 8.8,6 — типичный вид V-образной и телоцентриче-
ской хромосом. Для данного конкретного случая оператор «•»
означает просто связность отдельных частей хромосомы, фик-
фиксируемую при продвижении вдоль ее границы по направлению
i У
b с d
a
W
abcbabdbabcbabdb
Рис. 8.8. а — непроизводные элементы грамматики, предназначенной для опи-
описания изображений хромосом; б — телоцентрическая и V-образная хромосомы
и соответствующие им терминальные цепочки. Иллюстрация заимствована из
статьи Ледли «Высокоскоростной автоматический анализ биомедицинских
изображений», Science, 146, No. 3641, 1964 (R. S. Ledley, High-Speed Automa-
Automatic Analysis of Biomedical Pictures).
часовой стрелки. Начальные символы S и Т представляют V-об-
разную и телоцентрическую хромосомы соответственно. Инте-
Интересно отметить, что для разделения объектов на два класса
в данном случае используется одна грамматика с двумя на-
начальными символами. Если, например, грамматический разбор
снизу вверх приводит к Т, хромосому относят в класс тело-
центрических. Если грамматический разбор приводит к S, хро-
хромосома классифицируется как V-образная. Должно быть оче-
очевидно, что применение одной грамматики для распознавания —
в сущности, не что иное, как объединение двух классифика-
классификационных грамматик с различными начальными символами.
И хотя это можно сделать всегда, имеет смысл объединять
358
Гл. 8. Синтаксическое распознавание образов
только достаточно похожие грамматики, поскольку объединение
значительно отличающихся грамматик ничего не дает.
Проиллюстрируем грамматический разбор снизу вверх, не-
несколько подробнее рассмотрев использование этой схемы в со-
сочетании с приведенной выше грамматикой классификации хро-
хромосом. В качестве первого шага процесса распознавания за-
заданного цифрового изображения хромосомы необходимо найти
Пара плеч
Пара
плеч.
Сторона
Рис. 8.9. Восходящий грамматический разбор представляющей хромосому ie-
почки abcbaodbabcbabdb.
точку на границе хромосомы и затем осуществлять продвиже-
продвижение вдоль границы по направлению часовой стрелки. По мере
продвижения система процедур распознавания обеспечит обна-
обнаружение непроизводных элементов {а,Ь, с, d, е). В результате
такого отслеживания границы хромосома оказывается эффек-
эффективно сведенной к цепочке непроизводных элементов и образует
терминальное предложение, как показано на рис. 8.8, б.
После сведения хромосомы к терминальному предложению
начинается процесс синтаксического распознавания. Рассмот-
Рассмотрим, например, предложение, полученное для V-образной хро-
хромосомы, показанной на рис. 8.8, б. Грамматический анализатор,
работающий по принципу снизу вверх, начинает с применения
грамматических правил в обратном порядке. Проследим об-
обратный порядок применения правил подстановки, начиная
с правила Плечо—*¦ а. Так, если анализатор находит а, он вы-
выдает нетерминал Плечо. Как показано на рис. 8.9, символ а
обнаруживается четыре раза, что приводит к появлению четы-
четырех нетерминалов Плечо на первом уровне поиска, считая
8.5 Грамматики, используемые в распознавании образов 359
снизу. Следующее правило подстановки сочетает нетерминал
Плечо с терминалом Ъ. Как следует из рассмотрения дерева
на рис. 8.9, на следующем уровне порождаются только Плечи.
Количество проб в грамматическом разборе можно сократить,
следуя определенной заранее упорядоченной последовательно-
последовательности. «Наилучший» порядок устанавливается экспериментально.
Следующие правила подстановки порождают нетерминал Сто-
Сторона. Из трех порожденных Сторон два нетерминала порож-
порождаются при помощи символов d и один при помощи единствен-
единственного оставшегося неиспользованным символа Ъ. На следующих
двух уровнях комбинация Плеча и символа с порождает Пра-
Правую часть, и комбинация Правой части с Плечом порождает
Пару плеч. Наконец, комбинация символов Пара плеч и Сто-
Сторона порождает два символа Пара плеч, которые затем, объ-
объединяясь, порождают символ S, завершая, таким образом,
грамматический разбор снизу вверх. Следовательно, хромосома
была правильно классифицирована как V-образная.
Необходимо отметить, что в зависимости от способа обхода
границы хромосомы, получающиеся в результате цепочки сим-
символов, не всегда бывают правильно упорядочены с точки зрения
разбора. Эту трудность тем не менее легко преодолеть, заме-
заметив, что начало и конец цепочки в действительности примы-
примыкают друг к другу, так как, в конце концов, цепочка образована
в результате полного обхода вдоль границы хромосомы. Если
бы, например, на рис. 8.8,6 была приведена цепочка
bcbabdbabcbabdba, то для образования символа Плечо первый
терминальный символ b был бы объединен с последним симво-
символом а.
Приведенный грамматический разбор привел к искомому
результату при первой реализации. Конечно, далеко не всегда
получается так, поскольку обычно бывают необходимы частые
возвраты. Их число, однако, можно минимизировать упорядо-
упорядочением, упоминавшимся ранее, а также с помощью введения
в процесс поиска эвристических правил, указывающих грамма-
грамматическому анализатору способ действия в ситуациях, когда воз-
возможны несколько вариантов продолжения.
8.5.3. Распознавание древовидных структур
Для того чтобы обрабатывать древовидные структуры, необ-
необходимо слегка модифицировать наше определение грамматики.
Грамматика деревьев определяется как пятерка
G = (VN, VT,P,R,S), (8.5.1)
где Vn и Vt, как и раньше, — множества нетерминалов и тер-
терминалов соответственно, 5 — начальный символ, который во-
360 Гл. 8. Синтаксическое распознавание образов
обще говоря, может быть деревом, Р — множество грамматиче-
грамматических правил вида Q-*XF, где Q и 4я — деревья, и R — функция
ранжирования, обозначающая количество прямых потомков
узла, метка которого является терминальным символом данной
грамматики.
В качестве примера грамматики деревьев рассмотрим элек-
электрическую схему, представленную на рис. 8.3,6. Грамматика,
порождающая этот объект, состоит из следующих элементов:
VK = {A.S}, VT = {r,e,l,c,g}
Pi S ->r A -/ A -I
e А с А
I I
R(r) = 2
R(l) = {2, 1}
R(e) = 1
R[g) = 0
R[c) = 1
Для того чтобы породить конкретный образ, необходимо пере-
переписать все нетерминальные символы на узлах дерева таким
образом, чтобы сформировать дерево, все узлы которого имеют
терминальные метки (в данной грамматике).
Распознавание древовидных структур может производиться
методами, обсужденными ранее в этом разделе, за исключе-
исключением, конечно, правил подстановки, которые, отражая специ-
специфику грамматики деревьев, должны иметь древовидную
структуру.
8.6. СТАТИСТИЧЕСКИЙ АНАЛИЗ
Для определения и описания переменных, представляющих
случайную среду, должны быть привлечены статистические по-
понятия и методология. В распознавании образов случайность
появляется в основном в результате воздействия двух принци-
принципиальных факторов: шума, возникающего при измерении харак-
характеристик объекта, и неполноты информации о характеристиках
8.6. Статистический анализ 361
классов образов. В этом разделе внимание сосредотачивается
на обобщении основной модели формальной грамматики G =
= (Vn,Vt,P,S) распространением ее на ситуации статистиче-
статистического характера. Полученная в результате стохастическая мо-
модель грамматики затем может быть использована в качестве
статистического аппарата в процессе распознавания.
8.6.1. Стохастические грамматики и языки
Для придания статистического характера нашим моделям
грамматик весьма целесообразно воспользоваться следующим
приемом — считать недетерминированными правила подста-
подстановки и ставить в соответствие каждому из них некоторую ве-
вероятностную меру. Основываясь на этом приеме, мы определяем
стохастическую грамматику следующим образом:
G = (VX, VT, P, Q, S), (8.6.U
где Vn, Vt, Р и S, как и прежде, — множества нетерминалов,
терминалов, правил подстановки и начальный символ соответ-
соответственно, a Q — множество вероятностных мер, заданных на
множестве правил подстановки Р. Основные определения не-
неограниченной грамматики, грамматики непосредственно состав-
составляющих, бесконтекстной и регулярной грамматик остаются
в силе также и для стохастических грамматик. Как и прежде,
тип грамматики зависит от типа допустимых правил подста-
подстановки из множества Р.
Рассмотрим следующий процесс порождения терминальной
цепочки х, начинающийся с S:
^a2=>- . .. =^am = x, (8.6.2)
где {г\, г2, ¦ ¦ ¦, rm} представляют любые т правил подстановки
из множества Р и ai, осг, •••, am-i — промежуточные цепочки.
Пусть различные правила подстановки применяются с вероят-
вероятностями р(г\), р(г2), .-., р{гт). Тогда вероятность порождения
цепочки х определяется как
P(x) = p(r1)p(r2|ri)p(r3|r1r2) ... p{rm\r\r2 ... гт_1), (8.6.3)
где р{г]\г\г2. ¦. rj-i) — условная вероятность, поставленная в со-
соответствие правилу г,- при предварительном применении правил
гь г2, ..., /-/-1.
Если р (г,\ г\г2... г/_1) = р (г/), распределение вероятностей,
поставленных в соответствие правилу г,-, называется неограни-
неограниченным; множество Q неограниченно, если все составляющие
его распределения вероятностей неограниченны. Стохастиче-
Стохастическую грамматику называют неоднозначной, если существует п
362 Гл. 8. Синтаксическое распознавание образов
различных путей порождения цепочки х, характеризующихся
вероятностями Pi(x), P2(x), ..., рп(х), м>1. Таким образом,
вероятность порождения цепочки х неоднозначной стохастиче-
стохастической грамматикой определяется как
/>(*)= ZM*). (8.6.4)
Множество Q совместно, если
Z р(х)=1. (8.6.5)
xe=L(G)
Стохастический язык L(G)—это язык, порожденный стоха-
стохастической грамматикой G. Каждая терминальная цепочка х
языка L(G) должна обладать вероятностью р(х) порождения
данной цепочки. Стохастический язык, порожденный стохасти-
стохастической грамматикой G, формально можно определить так:
L (G) = | [х, р (х)] \xe=V?,S=^x,p(x)= t Pt (x)} , (8.6.6)
где Vf — множество всех терминальных цепочек, исключая
пустую, порожденных грамматикой G; обозначение S =Ь> х ис-
используется для обозначения выводимости цепочки х из на-
начального символа 5 посредством соответствующего применения
правил подстановки из множества Р. Короче говоря, выраже-
выражение (8.6.6) означает, что стохастический язык — это множество
всех терминальных цепочек, каждой из которых поставлена
в соответствие вероятность ее порождения, причем все цепочки
выводимы из начального символа 5. Вероятность порождения
р(х) задается суммированием вероятностей всех различных
способов порождения цепочки х. Заметим, однако, что при
п > 1 стохастический язык становится неоднозначным. Рас-
Рассмотренные выше понятия иллюстрируются следующим при-
примером.
Пример. Рассмотрим стохастическую бесконтекстную грам-
грамматику
G(VN, VT,P,Q,S),
где
VT = {a,b}, VN = {S),
Р, Q: 5 -^ aSb,
Заметим, что каждому правилу подстановки поставлена
в соответствие вероятность его применения. В данном случае
8.6 Статистический анализ 363
первое правило применяется с вероятностью р, в то время как
второе — с вероятностью 1 — р.
Дважды применив первое правило, а затем один раз второе,
получим последовательность
5 =>- aSb =*¦ aaSbb =p- aaabbb.
Обозначив терминальную цепочку aaabbb через х и используя
(8.6.3), имеем
Язык, порожденный грамматикой G, задается в данном слу-
случае следующим образом:
Каждая цепочка а'Ь' имеет, как мы видим, связанную с ней
вероятность /?(~'A— р)- Отметим также, что эта стохастическая
грамматика не является неоднозначной, так как существует
всего одна последовательность правил подстановки, ведущая
к каждой терминальной цепочке. В качестве упражнения
в конце этой главы предлагается доказать, что множество Q
в данном случае совместно. |
В стохастических языках используются те же методы грам-
грамматического разбора, что были рассмотрены в предыдущем па-
параграфе. Однако для облегчения процесса разбора могут при-
привлекаться знания о вероятности применения правил подста-
подстановки. Предположим, например, что на определенном шаге про-
процедуры восходящего грамматического разбора имеется несколько
правил-кандидатов, одно из которых следует выбрать и приме-
применить. Очевидно, что правилом, имеющим наибольшую вероят-
вероятность успешного применения, будет правило с наибольшей ве-
вероятностью применения для порождения анализируемой терми-
терминальной цепочки. В общем случае вероятности применения
грамматических правил должны использоваться в грамматиче-
грамматическом разборе для увеличения скорости распознавания стохасти-
стохастических систем.
8.6.2. Оценка вероятностей правил подстановки
с помощью процедур обучения
Переход от детерминированной к стохастической грамма-
грамматике осуществляется относительно просто. Единственное разли-
различие между этими двумя типами грамматик заключается в на-
наличии или отсутствии множества вероятностных мер для правил
подстановки Q. Естественно, если мы хотим использовать сто-
стохастические грамматики, необходимо обладать механизмом
оценки этих вероятностей.
364 Гл. 8. Синтаксическое распознавание образов
Рассмотрим задачу разделения М классов, характеризую-
характеризующуюся стохастическими грамматиками
G, = (Kv VTq, Pq, Qq, Sq), 9 = 1, 2, ..., M. (8.6.7)
Предполагается, что VN , Кг , Я, и S9 известны и грамматики
однозначны. Так как все еще существует множество нерешен-
нерешенных задач, связанных с оценкой вероятностей правил подста-
подстановки, мы сосредоточим наше внимание только на бесконтекст-
бесконтекстных и регулярных грамматиках. Учитывая это ограничение, тре-
требуется оценить вероятности правил подстановки Qq, q=l,
2, ..., М, при помощи множества выборочных терминальных
цепочек
Т = {хи хъ ..., хт), (8.6.8)
где каждая цепочка принадлежит языку, порожденному одной
из стохастических грамматик вида (8.6.7).
Собрав все цепочки, перенумеруем их н обозначим через
n(xh) количество появлений цепочки хн. Каждая цепочка под-
подвергается также разбору с помощью каждой грамматики,
н число Nqij(xh) обозначает, сколько раз при грамматическом
разборе цепочки хн применялось правило подстановки Л,-—«-р1,-
грамматики Gq. Хотя вероятности правил подстановки грамма-
грамматик (8.6.7) нам не известны, предполагается, что сами правила
подстановки мы знаем, поэтому грамматический разбор воз-
возможен.
Математическое ожидание пЧ{,- числа вхождений правила
подстановки Л,-->|3/ грамматики GQ в грамматический разбор
данной цепочки можно аппроксимировать следующим выра-
выражением:
nql!= ? n(xh)p(Gq\xh)Nqii(Xfl), (8.6.9)
где p(Gq\xh) — вероятность порождения данной цепочки хц
грамматикой Gq. В процессе обучения эта вероятность должна
быть определена для каждой цепочки.
Вероятность pqr, применения правила подстановки Л,--»-|3,-
в грамматике Gq может теперь быть аппроксимирована соот-
соотношением
где pqij — оценка вероятности pqrh а суммирование в знамена-
знаменателе (8.6.10) выполняется по всем правилам подстановки грам-
грамматики Gq, имеющим вид Л;->рй, т. е. для всех правил под-
подстановки грамматики Gq с одинаковой нетерминальной левой
частью Ai.
8.6. Статистический анализ 365
Как было показано Ли и Фу [1972], по мере приближения
числа цепочек в Т к бесконечности оценка вероятности рчц при-
приближается к истинной вероятности правила подстановки ряц
при выполнении следующих условий:
1. Множество Т — репрезентативное подмножество языков
L(Gq), q = I, 2, ..., М, в том смысле, что Т -> L, где L — объ-
м
единение языков, т. е. L = [} L (Gq).
q = \
2. Оценка вероятности появления цепочки xh в множестве Т,
определяемая соотношением
приближается к истинной вероятности р(хн).
3. В процессе обучения для каждой цепочки xh может быть
определена вероятность p(Gq\xh).
Вероятность p(Gq\xh) того, что данная цепочка Хц принад-
принадлежит классу со,,, обычно без труда может быть установлена
в обучающей фазе. Если определенно известно, что данная це-
цепочка принадлежит исключительно классу соч, то p(Gq\xfl) — 1.
Аналогично, если известно, что хн не может принадлежать со;,,
то p(Gq\xh) = 0. Часто, однако, вследствие обсужденных в на-
начале этого раздела причин некоторые цепочки могут принад-
принадлежать более чем одному классу. В этом случае можно полу-
получить простую оценку вероятности p{Gq\xh), <7=1, 2, ..., М,
для этих цепочек, фиксируя относительную частоту, с которой
они встречаются в каждом классе. При этом, конечно, необхо-
необходимо, чтобы
м
I p(Gq\xh)=l. (8.6.12)
G=1
Когда невозможно определить относительную встречаемость
«неоднозначных» цепочек в каком-либо определенном классе,
наиболее оправданным для этих цепочек считается обычно до-
допущение p(Gq\Xn)= l/M.
Пример. Проиллюстрируем представленные в этом пара-
параграфе понятия простым числовым примером. Рассмотрим сто-
стохастические грамматики
G, = (l/,v, VT, P, Qi, S),
G2 = (Vn, VT,P,Q2, S),
36G Га 8. Синтаксическое распознавание образов
где для обеих грамматик
VT={a,b), VN = {S).
Правила подстановки и соответствующие им вероятности за-
заданы следующим образом:
Р: S -+aS
S ^а
S -+bS
S -&
<?i
Ри
Р\г
Pl3
Ри
Qz
Р21
Р22
Ргг
Pit,
Требуется определить с помощью обучающей процедуры ве-
вероятности, входящие в Qi и Q2.
Для того чтобы не отклоняться от принятой ранее системы
обозначений, можно изменить приведенные выше обозначения
следующим образом:
Qi Qz
Р: Ai -*РХ Pui Рш
Ai —¦ fa Риг Риг
Ai-i-fis Риг Ргп
Аг —-fii Рш Рш
где мы задаем S = Alt Pi = aS, p2 = a, fc — bS, р4 = Ь. Ин-
Индексы вероятностей интерпретируются так же, как и раньше,
т. е. первый индекс представляет класс, второй означает индекс
левой части правила подстановки, третий — индекс правой ча-
части правила подстановки. В данном случае все левые части
идентичны.
Для наглядности предположим, что класс o)i включает
в себя только цепочки, составленные из символов а, а класс
0J — только цепочки из символов Ь. Однако вследствие вмеша-
вмешательства шума иногда могут встречаться и смешанные цепочки.
Отметим, что, хотя обе грамматики G\ и G2 могут порождать
смешанные цепочки, в этом примере мы будем считать, что G\
используется только для порождения цепочек, состоящих из а,
8.6. Статистический анализ 367
и G2 используется только для порождения цепочек, состоящих
из Ь. Предположим далее, что обучающая выборка состоит из
100 образов-цепочек со следующими характеристиками:
цепочно
а
аа
ааЬЪЬ
ЪЬ
Ъ
Число появлении цепочки
30
20
5
25
20
Обозначив первый тип цепочки х\, второй — х2 и т. д., получаем
Для оценки вероятностей рчц по формуле (8.6.10) необходимо
сначала вычислить значения пчц. Согласно (8.6.9),
= ? п (хн) р (G, | xh) Nqil (xh),
где Т состоит из 30 цепочек хи 20 цепочек х2 и т. д. Используя
это соотношение, мы получаем для дласса o)i
«ш = п (х{) р (G, | *,) Nm (Xl) + и (x2) p (d | x2) Nm (x2) +
+ n (x3) p (G, | x3) Nm (x3) + n (x4) p (G, | xt) Nm (xj +
+ n(x5)p(Gl\x5)Nm(x5).
Проанализируем это выражение более подробно. Величина
n(jci) известна, a p(Gi\xi) есть вероятность того, что цепочка
xi принадлежит к классу соь Можно предположить, что эта ве-
вероятность равна 1, поскольку Xi состоит только из элементов а.
Коэффициент iVm(*i) — число использований в грамматическом
разборе цепочки х\ правила А\-*-$\. Так как видно, что это
правило подстановки не участвует в разборе хи то Nui(xi) = 0.
Аналогичным образом вычисляется второе слагаемое. Третья
цепочка содержит как символы а, так и Ъ и поэтому может
принадлежать любому из двух классов. Допуская, что вероят-
вероятности ее принадлежности клаёсу o)i и классу «г равны, считаем
p(Gi\x3) = 0,5. В общем случае, как упоминалось ранее, знание
368 Гл. Я. Синтаксическое распознавание образов
конкретной информации о задаче помогает определять эти ве-
вероятности более осмысленно. Цепочки ^ и й в четвертом и пя-
пятом слагаемых относим к сог, поскольку они состоят исключи-
исключительно из символов Ь. Отметим также, что N\u(x.i) =
= Nm (x5) = 0, поскольку правило /4i—»|3i не участвует в грам-
грамматическом разборе этих цепочек. Учитывая все эти соображе-
соображения, получаем
яш = C0)A)@) ~ B0)A)A) + E)@.5)B) + B5)@)@) + B0)@)@) =
= 25.
Используя простую нисходящую схему грамматического раз-
разбора, получаем следующие значения Ni,f(xn):
xh
xl
хг
XA
V5
0
1
2
0
0
I
1
0
0
0
k) Nm(*
0
0
2
I
0
») AT,mW
0
0
1
I
I
Подставляя эти значения, вычисляем остальные nqij, что при-
приводит к
пп, = (Щ(Щ1) -f- B0)A)A) - E)@.5)@) + B5)@)@) - B0)@)@) =
= 50,
пи, = C0)A)@) 4- B0)A)@) ~ E)@.5)B) + B5)@)A) + B0)@)@) -
= 2,5.
Теперь можно подсчитать все вероятности для класса coi по
формуле
где суммирование производится по всем правилам подстановки
грамматики G\ с одинаковой нетерминальной левой частью А{.
S.6. Статистический анализ 369
В нашем примере все левые части правил подстановки иден-
идентичны. Следовательно,
! "lit «111
Рш = ^п
1п. "Ill -f «112 "I" 13 + «114-
Pus = ^112-«^ = 0,061,
=^- =Й = 0,030.
2 8o
Как и ожидалось, правила подстановки класса щ, связанные
с порождением цепочек из элементов а, обладают большей ве-
вероятностью.
Вычисление вероятностей правил подстановки для класса оJ
аналогично только что проделанной процедуре. Из того, что
правила подстановки этих двух грамматик идентичны, вытекает
N2ij(xh) = Nnj(Xh). Использование для этих величин значений,
приведенных ранее в таблице, приводит к следующим n2i/--
«211 = 1 (*l) Р (Р2 | Xi) N2n (jCi) + П (Х2) р (G2 | Х2) УУ2Ц (Х2) +
+ п (х3) р (G21 х3) N2U (х3) + п (х4) р (G21 х4) N2n M +
+ n(x5)/?(G2ix5)A'211(x5).
В данном случае х\ и х2 несомненно принадлежат классу coj,
поэтому можно предположить, что p(G2\xi) = p(G2\x2) = 0.
Аналогичным образом p(G2|x4) = p(G2\xs) = 1. Кроме того, из
нашего допущения о разбиении точно на два класса вытекает,
что р(О2|хз)=1 — p{G\\xz) = 0,5. Используя эти вероятности,
а также табличные значения, получаем
¦ BOJ(O)A) -г E)@,5)B) + (
370 Гл. 8. Синтаксическое распознавание образов
«212 = C0)@)(l) 4- B0)@)(l) + E)@,5)@) -
= 0,
«213 = C0)@)@) + BO)@J@) + E)@,5)B) + B5)A)A) + B0) A) @)-
= 30,
«214 = C0)@)@) + B0)@)@) + E)@,5)(l)- + B5)A)A) + B0)(l)(l) =
= 47,5.
Вероятности правил подстановки могут теперь быть вычислены
при помощи соотношения
п2И
где, как и ранее, суммирование происходит по всем правилам
подстановки грамматики бг, имеющим одинаковую нетерми-
нетерминальную левую часть Л,-; в данном случае это верно для всех
правил подстановки. Использование приведенного соотношения
дает следующий результат:
2 г\к «214
= о,
_ 13 30,0
= ^ = Т = °»364
= 0,576.
Вычислив по выборочным цепочкам вероятность всех пра-
правил подстановки, теперь можно полностью определить стохасти-
стохастическую грамматику для данного примера:
t, Vt,P,Qi,S).
= (VN, VT,P,Q2,S),
8.7 Обучение и грамматический вывод 371
где для каждой грамматики
VT = {a, b}, VN = {S)
и
P: S -*aS 0,303 0,061
•S — л 0,606 0
S -*bS 0,061 0,364
S -*b 0,030 0,576
8.7. ОБУЧЕНИЕ И ГРАММАТИЧЕСКИЙ ВЫВОД
Главы 3—6 были посвящены в основном проблеме построе-
построения решающих функций с помощью обучающих выборок.
В этой главе эта задача до сих пор умышленно не упомина-
упоминалась. Используя лингвистическую терминологию, процедуру
получения решений с помощью обучающей выборки легко ин-
интерпретировать как задачу получения грамматики из множе-
множества выборочных предложений. Эта процедура, обычно назы-
называемая грамматическим выводом1), играет важную роль в изу-
изучении синтаксического распознавания образов в связи с ее
значением для реализации автоматического обучения. Тем не
менее, как это станет ясно из последующего обсуждения, об-
область грамматического вывода находится еще в начальной ста-
стадии развития. Мы имеем в виду возможности обучения, которые
можно было бы считать приемлемыми для синтеза универсаль-
универсальных методов построения систем синтаксического распознавания
образов. Этот параграф посвящен в основном введению понятий
грамматического вывода, рассматриваемых с двух точек зре-
зрения. В п. 8.7.1 строится алгоритм для вывода некоторых клас-
классов цепочечной грамматики. Затем в п. 8.7.2 достаточно по-
подробно разбирается задача вывода двумерных грамматик. Хотя
грамматики деревьев быстро становятся важной темой иссле-
исследований в синтаксическом распознавании образов, алгоритмы
вывода подобных грамматик, на наш взгляд, еще не достигли
уровня, позволяющего включать их в учебник. В качестве вве-
введения в эту область можно рекомендовать читателям работу
Гонсалеса и Томасона [19746].
') В литературе можно встретить также термин «восстановление грамма-
грамматики».— Прим. перев.
372 Гл 8. Синтаксическое распознавание образов
8.7.1. Вывод цепочечных грамматик
На рис. 8.10 представлена модель вывода цепочечных грам-
грамматик. Задача, показанная на этом рисунке, заключается
в том, что множество выборочных цепочек {х,} подвергается
обработке с помощью адаптивного обучающего алгоритма,
представленного на рисунке блоком. На выходе этого блока
в конечном счете воспроизводится грамматика G, согласован-
согласованная с данными цепочками, т. е. множество цепочек {х,} яв-
является подмножеством языка L(G). К. сожалению, ни одна из
известных нам схем не в состоянии решить эту задачу в общем
виде, представленном на рис. 8.10. Вместо этого предлагаются
АЛГОРИТМ
ВЫВОДА
^'Грамматика G
Рис. 8.10. Модель вывода цепочечных грамматик.
многочисленнные алгоритмы для вывода ограниченных грам-
грамматик. Алгоритм, рассматриваемый в этом пункте, является во
многих отношениях типичным отражением результатов, полу-
полученных в данной области. Этот алгоритм, являющийся модифи-
модификацией процедуры, разработанной Фельдманом [1967,1969], для
заданного множества терминальных цепочек выводит автомат-
автоматную грамматику. Основная идея метода Фельдмана заключается
в том, чтобы сначала построить нерекурсивную грамматику,
порождающую в точности заданные цепочки, а затем, сращи-
сращивая нетерминальные элементы, получить более простую рекур-
рекурсивную грамматику, порождающую бесконечное число цепочек.
Алгоритм можно разделить на три части. Первая часть форми-
формирует нерекурсивную грамматику. Вторая часть преобразует ее
в рекурсивную грамматику. Затем в третьей части происходит
упрощение этой грамматики. Эту процедуру лучше всего пояс-
пояснить на примере.
Рассмотрим выборочное множество терминальных цепочек
{caaab, bbaab,caab, bbab,cab, bbb,cb}. Требуется получить ав-
автоматную грамматику, способную порождать эти цепочки. Ал-
Алгоритм построения грамматики состоит из следующих этапов.
Часть 1. Строится нерекурсивная грамматика, порождающая
в точности заданное множество выборочных цепочек. Выбороч-
Выборочные цепочки обрабатываются в порядке уменьшения длины.
8.7 Обучение и грамматический вывод 373
Правила подстановки строятся и прибавляются к грамматике
по мере того, как они становятся нужны для построения соот-
соответствующей цепочки из выборки. Заключительное правило
подстановки, используемое для порождения самой длинной вы-
выборочной цепочки, называется остаточным правилом, а длина
его правой части равна 2. Остаточное правило длины п имеет
вид
А .. ап,
где Л — нетерминальный символ, а а\, й2, • .., а.п-—терминаль-
а.п-—терминальные элементы. Предполагается, что остаток каждой цепочки
максимальной длины является суффиксом (хвостовым концом)
некоторой более короткой цепочки. Если какой-либо остаток
не отвечает этому условию, цепочка, равная остатку, добав-
добавляется к обучающей выборке. Из последующих рассуждений
будет ясно, что выбор остатка длины 2 не связан с ограниче-
ограничением на алгоритм. Можно выбрать и более длинный остаток,
но тогда потребуется более полная обучающая выборка в связи
с условием, что каждый остаток является суффиксом некото-
некоторой более короткой цепочки.
В нашем примере первой цепочкой максимальной длины
в обучающей выборке является цепочка caaab. Для порожде-
порождения этой цепочки строятся следующие правила подстановки:
S ->сАх
Л2 *аА3
Ля — ab
где Л3—правило остатка. Вторая цепочка — ЪЬааЪ. Для по-
порождения этой цепочки к грамматике добавляются следующие
правила:
5 -> ЬАХ
А, -&Л3
А5 -аАй
Л с -*ah
Поскольку цепочка bbaab и предыдущая цепочка caaab имеют
одинаковую длину, требуется остаточное правило длины 2. За-
Заметим также, что работа первой части алгоритма приводит
374 Гл 8. Синтаксическое распознавание образов
к некоторой избыточности правил подстановки. Например, вто-
вторая цепочка может быть с равным успехом получена введением
следующих правил подстановки: S—>6Л4, А4 —*ЬА2. Но в пер-
первой части мы занимаемся лишь определением множества пра-
правил подстановки, которое способно в точности порождать обу-
обучающую выборку, и не касаемся вопроса избыточности. В слож-
сложных ситуациях трудно соблюдать выполнение этого условия
и одновременно уменьшать число необходимых правил подста-
подстановки. Значительно проще просматривать введенные правила
слева направо, чтобы определить, будут ли они порождать но-
новую цепочку, не стремясь при этом минимизировать число пра-
правил подстановки. Об устранении избыточности речь пойдет
в третьей части алгоритма.
Для порождения третьей цепочки caab требуется добавле-
добавление к грамматике только одного правила
А3-+Ь.
Рассмотрев остальные цепочки из обучающей выборки, уста-
устанавливаем, что окончательно множество правил подстановки,
построенных для порождения обучающей выборки, выглядит
следующим образом:
S — сАх As -*ab
S -*ЬАь At — ЬА3
Л, -*b Аь -*Ь
Ax -+aA2 Аь -+аА0
A2-b Л„— b
A2 -* aA3 Aq -* ab
A3^b
Часть 2. В этой части, соединяя каждое правило остатка
длины 2 другим (неостаточным) правилом грамматики, полу-
получаем рекурсивную автоматную грамматику. Это происходит
в результате слияния каждого нетерминального элемента пра-
правила остатка с нетерминальным элементом неостаточного пра-
правила, который может порождать остаток. Так, например, если
Аг — остаточный нетерминал вида Ar-*-a\ai и Ап — неостаточ-
неостаточный нетерминал вида Ап-*а\Ат, где Ат-*а% все встречаю-
встречающиеся Аг заменяются на Ап, а правило подстановки Ar->a\u2
8.7. Обучение и грамматический вывод 375
отбрасывается. Таким способом создается автоматная грамма-
грамматика, способная порождать данную обучающую выборку,
а также обладающая общностью, достаточной для порождения
бесконечного множества других цепочек.
В рассматриваемом примере Л6 может сливаться с As, а А3
может сливаться с А2, образуя следующие правила под-
S
5
Ах
Аг
Аг
Л2
-*¦ с A i
-*ЬА4
-+Ь
-*аА2
-*Ъ
-* а А»
Аг
Л4
Аь
Аь
А,
-*Ь
-+ЪА5
-6
->-аА&
-ft
Рекурсивными правилами являются Ai-^-aAi и А^-^аА^.
Часть 3. Здесь грамматика, полученная во второй части,
упрощается объединением эквивалентных правил подстановки.
Два правила с левыми частями At и А/ эквивалентны, если со-
соблюдены следующие условия. Предположим, что, начиная с Ait
можно породить множество цепочек {x}i. Аналогичным образом
предположим, что, начиная с А/, можно породить множество
{*}/. Если {*},-s= {x}/, то два правила подстановки считаются
эквивалентными, и каждый символ А/ может быть заменен на
Ai без ущерба для языка, порождаемого этой грамматикой.
Формально два правила подстановки эквивалентны, если
{х| Л,-=>-*} s={*| Aj^-x}, где Ai^-x обозначает, что цепочка х
порождается из At соответствующим применением правил под-
подстановки.
В приведенном примере эквивалентны правила с левыми
частями А\ и Л2. После слияния Ai и А2 получаем
S -*cAi Л4 -*ЬА5
S -* bAt Л 5 -*Ь
Ах -*Ь Аь -*аА5 ,
376 Гл. 8. Синтаксическое распознавание образов
где исключены многократные повторения одного и того же пра-
правила. Точно так же, заметив, что А\ и А-а эквивалентны, по-
получаем
S —¦сА1 Ах ->¦ аА1
Л, -6
Дальнейшее слияние правил невозможно, поэтому алгоритм
в процессе обучения строит следующую автоматную грам-
грамматику:
G = (VN, VT,P,S),
где
•Vx ={S,A,B}, VT = {a,b,c)
P: S-*cA
S - <¦ bli
A -* aA
В - b A
A — h
Легко проверить, что эта грамматика может порождать обу-
обучающую выборку, использованную в процессе ее вывода.
8.7.2. Вывод двумерных грамматик
Вопросы, возникающие в связи с двумерными граммати-
грамматиками, применяемыми в распознавании, подробно обсуждались
в § 8.4 и 8.5. По существу, основная сложность применения этих
грамматик заключается в точном определении правил двумер-
двумерного соединения. В этом разделе мы представляем простой ал-
алгоритм, разработанный Эвансом [1971], иллюстрирующий по-
построение двумерной грамматики в процессе непосредственного
обучения. Алгоритм допускает, что соответствующие двумерные
позиционные дескрипторы задаются учителем. В сущности, ал-
алгоритм основывается на следующей процедуре. Имея множество
непроизводных элементов и позиционных дескрипторов, мы на-
начинаем с непроизводных элементов и, применяя дескрипторы,
строим более сложные структуры. Когда процесс завершается,
мы выводим грамматику, используя для этого шаги построения
структур. Рассмотрим эту схему на примере.
8.7 Обучение и грамматический вывод 377
На рис. 8.11 изображены простые ненроизводные элементы,
позиционные дескрипторы и выборочный образ. Выборочный
образ, несомненно, является комбинацией непроизводных эле-
элементов. Для упрощения системы обозначений назовем окруж-
окружность выборочного образа «объектом 1», левый глаз — «объек-
«объектом 2», правый глаз — «объектом 3», нос — «объектом 4»
и рот — «объектом 5». Начиная с непроизводных элементов
и последовательно применяя дескрипторы, можно построить
различные сложные объекты. Для того чтобы направлять
ДЕСКРИПТОРЫ ВЫ60Р0ЧНЫЙ ОБРАЗ
о: \^) Цх,у):х находится внутри у
в : \ А (х,у): х находится над у
8 : L (х,у): х находится следа от у
Рис. 8.11. Элементы двумерных грамматик.
этот процесс вплоть до получения полного описания этого об-
образа, используется выборочный образ. Первым сложным обра-
образом является
объект 6: / B,1),
т. е. просто объект 2, находящийся внутри объекта 1. Этому
условию удовлетворяет выборочный образ. Легко проверить,
что следующие объекты также соответствуют выборочному
образу:
объект 7: / C,1), объект 10: L B,3),
объект 8: / D,1), объект 11: А D,5).
объект 9: / E,1),
Очевидно, существуют и другие комбинации, которым также
удовлетворяет выборочный образ; продолжим, однако, работу
с теми, что перечислены выше.
На следующем шаге из порожденных объектов строятся бо-
более сложные структуры:
объект 12: / A0,1), объект 14: А A0,5),
объект 13: А A0,4), объект 15: А A0,11).
Следующий уровень сложности достигается дальнейшей
комбинацией ранее порожденных объектов:
объект 16: / A3,1), объект 18: / A5,1),
объект 17: / A4,1), объект 19: А A3,5).
378 Гл. 8. Синтаксическое распознавание образов
Заметим, что объект 18 является полным терминальным описа-
описанием исследуемого образа, т. е. объект 18 — это объект 15, на-
находящийся внутри объекта 1, представляющего собой окруж-
окружность. Объект 15 — это в свою очередь объект 10, расположен-
расположенный над объектом 11. Объект 10, с другой стороны, это один
глаз, расположенный слева от другого, а объект 11 — это нос,
расположенный над ртом. Таким образом, объект .18 представ-
представляет собой искомый образ лица.
Грамматика, порождающая выборочный образ, легко восста-
восстанавливается по шагам, ведущим к построению объекта. Так,
грамматика для этого примера выглядит следующим образом;
G = (VN, VT,P,S),
где
VK » {S, В, С, D], VT = {h, v. с)
Р: S-»I{B,c)
В -*A{C,D)
С - L(h, h)
D -*A[v,h)
Заметим, что множество правил подстановки является, в сущ-
сущности, множеством правил построения образа. Если предполо-
предположить, что S представляет лицо, то правила подстановки озна-
означают только следующее. Лицо представляет собой некоторый
объект В, расположенный внутри окружности. Этот объект В
представляет собой некоторый объект С, расположенный над
другим объектом D, причем С — горизонтальный отрезок, рас-
расположенный слева от другого горизонтального отрезка (глаза),
a D — это вертикальный отрезок, расположенный над горизон-
горизонтальным (нос и рот).
Если задано несколько выборочных образов, грамматика
выводится для каждого из них. Затем грамматики объеди-
объединяются, а эквивалентные правила «сливаются». Получаю-
Получающаяся в результате грамматика способна порождать всю обу-
обучающую выборку полностью. Эта процедура выглядит так же,
как и схема сращивания, обсуждаемая в предыдущем разделе.
Требуется разъяснить еще несколько моментов. Как отме-
отмечалось ранее, промежуточные объекты, порожденные в этом
примере, не исчерпывают всех возможностей. Хотя и нетрудно
задать алгоритм, порождающий все допустимые комбинации
для данных дескрипторов и выборочного образа, основной за-
задачей этой процедуры является порождение одного или более
8.8 Автоматы как распознающие устройства 379
множеств шагов процесса построения, приводящего от непроиз-
водных элементов к выборочному образу. Определение грамма-
грамматики образа является в таком случае несложным делом. Ставя
перед собой эту задачу, желательно, несомненно, порождать
как можно меньше промежуточных объектов. Конечно, для
этого может понадобиться более чем одна попытка. Тем не
менее если рассматривать этот алгоритм с точки зрения реали-
реализации в режиме диалога, то этот недостаток не является серьез-
серьезным препятствием для данной процедуры. Это особенно верно,
например, для алгоритма, реализуемого с помощью диалоговой
системы с дисплеями. Другим вопросом, на котором стоит еще
раз остановиться, является проблема определения позиционных
дескрипторов. Успех любой двумерной лингвистической схемы
в конечном итоге зависит от способности исследователя долж-
должным образом задать правила двумерного соединения структур.
Многие из известных в настоящее время методов граммати-
грамматического вывода по природе своей эвристические. Это особенно
верно для двумерного случая. Подходы, обсуждаемые в этом
разделе, должны дать читателю хорошее представление о не-
некоторых применяемых методах и задачах этого направления
в распознавании образов.
8.8. АВТОМАТЫ КАК РАСПОЗНАЮЩИЕ УСТРОЙСТВА
Грамматики, изученные в предыдущих разделах, были в ос-
основном схемами, порождающими цепочки. В этом параграфе
мы кратко коснемся теории автоматов и введем понятие авто-
автомата как системы распознавания цепочек. Связь между этой
теорией и распознаванием образов очевидна, поскольку, как
это было показано в предыдущих разделах, образы часто
можно выразить в виде терминальных цепочек. Хотя исчерпы-
исчерпывающий анализ автоматов лежит за пределами нашего обсуж-
обсуждения, мы рассмотрим несколько подробнее один специфический
тип автоматов — конечные автоматы — и покажем, что конеч-
конечный автомат способен распознавать автоматные языки (языки
типа 3).
Конечный автомат s4- над алфавитом 2 определяется как
пятерка
sfi = (K, 2, б, <7о, F), (8.8.1)
где К — конечное непустое множество состояний, 2 — конечный
входной алфавит, б — отображение К X 2 в К, <7о е К — на-
начальное состояние и F^K — множество заключительных со-
состояний. Терминология и система обозначений иллюстрируются
следующим примером.
380 Гл. 8 Синтаксическое распознавание образов
Пример. Рассмотрим автомат, заданный набором (8.8.1),
где
2 = {0, 1},
K={q0, q\, qi),
и б — отображение
в К—задается таким образом:
Если, например, автомат находится в состоянии q0 и на вход
поступает символ 0, то автомат переходит в состояние q2. Если
далее на вход поступает сим-
символ 1, то автомат переходит в
состояние <7i и т- Д- Заметим,
что в данном случае заключи-
заключительное состояние равно на-
начальному состоянию.
Диаграмма состояний этого
автомата, приведенная на
рис. 8.12, состоит из вершин,
соответствующих каждому из
возможных состояний, и ори-
ориентированных ребер, соединя-
соединяющих взаимно достижимые
состояния. В данном примере,
если состояние q\ было бы
Рис. 8.12. Конечный автомат.
недостижимо из состояния q2
и обратно, на диаграмме не существовало бы ребра между этими
двумя состояниями. Каждое ребро диаграммы обозначается соот-
соответствующим символом из множества 2, обусловливающим пере-
переход автомата в указанное состояние.
Предположим, что автомат находится в состоянии <7о и на
вход подается цепочка х = 00110011. Автомат просматривает
цепочку слева направо по одному символу за такт. Встретив
первый 0, автомат переходит в состояние q%. Следующий 0 за-
заставляет его вернуться в состояние q0. Точно так же следующий
символ, которым является 1, меняет состояние автомата на q\,
а вторая 1 возвращает его в исходное состояние qu. Завершение
этой процедуры не требует разъяснений. Совершенно очевидно.,
что после прочтения цепочки х автомат будет находиться в со-
состоянии <7о- I
Если в результате просмотра цепочки или предложения х ав-
автомат находится в одном из возможных заключительных состоя-
8.9. Заключительные замечания 381
ний, то говорят, что цепочка х допускается автоматом .9/. Мно-
Множество всех цепочек х, допускаемых автоматом «s^, обозначается
T(s4-), т. е.
T(st) = {x\6(q, x) находится в F}, (8.8.2)
где b(q,x) обозначает состояние автомата после прочтения
цепочки х.
Если цепочками {х} представлены образы, то нам удобно
рассматривать конечный автомат как устройство, обеспечиваю-
обеспечивающее разделение на два класса: цепочка приписывается к классу
(Оь если она допускается, и к классу «г, если она не допускается
автоматом.
Можно показать, что если задана автоматная грамматика
G — A/дг, VT, Р, S), то существует конечный автомат з4- =
— (K,Vr,b,S,F), такой, что T(s4-) = L(G). И обратно, если
задан конечный автомат s&, то существует автоматная грамма-
грамматика G, такая, что L(G)= T{$$¦).
Исследования в теории автоматов показывают, что неогра-
неограниченная грамматика, грамматика непосредственно составляю-
составляющих и бесконтекстная грамматика могут распознаваться дру-
другими типами автоматов. Неограниченные языки допускаются
машинами Тьюринга; языки непосредственно составляющих —
линейно ограниченными автоматами; бесконтекстные языки —
магазинными автоматами. Кроме того, теория автоматов легко
допускает статистические постановки, как показано в работе
Фу [1970]. Стохастические автоматы могут использоваться для
распознавания стохастических языков. Можно также задать
такой автомат, который будет допускать не цепочечные, а дре-
древовидные структуры. Читателю, заинтересованному в углубле-
углублении своих познаний по этому вопросу, можно порекомендовать,
например, работы Фу и Бхаргавы [1973], Тэтчера [1973], Гон-
салеса и Томасона [1974а].
8.9. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Материал данной главы иллюстрирует на примерах основ-
основные идеи использования лингвистических понятий в распозна-
распознавании образов. Ставятся и обсуждаются некоторые ключевые
проблемы. Задача выбора непроизводных элементов непосред-
непосредственно связана с задачей выбора структурных признаков, по-
подробно обсуждаемой в гл. 7. Тем не менее непроизводные эле-
элементы в этой главе рассматриваются как терминалы некоторой
грамматики. Это позволяет интерпретировать образы как пред-
предложения соответствующего языка.
Выбор соответствующей двумерной грамматики ослож-
осложняется изменчивостью, неизбежно возникающей при соединении
382 Гл. 8. Синтаксическое распознавание пбпазоп
двумерных структур. Эту сложность можно и какой-то степени
обойти, каким-либо предварительно установленным образом
ограничивая правила соединения. В п. 8.5.2 приводятся примеры
.эффективного сведения двумерных объектов к терминальным
цепочкам. Другой метод обработки многомерных образов за-
заключается в использовании грамматик деревьев, как было ука-
указано в п. 8.5.3.
Было показано, как при помощи грамматического разбора
можно проводить распознавание синтаксических структур.
В процессе распознавания можно применять нисходящие и вос-
восходящие схемы грамматического разбора. Эффективность раз-
разбора существенно возрастет, если вместе с анализируемым
предложением использовать синтаксис грамматики.
Статистический аппарат привлекается в сферу синтаксиче-
синтаксического распознавания при помощи стохастических грамматик.
Правила подстановки в этих грамматиках подчиняются ве-
вероятностным факторам. Следовательно, основной проблемой
использования стохастических грамматик является получение
вероятностей правил подстановки с помощью обучения. Метод,
рассмотренный в п. 8.6.2, показывает, что эти вероятности мо-
могут быть получены с помощью обучающей выборки.
Задача вывода грамматики является лингвистическим экви-
эквивалентом алгоритмов обучения, изложенных в предыдущих гла-
главах. Однако, как отмечалось ранее, известные схемы вывода
грамматики все еще имеют ограниченную область приложения.
Алгоритмы из § 8.7 типичны для подходов, которые могут при-
применяться при получении грамматики с помощью обучающей
выборки предложений.
Синтаксическое распознавание образов может быть связано
с некоторыми аспектами теории автоматов. Эта связь кратко
освещена в § 8.8, где конечные автоматы выступают в роли эф-
эффективного распознающего устройства для автоматных языков.
В этом параграфе также отмечено, что другие виды автоматов
могут быть использованы для распознавания неограниченных,
бесконтекстных языков и языков непосредственно состав-
составляющих.
Библиография
Исчерпывающее введение в формальные языки можно найти в книге
Хопкрофта и Ульмана [1969]. С середины 60-х годов быстрыми темпами
растет поток литературы по синтаксическому распознаванию образов. Первые
достижения в этой области принадлежат Идену [1961], Нарасимхану [1969],
Киршу [1964], Ледли [1964, 1965] и Ханкли и Ту [1968]. Представление об
основных тенденциях в синтаксическом распознавании образов можно полу-
получить при изучении обзорных статей Миллера и Шоу [1968], Фу и Суэйна
[1971] и Гонсалеса [1972].
Язык описания изображений, приведенный в п. 8.5.2, — результат работы
Шоу [1970], а грамматика распознавания хромосом создана Ледли [1964,
Задачи 383
1965]. Исчерпывающее изложение методов грамматического разбора можно
найти в книге Ахо и Ульмана [1978]. Великолепным справочником по древо-
древовидным системам является монография Кнута [1976]. Дополнительный ма-
материал по грамматикам деревьев можно найти в работах Фу и Бхаргавы
[1973], Тэтчера [1973] и Гонсалеса и Томасона [1974а]. Сведения о стохасти-
стохастических грамматиках —в работах Фу [1971а], Ли и Фу [1971, 1972] и Бута
[1969]. Алгоритм для цепочечных грамматик, представленный б п. 8.7.1, яв-
является адаптацией результатов Фельдмана [1967, 1969], а алгоритмом, при-
приведенным в п. 8.7.2, мы обязаны Эвансу [1971]. Дополнительная информация
о выводе грамматик — работы Фельдмана, Джипса, Хорнинга и Ридера
[1969], Фу [1972], Голда [1967], Хорнинга [1969], Пао [1969] и Креспи-
Регицци [1971]. Введение в проблему вывода грамматик деревьев может
быть найдено в книге Гонсалеса и Томасона [19746]. В качестве справочного
материала к § 8.8 рекомендуются работы Хопкрофта и Ульмана [1969] и Фу
[1970].
Задачи
8.1. Опишите бесконтекстную грамматику с терминальным множеством
Vt = [а, Ь), язык которой представляет собой цепочки, составленные из
чередующихся элементов а и Ь и из чередующихся элементов Ь и а, т. е.
L(G)= {ab, ba, aba, bob, abab, baba, ...}.
8.2. Можно ли породить язык, описанный в задаче 8.1, при помощи авто-
автоматной грамматики?
8.3. Используя непроизводные элементы, подобные изображенным на рис. 8.7,
постройте грамматику PDL, способную порождать цифры от 0 до 5.
Полезно было бы рассмотреть общий исходный символ и определить
один или несколько пустых символов.
8.4. Проведите процесс распознавания образов, заданных в задаче 8.3, ис-
используя синтаксически ориентированную схему грамматического разбора
сверху вниз.
8.5 Выполните задачу 8.4 при помощи синтаксически ориентированного вос-
восходящего грамматического анализатора.
8.6 К какому классу хромосом — V-образных или телоцентрических — от-
отнесет цепочку acabdabcabd хромосомный анализатор Ледли?
8.7 Опишите грамматику деревьев для единичного куба. В качестве непро-
непроизводных элементов возьмите ребра куба.
8.8. Покажите, что множество Q в примере из п. 8.6.1 совместно.
8.9 Рассмотрите стохастические грамматики Gi=(Vv, Vt, P, Qt, S) и
Gs=(V«, VT, P, QjS), где VN = {S}, VT = {a, b, с] и P = {S-+aS,
S-*-a, S-*-bS, S-*-b, S-*~cS, S-»-e}. В результате проведения 200 на-
наблюдений два класса образов, представленных этими грамматиками, по-
породили следующие цепочки:
цепочно
«1-
х2:
х3:
*4:
хь:
аассас
ааасса
aabcbc
сЪссЬс
bbbcbc
Число появлений цепочки
50
40
20
50
40
384
Гл. 8. Синтаксическое распознавание образов
Известно, что p(<ji|a:i) = 1,0, p(Gi|x2) = 1,0, p(Gi\x3) =0,25, p(|4)
= 0, p(Gi\Xi)= 0. Используя методы из а. 8.6.2 посредством обучения
определите вероятности правил подстановки.
8.10. Используя алгоритм из п. 8.7.1, определите посредством обучения авто-
автоматную грамматику, способную порождать следующие цепочки: {ааасс,
aaacb, aacc, bacb, aaa, abc, bb, ее].
8.11. Применяя алгоритм Эваиса, определите посредством обучения двумер-
двумерную грамматику для образа
Используйте непроизводные элементы и символы, изображенные на
рис. 8.11.
В. 12. Опишите конечный автомат, который будет допускать только цепочки,
составленные из четного числа символов а и/или четного числа сим-
символов Ь.
СПИСОК ЛИТЕРАТУРЫ
Браверман (Abramson N., Braverman D.)
[1962] Learning to Recognize Patterns in a Random Environment. IRE
Trans. It Th IT8 N 5 S58S63
Абрамсон и Браверман (Abramson N., Braverman D.)
[1962] Learning to Recognize Patterns in a Ra
Into. Theory, IT-8, No 5, pp. S58—S63.
Агмон (Agmon S.)
[1954] The Relaxation Method for Linear Inequalities, Can. J. Math., 6,
3, pp. 382—392.
Айзерман М. А., Браверман Э. М. н Рсзоноэр Л. И.
[1964а] Теоретические основы метода потенциальных функций в задаче
об обучении автоматов разделению входных сигналов иа классы, Автома-
Автоматика и телемеханика, 25, № 6, 917—936.
[19646] Метод потенциальных функций в задаче о восстановлении ха-
характеристик функционального преобразователя по случайно наблюдаемым
точкам, Автоматика и телемеханика, 25, № 12, 1705—1714.
[1965] Процесс Роббинса — Монро и метод потенциальных функций, Авто-
Автоматика и телемеханика, 26, № 11, 1951—1954.
Андерберг (Anderberg M. R.)
[1973] Cluster Analysis for Applications, Academic Press, New York.
Андерсон (Anderson T. W.)
[1963] Введение в многомерный статистический анализ, Физ.матгиз, М.
Андерсон и Бахадур (Anderson Т. W., Bahadur R. R.)
[1962] Classification into Two Multivariate Normal Distributions with
Different Covariance Matrices, Ann. Math. Stat., 33, pp. 420—431.
Ахо и Ульман (Aho A. V., Ullman J. D.)
[1978] Теорий синтаксического анализа перевода и компиляции. Синтак-
Синтаксический анализ, т. 1, «Мир», М.
Бабу (Babu С. Chitti)
[1973] On the Application of Probabilistic Distance Measures for the
Extraction of Features from Imperfectly Labeled Patterns, Internat. J.
Computer and Infor. Sci., 2, 2, pp. 103—114.
Батт и др. (Butt E. В. et al.)
[1968] Studies in yisual Texture Manipulation and Synthesis, Tech. Rept.
68-64, Computer Science Center, University of Maryland, College Park.
Батчилор и Уилкинс (Batchelor В. G., Wilkins В. R.)
[1969] Method for Location of Clusters of Patterns to Initialize a Learn-
Learning Machine, Electronics Letters, 5, 20, pp. 481—483.
Блейдон (Blaydon С. С.)
^1967] Recursive Algorithms for Pattern Classification, Office Naval Res.
'ech. Rept. 520, Division of Engineering and Applied Physics, Harvard
University, Cambridge, Mass.
Блекуэлл, Гиршик (Blackwell D., Qirshick M. A.)
[1958] Теория игр и статистических решений, ИЛ, М.
Блок (Block H. D.)
[1962] The Perceptron: A Model for Brain Functioning I Rev Mod
Phys., 34, 1, pp. 123—135. '
Блок, Нильсои и Дуда (Block H. D., Nilsson N. J., Duda R. O.)
[1964] Determination and Detection of Features in Patterns in "Computer
13 3aKs594
386 Список литературы
and Information Sciences — I" (J. T. Tou and R. H. Wilcox, eds.), Spartan
Books, Washington, D. С
Блюм (Blum J. R.)
[1954a] Approximation Methods Which Converge with Probability One,
Ann. Math. Stat, 25, pp. 382—386.
[19546] Multidimensional Stochastic Approximation Methods, Ann. Math.
Stat., 25, pp. 737—744.
Бодевиг (Bodewig E.)
[1956] Matrix Calculus, lnterscience Publishers, New York.
Болл (Ball G. H.)
[1965] Data Analysis in the Social Sciences: What about the Details?
Proceedings of the Fall Joint Computer Conference.
Болл и Холл (Ball G. H., Hall D. J.)
[1965a] Isodata, an Iterative Method of Multivariate Analysis and Pattern
Classification, Proceedings of the IFIPS Congress.
[19656] Isodata, a Novel Method of Data Analysis and Pattern Classifica-
Classification, NTIS Rept. AD699616.
Боннер (Воппег R. E.)
[1969] Некоторые методы классификации, в сборнике переводов «Авто-
«Автоматический анализ сложных изображений», «Мир», М., 205—234.
Браверман Э. М.
[1965] О методе потенциальных функций, Автоматика и телемеханика, 26,
№ 12, 2205—2213.
Браун (Brown R.)
[1963] Logical Properties of Adaptive Networks, Stanford Electronics Lab.
Quart. Res. Rev., No 4, Ш-6—III-9.
Бут (Booth T. L.)
[1969] Probabilistic Representation of Formal Languages, IEEE Conference
Record of the 10th Annual Symposium on Switching Automata.
Ван Трис (Van Trees, H. L.)
[1972] Теория обнаружения, оценок и линейной модуляции, т. I, «Совет-
«Советское радио», М.
Ватанабе (Watanabe S.)
[1969а] Разложение Карунена — Лоэва и факторный анализ. Теория и
приложения, в сборнике переводов «Автоматический анализ сложных
изображений», «Мир>, М., 254—275.
[19696] Methodologies of Pattern Recognition, Academic Press, New York.
[1970] Feature Compression, in Advances in Information Systems Science,
vol. 3 (J. Tou, ed), Plenum Press, New York.
[1971a] Ungrammatical Grammar in Pattern Recognition, Pattern Recogni-
Recognition, vol. 3, No. 4, pp. 385—408
[19716] Frontiers of Pattern Recognition, Academic Press, New York.
Гинзбург (Ginsburg S.)
[1970] Математическая теория контекстно-свободных языков, «Мир», М.
Голд (Gold Е. М.)
[1967] Language Identification in the Limit, Information and Control, 10,
5, pp. 447—474.
Гонсалес (Gonzalez R. C.)
[1972] Syntactic Pattern Recognition — Introduction and Survey, Proceed-
Proceedings of the National Electronics Conference, 27, 1, pp. 27—32.
[1973] Generation of Linguistic Filter Structures for Image Enhancement,
Proceedings of the ACM Conference.
Гонсалес, Лейн, Бишоп и Уилсон (Gonzalez R. С, Lane M. С, Bishop А. О.,
Jr., Wilson W. P.)
[1972] Some Results in Automatic Sleep-State Classification, Proceedings
of the Fourth Southeastern Symposium on System Theory.
Список литературы 387
Гоисалес и Томасон (Gonzalez R. С, Thomason M. Q.)
[1974а] Tree Grammars and Their Application to Pattern Recognition,
Tech. Rept. TR-EE/CS-74-10, Electrical Engineering Dept., Univ. of Ten-
Tennessee, Knoxville.
[19746] Inference of Tree Grammars for Syntactic Pattern Recognition,
Tech. Rept. TR-EE/CS-74-20, Electrical Engineering Dept., University of
Tennessee, Knoxville.
Гонсалес и Ту (Gonzalez R. С, Той J. Т.)
[1968] Some Results in Minimum-Entropy Feature Extraction, IEEE Con-
Convention Record — Region 111.
Гонсалес, Фрай и Крайтер (Gonzalez R. С, Fry D. N., Kryter R. C.)
[1974] Results in the Application of Pattern Recognition Methods to
Nuclear Reactor Core Component Surveillance, IEEE Trans. Nucl. ScL, 21,
1, pp. 750-757.
Гузмаи (Guzman A.)
[1967] Some Aspects of Pattern Recognition by Computer, Project MAC,
Rept. MAC-TR-37, MIT.
[1968] Decomposition of a Visual Scene into Three Dimensional Bodies,
Proceedings of the Fall Joint Computer Conference.
Дайдей (Diday E.)
[1973] The Dynamic Clusters Method in Nonhierarchical Clustering, Interna-
International J. Computer and Info. ScL, 2, 1, pp. 61—88.
Дворецки (Dvoretzky A.)
[1956] On Stochastic Approximation, in Proceedings of the 3rd Berkeley
Symposium on Mathematical Statistics and Probability (J. Neyman, ed.),
University of California Press, Berkely, pp. 39—55.
Девятериков И. П., Пропой А. И. и Цыпкин Я. 3.
[1967] О рекуррентных алгоритмах обучения распознаванию образов,
Автоматика и телемеханика, 28, 1, 122—132.
Джардин и Сибсон (Jardine N, Sibson R.)
[1968] The Construction of Hierarchic and Non-hierarchic Classifications,
Computer J., 11, pp. 177—184.
Джозеф (Joseph R. D.)
[I960] Contributions to Perceptron Theory, Cornell Aeronaut. Lab. Rept.
VG-1196-G-7.
Дуда и Фоссум (Duda R. О., Fossum H.)
[1966] Pattern Classification by lteratively Determined Linear and Piece-
wise Linear Discriminant Functions, IEEE Trans. Electronic Computers,
EC-15, 2, pp. 220—232.
Дуда и Харт (Duda R., Hart P.)
[1976] Распознавание образов и анализ сцен, «Мир», М.
Зан (Zahn С. Т.)
[1971] Graph-Theoretical Methods for Detecting and Describing Gestalt
Clusters, IEEE Trans. Computers, C-20, 1, pp. 68—86.
Идеи (Eden M.)
[1961] On the Formalization of Handwriting, in "Structure of Language
and Its Mathematical Aspect", Proceedings of the 12th Symposium on
Applied Mathematics. American Mathematical Society, Rhode Island, pp.
83—88.
Карунен (Karhunen K.)
[1947] Ober lineare Methoden in der Wahrscheinlichkeitsrechnung, Ann.
Acad. Sci. Fennicae, Ser. A137 (trans, by I. Selin in "On Linear Methods
in Probability Theory", T-131, 1960, The RAND Corp., Santa Monica. Calif.)
Кип (Keehn D. G.)
[1965] Обучение гауссовым свойствам, Экспресс-информация, серия «Тех-
«Техническая кибернетика», № 34, ВИНИТИ, 30—39.
388 Список литературы
Кирш (Kirsch К. А.)
Г19641 Computer Interpretation of English Text and Picture Patterns, IEEE
Trans. Electronic Computers, EC-13, 4, pp. 363—376.
Клауз (Clowes M. B.)
[19691 Transformational Grammars and the Organization of Pictures, in
Automatic Interpretation and Classification of Images (A. Qrasseli, ed.),
Academic Press, New York.
Кнут (Knuth D. E.)
[1976] Искусство программирования для ЭВМ, т. I, Основные алгорит-
алгоритмы, «Мир». М.
Ковалевский В. А.
Г1970"! Распознавание образов: эвристика или наука? Обзор, АН УССР,
Научный совет по кибернетике, Институт кибернетики, Киев.
Konen (Cover Т. М.)
[1964] Classification and Generalization Capabilities of Linear Threshold
Units, Rome Air Develop. Center Tech. Doc. Rept. RADC-TDR 64-32.
[1965] Geometrical and Statistical Properties of Systems of Linear Ine-
Inequalities with Applications to Pattern Recognition, IEEE Trans. Electronic
Computers, EC-14, 3. pr>. 326—334.
[1969] Learning in Pattern Recognition, in Methodologies of Pattern
Recognition (S. Watanabe, ed.^. Academic Press, New York.
Ковер и Харт (Cover Т. M . Hart P. E.)
Г.19671 "Nearest Neighbor Pattern Classification", IEEE Trans. Info.
Theory, 1Т-П, 1, pp. 21—27.
Кофер (Cofer R H.)
[1972] Picture Acquisition and Graphical Preprocessing System, Proceed-
Proceedings of the 9th Annual 1FHE Region III Convention, Charlottesville, Va.
Кофер и Tv (Cofer R. H., Tou J. T.)
[1971] Preprocessing for Pictorial Pattern Recognition, Proceedings of the
21st NATO Technical Symposium on Artificial Intelligence, Italy.
[1972] Automated Map Reading and Analysis by Computer, Proceedings
of the Fall Joint Computer Conference
Кофорд (Koford J.)
[1962] Adaptive Network Organization, Stanford Electronics Lab. Quart.
Res. Rev., No. 3, ITI-6.
Крамер fCramer H.)
[1975] Математические методы статистики. «Мир», М.
Креспи-Регишш (Crespi-Reprhizzi S.)
[1971] An Effective Model for Grammar Inference, IFIP Congress-71,
Yugoslavia.
Кульбак (Kullback S.)
[1967] Теория информации и статистика, «Наука», М.
Купер Д. и Купер П. (Cooper D. R., Cooper P. W.)
[1965] Неконтролируемая самообучающаяся система обнаружения и за-
задач распознавания образов. Экспресс-информация, серия «Техническая
кибернетика», 1965. № 8, 1—20.
Купеп П. ( Cooper P. W.)
[1964J Hyperplanes, Hyperspheres, and Hyperquadrics as Decision Bounda-
Boundaries, in Computer and Information Sciences — I (J. T. Tou and R. H. Wil-
cox, eds.), Spartan Books, Washington, D. С .
[1967] Some Topics in Nonsupervised Adaptive Detection for Multivariate
Normal Distributions, in Computer and Information Sciences —II
(J. T. Tou, ed.), Academic Press, New York.
Курант и Гильберт (Courant R., Hilbert D.)
[1951] Методы математической физики т. I, ГТТИ, М. — Л.
Кэнэл (Kanal L., ed.)
[1968] Pattern Recognition, Thompson Book Co., Washington, D. C.
Список литературы 389
Кэнэл, Рандл (Kanal L N., Randall N. С.)
[19641 Recognition System Design by Statistical Analysis, Proceedings of
the 19th ACM National Conference.
Ледли (Ledley R. S.)
[1964] High-Speed Automatic Analysis of Biomedical Pictures, Science,
146, 3641. pp. 216—223.
Ледли и др. (Ledley el al.)
[1965] FIDAC: Film Input to Digital Automatic Computer and Associated
Syntax-Directed Parrern Recognition Programming System, in Optical and
Electro-Optical Information Processing Systems (J. Tippet, D. Beckowitz,
L. Clapp, С Koester, A. Vanderbuig, Jr., eds.), MIT Press, Cambridge,
Mass., Chapter 33.
Ли и Фу (Lee H. С, Fu К. S.)
[1971] A Stochastic Syntax Analysis Procedure and Its Application to
Pattern Classification, Proceedings of the Two-Dimentional Digital Signal
Processing Conference, University of Missouri, Columbia.
[1972] A Syntactic Pattern Recognition System with Learning Capability,
in Information Systems — COINS-72 (J. T. Tou, ed.), Plenum Press, New
York.
Логинов Н. B.
[1966] Методы стохастической аппроксимации, Автоматика и телемеха-
телемеханика, 27, 4, 185—204.
Льюис (Lewis P. M.)
[1962] The Characteristic Selection Problem in Recognition Systems, IRE
Trans. Info. Theory, IT-8, 2, pp. 161—171.
Майзел (Meisel S. M.)
[1972] Computer-Oriented Approaches to Pattern Recognition, Academic
Press, New York.
Маккарти (McCarthy J.)
[1963] A Basis for a Mathematical Theory of Computation, in — "Computer
Programming and Formal Systems" — (P. Braffort. and D. Hirschberg,
eds.), North Holland, Amsterdam.
Маккуин (MacQueen J.)
Г1967] Some Methods of Classification and Analysis of Multivariate
Data, Proceedings of the 5th Berkeley Symposium on Probability and
Statistics, University of California Press, Berkeley.
Марилл и Грин (Marill Т., Green D. M.)
[19631 On the Effectiveness of Receptors in Recognition Systems, IEEE
Trans. Info. Theory, IT-9, 1, pp. 11—27.
Миллер и Шоу (Miller W. F., Shaw A. C.)
[1968] Linguistic Methods in Picture Processing — A Survey, Proceedings
of the Fall Joint Computer Conference.
Минский (Minsky M. L.)
[1961] На пути к искусственному мышлению, Труды института радиоин-
радиоинженеров, 49, No 1, 13—36.
Моцкин и Шёнберг (Motzkin Т. S., Schoenberg I. J.)
[1954] The Relaxation Method for Linear Inequalities, Can. J. Math., 6, 3,
pp. 393—404.
Надь (Nagy G.)
[1968] Распознавание образов. Обзор, Труды Института инженеров по
электротехнике и радиоэлектронике, 56, 5, 57—86.
Нарасимхан (Narasimhan R.)
[1969] Лингвистический подход к распознаванию образов, в сборнике
переводов «Автоматический анализ сложных изображений», «Мир», М.,
22—49,
390 Список литературы
Нильсон (Nilsson N. J.)
[1967] Обучающиеся машины, «Мир», М.
Новиков (Novicoff A.)
[1963] On Convergence Proofs for Perceptrons, Symposium on Mathema-
Mathematical Theory of Automata, Polytechnic Institute of Brooklin, 12, pp. 615—
622.
Огастсон и Минкер (Augustson J. G., Minker J.)
[1970] An Analysis of Some Graph-Theoretical Cluster Techniques, I. ACM,
17, 4, pp. 571—588.
Остин и Ту (Osteen R. E., Tou J. T.)
[1973] A Clique Detection Algorithm Based on Neighborhoods in Graphs,
Internat. J. Computer Info. Sci., 2, 4, pp. 257—268.
Пао (Pao T. W.)
[1969] A Solution of the Syntactical Induction-Inference Problem for a
Non-Trivia! Subset of Context-Free Languages, Interim Tech. Rept. 78-19,
Moore School of Electrical Engineering, University of Pennsylvania, Phila-
Philadelphia.
Патрик (Patrick E. A.)
[1972] Fundamentals of Pattern Recognition, Prentice-Hall, Englewood
Cliffs, N. J.
Паттерсон, Вагнер и Вумак (Patterson J. D., Wagner T. J., Womack B. F.)
J1967] A Mean-Square Performance Criterion for Adaptive Pattern Classi-
ication, IEEE Trans. Automatic Control, 12, 2, pp. 195—197.
Пфальц и Розенфельд (Pfaltz J. L., Rosenfeld A.)
[1969] Web-Grammars, Proceedings of the Joint International Conference
on Artificial Intelligence, Washington, D. С
Райе (Rice J. R.)
[1961] An Introduction to Information Theory, McGraw-Hill Book Co.,
Reading, Mass.
Реза (Reza F. M.)
[1961] An Introduction to Information Theory, McGraw-Hill Book Co.,
New York.
Риджуэй (Ridgv/ay W. C.)
[1962] An Adaptive Logic System with Generalizing Properties, Stanford
Electronics Lab. Tech. Rept. 1556-1, Stanford University, Stanford,
Calif.
Роббинс и Монро (Robbins H., Monro S.)
[1951] A Stochastic Approximation Method, Ann. Math. Stat., 22, 400—407.
Роджерс и Танимото (Rogers D., Tanimoto T.)
[1960] A Computer Program for Classifying Plants, Science, 132,
pp. 1115—1118.
Розенблатт (Rosenblatt F.)
[1957] The Perceptron: A Perceiving and Recognizing Automaton, Project
PARA, Cornell Aeronaut. Lab. Rept. 85-460-1.
[1960] "On the Convergence of Reinforcement Procedures in Simple Per-
Perceptrons», Cornell Aeronaut. Lab. Rept. VG-1196-G-4.
[1965] Принципы нейродинамики. Перцептроны и теория механизмов
мозга, «Мир», М.
Розенфельд (Rosenfeld A.)
[1969] Picture Processing by Computer, Computing Surveys, 1, 3,
pp. 147—176.
Саймоннард (Simonnard M.)
[1966^ Linear Programming, Prentice-Hall, Englewood, Cliffs, N. J.
Себестиан (Sebestyen G. S.)
[1965] Процессы принятая решений при распознавании образов, «Техш-
ка», Киев.
Список литературы 391
Синглтон (Singleton R. С.)
[1962] A Test for Linear Separability as Applied to Self-Organizing Ma-
Machines, in Self-Organizing Systems-1962 (M. С Yovits, G. T. Jacobi, and
G. D. Goldstein, eds.) Spartan Books, Washington, D. С
Скиннер и Гонсалес (Skinner С. W., Gonzalez R. С.)
[1973] On the Management and Processing of Earth Resources Informa-
Information, Proceedings of the Conference on Machine Processing of Remotely
Sensed Data, Purdue University. Lafayette Ind.
Спект (Specht D. F.)
[1967] Generation of Polynomial Discriminant Functions for Pattern Re-
Recognition, IEEE Trans. Electronic Computers, EC-16, 3, pp. 308—319.
Спреигинс (Spragins J.)
[1966] Learning Without a Teacher, IEEE Trans. Info. Theory, IT-12, 2,
pp. 223—230.
Суэйн (Swain P. H.)
[1970] On Nonparametric and Linguistic Approaches to Pattern Recogni-
Recognition, Ph. D. Dissertation, Purdue University, Lafayette, Ind.
Ту (Той J. Т.)
[1968a] Information Theoretic Approach to Pattern Recognition, IEEE
International Convention Record.
[19686] Feature Extraction in Pattern Recognition, Pattern Recognition, 1,
1, pp. 3—11.
[1969a] Engineering Principles of Pattern Recognition, in Advances in In-
Information Systems Science, vol. 1 (J. T. Tou, ed.), Plenum Press, New
York.
[19696] On Feature Encoding in Picture Processing by Computer, Proceed-
Proceedings of the Allerton Conference on Circuits and System Theory, University
of Illinois, Urbana.
[1969b] Feature Selection for Pattern Recognition Systems, in Methodolo-
fies of Pattern Recognition (S. Watanabe, ed.), Academic Press, New York.
1969r] (ред.) Advances in Information Systems Science, vol. 2, Plenum
Press, New York.
[1970] (ред.) Advances in Information Systems Science, vol. 3, Plenum
Press, New York.
[1972a] Automatic Analysis of Blood Smear Micrographs, Proceedings of
the 1972 Computer Image Processing and Recognition Symposium, Uni-
University of Missouri, Columbia.
[19726] CPA: A Cellular Picture Analyzer, paper presented at the IEEE
Computer Society Workshop on Pattern Recognition, Hot Springs, Va.
Ту и Гонсалес (Tou J. Т., Gonzalez R. С.)
[1971] A New Approach to Automatic Recognition of Handwritten Charac-
Characters, Proceedings of the Two-Dimensional Signal Processing Conference,
University of Missouri, Columbia.
[1972a] Automatic Recognition of Handwritten Characters via Feature
Extraction and Multi-level Decision, Internal. J .Computer and Info. Sci.,
1, 1, pp. 43—65.
[19726] Recognition of Handwritten Characters by Topological Feature
Extraction and Multilevel Categorization, IEEE Trans. Computers, C-21, 7,
pp. 776—785.
Ту и Унлкокс (Tou J. Т., Wilcox R. H., eds.)
[1964] Computer and Information Sciences-I, Spartan Books, Washing-
Washington D. С
T> и Хейдорн (Tou J. Т., Heydorn R. P.)
[1967] Some Approaches to Optimum Feature Extraction, in Computer
and Information Sciences-11 (J. T. Tou, ed.), Academic Press, New York,
392 Список литературы
Тэтчер (Thatcher J. W.)
[1973] Tree Automata: An Informal Survey, in Currents in the Theory of
Computing (A. V. Aho, ed.). Prentice-Hall, Englewood Cliffs, N. J.
Уайлд (Wilde D. J.)
[1964] Optimum Seeking Methods, Prentice-Hall, Englewood Cliffs, N. J.
Уидроу (Widrow B.)
[1962] Generalization and Information Storage in Networks of Adaline
Neurons, in Self-Organizing Systems—1962 (M. C. Yovits, G. T. Jacobi,
G. D. Goldstein, eds.), Spartan Books, Washington, D. С
Уиндер (Winder R. O.)
[1962] Threshold Logic, Ph. D. Dissertation, Princeton University, Prince-
Princeton, N. J.
[1963] Bounds on Threshold Gate Realizability, IEEE Trans. Electronic
Computers, EC-12, 5, pp. 561—564.
[1968] Fundamentals of Threshold Logic, in Applied Automata Theory
(J. T. Tou, ed.), Academic Press, New York.
Ульман (Ullman J. R.)
[1973] Pattern Recognition Techniques, Crane-Russak, New York.
Уормак н Гонсалес (Warmack R. E., Gonzalez R. C.)
[1972] Minimum-Error Pattern Recognition in Supervised Learning Envi-
Environments, IEEE Convention Record — Region III.
[1973] An Algorithm for the Optimal Solution of Linear Inequalities and
Its Application to Pattern Recognition, IEEE Trans. Computers, C-22, 12,
pp. 1065—1075.
Фельдман (Feldman J.)
[1967] First Thoughts on Grammatical Inference, Artificial Intelligence
Memo. 55, Computer Science Dept., Stanford University, Stanford, Calif.
[1969] Some Decidability Results on Grammatical Inference and Comple-
Complexity, Artificial Inteligence Memo., 93, Computer Science Dept., Stanford
Univ., Stanford, Calif.
Фельдман, Джине, Хорнинг и Ридер (Feldman J., Gips J., Horning J., Re-
der S.)
[1969] Grammatical Complexity and Inference, Artificial Intelligence
Memo. 89, Computer Science Dept., Stanford University, Stanford, Calif.
Фикс и Ходжес (Fix E., Hodges J. L., Jr.)
[1951] Discriminatory Analysis, Nonparametric Descrimination, Project
21-49-004, Rept 4, USAF School of Aviation Medicine, Randolph Field,
Texas (Contract AF41 A28)-31).
Фишлер (Fischler M. A.)
[1969] Machine Perception and Description of Pictorial Data, Proceedings
of the Joint International Conference on Artificial Intelligence, Washing-
Washington, D. С
Фу (Fu К. S.)
[1970] Stochastic Automata as Models of Learning Systems, in Adaptive,
Learning and Pattern Recognition Systems (J. M. Mendel and K. S. Fu,
eds.) Academic Press, New York.
[1971a] On Syntactic Pattern Recognition and Stochastic Languages, Tech.
Rept. TR-EE-71-21, School of Electrical Engineering, Purdue University,
Lafayette, Ind.
[19716] (ред.) Pattern Recognition and Machine Learning, Plenum Press,
New York.
[1971в] Последовательные методы в распознавании образов и обучении
машии, «Наука», М.
[1972] A Survey of Grammatical Inference, Tech. Report. TR-EE-72-18,
School of Electrical Engineering, Purdue University, Lafayette, Ind.
[1977] Структурные методы в распознавании образов, «Мир», М.
Список литературы 393
Фу и Бхаргава (Fu К. S., Bhargava В. К.)
[1973] Tree Systems for Syntactic Pattern Recognition, IEEE Trans. Com-
Computers, C-22, 12, pp. 1087—1099.
Фу и Суэйн (Fu К. S., Swain P. H.)
[1971] On Syntactic Pattern Recognition, in Software Engineering
(J. T. Tou, ed.), Academic Press, New York.
Фукунага (Fukunaga K.)
[1972] Introduction to Statistical Pattern Recognition, Academic Press,
New York.
Хайлиман (Highleyman W. H.)
[1962] Линейные решающие функции и их применение для распознавания
образов, Труды Института радиоинженеров, 50, 6, 1567—1580.
Ханкли и Ту (Hankley W. J., Tou J. Т.)
[1968] Automatic Fingerprint Interpretation and Classification via Contex-
Contextual Analysis and Topological Coding, in Pictorial Pattern Recognition,
(Q. С Cheng, et al., eds.), Thompson Book Company, Washington, О С.
Харари (Harary F.)
[1973] Теория графов, «Мир», М.
Хелстром (Helstrom С. W.)
[1963] Статистическая теория обнаружения сигналов, ИЛ, М.
Хо и Агравала (Но Y. С, Agrawala А. К.)
[1968] Об алгоритмах классификации образов. Введение и обзор, Труды
Института инженеров по электротехнике и радиоэлектронике, 56, 12,
5—19.
Хо и Кашьяп (Mo Y. С, Kashyap R. L.)
[1965] An Algorithm for Linear Inequalities and Its Applications, IEEE
Trans. Electronic Computers, EC-14, 5, pp. 683—688.
Хокиис (Hawkins J. K.)
[1970] Image Processing Principles and Techniques, in Advances in Infor-
Information Systems Science, vol. 3 (J. T. Tou, ed.), Plenum Press, New York.
Хомский (Chomsky Noam)
[1961] Три модели описания языка, Кибернетический сборник, No 2, ИЛ,
М., 237—266.
Хонкрофт и Ульман (Hopcroft J. E., Ullman J. D.)
[1969] Formal Languages and Their Relation to Automata, Addison-Wesley
Publishing Co., Reading, Mass.
Хорнииг (Horning J. J.)
[1969] A Study of Grammatical Inference, Tech. Rept. CS-139, Computer
Science Dept., Stanford University, Stanford, Calif.
[1971] A Procedure for Grammatical Inference, IFIP Congress-71, Yugo-
Yugoslavia.
Цзянь и Рибак (Chien Y. Т., Ribak R.)
[1971] Relationship Matrix as a Multi-Dimensional Data Base for Syntactic
Pattern Generation and Recognition, Proceedings of the Two-Dimensional
Signal Processing Conference, University of Missouri, Columbia.
Цзянь и Фу (Chien Y. Т., Fu К. S.)
[1967] On the Generalized Karhunen-Loeve Expansion, IEEE Trans. Info.
Theory, IT-13, 3, pp. 518—520.
Цыпкин Я. З.
[1965] О восстановлении характеристики функционального преобразова-
преобразователя по случайно наблюдаемым точкам, Автоматика и телемеханика, 26,
11, 1947—1950.
Чарис (Charnes A.)
[1964] On Some Fundamental Theorems of Perceptron Theory and Their
Geometry, in Computer and Information Sciences —I (J. T. Tou, R. Wil-
cox, eds.), Spartan Books, Washington, D. С
394 Список литератипы
Чини (Cheney E. W.)
Г.19661 Introduction to Approximation Theory, McGraw-Hill Book Co., New
York.
Шо> i Shaw A. C.)
fl9701 Parsing of Graph-Representable Pictures, J. ACM, 17, 3, pp. 453—
481.
Эванс (Evans T. G.)
[19711 Grammatical Inference Techniques in Pattern Analysis, in Software
Engineering (J T Ton. edi. Academic Press, New York.
Эндрюс (Andrews H Г.)
[1972] Introduction to Mathematical Techniques in Pattern Recognition,
John Wiley and Sons, New York.
Юр (Uhr L.)
Г19691 Pattern Recognition, John Wiley and Sons, New York.
f 19711 Flexible Linguistic Pattern Recognition. Pattern Recognition, 3, 4
np 363—383
Янг и Колперт (Young T Y. Calvert T W.)
f 19741 Clarification Estimation and Pattern Recognition, American Else-
vier Publishing Co., New York.
СПИСОК ОБОЗНАЧЕНИЙ
Ниже приведен перечень основных символов, используемых
в данной книге.
Обозначение
x =
x =
X\
*:
xn
X\
Xt
Xn
1
ь хг хп)
[п -IV»
х =
х,\
А, В, С, X, ...
|А|
п
Еп
N
»/
М
w
Пояснение
вектор; кроме того, образ или вектор
образа. Для обозначения векторов на
протяжении всей книги используются
строчные буквы, выделенные жирным
шрифтом, — а, Ь, х, у, z, w, ...
пополненный вектор
транспонированный вектор
вектор, снабженный индексом
евклидоза норма или модуль векто-
вектора х
вектор, компонентами которого явля-
являются абсолютные значения компонент
вектора х
матрицы
определителе матрицы А
размерность векторов образов
га-мериое евклидово пространство
количество образов
1-й класс образов
количество классов образов
количество образов, принадлежащих
классу сог
вектор весов; кроме того, вектор ко-
коэффициентов
396 Список обозначений
Обозначение Пояснение
w; вектор весов для класса оя
Z скалярное или внутреннее произведе-
/ / иие векторов w и х
|w'x| модуль скалярного произведения w'x
d (x) решающая или дискриминантная
функция
di (х) решающая функция для класса ai
di (x) = w^x линейная решающая функция
р (coj) априорная вероятность для класса
wj; скалярная величина, характери-
характеризующая вероятность появления обра-
образов, принадлежащих классу со<
р (х) = р (х\, х2, .... хп) плотность распределения образов х
р (х | (Of) плотность распределения образов х,
принадлежащих классу со*; эта функ-
функция иногда обозначается как р,(х)
р (со; | х) плотность условного распределения
для класса со*
\ dx = \ \ ... \ dx\ dx2 ... dxn кратный интеграл
X хх хг хп
Е (/ (х)( = \ I (х) р (х) dx математическое ожидание функции
X ' *¦ '
m= ?(x}== \ xp(x)dx= вектор средних значений; к|)оме того,
математическое ожидание вектора х
xip (x) dx
\ xnp(x)dx
X
mi вектор средних значений для клас-
класса @1
С = Е {(х — т) (х — т)'} = ковариационная матрица
х
С/ ковариационная матрица класса wj
N (пц, Cj) обозначение плотности нормального
или гауссовского распределения для
класса со*; эта плотность распределе-
распределения полностью определяется парамет-
параметрами ttii и С(
Список обозначений 397
Обозначение Пояснение
К (X, X/) потенциальная функция выборочного
образа Х|
G — (VN. Vr P, S) грамматика: Vn — множество нетер-
нетерминальных символов, Vr — множе-
множество терминальных символов, Р —
множество правил подстановки и
S — начальный символ или предложе-
предложение
G = {VN, V-, Р, Q, S) стохастическая грамматика: VN, Vt,
Р и S имеют те же значения, что
и выше, a Q — множестьо вероятно-
вероятностен, поставленных в соответствие
правилам подстановки, входящим в
множество Р
G = (Vjy, Vт, Р, R, S) грамматика деревьев: VN, Vt и S
имеют те же значения, что и выше,
Р — множество правил подстановки
для деревьев и R — ранжирующая
функция
Gi грамматика класса со*
L (G) язык, порожденный грамматикой G
k итерационный индекс
Cq ~ ~П—_ w биномиальный коэффициент
Э квантор существования (читается:
«существует»)
е читается: «принадлежит множеству»
0 читается: «не принадлежит множе-
множеству»
V квантор общности (читается: «для
всех»)
i>lj дельта Кронекера: б,-/ = 0, если l?=j,
и бг/ = 1, если i = j
ИМЕННОЙ УКАЗАТЕЛЬ
Абрамсон (Abramson N.) 174, 385
Агмон (Agmon S.) 385
Агравала (Agrawala А. К.) 86, 259,
393
Айзерман М. А. 234, 259, 385
Андерберг (Anderberg M. R.) 385
Андерсон (Anderson T. W.) 147, 156,
174, 385
Ахо (Aho A. V.) 383, 385
Бабу (Babu С.) 334, 385
Батт (Butt E. В.) 385
Батчилор (Batchelor В. G.) 125, 386
Бахадур (Bahadur R. R.) 147, 174,
385
Бишоп (Bishop А. О.) 386
Влейдон (Blaydon С. С.) 234, 252,
259, 385
Блекуэлл (Blackwell D.) 174, 385
Блок (Block H. D.) 234, 335, 385
Блюм (Blum J. R.) 240, 241, 259, 386
Бодевиг (Bodewig E.) 197, 334, 386
Болл (Ball G. Н.) 125, 386
Боннер (Воппег R. Е.) 123, 386
Браверман (Braverman D.) 174, 385
Браверман Э. М 234, 259, 385, 386
Браун (Brown R.) 87, 386
Бут (Booth Т. L.) 383, 386
Бхаргава (Bhargava В. К.) 381, 383,
393
Вагнер (Wagner T. J.) 390
Вальд (Wald N.) 10, 40
Ваи Трис (Van Trees H. L.) 174, 386
Эатанабе (Watanabe S.) 334, 335, 386
Вннер Н. (Wiener N.) 179
Вумак (Womack В. F.) 390
Гильберт (Hilbert D.) 81, 83, 87, 389
Гинзбург (Ginsburg S.) 386
Гиршик (Girshick M. А.) 174, 385
Голд (Gold E. М.) 383, 386
Гоисалес (Gonzalez R. С.) 5, 32, 48,
49, 125, 207, 335, 371, 381, 382,
383, 386, 387, 391, 392
Гренандер (Grenander U.) 179
Грии (Green D. М.) 389
Гудж (Googe J. M.) 10
Гузман (Guzman A.) 387
Дайдей (Diday E.) 387
Дворецки (Dvoretzky A.) 241, 259,
387
Девятериков И. П. 234, 387
Джардин (Jardine N.) 123, 387
Джипе (Gips J.) 383, 392
Джозеф (Joseph R. D.) 234, 387
Дуда (Duda R. О.) 125, 174, 259, 335,
385, 387
Дюран (Duran В. S.) 28
Журавлев Ю. И. 6, 29, 32, 129
Загоруйко Н. Г. 28
Зан (Zahn С. Т.) 123, 387
Идеи (Eden M.) 382, 387
Калаба (Kalaba R.) 7
Карунен (Karhunen К.) 387
Кашьяп (Kashyap R. L) 234, 293
Кин (Keehn D. G.) 174, 387
Кирш (Kirsch К. А.) 382, 388
Клауз (Clows M. В.) 388
Кнут (Knuth D. Е.) 383, 388
Ковалевский В. А. 334, 388
Ковер (Cover Т. М.) 87, 125, 206, 388
Колверт (Calvert T. W.) 394
Кофер (Cofer R. Н ) 388
Кофорд (Coford J.) 87, 388
Крайтер (Kryter R. С.) 48, 49, 125,
387
Крамер (Cramer H.) 388
Креспи-Регицци (Crespi-Reghizzi S.)
383, 388
Именной указатель
399
Кульбак (Kullback S.) 335, 388
Купер Д. (Cooper D. R.) 125, 388
Купер П. (Cooper P. W.) 125, 174,
334, 388
Курант (Courant Я.) 81, 83, 87, 388
Кэиэл (Kanal L.) 174, 389
Роджерс (Rogers D.) 125, 390
Розенблатт (Rosenblatt F) 8, 179,
234, 390
Розенфельд (Rosenfeld A.) 390
Розоноэр Л. И. 234, 259, 385
Рузвельт (Roosevelt F. D.) 14
Ледли (Ledley R. S.) 356, 357, 382,
389
Лейн (Lane M. С.) 386
Ли (Lee H. С.) 10, 365, 383, 389
Логинов Н. В. 335, 389
Лыоис (Lewis P. M.) 389
Майзел (Meisel S. М.) 174, 259, 389
Мак-Каллох (McCulloch W. С.) 179
Маккарти (McCarthy J.) 389
Маккуин (MacQueen J.) 125, 389
Марилл (МагШ Т.) 389
Миллер (Miller W. F.) 382, 389
Минкер (Minker J.) 123, 390
Минский (Minsky M. L.) 389
Монро (Monro S.) 240, 241 259, 390
Моцкин (Motzkin T. S.) 389
Надь (Nagy G.) 389
Нарасимхан (Narasimhan R.) 382
390
Нильсон (Nilsson N. J.) 85, 87, 125
174, 234, 335, 385, 390
Новиков (Novicoff A.) 234, 390
Огастсон (Augustson J. G.) 123 390
Оделл (Odell P. L.) 28
Остип (Osteen R. E.) 123, 390
Пао (Рао Т. W.) 383, 390
Патрик (Patrick E. A.) 125, 174, 259,
390
Паттерсон (Patterson J. D.) 390
Пирс (Pierce J. F.) 10
Пропой А. И. 234, 387
Пфальц (Pfaltz J. L.) 390
Райе (Rice J. R.) 335, 390
Рандл (Randall N. C.) 174, 389
Реза (Reza F. M.) 174, 335, 390
Рибак (Ribak R.) 393
Ридер (Reder S.) 383, 392
Риджуэй (Ridgway W. C.) 390
Роббиис (Robbins H.) 240, 241 259,
390
Саймоннард (Simmonard M.) 234,
390
Себестиан (Sebestyen G. T.) 334, 390
Сибсои (Sibson R.) 123, 387
Синглтон (Singleton R. C.) 234, 390
Скинпер (Skinner С W.) 391
Спект (Specht D. F.) 87, 391
Спремгинс (Spragins J.) 125, 391
Суонгер (Swonger С W.) 10, 42, 44,
45
Суэйн (Swain P. H.) 10, 382, 391, 393
Танимото (Tanimoto T.) 125, 390
Томасон (Thomason M. G.) 10, 371,
381, 383, 387
Ту (Той J. Т.) 5, 32, 123, 125, 174, 234,
259, 284, 334, 335, 382, 387, 388,
390, 391, 393
Тэтчер (Thatcher J. W.) 381, 383,392
Уайлд (Wilde D. J.) 259, 392
Уидроу (Widrow B.) 86, 392
Уилкинс (Wilkins B. R.) 125, 386
Уилкокс (Wilcox R. H.) 391
Уилсон (Wilson W. P.) 386
Уиндер (Winder R. O.) 78, 87, 392
Ульман (Ulman J. R.) 382, 383, 385,
392, 393
Уормак (Warmack R. E.) 207, 392
Фельдман (Feldman J.) 383, 392
Фикс (Fix E.) 392
Фишлер (Fischler M. A.) 392
Фоссум (Fossum H.) 125, 387
Фрай (Fry D. H.) 48, 49, 125 387
Фу (Fu K. S.), 10, 174, 259, 334, 335
365, 381, 382, 383, 388, 392, 393
Фукунага (Fukunaga K.) 125, 174,
259, 393
Хайлиман (Highleyman W. H.) 86,
234 393
Ханкли' (Hankley W. J.) 382, 393
Харари (Harary F.) 123. 393
Харт (Hart R.) 125. 174, 259, 387
Хейдорн (Heydorn R. P.) 284, 334
335, 392
Хелстром (Helstrom С W.) 174, 393
400
Именной указатель
Хо (Но Y. С.) 86, 234, 259, 393
Ходжес (Hodges J. L.) 392
Холл (Hall D J.) 125, 386
Хокиис (Hawkins J. К.) 393
Хомским (Chomsky Noam) 337, 393
Хопкрофт (Hopcroft J. E.) 382, 383,
393
Хорнииг (Horning J. J.) 383, 392, 393
Цзянь (Chien Y. Т.) 335, 393
Цыпкин Я. 3. 234, 387, 393
Чжэн (Chen W. H.) 10
Чини (Cheney E. W.) 178, 394
Шенберг (Schoenberg I. J.) 389
Шоу (Shaw А. С.) 352, 382, 389, 394
Эванс (Evans T. G.) 376, 383, 394
Эндрюс (Andrews H. С.) 394
Юр (Uhr L.) 394
Чарнс (Charnes A.) 234, 394
Чегис И. А. 29
Яблонский С. В. 29
Янг (Young Т. Y.) 394
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автокорреляционная матрица (auto-
(autocorrelation matrix) 295
— функция (autocorrelation function)
292, 295
Автоматы (automata) 379
— конечные (finite) 379
— линейно ограниченные (linear-
bounded) 381
— магазинные (с магазинной па-
памятью) (push-down) 381
Адаптивная схема, учитывающая на
каждом шаге информацию о всех
образах обоих классов (many-
pattern-adaption scheme) 197
Алгоритмы (algorithms)
градиентный (gradient) 247, 191
дробной коррекции (fractional-
correction) 188, 193
ИСОМАД (Isodata) 112
К внутригрупповых средних (К-
means) 109
корректирующих приращений (in-
(increment-correction) 247
коррекции абсолютной величины
(absolute-correction) 188
(основанный на принципе) макси-
миниого расстояния (maximin-
distance) 107
(основанный на принципе) миними-
минимизации среднеквадратичной ошиб-
ошибки (Ieast-mean-square-error)
— детерминистский (deterministic)
193
— статистический (statistical) 251
НСКО (LMSE) 194
перцептрон (perceptron) 181, 191,
192, 201
построение (derivation of) 189, 244
потенциальных функций (potential
functions) 207, 254
Роббинса — Монро (Robbins—Моп-
го) 237, 243
скорость сходимости (speed
of convergence) 242
Алфавит (alphabet) 337, 379
•— входном (input) 379
Апостериорная плотность распределе-
распределения (a posteriori density function)
158
Аппроксимация функциями (functio-
(functional approximation) 303
плотности распределения 163
Априорная вероятность 129, 134—136
Ассоциативные элементы (associative
units) 179
Байеса формула (Bayes' formula) 130
Байесовская обучающая процедура
(Bayesian learning) 157—163
оценка вектора средних зна-
значений (of mean vector) 157
— .. оценка ковариационной мат-
матрицы (of covariance matrix) 160
Байесовские
классификатор (classifier) 130, 135,
136, 236
решающее правило (decision rule)
131, 134
решающие функции (decision fun-
functions) 134, 236, 237
решающие функции для нормально
распределенных образов (decision
functions for normal patterns)
138
решающие функции для пирсонов-
ских плотностей распределения
VII типа (decision functions for
Pearson Type VII densities) 151
Биомедицинские приложения, приме-
примеры 39
БС правило см. Правило, основанное
на принципе ближайшего соседа
Вейерштрасса теорема о приближе-
приближении 306
Вектор градиента 190
— измерения (measurement vector)
21
— образа (pattern vector) 22. Си.
также Образ
402
Предметный указатель
Вектор средних значений (mean vec-
vector) 51, 137
определение 138
оценка 155, 157
Вероятность ошибки (probability of
error) 142, 144, 176
— — и Махаланобиса расстояния ве-
величина (versus Mahalanobis di-
distance) 145
статистической линейной ре-
решающей функции (of statistical
linear decision function 144
— правил подстановки (production
probability) 363—365
Весовой вектор (weight vector) 54
Внутриклассовые признаки (intraset
features) 24
Выбор двоичных признаков (binary
feature selection) 327—333
— — — параллельный алгоритм (pa-
(parallel algorithm) 330
¦— последовательный алгоритм
(sequential algorithm) 327
— признаков (feature selection appro-
approaches)
аппроксимация функциями
(functional approximation) 303
двоичные признаки (binary fea-
features) 327
Карунена— Лоэва дискретное
разложение (Karhunen — Loeve
expansion) 297
максимизация дивергенции (di-
(divergence maximization) 318
минимизация энтропии (entro-
(entropy minimization) 281
— ¦— разложение по системе ортого-
ортогональных функций (orthogonal ex-
expansion) 288
стохастичая аппроксимация
(stochastic approximation) 308
ядерная аппроксимация (ker-
(kernel approximation) 310
Вывод (inference) см. Грамматиче-
Грамматический пыпод
Выделение признаков (feature extrac-
extraction) 261, 263, 284
Выявление кластеров (cluster seeking)
алгоритм ИСОМЛД 112
— К виутригрупповых средних
109
— максиминного расстояния
107
—.— и распознавание образов без
учителя 123
оценка результатов 120
Выявление кластеров простой алго-
алгоритм 105
теоретико-графовый подход 122
Гармонический ряд (harmonic sequen-
sequence) 239
Гиперплоскость 70
— геометрические свойства 71
Грамматика дерева (tree grammar)
см. Грамматики
Грамматики (grammars) 337
— автоматные (finite-state) 341
— бесконтекстные (context-free) 341
— деревьев (tree) 359
— линейные (linear) 341
— неограниченные (unrestricted) 340
— непосредственно составляющих
(context-sensitive) 340
— нерекурсивные (nonrecursive) 372
— определение 337
— (используемые в) распознавании
образов 348
— регулярные (regular) 341
— рекурсивные (recursive) 372
— стохастические (stochastic) 361
— структуры составляющих (phrase-
structure) 341
— типы 340
— цепочек (string) 345
Грамматический вывод (grammatical
inference) 371—379
двумерные грамматики (two-di-
mentional grammars) 376—379
цепочечные грамматики (string
grammars) 372—376
Грамматическое правило (production)
338
— распознавание образов см. Син-
Синтаксическое распознавание обра-
образов
Граф образа (pattern graph) 123
Двоичная функция потерь (zero-one
loss function) 133
Дерево (tree) 347
— образа (pattern tree) 347
Диагональная матрица преобразова-
преобразований (diagonal transformation)
278
Диаграмма состояний (state diag-
diagram) 380
Дивергенция (divergence) 311, 313,
319
— максимизация 318
— свойства 314
Предметный указатель
403
Дискретные признаки ел. Выбор дво-
двоичных признаков
Дискриминаитные функции см. Ре-
Решающие функции
Дисперсии 276
— несмещенные 267
— смещенные 267
Дихотомизациоииая мощность (dicho-
tomization capacity) 74, 206
Дихотомии (dichotomies) 72
Древовидные структуры (tree struc-
structures) 347
— — распознавание 359
Евклидово пространство 22
— расстояние 91
Игра с нулевой суммой (game, zero-
sum) 128
Интегральные уравнения 291
Карунена — Лоэва разложение (Каг-
nunen — Loeve (/С—L) expansion)
289, 291, 293, 299
обобщенное (generalized) 297,
300
оптимальные свойства 294
применение 297
Класс (class, category) см. Класс об-
образов
Класс образов, определение 18
Классификатор, работающий по кри-
критерию минимального расстояния
(minimum-distance classifier) 91
для единственного
эталона (for single prototypes) 77
— множественных
эталонов (for multiprototypes) 93,
95
обобщение (exten-
(extension) 95
правило одного
ближайшего соседа A-NN classi-
classification rule) 95
• преде-
пределы ошибки (error bounds) 97
правило q ближай-
ближайших соседей (o-NN classification
rule) 95
сравнение с лиией-
иым классификатором (compari-
(comparison with general linear classifier)
93
Классификационная мощность (clas-
(classification capacity) см. Дихотоми-
зационная мощность
Классификация данных, полученных
дистанционно 37
Классификация для случая несколь-
нескольких классов (multicategory clas-
classification) 201, 231, 248
Классификация образов см. Распо-
Распознавание образов
— — построение алгоритмов (deriva-
(derivation of algorithms) 189, 244. См.
также Алгоритмы
Ковариационная матрица 51, 137
определение 137
оценка 156, 160
Конечный автомат (finite automaton)
379
Конкатенация 345. См. также Соеди-
Соединение
Контекстуальная информация 26
Корень дерева 346
Корневой символ (root symbol) 338
Корреляция 93
— матрица 296
— функция 291
Корректирующие ошибки (error-cor-
(error-correction)
— — выборочные образы (samples)
212
образ 229
последовательность образов
(sequence) 230
Коррекция весов (weight adjustment)
222
Koiuu — Шварца неравенство 186,
230
Критерии кластеризации (clustering
criteria) 104
Критерий разделимости (test of se-
separability) 195
Кумулятивный потенциал (cumulati-
(cumulative potential) 209
Кусочно-линейный классификатор
(piecewise-linear classifier) 94
Лагерра многочлены 83
Лагранжа множитель 270, 280
Лежандра многочлены 82
Лингвистическое распознапание обра-
образов см. Синтаксическое распозна-
распознавание образов
Линейное программирование 234
Лииейно-независимые функции (line-
(linearly-independent functions) 81
Линейно разделимые классы (linea-
(linearly-separable classes) 62
404
Предметный указатель
Линейные неравенства 67, 69, 178
— — несовместные 178
совместные 178
Лист 347
Максимум энтропии (maximum entro-
entropy) 152
Матрица потерь (loss matrix) 128
Махаланобиса расстояние (Mahala-
nobis distance) 102, 143, 144
и вероятность ошибки (and pro-
probability of error) 144
Меры сходства (similarity measu-
measures) 102
евклидовы (Euclidean) 102
Махаланобиса (Mahalanobis)
102
неметрические (nonmetric) 102
Танимото (Tanimoto) 103
Метод градиента 189
— потенциальных функций (potential
function method) 208, 222, 255
выбор функций 213
— — — геометрическая интерпрета-
интерпретация 222
— — — получение решающих функ-
функций 208
— сходимость алгоритмов 227
Методы стохастической аппроксима-
аппроксимации (stochastic approximation
methods) 237, 308
Минимаксный критерий (minimax cri-
criterion) 128, 135, 146, 147
Минимизация энтропии (entropy mini-
minimization) 281
Многогранный конус 69, 73
Миогодиапазонные спектральные раз-
развертывающие устройства (multi-
spectral scanner) 38, 39
Назначение весов признаков (feature
weighting) 268, 270
весовой коэффициент (coef-
(coefficient) 270
Начальный символ (start symbol) 338
Неймана — Пирсона критерий (Ney-
man — Pearson criterion) 136
Непроизводные символы (элементы)
(primitives) 343
Нетерминальные символы (nontermi-
(nonterminals) 338
Нетерминалы см. Нетерминальные
символы
Норма функции 79
НСКО-алгоритм см. Алгоритмы
Область отнесения объектов к опре-
определенному классу (decision re-
region) 57, 59, 60
Обобщение на случай нескольких
классов (multiclass generaliza-
generalization) 201, 231
Обобщенное обращение 194
Обобщенные решающие функции (ge-
(generalized decision functions) 62.
См. также Решающие функции
Образ (pattern) 16, 18
— определение 20—21
— предварительная обработка (prep-
(preprocessing) 261, 263
Обучающие образы (training pat-
patterns) 33
Обучение (learning, training) 25, 206
— вероятности правил подстановки
(production probabilities) 343
— и грамматический вывод (gram-
(grammatical inference) 371
— и обобщение (generalization) 206
— без учителя (learning without a
teacher) 33. См. также Распозна-
Распознавание образов без учителя
— с учителем (supervized pattern
recognition) 32
Оптимальный классификатор (opti-
(optimum classifier)
детерминистский (determinis-
(deterministic) 207
статистический (statistical) 127,
130
Ориентированные графы 352
Ортогональные функции 79
Ортонормированность 80, 215
Ортонормированные функции 79
построение из ортогональных
функций 80
Ортонормирующее преобразование
274, 275
Ортонормирующий множитель 215
Остаточное правило (residue produ-
production) 373
Отношение правдоподобия (likelihood
ratio) 131
и отношение среднеквадратич-
среднеквадратичного расстояния (versus mean-
square distance) 274
Отображение (mapping) 379
Параметрический вектор (parameter
vector) см. Весовой вектор
Перцептрои (perceptron) 179
— алгоритм см. Алгоритмы
— перцептроиный подход (perceptron
approach) 178
Предметный указатель
405
Поддерево 347
Позиционные дескрипторы (positional
descriptors) 377
Показатель класса (category index)
212
Полиномиальные функции см. Функ-
Функции
Пополненный (augmented)
— вектор образа (pattern vector) 55
— весовой вектор (weight vector) 55
Пороговое устройство (threshold
gate) 78
Порядковый номер шага итерации
325
Потенциальные функции (potential
functions) см. Функции
Правило классификации, основанное
на принципе ближайшего соседа
(БС правило) (nearest neighbor
classification rule) 94
— подстановки см. Грамматическое
правило
Преобразование подобия (similarity
transformation) 272
Преобразования кластеризации (clus-
(clustering transformations) 268, 269,
274, 276, 278
Признаки (features) 17, 23, 24, 261,
327
— математические (mathematical) 263
— структурные (structural) 263
— «физические» (physical) 263
Принцип кластеризации (clustering
concept) 30
— минимума энтропии (minimum-
entropy concept) 283
— общности свойств (common-proper-
(common-property concept) 29
— перечисления членов класса (mem-
(membership-roster concept) 28
— подкрепления — наказания (re-
(reward-punishment concept) 181
" Прирост эффективности (incremental
effectiveness) 315, 316
Проблема обработки информации (in-
(information-handling problem) 11
Просмотр таблиц (table look-up) 24
Пространство весов (weight space) 66
— образов (pattern space) 66
Процедура отыскания корня 239
Пустое предложение (empty senten-
sentence) 337
Радемахера — Уомиа полиномиаль-
полиномиальные функции (Rademacher —
Walsh polynomial functions)
170—171
Разбиение нд несколько классов, слу-
случай 1 (multiclass case 1) 55
случай 2 (multiclass
case 2) 57
случай 3 (multiclass
case 3) 44
Разделяющая граница (decision boun-
boundary) 53, 55, 59, 60
Разложение в ряд Фурье 289
Разложение по системе ортогональ-
ортогональных функций (orthogonal expan-
expansion) 288
Разложение по системе функций (fun-
(functional expansion) 303
Размещение общего типа (general
position) 74, 197
Распознавание (recognition). См.
также Распознавание образов
— грамматики см. Грамматики
— древовидных структур (of tree
structure) 359
Распознавание образов (pattern re-
recognition)
без учителя (unsupervised pat-
pattern recognition) 33. См. также
Выявление кластеров
концепция и методология 28
математические методы (mathe-
(mathematical methods) 31
определение 17
основные задачи, возникающие
при разработке систем распозна-
распознавания образов 21
понятия 16
представленных графами (of
graph-lijte patterns) 352
синтаксические методы (syntac-
(syntactic methods) 31. См. также Син-
Синтаксическое распознавание обра-
образов
эвристические методы (heuris-
(heuristic methods) 30
— отпечатков пальцев (fingerprint re-
recognition) 41
— речи (speech recognition) 18
— символов (character recognition)
18, 34
Расстояние (distance measure) 102"
265
— внутримножественное (intraset di-
distance) 266
— евклидово (Euclidean) 102
— Махаланобиса (Mahalanobis dis-
distance) 102,268,313,315
— между множествами (interset dis-
distance) 268
точками (point-to-point distan-
distance) 265
406
Предметный указатель
Расстояние между точкой и множе-
множеством (point-to-set distance) 265
— среднеквадратичное (mean-square
distance) 274
Решающие функции (decision func-
functions) 24, 53
геометрические свойства 69
два класса 55
дихотомизационная мощность
(dichotomization capacity) 74, 75
дихотомии (dichotomies) 72
для нормально распределенных
образов (for normal patterns) 138
— — квадратичные (quadratic form)
64,65
— — линеаризация (linearization) 63
— — линейные (linear) 51
обобщенные (generalized) 62
оценка методами стохастиче-
стохастической аппроксимации (stochastic
approximation) 244
— — построение (construction) 63, 85
представление в виде многочле-
многочленов (polynomial representation)
63
разбиение на несколько клас-
классов 55
реализация 76
число членов полиномиального
разложения 65
Сенсорные элементы (sensory units)
160
Синтаксис (syntax) 349—351
Синтаксически ориентированное рас-
распознавание (syntax-directed re-
recognition) 348—351
Синтаксическое описание образов
(syntactic pattern description)
324—348
— распознавание образов (syntactic
pattern recognition) 336—381
— постановка задачи 343—344
Системы распознавания образов, при-
примеры (pattern recognition systems)
33
— функций 79, 82
полные 81
Случайная переменная классифика-
классификации (random classification va-
variable) 245
Собственные векторы 271, 272, 275,
284,298, 317,322
— функции 291, 292
Соединение (juxtaposition) 345
Сопоставление (matching) 24
— с кластером (cluster matching) 93
Среднее значение 137
Среднеквадратичные отклонения 275
Статистические функции признаков
(statistical feature functions) 310
Стохастическая грамматика (stocha-
(stochastic grammar) 361
неоднозначная (ambiguous) 361
Стохастический язык (stochastic lan-
language) 361—363
Структурное распознавание образов
(structural pattern recognition)
см. Синтаксическое распознавание
образов
Сходимость (convergence)
алгоритма перцептрона 185, 188
алгоритма потенциальных функций
227
методов стохастической аппрокси-
аппроксимации 240, 241, 243, 244
НСКО-алгоритма 198
Терминальное предложение (terminal
sentence) 339
Терминальные символы (terminals)
338, 353
Технический надзор за состоянием
узлов ядерного реактора 46
Типы грамматического разбора (par-
(parsing techniques) 348—359
восходящий (bottom-up) 348,
358
нисходящий (top-down)
348—355
Тьюринга машина 381
Узел 347
Узел ветви 347
Упорядочение признаков (feature or-
ordering) 268
Условия ортогональности 79—81
функций многих переменных 79
одной переменной 79
Условные (средние) потери (condi-
(conditional loss) 113
Условный средний риск (conditional
average risk) 130
Формальные языки (formal langua-
languages)
определение 337
стохастические (stochastic) 361
Функции
— выбор потенциальных 213
— линейно независимые 81
— многих переменных 81
— норма 79
— оптимальное решение см. Опти-
Оптимальный классификатор
Предметный указатель
407
функции ортогональные 79, 81, 82
ортонормировамные 80, 82, 83
— полиномиальные 64
Лагерра 83
Лежандра 82
Радемахера — Уолша 170
Эрмита 84
— потенциальные (potential) 213, 214,
255
кумулятивный потенциал (cu-
(cumulative potential) 209
разбиение на несколько классов
231
типа 1 (of type 1) 214
типа 2 (of type 2) 215
— регрессии 237
— решение (decision) см. Решающие
функции
— скалярное произведение 79
Функция критерия (criterion functi-
function) 191
— — алгоритма корректирующих
приращений 247
наименьшей среднеквадра-
среднеквадратичной ошибки 251
перцептрона 191, 192
НСКО-алгоритма 193
— плотности распределения
— аппроксимация плотностей
распределения функциями 163—
173
второго пирсоиовского типа
(Pearson type 2) 149
— для двоичных образов (of
binary patterns) 170—173
— нормального распределения
136, 142, 149, 274
— оценка (estimation) 152
— вектора средних значений
157, 159
Функция плотности распределения,
оценка ковариационной матрицы
(estimation of the covariance mat-
matrix) 156, 160
Рэлея 175
— седьмого пирсоновского типа
150
третьего пирсоновского типа
150
Уишарта 161, 162
— потерь (loss function) 128
двоичная (zero-one) 133, 142
— правдоподобия (likelihood functi-
function) 130
— ранжирования (ranking function)
360
Характеристические числа 272, 284,
298, 317. 322
Хорошо размешенные точки (well-di-
(well-distributed points) 73, 74
Хромосомы 356, 359
— классификация 356—359
— телоцентрические 356
— V-образные 356
Цепочка (string) 337
— пустая (empty) 362
Энтропия (entropy) 152, 282. 294
— совокупности (population entropy)
281,282
Эрмита многочлены 84
Эталоны (prototypes) 91, 93
Ядерная аппроксимация 310
Язык (language) см. Формальные
языки
— описания изображений (Picture
Description Language) 352
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие редактора серии «Прикладная математика и яычислительные
процессы» . /
Предисловие «
Глава 1. Введение 11
1.1. Проблема обработки информации 11
1.2. Основные понятия распознавания образов 16
1.3. Основные задачи, возникающие при разработке систем распозна-
распознавания образов . 21
1.4. Краткое описание концепций и методологии 28
1.5. Примеры автоматических систем распознавания образов .... 33
1.6. Простая модель распознавания образов 49
Глава 2. Решающие функции 53
2.1. Введение 53
2.2. Линейные решающие функции 54
2.3. Обобщенные решающие функции 62
2.4. Пространство образов и пространство весов 66
2.5. Геометрические свойства 69
2.5.1. Свойства гиперплоскостей 69
2.5.2. Дихотомии 72
2.5.3. Дихотомизационная мощность обобщенных решающих
функций 74
2.6. Реализация решающих функций 76
2.7. Функции многих переменных 79
2.7.1. Определения 79
2.7.2. Построение функций многих переменных 81
2.7.3. Ортогональные и ортонормированные системы функций . . 82
2.8. Заключительные замечания 86
Библиография 86
Задачи 87
Глава 3. Классификация образов с помощью функций расстояния ... 89
3.1. Введение 89
3.2. Классификация образов по критерию минимума расстояния . . 90
- 3.2.1. Случай единственности эталона . . .- 91
1 3.2.2. Множественность эталонов 93
3.2.3. Обобщение принципов классификации по минимуму рас-
расстояния 95
3.42. Синтез системы распознавания. Пример 98
3.3. Выявление кластеров 101
3.3.1. Меры сходства 102
Оглавление '409
3.3.2. Критерии кластеризации 104
3.3.3. Простой алгоритм выявления кластеров 105
3.3.4. Алгоритм максиминного расстояния 107
3.3.5. Алгоритм К внутригрунповых средних 109
3.3.6. Алгоритм ИСОМАД 112
3.3.7. Оценка результатов процесса кластеризации 120
3.3.8. Кластеризация, основанная на теории графов 122
3.4. Распознавание образов без учителя 123
3.5. Заключительные замечания 124
Библиография 125
Задачи 125
Глава 4. Классификация образов с помощью функций правдоподобия . . 127
4.1. Введение 127
4.2. Классификация образов как задача теории статистических реше-
решений .... 127
4.3. Байесовский классификатор в случае образов, характеризующих-
характеризующихся нормальным распределением 136
4.4. Вероятности ошибок 142
4.5. Важное семейство плотностей распределения 148
4.6. Оценка функций плотности распределения 152
4.6.1. Вид плотности распределения 152
4.6.2. Оценка вектора средних значений и ковариационной мат-
матрицы . .155
4.6.3. Оценка вектора средних значений и ковариационной матри-
матрицы с помощью байесовской обучающей процедуры . . .157
4.6.4. Аппроксимация плотностей распределения функциями . . . 1вЗ
4.7. Заключительные замечания 173
Библиография 174
Задачи 175
Глава 5. Обучаемые классификаторы образов. Детерминистский подход 177
5.1. Введение 177
5.2. Перцептроппый подход 178
5.2.1. Принцип подкрепления — наказания 181
5.2.2. Доказательство сходимости 185
5.2.3. Разновидности перцептронного подхода 188
6.3. Построение алгоритмов классификации образов 189
5.3.1. Метод градиента 189
5.3.2. Алгоритм перцептрона 191
5.3.3. Алгоритм, основанный иа минимизации среднеквадратичной
ошибки 193
5.3.4. Доказательство сходимости НСКО-алгоритма 198
5.4. Классификация для случая нескольких классов ¦. . 201
5.5. Обучение и обобщение 206
5.6. Подход, основанный на использовании потенциальных функций . 207
5.6.1. Получение решающих функций 208
5.6.2. Выбор потенциальных функций 213
5.6.3. Геометрическая интерпретация коррекции весов 222
5.6.4. Сходимость алгоритмов обучения 227
5.6.5. Обобщение на случай нескольких классов 231
5.7. Заключительные замечания 232
Библиография 234
Задачи 234
410 Оглавление
Глава в. Обучаемые классификаторы образов. Статистический подход . 235
6.1. Введение 236
6.2. Методы стохастической аппроксимации 237
6.2.1. Алгоритм Роббинса — Монро 237
6.2.2. Скорость сходимости 242
6.2.3. Обобщение на многомерный случай 243
6.3. Построение алгоритмов классификации образов 244
6.3.1. Оценка оптимума решающих функций методами стохасти-
стохастической аппроксимации 244
6.3.2. Алгоритм корректирующих приращений 247
6.3.3. Алгоритм наименьшей среднеквадратичной ошибки .... 251
6.4. Метод потенциальных функций 254
6.5. Заключительные замечания 258
Библиография 259
Задачи 259
Глава 7. Предварительная обработка образов и выбор признаков . . .261
7.1. Введение 261
7.2. Расстояния 265
7.3. Преобразования кластеризации и упорядочение признаков . . . 268
7.4. Роль кластеризации в выборе признаков 278
7.5. Выбор признаков при помощи минимизации энтропии .... 281
7.6. Выбор признаков при помощи разложений по системе ортого-
ортогональных функций . 288
7.6.1. Разложение в ряд Фурье. Обзор 289
7.6.2. Разложение Карунена — Лоэва 290
7.7. Выбор признаков посредством аппроксимации функциями . . . 303
7.7.1. Разложение по системе функций 303
7.7.2. Метод стохастической аппроксимации 308
7.7.3. Ядерная аппроксимация 310
7.7.4. Использование функций признаков при классификации . .311
7.8. Концепция дивергенции 311
7.9. Выбор признаков на основе максимизации дивергенции .... 318
7.10. Выбор двоичных признаков 327
7.10.1. Последовательный алгоритм 327
7.10.2. Параллельный алгоритм 330
7.11. Заключительные замечания 333
Библиография 334
Задачи 335
Глава 8. Синтаксическое распознавание образов 336
8.1. Введение 336
8.2. Понятия теории формальных языков 337
8.2.1. Определения 337
8.2.2. Типы грамматик 340
8.3. Постановка задачи синтаксического распознавания образов . . 343
8.4. Синтаксическое описание образов 344
8.5. Грамматики, используемые в распознавании образов 348
8.5.1. Синтаксически ориентированное распознавание 348
.8.5.2. Распознавание образов, представленных графами . ... 352
8.5.3. Распознавание древовидных структур . 859
8.6. Статистический анализ 360
8.6.1. Стохастические грамматики и языки 361
8.6.2. Оценка вероятностей правил подстановки с помощью про-
процедуры обучения 363
Оглавление 411
8.7. Обучение и грамматический вывод 371
8.7.1. Вывод цепочечных грамматик 372
8.7.2. Вывод двумерных грамматик 376
8.8. Автоматы как распознающие устройства 379
8.9. Заключительные замечания 381
Библиография 382
Задачи 383
Список литературы 385
Список обозначений 395
Именной указатель 398
Предметный указатель 401
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформ-
оформлении, качестве перевода и другие просим присылать
по адресу. 129820, Москва, И-110, ГСП, 1-й Риж-
Рижский пер., д. 2, издательство «Мир».
Дж. Ту, Р. Гоноалес
ПРИНЦИПЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
Редактор И. Маховая
Художник В. Медников
Художественный редактор В. Шаповалов
Технический редактор Н, Манохина
Корректор Т. Пашковская
ИБ № 1025
Сдано в набор 14.03.78. Подписано к печа-
печати 20.10.78. Гарнитура литературная, печать вы-
высокая. Бумага тип. № 1. Формат 60X907 и-
Объем 13,06 бум. л., 26,13 усл. печ. л., в/ч вкл. 1.
Уч.-изд. л. 24,20. Изд. №1/9699. Тираж [3 500 экз.
Цена 2 р. 10 к. Зак. № 1057.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Отпечатано в типографии им. Котлякова изда
тельства «Финансы» Государственного Комитет
СССР по делам издательств, полиграфии и кииж
иой торговли. 191023, Ленинград Д-23, Садовая,
21 с матриц ордена Трудового Красного Зна-
Знамени Ленинградской типографии № 2 имени Ев-
Евгении Соколовой Союзполиграфпрома при Госу-
Государственном комитете СССР по делам изда-
издательств, полиграфии и киижиой торговли. 198052.
Ленинград, Л-52, Измайловский проспект, 29.
Заказ № 594.