Г. ШТЕ И Н ГАУЗ
МАТЕМАТИЧ ЕСКИЙ
Г. ШТЕЙНГАУЗ
МАТЕМАТИЧ ЕСКИ Й ^АЕ^°с/гос
МАТЕМАТИЧ ЕСКИ Й
КАЛЕЙДОСКОП
АВТОРИЗОВАННЫЙ перевод с польского
рели и Т&с!сяг£у1г4/И4.е.рсь-й4.
МОСКВА-ЛЕНИНГРАД
ПРЕДИСЛОВИЕ
Это — не систематический курс какой-нибудь области математики и не популярное изложение математических вопросов. Это—только книжка с картинками.
Содержание картинок взято, главным образом, из элементарной математики. Есть картинки, относящиеся и к высшей математике, но их смысл понятен будет всякому без больших затруднений. Есть и такие картинки, которые не имеют тесной связи с известными научными теориями.
Как надписи в кино-фильме, так и текст каждой «темы» служит только для пояснения рисунков и фотографий. Кто заинтересуется ими, тот, может быть, задумается над некоторыми вопросами и попытается на них ответить. Этих вопросов немного, и по большей части они нетрудны. Но есть и потруднее. Есть даже такие, на которые ни один человек сегодня не умеет ещё ответить.
Прогулка по зоологическому саду—не зоология в учебном смысле слова. Однако мне кажется, что нужно сначала заинтересоваться животными, а потом уже заниматься их классификацией и анатомией. Сад открыт для всех, в том числе и для тех, кто смотрит на животных только для развлечения. Поэтому не беда, если кто-нибудь скажет, что мои картинки—не математика. Кто их пересмотрит с начала до конца, тот, быть может, подметит то общее, что их объединяет. А это и есть математика.
Г. Штейнгауз
ОТ ИЗДАТЕЛЬСТВА
Популярная книжка известного польского математика Г. Штейнгауза «Kalejdoskop matematyczny» посвящена «занимательным» вопросам математики. Обычно в занимательных книгах по математике бывает много постороннего материала, шутливых рассказов и т. д., которые к математике не имеют никакого отношения. В этой же книге автор с большим вкусом подбирал только математический материал и преподнёс его читателю в форме, развивающей его любознательность и пытливость. Он выделил из большого количества математических идей и понятий такие, которые легче всего поддаются выпуклому, наглядному изображению, требующему лишь минимальных словесных пояснений.
Перевод к настоящему изданию был сделан под непосредственным наблюдением автора, который внёс ряд изменений и дополнений. Таким образом, некоторые из изложенных здесь «тем» появляются впервые. С другой стороны, здесь исключён материал, не имеющий специального математического интереса, например, стереоскопические двухцветные рисунки — анаглифы, хорошо известные советским читателям. Опущены также библиографические ссылки на источники, из которых автор черпал часть материала, так как перечень их далеко не полный и носит случайный характер.
1.	Из этих четырёх дощечек
составляется квадрат или равносторонний треугольник, смотря по тому, в какую сторону повернуть рукоятку.
2.	Из двух квадратов можно составить один, если бблыпий квадрат разрезать по двум прямым на четыре равные части.
3.	Из прямоугольного ковра, имеющего размеры 9X12, вырезан меньший ковёр размером 8X1; из остатка можно опять сшить прямоугольный ковёр, если сделать два разреза. (Как?)
4.	Квадратными плитками можно покрыть всю плоскость. Для этого могут быть взяты и неодинаковые плитки. Например, здесь
плоскость «вымощена» квадратами пяти различных величин.
Неизвестно, возможно ли вымостить плоскость такими квадратами, чтобы они все были попарно неравны, но не чересчур большие и не чересчур малые.
ш
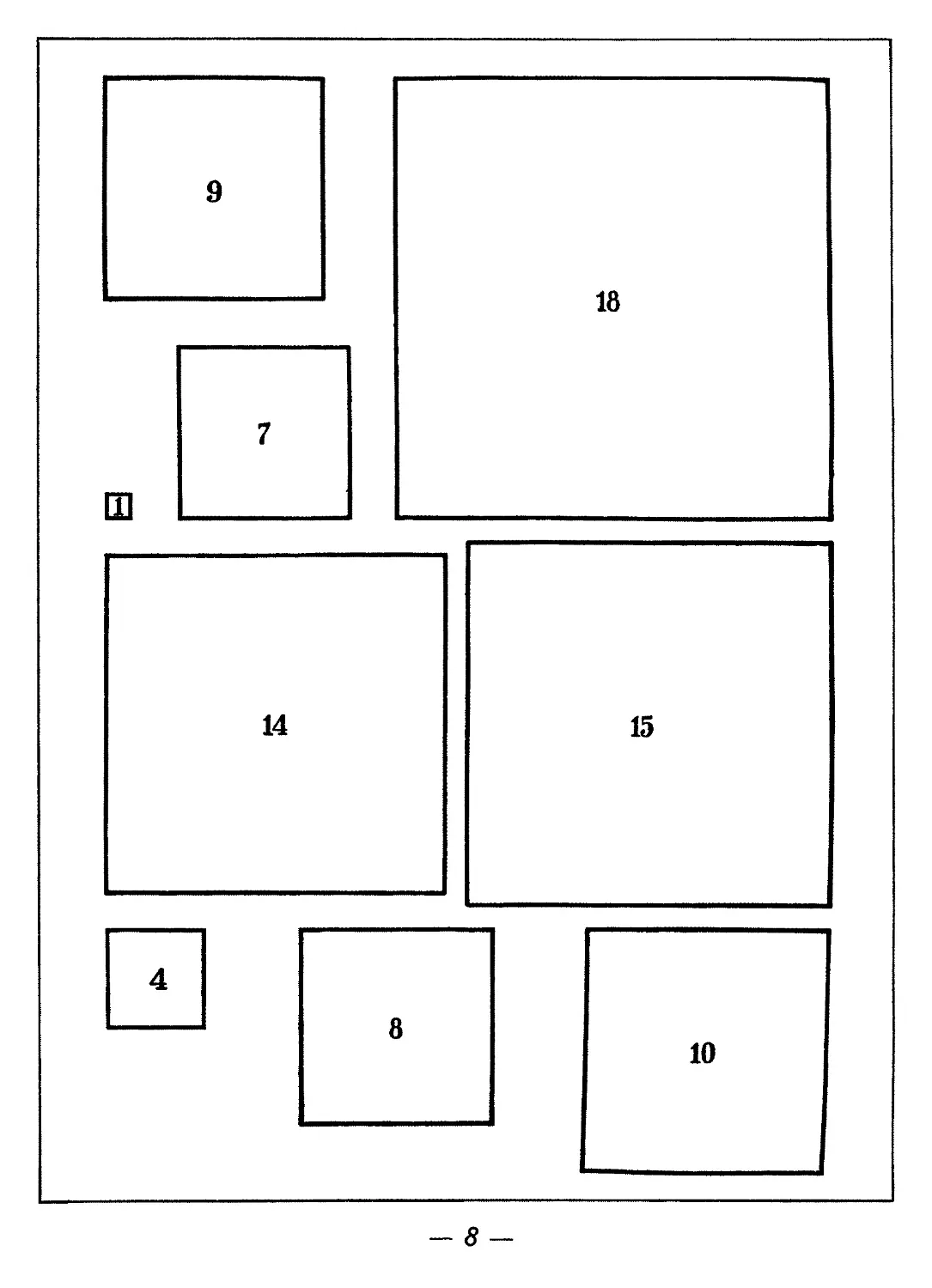
5.	Для составления прямоугольника из разных неповторяющихся квадратов необходимо иметь их по крайней мере девять (см. стр. 8). Такие квадраты имеют следующие стороны.
1, 4, 7, 8, 9, 10, 14, 15, 18.
Неизвестно, возможно ли составить прямоугольник из неповторяющихся квадратов с меньшими сторонами, длины которых выражаются целыми числами. Неизвестно также, можно ли разбить квадрат на неповторяющиеся квадраты.
6.	Тремя прямыми линиями Аа, ВЬ, Сс разбивают треугольник на семь частей.
С
Если отрезок АЬ равен у стороны АС и точно так же и другие стороны разбиты на три равные части, то площадь заштрихованного треугольника составляет ровно у площади всего треугольника. (Почему?)
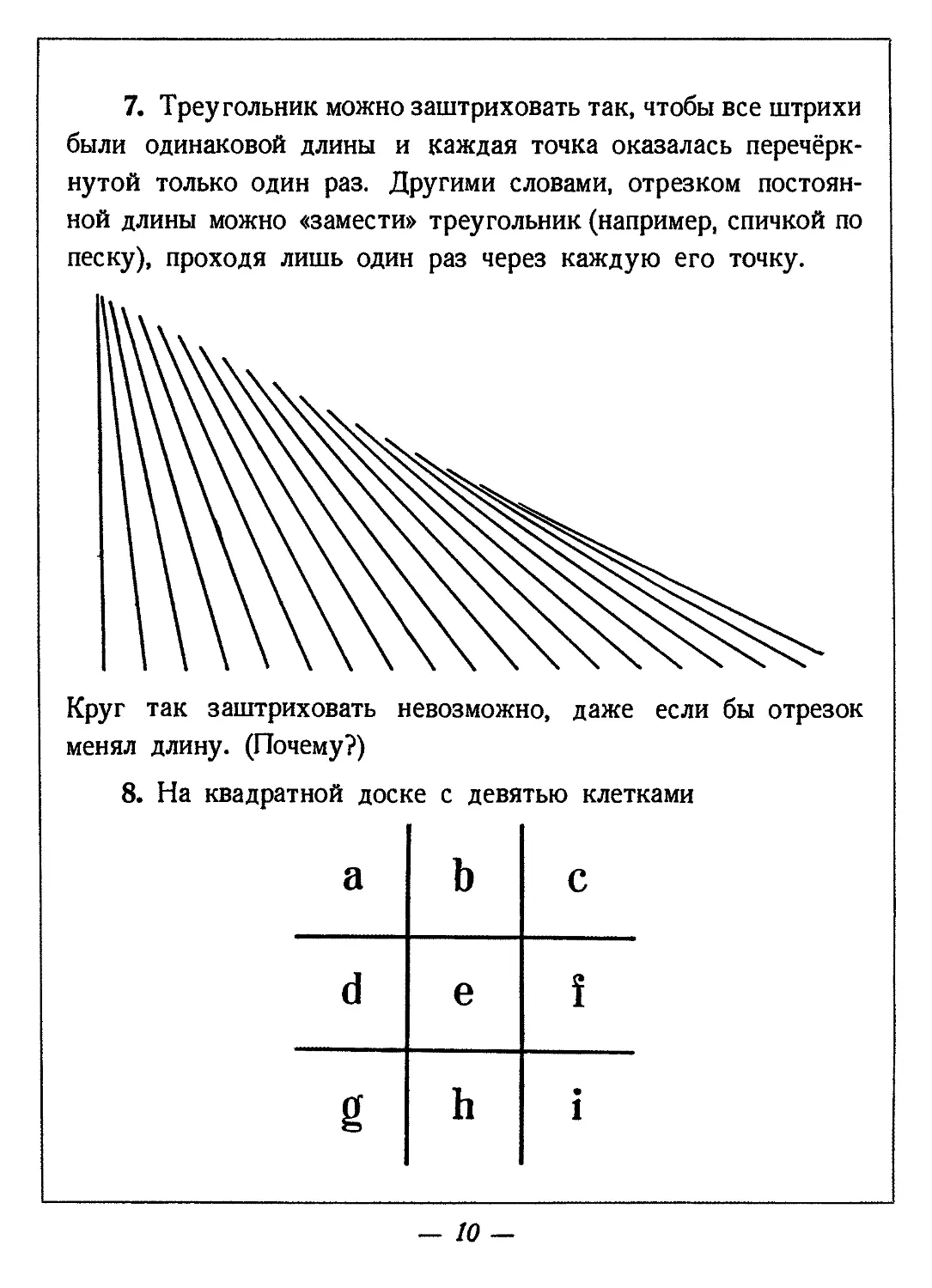
7.	Треугольник можно заштриховать так, чтобы все штрихи были одинаковой длины и каждая точка оказалась перечёркнутой только один раз. Другими словами, отрезком постоянной длины можно «замести» треугольник (например, спичкой по песку), проходя лишь один раз через каждую его точку.
Круг так заштриховать невозможно, даже если бы отрезок менял длину. (Почему?)
8.	На квадратной доске с девятью клетками
а	b	С
d	е	
g	h	• 1
можно играть в шашки следующим образом. У одного играющего три белые, у другого—три чёрные шашки. Они ставят поочерёдно свои шашки одну за другой на доску, и когда все шашки поставлены, их можно передвигать на соседние поля, но не наискось. Выигрывает тот, кто первый расположит свои шашки в столбец, строку или диагональ.
Выигрыш наверное останется за начинающим, если он сразу займёт центральную клетку и будет играть безошибочно, так как если белые займут е, то чёрные могут занять либо угловую, либо боковую клетку. Если они займут, например, а, то белые должны занять h\ этим они заставят чёрные занять Ъ и сами должны будут занять с, а это в свою очередь заставит чёрные занять g. Теперь двумя первыми ходами белые идут из h на Z и из е на / и, таким образом выиграют. Если бы чёрные заняли сначала боковую клетку Ь, то белые должны были бы занять g\ затем чёрные занимают с, белые—а, чёрные—d. Теперь белые пойдут из g на h и из h на Z, а чёрная шашка, стоящая на с, не успеет этому помешать.
Если игроки договорятся о том, что начинающий не имеет права занять клетку е, то при умелом проведении игры обоими противниками результат всегда будет ничейный.
9.	В известной игре «волк и овцы» всегда выигрывают овцы. Вообще, все игры, в которых участники делают ходы по очереди (например, игра, описанная в предыдущей теме), в том числе шашки и шахматы, теоретически или ведут к ничейному результату, или несправедливы к одной из сторон.
- И —
10.	Есть шахматные позиции, которые могут быть предметом точного исследования. Так, например, в этом эндшпиле (Бергера)
белые выигрывают, если они начнут ходом Ф Ы—Ь8, и не смогут выиграть, если начнут иначе (при условии, конечно, что чёрные будут правильно защищаться). При правильном первом ходе белые выиграют в 13 ходов (а при плохой защите чёрных—ещё раньше):
Белые	Чёрные	Белые	Чёрные
1. ФЬ8	Сс4	8. Kpg3	С13
2. Феб	Саб	9. Фс1	СЬб
3. Фе1	СЬ5	10. Фа1	Cg4
4. Фс1	СП	11. Ф118-|-	СЬЗ
5. Ф14	Саб	12. Ф:ЬЗ +	СЬ2
6. Фё4	СЬ7	13. Ф:Ь2Х	
7. Ф<11	Се4		
11.	Следующий эндшпиль имеет совсем математический характер. Белые должны сделать ничью.
Для решения задачи следует наложить на диаграмму кальку, приложенную к этой книге. Белые не позволят чёрному королю взять ни одной пешки, если они всегда будут занимать клетку, обозначенную на кальке той же буквой, что и клетка, на которую только что вошёл чёрный король. Поэтому белые могут начать только с хода В—F. Если они будут соблюдать это правило, то игра закончится вничью. Но если они сделают хотя бы одну ошибку, то чёрные форсируют проход X—Y или О—О.
Интересным был бы такой эндшпиль, при котором игра каждого из противников однозначно определялась бы ходами другого и при соблюдении обоими такой игры приводила бы к ничьей; в то же время игрок, который первый от неё отступит, неизбежно проигрывал бы (при соответствующей— опять-таки однозначно определённой—тактике другого).
11.	Следующий эндшпиль имеет совсем математический характер. Белые должны сделать ничью.
Для решения задачи следует наложить на диаграмму кальку, приложенную к этой книге. Белые не позволят чёрному королю взять ни одной пешки, если они всегда будут занимать клетку, обозначенную на кальке той же буквой, что и клетка, на которую только что вошёл чёрный король. Поэтому белые могут начать только с хода В—F. Если они будут соблюдать это правило, то игра закончится вничью. Но если они сделают хотя бы одну ошибку, то чёрные форсируют проход X—Y или О—О.
Интересным был бы такой эндшпиль, при котором игра каждого из противников однозначно определялась бы ходами другого и при соблюдении обоими такой игры приводила бы к ничьей; в то же время игрок, который первый от неё отступит, неизбежно проигрывал бы (при соответствующей— опять-таки однозначно определённой—тактике другого).
12.	По известному преданию, мудрец, который изобрёл шахматы, потребовал в награду от персидского шаха столько зёрен пшеницы, сколько их понадобится для покрытия всех клеток шахматной доски, если положить на первую клетку одно зёрнышко, на вторую — два, на третью четыре, на каждую следующую — вдвое больше зёрен, чем на предыдущую.
1	2	4	8	16 32 64 128
									
	X	ч X	ч ч ч ч	Ч Ч Ч ч ч ч ч ч	ч ч ч ч ч ч ч ч ч ч ч ч ч ч ч ч	чч \ч\ч ччч ччч			
									
									
									
									
									
									
									
									
Оказалось, что для этого нехватит пшеницы не только у персидского шаха, но и во всех амбарах мира: брамин скромно потребовал
1 +2 + 22+... + 263=264—1
зёрен. Это—двадцатизначное число. Оно — не простое, а составное, так как имеет делители. (Какие?)
Если не ограничиться одной шахматной доской в 64 клетки, а продолжать класть зёрна и на вторую шахматную доску, всё время удваивая число зёрен, и с последней клетки второй доски убрать одно зёрнышко, то на этой клетке останется
2Ш — 1 =
= 170141 183460469231 731 687303715884105727
зёрен. Это число уже не имеет делителей. Оно—наибольшее известное простое число, то-есть такое, которое не делится без остатка ни на какое другое целое число (кроме самого себя и 1).
Великий древнегреческий математик Евклид доказал, что простых чисел бесконечное множество, но до сих пор мы не знаем простого числа, которое превышало бы это 39-значное число.
Обозначим это число через L. Гораздо больше, чем L, следующее число М:
М= 22” — 1 = 8Z? +16L+7 =
=231 584178 474 632 390 847141970 017 375 845 706 539
969 331 281 128 078 915168 015 826 259 279 871.
Доказано, что это 78-значное число М—не простое, а составное, но до сих пор не удалось найти ни одного его делителя.
Таких чисел с ещё неизвестными делителями открыто много; среди них число М—самое большое, открытое до сегодняшнего дня.
13.	Шахматная доска является источником многих задач
и игр. Вот одна из них: расставить на доске восемь ферзей так, чтобы ни один из них не смог взять другого. Таких расстановок можно сделать 92; все они могут быть получены из 12 существенно различных расстановок путём поворотов и зеркальных отображений доски.
14.	На шахматной доске можно расставить пять ферзей так, чтобы под их боем были все поля доски. Эта задача имеет
4860 решений; их можно опять-таки получить из 638 существенно различных решений. Среди них можно найти и такое решение, чтобы, кроме того, ни один ферзь не смог взять другого. (Как?)
15. Всю шахматную доску можно обойти «ходом коня», возвращаясь на 64-м ходу на исходную клетку. Эта задача имеет много решений.
Вот одно из них, замечательное тем, что числа в клетках,
то-есть суммы чисел в каждой строке и в каждом столбце одинаковы. Эта сумма равна 260; иное значение невозможнс (Почему?)
- п —
16.	Великий математик Эйлер занимался задачей о ходе шахматного коня и другими подобными задачами. Вот ещё одна из задач Эйлера—задача о 36 офицерах. Как расставить в квадрате из 36 клеток делегацию от шести полков, в которую каждый полк выделяет полковника, майора, капитана, старшего лейтенанта, лейтенанта и младшего лейтенанта, если требуется, чтобы ни в одном горизонтальном и вертикальном ряду не повторялись ни полк, ни звание. Различая ранги при помощи букв, а полки по окраске, нетрудно расставить 25 офицеров из пяти полков по пять рангов,
но с 36 офицерами этого добиться невозможно.
17.	Математической теории шахматной игры ещё не существует. Но есть более простые игры, поддающиеся математическому анализу, например «игра в пятнадцать», одно время очень распространённая за границей. В плоской коробочке 16 клеток; из них 15 заняты квадратными плитками с номерами, а одна остаётся пустой. Плитки кладут в коробочку
в любом порядке и затем передвигают их одну за другой, занимая соседнюю пустую клетку (по горизонтали или вертикали). При помощи такого передвижения пытаются привести плитки в «нормальный» порядок, указанный на левом рисунке.
Математическая теория этой игры состоит в следующем. Обозначим пустое место числом 16; тогда каждое расположение плиток является некоторой перестановкой натурального ряда чисел: 1,2,3,.... 16. Всякую перестановку можно получить из натурального ряда, меняя несколько раз местами соседние числа; иногда вся перестановка требует чётного, а иногда нечётного числа таких «соседних перемен» (например, изображённое на правом рисунке расположение требует только одной соседней перемены). Оказывается, что если число перемен чётное, то задача разрешима, а если оно нечётное, то— неразрешима. Поэтому невозможно, например, получить друг из друга расстановки, указанные на этих двух рисунках.
Когда эта теория была опубликована (в 1879 году), игра вышла из моды.
18.	«Решётка целых чисел»—так называется расположение точек, расставленных как шесты для хмеля, вдоль и поперёк поля, на равном расстоянии друг от друга.
На этом рисунке наклонная прямая проведена через нижнюю левую точку и через ту точку, в которой дуга вспомогатель
ной окружности пересекает на чертеже вторую вертикальную линию. Радиусом окружности служит диагональ квадрата, а центром — вторая точка на нижней линии. Наклон этой прямой может быть измерен числом |/2 (тангенс угла, образуемого наклонной и горизонтальной прямыми). Это число—иррациональное, то-есть оно не является частным от деления двух целых чисел.
Наблюдатель который смотрит вдоль этой наклонной прямой, не увидит на ней ни одного шеста. (Почему?)
Число ]/2 можно написать в виде следующей непрерывной дроби:
/2=1+__1—
Отсюда получаются следующие приближённые значения для
2 7_ 17 *’ 2 ’ 5 ’ 12’’"
Можно проверить на решётке, что точка (2, 3), то-есть точка, удалённая на две единицы от левого и на три единицы от нижнего края, лежит вблизи прямой. Таким же образом и точки (5, 7), (12, 17), ... постепенно подходят к ней всё ближе и ближе.
19.	С рациональными и иррациональными числами связана проблема гаммы на рояле.
интервалы с — d, d—е. f—g, g—а и a — h (до-ре, ре-ми, фа-соль, соль-ля и ля-си) должны быть равны между собой — составлять один тон, а интервалы е—fn h—с (ми-фа и си-до — вдвое меньше (полутон).
На специальных приборах — монохордах —уже давно были исследованы простейшие аккорды (созвучия). При этом созвучие оказалось тем «чище», приятнее для слуха, чем более простой дробью выражается отношение чисел—колебаний в секунду, соответствующих высоте каждого звука. Так, вы
сокое с (до) имеет вдвое больше колебаний в секунду, чем низкое с: октава всегда выражается отношением 2:1. Отношение 3:2 даёт квинту (g—с), отношение 4:3—кварту (/—с}, отношение 5:4—большую терцию (е—с), а отношение 6:5—малую терцию (f—d).
Октава (с — с) состоит из 12 полутонов или четырёх малых терций. Вследствие этого должно было бы иметь место равенство
Но дробь в левой части этого равенства равна 2,074—несколько болыйе двух. Это противоречие устранить нельзя — невозможно подобрать высоту звуков так, чтобы все аккорды выражались отношениями целых чисел, независимо от тональности. Между / и g (фа и соль) лежит /Zs (фа диез — чёрная клавиша как раз посредине октавы). От с до fis и от fis до высокого с интервал один и тот же—увеличенная кварта. Поэтому, обозначая отношение числа колебаний fis — с через х, получим х-х—2, то-есть х=]/~2; это — иррациональное число.
На рояле гамма темперированная', все полутонные интервалы в ней выражаются отношениями, равными ]Л2, но зато аккорды на рояле не звучат чисто. Созвучия, которые даёт скрипач, руководясь своим слухом, отклоняются от созвучий рояля: у него увеличенная кварта на самом деле равняется 7:5, то-есть отличается от темперированной увеличенной кварты настолько, насколько точка (5, 7) на решётке целых чисел удаляется от наклонной прямой.
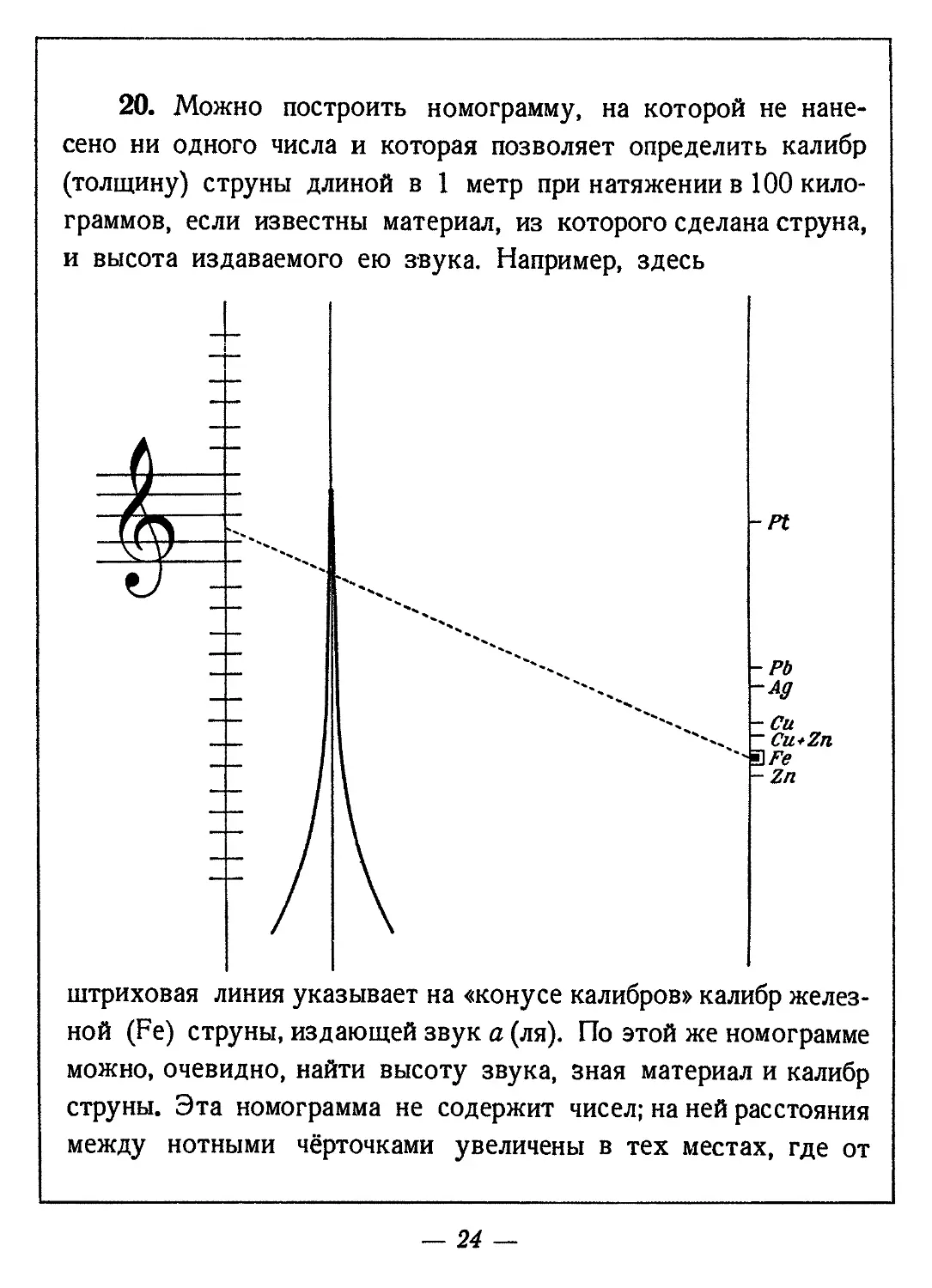
20.	Можно построить номограмму, на которой не нанесено ни одного числа и которая позволяет определить калибр (толщину) струны длиной в 1 метр при натяжении в 100 килограммов, если известны материал, из которого сделана струна, и высота издаваемого ею звука. Например, здесь
штриховая линия указывает на «конусе калибров» калибр железной (Fe) струны, издающей звук а (ля). По этой же номограмме можно, очевидно, найти высоту звука, зная материал и калибр струны. Эта номограмма не содержит чисел; на ней расстояния между нотными чёрточками увеличены в тех местах, где от
чёрточки до чёрточки большая терция, например, g—Л (соль— си). Номограмма построена по формуле Мерсена:
п И nr2d
(I—длина, Р—сила, г—радиус сечения, d—плотность материала; все величины, входящие в эту формулу, выражены в единицах системы COS—сантиметр-грамм-секунда).
21.	Бывают номограммы менее сложные, с обыкновенными (равномерными) масштабами. Такова, например, следующая номограмма смеси двух жидкостей:
Прикладывая к этой номограмме бумажную масштабную линейку (читатель найдёт её среди приложений к книге), можно прочесть на ней в точке её пересечения с левой вертикальной линией удельный вес более лёгкой жидкости (например, бензина), а в точке пересечения с правой вертикальной линией — удельный вес более тяжёлой жидкости (например, керосина). Если смешать обе жидкости и прочесть на наклонном масштабе чертежа (в точке пересечения с линейкой) процентное отношение объёма тяжёлой жидкости к объёму всей смеси, то в той же точке, на линейке определяется удельный вес смеси. (Почему?) Например, 55% керосина, удельный вес которого 0,830, и 45°/0 бензина, удельный вес которого 0,543, дают смесь, имеющую удельный вес 0,706. Если известны три из этих четырёх величин, то, прикладывая соответственным образом линейку, можно отыскать четвёртую. (Как?)
22. Ещё проще номограмма фотографов:
Расстояния f, g и h предмета, изображения и фокуса от линзы связаны известной формулой:
f g А •
Прикладывая прямую линию к двум из этих чисел, находим на номограмме третье:
о Линза
Здесь, например, предмет на расстоянии 7,5 дм (дециметров) от линзы. Так как её фокусное расстояние равно 3 дм, то изображение предмета получится на расстоянии 5 дм.
23.	Вернёмся к шахматной доске (рисунок на странице 14). В первом ряду лежит на ней 1, 2, 4, 8, 16, 32, 64, 128 зёрен. На первой и второй клетках вместе — 3 зерна, на первой и третьей—5, на второй и третьей—6 и т. д. С помощью сложения наших восьми чисел мы можем получить все числа от 1 до 255.
24. Для взвешивания тел весом до 4 килограммов с точностью до 1 гектограмма (100 граммов) достаточно иметь только 4 гири—в 1, 3, 9 и 27 гектограммов.
Это соответствует разложению чисел по троичной системе счисления. Имея ещё
1 = Z = 3 = ц в
1 3~1
3
9-3-1 9-3
6-7-
8-9-
10-11-
12-13-19-27-9-3-1 15-27-9-3 16-27+1-3-3 17-27-1-9 18-27-9 19-27+1-9
20 =27+3 - 9-1 21-27+3-9
22 - 27 +3 + 1-9 23 = 27 - 3-1 29-27-3
25 - 27+1-3
26 - 27-1
27 -27 28-27+1 29-27+3-1
30 - 27 +3
31 -27+3+1
32 =27+9-3-1
33 =27+9-3
39 - 27+9+1-3 35-37+9-1 36=27+9 37-27+9+1 38-27+3+9-1 39-27+3+9 90-27+1+3+9
9-1
9
одну гирю в 81 гектограмм, можно будет взвешивать тяжести до 12,1 килограмма. (Почему?)
25.	Обратимся снова к «решётке целых чисел» (рисунок на странице 20). Первый нижний квадрат мы можем рассматривать как бильярд, а наклонную прямую — как путь шара. Отскочив от верхнего борта по закону «угол падения равен углу отражения», шар пойдёт дальше; затем он ударится в правый борт и так далее. Ни в один угол бильярда шар не попадёт никогда, так как наша прямая проходит мимо всех точек решётки.
26.	Если бильярд прямоугольный и отношение его сторон есть число рациональное (на
пример, 5:3), то шар, пущенный из вершины под углом в 45°, попадёт в одну из вершин после нескольких ударов о борта (здесь— после шести). Объяснение даёт рисунок, заменяющий ломаный путь шара прямолинейным. Прямоугольники изображают последовательные зеркальные отражения бильярда в его бортах. Если p’.q (оба числа р и q целые) обозначает отношение сторон бильярда, то шар, прежде чем попасть в угол, испытает p+q—2 удара. (Почему?)
27.	Если нужно попасть на бильярде шаром А в шар В так, чтобы шар А раньше ударил поочерёдно в четыре борта— правый, передний, левый и задний,
то следует найти зеркальное отображение Вг точки В в заднем борту, затем—отображение Вг точки В} в левом борту, отображение В3 точки Вг в переднем борту и, наконец, отображение В* точки Ва в правом борту, а затем целить шаром А в точку В4. Все отображения мы получим, составляя прямоугольную решётку (как на предыдущем рисунке) и отмечая в каждом прямоугольнике отображения Ви Вг,... точки В. Соединив А с Bit мы получим длину всего пути шара в виде прямой линии.
28.	Задача о кратчайшем пути охотника очень похожа на предыдущую. Охотник, прежде чем вернуться в свою палатку, хочет накормить лошадь на пастбище и напоить её из реки. Что он должен сделать рань-ше, чтобы его путь был наиболее / j коротким?	,/	|
Палатка А, зеркально отражённая от берега реки, даёт точку ait а отражение последней от края пастбища даёт точку а2. Если же производить отражение в обратном порядке, то мы получим точки Аи и А2. Толстая зигзагообразная линия представляет кратчайший путь от охотника к пастбищу, реке и палатке; длина этой линии равна расстоянию Оа2 точки а2 от охотника. Если бы охотник захотел сначала напоить лошадь, то его путь был бы равен по меньшей мере расстоянию его от точки Д, а ОД больше чем Оа2.
Охотник не чертил плана; он просто прицелился своим ружьём в точку Р и, видя, что эта точка находится налево от палатки А, поскакал налево. (Почему?)
29.	Окаймлённые колоннами дворы Palazzo Cancellaria в Риме
имеют стороны, отношение которых близко к так называемому золотому сечению. Вопреки распространённому мнению, это отношение сторон встречается в архитектуре весьма редко. Золотое сечение заданного отрезка—такое, что отношение целого отрезка к большей части равно отношению большей части к меньшей. Если взять большую часть как длину прямоугольника, а меньшую — как его ширину, то получится прямоугольник, подобный двору Palazzo Cancellaria.
Если некоторый отрезок принять за единицу, то ббльшая /5 — 1 ПС1О часть его золотого сечения равняется —%— = 0,618. . . , а меньшая — 0,382	их отношение равняется
1,618 ... :1=1:0,618... =0,618... : 0,382.
Это число равно
Если в такой «золотой» прямоугольник
вставить наибольший возможный квадрат, то останется прямоугольник, подобный первоначальному. С этим новым «золотым» прямоугольником мы можем поступить так же и т. д. Такое разложение прямоугольника на бесконечный ряд квадратов и приводит к непрерывной дроби, состоящей из одних только единиц.
30.	Вычисление последовательных подходящих дробей предыдущей непрерывной дроби у, у, -|» 4 * • • • облегчается тем, что числитель и знаменатель каждой из них получается сложением числителей и знаменателей двух предшествующих дробей. Это—так называемые числа Фибоначчи:
1+1=2, 1+2=3, 2 + 3=5, 3 + 5=8, 5 + 8 = 13,...
31.	Если от ствола дерева отрастает в конце первого года одна ветвь, затем ствол «отдыхает» один год и даёт новую ветвь только в конце третьего года, и если от каждой ветви в свою очередь отрастают ветви по такому же закону,
то в первом году мы будем иметь лишь главный побег, во втором—2 побега, в третьем—3, затем 5, 8, 13 и т. д. как в последовательности Фибоначчи.
32.	Сетка, изображённая на странице 20, может покрыть всю плоскость квадрата. Снимок пчелиных сот

изображает покрытие всей плоскости правильными шестиугольниками.
33.	К такого рода сетке можно притти, решая задачу о сборной команде. В некотором городе имеются три спортивных клуба, из которых нужно составить одну сборную команду из пяти человек для участия в междугородних соревнованиях. Для установления числа мест, которое получит в команде каждый клуб, организованы отборочные соревнования, причём каждому клубу должно быть отведено число мест, пропорциональное числу очков из определённого общего числа возможных, набранных им в этих соревнованиях. При этом сначала учитывают только целые числа, а затем, расположив дробные остатки в убывающем порядке, добавляют каждому
клубу поочерёдно по одному представителю, пока хватит мест. Например, пусть из общего числа 1500 очков клуб А набрал 435, клуб В—690 и клуб С — 375 очков. Пропорциональное деление даёт для клуба А—1,45, для В—2,3 и для С—1,25 мест. Им отводят сначала 1, 2 и 1 место. Остаются дроби 0,45, 0,3 и 0,25; наибольшая из них 0,45 принадлежит клубу А и, следовательно, ему достанется одно оставшееся свободное место. Окончательный результат такой: А — 2 места, В — 2 места, С—1 место.
В равностороннем треугольнике, с высотой 10 см,
сумма расстояний любой внутренней точки от всех трёх его сторон постоянна и также равна 10 см. Пусть теперь отрезок длиной в 1 см изображает 1О°/о всех набранных клубами очков, а 2 см (2О°/о) изображают одно место в сборной команде. Всякая пропорция очков даёт какую-нибудь точку в треугольнике: например, точка, обозначенная чёрным кружком, соответствует подсчёту очков из приведённого примера, так как её расстояния от сторон А, В и С, выраженные в 2-сантиметровом масштабе, соответственно равны 1,45; 2,3 и 1,25. Все точки треугольника, которые в окончательном результате дадут одно и то же распределение мест, заполняют правильный шестиугольник (обозначенный здесь числами 2,2, 1). Таким образом, как только очки подсчитаны, можно сразу увидеть на рисунке окончательное распределение мест.
Стрелка в шестиугольнике указывает на возможность такого случая, что клуб А, которому ошибочно насчитали, скажем, слишком низкое количество очков за счёт другого клуба, после исправления ошибки не только не получит добавочного места, но даже не удержит прежнего числа представителей и потеряет одно место. (Почему?) Однако этого места не получит тот клуб, которому при проверке счёта количество очков будет убавлено. (Почему?)
34.	Если даны три сосуда, содержащие вместе 14 литров вина, то всякому распределению вина в этих сосудах отвечает точка равностороннего треугольника по тому же закону, как и в случае распределения мест в сборной команде из трёх клубов. Если высота треугольника равна 14 см, то расстояния
точки от его сторон, выраженные в сантиметрах, дают нам число литров вина в каждом сосуде.
Пусть 14 литров вина наполняют 14-литровый сосуд; требуется разделить вино пополам с помощью двух неградуиро-ванных сосудов: 9-литрового и 5-литрового. Как это сделать?
Выделим в нашем треугольнике параллелограм, стороны которого равны 9 и 5 см (рисунок немного уменьшен),
и проведём в нём ломаную линию, выходящую из левого нижнего угла сначала в горизонтальном направлении (по стороне параллелограма). Пусть точка, двигающаяся по этой ломаной, может итти только по трём направлениям, параллельным сторонам треугольника; при этом путь будет преломляться на сторонах параллелограма. Каждый отрезок этой ломаной изображает одно переливание вина (точек внутри параллелограма мы, конечно, не получим; в такой точке находится, например, центр нарисованной окружности). Мы видим, что для решения задачи необходимо произвести 13 переливаний (номер каждого переливания отмечен жирным шрифтом). Бильярдный шар, пущенный из левого нижнего угла вдоль большей стороны параллелограма, сам решит задачу и дойдёт до искомой точки на 13-м ходу. Пушенный вдоль меньшей стороны, этот шар найдёт другое решение (Какое?)
35.	Можно заполнить плоскость различными правильными многоугольниками; мы будем получать тогда разнообразные рисунки—«паркетажи». Если каждая вершина является общей точкой равного числа одинаковых многоугольников, то пар-кетаж называется однородным.
Так как каждый угол правильного n-угольника равен (2 — 4) прямым углам или, что одно и то же, (у—4) «пол-ному углу» (360°), то задача построения однородных парке-тажей требует нахождения таких целых положительных чисел n,p,q, .... г, ..., чтобы удовлетворялось равенство
(4—4)+(4~|)+(4~4)+ ••• +(4—4) + •••=!•
Таким образом, можно получить 17 решений (например, при n=4, jP = 4, <7=3 и г=6 получается паркетаж, изображённый на втором рисунке), но только 10 из них дают пар-кетажи, которые можно распространить на всю плоскость.
36. Неоднородные паркетажи красивее:
- -
37.	Начиная с правильного пятиугольника, наряду с выпуклыми многоугольниками, появляются звёздчатые (само-пересекающиеся).
Правильных пятиугольников может быть два: один выпуклый и один звёздчатый; правильных семиугольников может быть три: один выпуклый и два звёздчатых. (А сколько семнадцатиугольников?)
38.	Многоугольники играют весьма важную роль в статике. Известно, что если три силы уравновешиваются, то возможно нарисовать треугольник, стороны которого соответственно равны этим силам по величине и направлению. Это приводит нас к так называемым взаимным фигурам Кремоны.
Пусть имеется 10 стержней, соединённых шарнирами в точках А. В, С, D, Е и О.
———
Эти стержни разбивают всю плоскость на шесть областей: /, 2, 3, 4, 5, 6. Для этой системы стержней можно начертить следующий «взаимный многоугольник»;
В нём буквами будут уже обозначены области, а цифрами— вершины. На первом рисунке вершина С общая для областей 2, 3 и 6; она связана стержнями с вершинами
В, О и D-, в ней сходятся стержни ВС, ОС и DC. На втором же рисунке область С имеет вершинами точки 2, 3 и 6; она граничит с областями В, О и D вдоль отрезков, которые можно обозначить ВС, ОС и DC.
Во взаимном многоугольнике стороны ВС, ОС и DC соответственно параллельны стержням ВС, ОС и DC первого рисунка; на этом принципе и строится весь взаимный многоугольник.
Обойдём теперь какую-нибудь область взаимного многоугольника по его периметру, например, область С в направлении, указанном стрелками. Если теперь на точку С первого рисунка будут действовать три силы, равные по величине и по направлению сторонам области С на втором рисунке (или пропорциональные им), то точка С останется в равновесии. То же самое относится и к остальным точкам; например, три силы в точке D, оставляющие её в равновесии, определены сторонами области D. При этом стрелка вдоль стержня CD идёт теперь по направлению от С к D. (Почему?)
Весь взаимный многоугольник можно вычертить, зная лишь длину одной стороны и направление соответствующей стрелки. Из этого следует, что если в нашей стержневой конструкции, изображённой на первом рисунке, известно одно напряжение, то определены и все остальные. Если это напряжение изменится, то изменится только величина, но не форма взаимного многоугольника.
Можно заметить, например, что в данной конструкции стержень ОЕ испытывает всегда вдвое большее напряжение, чем стержень ВС, и что он растягивается, когда ВС сжимается.
39.	Для трёх деревень нужно построить общую школу. В первой деревне живут 50, во второй 70, в третьей 90 детей. Где нужно выбрать место для школы, чтобы сумма времени, которое придётся тратить всем детям на хождение в школу, была минимальной?
Для решения этой задачи достаточно положить на стол план местности,
затем пробуравить в столе отверстия в местах расположения деревень, пропустить через эти отверстия три верёвочки, верхние концы их связать в один узел, а к нижним подвесить нагрузки соответственно в 50, 70 и 90 единиц (например, 500, 700 и 900 граммов). Школа должна быть построена там, где окажется узел. (Почему?)
Можно решить эту задачу и не портя стола: начертить треугольник, имеющий стороны в 50, 70 и 90 единиц
и отыскать на плане местности точку, из которой прямые, соединяющие деревни, видны под углами, равными внешним углам вспомогательного треугольника.
(Как построить эту точку? Где здесь взаимные фигуры?)
Можно геометрически определить случаи, когда здание школы должно быть построено точно в одной из трёх деревень. (Когда это будет?)
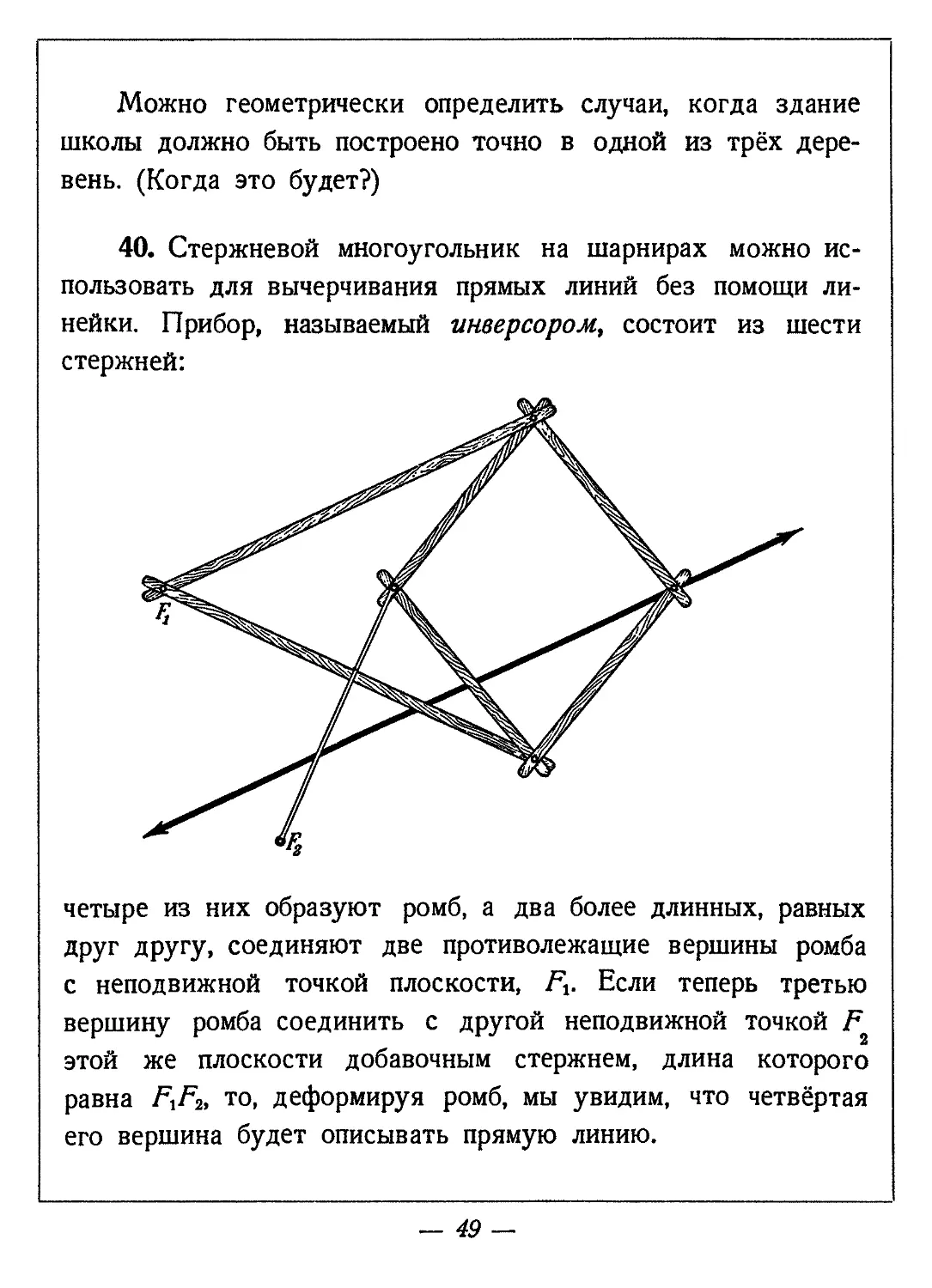
40.	Стержневой многоугольник на шарнирах можно использовать для вычерчивания прямых линий без помощи линейки. Прибор, называемый инверсором, состоит из шести стержней:
четыре из них образуют ромб, а два более длинных, равных друг другу, соединяют две противолежащие вершины ромба с неподвижной точкой плоскости, Fj. Если теперь третью вершину ромба соединить с другой неподвижной точкой F этой же плоскости добавочным стержнем, длина которого равна FiF2, то, деформируя ромб, мы увидим, что четвёртая его вершина будет описывать прямую линию.
41.	Все построения, для которых нужны циркуль и линейка, можно выполнить только одним циркулем—без помощи линейки. Желая, например, найти середину М отрезка 1—2, когда даны только его концы,
мы проведём сначала две равные окружности с центрами I и 2 радиусом 1—2-, затем из одной точки 3 их пересечения,
как из центра, проведём новую окружность тем же радиусом; в результате получим точку 4, и из неё, как из центра, проводим через точки 3 и 2 четвёртую окружность опять тем же раствором циркуля. Теперь из точки 5, в которой эта окружность пересекается со второй, чертим новую окружность, уже большим радиусом 5—3, а из точки 1—окружность новым радиусом 1 — 5. Эти две большие окружности пересекаются в точках 6 и 7. Наконец, из точек 6 и 7, как из центров, проводим две последние окружности, проходящие через точку 5. Вторая точка пересечения этих окружностей и есть искомая точка М—середина отрезка 1—2. Таким образом, наш чертёж состоит из восьми окружностей. (Может ли их быть меньше?)
42.	Имея две пересекающиеся окружности,
можно найти их центры без циркуля, при помощи только линейки. Проведём прямую линию через любую точку а, лежащую на одной окружности, и через точку пересечения обеих окружностей. Мы получаем на второй окружности точку Ь,
из которой возвращаемся через вторую точку пересечения окружностей снова на первую—в точку с. Затем выберем на первой окружности другую какую-нибудь точку А и таким же самым путём получаем В и С. Соединяя (на нашем чертеже—штриховыми линиями) а с с и А с С, а также А с а и С с с, мы получим две точки, которые соединяем прямой линией (на нашем чертеже—штрих-пунктирной). Эта прямая проходит через центр первой окружности аАсС. Повторяем такое же построение, начиная из другой точки, и находим вторую такую прямую и искомый центр.
43.	Нетрудно построить при помощи только одной линейки центр любой окружности, если нарисована другая окружность и её центр. (Как?)
Если же дана только одна окружность, то построить её центр только при помощи линейки, без циркуля, невозможно. Чтобы доказать это, рассмотрим эту окружность как основание наклонного конуса в пространстве (т. е. такого конуса, высота которого не падает в центр основания). На этом рисунке
изображена поверхность наклонного конуса, пересечённая двумя симметричными плоскостями; их плоскость симметрии здесь перпендикулярна к плоскости рисунка. Когда одно сечение является окружностью—мы этот случай и рассматриваем,—то другое, как симметричная фигура, тоже будет окружностью, равною первой. Вместе с тем мы видим, что прямая, соединяющая центр левой окружности с вершиной конуса, не попадает в центр правой. В этом и заключается доказательство невозможности построения центра окружности с помощью одной только линейки. Ибо если бы такое построение существовало, то, сделав его на плоскости левой окружности и проектируя всё построение через вершину конуса на плоскость правой окружности, мы получили бы на ней совершенно такое же построение, так как при проектировании прямые переходят в прямые, а их точки пересечения друг с другом и с окружностями — в такие же точки проекции. Поэтому центр левой окружности как одна из этих точек пересечения должен перейти в центр правой окружности. Но мы видим, что это не верно.
Это—пример одного из «доказательств невозможности», которые очень характерны для математики.
44.	Невозможно с помощью только циркуля и линейки «выпрямить окружность», т. е. точно построить отрезок, равный длине окружности данного радиуса. Отношение длины окружности к диаметру п = 3,141592 653 ... — число иррациональное.
В XVII веке Коханский нашёл следующее приближённое построение такого отрезка:
Из точки А, лежащей на данной окружности, как из центра, чертим окружность того же радиуса; получаем точку 1, из которой, как из центра, строим опять тем же радиусом новую окружность. Обе построенные окружности пересекаются в точке О и точке 2. Прямая О — 2 и касательная в точке А пересекутся в некоторой точке 3. Откладывая по касательной из точки 3 три раза радиус данной окружности, мы получаем точку 6. ОтрезокВ—6 равен приблизительно половине окружности. (С какой погрешностью?) Заметим, что для этого построения не потребовалось менять раствора циркуля.
45.	Для приближённого измерения длины кривых линий на плоскости можно пользоваться лонгиметром (прозрачная калька с наклонной квадратной сеткой, имеющаяся в числе приложений к этой книге). Желая, например, измерить по карте

длину Волги, следует наложить на карту кальку краем на край и переходить из клетки в клетку от истока к устью Волги ходом шахматной ладьи, считая при этом число переходов. Затем надо повторить такой счёт снова, предварительно перевернув лонгиметр на другую сторону. Наконец, для третьего подсчёта числа переходов надо положить на край карты одну из его наклонных линий, чтобы стороны квадратов оказались вертикальными и горизонтальными. Сумма всех трёх чисел даёт длину кривой в миллиметрах. Она равна приблизительно 280 мм.
По масштабу карты можно видеть, что здесь нужно умножить результат на 10, и тогда получается длина Волги в километрах, равная 2800 км. Но на самом деле длина Волги равна 3688 км. Мы получили такой ошибочный результат потому, что при большом уменьшении на карте совершенно не отражены многочисленные небольшие изгибы реки, которые в сумме и составят полученную разницу. (Если измерить длину Волги по карте, например, ниткой, то мы получим примерно 280 мм.) Из этого примера видно, что нельзя по карте с небольшим масштабом определять длину извилистой реки.
46.	Здесь изображено самое плотное расположение кругов на плоскости:
оно напоминает шестиугольный паркетаж—см. снимок пчелиных сот на стр. 35. Представим себе, что эти круги расширяются под действием внутреннего давления; тогда в результате действительно получится изображение пчелиных сот.
47.	Начертив систему всевозможных окружностей, проходящих через две точки,
можно видеть, что на плоскости существует такая другая система окружностей, что каждая окружность второй системы пересекает каждую окружность первой системы под прямым углом.
48.	Когда одна монета катится по краю другой такой же монеты,
то точка касания перемещается по контуру обеих монет: подвижной и неподвижной. Оба контура равны; следовательно, если точка касания опишет половину окружности неподвижной монеты, то она пройдёт и половину окружности подвижной. Однако опыт показывает, что подвижная монета опять очутится «головой» вверх. (Почему?)
49.	Если катить окружность по внутреннему краю вдвое большей окружности, то точка, закреплённая на меньшей окружности, опишет прямолинейный отрезок. Это можно видеть на картине 1 биоскопа, имеющегося в числе приложений к этой книге. Всю колоду карт биоскопа следует прижать к поверхности стола пальцами, левой руки и, приподняв левым большим пальцем правые края карт, быстро опускать их—«щелкнуть» колодой.
50.	Если круг — колесо—катится по прямой линии, то точка на его окружности (гвоздик Р) описывает линию с остриями — так называемую циклоиду.
Р
Длина одной дуги циклоиды равняется периметру квадрата, описанного около образующего её круга.
При таком качении круга по прямой всякая точка, находящаяся внутри круга (за исключением его центра) опишет кривую линию без остриёв {укороченную циклоиду),
а если точка закреплена вне круга на продолжении его радиуса, то—линию с петлями (удлинённую циклоиду):
Перевернём рисунок, на котором изображена циклоида, вверх ногами и представим себе, что тяжёлая точка Р будет падать по циклоидальному жолобу. При этом падении она
будет в каждый момент занимать точно такое же положение, какое отмечал бы на циклоиде воображаемый образующий круг, катящийся по прямой линии равномерно. На картине 2 биоскопа видно, что точка, падающая по циклоиде, перегоняет точки, падающие по наклонной плоскости, хотя даже ей приходится в конце пути подниматься вверх.
51.	Вернёмся опять к рисунку на стр. 59, изображающему колесо, точка Р которого описывает циклоиду. Пусть под колесом в начальном положении точки Р лежит камень. Колесо катится по земле (по прямой линии), и наблюдатель, находящийся на колесе, в движущейся точке Р, смотрит на этот камень. При этом камень будет от наблюдателя удаляться, одновременно с этим поворачиваясь. Наблюдателю будет казаться, что камень движется по спиральной линии:
Такую же спираль описывает конец натянутой нитки, которая сматывается с круглой неподвижной катушки. Поэтому такая спираль называется эвольвентой (что значит — развёрткой) окружности. Если бы какой-нибудь предмет внезапно перестал повиноваться закону тяготения (и если бы не было сопротивления воздуха), то мы бы увидели его улетающим с земной поверхности именно по такой спирали. (Почему?)
52.	Муха, ползающая равномерно по радиусу равномерно вращающейся граммофонной пластинки, описывает другую спираль—так называемую спираль Архимеда:
53.	Сердечник, составленный из двух дуг спирали Архимеда и насаженный на круглый диск, превращает равномерное вращательное движение диска в равномерное прямолинейное движение поршня—вперёд и назад. (Почему?)
54.	Из всех замкнутых кривых одной и той же длины окружность выделяется тем, что она ограничиваетнаиббль-шую площадь. Отсюда следует, что площадь, ограниченная £2 кривой, длина которой равна L, никогда не превышает .
55.	Площадь всякого (несамопересекающегося) многоугольника, вершины которого попадают в точки «решётки целых чисел» (см. стр. 20), содержит столько квадратных единиц, сколько точек решётки он содержит внутри своего контура плюс половина числа точек решётки, лежащих на его контуре, без единицы.
Так, площадь на этом рисунке
S=6+y—1 = 10,5.
56.	Возьмём какую угодно выпуклую центральную кривую, т. е. имеющую центр (так называется точка, делящая пополам все проходящие через неё хорды). Пусть площадь внутри этой кривой равна 4. Положим её на решётку целых чисел (в которой расстояние между соседними точками равно единице) так, чтобы центр упал на одну из точек решётки.
Тогда фигура захватит ещё по меньшей мере две точки (считая и те, которые очутятся на самом её контуре). Это—известная теорема Минковского.
57.	Любую фигуру всегда можно так положить на решётку целых чисел, что она захватит по крайней мере столько точек решётки, скольким клеткам равняется её площадь. Например, фигура, изображённая на рисунке,
имеет площадь, равную И клеткам. Бросим её на решётку как попало и разрежем вдоль линий решётки. Накладывая
теперь друг на друга квадратики, на которые распалась вся фигура, мы сможем проколоть их булавкой так, чтобы попасть по крайней мере 11 раз в заштрихованные участки. (Почему?)
Раскладывая квадратики опять один возле другого, как они лежали раньше, мы увидим внутри фигуры по крайней мере 11 следов прокола:
Теперь достаточно передвинуть фигуру параллельно самой себе так, чтобы один след прокола попал на точку решётки: тогда и все следы попадут на такие точки.
58.	Три фигуры могут быть случайно расположены на одной плоскости таким образом, что одна прямая разделит каждую из их площадей пополам. Но если они расположены не так, то всегда можно разделить их площади пополам с помощью одной окружности. Так, например, на карте, изображённой на следующей странице, разделены пополам озёра Иссык-Куль и Балхаш и Аральское море.

59.	Круг обладает постоянной шириной: круглый диск можно катить по столу, приложив ладонь сверху, и при этом ладонь не будет ни подниматься, ни опускаться. Но есть и другие фигуры, обладающие таким же свойством, — их ширина постоянна. Например, левая из этих двух фигур:
составленная из трёх дуг окружностей, центры которых находятся в вершинах равностороннего треугольника, также имеет постоянную ширину. (Почему?) Контур, ограничивающий эту фигуру, имеет три угловые точки.
Можно получить фигуру постоянной ширины, ограниченную и гладким контуром и отличающуюся от окружности; для этого достаточно продолжить стороны равностороннего треугольника за их вершины на одинаковые отрезки и затем описать из его вершин шесть дуг окружностей—одни радиусом, равным продолженной стороне, а другие — радиусом, равным её продолжению. Получается фигура, изображённая направо; она имеет постоянную ширину. (Почему?)
60.	Нескольким мальчикам сказали, чтобы каждый из них вышел из точки Р, перешагнул через канаву, находящуюся в 60 шагах от Р, и остановился точно в 30 шагах за канавой.
Каждый двигался по прямой линии и избрал своё направление; остановившись, ребята образовали изогнутую линию — так называемую конхоиду Никомеда (на чертеже это — правая кривая с намеченными на ней точками).
Затем ребятам велели вернуться на 60 шагов в обратном направлении (к точке Р), потом ещё на 30 шагов и, наконец, ещё на 30: Так возникли ещё три конхоиды—линия с изгибом, линия с остриём (на чертеже обе эти линии — жирные) и линия с петлёй. Точки на последней линии показывают, где в конце-кон нов очутились ребята.
61.	Такой же опыт с канавой, но имеющей форму круга, даёт новую кривую — так называемую улитку Паскаля.
Здесь ребята перешли на 30 шагов за канаву и затем отступили обратно за 60 шагов (поперечник круга больше 30 шагов).
62.	Плоские сечения кругового конуса мы можем видеть, когда свет падает на стену сквозь круглое отверстие или из-под круглого абажура. Граница тени образует
эллипс,
параболу
или гиперболу,
в зависимости от положения светового конуса по отношению к стене. (Когда получится парабола?)
63.	Эллипс—наиболее близкий «родственник» окружности. Когда мы держим наклонно стакан с водой,
то контур воды образует эллипс; плоское сечение круглого цилиндра является эллипсом.
64.	Пушечное ядро движется под влиянием тяжести по параболе, если не учитывать сопротивления воздуха (см. картину 3 биоскопа).
Согласно закону Кеплера, планеты движутся по эллипсам, причём Солнце находится в их фокусе, а отрезок, соединяющий Солнце с планетой, «заметает» в равные промежутки времени равные площади (см. картину 4 биоскопа).
65.	Если обернуть свечу несколько раз листком бумаги,
перерезать свечу наклонно острым ножом или бритвой,
затем разнять обе половины свечи
и, наконец, развернуть бумагу, то получится кривая линия,
которая называется—синусоида.
66.	Когда ребёнок, гуляющий по тротуару, тащит тележку по мостовой, то тележка описывает линию, которая называется «трактриса» (что значит: «линия влечения»}.
Принимая путь ребёнка за ось вращения и вращая вокруг него трактрису, мы получим поверхность вращения, обладающую замечательным свойством: если гибкая плёнка плотно
совпадёт с какой-нибудь частью этой поверхности, то она может скользить по ней в каком угодно направлении, изгибаясь, но не морщась и не отставая от бумаги. (Какие ещё поверхности обладают этим свойством?)
Эта поверхность называется псевдосферой. Для существ, живущих на псевдосфере, царят законы не нашей обыкновенной геометрии, а так называемой «неевклидовой геометрии Лобачевского^, открытой великим русским математиком Николаем Ивановичем Лобачевским. В этой геометрии, между прочим, сумма углов треугольника меньше 180°.
67.	На поверхности воды плывёт бревно — круглый цилиндр из однородного материала, более лёгкого чем вода. Так как поперечное сечение этого тела есть круг, то оно будет лежать на воде неподвижно, как бы мы ни поворачивали его вокруг оси. Но это свойство — не только круга. Цилиндрические тела, например, с такими поперечными сечениями;
обладают тем же самым свойством, если материал, из которого они сделаны, вдвое легче воды.
Форма этих сечений такова, что всякая хорда, делящая их периметр пополам, делит пополам и площадь; таким образом, это последнее свойство круга не является его «исключительной привилегией». Второй из этих контуров имеет три оси симметрии и в его состав входят три прямолинейных отрезка.
68.	Около любой замкнутой кривой можно описать квадрат:
Можно также вписать квадрат во всякую замкнутую кривую (то-есть найти на ней четыре точки, являющиеся вершинами квадрата).
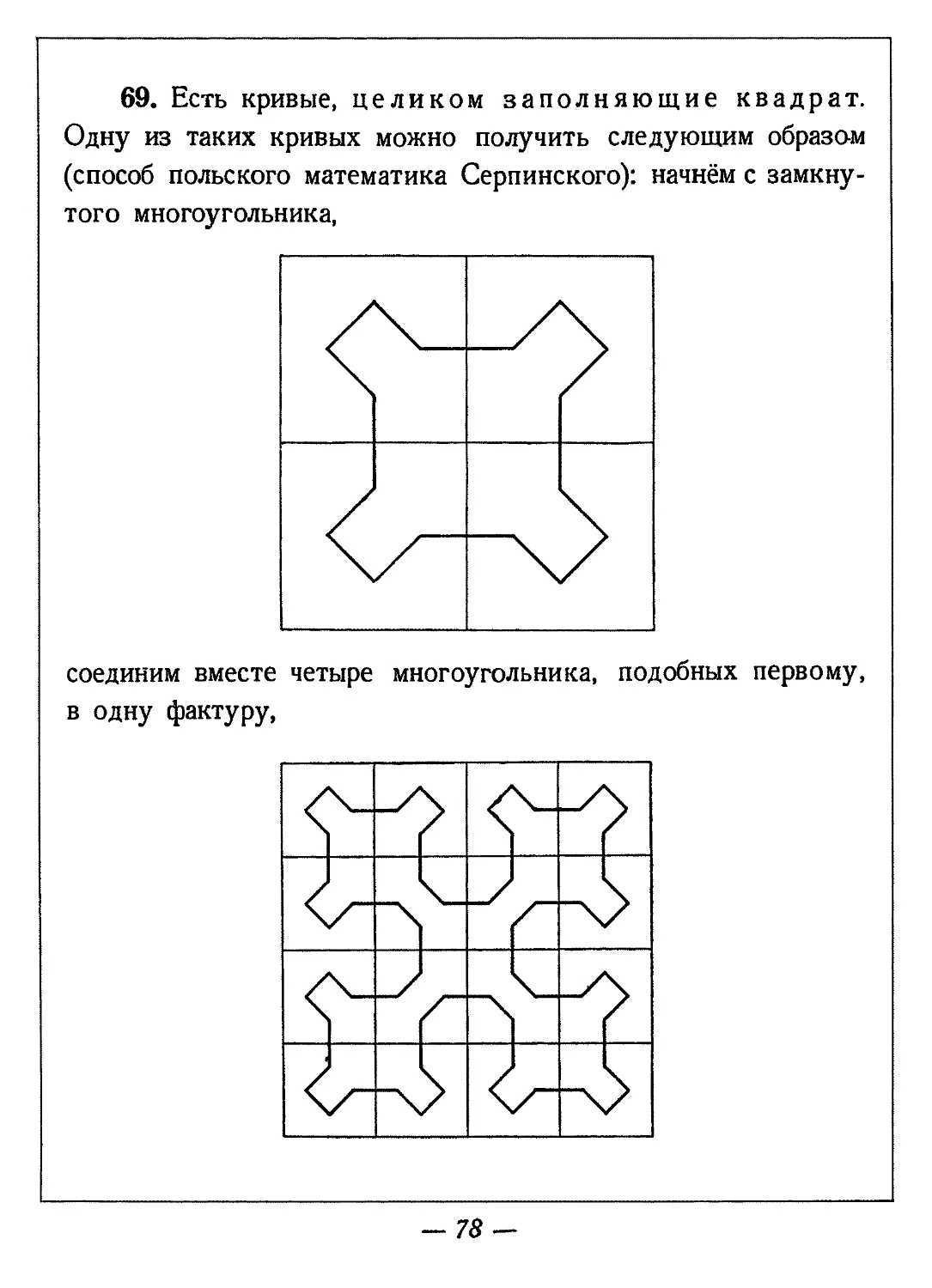
69.	Есть кривые, целиком заполняющие квадрат. Одну из таких кривых можно получить следующим образам (способ польского математика Серпинского): начнём с замкнутого многоугольника,
соединим вместе четыре многоугольника, подобных первому,
Получающаяся фигура приближается к некоторому пределу; этот предел и является той кривой, которая проходит через все точки квадрата. Но нарисовать эту кривую невозможно.
70.	Как из 6 спичек составить 4 треугольника? Надо сначала из 3 спичек сложить треугольник основания, а затем из 3 остальных — рёбра пирамиды. Так возникает правильный четырёхгранник {тетраэдр),
проекция которого на плоскость может принимать такие формы:
71.	Следующий правильный многогранник:
Его проекции могут быть такими:
Если диагональ куба поставить вертикально, то горизонтальная проекция примет вид правильного шестиугольника'.
72.	Согласно известной теореме Польке можно нарисовать три каких угодно отрезка, исходящих из одной точки, дополнить их параллельными отрезками (на чертежах они отмечены штриховыми линиями)
и полученную таким способом фигуру рассматривать как параллельную проекцию куба на некоторую плоскость (не обязательно перпендикулярно к направлению проектирования). Например, можно поместить проволочный куб так, чтобы солнце отбрасывало от него тень на стене в виде каждой из этих фигур.
73.	Сечение куба плоскостью, проходящей через его центр и перпендикулярной к его диагонали,
даёт правильный шестиугольник.
74.	Если паук сидит на середине ребра куба и хочет, двигаясь по кратчайшему пути, поймать муху, находящуюся в наиболее удалённой от него вершине куба,
При этом паук пересечёт одно ребро куба в точке, делящей это ребро в отношении 1:2. (Почему?)
Если муха хочет возможно быстрее обойти все 6 граней куба и вернуться на прежнее место, то на развёртке её путь должен опять-таки быть прямолинейным.
При этом оказывается, что для длины пути мухи положение исходной точки безразлично. (Почему?)
75.	В природе существуют тела, имеющие форму куба; это кристаллы соли (NaCl):
76.	Куб можно раскрасить шестью красками так, чтобы все грани были разных цветов. Оказывается, такую окраску можно осуществить тридцатью существенно различными способами. Если у нас есть 30 кубов, окрашенных различным образом, то выбрав наугад один из них, можно отыскать ещё 8 таких, что из полученных 9 кубов составляется большой куб, причём совпадающие грани будут одного и того же цвета.
Ti. Фотографируя на одной пластинке последовательные положения проволочной модели куба, вращающегося вокруг его диагонали, мы получим изображение, состоящее из двух конусов и поверхности, называемой однополостным гиперболоидом вращения. На снимке ясно видна гипербола, которая является меридианом этого гиперболоида.
78.	Уже Платону было известно, что существует 5 правильных многогранников. Два из них—тетраэдр и куб—мы уже рассмотрели (стр. 80—87). Следующим, по числу граней, правильным многогранником является октаэдр (восьмигранник), изображённый на следующей странице внизу. Он может быть составлен из 8 равносторонних треугольников. Развёртка его имеет следующий вид:
Ставя октаэдр на одну из граней и проектируя его на плоскость основания, мы получаем рисунок, изображённый на следующей странице наверху. Отмеченные на нём толстые штриховые линии показывают, что середины (центры) граней октаэдра являются в то же время вершинами куба. Но и наоборот: середины граней куба являются вершинами октаэдра (нижний рисунок на следующей странице).

79.	Следующий платонов многогранник—додекаэдр (двенадцатигранник)—имеет пятиугольные грани:
Додекаэдр легко склеить из его развёртки:
Если требуется раскрасить грани додекаэдра так, чтобы любые две смежные грани были различных цветов, то достаточно всего четырёх красок. Существует только два существенно различных способа распределения четырёх красок по граням додекаэдра; всякий другой способ получится из одного из них только заменой одних красок другими. Здесь изображена развёртка додекаэдра, выкрашенного первым способом. (А какой второй способ?)
80.	Последним правильным многогранником является икосаэдр (двадцатигранник), составленный из правильных треугольников. Вот его развёртка и проекция:
81. Из этого рисунка видно,
что середины граней додекаэдра являются вершинами икосаэдра, а из этого—
что середины граней икосаэдра являются вершинами додекаэдра.
Сопоставим эти два рисунка с рисунками на странице 89. Мы видим, что из всех правильных многогранников тетраэдр соответствует кубу, а додекаэдр—икосаэдру: середины граней одного многогранника являются вершинами другого и обратно. Только тетраэдр в этом смысле соответствует самому себе: середины его граней являются вершинами некоторого другого тетраэдра:
82. Кристалл пирита (FeS2) напоминает додекаэдр: он
имеет 12 пятиугольных граней, но эти пятиугольники — неправильные, хотя все они равны и имеют ось симметрии. Некоторые минералы имеют кристаллы в виде очень интересных неправильных многогранников. Здесь
первая модель изображает кристалл флюорита (CaF2); этот многогранник образуется из октаэдра отсечением его вершин при помощи куба; вторая—кристалл аргентита (Ag2S) — получается из октаэдра таким же образом, причём грани отсекающего куба проходят через середины его рёбер. Кеплер назвал этот многогранник кубоктаэдром.
Сфалерит (ZnS) даёт кристаллы в виде двенадцатигранника, ограниченного равными, но неправильными четырёхугольниками,
а куприт (CuO2)—в виде двадцатичетырёхгранника, ограниченного равными, но неправильными пятиугольниками.
83.	Если через каждое ребро правильного додекаэдра провести плоскость, перпендикулярную к плоскости симметрии, содержащей это ребро, то получится ромбоидальный три-дцатигранник:
Диагонали его граней являются рёбрами правильных многогранников. (Каких?)
84.	Здесь изображён многогранник, ограниченный двадцатью звёздчатыми пятиугольниками, изображёнными на странице 43.
85.	Кубы с соприкасающимися гранями могут заполнить всё пространство. Не все правильные многогранники пригодны для этого. Пространство можно заполнить правильными тетраэдрами и октаэдрами, как это изображено на рисунке на следующей странице.
86.	Проблема распределения мест в сборной команде для трёх клубов, решённая на плоскости с помощью рисунка на странице 36, приводит в случае четырёх клубов к этому рисунку. (Почему?)
87.	Шары одинаковой величины не могут заполнить пространства. При самом плотном размещении они заполнят около 74°/0 пространства. (Почему?)
Такое размещение получается следующим образом: первый слой шаров надо положить на плоскость так, чтобы они образовали рисунок, изображённый на странице 56. Затем можно положить на них второй такой же слой; при этом каждый верхний шар уложится в углубление, образованное тремя нижними шарами, но никогда не попадёт в углубление, соседнее с тем, которое уже занято другим шаром. Поэтому когда мы укладываем третий слой, то можем это сделать двумя
Первый способ.
способами: либо так, чтобы шары третьего слоя очутились над шарами первого, либо так, чтобы они очутились над теми углублениями в первом слое, которые шары второго слоя оставили свободными.
Каждый шар среднего слоя соприкасается с 12 шарами. Точки соприкосновения являются вершинами четырнадцати-гранника, который при первом способе состоит из 6 квадратов и 8 равносторонних треугольников, а при втором является кубоктаэдром Кеплера, изображённым на странице 94.
Второй способ.
88.	Правильные шары лучше всего получаются в виде мыльных пузырей: поверхностное натяжение жидкой плёнки стремится уменьшить её площадь; но так как пузырь содержит некоторый объём воздуха, то плёнка принимает форму такой поверхности, которая при данном объёме имеет наименьшую плошадь; эта поверхность и есть шар.
Подобно этому и на плоскости — из всех замкнутых кривых линий, ограничивающих фигуры с данной площадью, наименьшую длину имеет окружность. (Сравните тему 54 на стр. 62.)
89.	На этом рисунке
изображён воздушный шарик, освещённый лампой, а на этом —
«Луна в возрастающей фазе. Вот.— наглядное изображение фаз Луны и доказательство того, что Луна имеет форму шара.
90.	Земля тоже имеет вид, близкий к форме шара:
Из всех линий на земной поверхности, соединяющих два любых места, например, Лиссабон (Португалия) с мысом Фаруэлл (Гренландия), кратчайшей является дуга большого круга шара, называемая в данном случае ортодромой. (Все меридианы—тоже большие круги; из параллелей же только экватор является большим кругом). Те же самые два места можно соединить на поверхности Земли другой важной линией—локсодромой, или линией постоянного курса', эта линия пересекает все меридианы под одинаковым углом. Мореплаватель, который держится одного направления по компасу, плывёт по локсодроме; это для него—более простой, но не самый короткий путь.
91.	Географическая карта, изготовленная по принципу проекции Меркатора,
характерна тем, что на ней меридианы и параллели образуют прямоугольную сетку; при этом углы на земной поверхности воспроизводятся верно.
На такой карте локсодрома изображается прямой линией. (Почему?) Ортодрома же на этой карте изобразится кривой линией, имеющей перегиб.
92.	Если спроектировать поверхность шара (глобуса) из южного полюса на плоскость, касательную к шару в северном полюсе (это — так называемая стереографическая проекция), то мы получим географическую карту северного полушария,
в которой все меридианы изобразятся прямыми линиями, а параллели — кругами. Замечательно в этой проекции не только то, что в ней все углы на земной поверхности сохра
няются (как и в проекции Меркатора), но и то, что все окружности на земной поверхности (за исключением только меридианов) изображаются в виде окружностей. В частности и ортодрома, как дуга большого круга, перейдёт на этой карте в дугу окружности (довольно большого радиуса, и поэтому это можно обнаружить, только приложив к карте линейку). Локсодрома же в стереографической проекции перейдёт в логарифмическую спираль — так называется кривая, которая пересекает все лучи, выходящие из некоторой точки, под постоянным углом. На карте не изображено, но следует иметь в виду, что продолженная локсодрома обвивается вокруг полюса; на далёком севере она становится непригодной для мореплавания и воздухоплавания. (Почему?)
93.	Если логарифмическую спираль, изображённую здесь,
вращать (вместе с книжкой), то кажется, что она увеличивается или уменьшается в своих размерах.
94.	Будем теперь снова проектировать поверхность земного шара на плоскость, касающуюся его в северном полюсе, но уже не из южного полюса, а из центра шара (это — так называемая центральная проекция)-,
тогда мы получим на такой карте ортодрому в виде прямой линии. Это—самая подходящая карта для воздухоплавания в Арктике. (Почему?)
95.	Проекций шара на плоскость, которые сохраняли бы все расстояния на поверхности шара, не существует, и поэтому всякая географическая карта, по какому бы принципу она ни была составлена, искажает относительные размеры тех или иных расстояний на земной поверхности.
96.	Все линии на поверхности шара — кривые. Но существуют кривые поверхности, целиком «сотканные» из прямых линий. Например, куб, вращающийся вокруг диагонали, который мы видели на странице 87, скользит одними рёбрами по двум конусам, а другими—по однополостному гиперболоиду вращения. Самый общий однопо лестный гиперболоид также соткан из двух систем прямых линий:
Глядя на него сверху вниз, мы видим эллипс и систему прямых, касательных к этому эллипсу.
(Оба эти рисунка — не искусственные чертежи, а настоящие снимки проволочной модели гиперболоида.)
97.	Поверхность конуса также соткана из прямых линий. Если муха, сидящая на конусе, хочет обойти конус кругом возможно быстрее, то она должна итти по петлеобразной кривой линии и возвратиться к исходной точке под некоторым углом.
-ПО -
Если конус разрезать вдоль одной его образующей а и развернуть на плоскость, то мы получим развёртку конуса в виде кругового сектора:
На этой развёртке путь мухи изобразится в виде двух перпендикуляров, опущенных на её стороны. (Здесь разрез сделан вдоль образующей, противоположной той, на которой находится муха.)
Таков будет путь мухи, сидящей на поверхности конуса, развёртка которого даёт угол меньше 180°. Если же угол развёртки будет 180° или ещё больше, то решение задачи будет другое. (Какое?)
- Ill —
98.	Из прямых линий соткана также и поверхность цилиндра. Если разрезать её вдоль одной из этих прямых и развернуть на плоскость, то кратчайший путь на поверхности цилиндра перейдёт, очевидно, в некоторую прямую линию:
Если теперь навернуть эту развёртку обратно на цилиндр, то наша прямая перейдёт в винтовую линию'.
99.	Проекция винтовой линии на плоскость (например, эта фотография)
имеет в некоторых точках острия.
100.	Всякая пространственная кривая (т. е. кривая, которая не лежит в одной плоскости) обладает замечательным свойством: всегда возможно подходящим проектированием получить её изображение на плоскости
так, что любая точка пространственной кривой перейдёт в остриё плоской кривой—проекции.
101.	Винтовой линией является край обыкновенного штопора. Изображённый здесь прибор,
называемый бесконечным винтом, переводит равномерное вращательное движение в равномерное прямолинейное.
102.	Когда отрезок постоянной длины скользит одним концом по винтовой линии, а другим—по её оси, то образуется винтовая поверхность'.
Если не считать поверхностей вращения, то винтовая поверхность является единственной поверхностью, которая может скользить сама по себе. Поэтому эта поверхность играет большую роль в машиностроении.
103.	Каждая из трёх поверхностей—плоскость (которую можно причислить к поверхностям вращения — почему?), цилиндр и шар—может скользить по себе самой таким образом, что точка поверхности опишет при этом движении любой путь на поверхности. (Почему?) Поэтому эти три поверхности также играют исключительно важную роль в машиностроении.
104.	Если вершины любого пространственного четырёхугольника (т. е. такого, который не лежит в одной плоскости) нагружены одинаковыми грузами, то центр тяжести можно найти, определяя сперва центр тяжести одной пары грузов, затем—центр тяжести второй пары и, наконец, центр тяжести обоих центров (если сосредоточить в них массы обеих
пар). Этот центр тяжести находится, таким образом, в середине отрезка, соединяющего середины противолежащих сторон. Мы могли бы начать с другой пары противолежащих сторон и пришли бы, очевидно, к тому же самому центру тяжести. Таким образом, мы получаем из физических соображений следующую геометрическую теорему: отрезки, соединяющие середины противоположных сторон любого пространственного четырёхугольника, пересекаются и делят друг друга пополам. (Докажите эту теорему «чисто геометрически».)
105.	Если четыре нагрузки а, Ь, с и d в вершинах пространственного четырёхугольника не одинаковы, но пропорциональны (a:6=c:rf), то полученные подобным же образом отрезки также будут пересекаться, причём точка пересечения будет делить один отрезок в отношении а'.Ъ, а второй — в отношении b'.d. Изменяя величины а, Ь, с и d, но сохраняя условия пропорциональности, мы получим две системы линий, которые образуют поверхность, натянутую на контур четырёхугольника и вдвойне сотканную из прямых линий. На верхнем рисунке исходный четырёхугольник изображён красной краской, и прямые продолжены за его контур; поверхность ограничена произвольной кривой—металлической рамкой.
На нижнем рисунке эта поверхность изображена сбоку. Она имеет вид седла и называется гиперболическим параболоидом.
4M3$^X*>>X fc&’Jo ^ЗХХФ’ХЙ
' W
 ^^:»ж

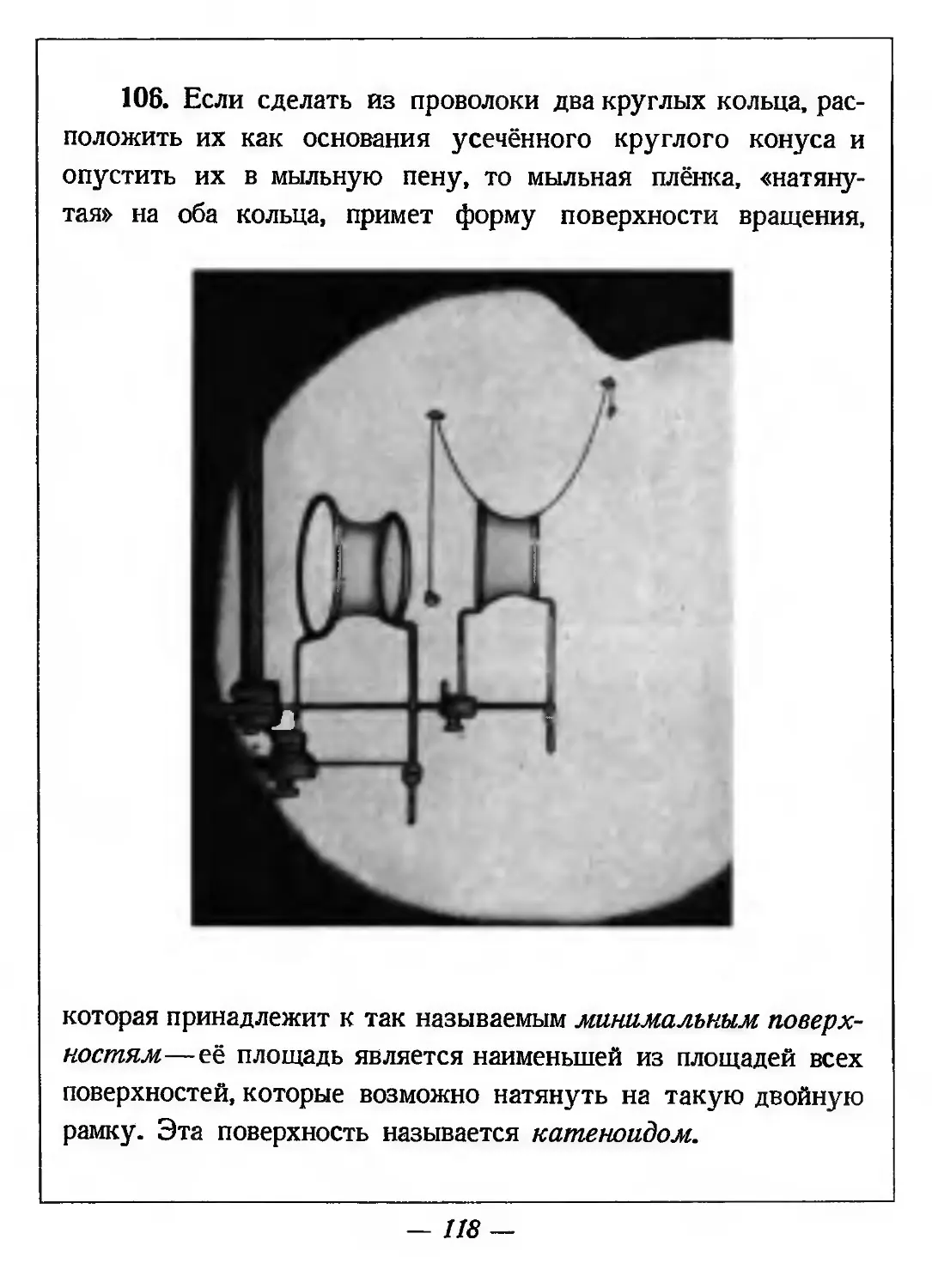
108. Если сделать из проволоки два круглых кольца, расположить их как основания усечённого круглого конуса и опустить их в мыльную пену, то мыльная плёнка, «натянутая» на оба кольца, примет форму поверхности вращения,
которая принадлежит к так называемым минимальным поверхностям— её площадь является наименьшей из площадей всех поверхностей, которые возможно натянуть на такую двойную рамку. Эта поверхность называется катеноидом.
107.	Параллели катеноида—круги, а его меридианы— кривые линии, которые мы отчётливо можем видеть на предыдущем рисунке, где изображена тень на стене от мыльного катеноида. Верхняя и нижняя линии этой тени и дают кривые, являющиеся меридианами нашего катеноида. Форму этой кривой принимает тяжёлая нить (цепочка), подвешенная на стене и свободно висящая на двух гвоздиках. Поэтому эта кривая носит название цепной линии.
108.	Какие фигуры можно вычертить непрерывным движением— «с одного почерка» (т. е. нарисовать, не отрывая карандаша от бумаги и не переходя два раза по одной и той же линии)?
Одной из известных задач этого рода является «задача о кёнигсбергских мостах». Ею занялся Эйлер, когда ему предложили вопрос о семи мостах города Кёнигсберга (ныне—Калининграда): возможно ли пройти по всем этим семи мостам, проходя по каждому из них только один раз?
Если обозначить через А остров, через В —левый берег реки, через С—правый и, наконец, через D — пространство между двумя рукавами верхнего течения, то задача сводится,
очевидно, к вычерчиванию с одного почерка следующего рисунка, состоящего из семи линий:

Но это невозможно: какие бы две из четырёх точек А, В, С и D мы ни выбрали как исходную и конечную, нам пришлось бы пройти по дороге ещё через две точки, и при каждом таком переходе мы вычертили бы линию, «входящую» в одну из этих точек и «выходящую» из неё. Но так как в каждой из четырёх точек нашего рисунка сходятся по три или пять (нечётное число) линий, то некоторые линии останутся не вычерченными и, значит, некоторые мосты — не пройденными.
109.	К этому же кругу вопросов принадлежит следующий.
На этом рисунке
изображены три домика, голубятня, колодец и навес. Требуется провести от каждого домика три тропинки к голубятне, колодцу и навесу так, чтобы ни одна из этих девяти тропинок не пересекалась другой.
Это оказывается невозможным. В самом деле, соединим самый левый домик с колодцем, навесом и голубятней и будем продолжать итти от них по тропинкам, ведущим к самому правому домику.
Мы получаем три линии между обоими домиками:
Эти три линии делят плоскость на три области: Cv Сг, Cs. Пропущенный средний домик лежит где-то в одной из этих областей. Если этот домик находится в то, значит, он будет вне замкнутой линии, окружающей навес; если этот домик в С2, то он—внутри замкнутой линии, не охватывающей голубятни, а если он в С3, то окружён замкнутой линией, вне которой находится колодец. В первом случае от него не будет дороги к навесу, во втором — к голубятне, в третьем— к колодцу.
Все эти вопросы принадлежат к области математики— топологии.
ПО. К топологии же относится и учение об узлах. Замкнутый шнур, изображённый здесь,
не имеет узла, а здесь
он имеет самый простой узел; такой узел может быть двух различных видов, которые невозможно превратить друг в друга, не разрезая шнура:
Один из этих узлов является зеркальным отображением другого.
111.	Два замкнутых шнура могут быть сплетены друг с другом. Этот же снимок
изображает три замкнутых шнура; никакие два из них не сплетены друг с другом, но, несмотря на это, все три сплетены вместе.
112.	Бумажная лента, скрученная на 180° и склеенная своими концами, образует так называемый лист Мёбиуса.
Он является односторонней поверхностью', муха, гуляющая по такой ленте, может переползти в любую её точку без неприятных для неё переходов через край ленты (например, из точки А в точку В). Эту поверхность невозможно выкрасить так, чтобы одна сторона была красная, а другая—зелёная: у неё есть только одна сторона. Край мёбиусова листа состоит из одной замкнутой кривой без узлов.
113.	Если мёбиусов лист разрезать вдоль чёрной линии, то он не распадётся, но образует новую двухстороннюю поверхность, край которой состоит уже из двух замкнутых
кривых, которые не имеют узлов, но двукратно сплетены друг с другом.
114.	Другую двухстороннюю поверхность, обладающую таким же свойством, легко получить, скручивая бумажную ленту на 360° и затем склеивая концы. Разрезанная вдоль средней линии, эта поверхность распадается на две замкнутые ленты, также без узлов, но однократно сплетённые друг с другом.
115.	Обыкновенный лист бумаги двухсторонен, но край его не имеет узлов. Возникает вопрос: существует ли двухсторонняя поверхность, край которой был бы одной замкнутой кривой с узлом? Такая поверхность была открыта недавно; вот она:
Её край снова имеет такой же узел, какой изображён на левом нижнем снимке на странице 124.
116.	Глобус—поверхность шара—можно раскрасить четырьмя красками таким образом, чтобы соседние страны были различного цвета. Это установлено многолетней практикой, но доказательства этой замечательной теоремы до сих пор ещё никто не нашёл.
117.	Для раскрашивания же тора, то-есть поверхности круглого кольца (например, автомобильной шины), требуется уже семь цветов: на нём можно нарисовать карту, состоящую из семи областей, которые имеют друг с другом общие границы.
В числе приложений к этой книге имеется картонная модель тора, на котором видно соседство таких семи стран. (Эту модель следует рассматривать как сплющенную шину.) Доказано, что для раскраски любой карты на торе семи красок всегда достаточно.
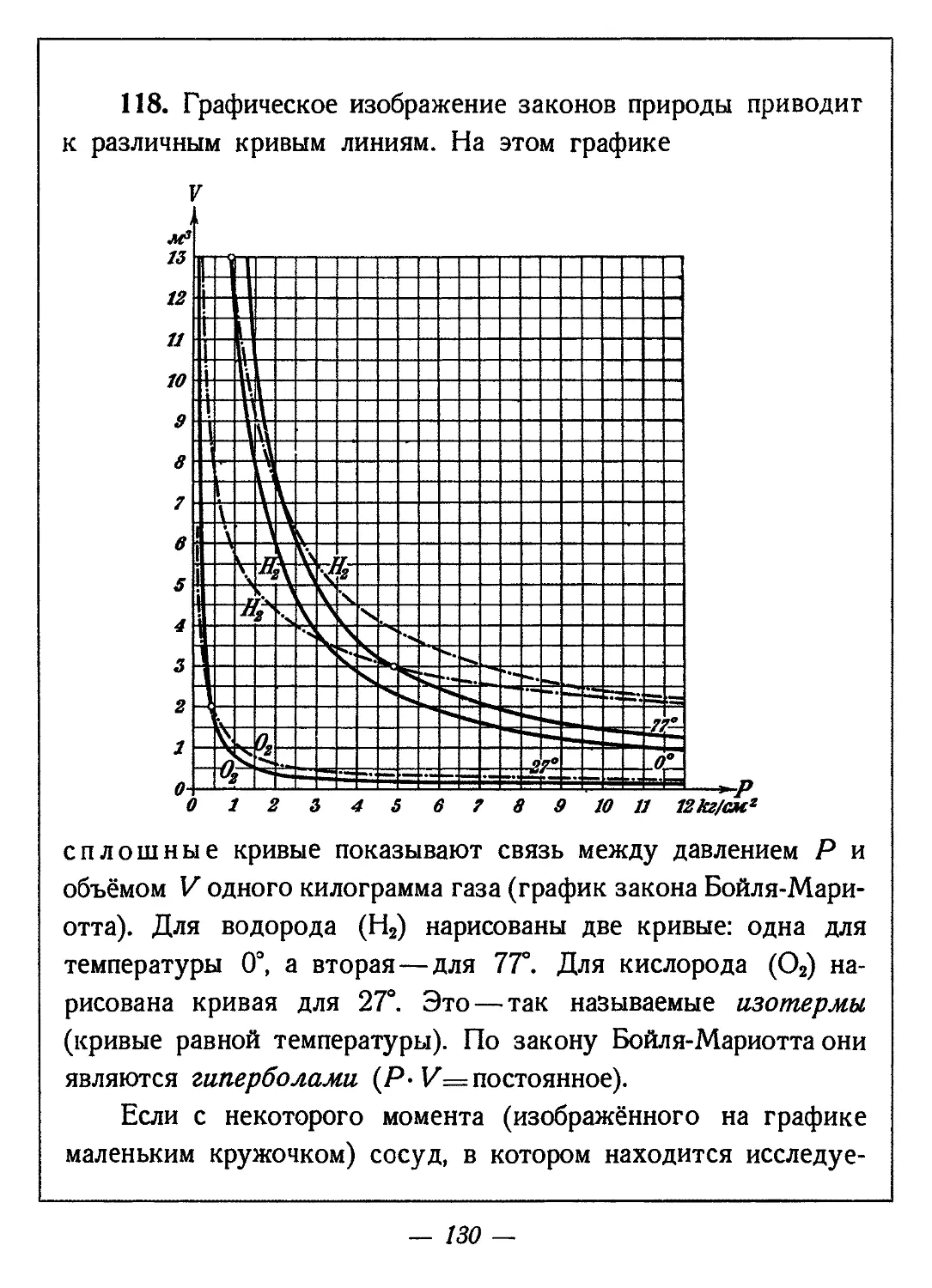
118.	Графическое изображение законов природы приводит к различным кривым линиям. На этом графике
сплошные кривые показывают связь между давлением Р и объёмом V одного килограмма газа (график закона Бойля-Мариотта). Для водорода (Н2) нарисованы две кривые: одна для температуры 0°, а вторая — для 77°. Для кислорода (О2) нарисована кривая для 27°. Это — так называемые изотермы (кривые равной температуры). По закону Бойля-Мариотта они являются гиперболами (Р- V= постоянное).
Если с некоторого момента (изображённого на графике маленьким кружочком) сосуд, в котором находится исследуе
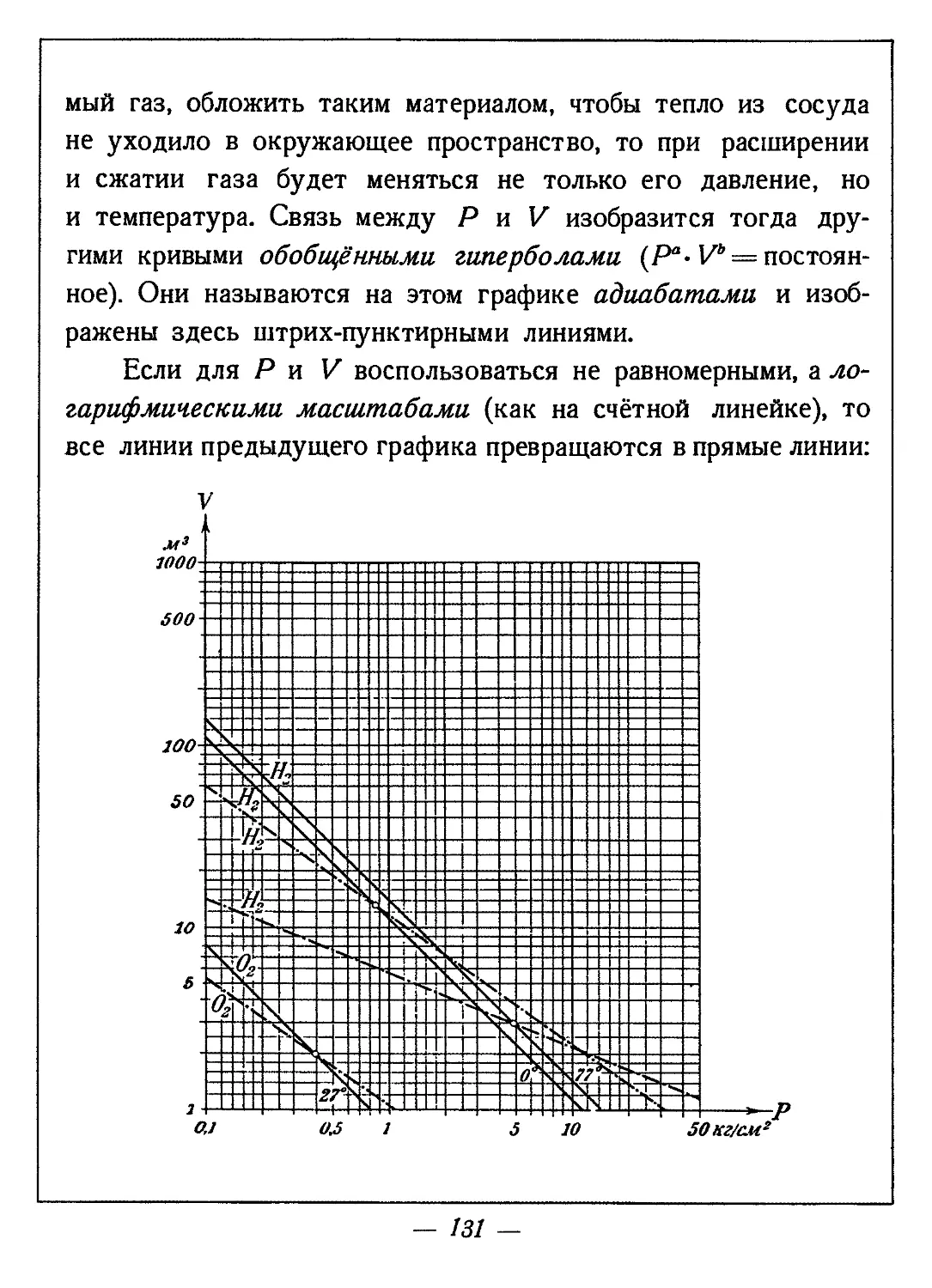
мый газ, обложить таким материалом, чтобы тепло из сосуда не уходило в окружающее пространство, то при расширении и сжатии газа будет меняться не только его давление, но и температура. Связь между Р и V изобразится тогда другими кривыми обобщёнными гиперболами (Р0- Vb = постоянное). Они называются на этом графике адиабатами и изображены здесь штрих-пунктирными линиями.
Если для Р и V воспользоваться не равномерными, а логарифмическими масштабами (как на счётной линейке), то все линии предыдущего графика превращаются в прямые линии:
119.	Приколотим к наклонной доске плитки, имеющие форму правильных шестиугольников, между которыми оставим каналы, ведущие от воронки (наверху) к продолговатым перегородкам (внизу).
Ружейные дробинки, которые насыпаются в воронку, могут попасть прежде всего в два вертикальных канала, обходя верхнюю шестиугольную площадку слева или справа. В следующие вертикальные каналы — а их три в одном ряду — дробь может попасть: а) в левый — только из верхнеголевого канала (один случай), б) в средний — из верхних левого и правого
каналов (два случая), в) в правый — только из верхнего правого канала (один случай).
Таким образом, во втором ряду имеется 1, 2, 1 возможных случаев. В следующем ряду уже 1, 3, 3, 1 возможностей, и эти, числа получаются из чисел 1, 2, 1, если складывать соседние и ставить по краям единицы. Так получается числовой треугольник Паскаля («биномиальные коэффициенты»),
1
1 1
1	2	1
13 3 1
1	4	6	4	1
1 5 10 10 5 1
1	6	15	20	15	6	1
1 7 21 35 35 21 7 1
1 8	28	56	70	56	28	8 1
1 9 36 84 126 126 84 36 9 1
в котором каждое число получается от сложения чисел, стоящих над ним (слева и справа). Последняя строка показывает, сколькими способами дробинки могут проникнуть в каждую из 10 перегородок нашего прибора.
Опыт, проведённый с этим прибором, показывает, что в перегородках вырастают столбики из дробинок; высоты этих столбиков приблизительно пропорциональны этим числам {закон Гаусса).
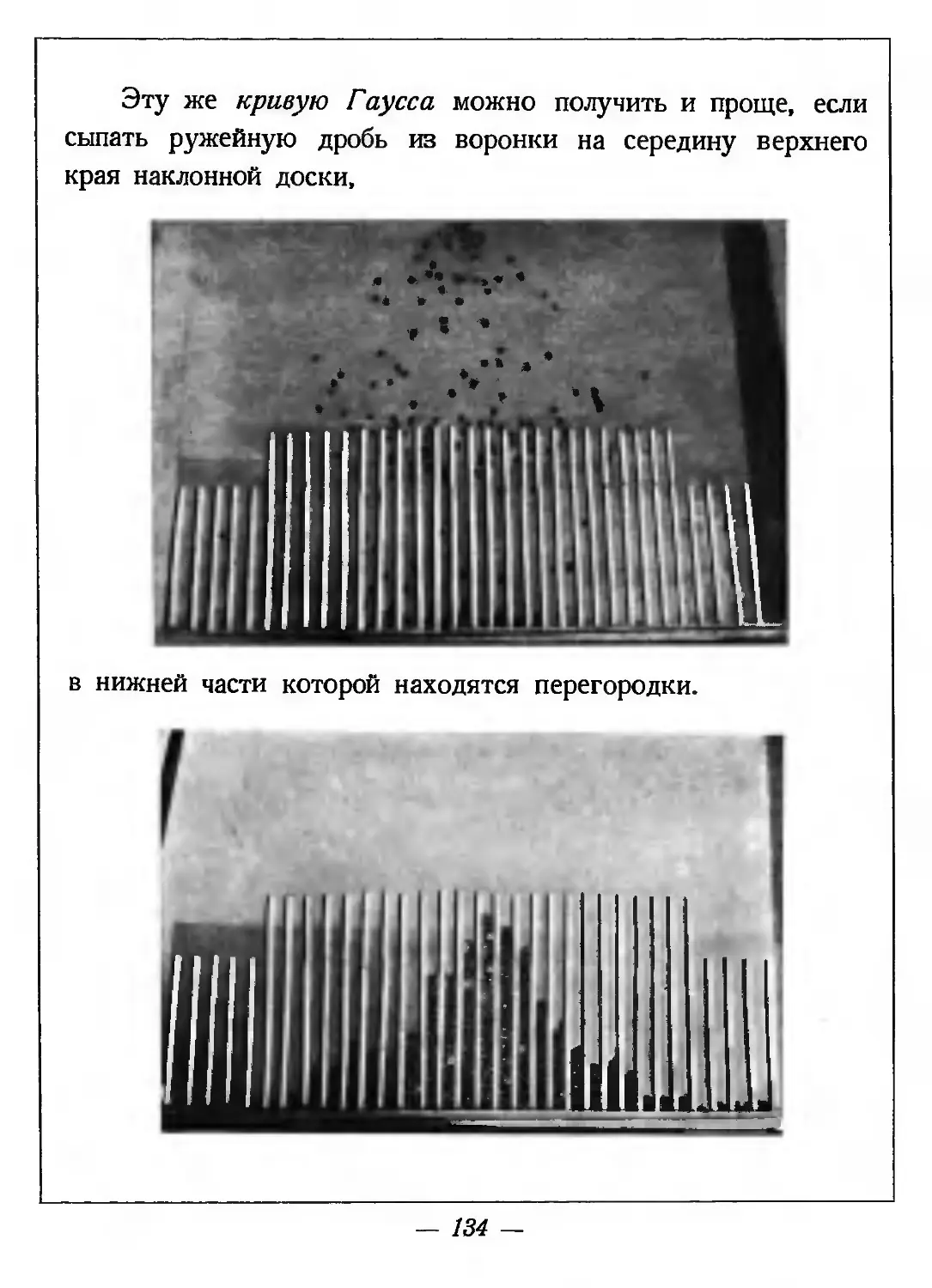
Эту же кривую Гаусса можно получить и проще, если сыпать ружейную дробь из воронки на середину верхнего края наклонной доски,
в нижней части которой находятся перегородки.
120.	Кривая Гаусса очень часто появляется при изучении явлений природы. Следующий график
изображает действие яда digitalis на лягушек. Было взято большое количество лягушек, которым дали некоторую дозу digitalis (вычисленную в кубических сантиметрах на 0,1 килограмма лягушечьего веса) и подсчитали, сколько лягушек из каждой сотни погибает в зависимости от дозы яда.
Здесь на горизонтальной нижней линии отмечены дозы яда от 0 до 1 ел? (в логарифмическом масштабе — как на счётной линейке). Если представить себе в точках деления перпендикуляры к этой линии, то влево от перпендикуляра, попадающего в точку масштаба, нарисовано столько лягушек, сколько погибает из каждой сотни от соответствующей дозы. Так, например, от впрыскивания 0,4 ел? погибает 6 лягушек от 0,6 сл? — 50 лягушек. (Эти числа, конечно, средние из большего количества опытов).
Кривая «лягушечьего строя» является опять кривой Гаусса.
121.	В вопросах, связанных с развитием организмов, выступает и другой тип кривых линий. Например, бациллы в замкнутом сосуде (вычисленные по занимаемой ими площади) размножаются с течением времени по закону, выражаемому графически следующей кривой линией.
Эта кривая имеет теоретическое обоснование; около неё написано уравнение кривой, полученное из теоретических соображений.
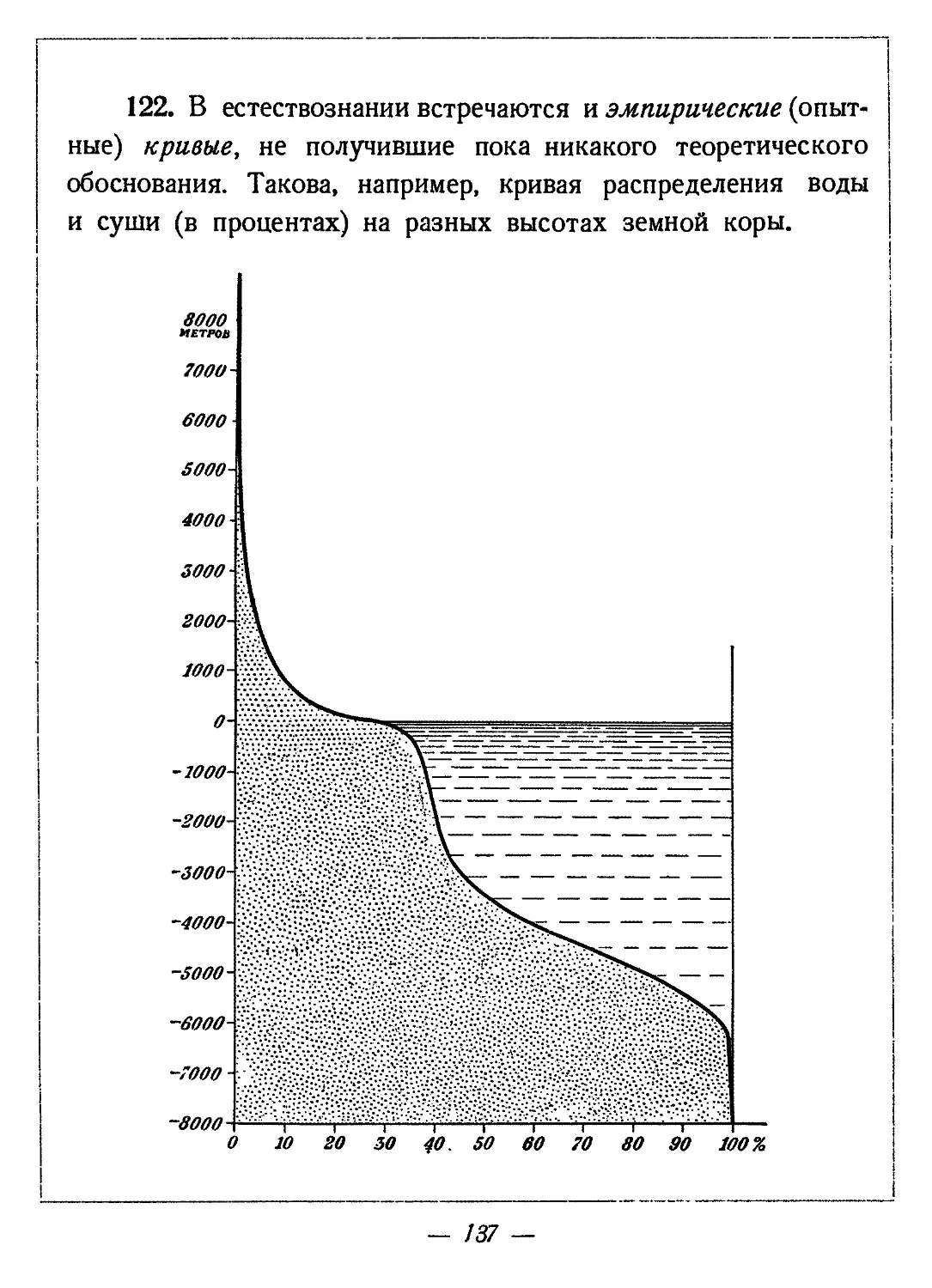
122.	В естествознании встречаются и эмпирические (опытные) кривые, не получившие пока никакого теоретического обоснования. Такова, например, кривая распределения воды и суши (в процентах) на разных высотах земной коры.
i
I
123.	С другой стороны, многие явления природы имеют строгое математическое объяснение. Таково, например, опытное определение центра тяжести гладкой палки. Если положить её горизонтально на края обеих ладоней и медленно сдвигать руки,
то они сойдутся всегда в центре тяжести, и палка не будет падать, каким бы способом ни сдвигать руки.
Это происходит от того, что при приближении одной руки к центру тяжести давление на неё очень сильно увеличивается по сравнению с давлением на вторую руку, удалённую от центра; так как одновременно с давлением возрастает сопротивление трения, то оно превзойдёт сопротивление трения второй руки; тогда движение палки относительно первой
руки прекратится и начнётся движение относительно второй. Таким образом, центр тяжести будет всё время находиться между ладонями и в конце концов будет ими «пойман».
124.	Немного математики требуется также для объяснения опыта с картонным диском, который имеется в числе приложений к этой книге. Если наколоть этот диск на остриё и привести в быстрое вращение, то при определённой скорости движения можно видеть оба кольца диска вращающимися независимо друг от друга и даже в противоположных направлениях. (Это явление особенно хорошо наблюдается только при электрическом освещении и то не при всяком).
125.	Наконец, прикрепив вертикально к столу кусок стекла, можно провести следующий опыт, основанный на законах геометрической оптики.
Перед стеклом, ближе к нам, положим на стол пуговицу и осветим её светом яркой лампы. Тогда в стекле мы увидим отражение этой пуговицы и можем положить позади стекла вторую точно такую же пуговицу так, чтобы она совпала как раз с отображением первой.
Теперь на вторую пуговицу положим комок из пласте-лина, глины или теста и, несмотря на это, мы будем видеть пуговицу сквозь стекло так, как будто бы наш комок был прозрачный.
Можно достать пуговицу сквозь комок при помощи щипцов. Мы на практике убедимся, до какой степени это «искусственное зрение» заменяет собой настоящее: мы сразу попадаем и захватываем закрытую пуговицу, как если бы она была действительно видима. При этом удача не зависит от положения нашей точки зрения перед стеклом. (Почему?)
СОДЕРЖАНИЕ
Предисловие.................... й
От издательства................ 4
1.	Четыре дощечки.............. 5
2.	Из двух квадратов — один ...	6
3.	Из одного ковра —два ....	6
4.	Заполнение плоскости различными квадратами................ 7
5.	Заполнение прямоугольника разными квадратами .................. 9
6.	Седьмая часть треугольника . .	9
7.	«Заметание» треугольника прямой линией..................... 10
8.	Игра в шашки на девяти клетках 10
9.	«Волк и овцы»............... 11
10.	Шахматный эндшпиль Бергера .	12
11.	Математический эндшпиль ... 13
12.	Числа — гиганты............ 14
13.	Задача о восьми ферзях .... 16
14.	Задача о пяти ферзях.......	16
15.	Ходом коня................. 17
16.	Расстановка 36 офицеров ...	18
17.	Игра в пятнадцать.......... 18
18.	«Решётка целых чисел» .... 20
19.	Темперированная гамма рояля . 22
20.	Номограмма без чисел...... 24
21.	Номограмма с масштабной линейкой ........................ 25
22.	Номограмма фотографов .... 26
23.	Суммы двоичных чисел .... 27
24.	Взвешивание четырьмя гирями . 28
25.	Вечное движение бильярдного шара........................ 28
26.	Когда шар попадёт в лузу? . . 29
27.	В шар от трёх бортов....... 30
28.	Кратчайший путь охотника . . 31
29.	Золотое сечение............. 32
30.	Числа Фибоначчи............. 34
31.	Числа Фибоначчи в растущем дереве......................... 34
32.	Заполнение плоскости шестиугольниками ................... 35
33.	Задача о сборной команде ... 35
34.	Переливание вина тремя сосудами .......................... 37
35.	Однородные паркетажи из правильных многоугольников. . 39
36.	Неоднородные паркетажи ... 41
37.	Звёздчатые правильные многоугольники ..................... 43
38.	Взаимные фигуры Кремоны . . 44
39.	Школа для трёх деревень ... 47
40.	Инверсор...................  49
41.	Построения без помощи линейки 50
42.	Построение без помощи циркуля 51
43.	Доказательство невозможности . 52
44.	Выпрямление окружности ... 53
45.	ДОнгиметр................... 54
46.	Форма пчелиных сот......... 56
47.	Две системы окружностей ... 57
48.	Загадка с монетой........... 58
49.	След движения точки на катящейся окружности................ 58
50.	Циклоиды.................... 59
51.	Эвольвента окружности .... 60
52.	Спираль Архимеда............ 61
53.	Переход вращательного движе-
ния в прямолинейное .... 62
54.	Наибольшая площадь при данном периметре....................... 62
55.	Новый способ вычислять площади ......................... 62
56.	Теорема Минковского о выпуклых фигурах................... 63
57.	Сколько точек решётки захватит фигура?................... 64
58.	Теорема о трёх любых фигурах 65
59.	Кривые постоянной ширины . 67
60.	Конхоида Никомеда......... 68
61.	Улитка Паскаля............. 69
62.	Конические сечения........ 70
63.	Эллипс..................... 71
64.	Парабола и эллипс на биоскопе 71
65.	Образование синусоиды ... 72
66.	Трактриса и псевдосфера ... 74
67.	Замечательные плавающие тела 76
68.	Описанный и вписанный квадраты ......................... 77
69.	Линия, целиком заполняющая квадрат....................... 78
70.	Тетраэдр.................. 80
71.	Куб....................... 81
72.	Теорема Польке............ 82
73.	Сечение куба по шестиугольнику 83
74.	Задача о пауке и мухе.... 83
75.	Кристаллы соли............. 86
76.	Окраска граней куба....... 86
77.	Вращение куба.............. 87
78.	Октаэдр................... 88
79.	Додекаэдр.................. 90
80.	Икосаэдр.................. 91
81.	Взаимное соответствие правильных многогранников .... 92
82.	Кристаллы — неправильные многогранники ................. 94
83.	Многогранник, ограниченный ромбами ....................... 97
84.	Звёздчатый многогранник . . 98
85.	Заполнение пространства правильными многогранниками. 98 86. Задача о сборной команде для четырёх клубов................. 99
87.	Различные кладки шаров ... 100
88.	Мыльные пузыри.............102
89.	Форма Луны.................103
90.	Локсодрома и ортодрома ... 104
91.	Карта Меркатора.............105
92.	Стереографическая проекция . 106
93.	Логарифмическая спираль . . 107
94.	Центральная проекция .... 108
95.	Дефект географических карт . 109
96.	Однополостный гиперболоид . 109
97.	Кратчайшая линия на конусе . ПО
98.	Винтовая линия..............112
99.	Кривая с остриями...........113
100.	Замечательное свойство про-
странственной кривой. ... 113
101.	Бесконечный винт...........114
102.	Винтовая поверхность .... 114
103.	Свойство плоскости, цилиндра и шара..........................115
104.	Пространственный четырёхугольник .......................115
105.	Гиперболический параболоид. 116
106.	Катеноид ..................118
107.	Цепная линия...............119
108.	«Кёнигсбергские мосты» ... 120
109.	Задача о девяти тропинках . . 122
ПО. Два вида узлов..............124
111.	Сплетённые шнуры...........125
112.	Лист Мёбиуса...............126
113.	Разрез листа Мёбиуса .... 126
114.	Двухсторонняя поверхность . . 127
115.	Замечательная поверхность . . 128
116.	Проблема четырёх красок . . 129
117.	Раскрашивание тора.........129
118.	Изотермы и адиабаты .... 130
119.	Треугольник Паскаля .... 132
120.	«Лягушечий строй»..........135
121.	Кривая размножения бацилл . 136
122.	Эмпирическая кривая........137
123.	Центр тяжести палки........138
124.	В разные стороны...........139
125.	Опыт с пуговицей...........140
Приложения:
1.	Ключ к шахматной задаче (к № 11)
2.	Масштабная линейка (к № 21)
3.	Лонгиметр (к № 45)
4.	Биоскоп (к № № 49,50 и 64)
5.	Тор (к № 117)
6.	Диск (к № 124)
Редактор И. Н. Бронштейн Технический редактор С. Н. Ахламов
•
Подписано к печати 12/IV 1949 г. А 07568 9 печ. л. + приложения. 7,47 уч.-изд. л.
25650 тип. зн. в печ. л:
•
Отпечатано в тип. М-111 с матриц 1-й Образцовой типографии имени А. А. Жданова Главполиграф-издата при Совете Министров СССР. Москва.
Опечатки
Страница	Строка	Напечатано	Должно быть
39	5—4 снизу	«полному углу»	«полного угла»
78	1 снизу	фактуру	фигуру
81	1 сверху	многогранник	многогранник—куб:
93	2 сверху	тетраэдр	октаэдр
Г. Штейнгауз. «Математический калейдоскоп».