Автор: Мордкович А.Г. Гусев В.А.
Теги: справочные издания по математике математика
ISBN: 5-09-002693-9
Год: 1990
Текст
Р А ГУСЕВ ЛГМОРДКОВИЧ
МАТЕМАТИКА.
ГРАФИК ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
У а 1 у=ах У <а>11 у=ах 1 (0<а<1)
0 1 х 0 1 "х
ГРАФИК ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ
У. y=Log0x <а>1) У y=log0x (0<а<1)
1 1 1
0 1 а х 0 а х
к = tgd=f'(x0)
ИНТЕГРАЛ
S = \ (f,(xi-f2ix>)dx
ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
В.А.ГУСЕВ А.ЕМОРДКОВИЧ
МАТЕМАТИКА.
Справочные
материалы
КНИГА
ДЛЯ УЧАЩИХСЯ
2-е издание
АЛГЕБРА
И НАЧАЛА
АНАЛИЗА
ГЕОМЕТРИЯ
ПРИЛОЖЕНИЯ
МОСКВА
«ПРОСВЕЩЕНИЕ»
1990
ББК 22.1я2я72
Г96
Рецензенты:
учитель-методист школы № 420 Москвы Б. П. Пигарев;
кандидат физико-математических наук.
доцент МГУ О. С. Ивашев-Мусатов
Раздел «Алгебра и начала анализа» написан А. Г. Мордковичем,
раздел «Геометрия» написан Б. А. Гусевым
Гусев В. А., Мордкович А. Г.
Г96 Математика: Справ, материалы: Кн. для учащих-
ся.— 2-е изд.— М.: Просвещение, 1990.— 416 с.: ил.—
ISBN 5-09-002693-9
В книге дано краткое изложение основных разделов школьных
курсов алгебры и качал анализа, геометрии. Книга окажет помощь в систе-
матизации и обобщении знаний по математике. Предыдущее издание
вышло в 1988 году.
г 4306030000-418 222_90
103(03)—90
ББК 22.1я2я72
Учебное издание
Гусев Валерий Александрович
Мордкович Александр Григорьевич
МАТЕМАТИКА
Справочные материалы
Зав. редакцией Р. А. Хабиб
Редактор Л. Н. Белоновская
Младший редактор Е. А. Буюклян
Художники Б. Л. Николаев,
Б. В. Костин
Художественный редактор
Е. Р. Дашук
Технический редактор И. Ю. Щукина
Корректоры Т. С. Крылова, Е. В. Мамитова
ИБ № 12625
Подписано к печати с диапозитивов 20.02.90. Формвт 60X90’/ (. Вум. типографская J* 1. Гариит.
школьн. Печать высокая. Уел. печ. л. 204-0.25 форз. Уел. кр.-отт. 26,69. Уч.-нзд. л.
21.844-0.42 форз. Тираж 1 000 000 экз. Заказ 769. Цена 65 коп.
РСФСР по делам издательств, полиграфии и книжной торговли. I2984E. Москва. 8-й проезд
Марьиной рощи. 41.
Саратовский ордена Трудового Краевого Знамени полиграфический комбинат Государственного
комитета РСФСР по делам издательств, полиграфии и книжной торговли. 410004. Саратов, ул. Чер-
нышевского, 59.
ISBN 5-09-002693-9
© Гусев В. А„ Мордкович А. Г., 1988
СЛОВО К УЧАЩИМСЯ
1. Что представляет собой этот справоч-
ник?
Б справочнике вы найдете основной материал всех разделов
школьного курса математики: математические понятия, опреде-
ления, аксиомы, теоремы, свойства и т. д. Кроме этого, в спра-
вочнике имеется много подробно разобранных задач и приме-
ров, но заметим, что в их решении используется иногда не
только материал того пункта, к которому относится пример нли
задача, но и материал из других разделов. Доказательств
теорем в большинстве случаев нет — их можно найти в тех
учебных пособиях, по которым вы учитесь или учились в
младших классах; те же немногие доказательства, которые
адесь приведены, мы даем потому, что либо нх нет в школьных
учебных пособиях, либо мы приводим их как образцы тех или
иных важных рассуждений.
В нашем справочнике весь материал, относящийся к тому
или иному понятию, помещен компактно, в одном разделе (в
школьных пособиях это не всегда так). Это поможет вам быстро
получить всю необходимую информацию об интересующем вас
понятии.
В некоторых пунктах справочника мы даем дополнитель-
ный материал, не входящий в программу курса математики
средней школы,— этот материал расширит ваши представле-
ния о некоторых известных вам понятиях. Такие пункты отме-
чены знаком *.
2. Зачем нужен справочник по матема-
тике?
Справочник поможет вам:
1) найти нужную информацию о том или ином понятии, о
той или иной теореме из школьного курса математики;
2) повторить соответствующий материал при подготовке
к уроку, к контрольной работе, к экзамену;
3) вспомнить, как решаются типовые задачи и примеры
школьного курса математики;
4) подготовиться к вступительному экзамену или собеседо-
ванию по математике при поступлении в вуз, техникум и дру-
гие учебные заведения.
3. Как пользоваться справочником?
Справочник состоит из трех частей: часть I — алгебра и
начала анализа, часть И — геометрия, часть III — приложения
(основные формулы и соотношения, предметный указатель).
Внутри первых двух частей материал изложен по главам:
7 глав по алгебре и началам анализа и 6 глав по геометрии.
Главы разбиты на параграфы, параграфы — на довольно мел-
кие пункты (так вам будет удобнее отыскать нужную инфор-
мацию) : 230 пунктов по алгебре и началам анализа и 84 пункта
по геометрии. Нумерация глав, параграфов и пунктов своя в
каждой части.
Необходимую вам информацию следует искать так: конкрет-
ное понятие удобно искать по предметному указателю, конкрет-
ный раздел курса — по оглавлению.
Приведем примеры использования предметного указателя.
Пусть вам понадобилось найти определение дробной части чис-
ла. В предметном указателе среди слов, начинающихся на бук-
ву «Д», вы находите: дробная часть числа — 39 (это значит,
что соответствующее определение помещено на странице 39).
Еще один пример: вам нужно найти определение бесконечной
десятичной периодической дроби. Дроби бывают разных типов,
всё они помещены в предметном указателе ниже слова «дробь».
Там, в частности, вы найдете:
Дробь
— десятичная 22
----бесконечная 27
-------- периодическая 28
Это значит, что интересующее вас понятие вы найдете на с. 28.
Аналогично термин «рациональное выражение» вы найдете
в алфавитном указателе под рубрикой «Выражение», «пря-
мой угол» — под рубрикой «Угол», «свойства модулей» —
под рубрикой «Свойства» и т. д.
Если вы будете читать тот или иной пункт с начала до
конца, то внутри текста вы тоже иногда найдете ссылки на
номера страниц или пунктов, где вводится понятие, исполь-
зуемое в этом пункте. Для удобства номера аксиом и тео-
рем выделены в тексте. Аксиомы геометрии пронумерованы в
соответствии с нумерацией, принятой в пособии А. Б. Пого-
релова «Геометрия, 6—10». Теоремы в справочнике нумеруются
так: Т.5.3 — это значит, что речь идет о теореме 3 из гла-
вы 5.
Мы надеемся, что справочник станет вашим добрым помощ-
ником, и желаем вам успехов!
Авторы
АЛГЕБРА
И НАЧАЛА АНАЛИЗА
ГЛАВА I. ЧИСЛА
f 1. Натуральные числа
1. Запись натуральных чисел 11
2. Арифметические действия
над натуральными числами —
8. Деление с остатком . . . 12
4. Признаки делимости . . 13
Б. Разложение натурального
числа на простые множите-
ли 14
6. Наибольший общий делитель
нескольких натуральных чи-
сел .......15
7. Наименьшее общее кратное
нескольких натуральных чи-
сел ........ 16
8. Употребление букв в алгебре.
Переменные............17
f 2. Рациональные числа
О. Обыкновенные дроби. Пра-
вильные и неправильные дро-
би. Смешанные числа ... 17
10. Равенство дробей. Основное
свойство дроби. Сокращение
дробей.......................18
11. Приведение дробей к общему
знаменателю ..... 19
12. Арифметические действия
над обыкновенными дробями 20
13. Десятичные дроби ... 22
14. Арифметические действия
над десятичными дробями 24
15. Проценты ...... 26
16. Обращение обыкновенной дро-
би в бесконечную десятичную
периодическую дробь . • 27
17. * Обращение бесконечной де-
сятичной периодической дро-
би в обыкновенную дробь 28
18. Координатная прямая . . 30
19. Множество рациональных
чисел .......31
§ 3. Действительные числа
20. Иррациональные числа . . 31
21. Действительные числа. Чис-
ловая прямая ..... 32
22. Обозначения некоторых чис-
ловых множеств .... 33
23. Сравнение действительных
чисел •«>•••. —
24. Свойства числовых нера-
венств ...................34
25. Числовые промежутки . . За
26. Модуль действительного чис-
ла ........ 36
27. Формула расстояния между
двумя точками координат-
ной прямой ..... 37
28. Правила действий над дейст-
вительными числами . . —
29. Свойства арифметических
действий над действитель-
ными числами .... 38
30. Пропорции................38
31. Целая часть числа. Дробная
часть числа ..... 39
32. Степень с натуральным пока-
зателем
33. Степень с пулевым показате-
лем. Степень с отрицатель-
ным целым показателем . . —
34. Стандартный вид положи-
тельного действительного
числа . ......................40
35. Определение арифметическо-
го корня. Свойства арифме-
тических корней .... —
36. Корень нечетной степени из
отрицательного числа . . 41
37. Степень с дробным показате-
лем ........ 42
38. Свойства степеней с рацио-
нальными показателями .
39. Приближенные значения чи-
сел. Абсолютная и относи-
тельная погрешности... 43
40. Десятичные приближения
действительного числа по
недостатку и по избытку . . 44
41.* Правило извлечения квад-
ратного корня из натураль-
ного числа ...... 45
42. Понятие о степени с иррацио-
нальным показателем . . 47
43. Свойства степеней с действи-
тельными показателями . • —
$ 4. Комплексные числа
44. Понятие о комплексном чис-
ле. ...... .47
45. Арифметические операции
над комплексными числами 48
46. Алгебраическая форма комп-
лексного числа .... 49
47. Отыскание комплексных кор-
ней уравнений .... 52
ГЛАВА П. АЛГЕБРАИЧЕСКИЕ
ВЫРАЖЕНИЯ
5 5. Основные понятия
48. Виды алгебраических выра-
жений .......53
49. Допустимые значения пере-
менных. Область определе-
ния алгебраического выра-
жения ....... —
60. Понятие тождественного пре-
образования выражения.
Тождество ..... 54
§ 6. Целые рациональные
выражения
51. Одночлены и операции над
ними .......65
52. Многочлены. Приведение
многочленов к стандартному
виду .......56
53. Формулы сокращенного ум-
ножения ...... 57
54. Разложение многочленов на
множители ..... 68
55. Многочлены от одной пере-
менной ...... 60
56. Разложение квадратного трех-
члена на линейные множи-
тели .........................—
57. Разложение на множители
двучлена Xя—ал . . . • 61
58. Возведение двучлена в нату-
ральную степень (бином Нью-
тона) —
$ 7. Дробные рациональные
выражения
59. Рациональная дробь и ее ос-
новное свойство .... 62
60. Сокращение рациональных
дробей ....•••63
61. Приведение рациональных
дробей к общему знаменате-
лю ........ —
62. Сложение и вычитание раци-
ональных дробей .... 64
63. Умножение и деление рацио-
нальных дробей .... 66
64. Возведение рациональной
дроби в целую степень . . 66
65. Преобразование рациональ-
ных выражений «... 67
§ 8. Иррациональные выраже-
ния
66. Простейшие преобразования
арифметических корней (ра-
дикалов) ...... 63
67. Тождество |а| . • • 69
68. Преобразование иррацио-
нальных выражений . • 70
ГЛАВА III. ФУНКЦИИ И ГРА-
ФИКИ
5 9. Свойства функций
69. Определение функции . . 71
70. Аналитическое задание
функции ...... —
71. Табличное задание функции 78
7
72. Числовая плоскость. Коорди-
натная плоскость, оси коор-
динат .......
73. График функции, заданной
аналитически .....
74. Четные и нечетные функции
76. График четной функции. Гра-
фик нечетной функции . .
76. Периодические функции.
77. Монотонные функции .
5 10. Виды функций
73. Постоянная функция.
79. Прямая пропорциональность
80. Линейная функция ...
81. Взаимное расположение гра-
фиков линейных функций
82. Обратная пропорциональ-
ность .......
83. Функция у=х4 ....
84. Функция у — х3 ....
85. Степенная функция с нату-
ральным показателем . .
86. Степенная функция с целым
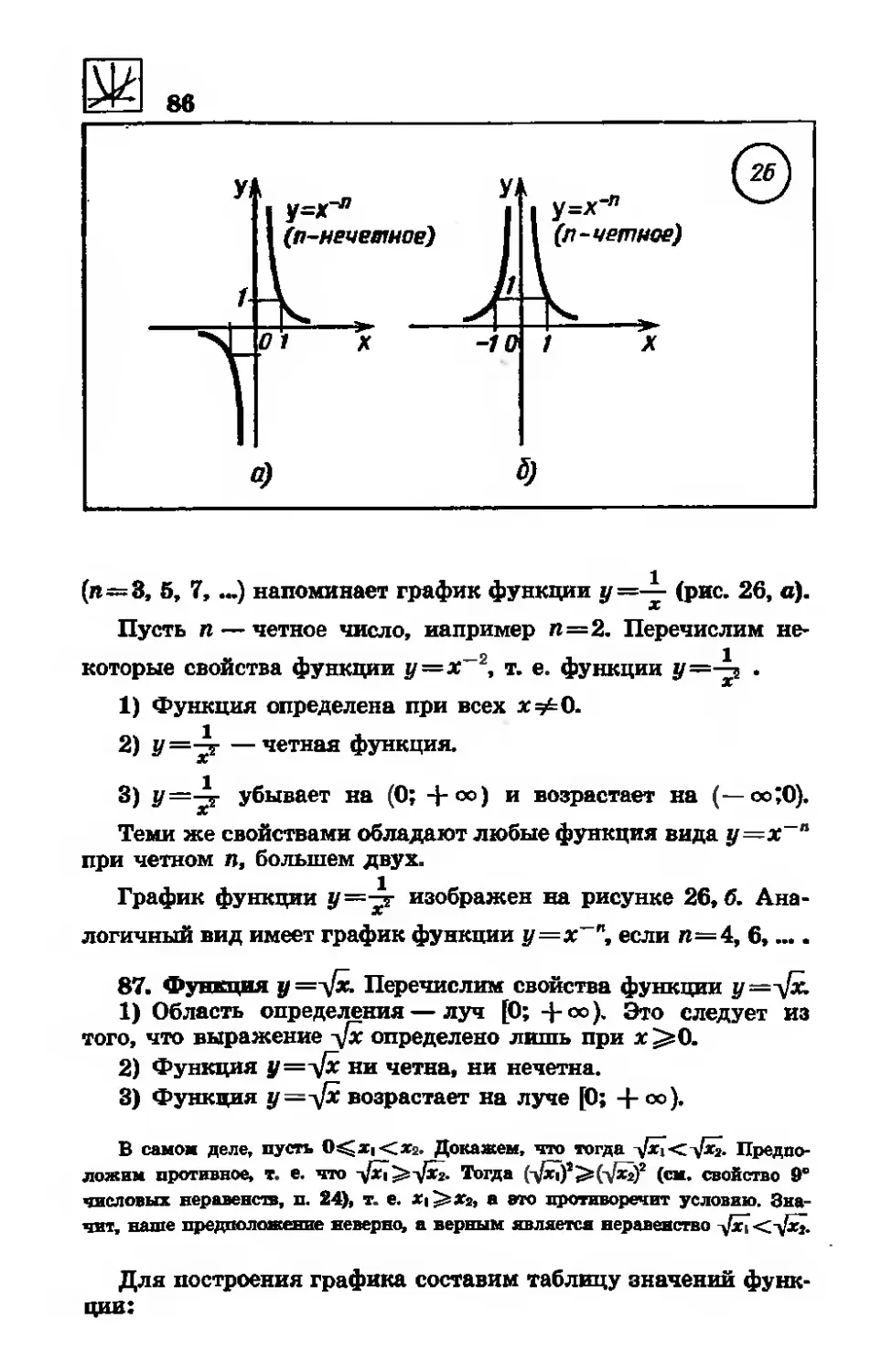
отрицательным показателем
37. Функция y=-yjx . . . .
83. Функция у—ух ....
39. Функция у—ух ....
90. Степенная функция с поло-
жительным дробным показа-
телем .......
©1. Степенная функция с отрица-
тельным дробным показате-
лем ........
©2. Функция у—Гх] ....
93. Функция у=(х} ....
94. Показательная функция .
©5. Обратная функция. График
обратной функции .
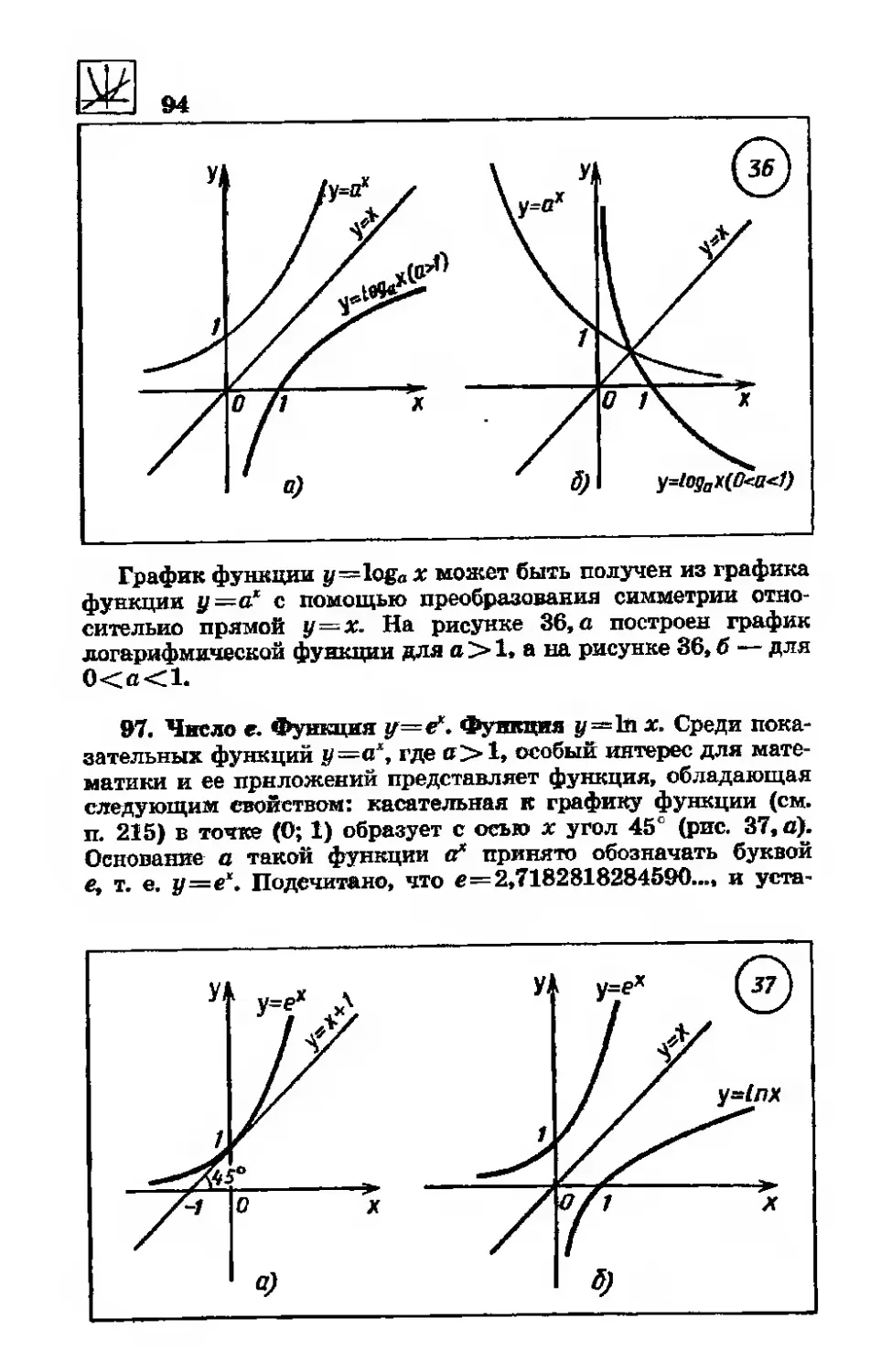
96. Логарифмическая функция
©7. Число е. Функция у=е*.
Функция у = Ln х .
98. Определение тригонометри-
ческих функций ....
99. Знаки тригонометрических
функций по четвертям . .
100. Исследование тригонометри-
ческих функций на четность,
нечетность .....
101. Периодичность тригономет-
рических функций ...
102. Свойства и граф ни функции
y=sinx ......
103. Свойства и график функции
у—соз х ..... .
104. Свойства и график функции
У=1£Х......................
105. Свойства и график функции
73
75
76
77
78
80
82
84
85
86
37
83
39
90
91
93
94
95
96
97
98
99
100
y=ctgx......................
106. * Функция у=агсвш х . . —
107.* Функция у=arccos х . .102
106.* Функция у — arctg х . . 103
109.* Функция у—arcctgx . .104
5 11. Преобразования графиков
110. Построение графика функ-
ции y=mf(x) .... 105
111. Графики функций у=дх2,
у=ОХ3.......................107
112. Построение графика функ-
ции y=f(x—m)+n. . . _
113. График квадратичной фун-
кции ....... 108
114. Способы построения гра-
фика квадратичной функ-
ции ....... 109
115. Построение графика функ-
ции y=f(kx). .... Ш
116. Сжатие и растяжение гра-
фиков тригонометрических
функций . . . • • .113
117. График гармонического ко-
лебания у=А sin (сох+а) 114
ГЛАВА IV. ТРАНСЦЕНДЕНТ-
НЫЕ ВЫРАЖЕНИЯ
5 12. Преобразование выраже-
ний, содержащих переменную
под знаком логарифма
118. Понятие трансцендентного
выражения ..... 116
119. Определение логарифма по-
ложительного числа по
данному основанию . . .117
120. Свойства логарифмов . . —
121. Переход к новому основа-
нию логарифма . . . .118
122. Логарифмирование и потен-
цирование • . . . .119
123. Десятичный логарифм. Ха-
рактеристика и мантисса
десятичного логарифма . .120
5 13. Формулы тригонометрии и
их использование для преобра-
зования тригонометрических вы-
ражении
124. Тригонометрические выра-
жения ...... 121
125. Формулы сложения и вы-
читания аргументов . .
126. Формулы приведения . . 123
127. Соотношения между триго-
нометрическими функция-
8
ми одного и того же аргу-
мента ...... 123
128. Формулы двойного угла . 125
129. Формулы понижения сте-
пени ....... 126
180. Преобразование суммы три-
гонометрических функций
в произведение .... 127
131. Преобразование произведе-
ния тригонометрических
функций в сумму . . .128
182.* Преобразование выраже-
ния ccost+bsint к виду
Asin(t-|-a) ..... —
188.* Примеры преобразований
выражений, содержащих об-
ратные тригонометрические
функции.................129
ГЛАВА V. УРАВНЕНИЯ И СИС-
ТЕМЫ УРАВНЕНИИ
§ 14. Уравнения с одной переменной
134. Определение уравнения.
Корни уравнения ... 131
135. Равносильность уравнений —
136. Линейные уравнения . . 132
137. Квадратные уравнения . . 133
138. Неполные квадратные урав-
нения .......134
139. Теорема Виета .... —
140. Системы и совокупности
уравнений . . . . .135
141. Уравнения, содержащие пе-
ременную под знаком моду-
ля........ 136
142. Понятие следствия уравне-
ния. Посторонние корни . 137
143. Уравнения с переменной
в знаменателе .... 138
144. Область определения урав-
нения ....... 139
145. Рациональные уравнения . 141
146. Решение уравнения р(х)=0
методом разложения его ле-
вой части на множители . —
147. Решение уравнений методом
введения новой переменной 142
148. Биквадратные уравнения 143
149. Решение задач с помощью
составления уравнений . . —•
150. Иррациональные уравнения 147
151. Показательные уравнения 149
152. Логарифмические уравне-
ния ....... —
153. Примеры решения покава-
тельно-логарифмических
уравнений . . . . .151
154 . Простейшие тригонометри-
ческие уравнения . . .152
155 . Методы решения тригоно-
метрических уравнений . 153
156 .* Универсальная подстановка
(для тригонометрических
уравнений) . . . . .156
157 .* Метод введения вспомога-
тельного аргумента (для
тригонометрических урав-
нений) . . . . . .157
158 . Графическое решение урав-
нений ...... 158
159 .* Уравнения с параметром . 160
§ 15. Уравнения с двумя пере-
менными
160. Решение уравнения с двумя
переменными . . . .168
161. График уравнения с двумя
переменными .... —
162. Линейное уравнение с дву-
мя переменными и его гра-
фик ....... —•
§ 16. Системы уравнений
163. Системы двух уравнений
с двумя переменными. Рав-
носильные системы . . .164
164. Решение систем двух урав-
нений с двумя переменными
методом подстановки . .166
165. Решение систем двух урав-
нений с двумя переменными
методом сложения . . . —
166. Решение систем двух урав-
нений с двумя переменными
методом введения новых
переменных ..... 167
167. Графическое решение систем
двух уравнений с двумя пе-
ременными ..... 169
163. Исследование системы двух
линейных уравнений с дву-
мя переменными . . .170
169 .* Решение систем двух урав-
нений с двумя переменными
методами умножения и де-
ления ....... 171
170 . Системы показательных и
логарифмических уравне-
ний ....... 173
171 .* Системы тригонометриче-
ских уравнений с двумя пе-
ременными ....................—
172 . Системы трех уравнений с
тремя переменными. . .175
173 - Решение задач с помощью
составления систем уравне-
ний ........................
ГЛАВА VI. НЕРАВЕНСТВА
§ 17. Решение неравенств е пе-
ременной
174. Основные понятия, связан-
ные о решением неравенств
с одной переменной .
175. Графическое решение нера-
венств с одной переменной
176. Линейные неравенства с од-
ной переменной ....
177. Системы неравенств с одной
переменной..................
178. Совокупность неравенств с
одной неременной .
179. Дробно-линейные неравен-
ства .......................
180. Неравенства второй степени
181. Графическое решение нера-
венств второй степени .
182. Неравенства с модулями .
183. Решение рациональных не-
равенств методом проме-
жутков ......
184, Показательные неравенства
185. Логарифмические неравен-
ства .......
186. * Иррациональные неравен-
ства .......
187. Решение тригонометричес-
ких неравенств ....
188. Неравенства и системы не-
равенств с двумя перемен-
ными .......
§ 18. Доказательство неравенств
189. Метод оценки знака раз-
ности .......
190. Синтетический метод дока-
зательства неравенств .
191. Доказательство неравенств
методом от противного . .
192. * Использование неравенств
при решении уравнений .
ГЛАВА УП. ЭЛЕМЕНТЫ МА-
ТЕМАТИЧЕСКОГО АНАЛИЗА
I 19. Числовые последователь-
ности
193. Определение последователь-
ности . ....................
176
178
179
180
181
182
183
185
187
189
191
193
195
196
199
200
201
201
194. Способы задания последова-
тельности ..... 202
195. Возрастание и убывание
последовательности ... —
196. Определение арифметичес-
кой прогрессии .... 203
197. Свойства арифметической
прогрессии ..... 204
198. Определение геометрической
прогрессии ..... 205
199. Свойства геометрической
прогрессии ..... 206
200. Понятие о пределе последо-
вательности . . . . .207
201. Вычисление пределов после-
довательностей . . . .209
202. Сумма бесконечной геомет-
рической прогрессии при
1С1<1.........................210
§ 20. Предел функции
203. Предел функции y—f(x)
при х->оо. Горизонтальная
асимптота . . . . .211
204, Вычисление пределов функ-
ций при Х~*-со .... 213
205. Предел функции в точке.
Непрерывные функции . .214
206. Вертикальная асимптота . 215
207. Вычисление пределов функ-
ций в точке ..... 216
§ 21. Производная и ее приме-
нения
208. Приращение аргумента. При-
ращение функции . . .218
209. Определение производной . —
210. Формулы дифференциро-
вания. Таблица производ-
ных ....... 220
211. Дифференцирование суммы,
произведения, частного . . —
212. Сложная функция и ее диф-
ференцирование . . . 221
213. Физический смысл произ-
водной ...... 222
214. Вторая производная и ее фи-
зический смысл .... 223
215. Касательная к графику
функции
216. Применение производной к
исследованию функций на
монотонность .... 226
217. Применение производной к
исследованию функций на
экстремум ..... 228
218. Отыскание наибольшего и
10
наименьшего значений не-
прерывной функции на от-
резке ....... 231
219.* Отыскание наибольшего
или наименьшего значения
непрерывной функции на
незамкнутом промежутке . 232
220. Задачи на отыскание наи-
больших или наименьших
значений величин . . .234
221. Применение производной
для доказательства тождеств 287
222. Применение производной
для доказательства нера-
венств ...... 238
223. Общая схема построения
графика функции' . . . 239
§ 22. Первообразная и интеграл
224. Первообразная .... 243
225. Таблица первообразных . . —
226. Правила вычисления перво-
образных ..... 244
227. Интеграл............246
228. Связь между интегралом и
первообразной (формула
Ньютона—Лейбница) . . 248
229. Правила вычисления инте-
гралов ......—
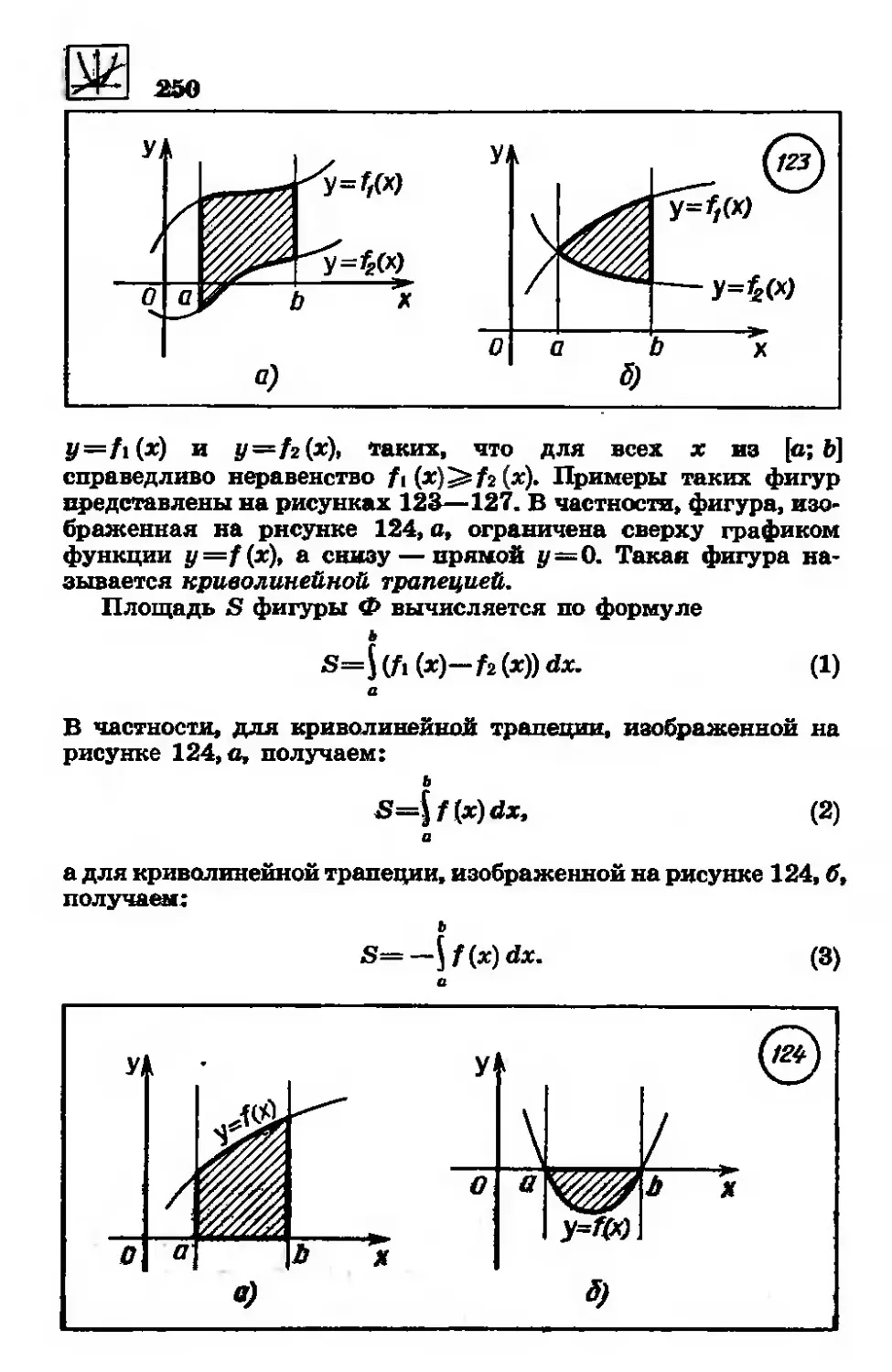
280. Использование интеграла
для вычисления площадей
плоских фигур .... 249
ГЛАВА I. ЧИСЛА
§ 1. Натуральные числа
1. Запись натуральных чисел. Числа 1, 2, 3, 4, 5, ... , ис-
пользующиеся для счета предметов или для указания поряд-
кового иомера того или иного предмета среди однородных пред-
метов, называются натуральными. Любое натуральное число в
десятичной системе счисления записывается с помощью цифр О,
1, 2, 3, 4, 5, 6, 7, 8, 9. Например, запись 2457 означает,
что 2 — цифра тысяч, 4 — цифра сотен, 5 — цифра десятков и
7 — цифра единиц, т. е. 2457=2 «1000 + 4 -100 + 5-10 + 7.
Вообще если а — цифра тысяч, Ь — цифра сотен, с — цифра
десятков н d— цифра единиц, то имеем а*1000-|-Ь’100-|-£>£
ХЮ + d. Используется также сокращенная запись abed
(написать abed нельзя, так как такая запись в соответствии
с принятым в математике соглашением означает произведение
чисел а, Ь, с, d). Аналогично запись abede означает число
о«10000-j-b’1000 +с-100+«2* 104-е, причем а=£0.
2. Арифметические действия над натуральными числами.
Результатом сложения или умножения двух натуральных чи-
сел всегда является натуральное число: если ш, п — натураль-
ные числа, то р=т-\-п тоже натуральное число, тип — сла-
гаемые, р — сумма; р = тп тоже натуральное число, т.п —
множители, р — произведение.
Справедливы следующие свойства сложения и умножения
натуральных чисел:
1 . а + Ь = 6+а (переместительное свойство сложения).
2°. (а + &)+с=о+(6+е) (сочетательное свойство сложе-
ния).
3°. аЪ = Ъа (переместительное свойство умножения).
4°. (аЬ) с=а (Ьс) (сочетательное свойство умножения).
5. а (Ъ +е)=а6+ас (распределительное свойство умноже-
ния относительно сложения).
В результате вычитания или деления натуральных чисел
не всегда получается натуральное число: например, 7—4=3—
натуральное число, тогда как 4 — 7 = — 3 — не натуральное чис-
ло; 21:7=3—натуральное число, тогда как 11:2 = 5,5 — не
натуральное число.
Если т, п, k — натуральные числа, то при т — n = k го-
ворят, что т — уменьшаемое, п — вычитаемое, k — разность;
при m:n = k говорят, что m — делимое, п — делитель, k —
частное, число m называют также кратным числа п, а число
п — делителем числа т. Если т — кратное числа п, то суще-
ствует натуральное число k, такое, что m = kn.
Из чисел с помощью знаков арифметических действий и
скобок составляются числовые выражения. Если в числовом
выражении выполнить указанные действия, соблюдая приня-
тый порядок, то получится число, которое называется значе-
нием выражения.
Напомним порядок арифметических действий в числовом
выражении: сначала выполняются действия в скобках; внутри
любых скобок сначала выполняют умножение и деление, а
потом сложение и вычитание. Например, если нужно найти зна-
чение выражения
(28-93+(1927—1873)-31): 6 — 710,
то порядок действий таков:
(28-93+(1927 —1873)*31):6 —710.
3. Деление с остатком. Если натуральное число т не де-
лится на натуральное число п, т. е. не существует такого
натурального числа fe, что m=nk, то рассматривают деление
с остатком. Например, при делении числа 43 на число 18 в
частном получается 2 и в остатке 7, т. е. 43 = 18-2 + 7. В общем
случае если т — делимое, п — делитель (m>n), р — частное
иг — остаток, то
m=np+r, (1)
где r<Zn. Здесь т, п, р, г— натуральные числа (исключение
составляет случай, когда m делится на п без остатка и г = 0). На-
пример, если п = 3, а г = 2, то получаем т=Зр+2. Это
формула чисел, которые при делении на 3 дают в остатке 2.
Пример. Найти частное и остаток от деления числа
36 421 на число 25.
Решение. Выполним деление «углом»:
36421|25
25 1456
_ 114
100
_142
125
.171
150
21
Итак, частное 1456, а остаток 21. Воспользовавшись ра-
венством (1), можем записать: 36 421 = 25*1456 + 21.
4. Признаки делимости. В некоторых случаях, не производя
деления натурального числа m на натуральное число /г, можно
ответить на вопрос: выполнимо деление m иа п без остатка или
нет? Ответ на этот вопрос можно получить с помощью различ-
ных признаков делимости.
Т.1.1. Если каждое слагаемое делится на некоторое число,
то и сумма делится иа это число (теорема о делимости
суммы).
Не следует, однако, думать, что если каждое слагаемое
суммы не делится на какое-то число, то и сумма не делится
на это число. Например, сумма 37 + 19 делится на 4, хотя нн 37,
ни 19 не являются кратными числа 4. Заметим, однако, что
если все слагаемые, кроме одного, делятся на некоторое число,
то сумма не делится на это число.
Т.1.2.
Если в произведении хотя бы один из сомножителей
делится на некоторое число, то и произведение де-
лится на это число (теорема о делимости произведе-
ния).
Например, ие выполняя умножения, можно утверждать, что
произведение 105-48-93-54 делится на 5, так как 105 делится
иа 5.
Т.1.3.
Т.1.4.
Т.1.5.
Т.1.6.
Натуральное число делится на 2 тогда и только тогда,
когда его последняя цифра делится на 2 (признак
делимости на 2).
Натуральное число делится на 5 тогда и только тогда,
когда его последняя цифра либо 0, либо 5 (признак
делимости на 5).
Натуральное число делится на 10 тогда и только тог-
да, когда его последняя цифра 0 (признак дели-
мости на 10).
Натуральное число, содержащее не менее трех цифр,
делится на 4 тогда и только тогда, когда делится
на 4 двузначное число, образованное последними
двумя цифрами заданного числа (признак делимости
на 4).
Доказательство проведем для пятизначного числа abcde. Имеем
ebcde=a-10000+b-1000+c-100 + d-10+e. Так как 100, 1000 и 10 000 де-
лятся на 4, то делится на 4 и сумма 10 000a -{-10006 + 100с. Значит, если
двузначное число d-10 +е делится на 4, то и abcde делится на 4; если же 104+е
не делится на 4, то и abcde не делится на 4.
14
Например, число 15 436 делится на 4, так как число 36 де-
лится иа 4. Число 372 514 не делится на 4, так как
14 не делится иа 4.
Т.1.7.
Натуральное число делится на 3 тогда и только тогда,
когда сумма его цифр делится на 3 (признак дели-
мости на 3).
Доказательство проведем для четырехзначного числа abed. Имеем
abed = 1000а 4-100 b 4- 10с 4- d=(999а 4- а) 4- (99Ь 4- Ь)+(9с 4- с)4- d=
=(999a+99Ь 4-9с)+(a 4-е 4-d)-
Числа 9, 99, 999 делятся на 3, поэтому 999а4~99Ь4-9с делится на 3, и сум-
ма (999a4-99&4-9c)4-(e4-b+®+4) будет делиться на 8 тогда и только тогда,
когда делится на 3 сумма цифр а4~Ь4-с-Н*-
Например, число 2742 делится на 3, так как делится на 3
сумма цифр этого числа 2 4-7 + 4 + 2 = 15. Число 17941 не
делится на 3, так как сумма цифр этого числа равна 22, а 22 не
делится на 3.
Т.1.8.
Натуральное число делится на 9 тогда и только тогда,
когда сумма его цифр делится на 9 (признак дели-
мости на 9).
5. Разложение натурального числа на простые множители.
Если число имеет только два делителя (само число и единица),
то оно называется простым; если число имеет более двух дели-
телей, то оно называется составным.
Так, число 19 простое, ибо оно имеет только два делителя:
1 и 19; число 35 составное, оно имеет четыре делителя: 1, 5, 7,
35. Простое число 19 можно представить в виде произведения
двух натуральных чисел только одним способом, не учиты-
вая порядок сомножителей: 19=1*19; составное число 35
можно представить в виде произведения даух натуральных
чисел более чем одним способом: 35 = 1-35 = 5*7.
Заметим, что число 1 не относится ни к простым, ии к
составным числам.
Т.1.9.
Любое составное натуральное число можно разло-
жить на простые множители, и только одним спо-
собом.
При разложении чисел на простые множители используют
признаки делимости и применяют запись столбиком, при кото-
рой делитель располагается справа от вертикальной черты, а
частное записывается под делимым. Так, для числа 360 эта
запись будет выглядеть следующим образом:
15
360
180
90
45
15
5
1
2
2
2
3
3
5
Если в разложении числа на простые миожители один и тот
же множитель а встречается п раз, то записывают коротко:
ап, т. е. ^g-g-- •а/=ап.
П множителей
Выражение а" называют степенью, а — основанием степе-
ни, п — показателем степени.
Поэтому можно записать: 360 = 2-2-2-3-3-5 = 23-32-5.
6. Наибольший общий делитель нескольких натуральных
чисел. Пусть даны числа 72 и 96. Выпишем все делители
числа 72:
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
Выпишем все делители числа 96:
1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96.
Среди выписанных чисел есть одинаковые:
1, 2, 3, 4, 6, 8, 12, 24.
Все эти числа называют общими делителями чисел 72 и 96,
а наибольшее среди них — наибольшим общим делителем.
Для любых заданных натуральных чисел а и Ь можно
найти наибольший общий делитель. Он обозначается D (а, Ь)
(читается: «D от а, Ь»). Если числа а и Ъ таковы, что D (а, Ь)=1,
то числа а и Ъ называются взаимно простыми.
Например, взаимно простыми будут числа 72 и 35 (хотя
каждое из них — составное число).
Чтобы найти наибольший общий делитель нескольких чисел,
надо разложить эти числа на простые множители и найти
произведение общих простых множителей, взяв каждый из них
с наименьшим (из имеющихся) показателем.
Пример 1. Найти D (48, 60, 72).
Решение. 48 = 24-3; 60 = 22-3-5; 72 = 23«32. Значит,
D (48, 60, 72)=22-3.
Ответ: D (48, 60, 72)= 12.
16
Пример 2. Найти В (3780, 7056).
Решение. Имеем:
3780 2
1890 2
945 3
315 3
105 3
35 5
7 7
1
7056 2
3528 2
1764 2
882 2
441 3
147 3
49 7
7 7
1
37 80 = 22-33-5 -7 7056 = 24-32-72
Тогда D(3780, 7056) = 22*32-7; взяты те простые множите-
ли, которые входят и в разложение числа 3780, и в разло-
жение числа 7056.
Ответ: D (3780, 7056)=252.
7. Наименьшее общее кратное нескольких натуральных чи-
сел. Пусть даны числа 12 и 18. Выпишем числа, кратные
12:
12, 24, 36, 48, 60, 72, ... .
Выпишем числа, кратные 18:
18, 36, 54, 72..
Среди выписанных чисел есть одинаковые:
36, 72, ... .
Все эти числа называют общими кратными чисел 12 и 18, а наи-
меньшее из них — число 36 — называют наименьшим общим
кратным чисел 12, 18.
Аналогично определяется наименьшее общее кратное произ-
вольных натуральных чисел а и Ъ, оно обозначается К (а, Ь)
(читается: «Кот а, Любое общее кратное чисел а и Ъ де-
лится на К (fl, Ь).
Чтобы найти наименьшее общее кратное нескольких чисел,
надо разложить эти числа на простые миожители и найти
произведение всех получившихся простых множителей, взяв
каждый из них с наибольшим (из имеющихся) показателем.
Пример. Найти К (3780, 7056).
Решение. Имеем 3780 = 22-3 - 5-7; 70 56 = 24*32-72 (см.
п. 6).
Тогда К(3780, 7056)=2 -33«5-7 , т. е. взяты все простые
множители, которые входят в разложение хотя бы одного из
чисел 3780 и 7056.
Итак, К (3780, 7056)=105 840.
Для любых натуральных а и Ъ справедливо равенство
В (о, 5)-К (о, Ъ)—аЪ.
Если, в частности, числа а и Ъ взаимно простые, т. е. D (а, Ь)=1,
то К (а, Ь)=аЪ. Это значит, что наименьшее общее кратное
двух взаимно простых чисел равно произведению этих чисел.
8. Употребление букв в алгебре. Переменные. В алгебре час-
то конкретные свойства чисел записывают с помощью букв.
Например, переместительное свойство сложения (от перемены
мест слагаемых сумма не меняется) записывают так:
о+5 = 5+с, где вместо а и Ь можно подставить любые числа:
3-|_ 5 = 5 + 3; 100 + 3501=3501 + 100 и т. д. Число, под-
ставляемое вместо буквы, называют ее значением. В некоторых
случаях (например, в уравнениях) вместо буквы можно подста-
вить только определенные числа, чтобы написанное равенство
было верным. Например, 7 + х=10 обращается в верное равен-
ство лишь при х=3. Употребляемые в алгебре буквы назы-
вают переменными; смысл такого названия состоит в том, что
числовое значение буквы можно изменить: например, в равенст-
ве с+5=5+с можно положить о=3, 5=5, а можно с = 7,
Ъ —19 и т. д.— во всех случаях равенство будет верно. В равенст-
ве 7+х=10 можно положить х=3, а можно х=5; разница в
том, что в первом случае числовое равенство будет верным, а
во втором — неверным. Равенство D (с, 5)=1 (см. п. 6) верно
при следующих значениях переменных а и 5:
о = 18, 5=25; с=100, 5 = 99; а=13, 5 = 1000 и т. д.
Это равенство неверно при следующих значениях переменных:
о=8, 5 = 6; о=25, 5 = 150; о = 7, 5 = 777 и т. д.
§ 2- Рациональные числа
9. Обыкновенные дроби. Правильные и неправильные дроби.
Смешанные числа. Обыкновенная дробь — это число вида —,
и
12 15
где тип — натуральные числа, например —, —. Число m
называется числителем дроби, п — знаменателем. В частности,
может быть п = 1, в этом случае дробь имеет вид -р, ио чаще
пишут просто т. Это означает, что всякое натуральное число
можно представить в виде обыкновенной дроби со знамена-
телем 1. Запись — другой вариант записи mtn.
Среди обыкновенных дробей различают правильные и непра-
18
вильные дроби. Дробь ~ называется правильной, если ее чис-
литель меньше знаменателя, и неправильной, если ее числи-
тель больше знаменателя или равен ему.
Всякую неправильную дробь можно представить в виде
суммы натурального числа и правильной дроби (или в виде на-
турального числа, если дробь — такова, что m кратно п,
16 ”
например —=4).
Пример. Представить неправильную дробь в виде суммы
„ -t , 28 48
натурального числа и правильной дроби: а) —; б) —.
____ .28 25+3 25 . 3 - . 3
Решение, а) -=-_^=-+-=5+-;
43_39+4_39 .44
7 13 13 13 ’13 ° т 13-
Принято сумму натурального числа и правильной дроби
записывать без знака сложения, т. е. вместо 5-|—пишут
к 3 О I 4 о 4 „
5—, а вместо 3-|-^ пишут 3~. Число, записанное в таком
виде, называется смешанным числом. Оно состоит из двух час-
тей: целой и дробной. Так, для числа 3~ целая часть равна 3,
J.O
4
а дробная — -jg. Всякую неправильную дробь можно записать
в виде смешанного числа (или в виде натурального числа).
Верно и обратное: всякое смешанное или натуральное число
можно записать в виде неправильной дроби. Например, 4-|- ~
. . 1 12 ,1 13 о 3
=4+-3-=-3-+-3-=V 3=Т-
10. Равенство дробей. Основное свойство дроби. Сокращение
дробей. Две дроби -у и считаются равными, если ad=bc.
Например, равными будут дроби и (так как 3-15 = 5-9),
и (так как 12-14=7-24).
Из определения равенства дробей следует, что равными бу-
дут дроби и так как а (Ът)=Ъ (ат\— здесь мы использу-
ем сочетательное и переместительное свойства умножения на-
туральных чисел (см. п. 2). Значит, т. е. если числи-
тель и знаменатель данной дроби умножить или разделить на
одно и то же натуральное число, то получится дробь, равная
данной. Это свойство называется основным свойством дроби.
Пользуясь основным свойством дроби, иногда можно заме-
нить данную дробь другой, равной данной, но с меньшим
числителем и меньшим знаменателем. Такую замену называют
сокращением дроби. Например, (числитель и знамена-
тель мы разделили на одно и то же число 3); полу-
ченную дробь снова можно сократить, разделив числитель и
_ 15 3
знаменатель на 5, т. е. gg=-£-.
В общем случае сокращение дроби возможно, если числи-
тель и знаменатель не взаимно простые числа (см. п. 6); если
же числитель и знаменатель — взаимно простые числа, то
„ 3
дробь называется несократимой: например, —--несократимая
дробь. Основная цель сокращения дроби — замена данной дро-
би равной ей несократимой дробью.
11. Приведение дробей к общему знаменателю. Пусть даны
две дроби и -у. Они имеют разные знаменатели: 3 и 8, но,
воспользовавшись основным свойством дроби (см. п. 10), можно
заменить эти дроби другими, равными им, причем такими,
что у полученных дробей будут одинаковые знаменатели. Такое
преобразование называется приведением дробей к общему зна-
2
менателю. Умножив числитель и знаменатель дроби -д- на
8, получим умножив числитель и знаменатель дроби
15 „ 15-3 45 т. *2 15
— на 3, получим Итак, дроби и — приведены к
о о-о Z4 О о
общему знаменателю:
_2__16. 15 = 45
3 24 * 3 24 '
Заметим, что это не единственное решение поставленной за -
дачи. Например, дроби можно было привести к общему зна-
менателю 48:
2_2-15_32, 15_15-6_90
3 3-16-48: 8 8-6 “ 43’
и к общему знаменателю 72:
2 2-24 48. 15__15-9_135
3 ~3-24~72’ 88-972’
и вообще к любому знаменателю, делящемуся одновременно на
3 и на 8.
Таким образом, привести дроби к общему знаменателю
можно многими способами, ио обычно стараются привести
дроби к наименьшему общему знаменателю, который равен
наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю
_ 7 11
ДР°бИ 24 И 30-
Решение. Найдем наименьшее общее кратное чисел 24 и
30, т. е. К (24, 30)= 120 (см. и. 7). Имеем 120:24 = 6,
7
поэтому, чтобы привести дробь — к знаменателю 120, надо
ее числитель н знаменатель умножить на 5:
7 _ 7-5 _ 35
24“ 24-5 ” 120 ’
Имеем далее 120:30 = 4, поэтому, чтобы привести дробь
к знаменателю 120, надо ее числитель и знаменатель
умножить на 4:
11114 44
30 “30-4“ 120 '
Дроби приведены к общему знаменателю:
7 35 11 _ 44
24“ 120 * 30“ 120 '
Числа 5 и 4 называют дополнительными множителями
соответственно для первой и второй дроби. Используется сле-
дующая запись:
7 _ 7& _ 35 11 _11А'_ 44
24 “ 24 “ 120 ’ 30 “ 30 “ 120 ’
Итак, чтобы привести дроби к наименьшему общему знаме-
нателю, нужно:
1) найти наименьшее общее кратное знаменателей дробей;
2) вычислить дополнительные множители, разделив наи-
меньшее общее кратное на каждый знаменатель;
3) умножить числитель и знаменатель каждой дроби на
соответствующий дополнительный множитель.
12. Арифметические действия над обыкновенными дробями.
Сложение обыкновенных дробей выполняется так:
а) если знаменатели дробей одинаковы, то к числителю пер-
вой дроби прибавляют числитель второй дроби и оставляют
а . с а+с
тот же знаменатель, т. е. -уН—Г=“&~’
21
б) если знаменатели дробей различны, то дроби сначала
приводят к общему знаменателю, предпочтительнее к наимень-
шему, а затем применяют правило а).
Пример 1. Сложить дроби и
Решение. Имеем:
7 . 11 У5, ц4'_ 35 . 44 35 + 44 79
24 ' 30 24 т’ЗО 120 ' 120 — 120 — 120 ’
Вычитание обыкновенных дробей выполняют следующим
образом:
а) если знаменатели дробей одинаковы, то
° с а~с -
b Ь ~ ь *
б) если знаменатели различны, то сначала дроби приводят
к общему знаменателю, а затем применяют правило а).
Умножение обыкновенных дробей выполняют следующим
образом:
а с ас
b d bd*
t. е. перемножают отдельно числители, отдельно знаменатели,
первое произведение делают числителем, второе — знаменате-
лем.
тт 3 2 3-2 6
Например,
Деление обыкновенных дробей выполняют следующим об-
разом:
а . с _ad
Ь ' d be*
т. е. делимое ~ умножают на дробь -у, обратную делителю
TJ „ 2 7 2 10 2-10 20
Например, т:-=_._=_=- .
Пример 2. Найти значение числового выражения
4 12 .
9 ‘ 5 ‘Г’ 8 ' 6 30‘
Решение. 1) • Сократив числитель и зна-
менатель на 3 (это полезно сделать до выполнения действий
умножения в числителе и знаменателе), получим т. е.
-л
— Итак -4-.12 -16
15- Итак» 9 V-15*
22
2) 7 • 5 —7’6—7‘3— 21
'3*6 ~8-б“4-5~ 20*
л. „ 16 . 21 11 „
3) При нахождении значения выражения уд+тод—30 дей“
ствия сложения и вычитания можно выполнять одновременно.
Наименьшим общим кратным чисел 15, 20, 30 является чис-
ло 60. Приведем все три дроби к знаменателю 60, использо-
вав дополнительные множители: для первой дроби 4, для
второй — 3, для третьей — 2. Получим:
16^ . г!*3, ll'2'- 64 .63 22 64 + 63 — 22 105 7 _1 3
15 + 20 30 бОТ’бО 60 ~ 60 60 — 4 4 *
1 2
Пример 3. Выполнить действия: а) 2— 4-З-д-;
б) 14.24.
Решение, а) Первый способ. Обратим каждое из
данных смешанных чисел в неправильную дробь, а затем вы-
полним сложение:
2“2+4=^
15 . о 2 —о. 2 9 2 11
7 ’ й3 + 3 3 + 8 3
15 11— 15^ 11-Z- —45 77 _ 122
7'3 7 ' 3 — 21 ' 2|~ 21 *
Обратим теперь неправильную дробь в смешанное
число*
122 105+17—105 . 1?_ к г 17—Г$ 17
21 ~ 21 — 21 “г 21^°"' 21 ° 21*
Второй способ. Имеем 2-|- + 3-|-'=^24—7‘)+(з +
+4)=(2+3)+(43+D=s+(^+^)=5+^=5^.
б) В случае умножения и деления смешанных чисел всегда
переходят к неправильным дробям:
1 2 __ 7 . „ 1 _ 15
1Т—5’ “7“ У
_ - 2 о 1 7 15 7-15 Q
Значит, 1 б *2 ? — б • ? Б 7 3.
13. Десятичные дроби. В виде десятичной дроби можно
записать правильную дробь, знаменатель которой равен 10,
100, 1000 н вообще 10”. Например, -^=0,3; ^-=0,48;
23
21-——Q.Q21 Таким же образом можно записать смешанное
1О00
число или неправильную дробь с указанным выше знамена-
телем (превратив ее предварительно в смешанное число). Напри-
мер, 2-fj=2,3; у55‘=3БЙ>=3,17' В этих слУчаях целую часть
смешанного числа отделяют нанятой от числителя дробной
части. Таким образом, десятичная дробь — это, по существу,
другая форма записи дроби со знаменателем 10".
В виде десятичной дроби можно представить любую обыкно-
венную дробь, знаменатель которой является делителем не-
которой степени числа 10. Например, 4 — делитель числа 100,
поэтому дробь можно представить в виде десятичной дро-
3 3-25 75
би: loo"0,75; 125 — делитель числа 1000, поэтому
_ 196 „ 196
дробь можно представить в виде десятичной:
196-8 1568 л Кйо
==12^8=1О00=1’568-
Общий вывод о представлении обыкновенной дроби в виде
десятичной таков: если в разложении анамеиателя дроби иа
простые множители содержатся только двойки и пятерки,
то эту дробь можно записать в виде десятичной; если же дробь
несократима и в разложение ее знаменателя на простые мно-
жители входят, кроме двоек и пятерок, другие простые множи-
тели, то эту дробь нельзя записать в виде десятичной дроби.
Рассмотрим десятичную дробь 7,234. Имеем:
у 234 = 7 234 _I 200 + 30+4__ . 200 . 30 4
’ 1000_ 1000 “ т-1000 т- юоо 1000:
1 100^1000
Значит, в дроби 7,234 содержится 7 единиц, 2 десятых, 3 со-
тых и 4 тысячных. Вообще в десятичной дроби после за-
пятой может быть сколько угодно разрядов: десятые, сотые,
тысячные, десятитысячные и т. д.
Дробь 7,234 можно записать так:
7-234=7^=7-^=7S. но Ч^=7.2340,
а 7iS=7-23400-
Значит, 7,234=7,2340=7,23400. Таким образом, если к деся-
тичной дроби приписать справа нуль или несколько нулей,
то получится равная ей дробь. Если десятичная дробь окан-
2
10
чивается одним или несколькими нулями, то эти нули можно
отбросить — получится равная ей дробь.
Для десятичных дробей вводится понятие значащей цифры
числа. Значащими цифрами числа называют все его цифры,
кроме нулей, стоящих в начале. Например, в числе 23,4009
шесть значащих цифр; в числе 0,1023 четыре значащие циф-
ры: 1, О, 2, 3; в числе 0,0004 одна значащая цифра: 4.
14. Арифметические действия иад десятичными дробями.
При сложении десятичных дробей надо записать их одну под
другой так, чтобы одинаковые разряды были друг под другом, а
запятая — под запятой, и сложить дроби так, как складывают
натуральные числа. Сложим, например, дроби 12,7 и 3,442. Пер-
вая дробь содержит одну цифру после запятой, а вторая — три.
Чтобы выполнить сложение, преобразуем первую дробь так, что-
бы после запятой было три цифры: 12,7=12,700, тогда
.12,700
3,442
16,142
Аналогично выполняется вычитание десятичных дробей.
Найдем разность чисел 13,1 и 0,37:
13,10
0,37
12?73
При умножении десятичных дробей достаточно перемно-
жить заданные числа, не обращая внимания на запятые (как
натуральные числа), а затем в результате справа отделить
запятой столько цифр, сколько их стоит после запятой в обоих
множителях суммарно.
Например, умножим 2,7 на 1,3. Имеем 27-13 = 351. Запя-
той отделим справа две цифры (сумма цифр у множителей
после запятой равна двум). В итоге получаем 2,7-1,3 = 3,51.
Если в произведении получается меньше цифр, чем надо
отделить запятой, то впереди пишут недостающие нули, на-
пример:
v 2,12
0,13
636
212
0,2756
У 3’43
х0,0002
0,000686
Рассмотрим умножение десятичной дроби на 10, 100, 1000
и т. д. Пусть нужно умножить дробь 12,733 иа 10. Имеем
12 733-10=127 330. Отделив справа запятой три цифры, по-
лучим 12,733-10 = 127,330. Но 127,330 = 127,33. Значит,
12 733-10=127,33. Таким образом, умножение десятичной дро-
би* на Ю сводится к переносу запятой на одну цифру
вправо.
Вообще чтобы умножить десятичную дробь на 10, 100,
1000, надо в этой дроби перенести запятую на 1, 2, 3 цифры
вправо (приписав в случае необходимости к дроби справа
определенное число нулей). Например, 1,47-10 000 = 14 700.
Деление десятичной дроби на натуральное число выполня-
ется так же, как деление натурального числа на натураль-
ное, а запятую в частном ставят после того, как закончено
деление целой части. Пусть надо разделить 22,1 на 13:
22,1 [13
13 1,7
91
91
0
Если целая часть делимого меньше делителя, то в ответе
получается нуль целых, например:
0,221113
13 0,017
91
91
о
Рассмотрим теперь деление десятичной дроби на десятич-
ную. Пусть нужно разделить 2,576 на 1,12. Для этого и в
делимом, и в делителе перенесем запятую вправо на столько
цифр, сколько их имеется после запятой в делителе (в дан-
ном примере на две). Иными словами, умножим делимое
и делитель на 100 — от этого частное не изменится. Тогда
нужно разделить дробь 257,6 на натуральное число 112, т. е.
задача сводится к уже рассмотренному случаю:
257,61112
224 2^Г
ззб
336
о
Чтобы разделить десятичную дробь на 10я, надо в этой
дроби перенести запятую на п цифр влево (при этом в случае
необходимости слева приписывается нужное число нулей).
Например, 27,344:104 = 0,0027344.
Как для натуральных чисел деление ие всегда выполни-
мо, так оно не всегда выполнимо и для десятичных дробей.
Разделим для примера 2,8 на 0,09:
26
280 [9_
27 ЗТД1-
10
9
10
9
1..
В результате получается так называемая бесконечная деся-
тичная дробь. В таких случаях переходят к обыкновенным
дробям. Например:
2,8:0,09=
28. 9 28-100 280 1
10*100” 10-9 ” 9 ” dl 9 *
Может оказаться так, что одни числа записаны в виде
обыкновенных дробей, другие — в виде смешанных чисел, тре-
тьи — в виде десятичных дробей. При выполнении действий
над такими числами можно поступать по-разному: либо об-
ратить десятичные дроби в обыкновенные и применить пра-
вила действий над обыкновенными дробями, либо обратить
обыкновенные дроби и смешанные числа в десятичные дро-
би (если это возможно) и применить правила действий над
десятичными дробями.
15. Проценты. Среди десятичных дробей особенно часто
на практике используется дробь 0,01, которая называется про-
центом и обозначается 1%. Так 1 % = 0,01, 2% = 0,02, 45% =
= 0,45, 350% = 3,5 и т. д. В хозяйственных и статистических
расчетах, во многих отраслях науки части величин принято
выражать в процентах. Чтобы найти, например, 23% от
60 цг, нужно 60 кг умножить на 0,23, т. е. 60-0,23 = 13,8.
Значит, 23% от 60 кг составляют 13,8 кг.
Пример 1. Рабочий должен был изготовить за смену
80 деталей. По окончании рабочего дия оказалось, что он
выполнил 150% сменного задания. Сколько деталей изгото-
вил рабочий?
Решение. 1) 150% = 1,5.
2) 80-1,5=120.
Ответ: 120 деталей.
Пример 2. Рабочий должен изготовить за смену 80 де-
талей. К 12 часам он изготовил 55 деталей. Сколько про-
центов задания выполнил рабочий к указанному времени?
Решение. К 12 часам дня выполнена часть задания,
выражающаяся дробью — , которую переводим в проценты:
27
55__,550 _ 550 1 _275 0, _co 750/
80 =Soo=-8" ioo-T % - 68175 /о-
Ответ: 68,75%.
Пример 3. Рабочий к 12 часам изготовил 55 деталей,
что составило 68,75% сменного задания. Сколько деталей
рабочий должен изготовить за смену?
Решение. Обозначим количество деталей, составляющих
сменное задание, буквой х. Из условия задачи следует, что
68,75%•*= 55, т. е. что х — 55, откуда Х^^^^БО.
Ответ: 80 деталей.
16. Обращение обыкновенной дроби в бесконечную деся-
тичную периодическую дробь. Пусть дана десятичная дробь
2,73. Ее значение не изменится, если справа приписать лю-
бое число нулей (см. п. 13): 2,73=2,730 = 2,7300=...=
= 2,73,000...О. Допускают также запись дроби 2,73 в виде
П цифр
десятичной дроби с бесконечным множеством нулей, т. е.
2,73=2,73000... . Здесь после запятой содержится бесконечно
много десятичных знаков. Такая десятичная дробь называет-
ся бесконечной десятичной дробью.
Т.1.10. I Любую обыкновенную дробь можно представить в
| виде бесконечной десятичной дроби.
3
Возьмем, например, число — и будем делить числитель
на знаменатель, постепенно получая десятичные знаки. При
этом заметим, что любое натуральное число можно предста-
вить как бесконечную десятичную дробь, т. е. 3 = 3,0000... .
Имеем: 3,00000000... 114 _______
28 0,214285714...
20
14
60
56
40
28
120
112
_ 80
70
_100
98
20
14
60...
1ZXIJ 28
Таким образом, -^ = 0,214285714... .
Выпишем последовательно остатки, которые получились
при выполнении операции деления:
2, 6, 4, 12, 8, 10, 2, 6, ... .
Ясно, что все эти остатки меньше делителя, т. е. меньше
числа 14. Это значит, что на каком-то шаге деления должен
неизбежно появиться снова такой остаток, который уже встре-
чался ранее. Так, на седьмом шаге появился остаток 2, кото-
рый был на первом шаге. Кроме того, ясно, что, как только
появится остаток, который уже встречался, за ним пойдут
остатки в той же последовательности, которая была ранее.
В нашем примере за остатком 2 идет остаток 6, за ним 4,
за ним 12 и т. д., т. е. мы получаем такую последователь-
ность остатков:
2, 6, 4, 12, 8, 10, 2, 6, 4, 12, 8, 10, ... .
Периодически повторяющиеся группы остатков приведут
соответственно к периодически повторяющейся группе цифр
в десятичной записи числа. Так, в нашем примере получим:
£ = 0,2142857142857142857... .
14
Последовательно повторяющаяся группа цифр (минимальная)
после запятой в десятичной записи числа называется периодом,
а бесконечная десятичная дробь, имеющая такой период в своей
записи, называется периодической. Для краткости принято
период записывать один раз, заключая его в круглые скобки:
0,2142857142857142857... = 0,2 (142857).
Если период начинается сразу после запятой, то дробь назы-
вается чистой периодической; если же между запятой и перио-
дом есть другие десятичные знаки, то дробь называется
смешанной периодической. Так, 2,(23)=2,2323232323...— чис-
тая периодическая дробь; 0,2 (142857) — смешанная периоди-
ческая дробь; 2,73 = 2,73000... —2,73 (0) — смешанная периоди-
ческая дробь.
17*. Обращение бесконечной десятичной периодической
дроби в обыкновенную дробь.
Чтобы бесконечную десятичную дробь умножить на 10,
100, 1000 и т. д., достаточно, как и в конечной десятичной
дроби, перенести запятую на один, два, три и т. д. знака
вправо.
Например, 0,1 (23). 100=0,1232323...-100=12,323232...=
= 12, (32).
Обращение периодической десятичной дроби в обыкновен-
ную рассмотрим на примерах.
Пример. Обратить в обыкновенную дробь число: а) 0,(13);
б) 2, (273); в) 0,2 (54); г) 3,254 (9).
Решение, а) Положим х=0, (13)=0,131313... . Умно-
жим чистую периодическую дробь х на такое число, чтобы
запятая переместилась ровно на период вправо. Поскольку
в периоде две цифры, надо перенести запятую на две цифры
вправо, а для этого достаточно умножить число х на 100,
тогда 100х =0,131313...-100 = 13,1313... = 13, (13). Теперь выч-
тем X из 100х, получим 100х—х=13, (13)—0, (13). Значит,
99х = 13, откуда находим
б) Положим х=2, (273). Эта чистая периодическая дробь
содержит три цифры в периоде. Умножив х иа 1000, получим
1000х = 2273, (273).
Далее имеем:
1000*—х=2273, (273)— 2, (273); 999х = 2271,
2271 757 91
Х 999 ЗЗЗ-Z333‘
в) Положим х=0,2 (54). Перенесем в этой смешанной пери-
одической дроби запятую вправо так, чтобы получилась
чистая периодическая дробь. Для этого достаточно х умножить
на 10, получим 10х=2, (54).
Положим у — 2, (54) и обратим эту чистую периодическую
дробь в обыкновенную так, как мы это делали в предыдущих
примерах.
Имеем у — 2, (54), откуда 100у = 254, (54);
100у-у = 254, (54)-2, (54); 99у = 252; у=^=^_ Зна-
чит, 10х=-|2, откуда находим x = ij7jo=^|-
г) Полагая х = 3,254 (9), получим 1000х = 3254, (9). Вве-
дем обозначение у = 1000г. Тогда имеем:
у=3254, (9), откуда 10у = 32 549, (9);
10у — у = 32 549, (9)—3254, (9); 9у=29 295; у = 3255;
1000х = 3255; х=^=3^.
Заметим, что 3,255 = 3,255 (0), т. е. мы получили ко-
нечную десятичную дробь, или бесконечную дробь с нулем в
периоде. Значит, 3,254 (9) =3,255 (0). Это обстоятельство имеет
30
место для любых десятичных дробей с девяткой в периоде:
такую дробь можно представить в виде дроби с нулем в пе-
риоде. Для этого достаточно лишь увеличить на единицу по-
следний десятичный знак перед периодом. Например, 0,45 (9)=
/ =0,46 (0); 14, (9)=15, (0) и т. д.
У 18. Координатная прямая. Проведем прямую Z, отметим на
ней точку О, которую примем за начало отсчета, выберем
направление и единичный отрезок [0; 1] (рис. 1).
В этом случае говорят, что задана координатная прямая.
Каждому натуральному числу или дроби соответствует одна
точка прямой I. Пусть, например, дано число 3. Отложим от
точки О в заданном направлении единичный отрезок три ра-
за, получим точку А — эта точка и соответствует числу 3.
Возьмем число 4—. Отложим от точки О в заданном направ-
лении единичный отрезок четыре раза, а затем еще -у- часть
• J
отрезка, получим точку В —• она и соответствует числу 4—.
Если точка 2W прямой I соответствует некоторому числу г, то
это число называется координатой точки, в таком случае
пишут Л/(г). Так, для точек J, А, В (рис. 1) можно указать
их координаты J (1), Л (3), В ^4-^-). Координатой точки О
считается число нуль.
Отложим теперь три раза единичный отрезок от точки О
в направлении, противоположном заданному. Получим точку
А', симметричную точке А относительно начала отсчета О.
Координатой точки А является число 3, а координату точ-
ки А* записывают так: —3— и читают: «Минус 3». Ана-
логично координатой точки В', симметричной точке В, на
рисунке 1 считается число —Числа 3 и —3, 4~ и — 4~
называют противоположными. Числа, которым соответству-
ют точки, расположенные на координатной прямой в задан-
ном направлении, называют положительными; так, 1, 3,
4—— положительные числа. Положительные числа пишут
Г?)
в А 0 J А в
-3 0 1 3
иногда со знаком «плюс»: +1, +3, + 4-^. Числа, которым со-
ответствуют точки, расположенные на координатной прямой в
направлении, противоположном заданному, называют от-
рицателъпыми-, так, —3, -4-1-— отрицательные числа. Чис-
ло О ие считается ни положительным, ни отрицательным;
точка О, соответствующая числу О, отделяет на координат-
ной прямой точки с положительными координатами от точек
с отрицательными координатами.
Заданное направление на координатной прямой называют
положительным (обычно оно идет вправо), а направление,
противоположное заданному,— отрицательным.
19. Множество рациональных чисел. Натуральные числа
1, 2, 3, 4, 5 ... называют также положительными целыми
числами. Числа —1, —2, —3, —4, —5, ..., противополож-
ные натуральным, называют отрицательными целыми числами.
Число О также считают целым числом. Итак, целые числа —
это натуральные числа, числа, противоположные натуральным,
и число О.
Целые числа и дроби (положительные и отрицательные)
составляют вместе множество рациональных чисел.
Заметим, что любое рациональное число может быть пред-
m
ставлено в виде отношения —, где тп — целое число, ал —
натуральное число, причем одно и то же число можно запи-
сать в виде отношения многими способами. Например:
2— — 4 — ’6 — ~100 . л о_ 3 _ 6 _ 300
2 3 50 * * ~10“20— 1000 *
Среди дробей, обозначающих данное рациональное число,
имеется одна и только одна несократимая дробь. Для целых
чисел — это дробь со знаменателем 1.
§ 3. Действительные числа
20. Иррациональные числа. Для измерения используются
не только рациональные числа, но и числа иной природы,
т. е. не являющиеся целыми или дробными. Все такие числа
называются иррациональными. Например, длина диагонали
квадрата со стороной 1 (рис. 2,а) должна выражаться некото-
рым положительным числом г, таким, что г~ —12-{-12 (по
теореме Пифагора, см. с. 281), т. е. таким, что' г2—2. Число г
ие может быть целым, так как 12=1; 22=4; 32=9 и т. д. Чис-
ло г не может быть и дробным: если г=-^ — несократимая
где п2^1; значит, не является целым числом, а потому
не может равняться 2. Поэтому длина диагонали квадрата
выражается иррациональным числом, оно обозначается -\/2
(читается: «Квадратный корень из двух»). На рисунке 2, б
изображена координатная прямая I, OABJ — квадрат, ОС—
=OB=OD. Тогда координатой точки С является число д/2,
а координатой точки D — число —-\/2. Обе точки С и D имеют
иррациональные координаты.
Аналогично не существует рационального числа, квадрат
которого равен 5, 7, 10. Соответствующие иррациональные
числа обозначаются д/б, д/7, д/10. Противоположные им числа
также иррациональны, они обозначаются — д/5, —\/7, —д/10.
Следует подчеркнуть, что к иррациональным числам при-
водит не только задача отыскания числа, квадрат которого
равен заданному положительному числу. Например, чис-
ло л, выражающее отношение длины окружности к диаметру,
нельзя представить в виде обыкновенной дроби — это ирраци-
ональное число.
Так как любое рациональное число можно записать в виде
бесконечной десятичной периодической дроби (см. п. 16) и в
свою очередь любая бесконечная десятичная периодическая
дробь представляет собой рациональное число (см. п. 17), то
каждое иррациональное число можно записать в виде беско-
нечной десятичной непериодической дроби н в свою очередь
любая бесконечная десятичная непериодическая дробь есть ир-
рациональное число.
21. Действительные числа. Числовая прямая. Рациональные
и иррациональные числа составляют вместе множество действи-
тельных чисел. Каждому действительному числу соответствует
единственная точка координатной прямой. Каждая точка коор-
динатной прямой соответствует единственному действительно-
33
му числу (достаточно найти расстояние до этой точки от нача-
ла отсчета и поставить перед найденным числом знак + или —
в зависимости от того, справа или слева от начала отсчета на-
ходится заданная точка). Для краткости обычно вместо фра-
зы «точка координатной прямой, соответствующая действи-
тельному числу а», пишут и говорят «точка а», а употреб-
ляя термин «число п», имеют в виду «действительное число а».
Множество действительных чисел называют также число-
вой прямой. Геометрической моделью числовой прямой служит
координатная прямая.
22. Обозначения некоторых числовых множеств.
А — множество натуральных чисел.
Z — множество целых чисел.
Q — множество рациональных чисел.
R — множество действительных чисел.
Запись n^N (читается: «п принадлежит множеству А»)
обозначает, что п — натуральное число. Аналогичный смысл
имеют следующие обозначения: mfzZ (т—-целое число);
(г — рациональное число); x(R (х — действительное чис-
ло).
23. Сравнение действительных чисел. Для любых нерав-
ных действительных чисел а и Ъ можно сказать, какое боль-
ше, а какое меньше.
Говорят, что число а больше числа Ь, и пишут: а>Ъ, если
разность а—Ъ — положительное число; если же разность
а — Ь — отрицательное число, то говорят, что число а меньше
числа Ь, и пишут: а<Ь. Согласно этому определению любое
положительное число больше нуля, любое отрицательное
число меньше нуля и меньше любого положительного числа.
Для любых заданных чисел а и Ь верно одно и только одно
из отношений: а > Ь, а <С Ъ, а — Ь.
С геометрической точки зрения неравенство a<Zb (а>Ь)
означает, что точка а расположена на координатной прямой
левее (правее) точки Ь.
Знаки <, > называются знаками строгих неравенств.
Иногда используются знаки — знаки нестрогих не-
равенств; запись а^Ъ означает, что верно одно из двух:
или число а меньше числа Ь, или число а равно числу Ь.
Например, 3<Z5, 5^5—верные неравенства. Неравенства
а>Ъ и c>d называются неравенствами одного знака;
неравенства а> Ь и c<d называются неравенствами противо-
положных знаков. Если числа а, Ь, с таковы, что а <_ Ь и b <Z с, то
используется запись а<_Ь<с.
Пример. Сравнить числа и 0,67.
2 Заказ 769
34
2
Решение. Составим разность —— 0,67 и найдем зна-
чение этой разности:
2__- fi7 ____67 2-100-67-3_____1
3 и,ъ‘ — 3 100 300 300'
Разность отрицательна, поэтому -~-<0,67.
24. Свойства числовых неравенств. Для любых действитель-
ных чисел й, b, с, d выполняются следующие свойства:
1". Если а>Ъ, то Ь<а.
2°. Если а>Ь и Ь>с, то а>с (свойство транзитивности).
3е. Если а>Ь, то a-t-c>b-\-c.
4°. Если а>Ь и с — положительное число (с>0), то
ас>6с. Это свойство имеет следующий смысл: если обе части
верного неравенства умножить на одно и то же положитель-
ное число, то получится верное неравенство.
Доказательство. Рассмотрим разность ас—be. Имеем ас—Ъс=
—с (а —Ь). По условию с — положительное число, а так как а> Ь, то и
а— Ь — положительное число. Но произведение двух положительных чисел
есть положительное число, значит, с (а—Ь)>-0. Таким образом, ас—Ьс>0.
Но если разность ас—Ьс — положительное число, то ctO-bc.
5П. Если а>Ъ и с — отрицательное число (с<О), то
ac<Zbc. Это свойство имеет следующий смысл: если обе части
верного неравенства умножить на одно и то же отрицатель-
ное число и изменить знак исходного неравенства на проти-
воположный, то получится верное неравенство.
6°. Если а>Ь и О&, то a+obj-d (если почленно сло-
жить два верных неравенства одного знака, то получится
верное неравенство).
7°. Ес ли а, Ъ, с, А — положительные числа, причем а>Ь
и О А, то ac>bd (если почленно перемножить верные
неравенства одного знака левые и правые части которых поло-
жительные числа, то получится верное неравенство).
Доказательство. Так как а>Ъ и с>0. то по свойству 4и ооЬе;
аналогично изt>d и Ь>0 следует bc>bd. Так как далее aObc и bc~>bd,
то по свойству 2е ec> bd.
8°. Если а>Ь и с<А, то а—с>Ь—А.
9°. Если а>Ь>О, то —
а Ь
10°. Если а>Ь>0, то для любого натурального числа п
выполняется неравенство а!!>Ьп.
35 IzTzJ
25. Числовые промежутки. Возьмем два числа а и Ь, такие,
что a<Zb, и отметим на координатной прямой соответствующие
им точки.
Произвольная точка х, лежащая между с и о, соответству-
ет числу, которое удовлетворяет неравенствам а<х<&. Мно-
жество всех чисел х, удовлетворяющих этим неравенствам, обо-
значают (а; Ь) и называют интервалом.
Множество всех чисел х, каждое из которых удовлетворяет
неравенствамобозначают [о; Ь] и называют отрезком.
Интервал и отрезок — это конечные числовые промежутки.
Конечные числовые промежутки бывают еще двух видов:
[а; Ь) — это множество чисел х, удовлетворяющих неравенствам
а^х<Ь,и(а; 6] — это множество чисел х, удовлетворяющих
неравенствам Эти промежутки называют полуинтер-
валами.
Бывают и бесконечные числовые промежутки. Множество
всех чисел х, удовлетворяющих неравенству х а, обозначают
[а; 4- оо) и называют лучом, а множество всех чисел х, удовлет-
воряющих неравенству х>а, обозначают (а; 4- оо) и называют
открытым лучом. Знак «4- оо» читается: «Плюс бесконеч-
ность».
Аналогично может быть луч вида (— оо; Ь| (числа, удовлет-
воряющие неравенству х^Ь) и открытый луч вида (— оо; Ь)
(числа, удовлетворяющие неравенству х < Ь). Знак « — оо » чита-
ется: «Минус бесконечность».
В приведенной ниже таблице для каждого вида числового
промежутка даны его геометрическое изображение, обозначение
и запись с помощью неравенств.
Вид промежутка Геометрическое изображение Обозна- чение Запись с помощью неравенств
Интервал а b (а; Ь) а<х<Ь
Отрезок !/////////'. а Ъ [а; »]
Полуинтервал _-&///////,, , а Ъ ) о («; Ч , V
Полуинтервал а b [а! Ь) с^х<6
36
Вид промежутка Геометрическое изображение Обозна- чение Запись С помощью неравенств
Луч ?////////////£ и [о; + оо) х^в
Луч '/////////////. х Ь (-»; Ц х<Ь
Открытый луч а (в; -Ьоо) х>а
Открытый луч (—оо; 6) х<Ь
На практике не всегда используют термины «интервал»,
«отрезок», «полуинтервал», «луч», заменяя их общим назва-
нием «числовой промежуток».
26. Модуль действительного числа. Модулем (абсолютной
величиной) действительного числа а называется само это число,
если а^О, и противоположное число —п, если с-С О. Мо-
дуль числа а обозначается |а|. Итак,
|а|= f а* если
1 —а, если а<0.
Например, |л—3| =л—3, так как л — 3>0 (л=3,14...);
| — 3,7| = —(— 3,7)= 3,7, так как —3,7 <0.
Геометрически |п| означает расстояние на координатной
прямой точки а от точки О (рис. 3).
Свойства модулей:
Iе. |а|>0.
2°. |о| = |-а|,
3°. |аЫ = |а|.|Ы.
Ь*°-
5°. |а!2=а2.
27. Формула расстояния между двумя точками коорди-
натной прямой. Если а и Ь — две точки координатной прямой,
то расстояние между ними р («; Ь) выражается формулой
р(а; &)=|с —Ь| (рис. 4). Ясно, что р(«; b)=p(fc: а). Так,
р(-2; 5)= I —2—5| = | —7| = —(—7)=7.
Пример. Найти все такие точки х, которые удовлетво-
ряют: а) уравнению (х —11=3; б) неравенству |х+И^2.
Решение, а) Уравнению удовлетворяют такие точки х,
расстояние которых от точки 1 равно 3. Это точки —2 и 4
(рис. 5). Значит, уравнение имеет два корня: —2; 4.
б) Неравенству удовлетворяют такие точки х, которые
удалены от точки —1 на расстояние, меньшее или равное 2.
Это точки из отрезка [—3; 1] (рис. 6).
28. Правила действий над действительными числами.
Сумма двух чисел одного знака есть число того же знака;
чтобы найти модуль такой суммы, надо сложить модули сла-
гаемых. Например, (+12)+(+8)= +20; (—12)+(—8)=—20.
Сумма двух чисел с разными знаками есть число, которое
имеет тот же знак, что и слагаемое с большим модулем; чтобы
иайти модуль этой суммы, надо из большего модуля вычесть
меньший. Например, (+12)+(—8)=+(12—8)=4; (—12)+
+(+8)=-(12-8)=-4.
Чтобы из одного числа вычесть другое, надо к уменьшае-
мому прибавить число, противоположное вычитаемому. На-
пример, 12-(—8)=12+8 = 20; 12-(+8)=12+(-8)=4.
Произведение (частное) двух чисел одного знака есть чис-
ло положительное, а произведение (частное) двух чисел раз-
ных знаков есть число отрицательное; чтобы найти модуль
произведения (частного), надо перемножить (разделить) моду-
ли данных чисел. Например, (—12) (—8) = +12 ♦ 8 — 96;
(_24):(+3)=-^ = -8.
29. Свойства арифметических действий над действитель-
ными числами.
1°. а-|-Ь = Ь+а.
2°. (а-гЬ)+с — а+(Ь+с).
3°. а + О^а.
4°. а+(—а)=0.
5°. а.&=Ьа.
6°. (аЪ)с==а(Ъс).
а(Ь-\-с)=аЬ+ас.
8°. о-1-с.
9°. а — =1, аАО.
а
Эти свойства называют иногда основными законами ал-
гебры, причем свойства 1° и 5° выражают переместительный
закон соответственно слежения и умножения, свойства 2° и
6° — сочетательный закон, а свойство 7° — распределитель-
ный закон умножения относительно сложения.
Из этих свойств выводятся другие свойства. Например,
а-0=0. В самом деле, имеем:
а>0—а (&+( — b))=ab-\~a(—b)=ab+(—ab)==Q.
30. Пропорция. Пусть о, Ь, с, d — действительные числа,
отличные от 0, и пусть имеет место равенство a‘.b=czd.
Это равенство называют пропорцией, числа а и d — край-
ними членами, а числа b и с — средними членами пропорции,
тг ас.
Для пропорции можно использовать и запись
Например, можно составить пропорцию из чисел 2,5; —4;
Справедливы следующие утверждения:
Т.1.11. I Произведение крайних членов пропорции равно про-
изведению ее средних членов.
Т 1 12 I КРа**ние члены пропорции можно поменять места-
° • । а с d с
ми, т. е. если -г-=-г, то —=—.
Ь . а b а
Т.1.13. I Средние члены пропорции можно поменять места-
а с а b
ми, т. е. если то —.
1 о а с а
39
31. Целая часть числа. Дробная часть числа. Пусть х —
действительное число. Его целой частью называется наиболь-
шее целое число, не превосходящее х; целая часть числа х
обозначается [х]. Дробной частью числа х называется раз-
ность между числом и его целой частью, т. е. х — [х]; дробная
часть числа обозначается {х}. Значит,
И=х—[х].
Например, [2,35]—2, а {2,35}—0,35;
[10]= 10, а (10)= 0;
[—0,85]=—!, а (—0,85}= —0,85-( —1) = 0,15.
32. Степень с натуральным показателем. Выше (см. п. 5)
определено понятие степени натурального числа с натураль-
ным показателем. Теперь обобщим это определение для лю-
бого действительного основания степени. Пусть а — действи-
тельное число, ап — натуральное число, большее единицы,
п-й степенью числа а называют произведение п множителей,
каждый из которых равен а, т. е. с"=д-а - Если п = 1, то
п множителей
полагают а'=а. Число а — основание степени, п — показа-
тель степени.
Например, 31 '
Справедливы следующие свойства степени с натуральным
показателем:
Г. an.ak = an+k.
2°. an:ak=an~\ если n>k.
3°. (an)k=ank.
4?. an-bn~(ab'f.
5°- £=(т)“’ 6*0'
Например, 23-25=23+5=28; (23)5=23 5=215;
= 125‘
33. Степень с нулевым показателем. Степень с отрица-
тельным целым показателем. Полагают по определению:
если а^0, то а° = 1. Например, (2,7)° =1; (—5)%=1. Нулевая
степень числа 0 не имеет смысла. г v
Полагают по определению: если а^=0 и п — натуральное
число, то
Например, 5 3=-^-=—— ; (—2} 2———- =-^-.
F F 53 125 (-2? 4
Справедливо равенство
(1ГЧ4)-
34. Стандартный вид положительного действительного
числа. Любое положительное число а можно представить в
виде ci-lO", где ап — целое число.
Пример 1. Пусть а = 395, тогда а = 3,95-102; здесь а\ —
= 3,95 и и=2.
Пример 2. Пусть а = 4,13, тогда а = 4,13 • 10°; здесь а i=
=4,13 и п~0.
Пример 3. Пусть а=0,0023, тогда а=2,3-10-3; здесь
а । = 2,3, п = — 3.
Если положительное число а представлено в виде я, 10”,
где l^Ci<10, п — целое число, то говорят, что число а за-
писано в стандартном виде; показатель п называют при этом
порядком числа.
Для того чтобы положительное число а представить в стан-
дартном виде, нужно поставить запятую так, чтобы в целой
части оказалась одна значащая цифра (см. п. 13), и умно-
жить полученное число на 10" так, чтобы в результате умно-
жения запятая вернулась на то место, которое она занимала
в числе а. Так мы действовали в примерах 1, 2, 3.
В примере 1, отделив в числе 395 первую значащую циф-
ру, получили 3,95; чтобы вернуться к исходному числу, надо
запятую передвинуть на две цифры вправо — это равносиль-
но умножению на 102. Значит, 395 = 3,95 • 10s.
В примере 2 уже отделена запятой одна значащая цифра,
поэтому 4,13 = 4,13 -10°.
В примере 3, отделив запятой в числе 0,0023 первую зна-
чащую цифру, получили 2,3; чтобы вернуться к исходному
числу, надо запятую передвинуть на три цифры влево —
это равносильно делению на 103 или умножению на 10“3.
Значит, 0,0023 = 2,3-10 3.
35. Определение арифметического корня. Свойства арифме-
тических корней. Если а^0 и п — натуральное число,
большее 1, то существует, и только одно, неотрицательное
число х, такое, что выполняется равенство хп—а. Это число х
называется арифметическим корнем п-я степени из неотрица-
тельного числа а и обозначается *\[а. Число а называется
подкоренным числом, п — показателем корня. Если п = 2, то
обычно пишут -\/а (опуская показатель корня) и называют
41
ЭТО выражение квадратным корнем. Часто вместо термина
•кооень» употребляют термин «радикал».
Итак, согласно определению запись -^а — х, где озна-
чает, во-первых, что х>0 и, во-вторых, что х =а. т. е.
Например, д/49 = 7, ^/125—'^/О — О.
Если а>0 и Ь>0, то справедливы следующие свойства:
Г. ^Л=^а^Ь.
2». t/Z=5£, ь^о.
v а Ч/а
3°.
4°. д^5="Ш
5°.
Свойство 1° распространяется на произведение любого
числа миожителей. Например, ^/8-327-"125=^8* А/27*д/125=
=2-3-5 = 30. 5 ,---
Пример. Упростить: а) у 7-Ц; б) (^/о5)3; в> пДЙ; г) Sja*.
б) (^)3=\₽p=W;
в) ^/^й=4дДв=1^;
г) (показатели корня и подкоренного выражения
разделили на 2).
36. Корень мечетной степени из отрицательного числа.
Пусть а<С0, а п — натуральное число, большее 1. Если п —
четное число, то равенство хп = а не выполняется ни при ка-
ком действительном значении х. Это значит, что в области
действительных чисел нельзя определить корень четной сте-
пени из отрицательного числа. Если же п — нечетное число,
то существует одно и только одно действительное число х,
такое, что х"=а. Это число обозначают дй и называют кор-
нем нечетной степени п из отрицательного числа а.
Например, V—8= — 2, так как ( —2)3=—8; V-243=— 3,
так как (—3)5=—243.
В случае нечетных показателей корней свойства радика-
лов, справедливые для неотрицательных значении подкорен-
ных выражений (п. 35), верны и для отрицательных значе-
ний подкоренных выражений.
Например, ^/аЬ=уа^Ь для любых а и Ъ.
37. Степень с дробным показателем. Полагают по опре-
делению: если «>0 и т, п — натуральные числа, п^2, то
если с>0, то
Нецелая степень отрицательного числа не имеет смысла.
2 Л —2
Пример. Вычислить 8 3,81 4, 4 2.
Решение. 8 3=V8=2;
_з ____
81 4=^81?=изУ=А/8Т?=33=27;
38. Свойства степеней с рациональными показателями.
Для любого числа а определена операция возведения в на-
туральную степень (см. п. 32); для любого числа а =£0 опре-
делена операция возведения в нулевую и целую отрицательную
степень (см. п. 33); для любого а^О определена операция
возведения в положительную дробную степень (см. п. 37),
и, наконец, для любого а>0 определена операция возведе-
ния в отрицательную дробную степень (см. п. 37).
Пример. Вычислить (6,25)°5 —( — 4)"1 -(0,343)°.
Решение. (6,25)-&Г=(^=
=Vi=4: (-4)“'=4-4=-4-: (0.343)»=1.
В итм'е получаем:
(6,25)- .(i)°26 -( - 4)~' •(0,343)»=44-( --$ • 1 = 1,5.
Если а>0, Ь>0 и г, s— любые рациональные числа, то:
1°. a'-as=a'+s.
2°. ar‘.as~ar \
3е. (аУ=а'\
4°. аг Ьг=(аЬ)'.
’•Нт)'-
39. Приближенные значения чисел. Абсолютная и отно-
сительная погрешности. При округлении десятичной дроби
до какого-нибудь разряда все следующие за этим разрядом
цифры заменяют нулями, а если они стоят после запятой,
«го их отбрасывают. Если первая следующая за этим раз-
рядом цифра больше или равна пяти, то последнюю остав-
шуюся цифру увеличивают на 1. Если же первая следующая
за этим разрядом цифра меньше 5, то последнюю оставшуюся
цифру не изменяют.
Пример 1. Округлить число « = 2471,05624 с точностью
до: а) десятков; б) единиц; в) десятых; г) сотых; д) тысячных.
Решение, а) Цифра единиц, следующая за разрядом
десятков, равна 1, т. е. меньше 5. Значит, округлив до десят-
ков, имеем а «2470. Знак « называют знаком приближен-
ного равенства.
б) Цифра десятых равна 0, значит, округлив до единиц,
имеем ««2471.
в) Цифра сотых равна 5, значит, округлив до десятых,
имеем а «2471,1.
г) Цифра тысячных равна 6, значит, округлив до сотых,
имеем а «2471,06.
д) Цифра десятитысячных равна 2, значит, округлив до
тысячных, имеем а=2471,056.
Все найденные значения называются приближенными зна-
чениями числа «=2471,05624.
Приближенные значения появляются не только при округ-
лении чисел. Чаще они возникают при различных измере-
ниях (длин, масс, температур и т. д.). При этом зажно знать,
с какой точностью выполнено измерение.
Пусть а — приближенное значение числа «. Тогда модуль
разности чисел а и а, т. е. |а—а|, называется абсолютной
погрешностью приближенного значения числа а, а отноше-
ние абсолютной погрешности к модулю приближенного зна-
чения называется относительной погрешностью приближен-
ного значения. Относительную погрешность обычно выражают
в процентах.
Пример 2. Взвесив деталь, масса которой равна
54,12705 г, на весах с ценой деления шкалы 0,1 г, полу-
чили приближенное значение массы 54,1 г. Найти абсолют-
ную и относительную погрешности этого приближенного
значения.
Решение. Абсолютная погрешность равна 54,12705 —
— 54,1 = 0,02705.
Относительная погрешность равна °’°^71<15 -100% = 0,05%,
При намерениях, как правило, точные значения величин
44
бывают неизвестны, поэтому важны сведения об абсолютных
погрешностях приближенных значений. Если, например, де-
таль массы т взвесили на весах с ценой деления шкалы 0,1 г,
то это значит, что абсолютная погрешность измерения будет
не более 0,1 г. Так, если, взвесив деталь, получили 54,1 г, то
точное значение массы т может отклоняться от 54,1 в ту
нли иную сторону не более чем на 0,1, т. е. 54,1—0,1
С 54,1+ 0,1. Короче это записывают так; ш = 54,1 ±0,1.
Вообще если абсолютная погрешность приближенного зна-
чения а, найденного для интересующего нас числа <х, не пре-
восходит некоторого числа h, то пишут a=o±fc; говорят,
что а — приближенное значение числа а с точностью до h.
Пример 3. Найти приближенное значение числа
«=2471,05624 с точностью до 0,01.
Решение. Округлив число а до сотых, получим (см.
пример 1, г) а — 2471,06.
Абсолютная погрешность этого приближенного значения
равна 12471,05624 —2471,061 =0,00376 <0,01. Значит,
2471,06—приближенное значение числа а с точностью
до 0,01.
В математических таблицах обычно даются приближен-
ные значения величин. При этом считают, что абсолютная
погрешность не превосходит половины единицы последнего
разряда. Например, найдя по таблице для числа -у'2 значение
1,4142, мы должны понимать, что это — приближенное зна-
чение с точностью до 0,0001, т. е. что его абсолютная погреш-
ность не превосходит 0,00005:
^2 = 1,4142 ± 0.00005.
40. Десятичные приближения действительного числа но
недостатку и по избытку. Возьмем иррациональное число \2.
Имёем:
Г<2<22
1,42<2<1,5г
1,4Г<2<1,42г
1,4142<2<1,4152
1.41422 <2<1,41432
1<V2<2
1,4 <2 <1,5
1,41 <У§< 1,42
1,414 <д/2< 1,415
1,4142 <V2< 1,4143
Числа 1; 1,4; 1,41; 1,414; 1,4142 называются десятичными
приближениями числа \2 по недостатку с точностью соответ-
ственно до 1, до 0,1, до 0,01, до 0,001, до 0,0001. Числа 2;
1,5; 1,42; 1,415; 1,4143 называются десятичными приближе-
ниями числа \2 по избытку соответственно с той же точ-
ностью. _
Для числа у/2 используют представление в виде бесконеч-
ной десятичной дроби; -\/2 = 1,4142... . Вообще любое действа-
45
тельное число представимо в виде бесконечной десятичной
дроби, причем периодической, если число рациональное (см.
п 16),и непериодической, если число иррациональное.
Например, =0,2 (54)=0,2545454... (см. п. 17). Десятин-
14
ное приближение числа — с точностью до 0,001 по недостатку
равно 0,254, а по избытку равно 0,255.
Число л имеет вид л = 3,1415926... . Десятичное прибли-
жение числа л с точностью до 0,0001 по недостатку равно
3,1415, а по избытку —3,1416.
41*. Правило извлечения квадратного корня из натураль-
ного числа. Пусть нужно извлечь квадратным корень из на-
турального числа пг, причем известно, что корень извлека-
ется. Чтобы найти результат, иногда удобно воспользоваться
следующим правилом.
1. Разобьем число пг на грани (справа налево, начиная с
последней цифры), включив в каждую грань по две рядом
стоящие цифры. При этом следует учесть, что если пг состоит
из четного числа цифр, то в первой (слева) грани будет две
цифры; если же число пг состоит из нечетного числа цифр,
то первая грань состоит из одной цифры. Количество граней
показывает количество цифр результата.
2. Подбираем наибольшую цифру, такую, что ее квадрат
не превосходит числа, находящегося в первой грани; эта циф-
ра — первая цифра результата.
3. Возведем первую цифру результата в квадрат, вычтем
полученное число из первой грани, припишем к найденной
разности справа вторую грань. Получится некоторое число А.
Удвоив имеющуюся часть результата, получим число а. Те-
перь подберем_ та кую наибольшую цифру х, чтобы произве-
дение числа ах на х не превосходило числа А. Цифра х —
вторая цифра результата. __
4. Произведение числа ах на х вычтем из числа А, при-
пишем к найденной разности справа третью грань, получится
некоторое число В. Удвоив имеющуюся часть результата,
получим число Ь. Теперь подберем такую наибольшую циф-
ру У, чтобы произведение числа by на у не превосходило чис-
ла В. Цифра у — третья цифра результата.
Следующий шаг правила повторяет 4-й шаг. Это продол-
жается до тех пор, пока не используется последняя грань.
Пример 1. Вычислить -^138384.
Решение. Разобьем число на грани; 13'83'84— их три,
значит, в результате должно получиться трехзначное число.
Первая цифра результата 3, так как 32<13, тогда как
46
422>13. Вычтя 9 из 13, получим 4. Приписав к 4 следующую
грань, получим А =483. Удвоив имеющуюся часть резуль-
тата, т. е. число 3, получим а=6. Подберем теперь такую
наибольшую цифру х, чтобы произведение двузначного чис-
ла ах на х было меньше числа 483. Такой цифрой будет 7,
так как 67-7=469— это меньше 483, тогда как 68-8=544—
это больше 483. Итак, вторая цифра результата 7,
Вычтя 469 из 483, получим 14. Приписав к этому числу
справа последнюю грань, получим 6 = 1484. Удвоив имеющую-
ся часть результата, т. е. число 37, получим В=74. Подбе-
рем теперь такую наибольшую цифру у, чтобы произведение
трехзначного числа by на у не превосходило 1484. Такой циф-
рой будет 2, так как 742-2=1484. Цифра 2— последняя циф-
ра результата. В ответе получили 372.
_V13/83,84 = 372
9
v67] 483
Х 7 469
.,742 1484
х 2 1484
О
Пример 2. Вычислить д/45 369.
Решение. _^/^53y69 =213
Х 1 41
х 423] __ 1269
31 1269
О
Если корень не извлекается, то после последней цифры
заданного числа ставят запятую и образуют дальнейшие грани,
каждая из которых имеет вид 00. В этом случае процесс извле-
чения корня бесконечен; ои прекращается, когда достигается
требуемая точность.
Пример 3. Вычислить д/7 с точностью до 0,01.
Решение.
х46
х 6
..524
* 4
5
_ VW00...=2,645...
4
300
“276
2400
2096
30400
26425
3975"
Итак, с точностью до 0,01 имеем —2,65.
42 Понятие о степени с иррациональным показателем.
Пусть а__иррациональное число. Какой смысл вкладывается
в запись а“, где а — положительное число? Рассмотрим три
случая: а=1, а>1, 0<с<1.
1) Если а = 1, то полагают 1=1.
2) Пусть а>1. Возьмем любое рациональное число Г|<а
и любое рациональное число г2>а. Тогда r( <г2 и <£'
В этом случае под а“ понимают такое число, которое заклю-
чено между <хг' и аГг для любых рациональных чисел Г| и г2,
таких, что П«х, а г2>а. В математике доказано, что такое
число существует и единственно для любого а>1 и любого
иррационального а.
3) Пусть 0<а<1. Возьмем любое рациональное число
Г]<а и любое рациональное число г2>а. Тогда Г1<г2 и
ar'Z>aTi. В этом случае под аа понимают такое число, кото-
рое заключено между аГ2 и аг' для любых рациональных чисел
Гг и Гц удовлетворяющих неравенству п <а<г2. В математике
доказано, что такое число существует и единственно для любого
числа а из интервала (О; 1) и любого иррационального а.
43. Свойства степеней с действительными показателями.
Если а>0, Ь>0 и х, у-—любые действительные числа, то
справедливы следующие свойства:
1°. а^ау=ах+,<
2°. ах:ау=ах~у.
3°. [px)y=ax,J.
4°. a bK=(aby.
s°- £=(!)•
§ 4. Комплексные числа
44. Понятие о комплексном числе. Процесс расширения
понятия числа от натуральных к действительным был связан
как с потребностями практики, так и с нуждами самой мате-
матики. Сначала для счета предметов использовались нату-
ральные числа. Затем необходимость выполнения деления при-
вела к понятию дробных положительных чисел; далее, необхо-
димость выполнения вычитания — к понятиям нуля и отрица-
тельных чисел; наконец, необходимость извлечения корней
из положительных чисел — к понятию иррациональных чисел.
Все перечисленные операции выполнимы на множестве дейст-
вительных чисел. Однако остались и невыполнимые иа этом
множестве операции, например извлечение квадратного корня
из отрицательного числа. Значит, имеется потребность в даль-
нейшем расширении понятия числа, в появлении новых чисел,
отличных от действительных.
Геометрически действительные числа изображаются точ-
ками иа координатной прямой: каждому действительному
числу соответствует одна точка прямой («образ» действитель-
ного числа) и, обратно, каждая точка координатной прямой
соответствует одному действительному числу. Координатная
прямая сплошь заполнена образами действительных чисел, т. е.,
выражаясь фигурально, «иа ней нет места для новых чисел».
Возникает предположение о том, что геометрические образы
новых чисел надо искать уже ие на прямой, а на плоскости.
Однако каждую точку М координатной плоскости ху можно
отождествить с координатами этой точки. Поэтому естественно
в качестве новых чисел — их называют комплексными —
ввести упорядоченные пары действительных чисел (упорядо-
ченные в том смысле, что (а; Ь) и (Ь; а) — разные точки,
а значит, и разные числа).
Комплексным числом называется всякая упорядоченная
пара (а; Ь) действительных чисел а и Ь.
Два комплексных числа (а; Ь) и (с; d} называются равными
тогда и только тогда, когда а=с и b=d.
45. Арифметические операции над комплексными числами.
Суммой комплексных чисел z=(a; Ь) и w—(с; d) называет-
ся комплексное число (а-\-с; b-\-d).
Например, (2; 7)+(3; -4М2+3; 7—4)=(5; 3); (-1; 0) +
+(4; 7)=( —l-f-4; 0J-7)=(3; 7).
Комплексным нулем считают пару (0; 0). Числом, проти-
воположным числу z—(a; Ь), считают число (—а; —&); обозна-
чают его — z.
Разностью комплексных чисел z и w называют, как обычно,
такое число и, что 2 = и> + и. Разность всегда существует и един-
ственна. В самом деле, пусть z=(a; b], w=(c; d), и=(х; у). Тогда
(а; Ь)~(с; d)-p(x; г/), т. е. (а; Ь)~(с+х; d-}-*/). Это значит,
что a=c-i~x, b—d-\-y, откуда находим х=а—с, y~b—d. т. е.
к=(х; у)=(а—с; b—d).
Таким образом, получаем следующее правило вычитания
комплексных чисел: (о; b)—(с; d) = (a — с; Ь-d').
Например, (9; 10) —(8; 12)=(9—8; 10 —12)=(1; —2).
Произведением комплексных чисел z—{a\ b) и u?=(c; d)
называется комплексное число (ас — bd; ad-\-bc).
Например, если г=(2; 5), ia = (3; 1), то zw = (2'3—5-1;
2*14-5*3)—(1; 17).
Арифметические операции над комплексными числами
обладают теми же свойствами, что арифметические операции
иад действительными числами (см. п. 29).
49 1Z±=J
Пусть z=(a; b), w=(c; d)#=(0; 0). Существует, и только
одно, комплексное число а=(х; у), такое, что z = uw. Это чис-
ло и называют, как обычно, частным от деления z на w.
Имеем uw={x-, у) (с; d)=(xc—yd-, xd + yc), г=(а-, b). Так
как z = uw, то должны выполняться равенства
| ex— dy — а,
I dx+cy — b.
Из этой системы двух уравнений с двумя переменными
, ac+bd be—ad ,T
находим (см. п. 164) х—> У—c2+d2 ’ ^так»
, , / ac-i-bd bc—ad\
“=<*; »)=(.-?+?; vqqr).
Получили следующее правило деления комплексных чи-
сел: если (с; d)=#(0; 0), то
(о; 6) _/ се 4- . bc—ad\
\e"+dJ ’ c‘‘+d'‘)
Например,
(2; 8) /21+3-4 . 31-2 4\ /14 , 5\
(1; 4) l2+4-“ 5 l«+42 ) \17 * 17)'
46. Алгебраическая форма комплексного числа. Используя
введенные в п. 45 определения сложения и умножения комп-
лексных чисел, легко получить следующие равенства:
(0; 1)-(0; 1)=( —Г, 0), (1)
(a; д)=(а; 0)+(d; 0)-(0; 1), (2)
(а; 0)+(Ь; 0)=(а-|-6; 0), (3)
(а; 0).(6; 0)=(а6; 0). (4)
Условимся вместо (а; 0) писать просто а, а комплексное чис-
ло (0; 1) обозначать буквой i и называть мнимой единицей.
Тогда равенство (1) принимает вид i-i——1, т. е.
i2=-l, (5)
а равенство (2) — вид
(а; Ь)=а+Ы. (6)
Запись а 4- Ы называется алгебраической формой комплекс-
ного числа z=(a; b); при этом число а называется действитель-
ной частью комплексного числа 2, а Ы — его мнимой частью.
Например, (2; —4)=2—4i; (3; 2)=3 + 2i; —7+V3-i=
Если мнимая часть комплексного числа а-\-Ы отлична от
нуля, то такое число называется мнимым; если при этом а=0,
т. е. число имеет вид Ы, то оно называется чисто мнимым;
наконец, если у комплексного числа а + Ы мнимая часть равна
нулю, то получается действительное число а.
Алгебраическая форма существенно облегчает выполнение
арифметических операций над комплексными числами.
1) Сложение. Мы знаем, что
(а; Ь) + (с; d);(a\c; b+d). (7)
Выполнив сложение тех же чисел в алгебраической форме,
считая a + fei и с-{-di обычными двучленами, находим:
(а + bi)+(с+di)=(а + с)+(ft + d)i. (8)
Сравнивая равенства (7) и (8), замечаем, что получился вер-
ный результат.
2) Вычитание. Мы знаем, что
(а; Ъ) —(с; d)=(a—с; b—d). (9)
Выполнив теперь вычитание тех же чисел в алгебраической
форме, считая a + fei и c-\-di обычными двучленами, нахо-
дим:
(a+fei) —(c+di)=(a—с)4-(Ь—й)»- (10)
Сравнивая равенства (9) и (10), замечаем, что получился вер-
ный результат.
3) Умножение. Мы знаем, что
(а; 6) (с; d) — (ас — bd; ad Ъс). (11)
Выполнив теперь умножение тех же чисел в алгебраической
форме, считая а-\-Ы и с-{-di обычными двучленами, имеем:
(а + Ы) (с+di) —ас + bci-{-adi-j-bdi2.
Воспользуемся тем, что i2= — 1 (см. равенство (5)); тогда bdi2—
= — bd. В результате находим:
(а + Ы) (с+di) — (ас — bd) + (ad+bc)i. (12)
Сравнивая равенства (11) и (12), замечаем, что получился
верный результат.
£) Деление.-Мы рцдем, ч^о если (с; d)=A(0; О),.то
(а; 6) /ас-ЬЙ be ad]
Выполним теперь деление тех же чисел в алгебраической
форме, считая a-j-Ы и с-{-di обычными двучленами, а
51
a+bA. — обычной дробью. Умножив числитель и знаменатель
этой дроби иа с—di (предполагая, что значение дроби от этого
Ве изменится), находим:
а-]-Ы (а-{-Ы)(с—di) ac-^-bci—adi—bdi9
с-{-di (c-]-di)(c—di) c2—d2i2
___ac-{bd-{(bc—ad)i ac-j-bd be—ad .
<?+d2 ci+d' c9-^-d2 l'
Итак,
а-^-Ы ас-{-bd .be—ad .
c-{di e2+d2 c2+d2
(14)
Сравнивая равенства (13) и (14), замечаем, что получился
верный результат.
Подводя итоги, приходим к следующему важному практи-
ческому выводу: над комплексными числами, записанными в
алгебраической форме, можно осуществлять все арифмети-
ческие операции как над обычными двучленами, учитывая
лишь, что i2 =—1. Чтобы преобразовать в комплексное число
дробь вида 9 нужно и числитель, и знаменатель дроби
умножить на число с—di', числа c-j-di и с—di называются
комплексно-сопряженными.
Пример 1. Вычислить (2—£)2.
Решение. Применив формулу (а — Ъ)2=а2 ~2аЬ-\-Ь2, по-
лучим:
(2-i)2=4-4i4-i2=4-4i-l=3-4i.
Пример 2. Вычислить (l-j-2i)i— ,
Решение. 1) (l-|-2i) j=j-|-2i2= — 2+i.
2ч 3+2i (3+2i)(l +») 3-b2i-j-3i + 2i2 3+5i—2_ l+5i
' 1— I ~ (l-i)(l+0 1+1 — 2
1,5.
r+v'-
3) (-2+o-(-|-+Ai)=—f-i.
Пример 3. Найти действительный ‘ЧЙсла х и у, такие,
что выполняется равенство (2х — 8yi) (2x+3i/i) + 4xi=97 + 8i.
Решение. Имеем (2х — Syi) (2х + 3yi) = 4х2—Qy2i2=4Х2 +
+ 9j/ . Тогда заданное равенство можно переписать в виде
4х2 +9^ + 4x1 = 97 + 81.
Так как комплексные числа a+fei и c-\-di равны тогда
только тогда, когда равны их действительные части (а=с)
коэффициенты при мнимых частях (b=d\ то приходим к
системе уравнений
( 4х24-9г/2 = 97,
I 4х = 8,
S S
из которой находим Xi = 2, г/] = 3; х2 = 2, г/2 = —3.
Пример 4. Найти комплексные числа z, удовлетворяю-
щие равенству z2 = — 5 4- 12г.
Решение. Будем искать комплексное число z в виде
x-\-yi. Имеем:
(х+у if = — 5 +121; х2+2ху i+уЧ2 = — 5 + 12г;
х2—г/2+2xyi = — 5 4- 12г.
Из последнего равенства следует, что Г х2—у2= — 5.
t 2хг/ = 12.
Эта система имеет два решения (2; 3) и (— 2; —3). Значит,
21 = 2 Зг, г2 = — 2 — Зг.
Пример 5. Вычислить (1 + 2г)6.
Решение. Имеем (см. п. 58) (a+fe)6=a6+6a5fe-f-
। 6-5 4,2 । 6-5-4 з«3 । 6-5-4-3 2z.4 । 6-5-4-3-2 >5 . ,5
ТУ ° ь 6 +ттггт“ Ь +Г2^4Т5 аЬ +ь =
=а6 4- 6a5fe 15a462 -f- 20a353 + 15a2 b4 4- 6a65 + b6.
Значит, (14- 2г)6=I6 + 6 • I5 • (2г) +15 I4 • (2г)2+
4- 20 • Г • (2г)3 4-15 • l2 • (2if 4- 6 1 - (2г)5 4- (2if = 14-12i 4- 60г2 4-
4-160i3 4-240i4 4-192Г 4-64г6.
Далее, имеем г2=—1, г3=г-г= — г, г4 = г2-г2=(—1)Х
Х(-1)=1, г5=г4-г = 1г = г, г6=г4-г2=1-(-1)=-1.
Значит, (1 4- 2г)6 = 14-12г — 60 — 160г 4- 240 4- 192г - 64 =
= 1174-441.
47. Отыскание комплексных корней уравнений. Пусть а > 0.
Так как (д/а-г)2=а*г2=—а, то \—a=^/a-i. Тем самым мы
получаем возможность извлекать квадратные корни из отри-
цательных действительных чисел. Это позволяет находить не
только действительные, ио и мнимые кории уравнений.
Пример 1. Решить уравнение х2 —4x4-13 = 0. __ _
Решение. Имеем (см. п. 137) х- s = 2d_-\/4—13 =
=2 + V— 9=2Зг. Итак, Xi = 24-3i, Xs=2 —3i.
Пример 2. Решить уравнение х3 = 8.
Решение. Имеем х3 — 8 = 0; (х — 2)(х24-2x4-4) = 0. Зна-
чит, либо х —2 = 0, откуда находим Х]=2; либо х2 4-2x4-
4-4 = 0, откуда находим х2д= — 1 ±л/1_'4 = — 1±-7'Зг. Итак,
Х| = 2, Хг=—1-Ьд^г, Хз= —1—\^г.
53
ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
§ 5. Основные понятия
48. Виды алгебраических выражении. Из чисел и пере-
менных с помощью знаков сложения, вычитания, умножения,
деления, возведения в рациональную степень и извлечения
корня и с помощью скобок составляются алгебраические вы-
ражения.
Примеры алгебраических выражений:
1) 2а2Ь-ЗаЬ-1а + Ь); 2) а+6+-|-; 3) 11 ;
4) (4-+-Г—т)’: 5> +
Если алгебраическое выражение не содержит деления иа
переменные и извлечения корня из переменных (в частности,
возведения в степень с дробным показателем), то оно назы-
вается целым. Из написанных выше целыми являются выра-
жения 1, 2 и 6.
Если алгебраическое выражение составлено из чисел и
переменных с помощью действий сложения, вычитания, ум-
ножения, возведения в степень с натуральным показателем
и деления, причем используется деление на выражения с пе-
ременными, то оно называется дробным. Так, из написанных
выше дробными являются выражения 3 и 4.
Целые и дробные выражения называют рациональными
выражениями. Так, из написанных выше рациональными вы-
ражениями являются выражения 1, 2, 3, 4 и 6.
Если в алгебраическом выражении используется извлече-
ние корня из переменных (или возведение переменных в дроб-
ную степень), то такое алгебраическое выражение называет-
ся иррациональным. Так, из написанных выше иррациональ-
ными являются выражения 5 и 7.
Итак, алгебраические выражения могут быть рациональ-
ными и иррациональными. Рациональные выражения, в свою
очередь, разделяются на целые и дробные.
49. Допустимые значения переменных. Область определе-
ния алгебраического выражения. Значения переменных, при
которых алгебраическое выражение имеет смысл, называют
допустимыми значениями переменных. Множество всех до-
пустимых значений переменных называют областью опреде-
ления алгебраического выражения.
Целое выражение имеет смысл при любых значениях вхо-
дящих в него переменных. Так, при любых значениях пере-
менных имеют смысл целые выражения 1, 2, 6 из п. 48.
lz^-1 54
Дробные выражения не имеют смысла при тех значениях
переменных, которые обращают знаменатель в нуль. Так,
дробное выражение 3 из п. 48 имеет смысл при всех о, кроме
а=1, а дробное выражение 4 имеет смысл при всех а, Ь, с, кро-
ме значений а=0, Ь=0.
Иррациональное выражение не имеет смысла при тех зна-
чениях переменных, которые обращают в отрицательное число
выражение, содержащееся под знаком корня четной степени
или под знаком возведения в дробную степень. Так, иррацио-
нальное выражение 5 имеет смысл только при тех а, Ъ, при
которых a-j- а иррациональное выражение 7 имеет смысл
только при а^О и Ь^О (см. п. 48).
Если в алгебраическом выражении переменным придать
допустимые значения, то получится числовое выражение; его
значение называется значением алгебраического выражения
при выбранных значениях переменных.
Пример. Найти значение выражения
при о=5, 5 = 2.
га—о
Решение. Имеем
50. Понятие тождественного преобразования выражения.
Тождество. Рассмотрим два выражения f (х)=х2—2х и g(x)=
=4х—5. При х=2 имеем f (2) = 22 — 2-2 = 0; g(2)=4-2 —5 =
= 3. Числа 0 и 3 называются соответственными значениями
выражений х2 — 2х и 4.x—5 при х = 2. Найдем соответствен-
ные значения тех же выражений при х=1:
/(1)=12 —2-1 = — 1; g(l)=4-l-5 = -l;
при х=0:
/(0)=02—2 0=0; g (0)=4-0 —5 = —5.
Соответственные значения двух выражений могут быть равны-
ми друг другу (так, в рассмотренном примере выполняется
равенство /(l)=g(l)), а могут и отличаться друг от друга
(так, в рассмотренном примере f(2)=#g(2); f (0)=^=g (0)).
Если соответственные значения двух выражений, содержа-
щих одни и те же переменные, совпадают при всех допустимых
^ндчениях перегревших, то выражения называются тождествен-
но равными.
Тождеством называют равенство, верное при всех допусти-
мых значениях входящих в него переменных.
Так, тождественно равны выражения х5 и х2-х3, а-1-Ъ-|-с
и с4- 6+а, (2аЬ)2 и 4(тЪ2.
55
Примеры тождеств:
a-j~ fe = fe-f-a,
«+0=а,
(а + Ь) с=ас -|- Ьс,
а-1=с,
х5=х2-х3.
Пропорция (см. п. 30) есть тождество при
всех значениях а, кроме а = 1, поскольку при а—1 знаменатели
дробей обращаются в нуль, т. е. дроби ие будут иметь смысла.
Замена выражения выражением (сократили иа с) есть
_ ас
тождественное преобразование выражения при ограниче-
z- „ — ас а
ниях: Ь=#0, с=5>ь0. Значит, ~^=~^— тождество при всех зна-
чениях переменных, кроме Ь = 0, с = 0. Верные числовые ра-
венства также называют тождествами.
Замена одного выражения другим, тождественно равным
ему, называется тождественным преобразованием выражения.
§ 6. Целые рациональные выражения
51. Одночлены и операции над ними. Одночленом назы-
вают такое выражение, которое содержит числа, натуральные
степени переменных и их произведения и не содержит никаких
других действий над числами и переменными. Например,
За-(2,5а3), (5afe2)-(0,4c3d), x2y*(—2z)--|-—одночлены, тогда
как выражения a-|-fe, не являются одночленами.
Любой одночлен можно привести к стандартному виду, т. е.
представить в виде произведения числового множителя, стоя-
щего на первом месте, и степеней различных переменных.
Числовой множитель одночлена, записанного в стандартном
виде, называют коэффициентом одночлена. Сумму показате-
лей степеней всех переменных называют степенью одночлена.
Если между двумя одночленами поставить знак умножения,
то получится одночлен, называемый произведением исходных
одночленов. При возведении одночлена в натуральную степень
также получается одночлен. Результат' обычно приводят к
стандартному виду. • ' с«
Приведение одночлена к стандартному виду, умножение
одночленов — тождественные преобразования.
ът\Ме₽ 1* ПРивести к стандартному виду одночлен
Решение. За-(2,5а3)—(3-2,5) (а• а3)=7,5а4.
Пример 2. Выполнить умножение одночленов 24a52cd3 и
у~а~ь'с.
Решение. (24a62cd3)-(-|-a2b3c) — (24~).(а-а2)*(62.Ь3)Х
X(c-c)-d3=ia3bsc2d3.
Пример 3. Возвести одночлен (— За62с3) в четвертую
степень.
Решение. (— За62с3)4=(— З)4 а4-(52)4-(с3)4 — 81а4 68с12.
Одночлены, приведенные к стандартному виду, называются
подобными, если они отличаются только коэффициентом или
совсем не отличаются. Подобные одночлены можно складывать
и вычитать, в результате чего снова получается одночлен,
подобный исходным (иногда получается 0). Сложение и вы-
читание подобных одночленов называют приведением подоб-
ных членов.
Пример 4. Выполнить сложение одночленов 18x2i/z3 и
— 8x2yz3.
Решение. 18x2j/234-( — 8x2i/2!3)=(184-( —-8)) x2yz3 =
= 10x2yz3.
52. Многочлены. Приведение многочленов к стандартному
виду. Многочленом называют сумму одночленов. Еели все
члены многочлена записать в стандартном виде (см. п. 51) и
выполнить приведение подобных членов, то получится много-
член стандартного вида.
Всякое целое выражение можно преобразовать в многочлен
стандартного вида — в этом состоит цель преобразований
(упрощений) целых выражений.
Рассмотрим примеры, в которых целое выражение нужно
привести к стандартному виду многочлена.
Пример 1. 3a-554-3a54~2a*(— 45)4-6-5.
Решение. Сначала приведем к стандартному виду чле-
ны многочлена. Получим 15a54~3a5 — 8a5 + 52. После приве-
дения подобных членов получим многочлен стандартного ви-
да 10а5-|-52.
Пример 2. (За 4- 55 — 2с) 4- (2а — Ъ 4- 4с).
Решение. Если перед скобками стоит знак «плюс», то
скобки можно опустить, сохранив знаки всех слагаемых, за-
ключенных в скобки. Воспользовавшись этим правилом раскры-
тия скобок, получим:
За 4“ 5 5 — 2с 4- 2а — Ь 4- 4с
57
и далее (За + 2а) + (56-&)+(-2с+4с) = 5а + 46 + 2с.
Пример 3. (5а2b+ab2)—(За26—4а62).
Решение. Если перед скобками стоит знак «минус»,
то скобки можно опустить, изменив знаки всех слагаемых,
заключенных в скобки. Воспользовавшись этим правилом
па скрытия скобок, получим:
5a2b-\-ab2 — 3a2b + 4ab2 —(5a2b — За2Ь)+(ab2 + 4а62)=2а2Ь +
+5а&2- VI \
Пример 4. 4х2(х—^-х2 + 3J.
Решение. Произведение одночлена и многочлена соглас-
но распределительному закону равно сумме произведений
этого одночлена и каждого члена многочлена. Получаем
4х'(х —~х2 + 3) = 4х2 • х—4х2 • -|-х2 4- 4х2 • 3=4х3 — 2х4 4- 12х2.
Пример 5. (а + 6) (а — 6).
Решение. Имеем (а + 6) (а —6) = (а + 6)-а+(а + &)-(—Ь)=
=a2-\-ab—ab — b2=a2 — b2.
Примерб. (2х2у+3ху2)(2х+3у+ 1).
Решение. Имеем 2х2у (2х-\-Зу-\-1)-\-Зху2 (2х+3у + 1)=
= (4х3у 4- 6х2у2 4- 2х2у) 4- (6х2у2 4- 9ху3 4- Зху2)=4х3у 4- 6х2у2 4-
4- 2з?у 4- 6х2у2 + 9ху3 4- Зху2.
Осталось привести подобные члены (они подчеркнуты). По-
лучим:
4х3у 4- 12х?у2 4- 2х2у 4- Эху3 4- Зху2.
53. Формулы сокращенного умножения. В некоторых слу-
чаях приведение целого выражения к стандартному виду мно-
гочлена осуществляется с использованием тождеств:
\ \ <а + Ь) (а — Ъ)=а2~Ъ2. (1)
Г \Л\ (а4-Ь)2=а2+2а5 + Ь2. (2)
Ч \ v' J (а — Ъ)2=а2 — 2аЬ 4- Ъ2. (3)
(аЦ-Ь) (а2—аЬ4-Ь2)=а34-Ь3- (4)
(а-Ь) (а24-аЬ + Ь2)=а3-Ь3. (5)
(а 4- Ь)3=а3 4- За25 4- Sab2 4- Ъ3. (6)
(а — 5)3=а3-За254-За52 —Ь3. (7)
Эти тождества называют формулами сокращенного умно-
<ИССНИЯ,
Рассмотрим примеры, в которых нужно преобразовать за-
данное выражение в многочлен стандартного вида.
1?тгг1 58
П Р и м е Р 1. (Зх24-4р3) (Зх2—4у3).
Решение. Воспользовавшись формулой (1), получим:
(Зх2)2 -(V)2=9х4 - 16j/6.
Пример 2. (а+Ь—с)(а+Ь4-с).
Решение. (а4-&—с)(а4-Ь+с)=((в“Ь&)_“с) ((° + ^)4-с)=
=(а + bf—с2=а2 4- 2а Ъ 4- Ь2—с2.
Пример 3. (За2 —5&3)2.
Решение. Воспользовавшись формулой (3), получим:
(За2)2 — 2 • За2 - 5Ь3 4- (5&3)2=9а4 — ЗОа2 Ь3 + 25Ь6.
Пример 4. (За 4-1) (9а2 — За 4-1).
Решение. Воспользовавшись формулой (4), получим:
(За)3 4-1 = 27а3 4-1.
54. Разложение многочленов на множители. Иногда можно
преобразовать многочлен в произведение нескольких сомно-
жителей — многочленов или одночленов. Такое тождественное
преобразование называется разложением многочлена на мно-
жители. В этом случае говорят, что многочлен делится на
каждый из этих множителей.
Рассмотрим некоторые способы разложения многочленов
на множители,
1) Вынесение общего множителя за скобку. Это преобра-
зование является непосредственным следствием распредели-
тельного закона (для наглядности нужно лишь переписать
этот закон «справа налево»):
ас 4- Ьс—с(а 4- Ь).
Пример 1. Разложить на множители многочлен 28х3 —
__35х4
Решение. 28ж3—35У’ = 7х3-4—7х3-5*=7«3 (4—5ж).
Обычно при вынесении общего множителя за скобки каж-
дую переменную, входящую во все члены многочлена, выно-
сят с наименьшим показателем, который она имеет в данном
многочлене. Если все коэффициенты многочлена — целые
числа, то в качестве коэффициента общего множителя берут
наибольший по модулю общий делитель всех коэффициентов
многочлена.
2) Использование формул сокращенного умножения. Фор-
мулы (1) — (7) из п. 53, будучи прочитанными «справа нале-
во», во многих случаях оказываются полезными для разложе-
ния многочленов на множители.
Пример 2. Разложить на множители х6 —1.
Решение, Имеем х6 — 1 =(х3)2—I2. Применив форму-
лу (1) (разность квадратов), получим (х34-1)(*3—!)• Применив
теперь формулы (4) и (5) (сумма кубов, разность кубов),
получим: (х _|_ у (х2 _ Л-+ ц (х _ 1) (ж* _|_ ж_|_ 1).
Итак,
х6-1=(х+1)(х-1)(х2-х + 1)(х2+х-|-1).
Пример 3. 4а4Ь3 + 16а3Ь4-|-16а”Ь5.
Решение. Сначала вынесем за скобку общий множи-
тель. Для этого найдем наибольший общий делитель коэффи-
циентов 4, 16, 16 и наименьшие показатели степеней, с кото-
рыми переменные а и b входят в составляющие данный мно-
гочлен одночлены. Получим:
4a2b3(a1 + 4ab + 4b1).
Так как далее по формуле (2) a2-t-4ab-f-4b2 = (a~l-2b)2, то
окончательно получаем 4а4 Ь3 + 16а3Ь4 16а2Ь5 = 4а2Ьл (а+2Ь)2.
3) Способ группировки. Он основан на том, что переме-
стительный и сочетательный законы сложения позволяют груп-
пировать члены многочлена различными способами. Иногда
удается такая группировка, что после вынесения за скобки
общих множителей в каждой группе в скобках остается одни и
тот же многочлен, который в свою очередь как общий множи-
тель может быть вынесен за скобки. Рассмотрим примеры
разложения многочлена на множители.
Пример 4. х3 — Зх2 + 5х —15.
Решение. Произведем группировку следующим образом:
(х3 —Зх2)+(5х—15).
В первой группе вынесем за скобку общий множитель х2,
во второй — общий множитель 5. Получим х2 (х —3)+5(х — 3).
Теперь многочлен (х—3) как общий множитель вынесем за
скобку: (х — 3) (х2 + 5). Таким образом, получаем:
х3 — Зх2 + 5х -15=(х — 3) (х2 + 5).
Пример 5. 2Ох24-Зуз—15ху- 4x2.
Решение. 20х2 + Зуг — 15ху — 4хя = (20х2 — 15ху) +
+ (Зг/z - 4xz)= 5х (4х— Ъу)—2 (4х - Зу)=(4х—Зу) (5х - г).
Пример 6. a2 —Tab12b2.
Решение. Здесь никакая группировка не приведет к
появлению во всех группах одного и того же многочлена. В
таких случаях иногда оказывается полезным представить
какой-либо член многочлена в виде некоторой суммы, после
чего снова попробовать применить способ группировки. В на-
шем примере целесообразно представить —Tab в виде суммы
<5аЬ~-4аЬ. Получим a2 — Tab-\- 12b2=а2—ЗаЬ— 4ab + 12b2=
~~{а — ЗаЪ)—(4а Ь — 12Ъ2)=а(а~ ЗЬ)—4Ь(а — ЗЬ)=
=(а-ЗЬ)(а-4Ь).
Пример 7. x4-|-4jf4.
Решение. Прибавим и отнимем одночлен 4х2у2. Получим
х< + 4 у' = (х* + 4х V 4- 4/J - 4хУ=(х24-2у2)2 - (2xyf=
=(х2 4- 2у2 — 2ху) (х24- 2у2 4- 2ху).
55. Многочлены от одной переменной. Многочлен ах 4- 5,
где о, Ь — числа {а =^= О), а х—переменная, называется мно-
гочленом первой степени; многочлен ах2 -^-Ьх-^с, где а, Ь, с —
числа (а=#0), а х — переменная, называется многочленом вто-
рой степени или квадратным трехчленом; многочлен ах34-
+ bx2 + cx-\-d, где a, b, е, d — числа (а=#0), а х— перемен-
ная, называется многочленом третьей степени.
Вообще если а, 5, с,...» Z, m—числа (а^О), ах — переменная,
то многочлен
ахп-\-Ъхп 1 + схл-24-...4-/х4-лг
называется многочленом п-й степени (относительно х)\ ахп,
bxn lt..., lx, in—члены многочлена, a, b, с,...»I, m — коэффици-
енты, ах" — старший член многочлена, а — коэффициент при
старшем члене, пг — свободный член многочлена. Обычно
многочлен записывают по убывающим степеням переменной,
т. е. степени переменной х постепенно уменьшаются, в част-
ности, на первом месте стоит старший член, на последнем —
свободный член. Степень многочлена — это степень старшего
члена.
Например, 5xs—2х3-гЗх24-1— многочлен пятой степени,
в котором 5хБ — старший член, 1 — свободный член много-
члена.
Корнем многочлена Р(х) называют такое значение х, при
котором многочлен обращается в нуль. Например, число 2
является корнем многочлена Р(х)=х3-{-2х2— 7х—2, так как
Р(2)=234-2-22 — 7-2 — 2 = 0.
56. Разложение квадратного трехчлена на линейные мно-
жители. Если Х1И Хг—корни квадратного трехчлена ах24-
4-5x4-с (т. е. корни уравнения ах2 4-Ьх+с=0), то
ax2-\-bx-\-c=a (х—xi)(x—х2).
Эта формула применяется для разложения квадратного трех-
члена на множители.
Пример. Разложить на множители 6х2—х —2.
Решение. Применив формулу корней квадратного урав-
нения (см. п. 137) к уравнению 6х2 —х — 2=0, находим
1 2 п
Xi = —g-, x2=-g-. Значит,
6^_ж-2=б(ж+4-)(Ж-4-)=2(«+4-).8(Я-{.) =
=(2х + 1)(3х —2).
57. Разложение иа миожители двучлена х”—ап. Известно,
я2—а2—(х—в) (я 4-а), (1)
я3 —а3=(я—а) (я2 4- ха-4- а2). (2)
Если перемножить многочлены я—а и х3 -\-х2а-\-ха2 4-й3.
то получим:
я4 — а4=(я—а) (я3 4- я2а 4- ха2 4- а3)- (3)
Обобщением формул (1), (2), (3) является формула разло-
жения на множители двучлена я"—а":
х"-йя=(х-п)(хя-14-хя-2а4-ж"~3л24-...4-жа“-24-оп~1).
Если, в частности, а=1, то получаем:
хп — 1 =(я — 1) («"- 14- Хп~2 4- хи-34-.- 4- X 4-1).
Например, я7 — 1 =(я — 1) (я64-я54-я4 4-х34-х24-*4-1).
58. Возведение двучлена в натуральную степень (бином.
Ньютона). В этом пункте речь идет о том, как двучлен
(или бином) а-\-Ъ возвести в любую натуральную степень.
Если л = 1, то =а-\-Ь.
Если л=2, то (a-\-b)2=a2-$-2ab-\-b2.
Если п = 3, то (a4-fc)3=a34-3a2b-|-3al?24-l>3.
Воспользовавшись тем, что (а4-Ь)*=(а-|-Ь^ (а-|-Ь), можно
вывести формулу
(а 4- Ь)* =а4 4-4а3Ь 4- 6a2b2 + 4аЬ3 4- Ь4.
Вообще справедлива следующая формула (бином Ньютона):
(а + ЬУ = п" + та,^'Ь+.;1^)^-^ + "("-1)("-2).а.^зь-з +
4- ... I д(п—^(д-2)--•(”—* +
Пример. Для (а 4- bf по формуле бинома Ньютона полу-
чаем:
(aW=a'' + 6a5b+^a^+|±J!o3b= +^l±^aV +
.6-5-4-3.2 ч
+ ab +be=ae + Gasbz + ISa’b2 + Wa3b3 + 15a3 b' +
+6аЬ54-Ь».
62
§ 7. Дробные рациональные выражения
59. Рациональная дробь и ее основное свойство. Любое
дробное выражение (п. 48) можно записать в виде -£ , где
Р и Q — рациональные выражения, причем Q обязательно
р
содержит переменные. Такую дробь — называют рациональ-
ной дробью.
Примеры рациональных дробей:
—4- —
х+1 (х+2)(хг-3) Ь Г d
1 ’ а + 2Ь-±-5с * а— Ь
Основное свойство дроби выражается тождеством ♦
справедливым при условиях 1?=#0 и Q=?=0; здесь R— целое
рациональное выражение. Это значит, что числитель и знаме-
натель рациональной дроби можно умножить или разделить
на одно и то же отличное от нуля число, одночлен или много-
член.
_4х3—6хг+12
Зх24-2х + 6 *
Основное свойство дроби может быть использовано для пере-
мены знаков у членов дроби. Если числитель и знаменатель
р р р
дроби — умножить на —1, получим Таким обра-
У у —у
зом, значение дроби не изменится, если одновременно изменить
знаки у числителя и знаменателя. Если же изменить знак
только у числителя или только у знаменателя, то и дробь
изменит свой знак: -
Значит, •£-= -^=
тт Зх—2
Например,
—(Зх—2) _ 2—Зх
Зх+4 Зх+4
60. Сокращение рациональных дробей. Сократить дробь —
это значит разделить числитель н знаменатель дроби на общий
множитель. Возможность такого сокращения обусловлена ос-
новным свойством дроби.
Для того чтобы сократить рациональную дробь, нужно
числитель и знаменатель разложить на множители. Если ока-
жется, что числитель и знаменатель имеют общие множители,
то дробь можно сократить. Если общих множителей нет, то
преобразование дроби посредством сокращения невозможно.
“ д х?—3ху
Пример. Сократить дробь
Решение. Имеем х2— %ху=х (х — Зу);
9!/2-х2= -(x2-9y2)= -(x-3y)(x+3s/).
_ х2—Зху х(х—3у) _ х
Значит, х+Ьу-
Сокращение дроби выполнено при условии х— 3y=/=Q.
61. Приведение рациональных дробей к общему знамена-
телю. Общим знаменателем нескольких рациональных дробей
называется целое рациональное выражение, которое делится на
знаменатель каждой дроби (см. п. 54).
Например, общим знаменателем дробей и слу-
жит многочлен (х + 2) (х — 2), так как он делится и на х 4- 2, и на
х—2; и многочлен 3 (х-|-2) (х—2), и многочлен х (х+2) (х—2),
и многочлен 5х_/ (х4-2)2 (х—2)3 и т. д. Обычно берут такой
общий знаменатель, что любой другой общий знаменатель де-
лится на выбранный. Такой простейший знаменатель называют
иногда наименьшим общим знаменателем.
В рассмотренном выше примере общий знаменатель равен
(х + 2)(х—2). Имеем
х х(х —2) _ Зх—1 (Зх—1)(х+2)
*+2 — (х+2)(х—2) * я—2 —”(х+2)(х—2) '
Приведение данных дробей к общему знаменателю достигнуто
путем умножения числителя и знаменателя первой дроби на
х 2, а числителя и знаменателя второй дроби на х 4-2. Мно-
гочлены х—2 и х-|-2 называются дополнительными множи-
телями соответственно для первой и второй дроби. Дополнитель-
ный множитель для данной дроби равен частному от деления
общего знаменателя на знаменатель данной дроби.
Чтобы несколько рациональных дробей привести к общему
знаменателю, нужно:
1) разложить знаменатель каждой дроби на множители;
64
2) составить общий знаменатель, включив в него в качестве
сомножителей все множители полученных в п. 1) разложе-
ний; если некоторый множитель имеется в нескольких разло-
жениях, то он берется с показателем степени, равным наиболь-
шему из имеющихся;
3) найтн дополнительные множители для каждой из дро-
бей (для этого общий знаменатель делят на знаменатель
дроби);
4) домножив числитель и знаменатель каждой дроби на до-
полнительный множитель, привести дроби к общему знаме-
нателю.
Пример. Привести к общему знаменателю дроби
а & а+Ь
12а2-12^ ’ 18а3 + 18а2Ь ’ 24а*-24аЬ'
Решение. Разложим знаменатели на множители:
12а2- 12 b2 = 12 (а - Ь) (а + &);
18а3 + 18а2Ь=18а2 (а + &);
24а2 — 24а b — 24а (а — Ь).
В общий знаменатель надо включить следующие множители:
(а—&), (а-|-Ь), а2 — и наименьшее общее кратное чисел 12,
18, 24, т. е. К (12, 18, 24)= 72. Значит, общий знаменатель
имеет вид 72а2 (а — &) (а -|- &).
Дополнительные множители: для первой дроби 6а2, для
второй —4 (а—Ь), для третьей —За (а + Ь). Значит, получаем:
а _______ 8а3
12а2— 12Ьг~ 12аъ (а — &) (а+&) ’
b _ 4Ь(а—Ь)
18а3 + ISd'b 72аг(а-Ь)(а+&)
^За (o-f-fe)
а + & _ 3a(fi + 6)2
24а2 — 24а& — 72а2 (а - Ь) (а + Ь) ‘
62. Сложение и вычитание рациональных дробей. Сумма
двух (и вообще любого конечного числа) рациональных дро-
бей с одинаковыми знаменателями тождественно равна дроби
с тем же знаменателем и с числителем, равным сумме числи-
телей складываемых дробей:
Pl I Pi
Q Q Q *
65
Аналогично обстоит дело в случае вычитания дробей с одина-
ковыми знаменателями:
Pt Ра^_Р>-Р2
Q Q Q ’ .
X3 у3
Пример 1. Упростить выражение
Решение.
х3 , у3 __ х3+у3 (х+у) (*3—*У+у2)
х+у+х+у х+У х+у
=х!—ху+у2.
Для сложения или вычитания рациональных дробей с раз-
ными знаменателями нужно прежде всего привести дроби к об-
щему знаменателю, а затем выполнить операции над получен-
ными дробями с одинаковыми знаменателями.
„ 3 . 2х-1 2
Пример 2. Упростить выражение 2a.rq:2;+ дс?_1—— •
Решение. Имеем 2х2+2х—2х (х-|-1); х2 — 1 =
=(х —l)(x-f-l).
о 3 . 2х—1 2 3 . 2х—1
Значит, 2x,+2t. +х,_1 х 2х(х+1)+ (Х-1)(х+1)
2(*-1)(х+1)
Р-------^__3(х-1)+2х(2х-1)-4(Ж-1)(х+1)_ х+1 _
—— 2х(х-1)(х+1) 2х(х-1)(х+1)
1
2х(х—1) *
63. Умножение и деление рациональных дробей. Произве-
дение двух (и вообще любого конечного числа) рациональных
дробей тождественно равно дроби, числитель которой равен
произведению числителей, а знаменатель — произведению
знаменателей перемножаемых дробей:
Р. _Pg=Pi«P>
Qi ’q2 <?*<& *
Частное от деления двух рациональных дробей тождест-
венно равно дроби, числитель которой равен произведению
числителя первой дроби на знаменатель второй дроби, а зна-
менатель — произведению внаменателя первой дроби на числи-
тель второй дроби:
Pi .Pa^Pi Qa
Qi ' Qa Qi Ра '
3 Заказ 769
66
Сформулированные правила умножения и деления распро-
страняются и на случай умножения или деления на много-
член: достаточно записать зтот многочлен в виде дроби со
знаменателем 1.
Учитывая возможность сокращения рациональной дроби,
полученной в результате умножения или деления рациональ-
ных дробей, обычно стремятся до выполнения этих операций
разложить на множители числители и знаменатели исходных
дробей.
Пример 1. Выполнить умножение
Решение. Имеем
я’+2х+1_(к-3-1)2 . fix'* ftx*
18^ ’ ' 18г3 ’ хй-1--(х—1)(х4-1) ’
Использовав правило умножения дробей, получаем:
хг4-2х4-1 9х“ («4-1)2-9х4 _х(х+1)
18х4 Xй-1 18х3(х+1)(х—1)— 2(х—1)"
тт о D а3-2а2. аг-4
Пример 2. Выполнить деление „ , „ :ч-;_гя v „.
За |-3 За 4-Ьа+З
Решение.
т, а3—2вг а2 (а—2) а2—4
Имеем — 3(о+1) ; зй2+ба+з —
_Ja-2)(a+2)
3(а+1)2
Использовав правило деления, получаем:
а3 — 2ог. а2 — 4 а2 (а —2)-3 (о+1)2 а2 (с4-1)
3а+3”*3а24-6а + 3“3(а + 1)(а—2)(а+2)~ «4-2 ‘
64. Возведение рациональной дроби в целую степень. Чтобы
Р
возвести рациональную дробь — в натуральную степень п,
нужно возвести в эту степень отдельно числитель и знаменатель
дроби; первое выражение — числитель, а второе выражение —
знаменатель результата:
Пример 1. Преобразовать в дробь степень
Решение.
3 _(2х2у3)3 _8х6у3
1 (Зг5)3 ~ 27z,b
При возведении дроби в целую отрицательную степень ис-
пользуется тождество справедливое при всех
значениях переменных, при которых Р#=0 и Q=/=0.
Пример 2. Преобразовать в дробь выражение
Z(a+&f (а—Ь)Л ~5 *
V (а+2Ь)4 ) *
Решение.
/ (в+2Ь/ V (а+2Ь)20
\. (п+ЯЧ1 > ~\(a+bY(a-t>f) (а + Ц'^а-Ь)14'
6& Преобразование рациональных выражений. Преобразо-
любого рационального выражения сводится к сложению,
вычитанию, умножению и делению рациональных дробей, а
также к вовведени» дроби в натуральную степень. Всякое ра-
циовалыше выражение можно преобразовать в дробь, числи-
тель и знаменатель которой — целые рациональные выра-
жения; в этом, как правило, состоит цель тождественных
преобразований рациональных выражений.
Пример. Упростить выражение
/2а 4a2 \ / 2a 1 \ - J f 8а2
\2a4~b 4а^+4аЬ+Ьу \ 4a4—b2*b—2а) ’ 2a 4-Ь*
Решение.
2а + Ъ
ji 2a_______4a2 __ 2а 4а2 ___
‘ 2a-t-b 4a2+4ab+b2^ 2а±Ь (2а+ b)'2
__2a(2a + b)—4as 2ab
(2a 4-Ь)2 =(2а+Ь)г ’
2) -Д-,-1___1 — 2°________!__
‘ 4а! — ь2 Ь-2а (2а-Ь)(2а + Ь) 2а-Ь ~~
_ 2а—2а —&____ —ь
(2а- Ь) (2а+6)—(2а- Ь) (2а+ Ь) ’
( (2а- Ь)(2а + Ь))
(2а-Ь)(2а+Ь) ,
- 2“Ь „ ( (2а—Ь)(2° + Ь)\ 2аЬ (2а-Ь)(2а+Ь)
>(^+4)4 6-----)--------Г(2а+Ь/
,___2а(2а— &)_2аЬ—4а2 t
2а+ Ъ 2а+Ь ’
5) 2аЬ-4»8 , Sa2 2at.+4a; 2а(2а + М „
2а+* ~2a-f-fc 2a4-fc 2а-(-ь ^а'
EZZJ 68
§ 8. Иррациональные выражения
66. Простейшие преобразования арифметических корней
(радикалов). При преобразовании арифметических корней
используются их свойства (см. п. 35).
Рассмотрим несколько примеров на применение свойств
арифметических корней для простейших преобразований ра-
дикалов. При этом все переменные будем считать принимаю-
щими только неотрицательные значения.
Пример 1. Извлечь корень из произведения Уа?Ъ9.
Решение. Применив свойство 1°, получим:
Vo'lt’=Vei'V67-=“63-
Пр и м е р 2. Вынести множитель из-под знака корня
д/45<?.
Решение. -\/45а^=-^9а45с=-\§*-^*-^5а=3<1%/5а.
Такое преобразование называется вынесением множителя из-
под знака корня. Цель преобразования — упростить подко-
ренное выражение.
Пример 3. Упростить (^г2)5.
Решение. По свойству 3° имеем (^S5)5=^/(а2)6=^пг.
Обычно стараются подкоренное выражение упростить, для
чего выносят миожители за знак кория. Имеем =\а1) а=
Итак, (3-\^2)5=а3^/£.
Пример 4. Упростить д/х2 \[х.
Решение. Преобразуем выражение, х2^/х, внеся мно-
житель под знак корня: х2Ух=У(х2)3 -2\/x—\/xs-^Jx—:\jlxr‘x=
=Ух7. По свойству 4° имеем д/^/л:7 =
Пример 5. Упростить 3У2?.
Решение. По свойству 5° мы имеем право показатель
корня и показатель степени подкоренного выражения разде-
лить на одно и то же натуральное число. Если в рассматри-
ваемом; примере разделить указанные показатели иа 3, то
получим 3^29' — —1У8.
Пример 6. Упростить выражения: а) Уа-Уа?'г б)
в) Ух^'Ух?.
Решение, а) По свойству 1° получаем, что для пере-
множения корней одной и той же степени достаточно пере-
множить подкоренные выражения и из полученного результа-
та извлечь корень той же степени. Значит, Уа-Уа?=Уа-а2*=
б) Прежде всего мы должны привести радикалы к одному
показателю. Согласно свойству 5° мы можем показатель корня
и показатель степени подкоренного выражения умножить на
одно и то же натуральное число. Поэтому Далее
имеем А теперь в полученном результате раз-
делив показатели корня и степени подкоренного выражения
на 3, получим
Итак,
в) Приведем радикалы к одному показателю. Для этого,
очевидно, нужно найти наименьшее общее кратное чисел 8 и
12, т. е. К (8, 12)= 24. Значит, нам нужно показатели корня
и степени подкоренного выражения для первого из перемно-
жаемых радикалов умножить на 3, а для второго — на 2.
Получим:
‘V^=2^-2V^=2W^=2V^.
На практике при выполнении действий над радикалами
довольно часто переходят к дробным показателям. Например:
V? • W=х 7 • +
67. Тождество д£*=|а|. Упростим выражение дй*. Здесь
могут представиться два случая: аЗ>0 или g<0. Если сЗ>0,
то д^=о; например, д/22 =2, д/27*==27, д/02 =0. Если же
а<0, то д^= —а; например, дГ(—2)2= —(—2) = 2. Итак,
r~? f а» если а>0,
*а { —с, если а<0.
Но точно так же определяется модуль действительного числа
(см. п. 26). Таким образом,
д/^= 1а[.
Например, д/З2 = |3| =3; д/(—5)2= | —5| = —(—5)=5. Вообще
если п — четное число, т. е. п= 2k, то
Пример. Упростить выражение д/х2 —6х-|-9-|-д^2—х +
+«—3. _______________
Решение. Имеем д/х2—6х+9=д/(х—3)2 = |х--3|. По-
скольку заданное выражение содержит слагаемое \!2 — х, то
2— откуда находим, что Х^2. Значит, х — 3<0, а по-
тому |х — 31 = — (х — 3)=3— х. Итак, д/х2—6х+9=3—х, и
мы получаем:
V®1—6* + 9+т/2—X+х—3 = 3—Х++х — 3=л'2^х.
1=^-1 70
68. Преобразование иррациональных выражении. Для пре-
образования иррациональных выражений используются свой-
ства радикалов (см. п. 35) и свойства степени с рациональ-
ным показателем (см. п. 38).
Пример. Упростить выражение
/(«)=(
п Уё(УР-1)
' 1__1_________/L 1
2)
ftS)1 л»'
х+2-vS+i (л£й-1)!
5) (<^+1Г
(v'l+i)’-
(VS+if Ji+1 ‘
®)
Итак, f(x) =
Обычно стараются записать ответ т^к, чтобы в знаменателе
не содержалась иррациональность. Для избавления от ирра-
циональности в знаменателе дроби —±— умножим и числи-
-V^+i
тель, и знаменатель на -yfx— 1 — это .выражение называется
сопряженным для выражения -у/х-[-1. Получим:
tS+1 h£+l)6/i -1) ('/?)--1! X
71
Глава III. ФУНКЦИИ И ГРАФИКИ
§ 9. Свойства функций
69. Определение функции. Зависимость переменной у от пе-
ременной х называется функцией, если каждому значению х
соответствует единственное значение у. Переменную х назы-
вают независимой переменной или аргументом, а переменную
у______зависимой переменной. Значение у, соответствующее за-
данному значению х, называют значением функции.
Записывают: y=f (х) (читается: «Эф от икс»). Буквой / обоз-
начается данная функция, т. е. функциональная зависимость
между переменными х и у, / (х) есть значение функции, соот-
ветствующее значению аргумента х. Говорят также, что / (х)
есть значение функции в точке х.
Все значения, которые принимает независимая переменная,
образуют область определения функции.
Все значения, которые принимает функция / (х) (при х, при-
надлежащих области ее определения), образуют область зна-
чений функции.
Рассмотрим функцию у=х, где 1^х^3. Эта запись озна-
чает, что задана следующая функция: каждому числу х
из отрезка [1, 3] ставится в соответствие квадрат этого числа.
Например, /(1)=Г=1, /(2)= 22 = 4, /(2,3)=2,32 = 5,29 и т. д.
Запись f (4) в этом случае лишена смысла, так как число 4 не
принадлежит отрезку [1, 3]. Отрезок [1, 3] — область опреде-
ления функции.
70. Аналитическое задание функции. Чтобы задать функ-
цию, нужно указать способ, с помощью которого для каждого
значения аргумента можно найти соответствующее значение
функции. Наиболее употребительным является способ зада-
ния функции с помощью формулы y=f(x), где f(x)— неко-
торое выражение с переменной х. Б таком случае говорят, что
функция задана формулой или что функция задана аналити-
чески.
Пример 1. р=я х2+5х — 1, где х 0. Область определения
этой функции — луч [0; + со). Чтобы найти значение функции
в любой точке х 0, достаточно найти числовое значение
выражения х2+5х — 1 в выбранной точке. Функция задана
аналитически.
Для аналитически заданной функции иногда не указывают
явно область определения функции. В таком случае под-
разумевают, что область определения функции y=f(x} совпа-
дает с областью определения выражения f (х), т. е. с множест-
вом тех значений х, при которых выражение f (х) имеет
Пример
2. Функция y—f(x) задана аналитически фор-
мулой /(х)— * » Найти: a) f(— х); б) f(kx); в) f{X-\-dy,
г) /(|х|).
Решение, а) Чтобы найти /(—х), надо в /(х) всюду
вместо х подставить (— х). Получим:
/(-*)
^(-гУ-К-х)+1_<2-х4-1
(-х)4+3 «<+8
Итак,
к» ./.--Л (fatf+tM+l *gz,4-fa?+l
OJ (jx)<+3 Л'х' + З •
)/(*+а)=(х+^г;+1-
/ /1V h — 1х|*-Ь lxl + 1 __xa+1x1+1
U— |xl*+3 х’+з •
Пример 3. Найти область определения функции
= 1
х+2 *
Решение. Выражение —~ определено при всех х, кроме
x-f-z
того значения, которое обращает знаменатель в 0,— это
значение х— — 2. Значит, область определения функции состоит
из всех чисел, кроме х= —2.
Пример 4. Найти область определения функции
у^д/х—1.
Решение. Выражение д/х—1 определено при тех х,
при которых X—1^0, т. е. при х^1. Значит, область опре-
деления функции — луч [1; + оо)
Иногда функция задается на различных промежутках рав-
нинными формулами, например:
2х + 3, если —l^x^O,
х + 2, если 0<х^1.
Эта функция определена на отрезке [—1; 1} Для вы-
числения значений функции нужно лишь точно определить,
какой формулой следует воспользоваться для заданного
конкретного значения аргумента. Например, если нужно вы-
/(*)={
73
числить /(0,5), воспользуемся равенством / (х)=х + 2 и полу-
чим /(0,5) =2,5. Если же нужно вычислить /(—0,5), то
воспользуемся равенством / (х) = 2х+3, получим / (—0,5) = 2.
71. Табличное задание функции. На практике часто исполь-
зуется табличный способ задания функции. При этом способе
приводится таблица, указывающая значения функции для
имеющихся в таблице значений аргумента. Примерами таб-
личного задания функции являются таблица квадратов,
таблица кубов, таблица квадратных корней.
Во многих случаях табличное задание функции оказывается
удобным. Оно позволяет найти значения функции для значений
аргумента, имеющихся в таблице, без всяких вычислений. На
практике часто зависимость одной величины от другой находят
опытным путем. В этом случае одной величине придают оп-
ределенные значения, а потом из опыта для каждого из таких
значений находят значение (обычно приближенное) второй
величины. Таким образом опыт позволяет составить некоторую
таблицу значений функции. Существуют методы, позволяющие
по такой таблице подбирать формулы, задающие функции
(с определенной точностью).
72. Числовая плоскость. Координатная плоскость, оси коор-
динат. Множество всех пар’ действительных чисел называется
числовой плоскостью.
Как для множества всех действительных чисел (или число-
вой прямой) есть геометрическая модель — координатная пря-
мая (п. 18, 21), так и для множества всех пар действитель-
ных чисел (числовой плоскости) есть геометрическая модель —
координатная плоскость. Координатная плоскость Ху определя-
ется двумя взаимно перпендикулярными координатными пря-
мыми с общим началом О и одинаковым масштабом (рис. 7).
Точка О называется началом координат. Горизонтальная пря-
мая называется осью абсцисс или осью х, вертикальная —
осью ординат или осью у.
Если отметить на координатной плоскости все точки с абс-
циссой х=а, то получится прямая, параллельная оси у (рис. 7);
говорят, что х=а — уравнение этой прямой. Если отметить на
координатной плоскости все точки с ординатой у = Ъ, то по-
лучится прямая, параллельная оси х (рис. 7); говорят,
что у=Ъ — уравнение этой прямой.
73. График функции, заданной аналитически. Пусть функ-
ция задана аналитически формулой у=Цх). Если иа коорди-
Под парой чисел понимают два числа, которые рассматрива-
ются в определенном порядке.
натной плоскости отметить все точки, обладающие следующим
свойством: абсцисса точки принадлежит области определения
функции, а ордината равна соответствующему значению
функции, то множество точек (х; f(x)) есть график функции.
Например, графиком функции у=х является множест-
во точек вида (x*t X), т. е. точек, имеющих одинаковые
координаты. Это множество точек есть биссектриса I и III коор-
динатных углов (рис. 8).
На практике для построения графика функции составляют
таблицу значений функции при некоторых значениях аргумен-
та, наносят на плоскость соответствующие точки и соединяют
полученные точки линией. При этрм предполагают, что график
функции является плавной линией, а найденные точки доста-
точно точно показывают ход изменения функции.
Пример. Построить график функции р—я2.
Решение. Составим таблицу некоторых значений функ-
ции:
X —2,5 —2 — 1 -0,5 0 0,5 1 2 2,5
У 6,25 4 1 0,25 0 0Д5 1 4 6,25
Нанесем найденные точки (О; О); (0,5; 0,25); (—0,5; 0,25);
(1; 1); (—1; 1); (2; 4); (—2; 4); (3; 9); (—3; 9) на координатную
плоскость (рис. 9,а). Соединив эти точки плавной линией, по-
лучим график (а точнее, эскиз графика) функции у=х*
(рис. 9,6). Эта линия называется параболой. Вообще параболой
является график любой функции вида у^ах2, где а 5^0
(см. и. 111).
74. Четные и нечетные функции. Функция y=f(x) назы-
вается четной, если для любого х из области определения
функции выполняется равенство f(—x)=f(x).
Функция y=f(x) называется нечетной, если для любого х
из области определения функции выполняется равенство
/(-*)=-Г (х).
Например, у=х2, у=х4, у=х* — четные функции, а у=х3,
У=х\ у=х/ — нечетные функции.
Если функция y—f(x} такова, что хотя бы для одной
пары значений хи —X оказалось, что f (—х)=^= —f(x), и хотя
бы для одной пары значений х и — х оказалось, что /(—х)=А
=/=/(#), то функция ие является ни четной, ни нечетной.
Из определения следует, что область определения X как
четной, так и нечетной функции должна обладать следующим
свойством: если х£Х, то и — х£Х (т. е. X — симметричное отно-
сительно О множество).
Пример. Исследовать иа четность функции: а) I/—%20;
б) »=Х13; в) V=-£±.
Решение, а) Имеем f (х)=х20, /(—х)=(—х)20=х20. Зна-
чит» /(—x)—f(x) для всех х. Функция является четной.
б) Имеем /(х)=х’3, / (—х)=(—х),3= —х13. Значит,
f (—х)=—f(x) для всех х. Функция является нечетной.
в) ИмеемТак
как f (—x)=£f(x) и f (—х)^= —f(*)> то функция не является ии
четной, ни нечетной.
75. График четной функции. График нечетной функции.
Графики четной и нечетной функций обладают следующими
особенно стями:
Если функция является четной, то ее график симметричен
относительно оси ординат.
Если функция является нечетной, то ее график симметричен
относительно начала координат.
Пример 1. Построить график функции у— |х|.
Решение. Имеем f (—х)== I — *1 — |х| —f (х). Значит,
функция четна, а потому график ее симметричен относительно
оси ординат.
Если х^О, то |х|=х, т. е. при хЗ>0 имеем у—х. Графи-
ком функции у=х при х^еО служит биссектриса первого ко-
ординатного угла. Подвергнув ее преобразованию симметрии
относительно оси у, получим график функции у~ |х[ (рис. 10).
Пример 2. Построить график функции у=х |х|.
Решение. Имеем/(—х)=(—х) | —х| = —х |х| = —/(х).
Значит, функция нечетна, а потому график ее симметричен
относительно начала координат.
Если хЗ>0, то |х|=х, a f(x)—x- |х| =х-х=х2. Значит,
при х^О имеем у=х2. Графиком будет ветвь параболы. Она
изображена иа рисунке 11,а. Подвергнув ее преобразованию
симметрии относительно начала координат, получим график
функции у=Х |х| (рис. 11,6).
76. Периодические функции. Функция «/=/(#) называется
периодической, если существует такое отличное от нуля число Т,
что для любого х из области определения функции справедливо
равенство f(x-\-T)=f (x)=f(x—Т),
Число Т называется периодом функции y=f(x).
Из этого определения сразу следует, что если Т — период
функции y—f(x), то 2Т, ЗТ, 4Т, —Т, — 2Т, — ЗТ, — 4Т— пери-
оды функции. Значит, у периодической функции бесконечно
много периодов. Если, например, Т — период функции, то и
число вида НТ, где fe — любое целре число, также является пе-
риодом функции.
Чаще всего (но не всегда) средй множества положительных
периодов функции можно найти наименьший. Его называют
основным периодом.
Графики периодических функций обладают следующей осо-
бенностью. Если Т — основной период функции y—f (х), то для
построения ее графика достаточно построить ветвь графика на
одном из промежутков оси х длиной Т, а затем осуществить
параллельный перенос этой ветви Цо оси X на ±Т, ± 2Т, -1- ЗТ,...
(рис. 12). Чаще всего в качестве такого промежутка длиной Т
выбирают промежуток с концами в точках ( —(А и о\
или (0; 0) и (Т; 0). \ 2 / \ 2 /
Примеры периодических функций:
— основной период Т=1 (см. п. 93),
^=sinx— основной период Т—2 л (см. п. 102),
г/—cosx — основной период Т=2л (см. п. 103),
y=tgx— основной период Т=л (см. п. 104),
y=ctg х — основной период Т=л (см. п. 105).
77. Монотонные функции. Функция y—f (х) называется воз-
растающей на промежутке X, если для любых и х? из X,
таких,что Х\<Х2, выполняется неравенство f(Xi)<f(Xz) (ко-
роче : xt < х? => f (Xi) < f (x2)). Функция y=f(x) называется
убывающей на промежутке X, если для любых Х\ и х2 из X,
таких, что Xi<*2, выполняется неравенство f(x\)>f(x^ (коро-
че: Х|<Х2=>/(Х1)>/(хг)). Иными словами, функция возра-
стает (убывает) на промежутке X, если, какие бы два значе-
ния аргумента, принадлежащие этому промежутку, ни взять,
окажется, что большему значению аргумента соответствует
большее (меныпее) значение функции.
При движении вдоль оси абсцисс слева направо ордината
графика возрастающей функции увеличивается (рис. 13, а),
а ордината графика убывающей функции уменьшается
(рис. 13, б).
Возрастающие и убывающие функции объединяются терми-
ном < монотонные функции».
Пример. Исследовать на монотонность функцию
у=2х3-|-3.
Решение. Пусть Х1<Хг. Тогда по свойствам числовых
неравенств (см. п. 24) имеем Xi<xl, 2x3i<2xl, 2x?J-3-<
< 2xl+3, т. е. f (Xj) < f (x2).
Итак, Xi<X2=>/(Xj)</(x2), а это значит, что функция
у—2х3-ЬЗ возрастает на всей числовой прямой.
§ 10. Виды функций
78. Постоянная функция. Постоянной называется функция,
заданная формулой у=Ь, где Ь — некоторое число.
Графиком постоянной функции у = Ь является прямая, па-
раллельная оси абсцисс и проходящая через точку (О; Ъ) на
оси ординат. На рисунке 14 изображены графики нескольких
постоянных функций. В частности, графиком функции у=0
является ось абсцисс.
79. Прямая пропорциональность. Прямой пропорциональ-
ностью называется функция, заданная формулой y=kxt где
79
/?^0. Число k называется коэффициентом пропорциональ-
ности.
Перечислим свойства функции y = kx.
1) Область определения функции — множество всех дейст-
вительных чисел.
2) у—Ьх — нечетная функция (/(—х)=Ъ (—х}~ — hx=s
= -/(*))•
3) При fe>0 функция возрастает, а при fe<0 убывает
на всей числовой прямой.
Т.3.1. I Графиком прямой пропорциональности y=kx явля-
I ется прямая, проходящая через начало координат.
Доказательство
Проведем прямую через начало координат и точку А (1; к) и докажем,
что она является графиком функции y=kx.
Рассмотрим сначала случай, когда к>О (рис. 15).
Возьмем любую точку М (х; у), лежащую на прямой I. Из подобия
Мх Ох у х
треугольников OAJ н ОМх заключаем, что т- е- » откУДа
y—kx. Возьмем теперь точку Р(х; у), не лежащую на прямой I. Тогда коор-
динаты точки М] с той же абсциссой, но лежащей на прямой I, удовлетворяют
уравнению y=kx, значит, координаты точки Р этому уравнению не удовлет-
воряют. Итак, точки прямой I, и только они, удовлетворяют формуле
значит, прямая I — график функции y=kx.
Рассмотрим теперь случай, когда fe<0. Возьмем две функции y=kx к
У—— kx. При одной и той же абсциссе х ординаты графиков этих функций
равны по модулю, но противоположны по знаку. Значит, графики этих
функций симметричны относительно оси абсцисс. Но — fe>fi, и по доказан-
ному выше графиком функции р=—kx является прямая. Поскольку при
преобразовании симметрии прямая переходит в прямую, то и графиком
функции у—kx является прямая.
На рисунке 16, а изображен график функции y=kx при
fe>0, а на рисунке 16, б — график функции y=kx при fe<0.
Пример. Построить график функции у=2х.
Решение. Мы знаем, что графиком является прямая,
проходящая через начало координат. Для ее построения доста-
точно найти одну точку графика, отличную от начала коорди-
нат, и провести прямую через начало координат и найденную
точку. В качестве такой точки выберем точку (1; 2) (если Х=1,
то у=2-1 = 2). График функции у—2х изображен на рисун-
ке 16, с.
80. Линейная функция. Линейной функцией называется
такая функция, которая задана формулой y=kx-\-b, где
k и b—действительные числа. Если, в частности, fe = 0, то
получаем постоянную функцию у—Ь; если Ь=0, то полу-
чаем прямую пропорциональность y = kx.
Перечислим свойства линейной функции y=kx-\-b при
1) Область определения функции — множество всех дейст-
вительных чисел.
2) Функция y=kx-\-b ни четна, ни нечетна.
3) При fe>0 функция возрастает, а прн fe<0 убывает
на всей числовой прямой.
Т.3.2. I Графиком линейной функции y = kx-{-b является
I прямая.
Доказательство
Если k—Q, то получаем постоянную функцию у=Ь, ее графиком является
прямая, параллельная оси х (см. п. 78).
Если Ь—0, то получаем прямую пропорциональность y=kx, ее графиком
по теореме 3.1 является прямая, проходящая через начало координат
(см. п. 79).
81 W
Пусть k^O и bgto. Если точка (atj; yi) принадлежит графику функции
у=кх (т. е. выполняется равенство Vi — kXi), то точка (XiS^i+b) принадле-
жит графику функции у=кх + Ь (т. е. выполняется равенство yt + b=kxl + b).
Но преобразование фигуры F, при котором произвольная ее точка (xj; у()
переходит в точку (xj; jh4-b), является параллельным переносом (см. п. 112),
а при параллельном переносе прямая переходит в параллельную ей пря-
мую.
Итак, графиком функции y—kx+b является прямая, параллельная гра-
фику прямой пропорциональности y—kx.
На рисунке 17 изображен график функции y==kx-^~b. Это
прямая, параллельная прямой, служащей графиком функции
y=kx, и проходящая через точку (0; Ь) на оси ординат.
Число k называется угловым коэффициентом прямой, оно
равно тангенсу угла а между прямой и положительным лучом
оси х, т. е. fe=tg а.
Пример. Построить график функции у= —|-+4.
Решение. Графиком линейной функции является пря-
мая, а для построения прямой достаточно знать две точки
графика. Заполним таблицу:
х 0 4
У 4 2
(аргументу х дали значения 0 и 4 и по формуле у ——1-4
нашли соответствующие значения у). Отметим на координатной
плоскости точки (0; 4) и (4; 2) и проведем через эти точки
прямую (рис. 18).
81. Взаяшое раеввложение храфижов линейных функций.
Пусть даны две линейные функции y—kiX-^-bi и y~ksx-\-b/.
Их графиками служат прямые (см. п. 80). Эти прямые пере-
секаются, если ki =^к2 (рис. 19, а). Прямые параллельны, если
k\=k2. Последний случай, в свою очередь, можно разбить
на два: если Й1 = Й2 и 61 — 62, то прямые совпадают; если
fei — k2 и bi^b2, то прямые параллельны и не совпадают
(рис. 19,6).
82. Обратная пропорциональность. Обратной пропорцио-
нальностью называют функцию, заданную формулой ?/=“»
где fe#:0. Число k называют коэффициентом обратной про-
порциональности.
k
Перечислим свойства функции р=—.
1) Область определения — множество всех действительных
чисел, кроме нуля.
2) у=——нечетная функция (поскольку /( — х)=— =
. х —х
=-4=-/(«»•
* k
3) Если fc>0, то функция у —— убывает на промежутке
(0; 4-оо) и на промежутке (— со; 0). Если fe<0, го функция
у=-~- возрастает на промежутке (—°°;0) и на промежутке
(0; 4-оо). j
Построим график функции у——. Сначала построим ветвь
графика на промежутке (Ф; + сю). Составим таблицу значений
функции:
X 1 4 1 2 1 2 4
У 4 2 1 1 2 1 4
Нанесем полученные точки на координатную плоскость и
соединим их плавной 1фивой (рис. 20, а). Это и будет ветвь
графика функции на промежутке (0; -Ь сю).
х 1
Воспользовавшись нечетностью функции , добавим
к построенной ветви ветвь, симметричную ей относительно на-
чала координат. Получим график функции У=— (рис. 20,6).
Аналогичный вид имеет график функции У~~ при любом
положительном Л. На рисунке 21 изображен график функ-
2
Ции У=—.
Если fe<0, то ветви графика обратной пропорциональ-
ности расположены не в I и III координатных четвертях, как
в случае, когда fe>0, а во II и IV. На рисунке 22 изобра-
жены графики функций
у=_±. y=_4.
Графив обратной пропорциональности у—— называют ги-
перболой. х
83. Функция у — х2. Перечислим свойства функции у=х2.
1) Область определения функции — вся числовая прямая.
2) у=х2 — четная функция (/(—х)=(—х)2=х2=/!(х)).
3) На промежутке [0; 4- оо) функция возрастает.
В самом деле, если 0^Х|<Хг, то х?<Х®. а это и означает возрастание
функции (см. п. 77).
4) На промежутке (— оо; 0] функция убывает.
В самом деле, если Xi<Xs^0, то —Xi>—Х2$Э=0, а потому (—Xi)2>
>(—Xj)2, т. е. х?>х|, а это и означает убывание функции (см. п. 77).
Графиком функции у=х2 является парабола (см. п. 73).
Этот график изображен иа рисунке 9.
84. Функция у=х\ Перечислим свойства функции у=х3.
1) Область определения функции — вся числовая прямая.
2) у=х?— нечетная функция (/(—х)=(—х)3= — х?=
= -/(*))•
3) Функция возрастает на всей числовой прямой.
График функции у=х3 изображен на рисунке 23. Он на-
зывается кубической параболой.
85. Степенная функция с натуральным показателем. Функ-
ция у=х", где п — натуральное число, называется степен-
ной функцией с натуральным показателем. При п=1 полу-
85
чаем функцию у=х, ее свойства рассмотрены в п. 79, а гра-
фик (прямая) изображен на рисунке 8. Прн п=2
получаем функцию у=х2, ее свойства рассмотрены в п. 83, а
график (парабола) изображен на рисунке 9. Прн п=3 полу-
чаем функцию у=х3, ее свойства рассмотрены в п. 84, а гра-
фик (кубическая парабола) изображен на рисунке 23.
Пусть п — произвольное четное натуральное число, большее
двух: и=4, 6, 8, ... . В этом случае функция у=х” обладает
теми же свойствами, что и функция ^=х2. График такой функ-
ции напоминает параболу у—х\ только ветви графика при
|х| >1 тем круче идут вверх, чем больше п, а при |х| <1 тем
«теснее прижимаются» к оси х, чем больше п (рис. 24).
Пусть п — произвольное нечетное число, большее трех: П=
= 5, 7, 9 В этом случае функция у = хп обладает теми же
свойствами, что и функция у—хг. График такой функции на-
поминает кубическую параболу (только ветви графика тем
круче идут вверх, вниз, чем больше л) (рнс. 25). Отметим также,
что на промежутке (0; 1) график степенной функции у=хп
тем медленнее отдаляется от оси х с ростом х, чем больше п.
86. Степенная функция с целым отрицательным показа-
телем. Рассмотрим функцию у=Х~п, где п — натуральное чис-
ло. При п = 1 получаем у=х~1 или У~~- Свойства этой
функции рассмотрены в п. 82, а ее график (гипербола) изоб-
ражен на рисунке 20, б.
Пусть п — нечетное число, большее единицы, п=3, 5, 7,....
В этом случае функция у=х~п обладает в основном теми же
a) S)
(n—3, 5, 7,.«) напоминает график функции y—-^ (рис. 26, a).
Пусть n — четное число, например и=2. Перечислим не-
которые свойства функции у=х~\ т. е. функции у =~^ •
1) Функция определена при всех х=£0.
2) У=~^ —четная функция.
3) У—-^г убывает на (О; -Ь°°) и возрастает на (—оо;0).
Теми же свойствами обладают любые функция вида у=х~п
при четном п, большем двух.
График функции У~~^ изображен на рисунке 26,6. Ана-
логичный вид имеет график функции у=х~п, если п=4, 6,....
87. Функция у=д/х Перечислим свойства функции #=дйс;
1) Область определения — луч [0; оо). Это следует из
того, что выражение д/х определено лишь при х^О.
2) Функция у=^[х ни четна, ни нечетна.
3) Функция возрастает на луче [0; + оо).
В самом деле, пусть 0^Х|<я2. Докажем, что тогда Предпо-
ложим противное, т. е. что Тогда (см. свойство 9е
числовых неравенств, п. 24), т. е. Xt^Xs, а это противоречит условию. Зна-
чит, наше предположение неверно, а верным является неравенство
Для построения графика составим таблицу значений функ-
ции:
соединим их плавной кривой. Получим график функции у =-\/х
(рис. 27, а).
88. Функция Перечислим свойства функции у=^/х.
1) Область определения функции — вся числовая прямая.
2) Функция y—^Jx нечетна, так как %J—x = —^/х.
3) Функция y—^Jx возрастает на всей числовой прямой.
Для построения ветви графика при составим табли-
цу значений функции y=^Jx'.
X 0 1 4 8
V 0 1 1,в 2
Нанесем полученные точки на координатную плоскость и
соединим их плавной кривой; затем к построенной ветви до-
бавим ветвь, симметричную ей относительно начала координат.
Получим график функции y=^jx (рис. 27, б).
89. Функция При четном п функция У=!у/х обла-
дает теми же свойствами, что и функция у=^[х (см. п. 87),
и график ее напоминает график функции (рис. 28, а).
При нечетном п функция y=!ylx обладает теми же свойст-
вами, что и функция y—^Jx (см. п. 88), и график ее напо-
минает график функции y=^Jx (рис. 28,6).
90. Степенная функция с положительным дробным показа-
телем. Рассмотрим функцию у=х\ где г — положительная
несократимая дробь. Перечислим некоторые свойства этой
функции.
1) Область определения — луч [0; 4- оо).
2) Функция ни четная, ни нечетная.
3) Функция у—хг возрастает на [0; Ч-оо).
На рисунке 29, а изображен график функции у=хй. Он за-
ключен между графиками функций у~хъ и у—Х3, заданных
на промежутке [0; + оо).
Подобный вид имеет график любой функции вида у=Хг,
где г>1. 2
На рисунке 29, б изображен график функции у~ х3. Подоб-
ный вид имеет график любой степенной функции у=хг, где
0<г<1.
91. Степенная функция с отрицательным дробным пока-
зателем. Рассмотрим функцию у=х~г, где г — положительная
несократимая дробь. Перечислим свойства этой функции.
1) Область определения — промежуток (0; + оо).
2) Функция ни четная, ни нечетная.
3) Функция у~х~г убывает на (0; Ч~°°)-
Построим для примера график функции у—х 2. Соста-
вим таблицу значений функции:
X 1 9 1 4 1 4 9
У 3 2 1 1 2 1 3
Нанесем полученные точки на координатную плоскость и
соединим их плавной кривой (рис. 29, в). Подобный вид имеет
график любой функции у=хг, где г—отрицательная дробь.
92. Функция у—[х]. Построим график функции у=[х]
(см. п. 31). Если 0<Ж1, то у=[я]=О; если 1<х<2, то
у=[х]= 1; если — 1 =Сх<0, то у=[х]= — 1 и т. д. График функ-
ции у=[х] изображен иа рисунке 30.
93. Функция у={х}. Построим график функции у={х}
(см. п. 31). Заметим, что {х + 1}={х), поэтому достаточно сначала
построить ветвь графика на любом промежутке длиной 1, на-
пример на [0; 1). Если O^xCl, то [х]=0, а потому {х}=х.
На рисунке 31, а изображен график функции у—{х) на
промежутке [0; 1), а иа рисунке 31, 6 изображен график функ-
ции у={х} на всей числовой прямой.
94. Показательная функция. Показательная функция за-
дается формулой у=а*, где а>Он0^=1.
Перечислим свойства функции у=ах при а>1.
1) Область определения функции — вся числовая прямая.
2) Область значений функции — промежуток (0; + оо).
3) Функция не является ни четной, ни нечетной. Это сле-
дует из того, что и а~хУ= — ах.
4) Функция возрастает на всей числовой прямой.
График функции у—о^ при а>1 выглядит так, как по-
казано иа рисунке 32, а. Отметим, что эта функция принимает
любые положительные значения.
Пример 1. Построить график функции у=2х.
Решение. Составим таблицу:
X —2 -1 0 1 3
У 1 т 1 2 1 2 В
С помощью найденных точек строим график функции у—2х
(рис. 32, б).
Свойства функции у=ах при 0<а<1.
1) Область определения функции — вся числовая прямая.
2) Область значений — (0; 4- оо).
3) Функция не является ни четной, ни нечетной.
4) Функция убывает на всей числовой прямой.
График функции у=ах при 0<а<1 выглядит так, как по-
казано на рисунке 33,а. Отметим, что эта функция принимает
любые положительные значения.
С помощью найденных точек строим график функции
у=(т)'(рис- 33>
95. Обратная функция. График обратной функции. Сравним
две функции y = f(x) и y=g(x), их графики изображены на
рисунке 34. Обе они определены на отрезке [а; Ь] и имеют
областью своих значений отрезок [с; d], Первая функция обла-
дает следующим свойством: для любого j/o из отрезка [с; d]
есть только одно значение Хо из отрезка [а; такое, что
/(aro)=Jfo. Геометрически указанное выше свойство означает
следующее: любая горизонтальная прямая, пересекающая ось
у между точками cad, пересекает график функции y—f{x)
только в одной точке. Вторая функция этим свойством не
обладает: например, для значения r/i прямая у=у\ пересекает
график функции y=g(x) в трех точках. Значит, в первом
случае при каждом фиксированном ро из отрезка [с; d] уравне-
ние f (x)=jfo имеет только один корень Хо, а во втором слу-
чае при некоторых у, например, при y=yi уравнение g(x)=yt
имеет более одного корня.
Если функция y—f(x) такова, что для любого ее значения
j/o уравнение f(x)=yo имеет относительно х единственный
корень, то говорят, что функция f обратима.
Так, функция y=f (я), график которой изображен на рисун-
ке 34, а, обратима, а функция y=g(x)i график которой изобра-
жен на рисунке 34, б, необратима.
Если функция у—fix') обратима, то, выразив X из формулы
y=f(x) и поменяв затем х к у местами, получим обратную
функцию.
Обратимся еще раз к рисунку 34. Сравнивая графики функ-
ций y=f{x} и y=g(x), замечаем, что y — f{x)—возрастаю-
щая функция (и у нее есть обратная функция), тогда как
функция y—g(x) не является ни возрастающей, ни убываю-
щей (и у нее нет обратной функции). Возрастание илн убыва-
ние функции обеспечивает существование обратной функции.
Т.3.3.
Если функция y=f(x) определена и возрастает (или
убывает) на промежутке X и областью ее значений
является промежуток У. то у нее существует обрат-
ная функция, причем обратная функция опреде-
лена и возрастает (или убывает) на У.
Пример. Доказать, что у функции у=2х— 1 есть обрат-
ная, и найтн ее.
Решение. Функция у=2х — 1 возрастает на всей число-
вой прямой, значит, у нее есть обратная функция. Чтобы найти
обратную функцию, надо из формулы у=2х~ 1 выразить х.
__ I/ Ч- 1 -н
Получим х=2-~-. Поменяв х и у местами, получим у—
. Это и есть искомая обратная функция.
Если точка (х; у) принадлежит графику функции y=f(x)t
то точка (у; х) принадлежит графику обратной функции. По-
этому график обратной функции получается из графика функ-
ции y=f{x) с помощью преобразования плоскости ху, пере-
водящего точку (у; х) в точку (х; у). Этим преобразованием явля-
ется симметрия относительно прямой у=х.
Таким образом, чтобы построить график функции, обратной
к функции y—f(x\ надо график функции y=f(x) подвергнуть
преобразованию симметрии относительно прямой у=х
(рис. 35, а).
Например, если у—хп, где х^О, п — натуральное, п> 1, то
x—^Jy. Поменяв х и у местами, получим y=ttfx. Графики двух
взаимно обратных функций у — хп и у=^/х симметричны отно-
сительно прямой у=х (рис. 35,6).
96. Логарифмическая функция. Показательная функция
у=ак, где а>0, а#=1, обладает всеми свойствами, которые га-
рантируют существование обратной функции (см. теорему 3.3).
1) Область определения —(—оо- 4-оо).
2) Область значений — (0; + оо).
3) Функция у=а* возрастает при а>1 и убывает при
0<а<1.
Эти свойства обеспечивают существование функции, обрат-
ной показательной, определенной на (0; 4-оо) н имеющей об-
ластью своих значений множество (— оо; + оо).
Эта обратная функция обозначается так: y=logc х (чита-
ется: ^Логарифм числа х по основанию о»). Итак, логариф-
мическая функция y=loga х, где «>0и а=Л1,— это функция,
обратная к показательной функции у=ак.
Логарифмическая функция y=loga х обладает следующими
свойствами (они вытекают из теоремы 3.3):
1) Область определения — (0; + оо).
2) Область значений — (—оо; 4- оо).
3) Функция ии четная, ии нечетная.
4) Функция возрастает иа промежутке (0; + оо) при а > 1,
убывает иа (0; 4- со) при 0<о<1.
График функции y~loga х может быть получен из графика
функции у—а* с помощью преобразования симметрии отно-
сительно прямой у=х. На рисунке 36, а построен график
логарифмической функции для а>1, а на рисунке 36,6 — для
0<а<1.
97. Число е. Функция Функция у=1п х. Среди пока-
зательных функций р“Ох, где а> 1, особый интерес для мате-
матики и ее приложений представляет функция, обладающая
следующим свойством: касательная к графику функции (см.
п. 215) в точке (О; 1) образует с осью х угол 45е (рис. 37, а).
Основание а такой функции о* принято обозначать буквой
е, т. е. у=е\ Подсчитано, что е=2,7182818284590..., и уста-
новлено, что е — иррациональное число. Логарифмическую
функцию, обратную показательной функции у=ек, т. е. функ-
цию y=loge х, принято обозначать у=1п х (In читается «нату-
ральный логарифм*). Графики функций у—е* п у=In х сим-
метричны относительно прямой у=х (рис. 37, б).
96. Определение тригонометрических функции. Для угла а,
такого.что 0° < а < 180°, понятия sin а, cos а, tg а определены
в курсе геометрии (см. часть II). В алгебре рассматривают
повороты отрезка ОА около точки О на любой угол, при этом
отрезок ОА называют начальным радиусом. Поворот на поло-
жительный угол осуществляется в направлении против часо-
вой стрелки, поворот на отрицательный угол — по часовой
стрелке. На рисунке 38 показаны повороты на углы 180°,
300°, —225°; начальный радиус ОА в результате поворота
переходит в радиус ОВ. При повороте на 360° отрезок О А
возвращается в первоначальное положение.
Пусть а — произвольный угол. Возьмем отрезок ОА в ко-
ординатной плоскости ху так, чтобы точка А принадлежала
положительной полуоси X (рнс. 39, а). Пусть при повороте
96
около точки 0 на угол а начальный радиус О А переходит
в радиус ОВ (рис. 39, б). Тогда синусом угла а называют отно-
шение ординаты точки В к радиусу и обозначают sin а; коси-
нусом угла а называют отношение абсциссы точки В к радиу-
су и обозначают cos а; тангенсом угла а называют отноше-
ние ординаты точки В к ее абсциссе и обозначают tg а; котан-
генсом угла а называют отношение абсциссы точки В к ее орди-
нате и обозначают ctg а.
Приведем таблицу значений синуса, косинуса, тангенса н
котангенса некоторых углов:
Функция Аргумент а
0” 30" 45° 60° 90° 180° 270°
81д а 0 1 2 2 уз 2 1 0 1
сова 1 £ 2 2 1 2 0 -1 0
tga 0 Уз 3 1 Vs - 0 -
ctg а - Уз 1 3 0 - 0
Из определений следует, что не существует тангенс углов,
косинус которых равен 0, и котангенс углов, синус которых
равен 0.
Можно говорить о синусе, косинусе, тангенсе и котангенсе
не только угла, но и числа, используя радианную меру угла:
1 рад=(^)"«57“, 1°=т=5 рад«0,017 рад.
Например, sin 4«sin (4 • 57°)=sin 228°,
cos 225“=cos (225--^)=cos
Функции y=sinx, s/=cosx, j/=tgx, #=ctgx называют
тригонометрическими функциями.
99. Знаки тригонометрических функций по четвертям.
Пусть при повороте около точки О на угол х начальный радиус
ОА переходит в радиус ОВ. Из определений тригонометри-
ческих функций (см. п. 98) следует, что знак sin х совпадает со
знаком ординаты точки В, а знак cos л совпадает со знаком
абсциссы точки В. Знаки тригонометрических функций по
четвертям указаны на рисунке 40.
100. Исследование тригонометрических функции на чет-
ность, нечетность. Если при повороте около точки О на угол а
начальный радиус ОА переходит в радиус ОВ, то при повороте
на угол — а начальный радиус ОА перейдет в радиус ОВ', сим-
метричный ОВ относительно оси абсцисс (рис. 41). Абсциссы
точек В и В' равны, а ординаты равны по модулю, но противо-
положны по знаку. Это значит, что
cos(— х)—cos x, tg(—х)=—tgx,
sin(~x)= — sin я, ctg (—x)==—ctgx.
Таким образом, функции j/ = sinx, j/='tgx, j/=ctgx нечет-
ные, а функция j/=cosx четная (см. п. 74).
101. Периодичность тригонометрических функций. Если
при повороте около точки О на угол х начальный радиус ОА
переходит в радиус ОВ, то при повороте иа угол х + 360°
начальный радиус ОА также перейдет в радиус ОВ. Значит,
4 Заказ769
98
sin (x4-360°)=sin x,
cos (x-|-360°)—cos x.
Более общими являются равенства
sin (x-|-360ofe)=sin x,
cos (x+360° k)=cos x,
где k — любое целое число.
Если аргумент х выражен в радианах, то
sin (x+2%ft)s=sin х,
COS (х-|- 2л&)=СО8 X,
где k — любое целое число.
Для функций z/=tgx и j/=ctgx справедливы равенства
tg(x4-nfc)=tgx,
ctg (х-|- nfe)=ctg X,
где k — любое целое число.
Таким образом, любое число вида 2л& является периодом
функций sin х, cos х, а число вида nk — периодом функций
tg х, ctg х. При этом 2л — основной период sin х, cos х,
ал — основной период tg х, ctg х (см. и. 76).
Используя свойства четности, нечетности, периодичности,
можно тригонометрическую функцию интересующего нас угла
свести к тригонометрической функции угла, заключенного в
пределах от 0° до 180°.
Пример. Вычислить sin 945°.
Решение. Имеем sin945°==sin(720° + 225°)=
=sin (225°+ 360° • 2) = sin (225°—360°)=sin (—135°)=
=—sin 135°. Далее, sin 135°=sin (180°—45c)—sin 45° (cm.
n. 126), но sin 45°=~(cm. n. 98), значит, sin 945°= —sin 135° =
= — sin 45°= - y-.
102. Свойства и график функции у—sin х.
1) Область определения — множество всех действительных
чисел.
2) Область значений — отрезок [—1; 1}
3) Функция периодическая; основной период равен 2л
(см. п. 101).
4) Функция нечетная (см. п. 100).
5) Функция возрастает на промежутках !—^--|-2лп;
y-4-2nnJ и убывает на промежутках }-2лп; ^4*2лп|,
n£Z (рис. 42).
Взяв контрольные точки (0; 0), -0, 1), (л; 0),
построим график функции jr=sin х на отрезке [0; л] (рис. 43,а).
Так как функция у—sinx мечетная, то, выполнив симметрию
построенного графика относительно начала координат, полу-
чим график функции на отрезке [—л; л] (рис. 43,6). Наконец,
воспользовавшись периодичностью функции y=sin х, можно
построить график на всей области определения (рис. 43, в).
103. Свойства и график функции у=созх. Исследование
функции у=созх проводится аналогично исследованию функ-
ции ^=sinx (см. п. 102). Перечислим свойства функции
y=cosx:
1) Область определения функции — множество всех действи-
тельных чисел.
2) Область значений — отрезок [— 1; 1J
3) Функция периодическая с основным периодом 2л.
4) Функция четная.
5) Функция убывает на промежутках [2лп; л+2лп] и
возрастает иа промежутках [—л-Ь2лп; 2лл], n£Z.
График функции у—созх изображен на рисунке 44.
100
104. Свойства и график функции y=tg х.
1) Область определения: х^=-^~f-nfe, k£Z.
2} Область значений — вся числовая прямая.
3) л — основной период функции.
4) Функция нечетная. / п я
5) Функция возрастает иа промежутках (—2*+лп;-|—}-
4-лп) .
Выбрав несколько контрольных точек (0; 0), (-j-; 1),
(“5“ 5 л/^)’ строим график функции y=tgx на промежутке
[0; 4г) (рис. 45,а). Воспользовавшись нечетностью функции
, ' , / л л \
i/=tgx, построим график на интервале I —у; -^-1
(рис. 45,6). Наконец, воспользовавшись периодичностью функ-
ции y=tgx, построим график на всей области определения
(рис. 45,в).
105. Свойства и график функции y=ctgx.
1) Область определения функции: x=£nk, k£Z.
2) Область значений функции —- вся числовая прямая.
3) Функция периодическая с основным периодом л.
4) Функция нечетная.
5) Функция J/=ctgx убывает на промежутках (лп; л-Ьяп).
График функции p=ctgx изображен на рисунке 46.
106*. Функция j/=arcsinx. Функция y=sinx возрастает
иа отрезке £—принимает на нем все свои значения
от —1 до 1 (рис. 43). Значит, для функции z/ = sinx,
—существует обратная функция (см. п. 95). Эту
функцию обозначают j/=arcsinx (читается «арксинус х«).
График функции у — arcsin х может быть получен из
образования симметрии последнего относительно прямой
У—* (рис. 47).
Перечислим некоторые свойства функции jr=arcsinx:
1) Область определения— отрезок [—1; 1].
2) Область значений — отрезок
3) Функция нечетная: arcsin(—х)~ — arcsin х.
4) Функция возрастающая.
Из сказанного выше следует, что записи у = arcsin х и
X=siny, —эквивалентны. Подставив в равен-
ство x = sin у вместо у его выражение, т. е. arcsin х, по-
лучим x=sin (arcsin х). Следовательно, для любого х из [— 1; 1]
имеем:
sin (arcsin х)=х, —^-^arcsin x=^-|-.
Последние два соотношения позволяют истолковать arcsin m,
где — так: arcsin т — это число, взятое в пре-
л л
делах от —— до — и такое, что его синус равен т.
Пример. Вычислить: a) arcsin ; б) arcsin ( —.
Решение, а) По определению у—arcsin ----это такое
число, что sin у=^-и —уСУОтсюда следует, что у=-~-.
Таким образом,
. д/з л
arcsin -^-=—.
б) Рассуждая аналогично, получаем arcsin • Но
по свойству нечетности имеем arcsin^——arcsin
следовательно, arcsin (—f)=—£“
107*. Функция jr=arccos х. Функция у—cos х убывает на
отрезке [О; л], принимает на нем все значения от —1 до 1
(рис. 44). Значит, для функции у=cos х, рассматриваемой на
отрезке [О; л], существует обратная функция (см. п. 95). Она обо-
значается arccos х (читается «арккосинус х>).
График функции у=arccos х получается из графика
функции у = совх, О^х^л, с помощью преобразования сим-
метрии относительно прямой у = х (рис. 48).
Перечислим некоторые свойства функции у = arccos х:
1) Область определения — отрезок [—1; 1J
2) Область значений функции — отрезок [0; л].
3) Функция не является ни четной, ни нечетной.
4) Функция убывающая.
Из сказанного выше следует, что записи у=arccos х и
x = cos у, эквивалентны. Подставив в равенство
х —cos у вместо у выражение arccos х, получим cos (arccos х)= х.
Следовательно, для любого х из промежутка [—1; 1] имеем:
cos (arccos х)=х, 0^ arccos х^л.
Последние два соотношения позволяют истолковать arccos т,
где —так: arccos т —это число, взятое в пределах
от 0 до л и такое, что его косинус равен т.
Отметим, что имеет место следующее тождество:
arccos (—х)=л—arccos х. (1)
103 Lz_*l
В его справедливости можно убедиться с помощью графика
функции у=arccos х (рис. 49).
Пример. Вычислить: a) arccos б) arccos (—
д/2
Решение, а) По определению arccos —— это такое
число у, что cos у и ОСу^л. Отсюда следует, что jr=-“.
Таким образом, arccos
б) По формуле (1) имеем arccos =л—-arccos^-.
_ / -у/2\ я Зя
Значит, arccos I —yJ = я —4~~ “4" •
108*. Функция у = arctg х. Функция y=tgx возрастает
на интервале ( —; 40 , принимает на нем все свои значения
(рис. 45). Поэтому на указанном интервале для функции
ff=tgx существует обратная функция (см. п. 95). Она обозна-
чается у=arctg х (читается «арктангенс х»).
График функции jf=arctg х получается из графика функ-
ции y=tg х, —с помощью преобразования сим-
метрии относительно прямой У = х (рис. 50).
Перечислим некоторые свойства функции # = arctg я:
1) Область определения — множество всех действительных
чисел.
2) Область виачений функции — интервал (—у; 40.
3) Функция нечетная: arctg (—х)— — arctg х.
4) Функция возрастающая.
Из сказанного выше следует, что записи =arctg х и
X — tg у, —~-<у<4р эквивалентны. Для любого х имеем:
tg (arctg х)=х, —^-<arctg х<-~.
Последние соотношения позволяют истолковать arctg т так:
arctg т — это число, взятое в пределах от —до (исклю-
чая сами значения —и -~) и такое, что его тангенс равен т.
Пример. Вычислить: a) arctg 1; б) arctg (—д/3).
Решение, а) По определению у=arctg 1—это такое
число, что tgy=l и —Отсюда следует, что
У=~г-* Таким образом, arctg 1—
104
б) Рассуждая аналогично, получим arctg д/3=-^-. Но
arctg (—д/3)= — arctg д/3. Значит, arctg (—д/3)— —
109*. Функция у=arcctg х. Функция y=ctgx У^1^вает
иа интервале (0; л), принимает на нем все свои зна^ения
(рис. 46). Следовательно, иа этом интервале для Функции
У—ctg х существует обратная функция (см. п. 95). Она обозна-
чается у—arcctg х (читается «арккотангенс х»).
График функции у— arcctg х получается из графика
функции i/=ctgx, 0<х<л, с помощью преобразования сим-
метрии относительно прямой у—х (рис. 51).
Перечислим некоторые свойства функции у = arcctg х:
1) Область определения — множество всех действительных
чисел.
2) Область значений функции — интервал (0; л).
3) Функция не является ни четной, ни нечетной.
4) Функция убывающая.
Из сказанного выше следует, что записи у = arcctg х и
x—ctgy, 0<у<л, эквивалентны. Для любого х иьхеем:
ctg (arcctg х)=х, OCarcctg х<п.
Последние соотношения позволяют истолковать arcctg т
так: arcctg т — зто число, взятое в пределах от 0 я
(исключая сами значения 0 и л) и такое, что его котангенс
равен т.
Имеет место тождество
arcctg (—я)=л—arcctg х. (1)
Пр и м е р. Вычислить arcctg (— д^).
Ре шение. Сначала вычислим у — arcctg д/3. Это 'Оакое
число, что ctg у=-\/3 и 0<у<л. Значит,
105 IzXd
По формуле (1) имеем arcctg (—^3)=я —arcctgЗначит,
arcctg (—\/3)=л—•
§ 11. Преобразования графиков
110. Построение графика функции y—mf (х). Решим не-
сколько задач.
Задача 1. Построить график функции y — mf (х), где
т>0, т^1, если задан график функции y—f (х).
Решение. Ординаты точек графика функции y—mf(x)
получаются умножением на т соответствующих ординат
точек графика функции y—f(x). Такое преобразование тра-
фика функции y=f(x) называется его растяжением от оси х
с коэффициентом т, если т>1, и сжатием к оси х, если
0<т<1,
Задача 2. Построить график функции y——f(x'), если
задан график функции y—f (х).
Решение. При одном и том же значении х ординаты
точек графика функции y=f(x) и функции у=—/(х) отли-
чаются только знаком. Значит, график функции у=—f (х)
можно получить из графика y=f(x) преобразованием сим-
метрии последнего относительно оси х (рис. 52, а).
На рисунке 52, б изображены графики функций .у = 10* и
У=—10х.
Задача 3. Построить график функции y=mf(x\ где
т<0, тп^=—1, если задан график функции y—f{x\
Решение. Так как mf (х)= — |?п|/(х), то график
функции y-mf(x') может быть получен при помощи растя-
женил (сжатия) графика функции y=f(x) от оси х с коэф-
фициентом 1т| и последующим преобразованием симмет-
рии относительно оси х (см. задачи 1 и 2).
На рисунке 53, а изображены графики функции у—х4 и
у = — Зле4.
На рисунке 53, б изображены графики функции p=log2*
и y=^-log2x.
111. Графики функции у=пх2, у—ах3. Графиком функции
у=х2 является парабола, Чтобы построить график функции
у=ах3, нужно осуществить растяжение (сжатие) параболы
у=х3 от оси х с коэффициентом |а|; при этом если о<с0, то
график функции у=|а|х2 нужно еще подвергнуть преобразо-
ванию симметрии относительно оси х (см. п. 110).
На рисунке 54, а изображены графики функции у=ах2 для
а, равного 1; —1; 3; —Все эти графики называют па-
раболами. При а>0 ветви параболы, служащей графиком
функции у—ах2, направлены вверх, а при с<0 — вниз.
Аналогично, зная график функций у = х3, можно построить
график функции вида у—ах3. На рисунке 54, б изображены
эти графики для случаев а, равного 1; —1; 3.
112. Построение графика функции y=f (х — Пусть
известен график функции y—f(x), а построить нужно
график функции y~f(x—
Положим х’—х—т, у'=у—п. Тогда формулу y=f(x—т)+п, или,
что то же самое, y—n=f(x~m), можно переписать в виде У'=/(*'). Таким
образом, график функции y=f(x —т)+п, построенный в координатной
плоскости ху, совпадает с графиком функции y'=f(x'), построенным в ко-
ординатной плоскости х'у’.
Формулы х'=х—т, у'=у—п, или, что то же самое, х=х’+т, у=*у'-\-п,
надают параллельный перенос, при котором любая точка (х; у) переходит
в точку (x-f-m;y + n) и, в частности, начало координат переходит в точку
(»»; п).
Чтобы построить график функции y=f (х — т)+п, нужно:
1) выполнить параллельный перенос плоскости, выбрав на-
чалом новой системы координат х'у' точку О' (т; п);
2) в плоскости х'у' построить график функции y'=f(x').
Пример. Построить график функции у— дбс —2+4.
Решение. 1) Выполним параллельный перенос плоско-
сти, поместив начало новой системы координат х'у' в точку
О' (2; 4).
2) В плоскости х'у' построим график функции у =-\’х.
Это и есть требуемый график (рис. 55).
На рисунке 56,а изображены графики функции y=f(x),
f (х) — 2, f (х)+3, а на рисунке 56, б — графики функций
У=/(Д y=f(x—2\ y=f(x+3).
113. График квадратичной функции. Квадратичной назы-
вают функцию, которую можно задать формулой вида у~
—ax2-\-bx-\~c, где а, Ь, с — любые действительные числа,
причем а=^0. Для построения графика этой функции выпол-
ним следующие преобразования (называемые «выделением
полного квадрата») квадратного трехчлена ах2 + &х+с:
ахг + 6х + с=О(хг+Лх)+с=а((«г+2-^х+^г)-
2 . t । I । b\2 । 4ae—b2
Итак, + a\x+to) 4----------------•
Для построения графика функции
нужно (см. п. 112) выполнить параллельный перенос плоско-
сти, поместив начало новой системы координат х'у' в точку
график функции у'=а (x'f\ Прямая х— —— называется осью
симметрии параболы, служащей графиком квадратичной
, 2 1 l 1 { Ь 4ас— Ь2 X
функции у=ах -j-bx-j-c, а точка О I —— точка
пересечения параболы с ее осью симметрии — называется
вершиной параболы.
Если а>0, то ветви параболы, служащей графиком функ-
ции у—ах~-\-Ьх-}-с, направлены вверх (рис. 57, а); в этом слу-
чае функция убывает на промежутке (— оо; —] и во3'
растает на промежутке £—; -|-оо^. Если а<0, то ветви
параболы направлены вниз (рис. 57, б); в этом случае функция
возрастает на промежутке — оо; —J и убывает на про-
межутке 4- 00 ) •
Пример. Построить график функции у=-|- х2 4~ 5.
Решение. Имеем у=-^-хг4-4х + 5=-^-(х2-|-8х) + 5 =
=-|- ((х2 + 8х +16) —16) + 5 = -у (х 4- 4)2 — 3. Выполним парал-
лельный перенос плоскости, поместив начало новой системы
координат х'у' в точку О'(—4; —3), и построим в коорди-
натной плоскости х'у' параболу — график функции у'=-^-(х')2.
Это и есть график функции у=-|-х2-|-4х4-5 (рис. 58).
114. Способы построения графика квадратичной функции.
Графиком функции у—ах2 4- Ьх-\- с, где а=/=0, является парабо-
110
ла (см. п. 113). Для ее построения на практике используются
трн способа.
Первый способ — отыскание координат вершины па-
раболы по формулам.
Ь 4а с— Ь2
Х°~ —2^; У°~ 4^ '
Пример 1. Построить график функции у=2х2—4x4-1.
Решение. Здесь а=2, Ъ= — 4, с= 1. Значит,
b 4ас— b2 - -rr z- - к
Хо=—‘2д'=1» У°~—4^—= —1. Итак, (1; — 1) — вершина па-
раболы. Для построения графика надо знать координаты еще
нескольких точек:
X 0 2 3
V 1 1 7
Отметив вершину параболы, полученные точки и точки,
симметричные им относительно оси параболы, строим требуе-
мый график (рис. 59, а}. Заметим, что запоминать формулы
координат вершины параболы не следует. Достаточно вос-
пользоваться тем, что если х0 — абсцисса вершины параболы, то
в этой точке у' (хо)=О (см. п. 217). Иауравнения (ох24- Ъх-\-с)'=
=0, т. е. 2ах-}-Ъ — 0, находим х=—— абсцисса вершины
параболы.
Второй способ — построение параболы по точкам с
ординатой, равной свободному члену квадратного трехчлена
ах2-}-Ьх-]-с.
Пример 2. Построить график функции у—х2 —4х-|-5.
Решение. Найдем точки графика, имеющие ординату,
равную свободному члену квадратного трехчлена, т. е. рав-
ную пяти. Для этого решим уравнение х2—4х-|-5 = 5. Имеем:
х2—4х=0, х(х—4)=0, откуда Xi=0, х2 = 4.
Итак, мы нашли две точки графика А (0; 5) и В (4; 5).
Отметим их на координатной плоскости (рис. 59, б). Мы знаем,
что графиком является парабола. Точки А и В лежат на этой
параболе и имеют одинаковую ординату. Значит, точки А п В
симметричны относительно оси симметрии параболы, а потому
ось симметрии параболы проходит перпендикулярно отрезку
АВ через его середину. Так как абсцисса точки А равна нулю,
а абсцисса точки В равна четырем, то уравнение оси параболы:
х = 2. Подставив значение х=2 в формулу у=х2 — 4х 4- 5, полу-
чим у=4— 84-5 = 1. Значит, вершина С параболы, т. е. един-
ственная точка параболы, лежащая на ее оси симметрии, имеет
координаты Хо=2, уо=1. Отметив иа координатной плоскости
точку С (2; 1), построим параболу, проходящую через три точки
А, В, С.'Это и будет график функции у—х?—4x4-5 (рис. 59, б).
(Для более точного построения можно найти координаты еще
нескольких точек и построить их.)
Третий способ — построение параболы по корням
квадратного трехчлена.
Пусть Х| и Х2 — корни квадратного трехчлена axz + bx+e
(о решении уравнения ах2-}~Ьх-}-с = 0 см. п. 137). Тогда па-
рабола, служащая графиком функции у~ах2-}- Ьх-[-с, пере-
секает ось абсцисс в точках А (xi; 0) и В (хг; 0), а ось симметрии
параболы проходит перпендикулярно отрезку АВ через его
середину. Зная абсциссу Хо вершины С параболы (точка С
лежит на оси симметрии параболы, поэтому хр—*' »
найдем по формуле у=ах24~ fex-J-c ее ординату, а затем постро-
им параболу по трем точкам А, В, С.
Пример 3. Построить график функции у= —х2 + 6х — 5.
Решение. Из уравнения —х24-6х—5=0 находим Х| =
= 1, ха=5. Значит, мы знаем две точки искомой параболы:
А (1; 0) п В (5; 0). Уравнение оси симметрии параболы тако-
во: х=3. Подставив значение 3 вместо х в формулу у= —х2+
4-6х —5, находим у = 4. Значит, вершиной параболы служит
точка С (3; 4). По трем точкам А, В п С строим параболу —
график функции у— — х24-6х— 5 (рис. 59, б).
115. Построение графика функции y=f(kx). Решим не-
сколько задач.
Задача 1. Построить график функции y — f (fex), где k > 0,
fe=/=l, если задан график функции y = f(x).
Решение. Ордината графика функции у =f (kx) в точке х
равна ординате графика функции y=f(x) в точке kx. Это
значит, что график функции y=f(kx) получается из графика
функции y—f(x) сжатием с коэффициентом k к оси у (если
0<fe<l, то фактически получается растяжение от оси у с ко-
эффициентом .
На рисунке 60 изображены графики функций у=агссозх
и у=агссоз 2х, на рисунке 61 — графики функций у=-у[х иу~
__/ X
у 3 ‘
Задача 2. Зная график функции y~f(x)f построить гра-
фик функции y = f{ — х).
Решение. Ордината графика функции y=f (—х) в точке
X равна ординате графика функции y=f(x) в точке — х. Это
значит, что график функции y = f(—х) может быть получен
из графика функции y—f(x) преобразованием симметрии
последнего относительно оси у.
На рисунке 62 изображены графики функций j/ = log3X н
из
Задача 3. Зная график функции y=f (х), построить
график функции y=f(kx), где fe<0.
Решение. Имеем f (kx) — f (— I k | x). Поэтому график
функции y — f(kx) может быть получен сжатием графика
функции y=f(x) с коэффициентом |fe| к оси у и симметрией
полученного графика p=f (|й| х) относительно оси у.
з
На рисунке 63 изображены графики функций у~х2 и
3_
у=(-2х)2.
116. Сжатие и растяжение графиков тригонометрических
функций. Здесь речь идет о построении графиков функций
вида у = т sin kx, у=т cos kx, у=т tg kx, y=m ctg kx.
Вообще говоря, построение графика функции у — т sin kx
осуществляется в три этапа: 1) строят график функции у=sin х
(см. п. 102); 2) строят график функции у= sinfex (см. п. 115);
3) строят график функции у=т sin kx (см. п. 110). Аналогич-
но обстоит дело с другими тригонометрическими функциями.
На практике обычно при построении графика функции
у—т sin kx (у = т cos kx) выполняют растяжение и сжатие
Для одной полуволны графика функции у—sinx (y=cosx),
а затем строят весь график. При построении графика функции
У~ т tg kx (у~ т ctg kx) выполняют растяжение и сжатие для
одной ветви графика функции y=tgx (y=ctgx), а затем
строят весь график.
Пример. Построить график функции у= —3 cos 2х.
Решение. Построим одну полуволну графика функции
J/==cosx. Осуществив ее сжатие к оси у с коэффициентом 2,
получим график функции y=cos 2х. Теперь осуществим растя-
экение полученного графика от оси х с коэффициентом 3, а
затем преобразование симметрии относительно оси х. В резуль-
тате мы получим график функции у= — 3 cos 2х. На рисунке
64, а показана одна полуволна графика, а на рисунке 64, б —
весь график.
117. График гармонического колебания у—A sin (cox-f-a).
Тригонометрические функции используются для описания коле-
бательных процессов. Один из наиболее важных процессов
такого рода описывается формулой
у=A sin (сох + а). (1)
Эта формула называется формулой гармонических или
синусоидальных колебаний. Величина А называется ампли-
тудой колебания, она характеризует размах колебания. Вели-
чина <о называется частотой колебания. Чем больше to, тем
больше число колебаний за единицу времени (число колеба-
ний за единицу времени равно — } . Наконец, а называется
начальной фазой колебания. л
Если, например, груз, висящий на пружине, вывести из
положения равновесия, то ои начнет совершать вертикаль-
ные колебания. Вакой движения выражается формулой (1), где
у — отклонение груза от положения равновесия, а х —
время. Тот же закон встречается в теории переменного электри-
ческого тока. При вращении прямоугольной рамки, сделанной
из проводящего электрический ток материала, в магнитном
поле по ней идет переменный ток. Если рамка вращается равно-
мерно, величина тока меняется по закону гармонических коле-
баний (1).
Построим график функции у=А ein (сох 4- а). Прежде всего
преобразуем функцию к виду у—A sin (со (х4~ ))- Построе-
ние графика этой функции выполним в несколько этапов.
1) Осуществим параллельный перенос системы координат,
поместив начало новой системы х'у' в точку О' (—; 0^ .
2) В системе х'у' построим график функции у' —sin х'
(при этом можно ограничиться одной полуволной).
3) Осуществив сжатие построенного графика к оси у' с ко-
эффициентом to, получим график у'=sin cox'.
4) Осуществив растяжение последнего графика от оси х' с
коэффициентом А, получим требуемый график.
Пример 1. Построить график функции у = 2 sin ( -|—
Решение. Имеем y = 2sin(-|-(x—£-)). Построение
графика выполним в несколько этапов.
1) Осуществим параллельный перенос системы координат,
выбрав началом новой системы точку О' ; 0^ .
В системе х'у' нам нужно построить график функции у'=
=2 sin-g-x'.
2) Строим график функции у'=в1п.х'.
3) Выполним сжатие графика к оси у' с коэффициентом —
(т. е. растяжение с коэффициентом 3), получим график функ-
ции y'=sin^-.
4) Осуществим растяжение последнего графика от оси х' с
коэффициентом 2. Полученный график является графиком
функции у = 2 sin (рис. 65).
На практике вместо сжатия, растяжения и параллельного
переноса часто поступают иначе: отыскивают значения х, при
которых заданная функция обращается в нуль, и значения, при
которых она принимает наибольшее п наименьшее значения.
Далее строят график по точкам.
Пример 2. Построить график гармонического колебания
у = 3 sin (2х+-у) .
Решение. Решим сначала уравнение 3sin^2x-|—J-)=0.
Имеем (см. п. 154) 2x+~=nfe, х=—k^z- Дадим
параметру k два значения: 0 и 1. При k—O имеем х = —
при fe = l имеем х=-^-. Значит, точки Ai (—0^ и
Аг ( ; 0^ служат концами одной полуволны искомой сину-
соиды. Далее, серединой отрезка [ —; -|-j является точ-
ка в которой функция 3sin^2x-|—принимает макси-
мальное значение, равное трем. Значит, М ; 3^ — точка
максимума (см. п. 217). Отмечаем на координатной плоскости
точки Ai ( —О) , -у; б) и М ( — ; з) и строим полу-
волну искомого графика (рис. 66, а). После этого строим гра-
фик заданного гармонического колебания (рис. 66, б).
ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ
§ 12. Преобразование выражений, содержащих переменную
под знаком логарифма
118. Понятие трансцендентного выражения. Трансцендент-
ным называется выражение, содержащее переменные под зна-
ком трансцендентной функции, т. е. под знаком показатель-
ной, логарифмической, тригонометрических или обратных три-
гонометрических функций. Примеры трансцендентных выраже-
ний: logs а+log2 Ъ\ sin а-cos p-cos у; arcsin (х2 —х).
119. Определение логарифма положительного числа по
данному основанию. Логарифмом положительного числа х по
основанию а(а>0, п=/=1) называется показатель степени, в
которую нужно возвести число а, чтобы получить число х:
Равенство logax = у означает, что ау=х.
Например, logs 81 = 4, так как 34=81; logic 0,001= — 3,
таккак 10~3=0,001; log 1 -у2=—— ,таккак^—} =22=-у2.
Из определения логарифма вытекают следующие важные
равенства:
log0 1=0,
logea=l.
Первое следует из того, что а°=1, а второе — из того,
что а1 —а.
Вообще имеет место равенство logaar—r.
В записи logflx число а — основание логарифма, х — лога-
рифмируемое число.
120. Свойства логарифмов.
1°. Если Х|>0 и Х2>0, то
loge xtx2=loge xt 4- loge x2
(логарифм произведения равен сумме логарифмов сомножите-
лей).
Например, log3 15=log3 (3*5)=log3 3 4- logs 5 = 1 + logs 5.
2°. Если Xi>0 и X2>0, то
log. =log. x, — log,
*2
(логарифм частного равен разности логарифмов делимого и
делителя).
Например, log2 1,25 = log2 = logs 5 — logs 4=log25 — 2.
Если х1 <О и х2<0, то написать
logo x1x2=loga Xi Ч-Ioga Xi
нельзя, так как правая часть такого «равенства» не имеет смысла
(логарифм отрицательного числа не существует). Здесь можно рассуждать
так: Xi и I; — отрицательные числа, следовательно, XiX2>0. Но тогда х}х2=
=а|Х1Х2] =]Х1| • |Хг|. Значит, logo Х]Х2 = logu ]X||-lx2|.
Так как |Х||>0 и IXsI^O, то, применив свойство 1°, получим
log» |Х,| .]Х2| =loga |х,| +loga |х2|.
118
Итак, если XjXi>0, то
10ga X,Xi=lOga Ixi I +loga !Xil
и аналогично logo —=loge |xj| — loga |x2!
Xj
(нетрудно заметить, что оба последних равенства справедливы и в случае,
когда Xi>0, Xi>0>.
3°. Если х>0, то
log. х*=r log. х
(логарифм степени равен произведению показателя степени на
логарифм основания степени).
Пример 1. logs 8I=logB 3*=4 log5 3.
__ "s 1
Пример 2. log3 -V2~log3 2 logs 2.
з I о
Пример 3. Вычислить logs уесли logs 3=a.
Решение. Имеем:
logs =logs = - j- (logs 3 — logs 4)=(a — 2).
Справедливо следующее утверждение: если k — четное чис-
ло, то log0xfe=felog0 |х| для любого XqtO.
Например:
logs хА=4 log2 |х|; log3 х2—2 log3|xl.
121. Переход к новому основанию логарифма. Справедливы
следующие два свойства, позволяющие перейти к новому осно-
ванию логарифма: ____
1°. Если х>0, то
iogj G
(формула перехода к новому основанию).
Например:
1овг3=йН:
OKs z togs a logs а
2°. Если х>0, то
logD x=log0» X*.
Например, logs 5= logs3 53=log^-^5.
119 Izxd
Пример 1. Вычислить logs 6, если log2 3— a, logs 10=^6.
Решение. Перейдем в log56 к основанию 2. Восполь-
зовавшись свойством Iе, получим:
1он 6—log2 6_log2 (2'3)=.loga 2+fog23_14-o
logs 6 , 10 logs 10—logs 2 6—1*
loe2~2
Пример 2. Вычислить log^ \/32.
Решение. Согласно свойству 2° можно основание лога-
рифма и логарифмируемое число возвести в одну и ту же сте-
пень, при этом числовое значение выражения не изменится.
Имеем:
5
________ _ _________ 2 5
togi5V32=tofel4W=tog2 V32=log2 2 =-£
122. Логарифмирование и потенцирование. Если некоторое
выражение А составлено из положительных чисел с помощью
операций умножения, деления и возведения в степень, то,
используя свойства логарифмов, можно выразить loga А через
логарифмы входящих в выражение А чисел. Такое преобразо-
вание называется логарифмированием.
Пример 1. Прологарифмировать по основанию 5 выра-
126asfc2 . „
жение ———, где а, о, с — положительные числа.
Решение. Используя свойства логарифмов (см. п. 120),
получим logs 12^.& =log5 (12 5а3Ъ?) — log5 -\£=logs 125+
1_
4-logs o34-10gs Ь2—logs с2 =34-3 logs о4-2 tog5 Ь—log6 с.
Часто приходится решать обратную задачу: находить вы-
ражение по его логарифму. Такое преобразование называется
потенцированием.
Пример 2. Найти х, если log3 х= 2 log3 5 +-|- log3 8 —
— 3 log3 10.
i
Решение. log3 х= log3 25+log3 8 —log3 10®=
=log3g.-2^=log3^
K 1000 83 20
Из равенства log3x — log3^| находим, что х^=~.
120
123. Десятичный логарифм. Характеристика и мантисса де-
сятичного логарифма. Если основание логарифма равно 10, то
логарифм называется десятичным. Вместо записи logic х при-
нята запись 1g х. На рисунке 67 изображены графики функций
у=1П* м y^lgx.
В частности, для десятичных логарифмов справедливы ра-
венства:
101£О=а
1g 1=0, 1g 0,1= 1,
lgl0=l, lg0,01= — 2,
1g 100=2, 1g 0,001-- 3,
1g 1000=3, 1g 0,0001 = - 4,
lgl0"=n.
Пусть положительное число а представлено в стандартном
виде (см. п. 34): a=ai«10", где l^aiClO, (л — поря-
док числа о). Прологарифмируем число а по основанию 10, вос-
пользовавшись свойствами логарифма (см. п. 120).
Имеем 1g a = lg(aj • 10n)=lgai4-lg 10"=lg си+п. Итак,
Iga^lgai+n. (1)
Поскольку 1 < 10, то 1g 1 =Clg aj <lg 10, t. e.
O^lgaiCl. Поэтому из равенства (1) следует, что п
есть наибольшее целое число, не превосходящее число 1g а,
иначе п есть целая часть числа 1g а, т. е. n=[lga] (см. п. 31).
Слагаемое 1g в! есть дробная часть числа 1g а, т. е. 1g ai =
121
={lga} (см. п. 31). Целая часть числа 1g а, т. е. порядок числа
а, называется характеристикой 1g а, а дробная часть числа
Ig а — его мантиссой.
Имеет место следующее утверждение: если число а2>0 ум-
ножить на 10*, где k — целое число, то мантисса логарифма
не изменится, иными словами, 1g а и 1g (а-10й) имеют одина-
ковые мантиссы.
Б самом деле, имеем:
(с- 10t)=lg а+10*=lg(ai‘10")4-fe=lgai+n+fc'
Мантиссой числа lg (а-10*) является Igfli, т. е. то же число, которое
служит мантиссой для 1g а.
§ 13. Формулы тригонометрии и их использование
для преобразования тригонометрических выражений
124. Тригонометрические выражения. Выражение, в кото-
ром переменная содержится под знаками тригонометриче-
ских функций, называют тригонометрическим. Для преобра-
зования тригонометрических выражений используют свойства
тригонометрических функций, отмеченные в п. 100—105
и формулы тригонометрии, указанные в п. 125—131.
125. Формулы сложения и вычитания аргументов. Для
любых действительных чисел аир справедливы формулы:
cos (а 4-0)=cos a cos 0—sin a sin 0, (1)
cos (a—0)=cos a cos 04-sin a sin 0, (2)
sin (a4-0)=sin a cos 04-cos a sin 0, (3)
sin (a—0)=sin a cos 0—cos a sin 0, (4)
<5)
Формула (5) верна при a, 0, a 4-0, отличных от
k(-Z. Формула (6) верна при a, 0, a —0, отличных от -£-4-nit,
fefEZ.
Пример 1. Вычислить sin 75°.
Решение. Имеем sin 75°=sin (30° 4-45°). Воспользовав-
шись формулой (3) при а =30°, 0=45°, получим:
sin (30° 4-45°)=sin 30° cos 45° 4-cos 30° sin 45°.
122
Известно, что sin 30° — ~ r cos 45°=sin 45Q=-^, cos 30°=-—
(cm. n. 98). Значит, sin(30° + 45°)=i—4-^-;^=:!^±^.
Итак, sin 75° =£±£=£<1±A.
4 4
йп(-?+“)-COS( 4+%
Пример 2. Упростить выражение —--г---------
вь(Л+«)+ео.(^+а)
Решение. Воспользуемся для sin (—+“) и «оз
формулами (3) и (1) и учтем, что sin-?-=соз 4-—.
4 4 2
Получим
ein^-| 4-а)—cos(-j 4-а)
ein^-j +«)4-cos^ -J 4-а)
^sln^ cos а+cossina^—(COS-J cosa—ein-^ sina^
(. Я n - \ . ( я 31 \
sin— cosa+coe — einaj+i cos — cos a—sin— sin a)
д/2 .
— (cosa+eina—cosa+ein a) _ .
__ 2 Sin ex , _
—12~. ~ ~ 7 7 2coea — tg “•
— (cos a+sin a+cos a — sin a)
Пример 3. Вычислить cos 15°.
Решение. Имеем 15° = 45° — 30°. Воспользовавшись фор-
мулой (2) при a=45°, 0=30°, получим:
cos 15° =cos (45° — 30°)=cos 45° cos 30°+sin 45° sin 30° =
(д/з ц_ 1).
2 2^ 2 2 4
Пример 4. Найти tg (_^_4"cc)» если tg a=-|-.
Решение. Воспользуемся формулой (5) и учтем, что
te-bl.
Имеем
tg(v+“) =
tg^ +tg a
1— tg-4 tga
4
1+tga 1+4
_____4
1 —tK“ J___3
123
126. Формулы приведения. Под формулами приведения
понимают обычно формулы, сводящие значение тригонометри-
ческой функции аргумента вида — ±сс, n£Z, к функции ар-
гумента а.
Пусть, например, нужно вычислить sin(-^—l-a). Имеем:
sin = sin -у- cos «4-cos-y sin a = l-cos ct + O-sin а=
=cos а.
Аналогично sin {л — ct)—sin л cos а — cos л sin а = 0 • cos а —
— (—l)-sin a = sin а.
(Зл , \ Зя . Зя -
cos (-£*+ а I —cos — cos а — sin~sin а — О • cos а —
—(—l)-sin a=sin а.
Подобным же образом выводятся и остальные формулы приве-
дения, эти формулы даны в следующей таблице:
Функция Аргумент t
1 0 л . 2+“ я—a «4-a 3л 2-“ 8л , -2+“ 2л—a
sin t сое а сое а sin a —sin a —сое a —cos a —sin a
сое t sin а —sin a —cos a —cos a —sin a sin a cos a
tet ctg а —ctg a —tga tga ctg a —ctg a —tga
ctg* tga —tga —ctg a ctg a tga —tga —ctg a
127. Соотношения между тригонометрическими функциями
одного и того же аргумента. Если в формуле (2) из п. 125 по-
ложить a = P=t, то получим:
cos2t4-sin21 — 1, (1)
откуда, в свою очередь, находим, что
(2)
1+^4=^. (3)
го 124
Тождество (2) справедливо при n£Zt а тождество
(3) — при t^nn, n£Z.
Равенства (1), (2), (3) связывают между собой различные
тригонометрические функции одного и того же аргумента.
Известны еще два равенства, связывающие между собой раз-
личные тригонометрические функции одного и того же аргу-
мента. Это
* — « Bin t . cos t
tgt=----ctgt=——
cost slnt
Перемножая эти равенства, получаем равенство
tgtctgt=l, (4)
справедливое при t=^-g » k£Z.
Пример 1. Известно, что sin t= —|-, причем л •< .
Найти cos t, tg t, ctg t.
Решение. Из формулы (1) получаем cos2t = 1 — sin2 t.
Подставив вместо sin t его значение, получим:
2, л l 3\2Л э ie
cos t =
Итак, cos21=—, значит, либо cost=-“, либо cost=—
По условию n<t * т. e. аргумент t принадлежит III чет-
верти. Но в III четверти косинус отрицателен, значит, из двух
4
указанных выше возможностей выбираем одну: cos t=—g-.
Зная sin t и cos t, находим tg t и ctg t:
_____________________3
, . e in t 5 3 . . 4
tel=«=—=T’ ctgt=-j-.
5
„ ж 4 . . 3 . . 4
Итак, cost=——, tgt==-^-, ctgt=-g-.
Пример 2. Известно, что ctg t = —, причем <t<
< л. Найти sin t, cos t, tg t.
Решение. Из формулы (3) находим sin2 t=-—i-,-.
14-ctg t
Подставив вместо ctg t его значение, получим:
Итак, sin2t=^|^. Значит, либо sint=“, либо sint =
109
== — -Ц. По условию Значит, t принадлежит II чет-
верти, а во II четверти синус положителен. Поэтому из двух
- . . 12
указанных возможностей выбираем одну: sin t=-jg .
Для отыскания значения cos t воспользуемся определением
, . СОЗ I ТГ
котангенса: ctg t —7^77 • Из этого равенства находим:
. _ . , 5 12 5
COSt=ctgt-S1nt=-I2.I3=-I3.
Осталось вычислить значение tg t. Из равенства tg t =
=cfet находим, что tg t = ——.
Итак,
slnt=j3’ C0St=~13’ tg‘=—5-
128. Формулы двойного угла. Если в формулах (3), (1), (5)
из п. 125 положить a = t, p=t, то получим следующие тожде-
ства:
sin 2t==2 sin t cos t, (1)
cos 2t = cos2 t—sin2 t, (2)
tg2t=rHh- (3)
С помощью формул (1), (2) и (3) можно выразить синус,
косинус, тангенс любого аргумента через тригонометрические
функции вдвое меньшего аргумента. Например, справедливы
следующие равенства:
sin х==2 sin cos ,
sin 5х=2 sin cos ~,
cos 8t=±cos2 4t —sin2 4t.
В ряде случаев полезным оказывается использование полу-
ченных формул «справа налево», т. е. замена выражения
2 ein t cos t выражением sin 2t (или выражения sin t cos t выра-
жением -^2t выражения cos2 t—sin2 t выражением cos2t
и, наконец, выражения выражением tg2t.
Пример. Упростить выражение tg t—ctg t.
Решение, tg t—ctg t —
cos t sin* t—cos21
ain t ~ ein t cos t
=_2^g_=_2cte2t,
— ein 2t
129. Формулы понижения степени. Зная, что cos2 t+sin2t—
— 1 (см. п. 127), а сов2 t— sin2 t=cos2 t (см. п. 128), находим,
что
€08*1=1^?, (1)
Аналогично находим, что
sin^l--^82*. (2)
Формулы (1) и (2) называются формулами понижения степени.
Они позволяют преобразовывать sin21 и cos2t в выражения,
содержащие первую степень косинуса двойного аргумента.
Например, используя формулы (1) и (2), можем получить
следующие равенства:
sin
X _1—COSX
2 — 2
COS2
Формулы используются и «справа налево* для преобразова-
ния сумм 1 + cos 2t, 1 — cos 2t в произведения. Например, верны
следующие равенства: 14-cos 5х = 2 cos2 ~ , 1 — cos (“+₽)=
=2sin2^±J.
Пример 1. Доказать тождество tg .
127
Решение. Знаменатель правей части преобразуем но
формуле (1), а числитель — по формуле синуса двойного угла
2sln — cos— sin —
. _ ч тт sin * 2 2 2.1
(см. п. 128). Получим —------=---------——-------— = tg -s-
J- "J COS t о t t
2CO82- cos-
Прн мер 2. Вычислить sin4 x-J-cos4 x, если известно, что
cos 2x=~.
Решение. Воспользовавшись тем, что sin4 х—(sin2x)2 и
cos4x=(cos2x)2, применим формулы понижения степени.
Получим sin4 x-l-cos4 x=(sin2 x)24-(cos2x)2=(-^—х^2-j-
25
l-j-cos 2х \ 2 _ 2+2cosg23: 14-cos22x_ +169 _ 97
2 / 4 2 — 2 ~ 169 ’
130. Преобразование суммы тригонометрических функций
в произведение. Имеют место следующие формулы:
sin сс -]-sin Д=2 sin cos ,
sin a—sin 0=2 sin cos
cos а 4-cos р=2 cos сов,
cos а —cos Р= —2 sin sin ,
tga+tgp = eln(ct+P),
cos а cos р
tga-tg₽=^<^.
cos a cos р
Пример 1. Преобразовать в произведение cos 48” —
—cos 12°.
Решение. Применив формулу разности косинусов при
«=48°, 0 = 12°, получим:
cos 48° — cos 12° = — 2 sin —°sin ~~12<,=
2 2
~ — 2 sin 30° sin 18°.
Поскольку sin30°=~~, то окончательно получим:
cos 48° — cos 12°= —sin 18°.
Пример 2. Преобразовать в произведение sin x-j-cos 2х —
—sin Зх.
Решение. Имеем sin x-f-cos 2х —sin 3x = cos 2х—
—(sin Зх—sinx)—cos 2x—2 sin x cos 2x—
= 2 cos 2x^ —sin x^=2 cos 2x( sin-^—sin x) = 2 cos 2xX
n x Л 4-x
X 2 sin cos =4 cos 2x sin (^—) cos ( ^+y-) .
131. Преобразование произведения тригонометрических
функции в сумму. Справедливы следующие формулы:
sin a cos ₽=°ш(°-Р>+«1°(°+Р), (1)
sin a sin p^fr-Pi-^fr+P), (2)
cos a cos ₽^(‘-РН^+Р). (3)
Пример. Преобразовать в сумму произведение
sin 43° cos 19°.
Решение. Воспользовавшись формулой (1) при а ==43°,
Р = 19с, получим:
sin 43° cos 19°=BiP (43°-19‘)+е1п (43°+19°)__
(sin 24°+sin 62°).
132*. Преобразование выражения a cos t 4- b sin t к ви ду
Asin(t+a). Любое выражение вида a cos 14-Ь sin t можно
представить в виде A sin(t-}-a). Для этого вынесем за скобки
выражение -^a2-f-b2 и получим:
a cos 14- b sin t =^а2Л-Ъ2( . ° . cos 14—* „ sin t
Ho ( a^|.y)24-( 2^,'bi)2—1* ®то значит’ что точка c коорди-
129 1Z2±J
натами , .° . и лежит на единичной окружности,
V<P-| ₽
поэтому существует такое а, что
а Ь
— —--sin а, -- =cos а.
Ь2 -у/а? 4" Ь2
Обозначив для краткости -\/а2 + Ь2 через А, получаем:
a cos t -|- b sin t = A (sin a cos 14-cos a sin t).
Применив к выражению в скобках формулу (3) из п. 125, по-
лучим:
a cos t-j-b sin t ~A sin (t 4-a).
Числа a, b, A, a связаны друг с другом соотношениями
a—A sin a, b= A cos a, А=д/а24-Ь*» sin а= , -° - ,
v -v^lP
cos a=-_
y/a^+b2
Например, 3 sin 2t + 4 cos 2t = 5 sin (2t4* ct), где sin a =-£-»
3
cos a=—.
о
133*. Примеры преобразований выражении, содержащих
обратные тригонометрические функции.
Пример 1. Упростить выражение cos (arcsin х), где
— 1<х<1.
Решение. Положим arcsin х = у. Тогда sin у = х, —
• Нужно найти cos у.
Известно, что cos2y = l— sin2 у, значит, cos2 г/ — 1 — х2.
Но —а на отрезке J—Т’1г] КОСИНУС принима-
ет лишь неотрицательные значения. Поэтому cos y=-Jl — x2,
т. е. cos (arcsin x)=-Jl—x2.
Пример 2. Вычислить tg ( arccos ( —
Решение. Положим а = arccos . Тогда cos а=
— —-7г<а<л. Нужно вычислить tg~ .
5 Заказ 75.9
Имеем cos2 1+^» а, значит, cos2-y=-—2^-=Т'* ^ак
как, далее, 1 + tg2 ~ , то 14-tg2 = 5, откуда tg2 -|-=
СО9?Т
= 4, т. е. tgy=2 или tg-|-=—2.
По условию —-<сс<л, значит, а в интерва-
ле (-2-; имеем tg-|->0. Итак, 2, т. е.
tg(-l-arcc0S(—1-)) = 2.
Пример 3. Доказать, что для любого х из [—1; 1] спра-
ведливо тождество
arcsin х=-|—arccos х. (1)
Решение. Вычислим значение синуса левой и правой
части проверяемого равенства:
sin (arcsin х)==х;
sin ( -g- — arccos xj —cos (arccos x)=x.
Синусы, как мы видим, равны, поэтому, чтобы убедиться в
справедливости равенства (1), осталось показать, что arcsin х и
— arccos х принадлежат одному и тому же промежутку мо-
нотонности функции у = sinx (без проверки этого условия
можно получить неверный результат, ведь тригонометриче-
ские функции могут принимать одинаковые значения и для
„ Г. , бл
различных значении аргумента, например, но
. л . бл 1 \
sinv=em-=-r).
Имеем —arcsin х<С-^- . Далее,© arccos х^ л, а поэто-
му —arccos х<-у. Итак, arcsin х и —arccos х
принадлежат одному промежутку монотонности [—~; -^-J
функции у —sin х. Теперь можно считать, что тождество
(1) доказано.
Аналогично можно доказать, что
arctg х=-~—arctg х.
131
ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИИ
$ 14. Уравнения с одной переменной
134. Определение уравнения. Корни уравнения. Равенство
с переменной f (x)~g{x) называется уравнением с одной, пере-
менной х. Всякое значение переменной, при котором» выраже-
нии f (х) и g (х) принимают равные числовые значения^ назы-
вается корнем уравнения. Решить уравнение— это значит най-
ти вое его корни или доказать, что их нет.
Пример 1. Уравнение 3 4- х = 7 имеет единственный ко-
рень 4, так как при этом и только при этом значении пере-
менной 34-х=7 — верное-равенство.
Пример 2. Уравнение (х—1) (х —2)=0 имеет два корня:
1 и 2.
Пример 3. Уравнение х2 4-1 = 0 не имеет действитель-
ных корней.
Заметим, что можно говорить и о мнимых корнях уравне-
ний. Так, уравнение х24-1=0 имеет два мнимых корня: Xi=i,
x-i~—I (см. п. 47). Всюду ниже речь идет только о действи-
тельных корнях уравнений.
135. Равносильность уравнений. Уравнения, имеющие одни
и те же кории, называются равносильными. Равносильными
считаются и уравнения, каждое из которых не имеет корней.
Например, уравнения х4-2=5 и х4-б=8 равносильны,
так как каждое из них имеет единственный корень — число 3.
Равносильны и уравнения х24-1 = 0 и 2х2 4-5 = 0 — ни одно из
них ие имеет корней.
Уравнения х — 5 = 1 и х2 = 36 неравносильны, так как пер-
вое имеет только один корень х = 6, тогда как второе имеет
два корня: 6 и —6.
В процессе решения уравнения его стараются заменить бо-
лее простым, но равносильным данному. Поэтому важно знать,
при каких преобразованиях данное уравнение переходит в
равносильное ему уравнение.
Т.5.1.
Если в уравнении какое-нибудь слагаемое перенести
из одной части в другую, изменив его знак, то полу-
чится уравнение, равносильное данному.
Например, уравнение х24-2 = 3х равносильно уравнению
х24-2-Зх=0.
Т.5.2.
Если обе части уравнения умножить или разделить
на одно и то же отличное от нуля число, то полу-
чится уравнение, равносильное данному.
Например, уравнение ——=2х равносильно уравнению
х2 —1=6х (обе части первого уравнения мы умножили на 3).
136. Линейные уравнения. Линейным уравнением с одной
переменной х называют уравнение вида ах=Ь, где а и Ь —
действительные числа; а называют коэффициентом при пере-
менной, Ь — свободным членом.
Для линейного уравнения ах = Ь могут представиться
три случая:
1) а=#0; в этом случае корень уравнения равен
2) а —О, Ь = 0; в этом случае уравнение принимает вид
0«х=0, что верно при любом х, т. е. корнем уравнения служит
любое действительное число;
3) а=0, в этом случае уравнение принимает вид
0«х = 5, оно не имеет корней.
Многие уравнения в результате преобразований сводятся
к линейным.
Пример 1. Решить уравнение х~}-у^=О-
Решение. По теореме 5.1 (п. 135) данное уравнение рав-
1 2
несильно уравнению — х=—Если разделить обе части
этого уравнения на коэффициент при х, то по теореме 5.2 по-
2 1
лучим равносильное данному уравнение х=—т. е.
15 о
2 „ 2
Х = ——. Итак, — g — корень уравнения.
Пример 2. Решить уравнение 1.
о 4 6 12
Решение. Это уравнение сводится к линейному уравне-
нию. Умножив обе части уравнения на 12 (наименьшее общее
кратное знаменателей 3, 4, 6, 12), получим:
12(4+4-+1fi)=12(g-i)
и далее
8+Зх + 2-2х = 5х-12,
84-2 +12= 5х — 3x4- 2х,
4х = 22,
х=5,5.
133
137. Квадратные уравнения. Уравнение вида
ах2-|-Ьх+с==0,
(1)
где a, Ь, с—действительные числа, причем называют
квадратным уравнением. Если а=1, то квадратное уравне-
ние называют приведенным; если а =£ 1,— то неприведенным.
Числа а, Ь, с носят следующие названия: а — первый коэффи-
циент, Ъ — второй коэффициент, с — свободный член.
Корни уравнения ах24-Ьх + с=0 находят по формуле
__~Ь±-\/ь2—4вс
--------«« • (2)
Выражение D=b2 — 4ас называют дискриминантом квад-
ратного уравнения (1). Если D<zO, то уравнение (1) не имеет
действительных корней; если D=0, то уравнение имеет один
действительный корень; если то уравнение имеет два
действительных корня.
В случае, когда £)=0, иногда говорят, что квадратное
уравнение имеет два одинаковых корня.
Используя обозначение D—b2—4ас, можно переписать фор-
— b±-v®'
мулу (2) в виде х=-----.
Если b=2k, то формула (2) принимает вид:
, —2k±~\f4k2—4ас — 2fe ± 2->Jk2—ас ——ос
Х 2а 2а а ’
—k-*z-yfk'2—ac ь
Итак, х=------------, где (3)
Формула (3) особенно удобна в тех случаях, Когда -це-
лое число, т. е, коэффициент b — четное число.
Пример 1. Решить уравнение 2х2—5х + 2 = О.
Решение. Здесь а=2, Ь= —5, с=2. Имеем Х>=&2—
— 4ае=(—б)2—4-2-2 = 9. Так как D>-0, то уравнение имеет
два корня, которые мы иаидем по формуле (2):
х _5±т/»_5±3
2а 4 4
Итак, Х1=-Ц^=2, х2=-~^-=-|-, т. е. *i=2 и х2=-|- —
корни заданного уравнения.
Пример 2. Решить уравнение Xs—6х~}-9=О.
Решение. Здесь а=1, Ъ=— 6, с=9. По формуле (3)
находим х= -9"1 =8^°=3, т. е. х=3 — корень урав-
нения.
Пример 3. Решить уравнение 2л2—Зх 4-5=0,
Решение. Здесь а=2, Ь=— 3, с=5. Находим дискри-
минант D—1?—4tac={—З)2—4-2-5 =—31. Так как Л<0, то
уравнение не имеет действительных корней.
138. Немодные ад гшле уравнения. Если в квадратном
уравнении ах2-}-Ьх-}-с=0 второй коэффициент b или свобод-
ный член с равен нулю, то квадратное уравнение называют
неполным. Неполные уравнения выделяют потому, что для
отыскания их корней можно ие пользоваться формулой кор-
ней квадратного уравнения — проще решить уравнение мето-
дом разложения его левой части иа множители.
Пример 1. Решить уравнение 2х2—5х=0.
Р ей е н ие. Имеем х (2х—5)=0» Значит, либо Х=0» либо
2х—5 = 0, т. е. х=2,5. Итак, уравнение имеет два корня;
0 и 2,5.
Пример 2. Решить уравнение Зх2—10=0.
Решение. Разделив обе части уравнения на 3, получим
«2-™=0, ». е. (х-дС
бо х— “^^=0, откуда х=
-./10
х=-V-3 •
О. Значит,
/10 п
Г-^-=0, откуда
з
V10 -,/ю
з" и — »Т'
Пример 3. Решить уравнение 2х2 4-5 = 0.
Решение. Поскольку 2х2 4-б> О при любых х, то урав-
нение 2х24~5=0 не имеет корней.
139. Теорема Виета.
Т.5.3.
Если приведенное квадратное уравнение х2+рх +
4-5 = 0 имеет действительные корни, то их сумма
равна —р, а произведение равно д, т. е.
Xl“}-*2=—р,
х>х2=д (1)
(сумма корней приведенного квадратного уравнения
равна второму коэффициенту, взятому с противо-
положным знаком, а произведение корней равно
свободному члену).
Выведем еще некоторые соотношения между корнями и
коэффициентами приведенного квадратного уравнения
х2+рх+9=€.
Найдем сумму квадратов корней: xj4-х%=(xj4-2xiX2+х2)—
— 2xiX2=(xi +х2)2—2xix2.
Воспользовавшись формулами (1), получим:
х?+х1=р2-25. (2)
Рассмотрим сумму кубов корнем. Имеем:
X? 4- х!=(Х14- х2) (х?—Х|Х2 4- Х?)=(Х14- х2) ((xi 4- x2f—8xix2).
Воспользовавшись формулами (1) и (2), получим:
х?+ха=-р(р2-3д).
Справедлива теорема, обратная теореме Виета.
Т-5.4. 1 Если числа Xi и х2 таковы, что Xj 4-х2= — A XiX2=
I =^, то X j и х2 — корни квадратного уравнения
I x24-J3Uc4-9~Q«
Эта теорема позволяет в ряде случаев находить корни квад-
ратного уравнения без использования формулы корней.
Пример 1. Решить уравнение х2 — 9x4-14=0.
Решение. Попробуем найти два числа Xi и Хг, такие, что
Xi4-x2=9,
XiX2 = 14.
Такими числами являются 2 и 7. По теореме 5.4. они и слу-
жат корнями заданного квадратного уравнения.
Пример 2. Решить уравнение х24~3х — 28=0.
Решение. Попробуем найти такие два числа Х| и х2, что-
бы выполнялись равенства
Xj 4-х2= —3,
XjX2 = — 28.
Нетрудно заметить, что такими числами будут — 7 и 4. Они и
являются корнями заданного уравнения.
140. Системы и совокупности уравнении. Рассмотрим урав-
нение
(х"-1)’+((х-1)(х-2))»=0.
Ясно, что (Xs—1)!>0 и ((х—1)(х—2))s5s0, а сумма двух не-
отрицательных чисел равна нулю тогда и только тогда, когда
каждое слагаемое равно нулю. Поэтому сначала надо решить
уравнения (xs—1^=0 и ((х—1)(х —2)f=0, а затем найти их
общие корки. Кернями уравнения (Xs—1)!= О служат числа 1 и
— 1. а корнями уравнения ((к— 1)(х— 2))’^0 — числа 1 я 2.
Общим является число 1 — это корень исходного уравнения,
В случае, когда нужно найти значения переменной, удовлет-
воряющие обоим заданным уравнениям, говорят, что задана
система уравнений. Для обозначения системы используется
фигурная скобка:
{ (х2 —1)2=0,
1((х-1)(х-2))2=0.
Рассмотрим теперь уравнение (х2—1) (х2— 4) = 0. Произве-
дение двух чисел равно нулю тогда и только тогда, когда хотя
бы одно из чисел равно нули». Поэтому сначала надо решить
уравнения х2 —1 = 0 и х2—4=0, а затем объединить их корни.
Корнями первого уравнения являются числа 1 и — 1, а корня-
ми второго — числа 2 и —2. Значит, 1, —1, 2, —2 — корни
исходного уравнения.
Несколько уравнений с одной переменной образуют совокуп-
ность уравнений, если ставится задача найти все такие значе-
ния переменной, каждое из которых является корнем хотя бы
одного из данных уравнений. Для обозначения совокупности
иногда используется квадратная скобка:
141. Уравнения, содержащие переменную под знаком мо-
дуля. Модуль числа а определяется следующим образом
(см. п. 26).
if ° прн
t — а при а<0.
Пример 1. Решить уравнение |3х—5|=2.
Решение. Если |а|=2, то либо а=2, либо —а=2. Это
значит, что заданное уравнение равносильно совокупности
двух уравнений: Зх—5=2; — (Зх—5)=2. Из уравнения
3x 5=2 находим Х|=-|-; из уравнения — (Зх — 5)=2 нахо-
дим х2=1.
7
Ответ: Xi = —, х2 = 1.
Пример 2. Решить уравнение |2х — 8| =Зх-|-1.
Решение. Если 2х—8^0, то |2х—8|=2х —8 и данное
уравнение примет вид 2х—8=3x4-1- Это можно записать
так:
( 2х —8>0,
( 2х —8 = 3x4-1.
Из уравнения 2х — 8= 3x4-1 находим х= — 9. Однако при этом
значении переменной неравенство 2х — 8^0 не выполняется,
137
значит, найденное значение не может быть корнем данного
уравнения.
Если 2х — 8<0, то |2х — 8| = — (2х— 8) и данное уравнение
примет вид 8 —2х = Зх4-1- Это можно записать так:
( 2х— 8<0,
t 8—2х=3x4-1.
Из уравнения 8 — 2х=3x4-1 находим х=-|-. Неравенство
2*( — —8<0 верно, значит, х=-|-----корень данного урав-
нения.
7
Ответ: х=—.
5
Уравнение вида jx—а|=Ь можно решать и геометриче-
ски (см. п. 26).
142. Понятие следствия уравнения. Посторонние корни.
Пусть даны два уравнения
Л (x)=gi (*), (!)
6(x)=g2(x). (2)
Если каждый корень уравнения (1) является одновременно
и корнем уравнения (2), то уравнение (2) называется следстви-
ем уравнения (1). Заметим, что равносильность уравнений
означает, что каждое из уравнений является следствием
другого.
В процессе решения уравнения часто приходится приме-
нять такие преобразования, которые приводят к уравнению,
являющемуся следствием исходного. Уравнению-следствию
удовлетворяют все корни исходного уравнения, но, кроме них,
уравнение-следствие может иметь и такие решения, которые не
являются корнями исходного уравнения, это так называемые
посторонние корни. Чтобы выявить и отсеять посторонние
корни, обычно поступают так: все найденные корни уравне-
ния-следствия проверяют подстановкой в исходное уравнение.
Если при решении уравнения мы заменили его уравнением-
следствием, то указанная выше проверка является неотъемле-
мой частью решения уравнения. Поэтому важно знать, при
каких преобразованиях данное уравнение переходит в следст-
вие.
Рассмотрим уравнение
А (*)=«?(*) (3)
и умножим обе его части иа одно и то же выражение Л (х),
имеющее смысл при всех значениях х. Получим уравнение
/ (х)-Л(х)=в(х)-Л(х), (4)
корнями которого служат как корни уравнения (3|, так и корни
уравнения h(x)=Q. Значит, уравнение (4) есть следствие
уравнения (3). Ясно, что уравнения (3) и (4) равносильны,
если «постороннее» уравнение h (х)=0 не имеет корней.
Итак, если обе части уравнения умножить на выражение
h(x), имеющее смысл при любых значениях х, то получится
уравнение, являющееся следствием исходного. Полученное
уравнение будет равносильно исходному, если уравнение
h (х)=0 не имеет корней. Заметим, что обратное преобразова-
ние, т. е. переход от уравнения (4) к уравнению (3) путем
деления обеих частей уравнения (4) на выражение Л(х), как
правило, недопустимо, поскольку может привести к потере
решений (в этом случае могут «потеряться» корни уравнения
h(x)~О). Например, уравнение (х—2)(х—3)=2(х—3) имеет
два корня: 3 и 4. Деление же обеих частей уравнения на х—3
приводит к уравнению х—2=2, имеющему только один
корень 4, т. е. произошла потеря корня.
Снова возьмем уравнение (3) и возведем обе его части в
квадрат. Получим уравнение
tf («))’=(»«. (5)
корнями которого служат как корни уравнения (3), так и корни
«постороннего» уравнения f(x)= — g{x), т. е. уравнение (5) —
следствие уравнения (3).
Например, уравнение х—1=3 имеет корень 4. Если обе
части уравнения х—1=3 возвести в квадрат, то получится
уравнение (х—1)2=9, имеющее два корня: 4 и —2. Значит,
уравнение (х—1)2=9— следствие уравнения х—1=3. При
переходе от уравнения х—1=3 к уравнению (х—1)2=Э по-
явился посторонний корень х=2.
Итак, при возведении обеих частей уравнения в квадрат
(и вообще в любую четную степень) получается уравнение,
являющееся следствием исходного. Значит, при указанном
преобразовании возможно появление посторонних корней. За-
метим, что возведение обеих частей уравнения в одну и ту же
нечетную степень приводит к уравнению, равносильному
данному.
143. Уравнения с переменной в знаменателе. Рассмотрим
уравнение вида
т$-=°- «
Решение уравнения вида (1) основано на следующем утверж-
дении: дробь — равна нулю тогда и только тогда, когда ее
числитель равен нулю» а знаменатель отличен от нуля (на О
делить нельзя!). Записывают это так: ( т=0,
( л=#0.
В соответствии со сказанным решение уравнения О
проводится в два этапа: сначала нужно решить уравнение
р(х)=О, а затем для каждого корня выяснить, обращается ли
при найденном значении переменной х знаменатель q (х) в нуль.
Если q(x)^O, то найденный корень уравнения р(х)=О явля-
ется и корнем уравнения (1); если q (х)==0, то получен-
ный корень уравнения р(х)=О не является корнем уравне-
ния (1).
Таким образом, уравнение р(х)=О является следствием
(см. в. 142) уравнения j-=0. При переходе от уравнения
~~ =0 к уравнению р(х)=0 (этот переход называется осво-
бождением от знаменателя} могут появиться посторонние
корни. Отсеять их можно с помощью условия q (х)#^0 (или с
помощью непосредственной подстановки каждого корня урав-
нения р(х)=0 в уравнение (1)).
Пример. Решить уравнение 0.
Решение. Из уравнения Зх—6=0 находим х = 2. Так
как при х=2 знаменатель х2 —х —2 обращается в нуль, то
заданное уравнение не имеет корней.
144. Область определения уравнения. Областью определе-
ния уравнения f (х)=< (г) называют множество всех тех значе-
ний переменной х, при которых и выражение f (х), и выражение
g (х) имеют смысл.
Прнмер. Найти область определения уравнения:
а) х2—5х=1+2х; б)"х^“1+х^2=3;
в) V*—V*—1=V* —2; Г) log3(x—3)=log3(5 —х).
Решение, а) Выражения х’—Ъх и 1 + 2х определены
при веех X. Значит, область определения уравнения — вся
числовая прямая.
б) Выражение не определено при х—1, а выражение
^~2 не определено при X—2. Значит, область определения
уравнения можно задать условиями: х^1, х#=2.
в) Корень четной степени имеет смысл лишь при неотрица-
тельных значениях подкоренного выражения. Значит, одновре-
менно должны выполняться условия: х^О, х—1^0 и
х— 2^0. Все эти неравенства справедливы при х^2, т. е.
[2; + оо) — область определения уравнения.
г) Логарифм имеет смысл лишь в случае положительного
числа под знаком логарифма. Значит, должны одновременно
выполняться два неравенства: х— 3>0, откуда х>3, и
5—х>0, откуда х<5. Итак, (3; 5) —область определения
уравнения.
Ясно, что корни уравнения f{x)=g{x) должны принадле-
жать его области определения. Но иногда бывает так, что в про-
цессе преобразований уравнения его область определения
меняется (чаще всего она расширяется) и из найденных в
итоге всех преобразований значений переменной одни значения
принадлежат области определения уравнения f(x)=g (х), а дру-
гие не принадлежат. Тогда первые являются корнями уравне-
ния, а вторые нет (это посторонние корни).
Так, при решении уравнения (п. 143), область
определения которого задается условием х2—х—2=/=0, мы
перешли к уравнению Зх—6 = 0, областью определения которо-
го является вся числовая прямая (область определения расши-
рилась). Уравнение Зх—6=0 имеет корень х=2, который не
принадлежит области определения исходного уравнения и, сле-
довательно, является посторонним корнем.
Общий вывод таков: если в процессе преобразований
уравнения его область определения расширилась, то могут
появиться посторонние корни. Поэтому все найденные зна-
чения переменной надо проверить подстановкой в исходное
уравнение или с помощью области определения исходного
уравнения.
Пример. Решить уравнение 1g (х — 5)=1g (2х—9). (1)
Решение. Если lg а=1g b, то в силу монотонности ло-
гарифмической функции а=Ь (если а Ф Ъ, например, а < Ь, то и
lg e^lg b, а именно lg а < lg b). Значит, от заданного уравне-
ния можно перейти к уравнению
х—5=2х—9, (2)
откуда находим х=4. Но при переходе от уравнения (1) к
уравнению (2) область определения расширилась: в уравнении
(1) она задается неравенством х>5, тогда как для уравнения
(2) областью определения служит вся числовая прямая. Поэто-
му найденное значение х=4, являющееся корнем уравнения
(2), может оказаться посторонним корнем для уравнения (1).
В данном случае именно это н происходит, поскольку х=4 не
принадлежит области определения уравнения (1) (не удовлет-
воряет неравенству х>5). Итак, х=4 — посторонний корень,
т. е. заданное уравнение не имеет корней.
145. Рациональные уравнения. Уравнение f(x)~g(x) назы-
вается рациональным, если / (х) и g(x)—рациональные вы-
ражения. При этом если f (х) и g (х) — целые выражения, то
уравнение называется целым; если же хотя бы одно из выраже-
ний f (х), g(x) является дробным, то рациональное уравнение
/(x)=g(x) называется дробным.
Например, целыми являются линейные (п. 136), квадратные
(и. 137) уравнения.
Чтобы решить рациональное уравнение, нужно:
1) найти общий знаменатель всех имеющихся дробей;
2) заменить данное уравнение целым, умножив обе его
части на общий знаменатель;
3) решить полученное целое уравнение;
4) исключить из его корней те, которые обращают в нуль
общий знаменатель. 2 1 4
Пример. Решить уравнение 2^+~2=х(2—х) ’
Решение. Общим знаменателем имеющихся дробей яв-
ляется 2х(2—х). Найдя дополнительные множители для
каждой дроби, освободимся от знаменателей. Имеем:
^[2-^
2 ! _ 42
2-ж’’- 2 ~ х(2-х) '
4«4-х(2 — х)=8;
х2-6х 4-8 = 0.
Из уравнения х2— бх^-8=0 находим х>=2, хг=4 (см. п. 137).
Осталось проверить, обращают ли найденные корни в нуль вы-
ражение 2х (2 — х), т. е. проверить выполнение условия
2х (2—х)=#0. Замечаем, что 2 не удовлетворяет этому условию,
а 4 удовлетворяет. Значит, х = 4 — единственный корень урав-
нения.
146. Решение уравнения р(х)=0 методом разложения его
левой части иа множители. Суть этого метода состоит в сле-
дующем. Пусть нужно решить уравнение р(х)=0, где р(х) —
многочлен степени п. Предположим, что нам удалось разло-
жить многочлен на множители: р (x)=pt (х)-Рг (х)-рз (х), где
А (х), рч (х), ръ (х) — многочлены более низкой степени, чем п.
Тогда уравнение р(х)=0 принимает вид р\ (х)’р2 (х)«рз (х)=0.
Если а — корень уравнения р(х)=0, то р\ (а) рч (а) Рз (а)=0, а
потому хотя бы одно из чисел а (а), р2 (а), рз (а) равно нулю.
142
Значит, а — корень хотя бы одного из уравнений
Р\ (х)=0, р2 (х)=0, рз (х)=О.
Верно и обратное: если x=ft — корень хотя бы одного из
уравнений р> (я)=0, р2(я)=О, р2(х)=О, то Ь — корень урав-
нения pi (х)«р2 (х)«Рг(х)=О, т. е. уравнения р(х)=О.
Итак, если р (x)=pi (х)-р4 (х)-р3 (х), где pt (х), р2 (я), р3 (я) —
многочлены, то вместо уравнения p(x)=Q нужно решить
совокупность уравнений р (я)—0, (х)=0, Рз (х)=0. Все най-
денные корни этих уравнений, и только они, будут корнями
уравнения р (х)= 0.
Пример 1. Решить уравнение я3+2х2+Зх+6=0.
Решение. Разложим на множители левую часть уравне-
ния. Имеем х2(х+2)+3(х+2)=0, откуда (х+2) (я2 -|-3)=0.
Значит, либо х+2=0, либо я2+3=0. Из первого уравнения
находим я= —2, второе уравнение не имеет корней. Ответ:
— 2.
Метод разложения ня множители применим к любым уравнениям вида
р(х)=0, где р(х) необязательно многочлен; пусть p(x)=pi (х)р2(х)₽э(х),
но среди выражение pt (х), р2 (х), р2 (х) есть выражения более сложного вида,
чем многочлены (например, иррациональные, логарифмические и т. д.).
Среди корней уравнений pi (х)=0, pj(x)=O, р2(х)=0 могут быть посторонние
для уравнения р (х)=0.
Пример 2. Решить уравнение Xе д/х— 9 -у/х= О.
Решение. Имеем -\£ё(х4—9)=0, значит, либо \/х=0, либо хг—9=0.
Из уравнения V*=0 находим х=0, из уравнения х4—9=0 находим х= ±3.
Но х=— 3 не удовлетворяет исходному уравнению, так как при этом
значении не определено выражение -у/х. Это посторонний корень.
Итак, уравнение имеет два корня: 3; 0.
147. Решение уравнений методом введения новой перемен-
ной. Суть этого метода поясним на примерах.
Пример 1. Решить уравнение (я2 — Зх)2 + 3 (я2—Зх)—
-28=0.
Решение. Положив X2—Зя=у, получим уравнение
У2+Зу—28=0, откуда находим у, = — 7, у,=4. Теперь за-
дача сводится к решению совокупности уравнений
я2—Зх— —7; я2—Зх=4, т. е.
х!—Зх+7=0; х2—Зх—4=0.
Первое квадратное уравнение не имеет действительных
корней, так как его дискриминант отрицателен.
Из второго квадратного уравнения находим Я1 =4, х2= — 1.
Это действительные корни заданного уравнения.
Пример 2. Решить уравнение х^_^2х—&~'я?+2х~3~2“
Решение. Положим х2 + 2х—3=у, тогда х24-2х — 8=
=(л^-}-2х—3)—5=р—5 и уравнение примет вид
—15=2.
У
Решив вто уравнение (см. п. 145), получим уi =12,5 и
{/ = — 3.
Но у=х2+2х—3. Значит, нам остается решить уравнения
х2 + 2х—3 = 12,5 и х2+2ж-3=—3,
или э?+2х—15,5=0 и х2+2х=0.
-2-Н/бв
Из первого уравнения находим Xi =-,
-2-V66
Х2=---g---; из второго уравнения получаем х3=0, х4= — 2.
Тем самым найдены четыре корня заданного уравнения.
148. Биквадратные уравнения. Биквадратным называется
уравнение вида ахА-^Ьх2-[-с—01 где а =£0. Биквадратное урав-
нение решается методом введения новой переменной: поло-
жив х2=у, придем к квадратному уравнению fly2+fej/+<?=0.
Пример. Решить уравнение хА -f-4xs—21 =0.
Решение. Положив х2=у, получим квадратное уравне-
ние у2+4у —21=0, откуда находим yi=— 7, уг—3. Теперь
задача сводится к решению уравнений э?= — 7, х2=3. Пер-
вое уравнение не имеет действительных корней, из второго
находим Л1=д/3, х2— —^3, которые являются корнями задан-
ного биквадратного уравнения.
149. Решение задач с помощью составления уравнений. С
помощью уравнений решаются многочисленные аадачи, к ко-
торым приводят самые разнообразные вопросы физики,
механики, экономики и многих других прикладных наук.
Прежде всего напомним общий порядок решения задач с
помощью уравнений.
1) Вводят переменные, т. е. буквами х, у, z обозначают
неизвестные величины, которые либо требуется найти в за-
даче, либо они необходимы для отыскания искомых величин.
2) С помощью введенных переменных и данных в задаче чи-
сел и их соотношений составляют систему уравнений (или
одно уравнение).
3) Решают составленную систему уравнений (или уравне-
ние) и из полученных решений отбирают те, которые под-
ходят по смыслу задачи.
4) Если буквами х, у, г обозначили ие искомые величины,
то с помощью полученных решений находят ответ на вопрос
задачи.
Задача 1. Для перевозки 60 т груза из одного места в
другое затребовали некоторое количество машин. Ввиду неис-
правности дороги на каждую машину пришлось грузить на 0,5 т
меньше, чем предполагалось, поэтому дополнительно потребо-
вались 4 машины. Какое количество машин было затребовано
первоначально?
Решение. Обозначим через х количество машин, затре-
бованных первоначально. Тогда на самом деле было вызвано
(х-|-4) машин. Так как надо было перевезти 60 т груза, то
_ 60
предполагалось, что на одну машину будут грузить — тонн
60 „ г
груза, а на самом деле грузили тонн груза, что на 0,5 т
меньше, чем предполагалось. В результате мы приходим к
уравнению
60 60 ПК
------г"т=6,5.
х Х4-4
Это уравнение имеет два корня: —24 и 20. Ясно, что по
смыслу задачи — 24 не подходит. Таким образом, первоначаль-
но было затребовано 20 машин.
Задача 2. Моторная лодка, обладающая скоростью дви-
жения 20 км/ч, прошла расстояние между двумя пунктами
по реке туда и обратно без остановок за 6 ч 15 мнн. Расстояние
между пунктами равно 60 км. Найти скорость течения реки.
Решение. Пусть х километров в час — скорость течения
реки. Тогда лодка, обладающая собственной скоростью 20 км/ч,
идет по течению со скоростью (20-j-x) километров в час, а
против течения со скоростью (20—х) километров в час. Вре-
60
мя, затраченное на путь по течению, составит 2Q [_х часов,
„ 60
а время, затраченное на обратный путь, составит ча-
сов. Так как на путь туда и обратно затрачено 6 ч 15 мнн, т. е.
25
ч, приходим к уравнению
60 । 60 _ 25
20-1-х“*"20-х‘“ 4 ’
решая которое, находим два корня: х=4, х=—4. Ясно, что
значение х= —4 не подходит по смыслу задачи. Итак, скорость
течения реки равна 4 км/ч.
Задача 3. Найти двузначное число, зная, что цифра его
единиц на 2 больше цифры десятков и что произведение иско-
мого числа на сумму его цифр равно 144.
Решение. Напомним, что любое двузначное число может
быть записано в виде 10х-|-у, где х — цифра десятков, а у —
цифра единиц. Согласно условию если х — цифра десятков, то
цифра единиц равна хЦ-2, и мы получаем
(10х+(х+2)) (х+(х+2))= 144.
Решив это уравнение, находим xi = 2, Хг= — 3-— . Второй ко-
рень не подходит по смыслу задачи.
Итак, цифра десятков равна 2, цифра единиц равна 4; зна-
чит, искомое число равно 24.
Задача 4. Двое рабочих, работая вместе, выполнили не-
которую работу за 6 ч. Первый из них, работая отдельно,
может выполнить всю работу на 5 ч скорее, чем второй ра-
бочий, если последний будет работать отдельно. За сколько ча-
сов каждый из них, работая отдельно, может выполнить всю
работу?
Решение. Прежде чем решать эту задачу (или другие
аналогичные задачи «на работу»), заметим следующее: произ-
водительность труда, т. е. часть работы, выполняемая в еди-
ницу времени (обозначим ее через А), и время, необходимое
для выполнения всей работы (обозначим его через t),— взаимно
обратные величины, т. е. At = l. Поэтому если обозначить через
х часов время, необходимое для выполнения всей работы пер-
вому рабочему, а через (x-J- 5) часов — второму, то часть работы,
- 1 1
выполняемая первым рабочим за 1 ч, равна —, а часть ра-
боты, выполняемая вторым за 1 ч, равна Согласно ус-
x-f-э
ловию они, работая вместе, выполнили всю работу за 6 ч. Часть
работы, выполненная за 6 ч первым рабочим, есть ~, а часть
работы, выполненная за 6 ч вторым рабочим, есть По-
скольку вместе они выполнили всю работу, т. е. доля выполнен-
ной работы равна 1, то мы получаем уравнение
6 1 6 1
решив которое иайдем х=10.
Итак, первый рабочий может выполнить всю работу за 10 ч,
а второй — за 15 ч.
Задача 5. Из сосуда емкостью 54 л, наполненного кисло-
той, вылили несколько литров и долили сосуд водой, потом
опять вылили столько же литров смеси. Тогда в оставшейся в
сосуде смеси оказалось 24 л чистой кислоты. Сколько кислоты
вылили в первый раз?
Решение. Пусть в первый раз было вылито х литров
кислоты. Тогда в сосуде осталось (54—х) литров кислоты. До-
лив сосуд водой, получили 54 л смеси, в которой раствори-
лось (54—х) литров кислоты. Значит, в 1 л смеси содержится
54—х . . „
- 54 литров кислоты (концентрация раствора). Во второй раз
из сосуда вылили х литров смеси, в этом количестве смеси
содержалось литров кислоты. Таким образом, в пер-
вый раз было вылито х литров кислоты, во второй 5^~ж-х
литров кислоты, а всего за два раза вылито 54—24=80 литров
кислоты. В результате приходим к уравнению
х+^-х=30.
Решив зто уравнение, найдем два корня: х(=90 и х2=18.
Ясно, что значение 90 не удовлетворяет условию задачи.
Итак, в первый раз было вылито 18 л кислоты.
Задача 6. Имеется кусок сплава меди с оловом массой
12 кг, содержащий 45% меди. Сколько чистого олова надо при-
бавить к этому куску, чтобы получившийся новый сплав содер-
жал 40% меди?
Решение. Пусть масса добавленного олова составляет х
килограммов. Тогда получится сплав массой (12+х) кило-
граммов, содержащий 40% меди. Значит, в новом сплаве имеет-
ся 0,4 (12+я) килограммов меди. Исходный сплав массой 12 кг
содержал 45% меди, т. е. меди в нем было 0,45-12 кг. Так
как масса меди и в имевшемся, и в новом сплаве одна и та же,
то приходим к уравнению
0,4 (12+х)=0,45-12.
Решив это уравнение, получим х=1,5. Таким образом, к
исходному сплаву надо добавить 1,5 кг олова.
Задача 7. Имеется сталь двух сортов с содержанием ни-
келя 5% и 40%. Сколько стали того и другого сорта надо
взять, чтобы после переплавки получить 140 т стали с содер-
жанием никеля 30%?
147
Решение. Пусть масса стали первого сорта равна х тонн,
тогда стали второго сорта надо взять (140—х) тонн. Содержа-
ние никеля в стали первого сорта составляет 5%; значит, в х
тоннах стали первого сорта содержится 0,05х тонн никеля. Со-
держание никеля в стали второго сорта составляет 40%; зна-
чит, в (140—х) тоннах стали второго сорта содержится
0,4 (140—х) тонн никеля. По условию после соединения взятых
двух сортов должно получиться 140 т стали с 30%-ным
содержанием никеля, т. е. после переплавки в полученной
стали должно быть 0,8 • 140 т никеля. Но это количество никеля
складывается из 0,05х тонн, содержащихся в стали первого
сорта, и из 0,4(140—х) тонн, содержащихся в стали второго
сорта. Таким образом, приходим к уравнению
0,05х-}-0,4(140—х)=0,3-140,
из которого находим х=40. Следовательно, надо взять 40 т
стали с 5%-ным и 100 т стали с 40%-ным содержанием никеля.
150. Иррациональные уравнения. Иррациональным назы-
вают уравнение, в котором переменная содержится под знаком
радикала или под знаком возведения в дробную степень. Так,
иррациональными являются уравнения V*~2 = 2х — 1,
£
х —5=0 н т. д.
Рассмотрим два метода решения иррациональных уравне-
ний: метод всеведения обеих частей уравнения в одну и ту же
степень и метод введения новых переменных (см. п. 147).
Метод возведения обеих частей уравнения в одну и ту же
степень состоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду
б) возводят обе части полученного уравнения в n-ю сте-
пень:
в) учитывая, что (^а)п=а, получают уравнение
/(*)=«(*);
г) решают уравнение и делают проверку, так как возведение
обеих частей уравнения в одну и ту же четную степень
может привести к появлению посторонних корней (см. п. 142).
Эта проверка чаще всего осуществляется с помощью под-
становки найденных значений переменной в исходное урав-
нение.
Пример 1. Решить уравнение tyc—3 — 2.
Решение. Возведем обе части уравнения в шестую сте-
пень, получим х—3=64, откуда х —67.
Проверка. Подставив 67 вместо х в данное уравнение,
получим ^/67 — 3 =2, т. е. 2 = 2 — верное равенство.
Ответ: 67.
Пример 2. Решить уравнение 4--\/2х-{-6 = 6.
Решение. Преобразуем уравнение к виду
и возведем обе части его в квадрат. Получим:
6/2i+6f=(6—
далее
2x4-6=36 —12 V* —1 + х—1. т. е.
12 Vх —1—29 —х.
Еще раз возведем обе части уравнения в квадрат:
144 (х—1)=(29—х)2, т. е. х2-202x4-985=О,
откуда Xi = 5, Ха = 197.
Проверка. 1) При х=5 имеем:
-/5^1+Л/2-5 + 6=6.
Таким образом, х=5 является корнем заданного уравнения.
2) д/197—-1 197 4-6 ^=6. Таким образом, х=197 —
посторонний корень.
Ответ: 5.
2 1
Пример 3. Решить уравнение (х — 2)5 — (х—2)5 = 2.
Решение. Применим метод введения новой переменной.
1 2
Положим у=(х—2)5. Тогда (х—2)5=у2, н мы получаем
уравнение у2—у—2 = 0, откуда находим jn=2, уг= — 1.
Теперь задача свелась к решению двух уравнений:
2 2
(х — 2)5 = 2; (х—2)5 = — 1. Возведя обе части уравнения
2
(х —2)5=2 в пятую степень, получим х—2=32, откуда
х=34.
Уравнение (х —2)5 = —1 не имеет корней, поскольку под
знаком возведения в дробную степень может содержаться
только неотрицательное число, а любая степень неотрица-
тельного числа неотрицательна.
Ответ: 34.
151. Показательные уравнения. Показательное уравнение
вида
а’ Ы=ае Ч
где а>0, а=?Ы, равносильно уравнению f(x)=g(x).
Имеются два основных метода решения показательных
уравнений: 1) метод уравнивания показателей, т. е. преобра-
зование заданного уравнения к виду a,w=agW, а затем к
виду f(x)=g(x); 2) метод введения новой переменной.
Пример 1. Решить уравнение 23х2+3=2|Ох.
Решение. Данное уравнение равносильно уравнению
Зх24-3 = 10х, откуда находим Зх2—10x4-3=0. Решив это
квадратное уравнение, получим Xi = 3, х2=-|-.
Пример 2. Решить уравнение
<°-2ГЦ=5-0.04«-'.
Решение. Приведем все степени к одному основанию —.
Получим уравнение
(4Г5-(4-Г=(4)"'-((4)2)”'
которое преобразуем к виду
(4-Н4-Г-
Полученное уравнение равносильно уравнению х=2х—3,
откуда находим х=3.
Пример 3. Решить уравнение 4*4-2*+' —24=0.
Решение. Применим метод введения новой переменной.
Так как 4Х=(2Х)2, 2х’1—2-2\ то данное уравнение можно
переписать в виде
(2*)24-2-2х—24=0.
Введем новую переменную, положив 2х = у. Получим квад-
ратное уравнение ^4-2^—24=0 с корнями yi=4, у2=—61
Теперь задача сводится к решению совокупности уравнений
2Х=4, 2х=-6.
Из первого уравнения находим, что х=2. Второе урав-
нение не имеет корней, так как 2х > 0 при любых значениях х.
Ответ: 2.
152. Логарифмические уравнения. Простейшее логарифми-
ческое уравнение имеет вид:
1о£а f {х)=1о& g (х\ где а > 0, а^=1.
Чтобы решить уравнение logaf (x)=loga g (х), нужно:
1) решить уравнение f(x)=g(x);
2) из найденных корней отобрать те, которые удовлетво-
ряют неравенствам /(х)>0 и g (х)>0; остальные корни урав-
150
неш f(x)=^g(x) являются посторонними для уравнения
logcf (x)=lo&g(x).
Имеются два основных метода решения логарифмических
уравнении: 1) метод, заключающийся в преобразовании урав-
нения к виду loge f (x)=\&gag (х\ затем к виду /(x)=g(x);
2) метод введения новой переменной.
Пример!. Решить уравнение 1о#з (х2—Зх — 5)=log3 (7—
—2х).
Решение. Перейдем от заданного уравнения к уравне-
нию х2 — Зх—5=7 — 2х и решим его. Имеем X2—х—12=0,
откуда Xj=—8, Хг—4. Проверку найденных значений х вы-
полним с помощью неравенств х2—Зх—5>0 и 7 — 2х>0.
Число —3 этим неравенствам удовлетворяет, а число 4 нет.
Значит, 4 — посторонний корень.
Ответ: —3.
Пример 2. Решить уравнение lg (х-J-4)4-1g (2x4-3)=
=Ig(l-2x).
Решение. Воспользовавшись тем, что сумма логариф-
мов равна логарифму произведения (см. п. 120), преобразуем
уравнение к виду
Ig(x4-4)(2x4-3)=lg(l-2x)
и далее
(х4-4)(2х4-3)=1-2х.
Из последнего уравнения находим xj = — 1, х2= —5,5.
Осталось сделать проверку. Ее можно выполнить с помощью
системы неравенств ( х4-4>0,
< 2х4-3>0,
I 1 —2х>0.
Подставив поочередно найденные значения —1 и —5,5 в
эти неравенства, убеждаемся, что —1 удовлетворяет всем не-
равенствам, а —5,5 нет,— например, при этом значении ие
выполняется первое неравенство. Значит, — 5,5 — посторонний
корень.
Ответ: —1.
Пример 3. Решить уравнение log2 х 4- log2 х 4-1 =
7
logs 0,5г *
Решение. Так как logs 0,5x=log2 х 4-logs 0,5=log2 х—
— 1, то заданное уравнение можно переписать следующим
образом:
logs a?+log2»+l= т '
lOgiX — 1
i6i
Введем новую переменную, положив logiX=y. Получим
!/2+»+1=уГ1ИЛал<*(у—1)(/+у+1)=7;у3—1=7; у3=8;
у—2. Но у=log2x, поэтому из уравнения logsх—2 находим
х=4.
Ответ: 4.
153. Примеры решения показательно-логарифмических
уравнений.
Пример 1. Решить уравнение
х1-1<*=0,01. (1)
Р еш е н и е. Область определения уравнения: «2>0. В этой
области выражения, входящие в обе части уравнения (1), при-
нимают только положительные значения; поэтому, пролога-
рифмировав обе его части по основанию W, получим урав-
нение
lg х1—,,x=lg 0,01,
равносильное уравнению (1). Далее имеем (1—lg «)lg х— — 2.
Полагая u=lgx, получим уравнение (1—и)и=—2, отку-
да in ——1, U2=2. Остается решить совокупность уравнений
1g Х=—1, 1g Х = 2. Из ЭТОЙ совокупности получим Х]=0,1,
«2—ЮО—корни уравнения (1).
Здесь применен метод логарифмирования, заключающийся
в переходе от уравнения f(x)=g(x) к уравнению loga/(x)=
=logflg(«).
Пример 2. Решить уравнение
log, (Зх,оеБ*+ 4)=21ogsx. (2)
Решение. Воспользовавшись определением логарифма,
преобразуем уравнение (2) к виду
хЯо<6Х=Зх,ч,6Х+4.
Полагая н=х1ВДвЖ, получим уравнение и2—3 и~ 4=0, корни
которого И] = —1, н2=4.
Теперь задача сводится к решению следующей совокуп-
ности уравнений: х,адвЖ=— 1, х1адвЖ=4. Так как х’°Я6Х>0,
а —КО, то первое уравнение совокупности не имеет реше-
ния. Прологарифмировав обе части второго уравнения со-
вокупности по основанию 5, подучим:
log| x=log5 4, т. е. log6 х= ±Vlogs 4,
откуда находим х1>2=— корни уравнения (2).
154. Простейшие тригонометрические уравнения. Уравне-
ние sin х~а, где |а|<Л, имеет бесконечно много корней. На-
пример, уравнению sin х =-^- удовлетворяют следующие зна-
л 5л л । о л г» 5л । с»
чения: х\=-^, х2=~^-, Хз=-р-4-2л, х4=-^—2л, х5=—4-2л,
х6=^—2л н т. д. Общая формула, по которой находятся
все корни уравнения sinx=a, где |а| такова:
arcsin а 4-лп. (1)
Здесь п может принимать любые целые значения, каждому
из них соответствует определенный корень уравнения; в этой
формуле (равно как и в других формулах, по которым ре-
шаются простейшие тригонометрические уравнения) п назы-
вают параметром. Записывают обычно n£Z, подчеркивая
тем самым, что параметр п может принимать любые целые
значения.
Решения уравнения cosx=a, где |а| находят по фор-
муле
х = ± arccos а4-2лп, п £ Z. (2)
Уравнение tg х=а решается по формуле
х—arctg а 4- лп, п Е Z, (3)
а уравнение ctg х = а — по формуле
х = arcctg а 4- лп, п £ Z. (4)
Пример 1. Решить уравнение sinx=-|-.
Решение. По формуле (1) имеем:
x=(—l)n arcsin-|-4-лп, n£Z.
Так как arcsin-|-=-^- (см. п. 106), то окончательно получа-
ем х = (—1)”~4-лп, n£Z.
' о
Пример 2. Решить уравнение cos Зх— — ~.
Решение. Воспользовавшись формулой (2), получим:
Зх = ±arccos ( — + 2лп, nQZ.
153
(л/2\ т/2 л Зл .
—^-1=л — arccos-^-= л—Т~~4 (см* П' ЮТ),
то получаем Зх= ±^4-2лл,
л . 2лп - „
*=±т+Т’ ngz.
Пример 3. Решить уравнение tg —=2.
Решение. Воспользовавшись формулой (3), получим:
-|-=arctg 2+лп,
откуда находим:
х=2 arctg 24-2лл, n£Z.
Заметим, что в некоторых случаях удобнее пользоваться
частными формулами:
1) sinx—О; х=лл.
2) sinx=l; х=-|-4-2лл.
3) sinx=—1; х=—^-4-2лл.
4) cosx = 0; х=-^-4-лл.
5) cosx=l; х = 2лл.
6) cosx= —1; х=л4-2лл.
7) tgx = O; х=пп.
8) ctgx=O; х=-|-4-лл.
Во всех формулах п — любое целое число.
155. Методы решения тригонометрических уравнений.
Имеются два основных метода решения тригонометрических
уравнений: 1) метод разложения на множители; 2) метод
введения новой переменной.
Пример 1. Решить уравнение sin 5x4-sin x4-2sin2x=l.
Решение. Перенесем 1 в левую часть и, выполнив пре-
образования левой части, разложим ее на множители.
Применим к sin5x4-sinx формулу для суммы синусов
и воспользуемся тем, что 2 sin2 х — 1 — cos 2х. Тогда уравнение
примет вид 2 sin Зх cos 2х 4- (1 — cos 2х)—1=0 и далее
cos 2х (2 sin Зх—1)=0. Теперь задача свелась к решению сово-
купности уравнений: cos2x=0; 2 sin Зх—1=0.
Из уравнения eos2x=0 находим 2х=~+пп, т. е. х=
л лл « ~v
=T+^-,n£Z.
Из уравнения 2 sin Зх—1 = 0 находим sin3x=-|- и далее
Зх=(—1/ arcsin так как arcsin, то Зх =
=(-1)‘-^+як’ *=<-1>‘^+4’ *€*•
Таким образом, решение заданного уравнения таково:
*=Т+^- х==(-1>‘-е+41 »€Z,*€Z.
Пример 2. Решить уравнение 2 cos2 х +14 cos х=3 sin2 х.
Решение. Так как sin*x=1 —cos2x, то уравнение мож-
но переписать следующим образом:
2 cos2 x-f-14 cos х—3 (1—cos2 х)=0
и далее 5 cos2x-f-14 соех—3=0.
Положив cosx=y, получим квадратное уравнение 5у2Ц-
+14^—3 ==0. Решая это уравнение, находим у 2= — 3.
Значит, либо созх=-|“, откуда находим х= ± arccos-|-+
+2лп, либо созх =— 3 — это уравнение ие имеет решений,
так как |cosx|<Cl.
Ответ: х= ±arccos -g—Ь 2лп, п £Z.
Метод введения новой переменной полезен при решении
так называемых однородных уравнений, т. е. уравнений вида
a sin х+b cos х=0 (однородное уравнение 1-й степени),
a sin2 х+b sin х cos х+с cos2 х=0 (однородное уравнение
2-й степени).
Рассмотрим случай, когда а=^0. Разделим обе части первого
уравнения на cosx, а обе части второго уравнения на cos2 х.
В результате получим следующие уравнения, алгебраические
относительно tg х, а потому решаемые подстановкой tg х=у t
atg x-\-b=Q,
a t^x-f-b tgx+c=O.
При однородному уравнению не удовлетворяют те
значения х, при которых созх=0. Поэтому деление на
cos х (или cos2 х) обеих частей однородного уравнения в слу-
чае а=/=0 не приводит к потере Кореей.
Пример 3. Решить уравнение 8 sin х —7 cos х=0.
Решение. Разделив обе части уравнения почленно на
cos х, получим 8tgx—7=0. Далее имеем tgx^~, откуда
х=arctg -|-+пп, n£Z
Пример 4. Решить уравнение sin2 х 4- 2 sin х cos х—
— 3 cos2 х=0.
Решение. Разделив обе части этого однородного уравне-
ния второй степени на соз2х, получим tg2 x-f-2 tg х— 3=0.
Далее положим u=tg х, тогда приходим к квадратному урав-
нению u24-2u—3=0, откуда ut — ~ 3, На=1.
Решив совокупность уравнений tg х= — 3, tg х=1, полу-
чим х=arctg (-3)4-nk', х=~\-пп, k(;Z, n^Z.
Пример 5. Решить уравнение 5 sin2 x-\^3 sin х cos х4-
4-6 cos2 х=5.
Решение. Имеем:
5 sin2 х 4- т/3 sin х cos х 4- 6 cos2 х—5 (sin2 х 4- cos2 х);
sin х cos х 4- cos2 х=0. (1)
В полученном уравнении отсутствует член вида a sin2 х,
т. е. в=0. Здесь делить обе части уравнения на еоз2 х нельзя,
так как те значения ж, прн которых сов2 х=0, удовлетворяют
уравнению (1), а потому деление на cos2 х приведет к потере
корней. Поступим мяаче: раалажив левую часть уравнения (1)
на множители, получим еоех (д/Зйп я 4-боа х)=0.
Теперь задача сводится к решению совокупности урав-
нений
совх=0; т/3 sinx4-cosjc=0.
(2)
Из первого уравнения совокупности (2) находим х=-^-+
4-л ft, k£Z. Разделив обе части однородного уравнения первой
степени sin х4-cos х =0 на cos х, имеем д/З tg х4-1 =0,
откуда tgx =—x=arctgf—У+лп, т. е. х= —J-4-
V3 \ т/з/ 6
4-лп, n£Z.
Итак, получаем две серии решений: x=~+nk, х = —
Л 6
4-пл, k£Z, n£Z.
156 . Универсальная подстановка (для тригонометрических
уравнений). Если х=^=л-}-2лп, то справедливы следующие тож-
дества:
l-tfy 2tg-|
cos х—-————; sin х--------—.
l+tg2-|- l+tfT
В самом деле, имеем:
cos —— sin —= cos x,
2tgT
sin4
x
COS -— XX
—------— 2 sin -|- cos sin x.
Итак, sin x и cos x рационально выражаются через u=tg-^-,
поэтому подстановка tg -|-= и называется универсальной. Она
может быть использована в уравнении вида R (sin ж; cos х)=0,
где R (sin ж; cos х) — рациональное выражение относительно
sin х и cos х.
Поскольку использование универсальной подстановки воз-
можно лишь при х^л4-2лл, то нужно проверять, не являют-
ся ли числа вида ж=л+2лл решениями заданного уравнения.
Пример 1. Решить уравнение 3 sin ж+ 4 cos х—5.
Решение. Выражая sin х и cos х через tg по форму-
лам (1) н полагая tg-^-=ut придем к рациональному урав-
нению
Решив это уравнение, получим Из уравнения tg~—
1
=-д- находим:
1 1
-=-= arctg —-f- лп, т. е. х—2 arctg 2лл, n£Z.
157
Проверкой убеждаемся, что значения х~ л 4-2лп не удовлет-
воряют заданному уравнению. Итак, получаем ответ:
х = 2 arctg -|-4-2лп, n£Z.
Пример 2. Решить уравнение 3 sin 2х 4- cos 2х 4-1 = 0.
Решение. Воспользуемся универсальной подстановкой.
Выражая sin 2х и cos 2х через tg х н полагая tg х=и, получим
рациональное уравнение
в^+4=4+1=о,
l-J-IT 1-|-и2 *
откуда и——Из уравнения tgx =—находим х=
s=arctg( —-^4-лЛ, k£Z.
Однако нужно еще проверить, не удовлетворяют ли задан-
ному уравнению те значения х, при которых 2х=л4-2лп,
т. е. значения x=-^--jrnn. Имеем:
3 sin (л 4- 2лп) 4- cos (л 4- 2лп) 4-1 =
= 3 sin л4-соз л 4-1=3-0—14-1=0.
Проверка показывает, что значения -^-f-лп являются ре-
шениями уравнения. Итак, заданное уравнение имеет следую-
щие решения:
х=arctg (—04-лй; х=-^-4-лп, k£Z, n£Z.
157*. Метод введения вспомогательного аргумента (для
тригонометрических уравнений). Иногда при решении тригоно-
метрических уравнений оказывается полезным заменить выра-
жение a cos х4- b sin х на A sin (x-f-ф)» где А =-^а24-Ь>
а Ъ
sin tp=—-—-, cos ф= . - —
(см. п. 132). В этом случае ф
называют вспомогательным аргументом.
Пример 1. Решить уравнение 8 cos х 4-15 sin х = 17.
Решение. Разделив обе части уравнения на -\/824-152 =
= 17, получим:
3 । 15 • 1
— cosx4-j^sinx=l.
Так как +(41) =1> то существует такое ф, что -^=
= sin ф н -||=cos ф. Перепишем последнее уравнение следую-
щим образом:
sin ф cos х4-sin х cos ф= 1.
Ho sin ф cos х+sin x со» ф=sin (x + ф). Значит, sin (x+<p)=1,
JT s
откуда x=—-[-2лп- ф. Так как ф—arcsm—, то окончательно
“ я
получаем следующие решения заданного уравнения: х—-%—
—arcsin ^+2лп, n£Z.
Пример 2. Решить уравнение 5 sin х —12 cos хЦ-
4-13 sin Зх=0.
Решение. Имеем:
-JS2+122' f - - sin х —— £2-"—cos х) = —13 sin Зх,
VV5 +12 V6’+12* '
5 . 12 . „
13 Sin X— 13 cos X— —sin Зх.
гт 5 12 .
Полагая -^j=cos ф, 1з=81П Ф» полУчим:
sin х cos ф—cos xsin ф = —sin Зх
н далее
sin(x—ф)+з1п Зх—0; 2sin(2x—|-) cos(x-|—J-)=0.
Решая совокупность уравнений sin ^2х—=0, сов (х+-|-) =
=0, получим х=-~+ф, х=-£----------4-лЛ. Учитывая, что
5
Ф=агссоз , в итоге получаем следующие решения задан-
ного уравнения:
x=-^arccos^-f-^t х=-£-----arccos + л/г, n£Z, k£Z.
4 lo< Z Л. £> Ю
158. Графическое решение уравнений. На практике до-
вольно часто оказывается полезным графический метод реше-
ния уравнений. Он заключается в следующем: для решения
уравнения f (х)=0 строят график функции y=f (х) и находят
абсциссы точек пересечения графика с осью х; эти абсциссы и
являются корнями уравнения. Так, для решения уравнения
ах2 + Ьх-|-с=0 достаточно построить график квадратичной
функции р=ах2-ЬЬх + с и найти абсциссы точек пересече-
ния этого графика с осью х.
Например, график функции у= — х2+6х —5 (рис. 59, в) пе-
ресекает ось х в точках (1; 0) и (5; 0), значит, уравнение
—х2+'6х —5=0 имеет два корня: Xi = l и Хг=5, График
функции у=х2 — 4я-(-5 (рнс. 59) не пересекает ось абсцисс,
значит, уравнение х2—4х+5=0 не имеет действительных
корней.
Часто уравнение f(x)—O заменяют равносильным в(х)=
— h (я), затем строят графики функций у=g (х) и у = h (х) (если
это проще, чем построение графика функции y—f (х)) и нахо-
дят абсциссы точек пересечения построенных графиков.
Так, для решения уравнения х3—'Зх+1=0 можно преоб-
разовать уравнение к виду я3=8я—1, затем построить гра-
фики функций у—х? и у=3х— 1 и найти абсциссы точек
пересечения этих графиков.
Пример 1. Решить графически уравнение я2 —х— 2=0.
Решение. Уравнение целесообразно переписать в виде
x®=x-t-2.
Теперь решение уравнения может быть сведено к нахожде-
нию абсцисс точек пересечения графиков функций у=з? и
У = х+2 (рис. 68, а, б).
На рисунке 68, в построены в одной системе координат
графики функций у=х2 и р=я-|-2. Определяем абсциссы
точек А я В пересечения этих графиков: хА=— 1, хв=2. Та-
ким образом, заданное уравнение имеет два корня: —1; 2.
Пример 2. Решить уравнение -Jx— |я—2|.
Решение. Построим в одной системе координат графики
функций у=^[х и у= |я — 2|. График функции у=-^х изобра-
жен на рисунке 69, а. Чтобы построить график функции у—
= |я—2|, рассмотрим два случая: если я>2, то х~ 2^0,
и потому |я—2|=х—2; если же х<2, то х—2<0, и пото-
му |я—2] =2—х. Таким образом, запись р=|я-—2| эквива-
лентна записи
Г х—2, если х >2,
у ( 2—я, если я <2.
График этой функции изображен на рисунке 69, б. На рисун-
ке 69, в оба графика изображены в одной системе координат.
Они пересекаются в двух точках с абсциссами Xi=l, Хг=4.
Это два корня данного уравнения.
С графическим методом решения уравнения f{x)=g{x) связан функцио-
нальный метод решения уравнения, основанный ня том, что если одна на
функций y=f(x) и У=в{х) возрастает, а другая убывает, то уравнение
f(x)=g(x) либо не имеет корней (рис. 70, с), либо имеет единственный ко-
рень (рис. 70, в).
Пример 3. Решить уравнение 2’=6—х.
Решение. Легко заметить, что х~2 — корень уравнения. Так как
функция у = 2к возрастает, а функция г/=6—X убывает, то других корней
это уравнение не имеет (рис. 71).
159*. Уравнения с параметром. Пусть дано равенство с
переменными х, а:
Цх; а)=0.
Если ставится задача для каждого действительного зна-
чения а решить это уравнение относительно х, то уравнение
161
/(х; а)=0 называется уравнением с переменной х и парамет-
ром а.
Решить уравнение с параметром а — это значит для каж-
дого значения а найти значения х, удовлетворяющие этому
уравнению.
Пример 1. Решить уравнение
2а (а—2) х—а—2.
Решение. Рассмотрим прежде всего те значения пара-
метра, которые обращают в нуль коэффициент прн х (при
этих значениях параметра невозможно деление обеих частей
уравнения на коэффициент при х, а прн остальных значе-
ниях параметра такое деление возможно). Такими значения-
ми являются а = 0, а = 2. При а = 0 уравнение принимает
вид 0-х=—2. Это уравнение не имеет корней. При а = 2
данное уравнение принимает вид О • х = 0, корнем его служит
любое действительное число. При а^О и а =/=2 уравнение
- а—2
можно преобразовать к виду х=(с—2)’ откуда находим
Таким образом, если а=0, то уравнение не имеет корней;
если а=2, то корнем служит любое действительное число;
если и а#= 2, тох =^-.
2а
Пример 2. Решить уравнение
(о — 1) х2 4-2 (2а 4-1) х+4а+ 3=0.
Решение. Выделим особо значение параметра а— 1. Де-
ло в том, что прн а=1 данное уравнение не является квад-
ратным, а при а^1 оно квадратное. Значит, решать его в
каждом из этих случаев надо по-своему. Прн а = 1 уравне-
ние принимает вид 6х + 7 = 0, откуда находим х = — Z-. В
V
случае а ф 1 для квадратного уравнения выделим те значения
параметра, прн которых дискриминант уравнения обращается
в нуль. Имеем —=5а + 4. Значит, а=—-|-----значение пара-
метра, на которое нам надо обратить внимание.
Если а<—то О<0, и, следовательно, уравнение не
4
имеет действительных корней; если а> —— н а#=1, то D>0
н мы получаем:
х^-(2д-Ц)±-уг5с+4.
6 Заказ7Б9
если а=—то 0 = 0 н мы получаем х— — , т. е.
1
3 ' 4
Итак, если а < —, то действительных корней нет; если
1 7 4 1^4
а=1, то х— —2- ; если а = —=-, то х= —+-; если О —=-и
О О d 5
а=£ 1, то
У__ -(2а+ 1)±л/&в+7
П р н м е р 3. Прн каких значениях параметра а уравнение
х24-2 (а-|-1)х+9а—5=0
имеет два различных отрицательных корня?
Решение. Так как .уравнение должно иметь два раз-
личных действительных корня Х| и х2, его дискриминант
должен быть положительным. Имеем:
D = 4 (а + 1)2 —4 (9а-5)=4а2-.28а+24 = 4 (а- 1)(а-6).
Значит, должно выполняться неравенство 4 (а— 1) (а—6)>0.
По теореме Виета имеем:
Xt + x2= — 2 (а + 1),
Х1Х2=9а—5.
Поскольку по условию Xi<0 и Хг<0, то — 2(а-|-1)<0 и
9а — 5 > 0.
В итоге мы приходим к системе неравенств (см. п. 177):
{4 (а — 1) (а — 6) > О,
-2(а+1)<0,
9а—5>0.
Из первого неравенства системы находим (см. п. 180, 183):
а<1; а>6; из второго: а>—1; нз третьего: а>-^-. С по-
мощью координатной прямой (рис. 72) находим, что либо
-|-<л<1, либо а>6.
163
§ 15. Уравнения с двумя переменными
160. Решение уравнения с двумя переменными. Рассмот-
рим уравнение с двумя переменными f(x; у)=®-
Пара значений переменных, обращающая уравнение с дву-
мя переменными в верное равенство, называется решением
уравнения. Если дано уравнение с двумя переменными х и у,
то принято в записи его решения на первое место ставить
значение переменной х, а на второе — значение у.
Так, пары (10; 0), (16; 2), (—2; —4) являются решениями
уравнения X— 3</ = 10. В то же время пара (1; 5) решением
уравнения не является.
Это уравнение имеет и другие решения. Для их отыскания
удобно выразить одну переменную через другую, например
х через у, получив уравнение х =10 + 3</. Выбрав произволь-
ное значение у, вычислим соответствующее значение х. Напри-
мер, если у=7, то х= 10+3 -7=31, значит, пара (31; 7) являет-
ся решением уравнения; если у= — 2, то х = 10 + 3 (—2)=4,
значит, пара (4; —2) также является решением заданного
уравнения и т. д.
Уравнения с двумя переменными называются равносиль-
ными, если они имеют одни и те же решения.
Для уравнений с двумя переменными справедливы теоре-
мы 5.1 н 5.2 (см. п. 135) о равносильных преобразованиях
уравнения.
161. График уравнения с двумя переменными. Пусть даио
уравнение с двумя переменными f(x;jf)=O. Если все его ре-
шения изобразить точками на координатной плоскости, то
получится некоторое множество точек плоскости. Это мно-
жество называется графиком уравнения f(x; у)=0.
Напрнмер, графиком уравнения у—х2=0 является пара-
бола у = х2 (рис. 9); графиком уравнения у— х = 0 является
прямая (биссектриса первого и третьего координатных углов,
рис. 8); графиком уравнения у — 3=0 является прямая,
параллельная осн X (рис. 73, а), а графиком уравнения х + 2 =
=0—прямая, параллельная оси у (рис. 73,6). Графиком
уравнения -\]х—1 + Vl/— 2=0 является одна точка (1; 2), так
как координаты только этой точки удовлетворяют уравнению.
162. Линейное уравнение с двумя переменными и его гра-
фик. Уравнение вида ах-\-Ьу = с, где X, у — переменные, а
а, Ь, с — числа, называется линейным’, числа а и b называют-
ся коэффициентами при переменных, с — свободным членом.
Графиком любого линейного уравнения ах-[-Ьу=с, у ко-
торого хотя бы один ив коэффициентов при переменных отли-
чен от нуля, является прямая; если Ь = 0, то эта пря-
мая параллельна осн у, если а=0, то эта прямая параллель-
на ОСИ X.
Пример. Построить график уравнения 2х ~ 31/ — — 6.
Решение. Графиком этого линейного уравнения явля-
ется прямая. Для построения прямой достаточно знать две
ее точки. Подставив в уравнение 2х — 31/ = — 6 вместо х зна-
чение 0, получим —3j/=—6, откуда у 2. Подставив в урав-
нение 2х — 3j/= — 6 вместо у значение 0, получим 2х= — 6,
откуда х= —- 3.
Итак, мы нашли две точки графика: (О; 2) и (— 3; 0). Про-
ведя через них прямую, получим график уравнения 2х—
— Зу=—6 (рис. 74).
Если линейное уравнение имеет вид 0-х-|-0-у=с, то могут представиться
два случая:
1) с=0; в этом случае уравнению удовлетворяет любая пара (х; у}, а по-
тому графиком уравнения является вся координатная плоскость;
2) в этом случае уравнение не имеет решения, значит, его график
не содержит ни одной точки.
§ 16. Системы уравнений
163. Системы двух уравнении с двумя переменными. Рав-
носильные системы. Пусть даны два уравнения с двумя пе-
ременными f (х; у)=0 н £(х; у)—0.
Если ставится вадача найти все общие решения двух урав-
нений с двумя переменными, то говорят, что надо решить
систему уравнений. Каждая пара значений переменных, об-
ращающая в верное равенство каждое уравнение системы,
называется решением системы уравнений. Решить систему —
значит найти все ее решения или доказать, что их нет.
165
Уравнения, образующие систему, объединяются фигурной
скобкой. Например, запись
( х— 30 = 10,
1 Зх-2у = 2
означает, что уравнения х— 30=10 и Зх —20 = 2 образуют
систему.
Две системы уравнении называются равносильными, если
эти системы имеют одни и те же решения. Если, в частности,
обе системы не имеют решений, то они также считаются рав-
носильными. При решении системы уравнений обычно заме-
няют данную систему другой, более простои или по каким-
либо причинам более «удобной», но равносильной перво-
начальной. Возможность такой замены обусловлена следующи-
ми двумя теоремами.
Т.5.5. Пусть дана система двух уравнений с двумя пере-
менными. Если одно уравнение системы оставить
без изменения, а другое уравнение системы заме-
нить уравнением, ему равносильным, то полученная
система будет равносильна заданной.
Так, системы
{х=Зу4-10,
(Зх—20 = 2
равносильны.
Следствие. Если каждое уравнение системы заменить рав-
носильным уравнением, то получится система, равносильная
данной.
Так, равносильными будут следующие системы:
Г х —30 = 10, и [х=Зу+10,
|ЗХ-2У = 2 2„+4
Т»+Т •
Т.5.6. Пусть дана система двух уравнений с двумя пере-
менными. Если одно уравнение системы оставить
без изменения, а другое уравнение заменить суммой
или разностью обоих уравнении системы, то полу-
ченная система будет равносильна заданной.
Так, системы
fx-3i/=10, Г (X-3у)+(3х-2у) = 10 + 2,
I Зх-2у=2 и { Зх—2у = 2
равносильны: мы заменили уравнение х — 30 = 10 суммой
двух уравнений заданной системы, а уравнение Зх — 2у = 2
оставили неизменным.
164. Решение систем двух уравнении с двумя перемен-
ными методом подстановки. Метод подстановки ваключается
в следующем:
1) Одно из уравв ний системы преобразуют к виду, в ко-
тором у выражено через х (или х через у).
2) Полученное выражение подставляют вместо у (или вме-
сто х) во второе уравнение. В результате получается уравне-
ние с -одной переменной,
3) Находят корни этого уравнения.
4) Воспользовавшись выражением .у -через х (нли х через
у), находят соответствующие значения х (или у).
Пример. Решить систему уравнений
х- 3# —10,
х2- 24#=100.
Решение. Из первого уравнения находим X — Зу +10.
Подсташим вырааюешзе Зр4~Ь0 вместо х ®о второе уравнение
-системы. .Получим (Зу4-1Ю)2—24#= 100, откуда находим
урал.О, #2=-~ 4. Соответствующие значения х найдем из урав-
ненияjr=s3y4-10.1 Если# =0,то;х==10; если у= —4, то х = —2.
Итак, система имеет два решения: (—2; — 4) ,и (10; 0).
165. Решение систем двух уравнении с двумя переменны-
ми методом сложения. Метод сложения основан на
мах 5.5 н 5.6 (п. 163). Суть его поясним на примерах.
Пример 1. Решить систему уравнений
2х + 3# = 7
Зх—#-16.
Решение. Умножив обе части второго уравнения
мы на 3, получим систему
2х+3#=7,
9х—3#=48,
равносильную данной по теореме 5.5.
Сложим теперь оба уравнения полученной системы. По
-теореме 5.6 система
(2х+3#=7, ,3>
I (2х + 3#)+(9х-3#)=7-|-48
равносильна системе (2). Система (3), в свою очередь, пре-
образуется к виду
( 2х + 3# = 7,
I 11х=55.
Из уравнения 11х=55 находим х=5. Подставив это эна-
чение в уравнение 2х-|-3# = 7, находим •#=—1.
теоре-
(1)
систе-
(2)
167
Итак, (5; — 1) — решение системы (3), а значит, н реше-
ние равносильной ей системы (1).
Пример 2. Решить систему уравнений
(х2+у2-2х+У=0,
I 2x2+2i/s+x—Зу—5 = 0.
Решение. Если обе части первого уравнения системы
умножить на 2 и вычесть полученное уравнение из второго
уравнения системы, то взаимно уничтожатся члены, содер-
жащие переменные во второй степени:
(2Х2 -Ь 2у2 4- х—Ъу - 5)-(2х2 + 2у2 - 4х + 2у)=0,
5х—5у—5=0,
х—у—1=0.
Мы приходим к более простой системе
f х!+9!-2х+9=0,
{х-у-1=0,
которую нетрудно решить методом подстановки. Имеем у=
= Х—1, значит,
х2+(х— I)2—2х+(х-1)=0,
2л2—Зх=0,
Х|=0, х2=1»б.
Если х=0, то у=х—1=0—1= —1; если Х=1,5, то р=
=х—1 = 1,5 —1=0,5.
Ответ: (0; — 1) н (1,5; 0,5).
166. Решение систем двух уравнений с двумя переменными
методом введения новых переменных. Метод введения новых пе-
ременных применяется при решении систем двух уравнений
с двумя переменными одним из следующих способов: 1) вво-
дится одна новая переменная только для одного уравнения
системы; 2) вводятся две новые переменные сразу для обоих
уравнений.
Пример 1. Решить систему (
I х+у=5.
Решение. Положим ~"=2> тогда *“=“ и первое урав-
нение системы примет вид z-|—^-=-—. Решим полученное
уравнение относительно новой переменной z:
168
6г2—13г-J-6=О, откуда
2 з
Zi — 3 , г2— 2 •
„ - х 2 Зх ~ х 3
Таким образом, либо т« е« У —-*г» либо —,
2х
т. е. у=^-.
Итак, первое уравнение заданной системы распалось на два
Зх 2х т,
уравнения: У=~£ и У~-&• В соответствии с этим нам пред-
стоит теперь решить совокупность двух систем:
z „ Зх z 2х
/»=-2- р=-3’
| x+ji=S и I х+у = 5.
Из первой системы находим х=2, i/ = 3, из второй я = 3, у=2.
Ответ: (2; 3) и (3; 2).
Пример 2. Решить систему уравнений
/ х2+у2 + х-Н=32,
I ху±2 (х+у)=26.
Решение. Положим х-[-у = и, ху = о. Тогда х2 + у2 =
=(х-[-у)2 — 2ху = и2—2v и система примет вид
I и2 —2v-|-u = 32,
{ i?-|~2u=26. W
Полученную систему можно решить методом подстановки. Вы-
разив из второго уравнения v через а, получим п=26— 2и и,
подставив результат в первое уравнение, получим и2—2(26 —
—2и)4~«—32,
u2+5u —84 = 0,
«i = — 12, w2=7.
Соответственно находим t>i = 50, у2=12.
Итак, нашли два решения системы (I):
f U\= —12, J u2=7,
11Л = 50 н (и2=12.
Возвращаясь к исходным
купность двух систем:
I х + у=-12,
1хУ=50
переменным, получим сово-
(х + » = 7,
1х»=12,
каждую из которых нетрудно решить методом подстановки
169
(выразив, например, у через х из первого уравнения). Первая
система не имеет действительных решений, а вторая имеет два
решения: (3; 4) и (4; 3). Они и будут решениями исходной
системы.
167. Графическое решение систем двух уравнений с дву-
мя переменными. Для того чтобы графически решить систему
двух уравнений с двумя переменными, нужно в одной системе
координат построить графики уравнений и найти координаты
точек пересечения этих графиков.
Пример 1. Решить графически систему линейных урав-
нений
f Зх + 2у = 5,
1 2х-р = 8.
Решение. Построим график уравнения Зх -f- 2у = 5 по
двум точкам, например (1; 1) и (3; —2) (рис. 75).
Построим график уравнения 2х —у = 8 по точкам (О; —8) и
(4; О) (рис. 75).
Полученные прямые не параллельны, их пересечением слу-
жит точка М ( 3; — 2). Значит, (3; — 2) — решение заданной
системы.
Пример 2. Решить графически систему уравнений
(х2+у2=25,
\ху=12.
Решение. Графиком уравнения х2-|-у2 = 25 является ок-
ружность с центром в начале координат н радиусом, рав-
ным 5. Графиком уравнения х?/=12 является гипербола
У=~~ (см. п. 82). Построив графики в одной системе коорди-
нат (рис. 76), найдем координаты точек А, В, С, D пересечения
окружности и гиперболы: А (4; 3), В(3;4), С (—4;—3),
Х>(—3; —4). Значит, решения заданной системы таковы:
(4; 3), (3; 4), (-4; -3), (-3; -4).
168. Исследование системы двух линейных уравнений
с двумя переменными. Пусть даны два линейных уравнения
с двумя переменными и все коэффициенты при переменных
отличны от нуля:
aix-[-b\y=C} и а2х+Ь2У = с2.
Графиком каждого из этих линейных уравнений является пря-
мая (см. п. 162). Если ♦ то эти прямые пересекаются в
одной точке; если то прямые совпадают; если
02 02 02
то прямые параллельны н не совпадают.
Отсюда следует, что система двух линейных уравнений с
двумя переменными
Г aix4-bij/4-Ci=O,
Iа2*Ч-М+с2=О
имеет единственное решение, если —У=Ф-,
02 ©2
имеет бесконечно много решений, если
<12 02 С-2
не имеет решений, если —=ф-у=—.
02 02 С2
Например, система
f 5х-Ь2у—3 = 0,
( Зх4-4у-7=0
5.2 Л
имеет одно решение, так как 4~ . Система
(2х-4у + 1=0,
( 4х — 8у4-3=0
„ 2 — 4 , 1 „
не имеет решении, поскольку Система
( Зх—?/ —4=0,
I -9x4-3?/4-12=О
171
имеет бесконечно много решений, поскольку
3 —1 —4
—9 3 12 •
169*. Решение систем двух уравнений с двумя переменными
методами умножения и деления. Методы умножения и деления
при решении систем уравнений основаны на следующем
утверждении:
Т.5.7.
Если обе части уравнения /2(х; y)=gz (х; у) ни при
каких значениях (х; у) одновременно не обращают-
ся в нуль, то системы
/i(x;»)=gi(x; у),
h(x-, y)—gn(x; у),
h (х; (*; уЪ
fl (х; у) h (х; y)=g\ (х; y)g2 (х; у),
fi (х; y)=gi (х; у},
ft (*; у) __ gi to у)
h (х; у) 8г (х; у)
равносильны.
Пример 1. Решить систему уравнений
Решение. Рассмотрим первое уравнение. Левая его часть
обращается в О при у = О. Если у = 0, то правая часть обраща-
ется в 0 при х=0. Но при х=0 левая часть не имеет смысла.
Значит, нет таких пар (х; у), при которых обе части первого
уравнения системы обращаются в О. Поэтому можно заменить
первое уравнение произведением обоих уравнений системы,
оставив второе уравнение системы без изменении.
Получим:
A^-V^=(Vx+7+ ^=у) (vS+^-^й.
Преобразовав первое уравнение этой системы, получим 8=
=(х+$/)—(х—у), т. е. у=4. Подставив найденное значение у
во второе уравнение системы, получим:
Решим это иррациональное уравнение (см. п. 150). Имеем по-
следовательно :
(V^2“(^+4-^4)2.
^=х-Ь4 —2-V^2—164-х —4,
5 д/х^^16=3х,
25 х2 — 400=9х2,
х2 = 25, Х| = 5, Х2=—5.
Второе значение не удовлетворяет уравнению (1), т. е. являет-
ся посторонним корнем. Значит, система имеет одно решение
(5; 4).
Пример 2. Решить систему уравнений
f(x-!/)xi/-30,
I (х+у)ху = 120.
Решение. Ни при каких значениях (х; у) обе части вто-
рого уравнения системы не обращаются в 0 одновременно.
Значит, можно применить метод деления, перейдя от заданной
системы к системе
(х—у)ху = 30,
_ 30
(х+у)ху 120 ‘
Из второго уравнения этой системы находим, что
^=4- 4x-4j/ = x+y, Зх —51/, у=%.
Подставим найденное выражение у через х в первое уравнение
системы. Получим (х—— х)«х-— х = 30 и далее -^-х3 = ЗО,
х3=125, х=5. Из уравнения у—^-х находим, что если х=5,
то J/=3. Итак, (5; 3) — решение системы.
173
170. Системы показательных и логарифмических уравне-
ний. Решение систем показательных и логарифмических
уравнений не содержит каких-либо принципиально новых
моментов. Используются обычные приемы решения логарифми-
ческих и показательных уравнений (см. п. 151, 152) и обычные
приемы решения систем уравнений (см. п. 1G4—166, 169).
Пример. Решить систему уравнений
( log2 X-Mog4 у=4,
I 3“J=9.31Sj,+z.
Решение. Рассмотрим первое уравнение системы. Вос-
пользуемся тем, что log^x — log2> x2=log4 х2 (см. п. 121). Тогда
уравнение можно записать в виде log< х2 log4 у = 4 и далее
logix2y = 4 (см. п. 120), откуда х2у = 4\ т. е. х2у = 256.
Теперь рассмотрим второе уравнение системы. Имеем:
3x*=32-3,6ff+2, x2 = 15i/4-4.
Задача свелась к решению следующей системы уравнений:
f х2г/=256,
( x2=15j/+4.
Подставим 15i/-|-4 вместо х2 в первое уравнение:
(15i/+4)iZ = 256, 16^ + 4^-256 = 0, 1/, = 4, ₽2= —.
Если у — 4, то х2 = 15у4-4=15-4-}~4 —64, т. е. х2 = 64, отку-
да находим Х| = 8, хз = —8. Если у — — , то x2=15j/4~4=
= 15-(—-|^4-4 =—60, т. е. х2=—60— это уравнение не
имеет действительных корней.
Итак, мы нашли две пары значений переменных:
|Х! = 8, Гх2=—8,
lyi = 4; 1</2=4.
Так как заданная система содержит выражения log2 х,
то должны выполняться условия х>0, у>0. Поэтому
пара ( Х2 = - 8, _ . „
(^2 = 4 исходной системе не удовлетворяет.
Ответ: (8; 4).
171*. Системы тригонометрических уравнений с двумя
переменными. Прн решении систем тригонометрических урав-
нений используются обычные приемы решения систем уравне-
ний и формулы тригонометрии.
Пример. Решить систему уравнений
{sin x-f-соз w = l,5»
sin2 x-j-cor у—1,25.
Решение. Положим sin х=и, созу=п. Тогда получим
систему ( первого уравнения этой системы
i и V —_L,ZO.
v=——и. Подставив найденное выражение вместо v во второе
уравнение системы, получим:
2иг —Зи + 1 = 0,
U| = l, В2 = -|-.
Если и=1, то и=-|—и=-|—1=-^-. ®сли и~ТГ’ т0
«1 = 1,
U2 = -g
tfl== ( »2 —1.
Итак, мы получили две пары решений:
Так как u—sin х, v—cos у, то нам остается решить две систе-
{sinх— 1, Г sinx=-i-»
„ 1 и { г1 ,
созу=— созу = 1.
Из уравнения sinx = l находим x=-~+-2jik, k£Z. Из урав-
нения cos У—-^- находим у= ±-у4-2лп, n£Z.
{sin х=1,
cog ____1
имеют вид J x—~+2nk, k£Z,
|j/=±^-4-2nn, п&г.
Из уравнения sin находим х = (— 1)*-f-xfe, k£Z.
Из уравнения созу—1 находим у=2лп, n£Z. Значит, реше-
{sin х =-^-,
2
cos у=1
имеют вид
х = (_1)*±+пй, k£Z,
у~2лп, n£Z.
Замечание. При решении систем тригонометрических
уравнений существенно использование различных обозначений
для параметра (n, т,...) в записи решений первого и второго
уравнений системы. Иными словами, если в первом уравнении
системы при записи решения в качестве параметра использо-
вана буква k, то для второго уравнения эту букву уже использо-
вать нельзя — в рассмотренном примере для этой цели исполь-
зовалась буква п.
172. Системы трех уравнения с тремя переменными. Рас-
смотрим систему трех уравнений с тремя переменными
( f(x-, у, z)=0,
< g (x-, J/;z)=O,
IЛ (х; у; г)=0.
Решением такой системы называется всякая тройка чисел,
удовлетворяющая каждому уравнению системы.
Для систем трех уравнений с тремя переменными при-
меняются методы решения, аналогичные тем, что использу-
ются для систем двух уравнений с двумя переменными.
Пример. Решить систему уравнений
{x + y4-z = 2,
2х4-3^+г=1,
xI 2+(» + 2)2+(z-l)2=9.
Решение. Применим метод подстановки. Выразим из
первого уравнения х через у и г и подставим результат во
второе и третье уравнения системы. Имеем:
х=2—у—2,
2(2-у-2) + 3У4-2=1,
(2 г)2+(У+2)2+(z -1)2 = 9
и далее
х = 2 — у — Z,
у — z= —3,
уг + гг + уг—3z=0.
Последние два уравнения полученной системы в свою очередь
образуют систему двух уравнений с двумя переменными. Ре-
шим эту систему методом подстановки. Имеем:
I У=г — 3,
l(z—3)2+z2+z(z-3)-3z = 0,
т. е.
f y=z—3,
|z2-4г 4-3=0.
Из уравнения г2 — 4г 4-3=0 находим zi=l, Z2=3. Из уравне-
ния y=z—3 получаем соответственно yi = —2, j/2=0, а из
уравнения х=2 — у — z находим Х| = 3, х% =—1.
Итак, получили следующие решения: (3; — 2; 1) и ( — 1; О; 3).
173, Решение задач с помощью составления систем урав-
нений.
Задача 1. Два пешехода идут навстречу друг другу из
двух пунктов, расстояние между которыми равно 30 км. Если
первый выйдет на 2 ч раньше второго, то встреча произойдет
через 2,5 ч после выхода второго. Если же второй пешеход
выйдет на 2 ч раньше первого, то встреча произойдет через
3 ч после выхода первого. С какой скоростью идет каждый
пешеход?
Решение. Пусть х километров в час — скорость первого
пешехода, а у километров в час — скорость второго пешехода.
Если первый выйдет на 2 ч раньше второго, то согласно условию
он будет идти до встречи 4,5 ч, тогда как второй — 2,5 ч. За
4,5 ч первый пройдет путь 4,5х километров, а за 2,5 ч второй
пройдет путь 2,5{/ километров. Их встреча означает, что
суммарно они прошли путь 30 км, т. е. 4,5х 4-2,5^ = 30 —
первое уравнение.
Если второй выйдет на 2 ч раньше первого, то согласно
условию он будет идти до встречи 5 ч, тогда как первый —
3 ч. Рассуждая, как и выше, придем ко второму уравнению:
3x-}~5i/=30.
“ В итоге получаем систему уравнений
Г 4,5x4-2,51/= 30,
I 3x4- 5^=30.
откуда получим х=5, j/=3.
Ответ: первый пешеход идет со скоростью 5 км/ч, а
второй — 3 км/ч.
Задача 2. Вкладчику на его сбережения через год сбер-
касса начислила 6 р. процентных денег. Добавив 44 р., вкладчик
оставил деньги еще на год. По истечении года вновь было про-
изведено начисление процентов, и теперь вклад вместе с про-
центами составил 257,5 р. Какая сумма была положена на
сберкнижку первоначально и сколько процентов начисляет
сберкасса?
Решение. Пусть х рублей — первоначальный вклад, а
сберкасса в год начисляет */%. Тогда к концу года к перво-
177
начальному вкладу добавится рублей. Из условия полу-
чаем уравнение у^=6.
В конце года вкладчик внес в сберкассу еще 44 р., так что
вклад в начале второго года составил х4~6+44, т. е. (х4~50)
рублей. Сумм;а, которая получилась к концу второго года с
учетом начисления, составляет (x-}~50-f—^(х4-50)) руб-
лей, и по условию она равна 257,5 р. Это позволяет составить
второе уравнение:
х + 50 FjIo(х +50) = 257,5.
Итак, мы пришли к следующей системе двух уравнений
с двумя переменными:
ж+5О+155<ж + 5О) = 257’5-
Выполнив преобразования обоих уравнений, получим:
( ху-=600,
I ЮОх 4- 50у 4- ху = 20 750.
Заменив второе уравнение системы разностью второго и перво-
го уравнений, получим;
| xz/ = 600,
( ЮОх 4-50g = 20 150.
Эту систему можно решить методом подстановки. Из вто-
рого уравнения находим у = 403 — 2х. Подставив выражение
403 —2х вместо у в первое уравнение системы, получим
х(403—2х)=600, откуда находим два кория: 200 и 1,5. Яс-
но, что только первое значение удовлетворяет смыслу
задачи.
Подставив в уравнение д = 403 — 2х вместо х найденное
значение 200, получим у — 3. Итак, первоначальный вклад
составлял 200 р., а сберкасса в год начисляет 3%.
178
Глава VI. НЕРАВЕНСТВА
§ 17. Решение неравенств с переменной
174. Основные понятия, связанные с решением неравенств
с одной переменной. Пусть дано неравенство / (х) > g (х). Вся-
кое значение переменной, прн котором данное неравенство с
переменной обращается в верное числовое неравенство, назы-
вается решением неравенства. Решить неравенство с перемен-
ной — значит найти все его решения или доказать, что их нет.
Два неравенства с одной переменной называются равно-
сильными, если решения этих неравенств совпадают; в част-
ности, неравенства равносильны, если оба не имеют решений.
Прн решении неравенств обычно заменяют данное неравен-
ство другим, более простым, но равносильным данному; полу-
ченное неравенство снова -заменяют более простым, равно-
сильным данному неравенством и т. д. Такие замены осуще-
ствляются на основе следующих утверждений.
Т.6.1. I Если из одной части неравенства перенести в другую
слагаемое с противоположным знаком, то получит-
I ся неравенство, равносильное данному.
Т.6.2.
Т.6.3.
Если обе части неравенства с одной переменной ум-
ножить или разделить на одно и то же положитель-
ное число, то получится неравенство, равносиль-
ное данному.
Если обе части неравенства с одной переменной ум-
ножить или разделить на одно н то же отрицатель-
ное число, изменив при этом знак неравенства на
противоположный, то получится неравенство, равно-
сильное данному.
Например, неравенства х24-5х<6 и х24-5х—6<0 равно-
сильны по теореме 6.1. Неравенства Зх2-|-6х<9 и х2-[-2х<3
равносильны по теореме 6.2 (обе части неравенства Зх2-|-6х<9
мы разделили на положительное число 3, оставив без измене-
ния знак < исходного неравенства). Неравенства — 6х<12 и
х> —2 равносильны по теореме 6.3 (обе части неравенства
— 6х<12 мы разделили на отрицательное число —6, изменив
прн этом знак < исходного неравенства на знак >•).
На практике иногда полезны теоремы, являющиеся обоб-
щениями теорем 6.2 н 6.3.
Т.6.4. I Если обе части неравенства умножить или разделить
I на одно и то же выражение, принимающее при всех
(значениях переменной положительные значения, то
получится неравенство, равносильное данному.
Т.6.5.
Если обе части неравенства умножить нлн разделить
на одно и то же выражение, принимающее прн всех
значениях переменной отрицательные значения, из-
менив при этом знак неравенства на противополож-
ный, то получится неравенство, равносильное дан-
ному.
175. Графическое решение неравенств с одной переменной.
Для графического решения неравенства /(x)>g(jr) нужно по-
строить графики функций y=f(x) и y=g(x) и выбрать те
промежутки оси абсцисс, на которых график функции у~ f(x)
расположен выше графика функции y = g(x).
Пример. Решить графически неравенство
1 2
lOg2X=—.
Решение. Построим в одной системе координат графики
функций j/=log2 х и У=-^- (рис. 77). Из рисунка видно, что
график функции j/=log2 х расположен выше графика функции
У=~ при х>2.
Ответ: (2; -J- оо).
176. Линейные неравенства с одной переменной. Линейным
называется неравенство вида ах > Ъ (нлн соответственно ах < 6,
ах^Ь, ах Ь). Если а > О, то неравенство ах>• Ъ равносильно
неравенстэу (см. Т. 6.2), значит, множество решений
неравенства есть промежуток ( ~ ; + оо). Если а<0, то нера-
180
веиство ах>Ъ равносильно неравенству х<~ (см. Т.6.3),
значит, множество решений неравенства есть промежуток
Г — оо; ~ J . Если а = О, то неравенство принимает вид О х > Ь,
т. е. оно не имеет решений, если 6^0, и верно при любых
х, если Ь<0.
Многие неравенства в процессе преобразований сводятся
к линейным.
Пример. Решить неравенство
2(х-3)+5(1-х)>3(2х-5).
Решение. Раскрыв скобки, получим:
2х-6-Ь5-5х>6х-15,
-Зх-1>6х-15.
Далее имеем
— Зх-6х> —15 + 1,
— 9х>-14. (1)
По теореме 6.1 это неравенство равносильно заданному нера-
венству. Разделим теперь обе части неравенства (1) на отрица-
тельное число — 9 и изменим знак неравенства. Получим
согласно теореме 6.3 неравенство, равносильное неравенст-
ву (1): х^.^-. Значит, множество решений заданного нера-
/ 141
венства есть промежуток ( — ею; — j.
177. Системы неравенств с одной переменной. Говорят,
что несколько неравенств с одной переменной образуют систему,
если ставится задача найти все общие решения заданных
неравенств.
Значение переменной, при котором каждое неравенство сис-
темы обращается в верное числовое неравенство, называется
решением системы неравенств.
Неравенства, образующие систему, объединяются фигурной
* f 2х__1 > 3
скобкой. Например, запись | _2 <11 означает» что неРа‘
венства 2х—1>3 и Зх — 2 >11 образуют систему.
Иногда используется запись в виде двойного неравенства.
„ (2х + 1>1,
Например, систему неравенств | 2х +1 < 5 можно 3airacaTb
в виде двойного неравенства 1<2х+1<5.
181
70
2
Пример 1. Решить систему неравенств
Г 5х + 2>3х— 1,
[ Зх-Ь1>7х-4.
Решение. Первое неравенство системы преобразуется в
_ 3
равносильное ему неравенство х >• ——, а второе — в нера-
венство Таким образом, задача сводится к решению
системы
__3^
Л 2
4 '
С помощью координатной прямой (рнс. 78) находим, что
/ 3 5 \
множество решении системы есть интервал ( —; у ) .
Пример 2. Решить систему неравенств
( 3(х + 1)-^<5х-7.^,
2х—|- + 6<4х-3.
Решение. Выполнив преобразования каждого из нера-
венств системы, получим:
56
5
27
Значений х, удовлетворяющих одновременно неравенствам
___ 56 27
х<~—$ и иет, значит, заданная система неравенств
не имеет решений.
178. Совокупность неравенств с одной переменной. Говорят,
что несколько неравенств с одной переменной образуют сово-
купности если ставится задача найти все такие значения пере-
менной, каждое из которых является решением хотя бы одного
из данных неравенств.
Значение переменной, при котором хотя бы одно из нера-
венств, образующих совокупность, обращается в верное число-
вое неравенство, называется решением совокупности нера-
венств.
Пример. Решить совокупность неравенств
2х—3 Зх—2
5^2
Решение. Преобразовав каждое из неравенств, получим
4 6
совокупность, равносильную заданной: С по-
мощью числовой прямой находим, что решением ааданной сово-
купности служит промежуток (— со; —) (рис. 79).
179. Дробно-линейные неравенства. Рассмотрим примеры
решения неравенств.
Пример 1. Решить неравенство
Решение. Дробь положительна, если числитель и знаме-
натель ее имеют одинаковые знаки, т. е. либо оба положи-
тельны, либо оба отрицательны. Значит, мы получаем совокуп-
ность двух систем неравенств:
2х + 1>0,
Зх — 2>0
или
2х + 1<0,
Зх —2<0.
Из первой находим
Из второй находим Л х <—,
1^2 1
*<“3 • т. е. .
183
В итоге получили следующие решения заданного неравен-
ства:
Пример 2. Решить неравенство
Решение. Имеем последовательно — 5^0,
3x4-7-lOx+35-. „
2х —7
",7х+/2>°-
2х—7
Умножим обе части неравенства на —1, изменив при этом
знак неравенства (см. Т. 6.3, п. 174). Получим:
^<о.
2х—7
Дробь меньше или равна нулю в двух случаях: 1) если числи-
тель меньше или равен нулю, а знаменатель больше нуля;
2) если числитель больше или равен нулю, а знаменатель
меньше нуля. Значит, мы получаем две системы неравенств:
(7х — 42 < 0, (7х—42>0,
(2х—7>0; { 2х — 7<0.
Из первой находим ( х=Сб,
{ т- е. -^-<*<6.
Из второй находим ( х^б,
( х<—, т. е. система не имеет реше-
ний.
Значит, множество решений заданного неравенства есть
промежуток ( ; 6j.
Т.6.6.
180. Неравенства второй степени. Здесь, речь идет о нера-
венствах вида ах24-Ьх4-с>0 илн ах2-|-6х-|-е<0, где а=£0.
Если дискриминант D=b2—4ас квадратного трех-
члена ах2 -\-bx-\-c отрицателен, а старший коэффи-
циент а положителен, то при всех значениях х вы-
полняется неравенство ах2 Ъх -|- с > 0.
Рассмотрим теперь случай, когда D^O. Для решения
неравенства ах2 4- Ъх4-с > О (или ах2 4- Ьх+с СО) нужно разло-
жить квадратный трехчлен ах2-}-Ьх-]-с на множители по
формуле ах2 4- bx-[-c=a (х—Xi) (х—Х2) (см. п. 56), затем разде-
лить обе части неравенства а (х — Xi)(x— Ха)>0 (или а(х—Xi)X
Х(х—Хг)СО) на число а, сохранив знак неравенства, если О О,
и изменив знак неравенства на противоположный, если с<0
(см. п. 174), т. е. перейти к неравенству (х—Xi)(x—Хг)>0
(или (х — Xi)(x — Хг)СО). Теперь остается воспользоваться тем,
что произведение двух чисел положительно (отрицательно),
если сомножители имеют одинаковые (разные) знаки.
Пример 1. Решить неравенство 2х2 4- 5х + 2 > О.
Решение. Найдем корни трехчлена 2х2 4- 5х4-2. Из урав-
нения 2х24-5х4-2 = 0 получаем Х] = —2, Хг=—Значит,
2х24-5х4-2 = 2 (х4-2) (х4—н мы приходим к неравенству
2 (х4-2)(х4—1-)>0 и далее (х4-2) (х4—1-)>0. Выражения х4-2
и х4—должны иметь одинаковые знаки, т. е.
( х4-2>0, ( * + 2<0,
J , ИЛИ { 1
I х4--|->0 I *+-2-<°-
т, 1
Из первой системы находим, что х>—а из второй, что
х<—2.
Пример 2. Решить неравенство 7x-j-10^3x2.
Решение. Преобразуем неравенство к виду 7x4*10—
— Зх2^0 н, умножив обе части последнего неравенства на —1,
получим Зх2 —7х—10^0. Корни квадратного трехчлена
Зх2—7х —10 таковы: Xi =— 1, Хг=—. Разложим трехчлен на
множители, в результате чего получим неравенство 3(х4*1)Х
х(*~|r)^0 н далее (х4-1)^х — От последнего нера-
венства переходим к совокупности систем неравенств:
Первая система не имеет решений, а из второй находим, что
185-
Пример 3. Решить неравенство х2 — 6х -|- 9 > О.
Решение. Квадратный трехчлен х2 — 6х + 9 имеет два
одинаковых корня: xi=x2 = 3. Значит, х2—6x-|-9=(x—З)2, и
неравенство принимает вид (х—3)2>0. Это неравенство вы-
полняется при всех х, кроме х = 3.
Пример 4. Решить неравенство х2 25.
Решение. Последовательно имеем х2 — 25 О, (х—5) X
Х(*4-5)>0, откуда
( х—5>0, f х — 5^0,
I х+5>0 или (х-|-5<0.
Из первой системы получаем х^>5, из второй х=С—5.
181. Графическое решение неравенств второй степени. Гра-
фиком квадратичной функции у —ах2 + Ьх + с является парабо-
ла с ветвями, направленными вверх, если а>0, и вниз, если
п<0. При этом возможны три случая: парабола пересекает ось
х (т. е. уравнение ах2-\-Ьх-\-с=О имеет два различных корня),
парабола имеет вершину на оси х (т. е. уравнение ах24- Ьх + с=
=0 имеет одни корень), парабола не пересекает ось х (т. е.
уравнение ах2-}-fex-f-c=O не имеет корней). Итого возможны
шесть положений параболы, служащей графиком функции
у = ах2-\-Ьх-\-с относительно оси х,— они представлены на ри-
сунках 80—81. Опираясь на эти графические иллюстрации,
можно решать квадратные неравенства.
Пример 1. Решить неравенство 2х2 + 5х + 2 > О.
Решение. Уравнение 2х2-|-5х-|-2=0 имеет два корня:
Х| = — 2, х2 =—g-. Парабола, служащая графиком функции
у = 2х2-|-5х-|-2, имеет вид, изображенный на рисунке 80, а.
Неравенство 2х2 4- 5х 4- 2 > О выполняется при тех значениях х,
прн которых точки параболы лежат выше осн х: это будет
186
при х<х( или при х>х2, т. е. при х< —2 или при х> —
Значит, решения неравенства таковы: х<—2, х>—|-
(см. пример 1 из п. 180).
Пример 2. Решить неравенство Зх2—7х—10^0.
Решение. Уравнение Зх2—7х —10—0 имеет два корня:
Xi = —1, х2=-^. Парабола, служащая графиком функции
y=Sx2—7х—10. имеет вид, изображенный на рисунке 80, а.
Неравенство Зх2—7х—10^0 выполняется при тех значе-
ниях х, при которых точки параболы лежат на оси х или
ниже ее: это будет при х из промежутка [xi; х2]. Значит,
Г 1 10 1
множество решении неравенства есть отрезок I—l»-^" I
(см. пример 2 из п. 180).
Пример 3. Решить неравенство — х2+4х—4 > 0.
Решение. Уравнение — х2-|-4х —4 — О имеет один корень
х=2. Парабола, служащая графиком функции у— — х2-}-
4-4х—4, имеет вид, изображенный на рисунке 81,6. Нера-
венство — х2-}-4х—4>0 выполняется при тех значениях х, при
которых точки параболы лежат выше оси х. Таких точек нет,
значит, неравенство не имеет решений.
Пример 4. Решить неравенство —Зх2-|-х—5<0.
Решение. Уравнение — Зх2 х — 5=О не имеет действи-
тельных корней. Парабола, служащая графиком функции
у=—Зх2+х—б, имеет вид, изображенный на рисунке 81, в.
Неравенство — Зх2-|-х—5<0 выполняется при тех значениях
х, при которых точки параболы лежат ниже оси х. Поскольку
вся парабола лежит ниже оси х, то неравенство выполняется
прн любых значениях х.
182. Неравенства с модулями. При решении неравенств,
содержащих переменные под знаком модуля, используется
определение модуля:
IГ Г.М — ! f (*> если f W °’
-/(х), если /(х)<0.
Иногда полезно воспользоваться геометрической интер-
претацией модуля действительного числа, согласно которой
|а| означает расстояние точки а координатной прямой от
начала отсчета О, a |а—означает расстояние между точками
си Ь на координатной прямой (см. п. 27).
Кроме того, можно использовать метод возведения в
квадрат обеих частей неравенства, основанный на следующей
теореме.
Т.6.7. | Если выражения f(x) и g(x) при любых х прини-
мают только неотрицательные значения, то иера-
1 эенстеа ?(х)>*(х) и (/(х))2>(₽(х))2 равносильны.
Применяется эта теорема при решении неравенств с
модулями так.
Пусть нужно решить неравенство
1Г(х)|> 1к(х)1-
Так как при любых х из области определения выражений
f(x) н g(x) справедливы соотношения |f(x)|S>.O, lsr(x)|^O,
(I/ (х)|)2=(/ (х))2 и (]g (x)|)2=(g (х))2, то данное неравенство
равносильно неравенству (/(x))2>(ff (х))2.
Пример 1. Решить неравенство |х—1| <5.
Решение.
Первый способ. |х—1| можно рассматривать как
расстояние на координатной прямой между точками х и 1.
Значит, нам нужно указать на координатной прямой все точки
х, которые удалены от точки 1 меньше чем на 2 единицы.
С помощью координатной прямой (рис. 82) устанавливаем,
что множество решений неравенства есть интервал (—1; 3).
Второй способ. Возведя обе части данного неравен-
ства в квадрат, получим равносильное ему неравенство
(х—1)2<4. Решая последнее неравенство, получим х2—2х—
— 3 < О, откуда находим, что — 1 < х < 3 (см. п. 180 или п. 181).
. ( 82
-7 t 3
188
'///////////4 '//////'.
-6 -2,5 1
Третий способ. По определению модуля числа
, 11 х—1, если х—1^0,
I —(х—1), если х—1<0,
поэтому данное неравенство можно заменить совокупностью
двух систем неравенств:
fx-l>0, ( х—1<0,
(х—1<2; 1 —(х —1)<2.
Из первой системы получаем 1^х<3, из второй системы
— 1<х<1. Объединив эти решения, получим промежуток
(-1:3).
Пример 2. Решить неравенство |2х + 5|^7.
Решение. Имеем |х+2,51 ^3,5. Нам нужно указать
на координатной прямой все такие точки х, которые удалены
от точки —2,5 на расстояние, большее или равное 3,5. С по-
мощью координатной прямой (рис. 83) находим решения:
х<^ —6; х^1.
Пример 3. Решить неравенство |2х—1|^|Зх+1|.
Решение. Возведя обе части неравенства в квадрат,
получим неравенство (2х—1)2^(3х+1)2, равносильное дан-
ному. Преобразовав последнее неравенство, получим 5эг-}-
4-10x^0, откуда находим: х^—2; х^О.
Пример 4. Ранить неравенство 12х+4| ^Зх+2.
Р е ш е н и е. Если 2x+4J>0, то |2х-}-4] — 2х+4, и,
следовательно, неравенство примет вид 2х + 4^3х + 2.
Если же 2х4-4<0, то |2х-]-4| — —(2x4-4), и неравенство
принимает вид — (2х-|-4)<: Зх-]-2. Таким образом, данное
неравенство можно заменить совокупностью двух систем: 1
2х + 4>0,
2x4-4 С Зх-)-2;
2х-]-4<0,
—(2х4-4)<Зх-)-2.
Из первой системы находим х^2, вторая система не
имеет решений. Значит, множество решений неравенства —
луч [2; оо).
183. Решение рациональных неравенств методом про-
межутков1. Решение рациональных неравенств вида ^^->0
(вместо знака >• может быть и любой другой знак неравен-
ства), где р (х) и q (х) — многочлены, основано на следующем
рассуждении.
Рассмотрим функцию &(*)—^Z^^Zj) * где
Если x2>d, то каждый из сомножителей х—а, х— Ь, х—с,
х—d положителен, и, следовательно, на промежутке (d; +°°)
имеем й(х)>0. Если c<x<d, то х— d<0, а остальные со-
множители по-прежнему положительны. Значит, на интервале
(с; d) имеем Л(х)<0. Аналогично на интервале (Ь; с) будет
Л(х)>0 и т. д. (рнс. 84, а).
Изменение знаков функции h (х) удобно иллюстрировать
с помощью волнообразной кривой (ее называют «кривой
знаков»), которую чертят справа налево, начиная сверху
(рис. 84,6). Эту иллюстрацию нужно понимать так: на тех
промежутках, где эта кривая проходит выше координатной
прямой, выполняется неравенство й(х)>0, на тех же проме-
жутках, где кривая проходит ниже прямой, имеем й(х)<0.
Для проведенного выше рассуждения было несущественно
количество линейных множителей в числителе и знаменателе,
а также взаимное расположение корней числителя н знамена-
теля дроби на координатной прямой. Поэтому оно применимо
и для функции вида
f °’) ад—(х с") (1 \
'w W
где числа fli, «2,...»ал, 2>i, Ь2,..., попарно различны. Изменение
знаков функции f (х) мы также можем иллюстрировать с
помощью кривой знаков, которую чертят справа налево, начи-
ная сверху, и проводят через все отмеченные иа координатной
прямой точки fli, аг, ...» йп, fe], 1>2, —» На этом основан метод
промежутков, который с успехом применяется для решения
рациональных неравенств.
Этот метод иногда называют методом интервалов.
190
Пример
1. Решить неравенство
(х+5)(х-д^)(х+-У2)
(2х—3) (4х + 5) '
Решение. Выполним преобразования левой части не-
равенства
(x + 5)(x-t/3)(x+V2)
и умножим обе части неравенства на 8; получим неравенство
(х 4-5) (х—-/3) (х4- /2) < д, равносильное данному.
М)(*+4)
„ А х (х4-5)(х—^)(х4-л/2)
Изменение знаков функции f(x)=——\ , < нл-
(’-4)(‘+4)
люстрируем с помощью кривой знаков (рис. 85, а). Значения х,
при которых f(x)<0 (заштриховано), удовлетворяют следую-
щим неравенствам:
х<-5; -^2<х<-~; -^<х<^3.
Это решения исходного неравенства.
„ от, (х-3)(х4-2)_^-
Пример 2. Решить неравенство ----<С 1.
Х^ — X 6
Решение. Имеем — д.г_1-------1 < 0
и далее -—
(х-1)(х4-1) ж+б
Начертим кривую знаков для функции f (х)=
(рис. 85, б). С ее помощью находим решения неравенства:
-5<х< —1; х>1.
~ - (х-1)5(х4-2)2
Пример 8. Решить неравенство-—------<0.
Решение. Выражение (х—1)* (Х4-2)5 обращается в нуль при х=1
и при х= — 2, а при остальных значениях х оно положительно. Значения
191
Х=1 и х=— 2 удовлетворяют данному нестрогому неравенству, т. е. яв-
ляются его решениями. Пусть теперь х=/=1,хф-2, тогда (х — I)4(x-f-2)?2>0,
а потому, разделив обе части заданного неравенства на (х-~ 1)* (x-f-2)2
х—1
н сохранив знак заданного неравенства, получим неравенство —— рав-
носильное исходному (ем. п. 174). Полученное неравенство имеет следую-
щие решения: 0<х^1. В ответ нужно включить и отмеченное выше
решение х—— 2.
184. Показательные неравенства. При решении неравенств
вида af м > ag м следует помнить, что показательная функция
у=а* возрастает при а>1 и убывает при 0<аС1 (см. п. 94).
Значит, в случае, когда а>1, от неравенства следует
переходить к неравенству того же смысла f (x}Z>g (х). В случае
же, когда 0<а<1, от неравенства a^w>agW следует пере-
ходить к неравенству противоположного смысла f(x)<g(x).
Пример 1. Решить неравенство 23*+? <22*“|.
Решение. Здесь основание степени больше 1, поэтому,
сравнивая показатели, запишем неравенство того же смысла:
3x-f-7<2x —1. Решив это неравенство, получим x<L—8.
Пример 2. Решить неравенство (0,04)6*~х -8^625.
Решение. Так как 625 =252=( ) ~2=(0,04)~2, то за-
данное неравенство можно записать в виде
(0,04)51"*^8 < (0,04)“2.
Так как О С 0,04 с 1, то, сравнивая показатели, запишем
неравенство противоположного смысла 5х — х2—8 — 2.
Имеем последовательно
5х-х2 —8-)-2>0,
—х2+5х—6>0,
х2 — 5х4-бС0»
(х—2) (х—3)<0.
Решив последнее неравенство (см. п. 183 или п. 180), полу-
чим 2^х^3.
Таким образом множество решений заданного неравенства
есть отрезок [2; 3].
185. Логарифмические неравенства. При решении нера-
венств вида logD f (x)Z> log« g (x) следует помнить, что логариф-
мическая функция у=loge х возрастает при а>1 и убывает
при 0<о<1 (см. п. 96). Значит, в случае, когда а>1, от
исходного неравенства следует переходить к неравенству того
же смысла f(x)>g(x). В случае же когда 0<д<1, от исход-
ного неравенства следует переходить к неравенству противо-
положного смысла f(x)<.g(x). При этом следует учитывать,
что логарифмическая функция определена лишь на множестве
положительных чисел. Значит, должны выполняться нера-
венства f(x)>0 н £(х)>0. В итоге от неравенства logo f (х)>
> logc g (х) мы переходим к системе неравенств
Цх)>0, ( /(х)>0,
g(x)>0, или { g(x)>0,
f(x)>g(x) I f(x)<g(x).
Заметим, что первую систему можно упростить: неравен-
ство f(x)>0 вытекает из неравенств f(x)>g(x), g(x)>0, поэ-
тому неравенство f (х)>»0 можно опустить, т. е. переписать
систему в виде
I f(x}>g(x).
Аналогично вторую из написанных выше систем можно
переписать в виде
/(х)>0,
/(x)<g(x).
Пример. 1. Решить неравенство log] (2х-)-59)2>—2.
‘з
Решение. Так как — 2 = logi 9, то данное неравенство
“з
можно переписать в виде log^ (2x-}-59)>log । 9. Далее имеем:
з з
f 2x-f-59>0, Jx> —29,5,
(2х + 59<9; |х< —25;
откуда —29,5 <х<—25.
Пример 2. Решить неравенство 1g (х-}- 2) <2 — 1g (2х —6).
Решение. Чтобы все логарифмы имели смысл, должны
выполняться неравенства x+2z>0 и 2х 6>0. Используя
свойства логарифмов, преобразуем заданное неравенство:
lg(x+2)+lg(2x-6)<2, lg (х + 2)(2х-6)< 1g 100.
Таким образом, заданное неравенство равносильно системе
неравенств
х+2>0,
2х —6>0,
(х+2)(2х-6)<100.
193
Имеем последовательно:
х> — 2,
х>3, f х>3,
х2—х—56<0; Цх+7)(х—8)<0;
С помощью координатной прямой (рнс. 86) устанавливаем,
что множество решений последней системы, а значит, и задан-
ного неравенства есть промежуток (3; 8).
Т.6.8.
186*. Иррациональные неравенства. При решении иррацио-
нальных неравенств используется следующее утверждение:
Если обе части неравенства на некотором множест-
ве X принимают только неотрицательные значения,
то, возведя обе части неравенства в квадрат (или
в любую четную степень) и сохранив знак исход-
ного неравенства, получим неравенство, равносиль-
ное данному (на множестве X). Возведение обеих
частей неравенства в одну и ту же нечетную степень
(с сохранением знака неравенства) всегда является
равносильным преобразованием неравенства.
Рассмотрим неравенство вида (1)
Ясно, что решение этого неравенства является в то же
время решением неравенства /(х)^>0 и решением неравен-
ства g(x)>0 (из неравенства (1) следует, что g (х)>-д/Дх)^О).
Значит, неравенство (1) равносильно системе неравенств
Г(х)^О,
g(x)>0,
V/W<g(x).
Так как при выполнении условий, задаваемых первыми двумя
неравенствами этой системы, обе части третьего неравенства
системы определены и принимают только неотрицательные
значения, то их возведение в квадрат есть равносильное пре-
образование неравенства. Выполнив это преобразование, при-
дем к системе ,
( Г(х)>0,
{ g(x)>0,
I /(z)<(g(x))2.
7 Заказ 769
Итак, неравенство д//(х)<£(х) равносильно системе не-
равенств
Z(x)>0,
g(x)>0,
f &<&&)?.
Рассмотрим теперь неравенство вида g (х). (2)
Как и выше, заключаем, что но в отличие от
предыдущего случая здесь g (х) может принимать как неотри-
цательные, так и отрицательные значения. Поэтому заданное
неравенство (2) рассмотрим в каждом из следующих случаев:
^(х)<0, g(xy^O. Получим совокупность систем
g(x)<0, р(х)>0,
Г(х)>0, J Г(х)>0,
V/ (*)> е О); I V/W>
В первой из этих систем можно опустить последнее нера-
венство — оно вытекает из первых двух неравенств системы.
Во второй системе можно выполнить возведение в квадрат обеих
частей последнего неравенства.
В итоге приходим к следующему результату: неравенство
V/ (*) > ё (х) равносильно совокупности двух систем!
g(x»O,
Л*)>0,
/(x)>(g(x)/.
[g (х)<0,
Пример 1. Решить неравенство -фс2 — х — 12 <х.
Решение. Это неравенство равносильно следующей сис-
теме Неравенств:
{х2—х —12 > О,
Х>0,
х2-х-12<х2.
Решив систему, находим xj>4.
Пример 2. Решить неравенство д/х2—Зх+2 > х + 3.
Решение. Данное неравенство равносильно совокупно-
сти двух систем:
f х + 3<0, ( х+3>0,
1х2—Зх+2>0; < х2—Зх+2>о,
I х2—3x-j-2>(x + 3)2.
Второе неравенство второй системы можно опустить как
следствие третьего неравенства той же системы.
Решив первую систему, получим x<Z —8, из второй систе-
мы получаем —3^х< —Объединив найденные решения.
1
получим х<—g-.
187. Решение тригонометрических неравенств. Рассмотрим
примеры графического решения простейших- тригонометри-
ческих неравенств, т. е. неравенств вида f{x)>a (или / (х)<п),
где f (х)—одна из тригонометрических функций.
Пример 1. Решить неравенство sin х>0.
Решение. Построим график функции y=sinx и вы-
берем на оси х значения аргумента х, которым соответствуют
точки графика, лежащие выше оси х. Одним из промежутков,
содержащих такие точки оси х, является интервал (О; л)
(рис. 87), а всего таких интервалов будет бесконечно много,
причем в силу периодичности функции i/=sinx каждый из
них получается из (О; л) Сдвигом по оси х на 2stk, где k£Z.
Таким образом, решением заданного неравенства служит объ-
единение интервалов вида (0+2л/?; л+2«fe), т. е. (2я/?; л+2лй),
k £ Z. Это можно записать так: 2лй <Сх«<л + 2лЛ, k С Z.
Пример 2. Решить неравенство cos х<-|-.
Решение. Построим график функции у — cos х и про-
ведем прямую у—Нас интересуют те значения аргумента х,
которым соответствуют точки графика, лежащие ниже пря-
мой Одним из нужных нам промежутков является
интервал ; -у) (рис. 88). Воспользовавшись периодич-
ностью функции у—соз х, запишем ответ:
|-+2nfe<x<^+2nfe, k £ Z.
Пример 3. Решить неравенство tg х^ — 1.
Решение. Построим график функции y=tg х и прове-
дем прямую у=— 1. Нас интересуют те значения х, которым
соответствуют точки графика, лежащие не ниже прямой у= —1.
Одним нз нужных нам промежутков является £—
(рис. 89), а всего таких промежутков будет бесконечно много,
причем в силу периодичности функции #=tgx каждый по-
лучается из £—СДВИГОМ по оси х на гДе & 6 Я.
Это позволяет записать решение следующим образом:
—^--|-nfc<x<-~+nfe, k Е Z.
188. Неравенства и системы неравенств с двумя перемен-
ными. Рассмотрим неравенство f(x;y)^>g(x; у). Решением не-
равенства с двумя переменными называется пара значений
переменных, обращающая неравенство в верное числовое не-
равенство. Известно, что пара действительных чисел (х; у)
однозначно определяет точку координатной плоскости. Это
дает возможность изобразить решения неравенства или систе-
мы неравенств с двумя переменными геометрически, в виде
некоторого множества точек координатной плоскости.
Пример 1. Изобразить на координатной плоскости мно-
жество решений неравенства х-]-у —1>0.
Решение. Преобразуем данное неравенство к виду
—х+1. Построим на координатной плоскости прямую
у=—х-Ь1. Так как ордината любой точки, лежащей выше
прямой у =—х-)-1, больше, чем ордината точки, имеющей
такую же абсциссу, но лежащей на прямой, то множество
точек плоскости, расположенных выше этой прямой, и будет
геометрическим изображением решений заданного неравен-
ства (рис. 90).
Пример 2. Изобразить на координатной плоскости мно-
жество решений неравенства х{х—— 3.
Решение. Преобразуем неравенство к виду —2x4-3.
Построим на координатной плоскости параболу — график
функции у=х‘г — 2x4-3.
Так как ордината любой точки, лежащей выше парабо-
лы у=х2—2x4^3, больше, чем ордината точки, имеющей ту же
абсциссу, но лежащей на параболе, и так как неравенство
у ^Х2—2x4-3 нестрогое, то геометрическим изображением ре-
шений заданного неравенства будет множество точек плос-
кости, лежащих на параболе у=х1~ 2х4-3и выше нее (рис. 91).
Пример 3. Изобразить на координатной плоскости мно-
жество решений системы неравенств
( х>0,
I i/>0,
I ху>±,
Vx4-i/<5.
Решение. Геометрическим изображением решений сис-
х>0,
i/>0
темы неравенств
является множество точек первого
координатного угла (рис. 92, а}. Геометрическим изображени-
ем решений неравенства x+j/<5 или у <5—х является мно-
жество точек, лежащих ниже прямой, служащей графиком
функции у—5—х (рис. 92, б). Наконец, геометрическим изо-
бражением решений неравенства хуЗ>4 или, поскольку х>0.
4
неравенства 1/>-— является множество точек, лежащих выше
ветви гиперболы, служащей графиком функции у =—
(рис. 92, е). В итоге получаем множество точек координатной
плоскости, лежащих в первом координатном углу ниже пря-
мой, служащей графиком функции у—5—х, и выше гипер-
4
болы, служащей графиком функции У=— (рис. 93).
§ 18. Доказательство неравенств
189. Метод оценки знака разности. Суть этого метода за-
ключается в следующем: для того чтобы установить спра-
ведливость неравенства f (х; у; z)>g (х; у; z) (f <Zg, fZ^g, f^.g),
составляют разность f (х; у; z)—g (x; y; z) и доказывают, что
она положительна (соответственно отрицательна, неотрица-
тельна, неположительна).
Пример. Доказать, что если х^О, то
(среднее арифметическое двух неотрицательных чисел не мень-
ше их среднего геометрического; это неравенство называется
неравенством Коши).
Решение. Составим разность ^~~—^ху- Имеем
*+у
~2~ Л У ~ 2 — 2 ‘
Неравенство (д/х—верно при любых неотрицательных
значениях х и у. Значит, X^V^^xyt причем равенство имеет
место лишь в случае х=у.
Из неравенства Коши, в частности, следует неравенство
х+-справедливое для всех х>0.
190. Синтетический метод доказательства неравенств.
Суть этого метода заключается в следующем: с помощью ряда
преобразований выводят требуемое неравенство из некоторых
известных (опорных) неравенств. Опорными неравенствами яв-
ляются, например, такие:
1) где х^О, (неравенство Коши);
2) х+-^->2, где х>0;
3) —1<вша<1;
4) - l^coscc^l.
Пример. Доказать, что Vqbcd> где а, Ь. с,
d — неотрицательные числа.
Решение. Используем здесь в качестве опорного нера-
венство Коши, составленное для неотрицательных чисел
200
д+Ь c+d ,---------
а + Ь c+d „ 2'2 /а + b c+d „
Х=-^~, Имеем -----2---> V-5-----2 • П₽ИМе-
нив теперь неравенство Коши к числам а и Ь, а также с и d,
получим
*л/ДНо -^-^ab •~\[cd=^abcd.
Таким образом, fl+b^c+d^\/qbc^
Равенство имеет место в случае, когда a = b~c=d.
191. Доказательство неравенств методом от противного.
Суть этого метода заключается в следующем. Пусть нужно дока-
зать истинность неравенства
f&l у; z)>g(x; у, z). (1)
Предполагают противное, т. е. что хотя бы для одного набора
переменных справедливо неравенство
f(x; у; 2)<я(х; у; z). (2)
Используя свойства неравенств, выполняют преобразования не-
равенства (2). Если в результате этих преобразований получает-
ся ложное неравенство, то это означает, что предположение о
справедливости неравенства (2) неверно, а потому верно нера-
венство (1)
Пример 1. Доказать, что если а^О, Ь^О, d^O,
то д/(а+с)
Решение. Предположим противное, т. е. что для некото-
рого набора значений а, b, с, d справедливо неравенство
*^(а+с) {b\d)<z^ab\^cd.
Возведем обе его части в квадрат. Получим:
at> + bc-|-ad4-cd<:flb-|-2 ^/abcd+cd,
откуда bc4-ad<2 \/abcd и далее ^~^<Z-\[abcd. Но это проти-
воречит неравенству Коши, составленному для неотрицатель-
ных чисел Ьс и ad.
Значит, наше предположение неверно, т. е. для любых неот-
рицательных значений о, Ь, с, d справедливо неравенство
-^(a+c)(b4-dj ^Jab+^jcd.
Пример 2. Доказать неравенство cos (а -|- 0) cos (а — 0)^
^cos2a.
Решение. Предположим противное, т. е. предположим,
что существуют такие а и 0, для которых выполняется нера-
венство cos (а -|- 0) cos (а — 0)> cos2 а.
Воспользовавшись формулами cos (а+0) cos (а—0)=
= Ив2£±ои2а ((,м Ш) и д = l+cos 2а (см п nQ
лучим *”* 2Р+С°° 2g >—+|”-2- , откуда cos 2₽>1. Поскольку на
самом деле cos 20^1 при любых значениях 0, то мы получили
противоречие. Значит, наше предположение неверно, а поэтому
справедливо неравенство cos (a-f-0) cos (a —0)^cos2 а.
192*. Использование неравенств при решении уравнений.
Пусть нужно решить уравнение f (x)—g(x), и пусть существует
такое число А, которое является одновременно наибольшим зна-
чением функции y=f(x) и наименьшим значением функции
y—g (х). Тогда корнями уравнения f{x)=g (х) являются общие
корни уравнений /(х)=А, g (х)=А, и только они. Этот метод
является частным случаем функционального метода решения
уравнений (см. п. 158).
Пример. Решить уравнение x2-j—=2—(х—I)4.
Решение. С одной стороны, х2+-j?^2 при всех х^=0
(см. п. 189). С другой стороны, при всех х выполняется не-
равенство 2—(х—1)4^2. Значит, корнями данного уравнения
будут общие корни уравнений х2 4—^=2 и 2—(х —1)4 = 2
(если, конечно, такие общие корни есть; если их нет, то уравне-
ние не имеет корней).
Из уравнения х24--^==2 находим х> = 1, х2= —1. Из урав-
нения 2—(х —1)4=2 находим х=1.
Общим корнем этих уравнений является значение х=1, оно
и является единственным корнем заданного уравнения.
ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
§ 19. Числовые последовательности
193. Определение последовательности. Пусть каждому нату-
ральному числу поставлено в соответствие определенное дей-
ствительное число: числу 1 соответствует число oi, числу 2 —
ЧИСЛО О2, числу 3 — число Оз, ...» числу п — число ап и т. д.
202
Тогда говорят, что задана числовая последовательность, и пи-
шут: ai, я2» —*яя,.... Иначе можно записать (яп). Числа Я1, яг, яз,
...» яп, ... называются членами числовой последовательности-.
Я] — первый член, я2 — второй член,..., ял — n-й член последо-
вательности.
Пример 1. I2, 22, З2, ..м п2, ... . Эта последователь-
ность построена следующим образом: каждому натуральному
числу соответствует его квадрат. Здесь ап = п2.
Пример 2. Для любой бесконечной десятичной дроби
можно построить последовательность ее десятичных прибли-
жений по недостатку или по избытку. Например, для числа
€ = 2,71828... последовательность десятичных приближений по
недостатку имеет вид:
2; 2,7; 2,71; 2,718; 2,7182; 2,71828; ... .
194. Способы задания последовательности. Имеется три
основных способа задания последовательности.
1. Аналитический — последовательность задается форму-
лой п-го члена. Например, формулой ая=~-^
следовательность Яь я2, Яз, ...» ап» у которой
задается по-
„ 11. 22. 33
1 14-1~ 2 ’ °2-3 * Сз“34-1"“ 4 *
12 3 п
т. е. последовательность —, , ..., ——, ... .
Z о 4 п-}-1
2. Рекуррентный — любой член последовательности, начи-
ная с некоторого, выражается через предшествующие члены.
При stom способе задания последовательности указывают ее
первый член (или несколько начальных членов) и формулу,
позволяющую определить любой член последовательности по
известным предшествующим членам.
Пример. aj = 1, я2=1, яи+2=я«+яп+1.
Имеем Яз=Я1+я2 = 1 + 1 = 2; яе=я4+я6=3+5 = 8;
Я4=Я2-|-Яз= 1+ 2=3; я7=яБ+я6=б+8 = 13;
а5=аз+а4 = 2 + 3—5; я8=я6-|-я7 = 8-|-13 = 21 ••• •
В итоге получаем последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34.
Каждый ее член, кроме первых двух, равен сумме двух
предшествующих ему членов.
3. Словесный — задание последовательности описанием.
Такова, например, последовательность десятичных приближе-
ний по недостатку числа е (см. п. 193).
195. Возрастание п убывание последовательности. Последо-
вательность (яя) называется возрастающей, если каждый ее
член меньше следующего за ним, т. е. если ап<оп+1 для лю-
бого п. Последовательность (ап) называется убывающей, если
каждый ее член больше следующего за ним, т. е. если ап>ап±1
для любого п.
Рассмотрим примеры:
1) 1, 4, 9, 16, 25, ...» л2, ...— возрастающая последо-
вательность.
2) 2, 5, 8, 11, 14, ..., Зл— 1, ...— возрастающая последо-
вательность.
„.1234 п
3) -г-, , —, ...» ——...— возрастающая последова-
о 4 а П-[-1
тельность.
4) —1, —2, —3, —4, .... —и, ...— убывающая последо-
вательность.
, 1 1 1 1 -
5) 1, -g-, -g-, ...» ...— убывающая последовательность.
6) —1, 2, —3, 4, —5, 6, ...» (—1)"-п, ...— эта последова-
тельность не является ни возрастающей, ни убывающей.
7) 3, 3, 3, 3, ...» 3, ...— здесь мы имеем постоянную или
стационарную последовательность.
196. Определение арифметической прогрессии. Последова-
тельность (а„), каждый член которой, начиная со второго, равен
предыдущему, сложенному с одним и тем же числом d, назы-
вается арифметической прогрессией. Число d — разность
прогрессии. Таким образом, арифметическая прогрессия есть по-
следовательность, заданная рекуррентно (см. п. 194) равенст-
вом On+i—an+d. Например, o5=O4-|-d; aS4=aQ3-}-d и т. д.
При d>0 арифметическая прогрессия возрастает, при d<ZO
убывает.
Пример 1. Последовательность 3, 5, 7, 9, 11, 13, ...—
арифметическая прогрессия, у которой ai=3, d=2.
Пример 2. Пусть даны aj = — 2, d=0,5. Этими условия-
ми задается арифметическая прогрессия, у которой аг= —2 +
+ 0,5 =—1,5; —1,5 + 0,5= — 1; в4=Пз + <2^
= —1+0,5=—0,5; a5 = a4 + d= — 0,5 + 0,5=0; a6=a5 + d—
=0+0,5=0,5.
Получаем арифметическую прогрессию —2; —1,5; —1;
— 0,5; 0; 0,5; ....
Пример 3. Постоянная последовательность 2, 2, 2, 2, ...»
2, ... является арифметической прогрессией, у которой ai = 2,
d=0.
Иногда рассматривают не всю последовательность, являю-
щуюся арифметической прогрессией, а лишь ее первые не-
сколько членов. В этом случае говорят о конечной арифмети-
ческой прогрессии.
Для указания того, что последовательность (ап) является
арифметической прогрессией, иногда используется обозна-
чение
-т-Ol, 02, Оз, —» Оп.........
197. Свойства арифметической прогрессии
1°. Формула п-го члена арифметической прогрессии:
an—ax+d (n—1).
2°. Формулы суммы п первых членов арифметической про-
грессии:
S„=2L±^.„; (1)
Я„^+а2<Д--».п. (2)
Здесь Si =ai, Sn=Oj -|-02-|-Оз +ал.
3°. Характеристическое свойство арифметической прогрес-
сии: последовательность является арифметической прогрессией
тогда и только тогда, когда каждый ее член, кроме первого
(и последнего в случае конечной арифметической прогрессии),
равен среднему арифметическому предыдущего и последующе-
го членов:
лл_1+ая+1
°”-----2 •
Пример 1. Бегун за первую минуту бега пробежал 400 м,
а в каждую следующую минуту пробегал на 5 м меньше, чем
в предыдущую. Какой путь пробежал он за 1 ч?
Решение. За первую минуту бегун пробежал 400 м, за
вторую — 395 м, за третью — 390 м и т. д. Числа 400, 395,
390, ... образуют арифметическую прогрессию, у которой
aI = 400, d=—5. Путь за 1 ч, т. е. за 60 мин, равен сумме
первых 60 членов прогрессии. Применив формулу (2), получим:
S60 = 2°'+2J'59-60 = 30-~59'5-60 = 15 1 50.
Итак, за 1 ч бегуи пробежит 15 км 150 м.
Пример 2. При делении 13-го члена арифметической про-
грессии на ее 3-й член в частном получается 3, а при делении
18-го члене на 7-й член в частном получается 2 и в остатке 8.
Найти 20-й член прогрессии.
Р е ш е и н е. Из условия следует, что ап = За3, а а!8=2а7+8
(см. п. 3). По формуле n-го члена имеем a3=ai-|-2d, П]з=
=ai4-12d, a7 = ai+6d, aI8=ai-f-17d и приходим к системе
двух уравнений с двумя переменными oi и d:
( 014-12^=3(0! 4-2d),
t ai4-17d=2(o!4-6d)4-8.
Решая эту систему, получаем:
( Oj = 3d,
tai = 5d— 8,
откуда d = 4, at = 12. Зная ai и d, нетрудно найти а2о:
020=014-19d = 124-19-4 = 88.
198. Определение геометрической прогрессии. Последова-
тельность (Ьп), первый член которой отличен от нуля и каждый
член, начиная со второго, равен предыдущему, умноженному на
одно и то же отличное от нуля число Q, называется геометри-
ческой прогрессией. Число q — знаменатель прогрессии. Таким
образом, геометрическая прогрессия есть последовательность,
заданная рекуррентно (см. п. 193) равенством bn+i — bnq, где
bi^O, Например, b7=b6Q, Ь54 = Ь535-
Пример 1. Последовательность 1, 2, 4, 8, 16, 32, ...—
это геометрическая прогрессия, у которой bi —1, q=2.
Пр и мер 2. Последовательность 100, 30, 9,
Урод, ...— это геометрическая прогрессия, у которой bi = 100.
Пример 3. Пусть даны = 2, q = — 3. Этими условиями
задается геометрическая прогрессия, у которой &2=biQ = 2X
Х(— 3)=—6; Ь3=Ь2д=(—6)-(—3)=18; Ь4= Ьз9 = 18-(-3)=
= — 54; Ь5 = Ь4д=(—54)«(— 3) = 162, ... . Получаем геометри
ческую прогрессию 2, —6, 18, —54, 162, ... .
Пример 4. Постоянная последовательность 2, 2, 2, 2, ...»
2, ... является геометрической прогрессией, у которой bi=2,
g = l.
Иногда рассматривают не всю последовательность, являю-
щуюся геометрической прогрессией, а лишь ее первые несколько
членов. В этом случае говорят о конечной геометрической про-
грессии.
Для указания того, что последовательность (5П) является гео-
метрической прогрессией, иногда используется обозначение
— bi, Ьг» Ьм
199. Свойства геометрической прогрессии.
1°. Формула п-го члена геометрической прогрессии:
bn^biqnl.
2°. Формулы суммы первых п членов геометрической про-
грессии:
а ьпд—bt .
—5=1—
Здесь Si = bi, = bi + £>2+&з+ — + &«> дУ=1; если Q = l, то
Sn=nbi.
3°. Характеристическое свойство геометрической прогрес-
сии: последовательность является геометрической прогрессией
тогда и только тогда, когда каждый ее член, кроме первого (и
последнего в случае конечной геометрической прогрессии), свя-
зан с предыдущим и последующим членами формулой
бя=Ьп~ 1 • бя-|- ]•
Пр и м е р 1. Найти 8-й член геометрической прогрессии,
у которой bi —3, Ья=96, S„=189.
Решение. Так как bn“big*_| (свойство 1°), то полу-
чаем 96 = 3qr_1, qb-1 = 32 или q"=32q.
С другой стороны, по свойству 2°
„ Ь1 (<?"—1)
Sn~—• откуда находим:
189^3(l?"~1), или 5-^=63. (1)
q—1 9 — 1 v '
Но q”=32q (см. выше). Подставив это выражение в равенство
(1), получим:
5|^р=63, 32g —1 = 63д—63, д=2.
Зная bi и д, найдем ЬЁ. Имеем:
Ьв = Ь1д7=3-27=384.
Пример 2. Три числа образуют конечную геометриче-
скую прогрессию. Если второе число увеличить на 2, то новая
тройка чисел будет представлять собой конечную арифмети-
ческую прогрессию. Если третье число этой новой тройки
увеличить на 9, то снова получится геометрическая прогрес-
сия. Найти первую тройку чисел.
Решение. Обозначим искомые три числа bi, b2, Ьз.
Используя обозначения -=- для арифметической прогрессии
и -ff- для геометрической прогрессии, запишем условие за-
дачи следующим образом:
1) -г Ьь Ь2, Ьз.
2) ~ Ьь Ь2Ц-2, Ь3.
3) bi, Ъг ЧН 2, Ьз + 9.
Воспользовавшись характеристическими свойствами ариф-
метической (свойство 3°, п. 197) и геометрической (свойство 3°,
п. 199) прогрессий, получим соответственно: 1) Ь2=Ь|«Ьз;
2) b2 + 2=il±^; 3) (Ь2 + 2)2 = Ь,(Ьз + 9).
Так как b2 = biQ, а Ьз—biQ2, то:
1) b?g2 = 6,b,g2; 2) b1Q + 2=il^^;3)(big + 2)2 = b1 (b,g2 +
-j- 9). Первое условие как тождественное равенство можно опу-
стить. Мы приходим к системе даух уравнений с двумя пере-
менными bi и q:
f 2(big+2)=b.4-b1g2,
I (b,g + 2)2=b, (b,g2+9).
Имеем далее:
bi (1 + g2-2g) = 4,
bi (9 —4g)=4.
Выразив bi через q из второго уравнения
bi=-=-^-?----и подставив это выражение вместо bi
» — 4Q
уравнение системы, получим —77^—7—~=1» откуда
Н — 4Q
Qi = 2, q2— — 4.
системы:
в первое
находим
Следовательно, bi = 4 при q = 2 и при q — —4.
Значит, условию задачи удовлетворяют две тройки чисел:
1) 4, 8, 16 (при bi = 4, 5 = 2);
4 16 64 , , 4 ..
2) 25’ — 26’ 25 ^ПрИ 6| — 25’ в 4)’
200. Понятие о пределе последовательности. Число b назы-
вается пределом последовательности (сп)> если, какое бы поло-
208
b-E Ь Ь+Е
жительное число ни взять (это число обычно обозначают с —
греческая буква ♦эпсилон»), найдется номер N, начиная с ко-
торого (т. е. при n^N) отличие ап от Ь по модулю будет
меньше е, т. е.
Пишут: lim ап=Ъ, или ап->Ь. Говорят, что последователь-
ность (пп) сходится к Ъ.
Геометрический смысл предела последовательности: если
Ъ — предел последовательности (ал), то, какую бы окрестность
точки Ь ни выбрать, вся последовательность, начиная с неко-
торого номера N, будет изображаться точками, лежащими
в этой окрестности (рис. 94); окрестность точки Ъ — это ин-
тервал с центром в точке Ь.
Примеры. Рассмотрим последовательности:
1) 1, -j—, ...» —, .... Чем больше номер члена последо-
вательности, тем меньше этот член отличается от числа 0. Эта
последовательность сходится, предел ее равен 0, т. е.
lim 1 =0.
Л->со П
1 2 3 4 п ,т
2) -5"» “5“» -зг. "к"» тг» — • Члены этой последователь-
' 2 о 4 о 71-J-1
ности по мере увеличения номера все меньше и меньше отли-
чаются от числа 1. Эта последовательность сходится, причем
т п 1
lim -гт=1.
n
В самом
Какое бы е>0 ни взять, найдется
номер N, такой, что для всех n^N выполняется неравенство -<С £.
Чтобы найти такое N, достаточно решить неравенство —-^-<е и взять в ка-
п 4-1
честне N любое натуральное число, удовлетворяющее атому неравенству.
Эта последовательность сходится,
Q\ 2_ _L _L _L
' з ’ з'
ее предел равен 0, т. е. Ит-^=0.
209
4) 2, 0, 3, 2, О, 3, 2, О, 3, ... . Эта последовательность
ие сходится, не имеет предела.
5) Постоянная последовательность а, а, а,...»а,... сходится к
пределу а, т. е. lim а—а.
201. Вычисление пределов последовательностей. Для вы-
числения пределов последовательностей используются следую-
щие утверждения:
1) Последовательность сходится к числу 0 (см. пример
1 из п. 200):
lim -i-=0.
2) Последовательность qn, где | q | < 1, сходится к числу 0
(см. пример 3 из п. 200, где
lim Qn=0, если |g| <1.
3) lim a=a (см. пример 5 из п. 200).
4) Это утверждение носит название теоремы об арифмети-
ческих операциях над пределами.
Т.7.1.
Если lim с„=а, a lim 6Л = Ь, то:
a) lim (ап±6л)=а±Ь; б) lim апЬп=аЬ\
П-^оо П~>оо
в) если Ь=/=0, то lim-^=-^-.
П-^со Оп О
Пример 1. Вычислить lim
Решение. Так как -^=———, а ——>0, то
п п п п п
—>0 «0 — 0. Итак, lim — 0.
П—>оо Л
Аналогично устанавливается, что >0 для любого нату-
рального k.
Пример 2. Вычислить lim •
п-*<» 2п — л—1
Решение. Разделим почленно и числитель, и знаменатель
данной дроби на наивысшую (из имеющихся) степень перемен-
ной п, т. е. на п2. Получим:
210
Воспользовавшись теперь тем, что Нт —=0, Нт -4-=0,
П-*-ео Л л-><х> П
Нт с—а, и теоремой об арифметических операциях иад преде-
лами, получим:
Г и8+и+2 _ 1-Ю+2-0 1
2ла—п—1 — 2—0—0 — 2 *
202. Сумма бесконечной геометрической прогрессии при
Igl <1. Пусть 61, Ь2> Ьз,.... Ьп,...— бесконечная геометрическая
прогрессия, у которой |д|<1. Рассмотрим сумму первых ее п
членов: Sn= 61 + 62 + ... + 6п. Имеем (см. п. 199):
sn=bt{Qn~1}.
Вычислим lim Имеем (см. п. 201):
lim S„=lim -^-(^-1).=
П-r-co пч-со Q 1 Л->-ео Q 1
=+(0-1)=+--
q —1 ' ’ 1— q
Итак, для бесконечной геометрической прогрессии, у которой
|Q|<1, существует lim Sn, где Sn= bi + 62 + 63+... + 6и.
Этот предел называют суммой бесконечной геометрической
прогрессии и обозначают S:
s=±-.
Пример. Сумма бесконечной геометрической прогрессии
при 1g] <1 равна 9, а сумма квадратов ее членов равна 40,6.
Найти сумму первых 6 членов прогрессии.
Решение. Обозначим заданную прогрессию так: 6i, 62,
63, ...» Ьп, ... . По условию ее сумма равна 9, т. е. 37“—9.
Рассмотрим последовательность 6?, 61 2» 62,Ьп,.... Каждый
ее член получается из предыдущего умножением на д2, т. е. это
геометрическая прогрессия В|, В2, Вз, ...» Bnt .... у которой пер-
вый член равен 6?, т. е. Bi = 62, а знаменатель Q равен д2,
т. е. Q=g2. Так как |д2|<1, т. е. |Q|<1, то сумма новой
прогрессии равна . По условию эта сумма равна 40,5.
Значит, в итоге мы приходим к системе двух уравнений с
двумя переменными:
1 7^5=40,5.
' 1 —
211 W
Выразив bi из первого уравнения bi=9(l — q) и подставив
«1(1 —в)2 81
результат во второе уравнение, получим a =-7р отку-
1—q 1 1
да 1+д 2 ’ 9 — 8
Тогда bi = 9(l — g)=9^1—6. Теперь можно найти сум-
му первых 6 членов прогрессии:
, _ь,(в’-1) ®((а) х) й80
Г~ 8 81-
§ 20. Предел функции
203. Предел функции y~f{x) при х-+оо. Горизонтальная
асимптота. Число Ъ называется пределом функции y=f(x'}
при стремлении х к + оо, если, какое бы число е>0ни взять,
найдется число Af>0, такое, что для всех х>М выполняется
неравенство |/(х) —Ь|<е. Пишут: lim f(x)=b.
Геометрически это означает, что график функции y—f{xj
при выборе достаточно больших значений х безгранично при-
ближается к прямой у = Ъ (рис. 96), т. е. расстояние от точки гра-
фика до прямой у = Ъ по мере удаления точки в бесконечность
может быть сделано меньше любого числа е>0. Прямая у~Ь
называется в этом случае горизонтальной асимптотой графика
функции y=f(x).
Возьмем для примера функцию • Для этой функции
имеем /(6)=i; /(10)=^; /(100)=^; /(Ю00)=^к. За-
мечаем, что, чем больше выбирается значение аргумента, тем
меньше отличается от нуля значение функции, причем это
отличие можно сделать меньше любого наперед заданного по-
ложительного числа е. Значит, lim =0. Это подтвер-
ждается и геометрически: прямая у = 0 является горизонталь-
ной асимптотой графика функции У=(^г) (рис. 96).
Прямая у = Ъ может быть горизонтальной асимптотой гра-
фика функции y = f(x) и при выборе достаточно больших по
модулю, но отрицательных значений аргумента (рис. 97). Тогда
говорят, что число Ь является пределом функции y=f{x) при
стремлении х к —оо, и пишут: lim f(x)=b. Например,
lim (3+2*)=3 (рис. 98).
Наконец, прямая у=Ъ может быть горизонтальной асимп-
тотой графика функции y=t (х) и при х—► + оо, и при х—^— оо.
Так, прямая у — 1 — горизонтальная асимптота графика функ-
ции (рис. 99). В этом случае говорят, что число Ь
является пределом функции y=f(x) при стремлении х к оо,
х2
и пишут: lim f (х)= Ъ. Так, верны равенства lim s—1,
*-> со со 1 I X
lim — = 0.
«-►со X
Число Ь называется пределом функции y—f{x) при стрем-
лении х к — оо, если, какое бы число е>Они взять, найдется
число Af>0, такое, что для всех x<Z—М выполняется нера-
венство | f (х) — Ь | с е.
Число Ь называется пределом функции y—f(x) при стремле-
нии х к оо, если,какое бы число е>0 ни взять, найдется число
Af>0, такое, что для всех х, таких, что |х!>Л1, выполня-
ется неравенство | f (х)— Ь | <е.
Зная предел функции при х->оо, можно построить горизон-
тальную асимптоту графика (если предел равен Ь, то у = Ь — го-
ризонтальная асимптота); обратно: если известна горизонталь-
ная асимптота графика функции, можно сделать вывод о ее пре-
деле при х—>оо (если у — Ь— горизонтальная асимптота, то
lim f (x)=b).
X-t-co
204. Вычисление пределов функций при х->оо. Для вы-
числения пределов функций прн х->-оо используются следую-
щие теоремы об операциях над пределами:
Т.7.2.
Т.7.3.
Если lim f{x)—at lim g(x)=b, то lim (/(х)-pg (*)) =
X-► оо Х“*со X—
=а + Ь (теорема о пределе суммы).
Если lim f[x)—at Iimg(x)=b, то lim f(x)g(x)=ab
X-f-oo X-.CO X—►<*>
(теорема о пределе произведения).
Т.7.4. I Если lim /!(х)=а, то lim kf(x)—ka (теорема о вы-
I несении постоянного множителя за знак предела).
Т.7.5.
Если lim f(x)=a, lim g(x)~b и Ь^О, то lim-®=
X—►со Х—со Х--<х>£Г(Х)
=-|- (теорема о пределе частного).
Пример 1. Вычислить lim ——.
Решение. Разделив числитель и знаменатель почленно
3 24-14-3
на х , получим lim-----------и далее
1+£
214
Так как lim —=0 (см. п. 203), то, воспользовавшись теоре-
*->ео X
мамн Т.7.2 — Т.7.5, получим ~0 ° ~
Итак, lim Зж3~^+х+-8=3.
Пример 2. Найти горизонтальную асимптоту графика
функции I/—д/х+2—Vx при х—>-|-со.
Решение. Чтобы найти горизонтальную асимптоту,
надо вычислить предел функции при х->+ оо. Имеем
Um (V^-t/S)= Um
*-►+«» * -++&> 7x4-24-7^
= цт = Um -----5----=0.
7*4-2 +Vx *->+«7*4-2 4-7*
Значит, у—С — горизонтальная асимптота графика функ-
ции у—^х-^-2—-у/х.
205. Предел функции в точке. Непрерывные функции. Рас-
смотрим функции у = f (х), у=g (х) и у—h (х), графики которых
изображены на рисунке 100. Это разные функции, они отли-
чаются своим поведением в точке х~а. Если же х=/=а, то /(х)=
= ff(x)=A(x). Во всех трех случаях замечаем, что, чем ближе
х к а, тем меньше отличается значение функции f (х), или g (х),
или h (х) от числа b — это отличие характеризуется выражени-
ем соответственно I f (х) — Ъ |, | g (х)—Ы, | h (х)—Ы. Для любой из
рассматриваемых функций говорят, что предел функции при
стремлении х к а равен Ь; пишут соответственно: lim f (х)=5,
lim g (х)—Ь, lim h (х)=Ь- Подчеркнем еще раз, что при этом
значение функции в самой точке а (и даже сам факт сущест-
вования или несуществования этого значения) не принимается
во внимание.
Определение формулируется так: число Ь называется пределом функции
y=f(x) при стремлении х к а, если, какое бы число е>0 ни взять, для
всех достаточно близких к а значении х, т. е. для всех х из некоторой окрест-
ности точки а, исключая, быть может, саму эту точку, будет выполняться
неравенство 1/(х)—Ь|<е.
Вернемся еще раз к рисунку 100. Замечаем, что для
функции у=f (х\ график которой изображен на рисунке 100, а,
выполняется равенство b=f(a), т. е. lim f(x)—f(a). Если
Hm f(x)—ffaY то функция называется непрерывной в точке а.
Если функция непрерывна в каждой точке интервала (а; Ь), то
она называется непрерывной на этом интервале. Если функция
непрерывна на интервале (а; Ь), определена в точках а и Ь и при
стремлении точки х интервала (а; Ь) к точкам а и b значения
функции y=f(x) стремятся соответственно к значениям / (а),
f(b), то функция y—f(x) называется непрерывной на отрезке
[а; Ь).
206. Вертикальная асимптота. График функции y=f(x),
изображенный на рисунке 101, а, обладает следующей осо-
бенностью: какое бы число р>0 ни взять, Можно указать та-
кую окрестность точки а, что для любого х из этой окрест-
ности (х=/=а) соответствующая ордината графика по модулю
будет больше р, т. е. I/(ж)| >р. Говорят, что прямая х=а явля-
ется вертикальной асимптотой графика функции y~f(x)t и
пишут: lim f (х)~ оо.
1
Например, график функции у—— имеет вертикальную
асимптоту х=0 и горизонтальную асимптоту у=0 (рис. 101, б);
график функции у=log 2 х имеет вертикальную асимптоту
я
хг=0 (рис. 101, в); график функции у—tgx имеет вертикаль-
ные асимптоты X—х— —х=-^, х=—~ и т. д.
Если f (х)= pq и в точке а функции р(х), д(х) непре-
рывны, причем р (a)^fcO, q (а)=О, то х=а — вертикальная асим-
птота графика функции y—f{x).
Например, график функции имеет две вертикаль-
ные асимптоты: х=3 и х= — 3 (рис. 102) — при указанных
значениях х знаменатель х2—9 обращается в нуль.
207. Вычисление пределов функций в точке. Для вычисле-
ния пределов функций в точке основными являются следующие
факты:
1) любая элементарная функция, т. е. функция, заданная
аналитически рациональным (см. п. 48), иррациональным (см.
п. 48), трансцендентным (см. п. 118) выражением или выраже-
нием, составленным из перечисленных с помощью конечного
числа арифметических операций, непрерывна в любой внутрен-
ней точке области определения функции (т. е. в любой точке,
принадлежащей области определения функции вместе с
некоторой своей окрестностью); если х=а — внутренняя точка
области определения сложной функции f (g (х)), то и сложная
функция f (g (х)) непрерывна в точке а;
2) если функция y=f{x) непрерывна в точке х—а, то
Um f(x)=f(a).
Пример 1. Вычислить lim ——х- .
*-* 3x4-1
Решение. Точка х = 4 — внутренняя точка области оп-
ределения функции f(x)=значит, функция непре-
т/44-45
рывна в этой точке. Имеем f (4)—4^1~=2.
Значит,
Пример 2. Вычислить lim —5sin,x—
х-^-п cos x+tgx
Решение. Функция f (х) х непрерывна в точке
х=л. Имеем:
f / ч Sinn 0 _п
' ' cos2 n-J-tgn 14-0
Значит,
um - =0.
Х-+я COS^x+tgX
xs4-9
Пример 3. Вычислить Пт —,—Т .
х->3 X —ЭХ4-*1
I 9
Решение. Функция f (х)=——не определена в
точке х=3» так как в этой точке знаменатель дроби обра-
щается в нуль. Поскольку числитель х2+9 отличен от нуля
хг4-9
в точке х=3, то пишут: lim—?—~— сю (см. п. 206); лря-
х-ьЗ X —0X4-6
мая х=3 является вертикальной асимптотой графика функ-
х24-9
ции »=*°-6*+в-
я2—9
Пример 4. Вычислить lim —?—-——.
х-*8 я —5x4-6
Решение. Здесь в отличие от предыдущего примера и
числитель, и знаменатель обращаются в 0 при х=3. В подоб-
ных случаях для вычисления предела необходимы тождест-
венные преобразования выражения, задающего функцию,
тх х2—9 (х—8)(х4-8) „ о
Имеем —у— д=-7~—50-—Поскольку при х->3 значение
X —OX-f-o (X—о) (X—
функции в самой точке х=3 не принимается во внимание
(см. п. 205), дробь можно сократить на х—3, получим
• Итак,
(х-8)(х4-8) _.. Х4-8 84-8_р
Х^з х2—5x4-6 х™ (х—8)(х—2) Йх-2 8-2 6‘
Пример 5. Вычислить lim - .
*^-г-/7^х-8
Решение. При х— —2 и числитель, и знаменатель обра-
щаются в нуль. Выполним следующие преобразования задан-
ного выражения:
х+2 _ (х+2)(У7-х+3) = (х+2)(У7^+3) _
V7—*—3 ЗИ^Т^х+З) (V7— х)г-32
= -<V7=S+8).
1* + ^;
ИТМПт2-^=У-^= limj—#—ж—3)= -(#+2 + 3)= -6.
§ 21. Производная и ее применения
208. Приращение аргумента. Приращение функции. Пусть
функция y=f(x) определена в точках х и Хь Разность Х\ — х
называется приращением аргумента, а разность f {x\)—f {х) —
приращением функции при переходе от значения аргумента х
к значению аргумента Xi. Приращение аргумента обозначают
Ах; значит, Ах = х»— х, т. е. Xi = x+Ax. Приращение функции
обозначают А/ или Ау; значит, A/=/(xi)—/(х)=/(х4-Ах)—
-/(*)
Пример 1. Найти приращение функции у = х при пере-
ходе от значения аргумента х к значению х4-Ах.
Решение. Имеем /(х)=х3, /(х4-Ах)=(х4-Ах)3. Значит,
А/= f fx + Ах)—f (х)=(х + Ах)3 - х5=Xs 4- Зх2 Ах4-Зх (Ах)2+
4- (Ах? - х3=Зх2 Ах 4- Зх (Ах)2 4- (Ах)3.
Итак, А/=(Зх24-Зх- Ах 4-(Ах)2) &х. По этой формуле можно
вычислять значение А/ для любых заданных х и Ах. Напри-
мер, при х = 2, Ах—0,1 имеем:
А/=/(2,1)-/(2)=(3-22 4-3-2-0,14-0,12)-0,1 = 1,261;
при х=1, Ах =—0,2 получаем А/=/(0,8)—/(1)=
=(3 -12 4- 3.1.(- 0,2) 4-( - 0,2?) (- 0,2) = - 0,488.
Пример 2. Доказать, что для линейной функции у —
=kx-\-b справедливо равенство k—
Решение. Имеем /(х)=Лх4-Ь» /(х4-Ах)=Л (х4-Ах)4-Ь-
Значит, А/=f (х 4- Ах)—f (х) ~ (Л (х 4- Дх)4- Ь)—(*х 4- Ь) = ЛАх,
откуда получаем что и требовалось доказать.
Геометрический смысл доказанного равенства проиллюст-
рирован иа рисунке 103.
209. Определение производной. Пусть функция у = /(х)
определена в точке х и в некоторой окрестности этой точки.
Пусть Ах — приращение аргумента, причем такое, что точка
х4-Дх принадлежит указанной окрестности точки х, а А/ —
соответствующее приращение функции, т. е. А/=/(х4-Дх)—
— f (x). Если существует предел отношения приращения функ-
ции А/ к приращению аргумента Ах при условии, что Ах—>0,
то функция y—f(x) называется дифференцируемой в точке
х, а этот предел называется значением производной функ-
ции y=f(x) в точке х и обозначается f (х) или у'. Итак,
f (х)=у‘ = lim Um _
Дх—О Дх Дх—О Дх
/' (х) — это новая функция, определенная во всех таких
точках х, в которых существует указанный выше предел;
эту функцию называют производной функции y=f(x).
Пример 1. Найти f (2), если f (х)=х2.
Р е ш е н и е. Имеем /(2) = 22=4, f (24-Дх)=(2-|- Ах)2,
Д/^/(24-Ах)-/(2)=(24-Аху-4=4Ах+(Ах)\
Тогда 4Axj-(Ax)2 __-4_|_дх а Jimlim (4-|-Дх)=4.
Дх Дх г Дх-»о Дх д*-ок г 1
Значит, f (2) =4.
Опираясь на определение, можно рекомендовать следующий
план отыскания производной функции у =/(х):
1) Фиксируем значение х, находим /(х).
2) Даем аргументу х приращение Ах, находим /(х-{-Ах).
3) Вычисляем приращение функции А/—/(хЦ-Дх)—/(х).
4) Составляем отношение 4^*
' Дх
5) Находим предел отношения ~ при Ах->-0.
Пример 2. Найти производную функции у=х3.
Решение.
1) /(х)=х3.
2) /(х+Дх)=(х4-Ах)3.
3) А/=/(х + Ах)-/(х)=(х + Ах)3-х3=(Зх2+Зх.Дх +
4-(Ах)2)Дх (см. п. 208).
4) ^-=Зх2+Зх.Дх+(Дх)2.
5) lim = lim (Зх2 + Зх • Дх+(Дх)2) = Зх2+Зх • 0 + О2 = Зх2.
Дх—О Ах Дх-*О
Итак, (х3)' —Зх2.
210. Формулы дифференцирования. Таблица производных.
Операцию отыскания производной называют дифференциро-
ванием. В п. 209 получена одна из формул дифференциро-
вания: (х3)'—Зх2. По такому же плану можно вывести осталь-
ные формулы, которые приведены ниже.
1. (С)'=о. 10-
2. (kx+b)=fc.
3. (x’J'—rx'-'. “•(ctgxy
4. (е’)'=е*.
5. (aY=a*lna. 12. (arcsin x)' = 1 -. -yl — X
6. (lnx)'=i. 13. (arccos x)' — — _
7. (logox)'=-L_.
14. (arctg х)'=-^-г.
3. (sin x)'=cos x.
9. (cos x)' = — sin x. 15. (arcctg x)'=— yppr-
Например, (2х — 3)' = 2 (формула 2); (х1°)' = 10х9, (Д,) =
=(х~2)' = — 2х“3, (\/ху)/ = (хб) 6 (формула 3); (5*)' =
= 5'In 5 (формула 4); (1g «)' = -,* 10 (формула 7).
211. Дифференцирование суммы, произведения, частного.
Если функции и и v дифференцируемы в точке х, то:
1°. Их сумма дифференцируема в точке х и
(«4-»)'=»'+»' (теорема о дифференцировании суммы);
2°. Функция Си» где С — постоянная, дифференцируема в
точке х и
(CuY—Cu* (теорема о вынесении постоянного множителя
за знак производной);
3°. Произведение функций и и v дифференцируемо в точ-
ке х и
(uv)'=u'v+uv' (теорема о дифференцировании произве-
дения);
221
4°. Частное функций и и v дифференцируемо в точке х, если
v (х) Ф О, и
=ц(теорема о дифференцировании частного).
Пример 1. Найти производную функции у =2 sin х—
СОЗ х . -
3~+5-
Решение. Воспользовавшись теоремами 1° и 2°, получим:
(2 3in х —5)*—(2 sin х)'4-( —cos х) + 5' —
=2 (sin х)'—|-(cos х)'4- 5'.
Осталось применить соответствующие формулы дифференци-
рования (см. п. 210). Получим 2cosx——(—sin х)4-0 =
= 2 cos х-р-sin х.
Итак, 2sinx —~Р б)' = 2 cos х+-S1g —.
2
Пр и м е р 2. Найти (х 5 log3x)'.
Решение. Воспользовавшись теоремой о дифференциро-
вании произведения, получим (х5 log3x)'=(xs) log3 х-р
2
+ X5 (log3 х)'. Осталось применить соответствующие форму-
лы дифференцирования (см. п. 210). Получим ~х 5 log3X-P
— / 3 ““
Итак, (х 5 log3«) =4* 5 logs *+^—=-°:41," *+1- •
\ /5 In 3 V^-ЬЗ
Пример 3. Вычислить f (0), если f (х)~
Решение- Сначала найдем f' (х). Воспользовавшись тео-
ремой о дифференцировании частного, получим f (х)=
_(27(*я+1)-У(ж»+1Г 2-ln2.(xz+l)-2x-2x
-------p+ip и далее (s)+i)2 ------------------•
Теперь вычислим f (0). Имеем:
r(0)=-^-.(g + >)-2°-2.0=hi2-
212. Сложная функция и ее дифференцирование. Рассмот-
рим функцию у—sin х2. Чтобы найти значение этой функции
222
в фиксированной точке х, нужно: 1) вычислить х2; 2) найти
значение синуса при полученном значении х2. Иными слова-
ми, сначала надо найти значение функции g(x)=x2, а потом
найти sin g (х). В подобных случаях говорят, что задана слож-
ная функция f{g{x)). В нашем примере u=g(x)=x2, а/(в)=
=sin и. Рассмотрим еще два примера.
Пример 1. Составить сложную функцию f (g (х)), если
в(х)=1пж, f(u)=yu.
Решение. f(g (х))=-^g (х) =ylln х.
Пример 2. Из каких функций составлена сложная функ-
ция y=tg5(2x+l)?
Решение. Эта функция состоит из трех функций: g (х)=
= 2x4-1, ft(u)=tgu, /(z)=z5. В самом деле, /(ft(g(x)))=
“(Л (8 (x)))^=(tg (8 (*)))5=(tg (2x4-l))5=tg5 (2x4-1)-
Пусть y=/(g(x))— сложная функция, причем функция
и—g (х) дифференцируема в точке х, а функция у—f (и) диффе-
ренцируема в соответствующей точке и. Тогда функция
y=f(g (х)) дифференцируема в точке х, причем
y'~f' (g (x))*g'(x)-
Запись f {g (х)) означает, что производная вычисляется по
формуле для f (х), но вместо х подставляется g (х).
Пример 3. Найти ((Зх 4- б)4)'.
Решение. Здесь g (х)= 3x4-5, f (и)~и\ f (g (х)) =
= (Зх 4- 5)4. Значит, у' = f' (g (х)) g' (х)=4 (Зх 4- 5f (Зх 4- 5)' =
= 4 (3x4- б)3 3 = 12 (3x4- 5)3.
Пример 4. Найти (tg (х24-х4-1))'.
Решение. Так как (tg и)' • то (tg (х24- х4-1))'=
~ соз2(х2Н-х+1) +* + !) = cos4 (ж2+X +1) •
213. Физический смысл производной. Если 8—s(t)— за-
кон прямолинейного движения, то s' (i) выражает скорость
движения в момент времени t, т. е. v=s'(i) (мгновенная
скорость).
Например, закон свободного падения тела выражается за-
висимостью s=-g- * ^orAa скорость падения в момент t такова:
"=»'=(4-)'
Вообще производная функции y—f(x) в точке х выражает
скорость изменения функции в точке х, т. е. скорость про-
223
текания процесса, описываемого зависимостью y=f(x). В этом
состоит физический смысл производной. Например, для функ-
ции у —х2 имеем /' (х)=2х, при х=2 имеем /'(2)=4, а при
х=3 имеем /'(3)=6. Это значит, что в точке х=2 функция
изменяется в 4 раза быстрее аргумента, а в точке х=3— в
6 раз быстрее.
214. Вторая производная и ее физический смысл. Пусть
функция y=f(x) имеет производную /'(х). Это новая функция,
которая, в свою очередь, может иметь производную. Произ-
водная функции f (х) называется второй производной функции
y = f(x) и обозначается /"(х) или у".
Пример 1. Найти у", если у = х10.
Решение. Имеем (х10)'=10х9, a (10х9)'=90х8. Итак,
(х,0)"=9Ох8.
Пусть s=s (i) — закон прямолинейного движения. Тогда
вторая производная выражает скорость изменения скорости
этого движения, т. е. ускорение c=s"(t). В этом состоит физи-
ческий смысл второй производной.
Пример 2. Материальная точка движется прямолинейно
по закону a—2t—i • Докаэать, что сила, действующая на тело,
пропорциональна кубу пройденного пути.
Решение. По второму закону Ньютона F—mat где F —
сила, действующая на тело, а — ускорение, m — масса; а—з".
Имеем a'=((2t— (21-1)"2-(21-1)'= — 2(2t —1)~2;
s"=(--2 (2t—1)-2)' =—2-(—2)-(2t--l)“8*(2t—1)' =
=8(2»-1)-3=^.
Значит, F=ma= * 5=8 zns3, т. e. сила F пропорциональ-
l)
на a3 (8m — коэффициент пропорциональности).
215. Касательная к графику функции. Касательной к графи-
ку функции y—f(x)t дифференцируемой в точке х=а, назы-
вается прямая, проходящая через точку (а; / (а)) и имеющая
угловой коэффициент f' (а). Геометрический смысл этого опреде-
ления состоит в следующем. Рассмотрим график функции
у=/(х), дифференцируемой в точке о, выделим на нем точку
М (a; f (а)) и проведем секущую МР2, где Р2 — точка графика,
соответствующая значению аргумента о-|-Дх (рис. 104» а). Уг-
ловой коэффициент прямой МРг вычисляется по формуле
(см. п. 208).
Если точку Р каиго.тъ по графику, приближая ее к точке Л/,
то прямая МР начнет поворачиваться вокруг точки М. Чаще
всего в этом процессе секущая МР стремится занять некоторое
предельное положение. Это предельное положение представля-
ет собой прямую, с которой практически сливается график
функции y~f (х) в некоторой окрестности точки а; эта прямая
и есть касательная к графику функции y=f(x) в точке х=а.
В самом деле, угловой коэффициент такой предельной прямой
(обозначим его k) получается из углового коэффициента секу-
щей в процессе предельного перехода от Р к М:
fe = lim Лсек.
р-^м
Но условие Р-^М можно заменить условием Ах->0, а
вместо Лсек написать 4^-. В итоге получаем:
Но lim —-----это значение производной функции y=f(x)
дд-но Дх
в фиксированной точке х—а, т. е. f'(a) (см. п. 209).
Итак, т. е. значение производной функции y^f(x)
в точке х=а равно угловому коэффициенту касательной к гра-
фику функции y — f{x)e точке х =*а (рис. 104, б). В этом состоит
геометрический смысл производной.
Если функция y=f(x) дифференцируема в точке х=а, то
в этой точке к графику можно провести касательную; верно и
обратное: если в точке х=а к графику функции у = f (х) можно
провести невертикальную касательную, то функция дифферен-
цируема в точке х.
Это позволяет по графику функции находить точки, в кото-
рых функция имеет или не имеет производную. Так, функция,
график которой изображен на рисунке 105, дифференцируема
во всех точках, кроме точки х=1; в этой точке график имеет
заострение и касательную провести нельзя.
Уравнение касательной к графику функции V=f(x) в точке
х=а имеет вид:
У=/(«)+/' (а)(х—а).
(1)
Пример 1. Составить уравнение касательной к графику
функции в точке х=4.
Решение. Имеем f (х)=-\[х, f (х)~—а=4, /(а)=
Г- 11 2дх
=-^4=2, . Подставив найденные значения
a, f (а) и f (а) в уравнение (1), получим:
У = 2+-1-(к-4), т. е. у=-1-«+1.
Пример 2. Найтн угол, который образует с осью х каса-
тельная к графику функции y=-^sin3x, проведенная в точ-
ке х=0.
Решение. Имеем f (х)=— sin Зх, f (х)=— cos Зх «3 =
=-\/3 cos Зх; а=0, f (а)=-\/3 cos 0=-\/3. Значит, kMC =tg а=-^,
откуда заключаем, что искомый угол а равен 60°.
Пример 3. К графику функции у= провести ка-
сательную так, чтобы она
У=-х+2.
была параллельна прямой
8 Заказ 769
226
Решение. Две прямые параллельны тогда и только тогда,
когда их угловые коэффициенты равны (рис. 106). Угловой
коэффициент заданной прямой равен —1, а угловой коэффи-
циент касательной равен f (а). Значит, точку касания мы
можем найти из уравнения f'(d)=— 1.
Имеем /(*)=i±|; f =
Решим уравнение—. 4„.г—— 1. Имеем (а—2)2=4, зна-
Iй—
чит, либо а—2 = 2, откуда си =4, либо а — 2=— 2, откуда
02 = 0.
Если а = 4, то /(а)= * =3 и уравнение касательной
имеет вид у=3— (х—4), т. е. у~7 — х.
Если а=0, то /(а)=в+| = — 1 и уравнение касательной
имеет вид у= — 1—(х—0), т. е. у= — х—1.
Пример 4. Через точку 0(0; 0) провести касательную к графику
функции у=1п X.
Решение. Здесь, как и в предыдущем примере, неизвестна точка
касания х=а. Чтобы ее найти, составим уравнение касательной в общем
виде. Имеем f(x)=\nx, f (я)=-^ , значит, /(«)=1па, и
уравнение касательной имеет вид:
у=In a +-i (X—а). (2)
По условию касательная должна проходить через точку 0(0; О), т. е.
координаты точки О (О; О) должны удовлетворять уравнению (2). Подста-
вив х=О, у=0 в уравнение (2), получим О=In о+-~ (О—в), откуда 0=1п а—1,
1пв~1, а~е. Если теперь в уравнение (2) подставить найденное значение
1 XX
точки касания а=е, получим у=1пе-h—(х—е), т. е. у = 1+—— 1, У~~•
Это — уравнение искомой касательной (рис. 107).
216. Применение производной к исследованию функций иа
монотонность. Производная позволяет во многих случаях срав-
нительно просто исследовать функцию на монотонность. Дости-
гается это с помощью следующих двух теорем:
Т.7.1.
Т.7.2.
Пусть функция у—f(x) определена и непрерывна
в промежутке X и во всех внутренних точках этого
промежутка имеет неотрицательную производную
(/' (*)^0), причем равенство f (х)=0 выполняется не
более чем в конечном числе точек этого промежутка.
Тогда функция y=f(x) возрастает иа промежутке X.
Пусть функция у=/(х) определена и непрерывна
в промежутке X и во всех внутренних точках этого
промежутка имеет неположительную производную
(Г(ж)^О)» причем равенство f (х)=0 выполняется
не более чем в конечном числе точек этого проме-
жутка. Тогда функция y=f(x) убывает на проме-
жутке X.
Пример 1. Исследовать на монотонность функцию
у=хЧ-хЧ-1.
Решение. Имеем ^'=5х44-3х2. Справедливо неравен-
ство причем знак равенства имеет место лишь в
одной точке х=О. Значит, по теореме 7.1 функция у =х5+ х3 +1
возрастает на всей числовой прямой.
Пример 2. Исследовать на монотонность функцию
у = 2 sin х—Зх.
Решение. Имеем у';=2созх—3. Так как Icosxl^l,
то 2 cos х—3<0 при всех х. Значит, по теореме 7.2 функция
у—2 sin х—Зх убывает на всей числовой прямой.
Пример 3. Исследовать на монотонность функцию
31п(х —2).
Решение. Имеем у'=-^-2х—3——=х----------——
2 х—2 х—2
т=х2-2х-3^(х-3)(х+1)
л—2 Jt—2
228
_ (х—3)(х+1)
Знаки выражения —- меняются так, как показано
на рисунке 108 (см. п. 183). Но область определения исследуе-
мой функции задается неравенством х>2. Значит, из показан-
ных на рисунке четырех промежутков нас интересуют только
два: промежуток (2; 3) — на нем у'<0, значит, функция на
этом интервале убывает — и промежуток (3; + оо) — на нем
у'>0, значит, функция иа этом промежутке возрастает.
217. Применение производной к исследованию функций на
экстремум. Говорят, что функция y=f(x) имеет максимум
(минимум) в точке х—а, если у этой точки существует окрест-
ность, в которой f(x)</(a) (f(x)>f(o)) для х^а.
Так, функция, график которой изображен на рисунке 109,
имеет максимум в точках Xt и хз и минимум в точках Хг и
Х4.
Точки максимума и минимума объединяются общим терми-
ном — точки экстремума.
Обратимся еще раз к рисунку 109. Замечаем, что в точках
Xi и Х4 к графику функции можно провести касательные, при-
чем эти касательные будут параллельны оси х, а значит, угло-
вой коэффициент каждой из касательных равен нулю; итак,
/' (Х|)=0, Г (х4)=0. В точках же х2 и х3 к графику касательной
провести нельзя, значит, в этих точках производная функции
f (х) не существует (см. п. 215). Таким образом, в точках экстре-
мума на рисунке 109 производная либо равна нулю, либо
не существует. Это — общее положение, подтверждаемое сле-
дующей теоремой:
Т.7.3. I Если функция y—f(x) имеет экстремум в точке х=а
то либо f (а)=0, либо /' (а) ие существует (необходи-
I мое условие экстремума).
Точки, в которых f (а)=0 или /' (а) не существует и которые
принадлежат области определения функции, называются
критическими. Теорема 7.3 означает, что экстремумы функций
могут достигаться только в критических точках. Обратная тео-
рема, однако, неверна: не во всякой критической точке функция
имеет экстремум. Так, функция у = Xi имеет одну критическую
точку х=0 (в этой точке у' = 3х5—О), ио в этой точке функция
не имеет ни максимума, ни минимума. Функция, график кото-
рой изображен на рисунке 110, имеет критическую точку
х=а — это точка излома, в ией у' не существует, но в этой точке
нет ни максимума, ни минимума.
Как узнать, когда критическая точка функции является
точкой экстремума? Ответ на этот вопрос дает следующая
теорема:
Т.7.4.
Пусть х=а — критическая точка функции y^f{x\
и пусть существует интервал (Ь; с), содержащий точку
а внутри себя и такой, что на каждом из интервалов
(6; а) и (а; с) производная f (х) существует и сохраняет
постоянный знак. Тогда:
1) если на (Ь; а) производная у'>0, а на (о; с)
производная у' <0, то х=о — точка максимума
функции y=f(x);
2) если на (&; а) производная у' < 0, а на (а; с)
производная ^>0, то х=а— точка минимума
функции y=f{x)\
3) если и на (fe; о), и на (а; с) производная у' <0
или у'>0, то х—а не является точкой экстремума
функции y—f(x) (достаточное условие экстремума).
Из теорем 7.3 и 7.4 вытекает следующее правило ис-
следования функции y~f{x) на экстремум:
1) Найти область определения функции.
2) Найти f (х).
3) Найти точки, в которых выполняется равенство f (х)—0.
4) Найти точки, в которых f' (х) ие существует.
5) Отметить на координатной прямой все критические точки
и область определения функции J/=f(x); получатся проме-
жутки области определения функции, на каждом из которых
производная функции y = f (х) сохраняет постоянный знак.
6) Определить знак у' на каждом из промежутков, полу-
ченных в п. 5.
7) Сделать выводы о наличии или отсутствии экстремума в
каждой из критических точек в соответствии с теоремой 7.4,
Пример 1. Исследовать на экстремум функцию
у = 2х3—15х’+36х+1.
Решение. 1) Функция определена при всех х.
2) у'=6х2-30x4-36.
3) Из уравнения 6х2—30x4-36=0 находим Xi=2, х2=3.
4) д' существует при всех х.
5) Отметим точки Х]=2, *2 = 3 на координатной пря-
мой (рис. 111}.
6) д'= 6 (х — 2)(х— 3). Знаки производной иа полученных
промежутках отмечены на рисунке 111.
7) При переходе через точку х=2 слева направо производ-
ная у' меняет знак с «4-» иа ♦ — », значит, х=2 — точка мак-
симума; при переходе через точку г—3 производная меня-
ет знак с • —» на «4-», значит, х=3— точка минимума.
В точке х=2 имеем у,™, = 29, в точке х=3 имеем ymln = 28.
Пример 2. Исследовать на экстремум функцию
у=1п (г—2)4- Ln х.
Решение. 1) Область определения функции задается не-
равенством х>2.
2) yz=—4~—— 2х~2
’ у х—2 ' х х(х—2) ’
3) В области определения функции, т. е. при х> 2, критиче-
ских точек и тем более точек экстремума у функции нет.
Пример 3. Исследовать на экстремум функцию
^-бх+9
у х—1 ‘
Решение. 1) Область определения: х^1.
2) у' —(ж- l)-(x*-6x+S) (ж—1У
_(2х-6) (х-1)-(х2—6х + 9) 1 (х-3;(2 (х-1)-(х~31) _ (х-3)(х+1)
, (x-lj4 (х-1)4 *
3) у' = 0 при х=3 или при х= —1.
4) j/ ие существует при х=1, но эта точка не принадлежит
области определения функции.
5) Отметим на координатной прямой критические точки
х= —1, х = 3 и точку х=1 (рис. 112).
6) Знаки производной на полученных промежутках отме-
чены на рисунке 112.
7) х= — 1 — точка максимума, —8.
х—3 — точка минимума, уЮ1П = 0.
218. Отыскание наибольшего и наименьшего значений
непрерывной функции на отрезке. Говорят, что функция
y = f(x), определенная на промежутке X, достигает на нем
своего наибольшего (наименьшего) значения, если существует
точка с, принадлежащая этому промежутку, такая, что для
всех х из X выполняется неравенство f(x)^f(a) (f (х)^ f (а)).
Т.7.5.
(Функция, непрерывная на отрезке, достигает на нем
своего наибольшего и наименьшего значений.
Наибольшее значение М н наименьшее значение т непре-
рывной функции могут достигаться как внутри отрезка, так и
на его концах (рис. 113). Если наибольшего (наименьшего)
значения функция достигает во внутренней точке отрезка, то
эта точка является точкой экстремума; впрочем, для практики
достаточно того, что эта точка критическая.
Алгоритм отыскания наибольшего и наи-
меньшего значений непрерывной функция
у = f (х) и а отрезке [а; Ь].
1) Найти /'(х).
2) Найти точки, в которых /' (х)=0 или f (х) не существует,
и отобрать из них те, что лежат внутри отрезка [а; Ь].
3) Вычислить значения функции y — в точках, полу-
ченных в п. 2, и на концах отрезка и выбрать из них наиболь-
232
шее и наименьшее; они и будут соответственно наибольшим и
наименьшим значениями функции y=f(x) на отрезке [а; Ь],
которые можно обозначить так: унви6, упвим-
Пример. Найти наибольшее и наименьшее значения не-
прерывной функции у=х3 — Зх2—45х-|-225 на отрезке [0; 6].
Решение. 1) у'=3х2 —6х —45.
2) у' существует при всех х. Найдем точки, в которых
у'=0. Имеем:
Зх2 — 6х — 45=0,
х2—2х—15=0,
Xi = — 3, ха=5.
Отрезку [0; 6] принадлежит лишь точка х=5.
3) Вычислим значения функции в точках 0, 5, 6.
X 0 5 6
У 225 50 63
Наибольшим из найденных значении функции является
число 225, наименьшим — число 50. Итак, унви6=225, уивии=
=50.
219*. Отыскание наибольшего или наименьшего значения
непрерывной функции на незамкнутом промежутке. Задача
отыскания наибольшего (наименьшего) значения непрерывной
функции на незамкнутом промежутке, например на интервале
(а; 5), не всегда имеет решение. Так, на рисунке 114 изображены
графики непрерывных на (а; Ь) функций. Функция y = fi (х)
достигает и наибольшего, и наименьшего значений, функция
y=fz{^ достигает наибольшего значения, а наименьшего зна-
чения на (а; Ь) у нее нет, у функции y=fa(x) на (о; Ь) нет ни
наибольшего, ни наименьшего значений.
Если поставлена задача найти </яви6 (уняим) Для непрерыв-
ной на (а; Ь) функции y=f (х), то она решается по тому же
правилу, что соответствующая задача для отрезка [а; Ь]
(см. п. 218). Отличне: на третьем этапе вместо вычисления
значений функции на концах отрезка находят пределы функ-
ции при приближении к концам интервала.
Пример. Найти наименьшее значение функции
у=( 2+c°sx)2 на интервале (0; л).
Решение. 1) Найдем производную данной функции:
, __ g / 2-bcosx \ / 2+со8Дс\/ Q 2+cosx^
У \ sin х / \ sin х / sin X
(2 -J- cos х}' sin х—(2+cos x) (sin x)' £. 2+cos x
* sin2* sin x
X
x (—sin x) sin x—(2+cos x) cosx 2 (2+cos x) (—sin2 x—cos2 x— 2 cos x)
74 ~~ sin2 x sin2 x
__—2 (2 +cosx)(1 + 2 cosx)
2) y'=0, если l+2cosx=0 или 2-)-созх=0. Но второе
уравнение не имеет решений, так как [созх] ^1, а из первого
находим соз х=—; х= ±-^4-2лЛ (см. п. 154). Из этих
значений интервалу (0; л) принадлежит лишь значение х=~^ •
Производная у' не существует, если sin3x=0. Но на
(0; л) это уравнение не имеет решений.
Итак, внутри интервала (0; л) функция имеет лишь одну
2л
критическую точку х—-g-.
(_ . 2л \ 2
2 + cos— \
----2^---/
2-4 Y
= 3.
J3
2
При приближении к концам интервала, т. е. при х-»-0 или при
х->л, знаменатель дроби ^д?^- стремится к 0, а числитель
соответственно к 9 или к 1. Значит, и в том и в другом случае
-f- оо (см. п. 206).
234
Поскольку при приближении к концам интервала (0; л) зна-
чения функции неограниченно увеличиваются, наименьшее
значение функция достигает в единственной критической точке,
т. е. в точке х=-^ . Итак, </нанм=3.
Иногда для отыскания наибольшего или наименьшего зна-
чения непрерывной функции y = f(x) на промежутке (а; Ь) по-
лезны два утверждения:
1°. Если функция y=f{x) имеет в промежутке X только одну
точку экстремума х=а, причем это точка максимума, то
f (о) — наибольшее значение функции на промежутке X.
2°. Если функция y=f(x) имеет в промежутке X только
одну точку экстремума х=а, причем это точка минимума, то
f (а) — наименьшее значение функции на промежутке X.
Так, в рассмотренном выше примере функция имела в интер-
вале (0; я) лишь одну критическую точку х=~ . При переходе
через эту точку знаки производной меняются с « — » на ♦ 4- ».
Значит, — точка минимума, а потому —
наименьшее значение функции на интервале (0; л).
220. Задачи на отыскание наибольших или наименьших
значений величин. Задачи на отыскание наибольших или
наименьших значении величии удобно решать по следующему
плану:
1) Выявляют оптимизируемую величину (т. е. величину,
наибольшее или наименьшее значение которой требуется иайти)
и обозначают ее буквой у (или S, р, г, Л и т. д. в зависимости от
сюжета задачи).
2) Одну из неизвестных величин (сторону, угол и т. д.) объ-
являют независимой переменной и обозначают буквой х: уста-
навливают реальные границы изменения х в соответствии с
условиями задачи.
3) Исходя из конкретных условий данной задачи выража-
ют у через х и известные величины.
4) Для полученной на предыдущем этапе функции y—f{x)
находят наибольшее или наименьшее значение (в зависимости
от требований задачи) по промежутку реального изменения х,
найденному в п. 2.
5) Интерпретируют результат п. 4 для данной конкретной
задачи.
На первых трех этапах составляется, как принято говорить,
математическая модель задачи. Здесь часто успех решения
зависит от разумного выбора независимой переменной. Важно,
чтобы было сравнительно нетрудно выразить у через х. На
четвертом этапе составленная математическая модель исследу-
ется чаще всего с помощью производной, реже элементарным
способом. В момент такого исследования сюжет самой задачи,
послужившей отправной точкой для математической модели,
исследователя не интересует. И лишь когда закончится реше-
ние задачи в рамках составленной математической модели,
полученный результат интерпретируется для исходной задачи
(пятый этап).
Пример 1. В степи, в 9 км к северу от шоссе, идущего с
запада на восток, находится поисковая партия. В 15 км к
востоку от ближайшей к поисковой партии точки, лежащей на
шоссе, находится райцентр. Поисковая партия отправляет
курьера-велосипедиста в райцентр. Каков должен быть
маршрут следования курьера, чтобы ои прибыл в райцентр
в кратчайший срок, если известно, что по степи ои едет со
скоростью 8 км/ч, а по шоссе 10 км/ч?
Решение. Сделаем чертеж. На рисунке 115 точка Р озна-
чает местонахождение поисковой партии, прямая I — шоссе,
В — райцентр, РА = 9 км, АВ =15 км, РМВ — маршрут следо-
вания курьера, причем положение точки М между А и В пока
неизвестно.
1) Оптимизируемая величина — время t движения курьера
из Р в В; надо найти £ивим.
2) Положим АМ=х. По смыслу задачи точка М может
занять любое положение между А и В, не исключая самих
точек А и В. Значит, реальные границы изменения х таковы:
0<х<15.
3) Выразим t через х. Имеем РМ=-\]РА2+AAf2 =-\/81 х2.
Этот путь велосипедист едет со скоростью 8 км/ч, т. е. время
ii, затраченное на этот путь, выражается формулой
= . Далее, МВ =15—х. Этот путь велосипедист едет
^♦1 236
со скоростью 10 км/ч, т. е. время ti, затраченное на этот путь,
15__________________________х
выражается формулой £2 = 10 1» Суммарное время £, затра-
те! 4-х2 । 15—х
ченное на весь путь, равно й+$2> т. е. t — 8 ' ю *
4) Нужно найти наименьшее значение функции
t s=~^81+на отрезке [0; 15]. Используем для этого план
из п. 218.
2. t' существует при всех х. Найдем точки, в которых
£' = 0. Имеем —, * —Дг=О»
8 л/814-х 10
5х=4Л/81+х2,
25х2=16(81 + х2),
9х2 = 16-81,
х = 4-3 = 12.
Значение х=12 принадлежит отрезку [0; 15].
3) Составим таблицу значений функции, куда включим
значения функции на концах отрезка и в найденной критиче-
ской точке.
X 0 12 15
t 105 40 87 40 5^306 40
t =21
‘•ияим 4Q
Четвертый этап решения задачи закончен, нам осталось ин-
терпретировать полученный результат применительно к исход-
ной задаче.
5) Лмиш достигается при х= 12. Значит, велосипедисту надо
ехать по такому маршруту РМВ, чтобы расстояние между
точками А и М по шоссе было равно 12 км.
Пример 2. Через фиксированную точку М внутри угла
провести прямую, отсекающую от угла треугольник наимень-
шей площади (рис. 116).
Решение.
1) Оптимизируемая величина — площадь S треугольника
АОВ.
2) Проведем DM || ОВ, МК || ОА. Положим КВ=х\ реаль-
ные границы изменения х таковы: 0<х< + 00-
3) Поскольку М — фиксированная точка, отрезки DM и КМ
тоже фиксированны; положим DM=a, КМ=Ь и выразим S
через х, а, Ъ.
Рассмотрим треугольники МКВ и AOBt они подобны, зна-
МК КВ b х Л Ь(в4-х)
чит’ АО=О^Т’ е- AO=^+i' Отск>Да находим АО=-^-<
Далее имеем <S=^-AO-OB-sin а, где а= ZAOB.
Значит,
SI b(a+x) f . v _ bsina (a-f-x)2.
=-g--——- • (а+х) sin а—— —^-(математическая мо-
дель задачи составлена).
4) Рассмотрим функцию S = , 0<x<-j-co, где
, b sin a -r-r «,
k =—-—. Найдем ее наименьшее значение.
j gf =.% 2(о+х)х—(д+х)2_ . (о+х) (х—о).
2. Производная не существует в точке х~ О, а обращается
в нуль в точках х= —а, х—а. Из этих трех точек промежутку
(О; —|—со) принадлежит лишь точка х=а.
3. И при х->0, и при х->+ со £->-|- со. Значит, наименьшее
значение функции достигается в точке х=а.
5) Вернемся к исходной геометрической задаче. Если х=
=ЯВ—а, то, поскольку ОК=а, МК — средняя линия тре-
угольника АОВ, значит, М — середина АВ. Таким образом,
чтобы от сторон угла отсечь треугольник наименьшей площади,
надо провести через точку М прямую так, чтобы ее отрезок,
заключенный между сторонами угла, делился в точке М попо-
лам.
221. Применение производной для доказательства тождеств.
Доказательство тождеств с помощью производной основано на
следующей теореме:
Т.7.6.
Для того чтобы непрерывная на промежутке X функ-
ция y=f(x) была постоянна на этом промежутке,
необходимо и достаточно, чтобы ее производная во
всех внутренних точках промежутка была равна
нулю (условие постоянства функции).
Пример. Доказать тождество
sin2 x+cos(x—£-) Cos(x+-|-)=-i-.
Решение. Рассмотрим функцию f (x)=sin2 х4-
4-cos^x—«cos (я 4—и найдем ее производную.
Имеем /'(x)=2sinx cos х—sin (х—^cos(x4—
-cos(x-i-) sin(х+-=-) = sin 2х- sin=
=sin 2х—sin 2х = 0. Значит, f (х)=0 при всех х, а потому
fix) — постоянная функция, f (х)=С. Осталось найти значение
постоянной С. Для этого достаточно вычислить значение
f(x) при любом значении х, например при х—0. Имеем:
f (O)=sin2 O+cos ( —I) cos -2- =0+4- 4 =4
\ o / 0 Z Z 4
Итак, /(0)=-|-, а потому 0=-^-. Значит, справедливо тож-
дество
sin2x+cos(x—2-)cos(x+-2-)=-l-.
222. Применение производной для доказательства иера-
венств.
Пример 1. Доказать, что при 0<х<-|- справедливо
неравенство
2х+-р->5.
Решение. Рассмотрим функцию f (х)=2х 4-— и найдем ее
2 2 (х3_1)
производную: f (х)=2—^г=—4^5—• • Замечаем, что на интер-
вале (О; 1) производная f (х)<0, значит, функция f (х) убывает
на этом интервале (см. п. 216). Поэтому, в частности, при
О < х <“ справедливо неравенство f (х) > f [ . Но f =
=24+(TF6’
Итак, f (х)> 5, т. е. 2х 4-р- > 5, что и требовалось доказать.
Пример 2. Доказать, что если сс<0, то cc-j-cos сс<р4-
4-cos р.
Решение. Рассмотрим функцию / (х)=х4-соз х и найдем
ее производную f (х)=1—sinx. Замечаем, что f (х)^0, т. е.
239
функция f (х) возрастает на всей числовой прямой. Значит, из
а<Р вытекает /(«)</(₽), т. е. a + cos a<₽+cos 0.
Пример 3. Доказать, что при всех х справедливо нера-
венство
x6+(l-x)5>i .
Решение. Рассмотрим функцию f (х)=х5+(1 —х)5 и ис-
следуем ее на экстремум. Имеем:
f (х)=5х4-5 (1-х)4=5 (х2-(1-х)2) (х2+(1-х)2)=
= 5 (2х—1) (2х2 — 2х +1).
Г (х)=0 при х=~. Других критических точек у функции
нет (уравнение 2х2 —2x4-1=0 не имеет корней). /' (х)<0 при
х<-~, a f (х)>0 при х^-—, значит, х=-|-----точка мини-
мума функции. Поскольку других точек экстремума у данной
непрерывной функции нет, то f — наименьшее значение
функции (см. утверждение 2° из п. 219). Но У(^")=("у) 4-
+(1М-
Итак, f т. е. х5+(1—
223. Общая схема построения графика функции. Пусть нуж-
но построить график функции y=f (х). Для этого нужно рас-
смотреть некоторые свойства функции, что обычно сопровожда-
ется соответствующей иллюстрацией на координатной плоскос-
ти. Это помогает создать графический образ функции и обратно:
графические представления помогают лучше понять свойства
функции, а иногда и предвидеть нх. Для этого полезно при-
держиваться следующего плана:
1) Найти область определения функции y=f (х).
2) Найти точки, в которых f (х)=0 (это будут точки пере-
сечения графика с осью абсцисс).
3) Отметить на оси х точки, найденные в п. 2, и точки,- в
которых функция не определена, найденные в п. 1; эти точки
разбивают ось абсцисс на несколько промежутков, на каждом нз
которых функция сохраняет постоянный знак. Установить знак
функции на каждом из промежутков.
4) Исследовать функцию на четность и нечетность (в случае
четности или нечетности функции можно ограничиться иссле-
дованием и построением графика прн х^О, а затем восполь-
зоваться симметрией графика — см. п. 74, 75).
240
5) Найти вертикальные и горизонтальные асимптоты (см.
п. 203, 206).
6) Исследовать функцию на экстремумы.
7) Найти несколько дополнительных контрольных точек и
построить график.
Для периодических функций полезно с самого начала найтн
основной период Т (см. п. 76), с тем чтобы, исследовав
[7 71
----------------------------------------------2~* ~2~I ’
построить затем, воспользовавшись периодичностью, весь гра-
фик.
Если выполнение каких-либо шагов предложенной схемы со-
пряжено с техническими трудностями, их иногда можно опус-
тить.
Пр и м ер. Построить график функции у=х?— 4х.
Решение. 1) Функция определена при всех х.
2) Из уравнения х3 — 4х=0 находим х(х2— 4)=0, Xi =
= 0, Х2=2, хз=—2.
3) Точки — 2; 0; 2 разбивают ось абсцисс на 4 промежутка.
Изменение знаков функции у—х3— 4х на промежутках отраже-
но иа рисунке 117. Соответствующая иллюстрация на коорди-
натной плоскости представлена на рисунке 118, а (заштри-
хованы те полуполосы, где графика не будет).
4) /(—х)=(—х)3—4 (—х)= —х3 + 4х=—(х3—4х)= —/(х),
значит, функция нечетна, ее график симметричен относи-
тельно начала координат.
5) Асимптот у графика иет.
6)^ = 3^_4 = 3(Ж_А)(Ж+А).
у' = 0 при »|=Л. х2=—L
Точка ~ принадлежит отрезку [0; 2]» из рисунка 118, а ясно,
что в этой точке функция будет иметь минимум (здесь мы
как раз имеем тот случай, когда графические представ-
ления позволяют сделать вывод о свойствах функции).
/ 2 \3 2 16 о 1
4д/з_ 3,1‘
A 2 ,
Аналогично в точке х=-----— функция имеет максимум:
Угаах«3,1.
7) В качестве дополнительных возьмем две точки х=3,
х= — 3. Имеем /(3)^15, /(—3)= —15.
Использовав найденные 7 точек, строим график функции
(рис. 118,6).
Пример 2. Построить график функции у=^ .
Решение. 1) Область определения: х=/= ±2.
2) Из уравнения О находим Xi = 3, xz= — 3.
3) Точки 2, —2, 3, —3 разбивают ось абсцисс на 5 проме-
х2—9
жутков. Изменение знаков функции у=р_~4 по промежут-
кам представлено на рисунке 119, соответствующая иллюстра-
ция на координатной плоскости дана на рисунке 120,а.
4) Функция четна, так как /(—x)=f(x). Значит, гра-
фик функции симметричен относительно оси ординат.
5) х=2, х=—2— вертикальные асимптоты (см. п. 206).
119
~3 ~2
2 3
а) б)
Чтобы иайти горизонтальную асимптоту, вычислим
~з_д
lim ~j. Для этого числитель и знаменатель дроби разделим
х—+ оо х —4
почленно иа х2 (см. п. 204).
х’_9 г_9
Получим Hm Кт Кт —^=1=5=1.
-.3_g
Итак, lim уз_4=1» значит, у=1 — горизонтальная асимп-
тота графика функции (см. п. 203).
, (х3—9)'(х2—4)—(х2—9)(х!—4)' 2x(x3-4)-(xs-9)-2x_
6) у =---------^гТ4)5---------------^4?---------
1Ох
-(?=4Г
Производная обращается в нуль в точке х = 0 и ие суще-
ствует в точках х= ±2. Но эти последние не принадлежат-об-
ласти определения функции, значит, функция имеет лишь одну
критическую точку х=0. При переходе через эту точку про-
изводная меняет знак с «—* на « + », значит, х=О—точка
g
минимума: y^iD=f (О)—-^-.
7) В качестве дополнительных возьмем следующие точкиг
*=.±1, х=±4. Имеем /(1)=/(-1)=4- Л4)=/(-4)=^.
Использовав найденные 7 точек, строим график функции
(рис. 120, б)<
243
i 22. Первообразная и интеграл
224. Первообразная. Функция F (х) называется первообраз-
ной для функции f (х) на промежутке X, если для любого х из X
выполняется равенство F' (x)=f(x).
Примеры.
1. Пусть /(х) = х3. Тогда первообразная У(х) имеет вид
так как F’ (*)=(4)=*3=^ w-
2. Пусть /(x)=sin Зх. Тогда первообразная F (х) имеет вид
F (х)= —|- cos Зх, так как F' (х)=(—|-cos ~ —|-Х
Х3(—sin 3x)=sin 3x = f(x).
Для функции /(х) = х3 в примере 1 мы нашли первообраз-
ную F (я)=-^-. Это не единственное решение задачи. Так, в
качестве первообразной можно было взять и функцию Fi (х)=
=7j-+3 (поскольку (^-+3^ =х3), и функцию F2(x)=~—5
(поскольку — б) — х3), и вообще любую функцию вида ^-+ С.
Так же обстоит дело в примере 2, где в качестве первообразной
можно было взять любую функцию вида —|- cos 3x4-С. Спра-
ведлива следующая теорема:
Т.7.7.
Если F (х) — первообразная для функции / (х) иа про-
межутке X, то у функции f (х) бесконечно много
первообразных, и все эти первообразные имеют вид
F (х)4-С, где С — произвольная постоянная (основное
свойство первообразной).
Пример. Найта общий вид первообразных для функции
f (х)=хг, где г=/= —1.
Решение. Одной из первообразных будет функция F (х)=
так как F'(x)=(^0 =/>-р^-(г-|-1)хг=хг=/(х). Зна-
чит, общий вид первообразных:
225. Таблица первообразных. Учитывая, что отыскание пер-
вообразной есть операция, обратная дифференцированию, и от-
талкиваясь от таблицы производных, (см. п. 210), получаем
следующую таблицу первообразных (для простоты в таблице
приведена одна первообразная F (х), а не общий вид перво-
образной F (х)4-С):
Функция Первообразная Функция Первообразная
S Л W ,м н S Е "ff 1S Е л Т । л л °. «1- -В*. * £xt .3 л л л л л S S S S S Ь. Ь. ь. ь. ь. X X L* IT Jill .S 8 li + tn u | to 1 и 1 r IH H II II II 1 Д 3 3 3 3 3 3 to t? а? о о н H X X X „ H ь ? 1 и 1 a s 1 1 11 11 11 11 3 3 3 3 3 3 k, Й. k. Й, %
226. Правила вычисления первообразных. Пусть нужно
найти первообразную функции y=f (х). Иногда это можно сде-
лать с помощью таблицы первообразных из п. 225; например,
з_
для функции f (х) = Х5 по второй строке указанной таблицы нахо-
J+i 6 4
дим F {х)=—=---, т. е. F (х)=—X, а общий вид первообраз-
Л+1
5 Т
ных: -g-x 5 +С. Но чаще, прежде чем воспользоваться табли-
цей, приходится применять правила вычисления первообраз-
ных.
1°. Если F (х) — первообразная для f (х), а Н (х) — перво-
образная для h (х), то F (х)+Н(х) — первообразная для f(x)+
+h(x).
Иными словами, первообразная суммы равна сумме пер-
вообразных.
2*. Если F (х) — первообразная для f (х) и k — постоянная,
то kF (х) — первообразная для kf (х).
Иными словами, постоянный множитель можно вынести за
знак первообразной.
3°. Если F (х) — первообразная для f(x) и k, Ь — постоян-
ные, причем k-т^О, то -^-F(kx-j-b)— первообразная для
f(kx + b).
Пример 1. Найти общий вид первообразных для функции
/ (х) = 2 л/х+З sin х — 2’+^.
Решение.
1) Воспользовавшись таблицей первообразных (п. 225), най-
дем первообразную для каждой из четырех функции, входящих
в состав f (х):
fi (x)=-Jx, (x)=sin x, /з (x) = 2\ /4 (x)=cos x.
Д 1+1 -
Для функции fi (х)==д/х=х2 имеем F, (x)~2 •
_ *2"+1
Для функции £г(х)=е1пх имеем F2(x)=s — cos X.
Для функции /3(х)=2х имеем Fa(x)—
Для функции ft (x)=cos х имеем F4 (x)=sin х.
2) Воспользовавшись правилом 2°, получим, что для 2fi (х)
з 2
первообразной будет 2Fj (х), т. е. 2~х2 =~х2 ; для 3/2 (х)
первообразной будет 3F2 (х), т. е. — 3 cos х; для — /з (х) пер-
2х 1
вообразной будет — F3(x), т. е. —Для -у А (х) первооб-
разной будет Р4 (х), т. е. sin х.
3) Воспользовавшись правилом 1°, получим, что для f (х)
первообразной будет следующая функция: 3
F(x)=2F, (x)+8F2(x)-F3(x)+±Ft (х)=~х^ -Зсовх-
2' . 1 .
-E2+7sml'
4) Общий вид первообразных для заданной функции:
4x^-3cosx-j^+^+C.
Пример 2. Найти общий вид первообразных для функции
/(х)=(2х-1)5.
Решение. Для функции h (х)—хБ первообразной будет
хв
H(x)=-g-. Тогда по правилу 3 для функции Л(2х-—1)=
=(2х—I)8 первообразной будет Н (2х— 1)—«
Итак, F (х)=^—, а общий вид первообразных для заданной
функции: (2х~1> +С.
246
Пример 3. Найти общий вид первообразных для функции
f(x)=sin23x.
Решение. Воспользуемся тем, что sin2 Зх ~—c°s 6х(см.
п. 129). Тогда /(х)—~—|-соз 6х. Для функции /1 (х)=-~
иервообразной будет -|-х, а для функции f2(x)=cos6x в
соответствии с правилом 3° первообразной будет 81п 6х. Тог-
6
да для функции 7(х)=Л (х)—по правилам 1° и
2° первообразной будет -|-х—я-'"”.6*, т. е. -1- х—Об-
л Z о Z 1Z
„ — х sin 6х ,
щии вид первообразных; -g------——|-С.
227. Интеграл. Пусть функция y=f(x) непрерывна на отрез-
ке {а; Ь]. Разобьем отрезок [а; Ь] на п частей точками х>, х2, ...,
xn-i? для однородности обозначений положим а=х0, Ь~хп
(рис. 121). Введем обозначения: xt—хо=Ахс, х2—Xi = Axi, Хз—
— х2 = Ах2, хп—Хи— 1 = Дхп-1 и рассмотрим сумму
f (Хо) Дхо+ f (Xi) Ax,-h / (Х2) Ах2 + ... + /’ (хп_,) Ах„_ I. (1)
Она называется интегральной суммой для функции y=f(x} по
отрезку [а; Ь}
Наряду с интегральной суммой (1) рассматривают н инте-
гральную сумму вида
f (xi) Ахо+f (х2) Axi +.«+/’ (х„) Дх„_ i. (2)
Отличие суммы (1) от суммы (2) состоит в том, что в пер-
вом случае на каждом из отрезков [хс? Xi], [хи х2],...»[xn-i; хп]
выбирается значение функции в левом конце отрезка, а во
втором случае — в правом.
На практике удобнее делить отрезок {а; Ь] на п рав-
ных частей. Тогда Дх0=Axi=Ax2=...=Axn-i=^^ и сумма
(1) принимает вид ^5(/(x0)-|-7(xl)-|-/(x2)-|-.--l-/(x»-i)). Зна-
V
X,. х2 х3
*П-1
247
чение суммы зависит только от числа п, поэтому эту еумму
можно обозначить 2П (2 — греческая буква «сигма»).
Рассмотрим последовательность интегральных сумм Si,
Е2» •••> В математике установлено, что для непрерыв-
ной на отрезке [а; Ь] функции р=/(х) эта последователь-
ность сходится (см. п. 200). Ее предел называют интегралом
функции f (х) от а до Ь и обозначают J f (х) dx (читается:
«Интеграл^от а до Ъ эф от икс дэ икс»). °
Итак, \/,(x)dx=lim Sn. Числа а и Ъ называют соответ-
а
ственно нижним и верхним пределами интегрирования, знак
5 — знаком интеграла, функцию f (х) — подынтегральной функ-
цией.
Пример. Найти J xdx.
о
Решение. Составим интегральную сумму 2« для функции
/(х)=х на отрезке [0; 1J, Для этого разобьем отрезок [0; 1]
иа п равных частей точками , ...» "~1 (рис. 122).
Имеем /(0)=0, /(4)=f ’ '(4)=4..........
fl----) =---. Интегральная сумма Srt имеет вид:
2„=± (о+4+4+4+_.+^)=1±2±2±;=±&!^)
п \ п П п п f п
248
В числителе содержится сумма первых (л—1) членов арифмети-
ческой прогрессии, у которой первый член равен 1, а (л — 1)-й
равен л —1. Тогда сумма Sn-t вычисляется по формуле (см.
п. 197).
2п(п—1) п— 1 1 1
2Л-
1
Далее имеем lim lim —^)==4-’ Значит»
228. Связь между интегралом и первообразной (формула
Ньютона—Лейбница). Если F (х) — первообразная для f (х) на
отрезке [а; &], то
ь
\fMdx=FV>)-F(d) (1)
(формула Ньютона—Лейбница). На практике в формуле (1) удоб-
но вместо F (Ь)—F (а) писать F (х) | а.
Пример 1. Вычислить J x7dx.
о
Решение. Для функции f (х)=х7 первообразной является
Значит- S*7d*=4lo=4~o=4-
о
2
Пример 2. Вычислить J 2х+Ъ ’
Решение. Для функции f(x)—„ * первообразной яв-
zx-f-o
ляется F (х)=— In 12х 4- 31. Значит,
( 2ГГЗ=4 to I2X+3II; =i(ln 7-1п 5)=2-1п-|-.
J 2SX-|-o Z • 1 Z ZD
229. Правила вычисления интегралов.
1*. Интеграл суммы равен сумме интегралов.
J (/i (x)+ft (*)) dx=\f, (х) dx+J ft (х) dx.
249 1^-
2°. Постоянный множитель можно вынести за знак ин-
теграла
ь ь
\kf (х) dx=k\f (х) dx.
а а
Пример 1. Вычислить J (2Х3 4- Зх — 4)dx.
— 2
Решение. Воспользовавшись правилами 1° и 2°, полу-
чим:
j (2х3+Зх—4)dx= j 2x3dx-b j 3xdx4- j — 4dx =
— 2 —2 — 2 —2
= 2 j x3dx4-3 j xdx — j 4dx=2«^-| La + 3*^-1 _2—4x| _2=
—2 -2 —2 4
= 2 (4-4) +4 (1 -4)-4 (1 4-2)= - 24.
Пример 2. Вычислить J tg2 xdx.
Решение. Представим подынтегральную функцию в виде
суммы функций, первообразные от которых можно найти по
таблице (см. п. 225).
Имеем:
tg2 —г—~~4-----1.
COS X COS X COS X
4 (3—V3)—л
12
230. Использование интеграла для вычисления площадей
плоских фигур. Рассмотрим плоскую фигуру Ф, представляю-
щую собой множество точек координатной плоскости ху, ле-
жащее в полосе между прямыми х=а, x—b(a<Zb), имеющее
в своем составе точки с абсциссами х—о, х = Ь н ограничен-
ное сверху и снизу графиками непрерывных на [а; Ь] функций
y=fi(x) и таких, что для всех х из [а; Ь]
справедливо неравенство Примеры таких фигур
представлены на рисунках 123—127. В частности, фигура, изо-
браженная на рисунке 124, а, ограничена сверху графиком
функции y=f(x), а снизу — прямой у—О. Такая фигура на-
зывается криволинейной трапецией.
Площадь S фигуры Ф вычисляется по формуле
ь
s=j (A (*)—h (*)) dx. (1)
В частности, для криволинейной трапеции, изображенной на
рисунке 124,0, получаем:
S=^(x)dz, (2)
Пр и м ер 1. Вычислить площадь фигуры, ограниченной
линиями у=4—х2, 1у=0-
Решение. Фигура, площадь которой надо иайти, изобра-
жена иа рисунке 125. Воспользовавшись формулой (2), по-
лучим:
2 2 2 v
S= J (4—x2)dx= J 4dx — J x2dx = 4x|^_2—у
-2 -2 —2
= 4(2 + 2)—L(8 + 8)=^.
Пример 2. Вычислить площадь фигуры, ограниченной
линиями у~х, у=&—х, Х=1, х—2.
Решение. Фигура, площадь которой надо найти, изо-
бражена на рисунке 126. По формуле (1) получим:
2 2 2 2
S=J ((5—*)—х) J (5—2*) dx=\ 5dx—2 j xdx=5x 12_
I I If1
-2-^|*=5(2-l)-(4-l)=2.
Пример 3. Вычислить площадь фигуры, ограниченной
линиями у—х—2, у=х12 — 4x4-2.
Решение. Построив прямую у=х—2 и параболу у —
=я?—4x4-2 (см. п. 114), получим фигуру, площадь ко-
ь
торой требуется вычислить (рис. 127). Значит, (ft (х)—
— fz (х)) где Л (х)—х—2, (х)=х2—4х 4- 2, а пределы инте-
грирования а и Ь суть абсциссы точек пересечения параболы
и прямой. Для отыскания этих абсцисс решим уравнение
Л (х)=Л(х), т. е. х—2=х2 —4x4-2, откуда х(— 1, х2=4.
S=J ((x-2)-(x2-4x + 2)) dx=J (5x-x?-4) dx =
= 5rR-4K-4»K=4(16-1)—§"(64 —1)—4(4 —1) = 4,5.
Пример 4. Вычислить площадь фигуры, ограниченной
линиями у = \х— 2|.
Решение. Фигура, площадь которой требуется найти,
изображена на рисунке 128 (см. п. 158). Проведем прямую
х=2. Тогда площадь S интересующей нас фигуры равна сумме
Si + Sa, где Si — площадь фигуры, заштрихованной на рисун-
ке 128 горизонтальной штриховкой, a Sz — площадь фигуры,
заштрихованной на рисунке 128 вертикальной штриховкой.
з
2 2 J. 2
Имеем Si=J(Vx—(2—x))dx=\lx2 +х—2)dx=^-| ,+
1 ' ~2
+4|“-2x|;=-|-(^-l)+-|-(4-l)-2(2-l)=^|=I;
4 4 1 —
&=J b/x-(x-2)) dx=J (х 2 -х + 2) dx=4| 1 г+
2 2 —
2
+ 2x|2=4(8-V8)-4(16-4) + 2(4-2)=itV^-
о Л « СУ I СУ 8-^—7 . 10 —4-J2 13
Значит, S—Si + S2 =—\-1--—>-=—.
о ЙО
ГЕОМЕТРИЯ
ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ
ФИГУРЫ НА ПЛОСКОСТИ
§ 1. О строении курса геометрии
1. Геометрические фигуры • . 255
2. Точка. Прямая. .... 256
3. Определения. Аксиомы. Тео-
ремы ........ 257
§ 2. Основные свойства простей-
ших геометрических фигур
4. Отрезок ...... 259
5. Луч......................261
6. Окружность. Круг .... 262
7. Полуплоскость .... 263
3. Угол. Градусная мера угла. . —
9. Смежные и вертикальные уг-
лы ..........................266
10. Центральные и вписанные уг-
лы .........................267
11. Параллельные прямые. . 268
12. Признаки параллельности
прямых................... . 271
13. Перпендикулярные пря-
мые .........................272
14. Касательная к окружности.
Касание окружностей ... 274
15. Треугольники ..... 275
16. Равенство треугольников . 277
17. Равнобедренный треуголь-
ник ......... 278
16. Сумма углов треуголь-
ника . ......................279
19. Прямоугольный треугольник.
Теорема Пифагора. .... 230
20. Окружности, вписанные в
треугольник и описанные около
треугольника ...... 282
§ 3. Геометрические построения
на плоскости
21. Чертежные инструменты. 284
22. Простейшие задачи на по-
строение ...................235
23. Геометрическое место точек
на плоскости ...... 288
§ 4. Четырехугольники
24. Выпуклые четырехугольни-
ки......... 290
25. Параллелограмм ... 291
26. Прямоугольник. Ромб. Квад-
рат .......................293
27. Трапеция................294
§ 5. Многоугольники
23. Ломаная ...... 296
29. Выпуклые многоуголь-
ники .......................297
30. Правильные многоугольни-
ки ........ . 293
31. Длина окружности ... 300
§ 6. Решение треугольников
32. Косинус, синус и тангенс. . 302
33. Соотношения между сторона-
ми и углами в прямоугольном
треугольнике ...............304
34. Теорема косинусов. Теорема
синусов ........ 305
35. Решение треугольников. . 307
§ 7, Площади плоских фигур
36. Понятие площади простых
фигур.......................зоз
37. Площади многоугольни-
ков ........................309
38. Площади подобных фи-
гур .......................311
39. Площадь круга .... 312
ГЛАВА II. ПРЯМЫЕ И ПЛОС-
КОСТИ В ПРОСТРАНСТВЕ
254
4 3. Аксиомы стереометрии и
некоторые следствия из них
40. Основные понятия стереомет-
рии ....•••• 314
4 9. Параллельность прямых и
плоскостей
41. Скрещивающиеся пря-
мые ......... 317
42. Параллельность прямой и
плоскости ....... 313
43. Параллельные плоскости 319
4 10. Перпендикулярность пря-
мых п плоскостей
44. Перпендикулярность прямой
и плоскости ..... 321
45. Перпендикуляр и наклонная
к плоскости ...... 323
46. Перпендикулярность плос-
костей ........ 325
ГЛАВА III. ТЕЛА В ПРО-
СТРАНСТВЕ
4 11. Многогранники
47. Тело и его поверхность. . 326
48. Многогранные углы. Мно-
гогранники ...... 327
49. Призма. Параллелепипед.
Куб.....................328
50. Пирамида ..... 331
51. Правильные многогрании-
........................333
4 13. Тела вращения
53. Цилиндр ...... 333
53. Конус....................336
54. Шар ....... 337
4 13. Изображение пространст-
венных фигур ма плоскости
55. Параллельная проекция. . 340
56. Ортогональное проектирова-
ние ........ 341
57. Геометрическое место точек в
пространстве ...... 342
4 14. Объемы тел
58. Понятие объема простых
тел..........................844
59. Объем параллелепипеда,
призмы и пирамиды ... 345
60. Объем цилиндра и конуса 346
61. Общая формула объемов тел
вращения. Объем шара и его
частей ........ 347
4 15. Площади поверхностей тел
63. Площади поверхностей мно-
гогранников . • . < • . 348
68. Понятие площади поверхнос-
ти ......... 349
64. Площади поверхностей тел
вращения ....... 350
ГЛАВА IV. ДЕКАРТОВЫ КО-
ОРДИНАТЫ
4 19. Координаты на плоскости
и в пространстве
65. Введение координат па плос-
кости и в пространстве. . . 351
66. Координаты середины отрез-
ка. Расстояние между точка-
ми ........................353
4 17. Уравнения фигур на плос-
кости
67. Уравнение окружности. . 355
63. Пересечение двух окружнос-
тей ......... 356
69. Уравнение прямой ... 357
70. Пересечение прямой и окруж-
ности ........ 359
§ 13. Уравнения фигур ® прост-
ранстве
71. Уравнение плоскости. . . 360
72. Уравнение сферы .... 361
73. Взаимное расположение сфе-
ры и плоскости. ..... 362
74. Пересечение двух ефер. . 363
ГЛАВА V. ПРЕОБРАЗОВАНИЯ
ФИГУР
§ 19. Движение
75. Примеры преобразований фи-
гур .......................364
76. Понятие движения. Свойства
движений ....... 369
4 20. Подобие фигур
77. Преобразование подобия. . 374
78. Подобные фигуры. ... 375
ГЛАВА VI. ВЕКТОРЫ
4 21. Введение понятия вектора
79. Параллельный перенос- . 377
80. Понятие вектора. . . . 378
81. Координаты вектора. . . 380
4 22. Операции над векторами
82. Сумма векторов .... 380
83. Умножение вектора на число.
Коллинеарные векторы. . . 882
84. Скалярное произведение век-
торов ........ 384
Г Л А В A I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ
§ 1. О строении курса геометрии
1. Геометрические фигуры. Геометрия — это наука о свойст-
вах геометрических фигур', треугольника, квадрата, круга, пи-
рамиды, сферы и др.
Слово «геометрия» греческое, в переводе на русский язык
означает «землемерие».
Геометрия, которая изучается в школе, называется евкли-
довой по имени древнегреческого ученого Евклида, живше-
го в III в. до н. э.
Школьная геометрия состоит из двух частей: планиметрии
и стереометрии. С первой частью геометрии вы знакомитесь в
восьмилетней школе, со второй — в старших классах. Плани-
метрия — это раздел геометрии, в котором изучаются геомет-
рические фигуры на плоскости. Стереометрия — это раздел гео-
метрии, в котором изучаются фигуры в пространстве (см. гла-
ву II).
На рисунке 1 изображены различные фигуры на плоскости.
Всякую геометрическую фигуру мы представляем себе состав-
ленной из точек. Часть любой геометрической фигуры также
является геометрической фигурой. На рисунке 2, а отрезок АВ
есть часть прямой а, и на рисунке 2, б круг <£>1 есть часть круга со.
Объединение нескольких геометрических фигур есть снова
геометрическая фигура. На рисунке 3 фигура составлена из
треугольника и трех квадратов, на рисунке 4 фигура состоит
из трех кругов.
В этой главе мы будем рассматривать только фигуры на
плоскости.
Треугольник Окружность Четырехугольник Многоугольник
2. Точка. Прямая. Основными геометрическими фигурами
на плоскости являются точка и прямая.
Точки обозначаются прописными (заглавными) латинскими
буквами:
A, В, Cf D...
Прямые обозначаются строчными латинскими буквами:
а, Ь, с, ... .
Прямую можно обозначить также двумя буквами, соответ-
ствующими точкам, лежащим на ней. Например, прямую а
на рисунке 5 можно обозначить АВ, & прямую Ь обозначить
МК.
На рисунке 5 изображены прямые а и Ъ н точки А, В, М и К,
Про точки М и К говорят, что они лежат на прямой Ь или что
точки М и К принадлежат прямой Ь. Аналогично точки А и В
лежат на прямой а или принадлежат прямой а.
Про прямую иногда говорят, что она проходит через точки.
257
Так, прямая а на рисунке 5
проходит через точки А н В,
а прямая b проходит через
точки М, К и А. Можно так-
же сказать, что прямая а не
проходит через точку М или
что точка К не принадлежит
прямой а.
3. Определения. Аксиомы.
Теоремы. В последующих пунк-
тах будут дамы определения
многих геометрических фигур
и других понятий. Дать определение чему-либо — значит объяс-
нить, что это такое. При определении любого понятия употреб-
ляются другие понятия, которые должны быть уже известны.
Однако нельзя дать определения всех понятий, поэтому неко-
торые из них принимают без определений и называют их не-
определяемыми. К таким понятиям относятся, например, точка
и прямая (см. п. 2).
На рисунке 5 прямые а н Ь имеют одну общую точку А.
Прямые, имеющие одну общую точку, называются пересекаю-
щимися, а точка А — точкой пересечения прямых а и Ь.
Рассуждение, с помощью которого устанавливается пра-
вильность утверждения о свойстве геометрической фигуры,
называется доказательством.
Предложение, выражающее свойство геометрической фигу-
ры, истинность которого доказывается, называется теоремой.
Совершенно ясно, что невозможно доказать все свойства
геометрических фигур, не приняв некоторые из них за основ-
ные, являющиеся отправными в доказательствах других
свойств фигур.
Принимаемые без доказательства свойства фигур называют
аксиомами.
По ходу изложения материала будут сформулированы
аксиомы, на основе которых построен школьный курс плани-
метрии. Эти аксиомы обозначены буквой А.
В главе II будет рассмотрена группа аксиом стереометрии.
К аксиомам планиметрии относятся, например, основные
свойства принадлежности точек и прямых на плоскости.
А—Ij. I Какова бы ни была прямая, существуют точки, при-
надлежащие этой прямой, и точки, ие принадле-
| жащие ей.
А—12. I Через любые две точки можно провести прямую, и
| только одну.
9 Заказ 769
Используя уже имеющиеся определения и аксиомы» можно
доказать первую теорему планиметрии.
Т. 1. 1. I Две различные прямые либо не пересекаются, либо
I пересекаются только в одной точке.
Если бы две различные прямые имели две точки пересече-
ния, то получилось бы, что через эти точки проходят две раз-
личные прямые. А это невозможно, так как согласно А—12
через две точки проходит только одна прямая.
Эта теорема доказывается методом доказательства от про-
тивного. Этот метод состоит в том, что сначала делается пред-
положение, противоположное тому, что утверждается теоре-
мой. Затем путем рассуждений, опираясь на аксиомы, а не-
редко на доказанные ранее теоремы, приходят к выводу, проти-
воречащему либо условию теоремы, либо одной из аксиом,
либо известной ранее теореме. На этом основании заключают,
что предположение было неверным, а значит, верно утвержде-
ние теоремы.
Строение курса геометрии можно охарактеризовать так:
1. Перечисляются основные геометрические понятия, они
вводятся без определения.
2. На основе введенных понятий даются определения всем
остальным геометрическим понятиям.
3. Формулируются аксиомы.
4. На основе аксиом и определений доказываются теоремы,
которые, в свою очередь, используются для доказательства
других теорем курса геометрии.
Построение геометрии с учетом выполнения всех этих пунк-
тов называется аксиоматическим.
Пример. Даны четыре точки. Сколько различных пря-
мых могут определять эти точки?
Решение. Воспользуемся аксиомой геометрии А—12. Су-
щественным здесь является рассмотрение различных возмож-
259
ностей расположения точек. Принципиально различными явля-
ются три случая расположения четырех точек (рис. 6). В первом
случае (рис. 6, а) мы имеем одну прямую, во втором случае
(рис. 6, б) — четыре прямые, в третьем случае (рис. 6, в) —
шесть прямых.
§ 2. Основные свойства простейших геометрических фигур
4. Отрезок. На прямой а (рис. 7, а) взяты точки А, В и С.
Точка В лежит между точками А и С, Можно также сказать,
что точки А и С лежат по разные стороны от точки В. Точки А и
В лежат по одну сторону от точки С, они не разделяются точкой
С. Точки В и С лежат по одну сторону от точки А.
Отрезком называется часть прямой, которая состоит из
всех точек этой прямой, лежащих между двумя данными ее
точками. Эти точки называются концами отрезка. Отрезок
обозначается указанием его концов.
На рисунке 7, б отрезок АВ является частью прямой а. Точка
М лежит между точками А и В, а поэтому принадлежит отрезку
АВ; точка К не лежит между точками А и В, поэтому не при-
надлежит отрезку АВ.
Аксиома (основное свойство) расположения точек на прямой
формулируется так:
А—Пр I Из трех точек на прямой одна и только одна лежит
| между двумя другими.
Следующая аксиома выражает основное свойство измере-
ния отрезков.
А—Шр
Каждый отрезок имеет определенную длину, боль-
шую нуля. Длина отрезка равна сумме длин частей,
на которые он разбивается любой его точкой.
Это значит, что если на отрезке МК взять любую точку С, то
длина отрезка МК равна сумме длин отрезков МС и СК (рис.
7, а).
Длину отрезка МК называют также расстоянием между
точками М и К.
П р и м е р 1. На прямой даны три точки О, Р и М. Известно,
что ОМ = 14 см, ОР =8 см, РМ=6 см. Лежит ли точка Р между
О н М? Может ли точка В принадлежать отрезку РМ, если
ВМ=5 см, РВ=4 см? Объяснить ответ.
Решение. Точка Р лежит между точками О и М, если
ОР-{-РМ=ОМ. Проверим выполнение этого условия: 8 см 4-
4-6 см = 14 см. Вывод: точка Р лежит между точками О и М.
Точка В принадлежит отрезку РМ, если оиа лежит между
точками Р и М, т. е. РВ-^-ВМ=РМ. Проверим: 4 см-|-5 см=
=9 см, а по условию РМ=6 см. Вывод: точка В не принад-
лежит отрезку РМ.
П р и м е р 2. Можно ли на плоскости расположить 6, 7 и 8
отрезков так, чтобы каждый из них пересекался ровно с тремя
другими?
Решение. 6 отрезков расположить так можно (рис. 8, а).
8 отрезков так расположить тоже можно (рис. 8, б). 7 отрезков
так расположить нельзя.
Докажем последнее утверждение. Предположим, что такое расположе-
ние семи отрезков возможно. Занумеруем отрезки и составим такую табли-
цу 7X7: в клетке (J; j) на пересечении i-й строки и /го столбца поставим «-Ь»,
если i-й стрезок пересекается с j-м, и если не пересекается. Если i—j,
то тоже ставим «—». Подсчитаем двумя способами, сколько знаков « + » в
таблице.
С одной стороны, в каждой строке их 3, поэтому всего знаков « +» 3-7=21.
С другой стороны, таблица заполнена симметрично относительно диагонали:
если в клетке (i; j) стоит • + », то в клетке (;; i) тоже. Значит, общее количество
знаков « +» должно быть четным. Получили противоречие.
Здесь мы воспользовались доказательством методом от противного.
5. Луч. Полупрямой или лучом называется часть прямой,
которая состоит из всех точек этой прямой, лежащих по одну
сторону от данной ее точки. Эта точка называется начальной
точкой полупрямой или началом луча. Различные полупря-
мые одной и той же прямой с общей начальной точкой назы-
ваются дополнительными.
Полупрямые обозначаются строчными латинскими буквами.
Можно обозначить полупрямую двумя буквами: начальной и
еще какой-нибудь буквой, соответствующей точке, принадле-
жащей полупрямой. При этом начальная точка ставится на
первом месте. Например, на рисунке 9, а изображены лучи
АВ и АС, являющиеся дополнительными, на рисунке 9, б
изображены лучи МА, МВ и луч с.
Следующая аксиома отражает основное свойство отклады-
вания отрезков-.
А—IVj.l На любой полупрямой от ее начальной точки можно
| отложить отрезок заданной длины, и только один.
Пример. Даны две точки А и В. Сколько прямых можно
провести через точки А и В? Сколько существует на прямой АВ
лучей с началом в точке А, в точке В? Отметить на прямой АВ
две точки, отличные от А и В. Принадлежат ли онн отрезку АВ?
Решение. 1) По аксиоме А—12 через точки А и В всегда
можно провести прямую, и только одну.
2) На прямой АВ с началом в точке А существуют два луча,
которые называются дополнительными. Аналогично и для
точки В.
3) Ответ зависит от расположения отмеченных точек. Рас-
смотрим возможные случаи (рис. 10). Ясно, что в случае а) точ-
ки М и N принадлежат отрезку АВ; в случаях б), в) одна точка
принадлежит отрезку, а другая иет; в случаях г) и д) точки
М и N не принадлежат отрезку АВ.
6. Окружность. Круг. Окружностью называется фигура, ко-
торая состоит из всех точек плоскости, находящихся на дан-
ном расстоянии от данной точки. Эта точка называется центром
окружности.
Расстояние от точек окружности до ее центра называется
радиусом окружности. Радиусом называется также любой
отрезок, соединяющий точку окружности с ее центром.
Отрезок, соединяющий две точки окружности, называется
хордой. Хорда, проходящая через центр, называется диамет-
ром.
На рисунке 11, а изображена окружность с центром в точке
О. Отрезок ОА — радиус этой окружности, BD — хорда окруж-
ности, СМ — диаметр окружности.
Кругом называется фигура, которая состоит из всех точек
плоскости, находящихся иа расстоянии, не большем данного,
от данной точки. Эта точка называется центром круга, а данное
расстояние — радиусом круга. Границей круга является окруж-
ность с теми же центром и радиусом (рис. 11, б).
263
Пример. На какое наибольшее число различных частей,
не имеющих общих точек, кроме своих границ, могут разби-
вать плоскость: а) прямая и окружность; б) две окружности;
в) три окружности?
Решение. Изобразим на рисунке соответствующие усло-
вию случаи взаимного расположения фигур. Запишем ответ:
а) четыре части (рис. 12, а); б) четыре части (рис. 12, б); в) во-
семь частей (рис. 12, в).
7. Полуплоскость. Сформулируем еще одну аксиому гео-
метрии.
А—П2. | Прямая разбивает плоскость на две полуплоскости.
На рисунке 13 прямая а разбивает плоскость на две полу-
плоскости так, что каждая точка плоскости, не принадлежа-
щая прямой а, лежит в одной из них. Это разбиение обладает
следующим свойством: если концы какого-нибудь отрезка
принадлежат одной полуплоскости, то отрезок не пересекает-
ся с прямой; если концы отрезка принадлежат разным полу-
плоскостям, то отрезок пересекается с прямой. На рисунке 13
точки А и В лежат в одной из полуплоскостей, на которые пря-
мая а разбивает плоскость. Поэтому отрезок АВ не пересека-
ется с прямой а. Точки С и D лежат в разных полуплоскостях.
Поэтому отрезок CD пересекает прямую а.
8. Угол. Градусная мера угла. Углом называется фигура,
которая состоит из точки — вершины угла тл двух различных
полупрямых, исходящих из этой точки, — сторон угла (рис. 14).
Если стороны угла являются дополнительными полупрямыми,
то угол называется развернутым.
Угол обозначается либо указанием его вершины, либо ука-
занием его сторон, либо указанием трех точек: вершины и двух
точек на сторонах угла. Слово «угол» иногда заменяют сим-
волом Z. Угол на рисунке 14 можно обозначить тремя спосо-
бами:
ZO, Z(ab), ZAOB-
Говорят, что луч с проходит между сторонами угла (оЬ),
если он исходит из его вершины и пересекает какой-нибудь
отрезок с концами на сторонах угла.
На рисунке 15 луч с проходит между сторонами угла (аЬ),
так как он пересекает отрезок АВ.
В случае развернутого угла любой луч, исходящий из его
вершины и отличный от его сторон, проходит между сторонами
угла.
Углы измеряются в градусах. Если взять развернутый
угол и разделить его на 180 равных углов, то градусная мера
каждого из этих углов называется градусом.
Основные свойства измерения углов выражены в следую-
щей аксиоме:
А—Ш2.
Каждый угол имеет определенную градусную меру,
большую нуля. Развернутый угол равен 180°. Гра-
дусная мера угла равна сумме градусных.мер углов,
на которые он разбивается любым лучом, проходя-
щим между его сторонами.
Это значит, что если луч с проходит между сторонами угла
(аЬ), то угол (ab) равен сумме углов (ас) и (сЬ), т. е. Z(ab)=
= Z (oc)4-Z (cb).
Градусная мера угла находится при помощи транспортира.
Угол, равный 90°, называется прямым углом. Угол, меньший
90°, называется острым углом. Угол, больший 90° и меньший
180° называется тупым.
A—IV2.
Сформулируем основное свойство откладывания углов.
От любой полупрямой в заданную полуплоскость
можно отложить угол с заданной градусной мерой,
меньшей 180°, и только одни.
Рассмотрим полупрямую а. Продлим ее за начальную
точку А. Полученная прямая разбивает плоскость на две полу-
плоскости. На рисунке 16 показано, как с помощью транспор-
тира отложить от полупрямой а в верхнюю полуплоскость угол
с данной градусной мерой 60°.
Т. 1. 2.
Если от данной полупрямой отложить в одну полу-
плоскость два угла, то сторона меньшего угла, от-
личная от данной полупрямой, проходит между
сторонами большего угла.
Пусть А(аЪ) и Z(ac) — углы, отложенные от данной полу-
прямой а в одну полуплоскость, и пусть угол (ab) меньше угла
(ас). В теореме 1. 2 утверждается, что луч Ь проходит между
сторонами угла (ас) (рнс. 17).
Биссектрисой угла называется луч, который исходит из
его вершины, проходит между его сторонами и делит угол
пополам. На рисунке 18 луч ОМ — биссектриса угла АОВ.
В геометрии существует понятие плоского угла. Плоским
углом нгсзыв&егся часть плоскости, ограниченная двумя раз-
личными лучами, исходящими из одной точки. Эти лучи назы-
ваются сторонами угла. Существуют два плоских угла с дан-
ными сторонами. Они называются дополнительными. На ри-
сунке 19 заштрихован один из плоских углов со сторонами
а и Ъ.
266
Если плоский угол является частью полуплоскости, то его
градусной мерой является градусная мера обычного угла с те-
ми же сторонами. Если плоский угол содержит полуплос-
кость, то его градусная мера равна 360° — а, где а — гра-
дусная мера дополнительного плоского угла.
Пример. Между сторонами угла (cd), равного 120°, про-
ходит луч а. Найти углы (са) и (da), если их градусные меры от-
носятся как 4:2.
Решение. Луч а проходит между сторонами угла (cd),
значит, по основному свойству измерения углов (см. п. 8)
Z (са) 4- Z (ad) = Z (cd).
Так как градусные меры Z(ca) и Z(da) относятся как 4:2, то
Z. (са)=-Цр-4 = 80°, Z. (da) = 2^1-2 = 40°.
9. Смежные и вертикальные углы. Два угла называются
смежными, если у них одна сторона общая, а другие стороны
этих углов являются дополнительными полупрямыми. На
рисунке 20 углы (ас) и (cb) смежные.
Т. 1. 3. | Сумма смежных углов равна 180°.
Из теоремы 1. 3 следуют свойства:
1) если два угла равны, то смежные с ними углы равны;
2) угол, смежный с прямым углом, есть прямой угол;
3) угол, смежный с острым, является тупым, а смежный с
тупым — острым.
Два угла называются вертикальными, если стороны одного
угла являются дополнительными полупрямыми сторон дру-
гого. На рисунке 21, а углы (ab) и (а^) вертикальные.
Т. 1. 4. | Вертикальные углы равны.
Очевидно, что две пересекающиеся прямые образуют
смежные и вертикальные углы. Смежные углы дополняют
Друг Друга до 180°. Угловая мера меньшего из них называ-
ется углом между прямыми.
Пример. На рисунке 21, б угол COD равен 30.° Чему равны
углы АОК и DOK?
Решение. Углы COD и АОК вертикальные, следователь-
но, по теореме 1.4 они равны, т. е. ААОК — 30е. Угол DOK
смежный с углом COD, значит, по теореме 1.3
Z DOK= 180°— A COD = 180° —30° = 150°.
10. Центральные н вписанные углы. Центральным углом
в окружности называется плоский угол с вершиной в ее центре.
Часть окружности, расположенная внутри плоского угла, назы-
вается дугой окружности, соответствующей этому централь-
ному углу. Градусной мерой дуги окружности называется гра-
дусная мера соответствующего центрального угла.
На рисунке 22 угол АОВ — центральный угол окружности,
его вершина О является центром данной окружности, а стороны
О А и ОВ пересекают окружность. Дуга АВ является частью
окружности, расположенной внутри центрального угла.
Градусная мера дуги АВ на рисунке 22 равна градусной
мере угла АОВ. Градусная мера дуги АВ обозначается о АВ.
Угол, вершина которого лежит на окружности, а стороны
пересекают эту окружность, называется вписанным в окруж-
ность. На рисунке 23 изображены вписанные углы.
Т. 1.5.
Вписанный в окружность угол, стороны которого
проходят через две данные точки окружности, равен
половине угла между радиусами, проведенными
в эти точки, или дополняет эту половину до 180°.
При доказательстве теоремы 1. 5 необходимо рассмотреть
три разных случая, которые изображены на рисунке 23: одна
из сторон вписанного угла проходит через центр окружности
(рис. 23, а); центр окружности лежит внутри вписанного угла
(рис. 23, б); центр окружности лежит вне вписанного угла
(рис. 23, в).
Из теоремы 1. 5 вытекает следствие: все вписанные в окруж-
ность углы, стороны которых проходят через две данные точ-
ки окружности, а вершины лежат по одну сторону от прямой,
соединяющей эти точки, равны; вписанные углы, стороны
которых проходят через концы диаметра окружности, прямые.
На рисунке 24 стороны вписанного угла АВС проходят
через концы диаметра АС, поэтому Z. АВС—99°.
Пример. Точки А, В и С лежат на окружности с центром
О. Найти угол АОС, если Z. АВС = 66°.
Решение. Угол АВС, вписанный в окружность, опира-
ется на дугу AC, a Z.AOC — центральный угол данной ок-
ружности (рис. 25). Z. АВС=66°, значит, АС=132° по
теореме 1. 5, а так как угол АОС центральный, то его градус-
ная мера равна градусной мере дуги АС, т. е. Z. АОС= 132°.
11. Параллельные прямые. Две прямые на плоскости назы-
ваются параллельными, если они не пересекаются.
269
На рисунке 26 показано, как с помощью угольника и ли-
нейки провести через данную точку В прямую Ь, параллель-
ную данной прямой а.
Для обозначения параллельности прямых используется
символ ||. Запись аЦЬ читается: «Прямая а параллельна пря-
мой Ь».
Аксиома параллельности выражает основное свойство па-
раллельных прямых.
А—V.
Через точку, не лежащую на данной прямой, можно
провести на плоскости не более одной прямой, парал-
лельной данной.
Т. 1. 6.1 Две прямые, параллельные третьей, параллельны
I друг другу.
На рисунке 27 прямые а и Ь параллельны прямой с. Теоре-
ма 1. 6 утверждает, что а||6.
Можно доказать, что через точку, не принадлежащую
прямой, можно провести прямую, параллельную данной. На
рисунке 28 через точку А, не принадлежащую Ь, проведена
прямая а, параллельная прямой Ь.
Сопоставляя это утверждение и аксиому параллельных,
приходят к важному выводу, на плоскости через точку, ие
лежащую на данной прямой, можно провести параллельную
ей прямую, и только одну.
Аксиома параллельности в книге Евклида «Начала» назы-
валась «пятый постулат». Геометры древности пытались до-
казать единственность параллельной. Эти безрезультатные
попытки продолжались более 2000 лет, вплоть до XIX в.
Великий русский математик Н. И. Лобачевский и не-
зависимо от него венгерский математик Я. Бойяи показали,
что, приняв допущение о возможности проведения через точку
нескольких прямых, параллельных данной, можно построить
другую, столь же «правильную» «неевклидову геометрию». Так
родилась геометрия Лобачевского.
Примером теоремы, которая использует понятие параллель-
ности, а ее доказательство опирается на аксиому параллель-
ных, служит теорема Фалеса. Фалес Милетский —
древнегреческий математик, живший в 625—547 гг. до н. э.
Т. 1. 7.
Если параллельные прямые, пересекающие стороны
угла, отсекают на одной его стороне равные отрезки,
то они отсекают равные отрезки и на другой его сто-
роне (теорема Фалеса).
Пусть Alt Д2, А3 — точки пересечения параллельных пря-
мых с одной из сторон угла и А2 лежит между А] и А3 (рис. 29).
Пусть Blt В2, В3 — соответствующие точки пересечения этих
прямых с другой стороной угла. Теорема 1.7 утверждает,
что если А1А2=А2А3, то В1В2=В2В3.
Пример 1. Могут ли семь прямых пересекаться в восьми
точках?
Решение. Могут. Например, на рисунке 30 изображены
семь таких прямых, три из которых параллельны.
Пример 2. Произвольный отрезок АС разделить иа 6
равных частей.
Решение. Начертим отрезок АС. Проведем из точки А луч
AM, не лежащий на прямой АС. На луче AM от точки А после-
довательно отложим 6 равных отрезков (рис. 31). Концам от-
резков дадим обозначения Alr А2, А3, А4, А6, Ае. Соединим
точку Ае отрезком с точкой С и через точки Alt As, А3, А 4, А5
проведем прямые, параллельные прямой А6С. Точки пересе-
чения этих прямых с отрезком АС разделят его на 6 равных
частей (по теореме 1. 7).
12. Признаки параллельности прямых. Пусть АВ и CD —
две прямые. Пусть АС — третья прямая, пересекающая
прямые АВ и CD (рис. 32, а). Прямая АС по отношению
к прямым АВ и CD называется секущей. Образованные этими
прямыми углы часто рассматриваются попарно. Пары
углов получилн специальные названия. Так, если точки
В и D лежат в одной полуплоскости относительно прямой АС,
то углы ВАС и DCA называются внутренними односторонними
(рис. 32, а). Если точки В и D лежат в разных полуплоскостях
относительно прямой АС, то углы ВАС и DCA называются
внутренними накрест лежащими (рис. 32, б).
272
Секущая АС образует с прямыми АВ и CD две пары внут-
ренних односторонних (Z4h Z.6, Z.3 и Z5)h две пары внут-
ренних накрест лежащих углов (Z.4 и Z.б, Z.3 и Z.6, рис.
32, в).
Т. 1. 8.
Если внутренние накрест лежащие углы равны или
сумма внутренних односторонних углов равна 180°,
то прямые параллельны.
На рисунке 32, в обозначены цифрами четыре пары углов.
Теорема 1.8 утверждает, что если Z.3=Z,6 или Z.4= Z.5,
то прямые а и Ь параллельны. Теорема 1.8 также утверждает,
что если Z. 44-Z. 6 =180° или Z.3+Z. 5 = 180°, то прямые
а и Ь параллельны.
Теоремы 1.6 и 1.8 являются признаками параллельности
прямых. Верна и теорема, обратная теореме 1.8.
Т. 1. 9.
Если две параллельные прямые пересечены третьей
прямой, то внутренние накрест лежащие углы равны,
а сумма внутренних односторонних углов равна 180°.
Пример. Один из внутренних односторонних углов, обра-
зовавшихся при пересечении двух параллельных прямых треть-
ей прямой, в 4 раза больше другого. Чему равны эти углы?
Решение. По теореме 1.9 сумма внутренних односто-
ронних углов при двух параллельных прямых и секущей
равна 180°. Обозначим эти углы буквами а и 0, тогда а + 0=
= 180°; известно, что а больше 0 в 4 раза, значит, а = 40, а
тогда 50=180°, т. е. 0=36°, 40=а = 144°. Итак, а = 144°, 0=
= 36°.
13. Перпендикулярные прямые. Две прямые называются
перпендикулярными, если они пересекаются под прямым
углом (рис. 33).
Перпендикулярность прямых записывается при помощи
символа _1_. Запись a_Lb читается: «Прямая а перпендику-
лярна прямой Ь*. '
Перпендикуляром к данной прямой называется отрезок
прямой, перпендикулярной данной, имеющий концом их точ-
ку пересечения. Этот конец отрезка называется основанием
перпендикуляра.
На рисунке 34 перпендикуляр АВ проведен из точки А к пря-
мой а. Точка В — основание перпендикуляра.
Т. 1.10.
Т. 1.11.
Через каждую точку прямой можно провести перпен-
дикулярную ей прямую, и только одну.
Из любой точки, не лежащей иа дайной прямой,
можно опустить на эту прямую перпендикуляр, и
только один.
Длина перпендикуляра, опущенного из данной точки на
прямую, называется расстоянием от точки до прямой.
Расстоянием между параллельными прямыми называется
расстояние от какой-нибудь точки одной прямой до другой
прямой.
Пусть ВА — перпендикуляр, опущенный из точки В на
прямую а, и С — любая точка прямой а, отличная от А. Отре-
зок ВС называется наклонной, проведенной из точки В к пря-
мой а (рис. 35). Точка С называется основанием наклонной.
Отрезок АС называется проекцией наклонной.
Прямую, проходящую через середину отрезка перпенди-
кулярно к нему, называют серединным перпендикуляром.
На рисунке 36 прямая а перпендикулярна к отрезку АВ
и проходит через точку С — середину отрезка АВ, т. е. а —
серединный перпендикуляр.
Пример. Равные отрезки AD и СВ, заключенные меж-
ду параллельными прямыми АС и BD, пересекаются в точке
О. Доказать, что АО=СО и ВО—DO.
Решение. Проведем из точек А и С перпендикуляры к
прямой BD (рис. 37). АК—СМ как расстояние между парал-
лельными прямыми. £\AKD и £\СМВ прямоугольные, они
равны по гипотенузе и катету (см. Т. 1. 25), а значит, Z_CBM=
= Z-ADK. ABOD равнобедренный (Т. 1.19), а значит, ВО=DO.
Из равенства треугольников AKD и СМВ следует, что /LDAK=
— 2 BCM, а тогда АСАО~ /-АСО, т. е. ЛАОС равнобедрен-
ный, а значит, А О=СО.
14. Касательная к окружности. Касание окружностей.
Прямая, проходящая через точку окружности перпендику-
лярно к радиусу, проведенному в эту точку, называется ка-
сательной. При этом данная точка окружности называется
точкой касания. На рисунке 38 прямая а проведена через точку
А окружности перпендикулярно к радиусу О А. Прямая а явля-
ется касательной к окружности. Точка А является точкой каса-
ния. Можно сказать также, что окружность касается прямой а
в точке А.
Говорят, что две окружности, имеющие общую точку, ка-
саются в этой точке, если они имеют в этой точке общую каса-
тельную. Касание окружностей называется внутренним, если
центры окружностей лежат по одну сторону от их общей каса-
тельной. Касание окружностей называется внешним, если
центры окружностей лежат по разные стороны от их общей
276 SZ
касательной- На рисунке 39, а касание окружностей внутрен-
нее, а на рисунке 39, б — внешнее.
Пример 1. Построить окружность данного радиуса, ка-
сающуюся данной прямой в данной точке.
р е щ е и и е. Касательная к окружности перпендикулярна
к радиусу, проведенному в точку касания. Поэтому центр
искомой окружности лежит на перпендикуляре к данной пря-
мой, проходящем через данную точку, и находится от данной
точки иа расстоянии, равном радиусу. Задача имеет два реше-
ния — две окружности, симметричные друг другу относи-
тельно данной прямой (рис. 40).
Пример 2. Две окружности диаметром 4 и 8 см касают-
ся внешним образом. Чему равно расстояние между центрами
этих окружностей?
Решение. Радиусы окружностей ОА и ОУА перпендику-
лярны их общей касательной, проходящей через точку А
(рис. 41)- Поэтому ОО, =OA-\-AOi — 6 см.
15. Треугольники. Треугольником называется фигура,
которая состоит из трех точек, не лежащих на одной прямой, и
трех отрезков, попарно соединяющих эти точки. Точки назы-
ваются вершинами треугольника, а отрезки — его сторонами.
Треугольник обозначается его вершинами. Вместо слова «тре-
угольник» употребляется символ Д.
На рисунке 42 изображен треугольник АВС; А, В, С —
вершины этого треугольника; АВ, ВС и АС — его стороны.
Углом треугольника АВС при вершине А называется угол,
образованный полупрямыми АВ и АС. Так же определяются
углы треугольника при вершинах В и С.
Т. 1.12.
Если прямая, не проходящая ни через одну из вер-
шин треугольника, пересекает одну из его сторон,
то она пересекает только одну из двух других сторон.
Высотой треугольника, опущенной из данной вершины,
называемся перпендикуляр, проведенный из этой вершины к
прямой, содержащей противолежащую сторону треугольника.
На рису15хе 43, а отрезок AD — высота остроугольного ДАВС,
а на рисунке 43, б основание высоты тупоугольного ДАВС —
точка D — лежит на продолжении стороны ВС.
Биссектрисой треугольника называется отрезок биссектри-
сы угла треугольника, соединяющий вершину с точкой иа
противолежащей стороне. На рисунке 44 отрезок AD — бис-
сектриса треугольника АВС.
Медианой треугольника, проведенной из данной вершины,
называется отрезок, соединяющий эту вершину с серединой
противолежащей стороны треугольника. На рисунке 45 отре-
зок AD — медиана треугольника АВС.
Средней линией треугольника называется отрезок, соеди-
няющий середины двух его сторон.
Т. 1.13.
Средняя линия треугольника, соединяющая сере-
дины двух данных сторон, параллельна третьей
стороне и равна ее половине.
Пусть DE — средняя линия треугольника АВС (рис. 46).
Теорема утверждает, что DE\\AC и DE=-^-AC.
Неравенством треугольника называется свойство расстоя-
ний между тремя точками, которое выражается следующей
теоремой:
Т. 1.14.
Каковы бы нн были три точки, расстояние между
любыми двумя из этих точек не больше суммы рас-
стояний от иих до третьей точки.
Пусть А, В, С — три данные точки. Взаимное расположе-
ние этих точек может быть различным: а) две точки из трех
или все три совпадают, в этом случае утверждение теоремы
очевидно; б) точки различны и лежат иа одной прямой (рис. 47,
а), одна из иих, например В, лежит между двумя другими, в
этом случае АВВС = АС, откуда следует, что каждое из трех
расстояний ие больше суммы двух других; в) точки ие лежат
на одной прямой (рис. 47, б), тогда теорема 1.14 утверждает,
что АС<АВ+ВС.
В случае в) три точки А, В, С являются вершинами тре-
угольника. Поэтому в любом треугольнике каждая сторона
меньше суммы двух других сторон.
Пример 1. Существует ли треугольник АВС со сторо-
нами: а) АВ=5 см, АС = 18 см, ВС—12 см; б) АВ=7 см, АС—
=8 см, ВС = 12 см?
Решение. Для сторон треугольника АВС должны вы-
полняться неравенства:
АВ^АС+ВС (1)
АС<АВ+ВС, (2)
ВС С АВ+АС. (3)
В случае а) неравенство (2) ие выполняется, значит, такого
расположения точек быть ие может; в случае б) неравенст-
ва (1)—(3) выполняются, т. е. треугольник существует.
Пример 2. Найти расстояние между пунктами А и В,
разделенными препятствием.
Решение. Для нахождения расстояния провешиваем
базис CD н проводим прямые ВС и AD (рис. 48). Находим точ-
ку М — середику CD. Проводим MN\\BD и MP\\AD. Из Д АВС
следует, что PN — средняя линия, т. е. PN=±-AB (Т. 1. 13).
Измерив PN, нетрудно найти АВ.
16. Равенство треугольников. Два отрезка называются
равными, если они имеют одинаковую длину. Два угла назы-
ваются равными, если они имеют одинаковую угловую меру
в градусах.
Треугольники АВС и А1В1С1 называются равными, если
АВ^А^, ВС=^ВуСи АС=А£и
Z.A = £Alt AB=Z.Blt Z.C=ACX.
278
Кратко это выражают словами: треугольники равны, если
у них соответствующие стороны и соответствующие углы равны.
Сформулируем основное свойство существования равных
треугольников (аксиому существования треугольника, равного
данному):
A-IV3.
Каков бы ни был треугольник, существует равный
ему треугольник в заданном расположении отно-
сительно данной полупрямой.
Справедливы три признака равенства треугольников:
Т. 1.15.
Т. 1.16.
Т. 1.17.
Если две стороны и угол между ними одного тре-
угольника равны соответственно двум сторонам и
углу между ними другого треугольника, то такие
треугольники равны (признак равенства треуголь-
ников по двум сторонам и углу между ними).
Если сторона и прилежащие к ией углы одного тре-
угольника равны соответственно стороне и приле-
жащим к ней углам другого треугольника, то такие
треугольники равны (признак равенства треуголь-
ников по стороне и прилежащим к ней углам).
Если три стороны одного треугольника равны соот-
ветственно трем сторонам другого треугольника, то
такие треугольники равны (признак равенства тре-
угольников по трем сторонам).
Пример. Точки В и D лежат в разных полуплоскостях
относительно прямой АС (рис. 49). Известно, что АВСА —
= ADAC и ADCB= ABAD. Доказать, что ААВС= ACDA.
Решение. АВСА = Z. DAC по условию, и ABAC—
= ADCA, так как эти углы получены вычитанием из равных
углов BCD и DAB равных углов ВС А и DAC. Кроме этого, в
указанных треугольниках сторона АС общая. Эти треугольники
равны по стороне и прилежащим к ией углам (Т. 1.16).
17. Равнобедренный треугольник. Треугольник называется
равнобедренным, если у него две стороны равны. Эти равные
стороны называются боковыми сторонами, а третья сторона
называется основанием треугольника.
В треугольнике АВС (рис. 50) АВ=СВ, значит, А АВС
равнобедренный с основанием АС.
Т. 1.18. I В равнобедренном треугольнике углы при осно-
| вании равны.
279
Т. 1.19.1 Если в треугольнике два угла равны, то он равно-
| бедренный (обратная теореме Т. 1.18).
Т. 1.20.
В равнобедренном треугольнике медианз, прове-
денная к основанию, является биссектрисой и вы-
сотой.
Можно также доказать, что в равнобедренном треуголь-
нике высота, проведенная к основанию, является биссектри-
сой и медианой. Аналогично биссектриса равнобедренного
треугольника, проведенная из вершины, противолежащей ос-
нованию, является медианой и высотой.
Треугольник, у которого все стороны равны, называется
равносторонним.
Пример. В треугольнике ADB угол D равен 90°. На про-
должении стороны AD отложен отрезок DC=AD (точка D ле-
жит между точками А и С) (рис. 51). Доказать, что треугольник
АВС равнобедренный.
Решение. В треугольниках ADB и CDB известно, что
AD=CD, BD — общая сторона, a Z. BDA = A BDC=90°. Следо-
вательно, /\ADB= £\CDB по двум сторонзм и углу между
ними (Т. 1.15). Из равенства треугольников следует, что ВС=
=АВ, т. е. Л АВС равнобедренный.
18. Сумма углов треугольника. В любом треугольнике
справедлива теорема о сумме его углов.
Т. 1.21. | Сумма углов треугольника равна 180°.
Из теоремы 1.21 следует, что у любого треугольника хотя
бы два угла острые.
Внешним углом треугольника при данной вершине назы-
вается угол, смежный с углом треугольника при этой вершине.
На рисунке 52 изображен A BCD — внешний угол треуголь-
ника АВС. Чтобы не путать угол треугольника при данной
вершине с внешним углом при этой же вершине, его называ-
ют внутренним углом.
Т. 1.22. | Внешний угол треугольника равен сумме двух внут-
| ренних углов, не смежных с ним.
Из теоремы 1.22 следует, что внешний угол треугольника
больше любого внутреннего угла, не смежного с ним.
Пример. В треугольнике АВС (рис. 53) АА =60°,
= 80°. Биссектриса AD этого треугольника отсекает от него
ДАСО. Найти углы этого треугольника.
Решение. A DAB=30°, так как AD — биссектриса
угла А (см. п. 15). Z.ADC = 30°-|-80o = 110° как внешний угол
ДАВВ (Т. 1.22). Z.C= 180° —(110°-|-30о) = 40° по теореме о
сумме углов ДАСО (Т. 1.21).
19. Прямоугольный треугольник. Теорема Пифагора. Тре-
угольник называется прямоугольным, если у него есть прямой
угол. Так как сумма углов треугольника равна 180°, то у пря-
моугольного треугольника только один прямой угол. Два
других угла прямоугольного треугольника острые, причем
они дополняют друг друга до 90°. Сторона прямоугольного
треугольника, противолежащая прямому углу, называется
гипотенузой, две другие стороны называются катетами. А АВС,
изображенный на рисунке 54, прямоугольный, АВ прямой,
С А — гипотенуза, СВ и В А — катеты.
281
Для прямоугольных треугольников можно сформулировать
свои признаки равенства.
Т. 1.23.
Т. 1.24.
Т. 1.25.
Если гипотенуза и острый угол одного прямоуголь-
ного треугольника соответственно равны гипотенузе
и острому углу другого треугольника, то такие тре-
угольники равны (признак равенства по гипотенузе
и острому углу).
Если катет и противолежащий ему угол одного
прямоугольного треугольника соответственно равны
катету и противолежащему углу другого треуголь-
ника, то такие треугольники равны (признак ра-
венства по катету и противолежащему углу).
Если гипотенуза и катет одного прямоугольного
треугольника соответственно равны гипотенузе и
катету другого треугольника, то такие треугольники
равны (признак равенства по гипотенузе и катету).
В прямоугольном треугольнике с углом 30° катет, противо-
лежащий атому углу, равен половине гипотенузы.
В треугольнике АВС, изображенном на рисунке 55, Z.C
прямой, Z.B=30°. Значит, в этом треугольнике СА——АВ.
В прямоугольном треугольнике справедлива теорема Пифа-
гора, названная в честь древнегреческого ученого Пифагора,
жившего в VI в. до н. э.
Т. 1.26. В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов (теорема Пифагора).
Пусть АВС — данный прямоугольный треугольник с пря-
мым углом С, катетами а и b и гипотенузой с (рис. 56). Теоре-
ма утверждает, что а2 + Ь2=с2.
Из теоремы Пифагора следует, что в прямоугольном тре-
угольнике любой из катетов меньше гипотенузы.
Из теоремы Пифагора следует, что если к прямой из одной
точки проведейы перпендикуляр и наклонная, то наклонная
больше перпендикуляра; равные наклонные имеют равные
проекции; из двух наклонных больше та, у которой проекция
больше.
На рисунке 57 из точки О к прямой а проведен перпенди-
куляр ОА и наклонные ОВ, ОС и OD, при этом OC=OD, а
ОВ>ОС. На основании вышесказанного: а) ОАС.ОВ,
ОА <ОС, ОА <OD; б) AC=AD, так как OC=OD; в) АВ> АС,
так как ОВ>ОС.
Пример 1. В треугольниках АВС и DMC, изображенных
на рисунке 58, АВ =DM, АВ X А С, MD X CD. Доказать равенство
этих треугольников.
Решение. У треугольников АВС и DMC по условию
AB=DM vl ЛВАС= Z.MDC -\ а /_ВСА= AMCD как
вертикальные (Т. 1. 4). Треугольники равны по катету и про-
тиволежащему углу (Т. 1. 24).
Пример 2. В прямоугольном треугольнике через сере-
дину его гипотенузы проведены прямые, параллельные его
катетам. Найти периметр образовавшегося прямоугольника,
если катеты треугольника равны 10 и 8 см.
Решение. В треугольнике АВС (рис. 59) /_А прямой,
АВ=10 см, АС=& см, KD и MD — средние линии треуголь-
ника АВС, откуда KD—^-AC — 4 см, MD=~AB=5 см (Т.
1. 13). Периметр прямоугольника KDMA равен 18 см.
Пример 3. В окружности, радиус которой 25 см, прове-
дены по одну сторону от ее центра две параллельные хорды
длиной 40 и 30 см. Найти расстояние между этими хордами.
Решение. Проведем радиус ОК, перпендикулярный
хордам АВ и CD, соединим центр окружности О с точками
С, A, D и В (рис. 60). Треугольники COD и АОВ равнобедрен-
ные, так как OC=OD и ОА = ОВ (как радиусы); ОМ и ON —
высоты этих треугольников. По теореме 1.20 каждая из высот
является одновременно медианой соответствующего треуголь-
ника, т. е. DM—MC и BN=NA.
Треугольники ОСМ и О AN прямоугольные, в них ОС —
=0,4 = 25 см, СМ=20 см, A2V=15 см. ON и ОМ найдем по
теореме Пифагора (Т. 1. 26): ON —152= 20 см, ОМ=
=V25 — 2°2=15 см-
MN=ON—ОМ, т. е. MN=$ см.
20. Окружности, вписанные в треугольник и описанные
около треугольника. Окружность называется описанной око-
ло треугольника, если она проходит через все его вершины.
283
Т. 1.27.
Центр окружности, описанной около треугольни-
ка, является точкой пересечения серединных пер-
пендикуляров к сторонам треугольника.
На рисунке 61 окружность описана около треугольника
АВС. Центр этой окружности О является точкой пересечения
серединных перпендикуляров СМИ, ON и ОК, проведенных
соответственно к сторонам АВ, ВС и С А.
Окружность называется вписанной в треугольник, если
она касается всех его сторон.
Т. 1. 28.1 Центр окружности, вписанной в треугольник, явля-
| ется точкой пересечения его биссектрис.
На рисунке 62 окружность вписана в треугольник АВС.
Центр этой окружности О является точкой пересечения бис-
сектрис АО, ВО и СО соответствующих углов треугольника.
Пример. В прямоугольном треугольнике катеты равны
12 и 16 см. Вычислить радиусы: 1) вписанной в него окруж-
ности; 2) описанной окружности.
Решение. 1) Пусть дан треугольник АВС, в котором
Z.C=90°, ВС =12 см, АС= 16 см, О — центр вписанной ок-
ружности (рис. 63, а). Периметр треугольника АВС равен
сумме удвоенной гипотенузы и диаметра вписанной в тре-
угольник окружности (используйте определение касательной
к окружности и равенство прямоугольных треугольников
АОМ и АОК, МОС и LOC по гипотенузе и катету).
Таким образом, АВ-\-ВС+АС—2АВ-}-2г, откуда 2г=
=АВ+ВС+АС — 2АВ=ВС+АС - АВ.
АВ =20 см по теореме Пифагора (Т. 1. 26), 2г= 8 см, т. е.
г=4 см.
2) Центр описанной около прямоугольного треугольника
окружности совпадает с серединой гипотенузы, откуда ради-
ус описанной окружности В=10 см (рис. 63, б).
§ 3. Геометрические построения на плоскости
21. Чертежные инструменты. В геометрии постоянно при-
ходится решать задачи на построение геометрических фигур
с помощью чертежных инструментов.
В некоторых случаях в задаче сказано, какие чертежные
инструменты можно применять при построении. В случаях,
когда это не оговорено, можно самим выбирать нужные для
построения инструменты.
В школьном курсе геометрии мы пользуемся такими чер-
тежными инструментами, как линейка (односторонняя), цир-
куль, угольник, транспортир.
Существуют различные типы задач на построение в за-
висимости от набора инструментов: построения циркулем
и линейкой; построения только одним циркулем (построения
Мора-Маскерони); построения только одной линейкой, ес-
ли на плоскости начерчена окружность и ее центр (пост-
роения Штейнера); с помощью угольника; с помощью транспор-
тира и т. д.
С помощью линейки можно начертить (в виде отрезка)
изображение: а) произвольной прямой; б) прямой, проходя-
щей через данную точку; в) прямой, проходящей через две
данные точки. С помощью линейки нельзя откладывать отрез-
ки, даже если на ней имеются деления, нельзя пользоваться
обоими краями линейки.
С помощью циркуля можно: а) построить окружность дан-
ного радиуса с центром в данной точке; б) отложить данный
отрезок на данной прямой от данной точки.
С помощью угольника можно выполнить те же построения,
что и линейкой; кроме того, можно совместить одну из сто-
рон угольника с данной прямой и провести прямую по другой
стороне угла. С помощью угольника можно также построить
прямой угол. В п. 11 (рнс. 26) рассказано, как с помощью уголь-
ника и линейки можно построить параллельные прямые.
С помощью транспортира можно построить точку на луче,
образующем некоторый данный угол с данной прямой с вер-
шиной в данной точке. На рисунке 16 (п. 8) показано, как с
помощью транспортира можно отложить от полупрямой в
верхнюю полуплоскость угол с заданной градусной мерой.
В геометрии, как правило, точными считаются построения,
выполняемые с помощью циркуля и линейки.
Есть задачи на построение, про которые известно, что они
не разрешимы с помощью циркуля и линейки.
1) Задача о трисекции угла. Дан угол а. Постро-
ч-
ить угол -д-сс.
2) Задача об удвоении куба. Дан куб (т. е. дан
отрезок, равный ребру куба). Построить другой куб (т. е. постро-
ить ребро такого куба), объем которого вдвое больше объема
данного куба.
3) Задача о квадратуре круга. Дан круг. Постро-
ить квадрат, равновеликий этому кругу.
Доказательство неразрешимости этих задач требует глубо-
ких математических знаний. Глава «Декартовы координаты
на плоскости* познакомит вас с аналитическим методом реше-
ния геометрических задач, когда задача переводится на язык
формул. Доказано, что если геометрическая фигура, которую
мы хотим построить, может быть выражена формулой, со-
держащей только рациональные функции и действие извле-
чения квадратного корня, то тогда этот объект можно постро-
ить с помощью циркуля и линейки.
22. Простейшие задачи иа построение. Во всех рассматри-
ваемых здесь задачах можно пользоваться только двумя чер-
тежными инструментами — линейкой и циркулем.
В школьном курсе геометрии при решении задач на построе-
ние прежде всего нужно знать, как выполнить построение,
а уже потом его выполнять. Кроме этого, важно уметь дока-
зать, что предложенное построение привело к построению
фигуры с требуемыми свойствами.
Рассмотрим простейшие задачи на построение.
Задача 1. Построить треугольник с данными сторонами
а, b и с.
На рисунке 64 построение ДАВС выполнено так: с по-
мощью линейки провели прямую и с помощью циркуля — три
окружности: радиусами ВС=а и ВА=с с центром в точке В,
радиусом СА = Ь с центром в точке С.
Эта задача не всегда может иметь решение. Для сторон
а, Ь, с треугольника должны выполняться условия:
а<Ь + с, Ь<а+с, с<а + Ь (см. п. 15).
Задача 2. Построить угол, равный данному.
На основании аксиомы А—IV2 (см. п. 8) от данной полу-
прямой в данную полуплоскость можно отложить угол, рав-
ный данному углу. Как это сделать с помощью циркуля и
линейки?
На рисунке 65 построение выполнено так: Z.A — данный
угол, ОВХ — данная полупрямая. Провели две окружности с
центрами А и О одинакового произвольного радиуса и окруж-
ность с центром Bi радиуса ВС. Очевидно, Л ВАС= Л В\ОС\ по
третьему признаку равенства треугольников (Т. 1. 17), откуда
Z.A = Z_O.
Задача 3. Построить биссектрису данного угла.
На рисунке 66 построение биссектрисы AD данного угла
ВАС выполнено так: построили три окружности с центрами
в точках А, В и С одного произвольного радиуса. Точку пе-
ресечения окружностей с центрами в точках В и С — точку
D соединим с точкой А, Полупрямая AD — биссектриса угла
ВАС. Доказательство этого факта основано иа равенстве тре-
угольников ABD и ACD по третьему признаку равенства тре-
угольников (Т. 1. 17).
Задача 4. Разделить отрегок пополам.
На рисунке 67 построение середины отрезка АВ выполнено
так: строим две окружности с центрами в точках А п В ра-
диусом АВ. Точки С и Cj лежат в разных полуплоскостях, поэ-
тому отрезок ССХ пересекает АВ в точке О — середине отрезка
АВ.
Доказательство основано на рассмотрении равных тре-
угольников: дСАС1=дСВС] (Т. 1. 17), А АСО— £\ВСО
(Т. 1. 15).
Задача 5. Через данную точку О провести прямую, пер-
пендикулярную данной прямой а.
Возможны два случая:
1) Точка О принадлежит прямой а. Построение изобра-
жено на рисунке 68. Строим три окружности: с центром в
точке О произвольного радиуса (она пересекает прямую а
в точках А и В), с центрами в точках А и В радиусом АВ. Точку
пересечения двух последних окружностей — точку С соединим
с точкой О. Прямая ОС искомая.
Перпендикулярность прямых следует из равенства тре-
угольников АСО и ВСО (Т. 1. 17).
2) Точка О не принадлежит прямой а. Построение, изобра-
женное на рисунке 69, выполнено так: построили три окруж-
ности: с центром в точке О произвольного радиуса, А и В —
точки пересечения этой окружности с прямой а; с центрами в
точках А и В тем же радиусом, — точка их пересечения,
лежащая в полуплоскости, в которой не лежит точка О. Пря-
мая ОО{ — искомый перпендикуляр.
Доказательство проводим так:
1) /\АОВ-~лАО}В (Т. 1. 17), отсюда /_ОАС=/_ОХАС.
2) ААОС=ДАО,С (Т. 1. 15), отсюда Z_ACO= ААСОХ.
3) ААСО и ААСОХ смежные, а так как они равны, то оии
прямые. Значит, ОС — перпендикуляр, опущенный из точки
О на прямую а.
Рассмотренные задачи применяются при решении более
сложных задач на построение.
Пример. Построить окружность данного радиуса R,
касающуюся данной прямой а н проходящую через данную
точку М, не лежащую на этой прямой.
Решение. Предположим, что задача решена и построена
окружность с центром О данного радиуса Я, касающаяся пря-
мой а и проходящая через точку М (рис. 70). Ее центр лежит
на прямой Ь [| а, находящейся от а на расстоянии R, а точка
О есть точка пересечения окружности того же радиуса с центром
в точке М и прямой Ъ.
Построение выполняем в такой последовательности:
1) Проводим прямую Ь, параллельную а и находящуюся
от а на расстоянии R.
2) Проводим окружность с центром в точке М радиусом R.
Точка пересечения О прямой Ь и проведенной окружности —
центр искомой окружности. Доказательство очевидно: постро-
енная окружность касается прямой а, имеет радиус R и про-
ходит через точку М. Задача может иметь два, одно решение
или ие иметь решений. (Рассмотрите различные случаи сами.
На рисунке 70 приведены два решения.)
23. Геометрическое место точек иа плоскости. Геометри-
ческим местом точек на плоскости называется фигура, которая
состоит из всех точек плоскости, обладающих определенным
свойством.
Т. 1.29.
Геометрическое место точек, равноудаленных от
двух данных точек, есть серединный перпендику-
ляр к отрезку, соединяющему эти точки.
На рисунке 71 к отрезку АВ проведен серединный перпен-
дикуляр СС|. Т. 1. 29 утверждает, что: а) каждая точка пря-
мой ССХ равноудалена от А и В; б) каждая точка плоскости,
равноудаленная от А и В, лежит на прямой ССХ.
Ниже перечислены несколько геометрических мест точек
на плоскости.
1. Геометрическое место точек, находящихся на данном
расстоянии от данной точки, есть окружность с центром в этой
точке и радиусом, равным данному расстоянию.
2. Геометрическое место точек, находящихся на данном
расстоянии от данной прямой, состоит из двух прямых, каж-
дая из которых параллельна данной и отстоит от нее иа дан-
ное расстояние.
3. Геометрическое место точек, равноудаленных от двух
пересекающихся прямых, состоит из двух прямых, на кото-
рых лежат биссектрисы всех углов, полученных при пересе-
чении данных прямых.
4. Геометрическое место точек, из которых отрезок АВ виден
под данным углом а и которые лежат по одну сторону от пря-
мой АВ, есть дуга окружности с концами в точках А и В.
Метод геометрических мест, применяемый при решении
задач на построение, основан на следующем.
Пусть нам надо построить точку X, удовлетворяющую двум
условиям. Геометрическое место точек, удовлетворяющих пер-
вому условию, есть фигура Fx, а геометрическое место точек,
удовлетворяющих второму условию, есть фигура Fz. Иско-
мая точка X принадлежит Fx и F2, т. е. является их общей
точкой.
Пример 1. Построить ДАВС по периметру р, углу В,
равному и высоте h, опущенной из вершины А.
Решение. Пусть задача решена и А АВС построен (рис.
72). Отложив на прямой ВС отрезки DB=AB и СЕ=АС, полу-
чим равнобедренные треугольники ABD и АСЕ.
Исходя из приведенных выше рассуждений построение мож-
но осуществить в следующей последовательности:
10 Заказ 760
1) Проводим прямую и на ней откладываем отрезок DE~p.
2) На расстоянии й от прямой DE проводим прямую I, па-
раллельную DE. о
3) С вершиной в точке D строим угол ADE, равный Точка
А — одна из вершин искомого треугольника.
4) Проводим серединные перпендикуляры к отрезкам AD
и АЕ. Точки В и С пересечения этих серединных перпен-
дикуляров с прямой DE — две другие вершины искомого тре-
угольника.
Доказательство того, что Л АВС искомый, проводим так:
высота этого треугольника равна й по построению, Z_ABC=
=2 Z. ADB ~ Р ( Л A BD равнобедренный, Z. АВС — внешний
угол этого треугольника, см. Т. 1. 22), AB-f-BC-f-CA —р по
построению.
Пример 2. Построить окружность, касающуюся сторон
данного утла, причем одной нэ них в данной точке К.
Решение. Пусть задача решена и окружность с центром
О искомая. Центр окружности — точка О принадлежит, с од-
ной стороны, биссектрисе ВО данного угла, а с другой — пер-
пендикуляру КО, проведенному к прямой ВС в данной точке К
(рис. 73).
Порядок построения таков:
1) Проводим биссектрису ВО данного угла АВС.
2) Из точки К к стороне ВС угла АВС проводим перпенди-
куляр KL.
3) Из точки О пересечения KL и ВО как из центра прово-
дим радиусом, равным ОК, окружность.
Построенная окружность искомая.
§ 4. Четырехугольники
24. Выпуклые четырехугольники. Четырехугольником на-
зывается фигура, которая состоит из четырех точек и четырех
последовательно соединяющих их отрезков. При этом никакие
три из данных точек не должны лежать иа одной прямой, а
соединяющие их отрезки не должны пересекаться. Данные
точки называются вершинами четырехугольника, а соединяю-
щие их отрезки — сторонами четырехугольника.
Четырехугольник обозначается его вершинами. Например,
на рисунке 74, а изображен четырехугольник MKCD.
Вершины четырехугольника называются соседними, если
они являются концами одной из его сторон. Вершины, ие яв-
ляющиеся соседними, называются противолежащими. Отрезки,
соединяющие противолежащие вершины четырехугольника, на-
зываются диагоналями. У четырехугольника ABCD на рисунке
74, б вершины А н В являются соседними, а вершины В и
D — противолежащими; диагоналями являются отрезки АС
и BD.
Стороны четырехугольника, исходящие из одной вершины,
называются соседними сторонами. Стороны, не имеющие об-
щего конца, называются противолежащими сторонами. У четы-
рехугольника ABCD на рисунке 74, б противолежащими яв-
ляются стороны АВ и DC, ВС и AD, а стороны АВ и AD явля-
ются соседними.
Четырехугольник (как и любой многоугольник) называ-
ется выпуклым, если он расположен в одной полуплоскости
относительно прямой, содержащей любую его сторону. При
этом сама прямая считается принадлежащей полуплоскости.
На рисунках 74, а и 74,6 четырехугольники выпуклые, а на
рисунке 74, в невыпуклый многоугольник.
Дальше мы будем рассматривать только выпуклые четы-
рехугольники. Углом выпуклого четырехугольника ABCD
цри вершине А называется угол, образованный полупрямыми
АВ и AD. На рисунке 74, г Z.BAD — угол выпуклого четырех-
угольника.
25. Параллелограмм. Параллелограмм — это четырех-
угольник, у которого противолежащие стороны параллельны,
т. е. лежат на параллельных прямых. На рисунке 75 четы-
рехугольник ABCD — параллелограмм, у которого AB||DC и
ВС||AD. Можно доказать следующий признак параллелограм-
ма:
т. хла
Если диагонали четырехугольника пересекаются
и точкой пересечения делятся пополам, то этот че-
тырехугольник — параллелограмм.
Сформулируем обратную теорему.
Т. 1. 31.
Диагонали параллелограмма пересекаются и точкой
пересечения делятся пополам.
Следующая теорема формулирует еще одно свойство па-
раллелограмма.
Т. 1.32.1 У параллелограмма противолежащие стороны
| равны, противолежащие углы равны.
Пусть ABCD — параллелограмм. Из вершины А на пря-
мую CD опущен перпендикуляр АЕ (рис. 76). Отрезок АЕ на-
зывается высотой параллелограмма, соответствующей сторо-
нам АВ и CD.
Пример 1. Периметр параллелограмма равен 122 см.
Одна из его сторон больше другой на 25 см. Найти стороны
параллелограмма.
Решение. По теореме 1.82 противолежащие стороны па-
раллелограмма равны. Обозначим одну сторону параллело-
грамма х, яругуяо У- Тогда по условию
Г 2x4-2^=122,
I х-у=25.
Решая эту систему, получим х —43, у=18. Таким образом,
стороны параллелограмма равны 18, 43, 18 и 43 см.
Пример 2. Построить параллелограмм по периметру,
диагонали и противолежащему ей углу.
Решение. Предположим, что задача решена и параллело-
грамм ABCD построен (рис. 77). Продолжив АВ и отложив
ВЕ-=ВС, получим ДАСЕ, в котором Z_E=—А АВС, так как
£\ВСЕ равнобедренный, a Z-B — его внешний угол. Реше-
ние задачи сводится к построению ДАСЕ по стороне АС,
углу Е и стороне АЕ, равной полупериметру параллело-
грамма. Далее строим ДАВС и дополняем его до паралле-
лограмма.
293
Пример 3. Найти расстояние между недоступными точ-
ками А и В, используя признак параллелограмма (Т. 1. 30).
Решение. Провешиваем базис CD (рис. 78). О — сере-
дина отрезка CD. По стороне и двум прилежащим углам строим
AA,OI>= ААОС и ДВ}ОС= &BOD. Из равенства треуголь-
ников следует, что АО=АХО и ВО=ВХО. Так как диагонали
AAi и ВВ1 четырехугольника ABAtB| точкой О делятся по-
полам, полученный четырехугольник АВА}В{ есть паралле-
лограмм (Т. 1. 30), т. е. AB=AjBt (Т. 1. 32). Остается измерить
AjBj.
26. Прямоугольник. Ромб. Квадрат. Прямоугольник — это
параллелограмм, у которого все углы прямые. На рисунке
79, а изображен прямоугольник ABCD (АА=/_В=АС=
= ZD=90°).
Можно доказать теорему о свойстве прямоугольника.
Т. 1.33. | Диагонали прямоугольника равны.
Ромб — это параллелограмм, у которого все стороны равны.
На рисунке 79, б изображен ромб ABCD (AB=BC=CD=
=AD).
Справедлива теорема о свойствах ромба.
Т. 1. 34.1
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являютсй биссектрисами его углов.
Квадрат — это прямоугольник, у которого все стороны
равны.
На рисунке 79, в изображен квадрат ABCD. Квадрат яв-
ляется и ромбом, поэтому обладает свойствами как прямо-
угольника, так и ромба.
Пример 1. Сторона прямоугольника равна 4 см и обра-
зует с диагональю угол 60°. Найти эту диагональ.
Решение. Л АВС прямоугольный, в нем катет ВС = 4 см,
a Z- ВАС = 30° (рис. 80). По свойству катета, лежащего в прямо-
угольном треугольнике против угла 30°, ВС=-^-АС (см. п. 19).
Итак, АС =8 см.
Пример 2. Найти углы ромба, если основание перпен-
дикуляра, опущенного из вершины тупого угла, делит сторону
ромба пополам.
Решение. Рассмотрим /\ABD (рис. 81). В нем AB—AD
как стороны ромба; его высота по условию является и его медиа-
ной. Следовательно, £\ABD является равнобедренным и при
основании AD. Значит, AB=BD. Итак, &ABD равносторон-
ний, а значит, Z. А — 60°. Таким образом, в ромбе ABCD мож-
но найти утлы: Z.A — Z.C=60°, Z_B= Z_D~120° (Т. 1. 32).
27. Трапеция. Трапецией называется четырехугольник, у
которого только две противолежащие стороны параллельны.
Эти параллельные стороны называются основаниями трапеции.
Две другие стороны называются боковыми сторонами.
295
На рисунке 82, а изображена трапеция ABCD. Стороны ВС
и AD — основания трапеции, АВ и CD — боковые стороны
трапеции. Трапеция, у которой боковые стороны равны, назы-
вается равнобокой. У трапеции KMDC (рис. 82, б) KM=DC,
а значит, эта трапеция является равнобокой.
Отрезок, соединяющий середины боковых сторон, назы-
вается средней линией трапеции. На рисунке 82, в отрезок
MN — средняя линия трапеции ABCD.
Сформулируем теорему о свойстве средней линии трапе-
ции.
Т. 1.35.
Средняя линия трапеции параллельна основаниям
и равна их полусумме.
На рисунке 83, а изображена трапеция ABCD. Из точек
А и В опущены перпендикуляры АЕ и BF иа прямую CD. От-
резки АЕ и BF равны расстоянию между параллельными
прямыми АВ и CD. Это расстояние называется высотой тра-
пеции.
Пример 1. В равнобокой трапеции диагональ перпенди-
кулярна к ее боковой стороне и образует с основанием угол
15°. Найти углы трапеции.
Решение. Углы при основаниях равнобокой трапеции
равны, т. е. Z^ABC— Z_DCB, Z_BAD~ Z_CDA (рис. 83, б);
A BCD = А ВС А + / ACD = 15° + 90° = 105°, A CD А = 180° —
— Z. BCD —180° —105° = 75°. Итак, углы при основании ВС
равны по 105°, а углы при основании AD равны по 75°.
Пример 2. Доказать, что середины сторон равнобокой
трапеции являются вершинами ромба.
Решение. Точки М, Nt Р и К — середины сторон АВ,
ВС, CD и DA равнобокой трапеции ABCD (рис. 83, в). Отрезки
MN и КР параллельны АС и равны ее половине как средние
линии треугольников АВС и ADC (Т. 1. 13); аналогично МК
и NP параллельны BD и равны ее половине. Поэтому четырех-
угольник MNPK — параллелограмм.
&ABD= Z\DCA (Т. 1. 15), МК и РК—средние линии
этих треугольников, значит, МК—РК. Аналогично MN=NP.
Таким образом, в параллелограмме MNPK все стороны
равны, а значит, он является ромбом.
§ б. Многоугольники
•
28. Ломаная. Ломаной AtA2...An называется фигура, ко-
торая состоит из точек А„ А2,..., Ап и соединяющих их отрез-
ков AtA2, А^з, ..., Ап-}АП. Точки Alf А2, Ап называются
'вершинами ломаной, а отрезки АуА2, ..., An_tAn —
звеньями лхялвикял. Ломаная называется простой, если она не
имеет самопересечений. На рисунке 84, а показана простая
ломаная. Ломаная на рисунке 84, б имеет самопересечения.
Ломаная называется замкнутой, если у нее концы совпада-
ют. На рисунке 85 изображены замкнутые ломаные.
Длиной ломаной называется сумма длин ее звеньев.
Т. 1. 36.
Длина ломаной не меньше длины отрезка, соединяю-
щего ее концы.
Пример. Звенья ломаной EFMO таковы: EF = 1 см, FM=
= 4 см, МО~2 см. Может ли отрезок ЕО равняться: а) 0,5 см;
б) 8 см?
Решение. Воспользуемся теоремой 1. 36. Исходя из этой
теоремы длина ломаной EFMO должна быть ие меньше длины
отрезка ЕО, соединяющего ее концы (рис. 86). Длина ломаной
EFMO равна 7 см, а значит, отрезок ЕО должен быть не боль-
ше 7 см.
Итак, отрезок ЕО может быть равен 0,5 см и не может быть
равен 8 см.
29. Выпуклые многоугольники. Простая замкнутая лома-
ная называется многоугольником^ если ее соседние звенья
не лежат иа одной прямой.
На рисунке 87 изображены различные многоугольники.
Вершины ломаной называются вершинами многоугольника,
а звенья ломаной — сторонами многоугольника. Отрезки,
соединяющие несоседиие вершины многоугольника, назы-
ваются диагоналями. Многоугольник с п вершинами, а значит,
и с га сторонами называется п-угольником.
298
Плоским многоугольником или многоугольной областью
называется конечная часть плоскости, ограниченная много-
угольником. На рисунке 88 изображены плоские многоуголь-
ники или многоугольные области.
Многоугольник называется выпуклыл, если он лежит в
одной полуплоскости относительно любой прямой, содержа-
щей его сторону. При этом сама прямая считается принадле-
жащей полуплоскости. На рисунке 88, а изображен выпуклый
многоугольник, а на рисунке 88, б — иевыпуклый. Углом вы-
пуклого многоугольника при данной вершине называется
угол, образованный его сторонами, сходящимися в этой вер-
шине.
Т. 1.37.1 Сумма углов выпуклого n-угольника равна
| 180° (п — 2).
Внешним углом выпуклого многоугольника при данной
вершине называется угол, смежный внутреннему углу мно-
гоугольника при этой вершине. На рисунке 89 Z-CDA —
внутренний угол выпуклого многоугольника Л BCD, a Z.CDM. —
внешний.
Пример. Найти углы выпуклого пятиугольника, если
они пропорциональны числам 1, 3, 5, 7, 11.
Решение. Сумма углов выпуклого пятиугольника равна
180°-3 = 540° (Т. 1. 37). Приняв за х меньший из углов, соста-
вим уравнение: х + Зх+5х+7х + 11х=540, откуда х=20.
Таким образом, углы пятиугольника равны 20°, 60°, 100°,
140°, 220°.
30. Правильные многоугольники. Выпуклый многоуголь-
ник называется правильным, если у него все стороны равны
и все углы равны. На рисунке 90 изображены правильные
многоугольники: треугольник, четырехугольник (квадрат),
пятиугольник и шестиугольник.
Многоугольник называется вписанным в окружность, если
все его вершины лежат иа некоторой окружности. Много-
угольник называется описанным около окружности, если
все его стороны касаются некоторой окружности.
На рисунке 91 многоугольник ABCDE вписан в окруж-
ность, а многоугольник A]B|C|Z>|EiF| описан около окруж-
ности.
Правильный выпуклый многоугольник является
вписанным в окружность и описанным около окруж-
ности.
Т. 1.38.
Для правильного равностороннего треугольника (л = 3)
р___
л— 3 , г— 6 .
Для правильного четырехугольника (квадрата) (п=4)
„ а-у/2 а
R---2~ ’ Г—2‘
Для правильного шестиугольника (п=6)
R=at
Пример. Вписать в данную окружность правильный вось-
миугольник.
Решение. Два перпендикулярных диаметра делят ок-
ружность иа четыре равные части. Для построения правиль-
ного восьмиугольника необходимо каждую из этих частей раз-
делить пополам, т. е. провести биссектрисы прямых углов, и
полученные 8 точек окружности последовательно соединить
отрезками. Получим вписанный в окружность восьмиугольник
(рис. 92). Равенство сторон и равенство углов восьмиуголь-
ника следует из равенства всех восьми треугольников, ко-
торые равны по двум сторонам и углу между ними (Т.1.15). Сле-
довательно, полученный восьмиугольник правильный.
31. Длина окружности. Из наглядных соображений ясно,
что длина окружности сколь угодно мало отличается от
периметра вписанного в иее выпуклого многоугольника с до-
статочно малыми сторонами. Имеет место такое свойство
длины окружности:
301
Т.1.39.
Отношение длины окружности к ее диаметру не зави-
сит от окружности, т. е. одно и то же для любых
двух окружностей.
Отношение длины окружности к диаметру принято обозна-
чать греческой буквой л (читается «пи»): 2д=л, где С —
длина окружности, R — ее радиус. Число л иррациональное,
л «3,1416.
Таким образом, длина окружности вычисляется по формуле
С = 2лЯ.
На рисунке 93 изображена дуга АВ окружности с центром О.
Длина дуги окружности, соответствующей центральному уг-
лу в п°, находится по формуле
Радианной мерой угла называется отношение длины соот-
ветствующей дуги к радиусу окружности. Из формулы длины
I л
дуги окружности следует, что — т. е. радианная мера
угла получается из градусной умножением на —; в частности,
радианная мера угла 180° равна л, радианная мера прямого уг-
ла равна
Единицей радианной меры углов является радиан. Угол в
один радиан — это центральный угол, у которого длина ду-
ги равна радиусу. Градусная мера угла в один радиан равна
л
Пример 1. Точки М и N делят окружность иа две дуги,
разность градусных мер которых равна 90°. Чему равны гра-
дусные меры каждой ив дуг?
Решение. Сумма градусных мер дуг равна 360°, а раз-
ность равна 90°. Обозначим градусные меры этих дуг х и у.
Имеем:
/ x+jf=360,
lx — у = 90.
Решая зту систему, получим х = 225°, у = 135°.
Пример 2. Сторона квадрата равна 4 см. Вычислить
длину окружности: 1) вписанной в него; 2) описанной око-
ло него.
Решение. 1) Радиус вписанной в квадрат окружности ра-
вен 2 см, тогда длина окружности равна С= 2лЯ, т. е. С = 4л см.
302
2) Радиус окружности, описанной около квадрата, равен
д Л а—
— . Поэтому К=—=2-J2, а длина окружности равна С=
— 4д/2л см.
§ 6. Решение треугольников
32. Косинус, синус и тангенс. Косинусом острого угла
прямоугольного треугольника называется отношение при-
лежащего катета к гипотенузе. Косинус угла а обозначается
так: cos а. На рисунке 94
Т.1.40. I Косинус угла зависит только от градусной меры
| угла.
Синусом острого угла а (обозначается sin а) называ-
ется отношение противолежащего катета ВС к гипотенузе АВ
(рис. 94):
Тангенсом острого угла а (обозначается tga) называется
отношение противолежащего катета ВС к прилежащему АС
(рис. 94):
Синус и тангенс угла, так же как и косинус, зависят
только от величины угла.
Для sin a, cos a, tg а составлены специальные таблицы.
Эти таблицы позволяют по данному углу а найти sin a, cos a,
tg а или по значениям sin a, cos a, tg a найти соответ-
ствующий угол. Пояснения, как пользоваться этими табли-
цами, помещены там же (см.: Б р а д и с В. М. Четырех-
значные математические таблицы.— М.: Просвещение, 1988).
303
Для синуса, косинуса и тангенса углов имеют место сле-
дующие тождества:
sin2 a-f- cos2 ct= 1,
l+tg2a=-^-,
cos а
11
tg2 a sin2 а *
(1)
(2)
(3)
Значение этих тождеств заключается в том, что они поз-
воляют, зная одну из величин sin а, cos а или tg а, найти две
другие.
Т.1.41. I Для любого острого угла а справедливы равенства
| sin (90° — а)=cos а, cos (90° —а)—sin а.
Значения синуса, косинуса и тангенса некоторых углов
приведены в таблице:
Фу нКЦШТ Аргумент
80° 46’ 60е
itaa 1 2 £ 2 2
сова £ 2 £ 2 1 2
tga £ 3 1
Т.1.42. I При возрастании острого угла sin а и tg а воз-
| растают, a cos а убывает.
Значения синуса, косинуса и тангенса можно определить
не только для острых углов, но и для любого угла от 0° до
180° (см. часть I).
Т.1.43.
Для любого угла а, 0°-<а<:180с, выполняются ра-
венства:
sin (180° — а)=sin а,
cos (180° — а)= —сов а,
tg(180°— а)= — tg а для а =#9О°.
Пример 1. Записать- в порядке возрастания числа
sin 20°, sin 45% sin 90°, sin 30% sin 60°, sin 70%
Решение. По теореме 1.42 sin a (0° < a < 90°) возрастает
при возрастании ct. Поэтому sin 20° < sin 30° < sin 45° <
< sin 60° < sin 70° <sin 90%
Пример 2. Упростить выражение 2 sin2 tz+cos2 a—1.
Решение. 1-й способ. 2sin2 a4-cos2a—l=2sin2a-|~
+ cos2 a—(sin2 a 4-cos2 ct)=2 sin2 a-J-cos2 a—sin2 a—cos2 a=*=
—sin2 a.
2-й способ. 2 sin2 a4-cos2 a —1—sin2 a-J-sin2 a-{-cos2a —
— 1—sin2 a 4-1 — 1—sin2 a.
33. Соотношения между сторонами и углами в прямоуголь-
ном треугольнике. Из определений sin a, cos a, tg а получаем
следующие правила:
1. Катет, противолежащий углу а, равен произведению
гипотенузы иа sin a.
2. Катет, прилежащий к углу а, равен произведению
гипотенузы на cos a.
3. Катет, противолежащий углу а, равен произведению
второго катета на tg а.
Эти правила позволяют, зная одну из сторон прямоуголь-
ного треугольника и острый угол, находить две другие
стороны, а зная две стороны, находить острые углы (с помощью
специальных таблиц).
4. Катет прямоугольного треугольника есть среднее пропор-
циональное между гипотенузой и его проекцией на гипоте-
нузу.
5. Высота прямоугольного треугольника, опущенная из вер-
шины прямого углв, есть среднее пропорциональное между про-
екциями катетов на гипотенузу.
Название «среднее пропорциональное» объясняется тем, что
число х—^/аЪ является средним членом пропорции а:х—х:Ъ.
В прямоугольном треугольнике АВС (рис. 95) Z.C прямой,
AD и BD — проекции катетов АС и ВС на гипотенузу. Согласно
сказанному выше справедливы равенства
AC—^AB-AD,
BC=t[AB-BD,
CD=^[AD-BD.
Пример. Наблюдатель, находясь на высоте 18 м, заме-
тил под углом понижения в 6° 18' неизвестный объект. Най-
ти расстояние (по горизонтали) от основания наблюдательного
пункта до этого объекта.
Решение. По условию задачи ВС= 18 м, АМСА = 6°18'
(рис. 96). Следовательно, ААСВ— 83 °42'. В а.АВС известно,
что
АВ=ВС tg 83 ° 42'«18-9,0579;
АВ «163 м.
34. Теорема косинусов. Теорема синусов.
Т.1.44.
Квадрат любой стороны треугольника равен сумме
квадратов двух других сторон без удвоенного произ-
ведения этих сторон на косинус угла между ними
(теорема косинусов).
В Д АВС (рис. 97) по теореме косинусов
BC’=AB2 + AC2-2AB-AC-cos а.
Из теоремы косинусов вытекает несколько утверждений.
1. Квадрат стороны треугольника равен сумме квадратов
двух других сторон ± удвоенное произведение одной из них на
проекцию другой. Знак « + » надо брать, когда противоле-
жащий угол тупой, а знак « — », когда угол острый.
Для случая, изображенного на рисунке 97, можно записать,
что
ВС2=АДг+АС2-2АС-А1>.
2. Сумма квадратов диагоналей параллелограмма равна
сумме квадратов его сторон.
Для параллелограмма, изображенного на рисунке 98, мож-
но записать равенство АС2+BD2 == АЁ +ВС2 A-CD?+AD2.
Т.1.45. | Стороны треугольника пропорциональны синусам
| противолежащих углов (теорема синусов).
В а АВС иа рисунке 99 по теореме синусов мы имеем:
а Ъ с
sin а йп₽ sin у *
Из теоремы синусов следует, что в треугольнике против
большего угла лежит большая сторона, против большей сто-
роны лежит больший угол.
Если в треугольнике АВС (рис. 99) а < Ь, то а < 0; если 0 > у,
то b,Z>c.
Пример 1. Для измерения высоты предмета АС, основа-
ние А которого недоступно (рис. lOO^z), выбирают некоторые
точки F и В на прямой АВ и измеряют базис FB—та.
Из точек F и В измеряют углы а и 0, под которыми видна
наивысшая точка С этого объекта. Доказать, что
Н=
т ein a sin р
ein (а—Р)
4- h, где ft — высота угломерного инструмента,
А А —90°.
Решение. Н=АС+Л. Из треугольника СРВ по теореме
/т 1 . CF гп „„ т ein fl
синусов (Т.1.45) —, откуда СР=~
Из треугольника AFC получим АС=CF sin а
„ . „ main а sin Р . ,
ИТ!,К’ В= rtn(a-P) +Й-
Пример 2. По одну сторону реки отмечены две точки
А и В. Расстояние АВ—а—3784 м. Вычислить расстояние
а) Б) 6)
307
между точками С и Д находящимися на другом берегу реки,
если даны Z.BAC=a, Z.RAZ)=p, Z_ABC=6, Z.ABD=y (рис.
100,6).
Решение. Из A ACD ио теореме косинусов (Т.1.44)
CD2=AD2+ACZ—2АП-AC cos Z.DAC, ADAC=a—₽.
Из A ABD по теореме синусов (Т.1.45)
AD а „ . ~ a Bin у
81п?”йв(Р4-т)’ УДа — eto (₽-}-т») ’
Из ДАВС по теореме синусов
АС а .,, a Bin 6
dnS“«ta(«+«)’ откуда АС
CD=а v^д2Т t sin2 6_________о sin т sin fl cos (к~ Р)
V вт2(Р+“р) Biri2(a+6) sin (а -J- б) sin (р+т)
35. Решение треугольников. Решение треугольников состоит
в нахождении неизвестных сторон и углов треугольника по
некоторым известным его углам и сторонам. Будем обозна-
чать стороны треугольника через а, Ь, с, а противолежащие
им углы соответственно через а, р, у.
Перечислим основные задачи на решение треугольников.
Задача 1. Даны сторона а и два угла треугольника,
например р и у. Найти третий угол и остальные две стороны.
На рисунке ICO,в в треугольнике АВС дано: СВ=а> Z_B=p,
Z.C=y. Нужно найти 5, с, а.
Решение, а найдем по теореме 1.21, b и с — но теореме
1.45. Задача имеет решение, если Р + у<180°. Единственность
решения следует из теоремы 1.16.’
Задача 2. Даны две стороны, например а и Ь, и. угол
V между ними. Найти остальные два угла и третью сторону.
На рисунке lOl^z в треугольнике АВС дано: ВС=а, АС=Ь
и Z.C=y. Нужно найти с, а и р.
Решение. Сторону с найдем по теореме 1.44, аир — по
308
теореме 1.44 или йо теореме 1.45. Задача всегда имеет решение.
Единственность решения следует из теоремы 1.15.
Задача 3. Даны две стороны, иапример а и 5, и угол,
противолежащий одной из них, например а. Найти остальные
два угла и третью сторону.
На рисунке 101,6 в треугольнике АВС дано: ВС=а, АС=Ъ,
А А — а. Нужно найти с, ₽, у.
Решение. Угол р найдем по теореме 1.45, у — по тео-
реме 1.21, с — по теореме 1.45. Задача может не иметь решений,
иметь одно решение, два решения.
Задача 4. Даны три стороны треугольника. Найти его
углы.
На рисунке 101,6 в треугольнике АВС дано: АВ—с, ВС—а,
АС=Ъ. Нужно найти а, р, у.
Решение. Сначала найдем один из углов а, р или у по
теореме 1.44. Затем будем поступать, как в задаче 2. Задача
имеет решение, если ббльшая сторона меньше суммы двух
других (п. 15). Единственность решения следует из теоремы
1.17.
§ 7. Площади плоских фигур
36. Понятие площади простых фигур. На плоскости вводит-
ся понятие площади простых фигур.
Фигура называется простой, если ее можно разбить на ко-
нечное число треугольников. Треугольник мы понимаем как
треугольную область, т. е. конечную часть плоскости, огра-
ниченную треугольником.
На рисунке 102 изображен выпуклый многоугольник
ABCDE, который является простой фигурой, так как его можно
разбить на треугольники EAB, ЕВС, ECD.
Площадь простой фигуры — это положительная величина,
численное значение которой обладает следующими свойствами:
1. Равные фигуры имеют равные площади.
2. Если фигура разбивается на части, являющиеся простыми
фигурами, то площадь этой фигуры равна сумме площадей
ее частей.
3. Площадь квадрата со стороной, равной единице измере-
ния, равна единице.
37. Площади многоугольников. Площадь прямоугольника
вычисляется по формуле
S-ab,
где а и Ъ — стороны прямоугольника. На рисунке 103 изобра-
жен прямоугольник ABCD, в котором АВ=а, ВС=Ъ. Его
площадь находится по формуле
8=АВ-ВС.
Квадрат есть прямоугольник, у которого стороны равны (см.
п. 26), а аначит, площадь квадрата со стороной а равна а2,
т. е.
S=a2,
где а — его сторона. Площадь квадрата можно также вычис-
лить по формуле
где d — диагональ квадрата.
Площадь параллелограмма равна произведению его стороны
иа высоту, проведенную к этой стороне, т. е. вычисляется
по формуле
S—ah,
где а — сторона, h — высота, проведенная к этой стороне.
На рисунке 104 изображен параллелограмм ABCD, в кото-
ром BE — его высота. Площадь параллелограмма равна произ-
ведению АВ на BE'.
S-AB-BE.
Площадь параллелограмма можно вычислить по формуле
S=ab sin ct,
Me а и b — стороны, a — угол параллелограмма.
Ромб есть частный случай параллелограмма, следователь-
но, его площадь можно находить так же, как и площадь па-
раллелограмма. Кроме того, имеются н другие формулы пло-
щади ромба:
S=a2 sin сс,
где а — сторона ромба, а — угол ромба;
где di и th — диагонали ромба.
Площадь треугольника равна половине произведения его
стороны на высоту, проведенную к этой стороне, т. е. вычисля-
ется по формуле
S=~ah.
На рисунке 105, а изображен треугольник АВС, в котором
BD — высота, т. е. площадь его находится по формуле
S=±AC-BD.
Для нахождения площади треугольника имеются и другие
формулы:
absin у»
где а и Ь — стороны ДЛВС, а у — угол между этими сторо-
нами. Иначе эту формулу можно записать так:
S=± АВ-AC sin А А (рис. 105, б).
Следующая формула принадлежит Г е р о н у, древне-
греческому ученому, жившему в I в. н. э. в г. Александрии:
(р—ь)(р—с) (формула Верона),
где а, Ь, с — стороны треугольника, р — его полупериметр.
Площадь трапеции равна произведению полусуммы ее осно-
ваний на высоту:
где а и Ь — основания трапеции, h — высота.
На рисунке 106 изображена трапеция ABCD, в которой
АВ и CD — ее основания, а АЕ — высота. Площадь этой
трапеции находится по формуле
s=ab±cd.a£.
Пример 1. Дан параллелограмм ABCD со стороной АВ=
=12 см и диагональю АС = 16 см. Вершина D удалена от
диагонали АС на 4 см. Вычислить расстояние от точки D до пря-
мой АВ.
Решение. SASCD = 2S д ADC=AC64 см2 (рис. 107),
а так как £^^0=АВ-О/Г, то DK=^, т. е. DKа; 5,33 см.
Пример 2. Через центр О квадрата ABCD со стороной а
проведена прямая I, пересекающая сторону АВ, но не проходя-
щая через точки А и В. Выразить сумму расстояний от вер-
шин В и С квадрата до прямой I через а и Ъ, если Ъ —
длина отрезка прямой I, заключенного внутри квадрата.
Решение. Обозначим искомую сумму через с, тогда в си-
лу центральной симметрии фигуры с= 2 (hi + йг) (рис. 108).
0,25а2, SдЛОВ=0,2бЪ (Л, + й2),
откуда 0,25а2 = 0,25& (fci + йг) и
38. Площади подобных фигур.
Т.1.46. I Площади подобных фигур относятся как квадраты их
I соответствующих линейных размеров.
Пусть даны два подобных треугольника АВС и AiBiCi (рис.
109). Если коэффициент подобия k>l, то линейные размеры
треугольника A\BtCi в k раз больше соответствующих раз-
меров треугольника АВС. В частности, сторона и высота
^AJSiCi в k раз больше соответствующих сторон и высот
дАВС, т. е. A.Bx=hAB, BxCi=kBC. AiCt=kAC, B}Di=kBD.
«ал,Я1С,=4- A,C, B,Dt =i fcACfeBD=4 ^AC-BD^S^.
39. Площадь круга. Формулы площади правильного много-
угольника, описанного около круга (рис. 110), и правильного
многоугольника, вписанного в круг (рис. 111), позволяют вы-
вести формулу площади круга, радиус которого В.
Площадь круга вычисляется по формуле
Я=пЯ2.
где R — радиус круга.
Круговым сектором называется часть круга, лежащая внут-
ри соответствующего центрального угла (рис. 112).
Площадь кругового сектора вычисляется по формуле
где R — радиус круга, а — градусная мера соответствующего
центрального угла.
313
Круговым сегментом называется общая часть круга и полу-
плоскости, граница которой содержит хорду этого круга
(рис. 113).
Площадь кругового сегмента, не равного полукругу, вычи-
сляется по формуле
s=1ar“±s.
где В — радиус круга, а — градусная мера центрального
угла, который содержит дугу этого кругового сегмента, a SД —
площадь треугольника с вершинами в центре круга и в концах
радиусов, ограничивающих соответствующий сектор. Знак
надо брать, если а>130п (рис. 113, а), а знак « — », если
а <180° (рис. 113, б).
Пр и м е р 1. Произвести необходимые измерения и вычис-
лить площади фигур, изображенных на рисунке 114.
Решение, а) ААВС правильный (рис. 114, о), точки К
и L — середины его сторон, АКМ и CML — секторы, дуга
каждого из которых содержит 60°. Поэтому
где а — сторона А АВС.
a) S) t)
314
Например, при а» 16 мм, S«44 мм2.
б) Считая, что АОВ — сектор с углом 120°» О — центр
окружности (рис. 114, бу, получим:
Я=^+Я2 ein 120"=-£(2п + 8
где В — радиус окружности.
Например, при D«sl6 мм, S«122 мм2.
в) Считая, что дуга АОС (рис. 114, в) проходит
через центр окружности О, а ее радиус равен радиусу
окружности и £AOC = 12Q°, получим:
8=2 —1- Я2 sin 120°) я? 1,2Я2,
где В — радиус окружности.
Например, при D«16 мм, S«s77 мм2.
Пример 2. Доказать, что сумма площадей двух заштри-
хованных луночек (рис. 115) равна площади прямоугольного
треугольника АВС.
Решение. Обозначим катеты прямоугольного треуголь-
ника АВС через а и &, гипотенузу через с (рис. 115), а сумму
площадей заштрихованных фигур через S.
По теореме Пифагора а2 + Ь2=с2, т. е. а2 + &2—<?2=0.
—(тГ— ®ллвс) = (а2 + Ъ2—С2)+ЯДЛВС=ЯЛАВС1
S---S&ABC-
ГЛАВА IL Прямые и плоскости в пространстве
§ 8. Аксиомы стереометрии п некоторые следствия из них
40. Основные понятия стереометрии. Основными геометри-
ческими фигурами в пространстве являются точка, прямая я
плоскость. На рисунке 116 изображены различные фигуры в
пространстве. Объединение нескольких геометрических фигур в
пространстве есть тоже геометрическая фигура, на рисунке 117
фигура состоит из двух тетраэдров.
Плоскости обозначаются строчными греческими буквами:
а, р, у, ... .
На рисунке 118 изображены плоскость а, прямые а и Ъ и
точки А, В н С. Про точку А и прямую а говорят, что они
лежат в плоскости а или принадлежат ей. Про точки В и С
и прямую Ъ, что они не лежат в плоскости а или не принад-
лежат ей.
Введение основной геометрической фигуры — плоскости за-
ставляет расширить систему аксиом. Перечислим аксиомы, ко-
торые выражают основные свойства плоскостей в пространстве.
Эти аксиомы обозначены в пособии буквой С.
Ci.
Какова бы ни была плоскость, существуют точки,
принадлежащие этой плоскости, и точки, не принад-
лежащие ей.
На рисунке 118 точка А принадлежит плоскости а, а точки
В и С ие принадлежат ей.
Сг, | Если две различные плоскости имеют общую точку, то
| они пересекаются по прямой.
На рисунке 119 две различные плоскости аир имеют об-
щую точку А, а значит, по аксиоме С2 существует прямая,
принадлежащая каждой из этих плоскостей. При этом если
какая-либо точка принадлежит обеим плоскостям, то она при-
надлежит прямой а. Плоскости а и 0 в этом случае называют-
ся пересекающимися по прямой а.
Сз.
Если две различные прямые имеют общую точку, то
через них можно провести плоскость, и притом только
одну.
На рисунке 120 изображены две различные прямые о и Ь,
имеющие общую точку О, а значит, по аксиоме Сз существует
плоскость а, содержащая прямые а и Ь. При этом по той же
аксиоме Сз плоскость а единственная.
Эти три аксиомы дополняют рассмотренные в главе I ак-
сиомы планиметрии. Все они вместе являются системой ак-
сиом геометрии.
Пользуясь этими аксиомами, можно доказать несколько
первых теорем стереометрии.
Т.2.1. I Через прямую и ие лежащую на ней точку можно
| провести плоскость, и притом только одну.
Т.2.2. I Если две точки прямой принадлежат плоскости, то
| вся прямая принадлежит этой плоскости
317
Т-2-3- I Через три точки, не лежащие на одной прямой,
можно провести плоскость, и притом только одну.
Пример 1. Дана плоскость а. Доказать, что существует
прямая, не лежащая в плоскости а и пересекающая ее.
Решение. Возьмем в плоскости а точку А, что мож-
но сделать по аксиоме Ci. По той же аксиоме существует точ-
ка В, которая плоскости а не принадлежит. Через точки А
и В можно провести прямую (аксиома А — 1Д Прямая АВ не
лежит в плоскости а и пересекает ее (в точке А).
Пример 2. Дана плоскость а. Доказать, что существует
другая плоскость 0, пересекающая а.
Решение. Возьмем точки А и В, принадлежащие плоскос-
ти а, и точку С, не принадлежащую ей (аксиома Cj). Точки
А, В и С не лежат на одной прямой. Через них по теореме
2.3 можно провести плоскость 0, и притом только одну. Плос-
кости а и р имеют общую точку, а значит, по аксиоме Сз
плоскости аир пересекаются.
Замечание. Если допустить, что точка С лежит на пря-
мой АВ, то по теореме 2.2 она будет лежать и в плоскости а,
что противоречит выбору точки С.
§ 9. Параллельность прямых и плоскостей
41. Скрещивающиеся прямые. Определение параллельных
прямых и их свойства в пространстве такие же, как и на
плоскости (см. п. 11).
Вместе с тем в пространстве возможен еще один случай рас-
положения прямых — скрещивающиеся прямые. Прямые, ко-
торые ие пересекаются и ие лежат в одной плоскости, назы-
ваются скрещивающимися.
На рисунке 121 изображен макет жилой комнаты. Вы види-
те, что прямые, которым принадлежат отрезки АВ и BtCi, ВС и
PiCt, являются скрещивающимися.
Углом между скрещивающимися прямыми называется угол
между пересекающимися параллельными им прямыми. Этот
угол не зависит от того, какие взяты пересекающиеся прямые.
Градусная мера угла между параллельными прямыми счи-
тается равной нулю.
Общим перпендикуляром двух скрещивающихся прямых
называется отрезок с концами на этих прямых, являющийся
перпендикуляром к каждой из них. Можно доказать, что две
скрещивающиеся прямые имеют общий перпендикуляр, и при-
том только один. Он является общим перпендикуляром па-
раллельных плоскостей, проходящих через эти прямые.
Расстоянием между скрещивающимися прямыми называет-
ся длина их общего перпендикуляра. Оно равно расстоянию
между параллельными плоскостями, проходящими через эти
прямые.
Таким образом, для нахождения расстояния между скрещи-
вающимися прямыми а и Ъ (рис. 122) нужно провести че-
рез каждую из этих прямых параллельные плоскости аир. Рас-
стояние между этими плоскостями и будет расстоянием меж-
ду скрещивающимися прямыми а и Ь. На рисунке 122 этим
расстоянием является, например, расстояние АВ.
Пример. Прямые а и Ъ параллельны, а прямые end
скрещиваются. Может ли каждая из прямых а и Ь пере-
секать обе прямые end?
Решение. Прямые а и Ъ лежат в одной плоскости, и по-
этому любая прямая, пересекающая каждую из них, лежит
в той же плоскости. Следовательно, если бы каждая иа пря-
мых о, Ь пересекала обе прямые с nd, тс прямые end лежали
бы в одной плоскости с прямыми а и Ь, а этого быть не
может, так как прямые end скрещиваются.
42. Параллельность прямой и плоскости. Прямая и плос-
кость называются параллельными, если они не пересекаются,
т. е. не имеют общих точек. Если прямая а параллельна
плоскости а, то пишут: аЦа.
На рисунке 123 изображена прямая а, параллельная плос-
кости а.
Т.2.4.
Если прямая, № принадлежащая плоскости, парал-
лельна какой-нибудь прямой в этой плоскости, то она.
параллельна и самой плоскости (признак парал-
лельности прямой и плоскости).
Эта теорема позволяет в конкретной ситуации доказать,
что прямая и плоскость являются параллельными. На рисун-
ке 124 изображена прямая Ъ, параллельная прямой а, лежа-
щей в плоскости а, т. е. по Т.2.4 прямая b параллельна
плоскости а, т. е. Ь||а.
Пример. Через вершину прямого угла С прямоугольного
треугольника АВС параллельно гипотенузе на расстоянии
10 см от нее проведена плоскость. Проекции катетов на эту
плоскость равны 30 и 50 см. Найти проекцию гипотенузы иа
ту ясе плоскость.
Решение. Из прямоугольных треугольников BBiC и
AAiC (рис. 125) находим:
ВС = /10’ + 30s=-/1000; АС=/10' + 502 =/2600.
Из треугольника АВС находим:
А й= /1000 + 2600 =60.
Проекция гипотенузы АВ на плоскость а равна -Ai-Bj. Так
как АВ параллельна плоскости а, то АВ= AiB}. Итак, AiBi =
—60 см.
43. Параллельные плоскости. Две плоскости называются па-
раллельными. если они не пересекаются.
Т.2.5.
Две плоскости параллельны, если одна из них парал-
лельна двум пересекающимся прямым, лежащим з
другой плоскости (признак параллельности двух
плоскостей).
На рисунке 126 плоскость а параллельна пересекающим-*
ся прямым а и Ь, лежащим в плоскости р, тогда по Т.2-Л эти
плоскости параллельны.
Т.2.6.
Через точку вне данной плоскости можно провести
плоскость, параллельную данной, и притом только
одну.
Т.2.7. I Если две параллельные плоскости пересекаются
I третьей, то прямые пересечения параллельны.
На рисунке 127 изображены две параллельные плоскости
а и р, а плоскость у их пересекает по прямым а и Ь. Тогда
по теореме 2.7 можно утверждать, что прямые а и Ь парал-
лельны.
Т.2.8. I Отрезки параллельных прямых, заключенные между
I двумя параллельными плоскостями, равны.
По Т.2.8 отрезки АВ и CDt изображенные на рисунке
128, равны, так как а||₽ и а||Ь.
Пусть данные плоскости пересекаются. Проведем плоскость,
перпендикулярную прямой их пересечения. Она пересекает
данные плоскости по двум прямым. Угол между этими
прямыми называется углом между данными плоскостями
(рис. 129). Определяемый так угол между плоскостями не
зависит от выбора секущей плоскости.
Градусная мера угла между параллельными плоскостями
считается равной нулю.
Пример 1. Доказать, что углы с соответственно па-
раллельными сторонами или равны между собой, или в сумме
составляют два прямых угла.
Решение. На сторонах углов DAE и DiAiEi отложим
AB=AiBi, AC=AiCi. Точки А и Ai, В и Вь С и Ci соединим
отрезками AAt, BBi и CCi (рис. 130). Четырехугольник
ABBiAi — параллелограмм, так как у него стороны АВ и AiBi
равны и параллельны. То же самое можно сказать и о четырех-
угольнике ACCiAi. Из сказанного следует, что ВВ\ равно и
параллельно AAi, a AAi равно и параллельно CCi, откуда
BBi и CCi равны и параллельны, следовательно, BCCiBi —
параллелограмм, поэтому BC=BiCi.
Рассмотрим дАВС и &А1В1С1. Они равны по трем соот-
ветственно равным сторонам (Т. 1.17). Отсюда следует, что
АВАС= ABiAiCi. Далее, ANAC-j- ABAC—2d как сумма
смежных углов. Заменяя ABAC равным ему Z.B1A1C1, полу-
чим ANAC+ ABlAlCi=2d.
§ 10. Перпендикулярность прямых и плоскостей
44. Перпендикулярность ирямой и плоскости. Прямая, пере-
секающая плоскость, называется перпендикулярной этой плос-
кости, если она перпендикулярна любой прямой в плоскости,
проходящей через точку пересечения данной прямой н плос-
кости.
На рисунке 131 изображена прямая а, перпендикулярная
плоскости а.
Т.2.9.
Если прямая, пересекающая плоскость, перпендику-
лярна двум прямым в этой плоскости, проходящим
через точку пересечения, то она перпендикулярна
плоскости.
Эту теорему называют признаком перпендикулярности пря-
мой и плоскости или теоремой о двух перпендикулярах.
11 Заказ 769
На рисунке 132 изображена прямая а, перпендикулярная
прямым с и d, проходящим через точку пересечения плос-
кости а и прямой а и лежащим в плоскости а. Ио Т.2.9 мож-
но утверждать, что о Ха.
В следующих двух теоремах говорится о взаимосвязи парал-
лельности и перпендикулярности прямых и плоскостей.
Т.2.10. I Если плоскость перпендикулярна одной из двух па-
раллельных прямых, то она перпендикулярна
I н другой.
Т. 2.11. I Две прямые, перпендикулярные одной и той же
| плоскости, параллельны.
На рисунке 133 изображены такие прямые а и Ь и плос-
кость а, о которых говорится в теоремах 2.10 и 2.11.
Углом между прямой и плоскостью называется угол между
этой прямой и ее проекцией на плоскость.
На рисунке 134 изображены плоскость а и прямая а, ко-
тор а я ее пересекает. Прямая а' есть проекция прямой а на плос-
кость а. Тогда угол есть угол между прямой а и плоскостью
а. Угол между параллельными прямой и плоскостью счи-
тается равным нулю, а угол между перпендикулярными пря-
мой и плоскостью — равным 90°. Так как прямая а, ее проек-
ция о' на плоскость а н перпендикуляр к плоскости а в
точке ее пересечения с прямой а лежат в одной плоскости,
то угол между прямой и плоскостью дополняет до 90° угол
между этой прямой и перпендикуляром к плоскости.
Пример. Отрезок длиной 10 см пересекает плоскость,
причем концы его находятся на расстоянии 3 и 2 см от
плоскости. Найти угол между данным отрезком и плоскостью.
Решение. Опускаем из точки А (рис. 136) перпенди-
куляр АЕ на плоскость а. Через две пересекающиеся пря-
мые СА и СЕ проводим плоскость ₽, которая пересечет
плоскость а по прямой ED. Опускаем в плоскости ₽ перпенди-
куляр на прямую DE. Получаем Л АСЕ с^> Л BCD (докажите са-
мостоятельно). По условию АВ = 10 см, поэтому ВС = 10—АС и
ЗО-ЗЛС=2ЛС, АС=6.
Итак, в ДАСЕ катет АЕ = 3 см, т. е. равен половине ги-
потенузы АС=6 см, следовательно, он лежит против угла
30°, откуда А АСЕ—30°.
45. Перпендикуляр и наклонная к плоскости. Перпендику-
ляром, опущенным из данной точки на данную плоскость,
называется отрезок, соединяющий данную точку с точкой
плоскости и лежащий на прямой, перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется осно-
ванием перпендикуляра. Расстоянием от точки до плоскости
называется длина перпендикуляра, опущенного иэ этой точки
на плоскость.
324
Наклонной, проведенной иэ данной точки к данной плоскос-
ти, называется любой отрезок, соединяющий данную точку с
точкой плоскости н не являющийся перпендикуляром к этой
плоскости. Конец отрезка, лежащий в плоскости, называется ос-
нованием наклонной. Отрезок, соединяющий основания перпен-
дикуляра н наклонной, проведенных из одной н той же точки,
называется проекцией наклонной.
На рисунке 136 из точки А проведены к плоскости а пер-
пендикуляр АВ и наклонная АС. Точка В — основание перпен-
дикуляра, точка С — основание наклонной, ВС — проекция на-
клонной АС на плоскость а.
Так как расстояния от точек прямой до параллельной ей
плоскости одинаковы, то расстоянием от прямой до парал-
лельной ей плоскости называется расстояние от любой ее точки
до этой плоскости.
Т. 2.12.
Прямая, проведенная на плоскости через основание
наклонной перпендикулярно ее проекции, перпенди-
кулярна и самой наклонной. И обратно: если пря-
мая на плоскости перпендикулярна наклонной, то
она перпендикулярна и проекции наклонной (теоре-
ма о трех перпендикулярах).
На рисунке 137 к плоскости а проведены перпендикуляр
АВ н наклонная АС. Прямая а, лежащая в плоскости а,
перпендикулярна ВС — проекции наклонной АС на плоскость
а. По Т. 2.12 прямая а перпендикулярна наклонной АС. Если
было бы известно, что прямая а перпендикулярна наклонной
АС, то по Т. 2.12 она была бы перпендикулярна и ее про-
екции — ВС.
Пример. Катеты прямоугольного треугольника АВС рав-
ны 16 и 20 м. Из вершины прямого угла С проведен к
плоскости этого треугольника перпендикуляр CD =35 м (рис.
138). Найти расстояние от точки D до гипотенузы АВ.
Решение. Проведем DEJ_AB. По условию DC — пер-
пендикуляр к плоскости, т. е. DE — наклонная, СЕ — ее про-
екция, поэтому по теореме о трех перпендикулярах из условия
DE.LAB следует, что СЕ1.АВ.
Из А АВС находим АВ=-у/АС2 +В(?=д/152+20" =д/625,
т. е. АВ=25 м. Для отыскания высоты СЕ в А АВС находим
8Ллвс=~5=160 м2.
„ CJ АВ-СЕ „„ 23ЛЛВС
С другой стороны, 8лАВС=—-—, откуда С£= дв~ ’
т. е. СЕ=12 м.
Из AjDCB по теореме Пифагора
DE=^DC2-LCE\ т. е. РВ=37 м.
46. Перпендикулярность плоскостей. Две пересекающиеся
плоскости называются перпендикулярными, если какая-либо
плоскость, перпендикулярная прямой пересечения этих плос-
костей, пересекает их по перпендикулярным прямым.
На рисунке 139 изображены две плоскости аир, ко-
торые пересекаются по прямой а. Плоскость у перпендику-
лярна прямой а и пересекает аир. При этом плоскость у
пересекает плоскость а по прямой с, а плоскость р — по прямой
d, причем cJ_d, т. е. по определению aJLp.
Т. 2.13.
Если плоскость проходит через прямую, перпенди-
кулярную другой плоскости, то эти плоскости перпен-
дикулярны (признак перпендикулярности плос-
костей).
На рисунке 140 плоскость р проходит через прямую a-La»
т. е. по Т. 2.13 плоскости Р н а перпендикулярны.
326
Т. 2.14.
Если прямая, лежащая в одной из двух перпенди-
кулярных плоскостей, перпендикулярна их лини»
пересечения, то она перпендикулярна и другой
плоскости.
Пример. Треугольник АВС с прямым углом АСВ и ка-
тетом АС, принадлежащим плоскости а, образует с этой
плоскостью двугранный угол, равный 45°. Найти расстояние
от вершины В до плоскости а, если АС=20 см и АВ:ВС=3:1
(рис. 141).
Решение. По условию АВ: ВС = 3:1, АС—20 см, поэтому,
обозначив ВС — х, АВ=Зх, по теореме Пифагора из ДАВС
получим (Зх)2=202-|-х2, откуда х2=50, т. е. ВС2 =50.
Из точки В проведем ВЕХа (рис. 141), соединим Е и С. По
теореме о трех перпендикулярах AC X СЕ, так как AC J_BC. Сле-
довательно, А ВСЕ — линейный угол двугранного угла (п. 48),
равного по условию 45°. В ДСВЕ имеем Z.BCE=45°, АВЕС —
= 90°, поэтому ВЕ=СЕ, т. е. 2ВЕ2=ВС2 (по теореме Пифагора),
откуда 2ВЕ2 = 50, ВЕ = Б см.
ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ
§ 11. Многогранники
47. Тело и его поверхность. Изучая многоугольники, гово-
рят о плоском многоугольнике, понимая под ним сам много-
угольник и его внутреннюю область.
То же самое происходит и в стереометрии. По аналогии с
понятием плоского многоугольника вводится понятие тела и его
поверхности.
Точка геометрической фигуры называется внутренней, если
существует шар с центром в этой точке, целиком принадле-
жащий этой фигуре. Фигура называется областью, если все
327
ее точки внутренние и если любые две ее точки можно соединить
ломаной, целиком принадлежащей фигуре.
Точка пространства называется граничной точкой данной
фигуры, если любой шар с центром в этой точке содержит
как точки, принадлежащие фигуре, так и точки, не принад-
лежащие ей. Граничные точки области образуют границу об-
ласти,
Телом называется конечная область вместе с ее границей.
Граница тела называется поверхностью тела. Тело называ-
ется простым, если его можно разбить на конечное число
треугольных пирамид.
Телом вращения в простейшем случае называется такое тело,
которое плоскостями, перпендикулярными некоторой прямой
(оси вращения), пересекается по кругам с центрами на этой
прямой. Цилиндр, конус, шар являются примерами тел вра-
щения.
48. Многогранные утлы. Многогранники. Двугранным уг-
лом называется фигура, образованная двумя полуплоскостями
с общей ограничивающей нх прямой. Полуплоскости назы-
ваются гранями, а ограничивающая их прямая — ребром дву-
гранного угла.
На рисунке 142 изображен двугранный угол с ребром а и
гранями а и fJ.
Плоскость, перпендикулярная ребру двугранного угла, пере-
секает его грани по двум полупрямым. Угол, образованный
этими полупрямыми, называется линейным углом двугранного
угла. За меру двугранного угла принимается мера соответ-
ствующего ему линейного угла. Если через точку А ребра а
двугранного угла провести плоскость -у, перпендикулярную это-
му ребру, то она пересечет плоскости а и 0 по полу-
прямым end (рис. 142); Z(cd) — линейный угол данного
двугранного угла. Градусная мера этого линейного угла явля-
ется градусной мерой двугранного угла. Мера двугранного уг-
ла не зависит от выбора линейного угла.
Трехгранным углом (abc) называется фигура, составленная
из трех плоских углов (ab), (Ъс) и (ас) (рис. 143). Эти
углы называются гранями трехгранного угла, а их стороны —
ребрами. Общая вершина плоских углов называется вершиной
трехгранного угла. Двугранные углы, образуемые гранями и их
продолжениями, называются двугранными углами трехгранно-
го угла.
Аналогично определяется понятие многогранного угла
(щйгоз ... ал) как фигуры, составленной из плоских углов (аш),
(«2Лз)> ..» (а-пОл) (рис. 144). Для многогранного угла опреде-
ляются понятия граней, ребер и двугранных углов так же,
как и для трехгранного угла.
Многогранником называют тело, поверхность которого со-
стоит из конечного числа плоских многоугольников (рис. 145).
Многогранник называется выпуклым, если он расположен
по одну сторону плоскости каждого многоугольника на его по-
верхности (рнс. 145, а, б). Общая часть такой плоскости и
поверхности выпуклого многогранника называется гранью.
Грани выпуклого многогранника — выпуклые многоугольники.
Стороны граней называются ребрами многогранника, а верши-
ны — вершинами многогранника.
49. Призма. Параллелепипед. Куб. Призмой называется
многогранник, который состоит из двух плоских многоуголь-
ников, совмещаемых параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих многоугольников.
Многоугольники называются основаниями призмы, а отрезки,
соединяющие соответствующие вершины,— боковыми ребрами
призмы (рис. 146).
Так как параллельный перенос есть движение, то осно-
вания призмы равны. Так как при параллельном переносе
плоскость переходит в параллельную плоскость (или в себя), то
у призмы основания лежат в параллельных плоскостях. Так
как при параллельном переносе точки смещаются по парал-
лельным (или совпадающим) прямым на одно и то же рас-
стояние, то у призмы боковые ребра параллельны и равны.
На рисунке 147, а изображена четырехугольная призма
ABCDA\B\C\Di. Плоские многоугольники ABCD и AiB|CiDi
совмещаются соответствующим параллельным переносом н яв-
ляются основаниями призмы, а отрезки AAi, BBi, CCi и DDi
являются боковыми ребрами призмы. Основания призмы ABCD
и Л|В1С|Р1 равны (параллельный перенос есть движение и
переводит фигуру в равную ей фигуру, п. 79). Боковые
ребра AAi, BBi, CCt и DD, параллельны и равны.
Поверхность призмы состоит из оснований и боковой
поверхности. Боковая поверхность состоит из параллелограм-
мов. У каждого из этих параллелограммов две стороны яв-
ляются соответствующими сторонами оснований, а две дру-
гие — соседними боковыми ребрами призмы.
На рисунке 147, а боковая поверхность призмы состоит из
параллелограммов ABBiAi, BCCiBit ADDiAi, DCCtDi. Пол-
ная поверхность состоит из оснований ABCD и AiBiCiDi и
указанных выше параллелограммов.
Высотой призмы называется расстояние между плоскостями
ее оснований. Отрезок, который соединяет две вершины, не
принадлежащие одной грани, называется диагональю призмы.
Диагональным сечением призмы называется сечение ее плос-
костью, проходящей через два боковых ребра, не принадлежа-
щих одной грани.
На рисунке 147, а изображена призма ABCDAiBiCiDi,
BiK — ее высота, D(B — одна из ее диагоналей. Сечение ACC^Ai
является одним из диагональных сечений этой призмы.
Призма называется прямой, если ее боковые ребра перпен-
дикулярны основаниям. В противном случае призма называется
наклонной. Прямая призма называется правильной, если ее ос-
нованиями являются правильные многоугольники.
На рисунке 147, а изображена наклонная призма, а на ри-
сунке 147, б — прямая, едесь ребро АА[ перпендикулярно осно-
ваниям призмы. На рисунке 148 изображены правильные приз-
мы, у них основаниями являются соответственно правильный
треугольник, квадрат, правильный шестиугольник.
Если основания призмы — параллелограммы, то она назы-
вается параллелепипедом. У параллелепипеда все грани — па-
раллелограммы. На рисунке 147, а изображен наклонный па-
раллелепипед, а на рисунке 147, б — прямой.
Грани параллелепипеда, не имеющие общих вершин, назы-
ваются противолежащими. На рисунке 147, а грани ABBiAi и
CDD\Ci противолежащие.
Можно доказать некоторые свойства параллелепипеда.
Т.3.1. | У параллелепипеда противоположные грани парал-
| лельны и равны.
Т.3.2. | Диагонали параллелепипеда пересекаются в одной
| точке н точкой пересечения делятся пополам.
Точка пересечения диагоналей параллелепипеда является
его центром симметрии.
Прямой параллелепипед, у которого основанием является
прямоугольник, называется прямоугольным параллелепипе-
дом. У прямоугольного параллелепипеда все грани — прямо-
угольники.
Прямоугольный параллелепипед, у которого все ребра рав-
ны, называется кубом.
Цляпи непараллельных ребер прямоугольного параллеле-
пипеда называются его линейными размерами или измере-
ниями. У прямоугольного параллелепипеда три линейных раз-
мера.
Для прямоугольного параллелепипеда верна такая теорема:
Т.3.3. I В прямоугольном параллелепипеде квадрат любой
диагонали равен сумме квадратов трех его линей-
| ных размеров.
Например, в кубе ABCDA iBiCiPj (рис. 149) с ребром а
диагонали равны: BtD=BDi —ACi =AjC = a д/3.
50. Пирамида. Пирамидой называется многогранник, кото-
рый состоит из плоского многоугольника — основания пира-
миды, точки, не лежащей в плоскости основания,— вершины
пирамиды и всех отрезков, соединяющих вершину с точками
основания (рис. 150). Отрезки, соединяющие вершину пирами-
ды с вершинами основания, называются боковыми ребрами.
На рисунке 150, а изображена пирамида SABCD. Четырехуголь-
ник ABCD — основание пирамиды, точка S — вершина пира-
миды, отрезки SA, SB, SC и SD — ребра пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный
из вершины пирамиды на плоскость основания. На рисунке
150, a SO — высота пирамиды.
Пирамида называется л-угольной, если ее основанием явля-
ется п-угольник. Треугольная пирамида называется так-
же тетраздром.
На рисунке 161, а изображена треугольная пирамида, или
тетраэдр, на рисунке 151, б — четырехугольная, на рисунке
151, в — шестиугольная.
Т.3.4. I Плоскость, параллельная основанию пирамиды и пе-
| ресекающая ее, отсекает подобную пирамиду.
Пирамида называется правильной, если ее основанием явля-
ется правильный многоугольник, а основание высоты совпада-
ет с центром этого многоугольника. На рисунке 151 изображены
правильные пирамиды. У правильной пирамиды боковые ребра
равны; следовательно, боковые грани — равные равнобедрен-
ные треугольники. Высота боковой грани правильной пирами-
ды, проведенная из ее вершины, называется апофемой.
По Т.3.4 плоскость а, параллельная плоскости £ основа-
ния пирамиды и пересекающая пирамиду, отсекает от нее
подобную пирамиду. Другая часть пирамиды представляет
собой многогранник, который называется усеченной пирамидой.
Грани усеченной пирамиды, лежащие в параллельных плос-
костях аир, называются основаниями усеченной пирамиды,
остальные грани называются боковыми гранями. Основания
усеченной пирамиды представляют собой подобные (более того,
гомотетичные) многоугольники, боковые грани — трапеции. На
рисунке 152 изображена усеченная пирамида ABCDAtBiCiDi.
Усеченная пирамида, которая получается из правильной пи-
рамиды, также называется правильной. Боковые грани пра-
вильной усеченной пирамиды — равные равнобокие трапеции,
их высоты называются апофемами.
Пример. В тетраэдре ABCD ребро CD-LAD, CDJ-BD,
двугранный угол при ребре CD=1 равен 120°, a AD=BD~->j2.
Найти величину двугранного угла при ребре АВ.
Решение. Пусть К — середина ребра АВ (рис. 153).
Отрезок CD перпендикулярен двум пересекающимся прямым
BD и AD плоскости ABD, а значит, по Т.2.9 ребро CD пер-
пендикулярно плоскости ABD, откуда ZADB=120°. KD —
медиана равнобедренного треугольника ADB, а значит, н его
высота, KD.LAB. Следовательно, ЙГС-LAB по Т.2.12, а тогда
A CKD — линейный угол двугранного угла при ребре АВ. Не-
трудно найти его величину (сделайте это самостоятельно).
Ответ: ACKD=4S°.
51. Правильные многогранники. Выпуклый многогранник
называется правильным, если его грани являются правиль-
ными многоугольниками с одним и тем же числом сторон и
в каждой вершине многогранника сходится одно и то же число
ребер.
Существует пять типов правильных выпуклых много-
гранников (рис. 154): правильный тетраэдр, куб, октаэдр, доде-
каэдр, икосаэдр. Про правильный тетраэдр и куб сказано
раньше (п. 49, 50). В каждой вершине правильного тетра-
эдра и куба сходятся три ребра.
Грани октаэдра — правильные треугольники. В каждой его
вершине сходятся по четыре ребра.
Грани додекаэдра — правильные пятиугольники. В каждой
вершине сходятся по три ребра.
Грани икосаэдра — правильные треугольники, но в отличие
от тетраэдра и октаэдра в каждой вершине сходится по
пять ребер.
§ 12. Тела вращения
52. Цилиндр. Цилиндром (точнее, круговым цилиндром)
называется тело, которое состоит из двух кругов, совмещае-
мых параллельным переносом, и всех отрезков, соединяющих
соответствующие точки этих кругов. Круги называются осно-
ваннами цилиндра, а отрезки, соединяющие соответствующие
точки окружностей кругов,— образующими цилиндра. На ри-
сунке 165 изображен цилиндр. Круги с центрами О и О, яв-
ляются его основаниями, АА>, BBi, ССл — его образующие.
Можно доказать, что основания цилиндра равны и лежат в
параллельных плоскостях, что у цилиндра образующие па-
раллельны и равны. Поверхность цилиндра состоит из основа-
ний н боковой поверхности. Боковая поверхность составлена из
образующих.
Цилиндр называется прямым, если его образующие перпен-
дикулярны плоскостям оснований. На рисунке 155, б изображен
наклонный цилиндр, а на рисунке 155, а — прямой.
В дальнейшем мы будем рассматривать только прямой ци-
линдр, называя его для краткости просто цилиндром. Его мож-
но рассматривать как тело, полученное при вращении пря-
моугольника вокруг одной из сторон как оси (рис. 156).
Радиусом цилиндра называется радиус его основания. Высо-
той цилиндра нааывается расстояние между плоскостями
оснований. Осью цилиндра называется прямая, проходящая че-
рез центры оснований. Она параллельна образующим. Сечение
цилиндра плоскостью, проходящей через ось цилиндра, назы-
вается осевым сечением. Плоскость, проходящая через образу-
ющую прямого цилиндра и перпендикулярная осевому сечению,
проведенному через эту образующую, называется касательной
плоскостью цилиндра.
На рисунке 157 сечение ABBiAi проходит через ось ци-
линдра ООь т. е. является осевым сечением.
Плоскость, перпендикулярная оси- цилиндра, пересекает его
боковую поверхность по окружности, равной окружности осно-
вания.
Призмой, вписанной в цилиндр, называется такая призма,
основания которой — равные многоугольники, вписанные в ос-
нования цилиндра. Ее боковые ребра являются образующими
цилиндра. Призма называется описанной около цилиндра, если
ее основания — равные многоугольники, описанные около осно-
ваний цилиндра. Плоскости ее граней касаются боковой по-
верхности цилиндра.
На рисунке 158 изображена призма ABCDA iBiCiDi, впи
санная в цилиндр. На рисунке 159 призма ABCDEAiBiCtDiEi
описана около цилиндра.
Пример. В цилиндр вписать правильную четырехуголь-
ную призму.
Решение. 1) Впишем в основание цилиндра квадрат
ABCD (рис. 158).
2) Проведем образующие AAi, ВВ{, CCt и DD\.
3) Через соседние пары этих образующих проведем плоскос-
ти, которые пересекают верхнее основание по хордам
А1В1, BiCi, CiD(, DuA,.
4) Призма ABCDAiBiCiDt искомая (по определениям пра-
вильной и вписанной призмы).
53. Конус. Конусом (точнее, круговым конусом) называется
тело, которое состоит из круга — основания конуса, точки, не
лежащей в плоскости этого круга,— вершины конуса и всех
отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности
основания, называются образующими конуса. Поверхность ко-
нуса состоит из основания и боковой поверхности. На ри-
сунке 160, а изображен круговой конус. S — вершина конуса,
круг с центром в точке О — основание конуса, SA, SB и SC —
образующие конуса.
Конус называется прямым, если прямая, соединяющая вер-
шину конуса с центром основания, перпендикулярна плоскос-
ти основания. На рисунке 160, б изображен наклонный конус,
а на рисунке 160, а — прямой. В дальнейшем мы будем рас-
сматривать только прямой конус, называя его для краткости
просто конусом. Прямой круговой конус можно рассмат-
ривать как тело, полученное при вращении прямоуголь-
ного треугольника вокруг его катета как оси (рис. 161).
Высотой конуса называется перпендикуляр, опущенный из
его вершины на плоскость основания. У прямого конуса
основание высоты совпадает с центром основания. Осью прямого
конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его ось, на-
зывается осевым сечением. Плоскость, проходящая через обра-
зующую конуса н перпендикулярная осевому сечению, прове-
денному через эту образующую, называется касательной
плоскостью конуса.
На рисунке 162 изображено сечение конуса, проходящее
через его ось — осевое сечение конуса.
Плоскость, перпендикулярная оси конуса, пересекает конус
по кругу, а боковую поверхность — по окружности с центром на
оси конуса.
Плоскость, перпендикулярная осн конуса, отсекает от него
меньший конус. Оставшаяся часть называется усеченным кону-
сом (рис. 163).
Пирамидой, вписанной в конус, называется такая пирамида,
основание которой есть многоугольник, вписанный в окруж-
ность основания конуса, а вершиной является вершина конуса.
Боковые ребра пирамиды, вписанной в конус, являются обра-
зующими конуса. Пирамида называется описанной около кону-
са, если ее основанием является многоугольник, описанный око-
ло основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды являются ка-
сательными плоскостями конуса.
На рисунке 164 изображена пирамида, вписанная в конус, а
на рисунке 165 изображен конус, вписанный в пирамиду,
т. е. пирамида, описанная около конуса.
54. Шар. Шаром называется тело, которое состоит нз всех
точек пространства, находящихся на расстоянии, не большем
данного, от данной точки. Эта точка называется центром шара, а
данное расстояние — радиусом шара. На рисунке 166 изобра-
жен шар с центром в точке О и радиусом R. Заметим,
что точки А, В, М, D и О принадлежат данному шару. Граница
шара называется шаровой поверхностью или сферой. На рисун-
ке 166 точки А, В и D принадлежат сфере, а, например,
точка М ей не принадлежит. Таким образом, точками сфер»
являются все точки шара, которые удалены от центра на»
расстояние, равное радиусу. Любой отрезок, соединяющий
центр пгара о точкой шаровой поверхности, также назы-
вается радиусом. Отрезок, соединяющий две точки шаровой
поверхности и проходящий через центр шара, называется
диаметром. Концы любого диаметра называются диаметрально
противоположными точками шара.
Шар, так же, как цилиндр и конус, является телом вра-
щения. Он получается при вращении полукруга вокруг его диа-
метра как оси (рис. 167).
Т. 3.5. I Всякое сечение шара плоскостью есть круг. Центр это-
го круга есть основание перпендикуляра, опущенного
I из центра шара на секущую плоскость.
Если шар с центром О и радиусом R пересечен плос-
костью а, то в сечении по Т. 3.5 получается круг радиуса г о.
центром К. Радиус сечения шара плоскостью можно вычис-
лить по формуле
г-^пок.
Из формулы видно, что плоскости, равноудаленные от цент-
ра, пересекают шар по равным кругам. Радиус сечения теьа
больше, чем ближе секущая плоскость к центру шара, т. е„
чем меньше расстояние ОК. Наибольший радиус имеет сече-
ние плоскостью, проходящей через центр шара. Радиус этого
круга равен радиусу шара.
339
Плоскость, проходящая через центр шара, называется диа-
метральной плоскостью. Сечение шара диаметральной плос-
костью называется большим кругом, а сечение сферы — боль-
шой окружностью. На рисунке 168 плоскость а является
диаметральной плоскостью, круг радиуса R является большим
кругом шара, а соответствующая окружность — большой ок-
ружностью.
Т. 3.6.
Любая диаметральная плоскость шара является его
плоскостью симметрии. Центр шара является его
центром симметрии.
Плоскость, проходящая через точку А шаровой поверх-
ности и перпендикулярная радиусу, проведенному в точку А,
называется касательной плоскостью. Точка А называется точ-
кой касания (рис. 169).
Т. 3.7. I Касательная плоскость имеет с шаром только одну
I общую точку — точку касания.
Прямая, проходящая через точку А шаровой поверхности
перпендикулярно к радиусу, проведенному в эту точку,
называется касательной (рис. 169).
Т. 3.8.
Через любую точку шаровой поверхности проходит
бесконечно много касательных, причем все они ле-
жат в касательной плоскости шара.
Шаровым сегментом называется часть шара, отсекаемая от
него плоскостью. Шировым слоем называется часть шара, рас-
положенная между двумя параллельными плоскостями, пере-
секающими шар (рис. 170).
Шаровой сектор получается из шарового сегмента и коиуса
следующим образом. Если шаровой сегмент меньше полушара,
то шаровой сегмент дополняется конусом, у которого вер-
шина в центре шара, а основанием является основание
сегмента. Если же сегмент больше полушара, то указан-
ный конус из него удаляется (рис. 171).
§ 13. Изображение пространственных фигур иа плоскости
55. Параллельная проекция. Для изображения пространст-
венных фигур на плоскости обычно пользуются параллельным
проектированием. Этот способ изображения фигуры состоит в
следующем. Берем произвольную прямую I, пересекающую
плоскость, на которую проектируется данная фигура, и прово-
дим через произвольную точку А фигуры прямую, параллель-
ную I. Точка пересечения А । этой прямой с плоскостью чертежа
будет изображением точки А.
На рисунке 172 изображена параллельная проекция F' фигу-
ры F на плоскость а.
Такой способ изображения пространственной фигуры на
плоскости соответствует зрительному восприятию фигуры при
рассмотрении ее издали.
Параллельную проекцию некоторого объекта в природе
представляет, например, его тень, падающая на плоскую по-
верхность земли при солнечном освещении (лучи солнца мож-
но считать параллельными). На рисунке 173 изображена па-
раллельная проекция рамы окна, освещенной солнечными лу-
чами, на плоскость пола.
Из описанного построения изображения фигуры вытекают
некоторые свойства этого изображения (изображаемые отрез-
ки и прямые не параллельны направлению проектирования).
1. Проекция прямой есть прямая.
2. Проекция отрезка есть отрезок.
На рисунке 174 отрезок АС проектируется на плоскость а.
Все прямые, проектирующие точки отрезка АС, лежат в од-
ной плоскости, пересекающей плоскость чертежа по прямой
A|Ci. Произвольная точка В отрезка АС изображается точ-
кой Bi отрезка AiCi- Отрезок AtCi есть проекция отрезка АС иа
плоскость а. Еще раз отметим, что это утверждение спра-
ведливо, если проектируемый отрезок не параллелен направле-
нию проектирования.
3. Параллельные отрезки фигуры изображаются на плос-
кости чертежа параллельными отрезками или отрезками, ле-
жащими на одной прямой.
АС н A]Ci — параллельные отрезки фигуры. Прямые А'С'
и A'iCi параллельны, так как они получаются в пересечении
параллельных плоскостей е плоскостью а. Первая из этих
плоскостей проходит через прямые АС и АА', а вторая —
через прямые AtCi и Ai-Af. Таким образом параллельные от-
резки АС и AiCi переходят в параллельные отрезки А'С' и
А(С(.
4. Отношение отрезков одной прямой или параллельных
прямых сохраняется при параллельном проектировании.
Например, 45=4^ (рие. 174).
ПО
56. Ортогональное проектирование. Пусть дана плоскость а,
на которой нужно изобразить фигуру. Прн этом направление
проектирования задано прямой I, перпендикулярной а
(рис. 175). Такое проектирование называется ортогональным
(прямоугольным) проектированием на плоскость.
Ортогональной проекцией широко пользуются в техническом
черчении. За основу выполнения технических чертежей берется
способ ортогонального проектирования фигуры на две плос-
кости: горизонтальную р и вертикальную у (рис. 176). Про-
екции точки А иа эти плоскости обозначают а и а'.
Т. 3.9.
Площадь ортогональной проекции многоугольника
на плоскость равна произведению его площади на ко-
синус угла между плоскостью многоугольника и
плоскостью проекции.
На рисунке 177 дана ортогональная проекция Л АВС на
плоскость а. Проекцией треугольника АВС является тре-
угольник ABCi. По сформулированной теореме S^ABC,=*
~S^ABCCQSfp, где <р — угол между плоскостью треугольника
АВС и плоскостью проекции а, на рисунке 177 это Z.CDC1.
57. Геометрическое место точек в пространстве. Геометрии
ческим местом точек в пространстве называется фигура, ко-
торая состоит из всех точек пространства, обладающих опре-
деленным свойством.
Перечислим несколько геометрических мест точек в прост-
ранстве.
1. Геометрическим местом точек, равноудаленных от даух
данных точек А и В, является плоскость а, перпенди-
кулярная прямой АВ и проходящая через середину отрезка
АВ.
2. Геометрическим местом точек, отстоящих от данной плос-
кости а на расстоянии d, являются две плоскости, парал-
лельные данной плоскости и находящиеся от нее на расстоя-
нии d.
3. Геометрическим местом точек, удаленных на данном рас-
стоянии d от данной точки О, является сфера с центром
в точке О и радиусом d.
Пример 1. Найти в пространстве геометрическое место
точек, равноудаленных от трех данных точек, не лежащих на
одной прямой.
Решение. 1-й способ (рис. 178). Три данные точки
А, В и С определяют плоскость а, в которой лежит А АВС.
Мы знаем, что геометрическое место точек, равноудаленных
от точек А н В, есть плоскость Р, перпендикулярная отрезку
АВ и проходящая через середину D стороны АВ; анало-
гично для точек В и С таким геометрическим местом точек
будет плоскость Q. Точки, принадлежащие линии пересечения
MN плоскостей Р и Q, находятся на одинаковом расстоянии от
точек А, В и С. Прямая MN — искомое геометрическое место
точек.
Точка О пересечения прямой MN с плоскостью а принад-
лежит геометрическому месту, следовательно, она находится
на равном расстоянии от точек At В и С и является
центром окружности, описанной около треугольника АВС. Да-
лее, так как АВХР, то ABXM2V, откуда MN_La.
Вывод: искомое геометрическое место точек — прямая,
перпендикулярная плоскости, определяемой данными точка-
ми А, В и С, и проходящая через центр окружности, описан-
ной около А А ЯС.
2-й способ (рис. 179). Пусть М — одна из точек иско-
мого геометрического места точек, т. е. МА —МВ=МС, МО-Lee.
Наклонные МА, МВ и МС равны, следовательно, равны и их
проекции на плоскость а, т. е. ОА=ОВ—ОС.
Отсюда следует: 1) О — центр окружности, описанной око-
ло ДАВС; 2) точки геометрического места проектируются в
одну и ту же точку иа плоскости а, следовательно, все они
лежат на перпендикуляре к плоскости а, проходящем через
точку О.
Пример 2. Найти в пространстве геометрическое место
точек, равноудаленных от двух данных пересекающихся пря-
мых.
Решение. Пусть АС и BD — данные прямые (рнс. 180),
Р — плоскость, ими определяемая. Пусть М — произвольная
точка искомого геометрического места, т. е. MF ±АС, ME.LBD
и MF =МЕ. Опустим перпендикуляр MN на плоскость Р; тогда
NP—NE как проекции равных наклонных MF и ME на плос-
кость Р. Прямые АС н BD соответственно перпендикулярны на-
клонным, следовательно, они перпендикулярны их проекциям,'
т. е. AC1.NF и BD1.NE. Мы видим, что проекция произ-
вольной точки геометрического места точек на плоскость Р,
определяемую данными прямыми, находится на одинаковом
расстоянии от АС и BD. Как известно, геометрическим местом
точек, равноудаленных от двух пересекающихся прямых на
плоскости, являются две прямые КО и HL, которые делят
углы, образованные данными прямыми АС и ВО, пополам.
Все точки перпендикуляра MN, очевидно, принадлежат
геометрическому месту точек. Построим плоскость Q через пря-
мые MN н КО. Эта плоскость по Т. 2.9 перпендику-
лярна плоскости Р. Все точки плоскости Q принадлежат
искомому геометрическому месту точек.
Аналогично доказывается, что точки искомого геометри-
ческого места лежат также и на плоскости 7?, перпенди-
кулярной плоскости Р. Плоскости Q и В перпендикулярны
между собой, так как линейные углы KOL и КОН прямые.
Итак, искомым геометрическим местом точек являются две
плоскости Q и R, перпендикулярные плоскости Р, причем
плоскости Q и В перпендикулярны между собой и делят
углы между данными прямыми пополам.
§ 14. Объемы тел
58. Понятие объема простых тел. Для простых тел объем —
это положительная величина, численное значение которой обла-
дает следующими свойствами:
1. Равные тела имеют равные объемы.
2. Если тело разбито на части, являющиеся простыми
телами, то объем этого тела равен сумме объемов его частей.
3. Объем куба, ребро которого равно единице длины, равен
единице.
Если куб, о котором идет речь в определении, имеет ребро
1 см, то объем измеряется в кубических сантиметрах; если
ребро куба равно 1 м, то объем измеряется в кубических
метрах; если ребро куба равно 1 км, то объем измеряется в
кубических километрах н т. д.
На рисунке 181 изображено простое тело — четырехуголь-
ная пирамида SABCD. Объем этой пирамиды на основании
свойства 2 равен сумме объемов пирамид SABC и SADC.
59. Объем параллелепипеда, призмы и пирамиды. Объем
прямоугольного параллелепипеда находится по формуле
V ~abc,
где a, Ь, с — ребра прямоугольного параллелепипеда. Исхо-
дя из этой формулы можно получить формулу для объема
куба. Объем куба находят по формуле
где а — ребро куба.
Иногда говорят, что объем прямоугольного параллелепипеда
равен произведению его линейных размеров или произведению
площади его основания на высоту. Последнее утверждение
верно и для любого параллелепипеда.
На рисунке 182 изображен наклонный параллелепипед. Его
объем равен V=Sabcd-AiK, где SABCD — площадь основания,
а А\К—высота наклонного параллелепипеда.
Можно вывести правило нахождения объема любой призмы
(в том числе и наклонной).
Объем призмы равен произведению площади ее основания
па высоту:
В случае прямой призмы (рис. 183) высота ее совпадает с
боковым ребром н объем прямой призмы равен произведению
площади основания на боковое ребро.
Объем любой пирамиды накормтся по формуле
346
v==4 sH>
где S — площадь основания, H — высота пирамиды.
На рнсунке 184 изображен правильный тетраэдр SABC с
а3 д/2
ребром а. Его объем равен V= .
Пример. В наклонном параллелепипеде основание и бо-
ковая грань — прямоугольники, площади которых соответст-
венно равны 20 дм2 и 24 дм2, а угол между их плоскостями
равен 30°. Одна нз боковых граней параллелепипеда имеет
площадь 15 дм2. Найти объем параллелепипеда.
Решение. Пусть в параллелепипеде ABCDA1B1C1D1 грани
ABCD и ADDiAi — прямоугольники. Тогда ребро AD
перпендикулярно грани ABBtAt и V— SABBiAi-AD=(ABX
ХА Ai sin 30°) ‘AD. Дальнейшие вычисления можно выполнить,
не находя длин этих отрезков. Имеем АО-АВ=20; АА( -АО=
—24; АА। -АВ=15. Перемножив эти равенства почленно,
получим 2V2 = 15-24-20, откуда У=60 дм3.
60. Объем цилиндра и конуса. Объем любого тела определя-
ется следующим образом. Данное тело имеет объем V, если
существуют содержащие его простые тела и содержащиеся в нем
простые тела с объемами, сколь угодно мало отличающими-
ся от V.
Применив это определение к нахождению объемов цилиндра
н конуса, можно доказать теоремы.
Т.3.10. I Объем цилиндра равен произведению площади осно-
| вания на высоту, т. е. V=SH.
Если радиус основания цилиндра В, а высота Н, то формула
его объема такова:
У=лК2Н.
Т.3.11. I Объем конуса равен одной трети произведения пло-
I щади основания на высоту, т. е. V=-|-*S/7.
Если радиус основания конуса R, а высота Н, то объем
его находится по формуле
К=-|-лЯ2Я.
Объем усеченного конуса можно найти по формуле
V=-g- (Я2 + Яг+г2),
где Внг — радиусы оснований, Н — высота усеченного конуса.
Объем усеченного конуса, изображенного на рисунке 185,
находится по формуле ^=-3- nOOi (ОА2 -J-ОА • OiА<OiA?).
61. Общая формула объемов тел вращения. Объем шара и
его частей. Для вывода формулы объема тела вращения вводят
декартовы координаты в пространстве, приняв ось тела за ось х.
Плоскость ху пересекает поверхность тела по линии, для кото-
рой ось х является осью симметрии. Пусть y=f (х) — уравне-
ние той части линии, которая расположена над осью х
(рис. 186).
При вычислении объема части тела вращения, заключенной
между параллельными плоскостями х=а и х=&, пользуют-
ся формулой анализа (см. п. 228).
ь
V=V(b)—V(a)= $ nf(x)dx.
а
где a < Ь, f (х) — непрерывная на [a; Ь] функция.
С помощью этой формулы можно получить формулы
объемов конкретных тел вращения, выбрав соответственно
систему координат и определив функцию f (х).
В частности, формула объема шара радиуса R такова:
V=~nR‘.
Объем шарового сегмента, высота которого Н, а радиус
R, находится по формуле
Формула объема шарового сектора:
где R — радиус шара, Н — высота соответствующего шарово-
го сегмента.
§ 15. Площади поверхностей тел
62. Площади поверхностей многогранников. Площадью
поверхности многогранника называется сумма площадей всех
его граней (иногда говорят площадь полной поверхности).
Для некоторых многогранников, например для пирамиды,
призмы, рассматривается площадь боковой поверхности.
Площадью боковой поверхности призмы называется сумма
площадей боковых граней. Площадь полной поверхности приз-
мы равна сумме площадей ее боковой поверхности н площадей
ее оснований. Площадь боковой поверхности призмы, изобра-
женной на рисунке 147, равна сумме площадей параллелограм-
мов BCCiBit CDDiCi, AA1D1D. Площадь полной по-
верхности этой призмы равна площади боковой поверхности
плюс сумма площадей двух основании ABCD и AiBiCiPi.
Т.3.10. 1 Площадь боковой поверхности прямой призмы равна
I произведению периметра основания на высоту приз-
| мы, т. е. на длину бокового ребра.
349
т.3.11.
Площадь боковой поверхности призмы равна произ-
ведению периметра перпендикулярного сечения на
длину бокового ребра.
Из этих теорем вытекает, что площадь полной поверхности
куба с ребром а равна 6а2.
Площадью боковой поверхности пирамиды называется сум-
ма площадей ее боковых граней. Площадь полной поверхности
пирамиды равна сумме площадей ее боковой поверхности и
площади основания. Площадь боковой поверхности пирами-
ды, изображенной на рисунке 150, б, равна сумме площадей
трех треугольников SACt SCB, SBA. Площадь полной ее поверх-
ности состоит из боковой поверхности и площади основания
АВС.
Т.3.12.
Т.3.13.
Площадь боковой поверхности правильной пирамиды
равна произведению полупериметра основания на
апофему, т. е. S6=—t где р— периметр основания,
а I — апофема пирамиды.
Площадь боковой поверхности правильной усеченной
пирамиды равна произведению полусуммы перимет-
ров основания на апофему, т. е. S=-^-(an-j-bn)Z,
где ап и Ьп — периметры основания, а I — апофема.
Площадь поверхности правильного тетраэдра с ребром а
равна a2i/3, а, например, площадь поверхности октаэдра с
ребром а равна 2а2 -у/3.
Пример. Все ребра правильной пирамиды увеличились в
3 раза. Как изменится площадь полной поверхности пирамиды?
Решение. Пусть площадь полной поверхности п-уголь-
ной пирамиды S равна пвд+Д^, где Sfi — площадь одной
боковой грани, a S0CB — площадь основания. При увеличении
каждого ребра в 3 раза правильный многоугольник основа-
ния перейдет в подобный, а каждый из п треугольников
(по признаку подобия) перейдет в подобный, т. е. S'6=9S&,
S^n =9Soqn, отсюда S'= 9S. Площадь полной поверхности пира-
миды увеличится в 9 раз.
63. Понятие площади поверхности. Пусть F — данная по-
верхность. Построим тело F*, состоящее из всех точек прост-
ранства, для которых найдется точка поверхности F на рас-
стоянии, не большем h. Наглядно тело Fh можно представить
себе как тело, заполненное краской прн окрашивании поверх-
ности с обеих сторон слоем краски толщиной й.
Пусть Vh — объем тела Fh. Площадью поверхности тела F
мы будем называть предел отношения при h -> О, т. е.
S—lim
л-о
Ki
2й
64. Площади поверхностей тел вращения. Воспользовав-
шись данным в предыдущем пункте определением площади
поверхности, можно получить формулы, по которым вычисля-
ются площади поверхностей различных тел вращения.
Площадь сферы находится по формуле
Я=4лЯ2,
где R — радиус сферы.
Площадь поверхности сферического сегмента находится по
формуле
где R — радиус сферы, а Н — высота сегмента.
Площадь боковой поверхности цилиндра находится по фор-
муле
»S'--2.iKH,
где R — радиус основания цилиндра, а Н — его высота. Для
нахождения площади полной поверхности цилиндра надо к
площади боковой поверхности прибавить удвоенную площадь
основания.
Площадь боковой поверхности конуса находится по фор-
муле
S=nRlt
где R — радиус основания конуса, a Z — его образующая. Для
нахождения площади полной поверхности конуса нужно к пло-
щади его боковой поверхности прибавить площадь основания.
Площадь боковой поверхности усеченного конуса находится
по формуле
«=л(ЯЧ-г)Ь
где R к г соответственно радиусы основании, а I — его
образующая.
Пример 1. В коиус, радиус основания которого R н вы-
сота Н, вписан цилиндр. Найдите размеры цилиндра, при кото-
рых площадь его боковой поверхности имеет наибольшее зна-
чение.
Решение. Обозначим радиус основания цилиндра через
г, а его высоту через h (рис. 187). Из подобия Д.8АО к
A Ml AM следует, что ** Г—откуда h=^R . Подста-
вив в формулу £б=2лгЛ значение h, получим S6=2nrH~
R
Рассмотрим S6 как функцию г и исследуем ее на экстре-
мум. Для этого найдем ее производную S'6=2nH--R~'r*
Очевидно, S'—О прн В этой точке функция S6 имеет
максимум. Итак, наибольшее значение площадь боковой ПО-
fl Ь 1 V
верхности цилиндра принимает при г——, а л=—я.
Г Л А В А IV. ДЕКАРТОВЫ КООРДИНАТЫ
§ 16. Координаты на плоскости и в пространстве
65. Введение координат иа плоскости н в пространстве.
Проведем на плоскости через точку О две взаимно перпендику-
лярные прямые хну — оси координат. Ось х (оиа обычно гори-
зонтальная) называется осью абсцисс, а ось у — осью ординат.
Точка пересечения этих осей О называется началом ноординат.
Этой точкой каждая из осей разбивается на две полуоси. Усло-
вимся одну нз них называть положительной, отмечая ее
стрелкой, а другую — отрицательной. На рисунке 188, а изобра-
жены оси хну, точка О — начало координат.
Каждой точке А плоскости мы сопоставим пару чисел —
координаты точки — абсциссу (х) и ординату (г/) по такому
правилу.
Через точку А проведем прямую, параллельную оси орди-
нат (рис. 188, б). Она пересечет ось абсцисс х в некоторой точке
Ах. Абсциссой точки А мы будем называть число х, абсолют-
ная величина которого равна расстоянию от О до Ах. Это число
положительное, если Ах принадлежит положительной полуоси;
отрицательное, если Ах принадлежит отрицательной полуоси.
Если точка лежит на осн ордниат у, то полагаем х=0.
Ордината (у) точки А определяется аналогично. Через
точку А проведем прямую, параллельную оси абсцисс
(рис. 188, б). Она пересечет ось ординат у в некоторой точке
Ау. Ординатой точки А мы будем называть число у9 абсолют-
ная величина которого равна расстоянию от точки Ау но О.
Это число положительное, если Ау принадлежит положитель-
ной полуоси; отрицательное, если Ау принадлежит отрицатель-
ной полуоси. Если точка А лежит на оси абсцисс, то пола-
гаем у—О.
Координаты точки записываются в скобках рядом с буквен-
ным обозначением точки, например А (х; у) (на первом месте
абсцисса, на втором — ордината).
Оси координат разбивают плоскость на четыре части —
четверти I, II, III, IV (рис. 188, е). В пределах одной четверти
знаки обеих координат сохраняются. В первой четверти они
положительны, во второй — абсцисса отрицательна, а ордината
положительна, в третьей — абсцисса и ордината отрицательны,
в четвертой — абсцисса положительна, а ордината отрицатель-
на (рис. 188, в).
Точки оси х имеют равные нулю ординаты (у—О), а точки
оси у — равные нулю абсциссы (х=0). Абсцисса и ордината
начала координат равны нулю.
Плоскость, на которой введены описанным выше способом
координаты х и р, будем называть плоскостью ху. Произволь-
ную точку А этой плоскости с координатами х и у обозначают
А (х; у).
Введенные на плоскости координаты х, у называются декар-
товыми по имени французского математика Р. Декарта
(1596—1650).
Аналогично вводятся декартовы координаты в пространстве.
Возьмем три попарно перпендикулярные прямые х, у и г, кото-
У У. л, A U У (-;+) _ ш 0 Г® (+:+> zr * (+;-)
о х о а) В) Ах х 6)
рые пересекаются в одной точке О (рис. 189, а). Проведем
через каждую пару этих прямых плоскость. Плоскость, про-
ходящая через прямые х и у, называется плоскостью ху.
Две другие плоскости называются соответственно xz и J/2.
Прямые х, у, z называются координатными осями или осями
координат, точка их пересечения О — началом координат, а
плоскости ху, xz, yz — координатными плоскостями. Точка О
разбивает каждую из осей координат на две полупрямые. Одна
из них называется положительной, а другая — отрицательной.
Если через точку А проведем плоскость, параллельную плос-
кости yz (рис. 189, б), то она пересекает ось х в некоторой точке
Ах. Координатой х точки А будет число, равное по абсолютной
величине длине отрезка ОАХ. Оно положительное, если точка
Ах лежит на положительной полуоси, и отрицательное, если
она лежит иа отрицательной полуоси. Если точка Ах совпада-
ет с точкой О, то х—О. Аналогично определяются координаты
у и z. Точку А с координатами х, у, г обычно вписывают так:
А (х; у; z).
Итак, каждой точке А пространства сопоставляют три числа
X, у, z — координаты точки А в пространстве.
На рисунке 190, а точка В в пространстве имеет три коорди-
наты с, а, Ь, т. е. В (с; а', Ъ).
Можно по трем числам иайти положение точки в простран-
стве. Например, три числа 1, 1,—1 задают положение точки С
в пространстве (рис. 190, б).
66- Координаты середины отрезка. Расстояние между точка-
ми. Пусть А (xi; yi} н В (х2; yz) — две произвольные точки
плоскости н С (х; у) — середина отрезка АВ (рис. 191). Фор-
12 Чякяч 769
мулы, связывающие координаты точки С с координатами точек
А и В, таковы:
_____*1 +*2 и yi +У2
2 ’ у 2 '
Формулы верны и в случае, если отрезок АВ параллелен одной
нз осей координат.
Для точек А, В и С пространства эти формулы аналогичны.
Пусть А (х5; у г, 21) и В (х2; ул z2} — две произвольные точки.
Формулы, выражающие координаты х, у, z точки С — середины
отрезка АВ через координаты его концов А и В, таковы:
*1+*2 __ У1 +У2 +*3
2 * * 2 ’ 2 ‘
Существует формула для нахождения расстояния между
точками, заданными своими координатами.
Если точки А( (х»; у\) и А2 (х2; у2) (рис. 192) лежат на плос-
кости, то расстояние между Л и А2 находится по формуле
AA2=V(»—х,)2+(»2 —У1)г-
Эта формула верна для любого расположения точек Ai н
Аг.
Расстояние между двумя точками Ai (хи у^ Zi) и
Аг (х2; 2г) пространства находится по формуле
Л| А =7(XS—Х|)2 + (»2 — y>)2 + (Z2 — »l)2.
Пример 1. Найти координаты одного нз концов диаметра
окружности, если другим его концом является точка (2; 3), а
центром окружности — точка (0; 1).
Решение. Известно, что центр окружности является
серединой любого диаметра, поэтому, подставив в формулы для
нахождения координат точки (0; 1) середины отрезка коорди-
наты концов его (2; 3) и (х2; yz), получим:
q _ 2-Ь«а -J 3-|-р2
2 ’ 2 ’
откуда Х2- — 2, — 1— координаты другого конца диа-
метра.
Пример 2. Найти расстояние между точками плоскости
А(—1; 2) и В (2; 4).
Решение. По формуле АВ=V(x2—Х|)2 +(у2—полу-
чим, что АВ=-\1$-\-4
Пример 3. Найти расстояние от точки пространства
(1; 2; — 3)до: 1) координатных плоскостей; 2) осей координат;
3) начала координат.
Решение. 1) Пусть А (1; 2; —3) и AAi — расстояние от
А до плоскости ху, т. е. Ai (1; 2; О), так как AAi-Lxy н Ai при-
надлежит плоскости ху. Тогда по формуле
АА1 =д/(1”!)2+(2-—2)2+(04-3)2—3. Аналогично ААг=2,
АА3=1.
2) Пусть ААХ — расстояние от А до оси х, тогда Ах (1; О; 0),
откуда ААХ = д/02 4-(— 2)2+32= д/13. Аналогично АА//=\'1О,
ААк=л/5.
3) Так как 0 (0; 0; 0), то AO=Vla+22+(—3)2=д/14.
§ 17. Уравнения фигур на плоскости
67. Уравнение окружности. Уравнением фигуры на плоско-
сти в декартовых координатах называется такое уравнение с
двумя переменными х и у, что координаты любой точки фигуры
являются решением этого уравнения. И обратно: любые два
числа, удовлетворяющие этому уравнению, являются координа-
тами некоторой точки фигуры.
Окружность с центром Ао (а; Ъ) и радиусом R (рис. 193)
задается уравнением
(х-а)2 + (у-Ь)2=Я2.
Если центром окружности является начало координат, то
уравнение окружности имеет вид:
х2 + !/2=Я2.
Пример. Составить уравнение окружности с центром на
прямой у — 4, касающейся оси х в точке А (—1; О).
Решение. В системе координат ху построим прямую у=4
(рис. 194) и точку А (— 1; О). По условию окружность должна
касаться оси х в точке А, а ее центр должен лежать на прямой
у=4, т. е. центр окружности — точка будет иметь координа-
ты О, (—1; 4). Искомое уравнение есть уравнение окружности
с центром в точке (—1; 4) и радиусом 4:
(х+1)2+(у-4)2=16.
68. Пересечение двух окружностей. На рисунке 195 даны
две окружности с центрами О и О], расстоянием между
центрами ОО] = с и радиусами, соответственно равными а и Ъ.
Примем точку О за начало координат, а полупрямую ОО1
за положительную полуось х. Тогда уравнения окружностей
таковы:
х2+»2=а2, (х—с)2 + у2=Ь2.
Решив систему этих уравнений, можно сделать вывод:
если одно из чисел а, Ь, с больше суммы двух других, то
окружности не имеют общей точки (рис. 195, а); если одно из
этих чисел равно сумме двух других, то окружности касаются
(рис. 195, в, г); если каждое из этих чисел меньше суммы двух
других, то окружности имеют две общие точки, т. е. пересекаю-
тся (рис. 195, д).
357
69. Уравнение прямой, Любая прямая в декартовых коорди-
натах на плоскости задается уравнением
ах-\-Ъу 4-с=0.
Коэффициенты а и b в этом уравнении могут принимать
различные значения. В зависимости от этого прямая будет
по-разному располагаться на плоскости. Рассмотрим некоторые
частные случаи.
1. а=0, Ь^О. В этом случае уравнение прямой можно запи-
сать так; у= —|-. Все точки имеют одну н ту же ординату
( —у) , следовательно, прямая параллельна осн х (рис. 196, а).
В частности, если с=0, то прямая совпадает с осью х.
2. i>=0, а 5^0. В этом случае уравнение принимает вид
х— — . Прямая параллельна оси у (рис. 196, б) нли совпадает
с ней, если с=0.
3. С-0. Уравнение принимает вид ах ^Ьу—0. Прямая про-
ходит через начало координат (рис. 196, в).
Если в уравнении прямой ax-|-bi/-}-c=0 коэффициент Ь^О,
то можно записать у — —^-х—Обозначив ——?- =
о о Ь Ь
=q, получим y=kx~}-q. Коэффициент k в этом уравнении на-
зывается угловым коэффициентом прямой.
На рисунке 197 точки -A(xi;i/j) и В(х21у2) принадлежат
изображенным прямым, а значит,
yi—kxi + q, У2=кх2+дч
вычитая почленно из второго равенства первое, получим:
У 2—yi=k(X2—*1),
откуда .
Хг—Х|
В случае, изображенном на рисунке 197, с,
*=И=4в<х.
Х2 — Xi
В случае, изображенном на рисунке 197, б.
Угловой коэффициент прямой имеет следующий геометри-
ческий смысл: коэффициент к в уравнении прямой с точностью
до знака равен тангенсу острого угла, который образует пря-
мая с осью х.
Пример. Составить уравнение прямой, проходящей через
начало координат и точку А (4; — 2).
Решение. Уравнение прямой имеет вид y = kx + q. Надо
найти k и д.
Прямая проходит через начало координат, т. е. координаты
точки О (О; О) удовлетворяют уравнению прямой O=fe*O-|-g,
т. е. д=0.
Угловой коэффициент к иайдем по формуле
ft— У8-У1
Х2 — Х1 *
где О (Xi; yt) и А {х2\ у ?) — точки, через которые проходит пря-
Искомое уравнение прямой имеет вид у=—.
70. Пересечение прямой и окружности. На рисунке 198
изображена окружность радиуса R и прямая a, d — расстоя-
ние от центра этой окружности до прямой а. Если принять центр
окружности за начало координат, а прямую, перпендикуляр-
ную прямой а, за ось х (рис. 199), то уравнения окружности
и прямой таковы: xz-|-y2=K2, X=d. Решая полученную систе-
му, найдем x=d, y = 3^I$—d2.
Окружность и прямая имеют две общие точки, т. е. пересе-
каются, если R>d (рис. 199, а); прямая и окружность имеют
одну общую точку, т. е. касаются, если R—d (рис. 199,6);
прямая и окружность ие пересекаются, если R<d (рис. 199, в).
Пример 1. Окружность с центром в точке А (2; 3) ка-
сается оси у. Пересекает ли эта окружность ось х?
Решение. Из условия следует, что радиус окружности
равен 2, а уравнение имеет вид (х—2f+(y — 3)2=4. Далее
задачу можно решить по-разному.
LSZ.I 360
1-й способ. Для того чтобы окружность пересекла ось х,
должно выполняться условие B<d, где R — радиус окруж-
ности, ad — расстояние от центра окружности до прямой.
Так как Н=2, a d—3, то окружность не пересекает ось х.
2-й способ. При у—О имеем (х —2)2-|-(0 —3)2=4, (х—
— 2)2= —5, что невозможно. Поскольку условие приводит
к неравенству (х—2)2 <1 — 5, можем сделать вывод: окружность
(х—2)2+(у —З)2—4 не пересекает ось х.
Пример 2. При каком значении с прямая х+у^-с=О
касается окружности х2+у2 = 1?
Решение. Решим систему уравнений:
tx’+A=l. t(-e-S)=+jr!=l.
Преобразовав второе уравнение, получаем квадратное урав-
нение 2у2-\г2су-\-с—1—0, дискриминант которого равен
D= — 4сг-}“8. Для того чтобы прямая и окружность касались,
нужно, чтобы они имели единственную о$лцую точку, а это
значит, что полученное квадратное уравнение относительно
у должно иметь единственное решение. Это будет в том случае,
если D — 0, т. е. — 4с2+8 = 0, откуда с— Прямые
х+у+-\/2=0и х+у—^/2=0 касаются окружности х2 +у2=1.
§ 18. Уравнения фигур в пространстве
71. Уравнение плоскости. Уравнение фигуры в простран-
стве определяется так же, как и на плоскости.
Пусть Ао (хо; уе, £о) — точка плоскости а и п (а; Ь; с) —
вектор, перпендикулярный этой плоскости (рис. 200). Пусть
А (х; у; z) — произвольная точка плоскости а, т. е. AAo_Ln,
тогда ААо-п=0. Координаты точки А удовлетворяют уравне-
нию
п(х—Х|)+&(у—у|)+с(г—2i)—О. (1)
Берио и то, что если точка А (х; у; г) удовлетворяет уравне-
нию (1), то точка А лежит в плоскости а. Таким образом, урав-
нение (1) есть уравнение плоскости а.
Уравнение плоскости можно записать в виде
ах+йу+сг-|-d=О.
Коэффициенты а, Ъ, с в этом уравнении являются координа-
тами вектора, перпендикулярного этой плоскости.
72. Уравнение сферы. Пусть центр сферы находится в точке
А (а; Ь; с), а радиус сферы равен R. Точками сферы являются
те и только те точки пространства, расстояние от которых до
точки А равно R. Квадрат расстояний от любой точки В (х; у; я)
сферы до точки Л равен (х—а)2+(у—Ь)2+(я—с)2. Поэтому
уравнение сферы с центром А (а; д; с) и радиусом R имеет
вид:
(х-«.)2 + (»-6)2+(г-с)2=Я2-
Сфера с центром (2; —1; 3) и радиусом 5 задается урав-
нением (х—2)2+(y + l)2+(z—3)2=25.
Если центром сферы является начало координат, то уравне-
ние сферы с радиусом R таково:
х>+У2+га = Я2.
Шар задается не уравнением, а неравенством. Рассмотрим шар с центром
А (а; Ь; с) и радиусом Я. По определению шара (п. 54) ему принадлежат все
такие точки Af, для которых АМ^Н, т. е. AM^s^R"2. Учитывая, что А (в: Ь; с),
а М(х; у; г), получим:
(Ж_О)»4-(₽_Ь)2+(,-С)»Сй’.
Если центр шара находится в начале координат, то неравенство таково:
x'+rf+^R'2.
Аналогично круг радиуса г в прямоугольных координатах на плоскости
с центром А (а; Ь) или в начале координат задается неравенством
(х— н)2-Ну — ИЛИ +
Пример. Запишите уравнение сферы, проходящей через
точки А (О; О; 0), В (4; 0; 0), С (0; 4; О), если радиус ее равен 3.
Решение. Уравнение сферы с центром М (а; Ь; с) и ра-
диусом 3 имеет вид (х—а)2+(у—Ь)2+(я—с)2 =9. Ему должны
удовлетворять координаты точек А, В к С. Числа а, Ъ и с отыски-
ваются из системы трех уравнений, получающихся при под-
становке в уравнение сферы координат трех данных точек:
( a2+b2+cs=9t
{ (4—а)2 + д2 + с2=9,
I а2+(4-&)2+с2=9.
LS6 362
Почленно вычитая первое уравнение из второго и третьего,
получаем 16-8а=0, 16—86 — 0, откуда а=Ъ = 2, Значение
с отыскивается подстановкой найденных значений а и Ъ в первое
уравнение: 4+4-|-е2=9, с2=1, С| = 1, С2——1.
Таким образом, существуют две сферы, удовлетворяющие
условию задачи, их центры Oi (2; 2; 1) и О2 (2; 2; — 1), а уравне-
ния таковы: (х —2)2+(г/—2)2-j-(z—I)2—9 н (х — 2)2+(г/ — 2)2+
+(z+1)2 = 9.
73. Взаимное расположение сферы и плоскости. Пусть дана
сфера радиуса R, а расстояние от ее центра С до плоскости а
равно d. Введем систему координат так, как покавано на ри-
сунке 201: плоскость ху совпадает с плоскостью а, а центр С
сферы лежит иа осн 2. В этой системе координат точка С имеет
координаты (О; 0; d), поэтому уравнение сферы таково: хг-\-у2 +
+(2—df=Rz. Плоскость совпадает с координатной плоскостью
ху, поэтому ее уравнение 2=0.
Если координаты какой-нибудь точки М (х; г) удовлетво-
ряют обоим уравнениям, то точка М лежит как в плоскости а,
так и на сфере, т. е. является общей точкой плоскости и сферы.
Если же система этих двух уравнений ие имеет решений, то
сфера и плоскость не имеют общих точек. Таким образом, вопрос
о взаимном расположении сферы и плоскости сводится к иссле-
дованию системы уравнений:
Г 2=0,
1х2+У2+(г-<02=Лг.
Возможны три случая:
1. d<R. Система имеет бесчисленное множество решений,
все точки лежат иа окружности. Вывод: если расстояние от
центра сферы до плоскости меньше радиуса сферы, то сечение
сферы плоскостью есть окружность (рис. 201, а).
2. d~R. Система имеет единственное решение. Вывод: если
расстояние от центра сферы до плоскости равно радиусу сферы,
то сфера и плоскость имеют единственную общую точку —
точку касания (рис. 201, б).
3. R. Система не имеет решений. Вывод: если расстояние
от центра сферы до плоскости больше радиуса сферы, то сфера
и плоскость не имеют общих точек (рис. 201, в).
74. Пересечение двух сфер. Для отыскания условия пересе-
чения двух сфер примем прямую, соединяющую их центры,
за ось х. Пусть точка А (а; 0; 0) — центр первой сферы, а
Ri — ее радиус. Точка В (Ь; 0; 0) — центр второй сферы, a R$ —
ее радиус. Уравнениями сфер будут
(х-а)2+У2+г2=Я? и (х-Ь)8+г/2+г2=/?1
Решая эту систему, можно прийти к выводу:
Т.4.1. | Линия пересечения двух сфер есть окружность.
Пример. Радиусы шаров равны 25 н 29 дм, а расстояние
между их центрами 36 дм. Найти длину линии, по которой пере-
секаются их поверхности.
Решение. Рассмотрим на плоскости отрезок OOi длиной
36 дм и две окружности с центрами в точках О и Ot радиусами
25 и 29 дм. Если А — одна из точек пересечения этих окруж-
ностей (рис. 202), то радиус г окружности пересечения данных
в условии задачи сфер (поверхностей данных шаров) равен
высоте АН треугольника AOOi и его можно найти, предвари-
тельно вычислив площадь по формуле Герона (п. 37).
364
=~- (36 + 25 + 29)=45. ЯлАОО(=т/45^9-20.16 = 9-52-4 =
= 360. С другой стороны, 5>лЛО01=-^-г-36, откуда г=20 дм=
=2 м.
Длина окружности пересечения сфер равна С=2лг=4л м.
ГЛАВА V. ПРЕОБРАЗОВАНИЯ ФИГУР
§ 19. Движение
75. Примеры преобразований фигур. Преобразования фигур
изучаются в курсе геометрии на плоскости и в пространстве.
Если каждую точку данной фигуры на плоскости или в прост-
ранстве сместить каким-нибудь образом, то мы получим новую
фигуру. Говорят, что эта фигура получена преобразованием
из данной. Приведем несколько примеров преобразований
фигур.
1. Симметрия относительно точки (цент-
ральная симметрия). Симметрия относительно точки
определяется так. Пусть О — фиксированная точка и X —
произвольная точка. Точка Х'| называется симметричной точке
X относительно точки О, если точки X, О, Х\ лежат на одной
прямой и OX=OXi. Точка, симметричная точке О, есть
сама точка О. На рисунке 203 точки X и Хь Y н ¥н Z и Zi сим-
метричны друг другу относительно точки О.
Пусть F — данная фигура и О — фиксированная точка
плоскости. Преобразование фигуры F в фигуру F\, при котором
каждая ее точка X переходит в точку Xt9 симметричную X
относительно данной точки О, называется преобразованием
симметрии относительно точки О. На рисунке 204 изображен
ДА|В]С1, симметричный ДАВС относительно центра О.
На рисунке 205 изображены два куба, симметричные отно-
сительно точки О.
Если преобразование симметрии относительно точки О пере-
водит фигуру в себя, то фигура называется центрально-сим-
метричной, а точка О — ее центром симметрии. Например,
параллелограмм является центрально-симметричной фигурой.
Центром его симметрии является точка пересечения диагона-
лей (рис. 206, а). Окружность с центром О тоже центрально-
симметричная фигура с центром симметрии О (рис. 206, б).
Все перечисленные фигуры плоские.
В пространстве, так же как и иа плоскости, много примеров
центрально-симметричных фигур. Например, на рисунке 207
изображены такие фигуры: это куб, сфера, параллелепипед.
2. Симметрия относительно прямой (осе-
вая симметрия). Пусть I — фиксированная прямая
(рис. 208). Точка Xi называется симметричной точке X отно-
сительно прямой I, если прямая XXi перпендикулярна прямой
I и 0X1 =ОХ, где О — точка пересечения прямых XX t и I.
Если точка X лежит на прямой I, то симметричная ей точка
есть сама точка X. Точка, симметричная точке Xi, есть точка
X. На рисунке 208, а точки X и Xi, Y и Yi, Z и Z\ симметричны
относительно прямой I.
Преобразование фигуры F в Flt при котором каждая точка X
переходит в точку Х|, симметричную относительно прямой Z,
называется преобразованием симметрии относительно прямой
I. При этом фигуры F и Fi называются симметричными отно-
сительно прямой I. На рисунке 208, б изображены окружности,
симметричные относительно прямой I.
На рисунке 209 изображены две сферы, симметричные от-
носительно прямой I.
Если преобразование симметрии относительно прямой I пере-
водит фигуру F в себя, то фигура называется симметричной
относительно прямой I, а прямая I называется осью симметрии
фигуры.
Например, прямые, проходящие через точку пересечения
диагоналей прямоугольника параллельно его сторонам, явля-
ются осями симметрии прямоугольника (рис. 210, а). Прямые,
иа которых лежат диагонали ромба, являются его осями сим-
метрии (рис. 210, б). Окружность симметрична относительно
любой прямой, проходящей через ее центр (рис. 210, в). Все
эти фигуры плоские.
В пространстве, как и на плоскости, много примеров фигур,
имеющих оси симметрии. На рисунке 211 изображены такие
фигуры: это прямоугольный параллелепипед, конус, правиль-
ная четырехугольная пирамида.
3. Симметрия относительно плоскости.
Пусть а — произвольная фиксированная плоскость. Из точки X
опускают перпендикуляр иа плоскость а (О — точка пересе-
чения его с плоскостью а) и на его продолжении за точку О
откладывают отрезок OXi, равный ОХ. Точки X и Xi называют
симметричными относительно плоскости а (рис. 212).
Преобразование фигуры F в Fj, при котором каждая точка
X фигуры F переходит в точку Xi, симметричную X отно-
сительно плоскости а, называется преобразованием симметрии
относительно плоскости а. При этом фигуры F и F\ называют-
ся симметричными относительно плоскости а.
На рисунке 213 изображены две сферы, симметричные отно-
сительно плоскости а.
Если преобразование симметрии относительно плоскости пе-
реводит фигуру в себя, то фигура называется симметричной
относительно плоскости а, а плоскость а называется плоскостью
симметрии.
На рисунке 214 изображены две плоскости симметрии
сферы. Заметим, что у сферы таких плоскостей симметрии бес-
конечное множество. У куба также имеются плоскости симмет-
рии. На рисунке 215 изображены две из иих.
4. Гомотетия. Пусть F — данная фигура и О — фикси-
рованная точка (рис. 216). Проведем через произвольную точку
X фигуры F луч ОХ и отложим на ием отрезок OXi, равный
kOX, где k — положительное число. Преобразование фигуры F,
при котором каждая ее точка X переходит в точку Xj, построен-
ную указанным способом, называется гомотетией относительно
центра О. Число k называется коэффициентом гомотетии.
Фигуры F и Ft называются гомотетичными. На рисунке 216
четырехугольник XiYiZiUi гомотетичен четырехугольнику
XYZU с центром гомотетии О и коэффициентом гомотетии
Л=2.
На рисунке 217 ДА1В1С1 гомотетичен ДАВС с центром О
и коэффициентом гомотетии, равным 1,6.
На рисунке 218 изображены две гомотетичные сферы с
коэффициентом гомотетии 2.
Пример. В данную правильную четырехугольную пира-
миду вписать куб так, чтобы четыре его вершины лежали на
ребрах, а четыре — на основании пирамиды.
Решение. Проведем любое сечение Л-iBiCiDi пирамиды с
вершиной S, параллельное ее основанию (рис. 219). На этом
сечении (квадрате) как на верхнем основании строим куб
Л|В1С1П|Л2В2С2П2. Взяв в качестве центра гомотетии вершину
S пирамиды, проведем полупрямые SA2, SB2, SC2, SD2 (на
рисунке их нет). Точки А', В\ С', 1У их пересечения с основанием
пирамиды (точнее, с диагоналями основания) будут вершинами
одного из оснований искомого куба. Вершины А, В, С, D
другого основания получим, если через А', В', С'91У проведем
прямые, параллельные AsAj, В2В1, С2С1, D2D1 до пересечения
с ребрами пирамиды.
76. Понятие движения. Свойства движений. Определение
движения одинаково и в плоскости, и в пространстве. Преобра-
зование фигуры F в фигуру Fi называется движением, если оно
сохраняет расстояние между точками, т. е. переводит любые
две точки А и В фигуры F в точки Ai и Bi фигуры Fi так, что
AB=AiB\. Рассмотренные в п. 75 симметрии относительно
точки, прямой и плоскости являются движениями.
Т.5.1. I Преобразование симметрии относительно точки явля-
I ется движением.
Т.5.2. I Преобразование симметрии относительно прямой яв-
ляется движением.
370
Т.5.3. I Преобразование симметрии относительно плоскости
I является движением.
Сформулируем некоторые свойства движения.
Т.5.4. I При движении точки, лежащие на прямой, переходят
в точки, лежащие на прямой, и сохраняется порядок
I их взаимного расположения.
Из теоремы 5.4 следует, что при движении прямые пере-
ходят в прямые, полупрямые — в полупрямые, отрезки — в
отрезки.
При движении сохраняются углы между полупрямыми. При
движении плоскость переходит в плоскость.
Рассмотрим еще два движения — поворот на плоскости и
вращение вокруг осн в пространстве.
Поворотом на плоскости около данной точки называется
такое движение, прн котором каждый луч, исходящий из дан-
ной точки, поворачивается на одни н тот же угол в одном и том
же направлении (по часовой стрелке или против часовой
стрелки). На рисунке 220 ДАВС повернут на 60° по часо-
вой стрелке около данной токи О. Углы между лучами О А и
OAi, ОВ и OBi, ОС и OCi равны 60°.
Вращением вокруг оси на угол <р называется преобразова-
ние пространства, при котором:
1) имеется единственная прямая I, все точки которой пере-
ходят сами в себя;
2) любая точка А, ие принадлежащая I, переходит в такую
точку Ai, что:
а) точки А и А) лежат в плоскости а, перпендикулярной I;
б) AAOAi =<р является постоянным по величине и направ-
лению (точка О есть точка пересечения плоскости а с осью Z).
Прямую I называют осью вращения, угол <р — углом враще-
ния (рис. 221).
Неподвижными элементами вращения являются точки оси
вращения, а также все плоскости, перпендикулярные этой оси.
Если ср=2лт, m£Z, то вращение можно считать тождествен-
ным преобразованием.
Симметрию относительно прямой можно рассматривать как
частный случай вращения, когда <р=л.
Два движения, выполненные последовательно, дают снова
движение. Результат выполнения этих движений называется
композицией движений.
На рисунке 222 йзображено последовательное выполнение
двух движений, фигура F| получена из фигуры F симметрией
относительно оси р, а фигура F2 получена из фигуры Fi сим-
метрией относительно точки О, в результате последовательного
выполнения этих движений сохранились расстояния между
соответствующими точками, а значит, фигура F? получена из
фигуры F движением.
Композиция двух вращений с одной и той же осью есть
вращение.
Пусть преобразование фигуры F в фигуру Fi переводит
различные точки фигуры F в различные точки фигуры F\.
Пусть произвольная точка X фигуры F при этом преобразова-
нии переходит в точку Xi фигуры Fj. Преобразование фигуры
Fi в фигуру F, при котором точка Xj перейдет в точку X, назы-
вается преобразованием, обратным данному. Преобразование,
обратное движению, является также движением.
Как на плоскости, так и в пространстве рассматриваются
равные фигуры. Фигуры Р и F-, называются равными, если они
движением переводятся одна в другую. Для обозначения равен-
ства фигур употребляется знак равенства. Запись F=F\ озна-
чает, что фигура F равна
На рисунке 213 шары симметричны относительно плоскости,
а значит, они равны. На рисунке 205 кубы симметричны отно-
сительно точки, а значит, они равны. На рисунке 222 треуголь-
ники F, Fi, Рг равны, так как все они получены один из другого
в результате движения.
Пример 1. На рисунке 223 изображены два треугольни-
ка АВС и AiBtCi, у которых АА = AAi, АВ= АВ\, Z.C=Z.Ci,
AB=AiBi, BC=B\Ci, AC=A\Ci. Доказать, что эти треугольни-
ки совмещаются движением, причем вершина А переходит в
вершину Аь В — в В], С — в С].
Решение. Решение задачи зависит от расположения тре-
угольников.
1) На рисунке 223, а изображен один из возможных вари-
антов. AAiBaCs получен из ДАВС при симметрии относитель-
но серединного перпендикуляра к отрезку ААь Л AiBiCi полу-
чен из АА1В2С2 при симметрии относительно прямом, со-
единяющей точку А1 с серединой отрезка В2В1. Мы знаем,
что последовательное выполнение движений есть движение.
Таким образом, aAiBjCi получен из ДАВС движением.
2) На рисунке 223,6 изображен другой вариант. АА1В2С2
получен из А АВС параллельным переносом (см. п. 79) в
направлении, заданном лучом AAi на расстояние AAi. Далее,
A A1B1C1 получен из А А1В3С2 поворотом иа угол а против часо-
вой стрелки. Вывод аналогичен первому случаю.
Пример 2. Даны две концентрические окружности.
Построить ромб, отличный от квадрата, так, чтобы: 1) две
вершины его принадлежали одной окружности, а две остав-
шиеся — другой; 2) три вершины принадлежали одной
окружности, а одна — другой.
Решение. 1) Построим любой диаметр АВ одной окруж-
ности и перпендикулярный ему диаметр CD другой окружности
(рнс. 224, а). Диагонали полученного четырехугольника CBDA
в точке пересечения делятся пополам, значит, CBDA — парал-
лелограмм (п. 25). Из симметрии отрезков АС и ВС относи-
тельно оси CD следует равенство сторон параллелограмма, т. е.
CBDA — ромб (п. 26).
2) Диаметр АВ меньшей окружности продолжим до пере-
сечения в точке С с большей окружностью. Построим оси
симметрии отрезков АС и ВС (рнс. 224, б). Мы получим два
ромба, удовлетворяющие условию задачи: BMCMt и AKCKi.
Доказательство правильности построения проведите самостоя-
тельно.
Аналогично можно в первом случае построить еще один
ромб, а во втором — еще два.
Пример 3. Даны плоскость а и две точки А к В вне
ее. Найдите на плоскости а такую точку N, чтобы сумма ее
расстояний от А и В, т. е. AN-\-NB, была наименьшей.
Решение. Если точки А к В расположены по разные
стороны от плоскости а, то очевидно, что искомая точка N —
точка пересечения прямой АВ с плоскостью а (рис. 225, а).
Если же точки А и В расположены по одну сторону от
плоскости а (рис. 225, 6), то искомая точка N получится при
пересечении прямой AiB с плоскостью а, где А| — точка,
симметричная точке А относительно плоскости а. Докажем,
что точка N искомая N находится на прямой I, которая перпен-
дикулярна отрезку AAi и проходит через его середину
(AitN ± A A i), а поэтому AN=AiN, отсюда AN+NB=А iN -J- NB.
Возьмем на плоскости а произвольную точку К, отличную от
N (рис. 225,6). Соединив точки и К, получим отрезок
АоКу перпендикулярный отрезку AAi и проходящий через его
середину Ао, поэтому AK=AiK. Отсюда вытекает, что АК-\-
-\-КВ=AiK-\-КВ. Из &AiKB имеем, что KB>AiB.
Так как AiB=AN-[-NB, то ясно, что A\K-}-KB>AN+NB.
Таким образом, приходим к выводу, что сумма AN-\-NB
имеет наименьшее значение, и, следовательно, N — искомая
точка.
§ 20. Подобие фигур
77. Преобразование подобия. Определение преобразования
подобия одинаково и на плоскости, и в пространстве. Преобра-
зование фигуры в фигуру называется преобразованием подо-
бия, если при этом преобразовании расстояния между точками
изменяются (увеличиваются или уменьшаются) в одно и то же
число раз. Это значит, что если произвольные точки А и В
фигуры F при этом преобразовании переходят в точки Ai и В|
фигуры Fj, то AiBt=kABt где Л>0.
Число Л называется коэффициентом подобия (k > О).
При k = l преобразование подобия является движением.
Т.5.5. I Гомотетия есть преобразование подобия.
Рассмотри свойства преобразования подобия.
1. При преобразовании подобия три точки А, В и С, лежащие
на одной прямой, переходят в три точки Ав В| и Сь также
лежащие на одной прямой. Причем если точка В лежит между
точками А и С, то точка В, лежит между точками Ai и Ct.
2. Преобразование подобия переводит прямые в прямые, по-
лупрямые в полупрямые, отрезки в отрезки, плоскости в
плоскости.
3. Преобразование подобия сохраняет углы между полу-
прямыми.
4. Не всякое преобразование подобия является гомотетией.
На рисунке 226 фигура Ft получена из фигуры F гомоте-
тией, а фигура Fi получена из фигуры Ft симметрией относи-
тельно прямой 2. Преобразование фигуры F в F2 есть преобразо-
вание подобия, так как при нем сохраняются отношения рас-
стояний между соответствующими точками, однако это преобра-
зование не является гомотетией.
Для гомотетии в пространстве верна теорема:
Т.5.6. | Преобразование гомотетии в пространстве переводит
любую плоскость, не проходящую через центр гомо-
| тетин, в параллельную плоскость или в себя.
На рисунке 227 изображены два гомотетичных куба с коэф-
фициентом гомотетии, равным 2. По Т.5.6 плоскость ABCD
переходит в параллельную ей плоскость А'В'С'1У. Это же можно
сказать и о плоскостях других граней куба.
78. Подобные фигуры. Две фигуры F к Ft называются
подобными, если они переводятся друг в друга преобравова-
нием подобия. Для обозначения подобия фигур употребляет-
ся символ со. Запись Fi со F читается так: «Фигура Ft подобна
фигуре F».
376
Из свойств преобразования подобия следует, что у подобных
многоугольников соответствующие углы равны, а соответствую-
щие стороны пропорциональны.
В записи Л AiBiCi со &АВС предполагается, что вершины,
совмещаемые преобразованием подобия, стоят иа соответствую-
щих местах, т. е. А переходит в А], В — в В|, С — в С|.
Для подобных треугольников АВС и A iBtCf верны равенст-
ва: = ZC=rC„ .
Два треугольника подобны, если у иих соответствующие
углы равны и соответствующие стороны пропорциональны.
Сформулируем признаки подобия треугольников.
Т.5.7.
Два треугольника подобны, если:
1) два угла одного соответственно равны двум углам
другого;
2) две стороны одного пропорциональны двум сторо-
нам другого и углы, образованные этими сторонами,
равны;
3) стороны одного треугольника пропорциональны
сторонам другого.
Пример. Дан Д АВС, в котором АВ=90°4- А А. Найти
зависимость между сторонами а, Ь п с этого треугольника.
Решение. Проведем BD.LAB (рис. 228). Тогда АА =
= ADBC, ACDB — внешний угол дАВО, т. е. ACDB—90°-j-
+ А А, а значит, ACDB=ACBA, &АВС со дВВС по двум
углам (Т.5.7). Из подобия треугольников следует
=—, откуда CD=^-, BD=~, AD^AC-CD—^-^-. Из
а о о о
&ABD по теореме Пифагора ADZ=BD24-AB\ откуда
(Ь2-О2)2 = С2(024-Ь2).
ГЛАВА VI. ВЕКТОРЫ
§ 21. Введение понятия вектора
79. Параллельный перенос. Введем на плоскости декартовы
координаты. Преобразование плоской фигуры F, при котором
произвольная ее точка (х; у) переходит в точку (х4~а; у 4-Ь), где
а и Ь — постоянные, называется параллельным переносом
на плоскости.
На рисунке 229 фигура Fi получена из фигуры F параллель-
ным переносом. Точка А (х; у) переходит при этом преобразо-
вании в точку В(Х-\-а\ у-\-Ъ). Параллельный перенос задает-
ся формулами Х1=х-|-а, yi=y4-i>- Эти формулы выражают
координаты точки В (Xi; yi), в которую переходит точка А (х; у)
при параллельном переносе.
Параллельным переносом в пространстве называется такое
преобразование, при котором произвольная точка (х; у, z)
фигуры F переходит в точку (х4~а; у + Ь; z+c), где а, b и с —
постоянные. Параллельный перенос в пространстве задается
формулами Х1==х4-а, zi—z-j-c.
На рисунке 230 призма ABCAtBiCi при параллельном
переносе переходит в призму A'B'C'AiBiCi.
Сформулируем некоторые свойства параллельного переноса:
1. Параллельный перенос есть движение.
2. При параллельном переносе точки смещаются по парал-
лельным (или совпадающим) прямым на одно и то же расстоя-
ние.
3. При параллельном переносе прямая переходит в парал-
лельную прямую (или в себя).
4. Каковы бы ни были две точки А и Ai, существует,
и притом единственный, параллельный перенос, при котором
точка А переходит в точку Ai.
5. Преобразование, обратное параллельному переносу, есть
I v 378
параллельный перенос. Композиция двух параллельных пере-
носов есть параллельный перенос.
6. При параллельном переносе в пространстве каждая плос-
кость переходит либо в себя, либо в параллельную ей плос-
кость.
Пример 1. Прямые, которым принадлежат боковые сто-
роны трапеции, перпендикулярны. Доказать, что отрезок, конца-
ми которого являются середины оснований трапеции, равен
полуразности оснований.
Решение. Пусть AD и ВС — основания трапеции ABCD,
М — середина ВС, N — середина AD. При параллельном пере-
носе в направлении полупрямой ВМ на расстояние ВМ точка В
переходит в точку М, точка А переходит в точку А|. При парал-
лельном переносе в направлении полупрямой СМ на расстоя-
ние СМ точка С переходит в точку М, точка D — в точку
Di (рис. 231). Тогда
Aft^AN-AA^AN-BM; (1)
NDi=ND—DiD—ND-MC. (2)
Складывая равенства (1) н (2), получаем:
A {N+ND\ —AN-]-ND~(BM-\- MC)=AD~ ВС.
Ho AiN-}-NDi~A]Di, значит,
AtD\—AD— ВС. (3)
Так как AiN=NDit то MN — медиана образовавшегося
прямоугольного треугольника A\MD\. Поэтому MW=s=-|-(AiN+
Учитывая равенство (3), получаем:
MN=^AlDl
80. Понятие вектора. Некоторые физические величины, та-
кие, как сила, скорость, ускорение и др., характеризуются не
только числовым значением, но и направлением. В связи с
этим указанные физические величины удобно изображать
направленными отрезками.
Направленный отрезок называется вектором. Для обозначе-
ния векторов будем пользоваться строчными латинскими бук-
вами а, Ъ, с, ... . Иногда вектор обозначают указанием
концов отрезка, изображающего вектор. Например, на рисунке
232, а изображен вектор АВ. Точка А называется началом, а
точка В — концом вектора АВ. При обозначении вектора с
помощью концов изображающего его отрезка на первом месте
всегда ставится начало вектора. Над буквенным обозначением
ставится стрелка или черта. Например, запись а читается:
«Вектор а».
Две полупрямые называются одинаково направленными, ес-
ли они совмещаются параллельным переносом, т. е. существует
параллельный перенос, который переводит одну полупрямую
в другую.
Если полупрямые а н Ь одинаково направлены и полупря-
мые Ъ и с одинаково направлены, то полупрямые а и с одина-
ково направлены.
На рисунке 232, б полупрямые АВ и CD одинаково направ-
лены, CD н КМ тоже одинаково направлены, а значит, полу-
прямые АВ и КМ одинаково направлены.
Две полупрямые называются противоположно направлен-
ными, если каждая нз них одинаково направлена с полупря-
мой, дополнительной к другой.
Векторы АВ в CD называются одинаково направленными,
если полупрямые АВ и CD одинаково направлены. Аналогич-
но определяются противоположно направленные векторы.
Абсолютной величиной (или модулем} вектора называется
длина отрезка, изображающего вектор. Абсолютная величина
вектора а обозначается |а[.
Два вектора называются равными, если они совмещаются
параллельным переносом. Это означает, что существует парал-
лельный перенос, который переводит начало и конец одного
вектора соответственно в начало и конец другого вектора.
Равные векторы одинаково направлены н равны по абсолют-
ной величине.
Обратно: если векторы одинаково направлены и равны
по абсолютной величине, то они равны.
Начало вектора может совпадать с его концом. Такой вектор
называют нулевым вектором. Нулевой вектор обозначается ну-
лем с черточкой 0. О направлении нулевого вектора не говорят.
Абсолютная величина нулевого вектора считается равной нулю.
Все нулевые векторы по определению равны.
Из свойств параллельного переноса (п. 79) следует, что от
любой точки можно отложить вектор, равный данному векто-
ру, и только один.
Углом между ненулевыми векторами АВ и АС называется
угол ВАС. Углом между любыми двумя векторами а и Ь назы-
вается угол между равными им векторами с общим началом.
Угол между одинаково направленными векторами считается
равным нулю.
На рисунке 233 даны векторы а и Ь. Отложим от данной
точки О векторы ОА=а и ОВ—Ь. Тогда Z.AOB есть угол
между векторами а и Ь.
81. Координаты вектора. Пусть вектор а на плоскости име-
ет началом точку А (х(; jh), а концом точку В (х£ у2) (рис. 234).
Координатами вектора будем называть числа а(=Х2—Xi,
а2 = у2 — yi. Координаты вектора будем ставить рядом с буквен-
ным обозначением вектора, в данном случае а (а>; аг) или
просто («i; аз). Координаты нулевого вектора равны нулю.
Из формулы расстояния между двумя точками (см. п. 66)
следует, что абсолютная величина вектора (од а2) равна -у/а*+<&
На рисунке 234 вектор АВ имеет координаты ai я а2, где
ai=x2—a2—y2—yi.
АВ = — х,)2+(у2—у ,)2.
В пространстве координатами вектора с началом в точке
A (xi? yt; Zi) и концом в точке В (хг; ya z->) называются числа
х2 — X], у2—уъ Z2—Z1. Можно доказать такую теорему:
Т.6.1. I Равные векторы имеют равные соответствующие ко-
ординаты. И обратно: если у векторов соответствую-
I щие координаты равны, то векторы равны.
§ 22. Операции над векторами
82. Сумма векторов. Суммой векторов а и b па плоскости
с координатами (ai; а2) и (£ц; Ь2) называется вектор с с координа-
тами (ai + bi* вг + Ьг)» т. е. a (ai; аз)+Ь (bi; b2)=c(ai -J-a2; bi + Ьг).
Для любых векторов a (th; «2), Ъ(Ьг, М» c(ci» ct)
а+Б=Ь+«, а-НЬ4-с)==(а+Ь)-|-е.
Т.6.2. I Каковы бы ни были точки A, D, С, имеет место вектор-
I ное равенство AD\- DC—АС.
Эта теорема дает следующий способ построения суммы про-
извольных векторов а и Ь. Надо от конца вектора а отложить
вектор bi, равный вектору Тогда вектор, начало которого
совпадает с началом вектора а, а конец — с концом вектора Ъ\,
является суммой векторов а и b (рис. 235, а). Такой способ
сложения двух векторов называется правилом треугольника.
Имеет место такое векторное равенство: AB-\-AD=AC, где
А, В, С и D — вершины параллелограмма ABCD. Это еще одно
правило сложения векторов — правило параллелограмма.
Если даны два вектора О-A и ОВ, то суммой векторов ОА
и ОВ будет вектор ОС, где ОАСВ — параллелограмм (рис. 236).
Разностью векторов a (ar, аа) и b (bi; bi) на плоскости назы-
вается такой вектор с (ci; сД который в сумме с вектором
Ъ дает вектор а, т. е. координаты вектора с=а — Ь таковы:
Ci=ai — bi, С2=аг~Ь'2.
Если даны векторы АС н AD (с общим началом), то раз-
ностью векторов АС и. AD является вектор DC (рис. 235,0):
ЛС AD=DC.
Это правило следует использовать при нахождении разнос-
ти векторов. _ _
Суммой векторов o(aj; аг, аз) и. b (&i; Ьц Ьз) в прост ранет-
Так же как и на плоскости, доказывается векторное равен-
ство ___ ___ __
АВ\ВС^ЛС.
Правило параллелограмма для суммы двух векторов, непа-
раллельных одной прямой, в пространстве сохраняется.
Сумма трех векторов, непараллельных одной плоскости,
находится по правилу параллелепипеда. На рисунке 237 вектор
ACi равен сумме векторов а, Ъ и с, отложенных от одной точки
А, при этом отрезок ACi является диагональю параллелепипе-
да ABCDAiBiCiDi.
83. Умножение вектора на число. Коллинеарные векторы.
Произведением вектора (дн д2) и числа К называется вектор
(Xai; Хд2), т. е. (ди д2)Х=(Хаи Хда).
Из определения операции умножения вектора на число сле-
дует, что для любого вектора а и чисел X, р
(X-f-ji)’fl=Xa-f-|xa.
Для любых двух векторов а и b и числа X
Х(д+Ь)=Ха-|-Хд.
Т.6.3.
Абсолютная величина^ вектора Ад равна |Х|«|д|.
Направление вектора Ха при а=^= 0 совпадает с направ-
лением вектора д, если XX), н противоположно
направлению вектора д, если Х<0.
Вектор называется единичным, если его абсолютная величи-
на равна единице. Единичные векторы, имеющие направление
положительных координатных полуосей, называются коорди-
натными векторами или ортами.
__ Координатные _векторы на плоскости принято называть
е( (1; О) на оси х н е2 (О; 1) на оси у. Любой вектор а (аг, аг) пред-
ставляется в виде
д (au
Произведением вектора а (аг аг, аз) в пространстве и числа
1 называется вектор (Лдй Адг", Адз). Так же как и на плоскости,
абсолютная величина вектора Ад равна • |д|, а направле-
ние совпадает с направлением вектора а (д=/=0), если А<>0,
и противоположно направлению вектора а, если А<0.
Для вектора в пространстве имеет место разложение:
а (аг, аг, аз)=ai®i Н-агба+азвз,
где ci (1; О; 0), (0; 1; 0), ез (0; 0; 1) — координатные векторы.
Два отличных от нуля вектора называются коллинеарны-
ми, если они лежат на одной прямой или на параллельных
прямых. На рисунке 238 векторы а и Ь, b и с коллинеарные.
Т.6.4.
У коллинеарных векторов соответствующие коорди-
наты пропорциональны. И обратно: если у двух век-
торов соответствующие координаты пропорциональ-
ны, то векторы коллинеарны.
Пример 1. Доказать, что средняя линия треугольника
параллельна его третьей стороне и равна половине этой
стороны.
Решение. Рассмотрим ДАВС (рис. 239). Пусть АВ=с,
ВС=а, АС~Ь. Тогда по правилу треугольника с-\-а=Ь
(п. 82).
Пусть М и N — середины сторон АВ и ВС треугольника
АВС, тогда MN=MB+BN=^- AB+-1-BCU-1-C+-^-а =
=-И+«)=-|-ь.
Так как АС Ь и Ь, то AflV=-|-AC. Таким образом,
MN сонаправлен с АС, следовательно, _АС| \MN. Так как MN—
=~АС, то MN=±-AC.
I^i 384
Пример 2. Коллинеарны ли следующие векторы:
а) а (3; 6; 8) и ^(6; 12; 16); б)_с(1; — 1; 3) и d(2;3;15);
n)i(l;O;O) и fe(O;l;O); г) т (0; 0; 0) и п(5;7;-3);
д) —1; 5) и 5(-1; -3; -15)?
Решение, а) Координаты вектора а (3; 6; 8) пропорцио-
нальны координатам вектора Ь(6; 12; 16), так как =
== fe. Поэтому а — kb, и, следовательно, векторы а и b кол-
линеарны.
б) Координаты вектора с (1; — 1; 3) не пропорциональны
координатам вектора d (2; 3; 15); например, > поэтому
векторы с и d не коллинеарны. В самом деле, если предполо-
жить, что векторы с и d коллинеарны, то существует число k,
такое, что с=kd. Но в таком случае координаты вектора с про-
порциональны координатам вектора d, что противоречит усло-
вию задачи.
Остальные случаи рассматриваются аналогично.
84. Скалярное произведение векторов. Скалярным произве-
дением векторов a (ai; az) м b (Ь»; Ъ?) на плоскости называется
число ai Ь 1+02^2- Для скалярного произведения векторов
употребляется такая же запись, как и для произведения чисел.
Скалярное произведение а «а обозначается а2. Очевидно,
а2=|а|2.
Из определения скалярного пронзведения^векторов следует,
что для любых векторов а(в];аа), Ь (bi; Ьг), c(ci; сэ)
(а + Ь) • с=а • <?+Ь • с.
Т.6.5. 1 Скалярное произведение векторов равно произведе-
I нию их абсолютных величин на косинус угла между
I ними.
Пусть нам даны векторы АВ и CD, угол между которыми
АВ-CD
а, тогда АВ • CD=АВ -CD -cos а, откуда cos ст — АВ.СР
Из Т.6.5, следует, что скалярное произведение двух взаим-
но перпендикулярных векторов равно нулю. И обратно: если
скалярное произведение отличных от нуля векторов равно
нулю, то векторы перпендикулярны.
На рисунке 240 изображены векторы ОА и ОВ, для кото-
рых ОА-ОВ— 0. Если AB-CD=0, то угол между ними равен
90°, т. е. эти векторы лежат иа перпендикулярных прямых.
Скалярным произведением векторов а{а\\О2\а^ и
Ь (bi> Ьг; Ьз) в пространстве называется число ajbi +о2Ь2+«зЬз.
Для скалярного произведения двух векторов в пространстве
справедлива теорема 6.5.
Пример 1. Даны векторы а (1;_4) и Ь (— 3; 2). Найти такое
число X, при котором вектор а+15 перпендикулярен векто-
ру Ь- _ _ _
Решение. Векторы а+ХЬ н b перпендикулярны, если их
скалярное произведение равно 0.
Вектор «+ХЬ имеет координаты 1 —ЗХ и 4 + 2Х, тогда ска-
лярное произведение векторов а+15 н Ъ равно
(1 — 31) ( — 3)+(4+2Х)-2=5 + 13Х,
5+Ш=0, т. е. >.== —i .
Итак, при 1=—векторы а +15 и Ь перпендикулярны.
Пример 2. Доказать, что сумма квадратов диагоналей
параллелограмма равна сумме квадратов всех его сторон.
Р е ш е н ие. Пусть ABCD — параллелограмм (рис. 241).
Пусть АВ=а, AD=b, причем |AB|=]CD|=a, |АО| =
= |ВС|=б.
По правилам сложения и вычитания векторов (п. 82).
AC=AB+AD, db=ab~ad,
AC=a+b, DB=a—b.
Используя свойства скалярного квадрата, получим АС2-]-
+ЙР=(а + Ь)2 + (а--Ь)2=о2 + 2а.Ь + Ь’+а2^2а-Ь + Ь2 =
= 2аг + 2Ь2, т. е. АС'ПВ-=АВ^ \-ВС‘‘+CD'1+AD'.
Пример 3. В тетраэдре ABCD противоположные ребра
AD и. БС, а также BD к АС взаимно перпендикулярны. До-
13 Заказ 769
казать, что противоположные ребра CD и АВ также взаимно
перпендикулярны.
Решение. Пусть DA=a, BD= b, DC = c
(рнс. 242). Отсюда ВА = Ь+а, АС=с—а, ВС—с+Ь. По усло-
вию AD_L.BC и BD.LAC, поэтому DA_LBC и BDJ-AC. Следо-
вательно, a(c+ft)=O и Ь'(с—а)=0, откуда — а-с=а-Ь и
b-c=b‘O. Из этих двух равенств следует, что —а-с—Ь-с
или (64”й),с=0* Но b-\-a=BAt с—DC, поэтому BA-DC=O,
и, значит, ABJ-CD.
Пример 4. Дана правильная треугольная призма
ABCAiB]Ci, в которой AAjZAB—-^2 (рис. 243). Найти угол
между прямыми АС] и А [В.
Решение. Пусть АВ==а, тогда AAi~a ^2. Введем пря-
моугольную систему координат так, как показано на рисунке
243. Тогда вершины А, В, Аь Cj имеют следующие коорди-
наты: а(^; ; о), В(0;0;0), А,(^;
С> (0; а; а д/2) (объясните почему). Отсюда находим координаты
векторов ACi и ВАь
Векторы ACi и BAj принадлежат прямым ACi и ВА|, ис-
комый угол между которыми обозначим через <р. По Т.6.5 по-
ACi-ВА,
лучаем cos4>^ACi:BAl =
3 -2 . 1 J . 0-2
—~2» отсюда <p=60°.
ПРИЛОЖЕНИЯ
Основные формулы и соотноше-
ния .......................388
Предметный указатель . . . 405
ОСНОВНЫЕ ФОРМУЛЫ И СООТНОШЕНИЯ
АЛГЕБРА И НАЧАЛА АНАЛИЗА
I. Основные законы алгебры
Для любых действительных чисел a, Ь, с справедливы
равенства:
а4-& = а (переместительный закон сложения),
а-{-(& +с)=(а+ &)4-е (сочетательный закон сложения),
а4-0=а,
а4-(—а)=0,
ab=ba (переместительный закон умножения),
a(bc)=(ab)c (сочетательный закон умножения),
a (b-\-c)=ab-\-ac (распределительный закон умножения от-
носительно сложения),
а‘1—а,
a-i-=l («¥=0).
II. Деление с остатком
Если т, п, р, г — натуральные числа, причем т — делимое,
п — делитель, р — частное и г — остаток (г<п), то
т=пр-\-г.
III. Числовые неравенства
Если а > Ь, то Ъ <_а.
Если а >Ь и &>с, то а>с.
Если а>Ь, то а-[-с>Ь-]-с.
Если а>Ь и с>0, то ас>Ьс.
Если а>Ь и сСО, то ас<Ьс.
Если а>Ь и c>d, то a+obj-d.
Если а>0, &>0, с>0, d>0, причем а>Ъ и Od, то
ас Z> bd.
Если а> !>> 0 и п — натуральное число, то ап> Ьп.
IV. Модуль действительного числа и свойства модулей
I г если а^О,
с — ( —а, если а<О (определение модуля).
389
|а| >0, |a| = | — a|,
|a&| = |a|-|b|, |a|2=a2,
, b#O.
V. Расстояние p (Л; В) между двумя точками А и В
1) координатной прямой при А (а) и В(Ь):
р (А; В)= |с— Ы;
2) координатной плоскости при A(xi; <л) и В(хг; */г):
р (Л; В) = vz(xi —хгУ + (у, — Л/г)2-
VI. Разложение иа множители
а2 — Ь2 = (а—Ъ) (а -|- Ь),
а3 — Ь3 — (а — b) (а2 4- ab &2),
a3 + b3=(a-[-b) (a2—ab + b2),
а2 + 2аЬ + Ь2=(а + Ь)2,
с2 — 2аЬ 4- Ь2=(а— Ь)2,
а3+За2Ь + За Ь2 + Ъ3=(а 4- Ь)3,
а3—За2» 4- За Ь2 — Ъ3==(а—Ъ)\
ax2-j-bx~l-e=a (х—Xi)(x—х2), где Xi и х2 — корни уравне-
ния ах2 -^-Ъх-\-с—О,
хп—ап—(х—а)(хп-'+ахп~2+а2хп 34-.„4-ап 2х+ап ).
VII. Арифметический корень и его свойства
Если а^О, то ^=х означает: 1) х^О; 2) хп=а (опреде-
ление арифметического корня).
\^Ь = \а-^Ь,
->Ja2= lai.
VIII. Степень с рациональным показателем
ал=а-а-...-а, а'=а (определение степени с натуральным
п множителей Показателем),
а' где а^О (определение степени с положитель-
ным дробным показателем),
aQ=l, где а^О (определение степени с нулевым пока-
зателем),
Q
390
a r=— , где a>0 (определение степени с отрицательным
рациональным показателем),
ar> ’(f3=ar'+r\
ar‘ :(f3—ar,~r\
(аг'Г=апГз,
(ab}r—arbr.
(!)'=£
IX. Квадратное уравнение ах24-Ьх-|-е=О
— b±^Jb — Ь±-\}Ъ2 — 4ас „
хк2=——-----=------2а---- (формула корней квадратного
уравнения).
xii2=~-——где k=— (формула корней квадратного
уравнения в случае, если Ь — чет-
ное число).
Теорема Виета. Если Xi и х? — корни приведенного
квадратного уравнения х2+рх-{-д = 0, то
Xi+«2=—А
3CiX2 = ?.
X. Стандартный вид положительного числа
а=вг10л,
где l<Oi<10, п — целое число (порядок числа а).
XI. Погрешности
Если а — приближенное значение числа а, то
|а—а| — абсолютная погрешность,
Ю0% — относительная погрешность.
XII. Логарифмы
Запись logo&=x означает, что а*=Ь\ ъпесъ а>0, а^=1
(определение логарифма).
lg Ъ — сокращенная запись для logic b (десятичный лога-
рифм).
1g 1=0, 1g 10 = 1, 1g 100=2, 1g 1000 = 3, ...» 1g 10"=n.
1g 0,1 = — 1, 1g 0,01 = — 2, 1g 0,001 = — 3, ..., 1g 10 ' = — n.
In x — сокращенная запись для loge x (натуральный лога-
рифм). 6 = 2,7182818284590...; lne = l, In 1=0.
391
Q
alo<-b=b, 101в b=b, eln 6 = b,
logQ X]X2 = log aX\ + We *2,
logo ^-= logo X] — logo X2,
logo Xi =r logo Xi (Xi >0, x2 > 0),
logQ b = (формула перехода к новому основанию).
logo b = Log„* bk (fey=0).
ХШ. Арифметическая прогрессия
a„+]=a„+d (определение арифметической прогрессии),
an=ai + d(n— 1) (формула п-го члена),
ав=°я~1^'Ои+1 (характеристическое свойство),
SBs=g|+g*. п=2°‘ (формула суммы п первых чле-
нов).
XIV. Геометрическая прогрессия
6„+i = bnQ, bi=/=0, (определение геометрической про-
грессии),
bn=bvqn~^ (формула п-го члена),
bl=bn-i bn4-i (характеристическое свойство),
Sn—Ьп9у (формула суммы п первых членов),
S=j3~ (формула суммы бесконечной геометрической про-
9 грессии при ]?|<1).
XV. Тригонометрия
1. Свойства тригонометрических функций:
sin (—х) =—sin х,
cos(—x)=cos X.
tg(-x)=—tgx,
ctg( — x) = — ctg X,
sin (x4-2Ttfe)—sin x, k^Z,
cos (x + 2nfe)=cos x, k^Z,
tg (x+tg x, k €Z,
ctg (x 4- nk) = ctg x, k£Z.
392
2. Таблица значений тригонометрических функций некото-
рых углов:
Функция Аргумент
О п К л т п т л 2 л Зл 2
sin а 0 1 2 -у;2 2 3^ 2 1 О -1
сой а 1 3^ 2 Л'2 2 1 2 О —1 0
tea О 3^ 3 1 д/3 - 0 -
ctg а - V3 1 3 О - О
Примечание. Связь между градусной и радианной ме-
рами измерения угла:
iso рад-
3. Формулы, связывающие тригонометрические функции
одного и того же аргумента:
sin2 а cos2 а=1,
tgct =
sin а
cos а
ctg а —
COS Ct
sin ct
14-tg2a =—t—, 1 + ctg2 а=-гтг
1 s COS2 a 1 Sin2
4. Формулы двойного угла:
sin 2а == 2 sin a cos а,
cos 2а=cos2 a—sin2 а,
±_Л_. _ 2tga
5. Формулы понижения степени:
sin;K-1-^62a,
393
6. Формулы сложения аргументов:
sin (a±₽)=sin a cos ₽=bcos a sin 0,
cos (oc±p)—cos a cos 0 + sin a sin ₽,
tg(g + P)= *«**£..
U l=Ftgatg₽
7. Формулы преобразования суммы тригонометрических
функций в произведение:
• i-o Cl • Cl4-₽ tt — ₽
sin tx + sin P=2 sin—cos—
- • Cl a — ₽ a+₽
sin a—sin a=2 sin —cos —,
। о о a4-₽ a—6
cos cc + cos p = 2 cos 2 cos 2 ,
о о a4₽ •« a~₽
cos a—cos p= — 2 sin —^-i-sin——£-
tga±tg₽=i^2±S.
ь “» < cos a СОЗ ₽
8. Знаки тригонометрических функций по четвертям:
Функция Четверть
I II Ill IV
sin + + — -
cos — —
tg + - + —
ctg + - + -
9. Формулы приведения:
Функция Аргумент t
л i+“ л—a n-j-a 3л 2~a 3л ~2+a 2 л —a
Bin t сова соз a sin a —sin a —cos a —cob a —sin a
cos t sin a —sin a — cos a —cos a —sin a sin a coe a
tgt ctg a —Ctg a —tg a tga ctg a —ctg a —tga
ctgt tga —tg a —ctg a ctg a tga —tga — ctg a
10. Решение простейших тригонометрических уравнений:
sinx=a, |а|^1, х=(—1)" arcsin а-\-лп, n£Z:
cosx=a, |а|<1, х= ± arccos а-{-2л.п, n£Z;
tgx—a, x=arctga-|-nn, n£Z;
clgx=a, x—arcctg а-|-лл, nf-Z.
11. Обратные тригонометрические функции:
—g-Orcsin x<~-, 0 arccos x< л,
—< arctg *<-£-, 0 < arcctg x< я,
arcsin (—x) = — arcsin x; arccos (—x) ~ л—arccos x;
arctg (—x) = — arctg x; arcctg (—x)=л — arcctg x.
XVI. Асимптоты графика функции y=f(x)
Если lim f[x)=b, то y = b — горизонтальная асимптота.
Х-*-чо
Если lim f (х)~оо, то х=а — вертикальная асимптота.
х-*-а
XVII. Производная
у'=f (х)= lim “ = lim (определение про-
V V ' Дх-ОАХ Лх.О Дх
изводной).
1. Правила дифференцирования:
(и + vj == и' + и', (Си)'=Си',
, ч, . . . ( и \, u'v — uo'
(uv)' = u'v + uv', J = ,
2. Формулы дифференцирования:
С7=0,
(/?x4-b)'=fe,
(х’У=га'-’,
(е*)'=е*,
(а*)'=ах Ina,
(lnx)-=i.
(sin !X)' = COS X,
(cosx)'=~-sinx,
(ctg*)'=-8-^-
(arcsin x)'=(—arccos x)' >
(arctg x)'—(—arcctg x)' = t .
396
3. Уравнение касательной к графику функции y = f{x):
»=/(«)+/'(«)(«—«),
где х~а — абсцисса точки касания.
ХУШ. Первообразная и интеграл
Если F' (x)=f (х), то F (х) — первообразная для f(x) (опре-
деление первообразной).
1. Правила вычисления первообразных.
Если F (х) — первообразная для f (х), а Н (х) — первообраз-
ная для й(х), то
F(x)4-H(x)— первообразная для /(х)+Л(х);
kF (х) — первообразная для kf (х);
— F (kx -|- Ь) — первообразная для f (kx -|- 6).
2. Таблица первообразных (в таблице для каждой функции
дана одна из первообразных).
Функция Первообразная
/(*)=* /(x)=x,(r=jfc — 1) /(*)=“ /(х)=е* f (х)—а' г V(x}~In |х| F («)=-r- v 1аа
Функция Первообразная
f(x}~ sin х F (x)= - cos x
f (х)=соа х F(x)—sinx
F(x)= — ctgx
'(x>=i5?V F(x)=tgx
/(x,= ')T==j -yl — * F (x)= arcsin x
F(x)—arctg x
3. Вычисление интеграла:
ь
J f (x)dx=F (b)—F (а) (формула Ньютона—Лейбница).
4. Вычисление площади криволинейной трапеции, ограни-
ченной прямыми х—а, х = Ь, где а<Ь,и графиками функций
У=Л (*), У=к(х), где на [а; &]:
5 (/2(х)—Л (x))dx.
396
ГЕОМЕТРИЯ
I. Аксиомы геометрии
Основные свойства принадлежности точек и прямых
А — Ip Какова бы нн была прямая, существуют точки, при-
надлежащие этой прямой, и точки, ие принадлежащие ей.
А —-12. Через любые две точки можно провести прямую, и толь-
ко одну.
Основные свойства взаимного расположения точек на прямой
и на плоскости
А — II2. Из трех точек на прямой одна и только одна лежит
между двумя другими.
А — Цо. Прямая разбивает плоскость на две полуплоскости.
Основные свойства измерения отрезков и углов
А — Шь Каждый отрезок имеет определенную длину, боль-
шую нуля. Длина отрезка равна сумме длин частей, на которые
он разбивается любой его точкой.
А — III2. Каждый угол имеет определенную градусную меру,
большую нуля. Развернутый угол равен 180°. Градусная мера
угла равна сумме градусных мер углов, на которые он разби-
вается любым лучом, проходящим между его сторонами.
Основные свойства откладывания отрезков и углов
А — IV]. На любой полупрямой от ее начальной точки можно
отложить отрезок заданной длины, и только один.
А — IV2. От любой полупрямой в заданную полуплоскость
можно отложить угол с заданной градусной мерой, меньшей
180°, и только один.
Существование треугольника, равного данному
А — IV3. Каков бы ни был треугольник, существует равный
ему треугольник в заданном расположении относительно дан-
ной полупрямой.
Основное свойство параллельных прямых
А — V. Через точку, не лежащую на данной прямой, можно
провести иа плоскости не более одной прямой, параллель-
ной данной.
Основные свойства плоскостей в пространстве
С]. Какова бы ни была плоскость, существуют точки, при-
надлежащие этой плоскости, и точки, ие принадлежащие ей.
397
С2. Если две различные плоскости имеют общую точку, то они
пересекаются по прямой.
С3. Если две различные прямые имеют общую точку, то через
них можно провести плоскость, и притом только одну.
II. Треугольники
а, Ъ, с — стороны треугольника.
а, р, у — внутренние углы тре-
угольника.
а', У' — внешние углы тре-
угольника.
ha, hb, hc — высоты треугольника,
опущенные из вершин треугольника
на прямые, содержащие соответствующие противоположные
стороны а, Ъ, с.
та, тс — медианы треугольника, соединяющие вершины
треугольника с серединами противолежащих сторон а, Ь, с.
la, 1ь, 1с — биссектрисы треугольника, соединяющие вер-
шины треугольника с точками на противолежащих сторонах
а, Ь, с.
MN — средняя линия треугольника.
Р — периметр треугольника.
р — полупериметр треугольника.
R — радиус окружности, описанной около треугольника.
г — радиус окружности, вписанной в треугольник.
&лавс — площадь треугольника АВС.
Сумма углов треугольника
сс-|-₽-Ь7 = 180о.
Свойства внешних углов треугольника
а'=₽ + Ь ₽' = ос-Ьу, /=« + ₽,
а'>р, а'>у, р'>а, Р/>Т, ?'>а, у' >Р-
Неравенство треугольника
a<b-j-c, b<a+c, сСа-^-Ъ.
Соотношения между сторонами и углами треугольника
Если с<а, то у<а.
Если е<Ъ, то у<р.
Если то а<Ъ.
Если то Ь~>с.
Если а>с, то ct>y.
Если а<_Ь, то а<₽.
Если у<а, то c<za.
Если то а>с.
Теорема синусов
а ____ Ь___с
sin a Bin fl sin у"
Теорема косинусов
а2 = b2-f-c2 — 2bc cos а,
b2=a2-j-c2— 2ас cos fl,
с2=а2 4- b2 — 2ab cos у.
Периметр и полупериметр треугольника
Р=а + Ь+с,
Свойства средней линии треугольника
MN\\AC, MN=±-.
Площадь треугольника
S=~^-aha* S~-^-bhb* S=~^-chci
S ас sin fl, S—^-ab sin y, be sin a;
S=Vp (p— a) (p— b) (p—с) (формула Герона).
Равнобедренный треугольник
а=с, Z.a = Z.?,
hb — ть h
Равносторонний треугольник
a=b—c, a = fl=Y—60°;
ha — la — maf kb-—lb—~Uibt he — lc —
Прямоугольный треугольник
а = 90°, b, с — катеты, а — гипотенуза,
а2—Ъ2-\-с2 (теорема Пифагора)'*
R—^-=ma, S^=^-bc,
399
sin-у=-^-, cosy=-^-, tgy=-|-,
sin P=_~» cos Э=“» tg ₽=“|“-
III. Четырехугольники
Параллелограмм
a, b — стороны параллелограмма.
ha,hb — высоты параллелограмма,
опущенные из вершин параллело-
грамма на прямые, содержащие сто-
роны параллелограмма а, Ь.
di, ds — диагонали параллело-
грамма.
а, V — углы параллелограмма,
а--{-у=180°.
Площадь параллелограмма
S~aha, S=bhb, S=ab sin а.
Связь между сторонами и диагоналями параллелограмма
d? + d2=2(a2+&2).
Прямоугольник
а=у=90°,
di —ds,
S=ab,
dl=a2 + b2.
Квадрат
В а С
А а о
a=y=90°,
di =d2, di _Lc?2,
S=a2,
d,=a-^2.
d,±d2f
S=a2 sin ct,
S=^-did2,
Равнобокая трапеция
MN=a-~— средняя линия
трапеции;
AB=CD,
а=у,
di=d2.
IV. Окружность и круг
В — радиус окружности (круга),
С—2лй — длина окружности,
— длина дуги,
S=3iR2 — площадь круга,
SceKT -------площадь кругового сектора,
£сеги=зэд — площадь кругового сегмента.
V. Правильные многоугольники
8=-|-В!лвт^.’,
„ . 180е
2 sin----
_4 180 °
2 tg----
VI. Объемы и площади поверхностен тел
Наклонная призма
1. Объем наклонной призмы
V=SBCat
где с — площадь перпендикулярного сечения наклонной
призмы, а — боковое ребро.
Площадь боковой поверхности наклонной призмы
86=Ро<!о,
где Рп с — периметр перпендикулярного сечения наклонной
призмы, а — боковое ребро.
Площадь полной поверхности наклонной призмы
Sd = S64-2Soi;b,
где S- — площадь боковой поверхности наклонной призмы,
$осн — площадь ее основания.
Прямая призма
Объем прямой призмы
а,
где SDCH — площадь основания прямой призмы, а — боковое
ребро.
Площадь боковой поверхности прямой призмы
S6=Pосн а,
где Роси — периметр основания прямой призмы, а — боковое
ребро.
Площадь полной поверхности прямой призмы
^Se+aSocH,
где Se — площадь боковой поверхности прямой призмы, Яосн —
площадь основания.
Прямоугольный параллелепипед
Объем прямоугольного параллелепипеда
V=dbc,
где a, Ъ, с — измерения прямоугольного параллелепипеда.
Площадь боковой поверхности прямоугольного параллеле-
пипеда
^=2с(а4-6),
где а, Ь — стороны основания, с — боковое ребро прямоуголь-
ного параллелепипеда.
Площадь полной поверхности прямоугольного параллелепи-
педа
SB=2 (ab 4- Ьс 4- ас),
где а, Ь, с — измерения прямоугольного параллелепипеда.
Куб
V=a3, 3,=4аг. S„=6aJ,
где а — ребро куба.
Пирамида
Объем пирамиды
У=4-5.«Н.
где — площадь основания пирамиды, Н — высота.
Площадь боковой поверхности пирамиды равна сумме
площадей ее боковых граней.
Площадь полной поверхности пирамиды
|864-8<)<.и,
гда S6 — площадь боковой поверхности пирамиды, SOCH — пло-
щадь основания.
Площадь боковой поверхности правильной пирамиды
где — периметр основания правильной пирамиды, I — ее
апофема.
Усеченная пирамида
Объем усеченной пирамиды
V=-|(S, +&+1/&&),
где Si, Sb — площади основании усеченной пирамиды, а Н —
ее высота.
Площадь боковой поверхности усеченной пирамиды равна
сумме площадей ее боковых граней.
Площадь полной поверхности усеченной пирамиды
где S6—площадь боковой поверхности пирамиды, Si, S2—
площади оснований.
Площадь боковой поверхности правильной усеченной пира-
миды
s«=^.z,
где Pi, Ps — периметры оснований, а I — ее апофема.
Цилиндр
Объем цилиндра
У=лЯ2Н,
где R — радиус основания цилиндра, а Н — его высота.
Площадь боковой поверхности цилиндра
S6=2nRH,
где R — радиус основания цилиндра, Н — его высота.
Площадь полной поверхности цилиндра
Зп=2лЯД + 2л№,
где R — радиус основания цилиндра. И — его высота.
Конус
Объем конуса
V=-i- яЯ! Н,
где R — радиус основания конуса, Н — его высота.
Площадь боковой поверхности конуса
S6=3iR’L,
где R — радиус основания конуса, L — его образующая.
Площадь полной поверхности конуса
Sa=3iR(R+L),
где R — радиус основания конуса, a L — его образующая.
404
Усеченный конус
Объем усеченного конуса
V=-i пН (Л2+Яг+г2),
где R, г — радиусы основании усеченного конуса, Н — его
высота.
Площадь боковой поверхности усеченного конуса
£б—л£> (Z?-f-r),
где Я, г — радиусы оснований усеченного конуса, L — его
образующая.
Площадь полной поверхности усеченного конуса
Sn=лЕ (R+г)+лЯ2 + лг2,
где R, г — радиусы оснований усеченного конуса. L — его
образующая.
Сфера и шар
Объем шара
г=4яН3’
где R — радиус шара.
Площадь сферы (площадь поверхности шара)
Я=4лЯ2,
где R — радиус сферы.
Объем шарового сегмента
V=nH2(R—1н),
где Н — высота шарового сегмента, R — радиус шара.
Объем шарового сектора
У=-|-лН2.Н,
где Н — высота соответствующего шарового сегмента, R —
радиус шара.
предметный указатель
Абсолютная величина
----вектора 378
-----числа 36
Абсцисса 351
Аксиома 257
Алгебраическая форма комплексного
числа 49
Амплитуда колебания 114
Аналитическое задание
----------функции 71
-----числовой последовательнос-
ти 202
Апофема
— правильной пирамиды 332
--------- усеченной 332
Аргумент 71
— вспомогательный 157
Асимптота
— вертикальная 215
— горизонтальная 211
Бином Ньютона 61
Биссектриса
— треугольника 275
— угла 265
Боковые стороны
— — равнобедренного треугольни-
ка 278
-----трапеции 294
Вектор 378
— единичный 382
— нулевой 380
Векторы
— коллинеарные 383
— одинаково направленные 378
— противоположно направленные 379
— равные 379
Бертина
— конуса 336
— ломаной 296
— многогранника 328
— многоугольника 297
— параболы 108
— пирамиды 331
— треугольника 275
— угла 263
----многогранного 327
— — трехгранного 327
— четырехугольника 290
Вершины
— четырехугольника противополож-
ные 290
------ соседние 290
Вращение 370
Выделение полного квадрата 103
Вынесение множителя
--------из-под знака корня 63
----общего за скобку 58
Выражение
— алгебраическое 53
— — дробное 53
----иррациональное 53, 68
— — рациональное 53
— — целое 53
— сопряженное 70
— трансцендентное 116
— тригонометрическое 121
— числовое 12
Высота
— конуса 336
— параллелограмма 292
— пирамиды 331
— призмы 329
— трапеции 295
— треугольника 275
Вычитаемое 12
Вычитание
— дробей десятичных 24
----обыкновенных 21
------- рациональных 64
— комплексных чисел 50
Геометрические фигуры
-----основные в пространстве 314
-------на плоскости 256
Геометрический смысл производной
224
Геометрическое место точек
-------в пространстве 342
-------на плоскости 288
Геометрия 255
— Лобачевского 270
— евклидова 25Б
Гипербола 83
Гипотенуза 280
Гомотетия 367
Градус 264
Градусная мера
----- дуги 267
----- угла 264
Граница
— круга 262
— области 327
Грань
— многогранника 328
— угла двугранного 327
-----многогранного 327
-----трехгранного 327
График
— гармонического колебания 114
— обратной пропорциональности 33
— прямой пропорциональности 79
— уравнения с двумя переменны-
ми 163
— функции 74
-----квадратичной 107
— — линейной 80
-----логарифмической 94
----- нечетной 76
----- обратной 93
— —- показательной 90
----- постоянной 78
------степенной 85
------— тригонометрической 98
------ четной 76
Графическое решение
------неравенства с одной перемен-
ной 179
--------------втором степени 185
----системы уравнений 169
— — уравнения с одной перемен
ном 153
Движение 369
Действительная часть комплексного
числа 49
Деление
— дробей десятичных 25
----обыкновенных 21
----рациональных 85
— комплексных чисел 50
— с остатком 12
Делимое 12
Делитель 12
— общий 15
----наибольший 15
— числа 12
Десятичное приближение числа
------------ — по избытку 44
------недостатку 44
Диагональ
— многоугольника 297
— параллелограмма 291
— призмы 329
— прямоугольника 293
— ромба 293
— четырехугольника 290
Диагональное сечение призмы 329
Диаметр
— круга 262
— окружности 262
— шара 338
Диаметральная плоскость 339
Диаметрально противоположные точ-
ки шара 338
Дискриминант квадратного уравне-
ния 133
Дифференцирование 220'
— произведения 220
— сложной функции 221
— суммы 220
— частного 220
Длина
— дуги 801
— • ломаной 296
— окружности 801
— отрезка 259
Додекаэдр 333
Доказательство 257
— неравенств 199
Дополнительные
— лучи 261
— множители 20
— полупрямые 261
Допустимые значения переменной 63
Достаточное условие экстремума 229
Дробная часть числа 39
Дробь
— десятичная 22
бесконечная 27
периодическая 23
смешанная 23
— чистая 28
— неправильная 18
— несократимая 19
— обыкновенная 17
— правильная 18
— рациональная 63
Дуга окружности 267
Единица измерения
— объема 344
— площади 308
Звено ломаной 296
Знак
— интеграла 247
— неравенства нестрогого 33
— — строгого 33
— приближенного равенства 43
Знаменатель
— геометрической прогрессии 205
— дроби 17
— общий обыкновенных дробей 19
—---------наименьший 20
----рациональных дробей 63
Значащие цифры 24
Значение
— алгебраического выражения 64
— буквы 17
---— производной функции в точке 219
— функции 71
-------- наибольшее 231
------наименьшее 231
— числового выражения 12
Избавление от иррациональности в
знаменателе 70
Извлечение квадратного корня из на-
турального числа 45
Измерения прямоугольного паралле-
лепипеда 330
Икосаэдр 333
Интеграл 247
Интервал 35
Исследование системы двух линейных
уравнений с двумя переменными 170
Касательная
— к графику функции 223
— к окружности 274
— к шаровой поверхности 339
— плоскость конуса 336
----цилиндра 335
----шара 339
Касание окружностей
----внешнее 27 4
—---внутреннее 274
Катет 280
Квадрат 293
Квадратный трехчлен 60
Колебания
— гармонические 114
—- синусоидальные 114
Комплексный нуль 48
Композиция движений 371
Конец вектора 379
Концы отрезка 259
Конус 336
— прямой 336
— усеченный 337
Координата точки на прямой 30
Координатные
— векторы 382
— четверти 352
Координаты
— вектора 380
— декартовы в пространстве 352
---на плоскости 351
— середины отрезка 354
— точки в пространстве 353
---на плоскости 351
Корень
— арифметический 40
— квадратного трехчлена 60
— — уравнения 131
— квадратный 41
— многочлена 60
— нечетной степени из отрицательно-
го числа 41
— посторонний для уравнения 137
— уравнения 131
Косинус
— острого угла 302
— угла 96
— числа 96
Котангенс
— угла 96
— числа 96
Коэффициент
— гомотетии 368
— одночлена 55
— подобия 374
— при переменной 163
•— пропорциональности 79
--- обратной 82
Крайний член пропорции 38
Кратное 12
— общее 16
------наименьшее 16
Критическая точка 229
Круг 262
Круговой
— сегмент 313
— сектор 312
Куб 330
Линейка 284
Логарифм 117
- — десятичный 120
— натуральный 95
— произведения 117
— степени 118
- — частного 117
Логарифмирование 119
Логарифмируемое число 117
Ломаная 296
— замкнутая 296
— простая 296
Луч 35, 261
— открытый 35
Максимум 228
Мантисса десятичного логарифма 121
Медиана треугольника 275
Метод
— докавательства от противного 258
------ неравенства 199
— —— оценки знака разности 199
— промежутков 189
— решения системы уравнений 166
---------введения новых перемен-
ных 167
---------подстановки 166
---------— сложения 166
---------умножения и деления 171
----уравнения 142
------— введения новой перемен-
ной 142
----— возведения в степень 147
--------- графическим 159
---------разложения на множите-
ли 141
Минимум 228
Мнимая единила 49
— часть комплексного числа 49
Многогранник 328
— выпуклый 328
— правильный 333
Многоугольник 297
— вписанный в окружность 299
— выпуклый 298
— описанный около окружности 299
— плоский 297
— правильный 298
409
Многочлен 56
— второй степени 60
— первой степени 60
— третьей степени 60
— n-й степени 60
Множители 11
— дополнительные 63
Модуль
— вектора 379
— числа 36
Наклонная 273, 324
Направление координатной прямой 31
Начало
— вектора 379
— координат 73, 353
— луча 261
Начальная
— точка полупрямой 261
— фаза колебания 114
Необходимое условие экстремума 229
Неравенство
— • Коши 199
— с переменной 178
-------второй степени 183
-------дробно-линейное 132
-------иррациональное 193
-------линейное 179
-------логарифмическое 191
—------показательное 191
---— с модулями 187
------- — тригонометрическое 195
— треугольника 276
— числовое 33
Область 326
— значений функции 71
— многоугольная 298
— определения алгебраического вы-
ражения 53
--- уравнения 139
------ функции 71
Образующая
— конуса 336
— цилиндра 334
Объем
конуса 347
------ усеченного 347
— куба 345
— пирамиды 345
— призмы 345
— прямоугольного параллелепипе-
да 345
— тела вращения 348
— цилиндра 346
— шара 343
— шарового сегмента 343
— — сектора 348
Одночлен 55
Окрестность точки 208
Окружность 262
— вписанная в треугольник 288
— описанная около треугольника 282
Октаэдр 333
Определение 257
Ордината 351
Орты 382
Осевое сечение
— — конуса 336
---- цилиндра 335
Оси координат 351, 353
Основание
— конуса 836
— логарифма 117
— наклонной 273, 324
— перпендикуляра 273, 323
— пирамиды 331
---- усеченной 331
— призмы 329
— равнобедренного треугольника 279
— степени 15, 39
— трапеции 294
— цилиндра 334
Основное свойство
-------- дроби обыкновенной 18
------------------ рациональной 62
---------- первообразной 243
Остаток 12
Ось
— абсцисс 73, 351
— вращения 371
— конуса 336
— ординат 73, 351
— симметрии параболы 108
----фигуры 376
— цилиндра 335
Отрезок 259
— направленный 378
— не пересекающийся с прямой 263
— пересекающийся с прямой 263
Парабола 74
— кубическая 84
Параллелепипед 330
— прямоугольный 330
Параллелограмм 291
Параллельность прямой и плоскос-
ти 318
Параллельный перенос
----в пространстве 377
----на плоскости 377
Параметр 160
Первообразная 243
Перемена знаков у членов дроби 62
Переменная 17
— зависимая 71
— независимая 71
Переместительное свойство
----сложение 11, 38
•---умножения 11, 38
Период
— бесконечной десятичной периоди-
ческой дроби 28
— функции 77
---- основной 77
Перпендикуляр 273. 323
— общий двух скрещивающихся
прямых 318
— серединный 273
Пирамида 331
— вписанная в конус 337
— описанная около конуса 337
— правильная 332
— усеченная 332
•----- правильная 332
Планиметрия 255
Плоскости
— координатные 353
— параллельные 319
— пересекающиеся 316
— перпендикулярные 325
Плоскость 314
— координатная 73
— симметрия фигуры 367
— числовая 73
Площадь
— боковой поверхности конуса 350
-------пирамиды 349
-------призмы 343
------- цилиндра 350
— квадрата 309
— круга 312
— кругового сегмента 313
-------------- сектора 312
— параллелограмма 309
— поверхности тела вращения 350
— полной поверхности конуса 350
-------пирамиды 349
------- призмы 348
— —• — цилиндра 350
— простой фигуры 308
—• прямоугольника 309
— ромба 309
— трапеции 810
— треугольника 310
Поверхность тела 327
Поворот 370
Погрешность
— абсолютная 48
— относительная 43
Подкоренное число 40
Подобные
— одночлены 56
— треугольники 376
— фигуры 375
Покаватель
— корня 40
— степени 15, 39
Полуинтервал 35
Полуось
— отрицательная 351
— положительная 351
Полуплоскость 263
Полупрямая 261
Полупрямые
— дополнительные 261
— одинаково направленные 379
— противоположно направленные 379
411
Порядок
— арифметических действий 12
— числа 41
Последовательность числовая 202
---возрастающая 202
---постоянная 203
— — убывающая 203
Построения на плоскости 285
Потенцирование 119
Правила вычисления интегралов 243
---первообразных 244
Правило
— параллелепипеда 332
— параллелограмма 381
— треугольника 331
Предел
— интегрирования верхний 247
---нижний 247
— функции 213
---в точке 214
— числовой последовательности 207
Преобразование
— подобия 374
— рациональных выражений 67
— тождественное 55
— • фигур 364
Приближенное значение числа 43
Приведение
— дробей к общему знаменателю
19, 63
— подобных членов 56
Призма 328
— вписанная в цилиндр 335
— - наклонная 330
—- описанная около цилиндра 335
— правильная 330
— прямая 329
Признак
— параллелограмма 291
— параллельности двух плоскос-
тей 319
---прямой и плоскости 313
---прямых 272
— перпендикулярности плоскостей
325
---прямой и плоскости 321
Признаки делимости 13
— равенства треугольников 273
—------прямоугольных 261
Приращение
— аргумента 218
— функции 218
Прогрессия
— арифметическая 203
— геометрическая 205
Проекция
— наклонной 273, 324
— прямой иа плоскость 323
Произведение
— • вектора и числа 383
— одночленов 55
— чисел 11
---комплексных 48
Производная 219
— вторая 223
Пропорциональность
— обратная 82
— прямая 78
Пропорция 38
Простейшие задачи на построение 285
Процент 26
Прямая 256
— координатная 30
— перпендикулярная плоскости 321
— числовая 33
Прямоугольник 293
Прямые
— параллельные 268
— пересекающиеся 257
— перпендикулярные 272
— скрещивающиеся 317
Равносильные
— неравенства 178
— системы уравнений 165
— уравнения 131
Равные
— векторы 379
— дроби 18
— комплексные числа 48
— - отрезки 277
— треугольники 277
— углы 277
— фигуры 372
412
Радиан 301
Радианная мера угла 301
Радиус
— круга 262
— начальный 95
— окружности 262
---цилиндра 335
— шара 338
Разложение на множители
-------квадратного трехчлена 60
—-------- многочлена 58
------- натурального числа 14
Разность
— арифметической прогрессии 203
— векторов 381
— чисел 12
---комплексных 48
Распределительное свойство умноже-
ния относительно сложения 11, 38
Расстояние
—- между параллельными прямы-
ми 273
---скрещивающимися прямыми
313
---точками 259, 354
-------координатной прямой 37
— от прямой до параллельной ей
плоскости 324
---точки до плоскости 323
---------прямой 273
Растяжение графика 105
Ребро
— боковое пирамиды 331
---призмы 329
— многогранника 323
— угла двугранного 327
---многогранного 327
---трехгранного 327
Рекуррентный способ гадания число-
вой последовательности 202
Решение
— неравенства с двумя перемен-
ными 196
-------одной переменной 178
— системы неравенств 180
---уравнений 164
— совокупности неравенств 132
— треугольников 307
— уравнений с двумя наременны-
ми 163
------ — одной переменной 131
Ромб 293
Свободный член
----многочлена 60
— — уравнения 133
Свойства
— арифметических действии 11, 38
— — корней 41
— логарифмов 117
— модулей 36
— прогрессии арифметической 204
----геометрической 206
— степеней с показателями действи-
тельными 47
-------------натуральными 39
---------рациональными 42
— числовых неравенств 34
Свойство
— измерения отрезков 259
----углов 264
— откладывания отрезков 261
----углов 265
— параллельных прямых 289
— плоскостей в пространстве 315
— принадлежности точек и прямых
на плоскости 256
— расположения точек на пря-
мой 259
— существования равных треуголь-
ников 273
Секущая 271
Сжатие графика 105
Симметрия
— относительно плоскости 367
-------- прямой 365
------точки 364
Синус
— острого угла 302
— угла 96
— числа 96
Система
— неравенств 180, 196
— уравнений 138
Скалярное произведение векторов
413
Q
-------в пространстве 385
-------на плоскости 384
Скорость изменения функции в точ-
ке 222
Слагаемые 11
Следствие уравнения 137
Сложение
— векторов 380
— дробей десятичных 24
— — обыкновенных 20
---рациональных 64
— комплексных чисел 50
Совокупность
— двух систем уравнений 168
— неравенств с одной переменной
181
— уравнений 136
Сокращение
— дробей обыкновенных 19
--- рациональных 63
Соответственные значения выраже-
ний 54
Сочетательное свойство
---сложения 11, 38
---умножения 11, 38
Способ группировки 59
Среднее
— арифметическое двух чисел 199
— геометрическое двух чисел 199
— пропорциональное 304
Средний член пропорции 38
Средняя линия
---трапеции 295
---треугольника 276
Стандартный вид
---многочлена 56
---одночлена 55
---* положительного числа 40
Старший член многочлена 60
Степень 15, 39
— многочлена 60
— одночлена 55
— с показателем дробным 42
—--- иррациональным 47
— — натуральным 15
нулевым 39
отрицательным цевым 39
рациональным 42
Стереометрия 255
Сторона
— многоугольника 297
— треугольника 275
— угла 263
— четырехугольника 290
Сумма
— бесконечной геометрической про-
грессии 210
— векторов 380
— интегральная 246
— чисел 11
---комплексных 48
Сфера 339
Табличное задание функции 73
Тангенс
— острого угла 302
— угла 96
— числа 96
Тело 327
— вращения 327
— простое 327
Теорема 257
— Виета 134
— косинусов 305
— о двух перпендикулярах 321
---делимости произведения 13
-------суммы 13
— — пределах 209
---трех перпендикулярах 324
— Пифагора 281
— синусов 305
— Фалеса 270
Тетраэдр 332
Тождественно равные выражения 54
Тождество 54
Точка 256
— внутренняя 326
— граничная 327
— касания окружностей 275
------ плоскости и сферы 339
— лежит между двумя точками 259
— не принадлежит плоскости 315
-------прямой 257
— пересечения прямых 257
— принадлежит плоскости 315
---прямой 256
— симметричная точке относительно
прямой 365
— -------точки 364
Транзитивность 35
Транспортир 264, 284
Трапеция 294
— криволинейная 250
— равнобокая 295
Треугольник 276
— вписанный в окружность 263
— описанный около окружности 283
— прямоугольный 260
— равнобедренный 278
— равносторонний 278
Угловой коэффициент
— — касательной 224
---прямой 81. 357
Углы
— вертикальные 267
— внутренние накрест лежащие 271
------ односторонние 271
— равные 277
— смежные 266
Угол 263
— внешний треугольника 279
— внутренний треугольника 280
— вписанный в окружность 269
— вращения 371
— выпуклого многоугольника 298
------ четырехугольника 291
— двугранный 327
— линейный двугранного угла 327
— между двумя векторами 860
—---плоскостями 320
— — прямой и плоскостью 322
—. — прямыми на плоскости 257
------скрещивающимися 313
— многогранный 327
— острый 284
— плоский 265
— поворота 370
— прямой 264
— развернутый 263
— • трехгранный 327
— тупой 264
— центральный 267
Угольник 284
Уменьшаемое 12
Умножение
— вектора на число 382
— дробей десятичных 24
---обыкновенных 21
---рациональных 65
— комплексных чисел 50
• — одночленов 55
Уравнение
— биквадратное 143
— дробное 138
— иррациональное 147
— касательной к графику 225
— квадратное 138
------ неполное 184
— — неприведенное 133
—• — приведенное 133
— линейное с двумя переменны-
ми 163
------- одной переменной 132
— логарифмическое 149
— окружности 356
— плоскости 361
— показательное 149
— прямой 357
— рациональное 141
— с двумя переменными 163
------ одной переменной 131
--- параметром 160
---переменной в знаменателе 136
— сферы 361
— тригонометрическое 152
— фигуры в пространстве 360
----на плоскости 355
— целое 138
Условие постоянства функции 237
Фигура
— геометрическая 255
— симметричная относительно плос-
кости 367
—------прямой 366
— центрально-симметричная 365
Фигуры
415
— гомотетичные 368
—- основные геометрические 256, 314
— подобные 375
— равные 372
Физический смысл
---производной 222
------- второй 223
Формула
— Герона 310
— Ньютона — Лейбница 248
— п-го члена арифметической прог-
рессии 204
-------геометрической прогрес-
сии 206
— расстояния между двумя точками
в пространстве 355
------------координатной плоскос-
ти 354
• — суммы бесконечной геометричес-
кой прогрессии 210
---п членов арифметической прог-
рессии 204
---------геометрической прогрес-
сии 206
Формулы
— двойного аргумента 125
— дифференцирования 220
— понижения степени 126
— преобразования суммы тригоно-
метрических функций в произведе-
ние 127
— приведения 123
- — связывающие тригонометрические
функции одного аргумента 123
— сложения и вычитания аргумен-
тов 121
— сокращенного умножения 57
Функция 71
— возрастающая 77
— дифференцируемая в точке 219
— квадратичная 107
— линейная 30
— логарифмическая 98
— монотонная 78
- — непрерывная в точке 215
---на интервале 215
------- отрезке 215
— нечетная 75
— обратимая 92
— обратная 92
— периодическая 77
— подынтегральная 247
— показательная 90
— постоянная 78
— сложная 222
— степенная с показателем дробным
отрицательным 88
----------положительным 33
----------натуральным 84
----------целым отрицательным 35
— тригонометрическая 96
— убывающая 77
— четная 75
Характеристика десятичного лога-
рифма 121
Характеристическое свойство
---арифметической прогрессии 204
---геометрической прогрессии 206
Хорда 262
Целая часть числа 39
Центр
— гомотетии 367
— круга 262
— окружности 262
— симметрии параллелепипеда 330
— — фигуры 365
— шара 333
Циркуль 284
Цилиндр 333
— прямой 334
Частное 12
— от деления комплексных чисел 49
Частота колебания 114
Четырехугольник 290
— выпуклый 291
— иеныпуклый 291
Числа
— взаимно простые 15
— действительные 32
— иррациональные 31
— комплексно-сопряженные 51
— комплексные 48
— мнимые 50
— натуральные 11
— отрицательные 31
— положительные 30
— простые 14
— противоположные 30
— рациональные 31
— смешанные 18
— составные 14
— целые 31
— чисто мнимые 50
Числитель дроби 17
Числовой
— луч 36
— промежуток 36
Член числовой последовательнос-
ти 202
Шар 337
Шаровой
— сегмент 339
— сектор 340
— слой 339
Экстремумы 229
ТРЕУГОЛЬНИКИ
ОСТРОУГОЛЬНЫЙ
ПРЯМОУГОЛЬНЫЙ ТУПОУГОЛЬНЫЙ
РАВНОБЕДРЕННЫЙ РАВНОСТОРОННИЙ
ЧЕТЫРЕХУГОЛЬНИКИ
ВЫПУКЛЫЙ ПАРАЛЛЕЛОГРАММ ПРЯМОУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
РОМБ
КВАДРАТ
ТРАПЕЦИЯ
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ПРЯМЫХ И ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
ПАРАЛЛЕЛЬНЫЕ ПЕРЕСЕКАЮЩИЕСЯ СКРЕЩИВАЮЩИЕСЯ
ПРЯМЫЕ ПРЯМЫЕ ПРЯМЫЕ
ПРЯМАЯ
ЛЕЖИТ В
ПЛОСКОСТИ
ПРЯМАЯ И
ПЛОСКОСТЬ
ПАРАЛЛЕЛЬНЫ
ПРЯМАЯ И
ПЛОСКОСТЬ
ПЕРЕСЕКАЮТСЯ
ПАРАЛЛЕЛЬНЫЕ
ПЛОСКОСТИ