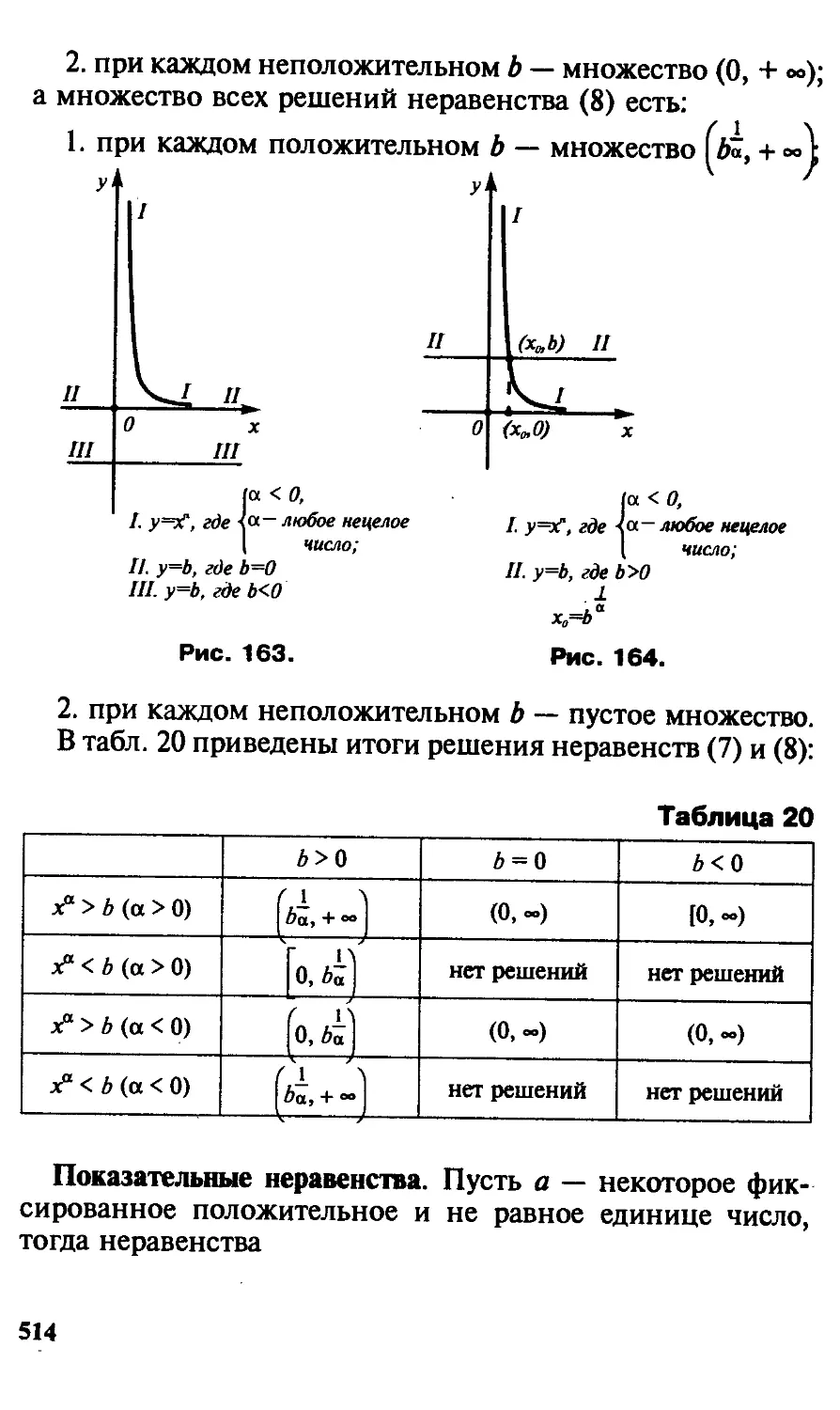
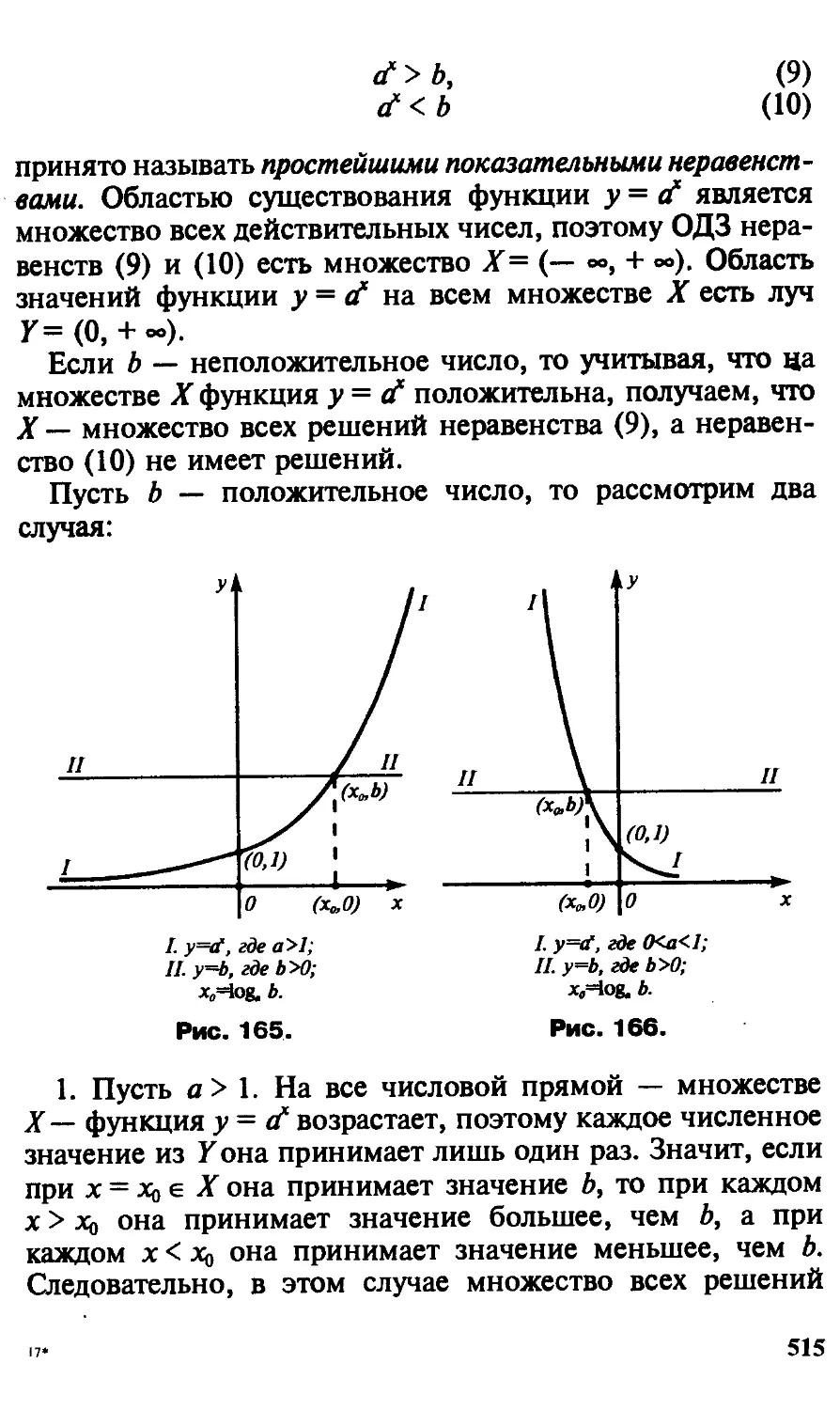
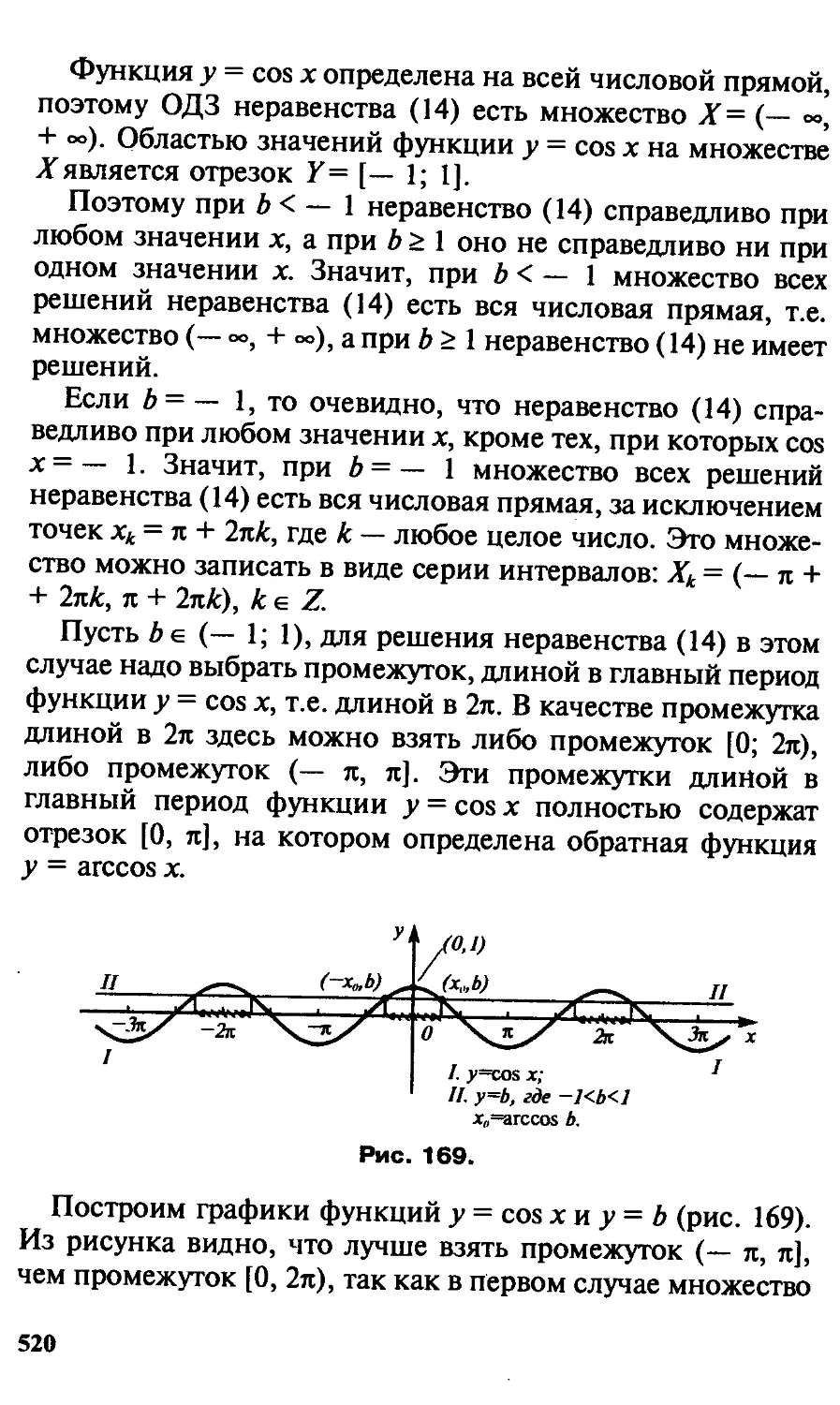
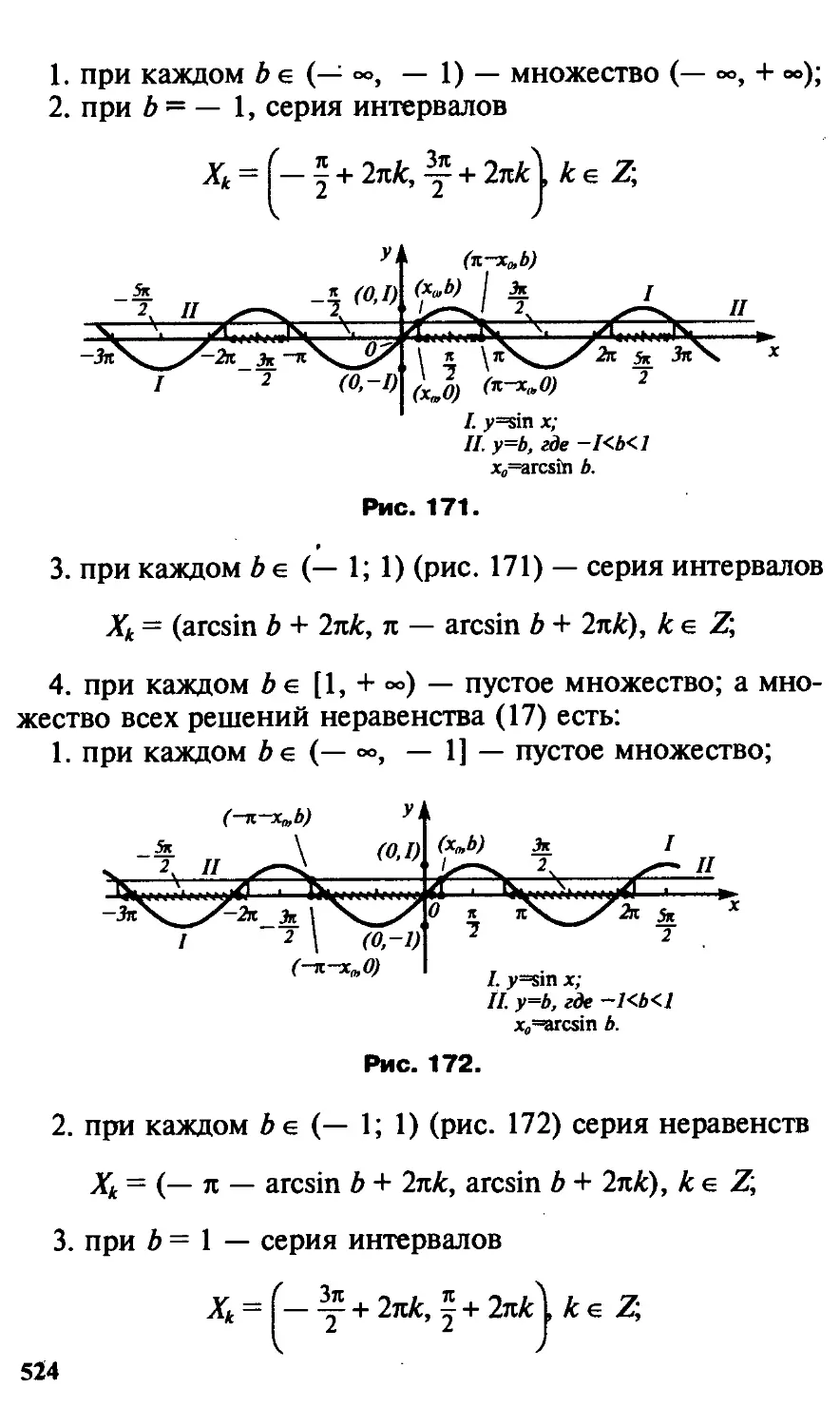
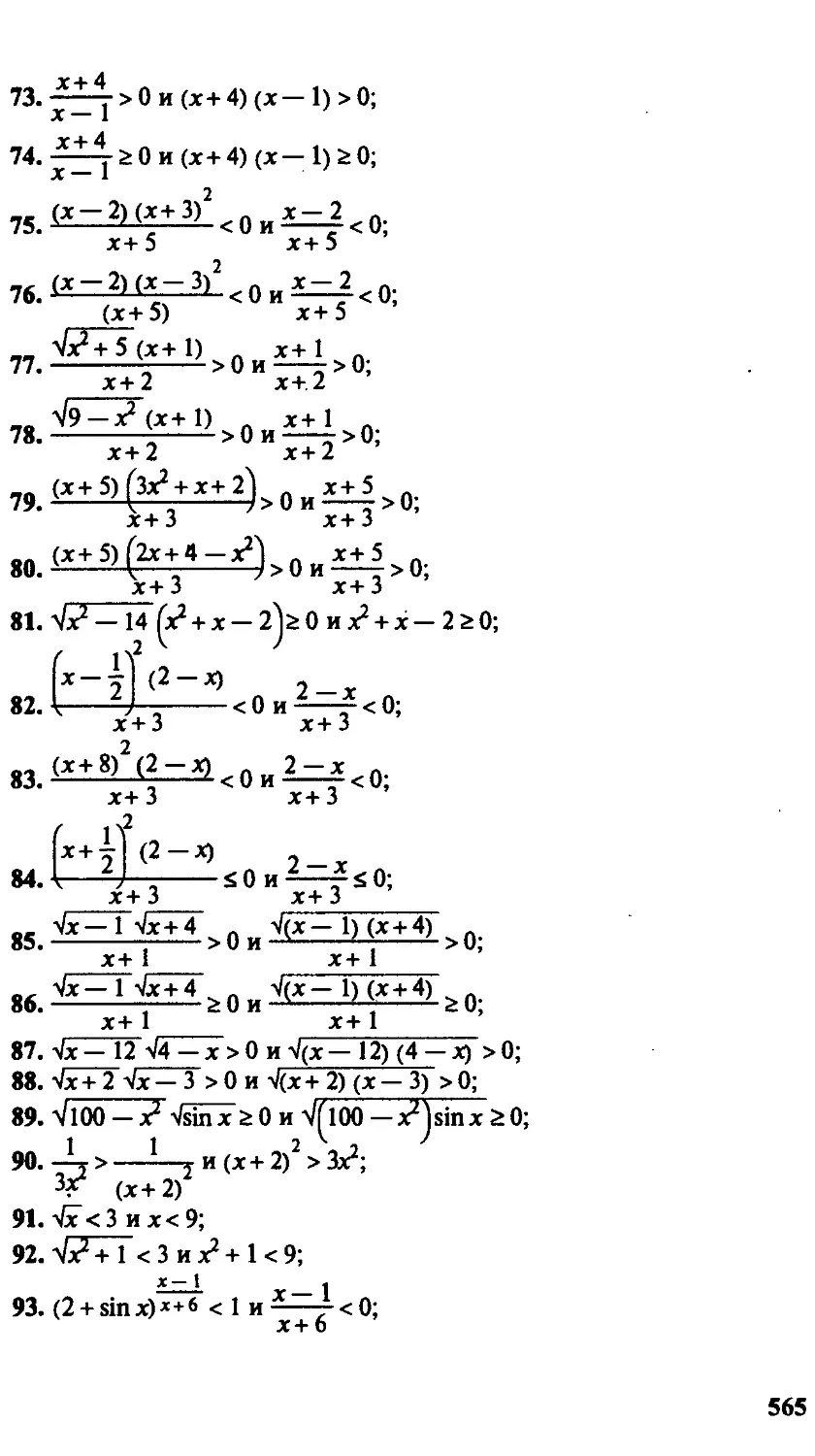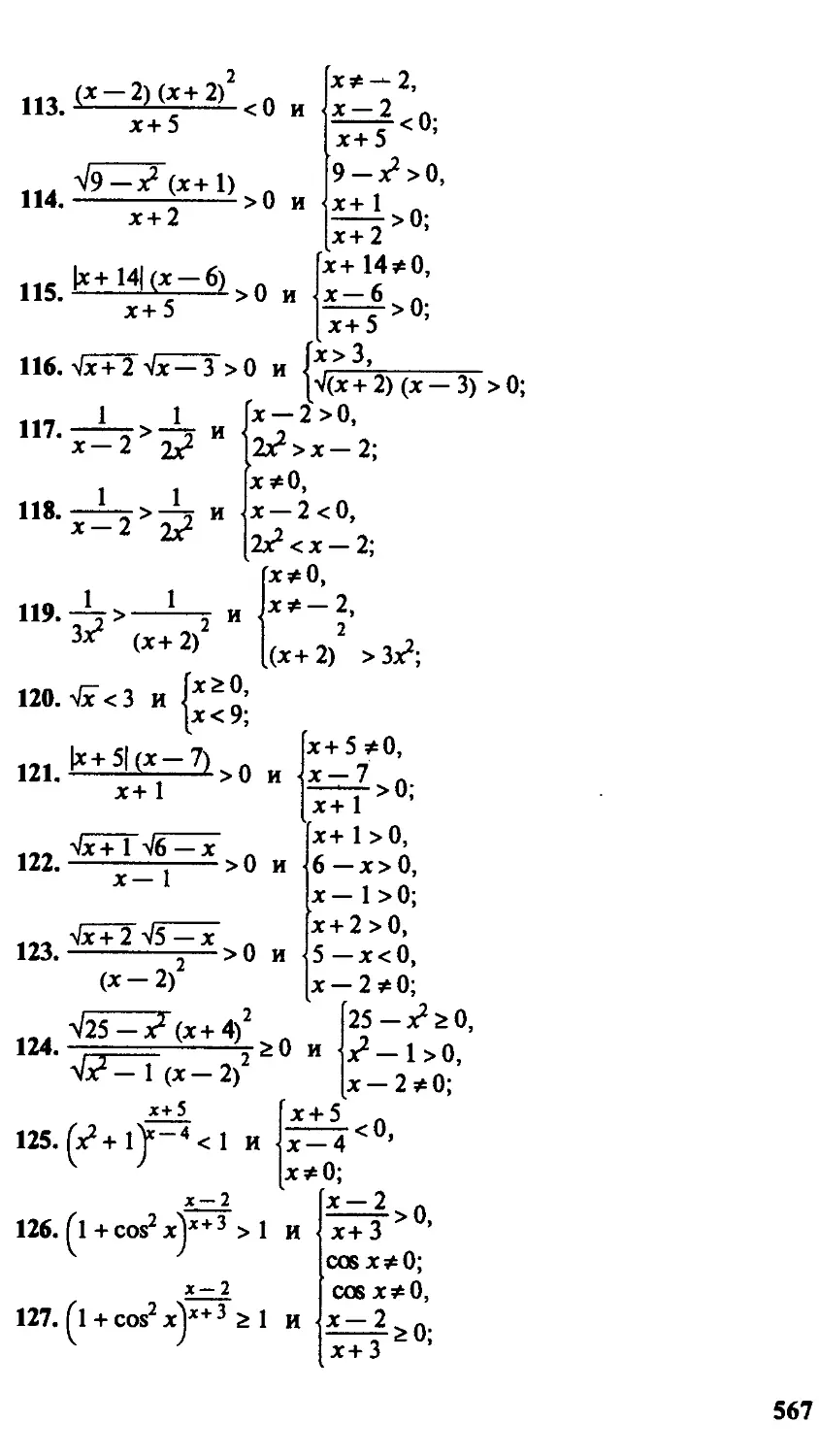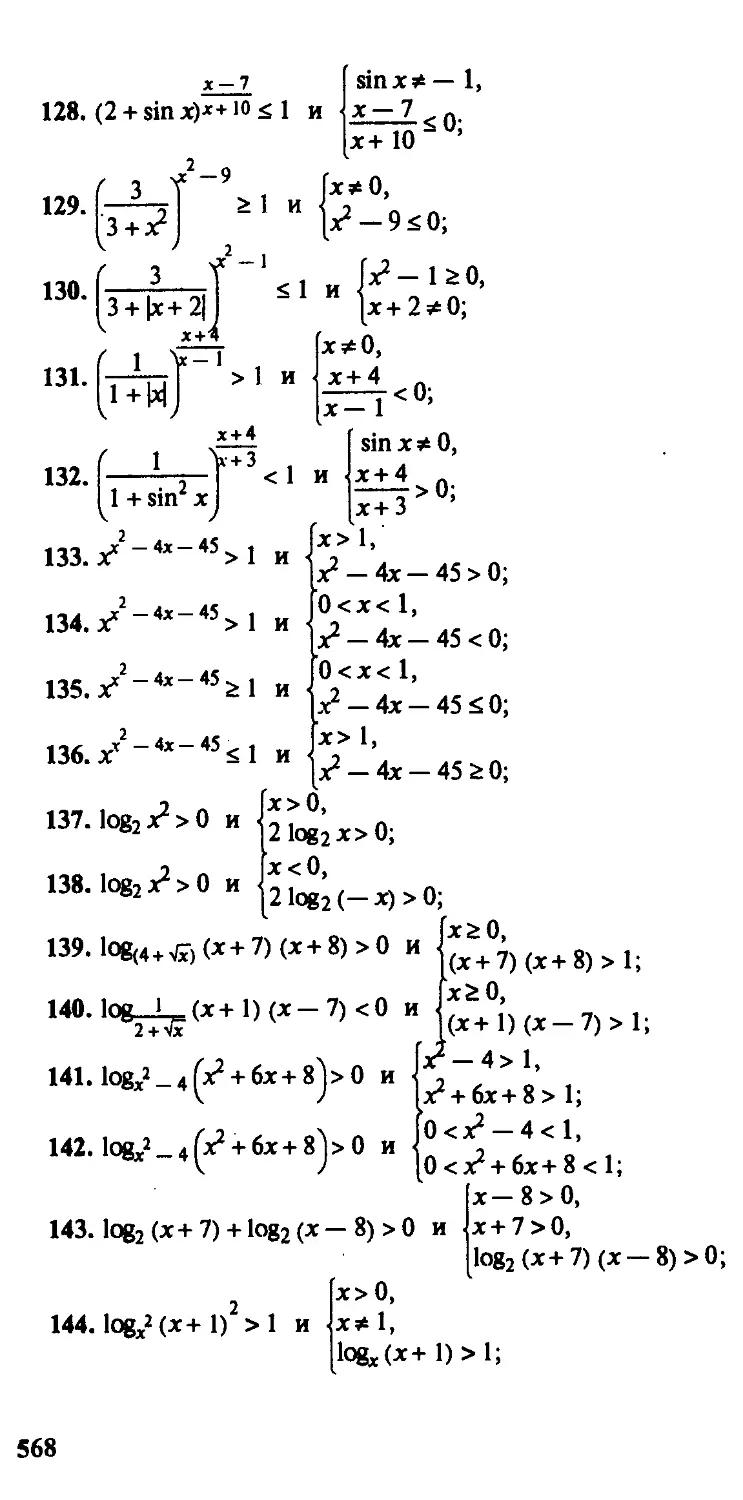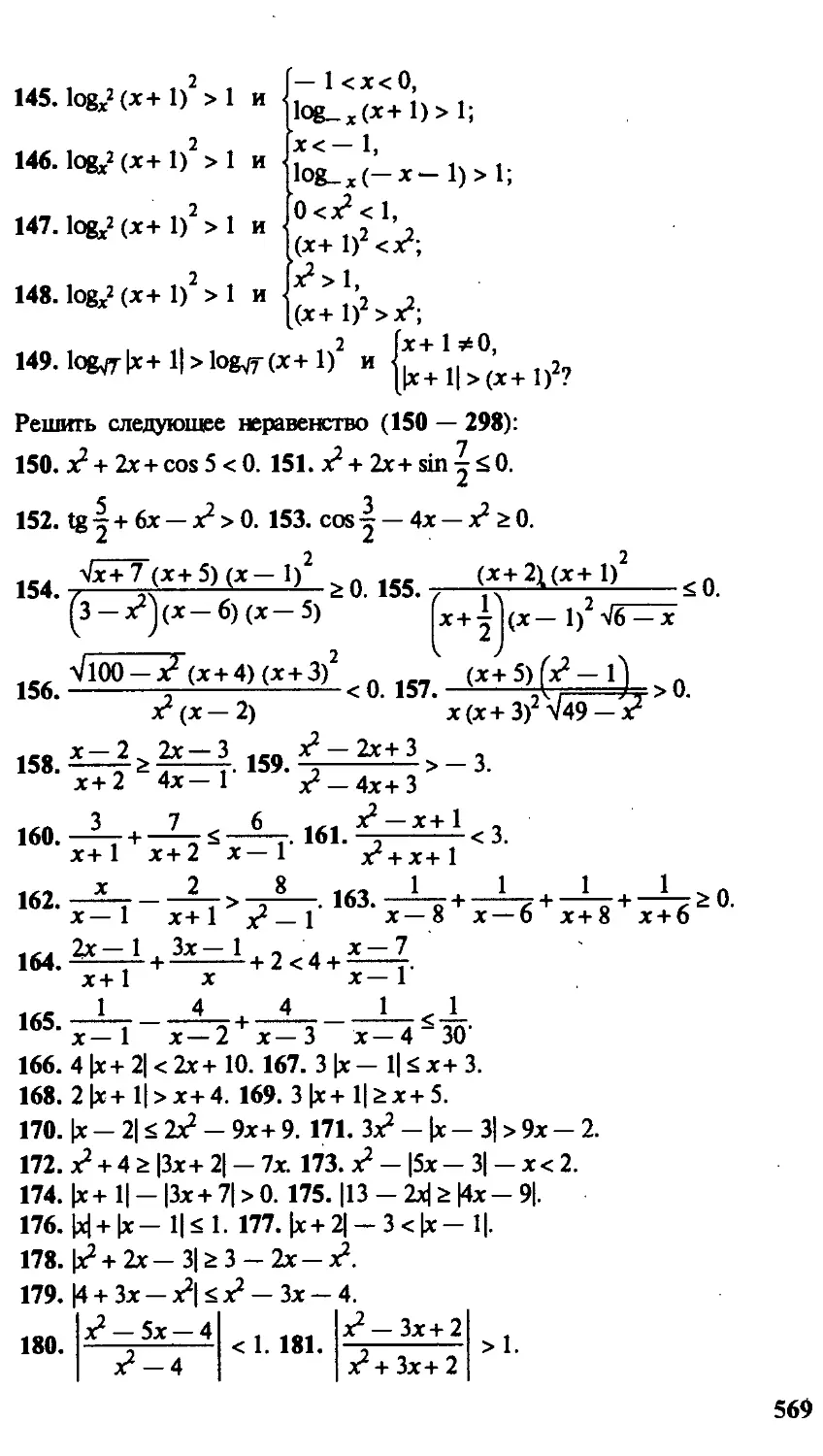Автор: Потапов М.К. Пасиченко П.И. Александров В.В.
Теги: алгебра математика тригонометрия
ISBN: 5-06-004178-6
Год: 2001
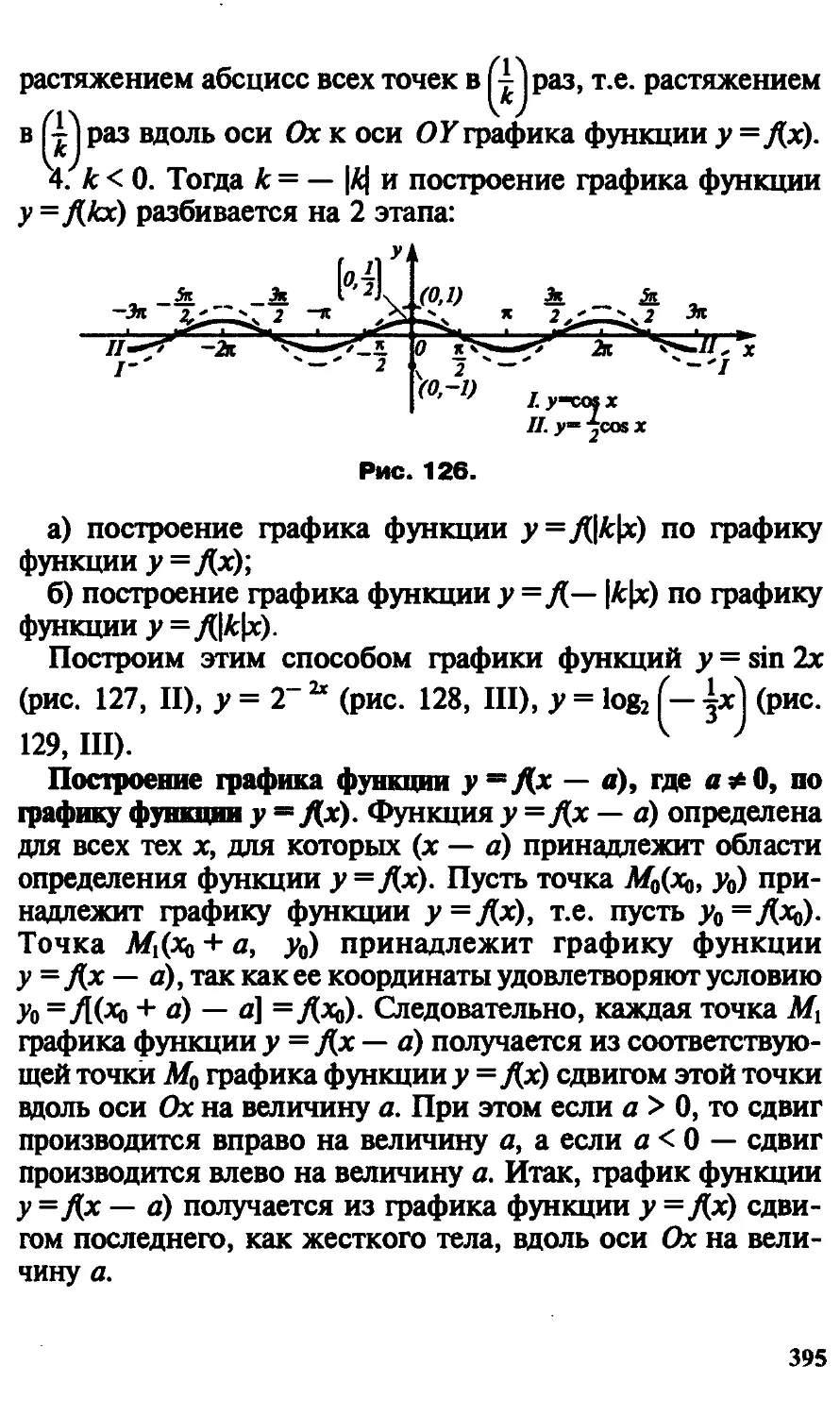
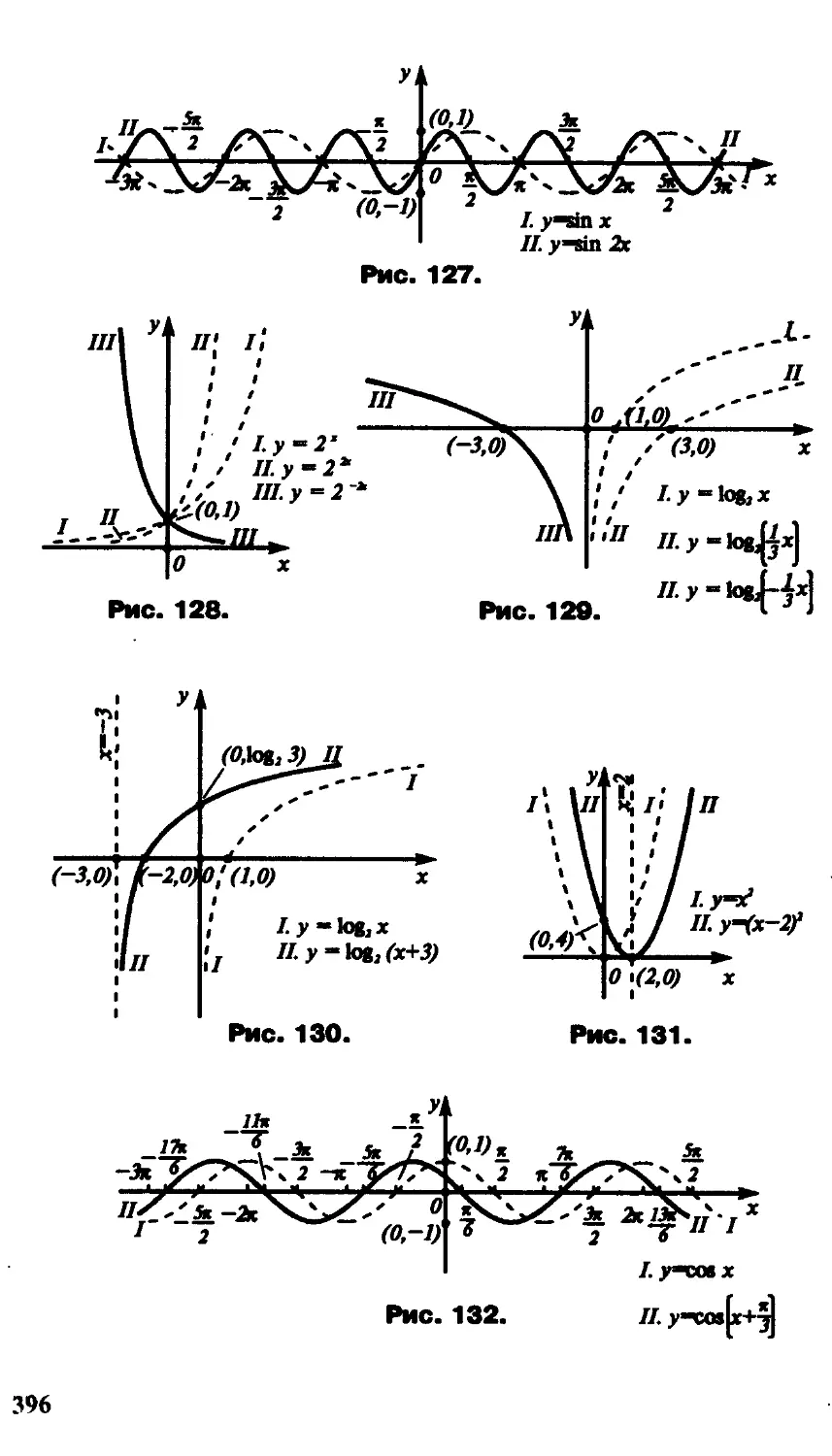
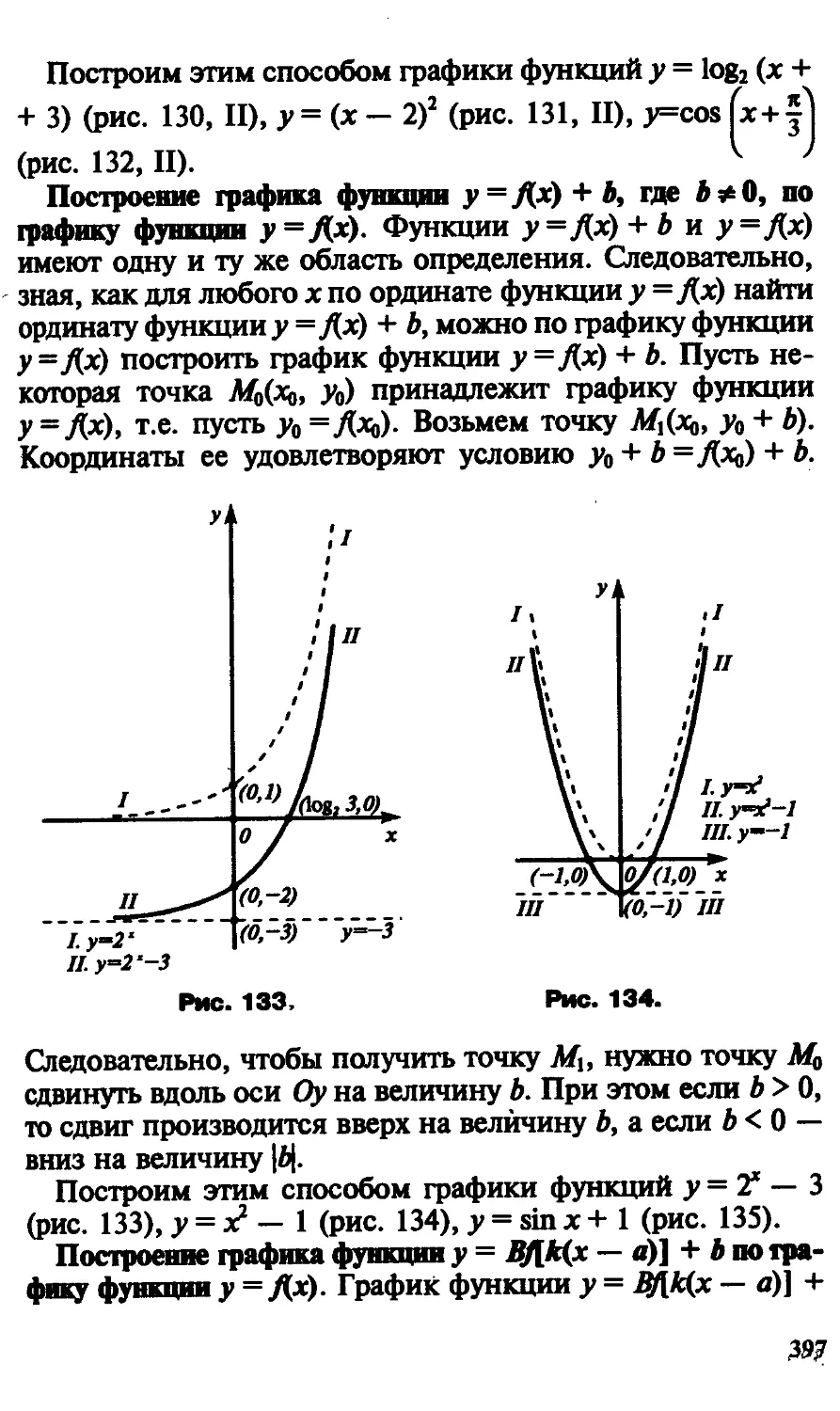
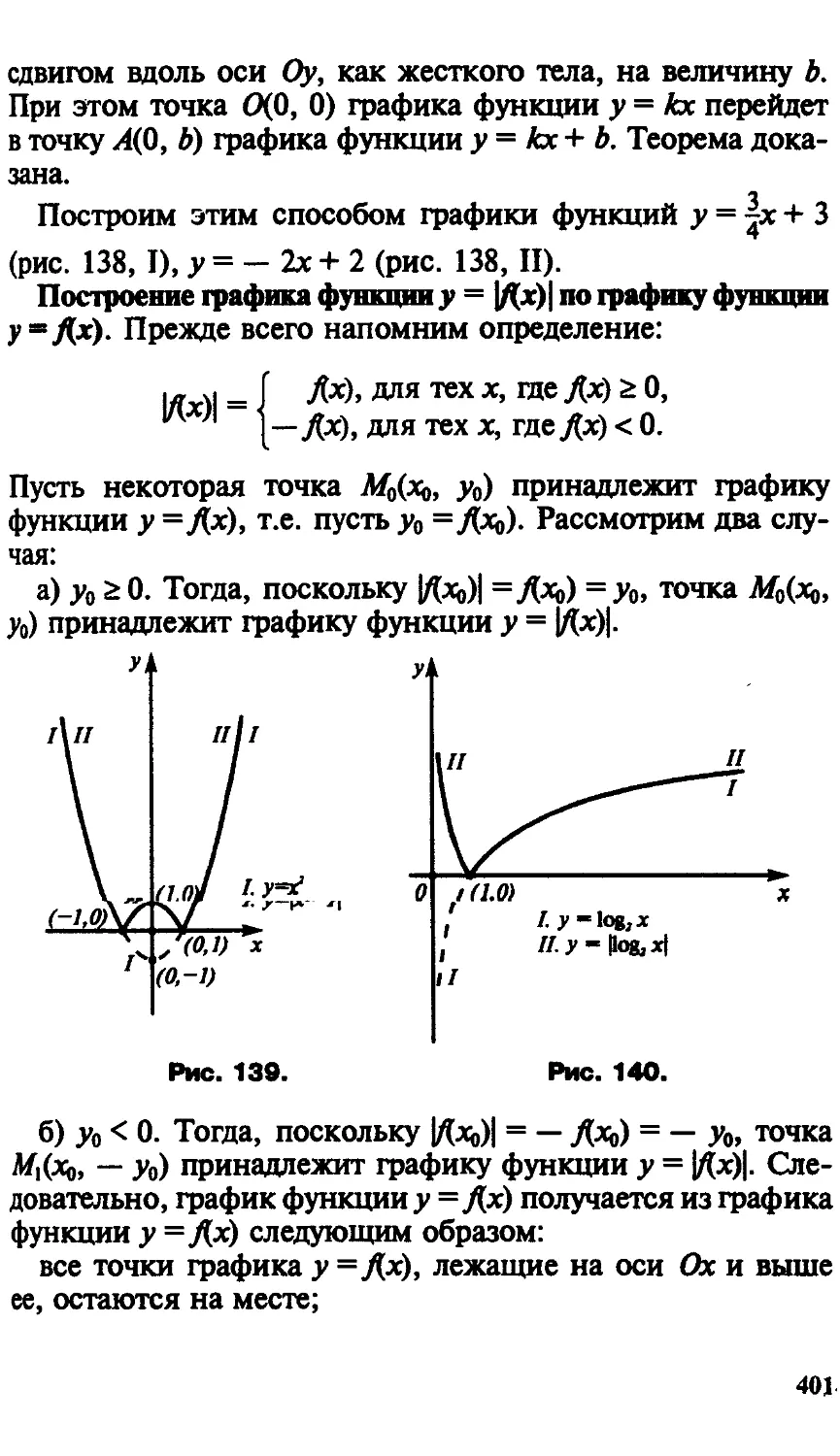
Текст
Высшая математика
Под общей редакцией
академика Российской Академии наук
В. А. Садовничего
Архипов Г.И., Садовничий В.А.,
Чубариков В.Н.
Лекции по математическому анализу
Виноградов И.М.
Элементы высшей математики
(Аналитическая геометрия.
Дифференциальное исчисление.
Основы теории чисел)
Привалов И. И.
Введение в теорию функций
комплексного переменного
Садовничий В.А.
Теория операторов
Гашков СБ., Чубариков В.Н.
Арифметика. Алгоритмы.
Сложность вычислений
Нечаев В. И.
Элементы криптографии.
Основы теории защиты информации
Виноградова И.А., Олехник С.Н.,
Садовничий В.А.
Задачи и упражнения по матема-
математическому анализу
Бахвалов НС, Лапин А.В.,
Чижонков Е.В.
Численные методы в задачах
и упражнениях
Яблонский СВ.
Введение в дискретную
математику
Благодатских В. И.
Введение в оптимальное
управление (линейная
теория)
M.K. ПОТАПОВ В.В .АЛЕКСАНДРОВ
П.И.ПАСИЧЕНКО
Алгебра,
тригонометрия
и элементарные
функции
Допущено
научно-методическим
Советом по математшсе и мехаввке
Учебно-методического объединения
университетов России
в качестве учебного пособия
для студентов университетов
и педагогических вузов
Москва
«Высшая школа» 2001
УДК 512
ББК 22.14
П64
Рецензент:
чл.-корр. РАН, проф. Ю. В. Нестеренко
Потапов, М. К.
П64 Алгебра, тригонометрия и элементарные функ-
функции: Учеб. пособие/М. К. Потапов, В. В. Алек-
Александров, П. И. Пасиченко; Под ред. В. А. Са-
довничего. — М.: Высш. шк., 2001. — 735 с: ил.
ISBN 5-06-004178-6
В книге систематизированы сведения по арифметике, алгеб-
алгебре, тригонометрии и началам анализа. Большое внимание уделе-
уделено теоретическому материалу, приведены основные понятия
и определения, необходимые при изучении математики.
Для студентов университетов и педагогических вузов. Мо-
Может быть полезна учителям, учащимся средних школ с углублен-
углубленным изучением математики, абитуриентам, слушателям подго-
подготовительных курсов и отделений вузов.
УДК 512
ББК 22.14
ISBN 5-06-004178-6 © ГУП «Издательство «Высшая школа»
2001
Оригинал-макет данного издания является собственностью издате-
издательства «Высшая школа», и его репродуцирование (воспроизведение)
любым способом без согласия издательства запрещается.
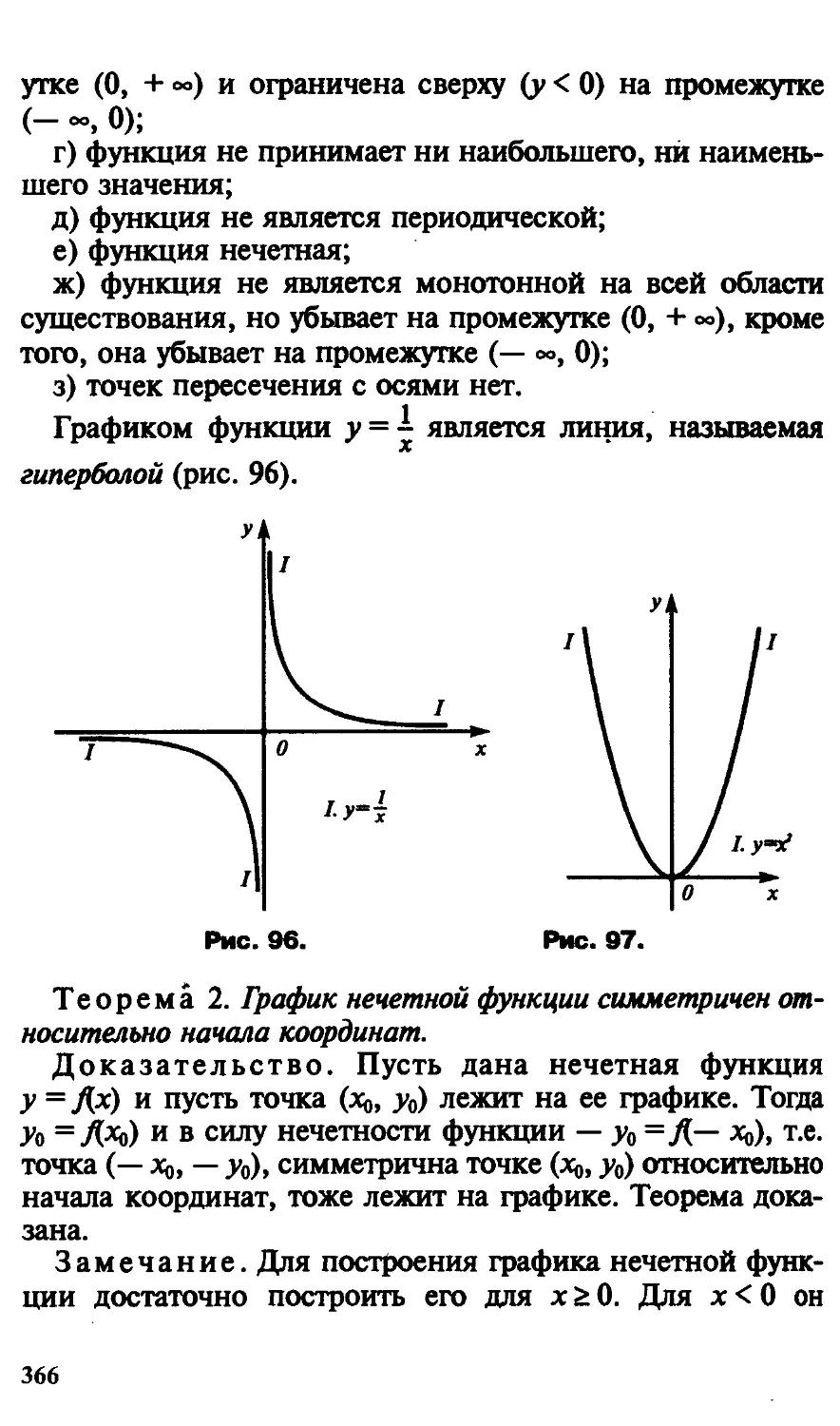
Предисловие
В России исторически сложилось так, что представле-
представление об образовании включает в себя органичное единство
школы как системы приобретения знаний, фундаменталь-
фундаментальной науки как показателя уровня подготовки специали-
специалистов и гуманитарной культуры как основы духовного
богатства человека.
Формулируя задачи образования, академик А. Н. Кры-
Крылов говорил : «Школа не может дать вполне закончен-
законченного знания, главная задача школы — дать общее раз-
развитие, дать необходимые навыки, одним словом... глав-
главная задача школы — научить учиться, и для того, кто
в школе научится учиться, практическая деятельность
всю его жизнь будет наилучшей школой».
Отметим, что особенность отечественной школы со-
состоит в сочетании четкости рассуждений с глубиной соде-
содержания и простотой, доступностью, конкретностью изло-
изложения материала, которые всегда предпочитаются фор-
формальным конструкциям. Практическое воплощение дан-
данных идей подразумевает наличие высококвалифициро-
высококвалифицированных и творчески мыслящих преподавателей.
Математическое образование и математическая
культура составляют стержень научного знания, и значе-
значение математики как основы фундаментальных исследова-
исследований постоянно возрастает.
Для решения этих задач требуются учебники, отража-
отражающие в определенной полноте современное состояние
исследований и мировоззренческие принципы данной об-
области науки.
Предлагаемые к публикации в серии «Высшая мате-
математика» учебники по математике реализуют указанный
выше подход. Они написаны, в основном, профессорами
Московского государственного университета им. М. В.
Ломоносова.
Книга «Алгебра, тригонометрия и элементарные фун-
функции» М. К. Потапова, В. В. Александрова и П. И. Па-
сиченко написана на основе лекций, прочитанных авто-
авторами в Московском государственном университете
им. М. В. Ломоносова.
В книге систематизированы сведения по арифметике,
алгебре, тригонометрии и началам анализа.
Книга способствует воспитанию активных знаний,
творческому усвоению навыков оперирования с матема-
математическими объектами, она призвана обеспечить повыше-
повышение уровня общеобразовательной подготовки читателя,
созданию у него прочного фундамента знаний.
Можно сказать, что книга содержит то количество
знаний по элементарной математике, которое необходи-
необходимо любому образованному человеку в течение всей его
сознательной жизни.
Так как в книге содержатся основы школьного курса
математики, то она будет полезна студентам педагоги-
педагогических вузов, учителям, школьникам, готовящимся к по-
поступлению в вузы, учащимся школ и классов с углублен-
углубленным изучением математики.
В данной серии уже изданы учебники Г. И. Архшюва,
B. А. Садовничего, В. Н. Чубарикова «Лекции по матема-
математическому анализу», И. М. Виноградова «Элементы выс-
высшей математики (Аналитическая геометрия. Дифферен-
Дифференциальное исчисление. Основы теории чисел)», И. И. При-
Привалова «Введение в теорию функций комплексного пере-
переменного», В. А. Садовничего «Теория операторов»,
C. Б. Гашкова, В. Н. Чубарикова «Арифметика. Алгорит-
Алгоритмы. Сложность вычислений», В. И. Нечаева «Элементы
криптографии (основы теории защиты информации)»,
И. А. Виноградовой, С. Н. Олехника, В. А. Садовничего
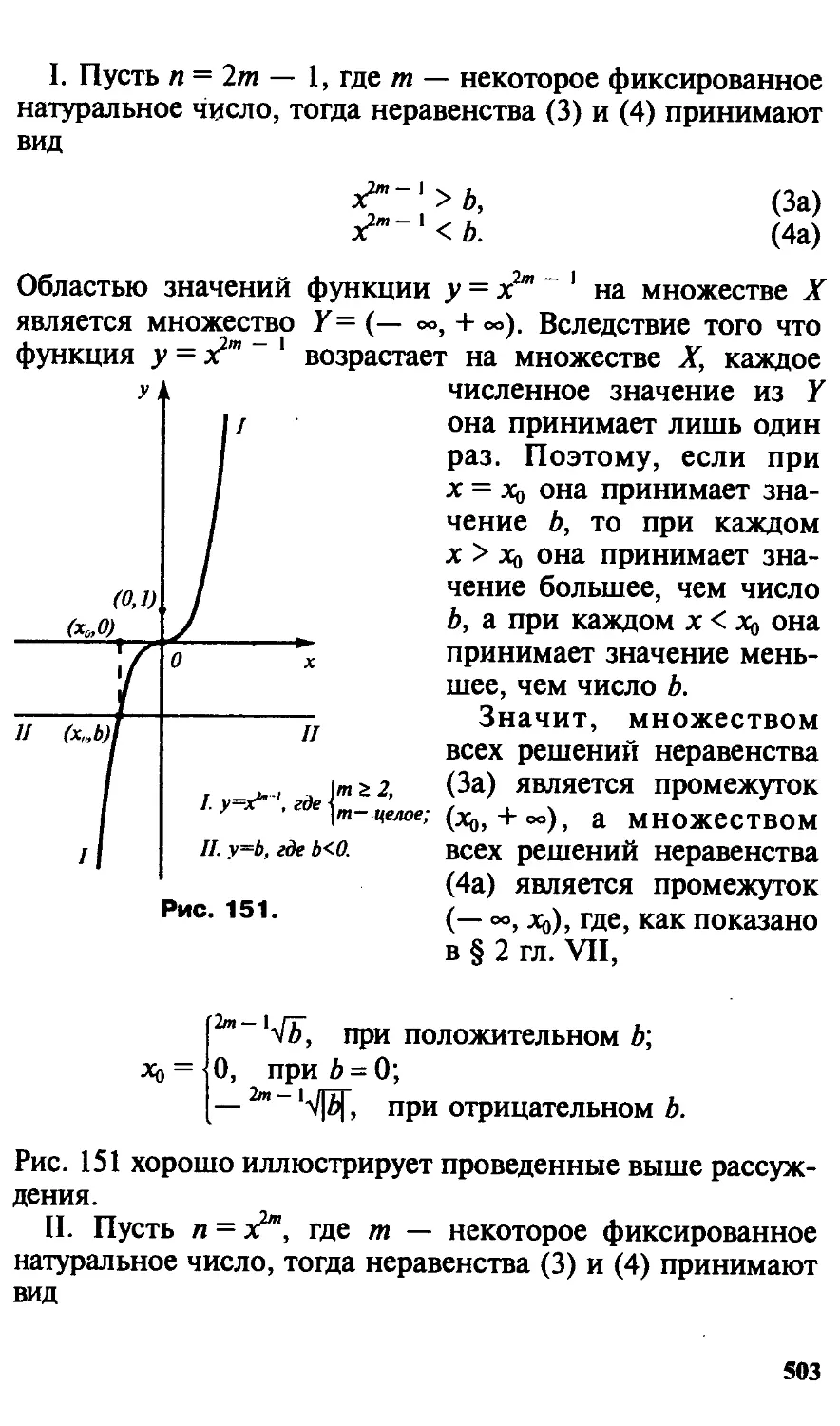
«Задачи и упражнения по математическому анализу» (то-
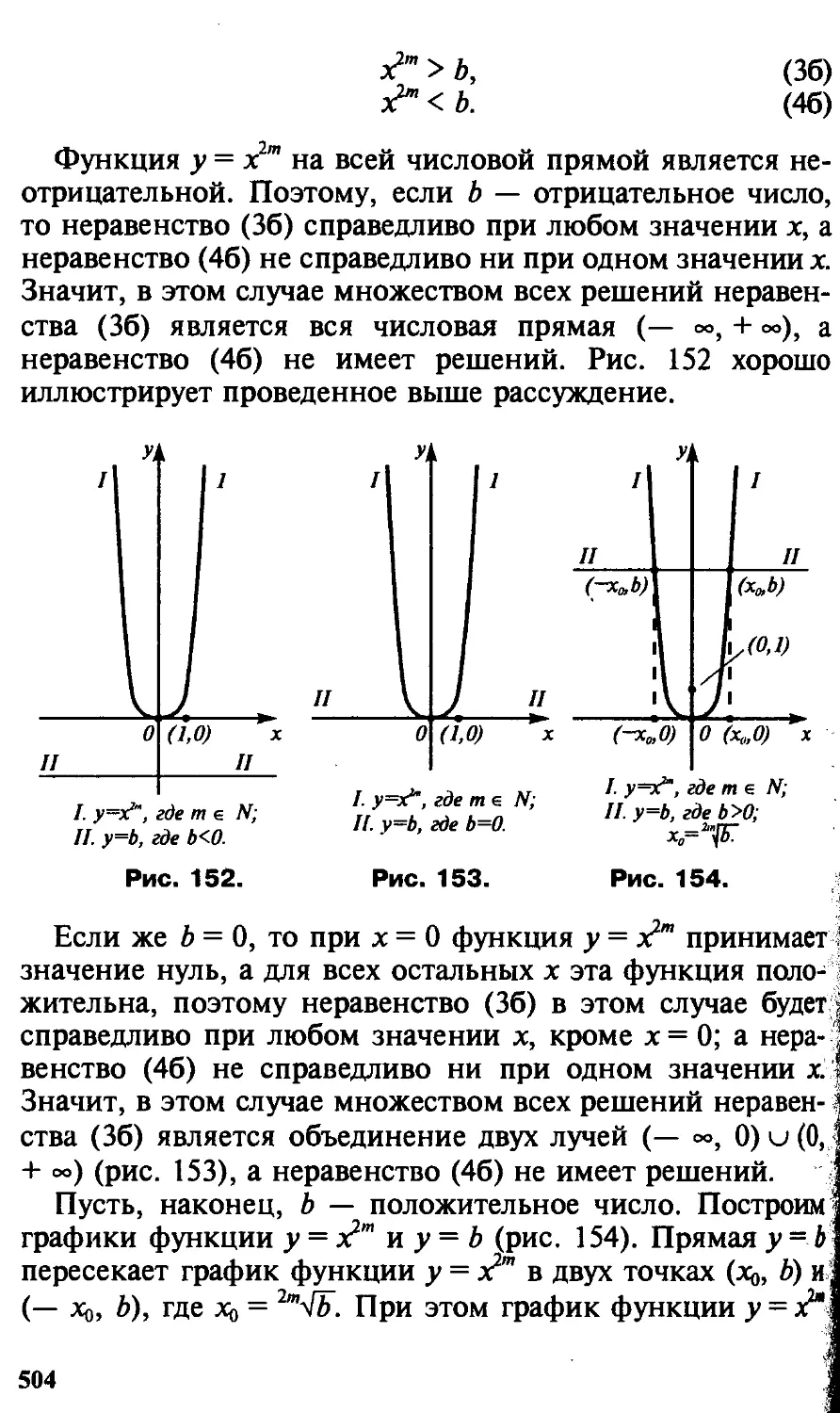
(тома 1 и 2), Н. С. Бахвалова, А. В. Лапина, Е. В. Чижонкова
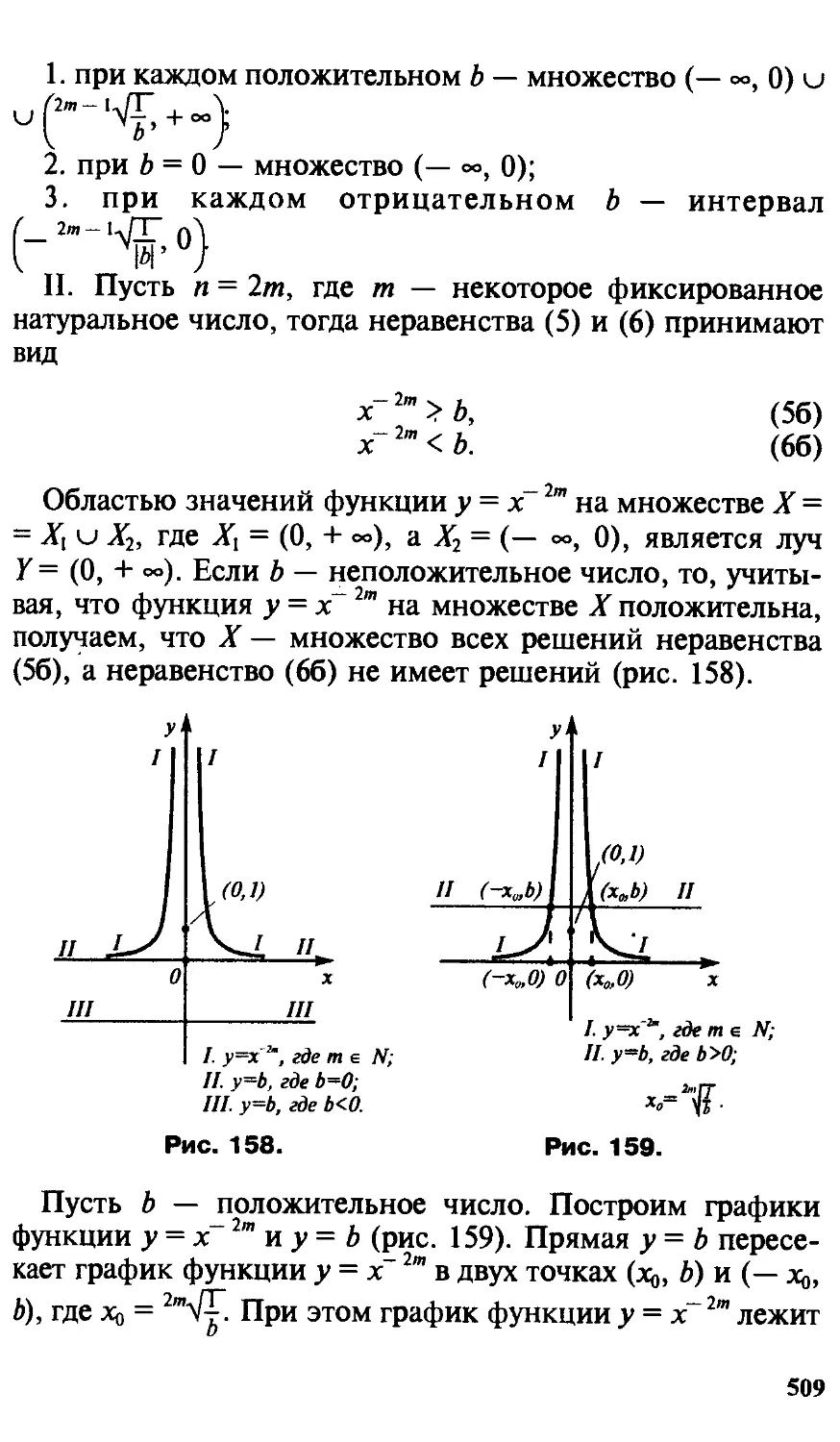
«Численные методы в задачах и упражнениях», С. В. Яб-
Яблонского «Введение в дискретную математику».
Кроме практической ценности эта серия призвана под-
подвести некоторые итоги работы российских ученых и педа-
педагогов-математиков по созданию базовых учебников по
математике на рубеже второго и третьего тысячелетий.
Серия не ограничивается указанными книгами. В даль-
дальнейшем предполагается продолжить отбор и издание как
современных, так и классических учебников, которые от-
отвечают изложенной выше концепции, не потеряли своей
новизны и актуальности и пользуются заслуженной попу-
популярностью и авторитетом у студентов и педагогов.
Академик Российской академии наук
В. А. Садовничий
Глава I. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
§ 1. Натуральные числа
Ряд натуральных чисел. Понятие натуральных чисел воз-
возникло из потребностей счета. Натуральные числа можно
сравнивать между собой, при этом ясно, какое из двух
чисел больше. Все натуральные числа, расположенные в
порядке возрастания, образуют ряд натуральных чисел:
первое число — единица, второе — два, третье — три и т.д.
У каждого натурального числа есть свое место в этом ряду.
В дальнейшем ряд натуральных чисел будем обозначать
буквой N.
Чтобы обозначить, что число т больше числа п, употреб-
употребляется запись т>п. Для обозначения того, что число т
меньше числа п, употребляется запись т< п. Называют эти
записи неравенствами натуральных чисел. Чтобы обозна-
обозначить, что число т и число п — одно и то оке число,
употребляют запись т = пи называют ее равенством нату-
натуральных чисел.
Сложение натуральных чисел можно определить, ис-
используя ряд натуральных чисел, следующим образом.
Сложить два натуральных числа т и п — значит найти
в ряду натуральных чисел число р{р> т), находящееся на
п-и месте от числа т, причем счет начинается с числа
т + 1. Это число р называется суммой чисел аи и л и
обозначается т + п, а числа тип называются слагаемыми.
Например, т + 3 — число, стоящее после числа т на
третьем месте. Чтобы сложить несколько натуральных
чисел, надо сложить сначала первые два, затем к получен-
полученной сумме прибавить следующее натуральное число и т.д.
Умножить натуральное число т на натуральное число
п — значит найти натуральное число q, равное: а) п, если
от = 1; б) сумме от чисел, каждое из которых есть л, если
от > 1. Это число д называется произведением чисел /пили
обозначается отл, а числа от ил называются сомножителями.
Например, умножить натуральное число 2 на число л —
значит найти натуральное число q, равное сумме двух
чисел, каждое из которых есть число л. Это число обозна-
обозначается 2л, т.е. q = 2/i. Чтобы перемножить несколько нату-
натуральных чисел, надо сначала перемножить первые два,
затем полученное натуральное число умножить на следую-
следующее натуральное число и т.д.
Приведем основные законы сложения и умножения
натуральных чисел:
а)от + л = л + от (коммутативность сложения);
б) (/ + от) + л = I + (от + п) (ассоциативность сложения);
в) отл = пт (коммутативность умножения);
г) Aт)п = /(от/i) (ассоциативность умножения);
д) (/ + т)п = In + mn (дистрибутивность сложения отно-
относительно умножения).
Если число от взято сомножителем к раз (к — натураль-
натуральное число, больше единицы), то произведение
отот... от
А раз
называют к-й степенью числа т и обозначают тк, т.е. по
определению
от ~ отот ... от
А раз
Кроме того, по определению
от1 = от.
Справедливы следующие свойства степеней:
а)от*от" = от*+";
б) (от*/= от*":
в) mt = (от/).
Эти свойства доказываются с помощью основных законов
сложения и умножения натуральных чисел.
Определим действия, обратные сложению и умножению
натуральных чисел, — действия вычитания и деления для
натуральных чисел.
Вычесть из натурального числа п натуральное число т —
значит найти натуральное число р такое, что
т+р = п. A)
Не для любых натуральных чисел пит существует такое
натуральное число р, что выполняется равенство A). Если
п > т, то такое число существует и единственно. Оно
называется разностью чисел лиши обозначается п — т,
число п называется уменьшаемым, а число т — вычитае-
вычитаемым.
Разделить натуральное число п на натуральное число
т — значит найти натуральное число g такое, что
mq = n. B)
Не для любых натуральных чисел пит существует такое
натуральное число д, что выполняется равенство B). Если
такое число существует, то числа т и д называются дели-
делителями числа п и обозначаются
g = п : т; т = п. д.
Опираясь на основные законы сложения и умножения
натуральных чисел и определения действий вычитания и
деления, можно доказать следующие утверждения или,
другими словами, теоремы.
Теорема 1. Если число т есть делитель чисел щ и п2, то
т есть делитель суммы щ + п2.
Доказательство. Поскольку т есть делитель числа пи
то и, = тдь Аналогично п2 = тд2. Применяя закон дистри-
дистрибутивности сложения относительно умножения натураль-
натуральных чисел, имеем пх + п2 = тдх + тд2 = т(дх + д2). Следова-
Следовательно, число щ + п2 делится на число т.
Теорема 2. Если число т есть делитель чисел щип2и
щ > п2, то число т есть делитель разности пх — п2.
Справедливость этого утверждения доказывается анало-
аналогично.
Отметим еще несколько очевидных свойств равенств
натуральных чисел:
а) если т = п, то т + к = п +к для любого натурального
числа к;
б) если т = п, тот— 1= п — I для любого натурального
числа / такого, что т > I;
в) если т = п, то тр = пр для любого натурального
числа р;
г) если т = п, то т: д = п: д для любого натурального
числа д, являющегося делителем числа т.
Расширенный ряд натуральных чисел. Рассмотрим новое
число — число нуль. Для его обозначения употребляется
символ 0. Нуль не является натуральным числом и счита-
считается числом, предшествующим всем натуральным числам.
Ряд натуральных чисел вместе с числом нуль называется
расширенным натуральным рядом. Расширенный натураль-
натуральный ряд будем обозначать буквой Zq.
В расширенном натуральном ряду можно определить
действия сложения и умножения; для этого к определениям
сложения и умножения натуральных чисел достаточно до-
добавить определения сложения и умножения, в которых
участвует число нуль:
аH + п = п + 0 = п;
б) 0 + 0 = 0;
в) 0 • п = п 0 = 0;
г) 0 • 0 = 0.
По определению нулевая степень любого натурального
числа т есть единица, т.е. т° = 1.
Деление на нуль и возведение нуля в нулевую степень
являются запрещенными действиями.
Чтобы производить действия над числами из расширен-
расширенного натурального ряда, надо уметь их записывать. Запись
одного и того же натурального числа зависит от системы
счисления.
В основе всякой системы счисления лежит следующий
принцип: некоторое количество единиц составляет новую
единицу следующего разряда. Это число называется осно-
8
ванием системы счисления. Если за основание системы
принято число два, то система счисления называется дво-
двоичной, если за основание принято число двенадцать —
система называется двенадцатиричной и т.д."
Дальше будем рассматривать только десятичную систему
счисления. В этой системе вводится десять знаков, назы-
называемых цифрами; для обозначения первых десяти нату-
натуральных чисел — знаки 1, 2, 3, 4, 5, 6, 7, 8, 9, а для числа
нуль — знак 0. В этой системе счисления число десять
обозначается символом 10, а каждое натуральное число р
представляется в виде
р~ а„ • 10" + ан_, • 10""' + ...+ а2 • 102 + а, • 10 + ай, C)
где п — число из расширенного натурального ряда, а„ —
одно из чисел 1, 2, 3 9, каждое из а^, аи а2 а„_х —
одно из чисел 0, Г, 2, 3 9. Заметим, что если число п
будет больше, чем число девять, то оно само должно быть
записано в виде C).
Для записи числа р обычно употребляется другая форма
записи, основанная на принципе позиционного значения
цифр. Суть этого принципа заключена в том, что каждая
цифра, кроме своего значения получает еще и так называе-
называемое позиционное значение. Например, цифра 5 может
иметь значения: пять единиц, если стоит в изображении
числа р на первом месте справа; пять десятков, если стоит
в изображении числа р на втором месте справа, и т.д. На
этом принципе и основана обычная запись натуральных
чисел. Запись 2705 означает, что число состоит из двух
тысяч, семи сотен, нуля десятков и пяти единиц, т.е.
2705 = 2 • 103 + 7 • 102 + 0 • 10 + 5.
Если взять число р, представленное в виде C), то его
запись, основанная на позиционном принципе, будет
такая:
(черта сверху ставится для того, чтобы отличать это число
от произведения а„а„ _ , ... а2аха^. В дальнейшем будут
употребляться две формы записи натурального числа р:
б)р = а„ • 10я + в„_, • 10я"' + ... + в2 • 102 + в, • 10 +
т.е. дальше будем пользоваться равенством
а„а„_х ...а2ахаъ =
= ап • 10я + в„_ , • 10я"' + ... + а2 • 102 + в, • 10 + % D)
Признаки делимости. Ранее уже отмечалось, что не всегда
одно натуральное число делится на другое. Поэтому пред-
представляет интерес выделение тех случаев, когда деление
возможно. Выделению этих случаев весьма помогают так
называемые признаки делимости. Приведем некоторые из
них. Заметим предварительно, что из вышеизложенного
вытекает, что:
а) нуль делится на любое натуральное число,
б) любое натуральное число делится на единицу.
Теорема 3 Чтобы натуральное число р =
= а„а„_х... ^одоо делилось на 2, необходимо и достаточно,
чтобы цифра единиц а$ этого числа делилась на 2.
Доказательство. Докажем, что если число а^ делится
на 2, то число р также делится на 2. Запишем число р в виде
/> = « + Р, E)
где
а = (а„ ¦ 10я"' + ап_, • 10я + ... + а2 • 10 + в,) • 10,
Каждое слагаемое в правой части равенства (S) делится
на 2, следовательно, и вся сумма делится на 2, т.е. число р
делится на 2.
Докажем обратное утверждение. Если число р делится
на 2, то число а^ также делится на 2. По свойству б)
равенств из равенства (S) вытекает, что
ю
До = />-(«„• Юя~1 + ая_110я-2+ ... + а2 • 10 + в,) • 10.
Каждый член разности правой части равенства делится
на 2, следовательно, вся разность делится на 2, т.е. число
4) делится на 2. Теорема доказана.
Натуральные числа, делящиеся на два, и число нуль
называют четными числами. Все остальные натуральные
числа называются нечетными. Теорему 3 можно перефор-
переформулировать так: для четности любого натурального числа
р = апа„_\ ... a2aia0 необходимо и достаточно, чтобы цифра
единиц Оо этого числа была бы числом четным.
Рассмотрим характерные черты доказательства теоре-
теоремы 3. В самой теореме сформулированы, а затем доказаны
два утверждения: а) из делимости числа Oq на 2 следует
делимость на 2 числа р {достаточное условие делимости
числа р на 2); б) из делимости числа р на 2 следует
делимость на 2 числа Oq (необходимое условие делимости
числа р на 2). Если свойство делимости числа а„ на 2
обозначим буквой А, а свойство делимости числа р на 2
обозначим буквой В, то первое утверждение можно кратко
сформулировать так: из А следует В (А=> В), а второе
утверждение — из В следует А (А <= В). Теорему с помощью
введенных символов можно записать так: А о В.
Запись А о В означает также, что свойство А, более
простое и легко проверяемое, является необходимым и
достаточным условием для выполнения более сложного
свойства В.
Так как свойство А является достаточным условием для
свойства В (А => В), то на практике, убедившись в том, что
цифра единиц числа является четной, можно быть уверен-
уверенным, что и все число делится на 2. Так как свойство А
является необходимым условием для свойства В (А<= В),
то, установив, что число воне делится на 2, можно утверж-
утверждать, что и число р не делится на 2, т.е. теорему 3 можно
сформулировать так: если цифра единиц числа р делится
на 2, то число р делится на 2, если она не делится на 2, то
число р не делится на 2.
п
Отметим, что если некоторое свойство С является доста-
достаточным условием для свойства D, то это еще не означает,
что нет чисел, обладающих свойством D, но не обладающих
свойством С. Например, достаточным условием делимости
числа р на 4 является условие в, = (ц = 0. Справедливость
последнего утверждения следует из представления числа р
в виде
р = (а„- 10я~2 + в„_,- 10"^+ ...+ в3- Ю + <h)- 102
и делимости числа 100 на 4. В то же время, например, число
252 делится на 4, хотя две последние его цифры не нули.
Если доказано, что некоторое свойство Е является необ-
необходимым условием для свойства D, то это еще не означает,
что нет чисел, обладающих свойством Е, но не обладающих
свойством D. Например, необходимым условием делимос-
делимости числа р на 4 является четность числа р. Справедливость
последнего утверждения очевидна, ибо если число р делит-
делится на 4, то тем более оно делится на 2. В то же время,
например, число 1222 не делится на 4, хотя оно четное.
Если же доказано, что свойство ? является необходимым
и достаточным условием для свойства Q, а свойство S легко
проверяется для любого числа р, то, найдя все числа,
обладающие свойством S, можно сказать, что найдены все
числа, обладающие более сложным свойством Q.
В дальнейшем для краткости будем часто пользоваться
символами =>,<=, о ъ следующем смысле: запись М=> L
будет означать, что из утверждения М, стоящего слева от
символа =>, следует утверждение L, стоящее справа. Запись
Q <= S будет означать, что из утверждения S, стоящего
справа от символа <=, следует утверждение Q, стоящее
слева. Запись Ео /"будет означать, что утверждения, сто-
стоящие слева и справа от символа о, равносильны, т.е.
одновременно и из утверждения F, стоящего справа от
символа о, вытекает утверждение Е, стоящее слева, и из
утверждения Е, стоящего слева от символа о, вытекает
утверждение F, стоящее справа.
Сформулируем и докажем признаки делимости нату-
натуральных чисел на 4 и на 9.
12
Теорема 4. Для того чтобы натуральное число р =
= а„а„_1... а2а1а0 делилось на 4, необходимо и достаточно,
чтобы число а,^) делилось на 4.
Доказательство. Достаточность. Пусть число
делится на 4. Запишем число р в виде
Р = Ф + V, F)
где
Ф = (в„ • 10я + ая_, • 10я + ... + а3 ¦ 10 + Ог) • 102,
Каждое слагаемое в правой части равенства F) делится на
4, следовательно, и вся сумма делится на 4, т.е. число р
делится на 4.
Необходимость. Пусть число р делится на 4. По
свойству б) равенств из равенства F) вытекает, что
= р - (ая ¦ 10я + ап_, • 10я-3 + ... + а3 • 10 + а2) ¦ 102.
Каждый член разности правой части равенства делится
на 4, следовательно, вся разность делится на 4, т.е. число
делится на 4. Теорема доказана.
Например, число 1232 делится на 4, так как число 32
делится на 4, а число 15126 не делится на 4, так как число 26
не делится на 4.
Теорема 5. Для того чтобы натуральное число р —
= а„а„-\... 020^ делилось на 9, необходимо и достаточно,
чтобы сумма всех цифр данного числа делилась на 9.
Доказательство. Достаточность. Пусть сумма
цифр данного числа делится на 9. Запишем число р в виде
р = ап ¦ 10я + ап_, • 10я"' + ... + а2 ¦ 102 + в, • 10 + д,,.
Легко видеть, что справедливо равенство
10* = 9 ¦ 10*"' + 9 • 10*~2 + ... + 9 • 10 + 9 + 1.
13
Пользуясь этим равенством, перепишем р в виде
Р = У + К G)
где
у = ак(9 ¦ 10*-' + 9 • К)* + ... + 9 • 10 + 9) +
+ а„_,(9- 10*-2 + 9-10*~3 + .„ + 9- 10 + 9) + ...
... + а2(9 • 10 + 9) + а, • 9,
Каждое слагаемое в правой части равенства G) делится
на 9, следовательно и вся сумма делится на 9, т.е. р делится
на 9.
Необходимость. Пусть число р делится на 9. По
свойству б) равенств из равенства G) вытекает, что
Каждый член разности правой части равенства делится
на 9, следовательно, вся разность делится на 9, т.е. число
(flo + fli + ... + а„) делится на 9. Теорема доказана.
Например, число 1215 делится на 9, так как 1 + 2 + 1 +
+ 5 = 9, а число 4232 не делится на 9, так как 4 + 2 + 3 +
+ 2=11, и 11 не делится на 9.
Простые и составные числа. Множество натуральных
чисел состоит из единицы, простых и составных чисел.
Натуральное число, большее единицы, называется про-
простым, если оно не имеет делителей, кроме единицы и
самого себя. Натуральное число, большее единицы, назы-
называется составным, если оно имеет хотя бы один делитель,
отличный от единицы и самого себя.
Пользуясь этим определением можно показать, что
любое составное число имеет хотя бы один делитель,
который является простым числом.
Теорема 6. Простых чисел бесконечно много.
Доказательство. Допустим, что существует лишь ко-
конечное число простых чисел ри р2, ..., р„. Тогда каждое
натуральное число, большее 1 и не совпадающее ни с одним
14
из этих чисел, будет составным. Число р = рх- рг- р3-...
... • рп + 1 не совпадает ни с одним из чисел А» Л» Л» •••» Рт
так как оно больше каждого из них. По нашему предполо-
предположению, простых чисел, кроме рх , р^, ..., р„, нет. Следова-
Следовательно, число р составное и поэтому делится на одно из
чисел рх, рг, ..., р„.
С другой стороны, число р не делится ни на одно число
из чисел Р\,рг, ..., рп, поскольку произведение рх ¦ р2 ¦... ¦ р„
делится на каждое из этих чисел, а число 1 ни на одно из
них не делится.
Таким образом, предположив, что существует лишь ко-
конечное число простых чисел, приходим к противоречию.
Следовательно, множество простых чисел бесконечно.
Теорема 6 доказана способом от противного. Этот способ
заключается в следующем: строится отрицание утвержде-
утверждения, сформулированного в теореме. Затем на основании
построенного отрицания приходим к выводу, который
либо не верен, либо противоречит сделанному отрицанию.
Тем самым из двух логически возможных ситуаций (либо
верно данное утверждение, либо его отрицание) остается
только одна — верно данное утверждение.
Всякое составное число р можно записать в виде произ-
произведения простых чисел: так, например, 221 = 13 • 17. В этом
случае говорят, что число р разложено на простые множи-
множители.
При разложении числа на простые множители некото-
некоторые из них могут встретиться в разложении не один раз.
Принято писать этот простой множитель в степени, пока-
показывающей, сколько раз он является сомножителем, напри-
например, 360 = 23 • З2 • 51.
Любое натуральное число р можно записать в виде
P = P>?...pl\ (8)
где Ри Рг, ¦-, Рк~ различные простые делители числа р, а
ось ос2, ..., ос* — соответственные числа их повторений в
разложении числа р. Разложение (8) натурального числа р
на простые множители единственно, т.е. не существует
15
других простых чисел, являющихся делителями числа р, и
степени а,, а2 а* не могут быть заменены другими
степенями. Итак, справедлива следующая теорема, прини-
принимаемая здесь без доказательства.
Теорема 7 (основная теорема арифметики). Для каж-
каждого натурального числа р > 1 существует единственное его
разложение на простые множители.
Если натуральные числа рх и р2 делятся на одно и то
же натуральное число р, то число р называется общим
делителем чисел р, и р2. Наибольшее натуральное
число, на которое делятся рх и р2, называется наиболь-
наибольшим общим делителем этих чисел (НОД). Например,
НОД чисел Pi = 132 = 22 • 3 • 11 и р2 = 90 = 2 • З2 • 5 равен
2-3 = 6.
Если НОД двух чисел равен 1, то они называются взаимно
простыми. Взаимно простыми являются, например, числа
33 = 3-11 и 35 = 5-7.
Теорема 8. Если натуральные числа р\ и р2 взаимно
простые, а натуральное число р делится и на р{ и на р2, то р
делится на произведение рфг.
Доказательство теоремы опустим.
Заметим, что если числа рх и /^ не являются взаимно
простыми, то утверждение теоремы не всегда верно. На-
Например, натуральное число 180 делится на 4 и на 6, но не
делится на их произведение — на 24.
Наименьшим общим кратным (НОК) двух натуральных
чисел рх, Ръ называется наименьшее натуральное число,
которое делится и на рх и на р2. Например, НОК чисел 132
и 90 есть число 22 • З2 • 5 • 11 = 1980.
Деление с остатком. Если в результате деления натураль-
натурального числа р на натуральное число т получилось натураль-
натуральное число q такое, что р = mq, то говорят, что р делится
на т. Как следует из вышеизложенного, не всегда в резуль-
результате деления получается такое число q. Однако всегда
возможно деление с остатком.
Разделить натуральное число р на натуральное число т с
остатком — это значит найти два числа q и г из расширен-
расширенного натурального ряда такие, что справедливо равенство
16
p= mq + г, причем г удовлетворяет условию 0 < г < т.
Число q называется частным, а число г — остатком. Если
г = О, что натуральное число р делится на натуральное
число т без остатка.
Теорема 9. Пусть р и т — любые натуральные числа.
Тогда существует единственная пара чисел q и г из расши-
расширенного натурального ряда, удовлетворяющая условиям: р =
= mq+ruO<r<m.
Доказательство. Если р<т, то пара чисел ^ = 0,
r — р удовлетворяет условиям теоремы.
Если р = т, то пара чисел q—l, r=0 удовлетворяет
условиям теоремы.
Если р > т и р делится на т, то существует натуральное
число qx такое, что р = mqx, тогда пара чисел q = qx и г = 0
удовлетворяет условиям теоремы.
Если р > т и р не делится на т, то пара чисел qx = 1 и
г, = р — т будет удовлетворять условиям
р = т ¦ 1 + г,, Г! > 0.
Поскольку р не делится на /и, то г, * т. Значит, либо гх < т,
либо гх > т. Если ^ < т, то пара чисел q = 1 и г = гх удов-
удовлетворяет условиям теоремы.
Если гх > т, то число г2 = гх — т таково, что г, = т + г2 и
0 < г2 < г,. А потому справедливо равенство
р = т-2 + г2.
Так как р не делится на т, то г2 ф т. Значит, либо г2 < т,
либо г2 > т. Если г2 < /л, то пара чисел q = 2 и г = г2 удов-
удовлетворяет условиям теоремы.
Если же г2 > /и, то повторяем этот процесс до тех пор,
пока на каком-то /с-м шаге окажется, что
р= mk+ rk, 0 < rk< т.
А это означает, что пара чисел q= /си r= rk удовлетворяет
условиям теоремы. Существование такого к-го шага выте-
вытекает из следующей аксиомы для натуральных чисел: для
17
любых натуральных чисел рит таких, что р> т, найдется
натуральное число I такое, что р< ml.
Итак, доказано существование пары чисел q и г, удовле-
удовлетворяющих условиям теоремы.
Теперь докажем единственность такой пары чисел.
Предположим, что есть две пары чисел q, г и q0, r0, удовле-
удовлетворяющие условиям теоремы, т.е. такие, что
р = mq+ г и 0 < г < т,
р = mq0 + г0 и 0 й г0 < т.
Следовательно, mq+ г= пщ + г0.
Предположим для определенности, что г0 > г, тогда
0<г0 — г< т и q — qo>O и m(q — q0) = r0 — г. В этом
случае в последнем равенстве в правой части стоит нату-
натуральное число, меньшее чем /я, а в левой части — большее
чем т или равное ему, и, следовательно, равенство m(q —
— Яо) = f0 — r является неверным. Аналогично, рассматри-
рассматривая случай г0 < г, приходим к противоречию. Следователь-
Следовательно, г = г0. Тогда из равенства m(q — q0) = r0 — г = 0 следует
равенство q = q0, т.е. пара чисел q и г, удовлетворяющая
условиям теоремы, единственна. Теорема доказана.
Приведем пример применения теоремы 9.
Докажем, что если р — простое число, большее трех, то
одно из двух чисел (р — 1) или (р + 1) делится на три.
Действительно, число р не делится на три, так как оно
простое и больше трех. Следовательно, остаток при деле-
делении на 3 может быть 1 или 2. Если остаток равен единице,
т.е. если p=3qi + 1, то ясно, что число р — 1 делится на 3.
Если остаток равен двум, т.е. если р = 3q2 + 2, то ясно, что
число р + 1 делится на 3.
Доказанная теорема дает способ нахождения наибольше-
наибольшего общего делителя (НОД) двух чисел. Возьмем два числа
р и т из расширенного натурального ряда и пусть, для
определенности, р> т. Если т = 0, то НОД(р; 0) = р. Если
т * 0, то р = mq+ г, причем, либо р делится на т без
остатка, т.е. г = 0, либо р делится на т с остатком г, где
0 < г < т. В первом случае НОД(р; т) = т, но НОД(/я; 0) =
18
= т, т.е. справедливо равенство НОД(р; т) = НОД(/я; г).
Оказывается, что аналогичное равенство
НОД(р;/я) = НОД(т;г) (9)
имеет место и в случае 0 < г < т.
Действительно, пусть / — общий делитель чисел р и т,
т.е. пусть р = 1к и т = In , где к, /, и п — натуральные числа.
Так как р = тд+ гиг > 0, то Ik— lnq> О, т.е. 1{к — щ) > 0.
Но тогда к — nq>0 и r= Is, где s= к— щ — натуральное
число, т.е. / является делителем числа г.
Значит, каждый общий делитель чисел р и m является
общим делителем чисел m и г. Рассуждая аналогично,
получим и обратное утверждение: каждый общий делитель
чисел /лиг является общим делителем чисел рит. Отсюда
следует, что совпадают и наибольшие общие делители этих
пар, т.е. что верно равенство (9). Так как т<ри г< т, то
задача нахождения НОД(/я; г) является более простой, чем
задача нахождения НОД(р; т).
Рассмотрим следующий пример. Найти НОДA428; 420).
Так как 1428 = 420 • 3 + 168, то НОДA428; 420) =
= НОДD20; 168).
Так как 420 = 168 • 2 + 84, то НОДD20; 168) = НОДA68;
84).
Так как 168 = 84 2, то НОДA68; 84) = НОД(84; 0) = 84,
т.е. НОДA428; 420) = 84.
Таким образом, способ нахождения НОД(р; т) заключается
в применении равенства (9).
После нахождения НОД(р; т) оказывается возможным
найти наименьшее общее кратное этих чисел: НОК(р; т).
Для этого надо воспользоваться теоремой 10, доказатель-
доказательство который мы опустим.
Теорема 10. НОД(р; т) ¦ НОК(р; т)=р т.
Например, найдем НОК A428; 420). Из предыдущего
примера следует, что НОДA428; 420) = 84. Следовательно,
НОКA428; 420) = 1428g4420 = 7140.
19
§2. Дроби
Выше отмечалось, что деление не всегда выполнимо в
множестве натуральных чисел. Например, в множестве
натуральных чисел нельзя 5 разделить на 4. Чтобы деление
было выполнимо всегда, приходится рассматривать новые
числа — части натуральных чисел, или дроби.
Обыкновенные дроби. Число, равное к-й части числа
единица (к — натуральное число, большее единицы), обо-
обозначают j-. Если эта часть берется т раз (т — натуральное
число), то получаемое в результате этого новое число
обозначают р Число, определяемое по этому правилу при
помощи двух натуральных чисел ри q(q> I) и записывае-
записываемое как ?, называют дробью или частным натуральных
чисел р и q, при этом р называют числителем этой дроби,
а число q — знаменателем.
Всякое натуральное число можно считать дробью со зна-
знаменателем единица, т.е. любое натуральное число п можно
записать как дробь у. Поэтому дальше ограничение q > 1
на знаменатель дроби снимается и говорят, что частное
двух любых натуральных чисел р и q есть дробь ^ и при этом
множество всех дробей содержит в себе множество всех
натуральных чисел.
Две дроби ? и ^ считаются равными, если произведение
числителя первой дроби на знаменатель второй равно
произведению числителя второй на знаменатель первой,
т.е. ? = j, если рк = qm.
Аналогично ^ > у, если рк > mq; ^ < у, если рк < mq.
Суммой двух дробей называется дробь, числитель кото-
которой равен сумме произведений числителя первой дроби на
знаменатель второй и числителя второй дроби на знамена-
знаменатель первой, а знаменатель равен произведению знамена-
знаменателей этих дробей, т.е.
20
P m_pk+qm
q+к qk ¦
Произведением двух дробей называется дробь, числитель
которой равен произведению числителей этих дробей, а
знаменатель — произведению знаменателей, т.е.
? т _рт
q' k~ qk-
Справедливы следующие основные законы сложения
и умножения дробей:
а)? + ^ = ^ + ? (коммутативность сложения);
б) [? + Щ-1+ - = ? + Г-т? + -1 (ассоциативность сложения);
' \q k\ n q \к пу "
ъ) Е. 01 = ?. Р. (коммутативность умножения);
г) Г ' Т Г ~ = ^" IT ' л I (асс°Циативность умножения);
д) \p- + 2f\-- = p-•- + %¦•- (дистрибутивность сложения
\q /с I n q п К п
относительно умножения).
Разделить дробь ? на дробь — — значит найти дробь -j-
q п к
такую, что
А. Ш
к п
В отличие от натуральных чисел, деление для дробей
всегда выполнимо. Используя определение равенства двух
дробей, легко показать, что
I _ рп
к~ qm
Вычесть из дроби ? дробь — — значит найти дробь -
такую, что
21
Вычитание так же, как и для натуральных чисел, не всегда
выполнимо. Если ^ < — или ^ = —, то не существует дроби,
которая бы при сложении с дробью — давала бы дробь 2.
Если же ? > —, то вычитание выполнимо и легко видеть,
г _ рп — mq
s nq
Из определения равенства двух дробей вытекает основное
свойство дробей: если числитель и знаменатель данной дроби
умножить и разделить на одно и то же натуральное число
к, то получится дробь, равная данной:
q qk'
Дробь ? называется несократимой, если числа р и q взаимно
простые.
Теорема 1. Если В- — несократимая дробь, то дробь —
равна ей тогда и только тогда, когда т = рк и п = qk, где
к — некоторое натуральное число.
Доказательство. Достаточность. Пусть т = рки
п = qk. Тогда дроби ? и — равны по основному свойству
дробей.
Необходимость. Пусть ? = —. По определению ра-
равенства дробей рп = mq. Левая часть этого равенства делит-
делится на число р, следовательно, согласно основной теореме
арифметики (см. § 1, теорема 7) и правая часть делится
на р. Так как числа р и q взаимно простые, а произведение
mq делится на р, то на р делится т (т.е. существует нату-
натуральное число к такое, что т = рк). Подставляя значение т
в равенство рп = mq, получаем пр = pkq, откуда п = qk.
Теорема доказана.
22
Конечные десятичные дроби. Рассмотрим те дроби ?, у
которых знаменатель q = 10*, где к — некоторое натураль-
натуральное число. Для каждой такой дроби принята специальная
форма записи, а именно: пишут числитель дроби и, отсчи-
отсчитав с правой стороны к цифр, отделяют их запятой; если в
числителе меньше цифр, чем к, например п цифр (и < к),
то пишут числитель и перед его первой цифрой дописыва-
дописывают к — п нулей, затем ставят запятую и перед ней еще один
нуль; если же в числителе к цифр, то пишут числитель,
перед его первой цифрой ставят запятую и перед ней
дописывают нуль.
Так, например, дроби Щ-, -^щ^ ^щ могут быть запи-
записаны так: 37,21; 0,0021; 0,131.
Дробь, записанная в таком виде, называется конечной
десятичной дробью.
Значит, дроби 37,21; 0,0021; 0,131 могут служить приме-
примерами конечных десятичных дробей. Вообще, каждую ко-
конечную десятичную дробь будем дальше обозначать так:
Oq, аха2аг ... ак, A)
где к — натуральное число, Oq — число из расширенного
натурального ряда, каждое из л,, аъ ..., ак — одно из чисел
0, 1,2, 3, 4, 5, 6, 7, 8, 9. Часто конечную десятичную дробь
называют просто десятичной дробью, опуская слово «ко-
«конечная».
Любая конечная десятичная дробь легко переводится в
обыкновенную. Для этого надо записать в числитель целое
число, которое получается, если отбросить запятую у деся-
десятичной дроби, а в знаменатель написать число 10 в такой
степени, сколько цифр стоит у десятичной дроби после
запятой, после чего дробь можно сократить на общий
множитель, если он есть, например 0,34 = -щ = ~^.
Записать обыкновенную дробь в виде конечной десятич-
десятичной — значит найти конечную дробь, равную данной.
Естественно поставить вопрос: любую ли обыкновенную
дробь можно записать в виде конечной десятичной дроби?
23
Оказывается, что дело здесь обстоит намного сложнее, чем
с переводом конечной десятичной дроби в обыкновенную.
Теорема 2. Всякая дробь ^, где натуральное число q не
имеет простых делителей, отличных от 2 и 5, может быть
записана в виде конечной десятичной дроби.
Доказательство. Пусть дана дробь ?, где q=2m ¦ 5".
По основному свойству дроби любая обыкновенная дробь
не изменится, если числитель и знаменатель ее умножить
на одно и то же число. Умножая числитель и знаменатель
дроби ? на 2m, получим
г _ , _ S р _ 2 5 р _25 р
Я 2'"-5я 2'" • 5" • 2" • 5™ 2"+'"-5"+т 10л+'"'
Так как произведение 2" ¦ 5тр — натуральное число, то,
обозначая его через /, запишем дробь в виде ? = —j^, откуда
видно, что дробь ? может быть записана конечной десятич-
десятичной дробью. Теорема доказана.
Теорема 3. Если данная несократимая дробь & может
быть записана конечной десятичной дробью, то ее знамена-
знаменатель не содержит простых множителей, отличных от 2 и 5.
Доказательство. Если q=l, то теорема очевидна.
Рассмотрим случай, когда q#l. Дробь ^ по условию пред-
представлена в виде конечной десятичной дроби, значит спра-
справедливо равенство ^ = -^, где / и к — натуральные числа.
Так как ^ несократимая дробь, то из теоремы 1 вытекает,
что 1 = рт и 10* = qm. Число 10* содержит только простые
множители 2 и 5. Значит, и число qm не имеет других
простых множителей, кроме 2 и 5, что вытекает из единст-
единственности разложения числа на простые множители. Сле-
Следовательно, число q не содержит других простых множите-
множителей, кроме 2 и 5. Теорема доказана.
24
Теорема 4. Для того чтобы несократимая дробь ^ могла
быть записана конечной десятичной дробью, необходимо и
достаточно, чтобы ее знаменатель не содержал никаких
других простых множителей, кроме 2 и 5.
Справедливость теоремы 4 вытекает из теорем 2 и 3.
Теперь рассмотрим дробь ?, где/» и q — взаимно простые
числа, и q содержит простые множители, отличные от 2 и 5.
Как вытекает из теоремы 4, эта дробь не может быть
записана конечной десятичной дробью. Но такие дроби
могут быть записаны при помощи так называемых беско-
бесконечных десятичных дробей.
Бесконечные периодические десятичные дроби. Выше ко-
конечной десятичной дробью была названа дробь, записан-
записанная в виде A), где после запятой стоит конечное число
цифр. Естественно бесконечной периодической десятичной
дробью назвать десятичную дробь, у которой после запятой
стоит бесконечно много цифр, причем одна цифра или
упорядоченная совокупность цифр, начиная с некоторого
места после запятой, повторяется. Более точно это можно
сказать так: бесконечной периодической десятичной дро-
дробью называется дробь, которая может быть записана в виде
оо, а,а2 - йк..., B)
где
1. Oq — число из расширенного натурального ряда;
2. в записи B) — для любого натурального числа т на
/и-м месте после запятой стоит одно из чисел 0, 1, 2, ..., 9,
при этом или ай отлично от нуля, или, если щ равно нулю,
то существует хотя бы одно натуральное число q такое, что
на 0-м месте после запятой стоит одно из чисел 1, 2, ..., 9;
3. существуют такие натуральные числа I и р, что для
любого натурального п > I справедливо равенство а„+р = а„,
при этом упорядоченная совокупность цифр {aflt+ х... а,+р_ х)
называется периодом бесконечной периодической десятичной
дроби B).
Обычно при записи бесконечной периодической деся-
десятичной дроби многоточие ставится после несколько раз
25
повторенного периода, т.е. тогда, когда становится понят-
понятным, какое число является периодом этой дроби.
Например, очевидно, что дробь
4,27131313 ... C)
есть бесконечная периодическая десятичная дробь с пери-
периодом A3).
Вместо того чтобы писать период несколько раз и потом
ставить многоточие, принято писать период один раз,
заключая его в круглые скобки:
4,27131313... =4,27A3),
0,454545 ... = 0,D5).
Справедлива следующая теорема, доказательство кото-
которой опускается.
Теорема 5. Всякая дробь е, гдер и q взаимно просты и q
содержит хотя бы один простой множитель, отличный от
2 и 5, может быть единственным образом записана в виде
бесконечной периодической десятичной дроби.
Объединяя теоремы 4 и 5, получаем, что любую обыкно-
обыкновенную дробь можно записать в виде либо конечной деся-
десятичной дроби либо бесконечной периодической десятич-
десятичной дроби. Приведем без доказательства правило перевода
бесконечной периодической десятичной дроби в обыкно-
обыкновенную (это правило будет доказано в гл. IX).
Чтобы сократить бесконечную периодическую десятичную
дробь в обыкновенную, надо из числа, стоящего до второго
периода, вычесть число, стоящее до первого периода, и сде-
сделать эту разность числителем, а в знаменателе написать
цифру 9 столько раз, сколько цифр в периоде, и после девяток
дописать столько нулей, сколько цифр между запятой и
первым периодом. Например:
26
11720-1172 _ 10 548 1172-9 _ 293 4 _ 293.
90000 90 000 9 10000 4 2500 2500'
?7M T> -
99 9 11 1Г
42 713 ~ 427 - 42 286 _ 2 ¦ 21 143 _ 21 143
9900 9900 " 2 4950 4950*
Пользуясь этим правилом, можно показать, что любую
конечную дробь также можно представить в виде бесконеч-
бесконечной периодической дроби, причем двумя способами.
Например:
0 172-0 172f(ft - 1720~ т - 1548 - т 9 -0
U,l/2-U,l/2(U)- 9fm -9000-9 1000" U'
0 172-0 17101 1719-171 _ 1548 _ 172 9 _q
и,1/2-и,1/1(У)- 5^ -9000-9 1000" U'
Чтобы не было двух разных представлений одной и той
же конечной десятичной дроби, принято не иметь число 9
в периоде. Тогда каждая десятичная конечная дробь может
быть единственным образом записана в виде бесконечной
периодической десятичной дроби с периодом 0 и, наобо-
наоборот, каждая такая дробь есть конечная десятичная дробь.
Итак, имеет место
Теорема 6. Каждая обыкновенная дробь е может быть
единственным образом представлена в виде бесконечной де-
десятичной периодической дроби и, наоборот, каждая бесконеч-
бесконечная десятичная дробь может быть единственным образом
представлена в виде обыкновенной дроби &.
Таким образом, можно сказать, что каждая бесконечная
периодическая десятичная дробь есть другая форма записи
некоторой вполне определенной обыкновенной дроби.
§ 3. Целые числа
Выше уже отмечалось, что вычитание не всегда выпол-
выполнимо в множестве натуральных чисел. Например, в мно-
множестве натуральных чисел нельзя вычесть из числа 3
27
число 5. Поэтому возникает необходимость в расширении
натуральных чисел.
Введем в рассмотрение новые числа — натуральные
числа со знаком минус, т.е. числа вида (— /я), где т —
натуральное число, и будем называть такие числа отрица-
отрицательными целыми числами. Отрицательное целое число
(— т) называют иногда числом, противоположным нату-
натуральному числу т.
Будем говорить, что два целых отрицательных числа
(— т) и (— и) равны, если равны натуральные числа тип.
Теперь рассмотрим множество чисел, состоящее из всех
натуральных чисел, нуля и всех целых отрицательных
чисел. Будем считать, что два числа из этого множества
равны, если либо они — равные натуральные числа, либо
они — равные целые отрицательные числа, либо каждое из
них есть нуль. Определим теперь действия сложения и
умножения для чисел из этого множества. Если оба числа,
которые надо сложить или умножить, есть числа из расши-
расширенного натурального ряда, то действия сложения и умно-
умножения для этих двух чисел определяются так же, как в § 1.
Если же одно число или оба числа, которые надо сложить
или умножить, есть отрицательные целые числа, то дейст-
действия сложения и умножения для этих двух чисел произво-
производятся следующим образом:
г)(-т) + (-п) = -(т + п);
б) (— т) + О = 0 + (— т) = — т;
— (т — п), если т > п;
в) (— т) + п =
п — т, если т < п;
О, если т = п;
г) (— т)п = т{— п) = — (тп);
д) (— т){— п) = тп;
е) (- т) ¦ О = 0 • (- т) = 0.
Множество чисел, состоящее из всех натуральных чисел,
нуля и всех отрицательных целых чисел, с только что
введенными определениями равенства и действий сложе-
сложения и умножения, называется множеством целых чисел и
обозначается буквой Z, а сами эти числа называются целы-
28
ми числами. Натуральные числа иногда называются также
целыми положительными числами.
Основные законы сложения и умножения целых чисел
аналогичны основным законам сложения и умножения
натуральных чисел и поэтому здесь не приводятся.
Для действий сложения и умножения целых чисел вво-
вводятся обратные действия — вычитание и деление (кроме
деления на нуль). При этом действие вычитания теперь
всегда выполнимо, а действие деления не всегда. Но как и
для натуральных чисел, для целых чисел всегда выполнимо
деление с остатком. Ниже рассматривается подробно лишь
деление с остатком целого числа на натуральное число.
Деление с остатком. Разделить целое число а на натураль-
натуральное число т с остатком — это значит найти два целых числа
qvi г таких, что справедливо равенство а = mq + г, причем
число г удовлетворяет условию 0 < г < т.
Если г = 0, то говорят, что целое число а делится нацело
на натуральное число т.
Теорема 1. Пусть а — любое целое число и т — любое
натуральное число. Тогда существует единственная пара
целых чисел q и г, удовлетворяющая условиям: а= mq + r и
Ойг<т.
Доказательство. Случай, когда а — натуральное
число, был разобран в § 1.
Если а = О, то пара чисел q = О и г = О удовлетворяют
условиям теоремы.
Пусть а = — п — целое отрицательное число. Тогда п —
натуральное число, и по уже доказанному получаем, что
существует пара целых чисел qx и г( такая, что п = mq{ + r(
и 0 < г( < т. В случае, если г( = 0, из равенства п = mq\ + г(
вытекает равенство а = mq, где q= (— q\), т.е. пара чисел
q = — q\ и г=0 удовлетворяет условиям теоремы. Если
О < г( < т, то из равенства п = mqx + r( вытекает равенство
а = (— 01 — \)т + (т — г,), и тогда пара чисел q = — qx — 1
и г = т — г( удовлетворяет условиям теоремы.
Итак, для любого целого числа а и любого натурального
числа т существует пара целых чисел q и г таких, что а =
29
Единственность пары целых чисел q и г доказывается так
же, как и в теореме 9 § 1. Так же, как и в § 1, целое число,
делящиеся на 2 нацело, будем называть четным числом, а
делящиеся на 2 с остатком г = 1 — нечетным.
Приведем некоторые следствия теоремы 1.
а) Любое четное число а может быть записано в виде а =
= 2q, где q — некоторое целое число.
б) Любое нечетное число а может быть записано в виде
а = 2qx + 1, где qx — некоторое целое число.
в) Любое целое число а, делящиеся нацело на три, может
быть записано в виде а = 3q, где q — некоторое целое число.
г) Любое целое число а, не делящиеся нацело на три, может
быть записано в одном из следующих видов: а = 31+ 1 или
а = Зл + 2, где I и п — некоторые целые числа.
д) Любое целое число а, делящиеся нацело на некоторое
натуральное число к, может быть записано в виде а = kg, где
q — некоторое целое число.
е) Любое целое число а, не делящиеся нацело на некоторое
натуральное число к, может быть записано в виде а = kq + г,
где г — одно из чисел 1, 2,..., (к — 1), a q — некоторое целое
число.
В зависимости от делимости целых чисел на данное
натуральное число к множество целых чисел можно разбить
на к классов. Например, если к = 2, то множество всех
целых чисел разбивается на два класса: четные числа и
нечетные числа.
Множество всех целых чисел можно разбить также и на
три класса:
а) числа, кратные числу три, т.е. числа вида 3q, где q —
любое целое число;
б) числа, имеющие при делении на три остаток единицу,
т.е. числа вида 3/+ 1, где / — любое целое число;
в) числа, имеющие при делении на три остаток два, т.е.
числа вида Ъп + 2, где п — любое целое число.
Из приведенных примеров ясно, как разбить множество
целых чисел на 4 класса, 5 классов и т.д.
Приведем примеры, показывающие, как разбиение
целых чисел на классы помогает решать ряд задач.
30
1. Доказать, что при любом целом Ъ число bBb + l)Gb +
+ 1) делится на три.
Доказательство. Разобьем множество всех целых
чисел натри класса: а) Ъц\ б) Зд + 1; в) Ъц + 2, где q — любое
целое число.
Пусть Ъ — любое число из класса а). Тогда bBb + l)Gb +
+ 1) = 3qFq + l)Blq+ 1), откуда видно, что при любом
целом q это число делится на 3.
Пусть b — любое число из класса б). Тогда bBb + l)Gb +
+ 1) = C? + 1) 3 Bq + l)Blq + 8), откуда видно, что при
любом целом q число делится на 3.
Пусть b — любое число из класса в). Тогда bBb + l)Gb +
+ 1) = C? + 2)Fq + 5) • 3 • Gq + 5), откуда видно, что при
любом целом q число делится на 3.
2. Доказать, что среди любых к последовательных целых
чисел есть число, делящееся нацело на к.
Доказательство. Все целые числа можно разбить на
следующие к классов:
kq, ....-->
kq+l,
kq+2,
где q — любое целое число.
Пусть даны к последовательных целых чисел, начинаю-
начинающихся с некоторого целого числа Ь, т.е. Ь, (Ь + 1), (Ь +
+ 2), ..., [Ь + (к — 1)], и пусть число Ъ содержится в классе
kq+ i для некоторого / [/=0, 1, 2 (к — 1)], т.е. пусть
b = kq + /, где q — некоторое целое число. Поскольку среди
к последовательных чисел есть число
[Ь + (к - I)] = [kq+ i+ (к - i)\ = k(q+ 1),
которое делится нацело на к, то утверждение 2 доказано.
минует, е. числа вида — — , где тип — натуральные числа,
называют иногда числом, противоположным
§ 4. Рациональные и иррациональные числа
Рациональные числа. Как уже отмечалось выше, в мно-
множестве натуральных чисел не всегда выполнимы действия
вычитания и деления. В § 2 множество натуральных чисел
было расширено до множества обыкновенных дробей, и в
этом множестве деление уже всегда выполнимо; однако
действие вычитания выполнимо не всегда. Поэтому возни-
возникает необходимость во введении новых чисел.
Введем в рассмотрение новые числа — дроби со знаком
Дробь (- fj
дроби —.
н
Теперь рассмотрим множество чисел, состоящее из всех
дробей, нуля и всех дробей со знаком минус. Можно
считать, что каждое число из этого множества есть отно-
отношение целого числа к натуральному. Поэтому будем счи-
считать, что это множество состоит из чисел вида ?, где q —
я
натуральное число, ар — целое число.
Будем считать, что два числа ? и — из этого множества
равны, если справедливо равенство рп = qm. Будем считать,
что сложение и умножение чисел из этого множества
производятся по следующим правилам:
Р т _pn + qm р m _рт
q п~ qn q n~ qn'
Множество чисел, состоящее из всех чисел вида ?, где
q — натуральное число, ар— целое число, с только что
введенными определениями равенства и действий сложе-
сложения и умножения, называется множеством рациональных
чисел и обозначается буквой Q, а сами эти числа называ-
называются рациональными числами.
32
Если р — натуральное число, то число ? называется
положительным рациональным числом, или положительной
дробью.
Если же/> — отрицательное число, то число ^ называется
отрицательным рациональным числом, или отрицательной
дробью. Ясно, что множество целых чисел — часть множе-
множества рациональных чисел.
Для действий сложения и умножения рациональных
чисел вводятся обратные действия — вычитание и деление,
при этом оба эти действия, за исключением запрещенного
деления на нуль, всегда выполнимы.
Основные законы сложения и умножения рациональных
чисел аналогичны основным законам сложения и умноже-
умножения целых чисел и поэтому здесь не приводятся.
Если рациональное число г взято сомножителем к раз
(к > 1), то произведение п... г называют к-й степенью
it раз
числа г и обозначают Л Кроме того, по определению ? = г.
Как и для натуральных чисел, справедливы следующие
свойства степеней рациональных чисел:
f +k
дL; = ^~Я1, если к> т, г*0.
г
По определению ? = 1 для любого рационального
числа г, кроме числа нуль.
В связи с понятием степени рационального числа часто
возникает задача: для данного натурального числа к и для
данного положительного числа гх найти другое положи-
положительное рациональное число г2 такое, что /? = г,.
Эта задача не всегда имеет решение.
Теорема 1. Не существует рационального числа, квад-
квадрат которого равен 2.
2 Алгебра, тригонометрия
и элементарные функции
Доказательство. Предположим, что существует ра-
циональное число ^ такое, что Мч = 2. Не ограничивая
общности, будем считать р и д взаимно простыми (если
числитель и знаменатель данного рационального числа
имеют общие множители, то число ?, полученное после
сокращения, равно данному). Пользуясь свойством г) сте-
степеней рациональных чисел, запишем наше предположение
2 «
в виде Ц - \.
я 1
Из определения равенства рациональных чисел вытека-
вытекает, что р2 = Iq2. Поскольку правая часть этого равенства
делится на 2, то и левая должна делится на 2. Но число р2
делится на 2 только в случае, если число р делится на 2
(если р не делится на 2, то р2 также не делится на 2).
Поскольку р делится на 2, то существует целое число к
такое, что р = 2к. Подставляя это значение р в равенство
р2 = Iq2, получаем, что q2 = 2k2. Поскольку правая часть
этого равенства делится на 2, то и левая делится на 2,
значит, число q делится на 2, т.е. q = 2т.
Итак, получили, что числа р и q имеют общий множи-
2
( Ч
тель — число 2, а по предположению в равенстве 1? ] = 2
числа/) и q взаимно простые. Это противоречие и означает,
что сделанное предположение неверно, а верно утвержде-
утверждение теоремы.
Таким образом, возникает необходимость ввести новые
числа, отличные от рациональных, такие, например, как
число, квадрат которого равен 2.
Иррациональные числа. В § 2 были введены в рассмотрение
бесконечные периодические десятичные дроби. Теперь расши-
расширим это понятие, введя в рассмотрение новые числа, которые
будем называть бесконечными десятичными дробями.
Бесконечной десятинной дробью назовем число, которое
может быть записано в виде
До, д,д2 ... ак ..., A)
или в виде
34
- до, а,а2... ак ..., B)
где щ — число из расширенного натурального ряда, аи
аъ ..., ак ... — числа из множества чисел 0, 1, 2, 3, 4, 5, 6,
7, 8, 9. Многоточие означает, для любого натурального
числа т на т — м месте после запятой стоит число ат.
Если среди чисел щ, аъ а2,..., а* ••• хотя бы одно отлично
от нуля, то число, записанное в виде A), будем называть
положительной бесконечной десятичной дробью, а число,
записанное в виде B), будем называть отрицательной бес-
бесконечной десятичной дробью. Если среди чисел щ, аи аъ ...,
ак ... нет чисел, отличных от нуля, то число, записанное в
виде A), будем считать равным числу, записанному в
виде B), и называть нулевой бесконечной периодической
десятичной дробью и обозначать так: 0,@). Очевидно, что
множество всех бесконечных десятичных дробей содержит
в себе:
1) множество всех положительных периодических беско-
бесконечных десятичных дробей;
2) множество всех отрицательных периодических беско-
бесконечных десятичных дробей;
3) нулевую бесконечную периодическую десятичную
дробь.
Покажем теперь, что только что перечисленными пери-
периодическими бесконечными десятичными дробями не ис-
исчерпывается множество всех бесконечных десятичных дро-
дробей.
Теорема 2. Бесконечная десятичная дробь
0, 1010010001000010000010000001 ...,
образуемая по правилу, за каждой единицей идет группа
нулей, содержащая на один нуль больше, чем предыдущая
группа, — не является периодической десятичной дробью.
Доказательство. Предположим, что это периодичес-
периодическая дробь. Пусть ее период состоит из п цифр и первый
период начинается с k-то места. Ясно, что в рассматривае-
рассматриваемой дроби с некоторого /я-го места, каждой единице будут
предшествовать Bл + 1) или более подряд идущих нулей.
Рассмотрим каждую из таких групп нулей, начинающуюся
2* 35
с любого р — го места, где р> к и р> т. Возьмем теперь
нуль, стоящий посередине этой группы. Этот нуль нахо-
находится либо в начале, либо в конце, либо внутри некоторого
периода длины п, но во всех перечисленных случаях этот
период целиком лежит на взятом отрезке из Bл +1) или
более нулей. Значит, период состоит из одних нулей, и,
следовательно, в записи дроби с к-то места должны быть
только нули, а это неверно. Теорема доказана.
Из вышеизложенного вытекает, что каждое рациональ-
рациональное число может быть записано в виде бесконечной пери-
периодической десятичной дроби. Поэтому естественно ирра-
иррациональным числом называть число, которое может быть
записано в виде бесконечной непериодической десятичной
дроби.
В дальнейшем будем считать, что любая бесконечная
периодическая десятичная дробь есть вполне определенное
рациональное число, а любая бесконечная непериодичес-
непериодическая десятичная дробь есть вполне определенное иррацио-
иррациональное число. Заметим, что в силу этих определений
нулевая бесконечная периодическая дробь есть число нуль.
§ 5. Действительные числа
Множество всех бесконечных десятичных дробей (с вво-
вводимыми ниже определениями равенства, суммы и произ-
произведения этих чисел) называется множеством действитель-
действительных чисел и обозначается буквой R, а каждая бесконечная
десятичная дробь называется действительным числом. По-
Положительная бесконечная дробь будет называться положи-
положительным действительным числом, отрицательная бесконеч-
бесконечная десятичная дробь — отрицательным действительным
числом, нулевая бесконечная периодическая дробь (с пери-
периодом нуль) — числом нуль. Поскольку бесконечные деся-
десятичные дроби есть периодические и непериодические, то
каждое действительное число является либо рациональ-
рациональным, либо иррациональным.
Два положительных действительных числа
36
До, аха7... ак ...,
60, bxb2 ••• At •••
равны, если 6* = а* для всех чисел & из расширенного
натурального ряда.
Из двух положительных действительных чисел
щ, аха2... ак ...,
b0, bxb2... Ък ...
первое больше второго, если либо щ > Ьо, либо если щ = bo,
но щ > Ьх, либо если а^ = bo, ах = Ьх, ..., а„ = Ь„ (для некото-
некоторого натурального числа л), но ая+ х > Ьн+ х.
Два действительных числа
щ, аха2... ак ... и — b0, bxb2... bk ...
называются противоположными, если Ьк = ак для всех к из
расширенного натурального ряда. Два отрицательных дей-
действительных числа равны, если равны противоположные им
числа. Из двух отрицательных чисел больше то, у которого
противоположное (положительное) число меньше. Поло-
Положительное число больше нуля и любого отрицательного
числа. Нуль больше любого отрицательного числа.
Рассмотрим приближенные значения бесконечных дробей.
Оборвем на каком-то месте бесконечную положительную
десятичную дробь, изображающую данное положительное
действительное число. Получим конечную десятичную
дробь (которую можно записать в виде бесконечной с
периодом нуль). Эта дробь будет меньше данного числа
(или равна ему). Такая дробь называется приближенным
значением данного положительного действительного числа с
недостатком.
Если положительную бесконечную десятичную дробь
оборвать на каком-то k-м месте и к полученной дроби
прибавить дробь -Ц, то получим конечную десятичную
дробь, которая больше данного действительного числа.
Такая дробь называется приближенным значением данного
положительного действительного числа с избытком.
37
Если отрицательную бесконечную дробь оборвать на
каком-то месте, то получим конечную десятичную дробь,
которая больше данного действительного числа (или равна
ему). Такая дробь называется приближенным значением дан-
данного отрицательного действительного числа с избытком.
Если отрицательную бесконечную дробь оборвать на
каком-то k-м месте и к полученной дроби прибавить дробь
[ К | , то получим десятичную дробь, которая меньше
данного действительного числа. Такая дробь называется
приближенным значением данного отрицательного числа с
недостатком.
Примеры. 1. Приближенным значением числа 0,4C1)
с недостатком будут следующие конечные дроби: 0,4; 0,43;
0,431; 0,4313; 0,43131; ... Приближенным значением этого
же числа с избытком будут дроби 0,5; 0,44; 0,432; 0,4314;
0,43132; ...
2. Приближенным значением числа — 3,2A7) с недостат-
недостатком будут следующие конечные дроби: — 3,3; — 3,22;
— 3,218; — 3,2172; — 3,21718;... Приближенным значением
этого же числа с избытком будут дроби — 3,2; —3,21;
- 3,217; - 3,2171; - 3,21717; ...
Определим теперь действия сложения и умножения для
действительных чисел.
Суммой двух действительных чисел называется число,
которое больше (или равно) суммы двух любых прибли-
приближенных их значений с недостатком, но меньше (или равно)
суммы двух любых приближенных их значений с избытком.
Без доказательства примем, что такое число всегда суще-
существует и притом только одно.
Отметим частный случай: сумма действительного числа
а и противоположного ему числа (которое будем обозна-
обозначать (— а)) есть число нуль.
Произведением двух действительных положительных
чисел щ, ага7 ... ак ... и b0, b^ ... Ьк ... называется число,
которое больше (или равно) произведения их значения с
недостатком, но меньше (или равно) произведения двух
любых приближенных их значений с избытком.
38
Без доказательства примем, что такое число всегда суще-
существует и притом только одно.
Произведение двух действительных отрицательных
чисел (— щ, аха2 ... ак ...) и (— Ьо, bxb2 ... Ьк ...) равно
произведению противоположных им положительных чисел
щ, аха2 ... ак ... и b0, bxb2 ... bk ... . Произведение двух
действительных чисел, имеющих разные знаки
Оо, аха2... ак ... и (— b0, bxb2... bk ...) или (— щ, аха2... ак ...)
и b0, bxb2... bk ..., равно отрицательному числу, противопо-
противоположному произведению чисел щ, аха2 ... ак ... и
b0, bxb2... bk ... .
Произведение двух чисел, одно из которых есть нуль,
равно нулю.
Справедливы следующие основные законы сложения
и умножения действительных чисел:
a)a+b = a + b (коммутативность сложения);
б) (а + Ь) + с = а + (Ь + с) (ассоциативность сложения);
в) ab = Ъа (коммутативность умножения);
г) (ab)c = a(bc) (ассоциативность умножения);
д) (а + b)c = ac + be (дистрибутивность сложения отно-
относительно умножения).
Для действий сложения и умножения действительных
чисел вводятся обратные действия — вычитание и деление.
Вычесть из действительного числа а действительное
число b — значит найти действительное число с такое, что
Ь + с=а.
Разделить действительное число а на отличное от нуля
действительное число Ъ — значит найти действительное
число d такое, что Ъй = а.
На множестве действительных чисел действия вычита-
вычитания и деления, за исключением запрещенного деления на
нуль, всегда выполнимы.
Если действительное число а взято множителем п раз
(и — натуральное число, п > 1), то произведение
аа ... а называют л-й степенью числа а и обозначают о".
л раз
Кроме того, по определению ах = а. Свойства степени
действительных чисел аналогичны свойствам степени ра-
рациональных чисел и поэтому здесь не приводятся. В связи
39
с понятием степени действительных чисел часто возникает
такая задача: для данного натурального числа п и для
данного неотрицательного действительного числа а найти
другое неотрицательное число b такое, что b" = а.
Неотрицательное число b такое, что его л-я степень есть
данное число а, т.е. Ь" = а, называется арифметическим
корнем степени п неотрицательного числа а и обозначается
Ча, т.е. b = Ча.
Теорема. Для любого натурального числа п > 1 и любого
неотрицательного числа а существует и притом единствен-
единственный в множестве неотрицательных чисел арифметический
корень степени п из числа а.
Доказательство теоремы опустим.
В случае п = 2 в обозначении корня цифру 2 не пишут;
в случае п = 1 корень 1-й степени из числа а есть само число
а. Арифметические корни могут быть рациональными и
иррациональными числами.
Например, ^ч~ есть рациональное число i; V2" — есть
иррациональное число (это вытекает из теоремы 1 § 4).
Заметим, что по определению арифметический корень
из числа 0 есть нуль.
Абсолютной величиной (или модулем) действительного
числа а называется: само это число, если а — положитель-
положительное число; нуль, если а — нуль; число противоположное
числу а, если а — отрицательное число. Абсолютная вели-
величина действительного числа а обозначается \а\. Сформули-
Сформулированное выше определение можно коротко записать так:
н=
а, если а > 0;
0, если а = 0;
— а, если а < 0.
Основные свойства абсолютных величин действительных
чисел будут приведены в главе П.
Заметим, что в силу определения арифметического
корня из неотрицательного числа для любого действитель-
действительного числа справедливо равенство *№ = \а\.
40
Поставим более общую задачу: для любого действитель-
действительного числа а и любого натурального числа п найти дейст-
действительные числа b такие, что b" = а. Если такие числа
существуют, то они называются действительными алгебра-
алгебраическими корнями п-й степени из действительного числа а.
Если число а неотрицательное, то, как говорилось выше,
существует одно неотрицательное число Ъ такое, что b" = а,
т.е. для любого неотрицательного числа а существует хотя
бы один алгебраический корень Ъ, для обозначения кото-
которого есть специальный символ Ча (арифметический ко-
корень). В случае существования других алгебраических кор-
корней, кроме арифметического корня, для их обозначения
нет специальных символов.
Рассмотрим вопрос существования алгебраического
корня из действительного числа. Заметим, что в этом
параграфе утверждения о количестве действительных кор-
корней для данного действительного числа принимаются без
доказательства. Их справедливость будет вытекать из
общей теоремы о количестве корней из комплексного
числа (гл. XI).
Пусть а = О, тогда для любого натурального числа п
существует и притом только один алгебраический корень
л-й степени — число Ъ, равное 0.
Пусть а — положительное число ил- нечетное нату-
натуральное число (п = 2к + 1). Тогда существует и притом
только один арифметический корень Ьх = 2к*Ча из этого
числа и других действительных алгебраических корней из
этого числа нет. Таким образом, существует только один
алгебраический корень нечетной степени из положитель-
положительного числа, а именно арифметический корень.
Пусть а — положительное число и п — четное натураль-
натуральное число (п = 2к). Тогда существует и притом только один
арифметический корень b{ = 2Ча и действительный алгеб-
алгебраический корень Ь2 = — Ча из этого числа. Таким обра-
образом, существуют два действительных алгебраических корня
четной степени из положительного числа а: Ьх = 2Ча и
Ь = v
41
Пусть а — отрицательное число и п — четное натураль-
натуральное число (п = 2к). Поскольку любое не равное нулю
действительное число в четной степени есть положитель-
положительное число, а число 0 в любой натуральной степени есть
нуль, то нет ни одного действительного числа Ъ такого, что
b — отрицательное число. Значит, нет действительного
алгебраического корня четной степени из отрицательного
числа.
Пусть а — отрицательное число ил- нечетное нату-
натуральное число (п = 2к + 1). Покажем, что есть одно дейст-
действительное отрицательное число Ъ такое, что Ь" = а. Обозна-
Обозначим с = — а. Тогда с > 0, и потому существует единствен^-
ный арифметический корень d степени Bк + 1) из числа с:
<?+1 = с, или </ = *+VF= *+V=^ = *+VH". Положим те-
теперь Ъ = - d. Тогда Ь2к+' = (- 1J*+ ld*+' = (- 1)с = (- 1) х
х (— а) = а. Значит, Ъ = — 2*+ty[aT есть отрицательное число
такое, что 62*+| = д, т.е. (— +Л/|яГ) — действительный
алгебраический корень из отрицательного числа а.
Примеры.1. Пусть а = — 7, п = 5, тогда вещественный
алгебраический корень 5-й степени из числа (— 7) есть
число Ъ = - 5VP7r= - 5^7"-
2. Пусть а = — 8, п = 3, тогда вещественный алгебраи-
алгебраический корень 3-й степени из числа (— 8) есть число b =
= VP8T= - V8~= - 2.
Замечание. Иногда корень нечетной степени из отри-
отрицательного числа а записывают в виде Ъ = Ча, понимая
под этим число Ъ = — и*ЧЩ. Например, вместо Ъ = — ЧТ
пишут Ъ = 5V— 7. Но в дальнейшем такая запись употреб-
употребляться не будет.
М N
Ъ -1 -1/4 0 13/2 а
Рис. 1.
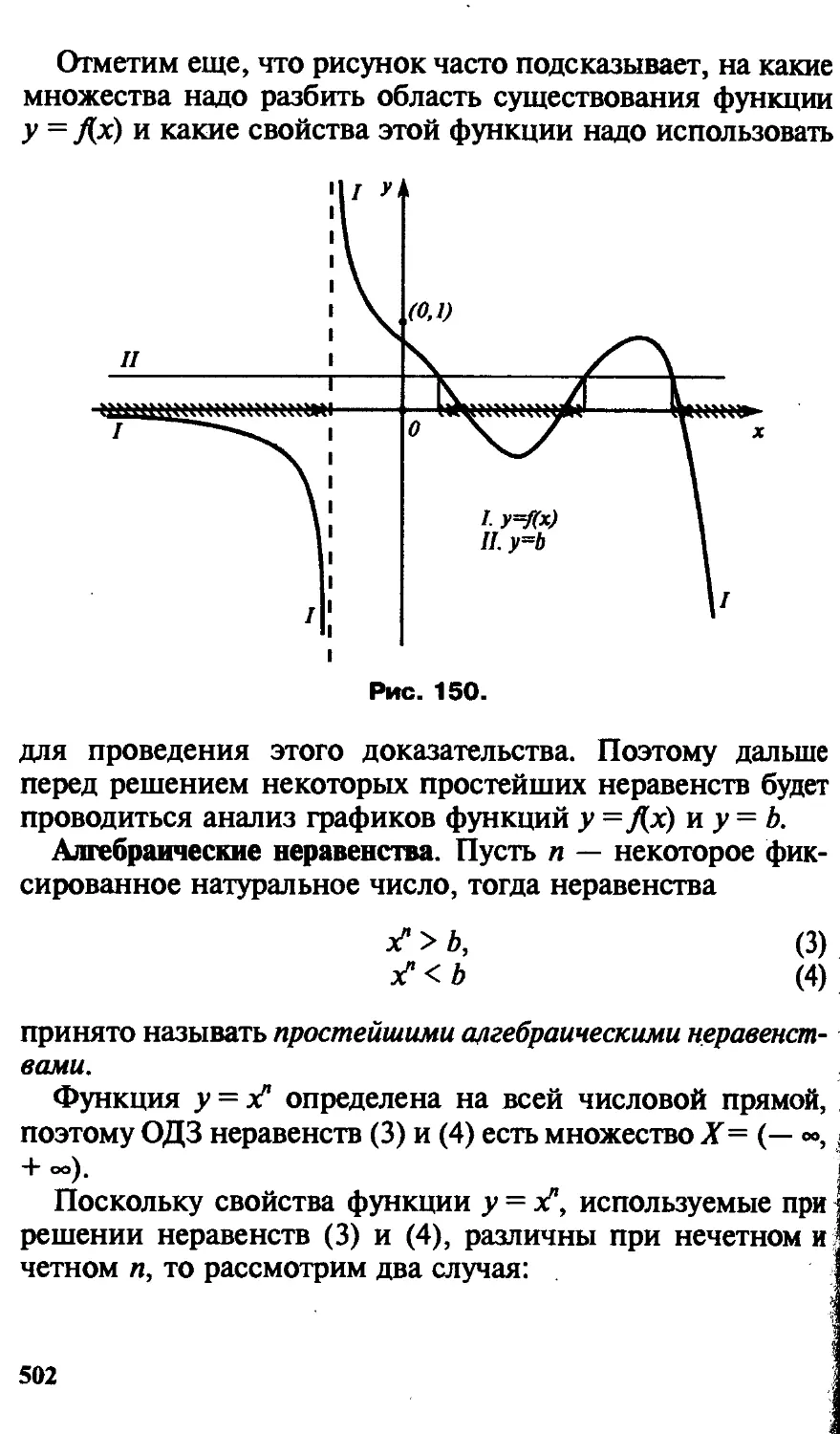
Перейдем теперь к геометрической интерпретации дей-
действительных чисел. Пусть дана горизонтальная прямая
(рис. 1). Она имеет два взаимно противоположных направ-
42
ления. Назовем одно из этих направлений положительным,
а другое отрицательным. Для определенности за положи-
положительное направление выберем направление вправо (если
смотреть по рисунку). Зафиксируем на прямой некоторую
точку О и назовем эту точку началом отсчета. Точка О
разбивает прямую на две части, называемые лучами. Луч,
направленный вправо, назовем положительным лучом, а
луч, направленный вправо, — отрицательным лучом.
Пусть задан отрезок, принятый за единицу длины; в таких
случаях говорят, что введен масштаб.
Прямую, на которой выбрано начало отсчета, положи-
положительное направление и введен масштаб, называют числовой
прямой.
Каждой точке числовой прямой можно поставить в соот-
соответствие действительное число по следующему правилу:
— выбранной точке О поставим в соответствие число
нуль;
— каждой точке N на положительном луче поставим в
соответствие положительное число а, где а — длина отрез-
отрезка ON;
— каждой точке М на отрицательном луче поставим в
соответствие отрицательное число Ъ, где |6| — длина отрез-
отрезка ОМ.
Таким образом, каждой точке числовой прямой (при
выбранном масштабе) поставлено в соответствие единст-
единственное действительное число.
Покажем, что этим процессом перебраны все действи-
действительные числа. Предположим противное, т.е. пусть неко-
некоторое действительное число с не поставлено в соответствие
некоторой точке на числовой прямой. Если число с поло-
положительное, то найдется отрезок, длина которого равна с.
Отложив этот отрезок вправо от точки О на числовой
прямой, получим точку, которой число с должно соответ-
соответствовать, т.е. получим противоречие. Если же число с
отрицательное, то найдется отрезок, длина которого
равна \с\, отложив этот отрезок влево от точки О на число-
числовой прямой, получим точку, которой должно соответство-
соответствовать число с, т.е. опять получим противоречие.
Итак:
43
1. каждой точке на числовой прямой поставлено в соот-
соответствие одно и только одно число;
2. разным точкам числовой прямой поставлены в соот-
соответствие разные числа;
3. нет ни одного действительного числа, которое не
соответствовало бы какой-либо точке на числовой прямой.
В таких случаях говорят, что между множеством всех
точек числовой прямой и множеством всех действительных
чисел установлено взаимно однозначное соответствие.
Отметим, что часто при этом точки числовой прямой
отождествляются с числами, которые им поставлены в
соответствие. Пользуясь этим, легко сформулировать,
какое из двухдействительных чисел больше: больше то,
которое расположено на числовой прямой правее другого.
Система координат на прямой. Если на прямой выбрано
начало отсчета, положительное направление и введен мас-
масштаб, то говорят еще, что на прямой задана система
координат. При этом сама прямая называется координат-
координатной осью, а точка О — началом координат. Каждой точке М
этой прямой ставят в соответствие число, называемое ко-
координатой точки М в заданной системе координат. Это
число определяется по правилу: если точка М находится на
положительном луче, то это число равно положительному
числу — длине отрезка ОМ; если точка М находится на
отрицательном луче, то это число равно отрицательному
числу — длине отрезка ОМ со знаком минус; если же
точка Мсовпадает с началом координат, то это число равно
нулю.
Пусть данная координатная ось расположена горизон-
горизонтально, причем так, что положительный луч направлен
вправо. Тогда любая точка, лежащая справа от начала
координат О, имеет положительную координату, а любая
точка, лежащая слева от начала координат О, — отрица-
отрицательную координату. Координата точки О, начала коорди-
координат, равна нулю. Легко видеть, что координата любой
точки М координатной оси равна действительному числу,
поставленному в соответствие точке на числовой прямой.
Если рассматривается несколько разных фиксированных
точек оси /, то часто их обозначают некоторой заглавной
44
буквой с разными номерами, например М\, М2, М3, ...,
М„, ... ; координаты этих точек обозначают буквой оси с
соответствующими номерами т.е. /,, t2, t3, ..., tn, ... Чтобы
указать, что данная точка имеет данную координату, запи-
записывают эту координату в круглых скобках рядом с обозна-
обозначением самой точки, например Mx{tx), M2(t2), ..., Mn(tn), ...
Говоря, что дана точка, понимают, что дана ее координата;
говоря, что надо найти точку, ищут ее координату.
Теорема 1. При любом расположении на координатной
оси двух разных точек Л^(/,) и M2(t2) расстояние d между
этими точками равно модулю разности их координат, т.е.
d=\U-h\.
Доказательство. Если точки Af, и М2 совпадают, то
утверждение теоремы очевидно. Пусть точки Л/, и М2 не
совпадают и пусть для определенности точка M2(t2) лежит
правее точки Л/,(/,) (если точка Л/,(/,) лежит правее точки
M2{t2), то доказательство повторяется с заменой t2 на /,, a t{
на t2).
А.
О@) 1
О@) 1
Рис. 2.
Рис. 3.
Пусть Mi(/i) и M2{t2) — любые не совпадающие точки,
лежащие правее нзчала координат О (рис. 2). Тогда длина
отрезка МХМ2 равна длине отрезка 0М2, которая равна t2,
минус длина отрезка 0Ми которая равна /,, т.е.
Пусть M\(t\) совпадает с началом координат 0@), т.е.
t\ = 0, a M2(t2) — любая точка, лежащая правее начала
координат О (рис. 3). Тогда длина d отрезка МХМ2 равна
длине отрезка ОМ2, которая равна t2, т.е.
45
Пусть А/,(/,) — любая точка, лежащая левее начала коор-
координат, а точка M2(t2) — любая точка, лежащая правее начала
координат (рис. 4). Тогда длина d отрезка МХМ2 равна длине
Шк) 0@) l
Рис. 4.
отрезка ОМ2, которая равна t2, плюс длина отрезка ОМи
которая равна (— /]), т.е.
Пусть Л/,(/,) — любая точка, лежащая левее начала коор-
координат, а точка M2(t2) совпадает с началом координат О@),
т.е. t2 = 0 (рис. 5). Тогда длина d отрезка МХМ2 совпадает с
длиной отрезка Л/, О, которая равна (— /]), т.е.
Пусть Л/,(/,) и M2(t2) — любые несовпадающие точки,
лежащие левее начала координат О (рис. 6). Тогда длина d
0@) Tt M,(to
JihU
0@) 1 t
Рис. 5.
Рис. 6.
отрезка М^М2 равна длине отрезка ОМи которая равна
(— /,), минус длина отрезка ОМ2, которая равна (— t2), т.е.
d=(- /,) _ (_ t2) = t2-t, = \t2 - tx\.
46
Итак, во всех случаях d=\t2— tx\. Теорема доказана.
Примеры. 1. Найти расстояние между точками М{Ъ) и
Л-2).
d= |з - (- 2)| = |3 + 2| = 5 или d= |- 2 - 3| = |- 5| = 5.
2. Найти расстояние между точками М(— 4) и Р{— 10).
</=|_4 — (- 10)| = |6| = 6 или
«/ = |(- 10) -(-4)| = |-6| = 6.
Итак, можно сказать, что модуль любого действительно-
действительного числа а, т.е. \а\, есть расстояние от точки М(а) до начала
координат.
§ 6. Числовые равенства и неравенства
В § 5 упоминалось о сравнении чисел и были приведены
определения, по которым можно выяснить, равны ли два
данных действительных числа или одно больше другого.
Все эти определения можно записать иначе, используя
сравнение действительных чисел с числом нуль, а именно
так: два действительных числа аи b равны тогда и только
тогда, когда их разность равна нулю, т. е. а = b<* a — Ь =
= 0; число а больше числа Ъ тогда и только тогда, когда
разность (а — Ь) положительна, т.е. а> Ь-» а — Ь> 0;
число а меньше числа Ъ тогда и только тогда, когда разность
(Ь — а) положительна или когда разность (а — Ь) отрица-
отрицательна, т.е. а< bo а — Ь<0 ¦» b — а> 0.
Если два числа соединены знаком равенства, то принято
говорить, что задано числовое равенство. Однако это ра-
равенство может быть и верным, и неверным. Например, 2 =
= 5 — 3, j = -j,— верные, аЗ = 5— 1,6 = | — неверные
равенства.
Аналогично, если два числа соединены любым знаком
неравенства, то принято говорить, что задано числовое
неравенство, которое может быть верным и неверным.
47
Например, 110,1 < II2, VT6"> 3 — верные, — 5 > VI,
j: > 3 — неверные неравенства.
Справедливость или несправедливость некоторых число-
числовых равенств и неравенств не всегда очевидна. Например,
справедливость неравенства
A00M0 < 1 2 3 4 ... 99 100
не очевидна. В таких случаях числовые равенства и нера-
неравенства надо доказывать. Большую роль при этом играют
рассмотренные ниже основные свойства неравенств..
1. Если числа а, Ъ и с таковы, что а = Ъ и Ъ= с, то а = с
(свойство транзитивности равенств).
2. Если числа а, Ъ, с, d таковы, что а = b и с = d, то а +
+ c=b + d.
3. Если числа а, Ь, с, d таковы, что а = Ъ, с = d, то ас =
= bd.
4. Для любых действительных чисел а,Ъи с равенства а= Ъ
и а + с= Ъ +с равносильны, т. е. из справедливости равен-
равенства а = Ъ следует справедливость равенства а + с= Ь + с,
и наоборот, из справедливости равенства а + с = Ь + с сле-
следует справедливость равенства а = Ъ, т. е. а= bo a + с =
= Ь + с.
5. Для любых действительных чисел а и Ъ и для любого
действительного отличного от нуля числа с равенства а= Ъ
и ас = be равносильны, т. е. если с * 0, то а = b о ас = be.
Приведем аналогичные свойства для числовых нера-
неравенств.
1. Если числа а, Ъ и с таковы, что а> Ъ и Ъ> с, то а> с
(свойство транзитивности неравенств).
Доказательство, а — с= (а — с) + (Ь — Ь) = (а —
— Ь) + (Ь — с). Так как а > Ъ, то а — Ъ > 0, так как Ъ > с, то
Ъ — с > 0, но сумма двух положительных чисел положитель-
положительна, поэтому а — с > 0 т.е. а > с.
2. Если числа а, Ъ, с, d таковы, что а> Ъ, с> d, moa+ с>
> b + d.
Доказательство, (а + с) — (b + d) = (а — Ъ) + (с —
— d). Так как а > Ъ, то (а — Ь) положительное число; так
48
как с > d, то (с — d) также положительное число; сумма
двух положительных чисел положительна, поэтому (а +
+ Ь) - (Ь + d) > О, т.е. а + с > Ъ + d.
2а. Если числа а, Ъ, с, d таковы, что а> Ъ и с < d, то а —
— с> Ъ — d.
Доказательство, (а —' с) — (Ь — d) — {а — b) + (d —
— с). Так как а > Ъ, то (а — Ь) — положительное число; так
как с < d, то (d — с) — также положительное число; сумма
двух положительных чисел положительна, поэтому (а —
— с) — (Ь — d) > 0, т.е. а— с> Ъ — d.
3. Если а, Ь, с, d — положительные числа и а> b и с > d,
то ас > bd.
Доказательство, ас — bd— (ас — bd) + (be — be) —
= (ас — be) + (be —bd) = c(a — b) + b(c — d). Так как а > b,
то (a — b) — положительное число; так как с — положи-
положительное число и так как произведение положительных
чисел положительно, то с(а — Ь) — положительное число;
' аналогично показывается, что b(c — d) — положительное
число; сумма положительных чисел положительна, поэтому
ас— bd> 0, т.е. ас> bd.
4. Для любых действительных чисел a, b и с неравенства
а> Ъ и а + с> Ь + с равносильны, т. е. из справедливости
неравенства а> Ъ следует справедливость неравенства а +
+ с> Ь + с и наоборот, из справедливости неравенства а +
+ с> Ь + с следует справедливость неравенства а> Ъ, т. е.
a>boa + c>b + c.
Доказательство. Пусть а> Ь. Тогда (а + с) — (Ь +
+ с) = (а — Ь) + (с — с) = (а — Ь)> 0, т.е. а + с> Ь + с.
Пусть (а + с)> (Ь + с). Тогда а — Ъ = (а — Ь) + (с — с) =
= (а + с) - (Ь + с) > 0, т.е. а > Ъ.
5. Для любых действительных чисел аи Ъ и любого поло-
положительного числа с неравенства а> Ъи ас> be равносильны,
т. е. если с > 0, то а > Ъ о ас > be.
Доказательство. Пусть а> Ъ, тогда ас— Ъс = (а —
— Ъ)с. Так как с и (а — Ъ) — положительное числа, то их
произведение положительное число, т.е. ас — be > 0, или
ас > be. Пусть ас > be, тогда (а — Ь)с = ас — be > 0.
49
Если произведение двух чисел положительно и одно из
них также положительно, то положительно и другое число,
т.е. так как с > 0, то а — Ъ > О, т.е. а > Ъ.
5а. Для любых действительных чисел а и Ь и для любого
отрицательного числа с неравенства а> Ъ и ас< be равно-
равносильны, т. е. если с< О, то а> bo ac< be.
Доказательство этого факта аналогично доказательству
свойства 5.
Итак, имеют место следующие основные свойства ра-
равенств и неравенств:
0) a = bob = a; 0)а> bob<a;
1) а = Ь, Ь = с=> а = с; l)a>b,b>c=>a>c;
2) a = b,c = d=>a + c=b + d; 2)а> b,c> d=>
=>a + c> b + d;
2a)fl> b, c< d=>
=> a — c> b — d;
3)a = b,c=d=>ac=bd; 3) a> b> 0, c> d> 0=>
=* ac > bd;
4)a = b*>a + c=b + c; 4) a< bo a + c> b + c;
5) a = b о ас = be при с ф 0; 5) а > b о ас > be при с > 0;
5а) а > b о ас < be при с < 0.
Выше употреблялись знаки равенства (=) и строго нера-
неравенства (< или >). Иногда этих знаков не хватает. Есть
задачи, где необходимы нестрогие неравенства.
Пример. Сегодня в Москве 0°, а в Ленинграде темпе-
температура не выше.
Если температуру в Ленинграде обозначить буквой Т,
тогда либо Т= 0°, либо Т< 0°. В таких случаях принято
писать Тй0°.
Приведем определения нестрогих неравенств atb и
а<Ь. Числовое неравенство а<Ь считается верным и при
а < b и при а = b и неверным лишь в случае а > Ь. Напри-
Например, неравенства 6^9и3^2 + 1 — оба верные неравен-
неравенства, а неравенство 7^6 неверное. (Запись айЬ читается
либо как «а не больше Ь», либо как *а меньше или
равно Ь».)
Числовое неравенство atb считается верным и при
а > Ь, и при а = Ь; оно считается неверным лишь в случае
50
a < b. (Запись a>b читается либо как *а не меньше Ь», либо
как «а больше или равно Ь».)
Для нестрогих неравенств справедливы свойства 1 — 5а,
если в них знак строго неравенства заменить на знак
нестрогого неравенства.
Будем говорить, что
справедливо двойное неравенство а< Ь< с, если одно-
одновременно справедливы два неравенства а < Ъ и Ъ < с;
справедливо двойное неравенство a?b< с, если одно-
одновременно справедливы два неравенства а < Ь и Ь < с;
справедливо двойное неравенство а< Ь<с, если одно-
одновременно справедливы два неравенства а < Ъ и Ъ ? с;
справедливо двойное неравенство айЬйс, если одно-
одновременно справедливы два неравенства а<,Ьи Ь<с;
§ 7. Числовые множества
Понятие множества и элемента множества относятся к
основным понятиям, т.е. к понятиям, которые не опреде-
определяются.
В этом параграфе рассматриваются числовые множества,
элементами которых являются действительные числа.
Если число а принадлежит множеству М, то пишут
ае М, если а не принадлежит множеству М, то пишут
аи М.
Например: 2 е N, 0 «ё N.
Выше были введены следующие числовые множества:
N — множество всех натуральных чисел (ряд натураль-
натуральных чисел);
Z— множество всех целых чисел;
Zq — множество всех неотрицательных целых чисел (рас-
(расширенный ряд натуральных чисел);
Q — множество всех рациональных чисел;
R — множество всех действительных чисел.
Приведем примеры других числовых множеств и усло-
условимся, как будем их обозначать дальше.
Множество, не имеющее элементов, называется пустым
множеством и обозначается 0.
51
Если множество состоит из конечного количества эле-
элементов, то такое множество принято записывать так: в
фигурных скобках записывают все элементы множества (в
любом порядке), отделяя их друг от друга точкой с запятой.
Например, множество М, состоящие из шести первых
чисел натурального ряда, можно записать так: М = {1; 2; 3;
4; 5; 6}, а множество L, состоящее из одного числа —^—,
запишется так: L = —¦;—.
4
Если множество состоит из бесконечного количества
элементов или из элементов, которые в свою очередь
являются множествами, то введенные фигурные скобки
сохраняются, а внутри них приводится краткое описание
множества. Например, множество всех пар чисел а и Ь, из
которых а есть любое целое число, а Ъ есть любое действи-
действительное число, записывается так:
M={(a;b)\aeZ, be R}.
Если каждый элемент множества А принадлежит множе-
множеству В, то множество А называется подмноокеством множе-
множества В. В этом случае принято писать А с В или Bz>A.
Например, NczZ; {(а; Ъ)\ае N; be 2) с {(a; b)\ae Z;
be R).
Множество всех действительных чисел /, для каждого из
которых справедливо двойное неравенство— 1 < t< 2, при-
принято обозначать (— 1; 2) и называть интервалом (— 1; 2).
В силу взаимно однозначного соответствия между множе-
множеством всех точек числовой прямой об интервале (— 1; 2)
принято говорить, что это есть множество всех точек
числовой прямой, расположенных между точками (— 1) и
B), не включая эти точки (рис. 7).
1 )
-1 0 1 2 t -2 0 1 4 t
Рис. 7. Рис. 8.
Множество всех действительных чисел /, для каждого из
которых справедливо двойное неравенство — 2 ? / < 4, при-
52
нято обозначать [— 2; 4) и называть полуинтервалом [— 2;4).
Принято также говорить, что полуинтервал [— 2; 4) есть
множество всех точек числовой прямой, расположенных
между точками (— 2) и D), включая точку (— 2) (рис. 8).
Множество всех действительных чисел /, для каждого их
которых справедливо двойное неравенство 0 < / < 3, приня-
принято обозначать @; 3] и называть полуинтервалом @; 3].
Принято также говорить, что полуинтервал @; 3] есть
множество всех точек числовой прямой, расположенных
между точками @) и C), включая точку C) (рис. 9).
0 1 3 t -2 0 1 t
Рис. 9. Рис. 10.
Множество всех действительных чисел /, для каждого их
которых справедливо двойное неравенство — 2 < / < 1, при-
принято обозначать [— 2; 1] и называть отрезком [— 2; 1].
Принято также говорить, что отрезок [— 2; 1] есть множе-
множество всех точек числовой прямой, расположенных между
точками (— 2) и A), включая обе эти точки (рис. 10).
В общем случае, если а < Ь, то
отрезком [а; Ь] называется множество всех действитель-
действительных чисел /, для каждого из которых справедливо двойное
неравенство a<t<b;
полуинтервалом [а; Ь) называется множество всех дейст-
действительных чисел /, для каждого из которых справедливо
двойное неравенство a<t<b;
полуинтервалом (а; Ь] называется множество всех дейст-
действительных чисел /, для каждого из которых справедливо
двойное неравенство a<t<b;
интервалом {а; Ь) называется множество всех действи-
действительных чисел /, для каждого из которых справедливо
двойное неравенство a<t<b;
лучом [а; + «) называется множество всех действитель-
действительных чисел /, для каждого из которых справедливо неравен-
неравенство t>a;
53
открытым лучом (а; + «>) называется множество всех
действительных чисел /, для каждого из которых справед-
справедливо неравенство t> а;
лучом (— °°; а] называется множество всех действитель-
действительных чисел /, для каждого из которых справедливо неравен-
неравенство / ? а;
открытым лучом (— °°; а) называется множество всех
действительных чисел /, для каждого из которых справед-
справедливо неравенство t< а;
Заметим, что иногда говорят — «промежуток*, понимая
под этим либо луч, либо отрезок, либо интервал, либо
полуинтервал. Наконец, иногда множество R всех действи-
действительных чисел обозначается так: (— °°; + °°).
Объединение и пересечение множеств.
Объединением множеств Аи В называется множество С,
состоящее из всех таких элементов, каждый из которых
содержится хотя бы в одном из данных множеств А и В.
Для объединения множеств употребляется символ:
С = A u А
Примеры. 1. ЕслиЛ={1; 2; 3; 4} и В={2; 3; 4; 5}, то
AvB={l;2;3;4;5}.
2.NkjZoKj{0} = Zo;3.(-1;2)kj@; 3] = (- 1; 3];
4. (- 1; 2)u[- 2; 1) = [- 2; 2); 5. [- 2; l]u@; 3] =
- [- 2; 3];
6.(-l;2]uB;4) = (-l;4);7.@;l)u(-l; + -) = (-l;
+ <*>).
Пересечением множеств Аи В называется множество L,
элементами которого будут те и только те элементы, кото-
которые одновременно являются элементами и первого и вто-
второго множества, т.е. пересечение двух множеств есть общая
часть этих множеств. Для пересечения множеств употреб-
употребляется знак : L = А о В.
Примеры. 1. Если А = {0; 1; 2; 3} и В= {2; 3; 4; 5; 6}, то
АпВ={2;3};
4. {1; 2; 3; 4} п {2; 3; 4; 5} = {2; 3; 4}; 5. (- 1; 2) о @; 3] =
- @; 2);
6. (- со; 1] п @; 3) = @; 1]; 7. (- 1; 3) о C; + -) = 0.
54
Упорядоченные множества. Перестановки и размещения.
При рассмотрении числового множества можно числа,
принадлежащие этому множеству, расположить в опреде-
определенном порядке. Тогда имеет смысл говорить об упорядо-
упорядоченном множестве. Одним из примеров упорядоченного
множества является ряд натуральных чисел. Если два упо-
упорядоченных множества содержат одни и те же элементы,
но расположенные в разном порядке, то будем говорить,
что эти упорядоченные множества отличаются порядком
расположения элементов. Например, из трех чисел 4, 7, 1
можно составить шесть различных упорядоченных мно-
множеств: {1; 4; 7}, {1; 7; 4}, {4; 7; 1}, {4; 1; 7}, {7; 1; 4}, {7; 4; 1}.
Рассмотрим более подробно этот вопрос для конечных
множеств, т.е. для множеств, состоящих из конечного
числа элементов, например чисел.
Определение. Установленный в конечном множестве
порядок называется перестановкой его элементов. Число
перестановок — это число различных упорядоченных мно-
множеств, составленных из одних и тех же элементов. Число
перестановок из п элементов обозначают через Р„. Для того,
чтобы ответить на вопрос, — чему равно число перестано-
перестановок из п элементов, рассмотрим общую задачу. Пусть дано
множество, состоящее из п элементов. Выделим т элемен-
элементов, где т < п, из этого множества и расположим их в
некотором порядке. Полученное конечное упорядоченное
множество будем называть размещением. Общую задачу
можно сформулировать так: «Сколько существует размеще-
размещений из п элементов по т элементов?» Ответим сначала на
вопрос, сколько существует размещений из п элементов по
два элемента. На первом месте такого размещения может
быть любой элемент из п элементов, на втором месте может
быть любой из (п — 1) оставшихся. Пусть на первом месте
стоит элемент аь тогда на втором месте может стоять любой
из элементов аъ а3, ..., а„. При этом получим (л — 1)
размещений. Если на первом месте стоит элемент аъ то на
втором месте может стоять любой из элементов аь а3, аА, ...
..., а„, т.е. будет еще (п — 1) размещений. Перебрав все
элементы д,, аъ а3, ..., а„, получим п групп, в каждой из
55
которых содержится Хл — 1) размещений. Следовательно,
число всех размещений из л элементов по два будет л(л— 1).
Если нужно узнать число размещений из л элементов по
три, то следует к каждому размещению из л элементов по
два добавить по очереди один элемент из (л — 2) оставших-
оставшихся. Тогда получится л(л — 1) групп, в каждой из которых
будет по (л — 2) размещений. Следовательно, всего разме-
размещений из л элементов по три будет л(л — 1)(л — 2). Если
число размещений из л элементов по т обозначить /С, то
можно записать следующие формулы:
1)(п-2). A)
Перепишем формулы A) в ином виде:
4 = п[п-B-1)], 4 = п(п-1)[п-C-1)]. B)
Можно подметить определенную закономерность в форму-
формулах B): число размещений равно произведению последова-
последовательных натуральных чисел начиная ели кончая [л —
— (к — 1)], где к =2,3. Рассуждая аналогично предыдуще-
предыдущему, получим
А? = л(л - 1)(л - 2) ... [л - (т - 1)], 1йтйп. C)
Пример. В 1-м классе 6 учебных предметов и 4 урока
в день. Сколькими способами можно составить расписание
одного учебного дня (более одного урока в день по каждому
предмету не допускается)?
Для того чтобы решить эту задачу, надо найти число
размещений из 6 элементов по 4: ^ = 6-5-4-3 = 360.
Итак, возможно 360 способами составить расписание на
день. Очевидно, что перестановка — это размещение из л
элементов по л. По формуле C)
Л = я(я-1)(я-2)...2-1. D)
Если воспользоваться символом л! (читается: «л фактори-
факториал»), который обозначает произведение л первых чисел
56
натурального ряда (л! = 1 • 2 ¦ 3 •... • п), то формулу D)
можно записать так:
Рп = п\. E)
Формулу C) тоже можно записать, используя этот символ:
«I _ я (я - 1)... [я - (от - 1)] [(я - от)... 2 1] _ я! ,^
п [(я-от)... 2 1] (я-от)!" К)
Чтобы формула F) совпадала с формулой E) при т = п,
принято считать, что 0! = 1.
Сочетания и их свойства. Часто возникают задачи, когда
из данного конечного множества из п элементов надо
образовать множество из т элементов (т < п), но во вновь
построенном множестве порядок следования элементов не
важен, а важно лишь их наличие.
Например, пусть спрашивается, сколькими способами
можно выбрать трех учеников из десяти для уборки класса.
В этом случае упорядоченность в группе из трех человек
необязательна. Такие множества из п элементов по т,
которые отличаются друг от друга только элементами, но
не порядком их расположения, называются сочетаниями, и
их число обозначается через С. Очевидно, что число
сочетаний из п элементов по п равно единице: С„=\.
Рассмотрим общий случай, когда 1 < т < п.
Пусть составлены все сочетания СЦ из п элементов по т.
Возьмем любое из этих сочетаний и переставим в нем
элементы всевозможными способами. Тогда число полу-
полученных всевозможных упорядоченных множеств из п эле-
элементов по т равно С^Р„. Покажем, что это число совпадает
с числом всех размещений из п элементов по т. Действи-
Действительно, возьмем всевозможные размещения и запишем их
по группам. В каждую группу включим размещения, со-
составленные из одинаковых элементов, отличающихся по-
порядком их расположения. Таким образом, в каждую группу
войдет столько размещений, сколько можно образовать
перестановок из данных т элементов, т.е. т\ размещений.
Все размещения, расположенные в одной группе, рассмат-
57
риваемые как сочетания, одинаковы, так как содержат
одинаковые элементы. Следовательно, число групп — это
число различных сочетаний из п элементов по т, т.е.
ДГ = Cm!. G)
Из равенства G) получим формулу для подсчета числа
сочетаний
или, используя формулу F):
(я-от)! от!'
(8)
Отметим, что в силу принятого соглашения: 0! = 1, фор-
формула (8) справедлива и при т = 0, а именно Сп = 1. Решим
сформулированную выше задачу о выборе трех учеников.
Число возможных способов выбора учеников равно
1-2-3-4-5-6-7-8-9-10
Если подсчитаем С^о, то получим тот же результат:
^10 ~ A • 2 3X1 -234-567)
Покажем в общем случае, что С? = С„~т @ й т й п). Дейст-
Действительно,
" [я — (я — от)]! (л —/и)! от! (я —от)!' v '
Формула (9) позволяет легко подсчитать число сочетаний
из п по т, когда т близко к п. Например,
Q= C9 = -gj- = 9.
58
Покажем справедливость еще одного свойства числа соче-
сочетаний:
A0)
Действительно, используя формулу (8) имеем
С+1+С = -
л!
л!
" (от+1)!(л — от — 1)! ' /я!(л — от)!
л! . л!
от! (от + 1) (л — от — 1)! от! (л — от — 1)! (л — от)
л! ( 1 . 1 V_ я!(я+1)
от!(л — от— 1)! |от+ 1 л —от| от!(л —от—1)!(от+1)(л —от)
(я+1)!
Используя еще раз формулу (8), получаем, что формула A0)
верна.
УПРАЖНЕНИЯ
Вычислить A — 10):
5.
||+0,0C) +0
5:[[4-0,8C)-2|j:^-7,91F)J
б.
К3,25. 3,125V 0,3411.
5,5 ' 341 J,875J'
2
| + 0,125
13
2-0,04
4-0.81-0'11'
59
@,3-|].3l]:0,05
Й
10.
Доказать следующие утверждения A1 — 33):
11. Для того чтобы натуральное число апап_ j... аха$ делилось на 5,
необходимо и достаточно, чтобы либо uq = 0, либо а$ = 5.
12. Для того чтобы натуральное число делилось на 6, необходимо, чтобы
оно делилось на 3.
13. Для того чтобы натуральное число делилось на 3, достаточно, чтобы
оно делилось на 6.
14. Для того чтобы натуральное число а„ап-1 ••• а!°о. "Si, делилось
на 4, необходимо и достаточно, чтобы число ща^ делилось на 4.
15» Для того чтобы натуральное число а„а„_ \... аха^, л 2 2, делилось
на 8, необходимо и достаточно, чтобы число fl2fliao делилось на 8.
16. Натуральное число тогда и только тогда делится на 11, когда
разность между суммой его цифр, стоящих на нечетных местах, и суммой
его цифр, стоящих на четных местах, делится на 11.
17. Для любого натурального числа л число
я(я+ 1)(я + 2)
— jr*
натуральное.
18. Произведение двух последовательных натуральных чисел при деле-
делении на три дает в остатке нуль или два.
19. Число, являющееся квадратом натурального числа, или делится на
три, или при делении на три дает в остатке единицу.
20. Число, являющееся кубом натурального числа, при делении на 9
дает в остатке либо 0, либо 1, либо 8.
21. При любом натуральном л число л(л2 + 5) делится на 6.
22. Сумма кубов трех последовательных натуральных чисел делится
на 3.
23. Произведение трех последовательных натуральных чисел, среднее
из которых есть квадрат натурального числа, делится на 60.
24. Для любых целых л и от число [лот(л — от)] является четным.
25. Произведение двух последовательных четных чисел делится на
восемь.
26. Разность между кубом нечетного числа и самим числом делится
на 24.
60
27. Квадрат всякого нечетного числа, уменьшенный на 1, делится на 8.
28. Сумма двух последовательных нечетных чисел делится на 4.
29. Два последовательных нечетных числа — числа взаимно простые.
30. Для любого натурального числа л числа л, л + 1 и 2л + 1 попарно
взаимно простые.
31. Сумма четырех последовательных натуральных чисел не может быть
простым числом.
-м v а х. 14/1+3 2Л+3
32. Каждая из двух дробей — и - несократима ни при каком
21л+ 4 5л + /
натуральном л.
33. Если данная дробь несократима, то дробь с числителем, равным
сумме числителя и знаменателя данной дроби, и знаменателем, равным
произведению числителя и знаменателя данной дроби, тоже несократима.
34. Сколько раз число 2 содержится множителем в разложении числа
100! на простые множители?
35. Сколько раз число 5 содержится множителем в разложении числа
1980! на простые множители?
1<№П 7100
36. Найти остаток от деления числа: ф) 2 на 5; б) 7 на 3.
37. Какой цифрой оканчивается число, получаемое в результате следу-
следующего возведения в степень: а) 21980; б) 71 .
38. Можно ли число 101010 представить в виде разности квадратов двух
целых чисел?
39. Делится ли число 1 • 1080 + 1 ¦ 1079 + 1 ¦ 107* + ... + 1 • 102 + 1 ¦ 10 +
+ 1на81?
40. Найти НОДB47, 221), НОДC23; 187; 209).
41. Найти числа анЬ, если: НОД(д;Ь) =¦ 13, НОК(д; Ь) = 1989.
42. При каких цифрах хну число 34х5>> делится на 36?
43. Разность двух чисел равна 5, а сумма квадратов равна 157. Найти
эти числа.
44. Найти все такие трехзначные числа, каждое из которых в 12 раз
больше суммы своих цифр.
45. Найти правильную дробь, не превышающую •=-, зная, что от увели-
увеличения ее числителя на некоторое целое число и умножения знаменателя
на то же число величина дроби не меняется.
46. Дробь-г несократима. Выяснить, сократима или несократима сумма
двух дробей — и -.
а а + b
47. Найти все такие натуральные числа л, для каждого из которых число
Зя + 4
—г натуральное число.
48. Верно ли утверждение: сумма двух натуральных чисел, каждое из
которых не делится на 7, также не делится на 7?
49. Найти наименьшее натуральное число, которое при делении на 7
дает остаток 6, а при делении на 9 дает остаток 8.
61
50. Найти наибольшее трехзначное число, которое при делении на 6
дает остаток 5, а при делении на 4 дает остаток 3.
51. Найти все натуральные числа, большие 200, но меньшие 1500,
каждое из которых как при делении на 7, так и при делении на 21, дает в
остатке 2.
52. Найти все натуральные числа, меньшие 150, каждое из которых как
при делении на 6, так и при делении на 8, дает в остатке 5.
53. Пусть р (р 2 5) — простое число. Доказать, что число (р2 — 1)
делится на 24.
54. Пусть р (р г 7) — простое число. Доказать, что число (р2 — 13) не
делится на 24.
55. Найти простые числа рн q такие, что /г — 2tf = 1.
56. Будет ли число Dр + 1) простым, если известно, что числа р и
Bр + 1) простые и р > 3?
57. Найти число р, если известно, что р, (р + 2) и (р + 4) — простые
числа.
58. Показать, что сумма (разность, произведение, частное) двух ирра-
иррациональных чисел может быть рациональным числом.
59. Доказать иррациональность чисел VF; ->/49~; (VT+ VT); (VT+ V3~).
60. Доказать, что бесконечная десятичная дробь 0, 1234567891011 ...,
где после запятой выписаны подряд все натуральные числа, является
непериодической дробью.
61. Дано: azb>0;c>d>0. Доказать, что^>-.
62. Доказать, что И = |— а|; И 2 а; И ? — а.
Найти множество всех чисел, для каждого из которых справедливо
равенство F3 — 73):
63. |- а\ = а. 64. |- а\ = - а. 65. а + И = 0. 66. а - И = 0. 67. а + И =
= 2а. 68. о|а| = - а2. 69. т| = 1. 70. щ = - 1. 71. л/?= - а. 72. <W2~ =
- V2?. 73.
74. Какие из следующих неравенств справедливы: 5 2 2; 3 2 3;
VTV9TI
Если два действительных числа а > Ь, то справедливо ли неравенство
G5, 76): 75. а2 > б2; 76. - < j?
а о
Найти множество всех чисел, для каждого из которых справедливо
неравенство G7 — 88):
77. |- о| й а. 78. И < - а. 79. И S |- а\- 80. a|a| 2 a2.
81. п^- 1.82. A>1.83.V?<-a. 84.
85. W s - aVT. 86. И - айО. 87. И + a<2a. 88. И + fl<0.
62
Найти пересечение следующих двух множеств (89 — 96):
91. [- VI; 2] и Ш; А 92. (- VT; 4] и [4; Ш).
93. fl; Д±1]и |^~-; г) 94. (- ~; 2) и (- >/Т; 10].
2
96. (-VITjVDh'^"
•y;VIT|.ie4.(-4;3)HB;4].
•0,2; 2].
Найти объединение следующих двух множеств (97 — 105):
97. [- 1,5; 4] и [- 2; 1]. 98. [1; 5] и [0; 6). 99. [2; 4] и [4; 7]. 100. (- 1;
4) и @; 3].
101. (- ~; 2] и [- 3; 5). 102. @; ., „ , 2>
103. (- с»; 2] и '
105. [- 1; 1) и
На числовой оси указать множество всех чисел, удовлетворяющих
условию A06 — 113):
106. W=l 107. W<3. 108. W22. 109. Кхй4. ПО. - 3sx<0.
111. (x - l)(x + 2) = 0. 112. (х - 1)\х + 3) й 0. ИЗ. (х - 2) V * 4) й 0.
114. Сколько различных четырехзначных чисел можно составить, ис-
используя цифры 1, 2, 3, 4, 5, если в записи каждого такого числа никакая
цифра не повторяется?
115. Сколько различных семизначных телефонных номеров можно
набрать с помощью диска, имеющего десять отверстий с номерами 1, 2,
3, 4, 5, 6, 7, 8, 9, 0?
116. Сколькими способами в группе из 25 человек можно выбрать
профорга, физорга и культорга?
117. Сколькими способами можно отобрать несколько книг (не менее
одной) из 5 одинаковых учебников алгебры и 4 одинаковых учебников
геометрии?
118. Рота состоит из 3 офицеров, 6 сержантов и 60 рядовых. Сколькими
способами можно выбрать наряд, состоящий из одного офицера, 2 сер-
сержантов и 20 рядовых?
119. Сколькими способами можно расставить 20 книг в книжном
шкафу с 3 полками, если каждая полка может вместить все 20 книг?
120. У одного человека есть 7 книг, а у другого 9. Сколькими способами
они могут обменять друг с другом по две книги?
Глава 11. АЛГЕБРАИЧЕСКИЕ
ВЫРАЖЕНИЯ
§ 1. Определения и основные свойства
Математические и алгебраические выражения. В предыду-
предыдущей главе были рассмотрены действительные числа и не-
некоторые действия над ними. С помощью чисел, знаков
действий и скобок составлялись различные числовые выра-
выражения. Приведем примеры некоторых числовых выраже-
выражений:
B7:9); V8+T;
fj. _Z\ii_(?... ГШ
11 2 71 |S 7 47.
(i ГШ '
[19 2 117
2 • 103 -F 7 • 10* + 10 - 5.
Если в числовом выражении можно выполнить все ука-
указанные в нем действия, то полученное в результате дейст-
действительное число называют числовым значением данного чис-
числового выражения, а о числовом выражении говорят, что оно
имеет смысл. В приведенных примерах каждое из первых
трех числовых выражений имеет числовое значение 3, а
четвертое — 2705.
Если числовое выражение состоит из одного действи-
действительного числа, то его числовым значением является само
это число.
Иногда числовое выражение не имеет числового значе-
значения, т.к. не все указанные в нем действия выполнимы; о
таком числовом выражении говорят, что оно не имеет
64
(лишено) смысла. Например, числовые выражения ,7 ;
V10 — 18 и B — 2)° лишены смысла.
Таким образом, любое числовое выражение либо имеет
одно числовое значение, либо лишено смысла.
Числовое выражение часто употребляют для описания'
какого-либо свойства числа, являющегося числовым зна-
значением этого выражения. Так, например, свойство числа
(— 17) давать при делении на 2 остаток 1 записывают
числовым выражением 2(— 9) + 1. Чтобы описать свойство
каждого нечетного числа из отрезка [— 2; 14] давать при
делении на 2 остаток 1, надо написать соответствующее
числовое выражение для каждого из чисел — 1, 1, 3, 5, 7,
9, 11 и 13, т.е. восемь следующих числовых выражений:
2. (-1) + 1; 2-0+1; 2-1 + 1; 2-2+1;
2-3+1; 2-4+1; 2-5+1; 2-6+1.
Это же свойство можно записать, используя буквенную
символику, следующим образом: 21+ 1, где 1е {— 1, 0, 1,
2, 3, 4, 5, 6}.
Приведенный пример говорит о том, что часто вместо
числовых выражений удобнее рассматривать выражения, в
которых на некоторых местах вместо чисел могут стоять
буквы. Всякое такое выражение называют математическим
выражением. Примеры математических выражений:
Отметим, что понятие «математическое выражение» явля-
является простейшим, и потому оно не определяется, а лишь
описывается, что и было сделано выше. Математическое
выражение, в котором над числами и буквами, входящими
в это выражение, производятся не более чем действия
сложения, вычитания, умножения, деления, возведения в
натуральную степень и извлечения арифметического
корня, называется алгебраическим выражением.
Примеры алгебраических выражений:
3 Алгебра, тригонометрия
и элементарные функции
a + b; f=f; 2 - if; V2^-1; ^~ *J>-+ abc.
a — b 13' ^ (от — n) + sxy
Алгебраическое выражение называется рациональным,
если в нем может быть участвуют относительно входящих
в него букв лишь действия: сложение, умножение, вычита-
вычитание, деление и возведение в натуральную степень (рацио-
(рациональное алгебраическое выражение может содержать
любые числа, в том числе и иррациональные). Примеры
рациональных алгебраических выражений:
7; ^L + VJa7; 2=±; -^- + ху; 2х - nab.
' 2от 'с — а' V5(ot —л) J'
Рациональное выражение называется целым относительно
данной буквы, если оно не содержит деления на данную
букву или на выражение, содержащее эту букву.
Дробное рациональное выражение относительно данной
буквы — это рациональное выражение, содержащее деле-
деление на некоторое выражение, содержащее эту букву, или
на саму букву.
Например, рациональное выражение а+ +с — целое от-
относительно буквы с, но дробное относительно букв аи Ь;
рациональное выражение Ц- + -?— целое относительно а,
но дробное относительно Ъ.
Алгебраическое выражение называется иррациональным,
если в нем участвует относительно входящих в него букв
действие извлечения арифметического корня.
Примеры иррациональных алгебраических выражений:
Действия над алгебраическими выражениями. Пусть даны
два алгебраических выражения, которые обозначены бук-
буквами А и В. Определим для них арифметические операции.
Сложить два алгебраических выражения А и В — значит
формально написать алгебраическое выражение А + В, ко-
которое называется суммой выражений Аи В.
66
Например, суммой алгебраических выражений ^—- и
?- будет алгебраическое выражение 2—^- + ?-.
2р с — а 1р
Умножить два алгебраических выражения А и В — зна-
значит формально написать алгебраическое вьфажение АВ,
которое называется произведением выражения Аи В.
Например, произведением алгебраических выражений
и (а2 — Ь2) будет алгебраическое выражение х
чх + у
х (а2 - Ь2).
Если надо сложить несколько алгебраических выраже-
выражений, то сначала складывают два первых выражения, затем
к полученной сумме прибавляют третье выражение и т.д.
Вот, например, как выглядит сумма пяти алгебраических
выражений: {[(А + В) + С\ + D) + Е. Аналогично определя-
определяется и произведение нескольких алгебраических выраже-
выражений.
Если в произведении одно и то же алгебраическое выра-
выражение А является множителем п раз (я > 1, п е N), то пишут
А" вместо произведения АА ... А.
Например, вместо произведения (а + Ь)(а + Ь)(а + Ь)
пишут (а + by. Вместо А обычно пишут А.
Вычесть из алгебраического выражения А алгебраичес-
алгебраическое выражение В — это значит формально написать алгеб-
алгебраическое выражение Л — В, которое называется разностью
выражений Аи В.
Например, разностью алгебраических выражений аЪсг и
-— будет алгебраическое выражение аЪс — -—.
Разделить алгебраическое выражение А на алгебраичес-
алгебраическое выражение В — это значит формально написать алгеб-
алгебраическое выражение А: В, которое называется частным от
деления выражения А на выражение В.
Например, частным отделения алгебраического выраже-
выражения (а — Ь2) на алгебраическое выражение ^ будет алгеб-
алгебраическое выражение (а — Ь2): ^. Отметим, что частное от
67
деления алгебраического выражения А на алгебраическое
выражение В часто записывается в виде 4-
о
Область допустимых значений алгебраического выраже-
выражения. Ясно, что под областью допустимых значений алгеб-
алгебраического выражения следует понимать ту область, в
которой это алгебраическое выражение имеет смысл. Од-
Однако это понятие необходимо уточнить.
Пусть дано некоторое алгебраическое выражение. Мно-
Множество всех букв, входящих в это выражение, называется
буквенным набором данного алгебраического выражения.
Если в алгебраическое выражение входит п букв аи а2, ...
..., а„, то буквенный набор этого алгебраического выраже-
выражения записывают в виде (а,, а2,..., а„). Каждая буква, сколько
бы раз она ни встречалась в алгебраическом выражении,
пишется в буквенном наборе только один раз. При состав-
составлении буквенного набора данного алгебраического выра-
выражения порядок следования букв может быть любым воз-
возможным, но раз навсегда зафиксированным.
Например, для алгебраического выражения ~?~ бук-
буквенным набором может служить набор (а, Ь, с), для алгеб-
алгебраического выражения V^ + с?Ък — ос — набор (к, а, а, Ь).
Если в буквенном наборе (а, Р, у) вместо буквы а взять,
например, число [ — -гА, вместо буквы р — число >B,
вместо буквы у — число 0,3, то набор чисел Г— ^ |, ^2, 0,3
называют числовым набором, соответствующим данному
буквенному набору (а, р, у), и записывают в виде
S— T7-, -^2, 0,з1. При этом говорят, что числовой набор
— -гг, ^12, 0,3 ] соответствует буквенному набору (а, Р, у)
а = --^, p = VT, y=0,3.
Аналогично определяется числовой набор, соответст-
соответствующий буквенному набору (а,, а2, ..., ая), и для любого
набора из п букв (п — любое натуральное число).
68
Одному и тому же буквенному набору можно поставить
в соответствие бесконечно много разных числовых набо-
наборов.
Два числовых набора считают разными, если хотя бы на
одном, но на одном и том же в каждом наборе, например,
/-м месте этих числовых наборов стоят неравные числа (т.е.
вместо одной и той же буквы, стоящей на /-м месте
буквенного набора, в этих двух числовых наборах взяты
неравные числа). Например, числовые наборы
fl,-3, — 5 —VT.^j и (l,-3, -4-V2,|V соответст-
соответствующие буквенному набору (а, Ь, с, d, e), разные, т.к. у них
на одном и том же третьем месте стоят неравные числа
(— 5) и (— 4) (т.е. в первом наборе с = — 5, а во втором
с = — 4). Числовые наборы Г— 3, — 11 и [— |, — 3 |, соот-
соответствующие буквенному набору (х, у), разные, так как у
них на первом месте стоят неравные числа (т.е. в первом
о
наборе х = — 3, а во втором х = — =); кроме того, они
разные, так как у них на втором месте стоят неравные числа
(т.е. в первом наборе у = — |, а во втором у = — 3).
Пусть даны некоторое алгебраическое выражение и его
буквенный набор. Рассмотрим некоторый числовой набор,
соответствующий этому буквенному набору. Этот числовой
набор называется числовым набором для букв данного ал-
алгебраического выражения. Если в это алгебраическое вы-
выражение подставить вместо каждой буквы, где бы она в нем
ни стояла, соответствующее ей число из данного числового
набора, то получим числовое выражение, которое либо
имеет смысл, либо лишено смысла. Например, рассмотрим
алгебраическое выражение ^~3а. Запишем его буквенный
набор в виде (а, Ь). Для числового набора D, 5), соответ-
соответствующего буквенному набору (а, Ь) (т.е. при а = 4, Ъ = 5),
это алгебраическое выражение записывается в виде число-
5 — 3 4
вого выражения ,- , и имеет числовое
^ V5 + 4
Для числового набора (— 6, 5) (т.е. при а
69
значение Г— у].
= — 6, Ь = 5) это
алгебраическое выражение запишется в виде числового
выражения ~7 _~ , которое лишено смысла.
Числовой набор, соответствующий буквенному набору
данного алгебраического выражения, называется допусти-
допустимым для этого выражения, если имеет смысл числовое
выражение, которое получается из данного алгебраическо-
алгебраического выражения, если вместо каждой буквы, где бы она в нем
ни стояла, подставить соответствующее ей число из данно-
данного числового набора.
Совокупность всех допустимых числовых наборов, соот-
соответствующих буквенному набору данного алгебраического
выражения, называется областью допустимых значений
(ОДЗ) данного алгебраического выражения.
Отметим, что существуют алгебраические выражения,
ОДЗ которых пуста. Например, пуста ОДЗ алгебраического
выражения -— , ибо для любого числового значения
буквы а, соответствующее числовое выражение лишено
смысла. Такие выражения называются выражениями, не
имеющими смысла, и в дальнейшем рассматриваться не
будут. Обычно ОДЗ алгебраического выражения записыва-
записывают в виде набора множеств, причем указывают, какой букве
соответствует, каждое множество. Так, например, ОДЗ ал-
алгебраического выражения ?~3 записывается в виде
{(a, ft) | ее (- 5; +«); Ье (- -.; + --)}.
Числовым значением, или числовой величиной, алгебраи-
алгебраического выражения для данного числового набора из ОДЗ
называют числовое значение того числового выражения,
которое получится, если в данное алгебраическое выраже-
выражение вместо каждой буквы, где бы она в нем ни стояла,
подставить соответствующее ей число из данного числово-
числового набора.
Например, числовым значением алгебраического выра-
выражения ,' при а = 4 и Ъ = 5 будет число \, а при а = 0 и
\Э + а 3
Ь = 4 — число -J-.
70
Часто алгебраические выражения рассматриваются не на
всей своей ОДЗ, а лишь на ее части — некоторой облас-
области М.
Например, рассмотрим алгебраическое выражение vt.
ОДЗ этого выражения {(v, t) | v е Я, t e R]. Пусть это алгеб-
алгебраическое выражение vt определяет путь, пройденный за
время t со скоростью v. Тогда по физическому смыслу
задачи следует наложить на v и t ограничения: v > 0 и t > 0.
Другими словами надо рассмотреть алгебраическое выра-
выражение v/ на следующей области М — части ОДЗ этого
выражения: М= {(v, t) ve [0; + °°); t<= [0; + ~)}. Алгебра-
Алгебраическое выражение обычно дается вместе с областью М, на
которой оно рассматривается. Если область М не указана,
то алгебраическое выражение следует рассматривать на
всей ОДЗ, которую предварительно надо найти.
Пусть даны два алгебраических выражения Аи В. Мно-
Множество всех букв этих двух выражений называют буквенным
набором двух выражений Аи В. Числовой набор, соответст-
соответствующий буквенному набору двух алгебраических выраже-
выражений, называют допустимым, если одновременно имеют
смысл оба числовых выражения, которые получаются из
данных алгебраических выражений, если в них вместо
каждой буквы, где бы она в них ни стояла, подставить
соответствующее ей число из этого числового набора.
Совокупность всех допустимых числовых наборов, соот-
соответствующих буквенному набору двух алгебраических вы-
выражений, называется областью допустимых значений (ОДЗ)
этих алгебраических выражений.
алгебраических выражений записывается в виде {(a, b)\as
е [-l;2)uB; + ~); Ье (- 3; + -)}.
Аналогично определяется ОДЗ л алгебраических выра-
выражений. Два алгебраических выражения можно рассматри-
рассматривать не на всей ОДЗ, а лишь на некоторой ее части —
некоторой области М. Поэтому дальше под областью М,
принадлежащей ОДЗ алгебраических выражений, будет
пониматься либо вся эта ОДЗ, либо какая-нибудь явно
указываемая ее часть.
71
§ 2. Равенства и неравенства алгебраических выражений
Равенства алгебраических выражений. Два алгебраичес-
алгебраических выражения называются тождественно равными на об-
области М, если для любого числового набора из области М
соответствующие числовые значения этих выражений
равны.
Например, два алгебраических выражения (а + IJ и
(а2 + 2а + 1) тождественно равны как на всей ОДЗ этих
выражений, т.е. на области {(а) \ а е (— ~; + «)}, так и на
любой ее части. Два алгебраических выражения т + d +
+ а~ и ( +с) + (а— ) т(ЮКдественно равны не на всей ОДЗ
3 + с 3 + с
этих двух выражений, которой является область {(а, Ь, от,
с, d) | a е R; be R; от е R; се (— ~; — 3) и (— 3; + ~);
d е R), а лишь на ее части — области М, где М = {(а, Ь, от,
с, d) | a g R; Ъ е R; от е {0}; с е (— ~; — 3) и (— 3; + ~); d e
Л}. Для записи тождественного равенства на области Мдвух
алгебраических выражений иногда употребляется знак ра-
равенства, над которым сверху написана буква М, т.е. если
буквами Аи В обозначены некоторые алгебраические вы-
ражения, то запись А = В обозначает, что алгебраические
выражения А и В тождественно равны на области М, а
область М входит в ОДЗ двух выражений Аи В.
Например, запись
а-* ода в ь
З+с 3+с 3+с
означает, что алгебраические выражения [^—-] и
1— zr— I тождественно равны на ОДЗ этих выражений,
3 + с 3 + с I
.е. на области {(а, Ь, с) \ а е R; Ь е R, с е (— ~; — 3) и
и (— 3; + °о)}, а запись V?" = а, где М= {(а) \ а е [0; + ~)},
означает, что утверждается тождественное равенство алгеб-
алгебраических выражений V? и а лишь на области М.
Замена алгебраического выражения А алгебраическим
выражением В, тождественно равным ему на области М,
72
принадлежащей ОДЗ выражений Аи В, называется тож-
тождественным преобразованием на области М алгебраического
выражения А. Если не указана область М, на которой
происходит тождественное преобразование, то принято
считать, что это преобразование происходит на ОДЗ двух
выражений: данного и преобразованного.
Например, замена алгебраического выражения (а + IJ
алгебраическим выражением а2 + 2а + 1 является тождест-
тождественным преобразованием на ОДЗ этих выражений, т.е. на
области М, где М= {(а) \ае К\.
Законен вопрос, а возможна ли запись Л = В без буквы М
над знаком равенства и что эта запись означает?
Конечно, формально можно сделать запись А = В, но
если рядом нет слов, поясняющих, как следует понимать
такую запись, то такая запись не несет никакой смысловой
нагрузки. Следовательно, такая запись должна употреб-
употребляться только с некоторыми сопровождающими эту запись
пояснениями, которые и разъяснят, как следует понимать
эту запись.
Приведем теперь наиболее часто встречающиеся случаи
употребления записи А = В с соответствующими поясне-
пояснениями, как следует понимать такую запись.
а) Пусть известно, что на некоторой области М, принад-
принадлежащей ОДЗ двух алгебраических выражений А и В, эти
два выражения тождественно равны. Тогда это утверждение
записывают так: «Известно (или дано), что А=Вна облас-
области М». В этом случае говорят также, что на области Мдано
тождественное равенство А= В.
б) Пусть требуется доказать справедливость утвержде-
утверждения: алгебраические выражения А и В тождественно равны
на области М, принадлежащей ОДЗ этих выражений. Тогда
пишут: «Доказать, что А=Вна области М». В этом случае
говорят также, что требуется доказать справедливость на
области М тождественного равенства А = В.
в) Пусть требуется найти область М, принадлежащую
ОДЗ двух алгебраических выражений А и В, такую, что для
любого числового набора из области М соответствующее
числовое значение выражения А равно соответствующему
числовому значению выражения В, а для любого числового
73
набора, не входящего в область М, но входящего в ОДЗ
этих выражений, соответствующие числовые значения дан-
данных выражений не равны. В таких случаях говорят: «Ре-
«Решить уравнение А = В».
Прежде всего отметим, что сложение и умножение ал-
алгебраических выражений производятся с использованием
следующих утверждений:
1. На ОДЗ двух выражений А и В справедливо тождест-
тождественное равенство А + В= В + А.
2. На ОДЗ трех выражений А, В, и С справедливо тожде-
тождественное равенство (А + В) + С = А + (В + С).
3. На ОДЗ двух выражений А и В справедливо тождест-
тождественное равенство АВ = ВА.
4. На ОДЗ трех выражений А, В и С справедливо тожде-
тождественное равенство (АВ)С = А(ВС).
5. На ОДЗ трех выражений А, В и С справедливо тожде-
тождественное равенство А(В + Q = АВ + АС.
Поскольку метод доказательства справедливости этих
утверждений один и тот же, то приведем здесь доказа-
доказательство лишь утверждения 1.
Возьмем некоторый числовой набор из ОДЗ двух выра-
выражений А и В и обозначим соответствующие числовые
значения этих выражений соответственно через Д, и Д>.
Тогда для чисел Д> и Д по свойству коммутативности
сложения чисел справедливо числовое равенство Д + Д, =
= Д + Д. Значит, показано, что для данного числового
набора из ОДЗ двух выражений А и В соответствующие
числовые значения выражений Д, + Д, и Д, + Ац равны. Так
как это рассуждение можно провести для любого числового
набора из ОДЗ двух выражений А и В, то справедливость
на ОДЗ этих выражений тождественного равенства Л + В =
= В + А доказана.
Аналогично доказываются и следующие утвержде-
утверждения.
6. На ОДЗ выражения А справедливы тождественные
равенства А + 0 = А,0+А = А.
7. На ОДЗ выражения А справедливы тождественные
равенства А- 1 = А, 1 А = А.
74
8. На ОДЗ выражения А справедливы тождественные
равенство А + (— А) = 0.
9. На области М — части ОДЗ выражения А, на которой
ни для одного числового набора соответствующее числовое
значение выражения А не равно нулю, — справедливо тож-
тождественное равенство А ¦ i = 1.
А
Используя утверждения 1 — 9, можно показать, что
действия вычитания и деления алгебраических выражений
являются соответственно обратными к действиям сложе-
сложения и умножения алгебраических выражений. А именно,
справедливы следующие утверждения.
10. На ОДЗ двух выражений А и В справедливо тождест-
тождественное равенство В + (А — В) = А.
П. На области М — части ОДЗ двух выражений А и В, на
которой ни для одного числового набора соответствующее
числовое значение выражения В неравно нулю, — справедливо
тождественное равенство В [ 41= А.
Приведем теперь утверждения, которые часто ис-
используются при доказательстве равенств алгебраических
выражений.
12. Если на некоторой области М, принадлежащей ОДЗ
трех алгебраических выражений А, В и С, одновременно
справедливы тождественные равенства А = В и В = С, то на
области М справедливо и тождественное равенство А = С
(транзитивность равенств).
13. Если на некоторой области М, принадлежащей ОДЗ
четырех алгебраических выражений А, В, CuD одновременно
справедливы тождественные равенства А = ВиС= Ь,тона
области М справедливо и тождественное равенство А+ С =
= B+D.
14. Если на некоторой области М, принадлежащей ОДЗ
четырех алгебраических выражений А, В, CuD одновременно
справедливы тождественные равенства А = В и С = D, то на
области М справедливо и тождественное равенство
АС = BD.
75
Метод доказательства утверждений 10—14 является тем
же самым, что и при доказательстве утверждений 1 — 9.
Докажем, например, утверждение 12.
Возьмем некоторый числовой набор из области М. Обо-
Обозначим соответствующие числовые значения выражений А,
В и С соответственно через Ад, Д> и Q. Из справедливости
на области М тождественных равенств А = В и В = С выте-
вытекает справедливость числовых равенств Ац = Д> и Д> = Q.
По свойству транзитивности числовых равенств тогда спра-
справедливо и числовое равенство Д> = Q. Таким образом,
показано, что для данного числового набора из области М
соответствующие числовые значения выражений А и С
равны. Поскольку это рассуждение можно провести для
любого числового набора из области М, то справедливость
на области М тождественного равенства А = С доказана.
Принято следующее соглашение: если не указана явно
область М, на которой рассматривается тождественное
равенство А = В, то оно рассматривается на ОДЗ двух
выражений Аи В. Поэтому слова «дано, что А = В* озна-
означают, что на ОДЗ двух выражений А и В справедливо
тождественное равенство А = В. Слова «доказать, что
А = В* означают, что сначала надо найти ОДЗ двух выра-
выражений А и В, а затем доказать тождественное равенство
А = В на этой ОДЗ.
В частности, исходя из этого, утверждения 1 — 5, назы-
называемые обычно законами сложения и умножения алгебра-
алгебраических выражений, можно переписать и так:
Справедливы следующие законы сложения и умноже-
умножения алгебраических выражений:
1.А + В=В + А (коммутативность сложения);
2. (A + B) + C=A + (B+Q (ассоциативность сложе-
сложения);
3. АВ = ВА (коммутативность умножения);
4. (AB)C = A(BQ (ассоциативность умножения);
5. (А + В) С'= АС + ВС (дистрибутивность сложения от-
относительно умножения).
Прежде чем рассмотреть применение данных утвержде-
утверждений для доказательства равенств, дадим определение рав-
равносильного перехода от одного равенства к другому.
76
Если на некоторой области М из справедливости одного
тождественного равенства вытекает справедливость второ-
второго, а из справедливости второго вытекает справедливость
первого, то говорят, что такие два тождественные равенства
равносильны на области М, а замену одного из них другим
называют равносильным переходом на области Мот первого
равенства ко второму.
В дальнейшем, если это не будет вызывать недоразуме-
недоразумений, для краткости слово «тождественное» будем опускать.
Равносильный переход на области Мот одного равенства
к другому обозначается двойной стрелкой, над которой
сверху написана буква М, т.е. запись А = В •» С = D озна-
означает, что на области М равенства А = В и С = D равносиль-
равносильны.
Тогда из справедливости утверждений 13, 14 следует
справедливость следующих равносильных переходов.
15. Пусть М — ОДЗ трех алгебраических выражений А, В
иС,тогдаА=вМ>А+ С=В+ С.
16. Пусть некоторая область М принадлежит ОДЗ трех
алгебраических выражений А, В и С и обладает следующим
свойством: ни для какого числового набора из области М
соответствующее числовое значение выражения С не равно
нулю. Тогда А= В<*>АС= ВС.
Докажем, например, утверждение 15. Так как С = С, то
из утверждения 13 следует справедливость перехода от
равенства А = В к равенству А+ С = В+ С. Обратно, имея
равенства А+ С- В+ С и (— С) = (— Q и используя
утверждения 13 и 8, получим справедливость перехода от
равенства (А + Q = (В + Q к равенству А = В. Следова-
Следовательно, справедлив равносильный переход
а = в?а + с=в+ с.
Приведенные утверждения 1 — 16 позволяют доказывать
равенства алгебраических выражений. Докажем, например,
что на ОДЗ двух выражений А и В справедливо равенство
А- В = А + (-В).
11
На основании утверждения 15 это равенство равносиль-
равносильно равенству
А- В+В = А + (- В) + В.
Согласно утверждениям 1, 2 и 10 справедливы следующие
равенства:
А — В+В=В+(А — В) и В+(А- В)=А.
Следовательно, А — В + В = А.
Аналогично, используя утверждения 2, 8, имеем А +
+ {-В) + В = А.
Таким образом, доказано, что равенство А — В+ В =
= А + (— В) + В справедливо на ОДЗ алгебраических вы-
выражений Аи В. Следовательно, на этой ОДЗ справедливо
и равенство А — В = А + (— В).
Неравенства алгебраических выражений. Перейдем теперь
к употреблению знака неравенства для алгебраических
выражений. Знак неравенства > (>, < или <) так же, как и
знак равенства, употребляется для алгебраических выраже-
выражений только с некоторыми пояснениями, как следует пони-
понимать такую запись. Приведем наиболее часто встречающие-
встречающиеся случаи употребления этих знаков.
а) Пусть известно, что на некоторой области М, принад-
принадлежащей ОДЗ двух алгебраических выражений Аи В, для
любого числового набора из М соответствующее числовое
значение выражения А больше соответствующего числово-
числового значения выражения В. Тогда это утверждение записы-
записывается так: «Известно (или дано), что А> В на области М».
В этом случае говорят также, что на области М справедливо
тождественное неравенство А> В.
б) Пусть требуется доказать справедливость утвержде-
утверждения: «Для любого числового набора из области М, принад-
принадлежащей ОДЗ двух выражений А и В, соответствующее
числовое значение выражения А больше соответствующего
числового значения выражения В». Тогда пишут: «Дока-
«Доказать, что А > В на области М». В этом случае говорят также,
что требуется доказать справедливость на области М тож-
тождественного неравенства А> В.
78
в) Пусть требуется найти область М, принадлежащую
ОДЗ двух алгебраических выражений А и В, такую, что для
любого числового набора из области М соответствующее
числовое значение выражения А больше соответствующего
числового значения выражения В, а для любого числового
набора из ОДЗ, не входящего в область М, соответствующее
числовое значение выражения А меньше или равно соот-
соответствующему числовому значению выражения В. В таких
случаях говорят: «Решить неравенство А> В».
. При доказательстве тождественных неравенств часто
приходится пользоваться следующими утверждения-
утверждениями.
17. Если на некоторой области М, принадлежащей ОДЗ
трех алгебраических выражений А, В и С, одновременно
справедливы тождественные неравенства А> В и В> С, то
на области М справедливо и тождественное неравенство
А> С (свойство транзитивности неравенств).
18. Если на некоторой области М, принадлежащей ОДЗ
четырех алгебраических выражений А, В, Си D, одновременно
справедливы тождественные неравенства А> В и О D, то
на области М справедливо и тождественное неравенство
А + О В + D.
19. Если для любого числового набора из некоторой облас-
области М, принадлежащей ОДЗ четырех алгебраических выраже-
выражений А, В, Си D, соответствующие числовые значения этих
выражений А, В, CuD положительны и если на этой области
одновременно справедливы тождественные неравенства
А> ВиО D,mo справедливо и тождественное неравенство
АО BD.
Дадим теперь определение равносильного перехода от
одного неравенства к другому.
Если на некоторой области М из справедливости первого
тождественного неравенства вытекает справедливость вто-
второго, а из справедливости второго вытекает справедливость
первого, то говорят, что такие два тождественные неравен-
неравенства равносильны на области М, а замену одного из них
другим называют равносильным переходом от первого нера-
неравенства ко второму. При этом употребляется знак равно-
равносильного перехода <*>.
79
Из справедливости утверждений 17 — 19 следует спра-
справедливость следующих равносильных переходов.
20. Пусть М — ОДЗ трех алгебраических выражений А, В
и С, тогда А> В&А+ О В+ С.
21. Пусть некоторая область М принадлежит ОДЗ трех
алгебраических выражений А, В и С и обладает следующим
свойством: для любого числового набора из области М соот-
соответствующее числовое значение выражения С положительно.
Тогда А> В & АО ВС.
Принято следующее соглашение, если не указана явно
область М, на которой рассматривается тождественное
неравенство А> В, то оно рассматривается на ОДЗ двух
выражений А и В. Поэтому слова «дано, что А> В» озна-
означают, что на ОДЗ двух выражений А и В справедливо
тождественное неравенство А > В; слова «доказать, что
А> В» означают доказать, что на ОДЗ двух выражений А и
В справедливо тождественное неравенство А > В (при этом
имеется в виду, что эту ОДЗ обязательно следует отыскать).
Если дано неравенство А > В, то ОДЗ двух выражений А и
В называют часто ОДЗ неравенства А> В.
Следует отметить, что утверждения 17 — 21 останутся
верными и в случае нестрогих неравенств. Например, свой-
свойство транзитивности неравенств может быть сформулиро-
сформулировано так.
17а. Если на некоторой области М, принадлежащей ОДЗ
трех алгебраических выражений А, В и С, одновременно
справедливы тождественные неравенства А^В и В> С, то
на области М справедливо и тождественное неравенство
А> С.
176. Если на некоторой области М, принадлежащей ОДЗ
трех алгебраических выражений А, В и С, одновременно
справедливы тождественные неравенства А> В и В^ С, то
на области М справедливо и тождественное неравенство
А> С.
Если оба неравенства являются нестрогими, то неравен-
неравенство, вытекающее из них, будет также нестрогим. Напри-
Например, в этом случае утверждение о транзитивности нера-
неравенств имеет вид.
80
17в. Если на некоторой области М, принадлежащей ОДЗ
трех алгебраических выражений А, В и С, одновременно
справедливы тождественные неравенства А 2: В и В^С, то
на области М справедливо и тождественное неравенство
А*С.
В дальнейшем, также, как и в случае равенств, слово
тождественное будем опускать.
Рассмотрим теперь некоторые способы доказательств
равенств и неравенств.
1. Перебор всех возможных случаев. Докажем этим спо-
способом свойства абсолютных величин действительных чисел
типа равенств и неравенств:
2.
3.
4.
A)
= jf, если Ь * 0.
Начнем, например, со свойства 3. Рассмотрим все воз-
возможные случаи:
о) {(в, Ь)\ае [0;+«>);?,€ [0; + -.)},
&){<«, ft) |«€ [0;+оо);6е(-оо;0]},
у) {(а, Ь)\ае(-°°,0];Ье [0; + -.)},
8) {(в, ft) |в€<-~;0]; ft€<--.;<)]}
и доказательство проведем отдельно в каждом случае.
В случае а) по определению абсолютной величины \а\ = а
и \t\ = b, поэтому \ab\ = ab. Значит, в случае а) равенство
\ab\ = \а\ \Ь\ может быть записано в виде ab = ab, после чего
оно становится очевидным.
В случае Р) ab < 0, поэтому по определению абсолютной
величины \а\ = а, \Ь\ = — b, \ab\ = — ab. Значит, в этом случае
свойство 3 может быть записано в виде — ab = а (— Ь) или
— ab= — ab, после чего оно становится очевидным.
В случае у) или 8) свойство 3 доказывается аналогично.
Из справедливости свойства 3 во всех возможных случаях
вытекает его справедливость в той формулировке, в кото-
которой оно записано.
81
Докажем теперь свойство 1. Рассмотрим следующие 6
случаев:
а) а > 0; Ъ > 0;
Р) a Z 0; Ъ й 0; а + Ъ > 0;
у) а ? 0; Ъ < 0; д + Ъ < 0;
8) а < 0; Л > 0; а + Ъ > 0;
X) а < 0; Ъ > 0; д + Ъ < 0;
v) а < 0; Л < 0.
В случае а) |а + й| = а + Ъ = |с| + |^, поэтому свойство 1 в
этом случае может быть записано в виде а + Ъ = |о| + \%
после чего оно становится очевидным.
В случае Р) \а + Ь\ = а + Ъ = а — (— Ь) = |с| — |?|, поэтому
свойство 1 в этом случае может быть записано в виде
а — b< a + b, после чего оно становится очевидным.
В случае у) \а + 1\ = - (а + Ь) = (- Ь) - а = Щ - |о|,
поэтому свойство 1 в этом случае может быть записано л
виде |6| — |с| < |с| + \t\, после чего оно становится очевид-
очевидным.
В случаях 8), X) и v) и доказательства свойства 1 анало-
аналогичны предыдущим. Из справедливости свойства 1 во всех
возможных случаях вытекает его справедливость в той
формулировке, в которой оно записано. Свойства 2 и 4
абсолютных величин A) доказываются аналогично.
2. Использование законов действий над алгебраическими
выражениями и вытекающих из них свойств A — 21). Дока-
Докажем этим способом равенство
(а + Ь)(а2 + Ь2) = а* + с?Ь + ab1 + b\ B)
Отметим, что равенство B) доказывается на ОДЗ трех
выражений (а + Л), (а2 + Ь2) и а3 + a2b + ab2 + b\ т.е. на
множестве {(a, b) \ a e R; b e R}. На основании закона ди-
дистрибутивности действий над алгебраическими выраже-
выражениями можно утверждать справедливость равенства
(а + Л)(д2 + Ь2) = а{а2 + Ь2) + Ь(с? + Ь2). C)
На основании закона коммутативности умножения спра-
справедливы равенства
82
atf + b2) = (а2 + Ь2)а, D)
b(a2 + b2) = (о2 + Ь2)Ь. E)
На основании закона дистрибутивности справедливы ра-
равенства
(а2 + Ь2)а = а*а + Ь2а, F)
(а2 + Ь*)Ь = a2b + Ь2Ь. G)
На основании законов коммутативности и ассоциативнос-
ассоциативности умножения справедливы равенства
eta = a\ (8)
Ъ\а = аЬ\ (9)
\ \ (9)
cth = A A0)
Ь2Ь = Ь\ A1)
Вследствие того что равенства можно складывать (см. свой-
свойство 13 равенств), складывая равенства (8) и (9), а затем
A0) и A1), получаем справедливость равенств
а1 а + Ь2а = д3 + ab2,
a2b + Ь2Ь = cth + Ь\
Складывая эти равенства, а затем равенства F) и G),
получаем справедливость равенств
аа + Ьа + аЬ + Ь2Ь= а3 + аЪ2 + a2b + b\ A2)
(а2 + Ь2)а + (а2 + Ь2)Ь = 0*0 + Ь2а + с?Ь + Ъ2Ъ. A3)
Складывая равенства D) и E), получаем справедливость
равенств
aid1 + Ь2) + Ь(<? + Ь2) = (о2 + Ь2)а + (а2 + Ь2)Ь. A4)
Применяя свойства транзитивности равенств, из спра-
справедливости равенств C), A4), A3) и A2) получаем справед-
справедливость равенства B).
Отметим, что все предшествующие выкладки записыва-
записывают в виде следующей цепочки равенств:
83
(a + b)(d + b2) =
= a{d +. b2) + b(a2 + b2) = (a2 + Ь2)а + (a2 + b2)b =
= da + b2a + a2b + b2b= a3 + a2b + ab2 + b\
Из справедливости этой цепочки равенств делается вывод
о справедливости равенства B). В дальнейшем при доказа-
доказательстве этим и другими способами будем писать лишь
цепочку очевидных равенств.
3. Прямое доказательство. Часто в процессе поиска до-
доказательства, переходя от данного неравенства к следую-
следующим, приходят в конце к очевидному неравенству. Если
при этом совершались только равносильные переходы, т.е.
в результате перехода каждый раз получали неравенство,
равносильное предыдущему, то тем самым получено дока-
доказательство исходного неравенства. Докажем этим способом
следующее неравенство: ~- > -fab на области М = {(a, b) |
| а е @; + °°); Ъ е @; + «>)}. Напишем цепочку равносиль-
равносильных на области М переходов:
Ц±* <а~Ь & а + Ъ - 2<аЬ *0 Д
Д (<аJ - 2<а~<Ь + {<bf * 0 Д {<а - <bf > 0.
Поскольку справедливость последнего неравенства очевид-
очевидна, то из равносильности первого и последнего неравенств
вытекает справедливость первого неравенства.
Доказанное неравенство часто формулируют так: среднее
арифметическое двух положительных чисел не меньше их
среднего геометрического.
4. Метод от противного. Этот метод уже использовался в
главе 1 при доказательстве теоремы о том, что простых
чисел бесконечно много. Можно его применять и при
доказательстве равенств и неравенств.
Докажем, например, этим методом, что для любого
положительного числа а справедливо неравенство а +
+ - ? 2. Предположим противное, т.е. предположим, что
существует хотя бы одно положительное число а такое, что
84
для него справедливо неравенство а + - < 2. Так как а —
положительное число, то это неравенство на основании
утверждения 21 равносильно неравенству (а + -)а < 2а, т.е.
неравенству я2 + 1 < 2д, которое на основании утвержде-
утверждения 20 равносильно неравенству (а2 + 1) — 2а < 2а — 2а,
т.е. неравенству а2 — 2а + 1 < 0. Перепишем последнее
неравенство в виде (а — IJ < 0. Приходим к противоречию
с очевидным фактом, что квадрат любого действительного
числа неотрицателен. Полученное противоречие говорит о
том, что сделанное предположение неверно. Следователь-
Следовательно, неравенство а + - > 2 выполняется для любого положи-
положительного а.
5. Использование свойства транзитивности неравенств.
Пусть требуется доказать на области М неравенство А < С.
Если известно или уже доказано, что на области М спра-
справедливы неравенства А< В, В< С, или неравенства А < В,
В< С, или неравенства А < В, В й С, то по свойству тран-
транзитивности неравенств будет справедливо и исходное не-
неравенство.
Докажем этим способом следующее неравенство:
-т + -т + -т+- + -т<2
I2 22 з2 л2
на множестве М = {(п) \ п е N}.
Для п = 1 неравенство очевидно. Рассмотрим теперь
любое натуральное л > 2. Каждое слагаемое суммы, начи-
начиная со второго, заменим на большее: — — -? • j < , где
к /с к к (к 1)
2йкйп. Таким образом, имеем справедливое неравенство
Л ^ ^ ? А ^2^3^
+ ... + ——-. Следует отметить, что неравенство Ан < Вн
л (л — 1)
является строгим при любом натуральном п ? 2.
85
Алгебраическое выражение В„ можно упростить, если
каждое слагаемое, начиная со второго, заменить алгебраи-
алгебраической суммой: * = ~—rr — -к
к(к— 1) (Л—1) А:
Получим
1 n
J 11=2-1
-1 П) * П
Неравенство Д, < 2 является, как легко заметить, спра-
справедливым для любого натурального п. Следовательно, по
свойству транзитивности неравенств имеем Ан < 2, что и
требовалось доказать.
Докажем в заключение свойства возведения алгебраи-
алгебраических выражений в натуральную степень, которые часто
используются при решении уравнений и неравенств (см.
гл. III).
Теорема 1. Пусть некоторая область Мпринадлежит
ОДЗ двух алгебраических выражений А и В и обладает
следующим свойством: для любого числового набора из облас-
области М соответствующие числовые значения выражений Аи В
положительны. Тогда на области М для любого натурального
числа п (п> 2):
а) равенства А — В и А" = В1 равносильны;
б) неравенства А> В и А" > В1 равносильны.
Доказательство. Обозначим алгебраическое выраже-
выражение А"~' + А"~2В + ... + АИ1'1 + В4'1 через С. В § 6 будет
доказана справедливость следующего равенства алгебраи-
алгебраических выражений:
Ая - В1 = (А - В)С. A5)
Очевидно, что для любого числового набора из области М
соответствующее числовое значение выражения С положи-
положительно.
Докажем утверждение а). Пусть дано, что А = В на об-
области М. Тогда на основании утверждения 15 на М спра-
справедливо равенство А — В = 0, а отсюда по утверждению 16
86
получим, что на М справедливо равенство (А — В)С=0.
По свойству транзитивности равенств из этого равенства и
равенства A5) вытекает, что А" — ЕС = 0, откуда по утверж-
утверждению 15 следует, что на области М справедливо равенство
Ап = ЕС.
Итак, доказано, что на области М из справедливости
равенства А = В следует справедливость равенства А" = ЕС.
Пусть теперь дано, что А" = ЕС на области М. Тогда на
области М по утверждению 15 справедливо равенство А" —
— ЕС = 0. Отсюда и из равенства A5) на области М на
основании свойства транзитивности равенств имеем, что
(А — В)С= 0, а отсюда по утверждению 16 вытекает, что
А — В = 0, и наконец, по утверждению 15 получаем, что
А = В. Значит, на области М из справедливости равенства
А" = ЕС вытекает справедливость равенства А = В. Утверж-
Утверждение а) доказано.
Докажем теперь утверждение б). Пусть дано, что А > В
на области М. Тогда на основании утверждения 20 на М
справедливо и неравенство А — В > 0, а отсюда по утверж-
утверждению 21 получим справедливость неравенства (А — В) О
> 0. Учитывая справедливость равенства A5) получим, что
А" — ЕС > 0. Наконец, по утверждению 20 получим, что на
М справедливо неравенство А" > ЕС.
Итак, доказано, что на области М из справедливости
неравенства А > В следует справедливость неравенства
Ап> ЕС.
Пусть теперь дано, что А" > ЕС на области М. Тогда на
области М по утверждению 20 справедливо неравенство
А" — ЕС > 0. Отсюда и из равенства A5) получим, что
(А — В)С> 0 на области М. Применяя теперь утвержде-
утверждение 21, находим, что А — В > 0 на М. Наконец, по утверж-
утверждению 20 имеем А > В на М. Итак, на области М из
справедливости неравенства А"> ЕС вытекает справедли-
справедливость неравенства А > В. Утверждение б) доказано. Теорема
доказана полностью.
87
§ 3. Многочлены
Рациональное выражение, содержащее относительно
входящих в него букв только два действия — умножение и
возведение в натуральную степень, называется одночленом.
Примеры одночленов: За, 2аЬсЦ^аЬс, Ц^-.
Рациональное выражение называется многочленом, если
оно является целым относительно каждой буквы, входящей
в это выражение.
Например, рациональное выражение л/ЗТдЛс — ^—- +
+ 0,3dc является многочленом, ибо это выражение являет-
является целым относительно букв а, Ь, си d.
В частности, рациональное выражение, содержащее
только одну букву и являющее целым относительно этой
буквы, называется многочленом относительно одной
буквы.
Из определения многочлена и правил действий над ал-
алгебраическими выражениями следует, что сумма, разность
и произведение двух многочленов будут многочленами.
Если в многочлен входит п букв, то многочлен имеет
смысл для любого числового набора из п чисел. Поэтому
обычно, рассматривая многочлен, не говорят о его ОДЗ.
Обычно одночлены тождественно преобразуют по законам
действий, приведенных в § 2, собирая вместе все числа,
входящие в одночлен, и записывая их перед буквами одно-
одночлена, а также собирая вместе одинаковые буквы, входя-
входящие в одночлен, и записывая их в виде натуральной степе-
степени этой буквы. После такого преобразования одночлен
считается записанным в стандартном виде, а числовой
множитель, стоящий перед буквами одночлена, называется
коэффициентом данного одночлена.
Например, одночлен ЪаЬЛсЩас преобразуется к стан-
стандартному виду уд2Л2с3, и число у есть его коэффициент.
Согласно правилам действий над алгебраическими вы-
выражениями многочлен всегда можно тождественно преоб-
преобразовать к виду, в котором многочлен состоит из несколь-
нескольких одночленов, записанных в стандартном виде и соеди-
88
ненных знаками сложения и вычитания; поэтому обычно
говорят, что многочлен есть алгебраическая сумма одночле-
одночленов.
Подобные члены многочлена — это его одночлены, запи-
записанные в стандартном виде и отличающиеся не более чем
коэффициентами. Привести подобные члены многочлена —
это значит заменить алгебраическую сумму подобных чле-
членов одним членом, тождественно равным этой сумме.
Исходя из правил действий над алгебраическими выра-
выражениями, можно следующим образом конкретизировать
законы действий над многочленами.
Чтобы сложить два многочлена, следует записать подряд
все члены первого многочлена, а затем все члены второго
многочлена, сохраняя у каждого члена знак, стоящий перед
его коэффициентом, после чего необходимо привести по-
подобные члены.
Например: (led + 5а) + (х+7а — 4cd) = 2cd+5a + x +
+ 7а — 4cd= \2a + x— led.
Чтобы вычесть из одного многочлена другой многочлен,
следует записать подряд все члены первого многочлена,
сохраняя у каждого одночлена знак, стоящий перед его
коэффициентом, затем все члены второго многочлена,
изменив на противоположные знаки, стоящие перед коэф-
коэффициентами одночленов второго многочлена, после чего
необходимо привести подобные члены.
Например: (х2 - у2) - (- Ix2 + Sy2 - 5а) = х2 - у2 +
+ Ix2 - Sy2 + 5а = Sx2 - Эу2 + 5а.
Чтобы умножить одночлен на многочлен, следует умно-
умножить этот одночлен на каждый член многочлена, записать
члены подряд с теми знаками, какие были у членов много-
многочлена, если перед коэффициентом одночлена стоит знак
плюс, и с противоположными знаками — если перед коэф-
коэффициентом одночлена стоит знак минус, каждый одночлен
произведения записать в стандартном виде, а затем привес-
привести подобные члены.
Например: (- 4аЬ)(ЗаЬ -2 + За2Ь2) = - Dab)Cab) +
+ DаЬ)-2 - Dab)Ca2b2) = - nftf + Sab - 12eV;
5cBab + 1 - 3b) = Ec)Bab) + Ec) ¦ 1 - Ec)Cb) = lOabc +
+ 5c- 156c.
89
Чтобы умножить многочлен на многочлен, следует каждый
одночлен (вместе со знаком, стоящим перед его коэффи-
коэффициентом) первого многочлена умножить на второй много-
многочлен, записать подряд все произведения, каждый получен-
полученный одночлен записать в стандартной форме, а затем
привести подобные члены.
Например: (ab — cd) • (ab + cd) = (ab)(ab) + (ab)(cd) —
- (cd)(ab) - (cd)(cd) = ctb2 + abed - abed - c2i = a2b2 -
Пользуясь правилами сложения и умножения многочле-
многочленов и свойствами равенств алгебраических выражений,
получим тождественные равенства, которые часто называ-
называют формулами сокращенного умножения.
Начнем с перемножения одинаковых многочленов вида
(а + Ь). Используя законы действий над алгебраическими
выражениями, можно написать следующую цепочку тож-
тождественных равенств:
(а + ЬJ = (а + Ь)(а + Ь) = (а)(а) + (а)(Ь) + F)(в) + (&)(&) =
= а2 + ab + ab + Ь2 = а2 + lab + Ъ2. A)
Формула A) имеет следующую словесную формулиров-
формулировку: квадрат суммы двух чисел равен квадрату первого числа,
плюс удвоенное произведение первого числа на второе, плюс
квадрат второго числа.
Теперь используя предыдущую формулу, можно напи-
написать следующую цепочку тождественных равенств:
(а + ЬK = (а + Ъ){а + ЪJ = (а + Ь^а2 + lab + Ъ2) =
= (а)(а2) + (а)AаЬ) + (а)(Ь2)
= а3 + Ictb + ab2 + a2b + lab2 + b3 = о3 + Ictb + ЪаЪ2 + Ь3.A)
Формула B) имеет следующую словесную формулиров-
формулировку: куб суммы двух чисел равен кубу первого числа, плюс
утроенное произведение квадрата первого числа на второе,
плюс утроенное произведение первого числа на квадрат вто-
второго числа и плюс куб второго числа.
Напишем еще одну цепочку тождественных равенств:
90
(a + bL = (a + b)(a + bK = (a + 6)(e3 + 3a2b + lab1 + b3) =
(a)Cab2) + (a)(b3)
= a4 + 3^6 + 3e262 + ab3 +
+ a3b + Ъ(?Ъг + ЪаЪ3 + b4 = a4 + 4a3b + 6c?b2 + 4a63 + b4.
Приведенные формулы позволяют заметить некоторую за-
закономерность, с помощью которой можно записать фор-
формулу для (в + Ь)", где п — любое натуральное число.
А именно легко заметить, что всех членов будет (л + 1);
первый член есть первое число в степени л; в каждом
последующем члене степень первого числа на единицу
меньше его степени в предшествующем члене, а в послед-
последнем члене оно в нулевой степени; второе число находится
в первом члене в нулевой степени, во втором члене в
первой степени, в каждом последующем члене степень
второго числа на единицу больше его степени в предшест-
предшествующем члене, а в последнем члене второе число в степе-
степени л.
Коэффициент же при каждом члене можно найти при
помощи «треугольника Паскаля»:
0
1
2
3
4
5
6
7
8
9
1
1
1 9
1
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
7 21 35 35 21 7 1
8 28 56 70 56 28 8 1
36 84 126 126 84 36 9 1
Правило образование строк «треугольника Паскаля»
простое. Каждая строка может быть получена из предыду-
предыдущей верхней строки следующим образом. В Промежутке
между любыми соседними числами верхней строки (но
ниже их) пишется сумма этих чисел, а по краям пишутся
единицы. Номер строки показывает, в какую степень воз-
возводится двучлен (в + Ь), а числа этой строки являются
91
коэффициентами соответствующих членов, записанных в
рассмотренном выше порядке.
Конечно, если надо написать формулу для (а + &)", где
п — большое число (например, 100), то ясно, что по
треугольнику Паскаля вычислять коэффициенты правой
части долго. Поэтому желательно знать общую формулу
вычисления (а + Ь)п. Эта формула носит название формулы
бинома Ньютона и имеет вид
C)
где <^=И(яи^), (следовательно, С?= С„~к), 0!=1, *! =
= 1 • 2 • 3 • ... • к для любого к е {1, 2, 3, ..., п).
Доказательство равенства C) будет дано в § 6.
Применим формулу бинома Ньютона, например, для
числения (а + Ь):
(а + b)s =
Вычислим коэффициенты С?, где т е {0, 1, 2}. Для вычис-
вычислением остальных коэффициентов воспользуемся равенст-
равенством.
доказанным в главе 1.
Таким образом,
?5=С$=1, 3=3 = ^=5,^= 3 = ^= 10.
Следовательно,
(а + b)s = 0s + 5а46 + lOoV + Wa2? + 5abA + b\
Из формулы бинома Ньютона легко получить формулу
для (а — Ь)п. Обозначим d = — Ь и применим формулу
бинома Ньютона:
92
'<?+... +ОТ.
Подставляя (— b) вместо d, получим
Частные случаи этой формулы для п = 2 и п = 3:
(a-bf = a2- lab + b2,
(a-bf = a3- lib + ЪаЪ1 - b\
Формула бинома Ньютона (a + Ь)" и вытекающая из нее
формула (a — b)" являются формулами сокращенного умно-
умножения, в которых берется произведение одинаковых много-
многочленов (биномов) п раз.
Докажем теперь некоторые формулы, в которых берется
произведение разных многочленов. Очевидна следующая
цепочка тождественных равенств:
(а - Ь)(а + Ь)
= а2 + аЪ - аЪ - Ь2 = а2 - Ь2.
Эта формула обычно запоминается в записи, где меняются
местами правая и левая части: а2 — Ь2 = (а — Ь)(а + Ь).
Приведем ее словесную формулировку: разность квадратов
двух чисел равна произведению разности этих чисел на их
сумму.
Выведем формулу разности кубов этих чисел (л3 — Ьъ).
Поскольку
(а - Ща2 + аЬ+ Ъ2) = Ша2) + (а)(аЬ) + (а)(Ь2) -
- (ЬКа2) - (Ь)(аЬ) - (Ь)(Ь2) = а3 + <tb + аЪ2 -
-a2b-ab2-bi = a3- b\
то
аЬ + Ъ2).
93
Приведем словесную формулировку этой формулы: раз-
разность кубов двух чисел равна произведению разности этих
чисел на неполный квадрат суммы этих чисел.
Приведенные формулы позволяют заметить закономер-
закономерность, с помощью которой легко записать формулу а" — Ь"
для любого натурального числа п. Эта формула имеет вид
а" - ЬЙ = (а - Ь) (dl~i + dl-2b+... + abn~2 + б").
Доказательство этой формулы будет проведено в § 6 мето-
методом математической индукции.
Наконец, выведем следующую формулу:
а3 + Ь3 = (в + Ь)(а2 -аЪ+ Ь2).
Действительно,
(а + Ь)(а2 -аЬ+ Ь2) =
- (a)(ab) + (а)(Ь2) + F)(а2) - (b)(ab)
= а3-а2Ь+ аЬ2 + ctb - аЬ2 + Ь3 = а3 + Ь3.
Словесная формулировка этой формулы следующая: сумма
кубов двух чисел равна произведению суммы этих чисел на
неполный квадрат разности этих чисел.
Приведем формулы, которые желательно запомнить:
(а + bf = а2 + lab + Ъ2,
(а + ЬK = а3+ За2*» + ЪаЪ2 + Ъ3,
(а - ЬJ = а2 - lab + Ь2,
(а - bf = а3 - Ъс^Ъ + ЪаЪ2 - Ь3,
a1-b1 = (a-b)(a+b),
а3 - Ь3 = (в - ЪШ + ab+ b\
а3 + Ь3 = (в + b)((? -ab+ b2).
Формулы, доказанные в этом параграфе, справедливы
для любцх числовых значений букв а и Ь. Иногда эти
формулы употребляются и тогда, когда буквами а и Ь
обозначены некоторые алгебраические выражения, но
тогда очевидно, что эти формулы будут справедливы уже
на ОДЗ двух алгебраических выражений а и Ъ.
94
В ряде вопросов при действиях с многочленами удобнее
рассматривать их не стандартном виде, а в-виде произве-
произведения.
Тождественное преобразование многочлена к виду про-
произведения многочленов называется разложением многочле-
многочлена на множители. Собственно говоря, все формулы сокра-
сокращенного умножения и есть формулы разложения много-
многочлена на множители.
Кроме применения формул сокращенного умножения,
есть и другие приемы для разложения многочлена на
множители, например, вынесение за скобки общего множи-
множителя, группировка. Для разложения многочлена на множи-
множители употребляются все приемы.
Рассмотрим пример разложения многочлена на множи-
множители. Группируя, вынося за скобки общий множитель и
пользуясь формулой сокращенного умножения, получаем
цепочку тождественных равенств:
а2 с + 2abc + b2c +(a + bfd = с(а2 + lab + b2) + d(a + bJ =
= c(a + bf + d(a + bJ = (a + b)\c + d).
§ 4. Алгебраические дроби
Алгебраической дробью называется дробное рациональное
выражение, являющееся частным от деления одного
многочлена на другой.
Алгебраическая дробь, которая есть частное от деления
многочлена А на многочлен В, обычно записывается в виде
4, причем многочлен А называется числителем алгебрам-
о
ческой дроби, а многочлен В — ее знаменателем.
Примеры алгебраических дробей:
b. ab — b. a + b . ху + бу
д3+1' d+a' а-Ь>
ОДЗ алгебраической дроби ^, в которую входит п букв,
есть множество всех числовых наборов, соответствующих
95
буквенному набору дроби 4» кроме тех, для каждого из
о
которых соответствующее числовое значение многочлена
В равно нулю.
2 ,2
Например, ОДЗ алгебраической дроби а _ь есть множе-
множество {(a, b)\ae R; be R; а*Ь}.
Докажем несколько утверждений о равенстве алгеб-
алгебраических дробей.
1. Если обозначить алгебраическую дробь 4 одной буквой С,
то на ОДЗ этой дроби равносильны тождественные равен-
равенства С=^иА= СВ.
о
Справедливость этого свойства вытекает из справедли-
справедливости утверждения 14 § 2.
2. Равенства jj = -^ и AD = ВС равносильны на ОДЗ первого
из них.
Это свойство часто формулируют так: две дроби 4 и -^
тождественно равны на ОДЗ тогда и только тогда, когда
на этой ОДЗ справедливо равенство AD = ВС.
Доказательство. Пусть область М— ОДЗ двух дро-
дробей 4 и ^. Рассмотрим случай, когда А = О на М. Тогда ^ =
= 0 и из равенства 4 = у. следует, что и -^ = 0 на М. Поэтому
С = 0 на М, а это значит, что AD = ВС на М.
Наоборот, пусть AD = ВС и А = 0 на М. Так как на М
D ф 0 и В * 0, то С = 0 на М. Следовательно, 4 = -^.
в и
Рассмотрим теперь случай, когда ни для одного набора
из области М многочлен А не обращается в нуль, т.е.
рассмотрим случай, когда Л*0 на М. Пусть ^ = -g, тогда
Л С
отсюда следует, что С * 0 на М. Обозначим 4 через а и -^
через р. По свойству 1 алгебраических дробей А = аВ и
= D. По утверждению 14 § 2 имеем
A$D=CaB. A)
96
Так как а = |5 ф О на М, что по утверждению 14 § 2 из A)
следует, что AD = СВ.
Наоборот, пусть AD = ВС, тогда, так как А ф О, D ф О и
В ф О на М, то и Сф О на М. Следовательно, а = ^ и |5 = —
не равны нулю на М. Тогда умножим данное равенство
AD = ВС на оф. Получим равносильное равенство
ос|Ш) = а$ВС. B)
Но oci? = A, PD = С, и равенство B) примет вид
C)
Используя утверждение 14 § 2, получим ос = |5, что и тре-
требовалось доказать.
Таким образом, свойство 2 алгебраических дробей дока-
доказано.
3. На ОДЗ алгебраической дроби 4 справедливы тождест-
тождественные равенства ^ = ^-| = — -^ = — z^-.
Каждое из этих равенств становится очевидным, если
воспользоваться только что доказанным свойством 2.
4. Для любого многочлена К, не обращающегося в нуль на
ОДЗ алгебраической дроби ~, справедливо тождественное
равенство ^ = —.
Поскольку на ОДЗ дроби 4 это равенство по свойству 2
о
равносильно равенству А(ВК) = В(АК), которое является
очевидным, то столь же очевидна и справедливость свой-
свойства 4.
5. На ОДЗ алгебраической дроби ^ справедливо тождест-
тождественное равенство 4 = Л 4-
Действительно, по утверждению 9 § 2
А_А(и Г
4 Алгебра,тригонометрия у/
и элементарные функции
Используя ассоциативность умножения алгебраических
выражений, имеем
Применяя утверждение 11 § 2 получаем, что
в л в-
6. На ОДЗ алгебраической дроби -^ справедливо тождест-
тождественное равенство — = ^ ¦ jj.
Действительно, на ОДЗ дроби -^ очевидна справедли-
справедливость цепочки тождественных равенств
Л R
7. На ОДЗ двух алгебраических дробей 4 м ^ справедливо
о А
тождественное равенство \ = \-
1
Действительно, применяя сначала свойство 5 дробей,
затем свойства действий над алгебраическими выражения-
выражениями, затем свойства 5 и 6 дробей, имеем цепочку тождест-
тождественных равенств
в А в А в \л i\{л л}\в 1
_ 1 _ 1
в а а
Напомним следующее соглашение: если не указана явно
область М, на которой рассматривается некоторое тожде-
тождественное равенство, то оно рассматривается на ОДЗ двух
выражений, стоящих в левой и правой частях равенства.
Поэтому дальше не будет явно указываться область, на
которой будет справедливо тождественное равенство, имея
в виду, что оно справедливо на ОДЗ двух выражений,
стоящих в левой и правой частях равенства.
98
Пользуясь свойствами сложения и умножения алгебра-
алгебраических выражений и свойствами алгебраических дробей,
легко доказать справедливость тождественных равенств
А С_АР+ВС. А С _АС
В Р BD ' В' Р ВР'
Действительно, используя свойства алгебраических дро-
дробей, получим
A C_AD , СВ
Применяя теперь свойства сложения и умножения алгеб-
алгебраических выражений, а затем опять свойства алгебраичес-
алгебраических дробей, имеем
что и требовалось доказать.
Аналогично доказывается второе равенство:
В D~{* В)[^ D)~A^ В Д-/М- BD BD
Так же доказываются и равенства
А С _ АР-ВС. А . С _ АР
В Р~ ВР ' В' Р~ ВС
Часто надо привести алгебраические дроби к общему
знаменателю, т.е. записать их так, чтобы у всех этих дробей
был один и тот же знаменатель. Для этого существует
следующий способ: надо разложить каждый знаменатель на
множители, а затем числитель и знаменатель каждой дроби
умножить на произведение тех множителей знаменателей
остальных дробей, которые не содержатся в данном знаме-
знаменателе, что по свойству дробей их не изменит.
Пример. Привести к общему знаменателю следующие
алгебраические дроби:
99
3 ,3» 2 ,2» 2 , ,2-
a — b a — b а + ab + b
Разлагая знаменатели на множители, перепишем дроби
так:
(а — Ь) (а2 + ab + b2)' (a — b)(a + b)' a+ab+b2'
Теперь, умножая числитель и знаменатель первой дроби на
{а + Ь), второй — на (а2 + ab + Ь2), третий — на (а — b) x
х (а+ Ь), получаем
а (а + Ь) . с(а+аЬ + Ь2)
(a — b)(a + b) (a2 + ab + b2) {a — b)(a + b) (a +ab+b2)'
(a — b)(a + b)(a +ab + b)
У этих дробей одинаковые знаменатели, т.е. первона-
первоначальные дроби приведены к общему знаменателю.
В ряде случаев требуется представить дробь в виде суммы
дробей с более простыми знаменателями. Это можно сде-
сделать только в том случае, когда многочлен, стоящий в
знаменателе дроби, разлагается на произведение многочле-
многочленов меньшей степени. Покажем на примере, как это дела-
делается.
Пусть надо разложить алгебраическую дробь -т^— на
х — 1
простейшие. Так как многочлен х2 — 1 разлагается на
произведение многочленов (х — 1) и (х + 1), то это можно
сделать. Для этого нужно найти алгебраические дроби
и —^-г такие, чтобы было выполнено тождественное
равенство -у^— = —^—г + -в-т. Рассмотрим сумму —~ +
х — 1 х—1 х+1 х- 1
-^ в-. По только что сформулированным правилам
х+
А . В _А(х+1) + В(х-1) _(А + В)х+(А-В)
100
Так как эта дробь должна тождественно равняться дроби
-5 (заметим, что эти рассуждения проводятся для любого
х — 1
х, кроме х = 1 и х = — 1), то по свойству 2 эти две дроби
равны только тогда, когда [(А + В)х + (А — В)](х — \)(х +
+ 1) = (х — 1)(х+ 1). Так как это равенство должно выпол-
выполняться для любого х, кроме х=1их=- 1, то, полагая,
например, х = 0, затем х = 2, получаем, что это будет верно
только тогда, когда одновременно А— В=1иЗА+В=1.
А эти два равенства справедливы одновременно только для
Л = ^ и В= — 2- Значит, данная дробь разложена на про-
простейшие, а именно, справедливо следующее тождественное
равенство:
Этот способ разложения дроби в сумму более простых
дробей называется способом неопределенных коэффициентов.
Действительно, полагая числа А и В вначале неизвестными,
получаем на ОДЗ равенство двух многочленов, один из
которых с известными коэффициентами, другой с неиз-
неизвестными, выраженными через А и В. Это дает возможность
выписать алгебраические равенства относительно неиз-
неизвестных коэффициентов (в данном случае А — В = 1, ЪА +
+ В= 1). Найдя числовые значения неизвестных коэффи-
коэффициентов, обращающие данные алгебраические равенства в
верные числовые равенства, тем самым решим поставлен-
поставленную задачу о представлении дроби в виде суммы более
простых дробей.
Неравенства алгебраических дробей. Докажем два ут-
утверждения, которые часто применяются при рассмотре-
рассмотрении алгебраических дробей.
8. На ОДЗ алгебраической дроби ^ равносильны следующие
неравенства: |>0и АВ > 0.
Докажем, что из справедливости первого неравенства
следует справедливость второго неравенства.
101
Доказательство. Обозначим алгебраическую дробь
^ одной буквой С, т.е. С = ^. На ОДЗ данной алгебраичес-
алгебраической дроби алгебраическое выражение С положительно, так
как любое числовое значение алгебраического выражения
Сявляется положительным числом. По свойству 1 равенств
алгебраических дробей имеем А = СВ на ОДЗ дроби. Сле-
Следовательно, алгебраическое выражение АВ равно СИ2:
АВ = СВ2. По определению на ОДЗ дроби 4 алгебраическое
выражение В в нуль не обращается, т.е. алгебраическое
выражение В2 положительно на ОДЗ дроби ^. Произведе-
Произведение положительных алгебраических выражений С и В2
будет также положительным. Аналогично доказывается,
что на ОДЗ алгебраической дроби 4 из справедливости
неравенства АВ > О следует справедливость неравенства
Л С1
9. На ОДЗ алгебраических дробей -= и -^ равносильны
О 1}
неравенства j>%uА&В> C&D.
Доказательство. Используя утверждение 20, полу-
получим равносильные неравенства: ^>^и4~^>0-
Выше было доказано равенство
А С _ АР- ВС
В D BD *
которое позволяет сделать еще один равносильный пере-
переход:
А ^ С „ АР- вс^п
В Р BD U>
Последнее неравенство по утверждению 8 на ОДЗ алгебра-
алгебраических дробей 4 и -т! равносильно неравенству (AD —
о и
— BQBD > 0, которое равносильно неравенству А1?В >
> C&D. Утверждение 9 полностью доказано.
102
Утверждения 8, 9 используются при доказательстве дру-
других неравенств.
Докажем, например, что неравенства а- . > а~ь и а> b
о — о а + о
равносильны для любых, не равных друг другу положитель-
положительных чисел а и Ь.
Действительно, по утверждению 9 равносильны следую-
следующие неравенства:
и (а2 - Ь2)[(а + ЬJ - {а- ЬJ) > 0.
Так как (а + ЬJ — (a — bJ = Aab, то последнее неравенство
равносильно неравенству (а — b)(a + b) Aab > 0, которое в
силу положительности а и Ъ равносильно неравенству
а > Ь. Следовательно, а+ , > g~f о а> Ь для любых, не
равных друг другу, положительных аи Ь.
§ 5. Многочлены относительно одной буквы
Многочлен относительно одной буквы х имеет одночле-
одночлены разных степеней, ибо в противном случае можно при-
привести подобные члены. Одночлены разных степеней можно
упорядочить относительно возрастания или убывания сте-
степеней буквы х. Обычно многочлен относительно одной
буквы записывают в порядке убывания степеней.
Многочлен, записанный в виде a^C + ахх" ~' + а-$С ~2 +
+ ... + а„ _ \Х + а„, называется расположенным многочленом.
Если Оц ф 0, то говорят, что этот многочлен имеет степень п.
Если не известно, равен или не равен нулю коэффициент
Oq, то говорят, что этот многочлен степени не выше, чем п.
Из этого определения в частности вытекает, что много-
многочлены нулевой степени — это отличные от нуля числа.
Число нуль также считается многочленом, причем это
единственный многочлен, степень которого не определена.
Для сокращенного обозначения многочленов обычно упот-
употребляют следующие записи:
Дх), Q(x), Цх), R(x), p(x), q(x), r{x),
103
при этом, если хотят подчеркнуть, что многочлен Р(х) —
степени п, то пишут Р„(х).
Для нахождения суммы многочленов Р„(х) и QJx) нужно
записать подряд все члены этих двух многочленов и затем
сделать приведение подобных членов.
Для нахождения произведения многочленов Р„(х) и Qm(x)
нужно каждый одночлен многочлена Р„(х) умножить на
каждый одночлен многочлена Qm(x), сложить полученные
произведения и привести подобные члены.
Теорема 1. Два многочлена относительно х тождест-
тождественно равны тогда и только тогда, когда равны их степени
и равны коэффициенты при одинаковых степенях х.
Доказательство этой теоремы опускается.
В этом параграфе для обозначения тождественного ра-
равенства двух многочленов Р(х) и Q(x) будет употребляться
запись Р(х) = Q(x), т.е. в этом параграфе знак «=», связы-
связывающий два многочлена, будет пониматься в смысле тож-
тождественного равенства этих многочленов. В частности,
запись Р(х) = О будет означать, что многочлен Р(х) тожде-
тождественно равен нулю, т.е. есть число нуль.
Теорема 1 может быть применена для разложения много-
многочлена на множители. Воспользуемся методом неопределен-
неопределенных коэффициентов. Суть применения этого метода состо-
состоит в следующем. Пусть дан многочлен Р„(х) степени п и его
надо представить в виде произведения многочленов степе-
степеней к и (п — к), где к < п. Тогда выписываются два много-
многочлена Рк(х) и Р„ _ к(х); первый — степени к и второй —
степени (п — к), с коэффициентами, обозначенными не-
некоторыми буквами, скажем, у первого осо, ось •••, щ, У
второго р0, Рь ••¦> Рл-*- Перемножая многочлены Рк(х) и
Рп - к(х) получаем многочлен Т„(х) степени п с коэффици-
коэффициентами, зависящими от а/(/=0, 1, ..., к) и ру(/ = 0, 1, ...
..., п — к). Из условия, что многочлены Р„(х) и Т„(х) тож-
тождественно равны, получаем п + 1 равенство, в которых
участвуют п + 2 коэффициента ос, и р7, которые надо найти.
Полагая, например, коэффициент cto = 1, приходим к п + 1
равенству, из которых надо найти п + 1 коэффициент ос,
104
(/ = 1, 2, ..., к) и ру (/ = О, 1, ..., п — к). Найдя их, найдем и
многочлены Рк(х) и Р„ _ к(х).
Пример. Разложить многочлен х3 + Зх + 4 на множи-
множители, среди которых один — многочлен первой степени, а
второй — многочлен второй степени. Будем искать много-
многочлены (х + ос,) и (роХ2 + р(х + р2) такие, что справедливо
тождественное равенство (х + а1)(рох2 + р,х + р2) = х3 +
+ Зх + 4. Применяя теорему 1, получаем четыре равенства:
р0 = 1, роа, + р, = 0, р,а, + р2 = 3, а,р2 = 4. Этим равенст-
равенствам удовлетворяют р0 = 1, а, = 1, р, = — 1, р2 = 4. Значит,
многочлен х3 + Зх + 4 разлагается на множители (х + 1) и
(х2 — х + 4), т.е.
х3 + Зх + 4 = (х + lKx2 - х + 4).
Заметим, что не всякий многочлен можно разложить на
множители. Например, многочлен х2 + х + 1 нельзя разло-
разложить в произведение двух многочленов первой степени.
Теорема 2. Если произведение двух многочленов тожде-
тождественно равно нулю, то хотя бы один из этих многочленов
тождественно равен нулю.
Доказательство этого утверждения опускается.
Вычесть из многочлена Р(х) многочлен Цх) — это значит
найти такой многочлен Q(x), что Р(х) = Т\х) + Q(x).
Нетрудно проверить, что для любых двух многочленов
Р(х) и Т\х) такой многочлен Q(x) существует и при этом
только один, он называется разностью многочленов Р(х) и
1\х) и обозначается Q(x) = Р(х) — 1\х).
Разделить нацело многочлен Р(х) на многочлен 1\х),
отличный от нуля — это значит найти многочлен Q(x)
такой, что Р(х) = T\x)Q(x).
Если такой многочлен Q(x) существует, то говорят, что
многочлен 1\х) является делителем многочлена Р(х), а
многочлен Q(x) является частным от деления многочлена
Р(х) на многочлен 1\х). Не всегда многочлен Р(х) можно
разделить нацело на многочлен 1\х). Например, многочлен
х2 + 1 не делится нацело на многочлен х+ 1. Значит в
множестве многочленов не всегда выполнимо деление на-
105
цело. Зато, как будет показано ниже, в множестве много-
многочленов всегда выполнимо деление с остатком.
Деление с остатком. Разделить с остатком многочлен
Р(х) на многочлен 1\х), отличный от нуля, — это значит
найти два многочлена q(x) и г(х) такие, что
Р(х) = Цх)Я(х) + г{х), A)
причем либо степень многочлена г(х) строго меньше сте-
степени многочлена Цх), либо г(х) есть нуль.
В случае, если выполнимо равенство A), говорят, что
многочлен Р(х) делится на многочлен 1\х) с остатком г(х)
и частным q(x)\ если г(х) = О, т.е. если остаток есть число
нуль, то говорят, что многочлен Р(х) делится на многочлен
7\х) с остатком нуль или многочлен Р(х) делится нацело на
многочлен 7\х).
Пример. Пусть Р(х) = х1 — х6 + Тх5 + х2,1\х) = х2 — х +
+ 2. Тогда легко видеть, что Р(х) = Дх)(х* + 1) + х — 2, т.е.
многочлен Р(х) делится на многочлен Т\х) с остатком г(х) =
= х — 2 и частным х5 + 1. Отметим, что из равенства
Р(х) = Дх)х* + х2 не вытекает, что многочлен Р(х) делится
на многочлен 1\х) с остатком х2, ибо нарушено условие:
степень остатка г(х) должна быть строго меньше степени
многочлена 1\х).
Теорема 3. Для любых двух многочленов Р(х) и 1\х), где
1\х) * 0, существует пара многочленов q{x) и г(х) таких, что
Р(х) = T\x)q{x) + rix), причем либо степень многочлена г(х)
строго меньше степени многочлена Т\х), либо г(х) есть нуль.
Доказательство. Пусть Р(х) = 0, а Цх) — любой от-
отличный от нуля многочлен, тогда многочлены q(x) = 0 и
г{х) = 0 удовлетворяют условиям теоремы.
Пусть Р{х) ф 0, а многочлен 1\х) имеет степень большую,
чем степень многочлена Р(х), тогда многочлены q(x) = 0 и
rix) = P(x) удовлетворяют условиям теоремы.
Наконец, пусть Р(х) фО,л многочлен 1\х) имеет степень,
меньшую или равную степени многочлена Р(х). Если
Т\х) = с, где с — константа, отличная от нуля, то много-
многочлены q(x) = Р(х)/с и г(х) = 0 удовлетворяют условиям тео-
теоремы.
106
Остается рассмотреть случай, когда многочлен Дх)
имеет степень п, причем п > 1, а многочлен 1\х) имеет
степень т, причем 0 < т < п. Пусть Дх) = Р„(х), Цх) =
= Тт(х), где 0 < т <, и, п > 1, т.е.
Рп(х) =
Тт(х) = boxT + blxm-l + ... + bm_lx+bl
7I>
где Oq ф 0, 60 * 0. Построим последовательность многочле-
многочленов Qnt(x) следующим образом. Положим
Тогда либо Qn{(x) = 0, либо &,(*) можно записать в виде
причем 4° * 0 и степень многочлена G.^x) меньше, чем п,
т.е. Wi < n; если окажется, что пх< т или Q,t(x) = 0, то
многочлены q(x) = —Xя ~ т и г(х) = G, (х) удовлетворяют
, (
"о '
условиям теоремы; если же я, > т, то делаем следующий
шаг: положим
-^'~'ад-
ясно, что либо б„2(х) = 0, либо п2 < Пх < п и G,2(x) можно
записать в виде
причем а?} * 0. Если окажется, что пг< т или &2(х) = 0, то
многочлены в(х) = &хч~" + %-хЧ|~", г(х) = Q.(х) удовле-
творяют условиям теоремы; если же п2>т, то делаем
следующий шаг и продолжаем этот процесс. Поскольку на
каждом шагу степень уменьшается: п > л, > п2 > ..., то на
107
некотором к-ъл шагу натуральное число пк станет меньше
натурального числа т или 0„к(х) = 0 и процесс закончится.
В результате получим, что
Тогда многочлены rix) = 0„к(х) и q(x) =
! rt) (t-D \
?*" " + =*-&'" + ... +\-хп'->~т удовлетворяют усло-
[м теоремы.
Итак, утверждение теоремы о существовании многочле-
многочленов q(x), r(x) доказано.
Теорема 4. Пара многочленов д(х), rix), удовлетворяю-
удовлетворяющая условиям теоремы 3, единственная.
Доказательство. Предположим противное, т.е. пред-
предположим, что существуют две пары многочленов q(x), rix)
и Я\(х), г,(х), таких, что Р(х) = T\x)q{x) = r(x) и Р(х) =
= T\x)qi(x) + r,(x). Пользуясь определением равенства
многочленов, имеем
Пх)Ых) - 9,(х)] = г,(х) - Кх). B)
Возможны два случая: либо г,(х) — rix) = 0, либо г,(х) —
— rix) * 0. В первом случае, так как Цх) ф 0, то q(x) —
— Q\(x) = 0, и единственность имеет место.
Во втором случае, так как степень r,(x) — rix) не больше
ни степени г,(х), ни степени rix), то степень г,(х) — rix)
меньше степени многочлена Т\х). В то же время степень
многочлена 7\x)[q(x) — qx(x)\ либо больше, либо равна
степени многочлена 7\х). Значит, в равенстве B) много-
многочлены, стоящие в левой и правой частях, имеют разные
степени, что противоречит теореме 1. Полученное проти-
противоречие означает, что г,(х) — г(х) = 0, а в этом случае
единственность уже доказана. Объединяя теоремы 3 и 4,
получаем справедливость следующей теоремы.
Теорема 5. Для любых двух многочленов Р(х) и Т\х), где
7\х) ф 0, существует и притом единственная пара многочле-
многочленов Q(x) и г(х) таких, что Р(х) = T\x)q(x) + r(x), причем либо
108
степень многочлена г(х) строго меньше степени многочлена
1\х), либо tix) есть нуль.
Для определения коэффициентов многочленов д(х), г{х)
существует несколько способов. Наиболее распространен-
распространенным среди них является метод неопределенных коэффици-
коэффициентов, уже рассмотренный раньше.
Пусть даны многочлены Р„(х) и Т„(х), где п > т. Поло-
Положим
„ ьл — mi
2+... + dm_u
где коэффициенты с, и dj пока не определены (отметим, что
их всего п + 1 и сь ф 0). Потребуем, чтобы было справедливо
равенство
Р„(х) = Tm(x)q(x) + г{х).
Раскрывая скобки и приравнивая коэффициенты при оди-
одинаковых степенях х в левой и правой частях, получим п + \
равенство, в которых участвует п + 1 коэффициент Со, сь
Съ •••> с„_„, 4,, du d2,.,., dm_u найдя их, тем самым найдем
многочлены q\x) и г(х).
Пример. Пусть Р{х) = 2х4 — 5*3 + 2, Дх) = 2x* — Зх
Полагая ^(х) = сьх2 + с^ + с2 (сь ^ 0), г(х) = d^c + dx, напи-
напишем равенство
2х4 - Зх3 + 2 = BХ2 - ЗхХсьх2 + с,х + с2) + (d«x + d,),
которое можно переписать в виде
2х4 - 5Х3 + 2 =
= 2с„х4 + Bс, - Зсь)^ + Bс2 - Зс,)^ + D. - Зс2)х + d{.
Согласно теореме 1 справедливы равенства
109
2co = 2,
2с,-Зсь = -5,
2c2 — 3c, = 0,
4 - 3c2 = 0,
dy = 2.
Из этих равенств находим сь = 1, с, = — 1, с2 = — |, 4 =
= — |, d\ = 2, и тогда получаем, что q(x) = х2 — х — |,
/<х) = -§х+2.
Схема Горнера. Рассмотрим деление многочлена на дву-
двучлен (х — а).
Пусть даны многочлен
где во ^ 0» я ^ 1, и двучлен (х — а). По теореме 5 существуют
многочлен q(x) и число г такие, что Р„(х) = (х — а)^(х) + г.
Степень многочлена q(x) равна (л — 1). Поэтому ^(х) =
= Ъд? ~ ' + 6,х" + ... + Ь„ _ гх + Ь„ _ ,, где *ь ?t 0. Найдем
числа 60, 6,, Ь2, .., 6Я _ , и г методом неопределенных
коэффициентов. Подставим Q(x) в равенство Дх) =
= (х — a)q(x) + г, получим, что
I- 1
i-2
а„ _ ,х + а„ =
1 -(Ь2-
(г-
По правилу равенства многочленов отсюда получаем, что
f
в, = bx — abo,
= bn_i — abn_2,
no
откуда
ab0,
C)
Итак, коэффициенты частного q(x) и остаток г выража-
выражаются через коэффициенты многочлена Р(х) и число а при
помощи действии сложения и умножения согласно форму-
формулам C), откуда следует:
а) если по, аи а2, ..., а„иа — рациональные числа, то Ьо,
bu Ьъ ..., Ь„_, и г — также рациональные числа;
б) если Оо> аи аъ —> ап и a — целые числа, то b0, bu Ь2, ...
..., Ь„ _, и г — также целые числа.
Из формул C) вытекает следующее правило для вычис-
вычисления коэффициентов Ьо, Ьх, Ь1? ..., Ь„_, и остатка г.
Выписать подряд, начиная с Oq, в строку все коэффици-
коэффициенты многочлена Р„(х). Во второй строке под Oq написать
коэффициент Ьо, равный коэффициенту Oq. Умножить а на
Ьо и, прибавляя произведение ab0 к аи получить коэффи-
коэффициент Ьх и написать его во второй строчке под а,. Умножить
а на ?>, и, прибавляя произведение а?>, к а2, получить
коэффициент Ь2 и написать его во второй строчке под а2.
Продолжая этот процесс, получить коэффициент Ь„ _ г и
написать его во второй строчке под а„ _ t. Умножить,
наконец, а на Ь„ _, и, прибавляя произведение abn _, к а„,
получить остаток г и написать его во второй строке под а„.
Это правило записывается в виде следующей таблицы,
которая называется схемой Горнера:
п'
п' о
Схема Горнера позволяет легко разделить многочлен Дх)
на двучлен х — а, т.е. найти коэффициенты частного q{x)
и остаток г.
Пример. Применяя схему Горнера, найдем частное а(х)
и остаток г при делении многочлена Дх) = 2Х5 — х4 — Зх +
+ х — 3 на многочлен Дх) = х — 3.
Схема Горнера имеет вид:
-1 -3
г\ п
3-5+(-3)
U
12Г
О 1
П. О
3-36+1
п
3 • 109+(-3)
4
324
Таким образом, 2Х5 — х4 — Зх' + х—3 = (х — 3)Bх4 + 5*3 +
+ 12Х2 + Збх + 109) + 324.
Теорема 6 (теорема Безу). Остаток от деления много-
многочлена Дх) на двучлен (х — а) равен значению многочлена Р(х)
при х = а, т.е. г = Да).
Доказательство. Подставив в равенство Р(х) =
= (х — v)q(x) + г вместо х значение, получим Р{х) =
= (а —а)^(а) + г, откуда и вытекает, что г= Р(а).
Теорема 7. Многочлен Р(х) делится нацело на двучлен
(х — а) тогда и только тогда, когда значение многочлена при
х = а равно нулю, т.е. Р(а) = 0.
Доказательство. Необходимость. Пусть много-
многочлен Дх) делится нацело на двучлен (х — а). Это значит,
что остаток г равен нулю. По теореме Безу остаток г = Р(а).
Следовательно, Р(а) = 0.
Достаточность. Пусть Да) = 0. С другой стороны, по
теореме Безу г = Да). Значит, г = 0, т.е. Дх) делится нацело
на х — а. к
Приведем несколько следствий из этой теоремы.
1. Многочлен Рп{х) = х" — а" делится нацело на двучлен
(х — а) при любом натуральном п.
Действительно, Р„(а) = а" — а" = 0.
2. Многочлен Р„(а) — х" — а" делится нацело на двучлен
(х + а) при любом четном п (т.е. п = 2т).
т
Действительно, Р-Л— а) = (— аJ — а2 = 0.
3. Многочлен Р„(х) = Xя + а" делится нацело на двучлен
(х + а) лри любом нечетном п (т.е. п = 2т+ I).
Действительно, P2m + i(- а) = (- аJ*' + а2т + ' = 0.
Приведем пример на применение этих следствий.
Требуется доказать, что при любом четном натуральном
п число B0я + 16я — 3я — 1) делится на 19. Так как п = 2т,
где те N, то воспользуемся формулами сокращенного
умножения:
20я + 16я - 3я - 1 = B02и - 1) + (I62m - 32w) = •
= B0я1 - 1) B(Г + 1) + A6й + 3m)A6m - 3й). D)
6 первом слагаемом первый сомножитель при любом
т е ^делится без остатка на число B0 — 1), т.е. на 19. Во
втором слагаемом первый сомножитель при т = 2к + 1,
ке N, делится без остатка на число A6 + 3), т.е. 19. При
т = 2к второй сомножитель можно представить в виде
произведения сомножителей A6* + 3*)A6* — 3*). Если к
нечетно, то разложение второго слагаемого на сомножите-
сомножители заканчивается. Если же к четно, то разложение продол-
продолжается. Через конечное число шагов, не превышающее
(л — 1), разложение будет закончено и один из сомножи-
сомножителей этого разложения будет иметь вид 16* + Ъ\ где s —
нечетное число. Тогда этот сомножитель делится на 19.
Таким образом, и первое и второе слагаемые в равенстве
D) при любом т е Nделятся на 19, значит, и B0я + 16я —
— 3я — 1) делится на 19 при любом четном натуральном п.
Корни многочлена. Число а называется корнем многочле-
многочлена Р(х), если Р(а) = 0. Переформулируем теорему 7, ис-
используя определение корня многочлена.
Теорема 8. Число а является корнем многочлена Р(х)
тогда и только тогда, когда многочлен Р(х) делится нацело
на двучлен х — а.
Докажем теорему о нахождении целых корней многочле-
многочлена.
Теорема 9. Если все коэффициенты многочлена степени
п, где л ? 1, — целые числа и корень а этого многочлена —
из
также целое число, то число а — делитель свободного члена
многочлена.
Доказательство. Пусть дан многочлен
Р„(х) = aQX? + arf-x + a^r~2 + ... + яя_,х + а„ (ао*0)
степени л, где п ? 1, и пусть а — корень этого многочлена.
Разделим с остатком многочлен Р~(х) на двучлен (х — а),
тогда частное есть многочлен q(x) = b^ ~ + bxx" ~ 2 + ...
... + Ь„ _,, а остаток — число г. Как показано выше, если
все коэффициенты многочлена Р„(х) и а — целые числа, то
числа Ьо, Ьи ..., Ь„_, и г — также целые числа. По схеме
Горнера г= а„ + айя_ ,, апо теореме 8, если а — корень
многочлена, то г = 0. Поэтому имеем равенство а„+оЛ^\ =
= 0, откуда а„ = ос(— Ь„_,). Так как а„, а, (— Ъп_,) — целые
числа, то отсюда вытекает, что а — делитель числа а„, и
теорема доказана.
Следствие. Целыми корнями многочлена с целыми коэф-
коэффициентами могут быть лишь делители свободного члена
многочлена.
Это следствие позволяет находить все целые корни
многочлена с целыми коэффициентами, применяя схему
Горнера.
Пример. Выяснить, имеет ли целые корни многочлен
Л(х) = х4 + 2х3 + 2х2-6х+5. E)
Делители свободного члена: 1, — 1, 5, — 5. Найдем
значение многочлена в этих точках:
РА(\) =1 + 2-2-6 + 5 = 0,
Л(- 1) =1-2-2+ 6 + 5 = 8* 0,
ЛE) = 625 + 250 - 50 - 30 + 5 = 800 * 0,
Л(- 5) = 625 - 250 - 50 + 30 + 5 = 360*0.
Итак, многочлен E) имеет целый корень х, = 1, а числа
5, — 5 и — 1 не являются его корнями. Применив схему
Горнера, разложим многочлен E) на множители. Схема
Горнера имеет вид:
114
1
2 -2
1-1+2 l-3+(-2
-6 5
()
Следовательно, х4 + 2Х3 + 2Х2 - 6х + 5 = (х - 1) (х3 + Зх2 +
+ х - 5).
Теперь будем искать корни многочлена Р?(х) = х3 + Зх2 +
+ х — 5. Делители его свободного члена: 1, — 1, 5, — 5. Нет
необходимости искать значение многочлена Р3(х) в точках
— 1, 5, — 5, так как эти числа заведомо не являются
корнями многочлена Р+(х), а значит, и многочлена Р3(х) в
силу того, что многочлен Л(х) в них не обращается в нуль.
Поэтому проверим только число 1:
Р3(х) =1+3 + 1-5 = 0.
Применив опять схему Горнера:
1
1
-5
11+3
о о
1-4+1
1
получим Р3(х) = (х — lXx2 + 4х + 5), а потому многочлен
можно записать так: Рл(х) = (х — 1J(х2 + 4х + 5).
Так как квадратный трехчлен х2 + 4х + 5 целых корней
не имеет, то следовательно многочлен РА(х) имеет два целых
корня х, = 1, Xj = 1. В таких случаях целесообразно ввести
понятие кратности корня. Если многочлен Р„(х) делится
нацело на (х — а)*, где к — некоторое фиксированное
натуральное число, но не делится нацело на (х — ос)*+', то
число а называется корнем кратности к многочлена Р„(х).
Корни кратности единица называются простыми корнями
многочлена. Таким образом, многочлен РА(х) в вышепри-
вышеприведенном примере E) имеет один корень х = 1 кратности
два.
115
Замечание. Если найден один кореньх( = ос многочле-
многочлена Р(х), то этот многочлен можно записать в виде Р(х) =
= (х — а)а(х), где коэффициенты многочлена q(x) легко
вычисляются по схеме Горнера. Чтобы найти другие корни
многочлена Р(х), следует найти корни многочлена q(x).
Важно отметить, что многочлен д(х) может иметь корнем
то же число а, которое находится также по схеме Горнера.
Если не искать корни многочлена д(х), а отыскивать
корни многочлена Р(х), то корень, который уже найден, во
второй раз этим же способом не будет обнаружен. Поэтому
после нахождения одного корня надо искать корни част-
частного, т.е. корни многочлена q(x).
Теорема 10. Если многочлен
с целыми коэффициентами и со старшим коэффициентом,
равным единице, имеет рациональный корень, то этот ко-
корень — целое число.
Доказательство. Доказательство этой теоремы про-
проведем методом от противного. Предположим, что много-
многочлен Р„(х) имеет корень а = p/q, где р и q — взаимно
простые целые числа. Так как число p/q — корень много-
многочлена Р„(х), то справедливо числовое равенство
а^ а/^2 ... ап_Л ап
я я я ч
которое можно записать в равносильной форме
Умножая это равенство на q" ~' получим равносильное
равенство
1= _ erff-« _ а#п-\-... - aH_lPq*-2- aj~\
116
Так как числа р и q — взаимно простые, то число ?— не
целое, а справа в последнем равенстве стоит целое число.
Такое равенство не возможно, значит, предположение не-
неверно, а верна теорема.
Следствие. Если у многочлена все коэффициенты —
целые числа, а старший коэффициент равен единице, то все
рациональные корни этого многочлена — целые числа.
Рассмотрим многочлен Р„(х) = а&С + ахх* ~ ' + а^С " 2 +
+ ... + а„_ хх + а„ с целыми коэффициентами и многочлен
QH(x) = яГ'ад = (оох)" + e,(flbx)""' + ... + аЛ~1.
Ясно, что многочлены Р„(х) и Qn(x) имеют одинаковые
корни. Обозначим у = а^х, тогда
Qn(x)=Tn(y)= yn + alyn-l +
Многочлен Т„(у) имеет по теореме 10 только целые корни,
которые можно найти. Пусть это будут числа уи уъ ... , у„,
тогда числа xk = yk/a0, где ке {1; 2; ... ; /и}, и только они
будут рациональными корнями многочлена Р„(х). Итак, у
любого многочлена с целыми коэффициентами можно
найти все его рациональные корни.
Если коэффициенты многочлена — рациональные
числа, то после приведения их к общему знаменателю
можно искать лишь корни числителя, который есть много-
многочлен с целыми коэффициентами.
Пример. Найти корни многочлена Р^х) = х3 + h? —
— \х — \. Рассмотрим многочлен Q3(x) = 8Р3(х) = BхK +
+ BхJ — 2х — 1 или T3(t) = ? + ? — t — 1, где /= 2х.
Делители свободного члена многочлена Г3(/): +1, — 1.
Найдем значение многочлена Г3(/) в этих точках:
1 + 1 - 1 - 1=0,
Т3(— 1) = - 1 + 1 + 1 - 1 = 0.
117
Применив схему Горнера, получим Г3(/) — {t— 1)(? + 2/ +
+ 1). Многочлен (Г2 + 2t + 1) есть полный квадрат бинома
(/+ 1). Следовательно, многочлен T3(f) имеет три корня:
U — 1» h = ~ 1» h = — 1» а многочлен Р3(х) — соответствен-
соответственно три корня: *i = |, Xj = — |, х3 = — |, или два различных
корня; один простой корень Xi = ^ и другой корень Xj = — 4
кратности два.
В заключение остановимся на корнях двучлена Р„(х) =
= х" — а. Как следует из § 5 предыдущей главы, при четном
п двучлен Р„(х) имеет если а > 0, то два корня: Ча и — 'VaT;
если а = 0, то один корень 0; если а < 0, то не имеет корней.
Если п — нечетное число, то двучлен Р„(х) имеет: если а ? 0 —
один корень *V^, если а < 0 — один корень (— *V|a|). Напри-
Например, двучлен х3 + 11 имеет один корень (— VTT).
§ б. Метод математической индукции
Существует очень много утверждений, зависящий от
натурального числа п. Как понимать такие утверждения?
Поскольку натуральных чисел бесконечно много, то на
самом деле каждое такое утверждение содержит в себе
бесконечно много утверждений. Например, утверждение —
сумма п первых натуральных чисел равна я(я2+1^ — содер-
содержит в себе следующие утверждения:
для п = 1: первое натуральное число, т.е. число еди-
единица, равно * A2+1);
для п = 2: сумма двух первых натуральных чисел,
т.е. сумма чисел единица и два, равна
2B+1).
2 '
для п = 3: сумма трех первых натуральных чисел,
т.е. сумма чисел единица, два и три, равна
3C+1).
2 '
118
для п = 10000: сумма десяти тысяч первых натуральных
чисел равна "> 000A0 000+1) и тд>
т.е. рассматриваемое утверждение действительно содержит
бесконечно много утверждений.
Аналогично и любое другое утверждение, зависящее от
натурального числа л, на самом деле есть простая форма
записи бесконечного числа утверждений.
Возникает вопрос, а как убедиться в справедливости
утверждения, зависящего от натурального числа?
Для доказательства утверждений, зависящих от нату-
натурального числа л, часто применяется общий метод доказа-
доказательства — метод математической индукции. Этот метод
основан на аксиомах натуральных чисел. Но поскольку
ранее эти аксиомы не приводились, то метод полной
математической индукции принимается здесь без доказа-
доказательства.
Для доказательства некоторого утверждения, зависящего
от натурального числа л, делается следующее:
1. Проверяется справедливость этого утверждения для
л = 1.
2. Предполагается справедливость этого утверждения для
л = к.
3. Доказывается справедливость этого утверждения для
л = к + 1 с учетом предполагаемой справедливости его для
п = к.
После чего делается вывод, что утверждение справедливо
для любого натурального числи л.
Пользуясь этим методом, докажем, что для любого на-
натурального числа л справедливо равенство
1 +2 + 3 + ... + л = ^Д A)
Проверяем справедливость равенства A) для л = 1. Для
п = 1 оно запишется так: 1 = A2+1\ и очевидно, что это
равенство верное. Предположим, что равенство A) спра-
справедливо для п = к, т.е. предположим, что справедливо ра-
равенство
B)
Используя равенство B), докажем, что равенство A) спра-
справедливо для п = к + 1, т.е. докажем справедливость равен-
равенства
1 + 2 + 3 + ... + <* + 1) - »+'Н»+'>+Ц. C)
Действительно, рассмотрим сумму 1+2 + 3 + ... + (Л+1).
Используя сначала свойство ассоциативности сложения,
затем равенство B) и делая простейшие преобразования,
получаем
1 + 2 + 3 + ... + (к + 1) = A + 2 + 3 + ... + к) + (к + 1) =
+ /Iул. 1ч-
т.е. получаем справедливость равенства C). На основании
метода полной математической индукции делаем вывод,
что равенство A) справедливо для любого натурального
числа п.
Рассмотрим еще пример. Докажем, что для любого
натурального числа п справедливо равенство
пйГ~\ D)
Доказательство. Для п= 1 неравенство D) превра-
превращается в верное числовое неравенство 1 й 21 ~'. Предполо-
Предположим, что неравенство D) справедливо для п = к, т.е. пред-
предположим справедливость неравенства
кй2к~\ E)
Используя неравенство E), докажем справедливость нера-
неравенства D) для п = к+1, т.е. докажем справедливость
неравенства
(*+1)?2(*+1)-'. F)
120
Действительно, очевидно, что к + 1 й 2к. Отсюда, исполь-
используя неравенство E) и свойство транзитивности неравенств,
получим, что к + 1 й 2 ¦ 2* ~ '. Правая часть последнего
неравенства может быть записана в виде 2(*+1} ~', откуда и
следует справедливость неравенства F). На основании ме-
метода полной математической индукции делаем вывод, что
неравенство D) справедливо для любого натурального
числа п.
Обобщенный метод полной математической индукции.
Часто метод полной математической индукции применя-
применяется к доказательству утверждений, справедливых не для
всех натуральных чисел п, а лишь для п, больших или
равных некоторого натурального числа р. Тогда формули-
формулировка сути метода полной математической индукции оста-
остается почти такой же, но с заменой пункта 1 на пункт 1а):
«Проверяется справедливость этого утверждения для
п= р». В этом случае для доказательства справедливости
утверждения для любого натурального п(п>р) делается
следующее:
1. Проверяется справедливость утверждения для п = р.
2. Предполагается справедливость этого утверждения для
п = к, (где к2р).
3. Доказывается справедливость этого утверждения для
п = к + 1 с учетом его справедливости для п = к. После
этого делается вывод, что утверждение справедливо для
любого натурального ntp.
Приведем пример доказательства неравенства с помо-
помощью обобщенного метода полной математической индук-
индукции: докажем, что если а — фиксированное число такое,
что ос>— 1 и ос * 0, то для любого натурального л > 2
справедливо неравенство Бернулли
A + о)" > 1 + оси. G)
Действительно, при л = 2 неравенство G) имеет вид
A + аJ > 1 + 2а. (8)
Неравенство (8) равносильно неравенству
121
a2 > 0. (9)
Неравенство (9) при a * 0 очевидно. Следовательно, нера-
неравенство (8) справедливо для рассматриваемых а. Предпо-
Предположим, что для рассматриваемых а при п = к (к ? 2) нера-
неравенство G) справедливо, т.е.
A + а)* > 1 + ак. A0)
Докажем, используя неравенство A0), справедливость не-
неравенства G) для п = к+ 1, т.е. докажем неравенство
A + ос)*+1>1 + ос(?+1). A1)
Для доказательства умножим обе части неравенства A0) на
положительное число A + а) (так как ос> — 1, то1 + ос>
> 0). Получим неравенство
A + сс)*+' > A + ak)(l + ос), A2)
равносильное неравенству A0), т.е. получим, что неравен-
неравенство A2) справедливо.
Докажем теперь справедливость неравенства
A + a*)(l + a) > 1 + <х(к + 1). A3)
Перенеся все члены неравенства A3) в одну сторону,
раскрыв скобки и приведя подобные члены, получим рав-
равносильное неравенство а2к > 0, которое справедливо, так
как a * 0 и к ? 2. Следовательно, неравенство A3) справед-
справедливо, но тогда, используя справедливость неравенств A2),
A3) и свойство транзитивности неравенств, получим, что
справедливо и неравенство A1). Таким образом, неравен-
неравенство Бернулли доказано для любого натурального п ? 2.
Это неравенство имеет смысл запомнить, так как с его
помощью можно доказать справедливость многих других
неравенств, например, справедливость для любого нату-
натурального п неравенства
л+1
A4)
V ") \ "T1J
122
Действительно, сделав несложные преобразования, полу-
получим цепочку равносильных неравенств:
" + 1 у я. II + 1 П
(я+? "
(л + 1)
1. A5)
Для доказательства неравенства A5) для п > 2 к выражению
Г1 "i" 1
. 1 j , считая а = —1г применим неравенство
I (я+1)Т (л+1>
Бернулли G). Получим
(л+1J (л+1J'
Умножая обе части этого неравенства на положительное
число ^—, получим
Поскольку
л + 2 Л п \ _ п + Зл2 + Зл + 2 s ,
то, используя свойство транзитивности неравенств, имеем
л+2 j
Таким образом, неравенство A5) доказано.
Так как неравенство A5) равносильно неравенству A4),
то и неравенство A4) справедливо для п 12. Поскольку при
п=\ оно очевидно, то справедливость неравенства A4)
доказано для любого натурального п.
123
Решение задач на делимость. Метод математической ин-
индукции применяется также и для решения задач на дели-
делимость.
Докажем, например, что для любого натурального числа
п число N(n) = п + 5п делится на 6.
Доказательство. Для п = 1 число NA) = 6, и потому
NA) делится на 6, т.е. утверждение справедливо, если п = 1.
Предположим, что утверждение справедливо для п = к, т.е.
предположим, что число Щк) = (к3 + 5к) делится на 6.
Используя то, что число N(k) делится на 6, докажем спра-
справедливость утверждения для п = к+ 1, т.е. докажем, что
число Щк + 1) = [(к + IK + 5(к + 1)] делится на 6.
Действительно, используя свойства коммутативности и
ассоциативности действий над числами и алгебраическими
выражениями, имеем
Щк + 1) = [(к + IK + 5(к + 1)] = к3 + Ък2 + Ък + 1 +
+ 5к+ 5 = (к3 + 5к) + 6 + Ък2 + Ък= Щк) + 6 + Щк+ 1).
Поскольку к и к + 1 — два рядом стоящих натуральных
числа, то одно из них четное, поэтому число Зк(к+ 1)
делится на 6. Учитывая, что число N(k) делится на 6 и
число 6 делится на 6, получаем, что число N(k + 1) также
делится на 6. На основании метода полной математической
индукции делаем вывод, что число N(n) = п3 + 5п делится
на 6 для любого натурального числа п.
Рассмотрим решение более сложной задачи на дели-
делимость, когда метод полной математической индукции при-
приходится применять несколько раз.
Требуется доказать, что при любом натуральном п число
(З2 — 1) не делится нацело на число 2"+\
При п = 1 утверждение очевидно, так как 8 не делится
на 16. Предположим теперь, что утверждение справедливо
при п = к, т.е. число (З2 — 1) не делится нацело на число
2*+ 3. Докажем тогда, что число C — 1) не делится нацело
на число 2*+\ т.е., что утверждение справедливо при
124
п = к + 1. Представим выражение C — 1) в виде произ-
произведения:
-1) = C2*-1)C2*+1).
По предположению первый сомножитель произведения не
делится нацело на число 2*+3, т.е. в представлении состав-
составного числа (З2 — 1) в виде произведения простых чисел
число два повторяется не более, чем (к + 2) раза. Таким
образом, чтобы доказать, что число C — 1) не делится
нацело на число 2*+4, надо доказать, что число (З2 + 1) не
делится на 4.
Для доказательства этого утверждения докажем вспомо-
вспомогательное утверждение: для любого натурального п число
C2" + 1) не делится на 4. Для п=\ это утверждение оче-
очевидно, так как 10 не делится на 4 без остатка. При предпо-
предположении, что (З2* + 1) не делится на 4, докажем, что и
C2<*+ ° + 1) не делится на 4. Представим последнее выра-
выражение в виде суммы C2<*+ ° + 1) = (З2* + 1) + 8 • З2*. Второе
слагаемое суммы делится на 4 нацело, а первое не делится.
Следовательно, вся сумма не делится на 4 без остатка.
Вспомогательное утверждение доказано.
Теперь ясно, что (З2 + 1) не делится на 4, так как число
2* является четным числом. Окончательно получаем на
основании метода полной математической индукции, что
число (З2 — 1) не делится нацело на число 2Л+3 ни при
каком натуральном п.
В заключение докажем методом математической индук-
индукции два утверждения, приведенные выше (§§ 2, 3 гл. II).
В § 3 была приведена формула бинома Ньютона:
(а + Ь)" = СУ + СУ~]Ь + ... + СУ~кЪк + ... + СпЬ".
A6)
Здесь С" — биномиальные коэффициенты, вычисляемые
по формуле с: = -r^-j.
125
Докажем равенство A6).
Для л=1 формула A6) запишется в виде (а+?I =
= С\ах + C\b\ Учитывая правило для вычисления бино-
биномиальных коэффициентов, перепишем эту формулу в виде
(а + ЬI = а1 + b , т.е. убеждаемся в справедливости форму-
формулы A6) для п =¦ 1. Предположим, что формула A6) справед-
справедлива для п = к, т.е. предположим, что справедлива формула
Ckk-Xabk~x
A7)
Докажем, используя справедливость формулы A7), что
формула A6) верна для п = к+ 1, т.е. докажем справедли-
справедливость формулы
... + Ckk:l)~xabk+ Ckk:\bk+\ A8)
Действительно, используя сначала свойства степени с на-
натуральным показателем, затем формулу A7), затем правило
перемножения многочленов, получим
= (a+b)(C°kak+ С
C'k-V~l'-nb'-l + С'как-1Ь'+
Ckk-labk-'
Ckkabk+ С°,
1. A9)
Приводя в этой сумме подобные члены, получим, что
126
у
c*~ V~V+1 +...
***+l- B0)
Так как коэффициент С * есть число сочетаний из п эле-
элементов по к элементов (см. § 7 гл. I), то
Св+1 I /-im /-rm+1
Пользуясь этим равенством, а также очевидными равен-
равенствами С°= 1 = Cj+, и С*= 1 = С**!, из справедливости
формулы B0) получим справедливость формулы A8). На
основании метода полной математической индукции дела-
делаем вывод, что формула бинома Ньютона A6) справедлива
для любого натурального числа п.
В § 2 было приведено равенство алгебраических выраже-
выражений
{А - ЩАп-' + А"-2В + ... + АВГ~2 + В"') =
= А" - ЕГ. B1)
Для доказательства этого равенства при п ? 2 воспользуем-
воспользуемся обобщенным методом полной математической индук-
индукции.
При п = 2 имеем следующую цепочку равенств: (А — В) х
х (А + В) = А2 + АВ — ВА — jB2 = А2 — В2, т.е. равенство B1)
верно.
Предположим, что при я = к (к> 2) равенство B1) спра-
справедливо, т.е. справедливо равенство
(А - ЩАк-х + Ак~2В+ Ак~3& + ... + AS1'2 + Вк"х) =
= Ак-Вк. B2)
Докажем, используя равенство B2), справедливость равен-
равенства B1) для п = к + 1, т.е. докажем равенство
(А - ЩАк + Ак-1В + А"-2В2 + ... +
= Л*+'_^+'. B3)
127
Действительно, используя свойства действий над алгебра-
алгебраическими выражениями и равенство B2), имеем цепочку
тождественных равенств
(А — В){Ак + Ак~ ХВ + Ак~2Вг + ... +
- Д)Я* = (А - В)(Ак~
- В)& = (Ак - #)А + {А
Тем самым равенство B3) доказано, а значит, доказано и
равенство B1) для любого натурального п ? 2.
УПРАЖНЕНИЯ
Найти числовое значение следующего алгебраического выражения при
IT fa+1 Л- 8fl+8fl 4. 4 1 М Л
4a2-!
Найти числовое значение следующего алгебраического выражения при
д=1и* = -2F- 10):
о2 (д + ft2) (g3 - ft3) (a2 - ft) a3 + ft (ft2 + 3a) - 1
(a2 + ft2) Ba-3ft2) " "fl(a-ft+l) + ft(ft + l)"
8
' ft (a + 2J - 4 (a - ft) - e2 - 8'
128
Найти числовое значение следующего алгебраического выражения при
m = 10, л = 4 и р = 5 A1 — 15):
Г »» + 2 Л
т + п+ 10
+ 4(Зл-3)т-2-32/>-'[:
: 41 ¦ {¦
sf
: [B0 - 4л) • 5Л+' • Bл + 2)т
10-л
13.
14.
6т+5 • [2 (л - 5)К+ 5 + C2 - 4рJ0
5 ¦ 43j> ¦ Bт - 11)" *5 - 4 (р - 4) ¦ 32т ¦ Bл)9
5 • г2" • 62т-' — 7 (т- 8Jт+9- 2710-"'
„ (т + 26)Cт- 12J0~4я-8-2"(р + лL — 3"+| {m-Af
' Bл + 4т-22у-2 "
Найти числовое значение следующего алгебраического выражения при
= — VT, Ь= \, с = Ъ, х = — ^ A6 — 20):
¦щ -^ (х — а) (х — &) Ь— с с — а а — b
" а*+ a{a — b) ~ b(a—b)+ be + ас + а*
л а2-4 х3-х ЗаЬ2 15&V 3* . 2
9(ГЬ
,9 Г а + * + ? 1.
[(а-Ь)(а-с) (Ь-с)(Ь-а) (с — а) (с — *)J"
. (х+1K —(х— IK
ff" — 1 а—1 х+с
Найти ОДЗ следующего алгебраического выражения B1 — 25):
'(а-Ь){а-с) (Jb-c){b-a) (с-а)(с-Ь)
2 • 6* 4 1_
-4а2-*2'
5 Алгебра, тригонометрия 129
и элементарные функции
23.
24.
25.
a2 — 2д + 1 J(g + 2J — a2
Г д t A |. tf-y]. от-4
I от (A — с) л (a — с) I' дА (m — с) I ' (m — 2) (д + 1)'
a+f 2д a—t] ad? b?
2 V
-Z4 ?-c?
(a-0 cf-f (t+ay
Найти ОДЗ двух следующих алгебраических выражений B6 — 30):
2д + 3
' г^-д-б '
, 2д . 1
—6
28. f--:--- и
[А с) [а с
а2-2а
?(а+\J — \
1 А
Ас ' д2_ 1 (т —о)(А+1)
Найти ОДЗ следующего алгебраического выражения и упростить это
выражение на его ОДЗ C1 — 40):
31. (За1х+ А-18А): [f - |+x- ^1
32. BАхУ • бх2/): (-3x4v 4х5у>ху)/
33. Cfl*AV • 5д3Ах (- бА2)]: A5дх
34.
35.
37.
. дАс V
12А2с'д3А2с1'
Г.2ь2 .„Л iiA
Ъ?-Ъа-2
„ А2-100 . А+10 а - А
JO. ——————— ^ ^ -
Ь2-аЬ
39.
40.
-%(с-2 8с3
с + д 'I 4c c2 + ac]J 2/»(a — с)"
д2 -
д2-4аА-21А2
- A3
130
2a-:
10a4 ас*
Упростить следующее алгебраическое выражение D1 — 65):
41. 3(х-2)-2(х-1).
42. 18-5(х+2)-3(х+ 1).
43. 6(х- 2) - 13(х - 3) - 2х+ 4.
44. 3(х-4) -4(х- 3) - 5(х- 2) -9(8 -х) + 20.
45. 2х- 5[7 - (х - 6) + Зх] - 21.
46. 1-х+2{3-2[х+2(х-2)]-х}.
47. 2 + 3[х - 4A - х)] - х - {(х - 1) - 3[х + 2(х - 1)] - 2х).
48.f+l±-f+f-4x.
« 8ГХ^Х xl n^f1^ xj.x>Lt(x x
56'3 4 + 8"i2 Г0'5!! T"T2 + 9 Г2 4-Т2
57. д ^ {2a - [W- 2Dc-la)] - 3(A -Jc)}. v
58. 2x - 4[5x - A \y - 3x)] - 3[5>< - 2Cx -
59. Ъу - (\by - 2[3x - 2(x - 12>>) - 5x] + x}.
60. - 2[д - 2(A - a)] - 3[b - 4Bд - ЗА)] + 2a.
61. 6{2a - 3[b - 2(c + a)] - ЗА} - 4{A - 2[a - 4(c - a) - 2c] + За}.
Следующий многочлен разложить в произведение не менее чем двух
многочленов F6 — 85):
66. 5тх + Ъпу — 5ту — Злх. 67. 5х + ху + Sy + у2.
5* 131
68. ах + Ьх+Ьу + су-сх-ау. 69. За5 - 6а4А + За3А2.
70. ЗбхУ - 100. 71. 25 - 49a2A6c4. 72. 4pV - 81*2.
73. Ba - ЗАJ - Ca - 2AJ. 74. (m + 2л/- 4Cm - лJ.
75. 9(a - ЗАJ - 16(A - 2aJ. 76. a4 - c2 + 9/ - 6a2*
77. ce- 6c3 - c2 - 2CX-X2 + 9. 78. <?b3 - 27m3.
79. 1 + 1000/. 80. m3A6c9 - 8*6. 81. 125a3 - 343A3.
82. 8a3 + (A - 2aK. 83. 64(m - лK + 1.
84. Ba - AK - (ЗА - aK. 85. 8(x - yK + 21{y - 2xK.
Следующий многочлен разложить в произведение не менее, чем четы-
четырех многочленов (86 —100):
86. 25А2 81/z2 - 121а2 81.Л2 - 25А2 169а2 + 121а2 169а2.
87. 144а2А8 25а10 - 49с4 25а10 - 144а2А8 + 49с4.
88. 125Х3 (а + АJ - 125Х3 (За - 2АJ - 8(а + АJ + 8Cа - 2АJ.
89. 25(а - ЗАJ - j (За + 7АJ - 125гУ(я - ЗАJ + ^-?у\Ъа + 7АJ.
90. 16Х2 ¦ 64абАб - 225Cт - лJ 64дбАб + 1бх* - 225Cт - лJ.
91. 9(х + уJ ¦ 27абА3 - 16(х + 2уJ 64а6Ь3 + 9(х + уJ ¦ 125т3 - .
- 16(х + 2>>J 125т3.
92. 2а2/ + аЬу5 - аЬу3 - 2а2/.
93. 13xY За - 39/ За - 13хУ 9а2 + 39/ 9а2.
94. 36а3 49Х2 - 9аА2 49Х2 + 36а3 1ху - 9аЬ2 1ху + 36а3 14х -
- 9аА2 14х.
95. 15А • 4а2 + 45тА2 4а2 + 15А 16аА + 15тА2 • 16аА.
96. A - xW - т2) + Fх - 9)(/ - т2) - A - х2) Bтл + л2) -
1 у 7 1111 Fх
97. B5Х2 + Ь2){сР- + 6аА) + 9B5x2 + А2) (А2 - с2) -
- 9(/ + 10хА)(А2 - с2) - (у2 + ЮхА) (а2 + 6аА).
98. (х + >-L(а3 + А3) - Л3 + (х +>-L(а + А) - (а + А).
99. (у3 - у2 + у)A21 - 25Х2 - 10х) - A21 - 25Х2 - Юх) -
100. ^(а3 - А3 - А)(9х3>' - Аху3) + 16a(9x3>- - 4хД
Привести к общему знаменателю следующие три алгебраические дроби
A01 - НО):
101. ' ' '
102.
103.
ху+х2'
(a+bf
а2-4'
(P' + a —
в»-Л
а2 + 3а +
2' а2-
2х2-2ху'
.' 7~?-
2' а2 + 2а
4а+3' сР-Х
X
ш« L_
20а-4' 50а2+ 2' 75А-Зс"
132
'9Ьх+4Ьу' Iicx+I2cy'
1 1 1
1
1
106
107.
108.
109.
ПО.
Найти ОДЗ следующего алгебраического выражения и упростить это
выражение на его ОДЗ A11 — 130):
1
1
1
Bл2 —ЗдАJ' Dд - 6АK> 4д2-9А2'
1 1 1
г' ох2: — ду2
112.
113.
114.
115.
116.
117.
119.
121.
д3 — 2д
а2+4д + 4 а4 — 4а2 + 4
А2 _ 4А - 5 '
х2-2х+1
—10"
А2 - 25 А2 - 8А - 9 ' ^ + 4А - 5'
с2-с-20 с^-с . Г с2 с*-3с-13
х2-4 4х-7.3х2-х-14
«-2 х + 4х2-14 4Х2
V_4o-4S . д2 — 12g-4S
e2-14e-15' e2-6o-27j'^A2-121 A + 2J'
Г 12а3 + 24Д2 . д2 + 2д\ Г 16Д2 - 49 . 2Д2 - а - Г
14д2-7д '2д-1 ГЦдЧд-М'
а « + Зд д +1
2х2 + 4х
A2-4
д + 2 4 —д2 Зд —6'
,22.6414^^-4
Зд2
'
^ + 64
1
я + 4 д2—4д+1б'
3.
(х+1)(х2 + 5х+6)'
133
124 (*~**H*~C) (* — c)(x— a) (x — g) (x — b)
'(a — b)(a — c) (b — c)(b — a) (с —д)(с —A)"
АтмШ+J ш * I - * g ^^^
e—b b—c c—a
: —.y x+yj"(x — у x+.yj"
[ + 7д+12
• A2) (a — b)
128.
129.
130.
Найти ОДЗ двух следующих алгебраических выражений А и В и
доказать, что на этой области справедливо тождественное равенство А = В
A31 - 160):
in л Д2-? 18А3 и ЗА2
131. Л = —т—т -I у, В— т.
6аА 5д4-10о2 5?
i« ^ а3-А3 а2-А2 и аг + аЬ+Ь1
cr — 2ab+lr ст + аЬ а
1*,*, л а2-16 .2о + 8 „ З(д-З)
„. . a + 9fl + 2Qg аЧУд+Ю
134. Л = —s •' —э > В = а.
сг + 5а + 4 сг + За + 2
ii« л 2g-3 4^-30-7 fl^+Sa-24
135. Л = —s "л й 1 < В=\.
2о2+13д-24 4д-7 ^~2а — 3
„, . 2а2 + ЗаЬ-2Ь2 J-Sb3 2а*-5аЬ + 2Ь _ ,
136. Л = —s s s х'.—s s—, В—а + Ь.
f 2b 4b1 * 3b2b2 2 2* А2
117 л f-9.(a + 3 2а-6) _ j.
137. А = —5—г-. j -.— , В = <го.
5Л3 [Юд4 дА4 J
138 л ( т3 + 4т2п + 4ггт2 (т + 2пK\ от2 —4л2
!-4от2 с2 + 2сот-8от2 „ 4/я2
<?-2ст с2-4от2 ' с(с + 2т)'
140.л=1 + о2^ + -°-=^27. Л-—L-r
1-й3 A — дK A - оJ
134
141. A:
142. И =
143. И =
UA. А--
145. А--
146. А--
147. Л =
148. А--
149. 4 =
150. 4 =
151. А--
152. А
153. А
154 .А ¦¦
155. А.
156. А
1ST. А-.
158. А.
a2 (a + xJ (a + yJ .
ху х*-ху ух-у-
3a —5 Зд + 5
3a2 - 2a - 5 3
5B6-3) |
llF62 + 6-l) 662 + 76-3 llD62 + 86+3)
4 2
76
, 5=2.
; B= 126+1.
a— 1 a+1
a-2 a + 2 4_
= 0.
1
48
_3___L_ + _3 ;_ B
x+1 x + 3 1-х 3-х' (x2 — 9) (x2 — 1)'
3a
1
(a-xJ x2 + ax-2a2 2a+x'
1+X 1 + V
X
(д-хJ
' — *)C —*) (г—х)(г—>»)
P'mn
; 5=0.
-, 5=0.
(/я — л) (jn — f) (n — /) (л — тя) (г — m) {f — л)
{ас + bmf — (aw + beK {ac + 6wK + {am + ocK
(a — 6) (c — m) (a + 6) (c + m) '
5 = 2(ac + bm)(am + be).
3 2c+15
2c-3 4c2 + 9 2c + 3 ' 81-16c4
5 x4
2 :+18Bc+i^> д=()
, В-
1
(x+yJ-(x—УJ'2^^ —>)' x + >''
x2 — (y — гJ >^ — {z — xJ _ (x — yf — z2
{x+zf-y2 {x+yf-z2
{x-y)*-xy{x-yJ-2x2y2
(х->')(х3-У!( + 2х2у2
Й_.
.-3 6-3) 76-4 62-14 _
76-4 6-4J 96-362 4-6 ' °
+ 6ac 1 Vr 1 1
5=1 —2c + a.
135
b -4 ¦ ( m 2b b-\b\ 6A + 4
-8 *2 + 2A + 4 2-A
0-mJ [m-3 27-
Для любых положительных чисел а к b доказать, что справедливо
неравенство A61 — 165):
161. (а2 - Ъ2J г> 4аЬ(а - ЬJ. 162. а* + Ь37>о2Ь + аЪ2.
163. (в + АL < 8д4 + 8А41б4.
т < +
1+д+А 1+в 1+А
Используя неравенство о среднем арифметическом и среднем геомет-
геометрическом, доказать, что для любых положительных чисел а, Ь, с справед-
справедливо следующее неравенство A66 — 168):
«„ be ас аЪ ,
166. — + т + — ? а + Ь + с.
а о с
167. {а + ЪМЬ + с)(а + с) г> 8дАс.
168. а2 + А2 + с2 г> дА + Ас + дс.
169. Доказать, что для любого действительного числа а справедливо
неравенство
а2 + 1 ;>
2д
V + 1"
170. Доказать, что если д?А?с>0, то
171. Доказать, что если at > 0, д2 > 0. —t Дя > 0 и Д) + д2 + ••¦ + дя = 1>
то
Доказать, что при любом натуральном п справедливо следующее нера-
неравенство A72 — 173):
+
Доказать, что для любых натуральных /и и /> справедливо следующее
неравенство A74 — 176):
" (от + 1) (т + 2) + (т + 2) (от + 3) + (т + 3) (от + 4) + "
136
(m+p)(m+p+1) m+Г
176.
Доказать, что для любого натурального л ? 2 справедливо следующее
неравенство A77 — 184):
. . f 1 + лТ 1а1 13 5 2л-1
2> й! К ["Г| • Ш- 2 4 6 - -2Г
184. -Ц- + -Ц + —Ц+ ...^
л+1 л + 2 л+3
Разложить по формуле бинома Ньютона A85 — 187):
( А6
185. « + 5| • 186- (« - ^/ЗO- 187. (а - VI)8 + (а + V3)8.
Найти 7-й член в разложении бинома Ньютона A88 — 191):
188. B + ft)9. 189. (За - 2I0. 190. (а2 - 2а)п. 191. у + За
Найти все к, при каждом из которых коэффициент при о* в разложении
бинома Ньютона есть рациональное число A92 — 194):
192. (VT+ УТ- аJ4. 193. D1- УТ- аI6. 194. (Vf- а + 12VT ш.
Найти коэффициент при Xs следующего многочлена A95 — 200):
х+^ .196. Bх-II7. 197. A+х-х2L.
1 - 2х + х2M. 199. A - хJ • B + хN. 200. A + 2хL • (х - IO.
Подобрать числа А, В, С так, чтобы было справедливо следующее
тождественное равенство B01 — 205):
201. х4 + 2Х3 - 16Х2 - 2х+ 15 = (х+ 1)(< + А* + Вх + С).
5 4 2 3 ^2 A
201. х + 2Х 16Х 2х+ 15 (х+ 1)(< + А* + Вх
202. Зх5 - х4 - Зх + 1 = (х2 + 1ХЗХ3 + ^х2 + At + Q.
203. *
204.
137
-2s+l A Bx+C
+
Применяя схему Горнера, найти частное и остаток при делении на
(х + 1) следующего многочлена B06 — 211):
б^ 3
20б.^ + 9х + 32х+16.
207. 14х - 4 + 27х4 - 9х7. 208. х5 - 7х - 6. 209. х4 + 19Х2 - 30.
210. 4(х + 5)(х + 6Нх + 10)(х + 12) - Зх2.
211. (х2 + 4х + 18J + Зх(х* - 4х + 8) + 3.
Применяя схему Горнера, убедиться, что и число (— 2) и число 1
являются корнями следующего многочлена B12 — 214):
212. (х2 + хJ + Цх2 + 1) - 12. 213. (х2 + х + Щх2 + х + 2) - 12.
214. 2х4 + 7Х3 - 2Х2 - 13х+ 6.
215. Применяя схему Горнера, убедиться, что многочлен
(X2 + 4х + ЗКх2 + 12х+ 35) + 15
делится на многочлен (х + 2)(х + 6), и найти частное.
216. Применяя схему Горнера, убедиться, что многочлен
Xs - 6х4 + 16Х3 - 32Х2 + 48х - 32
делится на многочлен (х — 2K.
217. Делится ли многочлен (х4 — lQx2 + 16) + (х4 — Их2+ 24) на
многочлен (х2 — 8)?
218. Доказать, что сумма одинаковых степеней х" + с* не делится на
разность их оснований х — с.
219. Доказать, что разность одинаковых нечетных степеней х2**' —
— с2 не делится на сумму их оснований х + с.
220. Доказать, что сумма одинаковых четных степеней х2* + с2* не
делится на сумму их оснований х+ с.
221. Найти целые корни многочлена х4 — х3 — Тх2 + 4х — 24.
Доказать методом математической индукции, что для любого натураль-
натурального п справедливо следующее равенство B22 — 241):
222. 1 + 2 + 3 + ... + л
+ 2 + 3 + ... + Я = >.
о
224. 22 + 42 + 82 + ... + BпJ = 2п (и + 1\Bи + *>.
225. I2 + З2 + 52 + - + Bп - IJ - "BИ ~ gBи + 1}.
226. 1 • 2 + 2 • 3 + 3 • 4 + ... + п(п + 1) - л(и + 1Ни + 2>.
227. 12-3 + 2-3-4 + 3-4-5 + ... + л(л+ 1)(л + 2) =
138
—
12
-2
229. I3 + 23 + З3 + ... + л3 ¦
230. 3 + З2 + З3 + ... + 3" =
231. 2 • 2° + 3 • 21 + 4 • 22 + ... + (л + 1) ¦ 2"~ 1 = л • 2".
— + — + — + 1 - "
2 • 3 + 3 • 4 + 4 • 5 + "¦+ (л + 1) (л + 2) 2 (л + 2)'
12 3 л - л + 2
* 2* 23 2" 2я
. _J_ _J_ 1 1 л_
'1-4 4-7 7 10 ¦" (Зл —2)(Зл+1) Зл+Г
. 1 + 1 + 1 1 _ п
' 1 10 + 10 • 19 + 19 28 + "¦+ (9л — 8) (9л + 1) ~ 9л + Г
111 1 л
238. -—- + -—- + -г—г + ... +
"¦ Fл — 1) Fл + 5) 5 Fл + 5)'
1 л
1-33-5 5-7
1 1
240.
241.
Bл —1)Bл+1) 2л + Г
л2 _ л (л + 1)
Bл —1)Bл+1) 2Bл+1)'
1 1
1-2-3 2-3-4 3-4-5
... "Г
л (л + 1) (л + 2)
12 3
357579
-1Г1. 1
2 [2 (л+1)(л + 2)
1-3-53-5-75-7-9
Bл— 1)Bл+1)Bл + 3)
л (л + 1)
2Bл+1)Bл + 3)'
Доказать (методом математической индукции), что для любого нату-
натурального л справедливо следующее равенство B42 — 244):
1
+ ... + ¦
1
245. До
ство2л>
л + Г
1
>/лТТ:
., что для любого натурального л ? 5 справедливо неравен-
139
246. Доказать, что для любого натурального л ? 3 справедливо неравен-
неравенство л! > 2"~'.
Доказать, что при любом натуральном л:
ТАТ. Число л3 + 5л делится на 6.
248. Число л3 + (л + IK + (л + 2K делится на 9.
249. Число 4" + 15л — 1 делится на 9.
250. Число З2" — 1 делится на 2я + 2 и не делится на 2" + 3.
251. Число л5 — л делится на 30.
252. Число А2" - У" - 7 делится на 84.
253. Число б2" + 19" - 2" +' делится на 17.
254. Число 42л +' + 3" + 2 делится на 13.
255. Число л (л — 1) делится на 60.
256. Число 6л + 15л + Юл3 — л делится на 30.
257. Число 20" +' + 16" +' - 3я +' - 1 делится на 323.
258. Число BлK + 20 Bл) делится на 48.
Глава III. АЛГЕБРАИЧЕСКИЕ
УРАВНЕНИЯ И НЕРАВЕНСТВА
Пусть даны два многочлена А и В. Если стоит задача
(гл. II) решить уравнение А = В, то говорят, что дано алгеб-
алгебраическое уравнение А = В. Если же стоит задача решить
неравенство А > В (А < В, А > В, А < В), то говорят, что дано
алгебраическое неравенство А> В(А< В, А>В, А<В).
В этой главе рассматриваются только алгебраические
уравнения и неравенства. Поэтому в этой главе часто
вместо слов «алгебраическое уравнение» будем писать про-
просто «уравнение», вместо слов «алгебраическое неравенство»
будем часто писать «неравенство».
§ 1. Уравнения с одним неизвестным
Основные понятия и определения. Пусть стоит задача
решить уравнение
A)
где R(x) и Q(x) — многочлены (см. гл. II) относительно
одной буквы х; тогда букву х называют неизвестной буквой,
или просто неизвестным, а уравнение A) — алгебраическим
уравнением с одним неизвестным.
Поскольку ОДЗ многочленов R(x) и Q(x) состоит из всех
действительных чисел, то задача о решении уравнения A)
может быть сформулирована так: найти все числовые значе-
значения неизвестного х, каждое из которого обращает уравнение
A) в верное числовое равенство. Каждое такое число назы-
называют корнем или решением уравнения A). Поэтому решить
уравнение A) — это значит найти множество всех его кор-
корней.
141
Если множество всех корней уравнения A) состоит из к
чисел х,, Хг, ..., хь среди которых нет равных, то говорят,
что уравнение A) имеет только к корней хи Хг, ..., хъ т.е.
множество всех решений уравнения A) есть множество
М= {хь *2, ..., хк}. Если же множество всех корней состоит
из одного числа х,, то говорят еще, что уравнение A) имеет
единственный корень или единственное решение х{.
В случае, если множество всех корней уравнения A) есть
пустое множество, то говорят, что уравнение A) не имеет
корней.
Например, очевидно, что уравнение х2 + 1 = — (х4 + 1)
корней не имеет, ибо ни для одного числового значения
неизвестного х это уравнение не превращается в верное
числовое неравенство.
Теперь рассмотрим простейшее алгебраическое уравне-
уравнение с одним неизвестным
х = а, B)
где а — некоторое фиксированное число. Очевидно, что
это простейшее уравнение имеет единственный корень —
число а, поэтому множество всех корней уравнения B)
состоит из одного числа а.
Не для всякого алгебраического уравнения с одним
неизвестным так же очевидно, как в двух рассмотренных
примерах, множество всех корней уравнения. Обычно для
нахождения множества всех корней уравнения это уравне-
уравнение равносильными переходами (определение равносиль-
равносильного перехода см. ниже) сводят к одному или совокупности
нескольких уравнений (определение совокупности уравне-
уравнений см. ниже), каждое из которых — либо простейшее
уравнение типа B), либо уравнение, для которого очевид-
очевидно, что оно не имеет корней.
В этом параграфе рассматриваются примеры равносиль-
равносильных переходов.
Пусть даны два алгебраических уравнения с одним не-
неизвестным R(x) = Q(x) и S(x) = Дх). Эти уравнения назы-
называются равносильными, если любой корень первого уравне-
уравнения является корнем второго уравнения, и наоборот,
142
любой корень второго уравнения является корнем первого
уравнения. В силу этого определения равносильны любые
два уравнения, не имеющие корней.
Замена одного уравнения равносильным ему другим
уравнением называется равносильным переходом от одного
уравнения к другому. Равносильный переход от одного
уравнения к другому обозначается двойной стрелкой <*.
Запись
ад = <2(х) <* ад = пх)
означает, что уравнения R(x) = Q(x) и S(x) = 7\х) равно-
равносильны.
Приведем некоторые утверждения, при помощи ко-
которых и будут совершаться равносильные переходы.
1. Уравнения R(x) = Q(x) и R(x) — Q(x) = О равносильны.
2. Уравнения R(x) = Q(x) и R(x) + a = Q(x) + а равносиль-
равносильны для любого действительного числа а.
3. Уравнения R(x) = Q(x) и aR(x) = aQ(x) равносильны для
любого отличного от нуля действительного числа а.
4. Пусть известно, что для любого действительного
числа х справедливо равенство R(x) = 1\х), тогда равносиль-
равносильны уравнения R{x) = Q{x) и Цх) = Q(x).
Доказательства справедливости этих утверждений похо-
похожи, поэтому докажем, например, утверждение 2. Пусть
число х, — некоторый корень уравнения R(x) = Q(x). Тогда
справедливо числовое равенство R(xx) = Q{xx). Поскольку
справедливость числового равенства не нарушается при
прибавлении к обеим его частям любого действительного
числа (см. гл. I), то справедливо числовое равенство
R(xx) + а = Q(xx) + а. Справедливость этого числового ра-
равенства означает, что число х, является корнем уравнения
R(x) + а = Q{x) + а. Поскольку такое рассуждение можно
провести для любого корня уравнения R(x) = Q(x), то тем
самым показано, что любой корень уравнения R(x) = Q{x)
является корнем уравнения R{x) + а = Q{x) + a.
Покажем теперь обратное. Пусть число х2 есть некото-
некоторый корень уравнения R(x) + а = Q{x) + а, тогда справед-
справедливо числовое равенство R(x2) + а = Q(x2) + а. Прибавим
143
к обеим частям этого числового равенства число (— а),
получим справедливость числового равенства Л(хг) = Qfo),
откуда вытекает, что число Xj есть корень уравнения
R(x) = Q(x). Поскольку такое рассуждение можно провести
для любого корня уравнения R(x) + а = Q(x) + а, то тем
самым показано, что любой корень уравнения R{x) + а =
— (?(*) + « является корнем уравнения R(x) = Q(x).
Из доказанного вытекает, что если уравнение R(x) = Q(x)
не имеет корней, то и уравнение R(x) + а = Q(x) + а также
не имеет корней. Действительно, предположим, что урав-
уравнение R(x) = Q(x) не имеет корней, а уравнение R(x) + а =
= Q(x) + а имеет хотя бы один корень. Из условия, что
уравнение R(x) + а - Q(x) + а имеет корень, по доказанно-
доказанному выше следует, что имеет корень и уравнение R(x) = Q(x),
что противоречит предположению. Значит, если уравнение
R(x) = Q(x) не имеет корней, то и уравнение R(x) + а =
= Q(x) + а корней не имеет.
Аналогично показывается, что если уравнение R(x) +
+ а = Q(x) + а не имеет корней, то и уравнение R(x) = Q(x)
корней не имеет.
Итак, показано, что в этом случае уравнения R(x) = Q(x)
и R(x) + a = Q(x) + а. равносильны. Тем самым утвержде-
утверждение 2 доказано полностью.
Пусть дан многочлен Р(х) степени п относительно
буквы х.
Р(х) = аохп + а1х"-1 + ... + а„_1х+ап (щ*0), C)
где буквами а^, а, а„ _ i, а„ обозначены некоторые
фиксированные действительные числа, называемые коэф-
коэффициентами многочлена 1\х).
Из утверждений 1 и 4 вытекает, что каждое алгебраичес-
алгебраическое уравнение с одним неизвестным можно привести к
виду Р{х) = 0, поэтому достаточно рассмотреть лишь урав-
уравнение
Р(х) = 0, D)
144
где Р(х) есть многочлен вида C). Всякое такое уравнение
называется алгебраическим уравнением степени п.
Из определений корня многочлена Р(х) (см. § 5 гл. II) и
корня (решения) алгебраического уравнения следует, что
любой корень многочлена Р(х) является корнем (решени-
(решением) уравнения D). Следовательно, нахождение всех корней
(решений) уравнения D) сводится к нахождению всех
корней многочлена Р(х). Следует только иметь в виду, что
при нахождении корней уравнения D) не учитывается
кратность корня многочлена J\x). Например, многочлен
Р(х) = х2 — 2х + 1 имеет корень хх = 1 кратности два, а
уравнение х2 — 2х + 1 = 0 имеет единственный корень
(единственное решение) х, = 1. Хорошо известно, что на-
нахождение корней многочлена является сложной задачей.
Поэтому рассмотрим только некоторые такие случаи, когда
удается найти все корни многочлена, т.е. решить уравне-
уравнение D).
Уравнение первой степени. Рассмотрим случай, когда Р(х)
есть многочлен первой степени, т.е. рассмотрим уравнение
аох + ах = О (яо * 0). E)
На основании утверждения 2 уравнение E) равносильно
уравнению
а^х = — ах (д0 * 0). F)
Поскольку число Оо * 0» то на основании утверждения 3
уравнение F) равносильно уравнению
* = -| <аь*О). G)
Все равносильные переходы от уравнения E) к уравнению
G) можно записать более коротко в виде следующей це-
цепочки равносильных переходов:
+ ах = 0 (яо * 0) о OqX = — ах (а0 ф 0) о
145
Простейшее уравнение х = — — имеет единственный
До
корень — число [ — — |. Так как уравнение E) равносильно
I ао I
простейшему уравнению G), то уравнение E) также имеет
единственный корень — число [ — — 1.
1 ао I
Таким образом, уравнение первой степени с одним неиз-
неизвестным E) имеет только один корень х, = — —.
Для решения алгебраических уравнений более высоких
степеней понадобится понятие совокупности уравнений.
Пусть дано т многочленов Pi(x), Р2(х), ..., Рт(х). Говорят,
что дана совокупность т алгебраических уравнений с одним
неизвестным х.
Рх{х) = О, Р2(х) = О, ..., Рт(х) = О, (8)
если требуется найти все числовые значения неизвестно-
неизвестного х, каждое из которых является корнем хотя бы одного
уравнения из этой совокупности (8) (уравнения совокуп-
совокупности обычно записываются в строчку).
Таким образом, решить совокупность уравнений (8) —
значит решить каждое уравнение Pfoc) — 0, где /= 1, 2, ...
..., т, т.е. найти множества Nu N2, ..., Nm всех корней
каждого из уравнений и затем взять объединение этих
множеств. Это объединение iV = Nt u N2 u ... u Nm будет
множеством всех корней совокупности уравнений (8), а
каждое число из множества Сбудет называться корнем или
решением совокупности (8). Если множество iV состоит из
к чисел: хьх2, ...,хк, среди которых нет равных, то говорят,
что совокупность уравнений (8) имеет только к корней хи
х2, ...,хк; если же множество /^состоит из одного числа хи
то говорят, что совокупность уравнений (8) имеет единст-
единственный корень хи
Часто возникает необходимость совершить равносиль-
равносильный переход от уравнения к совокупности уравнений.
Будем говорить, что уравнение
0 D)
146
равносильно совокупности уравнении
Л(х) = О, Р2(х) = О, ..., Рт(х) = О, (8)
если любое решение (любой корень) уравнения D) являет-
является решением (корнем) совокупности (8), и наоборот, любое
решение (любой корень) совокупности (8) является реше-
решением (корнем) уравнения D). Замена уравнения D) равно-
равносильной ему совокупностью (8) называется равносильным
переходом от уравнения D) к совокупности (8).
Например, уравнение
(Зх + 4)(- 7х + 2)Bх - л/Г)(- 12х - 16) = О (9)
равносильно совокупности уравнений
Зх + 4 = 0, -7х+2 = 0, 2х-л/Г=0, - !2х - 16 = 0.
Действительно, любой корень уравнения (9) обращает в
нуль хотя бы один из многочленов (Зх + 4), (— 7х + 2),
Bх — V5), (— 12х — 16), т.е. является корнем хотя бы
одного из уравнений совокупности, и, наоборот, любой
корень совокупности обращает в нуль хотя бы один из этих
многочленов, т.е. удовлетворяет уравнению (9). Совокуп-
4 2
ность уравнений имеет только три корня Xi = — |, Хг = j,
х3 = -у. Следовательно, в силу равносильного перехода эти
корни и только они являются корнями уравнения (9).
Рассмотрим алгебраическое уравнение второй степени, т.е.
уравнение
ах2 + Ьх + с = 0 (офО). A0)
Такие уравнения принято называть квадратными уравне-
уравнениями. Многочлен ах2 + Ъх + с, где а ф 0, называют обычно
квадратным трехчленом, число а {а ф 0), стоящее при х2, —
называется первым коэффициентом, число Ъ, стоящее при
х, — вторым коэффициентом, число с — свободным членом.
Кроме того, число D= b2 — 4ас называется дискриминан-
147
том квадратного трехчлена, а также дискриминантом квад-
квадратного уравнения A0).
Проведем тождественное преобразование квадратного
трехчлена. Так как а*0, то справедливо тождественное
равенство
ах2 + Ъх + с =
Теперь применим тождественное преобразование, которое
называется «выделением полного квадрата»:
~а I2el I2el a
2 - * ' ^*4ас-Ь2_
4а
Окончательно получаем справедливость следующего тож-
тождественного равенства:
На основании утверждения 4 уравнение A0) равносильно
уравнению
а на основании утверждения 3, учитывая, что а ф 0, полу-
получаем, что уравнение A1) равносильно уравнению
Более коротко это можно записать так:
148
ax2 + bx + с = 0 (a * 0),
0
В зависимости от дискриминанта D возможны три случая,
a) D< 0. Так как при любом числовом значении хь число
+ -%- неотрицательно, а число —^ — положительно,
то число хЬ + -т-| —=т также положительно и потому не
^ ^J 4в
может равняться нулю. А это означает, что уравнение A2)
не имеет действительных корней. Поскольку уравнение
A0) равносильно уравнению A2), то оно также не имеет
действительных корней.
б) D = 0. Тогда уравнение A2) принимает вид
Это уравнение равносильно уравнению первой степени
Следовательно, если D= 0, то уравнение A2) имеет един-
единственный корень х, = — jj.
в) D > 0. Тогда Z) = (VI)J, и поэтому выражение, стоящее
в левой части уравнения A2), можно рассматривать как
разность двух квадратов [х + у- ] и |у-1. Воспользовавшись
формулой сокращенного умножения, получим уравнение
149
[H>f][H)-f]=°
равносильное уравнению A2). Это уравнение, в свою оче-
очередь, равносильно совокупности двух уравнений
Каждое уравнение в этой совокупности является уравне-
уравнением первой степени и, следовательно, по доказанному
выше имеет только один корень. Решая каждое уравнение
совокупности A3), получаем, что совокупность уравнений
A3) имеет только два корня
A4)
В силу равносильных переходов, если D > 0, то уравнение
A0) равносильно совокупности A3) и потому имеет только
два корня Xi и хъ вычисляемые по формулам A4).
Итак, квадратное уравнение A0) не имеет действитель-
действительных корней, если его дискриминант отрицателен, имеет
только два действительных корня, если дискриминант поло-
положителен, и имеет только один действительный корень, если
дискриминант равен нулю.
Отметим, что если дискриминант квадратного уравнения
A0) положителен, то формулы A4) для нахождения корней
этого уравнения часто записывают в виде одной формулы:
Замечание. Если D = 0, то можно считать, что форму-
формула A5) остается справедливой, только надо помнить о том,
что в этом случае квадратное уравнение имеет только один
корень.
Приведенное квадратное уравнение. Квадратный трех-
трехчлен, у которого первый коэффициент равен единице,
называется приведенным квадратным трехчленом. Обще-
Общепринято второй коэффициент приведенного трехчлена
150
обозначать р, а его свободный член — q, т.е. приведенный
квадратный трехчлен имеет вид х2 + рх + q.
Квадратное уравнение вида
х2 + рх + q = О A6)
называется приведенным квадратным уравнением.
Очевидно, что квадратное уравнение A0) равносильно
соответствующему приведенному уравнению, а именно
Если дискриминант приведенного уравнения A6) положи-
положителен, то формула A5) для нахождения корней этого урав-
уравнения принимает вид
- q. A8)
Теорема (теорема Виета). Если приведенное квадратное
уравнение х2 + рх + q = О имеет положительный дискрими-
дискриминант, то сумма корней этого уравнения равна второму его
коэффициенту, взятому с противоположным знаком, а про-
произведение корней равно свободному члену, т.е. если хх и х2
корни уравнения X + рх+ q = 0, то х, + *2 = — р; х,х2 = q.
Доказательство. Так как 2)>0, то, используя фор-
формулы A8), получим
_?_Vffl -.1 —
-,?-«-Vf«l -«1-
Теорема доказана.
Замечание. При D = 0, как следует из доказательства,
теорема Виета верна, если рассматривать корень х, = — |
151
как два совпадающих корня х, = — | и Хг = — |. Теорема
Виета имеет место и при D< О, но в этом случае корнями
квадратного уравнения будут комплексные сопряженные
числа (см. гл. XI).
Теорема Виета часто применяется при решении различных
задач. Рассмотрим одну из них. Требуется найти неизвестный
свободный член q квадратного уравнения х2 + х + q = 0, если
известно, что это уравнение имеет два действительных корня
х, и х2 и сумма квадратов этих корней равна единице, т.е.
х\ + х\ = 1. Чтобы найти q, воспользуемся теоремой Виета.
Справедлива цепочка тождественных равенств
х\ + х\ = х\ + 2х,Х2 + х\ — 2х,Х2 = (х, + ХгJ
и потому х\ + х\ = 1 — 2q, т.е. 1 — 2q = 1, откуда q = 0.
Симметричное уравнение третьей степени. Алгебраическое
уравнение третьей степени называется симметричным урав-
уравнением, если оно имеет вид
йх2 + 6х + а = 0 (а*0). A9)
Преобразуем многочлен ах3 + Ьх2 + Ьх, + а, воспользо-
воспользовавшись способом разложения многочлена на множители.
Очевидна справедливость следующей цепочки тождествен-
тождественных равенств:
ах3 + Ьх2 + Ьх + а = а(х? + 1) + Ьх(х + 1) =
= а(х+ lXx2 - х+ 1) + Ьх(х+ 1) =
поэтому уравнение A9) равносильно уравнению
а] = 0 (а*0). B0)
Уравнение B0), в свою очередь, равносильно совокупности
уравнений:
х + 1 = 0 (а * 0), ох2 + (Ь - а)х + а = 0 {а ф 0). B1)
152
Следовательно, и уравнение A9) равносильно этой сово-
совокупности. Решение совокупности B1) легко находится, так
как она содержит только уравнения первой и второй сте-
степени.
Пример. Найти корни уравнения
х3 + 4х* + 4х + 1 = 0. B2)
Преобразуем левую часть уравнения:
х3 + 4х* + 4х + 1 = (х3 + 1) + 4х(х + 1) =
Очевидно, что уравнение B2) равносильно совокупности
уравнений
х + 1 = 0, х2 + Ъх + 1 = 0. B3)
Первое уравнение совокупности B3) имеет только один
корень *! = — 1; второе — только два корня Хг = —=— и
х3 = —^2—^ Следовательно, совокупность уравнений B3),
а значит, и данное уравнение B2) имеют только три корня
г у _3УГ
Симметричное уравнений четвертой степени. Алгебраичес-
Алгебраическое уравнение четверной степени называется симметрич-
симметричным, если оно имеет вид
axA + bx3 + cx2 + bx + a = 0 (д*0). B4)
Учитывая, что а ф 0, запишем это уравнение в равносиль-
равносильном виде:
(х4 + 1) + fax2 + 1) + Zx2 = 0 (а*0).
Очевидна справедливость следующей цепочки тождест-
тождественных равенств:
153
(x4 + 1) + ^(x2 + 1) +1*2 = (x4 + 2x* + 1) +?c(x2 + 1) +
4o2
Из справедливости этой цепочки получаем, что уравнение
B4) равносильно уравнению
J2J B5)
В зависимости от числа М = Ь2 — 4а(с — 2а) возможны три
случая:
а) М< 0. Уравнение B5), а значит, и равносильное ему
уравнение B4) действительных корней не имеют.
б) М= 0. Уравнение B5) в этом случае принимает вид
O B6)
Очевидно, что уравнение B6) равносильно уравнению
2 ^ 0 B7)
Следовательно, множество корней симметричного урав-
уравнения 4-й степени в этом случае совпадает с множеством
корней квадратного уравнения
х2 + ^х+1 = 0 (а*0) B8)
в) М > 0. Уравнение B5), а значит, и равносильное ему
уравнение B4) равносильны совокупности квадратных
уравнений
154
каждое из которых легко решить.
Пример. Решить уравнение
х4 + х* — х* + х+1 = 0. C1)
Приведем следующую цепочку тождественных равенств:
х4 + х3 - х2 + х + 1 =х4 + 2х* + 1 + х(х* + 1) - Зх2 =
| + (|| - Зх2 - | = (х 1
1 J + 2(х* + 1) | + (|| - Зх2 - | = (х2 +1 + 11 -
откуда следует, что уравнение C1) равносильно совокуп-
совокупности уравнений
Первое уравнение этой совокупности имеет только два
корня:
-VU-1+V2V13-2 — VIT— 1 — л/2л/13 -2 „^
X, ^ , Хг : 4 , C2)
а второе уравнение действительных корней не имеет, т.к.
его дискриминант отрицателен. Следовательно, уравнение
C1) имеет только два корня C2).
Двучленное уравнение. Алгебраическое уравнение назы-
называется двучленным уравнением, если оно имеет вид
х" - а = 0. C3)
Рассмотрим сначала двучленное уравнение C3) в частном
случае, когда а = 1:
х" - 1 = 0. C4)
155
При п = 1 уравнение C4) есть частный случай уравнения
первой степени и потому имеет единственный корень
Xi = 1. При п = 2 уравнение C4) есть частный случай
квадратного уравнения с положительным дискриминантом
и потому имеет только два корня: xt = 1 и дсг = — 1. Пока-
Покажем теперь, что при п > 3 для любого нечетного п уравнение
C4) имеет только один действительный корень Х\ = 1, а для
любого четного п уравнение C4) имеет только два дейст-
действительных КОРНЯ *i = 1 И X} — — 1.
Пусть п — фиксированное нечетное натуральное число,
п > 3, т.е. пусть п = 2к + 1, где А: — фиксированное нату-
натуральное число. Пользуясь формулой сокращенного умно-
умножения, получаем справедливость тождественного равенст-
равенства (см. гл. II):
Из справедливости этого тождественного равенства вы-
вытекает, что уравнение C4) при п = 2к + 1 равносильно
совокупности уравнений
Первое уравнение этой совокупности имеет только один
корень *j = 1, второе уравнение совокупности действитель-
действительных корней не имеет. Для доказательства этого покажем,
что для любого действительного х справедливо неравенство
х2к + х2к~1 + ... +х2 + х+1>0 C5)
Действительно, для любого х е [0, + «>) справедливость не-
неравенства C5) очевидна. При любом х е [— 1; 0), переписав
левую часть неравенства C5) в виде
х2* + Xй-2 (х + 1) + ... + х2 (х + 1) + (х + 1),
убеждаемся, что первое слагаемое этой суммы положитель-
положительно, а остальные — неотрицательны. Значит, для любого
хе [— 1; 0) неравенство C5) справедливо. Переписав
левую часть неравенства C5) в виде
156
Xй -' (x + 1) + Xй ~3 (x + 1) + ... + Xix + 1) + 1,
убеждаемся, что для любого хе (— «>, — 1) все слагаемые
этой суммы положительны. Значит, для любого хе (— «»,
- 1) неравенство C5) справедливо.
Итак, показана справедливость неравенства C5) для
любого действительного х, а это означает, что уравнение
действительных корней не имеет. Значит, уравнение C4)
при п = 2к + 1 имеет только один действительный корень
х, = 1.
Пусть теперь п = 2к (к — фиксированное натуральное
число и к > 2). Пользуясь формулой сокращенного умно-
умножения (см. гл. II), получаем справедливость тождественно-
тождественного равенства
- ¦>
1).
Из справедливости этого тождественного равенства выте-
вытекает, что уравнение C4) при п = 2к (к ? 2) равносильно
совокупности уравнений
x^-l-O, x2(*-1) + x2(*-2) + ...+*4 + x'+l-O.
Первое уравнение этой совокупности имеет два корня
Xi = 1hx2 = — 1, а второе уравнение действительных
корней не имеет, так как для любого действительного х
очевидна справедливость неравенства
Значит уравнение C4) имеет при п = 2к два действительных
корня: Xi = 1 и *2 = — 1.
Итак, уравнение C4) при любом нечетном п имеет
только один действительный корень хх= \, а при любом
четном п — только два действительных корня: Хх = 1 и
Да = -1.
Рассуждая аналогично, можно показать (см. § 1 гл. VII),
что:
157
— при любом положительном а уравнение C3) имеет:
1) при любом нечетном л только один действительный
корень х, = Ча, 2) при любом четном л — только два
действительных корня х, = Ча и х2 = — Ча;
— при а = 0 уравнение C3) имеет только один корень
х, = 0;
— при любом отрицательном а можно показать (см. § 1
гл. VII), что уравнение C3) имеет: 1) при любом нечетном
л только один действительный корень х, = — У— а, 2) при
любом четном л не имеет действительных корней.
Пример. Решить уравнение
х3 + 8 = 0.
Так как в данном случае п — нечетно (л = 3) и а —
отрицательно (а = — 8), то данное уравнение имеет един-
единственное решение х, = — 2.
Трехчленное уравнение. Алгебраическое уравнение вида
ох2" + ЬхГ + с = 0 C6)
при условии, что п ? 2, а * 0, Ь*0, с*0, называется трех-
трехчленным уравнением. При л = 2 трехчленное уравнение
имеет еще одно название «биквадратное уравнение». Дм
решения биквадратного уравнения
cot + ^ + 0 = 0 (а*0) C7)
его левая часть преобразуется способом «выделения пол-
полного квадрата»:
На основании этого тождественного равенства уравнение
C7) равносильно уравнению
158
0 <a*0)- •<3S)
Очевидно, что если b2 — 4ас < О, то уравнение C8), а
значит, и равносильное ему уравнение C7), корней не
имеют.
При Ъ2 — Аас = 0 уравнение C8) принимает вид
*0). C9)
Очевидно, что уравнение C9) равносильно уравнению
^ + ^ = 0 (д*0). D0)
Таким образом, при Ь2 — 4ас = 0 биквадратное уравне-
уравнение C7) равносильно квадратному уравнению D0), т.е. при
^- < 0 имеет только два действительных корня хх =
= V— ¦— и х2 = — "i—4-\ при у- = 0 — единственный корень
*i = 0; при у- > 0 — не имеет решений.
Если же Ь2 — Аас > 0, то уравнение C8), а значит, и
равносильное ему уравнение C7) равносильны совокуп-
совокупности уравнений
= 0 <«*0).
-Лас
Перепишем эту совокупность в равносильном виде:
— 4ас , ЛЧ 2 — Ь — VAZ —
(**0) ДГ =
Поскольку числа, стоящие в правых частях уравнений
совокупности D1), есть корни квадратного уравнения
a? + bt + c = Q (a*0), D2)
159
имеющего положительный дискриминант D= b2 — 4ас, то
совокупность уравнений D1) может быть записана в виде
J=tx (а*0), S = t2 (а*0), D3)
где tx и t2 — корни уравнения D2).
Таким образом показано, что для решения биквадратно-
биквадратного уравнения C7) надо сначала решить квадратное уравне-
уравнение D2), при этом, если квадратное уравнение D2) не имеет
действительных корней, т.е. его дискриминант отрицате-
отрицателен, то уравнение C7) также не имеет корней; если дис-
дискриминант уравнения D2) равен нулю, то уравнение C7)
равносильно квадратному уравнению D0), которое легко
решается; если же дискриминант уравнения D2) положи-
положителен, то уравнение C7) равносильно совокупности урав-
уравнений D1). Каждое из уравнений совокупности D1) —
квадратное, поэтому корни этой совокупности, а значит, и
корни равносильного этой совокупности уравнения C7)
легко найти.
Пример. Решить биквадратное уравнение
х4 - х2 - 6 = 0. D4)
Для решения уравнения D4) решим сначала квадратное
уравнение Г2 — t — 6 = 0. Корни этого уравнения tx = — 2,
t2 = 3. Поэтому уравнение D4) равносильно совокупности
уравнений
Первое уравнение этой совокупности действительных кор-
корней не имеет, а второе имеет только два корня: хх = VJ и
Хг = — V3~. Значит, и уравнение D4) имеет только два корня
Xi = VT и х2 = — V5".
При л > 2 для решения трехчленного уравнения
ох2" + ЬхГ + с = 0 (а * 0)
его левая часть также преобразуется способом «вьщеления
полного квадрата»
160
D5)
На основании этого тождественного равенства уравнение
C6) равносильно уравнению
Очевидно, что если Ь2 — 4ас < О, то уравнение D6), а
значит, и уравнение C6) корней не имеют.
Если же Ъ2 — 4ас = 0, то уравнение D6) равносильно
двучленному уравнению
У + ? = 0 (а*0). D7)
Следовательно, при Ь2 — 4ас = 0 трехчленно уравнение C6)
равносильно двучленному уравнению D7), решение кото-
которого рассматривалось в предыдущем пункте.
Если же b — 4ас > 0, то уравнение D6) равносильно
совокупности двучленных уравнений
<«*0), D8)
решение которых, как показано выше, можно найти.
Пример. Решить трехчленное уравнение
л* + Зх3 + 2 = 0. D9)
Так как данное уравнение равносильно совокупности двух
двучленных уравнений
^ + 2 = 0, ^ + 1=0,
то, решив их, получим, что уравнение D9) имеет только два
действительных корня х, = — 3V2~ и Хг = — 1.
Замечание. Выше было показано, как решить любое
уравнение первой степени и любое квадратное уравнение
6 Алгебра, тригонометрия 101
и элементарные функции
и были выведены формулы для Нахождения их корней. Что
касается уравнений, степени которых выше, чем два, то
были рассмотрены лишь отдельные примеры. Связано это
с тем, что хотя для уравнений третьей и четвертой степени
такие формулы есть, они очень громоздки и потому при-
применяются редко, а для уравнений пятой степени таких
формул нет. В то же время следует отметить, что если все
коэффициенты многочлена Р(х) в уравнении D) являются
целыми (или рациональными) числами, то для нахождения
целых (или рациональных) корней уравнения D) можно
применить теорему о целых (или рациональных) корнях
многочлена (см. гл. И).
§ 2. Неравенства с одним неизвестным
Основные понятия и определения. Пусть стоит задача:
решить неравенство
R(x) > Q(x) [или R(x) < Q(x)], A)
где R(x) и Q(x) — многочлены (см. гл. II) относительно
одной буквы х. Буквах называется неизвестной буквой, или
просто неизвестным, неравенство A) — алгебраическим не-
неравенством с одним неизвестным.
Поскольку ОДЗ многочленов R(x) и Q(x) состоит из всех
действительных чисел, то задачу о решении неравенства A)
можно сформулировать так: найти все числовые значения
буквы х, каждое из которых обращает неравенство A) в
верное числовое неравенство. Каждое такое числовое зна-
значение называется решением неравенства A). Поэтому ре-
решить неравенство A) — это значит найти множество всех
его решений. В случае, если множество всех решений
неравенства A) есть пустое множество, говорят, что нера-
неравенство A) не имеет решений.
Два алгебраических неравенства R(x) > Q(x) и 7\х) < S(x)
называются равносильными, если любое решение первого
неравенства является решением второго, и, наоборот,
любое решение второго неравенства является решением
первого. В силу этого определения равносильны любые два
неравенства, не имеющие решений. Замена одного нера-
венства равносильным ему другим неравенством называет-
называется равносильным переходом от одного неравенства к дру-
другому. Равносильный переход принято обозначать двойной
стрелкой о. Запись
R(x) > Q(jc) о Т\х) < S(x)
обозначает, что неравенства R(x) > Q(x) и 7\х) < S(x) рав-
равносильны.
Приведем некоторые утверждения, при помощи ко-
которых будут совершаться равносильные переходы.
1. Неравенства R(x) > Q(x) и R(x) — Q(x) > О равносильны.
2. Неравенства R(x) > Q(x) и R(x) + a > Q(x) + а равно-
равносильны для любого действительного числа ос.
3. а) Неравенства R(x) > Q(x) и oR(x) > a, Q(x) равносильны
для любого положительного числа ос.
б) Неравенства R(x) > Q(x) и aR(x) < aQ(x) равносильны
для любого отрицательного числа а.
4. Пусть известно, что для любого действительного числа
х справедливо равенство R(x) = 7\x), тогда равносильны не-
неравенства R(x) > Q(x) и 7\х) > Q(x).
Доказательства справедливости этих утверждений похо-
похожи, поэтому докажем, например, утверждение 1. Пусть
число х, есть некоторое решение неравенства R(x) > Q(x),
т.е. пусть справедливо числовое неравенство R(xt) > Q(xj).
Тогда по свойству числовых неравенств справедливо и
числовое неравенство R(x{) — 0(х{) > 0. Справедливость
этого числового неравенства означает, что число хх являет-
является решением неравенства R(x) — Q(x) > 0. Поскольку такое
рассуждение можно провести для любого решения нера-
неравенства R(x) > Q(x), то любое решение неравенства
R(x) > Q(x) есть решение неравенства R(x) — Q(x) > 0.
Покажем теперь обратное. Пусть число х^ есть некоторое
решение неравенства R(x) — Q(x) > 0, т.е. пусть справедли-
справедливо числовое неравенство R(x2) — Q(x2) > 0. Из справедли-
справедливости последнего неравенства следует справедливость чис-
числового неравенства Rfa) > Qfo). а это означает, что число
х2 — решение неравенства R(x) > Q(x). Поскольку такое
рассуждение можно провести для любого решения нера-
6* 163
венства R(x) — Q{x) > 0, то любое решение неравенства
R(x) — Q{x) > О есть решение неравенства R(x) > Q(x). Зна-
Значит, если каждое из неравенств R(x) > Q(x) и R(x) — Q(x) >
> О имеет решение, то эти неравенства равносильны.
Из доказанного вытекает, что если одно из неравенств
R(x) > Q(x) или R(x) — Q(x) > 0 не имеет решений, то и
другое не имеет решений, т.е. в этом случае неравенства
Л(х) > Q(x) и R(x) — Q(x) > 0 равносильны. Утверждение 1
доказано.
Из утверждений 1 и 4 вытекает, что каждое алгебраичес-
алгебраическое неравенство можно привести или к виду Р(х) > 0 или к
виду Р(х) < 0, поэтому достаточно рассмотреть лишь нера-
неравенства вида
Р(х) > 0 B)
и
т < о о)
где Р(х) — многочлен степени п относительно буквы х, т.е.
Такие неравенства называют алгебраическими неравен-
неравенствами степени п.
Неравенства первой степени. Метод интервалов. Пусть
надо решить неравенство
flox+a,>0 (flo*O), D)
которое называется неравенством первой степени. На осно-
основании утверждения 2 неравенство D) равносильно неравен-
неравенству
ОоХ > — a, (oq * 0). E)
Рассмотрим случаи ао>0 и Оо<0. Пусть ао> 0, тогда на
основании утверждения За) неравенство (S) равносильно
неравенству
*>-% ("o*O). F)
Очевидно, что любое х из промежутка [ — —, + ~ ] удовле-
I ^ I
творяет неравенству F). Следовательно, множество всех
решений неравенства F) есть промежуток ( — —, + «, |
I <h I
(рис. 11). Так как неравенство D) при во > 0 равносильно
неравенству F), то множество
всех решений неравенства D) -а/а„ х
также есть промежуток Рис. 11
. Все равносильные
переходы от неравенства D) к неравенству E), а затем к
очевидному неравенству F) записываются более коротко в
виде следующей цепочки равносильных переходов:
OqX + ах > 0 (во > 0) о аоХ > — ах (oq > 0) о
Аналогично справедливы следующие цепочки равносиль-
равносильных переходов:
+ ах > О (flo < 0) «> OqX > — ах {щ < 0) о
+ ах < 0 (оо > 0) о аоХ < — ах (ац > 0)
ax < 0 (Оо < 0) о atfc < — ах (оо< 0)
В каждой из этих цепочек из последнего неравенства легко
найти множество всех решений первого неравенства дан-
ной цепочки (при указанном ограничении на До). Итак,
решением неравенства а^х + ах > 0 при щ < О является про-
промежуток [ — ~, — — I; решением неравенства а^с+ ах<0
при До > 0 является промежуток | — «*>,— — ]; решением
неравенства а^х + ах < О при До < 0 является7 промежуток
(-*¦-)¦
v Все вышенаписанное о решении неравенств первой сте-
степени часто формулируют так: многочлен первой степени
atfc + ах (до * 0):
а) при До > 0 положителен для любого xef— —, +оо]и
I °о I
отрицателен для любого х е f — ~, — — ];
б) при До < 0 положителен для любого х е (— ~, — — 1 и
I ао I
отрицателен для для любого х е | — —, + <» I.
I «о I
В частности, двучлен (х — а) положителен для всех х,
находящихся на числовой оси справа от точки, изображаю-
изображающей число а, и отрицателен для всех х, находящихся слева
от этой точки. Другими словами, точка а делит числовую
ось на две части: в части, находящейся справа от точки а,
двучлен (х — а) положителен, а в части, находящейся слева
от точки а, отрицателен.
Это свойство двучлена (х — а) лежит в основе метода
интервалов и часто используется для решения алгебраичес-
алгебраических неравенств более высоких степеней.
Пусть требуется решить неравенство
(х — ах)(х — ос2) ... (х — а„ _ х)(х — а„) > 0, G)
где ось ос2, ..., ос„ _ 1, ос„ — фиксированные числа, среди
которых нет равных, причем такие, что ах < ос2 < ... < а„ _ i <
Рассмотрим многочлен
Р(х) = (х— ах)(х — Oj) ... (х — сс„ _ х)(х — а„). (8)
На основании сделанного выше замечания очевидно, что
для любого числа Xq такого, что Xq > а„, соответствующее
числовое значение любого сомножителя в произведении
(8) положительно, поэтому соответствующее числовое зна-
значение 1\хо) многочлена Р{х) также положительно. Для
любого числа хи взятого из интервала (а„_и а„), соответст-
соответствующее числовое значение последнего сомножителя отри-
отрицательно, а соответствующее числовое значение любого из
оставшихся сомножителей положительно, поэтому число
Р{хх) — отрицательно; аналогично для любого числа Xi из
интервала (а„_2, а„_,) число Р(х2) — положительно и т.д.
На этом рассуждении и основан метод интервалов, со-
состоящий в следующем: на числовую прямую наносят числа
а,, а2,..., а„_,, а„; над лучом справа от наибольшего из них
ставят знак плюс, под следующим за ним справа налево
интервалом ставят знак минус, затем — знак плюс, затем —
знак минус и т.д. (рис. 12). Тогда множество всех решений
неравенства G) будет объеденением всех промежутков, в
которых поставлен знак плюс.
Методом интервалов можно решать те алгебраические
неравенства, которые цепочкой равносильных переходов
можно свести к неравенствам вида G).
Пример. Решить неравенство
(х - 3)B + х)D - х) > 0. (9)
Умножая неравенство (9) на (— 1) получим равносильное
ему неравенство
[х-(-2)](х-3)(х-4)<0. A0)
Для решения неравенства A0) применим метод интервалов:
на числовую прямую наносим числа (— 2), 3, 4.В проме-
промежутках справа налево расставим знаки плюс и минус
(рис. 13). Множество всех х из промежутков (— «>, — 2) и
C, 4) — множество всех решений неравенства A0). По-
Поскольку неравенство (9) равносильно неравенству A0), то
множество всех решение неравенства (9) есть множество
(- оо, - 2) и C, 4).
Рис. 13.
Квадратное неравенство. Применим метод интервалов к
решению алгебраических неравенств второй степени. От-
Отметим, что обычно их называют квадратными неравенст-
неравенствами. Рассмотрим квадратное неравенство
а>? + Ьх+с>0 (а*0). A1)
Применяя тождественное преобразование «вьщеление пол-
полного квадрата» (см. § 1, гл. III), получаем
где D = b1 — 4ас. Поэтому неравенство A1) равносильно
неравенству
[(sf-3]>0 (а*0)-
Пусть а > 0. Тогда неравенство A2) равносильно нера-
неравенству
а) Если D< 0, то при любом числовом значении неиз-
неизвестного х = ль в левой части неравенства A3) стоит сумма
неотрицательного числа *ь + ¦?-] и положительного числа
I 2а)
Г) Л
—^j , т.е. неравенство A3) превращается в верное чис-
ловое неравенство. Следовательно, неравенство A3) спра-
справедливо при любом х. Другими словами, множество всех
решений неравенства A3) в этом случае есть множество
всех действительных чисел.
б) Если D = О, то очевидно, что неравенство A3) превра-
превращается в верное числовое неравенство для любого числа х,
кроме Xq = — ~. Следовательно, множество всех решений
неравенства A3) в этом случае есть множество
в) Если D > 0, то неравенство A3) равносильно неравен-
неравенству
(х — Xi)(x — Х2) > 0 (а >0), A4)
где хх = ~ 2~—, Хг = ~ 2* . Очевидно, что хх < х^, поэто-
поэтому, применяя метод интервалов, получим, что множество
всех решений неравенства A4) есть множество (— ~, хх) и
Пусть а < 0. Тогда неравенство A2) равносильно нера-
неравенству
--^<0 (а<0). A5)
а) Если D< 0, то очевидно, что для любого числа х это
неравенство превращается в неверное числовое неравенст-
неравенство, а потому неравенство A5) не имеет решений.
б) Если D = 0, то столь же очевидно, что неравенство A5)
не имеет решений.
в) Если D > 0, то неравенство A5) равносильно неравен-
неравенству
(х - хх)(х - хд < 0 (а<0), A6)
где JC! = ~ ~—, Хг = —-^—• Очевидно, что хх > х^, поэто-
поэтому, применяя метод интервалов, получим, что множество
всех решений неравенства A6) есть интервал fa; xx).
№
Аналогично проводится решение неравенства ах2 + bx +
+ с < О {а ф 0). Приведенные выше рассуждения можно
собрать вместе (см. табл. 1).
Таблица 1
^а
а>0
а>0
а>0
а>0
а>0
а>0
а<0
а<0
а<0
а<0
а<0
а<0
D
D>0
D>0
D = 0
D = 0
D<0
D<0
D>0
D>0
D = 0
Z) = 0
D<0
D<0
Неравенство
ax2 + bx + с > 0
ax2 + bx + с < 0
ax2 + bx + с > 0
ax2 + bx + с < 0
ax2 + bx + с > 0
ax2 + bx + с < 0
ax2 + &c + с > 0
ax2 + bx + с < 0
ax2 + bx+c>0
ax2 + bx+c<0
ax2 + bx+c>0
ax2 + bx + с < 0
Решение неравенства
( —b-<D) f—b + <D }
[ - 1° M 2a •¦"]
(—b-<D —Ь + <Г)Л
[ la ' la J
H-±M-*H
нет решений
(-«,+-)
нет решений
f—b + <D —b-<D)
{ la ' la j
( -b + <D] (~b-<D Л
[ - la H 2a .""]
нет решений
н-±м-*н
нет решений
( , + -)
Отметим, что запоминать эту таблицу не надо, для ре-
решения конкретного квадратного неравенства лучше каж-
каждый раз повторять те рассуждения, которые были сделаны
выше.
Пример. Решить неравенство
х2 _ х _. 6 < 0.
Поскольку корни квадратного трехчлена Р{х) = х2 — х —
— 6 есть х, = 3 и х2 = — 2, то Р{х) = (х — 3)(х + 2).
Значит, неравенство равносильно неравенству
(х - 3)(х + 2) < 0.
Применив метод интервалов к последнему неравенству
(рис. 14), получим, что множество всех решений исходного
неравенства есть интервал (— 2; 3).
Рис. 14.
Обобщенный метод интервалов. Некоторые алгебраичес-
алгебраические неравенства степеней, более высоких чем два, цепоч-
цепочкой равносильных переходов приводятся к виду
(х - а,)*' (х - а2)*>... (х - а„_ ,)*»' (х - а,,)*» > 0, A7)
где кикъ ...,к„_\,к„ — фиксированные натуральные числа,
а,, а2,..., а„_,, а„ — фиксированные действительные числа,
среди которых нет равных, и такие, что а, < а2 < ... < а„ _ j <
< а„ (отметим, что если хотя бы одно из чисел к, > 2, то для
решения неравенства A7) неприменим приведенный выше
метод интервалов). Тогда неравенства вида A7) решаются
так называемым обобщенным методом интервалов. Рассмот-
Рассмотрим многочлен
Р{х) = (х- а,)*'(х - а2)*>... (х - (хп_,)к-'(х - ап)\A8)
„,
Очевидно, что для любого числа Xq такого, что Xq > а
соответствующее числовое значение любого сомножителя
в произведении A8) положительно, поэтому числовое зна-
значение Р(хо) многочлена Р(х) также положительно.
Для любого числа хи взятого из интервала (а„_,, а„),
соответствующее числовое значение любого сомножителя,
кроме последнего, положительно; соответствующее число-
числовое значение последнего сомножителя положительно, если
к„ — четное число, и отрицательно, если к„ — нечетное
число. Поэтому число P(xi), положительно, если к„ — чет-
четное число, и число Р(хх) — отрицательно, если к„ — нечет-
нечетное число. Обычно в этих случаях говорят, что многочлен
Р(х) при переходе через точку а„ меняет знак, если к„ —
нечетное число, и не меняет знака, если к„ — четное число.
Аналогично показывается, что если известен знак много-
многочлена Р(х) на интервале (а/9 ai+1), то на интервале (а,_ ь а,)
знак определяется по правилу: многочлен Р(х) при переходе
через точку а, меняет знак, если к, — нечетное число, и не
меняет знака, если к, — четное число. На этом рассуждении
и основан обобщенный метод интервалов: на числовую ось
наносятся числа аь о^, ..., а„_ ь а„; над лучом справа от
наибольшего из этих чисел, т.е. справа от а„, ставят знак
плюс, над следующим за ним справа налево интервалом
ставят знак плюс, если к„ — четное число, и знак минус,
если к„ — нечетное число; над следующим за ним справа
налево интервалом ставят знак, пользуясь правилом:
многочлен Р(х) при переходе через точку а„ _ ] меняет знак,
если к„ _ ] — нечетное число, и не меняет знака, если
к„ _ | — четное число; затем рассматривается следующий за
ним справа налево интервал, в нем ставят знак, пользуясь
тем же правилом; таким образом рассматриваются все
промежутки.
Решением неравенства A7) будет объединение всех про-
промежутков, в которых поставлен знак плюс.
Пример. Решить неравенство
(х + 5)Bх - ЗM (- х + 7K (Зх + 8J < 0.
A9)
Прежде всего, умножая это неравенство на I— Ш Ш ,
получим равносильное ему неравенство ^ '
х - 7K > 0. B0)
Для решения неравенства B0) применим обобщенный
метод интервалов. На числовой оси отметим числа (— 5),
(— |\ |, 7 (рис. 15). Справа от наибольшего числа, т.е. от
числа 7, ставим знак плюс. При переходе через точку G)
многочлен
Р(х) = [х - (- 5)][x-(-ftf (х-фх - 7K B1)
меняет знак, так как двучлен (х — 7) содержится в произ-
произведении B1) в нечетной степени, поэтому под интервалом
|, 71 ставим знак минус. При переходе через точку Г|
многочлен Р(х) меняет знак, так как двучлен (х — | ] содер-
Рис. 15.
жится в произведении B1) в нечетной степени, поэтому
над интервалом [ — |, |"| ставим знак плюс. При переходе
через точку J — | Р(х) не меняет знака, так как двучлен
Гх— [ — | ]1 содержится в произведении B1) в четной сте-
пени, поэтому над интервалом — 5, — | ставим знак
плюс. Наконец, при переходе через точку (— 5) многочлен
Р(х) меняет знак, так как двучлен [х — (— 5)] содержится
в произведении B1) в первой степени, поэтому под лучом
(— оо, — 5) ставим знак минус. Итак, решение неравенства
B0) и равносильного ему неравенства A9) — совокупность
всех промежутков, где поставлен знак плюс, т.е. множество
всех решений неравенства A9) есть множество
Нестрогие неравенства. Перейдем теперь к решению не-
нестрогих неравенств
0, B2)
Р(х)?0. B3)
Если некоторое число % есть решение неравенства B2), то
справедливо числовое неравенство Р(хо) > 0. Тогда в силу
определения нестрогого знака неравенства справедливо
или числовое равенство Pix^) = 0 или числовое неравенство
Р(хо) > 0. Другими словами, если число х<, — решение не-
неравенства B2), то оно либо решение уравнения Р{х) = 0,
либо неравенства Р(х) > 0. Такое рассуждение можно про-
провести для любого решения неравенства Р(х) ? 0. Аналогич-
Аналогично показывается, что любое решение неравенства Р(х) > 0
и любое решение уравнения Р(х) = 0 также есть решение
неравенства B2).
Таким образом, множество решений нестрогого нера-
неравенства B2) является объединением двух множеств: мно-
множества всех решений строгого неравенства Р{х) > 0 и мно-
множества всех решений уравнения F\x) — 0.
Аналогично множество всех решений нестрогого нера-
неравенства B3) является объединением двух множеств, мно-
множества всех решений строгого неравенства Р{х) < 0 и мно-
множества всех решений уравнения Р{х) = 0.
На этом и основано правило решения нестрогих нера-
неравенств. Сначала решаются соответствующее строгое нера-
неравенство и соответствующее уравнение, а затем множества
решений строгого неравенства и уравнения объединяются;
объединение этих множеств и является множеством всех
решений нестрогого неравенства.
Примеры. I. Решим нестрогое неравенство первой
степени:
:+a,>0 (ao*O). B4)
Решаем сначала уравнение
Его единственное решение — число I — — |. Затем решаем
неравенство
а&+ах >0 (ао*О). B6)
f74
При Oq > О множество всех его решений — множество
( -, +то|, при а0 < О множество всех его решений —
множество [—«•,— — I; объединяя решения уравнения B5)
I °о I
и неравенства B6), получаем: для oq > 0 множество всех
решений неравенства B4) есть множество — —, +«>]
L "" J
(рис. 16); для пц < О множество всех решений неравенства
B4) есть множество (— «>, — — (рис. 17).
I а°1
-а/а0 х —а/а0 х
Рис. 16. Рис. 17.
2. Решить неравенство
(х2 - Ъх + 2)(>? - 3^D - х2) > 0. B7)
Поскольку справедливы следующие тождественные равен-
равенства
х2-Зх+2 = (х-2)(х-1),
х3 - Ъх1 = х2 (х - 3),
4 - х2 = - (х - 2)(х + 2),
то согласно утвержцениям 4 и 36) этого параграфа неравен-
неравенство B7) равносильно неравенству
[х - (- 2)] х1 (х - 1)(х - 2J (х - 3) < 0. B8)
Решим сначала уравнение
[х - (- 2)] х2 (х - 1)(х - 2J (х - 3) = 0. B9)
Оно имеет только пять корней: хх = — 2, х2 = 0, х3 = 1, х4 =
= 2, хъ = 3. Затем решаем строгое неравенство
[х - (- 2)] х2 (х - 1)(х - 2I (х - 3) < 0. C0)
ш
обобщенным методом интервалов (рис. 18). Множеством
всех его решений будет множество (— <*>; — 2) и A; 2) и B;
3). Объединяя множество всех решении уравнения B9) и
строгого неравенства C0), получим множество всех реше-
решений неравенства B8), а в силу равносильного перехода —
неравенства B7).
Итак, множество всех решений неравенства B7) есть
множество (— оо, — 2] и {0} и [1; 3].
§ 3. Уравнения с двумя неизвестными
Основные понятия. Пусть дано уравнение
R(x, У) = (Кх, у), A)
где R(x, у), Q(x, у) — многочлены (см. § 3 гл. II) относи-
относительно двух букв хиу. Тогда говорят, что дано алгебраичес-
алгебраическое уравнение с двумя неизвестными хиу. Упорядоченная
пара (х, у) называется набором неизвестных уравнения A).
ОДЗ уравнения A) является множество всех пар (х, у), где
буквы xvi у могут быть любыми действительными числами.
Числовой набор (xq, у0) соответствующий набору неиз-
неизвестных (х, у) называется решением уравнения A), если
равны числовые значения многочленов R и Q, соответст-
соответствующие этому числовому набору, т.е. если справедливо
числовое равенство R(xq, у0) = Q(xo, у0). Решить уравнение
A) — значит найти множество всех его решений, т.е. найти
все числовые наборы, каждый из которых обращает урав-
уравнение A) в верное числовое равенство. Если множество
всех решений уравнения A) состоит из к пар (среди кото-
которых нет равных) действительных чисел (хь ух); (Хг, у2)', —
••• ;(*ь Ук)> то говорят, что уравнение A) имеет только к
решений, т.е. множество всех решений есть множество
М= {(хь ух)\ (*2, Уг)\ — ; (*ь Ук)}- Если же множество всех
решений состоит из одной пары (хи у,), то говорят, что
уравнение A) имеет единственное решение. Например, урав-
уравнение х2 + у2 = 0 имеет единственное решение (х, у): (О, 0).
В случае, если множество всех решений уравнения A) есть
пустое множество, говорят, что уравнение A) не имеет
решений. Например, уравнение х2 + у2 = — 1 не имеет ре-
решений.
Пусть даны два алгебраических уравнения с двумя неиз-
неизвестными:
R(x, у) = Q(x, у) и Цх,у) = S(x, у).
Эти уравнения называются равносильными, если любое ре-
решение первого уравнения является решением второго урав-
уравнения и любое решение второго уравнения является реше-
решением первого уравнения. В силу этого определения равно-
равносильны любые два уравнения, не имеющие решении.
Замена одного уравнения равносильным ему другим
уравнением называется равносильным переходом от первого
уравнения ко второму.
Справедливы следующие утверждения:
1. Уравнения R(x, у) = Q(x, у) и R(x, у) — Q(x, y) = 0
равносильны.
2. Уравнения R(x, у) = 0(х, у) и R(xy у) + S(x, у) = Q(x, у) +
+ S(x, у), где S(x, у) — любой многочлен относительно букв
хиу, — равносильны.
3. Уравнения R(x, у) = Q(x, у) и aR(x, у) = aQ(x, у) равно-
равносильны для любого, отличного от нуля действительного
числа а.
4. Пусть известно, что справедливо тождественное равен-
равенство R(x, у) = 7\х, у), тогда уравнения R(x, у) = Q(x, у) и
7\х, у) = Q(x, у) равносильны.
Справедливость этих утверждений доказывается анало-
аналогично доказательству соответствующих утверждений § 1 и
потому опускается. Из утверждений 1 и 4 вытекает, что
каждое алгебраическое уравнение с двумя неизвестными х
и у можно привести к виду Р(х, у) = 0, поэтому можно
рассматривать лишь уравнения вида
Pix, у) = О, B)
где Р(х, у) — многочлен относительно букв х и у. Для
геометрической иллюстрации множества всех решений
уравнения B) целесообразно ввести систему координат на
плоскости.
Прямоугольная система координат на плоскости. Если
указан способ, позволяющий устанавливать положение
точек на плоскости заданием пар чисел, то говорят, что на
плоскости задана система координат. Плоскость в этом
случае называют координатной плоскостью. Рассмотрим
простейшую и чаще всего употребляемую систему коорди-
координат, которая называется прямоугольной.
Пусть дан отрезок, длина которого принята за единицу
измерения длины на плоскости, т.е. пусть введен масштаб.
Пусть даны две взаимно перпендикулярные прямые. Точку
пересечения прямых будем считать началом отсчета или
началом координат. На каждой прямой зададим положи-
положительное направление и отложим от начала координат за-
заданный единичный отрезок. Таким образом, на каждой
этой прямой введена своя система координат (см. § 5 гл. I);
эти прямые называют координатными прямыми, их часто
называют еще координатными осями, причем одну из них
принято называть осью абсцисс, а другую — осью ординат.
Если на плоскости введен масштаб и заданы две взаимно
перпендикулярные координатные оси и указано, какая из
этих осей является осью абсцисс, а какая осью ординат, то
говорят, что на плоскости задана прямоугольная система
координат.
Обозначим начало координат буквой О, ось абсцисс —
буквами Ох и ось ординат — буквами Оу. На рисунках
координатные оси обычно располагаются так, чтобы ось
абсцисс была горизонтальной* и ее положительная полуось
направлена вправо, а положительная полуось ординат —
вверх (рис. 19).
178
М(а,Ь)
t
N(a,O)
A,0)
Рис. 19.
Пусть М — любая точка координатной плоскости. Про-
Проведем через точку М прямые, параллельные координатным
осям. Пусть прямая, проходящая через точку М и парал-
параллельная оси Оу, пересечет ось
абсцисс в точке N, а прямая,
проходящая через точку М,
параллельная оси Ох, пересе-
пересечет ось ординат в точке L (см.
рис. 19). Так как на осях зада-
заданы системы координат, то
точка N имеет в системе ко-
координат на оси абсцисс коор-
координату а, точка L имеет в
своей системе координат на
оси ординат координату Ь.
Тогда координатами точки М
в выбранной системе коорди-
координат с осями Ох и Оу называют упорядоченную пару чисел
(а, Ь). Число а называется первой координатой, или абс-
абсциссой точки М, число Ъ называется второй координатой,
или ординатой точки М. Тот факт, что точка М имеет
абсциссу а и ординату Ъ записывается так: М(а, Ь) (при этом
сначала пишется абсцисса, затем ордината точки М).
Часто, когда рассматриваются несколько разных фикси-
фиксированных точек координатной плоскости, их обозначают
некоторой заглавной буквой с разными номерами, напри-
например, Ми М2, ..., М„, ... Координаты этих точек помечаются
соответствующими номерами: Мх{хх, ух), М2(х2, у2), ...
... М„(хя, уя), ...
Так как через любую точку плоскости можно провести
только одну прямую, параллельную данной оси координат,
а каждая такая прямая пересечет соответствующую перпен-
перпендикулярную ей ось только в одной точке, то каждой точке
координатной плоскости соответствует только одна упоря-
упорядоченная пара чисел — координаты этой точки.
Между точками, лежащими на любой оси, и множеством
действительных чисел имеется взаимно однозначное соот-
соответствие (см. гл. I), следовательно, разным точкам плос-
плоскости хОу будут соответствовать разные упорядоченные
179
пары действительных чисел. Итак, если на плоскости зада-
задана прямоугольная система координат хОу, то между мно-
множеством точек на плоскости и множеством упорядоченных
пар действительных чисел существует следующее соот-
соответствие:
1. Каждой точке плоскости соответствует одна упорядо-
упорядоченная пара действительных чисел.
2. Двум разным точкам плоскости соответствуют разные
упорядоченные пары действительных чисел.
3. Нет ни одной упорядоченной пары действительных
чисел, которая бы не соответствовала какой-нибудь точки
плоскости.
Такое соответствие называется взаимно однозначным со-
соответствием. Таким образом, введение на плоскости пря-
прямоугольной системы координат позволяет установить вза-
взаимно однозначное соответствие между множеством всех
точек плоскости и множеством упорядоченных пар дейст-
действительных чисел. Это соответствие дает возможность сво-
сводить изучение множества точек плоскости к изучению
множества пар действительных чисел, т.е. применять к
изучению вопросов геометрии алгебраические методы.
Сделаем несколько замечаний:
1. Абсцисса точки М равна нулю тогда и только тогда,
когда точка М лежит на оси Оу.
2. Ордината точки М равна нулю тогда и только тогда,
когда точка М лежит на оси Ох.
3. Точка О — начало координат (и только она) имеет обе
координаты, равные нулю.
4. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет положительную ординату (у > 0),
называется верхней полуплоскостью.
5. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет отрицательную ординату (у < 0),
называется нижней полуплоскостью.
6. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет положительную абсциссу (х > 0),
называется правой полуплоскостью.
180
7. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет отрицательную абсциссу (х < 0),
называется левой полуплоскостью.
8. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет положительную абсциссу (х > 0)
и положительную ординату (у > 0), называется первой ко-
координатной четвертью.
9. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет положительную ординату (у > 0)
и отрицательную абсциссу (х < 0), называется второй коор-
координатной четвертью.
10. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет отрицательную абсциссу (х < 0)
и отрицательную ординату (у < 0), называется третьей
координатной четвертью.
11. Множество всех точек координатной плоскости, каж-
каждая точка которого имеет отрицательную ординату (у < 0)
и положительную абсциссу (х > 0), называется четвертой
координатной четвертью.
12. Две точки M,(xi, у{)
@,1)
и М2(х2, у2) называются
симметричными относи-
относительно оси ординат, если
их координаты таковы, . т п , т
у 1^м **/ С/ \XjfWj X
что х, = — х2 и у, = у2 (рис. у1=у1 и Х=-Хз
20); симметричными отно-
сительно оси абсцисс, если с"
их координаты таковы,
чтох! = Хг и ух = — у2 (рис. 21); симметричными относитель-
относительно начала координат, если их координаты таковы, что
Xi = - Xj и у{ = — у2 (рис. 22).
Теорема 1. При любом расположении двух точек Мх(х\,
У\) и М2(х2, у2) на координатной плоскости квадрат рассто-
расстояния между ними (т.е. квадрат длины отрезка М\М2) опре-
определяется формулой а2 = (Хг — XiJ + (у2 — у{J, т.е. квадрат
расстояния между двумя любыми точками координатной
плоскости равен сумме квадратов разностей одноименных
координат.
>И1
181
Доказательство. Пусть даны две несовпадающие
точки М\(х\, у\) и М2(х2, у2). Прямая МХМ2 может быть:
а) параллельна оси Оу (или совпадать с ней);
б) параллельна оси Ох (или совпадать с ней);
ky
(х„0)
(х2,0)
@,У)
ЬУ
(о,у)
@,1)
(х»0)
0 х
х,=х2
1.
@,1)
О (х„0) х
Рис. 21.
Рис. 22.
в) не параллельна ни оси Оу, ни оси Ох. Доказательство
теоремы проведем для каждого из этих случаев отдельно.
а) Пусть прямая, на которой лежат точки М\(х\, У\) и
М2(х2, у2), параллельна оси Оу (или совпадает с ней). Тогда
у любой точки, лежащей на этой прямой, одна и та же
абсцисса, т.е. у точек Mj и М2 одинаковые абсциссы: jcj =
= Хг = т (рис. 23).
Эта прямая может быть рассмотрена как ось с положи-
положительным направлением вверх, с тем же самым единичным
отрезком, что и для системы координат хОу, и началом в
точке (т, 0). Координата любой точки этой оси будет
совпадать с ординатой той же точки, рассматриваемой как
точка плоскости. Согласно теореме 1 (§ 5 гл. I) расстояние
между точками Мх и М2, как точками этой координатной
прямой, равно d = y2 — У\, откуда
(Уг ~ Ух?-
182
б) Пусть прямая, на которой лежат точки Мх и Мъ
параллельна оси Ох (или совпадает с ней). Тогда у любой
точки, лежащей на этой прямой, одна и та же ордината,
т.е. у точек Мх и М2 одинаковые ординаты: ух = у2 — п
(рис. 24).
@,у)
@,1)
О
М/х„у,)
(т,0)
Рис. 23.
У>
(х„0)
М/х„у,)
@,1)
0 (x»0)
d
X
Q(O,n) M/x»yz
Рис. 24.
Эта прямая может быть рассмотрена как ось с положи-
положительным направлением вверх, с тем же самым единичным
отрезком, что и для систе-
системы координат хОу, и нача-
началом в точке @, л). Коорди-
Координата любой точки этой оси
будет совпадать с абсциссой
той же точки, как точки
плоскости. Согласно теоре- dMJC
ме 1 (§ 5 гл. I) расстояние
между точками Мх и Мъ как
точками этой координатной
прямой, равно d= X2 — Х\,
откуда
Рис. 25.
= \x2-xi\2 = (х2 - Xi)
2 + 0 =
- XiJ + (я - иJ
(У2 -
ш
в) Пусть теперь точки A/j и М2 не лежат ни на прямой,
параллельной оси ординат, ни на прямой, параллельной
оси абсцисс. Тогда одноименные координаты этих точек
будут разные числа, т.е. х, * Хг и ух ф уг (рис. 25). Проведем
через точку Л/, прямую, параллельную оси абсцисс, а через
точку М2 — прямую, параллельную оси ординат. Эти пря-
прямые пересекутся в точке К(х2, ух). Точка Мх и точка Улежат
на прямой, параллельной оси абсцисс, следовательно, как
было установлено в случае б), расстояние между этими
точками (длина отрезка МХК) равно dMiK=\x2 — х,|.
Точка М2 и точка Улежат на прямой, параллельной оси
ординат, следовательно, как было установлено в случае а),
расстояние между этими точками (длина отрезка М2К)
равно dMjK = \у2 — У\\. Так как треугольник МХКМ2 — пря-
прямоугольный, то по теореме Пифагора <? = а\^ + а\^к -
= \х2 — Xi\2 + \у2 — У\\2. На основании свойств абсолютной
величины получим
Теорема доказана полностью.
Следствие. Расстояние d между двумя любыми точками
М\(Х\, У\) и М2(х2, у2) на координатной плоскости определя-
определяется по формуле
Пример. Найти расстояние */межцу точками Л/,(— 3, — 2)
и М2(- 2, 1).
d= V[- 2 - (- З)]2 + [1 - (- 2)]' = Ш.
Геометрическая иллюстрация множества решений. Непус-
Непустое множество всех тех точек координатной плоскости,
координаты х и у каждой из которых являются решением
уравнения B): Р(х, у) = 0 есть некоторая фигура G. Говорят,
что уравнение Р(х, у) = 0 задает фигуру G или что оно
является уравнением фигуры G, если выполнены два сле-
следующих условия:
184
1. Координаты каждой точки M0(xq, у0) фигуры G явля-
являются решением уравнения Р(х, у) = О, т.е. удовлетворяет
числовому равенству 1\щ, у0) = 0.
2. Любому решению уравнения Р(х, у) = 0, т.е. любой
паре чисел (х,, у{), удовлетворяющей числовому равенству
Д*1> У1) = 0» соответствует на координатной плоскости
точка Mi(xi, y{), принадлежащая фигуре G.
Приведем некоторые примеры.
1. Пусть дано уравнение
(х-аJ + (у-ЬJ = #. C)
Покажем, что на координатной плоскости это уравнение
является уравнением окружности радиуса R с центром в
точке С(а, Ь).
Действительно, возьмем любую точку Мо с координатами
Xq и уо, лежащую на данной окружности. По определению
окружности расстояние от точки Мо до центра окружнос-
окружности — точки С — равно R. Используя следствие из теоре-
теоремы 1, получим, что R = V(xo — аJ + (у0 — bf. Из этого чис-
числового равенства вытекает числовое равенство
R2 = (яо - аJ + (у0 - ЬJ.
Следовательно, каждая точка, лежащая на данной ок-
окружности, имеет координаты, являющиеся решением урав-
уравнения C).
Возьмем теперь любое решение уравнения C), т.е. возь-
возьмем любую пару чисел \хи У\), такую, что справедливо
числовое равенство
(х, - аJ + (у, - bf = R2.
Это числовое равенство равносильно числовому равенству
Упорядоченной паре чисел (х{, у{) соответствует на коор-
координатной плоскости точка М\(хх, ух), причем из справедли-
вости числового равенства Vfo — аJ + (у, — bf =\R\ = R
следует, что точка A/j(xb yx) лежит на окружности радиуса
R с центром в точке С(а, Ь).
Значит, действительно, уравнение C) является уравне-
уравнением окружности радиуса R с центром в точке С(а, Ь)
(рис. 26). Пусть на координатной плоскости дана окруж-
@,1)
А(а,О)
M/a.yJ
I
Рис. 27.
О
I. х-а=О
ность радиуса г с центром в точке (а, р). Рассуждая анало-
аналогично, можно показать, что уравнение
есть уравнение этой окружности.
Итак, на координатной плоскости каждое уравнение
вида C) есть уравнение некоторой окружности, а каждая
окружность задается некоторым уравнением вида C).
Поэтому, говоря, что на координатной плоскости дана
окружность, имеют в виду, что дано уравнение этой окруж-
окружности, т.е. что дано уравнение вида C).
2. Пусть дано уравнение
х— д =
D)
Покажем, что на координатной плоскости это уравнение
является уравнением прямой, параллельной оси ординат и
проходящей через точку А(а, 0).
Действительно, возьмем любую точку Мо, лежащую на
этой прямой. Тогда абсцисса этой точки есть число Xq = a,
а ордината у0 есть какое-то фиксированное действительное
число.
Очевидно, что эти координаты д^и^о являются решени-
решением уравнения D), т.е. координаты любой точки, лежащей
на прямой, параллельной оси ординат и проходящей через
точку А(а, 0) являются решением уравнения D).
Возьмем теперь любое решение уравнения D), т.е. возь-
возьмем любую пару чисел (лгь ух), такую, что она удовлетворяет
числовому равенству х, — а = 0. Другими словами, возьмем
любую пару чисел (а, у^, где ух — любое фиксированное
действительное число.
Легко видеть, что точка М}(а, у}) лежит на прямой,
параллельной оси ординат и проходящей через точку
А(а, 0) (рис. 27). Значит, действительно, уравнение D)
является уравнением прямой, параллельной оси ординат.
Пусть на координатной плоскости дана прямая, парал-
параллельная оси ординат и проходящая через точку D(d, 0).
Рассуждая аналогично, можно показать, что уравнение
х — d= 0 является уравнением этой прямой.
Итак, на координатной плоскости каждое уравнение
вида D) есть уравнение некоторой прямой, параллельной
оси ординат, а прямая, параллельная оси ординат, задается
некоторым уравнением вида D).
Поэтому, говоря, что на координатной плоскости дана
прямая, параллельная оси ординат, имеют в виду, что дано
уравнение этой прямой, т.е. дано уравнение вида D).
3. Рассуждая аналогично, можно показать, что на коор-
координатной плоскости каждое уравнение вида
у-Ь = 0 E)
есть уравнение некоторой прямой, параллельной оси абс-
абсцисс (рис. 28), а каждая прямая, параллельная оси абсцисс,
задается некоторым уравнением вида E).
Поэтому, говоря, что на координатной плоскости дана
прямая, параллельная оси абсцисс, имеют в виду, что дано
уравнение этой прямой, т.е. дано уравнение вида E).
4. Пусть дано уравнение
у = кх+Ь, F)
где к ф 0.
W
В главе VI будет показано, что на координатной плос-
плоскости это уравнение является уравнением прямой, прохо-
проходящей через точку М@, Ь) и образующей с положительным
направлением оси Ох угол, тангенс которого равен к
(рис. 29).
О
@,Ъ)
A,0) х
I. у-Ъ=О
Рис. 28.
A,0) х
I. y=kx+b, где k=tg q>
Рис. 29.
Пусть на координатной плоскости дана прямая, прохо-
проходящая через точку Л/@, b^) и образующая с положительным
направлением оси Ох угол, тангенс которого равен ки где
кх ф 0; можно показать, что уравнение
у = кхх + h
является уравнением этой прямой.
Итак, на координатной плоскости каждое уравнение
вида F), где к * 0, есть уравнение прямой, не параллельной
ни одной из осей координат, а каждая прямая, не парал-
параллельная ни одной из осей координат, задается некоторым
уравнением вида F), где к*0.
Поэтому, говоря, что на координатной плоскости дана
прямая, не параллельная оси абсцисс и не параллельная
оси ординат, имеют в виду, что дано уравнение этой
прямой, т.е. дано уравнение вида F), где к* 0.
Уравнение первой степени. Уравнением первой степени с
двумя неизвестными называется уравнение вида
Ах+Ву+С=0,
где А2 + В1 * 0, или другими словами, где хотя бы один из
двух коэффициентов Аи В отличен от нуля.
Из вышеизложенного вытекает, что на координатной
плоскости каждое уравнение первой степени с двумя неиз-
неизвестными есть уравнение некоторой прямой, а каждая
прямая плоскости задается некоторым уравнением первой
степени с двумя неизвестными.
Действительно, пусть дано уравнение
Ах+Ву+С=0 (А2 + В2фО). G)
Если В = О, то учитывая, что АфО, уравнение G) равно-
равносильно уравнению
а выше показано, что это уравнение есть уравнение пря-
прямой. Если Вф О, то уравнение G) равносильно уравнению
а выше показано, что это уравнение есть уравнение пря-
прямой. Значит, действительно, уравнение G) является урав-
уравнением некоторой прямой. Кроме того, можно показать,
что если на координатной плоскости дана прямая, то она
задается некоторым уравнением вида G).
Поэтому, говоря, что на координатной плоскости дана
прямая, имеют в виду, что дано уравнение этой прямой,
т.е. что дано некоторое уравнение первой степени с двумя
неизвестными. Поскольку через две несовпадающие точки
проходит единственная прямая, то для того чтобы задать
прямую, достаточно задать две несовпадающие точки, ле-
лежащие на этой прямой.
Значит, если известны координаты двух несовпадающих
точек, лежащих на этой прямой, то можно написать урав-
уравнение этой прямой.
Пример. Написать уравнение прямой, проходящей
через начало координат и через точку М(р, д), где р2 + д2 ф
ф 0. Если р = 0, то очевидно, что эта прямая есть ось
ординат и ее уравнение есть х = 0.
Если q = О, то очевидно, что эта прямая есть ось абсцисс
и ее уравнение есть у = 0.
Если q ф 0 и р ф 0, то как указано выше, уравнение этой
прямой есть уравнение вида G), где А, В, С — некоторые
фиксированные числа, причем А1 + В7 ф 0.
Найдем эти числа, используя условие, что две точки
0@, 0) и М(р, q) лежат на этой прямой.
Так как прямая проходит через начало координат, то
пара @, 0) должна являться решением уравнения G), а это
возможно только если С = 0. Ясно, что ВфО, т.к. если бы
коэффициент В был равен нулю, то уравнение G) имело
бы вид Ах = 0, т.е. было бы уравнением оси ординат (А ф 0,
т.к. А2 + В2 ф 0), что противоречит условию р ф 0. Так как
В ф 0, то уравнение G) равносильно уравнению
у = кх,
где к = — jj. Так как прямая проходит через точку (р, q), то
справедливо числовое равенство
q = kp.
Следовательно, к = & и уравнение прямой, проходящей
через начало координат и через точку М(р, q), не лежащую
ни на одной оси координат, имеет вид
Совокупность уравнений. Пусть даны многочлены Р{(х, у),
Р2(х, у), ..., Р„(х, у) относительно букв хиу.
Говорят, что дана совокупность т алгебраических уравне-
уравнений с двумя неизвестными
Л(х, У) = 0, Р2(х, у) = 0, ..., Рт(х, у) = 0, (8)
если требуется найти все пары чисел (х, у), каждая из
которых является решением хотя бы одного уравнения из
совокупности (8), и которая называется решением сово-
совокупности (8). Таким образом, решить совокупность урав-
190
нений (8) — это значит решить каждое уравнение совокуп-
совокупности, т.е. найти множества Ми Мъ ..., Мт, где Mt —
множество всех решений уравнения Pfa, у) = О, а затем
найти множество Мо, являющееся объединением всех этих
множеств: Мо = Мх и М2 и ... и М„. Множество Мо и будет
множеством всех решений совокупности уравнений (8).
Уравнение A) равносильно совокупности уравнений (8),
если любое решение уравнения A) является решением
совокупности уравнений (8), а любое решение совокупнос-
совокупности уравнений (8) является решением уравнения A), иными
словами, если множества всех решений совпадают. Замена
уравнения A) равносильной совокупностью уравнений (8)
называется равносильным переходом от уравнения A) к
совокупности уравнений (8).
Часто с помощью таких равносильных переходов к со-
совокупности уравнений удается решить исходное уравнение.
Например, пусть требуется найти все корни уравнения
х2 - у2 = 0. (9)
Воспользуемся формулой сокращенного умножения (см.
гл. II) х2 — у1 = (х — у)(х + у). Тогда по утверждению 4
получим уравнение A0), равносильное уравнению (9):
(х-у)(х + у) = 0. A0)
Уравнение A0), как легко видеть, равносильно следую-
следующей совокупности уравнений:
х-у = 0, х + у = 0. A1)
Множество всех решений первого уравнения совокуп-
совокупности есть множество всех пар (/, /), где / — любое дейст-
действительное число: Мх = {(/, /) | / е R}. Множество всех реше-
решений второго уравнения совокупности есть множество всех
пар (q, — ф, где q — любое действительное число: М2 =
= i(q> — q) I q ^ ^}- Таким образом, множество всех реше-
решений совокупности A), а значит и уравнения (9), есть
объединение этих множеств М = Мх и Мъ т.е. М = {(/, /) |
\teR;(q,-q)\qeR}.
а 41
191
Рис. 30.
Как было показано
выше, каждое из урав-
уравнений совокупности
A1) есть уравнение
прямой. Поэтому фи-
фигура, задаваемая урав-
уравнением (9), представ-
представляет собой две пря-
прямые; причем легко ви-
видеть, что эти прямые
проходят через начало
координат и являются биссектрисами координатных углов
(рис. 30).
§ 4. Системы уравнений
Система двух уравнений с двумя неизвестными. Пусть
даны многочлены Р(х, у), Qix, у) относительно букв х и у.
Говорят, что дана система двух алгебраических уравнений
с двумя неизвестными хи^
\Дх, у) = О,
у)=о,
A)
если требуется найти числовые наборы, соответствующие
набору неизвестных (х, у), каждый из которых является
решением каждого из уравнений системы A), т.е. если
требуется найти все такие числовые наборы неизвестных
(х, у), при подстановке каждого из которых в оба уравнения
системы A) последние обращались бы в верные числовые
равенства. Каждый такой числовой набор называется ре-
решением системы A) (уравнения системы обычно записыва-
записываются в столбик, слева от которого пишется фигурная
скобка).
Решить систему уравнений A), это значит найти множе-
множество всех решений данной системы. Следует отметить, что
это множество является пересечением двух множеств: мно-
множества всех решений первого уравнения системы и множе-
множества всех решений второго уравнения системы. Рассмотрим
192
еще одну систему двух алгебраических уравнений с двумя
неизвестными:
JR(x,y) = 0,
[Sfr У) = О, U)
где R(x, у), S(x, у) — многочлены относительно букв хну.
Две системы алгебраических уравнений A) и B) называют-
называются равносильными, если любое решение первой системы
является решением второй системы и любое решение вто-
второй системы является решением первой системы. Другими
словами, системы A) и B) равносильны, если множества
их решений совпадают. Из определения следует, что две
системы равносильны, если множества их решений пусты.
Говорят, что дана совокупность к систем двух алгебраи-
алгебраических уравнений с двумя неизвестными:
jPl(x,y) = 0, jP2(x,y) = 0,..., {Рк(х,у) = О,
) = 0, \Q2(x,y) = 0,..., \Qk(x,y) = 0, V}
где Pi(x, у), Р2(х, у), ..., Рк(х, у), 0,(х, у), Q2(x, у), ...
••• Qkix, у) — многочлены относительно букв х и у, если
требуется найти все числовые наборы, каждый из которых
является решением хотя бы одной из систем уравнений
совокупности C). Каждый такой набор является решением
совокупности систем уравнений C).
Система уравнений A) равносильна совокупности систем
уравнений C), если любое решение системы уравнений A)
является решением совокупности систем уравнений C), а
любое решение совокупности систем уравнений C) явля-
является решением системы уравнений A).
Приведем некоторые утверждения о равносильности
систем уравнений:
1. л'ели изменить порядок следования уравнений системы
A), то полученная система равносильна системе A).
2. Если одно из уравнений системы A) заменить на равно-
равносильное уравнение, то полученная система равносильна сис-
системе A).
7 Алгебра, тригонометрия Л &\ '
и элементарные функции
3. Пусть в системе уравнений с неизвестными х и у одно
из уравнений записано в виде, где в левой части стоит одно
из неизвестных, например х, в первой степени, а в правой
части многочлен относительно у. Тогда говорят, что неиз-
неизвестное х выражено через другое неизвестное у. Если неиз-
неизвестное х выражено из первого уравнения системы A), то,
подставив в другое уравнение системы A) вместо х этот
многочлен от у, получим равносильную систему уравнений, т.е.
равносильны следующие системы:
jx = R(y), jx=R(y),
\ах,у) = 0, И \Q[R(y),y]=0.
Заметим, что второе уравнение Q[R(y), у] = О является
уравнением с одним неизвестным, и поэтому для нахожде-
нахождения его решений можно применить способы, рассмотрен-
рассмотренные в § 1.
4. Если первое уравнение системы A) заменить уравнением,
равным сумме первого уравнения, умноженного на некоторое
действительное число Р ф О, и второго уравнения, умножен-
умноженного на некоторое действительное число а, то полученная
система уравнений равносильна системе уравнений A), т.е.
при любых действительных р * О и а следующие системы
уравнений равносильны:
\Р(х,у) = 0,
\(Кх,у) = 0,
В качестве следствия утверждения 4 имеем утверждение:
5. Если первое уравнение системы A) заменить на сумму
(или разность) первого и второго уравнений системы, то
полученная система уравнений будет равносильна системе
уравнений A).
6. Если первое уравнение системы A) равносильно совокуп-
совокупности уравнений Рх{х, у) = 0, Р2(х, у) = 0, ..., Рк(х, у) = 0, то
система A) равносильна следующей совокупности к систем
уравнений:
= 0, \Q(x,y) = 0,..., \&х,у) = о'. D)
Если и уравнение Q(x, у) = 0, равносильно совокупности
т уравнений Qx(x, у) = 0, Q2(x, у) = 0, ..., Qm(x, у) = 0, то к
каждой системе совокупности D) применимо утвержде-
утверждение 6 и каждая система совокупности D) может быть
заменена своей совокупностью т систем.
Доказательство всех этих утверждений опускается.
Рассмотрим применение этих утверждений при решении
систем уравнений.
Система двух уравнений первой степени с двумя неизвест-
неизвестными. Рассмотрим систему двух уравнений первой степени
с двумя неизвестными:
E)
те ($ + Ь^фО и (% + Ь\ф0, другими словами, где хотя бы
один из двух коэффициентов ах и bu а также хотя бы один
из двух коэффициентов а2 и Ь2 отличны от нуля (в против-
противном случае по крайней мере один из многочленов ахх +
+ Ъуу + сх или fljX + ЬгУ + с2 не был бы многочленом первой
степени ни относительно неизвестного х, ни относительно
неизвестного у).
Каждое из двух уравнений системы E) (как было пока-
показано в § 3) является уравнением прямой на координатной
плоскости. Как известно, две прямые на плоскости могут
либо пересекаться в одной точке, либо совпадать, либо
быть параллельными, но не совпадающими. Следователь-
Следовательно, и при нахождении всех решений системы уравнений
E) могут возникнуть эти ситуации.
Рассмотрим их на примерах.
1. Пусть дана система уравнений
Система F), как легко видеть, равносильна системе
]*+>>+1=0.
G)
Используя утверждение 3, перейдем от системы G) к сис-
системе
\х=у,
\у+у + 1 = 0,
(8)
ей равносильной.
Второе уравнение системы (8) есть уравнение первой
степени с одним неизвестным и имеет единственное реше-
решение У\ — — 4. Следовательно, система (8), а значит и
. 2х+2у+2=0
I
Рис. 31.
равносильная ей система F) имеет единственное решение
(хи Ух): \ — \— j\ Точка с этими координатами является
точкой пересечения прямых задаваемых уравнениями F)
(рис. 31).
2. Пусть дана система уравнений
(9)
1=0,
\2х+2у + 2 = 0.
Разделив левую и правую части второго уравнения на 2,
перейдем к системе
\х+у+ 1=0,
\х + у+1=0,
A0)
равносильной исходной системе (9).
Система A0) состоит из двух одинаковых уравнений, что
соответствует двум совпавшим прямым на координатной
плоскости (рис. 32). Очевидно, что множество всех реше-
решений системы A0), а значит и равносильной ей системы (9)
есть множество всех пар вида (f, — 1 — f). где t — любое
действительное число.
3. Пусть дана система уравнений
(И)
\2к+2у+1=0.
Перейдем к равносильной ей системе
A2)
Воспользовавшись утверждением «3, получим систему
X— v
A3)
равносильную системе A2).
Второе уравнение
системы A3) равно-
равносильно числовому ра-
равенству 1 = 0, кото-
которое не верно. Следо-
Следовательно, система
A3), а значит и сис-
система A1) не имеют
решений, что соот-
соответствует двум не со-
совпадающим, но па-
параллельным прямым
на координатной
плоскости (рис. 33).
Способ решения систем уравнений F), (9) и A1), осно-
основанный на утверждении 3, называется способом подстанов-
подстановки или способом исключения неизвестного.
Рис. 33.
т
Рассмотрим его применение на более сложном примере,
когда одно из уравнений системы не является уравнением
первой степени:
ах + Ьу+с =
A4)
Рассмотрим случай, когда Ь = 0. Тогда первое уравнение
системы A4) есть уравнение прямой, параллельной оси
ординат. Второе уравнение системы A4) есть уравнение
окружности единичного радиуса с центром в начале коор-
координат. Применив метод подстановки (а ф О, так как Ъ = 0),
получим систему
х=—-
A5)
= 1,
равносильную исходной системе A4). Второе уравнение
системы A5) является квадратным уравнением. Если 1 —
— ^ < 0, то это уравнение не имеет корней и, следователь-
а
II
III. х=-| где |<-7
Рис.34.
но, система A5) и равносильная ей система A4) не имеют
решений. Это соответствует ситуации, когда прямая х =
= — - не пересекает единичную окружность х2 + у2 = 1
^198
(рис. 34). На рис. 34 прямая х = — - изображена и в случае
а
— -1 > 1, и в случае — -1 < — 1 . Если 1 — ¦% = 0, то второе
\ а) \ а) ) о
уравнение системы A5) имеет единственное решение у = 0.
Система A5), а значит, и система A4) имеют при этом
единственное решение (хъ ух): (— ^, 0 ]. Геометрически это
соответствует случаю касания прямой единичной окруж-
окружности в точке [ — -, 0 ](рис. 35). На рис. 35 прямая х = — -
изображена и в случае (— ~а ]= 1, и в случае [ — - ]= — 1.1
Если 1 — •% > 0, то второе уравнение системы A5) имеет
а
только два корня ух=\\— ¦% и>»2 = — vl— •%. Следова-
а а
тельно, системы A5) и A4) имеют при этом только два
решения (х„ >>,), (х2, у2): - ^, N1 - -^ , - -^ - 41 - ^ .
Геометрически это соответствует пересечению единичной
окружности прямой х = — - в двух точках: — -, "VI — ¦%
и [ — -а, — Vl —41 (рис. 36). | На рис. 36 прямая х = — ~а
изображена в трех случаях: 1) 0< — ~а< 1, 2) Г— ^]=
Если b * 0, то из первого уравнения системы A4) можно
выразить неизвестное у. у= — тх ~ т ~ и аналогично
вышесказанному применить способ подстановки. При
этом возможны только три ситуации:
1. Система A4) не имеет решений, т.е. прямая и окруж-
окружность не имеют общих точек (см. рис. 34);
2. Система имеет единственное решение, т.е. прямая
является касательной к данной окружности (см. рис. 35);
8**9
3. Система имеет только два решения, т.е. прямая пере-
пересекает окружность только в двух точках (см. рис. 36).
II
III
A,0) х
L х'+У'!1 с
II. х=-д, где а =-1
///.*=-?, где ?=;
Рис. 35.
Проведение соответствующих выкладок в этом случае
предоставляется читателю.
II. х=--а, где (К-а<1
III. х=-с-, где 0>с->-1
1У.х=-с-а,где\=0
Рис. 36.
Способ линейного преобразования (способ базируется на
утверждении 4 и заключен в равносильной замене первого
уравнения системы другим уравнением, равным сумме
Ш
первого уравнения, умноженного на число р ф О, и второго
уравнения, умноженного на число а).
Рассмотрим применение этого способа на примере ре-
решения следующей системы уравнений:
Вычитая из первого уравнения второе, получим на основа-
основании утверждения 5 систему
равносильную системе A6). Первое уравнение системы A7)
имеет единственное решение ух = — 1. Подставив это зна-
значение ух во второе уравнение системы A7), получим, что
эта система, а значит и равносильная ей система A6) имеет
только два решения: A, — 2) и (— 1, — 2). Отметим, что
часто эти решения записываются в виде множества: М=
= {A, - 2); (-^ 1, - 2)}.
Способ замены системы уравнений совокупностью систем
уравнений (способ базируется на утверждении 6 о равно-
равносильности системы уравнений совокупности систем урав-
уравнений).
Рассмотрим применение этого способа на примере ре-
решения следующей системы уравнений:
Поскольку первое уравнение этой системы равносильно
совокупности уравнений
х — у = 0, х + у— 1 = 0,
то система A8) равносильна совокупности систем
jx-y = 0, jx + y-1=0,
\ 2 \ 2
Каждая из систем совокупности A9) легко решается спо-
способом подстановки. Первая система имеет только два ре-
решения: A,1); (— 2, — 2); вторая система тоже имеет только
два решения: —j—> —^— ; —^—, —j— . Следовательно,
система A8) имеет только четыре решения: A, 1);
(- 2, - 2); (itS, Ц^; (Ц* Щ. Рассмотрим еще
применение этого способа на примере решения системы
двух уравнений с двумя неизвестными, если одно из этих
уравнений будет однородным уравнением второй степени.
Уравнение ах2 + Ьху + су2 = 0 называется однородным урав-
уравнением второй степени. Итак, решим систему уравнений
[ах2 + Ьху+су2 = 0,
[1\х,у) = 0,
где Р(х, у) — многочлен относительно хну.
1. Пусть а = 0. Очевидно, что система B0) равносильна
совокупности систем
Гу = О, (Ьх+су = 0,
\1\х,у) = 0, \Р(х,у) = 0.
Каждую из этих систем можно решить способом подста-
подстановки.
2. Пусть а * 0. Применим к левой части первого уравне-
уравнения системы B0) тождественное преобразование «выделе-
«выделение полного квадрата»:
ах2 + Ьху + су2 = а (х2 + ±
где D= b2 — 4лс.
В случае, если D > 0, левая часть первого уравнения
системы B0) представляется в виде произведения
Ж
и поэтому система B0) равносильна совокупности систем
1а-у = 0> B2)
Каждую из этих систем можно решить способом подста-
подстановки. В случае, если D = 0, совокупность систем B2)
состоит из двух одинаковых систем уравнений, т.е. на
самом деле есть только одна система уравнений.
В случае, если D < 0, из равенства B1) вытекает, что
уравнение системы B0) имеет единственное решение (х,,
3>,): @, 0) — и поэтому остается проверить, удовлетворяет
ли это решение второму уравнению системы B0).
Решим следующую систему уравнений:
Где2 + ху + у2 =19,
\х2-ху+у2 = 7.
Применим сначала способ линейного преобразования сис-
системы: умножая первое уравнение на 7, а второе на 19 и
вычитая затем из второго уравнения первое, приходим к
системе уравнений
B4)
равносильной системе B3). Применим к левой части пер-
первого уравнения тождественное преобразование «выделение
полного квадрата»:
На основании этого тождественного преобразования и
утверждения 6 можно утверждать, что система уравнений
B4) равносильна совокупности систем уравнении:
х —iy=U, х —^- = 1
х2-ху + у2 = 7,
Решая каждую из этих систем способом подстановки,
получаем, что первая система имеет только два решения:
B; 3) и (— 2; — 3); и вторая система имеет только два
решения: C; 2) и (— 3; — 2). Следовательно, система B3)
имеет только четыре решения: B; 3); (— 2; — 3); C; 2);
(- 3; - 2).
Иногда для решения системы уравнений утверждение 6
надо применить не один раз, а несколько раз. Например,
так надо поступать при решении системы уравнений
де3 -у3=\9(х -
Перепишем эту систему в следующем равносильном
виде:
\(х + у)(х2-ху + у2-7) = 0.
На основании утверждения б эта система равносильна
совокупности систем
Гх — у = 0, М + ху + у2— 19 = 0,
{ (х2 -ху + У2 - 7) = 0, \(х + у) (х2
Применяя к каждой системе опять утверждение б, получим,
что исходная система уравнений B5) равносильна совокуп-
совокупности систем уравнений
\ xy yl9 0,
\x2-xy + y2-7 = 0.
Первые три системы легко решаются способом подстанов-
подстановки, а четвертая система уже была решена выше. Собирая
вместе решения всех этих систем, получаем, что исходная
система B5) имеет только девять решений: @, 0); (V7~, V7);
(- V7~, - V7); (- VI9", VI9); (VI9", - Vl9); B; 3); (- 2; - 3);
C; 2); (- 3; - 2).
Отметим, что обычно для решения системы приходится
применять несколько способов.
Системы уравнений с несколькими неизвестными. На прак-
практике приходится решать системы уравнений не только с
двумя неизвестными, но и с большим количеством неиз-
неизвестных: с тремя, четырьмя и т.д. Поэтому приведем соот-
соответствующие определения и рассмотрим необходимые для
решения таких систем утверждения.
Пусть надо решить уравнение
R(x, у, z, ..., 0 = (Кх, у, z /), B6)
где R(x, у, z,.-, 0 и Q(x, у, z,..., t) — многочлены (см. гл. II)
относительно букв х, у, z, ..., t. Тогда говорят, что дано
алгебраическое уравнение с неизвестными х, у, z, —, t. Заме-
Заметим, что неизвестные х, у, z, ..., t представляют собой
множество всех неизвестных, содержащихся как в левой,
так и в правой частях уравнения B6). Например, уравнение
Ах2 = yz + бу2 есть уравнение относительно неизвестных х,
у, z, ибо многочлены, стоящие в левой и правой частях
этого уравнения, могут быть записаны в виде R(x, у, z) =
= 4x2 = 4x2 + 0y + 0z, (Кх, у, Z)=yz+5y2=0-x + yz +
+ Sy2, откуда видно, что обе части являются многочленами
относительно букв х, у, z.
Упорядоченный набор (х, у, z, —, 0 называется набором
неизвестных уравнения B6). ОДЗ уравнения B6) есть мно-
множество всех числовых наборов, соответствующих набору
неизвестных (х, у, z t), у каждого из которых на месте
№
каждого неизвестного может стоять любое действительное
число.
Числовой набор (ль, Уо, 3> *о)> соответствующий набору
неизвестных (х, у, z, ..., t), называется решением уравнения
B6), если равны числовые значения многочленов R и Q,
соответствующие этому числовому набору, т.е. если справед-
справедливо числовое равенство Л(*ь, Уо, 3> *о) = 0(хо, Уо, Zo к)-
Решить уравнение B6) — это значит найти все его реше-
решения, т.е. найти все числовые наборы, каждый из которых
обращает уравнение B6) в верное числовое равенство.
Пусть даны два алгебраических уравнения с одними и
теми же неизвестными:
R(x, у, z О = 0(х, у, z О
и
1\х, у, z, ..., f) = S(x, у, z О-
Эти уравнения называются равносильными, если любое ре-
решение первого уравнения является решением второго урав-
уравнения и, наоборот, любое решение второго уравнения
является решением первого уравнения. Замена одного
уравнения равносильным ему другим уравнением называ-
называется равносильным переходом от первого уравнения ко вто-
второму.
Справедливы следующие утверждения:
1. Уравнения R(x, у, z,..., i) = Q(x, у, z,..., i) u R(x, у, z,..., i) -
— (К*, У, Z,..., i) = 0 — равносильны.
2. Уравнения Щрс, у, z,..., i) = (Црс, у, z,..., t) и Щх, у, z,..., t) +
+ S(x, у, z, ..., i) = (Xx, у, z, ..., f) + S(x, y, z, ..., f), где S(x, y,
z,..., f) — многочлен относительно букв x,y,z,..., t, равносильны.
3. УравненияR(x,у, z,..., t) = Q(x,y, z,..., i) uaR(x,y, z,..., t) =
= aQ(x, y, z, ..., t) равносильны для любого, отличного от нуля
действительного числа а.
4. Пусть известно, что справедливо тождественное равен-
равенство R(x, у, z О = Т\х, у, z, ..., t)\ тогда уравнения
R(x, у, z О = <&х, у, z О и Т\х, у, z /) = (Кх, у,
Z t) — равносильны.
206
Справедливость этих утверждений доказывается анало-
аналогично доказательству соответствующих утверждений § 1 и
потому опускается.
Из утверждений 1 и 4 вытекает, что каждое алгебраичес-
алгебраическое уравнение можно привести к виду Р{х, у, z, ..., t) = О,
поэтому можно рассматривать лишь уравнения вида
Р(х, у, z, ..., О = 0, B7)
где Р{х, y,z,...,t) — многочлен относительно букв х, у, z, ...
..., t.
Пусть даны многочлены Р,(х, у, z,..., t), P2(x, у, z,..., f), ...
..., Р„(х, у, z, ..., t) относительно букв х, у, z, ..., t. Говорят,
что дана совокупность т алгебраических уравнений с неиз-
неизвестными х, у, z, —, ?.
Р,(х, у, z,..., f) = 0, Р2(х, у, z, ..., t) = 0, ...
..., Рт(х, у, z, ..., /) = 0, B8)
если требуется найти все числовые наборы, соответствую-
соответствующие набору неизвестных (х, у, z, ..., t), каждый из которых
является решением хотя бы одного из уравнений совокуп-
совокупности B8). Каждый такой набор называется решением со-
совокупности B8). Таким образом, решить совокупность
уравнений B8) — это значит решить каждое уравнение
Pfa, у, z, ..., t) = 0, где / = 1, 2, ..., т, а затем взять объеди-
объединение этих решений.
Уравнение B7) равносильно совокупности уравнений
B8), если любое решение уравнения B7) является решени-
решением совокупности B8), а любое решение совокупности B8)
является решением уравнения B7). Замена уравнения B7)
равносильной совокупностью B8) называется равносиль-
равносильным переходом от уравнения B7) к совокупности B8).
Пусть даны многочлены Р,(х, у, z,..., t), P2(x, у, z,..., t), ...
..., Р„(х, у, z, ..., t) относительно букв х, у, z, ..., t. Говорят,
что дана система т алгебраических уравнений с неизвест-
неизвестными х, у, z, ..., ?
Ж1
Pt(x, у, z,..., 0 = 0,
* z,..., 0 = 0,
Рт(х, у, z,..., 0 = 0,
если требуется найти все числовые наборы, соответствую-
соответствующие набору неизвестных (х, у, z, ...,(), каждый из которых
является решением каждого из уравнений системы B9), т.е.
если требуется найти все такие числовые наборы неизвест-
неизвестных (х, у, z, ..., t), при подстановке каждого из которых во
все уравнения системы B9) последние обращались бы в
верные числовые равенства. Каждый такой числовой набор
называется решением системы B9) (уравнения системы
обычно записываются в столбик, слева от которого пишет-
пишется фигурная скобка).
Две системы алгебраических уравнений с одними и теми
же неизвестными х, у, z, ..., t называются равносильными,
если любое решение первой системы является решением
второй системы и, наоборот, любое решение второй сис-
системы является решением первой.
Говорят, что дана совокупность k алгебраических систем
уравнений с неизвестными х, у, z, —, Л
Pn(x,y,z, ...,0 = 0,
Рц(х,у, z, ...,0 = 0,
Pmi(x,y,z,..., 0 = 0,
, у, z,..., 0 = 0,
,у,ъ ...,0 = 0,
., 0 = 0,
РцЦх,у, z, ...,0 = 0,
Pukx,y,z, ...,0 = 0,
C0)
Рикх,У, z, ...,0 = 0,
если требуется найти все числовые наборы, каждый из
которых является решением хотя бы одной из систем
уравнений совокупности C0). Каждый такой набор явля-
является решением совокупности систем уравнений C0). Сис-
Система уравнений B9) равносильна совокупности систем урав-
уравнений C0), если любое решение системы уравнений B9)
Ш
является решением совокупности систем уравнений C0), а
любое решение совокупности систем уравнений C0) явля-
является решением системы уравнений B9).
Приведем некоторые утверждения о равносильности
систем уравнений.
1. Если изменить порядок следования уравнений системы
B9), то полученная система равносильна системе B9).
2. Если одно из уравнений системы B9) заменить на
равносильное уравнение, то полученная система равносильна
системе B9).
3. Пусть в системе уравнений с неизвестными х, у, z, ..., t
первое уравнение записано в виде, где в левой части стоит
одно из неизвестных, например х, в первой степени, а в правой
части — многочлен относительно других букв. Тогда говорят,
что неизвестное х выражено из первого уравнения системы
через другие неизвестные. Если неизвестное х выражено из
первого уравнения системы через другие неизвестные, то,
подставив в другие уравнения системы вместо х этот много-
многочлен от других неизвестных, получим равносильную системы
уравнений, т.е. равносильны две следующие системы:
x=QHy,z 0,
Pi(x,y,z 0 = 0,
и
Pdx,y,z 0 = 0,
x=Q(y, z,..., 0,
f),y,z
Pm[QO>,z
Заметим, что если во второй системе рассмотреть только
уравнения Р2 = 0, Р3 = 0 Л|= 0, то они образуют систе-
систему уравнений с числом неизвестных на единицу меньшим,
чем в первой системе.
4. Если первое уравнение системы B9) заменить уравнени-
уравнением, равным сумме первого уравнения, умноженного на неко-
некоторое действительное число Р*0, и второго уравнения,
умноженного на некоторое действительное число ос, то по-
полученная система уравнений равносильна системе уравнений
B9), т.е. при любых действительных Р ф 0 и а две следующие
системы уравнений равносильны:
P\ix, y, z,..., 0 = 0,
и
Pm(X, У, Z, ..., 0 = 0,
p\P,(x, y, z,..., 0 + aP2(*> У, Z,..., 0 = 0,
PAx,y,z, ...,0 = 0,
,y, z, ...,0 = 0.
В качестве следствия утверждения 4 имеем утвержде-
утверждения:
5. Если первое уравнение системы B9) заменить на сумму
(или разность) первого и второго уравнений системы, то
полученная система уравнений будет равносильна системе
уравнений B9).
6. Если первое уравнение системы B9) равносильно сово-
совокупности уравнений Q,(x, у, z, ..., t) = 0, Q2(x, у, z, ..., 0 = 0,
..., Qt(x, у, г, ..., 0 = 0, то система B9) равносильна следую-
следующей совокупности систем уравнений:
Qi(x,y, z,..., 0 = 0,
У.г, ...,0 = 0,
г,..., 0 = 0,
».. 0 = 0,
-,0 = 0,
...,o=o,
Q*(x,y,z,..., 0 = 0,
с, у, z,..., 0 = 0,
C1)
Рт(Х, У, Z, -.., 0 = 0.
Если другие уравнения системы B9) равносильны своим
совокупностям уравнений, то к каждой системе совокуп-
совокупности C1) применимо утверждение 6 и каждая система
совокупности C1) может быть заменена своей совокупнос-
совокупностью систем уравнений. Полная совокупность систем урав-
нений, равносильная системе B9) получается перебором
всех логически возможных случаев.
Замечание. Системы линейных алгебраических урав-
уравнений подробно рассматриваются в гл. X.
Пример. Решим систему трех уравнений с тремя неиз-
неизвестными:
C2)
Первое уравнение заменим на разность первого и второ-
второго уравнений, второе уравнение заменим на разность вто-
второго и третьего уравнений. В результате по утверждению 5
получим систему, равносильную исходной:
— х — У =
— у — ^ =
C3)
Многочлены, стоящие в левой части первого и второго
уравнений системы C3), можно разложить на множители:
В результате, по утверждению 2, система C3) равносиль-
равносильна следующей системе:
C4)
Первое уравнение системы C4) равносильно совокупности
уравнений
х — у=0, х + у— 1 = 0.
Следовательно, по утверждению 6, система C4) равносиль-
равносильна совокупности систем
x-y=O,
(у- z)(y+z-
= 0,
x + y — 1=0,
C5)
Второе уравнение в системах совокупности C5) равносиль-
равносильно совокупности уравнений
y-z = 0t y + z-l=0.
Следовательно, первая система совокупности C5) равно-
равносильна совокупности систем
y-z=0,
Вторая система совокупности C5) равносильна совокуп-
совокупности систем
х + у — 1=0,
y-z=0,
х + у— 1=0,
z-l=0,
Таким образом, совокупность систем C5), а значит, и
равносильная ей система C2), равносильна следующей
совокупности систем уравнении
х+у—1 = 0, \х + у— 1=0,
Все системы этой совокупности легко решаются методом
подстановки. Первая система имеет только два решения
(х, у, z): (-1 + V3; - 1 + УЗ; -1 + VI); (-1- V3~; -1-VT;
— 1— л/3); вторая — только два решения (х, у, z): (— 1;
—1; 2); A; 1; 0); третья — только два решения (х, у, z):
@; 1; 1); B; — 1; — 1); четвертая — только два решения
(х, у, z): A; 0; 1); (— 1; 2 — 1). Следовательно, исходная
система C2) имеет только 8 решений (х, у, z): (— 1 + VT;
212
- 1 + VJ; - 1 + V3); (- 1 - VJ; - 1 - VJ; - 1 - V3);
@; 1; 1); A; 0; 1); A; 1; 0); (- 1; - 1; 2); (- 1; 2; - 1);
B; - 1; - 1).
УПРАЖНЕНИЯ
Применяя способ выделения полного квадрата, записать в виде алгеб-
алгебраической суммы квадратов многочленов следующий многочлен A — 14):
1. бх2 + 7х - 3. 2. 23 + 31х - 5x1 3. 27? - 15х - 112.
4. х2 - 6(х+ 12). 5. х(х+ 34) + 289. 6. - ^х2 + 2х+ 1.
7. jx2 - 4х+ 2. 8. 9 - Зх - j. 9. 4Х2 - 4х+ 1.
10. 4х4 + Зх2 + 1. 11. х4 - 4Х3 + бх2 - 4х+ 1.
12. х4 + Ъ? - х+ 14. 13. х4 - Ъ? + Щ- -1 + -^.
14. 16х6+16х7-4х8-4х9 + х10.
Следующий многочлен записать в виде квадратного трехчлена относи-
относительно х и найти его дискриминант A5 — 33):
15. 3 - ^ + 4Х2. 16. 23х - 120 - х2.
17. 13х - 11 - 8хA + х). 18. хB2 + х) - 2(х - 3).
19. 4 + х2 + 2Dх + 6). 20. (х - 1)C - 2х) - Зх2 + 2.
21. Bх - 3)Cх+ 1) - (х - 11). 22. 3(х+ ПBх+ 3) - (х - IJ.
23. 8х - Dх+ 3)(х - 2) - хBх - 1). 24. х2 - (х+ 2)C - х) - 2х - 8.
25. 5Dх2 + 4) - 3(х - 1) + 4(х + 1). 26. |A - х)B - х) -1.
29. 2/nx - mn - nx+ 2xf. 30. x2 + 2a(b - x) + ЪЪх.
31. x2 - *Bx - A) - 4A2.
32. 5a(x — a) + 8a(x + 2a) — x(x — a) + 2e(x — a).
33. (x - 3)Cx - a) - (x - 2a)Bx - 3).
Принадлежит ли множество {1; — 2} множеству всех решений следую-
следующего уравнения C4 — 41):
34. 2х+ 1 = 3(х- 2) - (х- 7); 35. (х- 1)(х+ 2) = 0;
36. 2х + х2 - 3 = 0; 37. х6 + 7Х3 = 8;
38. 4 + х4 = 5Х2; 39.х3 + 2хA -х) = х2;
40. х2 + Зх(х - 3) = 7х - 9; 41. (х2 + Зх - 5)(х2 + Зх+ 3) + 7 = 0?
Равносильны ли два следующих уравнения D2 — 54):
42. 2х+ 1 = 3 и 2х = 2; 43. ^у^ = 9,5 их(х — 1) = 2;
44. х2 = 4 и х4 - 16 = 0; 45. х2 + 1 = 0 и х4 + 1 = 0;
213
46. 9xBx - 3) = 26 и Fx - 13)Cx+ 2) = 0;
48. (х+4) = 0и(х+4)(х2 + 4х+100)\
49. x - 12 = 17 - 2x и (x - 12J = A7 - 2xJ;
50. x2 = 6 - xи*{x- 2) = F - x)(x- 2);
51. x2 + 6 = 5x и (д? + 6)(x + 4) = 5x(x+ 4);
52. 3 = 2x - x2 и 3 + (x2 + 5) = 2* - x2 + (x2 + 5);
53. |(x - 4) = 0 и 2(x+ l)(x+ 3) + 8 = Bx+ l)(x+ 5);
54. Cx+ 2)Bx- 7) = 6(x+ 2J + 7 и 3[5 - 2(X* - 2x+ 10)] = 5x?
Равносильны ли следующие уравнение и совокупность уравнений
E5 - 72):
ее
56.
57
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
Уравнение
1,- 4 4Gх+9) 4(б1Х-1)
J \ )
= (х+5)(х+3)
(Зх-2)(х-1) ,2.(х-3J
21 17 7
2х2-32 = х+4
(Зх-5)Bх-5) = х2 + 2х+3
2х(х + 7) = х2 + 3х
2х2-15=х
15- 11х=8хA+х)
8=Т
(х+1)Bх+3) = 4х2-22
(Зх+5J + 2х(Зх+5) = 0
|(х-±1+^(Зх-1J = 0
(х + IJ + (х - 2J = 2(х2 - 2,5)
хBх+1) (х+2)(х —4) Л
14 7 2
|Bх-7) = |(х-8J
Совокупность уравнений
iiv 92 — 0- х — 7 •
7х=18-2х; Зх+6 = 0;
2х- 5[7 - (х- 6)(х+ 1)] = 28;
х-4;
х 4; Зх+12 = 0;
х-4 = 0; х = |;
5х2 = бх; 5х+4 = 0;
2(х-1) = х+1; 2х+5 = 0;
8х-5 = 0; х+3 = 0;
2х=1; 2х+6 = 2(х+4)+1;
0,Зх-1,8 = 0,7-0,2х;
2х+5=0;
3{7 - 3[х - 2(х - 1)]} = бх;
2х = 5;
Зх - 1 = 0;
6 - C - х) = 4х - 4;
15-х(8-х) = (х-5J; х = 5;
0,5х + |-х 3; 2(х 5J~0;
г 11
— П 7Sr =!•=-• Or — — (\-
- — U.ZjX l-y *¦*¦ — 3
70.
71.
72.
3(x - 9J -
3x(x - 2) -
4Bx - 3J
Уравнение
-2(x-9)-
-(x+l)(x-
-4Bx-3)-
16
13)
f 1
= 0
= 0
= 0
Совокупность уравнений
3X+3 ГУ'
v yx2-14x + 49 =
x2 + 7 = 0; 13x2-14x + 9 =
VSx2 - x + 2 = 0;
3Bx—T)Q? + l)
4
= 0;
0;
= 0?
Решить следующее уравнение G3 — 123):
73. 5 - 4(х - 3) = х - 2(х - 1).
74. 4C + х) - 3Bх - 5) = 6 - х - 2C - х).
75. 3{ 15 - 2[х - 2(х - 4)] - х} = 5х - 20.
7U fi *-l-3-x х-2 „ 2х-5 х-2_
ЖЬ~ 2 " 4 3 <77< 11 ~ 7 "'
78. 0,2(х - 1) + О,5Cх - 9) = 4 - 2.
79.
0/75 -х
0,47 + 2х_4,4х
1,5-
3 5
80. (х + 2)(х - 1) = 0. 81. 2хCх - 4) = 0.
82.(Зх + 4)E-2х) = 0.
83. х2 - 7х + 6 = 0. 84. 2Х2 - 5х + 12 = 0.
85. Зх2-7х-1=0. 86. 2х(х+6) = х2-3х. -,~
87. 3(х2 + 20) = 21х. 88. х + 2х(х - 1) = 5.
89. Bх + 5J + 2хCх + 5) = 0. 90. (х+j?| + 2) - 1 = 0.
91. 7(х2 + 5х + 8) = 3(х + 1)(х — 2). '^ '
92. 3(х2 - Зх + 1) - 2х(* - 2) = 20 - 3(х + 1)Bх - 4).
93. 2(х - 3) - 3(х2 - 2х - 4) = 4Х2 - C - 5х)(х - 1) - 34.
94.3(x-2J-3B~x2)=x-ll
95. (х+ 2)(х - 3) + х(х+ 4) = (х - 3)(х- 7) + х2.
96. (х+ 1)(х + 2) + 9 + (х+ 2)(х+ 3) = (х+ 3)(х + 4).
97. B + 0,5х) f| - ll + 3j = 0,2 f| + 2Л.
98. 18 + (х + 4)(х - 4)(х - 11 = \х + 1)A + 3)(х + 2).
99. A - х)(х + 2)(х + 3) = 9Х2 - х3 + 4A - 7х).
100. х2 + 4х - 8V8"- х + 20 = 0. 101. х(х - 3) - 2x(V2 • х- 3) = 0.
102. (х + 1)(х - 3) - 2(х + V7) = 0.
103. Зх2 - 2х(х - к) + (х + 2)Cх - 1) = 0.
104. (VI - х)х - (V3x + 4)(х + 2) = 0. 105. (х + 2J = 2(х + 2) + 3.
106. (х2 + 5х - 7)Bх2 + 10х - 11) + 1 = 0. 107. х6 - Зх3 + 2 = 0.
108. х4 + 2Х2 - 8 = 0. 109. х9 - 2Х5 + х= 0.
НО. (х4 + х2 + 1)(х4 + х2 + 2) = 12. 111. (х2 + 2х + lXx2 - 5х + 7) = 0.
112. DХ3 - 19Х2 + 12х)Bх2 - 7х + 6) = 0.
113. (x2 - Шх2 - 5x - 6) = 0. 114. Зх3 - Зх(х - 1) = 7X2.
115. x3 - x2 + x - 1 = 0. 116. x3 + x - 2 - 0.
117. x3 - 2(x+ 1) =x. 118. x4 - 7X3 + 14X2 - 7x+ 1 =0.
119. (x + 9)(x - 1K2X2 + 16x - 20) = 12.
120. (x2 - 5x + 7J - 2(x - 2)(x - 3) = 1
121. x4 + x3 + x2 + x+ 1 = 0. 122. x4 - xCx2 - x+ 1) + 1 = 0.
123.x5 + x3 = x4.
Принадлежит ли множество {—2; 1} множеству всех решений следую-
следующего неравенства A24 — 134):
124. 7х- 3Bх + 3) > 2(х- 4); 125. ^< l\ - -^уЦ
126. —^ + ^— >5-х, 127. n-j< 0,3(х+ 7) + 2у;
128. х(х - 1) - 6 > 5х - х2; 129. х2 - 4х+ 3 < 0;
130. ^х2 - 3(х+ 5) < 0; 131. Эх2 - 6х+ 1 > 0;
132. х(х - 3) - 2 < Зх - (х2 + 2); 133. Ах2 + 6 (х-11> 2;
134. (х - 2)Cх + 4)(х2 + 1) > 0? ^ '
Равносильны ли два следующих неравенства A35 — 153):
135. х2 + 4х+ 12 > 0 и х — х2 — 3 > 0;
136. Bх- 5)Bх- 1)^|
137. (х- 1J>0и 1 -х<0;
138. 4х-3> 1иDх-3)(х+2)>х + 2;
139. 2Eх - 4) < 4 и 4Eх - 4J й 16;
140.х+3>0их3>-Зх2;
141. х-х2й2и(х- х2)(х + 4Х2 + 5) й 2(х+ Ах2 + 5);
142. 2х - 4 > 3 и 2х - 4 + 2(х+ 3) > 3 + 2(х+ 3);
143.x2 -5х+ б?0 и 1
144.х2-х-6^3х- 1иЗ§52х^
145. х+ 4 < Зх - 2 и х(х+ IJ > 3(х+ IJ;
146.|-з[2х- 1~2BХ~3I>х+5^их>3;
147. бх2 - 29х+ 30 < 0 и - Зх2 + 5х+ 2 > 0;
148. (х2 - 4)(х+ 1) > 0 и х2 - 2х - 3 > 0;
149. х2 —х+ 1>0и4х2 + х+3>0;
150.x3- 1<0их<1;
151. xs- 1 их3 + 1*0;
152. X8 - Xs + х2 - х + 1 ;> 0 и х2 - Зх + 10 2.0;
153. 2Х2- 1<;х4и4х4-4х3 + 5х2-4х+1;>0?
Решить следующее неравенство A54 — 205):
154. 21 - 7Bх - 9) > Зх. 155. 5C - х) - 3(х - 4) < 16х.
156. 2(х - 1) - 3Bх - 3) > 6 - 3(х+ 5).
157.
- 2x) - |D - 5x)
4) - 16.
,« x Dx-7)Cx-5) .2 Dx-9)(x-l)
IM3 15 *~ 5~ 5
159. |Bx + 24) - 0,1 (x + 1) > у - 0,3B - Зх).
160. -г(х-4)<4(х+4) + х.
161. Зх-4-
15
1 5Г 3 Г
162. Cx - 2)Bx - 3) - Bx -^ l)(x - Tf + бх > Bx - 3J.
343l 8ll2 62
163
( )(
Cx-4)Cx+l)
Лбх-1)Bх-3)
12
-2Cх+ 1).
165. Bх + 3)(х - 7) - B3х - 11) й 2(х + 8)(х - 2).
¦» 2 4x4-1 4
166. |Bх - 7) - |(х - 8) - 4 :> -^у1 + ^(х - 11).
167. X2 — х — 2 < 0. 168. Зх2 — 5х — 8 <. 0.
169. 15Х2 - 77х + 10 > 0 170. Зх2 + 13х - 30 :> 0.
171. 16х - 15х(х + 1) < 0. 172. 21 - 22х - 24Х2 й 0.
173. (х - 4J(х + 5) <. 0. 174. ^" Х)Х
> x + ^
175. (x - 3) :> (x - 3J. 176. 8x(x + 2) + 3(x + 1) > - 1.
177. Bx+2)(x-l)<5x+6.
Пв-^-гх+^^х- 1) + 4.
179. V6V - 2лЙх- VTx+ 2^0.
180. (x2 - 16xJ - 63 :> 2(x2 - 16x).
181. x2 + 2x+7^ D + 2x +x2)C + 2x +Д
182. (Зх2 - 4x + l)Dx4 - 5X3 + x2) ^ 0.
183. x3 + 2X2 > 6 + Зх. 184. (x+ 21(x - l)(x - ЗJй 0.
185. (x + 4)(x + 2K(x - 1)B - x?(x2 - 3x + 5) > 0.
186. (x2 - 4)(x2 - 4x + 4)(x2 - x - 2) <; 0.
187. (9 - xW - 2x - 31(x + 8) ^ 0.
188. (x3 - 2X2 - 3x + 4)(< - 3x+ 7) > 0.
189. B7 - 37X2 - 16x4)(x2 + x + 1) < 0.
190. (x2 - 4x - 12)(x3 - 7x - 6) :> 0. 191. (x2 + Юх + 25)B5 - x2) > 0.
192. BX2 - 3x - 14)Bx2 + 1 lx + 14) < 0.
193. (Зх3 - 24)Bx2 + бх - 20) :> 0.
194. (x2 + 4x - 45)Cx2 - 14x - 5)(x +1)^0.
195. Bx? + 2XKX2 - 2x + 1)(ЗхГ + 7x - 10) > 0.
196. (бх3 - x2 + 16)(8x3 - Их2 + 19x - 4) < 0.
197. xtf + 3x - 4) > 7X3 - Щ + 6x + 5.
198. 4X3 + Зх2 - 5Dx+ 3) > Ъ? - 5xB + 5x- x3).
199. (x - l)(x - 3)(x - 4)(x - 6) + 10 :> 0.
200. (x2 - Зх + 2ХХ2 - Sx + 6)A - х2) й 0.
201. (Sx2 - х - 4ХХ3 - 1)(х + 10) > 0.
202. ЗСх2 + Зх + 2) ;> (х + 1)(х + 2)(х + 3).
203. (х? - 16)Cх - 9) й (л? - 8х + 16)Г2х + 8).
204. (х2 + 4ХХХ2 + х - 6) > (х3 - 9х)(х* + 2х - 8).
205. (Зх2 - 7х+ 2КХ2 - 9) < BХ2 - 5х - 3) (9л2 - 6х+ 1).
В задачах №№ 206 — 213 под числовым набором (а; Ь) понимается
числовой набор, соответствующий набору неизвестных (х; у) при х = а и
у = А.
Принадлежит ли множество {B; 1)} множеству всех решений следую-
следующей системы уравнений B06 — 209):
Г1, М7 /95^-49 = 23х,
206
206..
208.
5x+7y=ll;
x+2y = 4,
209.
[14х+9у = 9,
2x+3y = 7; A1K'#\9x+4y = 4?
Является ли множество {B; 3), C; 2)} множеством всех решений
следующей системы уравнений B10 — 213):
\
210.
212.
х+у=5,
*
(
\х+у-5,
У
у ;
х2 + ху+у2=19,
=\Sx+3Oy,
ху=
В задачах N&Nb 214 — 221 по числовым набором (a, b, с) понимается
числовой набор, соответствующий набору неизвестных (х, у, z) при х = а,
y=b,z=c.
Принадлежит ли множество {C; 2; 1)} множеству всех решений сле-
следующей системы уравнений B14 — 217):
5х-3г=4A+у),
214.
5х-3у+2г=3, 215.
7х+у+Зг=20;
2у+3х=14 — г,
(х-1)(у+5)=14,
2yx-zx+2xy=l3, 217.
(у+5Х*+8) = 63,
216.
Является ли множество {C; 4; 1), (— 3; — 4; — 1)} множеством всех
решений следующей системы уравнений B18 — 221):
218.
220.
219.
ху+у*+уг=У2,
221.
хУг=48;
ху+2х+у = 2А,
yz+b+2z=\S,
гх+х+3г = 9?
Равносильны ли следующие две системы уравнений B22 — 229):
f3x+l 2x-y 2у-х
7 2 " 8 '
•|зх-2у=5 И '
4х—2 4у — 5х_х+у.
223.
224.
225. ^
226.
227.
228.
229.
х+у=11, Гх+у=11,
ху=12 [х2+ху+у2 = 91;
х+5у=26, Гх+2у=1,
х2- 25^=156 И [J + 8^=127;
7х —4у = 23, Jx+y=5,
49Х2-16^=1081 И
у-х = 2,
5 '
у+г=Ю, и
г+х=20
yz+zx= 16,
гх+ух=25,
+ ^ = —39
у+х — г= 14,
4х—5у+6г = 3,
8х-7у-3г=9,
7х—8у+9г=6;
х2 + ху+хг=48,
ху+у2+уг= 12,
и
и
(х+уJ-г2
2
х+у —г=5?
230.
232.
234.
236.
238.
240.
242.
244.
246.
Решить следующую систему уравнений B30 — 273):
4х+3у = 21, -Ч1 Jl3 + 2y = 9x,
4х-3у=3. [7х=3у.
9х+Зу-2 = 0, .„ /7х=8-7у,
10х+6у-4 = 0. 116у+16х-8 = 0.
5х-3 2у, fx+y=12,
6у + 15х=9. " [2ху=9(х — у).
х+у=5, |х+Зу=10,
х2у2-10ху + 24 = 0. '\х* + 27y^ = 280.
х+у=11,
х3 + у3 = 341.
*+У = 3, _ Гх-у = 2,
Xs+ /=1023. |(х2 + у2)(х3-у3) = 260.
|х+3ху = 35, м. |х3 = 5х+у,
\у = 22-2ху. Л-{у3 = х+5у.
лу=35, М5 Гху= 72,
2(х+уJ + 324 = 51(х+у). *{х2 + у2=145.
х2 + ху = 210, М7 J(x_yJ = 3-2x-2y,
3^ = 231-ху.
248.
250.
252.
254.
256.
258.
260.
262.
264.
266.
268.
270.
272.
2ху+ lOy2 = 145,
-х-30,
y3 = 351.
+ xy2 = 12
y3=152.
''[(х+уХу3-
-У2-*
10c-9z=19,
259J8x-y=10,
5х-
v-2z=3l, 261.
8х — iy — z=l.
-z=l,
-x=l, 263.
x + z —y= 1.
1, 265.
2x —
—6).
x —
2, 267.
ху+уг=Ю,
15.
= 42] 269.
zx+yz= 10.
хуг,
Z+x=xyz, 271.
273.
108.
Какую фигуру на координатной плоскости задает следующее уравнение
B74 - 281):
274. у = 1; 275.x- 2^ = 0; 276. Зх- 2у= 1; 277. ху = 0;
278. A - х)(х - у) - 0; 279 х2 + у2 = 5;
280. ? + /= 0; 281. х2 - / = 0?
220
Имеют ли общую точку следующие прямые B82 — 284):
284. 2х - .у - 3 = 0 и 2у + 9 = 4х?
Имеют ли общие точки следующие окружность и прямая B85 — 289):
2
8х / у ^
289. х2 + у*= 18 иу = х+ 3-U?
Глава IV. СТЕПЕНИ И ЛОГАРИФМЫ
§ 1. Степень с целым показателем
В первой главе было определено действие возведения
любого действительного числа в степень с натуральным
показателем. В этом параграфе повторяется это определе-
определение, а также приводятся определения возведения числа в
нулевую степень и в степень с отрицательным целым
показателем.
Пусть а — любое действительное число, п — любое на-
натуральное число, тогда степенью числа а с натуральным
показателем п (или п-й степенью числа а) называется число,
записываемое как а" и определяемое по правилу
\аа... а, если п > 2;
ап = \%-7^Г
[а, еслип=1.
Пусть а — любое отличное от нуля действительное
число, тогда нулевой степенью этого числа называется число
единица, т.е. по определению а0 = 1 для любого отличного
от нуля действительного числа а.
Нулевая степень числа нуль не определяется, и символ 0°
считается лишенным смысла.
Пусть а — любое отличное от нуля действительное
число, п — любое натуральное число, тогда степенью числа
а с целым отрицательным показателем (— п) называется
число -7, т.е. по определению а~" = ~ для любого отличного
а а
от нуля действительного числа а и любого целого отрица-
отрицательного числа (— п).
Целая отрицательная степень числа нуль не определяется,
и символ (Г" считается лишенным смысла.
222
Итак, натуральная (n-я) степень определяется для любо-
любого действительного числа, а нулевая и целая отрицательная
степени лишь для любого отличного от нуля действитель-
действительного числа.
Если а — любое отличное от нуля действительное число,
то можно дать определение степени с целым показателем,
которое есть объединение предыдущих определений.
Пусть а — любое отличное от нуля действительное
число, — любое целое число, тогда под числом аа понимают
число, определяемое по правилу
[а, если а= 1;
j да ... а, если а = т, т — натуральное число, т > 2;
I /яраз
а= i 1, если <х = 0;
-\, если а = — п, (— п) — целое
[ отрицательное число;
-О
при этом число а называется степенью с целым показате-
показателем, число а — основанием степени, число а — показателем
степени.
В первой главе были приведены основные свойства,
которыми обладает действие возведения в степень с нату-
натуральным показателем. Для действия возведения в степень
с целым показателем эти свойства также имеют место.
Именно, пусть а, Ъ — любые, не равные нулю, действи-
действительные числа, а, Р — любые целые числа, тогда:
г)а:а = ? = а;
Докажем справедливость этих свойств. Справедли-
Справедливость свойства а) при натуральном а (а = п, п е N) следует
из основных законов умножения действительных чисел:
(aby = (ab)" = (ab)(ab)... jab) =.a...a p... b =
л раз п раз п раз
n aa
Пусть a = 0, тогда (abf = (ab)° = 1 = 1 • 1 = a°b° = aaba,
т.е. (aZ»)a = aaba.
Пусть a = — m и /и — натуральное число. По определе-
определению степени с отрицательным показателем (ab)a = (ab)~m =
_ 1 _
(abf
по свойству степени с натуральным = _!_ =
показателем a"bm
по свойству дробей = ~s ¦ т^ =
о о
по определению степени с _ _ п,- « _ a,a
отрицательным показателем а
Следовательно, свойство а) справедливо.
Свойство б) доказывается аналогично.
Для доказательства свойства в) рассмотрим все шесть
возможных случаев: 1) a = п, р = т; 2) a = п, р = — т;
3) a = — п, р = т; 4) a = — п, р = — т (где пит — любые
натуральные числа); 5) a — любое целое число, Р = 0;
6) a = 0, р — любое целое число.
1. При a = п, р = т справедливость свойства в) следует
из основных законов умножения действительных чисел:
л раз /и раз (n + m) раз
¦}
'1
2. Пусть а = п, р = — т, где пит — натуральные числа,
тогда по определению степени с целым отрицательным '•
показателем
(X (* = о ' —«
а"
Применяя правило умножения дробей, имеем а" ¦ -^ = -^.
а а
224
Пусть п> т, тогда, применяя свойство степени с нату-
натуральным показателем, получаем
Пусть п = т, тогда по определению степени с нулевым
показателем получаем
Пусть п < т, тогда, применяя свойство степени с нату-
натуральным показателем и определение степени с целым от-
отрицательным показателем, получаем
О_ _ 1 _ 1 _ 1 _ - (т - и) _ - т + л _
ат в-.± аяа— а"-"
3. Пусть a = — п, р = /и, где пит — натуральные числа.
Этот случай аналогичен случаю a = n, р = — т.
4. Пусть a = — п, р = — /и, где п,т — натуральные числа.
Тогда аа^ = а~"а~т =
по определению степени с целым = J L =
отрицательным показателем а" а*
по правилу перемножения дробей
та,
по свойству степени с = 1 =
натуральным показателем а*т
по определению степени с целым = сГ(" + т) = сГ " ~ т =
отриц чтельным показателем = а(~ п) + (~ т) = аа+р.
5. Пусть а — любое целое число, р = 0, тогда, применяя
определение степени с нулевым показателем, получаем
Алгебра, тригонометрия ' ZZ3
н элементарные функции
6. Пусть а = О, |J — любое целое число, тогда, применяя
определение степени с нулевым показателем, получаем
Следовательно, свойство в) справедливо.
Для доказательства свойства г) при натуральных a, P
(а = п, р = т, n e N, m e N) рассмотрим три случая:
1. Если п>т, то п = т + 1, где Ы N. Воспользуемся
основными свойствами умножения и деления действитель-
действительных чисел:
/яраз /раз
аа: ? = (Г: сГ =<L=~
а - Д
m раз
2. Если п = /и, то
ираз
fla:op = 4 = ?^l? =1-
д д - д.
лтраз
По определению д° = 1. Следовательно,
аа:<? = <Г:<Г = а* = (Г-т = аа-*.
3. Если /и > п, то т = п + к, где hJV. Воспользуемся
основными свойствами умножения и деления действитель-
действительных чисел, а также определением возведения в отрицатель-
отрицательную степень:
д... а
л раз *раз
Следует отметить, что в этом случае (п — т) не является
натуральным числом.
Для остальных пяти случаев значений аир доказатель-
доказательство свойства г) аналогично доказательству свойства в).
226
Для доказательства свойства д) также как и в случае
свойств в) и г) рассмотрим все шесть возможных ситуаций:
1. Пусть а = п, р = т, где пит — натуральные числа.
Для доказательства свойства д) в этом случае воспользуемся
основными законами сложения и умножения действитель-
действительных чисел:
(aaf = (аУ = jari) (an]|... (an). =
/яраз
= (а... а)... (а... а) = аа... а = dT = в0*.
лраз лраз шяраз
<яраз
2. Пусть а = п, р = — /и, где п и т — натуральные числа.
Тогда (да)р = (сГ)~ т =
по определению степени с целым = 1 =
отрицательным показателем (а)"
по свойству степени с натуральным - 1 -
показателем в"
по определению степени с целым = а~ят =
отрицательным показателем = а*~ т) = а0*.
3. Пусть а = — п, р = т, где пит — натуральные числа.
Справедливость этого свойства доказывается аналогично
случаю а = п, р = — /и.
4. Пусть а = — п, р = — /и, где п, т — натуральные числа,
югда (а) — (а ) —
по определению степени с целым = 1 =
отрицательным показателем
по только что разобранному
случаю 3
по определению степени с целым
отрицательным показателем
по свойству дробей
по правилу деления дробей = d™ = а(~ ")(~ т) = я"*.
" 227
(а
_ 1
а~'
_ 1
nm
а
= 1:
У
. =
1 _
5. Пусть а — любое целое число, р4 = 0, тогда по опреде-
определению степени с нулевым показателем (да)р = (да)° = 1 =
6. Пусть а = О, Р — любое целое число, тогда по опреде-
определению степени с нулевым показателем (eff = (д°)р = A)р =
Следовательно, свойство д) справедливо.
Пример. Применим свойства степени с целым показа-
показателем для вычисления следующего числового выражения:
.¦WK
rfW'-S-lO-'
i
1 27 ifi 3
1_96416_4_1
§ 2. Степень с рациональным показателем
В главе I было дано следующее определение арифмети-
арифметического корня из положительного числа.
Пусть п — натуральное число, п 12, а — положительное
число. Тогда положительное число Ь, такое, что b" = a
называется арифметическим корнем п-й степени из числа а
и обозначается Ь = Ча.
Без доказательства было принято утверждение, что для
каждого положительного числа а существует и притом
единственный арифметический корень n-й степени.
По определению Ча справедливо следующее утвержде-
утверждение:
128
a — положительное число,
n — натуральное число,
Ча — положительное число,
Используя определение возведения в целую степень и
определение арифметического корня из положительного
числа, дадим теперь определение возведения положитель-
положительного числа в степень с рациональным показателем.
Пусть а — положительное число, г= ? — рациональное
число, причем q — натуральное число (q ? 2). Положитель-
Положительное число Ъ такое, что Ъ = >/</, называется r-й степенью
числа а и обозначается Ъ = J, т.е. at = VeV
ЯГ— I
Заметим, что у а = an. Пусть а и Ъ — любые положитель-
положительные числа, г, и г2 - любые рациональные числа, тогда
справедливы следующие свойства, называемые свойствами
степеней с рациональными показателями:
a) (ah)'1 =
Докажем справедливость этих свойств.
а) Пусть /*i = ?, причем q — натуральное число,
Рассмотрим
по определению рациональной степени = fi(abff =
по определению арифметического корня = (abY =
по свойству степени с целым
показателем
по определению арифметического корня = i
\ JK J
229
по определению рациональной степени _ f «Л* (, «Л* _
по свойству степени с натуральным
показателем
Итак, [(аЬ)г>]9 = [dbr>]9. По теореме 1 § 2 гл. II это
равенство равносильно равенству (ab)r> = dltfl и свойство а)
доказано.
Свойство б) доказывается аналогично.
2 m
в) Пусть г, = ?, г2 = ™. Тогда flV2 = а'а".
Рассмотрим Гд*д"Т" =
по свойству степени с , г^и , т^вя
натуральным показателем =(fl*J (а") =
по свойству степени с г/ ?x«t» r-r «s^
натуральным показателем =llfl*)J W0"
по определению рациональной _ rv«rjYf г^гш*^ _
степени ~L( JJ L( JJ =
по определению арифметического
корня
по свойству степени с целым
показателем
по свойству степени с целым
показателем
по определению арифметического
корня
по определению рациональной
степени
Итак, учитывая, что (рп + тФ = г, + г2, имеем (d'd1)*1 =
= (d1*'1)*1. По теореме 1 § 2 гл. II это равенство равносильно
равенству d'd1 = d>+ri и свойство в) доказано.
Свойство г) доказывается аналогично.
? —
д) Пусть г, = ?, г2 = —. Тогда (d'Y1 = {а9)".
230
—
Рассмотрим fffl'YT* =
по свойству степени с натуральным
показателем
по определению степени с K\lf 1Л TV
рациональным показателем = I Iе*J I =
по определению арифметического </ *v»i«
корня = {(а9)} =
по свойству степени с целым • *v»«
показателем = fa*J =
по свойству степени с целым
показателем
по определению степени с
рациональным показателем
по определению арифметического
корня
по свойству степени с целым _ « _
показателем
по определению арифметического
корня
по определению степени с • ??\«»
рациональным показателем = (a*" J .
Итак, [(d1I*]"9 = (лГЛ)"*- По теореме 1 § 2 гл. II из спра-
справедливости этого равенства вытекает справедливость свой-
свойства д).
Докажем еще одно свойство степени с рациональным
показателем.
е) Пусть а — положительное число, г, = ? — рациональ-
? ES.
ное число, ди п — натуральные числа, q12. Тогда ая=ая*.
Рассмотрим
по свойству степени с натуральным
показателем
231
по определению степени с рациональным
показателем
по определению арифметического корня = (сГ)" =
по свойству степени с целым показателем = сГ =
по определению арифметического корня = (*"л/д*"Т =
по определению степени с рациональным ?
показателем
Итак, fa*! = fa*"! , откуда и вытекает справедливость
свойства е).
Для арифметических корней доказанные свойства имеют
вид
а) ЧаЬ= Ча
в)
г) Ча: Ча= "л/о^"*;
е) 1/7- Ча~.
Пример. Упростить числовое выражение
А = BV8" + Зл/Г - 7V2)(V7l + V20" - 4л/2).
Применим рассмотренные свойства:
V8"= VF= 2V2"; V7l= V?T3r= V2rVF= 6V2";
V20"=
Следовательно,
= Dл/2~ + Зл/Г - 7л/2)Fл/2" + 2л/Г - 4л/2) =
= 3 • (VT- V2) • 2 • (л/2~+ VT) = 6(VT+ л/2)(л/Г+ V2) =
= 6E - 2) = 18.
232
Рассмотрим теперь основные свойства типа неравенства
для степени с рациональным показателем.
ж) Пусть а> 1, г = ? — положительное рациональное
число (q и п — натуральные числа, q ? 2). Тогда d > 1.
Рассмотрим («Y _
по определению степени с рациональным
показателем
по определению арифметического корня = d.
По теореме 1 § 2 гл. II условия а > 1 и d > lp равносиль-
равносильны, значит, из условия а > 1 вытекает, что d > lp, но тогда
J > 1*, т.е. (dL > Iя, откуда по тому же свойству получа-
получам, что d > 1. Свойство ж) доказано.
з) Пусть 0 < в < 1, г = ^ — положительное рациональное
число (р е N, q e N, q > 2). Тогда d < 1.
Доказательство этого свойства аналогично доказательст-
доказательству свойства ж).
и) Пусть а > 1 и г, и г2 — рациональные числа такие, что
г, > г2. Тогда л > л.
Доказательство. Поскольку (г, — г2) — рациональ-
рациональное положительное число, то по свойству ж) d'~ri>l.
Умножая это неравенство на положительное число d\ по
свойству 21 неравенств (см. 2 гл. II) получаем лГ2(лГ|~'2) >
> d\ Применяя к левой части свойство в) степени с раци-
рациональным показателем, получаем dx > d\ т.е. свойство и)
доказано.
к) Пусть 0 < а < 1, г,, г2 — рациональные числа такие, что
г, > г2. Тогда dl < d\
Доказательство этого свойства аналогично доказательст-
доказательству свойства и).
Пример. Доказать, что для любых положительных
чисел а и Ь справедливо неравенство
2 2 2
дз + Ьг > {а + Ь)з.
233
Доказательство. Обозначим а + Ъ через с и рассмот-
рассмотрим дроби ^и^. Таккак^ + ^=1, тоО<^<1, 0<-<1.
г г ' с с ее ее
I I
Используя свойство к), получим |^Т < 1, |м < 1 или
I I
^Т < 1, |м
(f) 3 < lf [т\ 3< f f
) [\ [] ff и f^ fef-
о свойству числовых неравенств справедливо и неравен-
неравенство
откуда, учитывая, что ~с + - — 1, получаем справедливость
неравенства
Учитывая, что с — положительное число, и умножая это
2
неравенство на сз, получаем справедливость неравенства
2 2 2
аз + Ьз> сз, что и требовалось доказать.
§ 3. Степень с иррациональным показателем
Возьмем приближенные значения числа VT с недостат-
недостатком:
1, 1,4, 1,41, 1,414, ...
и приближенные значения числа V2" с избытком:
2, 1,5, 1,42, 1,415, ...
По свойству и) степени с рациональным показателем
31<3М<3М1<3ММ<... A)
и
234
З2 > З1'5 > З1'42 > З1'415 > ... B)
В неравенствах A) и B) членов бесконечно много и
любой член неравенств A) меньше любого члена нера-
неравенств B). Естественно под числом 3^ понимать число,
которое больше любого члена неравенств A) и меньше
любого члена неравенств B). Значит, под числом 3 пони-
понимается число, которое больше чем 3 в любой рациональной
степени, приближающей V2~c недостатком, и которое мень-
меньше чем 3 в любой рациональной степени, приближающей
V2~ с избытком. Без доказательства здесь принимается, что
такое число существует и притом только одно.
Так же определяется и аа, где а > 1, а — иррациональное
положительное число. А именно, находятся рациональные
числа г„ приближающее число а с недостатком: г, < гг< г3 <
< ... < а, затем — рациональные числа 4, приближающее
число а с избытком: 1Х > /2 > /3 > ... > а, и составляются
неравенства: dl < d2 < d> < ... и dl > d2 > d' > ... Тогда под
tt понимается число, которое больше любого числа d' и
меньше любого числа dk. Это определение можно сформу-
сформулировать и так.
Пусть даны число а > 1 и положительное иррациональное
число а. Через г, обозначим рациональные числа, прибли-
приближающие а с недостатком, через 4 — с избытком. Под числом
аа понимается число у такое, что для любых г, и 4 справед-
справедливо неравенство d'<y< dk. Без доказательства здесь при-
принимается, что такое число существует и притом только
одно.
Пусть даны число а такое, что 0 < а < 1, и положительное
иррациональное число а. Через г, обозначим рациональные
числа, приближающие с недостатком, через 4 — с избыт-
избытком. Под числом аа понимается число у такое, что для любых
г, и 4 справедливо неравенство а\ > у > dk. Без доказатель-
доказательства здесь принимается, что такое число существует и
притом только одно.
Пусть даны положительное число а такое, что а* 1, и
отрицательное иррациональное число а. Под числом аа пони-
235
мается число, равное \, т.е. если а ф 1 и а — отрицательное
ег
иррациональное число, то в" = -^. Поскольку число а** не
а
равно нулю и в множестве действительных чисел деление
всегда выполнимо, то существует и притом единственное
число, равное частному -4. Это число называют числом аа.
(Г
Замечание. 1. Если а = 1, то аа = 1 для любого дейст-
действительного числа а. Поэтому в вышеприведенных опреде-
определениях случай а = 1 не рассматривается.
2. В силу вышеприведенных определений и определения
степени с рациональным показателем для а > 0 и любого
действительного числа а число аа всегда положительно.
Для степеней с иррациональным показателем справед-
справедливы следующие свойства. Пусть а > О, Ь > 0, а — ирраци-
иррациональное число, Р — рациональное или иррациональное,
тогда:
а) (аЬ)а = ааЬа;
Доказательство этих свойств проводится с помощью теории
пределов и поэтому здесь не приводится.
§ 4. Степень положительного числа
Изложенное в §§ 1 — 3 позволяет дать определение
действительной степени положительного числа. Заметим,
что число аа существует и притом только одно для любого
действительного а.
Определение. Пусть дано положительное число а и
действительное число а. Под числом аа 'понимают положи-
положительное число, определяемое по следующему правилу:
I. Если а > 0 и:
1. а = т, т — натуральное число, то
236
а, при т=1,
ярв
2. a = -, q — натуральное число, q2:2, то а* = V<T (ариф-
(арифметических корень q-й степени из положительного числа);
3. a = ?, где р, q — натуральные числа, qtl, то аа= Va^;
4. a — иррациональное число, тогда:
а) если а> 1, то аа — число большее, чем d' и меньшее, чем
dk, где rt — любое рациональное приближение числа а с
недостатком, lk — любое рациональное приближение числа a
с избытком;
б) если 0<а< 1,тоаа — число меньшее, чем а*' и большее,
чем а1* (г, и lk — me оке, что и выше);
в) если а=\,тоаа=\.
II. Если a = 0, то аа = 1.
III. Если а < О, то <t = ±
ег
Число аа называется степенью, число а — основателем
степени, число a — показателем степени.
Из §§ 1 — 3 вытекает, что степень положительного числа
обладает следующими основными свойствами: если а и Ь —
положительные числа, а и {$ — любые действительные
числа, то:
а) (аЬ)а = ааЬа;
— л« + р.
д) (af d.
Рассмотрим теперь основные свойства степени положи-
положительного числа типа неравенства. \
Теорема 1. Если а > 1 и a > 0, то аа > 1.
Доказательство. Если ос = ? — рациональное число
(р и q — натуральные числа), то свойство а* > 1 уже дока-
237
зано в § 2. Если а — иррациональное число, то возьмем
любое положительное рациональное число г, приближаю-
приближающее а с недостатком, тогда аа > d по определению ирраци-
иррациональной степени. В то же время по уже доказанному в § 2
свойству d > 1. По свойству транзитивности неравенств из
справедливости двух неравенств аа > d и d > 1 вытекает
справедливость неравенства аа > 1. Теорема 1 доказана.
Теорема 2. Если а > 1 и а < О, то аа < 1.
Доказательство. Число р = — а — положительное
число, поэтому, применяя теорему 1, имеем а9 > 1. Умно-
Умножим обе части этого неравенства на положительное число
аа. По свойству неравенств cPd* > d1' по свойству в) и
определению степеней а*аа = ae + p = a =1, поэтому а* < 1
и теорема 2 доказана.
Теорема 3. Если а> 1 и аа> I, тоа>0.
Доказательство. Предположим, что а > 1 иа° > 1,но
а й О, т.е. либо а = 0, либо а < 0. Если а = 0, то аа = 1 по
определению. Если а<0иа>1,то применяя теорему 2,
имеем аа < 1. Итак, если а < 0, то аа й 1, что противоречит
предположению аа > 1. Теорема доказана.
Теорема 4. Если а > 1 и аа < 1, то а < 0.
Доказательство теоремы 4 аналогично доказательству
теоремы 3.
Объединим теоремы 1—4.
Утверждение 1. Если а > 1, то условия аа > 1 и а > О
равносильны; кроме того, равносильны условия аа < 1 и а < О,
т.е. если а> 1, то
аа>1оа>0,
а'<1оа<0.
Теорема 5. ?Ъш 0 < а < 1 и a > 0, то аа < 1.
Доказательство. Рассмотрим число Ь>-. Так как
Ъ > 1, то применяя теорему 1, имеем Ьа=\. Умножим обе
части этого неравенства на положительное число аа. По
свойству неравенств baaa > d*. По свойствам степеней
Ьааа = (аЬ)а = A)" = 1, поэтому аа < 1.
Теорема 6. Если 0<а<1иа<0, тоаа> I.
238
Теорема 7. Если О < а < 1 и аа > О, то а < 0.
Теорема 8. Если 0 < а < 1 и аа < 1, mo a > 0.
Доказательство этих теорем аналогично доказательству
теоремы 5.
Объединим теоремы 5 — 8.
Утверждение 2. .Если 0 < а< 1, /по условия аа> 1 и
а < 0 равносильны; кроме того, равносильны условия аа <\ и
а > 0, т.е. если 0 < а < 1, то
а° > 1 о а < 0,
Из утверждений 1 и 2 легко получить следующее следст-
следствие:
Утверждение 3. Еслиа> 0 и а* 1, то условия аа= 1 и
а= 0равносильны, т.е. если а> 0 и а*1, то
Теорема 9. .Если а > 1 и ах > а2, то а°' > а.
Доказательство. Рассмотрим число Р = щ — a2. Так
как р > 0, то ар > 1. Умножим обе части этого неравенства
на положительное число а. По свойству 6 неравенств
(Pd4 > я; по свойству степеней Лт = а°1, поэтому
о > d4 и теорема 9 доказана.
Теорема 10. .Если а > 1 и ai < а2, то а < а.
Теорема 11. .Если а> 1 и а > а, то ^ > аг.
Теорема 12. .Если а > 1 и о < о, то ах < щ.
Доказательство этих теорем аналогично доказательству
теоремы 9. \
Объединим теоремы 9—12.
Утверждение 4. .Если а> I, то условия d*l>dh и
а, > а2 равносильны; кроме того, равносильны условия
а < л и ai < а2, т.е. если а > 1, то
rf1' < а о ai < a2.
239
Теорема 13. Если О < а < 1 и оц > а^, то cfr < cfr.
Теорема 14. Если О < а < 1 и ах < о^, то cfr > cfr.
Теорема 15. Если 0<а<1и(Р>> cfr, тощ< а2.
Теорема 16. Если 0 < а < 1 и а < а, то щ > щ.
Доказательство этих теорем аналогично доказательству
теоремы 9.
Объединим теоремы 13 — 16.
Утверждение 5. Если 0 < а < 1, то условия аа' > а и
а, < а2 равносильны; кроме того, равносильны условия
fl°i < а°» и а, > сс2) т.е. если 0< а<1, то
аа> > а <» а, < Ог,
аа' <аа%о а{> а2.
Из утверждений 4 и 5 легко получить следующее следст-
следствие:
Утверждение 6. Если а > 0 и а* 1, /по условия
a°i = а°» и ai = а2 равносильны, т.е. если а> 0 и а*\, то
Утверждения 4 и 5 словесно формулируются следующим
образом:
Если основание степени больше 1, то большему показа-
показателю соответствует большая степень и наоборот, большей
степени соответствует больший показатель.
Если основание степени меньше 1 @ < a < 1), то боль-
большему показателю соответствует меньшая степень и наобо-
наоборот, меньшей степени соответствует больший показатель.
Замечание. Если a > 0, то понятие действия возведе-
возведения в степень можно расширить на множество всех неот-
неотрицательных чисел, так как по определению 0" = 0, если
а>0.
Рассмотрим пример на применение свойств степеней
положительного числа. Пусть требуется доказать, что
240
По определению 3 < Зг, где г — рациональное прибли-
приближение иррационального числа V3~ с избытком. Возьмем
г = 1. Так как VJ" < J, то Ъ^ < 3*. Докажем, что 3* < 7.
Используя два раза теорему 5, получим равносильность
следующих неравенств:
у<1 и \j
Используя свойства степеней типа равенства, получим,
(зИ* з7
что неравенство у < 1 равносильно неравенству ^< 1,
которое является верным, так как З7 = 2187, 7* = 2401.
Следовательно, в силу равносильности переходов верно
и исходное неравенство У® < 7.
§ 5. Логарифмы
Рассмотрим основные задачи, которые возникают при
изучении степеней.
1. Даны действительные числа а и а. Найти действитель-
действительное число х такое, что х° = а. Это — задача о возведении
действительного числа в степень. Она разрешима для лю-
любого положительного числа а и любого действительного
числа а. Если а = 0 и а > 0, то х = 0 (см. § 4 гл. IV). При
а < 0 эта задача здесь рассматриваться не будет.
2. Даны действительные числа b и а. Найти действитель-
действительное число х такое, что Xй — Ъ.
Если b — любое положительное число й^Г^^юбое
отличное от нуля действительное число, то эта задача
сводится к предыдущей, ибо ответ дает число х = Ы. Дей-
(Ч 1а 1
ствительно, х° = I Ьа I = Ьа = b = b. Если а = 0и6=1,то
решением этой задачи является любое действительное от-
отличное от нуля число х. Если а = 0и6*1,то эта задача не
имеет решения. При Ъ < 0 эта задача здесь рассматриваться
не будет.
241
3. Даны действительные числа а и Ь. Найти действитель-
действительное число х такое, что а*= Ь. Будем рассматривать эту
задачу только для действительных положительных чисел а
и Ь- Если а ~ 1 и 6 = 1, то решением этой задачи является
любое действительное число х. Если а=1и6*1,то задача
не имеет решения. Рассмотрим случай пф\.
Теорема 1. Для любой пары действительных чисел аиЬ
таких, что а>0, a*l ub>0, существует и притом только
одно действительное число х такое, что d = Ь.
Доказательство существования такого числа х здесь не
приводится. Докажем единственность. Предположим, что
существуют действительные числа % и х^ такие, что а*1 = Ь,
а* = Ъ. Пр свойству транзитивности равенств а*х = а*1. На
основании утверждения 6 (см. § 4) х, = х2, что и требовалось
доказать.
Определение. Если а>0, пф\ и Ь>0, то действи-
действительное число ос называется логарифмом числа b no основанию
а и обозначается ос = \ogjb, если аа = Ь.
Заметим, что определение логарифма можно дать только
после доказательства теоремы 1, так как до нее было
неясно, существует ли такое число а, что аа = Ь, и единст-
единственно ли оно. Подчеркнем еще раз, что логарифм опреде-
определяется только для положительного числа по положитель-
положительному не равному единице основанию, т.е. для любого аи О,
а = 1 и любого ЬйО понятие логарифма лишено смысла.
Например, утверждение, что число 3 является логарифмом
числа (— 8) по основанию (— 2), лишено смысла. ,,.,,
Итак, в определении логарифма logj) всегда а > 0, а * 1,
Ь > 0. Из определения логарифма вытекает основное лога-
логарифмическое тождество
Пользуясь определением логарифма, получаем, что
= 1 и logel = 0.
Используя единственность логарифма, имеем, что если
ц > 0 и ц * 1, то всегда lojyi * 0,
142
Перейдем к рассмотрению основных свойств логариф-
логарифмов.
Пусть числа М, N, а, Ь, а и р таковы, что М> О, N> О,
а>0, 6 >0, а*\, 6*1, а я Э — любые действительные
числа О * 0). Тогда:
a) \ogaMN= \ogaM + logaN;
6)\ogJ%=\ogaM-\ogaN;
в)
д) logbM= т^-r (правило перехода от логарифма по одно-
му основанию к логарифму по другому основанию);
е) lo&M = \ogaNoM=N;
ж) если а > 1, то \о&№< \ogaNo M< N;
з) если 0 < а < 1, то logaM< logaW<s> M> N;
г') /
д')
Докажем эти свойства.
а) Рассмотрим
по основному логарифмическому _ жжът —
тождеству
по основному логарифмическому
тождеству
по свойству степени положительного
числа
Итак, ct*JIN= ^°t-M+lot"f/, Применяя к последнему ра
ству утверждение 6 свойств степеней, получим, что"
Свойство б) доказывается аналогично,
в) Рассмотрим
по основному логарифмическому _ _ .^ о _
тождеству = м=(а ) —
по свойству степени положительного _
числа . ~
243
Итак, a***} = d**^*. Применяя утверждение 6 свойств
степеней, получим 1о&,(А/") =
г) Рассмотрим
по основному логарифмическому _ , .-„ _ ,jc«^a _
тождеству \ ) к )
по свойству степени положительного _ jdat/n _
числа ~ <г^^ -
так как р ф 0, то 1 = р • |, поэтому = Г/ЛРч|Т1ов'л'=
по свойству степени положительного _ .«^
числа = Wp
Итак, (cP)Um*lMi = (flp)pk*^'. Применяя к последнему ра-
равенству утверждение 6 свойств степеней, получим, что
log,/ (Arf)e = ^logjl/.
д) Рассмотрим
по основному логарифмическому = м=
тождеству
по основному логарифмическому
тождеству
по основному логарифмическому
тождеству
по свойству степени положительного
числа
Итак, а10*^ = дк*^к***/. Применяя к последнему равенству
утверждение 6 свойств степеней, получим, что logJI/ =
= log^ lo&Af. По свойству равенств обе части этого равен-
равенства можно умножить на число —т (так как Ьф\, то
0) и получить справедливость равенства
244
е) По основному логарифмическому тождеству
М= aUm^tH N= я*0***, следовательно
М= Nod"* =<?**. A)
По утверждению 6 свойств степеней имеем
<?*•"= a**-"** log^Af = 1о&Д B)
Из A) и B) вытекает, что
M=No\ogaM=logaN.
ж) По основному логарифмическому тождеству
М= аи^ми N= a**^, следовательно
C)
На основании утверждения 4 свойств степеней имеем
а**-* < а*** о 1о&,А/< 1о&Д D)
Из C) и D) вытекает, что
М< No log.Af < log^.
Свойство з) доказывается аналогично.
Свойства ж) и з) имеют словесную формулировку:
При основании, большем единицы, меньшему из двух поло-
положительных чисел соответствует меньший логарифм и мень-
меньшему логарифму соответствует меньшее число.
^ При основании, меньшем единицы, меньшему из двух поло-
положительных чисел соответствует больший логарифм и боль-
большему логарифму соответствует меньшее число.
Логарифмы по основанию 10 называются десятичными
логарифмами, и вместо обозначения log10Af часто употреб-
употребляется обозначение lgM
Логарифмы по основанию е (е — иррациональное число,
приближенное значение которого 2,718281828459045...) на-
называются натуральными логарифмами, и вместо обозначе-
обозначения logfN часто употребляется обозначение ]nN.
иг
Свойства логарифмов используются для преобразования
различных логарифмических выражений как с числами,
так и с буквами.
Примеры. 1. Вычислить A = f^^
По свойству д') логарифмов ' _ = 4log35; по свойству
д) логарифмов log9V3-125 = log3* 53 = |log35. Используя свой-
свойства степеней и основное логарифмическое тождество,
получим
= 5" s = Щ
2. Доказать, что если а, Ь, с — действительные числа,
удовлетворяющие условию 0< Ьйс< а— 1, то справедли-
справедливо неравенство \о&,(а + Ь) < log,, _ &.
Доказательство. Поскольку д>0ис^6>0, то оче-
очевидна справедливость неравенства
в2 - (с - Ь)а - be < в2,
которое можно переписать так:
(а + Ь)(а - с) < в2. E)
Так как а > 1, то можно воспользоваться свойством ж) и
получить неравенство
/
F)
равносильное неравенству E).
Используя свойство а), получим неравенство
-c)<2, G)
равносильное неравенству F).
Каждое слагаемое в левой части неравенства C) положи-
положительно, так как {а + Ь) > 1 и (а — с) > 1. Следовательно,
246
можно воспользоваться теоремой 1 § 2 гл. II: возведя: щ
квадрат левую и правую части неравенства G) получим
равносильное неравенство.
Поэтому неравенство G) равносильно неравенству
которое равносильно неравенству
[кщАа + Ь) + \oga(a - с)}2 <
< 4 - 4 loge(a + Ь) + loga(a - с). (8)
Неравенство (S) равносильно неравенству E), которое
справедливо, значит, справедливо и неравенство (8).
Так как при Ь > О, с > 0 справедливо неравенство
О < DogJLa +b) + log,(fl - с)]2, (9)
то можно воспользоваться свойством транзитивности не-
неравенств.
Тогда из справедливости неравенств (8) и (9) будет
следовать справедливость неравенства
О < 4 — 4 logaia + b) + loge(fl — с),
которое можно записать так:
loge(a + Ь) + \oga(a - с) < 1.
Применяя свойство д') и учитывая, что а — с> 1иа> 1,
получим справедливость исходного неравенства.
УПРАЖНЕНИЯ
Найти числовое значение следующего числового выражения A — 19):
f (li J -,(- 0,5, V.
1. C!/ - К- Л V - (- 5'/. 2. ftf ¦ (li J -,(
5. (- 0.75K + @,3)" 3 ~ [~ f ] 6 К0.«) V - [(- 4,5)" V + Ш
247Г
2 [( 5)]2 [@l2f
8. f- 2^| • @,25J • [(- 5K]2 • [@,lJf \
10. 3-4:B4:32-22:l|)+f2i] (-0,295)
?[ -п
135 2163 [42 • 9J2 • 63 + 36 ¦ [32 • 42 • 34]2
Вынести за знак корня те множители числа, стоящего под знаком
корня, которые можно вынести B0 — 25):
20. л/Щ VhT, VIoT, V24T, V353". 21. 3V3T, 3V5T, 3>/5T7, 3VT5SO", 3V3l5".
22. 4VS0", 4V45T, 4V32T. 23. 5V4g?", 5V8OO~, V
248
24. Vl8D-Vl7J, V54B-VJ/. 25.
Внести под знак корня все множители, стоящие перед знаком корня
B6 - 30):
26. 4V3", 5V2, W|~, JVB". 27. 2 3V5", 3 л/4, 12 Vl^, 6 VlJ".
28. ^/8~, 1 JV6~, 1 jVijl 29. B - VI) • V2~, D - VI9) • VI.
30. (V3~- 2) • 4VT, A1 - Ш) ¦ 4V7.
Вынести за знак корня знаменатель дроби, стоящей под знаком корня
C1-33):
1
Записать в виде произведения двух чисел следующее число C4 — 37):
34. 7 + Vf, VTT+V4T+VII', S + tIS+Ш.
35. 5 - 3VT, VlF— 3V2T+ 3V20, 3 - 3Vf+ 3V2T.
36. 3VT2~- 3V6"+V36"-VU. 37. 3V4T- 3V7T+ 3V3T- 3V40.
Найти числовое значение следующего числового выражения C8 — 45):
38. 2V5V4T + 3V40VJT- 2V15V2T.
39. VT76"- 2V27T+ VI584"- V89T.
40. 2(V25l- VT75) - (VTTT- VST- V2T).
41. 15л/ТЖ-1^|"+ 6^~ EVp2"~ л/350).
42. 30 Ч^+ з| V^+ 5 3Vi44. 43. 2 >/ЬТ
44. 4VpS6T- SV0,00032. 45. (VS"- 2VI5) • у + V20.
Записать в виде корней одной и той же степени следующие четыре
числа D6 — 50):
46. 3V3", V2, 6VT и 4V7. 47. V5", VlJ, 8V50 и 16УГ7Г.
48. V2, 3V7, *Ш и I2VT67T. 49. ЧГ?, <4TW, УГ? и
so. vf, %; sf и vf:
Записать в виде степени с рациональным показателем следующие числа
E1 - 53):
5i.vr, Vt7", VIF, VIF, ViF.
249
52. VF1", VIF7", VF7", 'л/г77, VF5".
53. 2Л/421", 3 W, 7 VF, 3 VSt3", 9 VF".
Записать, используя знак корня, следующую степень с рациональным
показателем E4 — 57):
13 2 3 2 ,1
54. 2\ З4, S1, 77, 43, 55. З0-5, 40-25, 40'75, 71'25, 3 2.
- - 2±
56.3-23,4-34,5-60'25,7.32>25,2-92.
_! _2з _2
57.2-3 2,3-2-3>75,7-5 4, 6 ¦7~0'7, 8 • 10 2.
Заменив все знаки корней рациональными показателями степени,
найти числовое значение следующего числового выражения E8 — 64):
59. <Ш: p2Vf- ШГJ. 60. ЧъШ: ШШ:
61. fV^T]
62. V3V9V2W:
Найти числовое значение следующего числового выражения F5 — 78):
, i 1 1 3 1 _i 4 *
65. [273 • 83 ¦ 325 ¦ 814 Г. 66. (lOO 2 643 ¦ 0.250'5 • 16'75/.
2^
68.[B2.32):46]:{4 2:B 3-3
| Ir i i 1V
9. {з3 [
1 _2
64 3
Ч 5
):36}.
69. {з3 [5 2-3
70. 3 х-2
250
5 4
1 1 -Д
I i I
72.{32.53-24.[l6:B7-'.5 3 f [iS-32 :24)f.
_2 _I _1
73. 102-1000 3-(l00 2-0,027 5)-[б
--
74. [B7л/1K + (8V2K ] - Г| • C43>йK - 10 @,001 • л/2~Л
76. f4v^-0.5VIT+ л/0Ж-
77. p/5"-
Доказать справедливость следующего числового равенства G9 — 112):
79. V10-4V6* = t/S"- 2. 80. V3-
81.
83. ^n-
85. V
^T= 2VT. 82.
- 2. 84. "\Ы5*- >/з - V29 - 12V5" = 1.
86. V8 + V40+V20"+V8" =
87. V8
90. л/20+14^* + ^20-14^* = 4. 91. >/25 + 4VS"- ^1 + 2^/5" = 0.
93.
94.
2 §2".
95. л/28 + 4л/48" = л/3"+ 1. 96. л/17+12лЙ" = л/2~+ 1.
97. л[28 —
98.
= 2л/2".
251
. 102.
105.
106
107.
108
109
1B")(л/Т+ л/2").
VS"-\(l0
•л/2+л/3+л/5"~ 2
C0 - 2У30)(л/5'+ л/5~+ л/f)
26
111.
110. л/Т-
1.
112.
2 + л/З*
л/2~-^2--
113. Разность V|40>/2~— 57J — V4QVT+ 57 является целым числом.
Найти это целое число.
Какое из двух следующих чисел больше A14 — 123):
114. Ш или >6Г115.(^5ДГ3>5 или 1;
116. Ш или S*5T117. UV523~ или S*5T
118. B S^T' или 2" "; 119. 21л§- или 42Ш] j
120. ^/125 ¦ 343 или ^^ $9727121. V^^ или
122.
или
; 123.
или
252
Доказать справедливость следующего числового неравенства A24
132):
124. 334>251. 125. 202303 > 303202.
126.
128.
129. 6VI+
130. ( $5"+
131.
3.
+ 7 >fUf+
-W + л/9) > 9 >f5TT.
Найти числовое значение следующего числового выражения A33
170):
133. log2 %Ш+ log, ft-
134.
135. к*А V9~+ Iogw9 - Щ Ш+ log, V128V2".
3 % 8 ЧТ
136. к*з27 - togvr27 - tog, 27 -
138. logo Л
139.
140.
log
¦¦«
. Л/т V(V3"J
1. \TogJT \Ь?- + 1
141. VTog^V^ + log^
142.
143.2 logj ifT+i tog^25-logiV5"- 2.
144. ^^s*' -
145. tog3log>tog2l6.146
.147.
l+ 6 log2V2~+ 5].
148.
149.
151. 31+«о«з4 + 2«°«23-2 152.
153. 23-^Ч721^2Ч154Л6
155. 9* k*2+4 tog«|2 ¦ V32*!108316
156. (О,!
157.72-
": logo.2
gg g
160. 102
161. logvg-3 ¦ Iog336 + logvj« ¦ Iog481.
162. 72 logW|" log2s ^f2
163. 3J " ' ' " .164.@,2)
«« - R-31og^j5 —2log/j25 —log/j-10 + 21og,
165. (V2)
1
166. (Ig2 + Ig5 + Ig300 - Ig3) 3Sk)i53.
167.
169.
170. Iog32
• Iog54
Iog76 ¦ Iog87.
Имеет ли смысл следующее числовое выражение A71 — 173):
171. Vlog2l,4 + log20,7; 172. Vlgl5 + lg0,07; 173. lg Ig Igl 1?
254
Какое из двух чисел больше A74 — 188):
174. lgO,245 или 0; 175.l«pp-j или 0;
176. Ig ФкГ или log2V27 177.1о&»5 или 1о&5;
178. Iog910 или logioll; 179. Iog32 или Iog23;
180. Iog42 или logo,o62s0.2S; 181. log|891323 или 1о&3147;
182. logjll или logjV7T;183. i + lg3 или Igl9-lg2;
1в5 + 1ел/7
184. logo,20,8 + logo>25 или 0; 185.-s^-^- или j
186. 3 (Ig7 - igS) или 2 (±lg9 - jlg8]; 187. Ig Ig Ig5 или Ig35;
188. logj^log^ или Iog^-logv3? •.
2
Доказать справедливость следующего числового неравенства A89 —
205):
189. logs32 < Iog25. 190. Iog514 > Iog718.
191. log,6729 < Iog316. 192. кщ^/Тк logp/T.
2 3
193. logtog^j > 0. 194. ~- + T—i— < 2.
^**^2 logn Iog«
195. A + Iog25) flog2Vj5 + ll> 2 Iog25.
A )
A , \
196. logvr/35" 1+7 , - >4.
w [ logvj-7 • logvjfj
197. logjV Iog23 Iog25 < z}=. 198. 3 Iog57 + Iog75 + 1оь»5 > 4.
199. log7 ^4T-log7D5V3) > 24 log7 fe
4UV.
201.
202.
203.
4
,J. lgl + 1
lQg2log3g<
Iog62 ¦ log|2
5 5
log)
2
— ^
Ig3 + lg
6
log.f.
*2y>
3
1.204.
•
Iog,7>log73-|.
3
205. log,,( J
206. Зная, что 1о&2 = в, найти Iog2472.
207. Зная, что log^S = Ь, найти к%3б9.
208. Зная, что log4l2S = с, найти log|064.
209. Зная, что Iog|oo3 = а и Iogl0o2 = Р, найти Iogj6.
210. Зная, что 1о^15 = т и logJ18 = л, найти Iog2s24.
Глава V ТРИГОНОМЕТРИЯ
§ 1. Углы и их измерение
Понятие угла. Пусть даны два совпадающих луча: луч ОА
и луч ОВ (рис. 37).
Пусть луч ОА, поворачиваясь в плоскости вокруг точки
О, совершит некоторый поворот. Тогда для любого такого
поворота луч ОВ считается неподвижным (начальным)
лучом поворота, а луч ОА — подвижным, совершившим
данный поворот.
Любой поворот подвижного луча ОА от неподвижного
луча ОВ может быть совершен в двух противоположных
^ ^ направлениях (по часоьсй и про-
О А В тив часовой стрелки). Если на по-
Рис. 37. движном луче ОА приспособить
пишущее устройство, равномерно
удаляющееся от точки О вдоль
луча ОА, то при вращении луча ОА оно будет оставлять след
на плоскости. После того как луч ОА совершит некоторый
поворот, этот след будет представлять собой раскручиваю-
I
Рис. 38. Рис. 39.
щуюся вокруг точки поворота О кривую, которая начина-
начинается у неподвижного луча ОВ и оканчивается у подвижного
луча ОА. С помощью такой кривой на рисунках показывают
повороты. При этом возле подвижного луча кривая обяза-
256
тельно оканчивается стрелкой, указывающей направление
совершенного поворота.
На рис. 38 показан один из поворотов по часовой стрел-
стрелке.
На рис. 39 показан один из поворотов против часовой
стрелки.
Пусть подвижный луч ОА совершил такой поворот по
часовой стрелке, что луч ОА впервые совпал с начальным
лучом ОВ. Этот поворот принято называть полным оборотом
по часовой стрелке (рис. 40).
Пусть подвижный луч ОА совершил такой поворот про-
против часовой стрелки, что луч ОА впервые совпал с началь-
начальным лучом ОВ. Этот поворот принято называть полным
оборотом против часовой стрелки (рис. 41).
А В \О__У А В
Рис. 40. Рис. 41.
На рис. 42 показан поворот, равным трем полным обо-
оборотам против часовой стрелки.
На рис. 43 показан поворот, равным двум полным обо-
оборотам по часовой стрелке.
Итак, из рассмотренных примеров ясно, как изобразить
на рисунке любой поворот.
Пусть подвижный луч ОА совершил некоторый поворот
в плоскости вокруг точки О от неподвижного луча ОВ.
В
А В
Рис. 42. Рис. 43.
Тогда принято считать, что тем самым образован некото-
некоторый угол а, и в таком случае говорят, что подвижный луч
ОА задает угол а, соответствующий этому повороту. Точку
9 Алгебра, тригонометрия 257
ы элементарные функции
О называют вершиной угла а, неподвижный луч ОБ —
началом отсчета угла а, подвижный луч ОА — подвижным
лучом, задающим угол а. Неподвижный луч ОВ (начало
отсчета для любого угла) на рисунках принято располагать
горизонтально вправо. Принято считать: если подвижный
луч совершил некоторый поворот против часовой стрелки,
то он задает соответствующий положительный угол; если
подвижный луч совершил некоторый поворот по часовой
стрелке, то он задает соответствующий отрицательный угол;
если подвижный луч не совершил поворота, то он задает
нулевой угол.
Например, если подвижный луч ОА совершил полный
оборот против часовой стрелки, то он задает положитель-
положительный полный угол; если подвижный луч ОА совершил полный
оборот по часовой стрелке, то он задает отрицательный
полный угол.
Градусная мера угла. Пусть подвижный луч ОА совершил
поворот, равный ^ части полного оборота против, часовой
стрелки. Тогда говорят, что подвижный луч ОА задает угол,
градусная мера которого равна одному градусу, или коро-
короче — угол в один градус (Г). Следовательно, положитель-
положительный полный угол и угол в 360° — это один и тот же угол —
угол, который задает подвижный луч ОА, совершивший
полный оборот против часовой стрелки (см. рис. 41).
Для частей угла в один градус приняты специальные
наименования — минута и секунда.
Пусть подвижный луч ОА совершил поворот, равный
^ части поворота, соответствующего углу в один градус,
против часовой стрелки. Тогда говорят, что подвижный луч
• ОА задает угол в одну минуту (Г). Следовательно, угол в Ш
и угол в Г — это один и тот же угол.
Пусть подвижный луч ОА совершил поворот, равный
— части поворота, соответствующего углу в одну минуту,
против часовой стрелки. Тогда говорят, что подвижный луч
ОА задает угол в одну секунду A"). Следовательно, угол в
60" и угол в Г — один и тот же угол.
258
Пусть подвижный луч ОА совершил поворот, равный ^
части полного оборота против часовой стрелки. Тогда
говорят, что подвижный луч ОА задает положительный
прямой угол, или угол в 90" (рис. 44).
В
о в
Рис. 44. Рис. 45.
Пусть подвижный луч ОА совершил поворот, равный j
части полного оборота против часовой стрелки. Тогда
говорят, что подвижный луч ОА задает развернутый поло-
положительный угол, или угол в 180° (рис. 45).
Пусть подвижный луч ОА не совершил никакого пово-
поворота, тогда говорят, что подвижный луч ОА задает нулевой
угол, или угол в 0е (см. рис. 37).
В таких случаях иногда говорят, что подвижный луч ОА
совершил нулевой поворот. q
Пусть подвижный луч ОА совер- '
шил поворот, равный ^ части полно-
полного оборота по часовой стрелке. Тогда
говорят, что подвижный луч ОА за-
задает развернутый отрицательный
угол, или угол в (—180°) (см. рис. 45). А
Пусть подвижный луч ОА совер- Рис. 46.
шил поворот, равный j части полно-
полного оборота по часовой стрелке. Тогда говорят, что подвиж-
подвижный луч ОА задает отрицательный прямой угол, или угол в
(- 90е) (рис. 46).
Радианная мера угла. Пусть подвижный луч ОА совпадает
с неподвижным лучом ОВ, не совершив поворота. Возьмем
,. 259
произвольную точку М на неподвижном луче ОВ и точку
N подвижного луча ОА, которая совпадает с точкой М.
Проведем окружность с центром в точке О радиусом R,
равным длине отрезка ON (рис. 47).
В
В
Рис. 47.
Рис.48.
Если подвижный луч ОА будет вращаться вокруг точки
О, то точка N будет двигаться по этой окружности.
Пусть подвижный луч ОА совершил такой поворот про-
против часовой стрелки, что точка N, двигаясь по окружности,
прошла расстояние, равное радиусу этой окружности.
Тогда говорят, что подвижный луч ОА задает угол, радиан-
ная мера которого равна одному радиану, или короче —
угол в один радиан (рис.48).
Пусть дано положительное число р. Пусть подвижный
луч ОА совершил такой поворот против часовой стрелки,
что точка N, двигаясь по окружности, прошла расстояние
S, равное р/?, тогда говорят, что подвижный луч ОА задает
угол в р радиан.
Пусть дано отрицательное число р. Пусть подвижный луч
ОА совершил такой поворот по часовой стрелке, что точка
N, двигаясь по окружности, прошла расстояние S, равное
|Р|Л, тогда говорят, что подвижный луч ОА задает угол в Р
радиан.
Таким образом, радианную меру любого угла определяют
следующим образом. Пусть дан некоторый угол а, задавае-
задаваемый подвижным лучом ОА. Радианной мерой угла а назы-
называют такое число, абсолютная величина которого равна
отношению расстояния S, пройденного по окружности
260
радиуса R точкой N подвижного луча ОА, к радиусу R и
знак которого определяется направлением совершенного
поворота, другими словами, радианной мерой угла а назы-
вают положительное число ^, если поворот совершен про-
против часовой стрелки, или отрицательное число Г— ^\ если
поворот совершен по часовой стрелке.
Если угол задается подвижным лучом ОА, не совершив-
совершившим поворота, то угол а будет нулевым и радианную меру
этого угла полагают равной нулю.
Пусть подвижный луч ОА совершил полный оборот
против часовой стрелки, тогда точка N подвижного луча
ОА, двигаясь по окружности радиуса R, прошла расстояние
2nR. Значит, в этом случае подвижный луч ОА задает угол,
радианная мера которого равна 2л радиан, или короче, угол
в 2я радиан (рис. 49), т.е. угол в 360е и угол в 2я радиан, —
один и тот же угол (см. рис. 41 и рис. 49).
В
А Б
Рис. 49.
Рис. 50.
Если подвижный луч ОА совершил полный оборот по
часовой стрелке, то он задает угол в (— 2я) радиан (рис. 50),
т.е. угол в (— 360") и угол в (— 2я) радиан, — один и тот
же (см. рис. 40 и рис. 50).
Пусть подвижный луч ОА совершил А часть полного
оборота против часовой стрелки. Тогда точка N подвижно-
подвижного луча, двигаясь по окружности радиуса R, прошла рас-
стояние -у. Следовательно, если подвижный луч ОА совер-
совершил i часть полного оборота против часовой стрелки, то
261
он задает угол в | радиан (рис. 51), т.е. угол в 90° и угол в
| радиан, — один и тот же угол (см. рис. 44 и рис. 51).
Если подвижный луч ОА совер-
совершил j часть полного оборота по
часовой стрелке, то он задает угол в
!— 11 радиан (рис. 52), т.е. угол в
J f \
— 90°) и угол в ( —|] радиан, —
один и тот же угол (см. рис. 46 и
рис. 52).
Пусть подвижный луч ОА совер-
совершил ^ часть полного оборота против
часовой стрелки. Тогда точка N подвижного луча ОА,
двигаясь по окружности радиуса R, прошла расстояние nR,
следовательно, в этом случае, задаваемый подвижным
лучом ОА угол, будет углом в я радиан (рис. 53), т.е. угол в
180° и угол в я радиан — один и тот же угол (см. рис. 45 и
рис. 53).
В
Рис.51.
В
Рис. 53.
Аналогично угол в (— 180°) и угол в (— я) радиан — один
и тот же угол — угол, задаваемый подвижным лучом ОА,
совершившим ^ часть полного оборота по часовой стрелке
(см. рис. 45 и рис. 53).
262
Если радианная мера некоторого угла есть В радиан, а
градусная мера того же самого угла равна а градусов, то эти
числа связаны пропорцией
ос°: 360° = В : 2я.
Пользуясь этой пропорцией, можно переводить радиан-
ную меру угла в градусную и наоборот — градусную меру
в радианную. Рассмотренные выше примеры — частные
случаи этой пропорции. Приведем еще примеры.
Угол в 30° и угол в ? радиан есть один и тот же угол. Это
вытекает из справедливости пропорции 30°: 360° = |: 2я.
Угол в 45° и угол в ^ радиан есть один и тот же угол. Это
вытекает из справедливости пропорции 45°: 360° = ^ : 2я.
Угол в 60° и угол в | радиан есть один и тот же угол. Это
вытекает из справедливости пропорции 60°: 360° = |: 2я.
Замечание. Всюду в дальнейшем будет использоваться
только радианная мера угла. В обозначениях меры угла в
радианах почти всегда будет опускаться слово «радиан».
Поэтому в дальнейшем
— под углом я понимается угол в я радиан, т.е. угол,
радианная мера которого равна я радиан;
— под углом | понимается угол в | радиан, т.е. угол,
радианная мера которого равна ^ радиан;
— под углом а (где а — некоторое фиксированное число)
понимается угол в а радиан, т.е. угол, радианная мера
которого равна а радиан;
— под углом (а + В) понимается угол, радианная мера
которого равна (а + В) радиан;
— под углом (а — В) понимается угол, радианная мера
которого равна (а — (J) радиан.
Отметим еще, что под словами «угол а такой, что а ф В +
+ ку, ке 2» понимается, что угол а такой, что его радиан-
263
(-1,0)
ная мера не равна числу (Р + ку) ни при каком целом
числе к.
Единичная окружность. Пусть на плоскости введена пря-
прямоугольная система координат хОу с положительно полу-
полуосью абсцисс Ох, направленной вправо, и положительной
полуосью ординат Оу, направленной вверх. Пусть дана
окружность радиуса, равно-
@,1) го единице измерения
длин, и с центром в начале
координат (рис. 54). Такую
окружность принято назы-
называть единичной окружнос-
окружностью.
Примем за вершину лю-
любого угла начало коорди-
координат — точку 0@, 0). Поло-
Положительную полуось абсцисс
примем за неподвижный
луч, т.е. за начало отсчета
для любого угла а.
Пусть дан любой угол а; очевидно, что подвижный луч
ОА, задающий этот угол а, обязательно пересекает единич-
единичную окружность в некоторой точке QXa, b). Столь же
очевидно, что для любой точки R(c, d) единичной окруж-
окружности обязательно найдется угол р такой, что подвижный
луч ОА, задающий этот угол Р, пересекает единичную
окружность именно в этой точке R(c, d).
Определим координаты некоторых точек единичной ок-
окружности.
Прежде всего ясно (рис. 55), что: подвижный луч ОА,
задающий нулевой угол, пересекает единичную окружность
в точке М(\; 0); подвижный луч ОА, задающий угол тс,
пересекает единичную окружность в точке Р{— 1; 0); по-
подвижный луч ОА, задающий угол |, пересекает единичную
окружность в точке ДО; 1); подвижный луч ОА, задающий
угол | —1\ пересекает единичную окружность в точке
264
Пусть подвижный луч ОА, задающий угол ^, пересекает
единичную окружность в точке К (рис. 56). Вычислим ее
координаты. Проведем через точку К прямую, параллель-
параллельную оси Оу, пусть она пересекает ось Ох в точке Ки
ЦО-1)
Рис. 55.
Рис. 56.
Поскольку обе координаты точки ^положительны, то они
соответственно равны длинам катетов равнобедренного
прямоугольного треугольника ОКХК. Согласно теореме Пи-
Пифагора |OAJ2 = \ОК$ + {КК?; так как \ОКХ\ = |ЗД, то отсюда
получаем, что \ОКХ\ = \ККХ\ = -у. Поэтому абсцисса точки К
равна ординате точки К и равна -=-. Значит, подвижный луч
ОА, задающий угол |, пересекает единичную окружность в
Пусть подвижный луч ОА, задающий угол |, пересекает
единичную окружность в точке S (рис. 57). Вычислим ее
координаты. Проведем через точку S прямую, параллель-
параллельную оси Оу, пусть она пересекает ось Ох в точке Si.
Поскольку обе координаты точки S положительны, то они
соответственно равны длинам катетов прямоугольного тре-
треугольника OSiS. Из геометрии известно, что в прямоуголь-
прямоугольном треугольнике длина катета, лежащего против угла |,
265
равна половине длины гипотенузы. Значит, \SS\\ = L По
теореме Пифагора \OSi\2 = |OSJ2 — \SSi\2. Откуда \OSi\ = у.
Поэтому абсцисса точки S равна у, а ее ордината
равна |.
Значит, подвижный луч CU, задающий угол ^, пересекает
о
единичную окружность в точке si-^, т
^}
Рис. 57.
Рис.58.
Пусть подвижный луч ОА, задающий угол |, пересекает
единичную окружность в точке F (рис. 58). Вычислим ее
координаты. Проведем через точку F прямую, параллель-
параллельную оси Оу, пусть она пересекает ось Ох в точке Fx.
Поскольку обе координаты точки /"положительны, то они
соответственно равны длинам катетов прямоугольного тре-
треугольника. Используя сформулированное выше утвержде-
утверждение о длине катета, лежащего против угла ^, получаем, что
lO^I = -у, но тогда, применяя теорему Пифагора, находим,
что \F\J\ = -у. Поэтому абсцисса точки F равна L а ее
ордината равна -^.
246
Значит, подвижный луч ОА, задающий угол ^, пересекает
единичную окружность в точке f(-|, -у \
Пусть подвижный луч ОА, задающий угол а, пересекает
единичную окружность в некоторой точке QXa, b). Тогда
легко видеть справедливость следующих утверждений:
у,.
Рис. 59.
Рис. 60.
1. Подвижный луч ОА, задающий угол (ос + 2п), пересекает
единичную окружность в той же точке Q(a, b) (рис. 59).
2. Подвижный луч ОА, задающий угол (а — 2п), пересекает
единичную окружность в той же точке Q(a, b) (рис. 60).
Рис. 61.
Рис. 62.
3. Подвижный луч, задающий угол (а + я), пересекает
единичную окружность точке 0г(— а, — Ь), симметричной
точке Q(a, b) относительно начала координат — точки
0@, 0) (рис. 61).
267
Рис.63.
4. Подвижный луч, задающий
угол (— а), пересекает единичную
окружность точке (?,(а, — Ь),
симметричной точке Q(a, b) от-
относительно оси Ох (рис. 62).
5. Подвижный луч, задающий
угол (я — а), пересекает единич-
единичную окружность точке Q3(— a,
Ь), симметричной точке Q(a, b)
относительно оси Оу (рис. 63).
§ 2. Синус и косинус угла
Пусть на плоскости введена прямоугольная система ко-
координат хОу с положительной полуосью абсцисс Ох, на-
направленной вправо, и положительной полуосью ординат
Оу ординат, направленной вверх (рис. 64). Пусть дана
единичная окружность.
Примем за вершину любого угла начало координат —
точку 0@, 0). Положительную полуось абсцисс примем за
неподвижный луч ОВ, т.е. за нача-
начало отсчета для любого угла а.
Пусть точка Месть общая точка
неподвижного луча ОВ и единич-
единичной окружности. Тогда часть не-
неподвижного луча ОВ — отрезок
ОМ— будем называть единичным
неподвижным радиусом, или на-
началом отсчета углов.
Пусть подвижный луч ОА со-
совпадает с неподвижным лучом ОВ,
не совершив поворота. Точку по-
подвижного луча ОА, которая совпадает с точкой М непо-
неподвижного луча ОВ, обозначим через N. Тогда часть подвиж-
подвижного луча ОА — отрезок ON— будем называть единичным
Рис.64.
268
подвижным радиусом, а точку N — концом единичного
подвижного радиуса.
Если подвижный луч ОА совершит некоторый поворот,
то вместе с ним совершит этот же поворот и единичный
подвижный радиус ON. Поэтому можно считать, что не
только подвижный луч ОА задает некоторый угол а, но и
единичный подвижный радиус ON задает этот же угол а.
Условимся в дальнейшем говорить: единичный подвиж-
подвижный радиус ON задает угол а, понимая под этим, что
соответствующий подвижный луч ОА задает тот же самый
угол а.
Пусть конец подвижного единичного радиуса ON, зада-
задающего угол а, совпадает с точкой Q{a, b) единичной
окружности; тогда координаты точки Q будем называть
координатами конца единичного подвижного радиуса, за-
задающего угол а, и будем писать: N(a, b).
Синус угла. Пусть дан любой угол а. Число, равное
ординате конца подвижного единичного радиуса, задающе-
задающего этот угол а, называется синусом угла а и обозначается
sin а (рис. 65).
N(-1,0)
Рис. 65.
РИСа 66а
Из определения следует, что для любого угла а, сущест-
существует синус этого угла и притом единственный.
Примеры.
Ордината конца единичного подвижного радиуса, зада-
задающего нулевой угол, равна нулю (рис. 66), следовательно,
sin 0 = 0.
269
Ордината конца единичного подвижного радиуса, зада-
задающего угол я, равна нулю (см. рис. 66), следовательно,
sin я — 0.
Ордината конца единичного подвижного радиуса, зада-
задающего угол |, равна единице (рис. 67), следовательно,
sin |=1.
у,
N@,1)
Рис. 68.
Ордината конца единичного подвижного радиуса, зада-
задающего угол Г — 11 равна (—1) (см. рис. 67), следовательно,
У1
[
(
А.7
0
щ
\
\M(l,Ofx,
Рис. 69.
Рис. 70.
Ордината конца единичного подвижного радиуса, зада-
задающего угол ^, равна ^ (рис. 68), следовательно, sin ? = ^.
270
У i ,
N(a,b)
Рис.71.
Ордината конца единичного подвижного радиуса, зада-
ющего угол -т, равна -=- (рис. 69), следовательно, sin 7 = ~т-
Ордината конца единичного подвижного радиуса, зада-
задающего угол |, равна у (рис. 70), следовательно, sin | = -у.
Отметим некоторые свойства синуса угла.
Так как для любого угла а
ордината конца единичного по-
подвижного радиуса, задающего
этот угол а, не может быть
меньше, чем (— 1), и больше,
чем 1, а заключена между ними,
включая (— 1) и 1, то для любо-
любого угла а справедливо двойное N(a>~~b>
неравенство — 1 < sin a < 1.
Пусть ордината конца еди-
единичного подвижного радиуса,
задающего угол а, есть число Ь,
тогда, как указано выше, ордината конца единичного по-
подвижного радиуса, задающего угол (— а), есть число (— Ь)
(рис. 71). Поэтому для любого угла а справедливо равенст-
равенство
sin (— а) = — sin а.
Это свойство синуса угла можно сформулировать так:
знак минус можно выносить за знак синуса или вносить
под знак синуса, т.е.
sin (— а) = — sin а = sin (— а).
Примеры.
sin | — - | =
sin
sin
• я _
sin ^ —
. я
- Sin 4 =
• я
— sin у =
1.
V
_VT
V3~
2
27Д
Как указано выше, ордината конца единичного радиуса,
задающего угол а, равна ординате конца единичного ра-
радиуса, задающего угол (я — а) (рис. 72). Поэтому для
любого угла а справедливо равенство
sin (я — а) = sin а.
Примеры.
sin -f = sir
sin -?¦ = si
sin у = sin f re — |
=sinf
Пусть ордината конца единичного подвижного радиуса,
задающего угол а, есть число Ъ, тогда, как указано выше,
N(-a,
N(a,b)
N(a,b)
N(-a-b)
Рис. 72.
Рис. 73.
ордината конца единичного подвижного радиуса, задающе-
задающего угол (я + а) есть число (— Ь) (рис. 73). Поэтому для
любого угла а справедливо равенство
sin (я + а) = — sin а.
272
Примеры.
sin
sin
sin
5я
4
7я
6
4я
3
= sin
= sin
= sin
(
Y
я'
fl
= — sin
= — sin
= — sin
я _
4
я
6~
я _
3
2'
1
~~ 2'
Г"
Как указано выше, ордината конца единичного радиуса,
задающего угол а, равна ординате конца единичного ра-
радиуса, задающего угол (а + 2л), и равна ординате конца
единичного радиуса, задающего угол (а — 2я). Поэтому для
любого угла а справедливы равенства
sin a = sin (а + 2я),
sin а = sin (а — 2я).
Используя эти равенства и применяя метод математичес-
математической индукции, можно показать, что для любого целого
числа п и любого угла а справедливы равенства
sin a = sin (а + 2пп) = sin (а — 2тсл).
Это свойство синуса угла можно сформулировать так:
синус любого угла а повторяется при изменении угла на
2тш, где п — любое целое число.
Примеры.
9л
sin ^p = sin
sin у = sin
sin -^ = sii
о
sin -j = sin
sin у = sin
= sm
= sin
2 '
T'
273
sinff+K
sinf|+10«|=«siii|=l;
Пусть дано число ре @, я). Рассмотрим угол, радианная
мера которого есть это число р. Конец единичного подвиж-
подвижного радиуса, задающего этот угол, совпадает с некоторой
точкой единичной окружности, лежащей или в I или во II
четвертях, или на положительной полуоси ординат. Поэто-
Поэтому ордината конца единичного подвижного радиуса, зада-
задающего этот угол, положительна, другими словами, синус
этого угла положителен.
Учитывая, что sin p = sin (p + 2пп) для любого целого
числа л, можно утверждать, что sin а положителен для
любого угла а такого, что его радианная мера — число а —
принадлежит при некотором целом п соответствующему
интервалу Bпп, п + 2пп). На числовой прямой (рис. 74)
указаны такие интервалы, что для каждого числа а из
любого такого интервала sin а положителен.
п=-1 п=0 п=1
-2х -?¦ -к -3 О ? и % 2х &¦ Эк х
Рис. 74.
Аналогично показывается, что справедливо и такое ут-
утверждение: sin a — отрицателен для любого угла а такого,
что его радианная мера — число а — принадлежит при
п=-2 п=-1 п=0
-у -2к -у -к -§ 0 f к Щ- 2к х
Рис.75.
некотором целом п интервалу (я + 2тш; 2я + 2тш). На чис-
числовой прямой (рис. 75) указаны такие интервалы, что для
каждого числа а из любого такого интервала sin а отрица-
отрицателен.
274
Наконец, учитывая, что sin a = sin (а + 2пп) для любого
целого числа п и что sin 0 = sin я = 0, получаем, что sin a
равен нулю для любого угла а такого, что его радианная
мера — число а — равно при некотором целом т числу пт.
На числовой прямой (рис. 76) указаны такие числа а, для
каждого из которых sin а равен нулю.
т=—1 т=0 т=1 т=2 т=3
т=-2
i
м=1
i
-2к
О я
Рис. 76.
2к
Арксинус числа. Часто возникает такая задача: для любого
действительного числа а найти угол а такой, что его синус
равен этому числу а.
Сразу отметим, что если а > 1, а также если а < — 1, то
эта задача не имеет решения, так как по определению
синуса угла нет такого угла, синус которого был бы больше,
чем 1, или меньше, чем (—1).
Если же а € [— 1; 1], то можно показать, что существует
бесконечно много углов таких, что синус каждого такого
угла равен числу а. Действительно, прямая у = а при а €
е [— 1, 1] пересекает единичную окружность либо в двух
точках (рис. 77), либо в одной (рис. 78). Но, как указано
arcsn a
Рис. 77.
Рис
выше, для каждой такой точки единичной окружности
существует угол а такой, что синус этого угла равен орди-
ординате этой точки, т.е. равен а. Далее, по свойству синуса
275
sin a = sin (a + 2nn)
для любого угла a и любого целого числа п. Поэтому для
любого целого числа п синус угла (а + 2пп) равен числу а.
Принято следующее соглашение: тот угол, синус кото-
которого равен числу а и который взят из отрезка — f, §
называть главным углом и обозначать arcsin а (ч
арксинус числа а). Таким образом, по определению
arcsin a — есть угол, удовлетворяющий одновременно двум
условиям:
— | й arcsin а й |, sin (arcsin a) = а.
Легко видеть, что для любого числа а е [— 1; 1] арксинус
этого числа существует и притом единственный. Для лю-
любого числа а € (— оо, — 1) и A, + «>) арксинус этого числа
не существует.
Примеры.
1. arcsin 0 есть такой угол а, что — | й а й ^ и sin а = 0;
ясно, что это есть нулевой угол, следовательно,
arcsin 0 = 0.
2. arcsin 1 есть такой угол а, что —|^a^|nsina = l;
ясно, что это есть угол ^ (см. рис. 78), следовательно,
arcsin 1 = |.
3. arcsin (— 1) есть такой угол а, что — | ? а ? | и sin а =
= — 1; ясно, что это есть угол | — ^ | (см. ри. 78), следова-
следовательно, ^ '
arcsin (— 1) = — ^.
276
4. arcsini есть такой угол а, что — |^а^|и sin а = ^;
ясно, что это есть угол |, следовательно,
arcsin \ = %.
5. arcsin |—2" | есть такой угол а, что — |
^ ' ( IT I
= —у; ясно> что это есть угол | — ^ \ следовательно,
arcsin (- fl=-|.
V3" к к
6. arcsin-=- есть такой угол а, что — ^^а^^ и sina =
= -j-; ясно, что это есть угол |, следовательно,
arcsin -у- = j.
Отметим некоторые свойства арксинуса числа, вытекаю-
вытекающие из его определения. Для любого числа а, большего
чем 1, а также Для любого числа а, меньшего чем (—1),
лишена смысла запись arcsin а. Например, лишены смысла
записи
arcsin 2, arcsin (— 3), arcsin (— V5),
arcsin я, arcsin (—Зя), arcsin V|.
Для любого числа ае [— 1; 1] справедливо двойное
неравенство
— | ? arcsin аи*.
Для любого числа ае. [— 1; 1] справедливо равенство
sin (arcsin a) = а.
277
Для любого угла а е — |; | справедливо равенство
arcsin (sin a) = а.
Примеры.
1. Вычислить sin Гarcsin А Поскольку -| е [— 1; 1], то
sin [arcsin ~\ = -|.
2. Вычислить arcsin (sin V|j Поскольку V|~e Г— |; |~|, то
arcsin (siiW|)=V§.
Поскольку ^ <ё Г-1; |1 то
3. Вычислить arcsin sin -g-
нельзя написать, что arcsin
-^ =-4р. Однако легко
0 0
видеть, что sin-т- = siri|2n + 51= sin 5- Поэтому
обо
arcsin
arcsin
sin -^ ] = arcsin fsin 11 Поскольку | e — |; ^ , то
sin fsin 11 Поскольку | e — |; ^ ,
sin f\ = |. Итак, arcsin fsin ^\ = J.
4. В-ьгчислить arcsin [sin (— 5)]. Легко видеть, что sin
(— 5) = sin Bя — 5) и Bn — 5) e Г— |; |1. Поэтому arcsin
[sin (— 5)] = arcsin [sin Bя — 5)] = /я — 5: Итак, arcsin [sin
(— 5)] = 2я — 5. Наконец, отметим еще одно свойство
арксинуса числа а: для любого числа ее [— 1; 1] справед-
справедливо равенство
arcsin (— а) = — arcsin a.
Действительно, по определению
arcsin а = а, причем sin а = а и а е — |; | ,
arcsin (— а) = р, причем sin р = — а и р е — ^; |.
Отсюда очевидно, что р = — а, т.е.
arcsin (— а) = — arcsin a.
278
Примеры.
1. arcsin
2. arcsin
3. arcsin
Косинус
(-8;
-f|=-arcsin| = -f,
= — arcsin у = — J,
= - arcsin 5= —•?•
угла. "Пусть дан любой угол а. Число, равное
абсциссе конца подвижного единичного радиуса, задающе-
задающего этот угол а, называется косинусом угла а и обозначается
cos a (рис. 79).
Из определения следует, что
для любого угла а существует
косинус этого угла и притом
единственный.
Примеры.
Абсцисса конца единичного
подвижного радиуса, задающе- N(abj
го угол |, равна нулю (см.
рис. 67), следовательно,
Рис. 79.
cos 1 = 0.
Абсцисса конца единичного подвижного радиуса, зада-
задающего угол [ — 11 равна нулю (см. рис. 67), следовательно,
Абсцисса конца единичного подвижного радиуса, зада-
задающего нулевой угол, равна 1 (см. рис. 66), следовательно,
cosO= 1.
Абсцисса конца единичного подвижного радиуса, зада-
задающего угол я, равна (— 1) (см. рис. 66), следовательно,
cos я = — 1.
Абсцисса конца единичного подвижного радиуса, зада-
задающего угол |, равна -у (см. рис. 68), следовательно, cos | -
2'
279
Абсцисса конца единичного подвижного радиуса, зада-
задающего угол ^, равна -у (см. рис. 69), следовательно, cos ^ =
2'
Абсцисса конца единичного подвижного радиуса, зада-
1Г 1 * 1Г
ющего угол у, равна ^ (см. рис. 70), следовательно, cos -= =
_!
2"
Отметим некоторые свойства косинуса угла.
Так как для любого угла а абсцисса конца единичного
подвижного радиуса, задающего этот угол а, не может быть
меньше чем (— 1) и больше чем 1, а заключена между ними,
включая (— 1) и 1, то для любого угла справедливо двойное
неравенство
— 1 й cos а й 1.
Как показано выше, абсцисса конца единичного по-
подвижного радиуса, задающего угол а, равна абсциссе конца
единичного подвижного радиуса, задающего угол (— а).
Поэтому для любого угла а справедливо равенство
cos (— а) = cos а.
Это свойство косинуса угла можно сформулировать так:
знак перед углом, стоящим под знаком косинуса, можно
менять, не меняя значения косинуса угла, т.е.
cos (— а) = cos а = cos (— а).
Примеры.
cos
cos
cos б 2,
=«*!=т;
±
280
Пусть абсцисса конца единичного подвижного радиуса,
задающего угол а, есть число а; тогда, как показано выше,
абсцисса конца единичного подвижного радиуса, задающе-
задающего угол (я — а), есть число (— а) (см. рис. 72). Поэтому для
любого угла а справедливо равенство
cos (я — а) = — cos а.
Примеры
cos
cos
cos
Зя_
4
5я_
6
2я_
3
COS
COS
COS
HI
с я)
71 — z
T'-f
= — COS
= — COS
1= — cos
JC _
4
JC _
6 ~
я _
3
2'
V3".
2'
1
V
Пусть абсцисса конца единичного подвижного радиуса,
задающего угол а, есть число а; тогда, как указано выше,
абсцисса конца подвижного единичного радиуса, задающе-
задающего угол (я + а), есть число (— а) (см. рис. 73). Поэтому для
любого угла а справедливо равенство
cos (я + а) = — cos а.
Примеры.
-5
COS ^ = COS
4
COS -# = COS
4я
COS у = COS
Как указано выше, абсцисса конца подвижного единич-
единичного радиуса, задающего угол а, равна абсциссе конца
подвижного единичного радиуса, задающего угол (а + 2я),
и равна абсциссе конца единичного подвижного радиуса,
задающего угол (а — 2я). Поэтому для любого угла а
справедливы равенства
281
cos a = cos (a + 2л),
cos a = cos (a — 2л).
Используя эти равенства и применяя метод математичес-
математической индукции, можно показать, что для любого целого
числа п и любого угла а справедливы равенства
cos a = cos (a + 2тш) = cos (a — 2nn).
Это свойство косинуса угла можно сформулировать так:
косинус любого угла а повторяется при изменении угла на
2лл, где п — любое целое число.
Примеры.
cos
= cos Bл + !"] = cos | = ^;
COS -7- =
о
COS — = COS I — j
— -7 =COS
= cos
6
4
2 '
cos $ = cos
-5 + 2^-e«Y-*l-l:
-4 2'
COS
Пусть дано число ре (~ ?> f I Рассмотрим угол, радиан-
ная мера которого есть число р. Хонец единичного подвиж-
подвижного радиуса, задающего этот угол, совпадает с некоторой
точкой единичной окружности, лежащей в I или в IV
четвертях, или на положительной полуоси абсцисс. Поэто-
Поэтому абсцисса конца единичного подвижного радиуса, зада-
задающего этот угол, положительна; Другими словами, косинус
этого угла положителен. Учитывая, что cos р = cos (р + 2тси)
282
для любого целого числа п, можно утверждать, что cos a
положителен для любого угла а такого, что его радианная
мера — число а — принадлежит при некотором целом п
На числовой прямой
ы, что для каждого числа
а из любого такого интервала cos а положителен.
п=-1 п=0 п=1
-т -А -т -я 0 ¦ \ я т А т х
Рис. 80.
Аналогично, показывается, что cosy отрицателен для
любого угла у такого, что его радианная мера — число у —
принадлежит при некотором целом п интервалу
|| + 2тш, •у + 2тш1 На числовой прямой (рис. 81) указаны
такие интервалы/ что для каждого числа у из любого такого
интервала cos у отрицателен.
п=-1 п=0 п=1
-f те -J 0 $ к & 2к & Зк Ц- х
Рис.81.
Наконец, учитывая, что cos a = cos (а + 2тш) для любого
целого числа п и что cos^ = cos[— f |= 0, получаем, что
п=-3 п=-2 п=-1 п=0 п=1 п=2
1 1 1 1 1 1 >
~2 2 7 ? 2 1 Х
Рис. 82.
cos а равен нулю для любого угла а такого, что его ради-
радианная мера — число а — равно при некотором целом п
283
числу inn +11 На числовой прямой (рис. 82) указаны такие
числа ос, для тсаждого из которых cos а равен нулю.
Арккосинус числа. Часто возникает такая задача: для
любого действительного числа а найти угол а такой, что
его косинус равен этому числу а.
Сразу отметим, что если а > 1, а также если а < — 1, то
эта задача не имеет решения, так как по определению
косинуса угла нет такого угла, косинус которого был бы
больше, чем 1, или меньше, чем (— 1).
Если же а е [— 1; 1], то можно показать, что существует
бесконечно много углов таких, что косинус каждого такого
угла равен числу а.
Действительно, прямая х = а при а е [—1,1] пересекает
единичную окружность либо в двух точках (рис. 83), либо
в одной (рис. 84). Но, как указано выше, для каждой такой
Рис.83.
Рис.84.
точки единичной окружности существует угол а такой, что
косинус этого угла равен абсциссе этой точки, т.е. равен а.
Далее, по свойству косинуса
cos a = cos (а + 2пп)
для любого угла а и любого целого числа п. Поэтому для
любого целого числа п косинус угла (а + 2тм) равен
числу а.
Принято следующее соглашение: тот угол, косинус ко-
которого равен числу а и который взят из отрезка [0, тс],
284
называть главным углом и обозначать arccos а (читается:
арккосинус числа а). Таким образом, по определению
arccos а есть угол, удовлетворяющий одновременно двум
условиям:
О й arccos a<n, cos (arccos a) = а.
Легко видеть, что для любого числа ае [— 1; 1] арккосинус
этого числа существует и притом единственный. Для лю-
любого числа де (— «», — 1)иA, +<») арккосинус этого
числа не существует.
Примеры.
1. arccos 1 есть такой угол а, что Ойайп и cosa=l.
Очевидно, что это есть нулевой угол (см. рис. 84), следова-
следовательно, arccos 1=0.
2. arccos 0 есть такой угол а, что 0 й а й я и cos а = 0.
Очевидно, что это есть угол | и, следовательно, arccos 0 =
_ п
Г
3. arccos (— 1) есть такой угол а, что 0?<x?jtHCosa =
= — 1. Очевидно, что это есть угол я (см. рис. 84) и,
следовательно, arccos (— 1) = п.
4. arccos ^ есть такой угол а, что Ойайп и cos а = ^.
Ясно, что это есть угол | и, следовательно, arccos ^ = |.
5. arccos -j есть такой угол а, что 0?<x?jtHcosa = -y.
Ясно, что это есть угол | и, следовательно, arccos -у = j.
6. arccos -у есть такой угол а, что 0?a?jtHcos<x = y-
Ясно, что это есть угол ? и, следовательно, arccos ^r = т.
О 2. о
Отметим некоторые свойства арккосинуса числа, выте-
вытекающие из его определения.
Для любого числа а, меньшего чем (— 1), а также для
любого числа а, большего чем 1, лишена смысла запись
arccos а. Например, лишены смысла записи
285
arccos VT, arccos f—|\ arccos л,
cos j — -ji I arccos V-^C arccos f—1
Для любого числа ае [— 1; 1] справедливо двойное
неравенство
О < arccos а<п.
Для любого числа а е [— 1; 1] справедливо равенство
cos (arccos a) = а.
Для любого угла а е [0; я] справедливо равенство
arccos (cos a) = а.
Примеры.
1. Вычислить cos (arccos 0). Поскольку 0 е [— 1; 1], то
cos (arccos 0) = 0.
2. Вычислить cos [arccos А Поскольку |е [— 1, 1], то
cos farccos V)= ?•
3. Вычислить arccos (cos "ЛГ). Поскольку "ЛГе [0, я], то
arccos (cos) = VJT.
4. Вычислить arccos [cos (— 6)]. Так как (— 6) ё [0, п], то
нельзя написать, что arccos [cos(— 6)] = — 6. Однако легко
видеть, что cos (— 6) = cos Bя — 6) и Bл — 6) е [0, я].
Поэтому arccos [cos (— 6)] = arccos [cos Bя — 6)] = In — 6.
Наконец, отметим, еще одно свойство арккосинуса
числа: для любого числа ае [—1,1] справедливо равенство
arccos (— а) = п — arccos a.
Действительно, по определению
arccos а = а, причем cos а = а и а е [0, я],
arccos (— а) = р, причем cos р = — а и р е [0, я].
Отсюда видно, что р = я — а, т.е. arccos (— а) = я — arccos а
286
Примеры.
1. arccos
2. arccos
3. arccos
— -П = n — arccos | = n — f = ^,
= 7t — arccos -=- = я; — т = ~r>
z 4 4
л/Т я 5л
у = п — arccos — = п — •? = ^.
§ 3. Тангенс и котангенс угла
Тангенс угла. Пусть дан любой угол а такой, что а ф ^ +
+ пк, к& Z. Тангенсом этого угла а называется число,
равное отношению синуса этого угла а к косинусу того же
угла а и обозначается tg a, т.е.
cosa
Из определения следует, что для любого угла а такого, что
а ф j + пк, к е Z, тангенс этого угла а существует и притом
единственный.
Примеры.
cosre
COS?
я 3
COS-г
Отметим некоторые свойства тангенса угла.
Для любого угла а такого, что а * ^ + пк, к е Z, справед-
справедливо равенство
tg (- а) = - tg а.
287
Действительно, для любого угла а справедливы равенства
sin (— а) = — sin а и cos (— а) = cos а, поэтому для любого
угла такого, что а * | + пк, к е Z, по определению тангенса
tg (_ „) =
tg a.
cos (— a) cos a cos а
Это свойство тангенса угла можно сформулировать так: для
любого угла а такого, что а * | + пк, к& Z, знак минус
можно выносить за знак тангенса или вносить под знак
тангенса, т.е. если <х*| + тс?, fceZ, то
tg (- а) = - tg а = tg (- а).
Примеры.
4
tg Я>
С
6
6
Используя свойства синуса и косинуса угла, можно
показать, что для любого угла а такого, что а * | + пк, к е
е Z, справедливы равенства
tg a = tg (а + п) = tg (а — п).
Действительно, для любого такого угла справедливы цепоч-
цепочки равенств
cos (a + я) — cos a cosa
cos (a — я) —cosa cosa
288
Примеры.
5я_
-¦„Я-
tgi-tg hc + 5 =tgj=l;
LY
= tg
Используя равенства
tg a = tg (а + я) = tg (а — я)
и применяя метод математической индукции, можно по-
показать, что для любого целого числа л и любого угла а
такого, что а * | + ял, л е Z, справедливы равенства
tg a = tg (а + ял) = tg (а — ял).
Это свойство тангенса угла можно сформулировать так:
тангенс любого угла а такого, что а * | + ял, л е Z, повто-
повторяется при изменении угла на ял, где л — любое целое
число.
Примеры.
= to 7те = to — = ——
10 Алгебра, тригонометрия
н элементарные функции
tgff- I5nl=tgf =
t
Для любого угла а, синус и косинус которого одного
знака, тангенс угла а положителен, т.е. tg a положителен
для любого угла а, задаваемого подвижным единичным
радиусом, конец которого совпадает с точкой единичной
окружности, лежащей в I или III четвертях [т.е. для любого
числа а как радианной меры соответствующего угла а,
принадлежащего при некотором целом п интервалу
!7Ш, ^ + пп ||. На числовой прямой (рис. 85) указаны такие
[нтервалы, что для каждого числа а из любого такого
интервала tg a положителен.
-ill
—3
-f
n=-2
_¦}_ 3n
n=-l
-it —5
Рис.
n=0
0 1
85.
n-1
я -
n=2
X
Для любого угла а, синус и косинус которого разных
знаков, тангенс угла а отрицателен, т.е. tg a отрицателен
для любого угла а, задаваемого подвижным единичным
п=-2 п=-1 п=0 п=1 п=2 п=3
Ьня* Ьяя«1 Ьяя* fen* Нна* hmrt >
-4* -2п -—¦ -к -j 0 f я уйгуЗкх
Рис. 86.
радиусом, конец которого совпадает с точкой единичной
окружности, лежащей в II или IV четвертях [т.е. для любого
числа а как радианной меры соответствующего угла а,
принадлежащего при некотором целом п интервалу
— ^ + пп, пп 1]. На числовой прямой (рис. 86) указаны
290
такие интервалы, что для каждого числа а из любого такого
интервала tg а отрицателен.
Для любого угла а, синус которого равен нулю, тангенс
угла а тоже равен нулю, т.е. tg а = 0 для любого угла а,
задаваемого подвижным единичным радиусом, конец ко-
которого совпадает или с точкой МA; 0) или с точкой
Р(— 1; 0) (т.е. для любого числа а как радианной меры
соответствующего угла а, равного при некотором целом п
числу юг). На числовой прямой (см. рис. 76) указаны такие
числа а, для каждого из которых tg а равен нулю.
Ща,Ь)
Рис. 87.
Рис. 88.
Приведенное выше определение тангенса угла можно
переформулировать так:
пусть дан (рис. 87) любой угол а такой, что а ф j + таг,
пе Z, и пусть конец подвижного единичного радиуса,
задающего этот угол а, есть точка N(a, b) [причем аф0,
вследствие того что а ф ^ + пп, п е z\ тангенсом этого угла
называется число, равное отношению ординаты точки N
к абсциссе той же точки N, т.е.
tga-|.
Легко видеть (см. рис. 87), что прямая, проходящая через
начало координат и точку N(a, b), пересекает прямую х = 1
в точке ЛШ,А Другими словами, прямая, проходящая
через начало координат и конец подвижного единичного
радиуса, задающего угол а |<х ф^ + пп, п е Z\, пересекает
прямую х = 1 в точке К A, tga). Поэтому прямую х= 1
часто называют линией тангенсов.
Арктангенс числа. Часто возникает такая задача: для
любого действительного числа к найти угол а такой, что
его тангенс равен этому числу к.
Можно показать, что существует бесконечно много углов
таких, что тангенс каждого такого угла равен числу к.
Действительно, можно видеть (рис. 88), что прямая, про-
проходящая через начало координат и точку СA; к), лежащую
на прямой тангенса, пересекает единичную окружность в
двух точках: | . * ., ¦ * ,) и ( ,~ ?,, .""*.,\ Но, как ука-
IVTTFWi+FJ IVTTFVTiTj
зано выше, для каждой такой точки единичной окружности
существует угол а такой, что тангенс этого угла равен
отношению ординаты этой точки к абсциссе этой же точки,
т.е. равен к. Далее по свойству тангенса
tg a = tg (a + nt)
для любого угла а такого, что аф| + пт, те Z, и любого
целого числа /. Поэтому для любого целого числа / тангенс
угла (a + nl) равен числу к. Принято следующее соглаше-
соглашение: тот угол, тангенс которого равен числу к и который
взят из интервала [ — ?, ^ I называть главным углом и обо-
обозначать arctg к (читается: арктангенс числа к).
Таким образом, по определению arctg к есть угол, удов-
удовлетворяющий одновременно двум условиям:
292
— I < arctg к < |, tg (arctg к) = к.
Легко видеть, что для любого действительного числа к
арктангенс этого числа существует и притом единствен-
единственный.
Примеры.
1. arctg 0 есть такой угол а, что — |<a<|ntga = 0.
Ясно, что это есть нулевой угол, следовательно, arctg 0 = 0.
2. arctg 1 есть такой угол а, что — ^<oc<^Htga=l.
Ясно, что это есть угол ^, следовательно, arctg I = т-
3. arctg VT есть такой угол а, что — |<a<^Htga = VT.
Ясно, что это есть угол у. Следовательно, arctg VT = у.
VT я я VT
4. arctg -^ есть такой угол а, что — ^<a<^Htga = --f.
Ясно, что это есть угол ^. Следовательно, arctg -у- = ^.
5. arctg (— 1) есть такой угол а, что — ^<a<?ntga =
= — 1. Ясно, что это есть угол I — ^1 Следовательно,
( 1Л V )
arctg(-l)= -J
Отметим некоторые свойства арктангенса числа, выте-
вытекающие из его определения.
Для любого действительного числа к справедливо двой-
двойное неравенство
- |< arctgk<\
Для любого действительного числа к справедливо равен-
равенство
tg (arctg к) = к.
Для любого угла а е | — j, j] справедливо равенство
293
arctg (tg a) = a.
Примеры.
1. Вычислить tg (arctg 10). Получаем tg (arctg 10) = 10.
2. Вычислить arctg [ tg * \ Поскольку f e [ — 5, * \ то
)
(tg11
« | — j, j I to
Ш = tg (rO —
3. Вычислить arctg (tg Зя). Поскольку Зя е Г— ^, ^1 то
нельзя написать arctg (tg Зя) = Зя. Однако tg Зя - tg 0. Сле-
Следовательно, arctg (tg Зя) = arctg (tg 0) = 0.
4. Вычислить arctg (tg 10). Поскольку 10 « f — Ц, Ц \
нельзя написать arctg (tg 10) = 10. Однако tg
— Зя). Так как A0 — Зя) е (— j, j[ то arctg (tg 10) =
= arctg [tg A0 - Зя)] = 10 - Зя> '
Наконец, отметим еще одно свойство арктангенса числа:
для любого действительного числа к справедливо равенство
arctg (— к) = — arctg к.
Действительно, по определению
arctg к = а, причем tg а = к и а е | — j, j I
arctg (- к) = p, причем tg p = - к и р е (-1, fi
отсюда очевидно, что р = — a, т.е.
arctg (— k) = — arctg k.
Примеры.
1. arctg (— 1) = — arctg 1 = — ^.
2. arctg (— V3) = — arctg V3~= — |.
3. arctg [ —5~ 1= — arctg ~«~ = — ~?.
Котангенс угла. Пусть дан любой угол а такой, что
а ф пт, те Z. Котангенсом этого угла а называется число,
^294
равное отношению косинуса этого угла а к синусу того же
угла а и обозначаемое ctg a, т.е.
sina
Из определения следует, что для любого угла а такого,
что а фпт, те Z, тангенс этого угла а существует и
притом единственный.
Примеры.
COS7
sm4 T
з . я vt з-
япз Т
Отметим некоторые свойства котангенса угла.
Для любого угла а такого, что а ф nm, me Z, справедливо
равенство
ctg (— a) = — ctg a.
Действительно, для любого такого угла справедлива цепоч-
цепочка равенств
' sin (—a) — sin a sina
Это свойство котангенса угла можно сформулировать так:
для любого угла а такого, что а ф пт, знак минус можно
выносить за знак котангенса или вносить под знак котан-
котангенса, т.е. если а Ф пт, т е Z, то
ctg (— a) = — ctg a = ctg (— a).
Примеры.
J4^ _
з •
Используя свойства синуса и косинуса угла, можно
показать, что для любого угла а такого, что а ф я/и, те Z,
справедливы равенства
ctg a = ctg (а + я) = ctg (а — я).
Действительно, для любого такого угла справедливы
цепочки равенств
ctg (а + п) = ?<*i«±^ = zz?5*« = «*« = ctg а>
sm(a+K) — sin a sina
ctg (a -n) = со8(«-Я) =Izcos« = cos» =
v 7 sin(a — я) — sina sma
Примеры.
Используя равенства
ctg a = ctg (а + я) = ctg (а — я)
и применяя метод математической индукции, можно по-
показать, что для любого целого числа л и любого угла а
такого, что а ф я/и, те Z, справедливы равенства
ctg a = ctg (а + ля) = ctg (а — ля).
Это свойство котангенса можно сформулировать так: ко-
котангенс любого угла а такого, что а ф я/и, те Z, повторя-
повторяется при изменении угла на ял, где л — любое целое число.
Примеры.
Для любого угла а, косинус и синус которого одного
знака, котангенс угла а положителен, т.е. ctg а положите-
положителен для любого угла а, задаваемого подвижным единичным
радиусом, конец которого совпадает с точкой единичной
окружности, лежащей в I или III четвертях [т.е. для любого
числа а как радианной меры соответствующего угла а,
принадлежащего при некотором целом / интервалу
^ На числовой прямой (см. рис. 85) указаны такие интер-
интервалы, что для каждого числа а из любого такого интервала
ctg а положителен.
Для любого угла, косинус и синус которого разных
знаков, котангенс угла а отрицателен, т.е. ctg а отрицате-
отрицателен для любого угла а, задаваемого подвижным единичным
радиусом, конец которого совпадает с точкой единичной
окружности, лежащей в II или IV четвертях [т.е. для любого
числа а как радианной меры соответствующего угла а,
принадлежащего при некотором целом к интервалу
2?7
На числовой прямой (см. рис. 86) указаны такие интер-
интервалы, что для каждого числа а из любого такого интервала
ctg а отрицателен.
Для любого угла а, косинус которого равен нулю, котан-
котангенс угла а тоже равен нулю т.е. ctg а = 0 для любого угла
а, задаваемого подвижным единичным радиусом, конец
которого совпадает или с точкой ДО; 1), или с точкой ДО;
— 1) [т.е. для любого числа а как радианной меры соответ-
соответствующего угла а, равного при некотором целом п числу
i—}
v На числовой прямой (см. рис. 82) указаны такие числа
а, для каждого из которых ctg а равен нулю.
Приведенное выше определение котангенса угла можно
переформулировать так:
пусть дан (рис. 89) любой угол а такой, что а Ф пт, те Z,
и пусть конец подвижного единичного радиуса, задающего
этот угол а, есть точка N(a, b) (причем ЬфО, вследствие
Рис. 89.
Рис. 90.
того что а ф пт, те Z); котангенсом этого угла а называ-
называется число, равное отношению абсциссы точки N к орди-
ординате той же точки N, т.е. ctg a = |.
Легко видеть (см. рис. 89), что прямая, проходящая через
начало координат и точку N(a, b), пересекает прямую у= \
298
в точке F\j, 11 Другими словами, прямая, проходящая
6'
через начало координат и конец подвижного единичного
радиуса, задающего угол а (а * я/и, т е Z), пересекает
прямую у = 1 в точке F (ctg a, 1). Поэтому прямую у=\
часто называют линией котангенсов.
Арккотангенс числа. Часто возникает такая задача: для
любого действительного числа d найти угол а такой, что
его котангенс равен этому числу d.
Можно показать, что-существует бесконечно много углов
таких, что котангенс каждого такого угла равен числу d.
Действительно, можно видеть (рис. 90), что прямая,
проходящая через начало координат и точку D(d; 1), лежа-
лежащую на линии котангенсов, пересекает единичную окруж-
окружность в двух точках: ( , .., ¦ Л \ Г ,, ,~ , I Но, как
j ?j
указано выше, для каждой такой точки существует угол
такой, что котангенс этого угла равен отношению абсциссы
этой точки к ординате этой же точки, т.е. равен d. Далее
по свойству котангенса
ctg a = ctg (а + ял)
для любого угла а такого, что а ф пт, т е Z, и любого
целого числа п. Поэтому для любого целого числа п котан-
котангенс угла (а + ял) равен числу d.
Принято следующее соглашение: тот угол, тангенс кото-
которого равен числу d и который взят из интервала @, я),
называть главным углом и обозначать arcctg d (читается:
арккотангенс числа d).
Таким образом, по определению arcctg d есть угол, удов-
удовлетворяющий одновременно двум условиям:
0 < arcctg d < я, ctg (arcctg d) = d.
Легко видеть, что для любого действительного числа d
арккотангенс этого числа существует и притом единствен-
единственный.
29?
Примеры.
1. arcctg 0 есть такой угол а, что 0 < а < п и ctg а = 0.
Ясно, что это есть угол ^, следовательно, arcctg 0 = \
2. arcctg VJ есть такой угол а, что 0<<x<jiHctg<x = V3~.
Ясно, что это есть угол ?. Следовательно, arcctg VT = 5.
о о
3.. arcctg 1 есть такой угол а, что 0 < а < п и ctg а = 1.
Ясно, что это есть угол ^, следовательно, arcctg l=j-
4. arcctg -г- есть такой угол а, что 0<a<jiHctga = -r-.
Ясно, что это есть угол -j. Следовательно, arcctg -у = ^.
5. arcctg (— 1) есть такой угол а, что 0<<x<jiHctg<x =
/"ЗиЛ
= — 1. Ясно, что это есть угол -^-1 Следовательно,
arcctg (- 1) = (f \
Отметим некоторые свойства арккотангенса числа, вы-
вытекающие из его определения.
Для любого действительного числа d справедливо двой-
двойное неравенство
0 < arcctg d < п.
Для любого действительного числа d справедливо равен-
равенство
ctg (arcctg d) = d.
Для любого угла а е @, я) справедливо равенство
arcctg (ctg a) = а.
Примеры.
1. Вычислить ctg (arcctg 10). Получаем
ctg (arcctg 10) = 10.
300
2. Вычислить arcctg |ctg^j Поскольку ye @, те), то
arcctg (ctg fW.
3. Вычислить arcctg I ctg
то нельзя написать arcctg
— у ] • Поскольку J — у |е @, те),
ctg -T
легко
= ctgf и ^е@, те).
видеть, что ctg — у = ctg — у
Следовательно, arcctg [ctg | — у jj = arcctg | ctg у | = y.
Наконец, отметим еще^ одно свойство арккотангенса
числа: для любого действительного числа d справедливо
равенство
arcctg (— d) = те — arcctg d.
Действительно, по определению
arcctg d = а, причем ctg а = d и а е @, те),
arcctg (— d) = р, причем ctg р = — d и р е @, те),
отсюда вытекает, что р = те — а, т.е.
arcctg (— d) = — arcctg d.
Примеры.
1. arcctg (— 1) = те — arcctg 1 = те — j = -г-.
2. arcctg (— V3) = те — arcctg V3"= те — | = y.
3. arcctg |—y-] = те — arcctg -у = те — у = у.
§ 4. Основное тригонометрическое тождество
Теорема. Для любого угла а справедливо равенство:
sin2 a + cos2 а = 1, A)
которое называется основным тригонометрическим тожде-
тождеством.
301
N(cos a, sina)
Эту теорему можно сформулировать так: квадрат синуса
любого угла плюс квадрат косинуса того же угла равен
единице.
Доказательство. Пусть
дан некоторый угол а. Тогда
координаты конца единичного
подвижного радиуса, задающе-
задающего угол а, будут (cos а, sin а)
(рис. 91). Так как квадрат рас-
]МA,о) х стояния между любыми двумя
точками плоскости, заданны-
заданными своими координатами,
равен сумме квадратов разнос-
разности одноименных координат, то
для точки (cos a, sin а) и точки
(О, 0) имеем
Рис.91.
ИЛИ
(cos a — ОJ + (sin a — ОJ = I2
sin2 а + cos2 а = 1
и теорема доказана.
Основное тригонометрическое тождество показывает, в
какой зависимости находятся синус и косинус одного и
того же угла. Зная одну из величин, входящих в основное
тригонометрическое тождество для некоторого угла а,
можно найти другую величину того же угла а. Действитель-
Действительно, основное тригонометрическое тождество равносильно
равенству cos2 а = 1 — sin2 а, которое равносильно следу-
следующему:
|cos ot| = Vl — sin2 a.
B)
Из равенства B) имеем
cos а = VI — sirf а. Ba) cos a = -Vl — sirf а<2б)
302
для любого угла а, для для любого угла а, для
которого cos а не которого cos а не
отрицателен (т.е. для положителен (т.е. для
любого а, принадлежащего любого а, принадлежащего
при каждом ке Z отрезку при каждом ке Z отрезку
Ълк - f; f + 2яЛ Ълк+f; f + 2я*Т).
Далее основное тригонометрическое тождество равно-
равносильно равенству
sin2 а = 1 — cos2 а,
которое равносильно следующему:
|sin <х| = VI — cos'a. C)
Из равенства C) имеем
sin a = Vl —cos2 a. (За) sin a = -Vl — cos2ajC6)
для любого угла a, для для любого угла а, для
которого sin а не которого sin а не
отрицателен (т.е. для положителен (т.е. для
любого а, принадлежащего любого а, принадлежащего
при каждом те Zотрезку при каждом те Zотрезку
[2гои; я + 2пт\). [п + 2пт; 2я + 2пт]).
Замечание. Формулы Bа) и B6) при граничных зна-
значениях угла а, т.е. при а = | + жк, где к е Z, дают одно и
то же значение cos a = 0; формулы (За) и C6) при гранич-
граничных значениях угла а, т.е. при а = пт, где те Z, дают одно
и то же значение sin a = 0.
Примеры.
1. Вычислить sin a, если cos a = — -jy и a e e J я, -у I
Для любого угла а из указанного промежутка sin ос отрица-
отрицаa = - Vl —cos2 a = — \ 1 — J— -^ j =
телен, и поэтому sin
J— -^ j
11
2. Вычислить cos а, если sin а = — ^ и а е | —
Для любого угла а из указанного промежутка cos
цателен, и поэтому cos а = — Vl — sin2 а = — V1 — [— -j J =
Зя _п\
2' 2\
хюаотри-
з *
Следствие \.Дпя любого угла а. такого,
ke Z, справедливо равенство
1 + tg2 а = —V-. D)
cos а
Доказательство. Так как а*^ + пк, ке Z, то
cos а * 0, и поэтому основное тригонометрическое тожде-
тождество A) можно почленно разделить на cos2 а. Тогда для
любого такого а имеем
cos2 а + sin2 а _ 1
cos а cos2 а'
о cos2 а | sin2 а _ 1 ^
cos2 а cos2 а cos а'
1 + tg2 а =
_ 1
cos а
Равенство D) доказано.
Равенство D) показывает, в какой зависимости находят-
находятся тангенс и косинус одного и того же угла а (а ф | + пк,
ке Z). Зная одну из величин, входящих в равенство D),
для некоторого такого угла а можно найти другую величину
того же угла. Действительно, так как а*^ + пк, ке Z, то
равенство D) равносильно равенству cos2 а = —Ц—, кото-
l+tg а
рое равносильно следующему:
E)
304
Из равенства E) имеем
1 Eа)
cos а =
l+tg a
для любого угла а, для
которого cos а положителен
(т.е. для любого а,
принадлежащего при
каждом к е Z интервалу
cos a =
E6)
для любого угла а, для
которого cos а отрицателен
(т.е. для любого а,
принадлежащего при
каждом к е Z интервалу
(
\ Р \ Р ,
Далее равенство D) равносильно равенству tg a =
_ 1 — cos а
cos2 а
, которое равносильно следующему:
|tgo| =
— cos a
F)
Из равенства F) имеем
Fа>
Vl —
cos a
cos a
для любого угла a, для
которого tg a и cos a одного
знака (т.е. для любого угла
а, принадлежащего при
каждом те Zмножеству
tg(X=
— VT—
cosa
и (| + 1пт\ п
cos a
для любого угла а, для
которого tg а и cos а разных
знаков (т.е. для любого угла
а, принадлежащего при
каждом т е Z множеству
[2пт — п; — ^ + 2пт | и
/ _ )
и — х + 2пт; 2%т
Замечание. Формулы Fа) и F6) при граничных зна-
значениях угла а, т.е. при а = пт, где те Z, дают одно и то
же значение tg a = 0.
Примеры.
1. Вычислить tg a, если cosa= —г-иае я;4г
305
Для любого угла а из указанного интервала tg а положи-
телен, a cos а отрицателен, и поэтому tg a =
- = 2.
cos a
2. Вычислить cos а, если tg а = — 3 и а е | — |; 0 \
Для любого угла а из указанного интервала cos a поло-
положителен, и поэтому cos а = , ,. — -^г-.
Vl+tg а ш
Следствие 2. Для любого угла а такого, что а*пк,
ke Z, справедливо равенство
1 + ctg2 а = —\-. G)
sin а
Доказательство. Так как а*пк, ke Z, то sin афО, и
поэтому основное тригонометрическое тождество A)
можно почленно разделить на sin2 а. Тогда для любого
такого а имеем
cos2 а + sin2 ct _ 1
sin2 а sin2 а'
<> cos2 а sin2 а _ 1
sin2 а sin а sin2 а'
о 1 ¦+ ctg2 а = Ц-.
sin а
Равенство G) доказано.
Равенство G) показывает, в какой зависимости находят-
находятся котангенс и синус одного и того же угла а(а*пк,ке 2).
Зная одну из величин, входящих в равенство G), для
некоторого такого угла а можно найти другую величину
того же угла а. Действительно, так как а.Фпк, ke Z, то
равенство G) равносильно равенству
2 1
sin2 a =
1 + ctg2 a'
которое равносильно следующему:
№
|sin ct| =
(8)
Из равенства (8) имеем
sin а = -==Ц= (8a)
fl+ctg ot
для любого угла а, для
которого sin а положителен
(т.е. для любого а,
принадлежащего при
каждом п е Z интервалу
Bт; п + 2т)).
Далее, так как а *л&, ке Z,
равенству
ctg2 а = -
sin<x =
(86)
—1
+ ctg'ot
для любого угла а, для
которого sin а отрицателен
(т.е. для любого а,
принадлежащего при
каждом п е Z интервалу
(я + 2ял; 2я + 2пп)).
то равенство G) равносильно
sin2 a
которое равносильно следующему:
— sin а
1*4-^
Из равенства (9) имеем
ctga =
VT-
sin a
sin a
(9a)
ctga =
— у 1 — sin а
sin а
(9)
(96)
для любого угла а, для
которого ctg а и sin а одного
знака (т.е. для любого а,
принадлежащего при
каждом ке Zмножеству
для любого угла а, для
которого ctg а и sin a
разных знаков (т.е. для
любого а, принадлежащего
при каждом ке Z
множеству
\
\
Замечание. Формулы (9а) и (96) при граничных зна-
я
2
чениях угла а, т.е. при а = ~ + пк, к е Z, дают одно и то же
значение ctg a = 0.
Примеры.
1. Вычислить ctg а, если sin а = — Ц и ае
€ I~~~ TCj ~~~ "Z
у
для любого угла а из указанного интервала ctg а поло-
положителен, a sin а отрицателен, и поэтому
2. Вычислить sin а, если ctg а = 4 и а е [я, у I
Для любого угла а из указанного интервала sin а отри-
отрицателен, и поэтому
sina = __L_ = -f.
Из определения тангенса и котангенса одного и того же
угла следует справедливость следующего утверждения:
для любого угла а такого, что а^у, ле Д справедливы
равенства
tgactga=l, A0)
A2)
Равенства A1) и A2) показывают, в какой зависимости
находятся тангенс и котангенс одного и того же угла a
!« ^ у, л € Z]. Зная одну из величин, входящих в равенства
11) и A2), для некоторого такого угла а можно найти
другую величину того же угла а.
308
Примеры.
1. Вычислить cos a, tga и ctga, если sin а = — | и
ае | —я; —1\
Для любого угла а из указанного интервала cos a отри-
отрицателен, и поэтому
cos a = -Vl — sin2 a = — |.
Так как cos a * 0, то
6 cosa 4'
Аналогично, так как sin a ф О, то
ana 3
2. Вычислить cos a, sin a и tg a, если ctg a = — 7 и
aefenj
Так как ctg a * 0, то tg a = —i- = — j-
Для любого угла a из указанного интервала sin a поло-
положителен, а cos a отрицателен, следовательно,
10"
§ 5. Формулы сложения
Пусть дан некоторый угол а и некоторый угол В, т.е.
пусть даны число а, представляющее радианную меру угла
а, и число В, представляющее радианную меру угла В. Тогда
под углом (а — В) понимается угол, радианная мера кото-
которого есть число (а — В); угол (а — В) называется разностью
двух данных углов. Под углом (а + В) понимается угол,
радианная мера которого есть число (а + В); угол (а + В)
называется суммой двух данных углов.
309
Косинус разности и косинус суммы.
Теорема. Для любых углов аир справедливо равенство
cos (а — р) = cos а cos р + sin а sin p,
A)
которое называется формулой косинуса разности двух углов.
Эту теорему можно сформулировать так: косинус разнос-
разности двух любых углов равен произведению косинуса уменьшае-
уменьшаемого угла на косинус вычитаемого угла плюс произведение
синуса уменьшаемого угла на синус вычитаемого угла.
Доказательство. Пусть на плоскости даны прямо-
прямоугольная система координат хОу и единичная окружность.
Будем считать началом отсчета неподвижный единичный
радиус ОМ этой окружности, где Af(l, 0).
Пусть угол а задается подвижным единичным радиусом,
конец которого совпадает с точкой N(cos a, sin а) единич-
единичной окружности; угол р — подвижным единичным радиу-
радиусом, конец которого совпадает с точкой P(cos p, sin p)
единичной окружности.
Возможны два случая расположения точек N и R они
или совпадают (рис. 92), либо не совпадают (рис. 93).
Рис. 92.
Рис.93.
Доказательство теоремы проведем отдельно в каждом из
этих случаев.
1. Пусть точки N и Р совпадают. В этом случае углы а и
р таковы, что а = р + 2пк, т.е. (а — р) = 2л ? для некоторого
310
фиксированного целого числа к, и равенство A) можно
переписать в виде
cos Ink = cos р cos (р + Ink) + sin p sin (p + 2nk)
или, поскольку
cos 2nk = 1
cos (p + 2nk) = cos p,
sin (p + Ink) = sin p,
в виде
1 = cos2 p + sin2 p,
т.е. в рассматриваемом случае равенство A) есть равносиль-
равносильная форма записи основного тригонометрического тожде-
тождества, следовательно, равенство A) справедливо.
2. Пусть углы аир таковы, что а * р + Ink ни для какого
целого числа к. Вычислим двумя способами длину отрезка
PN.
В данной системе координат координаты точек N и Р
известны, поэтому по теореме о длине отрезка, координаты
концов которого заданы, имеем
(cos а — cos рJ + (sin а — sin рJ.
B)
Введем теперь другую прямоугольную систему координат
так, чтобы единица масштаба совпадала с уже выбран-
выбранной ранее единицей длины;
положительная полуось абс-
абсцисс {Ох!) была бы продолже-
продолжением радиуса ОР\ положитель-
положительная полуось ординат (О/) об-
образовывала бы положительный
угол | с положительной полу-
полуосью абсцисс (Ох?) (рис. 94).
В новой системе координат
точка Р будет иметь координа-
94.
311
ты РA, 0). Примем теперь радиус ОР за неподвижный
единичный радиус, т.е. за новое начало отсчета углов.
Система координат х?О/ вводится так, чтобы новое начало
отсчета углов (единичный неподвижный радиус ОР) было
смещено на угол Р относительно предыдущего начала от-
отсчета углов (единичного неподвижного радиуса ОМ). Тогда
относительно нового начала отсчета углов подвижный еди-
единичный радиус Отбудет задавать угол (а — Р) и в системе
координат коу точка N будет иметь координаты
JV(cos (а — р), sin (а — р)). По теореме о длине отрезка,
координаты концов которого заданы (см. § 3 гл. III), имеем
&„ = [1 - cos (а - р)]2 + [0 - sin (а - Р)]2. C)
Так как квадрат расстояния между двумя фиксирован-
фиксированными точками плоскости, найденный в двух разных пря-
прямоугольных системах координат с одной и той же единицей
длины, есть одно и то же число, то d2NP = <fNP.
Используя свойство транзитивности равенств, из ра-
равенств B) и C) имеем
(cos а — cos рJ + (sin а — sin pJ =
= [1 - cos (а - р)]2 + [sin (а - р)]2.
Раскрывая скобки и группируя, имеем
(cos2 a + sin2 а) + (cos2 р + sin2 р) — 2(cos а cos p +
+ sin а sin р) = 1 + [cos2 (а — р) + sin2 (а — р)] —
— 2cos (а — Р).
Применяя трижды основное тригонометрическое тождест-
тождество, перепишем это равенство в виде
2 — 2[cos a cos р + sin a sin р] = 2 — 2cos (а — р).
Откуда следует справедливость теоремы во втором случае.
Теорема доказана.
312
Пример.
ВЫЧИСЛИТЬ COS yj.
ПОСКОЛЬКУ jz = у — j, TO
COStx =
2' 2 + 2 ' 2 4
Итак, cos ^ = ^
Приведем несколько следствий из доказанной теоремы.
Следствие 1. Для любых углов аир справедливо равен-
равенство
cos (а + р) = cos а cos р — sin а sin p,
которое называется формулой косинуса суммы двух углов.
Это следствие можно сформулировать так: косинус суммы
двух углов равен произведению косинуса первого угла на коси-
косинус второго угла минус произведение синуса первого угла на
синус второго угла.
Доказательство. Представим (а + р) в виде [а—
— (а — р)] и применим теорему. Затем, пользуясь тем, что
cos (— а) = cos а и sin (— а) = — sin а для любого угла,
имеем
cos (а + р) = cos [а — (а — р)] = cos а cos (— р) +
+ sin а sin (— р) = cos а cos р — sin а sin p,
что и требовалось доказать.
Примеры.
1. ВЫЧИСЛИТЬ COS jx.
Поскольку ^ = | + J, то
313
2 2 22
2. Вычислить cos —.
Поскольку Ц = | +1, то
cos ^ = cos (| + J |= cos | cos | — sin I sin J =
2 2 2 2
Итак, cosg-
Формулы для дополнительных углов. Два угла аир, в
сумме составляющие |, т.е. такие, что а + р = |, называют-
называются дополнительными один к другому. Так, угол а дополни-
тельный к углу [ | — а | и наоборот.
Следствием. Для'любого угли а справедливы равенства
cos 1^ —а |= sin а, sinf| — а|= cos а,
которые называются формулами для дополнительных углов.
Действительно, применяя равенство A), имеем
cos || — а |= cos| cos а + sin | sin а =
= 0 • cos а + 1 • sin а = sin а,
т.е. получаем справедливость первой формулы.
Обозначая | ~ — а | = р, получаем из уже доказанной пер-
первой формулы, что sin р = cos|| — Р| Так как || — р |= а,
то \ J \ J
314
r — p = cos a.
Следствие 2 можно сформулировать так:
— синус любого угла равен косинусу дополнительного угла, а
— косинус любого угла равен синусу дополнительного угла.
Пример.
Вычислить sin -jj.
Поскольку ^ = f — "fj. то sin ^ = sin ^ — -^ = cos -^.
Значение cos-^ было найдено выше и равно —^—-.
Следовательно, sin -^ = —^j-—-.
Следствие 3. а) Для любого угла а такого, что а
к е Z, справедливо равенство
т-а =ctga.
б) Для любого угла а такого, что а^ + ят,
справедливо равенство
^-a]=tga.
Эти равенства также называются формулами для дополни-
дополнительных углов. Справедливость этих формул следует из
определений тангенса и котангенса и следствия 2.
Пример.
Вычислить tg§. Так как -^ = | - Ц, то tg -^ =
= * (f ~ ll]= ctg TI= —5^' Значения cos || и sin § были
¦JT rJT \\
найдены выше и соответственно равны —^-j и
f^. Следовательно, tgi-^f или tg? = 2 - VI.
315
Синус суммы и синус разности.
Следствие Л. Для любых углов аир справедливо равен-
равенство
sin (а + р) = sin а cos p + cos а sin p,
которое называется формулой синуса суммы двух углов.
Это следствие можно сформулировать так: синус суммы
любых двух углов равен произведению синуса первого угла на
косинус второго угла плюс произведение косинуса первого угла
на синус второго.
Доказательство. Используя следствие 2, затем равен-
равенство A) и еще раз следствие 2, имеем
sin (а + р) = cos fe — а — р1=
cos
=cos f — a cos p + sin
что и требовалось доказать.
Примеры.
1. Вычислить sin -jj.
Поскольку ^ = ? + т, то
12 О 4
fit Y
f — a sinp =
J
= sin a cos p + cos a sin p,
cos ^ sin -г =
6 4
1 V2
2 TH
VT V2
2 ¦ 2
Итак, sin Ц =
2. Вычислить sin т5.
Поскольку Щ = | + J, то
316
VT jT i V2~_ У2(УУ+1)
2 ' 2 +2" 2 4
Итак, sin Ъ =
Следствие 5. Для любых углов а и р справедливо равен-
равенство
sin (а — р) = sin а cos р — cos а sin p,
которое называется формулой синуса разности двух углов.
Это следствие можно сформулировать так: синус разнос-
разности любых двух углов равен произведению синуса уменьшаемого
угла на косинус вычитаемого угла минус произведение коси-
косинуса уменьшаемого угла на синус вычитаемого угла.
Доказательство. Представим (а — р) в виде [а +
+ (— р)] и применим следствие 4. Затем, пользуясь тем, что
cos (— р) = cos р и sin ( — р) = — sin p для любого угла р,
имеем
sin (а — р) = sin [а + (— р)] = sin а cos (— р) +
+ cos а sin (— р) = sin а cos р — cos а sin p,
что и требовалось доказать.
Пример.
Вычислить sin -^.
Поскольку 75 = ? ~ i> т0
sin|cosj-cosfsinj =
I V2~_ V2(VT-1)
2' 2 4
Итак, sin i =
317
Тангенс суммы и тангенс разности.
Следствие 6. Для любых двух углов аир таких, что
_, . Я | _К 1. f Q . Я | ».-- 7*<#v-l-A.A^-l- «там ^ *- Т
(X ^ ¦«• т ТИС, КЕ ^, р ^ -z т ИИ, п€ Z и Отр^ут ftjff, fflE ?
справедливо равенство
которое называется формулой тангенса суммы двух углов.
Доказательство. Для любых двух таких углов спра-
справедлива цепочка равенств
45 ^ Р' cos(a+P) cos a cosp — sin asm p
sinacosp + cosasinp sin a cos p cos a sin p
cos a cos p cos a cos p cos a cos P _
cos a cos p — sin a sin p cos a cos p sin a sin p
cos a cos p cos a cos p cos a cos p
ana sinp
'•¦-*¦ r? v ч_ cos a cosp _ tga + tgP
_ sina sinp 1— tgatgp'
cos a cosp
которая и доказывает следствие 6.
Примеры.
5it
1. Вычислить tg -J2-
Поскольку 31 = 5 + f» то
12 е 4 6 1 . . к. к
<3
-1 (V3 -1) (VT+1)
_?. «•
Итак, tgff = 2
2. Вычислить tg -j|. Имеем
12 lg 3+4 я x 1-V3M
Итак, tg g = - B + VJ).
Следствие 7. Для любых двух углов а м р таких, что
а * ! + refc, Jfc е Д р * | + тш, л е Zm а — р ^ | + nm, m e Z,
справедливо равенство
(а - В) =
(a P) l
+tgatgp'
которое называется формулой тангенса разности двух углов.
Доказательство. Для любых двух таких углов спра-
справедлива цепочка равенств
te (а — Н) = te Га + (— fttl = *ga + tg(-P). - tga-<&p
tg(a p) tgla+( p)j ^^^^р, i + tgatgp'
которая и доказывает следствие 7.
Пример.
ВЫЧИСЛИТЬ tg jr.
Поскольку ^ = | — J, то
18 12 lg 3 4 I
^31
l+VT
Котангенс суммы и котангенс разности.
Следствие 8. Для любых двух углов ос и В таких, что
а ф пк, к е Z, В * пп, п е Z u (а + (J) * тш, те Z, справед-
справедливо равенство
cte Га + ВЪ =
ctgp + ctga
которое называется формулой котангенса суммы двух углов.
Следствие 9. Для любых двух углов акр таких, что
а ф пк, ке Z, В ф пп, п е Z и (а — В) * тш, т е Z, справед-
справедливо равенство
которое называется формулой котангенса разности двух
углов.
Доказательство этих следствий аналогично доказательст-
доказательству следствий 6 и 7 и потому опускается.
Примеры.
1. Вычислить ctg -j|.
Поскольку Щ = J + |, то
14 6 | % %
• 1) />
Итак, ctg|| = 2-VJ.
2. Вычислить ctg -^j. Имеем
320
12 ~*е 3 ' 4
Итак, ctg -^ = 2 + VJ.
Формулы для вычисления произведений.
Следствие 10. Для любых двух углов а и C справедливо
равенство
cos а cos p =
которое называется формулой для вычисления произведения
косинусов.
Следствие 10 можно сформулировать так: произведение
косинуса любого угла а на косинус любого угла р равно
полусумме косинуса разности этих углов и косинуса суммы
этих углов.
Следствие 11. Для любых двух углов аир справедливо
равенство
которое называется формулой для вычисления произведения
синусов.
Следствие 11 можно сформулировать так: произведение
синуса любого угла а на синус любого угла р равно полуразнос-
полуразности госинуса разности этих углов и косинуса суммы этих
углов.
Доказательство. Выше было показано, что для
любых углов и справедливы следующие равенства:
cos (a — Р) = cos a cos p + sin a sin p,
cos (a + P) = cos a cos p — sin a sin p.
11 Алгебра, тригонометрия 321
и элементарные функции
Складывая и вычитая эти равенства, получаем формулы
для вычисления произведения косинусов и произведения
синусов:
cos<aP>+cos<a+P> D)
E)
Замечание. В формулах D) и E), в силу того что
cos (— a) = cos a для любого угла а, при взятии косинуса
разности двух углов можно брать косинус угла (а — Р) и
угла (Р — а).
Примеры.
i.c«(f+;Wf-§)-
-НИ-ИНИ+f-f)-
cosa + cosf
—2p) — cos
fj=cos2p.
4 4sin7sin8 _ 4 [cos G - 8) - cos G + 8I _ 2 [cos 1 - cos 151
5 5 2 5
Следствие 12. Для любых двух углов а и р справедливо
равенство
которое называется формулой для вычисления произведения
синуса одного угла на косинус другого угла.
Следствие 12 можно сформулировать так: произведения
синуса любого угла а на косинус любого угла р равно полусумме
322
синуса суммы углов а и Р и синуса разности углов а и р, причем
разность берется так, что от угла, стоящего под знаком
синуса, вычитается угол, стоящий под знаком косинуса.
Доказательство. Выше было показано, что для
любых углов аир справедливы следующие равенства:
sin (а + Р) = sin a cos P + cos a sin P,
sin (а — Р) = sin а cos р — cos а sin p.
Складывая эти равенства, получаем формулу для вычисле-
вычисления произведения синуса угла на косинус другого угла:
_ sin (a + P) + sin (a — P)
2
F)
Примеры.
1. Вычислить 4 sin
Применяя форму
in | l + ||cos| 1 +
улу (б), имеем
4sin|l+
6
sin
sin
cos
«in
= 2
= 2|"si
Итак, 4 sin I l+||cos| 1+f ]:
sin
1+f-'-f)
f — (— 2I— i| = 2 cos (— 2) — 1 = 2 cos 2 — 1.
")=2cos2-l.
2. Вычислить icos ^ sin ^.
Применяя формулу F), имеем
= smT+sin—t=i —=- =
Итак, 2cos ^ sin -^ =
ч 3sin4cos5 _ 3[sinD + 5) + sinD-5)] _ 3(sin9-sinl)
J- 7 7 2 14
323
Формулы суммы и разности синусов и косинусов.
Следствие 13. Для любых двух углов а и р справедливо
равенство
cos a + cos P = 2 cos —к-* cos —y>
которое называется формулой суммы косинусов.
Следствие 13 можно сформулировать так: сумма косину-
косинусов любых двух углов равна удвоенному произведению косинуса
полусуммы этих углов на косинус полуразности этих углов.
^Следствие 14. Для любых двух углов а и р справедливо
равенство
cos a — cos p = 2 sin ^j? sin ^y^,
которое называется формулой разности косинусов.
Следствие 14 можно сформулировать так: разность коси-
косинусов любых двух углов равна удвоенному произведению синуса
полусуммы этих углов на синус обратной полуразности этих
углов (под обратной разностью углов понимается такая
разность, когда из угла, стоящего под знаком вычитаемого
косинуса, вычитается угол, стоящий под знаком уменьша-
уменьшаемого косинуса).
Следствие 15. Для любых двух углов а и р справедливо
равенство
sin a + sin p = 2 sin ^t^ cos
которое называется формулой суммы синусов.
Следствие 15 можно сформулировать так: сумма синусов
любых двух углов равна удвоенному произведению синуса полу-
полусуммы этих углов на косинус полуразности этих углов.
Следствие 16. Для любых двух углов аир справедливо
равенство
sin a — sin p = 2 sin ^-^ cos
которое называется формулой разности синусов.
324
Следствие 16 можно сформулировать так: разность сину-
синусов любых двух углов равна удвоенному произведению синуса
полуразности этих углов на косинус полусуммы этих углов,
при этом синус полуразности берется так, что из угла,
стоящего под знаком уменьшаемого синуса, вычитается угол,
стоящий под знаком вычитаемого синуса.
Доказательство. Обозначая
складывая эти равенства и вычитая второе из первого,
получим
R sLz (8)
Из равенств (8) следует, что для любой пары хиу всегда
найдется пара аир такая, что справедливы равенства G).
Если в формулах D), E) и F) произвести замену аир
на х и у по формулам G) и (8), то получим справедливость
следующих формул:
|:=J:, (9)
cos x — cos у = 2 sin ^^ sin ^y^, A0)
sin x + sin j> = 2 sin ^i^ cos ^-j^- A1)
Пользуясь тем, что sin (— ,y) = — sin у для любого угла у, из
формулы (И) получим
sinx — sinj> = sinx + sin(— j>) = 2 sin =-^- cos -у%
т.е. получим, что справедлива следующая формула:
A2).
325
Из справедливости формул (9), A0), A1) и A2) вытекает
справедливость следствий 13, 14, 15 и 16.
Примеры.
1. cos 4а + cos 6а =
= 2 cos *Ц^ cos ^=^ = 2 cos 5а cos(- а) =
= 2 cos 5а cos а.
icosff-pUcosff+pV
— 2 Sin = Sin = I Sin т Sin В — tt —
3. sin у + | = sin у + sin | = 2 sin || + ^ jco
4. sin a — cos || — 5a |= sin a — sin 5a =
= 2 sin ^2 cos ^^ = 2 sin (- 2a) cos 3a =
= — 2 sin 2a cos 3a.
§ б. Формулы для двойных и половинных углов
Формулы для двойных углов. Пусть дан некоторый угол
а, т.е. пусть, например, дано некоторое число а, представ-
представляющее радианную меру этого угла. Тогда под углом 2а
понимается угол, радианная мера которого есть число 2а;
угол 2а часто называют двойным углом.
1. Для любого угла а справедливо равенство
sin 2a = 2sin a cos a, A)
которое называется формулой синуса двойного угла.
Это утверждение можно сформулировать так: синус двой-
двойного угла 2а равен удвоенному произведению синуса угла а на
косинус угла а.
326
Доказательство. Полагая а = C в формуле для синуса
суммы двух углов
sin 2a = sin (a + a) = sin a cos a + cos a sin a =
= 2 sin a cos a,
получаем справедливость утверждения 1.
2. Для любого угла 2а справедливо равенство
cos 2а = cos2 a — sin2 a, B)
которое называется формулой косинуса двойного угла.
Это утверждение можно сформулировать так: косинус
двойного угла 2а равен квадрату косинуса угла а минус
квадрат синуса угла а.
Доказательство. Полагая C = а в формуле для коси-
косинуса суммы двух углов
cos 2a = cos (a + a) = cos a cos a — sin a sin a =
= cos2 a — sin2 a,
получаем справедливость утверждения 2.
3. Для любого угла а такого, что a * j + nk, k e Z и
a * ? + Т' * € ^* справедливо равенство
^, C)
1 — tg о
которое называется формулой тангенса двойного угла.
Доказательство. Представляя 2а как (a + a) и при-
применяя формулу тангенса суммы двух углов, имеем
tg 2a = tg (a + a) =*" + *" = -Щ-,
что и требовалось доказать.
4. Для любого угла а такого, что а.фЩ,къ Z, справедливо
равенство
327
которое называется формулой котангенса двойного угла.
Доказательство. Представляя 2а как (а + а) и при-
применяя формулу котангенса суммы двух углов, имеем
что и требовалось доказать.
Примеры.
1. Вычислить sin 2a и cos 2a, если sin a = | и a e 11, n 1
Для любого угла a из указанного интервала cos оготри-
цателен, и поэтому
cos a = — Vl — sin* a = — у.
Применяя формулы A) и B), получаем
sin 2a = 2 sin a cos a = — Щ,
cos 2a = cos2 a — sin2 a = ¦!=.
2. Вычислить tg Гj + a | — tg | j — a l если tg 2a = 3. При-
Применяя формулы для тангенса буммьгдвух углов, затем для
тангенса двойного угла, получаем
tgff + a|-tgff-a| Щ-
V ) V ) 1-tg^tg
tgj-tga
tga l + tgjtga
_ 1 + tgot 1 — 1
1-tga 1+tga i_tg2a ~'° ~~ "
Рассмотрим угол па, где п — любое натуральное число.
Под углом па понимается угол, радианная мера которого
есть число па, если а есть радианная мера угла а. Можно
328
вывести формулы, выражающие sin ла и cos ла (пе N)
через sin а и cos а. В качестве примера приведем формулы
для sin За и cos За:
sin За = sin Bа + а) = sin 2а cos а + cos 2а sin а =
= 2 sin а cos2 а + (cos2 а — sin2 а) sin а =
= 3 sin а cos2 а — sin3 а = 3 sin а — 4 sin3 а.
Итак, sin За = 3 sin а — 4 sin3 а;
cos За = cos Bа + а) = cos 2а cos а — sin 2а sin а =
= (cos2 а — sin2 а) cos а — 2 sin2 а cos а =
= cos3 а — A — cos2 а) cos а — 2A — cos2 а) cos а =
= cos3 а — cos а + cos3 а — 2 cos а + 2 cos3 а =
= 4 cos3 а — 3 cos а.
Итак, cos За = 4 cos3 а — 3 cos а.
Примеры.
1. Вычислить sin За, если sin а = |. Используя формулу
для sin За, получим
sin За = 3 • 1 - 4 (^ = З67 = -2-
sinia 3-4-4^4j 16 -jg.
2. Вычислить (sin За + cos За), если sin a — cos a = tL
Используя формулы для sin За и cos За, имеем
sin За + cos За = 3(sin а — cos a) — 4(sin3 a — cos3 a).
Применим формулу сокращенного умножения:
(sin3 a — cos3 a) =
= (sin a — cos a) (cos2 a + sin a cos a + sin2 a)
Таким образом, при sin a — cos a = i имеем
329
sin За + cos За = Нз= — 4 • 4? A + sin a cos a) =
= -i= (— 1 — 4 sin a cos a).
Дополним получившееся выражение до полного квадрата
разности:
— 1 — 4 sin a cos a = — 3 + 2A — 2 sin a cos a) =
= — 3 + 2(cos2 a + sin2 a — 2 sin a cos a) =
= - 3 + 2(sin a - cos aJ = - 3 + 2 • i = - 2.
Окончательно получаем, что sin 3a + cos 3a = — V2~.
Формулы для половинных углов. Пусть дан некоторый
угол а, т.е. пусть, например, дано некоторое число а,
представляющее радианную меру этого угла. Тогда под
углом | понимается угол, радианная мера которого есть
число |; угол | часто называется половинным углом.
5. Для любого угла а справедливо равенство
E)
которое называется формулой квадрата косинуса половинно-
половинного угла.
Д о к а з а т е л ь с т в о. Очевидно, что угол а можно считать
двойным углом по отношению к углу ^. Поэтому для
любого угла а справедливо следующее равенство:
cos a = cos2 ^ — sin2 j,
кроме того, для любого угла а справедливо основное три-
тригонометрическое тождество:
l=cos2f + sin2f.
330
Складывая эти два равенства, получаем равенство E).
Равенство E) равносильно равенству
=4
l + cosot
Из последнего равенства имеем:
Eа)
для любого угла а, для для любого угла а, для
которого cos ^ которого cos ^
неотрицателен (т.е. для неположителен (т.е. для
любого а, принадлежащего
при каждом к е Z отрезку
[- я + 4яАг, я + 4пк\).
любого а, принадлежащего
при каждом к е Z отрезку
[я + 4яЛ; Зя + 4я*]).
Замечание. Формулы Eа) и E6) для граничных зна-
значений угла а, т.е. при а = я + 2пт, где т е Z, дают одно и
то же значение: cos ^ = 0.
Примеры.
_ 2_
1. Вычислить cos j. Так как cos ^
2. Вычислить cos j, если sin a = | и а е f—р — я I
Прежде всего найдем cos а. Поскольку для любого угла
а из указанного интервала cos а отрицателен, то
cos а = — Vl — sin2 а = — |.
Ц, — я\то|е (— ^, —1\ Для любого угла
ервала cos ^ также отрицателен и поэтому
Так как а е Г— Ц, —
^ из этого интервала cos ^ также отрицателен, и поэтому
cos ? = —
331
Итак, cos j = —j-.
6. Для любого угла а справедливо равенство
•'!=
— cosoc
F)
которое называется формулой квадрата синуса половинного
угла.
Доказательство. Выше уже было отмечено, что для
любого угла справедливы равенства
sin2 ^ + cos2 f = 1» — sin2 у + cos2 ^ = cos a.
Вычитая из первого равенства второе, получаем равенство
F). Равенство F) равносильно равенству
_ л/1 — cos a
Из последнего равенства имеем
Fа)
sinf = V
1 —cosa
Sin ^ = —
— cosa
F6)
для любого угла а, для для любого угла а, для
которого sin ^ которого sin ^
неотрицателен (т.е. для неположителен (т.е. для
любого а, принадлежащего любого а, принадлежащего
при каждом т е Z отрезку при каждом т е Z отрезку
[Акт; 2я + 4я/я]).
[— 2я + 4я/я; Акт]).
Замечание. Формулы Fа) и F6) для граничных зна-
значений угла а, т.е. при а = Ink, где k e Z, дают одно и то же
значение: sin ^ = 0.
Примеры.
1 — cos-7 I —y
1. Вычислить sin -g. Так как sin j =
1=Л. TOSin« =
4 , то sin 8
7
=
332
2. Вычислить sin ^, если sin а = g=- и а е | я, у j
Поскольку для любого угла а из указанного интервала
cos а отрицателен, то
cos а = — VI — sin2 а = — |.
Так как а е (я, у\то|е Г|, ^| Для любого угла | из этого
интервала sin ^ положителен, и поэтому
2g;
3 *
7. Для любого угла а такого, что а *¦ я + 2nk, k e Z спра-
справедливо равенство
t_ 2 а _ 1 — cosot ,-v
18 G)
которое называется формулой квадрата тангенса половин-
половинного угла.
Доказательство. Используя определение тангенса
угла и равенства E) и F), получаем равенство G).
Равенство G) равносильно равенству
_ л /1 — cos a
+ cosa
Из последнего равенства имеем:
333
Ga)
tg V Ga) tg? V^
°2 1 + cosa v ' 1 + cosa
для любого угла a, для для любого угла а, для
которого tg у которого tg у
неотрицателен (т.е. для неположителен (т.е. для
любого а, принадлежащего любого а, принадлежащего
при каждом п е Z при каждом п е Z
промежутку промежутку
[2пп; п + 2тш)). (— я + 2яи; 2ял]).
Замечание. Формулы Gа) и G6) для граничных зна-
значений угла а, т.е. при а = 2ял, где пе Z, дают одно и то же
значение: tg ^ = 0.
Примеры.
1. Вычислить tg |. Так как
¦COS-7
4
2-1
ТО
tg f = V3 — 2V2 . . .
2. Вычислить tg f, если cos 2a = ^ и a e (— я, —j-
Поскольку для любого угла а из указанного интервала
cos a отрицателен, то
Так как а е [ — л, —^\ то ^ е j — |, —g-1 Для любого угла
^ из этого интервала tg у отрицателен, и поэтому
334
ё 2 V 1
— со8оГ
+ cos a
Для тангенса половинного угла можно вывести и другие
формулы.
8. Для любого угла а такого, что a*nk, ke Z, справедливо
равенство
a = b^cosa (g)
2 sin a
Доказательство. Так как аФ-пк, ке Z, то siny*0 и
cos ^ * 0. Значит, справедлива цепочка равенств
sin ¦= sin — 2 sin -г- 2 sin -г-
tg?= 2" 2 2" 2
2 а о _ . о _ . о а*
cos -у cos -у • 2 sin -=• 2 sin -у cos -у
Применяя теперь формулы F) и A), получаем справед-
справедливость равенства (8).
9. Для любого угла а такого, что а ф п + 2я&, ke Z,
справедливо равенство
Доказательство этой формулы аналогично доказательст-
доказательству формулы (8) и потому опускается.
Примеры.
1. Для любого угла а такого, что ос*я + 2пк, ке Z, и
a * ^ + лл, п е Z упростить выражение
^ _ sin 2a cos a
1+cosa 1+cos 2a'
Поскольку для рассматриваемого угла a
335
cos o^O, cos a * — 1, cos 2a * — 1,
то
j _ 2 sin a cos a cos a _ sin a
1 + cosa 2 cos2 a 1 + cosoT
Так как в данном случае применима формула (9), то
2. Вычислить tg f, если cos a = | и a e [ — ?, 01
I i
Для любого угла а из указанного интервала sin a отри-
отрицателен, поэтому
sin a = — Vl — cos2 a = — |.
Теперь применяя формулу (9), имеем
a sin a J_
8 2 1+coso ~ 3*
Итак, tg I = — j.
Приведем еще формулы, выражающие синус, косинус,
тангенс и котангенс угла через тангенс половинного угла.
10. Для любого угла а такого, что a*n + 2nk, ke Z,
справедливо равенство
l-tg2f
cos a = -. A0)
1 + tg -j
Доказательство. Для любого угла а такого, что
а ф п + 2пк, ке Z, справедлива цепочка равенств:
336
COS ОС
cos a
1
cos
cos
a
a
. 2
+ sin
a
a
cos2
COS
a
~2~
cos
• sin2
a
2
a . 2
¦j + sm
cos
a
a
2
a
cos
cos2
COS
a
a
a
I
sin
cos
sin
a
2
a
a
2
1-
2 a 2 a
cos 2" c<k -j
1 +
a
л
a
. a
sin y
a
COS у
из которой вытекает справедливость равенства A0).
11. Для любого угла а такого, что а#я + 2л&, ke Z,
справедливо равенство
sin-а =
2tgf
(И)
Доказательство. Для любого угла а такого, что
a * л + 2пк, ке Z, справедлива цепочка равенств:
337
sin a =
sin a
1
„ . a a
2 sin у cos у
2a .2a
cos y + sm у
2
cos
. a
sin у
a
cosy
2a
COS у
a
cos
a
cos
cos
cos
sin
cos
a
2
sin
a
a
I
a
2
a
a
2
г a
2
2tgf _ 2tgf
2a 2 a
cos у cos у
1 +
sin
cos
V
a
2
a
I
J
из которой и вытекает справедливость равенства A1).
12. Для любого угла а такого, что a * я + 2я&, ke Z и
а Ф ^ + пп, п е Z, справедливо равенство
tga =
A2)
Это равенство есть следствие формулы тангенса двойно-:
го угла.
13. Для любого угла а такого, что а ф пк, & е Z, справед-
справедливо равенство
ctg a =
03)
Доказательство. Для любого угла а такого, что
а ф пк, к е Д справедлива цепочка равенств:
338
2(X . 2И
sin а - . а а
2 sin -у cos
2 а
cos -г
2 а
cos
. а
sin-»
•> *•
L " '
а
cos-у
cos2f-
cos2
. 2 re
sin -»
а
2
- . а а
2 sin ¦_- cos ¦--
cos2
. 2 а
sin ¦=¦
2 а
cos 2
а
cos-j
а
cos-_-
а
t
2
. а
sin -z
а
cos-у
'-«4
из которой и вытекает справедливость равенства A3).
Пример.
Вычислить - —:—, если tg ^ = 2.
2 + cos a + sin a 2
По формуле A0) cos a =
— = -j^. По формуле A1)
sma =
Значит,
5"
l
_
2 + cos a + sin a 11"
УПРАЖНЕНИЯ
Определить знак следующего числа A — 21):
1. sin 2 sin 4 sin 6. 2. cos 5 • cos 7 ¦ cos 8.
3. tg (- 1) ¦ tg 3 tg 6 tg (- 3). 4. ctg 1 ¦ ctg (- 2) ¦ ctg 9 ¦ ctg ( - 12).
, sin (— 3) ¦ cos 4 ¦ tg (— 5) - sin 7 ¦ cos (— 8)
ctg 6 tg 6 ¦ ctg (— 5) '
_ sin 6 +cos (—4) sin (— 8) + cos 9
' tg( —2)+ctg(—10)' ' cos 11 tg(—9)'
C05l0-sin7-tgl0 1Q tg7sin|f-co5f
" cos (— V2) • ctg (— 4)' ' cos (— 2) • sin VIT— tg V70~ '
. V2"
1 VI . 9 smT
llcossm
sin о
13. arcsin —' — arctg (— 10) + arccos — -? .
1 ( n\
¦rr • arcctg (— 11,5) — arcsin — т I
• ( П ЧТ
.. ЯГГ.С1П — —=i I. arorfvz — —
14. arccos
I N2 I
15. arcctg — -=- +
arcsin —
16. arcsin tg I — -~ + arctg [cos (— 4)]
17.
arcctg (sin 10) — arctg (cos 10)
arcsin [cos (— 8)] • arccos (sin 5)'
arcsin (cos 12) + arctg (sin 7) _
lo. i—^r^ -,—гт;— + ctg (— 7).
sin
19. arccos
arctg (cos 4) sin (— 10)
arcctg 115 + tg 12 "
20 arcs tct8 (-0,3)] • sin (- 9) t ctg (- 1) cQ? 13
arcsin [tg ( — 0,4I • cos E,8) sin V3~ 2 '
21.
arctg (sin 10) + tg
ctg arccos
arcsin | — -j
4
tg(-ll) sin^-
cos (— 3,5) '
Найти числовой значение следующего числового выражения B2
101):
„„ . л I л \
22. sin :г cos — -? — cos--
24.
2л . 5л
cos — + sin -7-
3 о
•i-f
2л
ctgy
. л '
Sin -z
-т1 sin^
340
25.
. Зл
sm —г
4
5л
cos -г
о
л . I Зл1 л
COS у + SUM 7- Ctg -z
Л Л
' sin (— л) + cos л 6'
fn\ (
— 100л +-г sin 20л — •
.,„ л) [17л л)
112л + j COS Hj~ + ?
^pltg (l 1л + J
. 13л J .., П8л
33. sin ^-cos A13л) + tg-j-cos —r-
34. sm|--g- cos -j- +tg 4~l 35.
,, . 63л ( 85л\ ( Пл^ 49л
36.sm^-cos _ —]tg|_ —Jctg-^
181л .
37. cos . sm
. 44л ( 15л"!
sm^-cos| ^|
-тУ
38. cos -~ sin | —
4
cos
39.
40.
tg3 (-^- 112л) — cos2 A15л)
. 2
sm
t 53л
5 + ctg -r-
341
41.
42. arccosj—x I+arcsin •«+arctg VT.
43. 2 arccos —=- + arcctg (— 1) — я.
. 44. 3arcsin[- ±1- 2arccosf-y|+ J.
45. 4 arctg (-1) + arctg 1 - y.
46. sin
47. sin
49. sin
51. tg
53. tg
55. ctg
arcsin-y |+cos[ji— arctg (—1)].
--^ - 2 arccos
Затесов
Г_1|.48.ш[-
+ 2 arcctg (-
sin 4 arccos (— 1) —
I VT|y 23я1 „ 4 Л,L n 9k1
6arccosl—5" r~3~r ^ arccos 0 — -r t
- ^ - 2 arccos ^ 54. tg [aresin f-y|+arccos o|
I.
56. ctg
57. ctg
59. cos
60. cos
61. cos
2 arcsin |——1+ arccos •=
3 arcsin (— 1) + arccos -=-
arcsinO
¦ 2 arctg --^
4 arcsin X — 3 arctg (—
5 arcsin -у — 2 arctg (— 1)
— 3 arcsin -=- + cos (— 2 arctg 0).
+ arctg 1
62.
cos (it — arcsin 0) — cos [6 arcctg (— 1)]
63.
sin Bit — arcctg 1)
sin pi5 - arcctg з]+ cos \l arcctg ^j
tg(-115n-arc<igl) 3^'
sin —2 arcctg [—r-| + cos (—5 arcctg 0)
L \ Д-Л
VJtgj^-Khc+JJ
342
65. sin | arcsin-rx I— cos I arccos |
66. tg (arctg 31) Vctg (arcctg5).
67. tg | arcsin^
V 1;
l arccos 7
70. sin
29 68. tg агссовЦ 69.
— cos
arccos — L 69. tg (arcctg 7).
arcsinU].
rcctg(-2)]r
73. cos |Ж
31
71. sin farctg 12) + cos [arcctg (-
72. cos [arctg (— 5)] — sin (arcctg 3).
in-rl 74. cos (it — arctg 17). 75. cos -=- +arcctg (—4) .
* ( л/TYI ( r\ ^
2ж - 2 arccos - у . 77. sin j - arccos ^ I
ж + arctg yl 79. sin |y - arcctg 81]
76. cos
78. sin
- - - i i
80. sin
2k - 3 arcsin Щ 81. tg f| - arccos f-1|.
Щ
82. tg fy + 4 arctg у! 83. tg [к + arcsin f- ^11
84. tg [2ж — arcctg(— 5)]. 85. ctg [f — arcsin — I
V K)
86. ctg Гк + arccos (- ^tll. 87. ctg Iу - 5 arcctg (- 1) L
88. ctg [2it + arctg (—11)]. 89. arccos (cos 2) + arcsin [sin (— 1)].
^ 1 — arcctg I ctg ? I
-=- + 2 arcsin sin — -g II.
90. arcctg (ctg 3) — arctg (tg 1). 91. arccos cos
92. arccos
arcsin
93.
cos
sin| — |
94.
it —arctg tg-j
arccos (cos it) — arcsin I sin
¦» I
j
^ )
gfctg^j+arctgjtgj-fj
sm 2) + arccos (cos 10).
^arcctgfctg^
95. arcsin (s (
96. arccos [cos (— 9)] — arcsin(sin 7).
97. arctg [tg (— 6)] — arcsin (sin 8).
( 13яЛ
98. arccos cos —r- + arcsin [sin (— 7)].
99 arcsin (sin V2T) ч- 2я
' arctg [tg (- 8)] - Зя"
343
100. arctg ftg -=- ] — 2 arcctg [ ctg Ц-1
I J l э 1
101. arcco? [cos (— 5)] + arccbs [cor (— 8)].
Доказать справедливость следующего числового равенства A02 —197):
102. sinf = V2~V-. 103. tg| = ^/T- 1.
104 • * УГ—1 ^ . ж Уб~—2
106 сад * УЮ + 2У5 107 fxa ж Уб~-2
K9ir 4ie лм" ж Sir 7ir _
. stog sin-Q-sin-Tg=-r-. 109. 8cosT^cos-jg a»Tg = \3.
ji^ Ui± 7ж ._ ж 1
111 cos —cos —cos —
,«_ ж 2ж Зж 4ж 5я 6к 7ж 1
112. COS -ГЦ COS -ГЦ COS jr COS j= COS -Те С08 Тс COS Тс = Too1
. tg^-гtgr-z-= 5.114. cos^cos-=-cos-=- = -j.
Э Э / / / 8
..<v ж 7ж . 7ж /=- ,„Л 2ж 4ж 6л
119. ctg^g + 4cos^g = V3.120. cosy+ cosy + cosy
... 2ж 4ж 7д ж 1
121. COSye + COSTT — COStt — Cos-res-».
„. к Зж 5ж 7ж 9я 1
124. COS -jj + COS JT + COS -jj + COS jr + COS ТГ = ^.
«.- . 4 Л . 4 Зж . 4 5я . 4 7ж 3
125. sin -jg + яп -^ + sm -jg + яп -^ = т
tic sin810 cos810 sin6 10 cos6 10 sin4 10 1
1Z6~8 8^ 3~ + ~T~+~4 24*
127. —!— -—Ц-+—Ц--1M- arcan[sin^|=7.
. ж . 2ж . Зж I 4 14
suiy siny smy v J
K 2 ( ( 10я^ ж
129. arcsin(cos 1)=—z—. 130. arcsin cos j- = —"g-
344
131. area»
sin т? = v
133
135. sin
sin т? = v. 132. arccos I sin
;i-j. -«и»р ~f =y-
.area» cos - у = у. 134. sm 2 area» ± = у.
arccos x + area» 7 = _
( lYl 4'
2arctg -T =T.
136. cos
с
137. a»
area» тт —
138. tg (arctg 2 + arctg 3) = — ]
139. arctg (tg 6) = 6 — 2*. 140. aresin (sin (— 5)) = — 5 + 2il
141. area»(cos9) = 9 — 2n. 142. arctg 2 + arctg| —1]=7-
3it
143. arctg (— 2) +arctg (— 3) = — -j-.
144. aresin 7 +aresin 7=- +aresin 77 = «.
j и to
145. arctg ¦=¦ + arctg 7 + arctg ¦= + arctg f = 7.
4 5 16 я
146. aresin 7 +aresin Т-Г +aresin 77 = x.
5 U 05 2
147. arctg 1 + arctg 2 + arctg 3 = я.
148. 2 aresin j = area» jr. 149. arccos Vj—area»-»i- = 5.
1 ._ 1 ^-3 151 щ^ i + 2 aretg I = arctgi?.
154. irtZ^3-i5S r!?
2sin6 — sin 12 ^ srno — sin9 + sm 12
155 sin 8 — sin 10 — sin 12 + sin 14 sin 11
cos4 — cos6 — cos8 + coslO~cos7'
157. sin6 Vf+cos6 Vf+-|sin2 2V7 = 1.
158. sin V2"sin B - V2) + cos2 1 + sin2 A - VJ) = 1.
^+1 2
~
l-2sh?2rfT 1-
o»|t-V6 |a»|? + V6"|+sin2V6"
sin22VS"-sin 2Vg"-| a» 2VS"-|
sin8cos8tg4 tg2 ^ ^
161. sin 8 — cos 8 tg 4:
345
162.
163.
164.
165.
166.
167.
168.
169.
171.
172.
173.
174.
175.
176.
177.
178.
179.
4 sin (VT+ ж) sin (vf+у Icos 11 - Vf|=
l-sjn6l-cos6l j {
l-2sin22-V3"sin4~2'
cos 2VTT- cos 6VTT+ cos KWTT- cos 14VTT
sin 2-ЛТ+ sin 6VIT+ sin HWIT+sin 14-ЛГ
sin 23 + cos 23 — sin 69 — cos 69
=tg2VTT.
= sin 23.
2 sin 46+4 sin2 23-2
1+cos 17 +cos 34 +cos 51 ,_
ч = cos 17.
2cosl7 + 4cos217-2
Sin2 + sin4 + sin6 = 4sin3cos2cosl.
sin 2VU+ sin 4VU- sin 6VTT= 4 sin 3VUsin 2Шsin VU.
tgl + ctgl
l+tg2tgl
= 2ctg2.17O.r
3 —4cos2 + cos4
gg
sin2 2 cos 6 + cos2 2 sin 6
sin3 1 cos 3 + cos3 1 sin 3
3 + 4cos2 + cos4
= 2 cos 4.
cos
2 sin кг
+ 2 cos 1 —
~T
V(l— tg2 l)(ctg* 1 — 1)= — 2ctg2.
(cos2tgl — Sin4)(cos4ctg2 + sin4) =
sin 13 +sin 14 +sin 15 +sin 16 29
cos 13 + cos 14 + cos 15 + cos 16 2'
sin B>/Г+ 1) + sin B-й- 1) - cos [з| - 2V2"
cos BVI+1) + cos BVI - 1) - sin 13| + 2л/2"
1 + cos D — 2it) + cos 14—? I
[374|
t2)(l
= ctg2.
sin 2(l+cosec2 + ctg2)(l —cosec2 + ctg2)
cos2(l+sec2 + tg2)(l—sec2 + tg2)
=COS
1.
346
181. 8 cos jl - jlsin f| - 2 jsin 3 cos 9 = sin 18.
182. tg 3 - tg 2 - tg 1 = tg 3 <g 2 tg 1.
183.
l-2cos27
1.
184. l+sin2-2cos2l = V2sin|2-j|
185. 1 - sin [у - 2)- cos B - -yl= 2V2"sin 1 cos f 1 -j]
186. 6sin2 1 -cos 2- 1 =- 8cos(l + |jcosjl -|)
187. 2cos23 + 2cos6-3 = 8cos 3 + y cos 3-jl .
188.
sm||-6|+sin(it-6)T
192.
tg2tgfe- 1 j+tg2tgf|- 11+tgf|- lltgff -ll= 1.
sin (ctg 5) + sin (tg 5) = 2 suihr^jg cos (ctg 10).
193. sin (ctg 5) + sin (tg 5) = 2 suihr^jg cos (ctg 10).
194. 1 + cos 2 + cos 4 + cos 6 = 4 cos 1 cos 2 cos 3.
195. sin 2 + sin 4 — sin 6 = 4 sin 1 sin 2 sin 3.
196. sin2 5 + sin2 V2~+ 2 sin 5 sin V2~cos E + V2) = sin2 E + V2~).
cos 1+sin 1 l + 2cos2l 2
1Q_
1!"
sinl-cosl
Доказать справедливость следующего числового неравенства A98 —
244):
198. sin I + cos 1 > 1.199. sin 1 + tg 1 > 2.
sinVT
,„ . 2 + V3"
200. sin—=—>
201. cos
2
VI
VI
-шл • ( ^ ( . VT,
202. smlcos-^r- kcos lsui-=-1
203. sin pin V2) < cos (cos V2).
347
204.
205.
206.
207.
208.
209.
210.
211.
213.
214.
216.
218.
220.
222.
224.
225.
226.
227.
228.
230.
231.
232.
^| sin
l+^s~VI
2
4VT
"Г*
>3 + 2VI.
sinl sinVl . 1+VT
sin—2—
cos 1 + cos VI+ cos (it — 1 — VI) <-=.
sin2 (it — VI—V5) > sin 2VIsin 2VT.
. 1 . VI . it-1-УГ 1
sin -z sin -z- sin = <¦$.
Li. i. Ъ
(
1
-4 < cos 2V7 + 3 sin V7"<y. 212. i < sin6 12 + cos6 12 < 1.
1,1,
VI+ V?
cos-
cos-
cos-
3 3 1
¦=. 215. arccos у < arccos j.
arctg | S arctg у 217. arcctg CVI) < arcctg 4.
2arcctg4 + arcctg3>^. 219. 2 2 *
2^1
21
< arccos I —т I 221. arctg-=->arctgV3~—-r-
I of i э
о v л' 8
j+arcsiri |. 223. arcctg (— 3) < | — arctg 3
arccos
arccos
, V -2VT\ - . Г 2VT\ 2k
3 arccos —j- — 2arcsin—j- >-y.
4 1 Зя
arectg ¦? + arcctg-^ <-J-.
2 arocos 2 > arccos -= — arcsin ^.
arccos-j+arccos-r?+arcsin-T >?.
5 13 4 2
¦rjr + 7sin-7jr<13. 229. sin4 + cos4> —VI.
ctg3 3 + ctg2 3 — ctg3 — 1 <0.
cos VI+ cos 2VI+ cos 3VI< 0.
2cosl+ sin 1 >tg^. 233. tg27 + ctg27>2.
348
234.2cos-yfcos-^-V8"tgyl<5.235.
cos2!
236.
1^->2.237.4sin|sin|sin|<sin|.
238. 2cos2 VJ-sin Vl+sin 3VI< 1.
239. 6 cos2 y «8* ^< 2 sin2 <2 + 3 tg2 VT.
242. VsS7"+V55s7>l.
244. cosl + cos3>cos2 + coe4.
Упроспггь B45 - 262):
245. sin2 (я - 9) + tg2 (* - 9) tg2 Гз|+9 ]+ sin f| + 9] cos (9 - 2*).
24«. 1 - sin A - 2*) cos fl - -yJ- tg (к -1) fcfy - ll-
— 2сов2(я+1).
_*. . к . 7к . гНя _2 25ж . г29к 134к
8ШD — ж) cos D — 2к)8ШBк — 4)
sinb-4 ctg(it-4)ctg
251. сое B>/2~- 2к) + cos 11 - лйг|а1п (л + VI).
254. 2arfVl9" Idn 2VI9~+ 2 cos 4VI9" со» 10VI9".
349
255. sin 3V2T+ 2 • sin5V2T cos 2V2T.
fe-llsinlcOs2.2S7. gifgg.
.„ sin2VT+tg2VT M- sin4 1 + cos4 1 — 1
' sin6l + cos6l —l'
„„ cos2V5"-rin2^S"c
zov. z
к 2к
COS COS -jr
261. ctg2 10 -1^ 10 - 8 cos 20 ctg 20.
3 V3~i3
Найти наиболыиее А и наименьшее Л такие, что при любом справед-
справедливо следующее Двойное неравенство B63 — 265):
263. Л*sinpcospcos 2р cos40S Д.
644 2
265. >ls4sin2p- 3cos
266. Доказать, что равенство (sinx)a + (cosx)a= 1 выполняется при
любом х в том и только в том случае, когда a = 2.
Глава VI. ФУНКЦИИ И ИХ ГРАФИКИ
При рассмотрении количественных отношений явлений
реального мира приходится иметь дело с численными зна-
значениями различных величин, например времени, пути,
скорости, ускорения, объема и т.д. .JJ зависимости от рас-
рассматриваемых условий одни из величин имеют постоянные
числовые значения, у других — эти значения переменные.
Такие величины называют соответственно постоянными и
переменными. Например, при равномерном движении ско-
скорость v постоянна, время t и путь S переменные, причем
S = vt. При свободном падении тела, брошенного без на-
начальной скорости, ускорение силы тяжести g постоянное,
время движения t и пройденный путь S переменные, при-
причем 5"=^.
Изучение окружающих явлений показывает, что пере-
переменные величины изменяются не независимо друг от друга,
а изменение численных значений одних из них влечет за
собой изменение значений других. Здесь будут рассматри-
рассматриваться лишь пары переменных, значения одной (зависимой)
из которых изменяются в зависимости от значений другой
(независимой). При этом в рассматриваемую зависимость
двух переменных величин кроме этих переменных могут
входить и некоторые постоянные величины, которые обыч-
обычно называют константами. В приведенных выше примерах
естественно считать t независимой переменной, S — зави-
зависимой переменной, а | и v — константами. Приведем
другие примеры таких пар переменных величин: площадь
круга S = nR2 (R — радиус, л — константа), где S меняется
в зависимости от R; закон Бойля — Мариотта: p — %(V—
351
объем некоторого количества газа, р — давление этого газа,
с — константа), где р меняется в зависимости от V.
Независимая переменная может принимать не любые
числовые значения, а лишь значения, продиктованные
условиями рассматриваемой задачи. Например, при сво-
свободном падении тела, брошенного без начальной скорости
с высоты Н, время движения / можно брать только из
промежутка Го, V— J.
Подчеркнем, что в приведенных примерах каждому зна-
значению независимой переменной соответствует только одно
значение зависимой переменной. Ниже будет рассматри-
рассматриваться только такая зависимость пар переменных.
§ 1. Определения и примеры
Понятие функции. Пусть дано некоторое множество
чисел X и пусть указано некоторое правило (закон), обо-
обозначаемое буквой/, по которому каждому значению величи-
величины х (независимой переменной) из множества X ставится
в соответствие единственное значение величины у (зависимой
переменной), обозначаемое Дх). Тогда принято говорить, что
дана функция у = Дх) с областью определения X, или что дана
функция у =fix), определенная на множестве X. Множество
Y — множество всех значений, которые принимает при
этом переменная, называется областью изменения функции
У=Лх).
В этой книге в основном будут рассматриваться такие
функции, для которых закон, устанавливающий соответст-
соответствия, задается посредством формул. Такой способ задания
функции называется аналитическим.
Примеры функций.
1. Пусть п — некоторое фиксированное натуральное
число, тогда каждому действительному числу а можно
поставить в соответствие (см. гл. IV) одно действительное
число а". Значит, можно сказать, что указан закон, по
которому каждому значению х из множества всех действи-
действительных чисел ставится в соответствие одно числовой
значение х". Другими словами, задана функция у=х* с
352
областью определения — множеством всех действительных
чисел.
2. Пусть (— п) — некоторое фиксированное целое отри-
отрицательное число, тогда каждому отличному от нуля дейст-
действительному числу а можно поставить в соответствие (см.
гл. IV) одно действительное число сГ ". Значит, этим
соответствием задана функция у = х~" с областью опреде-
определения — множеством всех отличных от нуля действитель-
действительных чисел.
3. Пусть а — некоторое фиксированное положительное
нецелое число, тогда каждому неотрицательному числу а
можно поставить в соответствие (см. гл. IV) одно действи-
действительное число аа. Значит, этим соответствием задана функ-
функция у = Xй с областью определения — множеством неотри-
неотрицательных чисел.
4. Пусть (— а) — некоторое фиксированное отрицатель-
отрицательное нецелое число, тогда каждому положительному числу
а можно поставить в соответствие (см. гл. IV) одно число
а~а. Значит, этим соответствием задана функция у — х~а с
областью определения — множеством всех положительных
чисел.
5. Пусть а — некоторое фиксированное положительное,
не равное единице число, тогда каждому действительному
числу Ь можно поставить в соответствие (см. гл. IV) одно
число д*. Значит, этим соответствием задана функция
у= cf с областью определения — множеством всех дейст-
действительных чисел.
6. Пусть а — некоторое фиксированное положительное,
не равное единице число, тогда каждому положительному
числу Ь можно поставить в соответствие (см. гл. IV) одно
число log,A Значит, этим соответствием задана функция
у = logpc с областью определения — множеством всех по-
положительных чисел.
7. Каждому действительному числу а (как радианной
мере угла а) можно поставить в соответствие (см. гл. V)
одно число sin а. Значит, этим соответствием задана функ-
функция у - sin х с областью определения — множеством всех
действительных чисел.
12 Алгебра, тригонометрия 353
и элементарные функции v'
8. Каждому действительному числу а (как радианной
мере угла а) можно поставить в соответствие (см. гл. V)
одно число cos а. Значит, этим соответствием задана функ-
функция у = cos х с областью определения — множеством всех
действительных чисел.
9. Каждому действительному числу а (как радианной
мере угла а), такому, что а * | + пк, где к — любое целое
число, можно поставить в соответствие (см. гл. V) одно
число tgcc. Значит, этим соответствием задана функция
у — tg х с областью определения — множеством всех дей-
действительных чисел, кроме чисел ос * ? + кк, где к — любое
целое число.
10. Каждому действительному числу а (как радианной
мере угла а), кроме а = пт, где т — любое целое число,
можно поставить в соответствие (см. гл. V) одно число
ctg а. Значит, этим соответствием задана функция у = ctg x
с областью определения — множеством всех действитель-
действительных чисел, кроме чисел а = лт, где т — любое целое число.
11. Каждому действительному числу а из отрезка — 1 й
й а < 1 можно поставить в соответствие (см. гл. V) одно
единственное число arcsin а. Значит, этим соответствием
задана функция у = arcsin x с областью определения —
множеством всех действительных чисел, принадлежащих
отрезку [— 1; 1].
12. Каждому действительному числу а из отрезка — 1 й
<,ай\ можно поставить в соответствие (см. гл. V) одно
единственное число arccos а. Значит, этим соответствием
задана функция у = arccos x с областью определения —
множеством всех действительных чисел, принадлежащих
отрезку [— 1; 1].
13. Каждому действительному числу а можно поставить
в соответствие (см. гл. V) одно единственное число arctg a.
Значит, этим соответствием задана функция у = arctg x с
областью определения — множеством всех действительных
чисел.
14. Каждому действительному числу а можно поставить
в соответствие (см. гл. V) одно единственное число arcctg a.
Значит, этим соответствием задана функция у = arcctg x с
областью определения — множеством всех действительных
чисел.
Замечание. Функции, рассмотренные в примерах 1 —
14, называются основными элементарными функциями.
15. Рассмотрим функцию, определенную для любого
действительного х по правилу: у = 1, если х — рациональ-
рациональное число; у = 0, если х — иррациональное число. Эта
функция называется функцией Дирихле. Коротко эту
функцию записывают так:
-it
если х — рациональное число,
если х — иррациональное число.
16. Рассмотрим функцию, определенную для любого
действительного х по правилу: у=1, если х — положитель-
положительное число; у = — 1, если х — отрицательное число; у = О,
если х = 0. Эта функция называется знаком х и обознача-
обозначается так: у = sign x. Определение этой функции коротко
записывают так:
у = signx =
— 1, если х<0,
0, если х = 0,
1, если х>0.
17. Рассмотрим функцию, определенную для любого
действительного х по правилу: у = п, если х — положитель-
положительное число, причем х = п + а, где п — натуральное числа и
0^а<1;у=— т, если х — отрицательное число, причем
х = — т + р, где т — натуральное число и0?{*< 1; у=0,
если 0 й х < 1. Эта функция называется целой частью х и
обозначается так: у = [х]. Коротко функцию у = [х] можно
определить так: [х] — есть наибольшее целое число, кото-
которое меньше или равно х.
18. Если каждому действительному числу поставлено в
соответствие одно и то же действительное число с, то
говорят, что задана функция у = с с областью определе-
определения — множеством всех действительных чисел.
355
Область существования и область изменения функции.
Первый вопрос, на которых надо ответить при исследова-
исследовании функции, — это вопрос об области определения и
области изменения этой функции.
Из определения функции вытекает, что функция у =/(х)
должна задаваться вместе с ее областью определения X. При
этом подчеркнем, что область определения функции может
задаваться либо условиями решаемой задачи, либо физи-
физическим смыслом изучаемого явления, либо математичес-
математическими соглашениями.
Однако часто, задавая функцию у =Дх) аналитически,
не указывают явно ее область определения. В таких случаях
принято рассматривать функцию в ее естественной области
определения.
Естественной областью определения, или областью суще-
существования функции у =Дх), заданной аналитически, назы-
называют совокупность всех действительных значений незави-
независимой переменной х, для каждого из которых функция
принимает действительные значения. Итак, область суще-
существования функции определяется самим законом (форму-
(формулой), задающим функцию, а область определения ее зада-
задается условиями или смыслом решаемой задачи, т.е. облас-
областью определения функции может быть любая часть области
существования функции или они могут полностью совпа-
совпадать. Например, для функции У = Щ- область существова-
существования — (— со; + со), а область ее определения при падении
тела с высоты Несгь отрезок Го, V— .
Таким образом, всегда, когда говорят, что дана функция
у =Дх), считают, что уже дана область ее определения X—
она либо указана явно, либо есть область существования
этой функции (и тогда ее надо предварительно найти).
Что касается области изменения функции у =Дх), то она
вычисляется по уже заданной области определения.
Примеры.
1. Пусть дана функция у = Vsin х — 3. Область существо-
существования этой функции — пустое множество, т.е. Х= 0, сле-
356
довательно, и область изменения — пустое множество, т.е.
Y= 0.
2. Пусть дана функция у = Vlog2 sin х. Область существо-
существования этой функции — множество всех чисел хк = | +• Ink,
где к — любое целое число, т.е. Х= Щ + Ink | к е Z. Легко
видеть, что область изменения состоит из одного числа
нуль, т.е. Y= {0}.
3. Пусть дана функция у = Vl — х2. Область существова-
существования этой функции есть отрезок [— 1; 1], т.е. Х= [— 1; 1].
Легко видеть, что область изменения есть отрезок [О; 1],
т.е. Y= [0; 1].
4. Пусть дана функция у = . 1 2. Область существова-
существования этой функции есть интервал (— 1; 1), т.е. Х= (— 1; 1).
Легко видеть, что область изменения есть промежуток [1:
+ оо), т.е. У=[1; + оо).
5. Пусть дана функция у = , ! , с областью определе-
"VI-ж
ния Х= 0; -у , тогда легко видеть, что область изменения
есть отрезок [i; 2], т.е. Y= [1; 2].
Ограниченные функции. Функция у=Лх), определенная
на множестве X, называется ограниченной снизу, если суще-
существует число А такое, что А й/{х) для любого х е X.
Пример. Функция у= а* ограниченная снизу на всей
области существования, так как (см. гл. IV) 0 < а* для
любого действительного х.
Функция у=Ах), определенная на множестве X, назы-
называется ограниченной сверху, если существует число В такое,
что/х) й В для любого х е X
Пример. Функция у = Vl — x2 ограничена сверху на
всей области существования, так как Vl — х2 й 1 для любо-
любого х такого, что х е [— 1; 1].
Функция у=Лх), определенная на множестве X, назы-
называется ограниченной, если существует число М > 0 такое, что
|Дх)| < М для любого х е X
357
Пример. Функция .у = sin x ограничена на всей области
существования, так как |sin xj < 1 для любого действитель-
действительного X.
Можно доказать, что функция у =fix), определенная на
множестве X, ограничена на этом множестве тогда и только
тогда, когда она одновременно ограничена и снизу и сверху
на этом множестве.
Пример. Функция у = Vl — х2 ограничена на области
существования Х= [— 1; 1], так как на этом множестве она
снизу ограничена нулем, а сверху — единицей.
Четность и нечетность функций. Говорят, что множество
X симметрично относительно начала координат, если мно-
множество X таково, что (— х) е Хддя любого х е X.
Функция у—fix) называется четной, если область ее
определения есть множество, симметричное относительно
начала координат, и если fix) =Д— х) при любом х е X.
Примеры четных функций:
= х2, y=cosx, y = Vl-
Ч
l+x
О любой четной функции у =fix) с областью определе-
определения X говорят, что она симметрична относительно оси
ординат, так как для любого х е Xточки плоскости (x,fix))
и (— х, fi— х)) симметричны относительно оси Оу.
Функция у = fix) называется нечетной, если область ее
определения есть множество, симметричное относительно
начала координат, и если Д— х) = —Дх) при любом х е X.
Примеры нечетных функций:
у = х, y = sinx, y = ±, у = з?, y = aictgx.
О любой нечетной функции у —Дх) с областью опреде-
определения Xговорят, что она симметрична относительно начала
координат, так как для любого х е X точки плоскости (х,
fix)) и (— х, fi— x)) симметричны относительно начала
координат.
Наряду с четными и нечетными функциями есть функ-
функции, не являющиеся ни теми, ни другими, например,
358
такими являются функции у = Т, y = ]gx, у = arccos х,
y = *Jx.
Теорема 1. Всякую функцию, определенную на множест-
множестве X, симметричном относительно начала координат, можно
представить в виде суммы функций, каждая из которых
определена на том же множестве X и одна из которых
четная, а другая нечетная.
Доказательство. Пусть функция у=Дх) имеет об-
область определения X, симметричную относительно начала
координат. Покажем, что существуют функции у = ф(х) и
у = у(х), каждая из которых определена на том же множе-
множестве X, и они такие, что у = ф(х) + \j/(jc) =fix), где у = ф(х) —
четная, а у = \|/(х) — нечетная функция. Положим
Ясно, что каждая из этих функций определена на множе-
множестве Хи что ф(— х) = ф(х), \|/(— х) = — \|/(х) и fix) = ф(х) +
+ \|/(jc). Теорема доказана.
Пример. Функцию у = 2" можно представить в виде
2 + 2
суммы двух функций у = ф(х), где ф(х) = —^—> и У =
2х — 2~х
где \|/(jc) = -—y—» причем функция у = ф(х) — четная, а
функция у = \|/(х) — нечетная.
Замечание. Наряду с понятием четной функции, т.е.
функции, симметричной относительно оси ординат,
можно ввести более общее понятие функции, симметрич-
симметричной относительно вертикальной прямой, проходящей через
точку (а, 0). Говорят, что множество X симметрично отно-
относительно точки (а, 0), если множество X таково, что точка
Bа — х) е Хрдя любого х е X.
Функция у =Дх) называется симметричной относительно
вертикальной прямой, проходящей через точку с координата-
координатами (а, 0), если область ее определения есть множество,
симметричное относительно точки (а, 0) и при любом х из
области определения J{2a — х) =/(х).
359
Пример. Функция у - sin х симметрична относительно
вертикальной прямой, проходящей через точку (я/2, 0).
Действительно, областью определения этой функции явля-
является вся числовая прямая, следовательно, это множество,
симметричное относительно любой точки, в том числе и
относительно точки я/2, а равенство sin [2(я/2) — х] = sin x
для любого действительного х очевидно.
Возрастание и убывание функций. Функция у =Дх), оп-
определенная на множестве X, называется возрастающей на,
этом множестве, если для любой пары чисел Х\ и х2 этого
множества из неравенства х{ < Хг следует, что Дхх) <flxi)-
Примеры. 1. Функция у = х возрастает на промежутке
(— оо; + оо).
2. Функция у = х2 возрастает на промежутке [0; оо).
3. Функция у = sin х возрастает на отрезке [— я/2, я/2].
Функция у=Ах), определенная на множестве X, назы-
называется убывающей на этом множестве, если для любой пары
чисел х, и Хг этого множества из неравенства х, < Xj следует,
Примеры. 1. Функция у = A/2)* убывает на промежут-
промежутке (— оо; + оо).
2. Функция у = sin х убывает на отрезке [я/2; Зя/2].
Функция у = J{x), определенная на множестве X, назы-
называется неубывающей на этом множестве, если для любой
пары чисел х1 и Хг этого множества из неравенства X\<Xj,
следует, что Дх^ <,Лхг)-
Пример.
Функция у = VxTJxf является неубывающей на проме-
промежутке (— оо; + оо).
Функция у = Дх), определенная на множестве X, назы-
называется невозрастающей на этом множестве, если для любой
пары чисел х1 и Хг этого множества из неравенства х1 < Xj
следует, что Дх,) >Дхг).
Пример.
Функция у = \п ^^ п' является невозрастающей на
[0, для х > 0
промежутке (— оо; + оо).
-160
, Функции возрастающие, убывающие, невозрастающие и
неубывающие называются монотонными функциями. Функ-
Функции возрастающие и убывающие называются строго моно-
монотонными функциями.
Периодичность функций. Функция у=Ах) называется
периодической, если существует число 7V 0 такое, что для
любого х из области определения функции у=Ах) числа
(х + 7) и (х — 7) также входят в область определения и для
любого х из области определения Дх + 7) =Ах).
Замечание. Для периодической функции имеет место
равенство Дх — 7) =Дх). Действительно, функция у =Дх)
в точке (х — 7) определена и fix) =Л(* — 1) + Л =Ах —
-Г).
Теорема. 2. Если число Тесть период функции у = Дх),
то число Q= тТ, где m — любое фиксированное отличное от
нуля целое число, будет периодом этой функции.
Доказательство. Докажем, что для любого х из об-
области определения функции у =Ах) и любого натурально-
натурального п:
а) точки (х + пТ) и (х — пТ) принадлежат области опре-
определения функции у = Дх);
б) Ах) =Ах + пТ) и Ах) =Ах - пТ).
Пусть п = 1, тогда согласно определению и замечанию:
а) точки (х + 7) и (х — 7) принадлежат области опреде-
определения функции у =АХУ,
б) Ах) =Ах + 7) и Ах) =Ах - 7).
Предположим, что для п = к справедливо утвержде-
утверждение а). Докажем справедливость утверждения для п—к +
+ 1. Действительно, по предположению точки (х + кТ) и
(х — кТ) принадлежат области определения функции
у=Ах) и Т есть ее период. Следовательно, точки [(х +
+ кТ) + 7] и [(х — кТ) — 7], т.е. точки [х + (к + 1O] и [х —
— (к + 1O], принадлежат области ее определения.
Итак, для любого х из области определения функции
У=Ах) при любом целом отличном от нуля m точка
(х + тТ) принадлежит области ее определения.
Предположим, что утверждение б) справедливо для лю-
любого п = к, т.е. Ах) =А + кТ) и Ах) =АХ — кТ). Докажем
справедливость утверждения б) для п = к+ 1. Действитель-
361
но, так как Г является периодом функции у =Дх), то для
точки (х + кТ) имеем Л (х + к!) + Т=Дх + кТ), но по пред-
предположению Дх) =Дх + кТ), следовательно, fix) =fix + (к +
+ 1O]. Аналогично для точки (х — к!) доказывается, что
Дх) =fix— (к + 1O], т.е. для любого целого отличного от
нуля m утверждение б) доказано.
Итак, теорема 2 доказана.
Примеры. 1. Функция у = sin x имеет периодом число
Т = 2я, так как для любого х числа (х + 2я) и (х — 2я) входят
в область определения этой функции и sin (х + 2я) = sin x.
2. Функция у = х — [х] имеет период Т= 1, так как она
определена для любого х и (х + 1) — [х + 1] = х — [х].
3. Функция, определенная следующим образом:
-{к
если х — любое рациональное число,
если х — любое иррациональное число.
имеет периодом любое рациональное число.
4. Функция у = sin Vx не является периодической, так
как, например, для числа х = 0 число х — Т (если Г> 0)
или число х+ Г (если Г<0) не принадлежит области
существования этой функции.
Число Гназывается главным периодом, если оно положи-
положительно и является наименьшим среди всех положительных
периодов.
Заметим, что функция, приведенная в примере 3, не
имеет главного периода.
Наибольшее и наименьшее значение функций. Пусть функ-
функция у=Дх) определена на множестве X. Если существует >
такое *о е X, что для любого х е ^справедливо неравенство
Дх) ^Дхо), то говорят, что функция у = fix), определенная j
на множестве X, принимает наименьшее значение у0 =
ПРИ X = Xq.
Если существует такое Xq е X, что для любого х е X
справедливо неравенство fix) ^Дхь)» т° говорят, что функ-
функция у—Ах), определенная на множестве X, принимает!
наибольшее значение у0 =Аха) ПРИ * = *о-
362
Примеры. 1. Функция ^ = smx на отрезке [0, 2я]
принимает наибольшее значение у = 1 при х = я/2 и на-
наименьшее значение у = — 1 при х = Зя/2.
2. Функция у = х2 на промежутке (— «>; + «>) принимает
наименьшее значение у = О при х = О, но нет такого х из
области существования функции, где она приминает наи-
наибольшее значение.
3. Функция у = 2х на промежутке (— «>; + «>) не прини-
принимает ни наибольшего, ни наименьшего значения.
4. Функция у = 2х на отрезке [0; 1] принимает наимень-
наименьшее значение у = 1 при х = 0 и наибольшее значение у = 2
при х= 1.
График функции. Введем на плоскости прямоугольную
систему координат хОу и рассмотрим функцию у =fix).
Придавая х последовательно значения хи Xj, ..., х„, ...,
получим соответствующие значения уи уъ ..., у„, ... . Отме-
Отметим на плоскости точки с координатами (хи yj, (x2, у2), ...
-, (х„, у„), ... .
Графиком функции у = Дх), х е М называется множество
точек на плоскости, удовлетворяющее следующим услови-
условиям:
а) всякая точка с координатами (xq, у0), где у0 = Дхь).
Хо е М принадлежит этому множеству;
б) всякая точка, принадлежащая этому множеству точек,
имеет координаты (хи ух) такие, что у{ = Лх\), *i e M.
Другими словами, график функции у = Дх), х е М — это
множество всех точек плоскости, координаты которых
удовлетворяют условию у=Д.х), х<= М и не содержащее
других точек.
Например, графиком функции у = Vlog2 sin x будет мно-
множество точек плоскости 11 + 2кк, 01 где к — любое целое
число, и только эти точки. ^
Исследование функции. Если для данной функции у = fix)
изучены все перечисленные выше свойства, то говорят, что
проведено исследование функции у = fix).
Итак, при исследовании функции необходимо ответить
на следующие вопросы:
363
а) Какова область существования функции?
б) Какова область изменения функции?
в) Ограниченная ли это функция?
г) Принимает ли функция наибольшее и наименьшее
значения?
д) Периодическая ли она?
е) Является ли эта функция четной или нечетной, или
ни той и ни другой?
ж) Есть ли у нее промежутки, где она монотонна?
з) Есть ли точки пересечения графика с осями коорди-
координат?
и) Какой график этой функции?
Замечание. Наглядность графика является незамени-
незаменимым вспомогательным средством исследования функции,
но он только иллюстрирует свойства функции, а не дока-
доказывает их.
§ 2. Основные элементарные функции
В этом параграфе будет проведено исследование всех
основных элементарных функций.
Линейная функция у = х. Зависимость у = х называется
прямой пропорциональной зависимостью. Легко проверяются
следующие свойства этой функции:
а) область существования ¦(— °°; + °°);
б) область изменения (— «>; + «>);
в) функция не ограничена ни сверху, ни снизу;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не периодическая;
е) функция нечетная;
ж) функция возрастает на всем промежутке (— «>; + »);
з) точка @, 0) — единственная точка пересечения с
осями координат.
Теорема 1. График функцииу = х есть прямая, проходя-
проходящая через начало координат и являющаяся биссектрисой
первого и третьего координатных углов (рис. 95).
Доказательство. Пусть точка Mfa, Ух) такова, что ее
координаты удовлетворяют условию ух = дс,. Если хх = ух =
364
= 0, то точка Мх совпадает в началом координат. Если хх =
= ух * 0, то числа х, и ух либо оба положительны, либо оба
отрицательны, т.е. точка Мх лежит либо в первом, либо в
третьем координатном угле. Поскольку из условий ух = х,
следует, что |j>i| = |х,|, то точка Мх рав-
равноудалена от осей координат. Следова-
Следовательно, она лежит либо на биссектрисе
первого координатного угла (если ее
координаты положительны), либо на
биссектрисе третьего координатного
угла (если ее координаты отрицатель-
отрицательны). Итак, любая точка Мх(хх, ух), где
ух — хх, либо совпадает с началом коор-
ух х, р
динат, либо лежит на одной из биссект- РмОт 95-
рис первого или третьего координатных
углов.
Очевидно, что координаты начала координат удовлетво-
удовлетворяют условию 0 = 0. Если точка М2(х2,'у2) лежит на одной
из биссектрис либо первого, либо третьего координатных
углов, то |xd = lyj (расстояние до осей координат равны).
Так как числа Xj и у2 или оба положительны (если точка М2
лежит в первом координатном угле) или оба отрицательны
(если точка М2 лежит в третьем координатном угле), то из
условий lyj = IxJ следует у2 = Хг, т.е. точка М2(х2, у2) такова,
что у2 = Xj. Итак, начало координат и любая точка, лежащая
на одной из биссектрис либо первого, либо третьего коор-
координатных углов, имеет координаты (Хз, уг) такие, что^з = х3.
По определению графика функции прямая, проходящая
через начало координат и являющаяся биссектрисой пер-
первого и третьего координатных углов, есть график функции
у = х (см. рис. 95). Теорема доказана.
Гипербола у = К Зависимость у = - называется обратной
пропорциональной зависимостью. Легко проверяются сле-
следующие свойства этой функции:
а) область существования (— «>, 0) и @, +«»);
б) область изменения (— «>, 0) и @, + «>);
в) функция не является ограниченной на всей области
существования, но ограниченна снизу (у > 0) на промеж-
365
утке @, + оо) и ограничена сверху (у < 0) на промежутке
(- ~, 0);
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не является периодической;
е) функция нечетная;
ж) функция не является монотонной на всей области
существования, но убывает на промежутке @, + оо), кроме
того, она убывает на промежутке (— оо, 0);
з) точек пересечения с осями нет.
Графиком функции у = - является линия, называемая
гиперболой (рис. 96).
1.уч!
О х
Рис.96.
Рис.97.
Теорема 2. График нечетной функции симметричен от-
относительно начала координат.
Доказательство. Пусть дана нечетная функция
у = fix) и пусть точка (xq, y0) лежит на ее графике. Тогда
Уо =Лхо) и в силу нечетности функции — у0 =fi— Xq), т.е.
точка (— Xq, — у0), симметрична точке (xq, y0) относительно
начала координат, тоже лежит на графике. Теорема дока-
доказана.
Замечание. Для построения графика нечетной функ-
функции достаточно построить его для х 10. Для х < 0 он
366
получается симметричным отображением построенной
части графика относительно начала координат.
Парабола у = х2. Зависимость у = х2 называется квадра-
квадратичной зависимостью. Легко проверяются следующие свой-
свойства этой функции:
а) область существования: (— °°, + °°);
б) область изменения: [0, + «>);
в) функция ограничена снизу: у ? 0;
г) функция принимает наименьшее значение у = 0 при
х=0;
д) функция не является периодической;
е) функция четная;
ж) функция не является монотонной на всей области
существования, но убывает на промежутке (— °°, 0] и
возрастает на промежутке [0, + °°);
з) точка @, 0) — единственная точка пересечения с
осями координат.
Графиком функции у = х2 является линия, называемая
параболой (рис. 97).
Теорема 3. График четной функции симметричен отно-
относительно оси Ох.
Доказательство. Пусть точка (Хо, у0) лежит на графи-
графике четной функции у=Ах), т.е. пусть уо=Ахо)- В силу
четности функции у0 = Д— Хо), т.е. точка (— Хо, у0), симмет-
симметричная точке (хо, у0) относительно оси Оу, тоже лежит на
графике функции у —Дх). Теорема доказана.
Замечание. Для построения графика четной функции
достаточно построить его для х ? 0. Для х < 0 он получается
симметричным отображением построенной части графика
относительно оси Оу.
Степенные функции у = ха. Рассмотренные выше функ-
функции у = х, у-х1, у-\ являются частными случаями этой
функции.
Рассмотрим другие случаи:
I. у — х (т — некоторое фиксированное натуральное
число).
Тогда
а) область существования: (— «>; + «>);
367
б) область изменения: [0, + «>);
в) функция ограничена снизу: у 10;
г) функция принимает наименьшее значение у = 0 при
х = 0;
д) функция не является периодической;
е) функция четная;
ж) функция не является монотонной на всей области
существования, но убывает на промежутке (— «>, 0] и
возрастает на промежутке [0, + «>);
з) точка @, 0) — единственная точка пересечения с
осями координат.
Графики функций у = х2, у = х*, у = х6 изображены на
рис. 98.
у,
(-1.-1)
П. уз?
III. у-*?
Рис. 99.
2. у ш jc*"~ ! (т — некоторое фиксированное натуральное
число).
Тогда
а) область существования: (— «>; + «>);
б) область изменения: (— «>; + «>);
в) функция не является ограниченной ни сверху, ни
снизу;
368
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не является периодической;
е) функция нечетная;
ж) функция возрастает на всей области существования;
з) точка @, 0) — единственная точка пересечения с
осями координат.
Графики функций у = х, y = x*, у = х* изображены на
рис. 99.
3. у — х~ ** (т — некоторое фиксированное натуральное
число).
Тогда
а) область существования: (— «>, 0) и @, + «>);
б) область изменения: @, + «>);
в) функция ограничена снизу: у > 0;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не является периодической;
е) функция четная;
ж) функция не является монотонной на всей области
существования, но возрастает на промежутке (— «>, 0) и
убывает на промежутке @, + «>);
з) точек пересечения с осями нет.
Графики функций у = х~~ 2, у = х~ 4 изображены на
рис. 100.
4. у — х~ *" +! (т — некоторое фиксированное натураль-
натуральное число).
Тогда
а) область существования: (— «>, 0) и @, + «>);
б) область изменения: (— «», 0) и @, + «>);
в) функция не является ограниченной ни сверху, ни
снизу;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не является периодической;
е) функция нечетная;
369
ж) функция не является монотонной на всей области
существования, но убывает на промежутке (— «>, 0), кроме
того, она убывает на промежутке @, + <*>);
з) точек пересечения с осями координат нет.
Графики функций у = х~\ у = х , у = х~5 изображены
на рис. 101.
!\п
т
Рис. 100.
5. у = ха (ос — фиксированное положительное нецелое
число).
Тогда
а) область существования: [0, + «»);
б) область изменения: [0, + «»);
в) функция ограничена снизу: у 2:0;
г) функция принимает наименьшее значение у = 0 при
х = 0;
д) функция не является периодической;
е) функция не является ни четной, ни нечетной;
ж) функция возрастает на всей области существования;
з) точка @, 0) — единственная точка пересечения с
осями координат.
Графики некоторых функций изображены на рис. 102.
370
6. у — х а (ос — фиксированное положительное нецелое
число).
Тогда
а) область существования: @, + <»);
б) область изменения: @, + «»);
//. у=хщ
III. у=°х
У.
У,
(Хл,<а2<1
а, а,
ш/
HI
1 1
ш
0 IV
У iv
1 !
1 1
1 / /
A,1)
г
III
/
II
7
X
Рис. 102.
в) функция ограничена снизу: у > 0;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
-J.
IV. у=х "¦
i_
V. у-х "'
У1
Ка,<аг<1
Х>)
III
1\1У
JJIk
A-ii
т1
\
0
A,1)
У IV
__! и
т
X
Рис. 103.
д) функция не является периодической;
е) функция не является ни четной, ни нечетной;
371
ж) функция убывает на всей области существования;
з) точек пересечения с осями координат нет.
Графики некоторых функций изображены на рис. 103.
Показательная функция у= а*. Функция у = <?, где а —
фиксированное число такое, что а > 0 и а * 1, называется
показательной функцией. Показательная функция обладает
следующими свойствами:
а) область существования: (— °°; + «>);
б) область изменения: @, + «»);
в) функция ограничена снизу: у > 0;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не является периодической;
е) функция не является ни четной, ни нечетной;
ж) если а> 1, то функция у = а^ возрастает на всей
области существования; если 0 < а < 1, то функция у = <?
убывает на всей области существования;
з) точка @, 0) — единственная точка пересечения с
осями координат.
Графики некоторых показательных функций изображе-
изображены при а > 1 на рис. 104, при 0 < а < 1 на рис. 105.
Ь iv т и II и ш iv
Рис. 104.
Рис. 105.
Логарифмическая функция у = log^c. Функция у = logjc,
где а — фиксированное число такое, что а>0 и пф\,
называется логарифмической функцией. Логарифмическая
функция обладает следующими свойствами:
372
а) область существования: @, + <*>);
б) область изменения: (— °°; + °°);
в) функция не является ограниченной ни сверху, ни
снизу;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значений;
д) функция не является периодической;
е) функция не является ни четной, ни нечетной;
ж) если а > 1, то функция у = logjc возрастает на всей
области существования; если 0 < а < 1, то функция у = logoX
убывает на всей области существования;
з) точка A, 0) — единственная точка пересечения с
осями координат.
Графики некоторых логарифмических функций изобра-
изображены при а > 1 на рис. 106, при 0 < а < 1 на рис. 107.
I. у = logj^ x
II. у = log, x
III. у=Ых
Рис. 106.
Рис. 107.
Основные тригонометрические функции. Прежде чем
переходить к исследованию тригонометрических функций,
докажем теорему.
Теорема 4. Для построения графика функции, имеющей
главный период Т, достаточно построить его на отрезке
длины Т, а затем продлить периодически.
Доказательство вытекает из определения графика функ-
функции и определения периодичности функции. Так, если
373
fix + nT) = fx), то вместе с точкой (xq, y0) графику принад-
принадлежат точки (xq + Тп, у0) при всех целых п.
Синусоида у — sin x Используя свойства синуса угла,
получим следующие свойства функции у = sin х.
а) область существования: (— «>; -*- «>);
б) область изменения: [- *• ?.]:
в) функция ограничена и сверху и снизу;
г) функция принимает наименьшее значение j> = — 1 при
каждом хк = — | + 2кк, где к — любое целое число, и
наибольшее значение у=\ при каждом х,-1 + 2кт, где
т — любое целое число;
д) функция периодическая, главный период 2л;
е) функция нечетная;
ж) функция не является монотонной на всей области
существования, но функция возрастает на каждом отрезке
[— | + 2я&, j + 2nk \, где к — любое целое число, и функция
Гк Зя 1
убывает на каждом отрезке у + 2кк, у + 2пк , где к —
любое целое число.
Покажем, например, что на отрезке — ^, ^ функция
у = sin х возрастает, т.е. что для любой пары чисел X; и Xj
такой, что — | й X; < Хг ^ §» будет справедливо неравенство
sin X; < sin х2.
Для любой пары чисел X: и Хг по формуле разности
синусов
sin хх — sin Хг = 2 sin ^-=-^ cos ^y^. A)
Докажем, что правая часть равенства A) отрицательна, если
— ^ < Xi < Xi < j. Условие Xi < ^ равносильно условию —| ^
^ — х2. Сложив это неравенство с неравенством — ^ й хх,
получим — пйхх — Хг. Учитывая, что неравенство хх <xj
равносильно неравенству xl—x2<0, имеем — пйх1—х1<
374
| й ^
< 0 или — | й ^у^ < 0. Следовательно, sin ^y^ < 0. Скла-
Складывая неравенства — ^ ^ Xi < ^ и — ^ < Хг ^ ?, получаем
— n<Xi+ Х2<п или — f < **2^ < f • Следовательно,
Итак, правая часть равенства A) меньше нуля, следова-
следовательно, sin Xi < sin Хг.
Покажем, что на отрезке §> у функция у = sin x убы-
убывает, т.е. что для любой пары дс, и Хг такой, что ^йхх<
< Xi й -г-, справедливо неравенство sin Х\ > sin Хг. Прибав-
ляя (— я) к неравенствам т- ^ *i < *2 ^ у, имеем — -= й хх —
-я<Х2-я^.В силу того что на отрезке — f. f функ-
функция у = sin х монотонно возрастает, то для (xi — я) и
(*2 — я) имеем sin fa — я) < sin fo — я). Далее справедлива
цепочка равносильных неравенств:
sin (хх — я) < sin fa — я) о
<* sin [— (я— дс,)] < sin [— (я— Хг)] **
о — sin (я— х,) < — sin (я— Хг) <*
<* sin (я— Xi) > sin (я— Хг) <* sin хх < sin Хг-
Значит справедливо неравенство sin xx < sin Хг, что и требо-
требовалось доказать.
Аналогично доказывается, что функция у = sin x являет-
является возрастающей на каждом отрезке — | + 2яЛ, ^ + 2пк ,
где к — любое целое число, и убывающей на каждом
отрезке | + 2яЛ, у + 2пк , где Л — любое целое число;
з) Точки пересечения с осями координат — точки (пк,
0), где к — любое целое число.
Учитывая периодичность, можно построить график
функции у = sin х, называемой синусоидой (рис. 108).
375
Косинусоида у = cos x Используя свойства косинуса
угла, получим следующие свойства функции у = cos x.
а) область существования: (— «»; + «»);
б) область изменения: [— 1; 1];
в) функция ограничена и сверху и снизу;
г) функция принимает наименьшее значение у= — \ при
каждом хк = п + 2к, где к — любое целое число, и наиболь-
@,1)
2
@,-1)
Рис. 108.
шее значение у = 1 при каждом хт = 2пт, где т — любое
целое число;
д) функция периодическая, главный период 2л;
е) функция четная;
ж) функция не является монотонной на всей области
существования, но функция возрастает на каждом отрезке
[2пк — п, 2пк], где к — любое целое число, и функция
убывает на каждом отрезке [2пк, 2к + п], где к — любое
целое число;
@,-1)
Рис. 109.
з) Точки пересечения с осью Оу — @, 1); с осью Ох точек
пересечения бесконечно много, каждая из точек
[|+ яЛ, 0 \ где к — любое целое число, есть точка пересе-
сения с сюью Ох.
Учитывая периодичность, можно построить график
функции у = cos х, называемой косинусоидой (рис. 109).
376
Тангенсоида y — tgx. Используя свойства тангенса угла,
получим следующие свойства функции у = tg х
а) область существования: любое х, кроме хк = | + пк, где
к — любое целое число;
б) область изменения: (— °°, + «>);
в) функция не является ограниченной;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция периодическая, главный период я;
е) функция нечетная;
ж) функция не является монотонной на всей области
существования, но функция возрастает на каждом из сле-
дующих интервалов I пк — ^, яЛ+^ I где к — любое целое
число; ^ '
з) точки пересечения с осями координат — точки (пт,
0), где т — любое целое число.
Учитывая периодичность, можно построить график
функции y = tgx, называемой тангенсоидой (рис. 110).
377
Котангенсоида у — ctg x. Используя свойства котангенса
угла, получим следующие свойства функции у = ctg x.
а) область существования: любое х, кроме х„ = пт, где
т — любое целое число;
б) область изменения: (— <*>, + <*>);
в) функция не является ограниченной;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция периодическая, главный период п;
е) функция нечетная;
ж) функция не является монотонной на всей области
существования, но функция возрастает на каждом из сле-
следующих интервалов {пт, п + пт), где т — любое целое
число;
з) точки пересечения с осями координат — точки
1 + пт, ОI где т — любое целое число.
Учитывая периодичность, можно построить график
функции у = ctg х, называемой котангенсоидой (рис. 111).
Рис. 111.
378
Основные обратные тригонометрические функции. Функ-
Функции у - arcsin х, у = arccosx, у = arctg х, у = arcctg x называ-
называются основными обратными тригонометрическими функция-
функциями.
Обратная тригонометрь *?с*ая функция j> — arcsin x Ис-
Используя свойства арксинуса числа, получим следующие
свойства функции у = arcsin х.
а) область существования: [— 1, 1];
б) область изменения: — -|, -|;
в) функция ограничена и снизу и сверху;
г) функция принимает наименьшее значение у = — ^ при
х = — i и наибольшее значение У~\ при дс = 1;
д) функция не является периодической;
е) функция нечетная;
ж) функция возрастает на всей области существования.
Докажем это свойство. Для этого докажем, что если
— 1 uxi <х2< 1, то arcsin Xi < arcsinXj. Обозначим
^ = arcsin ^ и а2 = arcsin Xj. Ясно, что sin oci = xx и
sin (Хг = *2* т.е. надо доказать, что если sin <Xi < sin 02, то
^ < а2. Доказательство проведем от противного: пусть
^ ? а2. Так как на отрезке — f» f функция у = sin x воз-
возрастает, то из условия <xi > ос2 следует, что sin c^ ? sin <х2, что
противоречит условию sin oci < sin <%. Значит предположе-
предположение неверно, т.е. функция у = arcsin x возрастает.
з) Точка @, 0) — единственная точка пересечения с
осями координат.
График функции у = arcsin x изображен на рис. 112.
Обратная тригонометрическая функция у = arccos x. Ис-
Используя свойства арккосинуса числа, получим следующие
свойства функции у = arccos x.
а) область существования: [— 1, 1];
б) область изменения: [0, тс];
в) функция ограничена и снизу и сверху;
г) функция принимает наибольшее, значение у = тс при
х = — 1 и наименьшее значение у = 0 при х = 1;
379
д) функция не является периодической;
е) функция не является ни четной, ни нечетной;
ж) функция убывает на всей области существования.
з) точки [0, f и A; 0)
точки пересечения с осями
I * I
координат.
График функции у = arccos x изображен на рис. 113.
'' /. j>=arcsin x
И
(-1,0).
у.
\/
О A,0)
И
Рис. 112.
(-1,0)
И)
О A,0) х
/. jHarccos x
Рис. 113.
Обратная тригонометрическая функция у — arctg x. Ис-
Используя свойства арктангенса числа, получим следующие
свойства функции у = arctg x.
а) область существования: (— «>, + «>);
б) область изменения: — |, |;
в) функция ограничена" и снизу и сверху;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
д) функция не является периодической;
е) функция нечетная;
ж) функция возрастает на всей области существования;
з) точка @, 0) — единственная точка пересечения с осью
координат.
График функции у = arctg х изображен на рис. 114. ]
Обратная тригонометрическая функция у= arcctgx. Ис-
Используя свойства арккотангенса числа, получим следующие
свойства функции у = arcctg x. \
а) область существования: (— «>, + «>);
б) область изменения: @, п);
380
в) функция ограничена и сверху и снизу;
г) функция не принимает ни наибольшего, ни наимень-
наименьшего значения;
J^ __
У,
и
0
И
/. JTC«gX
X
У~\
Рис. 114.
д) функция не является периодической;
е) функция не является ни четной, ни нечетной;
ж) функция убывает на всей области существования;
У;
у-к
у-0
0
I. y-arcctgx
— /
Рис. 115.
з) точка 0, j \~ единственная точка пересечения с осью
координатЛ ^
График функции у — arcctg x изображен на рис. 115.
§ 3. Обратные функции
Взаимно однозначное отображение. Каждая функция
у=Ах) производит отображение области существования
функции на область ее изменения так, что каждому х из
области существования соответствует единственное значе-
значение у из области изменения.
Рассмотрим несколько функций вместе с их областями
существования и изменения (табл. 2).
381
Некоторые из приведенных функций разным х из области
существования ставят в соответствие разные у. Например,
для функции у = 2х каждое значение у из области измене-
изменения получается лишь при одном значении х из области
существования. В таких случаях говорят, что функция
осуществляет взаимно однозначное отображение своей об-
области существования на область изменения. Заметим, что
все остальные функции, приведенные в таблице, таким
свойством не обладают:
Таблица 2
Функция
у = Г
Область
существования
(- -, -)
[-1; И
(- -, -)
(- -, -)
Область
изменения
№;-)
[0;1]
@;Ц
@;-)
функция у = х2 при х = 1 и при х =
и то же значение у=1;
1 принимает одно
=
функция у = VI —х2 при х = i и при х = — ~ принимает
одно и то же значение у = -=-;
при х = 2 и при х = — 2 принимает
функция }> = —-Ц
1+х
- 1
одно и то же значение y — j-
Итак, функции можно разделить на два класса:
1) функции, осуществляющие взаимно однозначное ото-
отображение области существования на область изменения;
2) функции, не обладающие этим свойством.
Если функции второго класса рассматривать не на всей
области существования, то часто удается выбрать такую
область определения (часть области существования), что
функция будет отображать эту область определения на
соответствующую область изменения уже взаимно одно-
382
значно. Заметим, что любая функция у = Дх) на той части
области определения X (из области существования функ-
функции), где она является строго монотонной (т.е. возрастаю-
возрастающей или убывающей), принадлежит к первому классу.
Например, для функции у = х2 такой областью будет про-
промежуток [0, + <») или промежуток (— °°, 0].
Рассмотрим функцию у = х* на области определения
Х= (_ те> 0] (соответствующая ей область изменения —
Yi = [0; + °°))- Эта функция осуществляет взаимно одно-
однозначное отображение области Хх на область Yx. При этом
по каждому у из области У, можно однозначно восстано-
восстановить х из области Хх. Действительно, если уое Уь то соот-
соответствующее значение Xq такое, что у0 = xl, ищется по
правилу Xq = — УйГ. При этом, если у0 *%, то Xq * х^, где
Хо = — Vy7» а х^ = — Vy7- Другими словами, можно устано-
установить взаимно однозначное отображение области У, на
область Хх по правилу х = — ^у.
Итак, функция у = х2 осуществляет взаимно однозначное
отображение области Хх на область Yx, а правило х = — ^у
осуществляет взаимно однозначное отображение области
Yx на область Хх. Правило х —— ^у назовем обратным
правилом для функции у = х2 на области определения Хх и
области изменения Yx.
Функция у = х2 и правило х = — Vy, если х € Хх = (— °°,
0], а у € У, = [0, + с»), выражают одну и ту же связь между
переменными х и у; только для любой пары (xq, y0) из
рассматриваемых переменных величин функция у = х дает
возможность, зная Xq, найти у0, а правило х = — Vy — зная
j>o, найти Xq.
Обратная функция. Если в обратном правиле заменить х
т у, а у на х с одновременной заменой области определе-
определения на область изменения и области изменения на область
определения функции у е х2, хе X, то получим новую
функцию у = — Vx, у которой область определения Х2 = [0,
+ со) = у, и область изменения У2 = (— °°, 0] = Хх. Новую
функцию у = — Vx с областью определения -ЛТ2 и областью
383
изменения Y2 называют обратной функцией к функции
у = х2 с областью определения Хх и областью изменения Yu
Для функции у = х2 с областью определения Х3 = [0; 10)
и областью изменения У3 = [0; Ю0) обратной функцией
будет функция у = ^хс областью определения Л^ = [0; 100)
и областью изменения У4 = [0; 10).
Приведем определение обратной функции в общем слу-
случае.
Пусть область определения функции у =fix) такова, что
функция осуществляет взаимно однозначное отображение
области ее определения X на область изменения Y. Тоща
по каждому у из области У можно однозначно восстановить
х из области, X следующим образом: в равенстве fix) —y =
= 0 считают каждое ye Yфиксированным и отыскивают
х е X, удовлетворяющее этому равенству. Найденное каж-
каждое х е ЛГ обозначается,/~ '(у). Равенство х =f 1(у) называ-
называется обратным правилом. Обратной функцией к функции
у = fix) (х е X, у е Y) называется функция, которая получа-
получается из обратного правила x=f (у) заменой х на у, а у на
х с одновременной заменой области определения на об-
область изменения, а области изменения на область опреде-
определения. После такой замены область изменения функции
у = fix) становится областью определения обратной функ-
функции y=f l(x), а область определения функции y=fix)
становится областью изменения обратной функции у =
= /~\х). Итак, две функции: функция у =fix) с областью
определения X и областью значений У и функция у=/~1(х)
с областью определения Y и областью значений X, где
ДГ 1(х)] = х для любого хе Y и f '[Дх)] = х для любого
х е X, такие, что одна из них является обратной к другой.
Покажем на нескольких примерах, как отыскивается
обратное правило и обратная функция. Во всех ниже
приведенных примерах области определения выбраны так,
что соответствующие функции осуществляют взаимно
однозначное отображение области определения на область
изменения (табл. 3).
384
Функция у =Л*)
Область
определения Л*)
Область
изменения
Таблица 3
Обратное правило
x=rf(y) ~
0<у<
Ouyul
Ойу<со
Функция у =J[x)
Обратная
функция
У=ГТ(х)
Область
определения
Область
изменения
0<х<~
— «о<уйО
— оо < у< оо
— оо<>.<
Замечание. Не для всякой функции удается найти
такую область определения, которую она взаимно одно-
однозначно отображает на соответствующую область измене-
изменения. Например, функция у = 1 не отображает взаимно
однозначно никакой промежуток числовой прямой на со-
соответствующую область изменения. В качестве другого
примера можно привести функцию Дирихле.
13 Алгебра, тригонометрия
и элементарные функции
385
A,0)
if
Рис. 116.
График обратной функции. Прежде всего выясним, как
расположены точки, координаты одной из которых полу-
получаются из координат другой заменой х на у, а у на х.
Теорема. Любые точки A(xq, у0) и В(у0, Xq) симметричны
относительно прямой у = х.
Доказательство. Если
Хо = уо, то точки А и В
(рис. 116) совпадают и лежат
на прямой у = х, т.е. в этом
случае утверждение теоремы
верно. Пусть Хо*уо и пусть
точка А (хо, у0) лежит в первой
четверти и Хц > у0. Проведем
из точки А параллельно оси
Ох прямую ААи т.е. прямую
у — у0; из точки В — прямую
ВВХ параллельно оси Оу, т.е.
прямую у = х0. Прямые ААХ и
ВВХ пересекаются в точке С(у0, у0) т.е. в точке, лежащей на
прямой у = х. Рассмотрим треугольник ВСА; он прямо-
прямоугольный (прямой угол ВСА) и равнобедренный <\АС\ =
= \ВС\ = |хо — ^ol)- Биссектриса (CD) угла ВСА совпадает с
прямой у = х. Поскольку треугольник ВСА равнобедрен-
равнобедренный, то его биссектриса (CD) является и высотой и медиа-
медианой, следовательно (CD) I (AB) и \AD\ = \BD\. Это означает,
что точки А и В симметричны относительно прямой у = х.
Аналогично проводится доказательство теоремы в случае,
когда точка Afa, у0) лежит в первой четверти и Xq < у0, а
также в случае, когда точка A(xq, yQ) лежит не в первой
четверти. Теорема доказана.
Пусть функция у =Ах) взаимно однозначно отображает
область определения X на область изменения У. Тогда
график этой функции таков, что по любому х, однозначно
находится ух =Лх,) и, наоборот, по любому у2 однозначно
находится Xi=f~ (y2) (рис. 117).
Если точка Af(*b> Уо) лежит на графике функции у =Дх),
то ее координаты удовлетворяют условию у0 =Ахо)> а сле-
следовательно, и условию Хо =f l(y0). Другими словами, все
точки (и только они) графика у = f(x) удовлетворяют уело-
вию x=f~x(y). Так как для получения обратной функции
надо в обратном правиле x=f (у) заменить х на у, а у на
х, то каждая точка графика у =f (x) получается из точки
графика функции у =/(х) заменой х на у, а у на х, т.е. если
точка К(х, у) — точка графика у =/(х), то точка Ki(y, x) —
точка графика у =f l(x). Из этого рассуждения и теоремы
вытекает, что график обратной функции у =f \x) получа-
получается из графика функции у=Лх) симметричным отобра-
отображением последнего относительно прямой у = х (см.
рис. 117).
Рис
Замечание. Часто возникает ситуация, когда вид об-
обратной функции получается непростым. Например, функ-
функция у = Xм ~ \ где т — фиксированное натуральное число,
взаимно однозначно отображает свою область существова-
существования (всю числовую прямую) на область изменения Y=
= (—«>,+ оо). Для того чтобы найти обратное правило, с
помощью которого строится обратная функция, необходи-
необходимо отыскать х, удовлетворяющее равенству х2" ~1 — у = 0.
Как известно (см. гл. IV) для неотрицательного у такое х
существует, а именно х=ъ>~1^у\ и для отрицательного у
Поэтому
387
такое х существует, а именно х=— 2т
обратное правило задается следующим образом:
I2" 'Vy, если уе [0, + <
-
'V^f, если у е (— °о, 0).
Следовательно, и обратная функция будет иметь вид
0, + оо);
Иногда обратную функцию к степенной функции
y = j^m~i записывают с помощью одной формулы
у = Ъп~ 'Vx, но мы так поступать не будем, так как символ
">fa употребляется у нас только для неотрицательных
чисел а.
Функции, обратные к основным тригонометрическим функ-
функциям. Для любой из основных тригонометрических функ-
функций, у = sin х, у = cos х, у = tg х, у = ctg х, можно выделить
много областей определения, каждую из которых соответ-
соответствующая тригонометрическая функция отображает взаим-
взаимно однозначно на соответствующую область изменения.
При этом если рассмотреть основную тригонометрическую
функцию на своей специально выбранной области опреде-
определения, то обратной к ней будет соответствующая обратная
тригонометрическая функция (см. табл. 4).
388
Таблица 4
Функция у = Дх)
j> = sinx
J> = COSX
j> = tgx
y = dgx
Функция у =J{x)
у = апх
У = СО6Х
y = tgx
y = ctgx
Область
определения Л*)
я^ я
SXS2
0?х?х
--<х<-
2<Х<2
0<х<ж
Обратная
функция
3> = aresin.x
j> = arccosx
j> = arctgx
j> = arcctgx
Область
изменения
У=Лх)
-luyul
- luyul
— е»< у< ео
— е»< у< оо
Область
определения
У=ГГ(х)
- 1SXS1
- lSXSl
— »» <Х<"»
— ов<Х<«>
Обратное правило
х=ГЧу)
х = arcane
х = агесову
x = aictgy
x = atcctgy
Область
изменения
У=ГЧх)
я ^я
S^2
О?у?1С
я .я
-2<у<2
0<^<я
Очевидно, что любая основная обратная тригонометри-
тригонометрическая функция отображает взаимно однозначно свою об-
область определения на свою область изменения. Поэтому у
каждой из этих функций есть обратная функция — соот-
соответствующая основная тригонометрическая функция, но
рассматриваемая только на соответствующей области оп-
определения.
Например, для функции .y = arccosx обратной к ней
будет функция у = cos x, рассматриваемая только на отрез-
отрезке [0, я]; для функции 3'=arctgx обратной к ней будет
функция y = tgx, рассматриваемая только на интервале
(}
ючение найдем обратную функцию к функции у
= sinx с областью определения Х= if, у • Легко видеть,
что функция у = sin x взаимно однозначно отображает от-
отрезок .Уна отрезок Y= [— 1; 1]. Поэтому у этой функции
есть обратная функция. Для ее нахождения возьмем про-
389
извольное уое Y и найдем ^еХиз равенства sin Xq —
— у0 = 0. Очевидно, что число Xq = я — arcsin у0 удовлетво-
ряет этому равенству и принадлежит отрезку ^, —¦. Поэ-
Поэтому обратное правило будет такое: х = % — arcsin у. Зна-
Значит, обратной функцией будет функция у = п — arcsin x
Итак, для функции y = sinx с областью определения
^ = §' Т обр*™0* к неи будет функция у = — arcsin x +
+ % с областью определения [— 1; 1] и с областью измене-
изменения
[§' У] fr
ис. 118).
У
(о,*)
(*.О)
и
I. yarcsin x+it;
ywax,
§ 4. Суперпозиции функций и их графики
Сложная функция. Пусть функция и = <р(х) определена на
множестве Хи множество значений этой функции входит
в область существования функции
у = Ди). Тогда любому х из области
определения X функции м = <р(х)
соответствует определенное значе-
значение переменной и, а этому значе-
значению и функция у = F{u) ставит в
соответствие определенное значе-
значение переменной у, т.е. переменная
у является функцией от х на мно-
множестве X: у= /1<р(х)]. Полученная
функция от функции называется
сложной функцией переменной х
Функцию и = <р(дс) называют внут-
внутренней функцией, яу= f{u) — внешней. Сложную функцию
у = /1<р(х)] называют часто суперпозицией двух функций:
внутренней и = <р(х) и внешней у = F{u). Например, если и
= cosjc и у = 2й, то для любого действительного х опреде-
определена сложная функция у=2со". Сложными функциями
будут, например, функции
у = sin Bх + 4), у = log2tg х, у =
Рис. 118.
390
Функции, полученные из основных элементарных функ-
функций с помощью конечного числа алгебраических операций
и применения конечного числа суперпозиций, принято
называть элементарными функциями. Элементарными
функциями будут, например, функции
У = tgVl-x", У = log2sin 3х,
У = ^ г \ , + 2 sin2 (х - 5).
х +4х+ 1
Рассмотрим примеры, показывающие, как построить
график сложной функции у = F[y(x)], зная график внут-
внутренней функции и = ф(дс) и свойства внешней функции у =
F{u) (из рассмотренных примеров будет ясно, как постро-
построить график любой элементарной функции, зная свойства и
графики основных элементарных функций).
Построение графика функции у — — fix) по графику функ-
функции у =Лх). Пусть некоторая точка Мо(хо, у0) принадлежит
графику функции y=fix), т.е. пусть yo=fixo). Возьмем
точку Mi(pco, — Уо), симметричную точке Мо(хо, у0) относи-
относительно оси Ох. Координаты точки Mfa, — у0) удовлетво-
удовлетворяют условию — уо = — fixo), поэтому точка М^Хц, — у0)
принадлежит графику функции у = — fix). Так как точка
Щхо, Уо), принадлежащая графику функции y=fix), бра-
бралась любая и функция у = fix) и у = — fix) имеют одну и ту
же область определения, то график функции у = — fix)
получается из графика функции y=fix) симметричным
отображением последнего относительно оси Ох. Построим
этим способом графики функций у = — х2 (рис. 119),
У=-\ (Рис 120), у = - log2 х (рис. 121).
Построение графика функции у — Д — х) по графику функ-
функции у "fix). Пусть некоторая точка Мо(хо, у0) принадлежит
графику функции y=fix), т.е. пусть yo=fixo). Возьмем
точку Mi (— Хо, Уо), симметричную точке Мо(хо, у0) относи-
относительно оси Оу. Координаты точки Мх{— л*,, у0) удовлетво-
удовлетворяют условию уо =Л— (— Хо)), поэтому точка М,(— хь» Уо)
принадлежит графику функции y=fi— x). Так как точка
Уо), принадлежащая графику функции y=fix), бра-
IУ log, х
II.y--\og2x
РИС. 121.
Рис. 122.
Рис. 123.
392
лась любая и функция у =/(х) и у =/(— х) имеют области
определения, симметричные относительно начала коорди-
координат, то график функции у —/{— х) получается из графика
функции у =Лх) симметричным отображением последнего
относительно оси Оу.
Построим этим способом графики функций у = 2~ х
(рис. 122), у = log2 (- jc) (рис. 123).
Построение графика функции у — ВДх), где ВфО,по гра-
графику функции у -Дх). Функции у =Дх) и У - Щх) имеют
одну и ту же область определения. Следовательно, зная, как
для любого х по ординате функции у =/(х) найти ординату
функции у = Bflx), можно по графику функции у =Дх)
построить график функции у = Bfoc). Пусть некоторая
точка Afofo,, уо) принадлежит графику функции у =Дх), т.е.
пусть у0 =Дхо). Возьмем точку A/ifo, Ву0). Координаты ее
удовлетворяют условию Ву0 = ВДхо), поэтому точка A/jfo,,
Ву0) принадлежит графику функции у = ВДх). Рассмотрим
возможные случаи в зависимости от числа &.
1. В > 1. Точка A/i(*o, Ву0) получается из точки А^(ло, у0)
растяжением ординаты точки МоъВ раз и график функции
у = ВДх) получается из графика функции у =Ддс) растяже-
растяжением в В раз вдоль оси Оу графика функции у =Лх).
2. В = 1. Все точки графика у =/(х) остаются на месте.
3. О < В < 1. Поскольку В = у, то точка A/jfo,, Ву0) полу-
чается из точки Мо(хо, у0) сжатием ординаты точки Мов^
раз и график функции у = ВДх) получается из графика
функции у =Дх) сжатием ординат всех точек в ^ раз, т.е.
сжатием в ^ раз вдоль оси Оу графика функции у =.Дх).
4. В < 0. Тогда В= — \В\и построение графика функции
у = Ж*) разбивается на 2 этапа:
а) построение графика функции у = |5|Дх) по графику
функции ^ =.Дх);
б) построение графика функции у = — |5|Дх) по графику
функции у = ||
„.. Построим этим способом графики функций у = 2 sin х
(рис. 124), у= — 2х2 (рис. 125), у = ^cos х (рис. 126).
II, i I
х
II. y=sin 2x
Построение графика функции у =fijac), где к ф 0, по гра-
графику функции у=Дх)- Функция у=Ак*) определена для
всех тех х, для которых число кх принадлежит области
определения функции у = fix). Пусть некото-
некоторая точка M0(Xq, yQ) принадлежит графику
функции у=Лх), т.е. пусть у0 =Яхо)- Точка
AfAxo,tf>l принадлежит графику функции
у =fljcx), так как ее координаты удовлетво-
ряют условию уо =f\k^\ Рассмотрим раз-
I )
личные случаи в зависимости от числа к.
1. к> 1. Точка Л/Дло,уо\ получается из
V )
111
II.
111. У-2Х1
Рис.125.
V ) m
v0) растяжением абсциссы точки Мо в |х1 раз, и график
V J
функции у =/{кх) получается из графика функции у =f(x)
\
V )
точки М0(хц, у0) сжатием абсциссы точки Мй
в к раз и график функции у = /{кх) получает-
получается из графика функции у =f(x) сжатием абс-
абсцисс всех точек в к раз вдоль оси Ох к оси
О У графика функции у = fix).
2. к = 1. Все точки графика у=Лх) остают-
остаются на месте.
3. О < к < 1. Точка mJjXq, уА получается из точки Afo(jtb,
е )
394
растяжением абсцисс всех точек в (Т)раз> т.е. растяжением
в |-н раз вдоль оси Ох к оси OYграфика функции у =fix).
4. к < 0. Тогда к = — Щ и построение графика функции
у =ДЛзс) разбивается на 2 этапа:
у,,
5л
-Эк
а) построение графика функции y=fl\k\x) по графику
функции у=Ах)\
б) построение графика функции у =Л— \к\х) по графику
функции y=fl\k\x).
Построим этим способом графики функций у = sin 2x
(рис. 127, II), у = 2~ * (рис. 128, III), у = log2 Г- ?с) (рис.
129, III).
Построение графика функции у —Лх — в), где а ф 0, по
графику функции у — Дх). Функция у=Дх— а) определена
для всех тех х, для которых (х — а) принадлежит области
определения функции у =Ддс). Пусть точка Мо(хо, у0) при-
принадлежит графику функции у=Ях), т.е. пусть Уо=Ахо)-
Точка Mi(Xq + а, у0) принадлежит графику функции
у = fix— а), так как ее координаты удовлетворяют условию
Уо =Л(хо + а) — а] =/Чхо)- Следовательно, каждая точка Мх
графика функции у = fix — а) получается из соответствую-
соответствующей точки Мо графика функции у = Дх) сдвигом этой точки
вдоль оси Ох на величину а. При этом если а > 0, то сдвиг
производится вправо на величину а, а если а < 0 — сдвиг
производится влево на величину а. Итак, график функции
у = fix— а) получается из графика функции у =fix) сдви-
сдвигом последнего, как жесткого тела, вдоль оси Ох на вели-
величину а.
395
@,1)
(o-i)
Рис. 127.
/Э?!
I.
//. y-sin 2c
i У
/\ \ii\4i'' In
Рис. 130.
Рис. 131.
\i
/У* -2c
ч ^ *
Iх
I.y-aatx
Рис. 132.
396
(рис. 131, II), y=cos (x+f\
Построим этим способом графики функций у = log2 (x +
+ 3) (рис. 130, II), у= (х - 2J (f
(рис. 132, II).
Построение графика функции у=Лх) + *» где 6*0, по
графику функции у=Дх)- Функции у=А*) + b и у=Ах)
имеют одну и ту же область определения. Следовательно,
зная, как для любого х по ординате функции у = Дх) найти
ординату функции у =.Дх) + Ь, можно по графику функции
у=Лх) построить график функции у=Дх) + Ь. Пусть не-
некоторая точка Mita,, у0) принадлежит графику функции
у = Лх), т.е. пусть у,, =Ахо). Возьмем точку М^Хц, у0 + Ь).
Координаты ее удовлетворяют условию у0 + Ь =А*о) + Ь.
1.у-2х
П.у=2'-3
Рис*
Рис. 134.
Следовательно, чтобы получить точку М\, нужно точку
сдвинуть вдоль оси Оу на величину Ь. При этом если Ь > 0,
то сдвиг производится вверх на величину Ь, а если Ъ < 0 —
вниз на величину Щ.
Построим этим способом графики функций у = 2х — 3
(рис. 133), у = х2 — 1 (рис. 134), у = sin х + 1 (рис. 135).
Построение графика функции у = Bf[k(x — а)] + Ь по тра-
трафику функции у = fix). График функции у = ЩЦх — а)] +
39?
+ b строится по графику функции у=Лх) последователь-
последовательным применением предыдущих способов.
Например, так:
У =Ах) -» У =Акх) -» у = ВЛкх) -» у = В/[к(х - а)] -»
->y = Bf[k{x-a)\+b.
Покажем применение этого способа на нескольких при-
примерах.
I.y-w\x
II. y=sin x +1
Рис. 135.
Построить график функции у = ах2 + Ьх + с, где а * 0.
Преобразуем квадратный трехчлен ах2 + Ьх + с, выделив
полный квадрат:
Итак, надо построить график функции
— \ — zr-\\ +
4ac-b
4a ¦
Сначала построим график функции у = х2. Затем растяже-
растяжением его вдоль оси Оу в \а\ раз — график функции у = \а\х?.
Если а > О, то возьмем построенный график функции
у = ах2; если а < О, то отобразим график функции у = |а|х*
относительно оси Ох и получим график функции у = ах.
Наконец, сдвигом графика функции у= ах вдоль оси Ох
(— j-\ а затем сдвигом полученного графика функции
на
498
y=
At
2a)
вдоль оси Оу на
Aac-b2
4a
получим график
функции у = ах2 + bx + с.
Покажем все эти этапы построение графика квадратного
трехчлена на следующем примере: построить график функ-
функции у = — 2Х2 + Зх+ I. Преобразуем квадратный трехчлен
3x+l= — 2 (х
j\ +уи построим по изложен-
}
4 +
17
(рис. 136).
III
ной схеме график функции у = -
Теорема I. График функции
у= кх+ Ъ есть прямая линия,
пересекающая ось Оу в точке r n yi<
М@, Ь) и образующая с положи-
положительным направлением оси Ох
угол, тангенс которого равен к.
Доказательство. Дока-
Докажем, что график функции
у = кх есть прямая, проходящая
через начало координат и обра-
образующая с положительным на-
направлением оси Ох угол, тан-
тангенс которого равен к.
Рассмотрим несколько случа- щ /к
ев:
а) к = 0. Тогда график функ-
функции у = 0 есть ось Ох — прямая
линия и tg a = 0.
б) к > 0. Тогда все точки графика функции у = кх лежат
в I и III четвертях. Начало координат принадлежит графику
функции у = кх. Возьмем некоторую точку Мо(хо, у0), от-
отличную от начала координат, принадлежащую графику
функции у = кх, т.е. такую, что у0 = кх^. Проведем через
точки Мо(хо, у0) и О@, 0) прямую и покажем, что эта и
прямая и будет графиком функции у = кх.
Пусть построенная прямая образует с положительным
направлением оси Ох угол, тогда
Рис. 136.
= — = — = к.
Возьмем некоторую точку А/^х,, у,), отличную от точек О
и Мо на этой прямой (пусть для определенности точка Мх
лежит в I четверти). Из прямоугольного треугольника ОАМХ
(рис. 137) находим, что \АМ\ = \ОА\ tg а. Так как АМ{ = уи
ОА = хи tg a = к, то у\ = кх\. Это означает, что координаты
любой точки построенной прямой удовлетворяют условию
у = кх.
Рис. 137.
? t-tg a-? Ь-3;
II. у—2х+2, *-tg <р—2, Ь-2.
Рис. 138.
Пусть теперь Хх и у2 таковы, что у% = кхг (пусть для
определенности Хх > 0 и, следовательно, у2 > 0). Построим
точку М2(хх, у2). Точка М2 должна оказаться на построенной
прямой, ибо если точка М2 не попадает на эту прямую, то
через начало координат будут проведены две различные
прямые, образующие один и тот же угол а с положитель-
положительным направлением оси Ох, что невозможно.
Итак, точки построенной прямой и только они удовле-
удовлетворяют условию у — кх, т.е. график функции у = кх есть
построенная прямая.
в) к < 0. Тогда график функции у = \к\х есть прямая,
проходящая через начало координат и образующая с поло-
положительным направлением оси Ох угол, тангенс которого
равен \к\. График функции у — — \к\х получается из этого
графика симметричным отображением относительно оси
Ох, поэтому этот график есть прямая, образующая с поло-
положительным направлением оси Ох угол, тангенс которого
равен — \к\ = к.
Для завершения доказательства остается сказать, что
график функции у = кх + Ъ получается из прямой у — кх
400
сдвигом вдоль оси Оу, как жесткого тела, на величину Ь.
При этом точка 0@, 0) графика функции у= кх перейдет
в точку А@, Ь) графика функции у = кх + Ь. Теорема дока-
доказана.
Построим этим способом графики функций у = |х + 3
(рис. 138, I), у = - 2х + 2 (рис. 138, И).
Построение графика функции у = |Дх)| по графику функции
У~ЛХ)- Прежде всего напомним определение:
1* ч| = J Ах), для тех х, где Ах) * О,
[—/л), Для тех х, где/х) < 0.
Пусть некоторая точка М0(хь, .у0) принадлежит графику
функции у =Ах), т.е. пусть у0 =Ахо)> Рассмотрим два слу-
случая:
а) у0 2:0. Тогда, поскольку |Дль)| =Axq) = Уо, точка М0(ль,
у0) принадлежит графику функции у = |Дх)|.
1A.0)
I
I
I
II
¦log,*
y
II. у
Рис. 140.
Рис. 139.
б) уо < 0. Тогда, поскольку |Дль)| = — Ахо) = — Уо, точка
, — у0) принадлежит графику функции у = |Дл:)|. Сле-
Следовательно, график функции у =А.х) получается из графика
функции у =Ах) следующим образом:
все точки графика у =Ах), лежащие на оси Ох и выше
ее, остаются на месте;
40J
все точки графика у =Ах), лежащие ниже оси Ох, сим-
симметрично отображаются относительно оси Ох.
Заметим, что график функции у = |Дх)| не имеет точек
ниже оси Ох.
/. y*sin x
II. y=|sin x\
Рис. 141.
Построим этим способом графики функций у = (дс2 — 1|
(рис. 139), у = Щ (см. рис. 104, II), y = |log2xl (рис. 140),
у = |sin;xj (рис. 141).
Построение графика функции у — /flxj) по графику функции
у —Ах)- Заметим, что функция у=АЫ) четная функция,
так как f(\— xj) = Л|х|). График четной функции строится
так: строится график этой функции для всех х 2:0; для
построения графика этой функции для х < 0 построенная
часть отображается симметрично относительно оси Оу.
Поскольку |х| = х для х 2:0, то для х > 0 график функции
у =.ДН) совпадает с графиком функции у=Ах). Для по-
построения графика функции у=ЛН) Для х< 0 надо часть
графика функции у=ЛН)> У^ построенного для х^О,
симметрично отобразить относительно оси Оу. Для постро-
построения графика функции у = ЛН) существенную роль играют
точки графика функции у=Ах)> лежащие на оси Оу или j
справа от нее; точки графика, лежащие слева от оси Оу,.]
никакой роли не играют, следовательно, для построения •
графика функции у = ЛН) надо: J
а) стереть все точки графика функции у =Дх)> лежащие ]
слева от оси Оу;
б) оставить на месте все точки графика функции, лежа-
лежащие на оси Оу и справа от нее;
в) отобразить правую часть графика симметрично отно-;
сительно оси Оу.
Построим этим способом графики функций у=2м
(рис. 142), у = log2 |х| (рис. 143), д' = sin |x| (рис. 144).
Построение графика функции у — ДДх» по графику функ-
функции у = Дх). В случаях, более сложных, чем рассмотренные
выше, график функции у = F(j{x)) строят, используя гра-
log, x
II II. у - log, |x|
I.y-2'
II. у-2*
Рис. 142.
Pifc. 143.
фик у =Лх) и свойства функции у = fix). He давая общих
рекомендаций, покажем как это делать, на нескольких
примерах.
ш
Рис. 144.
Используя график функции у = sin x (см. рис. 108), по-
построить графики функций:
403
а) область определения
функции у=2 х — все
действительные х;
б) поскольку функция
у = sin х — периодическая с
главным периодом 2я, то
функция у = 2тх тоже
у = log2 sin x
а) область определения
функции у = log2 sin x — все
те х, для которых sin x > О,
т.е. все те х, где график
функции y = sinx лежит
выше оси Ох;
б) поскольку функция
у = sin х — периодическая с
главным периодом 2я, то
функция у = log2 sin x тоже
периодическая с главным
периодом 2л;
t
функция у = 2'*пХ на этом
промежутке возрастает от 1
до 2; на
в) поскольку на
промежутке [0,?| функция
у = sin х возрастает от 0 до 1,
периодическая с главным
периодом 2я;
Поэтому будем строить графики обеих функций только
на отрезке [0, 2я], а потом продолжим графики периоди-
периодически.
в) поскольку на отрезке
|, ? функция y = sinx
взрастает от 0 до 1, то
то функция у = log2 sin х на
этом промежутке возрастает
отрезке |у,у| от (-о») до 0; на промежутке
функция y = sinx убывает Т'Л] ФУНКЦИЯ У = ®пх
от 1 до (— 1), а функция убывает от 1 до 0, а функция
у = log2 sin x убывает от 0 до
(— ее); на отрезке [я, 2я]
функция у = sin х
неположительна, поэтому на
этом промежутке функция
у = log2 sin х не определена (и
у = 2 убывает от 2 до ^; на
Зя
"»2я функция
отрезке
у = sin х возрастает от (— 1)
до 0, а функция у=2йпх
возрастает от ^ до 1.
точек графика этой функции
здесь нет).
Перечисленные свойства позволяют нам построить тре-
требуемые графики на отрезке [0, 2я] и продолжить их пери-
периодически (рис. 145, 146).
404
Предыдущие рассуждения показывают, как график
функции помогает выбрать необходимые промежутки для
исследования свойств сложных функций и тем с*мым
помогает построить график сложной функции.
II. у-2
finx
I //. y^og, sin x
Сложение графиков. Пусть даны функции у=Ах) и
У — i(x). Тогда на общей части их областей существования
определена функция у -Ах) + g(x). Пусть точка М^Хо, yi)
принадлежит графику функции у =Ах), а точка М2(хо, у2)
принадлежит графику функции у — g(x), причем число дь
принадлежит общей части областей существования функ-
функций у -Ах) и у - g(x). Тогда точка М3(хо, yt + y2) принадле-
принадлежит графику функции у =Ах) + g(x). Значит, для постро-
построения графика функций у =Ах) + g(x) надо:
405
' к
а) оставить те точки графиков у =Дх) иу = g(x), у кото-
которых х входит в общую часть областей существования этих
функций;
б) для каждого такого х произвести алгебраическое сло-
сложение ординат (соответствующих данному х) этих двух
графиков.
Построим этим методом график функции у = х + sin x
(рис. 147).
Умножение 1рафиков. Пусть даны функции у=Лх) и
У = g(x). Тогда на общей части их областей существования
определена функция y=Ax)g(x). Пусть точка М,(дь, ух)
принадлежит графику функции у-Ах); а точка М2(хо, Уг)
принадлежит графику функции у = g(x). Ясно, что число Хо
принадлежит общей части областей существования функ-
функций у =Ах) иу = g(x). Тогда точка Мз(хо,У\Уг) принадлежит
графику функции у =Ax)g(x). Значит, для построения гра-
графика функций у =f[x)g(x) надо:
а) оставить те точки графиков у =АХ) иу = g(x), у кото-
которых х входит в общую часть областей существования этих
функций;
б) для каждого такого х произвести умножение ординат
(соответствующих данному х) этих двух графиков.
Построим этим методом график функции y = xsinx
(рис. 148).
УПРАЖНЕНИЯ
Найти область определения и область изменения функций A — б):
2
4. j»=
Совпадают ли области определения функций (если нет, то найти общую
часть областей определений сравниваемых функций) G — 14):
7. у=х и у = —; 8. у= sin пх и у = tgгот,
9. ,y=cos лх и у = ctg ях; 10. у = tg х и у = ctg x;
П. у = arcsin х и у = arctg x, 12. >'=arcsinxH>' = aiccosx;
13. у= arcsin х и y = arcctgx; 14. у = arccos х и у = arcctg xl
407
15. Что значит:
— функция ограничена сверху (снизу);
— функция не является ограниченной сверху (снизу);
— функция ограничена;
— функция не является ограниченной?
16. Показать, что функция у= — не является ограниченной ни сверху,
ни снизу.
17. Показать, что функция у=х2 не является ограниченной сверху.
18. Показать, что функция у=х* не является ограниченной.
19. Приведите пример функции, которая не является ни четной, ни
нечетной.
20. Всякая ли функция может быть представлена в виде суммы четной
и нечетной функций?
Рассмотреть примеры: 1)у*=^х, 2) у=log2 х.
Доказать монотонность функций B1 — 24):
22.у=2*; 23..у=л?; 24.у=х>.
Является ли монотонной функция (если нет, то найти интервалы
монотонности) B5 — 43):
25. jp-^j 26.у=х- М; 27. j-signIgx;
28. у= 3^lxT; 29. ?=1сод arccos x, 30. у=aretg х2;
31. у=^5 — 4*; 32. ^=sinarccosx; 33. >>=tg2x;
34. >» = signx; 35. ^«Igcosr, 36. y=Vctgx;
37. y=arctgr, 38. >^=|^; 39. >^-Ix2 - 3x+2|;
40. >'=Vl-x2; 41. y= [sin *]; 42. >»=24*;
43.^=—^—?
' arcsinx
44. Может ли сумма двух монотонных функций быть немонотонной
функцией? э
45. Всегда ли произведение монотонно возрастающих функций есть
монотонно возрастающая функция?
46. Пусть на отрезке [0; 2] дана функция
у = Х*, еслиО?х< 1,
S, еслих=1,
х+3, если1<х?2.
Представить ее в виде разности двух монотонно возрастающих функ-
функций.
47. Можно ли немонотонную функцию представить в виде разности
двух монотонных функций? <
48. Доказать, что функция у = [х] (дробная часть х) является периоди-
ческой функцией. Найти ее период и построить график этой функции. ]
408 ;
49. Привести пример функции, не являющейся монотонной, периодом
которой является любое рациональное число.
50. Найти период функций y=cos (sinx) и у=Vsinx.
51. Дана периодическая функция с периодом Т= 2л, которая задается
на отрезке [— я; я] следующим образом:
{0, если — п?х?0,
х, если 0<х?я.
Построить ее график.
52. Периодическая функция с периодом Т= 2 определяется на отрезке
[— 1; 1] следующим образом:
{х+ 1, если — 1?х?0,
х, если 0<х<1.
Построить ее график.
53. Периодическая функция с периодом Т= 3 задана следующим обра-
образом: у=2 — х, если 0 <х? 3. Построить ее график.
54. Показать, что любое число Т такое, что 0 < Т< 2к, не является
периодом функции у=sin x.
55. Показать, что число Г=л является наименьшим периодом для
функции y=tgx.
56. Показать, что любое число Т такое, что 0 < Т< к, не является
периодом функции у = ctg x
57. Показать, что число Т= 2к является наименьшим периодом для
функции у=cos х.
58. Доказать, что для любого х справедливо неравенство (sin aj ? |xj.
59. Доказать, что для любого х из интервала I — -г; ? I справедливо
неравенство |tg *j 2 [х|.
В одной и той же системе координат построить график указанных групп
функций и выяснить их взаимное расположение F0 — 65):
60. у = х, у=Х*,у=х3, у=х4, у=х5.
61. ,у=х, >> =
62. ,y=x,>'
64. >»= — х+у, у = cos х
65.,у= — х+|,
Построить график следующей функции F6 — 143):
66. у= Vcosx. 67. y=-Hgx. 68. у=Ф-.
409
69. у=
72. у=
75. у ¦-
%\.у-.
ЪА. у.
87. у=
90. у=
93. у=
96. y-
¦ V2*. 70. у- sin2 х 71. у- ctg2 х
:cos3x 73. ^=lo^x 74. ^
1
: arctg-. 76.
[smx].77.y=[A
[2*1. 79. у= [log2x]. 80. ?= [arcsinxl.
[arctgx]. 82. у* [atccosx]. 83. у» [arcctgx].
signarccosx. 85. у=sign arctgx 86. y= sign cosx
signx2. 88. y= [x2]. 89. y-sign-.
98.
99. j> =
: sign lg x 91. ^
= log2[tg*]. 94.y=logv2[sin
2х, еслих? — 1,
-, если — 1<х<0, 97.у¦¦
х2, еслих^О.
Зя
signx, еслих^—=",
cosx, если—=-
arcctgx, если0<х<1,
log2x, если 1 их.
х2, еслих? — 2,
-=•, если —2<х<0,
яг
Vx, если
log2 х, если 4 < х
[sinx], еслих< —я,
100. у =
tgx, если — я?х?—г-,
ctgx, если—г-<х<0,
sinx. еслиО?х<-?-,
о
sign cosx, если-т-sx
о
:arcsincosx
—, если х ? — 1,
х
если — 1<х? 1,
IX, если 1<х
101. у
102.
103. у -
104. у-
105. у ¦¦
1-х) , еслих? — 2,
cosx, если —2<х<—1,
х2, если —Isx<2,
Vx, если 2 S х
2х, еслих? — 1,
arccosx, если —1<х?0,
arcsinx, еслиО<х?1,
-, если 1 < х
х
arcctgx, еслих^ — 1,
arcsinx, если — 1<х<0,
arccosx, если 0sxl7,
5я
ctgx, еслих^— -J-,
sinx, если——<х?— 1,
2х, если —1<х^0,
I
tagu х, если 0 < х ? j,
4
V5T, если -г<х.
4
[arctgx], еслих^ —^,
cosx, если —5
tgx, —"
106. у-
Зя
sinx, еслия^х^-г-,
Зя
ctgx, если-г-<х
х* + 5|х - 1| + 1. 107. у=|- Зх+ 2| - |2х- 3|.
ПО. у-
114. ^=
116. >-=
118. У-
1 - 1. 115. уж 10гМ.
I я I
119. у ¦ sin2 х — cos2 x
120. ;y=VTsin2x + cos2x. 121. у = arcsintgx
122. v=arccos [-:—1123. y=—sinx.
1 S1Q X I X
124. ;y= cos lgx. 125. ^= 2 sin |2xj.
Trarctg(x—1). 127. ^=^ arccos (x—1) + 1.
= arcsin(x+l)— 1.
130.
132.
¦1-х*
134. ^ « sin 2 arccos x 135. у=| \ |
136. ^=arccos cos x 137. y:
138.
140. ^= 3 + 23cMf. 141. ybarctg ^
142. ^=^4.143. y=aa\.
412
Найти обратные функции и построить их графики для функции с
заданной областью определения A44 — 153):
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
Функция
y=3x-2
у=-(х+\J-2
у=&~Ц
y=-^ZTxT
y=log^x+l)
"d?
y-dnfx+f]
,= ~2 + cos*
y=2tgx
Область определения
(- -; -)
(-~;-D
О;-)
[2;-)
[- 2; 01
(- 1; ->
(—;0J
[-f-z]
[0;я1
L'fi
Глава VII. УРАВНЕНИЯ С ОДНИМ
НЕИЗВЕСТНЫМ
Пусть даны две функции: функция у =fix) с областью
существования Р и функция у = g(x) с областью существо-
существования L. Пусть область Месть пересечение областей суще-
существования этих функций, т.е. М= PnL (в частности, об-
область М может быть пустым множеством).
Пусть стоит задача: найти все числа а из области М, для
каждого из которых справедливо числовое равенство
Да) = g(a). В таких случаях говорят, что стоит задача
решить уравнение fix) = g(x) с одним неизвестным х или что
дано уравнение fix) = g(x) с одним неизвестным х.
В этой главе рассматриваются некоторые способы реше-
решения таких уравнений, поэтому дальше вместо слов «урав-
«уравнение fix) = g(x) с одним неизвестным х* будем говорить
просто «уравнение fix) = g(x)*.
§ 1. Основные определения и утверждения
равносильности уравнений
Областью допустимых значений (ОДЗ) уравнения
fix) = g(x) называется общая часть (пересечение) областей
существования функций у =fix) и у = g(x), т.е. множество'
всех числовых значений неизвестного х, при каждом из
которых имеют смысл (определены) и левая, и правая часта1
уравнения. Всякое число х из ОДЗ уравнения называется
допустимым значением для данного уравнения.
Число а из ОДЗ уравнения называется решением (или
корнем) уравнения fix) = g(x), если при подстановке enr
вместо неизвестного х уравнение превращается в верное1
числовое равенство Да) = g(a).
414
Решить уравнение fix) - g(x) — это значит найти множе-
множество всех его корней. Отметим, что это множество может
оказаться и пустым множеством, что возможно только в
двух случаях: а) если ОДЗ уравнения fix) = g(x) есть пустое
множество; б) если ОДЗ уравнения fix) = g(x) есть непустое
множество М, но ни для одного числа а е М не выполня-
выполняется числовое равенство Да) = g(a). Если множество всех
корней уравнения fix) = g(x) — пустое множество, то обыч-
обычно говорят, что уравнение fix) = g(x) не имеет корней,
поэтому иногда говорят так: решить уравнение fix) = g(x) —
это значит найти все его корни или доказать, что это
уравнение не имеет корней. Если множество всех корней
уравнения fix) = g(x) состоит из к не равных между собой
чисел х,, Хг,..., хк, то говорят, что уравнениеfix) = g(x) имеет
только к корней: хи Xj,..., xk, т.е. множество всех его корней
есть множество {х,, Хг, ..., хк}. Если множество всех корней
уравнения fix) = g(x) состоит из одного числа хи то говорят
еще, что уравнение fix) — g(x) имеет единственный корень хх.
Пусть даны два уравнения: fix) = g(x) и р(х) = <р(х). Если
любой корень первого уравнения является корнем второго
уравнения, то второе уравнение называется следствием
первого.
Отсюда следует, в частности, что если первое уравнение
не имеет корней, то второе уравнение есть его следствие.
Другими словами, все это можно сказать так: если множе-
множество всех корней первого уравнения есть часть (подмноже-
(подмножество) множества всех корней второго уравнения, то второе
уравнение является следствием первого.
Пусть даны два уравнения: Дх) = g(x) p(x) = ф(х). Если
любой корень первого уравнения является корнем второго
уравнения, а любой корень второго уравнения является
корнем первого уравнения, то такие два уравнения назы-
называются равносильными (или эквивалентными). Другими сло-
словами, два уравнения равносильны, если каждое из них
является следствием другого. При этом, в частности, под-
подразумевается, что если каждое из этих уравнений не имеет
корней, то такие два уравнения равносильны. Замена одно-
одного уравнения другим уравнением, ему ^равносильным, на-
зывается равносильным переходом от одного уравнения к
другому.
Пусть даны уравнения Дх) = g(x) p(x) = ф(х) и пусть дано
некоторое множество М значений неизвестного х Если
любой корень первого уравнения принадлежащий множе-
множеству М, является корнем второго .равнения, а любой
корень второго уравнения, принадлежащий множеству М,
является корнем первого уравнения, то такие два уравне-
уравнения называются равносильными на множестве М. При этом,
в частности, подразумевается, что если каждое из этих
уравнений не имеет корней на множестве М, то такие два
уравнения равносильны на множестве М.
Замена одного уравнения другим уравнением, равно-
равносильным ему на множестве М, называется равносильным
переходом на множестве Мог одного уравнения к другому.
Приведем несколько примеров, иллюстрирующих вве-
введенные понятия. Пусть дано уравнение
VI - х = log2 (x - 1).
Область допустимых значений этого уравнения есть пус-
пустое множество. Действительно, область существования
функции у = VI — х есть множество Хх = (— ~; 1], а область
существования функции у = log2 (х — 1) — множество
Хг = A; + «>). Общая часть (пересечение) этих областей —
пустое множество.
В данном примере, после того как найдена ОДЗ уравне-
уравнения, оно уже решено, ибо установлено, что уравнение не
имеет корней.
Пусть дано уравнение
Область допустимых значений этого уравнения есть мно-
множество, состоящее из двух чисел: — 2 и 2. Действительно,
область существования функции у = Vx2 — 4 есть множест-
множество JST, = (— оо, — 2] и [2, + с»), а область существования
функции у = V4 — х2 — множество Х2 = [— 2; 2]. Общая
часть (пересечение) этих областей — множество Х=
416
= Xt n X2 = { — 2; 2). Подстановкой числа (— 2) и числа 2
в данное уравнение убеждаемся, что оба эти числа являют-
являются его корнями. Следовательно, данное уравнение имеет
только два корня х, = — 2 и х2 = 2. Значит, и в этом
примере, после того как найдена ОДЗ уравнения, оно уже
решено.
Приведенные примеры показывают, что при решении
уравнения бывает полезно знать ОДЗ этого уравнения.
Однако можно привести примеры уравнений, для реше-
решения которых не обязательно знать их ОДЗ.
Например, пусть дано уравнение
Vlog2(x+sin2jc) = — 1.
Это уравнение не имеет корней, так как при любом
значении х из ОДЗ уравнения имеем неверное числовое
равенство. В то же время вычисление ОДЗ этого уравнения
было бы непростой задачей.
Два уравнения х + 4 = 0 и (х2 + 1)(х + 4) = 0 равносиль-
равносильны на множестве всех действительных чисел, ибо каждое
из этих уравнений имеет только один корень — число
(- 4).
Рассмотрим два уравнения: ~Jx = 1 и х = 1. Первое урав-
уравнение имеет только один корень — число 1, которое явля-
является и корнем второго уравнения. Поэтому уравнение
х = 1 есть следствие уравнения Vx = 1. Но уравнение х2 = 1
тасеет еще один корень — число (— 1), которое не только
не является корнем уравнения \Gc = 1, но даже не входит в
его ОДЗ. Таким образом, данные уравнения не являются
равносильными на множестве всех действительных чисел.
Но эти уравнения равносильны на ОДЗ первого уравнения
(т.е. на множестве неотрицательных чисел), ибо на этом
множестве каждое из них имеет только один корень —
число 1.
Приведем некоторые утверждения равносильности
уравнений.
1. Уравнения fix) = g(x) и fix) — g(x) = 0 равносильны.
2. Уравнения fix) = g(x) и fix) + a = g(x) + а равносильны
для любого действительного числа а.
14 Алгейра, тригономе-фия
и элементарные функции
3. Уравнения fix) = g(x) и afix) = ag(x) равносильны для
любого действительного отличного от нуля числа а.
4. Уравнения fix) = g(x) ua™ = а** равносильны для любого
фиксированного положительного и не равного единице
числа а.
Доказательства справедливости утверждений сходны
между собой, поэтому докажем, например, утвержде-
утверждение 4.
Пусть число х, является некоторым корнем уравнения
дЛ*> _ ^gM^ т е лусть существуют числа fixx) и g{xx), для
которых справедливо числовое равенство <№ = л*Ч По-
Поскольку фиксированное число а удовлетворяет условиям
а > 0 и а*1, то из справедливости числового равенства
д"*|) = д**1> вытекает справедливость числового равенства
А*\) = g(xi). Следовательно, число х, является корнем урав-
уравнения fix) = g(x). Такое рассуждение можно провести для
любого корня уравнения а™ = а**\ Значит, любой корень
уравнения а™ = а800 является корнем уравнения fix) = g(x).
Покажем теперь обратное. Пусть число х^ является не-
некоторым решением уравнения fix) = g(x), т.е. пусть суще-
существуют числа Дхг) и gfa), для которых справедливо число-
числовое равенство fix^ = gfa). Тогда на основании свойства
числовых равенств для любого фиксированного числа а
такого, что а>0 и аф\, то из справедливо равенство
д«*1> = д^) Следовательно, число Хг является корнем урав-
уравнения 0м = а800. Такое рассуждение можно провести для
любого корня уравнения fix) = g(x). Значит, любой корень
уравнения fix) = g(x) является корнем уравнения сР* = ^
Итак, если каждое из уравнений fix) = g(x) и eF* =
(а > 0, а *¦ 1) имеет корни, то эти уравнения равносильны.
Заметим, что из доказанного вытекает, в частности, что
если одно из этих уравнений не имеет корней, то и другое
не имеет корней, т.е. и в этом случае уравнения fix) = g(x)
и 0м = а*х) (а > 0, а *¦ 1) равносильны. Утверждение 4 тем
самым доказано полностью.
Приведем некоторые утверждения, когда одно урав-
уравнение является следствием другого.
418
5. Пусть п — натуральное число, тогда уравнение [Дх)]л =
= [g(x)]n — следствие уравнения Дх) = g(x).
Доказательство. Согласно утверждению 1 уравнение
[Д*)Г = ШГ
равносильно уравнению
[Д*)Г - ШГ = О,
которое на основании формул сокращенного умножения
равносильно уравнению (см. гл. II)
№0 -
... + Ь<а)Г~'>-<>. A)
Пусть число Xq является некоторым корнем уравнения
fix) = g(x), т.е. пусть существуют числа flxo) и gfo), для
которых справедливо равенство Дхо) = gfo). Но тогда спра-
справедливо и числовое равенство
Следовательно, число Xq является корнем уравнения A),
которое равносильно уравнению [Дх)]л = [g(x)]n, а потому
число Xq является его корнем. Такое рассуждение можно
провести для любого корня первоначального уравнения.
Значит, любой корень уравнения Дх) = g(x), есть корень
уравнения [Дх)]л = [g(x)]n, т.е. в этом случае, действительно,
уравнение [Дх)]л = [g(x)]" есть следствие уравнения
ftx) = g(x). Если же уравнение Дх) = g(x) не имеет корней,
то тогда очевидно, что уравнение [Дх)]" = [g(x)]n есть его
следствие. Утверждение 5 доказано полностью.
6. Уравнение Дх) = g(x) — следствие уравнения ю&Дх) =
= loge g(x), где а > 0 и а ф 1.
Д о к а з а т е л ь с т в о. Пусть число Хо — некоторый корень
уравнения log,,Дх) = log,, g(x), т.е. пусть существуют числа
iogayfo)) и log^Xo), для которых справедливо числовое
равенство loge^Xo) = \ogag(x0). Из равенства логарифмов
14* 419
двух чисел по одному и тому же основанию следует равен-
равенство самих этих чисел, т.е.fixo) = g(*b)» следовательно число
Ло является корнем уравнения Дх) = g(x). Такое рассужде-
рассуждение можно провести для любого корня уравнения loge fix) =
= log,, g(x). Значит, любой корень уравнения log,,fix) =
= log,, i(x) является корнем уравнения fix) = g(x), т.е. в этом
случае, действительно, уравнение fix) = g(x) есть следствие
уравнения log^x) = logag(x). Если же уравнение loggfix) =
= loge g(x) не имеет корней, то тогда очевидно, что уравне-
уравнение fix) = g(x) есть его следствие. Утверждение 6 тем самым
доказано полностью.
Приведем примеры утверждений о равносильности
уравнений на множестве.
7. Пусть п — натуральное число и пусть на некотором
множестве М функции у =fix) и у = g(x) неотрицательны.
Тогда на этом множестве уравнения fix) = g(x) и [Дх)]л =
= [gix)]n равносильны.
Доказательство. Выше уже доказано (см. утвержде-
утверждение 5), что уравнение [Дх)]л = [g(x)]H есть следствие уравне-
уравнения fix)=g(x).
Докажем теперь обратное. Пусть число Xq e Месть неко-
некоторый корень уравнения [Дх)]л = [#(х)Г, т.е. пусть сущест-
существуют неотрицательные числа fixo) и ?fo>), ДЛЯ которых
справедливо числовое равенство
Предположим, что число Хо таково, что одно из чисел yfo)
или g(xo) равно нулю. Тогда из равенства B) следует, что и
другое из этих чисел равно нулю, т.е. в этом случае
fixo) = g(xo). Следовательно, в этом случае число Хо является
корнем уравнения fix) = g(x). Предположим теперь, что
число Хо таково, что одно из чисел fixo) или #(хо) не равно
нулю. Тогда из числового равенства B) следует, что и
другое из этих чисел также не равно нулю, и согласно
условию утверждения 7 оба числа fix^) и gfo) положитель-
положительны. Числовое равенство B) равносильно числовому равен-
равенству
420
-1} = о. C)
Поскольку любая натуральная степень некоторого положи-
положительного числа есть положительное число, произведение и
сумма положительных чисел есть положительное число, то
число {[Яхо)]"-1 + 1Лль)Гgib) + ... + [?(*>)]""'} положи-
положительно, следовательно, числовое равенство C) равносильно
числовому равенству Дхо) — gfo) = О или равенству
fix<>) = Ж*)- Последнее числовое равенство означает, что
число Ло является корнем уравнения Дх) = g(x). Такое рас-
рассуждение можно провести для любого корня, принадлежа-
принадлежащего множеству М, уравнения [Дх)]и = \g(x)]H. Значит,
любой принадлежащий множеству М корень уравнения
[Л*)Г = [#(*)]" является корнем уравненияДх) = g(x), т.е. на
множестве М уравнение Дх) = g(x) есть следствие уравне-
уравнения [Дх)Г = Ш]н.
Если же уравнение [fix)]" = [g(x)]n не имеет корней, то
тогда очевидно, что уравнение Дх) = g(x) есть его следствие
в силу определения.
Итак, доказано, что в условиях утверждения 7 уравнения
fix) = g(x) есть следствие уравнения [Дх)]и = \g(x)]H, чем и
завершается доказательство утверждения 7.
8. Пусть фиксированное число а таково, что а > 0 и а * 1,
и пусть на некотором множестве М функции у=Дх) и
У — s(x) положительны. Тогда на множестве М уравнения
fix) = g(x) и log,, fix) = log,, g(x) равносильны.
Доказательство. Выше уже доказано (см. утвержде-
утверждение 6), что уравнение Дх) = g(x) есть следствие уравнения
1о&, Ах) = 1о&, g(x).
Докажем теперь обратное. Пусть число Хо е М является
некоторым корнем уравнения Дх) = g(x), т.е. пусть Дхо) > О,
gfo) > 0 и Дхо) = gixa). Но тогда равны и логарифмы этих
чисел по одному и тому же основанию, т.е. тогда справед-
справедливо числовое равенство log,, Дхо) = loge gfo). Следователь-
Следовательно, число Хо является корнем уравнения log,, Дх) = log,, g(x).
Такое рассуждение можно провести для любого корня
уравнения Дх) = g(x) из множества М.
421
Итак, любой из множества М корень уравнения fix) =
= g(x) является корнем уравнения logafix) = logag(x), т.е. в
этом случае, действительно, уравнение logafix) = ]ogag(x)
есть следствие уравнения fix) = g(x). Если же уравнение
fix) = g(x) не имеет корней, то тогда очевидно, что уравне-
уравнение log,, fix) = log,, g(x) есть его следствие в силу определе-
определения.
Итак, доказано, что в условиях утверждения 8 уравнение
logafix) = logagix) есть следствие уравнения fix) = g(x), чем
и завершается доказательство утверждения 8.
9. Пусть на некотором множестве М, принадлежащем
ОДЗ уравнения fix) = g(x), функция у = ф(х) определена и при
любом х е М ф(х) Ф 0. Тогда на множестве М уравнения
fix) = g(x) и Дх)ф(х) = ^(х)ф(х) равносильны.
Доказательство. Пусть число хх е Мявляется неко-
некоторым корнем уравнения fix) = g(x), т.е. пусть существуют
числа fixi) и gC*i)> Для которых справедливо числовое
равенство ДхО — ^fa) = 0. Так как по условию существует
число ф(хО и ф(хО * 0, то справедливо и числовое равенство
ф(х1)[Дх1) — gfo)] = 0. которое равносильно числовому ра-
равенству yixijfixt) = ф(х,)#(х,). Последнее числовое равенст-
равенство означает, что число хх является корнем уравнения
Дх)ф(х) = #(х)ф(х). Такое рассуждение можно провести для
любого корня из множества М уравнения fix) = g(x). Зна-
Значит, любой корень из множества М уравнения fix) = g(jc)
является корнем уравнения Дх)ф(х) =#(х)ф(х).
Докажем обратное. Пусть число Хг е Мявляется некото-
некоторым корнем уравнения Дх)ф(х) = ^(х)ф(х), т.е. пусть суще-
существуют числа Дхг), gfcxj) и cpfo), для которых справедливо
числовое равенство Лх2)ф(хг) = ?С*2)ф(*2)> равносильное
числовому равенству ф(х2)[Дх2) — gfa)] = 0. По условию
число ф(х2) * 0, следовательно, последнее числовое равен-
равенство равносильно числовому равенству fix^ — g{x^ =0,
которое равносильно равенству fixj) = gfe). Последнее
числовое равенство означает, что число х^ — корень урав-
уравнения fix) = g(x). Такое рассуждение можно провести для
любого корня из множества М уравнения Дх)ф(х) =
= #(х)ф(х). Значит, любой корень из множества Муравне-
422
ния .Дх)ф(х) = g(x)<p(x) является корнем уравнения
Л*) = g(x). Итак, если каждое из уравнений Дх) = g(x) и
Дх)ф(х) = g(x)<p(x) имеет корни на множестве М, то эти
уравнения равносильны на этом множестве. Заметим, что
из доказанного вытекает, в частности, что если одно из этих
уравнений не имеет корней на множестве М, то и другое
не имеет корней на этом множестве, т.е. и в этом случае
уравнения Дх) = g(x) и .Дх)<р(х) = g(x)<p(x) равносильны на
множестве М. Утверждение 9 тем самым доказано полнос-
полностью.
Пусть дано п уравнений /i(x) = gj(x), /2(x) = &(*), •••
-,fn(x) = &,(*)• Обозначим через Q область, являющуюся
пересечением областей допустимых значений всех этих
уравнений. Если стоит задача найти все числа из области
Q, каждое из которых является корнем хотя бы одного из
этих уравнений, то говорят, что дана совокупность п урав-
уравнений
Л(х) = g,(x), /2(х) = &(х) /и(х) = gn(x) D)
и область Q называется областью допустимых значений
(ОДЗ) этой совокупности.
Отметим, что обычно уравнения совокупности записы-
записываются в строчку. Может оказаться, что в совокупности
уравнений D) содержится бесконечно много уравнений.
Число а из ОДЗ совокупности D) называется решением
(или корнем) этой совокупности, если оно является корнем
хотя бы одного уравнения из совокупности.
Решить совокупность уравнений D) — это значит найти
множество всех его корней. Если это множество оказыва-
оказывается пустым множеством, то говорят, что совокупность
уравнений D) не имеет корней.
Совокупность уравнений D) обычно решают следующим
образом. Сначала решают каждое уравнение на ОДЗ этой
совокупности, т.е. находят множества Ми Мг, ..., Мп, где
М/ — множество всех корней уравнения /foe) = gfec), при-
принадлежащих ОДЗ этой совокупности. Затем находят мно-
множество Мо, являющееся объединением всех этих множеств
Ми Мг, ..., Мн, т.е. М= М,иАГ2и ... и Мп. Это множество
и будет множеством всех корней совокупности уравнений
D). Если множество Мо состоит из к не равных между собой
чисел: Мо — {хи х^ хк}, то говорят, что совокупность
уравнении D) имеет только к корней хи х^ хк.
Говорят, что уравнение
Р(х) = Ф(х) E)
равносильно совокупности уравнений D), если любой ко-
корень уравнения E) является корнем совокупности D), а
любой корень совокупности D) является корнем уравнения
E).
При этом, в частности, подразумевается, что если урав-
уравнение E) не имеет корней и совокупность уравнений D)
не имеет корней, то уравнение E) равносильно совокуп-
совокупности уравнений D). Замена уравнения E) равносильной
ему совокупностью D) называется равносильным переходом
от уравнения E) к совокупности D).
Иногда возникает необходимость совершить равносиль-
равносильный переход от уравнения к совокупности уравнений на
некотором множестве М.
Говорят, что уравнение E) равносильно на множестве М
совокупности уравнений D), если любой корень уравнения
E) принадлежащий множеству М, является корнем сово-
совокупности D), а любой корень совокупности D), принадле-
принадлежащий множеству М, является корнем уравнения E).
Замена уравнения другим уравнением или совокупнос-
совокупностью уравнений будет в дальнейшем называться преобразо-
преобразованием уравнения.
§ 2. Простейшие уравнения
Пусть у=Ах) — основная элементарная функция, Ъ —
некоторое фиксированное действительное число. Тогда
уравнение
принято называть простейшим уравнением.
424
Очевидно, что ОДЗ простейшего уравнения совпадает с
областью существования основной элементарной функции
y=fix). Рассмотрим простейшее уравнение fix) = b на не-
некотором множестве X, принадлежащем ОДЗ, причем в
качестве множества Сбудем брать либо отрезок [хи д^], либо
интервал (хи д^), либо полуинтервалы (хи д^], [хи д^), либо
ЛУЧИ [х,, + оо), (X,, + оо), (— оо, X,), (— оо, X,], ЛИбО ВСЮ
числовую прямую (— оо, + оо). Через У обозначим область
значений функции у =fix), определенной на множестве X.
Пусть основная элементарная функция у =fix) строго мо-
монотонная на множестве X; тогда если b e Y, то уравнение
fix) = b имеет единственный корень на множестве X, а если
Ъ ? Y, то уравнение fix) = b не имеет корней на множестве
X, так как fixo) e Y при любом Xq e X и, следовательно,
Дх<,) ф b при любом Ло е X. В дальнейшем, решая простей-
простейшие уравнения, будем применять это утверждение.
Алгебраическое уравнение. Пусть п — некоторое фикси-
фиксированное натуральное число, тогда уравнение
х" = Ь A)
принято называть простейшим алгебраическим уравнением.
Функция у = Xя определена на всей числовой прямой,
поэтому ОДЗ уравнения A) есть множество Х= (— оо, + <»).
Поскольку свойства функции у =fix), используемые при
решении уравнения A), различны при нечетном и четном
л, то рассмотрим два случая:
1. Пусть п=2т— 1, где т — некоторое фиксированное
натуральное число, тогда уравнение A) принимает вид
^Ь. Aа)
Функция у = х2 ~ ' на всей числовой прямой является
строго возрастающей функцией, и область ее значений Y
также есть вся числовая прямая Y=(— оо, + <»). Поэтому
при каждом b уравнение Aа) имеет единственный корень,
который обозначим через х,. Согласно определению корня
уравнения справедливо числовое равенство xf" = b. Это
числовое равенство равносильно:
425
числовому равенству xl = 2m 'VZT, если b — положитель-
положительное число;
числовому равенству хх = О, если b = 0;
числовому равенству хх = — 2т~1'Щ, если b — отрица-
отрицательное число.
Итак, при каждом b множество всех корней уравнения
Aа) состоит из единственного числа хи другими словами,'
уравнение Aа) имеет единственный корень хь причем хх =
= 2т~ 'V5", если Ь > 0, х, = 0, если b = О, х, = — 2т~ 1Щ, если
Ь<0.
2. Пусть п = 2т, где т — некоторое фиксированное
натуральное число, тогда уравнение A) принимает вид
х2т = Ь. A6)
Разобьем ОДЗ уравнения A6) на два множества: Aj = [0,
+ оо) и Хг = (— оо, 0), и решим уравнение A6) на каждом из
них.
На множестве Хх функция у = х2т является строго возрас-
возрастающей функцией и областью ее значений является луч
Y= [0, + оо). Следовательно, если b — отрицательное
число, то на множестве Хх уравнение A6) не имеет корней,
а если b — неотрицательное число, то на множестве AJ
уравнение A6) имеет единственный корень, который обо-
обозначим через X]. Согласно определению корня уравнения
справедливо числовое равенство х\т = Ь. Это равенство
равносильно:
числовому равенству хх = 0, если b = 0;
числовому равенству хх = ЫлШ, если b — положительное
число.
На множестве Х2 функция у — х^ является строго убы-
убывающей функцией и областью ее значений является луч
Y = @, + оо). Следовательно, если b — отрицательное число
или нуль, то на множестве Хг уравнение A6) не имеет
решений, если b — положительное число, то на множестве
Х2 уравнение A6) имеет единственный корень, который
обозначим через Xj. Так как функция у = лг" на всей ОДЗ
является четной функцией, то Хг = — хь т.е. Хг = — 2NF.
Итак, при каждом отрицательном Ъ уравнение A6) не
имеет корней, при 6 = 0 уравнение A6) имеет единствен-
единственный корень х, = 0, а при каждом положительном Ь множе-
множество всех корней уравнения A6) состоит из двух чисел
2 ь
В табл. 5 приведены итоги решения уравнения A).
Таблица 5
х^-^Ь
х*" = Ь
Ь>0
ь = о
х,=0
х,=0
нет решений
Дробное уравнение. Пусть п — некоторое фиксированное
натуральное число, тогда уравнение
„— л _
B)
= Ь
принято называть простейшим дробным уравнением.
Функция у = х~ " определена на множестве всех отлич-
отличных от нуля действительных чисел, поэтому ОДЗ уравнения
B) есть множество Х= (— «, 0)и@,+ »). Поскольку
свойства функции у = х~ ", используемые при решении
уравнения B), различны при нечетном и четном и, то
рассмотрим два случая:
1. Пусть п = 2т — 1, где т — некоторое фиксированное
натуральное число, тогда уравнение B) принимает вид
Bт - 1) _
Bа)
Разобьем ОДЗ уравнения Bа) на два множества: Хх = (— ~,
0) и Хг = @, + оо), и решим уравнение Bа) на каждом из
них. На множестве Хх функция у =х~2т+' является строго
убывающей функцией и областью ее значений является луч
У, = (— оо, 0). Следовательно, если Ь — неотрицательное
число, то на множестве Хх уравнение Bа) не имеет корней,
а если Ь — отрицательное число, то на множестве Хх
уравнение Bа) имеет единственный корень, который обо-
427
значим через х,. Согласно определению корня уравнения
справедливо числовое равенство xj*1 = *» которое, учи-
учитывая, что b — отрицательное число, равносильно число-
числовому равенству хх = — 2т~ '"Ущ.
На множестве Х2 функция у = х~ 2m+i является строго
убывающей функцией и областью ее значений является луч
Y2 = (О, + «*>). Следовательно, если b — отрицательное
число или нуль, то на множестве Х2 уравнение Bа) не имеет
корней, а если b — положительное число, то на множестве
Хг уравнение Bа) имеет единственный корень, который
обозначим через хх. Поскольку х, — корень уравнения Bа),
то справедливо числовое равенство хГ2*1 = b, которое,
учитывая, что b — положительное число, равносильно чис-
числовому равенству Х\ = 2m~iy^.
Итак, если b = О, то уравнение Bа) не имеет корней, а
при каждом отличном от нуля b уравнение Bа) имеет
единственный корень хи причем хх = — 2т~ WjF, если b < О,
Г
2. Пусть п = 2т, где т — некоторое фиксированное
натуральное число, тогда уравнение B) принимает вид
x~2m = b. B6)
Разобьем ОДЗ уравнения B6) на два множества: Хх =
= (— оо, 0) и Хг = @, + «О, и решим уравнение B6) на
каждом из них.
На множестве Х2 функция у = х~ *" является строго
убывающей функцией и областью ее значений является луч
Y= @, + °о). Следовательно, если b — отрицательное число
или нуль, то на множестве Х2 уравнение B6) не имеет
корней, а если b — положительное число, то на множестве
Х2 уравнение B6) имеет единственный корень, который
обозначим через Xi. Поскольку хх — корень уравнения B6),
то справедливо следующее числовое равенство: хГ2" = А,
428
которое, учитывая, что b — положительное число, равно-
равносильно числовому равенству хх = 2l*V^.
На множестве Хх функция у = х~ *" является строго
возрастающей функцией и областью ее значений является
луч Y= (О, + ею). Следовательно, если b — отрицательное
число или нуль, то на множестве Хх уравнение B6) не имеет
корней, а если b — положительное число, то на множестве
Xi уравнение B6) имеет единственный корень, который
обозначим через х^. Так как функция у = х~ на всей ОДЗ
является четной функцией, то Xi = — хи т.е. хг = — W^.
Итак, при каждом неположительном b уравнение B6) не
имеет корней, при каждом положительном b множество
всех корней уравнения B6) состоит из двух чисел
Hx2 NT.
В табл. 6 приведены итоги решения уравнения B).
Таблица 6
х-Bл,-1) = й
х-2т = Ь
Ь>0
ь=о
нет решений
нет решений
нет решений
Степенные уравнения. Пусть а — некоторое фиксирован-
фиксированное положительное нецелое число, тогда уравнения
x~a = b
C)
D)
принято называть простейшими степенными уравнениями.
Естественной областью определения функции у = ха яв-
является множество всех неотрицательных чисел. Значит
ОДЗ уравнения C) есть множество Х= [0, + «). Функция
у = Xй на множестве А'является строго возрастающей функ-
429
цией, и областью ее значений является луч Y= [О, +~).
Поэтому уравнение C) при каждом отрицательном b не
имеет корней, а при каждом неотрицательном Ъ имеет
единственный корень, который обозначим через хх. Со-
Согласно определению корня уравнения справедливо число-
числовое равенство х\* = Ь. Это числовое равенство равносильно:
числовому равенству хх = 0, если b = 0;
числовому равенству хх = Ы, если b — положительное
число.
Итак, при каждом отрицательном Ъ уравнение C) не
имеет корней, а при каждом неотрицательном Ъ уравнение
C) имеет единственный корень хи причем хх = 0, если
b = 0; хх = Ы, если b > 0.
Естественной областью определения функции у = х~"
является множество всех положительных чисел. Значит
ОДЗ уравнения D) является множество X = @, + «»). Функ-
Функция у = х~ " на множестве X является строго убывающей
функцией и областью ее значений является луч Y=@,
+ оо). Поэтому уравнение D) при каждом неположительном
Ъ не имеет корней, а при каждом положительном b имеет
единственный корень, который обозначим через хх. По-
Поскольку х, — корень уравнения D), то справедливо следую-
следующее числовое равенство х\~ " = Ь, которое равносильно чис- j
I 1
ловому равенству хх = Сj-f.
Итак, при каждом неположительном Ъ уравнение D) не
имеет корней, а при каждом положительном b уравнение
D) имеет единственный корень хх = Сj- p.
В табл. 7 приведены итоги решения уравнений C) и D).
430
Таблица 7
Ь>0
1
*1 = Ьа
-(if
нет решений
нет решений
нет решений
Показательное уравнение. Пусть а — некоторое фикси-
фиксированное положительное и не равное единице число, тогда
уравнение
ах=Ъ
E)
принято называть простейшим показательным уравнением.
Естественной областью определения функции у = а* яв-
является множество всех действительных чисел. Значит ОДЗ
уравнения E) есть множество X = (— «>, + «>). Функция
у = 0х на множестве X является строго монотонной функ-
функцией, и областью ее значений является луч Y= @, + «>).
Следовательно, при каждом неположительном числе Ъ
уравнение E) не имеет корней, а при каждом положитель-
положительном Ъ уравнение (S) имеет единственный корень, который
обозначим через х,. Поскольку х, — корень уравнения E),
то справедливо числовое равенство а*1 = Ь, которое равно-
равносильно числовому равенству хх = 1о&, Ь.
Итак, при каждом неположительном Ь уравнение E) не
имеет корней, а при каждом положительном Ъ единствен-
единственный корень х, = logo Ъ.
В табл. 8 приведены итоги решения уравнения (S).
431
Таблица 8
ax"=b
b>0
x\ = loge b
ft = O
нет решений
b<0
нет решений
Логарифмическое уравнение. Пусть а — некоторое фик-
фиксированное положительное и не равное единице число,
тогда уравнение
logejc= Ъ
F)
принято называть простейшим логарифмическим уравнени-
уравнением.
Естественной областью определения функции у = logex
является множество всех положительных чисел. Значит
ОДЗ уравнения F) есть множество X = @, + «>).
Функция у = loge х на множестве X является строго мо-
монотонной функцией, и областью ее значений является вся
числовая прямая Y= (— «>, + <»).
Поэтому при каждом Ъ уравнение F) имеет единствен-
единственный корень, который обозначим через х,. Поскольку Xi —
корень уравнения F), то справедливо следующее числовое
равенство log,*, = b, которое равносильно числовому ра-
равенству *1 = а. Следовательно, при каждом Ъ уравнение F)
имеет единственный корень хх = аь.
В табл. 9 приведены итоги решения уравнения F).
logex
— b
b>0
Х\ =fl*
b
= 0
= 1
Таблица 9
b<0
Тригонометрические уравнения. Уравнения cosx = b,
sin x = b, tg x = b, ctg x = b принято называть простейшими
тригонометрическими уравнениями.
Сделаем несколько общих замечаний. Пусть надо ре-
решить простейшее уравнение .Дх) = Ь, где у =У(х) — основ-
основная элементарная тригонометрическая функция. Будем го-
говорить, что простейшее уравнение fix) = b имеет главный
432.
период Т, если функция у=/(х) имеет главный период Т.
Очевидно, что если для некоторого простейшего тригоно-
тригонометрического уравнения с главным периодом Т найдено
некоторое решение хь, то любое число хк = хь + кТ при
любом целом к также является решением этого уравнения.
При этом множество всех решений вида хк = Хо + кТ, где к
пробегает все целые числа, называется серией решений этого
уравнения и в дальнейшем будет записываться в виде
хк = Хо + кТ, ке Z.
Чтобы найти множество всех решений данного простейше-
простейшего тригонометрического уравнения fix) = Ь с главным пе-
периодом Т, надо найти все решения этого уравнения на
промежутке длиной в Т, затем для каждого найденного
решения выписать соответствующую серию решений. Если
получается п серий решений простейшего тригонометри-
тригонометрического уравнения .Дх) = Ь, то говорят, что множеством
всех решений уравнения fix) = Ъ является п серий решений
и затем выписывают все эти серии.
При решении простейшего тригонометрического урав-
уравнения промежуток длиной в главный период Т следует
выбирать таким, чтобы он содержал промежуток, на кото-
котором для функции у =Лх) определена обратная тригономет-
тригонометрическая функция, и таким, чтобы все решения уравнения
на этом промежутке можно было легко найти.
Заметим еще, что если простейшее тригонометрическое
уравнение Дх) = Ь на промежутке длиной в главный период
Г не имеет решения, то оно не имеет решений и на всех
числовой прямой.
Пусть дано простейшее тригонометрическое уравнение
cos х = Ь. G)
Естественной областью определения функции у = cos x яв-
является вся числовая прямая. Значит ОДЗ уравнения G) есть
множество Х= (— «>, + «>). Поскольку функция у = cos x на
этом множестве X является периодической функцией с
главным периодом 2л, то найдем сначала все решения
уравнения G) на полуинтервале (— л, л] длиной в главный
433
период. Разобьем этот полуинтервал на два множества:
Хх = (— я; 0) и Х2 = [0, я] и решим уравнение G) на каждом
из них.
На множестве Х2 функция у = cos x является строго убы-
убывающей функцией и областью ее значений является отре-
отрезок Y2 = [— 1; 1]. Следовательно, если число Ь такое, что
\Ь[ > 1, то на множестве Х2 уравнение G) не имеет корней,
а если число Ь такое, что Щ <> 1, то на множестве Хг
уравнение G) имеет единственный корень, который обо-
обозначим через хь- Поскольку хь е [0; я] и число Ъ е [— 1; 1],
то справедлива следующая цепочка равносильных число-
числовых равенств:
cos хь = Ъ о arccos (cos хь) = arccos Ъ *> хь = arccos Ъ.
На множестве Хх функция у = cos x является строго воз-
возрастающей функцией и областью ее значений является
интервал Y=\— 1; 1). Следовательно, если число 6такое,
что Щ>1, то на множестве Хх уравнение G) не имеет
корней, а если число Ъ такое, что Ъ < 1, то на множестве Хх
уравнение G) имеет единственный корень, который обо-
обозначим через Xq. Учитывая, что функция у = cos x на всей
числовой прямой является четной функцией, получаем, что
Хо = — Хо, т.е. Xq = — arccos Ъ.
Итак, на полуинтервале (— я, я] уравнение G) при
каждом Ъ таком, что \Ь\> I, не имеет решений; при Ь = \
имеет единственное решение хь = arccos 1, т.е.хь= 0; при
Ъ = — 1 имеет единственное решение хь = arccos (— 1), т.е.
хь = я; при каждом Ъ таком, что Щ < 1, имеет только два
решения хь = arccos Ъ и хь = — arccos Ь.
Каждое из этих решений дает серию решений уравнения
G) на всей числовой прямой. Значит, множеством всех
решений уравнения G) является:
при каждом Ъ таком, что Щ>\, пустое множество (дру-
(другими словами, при Щ > 1 уравнение G) не имеет решений);
при Ь = 1 — одна серия решений: хк = 2пк, ке Z;
при Ъ = — 1 — одна серия решений: хн = я + 2ял, п е 2,
434
при каждом Ь таком, что Щ<\, две серии решений:
Хщ = arccos Ъ + 2пт, те Z,nxp = — arccos b + 2пр, ре Z.
Заметим, что иногда две серии решений уравнения G)
записываются с помощью одной формулы хя = ± arccos Ъ +
+ 2щ, qe Z.
В табл. 10 приведены итоги решения уравнения G).
Таблица 10
cosx= Ъ
Ь<- 1
нет
решений
Ь = - 1
х„ = Bл+1)я,
Л€ Z
- I < А < I
х„ = arccos Ь +
+ 2лт, те Z
хр = — arccos b +
+ 2пр,ре Z
Ь=1
хк = Ink,
keZ
Ь>1
нет
решений
Пусть дано простейшее тригонометрическое уравнение
sin х = Ъ. (8)
Естественной областью определения функции y = smx
является множество всех действительных чисел. Значит,
ОДЗ уравнения (8) есть множество Х={— «>, + «>). По-
Поскольку функция у = sin х на этом множестве X является
периодической функцией с главным периодом 2л, то най-
найдем сначала все решения уравнения (8) на полуинтервале
— |, -у | длиной в главный период. Разобьем этот полуин-
полуинтервал на два множества: Хх =\ — |, | и Х2 =[ |, у | и
решим уравнение (8) на каждом из них. ^ ^
На множестве Х1 функция y = sinx является строго воз-
возрастающей функцией и областью ее значений является
отрезок У, = [— 1; 1]. Следовательно, если число Ь такое,
что |А| > 1, то на множестве Хх уравнение (8) не имеет
корней, а если число Ъ такое, что |6| й 1, то на множестве
Хх уравнение (8) имеет единственное решение, которое
обозначим через хь. Поскольку хь е — |, |, и число Ъ е
е [— 1; 1], то справедлива следующая цепочка равносиль-
равносильных числовых равенств:
35
sin До = b <» arcsin (sin х<>) = arcsin b о Xq = arcsin b.
На множестве Х2 функция у = sin x является строго убы-
убывающей функцией и областью ее значений является интер-
интервал Y2 = (— 1; 1). Следовательно, если число Ъ таково, что
\Ь\ > 1, то на множестве Х2 уравнение (8) не имеет корней,
а если число Ъ таково, что Ъ е (— 1; 1), то на множестве Х2
уравнение G) имеет единственное решение, которое обо-
обозначим через Xq. Учитывая, что функция у = sin x на всей
числовой прямой является функцией симметричной отно-
относительно вертикальной прямой, проходящей через точку
[ |, ОI получаем, что Хо = п — До, т.е. Хо = п — arcsin Ь. Итак,
на полуинтервале — |, -у ] уравнение (8):
при каждом Ъ таком, что Щ > 1, не имеет решений;
при Ъ = Г имеет единственное решение Хо = arcsin 1, т.е.
при Ь = — 1 имеет единственное решение Хо = arcsin(— 1),
т.е. ль = - f;
при каждом Ъ таком, что Щ < 1, имеет только два реше-
решения Хо = arcsin Ьи Хо = п — arcsin Ь. Каждое из этих реше-
решений дает серию решений уравнения (8) на всей числовой
прямой. Значит, множеством всех решений уравнения (8)
является:
при каждом Ъ таком, что Щ > 1, — пустое множество
(другими словами, при Щ > 1 уравнение (8) не имеет реше-
решений);
при Ь = 1 — одна серия решений: хк = Ц + Ink, ke Z;
при Ь = — 1 — одна серия решений: хн = — Ц + 2т,
п g Z;
при каждом Ъ таком, что Щ < 1 — две серии решений:
Хр = arcsinЬ + 2пр,ре Zh х„ = п — arcsinb + 2пт, те Z
Заметим, что иногда две серии решений уравнения (8)
записываются с помощью одной формулы: xq = (— 1)*х
х arcsin b + nq, q e Z.
436
В табл. 11 приведены итоги решения уравнения (8).
Таблица 11
sinx = ft
b<- 1
нет
решений
Ь = - 1
*-§¦
+ 2пп,
ле Z
- КЬ< 1
хр = arcsin ft +
+ 2*p,peZ
хт = я — arcsin й +
+ 2дая, m € Z
** =
= § + 2**,
fceZ
Ь>1
нет
решений
Пусть дано простейшее тригонометрическое уравнение
tgx=b. (9)
Естественной областью определения функции y = tgx
является множество всех действительных чисел, кроме
чисел | + пк, где к — любое целое число. Значит, ОДЗ
уравнения (9) есть множество X, состоящее из всех дейст-
действительных чисел, не равных | + пк, где к — целое число.
Поскольку функция у = tg х на этом множестве X является
периодической функцией с главным периодом я, то найдем
сначала все решения уравнения (9) на интервале [ — §> f I
длиной в главный период. На интервале [ — |, 11 функция
у = tg х является строго возрастающей функцией и облас-
областью ее значений является вся числовая прямая Y =(—«>,
+ ео). Следовательно, при каждом Ь уравнение (9) на ин-
интервале \ — \> f (имеет единственное решение, которое обо-
обозначим через х\. Так как ль — решение уравнения (9) и
ц g | — |, | \ то справедлива следующая цепочка равно-
равносильных числовых равенств:
tg Xq = Ъ *> arctg (tg ль) = arctg Ъ *> ль = arctg Ъ.
437
Итак, при каждом Ъ уравнение (9) на интервале
| ~ ?»? | имеет единственное решение хь = arctg Ъ. Это ре-
решение дает серию решений уравнения (9) на всей ОДЗ.
Значит, при каждом Ь множеством всех решений урав-
уравнения (9) является серия решений х, = arctg Ь + пп, пе Z.
В табл. 12 приведены итоги решения уравнения (9).
Таблица 12
tgx = b
-~<Ь<о.
х„ = arctg b + itn, л е Z
Пусть дано простейшее тригонометрическое уравнение
ctgx=b. A0)
Функция y = ctgx определена на всей числовой оси,
кроме точек х = пк, где к — любое целое число. Значит,
ОДЗ уравнения A0) есть множество X, состоящее из всех
действительных, не равных кк чисел, где к — любое целое
число. Поскольку функция y = ctgx на этом множестве X
является периодической функцией с главным периодом я,
то найдем сначала все решения уравнения A0) на интер-
интервале @, я), длиной в главный период. Функция у = ctg x на
интервале @, л) является строго убывающей функцией и
областью ее значений является вся числовая прямая Y=
= (— оо, + оо). Следовательно, при каждом Ь уравнение A0)
на интервале @, л) имеет единственное решение, которое
обозначим через Xq. Так как хь — решение уравнения A0)
и Хо е @, л), то справедлива следующая цепочка равносиль-
равносильных числовых равенств:
ctg Хо = Ъ о arcctg (ctg Xq) = arcctg b *> хь = arcctg b.
Итак, при каждом Ъ уравнение A0) на интервале @, к)
имеет единственное решение хь = arcctg Ь. Это решение
дает серию решений уравнения A0) на всей ОДЗ.
438
Значит, при каждом b множеством всех решений урав-
уравнения A0) является серия решений х9 = arcctg b + np,p e Z
В табл. 13 приведены итоги решения уравнения A0).
Таблица 13
ctgx- b
-*о<Ь<-
Хр = arcctg b + np,pe Z
Рассмотрим еще простейшие уравнения, содержащие
основные обратные тригонометрические функции, т.е. урав-
уравнения arccos х = b, arcsin x = b, arctg x = b, arcctg x = b.
Пусть дано простейшее уравнение
arccos х = b. A1)
Естественной областью определения функции у = arccos
хявляется отрезок Х= [— 1; 1]. Значит, ОДЗ уравнения A1)
есть множество Х= [— 1; 1]. Функция у = arccos x на мно-
множестве X является строго убывающей функцией, и облас-
областью ее значений является отрезок Y= [0, я]. Следовательно,
для каждого b такого, что b < 0 или Ъ > я, уравнение A1)
не имеет корней; если же число Ъ таково, что 0 й b й я, то
уравнение A1) имеет единственный корень, который обо-
обозначим через Xq. Поскольку Хо — корень уравнения A1),
Хо е [— 1; 1] и b e [0; я], то справедлива цепочка равно-
равносильных числовых равенств:
arccos Хо = b о cos (arccos хь) = cos b о Xq = cos b.
Итак, при каждом Ь таком, что 0<b<n уравнение A1)
имеет единственный корень хь = cos b, а при каждом Ъ
таком, что Ъ < 0 и Ъ > я, уравнение A1) не имеет корней.
В табл. 14 приведены итоги решения уравнения A1).
Таблица 14
arccos x = b
b<0
нет
решений
ft = 0
x, = l
0<ft<n
x\ = cos b
b = *
x, 1
b>%
нет
решений
Пусть дано простейшее уравнение
arcsin х = b.
A2)
Естественной областью определения функции у =
= arcsin х является отрезок [— 1; 1]. Значит, ОДЗ уравнения
A2) есть множество Х= [— 1; 1]. Функция у = arcsinx на
множестве X является строго возрастающей функцией, и
областью ее значений является отрезок Y= — ^, ^ . Сле-
Следовательно, для каждого b такого, что b < — | или b > |,
уравнение A2) не имеет решений; если же число b таково,
что — |<6^|, то уравнение A2) имеет единственный
корень, который обозначим через хи Поскольку Xi — ко-
корень уравнения A2), Xi е [— 1; 1] и b е | — |, 11 то спра-
справедлива цепочка равносильных числовых равенств:
arcsin Xi = b о sin (arcsin xx) = sin 6 о Xi = sin 6.
Итак, при каждом b таком, что — у й b й ^, уравнение
A2) имеет единственный корень xt = sin b, а при каждом 6
таком, что 6<— |и6>|, уравнение A2) не имеет корней.
В табл. 15 приведены итоги решения уравнения A2).
440
Таблица 15
arcsinx = i
»<-f
нет
решений
*-f
X, 1
-2<b<2
x{ = sin ft
* 2
x, = l
*»!
нет
решений
Пусть дано простейшее уравнение
arctg х = b.
A3)
Естественной областью определения функции у = arctg х
является множество всех действительных чисел. Значит,
ОДЗ уравнения A3) есть множество Х= (— ее, + ее), функ-
функция у = arctg х на этом множестве X является строго воз-
возрастающей функцией, и областью ее значений является
интервал Y= (— |, |j
Следовательно, для каждого b такого, что b й — | или
Ь>^, уравнение A3) не имеет решений; если же число b
таково, что — | < b < |, то уравнение A3) имеет единствен-
единственный корень, который обозначим через xt. Поскольку х, —
корень уравнения A3), х, е (— ее, + ее) и b е (— |, 11 то
справедлива цепочка равносильных числовых равенств:
arctg х, = b о tg (arctg x,) = tg b о х, = tg b.
Итак, при каждом b таком, что — | < b < | уравнение A3)
имеет единственный корень х{ = tg b, а при каждом b таком,
чю Ьй — |иб2:|, уравнение A3) не имеет корней.
В табл. 16 приведены итоги решения уравнения A3).
441
Таблица 16
arctgx = b
нет решений
я г иг я
~2<*<2
Xj=tgft
нет решений
Пусть дано простейшее уравнение
arcctg х = b.
A4)
Естественной областью определения функции у~
= arcctg х является множество всех действительных чисел.
Значит, ОДЗ уравнения A4) есть множество Х= (— ее, + <»).
Функция у = arcctg jc на этом множестве X является строго
убывающей функцией, и областью ее значений является
интервал Y= (О, я). Следовательно, для каждого b такого,
что b < О или b > n, уравнение A4) не имеет решений; если
же число b таково, что 0 < b < п, то уравнение A4) имеет
единственный корень, который обозначим через xt. По-
Поскольку X, — корень уравнения A4), хх е (— ее, + во) и b e
е @, я), то справедлива следующая цепочка равносильных
числовых равенств:
arcctg xi = b о ctg (arcctg xi) = ctg b о хх = ctg b.
Итак, при каждом b таком, что 0 < b < n, уравнение A4)
имеет единственный корень хх = ctg b, а при каждом b
таком, что b s 0 и b > n, уравнение A4) не имеет корней.
В табл. 17 приведены итоги решения уравнения A4).
Таблица 17
arcctg х = b
bzO
нет решений
0<b<n
xj = ctg b
Ь*к
нет решений
§ 3. Равносильные преобразования уравнений
В этом и следующем параграфах обсуждаются некоторые
преобразования уравнений, с помощью которых данное, не
442-
являющееся простейшим, уравнение может быть сведено к
одному или совокупности простейших уравнений.
Решая уравнение, не являющееся простейшим, обычно
приходится проводить довольно много преобразований.
При этом каждый раз уравнение заменяется на какое-либо
новое, а у нового уравнения, естественно, могут быть и
другие корни. Данное уравнение будет решено верно, если,
проводя преобразование уравнений, каждый раз уравнение
заменять новым уравнением, имеющим все корни
предыдущего и только их, т.е. чтобы не произошло потери
или приобретения корней. Если каждый раз заменять урав-
уравнение на ему равносильное уравнение, то корни последне-
последнего уравнения и будут корнями исходного.
В этом параграфе рассматриваются только равносильные
преобразования уравнений. Неравносильные преобразова-
преобразования уравнений будут рассмотрены в следующем параграфе.
Как уже отмечалось в § 1, утверждения 1—4 дают только
примеры равносильных преобразований. Приведем еще
несколько примеров равносильных преобразований
уравнений.
Преобразования, связанные с применением тождественных
равенств. Пусть дано уравнение
Ax)=g(x) A)
и пусть для любого действительного х справедливо тожде-
тождественное равенство g(x) — ф(х), тогда уравнение A) равно-
равносильно уравнению
А*) = Ф(х). B)
Это утверждение позволяет использовать различные
тождественные равенства, т.е. формулы, справедливые при
всех действительных значениях для проведения равносиль-
равносильных преобразований уравнений. Примерами таких тожде-
тождественных равенств являются формулы сокращенного ум-
умножения многочленов, основное тригонометрическое тож-
тождество и некоторые другие формулы. Отметим, что, прово-
проводя равносильное преобразование уравнений с помощью
формул сокращенного умножения многочленов, в гл. III
443
были решены квадратные и некоторые другие алгебраичес-
алгебраические уравнения. Приведем еще примеры, в которых прово-
проводятся равносильные преобразования уравнений при помо-
помощи тождественных равенств.
Пусть дано уравнение
cos3 2х = 1 — 2cos2 х. C)
Используя основное тригонометрическое тождество и фор-
формулу косинуса двойного угла, можно написать тождествен-
тождественное равенство
1 — 2cos2 х = — cos 2x,
справедливое для любого действительного х. Значит, урав-
уравнение C) равносильно уравнению
cos3 2х = — cos 2x.
Применяя утверждение 1 § 1 и делая группировку членов
левой части последнего уравнения, получим, что уравнение
C) равносильно уравнению
cos 2x (cos2 2х + 1) = 0.
Последнее уравнение равносильно совокупности двух про-
простейших тригонометрических уравнений:
cos2x=0, cos22x+l=0.
Множеством всех решений первого уравнения этой со-
совокупности является серия решений хк = ^ + -=-, к е Z, а
второе уравнение этой совокупности решений не имеет.
Следовательно, множество всех решений уравнения C)
состоит из серии хк = ^ + -^, к е Z
Рассмотрим теперь уравнение
a sin х + b cos x = с. D)
В случае, когда либо а = 0, либо Ь = 0, это уравнение при
помощи утверждений 2 и 3 § 1 сводится:
444
если а = О, b ф О, к простейшему уравнению cos x = |;
если а * 0, 6 = 0, к простейшему уравнению sin x = -.
Пусть теперь а ф О и 6 ф 0. Значит, <? + Ь2ф0. Применяя
утверждение 3, получаем, что уравнение D) равносильно
уравнению
1. Пусть а — положительное число. Рассмотрим два
случая: b > 0 и b < 0.
Пусть b > 0. Построим прямоугольный треугольник с
катетами длиной а и Ь. Угол, лежащий против катета
длиной Ь, обозначим ф,. Тогда имеем числовые равенства
а +Ь
из которых следует, что ф, = arcsin . / ;. = arccos
У +Ь
Теперь уравнение E) примет вид
cos ф! sin х + sin ф! cos x =
. / и-.
уа +Ь
По формуле синуса суммы двух углов имеем тождествен-
тождественное равенство
cos ф! sin х + sin ф! cos x = sin (x + Фх).
Применяя теперь сформулированное выше утверждение,
получаем, что уравнение D) равносильно уравнению
которое является простейшим уравнением.
Пусть b < 0. Построим прямоугольный треугольник с
катетами а и Щ. Угол, лежащий против катета длиной \Ь\,
обозначим ф2. Тогда имеем числовые равенства
445
из которых следует, что аь = arcsin >.: ¦ .. — ai^u» , ¦ ¦>
\о+Ь ча+Ь
Теперь, так как Ь = — Щ, то уравнение E) примет вид
cosф2sinх — sinф2cosх = цс д.
По формуле синуса разности двух углов имеем тождест-
тождественное равенство
cos фз sin 3f— sin Ф2 cos x = sin (x — ф2).
Применяя теперь сформулированное выше утверждение,
получаем, что уравнение D) равносильно уравнению
_ с
sin (x — ф2) =
которое является простейшим уравнением.
Если обозначить ф = arctg -, то легко видеть, что ф = ер,
для 6>0иф = - фз для Ь < 0. Поэтому можно написать,
что при а > 0 уравнение D) равносильно уравнению
которое тоже является простейшим уравнением.
2. Случай а < 0 сводится к рассмотренному выше умно-
умножением обеих частей уравнения D) на (— 1).
Пример. Решить уравнение
cos х + VTsin x + 1 = 0. F)
Поскольку уравнение F) таково, что а = VT, Ь=\,
л/а2+ Ь2 = 2, то оно равносильно уравнению
л/Т . 1 1
-у Sin X + ^ COS X = — ^.
44$
Найдем угол (р: ф = arctg i = ^. Значит, уравнение F)
равносильно уравнению
Решая это простейшее уравнение, получаем две серии
решений:
хк = — j + 2пк, ке Z и хт = п + 2пт, те Z.
Следовательно, множеством всех решений уравнения F)
являются две серии решений:
хк = — -| + 2я?, ке Z, и хт = я + 2я/и, те Z.
Преобразования, связанные с суперпозициями функций.
Пусть функция у =Лх) есть сложная функция у = P[g(x)],
являющаяся суперпозицией двух функций: внутренней
и = g(x) — основной элементарной функции, и внешней
у = Р(и), где Р(и) — квадратный трехчлен Р(и) = аи2 +
+ Ьи + с. В таких случаях уравнение Дх) = 0 записывают в
виде
a[g(x)]2 + bg(x) + c = 0. G)
и называют квадратным уравнением относительно g(x).
Уравнение G) решается следующим образом. Сначала
решают квадратное уравнение
a? + bt+c = 0. (8)
Находят дискриминант D = b2 — Лас уравнения (8). Если
D< 0, то уравнение (8) не имеет решений, следовательно,
и уравнение G) не имеет решений. Если D = 0, то уравне-
уравнение (8) имеет единственный корень: число [ — jA Следо-
Следовательно, в этом случае уравнение G) равносильно уравне-
уравнению
447
«to = - Та (9)
Затем решают уравнение (9). В силу равносильности урав-
уравнений G) и (9) множество всех решений уравнения (9)
является множеством всех решений уравнения G).
Если D > О, то уравнение (8) имеет только два действи-
действительных корня, которые обозначим /, и t2. Следовательно,
в этом случае уравнение G) равносильно совокупности
уравнений
&x) = tu g(x) = t2. A0)
Затем решают совокупность уравнений A0). В силу рав-
равносильности уравнения G) и совокупности уравнений A0)
множество всех решений совокупности уравнений A0)
является множеством всех решений уравнения G).
Отметим, что в гл. III этим способом решались трехчлен-
трехчленные уравнения, которые можно назвать квадратными урав-
уравнениями относительно х", где п — натуральное число и
ntl.
Приведем примеры.
Пусть дано уравнение
4х- 3- 2х + 2 = 0.A1)
Так как справедливо тождественное равенство 4х = BхJ, то
уравнение A1) равносильно уравнению
BхJ - 3 • 2х + 2 = 0.
Это уравнение есть квадратное уравнение относительно 2х.
Решая квадратное уравнение
получим, что оно имеет только два корня tx = 2, t2 = 1.
Следовательно, уравнение A1) равносильно совокупности
двух уравнений:
2х = 2, 2х =1.
448
Решая каждое простейшее показательное уравнение этой
совокупности, получаем, что эта совокупность имеет толь-
только два корня: хх = 1 и Хг = 0.
Следовательно, уравнение A1) имеет только два корня:
X] = 1 и х2 = 0.
Не всегда данное уравнение удается сразу преобразовать
к виду G). Часто для этого надо проделать дополнительные
равносильные преобразования.
Например, для решения уравнения
sin 2х — 12 (sin х — cos jc) + 12 = 0 A2)
в качестве g(x) можно взять (sin x — cos x). Чтобы предста-
представить уравнение A2) в виде G), воспользуемся тригономет-
тригонометрическими формулами
sin 2х = 2 cos xsin x, 1 = sin2 x + cos2 x,
затем тождественным равенством
sin2 х — 2sin xcos x + cos2 x = (sin x — cos xJ.
Получим, что уравнение A2) равносильно уравнению
— (sin х — cos jcJ — 12 (sin x — cos jc) + 13 = 0. A3)
Уравнение A3) является квадратным уравнением отно-
относительно (sin x — cos x). Решая квадратное уравнение
-Г1- Ш+13 = 0,
получаем, что оно имеет только два корня: tx = 1 и t2 =
= - 13.
Следовательно, уравнение A3) равносильно совокупнос-
совокупности уравнений
sinx— cosx= I, sin x — cos x = — 13. A4)
Воспользовавшись тождеством sinx — cosx = V2~x
xsin \x— -I получим, что совокупность уравнений A4)
равносильна совокупности простейших уравнений
15 Алгебра, тригонометрия 449
и элементарные функции
(.5)
Множеством всех решений первого уравнения совокупнос-
совокупности A5) являются две серии решении:
хк = 5 + 2пк, ке Z и х„=п + 2пт, те Z.
Второе уравнение совокупности A5) не имеет решений, так
Следовательно, множеством всех решений уравнения
A2) являются две серии решений:
хк = ^ + 2пк, ке Z и хт = п + 2пт, те Z.
Пусть функция у=Лх) есть сложная функция, являю-
являющаяся суперпозицией нескольких основных элементарных
функций. Пусть, например, функция у =fi,x) есть суперпо-
суперпозиция трех основных элементарных функций у = ?{<р[и(х)]}.
В таких случаях уравнение Дх) = 0 записывают в виде
8{ф(х)]} = 0 A6)
и решают следующим образом.
Сначала решают простейшее уравнение
АН = 0. A7)
Уравнение A7) может не иметь решений, тогда уравнение ¦
A6) не имеет решений. 1
Уравнение A7) может иметь конечное или бесконечное \
число корней. Пусть множество всех корней уравнения A7) J
состоит из чисел tu t2, Ц, ..., tn, ... . Тогда уравнение A6) j
равносильно совокупности уравнение 1
Ф(х)] = tx, ф(х)] = t2, ф(х)] = /3, ... • *
...„ ф(х)] = tn, ... . A8)
Теперь решают совокупность простейших уравнений
45ft
<P(V) = /„ ф) = h, q>(v) = t3 q>(v) = tH A9)
Совокупность уравнений A9) может не иметь решений,
тогда совокупность уравнений A8) не имеет решений, а
следовательно, и уравнение A6) не имеет решений.
Совокупность уравнений A9) может иметь конечное или
бесконечное число корней.
Пусть множество всех корней совокупности A9) состоит
из чисел vb v2, v3 vk, .... Тогда совокупность уравнений
A8) равносильна совокупности уравнений
и(х) = v,, и(х) = v2, и(х) = v3 и(х) = v*, ... . B0)
Множество всех корней совокупности простейших урав-
уравнений B0) является множеством всех корней уравне-
уравнения A6).
Рассмотрим, например, уравнение
2^=1. B1)
Решая простейшее уравнение 2'= 1, получаем его единст-
единственное решение tt = 0. Значит, уравнение B1) равносильно
уравнению
0. B2)
Решая простейшее уравнение
sin v = 0,
получаем, что множество всех решений является серия
решений vA = пк, к<= Z.
Значит, уравнение B1) равносильно бесконечной сово-
совокупности уравнений
<х = Ы, B3)
где к — любое целое число.
Каждое уравнение совокупности B3), в котором к —
отрицательно, не имеет корней, а каждое уравнение, в
котором к — неотрицательно, имеет единственный корень
хк = (якJ.
Следовательно, множество всех корней уравнения B1)
есть множество {(пкJ \ к е Zq).
§ 4. Неравносильные преобразования уравнений
В предыдущем параграфе рассматривались лишь равно-
равносильные преобразования уравнений. Однако не любое
уравнение удается решить при помощи лишь равносильных
преобразований, гораздо чаще при решении уравнений
приходится применять неравносильные преобразования. При
этом надо помнить, что из — за неравносильности преоб-
преобразований, вообще говоря, можно потерять некоторые
корни исходного уравнения или приобрести так называе-
называемые «посторонние корни» (всякий корень последующего
уравнения, не являющийся корнем исходного уравнения,
будем называть посторонним корнем).
Ниже приводятся примеры неравносильных преобра-
преобразований, приводящих как к потере корней исходного урав-
уравнения, так и к приобретению посторонних корней.
Преобразования, связанные с логарифмическими формула-
формулами. Пусть фиксированное число а таково, что а > 0 а* 1.
Рассмотрим следующие логарифмические формулы:
Ах) = а"*Л A)
log. Щ]7 = 2 \оёаЛх), B)
2 C)
log, [АхШ] = \ogaAx) + logo g(x), D)
log. WxfcCx)] = logo [~Ax)]+ logo [- g(x)], E)
, F)
log, gU log, [- Ax)] - logo [- g(x)]. G)
¦w
Если при решении уравнения ф(х) = h(x) формально при-
применить к левой или правой части этого уравнения любую
из рассматриваемых формул так, что левая часть этой
формулы будет заменена правой часть, то возможна потеря
4S2
корней исходного уравнения, поэтому такие преобразования
недопустимы.
Если к левой или правой части уравнения ср(х) = h(x)
формально применить любую из рассматриваемых формул
так, что правая часть формулы будет заменена левой, то
корни уравнения ф(х) = h(x) теряться не будут; любой ко-
корень уравнения ф(х) = h(x) будет корнем последующего
уравнения, но, вообще говоря, не всякий корень последую-
последующего уравнения будет являться корнем исходного уравнения,
и поэтому, если такие преобразования применялись, то в
конце решения обязательно необходима проверка, т.е. не-
необходимо каждый из найденных корней последней сово-
совокупности простейших уравнений или последнего простей-
простейшего уравнения подставить в исходное уравнение и убе-
убедиться, какие из них обращают исходное уравнение в
верное числовое равенство. Те из них, при каждом из
которых исходное уравнение превращается в неверное чис-
числовое равенство, нужно отбросить.
Ниже приводятся примеры, показывающие, что фор-
формальное применение этих формул приводит как к потере
корней исходного уравнения, так и к приобретению посто-
посторонних корней.
Пусть дано уравнение
log2(x+2J = 6.
Формально применяя формулу B), получим уравнение
log2(x+2) = 3,
которое имеет единственный корень хх = 6.
Поскольку в процессе решения исходного уравнения
проводилось такое преобразование, в результате которого
могли потеряться корни, то нельзя считать, что исходное
уравнение решено. И, действительно, корень исходного
уравнения — число (— 10) — был потерян при этом пре-
преобразовании.
Пусть дано уравнение
2-4x+3)_
_ п
453
Формально применяя формулу A), получаем уравнение
х2 — 4х+3=х— 3,
которое имеет только два корня: xt = 2 и Xj = 3.
Поскольку в процессе • решения исходного уравнения
было проведено преобразование, в результате которого
можно было приобрести посторонние корни, то необходи-
необходима проверка. Проверка показывает, что ни число 2, ни
число 3 не являются корнями исходного уравнения.
Следовательно, исходное уравнение не имеет корней.
Эти примеры показывают, что при решении уравнений
применять логарифмические формулы надо очень внима-
внимательно, помня о том, что формальное их применение может
привести и к потере и к приобретению посторонних кор-
корней.
Этого не может случиться, если применять каждую из
формул A) — G) на том множестве Mi из ОДЗ решаемого
уравнения, на котором имеет смысл правая часть соответ-
соответствующей формулы. Тогда такое преобразование приведет
к уравнению, равносильному исходному на множестве М{.
Найдя корни полученного уравнения и отобрав из них
те, которые принадлежат множеству Ми найдем все корни
исходного уравнения на этом множестве Мх.
При этом надо помнить, что таким образом исходное
уравнение решено не на всей ОДЗ, а только на множестве
Мх. Поэтому надо найти еще его решения на той части ОДЗ,
которая останется после выделения множества Мх.
Следовательно, если в процессе решения уравнения воз-
возникает необходимость провести преобразования с помо-
помощью некоторой логарифмической формулы, то такое урав-
уравнение можно решать по следующей схеме:
1. Найти ОДЗ уравнения.
2. Разбить ОДЗ на два множества: Мх и М2 (Mt — вся та
часть ОДЗ, где одновременно имеют смысл обе части
используемой формулы, М2 — та часть ОДЗ, которая оста-
остается после выделения множества Мх).
1*54
3. Решить уравнение на множестве Мх (учитывая, что
преобразование уравнения с помощью этой формулы есть
равносильное преобразование на множестве Мх).
4. Решить уравнение на М2.
5. Объединить множества корней, найденные на М{ и М2.
Решим по этой схеме рассмотренные выше уравнения.
Пусть дано уравнение
log2 (x + 2J = 6.
ОДЗ этого уравнения есть множество всех действитель-
действительных чисел, кроме х = — 2. Разобьем ОДЗ на два множества:
Мх = (- 2, + ~) и М2 = (- оо, - 2).
На множестве Мх справедливо тождественное равенство
log2 (х + 2J = 2 log 2 (х + 2).
Значит, на множестве Мх исходное уравнение равносильно
уравнению
log2(x+2) = 3,
которое равносильно на множестве Мх уравнению х + 2 =
= 8. Последнее уравнение имеет единственный корень
хх = 6. Так как этот корень входит в множество Л/,, то и
исходное уравнение на множестве Мх имеет единственный
корень хг = 6.
На множестве М2 справедливо тождественное равенство
log2(x+2J = 21og2[-(*+2)].
Значит, на множестве М2 исходное уравнение равносиль-
равносильно уравнению
1о&(-*-2) = 3,
которое в свою очередь равносильно на множестве М2
уравнению
- х - 2 = 8.
Последнее уравнение имеет единственный корень х^=
= — 10. Так как этот корень принадлежит множеству Щ
то и исходное уравнение на множестве М2 имеет единст-
единственный корень Xj = — 10. Объединяя множество корней,
найденное на Мх и Мъ получаем, что множество всех
корней исходного уравнения состоит из двух чисел: х, = 6
и ъ = — 10.
Пусть дано уравнение 31о*з(х ~4х+3) = х — 3.
ОДЗ этого уравнения есть множество всех тех х, для
каждого из которых х2 — 4х + 3 > 0, т.е. ОДЗ есть множе-
множество М= (— о°, 1) и C, + оо). Поскольку на этом множестве
справедливо тождественное равенство
то исходное уравнение равносильно на множестве М урав-
уравнению
х2 — 4х + 3 = х — 3,
которое имеет только два корня: х1 = 2их2 = 3.
Так как ни один из этих корней не входит в ОДЗ
исходного уравнения, а последнее и исходное уравнения
равносильны на ОДЗ исходного, то отсюда вытекает, что
исходное уравнение не имеет корней.
Итак, решить уравнения с помощью некоторой логариф-
логарифмической формулы можно двумя способами.
Первый способ. Совершить переход к уравнению,
которое является следствием данного уравнения. Найти все
корни полученного уравнения. Сделать проверку и устано-
установить, какие корни являются посторонними. Тогда все
найденные корни без всех посторонних корней составят
множество всех корней исходного уравнения.
Второй способ. Совершить равносильный переход
на множестве М, (М, — вся часть ОДЗ исходного уравне-
уравнения, где логарифмическая формула есть тождественное
равенство). Найти все корни полученного уравнения на Мх.
Затем найти все корни исходного уравнения на множестве
Мг (всей оставшейся части ОДЗ исходного уравнения после
4S6
выделения множества Мх). Наконец, объединить множест-
множества всех корней данного уравнения, найденные на Мх и Мъ
и тем самым получить множество всех корней исходного
уравнения.
Преобразования, связанные с тригонометрическими фор-
формулами. Рассмотрим следующие тригонометрические фор-
формулы:
^ (8)
f, (9)
l + tg х
1tg2x A0)
Если при решении уравнения ф(х) = h(x) формально при-
применить к левой или правой части этого уравнения любую
из рассматриваемых формул так, что левая часть этой
формулы будет заменена правой частью, то возможна потеря
корней исходного уравнения, поэтому такие преобразования
недопустимы.
Если к левой или правой части уравнения ф(х) = h(x)
формально применить любую из рассматриваемых формул
так, что правая часть формулы будет заменена левой, то
можно приобрести посторонние корни, а поэтому в конце
решения необходима проверка.
Приведем примеры, показывающие, что формальное
применение этих формул при решении уравнения может
приводить как к потере корней исходного уравнения, так
и к приобретению посторонних корней.
Пусть дано уравнение
sin 2х — 3 cos 2х = 3.
Формально применяя формулы (9) и A0), получим урав-
уравнение
,457
3(l-tg2x)_3
l+tg2x
Перепишем это уравнение в виде
2(tgs-3)_n
1+tg X
Отсюда очевидно, что множеством всех корней этого урав-
уравнения будет серия решений хр = arctg 3 + пр, р е Z
Однако нельзя утверждать, что найдены все корни ис-
исходного уравнения, ибо преобразования были такими, что
корни могли быть потеряны. Действительно, при этих
преобразованиях была потеряна целая серия решений
х„ = ~ + пт, те Z.
Пусть дано уравнение
tgx+l
Поскольку 1 = tg т. то уравнение можно переписать так:
1 + tgXtgj
Формально применяя формулу A1), получаем уравнение
откуда очевидно, что множеством всех корней этого урав-
уравнения будет серия решений х, = ^ + я/, / е Z
Поскольку преобразование было таким, при котором
могли появиться посторонние корни, то необходима про-
проверка. Проверка показывает, что ни один из этих корней
не будет корнем исходного уравнения.
Следовательно, исходное уравнение не имеет корней.
т
Эти примеры показывают, что при решении уравнений
применять тригонометрические формулы надо вниматель-
внимательно, помня о том, что формальное их применение может
привести и к потере и к приобретению корней.
Этого не может случиться, если применять каждую из
формул (8) — A1) на том множестве М{ из ОДЗ решаемого
уравнения, на котором имеет смысл правая часть соответ-
соответствующей формулы. Тогда такое преобразование приведет
к уравнению, равносильному исходному на множестве Мх.
Найдя корни полученного уравнения и отобрав из них
те, которые принадлежат множеству Ми найдем все корни
исходного уравнения на этом множестве Мх. При этом надо
помнить, что таким образом исходное уравнение решено
не на всей ОДЗ, а только на множестве Мх. Поэтому надо
найти еще его решение на той части ОДЗ, которая остается
после выделения множества Мх.
Поэтому уравнения, при решении которых применимы
эти тригонометрические формулы, часто решаются по той
же схеме, которая приведена при рассмотрении логариф-
логарифмических формул:
1. Найти ОДЗ уравнения.
2. Разбить ОДЗ на две части М{ и М2 (М{ — вся та часть
ОДЗ, где одновременно имеют смысл обе части используе-
используемой формулы, М2 — та часть ОДЗ, которая остается после
выделения множества Мх).
3. Решить уравнение на Mt (учитывая, что преобразование
уравнения с помощью этой формулы есть равносильное
преобразование на множестве М{).
4. Решить уравнение на М2.
5. Объединить множества корней, найденные на Mi и М2.
Решим по этой схеме рассмотренные выше уравнения.
Пусть дано уравнение
sin 2х — 3 cos 2х = 3.
ОДЗ этого уравнения есть множество всех действительных
чисел. Разобьем ОДЗ данного уравнения на два множества:
Mi — множество всех действительных чисел, кроме чисел
4SSL
хк = ^ + пк, где к — любое целое число, М2 — множество
чисел хк = j + пк, где к — любое целое число.
На множестве М{ формулы (9) и A0) являются тождест-
тождественными равенствами, поэтому на множестве Л/, исходное
уравнение равносильно уравнению
3(l-tg2s)_3
1+tg2*
Множеством всех корней последнего уравнения является
серия решений хт = arctg3 + я/я, те Z. Каждый корень
этой серии принадлежит множеству Ми поэтому множест-
множеством всех корней исходного уравнения на множестве Л/,
является серия хт = arctg3 + я/я, те Z.
Решим исходное уравнение на М2. Подставляя каждое
число хк = | + пк, к е Z, в исходное уравнение, убеждаемся,
что оно обращается в верное числовое равенство.
Следовательно, множеством всех корней исходного
уравнения на' множестве М2 является серия хЛ = | + яЛ,
ке Z
Объединяя множества корней, найденные на Л/{ и Мъ
получаем, что множеством всех корней исходного уравне-
уравнения являются две серии: хт = arctg 3 + я/я, /я е Z, и хк = ^ +
+ пк, ке Z.
Пусть дано уравнение
tgx+l
ОДЗ этого уравнения есть множество всех действитель-
действительных чисел, кроме чисел хт = — | + я/я, где /я — любое
целое число, и кроме чисел X/ = ^ + я/, где / — любое целое
число. Так как на ОДЗ формула (И) есть тождественное
469
равенство, то на ОДЗ исходное уравнение равносильно
уравнению
Множеством всех корней последнего уравнения на ОДЗ
является серия Хр = ^ + кр, где р — любое целое число.
Очевидно, что эта серия не входит в ОДЗ исходного урав-
уравнения.
Следовательно, исходное уравнение не имеет решений.
Итак, решить уравнения с помощью некоторой тригоно-
тригонометрической формулы можно двумя способами.
Первый способ. Совершить переход к уравнению,
которое является следствием данного уравнения. Найти все
корни полученного уравнения, сделать проверку и устано-
установить, какие корни являются посторонними. Тогда все
найденные корни без всех посторонних корней составят
множество всех корней исходного уравнения.
Второй способ. Совершить равносильный переход
на множестве Мх (М, — вся часть ОДЗ исходного уравне-
уравнения, где тригонометрическая формула есть тождественное
равенство). Найти все корни полученного уравнения на Мх.
Затем найти все корни исходного уравнения на множестве
Мг (всей оставшейся части ОДЗ данного уравнения после
выделения множества Мх). Наконец, объединить множест-
множества всех корней данного уравнения, найденные на Л/, и М2,
и тем самым получить множество всех корней исходного
уравнения.
Преобразования, связанные с возведением в натуральную
степень. Пусть п — фиксированное натуральное число и
пусть п > 2. Пусть дано уравнение
Ах) = g(x)
Замена этого уравнения уравнением
называется возведением уравнения в натуральную степень п.
461
Как следует из утверждения 5 § 1, при возведении в
натуральную степень уравнения нельзя потерять корни, а
можно лишь приобрести посторонние кони. Поэтому, если
применять такое преобразование, то в конце необходима
проверка найденных корней.
Приведем пример, показывающий, что применение
этого преобразования действительно может привести к
приобретению посторонних корней.
Пусть дано уравнение
2 cos х = 3 sin x — 2.
Возведя в квадрат это уравнение и используя основное
тригонометрическое тождество, получим уравнение
4A — sin2x) = 9sin2x— 12sinx + 4,
которое равносильно совокупности двух уравнений:
sin х = 0, sin х = Ц.
Множеством всех корней первого уравнения этой совокуп-
совокупности являются две серии: хт = 2пт, те Zn x9 = n + 2nq,
де Z. Множеством всех корней второго уравнения также
являются две серии: х,, = arcsin-Ц + 2кр, ре Z, и хк = к —
arcsin || + 2nk, ke Z Поскольку в процессе решения ис-
исходного уравнения проводилось возведение уравнения в
квадрат, то возможно, что среди найденных корней есть
посторонние корни, следовательно, необходима проверка.
Проверка показывает, что каждый корень серии х„ = 2юп,
те Z, является посторонним корнем, а каждый корень
серии х9 = п + 2nq, qeZ, — есть корень исходного уравне-
уравнения.
Кроме того, проверка показывает, что каждый корень
серии хк = к — arcsin Щ + 2пк, ke Z, является посторонним
19
корнем, а каждый корень серии хр = arcsin-rz + 2пр, ре Z,
есть корень исходного уравнения.
462
Поэтому множеством всех корней исходного уравнения
являются две серии: дс, - к + 2кд, де Z, и дс, = arcsin -j| +
+ 2кр, ре Z.
Заметим еще, что часто, провода возведение уравнения
в натуральную степень, используют следующую формулу
("ШУ =Лх).
Ясно, что если при решении уравнения заменить
наДдс), то можно приобрести посторонние корни, и поэто-
поэтому в конце решения необходима проверка.
Приведем пример такого преобразования уравнения.
Пусть дано уравнение
Возводя это уравнение в квадрат и заменяя (Vj^ + x— 5J
на (х2 + х — 5), а (V* — 1 J на (х — 1), получаем уравнение
х* + х— 5 = х— 1.
Множество всех корней последнего уравнения состоит из
двух чисел: дс, = 2 и х2 = — 2. Поскольку в процессе реше-
решения исходного уравнения проводилось возведение уравне-
уравнения в квадрат и проводилась замена С^Дх))" наДдс), то могла
появиться посторонние корни, поэтому необходима про-
проверка. Проверка показывает, что корень Хг = — 2 не явля-
является корнем исходного уравнения, а корень дс, = 2 является
корнем исходного уравнения.
Следовательно, исходное уравнение имеет единствен-
единственный корень дс, = 2.
Заметим, что обычно замена (и^Ддс))и на Ддс) при возведе-
возведении уравнения в натуральную степень п не оговаривается.
Вместо этого способа решения можно предложить и
другой, основанный на применении утверждения 7 § 1.
При этом способе уравнение можно решать по следую-
следующей схеме:
1. Найти ОДЗ уравнения.
463
2. Разбить ОДЗ на два множества Мх и М2 (М, — вся та
часть ОДЗ, где одновременно обе части уравнения либо;
неотрицательны, либо неположительны, М2 — вся та часть
ОДЗ, на которой правая и левая части уравнения имеют
разные знаки).
Тогда очевидно, что на М2 уравнение не имеет корней,
следовательно, множество всех корней исходного уравне-
уравнения содержится вМ|.
3. Решить уравнение на множестве М{. Множество всех
корней, найденное на Мь будет множеством всех корней
исходного уравнения (здесь учитывается то, что возведение
в натуральную степень исходного уравнения приводит к
равносильному ему на множестве Мх уравнению).
Решим по этой схеме уравнение
V2x+29 = 3-x.
ОДЗ этого уравнения есть множество Х= Г— у, + «Л
Разобьем ОДЗ на два множества Мх = Г— у, 3*1 и М2 = C,
+ оо). На множестве М2 исходное уравнение не имеет кор-
корней, ибо для каждого х е М2, левая часть уравнения поло-
положительна, а правая — отрицательна. Решим уравнение на
множестве Мх. Так как на этом множестве обе части
исходного уравнения неотрицательны, то после возведения
в квадрат исходного уравнения получим равносильное ему
уравнение
2х + 29 = C - хJ.
Множеством всех корней последнего уравнения являют-
являются два числа Xi = — 2 и Xj = 10. Так как число хь = 10 не
принадлежит множеству Мь то оно не является корнем
исходного уравнения.
Так как число х, = — 2 принадлежит множеству Ми то
оно является корнем исходного уравнения.
Следовательно, исходное уравнение имеет единствен-
единственный корень Xi = — 2.
464
Итак, решить уравнение, возводя его в натуральную
степень, можно двумя способами:
Первый способ. Совершить переход к уравнению,
которое является следствием исходного уравнения. Найти
все корни полученного уравнения. Сделать проверку и
установить, какие корни являются посторонними. Из мно-
множества всех найденных корней те корни, которые не явля-
являются посторонними, и составят множество всех корней
уравнения.
Второй способ. Совершить равносильный переход
на множестве Мх (Мх — вся та часть ОДЗ исходного урав-
уравнения, где обе части исходного уравнения одновременно
или неотрицательны, или одновременно неположительны).
Найти все корни полученного уравнения на Ми Все эти
корни и составляют множество всех корней исходного
уравнения.
Преобразования, связанные с освобождением от знамена-
знаменателя. Пусть дано уравнение
Замена этого уравнения на уравнение
Ах) = g(x)y(x)
называется освобождением уравнения от знаменателя.
Ясно, что при таком преобразовании уравнения возмож-
возможно появление посторонних корней. Поэтому, если в про-
процессе решения некоторого уравнения проводилось осво-
освобождение уравнения от знаменателя, то необходима про-
проверка всех найденных корней.
Приведем пример применения этого преобразования.
Пусть дано уравнение
2(х-7) _ j
j^-fce-7
Освобождаясь от знаменателя, получим уравнение
2х - 14 = х2 - 6х - 7.
46Г
Множество всех корней последнего уравнения состоит
из двух чисел: хх = 1 и хь = 7.
Так как в процессе решения исходного уравнения про-
проводилось преобразование, в результате которого могли
появиться посторонние корни, то необходима проверка.
Проверка показывает, что число д^ = 7 не является корнем
исходного уравнения, а число хх = 1 есть корень исходного
уравнения. Итак, уравнение имеет единственный корень
Х\ ~ 1.
Заметим, что согласно утверждению 9 § 1 уравнение
равносильно на своей ОДЗ уравнению
Ах) = g(xMx).
Поэтому решать такие уравнения можно по следующей
схеме:
1. Найти ОДЗ уравнения «& = ф(дс).
2. Решить на ОДЗ данного уравнения равносильное ему
уравнение fix) = g(x)y(x).
Поскольку уравнения «^ = ф(дс) и fix) = g(x)y(x) равно-
сильны на ОДЗ первого уравнения, то все корни уравнения
Л*) ~ ?(*)ф(*)> входящие в ОДЗ первого уравнения, соста-
составят множество всех корней уравнения ^| = ф(дс). .
Решим по этой схеме уравнение '
sin4x— 1 _ 1 x.:i
cos x
ОДЗ этого уравнения есть множество М — множество
всех действительных чисел, кроме чисел хт = ^ + я/и, где
т — любое целое число. На множестве М исходное урав-
уравнение равносильно уравнению
466
sin4 x — 1 = cos4 x.
Поскольку на множестве всех действительных чисел
справедливы следующие тождественные равенства:
cos4 х — sin4 x = (cos2 x + sin2 x)(cos2 x — sin2 x),
cos2 x + sin2 x = 1, cos2 x — sin2 x ?= cos 2x,
то на множестве всех действительных чисел справедливо и
тождественное равенство
cos4 х — sin4 x = cos 2x.
Поэтому исходное уравнение равносильно на множестве М
уравнению
cos 2х = — 1.
Множество всех решений последнего уравнения есть серия
хк = ^ + пк, ке Z Так как эта серия не принадлежит мно-
множеству М, то уравнение не имеет корней.
Итак, решить уравнение, освобождаясь от знаменателя,
можно двумя способами:
Первый способ. Совершить переход к уравнению,
которое является следствием исходного уравнения. Найти
все корни полученного уравнения, сделать проверку и
установить, какие корни являются посторонними. Из мно-
множества всех найденных корней те корни, которые не явля-
являются посторонними, и составят множество всех корней
уравнения.
Второй способ. Совершить равносильный переход
на ОДЗ исходного уравнения. Найти все корни полученно-
полученного уравнения. Все эти найденные корни составят множе-
множество всех корней исходного уравнения.
Преобразования, связанные с потенцированием уравнения.
Пусть а — любое фиксированное положительное и нерав-
неравное единице число. Пусть дано уравнение
Замена этого уравнения уравнением
А*) = g(x)
называется потенцированием уравнения.
Как следует из утверждения 6 § 1, при потенцировании
уравнения потерять корни нельзя, а можно лишь приобрести
посторонние. Поэтому, если при решении уравнения при-
пришлось его потенцировать, то в конце решения необходима
проверка.
Решим таким способом уравнение
1о& (х2 - А) = 1о& (Ах - 7).
Потенцируя данное уравнение, получим уравнение
х2 _ 4 = Ах - 7.
Множество всех корней последнего уравнения состоит
их двух чисел хг = 3 и Xi = 1.
Поскольку в процессе решения исходного уравнения
применялось потенцирование уравнения, то могли по-
появиться посторонние корни, поэтому необходима провер-
проверка. Проверка показывает, что число Xi = 1 не является
корнем исходного уравнения, а число хг = 3 есть корень
исходного уравнения. Поэтому, исходное уравнение имеет
единственный корень хх = 3.
Заметим, что согласно утверждению 8 § 1 уравнение
равносильно на своей ОДЗ уравнению
Ах) = g(x).
Поэтому уравнение logo Ax) - logo g(x) можно решить по
следующей схеме:
1. Найти ОДЗ уравнения Хо&Ах) = 1о&, g(x).
2. Решить на ОДЗ этого уравнения равносильное ему
уравнение Ах) = g(x).
468
Все корни последнего уравнения и будут составлять
множество всех корней уравнения logaj(x} - '^ g(x).
Решим по этой схеме рассмотренный выг :е пример.
Пусть дано уравнение
log2 (х2 - 4) = log2 Dx - 7}
ОДЗ этого уравнения есть множество М— B,+<»). На
множестве М данное уравнение равносильно уравнению
х2 - 4 = Ах - 7.
Множество всех решений последнего уравнения состоит
из двух чисел: хх = 3 и Хг=\. Поскольку число д^ = 1 не
принадлежит множеству М, а число х, = 3 принадлежит
множеству М, то последнее уравнение на множестве М
имеет только один корень хх = 3. Так как последнее и
исходное уравнения равносильны на множестве М, то
отсюда вытекает, что исходное уравнение имеет единствен-
единственный корень хх = 3.
Итак, решить уравнение, применяя потенцирование
уравнения, можно двумя способами.
Первый способ. Совершить переход г уравнению,
которое является следствием исходного уравнегшя. Найти
все корни полученного уравнения, сделать пгюверку и
установить, какие корни являются посторонними. Из мно-
множества всех найденных корней те корни, которые не явля-
являются посторонними, и составляют множество вогх корней
уравнения.
Второй способ. Совершить равносильный переход
на ОДЗ исходного уравнения, найти все корни полученного
уравнения на ОДЗ исходного уравнения Все эти найден-
найденные корни составляют множество всех корр^-й исходного
уравнения.
Преобразование, связанное с логарифмЕ^г-ж^гг.: уравне-
уравнения. Пусть а — фиксированное положительное и неравное
единице число. Пусть дано уравнение
Ах) = *Сх).
Замена этого уравнения на уравнение
469
называется логарифмированием уравнения.
Как следует из утверждения б § 1, при логарифмирова-
логарифмировании уравнения возможна потеря корней. Поэтому формаль-
формальное применение этого преобразования запрещается.
Заметим, что логарифмировать уравнение Дх) = g(x)
можно только на множестве М— всей той части ОДЗ, где
обе части этого уравнения положительны. При этом, как
следует из утверждения б § 1, на множестве М уравнения
А*) = g(x) и 1о&,Дх) = logag(x) равносильны.
Поэтому решить уравнение fix) = g(x), применяя лога-
логарифмирование уравнения, можно только по следующей
схеме:
1. Найти ОДЗ данного уравнения.
2. Разбить ОДЗ на два множества: Мх и М2 (Mi — вся та
часть ОДЗ, на которой обе части данного уравнения поло-
положительны, М2 — вся та часть ОДЗ, которая остается после
выделения множества A/j).
3. Решить уравнение на Мх (учитывая, что на A/j уравне-
уравнение fix) = g(x) равносильно уравнению 1о&,Дх) = log,^(x)).
4. Решить уравнение на М2.
5. Объединить множества всех корней, найденные на Мх и
М2.
Решим по этой схеме уравнение
ОДЗ этого уравнения есть множество М = [0, + ~). По-
Поскольку на множестве М обе части данного уравнения
положительны, то данное уравнение равносильно на мно-
множестве М уравнению
х2-х=1-(<хJ.
Полученное уравнение в свою очередь на множестве М
равносильно уравнению
470
Последнее уравнение имеет только два корня: хх = 1 и
Xi = — 1. Корень х, = 1 принадлежит множеству М, а
корень %i = — 1 не принадлежит множеству М. Следова-
Следовательно, последнее уравнение имеет на множестве М един-
единственный корень х, = 1. Так как исходное уравнение рав-
равносильно последнему уравнению на множестве М — всей
ОДЗ исходного уравнения, то исходное уравнение имеет
единственный корень х, = 1.
Преобразования, связанные с сокращением уравнения на
общий множитель. Пусть дано уравнение
<р(х)Д*) = Шх).
Часто это уравнение заменяют уравнением
Ax)=g(x),
т.е. сокращают исходное уравнение на общий множитель
ф(х). Это грубая ошибка, которая может привести как к
потере корней исходного уравнения, так и к приобретению
посторонних корней.
Рассмотрим пример. Пусть дано уравнение
Сокращая это уравнение на общий множитель Vx —2,
приходим к уравнению
х2 + 3 = 4х.
Множество всех корней последнего уравнения состоит
из двух чисел: хх = 1 и Хг = 3.
Однако легко видеть, что число х, = 1 не является корнем
исходного уравнения, т.е. это число является посторонним
корнем для исходного уравнения. В то же время легко
видеть, что число х3 = 2 является корнем исходного урав-
уравнения и этот корень был потерян при проведенном преоб-
преобразовании.
Значит, действительно, при сокращении уравнения на
общий множитель <р(х) можно и потерять корни исходного
уравнения, и приобрести посторонние корни.
471
Подобные уравнения надо решать только следующим
образом.
1. Найти ОДЗ уравнения у(х)Дх) = y(x)g(x).
2. Записать равносильное ему уравнение ф(х)[Дх) — g(x)] =
= 0.
3. Перейти от этого уравнения к равносильной ему на ОДЗ
исходного уравнения совокупности уравнений
<р(х) = 0, Ax)-g(x) = 0.
4. Решить эту совокупность уравнений на ОДЗ исходного
уравнения. Тогда множество всех тех корней этой совокуп-
совокупности, каждый из которых принадлежит ОДЗ исходного
уравнения, и составят множество всех корней исходного
уравнения.
Решим этим способом уравнение
=7 (х2 + 3) = 4х^1х~=2.
ОДЗ этого уравнения — множество М = [2, + «*»). Запи-
шем равносильное исходному уравнение
Это уравнение на множестве М равносильно совокупности
уравнений
Первое уравнение этой совокупности имеет единственный,<
корень хх = 2. Второе уравнение имеет только два корня:
Xi = 3, *j = 1. Значит, множество всех корней этой сово-
совокупности уравнений состоит из трех чисел: хх — 2, Хх = 3,5
х3 = 1. Корни Xi и *2 входят в множество М, а корень х3 не
входит в множество М.
Следовательно, исходное уравнение имеет только два
корня: хх =¦ 2, Xi - 3. j<
Преобразования, связанные с освобождением от знай;
абсолютной величины. Пусть дано уравнение 1
472
Шх)\ + Шх)\+ ... +Ux)\-\fm+x(x)\-...
~.-Шх)\ = 8(х), A2)
me/i(x),/2(x) f^x) — многочлены относительно х. Для
решения таких уравнений обычно необходимо избавиться
от знаков абсолютных величин. Отметим, что формальное
освобождение от знаков абсолютных величин может привес-
привести как к потере корней исходного уравнения, так и к
приобретению посторонних корней. Покажем это.
Пусть дано уравнение
Если формально освободиться от знака абсолютной вели-
величины, то получим уравнение
х - 1 = 2х - 4,
которое имеет единственный корень х, = — 5. Однако легко
видеть, что этот корень не является корнем исходного
уравнения, т.е. является для исходного уравнения посто-
посторонним корнем.
В то же время легко видеть, что число *2 = — 1 является
корнем исходного уравнения и этот корень был потерян
при проведенном преобразовании. Значит, действительно,
при формальном освобождении от знаков абсолютной ве-
величины возможно и потерять корни, исходного уравнения
и приобрести посторонние корни.
Для решения таких уравнений наиболее часто употреб-
употребляется так называемый метод интервалов. Суть этого ме-
метода состоит в следующем.
Пусть дано уравнение A2). Сначала решается совокуп-
совокупность уравнений
Л(х) = 0, Л(х) = 0 /т(х) = 0 Л(х) = 0, A3)
затем на числовой прямой отмечаются все корни этой
совокупности уравнений.
Таким образом, вся числовая прямая разбивается на
некоторое число промежутков, затем на каждом таком
41$
промежутке уравнение заменяется на другое уравнение, не
содержащее знаков абсолютной величины и равносильное
исходному уравнению на этом промежутке. На каждом
таком промежутке отыскиваются корни того уравнения,
которое на этом промежутке получается, и затем отбира-
отбираются их них те, которые попадают в данный промежуток.
Они и будут корнями исходного уравнения на рассматри-
рассматриваемом промежутке. Наконец, для того чтобы выписать все
корни исходного уравнения, собирают вместе (объединя-
(объединяют) все его корни, найденные на всех промежутках.
Продемонстрируем этот метод на нескольких примерах.
Пусть дано уравнение
|х-1| = 2х + 4. A4)
В этом случае совокупность уравнений A3) состоит из
одного уравнения
х - 1 = О,
имеющего единственный корень — число 1. Значит, чис-
числовая прямая разбивается на два промежутка: (— ~, 1) и [1,
+ ов).
Рассмотрим решение уравнения A4) на каждом из этих
промежутков.
1. На промежутке (— ~, 1) по определению абсолютной
величины
Поэтому на этом промежутке уравнение A4) равносильно
уравнению
имеющему единственный корень х{ = — 1. Этот корень
попадает в промежуток (— ~, 1). Значит, на этом проме-
промежутке уравнение A4) имеет единственный корень х{ = — 1.
2. На промежутке [1, + ~) по определению абсолютной
величины
\x- l\=x- 1.
Поэтому на этом промежутке уравнение A4) равносильно
уравнению
х- 1 = 2х+4,
имеющему единственный корень Хг = — 5. Этот корень не
попадает в промежуток [1, + ~). Значит, на этом промеж-
промежутке уравнение A4) не имеет корней.
Подводя итог, получаем, что исходное уравнение A4)
имеет единственный корень х, = — 1.
Пусть дано уравнение
1|-Н + |2х+3| = 4х-6. A5)
Рассмотрим совокупность уравнений
**-1=0, х=0, 2х+3 = 0.
Множество всех корней этой совокупности уравнений
состоит из четырех чисел: 1; — 1; 0; — |. Значит, числовая
прямая разбивается на пять промежутков: [ — <»; — | J,
[- §; — А [— 1; 0), [0; 1), [1; + со).
Рассмотрим решение уравнения A5) на каждом из этих
промежутков.
1. На промежутке [— <»; — 11 по определению абсолют-
абсолютной величины
|я>- 1|- (х? - 1), М = -х, |2х+3| = -Bх+3).
Поэтому на этом промежутке уравнение A5) равносиль-
равносильно уравнению
(х2 - 1) - (- х) - Bх + 3) = 4х - 6,
которое имеет только два корня:
475
Ни один из этих корней не входит в рассматриваемый
промежуток, поэтому уравнение A5) не имеет корней на
этом промежутке.
2. На промежутке Г—|; — 1 ] по определению абсолют-
абсолютной величины
l\ = tf-l), [х| = -*, \2х + 3| = Bх + 3).
Поэтому на этом промежутке уравнение A5) равносильно
уравнению
(х2 - 1) - (- х) + Bх + 3) = Ах - 6.
Это квадратное уравнение не имеет действительных кор-
корней. Значит, уравнение A5) не имеет корней на этом
промежутке.
3. На промежутке [— 1; 0) по определению абсолютной
величины
|^-lj = -(^-l), H = -*, |2х+3| = Bх + 3).
Поэтому на этом промежутке уравнение A5) равносильно
уравнению
- (х2 - 1) - (- х) + Bх + 3) = Ах - 6,
которое имеет только два корня:
v _
^Л»2
Ни один из этих корней не входит в рассматриваемый
промежуток, поэтому уравнение A5) не имеет корней на
этом промежутке.
4. На промежутке [0; 1) по определению абсолютной
величины
|х2-1| = -(х2-1), Н = *, |2х+3| = 2х+3.
Поэтому на этом промежутке уравнение A5) равносиль-j
но уравнению
476
- (x2 - 1) - x + Bx + 3) = Ax - 6,
которое имеет только два корня: л* = — 5, д% = 2. Ни один
из этих корней не входит в рассматриваемый промежуток,
поэтому уравнение A5) не имеет корней на этом промеж-
промежутке.
5. На промежутке [1; + «») по определению абсолютной
величины
Поэтому на этом промежутке уравнение A5) равносильно
уравнению
(х2 - 1) - х + Bх + 3) = Ах - 6.
Это квадратное уравнение не имеет действительных кор-
корней, поэтому уравнение A5) не имеет корней на этом
промежутке.
Подводя итог, получаем, что уравнение A5) не имеет
корней на всей числовой прямой.
В заключении отметим, что в этом параграфе рассмот-
рассмотрены не все возможные преобразования, а лишь наиболее
часто употребляемые. Конечно, можно привести примеры
и других неравносильных преобразований, как, например,
уничтожение подобных членов, переход к новому основа-
основанию логарифмов, содержащему неизвестную величину. Не
будем останавливаться на этом подробно, а сформулируем
лишь общее правило.
При решении уравнений надо пользоваться одним их
двух следующих способов:
1. Замена данного уравнения на уравнение, равносиль-
равносильное ему на некотором множестве; при этом явно указыва-
указывается и само множество и то, что уравнения равносильны
именно на этом множестве (в этом случае надо рассмотреть
все множества, на которое разбивается ОДЗ).
2. Замена данного уравнения на уравнение, являющееся
его следствием; при этом указывается, почему новое урав-
уравнение есть следствие предыдущего, и в конце решения
обязательно делается проверка.
477
УПРАЖНЕНИЯ
Является ли число 2 корнем следующего уравнения A — 15):
Щ]
Зх-4 (8х-11)(х+1) Fх-1)Bх-3)
3 4 " 12
3. 4л? + 5х- 2УЗх*-5х+2"=хA5 - 2х);
4. V14+ 25х - VIT47= VSxTT;
7. 3**+' + 9 = 28 • 3х. 8. 27* + З1 +х+З1 ~х+27=ЦШ,
9. (V2-V3)* + (V2T^5)X = 4;
10. (>/4 — V15)* =
|| iog2f=i;
14. sin2 - + cos — — 2 sin2? cos - = ^;
re j д i 8 re 2
15. 2arccos | =arccosC-х)?
Равносильно ли уравнение х=2и следующее уравнение (К — 30):
16. 3{10-2[Зх- 2 (х - 5)] + 7х|=Зх-4;
17.
18. (х2 — 5х- 7) - (х- 2) (х- 3) = 1;
+ J U
[ J
20.15X-X2-6| = х2- 5х+6. 21. Vx2-6x+9=(x-3J;
22. 2х+2 = 15 + 22-х.23.2х + 5х-1=5х
24. S2"-' + 5Х+' = 250. 25. 3х W- 36;
27. Iog4 B log3 [1 + log2 A + 3 log2 xjj = 1;
28. lg 2 + lg D*- 2 + 9)= 1 - lg (Г'2 + l
29. log2 (9х"' + 7J= 2 + Iog4 CX- * +1J;
см («0-1
Равносильны ли следующие два уравнения C1 — 66):
31. х + 1 = 0 и (х + 1) (х+ 4) = 0;
32. (х — 1) = 0 и (¦?"+1) (х — 1) = 0;
33. х2 = 2 -хи -^— = ^=^-;
34.х+4 = 0и , х+4— = 0;
х2-2х+9
35. х — 4 = 8 — хих — 4 +
х —6
—х+
¦?:
х —6
36. 2х —6
З7.х(х+4)=х+4и ?7.=
logJl-x2) ^
38. (х - 3) = 2х+ 1 и (х — 3) Vx+T= Bx+ 1)
39.x2-2 = 0 их4-4 = 0;
40. х2 - 4х + 3 = 0 и 4*.+ 3 = 0;
х— 1
41. х2 + 3 = 4х и Гх2 + 3Vx — 1) = 4х (х — 1);
43.
45.
х2 + 3 = 3х2;
х2-
46.
-10 и х-5 = -10;
^ = - 14 и х - 5 = - 14;
х+5
х2-2
-—^
х+5
47. (х+3)(х— 1) = 2(х— 1)их+3 = 2;
48. (х+2)(х— 1) = 3(х— 1)их+2 = 3;
49. х2 - 2х= 8 и Гх2 - 2x12^=8 • 2^;
50. Bх-3) = Зх- 2 и Bх- ЗJ = (Зх- 2J;
52. Ух+1 Ух+2=0и УA+х)(х+2Т=0;
53. -^c+TVx —3= -Жи V(x+2)(x —3)=
54. х2 -7 = 3log3faHx2 - 7 = 6х;
55. V(x+2) =1их+2=1;
56. Vp-4x + 4j = 4 и х2 - 4х+ 4 = 4;
479
57. \(х+1) =2и|х+1| = 2;
58. Iog4 (x — IJ = 0 и 2 Iog4 (x — 1) = 0;
60. log7 Xs = 0 и 5 log7 x = 0;
61. log(X+2J(x+1) =0и Iogx+2(x+l) = 0;
62. logi (x — 1) (x + 3) = 0 и logi (x — 1) + logi (x + 3) = 0;
64. ctgx+tg 2x=0 и sim3x=0;
65. sinxcosx=cos2xH-ctgx=ctg2x;
66. sinxcosx=cos2XH tgx=l?
Указать, какое из двух следующих уравнений является следствие»
другого F7 — 92):
67. (х+2) (х+IJ = 3 (х+IJ и х +2 = 3.
68. х2 + 4х+ 3 = 0 и (х2 + 4х+ 3\ 2ЛЙТГ=0.
хЗ_4х(х+2)=Оихз_4? = о
х+2 х
71.x2-7x=8hV4-x2(x2-7x)=8V4-x2.
72. х2 = 16 и х2 log2 (х— 5) = 16 • log2 (x — 5).
V5-X2 V5-X2
и^ = ^.
lgx lgx
75.x2 Ц + -Ц + Зх=Ои
x+3 x+3
76.х3-2х = 0их3- —= 0.
x
Ух —4=УЗО"иУ(х+3)(х —4) =V30".
78. Vx2-5x-6=4hx2 —5x-6 = 16.
79.
80.
81. V5" sinxcosx=cos2*и V3~tgx=l.
80. log2 (x+ 2) + log2 (x — 3) = 1 и log2 (x+ 2) (x — 3) = 1. j
83. cos2x V4 — x2 = sin4x• "^4 — x2 и cos2x = sin4x.
480
84.
1
1
H tgX= 1.
log2x log2x
85. cosx- Iog5(x— 1) = sin x- logs (x — 1) и cosx=sinx.
86. arcsin x2 = •=• и arosin— = — .
2 Iog3(-x) 21og3(-x)
87. arccosx=7t и т=— = -т=.
\x \x
88. [x2 - 1| = x+1 и x2 - 1 =x+1.
89. [x2 - 4| = x +2 и 4 - x2 = x+2.
90. \x+ 1| + [x — 1| = 6 и x = 3.
92. [x+l| + [x— 1| = — х2 + 2и2х= — х2 + 2.
Равносильны ли уравнения и совокупность уравнений (93 — 124):
Уравнение
Совокупность уравнений
93. (x2-l)(x+2) = O
94. 2х4 - Зх3 - 4Х2 + Зх+2 = О
95 5F-х)_1ОE-х)
х —2 3(х —4)
96. л/х + 4^/х = 12
ПF-х)
3(х-4)
98. Vx+1 =x— 1
99. V22 — х = 2 + V10 —х
100. Vx+1 = 1 — V2x + 3
101.x2-Vx2-9=21
102. V14 + 25х — Vl + 4х = V7T9~
= — 1,х= 1,
¦l.x-2;
«|,х-7;
= 81,х = 64;
= 1,х=5;
= 0,х=3;
= 4,х = 6;
— 1,х-3;
= -5,х=5;
= 1,х = 2;
= —2;
2 + 3x-2+V8x2-2x-l =
104. 3+х2-5 3-х
105. [х-3| = [х-3|2
106. |х-1| + |х+2| = 4 + |х-3|
х = — 1,х =
3-V2T
х = 3, х =
3 + V2T
х = 0, х = 2;
х = -8,х=2;
х = —4, х= —2, х = 2, х = 4;
х = 2, х = 0;
16 Алгебра, тригонометрия
н элементарные функции
481
Уравнение
109. 8177 = 4-32"х
110.2-4Ьс-17-4'+8 = 0
112. Xх + 139х~ х - Ю&Г ъ = 32
113.1og2(9-2x]=3-x
115. log. 2 log*. 2 = logi 2
116. log2 (9х-' + 7J= 2 + log2 (зх~' +
117. V3 log2 (— x) = log2 V?
118. Ig
x2-x-l
x2 + x—2
= 0
119. 4 cos3 x + 3 cos (я — x) = 0
120. sin4 x + cos4 x=¦?
121. ctgxsin3x( cosx — 2) = 0
4x
122. arccos x = я + arcsin -=-
123. cos D arccos x) = — -=
... ¦ x . V5x
124. arcsinx— arcsin¦= — arcsin-=- =
0
X
X
X
x
X
X
X
X
x
x
X
X
X
X
Совокупность уравнений
—
= T
= 2,
= 1,
= 0,
= 2,
= 4,
= 1,
= —
я
я
= f
= —
= —
= —
тг — —
х=3;
х = 2,х
*=3;
х=10;
х = 8;
х = 2;
Q
8,х = -
VS"
2'х"
— *:
+ — *
х =
+ Я/, / G
3
5'
V3"
2.х-
= 3;
1 VS"
2)Х" 2 '
я пт _
= — г + ~2". те Z;
Z;
х = ^ + 7гл, ле 2;
2
3'
1
2'
х=2-,х=-2-;
1,х = 0, х=1?
Решить следующее уравнение A25 — 326):
125. Bх+ l±Y3x-4W- 1.125) Bх- 1,25).
482
126.
?±1
x-S 2x-l Sx-1
2 + 2 + 3x 10
128.|__|=3?_3Л29.__* 2 + __П
4x —3 2x+5 x+2 x+4
130.
132.
134.
136.
137.
138.
~TTx~2x-
x-3
i
x*+x-12
«0.
x2-3jc-4 x2-x-
7
*-i ,,33.4--7jc+1°
x2 + 4x+5
1. 135.-—-+ 7
x2 + 3x-8>
6
1 :+-^ + -Ь + - *
x—8 x—6 x+6 x+8
2 5__ 2 5
x-14 x-13 x-9 Х-1Г
1 4.4 11
x+1 x+2 х-Г
= 0.
y' 2 7"
2х
x-1 x-2 x-3 x-4~30"
140. x3-x2- 100 = 0. 141.x3-7x2+14x-8 = 0.
142. 2x4-5x3 —5x2 + 18 = O. 143. 6x4-2x3 — 17x2 + 2x+11 = 0.
144. Зх5 - 5X3 + 2 = 0. 145. x7 - бх6 + 13X5 - 12x4 + 4X3 = 0.
146. 1 —14 = |. 147. |-x+2| = 2x+l.
148.^—-x=l3jcr5ll49. |x-l| + |x-2|=l.
150. |x-l| + |x+2|-|x-3| = 4. 151. |4A-
152. |1 — x2! = 1 — x2. 153. jx2 — 1| = 1 — Jxj.
154. Ix2 — 91 + lx2 — 4| = 5. 155.
156. Ix2 - 3x+ 2| = 4 - x2 +14 157.
T "T2
7
ix2-3x+4
.2
158. К~3л| + 5 = 1-159.
160. |3-|x+ 2| = 4.161.
x2-5x+4
х2-6Ы + 7
= 1.
162. >/x+T= V5x+20-2. 163. V10-x-Vx = Vx^T.
166.x"-3 = V4xi-
168.
169.
170.V9 + 4.
171. Vx2 -
4.165. V6-4x-xz= x+ 4.
167,^/x~T-V2x-l =3 + x2.
— 6+ V2x+3 = Vl — x.
-^-21 =2x+3,5.
-x*-4 = -11 -x\
483
172. V4x/ + 25-ldx-7 = lx - 2| -Зх.
173. (х+ 1) л/Юх-21-хТ=х2 -
174. Vx = 1-Vx-Vl^x".
175. A — VI + Vx) VI + Vx = Vx~.
176. Vx + 2-4Vx^2 = 1 - Vx+7-6Vx-2.
177. Vl+xVx^ + 24 =x+ 1.
178. , X+2 . = 1- *+2
V-l-x+1 Ух+Т-Г
179. Vx^T+Vx^T+Vx2* 1 +7 = 0.
180. V?+T+ Wx-l+2= 2.
181. Vx2-4x+4 -Vx2-6x+9=Vx2-2x+l.
182. x2 + 4x - 16 V2x + 20 = 0.
183. VVx+4 + l+ VV3—x + 2= x2 - x - 42.
184. 4V512"= 8Ь 21 - x. 185. 1252 ~ 3x=VJ. '
188. yfj
8x+ 5
189. 3*(*-2) 2~-9V24T=0.
г * + 2 -,3-x
190.[(VOjT) J =0,001331.
^ 1 v«+5 r x+17 ,—|—
191. [321^7J =[V0,0625BV4696j J* .
193. 2-5x+2-5x+3 = 375.194. 3-4x~2 = 2 256-l6~r)
195'6*-У~' •3X-2 2V515^W ^ J
196. 3V2*-31 -
197. 3^+ 2 - 3^+» - 3^~J = 68. 198.
199. 5xf3x+ 5X]=4 Cx+4). 200. 14 T~i = 3 ¦ 5'+2.
201. 3 • 13'+ 13'+1 -2*+2 = 5 •
202. 2Sx+l-j-4x+2-y Sx+2 = 3 • 4'-'.
203. 3 A0х - 6x+2)+4 • 10*+' = 5 (lO*-' + б'"
204. 9х"- 8 -3х +7=0.205. 4- 2х42 = 3.
206. 2*G -2*^=2 • 7log73. 207. 4*~l = 13 • 4X~2 - 21.
484
208.
210.
212.
214.
215.
216.
217.
219.
220.
221.
222.
223.
224.
225.
226.
227.
228.
229.
230.
231.
232.
233.
234.
235.
236.
237.
238.
239.
2*= 26 + 3 • 2T. 209. 2(У + 4Х)- 5 • 6х = 0.
v 1 ) 1 1
3- 16*+36*= 2-81*. 211. 4" + 6"=9~.
- 8 = 2 • 8*2+t. 213.
2*- 8*+11=0.
2*Г23*-2*+2>2-8*-1.218.5*-32=
I )
108~1395
25х
lQg2 (х+ 4) = log2 4 (log2 7 - log2 5\
log7x=21og7Bx-45). ;
logl(x+ 1) — logl(x— 3) = 1.
10B —VT)"
lQg3x+log3(x+2) = 1.
log3 log8 log2 (x+ 5) = log3 2 - 1.
lQgg B lOg/1 + lOg2 A + 3 lQg2 Xjjj= j.
1 + Ig (l + x* + 2x)- Ig (x2 + 6]= 2 Ig (x+ 1).
ч 2 ) \ 2 J
lgBx-3) -lgCx-2) =2.
^
log4(x2 - l)- log»(x- 1J =
B )^
log6 (x+ 1) = loge A - x) + logg Bx+ 3).
Ig2 + lgf4-5x-6x2l ,
lQgi(X—
2
= 0.
+ x-2
i(x+l)-lojH_G-x):
Ig Vl+x + 3 Ig VI—x = Ig Vl — x? + 2.
Vlog2x4+41og24V^"=2.
c-2 = 4.
485
240. Vlog9 [Эх3} log3 (9x) = log3 x2.
241. \2 log2-fj — 1 f2 + Iog4 (8x) | = log2 Bx).
242-5-41g(x+l)-3"l
243. log2 Ux+ 4]=x+ log2 B*+' -:
244. log3x+1О&Д-Х+ logix= 6.
245. log, 2 logJL 2 = logi 2.
16 64
249. 2 log2 Aog2 x]+ log^ Aog2 Q.<2x)\= 1.
250. log, _Цбх2 - 5x+ 1 j- log, _^Ux2 - 4x+ 1 j= 2.
251. logbc_, TlOx2 - 7x+ 1) = 2 + logj^, (iSx2 - \0x+ \\
2]^
253. log(J(_ „2 Г4 - 4x+x2)= 2 + lOg(J(_ „2
254. logx+ Лх2 + x — 6J = 4. 255.10&,[(x- II0**'*-'> J = 2.
256. log3 (З* - 1V log3 Гз*+' - 3у 6.
257. x+lg ("l + 2^J=x lg 5 + lg 6.
258. Iog4 lofe2 x+Iog2 log4 x = 2. 259. | log2 Wl = 2.
260. sin^ = — \. 261. VlOO — x2 sin 2x= 0.
262. cos Dx + 2) = - 4p 263. icos3x, = 0.
2M. tg 1^^-1= — 10. 265. ctg
266. V4x+77 —
VI 1
268. 4cosx+5sinx=-r-. 269. 2sinx— 3 cosx = — -=.
270. tgx2 = - VI. 271. ctgVx = - 1.
272. Vsin x = cos x. 273. V5 — 2 sin x = 6 sin x — 1.
274. V9-4V3 -A6-8V3)sinx = 4sinx-3.
275. sin |2x+y ]- 3 cosfx —y|= 1 + 2 sinx.
486
276. sin jc+ sin 3x+ 4 cos3 x = 0.
277. tg2x —4sinxcosx + 1 =4sin2*.
278. 4 + sin2x = C + VJj sin 2x — 2 B — >/3) cos2x.
279. sin 2x= 1 + VTcos x+cos 2x.
280. sin2x+sin3x=2.
281. 4 (sin 3x sin x) — sin 3x = 5.
282. cos402x-sin4°2x=l.
283. V
284. tg 2x tg 3x = 1. 285. sin4 x — cos4 x = sin 2x.
]
287. sin2x— h(sinx — cosx) + 12 = 0.
288. tgx+ctgx = sinx l
289. cos x + sin x = . c°S.2x- .
1 — sm2x
290. tg 2x cos 4x Г4 — sin2 7x)= 0.
291. 8cos4x=3 + 5cos4x
292. 2 (ctg x — tg x) = sin 4x
293. sin 4x sin 6x = 2 (sin x + sin 5x).
294. 1 — tg2x=4sin22x.
295. sin 5x sin 4x = — cos 6x cos 3x.
296. cos x= cos 3x+ 2 sin 2x.
297. sin4x + 5 cos2x+4 = 0.
298. tg2 x + 8 cos 2x ctg 2x = ctg2 x.
299. cos 7x — sin 5x = ->/3~ (cos 5x — sin 7x).
300. (cos x — sin x) 1 + -z sin 2x + sin x = 2 cos2 x.
301. 2sin22x + sin24x=|.
302. cos | - cos у = 3 sin21.
303. sinx— 2 sin 2x+sin 3x= 11 — 2 cos x+ cos 2x|.
... pf- (x к\ Г7- . (x n\ - . (x 2n\ _ . (Зх л
304. V2 cos -г — -ГГ — V6 sin т —Т7 =2sin + 2sin +
305. tg\-= cosx — ctg (л sinx) = 0.
v ( >' \
306. 2 sin 3x+^ = V1 + 8 sin 2x cos2 2x.
307. 2 — V3~cos 2x+sin 2x=4 cos2 3x.
487
309. sin2 lf=1 = \. 310. ing i sin x = \.
1 8cos2x l
311. |coHsinjt-2sinx+2 = 1. 312. 81sinjt + 81cosjt = 30.
313. 4tg2 x + 2^ - 80 = 0. 314. 21 + 2 cos 5x + 16si Iх = 9.
315 8i(sin2x~ 1) c0S3x n(sinx — cosx) _q
Iifi ^sin2x+2cos x т1 — sin 2x+2sin x _ ^o
317. x2 log3 x2 - (b? + 3j log, Bx + 3) = 3 log3
320. x2 Iog6 -45x?--2x-?> - x log)/e (V - 2x - 3 )= x2 + 2x.
321. 3-2 + 6-2 + l0E*sinx=2-2+l082C0Sx.
322. 4tg2x- ЛхтЬъ log23vr4 = - lOgsinx г ~ ^°S 2x.
323. 4 • 24V2cos(f-x)- 16,5 • |
324. sin jlc + sin[logxx31"j = cos jlc — cos(Iog3vi"***}
325. cos 2x + log4 xsinx +2 cosx- logi^ sinx =
326.
= 2 cos x + sin2 x • log2 sin2 x.
in
. 2 log25 E2 sin x - 4) = 2 sin x + sin у.
Глава VIII. НЕРАВЕНСТВА С ОДНИМ
НЕИЗВЕСТНЫМ
Пусть даны две функции: функция y=fx) с областью
существования Р и функция у = g(x) с областью существо-
существования L. Пусть область Месть пересечение областей суще-
существования этих функций, т.е. М= Рп L (в частности, об-
область М может быть пустым множеством).
Пусть стоит задача: найти все числа а из области М, для
каждого из которых справедливо числовое неравенство
fa) > g(a). В таких случаях говорят, что стоит задача:
решить неравенство fx) > g(x) с одним неизвестным х или
что дано неравенство fx) > g(x) с одним неизвестным х.
В этой главе рассматриваются некоторые способы реше-
решения только неравенств с одним неизвестным х. Поэтому
дальше вместо слов «неравенство fx) > g(x) с одним неиз-
неизвестным л» будем говорить просто «неравенство Дх) > g(x)».
Аналогично формулируются и понимаются задачи: решить
неравенство fix) < g(x); решить неравенство fx) > g(x); ре-
решить неравенство fx) < g(x).
§ 1. Основные понятия и утверждения равносильности
неравенств
Областью допустимых значений (ОДЗ) неравенства
fx) > g(x) называется общая часть (пересечение) областей
существования функций у =fx) к у = g(x), т.е. множество
всех числовых значений неизвестного х, при каждом из
которых имеют смысл (определены) левая и правая части
неравенств.
Число а из ОДЗ неравенства называется решением нера-
неравенства fx) > g(x), если при подстановке его вместо неиз-
489
вестного х неравенство превращается в верное числовое
неравенство Да) > g(a).
Решить неравенство Дх) > g(x) — это значит найти мно-
множество всех его решений. Отметим, что это множество
может оказаться и пустым множеством, что возможно
только в двух случаях:
а) если ОДЗ данного неравенства есть пустое множество;
б) если ОДЗ данного неравенства есть непустое множе-
множество Q, но ни для одного числа а е Q не выполняется
числовое неравенство Да) > g(a).
Если множество всех решений данного неравенства есть
пустое множество, то обычно говорят, что данное неравен-
неравенство не имеет решений. Поэтому иногда говорят так: решить
неравенство j{x) > g(x) — это значит найти все его решения
или доказать, что это неравенство не имеет решений.
Пусть даны два неравенства:^) > g(x) нр(х) > <р(х). Если
любое решение первого неравенства является решением
второго неравенства, а любое решение второго неравенства
является решением первого неравенства, то такие два не-
неравенства называются равносильными.
При этом, в частности, подразумевается, что если каждое
из этих неравенств не имеет решений, то такие два нера-
неравенства равносильны. Замена одного неравенства другим
неравенством, ему равносильным, называется равносиль-
равносильным переходом от одного неравенства к другому.
Пусть даны два неравенства/х) > g(x) и р(х) > (р(х) и пусть
дано некоторое множество М значений неизвестного х. Если
любое решение первого неравенства, принадлежащее множе-
множеству М, является решением второго неравенства, а любое
решение второго неравенства, принадлежащее множеству М,
является решением первого неравенства, то такие два нера-
неравенства называются равносильными на множестве М.
При этом, в частности, подразумевается, что если каждое
из этих неравенство не имеет решений на множестве М, то
такие два неравенства равносильны на множестве М.
Замена одного неравенства другим неравенством, равно-
равносильным ему на множестве М, называется равносильным
переходом на множестве Мот одного неравенства к другому.
490
Отметим, что аналогично формулируются задачи реше-
решения неравенств J{x) < g(x), J{x) > g(x), f{x) < g(x) и основные
определения для них.
Замечания. 1. В случае неравенств, в отличие от
уравнений, термин «корень» не употребляется.
2. Так как множеством решений неравенства обычно
является некоторый промежуток, а сделать проверку для
всех чисел данного промежутка практически невозмож-
невозможно, то понятие проверка при решении неравенств не исполь-
используется.
Приведем несколько примеров, иллюстрирующих вве-
введенные понятия.
Пусть дано неравенство
Vx+2 + Vx— 5 > V3 — х.
ОДЗ этого неравенства есть множество Л/, являющееся
пересечением областей существования функций
у = Vx+2, у = Vx — 5 и у = V3 — х, т.е. Месть пересечение
множеств [— 2, + °°), [5, + °°) и (— °°, 3]. Это пересечение
пусто. Следовательно, неравенство решено, так как нет ни
одного значения неизвестного, при котором все функции,
входящие в данное неравенство, имели бы смысл. Таким
образом, данное неравенство не имеет решений.
Пусть дано неравенство
л/х<-5.
Так как при подстановке в данное неравенство любого
числового значения из ОДЗ этого неравенства оно стано-
становится неверным числовым неравенством, то, следователь-
следовательно, данное неравенство не имеет решений.
Неравенства х + 5 > 0 и (х4 + 1)(х + 5) > 0 равносильны
на множестве всех действительных чисел; неравенства
¦^с > 1 и х2 > 1 не являются равносильными на множестве
всех действительных чисел, но равносильны, например, на
множестве положительных чисел.
Приведем некоторые утверждения равносильности
неравенств:
491
1. Неравенства f{x) > g(x) ufx) — g(x) > О равносильны.
2. Неравенства f{x) > g(x) и fix) + a > g(x) + а равносильны
при любом действительном а.
За. Неравенства fx) > g(x) и afx) > ag(x) равносильны для
любого положительного числа а.
36. Неравенства fix) > g(x) и afx) < ag(x) равносильны для
любого отрицательного числа а.
4а. Неравенства а^х) > а^х) и fx) > g(x) равносильны для
любого фиксированного числа а такого, что а > 1.
46. Неравенства а"*х) > а*(х) и fx) < g(x) равносильны для
любого фиксированного числа а такого, что 0 < а < 1.
Справедливость этих утверждений доказывается сход-
сходным образом, поэтому приведем доказательство лишь
утверждения За.
Пусть число х, есть некоторое решение неравенства
fx) > g(x), т.е. пусть существуют числа Дх,) и #(*,), для
которых справедливо числовое неравенство fx{) > g(x{).
Умножив это числовое неравенство на положительное
число а, получим, что справедливо числовое неравенство
аЛх\) > a?(*i)> а эт0 означает, что число хх есть решение
неравенства afx) > ag(x). Такое рассуждение можно про-
провести для любого решения неравенства fx) > g(x). Значит,
любое решение неравенства fx) > g(x) является решением
неравенства afx) > ag(x).
Покажем теперь обратное. Пусть число х2 есть некоторое
решение неравенства afx) > ag(x), т.е. пусть существуют
числа fx2) и g(x2), для которых справедливо числовое
неравенство afx2) > oig(x2). Из справедливости этого нера-
неравенства на основании свойств числовых неравенств выте-
вытекает справедливость числового неравенства fx2) > g(x2), a
это означает, что число х2 есть решение неравенства
fx) > g(x). Такое рассуждение можно провести для любого
решения неравенства afx) > ag(x). Значит, любое решение
неравенства afx) > ag(x) является решением неравенства
fx)>g(x).
Итак, если каждое из неравенств f x) > g(x) и afx) > ag(x)
имеет решения, то эти неравенства равносильны. Заметим,
что из доказанного вытекает, в частности, что если одно из
492
этих неравенств не имеет решений, то и другое не имеет
решений, т.е. и в этом случае неравенства Ах) > g(x) и
аДх) > ag(x) равносильны.
Утверждение За тем самым доказано полностью.
Приведем теперь несколько утве ржд ений равносиль-
равносильности неравенств на множествах.
5. Пусть п — натуральное число и пусть на некотором
множестве М одновременно обе функции у =АХ) и у = g(x)
неотрицательны, тогда на этом множестве равносильны
неравенства Дх) > g(x) и [Дх)]л > [g(x)]n.
ба. Пусть а — любое фиксированное число такое, что
а > 1, и пусть на некотором множестве М одновременно обе
функции у=Лх) и y = g(x) положительны, тогда на этом
множестве равносильны неравенства Ах) > g(x) и logo Ах) >
>logag(x).
бб. Пусть а — любое фиксированное число такое, что
О < а < 1, и пусть на некотором множестве М одновременно
обе функции у =ЛХ) иу = g(x) положительны, тогда на этом
множестве равносильны неравенства fix) > g(x) и logfl Ах) <
<\o%ag{x).
7a. Пусть на некотором множестве М функция у = ф(х)
положительна, тогда на этом множестве равносильны нера-
неравенства Ах) > g(x) иЛх)ф(х) > g(x)y(x).
76. Пусть на некотором множестве М функция у = ф(х)
отрицательна, тогда на этом множестве равносильны нера-
неравенства Ах) > g(x) «Лх)ф(х) < g(x)<p(x).
Приведем доказательство утверждения 5.
Если п = 1, то утверждение 5 верно.
Поэтому будем дальше считать, что п > 2. Пусть число х,,
принадлежит множеству М и является некоторым решени-
решением неравенства Ах) > g(x), т.е. пусть существуют неотрица-
неотрицательные числа Axi) и ?(*i) такие, для которых справедливо
числовое неравенство Ах{) > g(xi). Из справедливости этого
неравенства следует, в частности, что число Axi) положи-
положительно. Но тогда для любого натурального числа к число
[Дх[)]* положительно, а число [g(X[)]* — неотрицательно.
Значит, сумма
493
положительна, так как первое ее слагаемое — положитель-
положительно, а остальные — неотрицательны. Из числового неравен-
неравенства fiXi) > g(x{) вытекает еще, что число Ддс,) — g(x,) поло-
положительно. Так как произведение положительных чисел
положительно, то положительно и число
Применяя формулу сокращенного умножения (см. гл. II),
приходим к справедливости числового неравенства
[А*)]* - ЬК*,)]" > О,
откуда вытекает справедливость числового неравенства
[Л*)]" >
Итак, показано, что для любого числа хг из множества
М из справедливости числового неравенства Xxt) > g(xt)
следует справедливость числового неравенства [/fa)]" >
> [iK*,)]". Значит, любое решение неравенства fix) > g(x),
принадлежащее множеству М, является решением неравен-
неравенства [Лх)]я > ШУ-
Покажем теперь обратное. Пусть число Хг принадлежит
множеству М и есть некоторое решение неравенства
[Л*)Г > igix)]", т.е. пусть существуют неотрицательные
числа Дхз) и gixj), для которых справедливо числовое
неравенство [Дх^)]" > [jg(xj)]". Покажем, что число Дх^) по-
положительно. Предположим, что Дх^) равно нулю, тогда из
неравенства Ufa)]* > {sto)]" вытекает, что число \g(xd]H
отрицательно. Но так как число gixi) неотрицательно, то
неотрицательно и число [gixi)]". Полученное противоречие
означает, что число/fe) положительно. Но тогда положи-
положительна сумма
[/W + [/Wto + - + ЛхгШх,)]"-2 + bte)]-1.
Кроме того, из справедливости неравенства [Д*2)Г>
> {gixj)]" следует, что число [Дл*)]" — Mxi)]* положительно.
Рассмотрим теперь числовое равенство
494
+ №а)Г~2«(*а) +... +
В этом равенстве слева стоит положительное число, а
справа — произведение двух чисел, одно из которых поло-
положительно, значит, и второе число положительно, т.е. спра-
справедливо числовое неравенство/fo) — gfa) > 0. Из справед-
справедливости этого числового неравенства вытекает справедли-
справедливость неравенства /fa) > g(x^. Итак, показано, что для
любого числа Хг из множества Миз справедливости число-
числового неравенства [ffa)]n > [gifa)]", следует справедливость
числового неравенства /fa) > gfa). Значит, любое решение
неравенства [Дх)]л > [^(х)]л, принадлежащее множеству М,
является решением неравенства Дх) > g(x).
Итак, если каждое из неравенств fix) > g(x) и [/(*)]" >
> [#(х)Г имеет решения на множестве М, то эти неравен-
неравенства равносильны.
Заметим, что из доказанного вытекает, в частности, что
если одно из этих неравенств не имеет решений на множе-
множестве М, то и другое не имеет решений на этом множестве,
т.е. и в этом случае неравенства Дх) > g(x) и [Дх)]" > {gix)]"
равносильны, чем и завершается доказательство утвержде-
утверждения 5. Справедливость утверждений 6а, 66, 7а, 76 доказы-
доказывается аналогично.
Пусть дано т неравенств /(х) > &(х), f2(x) > g2(x), ...
...,fjx) > gjx). Обозначим через М область, являющуюся
пересечением областей допустимых значений всех этих
неравенств, если стоит задача: найти все числа а из области
М, каждое из которых является решением каждого из этих
неравенств, то говорят, что дана система т неравенств
/»(*)> gm(x)
и область М называется областью допустимых значений
(ОДЗ) этой системы. Отметим, что обычно неравенства
495
системы записывают в столбик, слева от которого ставится
фигурная скобка.
Число а из ОДЗ системы неравенств A) называется
решением этой системы, если оно является решением каж-
каждого из неравенств.
Решить систему неравенств A) — это значит найти мно-
множество всех ее решений. Если это множество оказывается
пустым множеством, то говорят, что система неравенств
A) не имеет решений. Систему неравенств A) обычно
решают следующим образом. Сначала решают каждое не-
неравенство на ОДЗ этой системы, т.е. находят множества Nu
N2, ..., Nm, где N, — множество всех решений неравенства
fix) > Six), принадлежащих ОДЗ этой системы. Затем на-
находят множество No, являющееся пересечением всех этих
множеств Nx, N2, ..., Nm, т.е. No = NinN2n ... n Nm. Мно-
Множество No и будет множеством всех решений системы
неравенств A).
Пусть числа а и Ь таковы, что а < Ь и пусть дана система
неравенств
B)
<Ь.
В этом случае иногда говорят, что дано двойное неравенство
а<Дх)< Ъ. C)
Отметим, что если у=Дх) — основная элементарная
функция, то часто проще решить двойное неравенство C),
чем систему неравенств B).
Пусть теперь дано к систем неравенств
fn(x)>gn(x),
/Ах)
D)
fafr) >
Обозначим через Q область, являющуюся пересечением
областей допустимых значений всех этих систем нера-
неравенств.
496
Если стоит задача: найти в области Q все числа а, каждое
из которых является решением хотя бы одной из этих
систем, то говорят, что дана совокупность к систем нера-
неравенств и область Q называется областью допустимых зна-
значений (ОДЗ) этой совокупности. Отметим, что обычно
системы неравенств из совокупности систем неравенств
записываются в строчку (см. D)).
Число а из ОДЗ совокупности систем неравенств D)
называется решением этой совокупности, если оно является
решением хотя бы одной системы неравенств из совокуп-.
ности D).
Решить совокупность систем неравенств D) — это значит
найти множество всех ее решений. Если это множество
оказывается пустым множеством, то говорят, что совокуп-
совокупность систем неравенств D) не имеет решений.
Совокупность систем неравенств D) обычно решают
следующим образом. Сначала решают каждую систему
неравенств на ОДЗ совокупности D), т.е. находят множе-
множества Mi, Мг, ..., Мк, где М, — множество всех решений
системы
Ux)>gpi(x),
на ОДЗ этой совокупности. Затем находят множество М„,
являющееся объединением всех этих множеств Ми М2, ...
..., Мк, т.е. Мо — Мх и М2 и М3 и ... и Мк. Множество Мо и
будет множеством всех решений совокупности систем не-
неравенств D).
Заметим, что если каждая из к систем совокупности D)
содержит только одно неравенство, то говорят, что дана
совокупность к неравенств.
Если к — 1, то совокупность D) является системой нера-
неравенств.
Говорят, что неравенство
Ах) > g(x) E)
497
равносильно совокупности систем неравенств D), если любое
решение неравенства E) является решением совокупности
D), а любое решение совокупности D) является решением
неравенства E).
При этом, в частности, подразумевается, что если нера-
неравенство E) не имеет решений, и совокупность D) не имеет
решений, то неравенство E) равносильно совокупности D).
В случае если в совокупности систем неравенств D)
п = т = ... = р =... = /= 1, то говорят, что неравенство E)
равносильно совокупности неравенств D).
В случае если в совокупности систем неравенств D)
к - 1, то говорят, что неравенство E) равносильно системе
неравенств D).
Замена неравенства E) равносильной ему совокупнос-
совокупностью D) называется равносильным переходом от неравенства
E) к совокупности D).
Иногда возникает необходимость совершить равносиль-
равносильные переход от неравенства к совокупности систем нера-
неравенств на множестве М.
Говорят, что неравенство E) равносильно на множестве
М совокупности неравенств D), если любое решение нера-
неравенства E), принадлежащее множеству М, является реше-
решением совокупности D), а любое, принадлежащее множест-
множеству М, решение совокупности D) является решением нера-
неравенства E).
Отметим, что в совокупности систем D) может оказаться
бесконечно много систем неравенств.
Замена неравенства другим неравенством или совокуп-
совокупностью систем неравенств будет дальше называться преоб-
преобразованием неравенства.
Наконец, приведем понятие смешанной совокупности —
совокупности уравнений и неравенств.
Пусть дано к уравнений /i(x) = g,(x), /2(х) = &(*), -
•••,/*(*) = gk(x) и т неравенств fk+i(x)> gk+l(x), fk+dx) > \
> gk+i(x), ...,fk+m{x)>gk+mix). Обозначим через Q область,
являющуюся пересечением областей допустимых значений
этих уравнений и всех этих неравенств. ,
Если стоит задача: найти в области Q все числа а, каждое;
из которых* является решением хотя бы одного из этих к
498 !
уравнений или хотя бы одного из этих т неравенств, то
говорят, что дана смешанная совокупность
A(x)=gi(x), /2(х) =&(*), ..., /*(*) =
Л+ i(x) > &+ i(x), Л+ г(х) > &+2(х), ... F)
и область Q называется областью допустимых значений
(ОДЗ) этой совокупности.
Отметим, что обычно уравнения и неравенства смешан-
смешанной совокупности записываются в строчку.
Число а из ОДЗ смешанной совокупности F) называется
решением этой совокупности, если оно является решением
хотя бы одного из к уравнений или хотя бы одного из т
неравенств этой совокупности.
Решить смешанную совокупность F) — это значит найти
множество всех ее решений. Если это множество оказыва-
оказывается пустым множеством, то говорят, что смешанная сово-
совокупность F) не имеет решений.
Смешанную совокупность F) обычно решают следую-
следующим образом. Сначала решают каждое уравнение и каждое
неравенство на ОДЗ этой совокупности, т.е. находят мно-
множества Ми Мъ ..., Мк_ и Мь где М, (/= 1, 2, ..., к) —
множество всех решений уравнения /Цх) = &(х), принадле-
принадлежащих ОДЗ этой совокупности, и множества Мк+и Мк+2,
..., Мк+т, где Mk+J(j=l, 2,.., т) — множество всех решений
неравенства fk+j(x) > gk+/x), принадлежащих ОДЗ этой со-
совокупности. Затем находят множество Мо, являющееся
объединением всех этих множеств Ми М2, ..., Мь Мк+и ...,
Мк+т, т.е. Мо = Mi^jМ20... и.Л/Ли Af*+iU ... uMk+m.
Множество Мо и будет множеством всех решений смешанной
совокупности F).
Будем говорить, что неравенство
Ax)*g(x) G)
равносильно смешанной совокупности F), если любое реше-
решение неравенства G) является решением смешанной сово-
совокупности F), а любое решение смешанной совокупности
F) является решением неравенства G).
499
При этом, в частности, подразумевается, что если нера-
неравенство G) не имеет решений и смешанная совокупность
F) не имеет решений, то неравенство G) равносильно
совокупности F).
Из вышесказанного вытекает, что нестрогое неравенство
(8)
равносильно смешанной совокупности
Ax)=g(x), Ax)>g(x). (9)
Так как решение нестрогого неравенства есть объедине-
объединение решений соответствующего уравнения и соответству-
соответствующего строгого неравенства, то достаточно рассмотреть
лишь решение строгих неравенств.
§ 2. Простейшие неравенства
Пусть у =Ах) — основная элементарная функция, Ь —
некоторое фиксированное действительное число. Тогда
неравенства
Ах) > Ь, A)
Ах) < Ъ B)
принято называть простейшими неравенствами.
Очевидно, что ОДЗ простейшего неравенства совпадает
с областью существования основной элементарной функ-
функции у =Ах).
Как отмечалось выше, нестрогое неравенство Ах) ? b
равносильно совокупности строгого неравенства Ах) > Ьп
уравнения Ах) = Ь, а нестрогое неравенства Ах) ? b равно-
равносильно совокупности строгого неравенства Ах) < Ъ и урав-
уравнения Ах) = Ь. Поэтому в этом параграфе будет рассмотре-
рассмотрено решение лишь простейших неравенств A) и B).
Прежде всего стоит сказать, что при решении неравен-
неравенства нельзя формально записывать решение соответствую-;
щего уравнения и затем заменить знак равенства на знак ,
неравенства. Как будет показано ниже, для решения про-
простейших неравенств A) и B) надо хорошо знать свойства
500
основной элементарной функции y=fix) и уметь пользо-
пользоваться ими.
Часто решение простейшего неравенства сопровождает-
сопровождается графиками функций у = fix) и у = Ь. При этом пользу-
пользуются следующим очевидным утверждением: если надо ре-
решить неравенство fix) > Ъ илиДх) < Ъ, где функция у =fix)
даже не обязательно основная элементарная функция, то
строят на одном рисунке графики функций у =fix) у = Ь.
Тогда решением неравенства fix) > Ъ будут те значения х,
для каждого из которых точка (х, fix)) графика функции
У = fix) лежит выше точки (х, Ь) прямой у = Ь (рис. 149), а
решением неравенства fix) < Ъ будут те значения х, для
каждого из которых точка (x,fix)) графика функции у =fix)
лежит ниже точки (х, Ь) прямой у = b (рис. 150).
Рис. 149.
Поэтому такой рисунок сразу подсказывает, какое мно-
множество является решением неравенства fix) > b, а какое
множество является решением неравенства^*) < Ь. Однако
подчеркнем, что наглядность графиков является лишь
вспомогательным средством при решении неравенств. Эти
графики только подсказывают ответ, а тот факт, что оче-
очевидное из рисунка множество является решением того или
иного неравенства, обязательно надо доказать.
501
Отметим еще, что рисунок часто подсказывает, на какие
множества надо разбить область существования функции
у = J{x) и какие свойства этой функции надо использовать
Рис. 150.
для проведения этого доказательства. Поэтому дальше
перед решением некоторых простейших неравенств будет
проводиться анализ графиков функций у =/(х) и у = Ь.
Алгебраические неравенства. Пусть п — некоторое фик-
фиксированное натуральное число, тогда неравенства
х">Ь,
х"<Ь
C)
D)
принято называть простейшими адгебраическими неравенст-
неравенствами.
Функция у = х" определена на всей числовой прямой,
поэтому ОДЗ неравенств C) и D) есть множество X-(—«>,
+ «>).
Поскольку свойства функции у = х", используемые при
решении неравенств C) и D), различны при нечетном и;
четном п, то рассмотрим два случая:
502
I. Пусть п = 2m — 1, где т — некоторое фиксированное
натуральное число, тогда неравенства C) и D) принимают
вид
г-\>ь,
(За)
Dа)
'
@,1)
Областью значений функции у = х2т ' на множестве X
является множество Y=(— », + «). Вследствие того что
функция у = ?т ~ ' возрастает на множестве X, каждое
численное значение из У
она принимает лишь один
раз. Поэтому, если при
х = Xq она принимает зна-
значение Ъ, то при каждом
х > Xq она принимает зна-
значение большее, чем число
Ь, а при каждом х < Xq она
принимает значение мень-
меньшее, чем число Ъ.
Значит, множеством
всех решений неравенства
(За) является промежуток
целое; (д^ + то)} а МНОЖеСТВОМ
всех решений неравенства
Dа) является промежуток
(— оо, Xq), где, как показано
в § 2 гл. VII,
п
¦у~ г \т- це
//. у=ь, где ь<о.
Рис. 151.
2™
при положительном Ь;
I
О, при Ъ = 0;
2 при отрицательном Ъ.
Рис. 151 хорошо иллюстрирует проведенные выше рассуж-
рассуждения.
II. Пусть п = х2*1, где т — некоторое фиксированное
натуральное число, тогда неравенства C) и D) принимают
вид
503
хЪп<Ь.
C6)
D6)
Функция у = х1т на всей числовой прямой является не-
неотрицательной. Поэтому, если Ь — отрицательное число,
то неравенство C6) справедливо при любом значении х, а
неравенство D6) не справедливо ни при одном значении х.
Значит, в этом случае множеством всех решений неравен-
неравенства C6) является вся числовая прямая (— °°, + оо), а
неравенство D6) не имеет решений. Рис. 152 хорошо
иллюстрирует проведенное выше рассуждение.
//
II
A,0)
II
II
I. у—х2", где т е N;
II. у=Ь, где Ь<0.
Рис. 152.
A,0)
I. y=xi", где т е N;
II. у=Ь, где Ь=0.
Рис. 153.
//
(-
¦ХсЬ)
У,
\
(~Xo,0)
J
0 (
I
II
(xab)
,@,1)
%,0) x
I. у=х3", где т е N;
II. у=Ь, где Ь>0;
Рис. 154.
Если же Ь = 0, то при х = 0 функция у = хЪп принимает !
значение нуль, а для всех остальных х эта функция поло-
положительна, поэтому неравенство C6) в этом случае будет j
справедливо при любом значении х, кроме х = 0; а нера- "I
венство D6) не справедливо ни при одном значении х. <
Значит, в этом случае множеством всех решений неравен- j
ства C6) является объединение двух лучей (— ~5 0) и @, м
+ оо) (рис. 153), а неравенство D6) не имеет решений.
Пусть, наконец, Ъ — положительное число. Построим;
графики функции у = х2т и у = Ь (рис. 154). Прямая у = Ь
пересекает график функции у = х2 в двух точках (х<,, Ь) и
(— Xq, b), где Xq = 2nVF. При этом график функции у = х2"
504
лежит ниже прямой у = Ъ на интервале (— Xq, Xq) и выше
на множестве (— «>, — Xq) u (xq, + »). Следовательно, эти
множества и должны быть множествами всех решений
неравенств D6) и C6). Однако это утверждение надо дока-
доказать. Рис. 154 показывает, что для доказательства надо
воспользоваться тем, что на промежутке Хх = [0, + »)
функция у = х2т возрастает, а затем воспользоваться чет-
четностью этой функции.
Разобьем область существования функции у = х2™ на два
множества Хх = [О, + «>) и Х2 = (— «, 0) и рассмотрим
решение неравенств C6) и D6) на каждом из этих мно-
множеств.
На множестве Хх функция у = х2т имеет область значений
Y= [0, + оо) и возрастает, поэтому каждое численное зна-
значение из У она принимает лишь один раз. Значит, если при
х = Xq е Хх она принимает значение Ь, то при каждом х > Xq
таком, что хе Хи она принимает значение, большее чем Ь,
а при каждом x<Xq таком, что хе Хх, она принимает
значение, меньшее чем Ь. Следовательно, на Хх множество
всех решений неравенства C6) есть промежуток (х<,, + <»),
а множество всех решений неравенства D6) есть проме-
промежуток [0, Xq). Так как функция у = х2т является четной
функцией, то на Х2 множество всех решений неравенства
C6) есть промежуток (— «>, — Xq), а множество всех
решений неравенства D6) — интервал (— Xq, 0). Объединяя
решения, найденные на Хх и Хъ получаем, что а этом случае
множество всех решений неравенства C6) есть объедине-
объединение двух лучей (— оо, — Xq) и (хо, + «>), а множество всех
решений неравенства D6) — интервал (— х<,, х<,), где
Ъ
Итак, множество всех решений неравенства C6) есть:
1. при каждом отрицательном Ь — числовая прямая
(— оо, + оо);
2. при Ъ = 0 — множество (— », 0) и @, + »);
3. при каждом положительном Ъ — множество (— »,
Множество всех решений неравенства D6) есть:
1. при каждом неположительном Ъ — пустое множество;
505
2. при каждом положительном Ъ — интервал (— ^VzT,
N5).
В табл. 18 приведены итоги решения неравенств C) и D):
Таблица 18
^fc/W —~ 1 v L
^fc/W "~~ 1 ? L
J»<b
A
{2m-
(-^
>0
1 ^—
2m-
/A~;
-)
'VF)
"VA)
A = 0
@;-)
(- -; 0)
(- ~; 0) u @; ~)
нет решений
A<0
(-2m-1VlAT;~)
(_«;_2—«VTAD
(- -; -)
нет решений
Дробные неравенства. Пусть п — некоторое фиксирован-
фиксированное натуральное число, тогда неравенства
х-я>Ь, E)
х-"<Ь F)
принято называть простейшими дробными неравенствами.
Функция у = х~" определена на всей числовой прямой,
кроме одной точки — нуля, поэтому ОДЗ неравенств E) и
F) есть множество Х= Хх и Хъ где Хх = @, + «>), а Х2 =
= (- -, 0).
Поскольку свойства функции у = х ", используемые при
решении неравенств E) и F), различны при нечетном и
четном п, то рассмотрим два случая:
I. Пусть п = 2т — 1, где т — некоторое фиксированное
натуральное число, тогда неравенства E) и F) принимают
вид
Eа)
Fа)
-2т+\
Областью значений функции у = х на множестве Хх
является луч 7, = @, + «), а на множестве Х2 — луч 72 =5
= (--, 0).
506
Если b = О, то, учитывая, что функция у = х
_ „- 2л» + 1
на
множестве Хх положительна, а на множестве Х2 отрицатель-
отрицательна, получаем, что Х{ — множество всей решений неравен-
неравенства Eа), а Х2 — множество всех решений неравенства Fа)
(рис. 155).
@,1)
и
J. IL
@,1)
I. у^х"", идете N;
II. у=Ь, где Ь=0.
Рис. 155.
(x«0) x
I. y^x"*', где т е N;
II. y=b, где b>0;
Рис. 156.
Пусть b — положительное число. Построим графики
функций y = x~2m+l и у= Ь (рис. 156). Прямая у = Ь пере-
пересекает график функции у = дГ2 +' в одной точке (*<,, Ь), где
хо = 2т~ 'лЯ" При этом график функции y = x~2m+l лежит
выше прямой на интервале @, х$) и ниже прямой на
множестве (— », 0) и (*<,, + »). Следовательно, эта множе-
множества и должны быть множествами всей решений неравенств
Eа) и Fа). Однако это утверждение надо доказать. Рисунок
показывает, что для доказательства надо рассмотреть реше-
решение неравенства отдельно на каждом множестве Хх и Х2 и
воспользоваться тем, что функция у = х~2т+' на множестве
Х2 — отрицательна, а на множестве Х{ — убывает.
Рассмотрим решение неравенств Eа) и Fа) на множестве
Х2. На этом множестве функция у = х'2™*1 отрицательна,
поэтому на множестве Х2 нет решений неравенства Eа), но
507
все множество Х2 содержится в множестве всех решений
неравенства Fа).
На множестве Хх функция у = х~ 2т +' убывает, поэтому
каждое численное значение из У, она принимает лишь один
раз. Значит, если при х = хь она принимает значение Ь, то
при каждом х < хь и таком, что
хе Хи она принимает значение у'
большее, чем Ь, а при каждом
х > хь и таком, что х е Хи она
принимает значение меньшее,
чем Ъ. Следовательно, на Хх
множество всех решений нера- (oj)
венства Eа) есть интервал (хм0)
(О, хь), а множество всех реше- TST" о
ний неравенства Fа) — луч (хь,
// (хяЬ)
II
I. у^х'*", где т е N;
II. у=Ь, где Ь<0;
Объединяя решения, найден-
найденные на Xi и Хъ получаем, что в
этом случае множество всех ре-
решений неравенства Eа) есть ин-
интервал @, хь), а множество всех Рис. 157.
решений неравенства Eа) —
объединение двух лучей (— °°, 0) и (хо, + °°).
Если Ь — отрицательное число, то, рассуждая аналогич-
аналогично (рис. 157), приходим к выводу, что в этом случае
множество всех решений неравенства Eа) есть объедине-
объединение двух лучей (— оо, Хо) и @, + °°), а множество всех
решений неравенства Fа) — интервал (хо, 0), где Xq =
_ _ Ъп - Ц/Т"
V
Итак, множество всех решений неравенства Eа) есть:
1. при каждом положительном Ь — интервал
2ю-1
о,
2. при Ь — 0 — множество @, + <»);
3. при каждом отрицательном
Ь — множество
2т -1
Множество всех решений неравенства Fа) есть:
508
1. при каждом положительном Ь — множество (— «>, 0) и
•_ . Л— N
(
2. при Ь = 0 — множество (— «>, 0);
3. при каждом отрицательном Ъ — интервал
И. Пусть п = 2т, где т — некоторое фиксированное
натуральное число, тогда неравенства E) и F) принимают
вид
х~2т>Ь,
х~2т<Ъ.
E6)
F6)
Областью значений функции у = х 2т на множестве X =
= Хх и Х2, где Хх = @, + оо), а Х2 = (— °°, 0), является луч
У= @, + оо). Если Ь — неположительное число, то, учиты-
учитывая, что функция у = х~2т на множестве X положительна,
получаем, что X — множество всех решений неравенства
E6), а неравенство F6) не имеет решений (рис. 158).
у>
т
/0,1)
II
II
(-хш0) 0
III
/0,1)
(х„Ъ) II
I. у=х 2", где т е N;
II. у=Ь, где Ь=0;
III. у=Ь, где Ь<0.
Рис. 158.
(хо,О) х
I. у^х2", где т е N;
II. у=Ь, где Ь>0;
Рис. 159.
Пусть Ь — положительное число. Построим графики
функции у = х~2т и у = Ъ (рис. 159). Прямая у = Ь пересе-
пересекает график функции у = х~2т в двух точках (*<,, Ь) и (—
Ь), где Xq = 2mV^. При этом график функции у = х
~2т
лежит
509
выше прямой у = Ъ на множестве (— Хо, 0) и @, Хо) и ниже
на множестве (— °°, — Xq) u (xq, + <*>). Следовательно, эти
множества и должны быть множествами всех решений
неравенств E6) и F6). Однако это утверждение надо дока-
доказать. Рисунок показывает, что для доказательства надо
воспользоваться тем, что на множестве Хх функция у = х~Ъп
убывает, а затем воспользоваться четностью этой функции.
Рассмотрим решение неравенств E6) и F6) на множест-
множестве Х{. На множестве Х{ функция у = х~2т имеет область
значений Y= @, + °°) и убывает, поэтому каждое числен-
численное значение из Y она принимает лишь один раз. Значит,
если при х = Хо е Х{ она принимает значение Ь, то при
каждом х < Хд и таком, что х е Хх, она принимает значение,
большее чем Ь, а при каждом х > Xq и таком, что хе Хи она
принимает значение, меньшее чем Ь. Следовательно, на Х\
множество всех решений неравенства E6) есть интервал (О,
Xq), а множество всех решений неравенства F6) — луч (xq,
+ оо).
Так как функция у = х~2т является четной функцией, то
на Х2 множество всех решений неравенства E6) есть ин-
интервал (— Хо, 0), а множество всех решений неравенства
F6) — ЛУЧ (— оо, — ХЬ).
Объединяя решения, найденные на Х{ и Х2, получаем,
что в этом случае множество всех решений неравенства E6)
есть объединение двух интервалов (— Xq, 0) и @, Xq), a
множество всех решений неравенства F6) есть объедине-
объединение двух лучей (— оо, — ль) и (хь, + °°).
Итак, множество всех решений неравенства E6) есть:
1. при каждом положительном Ъ — множество
2. при каждом неположительном Ъ — множество (— «>,
0) и @, + оо).
Множество всех решений неравенства F6) есть:
1. при каждом положительном Ь — множество
2. при каждом неположительном Ъ — пустое множество.
В табл. 19 приведены итоги решения неравенств E) и F):
510
Таблица 19
x~2'"+l>b
x-2m+l<b
x~2m>b
x~lm<b
b>0
(- <*>, 0) u
Bт-\л[Г }
[- 2mVT, o] u
ufo.Wj)
@,«)
(- -, 0)
(- -, 0) u @, ~)
нет решений
b< 0
( 2m - ЦГП
U @, ~)
Г W J
(- oo, 0) U @, oo)
нет решений
Степенные неравенства. Пусть а — некоторое фиксиро-
фиксированное нецелое действительное число, тогда неравенства
ха >Ь, ' r GJ
ха < Ъ (8)
принято называть простейшими степенными неравенствами.
Поскольку свойства функции у = ха, используемые при
решении неравенств G) и (8), различны при положитель-
положительном и отрицательном нецелом числе а, то рассмотрим дв"а
случая:
I. Пусть а — положительное нецелое число. Областью
существования функции у = ха является множество всех
неотрицательных чисел, поэтому ОДЗ неравенств G) и (8)
есть множество Х= [0, + °°). Областью значений функции
у = ха на всем множестве Хесть луч Y= [0, + «=).
Если Ъ — отрицательное число, то учитывая, что на
множестве Xфункция у = ха — неотрицательна, получаем,
что X— множество всех решений неравенства G), а нера-
неравенство (8) не имеет решений (рис. 160).
511
Если b = 0, то при х = О функция у = ха принимает
значение нуль, а для всех остальных х& X эта функция
у,,
[
, где <а-любое нецелое
[ число;
II. у=Ь, где Ь<0.
Рис. 160.
(а > 1,
I. у=х", где -la-любое нецелое
\ число;
II. у=Ь, где Ь=0.
Рис. 161.
положительна, поэтому неравенство G) в этом случае спра-
справедливо при любом значении х& X, кроме х = 0, а неравен-
неравенство (8) не справедливо ни при одном значении х& X.
Значит, в этом случае множе-
множество всех решений неравенств
G) есть луч @, + «=), а неравен-
неравенство (8) не имеет решений
(рис. 161).
Пусть, наконец, Ъ — поло-
положительное число. На множест-
множестве А" функция у = ха возрастает,
поэтому каждое численное зна-
значение из Уона принимает лишь
один раз. Значит, если при
х = Xq e X она принимает зна-
значение Ь, то при каждом х > Xq и
таком, что х е X, она принима-
принимает значение большее, чем b, a
при каждом х < Xq и таком, что
х е X, она принимает значение
512
/. y=tf, где j«~ любое нецелое
\ число;
II. у=Ь, где Ь>0.
1
хс=Ьа.
Рис. 162.
I
меньшее, чем b. Следовательно, в этом случае множество
всех решений неравенства G) есть луч (х^, + °°), а множе-
множество всех решений неравенства (8) есть промежуток [0, *<,),
где *о = Ьа (рис. 162).
Итак, если а > 0, то множество всех решений неравен-
неравенства G) есть:
1. при каждом положительном Ъ — множество I Ьа, + °° к
2. при Ь = 0 — множество @, + «>);
3. при каждом отрицательном Ь — множество [0, + «>);
а множество всех решений неравенства (8) есть:
Г Г\
1. при каждом положительном Ъ — множество 10, ba t
2. при каждом неположительном Ъ — пустое множество.
И. Пусть а — отрицательное нецелое число.
Областью существования функции у = Xй является мно-
множество всех положительных чисел, поэтому ОДЗ нера-
неравенств G) и (8) есть множество Х= @, + «>). Область зна-
значений функции у = т? на всем множестве А'есть луч Y = @,
+ оо).
Если Ъ — неположительное число, то учитывая, что на
множестве X функция у = э? положительна, получаем, что
X — множество всех решений неравенства G), а неравен-
неравенство (8) не имеет решений (рис. 163).
Пусть Ь — положительное число. На множестве А"функ-
А"функция у = ха убывает, поэтому каждое численное значение из
Y она принимает лишь один раз. Значит, если при х =
— Xq е А'она принимает значение Ь, то при каждом х < Хд и
таком, что х е X, она принимает значение большее, чем Ь,
а при каждом х> Хд и таком, что хе X, она принимает
значение меньшее, чем Ь. Следовательно, в этом случае
множество всех решений неравенства G) есть интервал @,
Xfl), а множество всех решений неравенства (8) есть луч (хд,
+ «О, где Xq = Ьа (рис. 164).
Итак, если а < 0, то множество всех решений неравен-
неравенства G) есть:
1. при каждом положительном Ъ — интервал [0, Ыл
17 Алгебра, тригонометрия
и элементарные функции
2. при каждом неположительном b — множество @, + «»);
а множество всех решений неравенства (8) есть:
1. при каждом положительном b — множество iba, + « \
У' ¦
III
II
1 II
III
(хиЬ)
их < О,
I. у=?, где <а~ любое нецелое
\ число;
II. у=Ь, где Ь=0
III. у=Ь, где Ь<0
Рис. 163.
<хю0)
(а < О,
С, где <а-любое нецелое
\ число;
II. у=Ь, где Ь>0
.1
Рис. 164.
2. при каждом неположительном b — пустое множество.
В табл. 20 приведены итоги решения неравенств G) и (8):
Таблица 20
У > b (а > 0)
У < b (а > 0)
У > b (а < 0)
У < b (а < 0)
Ь>0
[о, bi)
(о, ^j
@,-)
нет решений
@,-)
нет решений
Ь<0
[0,-)
нет решений
@,-)
нет решений
Показательные неравенства. Пусть а — некоторое фик-
фиксированное положительное и не равное единице число,
тогда неравенства
514
a*>b,
(9)
(Ю)
принято называть простейшими показательными неравенст-
неравенствами. Областью существования функции у= а* является
множество всех действительных чисел, поэтому ОДЗ нера-
неравенств (9) и A0) есть множество Х= (— <», + <»). Область
значений функции у = 0х на всем множестве X есть луч
У=@, + ~).
Если Ь — неположительное число, то учитывая, что ца
множестве X функция у = 0х положительна, получаем, что
X — множество всех решений неравенства (9), а неравен-
неравенство A0) не имеет решений.
Пусть Ъ — положительное число, то рассмотрим два
случая:
II
I _-
У*
@,1)
0
1
/ П
А(хяЬ)
1
(х„,0) х
II
I. у=а, где а>1;
II. у=Ь, где ЬХ);
Ь.
(ха0) О
I. у=а, где (Хо<1;
II. у=Ь, где Ь>0;
Рис. 165.
Рис. 166.
1. Пусть а> 1. На все числовой прямой — множестве
X — функция у = а* возрастает, поэтому каждое численное
значение из У она принимает лишь один раз. Значит, если
при х = Хо е X она принимает значение Ь, то при каждом
х > *о она принимает значение большее, чем Ь, а при
каждом х < Xq она принимает значение меньшее, чем Ь.
Следовательно, в этом случае множество всех решений
515
неравенства (9) есть луч (д%, + °о), а множество всех реше-
решений неравенства A0) — луч (— «>, д%), где л<, = 1о&,6
(рис. 165).
2. Пусть 0 < а < 1. На множестве X — всей числовой
прямой — функция у = <? убывает. Поэтому, рассуждая
аналогично, получим, что в этом случае множество всех
решений неравенства (9) есть луч (— «>, д%), а множество
всех решений неравенства A0) — луч (д%, + °°), где д% =
= logo b (рис. 166).
Итак, если а > 1, то множество всех решений неравенст-
неравенства (9) есть:
1. при каждом положительном Ъ — множество (log,, Ъ,
+ оо);
2. при каждом неположительном Ь — множество (— «}
+ оо);
а множество всех решений неравенства A0) есть:
1. при каждом положительном Ъ — множество (— <»}
loge b);
2. при каждом неположительном b — пустое множество.
Если 0 < а < 1, то множество всех решений неравенства
(9) есть:
1. при каждом положительном Ъ — множество (— <*>,
loge b);
2. при каждом неположительном Ъ — множество (— «}
+ оо);
а множество всех решений неравенства A0) есть:
1. при каждом положительном Ь — множество (log0A,
+ ¦»);
2. при каждом неположительном Ъ — пустое множество.
В табл. 21 приведены итоги решения неравенств (9) и
A0):
516
Таблица 21
д*>*(а>1)
а* < Ь (а > 1)
<? > Ь @ < а < 1)
д* < * @ < а < 1)
*>0
(loga*;~)
(--;loga*)
(--;ioga*)
(log,,*;-)
* = 0
(- -; -)
нет решений
(- -; -)
нет решений
*<0
(— •»; -)
нет решений
(- -; -)
нет решений
Логарифмические неравенства. Пусть а — некоторое фик-
фиксированное положительное и не равное единице число,
тогда неравенства
logo х > b,
logo х < b
(И)
A2)
принято называть простейшими логарифмическими неравен-
неравенствами.
Областью существования функции у = log,, x является
множество всех положительных чисел, поэтому ОДЗ нера-
неравенств A1) и A2) есть множество Х= @, + «>).
Областью значений функции у = logo x на всем множе-
множестве X является вся числовая ось Y =(—«>, + «>).
Поскольку используемые при решении неравенств A1)
и A2) свойства функции у = logax различны при а>1 и
при 0 < а < 1, то рассмотрим два случая:
1. Пусть а > 1. На множестве X функция у = log,, x воз-
возрастает, поэтому каждое численное значение из Y она
принимает лишь один раз. Значит, если при х = Xq e X она
принимает значение Ь, то при каждом х > Xq и таком, что
хе X, она принимает значение большее, чем Ь, а при
каждом х< Xq и таком, что хе X, она принимает значение
меньшее, чем Ь. Следовательно, в этом случае множество
всех решений неравенства A1) есть луч (д%, + «>), а множе-
множество всех решений неравенства A2) есть интервал @, д%),
где Xq = аь (рис. 167).
2. Пусть 0 < а < 1. На множестве X функция у = loge x
убывает. Поэтому, рассуждая аналогично, получим, что в
этом случае множество всех решений неравенства A1) есть
517
интервал @, х^), а множество всех решений неравенства
A2) есть луч (хь, + <»), где Xq = аь (рис. 168).
Итак, если а > 1, то при каждом Ь множество всех
решений неравенства A1) есть множество (д*, + «>), а мно-
множество всех решений неравенства A2) есть множество
(О, а");
I. у=1о$. х, где а>1;
II. у=Ь, где Ь>0;
х„=а>
Рис. 167.
/. ?=tog, x, где (Ка<1;
II. у=Ь, где Ь<0;
Рис. 168.
если 0 < а < 1, то при каждом Ъ множество всех решений
неравенства A1) есть множество @, а*), а множество всех
решений неравенства A2) есть множество (аь, + «>).
В табл. 22 приведены итоги решения неравенств A1) и
A2):
Таблица 22
logflx>*(a>l)
\OgaX< Ь(а> 1)
logox>*@<a<l)
logox<*@<a< 1)
— оо< b<°°
(а*;~)
@;д*)
@;<Л
(a*;-)
518
Тригонометрические неравенства. Неравенства
cos х > b, sin x > b, tg x > b, ctg x > b,
cos x < b, sin x < b, tg x < b, ctg x < b.
принято называть простейшими тригонометрическими не-
неравенствами.
Сделаем несколько общих замечаний.
Пусть у = Дх) — некоторая основная элементарная три-
тригонометрическая функция с главным периодом Т, и пусть
дано неравенство
Лх)>Ь (илиЛх)<г>). A3)
Выберем промежуток длиной Т и найдем решение нера-
неравенства A3) на этом промежутке. Пусть множество всех
решений неравенства A3) на этом промежутке есть интер-
интервал Хй = (а, Р), где а < Р и р — а< Г. Тогда, используя
периодичность функции у=Дх), получим, что множество
всех решений неравенства A3) есть объединение бесконеч-
бесконечного множества всех интервалов Хк = (ос + кТ, р + кТ), где
к — любое целое число. Это бесконечное объединение
будем называть серией интервалов и в дальнейшем будем
записывать в виде: Хк = (а + кТ, р + кТ), к& Z. Таким об-
образом, будем в дальнейшем говорить, что множество всех
решений неравенства A3) есть серия интервалов Хк =
= (ос + кТ,$ + кТ),к& Z.
Заметим еще, что интервал длиной в главный период Т
можно взять любым, но обычно его выбирают таким, чтобы
он удовлетворял двум условиям: он должен содержать
промежуток, на котором для данной функции у—Ах) оп-
определена обратная тригонометрическая функция и, чтобы
множество всех решений данного неравенства на этом
промежутке представляло собой один интервал.
Пусть дано простейшее тригонометрическое неравенст-
неравенство
cosx>6. A4)
519
Функция у = cos x определена на всей числовой прямой,
поэтому ОДЗ неравенства A4) есть множество Х= (— °°,
+ °о). Областью значений функции у = cos х на множестве
Xявляется отрезок Y=[— 1; 1].
Поэтому при Ъ < — 1 неравенство A4) справедливо при
любом значении х, а при Ъ > 1 оно не справедливо ни при
одном значении х. Значит, при Ъ < — 1 множество всех
решений неравенства A4) есть вся числовая прямая, т.е.
множество (— °о, + °о), а при Ъ > 1 неравенство A4) не имеет
решений.
Если Ь = — 1, то очевидно, что неравенство A4) спра-
справедливо при любом значении х, кроме тех, при которых cos
х=— 1. Значит, при Ь = — 1 множество всех решений
неравенства A4) есть вся числовая прямая, за исключением
точек хк = к + 2пк, где к — любое целое число. Это множе-
множество можно записать в виде серии интервалов: Хк = (— я +
+ 2пк, п + 2пк), ке Z.
Пусть Ъ g (— 1; 1), для решения неравенства A4) в этом
случае надо выбрать промежуток, длиной в главный период
функции у = cos х, т.е. длиной в 2л. В качестве промежутка
длиной в 2л здесь можно взять либо промежуток [0; 2л),
либо промежуток (— л, л]. Эти промежутки длиной в
главный период функции у = cos x полностью содержат
отрезок [0, л], на котором определена обратная функция
у = arccos х.
и
I. y=cos x;
//. у=Ь, где -1<Ь<1
;t,,=arccos Ь.
Рис. 169.
Построим графики функций у = cos х и у = Ъ (рис. 169).
Из рисунка видно, что лучше взять промежуток (— л, л],
чем промежуток [0, 2л), так как в первом случае множество
520
всех решений неравенства A4) представляет собой один
интервал, а во втором случае — объединение двух интер-
интервалов. Рисунок подсказывает еще, что промежуток (— л, л]
надо разбить на два промежутка: Мх = [0, л] и М2 = (— л,
0), а потом воспользоваться четностью функции.
На отрезке Мх = [0, л] функция у = cos х имеет область
значений Y= [— 1; 1] и убывает, поэтому каждое численное
значение из У она принимает лишь один раз. Значит, если
при х = Хо е Мх она принимает значение Ъ, то при каждом
х< Xq и таком, что хеМ,, она принимает значение боль-
большее, чем Ь, а при каждом х> Xq и таком, что хе Мх, она
принимает значение меньшее, чем Ъ. Следовательно, на Мх
множество всех решений неравенства A4) есть промежуток
[0, Xq). Так как на промежутке (— л, л) функция у = cos x
является четной функцией, то на М2 = (— л, 0) множество
всех решений неравенства A4) есть интервал (— Xq, 0).
Объединяя решения, найденные на Мх и М2, получаем,
что на промежутке (— л, л] множество всех решений
неравенства A4) есть интервал (— Xq, Xq), где, как показано
в § 2 гл. VII, Xq = arccos Ъ.
Используя периодичность функции у = cos x, получим,
что множество всех решений неравенства A4) есть серия
интервалов: Хк = (— arccos Ь + 2кк, arccos Ъ + 2кк), ке Z.
Итак, множество всех решений неравенства A4) есть:
1. при каждом be (— оо, — 1) — множество (— <», + <»);
2. при Ъ = — 1 — серия интервалов Хк = (— л + 2л&, л +
+ 2л&), к е Z;
3. при каждом be (— 1; 1) — серия интервалов Хк =
= (— arccos b + 2кк, arccos Ъ + 2пк), ке Z;
4. при каждом be [1, + °°) — пустое множество.
Пусть дано неравенство
cos х < Ъ. A5)
ОДЗ неравенства A5) есть множество Х= (— оо, + оо).
Областью значений функции у = cos x на множестве X
является отрезок Y= [— 1; 1].
521
Поэтому при Ъ > 1 неравенство A5) справедливо при
любом значении х, а при Ъ <, — 1 оно не справедливо ни
при одном значении х. Значит, при Ъ > 1 множество все*
решений неравенства A5) есть множество (— <», + <»), а при
Ъ й — 1 неравенство A5) не имеет решений.
Если Ь= 1, то очевидно, что неравенство A5) справед-
справедливо при любом значении х, кроме тех, при которых
cos х = 1. Значит, при Ь= 1 множество всех решений не-
неравенства A5) есть вся числовая прямая, за исключением
точек хк = 2пк, где к — любое целое число. Это множество
можно записать в виде серии интервалов: Хк = Bпк, 2я +
+ 2пк), к в Z
Пусть Ъ е (— 1; 1). Построим графики функций у = cos jc
и у = Ъ (рис. 170). Из рисунка видно, что в качестве
промежутка длиной в 2л здесь лучше взять промежуток [0,
2л), так как в случае множество всех решений неравенства
A5) представляет собой один интервал. Рисунок подсказы-
подсказывает еще, что промежуток [0, 2л) надо разбить на два
. у=со& х;
II. у=Ь, где -1<Ь<1
Ь.
Рис. 170.
промежутка М\ = [0, л] и Мг = (л, 2л), потом воспользовать-
воспользоваться убыванием функции y = cosx на промежутке [0, л], а
затем симметрией функции у = cos x относительно верти-
вертикальной прямой, проходящей через точку (л, 0).
Рассуждая аналогично предыдущему, получаем, что на
М, множество всех решений неравенства A5) есть промеж-
промежуток (xq, л]. Учитывая, что функция у = cos x симметрична
относительно вертикальной прямой, проходящей через
точку (л, 0), приходим к выводу, что на М2 множество всех
решений неравенства A5) есть интервал (л, 2л — Xq).
522
Объединяя решения, найденные на Мх и М2, получаем,
что на промежутке [0, 2л) множество всех решений нера-
неравенства A5) есть интервал (%, 2л — %), где, как показано
в § 2 гл. VII, Xq = arccos b.
Используя периодичность функции y=cosx, получим,
что множество всех решений неравенства A5) есть серия
интервалов: Хк = (arccos Ъ + 2пк, 2л — arccos b + 2пк),
ке Z.
Итак, множество всех решений неравенства A5) есть:
1. при каждом Z>e (— «>, — 1] — пустое множество;
2. при be (— 1; 1) — серия интервалов
Хк = (arccos b + 2кк, 2л — arccos b + 2кк), ке Z;
3. при Ь= 1 — серия интервалов
Хк = Bкк, 2л + 2кк), ке Z;
4. при каждом be A, + «>) — множество (— «>, + °°).
В табл. 23 приведены итоги решения неравенств A4) и
A5).
Таблица 23
cosx> b
cosx< b
b<- 1
(- ~; ~)
нет
решений
* = - 1
(- п + 2пк,
п + 2пк),
keZ
нет
решений
- 1<Ь< 1
(— arccos b + Ink,
arccos b + 2пк),
ке Z
(arccos b + 2пк,
2л — arccos b +
+ 2nk),keZ
*=1
нет
решений
Bnk,
2л + 2я*),
keZ
Ь>1
нет
решений
(— оо; во)
Пусть даны простейшие тригонометрические неравенст-
неравенства
sin х > b,
sin x < b.
A6)
A7)
Проведя аналогичные рассуждения получим, что множе-
множество всех решений неравенства A6) есть:
523
1. при каждом Ъ е (— «>, — 1) — множество (— «>, + ~);
2. при Ь~—\, серия интервалов
= (- f + 2лА:, у + 2пк\ ке Z;
I. II
±1
(n-Xo,b)
(xmb) I Эк
II
\5 V
(х„0)
I. y=5in x;
II. у=Ь, где -КЬ<1
jco=arcsin Ь.
Рис. 171.
3. при каждом be (— 1; 1) (рис. 171) — серия интервалов
Xk = (arcsin Ъ + 2пк, л — arcsin Ъ + 2пк), ке Z;
4. при каждом be [1, + °°) — пустое множество; а мно-
множество всех решений неравенства A7) есть:
1. при каждом be (— °°, — 1] — пустое множество;
" 2, II
(-ъ-хюЬ)
\
уь
@,1)
-Зп
(х„Ь) Эк
/. y=sm x;
II. у=Ь, где -1<Ь<1
jco=arcsin b.
Рис. 172.
2. при каждом be (— 1; 1) (рис. 172) серия неравенств
Хк = (— л — arcsin b + 2nk, arcsin b + 2пк), ке Z;
3. при Ъ = 1 — серия интервалов
Л ке Z;
-Г .1».
524
4. при каждом Ъ е A, + «>) — множество (— «>, + <»).
В табл. 24 приведены итоги решения неравенств A6)
и A7).
Таблица 24
sin х > b
sinx< b
b<- 1
(— oo; oo)
нет
решений
* = - 1
Г-f+bdk;
keZ'
нет
решений
- 1<А<1
(arcsin A +
+ 2лА,
я — arcsin b +
+ 2nk),keZ
(-71-
— arcsin b +
+ 2nk,
arcsin b +
+ 2nk), keZ
нет
решений
| + 2rtV
keZ*
b>\
нет
решений
(— oo; oo)
Пусть даны простейшие тригонометрические неравенст-
неравенства
tgx>Z>,
tgx<Z>.
A8)
A9)
Областью существования функции у = tg x является вся
числовая прямая, за исключением точек хк = j + nk, где
к — любое целое число. Поэтому ОДЗ неравенств A8) и
A9) есть множество X, состоящее из всех действительных
чисел, кроме чисел хк = j + пк, где к — любое целое число.
Областью значений функции у = tg x на множестве Л1"явля-
Л1"является множество Y= (— «>, + °°).
Построим графики функций y = tgxny=b (рис. 173).
Из рисунка видно, что надо сначала рассмотреть решение
неравенств A8) и A9) на промежутке I — ?, $1 длиной в
главный период функции у = tg x. Рисунок подсказывает
еще, что на этом промежутке надо воспользоваться возрас-
возрастанием функции у = tg х.
5?5.
На промежутке [—§>§] функция у = tg x имеет область
значений Y= (— *>, + °°/ и возрастает, поэтому каждое
численное значение из Y она принимает лишь один раз.
Значит, если при х = Xq е [ — ™, f ]она принимает значение
/. v=tg x;
II. y=b; jco=arctg b.
Рис. 173.
п п
Z>, то при каждом х > Хо и таком, что х е [ — f. f I она
принимает значение большее, чем Ъ, а при каждом х/< Xq и
таком, что х е | — §> я I она принимает значение меньшее,
чем Ъ. Следовательно, на | — |, тН множество всех решений
неравенства A8) (см. рис. 173) есть интервал f-Xb, fl a
множество всех решений неравенства A9) (рис. Г74) есть
интервал [ — ^, хЛ где, как показано в § 2 гл. VII, Xq =
= arctg b.
526
/• y=tg x;
II. y=b; x,,^arctg b.
Рис. 174.
/. y=ctg jc
//. y=b; x,,=arcctg b.
Рис. 175.
Используя периодичность функции у = tg х, получим,
что при каждом Ъ множество всех решений неравенства A8)
есть серия интервалов: Хк = | arctg Ъ + пк, ^ + пк\ ке Z, а
множество всех решений неравенства A9) естьхерия ин-
интервалов Хк = | — ^ + пк, arctg 6 + пк\ ке Z.
В табл/ 25 приведены итоги решения неравенств A8)
и A9). /
Таблица 25
tgx>b
tgx<b
— <»< b<<->
arctg b + пк, ? + я* , Ле Z
— 5 + пк, arctg * + я* , к е Z
Пусть даны простейшие тригонометрические неравенст-
неравенства
ctg x > b, B0)
ctgx<6. B1)
Проведя аналогичные рассуждения получим, что при
каждом Ъ множество всех решений неравенства B0) (рис.
175) есть серия интервалов Хк = (пк, arcctg b + пк), ке Да
множество всех решений неравенства B1) (рис. 176) есть
серия интервалов Хк = (arcctg Ь + пк, п + пк), ке Z.
В табл. 26 приведены итоги решения неравенств B0)
и B1).
528
Таблица 26
ctgx>*
ctg x < b
— oo< Ь<<*>
{nk, arcctg* + nk), ke Z
(arcctgb + nk, n + nk), ke Z
Рассмотрим еще простейшие неравенства, содержащие
основные обратные тригонометрические функции.
Пусть даны простейшие неравенства
arccos х > b,
arccos x < b.
B2)
B3)
Областью существования функции у = arccos x является
отрезок [— 1; 1]. Значит, ОДЗ неравенств B2) и B3) есть
множество Х=[— 1; 1]. Областью значений функции у =
= arccos x на всем множестве А'является отрезок У= [0, я].
Поэтому при Ъ отрицательном неравенство B2) справед-
справедливо при любом значении хе X, а неравенство B3) не
529
справедливо ни при одном значении х е X; если же Ъ > л,
то неравенство B2) не справедливо ни при одном значении
х е X, а неравенство B3) справедливо при любом значении
хеХ.
Значит, при Ъ отрицательном множество всех решений
неравенства B2) есть множество [— 1; 1], а неравенство
B3) не имеет решений; при Ъ > л неравенство B2) не имеет
решений, а множество всех решений неравенства B3) есть
множество [— 1; 1].
у,
Л
@,Ь)
II
и.
(~~lt%) f
(-1,0) 0 A,0) x
I. >>=arccos x;
II. y=b, где 0<b<n;
x,=cos b.
(О.Ь)
II
а)
(-1,0) 0 A,0) x
I. ,y=arccos x;
II. y=b, где 0<Ь<к;
б)
Рис. 177.
Если Ъ — 0, то неравенство B2) справедливо при любом
значении х е X, кроме х = 1, а неравенство B3) не справед-
справедливо ни при одном значении хе X. Значит, при 6 = 0
множество всех решений неравенства B2) есть множество
[— 1; 1), а неравенство B3) не имеет решений.
Если Ъ = п, то неравенство B2) не справедливо ни при
одном значении х е X, а неравенство B3) справедливо при
любом значении хе X, кроме х = — 1. Значит, при Ь = п
неравенство B2) не имеет решений, а множество всех
решений неравенства B3) есть множество (— 1; 1].
Пусть Ъ е @, я). Функция у = arccos x на множестве X
убывает, поэтому каждое значение из Y она принимает¦¦>
лишь один раз. Значит, если при х = Xq e X она принимает
значение Ъ, то при каждом х< Xq и таком, что хе X, она]
принимает значение большее, чем Ъ, а при каждом х > х^ и.]
530
таком, что х е X, она принимает значение меньшее, чем Ъ.
Следовательно, в этом случае множество всех решений
неравенства B2) (рис. 177, а) есть промежуток [— 1, *<,), а
множество всех решений неравенства B3) (рис. 177, б)
промежуток (Хо, 1], где, как показано в § 2 гл. VII, Xq = cos b.
Итак, множество всех решений неравенства B2) есть:
1. при каждом be (— °°, 0) есть множество [— 1; 1];
2. при Ь = 0 — множество [— 1; 1);
3. при каждом b е @, я) — множество [— 1; cos b);
4. при каждом be [я, + ~) — пустое множество;
а множество всех решений неравенства B3) есть:
1. при каждом b е (— ~, 0] — пустое множество;
2. при каждом Ъ е @, я) — множество (cos b, 1];
3. при b = — множество (— 1; 1];
4. при каждом Ъ е (я, + ~) — множество [— 1; 1].
В табл. 27 приведены итоги решения неравенств B2)
и B3).
Таблица 27
arccos x> b
arccos x < b
b<0
I- i; И
нет
решений
b = 0
I- i; i)
нет
решений
0<Ь<к
[- l;cosb)
(cos b; 1]
Ь = к
нет
решений
(-1; И
b>n
нет
решений
[-1; И
Пусть даны простейшие неравенства
arcsin х > b,
arcsin x < b.
B4)
B5)
Проведя аналогичные рассуждения, получим, что мно-
множество всех решений неравенства B4) (рис. 178, а) есть:
1. при каждом be I — ~,- — множество [— 1; 1];
I 2, I
2. при Ъ = — 2 — множество (— 1; 1];
3. при каждом be \~\>%\— множество (sin b, 1];
531
4. при каждом b e \j, + <» j — пустое множество;
а множество всех решения неравенства B5) (рис. 178, б)
есть:
@,Ь)
М
/s(Xo,b) Ц
@,Ь)
О A,0) х
I. >>=arcsin x;
П.у=Ъ,где ~<
Ь.
(-1,0O
-i,-W
?¦ (х„Ь) it
О A,0) х
I. >>=arcsin дс;
П.у=Ь,где -§<*<§;
Ь.
а)
б)
Рис. 178.
1. при каждом be
2. при каждом b e
К Jt
V2
— пустое множество;
— множество [— 1, sin b)\
3. при b — 2 — множество7!— 1; 1);
4. при каждом be ||, + •»| — множество [— 1; 1].
В табл. 28 приведены итоги решения неравенств B4)
и B5).
Таблица 28
arcsinx> b
arcsin x < b
t- i; i]
нет
решений
»-!
(-1; i]
нет
решений
-§<»<§
(sinfcl]
I— 1; sin Л)
»-!
нет
решений
[-1; 1)
»>!
нет
решений
I- 1; И
532
Пусть даны простейшие неравенства
arctg х > b, B6)
arctg х < b. B7)
Областью существования функции у = arctg x является
вся числовая прямая. Значит, ОДЗ неравенств B6) и B7)
есть множество Х= (— °°; + °°). Областью значений функ-
функции .у = arctg л: на множестве X является интервал Y=
= [ — f, я 1 Поэтому при 6 < — f неравенство B6) справед-
\ 1
ливо при любом значении х е X, а неравенство B7) не
справедливо ни при одном значении хе X, если же b > |,
то неравенство B6) не справедливо ни при одном значении
хе Х,а. неравенство B7) справедливо при любом значении
хеХ
Значит, при b < — | множество всех решений неравен-
неравенства B6) есть вся числовая прямая, а неравенство B7) не
имеет решений; при b > ^ неравенство B6) не имеет реше-
решений, а множество всех решений неравенства B7) есть вся
числовая прямая.
Пусть be [ — §> § 1 Функция у = arctg x на всей числовой
прямой возрастает/ поэтому каждое значение из Y она
принимает лишь один раз. Значит, если при х = Xq e Хона
принимает значение Ь, то при каждом х > Xq она принимает
значение большее, чем Ь, а при каждом х < Xq она прини-
принимает значение меньшее, чем Ь. Следовательно, в этом
случае множество всех решений неравенства B6) (рис. 179)
есть луч (Хо, + °°), а множество всех решений неравенства
B7) (рис. 180) есть луч (— °°, Хо), где, как показано в § 2 гл.
VII, хь = tg b.
Итак, множество всех решений неравенства B6) есть:
1. при каждом be [—«.,— -5 — множество (— «>, + «>);
2' 2
533
2. при be [ — ¦?,? 1 — множество (tg b, + °°);
3. при каждом be т» + °° j ~ пустое множество; а мно-
множество всех решений неравенства B7) есть:
. y=aictg x;
II. у=Ь, где -§<b<j;
1. при каждом be
2. при каждом b e
Рис. 179.
( Л
Ь.
пустое множество;
2>j\~ множество (—
II
J^
У,
@,b)
N
(xl$i^-
0
/.y=arc
j. ттг -
К ДС
Я y=i, где ~
Рис.180.
3. при каждом be ^, + •»| — множество (— •», + •»).
В табл. 29 приведены итоги решения неравенств B6)
и B7).
534
Таблица 29
arctg x > b
arctg x < b
"-!
(- ~, -)
нет решений
.-§<»<!
(tg b; ~)
(- ~, tg b)
**§
нет решений
(- ~, + со)
Пусть даны простейшие неравенства
arcctg х > b,
arcctg x < b.
B8)
B9)
Проведя аналогичные рассуждения, получим, что мно-
множество всех решений неравенства B8) (рис. 181) есть:
(х„,Ь)\
II
I. y=arcctg x;
II. у=Ь, где <КЬ<п;
x,,=ctg b.
Рис.
У,
I
II -»^.
(хтЪ)
181.
(O,iO
@,Ь)
0
и.
/=arcctg д
у—Ь, где
x,,=ctg Ъ
и
(КЬ<п,
Рис. 182.
1. при каждом be (— °°, 0] — множество (— •», + •»);
2. при b е @, п) — множество (— ~, ctg b);
3. при каждом Ъ е [п, + <») — пустое множество;
535
а множество всех решений неравенства B9) (рис. 182)
есть:
1. при каждом Ъ е (— оо, 0] — пустое множество;
2. при каждом Ъ е @, я) — множество (ctg b, + оо);
3. при Ъ — [п, + •») — множество (— оо, + оо).
В табл. 30 приведены итоги решения неравенств B8)
и B9).
Таблица 30
arcctg х > b
arcctgx < b
bzQ
(- -, -)
нет решений
0<b<n
(- «о, Ctg Ь)
(ctg b; oo)
bZn
нет решений
(--;-)
§ 3. Преобразования неравенств
В третьем и четвертом параграфах главы VII рассматри-
рассматривались соответственно равносильные и неравносильные
преобразования уравнений. Причем в случае неравносиль-
неравносильных преобразований отмечалось, что возможны два спосо-
способа решения уравнения. Первый способ — это совершать
равносильные переходы на множестве, принадлежащем
области допустимых значений, но не обязательно совпада-
совпадающем с ней. Второй способ — это переходы к уравнению,
являющемуся следствием предыдущего, с обязательной
проверкой полученных решений.
При решении неравенств второй способ на самом деле
невозможен, так как множество всех решений неравенства
чаще всего бесконечно и в связи с этим проверка решений
практически неосуществима. Поэтому при решении нера-
неравенств надо совершать только равносильные переходы и
при этом, в основном, переходы, равносильные на множе-
множестве. При этом необходимо каждый раз отмечать на каком
множестве совершается равносильный переход.
Ниже приводятся примеры равносильных и неравно-
неравносильных преобразований неравенств. I
Преобразования, связанные с применением тождеств.;
Пусть дано неравенство i
536 \
Лх)>8(х) A)
и пусть для любого действительного х справедливо тожде-
тождественное равенство ф(х) = g(x), тогда неравенство (I)равно-
(I)равносильно неравенству
Ах) > Ф(х). B)
Это утверждение позволяет для решения неравенств раз-
различные формулы, справедливые для всех действительных
х. Примерами таких тождественных равенств являются
формулы сокращенного умножения многочленов, основ-
основное тригонометрическое тождество и ряд других формул. В
гл. III с помощью формул сокращенного умножения
многочленов уже были решены некоторые алгебраические
неравенства.
Приведем пример равносильного преобразования нера-
неравенства при помощи тождественных равенств.
Пусть дано неравенство
sin4 х > cos4 x. C)
Применяя утверждение 1 § 1, получим неравенство
cos4 х — sin4 x < О, D)
равносильное неравенству C). Используя формулу разнос-
разности квадратов, основное тригонометрическое тождество и
формулу косинуса двойного угла, можно написать следую-
следующую цепочку тождественных равенств, справедливых для
любого действительного х.
cos4 х — sin4 x = (cos2 x + sin2 x)(cos2 x — sin2 x) = cos 2x
Значит неравенство D) равносильно неравенству
cos 2x < 0.
Множество всех решений последнего неравенства есть
серия интервалов Хк = [ ^ + пк, -^ + пк 1 к е Z
537
Поскольку последнее неравенство равносильно исход-
исходному, то множество всех решений неравенства C) есть
серия интервалов Хк = I ^ + пк, -? + пк 1 к е Z
Преобразования, связанные с суперпозициями функций.
Пусть функция у = Дх) есть сложная функция у = F\g{x)],
являющаяся суперпозицией двух функций: и = g(x) — ос-
основной элементарной функции, и у = Дм), где Дм) —
квадратный трехчлен (т.е. Дм) = аи2 + Ьи + с). В таких слу-
случаях неравенство Дх) > 0 записывают в виде
a[g(x)]2 + bg(x) + c>0 E)
и называют квадратным неравенством относительно g(x).
Неравенство E) решается следующим образом.
Сначала решают квадратное неравенство
а? + Ы+с>0, F)
находят его дискриминант D= b2 — Лас. В зависимости от
дискриминанта D и коэффициента а, возможны следую-
следующие четыре случая.
1. Если а<0 и D<0, то неравенство F) не имеет
решений. Следовательно, и неравенство E) не имеет реше-
решений.
2. Если а < 0 и D > 0, то множество всех решений нера^
венства F) есть интервал (tu t2), где tx и t2 корни квадратного
трехчлена а? + Ы+ с, причем tx < t2.
В этом случае неравенство E) равносильно системе
неравенств
Ш t2,
Следовательно, множество всех решений системы и будет
в этом случае множеством всех решений неравенства E).
3. Если а > 0 и D > 0, то множество всех решений нера-
неравенства F) есть объединение двух лучей (— •», /|) и (t2, + «),
где tx и t2 корни квадратного трехчлена а? + Ы+ с, причем
tx й t2 (если D = 0, то tx = t2).
538
В этом случае неравенство E) равносильно совокупнос-
совокупности неравенств
g(x)<tu g(x)>t2.
Следовательно, множество всех решений этой совокупнос-
совокупности и будет в этом случае множеством всех решений нера-
неравенства E).
4. Если а > О и D< О, то множество всех решений нера-
неравенства F) есть вся числовая прямая.
В этом случае множество всех решений неравенства E)
есть ОДЗ неравенства E), т.е. область существования функ-
функции у = g(x).
Приведем примеры.
Пусть дано неравенство
4 cos2 2х + 8 cos 2х — 5 < 0. G)
Это неравенство есть квадратное неравенство относитель-
относительно cos 2x Решая неравенство
4Z2 + 8/ - 5 < 0,
получаем, что множество всех его решений есть интервал
— т, т I Следовательно, неравенство G) равносильно сис-
2' 2j
теме неравенств
|cos2x> —|,
1cos2x<j.
Множество всех решений первого неравенства этой сис-
системы есть вся числовая прямая.
Множество всех решений первого неравенства есть
серия интервалов Хк = (j + пк, -?¦ + пк L к е Z
Значит, множество всех решений исходного неравенства
G) есть серия интервалов Хк = || + пк, ^ + я^I ke Z.
Пусть дано неравенство ^ '
539
4* - 3 • Т + 2 > 0. (8)
Это неравенство есть квадратное неравенство относитель-
относительно Т. Решая неравенство
Z2 — 3/ + 2 > 0,
получаем, что множество всех его решений есть объедине-
объединение двух лучей (— °°, 1) и B, + «>). Следовательно, неравен-
неравенство (8) равносильно совокупности неравенств
Г <1, Т > 2.
Множество всех решений первого неравенства этой со-
совокупности есть промежуток (— <», 0).
Множество всех решений второго неравенства — про-
промежуток A, + оо).
Значит, множество всех решений исходного неравенства
(8) есть множество (— «>, 0) и A, + °°).
Отметим, что приведенное выше утверждение о решении
квадратного неравенства относительно g(x) остается спра-
справедливым и в том случае, когда функция и = g(x) не явля-
является основной элементарной функцией.
Преобразования, связанные с логарифмическими и триго-
тригонометрическими формулами. Поскольку формулы, отмечен-
отмеченные в § 4 гл. VII, можно применять при решении нера-
неравенств лишь на том множестве изменения неизвестной, на
котором одновременно имеют смысл и левая и правая
части применяемой формулы, то неравенства, при реше-
решении которых хотят воспользоваться той или иной форму-
формулой, обычно решают по такой схеме:
1. Находят ОДЗ неравенства.
2. Разбивают ОДЗ на два множества Мх и М2 (М, — вся
та часть ОДЗ, где одновременно имеют смысл обе части
применяемой формулы, М2 — та часть ОДЗ, которая оста-
остается после выделения множества Л/,).
3. Решают неравенство на множестве Мх (учитывая, что
преобразование неравенства с помощью этой формулы есть
равносильное преобразование на множестве Мх).
4. Решают неравенство на М2.
540
5. Объединяют множества решений, найденные на Mi и М2,
и тем самым, получают множество всех решений исходного
неравенства.
Решим по этой схеме неравенство
log2(x2) + log2(x4)>3. (9)
ОДЗ этого неравенства есть множество (— «>, 0) и @, + <»).
Разобьем ОДЗ не два множества: Л^ = @, +»)и?2 = (- «>,
0) и решим неравенство (9) на каждом из этих множеств.
На множестве М] справедливы тождественные равенства
log2 (х2) = 2 log2 х, log2 (x4) = 4 log2 x
Значит, на А^ неравенство (9) равносильно неравенству
log2x>l/2.
Решая это простейшее неравенство, получаем, что множе-
множество всех его решений есть промежуток (VT, + <*>). Посколь-
Поскольку этот промежуток содержится в множестве Мь то мно-
множество всех решений неравенства (9) на Л^ есть промеж-
промежуток (VT, + о»).
На множестве М2 справедливы тождественные равенства
log2 (х2) = 2 log2 (- x), log2 (x4) = 4 log2 (- x).
Значит, на М2 неравенство (9) равносильно неравенству
log2 (- х) > 1/2.
Решая это простейшее неравенство, получаем, что множе-
множество всех его решений есть промежуток (— ~, — л/2).
Поскольку этот промежуток содержится в множестве М2,
то множество всех решений неравенства (9) на М2 есть
промежуток (— оо, — л/2).
Объединяя множества решений, найденные на М} и М2,
получаем, что множество всех решений неравенства (9)
есть множество (— ~, — л/2) u (V2~, + °°).
Преобразования, связанные с возведением в натуральную
степень. Пусть дано неравенство
541
Ax)>g(x) A0)
Замена этого неравенства неравенством
[Ах)Г > [g(x)Y (И)
(где п — фиксированное натуральное число и п > 2) назы-
называется возведением уравнения в натуральную степень п.
На основании утверждения 5 § 1 неравенства A0) и A1)
равносильны только на том множестве, на котором одно-
одновременно обе функции у =Лх) и у = g(x) неотрицательны.
Поэтому возведением в натуральную степень неравенства
обычно решают по такой схеме:
1. Находят ОДЗ неравенства, которое надо решить.
2. Разбивают ОДЗ на два множества Мх и М2 Шх — вся
та часть ОДЗ, где одновременно обе части неравенства
неотрицательны, М2 — вся та часть ОДЗ, которая остается
после выделения множества Мх).
3. Решают неравенство на множестве Мх (учитывая, что
возведение в степень п есть равносильное преобразование
на этом множестве).
4. Решают неравенство на М2.
5. Объединяют множества решений, найденные на Мх и Мъ
и тем самым, получают множество всех решений исходного
неравенства.
Решим по этой схеме неравенство
\х-4\>6 + х. A2)
ОДЗ этого неравенства — вся числовая прямая. Разобьем
ОДЗ на два множества: Мх = [— 6, + «>) и М2 = (— °°, — 6)
и решим неравенство A2) на каждом из этих множеств.
На множестве Мх обе части неравенства A2) неотрица-
неотрицательны, поэтому по утверждению 5 § 1 на этом множестве
неравенство A2) равносильно неравенству
(х - ЛJ > F + х)\
Множество всех решений последнего неравенства есть
промежуток (— оо, — 1). Из этого промежутка в множестве
Л/, содержится лишь промежуток [— 6, — 1). Поэтому
542
множество всех решений неравенства A2) на М, есть
промежуток [—6,-1).
Очевидно, что на множестве М2 левая часть неравенства
A2) положительна, а правая — отрицательна. Поэтому
множество всех решений неравенства A2) на М2 есть все
множество Мг.
Объединяя множества всех решений, найденные на М\
и М2, получаем, что множество всех решений неравенства
A2) есть промежуток (— «>, — 1).
Наиболее часто возведение в натуральную степень при-
применяется при решении следующих неравенств.
Пусть т — фиксированное натуральное число и пусть
даны неравенства
A3)
A4)
Неравенства типа A3) обычно решают по такой схеме:
1. Находят ОДЗ неравенства.
2. Разбивают ОДЗ на два множества Мх и Мг (Л^ — вся
та часть ОДЗ, где функция у = <р(;с) неотрицательна; М2 —
вся та часть ОДЗ, где функция у = <р(;с) отрицательна).
3. Решают на М\ неравенство fix) > [фС*)]2, равносильное
на этом множестве неравенству A3).
4. Отмечают, что на М2 множество всех решений нера-
неравенства A3) совпадает с множеством М2.
5. Объединяют множества всех решений неравенства fix) >
> [<p(x)]2m на Mi и множество М2, и тем самым, получают
множество всех решений неравенства A3).
Неравенства типа A4) решают по такой схеме:
1. Находят ОДЗ неравенства.
2. Разбивают ОДЗ на два множества Мх и М2 (Л^ — вся
та часть ОДЗ, где функция у = <р(х) положительна; М2 —
вся та часть ОДЗ, где функция у = <р(х) неположительна).
3. Решают на множестве Л/, неравенство fix) < [ц>(х)]2т,
равносильное на этом множестве неравенству A4).
4. Отмечают, что на множестве М2 нет решений нера-
неравенства A4).
543
5. Выписывают множество всех решений неравенства
J(x) < [<р(х)]2|Я на Мх; это множество и будет множеством
всех решений неравенства A4).
Покажем теперь на конкретных примерах, как решать
неравенства по этим схемам.
Пусть дано неравенство
-Jx~+2 >х. A5)
ОДЗ этого неравенства есть промежуток [— 2, + «>). Разо-
Разобьем ОДЗ на два множества: М, = [0, + «>) и М2 = [— 2, 0)
и решим неравенство A5) на каждом из этих множеств.
На множестве Мх обе части неравенства A5) — неотри-
неотрицательны, поэтому по утверждению 5 § 1 на этом множестве
неравенство A5) равносильно неравенству
х + 2 > х1.
Применяя теперь утверждение 1 § 1, получаем, что на
множестве Мх неравенство A5) равносильно неравенству
х2 - х - 2 < 0.
Множество всех решений последнего неравенства есть
интервал (— 1, 2). Из этого интервала в множестве Л/,
содержится лишь промежуток [0, 2). Поэтому множество
всех решений неравенства A5) на Мх есть промежуток [0,
2). Очевидно, что на множестве М2 левая часть неравенства
A5) неотрицательна, а правая — отрицательна, поэтому
множество всех решений неравенства A5) на М2 есть все
множество М2.
Объединяя множества всех решений, найденные на Л/,
и М2, получаем, что множество всех решений неравенства
A5) есть промежуток [— 2, 2).
Пусть дано неравенство
х+1>л/хТТ. A6)
ОДЗ этого неравенства есть промежуток [— 3, + «>). Разо-
Разобьем ОДЗ на два множества: М} = (— 1, + «>) и М2 = [— 3,
544
— 1] и решим неравенство A6) на каждом из этих мно-
множеств.
На множестве Мх обе части неравенства A6) неотрица-
неотрицательны, поэтому по утверждению 5 § 1 на этом множестве
неравенство A6) равносильно неравенству
(х + 1J>х+3.
Применяя теперь утверждение 1 § 1, получаем, что на
множестве Мх неравенство A6) равносильно неравенству
х2 + х-2>0.
Множество всех решений последнего неравенства есть
множество (— «., — 2) и A, + «>). Поэтому множество всех
решений неравенства A6) на М( есть интервал A, + «>).
Очевидно, что на множестве М2 левая часть неравенства
A6) неположительна, а правая — неотрицательна, поэтому
на М2 неравенство A6) не имеет решений.
Итак, множество всех решений неравенства A6) есть
промежуток A, + оо).
Преобразования, связанные с освобождением от знамена-
знаменателя.
Пусть дано неравенство
? A7)
Такие неравенства решаются по следующей схеме:
1. Находят ОДЗ неравенства.
2. Разбивают ОДЗ на два множества Мх и М2 (Мх — вся
та часть ОДЗ, где функция у = <р(х) положительна; М2 —
вся та часть ОДЗ, где функция у = <р(;с) отрицательна).
3. Решают на множестве Мх неравенство j{x) > g(x)<p(x),
равносильное на этом множестве неравенству A7) (см. § 1,
утверждение 7а).
4. Решают на множестве М2 неравенство Дх) < g(x)<p(x),
равносильное на этом множестве неравенству A7) (см. § 1,
утверждение 76).
18 Алгебра, тригонометрия
и элементарные функции
5. Объединяют множества решений, найденные на Мх и М2,
и тем самым, получают множество всех решений неравенст-
неравенства A7).
Решим по этой схеме неравенство
ОДЗ этого неравенства есть множество @; 1)иA, + «).
Разобьем ОДЗ на два множества: М2 = @; 1) и М, = A, + «).
На множестве Л/, функция у = log3 х положительна, поэто-
поэтому (см. § 1, утверждение 7а) на этом множестве неравенство
A8) равносильно неравенству
2 - (log3 хJ < log3 х A - log3 x),
которое можно записать в виде log3 x > 2. Множество всех
решений этого простейшего неравенства есть промежуток
(9, + оо). Поскольку этот промежуток содержится в множе-
множестве Ми то множество всех решений неравенства A8) на
Мх есть промежуток (9, + °°). На множестве М2 функция
у = log3 х отрицательна, поэтому (см. § 1, утверждение 76)
на этом множестве неравенство A8) равносильно неравен-
неравенству
2-(log3xJ>log3x(l-log3x),
которое можно записать в виде log3 x < 2. Множество всех
решений этого простейшего неравенства есть интервал @;
9). Из этого интервала в множестве М2 содержится лишь
интервал @; 1). Поэтому множество всех решений неравен-
неравенства A8) на М2 есть интервал @; 1).
Объединяя множества всех решений, найденные на Мх
и М2, получаем, что множество всех решений неравенства
A8) есть множество @; 1) и (9; + «.).
Метод интервалов. Решение неравенства
546
в случае, есть flx), g(x) и <р(х) будут многочлены, можно
провести иначе, а именно, неравенство A7) надо сначала
переписать в равносильном виде
fix) — <P(x)g(X) > q
Затем воспользоваться утверждением 7 § 1, умножить не-
неравенство A9) на ф2(х) и записать неравенство
ФМх) - ф(х)«(х)] > 0, B0)
равносильное неравенству A9) на его ОДЗ. Наконец, не-
неравенство B0) решить методом интервалов (см. § 2 гл. III).
Множество всех решений неравенства B0) и будет множе-
множеством всех решений неравенства A7).
Пусть дано неравенство
%fi<* B1)
Перенося х в левую часть неравенства, перепишем это
неравенство в равносильном виде
<0.
х+ 1
Пользуясь утверждением 7 § 1 получаем неравенство
-3(х+1) (* + })< 0,
равносильное неравенству B1) на его ОДЗ. Решая это
неравенство методом интервалов, получаем ответ: множе-
множество всех решений неравенства B1) есть множество (— °°,
Г
Преобразования, связанные с сокращением неравенства на
общий множитель. Пусть дано неравенство
Часто это неравенство заменяют неравенством
is* 547
Ax)>g(x),
т.е. сокращают исходное неравенство на общий множитель
Ф(х). Это грубая ошибка. Подобные неравенства надо ре-
решать только следующим образом:
1. Найти ОДЗ неравенства ф(х)Дх) > <p(x)g(x).
2. Переписать неравенство в равносильном виде
- «<*)] > о.
3. Перейти к совокупности двух систем неравенств
ГФ(х) > 0, Ых) < О,
f Ф(х) >
которая равносильна неравенству ф(х)Дх) > <p(x)g(x) на его
ОДЗ.
4. Решить эту совокупность на ОДЗ исходного неравенст-
неравенства.
Множество всех решений и будет множеством всех ре-
решений неравенства ф(х)Дх) > <p(x)g(x).
Решим этим способом неравенство
4х logs х > (х2 + 3) logs x. B2)
ОДЗ этого неравенства — множество М = @, + «>). Пере-
Перепишем неравенство B2) в равносильном виде
Dх - х2 - 3) logs х > 0
и решим на множестве М совокупность двух систем нера-
неравенств:
J4x-x2-3>0, J4x-x2-3<0,
[log5x>0, [log5x<0,
Множество всех решений первой системы есть интервал
A; 3), а множество всех решений второй системы есть
интервал @; 1). Поскольку и интервал A; 3) и интервал @;
1) содержатся в ОДЗ исходного неравенства, то получаем,
548
что множество всех решений неравенства B2) есть множе-
множество @; 1) и A; 3).
Преобразования, связанные с логарифмированием нера-
неравенств. Пусть а — фиксированное положительное и не
равное единице число.
Пусть дано неравенство
Ax)<g(x). B3)
Замена этого неравенства неравенством
logaAx)<logag(x), B4)
или неравенством
B5)
называется логарифмированием неравенства.
На основании утверждения 6 § 1 при а > 1 неравенства
B3) и B4) [а при 0 < а < 1 неравенства B3) и B5)] равно-
равносильны только на том множестве, на котором одновремен-
одновременно обе функции у=Ах) иу = g(x) положительны. Поэтому
применением логарифмирования неравенства обычно ре-
решают по такой схеме:
1. Находят ОДЗ неравенства.
2. Разбивают ОДЗ на два множества Мх и М2 (М\ — вся
та часть ОДЗ, на которой положительны обе части данного
неравенства, М2 — та часть ОДЗ, которая остается после
выделения множества М{).
3. Решают неравенство на множестве Мх (учитывая, что
логарифмирование есть равносильное преобразование на
этом множестве).
4. Решают неравенство на М2.
5. Объединяют множества решений, найденные на Л/, и Мъ
и тем самым, получают множество всех решений исходного
неравенства.
Решим по этой схеме несколько неравенств.
Пусть дано неравенство
2
X — X
B6)
549
ОДЗ этого неравенства есть множество М= [О, + «>). По-
Поскольку на множестве М обе части неравенства B6) поло-
положительны, то на основании утверждения 6 § 1 неравенство
B6) равносильно на М неравенству
которое равносильно на М неравенству
х2 -х<{\-х)\о%г2.
Множество всех решений последнего неравенства есть
интервал (— log3 2; 1). Из этого интервала в множестве М
содержится лишь промежуток [0; 1). Значит, множество
всех решений неравенства B6) есть промежуток [0; 1).
Пусть дано неравенство
¦(л? + х+1)х<1. B7)
ОДЗ неравенства B7) есть вся числовая прямая, так как
квадратный трехчлен х2 + х + 1 положителен для любого
действительного х.
Логарифмируя неравенство B7) по любому основанию,
например, по основанию 10, получим на основании ут-
утверждения 6а § 1, что неравенство B7) равносильно нера-
неравенству
Используя свойства логарифмов, перепишем это неравен-
неравенство в виде
Это неравенство равносильно совокупности двух систем
неравенств:
х < 0,
550
которая, в свою очередь, равносильна следующей совокуп-
совокупности двух систем неравенств:
Решая сначала первую систему, приходим к выводу, что
она не имеет решений, так как множество всех ее решений
есть пересечение двух множеств: @, + °о) — множества всех
решений первого неравенства и (— 1; 0) — множества всех
решений второго неравенства, а это пересечение пусто.
Множество всех решений второй системы есть проме-
промежуток (— «о, — 1). Следовательно, множество всех решений
неравенства B7) есть промежуток (— «>, — 1).
Отметим, что аналогично решаются неравенства более
общего вида
WT* < Ъ, B8)
где Ъ — данное положительное число. А именно, сначала
ищут ОДЗ неравенства, затем выбирают любое число а > 1.
Тогда на ОДЗ неравенство B8) равносильно неравенству
Ф(х) loga Дх) < loga Ь.
Далее остается решить последнее неравенство на ОДЗ
исходного неравенства B8).
Заметим еще, что простейшее показательное неравенст-
неравенство а>Ь при помощи логарифмирования неравенств
можно заменить равносильным ему алгебраическим нера-
неравенством первой степени:
1) при а > 1 неравенством х > loga b,
2) при 0 < а < 1 неравенством х < loga Ъ,
для которых легко выписываются множества всех их реше-
решений. Аналогично можно поступить и с неравенством <f < b.
Преобразования, связанные с потенцированием нера-
неравенств. Пусть а — некоторое фиксированное положитель-
положительное, не равное единице число.
Пусть дано неравенство
551
logaAx)<log.g(x). B9)
Замена этого неравенства неравенством
Ах) < &х)
или неравенством
Ax)>g{x)
называется потенцированием неравенства.
Учитывая утверждения 6а и 66 § 1, неравенства вида B9)
обычно решают по такой схеме:
1. Находят ОДЗ неравенства.
2. Решают неравенство на ОДЗ (учитывая, что потенци-
потенцирование есть равносильное преобразование на этом мно-
множестве).
Решим по этой схеме неравенство
logi (х2 - 4) > logi Dx - 7). C0)
ОДЗ этого неравенства определяется условиями:
Ux - 7 > 0,
[х2 - 4 > 0,
т.е. для нахбждения ОДЗ надо решить эту систему нера-
неравенств. Решая ее, получим, что ОДЗ есть промежуток B,
+ °°). Учитывая утверждение 66, получаем, что на ОДЗ
неравенство C0) равносильно неравенству
х2 - 4 < 4х - 1.
Решая это квадратное неравенство, находим множество
всех его решений — интервал A; 3). Из этого интервала в
ОДЗ неравенства C0) содержится лишь интервал B; 3).
Значит, множество всех решений неравенства C0) есть
интервал B; 3).
Рассмотрим еще некоторые частные случаи потенциро-
потенцирования неравенств.
552
Легко видеть справедливость следующих утвержде-
утверждений:
1. Пусть а — некоторое фиксированное число такое, что
а > 1, тогда неравенство logo/(x) > Ъ равносильно неравенст-
неравенству Лх) **¦ я*> а неравенство logfl fix) < b равносильно системе
неравенств
[Лх)>0,
или, что то же самое, двойному неравенству О < fix) < аь.
2. Пусть а — некоторое фиксированное число такое, что
О < а < 1, тогда неравенство logo^x) < Ъ равносильно нера-
неравенству fix) > аь, а неравенство logfl fix) > b равносильно сис-
системе неравенств
или, что то же самое, двойному неравенству 0 < fix) < аь.
Рассмотрим примеры.
Пусть дано неравенство
log| (х2 - Ъх + 5) < - 1.
На основании только что приведенного утверждения это
неравенство равносильно неравенству
у2 ^Y + S > Ш
которое равносильно неравенству
х2 — Зх + 2 > 0.
Множество всех решений последнего неравенства, а значит
и исходного неравенства, есть множество (— «>, 1) и B,
+ ~).
Пусть дано неравенство
553
log2 sin x < — j.
На основании только что приведенного утверждения это
неравенство равносильно системе неравенств
sin х > О,
VI
или, что тоже самое, двойному неравенству
О < sin х < --.
2*.
я/
II N.
О я
2
I. >=sin x;
II. у=0;
Т^
III. у
Л;
_I
Рис. 183.
Множество всех решений этого двойного неравенства
(рис. 183), а значит и исходного неравенства, есть две серии
интервалов:
ке Z;
гЪпк
Xm = \-r-+ 2кш,к + 2кш imeZ
Отметим, что потенцирование неравенств часто приме-
применяется и в более сложных ситуациях, чем рассмотренные
выше.
Пусть дано неравенство
554
2+ х)<1, C1)
ОДЗ этого неравенства определяется условиями
т.е. для нахождения ОДЗ надо решить эту систему нера-
неравенств. Решая ее, находим, что ОДЗ есть множество М =
= (— 2; — 1) и (— 1; 0) и @; 1) и A; + <~). Разобьем ОДЗ
на два множества: Мх — (— 2; — 1) и A, + °о) и М2 = (— 1;
0) и @; 1).
На множестве М, х > 1, поэтому на множестве Мх нера-
неравенство C1) по утверждению 6а § 1 равносильно неравен-
неравенству
2 + х < х2.
Решая это квадратное неравенство, находим, что множест-
множество всех его решений есть множество (— ~, — 1) и B, + «»).
Из этого множества в Мх содержится лишь множество (— 2;
— 1) и B, + оо). Следовательно, множество всех решений
неравенства C1) на Мх есть множество (—2; — 1) и B;
+ оо).
На множестве М2 0 < х2 < 1, поэтому на множестве М2
неравенство C1) по утверждению 66 § 1 равносильно
неравенству
2 + х > х1.
Решая это квадратное неравенство, находим, что множест-
множество всех его решений есть интервал (— 1; 2). Из этого
интервала в М2 содержится лишь множество (— 1; 0) и @;
1). Следовательно, множество всех решений неравенства
C1) на М2 есть множество (— 1; 0) и @; 1).
Объединяя множества решений, найденные на Мх и М2,
получаем, что множество всех решений исходного неравен-
неравенства C1) есть множество (— 2; — 1) и (— 1; 0) и @; 1) и B;
+ оо).
555
Аналогично решается и неравенство вида
log**, *(*)<*, C2)
где b— данное число. А именно, ищется ОДЗ неравенства.
Затем ОДЗ разбивается на два множества: Мх — всю ту
часть ОДЗ, где ф(дс) > 1, и М2 — всю ту часть ОДЗ, где 0 <
< ф(дс) < 1. Тогда неравенство C2) на множестве Мх равно-
равносильно неравенству
g(x) < [Ф(х)]А, C3)
а на множестве М2 неравенство C2) равносильно неравен-
неравенству
g(x) > [Ф(х)]А. C4)
Далее остается решить неравенства C3) и C4) на соответ-
соответствующих множествах и объединить получившиеся реше-
решения. Заметим, что простейшее логарифмическое неравен-
неравенство logfl х > b, при помощи потенцирования неравенств,
можно заменить при а > 1 равносильным ему алгебраичес-
алгебраическим неравенством первой степени х > аь, а при 0 < а < 1
равносильным ему двойным неравенством 0 < х < аь, для
которых легко выписываются множества всех их решений.
Аналогично можно поступить и с неравенством log, x <
<Ь.
Преобразования, связанные с освобождением от знака
абсолютной величины. Пусть дано неравенство
C5)
где fj(x), Мх), ..., fn(x), g[x) — многочлены, целые относи-
относительно X.
Для решения таких неравенств обычно употребляется
метод интервалов. Описание этого метода для неравенств
практически полностью повторяет описание этого метода
для уравнений (см. § 4 гл. VII), а именно, пусть дано
неравенство C5). Сначала решается совокупность уравнений
556
= О, Мх) = О fjx) = О Ux) = 0. C6)
Затем на числовой прямой отмечаются все корни этой сово-
совокупности уравнений.
Таким образом, вся числовая прямая разбивается на не-
некоторое число промежутков, затем на каждом таком про-
промежутке неравенство заменяется на другое неравенство, не
содержащее знаков абсолютной величины и равносилыюе
'исходному неравенству на этом промежутке. На каждом
таком промежутке отыскивают все решения того неравен-
неравенства, которое на этом промежутке получается, а затем
отбираются из них те, которые попадают в данный про-
промежуток. Они и есть множество всех решений исходного
неравенства на рассматриваемом промежутке. Наконец,
для того чтобы выписать множество всех решений исход-
исходного неравенства, собирают вместе (объединяют) все его
решения, найденные на всех промежутках.
Продемонстрируем применение метода интервалов на
примере решения неравенства
х2 + (х+1|-3>0. C7)
В этом случае совокупность уравнений C6) состоит из
одного уравнения
х + 1 = О,
имеющего единственный корень х, = — 1. Значит, число-
числовая прямая разбивается на два промежутка: (— °°; — 1) и
[— 1; + °о). Рассмотрим решение неравенства C7) на каж-
каждом из этих промежутков.
1. На промежутке (¦— <», — 1) по определению абсолют-
абсолютной величины
Поэтому на этом промежутке неравенство C7) равносиль-
равносильно неравенству
х1 - (х + 1) - 3 > 0.
557
Решая это квадратное неравенство, получаем, что множе-
множество всех его решений есть множество /—«»;¦
L + VI7 "\ т* ^
—2—; + °° I Из этого множества в рассматриваемом
) (
промежутке содержится лишь промежуток — —,
Следовательно, множество всех решений неравенства C7)
на промежутке (— °°; — 1) есть промежуток — —,
2. На промежутке [— 1; + ~) по определению абсол
ной величины
\х + 1| = (х + 1).
Поэтому на этом промежутке неравенство C7) равносиль-
равносильно неравенству
х2 + (х + 1) - 3 > 0.
Решая это квадратное неравенство, получаем, что множе-
множество всех его решений есть множество (— ~; — 2) и A;
+ °°). Из этого множества в рассматриваемом промежутке
содержится лишь промежуток A; + <»). Следовательно,
множество всех решений неравенства C7) на промежутке
[— 1; + «о) есть промежуток A; + «»).
Объединяя множества решений, найденные на рассмот-
рассмотренный промежутках, получаем, что множество всех реше-
решений неравенства C7) есть множество (— °°;^~—Iй О>
2
+ оо).
В заключение отметим, что выше рассмотрены не все
преобразования неравенств, а лишь наиболее часто исполь-
используемые. Кроме того, отметим, что при решении неравенств
часто приходится применять не одно, а несколько преобразо-
преобразований.
Проиллюстрируем это на двух следующих примерах.
Пусть дано неравенство
4V^7_6 2л/^7+8<0 C8)
558
Это неравенство является квадратным относительно
2 . Решая неравенство
получаем, что множество всех его решений есть интервал
B; 4). Следовательно, неравенство C8) равносильно систе-
системе неравенств
C9)
Решим сначала первое неравенство этой системы
2л?Т7<4 D0)
ОДЗ этого неравенства есть множество М=[— 3; 3]. На
этом множестве обе части неравенства D0) положительны,
поэтому логарифмируя неравенство D0) по основанию 2,
получим неравенство
равносильное неравенству D0) на множестве М. На мно-
множестве М обе части неравенства D1) неотрицательны,
поэтому возводя в квадрат это неравенство, получим нера-
неравенство
9 - х2 < 4,
равносильное неравенству D1) на множестве М. Решая это
простейшее неравенство, получаем, что множество его
решений есть множество (— °°, — V5) u (VfT, + °°). Из этого
множества в Мсодержится лишь множество [— 3; — V5) и
и (VfT; 3]. Значит, множество всех решений неравенства
D0) есть множество [— 3; — V5) u (VT; 3].
Решая аналогично второе неравенство системы C9),
получим, что множество всех его решений есть интервал
559
(— 2VX; 2V2). Следовательно, множество всех решений
системы C9) есть множество (— 2VT; — V5) u (VT; 2V2).
Пусть дано неравенство
tg-4>i.
1+Х
D2)
Функция у = tg —-Ц есть суперпозиция двух функций: про-
1 +х
стейшей элементарной функции у = tg v и функции v =
= 1
1+х2'
Решим сначала простейшее неравенство
tgv> 1.
II
Рис. 184.
Множество всех решений этого неравенства (рис. 184) есть
серия интервалов [ - + пк, ^ + пк I к е Z
Значит, исходное неравенство D2) равносильно беско-
бесконечной совокупности систем неравенств
560
If)'.
1 к <43>
l+x2 4 '
где к — любое целое число. (Проведенное преобразование
неравенства есть пример преобразования, не рассмотрен-
рассмотренного ранее вида).
Рассмотрим все системы в бесконечной совокупности
D3).
При любом положительном к ни одна из этих систем не
имеет решения, так как j + пк > 1 при любом натуральном
к, а ——2 ^ 1 при любом действительном х и поэтому второе
+х
неравенство в системе D3) не имеет решений.
При отрицательном к ни одна из систем также не имеет
решения, так как —Ч > 0 при любом действительном х, а
1 +.Х
+ пк < 0 при любом отрицательном целом к и поэтому
первое неравенство в системе D3) не имеет решений.
При к = 0 имеет систему
D4)
Поскольку —^-j й 1 < % при любом действительном х,
1 +х 1
множеством всех решений первого уравнения этой систе-
системы является вся числовая прямая. Для всех действительных
х функция у = 1 + х2 положительна, поэтому, освобождаясь
от знаменателя, получим неравенство
равносильное второму неравенству системы D4). Множе-
Множество всех решений этого простейшего неравенства есть
561
Г_ л/177, VIT
интервал I — \— — 1, "V— — 1 L Значит, множество всех ре-
Vя n )
шений системы D4) есть этот интервал.
Подводя итог, получаем, что множество всех решений
исходного неравенства D2) есть интервал
( WD — тс) тс УD — тс) тс'
УПРАЖНЕНИЯ
Является ли число (— 4) решением следующего неравенства A — 48):
хBх+1)(х-5) (х-1J(-х-5)C + хK
1' (х+3)(Зх-4) <0>2' B)(> 3) '
3
- Sx- lij (х- 2J A -х)
0 4 j ^Q
Sx-n ~ ' Y_ зх2 + 5х - 2х)(х+ 3) (х - 2)
+2 (х 2) (х7)
. х-2 х+2 (х- 2) (х-7)
5' Зх- 1 " 2х+ Г (х- 6) (х- 5) " "
8 ;8.1+А<-
' х— 1 х+1 х1— 1
• 9. |9-2х|?|4-Зх! + 1х-5|;10.
A х2 —5х+4
12 - х| - |х+ 3| S 4;
х2-4
13. Vx+T>x+1; 14.x-6<Vxz-7x+8;
17. л/25 - х2 > 3 - л/х2 + 7х; 18. V- 1 - х - V^-7 < VI^T;
х+ 1
F + х) V7 — х + G — х)
^-x 7.
6'
20. V5 (x+ 8) + 7 V2 (8 +x) + V5 (x+ 8) - 7 V2 (x+ 8) 2 4;
Л'3)
21. 4;
23.
x-l
si;
25.
26.
(М
562
29. lg 2 + lg D-*-' + 9)> 1 + lg B~x-' +
30. lg (x2 - l)<,lg (x- IJ + lg [x- 2|;
1
1
Vl — x — 1 VI—x + 1
32. log^ log5 fVx2 + 1 + x) > log3 log^ Nx2 + 1 — x\
33. log2 log3 ^
34
l+log_x3
2-log3(-x)'
36. lg\(x+l) <V2lg(-x-l);
37. 3sin2x— 1 >sinx + cosr, 38. |tgx + ctgx|<4VT;
39. 4 [x3 — 2x+ ll(sinx + 2 cosx) s 9 Ix3 — 2x+ 1|;
42. 4 sin x sin 2x sin 3x < sin 4r,
43. V3 + 2 tg x — ctg~ 2 x s 2 + ^ tg x,
44. cos x • sin ( sin x) + sin x • cos ( sin x) > 0;
я
> —;
4 t ., . 3
45. arccos ¦; < -z; 46. arcsin
1х 2
1-х 2
5
хг
47. arctg2 x — 4 arctgx+ 3 > 0; 48. 5 arcctgx — arcctg2x — 4 ? 0?
Является ли число -г решением следующей системы неравенств D9
59):
49К-29х + 30,0,50
[5x + 2>3x2;
5x ? 4 + x2,
19
51.
Зх+1
l-2x
<-2;
52.
3Vx+6-x2>2-4x,
563
54.
55.
56.
58.
log2(9-2*]>
>
59.
x2-2x-3S<0,
—9 + Vx —V6x —9
,x+l
- 1 1 - 3х
-г^з-г,
57.
lQgx2
-
16
108,3
V6x+1 +V4x+2
l<log
4х-2
ri|x-2|?
[x-51-3
Равносильны ли следующие два неравенства F0 — 104):
.л х(х+2)
б0-7Т
х2 х2
62. — < 0 и х < 0; 63. — ? О и х ? О;
X X
64.х+2>4их + 2 + —Ц->4+ *
65. х+2>4 их+2 +
х+4
1
х+4'
1
х-10 х-10'
66. Зх— 1<2х+3иCх— 1)(х+1)<Bх+3)(х+1);
67. Зх— 1<2х+3иCх— 1)(х+1)>Bх+3)(х+1);
68. ж2 + 1 > х и fx2 + lV|x| + 2) > х (W + 2);
69. х2 + 1 > х и (х2 + 1 |(Vx~+ 1) > х(Vx + 2);
0.^=4
х—3
х-3
72.
564
x+4
73. j^-y > 0 и (х+4) (x — 1) > 0;
r+4
74. J3-J;> 0 и (x+4) (x— 1) ;>0;
«=2
x+5 x+5
(x+5)
0
?=1 q.
x+5
x+2
x+2 '
87. л|х — 12 V4 — x > 0 иУ(х— 12) D — x) > 0;
88. Vx+TVx— 3 >0 и л/(х+2)(х—j>0;
89. VlOO — x2 Vsinx ?0 и Vf 100 — x^sinx SO;
90.-L>—L_^h(x+2) >3^;
& (x+2)
91. Vx<3 их<9;
93.
x+ 6
565
х-У
94. B + sinx)*+6 <
x-l
95. B + |sinx|)*+6
2 „
X— 1
x+6
x+6
97.
'-9
4 + |x-4|j
1 их2 —9^0;
?+1
100. ^x2 > 0 и 2 log2x> 0;
101. log2 x2 > 0 и 2 log2 (— x) > 0;
102. log2x2>0H2lQg2W>0;
103.
104.
>0 и
- 8)
- 8)
x+ 1
Q
]
Vx+1
log2(x+7) (x-8)
x+1
Являются ли равносильными неравенство и система неравенств A05 -
149):
х+
и
106. 2x+ z>x+4 + 7 и f. ' .
x —6 x —6 |2x>x+4;
107. Cx— 1) (x+ 1) < Bx+ 3) (x+ 1) и
I и
109.
110.
111.
3) > х
3) и
х+4
х+3
4
х+3
>3 и J
>3 и ^
Ш.^Ц-sO и
x —2
x+3>0,
(x+4)>3(x+3);
x+3<0,
x+4<3(x+3);
\x*2,
566
113.
(x — 2)(x+2)
x+5
<0 и
114.
>/9—x2 (x+l)
x + 2
[x+14[(x-6)
x+5
>0 и
хф — 2,
x-2 Q.
x+5 '
9-x2>0,
x+1 „
x+2
116.
117.
"*¦ 1=1*1?
119.
Л
Зх2
120. л/х<3 и
[x+5 '
) и f*>3'
и Ux + 2)(x-
x-2>0,
2x2>x-2;
х*0,
x-2<0,
2x2<x-2;
x*0,
X* —2,
2
+ 2) > Зх2;
3)>0;
x<9;
122.
123.
124.
x+l
Vx + 1 V6 — x
x-1
>0 и
(x-2)
^25-xz(x+4J
->0 и
x+
6-x>0,
x-l>0;
x + 2>0,
5-x<0,
20 и
x+5
x2-l>0,
и
x-2
x-2
125.
126.('l+cos2xjI+T>l и ¦
127.
x+J_<0
x —4 < '
и
x-2
x+3
cosx^O;
cosx^O,
Jc—2
x+3 ^ '
ж-7
128. B + sin x)*+10 й 1 и
sinx* — 1,
129.
130.
131.
132.
133.
3 + х2
' 3
-9
х+10
х*0,
[х+21
-1
х+2*0;
Х*0,
х+4 „
1
1 + sin2 x
!_4х-45.
+ 3
Х-1^"'
sin х * 0,
х + 4 л
134. Xх -4х-45>1 и
135.
!_4х-45.
г_4х-45;
1 и -
136. Xх
137.
138. log2 х2 > 0 и
139.
х+3'"'
1,
х2_4х-45>0;
х2_4х-45<0;
х> 1,
21og2(-x)>0;
О и
(х +
140. log 1 (х+1)(х-7)<0 и {
2 + Vx V
142.
0<х2-4<1,
0<х2 + 6х+8<1;
х-8>0,
143. log2 (х + 7) + log2 (x - 8) > 0 и
144. logx2(x+ 1)
х>0,
И Х*1,
х+7>0,
Iog2(x+7)(x—8)>0;
568
145.1ogx2(x+l)
146.
147.
(x+ 1) > 1 и
(x+ 1) > 1 и
148. logx2 (x+ 1) > 1 и
x< — 1,
log_x(-
0<x2<l,
(x+l^x
X2>1,
Решить следующее неравенство A50 — 298):
150.
152. tg|+6x-jc2>0. 153. cos|-4x-
,54. ;ETT(*+5)(*-liLj.o. ,55.
x + ^\x-lJ-l6-x
0_ 157;
. 159.
160.
162.
164.
165.
166.
168.
170.
172.
174.
176.
178.
179.
180.
x+2 4;
3,76
x+1 x+2 х-Г
x 2 8
>-3.
-. 163. —Ц + —X—7 + -^— + —Ц !
x—8 x —6 x+8 x + 6
2<4 +
x-7
х-Г
1
x-1 x+lV_i
2x-l | 3x-l
X+ 1 X
_J 4_ _4 ^_
x-1 x —2 x-3 x-40"
4 [x+ 2| < 2x+ 10. 167. 3 [x - 1| < x+ 3.
2[x+ l|>x+4. 169. 3[x+ l|^x+5.
[x — 2| < 2X2 — 9x+ 9. 171. Зх2 — |x — 3| > 9x — 2.
x2 + 4^|3x+2|-7x. 173. x2-|5x-3|-x<2.
[x + 1| — |3x + 7| > 0. 175. |13 — 2xi ? \4x — 9|.
|x| + |x— l|s 1. 177. |x + 2|-3<[x-l|.
[х^+гх-зиз-гх-х2.
K + 3x-x2|sx2-3x-4.
x2-Sx-4
x2-4
< 1. 181.
x2-3x+2
x2 + 3x+2
184.
186. [x+2| + [x+l| + [x— 1|
187. |5-x|<[x-2| + |7-:
1ЯЯ > 1 1RQ
' x2+Jx_5| ' ' J + \x+2\
190. 2>/x+T>x+ 2. 191. x+ 1 <4>/xT6".
192. Vl+4x-x2>x- 1. 193. V5-xz>x-l.
194. x+ 4 < V6 —4x —x2. 195. x — 2 < V4 + 2x-
196. Vx2-3x-10>x-2. 197.V4xz+16x+16<2x+ 10.
198. л/З^-бх+З*х+ 3. 199.
200. ^9x^+6x77<2 — x 201.
202. Vx2-x-2> x — 1. 203. V2x+T< 1 - Vx+T.
-З >x.
204. V— x — Vx+T> 4. 205. Vx+1 <Vx+ll — V2x—12.
206. V3^
_x_V_l_2x. 2O7.V2x+T<-
208.
1-V1-8X2
2-х
л/ZET лЩЕИ*1
214. 5x+3x?l25-5* 215. |л
216.
218. @,4)
x-2
x+2
27
< @,4) . 219. 5V7x "¦^ГЛ ^ 125VT.
220. 9х- 2 • 3*< 3. 221. 4X- 2*+1 S 3.
222.
224.3514
3*+I.223.22x+1-21 Л
+ 3
+ 2>0.
570
226.
235. 2^ - 21 - ^ >1.236.93^ - 2 ¦
244.
246.
247. lQgo,3 Ы + l)< logo,3 Bx - 5).
248. log3 fx2 - 5x+ 4]> 0. 249. log2 (x2 + 3x]< 2.
250. 2 Iog2 (x - 1) - log2 Bx — 4) > 1. '
251. log2 x+ log2 Bx — 1) < log2 Bx+ 2).
252. Iog2 x — 3 log2 x + 2 > 0.
253. log3 (x+ 2) (x - 3) ?4 log, Bx+ 1) - Iogvr7.
254. Iog4Г2Х2 + 3x+ \\> log2 Bx+ 2).
255. log? (x-Щ+ log1/5 fx-^j< 2.
256. Bjj
257. log^-^-6*C*f 258 1О^<СО8
260.
,0 26L й
M !og2X log2
262 loggx ^log23Vl + 2x
'Io(l 2JO log2x '
571
mi
264.
266.
268.
J
lQg*x
!0gD +
2x* — 3x+3
^-j> 1.265.
П —x
2x — x}\ 2
Гб + гх-х2^
., , г^-зх+з
L
lO^/2x + 3) ^ 1 •
k^. 267. log^+ijur + x— 61
;j.269.1og(x_3)(x2-4xf<4.
271. log(, _ ^(бх2 - 5x+ lj- log(i_ ад DХ2 - 4x+ 1 js 2.
272.10^2x41) [5 + 8x — 4X2 J+ logE _ 24 f 1 + 4x+4^]s 4.
273. log^. i) (lQx2.- 7x+ 1^ - log^. 1 B5x- 10x+ 1) > 2.
274. log^+7Г9+ 12x+ 4x2j+lQg2x+3 Гб^ч-23x+ 21 j<4.
5g
27б
2'7'7 °' I I °^ I I ^ Л
3 + X-2X2
logsfx2 -4x+ llf + log,, fx2-4x+ llf
г-5х-Ъ)?
мл 61о^2х— lllQg32x— 2 „ ,
279. , =r ^2 + logrxx.
log32x-2 623
зУ;^0.282. % ,<0.
3/5| + '/3 iog7 he2 — 2x+7Лб J
283. logv, - 3 log(x _ i) Ц > 2 |log^ (x - 1)|.
, Aog^(x2 — It+l)
284. Ш < 1. 285. lQgws-^*4' - 36x)s - 2.
286. 3 -9^ x - 10 ¦ 3log« *+log2 8 S 0.
287. ^' log^
288. ]
289. 4X2 + 3^+' + x ¦ 3^< 2X2 ¦ 3^+ 2x+6.
572
2x+l
10
2x—1
io
x —1 x—l'""" x—1
294. (x — 2J |cos д) ^ cos x 295. sin x + (x — 4J |sin д| i 0.
296. cos x < (cos д| (x+ViI. 297. i
298.
rx ? 0.
Глава IX. ПРЕДЕЛ
ПОСЛЕДОВАТЕЛЬНОСТИ И
ПРЕДЕЛ ФУНКЦИИ
§ 1. Числовые последовательности
Если каждому натуральному числу п поставлено в соот-
соответствие число хп, то говорят, что дана числовая последо-
последовательность хи х2,..., х„,..., или, короче, последовательность
{х„}. Чтобы задать числовую последовательность, надо за-
задать закон (правило), по которому каждому натуральному
числу ставится в соответствие некоторое число, т.е. каждая
числовая последовательность может рассматриваться как
функция, область определения которой — множество всех
натуральных чисел.
Если,функция у =Дх) такова, что множество всех нату-
натуральных чисел содержится в области ее существования,
тогда с помощью функции y=fipc) с областью определе-
определения — множеством всех натуральных чисел — можно за-
задать числовую последовательность Д1),Д2), ..., Дл), ... или
{Дл)}. Например, множество всех натуральных чисел содер-
содержится в области существования каждой из следующих
функций:
1. у = х; 2. у = 21-х; 3. у = - 2 - 3(х - 1);
На области определения — множестве всех натуральных
чисел — эти функции задают соответственно следующие
числовые последовательности:
1. 1, 2, ..., п, ... ;
574
2 l i (i
z. i, 2,..., i2
3. -2, -5,'.., — 2 — 3(я — 1), ... ;
4. 1,-1, ..„(-I)"-1,...;
5. 1, 1, ..., Г, ... ;
0. A 2, .... и
7.0, 1, ..., l^l-1" ... ;
n
8. 1, 2, ..-, -, ••¦ ,
9.1, 2,..., 2":',...;
10. 1, 4, ..., n\ ... .
Наиболее удобно задавать числовую последовательность
аи а2, ..., д„, ... при помощи формулы для ее общего члена.
Запишем, например, формулы общих членов последова-
последовательностей 1 — 10:
En"
-l)";
5.*„=1"; 6-fl» = ^
l.a =П + (-1)"] Ъа=\.
" п ' "л'
9.аЛ = 2"-1; 1О.ал = л2;
Нередко последовательность задают рекуррентным соот-
соотношением, т.е. формулой, выражающей а„ через некоторые
предшествующие ему члены последовательности, напри-
например:
11. Последовательность чисел Фибоначчи 1, 1, 2, 3, ...,
а„, ... задается формулой а„ = а„ _ г + а„ _ 2 для п > 2 и
условием а! = а2 = 1.
Последовательности могут задаваться и другими спосо-
способами, например:
12. Последовательность десятичных приближений числа
к с недостатком 3; 3,1; 3,14; 3,141; ... .
575
13. Последовательность {а„}, где а„ = -j=? ([а] — целая часть
числа а, т.е. наибольшее целое число, не превосходящее а).
Поскольку всякая числовая последовательность может
рассматриваться как функция натурального аргумента, то
на числовые последовательности переносятся понятия мо-
монотонности и ограниченности функций.
Числовая последовательность {а„} называется возрастаю-
возрастающей, если для любых натуральных чисел щ и п2 из условия
щ < п2 следует, что ащ < а^. Возрастающими являются, на-
например, последовательности 1, 9, 10, 12.
Числовая последовательность \а„} называется неубываю-
неубывающей, если для любых натуральных чисел щ и п2 из условия
щ < п2 следует, что ап% < а„г. Неубывающими являются, на-
например, последовательности 5 и 11.
Числовая последовательность {а„\ называется убываю-
убывающей, если для любых натуральных чисел щ и п2 из условия
«! < «2 следует, что а„х > а„г. Убывающими являются, напри-
например, последовательности 2, 3, 6, 8.
Числовая последовательность {а„} называется невозрас-
тающей, если для любых натуральных чисел щ и п2 из
условия «1 < «2 следует, что ап> > а„г. Например, последова-
последовательность 13 является невозрастающей, так как а, = 1,
а2 =1, а3= 1, а* = \ и т.д.
Числовая последовательность называется монотонной,
если она убывающая, или возрастающая, или неубываю-
неубывающая, или невозрастающая. Монотонными являются все
вышеприведенные последовательности, кроме последова-
последовательностей 4 и 7.
Последовательность {а„} называется ограниченной сверху,
если существует число В такое, что для любого натураль-
натурального числа п справедливо неравенство а„ < В. Ограничен-
Ограниченными сверху являются, например, последовательности ,2,
3, 4, 5, 6, 7, 8, 12 и 13.
Последовательность {а„} называется ограниченной снизу,
если существует число А такое, что для любого натураль-
натурального числа п справедливо неравенство а„ > А. Ограничен-
576
ными снизу являются, например, последовательности 2, 4,
5,6,7,8,9, 10, 11, 12 и 13.
Последовательность {а„} называется ограниченной, если
она ограничена и снизу и сверху. Ограниченными являют-
являются, например, последовательности 2, 4, 5, 6, 7, 8.
Из всевозможных последовательностей ниже подробно
будут рассмотрены лишь последовательности, называемые
арифметической и геометрической прогрессиями.
Арифметической прогрессией называется последователь-
последовательность чисел, каждый член которой, начиная со второго,
равен предыдущему, сложенному с одним и тем же посто-
постоянным для данной последовательности числом, т.е. такая
числовая последовательность {а„}, что для любого натураль-
натурального п an+i = а„ + d, где d — некоторое постоянное для
данной последовательности число, называемое разностью
прогрессии.
Например, последовательности
1,2, 3, 4,..., A)
3, 1, - 1, - 3, ... B)
— арифметические прогрессии. У арифметической про-
прогрессии A) разность d= I, ay прогрессии B) разность d =
= — 2. Для любой арифметической прогрессии член, сто-
стоящий на n-и месте, всегда можно выразить через первый
член и разность данной прогрессии
an=ai + (n-l)d. C)
Эта формула называется формулой общего члена арифмети-
арифметической прогрессии.
Доказательство ее проводится методом математи-
математической индукции.
Для п = 1 формула C) запишется в виде а{ = а{ + 0 • d,
т.е. оказывается справедливой. Предположим, что формула
C) справедлива для п = к, т.е. предположим, что к-й член
арифметической прогрессии вычисляется по формуле
D)
19 Алгебра, тригонометрия СТ7
и элементарные функции Э / /
Докажем, что формула C) справедлива для п = к + 1, т.е.
докажем справедливость формулы
д*+1 = д, + [(*+1)-1]Л E)
Действительно, по определению арифметической прогрес-
прогрессии аЛ+, = ак + d. Следовательно, используя формулу D),
можно написать, что аЛ+1 = а, + (к — X)d + d = а, + [(к +
+ 1) — l]d, т.е. получить справедливость формулы E). Тем
самым доказана справедливость формулы C) для любого
натурального числа п.
Используя формулу C) и свойства действий над числами,
легко проверить справедливость следующего утверждения:
для любой арифметической прогрессии {an} при т + п =
= к + I справедливо равенство
ат + а„ = ак + а,. F)
Действительно,
ат + ап = а, + d(m - 1) + в, + d(n - 1) =
= 2а, + d(m + п — 2) = 2а, + d(k + I — 2) =
= а, + (к — \)d+ а, + (/ — X)d= ak + а,.
Число, равное сумме первых п членов арифметической
прогрессии, обозначается Sn, т.е.
Sn = а, + а2 + ... + а„_, + ал;
члены а, и а„ называются крайними членами для суммы Sn.
Используя свойство F) и свойства действий над числами,
получим следующую формулу для Sn:
Действительно,
2Sn = Sn + Sn = (a, + a2 + ... + an) + (a, + a2 + ... + an) =
= (a, + а„) + (a2 + а„_,) + ... + (а„ + а,) = (a, + a>,
578
т.е. сумма первых п членов арифметической прогрессии равна
произведению полусуммы крайних членов на число суммируе-
суммируемых членов.
Сумму Sn арифметической прогрессии {ап} можно выра-
выразить через первый член и разность данной прогрессии:
\ —2 .
Пример. Найти сумму двузначных натуральных чисел,
не делящихся ни на 2, ни на 3.
Очевидно, что все двузначные натуральные числа обра-
образуют арифметическую прогрессию с первым числом ах = 10
и разностью d= 1, т.е. следующую последовательность
чисел: 10, И, 12, 13, ..., 97, 98, 99. Используя формулу G),
легко найти сумму 5°} всех этих чисел: «S0* = -—+2 —.
Двузначные числа, делящиеся на 2, составляют арифмети-
арифметическую прогрессию 10, 12, 14, ..., 96, 98 с суммой &2) =
_A0 + 98) 45
2
Аналогично числа, делящиеся на 3, образуют арифмети-
арифметическую прогрессию 12, 15, 18, ..., 96, 99 с суммой 50* =
_A2 + 99) 30
2
Легко заметить, что последние две арифметические про-
прогрессии имеют общие члены 12, 18, 24, ..., 96 — числа,
делящиеся одновременно и на 2 и на 3, т.е. делящиеся на
6. Сумма S всех двузначных чисел, не делящихся ни на 2,
ни на 3. находится следующим образом: S = &1) — &2) —
&3) + 5^ , где ^6) — сумма всех двузначных чисел, делящих-
делящихся и на 2, и на 3, т.е. делящихся на 6. Сумму •S<6) нужно
прибавить потому, что при вычитании сумм 5* и 5*3) сумма
чисел, делящихся на 6, вычитается дважды. Используя C),
найдем число членов арифметической прогрессии, состав-
составленной из таких чисел (очевидно, что разность этой про-
прогрессии равна 6): 96 = 12 + (п — 1) 6, откуда п = 15. Следо-
Следовательно, 5<6) = A2 + ^6) 15 и S= ^ A09 • 6 - 108 • 3 - 111 х
х 2+ 108) = 1620, т.е. S= 1620.
579
Геометрической прогрессией называется последователь-
последовательность чисел, каждый член которой, начиная со второго,
равен предыдущему, умноженному на некоторое, отличное
от нуля, постоянное для данной последовательности число,
т.е. такая числовая последовательность {а„}, что для любого
натурального п а„+1 = а„д, где д — некоторое постоянное
для данной последовательности и отличное от нуля число,
называемое знаменателем прогрессии.
Например, последовательности
2, 4, 8, 16, 32, ... ;
1, - 1, 1, - 1, ... ;
I __L ± L
7' 21' 63' 189' ¦"
— геометрические прогрессии соответственно со знамена-
знаменателями 2, (— 1), [ — А
Общий член геометрической прогрессии вычисляется по
формуле
ап = а4~\ (8)
Доказательство справедливости этой формулы для
каждого натурального числа п проводится методом мате-
математической индукции. Для п = 1 формула (8) запишется в
виде ах = atf0, т.е. оказывается справедливой. Предполо-
Предположим, что формула (8) справедлива для п = к, т.е. предпо-
предположим, что справедлива формула
ak = algk~\ (9)
Докажем, что формула (8) справедлива для п = к + 1, т.е.
докажем справедливость формулы
ak+l = aigik+l)~l. A0)
Действительно, по определению геометрической прогрес-
прогрессии ak+i = ад. Следовательно, используя формулу (9),
Можно написать, что
580
т.е. получить справедливость формулы A0). Тем самым
доказана справедливость формулы (8) для любого натураль-
натурального числа п.
С помощью формулы общего члена найдем формулу для
суммы первых п членов геометрической прогрессии:
Sn = ах + а2 + аъ + ... + а„_х + а„.
Если q = 1, то Sn = пах.
Если q* 1, то рассмотрим выражение
Sn — Snq = ах + axq + ... + a,4"~' — axq — arf — ...
... - axq"-l -axq"= ax - axq" = a,(l - q").
Следовательно, Sn(l — q) = ax(l — q"). Так как q± 1, то
e _ gi A — g")
§ 2. Предел числовой последовательности
Пусть дана числовая последовательность {а„}.
Число а называется пределом числовой последовательности
{а„\, если для любого положительного числа г найдется номер
N такой, что для любого п> N справедливо неравенство
\ап-а\< е.
Например, очевидно, что пределом последовательности
{а„}, где а„ = с, является число с.
Тот факт, что число а является пределом последователь-
последовательности {а„}, записывают так: lim а„ = а или а„ -» а при п -»«»
Примеры.
1. Доказать, что lim а„ = 0, если а„ = а" иО < q< 1.
Возьмем произвольное число е > 0.
а) Если е< 1, то положим Af= [log^e] + 1. Ясно, что
Л^ > log, е и для любого п > N \q" - 0| = \q\" < \q\N /
= е.
581
б) Если е > 1, то положим N= 1. Легко видеть, что для
любого п > 1 \д" — 0| = \д\" < 1 < е.
Итак, для любого е > 0 существует номер N такой, что
для любого п> N справедливо неравенство \<f — 0| < е, т.е.
доказано, что lim а„ = 0.
2. Доказать, что lim а„ = 1, если а„ = ^—.
Возьмем произвольное число е > 0. Положим N=\-
+ 1, тогда iV>l и для любого п > N
< j = е, что и требовалось доказать.
я+1
п
-1
= -< — <
п N
3. Доказать, что lim а„ = 0, если а„ = -.
Возьмем произвольное число - > 0. Положим N = - +
+ 1. Тогда для любого п > N
требовалось доказать.
Будем говорить, что последовательность {а„} имеет пре-
пределом (+ оо), и писать lim а„ = +<» или а„ -» + ~ при п -»«,
если для любого сколь угодно большого положительного
числа А найдется номер N такой, что для любого п > N
справедливо неравенство а„ > А.
Примеры.
1. Доказать, что lim а„ = + оо, если а„ = п1.
П—> + •"
Для любого положительного числа А положим N =
=([V>4 + 1 ] + 1). Тогда для любого п > N
аИ = п2> N* = (h/ITT] + \I>(^|ATTJ = А+\>А,
т.е. lim а„= + оо.
2. Доказать, что lim а„ = + <*>, если а„ = п.
582
Для любого положительного числа А положим N= ([A +
+ 1J + 1).
Тогда для любого п> N а„ = п > N= [А + 1] + 1 > А +
+ 1 > A, lim а„ = + «>.
^л — 1
n—>+->
3% Доказать, что lim а„ = + «>, если а„ = 2"
Для любого положительного числа Л положим N =
= [log2 (у4 + 1)] + 2. Тогда для любого п > N
+ l) = A+l>A,
т.е. lim а„= + oo.
Будем говорить, что последовательность {а„} имеет своим
пределом (— «>), и писать lim а„ = — «> или а„ -* — «>, при
п -» оо, если для любого отрицательного числа 5 такого, что
|5| — сколь угодно большое число, найдется номер Атакой,
что для любого п > N справедливо неравенство а„ < В.
Примеры.
1. Доказать, что lim а„ = — «>, если а„= — 2 — 3(л — 1).
и -> + ••
[In ||"|
1 ' + 1.
Гогда для любого п > N
а„= - 2 - 3(п - l)<-2-3(JV- 1) =
<-2-3fl^il-
- i)= — 2 — (I — В — 3) = В,
что и требовалось доказать.
2. Доказать, что lim а„ = — оо, если а„ = — 2".
Для любого отрицательного В положим N= [log2 \B\ + 1].
Тогда для любого п > N
an=-2n<-2N=- 2|l06W+" < - 21овгИ = - \В\ = В,
что и требовалось доказать.
583
3. Доказать, что lim а„ = — <», если а„ = log! п.
Для любого отрицательного В положим N= [2W +1].
Тогда для любого п > N
а„ = 1оЦп< log| N =1оц [2W + 1] < 1оц 21* = - |4| = В,
что и требовалось доказать.
Отметим, что существуют последовательности, не имею-
имеющие предела. Такой последовательностью является, напри-
например, последовательность {а„}, где а„ = (— 1)".
Теоремы о пределах числовых последовательностей. В
этом пункте будем рассматривать только те последователь-
последовательности, которые имеют конечный предел.
Теорема 1. Если последовательность {а„} имеет предел
А и число р < А, то найдется номер N такой, что для любого
п> N справедливо неравенство р < а„.
Доказательство. Поскольку А есть предел последо-
последовательности {а„}, то для любого е > 0 найдется номер N
такой, что для любого п > N справедливо неравенство
к - А < е-
Перепишем это неравенство в форме
А - е < а„ < А + е. A)
Положим, е = А — р > 0. Для этого е > 0 найдется номер N
такой, что для любого п > N будет справедливо двойное
неравенство A). Подставляя в левую часть неравенства A)
е = А — р, получаем, что р < а„, что и требовалось доказать.
Теорема 2. Если последовательность {а„} имеет предел
А и число q > А, то найдется номер N такой, что для любого
п> N справедливо неравенство q > а„.
Доказательство теоремы 2 аналогично доказательству
теоремы 1 и поэтому опускается.
Замечания.
1. Если lim а„ = А и А > 0, то найдется номер N такой,
что а„ > 0 для любого п> N.
584
2. Если lim а„ = А и А < О, то найдется номер N такой,
что а„ < О для любого п> N.
Теорема 3. Если последовательность {а„} имеет предел
А, то найдется положительное число М такое, что \ап\ < М,
т.е. последовательность, имеющая предел, ограничена.
Доказательство. Выберем число Мх так, чтобы оно
было больше \А\, т.е. чтобы было справедливо неравенство
— Мх < А < Мх. Обозначив р = — Мх, q = Мх, получим , что
А > р и А < q. По теореме 1 существует номер Nx такой, что
для любого п> Ni справедливо неравенство р < а„. По
теореме 2 существует номер N2 такой, что для любого п> N2
справедливо неравенство q > а„. Выберем номер N =
= тах(Л^, N2). Тогда для любого п > ^справедливо двойное
неравенство р< а„< q, или — Мх< а„< Мь т.е. \а„\ < Мх.
Неравенство |aj < Мх выполняется для любого п> N, т.е.
для п = N+ 1, п = N+ 2, п = N+ 3, п = N+ 4ит.д. Значит
неравенство \а„\ < Мх может не выполняться лишь для пер-
первых N членов последовательности.
Выберем среди чисел \ах\, \а2\, \а3\, ..., \aN _ ,|, 1^, Мх
наибольшее число и обозначим его через М. Тогда ясно,
что для любого п будет справедливо неравенство а„ < М, что
и требовалось доказать.
Теорема 4. Если последовательность {а„} имеет предел,
то этот предел единственный.
Доказательство. Предположим противное, т.е. пусть
одновременно ап -> А и а„-> В и пусть А < В. Возьмем
между А и В любое число С, т.е. А < С< В. Поскольку
а„ -*А и А < С, то по теореме 2 найдется такой номер Nx,
что для любого п> Nx будет выполняться неравенство
а„ < С. Поскольку а„-* Ви С < В, то по теореме 1 найдется
такой номер N2, что для любого п> N2 будет выполняться
неравенство а„ > С. Выберем номер N= max(Nx, N2). Тогда
член последовательности aN одновременно удовлетворяет
двум неравенствам aN > С и aN < С, что невозможно. Сле-
Следовательно, предположение неверно, а верно утверждение
теоремы 4.
Теорема 5.
585
Если lim а„ = А, то lim |aj = \А\.
Доказательство.
Пусть Л = 0. Тогда условие lim а„ = 0 означает, что для
любого е > 0 найдется номер Атакой, что для любого п> N
справедливо неравенство \а„ — 0| < е. Поскольку это нера-
неравенство можно переписать так: ||aj — 0| < е, то получаем,
что lim |aj = 0.
Пусть Л * 0. Тогда условие lim а„ = А означает, что для
любого е > 0 найдется номер Nt такой, что для любого
п > Nt справедливо неравенство \а„ — А\ < е.
Если А > 0, то по замечанию 1 к теореме 2 найдется,
номер N2 такой, что при п > N2, а„ > 0. Взяв номер
N= max(Nb N2), получим, что для любого п > JV справед-
справедливо неравенство ||aj — А\ < е, что и означает, что lim |aj =
я->+~
= \А\. Если же А < 0, то по замечанию 2 к теореме 2 найдется
номер N3 такой, что а„ < 0. Взяв номер N= max(JVb N3) и
учитывая, что а„ = — |ej и >4 = — |у4|, получим, что для
любого п> N справедливо неравенство |— (|а„| — |у4|)| < е,
которое можно записать так: ||а„| — |Л|| < е, а это означает,
что lim \а„\ = \А\.
Арифметические операции над последовательностями
{а„} и {Ь„} и сравнение последовательностей {ая} и {Ьп}
производятся также, как и над функциями, т.е. при одина-
одинаковых значениях аргумента, другими словами, почленно.
Теорема 6. Если последовательности {а„\ и {Ь„} таковы,
что а„ = Ь„ для любого п и а„ -»А, а Ь„ -»В, то А = В, т.е.
если а„ = Ь„ для любого п, то lim а„ = lim Ь„.
Доказательство. Условие а„ = Ь„ для любого п озна-
означает, что на самом деле имеется только одна последова-
последовательность, а по теореме 4 она не может иметь двух пределов;
значит, А = В и теорема 6 доказана.
586
Теорема 7. Если последовательности {а„\ и {Ь„\ таковы,
что а„ > Ь„ для любого п, ап-* А и Ь„-* В, то А> В, т.е. если
а„ > Ь„ для любого п, то lim а„ > lim Ь„.
л-» + ~ л-» + ~
Доказательство. Предположим противное. Пусть
А< В. Выберем число С такое, что А < С< В. Так как
а„ -» А и А < С, то по теореме 2 найдется номер Nx такой,
что для любого п> Nx справедливо неравенство а„ < С. Так
как Ь„ -»В и В> С, то по теореме 1 найдется номер N2
такой, что для любого п> N2 справедливо неравенство
Ь„ > С. Выберем номер N= max(Nu N2). Тогда для любого
п> N будут одновременно выполняться неравенства а„< С
и С < Ь„. Из них следует, что а„ < Ь„, что противоречит
условию теоремы. Значит, наше предположение неверное
и теорема 7 справедлива.
Замечание. Теорему 7 нельзя усилить, т.е. из строгого
неравенства а„ > Ь„ для членов последовательностей не
обязательно вытекает строгое неравенство для пределов,
например, если ап = \, Ь„ = —\, то ап > Ь„ для любого п,
но lim а„ = lim bn = 0.
л —> + «¦
Теорема 8. Если последовательности {а„}, {Ь„} и {с„}
таковы, что а„<Ь„< с„ для любого п и а„ -* а, и сп -* а, то
Ъ„-*а.
Доказательство. Возьмем произвольное е > 0. Поскольку
а„ -» а, то найдется номер Nx такой, что для любого п> Nx
справедливо неравенство а — е < а„< а + е. Поскольку
с„ -» а, то найдется номер N2 такой, что для любого п> N2
справедливо неравенство а — е< с„< а + е. Выберем номер
N= max(Nu N2). Тогда для любого п > Сбудут одновремен-
одновременно выполняться неравенства а — е < а„ < а + е, а — е< с„<
< а + е. Добавим к этим неравенствам неравенство а„<>Ьп<
< с„, верное для любого п. По свойству транзитивности
неравенств для любого п > N будет справедливо неравенст-
неравенство а — е < Ь„ < а + е, которое можно записать как \Ь„ — а\ <
< е. Итак, для произвольно выбранного е > 0 существует
номер Атакой, что для любого п > #справедливо неравен-
587
ство \Ь„.— а\ < е, а это означает, что lim Ь„ = а. Теорема
доказана.
Замечание. Если айЬ„йс„ для любого я и с,-> а, то
Теорема 9. ?слм последовательности {а„} и {Ь„} таковы,
что lim а„ = А и lim Ь„ = Д /ио последовательность {а„ + Ь„}
такова, что lim (а„ + Ь„) = А + В, т.е. если а„ -*А, Ь„-> В,
™{пп+Ьп)\1а + В).
Доказательство.
Поскольку lim а„ = А и lim Ь„ = В, то для любого гх > О
найдется номер JV, такой, что для любого п > JV, справед-
справедливо неравенство А — е{< а„<А + &i и найдется номер JV2
такой, что для любого п> N2 справедливо неравенство
В — ?i < Ь„ < В + е,. Выберем номер JV= max(JV,, N2). Тогда
для выбранного произвольно t\ > 0 существует номер JV
такой, что для любого п > N одновременно справедливы
неравенства А — е, < а„ < А + е, и В — е, < Ь„ < В + е,. На
основании свойств неравенств справедливо неравенство
(А + В) - 2е, < (а„ + 6„) < (А + В) + 2е,.
Возьмем произвольное е > 0 и обозначим е, = е/2. Тогда,
как следует из предыдущего, найдется номер Атакой, что
для любого п > /Сбудет справедливо неравенство (А + В) —
— е < (а„ + Ь„) < (А + В) + е, т.е. по определению предела
lim (а„ + Ь„) = (А + В). Теорема доказана.
Теорема 10. Если а„ -*А, Ь„ -»В, то (а„ — Ь„) -»(А —
-В).
Доказательство этой теоремы аналогично доказательству
теоремы 9 и поэтому опускается.
Теорема 11. Если а„ -»А, Ь„-> В, то (а„Ь„) -»АВ.
Доказательство.
588
Поскольку lim а„ = А, то для любого наперед заданного
л —> + ~
числа ?i > 0 найдется номер ЛГ, такой, что для любого п >
Nx будет справедливо неравенство
\ап-А< ei. B)
Поскольку lim Ъп = В, то для любого наперед заданного
л—> + ~
числа е2 >0 найдется номер N2 такой, что для любого п> N2
будет справедливо неравенство
\Ь„-Щ< е2. C)
Рассмотрим неравенство
\аА -АЦ = \а„Ь„ - а„В+а„В- АВ\<
< \ап\ \Ьп-В\ + \В\ \ап - А- D)
Оно справедливо для любого п. Поскольку по теореме 3
существует положительное число Мтакое, что \ап\ й М для
любого п, то, обозначая d = \В\ + 1 (d > 0), из неравенства
D) получаем неравенство
\а„Ьп - АВ\ < \М\ \Ьп - В\ + \d\ \an - А, E)
справедливое для любого п. Теперь берем произвольное
е > 0 и обозначим ?j = ^ и е2 = ^ Тогда для выбранного
?i существует номер Nx такой, что для любого п> N{ спра-
справедливо неравенство B), а для выбранного е2 существует
номер N2 такой, что для любого п> N2 справедливо нера-
неравенство C). Выберем номер N = max(Nu N2). Тогда для
любого п > N одновременно справедливы неравенства B),
C) и E). Подставляя в E) оценки B) и C), получаем, что
для любого п > N справедливо неравенство
\апЪп -АВ\<г. F)
Итак, для произвольного е > 0 найден номер N такой,
что для любого п> N справедливо неравенство F), т.е. по
589
определению предела lim (а„Ь„) = АВ = lim а„1ип Ъп.
л-»+~ л-»+~ л-»+~
Теорема доказана.
Теорема 12. ?слм последовательность {а„} имеет предел
АфО, то найдется номер N такой, что для любого п> N
справедливо неравенство |aj > ^-
Доказательство. Возьмем е = y. Так как последова-
последовательность {а„} имеет предел, то по определению предела для
этого е > 0 найдется номер N такой, что для любого п > N
справедливо неравенство \а„ — А\ < Щ.
Поскольку \а„ — А\ > |>4| — |aj, то получим, что для лю-
любого п> N справедливо неравенство (Л| — |aj < *^, откуда
Y < а„. Теорема доказана.
Теорема 13. Если а„ -> А,Ъп^> В, где Ь„фО для любого п
Доказательство.
Поскольку lim а„ = А, то для любого е, > 0 найдется
номер Ni такой, что для любого п> Nx справедливо нера-
неравенство
к - А < е- G)
Поскольку lim Ь„ = В, то для любого е2 > 0 найдется номер
N2 такой, что для любого п> N2 справедливо неравенство
\Ь„ - Ц < г2. (8)
По теореме 3 существует положительное число М такое,
что для любого п
\ап\ < М. (9)
По теореме 12 существует номер N3 такой, что для любого
п > N3 справедливо неравенство
590
К > f. A0)
Для любого п справедливо неравенство
_ \anB — ЬА _ \апВ — ajb,, + ajbn — AbJ
в \ъпв\ \ь,\\в\
К (В - Ь„)\ + \Ъп (а„ - А)\ ^ |aj \Ъп - В\ \а„ - А
\ъ,\\в\ - \ъм + \в\ •
Возьмем теперь произвольное е > 0 и обозначим zx = ^- и
е2 = -J^r. Тогда для выбранного ei существует номер Nx
такой, что для любого п> Nx справедливо неравенство G),
а для выбранного е2 существует номер #2 такой, что для
любого п> N2 справедливо неравенство (8). Выберем номер
N= тахGУ,, N2, N3). Тогда для любого п > TV одновременно
справедливы неравенства G), (8), (9), A0) и A1). Подстав-
Подставляя оценки G), (8), (9) и A0) в правую часть неравенства
A1), получаем, что для любого п > TV справедливо неравен-
неравенство
Итак, для произвольного е > 0 найден номер N такой, что
для любого п > N справедливо неравенство A2), а это и
означает справедливость теоремы 13.
Теорема 14. Если ап->А, Ъ — фиксированное положи-
положительное не равное единице число, то Ьа" -> ft*.
Доказательство. Поскольку ап->А, то для любого
е, > 0 найдется номер N такой, что для любого п > N
справедливо неравенство
А — е, < а„ < А + е,. A3)
Пусть Ь>\. Поскольку функция у= Ьх возрастающая, то
из неравенства A3) вытекает, что bl~Zi < If" < b1**1, т.е. для
любого ti > 0 найдется номер TV такой, что для любого п> N
591
справедливо неравенство Ь1 е' < ba" Kb1*4. Возьмем произ-
произвольное положительное число е и обозначим е, =
= log4 [ 1 + -^ 1 Тогда для выбранного е, существует номер N
такой, что для любого п > ТУ справедливо неравенство
ъЛ — 6i s №. s lA + e.
и v О V. о .
Ясно, что
>Ь-^г = ЬА-г;
,Л ,Л ,14 ЛА 2
1-е, _ о _ Ъ _й ^ b — е _
l+-*\ bA+t
Итак, показано, что для любого положительного е найдется
номер N такой, что для любого п > TV справедливо неравен-
неравенство Ь* - е < V- < ЬА + е, т.е. lim Ьа» = Ь*.
В случае 0 < Ъ < 1 доказательство теоремы проводится
аналогично.
Теорема 15. Возрастающая и ограниченная сверху пос-
последовательность {ап} имеет предел.
Теорема 16. Убывающая и ограниченная снизу последо-
последовательность {ап} имеет предел.
Доказательство этих теорем опустим.
Примеры применения теорем о пределах числовых
последовательностей.
1. Найти предел последовательности {ап}, если а„ =
_ (я + 1) (я + 2)
Перепишем формулу для общего члена в виде а„ =
i
Iv Применяя последовательно теоремы о пре-
I
1+-
п\\ п\
деле частного, произведения и суммы, получаем
592
lim a =lim
. lim
lim
lim fl+-l Um
.Л-H.il Л I ,,->+..
Л
lim 11 + — 1 lim fl+-
л „_+J л
_ I.S1.' +1!?Jfe.
i) _ (i+0) (i + 0) _ .
i A 0>A °) "
2. Найти предел последовательности dn, если dn =
2 ,
^Д;—! (а2 ф 0 и а2п2 + Ьгп + сг ф 0 для любого п).
Разделив числитель и знаменатель в выражении для dn
на п2 и применив те же теоремы, что и в предыдущем
примере, получим
а{ + й,— + с,— lim а, + Ь — + с,—
1- Ли л_, + „ Л п
= lim —5- = —t J—!U =
lim 4, = lim
>,— + с,-^- lim а, + fri~ + C2~7
и »-»+¦»! Л и
b с
lim a, + lim — + lim -r
л л
lim a2 + hm — + lim —
;i-» + - л-»+~ Л л-» + ~/1
a2 + 0 + 0
3. Выяснить, есть ли предел у последовательности {о„},
если а„ = A + IV
При изучении бинома Ньютона была показана справед-
ливость неравенства 1 + -1 < 1 + —- , т.е. показано,
что последовательность {а„} такова, что а„ < а„ +1 для любого
п. Из условия а„< а„ + 1 легко получить, что а„{ < а„г для
любых щ < п2, т.е. последовательность {а„} — возрастаю-
возрастающая. Покажем теперь, что для любого п справедливо нера-
593
венство ап < 3, т.е. что последовательность {а„} ограничена
сверху.
Действительно,
^ л (л - 1) (л - 2) (if , л(л-1)... [л-(л-1)]
3! ' Ы т - т п\ ' \п)
= 1 + й + П. я— 1 1 _j_ ? я— 1 я —2 1
л л л 1-2 п п
По теореме 15 возрастающая и ограниченная сверху
последовательность имеет предел. Этот предел принято
обозначать буквой е. Итак,
lim f 1 + -1 = e.
Определение числа е позволяет вычислить его с любой
степенью точности. В курсе математического анализа по-
показывается, что число е — иррациональное число.
4. Выяснить, есть ли предел у последовательности {а„},
которая задана рекуррентным соотношением ах = V2 и
а„ = V2 + an_i для любого п>2.
Прежде всего выясним, ограничена ли эта последова-
последовательность. Докажем, что а„ < 2. Доказательство проведем
методом математической индукции.
а) Для п = 1 неравенство ах < 2 справедливо, поскольку
б) Предположим, что неравенство справедливо для
п = к, т.е. ак < 2.
в) Покажем, что из этого вытекает справедливость нера-
неравенства для п = к + 1. Действительно, ak+l = V2 + ак <
< V2 + 2 = 2. Итак, неравенство а„ < 2 справедливо для лю-
любого п.
Покажем, что последовательность {а„} возрастающая.
Для этого достаточно показать, что а„< а„+ ь т.е. доказать
неравенство а„ < V2 + а„.
Это неравенство равносильно неравенству а\ < 2 + а„,
которое можно переписать так: (а„ + \){а„ — 2) < 0. По-
Поскольку 0 < а„ < 2, то последнее неравенство очевидно, а
значит, справедливо и равносильное ему неравенство а„ <
< а„+1. Итак, последовательность {а„} возрастает и ограни-
ограничена сверху; значит; она имеет предел, который обозначим
через с. Покажем, что с = 2. Действительно, воспользовав-
шись рекуррентным соотношением а„ = V2 + an_b имеем
lim а„ = lim V2 + an_i.
и—»+•• л—»+~
Воспользуемся теоремой (доказательство ее опускается):
если последовательность {Ь„} такова, что Ьп>0,и она имеет
предел, то lim V/>7= Vlim6n. Получаем lim а„ =
= lim V2 + а„_, = VBm 2 + limа„_ х. Поскольку lim а„ =
= lim д„ _ i, то получаем, что с надо искать из условия
с = V2 + c. Возводя это равенство в квадрат, получаем, что
с = 2.
5. Пусть а > 1 и а — положительное иррациональное
число. Вспомним определение аа. Поскольку любое ирра-
иррациональное число есть бесконечная десятичная дробь, то,
обрывая эту дробь на каком-то шаге, получаем приближен-
приближенное значение этого числа с недостатком, а прибавляя к
последней цифре единицу, получаем приближенное значе-
значение этого числа с избытком. Значит, для приближения
числа а, равного р, q^q-i... qn —, получаем две последова-
последовательности
595
Обозначим общий член первой последовательности через
Ь„, а общий член второй — через с„. Тогда очевидно, что
последовательность {Ь„} возрастающая и ограниченная
сверху (хотя бы числом (р + 1)), а последовательность с„
убывающая и ограниченная снизу (хотя бы числом р).
Рассмотрим последовательность аь\ Так как а > 1, то из
условия bn < bn+1 вытекает, что аь- < аь"*х. Поскольку после-
последовательность {Ь„} возрастающая, то последнее неравенство
означает, что последовательность {аь"} возрастающая.
Кроме того, аь" < <f + l, т.е. последовательность аь" ограни-
ограничена сверху. По теореме 15 последовательность аь- имеет
предел, который обозначим А. Аналогично показывается,
что последовательность ас" имеет предел, который обозна-
обозначим В. Докажем, что А= В.
Рассмотрим последовательность {ас" — аь") и покажем,
что lim (ас" — а4") = 0. Действительно, применяя теоремы
о пределах, имеем
lim (ас" - а4») = lim [abi<*c"-"" - 1)] =
= lim aK ¦ lim (ас"~ь- — 1) = lim aK ¦ |ViT5 ~ *J — lim f] =
V =А(а°-1) = 0,
так как lim (с„ — Ь„) = lim —^гт= 0- Далее, из условия
lim (cf" — ctn) = 0 получаем, что lim d" — lim a6" = 0, т.е.
А= В.
Итак, обе последовательности имеют один предел, кото-
который и называется числом аа.
В случае а > 1 и а < 0 или 0<а<1 иа — любое ирра-
иррациональное число рассуждения аналогичны.
596
6. Пусть задана последовательность {а„}. Тогда можно
построить другую последовательность {Sn} по правилу
S\ = аъ S2 = ах + аъ ..., Sn = а, + а2 + ... + а„, ... .
Формально можно написать бесконечную сумму
а, + а2 + ... + а„, ...,
которую называют рядом. Последовательность {Sn} называ-
называется последовательностью частичных сумм этого ряда. В
некоторых случаях последовательность {Sn} может иметь
конечный предел S. В таких случаях говорят, что ряд
сходится, а число S называется суммой ряда. Приведем
несколько примеров.
6.1. Пусть задана геометрическая прогрессия {а„} с пер-
первым членом ах и со знаменателем q таким, что 0 < q < 1.
Рассмотрим ряд а{ + axq + a^q1 + ... + aYq" ~ ' + ... и соста-
составим последовательность {Sn} частичных сумм этого ряда.
Формула для вычисления Sn для любого п следующая:
Применяя теоремы о пределах и учитывая, что 0 <
< 1, получаем, что lim Sn = lim U-^ a^_ ¦ q"
= уз lim q". Поскольку lim q" = 0 для 0 < \q\ < 1, то
получаем, что lim Sn = . J_ , т.е. по определению сум-
мой написанного ряда будет число а^_ . Следователь-
Следовательно, сумма геометрической прогрессии при 0 < \q\ < 1
равна первому члену, поделенному на разность едини-
единицы и знаменателя прогрессии, т.е. S = а^_ .
6.2. Пользуясь определением суммы ряда, можно дать
другое определение иррационального числа а.
Пусть положительное иррациональное число а равно
Р, Шг - Чп ••• Тогда
597
— последовательность десятичных приближений числа а с
недостатком, а
— последовательность десятичных приближений числа а с
избытком. Эти последовательности имеют один предел,
который называется числом а. Поэтому можно определить
а как сумму ряда
Заметим, что если а есть бесконечная периодическая дробь
то а тоже можно определить как сумму ряда
Pm+l i
-
6.3. Докажем правило перевода периодической десятич-
десятичной дроби в обыкновенную. Пусть дана положительная
периодическая десятичная дробь, целая часть которой, для
простоты, равна нулю. Тогда эта десятичная дробь равна
обыкновенной, у которой: числитель есть число, равное
разности чисел, составленных цифрами, стоящими до вто-
второго периода, и цифрами, стоящими до первого периода;
знаменатель есть число, в изображении которого цифра 9
повторяется столько раз, сколько цифр в периоде, а затем
после девяток нуль повторяется столько раз, сколько цифр
от запятой до периода.
598
Примеры.
-314-311-
990 990'
- 12731 — 127 _ 12604 _ 3151
Доказательство. Пусть дробь а имеет вид
a = 0, qxq2 ... gk(pip2... pm).
Запишем эту дробь в виде суммы ряда
„ + + + + + + +
a io+ioo + -+ 10* ш*-1 - to*-'
_j_ Рт*\ ^_ ^_ Plm
io*+m+1 ¦" io*+
Сделаем очевидные преобразования этого ряда:
a = -^ A0*- >
В этом ряде члены, начиная со второго, образуют гео-
геометрическую прогрессию со знаменателем -\. Применяя
формулу для суммы геометрической прогрессии со знаме-
знаменателем q таким, что 0 < \q\ < 1, получаем .
899
10
1 г 1 /V" — ^ 1 Л'" ~ 2
10"
Р|+10 Рг + -+Рт_
_ A0'"- 1)A0*~'ф,+ 10^2g2+. + g^+ Ю"~ р
10"**-Ч + 10" + *ft + ... + 10"'?,+ 10m~ p, + 10"~2pj + ... +рп
10
Я\ ¦*"
10*
по"'
10'
Яг
'A0"'
1)
-1)
- Як - Я1>
Чг ¦¦¦ ЯкР\Р2
999 ...
траз
-Рт—'
9000...
к раз
ЯхЯг
0
-Як
и правило перевода доказано.
§ 3. Предел функции
Пусть дана функция у=Д.х). Точка а (а — конечное
число) называется точкой сгущения области существования
функции у~Лх), если в любом сколь угодно малом про-
промежутке оси Ох, содержащем точку а, есть хотя бы одна
точка области существования этой функции, отличная от
точки а. Заметим, что сама точка а может и не принадле-
принадлежать области определения функции.
Примеры. 1. Для функции у = 2х любая точка оси Ох
есть точка сгущения этой функции, и все точки сгущения
принадлежат области существования функции.
2. Для функции у = - любая точка оси Ох есть точка
сгущения этой функции. Точка х = 0 также есть точка
сгущения , но она не принадлежат области существования
функции.
600
3. Пусть задана функция у = Vlog2 sin х; область сущест-
существования этой функции есть хк = ^ + 2пк, где к — любое
целое число. У этой функции нет точек сгущения.
Часто определение точки сгущения дается в несколько
других терминах. Для любого 8 > 0 промежуток а — 8 < х <
< а + 8 оси Ох называется 8 (дельта)-окрестностью
точки а.
Точка а {а — конечное число) называется точкой сгуще-
сгущения области существования функции у =Дх), если в каждой
8-окрестности точки а содержится хотя бы одно, отличное
от а, значение х из области существования функции.
Если точка а есть точка сгущения области существования
функции у =АХ)> то найдется, притом бесконечно много,
последовательностей {х„}, х„ ф а, из области существования
функции у — J{x), имеющих своим пределом точку а.
Примеры. 1. Пусть задана функция у = 2х и точка
а = 1 — точка сгущения области существования этой
функции. Последовательности точек {х„}, например, такие:
1;
n n
— последовательности точек из области существования
этой функции, причем в каждом случае lim х„ = 1.
2. Пусть задана функция у = - и точка а = О — точка
сгущения области существования этой функции. Последо-
Последовательности точек {*„}, например, такие:
г =1. v =J_- г =—L_-
Л" и' л 2"' 4% п
= _ I- = _ 1 = (— 1)"
*я и' *" 5"(" + 1)' Х" и
— последовательности точек из области существования
этой функции, причем lim х„ = 0.
60»:
Покажем, что для любой функции у = Дх) и любой точки
сгущения а области существования этой функции можно
построить хотя бы одну последовательность точек {х„} из
области существования такую, что х„ ф а и lim х„ = а.
Выберем положительное число 5t и возьмем окрестность
точки а, соответствующую числу Ьи и в ней возьмем любую
точку х, * а из области существования этой функции. Возь-
Возьмем теперь положительное число 82 такое, что 5г < 5i и
52 < \а — Xi|. В окрестности точки а, соответствующей числу
62, возьмем любую точку Хг * а из области существования
этой функции и т.д. В результате получим последователь-
последовательность точек:
Х\, Х2, Х3, ..., Х„,
Последовательность положительных чисел {5„} берется
такой, что кроме указанных условий она удовлетворяет
условию lim 5„ = 0. Покажем, что lim х„ = а. Действитель-
и—¦+¦» я—»+••
но, для любого е > 0 можно найти номер N такой, что
бдг < е. Для любого п > Nripn указанном способе выбора 5„
и х„ имеем 5„ < bN и |х„ — а| < 5„. Итак, для произвольно
выбранного е > 0 можно найти N такой, что для любого
п > N |х„ — <я| < е, а это означает, что lim х„ = а.
Из построения видно, что для любой функции у = Дх) и
любой точки сгущения а области существования этой
функции можно построить бесконечно много последова-
последовательностей точек из области существования таких, что
lim х„ = а.
х„
Заметим, что каждой такой последовательности хи
..., х„, ... соответствует последовательность Дх{),
-,Дх„), ...
Пусть точка а — точка сгущения области существования
функции у = Дх). Число А называется пределом этой функ-
функции при стремлении х к а, если для любой последователь-
последовательности точек из области существования функции {х„}, х„ * а,
«02
имеющей пределом число а, последовательность {Дх„)}
имеет пределом число А. При этом пишут lim fix) = A.
Пределом функции может явиться как конечное число
А, так и (+ оо) или (— оо): ИтДх) = +°° (ИтДх) = — <»),
если для каждой последовательности {х„} такой, что х„ -* а,
Дх„) -> + ~ (Дх„) -^ - со).
Примеры.
1. Доказать, что lim 2х = 2.
Для этого покажем, что lim 2х" = 2 для любой последо-
«-¦+«¦
вательности точек из области существования функции {х„},
х„ф\, такой, что lim х„=1; т.е. что для любой такой
л —¦+«¦
последовательности и любого е > 0 найдется номер N
такой, что для любого п > # справедливы неравенства 2 —
— е < 2*" < 2 + е. Заметим, что условие lim х„ = 1 означает,
что для любого числа е, > 0 найдется номер JVj такой, что
для любого п > Nt справедливы неравенства 1 — et < х„ <
< 1 + е,.
Пусть теперь дано положительное число е. Выберем
число ё! = log2 [ 1 +11 Ясно, что ?, > 0. Возьмем теперь
любую последовательность точек из области существова-
существования функции {х„}, х„ ф 1, такую, что lim х„ = 1. Тогда для
этой последовательности {х„} существует номер Ni такой,
что для любого п> Nx справедливы неравенства 1 — &i <
< хп < 1 + еь а следовательно, и неравенства
2х-< 21+Е- = 2 • 2е- = 2 • 21о4+!}= 2 fl +§]= 2 + е;
Итак, для любой последовательности точек из области
существования этой функции {х„}, хпф1, такой, что
603
lim х„ = 1, и для любого е > 0 найден номер N= JV, такой,
что для любого п > JV справедливо неравенство \Т" — 2| < е,
т.е. показано, что lim 2х" = 2 для любой последовательнос-
ти из области существования функции {хп}, х„ф 1, такой,
что lim х„ = 1. Следовательно, lim 2х" = 2.
2. Доказать, что lim A = + «>.
Пусть {х„}, х„ ф 0, — любая последовательность точек из
области существования функции такая, что lim х„ = 0. Это
означает, что для любого числа е, > 0 найдется номер N
такой, что для любого п > N справедливы неравенства 0 <
< W < ei- Возьмем произвольное положительное число В и
обозначим ?j = \. Тогда для любой последовательности {хл},
х„ ф 0, такой, что lim х„ = 0, найдется номер N такой, что
для любого п > N справедливы неравенства 0 < |xj < -|, т.е.
справедливо неравенство Л-. > В.
Итак, для любого В > 0 нашелся номер Атакой, что для
любого п > N справедливо неравенство Лт > В, т.е. lim Aj =
= + с» для любой последовательности точек из области
существования функции {xj, х„ ф 0, такой, что lim х„ = 0.
Следовательно, lim Л = + «>.
¦-»+-
Будем говорить, что (+ «>) является точкой сгущения для
области существования функии у=Ях)> если для любого
большого положительного числа В найдется хотя бы одно
значение х, принадлежащее области существования функ-
функции у = fix), такое, что х > В.
Будем говорить, что (— «>) является точкой сгущения для
области существования функии y=fix), если для любого
отрицательного числа В такого, что \В\ — сколь угодно
большое число, найдется хотя бы одно значение х, принад-
604
лежащее области существования функции y=fix), такое,
что х < В.
В случаях, когда (+ оо) или (— оо) являются точками
сгущения для области существования функции y=fix),
также легко показать, что можно построить последователь-
последовательность точек {х„} из области существования функции
у = fix), которая будет иметь своим пределом (+ оо) или
(— оо) соответственно, и определение предела функции
у = fix) можно распространить на случаи таких точек сгу-
сгущения.
Пример. Для функции у= 1 + - и (+ оо) и (— оо) явля-
являются точками сгущения и lim [ 1 + - ] = 1 = lim [1 + - \
*-*+-Л х) *-*— V х)
Пользоваться приведенным определением предела
функции для его отыскания трудно. Поэтому чаще пользу-
пользуются другим, эквивалентным ему, определением на так
называемом языке «е, 5».
Пусть точка а есть точка сгущения области существова-
существования функции у =fix) и а — конечное число. Число А
называется пределом функции у =fix) при стремлении х к а,
если для любого е > 0 найдется 5 > 0 такое, что для любого
х из области существования этой функции и такого, что
О < |х — в| < 5, выполняется неравенство |Дх) — А\ < е. При
этом пишут Mm fix) = A.
x-ta
Пусть (+ оо) есть точка сгущения области существования
функции y=fix). Число А называется пределом функции
у = fix) при стремлении х к (+ оо), если для любого е > О
найдется число М > 0 такое, что для любого х из области
существования функции у =fix), и такого, что М<х, вы-
выполняется неравенство |Дх) — А\ < е. При этом пишут
lim fix) = A.
Пусть (— оо) есть точка сгущения области существования
функции у =fix). Число А называется пределом функции
у = fix) при стремлении х к (— оо), если для любого е > О
найдется число М< 0 такое, что для любого х из области
существования функции у =fix), и такого, что х < М, вы-
605
полняется неравенство |Дх) — А\ < е. При этом пишут
lim fix) = A.
*-» —~
Аналогично можно дать определения: шпДх) = — «,,
х-*а
шпДх) = + со, Шп Дх) = — оо и т.д. В качестве примера
х-*а х-* — —
приведем одно из таких определений.
Пусть точка а есть точка сгущения области существова-
существования функции у =fix) и а — конечное число. Будем гово-
говорить, что функция у =fix) имеет пределом (+ оо) при стрем-
стремлении х к а, если для любого числа В > 0 найдется число
5 > 0 такое, что для любого х из области существования
функции и такого, что 0 < |х — в| < 5, будет выполняться
неравенство fix) > В. При этом пишут ШпДх) = + ~.
х-*а
Найдем пределы некоторых функций, используя опреде-
определение предела на языке «е, 5».
Примеры. 1. Дана функция у=Т и точка а= 1 —
точка сгущения области существования этой функции.
Доказать, что lim 2х = 2.
Возьмем произвольное положительное число е и выбе-
выберем число 5 > 0. Выберем, например, 5 = log211 +| \ ясно,
что 5 > 0. Возьмем теперь любое х, такое, чточ) < [х — 1| <
< 5, т.е. любое х* 1 из промежутка 1 — 5<х<1 + 5.
Ясно, что
Т < 21+8 = 2 • 28 = 2 • 2log41 + 2J= 2 |l+f|= 2 + е;
2* > 21"8 = 2 • 2~8 = 2 • 2-log41 +2j =
_ 2 _ 4 4-e2_
, e 2 + e 2 + e
1 + 2
Эти неравенства означают, что \2Х — 2| < е. Итак, для лю-
любого е > 0 нашлось 5 > 0, такое, что \Т — 2| < е для любого
606
х из области существования функции, и такого, что 0 < \х —
— 1| < 5. По определению это и означает, что Km 2х = 2.
х->1
2. Дана функция у = пи точка а = 0 — точка сгущения
области существования этой функции. Доказать, что
lim Л = + °°.
Возьмем произвольное число 5>0 и выберем число
5 > 0, например, 5 = -~ Ясно, что как только 0 < \х — 0| =?=
= Ы < 5, тОо>1 = -г = В. Итак, для любого Д > 0 нашлось
в
число 5 > 0, такое, что А > В для любого х из области
W
существования этой функции и такого, что 0 < \х — 0| < 5.
По определению это и означает, что lim А = + °°.
Выше даны два разных определения предела функции:
одно на языке последовательностей, другое — на языка «е,
5». Эти определения равносильны, т.е. если функция имеет
предел в смысле определения на языке последовательнос-
последовательностей, то она имеет тот же предел в смысле определения на
языке «е, 5» и наоборот.
Покажем равносильность двух определений предела
функции в случае, когда х = а — конечная точка сгущения
и когда функция имеет конечный предел А.
1. Пусть А — предел функции у =fl.x) при х, стремящемся
к точке а в смысле определения на языке «е, 5».
Возьмем произвольное е > 0. Тогда найдется число 5 > 0,
такое, что для любого х, принадлежащего области сущест-
существования функции и удовлетворяющего неравенствам 0 <
< \х — я| < 5, выполняется неравенство |Ддс) — А\ < е.
Рассмотрим любую последовательность {х„}, сходящуюся
к а, и такую, что х„ ф а и х„ принадлежит области сущест-
существования функции у =ЛХ) ПРИ любом п. Тогда для указан-
указанного числа 5 > 0, зависящего от е, существует число ./V
такое, что для любого п> N выполняются неравенства 0 <
< \х„ — я| < 5. Следовательно, при любом п> N будет вы-
Ш1
полниться неравенство |Дх„) — А\ < е. Но так как е > О
выбиралось произвольно, то это и означает, что Дх„) -»А,
т.е. для любой последовательности {х„}' (из области сущест-
существования функции у = Дх)), сходящийся к а, последователь-
последовательность Дх„) сходится к А; это и есть определение предела
функции на языке последовательностей.
2. Пусть KmДх) = А в смысле определения на языке
последовательностей. Покажем, что ШпДх) = А в смысле
определения на языке «е, 8».
Доказательство проведем от противного. Пусть Дх„) -> А
для любой последовательности {х„} точек из области суще-
существования функции такой, что х„ -» а, причем хп ф а. Пред-
Предположим, что для Дх)' число А не является пределом при
х —> а в смысле определения на языке «е, 8», т.е. существует
такое положительное число е, что для любого положитель-
положительного 8 найдется хотя бы одно число Зс такое, что 0 < |3с —
— я| < 8, но |ДЗс) — А\ > е.
Возьмем теперь последовательность {8„} такую, что
8„ —> 0. По предположению для любого 8„ существует число
х~„ такое, что 0 < |3^ — а| < 8„, но |ДЗ^) — А\ > е. Рассмотрим
последовательность х~„, х~„, ..., х~„, ... . Ясно, что х~„ -> а, но
ffa) не стремится к А, так как |Д5с^) — А\ > е для всех п.
Следовательно, нашлась последовательность {3^}, х~„ -» а,
из области существования функции у = Дх) такая, что
Шп 3^ = а, но последовательность {ДЗс^)} не стремится к А.
Это противоречит условию, что для любой последователь-
последовательности точек из области существования функции {х„}, х„ ф а,
такой, что lim х„ = а, обязательно lim Дхя) = А, т.е. наше
предположение неверно, а верно утверждение, что из схо-
сходимости на языке последовательностей следует сходимость
на языке «е, 8».
Равносильность двух определений предела функции до-
доказана в случае, когда точка сгущения а и Шп Дх) — конеч-
608
ные числа. В остальных случаях равносильность определе-
определений доказывается аналогично.
Для пределов функций справедливы свойства, аналогич-
аналогичные свойствам пределов последовательностей. Заметим,
что их практически не надо доказывать, ибо из определения
предела функции при помощи последовательностей выте-
вытекает, что все теоремы, доказанные для последовательнос-
последовательностей, справедливы и для функций. Сформулируем некото-
некоторые из них.
Теорема 1. Пусть точка а есть точка сгущения общей
части областей существования функций у = Дх) и у = g(x) и
пусть существуют оба конечных предела lim Дх) = А,
х~*а
lim g(x) = В. Тогда функции у = Дх) + g(x), y=fi.x) — g(x),
х-* а
У =Ax)g(x), у = 'Щк также имеют конечные пределы, соот-
ветственно равные А + В, А — В, АВ, ^ (В ф 0 в случае
частного).
Теорема 2. Пусть точка а (а — конечное число) есть
точка сгущения области существования функции у = Дх), и
если lim Дх) = А, где А > 0, то существует Ъ-окрестность
х~*а
точки а такая, что для любого хф а из области существо-
существования и принадлежащего этой окрестности, функция у = Дх)
положительна.
Аналогичное свойство справедливо, если А < 0.
Теорема 3. Если точка а (а — конечное число) есть
точка сгущения области существования функции у=Дх) и
если lim Дх) = А, где А — конечное число, то существует
х~*а
такая Ъ-окрестность точки а, что для любого хфа из
области существования и принадлежащего этой окрестнос-
окрестности функция у = Дх) будет ограниченной, т.е. найдется такое
число М>0 и такое 8>0, что для любого х из области
существования функции, такого, что 0 < |х — а\ < 8, будет
справедливо неравенство |Дх)| < М.
Теорема 4. Если точка а есть точка сгущения общей
части областей существования функций y=f{x), У = р(х) и
20 Алгебра, тригонометрия |%0Q
и элементарные функции WU7
У = Six) и для любого хфа, принадлежащего некоторой Ъ-ок-
рестности точки а и общей части областей существования
этих функций, справедливы неравенства f(x)<p(x)<'g(x).
Если Mm fix) = lim g(x) = А, тогда и lim g(x) = A.
x-*a x-*a
Пример.
Используя теорему 4, докажем, что lim ^^ = 1.
Х
х-*0
Функция у = ^^ четная, поэтому рассмотрим ее на
интервале @, я/2). Докажем, что на этом интервале имеет
место двойное неравенство
cosx<
sin л:
A)
Возьмем дугу AM единичной окружности, соответствую-
соответствующую углу, радианная мера которого равна х (рис. 185).
Тогда \ОА\ = 1, \МЦ = sin х, \ОЦ = cos x. Из подобия тре-
треугольников ОАТи ONM находим {0 |^ ^
Рис. 185.
= tg x. Так как площадь тре-
треугольника ONM меньше
площади сектора ОАМ, а
площадь этого сектора мень-
меньше площади треугольника
О AT, то имеем двойное нера-
неравенство
\\ОА\\МЩ<\\ОА?\АЩ<
<\\ОА\\А1\
или
sin х < х < tg x.
Разделим это двойное неравенство на sinx. Поскольку
sin х > 0, то знаки неравенства не изменятся и получим
справедливость двойного неравенства
610
sinx cosx*
Так как рассматривается интервал 10,1] и на нем х > О,
cos х > 0, sin х > 0, то имеем равносильные неравенства
sinx х sinx cosx х
что и доказывает неравенство A).
В силу четности функций у = cos х и у = ^^ двойное
неравенство A) будет иметь место и на интервале [— Ц, О
Действительно, если х е | — |, (И то 0 < (— х) < ^ ~и нера-
неравенство A) имеет вид ^ ^
Но cos (- х) = cos x, ^^> = =Ш* = Ж*. Следовательно,
неравенство A) справедливо и при х е [ — ^, ОI Итак, для
любого хе | — j, 0 |и [0, j |имеем cosх < ^^ < 1. Для того
чтобы теперь воспользоваться теоремой 4, необходимо
доказать, что limcosx=l. Воспользуемся определением
предела функции на языке «е, 5», т.е. докажем, что для
любого е > 0 найдется такое 8 > 0, что как только 0 < |х| <
< 8, то |1 — cos х| < е. В качестве 8 возьмем величину V2F,
тогда |1 — cosx| = 1 — cosx = 2sin21 = 2(sinЩ < 0f\
< е, что и требовалось доказать.
Итак, функция у = ^^ при х е [ — ^, 0 | и [ 0, ^ | заключе-
заключена между 1 и cos х, и поскольку lim cos х ^= 1,^то по теореме
4 получим lim ^^ = 1.
611
В определении предела функции у =Дх) в точке а (точке
сгущения области существования функции) х может при-
приближаться к а по любому закону.
Иногда приходится рассматривать предел функции
у=Ах), кргда х (из области существования функции),
стремясь к а, остается все время справа от точки а. Тогда
говорят, что функция у =Дх) имеет предел справа, и запи-
записывают lim Дх) = А, где lim Дх) — либо конечное число,
либо (+ °°), либо <— °°). Аналогично определяется предел
слева lim Дх) = A.
х-*а — 0
Примеры.
1. lim signx = I, lim sigiuc= — 1 (рис. 186).
jt-»O + O Jt-»O —О
2. lim —Ц = + во, lim —Ц = — °» (рис. 187).
*»2 0 0
3. Функция у = х2 имеет в любой точке а предел и справа
и слева, при этом lim x2 = lim x2 = а2.
х-*а + 0 х-*а — 0
Пусть дана функция у =Дх) и ее график. Если сущест-
существуют точка M(xq, Дхо)) и прямая, такая, что хотя бы при
одном из условий х->а, х->а + 0, x->a — 0, х-> + «>,
х _> _ оо начиная с точки М расстояние между точками
графика и прямой неограниченно уменьшается, то эта
прямая называется асимптотой функции у =flx).
Если выполняется хотя бы одно из условии:
= + оо, lim Дх) = + оо, lim Дх) = + оо,
х-*а + 0 х-*а — О
= — «о, lim Дх) = — оо, lim Дх) = — оо,
х-*а х-*а + 0 х-*а — О
то асимптота х = а называется вертикальной.
Примеры.1. Функция у = log2 (x + 3) имеет вертикаль-
вертикальную асимптоту х = — 3, так как lim log2 (x + 3) = — оо
(рис. 188).
2. Функция У = т^-п имеет вертикальную асимптоту
х = — 1, так как lim —-г. = + оо (рис. 189).
х-*-1 Iх" 1!
612
@,1)
A
@,-1)
J i
0 x
I. y=s\gn x
Рис. 186.
Kl
@,\og23)
@,1)
0
Рис. 188.
Рис. 187.
1-1
II. y~x-l
Рис. 190.
Рис. 191.
Если выполняется хотя бы одно из условий lim Дх) = Ь,
lim Дх) = b, то асимптота у = Ъ называется горизонтальной.
Х-* — "
Примеры. 1. Функция у = 2 + 3х имеет горизонталь-
горизонтальную асимптоту у = 2, так как lim B + 3х) = 2 (рис. 190).
х-* — ~
2. Функция у = - имеет горизонтальную асимптоту у = 0,
так как lim - = 0 и lim - = 0.
х-»-~Х *-» + - х
Если выполняется хотя бы одно из условий lim [Дх) —
— (кх + Ь)] = 0 или lim [Дх) — (кх+ Ь)] = 0, то асимптота
х-* — ~
.у = Азе + й называется наклонной.
Пример. Функция у = х + - — 1 имеет наклонную
асимптоту у = х — 1 (рис. 191).
§ 4. Непрерывность функции
Функция у =ЛХ) непрерывна в точке Хд, если:
1) Хо — точка сгущения области существования функции
У=Ах);
2) Хо принадлежит области существования функции
У=Лх);
3) существует Шп.Дх);
4) lim Дх) =Лхо) (т.е. lim Дх) = >>„, где у0 =Дхо)).
Примеры. 1. Функция у = 2х непрерывна, например, в
точке Хо = 1.
Действительно, Xq = 1 — точка сгущения области суще-
существования функции; точка Xq = 1 принадлежит области
существования функции, значит у0 = 2х = 2; существует
lim 2х = 2; наконец, lim 2х = 2 = у0.
Х-*\ Х-+1
2. Функция у = log3 х непрерывна, например, в точке
Хо = 3.
Действительно, Xq = 3 — точка сгущения области суще-
существования функции; точка Xq = 3 принадлежит области
614
существования функции, значит у0 = log3 3=1; существует
lim log3 х = 1; наконец, lim log3 х = 1 = у0.
х-*3 х-*3
3. Функция у = —Цг в точке Xq = 2 не является непрерыв-
ной, так как нарушено, например, условие 2, т.е. точка
Xq = 2 не входит в область существования функции.
4. Функция у = sign х в точке Xq = О не является непре-
непрерывной, так как нарушено, например, условие 3, т.е. не
существует lim sign x.
х-*0
5. Легко проверить, что каждая основная элементарная
функция является непрерывной в любой точке ее области
существования.
Учитывая вышеприведенные эквивалентные между
собой определения предела функции в точке, приведем еще
два определения непрерывности функции в точке.
Функция у =Дх) называется непрерывной в точке Xq, если
для любого числа е > 0 найдется такое число 8 > 0, что для
любого х из области существования, удовлетворяющего
неравенству \х — Хо| < 8, выполняется неравенство |/(х) —
-Ах<>)\<г.
Функция у =Дх) называется непрерывной в точке Xq, если
для любой последовательности {х„} значений аргумента из
области существования, сходящейся к точке хь, соответст-
соответствующая последовательность значений функции {Дх„)} схо-
сходится к значению Дхо).
Используя второе определение непрерывности функции
в точке, покажем, например, что функция у =2* является
непрерывной, например, в точке Xq = 1 (т.е. покажем, что
для любого е > 0 найдется такое 8 > 0, что для любого х,
удовлетворяющего неравенству |х — 1| < б, будет выпол-
выполняться неравенство \Т — 2'| < е). Действительно, для любо-
любого числа е>0 возьмем, например, число 8 = log2|l+||
Тогда для любого числа х, удовлетворяющего условию |х -*-
— 1| < 8, т.е. для любого х из промежутка A — 8; 1+8),
будут справедливы неравенства
615
T < 21+5 = 2 • 25 = 2 • 2log4I + 2J= 2f 1 +f ]= 2 + e;
_ 2 _ 4 >4-e2_2
e 2+e 2+e
1 + 2
Эти неравенства означают, что \2Х — 2'| < е для любого х
такого, что |х — 1| < 5, т.е. согласно второму определению
непрерывности функции в точке, функция у = 2х непре-
непрерывна в точке Хо = 1.
Используя третье определение непрерывности функции
в точке, покажем, например, что функция у = [х] не явля-
является непрерывной в точке х = 2, т.е. укажем хотя бы одну
последовательность значений аргумента {х„} такую, что
lim х„ = 2, но соответствующая последовательность значе-
ний функции {[х„]} такова, что lim [х„] * [2]. Такова, на-
например, последовательность значений аргумента с общим
членом х„ = 2 — -. Действительно, lim 12 — -1 = 2, но
lim |2 — -1 = 1 и, следовательно, lim Г2 — -1 = 1 ф 2 = [2],
что требовалось доказать.
Теорема 1. Пусть функция у ~ J[x) у = g(x) непрерывны
в точке Xq. Тогда в той же точке будут непрерывными и
функции у =Лх) + g(x), у = Лх) — g(x), у =Ax)gix), у =
(последняя при условии, что g(xo) * 0).
Эта теорема является следствием теорем о пределе функ-
функций в точке.
Например, согласно теореме 1 функция у = sin х + х2
является непрерывной, скажем, в точке хь = 1. Действи-
Действительно, точка Хо = 1 принадлежит области существования
функции у = sin х и функции у = х2. Так как любая основ-
основная элементарная функция непрерывна в каждой точке ее
области существования, то и функция у = sin x и функция
616
у = х2 непрерывны в точке Xq = 1. Тогда согласно теореме 1
и функция у = sin х + х2 непрерывна в точке Xq = 1.
Наряду с уже рассмотренной непрерывностью функции
в точке часто рассматривается так называемая односторон-
односторонняя непрерывность функции в точке. Приведем соответст-
соответствующие определения. -
Функция у =J[x) непрерывна справа в точке Xq, если:
1) Xq — точка сгущения области существования функции
У=Ях)\ . .
2) Xq принадлежит области существования функции
У=Лх);
3) существует Urn Лх), обозначаемый Дхо + 0);
Аналогично определяется непрерывность функции слева
в точке Xq. Ясно, что если функция y=J[x) непрерывна в
точке Хо, то она в этой точке одновременна непрерывна и
справа и слева и Дхо + 0) =Лхо) =/(хо — 0).
Примеры. 1. Функция у = [х] в точке Xq = 1 непрерыв-
непрерывна справа, так как lim [х] = 1 = [1].
х-»1+0
2. Функция у = sign х в точке Xq = 0 не является непре-
непрерывной ни справа, ни слева. Действительно, хотя функция
у = sign х в точке Xq = 0 имеет и предел справа (lim sign x =
х-»0+0
= 1) и предел слева (lim sign x = — 1), но ни один из этих
х-»0-0
пределов не совпадает со значением функции у = sign x в
точке Хо = 0 (sign 0 = 0).
3. Функция у = 2х в любой точке х непрерывна и справа
и слева.
Функция у =Лх) имеет в точке Xq разрыв, если не выпол-
выполняется хотя бы одно из условий 1 — 4 определения непре-
непрерывности функции в точке Xq.
Пример. Функция у = sign х имеет в точке Xq = 0 раз-
разрыв. Действительно, равенство lim sign x = sign 0 не выпол-
х-*0
няется, так как не существует предела функции у = sign x в
точке Хо = 0 (хотя и существуют односторонние пределы,
но они не равны друг другу и ни один из них не равен
значению функции в точке Xq = 0).
Пусть функция у=Дх) имеет разрыв в точке Xq. По
определению точка Xq называется точкой разрыва первого
рода, если в этой точке функция у =Дх) имеет конечный
предел как справа, так и слева. Во всех остальных случаях
разрыва точка Xq называется точкой разрыва второго рода.
Примеры. 1. Для функции у = [х] точка Xq = 1 является
точкой разрыва первого рода. Действительно, функция
у = [х] имеет в точке Хц = 1 разрыв, так как функция у = [х]
в точке Хо = 1 не имеет предела, но имеет конечный предел
и справа (lim [x] = 1) и слева (lim [x] = 0).
Jt-»1+O х-» 1 —0
2. Для функции у = - точка Xq = 0 является точкой раз-
разрыва второго рода. Действительно, функция у = -ъ точке
X
Xq = 0 имеет разрыв, так как точка Xq = 0 не принадлежит
области существования функции. Кроме того, функция
у = - в точке Хо = 0 не имеет конечного предела справа
X
(lim ±= + ~).
х-»0 + 0 х
3. Для функции у = sin |-1 точка Xq = 0 является точкой
разрыва второго рода. Действительно, функция у = sin - в
V J
точке Хо = 0 имеет разрыв, так как точка Xq = 0 не принад-
принадлежит области существования функции. Кроме того, функ-
функция у = sin [- ] в точке Xq = 0 не имеет предела справа, так
как можно указать две последовательности значений аргу-
аргумента справа {х„} и {х^,} такие, что lim х„ = 0, lim х„ = 0, но
соответствующие последовательности значение функции
{in f — 1 и I sin [ 4-1 таковы, что lim sin \ — | ф lim sin \4-1 Та-
б
sin f — [ 41
кими, например, будут последовательность с общим чле-
ном хп = и последовательность с общим членом
-х + 2тси
" тел'
Функция у=Л*) называется непрерывной на некотором
промежутке (а, Ь), если она непрерывна в каждой точке
этого промежутка. Другими словами, функция у=Дх) не-
непрерывна на промежутке (а, Ь), если:
1) весь промежуток:. входит в обларть существования
функции у =/00;
2) любая точка Xq этого промежутка есть точка сгущения
области существования функции у =/00;
3) в любой точке Xq этого промежутка существует lim /00;
4) в любой точке Xq этого промежутка справедливо ра-
равенство lim Лх) =Лхо), т.е. lim Дх) = у0, где у0 =Лхо)-
Примеры. 1. Функция y = cosx непрерывна на про-
промежутке (— °°, + «>).
2. Функция у = log3 х непрерывна на промежутке @,
+ °°).
3. Функция у = ^-j- непрерывна на промежутке A ; + «>);
кроме того, она непрерывна на промежутке (— °°, 1), но
она не является непрерывной, например, ни на промежутке
(— °°, + °°), ни на промежутке [1, + °°), ни на промежутке
§ 5. Производная функции
Рассмотрим функцию y=J{x). Пусть х — некоторая
точка сгущения функции, принадлежащая ее области су-
существования, J[x) — значение функции в этой точке. От
значения х переходим к другому значению аргумента xt * х,
которое также принадлежит области существования. Раз-
Разность хх — х (обозначим ее через Дх) называется прираще-
приращением аргумента в точке х. Значение функции, соответст-
соответствующее значению аргумента хх = х + Ах, обозначим
Ах + Ах).
619
Разность fix + Ах) — fix) называется приращением функ-
функции в точке х, соответствующим приращением аргумента
Ах в этой точке, и обозначается Ау или ДДх):
Ay = Afix)=fix + Ax)-fix).
В зависимости от вида функции, ее приращение Ау может
быть равно нулю, быть положительным или отрицатель-
отрицательным числом. Приращение аргумента Дх также может быть
положительным или отрицательным, но Ах ф 0.
Примеры. 1. Найти приращение функции .у = |х| в
точках х = 0, х=1их=— 1, считая, что |Дх| < 1.
а) Если х = 0, то
{А
[—Дх, еслиДх<0.
б) Еслих= 1, то
Ау = |1 + Дх1 — |1| = 1 + Дх — 1 = Дх, если fAxj < 1.
в) Если х= — 1, то
Ау = |— 1 + Дх| — |— 1| = 1 — Дх — 1 = — Дх, если |Дх| < 1.
2. Найти приращения функции у = sin х в точках х = 0,
х = ?, х= — |ив произвольной точке х.
а) Если х = 0, то Ay = sin @ + Дх) — sin 0 = sin Дх.
б) Если х = ^, то
Ay = sin (| + Дх) - sin | = 2 sin ^ cos [f + у
в) Если х = — |, то
Ay = sin Г-1 + Дх) - sin (- f\= 2 sin f cos (-1 + 4^
г) Если x — любая точка, то
620
Ay = sin (x + Ax) — sin x = 2 sin -y cos jx+ -r~
3. Найти приращения функции у = Vx~ в точках х = О,
х = 1 и любой точке х € @, + ~).
а) Если х = 0, то приращение Ах > 0 (в силу области
существования функции у = Vx), поэтому
Ау = л/О + Дх — V6" = VAx,
б) Если х= 1, то
где |Дх1 < 1.
в) Если х — любая точка (х > 0), то
NX + ДХ+Х
где |Дх| < х.
Пусть функция у = Лх) определена в некоторой окрест-
окрестности точки х. Дадим аргументу х приращение Дх (при этом
предполагается, что точка х + Дх принадлежит области
существования функции). Тогда функция получит прира-
приращение Ay =fix + Ах) — J{x).
Производной функции у = Дх) в точке х называется пре-
предел отношения приращения этой функции к приращению
аргумента в этой точке при стремлении приращения аргу-
аргумента к нулю, если такой предел существует и конечен.
Производная функции у = Дх) в точке х обозначается у
(читается «игрек штрих»), или -%¦ (читается «де игрек по де
икс»), или -??¦ (читается «де эф по де икс»). Нахождение
производной от функции называется дифференцировани-
дифференцированием.
Итак, по определению:
Дх->0 А* Дх-»0
т.е.
/()
Дх-»О Д*
Из определения следует, что производная функции
У = Лх) в точке х есть число, зависящее от рассматривае-
рассматриваемого значения х, но не зависящее от Ах. Кроме того,
производная функции y=flx) может существовать не во
всех точках области существования этой функции. Рас-
Рассмотрим множество М всех точек области существования
функции у =f(x), в которых эта функция имеет производ-
производную. Вычисляя производную функции y=J(x) в любой
точке х € М, получаем, что каждому числу х е М ставится
в соответствие одно число fix). Другими словами, этим
соответствием задана функция, обозначаемая У =/'(*)> с
областью определения — множеством М.
Найдем производные некоторых элементарных функ-
функций.
1. Пусть на некотором интервале (а; Ь) функция у =fix)
имеет постоянное значение с, т.е. у = с на (а; Ь). Тогда У =
= (с*) = 0 для любого х из (а; Ь).
Действительно, для любого х из (а; Ь): Ау = с — с = О,
следовательно, — = 0, откуда У = lim — = lim 0 = 0.
^ Дх^О^" Дх-»0
2. Пусть у = х, тогда У = 1 для любого х.
Действительно, для любого х Ау = (х + Ах) — х = Ах и
lim ^ = lim ^ = "т 1 = 1.
Дх->0 Д* Дх-^А* Дх->0
3. Пусть у = х" (п — фиксированное натуральное число),
тогда / = пх" ~ ' для любого х.
Действительно, для любого х по формуле бинома Нью-
Ньютона (см. гл. II)
622
... + (Ах)",
откуда
Дх
- i
и, следовательно, У = ton -^ = их" , т.е. (х4)' = пх"
Дх->0
Дх
4. Пусть >> = sin х, тогда У = cos x для любого х. Действи-
Действительно для любого х
Ay = sin (х + Ах) — sin х = 2 sin Щ- cos f x + 4р
и, следовательно,
У = ton & = ton
Дх-»0 Д* ¦ Дх-»0
. Дх
sin-=-
Дх
2
. Дх
яп-=-
Ранее было доказано, что ton —— = 1. Докажем, что
Дх->0 Д*
2
/ А \
lim cos |х + —|= cosx, т.е. докажем, что для любого е > О
Дх->0
найдется такое 6 > 0, что
ко
cos х +-=- — cos х
< е, как толь-
< 6. Для доказательства возьмем 6 = е и получим
следующую цепочку неравенств:
( ДхА
COS X + -у 1 — COS X
2 sin x + ^ sin^
<2
Дх
следовательно, (sin х)' = cos x.
5. Пусть у = cos х, тогда / - — sin x для любого х. Дей-
Действительно, для любого х
Ay = cos (х + Ах) — cos х = — 2 sin у sin Гх + у
Тогда
= lim^
Дх->0 Д*
= lim
Дх->0
. Дх
sin -=- , .„
и, поскольку lim
Дх
— =1и lim sin f x + 4^ ] = sin x (доказа-
« Дх->0 *
тельство такое же, как и в предыдущем примере), то У =
= — sin х, т.е. (cos х)' = — sin x.
Если нужно найти производную функции у =Дх) в не-
некоторой фиксированной точке х = Xq, to обычно сначала
находят производную этой функции в любой точке х, где
она существует, т.е. находят у =/'(х), а затем вместо про-
произвольного х подставляют х = Xq. Производную в фиксиро-
фиксированной точке Хо обозначают /'(xj,), /(xq), ^-^ или/'|х=д;),
Пример. Найти производную функции >> = sin x в точ-
Так как у = cos x, то
J =cos J =f,
fl=0.
Реиюние примеров на нахождение производных значи-
значительно упрощается, если использовать правила дифферен-
дифференцирования, которые вытекают из теорем для пределов.
Рассмотрим некоторые из них.
624
В дальнейшем предполагается, что аргумент х изменяет-
изменяется в общей части областей существования функций, участ-
участвующих в следующих утверждениях.
1. Если в точке х существуют конечные производные
функции у = v(x) и функции у = и(х), то в точке х производ-
производная суммы этих функций существует и равна сумме произ-
производных этих функций, т.е. (v(x) + w(x))' = v'(x) + i/(x).
Действительно, дадим х приращение Ах. Тогда функции
у = v(x) и у = и(х) получат приращение, соответственно
равные Av(x) и Ды(х), и функция у = v(x) + ы(х) получит
приращение Ay = [(v(x) + Av(x)) + (ы(х) + Ды(х))] — (v(x) +
+ ы(х)) = Av(x) + Аы(х). Поскольку
Ду __ AvC*) 4- ДиС*)
Дх Дх~ Дх '
ТО
л Дх-»0 I м °* I
так как предел каждого слагаемого существует и конечен.
Пример, (х2 + sin х)' = (х2)' + (sin х)' = 2х + cos x.
2. Если в точке х существуют конечные производные
функции у = v(x) и функции у = м(х), то в точке х производ-
производная разности этих функций существует и равна разности
производных этих функций, т.е. (v(x) — м(х))' = v^x) — м'(х).
Доказательство утверждения 2 аналогично доказательст-
доказательству предыдущего утверждения и поэтому опускается.
Пример, (х4 — cos х)' = (х4)' — (cos х)' = 4Х3 + sin x.
Используя формулы нахождения производной в точке
для суммы и разности двух слагаемых, легко получить
формулу для нахождения производной в точке для алгеб-
алгебраической суммы любого числа слагаемых. Напишем, на-
например, эти формулы для алгебраической суммы пяти
слагаемых:
625
Пример, (х + х5 — х* + sinх — cosx)' = 1 + 5х4 — 8х7 +
+ cos х + sin x.
3. Если в точке х существуют конечные производные
функции у = v(x) и функции у = и(х), то в этой точке суще-
существует производная функции у = v(x)u(x), при этом ,
У = (Цх)ы(х))' = У(х)ы(х) + v(x)i/{x).
Действительно, дадим приращение Дх. Тогда функции
у = v(x) и у = и(х) получат приращения, при этом
у = (v(x) + Ду(х))(ы(х) + Ды(х)) — v(x)m(x) =
= у(х)Ды(х) + м(х)Ду(х) + Ду(х)Ды(х),
и(х) + *f> v(x> + ^w Au{x)
Дх Дх v
и(х) f v(x> + ^
ДЛ Дх Дх Дх
Применяя теоремы о пределе суммы и произведения,
имеем
У = lim ^ = Шп (^и(х))+ lim
)
Аи(х)) = и(х) lim ^ + v(x) lim
J ЛХ-*О
+ lim ^ lim (Дм(х)).
Дх-»0 ^ Дх-»О
Учитывая, что lim ^ = V(x), lim ^ = i/(x), lim Ды(х) =
Дх-»0 ^ Дх-»О ДХ Дх-»0
= 0, получим У = (v(x)m(x))' = /(х)ы(х) + v(x)i/(Ax), что и
требовалось доказать.
В частности, если у = v(x) = с (с — константа), то
(си(х))' = <?и(х) + а/(х) = а/(х), т.е. постоянный множи-
множитель можно вынести за знак производной: У = (сы(х))' =
= Ы{х).
Пример, у = 5х + IX — 4.
У=Eх3 + 7х2- 4)' = Six3)' + 7(хУ - D)' = 15Х2 + 14х.
626
Используя формулу нахождения производной в точке
для двух сомножителей, легко получить формулу для случая
произведения нескольких сомножителей.
4. Если в точке х существуют конечные производные
функций у = v(x) и у= и(х) и функция у = и(х) отлична от
нуля в этой точке, существует и производная функции у =
= М при этом У = М = Г
«Ю [««J и(х)
Действительно, дадим х приращение Дг. Тогда функции
у = v(x) и у = и(х) получат приращения, при этом
д _
у
Применяя теоремы о пределах частного и произведения и
учитывая непрерывность функции у = и(х) в точке х, полу-
u\x)
Примеры. \.y = tgx.
./ _ /to vy _ fsinx^ _ (sin x)' cos x — (cos x)' sin x _
У Vlg х) Tcxr 2
[cosxj cos x
_ cos x + sin x _ 1
2 2 '
COS X COS X
т.е.
2
y-
T A
(tg*)' =
• J> = ctg
(ctgx)'
fr>ta vV z
1
cos2x
X.
_ /'cos хЛ _
1 sin x I
1
(cos x)' sin x —
sin2
(sin x)' cos x _
X
. 2 2
_ — sin x — cos x _
sin2x
1
. 2 '
sin x
sin x
627
Используя формулы производных основных элементарных
функций и правила дифференцирования, можно найти
производную любой функции, которая является суперпо-
суперпозицией основных элементарных функций. Приведем таб-
таблицу 31 производных элементарных функций:
Таблица 31
У=Лх)
у= с (с — const)
у = х
у^х2
у = х" (Л —
натуральное
число)
у = х~ " (п —
натуральное
число)
у = х~а(а>0)
у=а*(а>0,
У^
у = loga x(a>0.
а*1)
?=Г(х)
у = о
У=1
У = 2х
У=пх"~1
у = _лх-"-»
У = осса-1
У = -осс-°-1
У = д* In а
У = ^
1
xlna
у=Лх)
у= lnx
у = sin х
у = cos х
j> = tgx
у = ctg х
у = arcsin x
у = arccos x
у = arctg x
у = arcctg x
У =/'(*)
у4
У = cos х
У = — sin х
у 1
cos2x
у 1
sin2x
¦^ ^= '' ' "
л/ ^= *' ' "'
УПРАЖНЕНИЯ
Выписать десять первых членов последовательности, если ее общий
член задается формулой A — 6):
1. а„ = sin —, где х„ = .
2. а„ = яп—, гдех„ = —-
Х„ К
628
3. ^, = sin—,
х
п
2 + пп
. i,. t-2^ , Г3л+ 1 , ,
4. а„ = —— .5. а„ = —¦— .6. а„ =
Написать формулу общего члена последовательности, для которой
заданы восемь первых ее членов G — 12):
_ . i 1 J_ J_ J11
' 2' 6' 24' 120' 720'
2' 6' 24' 120' 720' 5040' 40320""
IIIIIIIJ.
3' 4' 5' 6' 7' 8' 9' 10'"
10. 1, 2, i 4,1 6, j, 8,...
11.1,-1,1,5,1,-5,1,9,...
и illlilil
' 2' 3' 4' 5' 2' 7' 8'"
13. Последовательность {сл} задана формулой общего члена:
с„ = Юл2 + 4. Найти ск+ 4-
14. Является ли число (—21) членом последовательности {*„}, заданной
формулой общего члена Ь„ = гг — Юл? В случае утвердительного ответа
найти его номер.
Выяснить, является ли монотонной последовательность, заданная сле-
следующей формулой общего члена A5 — 23):
15. а„ = л2 + 2л. 16. а„ = -^—.
пг + п
17. а„ = cos л. 18. а„ = **1п2 + л — л.
л
21. ал = 2л2 - 2л. 22. а„ = |10 - 2л2|.
23. ал = 3^л+Т—3^л".
Выяснить, является ли ограниченной последовательность, заданная
следующей формулой общего члена B4 — 29):
24.^ = ^1 +lJ. 25. ап-1.
Л + COS Л
, = (-1)^.29.^ = ^^3
629
Привести пример последовательности C0 — 35):
30. Ограниченной сверху, но не ограниченной снизу.
31. Ограниченной снизу, но не ограниченной сверху.
32. Не ограниченной ни сверху, ни снизу.
33. Ограниченной, но не имеющей предела.
34. Которая не является возрастающей.
35. Которая не является убывающей.
36. Существует ли числовой промежуток вида [а, Ь], которому принад-
принадлежат все члена последовательности {а„), заданной формулой общего
члена а„ = — ? В случае утвердительного ответа укажите такой проме-
2 + и
жуток.
37. Найти пятый член арифметической прогрессии {с„}, если
с, = -50и</=1,2.
38. Найти сумму 30 первых членов арифметической прогрессии {а„},
если ах = —2.5 и d= 3.
39. Известны два члена арифметической прогрессии {Ь„}: bj = 4,9 и
й17 = 10,9. Каково число членов прогрессии, каждый из которых мень-
меньше 20?
40. Является ли число 35 членом арифметической прогрессии — 47,
— 44, — 41,... ? В случае утвердительного ответа найти его номер.
41. Доказать, что если a, b и с есть три последовательных члена
арифметической прогрессии, то al + %bc= Bb + с) .
42. Найти 15-й член геометрической прогрессии {а„}, если
а, = — 0,001 и д= 10.
43. Известны 8-й член и знаменатель геометрической прогрессии {Ь„}:
Ag = 2,56 и q= 2. Найти сумму 16 первых членов прогрессии.
44. Известны два члена геометрической прогрессии {bn}: 6j = 0,l и
by = 2,5. Является ли эта прогрессия монотонной последовательностью?
45. Известны первый член и знаменатель геометрической прогрессии
{а„}: ax = — %\vid= — -=. Является ли эта прогрессия монотонной после-
последовательностью?
46. Доказать, что произведение п первых членов геометрической про-
л(л — 1)
грессии равно d[ q г , где а\ — первый член прогрессии, a q — ее
знаменатель.
47. Доказать, что если ab, b2, с2 — последовательные члены арифмети-
арифметической прогрессии, то Ь, с и BЬ — а) — последовательные члены геомет-
геометрической прогрессии.
48. Последовательности {а„}, {Ь„} и {с„} таковы, что
Ci = 5, сл+, = — Зс„.
630
Какая из последовательностей является: 1) арифметической прогрес-
прогрессией; 2) геометрической прогрессией?
49. Найти сумму бесконечной геометрической прогрессии с первым
членом а\ = V2~ и знаменателем q=-=.
Доказать, используя определение предела последовательности, следую-
следующие равенства E0 — 55):
50. lim —Ц = 0. 51. lim ^ 1
52. lim "~3я , 1. 53. lim
,_»+.Bи+!)(«+!) 2
54. lim ff^ = 1. 55. lim
Вычислить E6 — 76):
58. lim ^Щг-. 59. lim {^-r ?—
л-»+,5-0,9л л_>+42я~1 4и2-1
60. lim %-. 61. lim Nn2 — In — n\
n-»+- 2и— 1 + Зи n-»+-v /
62. lim 1^4-1- 63. lim f^rT.
5. lim
бб.Нт|.
л—»+~3 — 2и
68Ит iin%-6
3
70. lim tg x. 71. lim (sin 5x cos x — sin x cos 5x).
72. lim ^--. 73. lim >/x+T.
ДГ + Х x-»0
74. lim x2-5*^. 75. lim
(l)F)
76. lim (sin3xctg4x).
Найти производную следующей функции G7 — 90):
77.y=tgx + ctg(f — к). H.y = i'sin | —х + cosBx+ 1).
7* у = cos2xsin Cx+ 5). 80. y= Ц*-ЧР- 1)
' v l+tgxtg(x— 1)
81. у = logvj V2x-1. 82. у = log3Г2Х2 - 3x+ A
83. y= log10cosx 84. у = х~ЯТ—х1Т.
Глава X. СИСТЕМЫ ЛИНЕЙНЫХ
УРАВНЕНИЙ
„:__ч
В гл. Ill уже рассматривались системы алгебраических
уравнений с несколькими переменными. В этой главе
рассматривается общая теория решения систем линейных
уравнений с несколькими переменными.
Отметим, что алгебраическое уравнение Р(х, у, ...,/) = О
(см. гл. III) называется линейным, если Р(х, у, ..., /) есть
многочлен степени не выше первой, целый относительно
переменных х, у, ..., /.
§ 1. Матрицы
Матрицей размеров тхп называется совокупность тп
чисел, расположенных в виде прямоугольной таблицы из
т строк и п столбцов.
Например, прямоугольная таблица чисел
1 3
-5 7
есть матрица размеров 2x3; прямоугольная таблица чисел
есть матрица размеров 3x2.
Матрица размеров 1 х п, т.е. состоящая из одной строки,
называется матрицей-строкой. Например, матрица
A 3-4 5) есть матрица-строка.
633
Матрица размеров /nxl, т.е. матрица, состоящая из
одного столбца, называется матрицей-столбцом. Напри-
1 е
мер, матрица 1 есть матрица-столбец.
Матрица размеров пхп называется квадратной матри-
матрицей, а число п называется ее порядком. Например, матрица
есть квадратная матрица третьего порядка.
Квадратная матрица порядка 1 есть просто число.
Числа, из которых состоит матрица, называются элемен-
элементами матрицы.
Для записи матрицы в общем виде элементы матрицы
обозначаются буквами с двумя индексами, например av;
при этом первый индекс указывает номер строки, а второй
индекс — номер столбца, в которых содержится этот эле-
элемент.
Например, матрица размеров 3x4 записывается в общем
виде так:
«11 «12 «13 «14
1 «22 3 °ТА
<Н\ «32 «33 °34
A)
Часто матрицу, элементами которой являются, напри-
например, числа Ьф обозначают одной заглавной буквой В и для
записи этого факта употребляют знак равенства. Например,
матрицу с элементами av принято обозначать буквой А и
записывать этот факт так:
А =
«11 «12 «13 «141
°21 «22 «23 <*24
°i\ «32 3 °34
Пусть дана матрица С размером т х п:
634
c=
С„ C,2 С,, ... C^
<<2I - % *23 — С2л
^31 C32 C33 ••• C3»
сш1
Индексы i и у называются допустимыми для матрицы
размеров /и х и, если i — индекс строк есть любое из чисел
1, 2, ...^m;j — индекс столбца есть любое из чисел 1, 2, ...
..., п. t
Часто у матрицы-столбца и матрицы-строки их элемен-
элементы обозначаются одним индексом. Например,
Х=
= (Д /2 /3 /д.
Матрицы А и В, каждая из которых размеров /ихп,
называются равными, если равны их соответствующие эле-
элементы, т.е. если av = bv для любых допустимых индексов /
и j. В таких случаях пишут А = В. Например,
3 4
О 1
л/9 4
2^
0 1 f
Для любых матриц знаки сравнения >, >, < или < лишены
смысла, а для матриц разных размеров, кроме того, лишен
смысла знак равенства.
Суммой матриц Аи В, каждая из которых размеров /их п,
называется матрица С тех же размеров /и х п, каждый
элемент которой равен сумме соответствующих элементов
матриц А и В, т.е. С = А + В, если св = а# + bv для любых
допустимых индексов / и j. Например,
2
-1
0
31
4
fl
ко
1
-24)
-1
=
f 3
- 1
1
1
2
3
Для матриц А и В с разными размерами операция сло-
сложения лишена смысла.
«35
Легко видеть, что для любых матриц А, В, С, каждая из
которых размеров т х п, справедливы следующие утверж-
утверждения:
а) сложение матриц коммутативно: А+ В= В + А;
б) сложение Матриц ассоциативно: А + (В + Q = (А +
+ В) + С.
Из этих утверждений следует, что в любой сумме конеч-
конечного числа матриц, каждая из которых размеров тхп,
слагаемые можно записать в любом порядке и скобки,
указывающие порядок сложения, можно расставлять про-
произвольно. Например,
[A+(C+B)]+D=[(A+ Q + B] + D = A + B+ C+D.
Матрица размеров тхп, у которой каждый элемент
равен нулю:
0 =
называется нулевой матрицей размеров (т х п) или нуль-
матрицей размеров тхп. Эта матрица обладает тем свой-
свойством, что для каждой матрицы А размером тхп справед-
справедливы равенства А + 0 = 0 + А = А.
Например, матрица 0 = Г9 2 2 ] есть нуль-матрица разме-
размеров 2x3, матрица 0 = Г9 2] есть квадратная нуль-матрица
второго порядка.
Среди всех матриц, каждая из которых размеров тхп,
существует единственная нуль-матрица. Нуль-матрицы
разных размеров принято обозначать одним и тем же
символом 0, что не приводит к недоразумениям, ибо из
контекста ясно, какие размеры имеет нуль-матрица в рас-
рассматриваемом случае.
Пусть дана матрица А размеров тхп. Матрица (— А) тех
же размеров, каждый элемент которой есть элемент матри-
матрицы А, взятый с противоположным знаком, обладает тем
636
fo
О
О
О
О
О
О
О
О ..
О ..
О ..
О ..
. с
. О
. О
. О
свойством, что А + (— А) = (— А) + А = 0. Матрица (— А)
называется противоположной матрицей к матрице А. На-
Например, матрица Г Л противоположна к матрице
матрица (~^ ~^ _Л противоположна к матрице
E 6-гЛ ]
о -1 г)
Можно показать, что для любой матрицы А существует
единственная противоположная матрица, т.е. для матрицы
А только матрица (— А) такова, что А"+ (— А) = (— А) +
+ А = 0.
Сложение матриц обладает обратной операцией — вы-
вычитанием. Это значит, что для любых двух матриц А и В,
каждая из которых размеров тхп, существует единствен-
единственная матрица С тех же размеров и такая, что А + С = В.
Матрица С называется разностью матриц А и В и обозна-
обозначается А — В. Например,
D 0 П_ ( 2 1 П=B — 1 (П
13 5 7J 1-6 1 -ll 19 4 8J
Произведением матрицы А размеров тхп на некоторое
число а называется матрица С тех же размеров тхп,
элементы которой получаются из соответствующих эле-
элементов матрицы А умножением на это число а, т.е. С = аЛ,
если cv = аа^ для любых допустимых индексов i и/. Напри-
Например,
= Гб 8\ _ з (- П = р\
Из определения умножения матрицы на число следует,
что для любых матриц Аи В, каждая из которых размеров
тхп, и любых чисел аир справедливы равенства:
а) (а + р)Л = аЛ + $А;
б) (арМ = а(рЛ);
в) а(А + В) = аА + аВ.
Заметим, что противоположная матрица (— А) к матрице
А равна (- 1) А, т.е. (- А) = (- 1) А.
Пусть дана матрица-строка /"размеров 1 х г, т.е.
637*
F=(fu /2, /3, -.., /X
и матрица-столбец Хразмеров rxl, т.е.
X=
Произведением матрицы-строки F размеров 1 х г на мат-
матрицу-столбец X размеров rxl называется матрица, обозна-
обозначаемая FX, размеров 1x1, т.е. число, которое равно сумме
произведений соответствующих элементов этих матриц,
т.е. по определению
= /lXl +fyC2 +/3X3
или
, +/2X2
(fi,/г, .. ft
Примеры. 1. A 2) С" J]= 1 • (— 4) + 2 • 2 = 0;
7 - j • 2 + i • 3 + 0 • (- 7) + 1 • 1 +
С помощью произведения матрицы-строки размеров
1 х /• и матрицы-столбца размеров rxl определяется про-
произведение матрицы А размеров тхги матрицы В размеров
гхп, т.е. таких матриц, что первый сомножитель, матрица
А, имеет столько столбцов, сколько второй сомножитель,
матрица В, имеет строк.
По определению произведением матрицы А размеров тхг
на матрицу В размеров гхп называется матрица С размеров
638
m x n, обозначаемая АВ, у которой элемент сд равен произ-
произведению /-й строки первого сомножителя, матрицы А, на
у-й столбец второго сомножителя, матрицы В, т.е. С = АВ,
если сд = апЬи + aaby + ... + air _ xbr _ tJ + а,,Ь^ для любых
индексов / и у матрицы С.
ГО П
Примеры. 1. C 2 — 1)
= C0 + 21-1
1 3 1+20-1 1) = A 2).
3^1 =
0 3 + 1 (- 3) ] (- 3
1 3 + 0 • (- 3) = 3
1 3 + 1 (— 3) О
13 0 0^ J ¦ \ '
12 0 0 =
0 0 1 ll
1+4 03 3+1 2 + 4 03 0+10 + 4
1 + 5 02 3 + 0 2 + 5 02 0 + 0 0 + 5
1 3 0 + 0 0 + 4
1 2 0 + 0 0 + 5
= D 11
2 6
^
4
5
Итак, операция умножения двух прямоугольных матриц
выполнима только в том случае, когда число столбцов в
первом множителе равно числу строк во втором множите-
множителе, в остальных случаях произведение матриц не определя-
определяется. В частности, если матрицы А и В — квадратные
матрицы одного и того же порядка, то умножение матриц
всегда выполнимо при любом порядке, следования сомно-
сомножителей.
Однако заметим, что даже в этом частном случае не
всегда АВ = ВА. Например, пусть А = (J ^ I В = |q JI тогда
АВ =
lWl 0+1 0
II 10+0 0
= У0 1 + 11
0| 0 1 + 11
1-1+0-1
1-1+0-1
0 0+1
0 0+10
т.е. АВфВА.
Итак, умножение матриц некоммутативно, т.е. в общем
случае АВ ф ВА. Поэтому при перемножении матриц во
639
избежание ошибок следует строго придерживаться задан-
заданного порядка следования множителей.
Если АВ = ВА, то матрицы А и В называются перестано-
перестановочными, или коммутативными, между собой.
Например, матрицы А = (]2 *) и В = (~ъ2 _*) переста-
перестановочны между собой, так как АВ=\~1 ~^\ ВА =
Операция умножения матриц является ассоциативной, а
также дистрибутивной относительно сложения, т.е. для
любых прямоугольных матриц А, Ви С, для которых имеют
смысл соответствующие произведения, справедливы ра-
равенства:
а) (AB)C=A(BQ;
б) (А + В)С = АС+ ВС, С(А + В)= СА+ СВ.
Доказательство этих равенств опускается.
Операция умножения матриц соответствующим образом
распространяется на случай нескольких сомножителей. В
силу определения произведения матриц умножать матрицу
А на себя можно только в том случае, если это квадратная
матрица.
Пусть дана квадратная матрица А порядка п и натураль-
натуральное числор > 1. Матрица АА...А называется р-й степе-
/>раз
нью матрицы А и обозначается AF, т.е. для р > 1 по опреде-
определению А* = АЛ... А
рраэ
Кроме того, по определению А = А.
Пример. Найти куб матрицы А = \ \
-1
Из ассоциативного свойства умножения матриц следует,
что АРАЯ = АР + Я, где р и q — произвольные натуральные
числа.
640
Отметим, что для любой матрицы А размеров т х г
произведение матрицы А на нуль-матрицу 0 размеров г х п
есть нуль-матрица размеров т х п и произведение нуль-
матрицы 0 размеров / х т на матрицу А размеров т х г есть
нуль-матрица 0 размеров / х г. Например,
Го о о о)
0 0 0 0
0 0 0 0
т.е. в тех случаях, когда произведение матриц имеет смысл,
для любой матрицы А справедливы равенства АО = 0 и
О А = 0. В частности, для любой квадратной матрицы А
порядка п и квадратной нуль-матрицы 0 порядка п АО =
= 0/4 = 0.
Известно, что произведение двух чисел равно нулю тогда
и только тогда, когда хотя бы один из сомножителей равен
нулю. В отличие от чисел, произведение двух матриц может
быть равно нулю даже тогда, когда каждый из сомножите-
сомножителей не является нуль-матрицей, т.е. существуют матрицы
А ф 0 и В ф 0 такие, что АВ = 0.
Например, матрицы А = \\ q\*\q о 1и "^ = Ii l
ковы, что произведение АВ есть нуль-матрица. Дейс
™"».^--f.8)(??)-(J:X:J:!i:S:X::)-(SS)-o
Заметим, что деление матриц не рассматривается, т.е.
символ -^ для матриц не существует.
Квадратная матрица порядка п
и-
и1
0
0
0
0
0
1
0
0
0
0 ...
0 ...
1 ...
0 ...
0 ...
0
0
0
1
0
о
0
0
0
1
Е =
у которой элементы а„ = 1 для всех i= 1, 2, ..., л, а осталь-
остальные элементы равны нулю, обладает следующим свойст-
21 Алгебра, тригонометрия
и элементарные функции
641
вом: EA = А для каждой матрицы А размеров пхти АЕ = А
для каждой матрицы А размеров т х п. В частности,
АЕ = ЕА = А для каждой квадратной матрицы А порядка п;
EF= F для каждой матрицы-строки F размеров 1 х п;
ЕХ= X для каждой матрицы-столбца X размеров их 1.
Матрица Е в произведении матриц играет ту же роль, что
число 1 в произведении чисел, поэтому матрицу Е принято
называть единичной матрицей порядка п.
Транспонированием матрицы А называется перемена ро-
ролями строк и столбцов с сохранением их номеров. Таким
образом, строки данной матрицы А будут в той же после-
последовательности столбцами транспонированной матрицы,
обозначаемой АТ, а столбцы матрицы А будут в той же
последовательности строками транспонированной матри-
матрицы Ат.
(л Л\
( \ A. W т I —
Пример. Если i4=_!jgLTOi4=4 5
Ясно, что при транспонировании матрица^ размеров
m х п переходит в матрицу Ат размеров пхт. Если А —
квадратная матрица порядка п, то и транспонированная
матрица АТ является квадратной матрицей порядка п. За-
Заметим, что единичная матрица не меняется при транспо-
транспонировании. Легко проверяется, что транспонирование мат-
матриц обладает следующими свойствами:
а) (Ат)т'= А;
б) {А + В)Т = АТ+ Вт, (А-В)Т = АТ- Вт;
в) (Ы)т= ЫтСк — число);
г) (АВ)Т=ВТА.
§ 2. Определители
Пусть дана квадратная матрица второго порядка
А-=(а" Ч A)
Определителем второго порядка, соответствующем мат-
матрице A), называют число аиап — апап. Обозначается этот
определитель символом
642
«21 «22
B)
Например,
2
— 1
||
1) 1
-1
= 2
«и
«21
•О
&12
«22
_ f
или буквой Д, или символом \А\. Таким образом, по опре-
определению
- «11 «22 —
5) — (— 1) • 4 =
Элементы матрицы A) принято называть элементами
определителя B), строки и столбцы матрицы A) — строка-
строками и столбцами определителя B).
Рассмотрим простейшие свойства определителей второ-
второго порядка.
1. Определитель квадратной матрицы A) равен опреде-
определителю ее транспонированной матрицы. Действительно,
пусть
Д =
«II «12
«21 «22
АТ =
«II «21
«12 «22
Так как Д = аиа2г — агхахъ а Ат= а\\пгг — апагъ то Д = Дг.
Замена определителя матрицы A) на определитель
транспонированной матрицы называется транспонировани-
транспонированием определителя B). Поэтому свойство 1 можно сформу-
сформулировать так: определитель B) не меняется при его транс-
транспонировании.
Замечание. Так как по свойству 1 все строки опреде-
определителя можно, не меняя его значения, заменить соответст-
соответствующими столбцами, то, если доказана справедливость
некоторого утверждения для столбцов определителя, тем
самым будет доказана справедливость этого утверждения и
для строк. Исходя из этого рассматриваемые ниже свойства
определителей будут устанавливаться только для столбцов
определителя.
2. При перестановке столбцов (строк) определитель ме-
меняет только знак.
2* 643
Действительно, пусть Д =
«и «п
«21 «22
«12 «11
«22 «21
. Тогда Д =
= aua22 — a2iai2, Д, = al2a2i — o22au = — («11^22 — o2iai2), т.е.
Д, = — Д.
3. Если все элементы хотя бы одного столбца (строки)
определителя равны нулю, то определитель равен нулю.
О ап
Действительно, если Д =
= 0. Если Д, =
«и 0
«21 0
О я.
, то Д = 0 • а22 — 0 • ап =
, то по свойству 2 At = — Д, и поэтому
Д, = 0.
4. Определитель, имеющий два одинаковых столбца
(строки), равен нулю.
Действительно, если Д =
= 0. Если Д, =
«12 «12
«22 <*22
«И «И
, то Д - апа2х — а21аи -
«21 °21
ТО Д! = 012^22 ~~ °22аП = U-
5. Если все элементы некоторого столбца (строки) опре-
определителя умножить на одно и то же число а, то определи-
определитель умножится на это число.
Действительно, пусть, например, Д =
ош.
«и «и
«21 ^22
Тогда Д, = ап{аа22) — ап(аа12) = а(аиа22 —
«21 а«22
= СХД.
Свойство 5 иногда формулируется следующим образом:
если все элементы какого-либо столбца {строки) определите-
определителя содержат общий множитель а, то его можно вынести за
знак определителя.
Так, например, по доказанному
ош,
«21 ««22
= а
«11 «12
«21 «22
Свойство 5 выражает правило умножения определителя на
некоторое число.
6. Определитель, у которого элементы двух столбцов
(строк) соответственно пропорциональны, равен нулю.
и пусть, например,
|«21 «22
ап = Pai2> a2\ = Ря22- Тогда на основании свойств 5 и 4
определителя имеем
р) рр
Действительно, пусть Д=ГИ а"
|«21 «22
644
д =
«12
«11 «12
= 0.
7. Если каждый элемент какого-либо столбца (строки)
определителя есть сумма двух слагаемых, то определитель
равен сумме двух определителей, у одного из которых
элементами соответствующего столбца (строки) являются
первые слагаемые, у другого — вторые, а остальные эле-
элементы этих двух определителей те же, что и у данного.
ац+Ьп ап
«21 + *21 «22
Действительно, пусть, например, Д =
Д,=
«22
bU «12
Ь2\ «22
Тогда Д = (ап + Ьи)а22 — (а21 +
+ Ь21)а12 = (апагг — а2{ап) + (Ьиа22 — b2lan) = Д, + Д2. Свой-
Свойство 7 выражает правило сложения определителей.
8. Определитель не изменится, если к элементам како-
какого-либо столбца (строки) прибавить соответствующие эле-
элементы другого столбца (строки), умноженные на одно и то
же число.
Действительно, пусть, например,
А =
Покажем, что Д =
лителей имеем
«11 «12
«21 «22
й„ + ош12 ап
«21 + °Ш22 Оц
I. На основании свойств 7 и 6 опреде-
А. =
«11 «12
«21 «22
««12 «12
ош22 а22
= Д + 0 = Д.
Пусть дана матрица третьего порядка
А =
«11 «12
«21 «22
D)
Определителем третьего порядка, соответствующим матри-
матрице D), называется число
«22 «23
«32 «33
«12 «13
«32 «33
«22 «23
E)
645
Обозначается этот определитель символом
«11
«21
«31
«12
«32
Ol3
о23
«33
F)
или одной буквой Д, или символом |Л|. Таким образом, по
определению
«И
«21
«31
«12 fl13
#32 ^33
«22
«32
«23
«33
— «21
«12
«32
«13
«33
«31
«12
«22
«13
«23
G)
Например,
2 4-1
О 1 О
2 -3 1
= 2
1
-3
-О
4 - 1
-3 1
+ 2
4 - 1
1 О
= 2 A + 0) - 0 D - 3) + 2 @ + 1) = 4.
Элементы матрицы D) называются элементами опреде-
определителя F), строки и столбцы матрицы D) — строками и
столбцами определителя F).
Для изучения свойств определителя третьего порядка
введем некоторые новые понятия.
Минором любого элемента определителя третьего поряд-
порядка F) называется определитель второго порядка, соответ-
соответствующий матрице, полученной из данной матрицы D)
вычеркиванием столбца и строки, в которых содержится
данный элемент. Минор элемента av принято обозначать
Mv. Например, минор элемента аи обозначают А/,,, элемен-
элемента a3i — Л/31 и т.д. Таким образом, по определению
М12
«22
«32
«21
«31
«21
«31
«23
«33
«23
«33
«22
«32
М-» =
> ¦'1
м =
м =
«12
«32
«И
«31
«И
«32
«13
«33
«13
«33
«12
«32
м =
' 31
Мп =
j ¦'2
м =
«12
«22
«И
«21
«И
«21
«13
«23
«13
«23
«12
«22
646
Алгебраическим дополнением любого элемента av опреде-
определителя третьего порядка D) называют минор этого элемен-
элемента Мф умноженный на (— 1)н J. Алгебраическое дополнение
элемента ац обозначают заглавной буквой того же наиме-
наименования и с теми же двумя индексами, что и у данного
элемента.
Например, алгебраическое дополнение элемента а2х обо-
обозначают А2Х, элемента а^ — А23 и т.д. Таким образом, по
определению
Л / 1\1 + 1»^ _/ 1\1 + 1
\2+1
чЗ + 1
Л+2
Ч2 + 3
Ч3 + 3
Теорема 1. Определитель F) равен сумме произведений
элементов любого его столбца (строки) на соответствующие
им алгебраические дополнения, т.е.
А = аиАи + а21А21 + a3iA3U A = auAu+ ai2An + al3Al3,
А = ахъАп + Д22Л22 + дз*4з2> Д = а2\А2\ + 022^22 + вгтАп, (8)
Д = ахзАхз + агзАп + ai3A33, A = a3i4u + а31А32 + аЗУА33.
fl22
а32
ап
а32
а^
Q\\
ая
«и
а21
а23
«33
а33
а23
а23
а12
«32
а12
Докажем, например, четвертое из равенств (8). Для этого
преобразуем правую часть этого равенства:
апАп
vi + 2 a21 а23
а31 а33
(Д21<
— ЛпОзг^гз —
л + з
2 аЗЗ
а21 а22
а31 а32
«13@21^32 —
647
a13a21an — апапа22 = аи(а22а33 —
— а32а13) + а31(апа23 — а22а13)
«22
«32
«23
«33
21
«12
«32
«13
«33
31
«12
«22
«13
«23
Сравнивая полученное выражение с выражением E) опре-
определителя Д, заключаем, что апЛп + аХуАХ2 + а13А13 = А- Ана-
Аналогично устанавливается справедливость остальных ра-
равенств (8).
Запись определителя F) по любой из указанных формул
(8) называется разложением этого определителя по элемен-
элементам соответствующего столбца или строки. Эти разложения
удобно использовать для вычисления определителей
третьего порядка. Например, разложив определитель
Д =
2 3 1
1 0 -2
4 1 2
по элементам второй строки, получим
А= 1 (— 1)
2+1
3 1
1 2
+ 0 (- 1)
2 + 2
2 1
4 2
+ (- 2)(- 1)
2+3
2 3
4 1
= - F - 1) + 2B - 12) = - 25.
Для определителей третьего порядка остаются справедли-
справедливыми свойства 1 — 8, рассмотренные для определителей
второго порядка. Доказательство этих свойств непосредст-
непосредственно следует из теоремы 1 о разложении определителя
третьего порядка по элементам строки (столбца) и соответ-
соответствующих свойств определителей второго порядка. Так,
свойство 1, заключающееся в том, что определитель не
изменится, если его строки заменить столбцами, можно
доказать следующим образом. Пусть
Д =
Разлагая определитель Дг по элементам первой строки,
имеем
«11
«21
«31
«12
«22
«32
«13
^23
«33
т
,А =
«и
«12
«13
«21
«22
«23
«31
Д32
<*33
648
«22
«23
«32
«33
— a
21
«12
«13
«32
«33
+ «31
«12
«13
«22
«23
«22
«32
«23
«33
— a
21
«12
«32
«13
«33
+
/7,,
1
«12
Я22
«13
«23
Ат=аи
Учитывая, что определитель второго порядка от замены
строк столбцами не меняется, получим
Ат=ап
Сравнивая полученное выражение с выражением E) опре-
определителя А, заключаем, что Ат = А.
Аналогично устанавливается справедливость свойств
2-8.
Свойства 1 — 8 определителей в сочетании с теоремой 1
о разложении определителя по элементам строк и столбцов
часто позволяют упростить вычисления определителя
третьего порядка.
Пример. Вычислить определитель
д =
5 20 15
2 4 8
1 4 7
По свойству 5 определителей третьего порядка, вынося
•за знак определителя общий множитель 5 первой строки и
общий множитель 4 второго столбца, имеем
А=5-4-
1 1 3
2 1 8
1 1 7
Прибавим теперь к элементам второго столбца элементы
первого столбца, умноженные на (— 1), а к элементам
третьего столбца — элементы первого столбца, умножен-
умноженные на (— 3). По свойству 7 определитель не изменится и
равен
= 20-
1 о о
2-12
1 0 4
Разложив полученный определитель по элементам первой
строки, имеем
649
A = 201(- 1I + 1
0 4
= 20 (- 4 - 0) = - 80.
С помощью определителей третьего порядка можно
квадратной матрице четвертого порядка поставить в соот-
соответствие число — определитель четвертого порядка. Затем
с помощью определителей четвертого порядка ввести оп-
определители пятого порядка и т.д. Таким образом, для
введения определителей л-ого порядка надо иметь опреде-
определители (л — 1)-го порядка. Такое введение определителей
называется введением определителей по индукции. Приве-
Приведем теперь введение определителей л-го порядка индук-
индукцией по л.
Пусть л=1; определителем квадратной матрицы поряд-
порядка 1 (т.е. числа ап) считается само число ап. Будем считать,
что определители квадратных матриц порядка (л — 1) уже
введены и доказана справедливость их основных свойств
(свойств типа 1 — 8, доказанных выше для определителей
порядка 2). Рассмотрим квадратную матрицу л-го порядка
А =
«11
«21
«31
«12
«22
«32
«13
«23
«33
... Д,„
... Д2„
- «Зл
««1 ««2 ««3
(9)
Если в этой матрице вычеркнуть /-ю строку и у-й столбец,
а порядок элементов оставить прежним, то получится
квадратная матрица порядка (л — 1):
«и
«21
«12
«22
«2,-1
«/+1,1 «/+1,2 ••• aU\j—\
и»2
«„,-1
Определитель этой матрицы обозначается Мц и называется
минором элемента av матрицы (9).
Определителем матрицы (9) называется число
650
auMu — агхМгх + Д31Л/31 —
Определитель матрицы (9) обозначается символом
z
а,л
a"
z
a»2
z
... aln
... a3ll
- a,,,,
(И)
или буквой А, или символом \А\. Таким образом, по опре-
определению
= А =
a\\ а\г — <*1„
a2i an ... аъ
а„г
г„х. A2)
Элементы матрицы (9) называются элементами определи-
определителя A1), строки и столбцы матрицы (9) называются
строками и столбцами определителя A1). Миноры элемента
av матрицы (9) называются минорами элемента а0 определи-
определителя A1). Отметим, что определители второго порядка,
введенные по формуле C) и введенные по формуле A0),
будут одинаковыми. Определитель, получаемый из опреде-
определителя A1) заменой строк на столбцы, а столбцов на
строки, называется определителем, транспонированным с
определителем А, и обозначается АТ, а замена определителя
А на определитель Ат называется транспонированием опре-
определителя А.
Алгебраическим дополнением любого элемента at] опреде-
определителя л-порядка A1) называют минор My этого элемента,
умноженный на (— 1)'+у. Алгебраическое дополнение эле-
элемента аи обозначают заглавной буквой того же наименова-
наименования и с теми же двумя индексами, что и у данного элемента,
т.е. по определению Av = (— \)'+iMv.
651
Теорема 2. Определитель п-го порядка A1) равен сумме
произведений элементов любого его столбца {строки) на
соответствующие им алгебраические дополнения, т.е.
А = a^jAy + пуАу + ... + anjA^ для любого у = 1, 2. ..., п,
А = апАц + пцАа + ... + «йА, Для любого i = 1, 2, ..., п.
A3)
Доказательство теоремы 2 опускается.
С помощью теоремы 2 о разложении определителя л-го
порядка по элементам столбца (строки) и свойств 1 — 8 для
определителей (п — 1)-го порядка доказываются свойства
1 — 8 определителей л-го порядка.
Не останавливаясь на доказательстве, перечислим эти
свойства:
1. При транспонировании определителя его значение не
изменяется, т.е. А = АТ.
2. От перестановки двух столбцов (двух строк) определи-
определитель меняет знак.
3. Если все элементы хотя бы одного столбца (строки)
определителя равны нулю, то определитель равен нулю.
4. Определитель, имеющий два одинаковых столбца
(строки), равен нулю.
5. если все элементы какого-либо столбца (строки) оп-
определителя умножить на одно и то же число а, то опреде-
определитель умножится на это число (т.е. общий множитель
элементов какого-либо столбца (строки) можно выносить
за знак определителя).
6. Определитель, у которого элементы двух столбцов
(строк) соответственно пропорциональны, равен нулю.
7. Если каждый элемент какого-либо столбца (строки)
определителя есть сумма двух слагаемых, то определитель
равен сумме двух определителей, у одного из которых
элементами соответствующего столбца (строки) являются
первые слагаемые, у другого — вторые, а остальные эле-
элементы этих двух определителей те же, что и у данного.
8. Определитель не изменится, если к элементам како-
какого-либо столбца (строки) прибавить соответствующие эле-
652
менты другого столбца (строки), умноженные на одно и то
же число.
Сформулируем и докажем еще одно свойство определи-
определителей.
9. Сумма элементов некоторого столбца (строки) опре-
определителя порядка п, п > 2, умноженных на алгебраические
дополнения соответствующих элементов другого столбца
(строки), равна нулю, т.е.
(
= О | или
= О | для
^ )
любого п > 2 и любого / ф].
Доказательство. Пусть для определенности у> i,
тогда разложив определитель по элементам у-го столбца,
.получим
A4)
У определителя, стоящего в правой части равенства A4),
элементы /-го и у-го столбцов соответственно равны. По
свойству 4 определитель A4) равен нулю, следовательно,
л
г 1
:— 1
аН а\2 ••• аМ ••• а
а2\ а12 "• аЪ ••• &
Qj\ Qyi ••• aVi ••• а
Q л (X t ... Q ¦ .. С
Л1 fU ttl
,_,_, av ali/+,
2i/_, flj, a2J+1
nj-\ am aHJ*\
... au
... аь,
... а3я
— fl«/;
Для / > у доказательство аналогично. Свойство 9 доказано.
Пользуясь свойствами 1 — 8, вычислим определитель
единичной матрицы, единичную матрицу порядка к обо-
обозначим Ек. Пусть дана матрица Е„. Разлагая определитель
этой матрицы по первому столбцу, получаем
№ =
1
0
0
0
0
1
0
0
0 ...
0 ...
1 ...
0 ...
0
0
0
1
653
Повторяя это рассуждение для определителя \Е„ _ ,|, затем
для \Е„ _ 2| и т.д., приходим к выводу, что |Д,| = 1. Итак,
определитель единичной матрицы любого порядка п равен 1.
§ 3. Обратная матрица. Ранг матрицы
Если две квадратные матрицы А и В одного и того же
порядка п таковы, что АВ= ВА = Е (где Е — единичная
матрица порядка п), то говорят, что матрицы Аи В явля-
являются обратными друг другу и используют обозначение
В = А~' и А = ВТ'. Например, матрицы
А =
Г4 0 5
О 1 -6
3 0 4
И
являются обратными друг другу, поскольку АВ = ВА = Е,
где
Е =
(\ о О
0 1 0
0 0 1
т.е.
= В~
= А
~\
По определению обратной матрицей для данной квад-
квадратной матрицы А порядка п называется квадратная мат-
матрица А~' порядкап, обладающая свойствами АА~' = А~ХА =
= Е, где Е — единичная матрица порядка п.
Для каждой матрицы А порядка п, имеющей обратную
матрицу А~ ', обратная матрица А~' единственна.
Действительно, пусть некоторая матрица А порядка п
имеет обратную матрицу А~'. Пусть существует матрица С
порядка п, такая, что С А = АС= Е, тогда
С= ЕС=(А~ 1А)С=А~ \АС) = А' 1Е=А~'.
Обратные матрицы обладают следующими свойствами:
а)(Л-'г'=Л
г
'Г'
б) (АВ)~ l = B~lA'
в) (Ату' = (А~ У.
Доказательства этих свойств опускается.
Выясним, какие матрицы имеют обратные матрицы и
если матрица А имеет обратную А~', то как ее находить.
654
Пусть дана квадратная матрица А порядка п (п > 2)
А =
а„ an a,3
a2l a22 a2}
an an a33
Составим квадратную матрицу А порядка п следующим
образом: на место каждого элемента матрицы А поставим
алгебраическое дополнение этого элемента, т.е.
A =
A A
Лл\ Л?
Ац Aj
А„1 А„
Транспонируем матрицу А:
AT =
f A A
А\г А
АХп А
2 Аз
2 А23
2 А}}
2 4,3
и А31
п А32
ы А3п
.- Аи>
... А2п
... Агп
- Ат)
'.'.'. а
... Лз
••¦ Лот
Матрица АТ называется присоединенной „матрицей. Напри-
Например, найдем присоединенную матрицу Ат, если
А =
(\ О
6 2 О I
5 4 3
Так как
Л. = (- 1I + 1
Ап = (- О
Л22 = (- О
гг = (- О
1 +3
2 + 2
3+ 1
|
3 + 3
2 0| _
4 3
= 6, Ап = (- 1)
1 + 2
5 4
0 =3
5 3| -3'
О
= 14, Ап = (- 1)
2 +
6 0
5 3
= (~ 1)
2 + 3
6 2
= 0, Ап = (-1)
= 2,
3 + 2
= -18,
4 3
01 =
5 4
6 0
= 0,
= -4,
= 0,
ТО
655
A =
F - 18
3 — 4
0 2
И
Ат =
6 0 0)
-18 3 0
14 -4 2
Квадратная матрица А называется вырожденной (особен-
(особенной), если ее определитель равен нулю (\А\ = 0), и невырож-
невырожденной, если \А\ ф 0.
Теорема 3. Для любой невырожденной матрицы А
(\А\ ф 0) существует обратная матрица А~ \
Доказательство. Рассмотрим невырожденную мат-
матрицу первого порядка, т.е. число ап, отличное от нуля;
обратная матрица к этой матрице есть число —.
ап
Пусть дана некоторая невырожденная матрида А второго
порядка. Найдем произведение матриц ААТ и АТА, где Ат —
присоединенная матрица. Так как сумма произведений
элементов некоторого столбца (строки) матрицы А на ал-
алгебраические дополнения этих элементов равна определи-
определителю \А\ (см. теорему 2), а сумма произведений элементов
некоторого столбца (строки) матрицы А на алгебраические
дополнения элементов другого столбца (строки) (по свой-
свойству 9 определителей) равна нулю, то
a2iAu + anAn a2iA2i + a22A22
'Апап + А21а21 Апа12 + А^
Апап + А22а22
АТА =
Каждый элемент полученных матриц имеет общим множи-
множителем число \А\, следовательно,
ААТ= \А\ р Jj=
ТА = \А\ (J ^=
J
Отсюда, в силу невырожденности матрицы А (\А\ ф 0),
имеем
Следовательно, для невырожденной матрицы А второго
порядка матрица, элементами которой являются соответ-
656
ствующие элементы присоединенной матрицы Ат, делен-
деленные на определитель |Д является обратной матрицей А~1:
ИИ
А\г А22
И И1
Итак, для невырожденной матрицы А второго порядка
не только доказано существование обратной матрицы А, но
и указан способ ее построения.
Аналогично доказывается, что для любой невырожден-
невырожденной матрицы А порядка п, где п > 3, матрица, элементами
которой являются соответствующие элементы присоеди-
присоединенной матрицы Ат, деленные на определитель |Д является
обратной матрицей А~1:
А\\ Ai2
и и -
А21 Ап
ии -
Ап\ А„2
и и -
V
Теорема доказана.
Пример. Матрица
Ал
И
Аъ,
И
А,ш
и]
1
=
Ап
И
Ап
И
Аи
\А\
А21
и •
Ап
и •
А»,
И '
А,л
- и
Да
" И
Ат
¦¦ и
А =
1 о (Л
6 2 0
5 4 3
невырожденная, так как |/4| = 6 * 0. Ее присоединенная
матрица
следовательно,
657
Теорема 4. Определитель произведения двух квадратных
матриц Аи В порядка п равен произведению их определителей,
т.е. \АВ\ *=\А\ |Д (аналогичное свойство справедливо и для
любого конечного числа сомножителей).
Доказательство теоремы 4 опускается.
Так как определитель единичной матрицы Е порядка п
равен 1, то определители двух взаимно-обратных матриц
являются числами взаимно-обратными, т.е. \А\ \А~ '| = 1.
Любая вырожденная матрица А порядка п не имеет
обратной, так как по теореме 4 произведение вырожденной
матрицы А на любую матрицу порядка п будет снова
вырожденной матрицей.
Обратные матрицы часто применяются для решения
матричных уравнений.
Пусть даны матрицы А, В, С. Если поставлена задача
найти матрицу ЛГ такую, что справедливо матричное равен-
равенство АХ= В, то говорят, что дано матричное уравнение
АХ=В A)
с неизвестной матрицей X. Матрицу X, удовлетворяющую
уравнению A), называют решением уравнения A).
Если поставлена задача найти матрицу Y такую, что
справедливо матричное равенство УА = С, то говорят, что
дано матричное уравнение
YA=C B)
с неизвестной матрицей Y. Матрицу Y, удовлетворяющую
уравнению B), называют решением уравнения B).
Рассмотрим частный случай решения матричных урав-
уравнений A) и B). Пусть матрица А невырожденная, квадрат-
квадратная матрица порядка п; В т. матрица размеров пхт; С —
матрица размеров кхп, где п, т, к — любые натуральные
числа. В этом случае уравнения A) и B) имеют решения.
658
Действительно, умножим обе части первого уравнения
слева на матрицу Л~', что можно сделать в силу выбранных
размеров матрицы В. Проделав соответствующие действия:
А~ХАХ=А~ХВ, ЕХ=А~ХВ, Х=А~ХВ,
получим, что существует матрица Х=А~ ХВ размеров п х т,
удовлетворяющая уравнению A).
Умножим обе части второго уравнения справа на матри-
матрицу А~ ', что можно сделать в силу выбранных размеров
матрицы С, проделав соответствующие действия:
YAA~ ' = САГ \ YE= CA~ \ Y= CA~',
получаем, что существует матрица Y= CA~ ', размеров
к х п, удовлетворяющая уравнению B).
Отметим, что даже если В = С, но матрицы А~ ' и В не
перестановочны, то Хф Y, т.е. для одних и тех же матриц А
и В= С уравнения A) и B) имеют, вообще говоря, разные
решения.
Пример. Пусть
(} (}
Решим уравнения A) и B). Прежде всего найдем
!
_2
Тогда
Ранее (см. § 2) было дано понятие минора элемента а0
квадратной матрицы n-го порядка. В общем случае матри-
матрицы размеров тхп понятие минора элементов матрицы не
вводится, а вводится понятие минора порядка к данной
(&%
матрицы, где число к может принимать значения от еди-
единицы до наименьшего из чисел тип, т.е. 1 ? к ? min(m, п).
Пусть дана матрица А размеров тхпи пусть к — нату-
натуральное число такое, что 1 й к ? тт(т, п). Выберем произ-
произвольно к строк и к столбцов матрицы А. Из элементов,
стоящих на пересечениях этих строк и столбцов (не меняя
их порядка) образуем квадратную матрицу М порядка к.
Определитель матрицы М называется минором порядка к
матрицы А.
Пример. Пусть дана матрица
' 1 3
3 4
-3 О
размеров 3x2. Тогда миноры первого порядка матрицы
есть элементы этой матрицы, т.е. числа 1, 3, 3, 4, — 3, 0.
Миноры второго порядка есть определители
1 3
3 4
>
1 3
-3 0
>
3 4
-3 0
Миноров более высоких порядков эта матрица не имеет.
Если дана квадратная матрица А порядка п, то ее минор
порядка п есть определитель А, миноры порядка (п — 1)
есть миноры соответствующих элементов этой матрицы,
миноры порядка 1 есть элементы этой матрицы. Кроме
того, эта матрица имеет миноры порядка к, где 1 < к <
<п-\.
Рангом матрицы А размеров тхп называется наивысшей
порядок отличных от нуля миноров матрицы А.
Если все элементы матрицы А есть нули, то говорят, что
ранг матрицы равен нулю.
Ранг невырожденной матрицы А порядка п равен п.
Например, ранг матрицы А = (^ ? 2 11 равен единице,
так как миноры второго порядка этой матрицы равны нулю
(в силу пропорциональности строк матрицы), но есть ми-
миноры первого порядка — элементы матрицы А — отличные
от нуля.
660
Пусть дана матрица А размеров тхп и пусть дано
натуральное число / < min(m, п). Если все миноры порядка
/ матрицы А равны нулю, то и все миноры этой матрицы
порядка (/+1) также равны нулю.
Действительно, возьмем любой минор этой матрицы
порядка (/+1) и разложим его по элементам некоторой
строки. Каждое слагаемое разложения содержит множите-
множителем некоторый определитель порядка / — минор порядка /
соответствующего элемента выбранной строки определи-
определителя порядка (/+1). Поскольку каждый минор порядка /
равен нулю, то и( сумма разложения тоже равна нулю,
поэтому выбранный минор порядка (/+1) равен нулю.
Следовательно, если все миноры порядка / равны нулю, то
и все миноры порядка, большего чем /, также равны нулю.
Таким образом, для определения ранга матрицы разме-
размеров тхп надо сначала найти хотя бы один отличный от
нуля минор первого порядка, т.е. надо выяснить, есть ли
среди элементов матрицы хотя бы один, отличный от нуля.
Если такого элемента нет, то ранг матрицы равен нулю.
Если у матрицы есть элемент, отличный от нуля, то надо
найти хотя бы один отличный от нуля минор второго
порядка. Если такого минора нет, то ранг матрицы равен
1. Если есть отличный от нуля минор второго порядка, то
надо искать отличный от нуля минор третьего порядка и
т.д. до тех пор пока не найдется отличный от нуля минор
r-го порядка; но либо все миноры порядка г+ 1 равны
нулю, либо r= min(m, n). Тогда ранг матрицы равен /•.
Для нахождения ранга матрицы размеров тхп часто
поступают так. Берут любой отличный от нуля элемент
матрицы. Затем, дописывая некоторую строку и некоторый
столбец, отличный от тех, где лежит элемент, образуют
всевозможные миноры второго порядка до тех пор пока не
найдется минор второго порядка, отличный от нуля. Затем,
дописывая некоторую строку и некоторый столбец, отлич-
отличный от тех, где лежит найденный минор второго порядка,
образуют всевозможные миноры третьего порядка до тех
пор пока не найдется минор третьего порядка, отличный
от нуля. Продолжают этот процесс до тех пор пока не
найдется минор порядка г, отличный от нуля, для которого
661
все миноры порядка (г + 1), построенные указанным обра-
образом, равны нулю, любо таких миноров не будет вообще
(если матрица содержит г строк и г столбцов). Тогда ранг
матрицы равен г.
Доказательство справедливости этого способа определе-
определения ранга матрицы опускается.
Пример. Найти ранг матрицы
Минор первого порядка (число 1), лежащий на пересе-
пересечении первого столбца и первой строки, отличен от нуля.
Минор второго порядка, лежащий на пересечении первых
двух столбцов и первых двух строк, 1 ? = — 1 также
отличен от нуля. Все миноры третьего порядка этой мат-
матрицы равны нулю. Значит, ранг матрицы равен двум.
§ 4. Системы линейных уравнений
Рассмотрим систему т линейных уравнений с п неиз-
неизвестными:
а2]хх
= Ьъ
A)
= Ьт,
где хи х2, ..., х„ — неизвестные, av(i= 1, 2, ..., m,j= I, 2,
..., п) — коэффициенты, bu b2, ..., Ьт — свободные члены
системы уравнений A). Напомним, что числовой набор A,
2, ..., п), соответствующий набору неизвестных (хи х2, ...
..., х„), называется решением системы A), если при подста-
подстановке в каждое уравнение системы A) соответствующих
чисел вместо неизвестных получается т верных числовых
равенств. Решить систему A) — это значит найти все ее
решения или доказать, что их нет.
Система линейных уравнений называется совместной,
если она имеет хотя бы одно решение, и несовместной
662
(противоречивой), если она не имеет решений. Совместная
система называется определенной, если она имеет единст-
единственное решение, и неопределенной, если она имеет более
одного решения. Можно показать, что неопределенная
система линейных уравнений всегда имеет бесконечное
множество решений.
Примеры. Линейное уравнение с одним неизвестным
flux, = bx при аи * О имеет единственное решение х = —.
Линейное уравнение с двумя неизвестными
аихх + а12Х2 = Ьх при аи Ф О и при ап * О
имеет бесконечно много решений.
Действительно, пусть, например, ап * 0, тогда уравнение
аихх + а]2х2 = Ь\ равносильно уравнению
_ А, - апх,
которое имеет решением [а, — ^ + -0 где а — любое
I а\г а\г Г
действительное число.
Система двух линейных уравнений с одним неизвестным
А, А,
такая, что —L ^ —, несовместна.
Действительно, пусть число а — решение уравнения
аих= Ьи т.е. пусть справедливо числовое равенство
Ди<х = 6|. Тогда а = —L. Если бы а = —L было решением
уравнения a2ix = b2, то было бы справедливо числовое
равенство ^-^ = Ь2 или, в силу того что а21 ^ 0, числовое
аи
равенство —- = —, что противоречит условию. Итак, реше-
ние а уравнения аих = Ь\ не является решением уравнения
663
a2\X = b2, а это значит, что система двух уравнений с одним
А. *,
неизвестным, такая, что —- * —, несовместна.
«11 «21
Основной матрицей системы A) называется матрица А
размеров тхп, элементами которой являются коэффици-
коэффициенты при неизвестных системы уравнений A), т.е.
А =
«11 «12 •• «Ь
«21 «22 •" «2i
Матрицей неизвестных систем A) называется матрица-
столбец X, элементами которой являются неизвестные сис-
системы, т.е.
Х=
Матрицей свободных членов системы A) называется мат-
матрица-столбец В, элементами которой являются свободные
члены системы, т.е.
В =
ьт
Матричное уравнение
а11 «12
Д21 «22
«ml «ro2
л
*2
U
=
К
или
АХ=В
B)
664
называется матричным уравнением системы A), если мат-
матрица А, Хи В — соответствующие матрицы системы, A).
Поскольку любой числовой набор (аь а2, ..., а„), являю-
являющийся решением системы A), записанный в виде матри-
матрицы-столбца
о»
является решением матричного уравнения B), а любая
числовая матрица-столбец
ГР.1
Р2
являющаяся решением матричного уравнения B) системы
A), записанная в виде числового набора (рь р2, ...; р„),
является решением системы A), то говорят, что система
линейных уравнений A) равносильна матричному уравнению
B) системы A).
Рассмотрим частный случай системы A). Пусть дана
система п уравнений с п неизвестными
а21х{
Ьь
К
C)
= Ь„
и соответствующее матричное уравнение этой системы
«21 «22
аЛ
665
или
АХ=В D)
Определитель матрицы А системы C) будем называть
основным определителем и обозначать через Д, т.е. Д = |Л|.
Предположим, что основная матрица А (являющаяся квад-
квадратной матрицей порядка п) системы C) невырожденная,
т.е. пусть Д = \А\ ф 0. Тогда, как показано в § 3, существует
единственная обратная матрица А~ 1. Умножив левую и
правую части матричного уравнения D) системы C) слева
на обратную матрицу А~', получим, что Х= А~1 В, причем
матрица X— матрица размеров п х 1, т.е. матрица-столбец.
Итак, матричное уравнение D) системы C) в силу единст-
единственности обратной матрицы АГ ' имеет единственное ре-
решение — матрицу-столбец Х= А~' В.
Так как матричное уравнение D) равносильно системе
C), то, если определитель основной матрицы А линейной
системы C) не равен нулю (т.е. |Л| ф 0), тогда система C)
совместна и определена, т.е. имеет единственное решение.
Найти это единственное решение системы C) можно по
правилу Крамера, формулировка которого будет приведена
ниже.
Если в основной матрице А системы C) п линейных
уравнений с п неизвестными вместо у-го столбца коэффи-
коэффициентов системы C) поставить столбец свободных членов
этой системы, то полученную матрицу называют дополни-
j
тельной матрицей системы C) и обозначают ее А, т.е.
i
A =
аи ап ... аи_, *, alJ+
а21 ап ... a2j_t Ь^ о2_/+
ап\ ал — anj-i bn anJ+
E)
j
Определитель матрицы А обозначают обычно Д,, т.е. Д, =
= 14-
Перейдем теперь к решению системы уравнений C).
666
Пусть я=1, т.е. система C) состоит из одного уравнения
с одним неизвестным: апх= Ьи и пусть ап ф 0. Ясно, что
Ь,
это уравнение имеет единственное решение — число —.
ан
Пусть теперь п = 2. Рассмотрим систему двух уравнений
с двумя неизвестными:
\апхх
= Ьи
F)
Основной матрицей А, дополнительными матрицами А и
2
А этой системы являются соответственно матрицы
I /t \ 2
«22
Ч
Пусть определитель основной матрицы А не равен нулю
(Д = \А\ ф 0). Тогда существует единственная обратная мат-
матрица
И
и справедлива цепочка матричных равенств
И №21 ^аД^г! И I b\An +b-jA-n J
иг
Ml2 + M22
откуда
_
Xl
_ Мп+Ми _ A,(-i)uV,.+^(-iJ>4. _
и
и
667
и
Mn - bi (~
и
т.е. компоненты решения (хь Xj) системы F) находятся по
формулам
_ Д,
'
G)
где Д, Дь Д2 — определители матриц А, А, А системы F).
Рассмотрим систему трех линейных уравнения с тремя
неизвестными:
(8)
Основной матрицей А и дополнительными матрицами А,
2 3
А, А системы (8) являются соответственно матрицы
А =
А =
2
А =
«и
«21
«31
«И
«21
«31
«12
«22
«32
*1
*2
*3
«23
«33
«,з1
«23
«33
/
I
3
— «21 «22
«31 «32 *з|
Пусть определитель основной матрицы А не равен нулю
(Д = |Л| ф 0). Тогда существует единственная обратная мат-
матрица
и справедлива цепочка матричных равенств
668
и
А\ Ах Ах\
A\j Ац
Ьг
Аз
_ 1
откуда
X, =
и
_ А, (-
и
_ А, (-
M23 + Мзз _
я
+ Мзз
ЬхАи +
И
И
i + А2у42з + ЬуАу$
А'
«11
«21
«31
А.
*2
*з
«13
«23
«33
и
д'
А, (-
«11
«21
«31
«12
«22
«32
А,
*2
Аз
И
т.е. компоненты решения (хи х^, х3) системы (8) находятся
по формулам
669
_ V _
12 3
где А, Д,, Д2, A3 — определители матриц А, А, А, А системы
(8).
Докажем, что если определитель основной матрицы А
системы C) не равен нулю, то/-я компонента х} (/= 1, 2,
..., п) единственного решения (хь х2, ..., х„) системы D)
находится по формуле
где \А\ = А, — определитель дополнительной матрицы А
системы C), а \А\ = А — определитель основной матрицы А
системы C). РассмотримУ-ю компоненту матрицы-столбца
А~ 1В, являющегося единственным решением матричного
уравнения D) системы C). Имеем
И
_ Z>! (— l)l*JMv + bj (— lJ*JM2j-
И
<hj-\ bi а-
«nj-\ Ь„ а
И
что и требовалось доказать.
Правило, по которому находится решение системы C),
называется правилом Крамера. Сформулируем его.
Правило Крамера. Если система C) пуравнений сп
неизвестными такова, что определитель ее основной матри-
матрицы не равен нулю (А * 0), то система имеет единственное
решение (хь х2, ..., х„), каждая компонента которого нахо-
находится по формулам Крамера, т.е. Xj = -? (j = 1, 2, ..., л), где
с ¦>
670
A, — определитель дополнительной матрицы А, полученной из
основной матрицы Л системы C) заменой j-го столбца на
столбец свободных членов системы.
П р и м е р. Решить систему уравнений
[7л;, + Ъх2 + 2*з = 1,
= 4.
Определитель основной матрицы
А =
7 3 2
3 1 2
10 12 8
= -72*0.
Следовательно, система имеет единственное решение.
Найдем его по правилу Крамера:
Д. =
1 3 2
2 1 2
4 12 8
Аз =
= 0, А
7 3 1
3 1 2
10 12 4
2 ~~
7 1 2
3 2 2
10 4 8
-36,
}. т.е.
Следовательно, jct = — — 0* jc2 = — — — 4, х3 = -
Д Д I L
система имеет единственное решение: [ 0, — -i, 11
В случае, когда определитель |Л| основной матрицы А
системы C) равен нулю, правило Крамера не применимо.
Перейдем к изучению систем т линейных уравнений с
п неизвестными.
Расширенной матрицей системы уравнений A) называет-
называется матрица, получаемая добавлением к основной матрице
А системы A) столбца свободных членов, располагая его
последним столбцом и отделяя его вертикальной чертой,
т.е. матрица
671
в =
а2Х Oj2
«„« b,
h\
Отметим, что ранг расширенной матрицы В не меньше
ранга основной матрицы А системы A). Точнее, если ранг
основной матрицы равен г, а ранг расширенной — R, то
г < R. В то же время очевидно, что R< г+ 1.
Вопрос о совместности системы A) решает критерий
Кронекера — Капелли: система A) т линейных урав-
уравнений с п неизвестными совместна тогда и только тогда,
когда ранг расширенной матрицы В равен рангу основной
матрицы А системы A).
Доказательство этой теоремы опускается.
Пусть ранг основной матрицы системы A) равен г,
причем 1 < г < min(m, n). В этом случае любой отличный от
нуля минор порядка г основной матрицы системы A)
называют главным минором системы.
Решение системы линейный уравнений состоит в следу-
следующем. Вычисляем ранг основной матрицы А системы A)
и расширенной матрицы В.
Если ранг основной матрицы А системы A) не равен
рангу расширенной матрицы В, то согласно критерию
Кронекера — Капелли система несовместна, т.е. система
A) не имеет ни одного решения. На этом решение системы
A) заканчивается.
Если ранги основной и расширенной матриц равны
между собой и равны г, т.е. система A) совместна, то берут
любой отличный от нуля минор основной матрицы поряд-
порядка г и рассматривают г уравнений, коэффициенты которых
входят в этот главный минор, а остальные уравнения
системы отбрасывают. Неизвестные, коэффициенты кото-
которых входят в этот главный минор, объявляют главными, а
остальные неизвестные — свободными. Новую систему
переписывают так, что в левых частях всех уравнений
остаются только члены, содержащие г главных неизвест-
неизвестных, а все остальные члены уравнений, содержащие (п — г)
неизвестных, переносятся в правые части уравнений. Затем
672
по правилу Крамера находят главные неизвестные. Легко
видеть, что при этом главные неизвестные выражаются
через свободные неизвестные, каждое из которых может
принимать любое числовое значение. Полученные реше-
решения новой системы с /главными неизвестными называются
общим решением системы A).
Придавая всем свободным неизвестным некоторые чис-
числовые значения, из общего решения находят соответствую-
соответствующие числовые значения главных неизвестных и тем самым
находят находят решение исходной системы уравнений A),
которое называется частным решением при данных число-
числовых значениях свободных неизвестных. Указанным путем
можно получить любое решение системы A).
Примеры. 1. Рассмотрим систему
Ранг основной матрицы этой системы равен двум, так
как существует отличный от нуля минор второго порядка
этой матрицы, например
5 -1
2 1
= 7,
а все миноры третьего порядка равны нулю.
Ранг расширенной матрицы этой системы равен трем,
так как существует отличный от нуля минор третьего
порядка этой матрицы, например
5 -1 7
2 1 I
I -3 0
= 35
Согласно критерию Кронекера — Капелли система не-
несовместна, т.е. не имеет решений.
2. Рассмотрим систему
22 Алгебра, тригонометрия
и элементарные функции
673
f7x, + 3*2 — 2x3 = 2,
— 2x2 + 3x3 = 0,
[4x, + 9x2- Ilx3 = 2.
Ранг основной матрицы этой системы равен двум и ранг
расширенной матрицы тоже равен двум, так как, например,
минор второго порядка
1 -2
= -17
основной матрицы отличен от нуля, а все миноры третьего
порядка основной и расширенной матрицы равны нулю.
Значит, система совместна. Возьмем за главный минор,
например, минор
1 -2
. Так как третье уравнение системы
не содержит элементов этого главного минора, то третье
уравнение отбрасываем. Неизвестные х, и х2 объявляем
главными, ибо их коэффициенты входят в главный минор,
неизвестную х3 объявляем свободной.
Получаем систему, равносильную исходной:
J 7.x, + Зх2 = 2х3 + 2,
[х, — 2хг = — Зх3.
ь
Решаем ее по правилу Крамера:
-3*3 -2
= -4*3-4 + 9*3 = 5*з-4 _
- 17
7 2*з + 2
1 -3*з
— 17
_ — 21*з — 2*з — 2 _ —23*з — 2 _ 23 ,2
=Л7 ^Т7 Т7Хз Т7'
Итак, общим решением исходной системы является беско-
бесконечное множество наборов (х,, х2, х3) вида
[ — -р^/ + ^7, jjt + j~, Л где / — любое действительное число.
Частным решением исходного уравнения будет, например,
числовой набор (j^, -j^, 0\ получающийся при t = 0.
3. При каких к совместна система уравнений
674
x+ky=3,
Поскольку г * 0, то эта система совместна в двух случаях:
когда Д*0 и когда R = r=l. Поэтому рассмотрим два
случая.
а) Если А*0, т.е. если
1 к
к 4
), т.е. если Л2*4, то по
правилу Крамера система имеет единственное решение.
Значит, для любого к, кроме к=2 и к= — 2, система
имеет единственное решение.
б) Если R = г = 1, т.е. если
= 0,
т.е. если к = 2, то система совместна.
Подводя итог, получаем, что исходная система совместна
при любых к, кроме к = — 2.
Используя критерий Кронекера — Капелли, проведем
исследование системы двух линейных уравнений с двумя неиз-
неизвестными х и у.
1 к
к 4
3 к
6 4
=
1 3
к 6
lalx+b]y=cu
(9)
Основная матрица этой системы
имеет ранг г, причем 0 < г < 2.
Расширенная матрица
имеет ранг R, причем 0 < г <, R. Очевидно, что r<R<r+ 1.
Имеет место следующее утверждение.
Пусть дана система двух линейных уравнений с двумя
неизвестными (9). Тогда:
675
1. если г = R = О, т.е. если все коэффициенты аи а2, bu Ь2,
сх, с2 равны нулю, то любая пара действительных чисел
является решением системы (9);
2. если г = О, R = 1, т.е. а, = а2 = Ь{ = Ь2 = О и с\ + с\ ф О,
то система (9) не имеет решений;
3. если г= 1, R = \,то система (9) имеет бесконечно много
решений, но не любая пара действительных чисел есть ее
решение;
4. если r= 1, R = 2, то система (9) не имеет решений;
5. если г =2, R=2, то система (9) имеет единственное
решение, которое можно найти по правилу Крамера.
Справедливо и обратное утверждение.
1. Если система (9) имеет единственное решение, то
r= R=2;
2. если система (9) не имеет решений, то гф R, т.е. либо
г=0 и R= \,либог= 1 и R=2;
3. если любая пара действительных чисел является реше-
решением системы (9), то r= R=0;
4. если система (9) имеет бесконечно много решений, но не
любая пара действительных чисел является ее решением, то
r=R=\.
Приведем доказательство этих утверждений только
в том случае, когда оба уравнения системы (9) являются
уравнениями первой степени, т.е. когда выполняются ус-
условия а\ + Ь] ф 0, а\ + 1% ф 0. В этом случае каждое уравне-
уравнение этой системы в отдельности определяет прямую на
плоскости, где задана система координат хОу (см. гл. III).
Это дает возможность придать геометрический характер
дальнейшим рассуждениям при исследовании системы (9).
Теорема. Пусть две прямые заданы уравнениями
ахх + Ьху — сх = 0,
+ Ъ-у — с2 = 0. A0)
где а\ + Ь] ф 0 и а\ + $ ф 0.
1. Для того чтобы две прямые пересекались, необходимо и
достаточно, чтобы R = г = 2.
2. Доя того чтобы две прямые были параллельными, но не
совпадали, необходимо и достаточно, чтобы r= I, R=2.
676
3. Для того чтобы две прямые совпадали, необходимо и
достаточно, чтобы r= R = 1.
Доказательство. Сначала докажем достаточ-
достаточность условий.
1. Если r= R=2, то система A0) имеет единственное
решение, которое легко найти по правилу Крамера, а это
означает, что прямые имеют одну общую точку, т.е. пере-
пересекаются.
2. Если r= I, R=2, то система A0) несовместна, и
поэтому прямые не имеют общих точек, т.е. параллельны
и не совпадают.
3. Если r= R= 1, то все миноры второго порядка основ-
основной и расширенной матриц равны нулю, т.е.
а, Ь{
= 0,
с, Ь{
= 0,
а, с,
= 0.
Эти условия можно переписать так:
axb2 = Ьха2,
С\Ь2 = Ьхс2,
ахс2 = а2сх.
(И)
A2)
A3)
Рассмотрим теперь все возможные случаи.
а) если ах = 0, то Ьх*0, т.к. а^ + Ь^^О. Тогда из A1)
следует, что а2 = 0, а так как а\ + 1% * 0, то Ъ2 * 0. Тогда из
A2) находим, что -?- = % = а и при этом уравнения прямых
примут вид
Ъ\ (у - а) = 0, Ъ2 (у - а) = 0.
Поскольку Ъ\ * 0, и Ъ2 *¦ 0, то отсюда вытекает, что эти
прямые совпадают с прямой у — а = 0.
б) Если Ъ\ = 0, то ах * 0, а из A1) тогда следует, что Ъ2 = 0
С О
(причем а2 * 0). Тогда из A3) имеем — = — = р, и поэтому
уравнения прямых примут вид ах (х — р) = 0, а2 (х — р) =
= 0. Поскольку ах *0, а2*0, то отсюда вытекает, что эти
прямые совпадают с прямой х — р = 0.
677
в) Если ах ф О и Ъх ф О, то из A1) вытекает, что — = j- = у,
а из A2) и A3) вытекает, что с2 = ^с1= — с,. Таким обра-
зом, получаем что аг = уаи Ъг = ybu с2 = усь и поэтому
уравнения прямых примут вид
ахх + Ъху — с, = 0, у (агх + Ъ& — с,) = 0.
Поскольку у ф 0, то отсюда вытекает, что эти прямые со-
совпадают.
Теперь докажем необходимость условий. Доказа-
Доказательство проведем методом от противного.
1. Пусть прямые пересекаются. Докажем, что r= R=2.
Если бы оказалось, что r= I, R=2, то по доказанному
прямые были бы параллельны и не совпадали. Если бы
оказалось, что r= R= 1, то по доказанному прямые оказа-
оказались бы совпавшими.
Следовательно, г = R = 2.
2. Пусть прямые параллельны. Докажем, что г = 1, R = 2.
Если бы оказалось, что г = R = 2, то по доказанному пря-
прямые оказались бы пересекающимися. Если бы оказалось,
что r=R=l, то по доказанному прямые оказались бы
совпавшими.
Следовательно, r= I, R=2.
3. Пусть прямые совпадают. Докажем, что r=R=l.
Если бы оказалось, что г = R = 2, то по доказанному пря-
прямые оказались бы пересекающимися. Если бы оказалось,
что r=\, R=2, то по доказанному прямые были бы
параллельны.
Следовательно, r= R= 1. Теорема доказана полностью.
УПРАЖНЕНИЯ
1. Пусть Л = {
ЗА - 2В.
(I 2
(
2. Найти матрицу С, если А = 0 1 0
12 3 — 1
678
Г О 2
,В= -1 О 3
0 3 4
2С=ЗВ.
3. Найти произведения АВ и ВА, если А =
= Г1 о
_ Г1 0 — 1
п
U
(-2 О
,В=\ 3 2
4. Дана матрица А = L. _ . Найти все матрицы X, перестановочные А,
т.е. те, для которых АХ- ХА.
5. Матрица S = аЕ, где Е — единичная матрица порядка л, а а — число,
называется скалярной. Показать, что скалярная матрица Sперестановочна
с каждой матрицей порядка л, т.е. если А — матрица порядка л, то SA = AS.
, j-, . fcos a — sin сЛ и fcos В — sin B^
6. Показать, что матрицы А = \ . \ и В = \ . „ „
Isina cosal IsinB cos ВI
перестановочны. Найти их произведение.
7. Найти все квадратные матрицы В, для которых АВ = 0, если А =
Найти общий вид матрицы А третьего порядка, для которой
ГО 1 О
О 0 1 А = 0.
0 0 0
9. Пусть /= |_ У q |, Е = |\ УI. Показать, что / = — Е, Е2 = Е.
V / V ) с I л
10. Дан многочлен Р(х) = хг — 5х + 6 и матрица А = _ . .
Р(А) =А2-5А + 6Е. ^
Написать транспонированные матрицы для матриц A1 — 14):
. Найти
И. Л = B 1 3); 12. В =
; 13. С =
= f0 П.
3 4
; 14. D =
о
1 1
2 -2 1
15. Проверить выполнение свойства транспонирования на 'примере
Г %В = {\ 2Л.
^ ' @ 1
16. Показать, что при умножении матрицы В =
1 0 0
слева на
0 0 1
произвольную матрицу А третьего порядка меняются местами первые две
строки матрицы А. Установить, что произойдет при умножении справа.
(\ 0 0)
17. Показать, что при умножении матрицы D —
0 a 0 слева на
10 0 1 I
произвольную матрицу А третьего порядка 2-я строка матрицьгЛ умножа-
умножается на а. Установить, что происходит при умножении справа.
П 0 оЛ
18. Показать, что при умножении матрицы С =
0 1 0
на произволь-
0 0 1
ную матрицу А третьего порядка справа к первому столбцу матрицы А
добавляется 3-й столбец, умноженный на а. Установить, что происходит
при умножении слева.
679
Вычислить определители A9 — 25):
19.
23.
3
-2
2 3
.20.
1
3
-3
2
-4 7
12-15
-а - 1
1 — а
.24.
— а
а — а
— а — а
.21.
25.
a
- 1
a -
2 - 1
1 1
3 2
5 -2
1
a
1
—
—
a
1
a
3
2
1
1
.22.
- 1
4
3
-2
1
0
-ft
b 1
* 0
0 b
Найти ранг матрицы B6 — 28):
о -
26. А=
28. С =
29. Убедиться, что для А =
= 5-1-17
- 1
13
( </ -4
— be — с а
с d
i-l
если \А\ = ad — cb ф 0, то А =
30. Найти обратную матрицу А , если А =
31. Доказать, что если матрицы Л и В перестановочны, то перестано-
вочны и обратные матрицы А ' и В~ '.
32. Убедиться, что (АВ)~ ' = А~ 1Б~ \ если Л =
Решить систему уравнений C3 — 40):
5х\ — Зх2 = 7,
1 1
0 1
33.
35.
37.
39.
5х! + 2х2 + Зх3 + 7 = 0,
:] + 2х2 + Зх3 = 4.
- х, + 2х2 + Зх3 = 0,
х, — 4х2— 13х3 = 0,
— ЗХ] + 5x2 + 4хз = 0.
38.
40.
Зх+у— i= 1.
34. — 2х!+9х2 = 4,
л + 4*2 = ~.
2х — 4у + z = 1,
36. \х— 2y + 4z= 3,
Зх — у + 5z = 2.
4х! + 5х3 = 6,
+ 4х3 = 3.
2х— Ъу+z — 2 = 0,
х+ 5.у —
4х+.у—
5 = 0,
Глава XI. КОМПЛЕКСНЫЕ ЧИСЛА
При рассмотрении действительных чисел отмечалось,
что в множестве действительных чисел нельзя, например,
найти число, квадрат которого равен (—1). Чтобы подоб-
подобные задачи были разрешимы, понятие числа расширяется
с помощью введения комплексных чисел.
§ 1. Понятие комплексного числа
Пусть даны выражения вида а + Ы, где аи b — действи-
действительные числа, / — некоторый символ, смысл и связь
которого с действительным числом Ь, а также смысл знака
«+», соединяющего а и Ы, будут выяснены позже. Введем
определения равенства, суммы и произведения таких вы-
выражений.
Выражения а + Ы и с + di считаются равными в том и
только в том случае, если одновременно а = с и b = d.
Равенство выражений а + Ы и с + di принято записывать в
виде а + Ы = с + di.
Из определения равенства вытекает, что два выражения
а + Ы и с + di различны, т.е. а + Ыфс + di, если выполнено
хотя бы одно из неравенств а ф с или Ъ ф d.
Замечание. Из всех знаков неравенств ф, <, ?, й, > для
выражений вида а + Ы употребляется только знак ф.
Суммой выражений а + Ы и с + di называется выражение
(а + с) + (b + d)i. Сумму выражений а + Ы и с + di принято
обозначать через (а + Ы) + (с + di), т.е. по определению
(а + Ы) + (с + di) = (a+ c) + (b + dji.
Произведением выражений а + Ы и с + di называется вы-
выражение (ас — bd) + (ad + bc)i. Произведение выражений
681
a + Ы и с + d/ принято обозначать через (а + bi)(c + df), т.е.
по определению (д + Ы)(с + di) = (ос — bd) + (*м/ + 6с)/.
Множество всех выражений вида а + Z>/, которые разли-
различают, складывают и перемножают по только что сформу-
сформулированным определениям, называется множеством ком-
комплексных чисел, а каждый элемент этого множества, т.е.
выражение а + Ы, называется комплексным числом.
Часто комплексное число а + Ы обозначают одной бук-
буквой, например буквой z. В таких случаях пишут z = а + Ы.
Пусть даны комплексные числа Z\ — ах + bxi, Zi = a2 + b2i,
Zj = a3 + b3i, ..., zn = а„ + bni. Для того чтобы найти сумму
комплексных чисел Z\, Zi, Z3, ¦¦¦, zn, надо найти сумму первых
двух чисел, затем к полученной сумме прибавить третье
число, к полученной сумме прибавить четвертое и т.д., пока
не переберем все слагаемые.
Аналогично определяется и произведение нескольких
комплексных чисел.
Если комплексное число z взято сомножителем п раз
(п > 2), то произведение ZZZ ¦¦¦ Z называют л-й степенью
п раз
(л > 2) числа z и обозначают z", т.е. по определению
Кроме того, по определению zl = z.
Приведем основные законы сложения и умножения ком-
комплексных чисел:
а) Z\ + Z2 = Zi + Z\ (коммутативность сложения);
б) (z\ + Z2) + Zj = Z\ + (zi + Zi) (ассоциативность сложе-
сложения);
B) Z\Zi = ZiZ\ (коммутативность умножения);
г) (Z\Zi)Zi = Z\(.ZiZi) (ассоциативность умножения);
д) (Z\ + Zi)Zi = Z\Zi + Z2Z3 (дистрибутивность умножения
относительно сложения).
Справедливость этих законов следует из определения
суммы и произведения комплексных чисел и из справед-
справедливости аналогичных законов для сложения и умножения
682
действительных чисел (проверка их справедливости опус-
опускается).
Для действий сложения и умножения комплексных
чисел вводятся действия, обратные им.
Разностью комплексных чисел Z\ и z2 называется такое
комплексное число Zi, которое в сумме с ^дает Z\-
Покажем, что для любых комплексных чисел Z\ — ах + bxi
и z2 = o2 + b2i их разность Zi — Z\ — Zi существует, единст-
единственна и вычисляется по правилу Zi = (щ — а2) + (bx — b2)i,
т.е. существует единственное комплексное число Zi —
= х + yi, которое в сумме с z2 дает Z\- По определению
суммы комплексных чисел z2 + Zi = (a2 + jc) + (b2 + y)i. По
определению равенства комплексных чисел числа Z\, z2 + Zi
равны тогда и только тогда, когда одновременно справед-
справедливы равенства
а2 + х=аи Ь2 + у = Ьх.
Из этих равенств числа хиу всегда определяются и притом
единственным образом: х= ах — а2, у = Ьх — Ь2, т.е. суще-
существует и притом единственное комплексное число z-i —
= (я, — а2) + (Ьх — b2)i, которое и является разностью Z\
uz2.
Частным отделения комплексного числа Z\ на комплекс-
комплексное число z2 такое, что z2 *¦ 0 + 0/, называется такое ком-
комплексное число Zi, которое при умножении на z2 дает Z\-
Можно показать, что для любых комплексных чисел Z\ —
= ах + bxi, z2 = a2 + b2i (z2 ф 0 + 0/) их частное z-i = — сущест-
вует, единственно и вычисляется по правилу
b2 , bxa2— афг.
~ + '
Zi 2 Л~ + 2 J '•
а2 + о2 а2 + о2
Доказательство этого факта опускается.
Рассмотрим комплексные числа вида а + 0/. Каждое
такое число принято рассматривать как действительное
число а, т.е. каждое число вида а + 0/ отождествляется с
действительным числом а. Обычно числа а и а + 0/ не
различаются, и даже принято писать равенство а + 0/ = а.
683
В частности, числа 0 и 0 + О/ не различают; число 0 + О/
также называют нулем и пишут 0 + О/ = 0.
Рассмотрим теперь комплексные числа вида 0 + Ы. При-
Принято такие числа обозначать просто Ы и писать равенство
0 + Ы = Ы. В частности, комплексное число 0+1/ принято
обозначать просто / и писать равенство 0 + 1/= /. Ком-
Комплексное число / называется мнимой единицей. Покажем,
что мнимая единица обладает свойством /2 = — 1. Дейст-
Действительно, на основании принятых соглашений справедли-
справедливы следующие равенства: г2 = @ + I/J — @ + 10@ + 10 —
= @ • 0 - 1 • 1)@ ¦ 1 + 1 • 0)/ = - 1 + 0/ = - 1.
Комплексные числа вида 0 + Ы называют чисто мнимыми
числами.
Согласно принятым соглашениям любое чисто мнимое
число Ы представляет собой произведение двух комплекс-
комплексных чисел: числа b и мнимой единицы /. Действительно,
{Ь + 00@ + 10 = (Ь • 0 - 0 • 1) + (Ь • 1 + 0 • 0)/ = 0 + Ы = Ы.
Любое комплексное число а + Ы представляет собой
сумму двух комплексных чисел: числа а и чисто мнимого
числа Ы. Действительно, (а + 00 + @ + Ы) = (а + 0) +
+ @ + b)i =а + Ы.
Из определения действий сложения, вычитания и умно-
умножения комплексных чисел вытекает, что эти действия
можно проводить по правилам действий над многочленами
(см. гл. II), заменяя / на — 1 и объединяя затем члены,
содержащие и не содержащие /.
Примеры. B+ 30-4+ G- 130 + 4/= B - 4 + 7) +
+ C- 13 + 4)/= 5-6/:
D + 50 + (х + yi) - {а1 - Ы) = D + х - а2) +
+ E + у + b)i;
(а + Ы)(х + yi)= ax + ayi + bxi + byf = {ах — by) +
+ {ay + bx)i;
B + 40G - /) = 14 - 2/ + 28/ - 4/2 = 18 + 26/.
Пусть Z] и Z2 — любые комплексные числа, п — любое
натуральное число. Пользуясь правилами действий над
комплексными числами, легко доказать справедливость
формул сокращенного умножения:
684
и в частности формул
Ui + z2J = ? + 2Zlz2 + z\; z\-z\ =
- z2).
Геометрическая интерпретация комплексных чисел. Пусть
на плоскости дана прямоугольная система координат. Каж-
Каждому комплексному числу z — a + Ы поставим в соответст-
соответствие точку на плоскости с координатами а и Ь, т.е. точку
М(а, Ь) (рис. 192). Легко видеть, что тем самым между
множеством комплексных чисел и множеством точек плос-
@,1)
Рис. 192.
Рис. 193.
кости установлено такое соответствие, что каждому числу
соответствует только одна точка и разным числам соответ-
соответствуют разные точки. При этом на плоскости нет ни одной
точки, которая бы не соответствовала какому-нибудь ком-
комплексному числу. Значит, между множеством комплексных
чисел и множеством точек на плоскости установлено вза-
взаимно однозначное соответствие и поэтому можно считать,
что комплексное число z= а + Ы есть точка на плоскости
с координатами (а, Ь).
Модулем комплексного числа z — a + Ы называется дей-
действительное число г = \z\ — Vo^ + 62.
Поскольку комплексному числу z— я + Ы можно поста-
поставить в соответствие точку М плоскости с координатами а
и Ъ, то модулю комплексного числа можно придать следую-
685
щий геометрический смысл: \z\ — расстояние соответст-
соответствующей точки М(а, Ь) до начала координат. Рассмотрим
следующие задачи.
1. Найти множество точек плоскости, соответствующих
комплексным числам z таким, что \z\ = 1.
Согласно геометрическому смыслу модуля комплексно-
комплексного числа это будут точки, находящиеся от начала координат
на расстоянии единица, т.е. точки, которые лежат на ок-
окружности радиуса, равного единице, и с центром в начале
координат (рис. 193).
2. Найти множество точек плоскости, соответствующих
комплексным числам z таким, что 2 < \z\ < 3.
Согласно геометрическому смыслу модуля комплексно-
комплексного числа это будут точки, расположенные внутри кольца,
образованного окружностями с радиусами 2 и 3, и с цент-
центром в начале координат, включая окружность радиуса 2
(рис. 194).
М/а+с, b+d)
@,1)
2<\z\<3
Рис. 194.
Рис. 195.
Комплексное число z — a + Ы можно рассматривать как
вектор z, начало которого находится в начале координат, а
конец — в точке М(а, Ь), изображающей это число (см.
рис. 192). Далее, говоря о векторах, изображающих ком-
комплексные числа, будем подразумевать, что начало этих
векторов находится в начале координат.
Рассмотрим геометрическую иллюстрацию сложения и
вычитания двух комплексных чисел Z\ — а + Ы и z% ~ с + di
686
в том случае, когда три точки О@, 0), М,(я, Ь) и М2(с, d) не
лежат на одной прямой.
Пусть даны числа Z\ — а + Ы, z2 = с + di и Zs — (о + с) +
+ (b + d)i. Рассмотрим вектор Z\, конец которого находится
в точке М\(а, Ь), вектор zi, конец которого — в точке
М2(с, d), и вектор z-i, конец которого — точка М3(я + с,
Ъ + d). Вектор Zi является диагональю параллелограмма
0МхМгМ2 (рис. 195). Поскольку число Zj, есть сумма чисел
Z\ и Zi, то отсюда вытекает, что сложение двух комплексных
чисел можно геометрически интерпретировать как сложе-
сложение по правилу параллелограмма векторов Z\ и z2, начала
которых находятся в начале координат, а концы — в точках
М,(я, Ь) и М2(с, d), изображающих эти числа.
Векторы, изображающие комплексные числа z — а + Ы и
(— z) = — а — Ы, расположены симметрично относительно
начала координат, поскольку концы этих векторов, точки
М(а, Ь) и N(— a, — Ь), симметричны относительно начала
координат (рис. 196).
м,
Рис. 196.
Рис. 197.
Пусть даны числа Z\ = а + Ы и z2 = с + di. Рассмотрим
вектор Z\, конец которого находится в точке Мх{а, Ь), и
вектор z2, конец которого находится в точке М2(с, d)
(рис. 197). На этих векторах построим параллелограмм
0М\МгМ2. Рассмотрим вектор (— z2), конец которого нахо-
находится в точке М4(— с, — d). Складывая векторы Z\ и (— z2)
по правилу параллелограмма, получаем их сумму — вектор
687
Za, конец которого находится в точке М5(а — с, b — d).
Очевидно, что длина вектора г, равна длине отрезка МХМ2.
Поскольку длина вектора Za равна \z& = \z\ — z2\, то отсюда
вытекает, что длина диагонали МХМ2 равна \z\ — z2\ и модуль
разности двух комплексных чисел Zi и z2 представляет собой
расстояние между точками Мх и Мъ изображающими эти
числа.
Такое геометрическое толкование суммы и модуля раз-
разности двух комплексных чисел часто применяется при
решении задач.
Примеры 1. Найти множество точек плоскости, соот-
соответствующих комплексным числам z таким, что \z — г| =
= к+г
Расстояние от искомых точек до точек, соответствующих
комплексным числам / и (— 2), равны. Значит, искомое
множество состоит из точек прямой, перпендикулярной к
отрезку, соединяющему точки @; 1) и (— 2; 0), и проходя-
проходящей через середину этого отрезка (рис. 198).
\
(-2,0)
I
\
y,
•
v
\
\
@,1)
0 x
i. M-l
@,1),
\\3 3]
Рис. 198.
0 A,0) B,0)
1
Рис. 199.
2. Найти точки z, удовлетворяющие условию \z — 1| =
= |г-2| = |г-4.
Точки, соответствующие числам 1, 2, и /, образуют
треугольник. Условию задачи удовлетворяет единственная
точка — центр описанной окружности этого треугольника.
Так как она равноудалена от точек A; 0) и B; 0), то ее
координата л: = -|, а так как она равноудалена от точек A; 0)
688
и @; 1), то у = х = -у, т.е. условию задачи удовлетворяет
единственное число z = т + ji (рис. 199).
Аргументом комплексного числа z= a + Ы, отличного от
нуля, называется любое из чисел q>, являющихся решением
системы уравнений
COS ф =
Для числа z = 0 аргумент не определяется. Данная система
имеет бесконечное множество решений (так как на коор-
координатной плоскости пара чисел ( , ° а; , 2 Л определяет
\Уа + Ъ Sa + b \
точку единичной окружности), причем если <p0 есть одно
из ее решений, то все остальные решения получаются из
него по формуле ф = ф0 + Ink, где к — любое целое число.
Таким образом, любое комплексное число z ф 0 имеет бес-
бесконечно много аргументов, отличающихся друг от друга на
число, кратное 2я.
Главным аргументом, комплексного числа z — а + Ы ф 0
принято называть его аргумент из интервала [0; 2я) и
обозначать этот аргумент arg z-
Аргумент комплексного числа z имеет следующий гео-
геометрический смысл. Если комплексное число z = а + Ы ф 0
рассматривать как вектор z, конец которого — точка
М(а, Ь), то величина угла ф, на который нужно повернуть
против часовой стрелки положительную ось Ох до первого
совмещения ее с вектором z, является главным аргументом
комплексного числа z (см. рис. 192). Величина любого угла,
отличающегося от главного аргумента arg z на целое число
полных углов, является также аргументом рассматриваемо-
рассматриваемого числа z-
Пример. Найти на плоскости точки z, удовлетворяю-
удовлетворяющие условию ^ й arg z < -j--
689
Все точки, расположенные на каком-либо луче, выходя-
выходящем из начала координат, имеют один и тот же главный
аргумент, поэтому условию
задачи удовлетворяют все
точки той части плоскости,
которая расположена
между лучами, выходящи-
выходящими из начала координат
под углами ^ и -~, а также
точки, лежащие на первом
луче (рис. 200).
Сопряженные комплекс-
комплексные числа. Комплексное
число z— a — Ы называют
числом, сопряженным ком-
комплексному числу z— а + Ы.
По формулам сокращен-
сокращенного умножения
Рис. 200.
zz = (a + bi) x (a - bi) = a2 — (biJ = a2 + b2.
Это свойство сопряженных комплексных чисел позволя-
позволяет деление комплексного числа Z\ на комплексное число z2
{Zi * 0) свести к умножению комплексных чисел Z\ и ~z2.
Действительно, пусть Z\ — ах + bj, Zi = a2 + b2iwz2 * 0, тогда
Zx Z\Z2 (flj + bxi) {a2 — Aji) axa2 — axb2i+ bxa2i — bxb2i
г2 z2z2 a2 + b2 a2 + b2
axa2 + bxb2 , bxa2 — a^ .
2 ,2 + 2^ J—t-
a2 + b2 a2+ b2
Пример.
2+i _ B + i)D + i) _ 8 + 2/+4Z+;2 _ 7 . _6_-
4 — / D + /) D-/) 16+1 17 17
По определению, если z&0, то г° = 1; если z* 0 и п —
натуральное число, то z~" = \
z
(.90
о _
Примеры. 1. B + i) = 1;
2 ri- 1- -/--/-
/<-0 -z2
3.
~2=
/)~2=
B+/) 4 + 4/+/
_ 1 _ 1C-4/) _
3 + 4/ C + 4/) C - 4/)
= 3-4/ = J _4_.
9+16 25 25'
Легко видеть, что число, сопряжен-
сопряженное числу г, есть число z, т.е. ~z = z, и
поэтому числа ^иг называются вза-
взаимно сопряженными. В геометричес-
геометрической интерпретации комплексных
чисел взаимно сопряженные числа
представляют собой точки, симмет-
симметричные относительно действитель-
действительной оси Ох (рис. 201). Отметим ряд
свойств взаимно сопряженных чисел.
а) й = z.
Действительно, |г| =
т.е. й = |г|.
б) Если z= а, где а — действительное число, то z = z,
arg 1 = arg z.
в) Если г * Z, то arg г = 2те — arg z-
Действительно, если ф есть решение системы уравнений
f
а +
то число
= 2те —
sin ф = •
ф есть решение системы уравнений
а
г) Н =
691
Действительно, так как \z\ = Va2 + b2 и так как zz =
= (а + bi) (а — Ы) = а2 + Ъ2, то \z\ = "fzz.
д) Сумма и произведение взаимно сопряженных ком-
комплексных чисел есть действительное число.
Действительно, если z— a+ bi, то z + ~Z = 2а (действи-
(действительное число) и zz = а2 + Ъ2 (действительное число).
е) Число, сопряженное к сумме двух любых комплексных
чисел, равно сумме чисел, сопряженных к слагаемым, т.е.
Действительно, если Z\ = а + bi, Zi~ c+ di, то zi + zi =
= (а - bi) + (с - di) = (а+ с)-(Ь + d)i = [(а + с) + (b + d)i\ =
= Z\+ Zi-
ж) Число, сопряженное к произведению двух комплекс-
комплексных чисел, равно произведению чисел, сопряженных к
сомножителям, т.е. zizi = zi Z~i-
Действительно, если Z\ = а + Ы, Zi = c+ di, то Z\Zi =
= (ас — bd) + (ad + bc)i и (ад) = (ас — bd) — (ad + bc)i, a
z~x z~2 = (a — Ы)(с — di) = (ас — bd) + (— ad — bc)i =
= (ac — bd) — (ad + bc)i, т.е. ад = z~\Z~i-
з) Число, сопряженное к разности двух комплексных
чисел, равно разности сопряженных чисел, т.е. (zi — Zi) =
Свойство з) доказывается так же, как и свойство е).
и) Если z% *¦ 0, то
Свойство и) доказывается так же, как и свойство ж).
к) Число, сопряженное л-й степени комплексного числа
Z, равно л-й степени числа, сопряженного к числу z, т.е.
(?) — (?)", где п — натуральное число.
Докажем это свойство методом математической индук-
индукции. Для п = 1 теорема очевидна. Предположим, что она
справедлива для п = к, т.е. предположим, что справедливо
равенство (?) = (z)k, и докажем, что (^*+|) = (z)k+1. Дейст-
Действительно, (^+1) = (г* • z)- По свойству ж) сопряженных
чисел E*г) = (?) г. Используя теперь предположение для
692
п = к, получаем (?) z = (z)k Z = (z)k+ i и свойство к) доказа-
доказано.
В качестве следствия доказанных выше свойств (е, з, к)
получаем справедливость следующего утверждения.
Если число z выражено через комплексное число а при
помощи суммы и разности натуральных степеней этого
числа, то заменяя в этом выражении число а на ему сопря-
сопряженное число а, получим число 1, сопряженное с числом z-
§ 2. Тригонометрическая форма комплексных чисел
Пусть z= a+ Ы— некоторое комплексное число, отлич-
отличное от нуля. Обозначим через г его модуль, а через ф —
один из его аргументов. Тогда число z можно записать в
виде
Z= г(созф + /sin ф). A)
Правая часть равенства A) называется тригонометрической
формой комплексного числа z-
Тригонометрическая форма комплексного числа, отлич-
отличного от нуля, определена однозначно: это запись комплекс-
комплексного числа z в виде A), где г — положительное число,
равное модулю числя z, косинус и синус берутся от одного
и того же угла ф, равного аргументу числа z, при этом между
косинусом и синусом стоит знак плюс.
Ясно, что следующие комплексные числа записаны не в
тригонометрической форме:
Z\ = cos y + / sin я — j t Zi — — 2 cos -= + i sin -^
Zi = sin ^ + / cos ^; Za — cos ^ — i sin j.
Тригонометрическая форма этих комплексных чисел
следующая:
Z\ = cos ^ + i sin ^; zi = 2 cos у + / sin y
Zi = cos ^ + / sin Ц; Za = cos -? + / sin ~.
3 3 3 4 4
693
Действия умножения, деления, возведения в целую сте-
степень над любыми комплексными числами удобнее произ-
производить, если они записаны в тригонометрической форме.
Теорема 1. Модуль произведения двух комплексных чисел
равен произведению их модулей, а аргумент равен сумме
аргументов.
Доказательство. Пусть даны комплексные числя Z\ —
= r((cos cpi + /sin(pi) и Zi — r2(cosф2 + /sinф2). Рассмотрим
число Zy = Z\Z2- Применяя правила действия над комплекс-
комплексными числами и формулы для косинуса и синуса суммы
двух углов, имеем
Zi = Z\Zi = {r,(cos ф, + / sin Ф1)][г2(со8 ф2 + /sin ф2)] =
= r,r2[(cos Ф1 + / sin ф()(со8 ф2 + / sin ф2)] =
= rir2[(cos^icos ф2 — sin cpisin ф2) +
+ (sin ф^ов ф2 + cos q>isin ф2)/] =
= r,r2[(cos (ф, + фг) + /sin (ф, + ф2)].
Итак, Zi — r,r2[cos (ф, + ф2) + /sin (ф, + ф2)], т.е. число Zi
записано в тригонометрической форме и его модуль равен
гхгъ а аргумент равен (ф! + ф2), что и доказывает теорему.
Теорема 2. Модуль частного двух комплексных чисел Z\
и Zi (Zi * 0) равен частному их модулей, а аргумент равен
разности аргументов.
Доказательство этой теоремы проводится аналогично
доказательству теоремы 1, надо только предварительно
умножить числитель и знаменатель частного — на
Теорема 3. (формула Муавра). Пусть z — любое,
отличное от нуля, комплексное число, п — любое целое число,
тогда
z" = [г (cos ф + / sin ф)]Л = /(cos /ир + / sin жр). B)
Доказательство. 1. Для любого натурального л дока-
докажем эту формулу методом математической индукции.
694
Для п = 1 формула верна. Предположим, что формула B)
верна для п = к, т.е. предположим, что справедливо равен-
равенство
? = [г (cos ф + / sin ф)]* = /(cos kip + i sin kip). C)
Докажем, что из справедливости равенства C) вытекает,
что формула B) справедлива и для п = к+ 1. Применяя
формулу C), правила действия над комплексными числа-
числами, формулы для синуса и косинуса суммы двух углов,
имеем
/+' = zkz — [/(cos кар + i sin fop)][r(cos ф + / sin ф)] =
= /+ '[(cos kip cos ф — sin ktp sin ф) +
+ / (sin ktp cos ф + cos lap sin ф)] =
т, е, формула B) доказана для п = к + 1. Следовательно, по
методу математической индукции формула B) справедлива
для любого натурального п.
2. Если п = 0 и z* 0, то по определению z° = 1, поэтому
Z° = 1 • (cos Оф + i sin Оф), т.е. формула B) верна для п = 0.
3. Пусть п = — 1. Применяя определение степени с
целым отрицательным показателем и теорему 2, получим,
что
-1 = cos0 + /sin0 =1[COS(_ ф) + /sin(_ ф)]
Г(СО5ф + /81Пф) r l V "Г/ v f/J'
т.е. для п = — 1 формула B) верна.
4. Пусть п — любое целое отрицательное число, тогда
п = — т, где т = п — натуральное число. Применяя сна-
сначала определение степени с целым показателем, затем
справедливость формулы B) сначала для п = — 1, затем для
любого натурального т, имеем
695
[/¦[С08(+ф) + /МП(+ф)]|
= Д [cos (— ф) + / sin (— ф)]1 =
= [- ] [cos (— /яф) + / sin (— /иф)] = /(cos лф + / sin лф).
Итак, формула B) верна для любого целого л. Теорема
доказана.
Приведем пример на применение формулы Муавра. Вы-
Вычислим sin Зх и cos Зх через sin x и cos x. По формуле
Муавра
(cos х + / sin xK = cos Зх + / sin Зх.
В то же время по формуле бинома Ньютона
(cos х + / sin xK = cos3 x + / 3 cos2 x sin x +
+ 3 cos x (/ sin xJ + (i sin xK = (cos3 x — 3 cos x sin2 x) +
+ / Ccos2 x sin x — sin3 x).
Итак, по правилу равенства комплексных чисел имеем
sin Зх = 3 cos2 x sin x — sin3 x,
cos 3x = cos1 x — 3 cos x sin2 x.
Применяя основное тригонометрическое тождество, эти
формулы можно переписать так:
sin Зх = 3 sin х — 4 sin3 x, cos Зх = 4 cos3 x — 3 cos x.
Замечание. Эти же формулы были получены в гл. V
другим способом. Используя формулы Муавра и бинома
Ньютона, можно вычислить cos пх и sin пх для любого
натурального числа л.
Тригонометрическая форма комплексных чисел позво-
позволяет доказать свойства модулей комплексных чисел:
a) Izi^l = kil \z2\;
= р|, если Zi * 0;
696
в) к, + *аЫг,| + fcj;
д) Ikil — Ы\ ^ ki+ z2\;
е) Ikil — Ы\ ^ ki — zl
Докажем эти свойства. Свойство а) доказано в теореме 1,
а свойство б) — в теореме 2.
Докажем свойство в). Пусть z% — ^(cos ф] + /sin ф]),
Zi — /*2(cos ф2 + / sin ф2). Поскольку
(?i + Zi) — (^cos ф] + r2cos ф2) + / (risin ф1 + r2sin ф2),
то
= (/{cos2 ф] + 2r]r2cos ф]СО8 ф2 + /^cos2 ф2 +
+ /{sin2 ф] + 2r1r2sin q>isin ф2 + /^sin2 ф2I/2 =
= ^f\ + А + 2Г]Г2 COS (ф! — ф2)'.
Поскольку cos (ф] — ф2) < 1, то ki + zJi ^ V/{ + Аг + 2г]Г2 = гх +
+ Гг = kil + kd- Свойство в) доказано.
Свойство г) доказывается аналогично.
Свойство д) вытекает из свойства г). Действительно, kil =
= \{Z\ + Zi) — z2\ ? ki + z2\ + Ы, откуда
kil — k2|<k, + c2|- D)
Аналогично |^| = \(z2 + ^i) — Zi\ ^ \z2 + ^il + kil> откуда
k2|-kil^ki + 4 E)
Из справедливости неравенств D) и E) и вытекает спра-
справедливость свойства д).
Свойство е) доказывается аналогично.
Корни из комплексных чисел и их свойства. В главе IV
решалась задача: для любого данного числа а и любого
данного натурального числа п найти число Ъ такое, что
У = а. Такие числа Ъ принято называть корнями степени
п из числа а. Там было показано, что если число а —
действительное положительное число, а л — четное нату-
натуральное число, то существуют два действительных числа Ьх
697
и b2 таких, что b" = а и Ъ\ = а; если а — действительное
число, а л — нечетное натуральное число, то существует
одно действительное число Ъ такое, что Ь" = а.
Однако найти число, четная степень которого была бы
равна отрицательному числу, в области действительных
чисел уже нельзя. В области комплексных чисел это сделать
можно. Справедливо более общее утверждение: в множе-
множестве комплексных чисел можно найти корень любой нату-
натуральной степени из любого комплексного числа. Это ут-
утверждение является следствием следующей теоремы.
Теорема 4. Пусть z — комплексное число, z*Q, n —
натуральное число. Существует п различных комплексных
чисел щ, а2, а3, ..., а„ таких, что а? = z, где /= 1, 2, ..., п.
Эти числа называются корнями степени п комплексного
числа z- Для обозначения этих корней нет специальных
символов, подобных символу, которым обозначается ариф-
арифметический корень.
Доказательство. Для п = 1 теорема очевидна. Пусть
п > 2 и пусть z— r(cosф + /sin ф) (zф0). Будем искать
комплексное число а = р (cos у + / sin у) такое, что а" = z-
Покажем, что такое число а существует. Более того, пока-
покажем, что таких чисел бесконечно много, но различных
между собой их только п.
По формуле Муавра
Z = а" = р" (cos пу + i sin ny).
По определению модуля комплексного числа |г) = р", т.е.
г = р", откуда р = "Vr (по определению модуля комплексно-
комплексного числа z * 0 числа риг положительны, поэтому символ
арифметического корня здесь употреблен правильно).
Применяя определение равенства двух комплексных
чисел, получаем, что одновременно справедливы равенства
cos лу = cos ф,
sin n\\t = sin ф.
Эти равенства одновременно выполнены тогда и только
тогда, когда n\\t = ф + 2пк, где к — любое целое число, т.е.
698
для ш = ——, где к — любое целое число. Значит, числа
л
а такие, что каждое из них удовлетворяет равенству а" —
= г (cos ф + / sin ф), существуют и могут быть записаны в
виде
wsin^J, F)
где к — любое целое число. Обозначая через ар корень,
вычисляемый по формуле F) для к = р, получаем:
а2 =
a«-i =
cos
COS
COS
r*V/sinD
а_ i = а„_ i,
а_ 2 = а„_ 2,
Отсюда легко видеть, что для любого целого р справедливы
равенства ос,, = а^, а, = 0^+ „ а2 = 0^ + 2,..., аЛ_, = 0^+„ _,.
Итак, различных корней ровно я: Oq, а1} а2,..., аЛ_ j. Они
могут быть вычислены по формуле
G)
где к = 0, 1,2, ..., (я- 1).
699
Заметим, что из формулы G) можно получить все п
различных корней, если вместо к подставить в нее любые
п целых чисел, идущих подряд.
Пример. Найти корни третьей степени из числа
Поскольку г = 2, а ф = f, то
где к = 1, 2, 3, т.е.
0С2 =
cos
cos
cos
18
18
sin
sin
sin
18
18
18
Рассмотрим частный случай: отыскание корня п-й сте-
степени из единицы, т.е. найдем числа ак такие, что а"к= 1.
Поскольку г = 1 и ф = 0, то
(8)
где к = 0, 1, 2, ..., п- 1.
Если п = 2т (четное число), то среди этих корней суще-
существует два действительных корня осо=1 иосда = — 1. Если
п = 2т + 1 (нечетное число), то существует один единст-
единственный^ корень ОСо = 1.
Приведем еще другие свойства корней п-й степени из
единицы:
а) Ы = 1;
б)
г) a* = ocfon, где т — любое целое число (корень ос„
находится по формуле (8), где вместо к следует взять п).
700
Докажем эти свойства. Свойство а) вытекает из опреде-
определения модуля комплексного числа.
Для доказательства свойства б) воспользуемся теоремой
о произведении комплексных чисел в тригонометрической
форме:
Свойство в) доказывается аналогично.
Докажем свойство г). По формуле Муавра
Рассмотрим теперь геометрическую интерпретацию п-й
степени из единицы:
a, = cos
a2 = cos
a3 = cos
Л
л
л
+ '/sin
+ / sin
+ / sin
л
л
л
an _ 2 = cos
ос„ _, = cos
2я (я - 2)
'In (я -
+ /sin
+ /sin
Ъ. (я - 2)
и
In (л —
Очевидно, что точки ceo, a,, a2, ...,Чх„_, будут вершинами
правильного л-угольника, вписанного в единичную окруж-
окружность, одна из вершин которого — точка Д,A; 0).
Примеры. 1. Пусть п = 3, тогда осо= 1, a, = cos|y] +
+ /sinlyL a2 = cosly|+/sinfy] Точки 4,A; 0),
¦х, -у \ Щ~~5> —2~ ЯШ1ЯЮТСЯ вершинами правиль-
треугольника А^А\Аг{ вписанного в единичную окруж-
окружность (рис. 202).
701
2. Пусть п = 4, тогда oto = 1, а, = /, а2 = — 1, а3 = — /.
Точки 4,A; 0), Л@; 1), Н— 1; 0) и Л3@; — 1) являются
вершинами квадрата АъАхАтАг, вписанного в единичную
окружность (рис. 203).
А/0,1)
х А/-1.0)
A/0-1)
Рис. 202.
Рис. 203.
Приведем формулу для корня п-й степени из числа (—1).
Поскольку г = 1 и ф = п, то ак = cos fc±jk*V / sin p
гдеА:=0, 1, 2, .., n- 1. ' " '
Отсюда видно, что если п = 2т (четное число), то среди
ак нет ни одного действительного числа. Если п = 2т + 1
(нечетное число), то существует одно действительное число
аи = — 1.
Вообще для любого положительного числа а и любого
четного натурального числа п существует только два дей-
действительных числа Ьх и Ьг таких, что ti[ = Щ = а.
Действительно, поскольку для любого положительного
числа а = |а| (cos 0 + /sin 0), то все корни п-й степени из
этого числа вычисляются по формуле
Если п = 2т, то среди этих чисел будут только два
действительных числа Ьо = "-^Щи Ьт = — "^Щ, что и утверж-
утверждалось выше.
Аналогично можно доказать справедливость следующих
утверждений:
702
Для любого положительного числа а и любого нечетного
натурального числа п существует только одно действитель-
действительное число Ъ = "Vjof такое, что Ь" = а. < ^
Для любого отрицательного числа а и любого нечетного
натурального числа п существует только одно действитель-
действительное число Ъ = — "V|a[ такое, что Ь" = а.
Для любого отрицательного числа а и любого четного
натурального числа п не существует ни одного действитель-
действительного числа b такого, что Ь" = а.
§ 3. Числовые поля и кольца
В этом параграфе рассматриваются множества чисел,
причем под множеством чисел понимаются либо все ком-
комплексные числа, либо какая-нибудь их часть.
Ниже под операцией понимается одно из четырех ариф-
арифметических действий: сложение, умножение, вычитание и
деление.
Некоторое множество называется замкнутым относи-
относительно данной операции, если применение этой операции
к любой паре чисел из этого множества дает число из этого
же множества.
Примеры. 1. Множество натуральных чисел замкнуто
относительно операции сложения, так как сумма любых
двух натуральных чисел есть натуральное число.
2. Множество натуральных чисел не замкнуто относи-
относительно операции вычитания, так как разность двух наяу*-
ральных чисел не всегда есть натуральное число, например,
2 — 3 = — 1 (— 1 — не натуральное число).
3. Множество, состоящее из чисел 0, 1 и — 1, замкнуто
относительно операции умножения.
4. Множество целых чисел замкнуто относительно опе-
операции вычитания, но не замкнуто относительно операции
деления.
Множество чисел, замкнутое относительно операций
сложения, умножения, вычитания и деления (кроме деле-
деления на нуль), называется числовым полем.
Примеры. 1. Множество всех комплексных чисел об-
образует поле, называемое полем комплексных чисел.
703
2. Множество всех действительных чисел образует поле,
называемое полем действительных чисел.
3. Множество всех рациональных чисел образует поле,
называемое полем рациональных чисел.
4. Множество целых чисел не образует числового поля,
так как оно не замкнуто относительно операции деления.
5. Множество чисел вида (р + q4l), где р и q — любые
рациональные числа, образует числовое поле.
Доказательство, а) Поскольку
(А + qx<2) + (р2 + q2<2) = (рх + р2) + (qx + д2) VI,
а(рх + р2) и (qx + q2) — рациональные числа, то замкнутость
этого множества относительно операции сложения доказа-
доказана.
Аналогично доказывается замкнутость относительно вы-
вычитания.
б) Поскольку
(рх + qx<2){p2 + q2<2) = (рф2 + 2qxq2) + {pxq2 + p2qx) VI,
а (Р\Рг + 1qxq2) и (pxq2 + p2qx) — рациональные числа, то
доказана замкнутость этого множества относительно опе-
операции умножения,
в) Поскольку
(Pi + Я\&) _ (Pi + gi^) (P2 - Я2&) _ Р\Рг - 2gift + 9\Рг -Р\Чг
+ ^2
(Pi ~ ft>6) A-2ft A-2ft
и р\ — 2q\ ф 0, то замкнутость относительно операции деле-
деления очевидна.
Итак, множество чисел виде (р + q^2), гдер, q — любые
рациональные числа, является полем.
6. Множество чисел вида (р + gV2~), где р и q — любые
натуральные числа, не является полем, так как множество
натуральных чисел не замкнуто относительно операции
вычитания.
Множество чисел, замкнутое относительно операций
сложения, вычитания и умножения, называется числовым
кольцом.
704
Примеры. 1. Любое числовое поле есть числовое коль-
кольцо.
2. Множество целых чисел является числовым кольцом,
так как это множество замкнуто относительно операций
сложения, вычитания и умножения.
3. Множество четных чисел является числовым кольцом,
так как при сложении, вычитании и умножении четных
чисел вновь получается четное число.
4. Множество нечетных чисел не будет числовым коль-
кольцом, так как уже при сложении нечетных чисел получается
четное число, т.е. такое числовое множество не является
замкнутым относительно операции сложения.
5. Множество чисел вида (р + q^2), где р и q — любые
целые числа, является числовым кольцом, но не является
числовым полем. Действительно, так как множество целых
чисел замкнуто относительно операций сложения, вычита-
вычитания и умножения, то
(ft + <7iV2) + (ft + fcVf) = (д +p2) + (<?, + q2)
(ft + qx<2) - (ft + fcV2) = (ft - Pi) + (<7i - ft) ^2",
(ft + qx<2){p2 + q2<2) = (pip2 + 2qxq2) + {pxq2 + p2qx) <2,
где {px +p2), (qx + q2), {px - p2), (qx — q2), (PiP2 + 2qxq2),
(P\Q2 + PiQ\) — целые числа. Следовательно, множество
чисел вида (р + q^2) замкнуто относительно операции сло-
сложения, вычитания и умножения, то есть является числовым
кольцом.
Рассмотрим операцию деления. Поскольку
_ pj>2 - 2qxq2 + qj>2 - ptq2 ^-
и мнэжество целых чисел не замкнуто относительно опе-
операции деления, то при целых рх, р2, qx, q2 числовые выра-
выражения ?Щ ^т1, qtP2 ~Рх22 могут принимать и нецелые
Рг — 2ft Pi — 2ft
значения. Следовательно, множество чисел вида (р + q^2)
не замкнуто относительно операции деления, т.е. не явля-
является числовым полем.
23 Алгебра, тригонометрия
и элементарные функции
§ 4. Многочлены над полем комплексных чисел
Многочленом степени п(п — данное некоторое неотрица-
неотрицательное целое число) от переменного х над числовым полем
К называется выражение вида
fli/ + ахх"~1 + а2хп~2 + ... + а„_ хх+ а„,
где коэффициенты а„, аи а2,..., а„_ ь а„ — данные числа из
поля К, причем ай * 0.
Из этого определения, в частности, вытекает, что много-
многочлены нулевой степени — это отличные от нуля числа из
поля К. Число нуль считается многочленом, причем это
единственный многочлен, степень которого не определена.
Для сокращенной записи многочленов обычно употреб-
употребляют следующие символы: Р(х), Q(x), T\x), R(x), p(x), g(x),
г(х) и другие; при этом если хотят подчеркнуть, что много-
многочлен Р(х) степени п, то пишут Р„(х). В § 5 гл. II многочлены
рассматривались над полем действительных чисел.
В этом параграфе многочлены рассматриваются в основ-
основном над полем комплексных чисел, поэтому дальше под
многочленом понимается многочлен над полем комплексных
чисел. В тех случаях, когда многочлены рассматриваются
над другими числовыми полями, об этом будет сказано
особо.
Два многочлена Р(х) и Q(x) считаются тождественно
равными (иногда говорят кратко — равными) тогда и только
тогда, когда равны их степени и равны коэффициенты при
х в одинаковых степенях. Для записи тождественного ра-
равенства многочленов употребляется знак равенства, если
многочлены Р(х) и Q(x) тождественно равны, то пишут
Р(х) = Q(x). Значит, если
Р„(х) = аохп + а1хп~1 + а^-2 + ... + а„_хх+ а„,
Qm{x) = boxT+btx"-^ Ът?-1* ... + bm_xx+ bm,
тоР„(х) = Qm(x) тогда и только тогда, когда п = т и а„ _, =
= 6да_,для всех / = 0, 1, 2, .., п — 1, п.
Суммой двух многочленов
706
Pn(x) = д,/ + arf- \ + а^Г-2 + ... + an_lX+an,
Qm{x) = V + M" + V" + - + bm_lX+bm,
где п > m, называется многочлен Цх) = Cqx" + c{x" ~ ' +
+ c&?~2 + ... + с„_{х + с„такой, чтося_, = ая_, + 6да_,для
каждого / = 0, 1, 2, ..., п, причем Ът_, = 0 для каждого / =
= т + 1, т + 2,..., п, т.е. суммой многочленов Р„(х) и Qm(x)
называется многочлен Т\х), коэффициенты которого при
каждой степени переменного х равны сумме коэффициен-
коэффициентов при той-же степени х в многочленах Р„(х) и Qm(x),
причем если п > ш, то коэффициенты bm+u bm + 2, .-, Ь„
следует считать равными нулю. Для нахождения суммы
многочленов Р„(х) и Qm{x) нужно записать подряд все члены
этих двух многочленов и затем сделать приведение подоб-
подобных членов.
Произведением двух многочленов
Р„(х) =
Qm(x) = boxm + blxm-1 + bJn-2 + ... + bm_lX+ bm
называется многочлен
n-2
R(x) =
такой, что d, = ^ а„_рЬт_дДля каждого / = 0,1, 2,..., n + m,
т.е. произведением многочленов Р„(х) и Qm{x) называется
многочлен R(x), коэффициент которого d, есть результат
сложения всех произведений, в каждом из которых пере-
перемножаются такие коэффициенты ак и bt многочленов Р„(х)
и Qm(x), сумма индексов к + /которых равна п + т — i. Для
нахождения произведения многочленов Р„(х) и Qm{x) нужно
каждый член многочлена Р„(х) умножить на каждый член
многочлена Qm(x), сложить полученные произведения и
привести подобные члены.
Нетрудно проверить, что справедливы следующие ос-
основные законы сложения и умножения многочленов:
707
1. P(x) + Q(x) — Q(x) + P(x) (коммутативность сложе-
сложения);
2. [P(x) + Q(x)] + Цх) = P(x) + [Q(x) + Цх)) (ассоциа-
(ассоциативность сложения);
3. P(x)Q(x) = Q(x)P(x) (коммутативность умножения);
4. [P(x)Q(x)]T\x) = P(x)[Q(x)T\x)] (ассоциативность ум-
умножения);
5. №) + Q(x))Дх) = Р(х)Цх) + О(х)Цх) (дистрибутив-
(дистрибутивность сложения относительно умножения).
Вычесть из многочлена Р(х) многочлен Цх) — это значит
найти такой многочлен Q(x), что Р(х) = Цх) + Q(x).
Нетрудно проверить, что для любых двух многочленов
Р(х) и Цх) такой многочлен Q(x) существует и единствен-
единственный, он называется разностью многочленов Р(х) и Цх) и
обозначается Q(x) = Р(х) — Цх).
Если Цх) = а^х" + ахх"~' + а2х"~2 + ... + а„_,х + а„ и
Г(х) = —Цх) = (- ай)х" + (-
то Q(x) = Р(х) + Т*(х). Значит, в множестве многочленов
всегда выполнена операция вычитания, обратная к опера-
операции сложения.
Разделить нацело многочлен Р(х) на многочлен Цх),
отличный от нуля, — это значит найти многочлен Q(x)
такой, что Р(х) = Цх)B(х). Если такой многочлен Q(x)
существует, то говорят, что многочлен Цх) является дели-
делителем многочлена Р(х), а многочлен Q(x) называется част-
частным от деления многочлена Р(х) на многочлен Цх).
Не любой многочлен Р(х) можно разделить нацело на
многочлен Цх). Например, многочлен х2 + i не делится
нацело на многочлен х + 1. Значит, в множестве многочле-
многочленов не всегда выполнена операция деления нацело, обрат-
обратная к операции умножения. Зато в множестве многочленов
всегда выполнена операция деления с остатком.
Разделить с остатком многочлен Р(х) на многочлен Цх),
отличный от нуля, — это значит найти два многочлена д(х)
и г(х) такие, что
P(x) = ДхЫх) + r(x), A)
причем либо степень многочлена г(х) строго меньше сте-
степени многочлена Т\х), либо г(х) есть нуль.
В случае, если выполнено равенство A), говорят, что
многочлен Дх) делится на многочлен Цх) с остатком г(х)
и частным д(х). В частности, если фс) = О, то говорят, что
многочлен Р(х) делится на многочлен Т\х) с остатком нуль
или многочлен Р(х) делится нацело на многочлен Т\х).
Аналогично теореме 5 из § 5 гл. II доказывается теорема
о делимости многочленов, заданных над полем комплекс-
комплексных чисел.
Теорема. 1. Для любых двух многочленов Р(х) и Т\х), где
Т\х) Ф О, существует и притон единственная пара многочле-
многочленов д(х) и фс) таких, что Р(х) = Т\х)д(х) + г(х), причем либо
степень многочлена г(х) строго меньше степени многочлена
Т\х), либо г(х) есть нуль.
Для определения коэффициентов многочлена q(x) и фО
существует несколько способов. Наиболее распространен-
распространенным среди них является метод неопределенных коэффици-
коэффициентов, рассмотренный в § 5 гл. II. Там же был детально
рассмотрен вопрос о делении многочлена на двучлен (х —
а), где а — действительное число. Все результаты, получен-
полученные в § 5 гл. II, остаются верными и в том случае, когда
коэффициентами многочлена и число а являются любыми
комплексными числами.
В частности справедливы следующие теоремы.
Теорема 2 (теорема Безу). Остаток от деления
многочлена Р(х) на двучлен (х — а) равен значению многочлена
Р(х) при х = а, т.е. г = Р(а).
Теорема 3. Многочлен Р(х) делится нацело на двучлен
(х — а) тогда и только тогда, когда значение многочлена при
х = а равно нулю, т.е. когда Р(а) = 0.
Число а называется корнем многочлена Р(х), если
Да) = 0. Сформулируем теорему 3, используя определение
корня многочлена.
Теорема 4. Число а является корнем многочлена Р(х),
тогда и только тогда, когда многочлен Р(х) делится нацело
на двучлен (х — ос).
Возникает вопрос: всякий ли многочлен имеет корень?
Ответ на этот вопрос дает основная теорема алгебры.
Теорема (Основная теорема алгебры). Любой
многочлен степени п (п > 1) над полем комплексных чисел
имеет хотя бы один корень.
Эта теорема принимается без доказательств. Докажем в
качестве следствия этой теоремы такую теорему.
Теорема 5. Любой многочлен Р„(х) = а^х" + ахх"~ 1 + ...
... + а„ (ад ф 0) степени п(п>\) над полем комплексных чисел
разлагается в произведение п линейных множителей, т.е.
Рп(х) = Щ(х — а,)(х — а2)(х — а3) ... (х — а„). B)
Доказательство. Пусть Р„ — многочлен степени п.
Тогда по основной теореме алгебры у него есть корень.
Обозначим его а^ Тогда по теореме 4 Р„(х) = (х — ci^q^x),
где gi(x) — многочлен степени (п — 1). Для многочлена
д{(х) опять применима основная теорема алгебры, поэтому
gi(x) имеет корень ос2. Тогда по теореме 4 q^x) = (х —
— a2)q2{x), где q2(x) есть многочлен степени (л — 2). Про-
Продолжая этот процесс, получим, что qn _ i(x) = (х — а„ _ {) х
х qn{x), где qn(x) есть многочлен первой степени, т.е. qn(x) =
= bo(x — а„) (b0 Ф 0). Из этих рассуждений вытекает, что
Р„(х) = Ь0(х — а,)(х — а2)(х — а3) ... (х — ап). C)
Раскрыв скобки в произведении, стоящем в правой части
равенства C), получим, что у многочлена Р„(х) коэффици-
коэффициент при х" будет Ьо, но в то же время этот коэффициент
равен Оо, поэтому Ьо = а0.
Итак, показано, что Р„(х) = ао(х — at)(x — a2)(x — a3) ...
... (х — а„). Теорема доказана.
Заметим, что в равенстве C) некоторые из чисел оеь щ,
..., а„ могут быть равны между собой. Объединяя вместе
одинаковые линейные множители, равенство B) можно
переписать в виде
710
Р„(х) = aoix - а,)*1 <х - ос,)*1 (x - аз)*5 ... (х - aj\ D)
где кх + к2 + к3 + ... + к„= п, при этом предполагается, что
среди чисел at, а2, а3, ..., ат уже нет равных. Можно
показать, что в равенстве D) число а, является корнем
кратности к, многочлена Р„(х).
Из теоремы 2 вытекают следующие теоремы.
Теорема 6. Любой многочлен степени п над полем ком-
комплексных чисел имеет п корней, если каждый из корней
считать столько раз, какова его кратность.
Теорема 7 (формулы Виета). Если Р„(х) = х" +
+ а\х""' + ... + а„, т.е. если старший коэффициент много-
многочлена равен единице (щ = 1), а числа oct, oc2, ос3, ..., ос„ — его
корни, то справедливы равенства
ах = — (а, + а2 + а3 + ... + а„),
а2 = а(а2 + а(а3 + ... + а(а„ + а2а3 + ... + а2а„ + ...
... + а„ _,(*„,
а„ -1 = (— 1)" '(aioe2 ... а„ _, + а,а2 ... а„ _ 2а„ + ...
... + а2а3 ... ап),
а„ = (— 1)"(а,а2а3 ... а„_ ,ап).
Доказательство. По теореме 5
Р„(х) = (х— а,)(х — а2)(х — а3) ... (х — ап).
Раскрывая скобки и пользуясь правилом равенства
многочленов, получим справедливость этих равенств, ко-
которые называются формулами Виета.
Теорема 8. Если многочлен
Рп(х) = аохГ + а^-'агх"'2* ... + ап_,х+ а„ (щф0)
с действительными коэффициентами щ, аь ..., а„ имеет
комплексный корень а + Ы, то он обязательно имеет и корень
а — Ы, т.е. число, сопряженное к корню многочлена с дейст-
действительным коэффициентом, также является корнем этого
многочлена.
711
Доказательство. Пусть число а + Ы — корень много-
многочлена
Рп{х) =
Тогда Р„(а + bi) = 0, т.е. справедливо равенство
ао(а + Ы)" + at(a+ Ы)"" ' + а2(а + Ы)" ~2 + ...
Применяя формулу бинома Ньютона, левую часть этого
равенства можно записать в виде А + Bi, откуда по правилу
равенства нулю комплексного числа получаем, что А = О и
В=0.
Теперь рассмотрим
Р„(а - Ы) = ао(а - Ы)" + ах{а - Ы)"~ ' +
+ а2(а - ЫУ~2 + ... + а„_ ,(в - bi) + ап.
Выше было доказано, что произведение, степень и ал-
алгебраическая сумма чисел, сопряженных с данными ком-
комплексными числами, есть комплексное число, сопряжен-
сопряженное соответственно к произведению, степени и алгебраи-
алгебраической сумме данных чисел, поэтому Р„(а — bi) — A — Bi
(здесь еще учтено, что коэффициенты а0, аи ..., а„ —
действительные числа), то так как А = В = 0, то Р„(а — bi) =
= 0, а это значит, что число (а — Ы) является корнем
многочлена Р„(х). Теорема доказана.
Теорема 9. Если многочлен с действительными коэффи-
коэффициентами имеет комплексный корень а + bi, то он делится
нацело на квадратный трехчлен х2 + рх+ q, где p = —2a,q =
= а2 + Ъ2.
Доказательство. Если число Xi = a+bi — корень
многочлена Р(х), то согласно теореме 8 число х2 = а — Ы —
также корень этого многочлена. Тогда Р(х) делится нацело
и на двучлен (х — xt) и на двучлен (х — х2), значит, он
делится на их произведение
(х — Xi)(x — х2) = (х — а — bi)(x — а + bi) =
^х2 — 2ах + а2 + Ъ2 = х2 + рх + q,
712
что и требовалось доказать.
теорема 10. Всякий многочлен с действительными коэф-
коэффициентами разлагается на произведение либо двучленов
(х — а*), либо трехчленов х2 + р„х + д„, либо двучленов (х —
ак) и трехчленов х2 + р„х + qm, где аь рт, qm — действитель-
действительные числа, а трехчлены х1 + р„х + qm не имеют действитель-
действительных корней.
Теорема 10 есть следствие теоремы 5 и 9.
Пример. Известно, что многочлен Р(х) = х4 — 2Х3 +
+ 4х — 4 имеет корень хх = 1 + /. Разложить его на произ-
произведение двучленов и трехчленов с действительными коэф-
коэффициентами.
Поскольку многочлен Р(х) имеет корень х = 1 + /, то по
теореме 9 он делится на трехчлен х2 — 2х + 2. Разделив
многочлен Р(х) на этот трехчлен, получим х4 — 2х* + 4х —
— 4 = (х2 — 2х + 2)(л? — 2). Разлагая теперь многочлен х2 —
— 2 на линейные множители, получаем ответ:
Р(х) = (х2 - 2х + 2)(х - V2)(x + VI).
Пусть дан многочлен
а1хн-1а2хГ-2 + ... + ап (а„*0) E)
Выше было показано:
1. Многочлен E) над полем комплексных чисел может
быть записан в виде
Р„(х) = (х - аО(х - а2)(х - а3) ... (х - ая),
где числа а0, аи а2, а3 а„ из этого же поля.
2. Многочлен E) над полем действительных чисел может
быть записан в виде
— а2)(х — а3) ...
...(х —ак)(х2 + рхх + qx) ... (х2 + р„х + qm), F)
где к+2т = п, числа Oq, а,, а2 аъ ръ qx рт, qm —
действительные числа. При этом в разложении F) квадрат-
713
ные трехчлены нельзя представить как произведение двух
множителей (х — ос/)(х — а,) с действительными at и а,.
Перейдем теперь к вычислению корней многочленов.
Начнем с многочлена первой степени
Р,(х) = оох + а, (ао * 0).
В любом числовом поле этот многочлен имеет один
корень Xi = — —. Рассмотрим многочлен второй степени
°0
Р2(х) = Дох2 + д,х + д2 (оо 5* 0).
Как следует из теоремы 6, многочлен Р2(х) над полем
комплексных чисел имеет два корня. Для нахождения этих
корней преобразуем многочлен Р2(х), выделив полный
квадрат:
где D = й? — 4оо«2- Найдем комплексное число Р такое, что
Э2 = -4- Тогда
4а
откуда очевидно, что многочлен Р^х) имеет два корня:
Щ_ . г, О, -
Заметим, что если D ф 0, то существует два комплексных
1сла Pi и р2 таких, что Р2 = Р2 = -=7. Так как р, = — р2, то
для нахождения корней многочлена Р2(х) все равно, какой
числа
714
из них принять за р. Если D = О, то хх = х2 = — -^- и
многочлен Р2(х) имеет один корень кратности два.
В случае, если коэффициенты Oq, au а2 — действитель-
действительные числа, то D также действительное число и поэтому:
а) если D > 0, то многочлен Р2(х) имеет два действитель-
ных неравных корня: х{ = —^ , х^ = —5= ;
б) если D = 0, то многочлен Р2(х) имеет один единствен-
единственный корень кратности два: х, = х2 = — ?-;
в) если D< 0, то многочлен Р2(х) имеет два комплексных
корня: х, = - ^ + 2flo /, xj = - ^ - 2flo /.
Для любого многочлена третьей или четвертой степени
над полем комплексных чисел существуют способы нахож-
нахождения его корней. Эти способы здесь не приводятся, так
как они весьма трудоемки.
Что касается многочленов степени пять и выше, то для
них нет общих способов нахождения корней.
В частных случаях, пользуясь теоремами о целых и
рациональных корнях многочлена (см. § 5 гл. II), удается
представить данный многочлен в виде произведения
многочленов первого и второго порядков и, таким образом,
найти все его корни.
Пример. Найти корни многочлена Р3(х) = х3 + ^х2 +
Рассмотрим многочлен Шх) = 8Р3(х) = BхK + BхJ +
+ 2Bх) — 4 или Г3(/) = Г5 + Г + 2/ — 4, где / = 2х. Делители
свободного члена многочлена Г3(/): + 1, — 1, + 2, — 2, + 4,
— 4/
Найдем значения многочлена Г3(/) в этих точках:
Г3A) =1 + 1 + 2-4 = 0,
Г3(- 1) = -1 + 1-2-4 = -6*0,
Г3B) = 8 + 4 + 4-4=12*0,
Г3(- 2) = -8 + 4-4-4 = -12*0,
715
Г3D) = 64 + 16 + 8 - 4 = 84 * О,
Т3(- 4) = - 64 + 16 - 8 - 4 = - 60 * 0.
По теореме о целом корне (§ 5 гл. II) многочлен Г3(/)
имеет один целый корень 1. Поэтому его можно предста-
представить в виде произведения двучлена (/ — 1) и квадратного
трехчлена. Для нахождения коэффициентов квадратного
трехчлена применим схему Горнера:
1
1
t P
-4
п о
1-1+1
1-2+2
о
Итак, T3(t) = (/ - IX/2 + 2t + 4).
Квадратный трехчлен Г2 + 2/ + 4 имеет комплексные
корни t2 — — 1 + V37, /3 = — 1 — V3/. Следовательно, исход-
исходный многочлен .Рз(х) = х3 + ^х2 + ^х — ^ имеет один раци-
раци=
ональный корень Xi = -т и два комплексный корня Xj =
В заключение рассмотрим вопрос о нахождении корней
многочлена, заданного над другими числовыми полями.
Если многочлен задан над полем действительных чисел, то
из теоремы 6 следует, что число действительных корней
меньше или равно степени данного многочлена. О нахож-
нахождении действительных корней можно сказать то же самое,
что было сказано выше о нахождении комплексных кор-
корней. Если многочлен задан над полем рациональных чисел,
то,- используя теорему 9 (§ 5 гл. II), можно найти все
рациональные корни данного многочлена. Аналогично,
если многочлен задан над кольцом целых чисел, то все
целые корни данного многочлена можно найти, используя
теорему 8 из § 5 гл. И.
716
§ 5. Кольца, поля, группы
В предыдущих параграфах и главах наряду с числами
рассматривались и более сложные объекты: многочлены,
матрицы, функции и т.д.
Над этими объектами производились некоторые дейст-
действия или операции, аналогичные арифметическим операци-
операциям над числами. Например, рассматривались сложение
матриц, деление многочлена на многочлен и т.д. Поэтому
естественно расширить понятия числовых полей, колец на
множества, состоящие из более сложных объектив или
элементов. Но для этого надо определить операции над
элементами данного множества.
Пусть дано некоторое непустое множество элементов.
Будем говорить, что в этом множестве определена алгебра-
алгебраическая операция, если указан закон, по которому любой
паре элементов а и Ъ этого множества однозначным обра-
образом ставится в соответствие некоторый элемент с, также
принадлежащий этому множеству.
Если эта операция называется сложением, то элемент с
будет называться суммой аи 6 и обозначаться с = а + Ъ.
Если эта операция называется умножением, то элемент с
будет называться произведением элементов аи Ъ и обозна-
обозначаться с = аЪ.
Кольца. Непустое множество элементов называется коль-
кольцом, если в нем определены две операции — сложение и
умножение, обладающие свойствами:
1. Сложение коммутативно: а + Ъ = Ъ + а;
2. Сложение ассоциативно: а + (Ь + с) = (а + Ь) + с; <
3. Сложение и умножение связаны левым и правым
законом дистрибутивности: с(а + Ь) = са + сЪ, (а + Ь)с =
= ас + be;
4. Существует такой элемент этого множества, что при-
прибавление его к любому элементу этого множества не меняет
последнего. Этот элемент называется нулем кольца и обо-
обозначается символом 0; другими словами, существует эле-
элемент 0 такой, что а+ 0 = 0 + а = а;
5. Для любого элемента а этого множества существует
так называемый противоположный элемент, принадлежа-
717
¦4
щий этому же множеству, и такой, что сумма а и этого
элемента равна нулю кольца; обозначая этот элемент через
(— а), запишем это свойство в виде а + (— а) = 0.
Заметим, что из приведенного определения вытекают
следующие свойства кольца:
1. Любое кольцо имеет единственный нуль.
2. В любом кольце для каждого элемента а существует
единственный противоположный элемент.
3. Для любого элемента а кольца справедливы равенства
0 • а = а • 0 = 0.
Если в данном кольце операция умножения обладает еще
свойствами коммутативности, т.е. если для любых двух
элементов кольца а и b справедливо равенство ab = ba, то
кольцо называется коммутативным.
Если в данном кольце операция умножения обладает еще
свойствами ассоциативности, т.е. если для любых трех
элементов кольца а, Ъ и с справедливо равенство (ab)c =
= а{Ьс), то кольцо называется ассоциативным.
Числовые кольца, рассмотренные в § 3, представляют
собой простейшие примеры коммутативных и ассоциатив-
ассоциативных колец.
Приведем другие примеры колец.
1. Множество многочленов, целых относительно одной
буквы х, с коэффициентами из данного числового поля,
образует коммутативное и ассоциативное кольцо, которое
называется кольцом многочленов над данным полем.
Действительно, как указано в § 4, сумма и произведение
многочленов есть многочлен, т.е. в множестве многочленов
определены две операции: сложение и умножение. Причем
в § 4 указано, что обе эти операции коммутативны, ассо-
ассоциативны и связаны законом дистрибутивности. Нулем
этого кольца является многочлен, все коэффициенты ко-
которого равны нулю. Противоположный элемент для каж-
каждого многочлена есть многочлен, который получается ум-
умножением этого многочлена на число (— 1).
2. Множество всех функций, непрерывных на данном
отрезке [а; Ь], также образует коммутативное и ассоциатив-
ассоциативное кольцо.
718
Действительно, в гл. IX дано определение непрерывнос-
непрерывности на данном отрезке функции и указано, что сумма и
произведение двух непрерывных функций есть непрерыв-
непрерывная функция. Легко проверить, что операция сложения и
умножения непрерывных функций коммутативны, ассоци-
ассоциативны и связаны законом дистрибутивности. Нулем этого
кольца является функция, тождественно равная нулю, про-
противоположным элементом для функцииДх) является функ-
функция [-Ах)}.
3. Множество всех квадратных матриц данного порядка
п образует кольцо. Действительно, в гл. X показано, что
сумма и произведение квадратных матриц данного порядка
есть квадратная матрица того же порядка. Нулем этого
кольца является квадратная матрица порядка п, все элемен-
элементы которой суть нули. Противоположным элементом для
данной матрицы является матрица, все элементы которой
получены из элементов данной матрицы умножением на
число (—1).
В гл. X указано, что операция умножения матриц явля-
является ассоциативной, но не является коммутативной. Поэ-
Поэтому кольцо квадратных матриц данного порядка п будет
ассоциативным, но не коммутативным кольцом.
Поля. Множество элементов называется полем, если это
множество состоит не менее чем из двух элементов, и
является коммутативным и ассоциативным кольцом и если
в нем существует элемент (называемый единицей поля)
такой, что произведение любого элемента а поля на эту
единицу равно этому элементу а, и если в нем для любого
элемента а, отличного от нуля, существует элемент (назы-
(называемый обратным элементом) такой, что произведение
любого элемента а на его обратный элемент равно единице
поля.
Примерами полей могут служить все числовые поля,
рассмотренные в § 3.
Приведем другие примеры полей и колец.
1. Множество матриц вида
а
2b a
719
где числа а и b — любые числа из некоторого числового
кольца, образует коммутативное и ассоциативное кольцо
относительно обычных операций сложения и умножения
матриц. Действительно, рассмотрим сумму и произведение
матриц вида A). Ясно, что
а ЬЛ,( с d)-( а + с b + d)
2b a) Vld с) \2{b + d) a + cf
a b\( с tt\-f ac + 2bd ad+bc\
2b a)\2d c\ \2{ad+bc) ac + 2bd]
Поскольку числа, являющиеся элементами матриц, стоя-
стоящих в правых частях этих равенств, есть числа из данного
кольца, то это означает, что сумма и произведение матриц
вида A) есть матрицы вида A). Другими словами, показано,
что на множестве матриц вида A) определены операции
сложения и умножения.
Столь же легко показывается, что справедливы свойства
коммутативности, ассоциативности и дистрибутивности
сложения и умножения матриц вида A).
Матрица L J является нулем этого кольца, а матрица
— 2Ь —а\является противоположным элементом для мат-
р™ (»1}
Таким образом, показано, что множество .матриц вида
A), где числа аи Ъ — любые числа из данного числового
кольца, образует коммутативное и ассоциативное кольцо.
2. Множество матриц вида
U а
где аи b — рациональные числа, образуют поле.
Так как множество рациональных чисел есть числовое
кольцо, то, как показано выше, множество матриц вида B)
с рациональными а и b образует коммутативное и ассоци-
ассоциативное кольцо. Единицей этого кольца является матрица
Г 1 о)
20 1
720
Пусть теперь матрица I ° ь\ не является нулем кольца,
\2b a
т.е. хотя бы одно из чисел а и Ь отлично от нуля. Покажем,
что для любой матрицы найдется матрица вида B), т.е.
( х v\
матрица L у\ такая, что
\~у * I
а Ь\(х у\=( \ О
2Ъ а^\2у xj ^2-0 1
т.е. покажем, что у любого элемента этого кольца, отлич-
отличного от нуля, есть обратный элемент. Применяя правило
перемножения матриц, получаем, что справедливость ра-
равенства C) равносильна справедливости равенства
( ах+2Ьу Ьх+ау\= (\ 0
( ax+2by bx+ay)=(l 0)
[2(ау+Ьх) ах + 2Ьу) \0 1}
Равенство D) справедливо тогда и только тогда, когда
система уравнений
jax+2by=i,
\bx + ay = 0 K)
имеет решения. Вычислим определитель системы E)
= а - 2Ь\ F)
а 2Ъ
Ъ а
2
Поскольку а и b — рациональные числа, то выражение а —
— 2Ь2 * 0. Значит, для данных рациональных чисел а и b
существует единственная пара чисел х и у, удовлетворяю-
удовлетворяющая системе E).
Таким образом, показано, что существует и притом
только одна матрица вида B), удовлетворяющая условиям
C). Другими словами, показано, что отличный от нуля
элемент имеет единственный обратный элемент.
Значит, действительно, множество матриц вида B) с
рациональными аи b образует поле.
Замечание. Множество матриц вида B) с действитель-
действительными а и b поля не образует, так как для действительных
чисел определитель F) может обращаться в нуль, напри-
721
мер, если а = Irl2, и тогда у элемента, отличного от нуля,
нет обратного элемента.
3. Рассмотрим множество элементов, где каждый эле-
элемент — упорядоченная пара целых чисел (п, т). Введем
следующие определения.
Два элемента (п, т) и (р, q) равны тогда и только тогда,
когда п = р и т = д.
Суммой двух элементов (п, т) и (к, I) называется элемент
(п + к, т + I), т.е. (п, т) + (к, [) = (п + к, т + I).
Произведением двух элементов (п, т) и {к, I) называется
элемент (пк, ml), т.е. (п, т)(к, I) = (nk, ml).
Покажем, что так введенное множество есть коммута-
коммутативное и ассоциативное кольцо. Будем обозначать элемент
этого множества одной буквой А, т.е. А = (п, т). Проверим,
что операции сложения и умножения обладают следующи-
следующими свойствами:
\.А + В=В+А;
2.(A + B)+C = A + (B+Q;
Ъ.АВ=ВА;
4.{AB)C=A(BQ;
5. (А + В)С = АС+ВС.
Действительно, пусть А = (п, т), В=(к, I), C=(p, q).
Тогда, используя свойства коммутативности, ассоциатив-
ассоциативности и дистрибутивности сложения и умножения целых
чисел, получаем, что
А + В = (п, т) + (к, I) = (п + к, т + I),
В + А = (к, I) + (п, т) = {к + п, I + т) = (п + к, т + I),
откуда и вытекает, что А + В= В+ А, т.е. свойство 1 дока-
доказано.
Докажем свойство 5. По определению
(А + В)С=(п + к,т + 1){р, q) = (пр + кр, mq + lq),
АС=(п, т)(р, q) = (пр, mq),
BC=(l,k)(p,q) = (kp,lq),
AC+ BC= (пр, mq) + (кр, lq) = (пр + кр, mq + lq),
122
т.е. (А + В)С=АС + ВС. Остальные свойства доказываются
аналогично.
Нулем этого кольца является элемент @; 0). Для элемен-
элемента (п, т) противоположным элементом является элемент
(— п, — т). Покажем, что это кольцо не является полем.
Легко видеть, что единицей является элемент A; 1). Рас-
Рассмотрим, например, элемент C; 2) и покажем, что для него
нет обратного элемента.
Предположим противное: такой элемент есть. Пусть это
будет элемент (х, у). Тогда должно быть справедливо ра-
равенство C; 2)(х,у) = A; 1), откуда следует, что должны быть
справедливы равенства Зх= 1 и 2у= 1. Но в множестве
целых чисел эти равенства не выполняются. Значит, наше
предположение было неверным, а это и означает, что
рассматриваемое кольцо не является полем.
4. Рассмотрим множество, состоящее из трех элементов
Д), Аи А2. Под элементом Д> понимается класс всех целых
чисел, делящихся нацело на 3; под элементом Ах понима-
понимается класс всех целых чисел, которые при делении на 3 дают
остаток, равный 1; под элементом А2 понимается класс всех
целых чисел, которые при делении на 3 дают остаток,
равный 2.
Определим в множестве {Д>, Аи А2} операции сложения
и умножения следующими правилами:
ГДь+/, если?+/<3,
Лк Л' Ц+/-з, если*+/>3;
Л Л = \Akh еСЛИ к1< 3'
И/ [А,_з, если*/>3.
Можно показать, что операции сложения элементов Ак и А,
означает сложение любых чисел из классов Ак и А, и
отнесение их суммы в соответствующий класс Д, {к, I, т =
= 0, 1, 2); операция умножения элементов Ак и А, означает
умножение любых чисел из классов Ак и А{ и отнесение их
произведения в соответствующий класс Ат (к, 1,т = 0, 1, 2).
Легко также проверить, что операции сложения и умно-
умножения элементов Ак и А, обладают свойствами коммутатив-
коммутативности, ассоциативности и дистрибутивности.
723
Нулем в этом множестве является класс Aq. Противопо-
Противоположным элементом для элементом для элемента Ак являет-
является элемент А3 _ *.
Единицей в этом множестве является класс Ах. Для
элемента Ах обратным элементом будет он сам, т.е. Аь для
элемента А2 обратным элементом будет он сам, т.е. А2.
Значит, у любого, отличного от нуля, элемента этого мно-
множества есть обратный элемент. Все эти свойства легко
проверяются на основании правил сложения и умножения
этих классов. Значит, это множество есть поле.
Замечание. Если рассмотреть множество, состоящее
их к элементов (к > 2): Ао, Ах, А2,..., Ак_ и где под элементом
А, понимается класс всех целых чисел, которые при делении
на А: дают остаток, равный / (где /= 0, 1,2, ..., к — 1), то в
каждом таком множестве можно определить операции сло-
сложения и умножения аналогично рассмотренному примеру.
Для любого натурального к (к > 2) множество элементов Д>,
Аи А2, ..., Ак _ 1 с операциями сложения и умножения
элементов, определенными указанным образом, является
кольцом, а если число к будет простым числом, то такое
множество будет полем.
5. Рассмотрим множество упорядоченных пар натураль-
натуральных чисел (п, т). Разобьем это множество на классы,
относя в один класс А те и только те пары (п, т) и (к, I),
которые обладают свойством п + / = т + к. По определе-
определению пары, принадлежащие одному и тому же классу А,
называются равными и считается, что каждая пара опреде-
определяет класс А. В множестве, элементами которого будут
классы равных пар, определим операции сложения и ум-
умножения по следующим правилам.
Сложить два элемента Аи В — значит сложить любую
пару (п, т) из класса А и любую пару (р, д) из класса В по
правилу (п, т) + (р, д) = (п + р, т + д). Каждая такая пара
(п+ р, т + д) попадает к некоторый класс С, который
называется суммой элементов Аи В и обозначается А + В,
т.е. С = А+ В.
Умножить два элемента А и В — это значит умножить
любую пару (п, т) из класса А и любую пару (р, д) из класса
В по правилу (п, т)(р, д) = (пр + тд, пд + тр). Каждая такая
724
пара (пр + тд, пд + тр) попадает в некоторый класс D,
который и называется произведением Аи В и обозначается
АВ, т.е. D = АВ.
Введенное множество классов пар есть коммутативное и
ассоциативное кольцо. Действительно, легко проверить,
что операции сложения и умножения обладают свойствами
коммутативности, ассоциативности и дистрибутивности.
Докажем, например, свойство дистрибутивности:
(А + В)М= АМ+ ВМ. Пусть пара (п, т) е А, пара (к, I) e В,
пара (р, д) е М. Если А + В = С, то класс С определяется
парой (п + к, т + I). Если СМ = D, то класс D определяется
парой (пр + кр + тд + !д,пд + kq+ тр + 1р). Если АМ= Nu
то класс ty определяется парой (пр + тд, пд + тр). Если
ВМ= N2, то класс N2 определяется парой (кр + lg, kg+ tp).
Если Ni + N2 = N, то класс N определяется парой
(пр + тд + кр+ 1д, пд + тр + кд+ 1р).
Теперь очевидно, что классы DnNопределяются одной
парой, т.е. это один класс; таким образом, показано, что
(А + В)М=АМ+ ВМ. Аналогично доказываются и другие
свойства сложения и умножения.
Нулем в этом множестве является класс пар вида (к, к).
Покажем, что у каждого класса А, определяемого парой
(п, т) имеется противоположный класс. Выберем натураль-
натуральное число р такое, что р > п и р > т. Тогда числа х = р — п
и у — р — т есть натуральные числа. Покажем, что класс
В, определяемый парой (х, у), и есть класс, противополож-
противоположный классу А. Действительно, А+ В— С, где класс С опре-
определяется парой (р, р). Но пара (р, р) как раз и определяет
класс, являющийся нулем этого множества. Итак, у каж-
каждого элемента этого множества есть противоположный
элемент. Значит, рассматриваемое множество есть комму-
коммутативное и ассоциативное кольцо.
Замечание. При построении этого кольца были ис-
использованы только свойства натуральных чисел. Это коль-
кольцо можно использовать для конструктивного построения
кольца целых чисел на базе натуральных чисел. Делается
это так: класс А, определяемый парой (п, т), отождествля-
отождествляется:
а) с натуральным числом к, если п> тип — т = к;
725
б) с числом нуль, если п = т;
в) с отрицательным числом (— к), если п< оти т — п =
= к.
Полученное множество и будет кольцом целых чисел.
6. Рассмотрим множество упорядоченных пар целых
чисел [а, Ь] таких, что Ь*0. Разобьем это множество на
классы, относя в один класс а те и только те пары [а, Ь] и
[с, d], которые обладают свойством ad = be. По определе-
определению пары, принадлежащие одному и тому же классу,
называются равными и считается, что каждая такая пара
определяет класс а. В множестве, элементами которого
будут классы разных пар, определим операции сложения и
умножения по следующим правилам:
Сложить два элемента а и Р — значит сложить любую
пару [а, Ь] из класса а и любую пару [с, d\ из класса р по
правилу [а, Ь] + [с, d] = [ad + be, bd\. Каждая такая пара
[ad + be, bd] попадает в некоторый класс у, который и
называется суммой элементов а и р и обозначается а + Р,
т.е. у = а + р.
Умножить два элемента а и Р — это значит умножить
любую пару [а, Ь] из чисел класса а и любую пару [с, d] из
класса р по правилу [a, b][c, d] = [ас, bd\. Пара [ас, bd\
попадает в некоторый класс 5, который и называется
произведением элементов а и р и обозначается ар, т.е.
5 = ар.
Веденное множество классов пар есть поле. Действитель-
Действительно, легко проверить, что операции сложения и умножения
обладают свойствами коммутативности, ассоциативности
и дистрибутивности.
Докажем, например, свойство дистрибутивности:
(а + Р)ц = ац + Рц. Пусть пара [a, b] e а, пара [с, d] e P,
пара [l,J] g ц. Если а + Р = у, то класс у определяется парой
[ad + be, bd\, если уц = v, то класс v определяется парой
[adl + bcl, bdf\. Если ац = 5Ь то класс 5j определяется парой
[ol, bf\, если Рц = 52, то класс 52 определяется парой [с/, df\.
Если 5i + 62 = 5, то класс 5 определяется парой [aldf+ bfel,
bfdj]. Так как пары [aldf+ bfel, bfdj] и [ald+ bcl, bdj] удов-
удовлетворяют условию равенства пар, то они относятся к
726
одному и тому же классу, т.е. класс v и класс 8 есть один
и тот же класс. Таким образом, показано, что (а + р)ц =
= ац. + рц. Аналогично доказываются и другие свойства
сложения и умножения. Нулем в этом множестве является
класс у0, определяемый парой [0, 1].
Покажем, что для любого класса а имеется противопо-
противоположный класс р, т.е. такой, что а + р = у0. Пусть пара
[о, b] е а, тогда пара [— а, Ь] определяет класс р, который
и является противоположным классу а. Действительно,
если а + р = а, то класс а определяется парой [0, b\ где
Ь2 ф 0. Так как пары [0, Ь2] и [0, 1] удовлетворяют условию
равенства пар, то они относятся к одному и тому же классу,
т.е. класс а и класс у есть один и тот же класс, что и
означает, что а + р = у0.
Итак, у каждого элемента рассматриваемого множества
есть противоположный элемент. Значит, рассматриваемое
множество есть коммутативное и ассоциативное кольцо.
Единицей в этом кольце является класс Е, определяемый
парой [1; 1].
Покажем, что у каждого класса а, отличного от нуля,
есть обратный класс р, т.е. такой, что ар = Е. Пусть пара
[а, Ь] е а и а не нуль кольца, т.е. пусть а ф 0 и ЬфО.
Рассмотрим класс р, определяемый парой [Ь, а]. Если
ар = ц, то класс ц определяется парой [ab, ab]. Так как пары
[ab, ab] и [1; 1] удовлетворяют условию равенства пар, то
они относятся к одному и тому же классу. Значит, класс ц
совпадает с классом Е, т.е. ар = Е.
Итак, у любого отличного от нуля элемента рассматри-
рассматриваемого множества есть обратный элемент. Значит, это
множество есть поле.
Замечание. При построении этого поля были исполь-
использованы только свойства целых чисел. Это поле можно
использовать для конструктивного построения поля раци-
рациональных чисел на базе целых чисел. Делается это так:
класс х, определяемый парбй [а, Ь], отождествляется с
рациональным числом |; при этом если а = Ьп, где п —
целое число, то класс, определяемый парой [bn, b], отожде-
727
ствляется с целым числом п. Полученное множество и
будет полем рациональных чисел.
7. Рассмотрим множество упорядоченных пар действи-
действительных чисел {а, Ь). Будем считать, что два элемента этого
множества {а, Ь) и {с, d) равны тогда и только тогда, когда
а = си b = d. Введем в этом множестве пар действительных
чисел операции сложения и умножения: {а, Ь) + {с, d) =
= {а + с, b + d), {а, Ь) {с, d) = {ас — bd, ad + be}.
Можно показать, что это множество является полем.
Если отождествить пару {а, Ь] с комплексным числом
а + Ы, то получится поле комплексных чисел, рассмотрен-
рассмотренное выше в этой главе.
Группы. Рассмотрим теперь множества, в которых опре-
определена лишь одна операция. Если эта операция обладает
некоторыми определенными свойствами, то это множество
принято называть группой. А именно, имеет место следую-
следующее определение.
Непустое множество элементов называется группой, если
в нем определена операция, обозначаемая * и обладающая
свойствами:
а) ассоциативностью (а * Ь) * с = а * (Ь * с);
б) в этом множестве существует так называемый ней-
нейтральный элемент, обозначаемый символом е такой, что
а*е~е*а~а для любого элемента а этого множества;
в) для любого элемента а из этого множества существует
элемент b из этого же множества, такой, что a* b = b* a =
= е.
Поскольку наиболее распространены две операции —
сложение и умножение, то наряду с этим общим определе-
определением приведем еще два частных случая — определение
группы по сложению и группы по умножению.
Множество элементов называется группой по сложению,
если в нем определена операция, называемая сложением и
обладающая свойствами:
а) ассоциативностью сложения: (о + Ь) + с = а + (Ь + с);
б) в этом множестве существует элемент, называемый
нулем и обозначаемый символом 0', такой, что для любого
элемента а этого множества 0 + а = а + 0 = а;
728
в) для любого элемента а из этого множества существует
элемент b из этого же множества такой, что b+a=a+b=
= 0.
Элемент b называется противоположным для элемента а
и обозначается через (— а).
Множество элементов называется группой по умножению,
если в нем определена операция, называемая умножением
и обладающее следующими свойствами:
а) ассоциативностью умножения: (ab)c — а(Ьс);
б) в этом множестве существует элемент, называемый
единицей группы и обозначаемый символом е, такой, что
для любого элемента а этого множества ае= ае — а;
в) для любого элемента а из этого множества существует
элемент с из этого же множества такой, что ас — са = е.
Элемент с называется противоположным для элемента а
и обозначается через сГ'.
Если операция, определенная в группе, будет коммута-
коммутативной, то группа называется коммутативной группой.
Приведем примеры групп.
1. Отметим, что каждое кольцо является коммутативной
группой по сложению, каждое поле является коммутатив-
коммутативной группой по сложению.
Любое кольцо или любое поле не является группой по
умножению, однако если рассмотреть любое поле, исклю-
исключив из него нулевой элемент, то это новое множество уже
является коммутативной группой по умножению.
2. Рассмотрим множество, состоящее из числа нуль и
всех многочленов, целых относительно одной буквы х
степени не выше чем п, с коэффициентами из данного
числового поля.
На этом множестве определена лишь одна операция —
сложение многочленов (операция умножения многочленов
выводит произведение за пределы этого множества). Легко
видеть, что в этом множестве операция сложения много-
многочленов является коммутативной и ассоциативной, нулевой
элемент множества — многочлен, все коэффициенты ко-
которого равны нулю, и у любого многочлена есть противо-
противоположный элемент.
729
Значит, рассматриваемое множество образует коммута-
коммутативную группу по сложению.
3. Рассмотрим множество матриц, имеющих п строк и т
столбцов, причем п ф т. Легко видеть, что в этом множе-
множестве определена лишь одна операция — сложения матриц
(операция умножения для таких матриц не определена).
Легко видеть, что в этом множестве: а) операция сложения
является коммутативной и ассоциативной; б) существует
нулевой элемент — матрица, у которой все элементы равны
нулю; в) у любой матрицы есть противоположный эле-
элемент — матрица, все элементы которой получены из эле-
элементов данной матрицы умножением на число (—1).
Значит, множество таких матриц образует коммутатив-
коммутативную группу по сложению.
4. Рассмотрим множество, состоящее из всех чисел вида
2*, где к — любое целое число. Очевидно, что операция
умножения этих чисел не выводит за пределы этого мно-
множества, другими словами, на этом множестве определена
операция умножения элементов (обычная операция умно-
умножения чисел). Ясно также, что эта операция является
коммутативной и ассоциативной. Единичным элементом
является число 1, принадлежащее этому множеству, так как
1 = 2°; у каждого элемента 2* есть обратный элемент 2~ *.
Значит, это множество образует коммутативную группу по
умножению.
5. Рассмотрим множество всех положительных рацио-
рациональных чисел. На этом множестве определена операция
умножения. Причем эта операция является коммутативной
и ассоциативной. Число единица является нейтральным
элементом этого множества; у каждого элемента ? этого
множества есть обратный элемент ^. Значит, множество
всех положительных рациональных чисел образует комму-
коммутативную группу по умножению.
6. Рассмотрим множество всех положительных рацио-
рациональных чисел и выясним, образует ли это множество
группу относительно операции *, где * — деление рацио-
рациональных чисел. Хотя операция * не выводит за пределы
730
этого множества и в этом множестве есть нейтральный
элемент — число 1, ибо у каждого элемента 2 есть элемент
2 такой, что 2*2= \f это множество относительно введен-
введенной операции * не является группой, так как легко прове-
проверить, что операция * не будет ассоциативной.
7. Рассмотрим множество всех решений уравнения
У = 1, или, другими словами, рассмотрим множество всех
комплексных корней л-й степени из числа единица. Как
показано выше в этой главе, произведение любых двух
корней степени п из числа единица есть также корень
степени п из числа единица, причем эта операция является
коммутативной и ассоциативной. Единичным элементом
является элемент а0 = 1, обратным элементом для элемента
ак — элемент ос_ к. Значит, это множество образует комму-
коммутативную группу относительно операции умножения.
8. Рассмотрим множество вращений правильного тре-
треугольника вокруг его центра, совмещающих треугольник с
самим собой. Если за умножение двух вращений принять
их последовательное выполнение, то это множество обра-
образует коммутативную группу относительно этой операции.
Можно проверить, что выполнены все свойства, опреде-
определяющие коммутативную группу.
9. Рассмотрим множество вращений шара вокруг его
центра. В качестве произведения вращении естественно
взять последовательное выполнение двух вращений.
Можно показать, что это множество относительно введен7
ной операции образует некоммутативную группу.
УПРАЖНЕНИЯ
Выполнить указанные действия A — 4):
1. B + 30 C - 20 + B - 30 C + 20. 2. у^. + ^~^-.
3 _L_ + _1_ 4 A + 0C + 0 A-0C-0
* 1 + 4/ 4 — Г " 3 — i 3 + /
5. Построить на плоскости точки, изображающие следующие ком-
комплексные числа: 3 + 2/; 3; 2 + 4;; 3;; — 1 + 2;; — 4; — 2 — 3;; — 4/.
731
6. Концы отрезка заданы некоторыми комплексными числами Zi и ц-.
Найти комплексные числа, соответствующие: а) середине отрезка; б)
точке, делящей отрезок в отношении 1 : 3, считая от точки Z\-
7. Вершинами треугольника являются некоторые комплексные числа
Z\, Zj, Zy Найти все комплексные числа г, дополняющие этот треугольник
до параллелограмма.
8. Вычислить модули комплексных чисел /; 1 + /; — /; — 1; 3 — /; 1 + 2/.
9. Определить аргументы комплексных чисел 1 + /; 3 — /; /; 1; — /; — 1.
10. Дана точка z = а + Ы. Где расположена точка z — 2 + П
11. Пусть И = 1. Где расположены точки, изображающие комплексные
числа 1 + 2г?
12. Пусть И = 5. Где расположены точки, изображающие комплексные
числа 1 — 2/ + Зг?
Указать, где расположена точка, изображающая комплексное число г,
для которого выполняется следующее условие A3 — 18):
13. |/ - i = 1. 14. |г+ 1 - 2/| = 7.15. aiiz = - у.
16. |*-/| = |г+2|. 17. -n<argz<n. 18. 1<|г+2-3/|<2.
Записать в тригонометрической форме следующее число A9 — 21):
2
19. z = Г +2 ] • 20- Z = ctg а + /, где а б (я, 2я).
21. z = I + cos 40' + / sin 40°.
Найти все z, удовлетворяющие следующему равенству B2 — 24):
А
22. (г + О5 + (г - О5 = 1- 23. г5 = г5. 24. f-^Л | = 1.
25. Среди комплексных чисел, удовлетворяющих условию |г+ 3/|? 1,
найти число, имеющее наименьший главный аргумент.
26. Найти необходимое и достаточное условие того, что сумма двух
комплексных чисел а + Ы и с + di была бы действительным числом.
Доказать, что каждое из следующих множеств является кольцом B7 —
31):
27. Все целые числа, кратные данному натуральному числу п.
28. Все числа вида а + Ы, где а, Ь — целые числа.
29. Все числа вида а + irlJ, где a, b — целые числа.
30. Матрицы порядка п с целыми элементами (относительно сложения
и умножения матриц).
31. Многочлены от одного неизвестного с целыми коэффициентами.
Доказать, что каждое из следующих множеств образует поле C2 — 34):
32. Числа вида а + fr*/3~, где a, b — рациональные числа;
33. Числа вида а + Ы, где a, b — рациональные числа;
34. Множество из двух элементов а и р с операциями Фи®, задавае-
задаваемыми следующими правилами:
732
афос = а, а®а
= р,
35. Образует ли кольцо или поле множество пар (а, Ь) целых чисел а и
Ь с операциями Фи®, задаваемыми следующими правилами:
(а, Ь)Ф(с,ф=:(а + с,Ь + d); (а, Ь) ® (с, d) = (ас, W)?
Выяснить, образует ли группу каждое из следующих множество при
указанной операции над элементами C6 — 44):
36. Четные числа относительно сложения.
37. Целые числа, кратные данному натуральному числу п относительно
сложения.
38. Нечетные целые числа относительно сложения.
39. Целые числа относительно вычитания.
40. Рациональные числа, отличные от нуля, относительно умножения.
41. Невырожденные матрицы порядка п с действительными элемента-
элементами относительно умножения.
42. Матрицы порядка п с целыми элементами и определителем, равным
единице, относительно умножения.
43. Положительные действительные числа, если операция определяется
так: аФЬ — сР.
44. Действительные многочлены степени л от неизвестного х относи-
относительно сложения.
45. Образуют ли группу вращения квадрата вокруг своего центра на 0*,
90°, 180% 270°?
Содержание
Предисловие 3
Глава I. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА 5
§ 1. Натуральные числа 5
§ 2. Дроби 20
§ 3. Целые числа 27
§ 4. Рациональные и иррациональные числа 32
§ 5. Действительные числа 36
§ 6. Числовые равенства и неравенства 47
§ 7. Числовые множества 51
Глава П. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 64
§ 1. Определения и основные свойства . . . .• 64
§ 2. Равенства и неравенства алгебраических выражений .... 72
§ 3. Многочлены 88
§ 4. Алгебраические дроби 95
§ 5. Многочлены относительно одной буквы ЮЗ
§ 6. Метод математической индукции 118
Глава III. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА . Ш
§ 1. Уравнения с одним неизвестным 141
§ 2. Неравенства с одним неизвестным 162
§ 3. Уравнения с двумя неизвестными 176
§ 4. Системы уравнений 192
Глава IV. СТЕПЕНИ И ЛОГАРИФМЫ 222
§ 1. Степень с целым показателем 222
§ 2. Степень с рациональным показателем 228
§ 3. Степень с иррациональным показателем 234
§ 4. Степень положительного числа 236
§ 5. Логарифмы 241
Глава V. ТРИГОНОМЕТРИЯ 256
§ 1. Углы и их измерение 256
§ 2. Синус и косинус угла 268
§ 3. Тангенс и котангенс угла 287
§ 4. Основное тригонометрическое тождество 301
§ 5. Формулы сложения 309
§ 6. Формулы для двойных и половинных углов 326
Глава VI. ФУНКЦИИ И ИХ ГРАФИКИ 351
§ 1. Определения и примеры 352
§ 2. Основные элементарные функции 364
§ 3. Обратные функции . 381
§ 4. Суперпозиции функций и их графики 390
734
Глава VII. УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ ... 414
§ 1. Основные определения и утверждения равносильности
уравнений 414
§ 2. Простейшие уравнения 424
§ 3. Равносильные преобразования уравнений 442
§ 4. Неравносильные преобразования уравнений 452
Глава VIII. НЕРАВЕНСТВА С ОДНИМ НЕИЗВЕСТНЫМ . . 489
§ 1. Основные понятия и утверждения равносильности нера-
неравенств \ . . . 489
§ 2. Простейшие неравенства 500
§ 3. Преобразования неравенств 536
Глава IX. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ И ПРЕДЕЛ
ФУНКЦИИ 574
§ 1. Числовые последовательности 574
§ 2. Предел числовой последовательности 581
§ 3. Предел функции 600
§ 4. Непрерывность функции 614
§ 5. Производная функции 619
Глава X. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ 633
§ 1. Матрицы 633
§ 2. Определители 642
§ 3. Обратная матрица. Ранг матрицы 654
§ 4. Системы линейных уравнении 662
Глава XI. КОМПЛЕКСНЫЕ ЧИСЛА 681
§ 1. Понятие комплексного числа . -. . 681
§ 2. Тригонометрическая форма комплексных чисел .... 693
§ 3. Числовые поля и кольца 703
§ 4. Многочлены над полем комплексных чисел 706
§ 5. Кольца, поля, группы 717
Учебное издание
Потапов Михаил Константинович
Александров Владимир Васильевич
Паснчевхо Петр Иванович
АЛГЕБРА, ТРИГОНОМЕТРИЯ
И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Научный редактор М. К Потапов
Редактор Л. В. Честная
Художественный редактор Ю. Э. Иванова
Художник К. Э. Семенков
ЛР № 010146 от 25.12.96. Изд. № ФМ-220. Подп. в печать 17.05.2001
Формат 60x90'/i6- Бумага газетная. Гарнитура «Тайме»
Печать офсетная. Объем: 46,00 усл. печ. л., 46,00 усл. кр.-отт.,
37,78 уч.-изд. л. Тираж 6000 экз. Заказ № 1269
ГУП «Издательство «Высшая школа», 127994, Москва,
ГСП-4, Неглинная ул., д. 29/14
Факс: 200-03-01, 200-06-87
E-mail: V-Shkola@g23.relcom.ru http: // www.v-shkola.ru
Отпечатано во ФГУП ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул. Гончарова, 14