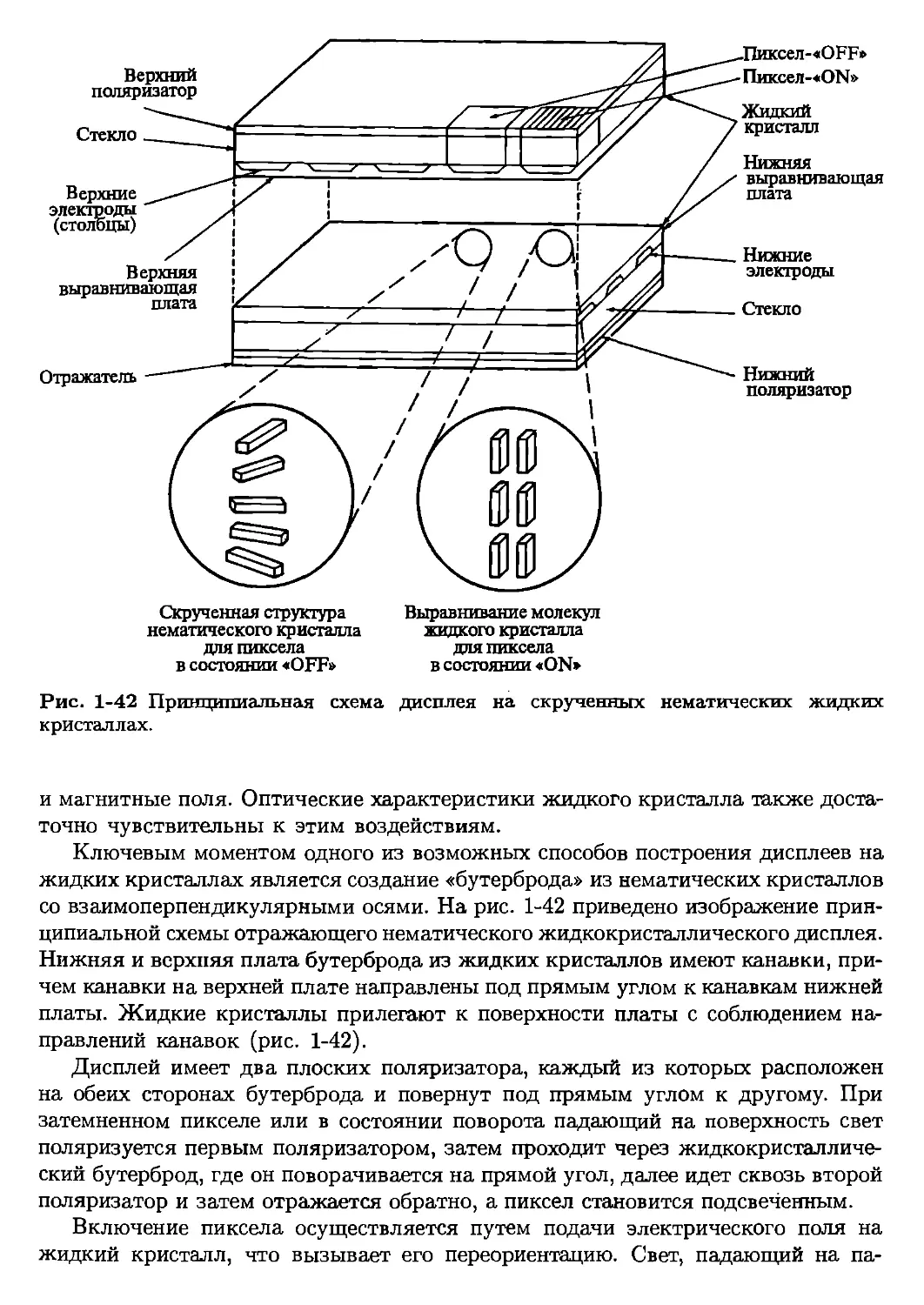
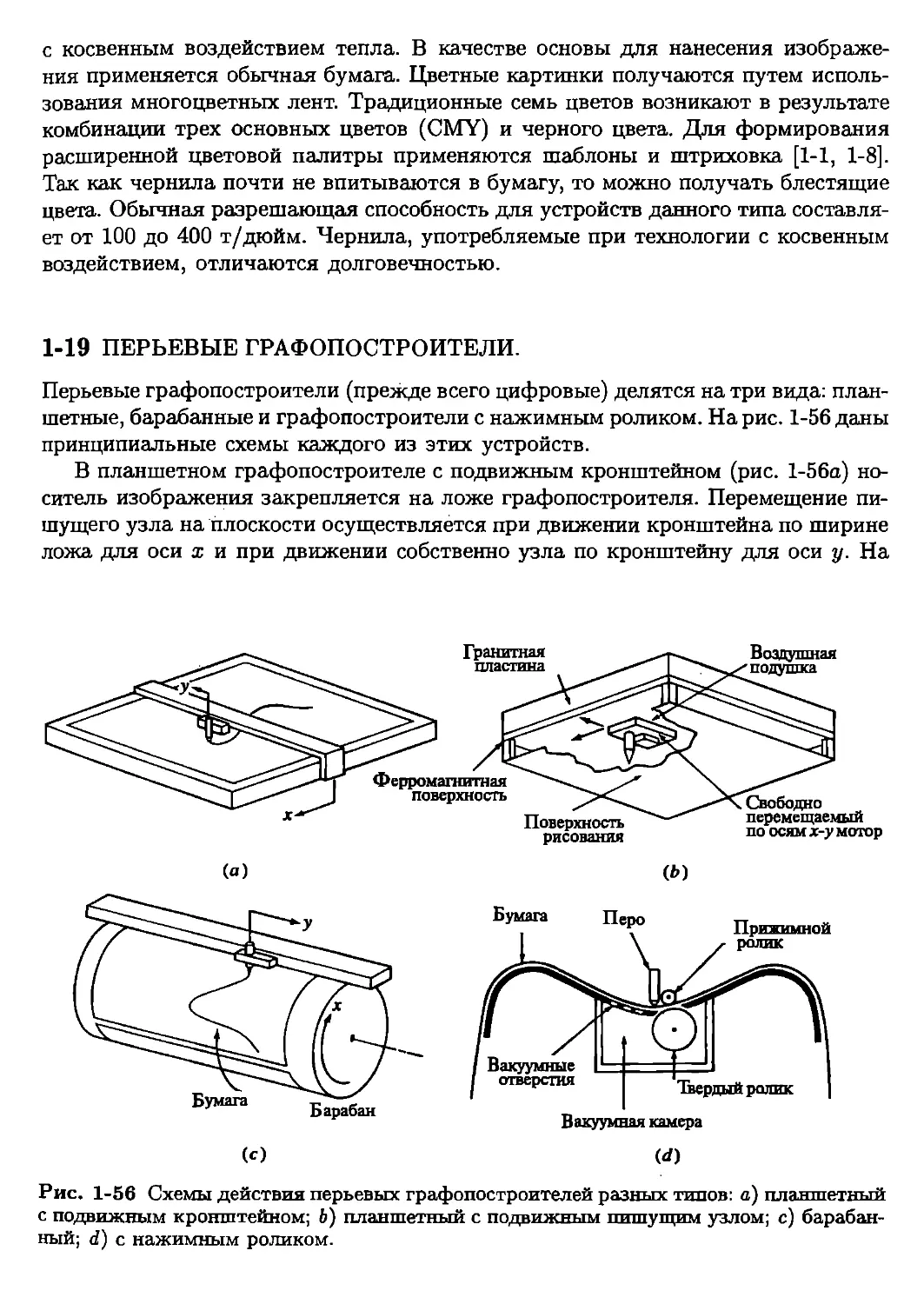
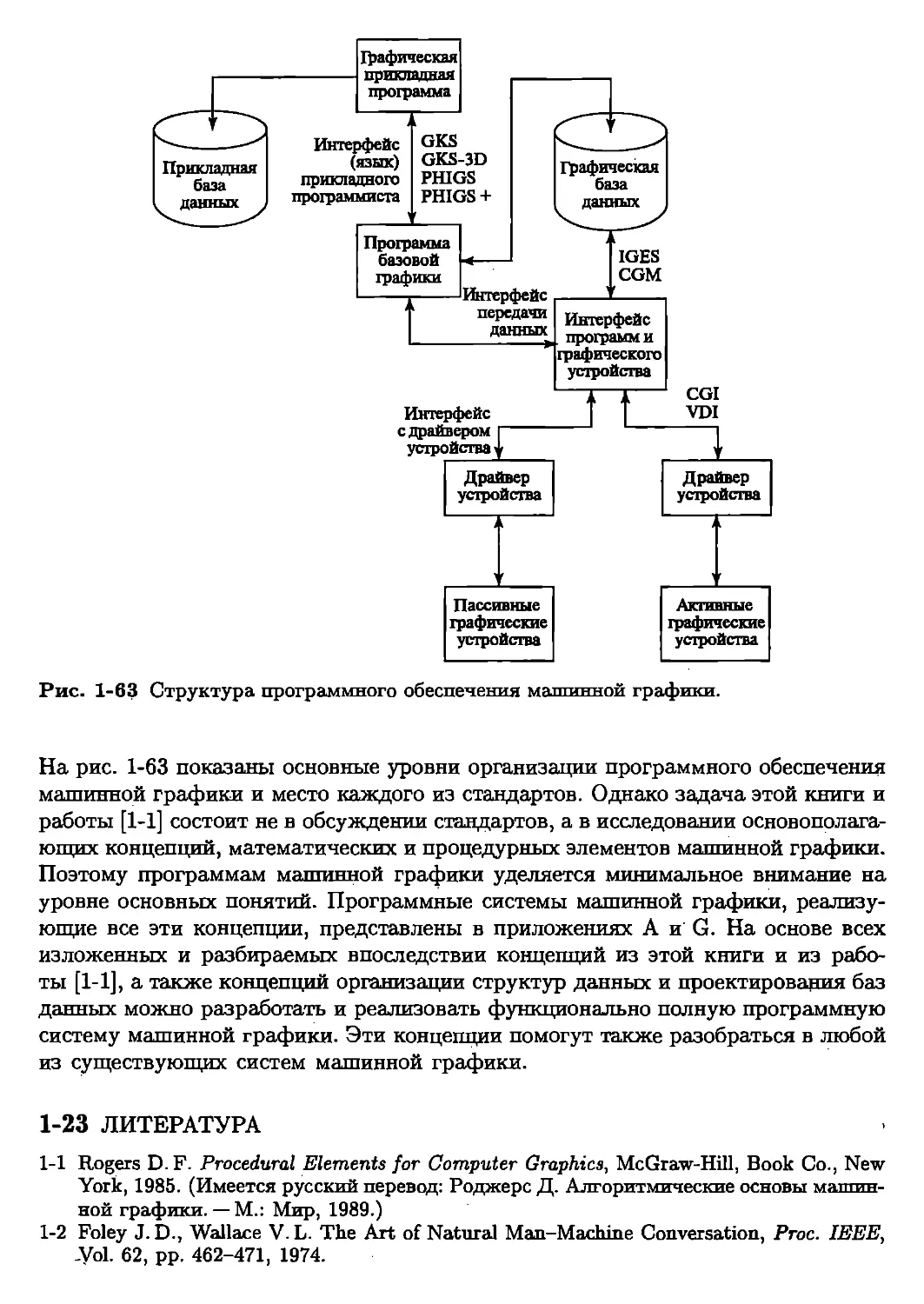
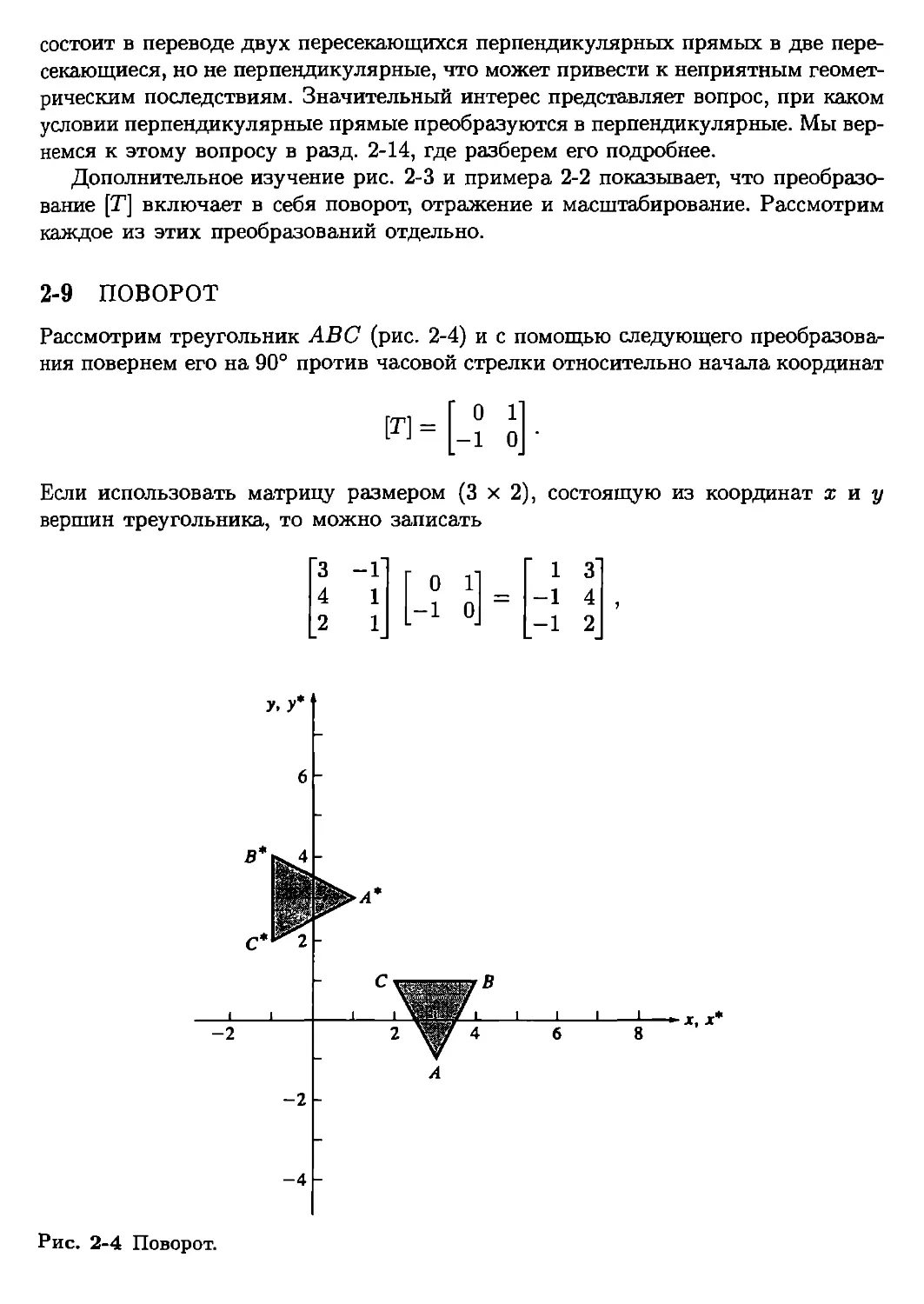
Текст
Д. Роджерс, Дж. Адаме
Математические
основы
МАШИННОЙ
ГРАФИКИ
ОТ РЕДАКТОРОВ
ПЕРЕВОДА
В 1990 г. в Далласе на конференции SIGGRAPH мы обсуждали с проф.
Д.Роджерсом планы перевода и издания на русском язьпсе данной книги. Уже
через год перевод книги был подготовлен, но в силу известных обстоятельств
выпуск ее задержался на много лет. И только теперь благодаря поддержке РФФИ
издание книги стало возможным. Безусловно это знаковое событие. Оно
свидетельствует о том, что происходит оживление и восстановление в российской
науке, технике, промышленности.
Материал, изложенный в книге, не устарел. Впервые на русском языке
появляется достаточно полное функциональное описание технических средств машинной
графики, систематическое изложение двумерных и трехмерных преобразований,
практическое руководство по геометрическому моделированию, включающее
такие объекты, как кривые, поверхности, сплайны. Всего этого так не хватает
нашим студентам, аспирантам, инженерам, научным работникам.
Мы искренне благодарны Д. Роджерсу за столь плодотворное сотрудничество
и надеемся, что оно будет продолжено.
Ю. М. Баяковский, В. А. Галактионов
Предисловие к
русскому изданию
Я с большой радостью узнал о выходе в свет в переводе на русский язык второго
английского издания «Математических основ машинной графики». Эта книга
составит прекрасный тандем вместе с ранее изданной в переводе на русский язык
книгой «Алгоритмические основы машинной графики». Я надеюсь, что в
совокупности эти две книги образуют фундаментальный материал по машинной графике
и в какой-то степени они скомпенсируют существующую нехватку публикаций по
этому предмету на русском языке.
Сегодня, даже в большей степени, чем в ту пору, когда была написана эта
книга, машинная графика глубоко проникает в искусство, технику, рекламу, связь. Я
упомянул лишь некоторые немногие области приложений, а список можно
продолжить. В частности, следует отметить Интернет, который возник как средство
быстрого и легкого обмена текстовой информацией между учеными, а в
настоящее время он сильно зависит от технологии машинной графики.
Почти на каждом вэб-сайте для представления информации используется
машинная графика. Многие спецэффекты в видео- и кинофильмах не обходятся без
применения средств машинной графики.
В индустриальном мире машинная графика играет огромную роль, особенно в
робототехнике, автоматизированном проектировании и производстве, в научной
визуализации. В наши дни обычный человек, не задумываясь, может послать
картинки своим друзьям и коллегам по электронной почте простым нажатием
на кнопку «мышки». Отмечу и такой факт: объем бизнеса в машинной графике
достиг 90 млрд. долларов.
За мои без малого три с половиной десятка лет деятельности в области
машинной графики произошли поистине удивительные изменения. Как
авиакосмический инженер я всегда восхищался прекрасными традициями замечательной
российской науки и техники. Я полон ожиданий, что и в новых условиях
становления и укрепления открытого общества русские ученые и инженеры внесут
значительный выдающийся вклад в дальнейшее развитие машинной графики.
Дэвид Ф. Роджерс
Аннаполис, Мэриленд, США
1 декабря 2000 г.
Введение к первому
изданию
Прошло уже более десяти лет с момента выхода в свет первого издания книги; за
это время машинная графика привлекла к себе пристальное внимание множества
специалистов из разных областей знания. В процентном отношении основное
внимание в среде увеличивающейся плеяды профессионалов по машинной графике
уделялось проблемам программирования, системного проектирования,
аппаратуре и т. п. Именно это обстоятельство отмечал Сазерленд в своем предисловии к
книге Принса «Interactive Graphics for Computer Aided Design», изданной в 1971 г.
Такая ситуация наблюдается и сегодня. Однако я считаю, что уделяется
недостаточно внимания именно прикладным проблемам, а это влечет за собой дефицит
информации, которую можно было бы использовать при создании действительно
работоспособных систем машинной графики. Основное принципиальное
требование к разработке систем машинной графики состоит в необходимости глубокого
понимания связи ее практических аспектов со спецификой конкретного
приложения. Фундаментом большинства приложений машинной графики являются
математические методы, особенно геометрия и способы преобразования. Тем не менее
многие программисты и аналитики, работающие в области машинной графики,
в своих работах обычно не рассматривают основы и не разбирают сложных
математических задач. Более того, потенциал машинной графики часто остается
полностью не реализованным именно вследствие неадекватного использования
математического аппарата с его ограничениями и допущениями. Ценность книги
профессоров Роджерса и Адамса состоит в ее практической ориентации. Четкий и
лаконичный стиль изложения значительно облегчает задачу читателей по
освоению материала. Книга является редким примером такой работы, которую многим
практикам следует поместить на видное место в своей библиотеке в качестве
неоценимого энциклопедического справочника. Она может быть также с успехом
использована и в качестве основы учебного курса.
Я поздравляю авторов с созданием яркой и полезной книги «Математические
основы машинной графики».
S.H. «ChastChasen
Lockheed Georgia Company, Inc.
Предисловие
За четырнадцать лет, прошедших с момента издания первой редакции данной
книги, машинная графика претерпела поистине грандиозные изменения и в
настоящее время представляет собой важнейшую дисциплину для специалистов
из многих областей знания, и в частности, для проектировпщков электронных
устройств, инженеров, математиков, физиков и художников. В это время
были в совершенстве разработаны прежние концепции машинной графики, а
также предложены новые идеи. Однако основополагающие математические понятия
остались неизменными. Глубокое овладение базовыми математическими
концепциями до сих пор остается главным ключом к пониманию и дальнейшему
развитию машинной графики. Предлагаемая книга содержит материал, необходимый
для усвоения этих концепций.
Данная редакция книги не является результатом простого пересмотра первого
издания, а представляет собой его полную переработку с включением множества
новых иллюстраций и более подробных примеров. В книге содержатся
формулировки проблем и концепций программных проектов. Алгоритмы, реализующие
математические теории, приведены в книге в виде псевдокодов.
Глава 1 содержит новые данные о растровых устройствах и дисплеях,
струйных и термических графопостроителях, цветных камерах. В главе приводится
также перечень литературы по аппаратному обеспечению машинной графики.
В главе 2 содержится подробное описание двумерных преобразований,
дополненное новыми разделами по преобразованиям сплошных тел, а также описание
и геометрическая интерпретация однородных координат.
Глава 3 была значительно расширена новыми разделами и дополнена
материалом по комбинированным преобразованиям, повороту вокруг произвольных осей,
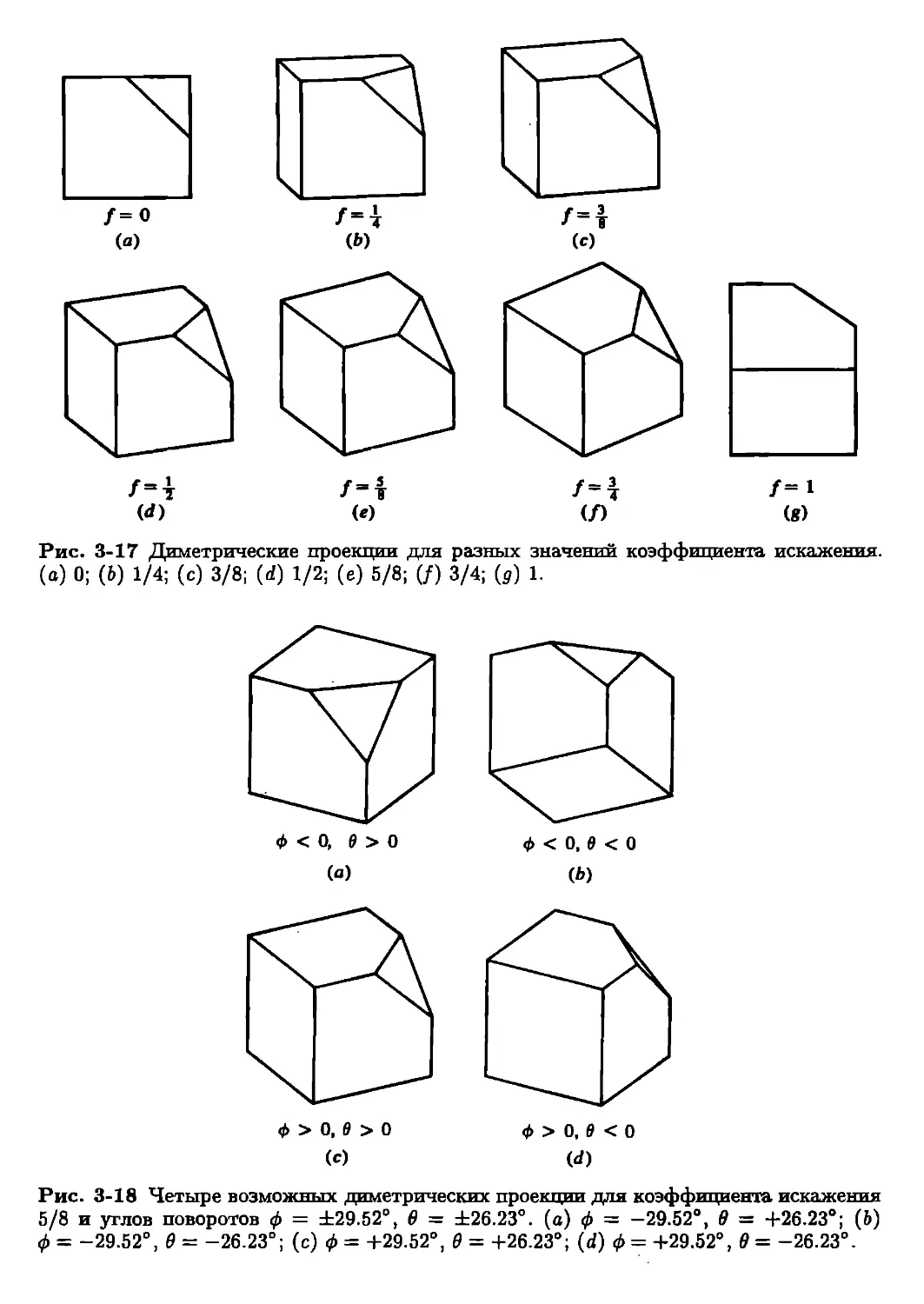
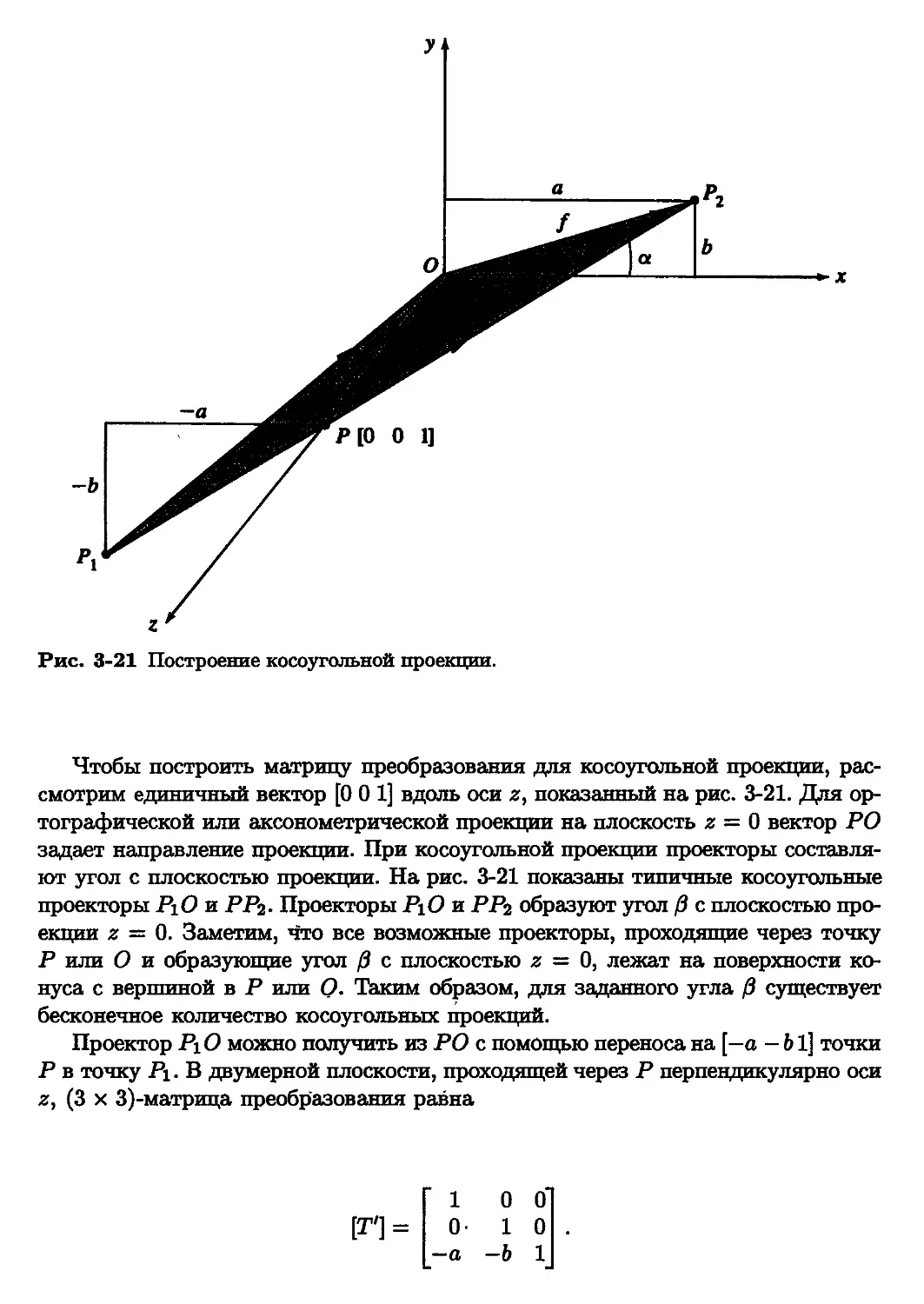
отражению относительно любой плоскости, косоугольным проекциям
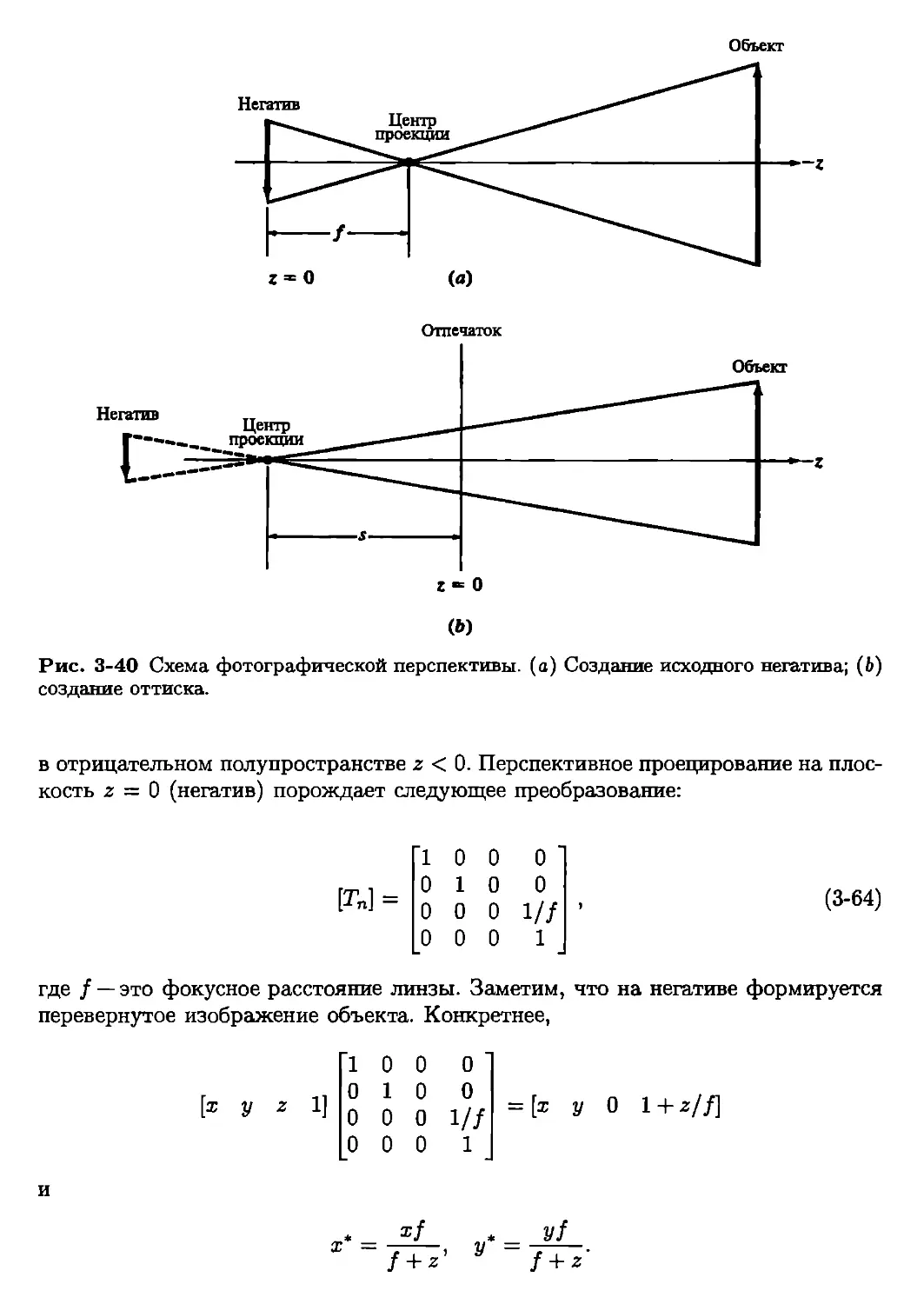
(проекциям кабине и кавалье), точкам бесконечности, фотографическим преобразованиям.
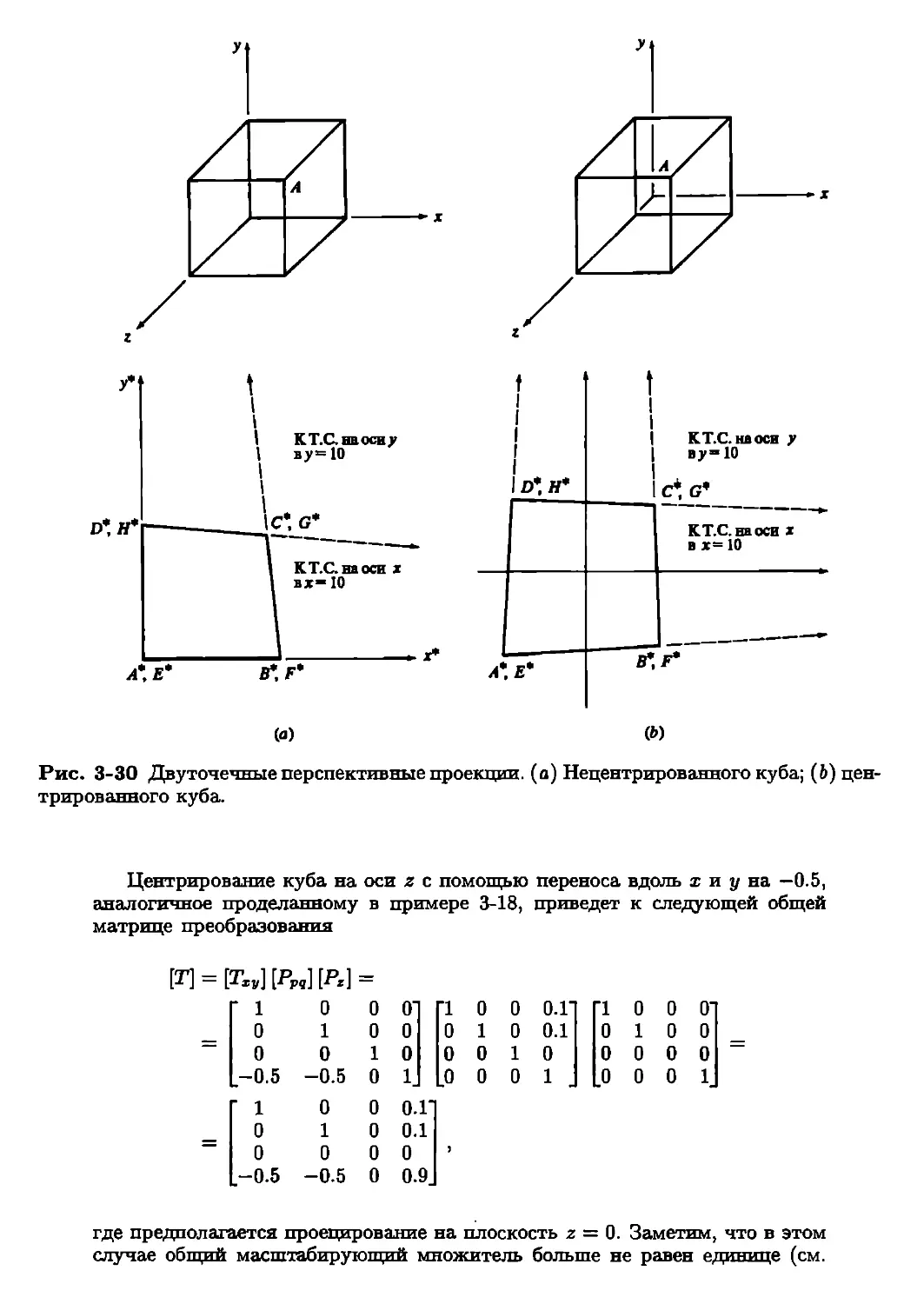
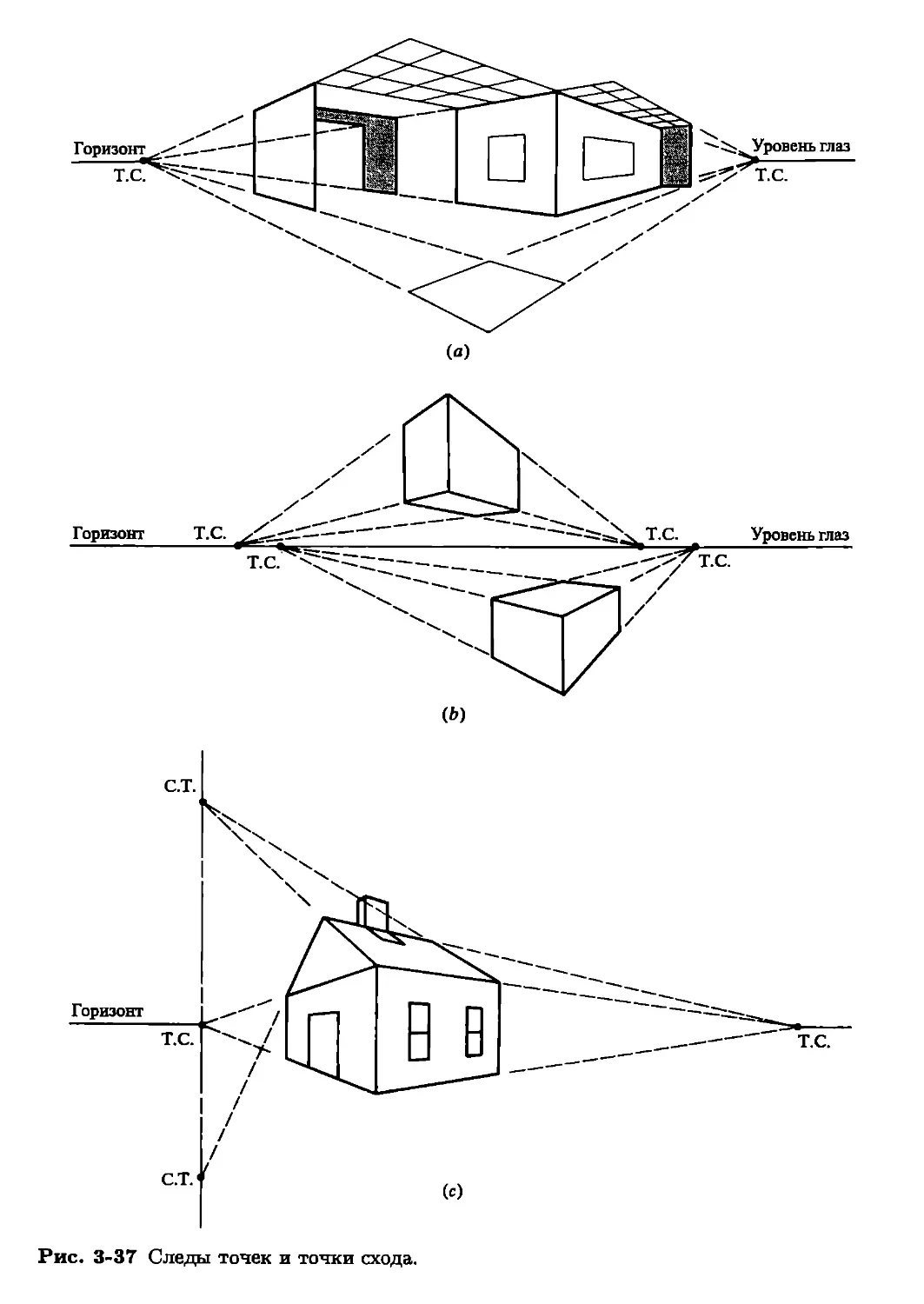
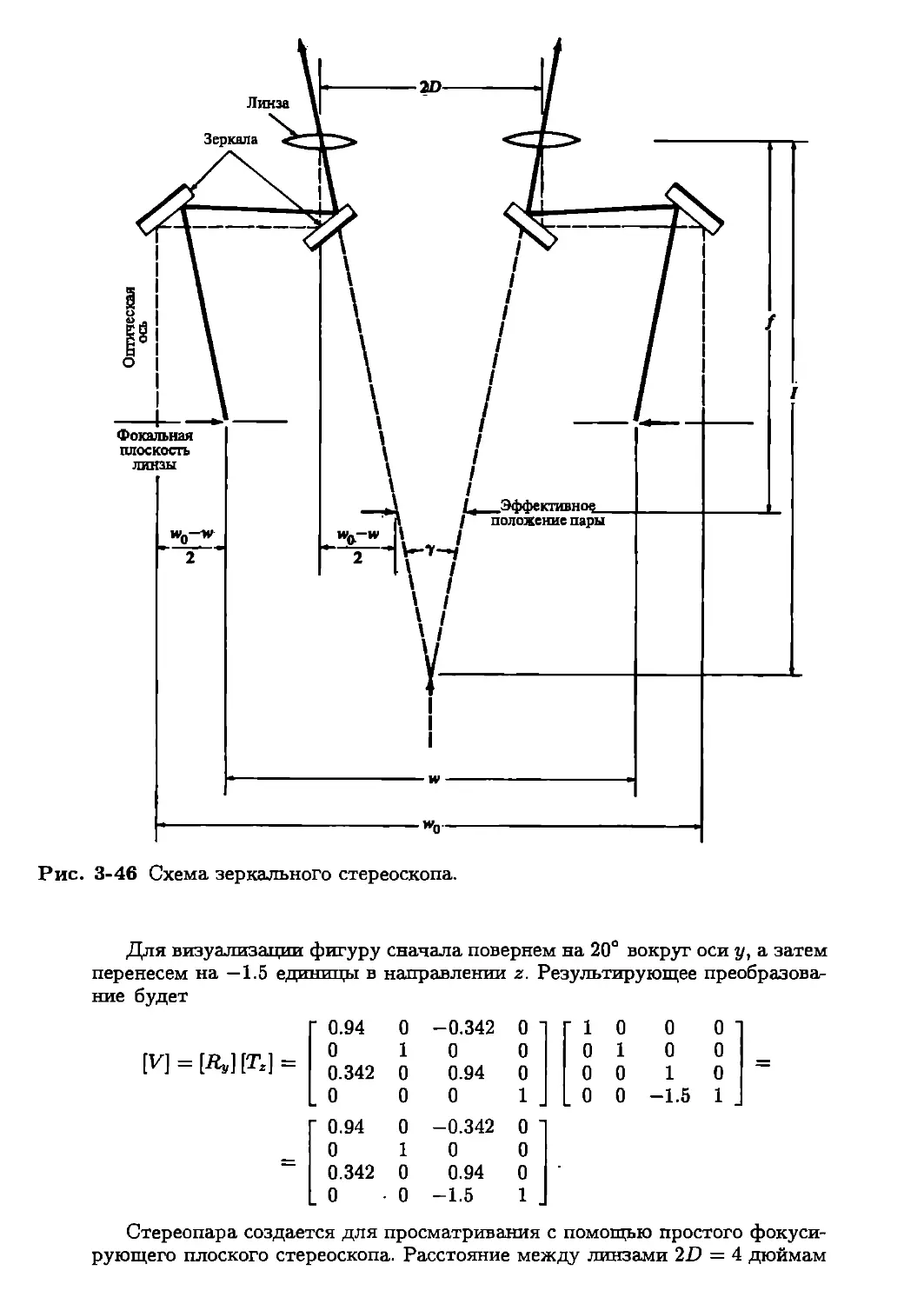
В главе подробно обсуждаются проблемы создания стереоизображений, а также
разбираются методы фиксированного и центрального проецирования.
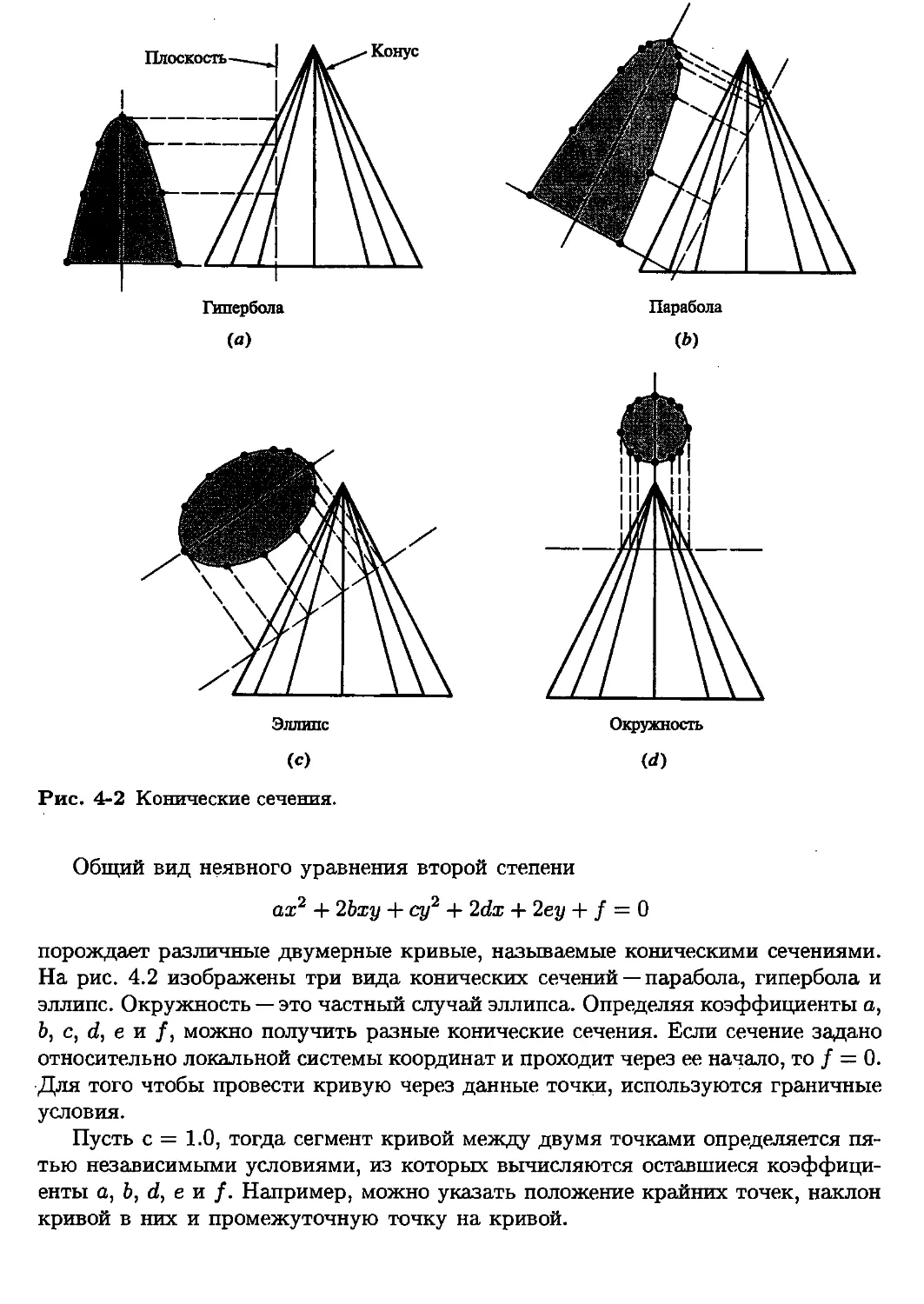
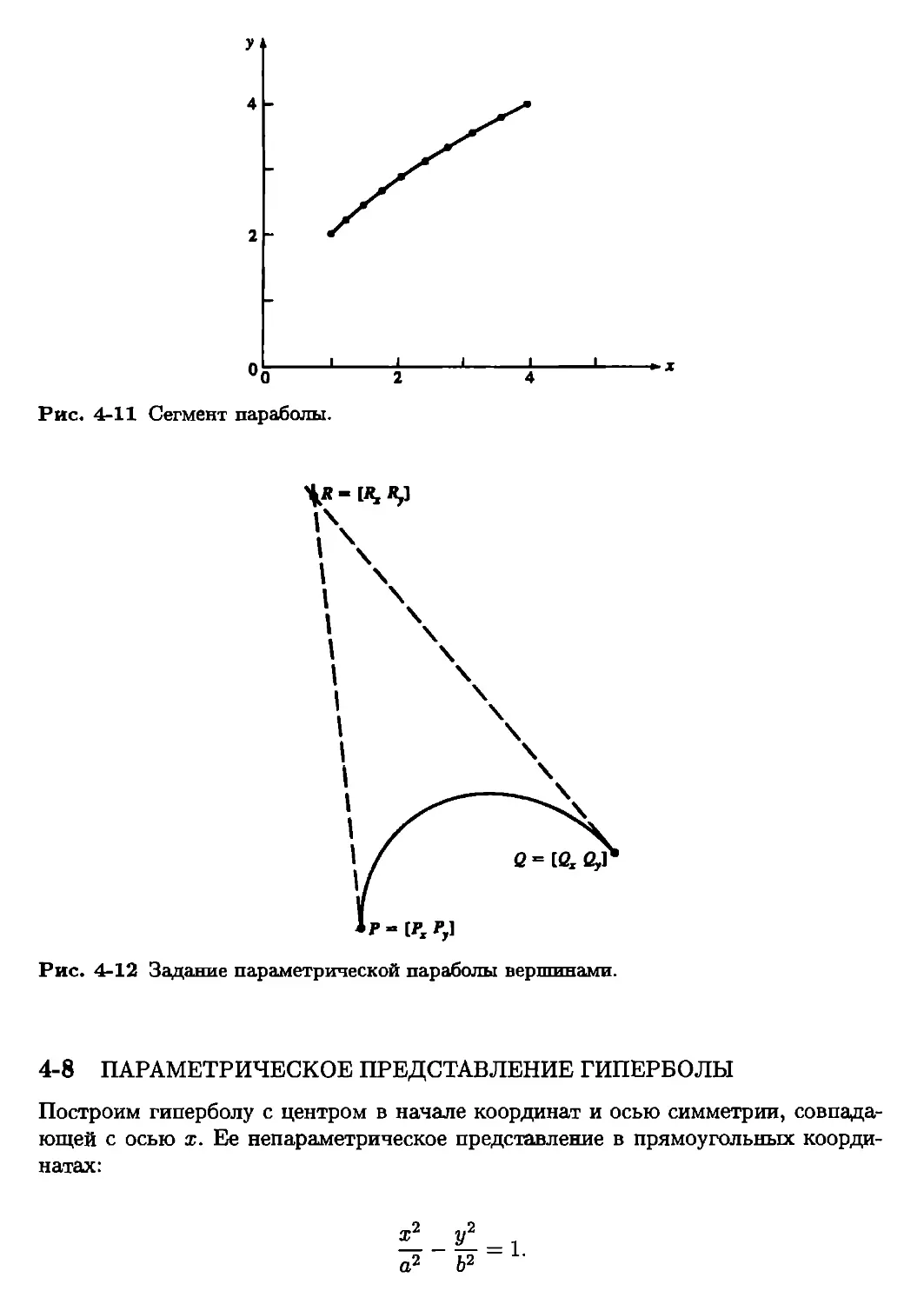
Глава 4 в настоящей редакции включает развернутое описание коник и
методов использования конических сечений.
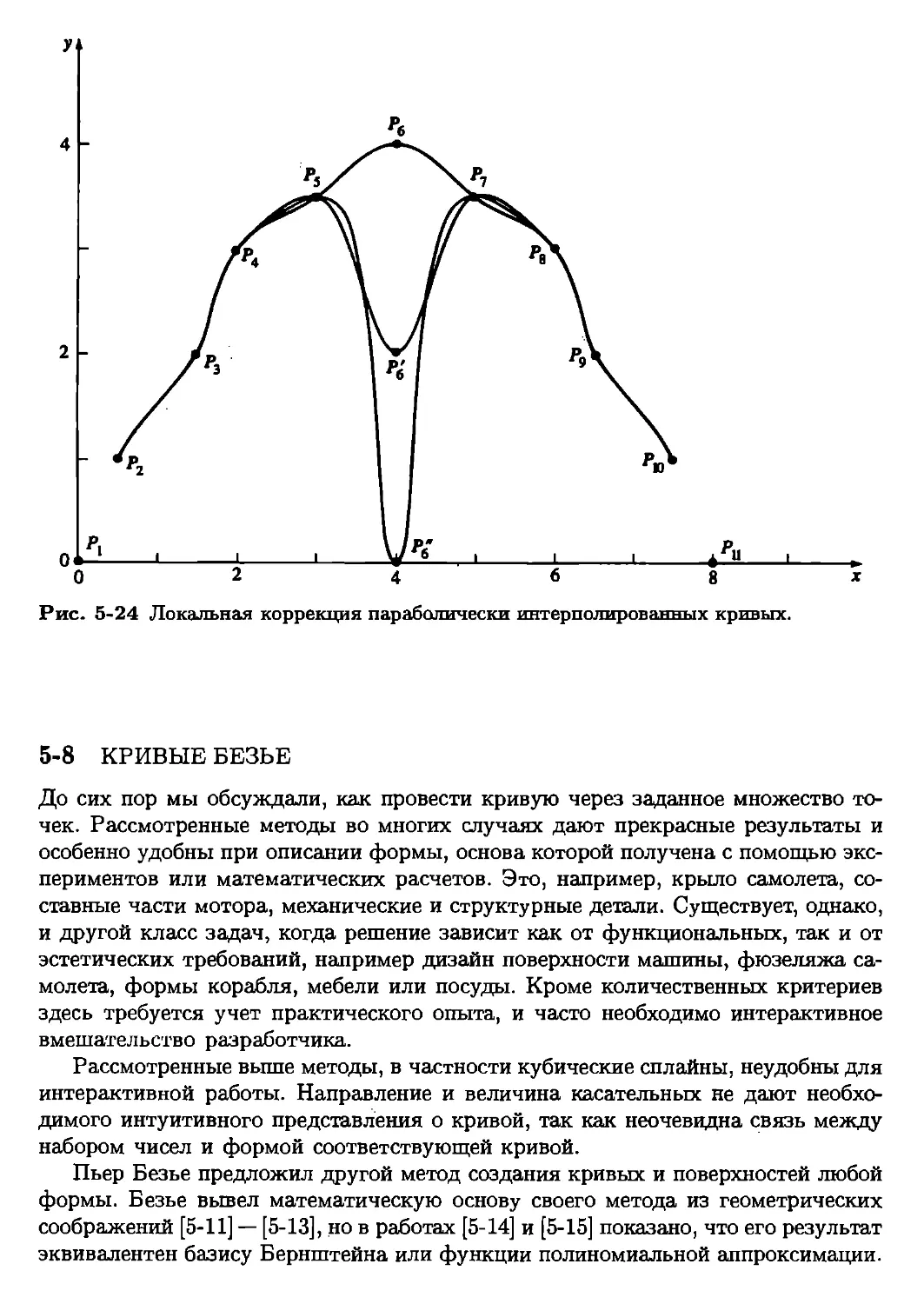
Глава 5 была полностью переработана. Для достижения большей ясности и
наглядности изложения в нее включено детальное рассмотрение вопросов
параболического сглаживания, кривых Безье и В-сплайнов, а также обсуждение
обобщенных параболических сплайнов. В главе исследуются согласования и
деления В-сплайнов, а также периодические униформные В-сплайны. В главу
включено развернутое обсуждение унифицированных и неунифицированных кривых
В-сплайна (NURBS).
Глава 6 также претерпела значительные изменения. Теперь она включает
изучение линейных и бикубических поверхностей, а также управляемых и
динамических поверхностей. В главе нашли отражение сведения о поверхностях
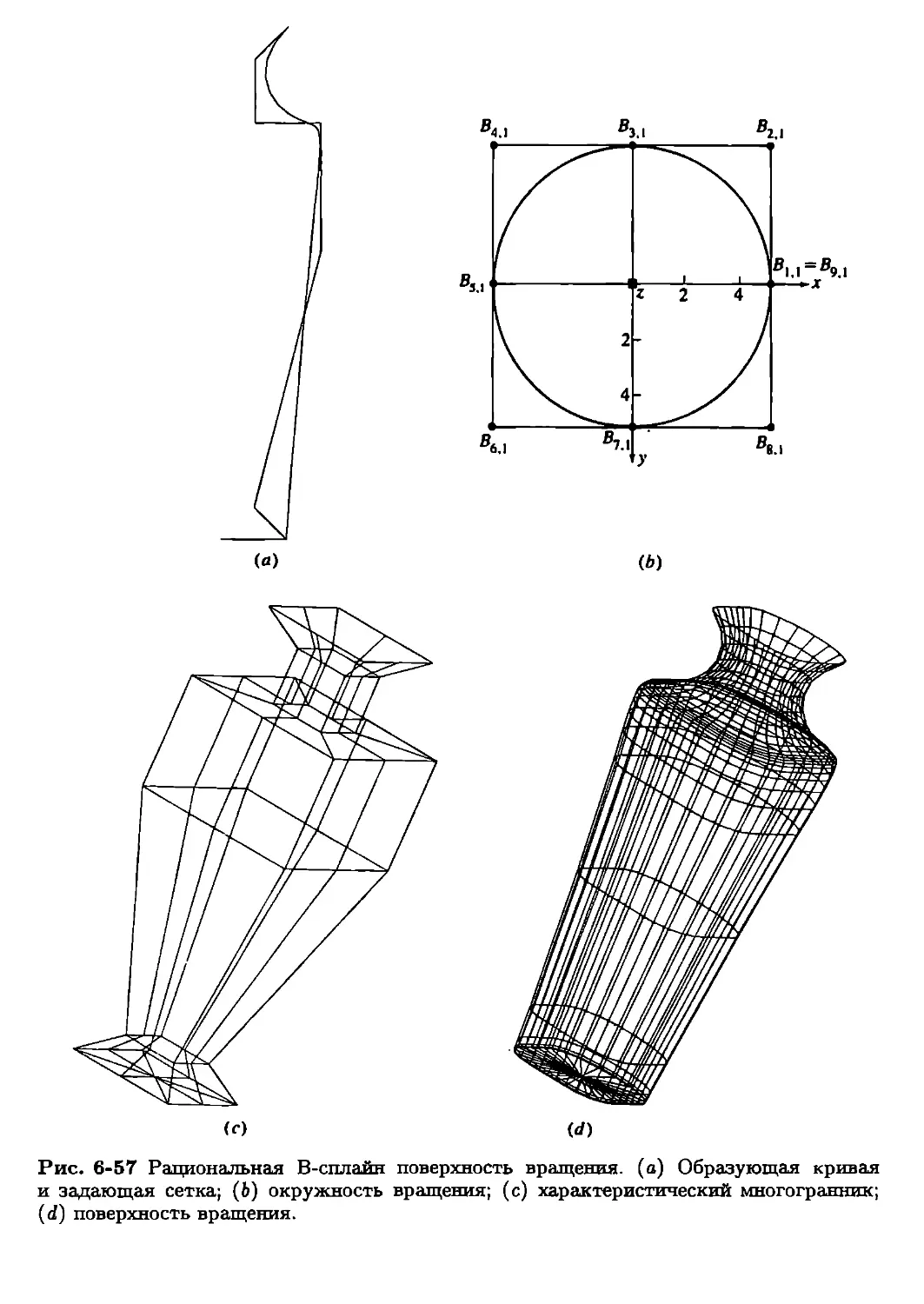
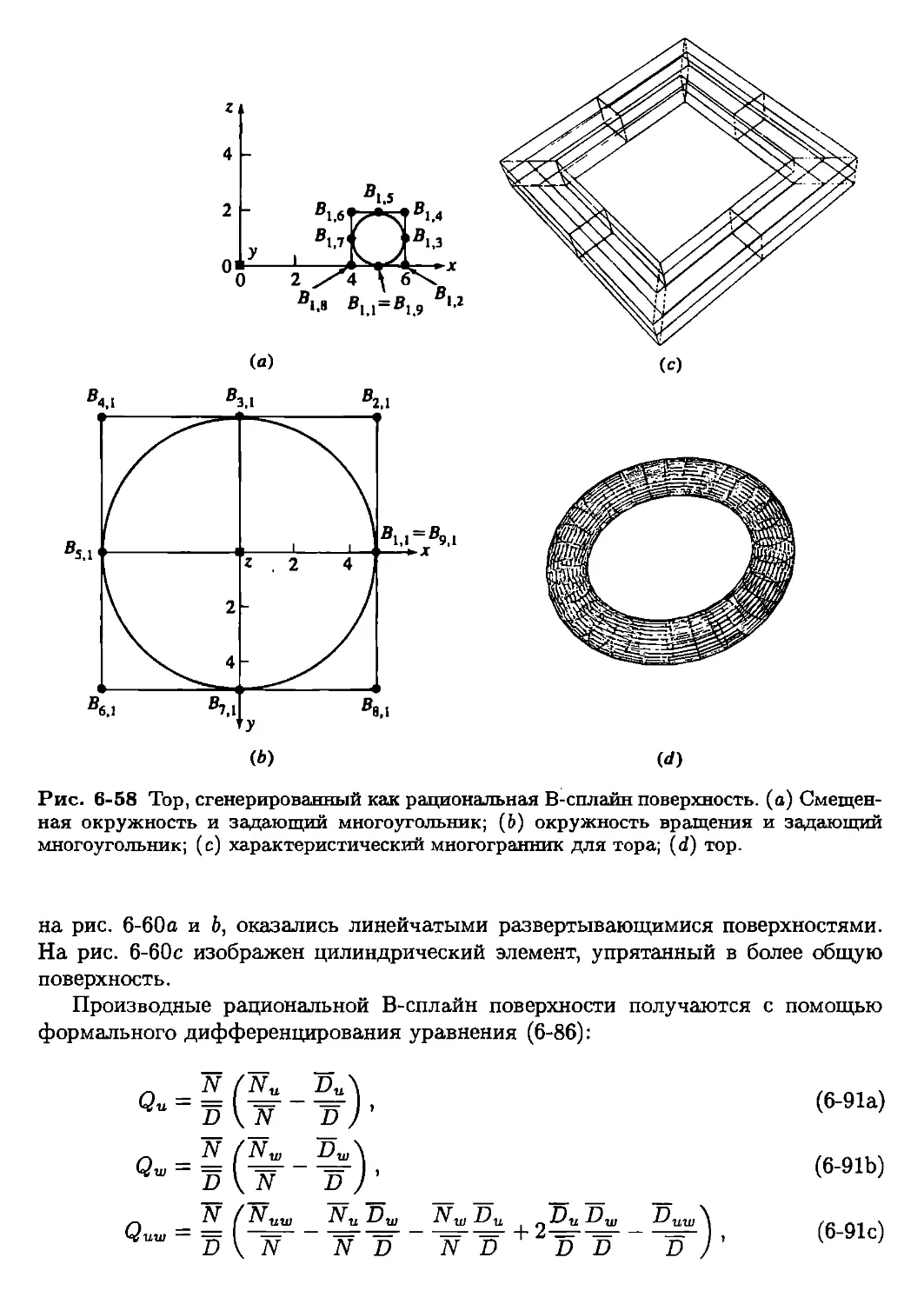
вращения, охвата и о квадратических поверхностях Безье и поверхностях В-сплайнов.
Рассматриваются вопросы сшивки поверхностей В-сплайна, деления
поверхности, а также вводятся понятия гауссовой кривизны и математически правильной
поверхности. Достаточно подробно в главе разбираются нерациональные и
рациональные, однородные и неоднородные поверхности В-сплайнов (NURBS).
Обширное приложение включает программы машинной графики, описание
методов работы с матрицами, псевдокоды, формат файла задания поверхности
В-сплайна, задачи, специфики программ и алгоритмы в виде псевдокодов.
Материал книги был тщательно подобран в расчете как на студентов, так и
на аспирантов. Книга может быть использована в качестве учебного пособия для
полугодового вводного курса машинной графики для студентов или аспирантов.
(Двухсеместровый курс основывается на другой книге «Алгоритмические
основы машинной графики», которая является естественным продолжением данной.)
Именно таким образом авторы и использовали книгу «Математические основы
машинной графики». Если в односеместровом курсе требуется изложение более
широкого круга вопросов, то можно использовать обе книги. В этом случае
предлагаются следующие темы: гл. 1 обеих книг, затем гл. 2 и 3 с отдельными
разделами из гл. 4 (например от раздела 4-1 до 4-8) данной книги, далее отдельные
разделы гл. 2 (например, от 2-1 до 2-5, 2-7 и от 2-15 до 2-19, 2-22, 2-23 и 2-28),
гл. 3 (например, с разд. 3-1, 3-2, 3-4 по 3-6, 3-9, 3-11, 3-15 и 3-16), гл. 4
(например, разд. 4-1, часть разд. 4—2 с алгоритмом отбрасывания невидимых граней,
разд. 4-3, 4-4, 4-7, 4-9, 4-11 и 4- 13) и гл. 5 (разд. с 5-1 по 5-3, 5-5, 5-6 и 5-
14) книги «Алгоритмические основы машинной графики». Д. Роджерс с успехом
использовал данный материал для вводного и обзорных курсов. Надеемся, что
наша книга пригодится также профессиональным программистам, инженерам и
научным работникам. Благодаря детальному изложению, примерам из практики
и многочисленным иллюстрациям, книга может быть полезна читателям разной
квалификации для самостоятельного изучения. Для усвоения материала
достаточно знания математики на уровне средней школы и знакомства с языком
программирования высокого уровня.
Возможно, читателю будет интересно узнать, как создавалась книга. Она была
набрана Нэнси А. Роджерс в системе обработки текстов TjjK. При работе
применялся комплекс шрифтов Computer Modern Roman. Все макроопределения,
необходимые для согласования с требованиями издательства, были написаны Дэвидом
Ф. Роджерсом. Для работы использовалось два компьютера: ШМ AT и Zenith 386.
Рукопись была введена непосредственно с бумажной копии. После ее
редактирования на экране дисплея были получены с помощью лазерного принтера
разрешением 300 точек на дюйм гранки, корректуры страниц и макеты.
Окончательный вариант, пригодный для включения иллюстраций, был передан на фотонабор
Американского Математического Общества в формате .dvi файлов системы ТеК.
Книга не появилась бы на свет без содействия многих людей. Мы
признательны студентам Центра прикладной физики Университета Джона Гопкинса,
которые просмотрели исходные варианты первых пяти глав книги. Многие
высказанные студентами предложения и замечания оказались очень полезными.
Отдельно хочется поблагодарить Джона Дилла и Фреда Манчмейера, двух
наиболее дорогих и близких нам коллег, прочитавших рукопись целиком с
красным карандашом в руках. Многие высказанные ими предложения и замечания
способствовали значительному улучшению книги. Особую признательность
следует выразить нашей коллеге Линде Эдлам, которая не только прочитала всю
рукопись, но и проверила все примеры. Огромное спасибо Стивену Д. Роджерсу,
прочитавшему рукопись и проверившему примеры из первых пяти глав.
Замечания Майка Джайгента об этих главах также были весьма ценными. Очень
полезным был обзор работ по кривым и поверхностям Безье, а также кривым и
поверхностям В-сплайна, проведенный Билом Гордоном.
Усилия Вирджинии Адаме по макетированию окончательного варианта
книги также были очень ценными. Мы благодарны Барбаре Битон за ее
неисчерпаемое терпение при консультировании нас по особенностям системы TjjjX.
Специально отдадим должное Джусту Залмстре, чьи выполненные весьма кстати
макроопределения для TjjjX'a существенно облегчили нашу задачу.
Традиционно высокий профессионализм бьш продемонстрирован редактором издательства
McGraw-Hill Джимом Брэдли. Наиболее сложные иллюстративные программы
проверены Мэлом Хабером. Особую благодарность заслуживает Б.Д.Кларк,
который вот уже около двадцати лет является нашим редактором в McGraw-Hill и
был весьма внимателен к нашим иногда неортодоксальным идеям.
Дэвид Ф. Роджерс, Док. Алан Адаме,
Аннаполис, февраль 1989
Предисловие к
первому изданию
Настоящее время характеризуется появлением новой быстро развивающейся
области знания — «машинной графики», которая включает в себя как
традиционные сферы знания, так и новые информационные технологии. Теперь компьютеры
используются не только крупными фирмами и организациями, уже достигшими
первых успехов в области программного и аппаратного обеспечения, но и
широким кругом пользователей-непрофессионалов. Такое широкое внедрение
компьютеров стало возможно благодаря недорогим графическим дисплеям, режиму
разделения времени, а также успехам в области мини- и микрокомпьютерной
технологии. Машинная графика является сегодня практическим, надежным,
эффективным и широкодоступным инструментом.
Задача данной книги состоит в том, чтобы на основе универсального
обобщения изложить математическую теорию основных методов машинной графики.
Несмотря на использование в книге новых приемов представления материала, в ней
нет совсем незнакомого читателю математического аппарата; в ней предпринята
попытка собрать воедино всю информацию по машинной графике, разбросанную
по разным техническим изданиям.
При отборе материала для книги мы уделяли особое внимание основным
математическим по своей природе методам, а не методам процедурного характера.
Именно по этой причине читатель обнаружит в данной книге прежде всего
достаточно развернутое изложение способов поворота, преобразования, построения
перспективных проекций, описание кривых и поверхностей, а не обсуждение
задач отсечения или удаления невидимых линий и поверхностей. Знание
математики в объеме первого курса колледжа является достаточной предпосылкой для
освоения основной части книги.
После обсуждения в гл. 1 современной компьютерной технологии дается
описание матричных операций над графическими элементами, заданными в
однородных координатах. В последующих главах содержится описание современных
способов представления точек, линий, кривых и поверхностей в цифровых
компьютерах. Приводятся также соответствующие программные процедуры
манипуляции и вывода графических изображений.
Вместе с математическими методами формирования аксонометрических и
перспективных видов приводятся методы поворота, преобразования и
масштабирования геометрических фигур. Процедуры определения кривых, заданных явно и в
параметрической форме, описываются как для двумерного, так и для
трехмерного пространства. Методы определения кривых предусматривают использование
конических сечений, круговой интерполяции дугами, кубических сплайнов,
параболического сглаживания, кривых Безье и кривых на основе В-сплайнов. В книгу
включено также введение в математическое описание поверхностей.
Приложение содержит подпрограммы на языке Бейсик, реализующие
алгоритмы большинства базовых модулей интерактивных пакетов машинной графики.
Однако эти алгоритмы преднамеренно оканчиваются такими командами или
подпрограммами реальной визуализации результатов, которые безусловно не
являются стандартными для конкретного графического устройства. Несмотря на то,
что в приложении А приводится некое предварительное описание графических
примитивов и элементов, пользователь в общем случае сочтет необходимым
ориентироваться на специфику конкретной физической конфигурации графических
устройств.
Главные концепции данной книги были положены в основу вводного курса
машинной графики для студентов высших учебных заведений научно-технической
специализации. Курс хорошо подходит как для университетов, так и для
технических школ. Книга полезна также и в качестве дополнительного материала для
более углубленных учебных курсов по программированию или математике.
Кроме этого, она может быть с успехом использована профессиональными
программистами для индивидуальной подготовки. В конечном счете хорошо
документированные программы могут быть полезны пользователям, заинтересованным в
развитии графических возможностей своего компьютера.
Благодарности
Авторы глубоко признательны Военно-Морской Академии США за поддержку
и внимание. Обеспеченная администрацией научная среда, предоставленное
оборудование и, особенно, участие курсантов оказало весьма благоприятное
воздействие на подготовку материала данной книги.
Ни одна книга не может быть написана без содействия многих людей, и мы
хотели бы выразить здесь благодарность некоторым из них. Прежде всего Стиву
Коонеу, просмотревшему всю рукопись и сделавшему множество ценных
предложений, Ричарду Рейзенфельду, изучившему материал по кривым и поверхностям
В-сплайна, профессору Пьеру Безье, который рецензировал материал по кривым
и поверхностям Безье, а также Ивану Сазерленду, предложившему нам включить
в гл. 3 обсуждение методов трехмерного преобразования. Особой благодарности
заслуживают бывшие и нынешние члены группы САПР в Кэмбриджском
университете. В первую очередь, это Робин Форест, Чарльз Ланг и Тони Нутбоурл,
проявившие глубокое понимание предмета машинной графики. Мы благодарим
также Лоя Кноппа, написавшего оригинальную программу на Фортране для
кривых В-сплайна.
Авторы хотели бы выразить признательность за содействие многим
сотрудникам Evans & Sutherland Computer Corporation и особенно Джиму Каллану,
который является автором документации, послужившей основой для многих идей по
подготовке изображений, их представлению и интерактивному взаимодействию с
ними. Особо отметим Ли Биллоу, подготовившего все векторные рисунки.
Большая часть работы по художественному оформлению гл. 1 была
проведена на рабочих станциях различных фирм-производителей. Отдельно выразим
благодарность следующим корпорациям:
Рис. 1-3 Evans & Sutherland Computer Corporation
Рис. 1-5 Adage Inc.
Рис. 1-7 Adage Inc.
Рис. 1-8 Vector General, Inc.
Рис. 1-11 Xynetics, Inc.
Рис. 1-12 CALCOMP, California Computers Products, Inc.
Рис. 1-15 Gould, Inc.
Рис. 1-16 Tektronix, Inc.
Рис. 1-17 Evans & Sutherland Computer Corporation
Рис. 1-18 CALCOMP, California Computers Products, Inc.
Дэвид Ф. Роджерс,
Док. Алан Адаме
Посвящается нашим женам:
Нэнси А. Роджерс и Вирджинии Ф. Адаме
и нашим семьям:
Стивену, Карен и Рэнсому Роджерс
и Линн, Дэвиду и Алану Адаме
Глава 1
Введение
в машинную графику
В настоящее время машинная графика представляет собой достаточно развитую
отрасль знания, однако некоторые термины и определения по-прежнему
трактуются очень широко. Например, такие понятия, как САПР, интерактивная
графика, машинная графика, АСТПП, часто используются либо в разных значениях,
либо так, что в значительной степени теряется их точный смысл. Наиболее
типичным термином такого рода является «САПР», что означает любое применение
компьютера для проектирования отдельных деталей, узлов или систем. Однако
такое использование компьютера необязательно предусматривает включение
машинной графики, ведь процесс проектирования может осуществляться на
концептуальном уровне, на уровне деталировки либо ориентироваться на интерфейс
с АСТПП.
В АСТПП компьютер используется для управления процессом
промышленного производства. Для АСТПП требуется язык программирования, позволяющий
задавать геометрию и траекторию перемещения обрабатывающего инструмента,
например язык APT (язык программирования станков с ЧПУ), для
генерирования команд управления инструментом станка. Контроллер станка, как правило,
представляет собой микро- или миникомпьютер, для которого САПР может
непосредственно формировать необходимые команды управления. Одновременно
можно создавать массив данных в стандартном формате, например IGES
(формат передачи графических данных). Для преобразования полученных данных в
формат команд конкретного станка используются специальные программы. На
рис. 1-1 показан типичный обрабатывающий центр с ЧПУ и контроллером.
Компьютер в машинной графике используется для описания изображений, их
хранения, манипулирования ими, их вызова и визуализации, т. е. в основном для
пассивных операций. Компьютер выводит на экран предварительно
подготовленное изображение, и наблюдатель не может непосредственно управлять
изображением, прежде чем оно появится на экране. В каждом конкретном случае изобра-
Рис. 1-1 Обрабатывающий центр с ЧПУ.
жение может быть либо таким простым, как, например, графики простых
функций, либо столь сложным, как визуализация результатов моделирования процесса
автоматического полета и посадки самолета или космического корабля.
В динамической интерактивной машинной графике (в дальнейшем просто
интерактивной графике) компьютер используется для подготовки и визуализации
графических данных. Однако интерактивная графика позволяет наблюдателю в
реальном масштабе времени влиять на весь процесс представления изображения.
Чтобы убедиться в серьезности ограничений, определяемых условиями работы в
реальном времени, рассмотрим задачу вращения объемного изображения,
состоящего из 1000 линий, со скоростью 15 град/с.
Как мы увидим в дальнейшем, картинка из 1000 линий в большинстве
случаев представляется матрицей 1000 х 4 однородных координат конечных точек
линий. Вращение, как правило, представляется путем умножения этой матрицы
на матрицу преобразования размером 4x4. Для проведения такого матричного
умножения требуется выполнить 16 тыс. операций умножения, 12 тыс. операций
сложения и 1 тыс. операций деления вещественных чисел. Если умножение
осуществляется программно, то для того чтобы выполнить все операции вращения,
может потребоваться значительное время. Обычный универсальный компьютер
с процессором вещественной арифметики, способным выполнять операции
умножения с быстродействием 3.6 мкс, сложения —за 2.6 мкс и деления со
скоростью 5.2 мкс, может выполнить такое матричное умножение за 0.1 с.
Поскольку для того, чтобы картинка на экране начала двигаться, она должна
перерисовываться не менее 30 раз в секунду, то становится очевидным, что в случае
с данным примером картинка не сможет непрерывно перемещаться по экрану.
Даже если предположить, что изображение обновляется только 15 раз в
секунду, т.е. при повороте на каждый градус, то и в этом случае программная
реализация не позволяет получить эффект непрерывного вращения и исключает
возможность получения действительно реалистичных изображений.
Существует множество способов достижения реального интерактивного режима
визуализации изображения: использование более мощного дополнительного компьютера
или более тщательное программирование, уменьшающее время выполнения
матричного умножения. Однако в любом случае обязательно будет достигнут
момент, когда всякое дальнейшее улучшение станет уже невозможным.
Уменьшение сложности изображения также не даст нужного эффекта, так как при этом
может оказаться неприемлемым качество картинки. Однако операция
матричного умножения, необходимая для манипулирования изображением из нашего
примера, для действительно очень сложных картинок может осуществляться на
уровне микропрограмм или с помощью специализированных цифровых
умножителей, применение которых всегда было наиболее эффективным и экономичным.
На основе введенной терминологии в следующих разделах главы предлагается
обзор машинной графики и обсуждаются различные типы современных
графических устройств.
1-1 ОБЗОР МАШИННОЙ ГРАФИКИ
Машинная графика —это сложная и многосторонняя дисциплина. Поэтому для
изучения ее необходимо разделить на более простые обозримые части, учитывая
при этом, что конечным результатом машинной графики является изображение,
которое, разумеется, можно использовать для самых различных целей:
технического чертежа, деталировки в справочном руководстве, изображения
архитектурной конструкции, как одного из возможных вариантов, так и эскиза проекта,
рекламной иллюстрации либо отдельного кадра из мультфильма. В машинной
графике фундаментальным связующим звеном является изображение,
следовательно, важно разобрать следующие вопросы:
представление изображений в машинной графике;
подготовка изображений для вывода;
визуализация предварительно подготовленных изображений;
взаимодействие с изображением.
В дальнейшем под термином «изображение» мы будем понимать множество
линий, точек, текстов и т.п., выводимых на графическое устройство.
1-2 ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
Многие алгоритмы интерпретируют изображения как набор многоугольников
или ребер, причем каждый многоугольник или ребро в свою очередь может
быть представлен с помощью точек (вершин). Таким образом, точки
являются основными строительными блоками изображения. Не менее важны
также и алгоритмы размещения таких точек. В качестве иллюстрации
рассмотрим единичный квадрат в первом квадранте координатной плоскости. Этот
квадрат может быть представлен своим четырьмя вершинами (см. рис. 1-2)
Pi(0,0), P2(l,0), -^(l)!), P4(0,l). Соответствующая алгоритмическая
нотация может выглядеть следующим образом:
Последовательно соединить PiP2PzPiPi-
Единичный квадрат можно также представить с помощью его четырех
ребер Ei = Р1Р2, Е2 = Р2Р3, Е3 = Р3-Р4, Ei = PiPi. Здесь алгоритмической
нотацией служит следующая запись-
Последовательно изобразить Ei E2 Е3 Е^.
И наконец, для описания единичного квадрата в виде многоугольника можно
использовать либо точки, либо ребра. Например, Si = P1P2P3P4P1, или Si =
PiPiP3P2Pi или Si = EiE2EzEi. В зависимости от размерности координатного
пространства основные строительные блоки (точки) можно представить либо как
пары, либо как тройки чисел. Таким образом, координаты (xi,yi) или (xi,yi,zi)
определяли бы точку на плоскости или в пространстве. Две точки задавали бы
отрезок или ребро, а совокупность из трех и более точек — многоугольник.
Построение кривых осуществляется обычно путем их аппроксимации короткими
отрезками. Символы представляются уже более сложным образом — они образуются
из совокупности различных кривых или определяются матрицей точек. Однако в
1.0
5 .
I н-= •
1.0
Рис. 1-2 Описание данных изображения.
основе представления символов по-прежнему лежат совокупности отрезков, точек
и соответствующие им алгоритмы. Если не надо создавать специальные шрифты
или проектировать графические устройства, то пользователю совсем
необязательно знать все детали описания символов текста, так как большинство графических
устройств имеют встроенные аппаратные или программные генераторы символов.
1-3 ПОДГОТОВКА ИЗОБРАЖЕНИЙ ДЛЯ ВЫВОДА
В конечном счете изображение определяется точками и алгоритмом их вывода.
Прежде чем информация об изображении будет использована для формирования
картинки, она хранится в файле, называемом базой данных. Для представления
очень сложных изображений нужны сложные базы данных, для которых
предполагается использование сложных алгоритмов организации доступа к ним. Данные
или структуры данных в таких базах могут быть организованы в виде кольца,
В-дерева, квадратичных структур и т. д. Сами базы данных могут содержать
указатели, подструктуры и другую негеометрическую информацию.
Организация баз данных и алгоритмы доступа к ним выходят за рамки изложения
данной книги. Однако многие конкретные реализации систем с машинной
графикой предназначены для работы с простыми изображениями, для которых можно
предложить простые структуры данных с простым способом доступа. Наиболее
элементарной структурой данных, безусловно, является линейный список. Может
показаться неожиданным, но оказалось, что с помощью этой структуры
представляются достаточно качественные изображения.
Точки — основные строительные блоки графической базы данных, именно
поэтому особый интерес представляют основные операции преобразования точек.
Существуют три типа операций, в которых точки используются как графические
примитивы: во-первых, перемещение пера и курсора, след курсора (в дальнейшем
просто курсор), невидимая точка; во-вторых, изображение линии между двумя
точками; в третьих, вывод точки в заданном месте. В общем случае
местоположение точки можно описать двумя способами: с помощью абсолютных и
относительных (инкрементальных) координат. В системе относительных координат
позиция точки определяется путем задания ее положения относительно
предыдущей точки. Все программное обеспечение машинной графики базируется на этих
основных понятиях и операциях. Более подробно основы построения программ
машинной графики излагаются в разд. 1-22 и в приложении А.
Местоположения точки могут быть описаны с помощью вещественных (с
плавающей точкой) или целых чисел. В случае применения целых чисел возникает
множество проблем, связанных с ограниченной длиной слова компьютера. Для
представления целых координат, как правило, используется полное машинное
слово. Наибольшее целое число, занимающее полное машинное слово и необходимое
для представления величин со знаком из положительного и отрицательного
диапазонов, равно 2n_1 — 1, где п — количество битов в слове. Для 16 битового слова
это число равно 32 767. Для многих приложений этого бывает вполне достаточно,
однако возникают серьезные проблемы, когда требуются большие числа, которые
невозможно представить с помощью одного слова компьютера. Эту трудность
можно преодолеть, например, воспользовавшись относительными координатами
в случае, когда их величина не превышает 60 000. При этом в абсолютной системе
координат устанавливаются точки с координатами (30000,30000), а затем с
помощью относительных координат (30 000,30 000) строится точка с координатами
(60 000,60 000). Однако этот способ обладает значительным недостатком: попытка
сохранить относительные координаты, превышающие максимально допустимую
величину, вызывает переполнение. В большинстве компьютеров результатом
целочисленного переполнения является генерация чисел с противоположным
знаком и неверным абсолютным значением.
От этого недостатка можно избавиться с помощью однородных координат, что
вызывает некоторые усложнения, уменьшение скорости выполнения и понижение
качества разрешения изображения. Однако все эти недостатки оправдываются
преимуществами, которые дают возможность представления больших чисел на
компьютерах с ограниченной длиной слова. Именно по этой причине, а также
в связи с другими преимуществами использования однородных координат, им
уделяется основное внимание в данной книге.
В системе однородных координат n-мерное пространство представляется
п 4- 1 измерением, т.е. трехмерные координаты, однозначно задаваемые тройкой
(x,y,z), выражаются через четыре координаты (hx,hy,hz,h), где h —
произвольный множитель. Если все координатное пространство в 16-битовом компьютере
представляется числами меньше 32 767, то h будет равно 1, а координаты
будут представляться путем прямых преобразований. Однако если хотя бы одна из
координат превышает число 32 767, например, х = 60000, то преимущества
использования однородных координат становятся очевидны. В данном случае мы
установили h = 1/2 и координаты точки теперь можно представить в 16-битовом
компьютере как (30 000, у/2, z/2, 1/2). Однако в этом случае неизбежно
снижение разрешающей способности, так как, например, значения х = 60 000 и 60 001
теперь представляются одинаковой однородной координатой. Фактически
разрешение ухудшается для всех координат даже в том случае, если только одна из
них превышает максимально допустимое для целых чисел значение.
1-4 ПРЕДСТАВЛЕНИЕ ПРЕДВАРИТЕЛЬНО ПОДГОТОВЛЕННОГО
ИЗОБРАЖЕНИЯ
Данные, используемые для подготовки рисунка, как правило, не совпадают с
данными, необходимыми для его визуализации (дисплейным файлом). В этом файле
содержится некоторая часть, вид или отдельная сцена целого изображения,
представленного в общей базе данных. Выводимое изображение обычно формируется
путем поворота, переноса, масштабирования и вычисления различных проекций.
Эти преобразования обычно выполняются с помощью матричных операций (4 х 4)
с данными, представленными в однородных координатах (гл. 2 и гл. 3). В случае,
когда требуется последовательность преобразований, матрица каждого
отдельного преобразования последовательно применяется к точкам рисунка. Однако
если таких точек очень много, данный метод становится неэффективным. Гораздо
удобнее другой способ, состоящий в использовании одной результирующей
матрицы комбинированных преобразований, полученной путем умножения матриц
каждого отдельного преобразования. Такая матричная операция называется кон-
Линия частично внутри окна:
часть а—Ь выводится,
часть Ь—с не выводится
/Линия полностью
внутри окна:
линия выводится
целиком
Линия полностью
вне окна:
не выводится
Линия частично внутри окна:
часть 6—с выводится,
части в—А и с—d не выводятся
Рис. 1-3 Двумерное отсечение.
катенацией. После этого вектор координат всех точек изображения умножается
на матрицу комбинированного преобразования размером 4x4 для получения
результирующих точек. Данный подход позволяет значительно сократить время
проведения сложных матричных операций над множеством точек.
Удаление невидимых линий или поверхностей, закраска, определение
прозрачности, текстуры или световые эффекты — все эти операции могут быть
выполнены еще до момента окончательной визуализации изображения. Если выводимое
изображение определено не на всей базе данных, в ней необходимо выделить
некоторую часть, соответствующую этому изображению. Данный процесс называется
отсечением. Отсечения бывают дву- и трехмерные. В ряде случаев окно и объем
отсечения могут иметь отверстия или быть неправильной формы. Стандартное
отсечение по границам дву- или трехмерных областей часто реализуется аппарат-
но. Подробное обсуждение особенностей реализации эффектов отсечения выходит
за рамки данного изложения. Более детальное описание приведено в работе [1-1].
С процессом визуализации изображений обычно связано два ключевых
понятия: окно и поле зрения. Процесс вывода с использованием окон предусматривает
извлечение части графических данных из базы путем их отсечения по границам
окна. Программная реализация операций отсечения и вывода окна, как правило,
требует значительного времени, что исключает возможность ее применения в
интерактивных графических системах. С другой стороны, в сложных графических
системах для этого используется специализированная аппаратура или
микропрограммные средства. Задача отсечения изображения включает выделение и
отбрасывание отрезков или их частей, лежащих вне окна. Отсеченные отрезки или их
части не передаются на графическое устройство вывода.
На плоскости окно задается левым, правым, верхним и нижним ребрами
ограничивающего прямоугольника. Координаты вершин ребер определяются в
системе координат пользователя или в мировой системе координат, т.е. именно в
Рис. 1-4 Трехмерная пирамида видимости.
той системе, в которой хранится вся информация из графической базы данных.
Как правило, координаты геометрических примитивов запоминаются в виде
вещественных чисел.
Процесс отсечения значительно упрощается в случае так называемых
регулярных окон, ребра которых параллельны осям координат. Нерегулярные
отсекающие окна также представляют определенный интерес для многих конкретных
приложений [1-1]. На рис. 1-3 показан процесс отсечения на плоскости. Линии
удаляются, выводятся на экран полностью или частично в зависимости от их
местоположения относительно границ окна. В трехмерном пространстве регулярное
окно или отсекающий объем представляет собой прямоугольный параллелепипед
(брус) или, для перспективных видов, усеченную пирамиду (пирамиду
видимости). На рис. 1-4 показана типичная пирамида видимости, ближайшая к
наблюдателю грань помечена символом N, наиболее удаленная — символом F, а стороны
образованы гранями SL, SR, ST и SB.
Поле зрения — это область на экране дисплея, предназначенная для
размещения попавшего в окно изображения. Регулярное поле зрения на плоскости
задается левым, правым, верхним и нижним ребрами ограничивающего
прямоугольника. Поле зрения может быть определено в реальных физических
координатах устройства, часто задаваемых в виде целых чисел. Координаты поля зрения
могут быть нормализованы по некоторому произвольному диапазону, например,
0<т<1,0<у<1и задаваться в виде вещественных чисел. Содержание
одного окна может быть выведено в нескольких полях зрения одного и того же
устройства (рис. 1-5). Сохранение пропорций окна и поля (полей) зрения
позволяет избежать искажений. Отображение на поле зрения графических данных,
попавших после отсечения в окно, предусматривает выполнение операций
переноса и масштабирования (приложение А).
Кроме графической информации, большинство изображений могут содержать
алфавитно-цифровые и символические данные. Существуют два основных
способа генерации символов: программный и аппаратный. Если при программной ге-
Устройство вывода
Поле зрения Л
-______^ Поле зрения А
Рис. 1-5 Несколько полей зрения для одного окна.
нерации символов используются линии, то они отсекаются обычным образом. Это
бывает необходимо в случае, когда символы подвергаются операции отсечения, а
затем операции преобразования. Однако многие графические устройства имеют
встроенные аппаратные генераторы символов, и в этом случае символы
идентифицируются только своим кодом, а их изображение формируется непосредственно
перед выводом на экран. Данная реализация намного эффективнее, но обладает
меньшей гибкостью, чем программная генерация символов, так как не позволяет
проводить отсечение и выполнять общие преобразования, ограничивающиеся в
этом случае поворотом и масштабированием.
При использовании аппаратного генератора управляющая программа
графического устройства должна установить размер, ориентацию и точку привязки
символа или строки текста. После этого в дисплейный файл заносятся коды символов,
имеющих установленные характеристики. Затем запускается генератор текстов,
который интерпретирует строку текста, задавая аппаратуре всю информацию,
необходимую для изображения каждого символа. После этого символы текста
пересылаются на устройство вывода.
1-5 ОРГАНИЗАЦИЯ ВЗАИМОДЕЙСТВИЯ С ИЗОБРАЖЕНИЕМ
После того как изображение на экране построено, возникает необходимость как-то
взаимодействовать с ним или модифицировать его. Для этого был разработан ряд
диалоговых устройств. Среди них можно назвать планшет, световое перо, рычаг,
мышь, ручки для ввода скалярных величин, функциональные переключатели или
кнопки и, разумеется, обычную алфавитно-цифровую клавиатуру. Прежде чем
перейти к обсуждению этих физических устройств, рассмотрим функциональные
возможности диалоговых графических устройств. Обычно насчитывается четыре
или пять функциональных логических классов [1-2] —[1-4]. Логическими
диалоговыми устройствами являются локатор, валюатор, селектор и кнопка. Из-за
широкой распространенности алфавитно-цифровой клавиатуры ее часто выделяют
в пятый класс, называемый клавиатурой. В действительности клавиатуру можно
концептуально и функционально считать набором кнопок.
Функцией локатора является выдача координатной информации в двух или
трех измерениях. Обычно выдаваемые значения координат являются нормализо-
Рис. 1-6 Алфавитно-цифровая клавиатура. (С разрешения фирмы Evans & Sutherland
Computer Corp.)
ванными и могут быть как относительными, так и абсолютными. Валюатор
применяется для ввода одиночной величины. Обычно это вещественное число между
нулем и некоторым вещественным максимумом. Кнопка используется для выбора
и активирования событий или процедур, управляющих сценарием диалога.
Кнопка обычно представляет двоичную («включено» или «выключено») цифровую
информацию. В функцию селектора входит идентификация или выбор объектов или
подкартинок в выведенном изображении. Логическая клавиатура обрабатывает
текстовую информацию. На рис. 1-6 показана типичная клавиатура.
Наиболее общим устройством класса локаторов является планшет (рис. 1-7).
Планшеты можно использовать либо отдельно, либо в комбинации с
графическим дисплеем на ЭЛТ. В первом случае их часто называют оцифровывателями.
Сам по себе планшет состоит из плоской поверхности и карандаша (похожего на
обычный карандаш), который используется для указания точки на поверхности
планшета. Обычно положение карандаша распознается, если он находится на
небольшом расстоянии от планшета. При работе с ЭЛТ обратная связь на экране
обеспечивается с помощью небольшого символа (курсора), отслеживающего
перемещение карандаша по поверхности планшета. В случае когда обратная связь
используется в качестве отдельного оцифровывателя, она обеспечивается с
помощью цифровых отсчетов.
Планшеты выдают координатную информацию в двух или трех
измерениях. На рис. 1-8 показан трехмерный планшет. Выдаваемые планшетом значения
представлены в координатах устройства. Они программно преобразуются в
пространство координат пользователя. Обычное разрешение и точность составляют
от 0.025 до 0.0025 см.
Рис. 1-7 Типичный планшет. (С разрешения фирмы Adage.)
Рис. 1-8 Трехмерный звуковой планшет. (С разрешения фирмы Science Accessories
Corp!)
При создании планшетов используется несколько различных принципов. BJ
первом планшете RAND [1-5] применялась ортогональная сетка из отдельных
проводов, расположенных под поверхностью. Каждый провод, кодируется таким
образом, чтобы карандаш, действующий как приемник информации, в каждой
точке пересечения проводов получал уникальный цифровой код. Декодирование
этого кода дает координаты карандаша х, у. Очевидными ограничениями на
разрешение таких матрично кодируемых планшетов является плотность размеще-
ния проводов и способность приемника обрабатывать уникальный код. Точность
ограничивается линейностью конкретных проводов, а также их параллельностью
в двух ортогональных направлениях.
В одной достаточно интересной реализации планшета применяются звуковые
волны. Карандаш используется для создания искры электрического разряда,
вызывающей звуковую волну. Она движется во всех направлениях от карандаша по
поверхности планшета, образуя круговой звуковой фронт. На его краях в
перпендикулярных направлениях смонтированы два чувствительных ленточных
микрофона. Координатные расстояния можно определить с помощью точного
измерения времени, за которое волна проходит с карандаша до микрофонов. Данную
методику можно распространить на три измерения (рис. 1-8).
Наиболее популярны конструкции планшета, в основе которых лежит
электромагнитный принцип. При этом электрические импульсы проходят через сетку
из проводов, расположенных под поверхностью планшета. Время, за которое
чередующиеся импульсы, параллельные координатным осям х, у, проходят от края
планшета до карандаша, определяется с помощью карандаша и соответствующих
индикаторов. Эти данные легко преобразуются в координаты х, у.
Сенсорная панель похожа на планшет и относится к классу локаторов. В
типичной сенсорной панели на двух смежных сторонах расположены источники
света, а на двух противоположных смежных сторонах смонтированы
светочувствительные элементы. Любой предмет, например палец, прерывая два
ортогональных луча света, позволяет определить пару координат х, у. Из-за низкого
разрешения этот прибор лучше всего использовать для грубых операций
указания. С этой целью сенсорную панель часто монтируют поверх экрана ЭЛТ.
В таких локаторных устройствах, как рычаг, шар и мышь, в качестве
делителя напряжения часто используются чувствительные переменные резисторы или
потенциометры. Аналогичным образом реализуются и ручки для ввода
скалярных величин, которые являются устройствами класса валюаторов. Точность всех
этих устройств зависит от качества потенциометра и обычно колеблется от 0.1
до 10% всего диапазона измерения. Несмотря на то что разрешение
потенциометра по существу бесконечно, его использование в цифровых системах требует
аналого-цифрового (АЦ) преобразования. Обычно разрешение АЦ
преобразователя изменяется в диапазоне от 8 до 14 бит, т. е. от 1/256 до 1/16384. Валюаторы
также реализуются с помощью цифровых преобразователей углового положения,
которые для каждого инкрементального угла поворота ручки выдают цифровой
результат. Типичное разрешение —от 1/256 до 1/1024.
Типичным валюатором является рычаг (рис. 1-9). Подвижный рычаг обычно
оборудуется двумя валюаторами — либо потенциометрами, либо
преобразователями углового положения, смонтированными на основании прибора. Валюаторы
выдают результаты, пропорциональные смещению ручки. В рычаг можно просто
добавить третью степень свободы, используя, например, третий валюатор для
измерения угла поворота. В качестве эха обратной связи рычага обычно
употребляется графический курсор.
Шар во многом аналогичен рычагу (рис. 1-10). Чаще всего его можно
встретить в радарных установках, например в системах управления воздушными
перевозками. Сферический шар смонтирован в основании прибора, причем над по-
Рис. 1-9 Рычаг. (С разрешения, фирмы Measurement Systems, Inc.)
Рис. 1-10 Шар. (С разрешения фирмы Measurement Systems, Inc.)
верхноствю возвышается только его часть. Шар может свободно вращаться в
любом направлении. В основании смонтированы два валюатора (потенциометры
или преобразователи углового перемещения), которые улавливают поворот шара
и выдают результаты, пропорциональные относительным величинам углов.
Кроме обычной обратной связи через курсор, пользователи получают тактильную
обратную связь в виде скорости поворота или углового импульса вращения шара.
Рычаг имеет фиксированное положение с фиксированным началом координат.
Мышь и шар, напротив, характеризуются только относительным положением ко-
Рис. 1-11 Мышь. (С разрешения фирмы Apple Computer, Inc.)
ординат. Обычная мышь состоит из шар'а, касающегося поверхности и
расположенного в маленьком, легком футляре. При движении мыши по поверхности шар
вращается и управляет осями двух валюаторов (потенциометров или
преобразователей углового перемещения). Совокупное движение осей дает координаты х,
у. Типичная мышь показана на рис. 1-11. Мышь можно поднять, переместить
в любом направлении л поставить на поверхность, по-другому ориентировав. В
этом случае изменяется система координат, в которой генерируются данные, т. е.
меняется положение мыши, но не система координат, связанная с данными.
Используемый для обратной связи курсор, не движется, когда мышь не
контактирует с поверхностью. Из-за проскальзывания шара возникает уменьшение точности.
Совсем недавно в продаже появились устройства,-работающие на оптическом или
на магнитном принципе. В обоих случаях исключаются неточности, связанные с
проскальзыванием.
Возможно, простейшими из валюаторов являются ручки для ввода скалярных
величин. Такие ручки, показанные на рис. 1-12, являются по существу
чувствительными вращающимися потенциометрами или точными цифровыми
преобразователями углового положения, которые обычно объединяются в группы. Такие
устройства особенно удобны при задании параметров для функций поворота, пе-'
реноса или масштабирования.
Кнопки и функциональные переключатели, показанные на рис. 1-13, являются
переключателями рычажного или нажимного действия. Они могут быть
постоянно нажаты, постоянно отжаты либо иметь кратковременный контакт. Наиболее
удобный тип функционального переключателя объединяет в себе обе эти
возможности. Обычно можно программно управлять световыми индикаторами',
указывающими, какие переключатели или кнопки в данный момент активны. Кнопки
Рис. 1-12 Набор ручек для ввода скалярных'значений. (С разрешения фирмы Evans
& Sutherland Computer Corp.)
Рис. 1-13 Функциональные кнопки. (С разрешения фирмы Adage.)
и переключатели часто «входят в состав других устройств. Например, на тонком
конце карандаша планшета обычно располагается переключатель,
срабатывающий при нажатии карандаша. На мьппи также находится одна или несколько
кнопок.
Единственным подлинным устройством указания является световое перо
(рис. 1-14), которое содержит светочувствительный фотоэлемент и
соответствующую электрическую цепы Основная информация, передаваемая световым пером,
связана с синхронизацией и зависит от того, что изображается на экране, и от
порядка, в котором происходит его заполнение. Это исключает использование све-
Поле зрения
Корпус ^__^_^ ,-'Т\
Переключатель
затвора
Пучок
световодов
(,t—^\/Фотоумножительная
\J лампа
Цепь формирования > К дисплейному
импульсов контроллеру
Рис. 1-14 Схема светового пера.
тового пера с дисплеями на запоминающей ЭЛТ (гл. 1-7). Его можно использовать
только при дисплеях с регенерацией — векторных или растровых.
В тот момент, когда активизированное световое перо оказывается над той
областью ЭЛТ векторного дисплея (гл. 1-8), в которой происходит рисование,
дисплейному контроллеру посылается сигнал. Он позволяет определить
конкретную команду в дисплейном буфере, выполняемую в данный момент времени, что
дает возможность идентифицировать отрезок, объект или подкартинку на
экране. Используя графический курсор, можно применять световое перо в качестве
локатора для векторного устройства с регенерацией изображения.
Так как в растровом дисплее изображение генерируется в фиксированной
последовательности, световое перо используется для определения горизонтальной
сканирующей строки (координаты у) и позиции в этой строке (координаты х).
Отслеживая программу в контроллере, можно снова определить, какой отрезок,
объект или подкартинка были указаны. Этот метод несколько усложняется в
случае чересстрочной развертки (гл. 1-12). Приведенное выше описание означает
также, что для растрового устройства световое перо может быть использовано
скорее всего как локатор, а не как устройство указания.
Несмотря на то что для всех логических устройств существуют
соответствующие физические устройства, в конкретной реализации некоторые из них могут
отсутствовать. Таким образом, необходимо уметь моделировать логические
интерактивные устройства ввода. На рис. 1-15 приведен пример, в котором световое
перо используется для моделирования функций логической кнопки путем выбора
из меню световых кнопок.
Планшет —одно из самых универсальных физических устройств. Его можно
использовать как оцифровыватель для получения координат х, у. Вдобавок к
этому оно прекрасно подходит для моделирования всяких логических
интерактивных функций (рис. 1-16). Из этого же рисунка видно использование планшета
в качестве локатора (позиция (а) на рис. 1-16). Используя графический курсор,
Рис. 1-15 С помощью выбора из меню световое перо используется для моделиров;
функции логической кнопки. (С разрешения фирмы Adage.)
(
1 2
5 6
9 0
Л
\
с)
3 1 Е
7 8 С
Экран ЭЛТ
(е)
t)
т
(а)
1
1
(Ь)
Rotate х
Rotate y
Rotate z
Trans x
Trans y
Trans z
Zoom
Scale
(d)
+ ^
Рис. 1-16 Использование планшета для моделирования всех логических интерактив-
; функций: (а) локатора, (Ь) кнопки, (с) клавиатуры, (d) валюатора, (е) селектора.
можно реализовать функцию кнопки. Для этого с помощью карандаша планшета
указываем курсором на кнопку меню (либо вблизи нее). Координаты, полученные
с планшета, сравниваются с известными координатами х, у кнопок меню. Если
обнаружено совпадение, то соответствующая кнопка активизируется (позиция (Ь)
на рис. 1-16). Аналогичным образом на планшете можно реализовать клавиатуру
(позиции (с) на рис. 1-16).
Отдельный валюатор обычно реализуется в сочетании с кнопкой. Конкретная
функция для определения значения выбирается кнопкой, как правило, из меню.
Затем валюатор можно смоделировать с помощью «числовой оси» (позиция (d)
на рис. 1-16). Перемещение курсора вдоль оси генерирует координаты х, у, одна
из которых интерпретируется как процентное отношение к диапазону валюатора.
Функцию указания можно реализовать с помощью локатора путем
определения относительных координат х и у небольшого «окна указания». Данное окно
становится затем графическим курсором, и для его позиционирования
используется карандаш планшета. Координаты х, у каждого из интересующих
отрезков, объектов или подкартинок сравниваются затем с текущим
местоположением. Если они попадают в пределы окна, то данный элемент считается указанным.
Для сложных изображений программная реализация данного алгоритма может
оказаться медленной, но при аппаратной реализации заметной задержки не будет.
Несмотря на то что световое перо нельзя использовать в качестве оцифровыва-
теля, его, подобно планшету, тоже можно применять для моделирования всех
логических интерактивных функций.
1-6 ТИПЫ ГРАФИЧЕСКИХ УСТРОЙСТВ
Существует много разнообразных устройств для вывода изображений,
построенных с помощью машинной графики. Наиболее типичными являются
электроннолучевые трубки (ЭЛТ), плазменные дисплеи, перьевые графопостроители,
матричные, электростатические и лазерные печатающие устройства, устройства для
фото и киносъемки. Кроме устройств визуализации большое развитие получают
устройства сохранения изображения.
Запоминающие ЭЛТ с прямым копированием изображения (рисование
отрезками), векторные дисплеи (рисование отрезками) и растровые сканирующие
дисплеи с регенераций (поточечное рисование) образуют три основных класса
дисплеев на ЭЛТ. Развитие электронной технологии позволило использовать в одном
дисплее несколько способов изображения. Класс устройств с плоским экраном
образуют газоразрядные плазменные, электролюминесцентные дисплеи, дисплеи
на жидких кристаллах и дисплеи, построенные на основе светодиодов. При
обсуждении различных дисплеев мы стоим на пользовательской или концептуальной
точке зрения, т. е. в основном рассматриваем функциональные возможности
дисплеев, а не особенности их электронной схемы.
1-7 ГРАФИЧЕСКИЕ ДИСПЛЕИ НА ЗАПОМИНАЮЩЕЙ ТРУБКЕ
Из всех дисплеев на ЭЛТ наиболее просто устроен дисплей на запоминающей
ЭЛТ с прямым копированием изображения. Запоминающую ЭЛТ, называемую
Рис. 1-17 Графический дисплей на запоминающей трубке. (С разрешения фирмы
Tektronix.)
также бистаб,ильной запоминающей трубкой, можно рассматривать как ЭЛТ,
покрытую люминофором с длительным временем послесвечения. Линия или символ
остаются на ней видимыми в течение длительного времени (до одного часа),
прежде чем станут окончательно неразличимыми. На рис. 1-17 показан типичный
дисплей такого типа. Чтобы нарисовать отрезок на дисплее, интенсивность
электронного луча увеличивают до такой величины, которая вызывает запоминание
следа луча на люминофоре. Для стирания изображения на всю трубку подают
специальное напряжение, снимающее свечение люминофора. Экран вспыхивает
и принимает исходное (темное) состояние. Весь процесс стирания занимает около
1/2 сек. Поскольку вспыхивает вся трубка, то стираются все отрезки и
символы. Таким образом, стереть отдельные линии и символы невозможно, и нельзя
осуществить динамическое изображение или анимацию. Иногда для обеспечения
возможности ограниченной регенерации используется промежуточное состояние
(режим рисования поверх изображения); см. ниже. В этом случае интенсивность
электронного луча принимает значение меньше того порогового, которое
вызывает запоминание, но достаточное для свечения люминофора. Поскольку в этом
режиме изображение не сохраняется, для его видимости необходима постоянная
перерисовка.
Дисплей на запоминающей трубке способен изображать фактически
неограниченное количество векторов, а мерцание изображения в принципе невозможно.
Его разрешение обычно составляет 1024 х 1024 адресуемых точек (10 бит) на
экране 8 х 8 дюймов (ЭЛТ с диагональю 11 дюймов) или 4096 х 4096 (12 бит)-либо на
экране 14 х 14 дюймов (ЭЛТ с диагональю 19 дюймов), либо на экране 18 х 18
дюймов (ЭЛТ с диагональю 25 дюймов). По вертикали обычно видно только 78%
адресуемой области.
Дисплей на запоминающей трубке —это векторный дисплей, или дисплей с
произвольным сканированием. Иначе говоря, отрезок (вектор) может быть
нарисован непосредственно из одной адресуемой точки в любую другую.
Относительно легко, быстро и,недорого можно получить твердую копию экрана. Дис-
плеи на запоминающей трубке в некоторой степени легче программировать, чем
векторные или растровые дисплеи с регенерацией изображения. Дисплеи на
запоминающих ЭЛТ можно объединять с микрокомпьютерами в сателлитные
графические системы или графические терминалы. В последнем случае алфавитно-
цифровая или графическая информация передается от главного компьютера в
терминал через интерфейс. Обычно используется последовательный интерфейс,
по которому за единицу времени передается только один бит информации,
однако может применяться и параллельный интерфейс. Уровень интерактивности
дисплея с запоминающей трубкой ниже, чем у векторного дисплея вследствие
небольшой скорости интерфейса и неудовлетворительных характеристик
стирания.
1-8 ГРАФИЧЕСКИЕ ДИСПЛЕИ С РЕГЕНЕРАЦИЕЙ ИЗОБРАЖЕНИЯ
В отличие от дисплея на запоминающей трубке в векторном (рисующем отрезки
или векторы) дисплее с регенерацией изображения используется люминофор с
очень коротким временем послесвечения. Такие дисплеи часто называют
дисплеями с произвольным сканированием. Из-за малого времени послесвечения
изображение на ЭЛТ за секунду должно многократно перерисовываться или
регенерироваться. Минимальная частота регенерации должна составлять по крайней
мере 30 кадров в секунду при рекомендуемой частоте от 40 до 50 кадр/с.
Частота меньше, чем 30 кадр/с, приводит к мерцанию изображения, как это бывает
при замедленном прокручивании кинофильма. На такое изображение неприятно
смотреть, и его трудно использовать.
Для векторного дисплея с регенерацией кроме ЭЛТ требуются еще два
элемента: дисплейный буфер и дисплейный контроллер. Дисплейный буфер —это
участок непрерывной памяти, содержащей всю информацию, необходимую для
вывода изображения на экран. Функция дисплейного контроллера состоит в
циклической обработке полученной информации со скоростью регенерации.
Сложность рисунка (количество изображаемых векторов) ограничивается двумя
факторами—размером дисплейного буфера и скоростью дисплейного контроллера.
Еще одним ограничением является скорость обработки геометрической
информации, например скорость выполнения таких операций, как преобразование,
отсечение и генерация текстов.
На рис. 1-18 представлены блок-схемы двух высокопроизводительных
векторных дисплеев. В обоих случаях предполагается, что такие геометрические
преобразования, как поворот, перенос, масштабирование, перспективное
проецирование и отсечение, реализованы аппаратно в геометрическом процессоре. В первом
случае (рис. 1-18а) геометрический процессор работает медленнее, чем это
необходимо при регенерации применяемых на практике изображений (4000-5000
векторов). Таким образом, геометрические данные (экранные координаты
векторов), посылаемые центральным процессором (ЦП) графическому дисплею,
обрабатываются до сохранения в дисплейном буфере. Следовательно, в нем
содержатся только те инструкции, которые необходимы генератору векторов и
символов. Обычно векторы задаются экранными координатами, а контроллер читает
информацию из буфера и передает ее генератору векторов и символов. При до-
стижении конца дисплейного буфера контроллер возвращается на его начало, и
цикл повторяется снова.
При использовании первой схемы реализуется концепция двойной
буферизации и независимого изменения изображения и его регенерации. Так как в этой
конфигурации геометрический процессор не успевает сгенерировать сложное
новое или измененное изображение за один цикл регенерации, то дисплейный буфер
делится на две части. В то время, когда измененное изображение обрабатывается
и записывается в одну половину буфера, дисплейный контроллер
регенерирует ЭЛТ из другой половины. При завершении изменения изображения буферы
меняются ролями и процесс повторяется. Таким образом, новое или измененное
изображение может генерироваться в каждый второй, третий, четвертый и т.д.
циклы регенерации. Использование двойной буферизации предотвращает
одновременный вывод части старого и части нового измененного изображения в
течении одного и более циклов регенерации.
Во второй схеме (рис. 1-186) геометрический процессор работает быстрее, чем
необходимо для регенерации достаточно сложных изображений. В этом случае
исходная геометрическая база данных, переданная из ЦП, сохраняется
непосредственно в дисплейном буфере, а векторы обычно задаются в мировых координатах
в виде чисел с плавающей точкой. Дисплейный контроллер за один цикл регене-
цп
Геометрический
процессор
Дисплейный
буфер
Дисплейный
контроллер
Генератор
векторов/
символов
-+/ ЭЛТ J
-*-[ ЭЛТ )
Рис. 1-18 Концептуальные блок-схемы векторных дисплеев с регенерацией
изображения.
ЦП
—»■
Дисплейный
буфер
Дисплейный
контроллер
—»-
Геометрический
процессор
—»■
Генератор
векторов/
символов
(а) (Ь)
Рис. 1-19 Динамическое движение.
(с)
(</)
Та
в
Рис. 1-20 Сегментация дисплейного буфера.
рации считывает информацию из буфера, пропускает ее через геометрический
процессор и передает генератору векторов. При таком способе обработки
геометрические преобразования выполняются «на лету» за один цикл регенерации.
При использовании любой конфигурации в дисплейном буфере содержатся
команды рисования каждого вектора, символа и подкартинки. Следовательно,
любой конкретный элемент изображения может быть изменен независимо от
другого. Эта особенность вместе с малым временем послесвечения люминофора ЭЛТ
позволяет выводить динамические изображения, что и показано на рис. 1.19, на
котором представлена последовательность из четырех циклов. Отрезок,
изображенный сплошной линией, — это отрезок, рисуемый для текущего цикла,
штриховой линией изображен отрезок из предыдущего цикла. Между двумя циклами
регенерации происходит изменение координат конца отрезка — точки В.
Создается впечатление, что отрезок вращается вокруг точки А.
В большинстве случаев лишь часть изображения является динамически
изменяемой. В действительности основная часть картинки остается статичной. Такое
разделение наводит на мысль о необходимости сегментации дисплейного буфера,
которая показана на рис. 1-20. Неподвижны, т. е. не изменяются от одного цикла
регенерации к другому: горизонтальный отрезок, заштрихованная часть и буква
А, используемые для показа опоры отрезка АВ. В то же время для получения
динамического изображения меняются положения конца отрезка АВ и буквы В. Эти
изолированные части базы данных помещены в отдельные сегменты дисплейного
буфера. Для конфигурации, показанной на рис. 1-18а, геометрический процессор
может пропускать статический сегмент в дисплейном буфере, так как он не
изменяется, и это существенно сокращает работу процессора при изменении рисунка.
В данном случае можно модифицировать изображение только в динамическом
сегменте. Еще одним достоинством подобного метода является сокращение
общего количества данных, передаваемых из ЦП в геометрический процессор при
каждом изменении изображения.
Для конфигурации, представленной на рис. 1-186, возможны разные типы
сегментации. Напомним, что для данного случая база данных изображения
сохраняется в дисплейном буфере в виде мировых координат, а обработка изображения
/А
Динамическая
кривая
В
Рис. 1-21 Интеллектуальная сегментация дисплейного буфера.
происходит «на лету», за каждый цикл регенерации. Для картинки, показанной
на рис. 1-20, в дисплейном буфере создаются два сегмента — статический и
динамический. В любом случае обработка совершается мгновенно. Информацию в
динамическом сегменте можно изменить с помощью функций, предоставляемых
геометрическим процессором. Таким образом, модификация изображения может
происходить локально в графическом устройстве, а для этого не требуется связь с
ЦП. В конкретном случае на рис. 1-20 единственной функцией, необходимой для
локального динамического изменения, является поворот вокруг точки А.
Для динамического изменения применительно к рис. 1-21 требуется связь с
ЦП, т. е. необходимо некоторое интеллектуальное изменение изображения. Снова
создаются два сегмента: статический, содержащий опорную линию,
заштрихованную часть и букву А, и динамический, состоящий из кривой АВ и буквы В.
Предположим, что форма кривой АВ должна изменяться от одного цикла
регенерации к другому в зависимости от физических факторов. Это изменение
выполняет прикладная программа в ЦП. Для модификации сегмента с динамически
изменяющимся изображением должны быть переданы и сохранены в дисплейном
буфере новые данные, например форма кривой.
Применение сегментации изображения не ограничивается только движением
или мультипликацией, хотя само понятие было введено с помощью примеров из
этой области. Сегментировано может быть любое изображение, что особенно
полезно для интерактивных графических программ. Понятие сегментации
аналогично модульному программированию. Выбор модульных сегментов
изображения, их размер и сложность зависят от конкретной прикладной области.
Сложность элементов изображения изменяется от отдельных точек до полных описаний
объектов. Типичный векторный дисплей с регенерацией изображения показан на
рис. 1-22.
Чтобы показать, насколько важна скорость передачи или ширина полосы
канала связи между ЦП и графическим устройством, рассмотрим затраты на
интеллектуальное изменение кривой, описываемой 250 отрезками или точками,
заданными тремя координатами. Пусть для представления чисел с плавающей точкой
используются шесть значащих цифр (литер), и пусть каждая литера задается
одним байтом (8 бит). Тогда при скорости регенерации 30 кадр/с и при уело-
Рис. 1-22 Векторный дисплей с регенерацией изображения. (С разрешения фирмы
Evans & Sutherland Computer Corp.)
вии, что модификация производится в каждом цикле, требуемая ширина полосы
связи составит
30[(кол-во точек) (кол-во коорд./точку) (кол-во знач. цифр/точку)(кол-во
бит/литера)] или
30(250) (3) (6) (8) = 1080 000 бит/с
Таким образом, необходимая скорость передачи данных может легко
превысить 1 Мбит/с. Для сложных трехмерных скульптурных поверхностей требуемая
ширина полосы может возрасти в 10 раз, т. е. достигнуть 10 Мбит/с. В
большинстве случаев для поддержки динамической графики в реальном масштабе
времени такие скорости.требуют применения между ЦП и графическим устройством
параллельного интерфейса или интерфейса с прямым доступом в память.
1-9 РАСТРОВЫЕ ГРАФИЧЕСКИЕ ДИСПЛЕИ С РЕГЕНЕРАЦИЕЙ
ИЗОБРАЖЕНИЯ
Как дисплеи на запоминающих ЭЛТ, .так и дисплеи с произвольным
сканированием являются устройствами рисования отрезков, т. е. отрезок прямой может
быть нарисован непосредственно из любой адресуемой точки в любую другую.
Графическое устройство на растровой ЭЛТ работает иначе. Растровое
устройство можно представить в виде матрицы дискретных ячеек (точек), каждая из
которых может быть подсвечена, т.е. оно является точечно-рисующим
устройством. Невозможно, за исключением специальных случаев, непосредственно на-
Элемент изображения (пиксел)
■Адресуемая точка
Растровая аппроксимация
отрезка AS
1
к
*
!?'
щ
л
к
Щ
Щ
%
щ
щ
р!
9
/^
Хк
$
щ.щ
.
ft
щ
шш
D
(*)
Рис. 1-23 Растровая развертка отрезка.
рисовать отрезок прямой из одной адресуемой точки или пиксела в матрице в
другую адресуемую точку или пиксел. Отрезок можно лишь аппроксимировать
последовательностями точек (пикселов), близко лежащих к реальной траектории
отрезка, что и проиллюстрировано на рис. 1-23а. Как видно из рис. 1-236, отрезок
прямой из точек получится только в случае горизонтальных, вертикальных или
расположенных под углом 45° отрезков. Все другие отрезки будут выглядеть как
последовательности ступенек. Это явление называется лестничным эффектом,
или «зазубренностью». Методы, позволяющие устранить лестничный эффект
обсуждаются в [1-1].
Чаще всего для графических устройств с растровой ЭЛТ используется буфер
кадра. Буфер кадра представляет собой большой непрерывный участок памяти
компьютера. Для каждой точки или пиксела в растре отводится как минимум
один бит памяти. Эта память называется битовой плоскостью. Для квадратного
растра размером 512 х 512 требуется 218 (29 = 512; 218 = 512 х 512), или 262144,
бита памяти в одной битовой плоскости. Изображение в буфере кадра строится
Рис. 1-24 Черно-белый буфер кадра (с одной битовой плоскостью) для растрового
графического устройства.
Регистр
Рис. 1-25 Полутоновый черно-белый буфер кадра с N битовыми плоскостями.
побитно. Из-за того что бит памяти имеет только два состояния (двоичные 0 или
1), при одной битовой плоскости можно получить лишь черно-белое
изображение. Битовая плоскость является цифровым устройством, тогда как растровая
ЭЛТ — аналоговое устройство, для работы которого требуется электрическое
напряжение. Поэтому при считывании информации из буфера кадра и ее выводе на
графическое устройство с растровой ЭЛТ должно происходить преобразование из
цифрового представления в аналоговый сигнал. Такое преобразование выполняет
цифро-аналоговый преобразователь (ЦАП). Каждый пиксел буфера кадра нужно
считать и преобразовать, прежде чем он будет отображен на растровой ЭЛТ. На
рис. 1-24 приведена схема графического устройства с черно-белой растровой ЭЛТ,
которое построено на принципе буферизации кадра в одной битовой плоскости.
Цвета или полутона серого цвета могут быть введены в буфер кадра путем
использования дополнительных битовых плоскостей. На рис. 1-25 показаны схемы
буфера кадра с N битовыми плоскостями для градации серого цвета.
Интенсивность каждого пиксела на ЭЛТ управляется содержимым соответствующих
пикселов в каждой из N битовых плоскостей. В соответствующую позицию регистра
загружается бинарная величина (0 или 1) из каждой плоскости. Получившееся в
результате двоичное число интерпретируется как уровень интенсивности между
О и 2N — 1. С помощью ЦАП это число преобразуется в напряжение между О
(темный экран) и 2N — 1 (максимальная интенсивность свечения). Таким образом
можно получить 2 уровней интенсивности. Рис. 1-25 иллюстрирует систему с
тремя битовыми плоскостями для 8 (23) уровней интенсивности. Для каждой
битовой плоскости требуется полный объем памяти при заданном разрешении
растра: например, буфер кадра с тремя битовыми плоскостями для растра 512 х 512
занимает 7864 32 (3 х 512 х 512) битов памяти.
Таблица 1-1 Комбинации цветов для простого 3-битового буфера кадра
Красный Зеленый Синий
Черный
Красный
Зеленый
Синий
Желтый
Голубой
Пурпурный
Белый
0
1
0
0
1
0
1
1
Зеленый
0
0
1
0
1
1
0
1
с
0
0
0
1
0
1
1
1
Число доступных уровней интенсивности можно увеличить, незначительно
расширив требуемую для этого память и воспользовавшись таблицей цветов, как
это схематично показано на рис. 1-26. После считывания из буфера кадра
битовых плоскостей получившееся число используется как индекс в таблице цветов,
в которой должно содержаться 2N элементов. Каждый ее элемент может иметь
W бит, причем W может быть больше N. В этом случае можно получить 2W
значений интенсивности, но одновременно могут быть доступны лишь 2N из них.
Для получения дополнительных значений интенсивности необходимо изменить
или перезагрузить таблицу цветов.
Поскольку существует три основных цвета, можно реализовать простой
цветовой буфер кадра с тремя битовыми плоскостями, по одной на каждый из цветов.
Отдельная битовая плоскость управляет индивидуальной электронной пушкой
для каждого из трех основных цветов, используемых в устройстве. Комбинации
их трех основных цветов дают восемь цветов на экране ЭЛТ, которые вместе с
соответствующими им двоичными кодами приведены в табл. 1-1. Схема простого
цветового растрового буфера кадра показана на рис. 1-27.
Для каждой из трех цветовых пушек могут использоваться дополнительные
битовые плоскости. На рис. 1-28 схематично показан цветовой буфер кадра с 8
битовыми плоскостями на каждый цвет, т. е. буфер кадра с 24 битовыми
плоскостями. Каждая группа плоскостей управляет 8-разрядным ЦАП и может
генерировать 256 (28) оттенков, или интенсивностей, красного, зеленого или синего
цвета. Их можно комбинировать для получения 16 777 216 [(28)3 = 224]
возможных цветов. Это «полноцветный» буфер кадра.
Полноцветный буфер кадра можно еще увеличить путем использования групп
битовых плоскостей в качестве индексов в таблицах цветов, как это показано на
рис. 1-29. При N битах на цвет и И^-разрядных элементах таблиц цветов
одновременно могут быть показаны (23)лг цветовых оттенков из палитры с (23)w
возможных цветов. Например, при буфере кадра с 24 битовыми плоскостями (N = 8) и
тремя 10-разрядными таблицами цветов (W = 10) могут быть получены 16 777 216
(224) цветовых оттенков из палитры 1 073 741 824 (230) цветов, т. е. около 17 млн.
оттенков из палитры немногим менее чем 1 млрд. цветов. Несмотря на то что на
рис. 1-29 схематически показаны три различных таблицы цветов, при небольшом
количестве физических битовых плоскостей (не более 12) более предпочтительной
является ситуация, когда изменение цветов осуществляется непрерывно в
таблице с (23)N элементами.
Таблица цветов
Рис. 1-26 Полутоновый черно-белый буфер кадра с N битовыми плоскостями и
^-разрядной таблицей цветов.
/
У
1=>
-^Т^-^ЦАп}-*-
Цветовые
Регистры пушки
синий
-*fl -*• ЦАП -*■ зеленый
О -*\ ЦАП —- красный
Рис. 1-27 Простой цветовой буфер кадра.
V
г
Регистры
синий 75
зеленый 172
—»■ 8-разр. ЦАП
красный 10
8-разр. ЦАП
8-разр. ЦАП
синий
♦ зеленый \
красный
Буфер кадра
Рис. 1-28 Цветовой буфер кадра с 24 битовыми плоскостями.
Из-за большого количества пикселов в растровых графических устройствах
трудно достигнуть производительности, необходимой для работы в реальном
масштабе времени, а также для работы с приемлемой частотой регенерации, или
смены кадра. Например, если среднее время доступа к каждому отдельному пикселу
равно 200 не (200 х Ю-9 с), то для организации доступа ко всем пикселам кадра
размером 512 х 512 потребуется 0.0524 с, что эквивалентно частоте регенерации 19
кадров (картинок) в секунду, а это значительно меньше минимально необходимой
частоты, равной 30 кадр/с. В буфере кадра размером 1024 х 1024 содержится
немногим более 1 млн. бит (1 Мбит), и при среднем времени доступа 200 не требуется
0.21 с для обращения ко всем пикселам, что составляет 5 кадр/с. Буфер кадра
размером 4096 х 4096 содержит 16.78 млн. бит на каждую битовую плоскость! Доступ
к ним займет 0.3 с. Для достижения скорости регенерации 30 кадров в секунду
при таком растре требуется средняя эффективная скорость доступа 2 не/пиксел.
Напомним, что за этот небольшой период времени свет успевает пройти два фута.
Работа в реальном времени с растровыми графическими устройствами
осуществляется путем одновременного доступа к группам по 16, 32, 64 и более пикселов.
В случае цветового буфера кадра каждый пиксел может содержать до 32 бит, при
этом все битовые плоскости для каждого пиксела доступны одновременно. При
среднем времени доступа для каждой группы пикселов 1600 не возможна работа
в реальном времени для буферов кадров размером 512 х 512 и 1024 х 1024.
Несмотря на то что для растровых устройств труднее достигнуть
производительности, необходимой для работы в реальном масштабе времени с приемлемыми
скоростями регенерации, чем на векторных дисплеях с регенерацией изображе-
Регистры
Таблица
' цветов
Ч Wpasp. ЦАП h Ч ^разр.ЦАП р.
«
Цветовые пушки
Рис. 1-29 Цветовой буфер кадра с 24 битовыми плоскостями и 10-разрядиой таблицей
цветов.
:::z l. : ::
ЙнЭ^Й^ЁЗЕ^ЕШ^^
§ щя iiiiisiiK
"г ЁЁ£ь1&^Ё^12^аЁ£ Г
Li ||sil^»%*SalS^2
H i i* я S S ? £ 5 В i В р8
"II* ЦШЦ^ЦЯ*
__ ll 1 ssSeI sli^is
Ь _:
Рис. 1-30 Изображение сплошной фигуры на растровом графическом устройстве.
ния, на них легче изображать сплошные фигуры с плавными переходами цветов.
Как показано на рис. 1-30, растровое представление сплошной «полигональной»
фигуры концептуально достаточно просто. Здесь представление сплошной
фигуры, ограниченной отрезками LI, L2, L3, L4, достигается установкой всех
пикселов внутри ограничивающего многоугольника в соответствующий цвет в буфере
кадра. Алгоритм «растровой развертки» сплошной области обсуждается в
работе [1-1].
1-10 УСТРОЙСТВО ЭЛЕКТРОННО-ЛУЧЕВОЙ ТРУБКИ
Описанный выше буфер кадра сам по себе не является устройством вывода, он
просто применяется для хранения рисунка. Наиболее часто в качестве устройства
отображения, используемого с буфером кадра, выступает видеомонитор. Для
того чтобы понять принципы работы растровых дисплеев и в некоторой степени
векторных устройств с регенерацией, нужно иметь определенное представление
об ЭЛТ и видеотехнике.
На рис. 1-31 схематично показана ЭЛТ, используемая в видеомониторах.
Катод (отрицательно заряженный) нагревается до тех пор, пока возбужденные
_ „ Отклоненный
Электронная Пластина электронный
фокусирующая горизонтального луч
линза отклонения
=—G>—-=
Катод
Пластина
вертикального
отклонения
Анод (слой
" люминофора)
Электронный
пучок
Рис. 1-31 Электронно-лучевая трубка.
электроны не создадут расширяющегося облака (электроны отталкиваются друг
от друга, так как имеют одинаковый заряд). Эти электроны притягиваются к
сильно заряженному положительному аноду. На внутреннюю сторону
расширенного конца ЭЛТ нанесен люминофор. Если бы электронам ничто не
препятствовало, то в результате их воздействия на люминофор весь экран ЭЛТ засветился
бы ярким светом. Однако облако электронов с помощью электронных линз
фокусируется в узкий, строго параллельный пучок, и теперь электронный луч дает
одно яркое пятно в центре экрана. Луч отклоняется, или позиционируется,
влево или вправо от центра и(или) выше или ниже центра с помощью усилителей
горизонтального и вертикального отклонения.
Именно в данный момент проявляется отличие векторных дисплеев —как с
запоминанием, так и с регенерацией — от растровых. В векторном дисплее
электронный луч может быть отклонен непосредственно из любой произвольной
позиции в любую другую позицию на экране ЭЛТ (аноде). Поскольку люминофор
нанесен на экран сплошным слоем, то в результате получается почти идеальная
прямая. В отличие от этого в растровом дисплее луч может отклоняться только в
строго определенные позиции на экране, образующие своеобразную мозаику. Эта
мозаика и составляет видеоизображение.
1-11 УСТРОЙСТВО ЦВЕТНОЙ РАСТРОВОЙ ЭЛТ
Цветная растровая ЭЛТ похожа на обычную черно-белую ЭЛТ, принцип
действия которой был описан в предыдущем разделе. Данная трубка содержит три
электронные пушки, по одной на каждый основной цвет: красный, зеленый и
синий. Электронные пушки часто объединены в треугольный блок,
соответствующий подобному треугольному блоку точек красного, зеленого и синего
люминофоров на экране ЭЛТ (рис. 1-32). Для того чтобы электронные пушки возбуждали
только соответствующие им точки люминофора (например, красная пушка
возбуждала только точку красного люминофора), между пушками и поверхностью
экрана помещена перфорированная металлическая решетка — так называемая
теневая маска стандартной ЭЛТ. Отверстия в маске образуют такие же треуголь-
WWWWWWWWW
D 0 0©А®©0 0 d
0 0 0 © (А) ® 0 0 0
^000^4)000(7
Рис. 1-32 Точечный люминофорный растр для ЭЛТ с теневой маской.
Теневая маска
Зеленый луч
Синий луч
-—Экран ЭЛТ;
красная,зеленая,
синяя точки
люминофора
Схождение
лучей
Рис. 1-33 Расположение электронной пушки и теневой маски цветной ЭЛТ.
ные блоки, как и точки люминофора. Расстояния между отверстиями
называются шагом. Цветовые пушки расположены таким образом, что их лучи сходятся
и пересекаются в плоскости теневой маски (рис. 1-33). После прохождения через
отверстие красный луч, например, защищен или маскирован от пересечения с
зеленой или синей точками люминофора. Он может пересечь лишь красную точку.
Изменяя интенсивность электронного луча для каждого основного цвета, можно
получить различные оттенки. Комбинация этих оттенков дает большое
количество цветов для каждого пиксела. Обычно в дисплее с высоким разрешением на
каждый пиксел приходится от двух до трех цветовых триад.
1-12 СИСТЕМЫ С ТЕЛЕВИЗИОННЫМ РАСТРОМ
Процесс преобразования хранящегося в буфере кадра растрового изображения
в упорядоченный набор точек на телеэкране называется растровой разверткой.
Сканируемый набор точек и частота воспроизведения основаны как на
особенностях визуального восприятия, так и на принципах электроники. Системе
визуального восприятия человека для рассмотрения элементов картинки требуется
конечное время. Однако обеспечить впечатление непрерывности позволит
только такой интервал, который настолько мал, что инерция зрительного
восприятия перекроет мерцание. На мерцание влияет ряд факторов, включая яркость
изображения и свойства конкретного люминофора, используемого для покрытия
экрана ЭЛТ. Опыт показывает, что для практических целей минимальной
скоростью вывода или изменения изображения является 25 кадр/с при условии, что
минимальная скорость регенерации или воспроизведения в два раза больше, т. е.
50 кадр/с. Аналогичная ситуация имеет место и при демонстрации кинофильма.
При этом показывается 24 кадр/с, но каждый кадр показывается дважды, и в
результате получается эффективная скорость воспроизведения 48 кадр/с. Таким
образом, для фильма скорость изменения равна 24 кадр/с, а скорость
регенерации—48 кадр/с. В телевидении тот же эффект достигается с помощью метода
чересстрочной развертки.
Телевидение использует метод растрового сканирования. В американской
стандартной видеосистеме используются в совокупности 525 горизонтальных строк с
кадровым, или видовым, отношением 4:3, т. е. высота видовой области равна трем
Рис. 1-34 Схема чересстрочной развертки для растра из семи строк. Нечетное поле
начинается со строки 1. Штриховой линией обозначен горизонтальный обратный ход
луча. Вертикальный обратный ход луча для нечетного поля начинается внизу в центре,
а для четного поля — внизу справа.
четвертям ее ширины. Скорость воспроизведения, или смены кадра, составляет
30 кадр/с. Однако каждый кадр делится на два поля, каждое из которых
содержит по половине картинки. Эти два поля чередуются или перемежаются. Они
попеременно показываются через каждые 1/60 с. Одно поле содержит все строки
с нечетными номерами (1,3,5,...), а другое — с четными (2,4,6,...).
Сканирование начинается в верхнем левом углу экрана с нечетного поля. Каждая строка в
поле сканируется или представляется слева направо. В то время как электронный
луч движется поперек экрана слева направо, он также перемещается вертикально
вниз, но с намного меньшей скоростью. Таким образом, «горизонтальная»
сканирующая строка в действительности немного наклонена. При достижении правого
края экрана луч становится невидимым и быстро возвращается к левому краю.
Такой горизонтальный возврат луча обычно занимает около 17% времени,
отведенного для одной сканирующей строки. Затем этот процесс повторяется со
следующей нечетной строкой. Так как половина от 525 равна 262.5 строки, то
при завершении сканирования поля нечетных строк луч окажется в центре
нижней строки экрана (рис. 1-34 и рис. 1-35). Луч после этого быстро переводится в
центр верхней стороны экрана. Так осуществляется вертикальный перевод луча
для нечетного поля. Время, затрачиваемое на него, эквивалентно времени,
затрачиваемому на сканирование 21 строки. Затем показывается поле четных строк,
после чего луч оказывается в нижнем правом углу. Перевод луча для поля четных
строк возвращает его в верхний левый угол, и весь процесс повторяется снова.
Таким образом, показываются два поля для каждого кадра, т. е. 60 полей в
секунду. Данный метод существенно уменьшает мерцание, так как глаз воспринимает
частоту воспроизведения полей.
Хотя в принятой в США стандартной видеосистеме предусмотрено 525 строк,
на самом деле видимы только 483 строки, так как время, затрачиваемое на
сканирование 21 строки, уходит на вертикальный перевод луча1. В течение этого
1 Во многих графических устройствах с растровым сканированием это время используется
для обработки другой информации.
Кадр
нечетное
поле сканирования
I видимые I
'нечетные строки'
I вертикальный I
I обратный ход ■
для нечетных строк
четное
поле сканирования
видимые
четные строки
1 Г
вертикальный I
обратный ход I
для четных строк
| 241у строки | I 21 строка i i 241у строки | | 21 строка |
262 \ строки
262 j строки
323 строк
Рис. 1-35 Схема 525-строчного стандартного кадра.
времени электронный луч невидим или отключен. Время, отпущенное на
каждую сканирующую строку, легко подсчитывается для частоты воспроизведения
30 кадр/с:
1/30 с/кадр х 1/525 кадр/строка = 63,5 мкс/строка.
Так как примерно 10,5 мкс расходуется на горизонтальный перевод луча, то
вывод видимой части каждой строки должен быть завершен за 53 мкс. В строке
при нормальном соотношении сторон видеообласти, равном 4:3, находятся 644
пиксела. Таким образом, время, отпущенное на считывание и вывод пиксела,
равно
53 мкс/строка х 1/644 строка/пиксел = 82 нс.
Во многих растровых дисплеях, построенных на основе буфера кадра,
применяется разрешение 512 пикселов на строку. Считывание и вывод пикселов при
таком разрешении происходит примерно за 104 не. Аналогичные результаты
получаются для 625-строчной видеосистемы с частотой воспроизведения 25 кадр/с,
используемой в Великобритании и большинстве стран Европы.
Метод чересстрочной развертки не является абсолютно необходимым при
выводе изображения, однако изображение без чередования строк будет
несовместимым со стандартным телевизионным приемником. При отсутствии чересстрочной
развертки придется для устранения мерцания увеличить частоту
воспроизведения до 60 кадр/с, а это, безусловно, в 2 раза сокращает время для обработки
пиксела. Более высокое разрешение по числу строк и количеству пикселов в строке
также уменьшает это время; например, при разрешении 1024 х 1024 на
считывание и вывод пиксела отводится в 4 раза меньше времени, чем при разрешении
512 х 512, —примерно 25 не! В этом случае потребуется очень быстрая память
для буфера кадра и такой же высокопроизводительный ЦАП.
1-13 ДИСПЛЕИ С ПЛОСКИМ ЭКРАНОМ
Несмотря на то что в настоящее время электронно-лучевые трубки (ЭЛТ) в
качестве устройств графического вывода находятся вне конкуренции, им присущ ряд
недостатков: большие габариты, тяжелый вес, хрупкость и ограниченные
размеры экрана (обычно 30 дюймов по диагонали). На фоне этих и других ограничений
ЭЛТ очень выигрышно выглядят плазменные дисплеи, принадлежащие к типу
растровых устройств с регенерацией изображения.
Плазменные дисплеи по способу формирования изображения делятся на два
принципиально различных класса устройств: активные (светоэмиссионные) и
пассивные (основанные на модуляции света). К первым устройствам относятся ЭЛТ,
дисплеи на газоразрядных панелях, электролюминесцентные и вакуумные
дисплеи. Жидкие кристаллы и светодиоды представляют класс пассивных устройств.
Среди устройств с активной генерацией света для решения задач
интерактивной машинной графики наиболее подходят плазменные и
электролюминесцентные дисплеи, которые способны генерировать большие изображения с высокой
разрешающей способностью. За исключением некоторых специальных
приложений, например в авиации, где дисплеи на светоэмиссионных диодах обладают
некоторыми преимуществами, дисплеи на жидких кристаллах являются наиболее
удачными устройствами из класса систем с пассивной регенерацией света.
Как показано на рис. 1-36, изображение на плоской ЭЛТ получается после
прохождения луча параллельно экрану и отражения под прямым углом.
Использование эффекта отражения позволяет значительно уменьшить протяженность
колбы ЭЛТ и, соответственно, габариты дисплея. ЭЛТ в форме плоской
панели обладают теми же преимуществами, что и обычные ЭЛТ, но при
значительно меньших габаритах. Большая длина «шейки» ЭЛТ ограничивает области ее
применения. Использование вакуумных флюоресцентных дисплеев также в
значительной степени сдерживается их габаритами.
Дисплеи на газоразрядных панелях, электролюминесцентные дисплеи и
дисплеи на жидких кристаллах имеют несколько общих характеристик. Все они
состоят из матрицы отдельных пикселов растра, в каждом из которых помещено
некоторое устройство или вещество, которые под воздействием напряжения или
тока начинают испускать свет либо модулировать падающий свет. Требуемое для
этого напряжение или ток подается каждому пикселу через отдельный
электрический вентиль, например тонкопленочный транзистор, диод или резистор типа
Отклоняющая
катушка Электростатические
Рис. 1-36 Схема ЭЛТ.
Рис. 1-37 Типичный плазменный дисплей. (С разрешения фирмы Thomson CSF
Electron Tubes & Device.)
металл—изолятор—металл, размещенный под каждым пикселом. Дисплеи,
основанные на данном принципе, называются матричными.
Другой способ, получивший широкое распространение, основан на
использовании адресации пикселов по строкам и столбцам, что позволяет значительно
уменьшить количество вентилей или драйверов генерации изображения. Данный
способ предполагает .наличие у материала, из которого изготовлен дисплей,
некоторого порога переключения. Эмиссия или модуляция света в таком элементе
возможна только при превышении такого порога переключения. На
соответствующую строку матрицы пикселов подается напряжение или ток, недостаточные для
активации отдельного пиксела, а на соответствующий столбец подается другое
напряжение или ток. Каждое в отдельности воздействие по строке или по
столбцу ниже порогового значения, а в сумме они превышают его..По этой причине
пикселы, не лежащие на пересечении нужной строки и столбца, оказываются в
невозбужденном состоянии и только один пиксел получает напряжение или ток
выше порогового значения становится активным.
При использовании такой адресации весьма желательно наличие для пикселов
бистабильной памяти, в которой однажды активизированный пиксел сохраняет
свое состояние, пока не произойдет его явное переключение. Бистабильная память
исключает необходимость в постоянной регенерации пикселов, и, как следствие
этого, не требуется внешней памяти для регенерации. Кроме того, значительно
упрощается устройство дисплейного контроллера.
Принцип работы плазменного или газоразрядного дисплея предельно прост.
Дисплей состоит из матрицы ячеек (растр), окруженных стеклянной оболочкой.
Каждая ячейка заполнена газом (обычно неоном или смесью аргона с неоном) под
давлением (ниже атмосферного). При действии достаточно высокого напряжения
происходит диссоциация газа, т. е. атомы лишаются своих электронов. Такой газ в
состоянии диссоциации называется плазмой, отсюда и возникло название — плаз-
менные дисплеи. При рекомбинации электронов происходит освобождение
энергии в форме фотонов и газ начинает светиться с характерным оранжево-красным
оттенком. На рис. 1-37 показан типичный плазменный дисплей.
Активация в плазменных дисплеях может быть типа АС (переменный ток) или
DC (постоянный ток) либо представлять комбинацию AC/DC. На рис. 1-38 а, Ъ и
с приведены схемы плазменных дисплеев с активацией типа AC, DC и гибридной
типа AC/DC соответственно. Дисплеи с типом DC являются более простыми, чем
АС, и состоят из полой диэлектрической панели, содержащей полости с газом,
которые помещены между панелями с матрицей проводников. Электронное поле
прилагается непосредственно к газу. Дисплеи с типом DC обладают достаточно
продолжительным циклом регенерации.
В дисплеях с типом АС слой диэлектрика размещается между проводником
и газом. Таким образом, единственный путь соединения между газом и
проводником — это емкость (конденсатор), и поэтому для получения диссоциированного
газа требуется использование напряжения. Плазменные дисплеи типа АС имеют
бистабильную память, что исключает необходимость в длительной регенерации.
Эффект бистабильной памяти достигается при использовании низкого АС
постоянного напряжения. Имеющейся емкости оказывается достаточно для
поддержания напряжения активации токопроводящих пикселов, но недостаточно для
активации непроводящих.
В гибридных дисплеях с типом активации AC/DC (рис. 1-38с) используется
DC-напряжение для «первичного» газа, а для облегчения активации применяется
АС-напряжение. Принципиальное преимущество гибридных AC/DC-плазменных
дисплеев — это снижение сложности управляющей схемы. На практике находят
применение как дисплеи больших размеров (3x3 метра с разрешением 4096 х
4096), так и системы высокого разрешения (100 пикселов на дюйм). На основе
использования данных принципов можно также создавать цветные и полутоновые
монохромные дисплеи.
В электролюминесцентном дисплее фосфоресцирующий материал излучает
свет под действием электрического поля от АС или DC. В качестве
фосфоресцирующего материала обычно используется сульфид цинка с добавками марганца,
поэтому эти дисплеи излучают желтый свет. Для адресации пикселов
используется такой же способ, как и в плазменных дисплеях. При подаче напряжения,
превышающего пороговое значение, возбуждаются электроны марганцевой
составляющей люминофора. Когда возбужденный атом возвращается на более низкую
энергетическую орбиту, он испускает фотон, вызывающий характерный желтый
цвет. Можно также получить хороший спектр серого цвета, так как уровень
люминесценции управляется напряжением и частотой приложенного электрического
поля. При использовании других типов добавок получаются различные цвета
свечения покрытия, следовательно, из совокупности нескольких фосфоресцирующих
слоев может быть сформирован цветной дисплей.
Люминофор представляет собой либо макроскопический субстрат,
напыляемый в виде толстого слоя, либо тонкую пленку частиц толщиной в одну
молекулу. Дисплеи с типом возбуждения тонкопленочного покрытия АС и DC получили
наибольшее распространение в системах машинной графики. Принципиальная
схема электролюминесцентного дисплея приведена на рис. 1-39, а на рис. 1-40
Стекло
Стекло
Отверстия
Проводники
Стеклянный
изолятор
Катоды
Плата
диэлектрика
Полости
стазом
Прозрачные
аноды
(а)
(Ь)
Стеклянная
лицевая панель
Прозрачный
тонкопленочный
проводник
Первичная плата
с тонкопленочным
покрытием
Светоизолятор
Тонкостенный
диэлектрик
с пленочным
покрытием
Расстеклованная
плата
Сканирующие
катоды
Сканирующие
аноды
Стеклянная
несущая панель
Рис. 1-38 Принципиальная схема плазменного газоразрядного дисплея: о) АС тип;
Ь) DC тип; с) AC/DC тип.
Черный слой
Стеклянное покрытие
Стеклянный уплотнитель
Металлические электроды
Слой люминофора
(Сульфид цинка: магнезия)
Прозрачные
электроды
Направление взгляда
Рис. 1-39 Принципиальная схема электролюминесцентного дисплея типа АС.
Рис. 1-40 Электролюминесцентный дисплей. (С разрешения фирмы Hewlett Packard.)
У +
У
4c
Прохождение
—x плоскополяриэованного
(а)
Поглощение
света
Рис. 1-41 Поляризация света: а) прохождение плоскополяриэованного света; 6)
поглощение света.
изображен типичный дисплей такого типа. Из рисунка видно, что дисплей с
разрешением 100 пикселов на дюйм имеет вполне компактные габариты.
Если плазменные и электролюминесцентные дисплеи представляют собой
примеры устройств, использующих активную панель, то дисплеи на жидких
кристаллах являются образцом пассивной технологии, основанной либо на пропускании,
либо на отражении падающего света. Для изменения характеристики падающего
света используются свойства поляризации, которыми обладают некоторые
органические вещества.
Рис. 1-41 наглядно иллюстрирует основные принципы поляризации света.
Некогерентный свет (рис. 1-41а) проходит через первый (на рисунке левый)
поляризатор и поляризуется по плоскости ху. Оси поляризации второго поляризатора
также ориентированы в плоскости ху, поэтому свет беспрепятственно проходит
дальше. На рис. 1-41Ь плоскость второго поляризатора повернута под прямым
углом относительно первого, и поэтому свет, поляризованный в плоскости
первого поляризатора, поглощается при прохождении через второй.
Органические вещества, способные сохранять стабильность в мезофазе при
температуре между жидким и твердым состоянием, называются жидкими
кристаллами. Различают три типа мезофазы: смектическую, нематическую и холе-
стерическую.
В нематической фазе оси молекул жидкого кристалла располагаются
параллельно, причем на их направление выравнивания влияют температура,
поверхностное натяжение, давление и, что особенно важно для дисплеев, электрические
Скрученная структура Выравнивание молекул
нематического кристалла жидкого кристалла
для пиксела для пиксела
в состоянии «OFF» в состоянии «ON»
Рис. 1-42 Принципиальная схема дисплея на скрученных нематических жидких
кристаллах.
и магнитные поля. Оптические характеристики жидкого кристалла также
достаточно чувствительны к этим воздействиям.
Ключевым моментом одного из возможных способов построения дисплеев на
жидких кристаллах является создание «бутерброда» из нематических кристаллов
со взаимоперпендикулярными осями. На рис. 1-42 приведено изображение
принципиальной схемы отражающего нематического жидкокристаллического дисплея.
Нижняя и верхняя плата бутерброда из жидких кристаллов имеют канавки,
причем канавки на верхней плате направлены под прямым углом к канавкам нижней
платы. Жидкие кристаллы прилегают к поверхности платы с соблюдением
направлений канавок (рис. 1-42).
Дисплей имеет два плоских поляризатора, каждый из которых расположен
на обеих сторонах бутерброда и повернут под прямым углом к другому. При
затемненном пикселе или в состоянии поворота падающий на поверхность свет
поляризуется первым поляризатором, затем проходит через
жидкокристаллический бутерброд, где он поворачивается на прямой угол, далее идет сквозь второй
поляризатор и затем отражается обратно, а пиксел становится подсвеченным.
Включение пиксела осуществляется путем подачи электрического поля на
жидкий кристалл, что вызывает его переориентацию. Свет, падающий на па-
нель дисплея, поляризуется теперь первым поляризатором, проходит через
жидкий кристалл без каких-либо изменений и оказывается полностью поглощенным
вторым поляризатором. Пиксел становится темным. Жидкокристаллические
дисплеи на повернутых нематических кристалах требуют для своей работы
постоянной регенерации.
Бистабильные дисплеи на жидких кристаллах могут быть построены на базе
смектических кристаллов, две устойчивые ориентации молекул которых обладают
различными оптическими свойствами, например уровнем отражения. Это
позволяет достигать оптических контрастов за счет приложения импульсного
напряжения, вызывающего изменение состояния молекул. Для дисплеев на кристаллах
данного типа не требуется регенерации.
Использование цветных фильтров или фосфоров позволяет строить цветные
дисплеи на основе повернутой нематическои технологии или с использованием
окрашивающих добавок. В дисплеях на кристаллах с добавками в основную жид-
кокристалическую подложку вносятся двухцветные посторонние молекулы,
спектральные характеристики которых используются для формирования различных
цветов. Под действием электрического поля происходит изменение ориентации
основных и привнесенных молекул, что дает возможность свету беспрепятственно
проходить сквозь кристалл. На рис. 1-43 схематически показан типичный жидкий
кристалл типа гость-хозяин. Отметим, что в этом случае требуется только один
поляризатор. На основе данного кристалла можно построить также дисплеи,
отражающие свет.
Дисплеи на жидких кристаллах имеют адресацию типа строка-столбец либо
содержат активные матричные элементы, например транзисторы или диоды в
каждом пикселе. Обычная разрешающая способность данных дисплеев
составляет 100 пикселов на дюйм.
1-14 ЭЛЕКТРОСТАТИЧЕСКИЕ ГРАФОПОСТРОИТЕЛИ
Электростатические графопостроители принадлежат к типу устройств с
растровым сканированием (см. разд. 1-9, 1-12). Основной принцип их
функционирования—это нанесение частиц краски на участки бумаги, обладающие
определенным электрическим зарядом. На рис. 1-44 представлена обобщенная схема
устройств данного типа. Специальное покрытие носителя изображения,
удерживающее электростатический заряд, помещается около записывающей головки,
которая содержит от 1 до 3 рядов пишущих узлов или перьев. Обычно на одном
дюйме располагается от 72 до 400 таких перьев. Чем больше рядов пишущих
узлов, тем выше плотность печати. При прохождении носителя под рядами перьев
каждое из них наносит отрицательно заряженную точку. Далее носитель
проходит через тоновый аппликатор, где положительно заряженные частицы краски
притягиваются к точкам изображения, имеющим отрицательный заряд, в
результате на носителе проступает видимое изображение. Затем частицы графитовой
краски просушиваются и фиксируются на носителе. В качестве материала
носителя изображения для графопостроителя может быть использована непрозрачная
или полупрозрачная пергаментная бумага и прозрачная или матовая
полиэфирная пленка.
Двухцветные
молекулы
Источник >^7
света ^-г
(неполяризованный)
Ж
Поляризатор
Молекулы
жидкого
кристалла
Наблюдатель
(о)
Наблюдатель
Включено
(6)
Рис. 1-43 Жидкие кристаллы типа гость-хозяин (закрашены). Молекулы
ориентированы для блокировки (о) и для свободного прохождения (6).
Накопитель
бумаги
Г
Записывающая
головка
Краскораспылитель
(пурпурный)
Краскораспылитель
(желтый)
Нанесение
тонера
Краско- |
распылитель I
(голубой)
Ведущий ролик
Краско-
распылитель Очиститель
(черный)
Нанесение Нанесение Нанесение
тонера тонера тонера
Рис. 1-44 Принципиальная схема цветного электростатического графопостроителя.
(a) (b) (с)
Рис. 1-45 Образцы размещения точек: а) без совмещения, 6) совмещение по оси у, с)
совмещение по осям хтиу.
Типичная ширина электростатических графопостроителей достигает 72
дюймов, а длина изображения ограничивается только длиной рулона материала
носителя (обычно это 500 футов). Разрешающая способность данных устройств
задается количеством точек на дюйм (dpi). Точность определяется несколькими
различными способами. Предполагается, что направление движения материала
может быть изменено на противоположное, точность в этом случае определяется
величиной ошибки, т. е. величиной расхождения в размещении двух точек,
нанесенных одним и тем же пером при двух последовательных проходах.
Электростатические графопостроители являются растровыми устройствами
вывода, поэтому для них имеет место лестничный эффект [1-1]. В устройствах с
высоким разрешением данный эффект устраняется за счет совмещения
отдельных точек. На рис. 1-45 показан типичный образец размещения точек. Обычный
уровень совмещенности точек составляет от 30% до 50%. В связи с тем что
электростатический графопостроитель является устройством с растровым
сканированием, элементы изображения, например линии и многоугольники, должны иметь
растровую развертку, а само изображение организуется по растровому принципу:
сверху вниз, слева направо. Изображение может быть подготовлено на главном
компьютере, однако необходимо соблюдать ряд требований организации
вычислений. Кроме этого, для получения высокой скорости обработки картинки
необходимо использовать быстрый интерфейс для передачи развернутого по растру
изображения. Например, для графопостроителя шириной 36 дюймов, имеющего
разрешение 400 точек на дюйм, требуется передавать данные от главного
компьютера со скоростью 360 Кб/с для получения скорости рисования, равной 1 дюйм/с.
С целью повышения быстродействия многие электростатические
графопостроители работают со специальным контроллером [1-6]. На рис. 1-46 изображен
типичный электростатический графопостроитель.
Существуют также цветные графопостроители, в которых используются три
основных субтрактивных цвета [1-1]—голубой (cyan), пурпурный (magenta) и
желтый (yellow) — (CMY) — и четвертый, черный, которые наносятся на материал
за один или четыре прохода. В случае одного прохода, отдельные ряды перьев
используются для нанесения' каждого из цветов. При нескольких проходах каждый
цвет наносится в течение одного прохода. Обычный графопостроитель
поддерживает 7 цветов. Цветовая закраска сплошных многоугольников
осуществляется путем псевдотонирования или заполнения узором [1-1]; Количество
возможных цветов зависит от размеров используемого узора (например, 2 х 2, 2 х 3
или 4 х 4) и от разрешения графопостроителя. Обычно при высоком
разрешении графопостроитель способен выводить несколько тысяч цветов. Стандартная
Рис. 1-46 а) Электростатический графопостроитель. (С разрешения фирмы Versatec
Corp.) b) Низкое разрешение 100 dpi; с) Высокое разрешение 400 dpi.
ширина электростатических графопостроителей — 42 дюйма, а разрешение — 400
точек на дюйм.
1-15 ЛАЗЕРНЫЕ ПЕЧАТАЮЩИЕ УСТРОЙСТВА
Несмотря на то что лазерные печатающие устройства (принтеры)
первоначально создавались для использования в типографском деле, они нашли достаточно
широкое применение и в машинной графике при решении задач вывода
графических изображений. Возможности этих устройств оказались особенно полезными
в различного рода издательских системах, где возникает необходимость в
компоновке на одной странице текстов и изображений [1-7]. Такие системы позволяют
комбинировать выведенные различными шрифтами тексты, художественные
иллюстрации и полутоновые изображения, как, например, представлено на рис. 1-47.
Лазерный принтер принадлежит к семейству растровых устройств.
Принципы его действия, схематично представленные на рис. 1-48, во многом подобны
принципам, применяемым при ксерокопировании. Печатающий механизм имеет
покрытый фоточувствительным веществом барабан, по поверхности которого
может перемещаться луч лазера (газоразрядного или полученного от
полупроводникового диода). При вращении барабана его покрытие получает электрический
заряд, который сохраняется до момента падения на него когерентного
лазерного луча. В результате прохождения луча на барабане появляются зоны (точки),
не имеющие заряда, которые в совокупности образуют негативное изображение
будущей картинки. Позиционирование луча на барабане осуществляется с
помощью вращающегося многогранного отражателя. Черный порошок на пластиковой
основе (тонер) притягивается к заряженным точкам на барабане, изображение с
которого переносится затем на лист положительно заряженной бумаги. На
завершающей стадии формирования изображения происходит фиксация тонера путем
его вплавления под действием температуры и давления.
Картинка наверху слева формируется Определяя переменную box, можно
командами rlineto и arc. Затем путем обеспечить вывод прямоугольника
масштабирования и поворота можно различными способами. Используя
получить различные изображения команды stroke, setgray, file, можно
выводить один и тот же
прямоугольник в разных видах и положениях
Рис. 1-47 Лазерный принтер позволяет формировать страницу путем комбинации
текстов, иллюстраций и полутоновых изображений. (С разрешения фирмы QMS, Inc.)
Рис. 1-48 Схема устройства лазерного принтера.
Обычно лазерный принтер имеет разрешение от 240 х 240 до 600 х 600 т/дюйм.
Наиболее типичное разрешение — это 300 х 300 т/дюйм. Лабораторные
эксперименты показывают, что практически высший предел возможностей данной
технологии—800 х 1000 т/дюйм. При более высоком разрешении происходит
спекание соседних точек тонера. Несмотря на то что лазерные принтеры
используются для типографского набора, их обычное разрешение значительно меньше,
чем разрешение, полученное при хорошем фотонаборе (1200-5000 т/дюйм).
Качество современных принтеров ограничено размерами отдельной точки, однако
лабораторные эксперименты по изменению размеров точки дают
обнадеживающие результаты. Изменение размеров точки позволяет увеличить гибкость при
формировании полутоновых изображений [1-1]. Хотя размеры лазерных
принтеров определяют формат используемой для них бумаги, в настоящее время
выпускаются устройства шириной 36 дюймов с разрешением 400 т/дюйм, которые
позволяют получать изображения форматов D (22 х 44) и Е (34 х 44) — формат
АО по ЕСКД.
Лазерная печать является достаточно продолжительным процессом. Вывод
страницы происходит с постоянной скоростью, так как для получения высокого
разрешения требуется и высокая скорость обработки. Например, при разрешении
300 х 300 для печати со скоростью 8 страниц в минуту при размере 8,5 х 11
дюймов, с печатным полем 7,5 х 10,5 обеспечение непрерывной бесперебойной работы
потребует скорости 1 Мбит/с. Для поддержания такой же высокой скорости, как
и в электростатических графопостроителях, используется специальный
контроллер, общая схема которого приведена на рис. 1-49. Главный компьютер выдает
описание страницы на языке высокого уровня [1-7]. Видеоконтроллер/процессор
отвечает за генерацию шрифтов, линий или полутоновых изображений и за
передачу всего необходимого потока битовой информации (точек) на печатающее
устройство.
Язык
Главный
компьютер
описания
страницы
Видеоконтроллер/
процессор
Поток
точек
Печатающее
устройство
Рис. 1-49 Конфигурация вычислительной системы лазерного принтера.
Рис. 1-50 Лазерный принтер. (С разрешения фирмы Toshiba America, Inc.)
Рис. 1-51 Примеры изображений, вьшодимых лазерным принтером: о) векторная
графика; Ъ) полутоновые поля.
На рис. 1-50 показан типичный лазерный принтер, а на рис. 1-51 приведены
примеры обычных векторных и полутоновых изображений.
1-16 МАТРИЧНЫЕ ГРАФОПОСТРОИТЕЛИ
Принтеры использовались еще на заре становления машинной графики, когда
применялись обычные строковые устройства, принадлежащие к типу устройств
с растровым сканированием. С помощью таких принтеров можно получать
изображения, графики и даже полутоновые картинки. Вполне естественно, что при
разрешении 1/6 дюйма по вертикали и 0.1 по горизонтали изображения были
довольно грубыми.
В машинной графике применяется множество принтеров, основанных на
использовании различных методов и принципов печати: ленточные или построчные
устройства, барабанные принтеры, цепные печатающие устройства и
лепестковые принтеры. Однако наибольшую популярность и распространение получили
именно матричные устройства.
Печатающий механизм в матричных принтерах представляет собой матрицу
из тонких перьев или иголок, закрепленную на печатающей головке, которая
перемещается вдоль страницы. Основу механизма составляет электромагнит для
одной или нескольких стальных пружин, смонтированных на иглах или
молоточках. В состоянии покоя молоточки удерживаются постоянным магнитом и не
соприкасаются с красящей лентой. Для нейтрализации действия этого постоянного
магнита используется электромагнит. При его включении стальные пружины
подают молоточки вперед, вызывая соприкосновение иголки с лентой. В результате
на бумагу, которая расположена между лентой и опорой, наносится точка. После
этого электромагнит отключается, молоточек возвращается в первоначальное
положение. В конструкциях со свободными молоточками их возврат и освобождение
происходит в состоянии возбуждения электромагнита.
Существует множество различных конфигураций расположения иголок
(рис. 1-52). При невысокой плотности размещения иголок размером от 0.012
до 0.013 дюйма получается изображение точки размером 0.014-0.015 дюймов,
что позволяет иметь разрешение от 60 до 80 т/дюйм. При большей плотности
размещения иголок размером 0.008 дюймов образуется точка размером 0.009-
0.010 дюйма, а разрешение составляет 180 т/дюйм. Таким образом, видно, что
при высокой плотности точек получается отпечаток с перекрытием. В зависимо-
7 иголок 9 иголок 9 иголок 9 иголок 18 иголок, 12 иголок
в шахматном в шахматном расположенных в шахматном
порядке порядке парами порядке
Рис. 1-52 Образцы размещения иголок в матричном печатающем устройстве.
Рис. 1-53 Сравнение качества вывода матричных печатающих устройств: о) 9 иголок —
разрешение 70 точек на дюйм; Ь) 24 иголки —разрешение 180 точек.
сти от плотности точек перекрытие может составить от 20 до 50%. Перекрытие
точек уменьшает уровень смещения или ступенчатый эффект [1-1], что
способствует улучшению качества изображения. На рис. 1-53 представлена картинка,
полученная на матричных принтерах с разрешением 70 и 180 т/дюйм и
иллюстрирующая данный эффект.
Цветное изображение на матричных печатающих устройствах получается с
помощью многоцветных красящих лент. Так как бумага обладает средней
отражающей способностью, то используется четырехцветная лента, на которой
имеются три основных цвета: голубой, пурпурный, желтый (CMY), а также черный
цвет. Использование методов псевдотонирования и заполнения узорами [1-1, 1-8]
позволяет получать оттенки разного цвета.
1-17 УСТРОЙСТВО СТРУЙНОЙ ПЕЧАТИ
Устройства струйной печати являются растровыми устройствами и
используются главным образом в недорогих системах формирования цветных изображений.
Основной принцип струйной печати состоит в распылении микроскопических
капель краски на носитель изображения. Существуют два типа устройств струйной
печати: с непрерывным распылением и с распылением по запросу.
Устройства первого типа формируют поток частиц путем распыления
краски через форсунку. Такой поток прерывается с помощью ультразвуковых волн.
Капельки краски, которые должны быть нанесены на бумагу, получают
электрический заряд. Специальные отражательные пластины управляют направлением
движения частиц. Все незаряженные частицы отклоняются таким образом, что
они попадают в желоб и возвращаются затем в резервуар. Обычно в качестве
носителя изображения используется бумага или прозрачная пленка. Типичная
система струйной печати показана на рис. 1-54а. В случае применения технологии
распыления по запросу, как следует из ее названия, выброс краски происходит,
только если требуется закрасить определенную точку. Краска поступает из ре-
Резервуар
с краской
Форсунка
Отклоняющие
электроды
Пьезоэлектрический
кристалл
Подача краски
!<=2
Рис. 1-54 Принципиальная схема технологии струйной печати: а) непрерывное
распыление; 6) распыление по запросу.
зервуара и попадает под давлением в форсунку. Далее с помощью
пьезоэлектрического кристалла, на который подается напряжение, происходит впрыскивание
краски через голову форсунки. Кристалл расширяется под действием
напряжения, уменьшая объем камеры с краской, что и вызывает ее выброс из форсунки.
При отключении напряжения кристалл сжимается, увеличивая объем резервуара,
и это приводит к всасыванию краски обратно в форсунку. На рис. 1-546
представлена иллюстрация данного процесса.
Разрешающая способность устройств струйной печати определяется
размерами капли краски, а следовательно, и форсунки. При использовании максимально
узкой форсунки, возникает ряд проблем с обеспечением свободного прохожде-
ния краски, предотвращением загрязнения форсунки, а также с удалением
пузырьков воздуха. Обычное разрешение устройств данного типа составляет 120—
400 т/дюйм. Лабораторные эксперименты показывают, что возможно разрешение
в 1000 т/дюйм.
Цветные устройства струйной печати имеют, как правило, четыре форсунки,
три для основных цветов — голубого, пурпурного, желтого — и одну для черного
цвета. Основное преимущество струйной технологии состоит в способности
смешивать цвета. Так как жидкие частицы краски наносятся за один проход
носителя, они успевают перемешаться еще до высыхания. Это позволяет получать
глубину и резкость цвета, не достижимую при использовании других технологий.
Применение методов псевдотонирования и узоров, как уже отмечалось, позволяет
получать несколько тысяч цветов [1-1, 1-8].
1-18 УСТРОЙСТВО ТЕРМОПЕЧАТИ
Различают два основных принципа термопечати: с прямым и косвенным
воздействием тепла. В первом случае используется специальная термочувствительная
бумага, которая изменяет свой цвет под действием тепла. Изображение на
такой бумаге формируется печатающим узлом, который воздействует на бумагу в
процессе движения. Устройство пишущего узла матричного принтера и
печатающие головки в виде полного ряда пишущих узлов аналогичны устройству узлов,
используемых в электростатических графопостроителях. Устройства
термопечати позволяют получать разрешение в 40 т/дюйм. Главные и наиболее серьезные
ограничения технологии с прямой передачей тепла связаны с необходимостью
применения специальной бумаги, которая имеет свойство выцветать с течением
времени.
В технологии с косвенным действием тепла используется тонкая пленка или
бумажная лента, покрытая чернилами на восковой основе. Тепловыделяющие
элементы, обычно располагаемые позади ленты, расплавляют восковое покрытие, и
пигменты чернил попадают на бумагу- Одинаково часто употребляются
матричные печатающие узлы, перемещающиеся вдоль бумаги, и печатающие головки в
виде полного ряда пишущих узлов. На рис. 1-55 представлена схема технологии
Красящий
состав
Термопечатающий \ Лента
узел
г
Чернила
в восковой оболочке
Обычная бумага Нанесенная краска
Рис. 1-55 Технология с косвенным тепловым воздействием.
с косвенным воздействием тепла. В качестве основы для нанесения
изображения применяется обычная бумага. Цветные картинки получаются путем
использования многоцветных лент. Традиционные семь цветов возникают в результате
комбинации трех основных цветов (CMY) и черного цвета. Для формирования
расширенной цветовой палитры применяются шаблоны и штриховка [1-1, 1-8].
Так как чернила почти не впитываются в бумагу, то можно получать блестящие
цвета. Обычная разрешающая способность для устройств данного типа
составляет от 100 до 400 т/дюйм. Чернила, употребляемые при технологии с косвенным
воздействием, отличаются долговечностью.
1-19 ПЕРЬЕВЫЕ ГРАФОПОСТРОИТЕЛИ.
Перьевые графопостроители (прежде всего цифровые) делятся на три вида:
планшетные, барабанные и графопостроители с нажимным роликом. На рис. 1-56 даны
принципиальные схемы каждого из этих устройств.
В планшетном графопостроителе с подвижным кронштейном (рис. 1-56а)
носитель изображения закрепляется на ложе графопостроителя. Перемещение
пишущего узла на плоскости осуществляется при движении кронштейна по ширине
ложа для оси х и при движении собственно узла по кронштейну для оси у. На
(а) (Ь)
(с) (</)
Рис. 1-56 Схемы действия перьевых графопостроителей разных типов: а) планшетный
с подвижным кронштейном; 6) планшетный с подвижным пишущим узлом; с)
барабанный; d) с нажимным роликом.
Рис. 1-57 Планшетный графопостроитель с подвижным кронштейном. (С разрешения
фирмы Xynetics, Inc.)
Рис. 1-58 Планшетный графопостроитель с подвижным пишущим узлом.
рис. 1-57 приведен типичный планшетный графопостроитель с подвижным
кронштейном.
В планшетном графопостроителе с подвижным пишущим узлом (рис. 1-566)
применяется устройство рисования, которое, находясь в подвешенном
состоянии, перемещается под действием магнитных сил. Данный принцип
обеспечивает почти полное отсутствие трения. Управление движением пишущего узла по
двум направлениям осуществляется на основе электромагнитного воздействия по
принципу сервомотора. Пример графопостроителя данного типа представлен на
рис. 1-58.
Крепление носителя изображения на ложе крупноформатных планшетных
графопостроителей осуществляется с помощью вакуума. Данные устройства
имеют разрешение не менее 0.004 дюйма и скорость 3600 дюйм/мин. Размеры
планшетных графопостроителей колеблются от 8.5 х 11 дюймов до нескольких
десятков футов в ширину и длину. В качестве носителя изображения может ис-
пользоваться множество материалов, таких, как бумага, пергамент, фотопленка,
копировальная поверхность, лист металла и ткани. Этим разнообразным типам
носителей соответствует множество устройств рисования, среди которых
шариковая ручка, фломастеры и обычные чернильные перья, световые и лазерные
лучи, инструменты для гравировки, копировальные резцы и резцы по ткани.
Такое разнообразие типов носителей и пишущих узлов предполагает широкий
спектр различных сфер применения планшетных графопостроителей. Кроме их
традиционного использования для рисования, крупноформатные
графопостроители применяются для создания шаблонов печатных плат и интегральных схем.
Носителем изображения в этом случае является фотопленка, а пишущим
инструментом луч света. Различные модификации планшетных графопостроителей
используются также и для раскройки мужской и женской одежды и даже парусов.
В качестве носителя здесь выступает соответствующая ткань, а пишущим узлом
является нож либо лазерный луч.
Более дешевые и небольшие планшетные графопостроители не обладают такой
гибкостью применения и имеют более низкую скорость и разрешающую
способность. Обычно в таких устройствах используется принцип электростатического
управления носителем, в качестве которого, как правило, применяется бумага,
пергамент или прозрачная пленка.
Барабанные графопостроители (рис. 1-56с) являются более сложными в
механическом плане устройствами, чем планшетные. Пишущий узел в них
перемещается вдоль неподвижного кронштейна в одном направлении. Сам носитель
вращается вперед и назад под кронштейном, обеспечивая таким образом отрисовку
по другому направлению.
Носитель закрепляется на барабане при помощи вакуума либо прижимных
роликов. Тип материала носителя определяется его свойствами легко вращаться.
Обычно это бумага или пергамент определенной ширины. Длина носителя
ограничена только длиной ленты в рулоне. Несмотря на то что разрешающая
способность графопостроителей данного типа примерно равна разрешению планшетных
устройств (0.0005 дюйма), скорость рисования в них, как правило, значительно
ниже.
Графопостроители с прижимным роликом представляют собой смесь
планшетных и барабанных устройств. Носитель изображения размещается в них между
прижимным роликом и цилиндрической поверхностью рисования (рис. l-56d).
При вращении прижимного ролика носитель движется вперед и назад под
неподвижным кронштейном, по которому, в свою очередь, перемещается пишущий
узел. В этих графопостроителях применяется накопитель для отдельных листов
либо для рулона, что и определяет формат бумаги, пергамента или прозрачной
пленки. Обычная разрешающая способность данных устройств составляет 0.001
дюйм, а скорость равна 180 дюйм/мин. На рис. 1-59 показан графопостроитель
с прижимным роликом.
Большинство перьевых графопостроителей работают в инкрементальном
режиме и приводятся в движение шаговым мотором. Пишущий узел в них
перемещается над поверхностью рисования по восьми возможным направлениям (рис.
1-60) за некоторое число небольших шагов. Результирующая линия, проведенная
в направлении, отличном от указанных на рис. 1-60, будет иметь ступенчатый ха-
Рис. 1-59 Графопостроитель с прижимным роликом. (С разрешения фирмы Hewlett-
Packard. Со.)
Рис. 1-60 Направления движения в инкрементальных графопостроителях.
рактер. Появление такой «лестницы», или зазубренной линии, является
следствием ключевого явления, получившего название лестничный эффект (алиазинг),
т.е. дефект изображения линии вследствие дискретности растра.[1-1]. Из всех
алгоритмов построения линии, имеющих наилучшие показатели < оптимальности
выбора из восьми возможных направлений, алгоритм! Брезенхема [1-1] является
наиболее удачным. Данный алгоритм, часто ассоциируемый с растровыми
устройствами, первоначально бьш разработан именно для цифровых инкрементальных
графопостроителей.
Рис. 1-61 Пример типичного изображения, получаемого иа цифровом
инкрементальном графопостроителе.
Корректность направления движения достигается путем использования
сервомоторов, которые управляют пишущим узлом графопостроителя. В этом случае
обратная связь в цепи постоянно корректирует одновременно оба мотора для
получения гладкой линии.
Скорость является важной, но не единственной существенной
характеристикой графопостроителя. В некоторых случаях ускорение оказывает гораздо
большее влияние на общее быстродействие. Дело в том, что чертеж состоит из
коротких сегментов линий и поэтому графопостроитель должен уметь стартовать и
останавливаться между сегментами. Большее ускорение позволяет
графопостроителю быстрее достигать нужной скорости. Возможная,в настоящее время
величина ускорения превышает 4 д. Многие контроллеры графопостроителей
комплектуются также специальными программами, позволяющими заранее избегать
лишних остановок, например, в случае, когда для представления кривой
используется последовательность соединенных друг с другрм коротких отрезков.
В отличие от многих графических устройств, перьевые графопостроители
позволяют получать достаточно высококачественные изображения, такие как на
рис. 1-61.
1-20 ЦВЕТНЫЕ ВИДЕОКАМЕРЫ
С появлением высококачественных цветных растровых дисплеев в сочетании с
цветными буферами кадров (§ 1-9), способных выводить свыше 16 млн. цветов,
возникла необходимость в способе представления полученных результатов. В
настоящее время существует единственная такая технология, основанная на
использовании цветной фотопленки. Цветная видеокамера—это наиболее часто
используемое в машинной графике устройство.
Совсем простая принципиальная схема цветной камеры приведена на
рис. 1-62. В методе, называемом записью последовательных полей, используется
небольшая, диаметром 5 дюймов, монохроматическая ЭЛТ с идеально плоским
ЭЛТ Диск
с белым люминофором с Цветными фильтрами
Цветная пленка
Рис. 1-62 Принципиальная схема цветной камеры.
экраном. На оптической оси от камеры к ЭЛТ сначала помещается красный
фотофильтр, пропускающий только красные лучи от ЭЛТ, которые и попадают
на пленку. После этого экран ЭЛТ гаснет, красный фильтр заменяется на
зеленый, открывающий путь только зеленым лучам. Пленка повторно экспонируется,
оставаясь в прежнем положении. В заключение процесс повторяется для синей
компоненты изображения. Такая трижды экспонированная пленка содержит
законченное изображения рисунка.
Успех всего процесса определяется качеством ЭЛТ [1-1], для уменьшения в
ней искажений применяется плоский, а не изогнутый экран, устанавливаемый на
большинство мониторов. Стекло ЭЛТ также должно быть высокого качества, без
пузырьков, царапин и других дефектов. Для того чтобы обеспечить примерно
одинаковую реакцию на все три сигнала (красный, зеленый, синий),
применяется широкополосный люминофор, слой которого должен быть без пятен и узоров,
иметь прекрасную зернистость и однородную текстуру. Размеры точки
электронного луча должны быть минимальными размеры для достижения повышенной
разрешающей способности, а электромагнитная фокусирующая система должна
быть отличного качества.
При условии аккуратной эксплуатации разрешение такого устройства
составляет 3000 х 5000 т/дюйм при диаметре монитора 5 дюймов. Отметим, что
разрешение и адресуемость — это не идентичные понятия. Разрешением измеряется
количество отдельных различимых точек, в то же время адресуемость указывает
число позиций, в которые может быть помещен электронный луч. Из-за
ограниченности возможностей человеческого глаза картинка может иметь адресуемость
выше порога, за которым глаз уже не различает отдельных точек изображения.
1-21 АКТИВНЫЕ И ПАССИВНЫЕ ГРАФИЧЕСКИЕ УСТРОЙСТВА
Разберем различия между пассивными и активными графическими
устройствами. Пассивные устройства просто формируют под управлением компьютера
изображения, т. е. они позволяют обеспечивать графический интерфейс между
компьютером и пользователем. Матричные принтеры, электростатические и
перьевые графопостроители, устройства записи на пленку, дисплеи с запоминающей
трубкой, а также мониторы с растровой ЭЛТ — все это примеры пассивных гра-
фических устройств. Некоторые образцы этих устройств вместе с типичными
картинками, которые они способны формировать, приведены на рис. 1-17, 1-22, 1-37,
1-40, 1-46, 1-50. 1-51, 1-53, 1-57, 1-58, 1-59 и 1-61.
Активные графические устройства позволяют пользователю
взаимодействовать с компьютером при помощи графики. Обычно это означает, что
пользователь получает координатную информацию в некотором преобразованном виде,
т. е. в виде, отличном от явного вывода соответствующих чисел. Так как
картинки, кривые или поверхности можно рассматривать в виде матрицы координат,
то пользователь получает достоверную иллюстративную информацию.
Обычно активные устройства обладают возможностью позиционирования курсора и
считывания его нового положения. Типичные активные графические устройства
включают алфавитно-цифровые клавиатуры (рис. 1-6), функциональные кнопки
(рис. 1-13), координатные колеса, наборы ручек для ввода скалярных значений
(рис. 1-12), оцифровывающий или аналоговый планшеты (рис. 1-7, 1-8),
световые перья (рис. 1-15), управляющие рычаги (рис. 1-9), координатный шар
(рис. 1-10) или мышь (рис. 1-11). Несмотря на то что эти устройства могут
использоваться самостоятельно, обычно они требуют применения каких-либо пассивных
устройств. Как правило это ЭЛТ.
1-22 ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ МАШИННОЙ ГРАФИКИ
Весь комплекс программного обеспечения машинной графики не только
реализует идеи, затронутые в данной книге и в работе [1-1], но и воплощает
алгоритмы организации структур данных, проектирования и управления базами данных,
идеологию и требования к человеко-машинному интерфейсу, охватывает языки
программирования и операционные системы. Исследование всех этих вопросов
выходит за рамки данной книги, однако они затрагиваются при обсуждении
вопросов проектирования систем машинной графики.
В настоящее время разработаны и продолжают создаваться многочисленные
графические стандарты, которые в общем случае можно объединить в три
группы. Первая группа —это графический прикладной интерфейс, преобразующий
идеи в форму, понятную компьютеру. Для этих целей применяются стандарты
представления данных: графическая корневая система (GKS), иерархический
интерактивный графический стандарт программиста (PHIGS, PHIGS+)
(приложение А).
Вторая группа относится к хранению и передаче данных между
графическими системами и между САПР и системами АСТПП. В данной области имеется
стандарт IGES (формат передачи графических данных).
В третью группу входит стандарт для определения интерфейса между
программными системами машинной графики или наборами данных и системой
передачи, а также стандарт определения требований к аппаратно зависимым
драйверам графических устройств. В данной области существуют стандарты: машин-
но графический метафайл (CGM) и виртуальный интерфейс устройств (VDI).
Все эти стандарты имеют очень важное значение и представляют собой
попытку обеспечения совместимости программ, пользователей и данных. В
приложении А эти стандарты рассматриваются более развернуто, но не очень детально.
Графическая
прикладная
программа
Интерфейс
(язых)
прикладного
программиста
GKS
GKS-3D
PHIGS
PHIGS +
Программа
базовой
графики
Графическая
база
данных
IGES
CGM
Интерфейс
передачи
данных
Интерфейс
программ и
графического
устройства
Интерфейс
с драйвером
устройства*'
"I ', L
CGI
VDI
Драйвер
устройства
Драйвер
устройства
Пассивные
графические
устройства
Активные
графические
устройства
Рис. 1-63 Структура программного обеспечения машинной графики.
На рис. 1-63 показаны основные уровни организации программного обеспечения
машинной графики и место каждого из стандартов. Однако задача этой книги и
работы [1-1] состоит не в обсуждении стандартов, а в исследовании
основополагающих концепций, математических и процедурных элементов машинной графики.
Поэтому программам машинной графики уделяется минимальное внимание на
уровне основных понятий. Программные системы машинной графики,
реализующие все эти концепции, представлены в приложениях А и G. На основе всех
изложенных и разбираемых впоследствии концепций из этой книги и из
работы [1-1], а также концепций организации структур данных и проектирования баз
данных можно разработать и реализовать функционально полную программную
систему машинной графики. Эти концепции помогут также разобраться в любой
из существующих систем машинной графики.
1-23 ЛИТЕРАТУРА
1-1 Rogers D.F. Procedural Elements for Computer Graphics, McGraw-Hill, Book Co., New
York, 1985. (Имеется русский перевод: Роджерс Д. Алгоритмические основы
машинной графики.— М.: Мир, 1989.)
1-2 Foley J. D., Wallace V. L. The Art of Natural Man-Machine Conversation, Proc. IEEE,
-Vol. 62, pp. 462-471, 1974.
1-3 Wallace V. L. The Semantics of Graphic Input Devices, Сотр. Graph., Vol. 10, pp. 61-65,
1976.
1-4 Olson M. System Design Considerations for Graphics Input Devices, Computer, pp. 9-18,
Nov. 1978.
1-5 Davis M.R., Ellis Т.О. The RAND Tablet: A Man-Machine Graphical Communication
Device, AFIPS Conf. Proc, Vol. 26, Part I, 1964 FJCC, pp. 325-332, 1964.
1-6 Ben-Dor A., Jones B. New Graphics Controller for Electrostatic Plotting, IEEE Сотр.
Graph. & Appi, Vol. 6, No. 1, pp. 16-25, 1986.
1-7 Adobe Systems Inc., Postscript Language Reference Manual, Addison-Wesley Publishing
Co., Reading, MA, 1985.
1-8 Kubo S. Continuous Color Presentation Using a Low-Cost Ink Jet Printer, Proc. Сотр.
Graph. Tokyo, 84, 24-27. Apr. 1984, Tokyo, Japan, T3-6, pp. 1-10, 1984.
1-9 Constantine J. M., Jr., Electron Optical Technique for an Ultra High Resolution Color
Film Recorder, Journal of Photooptical Instrument Engineers, 1984.
Глава 2
Двумерные
преобразования
2-1 ВВЕДЕНИЕ
Изучение математического аппарата, лежащего в основе машинной графики, мы
начнем с рассмотрения способов вывода и преобразования точек и линий. Эти
способы наряду с соответствующими алгоритмами рисования используются для
изображения объектов или визуализации графической информации. Возможность
проводить преобразования точек и линий является фундаментом машинной
графики. Нарисованный объект может быть представлен в нужном масштабе,
повернут, перемещен, преобразован или модифицирован в соответствии с требованиями
решаемой задачи. Все эти манипуляции с изображением можно выполнить,
используя математический аппарат, изложенный в данной и последующих главах.
2-2 ИЗОБРАЖЕНИЕ ТОЧЕК
Точка представляется на плоскости двумя своими координатами, которые
определяются как элементы матрицы размером 1 х 2 [х у]. В трехмерном пространстве
используется матрица размером 1 х 3 [х у z].
Иначе говоря, точка может задаваться в виде вектор-столбца И в двумерном
пространстве или в виде
х
У
z
в трехмерном. Строку [х у] или столбец х часто называют координатным
вектором. В этой книге для формирования такого вектора используется матрица-
строка, т. е. множество точек, каждая из которых определяет координатный
вектор в некоторой системе измерения. Данное множество хранится в компьютере
в виде матрицы или массива чисел. Положением точек можно управлять путем
манипулирования соответствующей матрицей. Линии, соединяющие точки,
формируют отрезки, кривые и картинки.
2-3 ПРЕОБРАЗОВАНИЯ И МАТРИЦЫ
В качестве элементов матрицы могут фигурировать различные величины:
числа, сетки или коэффициенты системы уравнений. Правила в матричной алгебре
определяют допустимые операции над элементами (приложение В). Многие
физические задачи удобно выражаются в матричном представлении. Для моделей
физических систем задача обычно ставится следующим образом: даны матрицы
[А] и [В], найти результирующую матрицу [Т], такую, что [А][Т] = [В]. В этом
случае решением является матрица [Т] = [А]"1 [В], где [А]-1 —матрица,
обратная к квадратной матрице [А].
В то же время матрицу [Т] можно интерпретировать как геометрический
оператор. В этом случае для выполнения геометрического преобразования точек,
представленных векторами положений в матрице [А], используется умножение
матриц. Предположим, что матрицы [А] и [Т] известны. Требуется определить
элементы матрицы [В]. Представление [Т] как геометрического оператора
является основой математических преобразований, используемых в машинной графике.
2-4 ПРЕОБРАЗОВАНИЕ ТОЧЕК
Рассмотрим результаты умножения матрицы [х у], содержащей координаты точки
Р, на матрицу общего преобразования размером 2x2:
[Х][Т]=[х у]
a b
с d
= [(ах + cy)(bx + dy)] = [х*у*\.
(2-1)
Данная запись означает, что исходные координаты точки х и у преобразуются
в х* и у*, где х* = ах + су, у* = Ъх + dy (приложение В). Представляют
интерес значения х*, у* —координаты результирующей, преобразованной точки Р.
Рассмотрим некоторые специальные случаи.
При а = а*=1ис = Ь = 0 преобразование сведется к единичной матрице
[Х][Т]=[х у]
1 О
О 1
= [х у] = [х* у*] ,
(2-2)
и координаты точки Р останутся неизменными. Как и следовало ожидать, в
линейной алгебре умножение на единичную матрицу эквивалентно умножению на
1 в обычной алгебре.
В случае d=l, b = c = 0
[Х)[Т\=[* У]
а О
О 1
= [ах у] = [х* у*],
(2-3)
где х* — ах —результат масштабирования координаты X. Эффект такого
преобразования показан на рис. 2-1а. Рассмотрим теперь еще случай b = с = 0, т. е.
[Х)[Т]=[х у]
а О
О d
= [ах dy] = [x* у*]
(2-4)
y'y
3 -
2-
P Р*
2
tfy
3
2
P*
'
-
-
P
i i
-1
1
>* = fcr + у
1 2 3
(«)
Рис. 2-1 Преобразовавие точек.
»x, х*
>*>
з -
2-
P*
/
4
2
(6)
(d)
if)
—x.x-'
y*y
3
2
1
- /
/
P*
1
-
P
/■ ■
1 2
-X, X"
уТу
3
2
1
n
L
"
<7
x*= cy + x
1 p p*
1 1
x.x*
Данное преобразование вызывает изменение обеих координат х и у вектора Р
(рис. 2-16). Если а ф d, то координаты масштабируются различным образом. При
а = d > 1 происходит растяжение вектора Р или масштабирование координат.
Если 0 < а = d < 1, то имеет место сжатие.
Если значение а или d отрицательное, то вектор отражается относительно
координатных осей или относительно плоскости. Чтобы убедиться в этом, возьмем
6 = с = О, d = 1 и а = 1, тогда
[Х][Т]=[х у]
-1
О
= [-х у] = [х* у*] ,
(2-5)
и в результате получаем симметричное отражение относительно оси у (рис. 2-1с).
Если Ь = с = 0, а = 1, d = —1, то выполняется симметричное отражение
относительно оси х. Если Ь = с = 0, а = d < 0, то происходит отражение относительно
начала координат, это показано на рис. 2-ld, где а = — 1, d = 1. Заметим, что обе
операции отражения и масштабирование зависят только от диагональных членов
матрицы преобразования.
Рассмотрим теперь случай с недиагональными членами. Возьмем сначала
значения а = d = 1, с = 0, тогда
[Х][Т]=[х у]
1 Ь
О 1
= [х (Ьх+у)] = [х* у*].
(2-6)
Заметим, что координата х точки Р осталась неизменной, тогда как
координата у* линейно зависит от исходных координат. Данное преобразование называется
сдвигом (рис. 2-1е). Аналогично, в случае, когдаа = d= 1,6 = 0, преобразование
приведет к сдвигу пропорционально координате у (рис. 2-1/). Таким образом,
видно, что недиагональные члены матрицы преобразования создают эффект сдвига
координат вектора точки Р.
Прежде чем закончить с преобразованием точек, разберем действие общего
преобразования, заданного выражением (2-1), когда начальный вектор лежит в
точке начала координат, т. е.
[z у]
= [(ах + су) (bx + dy)] = [x* у*]
или, в случае начала координат,
[0 0]
a b
с d
= [0 0] = [х* у*]
Видно, что начало координат инвариантно относительно преобразования общего
вида. Это ограничение устраняется при использовании однородных координат.
2-5 ПРЕОБРАЗОВАНИЕ ПРЯМЫХ ЛИНИЙ
Прямую линию можно определить с помощью двух векторов, задающих
координаты ее конечных точек. Расположение и направление линии, соединяющей две
У, У
Рис. 2-2 Преобразование отрезков.
X, X*
эти точки, может изменяться в зависимости от положений векторов. Реальный
вид изображения линии зависит от типа используемого дисплея. В этом разделе
мы рассмотрим только математические операции над конечными точками линии.
На рис. 2-2 изображена прямая линия, проходящая между двумя точками А
и В. Положение векторов точек А и В задается следующим образом: [А] = [0 1]
и [В] = [2 3].
Рассмотрим матрицу преобразования
Т =
1 2
3 1
(2-7)
которая, как следует из предыдущего обсуждения, приводит к сдвигу
изображения. Преобразование векторов А и В с помощью матрицы [Т] дает новое
положение векторов А* и В*
[А][Т}=[0 1]
1 2
3 1
= [3 1]=[А']
(2-8)
[В][Т}=[2 3]
1 2
3 1
= [11 7] = [В*].
(2-9)
Таким образом, результирующие координаты для точки А* — это х* = 3 и у* = 1.
Аналогично, В* —новая точка с координатами х* = 11, у* = 7. В более
компактном виде отрезок АВ может быть представлен матрицей размером (2x2):
L =
О 1
2 3
Умножим эту матрицу на [Г]:
[Ц[т] =
Го 1]
2 3
1 2'
3 1
[3 1]
11 7
= [L*],
(2-10)
где компоненты [L*] представляют собой преобразование координаты векторов
[А*] и [В*]. Результат преобразования А в А* и В в В* показан на рис. 2-2, где х
и у — это исходные оси координат, ах* и у* — преобразованные оси. Из рисунка
видно, что преобразование сдвига [Т] увеличивает длину отрезка и изменяет его
направление.
2-6 ПРЕОБРАЗОВАНИЕ СРЕДНЕЙ ТОЧКИ
На рис. 2-2 видно, что (2 х 2)-матрица преобразует прямую линию у = х +1,
проходящую между точками А и В в другую прямую у = |х — |, которая проходит
между точками А* и В*. Фактически с помощью (2 х 2)-матрицы осуществляется
преобразование любой прямой в другую прямую. Все точки преобразованной
линии непосредственно соответствуют всем точкам исходной линии. Это достаточно
очевидно для конечных точек линии. Рассмотрим теперь преобразование средней
точки прямой линии АВ. Допустим, что
[А].= [Х1 У1], [В] = [х2 у2] и [Т} =
a b
с d
Преобразуем одновременно две крайние точки:
А
В
[Т] =
xi У\
52 2/2.
a b
с d
=
ах± + cyi bx\ + dy\
ax2 + с
V2
bx2
+ dy2
A*
B*
(2-11)
Итак, конечные точки преобразованной линии А*В* имеют следующие
координаты
[А*] = [axi + cyi bxi + dyi] = [x{ yj],
[B*] = [ax2 + cy2 bx2 + dy2] = [x*2 y%\ .
(2-12)
Средняя точка отрезка А*В* выражается через преобразованные конечные точки
[хт Ут] =
Х\ + х\ yl+ yl
(axi + сух) + (ах2 + су2) (bxi + dyi) + (bx2 + dy2)
2 2
(xi + x2) (yi + y2) ,(a;i-|-X2) .(У1+У2)
+ c-
+ d±
(2-13)
Возвращаясь к исходной линии АВ, можно определить среднюю точку
следующим образом:
[хт ут] = [(xi +x2)/2 (yi+y2)/2]
(2-14)
Применив матрицу преобразования [Т] к средней точке линии АВ, получаем:
[хт Ут][Т] = р^1 Ц»]\*
(Д1 +Дг) , (Vi + Ы . (xi+хг) (2/1+J/2)
а 1- с о \- а
(2-15)
Из сравнения вьфажений (2-13) и (2-15) видно, что они одинаковы, и поэтому
средняя точка линии АВ преобразуется в среднюю точку линии А*В*. Такой
метод можно применить и к любым другим отрезкам разделенной линии. Таким
образом, при преобразовании путем умножения на матрицу гарантируется
соответствие всех точек линии АВ и А*В*.
Пример 2-1 Средняя точка прямой
Рассмотрим отрезок АВ из рис. 2-2. Положение векторов конечных точек
"1 2"
такое: [А] = [О 1], [В] = [2 3]. Преобразование [Т] =
перемещение вектора на линию А*В":
3 1
осуществляет
А
В
[Т] =
0 1
2 3
1 2
3 1
=
3 1
11 7
=
А"
В*
Средняя точка А*В* будет иметь координаты
[3 + 11 1 + 7
[*т Ут] = ["
2 2
Координаты средней точки линии АВ равны
ГО+ 2 1+3
] = [7 4].
[хт Ут] = I-
2 2
Преобразуем среднюю точку и получим
] = [1 2]
[as™ Ут] [Т] = [1 2]
1 2
3 1
[7 4] = [хт ут],
что полностью эквивалентно предыдущему результату.
Применением этих результатов в машинной графике любая прямая может
быть преобразована в любую другую прямую путем простого преобразования ее
конечных точек и восстановления линии между ними.
2-7 ПРЕОБРАЗОВАНИЕ ПАРАЛЛЕЛЬНЫХ ЛИНИЙ
Результатом преобразования двух параллельных линий с помощью (2x2)-
матрицы снова будут две параллельные линии. Это можно увидеть, рассмотрев
линию между точками [А] = [xi yi], [В] — [хг уг] и параллельную ей линию,
проходящую между точками Е и F. Покажем, что для этих линий любое
преобразование сохраняет параллельность. Так как АВ, EF и А*В* и E*F* параллельны,
то угол наклона линий АВ и EF определяется следующим образом:
тп =
2/2 -2/1
£2 — х1
(2-16)
Преобразуем конечные точки АВ, воспользовавшись матрицей общего
преобразования размером (2x2):
'А
В
[Т] =
-
х\ yi
Х2 2/2.
а
с
Ь
d
=
ах\ + cyi Ьх\ + dyi
ах2 + cj/2 Ьх2 + dj/г
'xi Vf
х2 2/2.
А*
В*
(2-17)
Наклон прямой А*В* определяется следующим образом:
тп =
(bx2 + dy2) - (bxi +dyx) _ b(x2 - xx) +d(y2 - yi)
(ax2 + cy2) - (aii + cyi) a(x2 - xi) + c(y2 - yx)
или
b + d
m —
(2/2-2/1)
(x2 — xi) _ b + dm
a + с
(2/2 - 2/i) a + cm'
(x2 - xi)
(2-18)
Так как наклон тп* не зависит от х\, х2, У\, j/г а тп, а, Ь, с и d одинаковы для
EF и АВ, то тп* одинаково для E*F* и А*В*. Таким образом, параллельные
линии сохраняют параллельность и после преобразования. Это означает, что при
преобразовании (2 х 2) параллелограмм преобразуется в другой параллелограмм.
Эти тривиальные вьтоды демонстрируют большие возможности использования
матрицы преобразования для создания графических эффектов.
2-8 ПРЕОБРАЗОВАНИЕ ПЕРЕСЕКАЮЩИХСЯ ПРЯМЫХ
Результатом преобразования с помощью (2 х 2)-матрицы пары пересекающихся
прямых линий также будет пара пересекающихся линий. Проиллюстрируем этот
факт на примере двух прямых, изображенных на рис. 2-3 штриховой линией и
заданных уравнениями
у = тп\Х + bi,
у = тп2х + b2.
10
у. У* б
(-Т'Т)Я
2
N.
-4 -2
(-1. -l)^*^
-2
-4
TF*
,'
>»В(3,|)
ч
/2» - Зу = I
-« "—л, л*
\
\* + У~ 1
^FCJ,-2)
Ifi*
Рис. 2-3 Преобразование пересекающихся прямых.
В матричном представлении эти уравнения будут иметь вид:
или
[Х][М] = [В]. (2-19)
Если существует решение этой системы уравнений, то линии пересекаются, в
противном случае они параллельны. Решение можно найти путем инверсии матрицы.
В частности,
[Xi]=[xi yi]=[B][M]-\
Матрица, обратная [М], имеет следующий вид:
1 7712
[М]"1 = Ш2 ~,т1 Ш2 "" т1
.7712 — т1 т2 — т1
(2-20)
(2-21)
так как [М][М] г = [J], где [Т\ —единичная матрица. Поэтому координаты точки
пересечения двух линий можно найти следующим образом:
1 7712
[Xi] = [ц yi] = [h bt]
[Х{] = [xi yt] =
ТП2 — ТП\ ТП2 — TTli
— 1 —mi
.7712 — ml m2 ~ ml
b\ — i>2 Ь\ТП2 — ЬгШ!
(2-22)
7712 — 77li 7712 — 77li
Если обе линии преобразовать с помощью (2 х 2)-матрицы общего
преобразования вида
[Т] =
a 6
с d
)
то их уравнения будут иметь вид
у* = тп\х* + £>*,
у = тп2х + о2.
Соответственно можно показать, что
b + dnii
mi = ,
a+ ami
и
h* - hAd ат.*~\ - Ь.- tt
-be
где
i = 1, 2.
(2-23)
(2-24)
a + crrii
Точка пересечения линий после преобразования отыскивается таким же образом,
как и в случае исходных линий:
[*;] = [*? v;] =
b* — i>2 Ь*тп*. — Щтп*'
ТПп — 771,
771, — ТП
1 J
Воспользовавшись вьфажениями (2-23) и (2-24), получим
a(bi — 62) + c(bi77i2 — 627711) b(b\ — Ь2) + d(bim2 — &2mi)
7712 — TTli
(2-25)
7712 — TTli
Возвращаясь теперь к точке пересечения [xj yi\ исходных линий и применяя
уже полученную матрицу преобразования, имеем
[х* yt] = [Xi yi][T} =
bi — 62 bi77l2 — i>277ll
a b
с d
7712 — TTli 7712 — TTli
a(b\ — 62) + C(bi77l2 — b277li) b(b\ — 62) + d(bi77l2 — i>2ml)
7712 — TTli
7712 — TTli
(2-26)
Сравнение уравнений (2-25) и (2-26) показывает, что они одинаковы. Итак, точка
пересечения преобразуется точно в другую точку пересечения.
Пример 2-2 Пересекающиеся прямые
Рассмотрим две штриховые линии АВ и EF на рис. 2-3, конечные точки
которых имеют координаты
[А]=[-1 -1], [В]=[3 5/3]
и
[Я] =[-1/2 3/2], [F]=[3 -2].
Уравнение прямой АВ имеет вид —(2/3) х + у = —1/3, а прямая EF
задается уравнением х + у = 1. В матричном виде пучок прямых представляется
в виде
[х у]
-2/3 1
1 1
= [-1/3 1].
Используя матрицу обратного преобразования (2-21), получим точку
пересечения этих прямых
-3/5 -3/5
3/5 2/5
[xt да] = [-1/3 1]
Теперь преобразуем эти линии с помощью матрицы
[Т] =
= [4/5 1/5].
1 2
1 -3
Результирующие прямые А*В* и E*F* показаны на рис. 2-3. В
матричном виде уравнения преобразованных линий имеют вид
[х* У']
1 О
О 1
[1 Ч
с точкой пересечения [х* у*] = [l l].
Преобразуя точку пересечения исходных линий, получим
[х* yt] = [Xi y<][T]= [4/5 1/5]
1 2
1 -3
= [1 1],
что тождественно точке пересечения преобразованных линий.
Из рис. 2-3 и примера 2-2 видно, что исходные штриховые прямые АВ и EF не
перпендикулярны друг другу. Однако преобразованные прямые А* В* и E*F*,
показанные сплошной линией, являются перпендикулярными. Таким образом,
преобразование [Т] переводит две пересекающиеся неперпендикулярные прямые в
две пересекающиеся перпендикулярные. Смысл обратного преобразования [Г]-1
состоит в переводе двух пересекающихся перпендикулярных прямых в две
пересекающиеся, но не перпендикулярные, что может привести к неприятным
геометрическим последствиям. Значительный интерес представляет вопрос, при каком
условии перпендикулярные прямые преобразуются в перпендикулярные. Мы
вернемся к этому вопросу в разд. 2-14, где разберем его подробнее.
Дополнительное изучение рис. 2-3 и примера 2-2 показывает, что
преобразование [Г] включает в себя поворот, отражение и масштабирование. Рассмотрим
каждое из этих преобразований отдельно.
2-9 ПОВОРОТ
Рассмотрим треугольник ABC (рис. 2-4) и с помощью следующего
преобразования повернем его на 90° против часовой стрелки относительно начала координат
[Г]
0 1
-1 0
Если использовать матрицу размером (3 х 2), состоящую из координат х и у
вершин треугольника, то можно записать
"3 -1"
4 1
2 1
0 1"
-1 0
=
1 3"
-1 4
-1 2
У, У
-2
-2
-4 -
J I I L
Рис. 2-4 Поворот.
что является координатами результирующего треугольника А*В*С*. Поворот на
180° относительно начала координат достигается путем следующего
преобразования
[Г]
-1 0
0 -1
0 -1
1 0
а на 270° относительно начала координат — преобразованием
[Г] =
Разумеется, что матрица тождественного преобразования
[Т} =
1 0
0 1
соответствует повороту вокруг начала координат на 0° или 360°. Обратим
внимание, что в этих примерах не встречаются ни масштабирование, ни отражение.
В этих примерах осуществляется преобразование в специальных случаях
поворота вокруг начала координат на углы 0°, 90°, 180° и 270°. Как осуществить
поворот вокруг точки начала координат на произвольный угол в? Для ответа
на этот вопрос рассмотрим вектор положения от начала координат до точки Р
(рис. 2-5). Обозначим г—длину вектора, а ф — угол между вектором и осью х.
Вектор положения поворачивается вокруг начала координат на угол в и попадает
в точку Р*. Записав векторы положений для Р и Р*, получаем:
Р = [х у] = [г cos ф г si
sm<
Р* = [х* у*] = [г cos(4> + в) г sin(4> + в)] .
Используя формулу для cos суммы углов, перепишем выражение для Р*
следующим образом
Р* = [х* у*] = [r(cos ф cos в - sin ф sin в) r(cos ф sin в + sin ф cos в)] .
Используя определения х и у, можно переписать Р* как
Р* = [х* у*] = [х cos в — у sin в х sin в + у cos в] .
Таким образом, преобразованная точка имеет координаты
х* = х cos в - у sin в, (2-27а)
у* = х sin в + у cos в. (2-27Ъ)
или в матричном виде
[X'] = [X\[T\=[f y'] =
cos в sin в
= [х у]
— sin в cos в
(2-28)
-x.x'
Рис. 2-5 Поворот координатного вектора.
Итак, преобразование поворота вокруг точки начала координат на произвольный
угол в задается матрицей
[Т] =
cos в sin в
— sin в cos в
(2-29)
Повороты являются положительными, если они осуществляются против часовой
стрелки относительно точки вращения (рис. 2-5).
Определитель общей матрицы поворота имеет следующий вид:
det[T] = cos2 в + sin2 0 = 1.
(2-30)
В общем случае преобразования по матрице с детерминантом, равным 1,
приводят к полному повороту.
Предположим теперь, что требуется возвратить точку Р* обратно в Р, т. е.
выполнить обратное преобразование. Очевидно, что требуемый угол поворота равен
—0. Из формулы (2-29) возьмем матрицу для выполнения необходимого
преобразования
[Г]"1 =
cos(-0) sin(-0)
• sin(-0) cos(-0)
cos в — sin в
sin в cos в
(2-31)
так как cos(—в) = cos0 и sin(—в) = — sin0. Выражение [Г] 1 является формальной
записью обратной матрицы [Т]. Можно показать, что матрица [Г]-1 является
обратной к [Т], если вспомнить, что результат умножения матрицы на обратную
дает единичную матрицу. В нашем случае:
СПРГ1 =
COS
0 sin0'
- sin 0 cos 0
COS0 -
sin0
cos2 в + sin2 0
— cos 0 sin в + cos в sin 0
"1 0'
0 1
= [I],
-sin0
COS0
— СОЕ
cos 0 sin 0 + cos 0 sin 0
cos2 0 + sin2 0
где [/] — единичная матрица.
Анализ выражений (2-29) и (2-31) приводит к другому интересному и
полезному результату. Вспомним, что транспонирование матрицы определяется заменой
ее строк столбцами. Обозначим транспонированную матрицу [Г] как [Г] .
Сравнивая ее с [Т]-1, видим, что
[Tf =
cos 0 - sin 0
sin в cos 0
= РГ
(2-32)
Обратная матрица вращения является транспонированной. Поскольку
формально определитель обратной матрицы вычисляется гораздо сложнее, чем
определитель транспонированной, то выражение (2-32) является достаточно важным
и полезным результатом. В общем случае обратной для любой матрицы
преобразования полного поворота, т.е. матрицы с определителем, равным +1, является
ее транспонированная матрица (такие матрицы называют ортогональными).
2-10 ОТРАЖЕНИЕ
В то время как полный поворот на плоскости ху обычно осуществляется в
двумерном пространстве относительно нормали к плоскости, отражение
представляет собой тот же поворот на угол 180° в трехмерном пространстве и обратно на
плоскость относительно оси, лежащей в плоскости ху. На рис. 2-6 приведены
примеры двух отражений на плоскости треугольника DEF. Отражение относительно
прямой у = 0 (ось х) получено с использованием матрицы
[Т} =
(2-33)
В этом случае новые вершины треугольника D*E*F* будут определяться
преобразованием
"8 1"
7 3
6 2
1 0'
0 -1
=
"8 -1"
7 -3
6 -2
Подобным образом отражение относительно оси у при х — 0 будет иметь вид
-1 0
[Т} =
0 1
(2-34)
У. У*
8
б
4
-2
i i
-2 ••
-2
D+ /
- Т /
: / .
: / л
'/ *
' II,'
2 4 6 8
<<
Е*
Рис. 2-6 Отражение.
Отражение относительно прямой у = х осуществляется спомощью матрицы-
[Т] =
0 1
1 О
(2-35)
Выполнив преобразования, получим координаты вершин треугольника D*E*F*
'8 1"
7 3
6 2
0 1"
1 0
=
"1 8'
3 7
2 6
Аналогичным образом отражение относительно оси х будет иметь вид
[Т] =
О -1
-1 О
(2-36)
У каждой из этих матриц определитель равен —1. В общем случае, если
определитель матрицы преобразования равен —1, то преобразование дает полное
отражение.
Если оба полных отражения осуществляются последовательно относительно
прямых, проходящих через начало координат, то результатом будет полный
поворот относительно начала координат. Это можно увидеть, обратившись к
следующему примеру.
\* У. У*
/ / / \. 2
1 I I |l 1 1 IN
-6 11 -4 -2
\\ \ "2
-6
■
\ Дрд
A
i i i i i ,
\ 2 4
\ c
Z^^tr \.
*•*,*'
Рис. 2-7 Выполнение отражения путем поворота.
Пример 2-3 Отражение и вращение
Рассмотрим треугольник ABC, показанный на рис. 2-7. Первоначально
отобразим его относительно оси х (уравнение 2-33), а затем относительно
прямой у,—,—х (см. выражение (2-36)). Результатом первого отображения
будет
[X'] = [Х][7\] =
Результатом второго будет
'4 1,
5 2
4 3
1 ' 0'
0 -1
=
4 -1"
5 -2
4 -3
[Х+] = [Х*][Т2] =
'4 -1'
5 -2
4 -3
0 -1
-1 0
=
"1 -4"
2 -5
,3 -4
Повернем треугольник относительно начала координат на угол в = 270°
(см. (2-29)) и получим аналогичный результат
[Х+] = [Х][Г3] =
'4 1"
5 2
4 3
0 -1'
1 0
=
'1 -4
2 -5
3 -4
Отметим, что матрицы отражения из (2-33)/и (2-36) ортогональны, т.е.
транспонированнная матрица одновременно является обратной. Например,
Г о
-1
-il
0
Г о
-1
-il
0
т
Г ° -11
-1 . 0
2-11 МАСШТАБИРОВАНИЕ
Из наших рассуждений относительно преобразования точек следует, что
величина масштабирования определяется значением элементов исходной диагональной
матрицы. Если матрица
-[Г] =
2 О
О 2
используется в качестве оператора воздействия на вершины треугольника, то
имеет место «двукратное» расширение или равномерное масштабирование
относительно точки начала координат. Если значения элементов не равны, то
треугольник искажается, что проиллюстрировано на рис. 2-8. Треугольник ABC,
преобразованный с помощью матрицы
[Т] =
2 О
О 2
О 2 4 б 8 1012 14
Рис. 2-8 Пропорциональное и непропорциональное масштабирование (искажение).
У. У*
i i—-*'х*
Рис. 2-9' Пропорциональное масштабирование без явного перемещения.
переходит в пропорционально увеличенный треугольник А*В*С*. Тот же
треугольник, но преобразованный с помощью матрицы
1/2 О
. О 3
переходит в треугольник D*E*F*, имеющий искажение, вызванное разными
коэффициентами масштабирования.
В общем случае при матрице
[Г] =
(2-37)
в которой а = d, Ь = с = 0, вьшолняется пропорциональное масштабирование; если
а ф d, Ь = с = 0, то масштабирование будет проведено непропорционально. В
первом случае для а = d > 1 происходит расширение, т. е. увеличение изображения.
Если а = d < 1, то происходит равномерное сжатие, т. е. фигура уменьшается.
Непропорциональное расширение и сжатие возникают в зависимости от значений
а и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.
Из рис. 2-8 видно также, что на первый взгляд преобразование треугольника
является перемещением. Это объясняется тем, что относительно начала
координат масштабируются координатные векторы, а не точки.
Для того чтобы лучше понять этот факт, рассмотрим преобразования ABC в
D*E*F* более внимательно. В частности,
[Х*\ = [Х][Т] =
4 2"
4 4
2 4'
"1/2 0'
0 3
=
'2 6'
2 12
1 12
Заметим, что каждая из компонент х координатных векторов треугольника
DEF умножалась на масштабный коэффициент 3, а компоненты у — на 2.
Для того чтобы получить чистое масштабирование без эффекта
перемещения, центр фигуры надо поместить в начало координат. Это видно из рис. 2-9,
на котором треугольник ABC увеличивается в два раза при масштабировании
относительно его центра с координатами, равными 1/3 основания и 1/3 высоты.
Конкретная матрица преобразования имеет вид
[X*] = [Х][Т] =
"-1 -1"
2 -1
-1 2
'2 0'
0 2
=
"-2 -2"
4 -2
-2 4
2-12 КОМБИНИРОВАННЫЕ ПРЕОБРАЗОВАНИЯ
Возможности матричного метода достаточно ясно описаны в предыдущих
разделах книги. С помощью матричных операций над координатными векторами,
определяющими вершины фигур, можно управлять формой и положением
поверхности. Однако для получения желаемой ориентации может потребоваться
более одного преобразования. Так как операция умножения матриц не
коммутативна, то важен порядок выполнения преобразования.
Для иллюстрации эффекта некоммутативности операции умножения матриц
рассмотрим преобразования поворота и отражения координатного вектора [х у].
Если вслед за поворотом на 90° (посредством [Ti]) производится отражение
относительно прямой у — —х (посредством рг]), то эти два последовательных
преобразования дают
[Х'] = [Х][Т1] = [х у]
0 1
-1 0
= [-У х]
и затем
[Х*] = [Х'][Т2] = [-у -х]
0 -1
-1 0
= [-х у] ■
С другой стороны, если отражение следует за поворотом, то получатся следующие
результаты:
[Х'] = [Х][Т2]=[х у]
0 -1
-1 0
= [-У -х]
[Х*] = [Х>][Т1]=[-у -х]
0 1
-1 0
= [х -у] ■
Оба результата различны, что подтверждает важность порядка применения
матричных преобразований.
Рис. 2-10 Комбинированное преобразование на плоскости.
Другое принципиальное обстоятельство иллюстрируется этими результатами
и приведенным ниже примером. Ранее отдельные матричные преобразования
применялись последовательно к результатам предыдущих преобразований, например
[х у] [Т{\ -> [х1 у1}
[*' у'][Т2]^[х* у*].
В приведенном ниже примере отдельные преобразования предварительно
комбинируются или конкатенируются, а затем полученная матрица применяется к
исходному вектору, т.е. [Ti][T2] ->■ [Т3] и [х у] [Т3] -> [х* у*].
Пример 2-4 Комбинированные преобразования на плоскости
Рассмотрим треугольник ABC на рис. 2-10. Выполним над ним два
преобразования: поворот на +90° вокруг точки начала координат
и отражение относительно линии у
РЧ =
0
-1
= —х
0 -
-1
1
0
-1
0
Результатом воздействия комбинированного преобразования [Тз]
[Ti][Tj] на треугольник ABC является
[х*\ = мрда] = [х][т3]
"2 2"
4 2
4 4
0 1"
-1 0
0 -1'
-1 0
=
"2 2
4 2
4 4
'-1 0'
0 1
=
'-2 2"
-4 2
-4 4
Получившийся треугольник А*В*С* является конечным результатом
данного преобразования, а треугольник А'В'С'—промежуточным результатом
(рис. 2-10).
Проведем преобразование в обратном порядке
[х*] = дорад = [х][т4]
'2 2
4 2
4 4
0 -1'
-1 0
0 1'
-1 0
=
"2 2
4 2
4 4
"1 0'
0 -1
=
'2 -2
4 -2
4 -4
Конечным результатом будет треугольник D*E*F*, а промежуточным
D'E'F' (рис. 2-10). Оба результата различны, тем самым снова
подтверждается важность порядка применения преобразований. Отметим также, что для
определителей справедливы равенства det [Тз] = — 1, и det [Т4] = — 1 и
поэтому оба результата могут быть получены с помощью единственного
отражения. Треугольник А*В*С* можно получить из ABC путем отражения
относительно оси Y (матрица [Тз] и уравнение (2-34), D* E* F* получается из
ABC при отражении относительно оси X (матрица [Tj] и уравнение (2-33).
2-13 ПРЕОБРАЗОВАНИЕ ЕДИНИЧНОГО КВАДРАТА
До сих пор мы рассматривали поведение точек и линий для определения
результатов простых матричных преобразований. Однако можно корректно
рассматривать применение матрицы к любой точке плоскости. Как было показано
ранее, единственная точка, остающаяся инвариантной при воздействии матричных
преобразований, — это точка начала координат. Все другие точки плоскости
подвержены преобразованию, которое можно представить как растяжение исходной
плоскости, системы координат и перевод в новую форму. Формально принято
считать, что преобразование вызывает переход от одного координатного
пространства к другому.
Рассмотрим координатную сетку, состоящую из единичных квадратов на
координатной плоскости ху (рис. 2-11). Четыре координатных вектора вершин
единичного квадрата, проходящие под одним углом к началу координат, имеют
следующий вид:
начало координат — А
единичная точка В на оси х
внешний угол С
единичная точка D на оси у
Го
1-й
1
0
0]
0
1—1
1
Такой идиничный квадрат изображен на рис. 2-Па. Применяя к нему (2 х 2)-
матрицу общего преобразования, получаем
А [О О'
В 1 О
С 1 1
D [о 1
Результаты этого преобразования показаны на рис. 2-116. Из выражения (2-38)
следует, что начало координат не подвергается преобразованию, т. е. [А] = [А*] =
[О 0]. Далее отметим, что координаты В* равны первой строке матрицы
преобразования, а координаты D* — второй. Таким образом, матрица
преобразования является определенной, если определены координаты В* и D*
(преобразование единичных векторов [1 0], [0 1]). Поскольку стороны единичного
квадрата первоначально параллельны и ранее было показано, что параллельные линии
преобразуются снова в параллельные, то результирующая фигура является
параллелограммом .
Влияние элементов а, 6, с и d матрицы 2x2 может быть установлено отдельно.
Элементы Ъ и с, как видно из рис. 2-116, вызывают сдвиг (см. разд. 2-4) исходного
квадрата в направлениях у их соответственно. Как отмечалось ранее, элементы а
и d играют роль масштабных множителей. Таким образом, 2 х 2-матрица задает
комбинацию сдвига и масштабирования.
Несложно определить также площадь параллелограмма A*B*C*D* из
рис. 2-116, которую можно вычислить следующим образом:
Ар = (a + c)(b+d) - l(oft) - \{cd) - |(6 + 6+d) - ^(c+a + c).
.
D
F^P""!
С
В
(a) W
Рис. 2-11 Общее преобразование единичного квадрата: а) до преобразования; 6) после
преобразования.
а 6
с d
■о
a
а + с
с
0
6
b + d
d
А
В
С
D
(2-38)
В результате получаем
Ар = ad — be = det
а Ь
с d
(2-39)
Можно показать, что площадь любого параллелограмма Ар, образованного
путем преобразования квадрата, есть функция от определителя матрицы
преобразования и связана с площадью исходного квадрата А8 простым отношением
Ар = As (ad - be) = As det [T]. (2-40)
Фактически, так как площадь всей фигуры равна сумме площадей единичных
квадратов, то площадь любой преобразованной фигуры At зависит от площади
исходной фигуры Ai
At = Ai(ad- be).
Это полезный способ определения площадей произвольных фигур.
(2-41)
Пример 2-5 Масштабирование области
Треугольник ABC с координатными векторами [1 0], [0 1] и [—1 0]
преобразуется матрицей
[Т] =
3 2
-1 2
образуя новый треугольник А'В'С* (рис. 2-12).
Площадь треугольника ABC равна
Ai = - (основание) (высота) = ^(2)(1) = 1.
Рис. 2-12 Масштабирование области.
Воспользуемся уравнением (2-41), тогда площадь преобразованного
треугольника А"В* С* будет равна
At = Ai{ad - be) = 1(6 + 2) = 8.
Векторы преобразованного треугольника А' В* С* теперь равны
1 0'
0 1
-1 0
Г 3 2]
-1 2
3
-1
-3
2"
2
-2
Вычислим площадь, образованную результирующими вершинами:
At = — (основание) (высота) = х(4)(4) = 8.
Это совпадает с полученным ранее результатом.
2-14 ПРЕОБРАЗОВАНИЯ ЖЕСТКИХ КОНСТРУКЦИЙ
Пришло время вернуться к поставленному в разд. 2-8 вопросу: когда
перпендикулярные прямые преобразуются в перпендикулярные прямые? Рассмотрим
сначала более общий вопрос: в каких случаях угол между пересекающимися прямыми
сохраняется?
Напомним, что скалярное произведение двух векторов равно
V1-V2 = VlxV2x + VlyV2y = \Vi | \V21 cos 9, (2-42)
а векторное произведение двух векторов, принадлежащих плоскости ху,
определяется как
Vi х V2 = (VlxV2y - V2xVly)k = |Vi| \V2\ksm9,
(2-43)
где индексы хну относятся к компонентам хну вектора, в — острый угол между
векторами, а к — единичный вектор, перпендикулярный к плоскости ху.
Проведем преобразование V\ и V2, используя (2 х 2)-матрицу общего
преобразования
v2
[Т] =
Vix V2y a b
V2x V2y\ С d
aVj.3 + cViy bVix + dViy
aV2x + cV2y bV2x + dV2y
V
(2-44)
Векторным произведением векторов V1 и V2 будет
V[ x У* = (ad-cb)(VlxV2y - V2xVly)k = |V^| \Vl\ksm9. (2-45)
Аналогично, скалярное произведение будет равно
V\-V*2 = (a2 + b2)VlxV2x + (С2 + d2)VlyV2y + (ас + bd)(VlxV2y + VlyV2x) =
= \Vl\\Vl\cos9. (2-46)
Требуется, чтобы значения векторов, как и угол между ними, оставались
постоянными. Сравнивая уравнения (2-42), (2-46) и (2-43), (2-45), а также приравняв
коэффициенты подобных членов, получим
а2 + Ъ2 = 1,
с2 + d2 = 1,
ас + bd = О,
ad — bc = +1.
(2-47а)
(2-47Ь)
(2-47с)
(2-48)
Выражения (2-47а, Ь, с) соответствуют условиям ортогональности матрицы, т. е.
[Т][Т}-1 = [Т}[Т}Т = [1]
или
а 6
с d
а с
Ь d
a2 + b2 ac+ bd
ac + bd с2 + d2
1 О
О 1
Выражение (2-48) требует, чтобы определитель матрицы преобразования был
равен + 1.
Таким образом, при полном повороте углы между пересекающимися прямыми
сохраняются. Данный результат распространяется также и на операцию
отражения, ортогональная матрица которого имеет определитель, равный —1. В этом
случае величины векторов сохраняются, но угол между преобразованными
векторами в действительности равен 2п — 9. (Следовательно, в общем случае угол
не сохраняется. Однако перпендикулярные прямые преобразуются в
перпендикулярные прямые. Поскольку sin(27r — в) = —sin9, ad — be = —1, полные
повороты и отражения называются преобразованиями жесткой конструкции. Кроме
того, несколько минут анализа или экспериментирования приводят к выводу, что
равномерное масштабирование также сохраняет неизменным угол между
пересекающимися прямыми, но не величину преобразуемых векторов. Поскольку
ортогональная матрица сохраняет угол между векторами и их величины, матрица
однородного масштабирования не является ортогональной.)
2-15 ПЕРЕМЕЩЕНИЯ И ОДНОРОДНЫЕ КООРДИНАТЫ
В предыдущих разделах был рассмотрен ряд преобразований, совершаемых с
помощью (2 х 2)-матрицы общего преобразования. Среди них поворот, отражение,
масштабирование, сдвиг и другие. Ранее отмечалось, что исходная система
координат инвариантна по отношению ко всем перечисленным преобразованиям.
Однако возникает необходимость изменять положение начала координат, т. е.
преобразовывать каждую точку на плоскости. Этого можно достичь путем
перемещения точки начала координат или любой другой точки на плоскости
х* = ах + су + т,
у* = bx + dy + п.
К сожалению, нельзя ввести константы перемещения тп и п в (2 х 2)-матрицу
преобразования, так как это не пространство!
Данное затруднение можно преодолеть, используя однородные координаты.
Однородные координаты неоднородного координатного вектора [х у]
представляют собой тройку [х' у' Л], где х = х'/h, у = y'/h, a h — некоторое
вещественное число. Заметим, что случай h = 0 является особым. Всегда существует один
набор однородных координат вида [х у 1]. Мы выбрали эту форму, чтобы
представить координатный вектор [х у] на физической плоскости ху. Все остальные
однородные координаты представляются в виде [hx hy h]. Данные координаты
не сохраняют однозначности, например, все следующие координаты [6 4 2], [12 8
4], [3 2 1] представляют физическую точку (3,2).
Матрица преобразования для однородных координат имеет размер 3 х 3. В
частности,
[Т} =
а Ь О
с d О
тп п 1
(2-49)
где действие элементов а, Ь, с и d верхней части (2 х 2)-матрицы точно
соответствует действиям, рассмотренным ранее. Элементы тип являются коэффициентами
перемещения в направлениях хну соответственно. Полная двумерная матрица
преобразования имеет вид
[х* у* 1] = [х у 1]
1 О О
О 1 О
тп п 1
= [х + тп у + п 1] .
(2-50)
Отметим, что каждая точка плоскости и даже начало координат х = у = 0 теперь
могут быть преобразованы.
2-16 ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ТОЧКИ
Ранее мы рассматривали вращение, совершаемое вокруг начала координат.
Однородные координаты предусматривают механизм выполнения поворотов
вокруг точек, отличных от начала координат. В общем случае поворот вокруг
произвольной точки может быть реализован посредством ее перемещения в начало
координат, выполнения требуемого поворота и последующего перемещения
результата обратно в исходный центр вращения. Таким образом, поворот вектора
[х у l] вокруг точки тп, п на произвольный угол можно осуществить
следующим образом:
[х* у* 1] = [х у 1]
1
0
тп
0
1
—п
0'
0
1
cos в sin 9 0
■ sin в cos 9 0
0 0 1
1 0 0
0 1 0
тп п 1
(2-51)
Выполняя действия над двумя внутренними матрицами, можно записать
cos 9 sin в
г * * л г il -sin0 costf
[х у 1] = [х у 1] r-m(cos0-l)l f-n(cos0-lV
+nsin0 J ]_ -msinO
Рассмотрим пример, иллюстрирующий данный результат.
(2-52)
Пример 2-6 Поворот относительно произвольной точки
Предположим, что центр объекта лежит в точке [4 3]. Требуется
повернуть объект на прямой угол против часовой стрелки вокруг центра.
Используя матрицу
"010'
-10 0
0 0 1
проведем поворот вокруг начала координат, не совпадающего с центром
объекта. Обязательной процедурой преобразования является прежде всего такое
перемещение объекта, чтобы желаемый центр вращения оказался в начале
координат. Это достигается с помощью следующей матрицы перемещения:
1 0 0
0 10
-4 -3 1
Далее применяем матрицу поворота и наконец с помощью матрицы
перемещения приведем результаты поворота обратно к первоначальному центру.
Вся операция
[х* у' 1] = [х у 1] =
1
0
4
0 0]
1 0
-3 1
0 1 0'
10 0
0 0 1
'1 0 0"
0 10
4 3 1
может быть реализована одной матрицей путем простого перемножения
отдельных матриц, т. е.
[х* у* 1] = [х у 1]
0 10
-10 0
7-11
2-17 ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ПРЯМОЙ
Ранее в разд. 2-10 обсуждалось отражение относительно прямых, проходящих
через начало координат. Иногда требуется выполнить отражение объекта
относительно прямой, не проходящей через точку начала координат. Это можно сделать,
воспользовавшись процедурой, аналогичной вращению вокруг произвольной
точки. Конкретно выполняются следующие действия:
— перемещение линии и объекта таким образом, чтобы линия прошла через
начало координат;
— поворот линии и объекта вокруг точки начала координат до совпадения с
одной из координатных осей;
— отражение относительно координатной оси;
— обратный поворот вокруг начала координат;
— перемещение в исходное положение.
В матричном виде данное преобразование имеет представление
[T] = [T'}[R}[R'][R}-'[T'}-\ (2-53)
где Т" — матрица перемещения, R — матрица поворота вокруг начала координат,
R1 — матрица отражения.
Перемещения, повороты и отражения также применяются для преобразования
произвольных фигур. Рассмотрим следующий пример.
Пример 2-7 Отражение относительно произвольной прямой
Рассмотрим прямую L и треугольник ABC (рис. 2-13о). Уравнение
прямой L имеет вид
у= ^(х + 4).
Координатные векторы [2 4 1], [4 6 1] и [2 6 1] задают вершины треугольника
ABC.
Прямая L пройдет через начало координат при перемещении ее на —2
единицы в направлении оси у. В результате этого при повороте вокруг
начала координат на — tg_1(l/2) = —26.57° прямая совпадет с осью х.
Выражение (2-33) используется для отражения треугольника относительно оси
х, затем преобразованные координатные векторы треугольника
поворачиваются и перемещаются к исходной ориентации. Комбинация преобразований
будет иметь вид
[Т] =
О
1
-2
[Т] =
2/ч/5
-1/л/5
О
3/5 4/5
4/5 -3/5
-8/5 16/5
2/%/5
1/У5
0
1Д/5
2Л/5
0
0'
0
1
-
1/л/5 0"
2/ч/5 0
0 1
0'
0
1
'1 0 0"
0 1 0
0 2 1
1
0
0
0
-1
0
0
0
1
и конкретно для координатных векторов треугольника А* В" С* имеем
Г2 4 *1
4 6 1
2 6 1
3/5 4/5 О
4/5 -3/5 О
-8/5 16/5 1
14/5 12/5 1
28/5 14/5 1
22/5 6/5 1
(рис. 2-13о). Рис. 2-13 6, с, d, e иллюстрируют различные этапы данного
преобразования.
' ' l_
-2
-2-
6 с в
С*
J I I „-I I l—njf»
(a)
1—i—I I I >x, jr*
,<*)
У.У'
2-
' ■ '
-2
-2-
j 1—| 1—|—1_», jt»
(O
У.У*
4
2
i i i
-2
-2
.
1
i
2
i i
4
С
L
1 ' >
6
(d)
(«)
Рис. 2-13 Отражение относительно произвольной прямой: о) исходное и конечное
положение; 6) перенос прямой в начало координат; с) поворот до совпадения с осью х; d)
отражение относительно оси х; е) обратный поворот; о) обратный перенос.
2-18 ПРОЕЦИРОВАНИЕ-ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ОДНОРОДНЫХ КООРДИНАТ
Матрицу преобразования размером 3x3 для двумерных однородных координат
можно разбить на четыре части
[Т] =
а Ъ
с d
т п
Р
Я.
(2-54)
Напомним, что а, Ь, с и d — коэффициенты масштабирования, вращения,
отражения и сдвига соответственно. Элементы тип задают перемещение. В двух
предыдущих разделах коэффициенты имели значения р = д = 0и«=1.
Установим величины р и q не равными 0. Какой эффект мы получим? В данном случае
полезно рассмотреть геометрическую интерпретацию.
При р = 9 = 0 и s = 1 однородные координаты преобразованных векторов
всегда равны h = 1. Геометрически данный результат интерпретируется как
ограничение преобразования физической плоскостью h = 1.
Для иллюстрации эффекта преобразования при р и q, отличных от нуля,
рассмотрим следующее выражение:
[X Y h] = [hx hy h] = [x у 1]
= [x у (px + qy +1)] .
"1
0
0
0
1
0
p
q
i_
(2-55)
Здесь X = hx, Y = hy и h = px + qy + 1. Преобразованный координатный вектор,
выраженный в однородных координатах, лежит теперь в трехмерном
пространстве, определенном как h=px + qy + l. Это преобразование показано на рис. 2-14,
где отрезок АВ, принадлежащий физической плоскости h = 1, преобразуется в
CD со значением h ф 1, т. е. рХ + qY — h + 1 = 0.
Однако представляют интерес результаты, принадлежащие физической
плоскости с h = 1, которые можно получить путем геометрического проецирования
прямой CD с плоскости h ф 1 обратно на плоскость h = 1 с использованием для
этого проецирующих лучей, проходящих через начало координат. Из рис. 2-14,
используя правило подобия треугольников, получим
X
X =
или в однородных координатах
[х* У* 1] =
*ч
V г 1
h h
>,У*п
X, X*
Рис. 2-14 Преобразовавие из физической плоскости (Л = 1) иа плоскость h ф 1 и
проецирование обратно на физическую плоскость.
После этого, нормализуя выражение (2-55) делением однородных координат
на величину h, получаем
или
х Y ll Г х у il
h h Ч \.px + qy + l px + qy+1 "J
x* - X - X
h px + qy + V
•-•?- ..'...
(2-56)
(2-57a)
(2-57b)
Детально действие преобразования рассмотрим на следующем примере.
Пример 2-8 Проецирование в однородных координатах
Для отрезка АВ из рис. 2-14 имеем р = q = 1, [А] = [1 3 1] и [В]
[4 1 1],
0-й"-
1 3 1
4 11
1 0 1
0 11
0 0 1
1 3 5
4 1 6
Таким образом, [С] = [1 3 5] и [D] = [4 1 6] на плоскости h—x+y+1.
Проецируя обратно на плоскость h = 1 путем деления на коэффициент
однородных координат, проведем двумерное преобразование точек
[С*]=[1 3 5] =.[1/5 3/5 1],
(D*] = [4 1 6] = [2/3 1/6 1] .
Результат показан на рис. 2-14.
2-19 ПРОПОРЦИОНАЛЬНОЕ МАСШТАБИРОВАНИЕ
Оставшийся необъясненным элемент s (3 х 3)-матрипы преобразования
соответствует пропорциональному масштабированию, при котором все компоненты
вектора изменяются пропорционально. Покажем это, рассмотрев следующее
преобразование:
[X Y h] = [x у 1]
Г1
0
0
6, чл
1 0
0 s
= [х у в].
(2-58)
где X = х, Y = у и h = s. После нормализации получим X* = xfs и У"*, = y/s.
Таким образом, преобразование [х у 1] [Г] = [x/s y/s l] является
равномерным масштабированием координатного вектора. Если s < 1, то происходит
растяжение, а если s > 1 — сжатие.
У, У*
А = 2
Рис. 2-15 Геометрическая интерпретация пропорционального масштабирования.
Заметим, что это преобразование осуществляется также в плоскости h = 1.
Здесь h = s — const, и поэтому плоскость h ф 1 параллельна плоскости h =
1. Геометрическая интерпретация данного эффекта показана на рис. 2-15. Если
s < 1, то h = const задает плоскость, лежащую между плоскостями h = 1 и
h = 0. Следовательно, когда преобразуемая прямая АВ проецируется обратно
на плоскость h = 1, то А*В* увеличивается. Аналогично, если s > 1, то h =
const определяет плоскость, расположенную за плоскостью h = 1 и проходящую
вдоль оси h. В случае проецирования прямой CD на плоскость h = 1 происходит
уменьшение прямой C*D*.
2-20 ТОЧКИ БЕСКОНЕЧНОСТИ
Однородные координаты предоставляют удобный и эффективный способ
нанесения точек из одной системы координат в соответствующие точки альтернативной
координатной системы. Бесконечная область в одной координатной системе часто
преобразуется в конечную область в альтернативной системе. При некорректном
выборе переноса параллельность прямых может не сохраняться. Однако точки
пересечения после преобразования оказываются снова в точках пересечения.
Данное свойство используется для определения однородных координат представления
точек бесконечности.
Рассмотрим пару пересекающихся прямых, заданных уравнениями
х + у = 1,
2х-3у = 0.
Прямые пересекаются в точке с координатами х = 3/5, у = 2/5. Запишем
уравнения в виде х + у — 1 = 0, 2х — Зу = 0 и представим их в матричной форме
[х у 1]
1 2
1 -3
-1 0
= [0 0]
или
[Х}[М'} = [R].
Если матрица [М'] квадратная, то пересечение может быть получено путем
обращения матрицы. Изменим систему исходных уравнений следующим образом:
х + у-1 = 0,
2х-3у = 0,
1 = 1,
или в матричной форме
[Х][М] = [Д],
т.е.
[х у 1]
1 2 0
1 -3 0
-1 0 1
= [0 0 1]
Квадратная матрица, обратная данной [2-1], имеет следующий вид:
'3/5 2/5 01 t [3 2 О'
[М]-1 = 1/5 -1/5 0 = - 1 -1 О
[3/5 2/5 lj 5 [з 2 5
Умножая обе части уравнения на [М]-1 и учитывая, что [М][М]-1 = [Г\ является
тождественной матрицей, получим
[х у 1] = - [0 0 1]
3 2 0
1 -1 О
3 2 5
= [3/5 2/5 1] .
Таким образом, точка пересечения опять имеет координаты х = 3/5, у = 2/5.
Рассмотрим теперь две параллельные прямые, заданные следующим образом:
х + у = 1,
х+у = 0.
По определению геометрии Евклида, точка пересечения двух параллельных
прямых расположена в бесконечности. Продолжая предыдущие рассуждения,
вычислим точку пересечения этих прямых, заданных в матричной форме,
[х у 1]
1 1 0
1 1 0
-1 0 1
= [0 0 1].
Однако несмотря на то что матрица квадратная, она не имеет обратной, так как
две ее строки тождественны. Такая матрица называется сингулярной. Возможна
иная формулировка с обратимой матрицей. Получим ее, переписывая систему
уравнений следующим образом:
х + у - 1 = 0,
х + у = 0,
или в матричной форме
[х у 1]
111
1 1 0
-10 0
= [0 0 х].
Таблица 2-1 Однородные координаты для
точки [4 3]
Л
1
1/2
1/3
ж*
4
8
12
У*
3
6
9
X
4
4
4
У
3
3
3
1/10 40 30 4 3
1/100 400 300 4 3
В данном случае матрица не является сингулярной и существует обратная ей
[М]
-1 _
о о
0 1
1 -1
-1
1
о
Умножая обе части выражения на обратную матрицу, получаем
[х у 1] = [0 0 х]
О 1 -1
0 1 1
1 -1 и О
= [х -х 0] = х [1 -1 0]
Результирующие однородные координаты [1 — 1 0] определяют точку
пересечения двух параллельных прямых, т.е. точку бесконечности. В частности, они
представляют данную точку в направлении [1 — 1] двумерного пространства. В
общем виде двумерный координатный вектор [а Ъ 0] представляет точку
бесконечности на прямой ау — Ъх = 0. Приведем несколько примеров:
точка на положительной оси ж,
точка на отрицательной оси х,
точка на положительной оси у,
точка на отрицательной оси у,
вдоль прямой у = х в направлении [1 1].
Вектор с однородной компонентой ft = 0 действительно представляет точку
бесконечности и может быть также интерпретирован как движение к пределу
(табл. 2-1).
Рассмотрим прямую у* = (3/4)х* и точку [X Y ft] = [4 3 1]. Напомним,
что в однородных координатах не существует единственного представления
координатного вектора (табл. 2-1). Точка [4 3 1] представлена в однородных
координатах по всем направлениям. Заметим, что в этой таблице при ft —> 0 отношение
у* х* остается равным 3/4, как и требуется для сохранения уравнения. Кроме
этого, обратим внимание на то, что следующая пара (х* у*), все точки которой
располагаются на линии у* = (3/4)х*, быстро приближается к бесконечности. Таким
[ 1
[-1
[ °
[ °
[ 1
0 0]
0 0]
1 0]
-1 0]
1 0]
образом, предел при h —> 0 и есть точка бесконечности, заданная в однородных
координатах как [X Y h] = [4 3 0].
Обратившись снова к рис. 2-15, легко продемонстрировать геометрическую
интерпретацию процесса движения к пределу при Л. —>- 0. Рассмотрим отрезок
единичной длины, проходящий от точки начала координат в направлении [1 0] на
плоскости h = s (s < 1). При s —> 0 проекция этой прямой обратно на
физическую плоскость h = 1 в направлении лучей, проходящих через начало координат,
становится бесконечной длины. Следовательно, конечная точка прямой должна
представляться точкой бесконечности на оси X.
2-21 ПРАВИЛА ВЫПОЛНЕНИЯ ПРЕОБРАЗОВАНИЙ
Для представления данных и выполнения преобразований с помощью
умножения матриц используются различные соглашения. Наибольшее внимание нужно
уделять формулировке задач и интерпретации результатов. Например, перед
выполнением поворота необходимо получить ответы на следующие вопросы.
В правосторонней или левосторонней системе координат определяются
поворачиваемые координатные векторы?
Вращается объект или система координат?
Как определяются положительный и отрицательный повороты?
Координаты записываются в виде строки или столбца матрицы?
Вокруг какой линии или оси осуществляется поворот?
В данном изложении используется правосторонняя система координат, объект
вращается в неподвижной координатной системе, положительный поворот
определяется правилом правой руки, т. е. поворот по часовой стрелке осуществляется
вокруг оси при наблюдении от начала вдоль положительной оси, и координатные
векторы представляются в виде строки матрицы.
Выражение (2-29) задает преобразование для положительного поворота
вокруг начала координат или оси z. Так как вектор задается строкой матрицы,
то матрицу преобразования следует разместить после данных или матрицы
координатных векторов. Это преобразование задается путем умножения справа. В
случае однородных координат для положительного поворота объекта на угол в
вокруг начала координат (оси z) использование умножения справа приводит к
следующему результату:
[X*] = [Х][Щ,
[х* у* 1] = [х у 1]
cos в sin в 0
■ sin в cos в 0
0 0 1
(2-59)
Если мы подставим координатные векторы, заданные в однородных координатах
в виде столбца матрицы, то поворот можно выполнить следующим образом:
[Х*] = [Д]-1[Х],
COS в
sind
0
— sin в
cos в
0
0
0
1
X
У
1
(2-60)
Выражение (2-60) называется преобразованием с умножением слева, так как
матрица преобразования расположена перед столбцом координатного вектора или
данных.
Заметим, что (3 х 3)-матрица в выражении (2-60) есть транспозиция (3 х 3)-
матрицы из выражения (2-59). Это свидетельствует о независимости строк и
столбцов матрицы.
Для того чтобы повернуть систему координат и оставить неизмененными
координатные векторы, необходимо в выражении (2-59) заменить в на —в. Вспомним,
что sin# = — sin(—в), a cos0 = cos(—в).
Теперь выражение (2-59) будет иметь вид
[х* у* 1] = [х у 1] =
cos в -sin в 0
sin в cos в 0
0 0 1
(2-61)
Рис. 2-16 Эквивалентность преобразования координатных векторов и систем
координат.
Заметим, что (3 х 3)-матрица опять имеет обратную и также транспонируется в
матрицу из (2-59).
Если вращается система координат и используется левосторонняя
координатная система, то замену в на —в надо производить дважды, а уравнение (2-59)
снова оказывается справедливым при допущении, что применяется последующее
умножение на строку матрицы данных.
Заметим, что, как показано на рис. 2-16, вращение против часовой стрелки
векторов, задающих объект, идентично повороту в том же направлении
координатных осей при неподвижном объекте. Опять нет необходимости в изменении
содержимого матрицы преобразования 3x3, если нет других причин для ее
редактирования. Эти несколько примеров показывают, насколько аккуратно
необходимо выполнять матричные преобразования.
2-22 ЛИТЕРАТУРА
2-1 Fox L. An Introduction to Numerical Linear Algebra, Oxford University Press, London,
1964.
2-2 Forrest A. R. Coordinates, Transformations, and Visualization Techniques, CAD Group
Document №. 23, Cambridge University, June 1969.
Глава 3
Пространственные
преобразования и
проекции
3-1 ВВЕДЕНИЕ
Способность визуализировать или изображать пространственный объект
является основой для понимания формы этого объекта. Кроме того, во многих
случаях для этого важна способность вращать, переносить и строить виды проекций
объекта. Все это легко демонстрируется на примере нашего знакомства с
относительно сложным незнакомым объектом. Чтобы понять его форму, мы тут же
начинаем вращать объект, отодвигать на расстояние вытянутой руки,
передвигать вверх и вниз, вперед и назад и т.д. Чтобы сделать то же самое с помощью
компьютера, мы должны распространить наш предшествующий двумерный
анализ на три измерения. Основьтаясь на полученном опыте, мы немедленно вводим
однородные координаты. Таким образом, точка в трехмерном пространстве [х у z]
представляется четырехмерным вектором
[х1 у' z' h] = [x у z 1] [Г],
где [Т] является матрицей некоего преобразования. Как и ранее, преобразование
из однородных координат в обычные задается формулой
[х* у*
1] =
°L К. £ 1
h h h
(3-1)
Обобщенную матрицу преобразования размерности 4x4 для трехмерных
однородных координат можно представить в следующем виде:
[Т] =
а Ь с р
d e f q
9 г j т
I тп п s
(3-2)
Матрицу преобразования 4 х 4 из (3-2) можно разделить на четыре отдельные
части:
3
3x3 : х
1
1x3
1x1
Верхняя левая (3 х 3)-подматрица задает линейное преобразование1 в форме
масштабирования, сдвига, отражения и вращения. Левая нижняя (1 х 3)-подматрица
задает перемещение, а правая верхняя (3 х 1)-подматрица—перспективное
преобразование. Последняя правая нижняя (1 х 1)-подматрица задает общее
масштабирование. Общее преобразование, полученное после применения этой (4 х 4)-
матрицы к однородному вектору и вычисления обычных координат, называется
билинейным преобразованием2. В общем случае данное преобразование
осуществляет комбинацию сдвига, локального масштабирования, вращения, отражения,
перемещения, перспективного преобразования и общего масштабирования.
3-2 ТРЕХМЕРНОЕ МАСШТАБИРОВАНИЕ
Диагональные элементы (4 х 4)-матрицы обобщенного преобразования задают
локальное и общее масштабирование. Для иллюстрации этого рассмотрим
преобразование
[Х}[Т} = [х у z 1]
а О О О
О е О О
О 0 j О
0 0 0 1
1],
(3-3)
= [ах еу jz 1] = [х* у*
которое показывает действие локального масштабирования. Ниже приводится
пример.
Пример 3-1 Локальное масштабирование
Рассмотрим прямоугольный параллелепипед (RPP), показанный на
рис. 3-1 а со следующими однородными координатами вершин:
0
2
2
0
0
2
2
0
0
0
3
3
0
0
3
3
1
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
[Х] =
Чтобы получить единичный куб из RPP с помощью локального
масштабирования, необходимы масштабные множители 1/2, 1/3, 1 вдоль осей х, j/, z
соответственно. Преобразование локального масштабирования задается
матрицей
[Т] =
1/2 0 0 0'
0 1/3 0 0
0 0 10
0 0 0 1
1 Линейное преобразование — это преобразование, переводящее линейную комбинацию
векторов в ту же самую линейную комбинацию преобразованных векторов.
2 Билинейное преобразование — это результат двух последовательных линейных
преобразований.
z («о
Рис. 3-1 Трехмерные масштабирования.
Результирующий куб имеет следующие однородные координаты вершин:
[Х'] = [Х][Т]
0
2
2
0
0
2
2
.0
■о
1
1
0
0
1
1
.0
0
0
3
3
0
0
3
3
0
0
1
1
0
0
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1-1
1
1
1
1
1
1
lj
1-1
1
1
1
1
1
1
lj
Г1/2
0
0
0
0
1/3
0
0
0
0
1
0
<r
0
0
1
Заметим, что однородный координатный множитель h равен единице для
каждой из преобразованных вершин. Результат масштабирования показан
на рис. 3-1 6.
Общее масштабирование можно осуществить, воспользовавшись четвертьш
диагональным элементом, т. е.
[X)[T\ = [xyzl]
10 0 0
0 10 0
0 0 10
0 0 0s
= [х' у' z' a].
(3-4)
Обычные или физические координаты имеют вид
Этот результат снова иллюстрируется на примере.
Пример 3-2 Общее масштабирование
Для общего масштабирования единичного куба, изображенного на
рис. 3-1 6, на множитель два (удвоение размера), необходимо
преобразование (см. (3-4))
[Т] =
10 0 0 ■
0 10 0
0 0 10
0 0 0 1/2
Полученный в результате параллелепипед RPP имеет следующие
однородные координаты вершин:
[Х'] = [Х*][Т] =
гО 0
1 0
1 1
0 1
0 0
1 0
1 1
.0 1
гО 0
1 0
1 1
0 1
0 0
1 0
1 1
.0 1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1-
1
1
1
1
1
1
1.
■1
0
0
0
0.5-]
0.5
0.5
0.5
0.5
0.5
0.5
0.5.
0
1
0
0
0
0
1
0
0
0
0
1/2
Заметим, что однородный координатный множитель h для каждой из
преобразованных вершин равен 0.5. Таким образом, для того чтобы получить
обычные или физические координаты, каждый вектор необходимо разделить
на h. Результат, показанный на рис. 3-1 с, равен
[X*]
0
2
2
0
0
2
2
0
0
0
2
2
0
0
2
2
2
2
2
2
0
0
0
0
1—1
1
1
1
1
1
1
1
Заметим здесь, что, как и в случае двумерного общего масштабирования,
однородный координатный множитель не равен единице. По аналогии с предыдущим
обсуждением (см. разд. 2-18) это означает преобразование из физического
объема h = 1 в другой объем в 4-мерном пространстве. Преобразованные физические
координаты получаются проецированием через центр 4-мерной координатной
системы обратно в физический объем h = 1. Как и ранее, если s < 1, происходит
однородное расширение. Если s > 1, происходит однородное сжатие
координатного вектора.
Такой же результат можно получить, используя одинаковые коэффициенты
локальных масштабирований. В этом случае матрица преобразования имеет вид
"1/а 0 0 0"
0 1/а 0 0
0 0 1/а 0
0 0 0 1
[Т] =
Отметим, что здесь однородный координатный множитель равен единице, т.е.
h = 1. Таким образом, все преобразование происходит в физическом объеме Л = 1.
3-3 ТРЕХМЕРНЫЕ СДВИГИ
Недиагональные элементы в верхней левой 3 х 3-подматрице обобщенной матрицы
преобразования размером 4x4 задают сдвиги в трех измерениях, т. е.
= [х у z 1]
= [х + yd + gz
1 b с 0
d 1 / 0
9 г 1 0
0 0 0 1
bx + y + iz
=
сх + fy + z
!]•
(3-5)
Поясним это на примере.
Пример 3-3 Сдвиги
Снова рассмотрим единичный куб, изображенный на рис. 3-1 Ь. Применив
преобразование сдвигов
[21 =
получаем
[Х'] = [Х][Т]
■ 1
-0.75
0.5
0
0 0
1 0
1 1
0 1
0 0
1 0
1 1
0 1
0.5
1.5
0.75
-0.25
0
1
0.25
-С
).75
1
1
1
1
0
0
0
0
-0.85 0.25
1
1
0
1-
1
1
1
1
1
1
1.
1
0.15
1.15
2
0
-0.85
0.15
1
0.7
1
0
■ 1
-0.75
0.5
0
1 1п
1.25 1
1.95 1
1.7 1
0 1
0.25 1
0.95 1
0.7 1.
0"
0
0
1.
>
-0.85 0.25
1
1
0
0.7
1
0
0
0
0
1
Этот результат показан на рис. 3-1 d. Заметим, что во всех трех примерах
остается неизменной вершина параллелепипеда, находящаяся в начале
координат.
3-4 ТРЕХМЕРНОЕ ВРАЩЕНИЕ
Прежде чем переходить к трехмерному вращению вокруг произвольной оси,
рассмотрим вращение вокруг каждой из координатных осей. При вращении вокруг
оси х остаются неизменными я-координаты координатного вектора. Фактически
J—►*
(*)
(о)
+90°
i 1 „д*
Рис. 3-2 Трехмерные повороты.
вращение происходит в плоскостях, перпендикулярных оси х. Аналогичным
образом вращение вокруг осей у и z происходит в плоскостях, перпендикулярных осям
у и z соответственно. Преобразование координатного вектора в каждой из этих
плоскостей задается указанной в (2-29) матрицей двумерного вращения. Эта
матрица и неизменность координаты х при вращении вокруг оси х позволяют
записать 4 х 4-преобразование однородных координат при повороте на угол в в виде
[Т] =
1
0
0
0
0
COS0
— sin0
0
0
sin0
COS0
0
0
0
0
1
(3-6)
Вращение считается положительным в смысле правила правой руки, т. е. по
часовой стрелке, если смотреть из начала координат в положительном направле-
нии оси вращения1. На рис. 3-2 Ь показан параллелепипед, полученный поворотом
на —90° вокруг оси х параллелепипеда с рис. 3-2 а.
Аналогично матрица преобразования для вращения вокруг оси z на угол ф
имеет вид
[Т} =
cos^ sini/i 0 0
— sini/) cos^ 0 0
0 0 10
0 0 0 1
(3-7)
При вращении на угол ф вокруг оси у преобразование имеет вид
[Т} =
COS0
0
sin$
0
0
1
0
0
— sin0
0
COS0
0
0
0
0
1
(3-8)
Заметим, что в (3-8) знаки у синусов противоположны знакам этих членов в
равенствах (3-6) и (3-7). Это нужно для того, чтобы вьшолнялось соглашение о
положительном направлении по правилу правой руки.
Из равенств (3-6)-(3-8) следует, что детерминант каждой из матриц
преобразований равен +1, что и необходимо для чистого вращения. Более полно эти
результаты проиллюстрирует пример.
Пример 3-4 Вращение
Рассмотрим прямоугольный параллелепипед, изображенный на
рис. 3-2 о. Матрица [X] координатного вектора имеет вид
[X]
0
3
3
0
0
3
3
0
0
2
2
0
0
2
1
1
1
1
0
0
0
1-1
1
1
1
1
1
1
О 2 0 1J
В данном случае строка, отмеченная буквой А в матрице [X], соответствует
точке А на рис. 3-2. Равенство (3-6) для поворота на в = —90° вокруг оси х
приводит к следующему преобразованию:
[Т] =
10 0 0-
0 0-10
0 1 0 0
0 0 0 1
1 Правило правой руки для вращения формулируется следующим образом: направьте
большой палец правой руки в положительном направлении оси вращения. Тогда естественное
спиральное движение пальцев указывает положительное направление вращения.
Применение этого преобразования дает новые координаты:
[Х'] = [Х)[Т] =
гО 0 1 1]
3 0 11
3 2 11
0 2 11
0 0 0 1
3 0 0 1
3 2 0 1
.0 2 0 1.
■1 0
0 0
0 1
0 0
Г0 1 0 1-1
3 1 0 1
3 1-21
0 1-21
0 0 0 1
3 0 0 1
3 0-21
.0 0 -2
1.
А'
0 О"
-1 0
0 0
0 1
Отметим, что, как и должно быть, т-компоненты [X] и [X*] идентичны.
Результат данного поворота изображен на рис. 3-2 Ь.
Для поворота на угол ф = +90° вокруг оси у уравнение (3-7) дает
следующую матрицу преобразования:
[Т'} =
Г0 0 -1 0
0 1 0 0
10 0 0
0 0 0 1
Снова применив преобразование к исходному параллелепипеду, получим
новые координаты:
[Х*'] = [Х][Т'] =
о
3
3
0
0
3
3
.0
1
1
1
1
0
0
0
.0
0
0
2
2
0
0
2
2
0
0
2
2
0
0
2
2
1 1-
1 1
1 1
1 1
0 1
0 1
0 1
0 1.
0 1]
-3 1
-3 1
0 1
0 1
-3 1
-3 1
0
1.
■о
0
1
.0
А'
0
1
0
0
-1
0
0
0
0
0
0
1
Заметим, что в этом случае идентичны у-компоненты [X] и [X"]. Результат
изображен на рис. 3-2 с.
Так как трехмерные вращения получаются с помощью перемножения матриц,
то они не коммутативны; т. е. порядок перемножения влияет на конечный резуль-
тат (см. разд. 2-12). Чтобы показать это, рассмотрим два последовательных
поворота на один и тот же угол — сначала вокруг оси х, затем вокруг оси у. Используя
уравнения (3-6) и (3-8) с в = ф, мы получим
[Т} =
О 0 0
cos в sin в 0
- sin в cos в 0
0 0 1
cos^ 0
0 1
sine 0
0 0
-sine 0
0 0
cose 0
0 1
cose
sin2e
cos e sin e
о
0 -sine 0'
cos e cos e sin e о
-sine cos2e о
о о 1
(3-9)
С другой стороны, обратная операция, т. е. поворот вокруг оси у, а потом вокруг
оси х с углом в = ф дает
[Т} =
cose
0
sine
0
cose
0
sine
0
0
1
0
0
—
— sine
0
cose
0
sin2e
cose
cos e sin e
0
0'
0
0
1
"1 0
0
о cos e sin e
о — sin e cos e
0 0 0
- cos e sin e о
sine 0
cos2 e о
0 1
0"
0
0
1
(3-10)
Сравнивая правые части (3-9) и (3-10), видим, что они не одинаковы. Если надо
сделать более одного поворота, то следует помнить о некоммутируемости
трехмерных вращений.
На рис. 3-3 с и 3-3 d штриховой линией изображен результат
преобразования, состоящего из двух поворотов на 90° при помощи произведения матриц из
(3-9) для объекта, показанного на рис. 3-3 а. Осуществляя повороты, заданные
(3-10), в обратном порядке, получим фигуры, нарисованные сплошными линиями
на рис. 3-3 Ь и 3-3 d. Рис. 3-3 d наглядно показывает, что при изменении
порядка вращения получаются различные результаты. Приведенный ниже численный
пример иллюстрирует это.
Пример 3-5 Комбинированные повороты
Объект на рис. 3-2 а имеет следующие координатные векторы:
Г0 0 1 1-1
2 0 11
2 3 11
0 2 11
0 0 0 1
2 0 0 1
2 3 0 1
.0 2 0 1.
[X]
+90°
(a)
+90°
+90°
(с).
Рис. 3-3 Некоммутативность трехмерных поворотов.
(<0
Общая матрица для вращения сначала вокруг оси х на угол в = 90°, а затем
вокруг оси у на угол ф = 90° задается уравнением (3-9) в виде
[Т} =
0 0 -1 0
10 0 0
0-1 0 0
0 0 0 1
Преобразованные координатные векторы равны
[Х'] = [Х][Т} =
0
2
2
0
0
2
2
0
0
0
3
2
0
0
3
.2
0 1
0 1
3 1
2 1
0 0
0 0
3 0
2 0
-1
-1
-1
-1
0
0
0
0
1-
1
1
1
1
1
1
1.
■о
1
0 -
0
0 1-
-2 1
-2 1
0 1
0 1
-2 1
-2 1
0
1.
А'
0
0
-1
0
-1
0
0
0
0
0
0
1
Преобразованный объект изображен штриховой линией на рис. 3-3 d.
Общая матрица для вращения сначала вокруг оси у на угол ф = 90°, а
затем вокруг оси х на угол в = 90° задается уравнением (3-10) в виде
[Х«] = [Х\[Т]:
301
0
2
2
0
0
2
2
0
[Т'] =
3cLHI
0
0
3
2
0
0
3
2
1
1
1
1
0
0
0
0
КС
1-
1
1
1
1
1
1
1.
0
1
0 0
1 0
0 0
ордш
"0
0
1
.0
0
1
0
0
!ать
1
0
0
0
0
0
0
1
1Ы€
0
1
0
0
■1
1
1
1
0
0
0
.0
0
2
2
0
0
2
2
0
0
0
3
2
0
0
3
2
1
1
1
1
1
1
1
1
А"
Преобразованный объект изображен сплошными линиями на рис. 3-3 d.
Сравнение двух числовых результатов также ясно показывает, что
ориентация преобразованных объектов совершенно различна. Следовательно,
порядок перемножения матриц очень важен.
3-5 ТРЕХМЕРНОЕ ОТРАЖЕНИЕ
Некоторые ориентации трехмерного объекта нельзя получить одними
вращениями, требуются преобразования отражения. В трехмерном пространстве
отражение происходит относительно плоскости. По аналогии с обсуждавшимся
ранее двумерным отражением (см. разд. 2-10), трехмерное отражение относительно
плоскости эквивалентно вращению вокруг оси в трехмерном пространстве в
четырехмерное пространство и обратно в исходное трехмерное пространство. Для
чистого отражения детерминант матрицы равен — 1.
•-*,**
Рис. 3-4 Трехмерное отражение относительно плоскости ху.
При отражении относительно плоскости ху изменяются только значения z-
координаты координатного вектора объекта. В самом деле, они изменяют знак.
Таким образом, матрица преобразования для отражения относительно плоскости
ху равна
[Т] =
10 0 0
0 1 0 0
0 0-10
0 0 0 1
(3-11)
На рис. 3-4 изображено отражение единичного куба относительно плоскости ху.
При отражении относительно плоскости yz
сп =
-10 0 0
0 10 0
0 0 10
0 0 0 1
а для отражения относительно плоскости xz
[Т\ =
0 0 0
-10 0
0 10
0 0 1
(3-12)
(3-13)
Эти результаты иллюстрируются в приведенном ниже численном примере.
Пример 3-6
Отражение
Параллелепипед ABCDEFGH, изображенный на рис. 3-4, имеет коор
динатный вектор
[Х] =
г1 0
2 0
2 1
1 1
1 0
2 0
2 1
.1 1
-1
-1
-1
1 1
to i->
-2
-2
-2
1-
1
1
1
1
1
1
1.
Матрица преобразования для отражения относительно плоскости ху
задается посредством (3-11). После отражения преобразованные координатные
векторы равны
[Х'] = [Х}[Т] =
Результат А* В'С* D* E* F*G' Я* показан на рис. 3-4.
3-6 ПРОСТРАНСТВЕННЫЙ ПЕРЕНОС
Матрица пространственного переноса имеет вид:
'10 0 0'
п 1
[Т) =
1
2
2
t-H
t-H
2
2
1
0
0
1
1
0
0
1
1
-1
-1
-1
-1
-2
-2
-2
-2
"1
0
0
0
0
1
0
0
0
0
-1
0
0]
0
0
lj
~"
t-H
2
2
t-H
1
2
2
1
0
0
1
1
0
0
1
1
1
1
1
1
2
2
2
2
1 0 0
0 1 0
тп п 1
(3-14)
Перемещенные однородные координаты получаются с помощью преобразования
[х' у' z' h] = [x у г 1]
0 0 0
1 0 0
0 1 0
тп п 1
Выполнив умножение, получим
[х1 у1 z1 h] = [(x + l) (у + тп) (z + n) 1].
Из этого следует, что преобразованные физические координаты равны
х* = х + 1,
у* = у + тп,
z* — z + n.
(3-15)
3-7 КОМПОЗИЦИИ ПРЕОБРАЗОВАНИЙ
Последовательные преобразования могут быть скомбинированы или объединены
в одно (4 х 4)-преобразование, дающее тот же самый результат. Так как
перемножение матриц является некоммутативной операцией, то важен порядок ее
выполнения (в общем случае [Л] [В] ф [В] [А]). Правильный порядок определяется
положением конкретной матрицы преобразования относительно матрицы
координатного вектора. Матрица, ближайшая к матрице координатного вектора, задает
первое преобразование, а последняя — последнее преобразование. Математически
это можно записать следующим образом:
где
[Х}[Т] = [Х№][Т2][Т3][Т4].
[Г] = [Г1][Г2][Тз][Г4]...
и [Ti] являются произвольной комбинацией матриц масштабирования, сдвига,
вращения, отражения, переноса, перспективного преобразования и проецирования.
Так как перспективные преобразования искажают геометрические объекты (см.
разд. 3-15), а преобразования проецирования приводят к потере информации (см.
разд. 3-12), то в случае наличия этих матриц они должны быть расположены
соответственно предпоследней и последней по порядку.
Эти идеи проиллюстрированы в приведенном ниже примере.
Пример 3-7 Композиции преобразований
Рассмотрим для заданного в однородных координатах координатного
вектора [12 11] результат переноса в направлениях x,y,z на —1,-1,-1
соответственно, а затем поворота на +30° вокруг оси х и поворота на +45°
вокруг оси у.
Сначала получим матрицу комбинированного преобразования. Из
равенств (3-14), (3-6) и (3-8) следует, что
[T] = [Tr][Rx][Ry] =
10 0 0
0 cos^ sine 0
о -sine cose о
0 0 0 1
о
1
о
771
о
1
о
тп
COS0
sin ф sin e
sin ф cos e
0
0
cose
— sine
о
COS0
0
sin$
0
— зтф
cos ф sine
cos фcos e
0
— зшф
0
СОБф
о
сояф 0 — sin0 0
sin^sine cose cos^sine 0
sin ф cose —sine cosqdcose 0
1ссюф m cose — fsin0 1
+771 sin ф sine —7i sine +m cos ф sine
_ +7i sin ф cose +n cos ф cose
где е и ф — соответственно углы вращения относительно осей х и у; а /, т,
п — величины переноса в направлениях х, у, z.
(3-16)
В общем случае для координатного вектора мы имеем
[Х][Т] = [х у z 1]
COS0
sin ф sin в
sin ф cos в
1сОБф
0
cos в
— sin в
771 COS 0
— зтф
cos ф sin в
cos ^ cos в
—1 sin 0
0
0
0
1
+msin0sin0 —n sin в +mcos0sin0
,+n sin ф cos б +7i cos ф cos б
(a: + i)cos0 (y + m)cos0 — (x + /)sin^> Г
+(у + 77i) sin 0 sin 0 — (z+n)sin0 +(у + тп)созфзт9
.+(z + n)sin0cos0 +(z + n)cos0cos0
Для конкретных значений 9 = +30°, ф = +45°, I = —1, т = 1, п = — 1
преобразуемый координатный вектор имеет вид [3 2 1 1].
[Х][Т] = [3 2 1 1]
Г 0.707 0 -0.707 0'
0.354 0.866 0.354 0
0.612 -0.5 0.612 0
1.673 -0.366 -0.259 1
[X] [Г] = [1.768 0.866 -1.061 1].
Чтобы убедиться, что общая матрица дает тот же самый результат, как и
последовательное применение матриц, рассмотрим
[Х'] = [Х][Тг] =
= [3 2 1 1]
= [210 1],
• 1 0 0 0'
0 10 0
0 0 10
-1 -1 -1 1
[X"] = [X'] [1Ц = [2 1 0 1]
10 0 0"
0 0.866 0.5 0
0 -0.5 0.866 0
0 0 0 1
= [2 0.866 0.5 1],
[Х'"\ = [Х"\ [Ry] = [2 0.866 0.5 1]
[Х'"] = [1.768 0.866 -1.061 1],
0.707 0 -0.707 0'
0 10 0
0.707 0 0.707 0
0 0 0 1
что доказывает наше утверждение.
3-8 ПОВОРОТЫ ВОКРУГ ОСИ,
ПАРАЛЛЕЛЬНОЙ КООРДИНАТНОЙ ОСИ
Преобразования, заданные равенствами (3-6)-(3-8), описывают вращение вокруг
координатных осей х, у и z. Однако часто бывает необходимо вращать объект
вокруг оси, не совпадающей с этими тремя. Мы рассмотрим частный случай для
оси, параллельной одной из координатных осей х, у или z. На рис. 3-5 изображено
тело в локальной системе осей x'y'z', параллельных фиксированной глобальной
системе xyz. Вращение тела вокруг любой из локальных осей х', у' или z'
выполняется с помощью следующей процедуры:
— переместить тело так, чтобы локальная ось совпала с координатной;
— повернуть вокруг указанной оси;
— переместить преобразованное тело в исходное положение.
Математически это можно записать так:
[X*) = [X][Tr][Rx}[Tr]-\
где
[X*] — преобразованное тело,
[X] — исходное тело,
[Тг] — матрица перемещения,
[Rx] — соответствующая матрица поворота,
[Тг]-1 —матрица, обратная к матрице перемещения.
Ниже приводится иллюстративный пример.
(а) <*)
Рис. 3-5 Поворот вокруг оси, параллельной одной из координатных осей.
Пример 3-8 Единственное относительное вращение
Рассмотрим параллелепипед, изображенный на рис. 3-5 а, заданный
координатными векторами
[Х] =
относительно глобальной системы координат xyz. Повернем
параллелепипед на в = +30° относительно локальной оси х', проходящей через центр
параллелепипеда. Предполагается, что начало локальной системы
координат находится в центре параллелепипеда. Координаты этого центра равны
[хс Ус zc 1] = [3/2 3/2 3/2 1]. Вращение осуществляется следующим
образом:
t-H
2
2
1
t-H
2
2
1
t-H
1
2
2
1
1
2
2
2
2
2
2
1
1
1
1
1-
1
1
1
1
1
1
1.
А
В
С
D
Е
F
G
Н
[Х'] = [Х][Тг][Щ[ТгГ
где
[Тт] =
1 0
0 1
о о
о -ус
0 О'
о о
1 0
10 о а
0 1 0 0
0 0 10
0 -3/2 -3/2 1
[Ях] =
10 0 0"
0 cos0 sine 0
0 -sin в cos в 0
0 0 0 1
10 0 О-
О 0.866 0.5 О
0 -0.5 0.866 0
0 0 0 1
[Тг]-1 =
10 0 0
0 10 0
0 0 10
.0 ус zc 1.
10 о а
0 10 0
0 0 10
0 3/2 3/2 1
Первая матрица [Тг] сдвигает параллелепипед параллельно плоскости х = 0
до тех пор, пока ось х' не совпадет с осью х. Вторая матрица [Rx] вьшолняет
требуемое вращение вокруг оси х, третья матрица [Тг]"1 переносит ось х',
а следовательно, и повернутый параллелепипед, обратно в исходное
положение.
Объединив эти три матрицы, получим
[Т] = [Тг][Д,][Тг]-1 =
■1 0
0 cos^
0 -sine
.0 ус(1 — cos в) + zc sin в zc{\ -
0 0
sine 0
cose о
- cos e) — yc sin e 1.
После подстановки числовых значений преобразованные координаты примут
вид:
[Х'] = [Х][Т] =
[Х'] =
1
1
2 1
2 2
1 2
1 1
2 1
2 2
1 2
-1
2
2
1
1
2
2
.1
2 1-1
2 1
2 1
2 1
1 1
1 1
1 1
1 1.
■10 0
0 0.866 0.5
0 -0.5 0.866
0 0.951 -0.549
0.817 1.683 IT A
0.817 1.683 1
1.683 2.183 1
1.683 2.183 1
1.317 0.817 1
1.317 0.817 1
2.183 1.317 1
2.183
1:317 1J
В
С
D
Е-
F
G
Н
0
0
0
1
Результат изображен на рис. 3-5 6.
В предыдущем примере требовалось только вращение вокруг единственной
оси, параллельной одной из координатных осей. Таким образом надо только
было сделать так, чтобы ось вращения совпала с соответствующей координатной
осью. Для того чтобы совершить несколько поворотов в локальной системе осей,
параллельных осям глобальной системы координат, надо совместить начала
локальной и глобальной систем. Конкретнее, повороты могут быть выполнены с
помощью следующей процедуры:
— переместить локальную систему осей так, чтобы начала локальной и
глобальной систем совпали;
— выполнить требуемые повороты;
— переместить локальную систему осей обратно в исходное положение. Ниже эта
процедура иллюстрируется на примере.
Пример 3-9 Несколько относительных вращений
Рассмотрим снова параллелепипед, изображенный на рис. 3-5 а. Пусть его
требуется повернуть сначала на угол ф = —45е вокруг оси у', а затем на угол
в = +30° вокруг оси х'. Для этого надо совместить начала систем координат
x'y'z' и xyz, выполнить необходимые повороты, а результат вернуть обратно
в исходное положение.
Объединенное преобразование имеет вид:
[X'] = [X][T] = [X][Tr][Rv][Rx][Tr]-
Конкретнее,
[Г] =
Г 1
0
0
_^Хс
0
1
0
~Ус
0
0
1
—z
'cos ф 0
0 1
sin<£ 0
0 0
1 0
0 cosfl
0 -sinfl
0 0
— sin ^
0
созф
0
0
sin6
cosd
0
О'
0
0
1.
О-
0
0
1
X
■1
0
0
_Хс
0
1
0
Ус
0
0
1
Zc
о-
0
0
1
где ф и в обозначают углы поворотов вокруг осей у' и х', соответственно.
Объединив эти матрицы, получим
[Т] =
созф
0
sin<£
хс(1 — cos$)
—zc sin ф
sin ф sin б
cos в
— cos $ sin в
—xcsin<£sm#
+J/c(l -COS 6)
+zc cos ^ sin б
— sin 0 cos в 0'
sin# 0
cos (^ cos Й 0
Xc sin 0 cos в 1
—j/c sin б
+2C(1 — COS$COS<?)
(3-17)
Тогда преобразованные координатные векторы равны
[Х'] =
Г1
2
2
1
1
2
2
L1
0.707
0
-0.707
1.5
-0.354
0.866
-0.354
1.262
0.612
0.5
0.612
-1.087
[Х'] =
Г0.793
1.5
1.5
0.793
1.5
2.207
2.207
.1.5
Результат изображен на рис. 3-6.
1.067
0.713
1.579
1.933
1.421
1.067
1.933
2.287
1.25
1.862
2.362
1.75
0.638
1.25
1.75
1.138
3-9 ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ В ПРОСТРАНСТВЕ
Обобщенный случай поворота вокруг произвольной оси в пространстве
встречается часто, например в робототехнике, мультипликации, моделировании. Следуя
логике предыдущего обсуждения, поворот вокруг произвольной оси в
пространстве выполняется с помощью переноса и простых поворотов вокруг
координатных осей. Так как метод поворота вокруг координатной оси известен, то основная
идея заключается в том, чтобы совместить произвольную ось вращения с одной
из координатных осей.
Рис. 3-6 Несколько поворотов относительно локальной системы координат.
Предположим, что произвольная ось в пространстве проходит через точку
(я0)2/0)2о) с направляющим вектором (cx,Cj,,cz). Поворот вокруг этой оси на
некоторый угол 6 выполняется по следующему правилу:
— выполнить перенос так, чтобы точка (xo,yo,Zo) находилась в начале системы
координат;
— выполнить соответствующие повороты так, чтобы ось вращения совпала с
осью z г;
— выполнить поворот на угол S вокруг оси z\
— выполнить преобразование, обратное тому, что позволило совместить ось
вращения с осью z\
— выполнить обратный перенос.
В общем случае для того, чтобы произвольная ось, проходящая через
начало координат, совпала с одной из координатных осей, необходимо сделать два
последовательных поворота вокруг двух других координатных осей. Для
совмещения произвольной оси вращения с осью z сначала выполним поворот вокруг
оси х, а затем вокруг оси у. Чтобы определить угол поворота а вокруг оси х,
используемый для перевода произвольной оси в плоскость xz, спроецируем сначала
на плоскость yz направляющий единичный вектор этой оси (рис. 3-7 а).
Компоненты у и z спроецированного вектора равны Су- и cz-компонентам единичного
направляющего вектора оси вращения.
Из рис. 3-7 а следует, что
d = yV + cz2 (3-18)
Выбор координатной оси (в данном случае z) произволен.
P{et, 0. d)
(e)
Рис. 3-7 Повороты, необходимые для совмещения с осью z единичного вектора ОР.
(а) Поворот вокруг х; (Ь) поворот вокруг у.
cos а =
(Г
sin a =
(3-19)
После перевода в плоскость xz с помощью поворота вокруг оси х, z-компонента
единичного вектора равна d, a i-компонента равна сх, т.е. i-компоненте
направляющего вектора, как это показано на рис. 3-7 Ь. Длина единичного вектора
равна, конечно, 1. Таким образом, угол поворота 0 вокруг оси у, необходимый
для совмещения произвольной оси с осью z, равен
cos/3 = d, sin/3 = Сх.
Тогда полное преобразование можно представить в виде
[М] = [Т] [Д.] [Ry] [Rs] [Ry]-1 [R*]-1 [Г]'1,
где матрица переноса равна
[Т]
10 0 0
0 10 0
0 0 10
-хо -j/o —го 1
Матрица преобразования поворота вокруг оси х
[Д-] =
1
0
0
0
0
cos a
— sin а
0
0
sin а
cos а
0
0
0
0
1
1
0
0
0
0
Cz/d
-Су/d
0
0
Cy/d
cz/d
0
0
0
0
1
(3-20)
(3-21)
(3-22)
(3-23)
и вокруг оси у
[Ry] =
cos(-/?) О -sin(-/?) О'
0 10 0
sin(-/?) О cos(-/3) О
0 0 0 1
d 0 сх О"
0 10 0
-сх 0 d О
0 0 0 1
(3-24)
И, наконец, вращение вокруг произвольной оси задается матрицей поворота
вокруг оси z
[Щ* =
— cos S sin 6 0 0
— sin 6 cos 6 0 0
0 0 10
0 0 0 1
(3-25)
На практике углы аи/?не вычисляются явньш образом. Элементы матриц
поворотов [Rx] и [Ry] в (3-21) получаются из уравнений (3-18)-(3-20) за счет
выполнения двух операций деления и извлечения квадратного корня. Хотя данные
результаты были разработаны для произвольной оси в первом квадранте, они
применимы во всех квадрантах.
Если компоненты направляющего вектора произвольной оси неизвестны, то,
зная вторую точку (xi,yi,zi) на оси, их можно определить, нормализовав вектор,
соединяющий первую и вторую точки. Более точно вектор оси из (xo,yo,Zo) в
(xi,yi,zi) равен
[V] = [(ii - х0) (j/i - 2/0) (zi - Zq)].
Нормализация дает компоненты направляющего вектора:
[(ii - х0) (2/1 - j/o) (zi - zo)}
[Cx Cy Cz\ —
[(ii - Z0)2 + (j/1 - J/o)2 + (Zl - Z0)2]*
Более полно этот метод иллюстрируется в следующем примере.
(3-26)
Пример 3-10 Поворот вокруг произвольной оси
Рассмотрим куб с одним отсеченным углом, изображенный на рис. 3-8 а.
Координатные векторы вершин равны
[Х) =
"2
3
3
2.5
2
2
3
3
2
3
1
1
1.5
2
2
1
1
2
2
2
2
2
2
2
2
1.5
11
1
1
1
1
1
1
1
1
1.
А
В
С
D
Е
F
G
Н
I
J
(a)
(с)
Рис. 3-8 Поворот вокруг произвольной оси.
Куб необходимо повернуть на —45° вокруг оси, проходящей через точку F и
противоположный угол на диагонали. Ось направлена из точки F в
противоположный угол и проходит через центр угловой грани.
Сначала определим компоненты направляющего единичного вектора оси
вращения. Учитывая, что угол, отрезанный треугольником CD J также
лежит на оси, из (3-26) следует, что
[Сх Су Сх\ —
[(3-2) (2-1) (2-1)]
((3 - 2)2 + (2 - I)2 + (2 - 1)2)1/2
= [1/^3 1/^3 1Д/3).
С помощью уравнений (3-18)-(3-20) получаем
d = У(1/^3)2 + (1/V3)2 = у/Щ
а = cos-1(l/V3/v^73) = cos-1(l/\/2) = 45°,
^ = cos-1(v^73)=35,26°.
Так как точка F лежит на оси вращения, матрица переноса равна
[Т} =
Г 1 0 0 0'
0 10 0
0 0 10
-2 -1 -1 1
Тогда матрицы поворотов, совмещающих произвольную ось вращения с осью
z, имеют вид:
[Л-] =
10 0 0'
0 1Д/2 1Д/2 0
0 -1Д/2 1/\/2 0
0 0 0 1
[Я,] =
2/V6 0 1/л/з 0'
0 10 0
-l/v/З О 2/\/б 0
0 0 0 1
Обратные матрицы [Д*]-1, [Л»]-1 и РП-1 получаются с помощью
подстановки значений —а, —(3 и (so, j/o, zo) для углов а, (3 и (—so, —уо, —го),
соответственно, в уравнения (3-22)-(3-24).
Объединив [Т], [Ля], [Ду], подучим
[M] = [T}[RX][RV] =
' 2/у/б 0 1/у/з 0
-1/л/б 1Д/2 1/л/З 0
-1/%/б -i/\/2 1/V5 о
.-1/V6 0 -4\/§ 1
Преобразованные промежуточные координаты равны
0.408
0.408
0.204
0.408
0.816
0
0.816
0.408
0.408
0.204
-0.707
-0.707
-0.354
0
0
0
0
0.707
0.707
0.354
0.577
1.155
1.443
1.443
0.155
0
0.577
1.155
0.577
1.443
1
1
1
1
1
1
1
1
1
1
[Х][М] =
Этот промежуточный результат изображен на рис. 3-8 6. Заметим, что точка
F равна (0,0,0).
Вращение вокруг произвольной оси теперь эквивалентно вращению
вокруг оси z. Следовательно (см. (3-7)),
у/2/2
л/2/2
0
0
-л/2/2 0 0"
л/2/2 0 0
0 10
0 0 1
т =
Преобразованный объект возвращается в его «исходное» местоположение в
пространстве с помощью преобразования
[мг^^]-1^]-1^]-
2/ч/б -1/\/б -1/\/б 0'
0 1/л/2 -1/л/2 0
1/л/З 1/л/З 1/л/З 0
2 111
Этот результат можно получить либо обращением и объединением матриц,
составляющих [М], либо обращением самой матрицы [М]. Заметим,
между прочим, что [Rx] [Ry] представляют только повороты. Верхняя левая
(ЗхЗ)-подматрица [М]-1 является точным транспонированием верхней левой
(3 х 3)-подматрицы [М].
Координаты результата равны
где
[X] [М] [Rs] [М-1
[MURs^M]-1 =
) =
"1.689
2.494
2.747
2.598
2.195
2
2.805
3.311
2.506
3.155
■ 0.805 -
0.506
-0.311
0.
195
1.506
1.195
1.598
2.155
2.311
1
0.689
1.494
1.805
1.747
-0.311
0.805
0.506
0.311
1.805
2.311
2.155
1.747
1.494
1
1.506
1.195
0.689
1.598
0.506
-0.311
0.805
-0.506
Г
1
1
1
1
1
1
1
1
1.
О-
0
0
1
На рис. 3-8 с изображен преобразованный объект.
3-10 ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ПЛОСКОСТИ
Преобразования, заданные в уравнениях (3-11)—(3-13), осуществляют отражение
относительно координатных плоскостей х = 0, у = 0, z = 0 соответственно.
Часто возникает необходимость отразить объект относительно произвольной
плоскости. И снова это можно сделать с помощью процедуры, объединяющей ранее
определенные простые преобразования. Один из возможных методов состоит в
следующем:
— перенести точку Р, принадлежащую плоскости отражения, в начало системы
координат;
— повернуть вектор нормали к плоскости отражения в начале координат до
совпадения с осью +z (см. разд. 3-9, уравнения (3-23) и (3-24)), теперь плоскость
отражения будет совпадать с координатной плоскостью z = 0;
— применяя уже известные преобразования, отразить объект относительно
координатной плоскости z = 0 (см. (3-11));
— чтобы получить результаты, необходимо выполнить преобразования,
обратные к описанным в первых двух пунктах.
Тогда общее преобразование описывается матрицей
[М] = [Г] [Дз] [Ry] [Rfltz] [Ry]-1 [Л*]-1 [Г]"1,
где матрицы [Т], [Rx], [Ry] задаются уравнениями (3-22)-(3-24)
соответственно, Rfltz — матрица отражения относительно плоскости z = О, (xo,yo,zo) =
(РХ,РУ, Pz) — координаты точки Р на плоскости отражения; а(Сх,Су, сг) есть
вектор нормали к плоскости отражения1.
Пример более подробно проиллюстрирует данный метод.
Пример 3-11 Отражение
Снова рассмотрим куб с одним отсеченным углом, как это показано на
рис. 3-8 а. Отразим куб относительно плоскости, содержащей треугольник
CDJ.
Выбрав точку С для перемещения в начало координат и вспомнив
координатные векторы для куба, получим матрицу переноса
[Т] =
' 1 0 0 0'
0 1 0 0
0 0 10
-3 -3/2 -2 1
1 Если известно уравнение плоскости отражения, ax + by + cz + d = 0, то единичный вектор
нормали к плоскости равен
Подробности можно найти в [3-1].
(2-1.5) (2-2)] =
1/4 1/4].
Нормаль к плоскости отражения получим, используя координатные векторы
С, D, J (см. [3-1]). Конкретнее, взяв векторное произведение векторов С J и
CD до переноса, получим
n=([J]-[C])x([D]-[C]) =
= [(3 - 3) (2 - 1.5) (1.5 - 2)] х [(2.5 - 3)
= [0 1/2 -1/2] х [-1/2 1/2 0] = [1/4
Нормализация дает
n=[l/V3 1/V3 1/л/З].
Используя уравнения (3-19) и (3-20), получим
d=y/nl+nl = ^(1/л/гу + (1/л/З)2 = v/2/З
и а = 45°, j3 = 35.26°. Матрицы поворотов для совмещения нормали в точке
С с осью z имеют вид (см. (3-23) и (3-24))
[Д*] =
Матрицы [Rx] l, [Ry] 1 и [Г] 1 можно получить подстановкой —а, —/3 и
[х0 уо z0] = [С] в (3-22)-(3-24).
Объединение [Г], [Rx] и [Ry] дает
1
0
0
0
0 0 0'
1/л/2 l/-v/2 0
-1/л/2 1/л/2 0
0 0 1.
, [Ry] =
2/V6 0 1/л/З 0"
0 10 0
-1/л/З 0 2/%/б 0
0 0 0 1
[М] = [Г][Л1][Д„] =
2/%/б 0 1/л/з 0'
-1/%/б 1/л/2 l/v/3 0
-1/л/б -1/л/2 1/л/з 0
-5/2л/б 1/2л/2 -13/2л/3 1
Преобразованные промежуточные точки равны
[Х][М] =
-0.612
0.204
0
-0.612
-1.021
-0.204
0.612
0.204
-0.612
0
-0.354
-0.354
0
0.354
0.354
0.354
0.354
1.061
1.061
0.707
-0.876
-0.287
0
0
-0.287
-1.443
-0.876
-0.287
-0.876
0
1
1
1
1
1
1
1
1
1
1
Этот промежуточный результат изображен на рис. 3-9 6. Заметим, что точка
С находится в начале системы координат, а ось z направлена на нас.
Отражение относительно произвольной плоскости теперь эквивалентно
отражению относительно плоскости z = 0. Следовательно (см. (3-11)),
[Rflt] =
10 0 0-
0 1 0 0
0 0-10
0 0 0 1
Рис. 3-9 Отражение относительно произвольной плоскости.
Для возврата преобразованного объекта в «исходное» положение в
пространстве требуется преобразование
[МГ1 = [Д,Г1[Д.Г1РГ1 =
'2/\/б -1/\/б -1/\/б О'
О 1/л/2 -1/л/2 О
1/-УЗ 1/-УЗ 1/л/З О
3 3/2 2 1
Результирующие координатные векторы таковы:
mwwituM]-1
где
[MURfitwr1 =
На рис. 3-9 с показан преобразованный объект.
=
Г 3 2
10/3 4/3
3 3/2
5/2 2
7/3 7/3
11/3 8/3
4 2
10/3 7/3
3 3
L 3 2
1/3 -2/3
-2/3 1/3
-2/3 -2/3
13/3 13/3
3
7/3
2
2
7/3
8/3
2
4/3
2
3/2
-2/3
-2/3
1/3
13/3
г
1
1
1
1
1
1
1
1
1.
о-
0
0
1
Как показано в этом и предыдущих разделах, сложные преобразования
можно легко построить с помощью простых базовых преобразований. Такой подход
даже предпочтительнее, так как он уменьшает вероятность появления ошибок и
более эффективен с вычислительной точки зрения, нежели прямой
математический подход.
3-11 АФФИННАЯ И ПЕРСПЕКТИВНАЯ (НАЧЕРТАТЕЛЬНАЯ)
ГЕОМЕТРИЯ
К настоящему времени разработана математическая теория как для
перспективной (начертательной), так и для аффинной геометрии. Теоремы аффинной
геометрии идентичны теоремам геометрии Евклида. И в той и в другой науках важным
понятием является параллелизм. В перспективной геометрии прямые в общем
случае не параллельны.
Аффинное преобразование есть комбинация линейных преобразований,
например поворота и последующего переноса. Для аффинного преобразования
последний столбец в обобщенной 4 х 4-матрице равен [0 0 0 1]т. В противном
случае, как это показано далее в разделе 3-15, преобразованная однородная
координата h не равна единице и нет взаимно однозначного соответствия между
аффинным преобразованием и (4 х 4)-матричным оператором. Аффинные
преобразования образуют полезное подмножество билинейных преобразований, так
Плоские геометрические
проекции
параллельная
ортографическая
перспективная
аксонометрическая
косоугольная
тримстрическая
кабине
димстрическая
изометрическая
одноточечная
двуточечная
трехгочечния
Рис. 3-10 Иерархия плоских геометрических проекций.
как произведение двух аффинных преобразований также аффинно. Это свойство
позволяет скомбинировать общее преобразование множества точек относительно
произвольной системы координат при сохранении значения единицы для
однородной координаты h.
Так как евклидова геометрия изучается в школах многие годы, то методы
рисования и черчения, основьгвающиеся на евклидовой геометрии, стали
стандартными методами графического сообщения. Хотя художниками и
архитекторами часто используются перспективные виды для создания более реалистического
изображения, в технической работе они используются редко из-за трудности их
ручного конструирования. Однако при использовании для задания объекта
однородных координат, аффинные и перспективные преобразования вычисляются
одинаково легко.
И аффинные, и перспективные преобразования трехмерны, т. е. являются
преобразованиями одного трехмерного пространства в другое. Однако для
наблюдения результатов на двумерной поверхности требуется проецирование из
трехмерного пространства в двумерное. Результат этого проецирования называется
плоской геометрической проекцией. На рис. 3-10 изображена иерархия плоских
геометрических проекций. Матрица проецирования из трехмерного пространства
в двумерное всегда содержит столбец из нулей, следовательно, детерминант
этого преобразования всегда равен нулю.
Плоские геометрические проекции объектов образуются пересечением
прямых, называемых проекторами, с плоскостью, называемой плоскостью проекции.
Проекторы — это прямые, проходящие через произвольную точку, называемую
центром проекции, и каждую точку объекта. Если центр проекции расположен в
конечной точке трехмерного пространства, получается перспективная проекция.
Если центр расположен в бесконечности, то все проекторы параллельны и
результат является параллельной проекцией. Плоские геометрические проекции пред-
Плоскостыпюекции
№>
Центр проекции
Рис. 3-11 Плоские проекции, (о) Фиксирован центр проекции; (6) фиксирован объект.
ставляют основу описательной геометрии. Неплоские и негеометрические
проекции также полезны; они широко используются в картографии.
Для разработки различных преобразований, представленных на рис. 3-10,
можно использовать два разных подхода. В первом предполагается, что центр
проекции или точка зрения фиксирована, а плоскость проекции перпендикулярна
каждому проектору, как это показано на рис. 3-11 о. Для получения требуемого
вида манипулируют объектом. Во втором подходе предполагается, что объект
фиксирован, центр проекции может как угодно перемещаться в трехмерном
пространстве, а плоскость проекции не обязательно перпендикулярна направлению
взгляда. На рис. 3-11 Ь приведен пример этого. Оба подхода математически
эквивалентны.
Первый подход напоминает действия наблюдателя, которого попросили
описать небольшой объект, например, книгу. Он берет объект в руки,
поворачивает и перемещает его для того, чтобы изучить все его стороны. В этом случае
центр проекции фиксирован и манипулируют объектом. Второй подход
напоминает действия наблюдателя, которого попросили описать большой объект, например
автомобиль. Наблюдатель ходит вокруг объекта, чтобы осмотреть его с разных
сторон, взбирается на лестницу для осмотра верха и опускается на колени для
осмотра его нижней части. В этом случае объект фиксирован, а центр проекции
и точка зрения перемещаются.
В процессе конструирования или изображения объекта на графическом
дисплее компьютера местоположение глаза обычно фиксировано, а плоскость
проекции, т. е. поверхность, обычно перпендикулярна направлению взгляда.
Следовательно, в данном случае более подходит первый подход. Тем не менее, если
графический дисплей используется для представления движения какого-нибудь
транспортного средства или наблюдатель движется в сгенерированной
компьютером модели, как в случае использования тренажера, или если наблюдатель
прогуливается в архитектурной модели, тогда больше подходит второй подход.
В этой книге используются фиксированный центр проекции и движущийся
объект. Метод с фиксированным объектом и движущимся центром проекции
хорошо проработан Калбомом и Пейсиореком ([3-2]).
Мы начнем наше обсуждение плоских геометрических проекций (см. рис.
3-10) с рассмотрения параллельных проекций.
3-12 ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
Самой простой из параллельных проекций является ортографическая проекция,
используемая обычно в инженерных чертежах. В этом случае точно
изображаются правильные или «истинные» размер и форма одной плоской грани объекта.
Ортографические проекции — это проекции на одну из координатных плоскостей
х — 0, у = 0 или z = 0. Матрица проекции на плоскость z = 0 имеет вид
[Рг} =
10 0 0
0 10 0
0 0 0 0
0 0 0 1
(3-27)
(a)
(Ь)
(с)
W)
Рис. 3-12 Ортографические проекции объекта на рис. 3-12а на плоскости: (6) у = О,
(с) г = 0 и (d) х = 0.
Заметим, что в третьем столбце (столбце z) все элементы нулевые. Следовательно,
в результате преобразования г-координата координатного вектора станет равной
нулю.
Аналогичным образом матрицы для проекций на плоскости х = 0 и у — 0
равны
[Р*] =
0 0 0 0
0 10 0
0 0 10
0 0 0 1
(3-28)
[Ру} =
10 0 0
0 0 0 0
0 0 10
0 0 0 1
(3-29)
Omi^w
Сверху
N
ч
\
N
_ N
Слева
Спереди
Справа
/
/
/
/
/
Снизу
Рис. 3-13 Многовидовая ортографическая проекция.
Ортографические проекции объекта на рис. 3-12 о на плоскости х — 0, у = О
и z = 0 из центров проекций, расположенных в бесконечности на -Ы-, +у- и
-f-z-осях соответственно, изображены на рис. 3-12 Ь, 3-12 с и 3-12 d соответственно.
Одна ортографическая проекция не дает достаточной информации для
визуального и практического воссоздания формы объекта. Необходимо,
следовательно, наличие нескольких ортографических проекций. Эти многовидовые
ортографические проекции обычно1 организуются так, как это показано на рис. 3-13.
Это соглашение относится к Соединенным Штатам.
У
1 2
(с)
Рис. 3-14 Построение вспомогательного вида, (а) Триметрический вид; (6) нормаль
совмещена с осью z; (с) спроецировано на плоскость z = 0.
Виды спереди, справа и сверху получаются проецированием на плоскости z = 0,
ж = 0иу = 0из центров проекции, расположенных в бесконечности на +z, +х
и +у осях. Виды сзади, слева и снизу получаются- проецированием на плоскости
z = 0, х = 0,' у = 0 из центров проекции, расположенных в бесконечности на —z,
—х и —у осях. Координатные оси обычно не изображаются на этих видах.
Как показано на рис. 3.13, невидимые линии принято изображать пунктиром.
Для адекватного представления формы объекта обычно не требуются все шесть
видов. Наиболее часто используются виды спереди, сверху и справа. Даже если
используются не все шесть видов, оставшиеся располагаются в указанных местах.
Виды спереди и с боков иногда называют главным и боковыми фасадами, вид
сверху иногда называют планом.
Интересно и важно отметить, что все шесть видов могут быть получены
комбинациями отражения, вращения и переноса с последующим проецированием на
плоскость z = 0 из центра проекции, расположенного в бесконечности на оси z.
Например, вид сзади получается отражением относительно плоскости z = 0 и
проецированием на эту плоскость. Аналогичным образом вид слева получается
вращением вокруг оси у на угол +90° и проецированием на плоскость z = 0.
Для объектов с гранями, не параллельными одной из координатных
плоскостей, стандартные ортографические виды не показывают правильную или
истинную форму этих граней. Для этих целей используются вспомогательные виды.
Вспомогательный вид образуется с помощью вращения и перемещения объекта
так, чтобы нормаль к грани совпала с одной из координатных осей (см. разд. 3-
9). Результат затем проецируется на координатную плоскость, перпендикулярную
этой оси. На рис. 3-14 с изображена вспомогательная плоскость, показывающая
истинную форму треугольного угла объекта на рис. 3.13.
Пример более полно объясняет эти построения.
Пример 3-12 Вспомогательный вид
Построим вспомогательный вид, изображающий правильную форму
треугольного угла объекта на рис. 3-14 о. Координатные векторы объекта равны
■ о
1
1
0.5
0
0
1
1
0
1
0
0.25
0.25
0
0
0.25
0.25
0
0
0
0.5
1
1
0
0
1
1
1
0
0
0.5
0.5
0
0
0.5
0.5
0
0
0
0
0.5
0.6
0.6
0.6
0.6
0.4
0.4
0.4
0.4
1 "
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Номера вершин, изображенные на рис. 3-14, соответствуют номерам строк
матрицы [X] координатных векторов.
Внешняя нормаль к треугольной грани имеет следующие направляющие
косинусы
[Х] =
[Сх Су CZ] = [1/V3 1/л/З 1/л/З]
и проходит через начало координат и точку [0.83333 0.83333 0.83333].
Вспомнив результаты разд. 3-9 и примера 3-10, получим, что нормаль
совмещается с осью z с помощью поворота вокруг оси х на угол
а = arccos(cz/d) = arccos(l/-\/2) = +45°
и последующего поворота вокруг оси у на угол
0 = arccos(d) = arccos(2/\/6) = +35, 26°.
Теперь общая матрица преобразования равна
[Т]
2/>/б 0 1/л/з 0'
— 1/л/б 1/%/2 1/л/з 0
-1/VE -i/\/2 1/уД о
0 0 0 1
Преобразованные координатные векторы равны
[Х'] = [Х][Т]
0.408
0.408
0.204
0.408
0.816
0
0.816
0.408
0.408
0.204
0.245
0.041
0.245
0.449
0.163
0.041
0.163
0.367
-0.707
-0.707
-0.354
0
0
0
0
0.707
0.707
0.354
-0.424
-0.424
-0.071
-0.071
-0.283
-0.283
0.071
0.071
0.577
1.155
1.443
1.443
1.155
0
0.577
0.155
0.577
1.443
0.354
0.491
0.779
0.635
0.231
0.375
.0.664
0.52
1
1
1
1
1
1
1
1
1—1
1
1—1
1—1
1
1
1—1
1
1
1—1
Результат изображен на рис. 3-14 6. Вспомогательный вид создается
проецированием этого промежуточного результата на плоскость z = 0 с помощью
(3-27), т.е.
[Р..
10 0 0-
0 10 0
0 0 0 0
0 0 0 1
Объединение матриц [Т] и [Pz] дает
2/у/Е
-1/у/Е
-1Л/3
0
[т'] = [т№] =
0 0 0'
1/ч/2 0 0
-1/\/2 0 0
0 0 1
Обратите внимание на столбец из нулей. Вспомогательный вид создается
затем с помощью
[Х"] = [Х][Т'}.
Матрица [X"] та же самая, что и [Х'\ за исключением вулевого третьего
столбца, т. е. действие проецирования состоит в отбрасывании координаты z.
Результат показан на рис. 3-14 с. Невидимые линии изображены сплошными.
Заметим, что показана правильная форма грани объекта—равностороннего
треугольника.
Часто бывает необходимо для сложных объектов показать внутренние детали.
Это выполняется с помощью сечений. Сечение образуется проведением через
объект так называемой, «секущей» плоскости, удалением части объекта по одну
сторону от этой плоскости и проецированием оставшейся части объекта на плоскость
сечения. Как и ранее, этот вид можно сделать с помощью совмещения с одной из
координатных осей нормали к плоскости сечения (см. разд. 3-9), отсечения
объекта с одной стороны от плоскости сечения (см. [3-1]) и, наконец, проецирования
результата на координатную плоскость, перпендикулярную этой оси.
(*)
(О
Рис. 3-15 Построение сечения, (о) Весь объект; (6) удалена часть между плоскостью
сечения и центром проецирования; (с) проекция на плоскость z = 0.
На рис. 3-15 изображена плоскость сечения, проходящая через выемку на
левой стороне объекта с рис. 3-13. Стрелки используются для показа плоскости
сечения и направления взгляда.
3-13 АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Одна ортографическая проекция не может дать представления об общей
трехмерной форме объекта. Это ограничение можно преодолеть с помощью
аксонометрических проекций. Аксонометрическая проекция образуется
манипулированием объекта с помощью поворотов и перемещений таким образом, что бы были
видны по крайней мере три соседние грани1. Результат затем проецируется с
центром проекции, расположенным в бесконечности, на одну из координатных
плоскостей, обычно на плоскость z = 0. Если грань не параллельна плоскости
проекции, то аксонометрическая проекция не показывает истинную форму этой
грани. Однако остаются постоянными относительные длины параллельных в
исходном пространстве линий, т. е. параллельные линии одинаково укорачиваются
(искажаются). Коэффициент искажения есть отношение длины проекции отрезка
к его истинной длине. Представляют интерес три аксонометрические проекции:
триметрическая, диметрическая и изометрическая, как это показано на рис. 3-
10. В триметрической проекции меньше всего ограничений, а в изометрической —
больше всего. В самом деле, как будет показано ниже, изометрическая проекция
есть частный случай диметрической, а диметрическая проекция есть частный
случай триметрической.
Триметрическая проекция строится произвольными поворотами вокруг
любых координатных осей, совершаемыми в произвольном порядке, с последующим
проецированием на плоскость z = 0. Большинство иллюстраций в этой книге
представлены триметрическими проекциями. На рис. 3-16 изображено несколько
таких проекций. Каждая из них построена с помощью поворота вокруг оси у,
затем вокруг оси х и, наконец, параллельного проецирования на плоскость z = 0.
В общем случае для триметрической проекции коэффициенты искажения по
каждой из проецируемых главных осей (х, у и z) не равны друг другу. Здесь
термин главная ось используется в том смысле, что ось (или ребро) объекта в
исходном пространстве параллельна одной из координатных осей х, у или z.
Наложение ограничений на коэффициенты уменьшает диапазон триметрических
проекций. Однако для любой конкретной триметрической проекции коэффициенты
искажения вычисляют с помощью применения общей матрицы преобразования к
единичным векторам вдоль главных осей. В частности,
[U)[T] =
1
0
0
0 0 1
1 0 1
0 1 1
[Т] =
х* У; о
*; у*У о
_*; yi о
1
1
1
(3-30)
1 Минимальное количество граней, встречающихся для простых кубовидных объектов,
подобных используемым в большинстве иллюстраций этой главы.
ф 15°
30°
45"
\
\
Рис. 3-16 Триметрические проекции.
где [17] есть матрица единичных векторов вдоль нетрансформированных осей х,
у и z соответственно, а [Т] —общая матрица триметрической проекции. Тогда
коэффициенты искажения вдоль спроецированных главных осей равны
/. = V*? + i
,*2
fv = yfi?
+
i,*2
В примере 3-13 триметрическая проекция рассмотрена более подробно.
(3-31 о)
(3-316)
(3-31 с)
Пример 3-13 Триметрическая проекция
Рассмотрим центральную иллюстрацию рис. 3-16, построенную с
помощью поворота на угол ф = 30° вокруг оси у, затем поворота на угол в = 45°
вокруг оси х и последующего параллельного проецирования на плоскость
z = 0. Координатный вектор куба с отсеченным углом
[X].
о
1
1
0.5
0
0
1
1
0
1
о
о
0.5
1
1
0
0
1
1
1
о
о
о
о
0.5
Общая матрица триметрической проекции равна (см. (3-8), (3-6) и (3-27)):
[T] = [Ry][Rz}[P:} =
~cos(p 0 — sin0 0'
0 1 0
sin 0 0 cos0 0
0 0 0 1
0
cos в
sin б
0
0
sin 9
cos в
0
01
0
0
lj
10 0 0
0 10 0
0 0 0 0
0 0 0 1
cos ф sin ф sin 0 0 0'
0 cosfl 0 0
sin0 — cos0sin0 0 0
0 0 0 1
V3/2 ч/2/4 0 0'
0 \/2/2 0 0
1/2 -VE/4 0 0
0 0 0 1
Таким образом, преобразованные координатные векторы имеют вид:
[Х'] = [Х][Т] =
0.5
1.366
1.366
0.933
0.5
0
0.866
0.866
0
1.116
-0.612 0
-0.259 0
0.095 0
0.272 0
0.095 0
0 0
0.354 0
1.061 0
0.707 0
0.754 0
а коэффициенты искажения —
[U][T] =
1
0
0
0
1
0
0
0
1
l"
1
1
v/3/2 л/2/4 О О'
О л/2/2 О О
1/2 -л/6/4 О О
О 0 0 1
V3/2 л/2/4 О 1
О л/2/2 О 1
. 1/2 -л/6/4 О 1
U = л/(\/3/2)2 + (л/2/4)2= 0.935,
/„ = л/2/2 = 0.707,
/2 = л/(1/2)2 + (-л/6/4)2 = 0.791.
Диметрическая проекция — это триметрическая проекция с двумя
одинаковыми коэффициентами искажения, третий коэффициент может иметь любое
значение. Диметрическая проекция строится с помощью поворота на угол ф вокруг оси
у, затем поворота на угол в вокруг оси х и проецирования на плоскость z = 0
с центром проекции, расположенным в бесконечности. Точные значения углов
поворотов еще не известны. Воспользовавшись (3-8), (3-6) и (3-27), получим
результирующее преобразование:
[T} = [Ry)[Rx}[Rz]
cos ф 0 — sin ф 0
0 10 0
Бшф 0 cos^ 0
0 0 0 1
10 0 0
0 cos0 sin0 0
0 -sin6 cos0 0
0 0 0 1
10 0 0
0 10 0
0 0 0 0
0 0 0 1
Объединение матриц дает
[Т] =
собФ sin^>sin0 0 0
0 cos в 0 0
sin ф — cos ф sin в 0 0
0 0 0 1
Единичные векторы на главных осях х, у и z преобразуются в
соБф sin^sinf? О 0
0 cos0 0 0
яшф — cos ф sin в 0 0
0 0 0 1
[U*] = [U][T} =
10 0 1
0 10 1
0 0 11
[U*] =
соБф sin<£sin# 0 1
0 cos^ 0 1
sin ф — cos ф sin в 0 1
(3-32)
(3-33)
Теперь квадрат длины подвергнутого преобразованию единичного вектора вдоль
оси х, т. е. квадрат коэффициента искажения, равен
fl = (х;2 + у?) = cos2 ф + sin2 ф sin2 в. (3-34)
Аналогично квадраты коэффициентов искажения по осям у и z равны
/2 = (x;2 + y;2) = cos4 (3-35)
/2 = (xf + у?) = sin2 ф + cos2 ф sin2 в. (3-36)
Приравнивание коэффициентов искажения по осям1 х и у дает одно уравнение с
двумя неизвестными углами поворота ф и в. А именно
cos2 ф + sin2 ф sin2 0 = cos2 в.
Используя равенства cos2 ф = 1 — sin2 ф и cos2 0 = 1 — sin2 в, получаем
sin2 ф = sin2 61/(1 - sin2 в). (3-37)
Второе соотношение между ф и в получим, фиксируя коэффициент искажения fz
вдоль оси z. Объединив уравнения (3-36) и (3-37) и воспользовавшись равенством
cos2 ф = 1 — sin2 ф, получаем
2 sin2 0-2 sin4 0 - (1 - sin2 0)/2 = О
или
2 sin4 в - (2 + /2) sin2 6» + /2 = 0. (3-38)
Положив u = sin2 в, получим решения sin20 = /f/2, 1. Решение sin20 = 1
отбросим, так как при подстановке его в (3-37) оно дает бесконечный результат.
Следовательно,
в = агсБш(±Л/л/2). (3-39)
Подстановка в равенство (3-37) приводит к
ф = arcsin(±/z/V2 - fl). (3-40)
Это показывает, что диапазон коэффициентов искажения равен 0 < / < I2.
Заметим далее, что каждый коэффициент искажения fz порождает четыре возможных
диметрических проекции.
На рис. 3-17 показаны диметрические проекции для разных коэффициентов
искажения. Для каждого коэффициента была выбрана диметрическая проекция,
соответствующая положительному вращению вокруг оси у и положительному
вращению вокруг х.
На рис. 3-18 показаны четыре возможных диметрических проекции для
коэффициента искажения 5/8.
Рассмотрим конкретный пример.
Могут быть использованы любые оси из трех.
Отрицательные коэффициенты искажения не имеют смысла.
/=0
(<0
Рис. 3-17 Диметрические проекции для разных значений коэффициента искажения.
(а) 0; (6) 1/4; (с) 3/8; (d) 1/2; (е) 5/8; (/) 3/4; (д) 1.
Рис. 3-18 Четыре возможных диметрических проекции для коэффициента искажения
5/8 и углов поворотов ф = ±29.52°, в = ±26.23°. (о) ф = -29.52°, в = +26.23°; (Ь)
ф = -29.52°, 9 = -26.23°; (с) ф = +29.52°, в = +26.23°; (d) ф = +29.52°, в = -26.23°.
Пример 3-14 Диметрические проекции
Для куба с отсеченным углом построим диметрическую проекцию для
коэффициента искажения по оси z, равного 1/2.
Из равенства (3-39)
в = axcsin(±fz/y/2)
= arcsin(±l/2-\/2)
= arcsin(±0.35355)
= ±20.705°.
Из равенства (3-40)
ф = arcsin(±/z/i/2-/|)
= arcsin(±l/2v/774)
= arcsin(±0.378)
= ±22.208°.
Выбрав ф = +22,208° и в = +20,705°, из (3-32) получаем следующую
матрицу диметрической проекции:
[Т] =
Вспоминая координатный вектор [X] для куба с отсеченным углом (см.
пример 3-13), получим координаты
0.926
0
0.378
0
0.134
0.935
-0.327
0
0
0
0
0
0
0
0
1
[Х-] = [Х][Г] =
0.378
1.304
1.304
0.841
0.378
0
0.926
0.926
0
1.115
-0.327
-0.194
0.274
0.675
0.608
0
0.134
1.069
0.935
0.905
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
Результат изображен на рис. 3-17 d.
Диметрическая проекция позволяет проводить измерения с одинаковым
масштабным множителем по двум преобразованным главным осям. Измерение вдоль
третьей оси требует другого масштабного множителя. Это может привести к
путанице и ошибкам, если требуется точное масштабирование размеров
спроецированного объекта. Изометрическая проекция решает эту проблему.
В изометрической проекции все три коэффициента искажения равны.
Вспомним уравнения (3-34)-(3-36) и приравнивая (3-34) и (3-35), снова получим ра-
венство (3-37), т.е.
sin2 ф =
sin20
(3-37)
1- sin2в'
Приравнивание равенств (3-35) и (3-36) дает
. ,л l-2sin20
sin20=- г-5—.
1 - sin2 в
Из (3-37) и (3-41) следует, что sin2 в = 1/3 или sin в = ±л/Т/3 и в = ±35,26°. Тогда
.2,
(3-41)
sin'
■Ч'ИИ
и ф = ±45°. Снова отметим, что существуют четыре возможных изометрических
проекции. Это показано на рис. 3-19. Коэффициент искажения для
изометрической проекции равен (см. (3-35))
/ = Vcos2 в = у/Щ = 0.8165.
В самом деле, изометрическая проекция есть частный случай диметрической с
Л = 0,8165.
Рис. 3-19 Четыре возможных изометрических проекции с углами поворотов ф = ±45°,
в = ±35.26°. (а) ф = -45°, в = +35.26°; (Ь) ф = -45°, в = -35.26°; (с) ф = +45°,
в = +35.26°; (<0 ф = +45°, в = -35.26°.
При построении изометрических проекций вручную важен угол, который
составляет проекция оси х с горизонталью. Преобразование единичного вектора
вдоль оси х с помощью матрицы изометрической проекции дает
[U*X} = [1 0 0 1]
cos0 sin ф sin в 0 0
О cos^ О О
sin ф — cos 0sin0 0 0
О 0 0 1
= [cos<^> sin<^>sin(? 0 1].
Тогда угол между проекцией оси х и горизонталью равен
yt sin ф sin в , . „
tga= ^ = __ ± = ±sin0,
(3-42)
cos<^>
поскольку sin 0 = cos0 для ф — 45°. Следовательно,
а = arctg(± sin 35.26439°) = ±30°.
Для построения изометрических проекций вручную обычно используется
пластмассовый прямоугольный треугольник с углами 30° и 60°. Ниже приводится
пример.
Пример 3-15 Изометрическая проекция
Снова рассмотрим куб с отсеченным углом (см. пример 3-13) и построим
изометрическую проекцию для ф = —45° и в = +35.26439°. Из равенства
(3-32) получаем, что преобразование изометрического проецирования имеет
вид:
[Т] =
0.707 -0.408 0 0
0 0.816 0 0
-0.707 -0.408 0 0
0 0 0 1
Вспоминая координаты [X], получим
[Х'] = [Х][Т] =
-0.707
0
0
-0.354
-0.707
0
0.707
0.707
0
0.354
-0.408
-0.816
-0.408
0.204
0.408
0
-0.408
0.408
0.816
0.204
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
Результат изображен на рис. 3-19 а.
3-14 КОСОУГОЛЬНЫЕ ПРОЕКЦИИ
В противоположность ортографическим и аксонометрическим проекциям, для
которых проекторы перпендикулярны плоскости проекции, косоугольная проекция
формируется параллельными проекторами с центром, лежащим в бесконечности,
и расположенными под косым углом к плоскости проекции. Общая схема
проекции изображена на рис. 3-20.
Косоугольные проекции показывают общую трехмерную форму объекта.
Однако истинные размер и форма изображаются только для граней объекта,
расположенных параллельно плоскости проекции, т.е. углы и длины сохраняются
только для таких граней. В самом деле, косоугольная проекция этих граней
эквивалентна ортографическому виду спереди. Грани, не параллельные плоскости
проекции, подвергаются искажению.
Особый интерес представляют две косоугольные проекции — кавалье и
кабине. Проекция кавалье получается, когда угол между проекторами и плоскостью
проекции составляет 45°. В этой проекции коэффициенты искажения для всех
трех главных направлений одинаковы. Результат этой проекции выглядит
неестественно утолщенным. Для «коррекции» этого недостатка используется проекция
кабине.
Проекцией кабине называется такая косоугольная проекция, у которой
коэффициент искажения для ребер, перпендикулярных плоскости проекции, равен
1/2. Как будет показано ниже, для проекции кабине угол между проекторами и
плоскостью проекции составляет arcctg(l/2) = 63.43°.
Рис. 3-20 Косоугольная проекция.
— X
Рис. 3-21 Построение косоугольной проекции.
Чтобы построить матрицу преобразования для косоугольной проекции,
рассмотрим единичный вектор [0 0 1] вдоль оси z, показанный на рис. 3-21. Для ор-
тографической или аксонометрической проекции на плоскость z = 0 вектор РО
задает направление проекции. При косоугольной проекции проекторы
составляют угол с плоскостью проекции. На рис. 3-21 показаны типичные косоугольные
проекторы Pi О и РРъ. Проекторы Pi О и РРъ образуют угол /? с плоскостью
проекции z = 0. Заметим, что все возможные проекторы, проходящие через точку
Р или О и образующие угол /? с плоскостью z = 0, лежат на поверхности
конуса с вершиной в Р или О. Таким образом, для заданного угла /? существует
бесконечное количество косоугольных проекций.
Проектор Pi О можно получить из РО с помощью переноса на [—а —Ы] точки
Р в точку Pi. В двумерной плоскости, проходящей через Р перпендикулярно оси
z, (3 х 3)-матрица преобразования равна
[Т'] =
10 0
010
-а -Ь 1
В трехмерном пространстве это двумерное преобразование эквивалентно сдвигу
вектора РО в направлениях х и у. Для этого необходимо преобразование
[Г"] =
1 0 0 0
0 10 0
-а -Ь 1 0
0 0 0 1
Проецирование на плоскость z = 0 дает
[Т} =
1 0 0
0 1 0
-а -Ъ 0
0 0 0
а = / cos a,
Ъ = / sin a,
0
0
0
1
Из рис. 3-21 получаем, что
где /—длина спроецированного единичного вектора на оси z, т.е. коэффициент
искажения, а а — угол между горизонталью и спроецированной осью z. Из рис. 3-
21 также ясно, что /J — угол между косыми проекторами и плоскостью проекции
равен
0 = arcctg(/).
Таким образом, преобразование для косоугольной проекции имеет вид:
[Г] =
1 0 0 0
0 10 0
—/cos a —/sin a 0 0
0 0 0 1
(3-43)
(3-44)
При / = 0, /J = 90° получаем ортографическую проекцию. Если / = 1, то не
подвергаются искажению ребра, перпендикулярные плоскости проекции. А это
является условием проекции кавалье. Из равенства (3-43) имеем:
Р = arcctg(l) = 45°.
Заметим, что в проекции кавалье а является все еще свободным параметром. На
рис. 3-22 показаны проекции кавалье для некоторых значений а. Наиболее часто
используются значения а, равные 30° и 40°. Также применяется значение 180° — а.
Проекцию кабине можно получить при коэффициенте искажения / = 1/2.
Отсюда
Р = arcctg(l/2) = 63.435°.
В этом случае снова угол а является переменной величиной, как это показано
на рис. 3.23. Наиболее часто встречаются значения 30° и 45°, применяется также
a -= -45
+45'
Рис. 3-22 Проекции кавалье. Сверху вниз угол а изменяется от —45° до +45° с
интервалом 15е, угол в = 45е.
: = -45'
-30°
-15е
+15'
+30с
а = +45'
Рис. 3-23 Проекции кабине. Сверху вниз угол а изменяется от —45е до +45° с
интервалом 15°, коэффициент искажения / = 0.5.
3
1
7
Рис. 3-24 Косоугольные проекции. Слева направо /
а = 45°.
= 1, 7/8, 3/4, 5/8, 1/2 при
(*)
Р
Рис. 3-25 Искажение, возникающее в косоугольных проекциях, / = 5/8, а = 45°.
(а) Круглая грань параллельна плоскости проекции; (Ь) круглая грань
перпендикулярна плоскости проекции; (с) длинная сторона перпендикулярна плоскости проекции;
(d) длинная сторона параллельна плоскости проекции.
значение 180° — а. На рис. 3-24 изображены косоугольные проекции для
коэффициентов искажения / = 1, 7/8, 3/4, 5/8, 1/2 с углом а = 45е.
Поскольку изображается истинная форма одной грани, косоугольные
проекции особенно подходят для иллюстрации объектов с круглыми или иными
искривленными гранями. Такие грани должны быть параллельны плоскости проекции,
чтобы избежать нежелательных искажений. Так же, как и в случае параллельных
проекций, объекты с одним измерением, существенно превосходящим другие,
подвергаются значительному искажению, если только это измерение не параллельно
плоскости проекции. Такие эффекты показаны на рис. 3-25.
Ниже приводится подробный пример.
Пример 3-16 Косоугольные проекции
Построим проекции кавалье и кабине для куба с одним отсеченным углом
(см. пример 3-13).
Вспомнив, что проекция кавалье - это косоугольная проекция с /3 = 45 е,
т. е. коэффциент искажения / = 1, и выбрав угол горизонтального наклона
а = 30е, из (3-44) получим матрицу преобразования
[Т] =
1 0 0 0"
0 10 0
—/cos a —/sin a 0 0
О 0 0 1
1
0
-0.866
0
0
1
-0.5
0
Преобразуем координаты [X] куба с отсеченным углом (см. пример 3-13)
[Х'] = [Х][Т] =
Г -0.866
0.134
0.134
-0.366
-0.866
0
1
1
о
0.567
-0.5
-0.5
0
0.5
0.5
0
0
1
1
0.75
Результат изображен на рис. 3-22.
Обратившись теперь к проекции кабине и вспомнив, что коэффициент
искажения равен 1/2, из равенства (3-43) получим
/3 = arcctg(l/2) = arctg(2) = 63.435°.
Снова выбрав а = 30е, из (3-44), имеем:
[Т] =
1
о
—/ cos a
0
0
1
-/sin a
0
1
0
-0.433
0
0
1
-0.25
0
Преобразованные координаты проекции кабине для этого куба равны
РП = [х][т] =
-0.433
0.567
0.567
0.067
-0.433
0
1
1
0
0.783
-0.25
-0.25
0.25
0.75
0.75
0
0
1
1
0.875
Этот результат изображен на рис. 3-23.
Отметим, что и для проекции кавалье, и для проекции кабине
треугольная грань не изображается с правильными размерами или формой, так как
она не параллельна плоскости проекции (г = 0).
3-15 ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
Перспективное преобразование имеет место, когда не равен нулю любой из первых
трех элементов четвертого столбца обобщенной (4 х 4)-матрицы преобразования
однородных координат. Как было упомянуто ранее (см. разд. 3-11),
перспективное преобразование — это преобразование одного трехмерного пространства
в другое. В отличие от обсуждавшихся ранее параллельных преобразований, в
данном случае параллельные прямые сходятся, размер объекта уменьшается с
увеличением расстояния до центра проекции, и происходит неоднородное
искажение линий объекта, зависящее от ориентации и расстояния от объекта до центра
проекции. Все это помогает нашему восприятию глубины, но не сохраняет форму
объекта.
Одноточечное перспективное преобразование задается равенством
[х у z 1]
10 0 0
0 10 0
0 0 1 г
0 0 0 1
= [х у z rz +1].
(3-45)
Здесь h = rz + 1 ф 1. Обычные координаты получаются делением на h:
[х* у* z* !]=[■
TZ+l TZ+\ TZ+l
Ч-
(3-46)
Перспективное проецирование на некоторую двумерную видовую плоскость
можно получить, объединив ортографическую проекцию с перспективным
преобразованием. Например, перспективное проецирование на плоскость z = 0 выполняется
с помощью преобразований
[T] = [Pr][Pz} =
"10 0 0"
0 1 0 0
~ 0 0 1 г
0 0 0 1
1
0
0
0
0
1
0
0
0
0
0
0
0]
0
0
1
10 0 0
0 10 0
0 0 0 г
0 0 0 1
(3-47)
[х у z 1]
Обычные координаты равны
[х* У*
10 0 0
0 10 0
0 0 0 г
0 0 0 1
Ч=[
= [х у 0 rz + 1].
0 1].
rz+1 rz-\-l
(3-48)
(3-49)
Чтобы показать, что равенство (3-47) выполняет перспективное проецирование
на плоскость z = 0, рассмотрим рис. 3-26 с геометрическими построениями для
перспективной проекции трехмерной точки Р на плоскость z = z* = 0 в точку Р*
Рис. 3-26 Перспективная проекция точки.
и с центром проекции, лежащим в z0 на оси z. Координаты точки проекции Р*
можно получить, используя подобие треугольников. Из рис. 3-26 следует:
или
zc zc- z
*—'Н)
у
У
или
л/я*2 + z\ у/х* + (zc - zf
У
У =
1-
z >
z* равно, конечно, нулю.
Полагая г = — l/zc, получим результаты, аналогичные полученным с помощью
(3-47). Таким образом, уравнение (3-47) осуществляет перспективное
проецирование на плоскость z = 0 с центром проекции в точке (—1/г) на оси z. Заметим,
Рис. 3-27 Проекция прямой, параллельной оси z.
что при приближении zc к бесконечности, г приближается к нулю и в результате
получаем аксонометрическую проекцию на плоскость z = 0. Заметим далее, что
на точки, лежащие в плоскости проекции, т.е. z = 0, перспективное
преобразование не действует. Отметим также, что начало координат (х = у = z = 0) остается
неизменным. Следовательно, если плоскость проекции (z = 0) проходит через
объект, то эта часть объекта изображается с правильным размером и формой.
Все другие части объекта искажаются.
Чтобы лучше понять действие перспективного преобразования, рассмотрим
рис. 3-27. На нем показано перспективное проецирование на плоскость z = 0
отрезка АВ, параллельного оси z, в отрезок А*В* на плоскости z = 0 с центром
проекции, расположенным в точке — 1/г на оси z. Преобразование можно
разделить на два этапа (см. (3-47)). На первом этапе отрезок АВ отображается в
отрезок А'В' (см. рис. 3-27). Затем с помощью ортографического
проецирования отрезок А'В' в трехмерном пространстве отображается в отрезок А*В* на
плоскости z = 0. Центр проекции расположен в бесконечности.
Исследование рис. 3-27 показывает, что прямые А'В' и АВ пересекают
плоскость z = 0 в одной и той же точке. Прямая А'В' также пересекает ось z в точке
z = +l/r. Далее, перспективное преобразование (см. (3-45) и (3-46)) отображает
расположенную в бесконечности точку пересечения параллельных прямых АВ и
оси z в конечную точку z = 1/г на оси z. Эта точка называется точкой схода 1.
Заметим, что точка схода лежит на том же расстоянии от плоскости проекции,
что и центр проекции, только с противоположной стороны от плоскости,
например, если z = 0 есть плоскость проекции, а центр проекции находится в z = —1/г,
тогда точка схода находится в z = +1/г.
Чтобы подтвердить это наблюдение, рассмотрим перспективное
преобразование точки, находящейся в бесконечности на оси +z, т. е.
[0 0 1 0]
10 0 0
0 10 0
0 0 1 г
0 0 0 1
= [001 г].
(3-50)
Соответствующая ей точка [х* у* z* 1] = [0 0 1/г 1] теперь является конечной
точкой на положительной оси z. Это означает, что все полубесконечное
положительное пространство (0 < z < оо) отображается в ограниченную область
0 < z* < 1/г. Далее, все прямые, параллельные оси z, теперь проходят через
точку [0 0 1/г 1] - точку схода.
Прежде чем перейти к примерам, для полноты изложения укажем
одноточечные перспективные преобразования с центром проекции и точкой схода,
расположенными на осях х и у. Одноточечное перспективное преобразование
[х у z 1]
1 0 0 р
0 10 0
0 0 10
0 0 0 1
[х у z (рх +1)]
(3-51)
с обычными координатами
г а; у z л
[х* у* z* 11= -т —^—г г 1
1 " ' Урх + 1 рх+1 рх+1 J
(3-52)
имеет центр проекции [— 1/р 0 0 1] и точку схода, расположенную на оси х в
[1/р 0 0 1].
Одноточечное перспективное преобразование
[х у z 1]
10 0 0
0 1 0 q
0 0 10
0 0 0 1
= [х у z (qy +1)]
(3-53)
1 Интуитивно точка схода — это такая точка «вдали», в которой параллельные прямые
«кажутся» сходящимися и исчезающими. В качестве примера приведем прямолинейную, уходящую
вдаль железнодорожную колею.
с обычными координатами
[х* у* z* 1] = [
У
1
(3-54)
имеет центр проекции [О
[О 1/д 0 1].
qy + 1 qy + 1 ду + 1
1/д О 1] и точку схода, расположенную на оси у в
Пример 3-17 Перспективное преобразование прямой,
параллельной оси z
Рассмотрим отрезок АВ на рис. 3-27, параллельный оси z, с концевыми
точками А [3 2 4 1] и В [3 2 8 1]. Выполним перспективное проецирование
на плоскость z = 0 с центром проекции в точке z = —2. Перспективное
преобразование АВ в А'В' при г = 0.5 равно
Г1 0 0 0
А
В
3 2 4 1
3 2 8 1
0 1 0
0 0 1
0 0 0
о
0.5
1
1 0.667 1.333
0.6 0.4 1.6
А'
В'
Параметрическое уравнение отрезка А'В'
Pit) = [А'\ + [В' - A']t, 0 < t < 1,
или РЦ) = [1 0.667 1.333 1] + [-0.4 - 0.267 0.267 0]t.
Пересечение этого отрезка с плоскостями a: = 0,y = 0Hjz = 0 дает
x(t) = 0 = 1- 0At —► t = 2.50
y(t) = 0 = 0.667 - 0.267* —► t = 2.50
z(t) = 0 = 1.333 + 0.267*—► t = -5.0.
Подставив значение t = 2.5 в параметрическое уравнение отрезка А'В',
получим
z(2.5) = 1.333 + (0.267)(2.5) = 2.0,
что является пересечением отрезка А'В' с осью z в точке z = +1/г, точке
схода. Теперь подстановка в уравнения для х- и у-компонент значения t =
—5.0 дает пересечение с плоскостью z — 0, т. е.
х(-5.0) = 1 - (0.4)(-5.0) = 3.0
у(-5.0) = 0.667 - (0.267)(-5.0) = 2.0,
что совпадает с пересечением прямой АВ с плоскостью z = 0. Проекция
отрезка А'В' в отрезок А'В* на плоскости z = 0 вычисляется следующим
образом
А'
В'
1
0.6
0.667
0.4
1.333
1.6
1
1
Г1 0 0 01
0 10 0
0 0 0 0
Lo о о 1
—
1
0.6
0.667
0.4
0 1
0 1
Л*
в'-
Ниже приводится пример с простым кубом.
Пример 3-18 Одноточечное перспективное преобразование куба
Выполним перспективное проецирование на плоскость z = О единичного
куба, изображенного на рис. 3-28 а, с центром проекции в точке % = 10 на
оси z.
Одноточечный перспективный множитель г равен
г = -l/ze = -1/10 = -0.1.
У
И -
'Л В
(а)
КЦЛ.вх=10
D'
У
И' G,
ДА
с
Уе~' ~/ ¥
И*
71 С*
Л* Е* F*B*
(Ь)
Л* В*. Е* F*
О?)
D'.C
х г —
КТ.С.вх=-10
a; w
л\ в' е; F'
'Л' В'
/
г W) (e)
Рис. 3-28 Одноточечная перспективная проекция единичного куба.
Из уравнения (3-48) получаем, что
[Х'] = [Х)[Т\ =
11 _
J -
■1 0
0
0 1 0
0 0 0-
0 0 0
0 0 11"
10 11
1111
0 111
0 0 0 1
10 0 1
110 1
.0 10 1.
■1
0
0
0
0 0 0 0.9-1
1 0 0 0.9
1 1 0 0.9
0 1 0 0.9
0 0 0 1
10 0 1
110 1
.0 1
0 1
0
0
-0.1
1
)
0 0
1 0
0 0
0 0
гО
1.11
1.11
0
0
1
1
.0
о ■
0
-0.1
1
0 0 1
0 0 1
1.11 0 1
1.11 0 1
0 0 1
0 0 1
1 0 1
1
0 1
Результат изображен на рис. 3-28 Ь. Отметим, что, поскольку центр
проекции находится на положительной оси z, проекция передней грани ABCD
куба больше проекции задней грани. Почему так происходит, показано на
рис. 3-28 с, на котором изображена параллельная проекция исходного куба
на плоскость х = 0.
Отметим также, что, поскольку точка схода лежит на оси z, прямая CG*
на рис. 3-28 6 проходит через начало координат.
В качестве альтернативного метода, эквивалентного первому, можно
было бы выполнить перспективное преобразование и получить искаженный
объект в трехмерном пространстве, а затем ортографически спроецировать
результат на некоторую плоскость. Искаженный объект получают следующим
образом:
[Х'] = [Х][РТ} =
г0 0
1 0
1 1
0 1
0 0
1 0
1 1
.0 1
■о о
1 0
1 1
0 1
0 0
1 0
1 1
.0 1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1-
1
1
1
1
1
1
1.
"1
0
0
0
0.9-
0.9
0.9
0.9
1
1
1
1
0 0
1 0
0 0
0 0
гО
1.11
1.11
0
0
1
1
.0
о ■
0
-0.1
1
0 1.11 1
0 1.11 .1
1.11 1.11 1
1.11 1.11 1
0 0 1
0 0 1
1 0 1
1
0 1
Результат, полученный с помощью косоугольной проекции показан на рис. 3-
28 d. Заметим, что «передняя» грань (A'B'C'D1) больше, чем «задняя»
грань (E'F'G'H1). Последующее ортографическое проецирование на
плоскость z = 0 дает тот же самый результат [X*], что был получен ранее и
который изображен на рис. 3-28 с.
На рис. 3-28 е, на котором представлена ортографическая проекция на
плоскость х = 0 искаженного объекта с рис. 3-28 d, показано, что ребра куба,
ранее параллельные оси z, теперь сходятся к точке схода z = —10.
Рис. 3-28 b не передает трехмерности куба. Как показано в следующем
примере, более удовлетворительный результат можно получить центрированием куба.
Пример 3-19 Одноточечное перспективное преобразование
центрированного куба
Изображенный на рис. 3-28 а куб может быть центрирован на оси z путем
его переноса на —1/2 вдоль направлений х и у. Результирующее
преобразование
[Т]:
[Trxv][Prz] =
~
Г 1
0
0
.-0.5
Г 1
0
0
-0.5
0
1
0
-0.5
0
1
0
-0.5
0 0]
0 0
1 0
0 1.
0 0
0 0
0 -0.1
0
1
Г1 0 0 0
0 10 0
0 0 1 -0.1
0 0 0 1
Сдвинутый куб изображен на рис. 3-29 а.
Преобразованные обычные координаты равны
[Х'] = [Х][Т] =
•о о
1 0
1 1
0 1
0 0
1 0
1 1
0 1
-0.5
0.5
0.5
-0.5
-0.5
0.5
0.5
-0.5
1 1]
1 1
1 1
1 1
0 1
0 1
0 1
0 lj
Г 1
0
0
-0.5
-0.5 0 0.9-]
-0.5 0 0.9
0.5 0 0.9
0.5 0 0.9
-0.5 0 1
-0.5 0 1
0.5 0 1
0.5
(
) 1 J
0 0
1 0
0 0
-0.5 0
Г-0.56
0.56
0.56
-0.56
-0.5
0.5
0.5
L-0.5
0 ]
0
-0.1
1
^
-0.56
-0.56
0.56
0.56
-0.5
-0.5
0.5
0.
5
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
Результат изображен на рис. 3-29 6. Заметим, что ранее параллельные оси
z прямые, соединяющие углы передней и задней граней, теперь сходятся к
оси z (х = 0, у = 0).
У
и
/
/
*^с—
/
/
А*
В
(а)
Я*
Е*
С*
F*
В*
(Ь)
Рис. 3-29 Одноточечная перспективная проекция центрированного единичного куба.
К сожалению, результирующее изображение все еще не дает адекватного
восприятия трехмерной формы объекта. Поэтому мы обратимся к более сложным
перспективным преобразованиям.
Если в четвертом столбце (4 х 4)-матрицы преобразования два элемента из
первых трех не равны нулю, то такое преобразование назьшается двуточечным
перспективным преобразованием. Двуточечное перспективное преобразование
[х у z 1]
1 0 0 р
О 1 0 q
0 0 10
0 0 0 1
= [х у z (рх + qy + 1)]
с обычными координатами
[х у z л
7 7 7 1\
px + qy + 1 px + qy + 1 px + qy + l J
(3-55)
(3-56)
имеет два центра проекции: первый на оси х в точке [—1/р 0 0 1] и второй на
оси у в точке [0 — 1/q 0 1], и две точки схода: на оси х в точке [1/р 0 0 1] и на
оси у в точке [0 1/д 0 1]. Заметим, что заданное уравнением (3-55) двуточечное
преобразование можно получить объединением двух одноточечных. Конкретнее,
[Рря] = [Рр][Ря] = [Ря][Рр],
где [Ppq] задается уравнением (3-55), [Рр] — уравнением (3-53) и [Ря] —
уравнением (3-51). Более подробно двуточечная перспективная проекция рассмотрена в
следующем примере.
Пример 3-20 Двуточечные перспективные преобразования
Снова рассмотрим куб, описанный в примере 3-18. Построим
двуточечную перспективную проекцию этого куба на плоскость z = 0 для центров
проекции, находящихся в точках х = — 10 и у = —10. Нужное
преобразование получим путем объединения (3-55) и (3-27). А именно,
т = [Рп][р.] =
•1
0
0
0
0
1
0
0
0
0
1
0
р]
я
0
1J
10 0 0'
0 10 0
0 0 0 0
0 0 0 1
1 0 0 р
0 1 0 q
0 0 0 0
0 0 0 1
Здесь р и q равны
р= -1/С-10) = 0.1, q = —1/(—10) = 0.1.
Преобразованные координаты куба имеют вид:
[Х'] = [Х][Т\ =
гО 0
1 0
1 1
0 1
0 0
1 0
1 1
.0 1
гО 0
1 0
1 1
0 1
0 0
1 0
1 1
.0 1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
1-
1
1
1
1
1
1
1.
■1
0
0
0
1 ■
1.1
1.2
1.1
1
1.1
1.2
1.
1.
0 0
1 0
0 0
0 0
гО
0.909
0.833
0
0
0.909
0.833
.0
0.1"
0.1
0
1
~~
0
0
0.833
0.909
0
0
0.833
0.J
109
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
Результаты изображены на рис. 3-30 а. Две точки схода находятся в х = 10
и у = 10.
/
/
A
У
/
/
\ \
\
\
\
\
Ic
КТ.Снаосиу
ву=10
К T.C. на оси z
bi-10
BT.F*
(о)
f
1
1
1
1
1
1 D* H*
A*E*
|
К T.C. на оси у
ву-10
C*G*
КТ.С.наоси z
вж=10
BT.F*
№)
Рис. 3-30 Двуточечные перспективные проекции, (а) Нецентрированного куба; (6)
центрированного куба.
Центрирование куба на оси z с помощью переноса вдоль х и у на —0.5,
аналогичное проделанному в примере 3-18, приведет к следующей общей
матрице преобразования
[T] = [Txy][PPq][Pz] =
1 0 0 0'
0 10 0
0 0 10
L—0.5 -0.5 0 1.
10 0 0.1'
0 1 0 0.1
0 0 0 0
-0.5 -0.5 0 0.9
10 0 0.1'
0 1 0 0.1
0 0 10
0 0 0 1
10 0 0"
0 10 0
0 0 0 0
0 0 0 1
где предполагается проецирование на плоскость 2 = 0. Заметим, что в этом
случае общий масштабирующий множитель больше не равен единице (см.
(3-4)), т.е. происходит очевидное масштабирование куба, вызванное его
перемещением. Преобразованные координаты равны
[Х*] = [Х][Т] =
0 0
1 0
1 1
0 1
0 0
1 0
1 1
0 1
-0.5
0.5
0.5
-0.5
-0.5
0.5
0.5
-0.5
1 1-1
1 1
1 1
1 1
0 1
0 1
0 1
0 1.
■ 1
0
0
-0.5
-0.5 0 0.91
-0.5 0 1
0.5 0 1.1
0.5 0 1
-0.5 0 0.9
-0.5 0 1
0.5 0 1.1
0.5
3 1 J
0 0 0.Г
1 0 0.1
0 0 0
-0.5 0 0.9
=
Г-0.56 -0.56
0.5 -0.5
0.46 0.46
-0.5 0.5
-0.56 -0.56
0.5 -0.5
0.46 0.46
.-0.5
0.5
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
Результаты изображены на рис. 3-30 6.
И снова полученное изображение не дает адекватного восприятия трехмерной
формы объекта. Поэтому обратимся к трехточечным перспективным
преобразованиям.
Трехточечная перспектива получается, если не равны нулю три первых
элемента четвертого столбца (4 х 4)-матрицы преобразования. Это трехточечное
перспективное преобразование
[х у z 1] =
1 0 0 р
0 1 0 q
0 0 1 г
0 0 0 1
= [х у z (px + qy + rz + 1)]
(3-57)
с обычными координатами
[*• у* z* 1] = [
У
px + qy + rz + 1 px + qy + rz + 1 px + qy + rz + 1 J
(3-58)
имеет три центра проекции: на оси х в точке [— 1/р 0 0 1], на оси у в
[О - 1/д 0 1] и на оси z в [0 0 — 1/г 1], а также три точки
схода: на оси х в [1/р 0 0 1], на оси у в [0 1/д 0 1] и на оси
z в [0 0 1/г 1].
Снова заметим, что трехточечное перспективное преобразование, заданное
равенством (3-57), может быть получено конкатенацией трех одноточечных
перспективных преобразований, по одному на каждую координатную ось. Создание
трехточечной перспективы иллюстрируется на следующем примере.
Пример 3-21 Трехточечное перспективное преобразование
Для описанного в примере 3-18 куба рассмотрим проекцию на
плоскость z = 0 после применения трехточечного перспективного
преобразования. Центры проекции находятся в точках х = —10, у = —10 и z = 10. Точки
схода находятся в х = 10, у = 10 и z = —10. Матрица преобразования равна
[Г] =
■1
0
0
0
Преобразованные координаты куба
[Х'] = [Х][Т] =
Г0 0 1
1 0 1
1 1 1
0 1 1
0 0 0
1 0 0
1 1 0
.0 1 0
"0 0 0
1 0 0
1 1 0
0 1 0
0 0 0
1 0 0
1 1 0
.0 1
0
0
0
1 0
0 0-
0 0
1-
1
1
1
1
1
1
1.
■1
0
0
0
0.9-1
1
1.1
1
1
1.1
1.2
1.
1.
о.г
0.1
0.1
1
0 0
1 0
0 0
0 0
гО
1
0.909
0
0
0.909
0.833
.0
О.Г
0.1
-0.1
1
0
0
=
0 1
0 1
0.909 0 1
1
0
0
0 1
0 1
0 1
0.833 0 1
0.909 0 1
Результат показан на рис. 3-31 6. Искаженный в результате перспективного
преобразования объект изображен на рис. 3-31 с. Отметим, что ребра на
рисунке сходятся.
И снова получившийся вид недостаточно информативен, хотя и математически
корректен. Соответствующие методы генерации перспективных видов
обсуждаются в разд. 3-16.
3-16 МЕТОДЫ СОЗДАНИЯ ПЕРСПЕКТИВНЫХ ВИДОВ
Предложенные в предыдущем разделе виды перспективной проекции были
неинформативны, так как во всех случаях из каждого центра проекции была видна
только одна грань куба. Для того чтобы наблюдатель воспринял трехмерную
форму объекта на основании только одного вида, надо, чтобы были видны несколько
граней этого объекта. Для простых объектов, подобных кубу, должны быть
видны как минимум три грани. Вид с несколькими гранями можно получить из
одноточечной перспективной проекции с фиксированным центром и с плоскостью
проецирования, перпендикулярной направлению взгляда, если предварительно
выполнен перенос и/или поворот объекта. Тогда получается реалистический вид,
если только центр проекции не находится слишком близко к объекту.
У
/
/
н
Е
/
/
/
С
/
G
F
В
(а)
У*
D*
К
?7f
/
К Т.С. на оси г
вг=-Ю
К Т.С. на оси у
bj>=10
'с*
1 К Т.С. на оси х
1 вх=10
Л*.Е*
F* В*
(с)
Рис. 3-31 Трехточечная перспектива, (а) Исходный куб; (6) перспективная проекция
на плоскость z = 0; (с) искаженный куб.
Для начала рассмотрим простой перенос объекта с последующим
одноточечным проецированием на плоскость г = 0ис центром проекции в точке z = zc.
Требуемое преобразование записывается в виде
[Т] = [Тг^уг][Ргг} =
10 0 0
0 10 0
0 0 0 г
1 тп 0 1 + тп
1
0
0
1
0
1
0
тп
0
0
1
п
0]
0
0
1
10 0 0
0 10 0
0 0 0 т-
0 0 0 1_
'10 0 0
0 10 0
0 0 1 -l/zc
1 тп 0 1 - n/zc
(3-59)
где т = -l/zc
У
4
2
I I I I |
-4 -2
/
О ~2
{ Q
-/
■ i i i i ,
2 4
Рис. 3-32 Одноточечная перспективная проекция с переносом в х, у направлениях.
Уравнение (3-59) вместе с рис. 3-32 показывает, что перенос в направлениях
х и у открывает дополнительные грани объекта. Перенос в обоих этих
направлениях необходим, чтобы открыть три грани простого кубообразного объекта. На
рис. 3-32 показаны результаты переноса вдоль прямой у = х отцентрированного
относительно начала координат куба и одноточечного проецирования на
плоскость z = 0. Заметим, что для передней грани показываются истинные размер
и форма.
Уравнение (3-59) также показывает, что перенос вдоль оси z, т.е. к центру
проекции или от него, приводит к явному изменению масштаба (из-за элемента
1 — n/zc). Этот эффект соответствует физической реальности, так как объекты,
находящиеся дальше от наблюдателя, выглядят более мелкими. Заметим, что при
приближении центра проекции к бесконечности явление масштабирования
исчезает. Этот эффект схематично показан на рис. 3-33. Как изображено на этом
рисунке, объект может находиться с любой стороны от центра проекции. Если
объект и плоскость проекции находятся по одну сторону от центра, то, как
показано на рис. 3-33, получается прямое изображение. Если же объект и плоскость
проекции лежат по разные стороны от центра, то получается перевернутое
изображение.
-z
Рис. 3-33 Эффект масштабирования при перемещениях вдоль оси z для одноточечной
перспективной проекции.
На рис. 3-34 показаны результаты перемещения объекта во всех трех
направлениях. Здесь куб перемещается вдоль трехмерной прямой от —х = — у = — z к
х = у = z. Заметно очевидное увеличение размера, а также на всех видах заметно
сохранение истинной формы, но не размера передней грани.
Эти идеи более подробно изложены в примере.
Пример 3-22 Одноточечная перспективная проекция с переносом
Рассмотрим г>тттрнт[»щ>пиаин«й относительно начала координат
единичный куб со следующими координатными векторами
[Х) =
Г-0.5
0.5
0.5
-0.5
-0.5
0.5
0.5
L-0.5
-0.5
-0.5
0.5
0.5
-0.5
-0.5
0.5
0.5
0.5
0.5
0.5
0.5
-0.5
-0.5
-0.5
-0.5
Переместим куб на 5 единиц в направлениях х и у и построим перспективную
проекцию на плоскость z = 0 с центром проекции в г = гс = 10.
Из уравнения (3-59) получаем общую матрицу преобразования
[Г] =
10 0 0
0 10 0
0 0 1 -0.1
5 5 0 1
Рис. 3-34 Одноточечная перспективная проекция, объединенная с переносами в х,
z направлениях.
Преобразованные координаты
[Х'] = [Х][Т] =
Г4.5
5.5
5.5
4.5
4.5
5.5
5.5
.4.5
4.5
4.5
5.5
5.5
4.5
4.5
5.5
5.5
0.95
0.95
0.95
0.95
1.05
1.05
1.05
1.05.
■4.737
5.789
5.789
4.737
4.286
5.238
5.238
.4.286
4.737
4.737
5.789
5.789
4.286
4.286
5.238
5.238
Правый верхний объект на рис. 3-32 изображает этот результат.
Бели исходный объект был перемещен на 5 единиц в направлениях х, у, z
и была построена одноточечная перспективная проекция на плоскость z = 0
с центром проекции в z — zc = 20, тогда из (3-59) следует, что общая матрица
преобразования записывается в виде
[Г] =
10 0 0
0 10 0
0 0 0 -0.05
5 5 0 0.75
Отметим общее масштабирование, задаваемое значением 0.75 в правом
нижнем элементе матрицы преобразования.
Преобразованные координаты равны
г4.5 4.5
5.5 4.5
5.5 5.5
4.5 5.5
4.5 4.5
5.5 4.5
5.5 5.5
U.5 5.5
0 0.7251
0 0.725
0 0.725
0 0.725
0 0.775
0 0.775
0 0.775
0 0.775J
Гб.207
7.586
7.586
6.207
5.806
7.097
7.097
1.5.806
6.207 0 1-1
6.207 0 1
7.586 0 1
7.586 0 1
5.806 0 1
5.806 0 1
7.097 0 1
7.097 0 lJ
[Х*) = [Х)[Т] =
Результат показан в виде верхнего правого объекта на рис. 3-34.
Несколько граней также будет видно, если использовать вращение объекта.
Один поворот откроет по крайней мере две грани объекта, тогда как два и более
поворотов вокруг разных осей откроют, как минимум, три грани.
Матрица преобразования для поворота вокруг оси у на угол ф и
последующего одноточечного перспективного проецирования на плоскость z = 0 с центром
проекции в z = zc:
cos0 0 -sin0 0
0 10 0
sin0 0 cos0 0
0 0 0 1
[T] = [Ry][Prz} =
1
0
0
0
0
1
0
0
0
0
0
0
0
0
-1/z
1
cos 0 0 0
0 1 0
sin ф 0 0
0 0 0
sin0
Zc
0
COS0
Zc
1
(3-60)
Аналогичным образом матрица преобразования для поворота вокруг оси х на угол
9 и последующего одноточечного перспективного проецирования на плоскость
z = 0 с центром проекции в точке z = zc имеет вид:
[Т] = [Дх] [Р„] =
1
0
0
0
1
0
0
0
0
cos в
-sinfl
0
0
cos в
— sinfl
0
0 0
sin 9 0
cosfl 0
0 1
0 0 "
о sm
Zc
о cos
Zc
0 1
0
в
1
0
0
0
0
1
0
0
0
0
0
0
0
0
-1/z
1
(3-61)
В обоих уравнениях (3-60) и (3-61) не равны нулю два отвечающих за
перспективное преобразование (перспективных) элемента в четвертом столбце матрицы
преобразования. Таким образом, один поворот вокруг главной оси,
перпендикулярной той оси, на которой лежит центр проекции, эквивалентен двуточечному
перспективному преобразованию. При повороте вокруг оси, на которой лежит
центр проекции, такого эффекта нет. Заметим, что для одного поворота
перспективный элемент для оси вращения остается неизменным, например, в уравнениях
(3-60) и (3-61) элементы q и р соответственно равны нулю.
В общем случае вращение вокруг главной оси не открывает необходимого для
адекватного трехмерного представления числа граней — как минимум, трех. Для
этого оно должно быть скомбинировано с перемещением вдоль оси. Следующий
пример иллюстрирует это.
Пример 3-23 Двуточечное перспективное проецирование
с использованием поворота вокруг одной главной оси
Рассмотрим проекцию на плоскость z = 0 с центром в точке z = zc = 2.5
куба с рис. 3-35 о, повернутого вокруг оси у на угол ф = 60°, чтобы открылась
левая грань, и перемещенного на —2 единицы вдоль у, чтобы открылась
верхняя грань.
Используя уравнение (3-38) с ф = 60°, уравнение (3-47)
уравнение (3-14) сп=1 — 0, тп= —2, получим
[T} = [Ry][Tr][PTZ} =
с ze = 2.5
■0.5
0
0.866
0
0
1
0
0
-0.866
0
0.5
0
01
0
0
1
Г1
0
0
0
0 0 0]
1 0 0
0 1 0
-2 0 1
Г1 0 0
0 1 0
0 0 0
0 0 0
0 '
0
-0.4
1
0.5 0 0 0.346
0 10 0
0.866 0 0 -0.2
.0 -201.
Преобразованные координаты равны
[Х-) = [Х][Т].
0 0 11
10 11
1111
0 111
0 0 0
1 0 0
1 1 0
О 1 0
0.5 0 0 0.346'
0 10 0
0.866 0 0 -0.2
0 -2 0 1
0.866
1.366
1.366
0.866
0
0.5
0.5
О
-2 0 0.8 ■
-2 0 1.146
-1 0 1.146
-1 0 0.8
-2 0 1
-2 0 1.346
-1 0 1.346
-10 1
1.083
1.192
1.192
1.083
0
0.371
0.371
.0
-2.5
-1.745
-0.872
-1.25
-2
-0.485
-0.743
-1
Результат показан на рис. 3-35 Ъ. Искажение появляется из-за того, что центр
проекции расположен слишком близко к кубу. Отметим схождение
параллельных осям х и z прямых линий к точкам схода, лежащим на оси х. Эти
точки схода определяются в примере 3-25 из разд. 3-17.
J
(*)
Рис. 3-35 Двуточечная перспективная проекция с поворотом вокруг одной оси.
Аналогичным образом трехточечное перспективное преобразование
выполняется с помощью вращения вокруг двух или более главных осей и последующего
одноточечного перспективного преобразования. Например, поворот вокруг оси у,
потом поворот вокруг оси х и перспективное проецирование на плоскость z = 0 с
центром проекции в точке z = zc имеет следующую матрицу преобразования
[T] = [Ry][Rx][PrA =
ссъф 0 -sin0 0 1 0
0 10 0 0 cosfl
зшф 0 cos0 0 0 -sine
0 0 0 lj [О 0
sin ф cos 9
0
sind
cos б
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
-1/z
1
cos^
0
з'тф
0
sin ф sin в
cos 9
- cos ф sin в
0
0
о
о
о
sin б1
cos фcos в
(3-62)
Отметим три ненулевых перспективных элемента. Объект можно также
переместить, если перемещение происходит после вращения, тогда результирующая
матрица преобразования равна
[T) = [Rv][Rx][Tr}[Prz] =
cos ф sin ф sin в О
0 cos0 0
sin ф — cos ф sin в О
1 m О
sin ф cos в
zc „
smfl
zc
cos фcos 0
ze .
(3-63)
Отметим здесь очевидный масштабирующий эффект перемещения вдоль z.
Результаты преобразования будут различными, если поменять порядок вьшолнения
поворотов или перенос выполнять до вращения.
Пример 3-24 Трехточечная перспективная проекция с поворотом
вокруг двух осей
Рассмотрим куб на рис. 3-35 о, повернутый вокруг оси у на угол ф = —30°,
вокруг оси х на в — 45° и спроецированный на плоскость z = 0 с центром
в точке z = ze = 2.5.
Из уравнения (3-62)
[Т] =
' 0.866 -0.354 0 -0.14Г
0 0.707 0 -0.283
-0.5 -0.612 0 -0.245
. 0 0 0 1
Преобразованные координаты равны
ГО 0 1
1 0 1
1 1 1
[**] = [*] PI =
0 111
0 0 0 1
10 0 1
110 1
.0 10 1.
0.866 -0.354 0 -0.141"
0 0.707 0 -0.283
-0.5 -0.612 0 -0.245
0 0 0 1
-0.5
0.366
0.366
-0.5
0
0.866
0.866
0
-0.612
-0.966
-0.259
0.095
0
-0.354
0.354
0.707
0
0
0
0
0
0
0
0
0.7551
0.614
0.331
0.472
1
0.859
0.576
0.717J
Г-0.662
0.596
1.107
-1.059
0
1.009
1.504
L о
-0.811
-1.574
-0.782
0.201
0
-0.412
0.614
0.986
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Результат изображен на рис. 3-36.
Рис. 3-36 Трехточечная перспективная проекция с поворотом вокруг двух осей.
Из этих результатов становится ясно, что одно-, дву- или трехточечное
перспективное преобразование можно сконструировать с помощью поворотов и
переносов вокруг и вдоль главных осей с последующим одноточечным перспективным
преобразованием с центром проекции, расположенным на одной из главных осей.
Эти результаты также справедливы для поворота вокруг произвольной оси в
пространстве. Следовательно, при использовании в графической системе парадигмы
с фиксированным центром проекции и малипулируемым объектом, необходимо
обеспечить только построение одноточечной перспективной проекции на
плоскость z = 0 с центром проекции на оси z.
3-17 ТОЧКИ СХОДА
Как показано на рис. 3-37 а при построении перспективного вида объекта
используется линия горизонта, расположенная обычно на уровне глаз. Главные точки
схода—это те точки на линии горизонта, в которые сходятся прямые,
параллельные в исходном пространстве главным осям. В общем случае различные
множества параллельных прямых имеют различные главные точки схода, как это
показано на рис. 3-37 Ь. Для плоскостей объекта, расположенных наклонно
относительно исходных главных осей, точки схода лежат выше или ниже линии
горизонта. Как показано на рис. 3-37 с, такие точки часто называются следом
точек.
Представляют интерес два метода определения точек схода. В первом просто
вычисляется точка пересечения пары преобразованных спроецированных
параллельных прямых. Второй метод сложен, но зато дает более точные результаты. В
Горизонт.^———
/
Горизонт Т.С. ^-^^—-~ ~~
т.е. ^г^:;"—-
\
"~"~—~-г-=г^^_Т.С. Уровень глаз
^Т.С.
Ф
/
/
./
(Ь)
— "" Т.С.
Рис. 3-37 Следы точек и точки схода.
этом методе в нужную позицию и ориентацию преобразуется объект, стороны
которого параллельны исходным главным осям. Потом применяется одноточечное
перспективное проецирование. Затем результирующая матрица преобразования
(см. уравнение 3-63) применяется к точкам, расположенным в бесконечности на
главных осях. Полученные в результате этого обычные координаты есть главные
точки схода для этого объекта. Для нахождения следов точек, возникающих для
наклонных плоскостей, сначала находят расположенные в бесконечности точки
на наклонной плоскости и затем подвергают их преобразованию.
Эти методы проиллюстрированы на нескольких примерах. В первом из них
для определения точек схода используется пересечение преобразованных прямых.
Пример 3-25 Главные точки схода, определяемые по пересечению
прямых
Из примера 3-23 преобразованные координатные векторы для пары
отрезков, один из которых проходит через точку А (см. рис. 3-35 а), и
первоначально параллельных соответственно осям х и z, равны
(5)
(3)
<8>
©
Г1.083
1.192
0
1.0.371
-1.25 0 1]
-0.872 0 1
-1 0 1
0.743 0 lj
Г1.192
0.371
1.083
Lo
-0.872 0 1]
-0.743 0 1
-1.25 0 1
-1 0 lj
(3)
(7)
(5)
®
Здесь цифры в кружках относятся к строкам исходной и преобразованной
матриц из примера 3-23. Уравнения пары прямых, параллельных в исходном
пространстве оси х таковы:
у = 3.468а; - 5.006,
t/ = 0.693x - 1.
Решение этой системы дает точку схода [VPX] = [1.444 0].
Уравнения пары прямых, параллельных в исходном пространстве оси z,
имеют вид:
у = -0.157х - 0.685
у = -0.231х - 1.
Решение дает точку схода [VPZ] = [—4.333 0].
Эти точки показаны на рис. 3-35 Ь.
Во втором примере для нахождения точек схода используется преобразование
расположенных в бесконечности точек на главных осях.
Пример 3-26 Главные точки схода, найденные с помощью
преобразования
Общая матрица преобразования из примера 3-24
[Г] =
' 0.866 -0.354 0 -0.14Г
0 0.707 0 -0.283
-0.5 -0.612 0 -0.245
0 0 0 1
Преобразование расположенных в бесконечности на осях х, у и z точек
дает
[VP][T] =
10 0 0"
0 10 0
0 0 10
"-6.142 2.5
0 -2.5
2.04 2.5
■ 0.866
0
-0.5
0
0 1"
0 1
0 1
-0.354 0
0.707 0
-0.612 0
0 0
-0.141
-0.283
-0.245
1
Эти точки схода показаны на рис. 3-36.
В третьем примере для нахождения следов точек используется преобразование
точек, расположенных в бесконечности на наклонных плоскостях.
Пример 3-27 Следы точек, полученные с помощью преобразования
Рассмотрим простую треугольную призму на рис. 3-38 а. Координатные
векторы призмы
0
1
0.5
0
1
0.5
0
0
0.5
0
0
0.5
1
1
1
0
0
0
1
1
1
1
1
1
[Х] =
Применяя общее преобразование из примера 3-24, получим
преобразованные координаты
[Х-] = [Х][Т] =
0 0
1 0
0.5 0.5
0 0
1 0
0.5 0.5
-0.5
0.366
-0.067
0
0.866
0.433
-0.662
0.596
-0.123
0
1.009
0.55
1 1"
1 1
1 1
0 1
0 1
0 1
—
-0.612 0
-0.966 0
-0.436 0
0 0
-0.354 0
0.177 0
-0.811 0
-1.574 0
-0.802 0
0 0
-0.412 0
0.224
0
0.866
0
0.5
0
0.755'
0.614
0.543
1
0.859
0.788
1"
1
1
1
1
1
-0.354
0.707
-0.612
0
=
0
0
0
0
-0.141
-0.283
-0.245
1
На рис. 3-38 Ь изображена преобразованная призма.
к С.Т.г
(*)
Рис. 3-38 Следы точек.
Объект
Негатив
Рис. 3-39 Фотография как перспективная проекция.
Направляющие косинусы наклонных ребер левой верхней плоскости
призмы до преобразования равны [0.5 0.5 0]. Таким образом, точка, лежащая
в бесконечности в этом направлении, имеет однородные координаты [1 10 0].
Аналогично [—0.5 0.5 0] —направляющие косинусы наклонных ребер
правой верхней плоскости призмы до преобразования. Таким образом, точка,
лежащая в бесконечности в этом направлении, имеет координаты [—1 1 0 0].
Применяя преобразование к только что полученным точкам и к точкам,
лежащим в бесконечности на главных осях, получим
[VP][T] =
1
0
0
1
1
0
1
0
1
1
0
0
1
0
0
0]
0
0
0
0
■ 0.866 -0.354 0 -0.141'
0 0.707 0 -0.283
-0.5 -0.612 0 -0.245
0 0 0 1
0.866
0
0.5
0.866
0.866
6.142
0
2.041
2.041
6.142
-0.354
0.707
-0.612
0.354
1.061
2.5
-2.5
2.5
-0.833
-7.5
0
0
0
0
0
0
0
0
0
0
—
0.1411
-0.283
-0.245
-0.424
-0.141.
11
1
1
1
1
VPX
VPy
VPZ
тр
TPr
Точки схода и следы точек изображены на рисунке 3-38 Ь. Как мы и
ожидали, точки VPX, VPy и VPZ совпадают с полученными в примере 3-26.
3-18 ФОТОГРАФИЯ И ПЕРСПЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ
Фотография — это перспективная проекция. Схема работы камеры в общем виде
изображена на рис. 3-39. Центр проекции — это точка фокуса линзы камеры.
Удобно рассматривать создание негатива и отпечатка с него как два разных процесса.
На рис. 3-40 а показана схема создания исходного негатива. Для удобства
поместим негатив в плоскость z = 0 так, чтобы центр проекции и сцена находились
Объект
Объект
Негатив ..
Центр
[■"«»« проекции
z-=0
(Ь)
Рис. 3-40 Схема фотографической перспективы, (а) Создание исходного негатива; (Ь)
создание оттиска.
в отрицательном полупространстве z < 0. Перспективное проецирование на
плоскость 2 = 0 (негатив) порождает следующее преобразование:
[Тп} =
10 0 0 '
0 10 0
0 0 0 1//
0 0 0 1
(3-64)
где / — это фокусное расстояние линзы. Заметим, что на негативе формируется
перевернутое изображение объекта. Конкретнее,
[х у z 1]
10 0 0
0 10 0
0 0 0 1//
0 0 0 1
= [х у 0 l + z//]
xf
yf
f + z'
Здесь для / + z < 0 значения х* и у* имеют противоположный знак по
сравнению с i и у, следовательно, на негативе образуется перевернутое изображение.
На рисунке 3-40 Ь изображена схема создания отпечатка с фотографического
негатива. Здесь s обозначает расстояние от фокуса линзы увеличителя до бумаги.
Предполагается, что бумага находится в z = 0. Тогда преобразование
перспективного проецирования имеет вид:
[ТР} =
1
0
0
0
0
1
0
0
0
0
0
0
0
0
-1/8
1
(3-65)
Заметим, что на отпечатке формируется прямое изображение. А именно,
[х у z 1]
1
0
0
0
0
1
0
0
0
0
0
0
0
0
-1/S
1
= [*
1-Й
XS
X =
У =
ys
s — z'
Для объекта значение z < 0, тогда s — z > 0 и координаты z*, у* имеют тот
же знак, что и х, у, т. е. формируется прямое изображение.
3-19 СТЕРЕОГРАФИЧЕСКАЯ ПРОЕКЦИЯ
Во многих приложениях важно увеличение восприятия трехмерной глубины
сцены. Для восприятия глубины у системы глаз-мозг существует два основных типа
подсказок: монокулярные и бинокулярные, в зависимости от того, сколько глаз
используется — один или два. Основными монокулярными подсказками являются:
— перспектива — схождение в одну точку параллельных прямых;
— параллакс движения —при горизонтальном движении головы кажется, что
ближние объекты сдвигаются на плоскости проекции больше, чем дальние;
— относительный размер знакомых наблюдателю объектов;
— перекрытие — более близкий объект загораживает остальные и располагается
перед более отдаленным;
— свет и тени;
— ослабление атмосферой и неспособность глаза из-за этого различить мелкие
детали удаленных объектов;
— фокусирующая аккомодация—для объектов, расположенных на разных
расстояниях, требуются разные усилия фокусирующих мускулов глаза;
Основными бинокулярными подсказками являются:
- углы сближения оптических осей глаз;
— несогласованность на сетчатке — разница в местоположении спроецированных
на стечатку глаза объектов интерпретируется как различие в расстоянии до
глаз.
Монокулярное зрение дает лишь слабое восприятие трехмерной глубины.
Однако бинокулярное зрение дает очень сильное восприятие глубины, потому что
система глаз-мозг смешивает в одно два различных изображения, созданных для
каждого глаза. Стереография пытается создать изображение с характеристиками,
аналогичными настоящему бинокулярному зрению. Для генерации
стереоизображений существуют несколько методов (см. [3-4] и [3-5]). Все они основываются на
том, что для левого и правого глаза готовятся разные изображения.
В двух методах, называемых цветовым анаглифом и поляризованным
анаглифом методами, для получения левым и правым глазами корректных и различных
изображений используются фильтры. Если рассказать в нескольких словах, то в
первом случае двумя разными цветами создаются два изображения — одно для
левого и другое для правого глаза. При просмотре через соответствующие фильтры
левый глаз видит левое изображение, а правый — только правое. Система глаз-
мозг объединяет оба двумерных изображения в одно трехмерное с правильными
цветами. Во втором случае вместо цветовых фильтров используются
поляризованные.
В третьем методе используется попеременное проецирование видов для левого
и правого глаза. Соответствующее устройство просмотра синхронизировано так,
чтобы свет не попадал в другой глаз.
В четвертом методе, автостереоскопии, никакого специального оборудования
для просмотра не требуется. Метод основан на использовании плоских или
линзообразных экранов. Изображения называются параллаксными стереограммами,
параллаксными панорамаграммами и панорамными параллаксными
стереограммами. Более полную информацию по этому вопросу можно найти в [3-5].
Во всех этих методах требуется проецирование объекта на плоскость из двух
различных центров проекции — одно для правого глаза и одно для левого. На
рис. 3-41 показано проецирование на плоскость z = О точки Р из центров проекции
в El (—е, 0, de) и Ец (е, 0, de), соответствующих левому и правому глазу.
Как показано на рис. 3-41 Ь, для удобства центр проекции для левого глаза
перенесен таким образом, чтобы он лежал на оси z. Используя подобные
треугольники, получим
de de — z
и
х*' = Х> = Х'
L l-z/de 1 + rz'
где
г = -l/de.
в
Т
е
е
L
£.
L
Р&*% У* Ф
——J^V^
• А
;
• dt z
Ъ'ЬуЬФ
с
>Р(х у г)
(а)
P(x',y,z)
Р(х% у, г)
Рис. 3-41 Стереографическая проекция на плоскость z = 0.
Аналогичным образом перенеся центр проекции для правого глаза на ось z (как
показано на рис. 3-41 с) и снова используя подобные треугольники, получим
XR -
1 — z/de 1 + rz
Так как для каждого глаза значение у = 0, то оба спроецированных значения
у имеют вид:
У =
У
У
z/de
l + rz
Эквивалентные матрицы преобразования 4x4 построения видов для правого
и левого глаза следующие:
[Sl] = [Trx] [Р„] =
1
0
0
е
0
1
0
0
0
0
1
0
0"
0
0
1
10 0
0 1 0
0 0 0
0 0 0
1 0 0
0 1 0
0 0 0
е 0 0
0
0
-l/de
1
о
о
-l/de
1
(3-66)
[SR] = [Trx] [P„] =
1 0 0
0 1 0
0 0 0
е 0 0
0
0
-l/de
1
(3-67)
Следовательно, стереографическая проекция получается при преобразовании
сцены с помощью уравнений (3-66), (3-67) и вывода обоих изображений.
Существует ряд методов для вывода изображений стереографических
проекций. Многие люди смогут создать стереоизображение без помощи каких-либо
технических средств. Один из методов, требующий некоторой тренировки, состоит
в следующем: сначала сфокусировать глаза в бесконечности, затем, не изменяя
фокуса, постепенно передвигая стереопары и держа их примерно на расстоянии
локтя, добиться стереоэффекта.
Бинокулярное смешение стереопар улучшается при использовании небольшой
непрозрачной маски, например полоски черного картона шириной
приблизительно в дюйм. Как показано на рис. 3-42, маску помещают между глазами и
стереопарой и передвигают вперед и назад до получения нужного положения. В этом
Левый глаз
Левое
изображение
Правое
изображение
Рис. 3-42 Простой метод просмотра стереопар.
(Ь)
Рис. 3-43 Стереоскопы, (а) Стереоптикон Брустера; (Ъ) типичный лабораторный
инструмент.
положении левый глаз видит только левое изображение стереопары, а правый
глаз — правое.
Два более специализированных устройства для просмотра стереопар
изображены на рис. 3-43 а и 3-43 6. На рис. 3-43 а показан популярный в начале нашего
века стереоптикон Брустера, а на рис. 3-43 6 — типичный современный
лабораторный стереоскоп. Оба устройства относятся к простым стереоскопам с
фокусирующими линзами.
Хотя уравнения (3-66) и (3-67) задают основное преобразование для
генерации стереопар, их надо модифицировать для приспособления к различным схемам
стереопросмотровых устройств. Схема простого фокального стереоскопа
приведена на рис. 3-44. Стереопары в нем располагаются на фокусном расстоянии / от
линз. Стереоизображение реконструируется на расстоянии / от линз. Как было
ранее упомянуто, стереоугол 7> очень сильно влияющий на бинокулярное
смешение, связан со сближением оптических осей глаз. У обычного человека расстояние
Рис. 3-44 Схема фокусного плоского стереоскопа.
между зрачками глаз приблизительно равно 60 мм. Эксперименты показали ([3-
4]), что наилучший стереоэффект наблюдается на расстоянии приблизительно
600 мм. Следовательно, наилучший стереоэффект достигается для tg(7/2) = 1/5.
Как показано на рис. 3-44, для достижения бинокулярного смешения стереопары
должны быть разнесены на расстояние 2w при условии, что они размещены на
фокусном расстоянии /.
Обозначив через 2D на рис. 3-44 расстояние между линзами стереоскопа, из
подобия треугольников получим
D-w
D
1
Таким образом, разнесение на расстояние
w = D-J-
5
(3-68)
дает наилучший стереоэффект. Для стереопары, просматриваемой через простой
линзовый стереоскоп, уравнения (3-66) и (3-67) записываются в виде
[Si
[Sr} =
1
0
0
w
1
0
0
-w
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
-1//
1
0
0
-1//
1
(3-69a)
(3-69b)
Рис. 3-45 Стереопара.
Типичная стереопара для простого линзового стереоскопа показана на
рис. 3-45.
Расстояние между стереопарой, полученное из уравнения (3-68) для типичных
значений D и /, довольно мало. Следовательно, можно просматривать только
маленькие стереоизображения. Чтобы увеличить размеры изображений для
увеличения расстояния между ними используются зеркала или призмы. Типичный
зеркальный стереоскоп изображен на рис. 3-43 Ь. Соответствующая схема
приведена на рис. 3-46. Снова используя подобие треугольников, получим расстояние
между стереопарой
wo — w _ D _ 1
/ ~Т~5
w =
W0 - f
(3-70)
Создание типичной стереопары проиллюстрировано на примере.
Пример 3-28 Создание стереопары
. Рассмотрим изображенный на рис. 3-45 простой трехмерный
проволочный объект с координатами
[Х] =
0
1
1
1
0
0
0
-1
-1
-1
-1
0
0
0
1
1
1
0
0
0
0
1
0
0
1
1
1
2
2
2
0
0
0
1
1
1
1
1
1
1
1
1
1
1
Рис. 3-46 Схема зеркального стереоскопа.
[V] = [Ry][Tz} =
Для визуализации фигуру сначала повернем на 20° вокруг оси у, а затем
перенесем на —1.5 единицы в направлении z. Результирующее
преобразование будет
0.94 0 -0.342
0 1 0
0.342 0 0.94
0 0 0
0.94 0 -0.342 0
0 10 0
0.342 0 0.94 0
0 • 0 -1.5 1
Стереопара создается для просматривания с помощью простого
фокусирующего плоского стереоскопа. Расстояние между линзами 2D = 4 дюймам
0 ]
0
0
1
Г 1
0
0
0
0
1
0
0
0
0
1
-1.5
0
0
0
1
и фокусное расстояние тоже равно 4 дюймам. Из уравнения (3-68) следует,
что расстояние между стереопарой
w = 2 - 4/5 = 1.2".
Используя уравнение (3-69), получим преобразования для левого и
правого стереоизображений
[Sl]
I 0 0 0 "
0 10 0
0 0 1 -0.25
1.2 0 0 1
и [Sr] =
1 0 0 0
0 10 0
0 0 0 -0.25
-1.2 0 0 1
Объединение этих преобразований с видовым дает
[Cl] = [V][Sl] и [Cr] = [V][Sr],
[Сь} =
0.94 0 0 0.086'
0 10 0
0.342 0 0 -0.235
1.2 0 0 1.38
[Cr] =
0.94 0 0 0.086-
0 10 0
0.342 0 0 -0.235
-1.2 0 0 1.375
Преобразованные координаты для левого и правого изображений
вычисляются следующим образом:
[Xl] = [X][GL] и [XR] = [X][CR],
[XI] =
0.873
1.465
2.025
2.025
1.353
2.081
2.081
1.152
0.202
0.202
0.202
0
0
0
0.816
0.877
1.105
0
0
0
0
0.775
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
и [XR] =
-0.873
-0.178
0.067
0.067
-0.753
-0.57
-0.57
-1.776
-1.659
-1.659
-1.659
0
0
0
0.816
0.877
1.105
0
0
0
0
0.775
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
Результат изображен на рис. 3-45. Заметим, что при создании
конечного изображения эти данные должны быть промасштабированы для каждого
конкретного устройства вывода, с тем чтобы обеспечить корректное
физическое значение для w.
3-20 СРАВНЕНИЕ ДВУХ МЕТОДОВ ПОСТРОЕНИЯ ПРОЕКЦИЙ-
С ФИКСИРОВАННЫМ ОБЪЕКТОМ И С ФИКСИРОВАННЫМ
ЦЕНТРОМ ПРОЕКЦИИ
Метод проецирования, в котором объект зафиксирован, а перемещается центр
проекции, может быть легко преобразован в обсуждавшийся ранее метод с
перемещающимся объектом и фиксированным центром. Представляет интерес два
случая. В первом, более простом, предполагается, что плоскость проекции
перпендикулярна направлению взгляда, направленного из центра проекции к сцене. Во
втором случае перпендикулярность не предполагается. Здесь будет рассмотрен
только первый случай.
Когда плоскость проекции перпендикулярна направлению взгляда, с
помощью описанной ниже процедуры построение проекции можно свести к случаю с
движущимся объектом и фиксированным центром проекции:
— найти пересечение линии взгляда и плоскости проекции;
— перенести точку пересечения в начало координат;
— повернуть вектор взгляда таким образом, чтобы он совместился с осью +z и
был направлен к началу системы координат (см. разд. 3-9);
— применить к сцене полученное преобразование;
— выполнить одноточечное перспективное проецирование на плоскость z = 0 из
преобразованного центра проекции, расположенного теперь на оси z.
В качестве иллюстрации этого метода приведем относительно простой пример.
Пример 3-29 Перспективное проецирование на перпендикулярную
плоскость проекции для фиксированного объекта
Рассмотрим обсуждавшийся ранее в примере 3-10 куб с отсеченным
углом. Спроецируем куб из центра в точке [10 10 10] на плоскость,
проходящую через точку [—1 — 1 — 1] и перпендикулярную направлению взгляда,
как это показано на рис. 3-47.
Уравнение плоскости проекции можно получить из ее нормали (другие
методы можно найти в [3-1]). В данном случае нормаль направлена в сторону,
противоположную вектору взгляда.
Направление вектора взгляда
И = [-1 -1 -1].
Тогда нормаль к плоскости проекции, проходящей через точку [—1 —1 —1]
перпендикулярно направлению взгляда, будет
[п] = [1 1 1].
Общее выражение уравнения плоскости имеет вид:
ах + by + cz + d = 0.
Нормаль к такой плоскости задается вектором
[п] = [о Ъ с].
Значение d в уравнении плоскости вычисляется по любой точке,
принадлежащей этой плоскости. Тогда уравнение плоскости проекции, проходящей
через точку [—1 — 1 — 1], примет вид:
x+y+z+d=Q
и
d=-x-y-z = l + l + l = 3.
Следовательно,
x+y+z+3=0
есть уравнение плоскости проекции.
Пересечение направления взгляда и плоскости проекции определяется с
помощью записи уравнения прямой в параметрическом виде, подстановки
его в уравнение плоскости и решения полученного уравнения.
Параметрическое уравнение вектора взгляда таково:
[S(t)] = [x(t) y(t) *(*)] =
= [10 10 10]+ [-11 -11 —11]*, 0 < i < 1.
Его подстановка в уравнение плоскости приводит к
*(*) + У{*) + *(*) + 3 = (10 - lit) + (10 - lit) + (10 - lit) +3 = 0.
Решение уравнения дает значение параметра для точки пересечения, т. е.
—33* + 33 = 0 -»• t = 1.0.
Саму точку пересечения получаем подстановкой t в [5(<)]. А именно,
[I] = [5(1)] = [10 10 10] + [-11 - 11 - 11](1.0) =
= [-1-1 -1].
Как и ожидалось из простых геометрических рассуждений, точка
пересечения находится в х = у = z = —1.
Требуемая матрица переноса (для переноса точки пересечения в начало
координат) следующая:
[Тг] =
10 0 0-
0 10 0
0 0 10
1111
После переноса центр проекции находится в точке [11 11 11], а
направление взгляда проходит через начало координат.
Используя результаты разд. 3-9, совместить вектор взгляда с осью z
можно с помощью поворота вокруг оси х на угол а = 45° и последующего
поворота вокруг оси Ъ на угол /3 = 35.26°. Матрицы поворотов записываются
в виде:
[R*} =
1
0
0
0
0
1/V2
-1/\/2
0
0 0
i/уД о
i/уД о
0 1
и [Ry] =
2/л/б 0 1/л/З 0'
0 10 О
-1Д/3 0 2/у/б 0
0 0 0 1
а суммарная матрица преобразования имеет вид
[М] = [Тг] [Д.] [R,]
2/уД, 0 1Д/3 0'
-1/\/б 1/\/2 1/л/З 0
-1Д/6 -1/%/2 1/л/З 0
0 0 З/л/3 1
Преобразование центра проекции дает
[Ср] [М] = [10 10 10 1]
2/у/б 0 1/V3 0'
-1/VG 1/%/2 1/л/З 0
-1/\/б -1/%/2 1/V3 0
0 0 З/л/3 1.
= [0 0 33/%/3 1].
Преобразование одноточечного центрального проецирования с центром в
точке z — 33/уЗ на плоскость z = 0 задается матрицей
[Р'Л =
10 0 0
0 10 0
0 0 0 -л/З/33
.0 0 0 1
Объединив с [М], получим, что
[T) = [M][PTZ) =
10 0
0 1 0
0 0 0
.0 0 0
о
о
-v/3/ЗЗ
2/л/б 0 1/л/З О
-1/л/б 1/л/2 1/л/З О
-1/л/б -1/\/2 1/л/З О
О 0 3/%/3 1
2/л/б 0 0 -1/33'
-1Д/6 1/\/2 0 -1/33
-1/л/б -1/\/2 0 -1/33
0 0 0 30/33
Преобразованные обычные координаты спроецированного объекта будут
[Х'] = [Х][Т} =
о
1
1
0.5
О
О
1
1
О
1
о
о
0.5
1
1
О
о
1
1
1
-0.408
0.408
0.204
-0.408
-0.816
О
0.816
0.408
-0.408
0.204
-0.465
0.481
0.245
-0.490
-0.962
О
0.929
0.481
-0.465
0.245
1
1
1
1
1
О
О
о
о
0.5
-0.707
-0.707
-0.354
О
О
О
О
0.707
0.707
0.354
-0.805
-0.833
-0.424
О
О
О
О
0.833
0.805
0.424
0.816 0 0 -0.0301
-0.408 0.707 0 -0.030
-0.408 -0.707 0 -0.030
О 0 0 0.909
О 0.879-
О 0.848
О 0.833
О 0.833
О 0.848
О 0.909
О 0.879
О 0.848
О 0.879
О 0.833.
О V
О 1
О 1
О 1
О 1
О 1
О 1
О 1
О 1
О 1
Результат изображен на рис. 3-48.
3-21 ВОССТАНОВЛЕНИЕ ТРЕХМЕРНЫХ ОБЪЕКТОВ ПО
ПРОЕКЦИЯМ
Задача восстановления трехмерной формы объекта или координат в пространстве
широко распространена. Например, она постоянно возникает при использовании
Рис. 3-48 Результат проецирования в примере 3-29.
чертежей, являющихся ортографическими проекциями. Хорошо известен метод
восстановления трехмерного объекта или координаты по двум или более
представленным на чертеже видам (ортографическим проекциям). Метод же
восстановления трехмерного координатного вектора по двум перспективным
проекциям, например по двум фотографиям, не столь хорошо известен. Конечно, если
метод пригоден для перспективных проекций, то он подходит также и для
более простых ортографических проекций и фактически для всех рассмотренных в
предыдущих разделах проекций. Как будет показано ниже, при наличии
определенной дополнительной информации не надо иметь точную информацию о самом
преобразовании.
Прежде чем рассматривать задачу в общем виде, обратимся к специальному
случаю восстановления трехмерных координат точки по двум или более
ортографическим проекциям. На рис. 3-49 представлены ортографические виды
(проекции) спереди, справа и сверху. При определении трехмерных координат точки А
вид спереди дает значения координат х и у, вид справа — у и z и вид сверху —
х и z, т. е.
спереди (front): Xf yf
справа (right side): yr zT
сверху (top): xt zt
Заметим, что для каждой координаты мы получаем два значения. В
математике в подобном случае говорят, что на задачу наложены избыточные условия.
Ведь надо найти только три независимые величины, тогда как известны шесть
определяющих их условий (уравнений). Для любой измерительной системы в
общем случае Xf ф xt, yf Ф yr, zr ф zt1- Так как неизвестно, какое из значений
верно, то наиболее разумным решением будет усреднить их.
Вернувшись теперь к восстановлению трехмерных координат по
перспективным проекциям, напомним, что обобщенное перспективное преобразование
представляется в виде матриц размера 4x4. Таким образом,
[х у z 1][Т'] = [х' у' z' h],
1 По этой причине в чертежах размеры указываются явным образом.
Рис. 3-49 Восстановление трехмерной формы по ортографическим проекциям.
где
rpl
Jll
rpl
J21
rpl
J31
rpl
J41
rpl
J12
rpl
J22
rpl
J32
rpl
J42
Пъ
rpl
J23
T'
-'зз
rpl
J43
T'
J14
^4
Ц,
rpl
J 44
[T'] =
Результаты могут быть спроецированы на двумерную плоскость, скажем на
плоскость z = 0, с помощью
[Т"\ =
Объединение двух матриц дает
10 0 0
0 10 0
0 0 0 0
0 0 0 1
[Т] = [Г"] [Г'] =
Гц Т12 0 Г14
Т21 Т22 0 Т24
Гз1 2з2 0 Т34
Г41 Г42 0 Т44
Полезно записать это преобразование в виде
[х у
Гц Т12 0 Ти
T2i Т22 0 Т24
Г31 ^32 0 Т34
Тц Ti2 0 Т44
= [х' у' 0 ft] = /i[z* у* 0 1]. (3-71)
Заметим, что х* и у* — это координаты перспективной проекции на плоскость
z = 0. Могли бы также использоваться проекции на плоскости х = 0 или у = 0.
Расписав в явном виде матричное уравнение (3-71), получим
Тих + Т21у + T31z + T4i = hx*,
Т12х + Т22у + T32z + Т42 = hy\
Т14х + Т24у + TMz + T44 = h.
(3-72 а)
(3-72 b)
(3-72 с)
Подставим значение h из (3-72 с) в уравения (3-72 а) и (3-72 Ь):
(Гц - Т14х*)х + (Т21 - Т24х*)у + (Гз1 - T34x*)z + (Г41 - Т44х*) = 0, (3-73а)
(Tia - Тиу*)х + (Т22 - Т24у*)у + (Т32 - T34y*)z + (Т42 - Т44у*) = 0. (3-73Ь)
По предложению Сазерленда [3-4] эту пару уравнений можно рассматривать
тремя разными способами. В первом предполагаются известными Т, х, у, z.
Тогда у нас есть два уравнения с двумя неизвестными х* и у*. Таким образом,
эти уравнения можно использовать для непосредственного вычисления координат
перспективной проекции. Именно этот подход применялся во всех предыдущих
рассуждениях в данной главе.
При другом подходе полагаются известными Т, х*, у*. В этом случае
получается два уравнения от трех неизвестных пространственных координат х, у, z. Эту
систему уравнений невозможно решить. Однако, если известны две
перспективные проекции, скажем две фотографии, тогда уравнения (3-73) можно записать
для обеих проекций. В результате получим
(Т& - Т1Ахл)х + (Т2\ - ПАх*)у + (Т3\ - Tl4x*)z + (I* - Г^х*1) = 0,
(Ik - T}4y*l)x + (Ti - T2V:)y + (П3 - Т^ул)г + (Г*, - Т^у*1) = 0,
(I* - Т?4х*2)х + (Г& - ТЪх*2)у + (Т& - n4x*2)z + (Г2, - Г24х*2) = 0,
(Т?2 - Т?лу*2)х + (Т22 - Т24у*2)у + (Т322 - T3V2)z + (I* - Т2,у*2) = 0,
где верхние индексы 1 и 2 обозначают первую и вторую перспективные проекции.
Заметим, что преобразования [Т1] и [Т2] не обязательно должны быть
одинаковыми. Эти уравнения можно переписать в матричной форме
где
А =
[А][Х] = [В],
"Т1 — Т1 т*1 Т1 — Т1 т*1 Т1 — Т1 т*1"
^12 — Тыу* Т22 — T2iy* Т32 — T3iy*
rpl rp2 »2 rp2 rp2 »2 гр2 гр2 *2
±\\ 1ЫХ J21 J24x ±Ъ\~ J34x
Th-Tly*2 т22-т2лУ*2 t322-t3V2.
»
[Х]т = [х у г\
[В]Т=[П4х
► 1 _ rpl rpl »1 rpl rp2 *2 _rp2 rp2
J4I 1ИУ J42 J44I J41 J44*l
•a.
-T422]
(3-74)
Уравнения (3-73) представляют четыре уравнения от трех неизвестных
пространственных координат х, у, z. Для нахождения решения [X] матрица [А] не
может быть инвертирована, так как она не квадратная. Снова, как и в случае
восстановления трехмерных координат по ортографическим проекциям, условия
избыточны и, таким образом, задача может быть решена только в некотором
усредненном или наиболее подходящем смысле.
Усредненное решение можно вычислить, вспомнив, что матрица,
умноженная на свою транспонированную матрицу, является квадратной. Таким образом,
умножив обе части уравнения (3-74) на [А]т, получим
[А]Т[А][Х] = [А]Т[В].
Вычислив обратную матрицу [[А]т [А]], получим усредненное решение для [X],
т.е.
[Х] = [{АУ[А]]-1[АУ[В}.
(3-75)
Если решения для [X] нет, то наложенные условия избыточны и не
существует единственного решения, обеспечивающего наименьшую ошибку. Этот метод
иллюстрируется на примере.
Пример 3-30 Трехмерное восстановление
Предположим, что обмеренные координаты точки на одной
перспективной проекции равны [0.836-1.836 0 1] и [0.6548 0 0.2886 1] на другой. Первое
преобразование перспективной проекции является результатом поворота на
60° вокруг оси у и последующего переноса на 2 единицы в отрицательном
направлении оси у. Точка проекции находится в z = —1, а результат
проецируется на плоскость z = 0. Это действительно является двуточечной
перспективной проекцией. Второе преобразование является результатом поворотов
на 30° вокруг каждой из осей х, у- Точка проекции находится в у = —1,
а результат проецируется на плоскость у = 0, т. е. является трехточечной
перспективной проекцией. Таким образом преобразования [Г1] и [Г2]
0.5
0
0.87
0
0
1
0
-2
0
0
0
0
-0.871
0
0.5
1
и
[Т2] =
Г0.87
0.25
0.43
0
0
0
0
0
-0.5
0.43
0.75
0
0 '
0.87
-0.5
1
рг1] =
Отметим, что последние две строки [А] и [В] должны быть переписаны,
чтобы учесть тот факт, что [Г2] является проецированием на плоскость у = 0.
Тогда матрица А
[А] =
[Bf = [
Г 1.22 0 0.45
-1.59 1 0.92
0.87 -0.32 0.76
.-0.5 0.18 0.89
D.84 0.16 0.65 0.2
Решив уравнение, получим [X] = [0.5 0.5 0.5], т.е. центр единичного куба.
В качестве третьего подхода к рассмотрению уравнений (3-73) отметим, что
если известны координаты нескольких точек в объектном пространстве и на
перспективной проекции, то можно найти элементы преобразования Тц. Эти
элементы впоследствии можно использовать для нахождения местоположения
неизвестных точек, используя описанный выше второй метод. Чтобы показать это,
перепишем (3-73) в виде
Тцх + Т21у + T3iz + Т41 - Т14хх* - Т24ух* - T34zx* - Т44х* = 0, (3-76а)
Т12х + Т22у + TZ2z + Г42 - ТцхУ* - Т24уу* - T3izy* - Т44у* = 0. (3-76 b)
В предположении, что известны х*, у*, х, у, z, уравнения (3-76 а) и (3-76 Ь)
представляют два уравнения с 12 неизвестными элементами Тц. Применяя эти
уравнения к 6 некомпланарным точкам в объектном пространстве и на
перспективной проекции, получим систему из 12 уравнений с 12 неизвестными. Эти
уравнения могут быть решены относительно Тц. Таким образом, находится
преобразование, породившее перспективную проекцию, например фотографию. Заметим,
что в этом случае не требовалось никакой предварительной информации о
преобразовании. Если, например, это бьши фотографии, то не требовалось знать ни
о местоположении, ни об ориентации фотокамеры. В матричном виде система
уравнений записывается в таком виде:
XI
0
Х2
0
хз
0
х4
0
хь
0
х%
0
0
Xl
0
Х2
0
хз
0
х4
0
Z5
0
х6
—XiX\
-Xiy{
-х2х2
-х2у2
-X3X3
-хзУз
х^х^
-х4у4
-х5х*5
-х5у£
— ХвХ6
-ХвУв
2/1
0
2/2
0
Уз
0
2/4
0
2/5
0
2/6
0
0
2/1
0
2/2
0
2/з
0
2/4
0
2/5
0
2/6
-У1Х\
-2/12/Г
-2/232
-2/22/2
-2/3^3
-2/32/3
-2/4^4
-2/42/1
-2/5^5
-2/52/5
-Увх%
-2/62/е
Z\
0
Z2
0
Z3
0
Z4
0
Zb
0
z6
0
0
Z\
0
z2
0
Z3
0
z4
0
Zb
0
z%
~Z\X\
-21У*
-z2x*2
-222/2
~Z3X\
-232/3
-z4x\
-242/4
-z5x*5
-252/5
~Z%X*%
-^бУе
1
0
1
0
1
0
1
0
1
0
1
0
0
1
0
1
0
1
0
1
0
1
0
1
-xl "
-1/1
—x2
-2/2
—x3
-2/3
-xl
-2/4
-'%
-2/5
—x6
-2/6* .
"Тц
Tl2
T14
T21
T22
T24
T31
T32
T34
T,i
T42
T44
(3-77)
где нижние индексы соответствуют точкам с известным местоположением.
Уравнения (3-77) записываются в более компактном виде:
[А'][Т} = 0.
Так как уравнения (3-77) являются однородными уравнениями, то они
содержат произвольный масштабный коэффициент. Следовательно, Т44 можно
приравнять единице и нормализовать результирующее преобразование. Система
сводится к 11 уравнениям или 5 1/2 точки. Если преобразование нормализовано, то
-2-
(*) (Ь)
Рис. 3-50 Восстановление преобразования по перспективной проекции.
последний столбец в [А1] переносится в правую часть и решается неоднородное
матричное уравнение. Ниже приводится пример.
Пример 3-31 Основы восстановления
В качестве конкретного примера рассмотрим единичный куб с шестью
известными угловыми точками
[Р} =
ГО
0
0
0
1
1
0
0
1
1
0
0
°1
1
1
0
0
1
Как показано на рис. 3-50, соответствующие им точки на проекции
отмечены жирными кружками. Преобразованные координаты этих точек таковы:
"О
0.34
0.34
0
0.44
0.83
-1
-0.8
-0.4
-0.5
-1.75
-1.22
Тогда (3-77) записывается в виде
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
-0.44
1.75
-0.83
1.22
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
-0.34
0.4
0
0.5
0
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
0
0
0
1
0
1
0
0
0
0
0
1
0
0
-0.34
0.8
-0.34
0.4
0
0
0
0
-0.83
1.22
1
0
1
0
1
0
1
0
1
0
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
-0.34
0.8
-0.34
0.4
0
0.5
-0.44
1.75
-0.83
1.22
Гц
Г12
Г14
Г21
Г22
Г24
Гз1
Гз2
Г34
Г41
Г42
Г44
= 0.
Решение относительно 12 неизвестных элементов Ту такое:
ГГц]
г12
Гц
Г21
Т22
г24
Гз1
Гз2
Г34
Г41
г42
Г44.
Г 0.25]
0
-0.43
0
0.5
0
0.43
0
0.25
0
-1
1
Подстановка этих результатов в матрицу [Г] 4 х 4 дает
[Г] =
0.25
0
0.43
0
0
0.5
0
-1
0
0
0
0
-0.43
0
0.25
1
3-22 ЛИТЕРАТУРА
3-1 Rogers, D. F., Procedural Elements for Computer Graphics, McGraw-Hill Book Co., New
York, 1985. (Cm. [l-l] на с. 74.)
3-2 Cailbom, I., and Paciorek, J., «Planar Geometric Projections and Viewing
Transformations», A CM Сотр. Surv., Vol. 10, No. 4, pp. 465-502, 1978.
3-3 Sutherland, I. E., «Three Dimensional Data Input by Tablets-, Proc. IEEE, Vol. 62, No. 2,
pp. 453-461, 1974.
3-4 Slama, C. (ed.), Manual of Photogrammetry, American Society of Photogrammetry, 1980.
3-5 Kingslake, R. (ed.), Applied Optics and Optical Engineering, Vol. 2, Academic Press,
New York, 1965.
Глава 4
Плоские кривые
4-1 ВВЕДЕНИЕ
Существует множество способов построения кривых вручную с помощью
карандаша, ручки, кисточки, ножа и разнообразных инструментов: линейки, лекала,
циркуля, плаза, шаблона и т. д. Каждый инструмент служит определенной цели,
причем нет ни одного абсолютного универсального. Точно так же в машинной
графике кривые строятся с помощью разных методов и инструментов. В этой
главе рассматриваются методы построения двумерных кривых, т.е. полностью
лежащих в одной плоскости. Здесь мы ограничимся коническими сечениями.
4-2 ПРЕДСТАВЛЕНИЕ КРИВЫХ
В предыдущих двух главах изучались преобразования точек. Кривая может быть
представлена совокупностью точек. Если точки расположены близко друг от
друга, то, соединяя их отрезками прямой, мы получим изображение кривой. На рис.
4.1 показаны два разных точечных представления одной кривой. Точки на
кривой 4.1а расположены равномерно по ее длине. В результате получается довольно
плохое представление кривой, особенно если мал радиус кривизны. Улучшить вид
можно, увеличивая плотность точек в таких участках, рис. 4.16.
Хотя, как показано выше, кривые могут быть достаточно хорошо
представлены совокупностью точек, аналитическое представление во многих отношениях
предпочтительнее. Его преимущества — это точность, компактность записи и
простота вычисления промежуточных точек. Аналитическое представление
позволяет без труда определить наклон и радиус кривизны, а при точечном представле-
Рис. 4-1 Точечное представление кривых, (а) Равномерная плотность точек вдоль
кривой; (Ь) плотность точек возрастает с уменьшением радиуса кривизны.
нии для этого требуется численное дифференцирование — чрезвычайно неточная
процедура. Сравните объем памяти для точечного представления окружности с
32 точками на ней и аналитическое представление — координаты центра и
радиус. При аналитическом представлении кривой можно точно определить
положение любой точки, а при точечном нужна интерполяция, причем в общем случае
результат интерполяции не принадлежит кривой.
Опыт показывает, что аналитически представленные кривые легче
изобразить на рисунке. Аналитическое представление выгоднее, когда для
удовлетворения заданному критерию необходимо непрерывно изменять форму кривой. Ниже
рассматриваются различные методы аналитического представления двумерных
кривых.
Часто требуется аналитическое представление кривой, первоначально
заданной точками. С математической точки зрения это проблема интерполяции. Для
того чтобы провести кривую через все заданные точки, применяется метод
кусочной полиномиальной аппроксимации. Для этого требуется определить
коэффициенты полинома некоторой степени. Вид кривой в промежуточных точках зависит
от степени полинома и граничных условий. Метод рассматривается в гл. 5.
Если же точки —только приблизительные значения величин, например
данные экспериментальных измерений или наблюдений, то нужна кривая, задающая
верное направление изменения. В общем случае кривая может не проходить ни
через одну точку данных. Здесь применяется метод наименьших квадратов [4-1].
Метод наименьших квадратов дает кривую в виде у = f{x), которая
минимизирует сумму квадратов отклонений по оси у между данными и полученной кривой.
Вид у = f(x) выбирают, исходя из характера изучаемого процесса.
Обычно для метода наименьших квадратов используются полиномы,
степенные и экспоненциальные функции: у = ахь, у = аеЬх или у = с\ + с^х + с^х2 +
■ ■ ■ + Сп+\хп, где а, 6 и Cj — константы. Независимо от выбора вида кривой метод
требует решения системы линейных алгебраических уравнений для определения
неизвестных констант. Более подробное описание приведено в работе [4-1] и
книгах по численному анализу.
4-3 НЕПАРАМЕТРИЧЕСКИЕ КРИВЫЕ
Математически кривая может быть представлена в параметрической или
непараметрической форме. Непараметрическая кривая задается в виде явной или
неявной функции. Для плоской кривой явное непараметрическое представление имеет
вид:
У = f{x).
Пример — уравнение прямой, у — тпх + Ь. При этом одному значению х
соответствует только одно значение у, поэтому замкнутые или многозначные кривые,
например окружность, явно представить нельзя. Неявное представление
/(*, У) = О
позволяет обойти это ограничение.
Гипербала Парабола
(«) (ft)
Эллипс Окружность
(с) (d)
Рис. 4-2 Конические сечения.
Общий вид неявного уравнения второй степени
ах2 + 2Ьху + су2 + 2dx + 2еу + f = О
порождает различные двумерные кривые, называемые коническими сечениями.
На рис. 4.2 изображены три вида конических сечений — парабола, гипербола и
эллипс. Окружность — это частный случай эллипса. Определяя коэффициенты а,
Ь, с, d, e и /, можно получить разные конические сечения. Если сечение задано
относительно локальной системы координат и проходит через ее начало, то / = 0.
Для того чтобы провести кривую через данные точки, используются граничные
условия.
Пусть с = 1.0, тогда сегмент кривой между двумя точками определяется
пятью независимыми условиями, из которых вычисляются оставшиеся
коэффициенты а, Ь, d, e и /. Например, можно указать положение крайних точек, наклон
кривой в них и промежуточную точку на кривой.
Если Ь = 0 и с = 1.0, то аналитическое представление кривой получается с
помощью только четырех дополнительных условий, например положения концевых
точек и наклона кривой в них. Кривая при а= 1.0, 6 = 0ис=1.0 еще проще:
х2 + у2 + 2dx + 2еу + f = 0.
Тремя условиями для вычисления d, e и / могут быть две концевые точки
и наклон кривой в одной из них или же две концевые точки и третья точка на
кривой.
При а = b = с = 0 получается прямая линия. Ее уравнение
dx + еу = f = 0
или
fd\ f
у = — \ - ) х = тх + о ,
\ej e
где т — наклон линии, 6' — пересечение с осью у.
Как явное, так и неявное непараметрическое представление осезависимо, т. е.
сложность обработки зависит от выбора системы координат. Например, если в
заданной системе координат граничным условием является вертикальный наклон,
нужно либо изменить ее, либо аппроксимировать бесконечный коэффициент
наклона наибольшей допустимой положительной или отрицательной величиной.
Кроме того, если точки на осезависимой непараметрической кривой
вычисляются с равномерным приращением по х или у, они не будет равномерно
распределены вдоль кривой. Это может повлиять на качество и точность
графического изображения. Тем не менее непараметрическое представление бывает
полезным. Теперь рассмотрим параметрическое представление, позволяющее обойти
эти ограничения.
4-4 ПАРАМЕТРИЧЕСКИЕ КРИВЫЕ
В параметрическом виде каждая координата точки кривой представлена как
функция одного параметра. Значение параметра задает координатный вектор
точки на кривой. Для двумерной кривой с параметром t координаты точки равны:
х = x(t),
У = y{t).
Тогда векторное представление точки на кривой:
P(t) = [x(t) y(t)).
Чтобы получить непараметрическую форму, нужно исключить t из двух
уравнений и вывести одно в терминах х и у.
Параметрическая форма позволяет представить замкнутые и многозначные
кривые. Производная, т.е. касательный вектор, есть
P'(t) = [x'(t) y'(t)],
где ' обозначает дифференцирование по параметру. Наклон кривой, dy/dx, равен
dy = dy/dt = y'(t)
dx dx/dt x'{t)'
Отметим, что при x'(t) = 0 наклон бесконечен. Параметрическое представление
не вызывает в этом случае вычислительных трудностей, достаточно приравнять
нулю одну компоненту касательного вектора.
Так как точка на параметрической кривой определяется только значением
параметра, эта форма не зависит от выбора системы координат. Конечные точки
и длина кривой определяются диапазоном изменения параметра. Часто бывает
удобно нормализовать параметр на интересующем отрезке кривой к 0 < t < 1.
Осенезависимость параметрической кривой позволяет с легкостью проводить с
ней аффинные преобразования, рассмотренные в гл. 2 и 3.
Самое простое параметрическое представление у прямой. Для двух векторов
положения Pi и Рг параметрический вид отрезка прямой между ними такой:
P(t) = Pi + (Р2 - Pi)*, 0 < * < 1.
Так как P(t) это вектор, у каждой его составляющей есть параметрическое
представление x(t) и y(t) между Pi и Р2:
x(t) =xi + (x2 -Xi)t, 0<t<l.
y(t) = 2/i+ (2/2-2/1К
Пример 4-1 Параметрическое представление прямой
Найти параметрическое представление отрезка между точками Р\[1 2]
и Рг[4 3], касательный вектор и наклон.
Параметрическое представление:
P(t) = Fi+(Ft-Pi)t = [l 2]+ ([4 3]-[1 2])*, 0<<<1,
P{t) = [1 2] + [3 \]t, 0 < t < 1.
Параметрическое представление составляющих х и у:
x{t) = xi + (xi-xi)t=\ + 3t, 0 < * < 1,
y(t) = yi + (y2-yi)t = 2 + t.
Дифференцируя P(t), получим касательный вектор:
Р'(*) = [*'(*) »'(*)] = [3 1]
или
где V\ —касательный вектор, a i, j — единичные векторы в направлениях х,
у соответственно.
Наклон отрезка равен
dy ^ dy/dt = у'jt) = 1
dx dx/dt x'(t) 3'
На рис. 4.3 сравниваются непараметрическое и параметрическое
представления окружности в первом квадранте. Непараметрический вид
У
= +у/\-х2, 0<х<1,
(4-1)
х = аяб у « юп 0 О < в < т/2
(ft)
1 + t1 ' 1 + »» - -
(с)
Рис. 4-3 Представление окружности для первого квадранта.
(1 - г2)
Рис. 4-4 Связь между параметрическими представлениями.
показан на рис. 4.3 а. Точки на дуге соответствуют равным приращениям х. При
этом дуга состоит из отрезков разной длины, и получается весьма
приблизительное графическое представление окружности. Кроме того, расчет квадратного
корня—вычислительно дорогостоящая операция.
Стандартная параметрическая форма единичной окружности:
x = cos0, О<0<2тг,
у = sin б,
или
Р(в) = [х y] = [cos0 sin б], О<0<2тг,
(4-2)
где параметр в — геометрический угол, отмеряемый против часовой стрелки от
положительной полуоси х. На рис. 3.4 Ь изображена дуга, построенная по равным
приращениям параметра в пределах 0 < в < тт/2. При этом точки
располагаются на одинаковом расстоянии вдоль окружности, и окружность выглядит гораздо
лучше. Недостаток такого представления — сложность вычисления
тригонометрических функций. (Более простой метод рассматривается ниже в разд. 4.5.)
Параметрическом представление кривой не единственно, например,
'(1-t2) 2t
P(t) =
(1-М2) (1 + *2)J'
О <i< 1
(4-3)
также представляет дугу единичной окружности в первом квадранте (рис. 4.3 с).
Связь между параметрическим представлением (3.4) и стандартным
параметрическим представлением (4.2) показана на рис. 4.4. Из него видно, что для
единичной окружности
х = cos в =
у = sin в =
1-t2
1 + Р'
2t
1 + i2'
О < в < 7г/2, 0 < t < 1,
О < в < тг/2, 0 < t < 1.
Факт, что уравнение 4.3 представляет дугу единичной окружности,
подтверждается следующим:
г2_д2|и2_Л-*2У , ( а У. l-^ + f + tf _(i + *2)2
~ у "Vi + *V U + *v ~ (i + *2)2 "(i + i2)2 '
где г —единичный радиус.
На рис. 4-Зс показан результат для равных приращений t. Он лучше, чем
у явного (4-1), но хуже, чем у стандартного параметрического представления
(4-2). Однако уравнение (4-3) проще с вычислительной точки зрения, т.е. это
компромиссное решение.
Пример 4-2 Определение точки на параметрической кривой
Пусть надо найти у для заданного значения х. Например, пусть х = 0.5,
и требуется вычислить у для единичной окружности. Для явного
представления (4-1) вычисляем непосредственно:
у = VI-х2 = у/1 - (0.5)2 = %/0?75 = 0.866.
Для параметрического представления сначала нужно выразить параметр
t через х, а затем с помощью полученного значения найти у.
Параметрическое представление уравнения (4-2)
х = cos в,
у = sin в.
Поэтому
в = arccos(i) = arccos(0.5) = 60°,
у = sin(60°) = 0.866.
С другой стороны, из уравнения 4-3
1-t2
Х~ 1-И2'
- 2t
V ~ 1 +t2'
Решаем первое из этих уравнений относительно
1/2
0.57735
и получаем
\1+х) л/3
2/v/3 v/3
у = Ж = т = °-866-
В случае более сложного параметрического представления бывает удобнее
искать значение явной переменной итеративными методами.
Параметрическое представление конических сечений осенезависимо и дает
более качественное изображение, чем непараметрическое; однако оба имеют свои
достоинства и недостатки и часто применяются в машинной графике.
4-5 ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОКРУЖНОСТИ
Параметрическое представление окружности радиуса г с центром в начале
координат:
X = fCOS0, О<0<27Г,
y = rsinO, (4-4)
где О — параметр. Ранее мы отмечали, что равномерное приращение дает отличное
изображение, но алгоритм неэффективен из-за частого вызова
тригонометрических функций. В работе [4-2] приводится более быстрый алгоритм.
Полной окружности соответствует диапазон изменения параметра в от 0 до
27г. Если рассматривать некоторое фиксированное число равномерно
распределенных точек по окружности, то приращение параметра между точками можно
считать константой. Координаты любой точки на окружности с центром в
начале координат
ц+1 = г cos(0j + 50),
3/i+i = rsm(0i+50),
где в{ — значение параметра для точки х<, у<.
По формуле суммы углов
Xi+i = r (cos 6i cos 50 — sin 6, sin 80),
yi+i = r (cos Oi sin 80 + cos 50 sin Oi) ■
Вспомним уравнение (4-4) для 0 = Oi
Xi = Г COS Oi,
yi = TsmOi
и получим рекурсивные уравнения
x»+i = xi cos 50 — j/i sin 50,
j/t+i = Xi sin 50 + у» cos 60, (4-5)
что соответствует повороту точки Xj, j/i на 50.
Так как 50 постоянно и равно 2тг/(п — 1), где п — количество равномерно
распределенных по окружности точек, значения sin и cos нужно вычислить только
один раз. Во внутреннем цикле используются только четыре умножения,
вычитание и сложение, поэтому алгоритм работает очень быстро1. Результат на рис. 4-5
соответствует расчетам по формуле (4-4).
Окружность с центром в произвольной точке получается переносом
окружности соответствующего радиуса с центром в начале координат. В некоторых
случаях можно упростить задачу: сначала строить единичную окружность с центром
в начале координат, а затем, комбинируя перенос и масштабирование, получить
окружности с любым радиусом и центром.
1 Замечание. Как и для всех рекурсивных алгоритмов результаты при больших п могут сильно
зависеть от конкретных данных.
>4
Рис. 4-5 Единичная параметрическая окружность с п = 8.
Пример 4-3 Генерация параметрической окружности
Построить окружность радиуса 2 с центром в точке (2,2). Рассмотрим
два метода. Первый: построить окружность радиуса 2 с центром в начале
координат и перенести на 2 единицы по х и у. Второй: построить единичную
окружность с центром в начале координат, увеличить в два раза и, наконец,
перенести. Воспользуемся вторым методом. Пусть для простоты на
окружности лежат восемь точек, хотя обычно требуется гораздо большее количество.
На самом деле количество точек зависит от радиуса.
Окружность — это замкнутая кривая, поэтому первая (в = 0) и последняя
(в = 2п) точки совпадают. Следовательно, чтобы получить п различных
точек на окружности, нужно вычислить п+1 точку. Для незамкнутых кривых
это необязательно.
Найдем 5в:
_ 27Г _ 27Г _ 27Г _ 7Г
~ (п + 1 - 1) ~ 7Г ~ Т ~ 4'
Исходные значения х и у из уравнения (4-4) при в = 0 таковы:
xi = r cos 01 = (l)cos(O) = 1,
ух = г sin Si = (l)sin(O) = 0.
Теперь по формуле (4-5) получим остальные семь точек. Для первой
sin 5в = sin —
4
cos 5в = cos —
2 '
у/2
2
Таблица 4-1 Результаты для единичной
окружности
г
1
2
3
4
5
6
7
8
9
я>
1
%/2/2
0
-%/2/2
-1
-V2/2
0
%/2/2
1
Vi
0
%/2/2
1
л/2/2
0
-%/2/2
-1
-л/2/2
0
12 = И cos50 - J/1 sin50 = (1)(л/2/2) - 0(л/2/2) = (л/2/2),
г/г = ц sin59 + 2/1 cos 5(9 = (1)(л/2/2) + 0(л/2/2) = (л/2/2).
Результаты для остальных точек собраны в таблице 4-1.
Вспоминая двумерные преобразования из гл. 2, определим 3x3
преобразование, которое масштабирует полученные результаты с коэффициентом 2
и переносит центр окружности в точку (2,2):
[Т] = [S\[Trxy] =
2 0 0
0 2 0
0 0 1
1 0 0
0 1 0
2 2 1
=
2 0 0
0 2 0
2 2 1
Применяя это преобразование к точке (х,у), получаем
[Х1 ух 1][Т] = [1 0 1]
2 0 0
0 2 0
2 2 1
= [4 2 1],
как и ожидалось. Полный результат приведен в таблице 4-2 и на рис. 4-5.
Таблица 4-2 Результаты для окружности
радиуса 2 с центром в (2,2)
г
1
2
3
4
5
6
7
8
9
Xi
4
3.414
2
0.586
0
0.586
2
3.414
4
Ш
2
3.414
4
3.414
2
0.586
0
0.586
2
Ограничивая диапазон параметра в, можно получить дуги окружности.
Например, 0 < в < 7г/2 соответствует четверти круга в первом квадранте, а
7Г < в < Зп/2 — четверти круга в третьем квадранте.
4-6 ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЭЛЛИПСА
Достаточно хорошее представление окружности получается, если соединить
отрезками некоторое количество равномерно распределенных на ней точек. Однако,
если рассчитывать точки эллипса через равные приращения угла, изображение
будет неверным, как показано штриховой линией на рис. 4.6. Особенно сильно
неточности проявляются на концах, где кривизна слишком велика и требуется
большее количество точек.
Другой метод основан на равных приращениях по периметру и дает хороший
результат для достаточно большого количества точек. Недостатки его в том, что
указывается слишком много точек на сторонах с малой кривизной, и вычисление
равных частей периметра требует сложного расчета эллиптического интеграла.
Что нам необходимо, это малые приращения параметра у концов, где кривизна
велика, и большие приращения параметра вдоль сторон с малой кривизной.
Такое распределение точек получается из параметрического представления
эллипса с центром в начале координат, большой полуосью а и малой полуосью Ь:
х = a cos в,
y = bsine, (4-6)
Рис. 4-6 Равноугольное представление сильно вытянутого эллипса.
где в — параметр. Диапазон от 0 до 27г задает полный эллипс. Требуемое
распределение точек порождается равномерными приращениями параметра в.
Рассматривая производные х и у:
dx = —asin6d6,
dy = b cos Ode, (4-7)
получаем, что при в, близком к 0 или 7г, т.е. у концов, \dx\ и 0 и \dy\ га bdO.
Если в близко к 7г/2 или 37г/2, т.е. вдоль сторон, то \dx\ га add и \dy\ га 0. Таким
образом, около концов, где кривизна более высокая, точки располагаются чаще,
а вдоль сторон, где кривизна меньше, — реже. Отношение приращений
периметра концов к приращениям вдоль сторон приблизительно равно Ь/а. Отметим,
что для окружности (Ь = а) достигается оптимальное представление — равные
приращения параметра или угла.
Если задано фиксированное количество точек на эллипсе, можно, пользуясь
формулами суммы углов, получить эффективный алгоритм [4-2]. Координаты
любой точки на эллипсе:
Xj+i = acos(6i + 56),
3/i+i = bsin(6i + 66),
где 66 = 2п/(п — 1) — фиксированное приращение в, п — количество точек на
периметре, 0j —значение параметра для точки Xj, j/j.
По формуле суммы углов
xi+1 = a(cos 6i cos 66 — sin 6i sin 66),
3/i+i = 6(cos 6{ sin 66 + cos 56 sin 6i).
Применяя уравнение (4-4) с в — в{, перепишем эти уравнения:
Xi+i = Xi cos 56 — f - J j/i sin 66,
j/i+i = I - I Xi sin 56 + yi cos 66, (4-8)
Так как 66, а и b— константы, полученный алгоритм содержит во внутреннем
цикле только четыре умножения, одно сложение и вычитание и достаточно
эффективен. В работе [4-2] показано, что алгоритм дает многоугольник максимальной
площади, вписанный в эллипс. Результат представлен на рис. 4-7.
Чтобы получить эллипс с центром не в начале координат и с главной осью,
расположенной под углом к горизонтали, его поворачивают вокруг начала
координат, а затем переносят.
Пример 4-4 Параметрическое построение эллипса
Построить эллипс с большой полуосью a = 4 и малой полуосью 6 = 1, под
углом 30° к горизонтали, с центром в точке (2,2).
Сначала построим эллипс с центром в начале координат с помощью 32
точек (п — 33, так как первая и последняя точки совпадают). Мы рассмотрим
только точки первого квадранта, т. е. диапазон параметра от 0 до 7г/2.
У
■ ,
_Z 1 1 1 1 1 1 j| ^x
^^2 2 /4
Рис. 4-7 Параметрическое представление эллипса.
Приращение параметра
59 =
2тг
2тг
32
7Г
16'
(п-1)
Пользуясь уравнением (4-6) с начальным значением 0 = 0, найдем х и у:
х\ = a cos 01 = (4) cos(O) = 4,
2д = 6sin0i = (l)sin(O) = 0.
Вычислим величины а/Ь = 4, Ь/а = 1/4 и
sin <50 = sinT^ =0.195,
cos 69 ■
: cos — = 0.981.
Теперь по формуле (4-8) найдем вторую точку
XI = X! cos 59 - (^) J/1 sin 59 = (4)(0.981) - (4)(0)(0.195) = 3.92,
2/2 = ( - ) xi sin50 + 2/1 cos 50 = (1/4)(4)(0.195) + (0)(0.981) = 0.195.
Результаты для оставшихся точек первого квадранта представлены в
таблице 4-3 и на рис. 4-7.
Нам требуется комбинированное двумерное преобразование (гл. 2)
поворота на 30° вокруг центра координат и переноса центра в точку (2,2).
Характерно, что
[Т] = [Щ[Ттху =
cos a
— sin а
0
0.866
-0.5
0
sin а
cos а
0
0.5
0.866
0
0
0
1
0 "
0
1
1
0
m
" 1
0
2
0 0
1 0
71 1
0 0
1 0
2 1
0.866 0.5 0
-0.5 0.866 0
Таблица 4-3 Точки эллипса с центром в
начале координат для первого квадранта
г
1
2
3
4
5
6
7
8
9
ц
4.0
3.923
3.696
3.326
2.828
2.222
1.531
0.780
0
Vi
0
0.195
0.383
0.556
0.707
0.831
0.924
0.981
1.0
Применим это преобразование для точек (xi,yi) и (х2,2/г):
XI
Х2
2/1
2/2
4
3.923
5.464
5.3
0
0.195
4
4.131
1 '
1
1 '
1
0.866
-0.5
2
0.5
0.866
2
0
0
1
Результаты приведены в табл. 4-4 и на рис. 4-8.
Таблица 4-4 Повернутый и перенесенный
эллипс
г
1
2
3
4
5
6
7
8
9
Xi
5.464
5.3
5.009
4.603
4.096
3.509
3.864
2.185
1.5
Vi
4.0
4.131
4.179
4.144
4.027
3.831
3.565
3.240
2.866
4-7 ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПАРАБОЛЫ
Рассмотрим параболу с вершиной в центре координат, раскрыв вправо, т. е. с осью
симметрии — положительной полуосью х. На рис. 4-9 изображена верхняя ветвь
такой параболы. В прямоугольных координатах непараметрическое
представление параболы:
У
2 = 4 ах.
Параметрическое представление имеет вид
х = tg2 ф,
у = ±2v/otg^,
У
' JcT' ■" ^^' ' ' ' ' ' ►*
-2"^v 2 4 6
Рис. 4-8 Эллипс после поворота и переноса.
где 0 < ф < 7г/2. Хотя оно обеспечивает достаточно хорошее изображение,
Смит [4-2] указал, что получаемая фигура не является фигурой с
максимальной вписанной площадью и поэтому это не оптимальный вариант. Другое
параметрическое представление действительно дает фигуру с наибольшей вписанной
площадью:
х = ав2,
У = 2ав, (4-9)
где 0 < в < со соответствует всей верхней ветви параболы. В отличие от эллипса
парабола не замкнутая кривая, поэтому изображаемая часть должна быть огра-
Вершина
Рис. 4-9 Парабола.
Рис. 4-10 Параметрически сгенерированная парабола.
ничена минимальным и максимальным значением параметра. Это можно сделать
несколькими способами. Если диапазон изменения координаты х ограничен, то
*min = ^, «U. = ^. (4-Ю)
Если ограничен диапазон изменения у, то
"min — -Z—, "max — — . V^>-4
Установив 0min и/или 9тах, можно построить параболу в первом квадранте.
Параболы в других квадрантах, со смещенным центром и в других ориентациях
строятся с помощью отражения, поворота и переноса.
Параболу можно построить также, пользуясь приращениями параметра.
Пусть на параболе задано фиксированное количество точек, т.е. приращение
параметра в постоянно. Для 0j+i = Qi + 59 уравнение (4-9) принимает вид
xi+i = ав2 + 2авг6в + а(6в)2,
2/i+i = 2a9i + 2a69.
Используя уравнение (4-9) с в = 6t, перепишем формулы
Xi+l = Xi + Угбв + а(5в)2,
W+1 =Vi + 2a66. (4-12)
Расчет очередной точки требует трех сложений и одного умножения во
внутреннем цикле алгоритма. На рис. 4-10 приведен пример параболы, сгенерированной
по рекурсивным формулам (4-12).
Пример 4-5 Параметрическое представление параболы
Построить параболический сегмент в первом квадранте при 1 < х < 4
для параболы
х = ав2 = в2, у = 2ав = 20
при а = 1.
Сначала найдем границы 9. В соответствии с уравнением (4-10) 0min и
#тах определяются так:
0,
/ Zmin /1 i
д / Дтах
"max — Д/ ж, .
у а VI
Пусть на сегменте расположено 10 точек, тогда
сд "max "min 2—1 1^
n-l — 10 - 1 — 9'
Начиная с в\ = 0min, xi = 1, из уравнения (4-9) получаем
2/1 = 2o0i = (2)(1) = 2.
Из уравнения (4712)
х2 = Х!+ У16в + (6в)2 = 1 + (2) Q) + Q) = 1.235,
у2 = У1+2бв = 2 + (2) Q) = 2.222.
Окончательный результат приведен в табл. 4-5 и на рис. 4-11.
Таблица 4-5 Результаты для сегмента
параболы
г
1
2
3
4
5
6
7
8
9
10
Xi
1.0
1.235
1.494
1.778
2.086
2.420
2.778
3.160
3.568
4.0
Уг
2.0
2.222
2.444
2.667
2.889
3.111
3.333
3.556
3.778
4.0
В некоторых случаях более удобны другие параметрические представления,
вид которых зависит от прикладной задачи и имеющихся данных. Например,
если надо нарисовать дугу параболы между двумя точками и учитывать наклон,
то предлагается следующее представление:
*(*) = (Qx - 2Rx + Rx)T2 + 2{RX - Px)t + Px,
y(t) = {Qy-2Ry + Py)t2 + 2(Ry-Py)t + Py, 0<t<1.0, . (4-13)
где t — параметр, а две конечные точки P = [Px Py] и Q = [Qx Qy]. Точка
R = [Rx Ry] это точка пересечения касательных в конечных точках. Три
вершины Р, Q, R определяют параболу, как показано на рис. 4-12. Более общий
метод построения кривых с помощью вершин незамкнутого многоугольника был
разработан Безье и рассматривается в следующей главе.
У*
4 -
Рис. 4-11 Сегмент параболы.
Рис. 4-12 Задание параметрической параболы вершинами.
4-8 ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ГИПЕРБОЛЫ
Построим гиперболу с центром в начале координат и осью симметрии,
совпадающей с осью х. Ее непараметрическое представление в прямоугольных
координатах:
При этом вершина находится в точке (а, 0), оси асимптот ±Ь/а. Вид
параметрического представления:
х — ±asec9,
У = ±btg0, (4-14)
где 0 < 6 < 7г/2, дает искомую гиперболу. Смит [4-2] указывает, что для такого
представления площадь вписанного многоугольника не максимальна. Однако она
близка к максимальной, и с помощью формулы суммы углов можно получить
эффективный алгоритм. Вспомним, что
1 1
sec(0 + 86)
cos (6 + 66) cos 6 cos 66 - sin в sin 66
tg(6 + 66)=it&e + t&6e\
Подставим в уравнения (4-14)
ab/ cos 6
Xi+i = ±asec(0 + 6в) = ±-
"bcos£0-6tg0sin£0'
Используя уравнения (4-14) с в = 0,, перепишем эти уравнения как
bxi
Xi+l = ±
Ъ cos 66 — у i sin 86'
Другое параметрическое представление гиперболы, дающее максимальную
вписанную площадь:
х = ach6,
y = bsh6. (4-16)
Гиперболические функции определяются как chd — (ев +е~в)/2 и sh0 = (ев —
е~в)/2. При изменении от 0 до бесконечности проходится вся гипербола. Формула
для суммы углов для и
ch(6 + 86) =ch6ch66 + sh6sh66,
sh{6 + 86) = sh0ch<50 + ch0sh<50.
Это позволяет записать уравнения (4-16) как
xi+i = a(ch в ch 66 + sh в sh 66),
yi+i = b{sh 6 ch 86 + ch в sh 86)
или
xi+i = цсЪбв + (-) yishSe,
Vi+i = (£) Xi sh 56 + Vi ch 86. (4-17)
Чтобы ограничить область гиперболы, необходимо установить минимальное
и максимальное значения. Пусть ветвь гиперболы лежит в первом и четвертом
квадранте и рассматривается часть при a;m;n < х < хтах. Тогда
0min = Arch (-^ j ,
6тах = Arch (£jp) , (4-18)
где обратный гиперболический косинус получен как
Arch а; = 1п(а; + \/х2 - 1). (4-19)
Остальные границы определяются аналогично. Пример части гиперболы в
первом квадранте, полученной этим методом, показан на рис. 4-13.
Пример 4-6 Параметрическая гипербола
С помощью параметрического представления (4-16) найти восемь точек
на сегменте гиперболы в первом квадранте при a = 2, Ь = 1, для 4 < х < 8.
Сначала определим границы параметра из уравнений (4-18) и (4-19)
ft.
Аналогично,
Итак,
=^(Т)^(^Ч(^У-1) =
= 1п(4 + л/16 - 1)
= 2.063.
ftnin = 1-317.
гд ftnax — ftnin 2.063 — 1.317
до = = = U.1U7
n-1 7
sh(Jft) = sh(0.107) =
ch(Jft)
е0ЛО7-е-
2
= 0.107,
= ch(0.107) ■
e0107+e
2
= 1.006.
-0.107
-0.107
0 2 4
Рис. 4-13 Параметрическая гипербола.
Уравнения (4-16) с 0i
— "min ДЗЮТ
xi — och(6min) =
= (2) ch(1.317) =
= 4.000,
j/i =6sh(0min) =
= (l)sh(1.317) =
= 1.732.
Затем из уравнений (4-17)
х2 = xi ch(J0) + (a/b)yi sh(66)
= (4)(1.006) + (2)(1.732)(0.107)
= 4.393.
у2 = (Ъ/а)Х1 sh(cJ0) + yi ch(cW)
= (1/2)(4)(0.107) + (1.732)(1.006) = 1.956.
Результаты вычислений приведены в табл. 4-6 и выделены жирной
линией на рис. 4-13.
Таблица 4-6 Результаты для сегмента
гиперболы
i Xi Vi .
1 4 L732
2 4.393 1.956
3 4.836 2.201
4 5.334 2.472
5 5.892 2.771
6 6.518 3.102
7 7.218 3.468
8 8 3.873
4-9 ПРОЦЕДУРА ИСПОЛЬЗОВАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
Плоские геометрические фигуры часто используются в прикладной машинной
графике, например для разработки деталей или в чертежных системах. Особенно
важны здесь проблемы определения положения конического сечения и его
пересечения и/или точек касания с другим коническим сечением или прямой. На
первый взгляд задача несложная, но для произвольно расположенных на
плоскости элементов могут существовать различные решения. Выбор правильного
решения не всегда очевиден, что приводит к нелинейным расчетам. Ниже
приводятся методы, исключающие нелинейную математику и упрощающие линейные
результаты. Кроме того, объясняется, как выбрать необходимое решение, если
оно неоднозначно.
Основная идея заключается в том, чтобы методами машинной графики, в
частности плоским поворотом и переносом, перевести расчеты в первый
квадрант в стандартной конфигурации. Если фигура включает коническое сечение,
его центр (для параболы и гиперболы — вершина) располагается в начале
координат. В общем случае неизвестные центры, вершины, точки касания и пересечения
вычисляются с помощью непараметрических уравнений, а параметрическое
представление используется для изображения фигур. Разделение расчета и построения
позволяет максимально использовать преимущества обоих представлений.
Рассмотрим подробный пример, чтобы лучше представить себе суть и
возможности этого метода. Одна из простейших и часто используемых задач —
построить окружность по трем точкам. Чертеж приведен на рис. 4-14, где Pi(xi,y{),
Рг{яг,Уг), Рз{хг,Уг) заданные точки. Необходимо определить центро и радиус
окружности. Для этого нужно решить систему из трех нелинейных уравнений с
переменными h, к, координатами центра (х, у) и радиусом R:
(xi - К)2 + (2/i - А;)2 = R2, (4-20а)
(х2 - h)2 + (2/2 - fc)2 = R2, (4-20Ь)
{х3 - h)2 + (2/3 - к)2 = R2. (4-20с)
У У
х"
Рис. 4-14 Окружность, проходящая через три заданные точки.
Вычитание уравнения (4-20Ь) из уравнений (4-20а) и (4-20с) устраняет
нелинейность. Собственно алгоритм решения — это [(а) — (Ь)][хз — х2) — [(с) — (Ь)]{х\ — х2),
где буквы в скобках взяты из уравнений (4-20). Уравнение, выраженное через
неизвестную, таково:
к =
[{x\-xl) + {yl-yl)]{x3-x2)
2[(2/1 - ЫО^з - х2) - {уз ~ 2/2)0*1 - х2)]
[(х$ - хр + (у$ - у%)](х1 - х2)
2[(2/i - 2/г)(а;з - х2) - (у3 - у2)(хг - х2)\'
(4-21)
Аналогично из [(а) — (Ь)] и уравнения (4-21) вычисляется
h =
(xl - х\) + (у\ - у%) - 2к(У1 - у2)
2(ц - хг)
(4-22)
R находится из любого из уравнений (4-20).
Уравнения (4-21) и (4-22) содержат ряд трудностей. В частности, если
знаменатель дроби равен нулю, требуются другие методы решения. Также необходимы
условия проверки на бесконечный радиус и коллинеарные точки.
Уравнения для h та к можно упростить переносом начала координат в точку
(см. рис. 4-14). Тогда
Ы2 + fc'2 = Д2, (4-23а)
{x2-hl)2 + {y'2-k')2 = R2, (4-23Ь)
(4 - К? + {у'3 - к')2 = Д2. (4-23с)
Вычитая (а) из (Ь) и (с), получаем систему из двух линейных уравнений.
Алгоритм решения: [(b) — (а)]х'3 — [(с) — (а)]х'2, что дает
. / _ [хгх2\х1 ~ ^з) + Уг хз ~ Уз х2\ (А-ОДЛ
2ft«-|«) ' 1 '
h, = *I±ylzMl, (4.25)
2х2
R={h'2+ti2)i. (4-26)
Преобразование h', к' обратно к первоначальной системе координат дает h,
к. При этом знаменатель уравнений (4-24) или (4-25) опять может обратиться
в нуль, и требуются условия проверки на бесконечный радиус и коллинеарные
точки. Эти трудности преодолеваются с помощью следующей процедуры:
Перенести начало координат в одну из точек.
Повернуть оси координат, чтобы одна из оставшихся точек лежала на
положительной полуоси х.
Проверить коллинеарность точек.
Найти центр и радиус окружности в перенесенной и повернутой системе
координат.
Повернуть обратно к ориентации промежуточной системы координат.
Перенести начало координат в первоначальное положение и найти центр
окружности в исходной системе координат.
На рис. 4-14 начало координат перенесено в точку Pi, а положительная
полуось х" проходит через точку Р2. Уравнения в координатах (х" ,у")\
h"2 + к"2 = Д2, (4-27а)
(x'2'-h")2+k"2=R2, (4-27b)
W-h")2 + (y'J-k")2=R2. (4.27c)
Вычтем уравнение (4-27а) из (4-27Ь)
х'{2 - 2x'2'h" = О,
или
h" = х'Ц2. (4-28)
Вычтем уравнение (4-27а) из (4-27с) и подставим уравнение (4-28):
*" = ||(*з'-4') + |, (4-29)
а из уравнения (4-27а) получим
R=(h"2 + k"2)^2. (4-30)
Уравнение (4-29) показывает, что при у% = 0 значение к бесконечно, однако это
случается только тогда, когда все три точки лежат на одной прямой. Проверка
этого условия очень проста.
Провести окружность через три точки достаточно легко. Здесь не требуется
выбора из множества решений, как в большинстве геометрических конструкций,
включающих конические сечения. Метод выбора предложен в работе
Роджерса [4-3].
Роджерс рассматривает левое, правое, ближнее, дальнее, внутреннее и
внешнее решение. Левое и правое существуют относительно направления от одной
известной точки к другой; ближнее и дальнее — относительно линии пересечения;
внутреннее и внешнее — относительно окружности.
Эти понятия справедливы как в ориентации пользователя, т. е. в любом месте
пространства, так и в стандартной конфигурации в первом квадранте. Простой
пример для иллюстрации понятий левое—правое и ближнее—дальнее это
определение центра и точек касания окружности известного радиуса R, касающейся
двух пересекающихся прямых Р и L. На практике задача возникает, например,
при изготовлении закругленных углов. Для любого радиуса всегда существует
четыре решения. Стратегия выбора такова:
Найти точку пересечения прямых. Если решения нет, прямые параллельны.
Перенести начало координат в точку пересечения.
Повернуть вокруг нового центра координат, чтобы одна из линий совпала с
осью х.
Найти угол между другой линией и осью х.
Повернуть вокруг нового начала координат, чтобы положительная полуось х
совпала с биссектрисой пересекающихся прямых.
Найти центр и точки касания.
Перевести в первоначальную систему координат.
На рис. 4-15 изображен этот случай в стандартной конфигурации. Две
пересекающиеся линии Р и L заданы точками Pi, Рг, L\, L^ соответственно. Для
каждого возможного решения одна из координат центра (h, к) лежит на оси
координат. Чтобы выбрать нужное решение, требуется указать, находится ли оно
слева или справа от линии Р, если смотреть от Pi и Рг, и ближнее оно или
дальнее относительно линии L с той же точки зрения. На рис. 4-15 С\— правое и
дальнее, а Сз — левое и ближнее. Центр
h = Д/sinfl,
к = 0,
где 9 — острый угол между положительной осью а; и Р. Точки касания с линиями
Р и L
xt = h — Rsin 9,
yt = ±Rcos9.
Рис. 4-15 Окружности, касающиеся двух пересекающихся прямых.
Таблица 4-7 Окружность, касающаяся двух пересекающихся линий
Ориентация
относительно
линии Р
Левая
Левая
Правая
Правая
Ориентация
относительно
линии L
Дальняя
Ближняя
Дальняя
Ближняя
Центр
Л = 0
к = fl/sin(90-
= R/ cos (в)
h= -R/sm(9)
fc = 0
Л= -R/sin(e)
fc = 0
Л = 0
к = -R/ sin(90
= -R/cos(9)
9) =
-в) =
Точки касания
xt = ±.Rcos(9O-0) =
= ±Rsin(9)
yt — к — Rcos(9)
xt = h + Rsin(9)
yt = ±Rcos(9)
xt = h — Rsin(6)
yt = ±Rcos(e)
xt = ±.Rcos(9O-0) =
= ±.Rsin(0)
yt = k + Rcos(9)
Полный перечень приведен в табл. 4-7. Более сложные примеры с
использованием понятий внутреннее-внешнее содержатся в работе [4-3]. Возможно
расширение для других конических сечений. В работе [4-4] рассматривается векторный
подход к решению подобных проблем.
4-10 ОБЩИЕ УРАВНЕНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
Все конические сечения из предыдущих разделов являются частными случаями
кривых, задаваемых общим уравнением второго порядка
Ах2 + Вху + Су2 +Dx + Ey + F = 0,
(4-31)
где А, В, С, D, Е, F — константы1. Коническое сечение —это любая плоская
кривая, удовлетворяющая уравнению (4-31). Уравнение интересно не только само по
себе, но и для последующего обсуждения рациональных конических сечений и
квадратичных поверхностей. Для простоты и полноты будем пользоваться
методами линейной алгебры.
Конические сечения являются центральными — эллипс и гипербола
(окружность это частный случай эллипса) или нецентральными — парабола. Кроме
того, существует ряд вырожденных форм, которые все центральны. Необходимо
определить для заданных значений констант, какое сечение задает уравнение (4-
31) — центральное или нецентральное. Также нужно выделить все вырожденные
случаи.
Заметим, что уравнение (4-31) можно записать в матричной форме
[х у 1]
или
A D/2 D/2
В/Ъ~~С Е/2
D/2 Е/2 F
[X][S][X]T = 0.
х
У
= 0
(4-32)
Отметим также, что [S] симметрична относительно главной диагонали.
Сначала приведем сечение к стандартному виду. Для центрального сечения
(эллипс или гипербола) это значит, что центр находится в начале координат, а
оси располагаются вдоль осей координат. Для нецентрального сечения (парабола)
ось симметрии параболы совпадает с положительной осью х, вершина находится
в начале координат, и парабола раскрывается направо. Сечение приводится к
стандартному виду переносом и вращением.
Для центральных сечений линейные члены уравнений (4-31) или (4-32)
уничтожаются переносом центра сечения в начало координат. После этого уравнение
(4-32) принимает вид
[X}[Tr][S}[Tr}T[Xf=0,
(4-33)
где матрица переноса [Тг] такова:
[Тт] =
1 0 0
0 1 0
тп n 1
1 Уравнение (4-31) —это модифицированная версия неявного уравнения из раздела 4-3 с А ■■
а, В = 26, С = с, D = 2d, Е = 2, F = /.
После конкатенации матриц переноса и коэффициентов уравнение
принимает вид
[X)[S'}[X]T = 0,
где
[S'} = [Tr][S][Tr]T = g)
2А! В' D'
D' 2C" Е1
D' E' 2F'
(4-34)
(4-35)
А' = А
В' = В
С = С
D' = 2Ат + Bn + D
Е' = Вт + 2Сп + Е
2F' = mD' + пЕ' + (Dm + En + 2F).
Заметим, что [S'\ также симметрична.
Следовательно, уравнение (4-31) преобразуется к
А'х2 + В'ху + Су2 + D'x + Е'у + F' = 0.
Коэффициенты переноса тип для уничтожения линейных членов
вычисляются из условия D' = Е' = 0. Отсюда
2Ат + Bn + D = 0,
Вт + 2Сп + Е = 0
или в матричном виде
[т п]
2А В
В 2С
-D
-Е
(4-36)
что можно записать как [M][L] = [Q].
Если [L] инвертируема, существует решение для [М], и сечение центрально,
т. е. это эллипс или гипербола. Если [L] не инвертируема, т. е. сингулярна, то
решения для [М] не существует, и сечение не центрально (парабола). Детерминант
сингулярной матрицы равен нулю:
det[L] = \L\ =
2А В
В 2С
= 0
(4-37)
или
В2 - AAG = 0.
Итак, уравнение (4-31) представляет параболу при В2—ААС = 0 и центральное
сечение при В2 — ААС ф 0. Если сечение центрально и В2 — ААС < 0, уравнение
представляет эллине, а если В2 — ААС > 0 — гиперболу.
Независимо от инвертируемости [L] оси сечения можно поворотом сделать
параллельными осям координат. Вернемся к уравнению (4-32). Используем матрицу
плоского поворота [R]
[X}[R][S][R]T[X]T = 0,
где для угла поворота в она такая:
[R} =
cos в sin в 0
- sin в cos в 0
0 0 1
Конкатенация матриц дает
[X][S"][X]T = 0,
(4-38)
(4-39)
где
[S"] = [R][S][R]T=(\)
2А" В" D"
В" 1С" Е"
D" Е" 2F"
А" = Acos2 в + Bcosflsinfl + Csin2 в,
В" = 2(С - A) cos в sin в + B(cos2 в - sin2 в),
С" = Asm2 6 - В cos6s\n6 + С cos2 в,
D" = D cos в + Е sin в,
Е" = Ecos6-Dsm6,
F" = F.
Опять заметим, что [S"] симметрична. Если оси сечения параллельны осям
координат, член Вху в уравнении (4-31) отсутствует. Поэтому нулевой
коэффициент дает угол поворота:
2(С - A) cos в sin в + B{cos2 в - sin2 в) = 0
или
(С - A) sin 2в + В cos 26» = 0.
Решим это уравнение относительно угла поворота в:
Н"*8^)-
(4-40)
Для этого угла [S"] принимает вид
м-®
2А" О D"
О 2(7" Е"
D" E" 2F"
e=i"Mtt)
Уравнение (4-37) позволяет узнать, центрально ли сечение. Центральное
сечение можно привести к стандартному виду комбинацией переноса и поворота:
[X][Tr][R][S][R]T[Tr]T[X]T = 0.
Конкатенация внутренних матриц дает
[S'"] = [Tr][R][S][R]T[Tr]T =
где
-а:
1 \
)
2/
А'"
0
0
" 2А'"
В'"
D'"
0
С"
0
В'"
2(7'"
Е'"
"
0
рт
D'" '
Е'"
2F'"
=
а
0
0
=
0
/з
0
0
—к
А'" = A cos2 в + В cos в sin в + С sin2 в,
В'" = 2(<7 - А) соз в sin в + B(cos2 в - sin2 в),
С'" = Asm2 в - Bcosflsinfl + Ccos20,
D'" = £ cos в + 77 sine,
.E"' = 77cos0-£sin0,
F'" = (m£ + 7771-1- C)/2
(4-41)
(4-42)
(4-43a)
(4-43b)
(4-43c)
(4-43d)
(4-43e)
(4-43f)
£ = 2Am + Bn + D,
T) = Вт + 2Cn + E,
С = Dm + En + 2F.
(4-43g)
(4-43h)
(4-43i)
Заметим, что это диагональная матрица, т.е. все недиагональные элементы
равны нулю. Поворот устраняет член (В'" = 0), а перенос — линейные члены
(D'" = Е'" = 0).
Угол вращения задается уравнением (4-40). Как и раньше, коэффициенты
переноса можно получить, приравняв D'" и Е1" к нулю, т. е. £ = т) = 0. Имеем
2Ат + Вп + D = 0,
Вт + 2Сп + Е = 0.
Отсюда получаем решение
2CD - BE
т = В' - ААС ' (4"44а)
2АЕ - BD
П = В>-4АС- (4"44Ь)
Вспомним, что для центрального конического сечения В2 — 4АС ф 0. Запишем
уравнение (4-41), используя (4-42):
ах2 + (Зу2 = к, (4-45)
что является стандартным видом конического сечения. Остается систематически
исследовать результат для различных значений а и /3.
Если к больше нуля, то а и /3 положительны, и сечение — эллипс. Если они
имеют разные знаки и ни один из них не равен нулю, то сечение — гипербола.
Если а и /3 отрицательны, решения не существует.
Оба а и /3 одновременно не могут быть равны нулю, так как в этом случае
уравнение (4-45) не содержит членов второго порядка. Однако один из
коэффициентов а или /3 может быть нулевым. Пусть /3 = 0 (если а = 0, замена х на у
дает /3 = 0), тогда уравнение (4-45) принимает вид
ах2 = —к.
Решением являются две параллельные линии х = ±^/—к/а при —к/а > 0.
Если —к/а < 0, то решения нет.
Если к = 0, есть две возможности: а и /3 имеют одинаковые или разные знаки.
В обоих случаях решение вырожденное. Если знаки а и /3 одинаковы, уравнению
(4-45) удовлетворяет только начало координат х = у = 0. Можно считать, что
это предельный случай эллипса.
Если знаки а и /3 различны, уравнение (4-45) принимает вид
2 а 2
V = —~^х
У 0
или
т. е. это пара прямых, пересекающихся в начале координат, — предельный случай
гиперболы.
Наконец, если /3 = 0 (если а = 0, замена х на у дает /3 = 0), то решение —
ось у для всех значений.
Для нецентрального сечения, параболы, оба линейных члена устранить
нельзя, однако можно убрать один линейный и один квадратичный член для х или
у. Применим оператор переноса к уравнению (4-39) — квадратному уравнению
после поворота:
2А+ 0 D+
0 2С+ Е+ , (4-46)
D+ Е+ 2F+
1*1-5
где
А+ = А", (4-47а)
С+ = С", (4-47Ь)
D+ = 2А"т + D", (4-47с)
Е+ = 2С"п + Е", (4-47d)
F+ = (m/2)D+ + (n/2)E+ + (mD" + nE" + 2F"). (4-47е)
Угол поворота задан уравнением (4-40). Здесь либо А+ = А", либо С+ = С"
обратится в нуль. Один из линейных членов для х или у устраняется, если D+
или Е+ приравнять к нулю. Пусть D+ = 0, тогда
-D"
т=^Г- (4-48а)
Если Е+ = 0, то
п = ^- (4-48Ь)
Заметим, что при А" = 0 значение m не определено, следовательно,
устраняются только линейные члены относительно у. Если С" = 0, не определено п и
устраняются только члены с х.
Предположим, что уничтожены линейный у- член (Е+ = 0) и квадратичный
х- член (А+ = 0) (если /3 = 0, замена х иу дает 7 = 0). Тогда [S+] принимает вид
[5+]
0 0 0
0/3 0
7 0 -к
Запишем уравнение конического сечения
/Зу2 + 271 = к. (4-49)
Чтобы привести параболу к стандартной ориентации с вершиной к в центре
координат, перенесем ее по оси х на
2 Ь , ,
у = —i-x = ах .
/3
Все вырожденные формы сечений центральны, т.е. парабола—это
единственное нецентральное сечение. Результаты собраны в табл. 4-8.
Пример 4-7 Сегмент гиперболы
Найти тип конического сечения, заданного формулой
2х2 - 72xj/ + 23j/2 + 140х - 20j/ + 50 = 0,
изображенного непрерывной линией на рис. 4-16. Нарисовать его сегмент для
3 < х < 5 для j/min- Сегмент должен быть нарисован с помощью
параметрического представления из предыдущих разделов. Для того чтобы определить
Таблица 4-8 Конические сечения
Название Уравнение Условия Тип
Чертеж
Эллипс ах +/3у = к к, а, /3 > 0 Центральный
Гипербола ах +/3у = к /3 < 0 < к, а Центральный
О
Парабола ау2 + /Зх = О
/Зх2 +ау = 0
Нецентральный ,,
Y
К
Пустое мно- ах2+/3у2 = к а,/3 < 0 < к (Центральный) (Чертеж
жество отсутствует)
Точка ах2+/3у2 — 0 а, /3 > 0 Центральный
Пара прямых ах +/3j/ =0 /3 < 0 < а Центральный
Параллель- ах2 = к
ные прямые
Пустое мно- ах2 = к
жество
«Повторя- ах2 = 0
ющаяся»
прямая
а, к > 0 Центральный
а < 0 < к (Центральный) (Чертеж
отсутствует)
Центральный
Эллипс, гипербола и парабола — это невырожденные сечения, остальные —
вырожденные.
значения параметрического представления, используются методы,
рассмотренные в данном разделе.
Сначала узнаем тип сечения
В2 - 4АС = (-72)2 - (4)(2)(23) = 5000 > 0,
т. е. это гипербола.
Приведем гиперболу к стандартному виду с помощью уравнений (4-40)-
(4-44). Угол поворота
в = \ •"* hch) = \ ™** (^з) = \ *«** (т) = 3687°-
Подставим значения cos в = 4/5, sin в = 3/5 и получим
А'" = Acos2 в + В cos6sm6 + С sin2 в =
= (2)(4/5)2 + (-72) (4/5) (3/5) + (23)(3/5)2 =
= -625/25 = -25,
С" = 4sin20-.Bcos0sin0 + C7cos20 =
= (2)(3/5)2 - (-72)(4/5)(3/5) + (23)(4/5)2 =
= 1250/25 = 50.
Коэффициенты переноса тип таковы:
_ 2CD-BE (2)(23)(140) - (-72)(-20) _ 5000 _
т~ В2- 4АС ~~ 5000 ~~ 5000 ~ '
_ 2АЕ -BD _ (2)(2)(-20) - (-72)(140) _ 10000
П ~ В2-4АС ~~ 5000 ~~ 5000 ~ '
Рис. 4-16 Гипербола 2х2 —72ху+23у2+140х —20у+50 = б. Сплошная линия —заданная
ориентация. Пунктир — стандартная ориентация.
Так как £ = т\ = 0, константа равна
с'" — £
F "2
(£>тп + En + 2F)
= (140)(1) + (-20)(2) + (2)(50) = 200 =
2 2
Уравнение гиперболы
-25х2 + 50у2 + 100 = 0.
В стандартной форме ах2 + (Зу + к = 0 имеем
-x2 + 2j/2+4 = 0:
2у2=4.
В форме
О" -й)"-:
2 2
4 2 '
что дает а = 2, Ь = -\/2.
Параметрическое представление параболы (4-16):
x = ach(t), j/ = 6sh(t),
где t — параметр. Для параметрического изображения гиперболы необходимо
найти величину t для х = 3,5. Заметим, что преобразования к стандартному
виду переносят оси координат, а не само сечение. Поэтому соответствующие
преобразованные значения х получаются обратными преобразованиями. В
результате
[TR] = [T][R] =
1
0
—771
0 0
1 0
-п 1
COS б
-sin(-0)
0
sin(-0) 0
cos6 0
0 1
cos б — sin в 0
sin 6 cos# 0
—(m cos в + 7i sin в) msin.6 — псозв 1
4/5 -3/5 О'
3/5 4/5 0
-2 -1 1
Преобразованные координаты х
3 2.871
5 2.476
4/5 -3/5 О'
3/5 4/5 0
-2 -1 1
2.123 -0.503 1
3.486 -2.019 1
где также включена у координата. Тогда параметрические значения
fmin = t\x=3 = Arch (|) = Arch №j?\ = 0-3486,
W = t|x=s = Arch (|) = Arch (^) = 11539.
Пользуясь этими значениями для t„
рис. 4-16 и в табл. 4-9.
и tmax, получаем результат на
Таблица 4-9 Сегмент гиперболы в
дартной ориентации
t
0.349
0.438
0.528
0.617
0.706
0.796
0.885
0.975
1.064
1.153
X
2.123
2.195
2.285
2.393
2.520
2.668
2.837
3.028
3.244
3.486
У
-0.503
-0.640
-0.781
-0.929
-1.084
-1.248
-1.422
-1.608
-1.806
-2.019
Затем эти результаты обратным преобразованием переводятся в исходное
положение:
[ТВ]'1 =
4/5 3/5 0'
-3/5 4/5 0
12 1
Результат приведен в табл. 4-10 и на рис. 4-16.
Таблица 4-10 Сегмент гиперболы в
исходной ориентации
t
0.349
0.438
0.528
0.617
0.706
0.796
0.885
0.975
1.064
1.153
X
3.000
3.140
3.297
3.472
3.667
3.883
4.123
4.387
4.679
5.000
У
2.871
2.805
2.746
2.693
2.645
2.602
2.564
2.531
2.502
2.476
4-11 ЛИТЕРАТУРА
4-1 Lancaster P. and SalkauskasK., Curve and Surface Fitting, An Introduction, Academic
Press, 1987.
4-2 Smith L. В., «Drawing Ellipses, Hyperbolas, or Parabolas With a Fixed Number of Points
and Maximum Inscribed Area», Сотр. J., Vol. 14, pp. 81-86, 1969.
4-3 Rogers D.F., «Interactive Graphics and Numerical Control», Сотр. Aid. Des., Vol. 12,
pp. 253-261, 1980.
4-4 Middleditch A. E. and Stacey T. W., «Robust Computation of Tangent Lines and Circles»,
Сотр. Aid. Des., Vol. 19, pp. 503-507, 1987.
Глава 5
Пространственные
кривые
5-1 ВВЕДЕНИЕ
Трехмерные, или пространственные, кривые широко используются в
проектировании и разработке самой различной продукции: автомобилей, кораблей,
самолетов, обуви, бутылок, зданий и т. д. Также они имеют большое значение для
описания и интерпретации физических явлений в геологии, физике и медицине.
До начала применения математических и компьютерных моделей в процессе
производства, дизайна и изготовления использовалась начертельная геометрия.
Многие ее методы были перенесены в машинную графику.
Поверхности часто изображаются как сеть кривых, лежащих в
ортогональных секущих плоскостях, с трехмерными контурами деталей. Пример приведен
на рис. 5-1. Здесь сечения бьши получены оцифровкой физической модели или
Рис. 5-1 Поверхность в виде сети ортогональных плоских кривых (Дж. Хейзен)
чертежа и математическим подбором кривой, проходящей через все заданные
точки. В данной главе рассматриваются два таких метода: кубические сплайны и
параболическая интерполяция. Существуют и другие реализации этого подхода,
рассмотренные, например, в работе [5-1].
Другой подход состоит в том, что математическое описание кривых
генерируется без изначального знания формы кривой. Его примеры —это кривые Безье и
их обобщение до В-сплайнов. Эти методы отличаются тем, что кривая может не
проходить ни через одну заданную точку. Контрольные точки определяют
только направление изгиба.
Как будет показано далее, оба подхода можно применить при любом способе
задания кривой.
5-2 ПРЕДСТАВЛЕНИЕ ПРОСТРАНСТВЕННЫХ КРИВЫХ
Трехмерные кривые можно представить параметрически или непараметрически.
Явное непараметрическое представление имеет вид
х = х,
У = /(*)>
z = д(х).
Неявное непараметрическое представление кривой как пересечения двух
поверхностей задается уравнениями:
f(x,y,z) =0,
g(x,y,z) = 0.
Пример 5-1 Пространственная кривая
Найти линию пересечения двух поверхностей второго порядка
f{x,y,z) = y-z2 = 0,
9(x,V<z) = zx-y2 = 0.
При условиях что
df df
det
Эх dy
9д dg
dx dy
/0,
z ф 0, x и у можно выразить относительно z и получить явный вид пинии
пересечения
х-У2 -z3
X = = Z .
Z
Заметим, что при пересечении двух поверхностей второго порядка
получается кривая третьего порядка. Поверхности и кривая пересечения
показаны на рис. 5-2.
Рис. 5-2 Пересечение кривых второго порядка.
Общий параметрический вид пространственной кривой можно записать в
виде:
х = x(t),
У = У(*),
z = z(t),
где параметр t изменяется в определенных пределах ti < t < £2- В
приведенном выше явном непараметрическом представлении х можно рассматривать как
параметр, х = t. Тогда эта же кривая имеет параметрическую форму
х = t,
У = /(«),
z = g(t).
Далее, пусть z = t в неявном непараметрическом представлении из примера
5-1, тогда
x = t3,
y = t2,
z = t.
Некоторые полезные параметрические трехмерные кривые имеют известное
аналитическое решение. Например, кривая шва на теннисном или бейсбольном
мяче имеет вид:
х = \[acos(6 + j) - Ьcos3(9 + j)],
у = n[asm(9 + j) - bsin3(0 + ^)],
z — csin(20),
Рис. 5-3 Примеры параметрических пространственных кривых, (о) Шов бейсбольного
мяча; (6) круговая спираль.
где
A = l + dsin(20) = l + d(-),
/i = l- dsin(20) = 1 - d (-) ,
параметр в = 2ivt и 0 < t < 1.0. Если d = 0 и с2 = АаЪ, то кривая лежит на сфере
радиуса а + Ь. На рис. 5-За приведен пример для а = 1, Ь = 1, с = 2, d = 0, где
кривая лежит на сфере радиуса 2.
Другой пример параметрической пространственной кривой — круговая
спираль:
х = г cos t,
у — г sin t,
z = bt
Рис. 5-4 Физические отвесы и сплайн.
для г, b ф О, —оо < t < оо. Эта кривая лежит на поверхности цилиндра
радиуса |г|. Уравнение z = bt отвечает за распространение спирали по оси z. После
каждого изменения параметра t на 2л- переменные х и у возвращаются к своим
первоначальным значениям, a z увеличивается или уменьшается на 27г|Ь| в
зависимости от знака Ь. Эта величина назьтается шагом спирали. Пример изображен
на рис. 5-ЗЬ.
5-3 КУБИЧЕСКИЕ СПЛАЙНЫ
В промышленном производстве, например, судо-, автомобиле- и авиастроении,
окончательная форма в реальном или близком к нему масштабе определяется в
процессе доводки1.
Автоматизация этого процесса представляла значительный интерес для
машинной графики. Форма математического сплайна повторяет контур
физического сплайна (рис. 5-4), т.е. гибкой деревянной или пластмассовой линейки,
проходящей через определенные точки. Для изменения формы сплайна используются
свинцовые грузики. Меняя их количество и расположение, получившуюся кривую
стараются сделать более гладкой, красивой и «приятной для глаза»2.
Если рассматривать физический сплайн как тонкую гибкую рейку, его форма
(отклонение у) определяется уравнением Эйлера (5-2) для момента изгиба М{х)
вдоль рейки:
где Е — модуль Юнга, зависящий от свойств материала рейки, I — момент
инерции, определяемый формой кривой, Щх) — радиус кривизны.
1 В судостроении, например, необходимо определить форму судна более точно, чем это
возможно на небольшом чертеже. Поэтому общепринято изображать контур судна в натуральную
величину на плазе.
2 Не существует общепринятого термина для оценки внешнего вида кривой. Мы не пытаемся
дать математического определения, потому что любая такая попытка вызовет волну протеста
по крайней мере у половины заинтересованных специалистов.
Для малых отклонений (у' <С 1) радиус приближенно равен
R(X) (l + y'2)3/2 У '
где штрих обозначает производную по х — расстоянию вдоль рейки, а у —
отклонение рейки. Уравнение Эйлера принимает вид
,, = М(х)
У EI '
Пусть грузики действуют как простые подпорки, тогда момент изгиба
между ними изменяется линейно. Подставляя М(х) = Ах + В в уравнение Эйлера,
получаем
„ Ах + В
и после двойного интегрирования
у = Aix3 + Bix2 + dx + £>!.
Таким образом, форма сплайна задается кубическим полиномом.
В общем случае математический сплайн это кусочный полином степени К с
непрерывной производной степени К — 1 в точках соединения сегментов. Так,
например, кубический сплайн имеет в точках соединения непрерывность второго
порядка. Кусочные сплайны из многочленов невысокого порядка очень удобны
для интерполяции кривых, так как они не требуют больших вычислительных
затрат и не вызывают численных отклонений, свойственных многочленам высокого
порядка. По аналогии с физическими сплайнами обычно используется серия
кубических сегментов, причем каждый сегмент проходит через две точки. Кубический
сплайн удобен еще и тем, что это кривая наименьшего порядка, допускающая
точки перегиба и изгиб в пространстве.
Уравнение одного параметрического сегмента сплайна таково:
4
P{t) = Y,Bitl-\ h<t<t2, (5-1)
t=i
где t\ и ti — значения параметров в начале и конце сегмента. P(t) — вектор к
любой точке сегмента. P{t) = [x(t) y(t) z(t)] —это векторно-значная функция, где
три составляющие P(t) —декартовы координаты вектора1.
1 P(t) = [r(i) e(i) z(t)], где r(t), 9(t), z(t) — компоненты цилиндрической системы координат,
также совершенно справедливо, как, впрочем, и представление в любой другой системе
координат. (См. задачу 5-8.)
Pi
Г
Pvh
Рис. 5-5 Один сегмент кубического сплайна.
Каждая составляющая имеет вид, похожий на P(t), т.е.
4
i=i
4
y(t)=Y,BHti~1> *1 < * < *2,
i=l
4
г(*) = ^В^-\ *1 < * < «а.
t=i
Постоянные коэффициенты В{ вычисляются исходя из четьфех граничных
условий для сегмента сплайна. Запишем уравнение (5-1) в виде
P(t) = Bi + B2t + B3t2 + B4t3, h<t<t2. (5-2)
Пусть Pi и P2 — векторы концов сегмента (см. рис. 5-5). Пусть также Р[ и Р2,
производные по t, будут касательными векторами в концах сегмента.
Дифференцируя уравнение (5-1), получим
4
P'(t) = [x'(t) y'(t) z,(t)] = Y,Bi(i-l)ti-2, h<t<t2. (5-3)
t=i
Запишем результат
P'(t) =B2+ 2B3t + W^2, h<t< t2. (5-4)
Предположим, без потери общности, что t\ = 0, и применим граничные
условия
Р(0)=Р1; (5-5а)
P(t2) = Р2, (5-5Ь)
Р'(0) = Р{, (5-5с)
P'(t2) = P'2. (5-5d)
Получим четыре уравнения для неизвестных Р,:
Р(0) = В1=Р1,
4
Р'(0) = У)(г - l)t*-2Bi| = В2 = Р[,
1=1
4
4=0
г=1
P(t2) = Y^Biti-1 _ =Bl + B2t2 + B3tl + Bit\,
t=t2
P'(t2) = J2(i-l)ti-2Bi _ =B2 + 2B3t2 + Witl
i=l
t=t2
(5-6a)
(5-6b)
(5-6c)
(5-6d)
(5-7a)
(5-7b)
Величины Bi, B2, Вз и P4 задают сегмент кубического сплайна. Очевидно, что
форма сегмента зависит от положения и касательных векторов в концах сегмента.
Далее, заметим, что в результатах присутствует значение параметра t = t2 в
конце сегмента. Так как каждая конечная точка и вектор касания имеют три
компоненты, параметрическое уравнение кубической пространственной кривой
зависит от двенадцати векторных компонент и значения параметра t2 в конце
сегмента.
Подставив уравнения (5-6) и (5-7) в (5-1), получим уравнение для одного
сегмента кубического сплайна:
Решения
для
В3
и
Bi
имеют вид:
Вз
Bi
3(Р2-
"~ t2
2(Pi-
~ t3
ъ2
Pi)
Р2)
2Р[
«2
Р{
Р'
Р'
t2 '
12
P{t) = i\+ P[t +
+
3(Р2 - PQ 2Р[
Щ «2
2{Р1-Р2) Р{
«2
Г
t\
J L J £
• .0 1 .0
ti
ti
(5-8)
"2 b2 J
Это уравнение для одного сегмента. Чтобы получить кривую целиком, нужно
соединить множество сегментов. На рис. 5-6 показаны два соседних сегмента.
Если известны векторы Pi, Р2, Р3, касательные векторы Р[, Р2, Р3 и значения
параметров t2, £3, то форма каждого сегмента определяется из уравнения (5-8).
Однако маловероятно, что известен касательный вектор Р2 в точке соединения.
К счастью, его можно вывести из условия непрерывности.
Вспомним, что кусочный сплайн степени К имеет непрерывность степени К— 1
в точках соединения; непрерывность кубического сплайна равна двум. Для этого
должна быть непрерывна вторая производная P^it) или кривизна линии. Дважды
продифференцировав уравнение (5-1), получим
4
P"(t) = Y^{i - l)(i - 2)В^~3, ti<t< t2.
(5-9)
i=l
^■'з
Pi
Pvh
Рис. 5-6 Два кусочно кубических сегмента сплайна.
Для первого куска сплайна параметр изменяется в пределах 0 < t < t2.
Подставим t = t2 в уравнение (5-9):
Р" = 6В4*2 + 2В3.
Для второго участка сплайна параметр изменяется в диапазоне 0 < t < t3.
Подставим в уравнение (5-9) значение t = 0 в начале второго участка
Р" = 2В3.
Приравнивая полученные результаты и пользуясь уравнениями (5-6а, 6) и
(5-7а), получим
6Ь
\2{Р,-Р2) ! Р[ ( РЦ
12 *2 *2 .
+ 2
=
3(Р2~Р1) 2Р[ Р!Л
t\ t2 t2_
2
"3(Р3 - -Р2) 2Р± 1
[ Ч t3 t
or
_3
3 .
Левая часть этого уравнения представляет кривизну в конце первого сегмента,
а правая —в начале второго. Домножим на t2t3 и сгруппируем члены:
t3P[ + 2(t3 + 12)Р<2 + hP^ = ^-[t\{P3 - P2) + t23(P2 - Рг)]. (5-10)
t2t3
Отсюда определяется Р2, неизвестный касательный вектор в точке
соединения. Отметим, что в окончательном уравнении опять присутствуют значения
параметра t в концах сегментов t2 и
Заполученную формулу можно обобщить для п точек, и для п — 1 сегментов
кубического сплайна получить непрерывность второго порядка в точках соедине-
Рис. 5-7 Обозначения множества кусочно кубических сегментов сплайна.
ния. Обобщенное уравнение для двух любых соседних сегментов сплайна Рк (£) и
Pjk+i(t)1 в обозначениях рис. 5-7 имеет вид:
Pk(t) = Рк + PLt +
+
для первого сегмента и
Pk+1(t) = Pk+1+P'k+1t +
+
3(Рк+1-Рк) 2Р'к Рк+1
t2
ък+1
tk+1 tk+1 .
2{Pk-Pk+i) PL P'k+i
t2 +
t3
4+1
t2
4+1
t2
ък+1
(5-11)
3(Pfc+2 ~ Pk+l) _ 2-Pfc+l _ P'k+2
tk+2 tk+2 .
PI
t2
lk+2
t< +
2(Pfe+l - Pk+2) Pk+l Pk+2
' .0 1
t3
lk+2
t2
lk+2
t2
lk+2 J
f
(5-12)
для второго, так как для каждого сегмента параметр начинает изменяться с нуля,
для первого 0 < t < tk+i и для второго —0 < t < tk+2-
Приравнивание вторых производных в точках стыковки для любых соседних
сегментов, Pk(tk) = -ffc+i(0), дает общий результат, эквивалентный уравнению
(5-10),
tk+2P'k + 2(ife+l + tk+2)P'k+i + tk+\P'k+2 =
= 7—^ \tl+l(Pk+2 - Pk+i) + tl+2(Pk+i -Pk)], 1 < к < n - 2, (5-13)
tk+ltk+2 L J
откуда определяется касательный вектор в точках соединения любых двух
сегментов Рк И Рк+1-
1 Чтобы не вводить лишних определений, условимся обозначать участок параметрической
кривой между точками Рь и Рк-\ как Pk(t).
Рекурсивное использование уравнения (5-13) для всех сегментов сплайна
порождает п — 2 уравнений касательных векторов PL 2 < к < п — 1. В матричной
форме:
*з 2(*2 + *з) *а О
О U 2{t3 + U) t3 О
0 0 tb 2(t4 + t5) U 0
0 tn 2{tn + tn-\) tn-i
Pi
Р'г
или
fr{t22(P3-P2)+tl(P2-P1)}
-£-{tl(P4-P3) + tl(P3-P2)}
Cn—1*71
{t2n_1(Pn - Pn-l) + t2n(Pn-l - Pn-2)
(5-14)
[M*][P>] = [R].
Матрица [М*] неквадратная, так как имеется только п — 2 уравнений для п
векторов, и ее нельзя обратить и получить решение для [Р1]. Если предположить,
что известны касательные векторы на концах кривой Р[ и Р'п, проблема
разрешается. Теперь матрица имеет вид
1
*3
0
0
2(t
0
2 +
и
0
*з)
*2
2(*з +
*Б
U)
2{t
0
*з
1 +
*б)
0
и
0 tn 2(tn + tn-i) t„_i
• • 0 1
PI
Pi
P'
P[
^r{tl(P3-P2)+tl(P2-P1)}
*2t3
-*-{tl{P4-Pb) + tl(P3-P,)}
ГЗГ4
*П—1*71
P'
{tl-l(Pn - Pn-l) + t2n{Pn-l - Pn-2)}
(5-15)
или
[M][P'} = [R],
где матрица [М] квадратная и обратимая. Заметим также, что [М] трехдиагональ-
ная1, что снижает вычислительные затраты на ее обращение. Далее, матрица [М]
диагонально доминантная2. Отсюда следует, что у нее существует единственное
решение:
[Р'] = [М]-'[Щ
(5-16)
Если нам известны Р'к, то легко определить коэффициенты В{ для каждого
сегмента сплайна. Обобщая уравнения (5-6)—(5-11), получим
В1к=Рк,
Вгк = Рк,
Взк = ЧРк+i-Pk)
tk+1 ifc+i tfc+i
в4к = 4Pk-Pw) , П , pUi
iP'k
к+1
f3
4+1
t2
lk+l
t2
Так как Pk и Рк — это векторные величины, то и В{ тоже векторные; если Рк
и Р'к имеют х, у, z составляющие, значит, и Bi также имеет эти составляющие.
1 У трехдиагональной матрицы элементы расположены только на главной диагонали, первой
верхней и первой нижней диагоналях.
2 У диагонально доминантной матрицы порядок членов на главной диагонали больше, чем
других членов в этом же ряду.
В матричной форме уравнение любого сегмента сплайна к таково:
[В} =
Bik
Bik
Взк
Bik
1
0
0
1
0
0
0
0
к+1
t3
lk+l
tk+1
1
ffc+l
t2
4
t3
lk+l
tk+1
1
t2
4+1
Pk
P'
rk
Pk+1
P'
(5-17)
Пусть требуется задать кубический сплайн, проходяпщй через п точек Рк, 1 <
к < п с касательными векторами на концах Р[ и Р^. Из уравнения (5-16) находим
внутренние касательные векторы Р'к> 2 < к < п — 1. Затем из уравнения (5-17) с
известными координатами концов каждого сегмента и касательными векторами
определяются Bik, 1 < * < 4, для каждого сегмента. Окончательное обобщение
уравнения (5-1)
Р*(0 = 5^В<*'*_1' 0 < * < **+!, l<fc<n-l,
(5-18)
используется для расчета сегмента сплайна.
В матричном виде уравнение (5-18) выглядит следующим образом:
Pk(t) = [l t t2 t3)
Ь
hk
Bin
Взк
Bik
0<* <**+!-
Подставляя уравнение (5-17) и перегруппируя члены,
Pk(r) = [F1(T) F2(t) F3(t) Fi(r)]
Рк
Рк+1
Р'
гк
Р'
. Гк+1 .
где
т = (t/tk+1),
Fu(r) = 2r3-3r2 + l,
F2*(t) = -2t3 + 3t2,
F3k(T)=T(T2-2T+l)tk+u
Fik(r) = т(т2 - r)tk+1
назьшаются весовыми функциями.
получим
0<т < 1
1< Jfe<n-1
(5-19)
(5-20)
(5-2 la)
(5-21b)
(5-21с)
(5-21d)
Рис. 5-8 Весовые функции кубического сплайна для tk+i = 1.0
Пользуясь этими определениями, запишем уравнение (5-20) в матричном виде
Pk{r) = [F)[G], (5-22)
где [F] — матрица весовой функции
[F] = [J\(r) F2(r) F3(r) ВД]
и
[C?]T = [Pfc Pfc+1 Р'к PUi] (5-24)
содержит геометрическую информацию. Как будет видно из дальнейшего,
уравнения типа (5-22), т.е. матрица весовой функции, умноженная на матрицу
геометрических условий, часто применяются для описания кривых и поверхностей.
Из уравнения (5-21) видно, что каждая весовая функция имеет третий
порядок. Любая точка на сегменте кубического сплайна это взвешенная сумма
конечных точек и касательных векторов. Коэффициенты Fik выступают в роли
весовых функций. На рис. 5-8 изобрежены Fi для tk+i = 1.0. Из рисунка видно, что
Fi(0) = 1 и F2(0) = -Рз(О) = Fi = 0, т.е. кривая проходит через вектор-точку Рг.
Аналогично F2(l) = 1 и Fi(l) = F3(l) = Fi(l) = 0, т.е. кривая также проходит
через вектор-точку Pi- Далее отметим симметрию F\ и F2, и F3 и Fi.
Фактически F2(t) = 1 — Fi(r). Наконец, обратим внимание на относительный порядок F\,
F2, F3 и Fi. Значительная разница величин говорит о том, что в общем случае
положение конечных точек имеет большее влияние, чем касательные векторы.
Вспомним, что кусочный кубический сплайн определяется точками,
векторами касательных и величинами параметра, т. е. £* в концах всех сегментов. Выбор
tk влияет на гладкость кривой.
(5-23)
Непрерывность второй производной в точках внутреннего соединения сама по
себе не обеспечивает гладкости кривой в смысле минимальности кривизны вдоль
нее. Подбирая соответствующие значения, можно минимизировать
коэффициенты Вз и В± для каждого сегмента и достичь большей гладкости кривой. Обычно
эти дополнительные вычисления не требуются. Для практческих целей
применяются более простые методы, наподобие рассмотренных здесь.
Один метод вычисления £* — установить величины параметров равными
длинам хорд между соседними точками. При этом качество кривой удовлетворяет
требованиям большинства прикладных задач. Другой метод состоит в том, что
для нормализации вариации £* полагается равным единице у каждого сегмента
сплайна. Такой выбор упрощает вычисления (см. разд. 5-4). Как видно из
приведенных выше уравнений, любой выбор £* приводит к другим коэффициентам,
и, следовательно, получаются различные кривые, проходящие через заданные
точки.
Рассмотрим пример1.
Пример 5-2 Кубический сплайн
Пусть даны четыре вектор-точки на плоскости: Pi [0 0], Рч. [1 1],
Рз [2 — 1], Р, [3 0] (см. рис. 5-9). Найти кусочный кубический сплайн,
проходящий через них, используя хордовую аппроксимацию tk-
Касательные векторы в концах: Р[ [1 1] и Р\ [1 1]. Найти промежуточные точки
при т = 1/3, 2/3 для каждого сегмента.
Сначала найдем
«а = л/(х2 - xi)2 + (уг - У1)2 = ч/(1)2 + (1)2 = %/2,
*з = ч/(хз - х2)2 + (уз - г/2)2 = ч/(1)2 + (-2)2 = ч/б,
и = \/(х4 - хз)2 + (г/4 - г/з)2 = \/(1)2 + (1)2 = V2.
Внутренние касательные векторы Р'ч и Р$ вычисляются из уравнения
(5-15):
Г 1 0 0
*з 2(*2 + *з) t2
0 U 2(*з + U)
L 0 0 0
0 1
0
*з
1 J
ГР>
И
Pi
IP'*
Pi
pf
{t22(P3-P2)+t23(P2-Pl)}
{tl(Pt-Pa) + tl(Pa-P2)}
1 На протяжении всей этой главы рассматриваются двумерные примеры. Это сделано только
для упрощения выкладок и представления результатов. Третье измерение вводится простым
расширением (см. вопросы к гл. 5).
Рис. 5-9 Кусочный кубический сплайн, (a) tk вычислены с помощью хордовой
аппроксимации; (6) tk нормализованы к 1.
Сделав подстановку, получим
[1 1]
3
у/2у/Е
3
у/Ел/2
[1 1]
10 0 0 ] Г Р[
у/Е 2(у/2 + у/Е) у/2 0 Pi
О у/2 2{у/Е+у/2) у/Е Pi
0 0 0 1 L Рл
{2([2 -1]-[1 1]) + 5([1 1]-[0 0])}
{5([3 0]-[2 -1]) + 2([2 -1]-[1 1])}
[1 1]
3
у/2~у/Е
3
у/Еу/2
[1 1]
{[2 -4]+ [5 5]}
{[5 5]+ [2 -4]}
[1
0.949 [7
0.949 [7
[1
1
1
1
1
"
.
1
2.236
0
0
0
7.300
1.414
0
0
1.414
7.300
0
о
о
2.236
1
Pi
Pi
Р'ь
1 1
6.641 0.949
6.641 0.949
1 1
С помощью инверсии и умножения вычисляются касательные векторы
Pi 1
PL
Pi
Ъ .
=
■ l
-0.318
0.062
0
■ 1
0.505
0.505
1
0
0.142
-0.028
0
1
-0.148
-0.148
1
0
-0.028
0.142
0
0
0.062
-0.318
1
■ 1
6.641
6.641
1
1
0.949
0.949
1
Из уравнения (5-21) находим весовые функции первого сегмента:
2П
Л(1/3) = 2(1/3)3 - 3(1/3)2 + 1=2?= 0.741,
F2(l/3) = -2(1/3)3 + 3(1/3)2 = ^ = 0.259,
Л(1/3) = (1/3)[(1/3)2 - 2(1/3) + \\у/2 = ^ = 0.210,
27
2^/2
Д(1/3) = (1/3)[(1/3)2 - 1/ЗЬ/2 = -Ц± = -0.105
27
и второго:
Fi(2/3) = 2(2/3)3 - 3(2/3)2 + 1 = ^- = 0.259,
27
F2(2/3) = -2(2/3)3 + 3(2/3)2 = ^ = 0.741
27
2%/2
F3(2/3) = (2/3)[(2/3)2 - 2(2/3) + 1]>/2 - ^ = 0.105,
F4(2/3) = (2/3)[(2/3)2 - 2/3]>/2 = -^- = -0.210.
Точка на первом сегменте сплайна при т = 1/3 получается из уравнения
(5-22), Р(т) = [F][G], т.е.
Р(1/3) = [0.741 0.259 0.210 -0.105]
= [0.416 0.484]
и при т = 2/3.
Р(2/3) = [0.259 0.741 0.105 -0.210]
= [0.740 0.876].
0 0
1 1
1 1
0.505 -0.148
0 0
1 1
1 1
0.505 -0.148
Полный результат приведен в табл. 5-1. Кубический сплайн показан на
рис. 5-9.
Таблица 5-1 Результаты для кубического
сплайна
Сегмент
1
2
3
т
1/3
2/3
1/3
2/3
1/3
2/3
P-W
0.416
0.740
1.343
1.657
2.260
2.584
Ру(т)
0.484
0.876
0.457
-0.457
-0.876
-0.484
Хотя из весовых функций (см. (5-21)) видно, что касательные векторы в
концах меньше влияют на форму сплайна, чем положение концевых точек, их
эффект может оказаться значительным. На рис. 5-10 изображен один симметричный
сегмент сплайна с одинаковым направлением касательных векторов, но разной
величины. Направления касательных векторов обозначены углом а, а их
относительная величина — длиной этих векторов. Если величина значительно меньше
длины хорды I, то кривая вьшукла на концах и лежит внутри треугольника из
хорды и касательных. При возрастании величины кривая постепенно становится
вогнутой и выходит за треугольник. В этом случае при величине вектора 3/ cos a
у кривой появляется вершина (см. рис. 5-10d). При еще больших величинах
появляется петля, как видно из рис. 5-10е. Иногда для улучшения формы кривой
величина вектора ограничивается длиной хорды.
5-4 НОРМАЛИЗОВАННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Рассмотрим другой подход к аппроксимации величин ^-нормализацию, т. е.. 0 <
t < 1 для всех сегментов.
В этом случае весовые функции (см. уравнение 5-21)1 имеют вид:
Fi(t) = 2t3-3t2 + l,
F2(t) = -2t3 + 3t2,
F3{t) = t3 -2t2+t,
Fi(t) = t3- t2.
(5-25a)
(5-25b)
(5-25c)
(5-25d)
Матрица весовых функций для нормализованного кубического сплайна
выглядит следующим образом:
[F] = [T][N] = [t3 t2 t 1]
2
3
0
-2
3
0
1
-2
1
1
-1
0
0 0 0
(5-26)
1 Данные функции являются кубическими весовыми функциями Эрмита на интервале
0 < t < 1.
l.Or
1/4/
1/4
X4
1/2
(<»)
1.0
(b)
1.0
(c)
(<*)-
—i XI
1.0
1.0
1.0
Рис. 5-10 Влияние величины касательного вектора на форму сегмента кубического
сплайна, а = 7г/4. (а) 1/4; (Ь) 1/2; (с) 1; (d) 3/cosq; (e) 5.
Матричное уравнение сегмента (уравнение (5-22) записывается как
P(t) = [F][G\ = [T][N][G].
(5-27)
Заметим, что [Т] и [N] — константы для всех сегментов сплайна. От сегмента
к сегменту меняется только матрица геометрии [G].
Уравнение (5-15) для определения внутренних касательных векторов,
необходимых в [G], приобретает вид:
10- • •
14 10- •
0 14 10 -
■ -0141
• • ■ 0 1.
[Pi I
■ К-
3{(P3-P2) + (P2-Pi)}
3{(Р4-Рз) + (Рз-Р2)}
3{(Р„ - Р„-1 + (Рп-1 - Рп-2)}
(5-28)
Решение опять дается уравнениями (5-16), но так как [М] — константа, ее
нужно обратить только один раз. При большом количестве точек это значительно
сокращает вычисления.
Рассмотрим пример.
Пример 5-3 Нормализованный кубический сплайн
Опять рассмотрим четыре вектор-точки на плоскости из примера 5-2, т. е.
Pi[0 0], Р2[1 1], -Рз[2 -1] и Р4[3 0] с касательными векторами Р[[1 1] и
Pi[l 1]. Найти нормализованный кусочный кубический сплайн, проходящий
через эти вектор-точки.
Величины параметров t2 — ^з = *4 = 1.0.
Касательные векторы в точках соединения рассчитываются из уравнения
(5-28), т.е.
[1 1]
1
1
0
0
0
4
1
0
0
1
4
0
0 1
0
1
1 J
[Pi
Pi
Pi
I Pi
3{[2 -1]-[1
3{[3 0]-[2 -
[1 1]
1
l]-[0 0]}
-1]-[1 1]}
-3
-3
1
Обращаем и умножаем:
Pi 1
Pi.
Pi
Pi J
Г 1
-0.267
0.067
L о
о о
0.267 -0.067
-0.067 0.267
0 0
0
0.067
-0.267
1
1 1
6 -3
6 -3
1 1
1 1
1 -0.8
1 -0.8
1 1
Отметим, что здесь внутренние касательные Р'2, Р'г существенно
отличаются от результатов хордовой аппроксимации в примере 5-2.
Таблица 5-2 Результаты для
нормализованного кубического сплайна
Сегмент
1
2
3
t
1/3
2/3
1/3
2/3
1/3
2/3
Px(t)
0.333
0.667
1.33
1.667
2/333
2/667
Py(t)
0.467
0.933
0.422
-0.422
-0.933
-0.467
Из уравнения (5-26) матрица весовых коэффициентов для первого
сегмента при t = 1/3 имеет вид:
[F] = [T][N] = [1/27 1/9 1/3 1]
2-211
-3 3 -2 -1
0 0 10
10 0 0
= [20/27 7/27 4/27 -2/27]
и при t = 2/3:
[F] = [7/27 20/27 2/27 - 4/27].
Точка на первом сегменте сплайна при t = 1/3:
P(t) = [F][G] = [20/27 7/27 4/27 -2/27]
= [1/3 63/135] = [0.333 0.467]
и при t = 2/3:
P(t) = [F][G] = [7/27 20/27 2/27 -4/27]
= [2/3 126/135].
Результаты собраны в табл. 5-2.
0 0
1 1
1 1
1 -0.8
0 0
1 1
1 1
1 -0.8
На рис. 5-9 изображены два сплайна—из примера 5-1 и 5-3. Кривые
получились разными, т. е. параметризация влияет на результат.
Если точки из набора данных распределены неравномерно, то опыт
показывает, что хордовая аппроксимация tk дает более гладкую кривую, чем
нормализация. Это видно из рис. 5-11. На рис. 5-11а показано упорядоченное множество
точек, представляющее контур петушка. На рис. 5-116 точки соединены отрезками
прямых. Рисунки 5- 11с и d представляют нормализованную и хордовую
аппроксимацию сплайна, соответственно. Обратите внимание на разницу в изображении
<*)
<*)
V/5
.«'
• •*
.*t«
V
(с)
• •""■•. ..-■
^ J / r±j)
V/ V
. ~рл :
■ • -\ :.
• •
./ ■•
.V • .
•
я т
• •
* •
• •
• •
•••
• *
■*•*..
-v :•*■••
• ■
*7 f
*•—•. :
:
4
V
4
.
• •
-;ф'-
\ -гчТ*.:
\
Ча •••■Ч \
/J '.
% .•
■*
4 i
w
Рис. 5-11 Сравнение кубических сплайновых аппроксимаций, (а) Данные; (6)
соединение прямыми; (с) нормализованная аппроксимация tk] (d) хордовая аппроксимация tk-
лапок и гребешка. Хордовая аппроксимация устраняет петли, заметные на рис.
5-11с на лапках, и дает более гладкое изображение гребешка. Несмотря на эти
недостатки, нормализованное представление применяется для создания кубических
ограничивающих кривых для кусков трехмерной поверхности (см. гл. 6).
Еще одно интересное замечание: если для нормализованного сплайна известна
матрица [В]т = [Pi B% B$ B^], то геометрическая матрица сегмента сплайна
[G] равна
[G] = [iV]-W,
где [iV]-1—обратная матрица [N]:
[N]-1 =
0 0 0 1
1111
0 0 10
3 2 10
(5-29)
Точки на сегменте рассчитываются из уравнения (5-27).
5-5 ДРУГИЕ ГРАНИЧНЫЕ УСЛОВИЯ
В предыдущих рассуждениях предполагалось, что известны касательные
векторы Р[ и Р'п в концевых точках кусочного кубического сплайна. Такое граничное
условие называется закрепленным. Неизвестные касательные векторы в
промежуточных точках вычисляются инверсией трехдиагональной матрицы [М] из
уравнения (5-15).
Если задано мало точек или физические ограничения требуют определенной
формы кривой у концов, возможны другие граничные условия. Например,
можно задать кривизну в концевых точках. Нулевая кривизна называется слабым
граничным условием. Аппроксимируя кривизну второй производной и вспоминая
уравнение (5-9), получаем
P"it) = Х> - 1)(» - 2)5if-3, 0 < t < tk+1.
i=l
В начале первого сегмента сплайна t = 0. Отметим, что на результат влияет
только член г = 3. Из уравнения (5-17)
-<°>^-№-f-§)
0.
После перегруппировки получаем
Теперь первая строка в матрицах [М] и [R] (см. (5-15)) такова:
(5-30)
Г1 1/2 0 •■■1ГР1'] =
£<*
Pi)
В конце последнего сегмента t = tn, к = п — 1. Здесь результат зависит от двух
членов i = 3 и «' = 4 в (5-9), а именно
P"(tn) = 2В3 + 6B4tn = О
или, используя уравнение (5-17),
После перегруппировки
2P;_i + 4Р; = f (Pn - Pn-i). (5-31)
Последняя строка матриц [М] и [Л] (см. (5-15)) выглядит теперь так:
6
L-- о 2 4jlp;j =
-{Pn-Pn-i)
Заметим, что для сплайна слабые и закрепленные граничные условия могут
меняться местами.
Пример 5-4 Кубический сплайн со слабым граничным условием
Пусть заданы три точки Pi [0 0], Рг[1 2] и Рз[3 2]. Найти кубический
сплайн, проходящий через них, со слабыми граничными условиями. Для tk
использовать хордовую аппроксимацию.
Коэффициенты tk таковы:
t2 = у/{Х2 - Xl)2 + (У2 - У1)2 = у/{1)2 + (2)2 = у/Е,
ta = >/(*а - х2)2 + (уз - у2)2 = л/(3 - I)2 + (О)2 = 2.
Модифицируя матрицы [М] и [R] с помощью уравнений (5-30) и (5-31),
получим уравнение внутреннего касательного вектора в Р^:
1 0.5 0
2 8.472 2.236
0 2 4
Pi
ф([1
5Л{5(Р
3([3 2]-
2]-[0 0])
2]-[1 2]) + 4([1
[1 2])
2]-[0 0]0)}
0.671 1.342
0.391 5.367
6 0
Инвертируя (3 х 3)-матрицу и умножая, найдем производные
—
1.157
-0.315
0.157
" 0.301
0.739
1.131
-0.079
0.157
-0.079
1.131 '
0.422
-0.211
0.044
-0.088
0.294
0.671
9.391
6
1.342
5.367
0
Из уравнения (5-21) весовые функции при г = 1/3 и 2/3 для первого
сегмента имеют вид:
[F]T=i/3 = [0.741 0.259 0.331 - 0.166],
[F]T=2/3 = [0.259 0.741 0.166 - 0.331].
Затем уравнение (5-22) дает точки на первом сегменте, т. е.
Р(1/3) = [0.741 0.259 0.331
= [0.237 0.823].
0.166]
0 0
1 2
0.301 1.131
0.739 0.422
Аналогично
Р(2/3) = [0.546 1.529].
Весовые функции при г = 1/3, 2/3 для второго сегмента таковы:
[F]T=1/3 = [0.741 0.259 0.296 - 0.148],
[Р]т=2/з = [0.259 0.741 0.148 - 0.296]
и уравнение (5-22) дает
Р(1/3) = [1.570 2.156],
Р(2/3) = [2.256 2.125].
Результаты показаны на рис. 5-12.
Интерес представляют еще два типа граничных условий: циклическое и
ациклическое. Циклическое условие порождает замкнутую кривую или часть
периодически повторяющейся кривой. Для этого необходимо, чтобы касательная
вектора и кривизна на обоих концах были нулевыми:
Р[(0) = P'n{tn),
(5-32)
(5-33)
Из уравнений (5-3) и (5-9), пользуясь уравнениями (5-17) и (5-32), получаем
ГЗ(Рп-Рп-1) 2P;_t Р'п
PL-Pk-i=*n
+ 3tn
tl
2(Pra_1 - Pn) P^ P'n
(5-34)
О 1 2
Рис. 5-12 Кубический сплайн для примера 5-4.
Аналогично, уравнение (5-33) приводится к виду
\3(Рп - Р„-0 2Рп_, Рп
[3(Р2 - Pi)
t2
2P[
t2
Pr
= 2
+ 6t,
'3
1
tl
tfl tfl
2(Pn-l ~ Pn) Pn-1 . PL
tl tl + tl
Умножив (5-35) на tn и вычитая его из (5-34), получим
[3(P2-Pi) 2P[ Р^
P[-Pn_^-2tn
= 3t2n
-6tl
t2
ъ2
tl
2(Рп-!-Рп) ,K-1,K
Ъ tl + tl,
2(Pn_! - Pn) PU P'n
tl +t2nJ
tl
Вспомним, что Р[ = Pn, к перегруппируем члены:
a (i + £) Ъ + 'fPk + PU = з|(р2 - Pi) - ^(Рп-i - Pn
(5-35)
(5-36)
Касательные векторы в точках внутреннего соединения опять получаются с
помощью уравнения (5-15). Однако из-за того, что касательные векторы линейно
зависимы (Р{ = Рп)), матрица [М] теперь имеет размер (п — 1) х (п — 1), где
первая строка состоит из коэффициентов уравнения (5-36):
2 (l +1) 't ° ° 1
h 2(t2 + t3) t2 ■
[Pi
P1
P'
0 tn 2(tn + tn-i) tn-i
З^Рг-Р^-^Р^-Р»)
{t22(P3-P2)+t23(P2-Pl)}
{iI)P4-P3)+ti(P3-P2)}
-{tl^Pn - Pn_!) + t\(Pn_! - Pn_2}
^3
*3*4
(5-37)
Эта матрица уже не трехдиагональная. Ациклический сплайн похож на
циклический за исключением того, что
Р[(0) = -РМ, (5-38)
Р['Ф) = -Pnitn). (5-39)
Та же процедура, что и для циклических граничных условий, дает
2 (l + £) Pi' + \Рк ~ К-х = з|№ - Pi) + £(Pn-i - Р„). (5-40)
Из уравнения (5-40) видно, что единственные отличия — это разные знаки у 1 в
М(1, п — 1) в матрице [М] и у второго члена Р(1, 1) в уравнении (5-37).
Ациклические спайны полезны при изображении кривых, у которых касательные векторы в
концах имеют одинаковую величину и противоположные направления, например
как у многослойной деревянной теннисной ракетки. В табл. 5-3 собраны
граничные условия для кубических сплайнов.
У кубических сплайнов первые и вторые производные непрерывны для любых
граничных условий, но с увеличением количества заданных точек время
обращения матрицы касательных векторов может стать слишком большим.
На рис. 5-13 изображены два кубических сплайна, проходящих через пять
точек: с закрепленными и слабыми граничными условиями. Касательные векторы
в закрепленных концах —[—1 1] и [1 1], соответственно. В этом случае различие
кривых несущественно. Другие касательные векторы, например [1 1] и [1 1],
могут существенно изменить форму сплайна с закрепленными концами.
На рис. 5-14 показано влияние изменения величины, а не направления
касательных векторов в концах замкнутого кубического сплайна. Эти кривые
симметричны, так как квадратная матрица в уравнении (5-15) трехдиагональна.
Таблица 5-3 Граничные условия для кубических сплайнов
Граничное
условие
Ненулевые элементы
в первой и последней
строках [М]
Первая и последняя
строки [Я]
Закрепленное
Слабое
Циклическое
Ациклическое
М(1, 1) = 1
М(п, п) = 1
М(1, 1) = 1
М(1, 2) = 1/2
М(п, п - 1) = 2
М(п, п) = 4
M(l,l) = 2(l + £)
М(1, 2)
*1
*2
М(1, п-1) = 1
М(1,1) = 2^1 + ^
М(1, 2) = £
М(1, п-1) = -1
Я(1, 1) = Р[
Щп, 1) = Р>п
R(l, 1) = £-(Р2 - Рг)
Щп, 1) = — (Pn-Pn-i)
Д(1,1) = з(|)(Р2-Р1)
-f(Pn-i-Pn)
Я(п, 1) не определено
Д(1,1) = 3^|)(Р2-Р!)
+^-(рп-1-рп)
R(n, 1) не определено
Закрепленное
Рис. 5-13 Сравнение закрепленного и слабого граничных условий
для'нормализованного кусочно кубического сплайна.
У
ю
8
б
4
2
О
-2 2 6 10 х
Рис. 5-14 Влияние величины касательного вектора на форму нормализованного
кусочно кубического сплайна, (а) Р{[0 1], Р^О - 1]; (Ь) Р{[0 10], Рг[0 - 10].
На рис. 5-15 через те же пять точек проходит сплайн со слабыми и
циклическими граничными условиями. Обратите внимание на то, что сплайн со слабыми
условиями симметричен, а циклический — нет.
На рис. 5-16 сравниваются слабое и циклическое граничные условия.
Циклическое условие можно использовать и для незамкнутых кривых: направление
начального касательного вектора должно совпадать с направлением касательного
вектора в конце.
Несмотря на то, что параметрические кусочные сплайны удобны и
применяются в ряде отраслей (производстве автомобилей, судостроении и авиастроении),
у них есть некоторые недостатки. Так, они неточно представляют конические
сечения и асимптотические кривые и часто приводят к видимой осцилляции.
Осцилляция возникает из-за того, что сплайн испытывает локальное влияние
каждой точки, а третья производная только кусочно постоянна. Разрывы третьей
производной порождают отклонения, и полученная кривая не является гладкой,
несмотря на то, что ее вторая производная непрерывна.
Один из методов борьбы с осцилляциями — математический аналог
приложения силы к концам сплайна. Пусть имеется физический сплайн — тонкая, гибкая
Циклическое
Рис. 5-15 Сравнение слабого и циклического граничных условий для
нормализованного кусочно кубического сплайна.
-1 -
Рис. 5-16 Сравнение слабого и циклического граничных условий для открытых
кривых.
♦ >
(о) (ft)
Рис. 5-17 Эффект напряжения кусочно кубического сплайна, (а) Без напряжения; (Ь)
с напряжением.
рейка, нагруженная в некоторых точках. Чтобы устранить малые колебания,
нужно приложить силу к концам рейки. Изучение нагруженных сплайнов выходит за
рамки этой книги, однако мы сделаем несколько замечаний. В первых
разработках [5-6] и [5-7] рассматривается экспоненциальный сплайн, требующий больших
вычислений. В работе [5-8] рассматривается другой полиномиальный вид
сплайна, ь'-сплайн. Эффект напряжения кубического сплайна показан на рис. 5-17.
5-6 ПАРАБОЛИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
Кубические сплайны — это мощное и удобное средство, но и они небезупречны:
необходимо учитывать влияние направления и величины касательных векторов,
указывать все точки кривой до ее изображения, невозможна локальная коррекция
кривой. Последнее особенно важно для интерактивной работы. Расчет
кубического сплайна требует обращения большой матрицы, зависящей от всех элементов
сплайна; т. е. изменение любого сегмента затрагивает все остальные сегменты.
Воздействие уменьшается при удалении от точки возмущения, но полностью
пренебречь им нельзя. Параболическая интерполяция разрешает большинство этих
проблем за счет того, что она только непрерывна, т. е. в точках соединения
сегментов сохраняется непрерывность лишь первой производной. Для многих
прикладных задач этого достаточно, причем параболическая интерполяция не требует
больших расчетов.
Параболическая интерполяция была разработана Оверхаузером1 [5-9]. Оверха-
узер строил кривую интерполяции, исходя из геометрических соображений. Идея
состоит в линейной интерполяции пересекающихся частей двух парабол.
Параболы заданы четырьмя последовательными точками: первая — тремя первыми
точками, вторая —тремя последними. Пересечение лежит между второй и третьей
1 В первом издании данной книги был рассмотрен метод Оверхаузера.
Рис. 5-18 Параболическая интерполяция.
точками. Несмотря на то, что параболы — плоские кривые, их линейная
интерполяция это кубическая пространственная кривая, как показано на рис. 5-18.
В работе [5-10] рассматривается метод построения одного из семейств
параболически интерполированных кривых с помощью матриц. Этот алгоритм требует
меньше вычислений. Рассмотрим обобщенный вывод для всего семейства.
Параболически интерполированная кривая имеет вид
G(t) = (l-t)p(r)+tq(s), (5-41)
где г, s, t — параметры, p(r), q(s)— параметрические параболы, проходящие через
Pi, Рг, Рз и Рг, Рз, Ра, соответственно, как показано на рис. 5-19. Для простоты
параболы на рис. 5-19 лежат в одной плоскости, но это не обязательно (рис. 5-18).
Параметрическое представление р(г) и q(s) следующее:
p{r) = [r2 r 1][В], (5-42)
q(s) = [s2 r 1][£>], (5-43)
где [В] и [£)] —матрицы, представляющие положение вектор-точек Pi, Рг, Рз и
Рг, Рз, Ра, соответственно. Результат интерполяции — кубическая кривая
C(t) = [t* t2 t 1}[A][G] = [T][A}[G\, (5-44)
Рис. 5-19 Обозначение для параболической интерполяции.
где [Г] [А] — матрица интерполяционных функций, a [G] — геометрическая
матрица вектор-точек Pi, Р2, Рз, Р*. Чтобы определить [В] и [D], а затем [А] и [G],
необходимо установить связь между параметрами г, s, t. Из рис. 5-19, замечая,
что г меняется от 0 до 1 на сегменте от Pi до Рз вдоль p(r), s меняется от О
до 1 на сегменте от Pi до Р± вдоль q(s), и t меняется от 0 до 1 на сегменте от
Рг до Рз вдоль С{€), разумно предположить, что г и t, а также s и t связаны
линейно. Отсюда
г = k\t + &2, s = k3t + ti, (5-45)
где кг — константы, заданные граничными условиями в вектор-точках Pi, Рг, Рз и
Р^. Предположим, что данные распределены равномерно или почти равномерно,
и диапазон параметров нормализован, т. е. О < r, s,t < 1. Тогда молено
условиться, что
р(0) = Рь р(1/2) = Р2, р(1)=Рз, (5-46а)
д(0) =Р2, 9(1/2) = Р3, <7(1) = Р4, (5-46Ь)
С(0)=Р2, С(1) = Р3. (5-46с)
Здесь основные предположения таковы: р(г) = Р2 для г = 1/2 и q(s) = P3
для s = 1/2. Эти предположения сделаны в работе [5-10]. В результате
получаем единственный член семейства параболически интерполированных кривых, как
будет показано ниже.
В предположениях уравнений (5-45)
@Р2: г = 1/2,*= 0 =^ А;2 = 1/2
@ Р3 : г = 1, t = 1 =^ кг + к2 = 1 => кг = 1/2
@ Р2 : s = 0, * = 0 => fc4 = 0
@Р3: в = 1/2,*= 1 =*■ *з = 1/2
Итак
r(t) = ±(l + t), s(t) = ±t. (5-47)
Вспомним уравнение (5-42) и используем уравнение (5-46а), чтобы выразить
[В] через Рь Р2, Рз,
р(0)=Рх = [0 0 1}[В], (5-48а)
р(1/2) = Р2 = [1/4 1/2 1][В], (5-48Ь)
р(1) = Р3 = [1 1 1][В]. (5-48с)
Запишем в виде одной матрицы
Pi
Р2
Рз
0 0 1
1/4 1/2 1
1 1 1
[В] = [М][В].
Отсюда
[В] = [МУ
Pl
р2
Рз
2
3
1
-4
4
0
2 "
-1
0
"Pi "
Р2
Рз
(5-49)
Аналогично через Рг, Рз, Pi находится выражение [D]. Пользуясь уравнением
(5-46Ь), получаем
(5-50а)
(5-50Ь)
(5-50с)
д(0) = Р2 = [0 0 l][D],
g(l/2) = P3 = [l/4 1/2 1][D],
g(l) = P4 = [l l 1][D].
Сравнение с уравнениями (5-48) сразу же дает
"Р2
[D] = [М]-1 Рз
Вспомним уравнение (5-41) и подставим уравнения (5-42) и (5-43):
С(«) = (1 - t)[r2 r l][B] + t[s2 а !][£>].
Используем уравнение (5-47), чтобы переписать это только в терминах
параметра t,
2
3
1
-4
4
0
2 "
-1
0
" Рг "
Рз
Pi
(5-51)
C{t) = [-\{t2 + t2-t-\) -\(t2-l) l-t][B] +
t3 i2
[D].
Подставив [В] и [D] из уравнений (5-49) и (5-51), получим
C{t) =
+
_L+f2_* t3_t2_t+1 _t +t
Pi
P2
Рз
+
t3 3 о
t3 + 2t2 *--*
з +2
2 2
P2
Рз
P4
Перепишем уравнение так, чтобы включить все четыре точки Pi, P2, Р3, Рц-
C(t) =
+
-у + |1-5 t3-t2-t + i -t + i о
t3 з.
t3 t2
0 J-^ + t -t3 + 2t> ---
Pi
Pi
Ръ
Pi
где
и-G)
-1 3-3 .1
2 -5 4 -1
-10 10
0 2 0 0
Pi
P2
Рз
P4
Наконец, перепишем результат в форме уравнения (5.44)
C(t) = [t3 e t 1][A][G\ = [T][A][G\,
(5-44)
(5-52)
[G]r = [Pi Р2 Рз Р4].
(5-53)
Заметим, что снова (см. разд. 5-3 и уравнение (5-22)) результат имеет вид
произведения матрицы интерполяционных функций и геометрической матрицы.
Интерполяционные функции [F] = [Т][А] показаны на рис. 5-20. Реализация алгоритма
очень проста. Рассмотрим подробности на примере.
Пример 5-5 Параболическая интерполяция
Рассмотрим снова четыре вектор-точки Pi[0 0], Рг[1 1], Рз[2 — 1] и
Pi[3 0] из предыдущих примеров 5-2 и 5-3 (см. рис. 5-21). Найти
параболическую интерполяцию между Рг и Рз. Вычислить промежуточные точки
при t = 1/3, 2/3.
Из уравнений (5-44), (5-52) и (5-53) для t = 1/3 получаем
с(1\ = П\\±. I I
\3J \2J [27 9 3
- \i i
-1
2
-1
0
3
-5
0
2
-3
4
1
0
1 1
-1
0
0
Г °
1
2
3
0
1
-1
0
Аналогично при t = 2/3 имеем С(2/3) — [5/3 — 4/9]. Полученная кривая
изображена на рис. 5-21.
0.4
J0FA
10F.
-1
Рис. 5-20 Весовые функции для параболически интерполированных кривых в случае
а = /3 = 0.5.
-1 -
Рис. 5-21 Параболически интерполированная кривая для примера 5-5.
5-7 ОБОБЩЕННАЯ ПАРАБОЛИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
В примере параболической интерполяции в разд. 5-6 предполагается, что
параметры г и s в точках Pi и Рз, соответственно, равны 1/2. Если данные распределены
неравномерно, кривая становится менее гладкой. Более общим предположением
была бы нормализованная хордовая аппроксимация. Пусть
а —
1[Р2] - [Pill
13 =
|[Рз]-[Р2]| + |[Р2]-[Р1]Г
|[Рз]-[Р2]|
|[Р4]-[Рз]| + |[РзЫР2]Г
Тогда уравнения (5-46) принимает вид
О < а < 1,
0</3< 1.
(5-54)
(5-55)
К0) = Рь
9(0) = Р2)
С(0)=Р2,
Р(о) = Р2,
<г(/3) = Р3,
Р(1) = Рз,
?(1)=Р4,
С(1) = Рз.
(5-56а)
(5-56Ь)
(5-56с)
В этих предположениях получаем линейные выражения r(t) и s(t) (см. (5-47))
r(t) = (1 - a)t + a,
Из уравнений (5-42) и (5-56а)
s(t) = 0t.
(5-57)
'l
\
\
=
0 0 1
а2 а 1
1 1 1
[В] = [М][В]
Отсюда
[В] = [М]
-1
"Pi'
р2
Рз
=
1_
-(1+в)
а
1
-1
а(1-а)
1
о(1-о)
0
1
1-а
—а
1-а
0
Pi
р2
Рз
(5-58)
Аналогично
Вспомним уравнение (5-41) и подставим уравнения (5-58) и (5-59):
C(t) = (1 -"<)[{(! -a)t + a}2 {l-a)t + a l] x
1
-1
1
а а(1 — a) 1 — а
-(1 + а) 1 -а
а а(1 — а) 1 — а
1 0 0
Pi
Р2
Рз
+
+ t[(0t)2 0t l]
-1
/3 /3(1-/3) 1-/3
-q + fl i -/?
/3 /3(1-/3) 1-/3
1 0 0
-Г2
Рз
p4
Так же, как в предыдущем разделе, это можно записать в матричном виде
C(t) = [t3 t2 t l][A][G\-[T][A][G\,
(5-44)
где
[A] =
-(1-a)2 (l-a)+a/3
a
2(1 - a)2
a
-q-g)2
a
0
-(1-a)-a/3
a 1-/3
-2(1 - a) - a/3 2(1 - a) - /3(1 - 2a)
a
(1 ~ 2a)
a
1
(1-/3)
a
0
/32
1-/3
0
0
(5-60)
и опять
[G\T = [Pl P2 P3 P4],
(5-53)
Fl{t) = (±—E¥{-t3 + 2t2-t),
a
Fa (0 = KlzfO+M,. + [-2d-g)-^ + (L^2o)f + lt
a
m = КГ-аНаД,, + [2(l-a)-/3(l-2a)]t2 +
1 — p a
(5-61a)
(5-61b)
(5-61c)
(5-61d)
Ha рис. 5-22 изображены интерполяционные функции Р»(£) для частного
случая /3 = 1 — а, т.е. когда длина хорды от Pi до.Рг равна длине от Рз до Pj:
i[p2-Piii = т-щ.
Рассмотрим это на примере.
Пример 5-6 Обобщенная параболическая интерполяция
Снова рассмотрим данные из предыдущего примера (рис. 5-22). Найти
параболическую интерполяцию между Рг и Рз в обобщенной формулировке.
Вычислить промежуточные точки при t = 1/3, 2/3.
Найдем а и /3 из уравнений (5-54) и (5-55):
С21 = |[Рг] - [Pi]\ = V(s2-si)2 + (j/2-J/i)2 =
= V(i - о)2 + (1 - о)2 = ^,
сз2 = |[Л>] - [Р2]\ = л/(хз - х2)2 + (г/з - г/г)2 =
= 7(2 - D2 + (-1 - I)2 = А
С4з = |[А] - [Рз]| = V(^4 - х3)2 + (г/4 - г/з)2 =
= ч/(3 - 2)2 + (0 + I)2 = л/2.
Итак,
С21
л/2
/9 =
С32 + С21
С32
V5 + V2
С43 + С32 у/2 + л/5
= 0.387,
= 0.613.
Заметим, что /9 = 1-
• а
Из уравнения (5-60)
[Л] =
Г -0.969
1.937
-0.969
0
2.194
-3.775
0.581
1
-2.194
2.806
0.387
0
0.969
-0.969
0
0
и из уравнения (5-44)
Г °
1
2
L 3
0 ]
1
-1
о J
= [1.360 0.496].
Аналогично, при t = 2/3, (7(2/3) = [1.640 - 0.496]. На рис. 5-23
изображена получившаяся кривая, а также кривые из примера 5-5. Заметен
большой изгиб около заданных точек
На рис. 5-24 показана локальная коррекция параболически
интерполированных кривых. Здесь имеется 11 заданных точек, или радиус-векторов, и 9
параболических составных сегментов. Центральная точка располагается в трех
положениях. Заметим, что влияние перемещения этой точки на форму кривой
ограничивается ±2-я сегментами.
-1 -
(о)
0«= 0.9
^^"^^ч
аз
Об
i
аэ
i"^i
IX» I
W
1Я I
(с)
W)
Рис. 5-22 Обобщенные параболические весовые функции, а = 1 — /?. (a) Fi; (b) F2;
(с) F3; (d) F4.
Рис. 5-23 Сравнение результатов параболической интерполяции, (а) Пример 5-5, а
Р = 1/2; (&) Пример 5-6, а = 1 - /9.
У+
2 -
OA-i
02468
Рис. 5-24 Локальная коррекция параболически интерполированных кривых.
5-8 КРИВЫЕ БЕЗЬЕ
До сих пор мы обсуждали, как провести кривую через заданное множество
точек. Рассмотренные методы во многих случаях дают прекрасные результаты и
особенно удобны при описании формы, основа которой получена с помощью
экспериментов или математических расчетов. Это, например, крыло самолета,
составные части мотора, механические и структурные детали. Существует, однако,
и другой класс задач, когда решение зависит как от функциональных, так и от
эстетических требований, например дизайн поверхности машины, фюзеляжа
самолета, формы корабля, мебели или посуды. Кроме количественных критериев
здесь требуется учет практического опыта, и часто необходимо интерактивное
вмешательство разработчика.
Рассмотренные выше методы, в частности кубические сплайны, неудобны для
интерактивной работы. Направление и величина касательных не дают
необходимого интуитивного представления о кривой, так как неочевидна связь между
набором чисел и формой соответствующей кривой.
Пьер Безье предложил другой метод создания кривых и поверхностей любой
формы. Безье вывел математическую основу своего метода из геометрических
соображений [5-11] — [5-13], но в работах [5-14] и [5-15] показано, что его результат
эквивалентен базису Бернштейна или функции полиномиальной аппроксимации.
я,
*2
Рис. 5-25 Кривая Безье и определяющие ее точки.
Кривая Безье задается многоугольником, как показано на рис. 5-25. Так как
базис Безье является бернштейновским, сразу же'известны некоторые свойства
кривых Безье. Например:
Функции базиса вещественны.
Степень многочлена, определяющего участок кривой, на единицу меньше
количества точек соответствующего многоугольника.
Основа формы кривой повторяет очертания многоугольника.
Первая и последняя точки кривой совпадают с соответствующими точками
определяющего многоугольника.
Векторы касательных в концах кривой по направлению совпадают с первой и
последней сторонами многоугольника.
Кривая лежит внутри выпуклой оболочки многоугольника, т. е. внутри самого
большого многоугольника, построенного по заданным точкам. На рис. 5-25
выпуклая оболочка обозначена штриховой и тонкой линиями.
Кривая обладает свойством уменьшения вариации. Это означает, что кривая
пересекает любую прямую линию не чаще, чем определяющий многоугольник.
Кривая инвариантна относительно аффинных преобразований.
На рис. 5-26 показано несколько четырехточечных многоугольников Безье и
соответствующих кривых. На основе перечисленных выше свойств можно легко
научиться предсказывать форму кривой по виду многоугольника.
Математическое параметрическое представление кривой Безье имеет вид
п
P(t) = Y,BiJn№, 0.<t<l, (5-62)
i=0
где базис Безье или Бернштейна, или функция аппроксимации
•М*) = (")*Ч1-*)"-' (5-63)
Рис. 5-26 Многоугольники Безье для кубических кривых.
Jn,i(t) —это г-я функция базиса Бернштейна порядка п. Здесь га — порядок
определяющей функции базиса Бернштейна — и, следовательно, сегмента
полиномиальной кривой, на единицу меньше количества точек определяющего
многоугольника. Как показано на рис. 5-25, вершины многоугольника Безье нумеруются от
О до га1. Поэтому (0)° = 1 и 0! = 1.
На рис. 5-27 изображены аппроксимирующие функции для разных значений га.
Заметим, что функции симметричны. Каждая функция имеет порядок п,
например все четыре функции на рис. 5-27Ь для га = 3 кубические, Максимум каждой
функции достигается при t = г/п и равен (5-14)
/г'\ _ /п\ г'г(п-г')"~*
(5-65)
1 Обозначения и отсчет выбраны в соответствии с традициями, принятыми в литературе по
кривым Безье и базису Бернштейна. Для программирования удобнее другое представление
N
1=1
где
(7-•') -
(JV - 1)8
(I-l)\(N-iy/
Точки многоугольника нумеруются от 1 до N. Для перехода к этим обозначениям положим
п=ЛГ-1иг = /-1.
(с)
(«О
Рис. 5-27 Весовые функции Безье/Бернштейна. (о) Многоугольник из трех точек, п ■
2; (6) из четырех точек, п = 3; (с) из пяти точек, п = 4; (d) из шести точек, и = 5.
Например, для кубической кривой п — 3. Максимум Js,i и 7з,2 достигается в
1/3 и 2/3, соответственно, и имеет значения
-73-1 G)=I и -^ (I)=J-
Рисунок 5-27Ь иллюстрирует этот пример.
Рассмотрим уравнения (5-62) и (5-64) для первой точки на кривой, т. е. при
t = О
п!(1)(1-0)"-°
Л.,0(0) = -; = 1,
= 0,
п!(0)'(1-0)"-'
Итак,
P(0) = BoJ„,o(0) = Bo,
первая точка кривой совпадает с первой точкой многоугольника.
Аналогично, для последней точки кривой, т. е. при t = 1
п!(1)"(0)"~" _
J"'"(1) = п!(1) ~ 1j г = "'
J"-'(1) = i!(^b)!ii(1 - ir_i = °' {фп-
Итак,
Р(1) = BnJB,„(l) = Вп
и последняя точка на кривой Безье совпадает с последней точкой определяющего
многоугольника.
Далее, можно показать, что для любого значения параметра t сумма базисных
функций равна 1, т.е.
п
]Г Jn,i(t) = 1. (5-66)
i=0
Рассмотрим метод построения Безье на примере.
Пример 5-7 Кривая Безье
Пусть заданы вершины многоугольника Безье Во[1 l],Bi[2 3], Вг[4 3]
и Вз[3 1]. Найти семь точек, лежащих на кривой Безье.
Рассмотрим уравнения (5-62) — (5-64):
п
P(t) = ^BiJ„,i(t)!
i=0
где
и
( п\ п!
V * / г!(п-г)
как имеется четыр
\ i ) = \ i ) = г!(3 - 1)!
г)!'
В нашем случае п = 3, так как имеется четыре вершины. Отсюда
Итак,
J3,o(t) = (l)t°(l-t)3 = (l-t)3,
J3,i(t) = 3*(l-t)2,
J3,2(t)=3t2(l-t),
P(t) = B0J3,o + BiJ3,i + B2J3,2 - B3J3.3
= (1 - t)3P0 + 3t(l - tfPx + 3t2(l - t)P2 + t2P3.
Таблица 5-4 Коэффициенты для кривой
Безье
t
0
0.15
0.35
0.5
0.65
0.85
1
J3,0
1
0.614
0.275
0.125
0.042
0.003
0
Лд
0
0.325
0.444
0.375
0.239
0.058
0
■^3,2
0
0 058
0.239
0.375
0 444
0.325
0
■^3,3
0
0.003
0.042
0.125
0.275
0.614
1
2-
_1_
О 2
Рис. 5-28 Сегмент кривой Безье, пример 5-7.
Значения Jn,i для различных значений t приведены в табл. 5-4.
Точки на кривой:
Р(0)=Во = [1 1],
Р(0.15) = 0.614-Во + 0.325Bi + 0.058Р2 + О.ООЗВз = [1.5 1.765],
Р(0.35) = 0.275Во + 0.444Bi + 0.239Р2 + 0.042В3 = [2.248 2 367],
Р(0.5) = 0.125В0 + 0 375Р! + 0.375В2 + 0.125Р3 = [2.75 2.5],
Р(0.65) = 0.042Ро + 0.239Pi + 0.444В2 + 0.275Р3 = [3.122 2.367],
Р(0.85) = 0 ООЗРо + 0.058Pi + 0.325В2 + 0.614Р3 = [3.248 1.765],
Р(1) = В3 = [3 1].
Эти точки показаны на определяющем многоугольнике на рис. 5-28.
Уравнение кривой Безье можно записать в матричном виде, так же как
уравнения для кубических сплайнов и параболической интерполяции (см. уравнения
5-27 и 5-44):
P(t) = [T][N][G] = [F][G].
(5-67)
Здесь [F] = [Jn>0 J„,x ••• J„,„] и [G]T = [B0 Вг ■■■ Bn].
Особенный интерес представляют матричные формы для малых значений п.
Для многоугольника из четырех точек (п = 3) кривая Безье имеет вид
P(t) = [(l-t)3 3t(l-t)2 3t2(l-t) t3}
Группируя коэффициенты, получим
P(t) = [T][N][G] = [t3 t2 t 1]
'B0 '
Bi
B2
B3
-1 3-3 1
3-6 3 0
-3300
10 0 0
Bo
Bi
B2
B3
(5-68)
Аналогично, кривая Безье четвертого порядка (тг = 4), заданная
многоугольником из пяти точек:
1
-4
6
-4
1
-4
12
-12
4
0
6
-12
6
0
0
-4 1 "
4 0
0 0
0 0
0 0 .
[В0 I
Bi
в2
в3
1в4 J
P(t) = [U t3 t2 t 1]
В работе [5-19] приводится обобщенное представление:
P(t) = [T][N][G],
(5-69)
где
71-1
[N) =
[Г] = [tn t
(оЮ(-1)п (aciix-i)-1
(оНЛК-!)"-1 (т)С:5)(-1)-я
t 1],
/_i\0
GDCVK-1)0
0
о
(5-70)
Матрица [G]T — это опять [В0 В\
таковы:
Вп]. Отдельные члены матрицы [N]
0 < i + j < п,
иначе
Уравнение (5-70) можно записать в более удобном виде
[N] = [C][D],
(5-71)
где
[С] =
ГК-i)1
o)(-i)°
[D} =
(о)
о
(S)
(?)(V)(-d0
о
о
(п)
С)(П)(-1)0П
о
о
о
Уравнения (5-70) или (5-71) удобнее для расчета при больших значениях п.
Заметим, что для всех п матрица [N] симметрична относительно главной
диагонали и правый нижний угол состоит из нулей.
Для каждой отдельной кривой Безье необязательно знать касательные
векторы в ее концах, но если необходимо соблюдать непрерывность кривизны и
наклона в точках соединения кривых, рассчитывать нормали к поверхности для
освещения, вычислять локальную кривизну, то требуется знать как первую, так
и вторую производную кривой Безье.
Из уравнения (5-62) первая производная кривой Безье имеет вид:
p'w = EB^«,iW-
г=0
Вторая производная такова:
P"(t) = ЁВД',4(«).
(5-72)
(5-73)
i=0
Формально дифференцируя уравнение (5-63), получаем производные
базисных функций
■£,<(*) = (") {^i_1d - О"-*.- (п - |У (1 - 'Г-'-1}
(г — 7г*)
*(1 " *)
■МО-
(5-74)
Аналогично, вторые производные имеют вид:
\2 _ „а
^м-{('-'%У~*)}*л'>- <5-75)
В начале и конце кривой Безье, т.е. при t = 0 и t = 1, численный расчет
уравнений (5-74) и (5-75) представляет затруднения1.
Другой способ вычисления г-й производной при t = 0:
^)=^в-1)г-<(;)* о*-*»)
и при t = 1:
^> = (^D-i>'(Ofl"-" f5-"»
Отсюда первые производные в концах будут
P'(0) = n(Bi-Bo) (5-78)
и
Р'(1) = п(Вп - Bn_i). (5-79)
Это показывает, что касательные к кривой Безье в первой и последней точках
параллельны соответствующим сторонам многоугольника.
Аналогично, вторые производные в концах таковы:
Р"(0) = п{п - 1)(В0 - 2Bi + В2) (5-80а)
Р"(1) = п(п - 1)(Вп - 2Bn_! + Bn_2). (5-80b)
Вторые производные в концах зависят от двух ближайших сторон, т. е. от трех
ближайших вершин. В общем случае, г-я производная в начальной и конечной
точках зависит от этих точек и г ближайших вершин многоугольника.
Подробнее рассмотрим это на примере.
Пример 5-8 Производные кривых Безье
Рассмотрим четырехточечный многоугольник Безье, например, как на
рис. 5-26 и 5-28. Вспомним представление кривой
P{t) = B0J3,o(t) +BiJ3,i(t) + B2J3,2(t) + B3J3,3(t)-
Отсюда первая производная
P(t) = B0f3fi{t) + BiJ'3tl(t) + B2J'3,2(t) + B3J3i3(t).
1 Правильный результат получается при алгебраическом вычислении и подстановке до
численного расчета (см. пример 5-8).
Вспомним пример 5-7 и непосредственно продифференцируем базисные
функции
J3,o(t) = (l-t)3 => Ja.oCO = -3(l-t)2,
J3,i(t) = 3t(l-t)2 =► 4,iW = 3(l-t)2-6t(l-t),
J3,2(«) = 3t2(l - t) => 4,2(0 = 6t(l-t)-3t2,
Js.s(*) = *S =* 4,з(0 = 3t2
Подставим £ = 0:
4,з(о) = -з, /s,i(o) = 3, 4,2(0) = 0, 4,3(0) = 0.
Подстановка дает
P'(0) = -ЗРо + 3Pi = 3(ft - Po).
Поэтому направление касательной в начале кривой совпадает с первой
стороной многоугольника (см. рис. 5-28).
В конце кривой t = 1 и
4,o(i) = o, Ji,i(i) = o, 4,2(1) = -з, 4,з(1) = з-
Аналогично, подстановка дает
Р'(1) = -ЗР2 + ЗРз = 3(Р3 - Р2)
и направление касательного вектора в конце кривой совпадает с последней
стороной многоугольника.
Чтобы вычислить производные вдоль кривой, воспользуемся функциями
базиса и уравнениями (5-74) и (5-75):
J5.o(*) = ^^(i-03 = -3(i-*)2,
J3.1 (0 = §ГЗ§(3*)(1 -t)' = 3(1 -3t)(l - 0 = 3(1 -4t + 3t2),
4,2W = Щ^Щ&'Ш - О = 3t(2 - 3t),
■*■-<*> = §г^=*я-
Результаты легко вычисляются как для t = 0, так и для t = 1. Подставляя
в уравнение (5-72), получаем первую производную в любой точке кривой.
Например, при t = 1/2 имеем
= -|д> - f £i +1 a + |вв = -|(д> + Bi - в2 - Вз).
Результат для точек Во, Bi, B2, Вз из примера 5-7 изображен на рис. 5-29.
Рис. 5-29 Кривая Безье и ее производные: P(t); P'(t); P"(t).
Аналогично, вторые производные имеют вид:
JUt) = ^-%-^-^mi -1? = -6(2 - »),
J'Ut) =
_ {(2 - 3t)2 - 3t2 - 2(1 - 2t)} /nx2
t2{l-t)2
(3r)(l-t) = 6(l-3t),
T» m - {(3~3t)2-3t2-3(l-2t)} з _ ,.
JaAt)- t2(1_t)2 * ~6t-
Уравнение (5-73) при t = 1/2 дает
= ЗВо - 3Bi - ЗВ2 + ЗВз = 3(В0 -Bi-B2+ В3).
Иллюстрация также приведена на рис. 5-29. Заметим, что вектор из
начала координат в любую точку на каждой из кривых представляет
соответственно направление и величину радиуса-вектора и приблизительную
кривизну в этой точке на кривой.
Условие непрерывности соседних кривых Безье формулируется очень просто.
Пусть кривая Безье P(t) степени п задана вершинами Bi, а соседняя кривая
Безье Q(s) степени тп — вершинами Cj. Тогда непрерывность первой производной
в точке соединения выражается соотношением
P'(l) = gQ'(0),
Рис. 5-30 Непрерывность первой производной для кубических кривых Безье.
где д — скаляр. Пользуясь уравнениями (5-78) и (5-79), получим
С\ — Со = —(Вп — Ai-i)-
тп
Из непрерывности кривой следует, что Со = Вп и
С\ = —(Вп — Bn-i) + Вп.
тп
Отсюда направления касательных на стыке совпадают, если три вершины
Вп-\, Вп = Со, С\ коллинеарны, т.е. Вп должна лежать на линии между Вп-\
и Ci.
Если совпадают еще и величины касательных векторов, то Вп = Со является
серединой отрезка от Bn-i до С\:
С\ — Со = Вп — Вп-\ = Cq — Bn-i
или
С\ + Bn-i — 2Cq — 2Вп.
На рис. 5-30 приведена иллюстрация для п — тп — 3, т. е. для двух кубических
кривых Безье.
Условие непрерывности вторых производных между соседними кривыми:
тп(тп - 1)(С0 - 2Ci + С2) = п(п - 1)(Вп_а - 2ВП_! + Вп).
Из условий С0 и С1 непрерывности в точке соединения получаем положение
третьей определяющей вершины второго многоугольника, выраженное через три
последние вершины первого многоугольника, а именно
C2 = ^^Bn.2-2\^^ + ^)Bn.1 + {l + 2^ + ^^)Bn
тп(тп — 1) {тп(тп — 1) тп) ( тп тп[тп—1))
Это означает, что вершины Вп-2, Вп-\, Вп = Со, С\, Сг должны либо составлять
выпуклый многоугольник, либо лежать на одной прямой, чтобы сохранить С2
Рис. 5-31 Непрерывность второй производной для кривых Безье четвертой степени.
непрерывность на стыке. Для кубических кривых Безье (п = та = 3) это условие
имеет вид
Сг = -Вп_! — 4(Bn_i - Вп).
Несколько карандашных набросков на бумаге покажут, что данное требование
существенно ограничивает множество кривых; поэтому на практике для
соблюдения непрерывности вторых производных используются полиномиальные кривые
более высокого порядка. На рис. 5-31 приведен пример непрерывности вторых
производных для двух пятиточечных кривых Безье.
Если необходима более гибкая кривая Безье, увеличивается количество
определяющих точек и степень полинома. Для каждой точки на кривой Безье с п
определяющими вершинами многоугольника В0,... , Вп та же самая точка на
новой кривой Безье ся+1 определяющими вершинами Bq,... ,5*+1 задается в
виде
71 71+1
P(t) = Y^BiJn<i(t) = J2 B!Jn+Ut), (5-81)
t=0 i=0
где
B0 = Bo,
B$ = ctiBi-! + (1 - ati)Bi, ati = -, i = l,...,n,
n + 1
-Sn+i -Bn.
Здесь можно с успехом применить методику из работы [5-14] . В предельном
случае многоугольник сходится к кривой. Дополнительную гибкость кривой можно
также получить разбиением кривой Безье на две новых таким образом, чтобы они
вместе совпадали с исходной кривой. В работах Барского [5-16, 5-18] было
показано, что любая кривая Безье может быть разбита с использованием произвольного
параметра в диапазоне 0 < t < 1. Простейший случай —это средняя точка, т.е.
t = 1/2 (см. [5-18]). При разбиении средней точкой получаются два специальных
вида кубических кривых Безье.
Кубическая кривая Безье (см. упражнение 5-7) задается в виде
P(t) = (1 - t)3B0 + 3t(l - t)2Bi + 3t2(l - t)B2 + t3B3, 0 < t < 1.
с определяющими вершинами Bo,Bi,B2, B3. Тогда многоугольник Co,Ci,C2,C3
определяет кривую Безье Q(u), 0 < и < 1, соответствующую первой половине
исходной кривой, а именно P(t), 0 < t < 1/2, как и требовалось. Подобным
образом, многоугольник Do,Di,D2,D3 определяет кривую Безье R(v), 0 < v < 1,
соответствующую второй половине исходной кривой, т.е. P(t), 1/2 < t < 1, как
и требовалось. Новые определяющие вершины многоугольника Сг и Бг
получаются путем приравнивания радиус-векторов и касательных векторов при и = О,
t = 0; и = 1, t = 1/2 и v = 0, t = 1/2; v = 1, t = 1. Из соотношений (5-62) и
(5-72) получаем
Со = Во,
3(C1-C0) = ^(Bi-Bo),
з
3(Сз — Сг) = д(^з + В2 — В\ — Во),
С3 = -(В3 + ЗВ2 + ZBi + Во).
о
Решение этих уравнений дает
Со = В0,
Сх = \{Вх + Во),
C2 = -(B2 + 2Bi+Bo),
С3 = -(В3 + ЗВ2 + 3Bi + В0).
о
Аналогично,
Do = - (В3 + ЗВ2 + ЗВ! + Во),
О
£»1 = ^(В3 + 2В2 + В1),
D2 = -(B3 + B2),
D3=B3.
Эти результаты обобщаются до
С« = ЕС)|г' < = 0,1,...,п,
^=е(;:;)#т- *=о,1,...,п
Дальнейшее применение определяющих многоугольников с помощью кривой Бе-
зье оставляем для самостоятельной работы.
5-9 В-СПЛАЙНЫ
С математической точки зрения кривая, заданная вершинами многоугольника,
зависит от интерполяции или аппроксимации, устанавливающей связь кривой и
многоугольника. Здесь основой является выбор базисных функций. Как было
отмечено в разд. 5-8, базис Бернштейна порождает кривые Безье вида (5-62), но он
обладает двумя свойствами, которые ограничивают гибкость кривых. Во-первых,
количество вершин многоугольника жестко задает порядок многочлена.
Например, кубическая кривая должна быть задана четырьмя вершинами и тремя
отрезками. Многоугольник из шести точек всегда порождает кривую пятого порядка.
Единственный способ понизить степень кривой —это сократить количество
вершин, а повысить степень кривой — увеличить их число.
Второе ограничение следует из глобальной природы базиса Бернштейна. Это
означает, что величина аппроксимирующих функций Jn,i{t) из уравнения (5-
63) ненулевая для всех значений параметна на кривой. Любая точка на кривой
Безье зависит от всех определяющих вершин, поэтому изменение какой-либо
одной вершины оказывает влияние на всю кривую. Локальные воздействия на
кривую невозможны.
Например, так как наклон концов кривой Безье задан соответствующими
сторонами многоугольника, можно передвинуть среднюю вершину пятиточечного
многоугольника, не меняя направления на концах. Однако из-за глобальности
базиса Бернштейна меняется форма всей кривой. Отсутствие локальной коррекции
может оказаться решающим в некоторых прикладных задачах.
Существует неглобальный базис, называемый базисом В-сплайна,
включающий базис Бернштейна как частный случай. В-сплайны неглобальны, так как с
каждой вершиной Bi связана своя базисная функция. Поэтому влияние каждой
вершины на кривую проявляется только при тех значениях параметра, где
соответствующая базисная функция не равна нулю. Базис В-сплайна также позволяет
менять порядок базисных функций и, следовательно, всей кривой без изменения
количества вершин. Теория В-сплайнов была предложена в работе [5-20].
Рекурсивное определение для численного решения было выведено независимо Коксом
[5-21] и де Буром [5-22]. Гордон и Ризенфельд [5-15], [5-23] определяли кривые
через базис В-сплайна.
(5-82а)
(5-82Ь)
Пусть P(t) определяет кривую как функцию от параметра t, тогда В-сплайн
имеет вид
п+1
P{t) = Y,BiNi,k(t)t t
min 2 < fc < n + 1, (5-83)
i=l
где Bi есть n + 1 вершина многоугольника, a Ni^ — нормализованные функции
базиса В-сплайна.
Для г-й нормализованной функции базиса порядка fc (степени fc — 1) функции
базиса Nitk(t) определяются рекурсивными формулами Кокса—де Бура:
Nti{t) = l l 6СЛИ x'^t<x™ (5-84a)
• v ' \ 0 иначе v '
N {t) = (t-XiW^t) + (*i+k-t)NiW(t)
^t+Jfe-l - ^i Xi+k - Xi+i
Величины Xi — это элементы узлового вектора, удовлетворяющие отношению
х^ < Xj+i- Параметр t изменяется от tm\n до tmax вдоль кривой Pit)1. Считается,
что 0/0 = 0.
Формально В-сплайн определяется как полиномиальный сплайн порядка к
(степени fc — 1), так как он удовлетворяет следующим условиям:
Функция P(t) является полиномом степени fc — 1 на каждом интервале ц <
t < Xi+l-
P(t) и ее производные порядка 1,2,..., fc — 2 непрерывны вдоль всей кривой.
Так, например, В-сплайн четвертого порядка — это кусочная кубическая
кривая.
Из того что В-сплайн задается базисом В-сплайна, сразу следует еще
несколько его свойств:
Сумма базисных функций В-сплайна для любого значения параметра t (см.
работы [5-15] и [5-22])
п+1
£>i>fc(t) = l. (5-85)
г=1
Каждая базисная функция положительна или равна нулю для всех значений
параметра, т. е. iVi|fc > 0.
Кроме fc = 1, все базисные функции имеют ровно один максимум.
Максимальный порядок кривой равен количеству вершин определяющего
многоугольника.
Кривая обладает свойством уменьшения вариации. Кривая пересекает любую
прямую не чаще, чем ее определяющий многоугольник.
1 Отметим, что в отличие от кривых Беэье вершины определяющего многоугольника
нумеруются от 1 до п + 1.
Общая форма кривой повторяет форму определяющего многоугольника.
Чтобы применить к кривой любое аффинное преобразование, необходимо
применить его к вершинам определяющего многоугольника.
Кривая лежит внутри выпуклой оболочки определяющего многоугольника.
Последнее свойство В-сплайна сильнее, чем у кривых Безье. У В-сплайна
порядка к (степени к — 1) точки кривой лежат внутри выпуклой оболочки к
соседних точек. Таким образом, все точки на В-сплайне должны лежать внутри
объединения всех выпуклых оболочек к последовательных вершин. На рис. 5-32
приводится иллюстрация для различных значений к, причем выпуклые оболочки
выделены серым цветом. В частности, при к = 2 выпуклая оболочка совпадает с
многоугольником, т. е. В-сплайн — это сам многоугольник.
С помощью свойства выпуклой оболочки легко показать, что если все точки
многоугольника коллинеарны, то соответствующий В-сплайн — прямая линия для
всех к. Далее, если в неколлинеарном определяющем многоугольнике
встречаются / коллинеарных вершин, то прямые участки кривой (если они есть) начинаются
и кончаются по крайней мере за к — 2 отрезка от начала и конца серии
коллинеарных вершин. Если последовательность коллинеарных вершин полностью лежит
внутри неколлинеарного многоугольника, число коллинеарных участков кривой
не меньше, чем / — 1к + 3. Если же эта последовательность находится на
конце неколлинеарного многоугольника, то число коллинеарных участков кривой не
меньше I — к + 1. Иллюстрация приведена на рис. 5-33.
Если имеется к — 1 совпадающих вершин, т. е. Bi = Bi+i = ■ ■ ■ = Bi+k-2, то
выпуклая оболочка вершин от В, до Bi+k-2 — это сама вершина. Отсюда следует,
что В-сплайн должен проходить через вершину Bi. На рис. 5-34 изображен пример
такой точки для к = 3. Далее, так как В-сплайн везде Ск~2 непрерывен, он также
Ск~2 непрерывен в Bi.
Наконец, заметим, что свойство непрерывности плавно переводит В-сплайн во
вложенные отрезки прямой, как показано на рис. 5-35.
Уравнения (5-84) указывают, что выбор узлового вектора оказывает
существенное влияние на базисные функции В-сплайна TVj^i) и, следовательно, на
сам В-сплайн. Единственное требование к узловому вектору: Xi < Xj+i, т.е. это
монотонно возрастающая последовательность вещественных чисел. Обычно
используются три типа узловых векторов: равномерные, открытые равномерные
(или открытые) и неравномерные.
Отдельные узловые значения равномерного узлового вектора распределены
на одинаковом расстоянии, например
[01234]
[-0.2 -0.1 0 0.1 0.2]
В частности, равномерные узловые векторы обычно начинаются в нуле и
увеличиваются на 1 к некоторому максимальному значению или нормируются в диапазоне
между 0 и 1 равными десятичными значениями, например,
[0 0.25 0.5 0.75 1.0].
* = 2
*=3
* = 4
* = 6
* = 8
Рис. 5-32 Свойства выпуклой оболочки В-сплайнов.
Кояинеарные сегменты кривой
к— Колинеарные вершины многоугольника
*=3
(а)
U—Колинеарные вершины многоугольника —J
[•—Колинеарные сегменты кривой —А
*=3
Ф)
Рис. 5-33 Свойства выпуклой оболочки В-сплайнов для коллинеарных сегментов
кривой, (о) Внутренние вершины определяющего многоугольника; (6) вершины в конце
определяющего многоугольника.
Для данного порядка к равномерные узловые векторы порождают периодические
равномерные функции базиса, для которых
Nitk(t) = Ni-ltk(t - 1) = Ni+1>k(t + 1).
То есть каждая функция базиса—это параллельный перенос другой функции,
см. рис. 5-36.
У открытого равномерного узлового вектора количество одинаковых
узловых значений в концах равно порядку к базисной функции В-сплайна.
Внутренние узловые значения распределены равномерно. Несколько примеров с целыми
Рис. 5-34 Выпуклая оболочка для кратных вершин, к = 3.
Рис. 5-35 Плавное (С ) превращение в отрезки прямой.
Рис. 5-36 -Базисные функции периодического равномерного'' В-сплайна, [X]
[О 1 2 3 4 5 6], п + 1 = 4, к = 3.
приращениями:
к = 2 [0 0 1. 2 3 4 4],
* = 3 [0 0 0 1 2 3 3 3],
к = А [0 000 1222 2]
Рис. 5-37 Базисные функции открытого равномерного В-сплайна, [X] =
[О 0 0 1 2 2 2], к = 3, п + 1 = 4.
или для нормализованных приращений
А; = 2 [0 0 1/4 1/2 3/4 1 1],
к = 3 [0 0 0 1/3 2/3 1 1 1],
А: = 4 [0 0 0 0 1/2 1111].
Формально открытый равномерный узловой вектор определяется как
Xi = 0 1 < г < к
Х{= г — к к+1 <i <п + 1
ц=п-к+2 n+2<i<n+k+l
Получающиеся базисные функции ведут себя примерно так же, как и
кривые Безье. Фактически, если количество вершин многоугольника равно порядку
базиса В-сплайна и используется открытый равномерный узловой вектор, базис
В-сплайна сводится к базису Бернштейна. Отсюда В-сплайн является кривой
Безье. В этом случае узловой вектор —это просто к нулей, за которыми следует к
единиц. Например, для четырех вершин открытый равномерный узловой вектор:
[00001111].
В результате мы имеем кубическую кривую Безье — В-сплайн.
Соответствующие базисные функции изображены на рис. 5-27Ь. На рис. 5-37 приведен еще
один пример открытых базисных функций.
Неравномерные узловые векторы отличаются тем, что их внутренние узловые
величины располагаются на разном расстоянии друг от друга и/или совмещаются.
Векторы могут быть периодическими или открытыми, например
[00011222],
[012234],
[0 0.28 0.5 0.72 1].
На рис. 5.38Ь-е показаны примеры неравномерных базисных функций В-
сплайна порядка к = 3. У соответствующих узловых векторов на концах
находится по к совмещенных одинаковых значений. Для сравнения на рис. 5-38а
приведены базисные функции для открытого равномерного вектора. Отметим,
что на рис. 5-38а и b функции симметричны, а также что у неравномерных
базисов симметрия нарушается: 5-38с-е. Кроме того, при совмещенных узловых
значениях у одной из функций появляется излом. На рис. 5-38d и е видно, что
положение излома зависит от расположения совмещенного значения в узловом
векторе.
Формула Кокса-де Бура (5-84) для расчета базисных функций В-сплайна
рекурсивна, поэтому функция порядка к зависит от базисных функций более
низкого порядка вплоть до 1. Пусть дана базисная функция Л^,*. Тогда эту зависимость
можно выразить в виде треугольника
Nlik
iVlifc_i JVl+i,fc_2 Nl+2,k-2
JV.,1 JVi+i,i Ni+2,i JV.+3.1 • iVi+fc-i.i
Тогда обратная зависимость, т.е. влияние одной базисной функции первого
порядка iVj,i на функции более высоких порядков, такова:
Ni-k+i,k • -Ni+it-i,*; Nt<k Ni+itk • Nt+k-i,k
N,-1,2 Nt>2 Nl+1>2
Рассмотрим пример расчета базисных функций.
Пример 5-9 Расчет периодических базисных функций
Найти четыре базисные функции Nt,a(t), г = 1,2,3,4, третьего порядка
(к = 3). Число п+1 в данном случае равно 4. Зависимость базисных функций
для 7Vt|3 изображается следующей диаграммой.
Ni,3 N2,3 N3,3 N4,3
N1,2 N2,2 N3,2 N4,2 N5,2
N1,1 N2,1 N3,1 N4,1 N5,1 N6,i
Рис. 5-38 Функции неравномерного базиса для п + 1 = 5, к = 3.
(а)[Х] = [0 0 0 1 2 3 3 3];
(Ь) [X] = [0 0 0 .4 2.6 3 3 3];
(с)[Х] = [0 0 0 1.8 2.2 3 3 3];
(d)[X] = [0 0 0 1 1 3 3 3];
(е) [X] = [0 0 0 2 2 3 3 3].
Обратные зависимости для г > 1:
Ni,3 N2,3 N3,3 N4,3 N5,3 Ne,3
N1,2 N2,2 N3,2 N4,2 N5,2
N1,1 N2,1 N3,1 N4,1
Каков диапазон узлового вектора, необходимый для этого расчета? Из
уравнения (5-84) следует, что для вычисления Ne,i необходимы узловые величины
хв и Х7, а для N\,i — xi и Х2, т. е. необходимы значения от 0 до п + к. Отсюда
количество узловых значений равно п + к + 1. Узловой вектор для заданных
периодических функций:
[X] = [0 1 2 3 4 5 6],
где xi = 0,... ,Х7 = 6. Диапазон параметра 0 < t < 6. Используя
уравнение (5-84) и приведенные выше диаграммы, получим базисные функции для
различных значений параметра:
О < * < 1
Ni,i(t) = l; Ni,i(t) = 0, i^l
ATi,a(t) = t; Nil2(t) = 0, i#l
Ni.s(t) = y; ЛГ4,в(*) = 0, i#l
1 < t < 2
JVa>I(t) = l; M,i(t) = 0, г #2
JVi,a(t) = (2-t); Na.a(t) = (t-1); Ni,a(t) = 0. * # 1,2
M.s(t) = |(2-t)+(^L*)(t-l);
ATa.s(t)= (*~Х) ; JV<lB = 0, i #1,2,3
2 <t<3
ATSli(t) = l; ЛГ<,,(*) = 0, г#3
Na,a(t) = (3-t); JVB>a(t) = (* - 2); AT,,2(t) = О, г #2,3
^a,3,W=(f-1)2(3-f) + (4-^-2);
N3,3(t) = ^¥-\ Ni,3(t) = 0, i #1,2,3
3<t<4
ЛГ«,1(*) = 1; ЛГ4,1(0 = 0, г#4
ЛГв,а(0 = (4-*); Ar«,a(0 = (*-3); JVil2(t) = 0, г #3,4
N m-(4"f)2- ЛГ /,ч_(*-2)(4-*) , (5-t)(t-3).
JV2,3(t) = —g ' ^,3(1) j h 2 '
N4.s(t) = ^Ц^; M.s(t) = 0, i# 2,3,4
4 <t< 5
jVb.i(*) = 1; Ni,i{t) = 0, 1фЪ
ЛГ4,2(0 = (5-*); A^,j(t) = (*-4); Nifi{t) = 0, г #4, 5
(t-3)(5-t) (6-t)(t-4).
^4.8(t) - J + ,
Ni,3(t) = 0, iфЗ,A
5 < i < 6
JVe>1(t) = l; Nt,i(t) = 0, 1ф6
N5,2(t) = (6-t); M,a(t) = 0, i^5
Знак < в определении Л^д приводит к тому, что при t = 6 все функции
равны 0.
Результаты показаны на рис. 5-36 и 5-39с. Отметим, что каждая из
базисных функций является кусочной параболической (квадратичной) кривой.
Параболические сегменты на интервалах ц —> Xi+i, Xi+i —> Z:+2, Z:+2 —> Xi+з
объединяются и составляют базисные функции Л^,з- Каждая функция
представляет собой параллельный перенос другой.
Пример 5-9 показывает, как построить базис N по функциям базиса более
низкого порядка. На рис. 5-39а изображены функции первого порядка из примера
5-9, на рис. 5-39Ь — второго порядка, и на рис. 5-39с — третьего порядка.
Обратим внимание на то, как растягивается диапазон ненулевых значений функций с
увеличением их порядка. Говорят, что функция базиса обеспечивает поддержку
на интервале от Xi до Хг+к-
Внимательно рассматривая рис. 5-36, можно заметить важное свойство
функций равномерного базиса. Из уравнения (5-85) известно, что J2Ni,k(i) = 1 для
любого значения параметра t. Отсюда следует, что все множество
периодических базисных функций для к = 3 определено только в диапазоне 2 < t < 4.
За его границами $2iVi,fc(i) Ф 1- Для равномерного начинающегося с 0 узлового
вектора с целыми приращениями пригодный диапазон параметра: к — 1 < t <
(п + к) — (к — 1) =п+1. Для более общих или нормализованных векторов
сокращение диапазона параметра соответствует потере к — 1 интервала узловых
значений на каждом конце вектора.
'■№..
ОПИВ I i L.
0 2 4
-*■ Г
ЛГ,
2.1
' ' » l_
N,
3.1
-►f
Na
4,1
J l_
\N,
J l_
(A)
■* Г
0
Ir
0
lr
N,
-I I L.
2 4
*2,2
2 4
4 -f
J 1 ► /
4.2
4
— r
tf,
3.2
Рис. 5-39 Построение периодических базисных функций п+1 = 4. (a) fc = 1; (b) fc = 2;
(с) fc = 3.
Пример 5-10 Расчет открытого равномерного базиса
Найти четыре (п = 3) базисные функции Nil3(t), i = 1,2,3,4, третьего
порядка (к = 3).
Напомним, что формально открытый узловой вектор с целыми
интервалами между внутренними узловыми значениями определяется как
Xi = 0, 1 < i < к,
х; = г — к, fc + l<i<n + l,
ц =п- к + 2, n + 2<i<n + k + l.
Диапазон изменения параметра 0 < t < п — к + 2, т. е. от 0 до
максимального узлового значения. Как и в примере 5-9, количество узловых значений
равно 71 + к + 1. Если брать узловые значения, то вектор для данного
примера примет вид
[X] = [0 0 0 1 2 2 2],
где х\ = 0,... ,хт = 2. Параметр t изменяется от 0 до 2.
Пользуясь уравнениями (5-84) и диаграммами зависимости, получаем
функции базиса для различных диапазонов параметра:
О < t < 1
N3A(t
N2<2(t
Ni,3(t
l<t<
^3,2 (*:
N2,3(t
N4,3 (*:
= 1; Mll(t) = 0, i^3
= l-t; N3,2{t) = t; Ni,2{t) = 0, i?2,3
= (l-t)2; N2,3(t)=t{l-t) + ¥^lt;
= ji Ni.s(*) = 0, 1ф 1,2,3
= 1; ЛГм(*) = 0, i^4
= (2-t); АГ4,а(*) = (*-1); Nit2(t) = 0, i ^3,4
= <Ц£; №,(0 = ^f^ + (2-0(*-Di
= (t-l)2; Nit3(t) = 0, i^2,3,4.
Эти результаты приведены на рис. 5-40.
Сравнивая результаты примера 5-10 (рис. 5-40) и 5-9 (рис. 5-39), мы видим,
что они существенно различаются для периодического и открытого равномерного
узловых векторов. В частности, отметим, что у открытых равномерных узловых
векторов на всем диапазоне изменения параметра определен полный набор
базисных функций; т.е. $2-ЭД,*(*) — 1 Для всех 0 < t < п — к + 2. У периодического
вектора диапазон параметра уменьшается.
N,
N,
1.2
-f 0
2 0
к"1.3
2 W0
W,
2.1
2 0 2 0
Ъ
4.1
*,
'5.1
N*
2 0 2 0 2
(c)
N.
5.2
_L.
"' °0 2
(ft)
0 2
(a)
Рис. 5-40 Построение открытых базисных функций п + 1 = 4. (о) А; = 1; (Ь) fc = 2; (с)
fc = 3.
Пример 5-11 Расчет неравномерных базисных функции
Найти пять (п+1 = 5) базисных функций Ni^it), г = 1, 2, 3,4, 5, третьего
порядка (А; = 3) с узловым вектором [X] = [0 001133 3],
содержащим повторяющееся внутреннее узловое значение. Из уравнений (5-84) и
диаграмм зависимости
0 < t < 1
Na,i(t) = l; Ni,i(t) = 0, 1ф2
N2,2{t) = \-t; N3,2{t)=t; Ni,2(t)=0, i #2,3
Ni,t(t) = (1 - *)2; ^а.з(*) = *(1 - *) + (1 - *)* = 2*(1 - *);
N3,3(t)=t2; Nt,a{t) = 0, i # 1,2,3
1 < * < 1
JVi,i(t) = 0. все г
Ni,2(t) - 0, все г
Ni,3(t) = 0, все г.
В частности, как следствие повторения узлового значения, N4,i(t) = 0
для всех t.
1 < * < 3
JVB,i(t) = 1; JVi,i(t) = 0, г #5
ЛЫ*) = *Ц^; WB,2(t) = ^^; ЛГ4,а(0 = 0, г #4,5
^з.з (*) =
2 ' '"•-^' 2
(з-о2.
4 '
#„,,(*) = С"1)^-') + (3-«)(«-!) = (3-р(«-1).
JVs.a(t) = ^"^ ; ^,з(*) = 0, i#3,4,5.
Результат приведен на pnc.5-38d.
Заметим, что для всех значений t имеем ^2Ni,k(t) = 1.0. Например, для
0 < t < 1,
5
53 JVi,3(t) = (1 - <)2 + 2*(1 -1) +12 = 1 - 2t +t2 + It - 2t2 +t2 = 1.
Аналогично для 1 < t < 3
£ ^.з(*) = J[(3 - *)' + 2(3 - *)(' - 1) + (t - l)2]
1=1
= h? - 6t + t2 - 6 + 8t - 2t2 + 1 - 2t +12]
Рис. 5-41 Зависимость формы В-сплайна от его порядка.
Из вышесказанного видно, какое влияние оказывает выбор узлового вектора
на вид базисных функций В-сплайна и, следовательно, на форму В-сплайна.
Гибкость базиса В-сплайна позволяет воздействовать на форму кривой
разными способами:
Изменяя тип узлового вектора и базиса: периодический равномерный,
открытый равномерный и неравномерный.
Меняя порядок к базисных функций.
Меняя количество и расположение вершин определяющего многоугольника.
Используя повторяющиеся вершины.
Используя повторяющиеся узловые значения в узловых векторах.
Рассмотрим эти способы сначала для открытых В-сплайнов, затем для
равномерных периодических и неравномерных В-сплайнов.
Открытый В-сплайн по своим свойствам во многом аналогичен кривым Безье.
Как уже отмечалось, если порядок В-сплайна равен количеству вершин
определяющего многоугольника, то базис В-сплайна сводится к базису Бернштейна, а
сам В-сплайн становится кривой Безье. У открытого В-сплайна любого порядка
(к > 2) первая и последняя точки кривой совпадают с соответственными
вершинами многоугольника. Далее, наклон кривой в первой и последней вершинах
многоугольника равен наклону соответственных сторон многоугольника.
На рис. 5-41 изображены три открытых В-сплайна различного порядка,
заданные одним набором из четырех вершин. Кривая четвертого порядка —это кривая
Безье — один кубический полиномиальный сегмент. Кривая третьего порядка
состоит из двух параболических сегментов, соединяющихся в центре второго
отрезка с непрерывностью С1. Кривая второго порядка совпадает с определяющим
многоугольником. Она состоит из трех линейных сегментов, соединяющихся во
второй и третьей вершинах с непрерывностью С0. Угол наклона на концах,
заданный наклоном сторон многоугольника, одинаков для всех трех кривых. Отметим
Три кратные вершины
Две кратные вершины
2 4 6 8
Рис. 5-42 Влияние кратности вершины на форму В-сплайна, к = 4.
также, что по мере возрастания порядка кривой, она все меньше напоминает
исходный многоугольник и становится более гладкой.
На рис. 5-42 изображается влияние повторяющихся или совпадающих вершин.
Все В-сплайны имеют порядок к = 4. Нижняя кривая определена четырьмя
вершинами с узловым вектором [0 0001111].У средней кривой пять определяющих
вершин, причем две из них повторяются во второй вершине многоугольника [3 9].
Узловой вектор — [0 0001222 2]. Верхняя кривая определена шестью
вершинами с тремя повторяющимися в точке [3 9]. Узловой вектор —[0 0 0 0 12 3 3
3 3]. Соответствующие многоугольники для трех кривых соответственно таковы:
В\,В<2,,В^,В^\ B\,B<2,,B<2,,Bz,Bi и Bi,B<2,,B<2,,B<2,,B^,Bi-
Нижняя кривая состоит из единственного кубического сегмента. Средняя
кривая состоит из двух сегментов, соединенных между Вг и #з- Верхняя кривая
состоит из трех сегментов: первый от В\ до В2, второй от Вг ДО середины между
Вч и Вз, третий от этой точки до В±. Обратим внимание на то, что с
увеличением кратности вершины Вч кривая все ближе подходит к Вг. Когда кратность
достигается к — 1, возникает острый угол в соответствии со свойством выпуклой
оболочки В-сплайнов. При внимательном изучении рис. 5-42 можно заметить, что
на обеих сторонах кратной вершины имеется линейный участок.
Несмотря на наличие углов, сохраняется Ск~2 дифференцируемость кривой.
На первый взгляд это может показаться противоречием, однако излом
определяется нулевым касательным вектором, что не исключает непрерывности его
изменения. Возможность включения острых углов и изломов в непрерывно Ск~2
дифференцируемые кривые это важное свойство В-сплайнов.
Наконец, заметим, что у всех кривых наклон в концах одинаков.
На рис. 5-43 показаны три В-сплайна четвертого порядка. Каждый
определяющий многоугольник состоит из восьми вершин. Кривые отличаются тем, что
точка Вь передвигается в В'5 и Вд. Передвижение точки В& воздействует на
кривую только локально: изменяются лишь сегменты, отвечающие отрезкам В3В4,
Рис. 5-43 Локальная коррекция В-сплайна.
В4В5 и В^Ве, BqBj. В общем случае затрагиваются только ±к/2 отрезков вокруг
сдвинутой точки.
Для иллюстрации рассмотрим пример.
Пример 5-12 Расчет открытого В-сплайна
Рассмотрим многоугольник из примера 5-7: Bi[l 1], В2[2 3], Вз[4 3],
.04 [3 1]. Найти В-сплайн второго и четвертого порядка. Для к = 2 открытый
узловой вектор
[001233],
где xi = 0, Х2 = 0,..., Хб = 3. Параметр t изменяется от 0 до 3. Кривая
состоит из трех линейных (к — 1 = 1) сегментов. Для 0 < t < 3 функции
базиса имеют вид:
0 < t < 1
N2,i(t) = l; JVu(t) = 0, *#2
N1<2(t) = 1 - t; N2,2(t)=t; Nit2(t) = 0, i^l.2
1 <t <2
7V3,i(t) = l; Wi,i(t) = 0, г^З
N2,2(t) = 2-t; N3l2(t) = (t - 1); Nil2(t)=0, г ^2,3
2<t <3
JV4,i(t) = 1; M,i(0 = 0, г #4
AM*) = (3-«); W4la(t) = (t-2); W,a(t) = 0, i#3,4
Из уравнения (5-83) получаем параметрический В-сплайн
P(t) = BiNi,2(t) + B2N2<2(t) + B3N3,2(t) + B«JV4la(t).
Для каждого из этих интервалов
P(t) = (1 - t)Bi + tB2 = Bi+ (B2 - Bi)t 0<t<l,
Pit) = (2 - t)B2 + (t- 1)B3 = B2 + (B3 - B2)t 1 < t < 2,
P(t) = (3 - t)B3 + (t- 2)B4 = B3 + (Рм - B3)t 2 < t < 3.
В каждом случае в результате получается уравнение прямой для ребра
многоугольника, т. е. кривая совпадает с многоугольником.
Последняя точка кривой (t = tma.x = 3) требует особого внимания. Из-за
того что интервал в уравнении (5-84а) открыт справа, все базисные функции
Nik при t = 3 равны нулю. Следовательно, последняя точка многоугольника
формально не лежит на кривой. Фактически же это не так. Рассмотрим t =
3-е, где е — бесконечно малая величина. Бели е стремится к нулю, то в
пределе последние точки кривой и многоугольника совпадают. На практике
либо явно добавляют последнюю точку в описание кривой, либо определяют
N(t = tmax) = 1.0.
Для к = 4 порядок кривой совпадает с количеством вершин
определяющего многоугольника, поэтому В-сплайн сводится к кривой Безье. Узловой
вектор с tmax = n — fc + 2 = 3 — 4 + 2 = 1 — [0 0001 1 1 1]. Функции базиса
таковы:
0 <t < 1
ЛМ*) = 1; W.i(*)=0, i#4
N3,2(t) = (1 - t); N4l2(t) = t; Ni,2(t) = 0, i #3,4
JV2l3(t) = (l-*)2; JVs.s(*) = 2t(l - t);
N4,3(t) = t2; Niti(t) = 0,i? 2,3,4
JVi,4(t) = (1 - t)3; N2A(t) = t(l - f)2 + 2t(l - t)2 = 3i(l - t)2i
JV3,4(0 = 2*2(! -*) + (!- О*2 = 3*2(1 - t); N*A(t) = f3
Из уравнения (5-83) получаем параметрический В-сплайн
P(t) = BiN1A(t) + B2N2A(t) + B3N3A(t) + BiNiA(t),
P(t) = (1 - t)3Bi + 3t(l - 02^2 + 3f2(l - t)B3 + t3B4.
Итак, при t = 0
P(0) = Bi
и при £ = 1/2
и
pGH[i l]+t[2 3]+*[4 3]+^[31]
= [11/4 5/2].
Сравнивая с примером 5-7, видим, что результаты одинаковы.
Получившаяся кривая изображена на рис. 5-28.
Рис. 5-44 Зависимость формы периодического В-сплайна от его порядка.
Теперь займемся периодическими В-сплайнами. На рис. 5-44 показаны три
периодических В-сплайна разного порядка. Все кривые определены теми же
вершинами, что и для открытых В-сплайнов на рис. 5-41. Для к = 2 В-сплайн опять
совпадает с определяющим многоугольником. Отметим, однако, что у
периодического сплайна при к > 2 первая и последняя точки на кривой не совпадают с
первой и последней точками многоугольника. Наклон в первой и последней
точках также может отличаться от наклона соответствующих сторон
многоугольника. Для А; = 3 В-сплайн начинается в середине первого ребра и оканчивается
в середине последнего, как отмечено стрелками. Это происходит из-за
сокращения диапазона параметра для базисных функций периодического В-сплайна. Для
к = 2 периодический узловой вектор — [0 1 2 3 4 5] с диапазоном
параметра 1 < t < 4. Для к = 3 периодический узловой вектор — [0 1 2 3 4 5 6]
с диапазоном параметра 2 < t < 4. Для А; = 4 периодический узловой вектор —
[О 123456 7] с диапазоном параметра 3 < t < 4.
Сравнение полученных результатов и результатов для открытых узловых
векторов на рис. 5-41 показывает, что кривую можно определить на полном
диапазоне параметра, задавая кратные узловые значения на концах векторов. При этом
кривая растягивается к концам многоугольника.
В данном случае кривая четвертого порядка опять состоит из единственного
кубического сегмента; кривая третьего порядка — из двух параболических
сегментов, соединенных в середине второго ребра с непрерывностью С1; кривая второго
порядка— из трех линейных сегментов, соединенных во второй и третьей
вершинах с С0 непрерывностью. Увеличение порядка опять сглаживает кривую, но в
то же время и укорачивает ее.
Рис. 5-45 показывает, что воздействие кратных вершин одинаково для
периодических и открытых В-сплайнов. Область вокруг точки изображена более
подробно.
Три кратные
вершины
0 2 4 6 8 *
Рис. 5-45 Влияние кратности вершины на форму периодического В-сплайна, к = 4.
Пример 5-13 Расчет периодического В-сплайна
Снова рассмотрим многоугольник на рис. 5-44. Вершины
многоугольника— В1 [0 0], Вг[3 9], Вз[6 3], £>4[9 6]. Найти периодический В-сплайн
четвертого порядка (к — 4), заданный этим многоугольником.
Для к = 4 на диапазоне 3 < t < 4 узловой вектор для периодических
базисных функций— [0 12 3 4 5 6 7]. Для этого диапазона базисные
функции первого порядка (см. уравнение (5-84а), (3 < t < 4):
JV4,i(t) = l; NiA{t) = Q, гфЬ
Из уравнения (5-84Ь) получаем базисные функции высших порядков:
W3,2(t) = (4-t); ЛГ4,2(*) = (*-3); Ni,2(t) = 0, г #3,4
*,,(*)-^
ЛГ4,з(0 =
N1A(t) =
(*-з)2,
2 '
(4-О3.
м т-(*~2)(4-*) , (5 -1)(* - 3).
Nil3(t) = 0, г ф2, 3,4
(t-l)(4-Q2 (5-t)(4-t)(t-2) (5-*)2(*-3),
2'4^ 6 6 6
_ (*-2)2(4-t) (t-2)(*-3)(5-t) (6-*)(t-3)2.
6 6 6
(*-з)3
Мм(0
^4,4(0 = g
При t = 3
/v ™ - (4 - 3)2 - x
W1|4(3) - —— - -
(3-l)(4-3)2 (5-3)(4-3)(3-2) (5-3)2(3-3) 2
W2p4(3) - + + = -
(3-2)2(4-3) (3-2)(3-3)(5-3) (6-3)(3-3)2 1
^3,4(3) - g + g + 6 - 6
ЛГ4)4(3) = ^^=0
Точка на В-сплайне при t = 3 имеет вид
Р(3) = Ы + ^В2+0В4 =
о J
= |[0 0] + |[3 9] + |[6 3] + 0[9 6] =
= [3 6.5]
Полная кривая приведена на рис. 5-44.
Периодические В-сплайны очень удобны для построения замкнутых кривых.
На рис. 5-46а изображен периодический В-сплайн четвертого порядка (к = 4),
построенный для замкнутого многоугольника B\B2B^BiB^B%BiB%Bi.
Первая вершина совпадает с последней. В-сплайн получается незамкнутым
из-за ограниченного диапазона параметра. Здесь периодический равномерный
узловой вектор: [0 12 ... 10 11 12] с диапазоном параметра 3 < t < 9.
Повторяя всего к—2 вершин в начале и/или конце замкнутого многоугольника,
получаем замкнутый периодический В-сплайн. (Далее в этом разделе
обсуждается другой метод в матричной формулировке.) Результат показан на рис. 5-46Ь, где
определяющий многоугольник — B%BiB2BjBiB^B^BfB%BiB2 с периодическим
равномерным узловым вектором [0 1 2 ... 12 13 14] и диапазоном
параметра 3 < t < 11. Альтернативные многоугольники BiB2B$BiBbB&BTB%BiB2B$
или B7BSB1B2B3B4B5B6B7B8B1 приводят к тому же самому результату.
На рис. 5-47 одна вершина многоугольника В4 передвинута на другое место.
Ее воздействие распространяется на сегменты кривой, соответствующие ±fc/2
ребрам многоугольника по обе стороны от сдвинутой точки. На рис. 5-48 показан
эффект кратной вершины В±. Область вокруг В^ изображена более подробно.
Опять отметим, что ее влияние распространяется также только на ±к/2 сегмента
кривой по обе стороны кратной вершины.
Теперь рассмотрим неравномерные В-сплайны. На рис. 5-49 кривая
изменяется под воздействием кратных внутренних узловых значений. Верхняя кри-
Рис. 5-46 Замкнутый периодический В-сплайн. (о) В\В2ВзВ^ВъВбВтВ»В\
определяющий многоугольник; (6) ВаВ\В2ВзВьВ$ВъВтВаВ\В2 —определяющий
многоугольник.
0 2 4
Рис. 5-47 Изменение формы В-сплайна после перемсщспия одной вершины
многоугольника.
вал третьего порядка (к = 3) рассчитана для открытого узлового
вектора [0 0 0 1 2 3 3 3]. Базисные функции для этой кривой
изображены на рис. 5-38а. Нижняя кривая третьего порядка построена с
неравномерным узловым вектором [0 0 0 1 1 3 3 3]. Ее базисные функции —на
Тройная вершина .
Двойная вершина.
О 2 4 *
Рис. 5-48 Влияние кратных вершин на форму замкнутого периодического В-сплайна.
рис. 5-38d. Такая же кривая получается с неравномерным узловым вектором
[О 002233 3] и базисными функциями на рис. 5-38е.
Из рис. 5-49 видно, что кратные внутренние узловые значения порождают
излом в вершине Вз- Кратное значение порождает ребро нулевой длины, поэтому
уменьшается диапазон поддержки базисных функций. Далее, кратные
внутренние узловые значения, в отличие от кратных вершин многоугольника, снижают
дифференцируемость базисной функции в Xi до Ск~т~1, где т < к — 1 равно
кратности внутреннего узлового значения. Локально неравномерная кривая на
рис. 5-49 С0 (к — т — 1 = 3 — 2— 1 = 0) непрерывная в окрестности В3, что и
приводит к появлению угла.
Открытые неравномерные В-сплайны третьего порядка (к = 3) на рис. 5-50
построены с помощью узлового вектора с внутренними значениями,
пропорциональными длинам ребер между вершинами многоугольника. Узловой вектор
имеет вид
xi = 0 1 < г < к,
ГО
Xi+k =
[4+г) Сг+1 + £ Cj
' j=l
\
(n-fc + 2), 1<г<п-£+1,
У
Хг = п — к+ 2, п+1 <г <п + к,
(5-86)
где Ci = |Bi+i — Bi\. Для вершин, находящихся на одинаковом расстоянии друг
от друга, узловой вектор имеет целые равномерно распределенные значения,
т. е. вектор является открытым и равномерным. В работе [5-25] предложен по-
Рис. 5-49 Неравномерные В-сплайны, к = 3. (а) [X] = [0 0 0 1 2 3 3 3];
(6) [X] = [О О О 1 1 3 3 3].
Рис. 5-50 Сравнение открытых неравномерных В-сплайнов: (а) равномерный узловой
вектор; (Ь) неравномерный узловой вектор, пропорциональный длинам хорд; (с)
неравномерный узловой вектор, пропорциональный длинам хорд, с двойной вершиной в Вг-
хожий метод, позволяющий получить отдельные внутренние узловые значения.
Для сравнения приведена кривая с открытым равномерным вектором, а также
кривая с парой совпадающих вершин Вз-
Отсюда следует, что неравномерные В-сплайны не сильно отличаются от
равномерных при небольшом изменении относительного расстояния между
вершинами. Рассмотрим пример.
Пример 5-14 Неравномерный В-сплайн
Найти открытый В-сплайн третьего порядка, заданный точками Si [0 0],
Вг[2 6], Вз[4 3], #4[6 6], Bs[8 6] с помощью неравномерного вектора с
узловыми значениями, пропорциональными длинам ребер многоугольника.
Сначала найдем длины хорд
d = v/(2 - О)2 + (6 - О)2 = V40 = 6.325
с2 = у/(4 - 2)2 + (3 - б)2 = у/п = 3.606
с3 = ^(6 - 4)2 + (6 - З)2 = у/п = 3.606
с4 = У(8 - б)2 + (6 - б)2 = у/1 = 2.0
Их суммарная длина
J2a = 15.537.
Из уравнения (5-86) получаем внутренние узловые значения
ц
хъ =
f +С1
15.537
= 1.453,
2са.
+ С1+С2
15.537
(3) = 2.382.
Узловой вектор имеет вид
[х] = [000 1.45 2.382 333]
где xi = 0, хъ = 0,... , ха = 3. Диапазон параметра 0 < t < 3. Кривая состоит
из трех параболических (А; — 1 = 2) сегментов.
функции базиса для 0 < t < 1.453 таковы
JV3>1(t) = l; JVi.i(*) = 0, гфЪ
NiAt) = (1'М530; " N*M = Li53; NiAt) = °' i Ф 2'3
JVi,s(t) =
JV3.a(*) =
(1.453 -*)2
(1.453)* "! ^.»(*) = 7г1й^(1-4БЗ-') +
(2.382 - t)t
(2.382)(1.453)'
(1.453)2 ^"™" "' ' (2.382)(1.453)'
iVi,3(t) = 0, гф 1,2,3
Функции базиса для 1.453 < t < 2.382:
(2.382 - i)
n3,2(0:
N2,3(0 =
(2.382 - 1.453)'
(2.382 - tf
2.382(2.382 - 1.453)'
_ t (2.382-Q (3-f) (*-1.453)
3,3K ; 2.382 (2.382 - 1.453) (3 - 1.453) (2.382 - 1.453)'
^■'W=(3-1.«3K2^?-1.463); ^3W = 0' ^W
Функции базиса для 2.382 < t < 3:
ЛГВ,1(*) = 1; ЛГм(«)=0, iV5
NiAt) ~ (3-2.382)'
N3,3(0= — (^)2- •
(3 - 1.453)(3 - 2.382)'
(t-1.463)(3-t) (3-t)(t-2.382)
4,3 W (3 - 1.453)(3 - 2.382) (3 - 2.382)2 '
N5.3W = §rf§ii -М.з(0=0, г *3,4,5
Вспомним, что любая точка кривой задается уравнением:
Р(0 = Ni,a{t)Bi + N2,3(0^2 + N3,3(t)B3 + N4,3(0B4 + N5,3(0^5
т.е. при i = 1/2
р f I j = 0.430Bi + 0.498В2 + 0.072Д, + (0)В4 + (0)В5
= 0.430[0 0] + 0.498[2 6]+0.072[4 3]
= [1.284 3.202]
и при t = 2
Р(2) = (0)Bi + О.О66В2 + 0.726Вз + O.2O8B4 + (0)Bs
= 0.066[2 6]+ 0.726(4 3]+0.208(6 6]
= [4.284 3.822]
Результаты приведены на рис. 5-50.
Уравнения В-сплайна можно записать в матричной форме, подобно
кубическим сплайнам, параболической интерполяции и кривым Безье (см. уравнения
(5-276), (5-44) и (5-67). У периодических В-сплайнов матричная форма особенно
проста.
Вспомним, что базисные функции периодического В-сплайна являются
параллельным переносом друг друга (см. рис. 5-36) и что влияние каждой функции
распространяется только на к интервале. Поэтому для целых узловых значений
все базисные функции на единичном интервале 0 < t* < 1 имеют один и тот же
вид N*k(t*), т.е. иногда удобно нормализовать параметризацию. Точка на
параметрическом В-сплайне на единичном интервале имеет вид
fc-i
*Ж) = I^;+1|fc(r)B,+i, l<j<n-k + l, О <Г<1,
(5-87)
i=0
где j — счетчик сегментов кривой, а п на единицу меньше количества вершин.
Заметим, что уравнение (5-87) содержит только к членов:
РЛП = KkBi + лад+i + • • • + KkBi+k-i-
Для к = 3 базисные функции на интервале параметра 0 < t* < 1
2t*z + 2t* + 1
Щ,3(П =
Nls(t*) = ^
Тогда уравнение (5-87) принимает вид
2Pj{f) = (1 - 2t* + t*2)Bj + {-2t*2 + It* + l)Bj+i + t,2Bj+2
t*2 ( Bj - 2Bj+1 + Bj+2)
+ t* ( -2В5 + 2Bj+1 + Q-Bj+2)
+ ( Bj + Bi+i + Q-Bj+2)
Перепишем в матричной форме:
P/(f) = [T*)[N*][G] =
= \[t*2 t* 1]
1-2 1
-2 2 0
1 1 0
B,
Bj+i
L Bi+2
(5-88)
Аналогично, для к = 4 базисные функции на интервале параметра 0 < t* < 1
таковы:
-г*3 + зг*2 - зг* +1
*Г,4(**) =
ЛГ*4(Г) =
^,4(П =
зг*л + б**2 + 4
б
*2
6
-i*J + Ы*1 + 3**4-1
**з
6
Матричная форма для к = 4 имеет вид
= №
**2 ^*
1]
-1
3
-3
1
3
-6
0
4
-3
3
3
1
1—1
0
0
0
Bi
Bj+i
Bj+2
. Bj+3
(5-89)
Уравнения (5-87) и (5-89) содержат произведение весовой функции и
геометрической матрицы (см. уравнения (5-27), (5-44), (5-67); т.е.
Pj(t*) = [T*][N*][G] = [F][G] l<j<n-k + l, 0 < £* < 1
(5-90)
где
[г*] = [г**-1 t*
Jfc-2
t* 1] 0 < t* < 1
[G]T = [Bj ... Bj+k-i] содержит геометрию — вершины многоугольника, a [F]
состоит из соответствующих базисных функций.
В работе [5-19] показано, что для периодических В-сплайнов общий вид [N]:
[N*] = [N*+ltj+1],
(5-91)
где
i+lj'+l
(*-1)!
п
_ ^"j+ij+i
-ггЬя(*71)§(*-(,+1))'И),"(|-^ "*'■ '-'-''
Вспомним, что у периодических замкнутых В-сплайнов необходимо повторить
некоторые вершины, чтобы ликвидировать разрыв. В матричном виде это очень
просто. Замкнутый периодический сплайн имеет вид
*-i
Pj+Л**) = £ ^i+i.fc(«*)B(U+<) mod (n+i)) + 1, 0 < J < п.
(5-92)
г=0
Или в матричном виде
Pi+1{t*) = [T*][N']
Bj mod (n+l))+l
B((j+1) mod (n+l))+l
B((j+l+n-k) mod (n+l))+l
(5-93)
где [Г*] и [N*] взяты из уравнения (5-90), a mod — остаток; например, 3 mod 2=1.
Открытые В-сплайны также можно записать в матричном виде, однако из-за
кратных узловых значений на концах это не так удобно, как для периодических.
В общем случае матричный вид открытого В-сплайна с целыми узловыми
значениями таков:
P(t) = [F][G\ = [T][N][G\,
(5-94)
где
[СГ = [Вх
Bn+i],
а элементы [F] и [N] получены по алгоритму Кокса-де Бура (уравнение (5-84))
для каждого ненулевого интервала вектора [X]. У В-сплайнов низкого порядка,
заданных большим количеством точек, большинство членов [F] равны нулю.
Используя это свойство, можно значительно сэкономить вычисления.1
В работе [5-19] приведена обобщенная формулировка для [N*] на
нормализованном интервале 0 < t* < 1; однако из-за кратности концевых узловых значений
первые и последние к — 1 N*] матриц являются частными случаями.
Рассмотрим пример матричного метода.
Пример 5-15 Расчет замкнутого В-сплайна
Найти замкнутый В-сплайн четвертого порядка (к = 4), заданный
многоугольником, изображенным на рис. 5-46. Записать результат в матричном
виде. Вершины многоугольника: Вг [2 0], В2[4 0], В3[4 2],В4[4 4], Б5[2 4],
В6[0 4], В7[0 2], В8[0 0], Вв[2 0], п = 8.
Для каждого единичного интервала 0 < t* < 1 из уравнений (5-89) и
(5-93) получим
р,+ЛП = 1р3 t'2 e 1]
-1 3-3 1
3-6 3 0
-3030
14 10
B(j mod 8)+l
5(0+1) mod 8)+l
В(0+2) mod 8)+l
-В(Ц+з) mod 8)+l
1 См. алгоритм из Приложения G.
При t* = 1/2 на первом сегменте (j = 0) кривой
= -[1 23 23 1]
-1
3
3 -6
-3 0
1 4
2 0 ]
4 0
4 2
4 4
-3
3
3
1
1 ]
0
0
о J
Г Bi
в2
Вз
L в4
= —[190 50] = [3.958 1.042].
При f = 1/2 на восьмом сегменте (j = 7) кривой
Рй(\)=Т8[1 23 23 1]
= -тг[1 23 23
48L
Вй
Вг
В2
L В3 j
0 0
2 0
4 О
4 2
= То [142 2] = [2.958 0.417].
Результат показан на рис. 5-46Ь.
Производная в любой точке В-сплайна вычисляется формальным
дифференцированием. Из уравнения (5-83)
первая производная:
и вторая производная:
п+1
п+1
p'(t) = y£BiN'>k(t)
i=l
п+1
»=i
(5-83)
(5-95)
(5-96)
Штрихи обозначают дифференцирование по параметру t.
Производные базисных функций также получают формальным
дифференцированием. После однократного дифференцирования уравнения (5-84) имеем
дад)
= W,fc-i (f) + (t - xjN^ (t) | (xi+k - t)iV/+1|fe_1 (f) - Ari+M_! (f)
^i+fc-l - I»
Xi+k — Xi+1
(5-97)
Из уравнения (5-84а) следует, что iV,'pl(£) = 0 для всех t. Следовательно, для
к = 2 уравнение (5-97) принимает вид
^a(t) = -JM0_. Ц»ДМ , (5-98)
Вторые производные базисных функций получаем, дифференцируя уравнение
(5-97),
N,,k{t) 2*Z,t-i(*)+ (*-««)*&-i(0 +
Zi+fc-i - а:»
xi+k - xi+1
Здесь как Щ\{£) = 0, так и N"2(t) = 0 равны нулю для всех t. Следовательно,
для к = 3 уравнение (5-97) имеет вид
ади-лГ *Ь(" _ "W) у (5.ш)
На рис. 5-51 изображены несколько базисных функций В-сплайна и их
производные для к = 4. Отметим, что при fc = 4 каждая базисная функция —
кусочно кубическая, первая производная — кусочно параболическая, вторая
производная — кусочно линейная. Третья производная разрывна и состоит из различных
констант.
Рассмотрим пример.
Пример 5-16 Расчет производных В-сплайна
Рассмотрим многоугольник из примера 5-12: Bi[l 1], В2[2 3], Вз[4 3],
В\ [3 1] и соответствующий сплайн. Найти первую производную кривой
второго порядка (к = 2).
Для к = 2 открытый узловой вектор имеет вид:
[001233],
где xi = 0, Х2 = 0,..., хв = 3. Диапазон параметра 0 < t < 3. Из уравнения
(5-95) получаем первую производную для п = 3, к = 2
P'{t) = BiN,lt2{t)+B2N'2t2(t) + BaNli2(t) + BiN'it2(kt).
Из уравнения (5-98) следует, что
N'i2(t)= "'■'<*> *±*W_.
Xi+Jfc-l — Xi Xi+k—Xi+l
Пользуясь результатами уравнения (5-12), для 0 < t < 1 получим
N2,i(t) = l; JVi.i(t) =0, t#2,
Рис. 5-51 Базисные функции В-сплайна и их первые и вторые производные, к = 4,
п = 6. (а) Базисные функции; (6) первая производная; (с) вторая производная.
и
N{,2(t) =-1; M,2(*) = l; K2(t) = 0, гф1.
Итак
P'(t) = B2-B1,
что является наклоном (касательным вектором) первого ребра
многоугольника, как оно и должно быть. Для 1 < t < 2
и
Л£,2(*) = -1; Aj,2(t) = l; K,2(i) = 0 г ^2,3
т.е.
Р'(*) = -Вз-В2)
что равно наклону (касательному вектору) второго ребра.
Наконец, для 2 < t < 3
JV«.i(t) = l; JVi,i(t) = 0 г ^4
и
Л£.2(*) = -1; Wji2(t) = l; <2W = 0 г ,4 3,4,
т.е.
Р'(<) = Bi-B3
— наклон последнего ребра.
При t = 3, Ni,i(3) = 0 для всех г. Следовательно, формально Р'(3) = 0, но
предел t = 3 — е, при £ —► 0 показывает, что на самом деле Р'($) = (В^ — Вз).
5-10 КОНЕЧНЫЕ УСЛОВИЯ ДЛЯ ПЕРИОДИЧЕСКИХ В-СПЛАЙНОВ
Как было показано ранее, конец и начало периодического В-сплайна не
совпадают с первой и последней вершинами определяющего многоугольника. Отсюда
возникают два вопроса. Во-первых, где же именно начинается и заканчивается
В-сплайн,.и каковы его граничные условия, т.е. производные в этих точках? Во-
вторых, что влияет на конечные точки и производные в них? В работе [5-24]
изучается этот вопрос для частного случая кубических (к = 4) В-сплайнов. Мы
рассмотрим более общий случай.
Произвольный периодический В-сплайн начинается в точке Ps = P(t = Xk)
и оканчивается в точке Ре = P(t = xn+i)- Для целых узловых значений,
начинающихся с нуля, Ps = P(t = к) и Ре = P(t - n). Из уравнений (5-87) и (5-91),
а также из того, что любая точка В-сплайна зависит от к ближайших вершин,
следует, что для преобразованного параметра 0 < t* < 1 начальная точка
соответствует t* = 0. Итак
р° = Тк^гу. {N*k'lBl + N*K2B2 + '" + N*k'hBk)-
Заметим, что N% к = 0 для всех к
Р* = 71^Гпт№В1 + ^МВ» + * ■ • + Nk,k-iBk-i), п>к. (5-101)
В конце интервала t* = 1. Известно, что Yli=i ^ti = ^> П0ЭТ0МУ конечная
точка
1 / к к к \
Ре = Jk^Ty. ( Е^В-*+3 + ЕNtsBn-k+4 + • • • + Х>£*Д.+1 1 " > *■
(5-102)
Для квадратичного (А; = 3) периодического сплайна уравнения (5-101) и
(5-102) принимают вид
i"e = ~^{Вп +Вп+{).
Следовательно, квадратичный периодический В-сплайн начинается и
кончается, соответственно, в середине первого и последнего ребер многоугольника.
Конечные точки кубического (к = 4) периодического сплайна таковы:
о
Ве = -(Вп_1+4Вп + Вп+1).
о
Из уравнения (5-90) первая производная в начальной точке
К = [T*']f=o[N*][G] =
= (jfeZ-Ijj^-M*! + ^-1.2Б2 + • • • NU.k-iBk-1) (5-103)
так как Nk_x k = 0 для всех к. Первая производная в конечной точке
Pi = [T*']t>=i[N*][G] =
= (^Т)т(Е^-^2В"-^з +
fc-1 fc-1 \
+ £> - i)N*3Bn_k+4 + ■ ■ ■ + £(fc - i)N£kBn+1 , (5-104)
i=l i=l /
где [Г*'] = [(к - l)t*(fc-2) (A; - г)**^"3) ... 1 0] - производная вектора
параметра.
В случае квадратических (А; = 3) периодических В-сплайнов эти результаты
сводятся к
Р^ = ±(-2В1+2В2)=В2-В1
Ре = 2^~^п + 2-Bn+l) = Bn+i - Вп,
т. е. векторам касательных (наклону) первого и последнего ребер.
Для кубических (к = 4) кривых
Pi = i(-3Bx + ЗВз) = \(.Вг- В,)
Ре = т(—З.Вп-2 + 3Bn+i) = -(Вп+\ — Bn-i)-
Здесь касательные векторы (наклоны) зависят от касательных к трем первым
и к трем последним сегментам кривой.
Вторые производные в конечных точках:
P'J = [T*"]f.=0[iV*][G] =
= Jk^V)\{NU'lBl + NZ~™B* + • • • + JViU,t-iflb-i) (5-Ю5)
^' = [T*"]f.=1[iV*][G] =
1 Л-2
fc-2
+ £(* ~ »)(* ~ » ~ V43Bn-k+4 +
i=l
Jfe-2 \
+ • ■ • + £(fc - i) (fc - i - l)N*kBn+l\ (5-106)
»=i /
где [Г*"] = [(к - l)t*(fc-2) (jfe - 2)t*(*-3) 1 0] - вторая производная
вектора параметра.
Для кубических (к = 4) сплайнов уравнения (5-105) и (5-106) дают
P'J = |(6Bi - 12Б2 + 6В3) = Bi - 2В2 + В3,
о
Р" = «№-1 - 12Вп + 6Bn+1) = Bn_i - 2Вп + Вп+1.
о
Существует два метода регулирования положения первой и последней точек, а
также конечных условий: кратные вершины и псевдовершины.
Кратные вершины на концах периодического В-сплайна притягивают концы
сплайна к соответствующим вершинам. Если определены к — 1 совпадающая
вершина, то конечные точки кривой совпадают с вершинами многоугольника и
касательные (наклон) совпадают с направлением соседних ненулевых ребер.
Например, для к = 3 с двойными вершинами на концах, т. е. В\ = В^ и Вп =
Bn+i из уравнений (5-101) и (5-102) следует
Р. = \{В1 + В2) = \(2В1)=В1,
Ре = ~^(Вп + Bn+i) = ~(2Bn+i) = Вп+х.
Для к = 4 с двойными вершинами на концах эти же уравнения дают
P. = \{5B1+Bi),
о
Pe = i(Pn_! + 5Pn+1).
Отсюда начальная точка находится на расстоянии от одной шестой ребра,
соединяющего точки В\ и Рз, а конечная точка находится на расстоянии в пять
шестых ребра от Bn-i до Pn+i.
Если в концах располагаются по три кратные вершины, т. е. Bi = Въ = Вз и
Pn_i = Вп = Вп+1 для к = 4, то
Ps = ^r(Pi+4P1+P1)=P1,
о
■Ре = т(Рга+1 + 4Рп+1 + Pn+l) = -Вп+1-
О
Кривая начинается и кончается в первой и последней вершинах многоугольника.
На рис. 5-52 изображено влияние кратных вершин.
С тремя кратными вершинами на концах первый и последний сегменты В-
сплайна для к = 4 (см. уравнение 5-89) имеют вид:
Pi (Г) = Bi + ^-[Р4 - Pi] = Рз + ^-[Р4 - В3] 0 < Г < О
(1 - г*3)
Рп(**) = Рп+1 Н 7 (Рга — Pn+l)-
При этом первый и последний сегменты линейны. Первый сегмент на одну
шестую длины ребра от Pi = Рг = Рз до Р4 совпадает с этим ребром. Последний
сегмент на одну шестую ребра от Р„_2 до Pn-i = Вп = Вп+\ совпадает с
соответствующим ребром.
Несмотря на то, что участки можно сделать как угодно малыми, в
некоторых прикладных областях это может быть неудобным. В таких случаях лучше
пользоваться открытыми В-сплайнами.
Псевдовершины в концах периодического В-сплайна, в отличие от кратных
вершин, позволяют управлять как положением конечных точек, так и
граничными условиями. В общем случае псевдовершины не обозначаются, и пользователь
не может контролировать их. Как показано на рис. 5-53, Во и Рп+2 —
псевдовершины в начале и конце В-сплайна. В этих обозначениях уравнения (5-101) и
(5-102) принимают вид
Ря =
(к-
Y£(KiB° + К*В^ + ■■■ + N*k,k-iBk-2) n > к (5-107)
Рис. 5-52 Совпадающие кратные вершины на концах определяющего многоугольника
(к = 4). (а) Кратных вершин нет; (Ь) две кратные вершины; (с) три кратные вершины
и соответствующие открытые В-сплайны.
Рис. 5-53 Псевдоверпшны определяют начальную и конечную точки периодического
В-сплайна.
Ре = Jk^ty. [ £ Ni,2Bn-k+i + Y, КзВп-к+5 + • • • + 53 NtkBn+2 J П>к
(5-108)
При Ps = Bi и Ре = Bn+i эти уравнения имеют вид
Bo = {(k-l)\-Nl2)B1 = (N*kt3B2 + --- + Nlk_lBk-2) п>к (5-109)
и
к
вп+2 = ((*- i)!-j>i%-i)B»+i -
i=l
^iV*2Bn_fc+4 + --- + ^iV^_2JBn] n>k (5-110)
S.x=l
t=l
где AT*, =1и^ = 1.
Для A; = 3 из уравнений (5-109) и (5-110) следует, что В0 = В^ и Bn+2 = -B„+i,
т.е. двукратные вершины на концах!
Для к = 4 аналогично
В0 = (6 - 4)Bi - £2 = 2Bi - £2
■Bn+2 = (6 — 4)Bn+i — Bn = 2Bn+i — Bn.
Пример изображен на рис. 5-53.
Первая и вторая производные в концах выражены уравнениями (5-103) и
(5-104) с соответствующими изменениями для учета псевдовершин. Например,
используя приведенные результаты для В0, из уравнений (5-103) и (5-104) для
к = 4 получаем
P's = \{В2 - В0) = ±{В2 - (2£?j - В2)} = В2-В1
и
Ре = ^(Вп+2 — Вп) = -{2Bn+i — Вп — Вп} — Bn+i — Вп.
Итак, кривая касательна к первому и последнему ребрам многоугольника.
Аналогично, для к = 4 и точек В0 и Вп+2 из уравнений (5-105) и (5-106)
следует
P'J = В0- 2Bi +B2 = 2Bi -В2- 2ВУ + В2 = 0,
Ре = Вп + 2Bn+i + Вп+2 = Вп — 2Bn+i + 2Bn+i — Вп = 0,
т.е. «кривизна» в концах нулевая.
Переписав уравнения (5-103) и (5-104), можно определить псевдовершины,
порождающие заданные граничные условия. В частности, из уравнения (5-103)
ВО = Jj^-{(k ~ W* - W-1.2Sl + • • • + *k-l,k-lBk-2)} П > к (5-111)
а из уравнения (5-104)
в»+> = 1=г-^ {(* ~ W ~
1=1
(fc-1 fc-1 \ "I
£(* - l)JV*aB„_t+4 + • • • + £> - ХЩь^В^ И п>к (5-112)
Для к = 4 уравнения (5-111) и (5-112) сводятся к
Во = В2- 2PJ,
Вп+2 = 2Ре + Вп.
Типичный пример изображен на рис. 5-54. Конечные точки кривой получены
подстановкой этих значений в уравнения (5-107) и (5-108). Из рисунка видно, что
первая и последняя точки кривой с заданными касательными на концах для
многоугольника BoBiB2BzBiB<a не совпадают с соответствующими точками кривой
для многоугольника BiB2B^Bi (отмечено крестиками).
Для управления второй производной или приблизительной кривизной в
концах кривой перепишем уравнения (5-105) и (5-106) в виде
Во = j^— { ^^Ps" - W_2>2Si + ■ ■ • + JV,Ut-iflb-a)} , n>k, (5-113)
Касательный
О 2 4 6 8
Рис. 5-54 Управление касательным вектором для периодического В-сплайна, к = 4.
Вп+2 ~ *П
E(k-l)(k-i-l)Nlk
г(
(fc-l)!Pe"~
/fc-2
- £(fc - l)(fc - г - l)N*2Bn-k+4 +
fc-2 >
+ • • • + J> - 1)(* - i ~ l)^fc-i£n+i
i=i
n > к
(5-114)
Для к = 4 из уравнений (5-113) и (5-114) следует
До = Д + 2Д — В2,
Вп+2 = Ре + 2Bn+i — Bn.
Чтобы получить конечные точки, надо подставить эти значения в уравнения
(5-107) и (5-108). Касательные векторы получаются аналогично, с помощью
уравнений (5-103) и (5-104), переписанных относительно В0 и Вп+2.
5-11 ПОДГОНКА В-СПЛАЙНОВ
В предыдущем разделе рассматривалось построение В-сплайна по
определяющему многоугольнику. Сейчас нам нужно найти многоугольник, порождающий
В-сплайн, для заданного множества точек кривой, как показано на рис. 5-55.
Точка, лежащая в В-сплайне, должна удовлетворять уравнению (5-83).
Запишем уравнение (5-83) для всех j заданных точек
Di(ti) = Ni,k{t1)Bi+N2tk(ti)B2-+-
D2(t2) = JVi,fc(*a)Bi + N2<k(t2)B2 +
■ +^n+l,fc(*l)-Bn+i,
+ Nn+iik(t2)Bn+\,
Dj(tj) = ^i.*(«j)Bi + N2ik(tj)B2 + ■■■ + Мп+11к(^)Вп+1,
где 2<fe<n+l<j, или в матричной форме
[D] = [N][B]
где
[D]T = [£>!(*!) D2{t2) ■■■ Dj(tj)]
[Bf = [Bl B2 ■■■ Bn+1]
Nhk Wn+i,'k(*i)
[N] =
Ni,k(W
JVn+i,fc(*j) .
(5-115)
При 2<fc<n+l=j матрица [N] квадратная, и определяющий
многоугольник вычисляется непосредственно обращением матрицы, т. е.
[В] = [N]_1[£>] 2<k<n+l=j. (5-116)
В этом случае В-сплайн проходит через все заданные точки, т. е. достигается
точная подгонка. Кривая на всем протяжении Ск~2 непрерывна, но при этом она
может быть недостаточно гладкой на вид и иметь нежелательные изгибы.
Если указать меньшее число вершин многоугольника, чем количество
заданных точек, т. е. 2 < к < п + 1 < j, кривая будет более гладкой. При этом
матрица [N] становится неквадратной, и можно найти только общее решение.
Воспользуемся тем, что произведение матрицы на транспонированную всегда дает
"1 "4
Рис. 5-55 Построение многоугольника В-сплайна для заданного множества точек.
квадратную матрицу (см. разд. 3-31). Вершины определяющего многоугольника,
сглаживающего кривую заданы условием
[D] = [N][B],
[Nf[D] = [Nf[N][B]
[B] = [[N]T [rf]]-1[mT[D] (5-П7)
Оба метода подразумевают, что матрица [N] известна. Базисные функции Niyk(tj)
и, следовательно, матрицу [N] можно получить, если задан порядок В-сплайна
к, количество точек многоугольника п + 1, а также величина параметра вдоль
кривой. При соблюдении условия 2 < к <п + 1< j порядок и количество вершин
произвольны.
Величина параметра tj для каждой заданной точки — это мера расстояния до
точки вдоль В-сплайна. Удобна аппроксимация параметра с помощью длин хорд
между заданными точками; в частности, для j точек величина параметра в точке I
h =0
Z\D3 -D3-!\
3=2
E|i>.--d.-i|
s=2
l>2.
Максимальное значение параметра imax обычно выбирается в качестве
максимальной величина узлового вектора. Подобные методы затрагиваются в работах
[5-15] и [5-22].
Для открытого равномерного узлового вектора с к кратными вершинами на
концах кривая Безье получается при п = к.
Рассмотрим пример.
Пример 5-17 Подгонка В-сплайна
Даны пять точек Di[0 0], D2[1.5 2], D3[3 2.5], D4[4.5 2], D6[6 0].
Найти определяющие многоугольники третьего порядка (к = 3) с пятью
и четырьмя вершинами для В-сплайна, проходящего через данные точки.
Использовать хордовую аппроксимацию параметра.
Сначала найдем длины хорд.
£>2i = \D2 - £>i| = i/(x2-x02 + (y2-yi)2 = V(l-5)2 + (2)2 = %/«Г25 = 2.5,
D32 = |1>з - D2\ = л/(1-5)2 + (.5)2 = 1.58,
D43 = \D4 - Dz\ = v/(1.5)2 + (-.5)2 = 1.58,
D64 = \DS - D4\ = л/(1-5)2 + (-2)2 = 2.5
и
5
J2(D° - D*-i) = Dm = 816.
Итак
h
t2
*max
и
*max
tmax
= 0
_ £>21
Asi
_ An
Ail
£>41
_ D51
D51
2.5
= 8l6=°-31
= (2.5 + 1.58)
8.16
_ (2.5 + 1.58 + 1.58)
8.16
= 1.
= 0.69
Для пятиугольника максимальное значение узлового вектора у В-сплайна
третьего порядка п — fc + 2 = 4 — 3 + 2 = 3. Здесь п на единицу меньше
количества вершин многоугольника. Узловой вектор с кратностью к на концах
имеет вид
[00012333].
Уравнение (5-115) с этими значениями выглядит следующим образом:
0
1.5
3
4.5
6
[D] = [N][B]
0 "
2
2.5
2
0
=
" 1
0.007
0
0
0
0
0.571
0.125
0
0
0
0.422
0.75
0.422
0
0
0
0.125
0.571
0
0
0
0
0.007
1
[В].
Решим относительно [В]
[B] = [N]-'[D]
=
" 1 0
-0.013 2.037
0.003 -0.387
-0.002 0.286
0 0
0
-307
1.769
-1.307
0
0
0.286
-0.287
2.037
0
0
-0.002
0.003
-0.013
1
' 0 0
1.5 2
3 2.5
4.5 2
6 0
[В] =
0
0.409
3
5.591
6
0
1.378
2.874
1.377
0
На рис. 5-56а изображены исходные точки, рассчитанные вершины
многоугольника и кривая.
Для четырехугольника узловой вектор с кратностью к на концах:
[0001222].
Рис. 5-56 Результаты для примера 5-17. (о) Пятиугольник; (6) четырехугольник.
Матрица [N]:
[N] =
10 0 0
0.15 0.662 0.188 0
О 0.5 0.5 0
0 0.188 0.662 0.15
0 0 0 1
Умножим на [N]T и обратим ее:
[[NflN]}-1 =
0.995 -0 21 0.106 -0.005
-0.21 2.684 -1.855 0.106
0.106 -1.855 2.684 -0.21
-0.005 0.106 -0.21 0.995
Тогда из уравнения (5-117) получим
[B} = [[Nf[N]]-1[N]T[D]
0 0
О 788 2.414
5.212 2.414
6 0
На рис. 5-56 6 изображены исходные точки, рассчитанные вершины
многоугольника и кривая.
Этот метод допускает произвольное расположение всех точек
определяющего многоугольника в трехмерном пространстве, но иногда бывает удобно
ограничиться плоскостью, например при подгонке В-сплайна под заданный контур
корабля. В работе [5-26] приведен соответствующий метод как для кривых, так и
для поверхностей. Его сущность состоит в том, что итеративно вычисляется
параметр для фиксированной координаты до тех пор, пока значение на кривой при
величине параметра, вычисленной по подогнанному многоугольнику, не попадает
в некоторую окрестность фиксированного значения, т.е. |xfixed — ^caid < error.
Подгонка получается менее точной, но более удобной для модификаций.
5-12 РАЗБИЕНИЕ В-СПЛАЙНОВ
Для того чтобы увеличить гибкость кривой Безье, необходимо добавить вершину
к определяющему многоугольнику, что повышает степень полиномиальной
кривой (см. разд. 5-8). Гибкость В-сплайна также растет с увеличением порядка его
базиса, т. е. полиномиальных сегментов. В работе [5-27] предлагаются теория и
алгоритм увеличения порядка В-сплайна.
Повысить гибкость В-сплайна можно другим способом: вставить
дополнительные узловые значения в определяющий узловой вектор. При этом
полиномиальный сегмент для некоторого интервала узловых значений (параметрического
интервала) локально разбивается на два. Есть два основных метода вставки узловых
значений. Первый, так называемый алгоритм Осло, разработанный Коэном и др.
([5-28] и [5-29]), вставляет сразу несколько узлвоых значений. Второй метод Бе-
ма ([5-30] и [5-31]) последовательно вставляет по одному узловому значению. Мы
рассмотрим только метод Осло.
Как повышение порядка, так и дополнительные узловые значения
увеличивают гибкость базиса кривой (поверхности) и, следовательно, кривой без изменения
ее формы. Это возможно потому, что один В-сплайн можно задать бесконечным
множеством многоугольников с более чем минимальным количеством вершин.
Форма кривой меняется путем передвижения вновь полученных вершин.
Рассмотрим исходную кривую P(t) = J27=i BiNi,k(t) c узловым вектором
[X] = [xi х2 ■■■ xn+k-i]- Вставив узел, получаем новую кривую R(s):
тп+1
R(s) = £ CjMj>k(s) (5-118)
с новым узловым вектором
[У] = [У1 У1 Ут+k+l],
где т > п. Надо найти новые вершины определяющего многоугольника Cj, такие,
что P{t) = R(s). По алгоритму Осло [5-29]
ЛГ+1
Cj = Y, atjBi> ! < г < n, 1 < j < m, (5-119)
где а*; заданы рекурсивным отношением
a\. = i I xi<Vi<*M> , (5.i20a)
l'3 у 0 в противном случае v '
* = yj+k-,-xiakl + xi+k-yj+k^aki
Xi+k-l - ^ ,J Xi+k - Щ+1
Отметим, что J2™+1 ai,j = *•
На первый взгляд может показаться, что равномерный исходный вектор,
неважно периодический или открытый, после вставки одного или более узловых
значений станет неравномерным. Равномерность вектора можно сохранить,
добавляя кратные узловые значения в середину каждого ненулевого интервала.
Рассмотрим разбиение подробнее на примере.
Пример 5-18 Глобальное разбиение В-сплайна
Пусть дан открытый В-сплайн третьего порядка (к = 3), изначально
заданный четырьмя (п + 1 = 4) вершинами Bi[0 0], Вг[1 1], -Вз[2 1],
.B-i [3 0]. Требуется провести разбиение с сохранением открытого
равномерного узлового вектора.
Исходный открытый равномерный вектор имеет вид:
[Х'\ = [0 0 0 1 2 2 2],
где два ненулевых интервала 0 —¥ 1 и 1 —¥ 2 соответствуют двум кусочно
параболическим сегментам, составляющим В-сплайн. Предположим, что после
разбиения мы должны иметь целочисленный равномерный вектор. Проведем
преобразование параметра, умножая каждое узловое значение в [X'] на 2, и
получим
[X] = [0 0 0 2 4 4 4]
с xi = 0, 12 = 0,..., хт = 4. Кривая при этом не меняется.
Для разбиения кривой с учетом поставленных условий необходимо
вставить узловые значения 1 и 3 в интервалы 0 —► 2 и 2 —¥ 4, соответственно.
Запишем новый узловой вектор:
[У] = [0 0 0 1 2 3 4 4 4]
с yi = 0, у2 = 0, ...,уд = 4.
Теперь В-сплайн состоит из четырех параболических сегментов.
Из уравнения (5-119) получим шесть новых вершин Cj. Значения a3j
вычисляются с помощью рекурсивных соотношений (5-120). В частности, из
уравнения (5-120а) видно, что единственное ненулевое a\j первого порядка
(к = 1) таково:
азд = аз,2 = а3|3 = аз,4 = а4|5 = ач,б = 1-
Из уравнения (5-120Ь) ненулевые q?j второго порядка (к = 2) таковы:
3=1
2 _ У2 - ХЗ _.1 _?-0/1\_п
2 14-1/2 1 2 — 0, .
Q2,l = —«3,1 = ^ nW =
Х4 — Хз Z — U
J =2
2 Х4 - УЗ .1 2 —0. ^
а2,2 = — <*з,1 = г—-(1) = 1,
Х4 — Хз I — U
2 _ УЗ ~ ХЗ _ 1 _ 0-0 .
Q3.2 = I I-Q3,2 = У. -ЛУ) = О,
Х4 — Хз 2 — 0
i=3
2 _ У4 ~ ХЗ _ 1 _1^2/1л_1
Q3'3-x7^IQ3'3-23o(1)-2'
2 X4-J/4 1 2-1, . 1
Q2,3 = ~а3,3 = X р:(1) = ^.
Х4 — Хз Z — U 2
i=4
2 _ У5-ХЗ 1 _ 2-°/i4 _ 1
°3-4 " хТ^Г3'4 - 2^0(1) - *'
2 _ д4 - У5 .1 _ 2-2
Q2'4 = xT^7Q3'4-^^(1) = 0'
j =5
о _ Уб - Х4 1 _ 3-2, 1
Q4'5 = x7^7Q4'5 - m(1) = г-
2 _ Х5 ~ Ув „1 _ 4-3,,,,, 1
Q3-5-x7^7Q4'5-4^2(1)=2'
j=6
2 _ У7 ~ Х4 _i _ 4-2
Q4,6 = а4,6 = -: г(1) = 1,
Хб — Х4 4 — Z
2 _ Х5 - У7 . 1 _ 4-4
аз,б = а4|6 = -:—~(1) = 0
Х5 — Х4 4 — Z
третьего порядка (к — 3)
J=l
3 УЗ-Х2 2 0-0/1Ч п
a2,i = £ Q2,i = ^—„0) = О,
14 — ^2 2 — U
2-0
Г,1 = —.<*2,i =
14 — £2
J =2
з Д4 -г/з„г _ 2-0, , _ п
«1,1 = Q2,l = ^ „(1) - 1>
3 14-1/4! _ 2-1/11 — 1
Ql,2 = Q2,2 - ^ prUJ - o>
14—12 2 — 0 2
3 2/4 ~ Д2 ,2 _ 1-0/-П _ 1
Q2,2 = а2,2 - ^—„UJ - о'
14—12 2 — U 2
3=3
..з _ys-i3 2 _ 2 —
-0 V2/ 4'
Q3,3 = Q3,3 ,,
15 — 13 4
3 У5-12 2 , ДБ -2/5..2 2-0 /1\ 4-2 /1\
Q2'3 = ^^7Q2'3 + ^^з""3'3 = 2^0 U) + 4^0 UJ
3 Z4 — г/5 2 2
Ql,3 = <*2,3 = Г
Х4 — ^2 2
3(£Ь
j=4
я г/е-дз j _ з-о, . з
аз,4 = а3,4 - -.—„(Д) - -г,
15—13 4 — 0 4
3 Д5 - г/6 .2 _ 4~3/тч _ 1
QM = i7^7Q3,4-rro(i)-i.
j =5
3 15 - 2/7 2 4
Q2,5 = tt3,5 = у
15 — 13 4
3 2/7 -13 2 . 16-J7 2 4-0 /1\ 4-4 /1\
Q3'5 = ^^7Q3'5 + ^^l"4'5 = 4^0 UJ + 4^2 \2)
W = 2*
3 _ 2/7 - Д?4 ^2 _ _ 4 - 2
XQ — Х4
a*.s = ^7^Г.а^ = 4-2
J =6
з г/в - Д4 j _ 4-2
<Чв = а4|6 = -.—г(1) = 1,
16 — 14 4 — 2
з Дб -г/а 2 4-4. .
а3,б = Q4,e = j—~(1) = 0.
хе —14 4 — 2
Новые вершины рассчитьшаются по уравнению (5-119):
п+1
Ci = 53 ^.i-8* = "Ь-01 + Q2,iB2 + af.iBs + Q3,iB4
i=l
= q?,iBi = Si = [0 0].
Аналогично
C2 = i(B1+B2) = i([0 0] + [l 1]) =
С3 = |в2 + |вз = |[1 1] + |[2 1] =
С* = \в2 + \в3 = \{1 1] + |[2 1] =
C6 = i(B3 + B4) = i([2 l] + [3 0]) =
С6 = В4 = [3 0].
В результате увеличивается гибкость всей кривой.
1
2
i 1
I 1
1.
2
В следующем примере в исходный открытый равномерный узловой вектор
вносится один узел, после чего вектор становится неоднородным.
Пример 5-19 Локальное разбиение В-сплайна
Рассмотрим открытый В-сплайн третьего порядка (к = 3) из примера
5-18. Провести разбиение, добавив узловое значение 1 на интервале 0 —> 1
вектора: [X] = [0001222], где х\ = 0,... ,хт = 2. Новый узловой
вектор имеет вид: [У] = [00011222], где у\ = О,...,да = 0.
Новый многоугольник имеет пять вершин С\... Сь ■
Ненулевые afj, необходимые для расчета Cj:
k=l
йз,1 = а3,2 = аз,з = аз,4 = а4,5 = 1
к =2
Q
к=3
2 2 2 2 2
<*2,i = Q2,2 = а3,3 = аз,4 = а4,5 = 1
„з _ з _ з з _, а з _ 1
Qi,i = а2,2 - аз,4 = а4,5 = 1, аз.з = ^г.з = j-
Новые вершины:
Ci = ai.iBi = Bi = [0 0],
С2 = ai,2S2 = В2 = [1 1],
Сз = аЬВ2+аз,звз = |(В2+Вз) = |([1 1] + [2 1]) =
С4 = а|,4Вз = Вз = [2 1],
С5 = а\5В* = В4 = [3 0].
Если Сз сдвинуть до совпадения с С2, т. е. С2 = Сз = [1 1], то получится
как двойная вершина, так и двойной узел для С2 = Сз- Для к = 3 В-сплайн
имеет острый пик в С2 = Сз (см. задачу 5-30).
5-13 РАЦИОНАЛЬНЫЕ В-СПЛАЙНЫ
Впервые в машинной графике описание рациональных кривых и поверхностей
было предложено в работе [5-32]. В литературе широко известны рациональные
формы кубических сплайнов и кривых Безье ([5-33]—[5-37]), а также конических
сечений [5-38]. Здесь мы рассмотрим только рациональные В-сплайны, так как они
составляют общепринятую основу, а также из-за пространственных ограничений.
Рациональные В-сплайны это единственное точное математическое
представление, охватьшающее все аналитические формы — прямые, плоскости, конические
сечения, включающие окружности, кривые произвольной формы, квадрики и
трехмерные поверхности, используемые в машинной графике и проектировании.
Первым рациональные В-сплайны изучил Весприлл [5-39]. Основа наших
рассуждений приведена в работах [5-40] и [5-41]. Стоит отметить, что неравномерные
рациональные В-сплайны (NURBS) с 1983 г. являются стандартом IGES (5-42).
IGES — это стандарт обмена проектной информацией между системами
машинного проектирования, а также между ними и системами автоматизированного
производства. Рациональные В-сплайны применяются в ряде систем
геометрического моделирования и реализованы аппаратно (СБИС или микрокод) в
некоторых графических рабочих станциях.
Рациональный В-сплайн это проекция нерационального (полиномиального) В-
сплайна, определенного в четырехмерном (4D) однородном координатном
пространстве, на трехмерное (3D) физическое пространство. В частности
71+1
Рф = £в*ад*), (5-121)
г=1
где В^ — вершины многоугольника для нерационального 4D В-сплайна в
четырехмерном пространстве, Ni^it) — функция базиса нерационального В-сплайна
из уравнения (5-84).
Рациональный В-сплайн получается после проектирования, т.е. деления на
однородную координату
ПЕ BihiN^it) n+1'
PW = ^+1 = Е В*ЪА*), (5-122)
Е hiNi>k(t) <=i
г=1
где Bi — вершины трехмерного многоугольника для рационального В- сплайна, а
PiAt) = n+fiAt) (5-123)
Е ЫЪ,к(!)
t=i
— базисные функции рационального В-сплайна. Здесь hi > 0 для всех г1.
1 Базисные функции рационального В-сплайна могут быть определены и для /i, < 0 (см. [5-
39]), но в данном случае это неудобно.
Как видно из уравнений (5-121) — (5-123), рациональные В-сплайны и их
базисы это обобщение нерациональных В-сплайнов и базисов. Они наследуют почти
все аналитические и геометрические свойства последних. В частности:
Каждая функция рационального базиса положительна или равна нулю для
всех значений параметра, т. е. Д^ > 0.
Для любого значения параметра t сумма базисных функций рационального
В-сплайна равна единице, т. е.
71+1
^2Ri,k(t) = l. (5-124)
i=i
Кроме к = 1 каждая рациональная базисная функция имеет ровно один
максимум.
Рациональный В-сплайн порядка к (степени к — 1) везде Ск~2 непрерывен.
Максимальный порядок рационального В-сплайна равен количеству вершин
определяющего многоугольника.
Рациональный В-сплайн обладает свойством уменьшения вариации.
Общая форма рационального В-сплайна повторяет очертания определяющего
многоугольника.
Любое проективное преобразование рационального В-сплайна производится
соответствующим преобразованием вершин определяющего многоугольника;
т. е. кривая инварианта относительно проективного преобразования. Это более
сильное условие, чем для нерационального В-сплайна, который инвариантен
только относительно аффинного преобразования.
Из уравнений (5-85) и (5-123) видно, что при всех hi = 1, Ri,k(t) = N^k^t), т. е.
нерациональные В-сплайны и их базисы являются частным случаем
рациональных. Легко показать, что открытый рациональный В-сплайн с порядком, равным
количеству вершин определяющего многоугольника, представляет собой
рациональную кривую Безье. В случае /ц = 1 рациональная кривая Безье сводится к
нерациональной. Таким образом, В-сплайны включают как рациональные, так и
нерациональные кривые Безье.
Рациональные В-сплайны — это четырехмерное обобщение нерациональных В-
сплайнов; поэтому алгоритмы повышения степени (работа [5-27] и пример 6-18),
разбиения (разд. 5-12 и работы [5-28] — [5-31]) и подгонки (разд. 5-11) для
нерациональных В-сплайнов справедливы и для рациональных при распространении
их на четырехмерное пространство.
Рациональные В-сплайны и их базисы можно получить с помощью открытых
равномерных, периодических равномерных и неравномерных узловых векторов.
Однородные координаты ft, (также называемые весами) в уравнениях (5-122) и
(5-123) предоставляют дополнительные возможности изгиба кривой; h = 1
называется аффинным пространством и соответствует физическому пространству. На
рис. 5-57 показано влияние однородных координат h на базисные функции
рационального В-сплайна, где [0 0 0 12 3 3 3] (тг +1 = 5, к = 3) — открытый
равномерный узловой вектор, hi = 1, г + 3 — вектор однородных координат. Значе-
Рис. 5-57 Базисные функции рационального В-сплайна для п+1 = 5, к = 3 с открытым
узловым вектором [X] = [0 0 0 1 2 3 3 3], [Я] = [1 1 h3 1 1]. (а) кз = 0;
(Ь) /is = 0.25; (с) к3 = 1.0; (d) /i3 = 5.0.
У
Рис. 5-58 Рациональные В-сплайны для п+1 = 5, к = 3 с открытым узловым вектором
[X] = [0 0 0 1 2 3 3 3], [Я] = [1 1 ft3 1 1].
ния Лз лежат в диапазоне от 0 до 5. Базисные функции рационального В-сплайна
на рис. 5.57с при h = 1 совпадают с соответствующими функциями
нерационального В-сплайна. Рациональный В-сплайн для кз = 1 на рис. 5-58 также совпадает
с соответствующим нерациональным. Отметим, что для h3 = 0 (рис. 5-57а) Дз,з
везде равно нулю; т. е. соответственная вершина Z?3 не оказывает никакого
влияния на форму соответствующей кривой. Это показано на рис. 5-58, где вершины
определяющего многоугольника B<l и В± соединены прямой. Из рис. 5-57 также
видно, что при увеличении Кз также возрастает Д3,з и, вследствие уравнения (5-
124), Яг.з и i?4,3 уменьшаются. На рис. 5-58 изображено воздействие на
соответствующие рациональные В-сплайны. В частности отметим, что с увеличением кз
кривая приближается к Вз- Отсюда, как уже отмечалось, следует, что однородные
координаты дают возможность увеличить гибкость кривой. Иллюстрация
аналогичных свойств рациональных В-сплайнов и базисов четвертого порядка (к = 4)
дана на рис. 5-59 и 5-60. Однако для кривых более высокого порядка на рис. 5-60
кривая при кз = 0 не вырождается в отрезок прямой между В2 и Bt.
На рис. 5-61 изображен периодический равномерный базис для п+1 = 5, А; = 3
и узлового вектора [X] = [0 123456 7] и вектора однородных
координат [Н] = [1 1 Нз 1 1] с 0 < h3 < 5. Здесь, как и в случае нерационального
базиса, допустимый диапазон параметра 2 < t < 5. На рис. 5-61 показан только
этот диапазон. Для Лз = 1 базисные функции рационального В-сплайна
совпадают с соответствующими нерациональными, но для ft3 ^ 1 они становятся
непериодическими и не являются параллельным переносом друг друга. На рис. 5-62
приведены соответствующие рациональные В-сплайны. Отметим, что конечные
точки всех кривых совпадают.
На рис. 5-63 и 5-64 показаны соответствующие В-сплайны четвертого порядка
(к = 4) и их базисы. Отметим, что начальные и конечные точки кривых лежат
на прямых.
О 1 2
(с)
Рис. 5-59 Базисные функции рационального В-сплайна для п+1 = 5, к = 4 с открытым
узловым вектором [X] = [0 0 0 0 1 2 2 2 2], [Я] = [1 1 h3 1 1]. (а) Л3 =
0; (Ь) Лз = 0.25; (с) h3 = 1.0; (d) h3 = 5.0.
Рис. 5-60 Рациональные В-сплайны для п+1 = 5, к = 4 с открытым узловым вектором
[X] = [0 0 0 0 1 2 2 2 2], [Я] = [1 1 Л3 1 1].
Вычисляя уравнения (5-122) и (5-123) для конечных точек кривой с
аргументом (tmax—e)e_+o из примера 5-12, получаем, что первая и последняя точки
открытого рационального В-сплайна совпадают с конечными точками определяющего
многоугольника:
Р(0) = Bi и P(imax) = Р{п - к + 2) = Вп+1.
Из рис. 5-65 видно, что перемещение одной вершины многоугольника влияет
на кривую так же, как и в случае рациональных В-сплайнов. В данном случае
[Н] = [1 1 0.25 1 1]. Если /is = 0, то передвижение В3 не оказывает никакого
воздействия. С увеличением /i3 растет влияние движения точки В$.
На рис. 5-66 показано воздействие кратных вершин в Вз на рациональный
В-сплайн четвертого порядка. Как и для нерациональных кривых, А; — 1
совпадающая вершина приводит к появлению острого угла или пика. Далее, кратная
вершина порождает ребра нулевой длины, поэтому существование угла не зависит
от значений h3 > 0, соответствующих ей (см. задачу 5-33).
Рассмотрим пример расчета рационального В-сплайна.
Пример 5-20 Расчет открытых рациональных В-сплайнов
Пусть дан многоугольник с вершинами Bi[0 1], Вг[1 2], Вз[2.5 0],
Й4[4 2], Вь[5 0]. Найти точку при t = 3/2 на открытом рациональном
В-сплайне третьего порядка (к = 3) с однородными векторами, заданными
[Я] = [1 1 Лз 1 1], Лз =0,1/4,1,5.
Узловой вектор —[0 0 0 12 3 3 3]. Диапазон параметра t: 0 <
t < 3. Кривые состоят из трех кусочно рациональных квадратичных кривых,
по одной на каждом внутреннем интервале узлового вектора.
(*)
1-
*« *W Л44
Рис. 5-61 Базисные функции рационального В-сплайна для n + l = 5, fc = 3c
периодическим узловым вектором [X] = [0 123456 7], [Я] = [1 1 Лз 1 1].
(а) Лз = 0; (Ъ) Лз = 0.25; (с) h3 = 1.0; (d) h3 = 5.0.
Рис. 5-62 Рациональные В-сплайны для тг + 1 = 5, fc = 4 с периодическим узловым
вектором [X] = [0 1 2 3 4 5 6 7], [Я] = [1 1 h3 1 1].
Из уравнения (5-84) на интервале 1 < t < 2 получим базисные функции
нерационального В-сплайна:
1 < t <2
ЛГ4,1(0 = 1; Nt,i(t) = Q, i?4
N3,2(t) = (2-t); N4,2(t) = (t - 1); Nit2(t) = О, i ^3,4
JV4|3(t)= ^"^ ; ЛГ4,з(0 = 0, t ^2,3,4
Отсюда и из уравнения (5-123) после определения знаменателя
п+1
S = Y,hiNi,k(t) = hiNifi(t) + h2N2,3(t) +UN*At) + ЛвЛЫО =
= h2N2,3(t) + Л4ЛГ4,з(0 =
_ (2 - t)2 (t - l)2 _ 2t2 - 6t + 5
2 2 ~~ 2
получим базис рационального В-сплайна:
1 <t < 2
Рис. 5-63 Базисные функции рационального В-сплайна для п + 1 = 5, к = 4 с
периодическим узловым вектором [X] = [0 1 2 3 4 5 6 7 8], [Я] = [1 1 h3 1 1].
(а) h3 = 0; (Ь) h3 = 0.25; (с) h3 = 1.0; (d) h3 = 5.0.
Рис. 5-64 Рациональные В-сплайны для тг + 1 = 5, fc = 4 с периодическим узловым
вектором [X] = [0 1 2 3 4 5 6 7 8], [Я] = [1 1 h3 1 1].
4 -
2 -
^
-
-
■- А
/в.
г '
/
/
/
/
/
/
/
Вэ,
А
/ \
/ \
/ \
\
\
\
*э. \
х \
/ ч \
/ / ч \
/ /
/ •
/ S>T
//^«-^Л
д.^о^—с
У>5^— *
/j&^* ч о
^^ ч
#^ ч
~ ч
ч
ч
ч
\
ч \
-^Л
^^v \
/ ^<§%4
/ ^^NS^
\ / ^^
* у ^V
S ^.
у X
s X
Ч /* X
1 1
"^ / . X.
—^ 1 Ji-
2 В,
Рис. 5-65 Влияние перемещения одной вершины многоугольника на рациональный В-
сплайн п + 1 = 5, к = 4, [Я] = [1 1 0.25 1 1].
Рис. 5-66 Влияние кратной вершины многоугольника Вз на рациональный В-сплайн
п + 1 = 5, к = 4. (а) Одна вершина [Я] = [1 1 0.25 1 1]; (Ь) двойная вершина [Я] =
[1 1 0.25 0.25 1 1]; (с) тройная вершина [Я] = [1 1 0.25 0.25 0.25 1 1].
fc3=0
Я1,з(*) = 0
Д2,з(<) - ^ 2t2_6t + 5
Дз,з(*) = 0
Й4,3(<) =
/l4JV4l3(t) _ С"1)2
S 2t2 - &t + 5
Rb,i(t) = 0
h3 =1/4
S = h2N2,3{t) + h3N3,3{t) + h4N4,3{t)
_(2-t)2 t(2-Q (3-f)(«-l) (<-l)2
-"~T~ + _8~+ 8 + ~~2~~
_ 6t2 - Ш + 17
8
Ri,i(t) = 0
«M(0-6t2_18+17
p m t(2-0 + (3-t)(t-l)
^•^-e^-m + i?
Дб,з(0 = 0
Лз = 1
S=l
Й1,з(0 = 0
R, ,(t) - N, ,(t\ - (2~^
-2t2 + 6t - 3
6t2 - 18* + 17
R>,(t) = N3At)=t-^+{3-t}{t-1)
R*A*) = ^4,3(*) :
R5,i(t) = 0
Л3 = 5
2
(t-l)2
(2-t)2 | 5t(2-f) { 5(3-*)(*-!) { (t-1)2
Й1,з(0 = 0
Й2,з(*)
Дз,з(*)
Й4.з(0
2
(2-О2
-4*2 + 12* — 5
2(-4*2 + 12* - 5)
5*(2-*) +5(3-*)(*-!)
2(-4*2 + 12* - 5)
(t-l)2
2(-4*2 + 12* - 5)
5(-2*2 + 6* - 3)
2(-4*2 + 12* - 5)
Д6>з(*)=0
Полностью результаты приведены на рис. 5-57.
При * = 3/2
Лз=0: Й1,з(3/2)=0; Дв,з(3/2) = ±; Дз,з(3/2) = 0;
Д4,з(3/2) = ±; Д6,з(3/2)=0
Лз = 1
Л3 = 1
Л3 = 5
Д1,з(3/2)=0; Д2,3(3/2) = §;
Д4,з(3/2) = f; Дб,з(3/2) = 0
«i.s(3/2)=0; Д2,з(3/2) = ±;
Д«.а(3/2) = £; Лв.а(3/2) = 0
Д1,з(3/2) = 0; Ла,а(3/2):
1 .
Л.»(3/2) = £; Д5.з(3/2)=0
Соответственные точки на рациональных В-сплайнах:
*з,з(3/2) = f;
Дз.з(3/2) = f;
Лв.а(3/2)
15.
16'
0:
P(3/2) = i[l 2] + i[4 2] =
Р(3/2)=Л[1 2] + ^
Лз
Лз = -.
4
Л3 = 1
Лз = 5
Полностью результаты приведены на рис. 5-58
!•
Р(3/2)
> *Л
I о
+ f[4 2] =
+ J[4 2] =
P(3/2) = ^[l 4 + S
I»
+
1 г, „! Г5 1"
3214 2^=[2 В.
Формально дифференцируя уравнения (5-122) и (5-123), получаем
производные рациональных В-сплайнов, а именно
р'(*) = Х>дЫ')
г=1
(5-125)
где
п+1
мял*) hiNi>k£>hiNU
KM = ^r^~ - ^ 2- (5-126)
1=1
Подставим t = 0nt = n — к + 2:
h2,
P'(0) = (k-1)-±(B2-B1), (5-127)
Ail
P'(n - к + 2) = (к - 1)-^ЧБп+1 - Bn), (5-128)
"■п+1
т.е. наклон кривой в концах совпадает с наклоном первого и последнего ребер
многоугольника, соответственно.
Аналогично рассчитьгоаются производные более высокого порядка (см. задачи
5-35 и 5-36).
Рассмотрим простой пример.
Пример 5-21 Производные открытых ргщиональных сплайнов
Пусть дан определяющий многоугольник из примера 5-16 с вершинами
Bi[l 1], Вг[2 3], Вз[4 3], В^[3 1]. Найти первую производную
рационального В-сплайна второго порядка (к = 2) с [Щ = [1 1/2 1 1].
Узловой вектор [X] = [0 0 1 2 3 3]. Параметр изменяется в
диапазоне 0 < t < 3. Из уравнения (5-125) первая производная
P'{t) = BiR!li2(t) + B2R^,2(t) + В3Дз,2 (0 + В4^,3(<)
Из уравнений (5-12) и (5-16) получаем нерациональные базисные функции
и их производные:
0<<<1
Ni.2(t) = 1 - t; ЛГ2,2(0 = *; N,2(0 = 0, i ф!,2
<2(0 = -i; n;,2(0 = 1; <2(0 = о, t#i,2
Используя уравнение (5-126), найдем рациональный базис и его производные
п+1 п . п+1
!>№.' = V: £wvb = -i
1 1=1
<2(0 = ^7{(-i)-(i-0(^} = ^
"О2
-2_
Л«.я(*) = 0, 154 1,2
Итак
P'^ = why^-B^
Отметим, что в отличие от нерационального В-сплайна из примера 5-16, при
сохранении наклона равным наклону первого ребра значение производной
теперь изменяется вдоль кривой. При t = 0, т. е. в начале кривой
P'(t) = \{В, - В,)
величина производной в два раза меньше, чем у нерационального В-сплайна
из примера 5-16.
На интервале
1 < * < 2
N'2j2(t) = 2-t; N3,2(t) = t - 1; JVil2(*) = 0, i 5*2,3
Здесь
^С)-(|)(|){С-Х)-С*-0(Ш—F
Л5.2(*) = 0, г ^2,3
Итак
F'(t) = |(B3-B2)
На интервале
2 < t < 3
JVSla(t) = 3-t; JV4,2(t)=t-2j Nit2(t) = О, г/3,4
^з,2(0 = -1; Ml.2(t) = l; <2(*)=0, г ^3,4
При этом
п+1 П+1
Дз,2(<) = Wa.a(0 = -i; R'iAt) = K2(t) = i;
л5,я(0 = о, *^з,4
To есть
При < = (3 — e), e —»■ 0, получаем тот же результат, что и при t = 3.
Как уже отмечалось, с помощью рациональных В-сплайнов можно
представить все конические сечения. Кроме того, это единственное математическое
описание, способное задать произвольную кривую, состоящую из конических сечений.
Коническим сечениям соответствуют квадратичные уравнения, поэтому удобно
сначала рассмотреть квадратичный рациональный В-сплайн (к — 3), заданный
тремя вершинами (п + 1 = 3) с узловым вектором [X] = [0 0 111]:
рт = /цДГ1,з(«)Д1 + h2N2i3(t)B2 + h3N3,3(t)B3
{> h.N^t) + h2N2}3(t) + h3N3t3(t) ' K ]
что фактически представляет собой рациональную кривую Безье третьего
порядка (см. рис. 5-67). Предположим, что h\ = h3 = 1. Тогда уравнение (5-129)
принимает вид
рт = N1<3(t)Bx + h2N2t3(t)B2 + N3,3(t)B3
W N!,3(t) + h2N2}3(t) + N3,3(t) ■ ( }
При h2 = 0 точки В\ и В3 соединены прямой линией. При h2 —> оо повторяется
контур определяющего многоугольника. Если h2 = 0 и t = 1/2, достигается
серединная точка отрезка BXB2, обозначенная на рис. 5-67 буквой М. Аналогично
при h2 —» оо, t = 1/2, достигается точка В2. Для 0 < h2 < оо точка S,
соответствующая точке кривой P(t) при t — 1/2, движется по прямой линии между М
и В2. S называется плечевой точкой. Значение h2 определяет тип конического
сечения. В работе [5-43] показано, что результат при
h2 = 0 — прямая линия,
О < h < 1 — эллиптический сегмент,
h2 = 1 — параболический сегмент,
h2 > 1 — гиперболический сегмент.
Воспользуемся уравнением (5-84) и подставим t = 1/2 в уравнение (5-130):
m (1 - г)2Вг + 2М(1 - t)B2 + t2B3
U (1 - i)2 + 2/i2t(l - t) + fi
При t = 1/2, P(t) = S, что дает
1 + h2 2 1 + h2 l + h2 l + h2
Запишем параметрическое уравнение прямой между М и В2
S = (1 - s)M + sB2, (5-132)
где s — параметр. Приравнивая коэффициенты уравнений (5-131) и (5-132),
получаем
s=t\~ и /г2 = -^ = ^. (5-133)
l + h2 1 - s S - В2 К '
yt
Bi
Рис. 5-67 Конические сечения, заданные рациональными В-сплайнами (кривыми
Безье); (а) прямая линия, Лг = 0; (Ь) эллипс, Лг = 0.25; (с) парабола, Ъч = 1; (d)
гипербола, /l2 = 3.
Параметр s определяет форму кривой и тип конического сечения, т. е. это удобное
средство разработки.
Так как окружность является частным случаем эллипса, можно подобрать
такое значение /i2, что уравнение (5-130) будет уравнением дуги окружности. Из-
за симметрии 2?i, В-з, и В% для дуги окружности формируют равнобедренный
треугольник, как показано на рис. 5-68. Требуемое значение Лг, определяется из
рис. 5-68.
Треугольник В\В^В% равнобедренный, поэтому S — максимум кривой и
касательная в точке S параллельна линии В\В$. Треугольник B\qS также
равнобедренный с равными углами ZSB%q и /.B\Sq у основания, обозначенными 9/2 на
рис. 5-68. Из параллельности касательной S линии В1В3 следует, что углы /.qSB\
и ASB\M равны. Поэтому угол /,SB\M = е/2 равен половине угла у основания
треугольника В\, 2?2 и Вз-
Отсюда и из уравнения (5-133) получаем
Ла =
M-S
"*(*)
S-B2 /8in0-etg(f)"
Подставляя тождество (9/2) = sin0/(l + cos0), получаем
/12 =
esin 8
1+cosfl
/sin0
esinff
l+cos9
/(l + cos0)-e /
= — = cos 9
(5-134)
Рис. 5-68 Дуга окруясности, построенная как рациональный В-сплайн.
Рис. 5-69 Рациональные В-сплайны — окружности, (а) Три сегмента по 120°; (Ь)
четыре сегмента по 90°.
0 2 4
Рис. 5-70 Сопряжение рациональных В-сплайнов.
Дуга покрывает часть окружности для удвоенного угла 9. Для дуги 120° угол
9 = 60° и /гг = 1/2. Для данного случая радиус окружности равен 2(5 — М).
Полная окружность получается соединением нескольких сегментов. В
частности, окружность можно составить из трех сегментов рационального
квадратичного В-сплайна, каждый из которых покрывает 120°. Определяющие точки
составляют равносторонний треугольник, как показано на рис. 5-69а.
Неравномерный узловой вектор и вектор однородных координат:
[Х] = [0 0 0 1 1 2 2 3 3 3]
[Я] = [1 1/2 1 1/2 1 1/2 1]
Аналогично, полная окружность также задается четырьмя рациональными
квадратичными сегментами В-сплайна, каждый по 90°, где определяющие вершины
составляют квадрат, рис. 5-69Ь. Неравномерный узловой вектор и вектор
однородных координат:
[X] = [0 0 0 1 1 2 2 3 3 4 4 4],
[Я] = [1 л/2/2 1 л/2/2 1 л/2/2 1 л/2/2 1].
Рассмотрим пример построения конических сечений с помощью В-сплайна и
объединения их в произвольные кривые.
Пример 5-22 Конические сечения, использующие рациональные
В-сплайны
Построить единственный рациональный В-силайн третьего порядка,
сопрягающий 90° дугу окружности, заданную квадратичным рациональным
В-сплайном с определяющими вершинами Bi[0 0], Вг[0 2], Вз[2 2] с ква-
дратическим рациональным В-сплайном третьего порядка, заданным
точками В3[2 2], В4[4 2], В5[6 3], В6[7 5] с Л, = 1, 4 < г < 7.
90° дуга окружности имеет узловой вектор [0001 1 1] и
вектор однородных координат [1 v2/2 1]. Соответственные векторы
рационального В-сплайна, заданного точками ВзВ^ВвВб- [0 0 0 1 2 2 2] и
[1 1 1 1].
Неравномерный узловой вектор комбинированной прямой: [X] = [0001
12 3 3 3]; вектор однородных координат: [1 -\/2/2 1111].
Результат изображен на рис. 5-70.
5-14 ЛИТЕРАТУРА
5-1 Bohm, W , Farin, G., and Kahmann, J. «A Survey of Curve and Surface Methods in
CAGD», Сотр. Aid. Geom. Des., Vol. 1, pp. 1-60, 1984.
5-2 Higdon, A., Olisen, E , Stiles, W., and Weese, J. Mechanics of Materials, 2d ed., John
Wiley & Sons, New York, 1967. 5-3 South, N.E., and Kelly, J P., «Analytic Surface
Methods», Ford Motor Company N/C Development Unit, Product Engineering Office,
December 1965.
5-4 Nutbourne, A.W., «A Cubic Spline Package Part 2 —The Mathematics», Сотр. Aid.
Des., Vol. 5, No. 1, January 1973.
5-5 Adams, J. A., «A Comparison of Methods for Cubic Spline Curve Fitting», Сотр. Aid.
Des., Vol. 6, pp. 1-9, 1974.
5-6 Schweikert, D. C, «An Interpolation Curve Using a Spline in Tension», J. Math. Phys.,
Vol. 45, pp. 312-317, 1966.
5-7 Cline, A. K., «Curve Fitting Using Splines Under Tension», Atmos. Tech., No. 3, pp. 60-
65, 1973.
5-8 Nielson, G., «Some Piecewise Polynomial Alternatives to Splines Under Tension»,
Computer Aided Geometric Design, Barnhill, R. E., and Riesenfeld, R. F. (eds.), pp 209-
235, Academis Press, New York, 1974.
5-9 Overhauser, A. W., «Analytic Definition of Curves and Surfaces by Parabolic Blending»,
Tech. Rep. No SL68-40, Ford Motor Company Scientific Laboratory, May 8, 1968.
5-10 Brewer, J. A., and Anderson, D. C, «Visual Interaction with Overhauser Curves and
Surfaces», Сотр. Graph., Vol. 11, pp. 132-137, 1977 (SIGGRAPH 77).
5-11 Bezier, P. E., «How Renault Uses Numerical Control for Car Body Design and Tooling»,
SAE paper 680010, Society of Automotive Engineers' Congress, Detroit, MI, 1968.
5-12 Bezier P. E., «Example of an Existing System in the Motor Industry: The Unisurf
System», Proc. Roy. Soc. (London), Vol. A321, pp. 207-218, 1971.
5-13 Bezier, P. E., Emploi des Machines a Commande Numerique, Masson et Cie, Paris, 1970.
Translated by Forrest, A R., and Pankhurst, A. F., as Bezier, P. E., Numerical Control
Mathematics and Applications, John Wiley &: Sons, London, 1972.
5-14 Forrest, A. R., «Interactive Interpolation and Approximation by Bezier Polynomials»,
Сотр. J., Vol. 15, pp. 71-79, 1972.
5-15 Gordon, W. J., and Riesenfeld, R. F., «Bernstein-Bezier Methods for the Computer Aided
Design of Free-from Curves and Surfaces», J. ACM, Vol. 21, pp. 293-310, 1974.
5-16 Bartels, R. H., Beatty, J. C, and Barsky, B. A., Splines for Use in Computer Graphics
& Geometric Modeling, Morgan Kaufman, Los Altos, CA, 1987.
5-17 Barsky, B. A., «Arbitrary Subdivision of Bezier Curves», TR UCB/CSD 85/265, Сотр.
Asi. Div., Univ. of Cal., Berkeley, November 1985.
5-18 Clark, J. H., «A Fast Scanline Algorithm for Rendering Parametric Surfaces», Сотр.
Graph., Vol. 14, pp. 7-12, 1979 [addendum to SIGGRAPH 79 Conf. Proc. — «papers to
be published in the С ACM»].
5-19 Cohen, E., and Riesenfeld, R. F., «General Matrix Representations for Bezier and B-
Spline Curves», Сотр. in Indus., Vol. 3, pp. 9-15, 1982.
5-20 Schoenberg, I. J., «Contributions to the Problem of Approximation of Equidistant Data
by Analytic Functions», Q. Appl. Math., Vol. 4, pp. 45-99; pp. 112-141, 1946.
5-21 Cox, M. G., «The Numerical Evaluation of B-Cplines», National Physical Laboratory
DNAC 4, August 1971.
5-22 de Boor, C, «On Calculation with B-splines», J. Approx. ТЪеогу, Vol. 6, pp. 50-62, 1972.
5-23 Riesenfeld, R. F., «Application of B-Spline Approximation to Geometric Problems of
Computer Aided Design», PhD dissertation, Syracuse Univ., Syracuse, NY, 1972. Also
available as U. of Utah, UTEC-CSc-73-126, March 1973.
5-24 Barsky, B. A., «End Conditions and Boundary Conditions for Uniform B-Spline Curve
and Surface Representations», Сотр. in Indus., Vol. 3, pp. 17-29, 1982.
5-25 Hartley, P. J., and Judd, C. J., «Parameterization of Bezier Type B-spline Curves and
Surfaces», Сотр. Aid. Des., Vol. 10, pp. 130-134, 1978.
5-26 Rogers, D. F., and Fog, N. G., «Constrained B-spline Curve and Surface Fitting», CAB J,
Vol. 21, pp. 641-648, 1989.
5-27 Cohen, E., Lyche, Т., and Schumacher, L. L., «Zlgorithms for Degree-Raising of Splines»,
ACM Trans, on Graph., Vol. 4, pp. 171-181, 1985.
5-28 Cohen, E., Lyche, Т., and Riesenfeld, R.. F., «Discrete B-Splines and Subdivision
Techniques in Computer Aided Geometric Design and Computer Graphics», Сотр.
Graph. Imag. Proc, Vol. 14, pp. 87-111, 1980.
5-29 Prautzsch, H., «A Short Proof of the Oslo Algorithm», Сотр. Aid. Geom. Des., Vol. 1,
pp. 95-96, 1984.
5-30 Bohm, W., «Inserting New Knots into B-spline Curves», Сотр. Aid. Des., Vol. 12,
pp. 199-201, 1980.
5-31 Bohm, W., and Prautzsch, H., «The Insertion Algorithm», Сотр. Aid. Des., Vol. 17,
pp. 58-59, 1985.
5-32 Coons, S. A., «Surfaces for Computer Aided Design of Space Forms», MIT Project MAC-
TR-41, 1967.
5-33 Farouki, R., and Hinds, J., «A Hierarchy of Geometric Forms», IEEE Сотр. Graph. &
Appl., Vol. 5, No. 5, pp. 51-78, 1985.
5-34 Piegl, L., «A Geometric Investigation of the Rational Bezier Scheme of Computer Aided
Design», Сотр. in Indust, Vol. 7, pp. 401-410, 1986.
5-35 Forrest, A. R., «The Twisted Cubic Curve: A Computer Aided Geometric Design
Approach», Сотр. Aid. Des., Vol. 12, pp. 165-172, 1980.
5-36 Bohm, W., «On Cubics: A Survey», Сотр. Graph. Imag. Proc, Vol. 19, pp. 201-226,
1982.
5-37 Forrest, A. R., «Curves and Surfaces for Computer-Aided Design», PhD Dissertation,
Cambridge Univ., 1968.
5-38 Ball, A. A., «Consurf I-III», Сотр. Aid. Des., Vol. 6, pp. 243-249, 1974; Vol. 7, pp. 237-
242, 1975; Vol. 9, pp. 9-12, 1977.
5-39 Versprille, K. J., «Computer-Aided Design Applications of the Rational B-spline
Approximation Form», PhD dissertation, Syracuse Univ., Syracuse, NY, February 1975.
5-40 Tiller, W., «Rational B-splines for Curve and Surface Representation», IEEE Сотр.
Graph. & Appl., Vol. 3, No. 6, pp. 61-69, September 1983.
5-41 Piegl, L., and Tiller, W., «Curve and Surface Constructions Using Rational B-splines»,
Сотр. Aid. Des., Vol. 19, pp. 485-498, 1987.
5-42 IGES 'Initial Graphics Exchange Specifications, Version 3.0', Doc. No. NB-SIR 86-3359
Nat. Bur. of Stds., Gaithersburg, MD, USA, 1986.
5-43 Lee, E., «Rational Bezier Representation for Conies», in Geometric Modeling, Farin, G.
(ed.), SIAM, pp. 3-27, 1986.
Глава6
Поверхности
6-1 ВВЕДЕНИЕ
Поверхности и их описание играют важную роль в конструировании и
производстве. Очевидными примерами этого являются разработка и производство
автомобильных кузовов, корабельных корпусов, авиационных фюзеляжей и крыльев;
пропеллеров, турбин, компрессоров и лопастей вентиляторов; посуды, мебели и
обуви. В этом случае сущность конструирования либо по функциональным, либо
по эстетическим причинам составляет форма или геометрия поверхности.
Описание поверхности также играет важную роль в представлении данных, полученных
в медицине, геологии, физике и других естественных науках.
Традиционным способом представления поверхности является использование
нескольких ортогональных проекций. По существу, поверхность задается сеткой
ортогональных плоских кривых, лежащих на секущих плоскостях, и
несколькими ортогональными проекциями определенных «характерных»
пространственных линий (см. рис. 5-1). Эти кривые первоначально могут быть созданы на
бумаге либо же взяты (оцифрованы) из трехмерной модели, например в
автомобильной промышленности дизайнерами традиционно используется глиняная
модель.
В машинной графике и автоматизированном проектировании выгодно
разрабатывать «настоящую» трехмерную математическую модель поверхности. Такая
модель позволяет на ранних стадиях и относительно легко провести анализ
характеристик поверхности, например кривизны, или физических количественных
характеристик, зависящих от поверхности, например объема, площади
поверхности, момента инерции и т.д. Упрощается визуализация поверхности (см. [6-1]),
применяемая для разработки или контроля за ходом разработки. Далее, по
сравнению с традиционным методом, использующим сетку линий, также существенно
упрощается генерация необходимой для изготовления поверхности информации,
например управляющих программ для станка с числовым программным
управлением. В ранних работах Безье [6-2], Сабина [6-3], Петерса [6-4] и других авторов
продемонстрирована осуществимость этого подхода. Разработанные в последнее
время методы описания поверхностей достигли такой стадии развития, что
позволяют «почти» исключить традиционное описание поверхности с помощью сетки
линий.
Существуют две основные идеи, лежащие в основе методов описания
поверхностей. В первой, связаной в основном с именем Кунса, математическую
поверхность стараются создать по заранее известным данным. Во второй, связанной
в основном с именем Безье, математическую поверхность стараются создать ab
initio (с самого начала). В первое время отрасли, связанные с числовыми
параметрами, например конструирование, тяготели к первому подходу, тогда как
отрасли, учитывающие визуальные, осязательные или эстетические факторы,
например дизайнеры и художники, тяготели ко второму. Последние работы
Роджерса ([6-5] — [6-7]) об интерактивных системах разработки корпусов кораблей и
Коэна ([6-8]) о разработке поверхностей показали, что эти два подхода
совместимы.
В следующих разделах представлены основы математического описания
параметрических поверхностей, используемых в машинной графике и
автоматизированном проектировании.
6-2 ПОВЕРХНОСТИ ВРАЩЕНИЯ
Возможно самым простым способом создания трехмерной поверхности является
вращение двумерного объекта, например прямой или плоской кривой вокруг оси в
пространстве. Такие поверхности называются поверхностями вращения. Сначала
для простоты предположим, что ось вращения совпадает с осью х и
положительно направлена. Предположим также, что объекты вращения — отрезок, прямая
или плоская кривая —лежат на плоскости ху. Позднее мы рассмотрим метод,
позволяющий избавиться от этих ограничений.
Самый простой объект, который можно вращать вокруг оси, —это точка. При
условии что точка не лежит на оси, вращение на угол 27г (360°) породит
окружность. Поворот на меньший угол даст дугу окружности.
Следующим по сложности являетсмя отрезок, параллельный, но не
совпадающий с осью вращения. Вращение на угол 27г (360°) породит в этом случае круговой
цилиндр. Радиусом этого цилиндра яляется длина перпендикуляра, опущенного
с отрезка на ось вращения. Длина цилиндра равна длине отрезка. Пример
изображен на рис. 6-1.
Если отрезок и ось вращения компланарны и отрезок не параллелен оси
вращения, то в результате вращения вокруг оси на угол 27г (360°) мы получим
усеченный круговой конус. Радиусы оснований усеченного конуса —длины
перпендикуляров, опущенных с концов отрезка на ось вращения. Высота конуса —это
длина спроецированного на ось вращения отрезка. Пример изображен на рис. 6-2.
И снова, если отрезок и ось вращения компланарны и отрезок
перпендикулярен оси вращения, то в результате вращения на угол 2п (360°) мы получим
плоский диск. Если отрезок пересекает (или касается) ось вращения, то
получится сплошной диск, в противном случае диск будет иметь круглое отверстие.
Примеры изображены на рис. 6-3.
И наконец, если отрезок наклонен к оси вращения, т. е. некомпланарен, то
вращение на угол 27г (360°) породит однополостный гиперболоид (см. разд. 6-4
и 6-7).
(я) (Ь)
Рис. 6-1 Цилиндрическая поверхность вращения, (о) Схема построения; (6) результат.
(я) (Ь)
Рис. 6-2 Коническая поверхность вращения, (о) Схема построения; (6) результат.
(а) (Ь)
Рис. 6-3 Диск в качестве поверхности вращения, (о) Схема построения; (6) результат.
(a) (b)
Рис. 6-4 Поверхность вращения из замкнутой ломаной, (о) Схема построения;
(Ь) результат.
Рис. 6-5 Бипараметрическая поверхность вращения.
Для создания поверхностей вращения могут быть также использованы
замкнутые и незамкнутые ломаные. На рис. 6-4 представлен конус с цилиндрическим
отверстием.
Параметрическое уравнение точки на поверхности вращения можно получить,
если вспомнить, что параметрическое уравнение вращаемого объекта, например
P(t) = [x(t) y{t) z{t)] 0<*<
есть функция одного параметра t. Вращение вокруг оси приводит к тому, что
координаты зависят также от угла поворота. Таким образом, точка на поверхности
вращения определяется двумя параметрами t и ф. Как показано на рис. 6-5, это
бипараметрическая функция.
Для рассматриваемого частного случая, т. е. вращения вокруг оси х объекта,
расположенного в плоскости ху, уравнение поверхности записывается1
Q(t, ф) = [x(t) y(t) cos ф y(t) sin ф]
(6-1)
Заметим, что здесь координата х не меняется. В качестве иллюстрации
приведем пример.
Пример 6-1 Простая поверхность вращения
Рассмотрим отрезок с концами Pi[l 1 0] и Рг[6 2 0], лежащий в
плоскости ху. Вращение отрезка вокруг оси х породит коническую
поверхность. Определим на поверхности координаты точки с параметрами t = 0.5,
ф = тг/3 (60°).
Параметрическое уравнение отрезка, соединяющего Pi и Рг, имеет вид
P(t) = [x(t) y{t) z(t)] = Pi + (Р2 - Pi)t 0 < t < 1
с декартовыми координатами
x(t) = Xl + (Х2 — Xl)t — 1 + 54,
y(t) = yi + (3/2 - yi)t = 1 +1,
z(t) = zi + (22 - zi)t = 0.
Используя уравнение (6-1), получим точку Q(l/2,ir/3) на поверхности
вращения
<Э(1/2, тг/3) = [1 + 5i (l + i)cos<£ (1 + 4)sin0]
"7 3 /ял 3 . /7гл'
= 2 2С08Ы 28ШЫ
3%/3
4
= [3.5 0.75 1.3].
Вращение плоских кривых также порождает поверхности вращения. Как
показано на рис. б-ба, сфера получается в результате вращения вокруг оси х
расположенной в плоскости ху полуокружности, центрированной относительно начала
координат. Вспомнив параметрическое уравнение окружности (см. разд. 4-5)
х = г cos в
у = г sin в
0 < в < тг
получим параметрическое уравнение сферы
<Э{в,ф) = [х{в) у(в)созф у(в)зтф]
— [г cos в г sin в cos ф г sin в sin ф]
0 < в < 7Г,
0 < ф < 2тг
1 Заметим, что Q(t,ф) являетя вектор-функцией, т.е. в векторной форме
Q(t, ф) = x(t)i + y(t) cos ф'} + y{t) sin фк,
где i, j, k —единичные векторы в х, у, z направлениях, соответственно.
(4-4)
(6-2)
(a) (*)
Рис. 6-6 Поверхности вращения, (о) Сфера; (Ь) эллипсоид.
Если вместо окружности подставить параметрическое уравнение
центрированного полуэллипса, расположенного в плоскости ху, получится эллипсоид вращения.
Напомнив параметрическое уравнение полуэллипса (см. разд. 4-6)
x = acos6 0<(9<тг (4-6)
у = b sin в
получим для любой точки эллипсоида следующее параметрическое уравнение:
Q(6,(j>) = [a cos б bsinOcoscJ) 6sin 0 sin 0] 0 < в < 7г,
О < ф < 2тг. (6-3)
При а = b = г уравнение (6-3) превращается в уравнение (6-2) для сферы.
Эллипсоид вращения показан на рис. 6-66.
Если ось вращения не проходит через центр окружности или эллипса, то в
результате вращения получается тор с сечением в виде окружности или эллипса,
соответственно. Параметрическое уравнение эллипса на плоскости ху с центром,
не совпадающим с началом координат, выглядит так
х = h + a cos в 0 < в < 27г,
у = к + bsind,
где (Л,к)— это х, у — координаты центра эллипса, тогда параметрическое
уравнение для любой точки тора имеет вид:
С}{6,ф) = [h + acosd (к + bsind) cos ф (к + bsind) sin ф], (6-4)
где 0 < в < 27г, 0 < ф < 27г. Если а = b = г, то уравнение (6-4) задает тор с
сечением в виде окружности. Если а ф Ь, то получится тор с сечением в виде
эллипса. На рис. 6-7 представлены оба типа торов.
(a) (6)
Рис. 6-7 Торы, (а) С сечением в виде окружности; (Ь) с сечением в виде эллипса.
Параболоид вращения получается при вращении параметрической параболы
(см. разд. 4-7)
х = ав2 0 < в < 0тах (4-9)
у = 2а0
вокруг оси х. Параметрическая поверхность задается уравнением
Q(6, ф) = [ав2 2aQcos ф 1айsin ф] 0 < в < (9тах,
О < Ф < 2тг. (6-5)
Гиперболоид вращения получается при вращении параметрической гиперболы
x = asec6 0<0<втах (4-14)
V = btg6
вокруг оси х. Параметрическая поверхность задается уравнением
Я(6,ф) = [asec6 btg(9cos</> btgвsmф], 0 < в < (9тах,
О < Ф < 2тг. (6-6)
Примеры показаны на рис. 6-8.
Для создания поверхности вращения можно использовать любую
параметрическую кривую, например кубический сплайн, параболический сплайн, кривую
Безье и В-сплайн. На рис. 6-9 изображена поверхность вращения, созданная из
относительно простого параболического сплайна. На рис. 6-10 изображен бокал,
(о) ф)
Рис. 6-8 Поверхности вращения, (а) Параболоид; (Ь) гиперболоид.
(о)
(*)
Рис. 6-9 Поверхность вращения из параболически интерполированной кривой, (а)
Создание кривой; (Ь) поверхность.
созданный как поверхность вращения с помощью незамкнутого В-сплайна.
Заметим, что бокал имеет как внутреннюю, так и внешнюю стороны. Вращение
производится относительно оси у
1 Метод, использованный при создании В-сплайна для бокала на рис. 6-10, может
представлять определенный интерес. Сначала набросок бокала был сделан на миллиметровке. Затем
тридцать четыре точки с этого рисунка были оцифрованы. С помощью описанного в разд. 5-11
итерационного процесса был получен исходный В-сплайн {к = 4, п + 1 = 21). После этого для
окончательной разработки в интерактивную систему (см. [6-7]) были переданы определяющие
точки кривой. Для изображенной поверхности вращения был использован В-сплаЙн,
полученный из окончательных 25 вершин. Определяющие точки кривой: [0, 0.684], [0.302 0.684], [0.302
0.684], [1.598 -0.288], [1.088 0.405], [0.374 0.773], [0.848 0.993], [1.232 1.446], [1.451 1.875], [1.502
2.631], [1.448 3.308], [1.226 4.076], [1.397 4.449], [1.398 4.592], [1.268 4.572], [1.241 4.485], [1.109 4.170],
[1.214 3.669], [1.313 2.889], [1.310 2.280], [1.172 1.575], [0.629 1.119], [0.281 0.882], [0.278 0.891], [0
0.897].
(*)
(с)
Рис. 6-10 В-сплайн поверхность вращения, (а) Вершины ломаной; (Ь) В-сплайн;
(с) поверхность.
Напомним, что в матричной форме параметрическая пространственная
кривая (см. уравнения (5-27), (5-44), (5-67) и (5-94)) задается следующим образом:
P(t) = [T][N)[G],
где [Г], [N] и [G] — соответственно матрица параметров, матрица функций
смешивания и геометрическая матрица. Таким образом, в общей форме матричное
уравнение поверхности вращения записывается в виде:
Q(t,<P) = [T][N}[G}[S},
(6-7)
где [S] представляет вклад вращения вокруг оси на угол ф. Для частного случая
вращения вокруг оси х имеем:
[S} =
10 0 0
0 совф sin 0 0
0 0 0 0
0 0 0 1
(6-8)
Эти методы иллюстрируются в следующем примере.
Пример 6-2 Поверхность вращения, созданная по параболической
кривой
Рассмотрим параболическую кривую, заданную точками Pi[0 1 0],
Рг[2 3 0], Рз[4 1 0], Р»[5 2 0]. Будем вращать эту кривую вокруг оси
х на угол 27г, чтобы получить поверхность вращения. Найдем на поверхности
точку с параметрами t = 0.5, ф = 7г/3 (60°).
Из уравнений (6-7) и (6-8) получим параметрическое уравнение
поверхности вращения
Q(t^) = [T][A][G][S],
где [5], [Т], [А] и G] задаются уравнениями (5-44), (5-52) и (5-53)
соответственно.
Конкретнее,
Q(t
^=G>3
t2 t 1]
10 0 0
0 cos</> sin^ 0
0 0 0 0
0 0 0 1
1
2
1
0
3
-5
0
2
-3
4
1
0
1 ]
-1
0
0
Г °
2
4
5
1
3
1
2
0
0
0
0
1
1
1
1
Q(t
,*)=(£)[*'
e t i]
-17 0 1
1 -11 0 1
4 0 0 1
4 6 0 1
Для t = 0.5 и ф = тг/3 (60°)
Q(0.5,tt/3)
- 1
-1
1
4
4
7 0
-11 0
0 0
6 0
10 0 0
0 cos<£ sin<£ 0
0 0 0 0
0 0 0 1
10 0 0
0 1/2 уД/2 0
0 0 0 0
0 0 0 1
49
16
33 33%/3
32
32
[3.0625 1.03125 1.786181 1].
Рис. 6-11 Поверхность вращения вокруг произвольной оси.
Результаты изображены на рис. 6-9. Такая поверхность может быть
результатом разработки кубка или даже газового канала двигателя или
ракетного сопла.
Предыдущие результаты были получены путем вращения точки, отрезка,
ломаной или кривой вокруг координатной оси, а именно вокруг оси х. К более
общему случаю поворота вокруг произвольной оси в пространстве поверхность
вращения, полученную в более удобной локальной системе координат, можно свести с
помощью переносов и поворотов, приводящих поверхность в нужное положение.
На рис. 6-11 показана параметрическая кривая P(t), повернутая вокруг
произвольной оси в пространстве, проходящей через точки ао и ai и направленной
от ао к а\. После того как поверхность создана в удобной системе координат
для приведения поверхности вращения в нужное положение, нужно совершить
следующие действия:
1. Перенести точку ао в начало координат.
2. Выполнить повороты, необходимые для совмещения осей а и +z (см. разд. 5-9).
3. Повернуть вокруг оси у на угол +90° для совмещения осей а и а;.1
1 Этот шаг необходим только для согласования с предыдущими рассуждениями. Поверхность
вращения может быть легко построена для поворотов вокруг оси z.
Эти три шага необходимы только для того, чтобы найти обратное
преобразование, размещающее поверхность вращения в нужном месте в трехмерном
пространстве. Получив поверхность вращения вокруг оси х, приведем ее в нужное
положение в пространстве:
1. Сдвинуть по оси х, чтобы переместить центр поверхности вращения в нужное
положение на оси а.
2. Применить к поверхности вращения преобразование, обратное к суммарному
преобразованию поворотов.
3. Применить к поверхности вращения обратный перенос точки а0.
Точка на поверхности вращения тогда задается уравнением:
О(*,0) = [днггр^-ЧДзГЧДхГВД
(6-9)
где [Тг], [Rx], [Ry] задаются уравнениями (3-22) — (3-24). [.Rj,] *■ задается
уравнением (3-8), и матрица [Q] задается в форме уравнения (6-7) с геометрической
матрицей [G], представленной в однородных координатах. [S] теперь является
матрицей 4x4, заданной в виде
[S} =
10 0 0
0 cos0 sin</> 0
0 0 0 0
0 0 0 1
(6-10)
Данный метод иллюстрируется на следующем примере.
Пример 6-3 Поверхность вращения вокруг произвольной оси
Найдем координаты точки с параметрами t = п/2, ф = 7г/6 на
поверхности вращения, образованной вращением эллипса с главной осью,
наклоненной относительно оси вращения. Ось вращения проходит через центр
эллипса и лежит в плоскости эллипса. Угол наклона г = 7г/4. Полуоси эллипса
а = 5, Ь = 1. Ось проходит через точки ао[0 10 10] и ai[10 10 0]. Центр
эллипса находится в точке ai.
Для начала найдем направляющие косинусы оси вращения (см.
уравнение 3-26)
\Сх Су Cz ] = [1/\/2 0 - 1/л/2]
и (см. уравнение 3-18)
•-Ф
2V+Cl
1/\/2.
Таким образом, используя уравнения (3-22) — (3-24)
[Мг] = рУ][Д,][Д»] =
10 0 0
0 1 0 0
0 0 10
0 -10 -10 1
1/V2
10 0 0
0-1 0 0
0 0-10
0 0 0 1
0 1Д/2 0
0 -10 0
1/уД 0 -1/уД О
-10/уД 10 10/уД 1
1/уД 0 1/л/2 О
О 10 О
-1/уД О 1/уД О
О 0 0 1
совместим ось вращения с осью z. Поворот вокруг оси у на угол 90°
приводит к
[Щ = рГг][Л,][Д,][Л,] =
1/уД
0 у/2
1/уД
-10/уД
1/уД
о у/г
-1/уД
ю/уД
0
-1
0
10
0
-1
0
10
i/уД о "
о уД о
-1/уД 0
10/уД 1 .
-i/уД о "
о уД о
-1/\/2 0
10/л/2 1
■ о о
0 1
1 0
0 0
-1 0
0 0
0 0
0 1
Используя преобразование [Мг] и однородные координаты, преобразуем
центр эллипса, находящийся первоначально в а:
[10 10 10 1]
1/уД 0
0 уД -1
1/уД 0
-10/уД 10
1/уД 0
0 уД 0
-i/уД о
ю/уД 1
= [20/уД 0 0 1]
т. е. в h = 20/уД на оси х.
Вспомнив пример 4-4 из разд. 4-6, получим параметрические уравнения
центрированного относительно начала координат эллипса, повернутого на
угол г:
х = a cos t cos г — bsin t sin i 0 < t < 27Г
у = a cos t sin г + 6 sin t cos г
которые могут быть записаны в форме уравнения (6-7)
[cost sin* 0 1]
а 0 0 0
0 6 0 0
0 0 0 0
0 0 0 1
— cos г sin j 0 0
— sin i cos» 0 0
0 0 10
0 0 0 1
Тогда поверхность вращения имеет вид:
[Q] = [T][N][G][ff\ =
[cost sint 0 1]
а О О О
О Ь О О
0 0 0 0
0 0 0 1
- cos г sin г О О
-sin г cos г О О
О 0 10
О 0 0 1
10 0 0
О coscj) зтф О
0 0 0 0
0 0 0 1
Для а = 5, b = 1, г" = 7г/4
[Q] = [cos t sint 0 1]
5\/2/2 5\/2/2 О О
—^2/2 л/2/2 О О
О 0 0 0
О 0 0 1
10 0 0
О созф зтф О
0 0 0 0
0 0 0 1
Эта центрированная относительно начала координат поверхность
вращения также показана на рис. 6-10.
Перенеся начало в (h, n) на оси х и заметив, что
[л*.Г1 = (я,Г1[Д»Гг[Д.Ггр,'Г1 =
л/2/2 0
0 -1
-л/2/2 0
0 10
-л/2/2 0
0 0
-л/2/2 0
10 1
получим
[Q] = тттятглм*]-1
Точка на поверхности Q(t, ф) имеет координаты
Q(f,0) - [cost sint 0 1]
0
1 0 0
0 созф sin</> 0
0 0 0 0
0 0 1
О
5\/2/2 5\/2/2 О О
-\/2/2 \/2/2 О О
О 0 0 0
О 0 0 1
1 0 0 0
О 10 0
О 0 10
20/\/2 0 0 1.
л/2/2 0 -\/2/2 о
0-100
-л/2/2 0 -\/2/2 О
О 10 10 1
Q{t
,ф) = 1-1 [cost sint 0 1] х
5(1- sin ф) -5\/2cos0 -5(1 + sin ф) О
-(l+sin</>) -\/2cos0 (l-sin</>) 0
О 0 0 0
20 20 0 0
Рис. 6-12 Сложная эллиптическая поверхность вращения из примера 6-3.
Для t = 7г/2, ф = 7г/6
ОС
7r/2,7r/6)=(i)[0 1 0 1]
5/2
-3/2
О
20
-5^/2 -15/2 0
-V6/2 1/2 0
0 0 0
20 0 1
= [37/4 10 - -Л/4 1/4 1] =
= [9.25 9.388 0.25 1]
Получившаяся в результате поверхность изображена на рис. 6-12.
Заметим, что эта поверхность самоперссекается и имеет сложную форму.
Формальное дифференцирование уравнения (6-7) дает параметрические
производные для поверхности вращения. А именно, производная в осевом
направлении равна
Qt(t^) = [T'][N][G}[S],
(6-П)
(6-12)
а производная в радиальном направлении
Q,(*,0) = PTOG1[n
где штрих обозначает соответствующее дифференцирование.
Нормаль к поверхности задается векторным произведением параметрических
производных, т.е.
n = Qtx (^ф.
(6-13)
6-3 ЗАМЕТАЮЩИЕ ПОВЕРХНОСТИ
Пространственную поверхность также можно получить путем перемещения
объекта, например отрезка, ломаной или кривой вдоль некоторой кривой, в
пространстве. Получающиеся в результате поверхности называются заметающими.
Генерация заметающих поверхностей часто используется в геометрическом
моделировании. Самый простой заметающий объект—точка. Результатом заметания точки
является, конечно, не поверхность, а пространственная кривая. Тем не менее на
этом примере хорошо иллюстрируется основная идея.
Рассмотрим координатный вектор Р[х у z 1], перемещаемый вдоль
кривой, заданной заметающим преобразованием [T(s)]. Координатный вектор Q{s),
представляющий получающуюся в результате кривую, задается выражением
Q(s) = P[T(s)] si<s<s2
(6-14)
Преобразование [T(s)] определяет форму кривой. Например, если направляющая
есть отрезок длины п, параллельный оси z, то (см. уравнение 3-14)
[Т(8)\ =
10 0 0
0 10 0
0 0 10
0 0 ns 1
0 < s < 1.
Если направляющая есть окружность с центром в начале координат, лежащая в
плоскости z = const, то (см. уравнение 3-8)
W(s)] =
(£) cos{2tt(s + Si)} 0 0 0
0 (j) sin{27r(s + s^} 0 0
0 0 10
0 0 0 1
0<s< 1,
где Si — (1/27г) a,Tctg(yi/xi) и для Р[х у z 1], г = у/х2 + у2. Здесь подстрочный
индекс i используется для обозначения начальной, или стартовой точки.
Сложные направляющие можно сконструировать с помощью объединения
более простых. Например, после объединения двух предыдущих преобразований
получим один оборот спирали вдоль оси z, т. е.
(§) cos{2tt(s + s^} 0 0 0
[T(S)]= ° (§) sin{27r(s + s,)} 0 0
0 0 10
0 0 ns 1
0< s < 1.
Самая простая заметающая поверхность получается в результате
перемещения отрезка вдоль направляющей. Напомним, что параметрическое уравнение
отрезка
P(t) = Рг + {Р2 - Pi)t 0 < t < 1. (6-15)
Соответствующая заметающая поверхность задается уравнением
Q(t, s) = P(t)[T(s)], 0 < t < 1, si < s < s2, (6-16)
где [T(s)] снова обозначает заметающее преобразование. Если оно состоит
только из переносов и/или локальных или общих масштабирований, то в результате
возникает плоская поверхность. Если заметающее преобразование включает
повороты, то поверхность не будет плоской. На рис. 6-13 изображена спиральная
заметающая поверхность, полученная из отрезка, в начальный момент
параллельного оси у, с помощью одновременного переноса вдоль оси х и вращения вокруг
нее. Более подробно этот метод объясняется в следующем примере.
Пример 6-4 Линейчатая заметающая поверхность
Рассмотрим отрезок, лежащий в плоскости ху, параллельный оси у и
заданный концевыми точками Pi [0 0 0] и Рг[0 3 0]. Найти точку с
параметрами t = 0.5, s = 0.5 на заметающей поверхности, образованной
одновременным переносом отрезка на 10 единиц вдоль оси х и его поворотом на
27Г вокруг оси х.
В данном случае матрица заметающего преобразования — переноса и
последующего поворота, задается матрицей
10 0 0
0 cos(27rs) sin(27rs) 0
0 — sin(27rs) cos(27rs) 0
Is 0 0 1
Параметрическое уравнение отрезка
[T(s)] =
P(t) = Pi + (Р2 - Pi)i = [0
= [0 3* 0 1]
0 0 1] + [0 - 0 3-0 0-0 1 — 1]*
Из уравнения (6-15) заметающая поверхность определяется следующим обра-
Q(t,s) = [P(t)][T(s)]
= [О U 0 1]
1
о
о
Is
0
cos(27rs)
— sin(27rs)
0
0
sin(27rs)
cos(27rs)
0
Q(0.5, 0.5) = [0 1.5 0 1]
= [5 -1.5 0 1].
Результат изображен на рис. 6-13.
10 0 0
0-1 0 0
0 0-10
5 0 0 1
Для создания заметающих поверхностей также могут быть использованы
параметрические кривые, например кубические сплайны, параболические сплайны,
Та же самая матрица получается для поворота и последующего переноса.
Рис. 6-13 Спиральная заметающая поверхность.
Рис. 6-14 Заметающая поверхность на основе кубического сплайна, (а) Кривая;
(Ь) поверхность.
кривые Безье и В-сплайны. В этом случае уравнение поверхности идентично
уравнению (6-15), где P(t) теперь представляет параметрическую кривую. На рис.
6-14 показана заметающая поверхность, созданная из одного сегмента
кубического сплайна, перенесенного вдоль оси z. Этот метод иллюстрируется примером.
Пример 6-5 Заметающая поверхность с кубическим сплайном в
качестве образующей
Рассмотрим поверхность, образованную в результате переноса на 10
единиц вдоль оси z кубического сплайна, определяемого следующими данными:
Pi [0 3 0 1], Р2 [3 0 0 1], Р[ [3 0 0 0], Pi [3 0 0 О].1
1 В однородных координатах касательный вектор имеет нулевой однородный координатный
множитель.
Заметающая поверхность задается формулами:
Q(t, з) = [C{t)][T{s)] 0 < t < 1, 0 < s < 1.
Нормализованный сегмент кубического сплайна задается (см. уравнение
5-27)
[C(t)] = [t3 t2 t 1]
Сегмент кривой изображен на рис. 6-14а.
Заметающее преобразование (см. уравнение 3-14) имеет вид:
2
3
0
1
-2
3
0
0
1
-2
1
0
1 1
1
0
0
Г °
3
3
3
3
0
0
0
0
0
0
0
1
1
0
0
Wis)] =
Следовательно,
Q{t, з) = [t3 t2 t
1]
10 0 0
0 10 0
0 0 10
0 0 пз 1
6 0 0
-9 0 0
0 0 0
3 0 1
10 0 0
0 10 0
0 0 10
0 0 10s 1
Для t = 0.5, з = 0.5
Q(0.5, 0.5) = [0.125 0.25 0.5 1]
= [3 1.5 5 1].
Результат изображен на рис. 6-146.
0 6 0 0
6-900
3 0 0 0
0 3 0 1
10 0 0
0 10 0
0 0 10
0 0 5 1
Следует позаботиться о том, чтобы избежать вырождения поверхностей или
их частей при генерации заметающих поверхностей из отрезков и кривых. Пример
этого приведен на рис. 6-15. Здесь s-образную кривую, расположенную в
плоскости ху, перемещают параллельно оси х. Заметим, что «хвосты» с левой и правой
сторон являются вырожденными частями поверхности (т. е. отрезками) с нулевой
площадью. Такие вырожденные части поверхности могут породить проблемы в
геометрических моделирующих системах.
Кроме незамкнутых кривых для создания заметающих поверхностей
используются замкнутые ломаные и кривые. При добавлении концевых поверхностей
заметающая поверхность ограничивает конечный объем в пространстве.
Подобным способом объемные примитивы создаются во многих геометрических
моделирующих системах. Перемещаемый вдоль прямой направляющий квадрат или
прямоугольник порождает прямоугольный параллелепипед. Окружность,
перемещаемая вдоль прямой направляющей, порождает цилиндр. Окружность с
уменьшающимся радиусом, перемещаемая вдоль прямой направляющей, порождает
конус. Также возможно вращение вокруг направляющей оси. На рис. 6-16 показана
Рис. 6-15 Заметающая поверхность с вырожденными участками.
Рис. 6-16 Заметающая поверхность, образованная квадратом, перемещаемым вдоль
оси х и одновременно вращаемым вокруг нее.
заметающая поверхность, образованная из плоского квадрата,
перпендикулярного оси х и перемещаемого вдоль оси х с одновременным вращением на 90° вокруг
этой же оси.
При перемещении плоского многоугольника или замкнутой кривой вдоль
произвольной направляющей кривой следует отметить два важных момента. Во-
первых, какая точка многоугольника постоянно лежит на направляющей? В
общем случае это может быть любая точка многоугольника или замкнутой кривой.
Для различных точек порожденные поверхности различаются.
Во-вторых, каково направление нормали многоугольника или замкнутой
кривой во время перемещения вдоль направляющей? В этом случае обычно
применяется два подхода. Нормаль может быть направлена как касательная к
направляющей кривой. Либо может задаваться независимо от направляющей. Последняя
альтернатива очень гибка. Два примера изображены на рис. 6-17, где показаны
заметающие поверхности, образованные квадратом, центрированным на оси х и
передвигаемым вдоль направляющей х — Is, у = cos(ns) — 1. На рис. 6-17а
нормаль направлена как ось х. На рис. 6-176 нормаль в каждой точке направлена так
же, как и касательная к направляющей. Отметим разницу между этими двумя
заметающими поверхностями. Детальный пример дополнительно иллюстрирует
эту идею.
Пример 6-6 Сложная заметающая поверхность
Поверхность создается перемещением плоского квадрата, заданного
вершинами Pi[0 - 1 1], Р2[0 - 1 - 1], Р3[0 1 - 1], Р4[0 1 1], вдоль
направляющей кривой х — 10s, у = cos(7rs) — 1. При этом направление
нормали к многоугольнику совпадает с касательной к образующей.
Направление касательной к образующей равно [10 — 7rsin(7rs) 0].
Таким образом, угол поворота вокруг оси z, необходимого для сонаправленно-
сти нормали многоугольника и касательной, равен
^ = aict4 ю J
Заметающее преобразование равно, таким образом,
1Т(з)]
cos ф sin ф 0 0
— sin ф cos ф 0 0
0 0 10
10s cos(7rs) - 1 0 1
При s = 0.5 угол поворота равен
ф = arctg
/-7rsin(7r/2)\
I Ю )
= arctg(-7r/10) = -17.44°
Тогда при s = 0.5 квадрат задается матрицей
Г °
0
0
. 0
Г 4-7
4.7
5.3
5.3
-1 1 1 1
-1 -1 1
1 -1 1
1 1 1 J
Г 0.954
0.3
0
L 5
-0.954 1 1 1
-0.954 -1 1
-0.046 -1 1
-0.046 1
1
-0.3
0.954
0
-1
0 0
0 0
1 0
0 1
Результат изображен на рис. 6-176
Рис. 6-17 Прямоугольник перемещается вдоль направляющей кривой, (а) Нормаль
направлена как ось X] (Ь) нормаль направлена так же, как касательная к направляющей
кривой.
Дополнительную информацию о заметающих поверхностях можно найти в
[6-9] и [6-10], а также в приведенной в них библиографии.
6-4 КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
Обычные квадратичные поверхности, такие как сфера, конус, цилиндр,
эллипсоид, параболоид вращения и гиперболоид вращения являются также и
поверхностями вращения (см. разд. 6-2). Эти квадратичные поверхности, особенно сфера,
конус и цилиндр, играют важную роль при изготовлении деталей механизмов,
а также в описании обрабатываемых поверхностей. Например, баскетбольные и
футбольные мячи имеют сферическую форму, воронки — коническую, банки для
пива — цилиндрическую, а спутниковые антенны — параболическую.
Квадратичные поверхности также важны и при описании более сложных поверхностей.
Например, фюзеляж истребителя North American P-51 времен второй мировой
войны бьш описан с помощью сегментов конических поверхностей [6-11]. Этот метод
называется методом построения плазов с помощью конических сечений.
Существует два метода представления квадратичных поверхностей —
алгебраический (включающий параметрические представления) и геометрический.
Геометрические описания обычно применяются для естественных квадратичных
поверхностей. Алгебраически квадратичная поверхность задается в общем виде
уравнением
Ах2 + By2 + Cz2 + Dxy + Eyz + Fxz + Gx + Ну + Jz + К = 0, (6-17)
где А, В, С, D, E, F, G, H, J, К — константы. Уравнение (6-17) является
обобщением уравнения конических сечений (см. уравнение 4-31) на три измерения. В
матричной форме обобщенное квадратичное уравнение можно записать как
[X][S][Xf = 0, (6-18)
где [X] = [х у z 1], а
2А D F G '
D 2В Е Н
F Е 2С J
G H J 2K
Как и в случае конических сечений, квадратичные поверхности бывают либо
центральными, либо нецентральными. Центральные квадрики —это эллипсоид
и гиперболоид1. Параболоиды — это нецентральные поверхности. Если квадрика
центральна, то ее центр можно перенести в начало координат. Если это
невозможно, то квадрика нецентральная, т. е. является параболоидом. Перенос центра
в начало координат приводит к исчезновению линейных членов уравнения (6-17).
После переноса уравнение (6-18) превращается в
[X][Tr][S][Tr]T[X]T = [X][S'][X)T = 0, (6-19)
1 Сфера есть частный случай эллипсоида. Цилиндр является предельным случаем для
эллипсоида либо гиперболоида.
[S] =
А
D/2
F/2
G/2
D/2
В
Е/2
Я/2
F/2
Е/2
С
J/2
G/2 '
Я/2
J/2
К
-G
где матрица переноса имеет вид:
[Тг] =
10 0 0
0 10 0
0 0 10
1 m n 1
Преобразованная матрица [S'} равна
[S'
41)
2А' D' F' G'
D' 2В' Е' Н'
F' Е' 2C" J'
G' H' J' 2К'
(6-20)
сА' = А,В' = В, С = С, D' = D, Е1 = Е, F' = F и
G' = 2А1 + Dm + Fn + G,
Н' = Dl + 2Bm + Еп + Н,
J' = Fl + Em + 2Сп + J,
IK' = 1С + mH' + nJ' + (Gl + Hm + Jn + 2K).
Исключение линейных членов, т. е. случай С" = Н' = J' = 0, приводит к
2А1 + Dm + Fn + G = 0,
Dl + 2Bm + En + H = 0,
Fl + Em + 2Cn + J = 0
или
[I m n]
2A D F
D 2B E
F E 2C
-G
-H
-J
что можно записать в следующем виде:
(6-21)
[M][L] = [G].
Если матрица [L] обратима, то решение существует и квадрика центральна,
т. е. является эллипсоидом или гиперболоидом. Если же [L] особенная
(вырожденная) матрица, то решения не существует и квадрика является параболоидом.
Приравнивание детерминанта [L] к нулю дает условие для параболоида. Таким
образом,
det[L] =
2F D F
D 2B Е
F E 2C
= 0
(6-22)
A(E2 - ВС) + B(F2 - AC) + C(D2 - AB) - {ABC + DEF) = О является условием
для параболоида. Далее, если det[L] > 0, то мы получаем гиперболоид, и если
det[L] < 0 —эллипсоид.
Как и для конических сечений (см. разд. 4-10), независимо от того, обратима
[L] или нет, оси квадрики с помощью поворотов можно сделать параллельными
координатным осям. Здесь требуется три поворота: два для того, чтобы сделать
одну из осей квадрики параллельной координатной оси (см. разд. 3-9) и последний
поворот вокруг этой же оси для того, чтобы сделать две другие оси квадрики
параллельными другим координатным осям. Для квадрики в обобщенном виде
решение получающихся уравнений для необходимых углов поворотов является
нетривиальной задачей и здесь не приводится.
Аналогичным образом, если квадрика нецентральна, т. е. является
параболоидом, то как было ранее упомянуто, нельзя исключить из уравнения все линейные
члены. Тем не менее, два их трех линейных членов могут быть исключены. И
снова, решение получающихся при этом уравнений является нетривиальной задачей
и здесь не приводится.
Результатом вышеперечисленных операций должно было быть приведение
квадрики к стандартному виду. Для центральной квадрики в стандартном виде
центр находится в начале координат, а оси направлены в соответствии с
координатными осями. Запишем получившееся стандартное уравнение в матричном виде
" а 0 0 0
г , 0 /3 0 0
L J 0 0 7 0
0 0 0 -к
или
ах2 + Ру2 + jz2 = к. (6-24)
Если а ф /3 ф 7 > 0, к > 0, то мы получим обобщенный эллипсоид (см.
рис. 6-18а). Наибольшее из значений а, /3, j определяет главную ось. Если две
из трех констант равны, например, а = /3 ф 7 > 0, то мы получим эллипсоид
вращения. Ось вращения связана с константой, отличной от двух остальных. Если
а = /Э = 7>0, то мы получим сферу радиуса \/к/а.
Переписав уравнение (6-24) в виде
х2 у2 z2
h — Ч =1
а2 Ь2 с2
и устремив одну из констант к бесконечности, получим цилиндр как предельный
случай эллипсоида. «Ось» этого эллипсоида, заданная отсутствующей
координатой, «бесконечно» длинна. Если две оставшиеся константы равны, например
а = /3, то мы получим круговой цилиндр. Если они не равны, например а ф /3, то
получим эллиптический цилиндр. В этом случае уравнение (6-24) превращается в
[Х]т = 0 (6-23)
ах2 + Ру2 = к.
Обобщенный
эллипсоид
(о)
Эллиптический
цилиндр
а * /3
Двуполостный
гиперболоид
а * 0
Конус,
асимптотический
к обоим
гиперболоидам
к = 0
(Ь)
Двойной
конус
а * 0
Эллиптический
параболоид
(в)
Г"Т"
KZ&.
Ы
I 1
i \
i \
\ \
Однополостный
гиперболоид
а * 0
Гиперболический
параболоид
V)
(А)
Рис. 6-18 Квадратичные поверхности, (о) Обобщенный эллипсоид а ф /3 ф у; (6)
эллиптический цилиндр а ф /?; (с) двойной конус а ф /3; (d) однополостный гиперболоид
а Ф /3] (е) двуполостный гиперболоид а ф /3; (/) конус, асимптотический к обоим
гиперболоидам к = 0; (д) эллиптический параболоид; (Л) гиперболический параболоид.
Посмотрим пример, приведенный на рис. 6-186. Если к = 0, то мы получим
мнимый цилиндр, потому что сумма квадратов двух вещественных чисел не может
быть равной нулю1.
Если к = О, одна из констант отрицательна, а две другие положительны,
например а, /3 > 0, 7 < 0, то мы получим двойной конус. Ось конуса связана с
координатой отрицательной константы. Если а = /3, то получится правильный
круговой конус. Если а ф /3, получится эллиптический конус. В этом случае
уравнение (6-24) превращается в
ах2 + /Зу2 = jz2.
Пример изображен на рис. 6-18с.
Если к = 0, а, Р, 'у ф 0, то конус мнимый, потому что сумма квадратов трех
вещественных чисел не может быть равной нулю.
Если а, /3, 7 > 0, а к < 0, получится мнимый эллипсоид, потому что опять
сумма квадратов трех вещественных чисел не может быть отрицательной.
Если одна из констант в уравнении (6-24) отрицательна, например 7 < 0>
а другие положительны, в результате квадратичная поверхность будет однопо-
лостным гиперболоидом. Ось гиперболоида связана с отрицательной константой,
например, если 7 < 0, то осью гиперболоида будет координатная ось z. На рис.
6-18d приведен пример. Если две положительные константы равны между собой,
например а = /3, то получается гиперболоид вращения. В противном случае
—эллиптический гиперболоид. Гиперболоид называется однополостным, потому что
можно соединить любые две точки поверхности, не выходя за ее границы. В
пределе, при приближении отрицательной константы к нулю, получится либо круговой,
либо эллиптический цилиндр. Однополостный гиперболоид является двулинейча-
той поверхностью (см. разд. 6-8). Двуполостный гиперболоид в некотором смысле
противоположен однополостному. Здесь отрицательны две из трех констант а, /3,
7, например а, /3 < 0, а третья положительна. Ось гиперболоида связана с
положительной константой. Пример приведен на рис. 6-18е. Соединить две любые
точки двуполостного гиперболоида, не покидая поверхность, невозможно. Для а,
/3 < 0, 7i к > 0 вершины двух полостей гиперболоида находятся в диапазоне
на оси z2. Если отрицательные константы равны, то получается гиперболоид
вращения. В противном случае получается эллиптический гиперболоид. Заметим,
что число отрицательных констант равно числу полостей гиперболоида.
Если к = 0, то оба гиперболоида вырождаются в конус, асимптотический к
обоим из них, как это показано на рис. 6-18/.
1 Кроме случая х = у = 0, т. е. прямой, совпадающей с осью г. — Прим. перев.
2 ± ( sMp- \ = ±с, когда уравнение двуполостного гиперболоида записано в менее общем
виде £ - ^ - £ = 1.
Теперь рассмотрим нецентральные квадратичные поверхности, а именно
параболоиды. В стандартном виде, где z является осью параболоида, имеем уравнение
' а О О О
Г XI ° Р ° °
1 J 0 0 0 0
_ 0 0 7 0
или
ах2 + Ру2 + jz = 0. (6-26)
Если а, /3 > 0, то, как показано на рис. 6-18д, получается эллиптический
параболоид. Если а = 0 > 0, то получим параболоид вращения. Вершина параболоида
находится в начале координат. При 7 < 0 поверхность «открыта» в
положительную сторону оси z. Аналогичным образом, при 7 > 0 поверхность открыта в
отрицательную сторону оси z. Если 7 = 0) поверхность превращается в эллипс1. Если
либо а, либо /3 < 0, то, как показано на рис. б-18/i, получается гиперболический
параболоид. Если а > 0, /3 < 0, то фокальной осью является ось у. Аналогично,
если а < 0, /3 > 0, фокальная — ось х. Если 7 < 0, то седло направлено вверх, как
это показано на рис. 6-18Л. Если 7 > 0, то поверхность отражена относительно
плоскости z = 0 и седло направлено вниз. Если 7 = 0, то поверхность
вырождается в гиперболу2. Гиперболический параболоид иногда назьшают седловой
поверхностью. Заметим, что даже при а = /3 гиперболический параболоид не
является поверхностью вращения. Тем не менее это двулинейчатая поверхность
(см. разд. 6-8).
И наконец, если либо а, либо 0 = 0, то получаем параболический цилиндр.
Дальнейшую информацию о квадратических поверхностях и их свойствах можно
найти в [6-12] - [6-14].
Хотя для нахождения свойств квадратичных поверхностей часто бывает
полезна явная форма их задания, но, аналогично случаю конических сечений,
параметрическое задание поверхностей позволяет получить более привлекательные и
доходчивые графические изображения. Для квадратичных поверхностей со
стандартной ориентацией параметрические представления задаются следующим
образом:
Эллипсоид:
х — a cos в sin ф, 0 < в < 27Г,
у = b sin в sin ф, 0 < ф < 27г,
z—c cos ф.
1 Так как знаки а и /3 одинаковые, то это прямая х = у = 0, т. е. совпадающая с осью 2. —
Прим. перев.
2 Так как у а, /3 разные знаки, то получается пара скрещивающихся плоскостей. — Прим.
перев.
[Х]т = 0 (6-25)
(6-27)
Однополостный гиперболоид:
х = a cos в ch ф,
у = 6sin0sh</>,
z = с sh ф.
Двуполостный гиперболоид:
х = ±а ch ф,
у = bsin#sh<£,
z = ccos#sh</>.
Эллиптический параболоид:
х = афсовв,
у = Ьф sind,
г = ф2.
Гиперболический параболоид:
х = афсЪв,
у = Ьф sh.6,
г = ф2.
Эллиптический конус:
х = афсовв,
у = Ьфвтв,
z = сф.
Эллиптический цилиндр:
х = a cos б,
у = b sin в,
О < в < 2тг,
—7Г < ф < 7Г,
О < 0 < 2тг,
-7Г <ф<Ж,
О < 0 < 2тг,
О < «А < «/'max,
—7Г < 0 < 7Г,
</>min <Ф<Ф max;
О < 0 < 2тг,
«/•miii < Ф < Ф max,
О < в < 2тг,
</>min < Ф < ф max,
Z = ф.
Параболический цилиндр:
х = ав2, 0<в< 0тах,
2/ =^ 2ав, фт\п <ф< фтах,
z = ф.
(6-28)
(6-29)
(6-30)
(6-31)
(6-32)
(6-33)
(6-34)
Параметрически заданные эллипсоид и часть гиперболического параболоида
показаны на рис. 6-19.
(а) Ф)
Рис. 6-19 Параметрические квадратичные поверхности, (о) Эллипсоид; (Ь)
гиперболический параболоид.
Хотя представлять все квадратичне поверхности удобно с помощью
обобщенного уравнения второй степени (см. уравнение (6-17)), а генерировать — с
помощью параметрического задания, описанного выше, но при компьютерном
моделировании квадратичные поверхности наиболее точно представляются
геометрически (см. [6-15] и [6-17]). Геометрически любая квадратичная поверхность
представляется точкой, двумя ортогональными (единичными) векторами и
тремя скалярами. Точка —либо центр, либо вершина, фиксирует местоположение
в пространстве. Вектора и их векторное произведение определяют оси
поверхности или ориентацию. Скаляры определяют ее измерения или размер.
Например, сфера определяется своим центром и радиусом, правильный цилиндр —
вектором, задающим его ось, точкой на оси и радиусом, эллипсоид
определяется центром, двумя векторами, представляющими две из его трех
ортогональных осей и тремя скалярами, представляющими длины вдоль этих осей,
и т.д. В табл. 6-1 перечислены геометрические описания квадратичных
поверхностей.
При работе с геометрически заданными квадратичными поверхностями
необходимо преобразовывать только определяющие точки и векторы. Скалярные
величины остаются неизменными и, таким образом, не накапливают при
вычислениях ошибок, возникающих из-за использования в компьютере арифметики с
ограниченной разрядной сеткой.
Например, геометрически заданный радиус сферы всегда равен R. А радиус
сферы, полученный путем преобразования алгебраического представления (см.
уравнение (6-17)) равен R±e, где е — небольшая числовая ошибка. Числовая
стабильность определяющих скаляров очень важна, например при определении
характера кривой пересечения двух квадратичных поверхностей или при
определении идентичности двух поверхностей (см. [6-15]).
Таблица 6-1 Геометрические описания квадратичных поверхностей
Поверхность
Плоскость
Сфера
Правильный
круговой конус
Правильный
круговой цилиндр
Правильный
эллиптический
цилиндр
Правильный
параболический
цилиндр
Эллиптический
конус
Эллипсоид
Эллиптический
параболоид
Гиперболический
параболоид
Однополостный
гиперболоид
Двупол остный
гиперболоид
Скаляры
Нет
Радиус
Половинный
угол
Радиус
Длины осей
эллипса (2)
Фокусное
расстояние
Длины осей
эллипса (2)
Длины осей (3)
Длины осей
эллипса
Гиперболический
и параболический
фокусы (3)
Длины осей
эллипса (2)
Гиперболический
фокус вдоль
главной оси
Длины осей (2)
Местоположение
вершины на оси
симметрии (1)
Точка
Любая точка
на плоскости
Центр
Центр
(вершина)
Любая точка
на оси
Любая точка
на оси
Вершина
Центр
Центр
Вершина
Вершина
Центр
Центр
Векторы
Единичная нормаль
Нет
Единичный вектор,
параллельный оси
Единичный вектор,
параллельный оси
Единичный вектор
оси
Единичный вектор,
параллельный оси
Два единичных вектора,
параллельных двум
из трех осей
Единичный вектор,
параллельный оси
Единичный вектор,
параллельный оси
Единичный вектор,
параллельный оси
Единичный вектор,
параллельный оси
6-5 КУСОЧНОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТЕЙ
В предыдущих разделах обсуждались создание и характеристики поверхностей,
для которых существуют известные аналитические описания. Однако есть
много поверхностей, для которых таких описаний сделать невозможно.
Типичными примерами являются автомобильные кузова, фюзеляжи и крылья самолетов,
корпуса кораблей, скульптуры, бутылки, башмаки и т.д. Эти поверхности
представляются в кусочном виде, т. е. похожем на лоскутное одеяло. В рассуждениях
используется векторное параметрическое представление, потому что оно не
зависит от осей, устраняет бесконечные значения углов наклона относительно
некоторой произвольной системы координат, устраняет неоднозначность представления
многозначных поверхностей и пространственных функций, облегчает представле-
ние поверхностей в однородных координатах, и такое представление совместимо
с использованием преобразований трехмерных однородных координат,
обсуждающихся в гл. 3.
Остаток этой главы будет посвящен обсуждению способов и методов
математического описания кусков поверхностей.
Наша цель заключается в том, чтобы для создания полной поверхности
объединить вместе отдельные куски вдоль их границ. Для кусочного представления
кривых мы будем придерживаться принятого в гл. 5 изложения. Мы начнем наше
обсуждение с достаточно интересного элемента или куска аналитической
поверхности, а именно сферы.
На примере сферической поверхности мы продемонстрируем некоторые
свойства кривых, полезные при описании поверхности. Определенные кривые на
поверхности задаются плоскостями, пересекающими сферу. В качестве примера
рассмотрим пересечение единичной сферы и плоскости, определяемое уравнением
поверхности z = cos</»i = a-\_ = constant и показанное на рис. 6-20а.
Получившаяся кривая является параллелью широты. Уравнение этой кривой получается
путем решения системы двух уравнений поверхностей. Непараметрическое
уравнение единичной сферы записывается в виде:
x2+y2 + z2 = 1.0.
Таким образом,
2 , 2 1 2
х + у - 1 - а\
определяет пересечение плоскости и сферы.
На рис. 6-20Ь плоскость в = во = constant задается уравнением
х sin во —у cos во = О
или
С\х — biy = 0.
Рис. 6-20 Пересечение плоскости и сферы, (а) Параллель широты; (6) меридиан
долготы.
Рис. 6-21 Кусок сферической поверхности.
В результате пересечения этой плоскости и сферы получается меридиан долготы.
Решение системы уравнений дает уравнение кривой пересечения; т. е.
+ 1
+ z2 = 1.0.
Как показано на рис. 6-21, границы куска сферической поверхности на
единичной сфере могут быть сформированы четырьмя плоскостями, двумя
параллелями и двумя меридианами, пересекающими сферу. Векторное параметрическое
уравнение для куска поверхности Q(6, ф)
<3(0,</>) = [cos в sin ф, sinflsin^ cos</>] в\ < в < 6%, ф\ < ф < фг- (6-35)
Кусок поверхности — это все возможные положения точки в трехмерном
пространстве, движущейся с двумя степенями свободы, управляемой двумя
параметрическими переменными в и ф, т.е. это бипараметрическая функция.
Параметрическое представление единичной сферической поверхности (см.
уравнение (6-27) с о = 6 = с = 1) таково:
х = cos в sin ф,
у = sin в sin ф,
z = cos ф.
Показанный на рис. 6-21 кусок поверхности задан для диапазонов изменения
параметров 0 < в < 7г/2 и 7г/4 < ф < тт/2. Границы или ребра его задаются кривыми
АВ, ВС, CD и DA. Для сферического куска на рис. 6-21 эти кривые являются
дугами окружностей. Каждая кривая может быть задана двумя конечными точками
и касательными векторами в концах. Следовательно, четыре граничных кривых
куска задаются четырьмя координатными векторами в углах и восемью
касательными векторами, по два в каждом углу. Для сферического куска на рис. 6-21
касательные вектора задаются параметрическими производными Q(6,ф), т.е.
Qe (Я. Ф) = S О9. Ф) = [- sin в sin ф cos в sin ф 0] (6-36)
Ои
(2ф(в,ф) = [cos в cos ф sin0cos</> -sin</>]. (6-37)
Касательные векторы в каждом углу показаны на рис. 6-21.
Форма внутренней части поверхности около каждого угла управляется
вектором кручения или смешанной производной в этом углу. Для куска сферической
поверхности на рис. 6-21 смешанная производная или вектор кручения
®9'ф(в,ф) = Шф = Шв = {~*{пвсо*ф С08вс08Ф °]- (6"38)
Подстановка значений параметров в углах куска поверхности дает векторы
кручения в них. Внутренняя форма куска задается уравнением (6-35). Это уравнение
можно считать сферической смешивающей функцией. Следовательно,
четырехугольный кусок поверхности может быть полностью описан 4 координатными
векторами в углах, 8 касательными векторами (по два в каждом углу), 4
векторами кручения в углах и смешивающей функцией, заданной в уравнении (6-35).
Нормаль в любой точке куска поверхности определяется векторным
произведением производных по параметрам. Например, для сферической поверхности
Qe х Яф =
i J k
— sin в sin ф cos в sin ф 0
cos в cos ф sin в cos ф — sin ф
— cos0sin2</> sin в sin2 ф — sin</>cos</>]. (6-39)
На куске поверхности изопараметрические линии, т. е. линии с постоянным
значением параметра, ортогональны. Следовательно, скалярное произведение
производных по параметрам равно нулю. Например, для сферической
поверхности
Qe • Яф — [— sin#sin</> cos6sin</> 0] • [cos в cos ф sin в cos ф — sin</>] = 0
= [— sin в sin ф cos в sin ф 0] [cos в cos ф sin в cos ф — sin ф]т = 0
= [— cos в sin в cos ф sin ф cos в sin в cos ф sin ф 0] = 0. (6-40)
6-6 ОТОБРАЖЕНИЕ ПАРАМЕТРИЧЕСКИХ ПОВЕРХНОСТЕЙ
Методы параметрического описания поверхностей наиболее удобно
представляются в терминах отображения двупараметрической плоской поверхности из
параметрического пространства uv в трехмерное объектное пространство xyz.
Ограничимся здесь обсуждением отображения прямоугольной плоской поверхности
w
C4
4
.
Рис. 6-22 Прямоугольная параметрическая плоская поверхность.
в параметрическом пространстве, показанной на рис. 6-22 и заданной
уравнениями
u = Ci
и = С2
w = С3
w = C\
C3<w< C4,
С3 < w < С4,
Ск < и < Сз,
Ci<u< C2.
Поверхность в объектном пространстве представляется функциями,
отображающими эту параметрическую поверхность в объектное пространство xyz, т. е.
х = x(u,w),
y = y(u,w),
z = z(u, w).
Простой двумерный пример послужит в качестве иллюстрации этого метода.
Пример 6-7 Двумерное отображение поверхности
Отобразить поверхность, описываемую в параметрическом пространстве
уравнениями
х = 3и + и> 0 < и < 1,
у = 2и + 3и> + ии> 0 < w < 1,
г = 0
в объектное пространство. Для начала заметим, что так как z = constant = 0,
то поверхность в объектном пространстве также является двумерной и лежит
на плоскости z = 0.
.
-
-
°У
///■
a/
V
/l
/ 1
/ i Л
/ 1 ''
/ 1 / 1
/ 1 / I
/ 1 / I
f у \
/ '7 /
i / i i
/ i У
1 / 1 у1
' 1 y^
1 /
/$
/■■4
1II
'»
1
(a)
(6)
Рис. 6-23 Двумерное отображение поверхности, (а) Параметрическое пространство;
(6) объектное пространство.
Границы поверхности в объектном пространстве определяются с
помощью отображения в объектное пространство границ прямоугольника в
параметрическом пространстве. Таким образом, для
и = 0; х = w, у = Зги и у = Зх,
и=1; x = w + 3, у -2{2w + l) и у - 2(2х - 5),
w = 0; х = Зи, у - 2и и у = (2/3)х,
w = 1; x = 3u+l, у = 3и + 3 и у = х + 2.
Во всех случаях для получения уравнения вида у = у(х) из соответствующего
выражения исключался параметр (и или w). Результаты представлены на
рис. 6-23.
Как показано в примере, задание постоянного значения одному из параметров
порождает кривую на поверхности в объектном пространстве. Такая кривая
называется изопараметрической или параметрической линией. Если задать один из
параметров как функцию другого в параметрическом пространстве, т. е. и = u(w),
то в результате также получится кривая на поверхности в объектном простран-
Рис. 6-24 Трехмерное отображение поверхности, (о) х компонента; (Ь) у компонента;
(с) z компонента; (d) результат.
стве. Например, функции
и = w, 0 < w < 1,
и = 1 — ги,
представляют диагонали единичного квадрата в параметрическом
пространстве.
Специфицирование значений обоих параметров задает точку на поверхности
в объектном пространстве. Другим способом задания точки (или точек) может
служить пересечение двух кривых в параметрическом пространстве, например
f(u,w) = 0 и g(u,w) = 0. Пересечение в параметрическом пространстве
отображается или преобразуется в пересечение в объектном пространстве.
В более сложном трехмерном примере дополнительно иллюстрируется
описываемая идея отображения.
Пример 6-8 Трехмерное отображение поверхности
Отобразить описанную в параметрическом пространстве поверхность
х(и, w) = (и — w)2, 0 < и < 1,
y(u,w) = и — w2, 0 < w < 1,
z(u, w) = uw
в объектное пространство. Вычислить координаты в объектном пространстве
точки на поверхности с параметрами и = w = 0.5.
Сначала найдем граничные кривые
и = 0
и = 1
w = 0
w = 1
х = w , у = —w2, z = 0 и х = — у, z = 0,
х = (1 - ш) , у = 1 — u;2, z = и; и х = (1 - z)2, у = 1 — z2,
х = и , у = и, z = 0 и х = у2, z = 0,
(и — 1) , у = и — 1, z = и и х
2
У , z
1+у.
Граничные кривые изображены на рис. 6-24d более толстыми линиями.
Записав параметрическую поверхность в виде векторной функции
Q(u, w) = [x{u, w) y(u,w) z(u,w)] = [(u — w)2 u — w2 uw]
получим
Q(0.5,0.5) = [0 0.25 0.25]
в качестве координат точки и = w = 0.5, отмеченной на рис. 6-24d жирной
точкой. Заметим, что каждая из компонент поверхности в объектном
пространстве является также функцией параметров и, w. Каждая из этих
отдельных компонент показана на рис. 6-24а, Ь, с. Поверхность, изображенная
на рис. 6-24d, является композицией всех преобразованных компонент.
И наконец, представляют интерес отображения вырожденных кусков,
соответствующих точке и прямой. Для точки отображение записывается
х = constant, у = constant, z = constant.
Для прямой отображение записывается в виде х = и, у = constant, z = constant.
6-7 БИЛИНЕЙНАЯ ПОВЕРХНОСТЬ
Одной из самых простых является билинейная поверхность. Билинейная
поверхность конструируется из четырех угловых точек единичного квадрата в
параметрическом пространстве, т.е. из точек Р(0,0), Р(0,1), Р(1,1) и Р(1,0). Любая
точка на поверхности определяется линейной интерполяцией между
противоположными границами единичного квадрата, как это показано на рис. 6-25. Любая
точка внутри параметрического квадрата задается уравнением
Q(u, w) = Р(0,0)(1 - u)(l -w) + Р(0,1)(1 - u)w + P(l, 0)u(l -w)+ P(1, l)uw.
(6-41)
В матричном виде
Q(u,w) = [1 — и и]
Р(0,0) Р(0,1)
Р(1,0) Р(1,1)
1 — w
w
(6-42)
Необходимо, чтобы интерполируемая поверхность удовлетворяла исходным
данным. В этом случае легко проверить, что угловые точки принадлежат этой
поверхности, т.е. (2(0,0) = Р(0,0) и т.д.
Уравнение (6-42) задано в обобщенном матричном представлении
интерполированной поверхности, а именно — матрица функций смешения по одной из бипа-
1
QtM,w)
i
Д1.1)
i >
P(0.0) P(1,0)
Рис. 6-25 Билинейная интерполяция в параметрическом пространстве.
раметрических переменных, геометрическая матрица, представляющая исходные
данные, и матрица функций смешения по другой параметрической переменной.
При изучении параметрических интерполированных поверхностей мы будем
постоянно пользоваться этим представлением.
Если координатные векторы четырех точек, определяющих билинейную
поверхность, заданы в трехмерном объектном пространстве, то будет трехмерна
и билинейная поверхность, получаемая в рузультате отображения
параметрического пространства в объектное. Если четыре определяющие точки не лежат в
одной плоскости, то и билинейная поверхность также не лежит ни в какой
плоскости. Действительно, в общем случае она сильно изогнута, пример этого
показан на рис. 6-26. Определяющие точки являются концами противоположных
диагоналей на противоположных гранях единичного куба. В результате получаем
гиперболический параболоид. В качестве иллюстрации рассмотрим следующий
пример.
Пример 6-9 Билинейная поверхность
Найти точку на билинейной поверхности, заданной точками Р(0,0) =
[0 0 1], Р(0,1) = [1 1 1], Р(1,0) = [1 0 0], Р(1,1) = [0 1 0], т.е.
концами противоположных диагоналей, лежащих на противоположных
гранях единичного куба в объектном пространстве. Искомая точка имеет
координаты и = w = 0.5 в параметрическом пространстве.
Напомним, что поверхность в объектном пространстве является
векторной функцией:
Q(u, w) = [х(и, w) y(u,w) z(u,w)]
Рис. 6-26 Билинейная поверхность, (а) Определяющие угловые точки; (6) поверхность.
тогда из уравнения (6-41) имеем
0(0.5,0.5) = [0 0 1](1 - 0.5)(1 - 0.5) + [1 1 1](1 - 0.5)(0.5)
+ [10 0](0.5)(1-0.5) + [0 1 0](0.5)(0.5)
= 0.25[0 0 1] + 0.25[1 1 1]
+ 0.25[1 0 0]+0.25(0 1 0]
= [0.5 0.5 0.5]
Вся поверхность изображена на рис. 6-266.
Заметим, что каждая изопараметрическая линия на билинейной поверхности
является прямой линией. В самом деле, эта поверхность является двулинейчатой
(см. разд. 6-8).
6-8 ЛИНЕЙЧАТЫЕ И РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ
Линейчатые поверхности часто используются в авиа- и кораблестроительной
промышленности. Например, большинство авиационных крыльев являются
цилиндрическими линейчатыми поверхностями. Линейчатая поверхность образуется
при движении прямой линии вдоль направляющей с одной степенью свободы.
Другой метод определения линейчатой поверхности состоит в следующем.
Выберем произвольную точку на поверхности и будем вращать вокруг нормали
плоскость, проходящую через нормаль к поверхности в этой точке (см. рис. 6-27).
Если существует такая ориентация плоскости, при которой каждая точка на
ребре плоскости контактируют с поверхностью, то поверхность линейчата в этом
направлении. Если ребро вращающейся плоскости полностью соприкасается с
поверхностью при более чем одной ориентации, то поверхность в этой точке мно-
голинейчата.
Самой простой линейчатой поверхностью является плоскость. Для
квадратичных поверхностей однолинейчаты конусы и цилиндры; однополостный
гиперболоид и гиперболический параболоид двулинейчаты.
В терминах отображения параметрического пространства и, w в объектное
пространство линейчатая поверхность получается с помощью линейного
интерполирования между двумя известными граничными кривыми, ассоциированными
с противоположными сторонами единичного квадрата в параметрическом
пространстве, скажем, между кривыми Р(и,0) и Р(и, 1). Поверхность задается
уравнениями:
Q(u, w) = Р(и, 0)(1 - w) + P(u, l)w (6-43)
или
[Q] = \x{x,w) y(u,w) z(u,w)] = [1 - w w]
Заметим, что снова Q(0,0) = Р(0,0) и т.д., то есть концы специфированных
кривых и углы поверхности совпадают. Кроме того, два края
интерполированной поверхности совпадают с заданными кривыми, т.е. Q(u,0) — P(u,0) и
0(«,1) = Р(и,1).
Теперь предположим, что известны кривые, соответствующие Q(0,w) и
P(l,w). Тогда линейчатая поверхность задается следующим образом:
Q(u, w) = Р(0, w){\ - и) + P(l, w)u (6-44)
или
[Q] = [x(x,w) y(u,w) z(u,w)] - [1-й и]
Рис. 6-27 Свойства линейчатой поверхности.
Р(и,0)
Р(и,1)
P(0,w)
P(l,w)
Рис. 6-28 Пример линейчатой поверхности.
В этом случае опять углы поверхности совпадают с концами заданных кривых, а
соответствующие края интерполированной поверхности совпадают с заданными
граничными кривыми. На рис. 6-28 приводится пример линейчатой поверхности.
Изображенные на этом рисунке отстоящими на некотором расстоянии от
поверхности граничные кривые являются В-сплайнами третьего порядка (см. разд. 5-9).
Описанная методика иллюстрируется на примере.
Пример 6-10 Линейчатая поверхность
Рассмотрим линейчатую поверхность, сформированную линейным
интерполированием кривых P(0,w) и P(l,w). Найдем координаты точки Q(u,w)
на поверхности с параметрами и = w = 0.5.
Р(0, w) является незамкнутым В-сплайном третьего порядка (к = 3)
с определяющими вершинами ломаной, заданными точками Bi[0 0 0],
В2[1 1 0], В3[1 1 0], Вл[2 1 0 и В5[3 0 0] (см. разд. 5-9). Отметим,
что вершины Вг = Вз совпадают, в результате чего на кривой
получается излом. Р(1,ш) также является незамкнутым В-сплайном третьей
степени. Его вершины определяющей ломаной равны Bi[0 0 6], Вг[1 1 6],
Вз[2 1 6], В4[3 0 6].
Вспоминая обсуждение В-сплайнов, получим незамкнутые однородные
узловые векторы для P(0,w) и P(l,w), соответственно,
[X] = [0 0 0 1 2 3 3 3],
[У] = [0 0 0 1 2 2 2].
Заметим, что ненормализованные диапазоны изменения параметров для этих
двух кривых различны, 0 < t < 3 для Р(0, w) и 0 < s < 2 для P(l,w).
«Нормализованное» значение параметра линейчатой поверхности Q в точке
w = 0.5 соответствует t = 1.5 для P(0,w) и s = 1.0 для Р(1, w).
Используя уравнения (5-83) и (5-84), получим
P(0,w) = P{t)
= BiNi,3(t) + B2N2,3(t) + B3N3j3{t) + B4N4,3(t) + BsNSiS(t).
В точке w = 0.5 или t = 1.5
P(0,0.5) = P(1.5) = (0)Bi + 0.125B2 + 0.75B3 + 0.125B4 + (0)B5
= 0.125[1 1 0]+0.75(1 1 0] +0.125(2 1 0]
= [1.125 1 0].
Аналогичным образом
P(l,w) = P(s)
= Si JVi,s(s) + B2N2,3(s) + B3N3,3(s) + В Jf 4,3(3).
В точке w = 0.5 или s = 1.0
P(l, 0.5) = P(1.0) = (0)Bi + 0.5B2 + 0.5B3 + (0)B4
= 0.5(1 1 6]+0.5(2 1 6]
= [1.5 1 6].
Использование уравнения (6-44) для получения точки на линейчатой
поверхности даст
Q(u,w) = P(0,w)(l - и) + P(l,w)u
0(0.5,0.5) = Р(0, 5.5)(1 - 0.5) + Р(1,0.5)(0.5)
= 0.5(1.125 1 0] + 0.5(1.5 1 6]
= [1.3125 1 3].
Результаты показаны на рис. 6-28. Жирной точкой отмечена точка
поверхности, соответствующая Q(0.5,0.5). Обратите внимание на то, что кривая
Р(0.ш), содержащая излом, плавно переходит в гладкую кривую P(l,w).
Особый практический интерес представляет вопрос, является ли линейчатая
поверхность развертывающейся? Не все линейчатые поверхности
развертывающиеся, однако все развертывающиеся поверхности являются линейчатыми.
Если поверхность развертывающаяся, то с помощью последовательности
небольших поворотов вокруг образующей линии она может быть без растяжений и
разрывов развернута или раскрыта в плоскость. Развертывающиеся поверхности
особенно важны для листопрокатной промышленности и в меньшей степени для
текстильной промышленности.
Ясно, что среди линейчатых квадратичных поверхностей развертывающимися
являются конусы и цилиндры. Однако после небольшого размышления
становится ясно, что ни однополостный гиперболоид (см. рис. 6-18d), ни гиперболический
параболоид (см. рис. 6-26) не являются развертывающимися поверхностями,
хотя они линейчатые.
Чтобы определить, будет ли развертывающейся поверхность или ее часть,
необходимо рассмотреть кривизну параметрической поверхности. В произвольной
Рис. 6-29 Кривизна бипараметрической поверхности.
точке Р на поверхности кривая пересечения поверхности и плоскости,
содержащей нормаль к поверхности в точке Р, имеет кривизну к (см. рис. 6-29). При
вращении этой плоскости вокруг нормали кривизна меняется. Великий
швейцарский математик Эйлер показал, что существуют только два направления, для
которых кривизна принимает минимальное и максимальное значения. Кривизны
в этих направлениях называются главными кривизнами, ктт и ктах. Кроме
того, направления главных кривизн ортогональны. Два сочетания главных кривизн
представляют особый интерес — средняя и гауссова кривизны:
= 2 ' ^ ^
(6-46)
Для развертывающейся поверхности гауссова кривизна К в любой точке равна
нулю, т. е. К = 0. Дил [6-18] показал, что для бипараметрических поверхностей
средняя и гауссова кривизны задаются выражением1
A\QW\2 - 2BQU ■ Qw + C\QU\2
H
К
2\QU x Qv
AC-В2
\Qu x Qw\4
(6-47)
(6-48)
где
(ABC) = [Qu x Qw] ■ [Quu Quw Qww].
1 Здесь подстрочные индексы используются для обозначения частных производных, т. е. Qu =
dQ/du и т. д.
Таблица 6-2 Типы поверхностей
Kmin» Kmax
Одинаковые
знаки
Противоположные
знаки
Одна или обе
кривизны равны
нулю
К
<0
>0
0
Форма
Эллиптическая
(выпуклость или впадина)
Гиперболическая
(седловая точка)
Цилиндрическая/коническая
(гребень, впадина,
плоскость)
Как показано в табл. 6-2, знак гауссовой кривизны характеризует локальную
форму поверхности: эллиптическую, гиперболическую, цилиндрическую или
коническую. Так как гауссова кривизна развертывающейся поверхности должна быть
нулевой, то поверхность должна быть скомпонована из цилиндрических,
конических или плоских кусков. Приведенный ниже пример поможет
проиллюстрировать эти рассуждения
Пример 6-11 Развертывающаяся поверхность
Показать, что эллиптический конус является развертывающейся
поверхностью.
Перепишем уравнение (6-32) для параметрического эллиптического
конуса в терминах и и ш:
Q{u, w) = [aucosuj businuj си].
Частные производные будут
Uguw =
QuxQw =
acosuj bsinu; с],
-ои sin w bu cos w 0],
—asinw bcosuj 0],
0 0 0],
-aucosuj — bus'mw 0],
-bcu cos w — acu sin ш abu],
\Qu xQu,|2 = {abu)2 I (- cosw\ + (j-sinwY + lX ф0
u> 0
A = [—bcu cos w — acu sin w abu] • [0 0 0] = 0,
В = [—bcu cos w —acu sin w abu] ■ [—a sin w Ьсовш 0]
= abcu sin w cos w — abcu sin w cos w = 0,
C=[—bcucosw — acu sin w abu] ■ [—au cos w -dusiniu 0]
= abcu cos w + abcu sin w = abcu .
Таким образом, используя уравнение (6-48), получим, что в любой точке
поверхности
К =
АС-В2 _ {0){аЪси2) - (0)
~~ \Qu х Qw\* ~ \QU x Q„|«
= 0
и, следовательно, поверхность является развертывающейся. Заметим, что
хотя \Q-u х Qui|z = 0 для и = 0, из правила Логшталя получаем, что К = 0/0 — 0
в и = 0.
6-9 ЛИНЕЙНАЯ ПОВЕРХНОСТЬ КУНСА
Если известны четыре граничные кривые Р(и,0), Р(и, 1), P(0,w) и P(l,w) и
для внутренней части куска поверхности используется билинейная
смешивающая функция, то в результате получаем линейную поверхность Кунса. На
первый взгляд можно предположить, что желаемый результат дает простая сумма
отдельных линейчатых поверхностей (уравнения (6-43) и (6-44)) в двух
направлениях и, w.
Q(u,w) = Р{и,0)(1 - w) + P(u,l)w + P{0,w){l - и) + P(l,w)u.
Однако, проверив этот результат в угловых точках куска поверхности, например
Q(0,0) = Р(0,0) + Р(0,0) = 2Р(0,0)
и на границах, например
Q(0, w) = Р(0,0)(1 -w) + Р(0,1)ш + Р(0, w)
получим, что ни одно из этих значений не соответствует исходным данным. Это
происходит из-за того, что угловые точки учитываются дважды, так как Р(0,0)
содержится в обеих граничных кривых Р(и, 0) и P(0,w).
Правильный результат можно получить с помощью вычитания
дополнительных членов, возникающих из-за удвоения угловых точек:
Q(u, w) =Р(и, 0)(1 -w)+ Р(и, l)w + Р(0, w)(l -и) + P(l, w)u
- Р(0,0)(1 - и)(1 -v))- Р(0,1)(1 - u)w
-P(l,0)u(l-w)-P(l,l)uw. (6-49)
Теперь в угловых точках
Q(0,0) = P(0,0) и т.д.
и вдоль границ
(9(0, ш) =Р(0,ш)
Q(u,l) = Р(и,1)
и т.д.
В матричной форме уравнение (6-49) имеет вид:
Q(u,w) = [1 - и w]
— [1-й w]
P{0,w) '
P(l,w) .
P(0,0)
P(1,0)
+ [Р(Щ
p(o,i) ■
P(U) .
0) P(u, ]
1 — w
w
0]
1-го
w
Рис. 6-30 Линейная поверхность Кунса.
или более компактно
Q(u,w) = [1 — и и 1]
-Р(0,0) -Р(0,1) P(0,w)
-Р(1,0) -P(l,l) P(l,w)
Р{и,0) Р{и,1) 0
1-го
w
1
(6-50)
Функции (1-й), и, (1 — w) и w называются функциями смешения потому, что
они смешивают граничные кривые для получения внутренней формы
поверхности. Линейная поверхность показана на рис. 6-30. Линейная поверхность Кунса
является самой простой из поверхностей Кунса. В разд. 6-10 обсуждается
более общая поверхность Кунса. Следующий пример иллюстрирует
использованный выше метод.
Пример 6-12 Линейная поверхность Кунса
Найти точку с координатами и = w = 0.5, расположенную на линейной
поверхности Кунса, если четыре граничные кривые Р(и,0), Р(и, 1), P(0,w),
P(l,w) задаются незамкнутыми Р-сплайнами третьего порядка (к = 3)
P(u,0):Pi[0 0 0],В2[1 1 0],В3[2 1 0],Р4[3 0 0],
Р5[3 0 3]
P(u,l):Bi[0 0 3],В2[1
P(0,™):Ci[0 0 3],С2[0
P(l,w):Ci[3 0 3],С2[3
СБ[3 0 0]
Вспоминая предыдущее обсуждение В-сплайнов (см. разд. 5-9), получим
узловой вектор для Р(и, 0) и P(l, w)
[X] = [0 0 0 1 2 3 3 3]
1
1
1
3],Вз[2
2],С3[0
2],Сз[3
1
1
1
3],Рм[2
1],С4[0
2], Са[3
1
0
1
3]
0]
1].
Таким образом, ненормализованный диапазон параметра есть 0 < t < 3. Для
(и, 1) и Р(0, w) узловой вектор с ненормализованным диапазоном параметра
О < s < 2 имеет вид
[У] = [0 0 0 1 2 2 2].
Соответствующими значениями для параметров в нормализованном
диапазоне 0 < и, w < 1 являются t = 1, 5 и s = 1.0.
Воспользовавшись уравнениями (5-83) и (5-84), получим
Р(и, 0) = P{t) = BiiVi,3(t) + B2N2,3{t) + B3N3i3{t) + B4N4l3(t) + B5N5,3{t)
P(0.5, 0) = P(1.5) = (0)Bi + 0.125B2 + 0.75B3 + 0.125B4 + (0)B5
= 0.125[1 1 3]+0.75[2 1 3]+0.125(2 1 3]
= [1.875 1 3]
P(u, 1) = P(s) = BiFi,3(e) + B2iV2,3(s) + B3iV3,3(s) + B4iV4,3(s)
P(0.5,1) = P(1.0) = (0)Bi + 0.5B2 + 0.5B3 + (0)B4
= 0.5[1 1 0] +0.5(2 1 0]
= [1.5 1 0]
P(0, io) = P(s) = VJfiA') + C2N2,3(s) + C3N3,3{s) + C4774,3(s)
P(0,0.5) = P(1.0) = (0)Ci + 0.5C2 + 0.5C3 + (0)C4
= 0.5[0 1 2]+0.5(0 1 1]
= [0 1 1.5]
P(l, w) = P(t) = CiNi,a(t) + C2N2,3(t) + C3N3,3{t) + C4N4,3(t) + C5N5,3(t)
P(l, 0.5) = P(1.5) = (0)Ci + 0.125C2 + 0.75C3 + 0.125C4 + (0)C5
= 0.125(3 1 2]+0.75(3 1 2]+ 0.125(3 1 1]
= [3 1 1.875]
Теперь, используя уравнение (6-50), имеем
Q(u, w) = [1 — и и 1]
-Р(0,0) -Р(0,1) Р(0,«;)
-Р(1,0) -P(l,l) P(l,w)
Р(щ,0) Р(и,1) 0
Q(0.5,0.5) = [0.5 0.5 1] х
'-(0 0 3
-[3 0 3
[1.875 1
-[0 0 0
-[3 0 0
3] [1.5 1 0]
[0 1 1.5]
[3 1 1.875]
0
1 — W
W
1
0.5
0.5
1
= [1.6375 2.25 1.6375].
Полученные результаты изображены на рис. 6-30. Отметим наличие плоского
участка на поверхности, гауссова кривизна в этой области равна нулю.
Следовательно, эта часть поверхности развертывающаяся. В остальной области
гауссова кривизна положительна и поверхность не является
развертывающейся.
6-10 БИКУБИЧЕСКАЯ ПОВЕРХНОСТЬ КУНСА
Хотя аналитические поверхности, например квадратичные, линейчатые и
простые куски линейно интерполированных поверхностей, обсуждавшиеся в
предыдущих разделах, и важны для конструирования и производства, но для многих
приложений они не обладают достаточной гибкостью. Описание поверхностей,
обсуждаемое в этом и дальнейших разделах главы, предоставляют необходимую
гибкость с помощью использования полиномов более высоких степеней как для
граничных кривых куска поверхности, так и для внутренних смешивающих
функций. Поверхности, сгенерированные с помощью объединения таких кусков,
называются скульптурными поверхностями. Для описания скульптурных
поверхностей фундаментальное значение имеет кусок бикубической поверхности Кунса
(см. [6-19]).
Для всех четырех граничных кривых куска бикубической поверхности Кунса
используются нормализованные кубические сплайны (см. разд. 5-4). Для задания
внутренней части куска используются кубические смешивающие функции. Таким
образом, каждую граничную кривую можно представить в общем виде
P(t) =£i + B2t + B3t2 + Brf3, 0<t<l.
(5-2)
Для одного сегмента нормализованного кубического сплайна с известными
касательными и координатными векторами на концах, каждая из четырех
граничных кривых, Р(и, 0), Р(и, 1), P(0,w) и P(l,w) задается следующим образом (см.
»*' Кубическая
граничная
кривая
Касательный
вектор
Касательный
вектор
Р(0,0)
Рис. 6-31 Геометрия для куска бикубической поверхности Кунса.
уравнения (5-24), (5-26), (5-27):
P(t) = [T][N][G\ =
= [t3 t2 t 1]
2
3
0
1
-2
3
0
0
1
-2
1
0
1
-1
0
0
Pi
Pi
P[
n
0<t< 1,
(5-27)
где t становится соответственно и или w, a Pi, Р2, P{, Pi —координатные и
касательные векторы на концах соответствующей граничной кривой (см. рис. 6-31).
Кубическая смешивающая функция, использованная для обоих параметрических
направлений, идентична функции, использовавшейся для интерполирования
внутренней части нормализованного кубического сплайна, т. е.
\F\ = \W) W Mt) F4(t)] = [T][N]
2-211
= [t3 t2 t 1]
-3
0
1
3
0
0
-2
1
0
-1
0
0
(5-26)
Расписывая смешивающие функции, имеем
Fi(t)=2t3-3*a + l>
F2(t) = -2t3 + 3t2,
F3(t) = t3 - 2t2 + t,
F4(t) = t3-t\
(5-25a)
(5-25b)
(5-25c)
(5-25d)
где t есть либо и либо ы, соответственно. Эти функции изображены на рис. 5-8.
Тогда определение куска бикубической поверхности Кунса записывается в виде
Q(u,w) = [F1(u) F2 (u) F3(u) F4(u)]x
Р(0,0)
Р(1,0)
Ри(0,0)
Ри{1,0)
Р(0,1)
Р(1,1)
ЗД,1)
Ри{1,1)
Рш(0,0)
Рш(1,0)
Риш(0,0)
Риш(1,0)
Рш(0,1) "
^(1,1)
Риш(0,1)
m«jj (,-!■) J-J
Fi(w)
F2(w)
F3(w)
F^w)
(6-51)
для 0<и<1и0<ш<1. С помощью уравнения (5-26) это можно записать
более компактно:
Q(u,w) = [U][N][P][N}T[W},
(6-52)
где [U]
= \и3
и 1] и [W]T = [w
w
w 1].
Матрица [Р] в уравнении (6-51) содержит всю геометрическую информацию,
необходимую для генерации одного бикубического куска поверхности Кунса.
Подматрицы размера 2 х 2 в каждом углу [Р] содержат
[Р] =
угловые
координатные
векторы
и-каса-
тельные
векторы
го-касательные
векторы
векторы
кручения
Таким образом, кусок бикубической поверхности определяется четырьмя
координатными векторами в угловых точках, восемью касательными векторами (по два
в каждом углу), четырьмя векторами кручения в углах и четырьмя кубическими
смешивающими функциями Fi, F2, F3 и F^.
Пример куска бикубической поверхности представлен на рис. 6-32. Заметим,
что каждая из изображенных на рис. 6-32 изопараметрических линий является
нормализованным кубическим сплайном. Несколько кусков могут быть
соединены вдоль С1-гладких границ для образования более сложных поверхностей,
являющихся С1-гладкими везде. Детально условия объединения кусков бикубических
поверхностей обсуждаются в [6-19].
Параметрические производные в любой точке на бикубической поверхности
получаются с помощью формального дифференцирования уравнения (6-52):
Qu(u, w) = [U][N][P}[N}T[Wl (6-53)
Qw{u,w) = [U][N][P][N]T[Wl (6-54)
Quw{u,w) = [U'][N][P][N]T[W'}, (6-55)
Quu{u,w) = [U"][N}[P}[N]T[W], (6-56)
Qww(u,w) = [U][N][P}[Nf[W"}, (6-57)
где штрихи обозначают дифференцирование по соответствующей переменной и
[[/'] = [Зи2 2и 1 0],
[W']T = [3w2 2w 1 0],
[U"] = [6u 2 0 0],
[W"f = [6w 2 0 0].
Нормаль к поверхности, используемая для определения невидимых поверхностей,
вычисления освещенности (см. [1-11)] и создания управляющих программ для
станков, задается выражением
п = Qu х Qw.
Рис. 6-32 Кусок бикубической поверхности Кунса.
Подробный пример иллюстрирует метод вычислений для бикубических
кусков.
Пример 6-13 Кусок бикубической поверхности Кунса
Определить точку на куске бикубической поверхности Кунса,
соответствующую параметрам и = w = 0.5. Вектор-точки для четырех углов
равны Р(0,0) = [-100 0 100], Р(1,0) = [-100 -100 -100], Р(1,0) =
[100 - 100 - 100], Р(1,1) = [100 0 - 100]. Касательные векторы
равны Ри(0,0) = [100 100 0], Р„(0,1) = [1 1 0], Р„(1,0) = [1 -1 0],
Р,(1,1) = [1 - 1 0], Р»(0,0) = [0 10 - 10], Р„(0,1) = [0 - 1 - 1],
Рш(1,0) = [0 1 — 1], Рш(1,1) = [0 — 1 — 1]. Векторы кручения равны
Р„ш(0,0) = [0 0 0], Р„ш(0,1) = [0.1 0.1 0.1], Риш(1,0) = [0.1 -0.1 -
0.1], Риш(1,1) = [0 0 0]. Определить параметрические производные Qgu,
Qw и вектор нормали для и = w = 0.5.
Используя матричную запись из уравнения (6-51), получим
Q(u,w) = [U][N]
-100 0 100]
100 -100 100]
100 100 0]
1 -1 0]
0 10 -10]
0 1 -1]
0 0 0]
0.1 -0.1 -0.1] [0 0 0]
-100 -100 -100]
100 0 -100]
1 1 0]
1 -1 0]
[0 -1 -1
[0 -1 -1
[0.1 0.1 0.1
[N]T[W?
Для и = 0.5 смешивающие функции по и имеют вид:
[U][N] = [и3 и2 и 1]
[0.125 0.25 0.5 1]
= [0.5 0.5 0.125 -0.125]
2
3
0
1
и
Ц
-2
3
0
0
Г 2
-3
0
1
1
-2
1
0
-2
3
0
0
1 1
-1
0
о J
1
-2
1
0
1
-1
0
0
Для w = 0.5 смешивающие функции по w:
[Nf[W] :
0.125
0.25
0.5
1
= [0.5 0.5 0.125 -0.125]т.
Таким образом, х компонента Q(u,w) при и = w = 0.5 равна
«23(0.5,0.5) = [0.5 0.5 0.125 - 0.125] х
2
-2
1
1
2
-2
1
1
-3
3
-2
-1
-3
3
-2
-1
0
0
1
0
0
0
1
0
1
0
0
0
1
0
0
0
Г ™3 1
w2
W
. 1 .
-100
100
100
1
-100
100
1
1
о
о
о
0.1
о
о
0.1
о
= [12.375 0 -0.0125 0.0125]
0.5
0.5
0.125
-0.125
0.5
0.5
0.125
-0.125
= 6.18
Аналогично у и г компоненты таковы:
Q„(0.5,0.5) = [0.5 0.5 0.125
■ 0.125] х
0
-100
100
-1
-100
о
1
-1
10
1
о
-0.1
-1
-1
0.1
о
= -42.75
Q*(0.5,0.5) = [0.5 0.5 0.125
100 -100
100
О
О
= -0.56
-100
О
О
- 0.125] х
-10 -1 "
-1 -1
О 0.1
-0.1 О
0.5
0.5
0.125
-0.125
0.5
0.5
0.125
-0.125
Следовательно, Q(0.5,0.5) = [6.18 — 42.75 — 0.56]. Вся поверхность
изображена на рис. 6-32.
Обратимся теперь к производным, вспомним уравнения (6-53)-(6-55) и
заметим, что
[U'][N] = [3и2 2и 1 0][ЛГ] =
2-211
= [0.75 1 1 0]
= [-1.5 1.5 -0.25 -0.25]
-3
0
1
3
0
0
-2
1
0
-1
0
0
[N]T[W'] = [N]T[3w2 1w 1 0]
■ 2-301"
-2 3 0 0
1-210
1-10 0
т _
■ 0.75 -
1
1
0
= [-1.5 1.5 -0.25 -0.25]T
['араметрические производные в и = w = 0.5 равны
QUl(0-5,0.5) = [-1.5 1.5 -0.25 - 0.25] х
X
■ -100 -100 0 0 "
100 100 0 0
100 1 0 0.1
1
1 0.1 0
" 0.5 ■
0.5
0.125
-0.125
= [274.75 299.5 -0.025 -0.025]
0.5
0.5
0.125
-0.125
= 287.13
Qiiv и QUt находятся аналогичным образом. В результате получим
Qu (0.5,0.5) = [287.13 -14.06 1.69].
Теперь
<ЭШ,(0.5,0.5)
[0.5 0.5 0.125
-100 -100
100
100
1
100
1
1
- 0.125] х
0 0
0
0.1
о
о
о
0.1
= [12.38 0 -0.0125 0.0125]
-1.5
1.5
-0.25
-0.25 ,
-1.5
1.5
-0.25
-0.25
= -18.56
Qwv и QWl находятся аналогичным образом, откуда
Q„,(0.5,0.5) = [-18.56 - 19.69 - 298.38]
И наконец, вектор нормали имеет вид:
i J k
n = Qu x Qw = QUl QUi/ QUl
ЧШа ЧШу Ун»!
= 4227.5i + 85641.2J - 5915.5k.
Единичная нормаль равна
n = [0.049 0.996 - 0.069]
Заметим, что векторы кручения в угловых точках слегка сместили нормаль
от направления у.
i
287.13
-18.56
J
-14.06
-19.69
k
1.69
-298.38
(я)
Ф)
(с) (rf)
Рис. 6-33 Действие на кусок бикубической поверхности варьирования величины
касательного вектора. Значения компонент касательного вектора равны (о) 1; (Ь) 10; (с) 100;
(d) 1000.
Одна из проблем, возникающих при использовании бикубических кусков
поверхности, заключается в несоответствии значений векторов положения,
кручения и касательных векторов. Все они в общем случае имеют различные порядки
величин. Например, для куска поверхности со стороной 10 единиц, касательные
векторы могут иметь значения порядка 10 единиц векторы кручения —100 единиц
и векторы положения —1000 единиц. Кроме того, не всегда очевиден результат
изменения величины и направления касательных векторов и/или векторов
кручения.
На рис. 6-33 показан результат варьирования величин касательных векторов в
угловых точках куска бикубической поверхности. Векторы положения углов
куска лежат в плоскости у = 0, отцентрированные относительно начала координат
в ±100а;,г. Касательные векторы лежат в плоскостях, расположенных
перпендикулярно плоскости угловых точек и содержащих смежные углы куска
поверхности. Направление касательных векторов выбрано таким образом, чтобы
сделать кубическую граничную кривую выпуклой вверх («горбом вверх»), например
-Р«(0,0) = [1 1 0], Р„(1,0) = [1 — 1 0], и т.д. Величина векторов кручения
равна нулю. Если значение компоненты у каждого касательного вектора равно
нулю, то кусок поверхности плоский; если не равно нулю, то кусок изогнут.
На рис. 6-33 о изображен кусок бикубической поверхности с единичными
значениями компонент касательного вектора. Хотя поверхность выглядит плоской,
на самом деле она слегка округлена. Компонента у в центре поверхности, т. е. в
х = z = 0 равна 0.5. На рисунках б-336-d показаны бикубические поверхности,
для которых значения компонент касательного вектора увеличены
соответственно на 1, 2 или 3 порядка величины, т.е. равны 10, 100 и 1000. Значения
компоненты у центральной точки теперь равны 5, 50 и 500. Заметим, что они также
увеличиваются на порядок величины всякий раз, когда увеличивается значение
касательного вектора.
Особый интерес представляет рис. 3-33 d. Изображенная на нем поверхность
является самопересекающейся. Чтобы лучше понять этот результат, можно
вспомнить обсуждение кубических сплайнов кривых в разд. 5-3 и в особенности рис.
5-10. Кроме того, заметим, что каждая изопараметрическая линия на поверхности
является кубической сплайновой кривой. Каждая из изопараметрических линий
образует петлю, показывая, что значение касательного вектора в угловой точке
превысило критическое значение.
Результат изменения направления касательного вектора в угловой точке
показан на рис. 6-34. Здесь изменены знаки компонент у касательных векторов Р(0,1);
их значения стали равны 100. Заметим, что на рис. 6-34 правый передний угол
поверхности теперь вогнутый, а не выпуклый, как на рис. 6-33с.
Кручение было ранее упомянуто в разд. 6-5 при обсуждении куска
сферической поверхности. Там оно определялось как смешанная производная поверхности
в угловых точках. В действительности вектор кручения в угловой точке позволяет
модифицировать внутреннюю форму поверхности без модификации касательных
векторов в этой точке. На рис. 6-35 показан результат модифицирования вектора
кручения в одной угловой точке Р(0,0) на поверхности. Для каждой из
поверхностей на рис. 6-35 Р(0,0) является нижней угловой точкой. Поверхность
аналогична представленной на рис. 6-336, за исключением ненулевого вектора кручения
в Р(0,0). На рисунках 6-35а и 6 со значениями компонент вектора кручения 10
и 100, соответственно, показан небольшой видимый эффект ненулевого вектора
кручения. На рис. 6-35с поверхность имеет выраженную выпуклую форму
благодаря ненулевому вектору кручения. Рис. 6-35d иллюстрирует действие больших
значений этого вектора. Заметим, однако, что в отличие от рис. 6-33 d поверх-
Рис. 6-34 Действие на кусок бикубической поверхности изменения направления
касательного вектора.
Рис. 6-35 Влияние вектора кручения на кусок бикубической поверхности. Значение
компоненты вектора кручения в точке Р(0,0) равно (о) 10; (Ь) 100; (с) 1000; {d) 10000.
ность не самопересекается. Дополнительное тщательное исследование рис. 6-35 d
показывает, что поверхность слегка вогнута в трех угловых точках с нулевым
кручением.
Поверхность с ненулевым кручением в угловой точке является в ней
локально «плоской». Поверхность с нулевым кручением во всех четырех углах, как это
показано на рис. 6-33, называется куском поверхности Ферпосона или F куском
[6-20]. При совместном объединении для формирования более сложных
поверхностей местоположение угловых точек кусков вполне очевидно. По этой причине
такие куски поверхностей редко используются на практике.
Хотя приведенное здесь обсуждение ограничивается четырехсторонними
кусками поверхностей, и другие формы кусков, как это показано на рис. 6-36, тоже
имеют значение. Треугольные куски поверхностей рассмотрены в [6-21] и [6-22].
Пятиугольные куски поверхностей обсуждаются в [6-23].
6-11 ПОВЕРХНОСТИ БЕЗЬЕ
Бикубические поверхности Кунса предоставляют гибкое и мощное средство
разработки поверхностей. Однако их практическое использование, как и для
кубических сплайновых кривых, затрудняется необходимостью задания точной,
интуитивно неочевидной математической информации, например координат точек,
(а) ф)
Рис. 6-36 Нечетырехугольные куски, (о) Пятиугольный; (Ь) треугольный.
касательных векторов и векторов кручения. Возникающие проблемы
иллюстрируются на рисунках 6-33 — 6-35. Большинство из этих проблем можно преодолеть,
распространив понятия кривых Безье на поверхности.
Декартово или тензорное произведение поверхности Безье задается в виде
п го
Q(u,w) = J2J2Bi,jJn,i{u)Km,j{w), . (6-58)
где Jn,i(u) и Kmj(w) есть базисные функции Бернштейна в параметрических
направлениях и и w (см. уравнения 5-63 и 5-64). Для удобства повторим здесь
определение, приведенное ранее в разд. 5-8
Jn»= Г")«*(1-и)""*, (5-63)
\т-з
О-
(7) =
п! (6-64)
i\(n-i)V
jl(m-j)\
Здесь элементы B^j являются вершинами задающей полигональной сетки, как
это показано на рис. 6-37. Индексы п и m на единицу меньше числа вершин
многогранника в направлениях и и w, соответственно. Для четырехсторонних кусков
поверхностей задающая полигональная сетка должна быть топологически
прямоугольной, т. е. должна иметь одинаковое количество вершин в каждом «ряду».
Снова, как и для кривых Безье, из-за того что для смешивающих функций
используется базис Бернштейна, многие свойства поверхности известны. Например:
Степень поверхности в каждом параметрическом направлении на единицу
меньше числа вершин задающего многогранника в этом направлении.
Рис. 6-37 Поверхность Безье и вершины характеристического многогранника.
D
В..з
А
В23
В1Л
ви
с"
с
а2д
В1Л
в
1
' 3,3
в,~
Дз,,
i >
'о,о Bi,o в2,о вз,о
Рис. 6-38 Схема задающей полигональной сетки 4x4 для поверхности Безье.
Гладкость поверхности в каждом параметрическом направлении на две
единицы меньше числа вершин задающего многогранника в этом направлении.
Поверхность отображает в общем виде форму задающей полигональной сетки.
Совпадают только угловые точки задающей полигональной сетки и
поверхности.
Поверхность содержится внутри вьшуклой оболочки задающей полигональной
сетки.
Поверхность не проявляет свойства затухания изменений. Это свойство не
определено и неизвестно для поверхностей двух переменных.
Поверхность инвариантна относительно аффинного преобразования.
Каждая из граничных кривых поверхности Безье является кривой Безье.
Запомним этот факт и рассмотрим задающую полигональную сетку для
бикубической поверхности Безье размера 4x4, изображенную схематично на рис. 6-38.
Легко видеть, что направление и величина касательных векторов в угловых
точках куска управляются положением соседних точек вдоль сторон сетки. А именно
касательные векторы в направлениях и, w в точке А управляются вершинами
полигональной сетки Бод и .Bi.o, соответственно. Аналогичным образом, вершины
полигональной сетки Бг,о, Бзд, Бз,2, Бг,з и 51,3, Д),2 управляют
касательными векторами в угловых точках Б, С, D, соответственно. Четыре внутренние
вершины полигональной сетки, Б1д, Бгд, Бг,2 и Б^ влияют на направление и
величину векторов кручения в угловых точках А, В, С, D куска поверхности.
Следовательно, пользователь может управлять формой куска поверхности, не зная
конкретных значений касательных векторов и векторов кручения.
На рис. 6-39 показано несколько бикубических поверхностей Безье и их
задающих полигональных сеток. Базовая полигональная сетка имеет размер 4 х 4 и
отцентрирована относительно начала координат с угловыми точками,
находящимися в ±15 по х, z. Компонента у угловых вершин равна нулю. У всех других
вершин эта компонента равна пяти. Базовая полигональная сетка и
соответствующая ей поверхность Безье изображены на рис. 6-39а. На рис. 6-39 точка Бо^
является левой угловой вершиной, а Б3(з —правой угловой вершиной. Заметим,
что центральные вершины базовой полигональной сетки образуют плоский крест
(показанный затененным). Следовательно, центр получившейся поверхности
минимально изогнут, хотя и не плоский.
На рис. 6-396 проиллюстрирован эффект увеличения в 2 раза величины
касательного вектора в точке Б0|о в обоих параметрических направлениях и и w с
помощью перемещения точек.Б^о и Бод. Вектор кручения не меняется.
Отметим увеличение кривизны граничных кривых, отвечающих значениям
параметров и = 0 и ш = 0, и соответствующее изменение внутренности поверхности.
На рис. 6-39 с показано действие изменения направления касательных векторов
в точке Бо,з в обоих параметрических направлениях и и w с помощью
перемещения точек Бо,2 и В\£. Отметим изменение знака кривизны граничной кривой
около точки Б0,з и формы внутренней части поверхности по сравнению с базовой
поверхностью.
На рис. 6-39 d проиллюстрирован результат удвоения величины вектора
кручения в точке Б0,о без изменения его направления. В этом случае перемещается
только точка Б1д. Эффект этого изменения неуловим, но тем не менее важен для
конструирования. Внимательное сравнение с базовой поверхностью на рис. 6-39 а
показывает, что параметрические линии вблизи точки Бо,о имеют большую
кривизну. Этот эффект распространяется приблизительно до центра поверхности.
В матричном виде декартово произведение поверхности Безье задается
выражением
Q(u,w) = [U][N][B][M]T[W], (6-59)
Рис. 6-39 Бикубические поверхности Безье. (о) Основная поверхность; (6) эффект
изменения величины обоих касательных векторов в Во,о; (с) эффект изменения
направления касательного вектора в Во,з; (d) эффект изменения величины вектора кручения в
Во.о-
где
[U] = [ип и"-1 1]
[W] = [wn гп™-1 ••■ 1]т
Boto B0
[В] =
Вп,о
Bn,i
а матрицы [N] и [М] задаются уравнением (5-70) или (5-71).
Для специального случая бикубической поверхности Безье размера 4x4
уравнение (6-59) сокращается до
Q(u,w) = [u3 и2
Bofl .Вод
Bi,o -Bi.i
-^2,0 -^2,1
Вз,о -Вз,1
Bq,2
Bl,2
В2,2
Вз,2
Во,з
Bi,3
В2,3
Вз,з
1]
-1
3
-3
1
-1
3
-3
1
3 -3 1
-6 3 0
3 0 0
0 0 0
3
-6
3
0
-3 1"
3 0
0 0
0 0
W3
W2
w
1
(6-60)
Поверхность Безье не обязательно должна быть квадратной. Для сетки
размера 5x3 уравнение (6-59) превращается в
Q(u,w) — [и4
3 2
и и и
Д),о Д)д
-#1,0 -^1,1
-^2,0 -^2,1
-^3,0 -^3,1
. ^4,0 -^4,1
1]
'
1
-4
6
-4
. 1
Во,2
Bl,2
В2,2
Вз,2
В.
1,2 -
-4
-12
-12
4
0
1
-2
1
6 -
-12
6
0
0
-2 1 '
2 0
0 0
4
1 I
4 0
0 0
0 0
0 0 .
w2
w
1
(6-61)
Поверхность Безье размера 5x3 состоит из полиномиальных кривых четвертой
степени в параметрическом направлении и и из квадратичных полиномиальных
кривых в направлении w. Пример такой поверхности Безье показан на рис. 6-40.
В данном случае, как это показано на рис. 6-406, изменение центральной вершины
стороны задающей сетки с пятью вершинами не влияет на касательные векторы
в угловых точках.
вз.з
Рис. 6-40 Поверхность Везье размера 5x3. (о) Основная поверхность; (Ь) эффект
изменения центральной вершины граничной ломаной с пятью вершинами.
Производные поверхности Безье получаются с помощью формального
дифференцирования уравнения (6-58) или (6-59). Если воспользоваться уравнением
(6-58), то первые и вторые параметрические производные будут
Qu(u,w) = Y^Y^Bi'0Jn,iiu)KmAw
i=0 j=0
n m
Qw{u,w) = J2J2Bi<iJn<i(u)K'm,j(W
i=0 j=0
n m
Qu,w(u,w) = ^2^2BitjJ'nti(u)KmtJ(w
i=0 j=0
n m
i=0 j=0
n m
Qw,w{u,w) = ^2^2BitJJnii(u)K'ntJ(w\
i=0 j=0
(6-62)
(6-63)
(6-64)
(6-65)
(6-66)
где штрих обозначает дифференцирование относительно параметрической
переменной. Производные функций базиса Бернштейна J'ni, J^'j, К'т^ и K'^j
приведены в уравнениях (5-74) и (5-75).
Легко найти соотношение между бикубическими поверхностями Безье и
Кунса. Приравнивая уравнения (6-52) и (6-59), получим
<ЭкУнс(и,ш) = <ЭБеэье(и,ш),
[U}[NC][P}[NC}T[W] = [U][NB][B}[NB}T[W]
где [Nc] задан уравнением (5-76) и [iV^] — уравнением (5-70). Следовательно
геометрическая матрица [Р] бикубической поверхности Кунса задается в терминах
полигональной сетки поверхности Безье следующим образом
[P} = [Nc}-1[NB}[B}[NB}T[[Ncf]-1
или
Р(0,0) Р(0,1) Рш(0,0) Рш(0,0)
Р(1,0) Р(1,1) Рш(1,0) Рш(1,1)
Ри(0,0) Р„(0,1) Риш(0,0) PutB(0,l)
Р„(1,0) Р„(1,1) Риш(1,0) PutB(l,l) _
=
3(-В0д — -Во,о)
3(-В3д - -В3,о)
9(.Во,о — Вх^ — Бод + .В1Д
9(-В2,о — -Вз.о — -Вгд + -Взд
-Во -Во,з
-Вз.о -Вз.з
3(-Bi,o — -В0,о) 3(^1,3 — -В0,з)
3(-В3,о — -Вг.о) 3(Б3,з — -Вг.з)
3(-Boi3 — -В0,2)
3(.Вз,з — -Вз.г)
) 9(Б0)2 - -Bli2 _ -Во.з + -В1,з)
) 9(Бг,2 — Бз,2 — -Вг.з "*" -^3.3)
(6-67)
Исследование правой нижней подматрицы размера 2 х 2 в уравнении (6-67)
подтверждает, что четыре центральные вершины задающей полигональной сетки
влияют на кручение в угловых точках куска бикубической поверхности Безье.
Тем не менее кручение в угловых точках управляется не только центральными
вершинами, но также и соседними касательными векторами. В самом деле,
кручение в угловой точке управляется формой неплоского четырехугольника,
сформированного угловой точкой, двумя соседними граничными точками и соседней
центральной точкой.
Из уравнений (6-62)-(6-64) следует, что
Р(0,0)
Р(1,0)
Ри(0,0)
ВД,о)
" Q(o,o)
0(1,0)
0«(о,о)
QuihO)
Р(0,1)
P(i,i)
PU(0,1)
ВД.1)
0(0,1)
Q(i,i)
Q„(o,i)
0«(i,i)
Рш(0,0)
Рш(1,0)
Риш(0,0)
Риш(1,0)
Qw(o,o)
Qw(i,o)
0™(o,o)
0«ш(1,о)
Рш(0,0)
рш(1Д)
Puw(0,l)
*UW \ •*■ 1 •*■ )
Qw(o,o)
0Ш(1,1)
Quw(o, i)
Ц/иш\*) •*■>
(6-68)
Аналогичным образом обратное соотношение между матрицами [Р] и [В],
выражающее вершины полигональной сетки Безье в терминах параметров
бикубической поверхности Кунса, равно
Ро,о Род Во,2 Во,з
g:
B\fl Pl,l Pi,2 Pl,3
Рг,о Ргд #2,2 Рг.з
Рз,о Рз,1 Рз,2 Рз,з
S)
' ЗР(0,0)
ЗР(0,0) + Р„(0,0)
ЗР(1,0)-Р„(1,0)
. ЗР(1,0)
ЗР(0,1)-Р«,(0,1)
ЗР(0,0) + Рш(0,0)
\ {Р„«,(0,0) + 9Р(0,0) - 3(PU,(0,0) + Р„(0,0))}
|{Рш»(1,0) + 9Р(1,0) + 3(Ри|(1|0)-Р„(1|0))}
ЗР(1,0) + Р«,(1,0)
ЗР(0,1)
\ {Р„«,(0, 1) + 9Р(0,1) + 3(Р„(0,1) - Рш(0,1))} ЗР(0,1) + Р„(0,1)
J {Pu«,(l, 1) + 9Р(1,1) - 3(Р„(1,1) + PW{1,1))} ЗР(1,1) - Р„(1,1)
ЗР(1,1)-Р«,(1,1) ЗР(1,1)
(6-69)
Более полно концепция поверхности Безье иллюстрируется на следующем
примере.
Пример 6-14 Поверхность Безье
Для изображенной на рис. 6-39 а поверхности Безье для значений
параметров и = w = 0.5 определить координаты точки на поверхности и
первые производные в и и w направлениях. Найти также координаты точки и
производные для модифицированной поверхности, показанной на рис. 6-39(2.
Сравнить полученные результаты. Вершины многогранника 4x4
поверхности Безье таковы:
[В]
[-15 0 15]
[-5 5 15]
[5 5 15]
[15 0 15]
-15 5
-5 5 5]
'5 5 5]
15 5 5]
5]
[-15 5 -5]
[-5 5 - 5]
[5 5 - 5]
[15 5 - 5]
-15 0 -15]
-5 5 -15]
5 5 -15]
15 0 -15]
Для модифицированной поверхности на рис. 6-39d изменяется только
вершина Bi,i[0 10 0], т.е. изменение сказывается лишь на кручении в угловой
точке Во,о-
Напомним матричное представление поверхности, заданное в уравнениях
(6-59) и (6-60), т.е.
Q(u,w) = [U][N][B][N]T[W].
Здесь
[N][B][N]T =
=
■ -1 3-3 1-
3-6 3 0
-3300
10 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0
0 -'
0 45
0 -1
[В]
0]
15 0]
0]
5 0
" -1 3-3 1
3-6 3 0
-3300
10 0 0
0 0 0] [
0 45 0]
0 -45 0] [
0 15 -30]
D 0 0]
) -15 0]
30 15 0]
-15 0 15]
Точка на поверхности, таким образом, будет
Q(0.5,0.5) = [0.125 0.25 0.5 1][ЛГ][В][ЛГ]Э
= [0 4.6875 0].
Производные по направлениям:
0.125
0.25
0.5
1
Qu (0.5,0.5) = [Zu2 2ч 1 Q][N][B][N]T
= [0.75 1 1 0][N][B][N]T
= [30 0 0]
Qw(0.5,0.5) = [u3 и2 и 1][N][B][N]T
w
w
. 1
0.125
0.25
0.5
1
Zw2
1w
1
L о
= [0.125 0.25 0.5 1][N][B][AT]3
= [0 0 - 30]
0.75
1
1
0
Заметим, что векторы Qu и Qw ортогональны.
В модифицированной поверхности на рис. 6-39d изменено значение
только точки Bi,i стандартной поверхности. Новое значение координат равно
■Bi,i[0 Ю 0]. Новое значение произведения:
[N][B][Nf =
[45 45 -45] [-90 -90 90] [45 45 -45] [0 0 0]
[-90 -90 90] [180 135 -180] [-90 -45 90] [0 -15 0]
[45 45 -45] [-90 -45 90] [45 0 -45] [30 15 0]
[0 0 0] [-0 -15 0] [0 -15 -30] [-15 0 15]
Новые координаты точки поверхности для и — w = 0.5:
Q(0.5,0.5) = [0.703 5.391 - 0.703].
Новые параметрические производные для и = w = 0.5:
<Э„(0.5,0.5) = [28.594 -1.406 1.406]
<Эш(0.5,0.5) = [-1.406 - 1.406 - 28.594]
Заметим в этом случае, что поскольку задающая полигональная сетка более
не симметрична относительно оси у, то поверхность теперь не симметрична
относительно этой оси. Далее, заметим, что хотя Qu и Qw все еще
ортогональны, но как их величины, так и направления отличаются. Данные результаты
показывают, что вектор кручения в одной угловой точке оказывает трудно
уловимое, но существенное влияние на форму всей поверхности.
Приведенное выше обсуждение поверхностей Безье касалось определения и
характеристик одного куска поверхности. Для того чтобы получить более
сложные поверхности, надо объединить несколько кусков поверхности Безье.
Подробное обсуждение этого вопроса лежит вне сферы данной книги. Интересующегося
читателя мы отсылаем к [6-24] и [6-25]. Проблемы, возникающие при
объединении кусков поверхности Безье с обеспечением гладкости вдоль соприкасающихся
сторон, иллюстрируются рис. 6-41 на примере объединения двух кусков
бикубической поверхности Безье вдоль одной стороны.
Для обеспечения непрерывности или С0 гладкости вдоль границы необходимо,
чтобы совпадали1 две граничные кривые, а следовательно, и две граничные
ломаные вдоль края поверхности. Для обеспечения непрерывности векторов наклона
или касательных векторов или С1 гладкости вдоль границы куска направление
нормали к поверхности вдоль граничной кривой должно быть одинаковым для
обоих кусков. Для этого можно использовать два условия. Первое требует, чтобы
четыре отрезка полигональной сетки, встречающиеся у границы и пересекающие
ее, были коллинеарными, как это показано выделенными линиями на рис. 6-41 а.
Второе, менее жесткое условие требует, чтобы только три ребра полигональной
сетки, встречающиеся в концевых точках граничной кривой, были
компланарными, как это показано выделенными линиями на рис. 6-416.
6-12 В-СПЛАЙН ПОВЕРХНОСТИ
Естественным расширением понятия поверхности Безье является декартово
произведение В-сплайн поверхности, определяемой выражением
n+l m-f 1
Q(u,w) = J^J^ BUjNi<k{u)Mu(w), (6-70)
t=l j=l
где Nitk (и) и Mjti (w) — базисные функции В-сплайна в бипараметрических
направлениях и и w соответственно (см. уравнение 5-84). Для удобства повторим
здесь определение базисных функций, данное ранее в разд. 5-9,
Nil(u) = i I' «*"*'<«<*<+!. (5-84а)
' v ' у 0, в противном случае, ч '
Ni к {и) = («-««W,*-i(») + (^-»)%U-i(«) (5.84b)
Вспомним обсуждение в разд. 5-8 гладкости сегментов кривой Безье.
Граничное ребро
(Ь)
Рис. 6-41 Гладкость стыковки кусков поверхности Безье. (о) Линии сетки коллинеар-
ны; (6) ребра ломаных компланарны.
Mjl(w) = {1> есливд<и,<»я.ь- (5_84а)
•'' ^ 0, в противном случае, х '
Mj ,(«,) ={W~ «ЛЦй-^) + {mi ~ w>M^-iM, (5-84b)
Vj+l-i ~ Vj Vj+l - Vj+i
где Xj и 2/j являются элементами узловых векторов, как это обсуждалось в разд.
5-9. Снова Bij являются вершинами задающей полигональной сетки. Для
четырехугольных «кусков» поверхности задающая полигональная сетка должна
быть топологически прямоугольной. Индексы п и тп на единицу меньше
числа вершин задающего многогранника соответственно в и и w параметрических
направлениях.
Как и для В-сплайн кривых на форму и свойства В-сплайн поверхности
существенно влияют узловые векторы [X] и [У], причем используются незамкнутые,
периодические и неоднородные узловые векторы. Хотя обычно для обоих
параметрических направлений применяют узловые векторы одного и того же типа, но
это не обязательно. Например, можно использовать незамкнутый узловой вектор
и его соответствующие В-сплайн базисные функции для одного параметрического
направления и периодический узловой вектор и его соответствующие В-сплайн
базисные функции для другого. Практическим примером служит цилиндрическая
поверхность с переменным сечением.
Так как для описания граничных кривых и для интерполирования внутренней
части поверхности используется В-сплайн базис, то сразу же можно перечислить
некоторые свойства В-сплайн поверхности:
Максимальный порядок поверхности в каждом параметрическом направлении
равен числу вершин задающего многогранника в этом направлении.
Гладкость поверхности в каждом параметрическом направлении на две
единицы меньше порядка поверхности в каждом направлении; т. е. Ск~2 и С'-2 в
ниш направлениях, соответственно.
Поверхность инвариантна относительно аффинного преобразования; т. е.
поверхность преобразуется с помощью преобразования задающей полигональной
сетки.
Свойство затухания изменений для В-сплайн поверхности в настоящее время
неизвестно.
Влияние одной вершины полигональной сетки ограничивается ±fc/2, ±1/2
интервалами в каждом параметрическом направлении.
Если число вершин задающей полигональной сетки равно порядку в
каждом параметрическом направлении и внутренних узловых величин нет, то В-
сплайн поверхность превращается в поверхность Безье (см. рис. 6-39).
При триангуляции задающая полигональная сетка образует плоскую
аппроксимацию поверхности.
Поверхность лежит внутри выпуклой оболочки задающей полигональной
сетки, образуемой объединением всех выпуклых оболочек к, I соседних вершин
полигональной сетки.
Из предыдущего обсуждения свойств выпуклой оболочки В-сплайн кривых
(см. разд. 5-9) сразу же следует, что В-сплайн поверхность может содержать
плоские области и линии резкого нарушения гладкости. Это свойство очень
полезно во многих ситуациях, возникающих при конструировании. На рис. 6-42а - d
изображена серия незамкнутых В-сплайн поверхностей и их характеристических
многогранников третьего порядка в каждом характеристическом направлении.
Отметим, что каждая из линий задающей полигональной сетки в направлении
w является прямой линией с четырьмя вершинами. Получающаяся поверхность
(b)
id)
Рис. 6-42 В-сплайн поверхности третьего порядка, (а) Гладкая линейчатая
поверхность; (6) небольшая внутренняя плоская область, вызванная коллинеарностью трех
вершин сетки в и направлении; (с) обширная внутренняя плоская область, вызванная
коллинеарностью пяти вершин сетки в и направлении; (d) плоская область внутри
скульптурной поверхности.
линейчата в направлении w. Изображенная на рис. 6-42а В-сплайн поверхность,
заданная четырьмя вершинами полигональной сетки в направлении и, плавно
изогнута в этом направлении.
Изображенная на рис. 6-426 В-сплайн поверхность задана пятью вершинами
полигональной сетки в направлении и. Три центральные вершины коллинеарны.
Заметим, что центр получившейся поверхности имеет плоскую форму.
Аналогичным образом коллинеарны пять из семи вершин задающей полигональной сетки в
направлении и для поверхности, изображенной на рис. 6-42с. И снова в
центральной области, которая имеет большие размеры, чем на рис. 6-426, поверхность
плоская.
На рис. 6-42 d показано, что эти очень сильные свойства выпуклой оболочки
распространяются на оба параметрических направления. Таким образом, плоская
область может быть встроена во внутреннюю часть скульптурной поверхности.
При увеличении порядка поверхности плоская область становится меньше.
На рис. 6-43 иллюстрируется эффект, возникающий при совпадении линий
сетки. На рис. 6-43а три совпадающие линии сетки используются для
образования линии складки в центре В-сплайн поверхности четвертого порядка. На рис.
6-436 показан результат совмещения трех линий сетки в обоих параметрических
направлениях. В этом случае В-сплайн поверхность четвертого порядка
содержит два гребня, поднимающихся к точке в центре поверхности. Так же как и
для В-сплайн кривых, линия складки возникает в том случае, когда совпадают
к — 1 или I — 1 линий сетки. Кроме того, так как В-сплайн поверхность везде
Ск~2/С'-2 гладка, то она гладка и на этой линии. Вдобавок данное свойство
также гарантирует Ск~2/С1~2 гладкость перехода изогнутой поверхности в
плоскую.
Превосходные свойства локального изменения В-сплайн кривых (см. разд.
5-9) переносятся на В-сплайн поверхности. Пример этого приведен на рис. 6-
44, где незамкнутая бикубическая (к = I = 4) В-сплайн поверхность
определена полигональной сеткой 9 х 9 (m = n = 8). Эта сетка, показанная как
верхняя поверхность на рис. 6-44, плоская везде, за исключением центральной
точки. Незамкнутый узловой вектор в обоих параметрических направлениях равен
[0 00012345666 6]. Таким образом, у нас есть шесть
промежутков параметров в каждом направлении, т. е. 0 — 1, 1 — 2, ..., 5 — 6. Каждый
параметрический четырехугольник, например 0<u<l,0<w<l, образует
подкусок1 В-сплайн поверхности. Средняя поверхность, изображенная на рис.break
6-44, составлена из параметрических линий на концах каждого параметрического
интервала, т. е. ви = ш = 0,1,2,3,4,5,6. Каждый четырехугольник представляет
подкусок поверхности. Отметим, что влияние смещенной точки ограничивается
±fc/2, 1/2 интервалами или подкусками.
1 Некоторые авторы обозначают каждый подкусок как В-сплайн поверхность. В данном
случае поверхность рассматривается как объект, заданный всей полигональной сеткой.
(в)
Рис. 6-43 В-сплайн поверхности четвертого порядка с несколькими совпадающими
линиями сетки.
Рис. 6-44 Локальное изменение В-сплайн поверхностей.
Параметрические производные В-сплайн поверхности получаются с помощью
формального дифференцирования уравнения (6-70):
71+1 7П+1
Qu(u,w) = J2J2 BitjNlk(u)Mjtl(w
г=1 j=\
П+1 7П+1
Qw{u,w) = J2J2 BijNi^M^iw
i=l J=l
n+1 m+1
Quw(u,w) = J2J2 BUiNlk{u)M^{w
i=l j=l
n+1 m+1
i=l J=l
П+1 7П+1
Qww{u,w) = Y, Y^ Bi.JNiA^)M-',l(w
i=l j=l
(6-71)
(6-72)
(6-73)
(6-74)
(6-75)
где штрих обозначает дифференцирование относительно соответствующего
параметра. Производные В-сплайн базисных функций задаются уравнениями (5-97)-
(5-100).
Приведенный пример иллюстрирует метод вычисления В-сплайн поверхности.
Пример 6-15 Вычисление незамкнутой В-сплайн поверхности
Рассмотрим В-сплайн поверхность, заданную полигональной сеткой
размера 4x4:
Bi.i
Bl,2
Bi,3
Bl,4
-15
-15
-15
[-15
0
5
5
0
15]
51
-51
-15]
B2,i[-5
B2>2[-5
B2,3[-5
B2,4[-5
5
10
10
5
-151
51
-5]
-15]
■03,1
■Вз.г
■Вз.з
■Вз,4
5 5 15] B4,i[15 0 15]
5 10 5] B4,2[15 5 5]
5 10-5] В4,з[15 5 -5]
5 5 -15] В4,4[15 0 -15]
Это поверхность четвертого порядка в направлении и (к = 4) и третьего
порядка в направлении w (1 = 3). Таким образом, поверхность составлена из
двух подкусков: один для 0 < и < 1, 0 < ш < 1 и другой для 0 < и < 1,
1 < w < 2. Надо найти точку в центре поверхности, т. е. при и = 1/2, w = 1.
Расписывая уравнение (6-70), получим
4 4
Q(u,w) = ^^В^М,4(и)Му,зН
i=i j=i
= JVi,4(Bi,iMi,3 + Bi,2M2,3 + ВизМ3,з + B1AMi<3)
+ N2,4(B2,lMl,3 + В2,2М2,3 + В2,зМз,3 + В2,4М4,з)
+ N3,4(53,1^,3 + Вз,2М2,з + В3,зМз,з + Вз,4М4,з)
+ JV4,4(B4,iMi,3 + В4,2М2,з + В4,зМ3,з + В4,4М4,3).
Здесь узловой вектор в и направлении [X] = [0 0 0 0 111 1].
Вспомнив пример (5-12), получим выражения для базисных функций, т.е.
4£)-<x-*-(i)4
NM(i)=3«(l-.r = (3)(i)(i)'4
№1<(1)=з„*<1-») = <з>(1)'(±)4
Аналогичным образом узловой вектор в направлении w имеет вид \У] =
[000122 2]. Вспомнив пример (5-10), получим выражения для
базисных функций, т. е.
Afi.a(l) = 0,
М2|3(1) _ —^— - -,
т_(2-Щ)(Зщ-2)_(2-1)(3-2) .1
М3,з(1) -,
М4|3(1) = (ш-1)2 = (1-1) = 0.
Таким образом,
Q(l/2,1) = i{(0)Bi,i + |Bi,2 + |bi,3 + (0)Bi,„}
+ |{(0)B2li + \в2,2 + |в2,3 + (0)В2>4}
+ |{(0)Вз,1 + ^Вз,2 + 2-Вз,з + (0)Вз,4}
+ |{(0)В4,1 + \вА,2 + £в4,3 + (0)В4,4>
0(1/2,1) = i(Bil2 + Bi,s) + ^(В2>2 + В2|3)
3 1
+ Т^(Вз,2 + Вз,з) + Гт(В4,2 + В4,з)
= ^{[-15 5 5]+ [-15 5 -5]}
+ ^{[-5 10 5]+ [-5 10 -5]}
+ ^{[5 10 5]+ [5 10 -5]}
+ -7j[15 5 5]+ [15 5 -5]}
lb
= [0 35/4 0]
Периодические В-сплайн поверхности легко генерируются с помощью
периодических базисных функций в уравнении (6-70), для получения которых
используются периодические узловые векторы. На рис. 6-45 показано несколько приме-
Рис. 6-45 Периодические В-сплайн поверхности для незамкнутых характеристических
многогранников, (а) Гладкая линейчатая поверхность третьего порядка; (6) большая
внутренняя плоская область третьего порядка, вызванная коллинеарностью пяти
вершин сетки в и направлении; (с) острый выступ на поверхности четвертого порядка,
вызванный пересечением нескольких совпадающих линий сетки.
ров периодических В-сплайн поверхностей, формируемых незамкнутыми
задающими полигональными сетками. На рисунках 6-45 а и Ь задающие полигональные
сетки соответствуют сеткам рисунков 6-42 а и с, а сетка рис. 6-45 с
соответствует сетке рис. 6-436. Заметим, что во всех случаях, так же как и для
периодических В-сплайн кривых, границы поверхности и многогранника не совпадают из-за
уменьшения диапазона параметра, используемого для периодических В-сплайн
базисных функций.
Замкнутые периодические В-сплайн поверхности демонстрируют свойства,
аналогичные свойствам замкнутых периодических В-сплайн кривых. На рис. 6-46
показаны примеры трех поверхностей третьего порядка. Задающая
полигональная сетка на рис. 6-46а образуется с помощью повторения через одинаковые
промежутки вдоль оси z От точки z = — 8 до z = 8 задающего многоугольника для
Рис. 6-46 Замкнутые периодические В-сплайн поверхности, (а) Прямая
цилиндрическая поверхность; (6) возмущенная волнистая цилиндрическая поверхность; (с) эффект
возмущения одной вершины сетки.
ф)
Рис. 6-47 Объединенные В-сплайн поверхности третьего порядка, (а) Незамкнутый
характеристический многогранник; (6) замкнутый характеристический многогранник.
замкнутой В-сплайн кривой на рис. 6-466. В результате получается
цилиндрическая поверхность. Отметим, что поверхность не касается плоскостей первого и
последнего задающих многоугольников. Характеристический многогранник для
рис. 6-466 получен с помощью увеличения на единицу х- и у-размеров второго
и четвертого задающих многоугольников на рис. 6-46 а. В результате получается
волнистый цилиндр. На рис. 6-46с показан локальный эффект возмущения одной
вершины задающей сетки.
В уравнении (6-70) можно комбинировать незамкнутые и периодические В-
сплайн базисные функции. Два примера этого представлены на рис. 6-47. Здесь
в одном параметрическом направлении используются незамкнутый узловой
вектор и базисная функция, а в другом направлении используются периодический
узловой вектор и базисная функция. На рис. 6-47а показана комбинированная
В-сплайн поверхность, заданная незамкнутой полигональной сеткой с рис. 6-42а.
На рис. 6-476 показана комбинированная В-сплайн поверхность, заданная
замкнутой полигональной сеткой с рис. 6-466. Отметим, что поверхность совпадает с
крайними линиями полигональной сетки в направлении и. Это свойство бывает
полезным в некоторых случаях.
Матричное выражение для периодических В-сплайн поверхностей имеет вид
Q(s,t) = [U*]{N*][B;it][M*]T[W*]T (6-76)
где [U*] и [W*] являются репараметризованными параметрическими
переменными в интервалах 0 < и* < 1 и 0 < w* < 1, заданными в уравнении (5-90). [N*] и
[М*] задаются уравнением (5-91). Матрица [B*t] представляет скользящую сетку
к х I вершин характеристического многогранника, задающего подкусок на
поверхности. Для периодических В-сплайн поверхностей, заданных незамкнутыми
полигональными сетками
где
1 < s <п — к+ 2, s<i<s + k — l,
l<t<m-l + 2, t<j <t + l-l (6-78)
(6-77)
(a) (*)
Рис. 6-48 Замкнутая тороидальная бикубическая (к = I = 4) В-сплайн поверхность,
(а) Характеристический многогранник; (6) поверхность.
и Bij представляет индивидуальные элементы задающей полигональной сетки.
Для полигональных сеток, замкнутых вдоль и = О, т. е. с совпадающими
первой и последней сеточными линиями в направлении и, скользящая сетка задается
так1
l<s <п-к + 2,
l<t<m + l,
s <i < s + к — 1,
je[{(t-l) mod (m + l)} + l :(t + l- 2) mod (m + 1) + 1]. (6-79)
Аналогичным образом, для полигональных сеток, замкнутых вдоль w = О,
скользящая сетка задается в виде
1 < s < п + 1,
1 <i <m-Z + 2,
z'e[{(s-l) mod (п + 1)} + 1 : (s + k-2) mod (тг + 1) + 1],
t < j < t + / - 1. (6-80)
1 j' £ [o : b] означает принадлежность множеству о... Ь. В данном случае списки вершин
многогранника должны рассматриваться как закольцованные. Например, если тп + 1 = 4, то
j £ [3 : 2] означает принадлежность множеству 3, 4, 1, 2 в указанном порядке.
И наконец, для полигональных сеток, замкнутых вдоль как и = 0, так иш = 0,
скользящая сетка задается так:
l<s<n-k + 2,
l<t<m-l + 2,
i£[{{s-l) mod (п + 1)} + 1 : (s + к - 2) mod (тг + 1) + 1],
j6[{(«-l) mod (m + l)} + l : (t + l-2) mod (m + 1) + 1]. (6-81)
В этом случае образуется полностью замкнутая поверхность. Пример изображен
на рис. 6-48. Задающая полигональная сетка, изображенная на рис. 6-48 а,
формируется с помощью переноса вершин задающего многоугольника для
периодической В-сплайн кривой на рис. 6-47 на —2 единицы по х и +4 единицы по у и
затем вращения на 360° вокруг оси х с шагом 45°. Замкнутая периодическая
бикубическая {к = I = 4) В-сплайн поверхность, изображенная на рис. 6-486, имеет
форму тора.
Матричное выражение для незамкнутых В-сплайн поверхностей имеет ту же
форму, что и уравнение (6-76). Однако, так же как и для матричного выражения
незамкнутых В-сплайн кривых, существование нескольких узловых значений на
концах узлового вектора делает этот результат менее компактным и менее
полезным, чем для периодических В-сплайн поверхностей. По этим причинам данный
вопрос не рассматривается здесь более подробно.
6-13 В-СПЛАЙН ИНТЕРПОЛЯЦИЯ
В предыдущих разделах обсуждались свойства и создание В-сплайн
поверхностей по известной задающей полигональной сетке. Также представляет интерес
и обратная задача: т. е. задано известное множество данных на поверхности,
надо найти задающую полигональную сетку для В-сплайн поверхности,
наилучшим образом интерполирующей эти данные. Так как границы поверхности,
представляемой этими данными, обычно известны, то здесь будут рассматриваться
только незамкнутые В-сплайн поверхности. Разработка аналогичного метода для
замкнутых поверхностей с помощью периодических В-сплайн поверхностей не
представляет труда. Обсуждение ограничивается топологически
прямоугольными сетками, т. е. данные умозрительно могут быть представлены как находящиеся
в точках пересечения прямоугольной решетки. Эта задача схематично
изображена на рис. 6-49, где показана задающая полигональная сетка размера 4x4 для
матрицы данных 8x8. Эта задача рассматривалась в [6-5] и в [6-26]. Для того
чтобы повысить эффективность вычислений, в работе [6-26] были использованы
известные свойства бикубических В-сплайн поверхностей. Применяемый нами
метод более прямолинеен, но имеет меньшую вычислительную эффективность (см.
разд. 5-11).
Вспомним уравнение (6-70) и заметим, что Q(u, w) в этом уравнении являются
известными точками на поверхности. Базисные функции Ni^iu) и Mjj(w) могут
быть определены для известного порядка и известного числа вершин задающей
полигональной сетки в каждом параметрическом направлении при условии, что
"1,4
и2.4
UU
1.2
В.
В,
ИЭ,4
1 ■ » 1 1 Ш » « ■ 1
• • • • • •
• • • • • •
В2,3 В3,3
• •
• •
• •
• •
• • • •
• • • •
В2Л ВЗЛ
• • • •
• • • •
De.l
в,
4,2
вА
1.1 "2,1 "3.1 "4,1
Рис. 6-49 Определение В-сплайн поверхности по известному набору данных.
известны значения параметров м,шв исходных точках. Следовательно, для
каждой известной точки поверхности уравнение (6-70) дает линейное уравнение от
неизвестных вершин Bij задающей полигональной сетки. В результате
расписывания уравнения (6-70) для исходной точки поверхности получим
£l,l(wi|U>l) =
Nltk(u1)[Mlti(w1)B1A + M2ti(w1)BU2 + --- + Mm+iAwi)Bi,m+i]+
Nn+hk{ui)[Mi,i(wi)Bn+lil+M2,i(w1)Bn+ii2 + --- + Mm+lii{wi)Bn+ltm+i]
где для топологически прямоугольного множества г х s данных вьшолняются
неравенства 2 < Кп + 1<ги2 <!<m+l <s. Записав уравнения такого
вида для всех исходных точек, мы получим систему уравнений. В матричном
виде данный результат записывается так:
[D] = [С][В], (6-82)
где С*j = Ni.kMjj. Для топологически прямоугольных исходных данных размера
rxs матрица [D] является матрицей г * s х 3, содержащей трехмерные координаты
исходных точек, [С] является матрицей r*sxn*m трехмерных координат искомых
точек полигональной сетки.
Если матрица [С] квадратная, то задающая полигональная сетка находится с
помощью обращения матрицы, т. е.
[B] = [C]-l[D]. (6-83)
В этом случае получившаяся поверхность проходит через все исходные точки.
Хотя эта поверхность будет везде Ск'2,С1~2 гладка, но она может быть непри-
Рис. 6-50 Интерполяция В-сплайн поверхностью, (а) Исходные точки и
интерполирующий характеристический многогранник; (Ь) исходные точки и сгенерированная
поверхность.
емлема с точки зрения пользователя. Опыт показывает, что в общем случае чем
меньше точек задающей полигональной сетки, тем лучше выглядит поверхность.
Если [С] не квадратная, то мы имеем избыточное количество исходных данных
и решение может быть получено в некотором усредненном смысле. В частности,
решение может быть получено в виде
[B] = [[cy[c}}-i[cy[D].
(6-84)
Параметрические значения и и w для каждой исходной точки поверхности
получаются с помощью аппроксимации длины хорды (см. разд. 5-11). Конкретнее,
для г исходных точек значение параметра в 1-й точке в параметрическом
направлении и равно
ui =0
J2 \Dg,s ~~ Dg-l,s
Щ д=2
J2 \Dg,s ~ Dg-l,s
д=2
Аналогично для s исходных точек в параметрическом направлении w
w\ = 0
J2 \Dr,g - Drig-i\
Wl g=2
W„
J2 \Dr,g - A-,s-l|
g=2
где umax и wmax являются максимальными значениями соответствующих узловых
векторов. На рис. 6-50а показаны исходные данные и задающая полигональная
сетка, сгенерированная с помощью данного метода. На рис. 6-506 изображена
В-сплайн поверхность, созданная по этой сетке.
Как было ранее отмечено для интерполяции с помощью В-сплайн кривой (см.
разд. 5-11), ни данный, ни указанный в [6-5] методы не могут привести к
появлению точек или линий складок (разрывов первой или второй производной) в
получаемой поверхности.
Отметим из рис. 6-50, что вершины задающей полигональной сетки,
полученные из уравнения (6-84), расположены произвольным образом в пространстве.
Это неудобно, если в дальнейшем поверхность предполагается модифицировать.
В работе [6-27] разработан итерационный метод, основанный на параметрических
значениях и, w, в результате которого вершины сетки располагаются на
плоскостях или вдоль кривых в трехмерном пространстве.
6-14 РАЗБИЕНИЕ В-СПЛАЙН ПОВЕРХНОСТЕЙ
В-сплайн поверхность разбивается с помощью отдельного разбиения каждой
линии задающей полигональной сетки в одном или обоих параметрических
направлениях. Может использоваться любой из методов разбиения В-сплайн кривой (см.
разд. 5-12). Лучше всего продемонстрировать это на примере.
Пример 6-16 Разбиение незамкнутой В-сплайн поверхности
Рассмотрим незамкнутую В-сплайн поверхность, заданную
полигональной сеткой размера 4x4:
Bi,i[-15 0 15] jB2.i[—5 5 15] B3,i[5 5 15] B4,i[15 0 15],
Bi,2[-15 5 5] В2,2[-5 10 5] B3|2[5 10 5] В4,2[15 5 5],
Bi,3[-15 5 -5] В2,з-5 10 -5] В3,з[5 10-5] В4,з[15 5 -5],
Bi,4[-15 0 -15] В2|4[-5 5 -15] Вз,4[5 5 -15] В4,4[15 0 -15].
Это поверхность четвертого порядка в обоих параметрических направлениях
(к = I = 4), состоящая из одного куска с диапазонами параметров 0 < и < 1,
0 < ги < 1. Требуется разбить поверхность на 4 подкуска. Следует сохранять
однородный незамкнутый узловой вектор.
Вспомним узловой вектор [00001111]; для обоих
параметрических направлений, найденных в разд. 5-12 и примере 5-18, репараметри-
зуем этот вектор в [0 0 0 0 2 2 2 2], тогда поверхность разбивается
с помощью вставки узлового значения 1 в интервале 0 —> 2. Таким образом,
новый узловой вектор задается координатами [0 0001222 2].
Применив уравнения (5-119) и (5-120) к каждой линии сетки в обоих
направлениях, получим сетку для разбитой на 4 куска поверхности. Например,
рассмотрим разбиение линии сетки в направлении w, заданной Bi,j, 1 < j' < 4.
Здесь только
Q4,l = Q4,2 = Q4,3 = а4|4 = Q4|5 = 1
не равны нулю.
Воспользовавшись уравнениями (5-120), получим
о=з,1 = аз,2 = а3|з = а3,5 = 1; аз,4 = а4|4 = I/2,
0=2,1 = 0=2,2 = 0=3,5 = 1; 0=2,3 = 0=3,3 = Q=3,4 = Q=4,4 = 1/2,
4 4 1 4 4 4 4 4 4 i /о
0=1,1 = а=з,5 = 1; Q=i,2 = а=2|2 = а2,3 = о=з,з = а=3|4 = о=4,4 = 1/^-
Тогда из уравнения (5-119) получим вершины нового характеристического
многогранника. В частности,
Cl,l = a^i-Bl,! + Q2|iBl,2 + Q3,1^1,3 + Q4,1-^1,4
= Bi,i = [-15 0 15]
Ci,2 = Qi,2-Bi,i + a2i2-Bi,2 + a32jBi,3 + a4|2jBi,4
= i(JBi,i+JBi,2) = [-15 2.5 10]
Ci,3 = a13jBi,i + q2,3jBi,2 + Q3,3-Bi,3 + a4|3jBi,4
= |(Bi,2 + Bi,3) = [-15 5 0]
Cl,4 = Ql,4jBl,l + a2,4^1,2 + 0:3,4^1,3 + Q4,4-Bl,4
= ^(Bi,3+Bi,4) = [-15 2.5 -10]
Cl,5 = a1|5jBl,l + Q2|5jBl,2 + Q3,5-Bl,3 + Q4|5jBl,4
= jBi,4 = [-15 0 -15]
Выполнив ту же операцию для каждой линии сетки в направлении w, мы
получим задающую полигональную сетку размера 4x5 для поверхности,
состоящей из двух подкусков в направлении w и одного в направлении и
Ci,i[-15
Ci,2[-15
Cll3[-15
Ci,4[-15
C1|5[-15
0 15] C2,i[-5
2.5 10] C2,2[-5
5 0] С2,з[-5
2.5 - 10] C2,4[-5
0 -15] C2,5[-5
5 15]
7.5 10]
10 0]
7.5 -10]
5 -15]
C3,i[5
Сз,2[5
С3,з[5
Сз,4[5
Сз,5[5
5 15]
7.5 10]
10 0]
7.5 - 10]
5 -15]
C4,i[15
С4,2[15
С4,з[15
С4|4[15
С4,5[15
0 15]
2.5 10]
5 0]
2.5 - 10]
0 -15]
Элементы а*.,-, приведенные выше, применяются также при разбиении
поверхности в направлении и. В этом случае задающая полигональная сетка
размера 5x4 такова:
Ci,i[-15 0 15] C2,i[-10 2.5 15]
Ci,2[-15 5 5] C2,2[-10 7.5 5]
Ci,3[-15 5 -5] С2,з[-Ю 7.5 -5]
Ci,4[-15 0 - 15] C2,4[-10 2.5 - 15]
Сзд[0
C3,2[0
C3,3[0
C3,4[0
5 15] C4,i[10
10 5] C4,2[10
10 -5] C4|3[10
5 - 15] C4,4[10
2.5
7.5
7.5
2.5
15] C75.i[15
5] C5,2[15
-5] C5,3[15
-15] C5,4[15
0
5
5
0
15]
5]
-5]
-15]
Здесь поверхность состоит из двух подкусков в направлении и и одного в
направлении w.
Разбиение поверхности как в и, так и в w направлениях приведет в
результате к задающей полигональной сетке размера 5x5, заданной в виде
Cl,2
Ci,3
Cl,4
Oi,i
-15
-15
-15
-15
-15
C3,i[0
Сз,2[0
Сз,з[0
Сз,4[0
Сз,5[0
5 15]
7.5 10]
10 0]
7.5 - 10]
5 -15]
C4,i[10
С4,2[10
С4,з[10
С4,4[10
С4,5[Ю
0 15]
2.5 10]
5 0]
2.5 - 10]
0 -15]
2.5 15]
5 10]
7.5 0]
5 -10]
2.5 -15]
С2,1
С2,2
Сг,з
Сг.4
С2,5
[-10
-10
-10
-10
[-10
C5.i[15
С5,2[15
С5,з[15
С5,4[15
С5,5[15
2.5 15]
5 10]
7.5 0]
5 -10]
2.5 -15]
0 15]
2.5 10]
5 0]
2.5 -10]
0 -15]
Заметим, что последняя сетка получается из первой или второй с помощью
уравнений (5-119) и (5-120).
Исходная поверхность и все три полученные при ее разбиении сетки
изображены на рис. 6-51. Каждая из поверхностей идентична исходной.
Ясно, что при дальнейшем разбиении поверхности задающая полигональная
сетка приближается к поверхности.
6-15 ГАУССОВА КРИВИЗНА И КАЧЕСТВО ПОВЕРХНОСТИ
В автоматизированном проектировании большой интерес представляет
разработка соответствующих методов для определения и/или визуализации качества или
гладкости поверхностей. Хорошо известно, что используемые обычно
бикубические поверхности (Кунса, Безье или В-сплайн), хотя и являются во всех точках
С2 гладкими, в некоторых местах могут быть плоскими или выпуклыми либо
волнистыми. В настоящее время самые лучшие математические методы определения
качества поверхности используют Эйлеровы (ортогональные) сетки минимальной
и максимальной кривизны (см. [6-28] и [6-29]) и гауссовой кривизны (см. [6-28] —
[6-32], и разд. 6-8).
Вспомним (разд. 6-8), что две комбинации главных кривизн, называемые
средней и гауссовой (общей) кривизнами, характеризуют локальную форму
поверхности. Средняя кривизна определяется как
Ла —
. + «п
(6-45)
Гауссова кривизна определяется как
(6-46)
где кт;п и Kmax являются главными кривизнами. Гауссова кривизна в точке на
поверхности показывает, является ли поверхность локально эллиптической,
гиперболической или параболической (гауссова кривизна положительна, отрицательна
или равна нулю).
Рис. 6-51 Разбиение В-сплайн поверхности, (а) Поверхность; (ft) исходная задающая
полигональная сетка; (с) сетка, разбитая в w направлении; (d) сетка, разбитая в и
направлении; (е) сетка, разбитая в обоих направлениях.
Интересно отметить здесь, что если гауссова кривизна равна нулю, то
поверхность является развертывающейся, т.е. она может быть развернута в плоскость.
Такая поверхность изогнута в одном направлении, например, конус или цилиндр.
Это подразумевает, что одна из главных кривизн, Kmin и ктах равна нулю.
Следовательно, равна нулю и гауссова кривизна.
Существуют несколько методов визуализации средней и гауссовой кривизн
поверхности. Если изобразительные возможности ограничены рисованием отрезков,
то наиболее полезны контурные чертежи (см. [6-28] и [6-29]). В работах [6-30] и
[6-32] показано, что эффективным методом этого является кодирование гауссовой
кривизны на растровом изображении с помощью цветов или набора полутонов
серого цвета.
На рис. 6-52 показаны закодированные1 с помощью полутонов серого цвета
изображения гауссовой кривизны для нескольких тестовых поверхностей вместе
с соответствующим характеристическим многогранником (слева) и проволочным
параметрическим представлением поверхностей (по середине). Все поверхности
являются бикубическими (к = I = 4) В-сплайн поверхностями. На рис. 6-52
изображены три поверхности по мере увеличения степени нарушения их гладкости.
На рис. 6-52а представлена совершенно гладкая поверхность, без изъянов. Два
ярко выраженных гребня уменьшенной гладкости на рис. 6-526 вызваны
совпадением на каждой стороне трех линий полигональной сетки. На рис. 6-52с удлиненная
линия «складки» в середине поверхности получилась из-за совпадения трех
линий полигональной сетки на участке, пересекающем несколько внутренних линий
сетки, что показано на характеристическом многограннике.
Вообще, изображения закодированной гауссовой кривизны более наглядно
показывают свойства поверхностей. Например, рисунки 6-52о и 6 демонстрируют
большое отрицательное значение кривизны в угловых точках. Эта
отрицательная кривизна является результатом ограничений на границы поверхности — они
должны быть прямыми и плоскими, тогда как внутренняя область выпукла и
положительно изогнута. Закодированное изображение гауссовой кривизны на рис.
6-526 подчеркивает уплощение области, расположенной между гребнями.
Отметим, что так как гауссова кривизна равна нулю в этой области, то эта часть
поверхности является развертывающейся. Отметим также, что задающая
полигональная сетка в этой области является развертьшающейся. И наконец, полоса
поперек середины закодированного изображения на рис. 6-52 с показывает, что
поверхность в этой области представляет собой плоскость, согнутую посередине.
Тот факт, что сгиб является прямой линией, объясняет исчезновение гауссовой
кривизны вдоль этой линии.
1 Эти изображения являются монохромными копиями цветных изображений из [6-33]. При
кодировании изображений гауссовой кривизны были усреднены значения кривизн в четырех
вершинах многоугольников, образуемых густой сеткой аппроксимирующих поверхность
четырехугольников. Эта усредненная величина была присвоена каждому многоугольнику. Диапазон
изменения кривизны был разделен на ряд одинаковых интервалов (за исключением концов),
соответствующих доступному диапазону интенсивностей. Справа от изображения указан список
полутонов и соответствующих им значений кривизны. Ступенчатость (границы между
различными интенсивностями) возникает из-за ограниченного числа доступных интенсивностей, а не
из-за аппроксимации с помощью многоугольников.
кшигональная
сетка
Поверхность
(<0
Гауссова кривизна
Полигональная
сетка
Поверхность
Гауссова кривизна
Полигональная
сетка
Поверхность
(с)
Гауссова кривизна
Рис. 6-52 Гауссова кривизна, (о) Гладкая поверхность; (6) короткая линия «складки»;
(с) более длинная линия «складки». (С разрешения Дж. Дилла и Д. Роджерса.)
Метод вычисления гауссовой кривизны будет проиллюстрирован на примере.
Пример 6-17 Гауссова кривизна
Найти гауссову кривизну в точке с параметрами и = 1/2, w = 1 для
незамкнутой В-сплайн поверхности, определенной ранее в примере 6-15.
Вспомним сначала базисные функции ЛГ^4 и М,,/ из примера 6-15. По
этим данным можно вычислить первую и вторую производные,
необходимые для нахождения Qu, Qw, Quvl, QUu и Qwvl, и последующего вычисления
гауссовой кривизны. А именно
JVM = (1 - и)3
N2,4 = 3u(l - и)2
N3,4.=3u2(l-u)
N4,4. :
-■и3
N'1A = -3(1 - и)2
Л^4=3(1-и)(1-3и)
N3A = 3u(2 - 3u)
Лй'4 = 3u2
»4,4
N1,4 = 6(1 - U)
N'4A = 6(3u - 2)
N'li = 6(1 - 3u)
N'li = Qu
и
Afi,3 = 0 M{i3 = О М[[3 = О
М2,з = ^li мЬ = ю-2 M'U = 1
Мз.з = (2-™)(3™-2? м3,з = 4 - Zw Мз'.з = -3
М4,з = (ш - I)2 М^з = 2(ш - 1) М^з = 2
Вычисление производных в точке и = 1/2, 1« = 1и подстановка в уравнения
(6-71) — (6-75) приводит к следующим результатам:
0(1/2,1) = [0 35/4 0],
0,(1/2,1) = [30 0 0],
Q™(1/2,1) = [0 0 10],
0«»(1/2,1) = [О О О],
О««(1/2,1) = [0 -30 0],
Оч™(1/2,1) = [0 -10 10].
Компоненты уравнения (6-48) для гауссовой кривизны таковы:
Qu х Qw = [30 0 0] х [0 0 10] = [0 - 300 0]
10» * 0™|" = (300)4
А = [Qu х Qw] ■ Quu = [0 - 300 0] ■ [0 - 30 0] = 9000
В = [0„ х Qw] ■ Quw = [0 - 300 0] • [0 0 0] = О
С = [Qu х О™] • Qww = [0 - 300 0] • [0 - 10 10] = 3000
Используя уравнение (6-48), получим гауссову кривизну
Кд = A£zB = POOP);3000) - (0) = ^ х 10-
9 \Qu х Qw\4 (300)4
Так как кд > 0, то поверхность является локально эллиптической.
6-16 РАЦИОНАЛЬНЫЕ В-СПЛАЙН ПОВЕРХНОСТИ
Так же как и для рациональных кривых, возможно существование рациональных
форм квадратичных поверхностей, бикубических поверхностей Кунса и
поверхностей Безье. Однако здесь будут рассмотрены только рациональные В-сплайн
поверхности, как из-за нехватки места, так и в связи с тем, что такие
поверхности являются обобщением всех этих форм.
Декартово произведение рациональной В-сплайн поверхности в
четырехмерном пространстве однородных координат задается формулой
n+l m+l
Q(u,w) = £ £ ВЪК,к(и)Ми(г»), (6-85)
i=i i=i
где В± • являются 4D однородными вершинами характеристического
многогранника, а Мг<к(и) и Mjti(w) являются нерациональными В-сплайн базисными
функциями, приведенными ранее в уравнении (5-84).
Проецирование обратно в трехмерное пространство с помощью деления на
однородную координату дает рациональную В-сплайн поверхность
п+1 тп+1
Е Е KiBi,jNi,k(u)Mjti(w) п+1т+1
Q(u,™) = '"^+1 = Е Е BijStJ(u,w), (6-86)
Е Е л*Л(«)м,м(«0 *=i >=i
i=l i=l
где B^j являются ЗБ-точками задающей полигональной сетки и Sij(u,w)
—базисными функциями от двух переменных рациональной В-сплайн поверхности
Е Е Лй,л^г1,*(«)М,-1,,(ш)
il=l J'l=l
Удобно положить /ijj > 0 для всех г, j.
Важно отметить здесь, что Sitj(u,w) не являются произведением Riie(w) и
Rjti(w) (см. уравнение 5-123). Тем не менее Sitj(u,w) имеют форму и
аналитические свойства, похожие на функцию произведения Niik(u)Mjti(w).
Следовательно, рациональные В-сплайн поверхности имеют аналитические и геометрические
свойства, похожие на их нерациональные двойники. Конкретнее,
Сумма базисных функций рациональной поверхности для любых значений и,
w равна
п+1 тп+1
£51 $,,■(«, «0 = 1. (6-88)
i=i i=i
Каждая базисная функция рациональной поверхности положительна или
равна нулю для всех значений параметров и, w, т. е. Sij > 0.
Кроме случая к = 1 или / = 1, каждая базисная функция рациональной
поверхности имеет ровно один максимум.
Максимальный порядок рациональной В-сплайн поверхности в каждом
параметрическом направлении равен числу вершин характеристического
многогранника в этом направлении.
Рациональная В-сплайн поверхность порядка к, I (степени к — 1,1 — 1) гладкая
во всех точках Ск~2, С1~2.
Рациональная В-сплайн поверхность инвариантна относительно проективного
преобразования; т.е. любое проективное преобразование может быть
применено к поверхности путем его применения к задающей полигональной сетке.
Отметим, что это условие является более строгим, чем для нерациональной
В-сплайн поверхности.
Поверхность лежит внутри выпуклой оболочки задающей полигональной
сетки, образуемой объединением всех выпуклых оболочек к, I соседних вершин
полигональной сетки.
Свойство затухания изменений для рациональных В-сплайн поверхностей
неизвестно.
Влияние одной вершины полигональной сетки ограничивается ±/с/2, ±1/2
интервалами в каждом параметрическом направлении.
При триангуляции задающая полигональная сетка образует плоскую
аппроксимацию поверхности.
Если число вершин задающей полигональной сетки равно порядку в каждом
параметрическом направлении и дублированных внутренних узловых величин
нет, то рациональная В-сплайн поверхность является рациональной
поверхностью Безье.
Из уравнений (6-86) и (6-87) ясно, что когда все hij = 1, тогда Sij(u,w) =
Nitk(u)Mjj(w). Таким образом, базисные функции рациональной В-сплайн
поверхности и сами поверхности превращаются в их нерациональные эквиваленты.
Следовательно, рациональные В-сплайн поверхности представляют
соответственно обобщение нерациональных В-сплайн поверхностей и рациональных и
нерациональных поверхностей Безье.
Снова, как и в случае рациональных В-сплайн кривых, алгоритмы для
увеличения степени, разбиения (см. разд. 6-14) и интерполяции (см. разд. 6-13)
нерациональных В-сплайн поверхностей можно применять просто путем их
использования для 4.0-вершин задающей полигональной сетки.
Незамкнутый однородный, периодический однородный и неоднородный
узловой векторы могут быть использованы для генерации рациональных В-сплайн
базисных функций и рациональных В-сплайн поверхностей. Типы узловых
векторов могут смешиваться. Например, в параметрическом u-направлении может
использоваться незамкнутый однородный узловой вектор, а в ш-направлении—
неоднородный узловой вектор. Сначала мы остановимся на незамкнутых
однородных узловых векторах.
На рис. 6-53 представлены бикубическая (/с = I = 4) рациональная В-сплайн
поверхность и ее задающая полигональная сетка для /ii_3 = /12,3 = 0,1,5.
Изображение на рис. 6-53с с hit3 = /12,3 = 1 идентично нерациональной В-сплайн
поверхности. Результаты варьирования значений однородной координаты можно
заметить, сравнивая рис. 6-53с с рис. 6-536 и d. Эти результаты аналогичны
полученным для рациональных В-сплайн кривых (см. разд. 5-13), но проявляются
не в столь сильной степени. В данном случае уменьшение эффекта обусловлено
тем, что Sij(u,w) является функцией смешения от двух переменных.
На рис. 6-54а и Ь иллюстрируется результат, полученный при присвоении всем
внутренним hij значений 0 и 500, соответственно; т. е. /12,2 = ^2,з = /13,2 = h3j3 —
/14,2 = /14,3 = 0 или 500. Все остальные hij = 1. Характеристический
многогранник изображен на рис. 6-53 а. Установка всех внутренних hij = 0 приводит
к игнорированию внутренних вершин характеристического многогранника.
Интерполируются только вершины граничных кривых. Напротив, присвоение всем
внутренним hi j = 500 сводит к минимуму влияние граничных вершин. Заметим,
что изменение hij влияет на параметризацию поверхности. Это иллюстрируется
скоплением параметрических линий около границ поверхности, когда внутренние
hij = 0 (см. рис. 6-54о), и во внутренней части поверхности, когда внутренние
hij = 500 (см. рис. 6-546).
Рис. 6-53 Рациональные В-сплайн поверхности с я + 1 = 5, т + 1 = 4, к = I = 4.
(а) Характеристический многогранник; (6) hi,a = /12,3 = 0; (с) /ii,3 = /12,3 = 1; (d) hi,3 =
/l2,3 = 5.
Рис. 6-54 Рациональные В-сплайн поверхности с n+1 = 5, тп + 1 = 4, fc +J = 4. (а) Все
внутренние hij — е = 0; (6) все внутренние hij — е = 500.
Рис. 6-55 Рациональный В-сплайн эллиптический цилиндр, сгенерированный
заметанием рациональной эллиптической кривой на рис. 5-676.
Результаты, возникающие при совпадении нескольких вершин или линий
сетки аналогичны результатам, полученным для нерациональных В-сплайн
поверхностей (см. разд. 6-12) и рациональных В-сплайн кривых (см. разд. 5-13). Также
аналогичны результаты смещения одной вершины на поверхности.
Одним из самых привлекательных свойств рациональных В-сплайн
поверхностей является их способность представлять квадратичные поверхности и плавно
переходить в скульптурные поверхности высоких степеней. В качестве простого
примера квадратичной поверхности рассмотрим обобщенный цилиндр,
образуемый заметанием кривой. Ясно, что в направлении заметания такая поверхность
должна быть второго порядка, т.е. прямой линией. Следовательно, для
заметаемой в направлении и поверхности формула выглядит (см. [6-33]) следующим
образом:
2 т+1
Q(u,w) = J2 J2 ВмЯ;(",«О, (6-89)
i=l j=l
где Sij(u,w) имеет в параметрическом направлении w тот же порядок, что и
кривая, и порядок 2 в направлении и. Кроме того, вершины характеристического
многогранника в направлении и равны B\tj = Bj и B2J = Bj + sD, где D
задает направление и расстояние заметания. Параметр s изменяется в диапазоне
О < s < 1. Элементы Bj являются вершинами задающего многоугольника для
заметающей кривой. Однородные координаты остаются неизменными в
направлении заметания; т.е. h\tj = hij = hj, где hj - это однородная координата для
заметаемой кривой. На рис. 6-55 изображен эллиптический цилиндр,
образованный с использованием эллиптической кривой, представленной на рис. 5-676. С
каждой стороны поверхности показана отодвинутая заметаемая кривая.
Рациональные В-сплайн поверхности используются также для создания
линейчатых поверхностей. Эллиптический цилиндр, изображенный на рис. 6-55,
является, конечно, линейчатой поверхностью. Для генерации с помощью рацио-
Рис. 6-56 Рациональная В-сплайн линейчатая поверхность.
нальных В-сплайнов линейчатой поверхности более общего вида требуется, чтобы
обе кривые имели одинаковый порядок (степень), одинаковый узловой вектор и
одинаковое число вершин задающего многоугольника. Если кривые имеют
разный порядок (степень), то степень кривой меньшего порядка увеличивают (см.
разд. 5-8 и пример 6-18). Требуемый узловой вектор является объединением
узловых векторов двух кривых. Любые кратные узловые значения для любой
кривой включаются в окончательный узловой вектор. Для обеспечения идентичности
обоих узловых векторов используется вставка узлов (см. разд. 5-12). Увеличение
степени и вставка узлов обеспечивают равенство числа вершин
характеристического многоугольника для обеих кривых. Получающаяся рациональная В-сплайн
линейчатая поверхность описывается уравнением (6-89) с
ТП+1 7П+1
Pi («О = Q{o,w) = £ В1.;Л;,<Н и P2(w) - J2 52,i-Rj,(H = Q(i,w).
На рис. 6-56 показан пример линейчатой поверхности, переводящей четверть
окружности в рациональную В-сплайн кривую четвертого порядка. Кривые и
их характеристические многоугольники изображены отодвинутыми от края
поверхности. Данный метод лучше проиллюстрировать на примере.
Пример 6-18 Рациональные В-сплайн линейчатые поверхности
Найти точку с параметрами u = id = 0.5 на линейчатой
поверхности, образованной смещением 120° дуги окружности и рациональной
кривой четвертого порядка. Дуга окружности представляется рациональной В-
сплайн кривой, заданной Bi,i[0 0 0], Bi,2[l -\/3 0], Й1,з[2 0 0] и [Н] =
[1 1/2 1]. Вторая кривая определяется #2,1 [0 0 10], В2^[1 1 10],
Вз,г[2 0 10], В4,2[3 1 10] с [Н] = [1 3/4 5 1].
Сначала необходимо увеличить степень дуги окружности. В
действительности дуга является рациональной кривой Безье. Обсуждавшийся в разд. 5-8
метод увеличения степени в рациональном случае применяется к 4D
однородным координатам. В результате получаем:
Bi"=Bi\
В?* =<*£?_! +(1 - ач)В? <*-4т t = 2,...,n,
п +1
n+1 — %■
После проецирования обратно в трехмерное пространство имеем:
В\ = Bi,
, Oi/ii-iBi-x + (1 - ai)hiBi .
Bi = п; T7i ITI г = 2,... , n,
ai/ii-i + (1 -ai)hi
h' = a>ihi-i + (1 — a>i)hi.
Использование данных результатов для увеличения степени 120° дуги
приведет к
^1,1 = /ii,i = 1,
Br,i=Bi,i = [0 0 0],
«-- (ж)« * (I) (I) -1-
«.-{1(1» о «4 + I(|)l» VS 4}/(§)-[! f о,
4., = (|)(i) + (i)(D = |,
*.-{(§)G> *"+5«12001}'(!)-[! т •]■
/lj 4 = /i13 = 1,
BJ.4 = Bi.s = [2 0 0].
Теперь каждая кривая имеет четыре вершины характеристического
многоугольника. Узловой вектор для каждой кривой равен [X] = [Y] =
[00001111]. Следовательно, включение узлов применять не
нужно.
Для и = w = 0.5 из уравнения (5-84) получим
Ni,2 = 0.5; N2,2 = 0.5
Mi,4 = 0.125; М2,4 = 0.375; Мз,4 = 0.375; М4,4 = 0.125
Тогда уравнение (6-87) приведет к следующим результатам:
5i,i = 0.0396 5i,2 = 0.0792 Si,3 = 0.0792 SM = 0.0396
52,i = 0.0396 52,2 = 0.0891 S2,3 = 0.594 52,4 = 0.0396
Координаты точки на поверхности
Q(0.5,0.5) = [1.634 0.266 7.624].
Вся поверхность изображена на рис. 6-56.
С помощью В-сплайнов могут быть также представлены поверхности
вращения. Предположим, что
771+1
P(w) = Y, BjBjtl(w)
3=1
с узловым вектором [Y] является рациональной В-сплайн кривой, и вспомним, что
полная окружность получается при объединении четырех четвертей окружности,
заданных девятью вершинами многоугольника (см. разд. 5-13). Это приводит нас
к рациональной В-сплайн поверхности вращения, задаваемой (см. [6-33])
9 771+1
Q(u, w) = J2J2 ^.A>, 4 (6-90)
г=1 j=l
где узловой вектор [X] = [0 0 0 1 1 2 2 3 3 4 4 4].
Предположимте вращение происходит вокруг оси z, кривая P{w) определена в плоскости
xz, элементы В^ задаются как B\j = Bj для фиксированного j с 1 < г < 9.
Вершины характеристического многоугольника образуют угловые и средние точки
квадрата, лежащего в плоскости, перпендикулярной оси z, и с размером стороны,
равным удвоенному радиусу окружности вращения. Однородные весовые
множители являются произведением множителей, необходимых для задания
рациональной В-сплайн кривой и для задания окружности вращения. Конкретнее, для
фиксированного j, hi j = hj, /i2j = /ijV2/2, haj = hj, h^j = /ijV2/2, ■•■ ,/ig,j = hj.
На рис. 6-57 показаны характеристический многоугольник и сама кривая для
окружности вращения и для вращаемой рациональной В-сплайн кривой. Также
на рисунке приведены объединенный характеристический многогранник
поверхности и сама поверхность.
На рис. 6-58 и 6-59 представлены обычные поверхности вращения — тор и
сфера, вместе со своими характеристическими многогранниками. Тор генерируется
путем вращения смещенной окружности вокруг одной из осей. Сфера
генерируется путем вращения полуокружности, составленной из двух 90° дуг вокруг оси,
проходящей через диаметр полуокружности.
Как было ранее упомянуто, одной из наиболее мощных характеристик
рациональных в отличие от нерациональных В-сплайн поверхностей является их
способность «упрятывать» (или включать) квадратичные элементы поверхности
внутри обобщенной скульптурной поверхности. Например, как часть более общей
поверхности, может быть включен цилиндрической элемент. На рис. 6-60
представлено три примера. Центральной частью каждой поверхности четвертого порядка
является секция кругового цилиндра. Рис. 6-60а мог бы изображать переднюю
кромку крыла или лопасти1 турбины, рис. 6-606 — цилиндрический нос корабля.
Обе поверхности генерируются с помощью задания дуги окружности третьего
порядка (см. разд. 5-13), увеличения степени дуги (см. пример 6-18), создания
из дуги линейчатой поверхности и ее включения между двумя крайними
элементами поверхностей четвертого порядка. Случайно обе поверхности, показанные
В аэродинамических профилях NACA для задания передней кромки используется дуга
окружности.
By,
"6,1
(с)
z 2
(b)
(</)
Bl.l-B9.1
—-X
Рис. 6-57 Рациональная В-сплайн поверхность вращения, (о) Образующая кривая
и задающая сетка; (Ь) окружность вращения; (с) характеристический многогранник;
(d) поверхность вращения.
Рис. 6-58 Тор, сгенерированный как рациональная В-сплайн поверхность, (о)
Смещенная окружность и задающий многоугольник; (6) окружность вращения и задающий
многоугольник; (с) характеристический многогранник для тора; (d) тор.
на рис. 6-60а и Ь, оказались линейчатыми развертывающимися поверхностями.
На рис. 6-60с изображен цилиндрический элемент, упрятанный в более общую
поверхность.
Производные рациональной В-сплайн поверхности получаются с помощью
формального дифференцирования уравнения (6-86):
z
6
У*
Bljs
Л
i
-J
>*1.з
i
—*-x
(a)
Вл-й
4,3'
В, .i
6,3'
язз
^
I
I
V1
У
л
\
1 1
z 2
■y
%; i
• R
,e2,3
Я1,3 = Я9,3
кЯв.з
(с)
(ft)
Рис. 6-59 Сфера, сгенерированная как рациональная В-сплайн поверхность, (а)
Смещенная окружность и задающий многоугольник; (6) окружность вращения и задающий
многоугольник; (с) характеристический многогранник и сфера.
п _N(NUU nNuDu D2u _DuA
Quu-d['W"'2n d +2d2 d )■
f*. I ww о w w i о HI -Uyivi
(6-91d)
(6-91e)
где N и D являются числителем и знаменателем, соответственно, уравнения
(6-86) с производными
П+1 771+1
Nu = Y, J2 KiBUiNlk{u)Mu{w),
Рис. 6-60 Элемент квадратичной поверхности внутри более общей рациональной В-
сплайп поверхности. Передняя кромка крыла, (а) Характеристический многогранник;
(6) поверхность. Корма корабля, (с) Характеристический многогранник; (<f)
поверхность. Цилиндр как часть более общей поверхности, (е) Характеристический
многогранник; (/) поверхность.
n+l m+1
W"> = Е Е hijBijN^i^M'^w),
t=i j=i
n+l m+1
я«» = E E ^-^ло^м.
i=i j=i
n+l m+1
t=i j=i
n+l m+1
Nww = J2 Y, hijBitJNitk(v)Mh(w),
i=l j=l
n+1 m+1
E E ълм^».
n+1 m+1
E E /^.*(")Mj»,
i=l j=l
n+1 m+1
E E /чХ* W»-
t=l j=l
n+1 m+1
E E ь A(«)^-.'H.
i=l j=l
n+1 m+1
E E /^ amm;».
t=i j=i
Штрих обрзначает производную относительно соответствующего параметра.
Функции Nlk(u)Mjtl(w), N"ik(u), М",(ш) задаются уравнениями (5-97)-(5-100).
Эти производные полезны при определении гауссовой кривизны поверхности
(см. разд. 6-15), а также других свойств поверхности.
6-17 ЛИТЕРАТУРА
6-1 Rogers, D. F., Procedural Elements for Computer Graphics, McGraw-Hill, New York,
1985. (Cm. [1-1] на с. 74.)
6-2 Bezier P. E., Emploi des Machines a Commande Numerique, Masson et Cie, Paris, France,
1970; Bezier, P. E., «Example of an Existing System in the Motor Industry: The Unisurf
System,»- Proc. Roy. Soc. (London), Vol. A321, pp. 207-218, 1971.
6-3 Sabin, M. A., «An Existing System in the Aircraft Industry. The British Aircraft
Corporation Numerical Master Geometry System,» Proc. Roy. Soc. (Longon), Vol. A321,
pp. 197-205, 1971.
6-4 Peters, C. J., «Interactive Computer Graphics Application of the Bicubic Parametric
Surface to Engineering Design Problems,» McDonnell Douglas Automation Company,
St. Louis, Missouri, presented at SIAM 1973 National Meeting, Hampton, Va., 18-21
June 1973.
6-5 Rogers D. F., and Satterfield S. D., «Dynamic B-Spline Surfaces,» Proc. of the Fourth
International Conference on Computer Applications in the Automation of Shipyard
Operation and Ship Design (ICCAS 82), 7-10 June 1982, Annapolis, Maryland, pp. 189-
196, North Holland, 1982.
6-6 Rogers, D. F., and Satterfield S. G., «B-Spline Surfaces for Ship Hull Design,» Сотр.
Graph., Vol. 14, pp. 211-217, 1980, (SIGGRAPH 80).
6-7 Rogers, D. F., Rodriguez, F., and Satterfield, S. G., «Computer Aided Ship Design and
the Numerically Controlled Production of Towing Tank Models,» Proc. of 16th Des.
Auto. Conf, San Diego, California, 24-27 June 1979.
6-8 Cohen, E., «Some Mathematical Tools for a Modeler's Workbench,» IEEE Сотр. Graph.
& Appl, Vol. 3, pp. 63-66, October 1983.
6-9 Tan, S. Т., Yuen, M. F., and Hui, К. С, «Modeling Solids with Sweep Primitives,»
Сотр. Mech. Eng., Vol. 6, pp. 60-72, 1987.
6-10 Coquillaxt, S., «A Control-Point-Based Seeeping Techique,» IEEE Сотр. Graph. &
Appl., Vol. 7, pp. 36-45, November 1987.
Du =
D,„ =
J^uw —
Dun =
i-^ww —
6-11 Patton, D., Dept. of Mech. and Prod. Engr., Royal Melbourne Inst, of Tech., Melbourne,
Australia, private communication, 1988.
6-12 Dresden, A., Solid Analytic Geometry and Determinants, Dover Publications, New York,
1964.
6-13 Sommerville, D. M. Y., Analytical Geometry of Three Dimensions, Cambridge Univ.
Press, 1959.
6-14 Snyder, V., and Sisam, C. H., Analytic Geometry of Space, Henry Holt and Co., New
York, 1914.
6-15 Goldman, R. N., «Two Approaches to a Computer Model for Quadric Surfaces,» IEEE
Сотр. Graph. & Appl, Vol. 3, pp. 21-24, September 1983.
6-16 Wilson, P. R., «Conic Representation for Shape Description,» IEEE Сотр. Graph. &
Appl., Vol. 7, pp. 23-30, 1987.
6-17 Miller, J. R., «Geometric Approaches to Non-planar Quadric Surfaces Intersection
Curves,» ACM Trans, on Graph., Vol 6, pp. 274-307, 1987.
6-18 Dill, J. C, «An Application of Color Graphics to the Display of Surface Curvature,»
Сотр. Graph., Vol. 15, pp. 153-161, 1981, (SIGGRAPH 81).
6-19 Coons, S., «Surfaces for Computer-Aided Design of Space Forms,» M. I. T. Proj. MAC,
MAC-TR-41, June 1967. (Also as AD 663 504).
6-20 Ferguson, J. C, «Multivariable Curve Interpolation,» J. ACM, Vol. 2, pp. 221-228, April
1964.
6-21 Barnhill, R. E., «Smooth Interpolation over Triangles,» in Computer Aided Geometric
Design, Barnhill, R. E., and Riesenfeld, R. F. (eds.), Academic Press, New York, pp. 45-
70, 1974.
6-22 Barnhill, R. E., «Coons Patches,» Сотр. in Ind., Vol. 3, pp. 37-43, 1982.
6-23 Charrot, P., and Gregory, J., «A Pentagonal Surface Patch for Computer Aided
Geometric Design,» Сотр. Aid. Geom. Des., Vol. 1, pp. 87-94, 1984.
6-24 Faux, I. D., and Pratt, M. J., Computational Geometry for Design and Manufacture,
Ellis Horwood (John Wiley & Sons), 1979.
6-25 Bezier, P. E., The Mathematical Basis of the Unisurf CAD System, Butterworth, London,
1986.
6-26 Barsky, B. A., and Greenberg, D. P., «Determining a Set of B-spline Control Vertices
to Generate an Interpolating Surface,» Сотр. Graph. Imag. Proc, Vol. 14, pp. 203-226,
1980.
6-27 Rogers, D. F., and Fog, N. G., «Constrained B-spline Curve and Surface Fitting,» С AD J,
Vol. 21, pp. 641-648, 1989.
6-28 Munr.hmeyer, F. C., Schubert, C, and Nowacki, H., «Interactive Design of Fair Hull
Surfaces Using B-splines,» Proc. of the Third International Conference on Computer
Applications in the Automation of Shipyard Operation and Ship Design (ICCAS 79), 18-
21 June 1979, University of Strathclyde, Glasgow, Scotland, pp. 67-76, North Holland,
1979.
6-29 Munchmeyer, F. C, «The Gaussian Curvature of Coons Biquintic Patches,» Proc. ASME
Century 2 Inter. Сотр. Tech. Conf, 12-15 August 1980.
6-30 Dill, J. C, «An Application of Color Graphics to the Display of Surface Curvature,»
Сотр. Graph., Vol. 15, pp. 153-161, 1981, (SIGGRAPH 81).
6-31 Forrest, A. R., «On the Rendering of Surfaces,» Сотр. Graph., Vol. 13, pp. 253-259,
1979, (SIGGRAPH 79).
6-32 Dill, J. C., and Rogers, D. F., «Color Graphics and Ship Hull Surface Curvature,» Proc.
of the Fourth International Conference on Computer Applications in the Automation of
Shipyard Operation and Ship Design (ICCAS 82), pp. 197-205, North Holland, 1982.
6-33 Piegl, L., and Tiller, W., «Curve and Surface Constructions Using Rational B-splines,»
Сотр. Aid. Des., Vol. 19, pp. 485-498, 1987.
Приложение А
Графическое
программное
обеспечение
А-1 ВВЕДЕНИЕ
Разрабатывая концепции графического программного обеспечения, удобно
мыслить в терминах схемы, показанной стрелками на рис. 1-63. Конвейер
начинается с прикладной программы и соответствующей ей базы данных, проходит через
пакет машинной графики и соответствующую ему графическую базу данных и
далее через соответствующий программный интерфейс внешнего устройства, для
генерации изображения на физическом графическом устройстве, с которым
пользователь может или не может взаимодействовать. На протяжении такого
конвейера существуют два критических программных интерфейса: интерфейс
прикладной программы и интерфейс внешнего устройства. В настоящее время
предпринимаются попытки привести оба интерфейса в соответствие с международными
стандартами.
Интерфейс прикладного программиста обычно оформляется как пакет
подпрограмм или функций, доступных из языка высокого уровня, такого, как
Фортран, Си, Бейсик или Паскаль. Интерфейс пользователя обычно пишется с
помощью подпрограмм и функций интерфейса прикладного программиста,
который в настоящее время представлен четырьмя основными стандартами
Графической корневой системой (the Graphical Kernel System GKS) [A-l-A-3], GKS-3D
[A-4] и Иерархической интерактивной графической системой программиста (the
Programmer's Hierarchical Interactive Graphics System PHIGS) [A-5, A-6] и PHIGS+
[A-7]. Многие программы и функции, предусмотренные для интерфейса
прикладного программиста, являются основным предметом данной книги и работы [А-8].
Примеры: поворот, перенос, перспективные проекции, отсечения, удаление
невидимых линий и невидимых поверхностей.
Интерфейс внешнего устройства работает на гораздо более низком уровне, чем
интерфейс прикладного программиста. Это связано с генерацией кодов
(двоичных битовых карт), требуемых для управления конкретным физическим или
виртуальным графическим устройством. Обычно системные программисты и
разработчики интерфейса прикладной программы имеют дело с интерфейсом
устройства. Примеры стандартов интерфейса устройства: Графический метафайл
компьютера (the Computer Graphics Metafile CGM) [А-9]-[А-11], Графический
интерфейс компьютера (the Computer Graphics Interface CGI) [A-10]-[A-12] и
Интерфейс виртуального устройства (the Virtual Device Interface VDI) [A-13].
Детальное обсуждение различных стандартов выходит за рамки данной
книги и проводится в цитируемой литературе. Здесь дается только краткое общее
описание.
GKS — двумерный стандарт визуализации, не включает моделирования,
предусмотрены только двумерные примитивы, такие, как ломаная, поворот, перенос,
масштабирование. Трехмерные преобразования должны выполняться за
пределами стандарта, т. е. трехмерный объект преобразуется в двумерную проекцию (см.
гл. 3) и результат отображается с использованием программ двумерной
графики GKS. GKS поддерживает широкий спектр устройств ввода/вывода (см. гл. 1),
таких, как монохроматические и цветные ЭЛТ-дисплеи, принтеры,
графопостроители, мыши, планшеты, устройства для ввода скалярных значений,
функциональные переключатели и т. д. Доступ к программам GKS обеспечен из ряда языков
высокого уровня: Фортран, Паскаль, Ада, Си, GKS — официальный стандарт как
Международной организации по Стандартам (ISO), так и Американского
национального института стандартов (ANSI) [A-1].
GKS-3D — расширение GKS, обеспечивающее возможности отображения и
определения трехмерных объектов. В нем также нет функций моделирования.
Включает невидимые линии и невидимые поверхности, а также параллельные и
перспективное проецирование. В настоящее время стандарт GKS-3D продолжает
дорабатываться [А-4].
В отличие от GKS и GKS-3D, стандарт PHIGS был изначально разработан
как двойной стандарт для трехмерного манипулирования и визуализации и для
трехмерного геометрического моделирования. Особо выделяется поддержка
высокоинтерактивного программного обеспечения, такого, как САПР/АСТПП,
молекулярное моделирование, моделирование сплошных тел, а также имитация и
управление. PHIGS позволяет строить, преобразовывать, модифицировать и
хранить трехмерные геометрические модели. Стандарт PHIGS продолжает
дорабатываться [А-5].
PHIGS-I—расширение PHIGS, включает модели освещения, обработку
полутонов, глубину, а также кривые и поверхности, такие, как рациональные
В-сплайны (см. разд. 5-13 и 6-16). PHIGS специально разработан применительно
к возможностям высокоинтерактивных графических рабочих станций. Стандарт,
например включает представление таких эффектов, как раскраска по методу Гуро
и Фонга, а также новые геометрические атрибуты, например нормали вершины.
CGI обеспечивает функциональное преобразование независимой от
аппаратуры информации, генерируемой стандартом интерфейса прикладного
программиста, в аппаратно зависимые данные, требуемые для управления конкретным
графическим устройством. CGI определяет виртуальный интерфейс устройства,
т. е. идеализированное стандартное графическое устройство, которое
поддерживает ввод от пользователя, генерирует графическую информацию и манипулирует
ею. Существует строго регламентированное взаимодействие между GKS и CGI.
CGM перехватывает и хранит информацию на уровне CGI. Результатом
является форматированный файл, содержащий «картинку», который может храниться
на диске или ленте и передаваться по телефонным линиям или компьютерным
сетям.
Прежде чем обсуждать каждый из стандартов во всех деталях и сравнивать
их, полезно получить представление об их функциональной и концептуальной
структуре.
А-2 ГРАФИЧЕСКИЕ ПРИМИТИВЫ МАШИННОЙ ГРАФИКИ
При создании любой системы графического программного обеспечения
физическое (виртуальное) графическое устройство управляется первичными аппаратно
зависимыми командами нижнего уровня (примитивами). Графический примитив
выполняет единичное действие. Графические примитивы обычно распадаются на
три группы: управление курсором, управление состоянием устройства и
графический ввод. Здесь понятия курсора и состояния используются в наиболее общем
смысле. Из этих графических примитивов формируются различные графические
команды (множественные действия), называемые элементарными графическими
функциями, они рассматриваются в разд. А-3. Графические элементарные
функции аппаратно независимы.
Существуют два графических примитива управления курсором:
переместить курсор —MOVE (x, у);
включить/выключить курсор ONOFF (i).
Функции этих примитивов не нуждаются в комментариях.
Графические примитивы управления устройством более многочисленны и
разнообразны. Они получили общее имя SET (установить). Некоторые примеры:
установить алфавитно-цифровой режим;
установить графический режим;
установить режим абсолютных координат;
установить режим относительных координат;
установить цвет (красный, зеленый, синий);
очистить экран
и т. д.
В принципе существует только один графический примитив SET с различными
аргументами. Перед тем как продолжить, кратко охарактеризуем функции
каждого из этих различных состояний устройства.
Алфавитно-цифровой и графический режимы, как правило, относятся к
устройствам, которые могут интерпретировать поток данных как в виде
алфавитно-цифровых (ASCII) символов, так и в виде графических команд. Режимы
абсолютных и относительных координат определяют, будут ли декартовы
координаты, объявленные в графических примитивах, интерпретироваться как
абсолютные или относительные. Команда установки цвета определяет цвет курсора
для последующих команд, таких, как линия, точка и т. д. Команда очистки экрана
перекрашивает экран дисплея в цвет фона.
Примитив графического ввода имеет общее имя GET (задать)
GET (значение).
Из сказанного ясно, что в принципе существуют только четыре графических
примитива. В общем виде они могут быть представлены следующим образом:
ONOFF (управляющая переменная);
MOVE (коорд., коорд.);
SET (упр. переменная, (арг.1), (арг.2), ...);
GET (значение).
Здесь угловые скобки () используются для обозначения необязательных
аргументов.
А-3 ЭЛЕМЕНТАРНЫЕ ГРАФИЧЕСКИЕ ФУНКЦИИ
Графические примитивы, которые обсуждались в разд. А-2, могут быть
объединены в графические элементарные функции. Вообще говоря, это составные
операции, т. е. они содержат более одного графического примитива. При аккуратной
реализации они не зависят от конкретного физического устройства.
Так же как и графические примитивы, элементарные графические функции
делятся на три группы: функции рисования, функции управления устройством
или картинкой и функции управления интерактивным вводом. Функции
рисования происходят от процесса рисования карандашом или перемещения карандаша
по листу бумаги. Карандаш может быть перемещен над листом без рисования.
Когда карандаш опускается на лист и перемещается, то он рисует линию.
Карандаш может быть перемещен в некоторую позицию, в которой будет поставлена
точка. Удобно иметь возможность задавать перемещения карандаша над
бумагой и рисования им как в абсолютных так и в относительных координатах. Эти
понятия проиллюстрированы шестью функциями рисования, или графическими
элементарными функциями:
MOVE ABSOLUTE (x, у);
MOVE RELATIVE (Дх, Ду);
DRAW ABSOLUTE (x, у);
DRAW RELATIVE (Дх, Ду);
РОШТ ABSOLUTE (x, у);
POINT RELATIVE (Дх, Ду).
Также нужна возможность вывести символ или текст на поверхности рисования,
сказав:
TEXT (строка).
Всегда удобно предполагать, что действие начинается от текущей позиции
курсора. Функционально каждая из этих графических элементарных функций может
быть описана в терминах графических примитивов. Например, алгоритм MOVE
ABSOLUTE можно представить следующим образом:
установить режим абсолютных координат;
установить графический режим;
выключить курсор;
переместить курсор в указанную позицию.
Алгоритм POINT ABSOLUTE представляется в следующем виде:
Установить режим абсолютных координат.
Установить графический режим.
Выключить курсор.
Переместить курсор в указанную позицию.
Включить курсор.
Алгоритм DRAW ABSOLUTE:
Установить режим абсолютных координат.
Установить графический режим.
Включить курсор.
Переместить курсор в указанную позицию.
Относительные алгоритмы аналогичны приведенным, но с установкой режима
относительных координат командой SET.
Элементарные функции управления устройством или картинкой инициируют
устройство и начинают новый фрейм или картинку. Например, для этих целей
могли бы служить функции:
Инициировать устройство.
Начать фрейм.
Функционально команда «Инициировать устройство» служит для установки
предопределенного состояния устройства. Команда «Начать фрейм» служит для
объявления регенерации графического устройства, при которой работа с
текущей картинкой завершается, устройство заполняется цветом фона и начинается
представление следующей картинки, очищается экран на запоминающей ЭЛТ,
устанавливается новый чертеж для перьевых или струйных устройств и т. д.
Управление графическим вводом должно быть более сложным, чем простой
графический примитив GET, обсуждавшийся в разд. А-2. Вот некоторые
примеры элементарных функций графического ввода:
GET MOUSE (x, у).
GET VALUATOR (значение).
GET TABLET (x, у).
GET FUNCTION SWITCH (i).
и т. д.
Для выполнения этих функций графические примитивы можно объединить.
Это иллюстрируют два примера алгоритмов. Первым является алгоритм GET
VALUATER, который мог бы иметь следующий вид:
Установить режим абсолютных координат.
Установить графический режим.
Задать (значение).
Алгоритм команды GET MOUSE:
Установить режим абсолютных координат.
Установить графический режим.
Задать (значение х).
Задать (значение у).
Выше ничего не говорилось о типе графического устройства, пикселях и т.д.
Читатель может удивиться, что не были включены команды SET PIXEL и GET
PIXEL. Однако после минутного размышления он обнаружит, что в контексте
графического устройства пиксел — это точка. Следовательно, команды для точек
концептуально достаточны для команд пикселов.
Вообще говоря, элементарные графические функции — самый нижний уровень
графических команд прикладного программиста. Во многих случаях
прикладной программист ничего не знает о графических примитивах, и они могут быть
ему фактически недоступны. Однако эти примитивы интересны для системного
программиста. Если всю графическую систему представить в виде уровней или
оболочек, то графические элементарные функции образуют первый уровень или
первую оболочку, а графические примитивы — нулевой уровень или нулевую
оболочку (нулевой, потому что они скрыты от прикладного программиста).
А-4 СИСТЕМЫ КООРДИНАТ
Для систем программного обеспечения машинной графики интерес представляют
три координатные системы: мировые координаты, или координаты пользователя,
псевдопространство с нормализованными координатами устройства и
координаты устройства. Мировые координаты служат для описания прикладной области.
Они обычно задаются в виде чисел с плавающей точкой. Координаты
устройства используются для работы с конкретным графическим устройством:
пиксели, адресуемые точки, дюймы, сантиметры и т. д. Они задаются целыми числами.
Нормализованным пространством координат устройства называется
псевдопространство, используемое для обеспечения независимости от устройства.
Нормализованные координаты задаются числами с плавающей точкой из первого
квадранта в интервалах 0 < ndcx < 1.0, 0 < ndcy < 1.0. Таким образом, начало
координат находится в левом нижнем углу.
Как показано на рис. А-1 и обсуждалось в гл. 1, описание, манипулирование
и отсечение базы данных происходит в мировых координатах. Сформированное
таким образом в базе данных «окно» преобразуется в нормализованные
координаты, а затем в координаты устройства. Размеры «окна» определяются в мировых
координатах. Размеры экранного окна задаются в нормализованных координатах,
чтобы обеспечить независимость от устройства. Оба преобразования из мировых
в нормализованные координаты и из нормализованных координат в координаты
устройства включают только простые перемещения и масштабирование1.
1 Предполагается, что преобразования перспективных проекций были выполнены перед
отсечением.
Пространство
пользователя
Окно
> (110,100)
(-30,-40)
Нормализованные
координаты
устройства __ -— -
Пространство
устройства
- ^Пг-_г-——__(°-8Д8)
(0.1.0.1)-
^
(1,1)
(0.5,0.5)
ТГ~1
'
у
Vs-
□
□
□
Окна
'просмотра^'
(0.0)
Рис. А-1 Преобразования в графическом конвейере.
Пример служит для иллюстрации различных систем координат и
преобразований.
Пример А-1 Преобразование координат
Отобразить квадрат с центром в начале координат, со стороной 36 единиц
в верхний левый квадрант устройства с разрешением 1024 х 1024.
Чтобы задать некоторое рабочее пространство вокруг квадрата,
определим окно со следующими левым, правым, верхним и нижним углами:
wleft = —20, wright = 20, wbottom = —20, wtop = 20. Это действительно
окно, а не изображение, которое определяет преобразование.
В нормализованных координатах верхний левый квадрант определяется
так: vie ft = 0, vright = 0,5, vbottom = 0,5, vtop = 1,0.
Преобразование из мировых координат в нормализованные требует
масштабирования оконных координат и затем приведения результата к первому
квадранту. Масштабные коэффициенты:
_1 1 _ J_
40'
xwacale =
wright — wleft
ywscale = ;
wtop — wbottom
Коэффициенты преобразования:
xwtran =
ywtran =
—wleft
20 - (-20) "
1
= 20 - (-20)
-(-20)
40'
wright - wleft 20 - (-20) ~ 2'
-wbottom _ -(-20) _ 1
wtop - wbottom ~ 20 - (-20) ~ 2'
Результирующее преобразование плоского окна в нормализованные
координаты:
xwscale О О
О ywscale О
xwtran ywtran l
[Г„] = [5»][Гг„] =
1/40
0
1/2
0 0
1/40 0
1/2 1
Преобразование из нормализованных координат в координаты устройства
вновь включает масштабирование и перенос. Когда координаты устройства
описаны в целых числах, требуется особое внимание при определении
масштабного и преобразующего множителей.
Хотя разрешение адресуемого в целых числах устройства составляет
xresolution х yresolution, адресуемый диапазон целых чисел расположен
между 0 и xresolution — 1 и между 0 и yresolution — 1, т. е. если
разрешающая способность равна 1024 х 1024, то адресуемый интервал по обеим осям
изменяется от 0 до 1023. Обозначив через xmaxdev и ymaxdev
максимальные числа соответственно по осям х и у, получим масштабный множитель и
величину переноса из нормализованных координат в координаты устройства:
xvscale — int{{vright — vleft)xmaxdev} = int{(0.5 — 0)(1023)} = 511,
yvscale = int{(vtop — vbottom)ymaxdev} = int{(l — 0.5)(1023)} = 511,
xvtran = int{(vleft)(xmaxdev + 1)} = mt{(0)(1024)} = 0,
yvtran = int{(vbottom)(ymaxdev + 1)} = rnt{(0.5)(1024)} = 512.
Результирующие преобразование нормализованных координат к
координатам устройства:
[Г.] = [S,][Tr,] =
xvscale 0 0
0 yvscale 0
xvtran yvtran 1
511 0 0
0 511 0
0 512 1
Использование этих результатов для координат углов квадрата с центром в
начале координат дает:
-18
18
18
-18
-18 1
-18 1
18 1
18 1
1/40 0 0
0 1/40 0
1/2 1/2 1
1/20 1/20 1
19/20 1/20 1
19/20 19/20 1
1/20 19/20 1
1/20 1/20 1
19/20 1/20 1
19/20 19/20 1
1/20 19/20 1
511 0 0
0 511 0
0 512 1
25.55 537.55 1
485.45 537.55 1
485.45 997.45 1
25.55 997.45 1
25 537
485 537
485 997
25 997
Целочисленная функция использована здесь для получения результирующих
целых адресуемых точек.
А-5 ПРОСТОЙ ГРАФИЧЕСКИЙ МЕТАФАЙЛ
К концепции хранения картинки в файле данных мы обращались при
обсуждении графических стандартов. Применимым для этого графическим стандартом
является Графический метафайл компьютера (CGM). Однако CGM более сложен
и детализован, чем это требуется для простых разработок и студенческих работ.
Простая альтернатива этому стандарту, называемая здесь стандартным
дисплейным файлом, дана в таблице А-11.
Первая строка стандартного дисплейного файла служит для идентификации.
Каждая последующая строка файла начинается с номера кода операции, за
которым следует информация, требуемая для данной операции. Все значения
координат определяются как числа с плавающей точкой в нормализованных
координатах, т.е. в интервалах 0 < а: < 1,0, 0 < з/ < 1,0. Все элементы данных разделены
запятыми.
Простой стандартный дисплейный файл для квадрата из примера А-1
имеет вид:
0, 0.05, 0.05
2, 0.95, 0.05
2, 0.95, 0.05
2, 0.05, 0.95
2, 0.05, 0.05
Такой формат настолько прост, что позволяет создавать картинку с помощью
текстового редактора. Обычно файл создается путем вызова графической
процедуры, образованной из обращений к командам установки либо отмены, например:
Set sdf on/off filename.
Программы вывода сохраненной в метафайле картинки на некоторое графическое
устройство достаточно элементарны. Такой формат допускает доступное
расширение за счет включения локальной функциональности.
Возможности нормализованных координат и графического метафайла
иллюстрирует рис. А-2. Изображения, включающие символы, были разработаны и
отлажены на устройстве с запоминающей трубкой. Результирующая картинка
заполнена в стандартном дисплейном файле, который был передан компьютером,
используемым как контроллер реального времени для обрабатывающего центра с
ЧПУ (рис. 1-1). Программа читает стандартный дисплейный файл и генерирует
код для драйвера обрабатывающего центра. Полученный результат показан на
рис. А-2.
А-6 ПРОСТЫЕ ФОРМАТЫ ГРАФИЧЕСКОГО ВВОДА
В некоторых системах графического программного обеспечения необходимы
стандарты форматов файла ввода. Для сложных или очень больших баз данных
требуются формализованные структуры данных и систем управления. Однако для
Подобная концепция используется более десятилетия в институте, где работают авторы.
Таблица А-1 Код стандартного дисплейного файла (.sdf)
■од
0
1
2
3
4
5
6
7
8
9
10
11
12
99
Операция
Абсолютное перемещение
Абсолютная точка
Абсолютное рисование
Относительное перемещение
Относительная точка
Относительное рисование
Текст
Установить цвет
Установить таблицу просмотра
Установить пиксел
Новый фрейм
Пауза
Установить разрешение
Печать сообщения
Параметры
х, У
х,У
х, У
Ах, Ау
Ах, Ду
Ах, Ду
Строка текста
красный, зеленый, синий
красные биты, зеленые биты, синие
х, у, красный, зеленый, синий
xresolution, yresolution
Строка сообщения
биты
х, у —числа с плавающей точкой в NDC, т.е. в диапазоне 0 < х,у < 1.0. Цвета
красный, зеленый, синий являются числами с плавающей точкой в диапазоне 0 <
красный, зеленый, синий < 1.0; при этом равенство нулю означает отсутствие
интенсивности, а равенство единице — полную интенсивность. Биты красного,
зеленого и синего цветов суть степени 2 (см. разд. 1-9, где обсуждаются соответствующие
таблицы).
относительно небольших баз данных вполне достаточны простейшие форматы,
основанные на файле с последовательным доступом. Приведем два таких
формата.
Первый формат файла ввода, называемый «стандартный графический
формат» (sgf) (табл. А.2), лучше всего подходит для простого рисования и для дву-
и трехмерного каркасного представления изображения. Второй, определяемый в
табл. А-3, называется «стандартный полигональный формат» и особенно полезен
для растровых дисплеев или для описания входной информации для
алгоритмов невидимых линий и невидимых поверхностей. Заметим, что когда формат
.spf используется для генерации каркасных изображений, каждая линия рису-
Рис. А-2 Гравюра, полученная из стандартного дисплейного файла.
Таблица А-2 Стандартный графический формат (.sgf)
Стандартный графический формат — это очень простой и
общеупотребительный формат для описания любых дву- или трехмерных данных, которые
могут быть представлены как список пар х, у или троек х, у, z. В файле
допускаются пустые строки. Общая форма:
строка описания строка описания
Xl, J/1 II, 2/1, 21
Х2, S/2 Х2, У2, Z2
Хп, Уп Хп j Уп, 2П
1е37, 1е37 1е37, 1е37, 1с37
Разделителем группы пар или троек является 1е37, 1е37 или 1е37, 1е37, 1е37 .
Последняя строка файла не должна быть разделителем.
Обычно этот формат интерпретируется следующим образом: графическое
устройство, начиная с первой точки группы, рисует все входящие в эту
группу точки и соединяющие линии, пока не встречает разделитель.
Значение разделителя сложилось исторически.
ется дважды. В обоих случаях такие атрибуты представления, как цвет линии
или многоугольника, коэффициент отражения многоугольника или тела и т.д.,
хранятся в отдельной группе файлов.
Оба формата заключают в себе уже готовый алгоритм рисования или
черчения.1 Рисование в соответствии с форматом .sgf:
В абсолютных координатах переместиться к первой точке и затем рисовать
каждую следующую точку, пока не будет обнаружен разделитель.
Повторять до конца файла.
Алгоритм рисования для .spf формата приводится как часть описания
многоугольника:
Переместиться в абсолютных координатах к точке, определенной первым
указателем.
Соединять точки, определенные каждым следующим указателем в списке.
Соединить точку, определенную последним указателем списка, с точкой,
определенной первым указателем, чтобы замкнуть многоугольник.
Вообще удобно иметь согласованное направление (по часовой стрелке или против)
для спецификации вершин многоугольника.
А-7 ПРОСТЫЕ АЛГОРИТМЫ СОЕДИНЕНИЯ
Оба формата (.sgf и .spf) определяют простой и ограниченный алгоритм
соединения или рисования. Практический интерес представляют два альтернативных, но
1 И стандартный графический формат (.sgf), и стандартный формат многоугольника (.spf)
более десятилетия используются в институте, где работают авторы.
Таблица А-3 Простой полигональный формат файла (.spf)
Прежде всего мы приведем общее описание формата, а затем подробный
пример. Файл естественным образом делится на две части. Первая часть
образует описание всех координатных векторов в изображении, вторая — описание
характеристик многоугольника. В файле допускаются пустые строки.
Построчное описание файла имеет следующую форму:
описательная (идентифицирующая) строка
число координатных векторов, многоугольников
список векторов х, у, z
список многоугольников
Каждая строка содержит два типа данных: число вершин многоугольника,
за которым следует список вершин в виде соответствующих номеров строк из
списка координатных векторов.
Характерный пример:
многоугольник с отверстием
14,2
4,4
4,26
20,26
28,18
28,4
21,4
21.8
10,8
10,4
10,12
10,20
17,20
21,16
21,12
9,1,2,3,4,5,6,7,8,9
5,10,11,12,13,14
Это простой многоугольник с отверстием.
Даны 14 координатных векторов или вершин многоугольника и 2
многоугольника.
Первый многоугольник содержит 9 вершин.
Второй многоугольник содержит 5 вершин.
Предполагается, что многоугольники замкнуты, т.е. первая точка не должна
быть переопределена в качестве последней точки списка, чтобы замкнуть
многоугольник.
отдельно описанных алгоритма рисования. Допустим, что база данных
трехмерных координатных векторов представлена в виде матрицы п х 4. Также определен
одномерный управляющий массив C(j), задающий алгоритм рисования
следующим образом:
Значение C(j) определяет номер строки в матрице координатных
векторов.
Знак C(j) используется для определения оператора рисования.
C{j) < 0 — перемещение в абсолютных координатах;
C(j) > 0 —рисование в абсолютных координатах.
Хотя такая схема достаточна, в некоторых отношениях она ограниченна. Более
гибкая и мощная схема использует двумерный управляющий массив C(i,j).
Алгоритм рисования определяется следующим образом:
значение C(i, 1) служит для определения строки в матрице координатных
векторов;
значение С(г,2) определяет оператор рисования (табл. А-1):
С (г, 2) = 0 — перемещение в абсолютных координатах;
С(г,2) = 1 —перемещение в относительных координатах;
С (г, 2) = 2 —рисование в абсолютных координатах;
С (г, 2) = 3 —рисование в относительных координатах;
С(г,2) = 4 —точка с абсолютными координатами;
С(г, 2) = 5 —точка с относительными координатами.
А-8 ПРОСТОЙ ГРАФИЧЕСКИЙ ПАКЕТ
В методике преподавания и изучения нового предмета, как правило, лучше
начинать с простых понятий и тем. Приведение здесь минимального множества
программ с использованием концепций, развивавшихся в этой книге и в работе
[А-8], преследует цели обучения. Графический пакет растрового дисплея (RDGP)
[А-14] представляет собой пример такого минимального множества графических
программ. Программы разработаны для четырех языков: ANSI Бейсик, Фортран
77, Си, Паскаль. Описание каждой программы дано для всех четырех языков,
сначала для ANSI Бейсика, потом для Фортрана 77, Си, Паскаля.
Спецификации каждой программы отделены горизонтальными линиями. Типы переменных
определены для каждого параметра каждой программы.
RDGP- ГРАФИЧЕСКИЙ ПАКЕТ РАСТРОВОГО ДИСПЛЕЯ1
Программы естественным образом распадаются на три группы: управления
состоянием дисплея, манипулирование пикселем и рисование линии. В таком
порядке они и обсуждаются.
1 Copyright © 1985 by David F. Rogers and Stephen D. Rogers. Пакет программ RDGP на TRUE
Бейсик, Фортран 77 и Си для IBM PC распространяется автором. За информацией обращаться
по адресу: Prof. D.F.Rogers, 817 Holly Dr. E., Rt. 10, Annapolis, MD 21401, USA.
имя:
назначение:
описание:
комментарии:
rdinit (Инициировать графический дисплей)
Инициализировать графический пакет растрового дисплея и
графическое устройство.
sub rdinit
subroutine rdinit
rdinit ()
procedure rdinit;
rdinit вызывается только один раз в начале программы.
имя: erase (Очистить экран)
назначение: Очистить графический экран указанным цветом.
описание: sub erase (г, g, b)
subroutine erase (г, g, b)
real r, g, b
erase (r, g, b)
double r, g, b;
procedure (r, g, b: real);
комментарии: г, g, b — красная, зеленая и синяя составляющие цвета. Их значения
задаются из интервала от 0 до 1. (г, g, b) = (0, 0, 0) —черный и (г, g,
b) = (l., 1., 1.)—белый.
имя: setrsl (Установить разрешение)
назначение: Установить псевдоразрешающую способность растрового дисплея.
описание: sub setrst (xres, yres)
subroutine, setrsl (xres, yres)
integer xres, yres
setrsl (xres, yres)
int xres, yres;
procedure setrsl (xres, yres: integer);
комментарии: xres — псевдоразрешающая способность растра по оси х или по
горизонтали. Она может изменяться от 1 до максимального значения
физической разрешающей способности растра по горизонтали.
yres — псевдоразрешающая способность растра по оси у или по
вертикали. Может изменяться от 1 до максимального значения
физической разрешающей способности растра по вертикали. Псевдорастр
располагается в центре физического пространства дисплея.
Пиксели имеют квадратную форму, насколько это позволяют ограничения
физического дисплея. Программа setrsl вызывается только один раз
в начале программы.
имя: setrgb (Установить rgb)
назначение: Установить текущий цвет для рисования.
описание: sub, setrgb (г, g, b)
subroutine setrgb (г, g, b)
real r, g, b
setrgb (r, g, b)
double r, g, b;
procedure setrgb (r, g, b: real);
комментарии: г, g, b — красная, зеленая и синяя составляюпще цвета. Их значения
задаются из интервала от 0 до 1. (г, g, b) = (0., 0., 0.). — черный и (г,
g, b) = (l., 1., 1.)—белый. Эта команда обычно используется, чтобы
установить цвет для команд рисования ma, pa, da, mr, pr, dr и text,
данных ниже. Заметим, однако, что вызов команд setpxl и setscn
может изменить цвет рисования.
имя: setlut (Установить таблицу просмотра)
назначение: Установить таблицу цветов просмотра,
описание: sub setlut (table, rbits, gbits, bbits)
subroutine setlut (table, rbits, gbits, bbits)
character table (*)
integer rbits, gbits, bbits
setlut (table, rbits, gbits, bbits)
rdString = lstring (255);
procedure setlut (table: rdString; rbits, gbits, bbitg: integer);
комментарии: Таблица — это строка, которая определяет специфику установленной
таблицы просмотра. Возможны следующие значения: по умолчанию
(таблица просмотра отсутствует), серый и цветной.
rbits, gbits и bbits —число бит, которые предполагается отвести под
красную, зеленую и синюю составляющие буфера кадра. Число
градаций каждого цвета 2Ьг'3. Каждый из параметров rbits, gbits, bbits
должен быть меньше или равен ширине таблицы цветов просмотра.
Их сумма должна быть меньше числа физических бит, отведенных
под буфер кадра. Общее число отображаемых в некоторый момент
времени цветов, равное 2^Tb't3+9btt'+bblta', выйдет за допустимую
палитру, значение которой равно 23*ш\ если w > n, где п — ширина
таблицы цветов просмотра. В случае использования таблицы серых
тонов просмотра значение градации серого цвета равно rbits.
Максимальное число градаций серого цвета —это w.
имя: setdm (Установить режим дисплея)
назначение: Управление режимом дисплея.
описание: sub setdm (str $)
subroutine setdm (str)
character str (*)
setdm (str)
char * str;
rdString — lstring (255);
procedure setdm (str: rdString);
комментарии: Предопределенными являются строки monitor (стандартное
алфавитно-цифровое устройство) и graphics (стандартное
графическое устройство).
имя: setpxl (Установить пиксел)
назначение: Установить единственный пиксел на линии развертки.
описание: sub setpxl (x, у, г, g, b)
subroutine setpxl (x, у, г, g, b)
integer x, у
real r, g, b
setpxl (x, у, г, g, b)
int x, y;
double r, g, b;
procedure setpxl (x, y: integer; r, g, b: real);
комментарии: Координаты х и у указывают левый нижний угол псевдопиксела,
который был определен программой setrsl. Пиксел покрывает
пространство правее и выше позиции, определенной х и у. г, g, b — красная,
зеленая и синяя составляющие цвета пиксела. Их значения задаются
из интервала от 0 до 1. (г, g, b) = (0., 0., 0.) —черный и (г, g, b) = (1.,
1., 1.) —белый.
имя: setscn (Установить линию развертки)
назначение: Установить группу пикселов на нинии сканирования.
описание: sub setscn (у, га, ga, ba, xstart, xstop)
subroutine setscn (у, га, ga, ba, xstart, xstop)
integer y, xstart, xstop
real ra (*), ga (*), ba (*)
setscn (у, га, ga, ba, xstart, xstop)
int y, xstart, xstop;
double ra Q, ga [], ba [];
rgScanline = array [0... x max] of real;
procedure setscn (y: integer; ra, ga, ba: rdScanline; xstart, xstop: integer);
комментарии: у — устанавливаемая псевдолиния развертки, xstart — начальная
позиция пикселов, xstop — позиция последнего пиксела, га, ga, ba —
массивы, содержащие красную, зеленую и синюю составляющие цветов
пикселов. Значения элементов га, ga, ba задаются из интервала от 0
до 1, где (0., 0., 0.)—черный и (1., 1., 1.)—белый. Первый элемент
каждого массива используется для цвета пиксела,
соответствующего xstart. Следующие пиксели линии развертки используют значения
следующих элементов массивов.
имя: getpxl (Задать пиксел)
назначение: Дать характеристики единственного пиксела линии развертки.
описание: sub getpxl (x, у, г, g, b)
subroutine getpxl (x, у, г, g, b)
integer x, у
real r, g, b
getpxl (x, у, г, g, b)
int x, y;
double *r, *g, *b;
procedure getpxl (x, g: integer; var r, g, b: real);
комментарии: Координаты х и у указывают левый нижний угол псевдопиксела,
который был определен программой setrsl. Пиксел покрывает
пространство правее и выше позиции, определенной х и у. г, g, b (для Си —
указатели на них) — красная, зеленая и синяя составляющие цвета
пиксела. Их значения находятся в интервале от 0 до 1. (г, g, b) = (0.,
0., 0.) —черный и (г, g, b) = (l., 1., 1.) —белый.
имя: getscn (Дать линию развертки)
назначение: Дать характеристики группы пикселов линии развертки.
описание: sub getscn (у, га, ga, ba, xstart, xstop)
subroutine getscn (у, га, ga, ba, xstart, xstop)
integer y, xstart, xstop
real га (*), ga (*), ba (*)
getscn (у, га, ga, ba, xstart, xstop)
int y, xstart, xstop;
double га [], ga [], ba Q;
rdScanline = array [0...x max] of real;
procedure getscn (y: integer; var га, ga, ba: rdScanline; xstart, xstop:
integer);
комментарии: у — псевдолиния развертки, . информацию о которой требуется
прочитать.
xstart — начальная позиция группы пикселов.
xstop — позиция последнего пиксела.
га, ga, ba —массивы, которые получают значения красного, зеленого
и синего компонентов цвета пикселов, о которых читается
информация. Их значения находятся в интервале от 0 до 1. (га, ga, ba) = (0., 0.,
0.) —черный и (1., 1., 1.) —белый. Первый элемент каждого массива
используется для цвета пиксела, соответствующего xstart.
Следующие элементы массива для следующих пикселов линии равертки.
имя: text (Текст)
назначение: Отобразить текст,
описание: sub text (str $)
subroutine text (str)
character str (*)
text (str)
char *str;
rdString = lstring (255);
procedure txt (str: rdString)
комментарии: Текст отображается, начиная с последней позиции курсора с
использованием предопределенного размера символов. Позиция
курсора указывает на левый нижний угол ячейки первого символа. Курсор
остается в нижнем правом углу ячейки последнего символа строки.
Замечание. В Фортране 77 текстовая/символьная строка должна
заканчиваться символом $, т.е. HELLOS служит для отображения на
экране HELLO.
Замечание. Так как text — это зарезервированное в Паскале слово,
используется аббревиатура txt.
имя: ma (Абсолютное перемещение)
назначение: Переместить курсор в позицию с абсолютным значением х и у.
описание: sub ma (x, у)
subroutine ma (x, у)
real х, у
та (х, у)
double х, у;
procedure та (х, у: real);
комментарии: х и у — действительные числа, х и у —абсолютные координаты для
псевдорастра, установленного программой setrsl. 0,0 — это левый
нижний угол псевдорастра.
имя:
назначение:
описание:
комментарии:
тг (Относительное перемещение)
Переместить курсор на dx, dy.
sub mr (dx, dy)
subroutine mr (dx, dy)
real dx, dy
mr (dx, dy)
double dx, dy;
procedure mr (dx, dy: real);
dx и dy — действительные числа. Перемещение происходит
относительно последней позиции курсора в размерах псевдорастра,
установленного программой setrsl.
имя: da (Абсолютное рисование)
назначение: Нарисовать тонкую линию в абсолютных координатах.
описание: sub da (x, у)
subroutine da (x, у)
real х, у
da (x, у)
double х, у;
procedure da (x, у: real);
комментарии: х и у — действительные числа, заданные в размерах псевдорастра,
установленного программой setrsl. Тонкая (шириной в один
физический пиксел) линия рисуется от текущей позиции курсора до
позиции х, у. Значения х, у — это абсолютные координаты, причем
начальная пара 0, 0 соответствует левому нижнему углу псевдорастра,
заданного программой setrsl. Для рисования линии
используется текущий цвет, который устанавливается с помощью программы
setrgb.
имя:
назначение:
описание:
dr (Относительное рисование)
Нарисовать тонкую линию, используя относительные координаты.
sub dr (dx, dy)
subroutine dr (dx, dy)
real dx, dy
dr (dx, dy)
double dx, dy;
procedure dr (dx, dy: real);
комментарии: dx и dy — действительные числа, заданные в размерах псевдорастра,
установленного программой setrsl. Тонкая (шириной в один
физический пиксел) линия рисуется от последней позиции курсора хО, уО
до позиции xO+dx, yO+dy. Значения dx и dy — это относительные
координаты, где хО, уО — последняя позиция курсора. Для рисования
"иннн используется текущий цвет. Текущий цвет устанавливается с
помощью программы setrgb.
имя: ра (Абсолютная точка)
назначение: Отобразить точку в абсолютных координатах.
описание: sub pa (x, у)
subroutine pa (x, у)
real х, у
ра (х, у)
double х, у;
procedure pa (х, у: real);
комментарии Значения х и у — действительные числа, заданные в размерах
псевдорастра, который установлен программой setrsl. Маленькая точка
(размером в один физический пиксел) отображается в позиции х,
у. Значения х, у представляют собой абсолютные координаты,
причем пара 0, 0 соответствует левому нижнему углу псевдорастра,
заданного программой setrsl. Для отображения точки
используется текущий цвет. Текущий цвет устанавливается с помощью
программы setrgb.
имя: рг (Относительная точка)
назначение: Отобразить точку, используя относительные координаты.
Описание: sub рг (dx, dy)
subroutine рг (dx, dy)
real dx, dy
pr (dx, dy)
double dx, dy;
procedure pr (dx, dy: real);
комментарии: Значения dx и dy —это действительные числа, заданные в
размерах псевдорастра, установленного программой setrsl. Маленькая
точка (размером в один физический пиксел) отображается в позиции
хО + dx, уО -I- dy. dx, dy — относительные координаты, а хО, уО —
последняя позиция курсора. Для отображения точки используется
текущий цвет. Текущий цвет устанавливается с помощью программы
setrgb.
А-9 ЛИТЕРАТУРА1
A-l «Graphical Kernel System (GKS)», ISO 7942, 15 August 1985; also, ANSI X3.124-1985,
24 June 1985.
A-2 Bono, P., and Herman, I. (eds.), GKS Theory and Practice, Springer-Verlag, Heidelberg,
1987.
A-3 Enderle, G., Kansy, K., and Pfaff, G., Computer Graphics Programming, GKS— The
Graphics Standard, Springer/Verlag, Heidelberg, 2nd ed., 1987.
A-4 «Graphical Kernel System for Three Dimensions (GKS-3D)», ISO DIS 8805, July 1987.
A-5 «Programmer's Hierarchical Interactive Graphics System (PHIGS)», ISO DIS 9592,
December 1987; also, dpANS X3.144.
A-6 Brown, M., and Heck, M., Understanding PHIGS, Megatek Corp., San Diego, 1985.
A-7 Van Dam, A., «PHIGS+, Functional Description Revision 3.0», Сотр. Graph., Vol. 22,
pp. 125-218, 1988.
A-8 Rogers, D.F., Procedural Elements for Computer Graphics, McGraw-Hill, New York,
1985. (Cm. [1-1] на с. 74.)
A-9 «Computer Graphics Metafile for the Storage and Transfer of Picture Description
Information (CGM)», ISO 8632-Parts 1 through 4: 1987; also, ANSI/X3.122-1986.
A-10 Arnold, D.B., and Bono, P.R., CGM and CGI, Springer-Verlag, Heidelberg, 1988.
A-ll McKay, L., CGI/CGM PRIMER, Nova Graphics International, Austin, TX 1987.
A-12 «Computer Graphics Interfacing Techniques for Dialogues with Graphical Devices
(CGI)», ISO DP 9636, 6 December 1986; also, dpANS X3.161.
A-13 International Organization for Standardization: Information Processing Systems —
Computer Graphics — Interface Techniques for Dialogues with Graphical Devices.
Baseline Document. ISO/TC97 N1511 (1985).
A-14 Rogers,'D.F., and Rogers, S.D., «A Raster Display Graphics Package for Education»,
IEEE Сотр. Graph. & Appl., Vol. 6, pp. 51-58, April 1986.
1 Эти документы имеются в различных источниках:
Опубликованные ANSI-стандарты (а именно GKS и CGM) и ISO-документы (CGI, CGM,
GKS, GKS-3D, PHIGS) можно получить в ANSI (1430 Broadway, New York, NY 10018).
Помимо США ISO-документы можно получить из национальных организаций по стандартам
(например, BSI в Великобритании, AFNOR во Франции, DIN в ФРГ и JIS в Японии).
Проекты ANSI-стандартов (CGI, GKS-3D и PHIGS) можно получить в секретариате ХЗ
фирмы СВБМА (311 First Street, Suite 500, Washington, DC 20001).
Документы IGES и PDES можно получить в фирме IGES (IGES Committee Chairman, Mr.
Bradford Smith, National Bureau of Standards, Gaithersburg, ND 20760).
Приложение В
Матричные операции
Это приложение содержит некоторые несложные правила из матричной алгебры.
Матрица — это прямоугольный массив чисел, операции над которыми подчинены
приведенным правилам.
В-1 ТЕРМИНОЛОГИЯ
Числа, которые составляют матрицу, называются ее элементами. Эти элементы
образуют строки и столбцы внутри матрицы. Если число строк равно числу
столбцов, матрица называется квадратной. Рассмотрим квадратную матрицу 4x4:
an ai2 ai3 an
a2l C22 023 ^24
^31 032 ОЗЗ 034
ац U42 0.43 0,44
Обозначим элементы матрицы через а^. Первый индекс — номер строки, второй —
номер столбца. Таким образом, а34 — элемент из третьей строки, четвертого
столбца. Матрица, состоящая из т строк и п столбцов, имеет размерность тхп. Для
квадратной матрицы выполняется равенство та— п. Элементы ац, агг, азз и а44
при i = j называются диагональными элементами. Сумма диагональных
элементов квадратной матрицы называется ее следом.
Диагональной матрицей называют матрицу, в которой отличны от нуля только
диагональные элементы, т.е. ац = 0, если i ф j. Единичной матрицей называют
матрицу, у которой а^ = 0 для г ф j и а^ = 1 для г = j. Пример единичной
3x3 матрицы:
"10 0"
0 10.
0 0 1
Каждый элемент нулевой матрицы равен 0, т. е. ay = 0. Две матрицы равны,
только когда каждый элемент первой матрицы равен соответствующему элементу
второй матрицы, т.е. а^ = Ьц.
Симметричной называется квадратная матрица, у которой ау = a^j.
Например,
"236
3 17 5
6 5 12
Строка матрицы является 1 х n-матрицей. Строки матрицы иногда называют
векторами строк или просто векторами. Столбец матрицы является п х 1-матрицей.
Столбцы матрицы иногда называют векторами столбцов или просто векторами.
Скаляр —это 1 х 1-матрица.
В-2 СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Если две матрицы имеют одинаковую размерность, то для них определены
операции сложения и вычитания. Чтобы сложить или вычесть две матрицы, надо
сложить или вычесть соответствующие элементы, т. е. су = ay + 6у или су = оу — 6у
соответственно. Например:
12 3
4 5 6
7 8 9
12 3'
4 5 6
7 8 9
+
—
1 4 7
2 5 8
3 6 9
"14 7'
2 5 8
3 6 9
=
=
2 6 10
6 10 14
10 14 18
" 0 -2 -4
2 0-2
4 2 0
Матрица [В] называется отрицанием матрицы А, если 6у = —ay.
В-3 УМНОЖЕНИЕ
Умножение матриц — это очень полезная операция для машинной графики.
Рассмотрим матрицу размера п х т и вторую матрицу размера г х s. Для умножения
этих матриц необходимо, чтобы т было равно г. Это значит, что число
столбцов первой матрицы должно быть равно числу строк второй матрицы. Правила
умножения матриц лучше всего описывает следующий пример. Если матрица [А]
имеет размерность 4 х 3, а [В] — квадратная 3 х 3-матрица, то произведение этих
матриц определяется следующим образом:
an
С21
С41
ai2
a22
аз2
a42
ai3
U23
азз
fl43
6ц
&21
631
&12
&22
&32
6l3
&23
633
"43 J "
Оцбц + 012&21 + a13&31 011612+012622+013632 011613 + 012623+013633
O21611 + 022621 + 023631 02l6l2 + 022622 + О23632 О21613 + 022623 + 023&33
0316ц + 032621 + 033631 О31&12 + 032622 + 033632 О31613 + 032623 + О33633
041611+042621+043631 041612+042622 + 043632 041613+042623 + 043633
Иначе говоря, каждая строка в матрице [А] поэлементно умножается на
соответствующий столбец матрицы [В], результаты складываются и записываются в
качестве элемента результирующей матрицы [С]. Заметим, что умножение 4x3-
матрицы на 3 х 3-матрицу, дает матрицу размерности 4x3. Вообще говоря, в
результате умножения п х m-матрицы на г х s-матрицу при т — г мы получим
п х s-матрицу. Рассмотрим численный пример:
1 3 -
4 2
1 1
6 4
3 2 .
Г 1 о 1
[alj =
■ 1 + 9
4 + 6
1 + 3
6 + 12
. 3 + 6
2 + 12 "
8 + 8
2 + 4
12+16
6 + 8 .
=
" 10 14
10 16
4 6
18 28
. 9 14
Операция умножения матриц не является коммутативной, т. е. в общем случае
произведение [А][В] не равно [В][.А]. Таким образом, важен порядок
(последовательность) умножения. Для операции умножения матриц верны первый и второй
дистрибутивные законы, т.е. А(В + С) = АВ + АС и (А + В)С — АС Л-ВС. Также
выполняется ассоциативный закон А(ВС) = {АВ)С.
В-4 ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
Определитель квадратной матрицы [А] обозначается |А|. В теории матриц
определитель имеет много полезных свойств. Для наших целей достаточно
проиллюстрировать метод вычисления определителя на примере квадратной 3x3-
матрицы. Для матриц
М =
определитель равен
ац ai2 щз
U2i a22 агз
аз1 ^32 а3з
■ ац
^22 агз
Озг азз
ац ai2 ai3
a2i C22 а2з
аз1 а32 азз
-0-12
U21
аз1
агз
азз
+ Ol3
121 а22
Й31 а32
= ац(а22азз - агзазг) - 012(021033 - 023031) + 013(021032 - 022031),
т.е. определитель имеет единственное численное значение. В качестве примера
подсчитаем определитель
9 4
1 8
5 3
В результате получим
3(3 - 40) - 9(18 - 16) + 4(30 - 2) = 3(-37) - 9(2) + 4(28) = -17.
В-5 ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
Транспонированная матрица — это исходная матрица, в которой строки заменены
на столбцы, т.е. b{j = а^. Например,
16 3 7
2 8 11 4
6 3 2 1
1 2 6
6 8 3
3 11 2
7 4 1
где специальный символ Т определяет операцию транспонирования. Заметим, что
если исходная матрица имела размерность m х п, то размерность
транспонированной матрицы будет п х т.
В-6 ОБРАЩЕНИЕ КВАДРАТНОЙ МАТРИЦЫ
В алгебре скаляров справедливо следующее утверждение, если ах = у, то х =
а~1у, где а-1 это просто обратная величина к а, т.е. а"1 = 1/а. В матричной
алгебре операция деления не определена и обратной матрицы в смысле скалярной
алгебры не существует, однако если [А][X] = [У], то [X] = [А]-1 [У], где [А]-1 —
матрица, обратная к квадратной матрице [А].
Обратная матрица существует для квадратной и неединичной матрицы.
Однако не каждая квадратная матрица имеет обратную. Но если определитель
квадратной матрицы не равен нулю, то обратная матрица существует и единственна.
Если обратная матрица существует, то [А][А]~г = [I], где [I] — единичная
матрица.
Рассмотрим произведение двух квадратных матриц, размерностью 3x3.
1 О О
О 1 О
О 0 1
Если произведение двух матриц [А][В] = [Г\, то [J5] = [А]-1, т. е. [В] — это матрица,
обратная к [А].
Существует много способов вычисления обратной матрицы. В большинстве
языков программирования есть функции или подпрограммы, позволяющие
вычислять значения элементов матрицы, обратной к данной. Описание таких
алгоритмов выходит за рамки нашего краткого изложения.
12 3
13 3
12 4
6
-1
-1
-2
1
0
-3
0
1
Приложение С
Псевдокод
Приведенный псевдокод призван помочь в понимании и реализации
представленных в тексте алгоритмов. Он не задумывался как точный, синтаксически
корректный и полный язык. Элементы псевдокода заимствованы из нескольких
общеизвестных языков программирования: Бейсика, Фортрана, Паскаля, Си и т. д.
Псевдокод содержит структурные конструкции, например if-then-else и while.
Для удобства включен оператор безусловного перехода go to. Оператор цикла
for-next взят из Бейсика. Псевдокод включает также подпрограммные модули и
матричные функции. Специальные функции и программы, такие, как Min, Max,
Push, Pop, определены в алгоритмах в индивидуальном порядке.
Кратко охарактеризуем общие соглашения, используемые при описании
алгоритмов. Все ключевые слова набираются жирным шрифтом строчными
буквами. Все операторы внутри тела оператора if-then-else или цикла for-next
выделяются отступом. Комментарии набираются курсивом и печатаются с таким
же отступом, как и операторы, к которым они относятся. Многолитерные имена
переменных, как правило, набираются строчными буквами. Однолитерные
переменные могут представляться как прописной, так и строчной буквами. Функции
выделяются жирным шрифтом и начинаются с прописной буквы. Далее следует
детальное описание этих соглашений.
С-1 КОММЕНТАРИИ
Комментарии набираются курсивом. Они располагаются с тем же отступом, что
и операторы, к которым они относятся. В начале алгоритма помещаются
комментарии, кратко описывающие назначение этого алгоритма и определяющие
используемые переменные.
С-2 КОНСТАНТЫ
Все константы являются десятичными числами, если в комментариях не
оговорено иное. Например: 9, -3, 6.732, 1 х Ю-9, 3.
С-3 ПЕРЕМЕННЫЕ
Переменная — это имя, используемое для хранения значения. Это значение может
изменяться. В длинных именах переменных используются, в основном, строчные
буквы; прописные используются в тексте книги лишь в тех случаях, когда это
способствует лучшему пониманию программы. Однолитерные переменные могут
набираться как строчной, так и прописной буквой. Для большей наглядности
можно употреблять литеры с индексами. Примеры переменных: flag, Pj, x, у.
С-4 МАССИВЫ
Массив —имя для индексированной совокупности значений. Для имен массивов
действуют те же соглашения, что и для переменных. Обращение ко всему массиву
осуществляется по его имени, а к отдельным элементам —по имени массива, за
которым в скобках следует список индексов. Примеры массивов: window, window
(1, 3).
С-5 ОПЕРАТОР ПРИСВАИВАНИЯ
Знак «равно» используется для присвоения переменной, расположенной в левой
части оператора, значения выражения из правой части этого оператора.
С-6 АРИФМЕТИЧЕСКИЕ ВЫРАЖЕНИЯ
Обычные арифметические операции умножения, деления, сложения, вычитания
и возведения в степень обозначаются знаками *, /, +, —,".
С-7 ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ОПЕРАЦИИ ОТНОШЕНИЯ
Логические операции and и ог выделяются жирным шрифтом, как это здесь
показано. Операции отношения «равно», «не равно», «меньше», «больше», «меньше
или равно», «больше или равно» обозначаются =, ф, <, >, <, > соответственно.
Эти операции используются для проверки условий. Результатом проверки
являются логические значения «истина» или «ложь».
С-8 ОПЕРАТОР finish
Оператор finish используется для обозначения конца работы алгоритма.
С-9 ОПЕРАТОРЫ while И end while
Операторы, расположенные внутри блока while-end while, выполняются
циклически, до тех пор, пока истинно некоторое условие. Условие проверяется в начале
блока. Когда условие перестает быть истинным, выполнение программы
продолжается с оператора, следующего за end while. Оператор end while используется
для обозначения конца блока. Все операторы внутри блока while-end while
располагаются с отступом. Общая форма оператора
while (условие)
[операторы, которые необходимо выполнить]
end while
Пример
i = 0
while (i < 5)
x = x + 5
i = i + l
end while
finish
C-10 ОПЕРАТОР if-then
Оператор if-then используется для выбора альтернативы пути выполнения
программы либо для присвоения переменной альтернативного значения в
зависимости от истинности некоторого условия.
Если аргументом then служит номер оператора и условие истинно, то
управление передается на оператор с этим номером. В противном случае вьшолняется
следующий по порядку оператор. Номера операторов являются их метками.
Если аргументом then служит оператор присваивания и условие истинно, то
присваивание вьшолняется. В противном случае присваивание не вьшолняется и
управление передается сразу на следующий оператор. Общая форма оператора:
if (условие) then (номер оператора)
if (условие) then (оператор присваивания)
Примеры
if (г < 10) then 3
if (г < 10) then x = х + 1
С-11 ОПЕРАТОРЫ if-then-else И end if
Оператор if-then-else используется для выбора одного из двух альтернативных
блоков операторов в зависимости от истинности некоторого условия. Для
обозначения конца блока оператора if-then-else используется оператор end if. Оператор
не подразумевает повторения. Вьшолняется только один из альтернативных
блоков. После этого выполнение программы продолжается с оператора, следующего
за end if. Все операторы внутри блока if-then-else располагаются с отступом.
Общая форма оператора
if (условие) then
[операторы, выполняемые, если условие истинно]
else
[операторы, выполняемые, если условие ложно]
end if
Пример
if (i > 0) then
x = x+ 1
else
x = x — 1
end if
Если оператор if-then-else записывается в одной строке, то оператор end if
опускается. Заметим, что если опускается else и вторая группа операторов, то в
результате получается блок оператора if-then.
С-12 ОПЕРАТОР for-next
Управление циклом можно организовать с помощью оператора for-next, как и с
помощью оператора while. Циклическое вьшолнение операторов, расположенных
внутри тела цикла for-next, происходит до тех пор, пока значение переменной
цикла находится в заданных пределах. Все операторы внутри блока for-next
располагаются с отступом. Общая форма оператора:
for (пер-цикла) = (нач_знач) to (кон_знач) step (шаг .цикла)
[операторы, которые надо выполнить]
next (пер-цикла)
Если шаг цикла отсутствует, то он полагается равным единице. Шаг цикла может
быть отрицательным. Начальное, конечное значение переменной цикла и шаг
цикла могут быть переменными.
Пример
for х = 1 to n step a
У = У + х
next х
С-13 ОПЕРАТОР go to
Оператор go to вызывает безусловный переход на оператор, определяемый
аргументом. Общая форма оператора:
go to (номер оператора)
Номера операторов являются метками. Они располагаются в крайней левой
позиции строки оператора.
С-14 ПОДПРОГРАММНЫЕ МОДУЛИ
Подпрограмма —отдельный программный модуль, который вызывается с
помощью оператора call. Начало подпрограммы определяет оператор subroutine.
Выход из подпрограммы определяется оператором return. После выхода из
подпрограммы управление возвращается оператору, следующему за оператором call
в вызывающей программе. Оператор subroutine содержит список входных и
список выходных переменных. Связь между вызывающей программой и подпро-
граммным модулем осуществляется только через эти переменные. Все остальные
переменные подпрограммного модуля локализованы в этом модуле. Общая
форма операторов call, subroutine и return:
call имя (входные переменные; выходные переменные)
subroutine имя (входные переменные; выходные переменные)
return
Списки входных и выходных переменных операторов call и subroutine
разделяются точкой с запятой и должны соответствовать друг другу. Имена подпрограмм
состоят из строчных букв, набранных жирным шрифтом. Пример подпрограмм-
ного модуля:
subroutine check (x, у; flag)
if х < у then
flag = О
else
flag=l
end if
return
C-15 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Тригонометрические функции, такие, как Sin (0), Cos (9), Tan (9) и обратные
к ним Arcsin (x), Arccos (s), Arctan (х) принимают и возвращают значения в
градусах, если установлен переключатель option angle degrees. Общепринятые
гиперболические функции и их обратные функции Sinh (9), Cosh (9), tanh (9),
Arcsinh (i), Arccosh (x), Arctanh (i) также принимают и возвращают
значения в градусах, если установлен этот переключатель. В противном случае они
принимают и возвращают значения в радианах. Имена этих функций начинаются
с прописной буквы и выделяются жирным шрифтом.
С-16 МАТРИЧНЫЕ ФУНКЦИИ
Матричные функции служат для выполнения типичных операций матричной
алгебры, например сложения, вычитания, умножения, обращения и
транспонирования матриц. Матричные функции манипулируют целыми массивами.
Размерность каждого массива, используемого в качестве аргумента матричной функции,
должна соответствовать выполняемой операции. Размерность результирующей
матрицы также соответствует выполненной операции. Например, в результате
умножения 3 х 2-матрицы на 2 х 3-матрицу получается 3 х 3-матрица. Массив
матрицы читается и записывается по строкам. Размерность матрицы может быть
изменена во время выполнения операций. Массив матрицы может быть
использован в обеих частях оператора присваивания. Имена матричных функций
начинаются с прописной буквы и выделяются жирным шрифтом. Матричные функции:
сложение
вычитание
умножение
обращение
транспонирование
вычисление определителя
единичная матрица
нулевая матрица
постоянная матрица
скалярное произведение
Mat
Mat
Mat
Mat
Mat
Значение
Mat
Mat
Mat
Значение
A
A
A
A
A
A
A
A
= B + C
= B-C
= B*C
= Inv(B)
= Trn(B)
= Det(B)
= Idn
= Zer(nl,n2)
= Con(nl)
= Dot(A,B)
Функция Zet формирует массив матрицы размерностью [nl х п2] и
заполняет его нулями. Функция Con заполняет массив заранее заданной размерности
константы nl.
С-17 СПЕЦИАЛЬНЫЕ ФУНКЦИИ
В алгоритмах, представленных в данной книге, определены разнообразные
специальные функции. Имена этих функций выделяются жирным шрифтом и
начинаются с прописной буквы. В качестве примера приведем функцию
Max(xi, х2),
результатом которой является большее из значений xi и хг-
Приложение D
Формат файла
в-сплайн поверхности
В связи с возникшим значительным интересом к В-сплайн поверхностям,
разработан ряд значительных форматов файлов для обмена их описания. Еще один
формат предложен в табл. D-1. Четырехмерные однородные координаты
используются для обозначения определяемых точек прямоугольной сетки. Это позволяет
объединить трехмерные физические позиции точек прямоугольной сетки и
однородный координатный (весовой) коэффициент в общем описании. Предлагаемый
формат, вообще говоря, достаточен для управления рациональными
однородными и неоднородными, периодическими и открытыми В-сплайн поверхностями.
Нерациональные сплайны поверхностей определяются установкой всех
однородных координатных коэффициентов (весов) равными единице. Рациональные
поверхности Безье определяются посредством однородных открытых связующих
векторов в виде [к нулей, к единиц] с подходящими однородными координатными
коэффициентами. Нерациональные поверхности Безье определяются с помощью
соответствующих связующих векторов и установкой всех однородных
координатных коэффициентов (весов) равными единице. Составные поверхности
определяются простым повторением полного описания для каждой поверхности. Заметим,
что такой подход позволяет описывать различные типы В-сплайнов и
поверхностей Безье в одном файле. Запятые должны быть проставлены, как показано в
таблице. В файле допустимы пробелы и пустые строки.
Таблица D-1 Формальное описание формата файла В-сплайн поверхности
Строка идентификации поверхности например, номер корпуса (рис. 6-50)
нерациональная рациональная рациональная, нерациональная в и, w
соответственно
открытая, периодическая открытая, периодическая, неоднородная в и, w
соответственно
порядок базиса, порядок базиса порядок в и, порядок в w
кол-во узлов сетки кол-во узлов сетки в направлении и
кол-во узлов сетки кол-во узлов сетки в направлении w
вектор связи в и последовательность чисел 1, 2, 3,...
вектор связи в w последовательность чисел 1, 2, 3,...
список 42?-точек сетки массив B(i,j) размерностью ((кол-во узлов сетки
в направлении и) х (кол-во. узлов сетки в
направлении w), 4). Элементы массива B{i,j)
располагаются с опережающим изменением индекса
j, т.е. по строкам. Каждая строка содержит
компоненты х, у, z, h, где h — однородный (весовой)
коэффициент для каждой точки сетки.
Замечание. Для нерациональных В-сплайнов все
Пример файла
Пример поверхности (см. рис. 6-50)
нерац., нерац.
открыта, открыта
4,4
8 8
0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5
О, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5
Поверхность, нерациональная в обоих
направлениях.
В обоих направлениях используются функции
открытого базиса.
Четвертого порядка в обоих направлениях.
Используется прямоугольная сетка 8x8.
Открытый однородный связующий вектор для
направления и.
Открытый однородный связующий вектор для
направления ш.
Точки сетки B(i,j), расположенные по строкам.
0
0
0
0
0
0
0
0
13.2994
8.6079
7.2922
-0.6518
1.5411
3.7183
7.87419
0.9025
17.0482
14.0925
11.067
3.0433
0.2289
3.5539
3.0443
-0.2092
29.2903
30.7639
21.1234
12.0645
9.0546
8.6407
5.1127
0.1572
62.7896
58.3546
50.7321
37.2752
24.6114
12.2841
0.9638
-0.02351
57.2518
50.7918
52.4931
33.3121
14.3331
13.4063
1.8224
-0.4589
57.6166
55.5365
48.282
40.1302
21.5281
7.0775
0.7293
0.08977
53.3467
54.1187
48.1403
35.461
17.3787
6.64932
-0.7182
-0.03143
-14.2345
-11.7746
-7.7246
-0.7445
0.2266
-.7321
-4.2096
-0.06207
0
0
0
0
0
0
0
0
13.5
13.5
13.5
13.5
13.5
13.5
13.5
13.5
54
54
54
54
54
54
54
54
37.8884
33.861
27.1525
23.2976
19.832
12.7107
5.5457
-0.01007
41.0213
39.6319
38.6344
33.8422
28.2826
18.2607
4.4469
0.1344
40.4748
41.1403
40.9666
41.4111
34.093
16.9322
5.55319
0.06208
40.536
40.8065
39.8169
41.8009
37.0837
13.1546
7.0730
0.07475
50.5464
47.4467
36.9685
19.6017
11.186
2.5924
-0.4150
-0.04313
48.1632
39.2661
30.4192
16.8768
6.96425
-1.0973
0.2564
0.01421
47.8315
43.5986
30.6183
14.9213
0.2635
0.9311
0.167384
-0.07885
47.9986
41.4721
33.6058
13.1977
0.3062
1.2999
-0.2726
-0.04795
108
108
108
108
108
108
108
108
162
162
162
162
162
162
162
162
216
216
216
216
216
216
216
216
270
270
270
270
270
270
270
270
Приложение Е
Задачи
Изучение компьютерной графики невозможно без ее практического
использования, поэтому здесь приводится ряд задач и спецификаций программ. Задачи в
основном направлены на то, чтобы подтвердить или развить концепции,
представленные в тексте, или на то, чтобы накопить определенный опыт работы в
соответствии с предлагаемой технологией. Как правило, задачи акцентируют
внимание на каких-то отдельных конкретных аспектах материала. Задачи могут
требовать, а могут и не требовать программирования.
Спецификации программ разработаны не только для иллюстрации концепций
и технологий, представленных в книге, но также чтобы передать некоторый опыт
создания достаточно сложных программ машинной графики. Хорошо
реализованные, они могут составить инструментарий полезных графических программ.
Результатом законченных программных проектов являются полезные
программы общего назначения.
Это приложение содержит задачи. Спецификации программ приводятся в
приложении F. Задачи и спецификации объединены в соответствии с главами
книги.
ГЛАВА 2
2-1. Показать, что зеркальное отражение в плоскости относительно оси х,
следующее за зеркальным отражением относительно прямой у = —х, эквивалентно
полному повороту вокруг точки начала координат.
2-2. Для плоского прямоугольника, заданного координатными векторами
своих вершин Pi [1 1], Р2 [3 1], Рз [4 2], Pi [2 3], определить единственную
матрицу преобразования, которая
1) зеркально отражает его относительно прямой х = 0;
2) осуществляет параллельный перенос на —1 в направлениях х и у;
3) осуществляет поворот на 180° относительно точки начала координат.
Используя эти преобразования, определить новые координатные векторы
вершин прямоугольника. Построить исходный и преобразованный прямоугольники
на каком-либо графическом устройстве.
2-3. Показать, что 2 х 2-матрица
1-i2
[Т} =
2t
1 + t2
-It
1+t2
1 + t2
1 + t2
осуществляет полный поворот.
2-4. Единичный квадрат преобразуется 2 х 2-матрицей. Результирующие
координатные векторы:
' 0
2
8
6
0 '
3
4
1
Найти матрицу преобразования.
2-5. Показать, что для х = t2, у = t результатом преобразования
[* У 1]
0-2 2
-2 2 -2
1 0 1
является множество точек, образующих единичную окружность.
ГЛАВА 3
3-1. Показать, что для достижения некоторого эффекта преобразования
объекта путем конкатенации некоторых матриц слева требуется, чтобы они были
применимы в обратном порядке, когда используется конкатенация справа, т. е.
[Tr][Rx][Ry][Data] = [Data][Ry][Rx][Tr],
где [Data] — матрица данных для объекта.
3-2. Вывести результирующую матрицу преобразования для перевода тп, п,
I в х, у, z соответственно; поворота вокруг оси у на угол ip; поворота вокруг
оси х на угол в, следующих за преобразованием центрального перспективного
проецирования на плоскость z = 0, с центром проекции на оси z в точке z = к.
Сравнить результат с (3-63).
3-3. Изменить порядок выполнения поворотов в задаче 3-2. Сравнить
результаты.
3-4. Для куба из примера 3-23 определить координатные векторы после
преобразования, использующего конкатенацию матриц из задачи 3-2 при тп = I = п =
0, (р = 60°, в = 30° и к = 2.5. Сравнить полученный результат с примером 3-23
после построения обоих результатов рядом на одном листе графической бумаги.
3-5. Изменить порядок выполнения поворотов в задаче 3-4. Сравнить
полученный результат с результатом задачи 3-4 и с примером 3-23 путем построения
этих результатов на одном листе графической бумаги.
3-6. Получить матрицу преобразования размера 4x4 для объекта, заданного
координатными векторами
■ о
2
2
1
0
0
2
2
0
2
0
0
1
2
2
0
0
2
2
2
2
2
2
2
2
0
0
0
0
1
1 ■
1
1
1
1
1
1
1
1
1
с алгоритмом соединения (разд. А-7)
C(j) = -1,2,3,4,5,1,-6,7,8,9,6,-1,6,-2,7,-5,9,-4,10,8,-10,3
для вида из точки наблюдения (центр проекции), расположенной на 50 единиц
правее, 60 единиц выше и выдвинутой на 150 единиц вперед от центра объекта.
Помните, что мы смотрим в перспективу.
3-7. Повернуть куб с отсеченным углом (задача 3-6) на 30° относительно оси,
проходящей через точки Pi [—3 —3 2]иРг[—3 —2 —2]. Определить
преобразованные координатные векторы. Нарисовать результат в диметрической
проекции с коэффициентом искажения 0.625. Оба диметрических угла вращения
считать положительными.
3-8. Показать, что любые комбинации полных поворотов и/или четное число
зеркальных отражений могут быть представлены не более чем тремя поворотами
вокруг координатных осей.
3-9. Продолжить анализ, приведенный в разд. 3-20 для случая, когда вектор
зрения из центра проекции не перпендикулярен плоскости проекции.
ГЛАВА 4
4-1. Получить отношение между числом точек, радиусом и толерантностью
(точностью приближения), в случае когда круг представляется вписанным в него
многоугольником. Толерантность определяется как наибольшее расстояние
между дугой и хордой, соединяющей две точки многоугольника на внешней
окружности.
4-2. Кривая Ламе описывается формулой
хп уп ,
— + — = 1.
Cl С2
Определить овал, проходящий через три точки Pi[0 6], Р2[5 5], Рз[6 0].
Определить точки пересечения овала и круга с радиусом 3 и центром в точке х = 6,
у = 0.
4-3. Вычислить равное число точек на внешней дуге четверти круга в
первом квадранте, используя непараметрический явно заданный (уравнение (4-1)),
параметрический тригонометрический (уравнение (4-2)) и параметрический
чередующийся (уравнение (4-3)) анализ. Построить и сравнить результаты.
4-4. Получить уравнение (4-13).
4-5. Разработать и реализовать алгоритм для определения вершин
параметрической параболы, заданной уравнением 4-13.
4-6. Доработать метод, предложенный в разд. 4-9, для случая круга,
касающегося заданной прямой.
4-7. Доработать метод, предложенный в разд. 4-9, для случая прямой,
касающейся круга заданного радиуса с центром в заданной позиции.
4-8. Доработать метод, предложенный в разд. 4-9, для случая окружности
заданного радиуса, касающейся двух окружностей заданного радиуса с центрами
в заданных позициях. Небольшая подсказка: существует 16 возможных решений.
Построение дерева возможных вариантов решения зависит от радиуса
касательной окружности и расстояния между двумя заданными окружностями.
4-9. Доработать метод, предложенный в разд. 4-9, для случая окружности
заданного радиуса, одновременно касающейся прямой и окружности заданного
радиуса с центром в заданной позиции. Небольшая подсказка: существует 8
возможных решений. Прямая может пересекать или не пересекать окружность.
4-10. Доработать метод, предложенный в разд. 4-9, для случая эллипса с
заданными большой и малой полуосями, касающегося двух пересекающихся
прямых. Какая дополнительная информация могла бы потребоваться?
4-11. Решить задачи 4-5-4-8, заменив все окружности эллипсами с заданными
большими и малыми полуосями. В каждом случае определить, если это
необходимо, какая дополнительная информация требуется.
4-12. Какой тип конического сектора представлен каждым из следующих
уравнений:
х2 + у2 + 4х - 2у = 10,
х2 + у2 + ху - х + у = 3,
х2 - 4ху + 4у2 + Зх = 6,
2х2 -у2 + 4ху + 2х-3у = 6,
х2 - 4ху + Зу2 + 5j/ = 7,
х2-у2 = 1.
4-13. Преобразовать каждое из уравнений задачи 4-12 к стандартной форме.
4-14. Показать, что уравнение (4-33) эквивалентно следующему:
А{х + тп)2 + В(у + п)(х + тп) + С{у + п)2 + F{x + m) +G(y + п) + Н = 0.
4-15. Показать, что следующее квадратное уравнение определяет параболу, и
нарисовать сегмент между х — 1 и х = 3 для ymi„:
16а;2 - 24ху + 9у2 - 60ж - 80j/ + 20 = 0.
4-16. Первый квадрант
виде
единичного круга параметрически представляется в
(1 - x/2)t2 + (y/2-2)t+l
х —
У =
(2 - уД)Ь2 + (уД - 2)t + 1'
(1 - y/2)t2 + s/2t
(2 - \/2)t2 + (\/2 - 2)t + 1
Определить значение у для х = О,5. Указание: использовать метод итераций и
сначала определить t для х = 0,5.
ГЛАВА 5
5-1. Сгенерировать параметрическую кривую, показанную на рис. 5-3.
5-2. Заданы четыре координатных вектора Рх [0 0 0], Рг [1 1 l]i Рз [2
-1 — 1],Р4[3 0 0], определить кусочно непрерывный кубический сплайн
кривой, проходящей через них, используя аппроксимацию хордами для tk-
Касательные векторы на концах: Р[ [1 1 1] и Р{ [1 1 1]. Вычислить 7 точек каждого
сегмента сплайна. Сравнить результат для г = 1/3, 2/3 с примером 5-2,
двумерным аналогом данной задачи на плоскости.
5-3. Используя координатные векторы из примера 5-2, вычислить и сравнить
формы кривой для кубического сплайна для касательных векторов в точке Pi
для Р[ [л/2 cos0, v^sinfl] при в = 0°, 22.5°, 45°, 67.5°, 90°, сохраняя Р2 [1 1].
Сравнить эти результаты с получаемыми в случае, когда оба касательных вектора —
переменные Р{ [л/2 cos вуД sin в] и P^v^cosflv^sinfl]. Заметим, что величина
касательных векторов постоянна, изменяется только их направление.
5-4. Используя координатные векторы из примера 5-2, вычислить и сравнить
формы кривой кубического сплайна для касательных векторов в точках Pi и Р2
для Р[[а а] и Р^[а а] при а = 1/4, 1/2, 1, 2, 4, 8. Заметим, что направление
касательных векторов постоянно, изменяется только их величина.
5-5. Используя координатные векторы из примера 5-2, вычислить и сравнить
формы кривых кубического сплайна при условии незакрепленного конца.
Сравнить результаты с теми, которые были получены в задаче 5-2 и в примере 5-2.
5-6. Заданы пять координатных векторов на плоскости
[Р] =
0 0
0.5 0.6
1.0 1.0
1.5 0.8
1.0 0
Положив касательные векторы концов равными P/fl 1] и Р2[0 - 1],
определить Р(0.5) для каждого из четырех сегментов кубического сплайна, используя
нормализованную аппроксимацию, т.е. приняв 0 < t < 1.
5-7. Повторить задачу 5-2, используя нормализованную аппроксимацию для
tk, т.е. приняв tk = 1.0. Сравнить результат с результатами, которые были
получены в задаче 5-2, и с примером 5-2, аналогом этой задачи для плоскости.
5-8. Определить кубический сплайн кривой через пять координатных
векторов Pi [1 тг/4 0],Ра[1 Зтг/4 1], Р3[1 5тг/4 2], Р4[1 7тг/4 3], Р5[1 тг/4 4],
где компоненты координатных векторов заданы в цилиндрических координатах,
т.е. Pi[r в z]. Использовать условия незакрепленного конца.
5-9. Вычислить параболически смешанную кривую, проходящую через точки,
данные в задаче 5-2. Использовать технологию, описанную в разд. 5-6. Сравнить
результаты с результатами задачи 5-2 и с примером 5-2.
5-10. Вывести матрицу [А] (см. равенство (5-60)) для параболически
смешанной кривой, используя длины хорд как максимальные значения параметров, т.е.
полагая
р(г) = [г2 г 1][В], 0<r<di3,
q(s) = [s2 s 1][D], 0 < s < d2i,
C(t) = [t3 t2 t lp][G], 0<t<d23,
ГДе di2, d23, d3i —ДЛИНЫ ХОРД ДЛЯ PlP2, Р2Рз, Р3Р4 И di3 = ^12 + ^23, ^24 = ^23+^34-
Заметим, что это не совсем точно соответствует результату Оверхаузера.
5-11. Вывести результат Оверхаузера, используя матричные методы из
разд. 5-7.
5-12. Определить кривую Безье, используя координатные векторы, заданные
в примере 5-2, как определение многоугольника. Вычислить результат для
следующих значений параметров: 0, 1/3, 2/3, 1.
5-13. Вычислить координатный вектор Р3, задающий касательный вектор,
проходящий вдоль кривой, соединяющей два сегмента кривой Безье, иначе
определяемых как Pi[0 0 0],Р2[2 2 -2],Р4[4 0 0]hQi[4 0 0], Q2[6 -2 1],
Q3[8 - 3 2], g4[10 0 1].
5-14. Для поверхности Безье, заданной вершинами многоугольника из
примера 5-7, найти определяющие вершины многоугольника, требуемые для генерации
поверхности Безье шестого порядка, эквивалентной поверхности четвертого
порядка из примера 5-7. Порядок наращивать последовательными шагами.
5-15. Найти определяющие вершины многоугольника, которые разбивают
поверхность Безье, определенную в примере 5-7, на две кубические поверхности
Безье.
5-16. Применить пошагово технологию разбиения к поверхности Безье и
определяющим ее вершинам многоугольника из примера 5-7 и показать на этом
примере, что определяющий многоугольник и поверхность сходятся.
5-17. Повторить пример 5-11 для узлового вектора [00022333].
Результат показан на рис. 5-38е. Сравнить этот результат с примером 5-11 и с
рис. 5-38d.
5-18. Определить алгебраические отношения для функций неоднородного
базиса, полученного с помощью узловых векторов [0 0 0 0.4 2.6 3 3 3] и
[0 0 0 1.8 2.2 3 3 3]. Результаты показаны на рис. 5-38Ь и с. Сравнить
эти результаты с рисунками 5-38d и 5-38е.
5-19. Проиллюстрировать зависимость базисных функций кривых В-сплайна
четвертого и пятого порядков, определенных шестью вершинами многоугольника.
Использовать технологию, подобную рассмотренной в разд. 5-9.
5-20. Определить В-сплайн кривой четвертого порядка, используя
координатные векторы примера 5-2 как определяющий многоугольник. Сравнить результат
с поверхностью Безье, полученной в задаче 5-12.
5-21. Определить В-сплайн кривой третьего порядка, используя
координатные вектора примера 5-2 как определяющий многоугольник. Использовать
параметрические значения 0, 1/2, 1, 3/2, 2.
5-22. Для определяющего многоугольника, заданного в примере 5-13,
определить псевдовершины, необходимые для совпадения конечных точек
периодического В-сплайна с В\ и Bi соответственно. Сравнить результат с рис. 5-54.
5-23. Для определяющего многоугольника из примера 5-13 определить
псевдовершины, необходимые, чтобы сделать касательные векторы концов кривой
равными [—1 1] и [1 — 1] соответственно. Вычислить также начальную и конечную
точки кривой. Результаты сравнить с рис. 5-54.
5-24. Используя аппроксимацию хордами, обсуждавшуюся в разд. 5-9, найти
открытый В-сплайн поверхности четвертого порядка для определяющего
многоугольника, заданного в примере 5-14. Сравнить результат с примером 5-14.
5-25. Используя аппроксимацию хордами, обсуждавшуюся в разд. 5-9,
найти периодический В-сплайн поверхности третьего порядка для определяющего
многоугольника, заданного в примере 5-14. Сравнить результат с примером 5-14.
5-26. Используя аппроксимацию хордами, обсуждавшуюся в разд. 5-9,
найти периодический В-сплайн поверхности четвертого порядка для определяющего
многоугольника, заданного в примере 5-14. Сравнить результат с примером 5-14
и результатом задачи 5-24.
5-27. Показать, что две кривые В-сплайна, заданные в примере 5-18
вершинами многоугольника Bi[0 0], Вг[1 1], -Вз[2 1], В±[3 0] с альтернативными
узловыми векторами [X'] = [0 0 0 1 2 2 2] и [X] = [0 0 0 2 4 4 4],
идентичны. Указание: вычислите число точек на первой кривой 0 < t' < 2 и на
второй кривой 0 < t = It' < 4 и сравните результаты.
5-28. Показать, что кривые В-сплайна разбиения из примера 5-18 такие же,
как и исходная кривая. Указание: вычислите несколько точек двух кривых и
постройте их на такой же шкале.
5-29. Показать, что кривые В-сплайна разбиения из примера 5-19 такие же,
как и исходная кривая. Указание: вычислите несколько точек двух кривых и
постройте их на такой же шкале.
5-30. Показать, что если после разбиения исходной кривой из примера 5-19
новую вершину многоугольника Cj переместить в позицию вершины Сг, то
результирующая поверхность будет иметь угловую форму в точке Сг = Сз-
5-31. Для лучшего понимания сущности функции оценки вектора, такой, как
P(t) = [x(t) y(t)], построить графики функций x(t) от t, y(t) от t и y(t) от x(t) для
В-сплайна кривой четвертого порядка (к = 4), определенной Bi[0 0], Вг[2 2],
В3[4 2], В4[6 0] с открытым узловым вектором [00001111].
Решить эту же задачу для В-сплайна кривой третьего порядка (к = 3) с открытым
узловым вектором [0001222].
5-32. Вывести аналитическое выражение для второй производной вдоль
кривой рационального В-сплайна. Оценить результат для t = 0nt = n + k — 2.
5-33. Сгенерировать кривые рационального В-сплайна для определяющих
вершин многоугольника Bi[0 0], В2[1 2], В3[2.5 0], В4[2.5 0], В5[2.5 0],
В6[4 2], В7[5 0], при [Я] = [1 1 h3 hi h5 1 1] для значений h3 = /i4 =
h5 = 0,0.25,1,5. Сравнить результаты с рис. 5-66.
5-34. Рассмотреть пример 5-20 при к = 4.
5-35. Найти первую и вторую производные при t = 0 и t = 3 для
определяющего многоугольника из примера 5-20.
5-36. Найти первую и вторую производные при t = 0 и t = 2 для fc = 4 для
определяющего многоугольника из примера 5-20.
5-37. Сгенерировать тор как поверхность рационального В-сплайна,
полученную вращением окружности радиуса 1 с центром в точке х = 5, z = 1
относительно оси z (рис. 6-58).
5-38. Сгенерировать сферу радиуса 1 как поверхность рационального В-
сплайна, полученную вращением полуокружности радиуса 1 с центром в точке
х = 0, z = 1 относительно оси z (рис. 6-59).
ГЛАВА 6
6-1. Сгенерировать поверхности, показанные на рис. 6-6.
6-2. Сгенерировать поверхности вращения для кривых, вычисленных в
задачах 5-6 и 5-9.
6-3. Сгенерировать «кружку», показанную на рис. 6-10.
6-4. Добавить точку к «кружке», показанной на рис. 6-10, используя
изогнутую поверхность.
6-5. Сгенерировать изогнутую поверхность, показанную на рис. 6-16.
6-6. Определить тип квадратичной поверхности, заданной каждым из этих
уравнений:
2х2 - 2yz + 2zx - 2ху - х - 2у + 3z - 2 - 0,
х2 + z2 + 2ху + 2xz - 2yz - 2х + 4у - 4 = 0,
х2 + 4У2 + z2 - 4yz - 12zx + 24xy + 4х + 16у - 26z - 3 = 0,
4х2 + у2 + z2 - Аху + 6z + 8 = 0,
4j/2 + 4z2 + 4ху -2х- Uy - 22z + 33 = 0.
6-7. Используя параметрическое представление, сгенерировать
гиперболический параболоид.
6-8. Нарисовать поверхности, составляющие отдельные компоненты, т.е.
Q(u, v,x), Q(u, v, у), Q(u, v, z) (рис. 6-24) и полную поверхность Q(x, у,z) для
точки, прямой и плоскости.
6-9. Для линейчатой поверхности с ребрами в виде кривых, заданных как
z = 0, у = 0.25cos(27r:r), 0 < х < 1,
z = 1, у = 0.25sin(27rz), 0 < х < 1,
определить поверхность в точке Q(0.5,0.5).
6-10. Построить билинейную поверхность, соответствующую четырем точкам
Р(0,0) = [0.25 0], Р(1,0) = [0.75 0], Р(0,1) = [0.75 0.9], Р(0,0) = [0.25 0.8].
6-11. Построить билинейную поверхность, которая соответствует четырем
точкам, определяемым противоположными концами диаметров двух единичных
окружностей, лежащих на параллельных плоскостях, отстоящих друг от друга
на единицу и поворачиваемых на 180° с интервалом 15°.
6-12. Сгенерировать полную линейчатую поверхность, показанную на рис.
6-28 и обсуждавшуюся в примере 6-10. Является ли такая поверхность
развернутой?
6-13. Сгенерировать полную линейчатую поверхность, показанную на рис.
6-30 и обсуждавшуюся в примере 6-12. Показать, что угловая часть этой
поверхности развернута.
6-14. Показать на примере, что плоская бикубическая поверхность Кунса
получается в том случае, когда координатные, касательные векторы и векторы
вращения лежат в одной плоскости.
6-15. Найти матрицу [Р], которая задает кусок цилиндрической бикубической
поверхности Кунса.
6-16. Найти матрицу [Р], которая задает кусок общей бикубической
поверхности Кунса.
6-17. Определить точку на поверхности с координатами и = w = 0.5 для
бикубической поверхности Кунса со следующими координатными векторами:
Р(0,0) = [-100 0 100],Р(0,1) = [100 -100 100], Р(1,1) = [-100 0 -100],
Р(1,0) = [-100 -100 - 100], u-касательные векторы Р^О.О) = [10 10 0],
pi.°(0,l) = [-1 - 1 0], Pll0(l,l) = [-1 1 0], P^l.O) = [1 - 1 0], w-
касательные векторы Р°л(0,0) = [0 - 10 - 10], Р°'1(0,1) = [01- 1],
Р^ЧМ) = [0 1 1], P^l.O) = [0 1 1], и векторы вращения Р^О.О) =
[0 0 0],Р1,1(0,1) = [0.1 0.1 0.1],Р1-1(1,1) = [0 0 0], Р1-1(1,0) = [-0.1 -
0.1 — 0.1]. Систематически изменить векторы вращения и касательные векторы
и сравнить результаты.
6-18. Продолжить анализ параболически смешанной кривой на случай
параболической смешанной поверхности [5-10]. Указание: использовать параболически
смешанные кривые для четырех граничных кривых и стиль задания линейной
поверхности Кунса со смешанными функциями, заданными как Fi(t) = 1 — 3£2 + 2£2,
F2(*) = 3t2 — 2tz. Заметим, что результирующая поверхность контролируется
четырьмя угловыми точками и двумя присоединенными векторами в концах
граничных кривых. Что является продолжением отдельных кусков? Какой порядок
продолжения может поддерживаться через границы кусков? Каково продолжение
влияния перемещения единственной точки поверхности, построенной из
множества кусков?
6-19. Показать для бикубической поверхности Безье 4x4, что для и = w = 0
Quw{0,0) = 9[(£i,i - Вод) - (Pi,o - Bo,o)].
Сравнить результат с уравнением (6-60).
6-20. Найти (4 х 4) определяющие вершины прямоугольной сетки Безье,
которые задают кусок бикубической поверхности Кунса из примера 6-13.
6-21. Сгенерировать поверхность Безье из примера 6-14, не используя
матричных методов.
6-22. Показать, что ни гиперболический параболоид, ни параболический лист
не являются развертывающимися поверхностями.
6-23. Для поверхности из примера 6-12 показать, что кривизна Гаусса равна
нулю для плоской области и положительна в остальной области.
6-24. Определить кривизну Гаусса при и = w = 0.5 для поверхности из
примера 6-14, показанной на рис. 6-39a-d. Сравнить результаты.
6-25. Сгенерировать закрытые периодические поверхности В-сплайна,
показанные на рис. 6-46.
6-26. Сгенерировать комбинированную открытую и периодическую
поверхность В-сплайна, показанную на рис. 6-47.
6-27. Сгенерировать закрытую периодическую тороидальную поверхность В-
сплайна, показанную на рис. 6-48.
6-28. Рассчитать поверхность В-сплайна четвертого порядка для
определяющей прямоугольной сетки 4x5, заданной так:
£i,i[o
51)2[0
Bi,3[0
BiA[0
0 100]
33 150]
66 50]
100 100]
B2,i [25
54,i[75
#2,2 [25
54l2[75
52]3[25
54,з[75
В24[25
0 150]
0 50]
33 200]
33 50]
66 25]
66 150]
100 50]
B3,i[50 0 100]
B5,i[100 0 100]
В3,2[50 33 100]
В5,2[Ю0 33 50]
В3,з[50 66 100]
В5,з[100 66 150]
В3)4[50 100 100]
В4,4[75 100 150] В5,4[100 100 100]
Определить вычислением вручную точку в центре параметрической сетки
поверхности 11 х 15.
Написать программу для вычисления двух диагональных параметрических
прямых и = 2w и и = 2(1 — w). Составить список точек от (0, 0) до (2, 1) для
и = 2w и от (0, 1) до (2, 0) для и = 2(1 —w). Составить список значений 15и и \\w.
Вычислить и изобразить параметрическую поверхность 11 х 15. Использовать
подходящее зрительное преобразование. Указание: вывести результаты в файл
в стандартном графическом формате (.sgf) или в стандартном полигональном
формате (.spf) и использовать трехмерные преобразования, разрабатываемые в
спецификации 3-1 для изображения поверхности.
Приложение F
Спецификации
программ
Спецификации программ разработаны не только для пояснения концепций и
методов, представленных в книге, но также для передачи некоторого опыта
создания достаточно сложных программ машинной графики. Хорошо выполненные,
они могут составить инструментарий полезных графических программ.
Законченные программные проекты дают в результате полезные программы общего
назначения. Спецификации сгруппированы по главам книги.
Особенно рекомендуются две из этих спецификаций. Первая —это научная
программа черчения (спецификация 2-4). Написание хорошей научной
программы черчения — нетривиальная задача, однако она вполне доступна студентам
старших курсов и дипломникам. Ее можно рекомендовать в качестве одного из
двух курсовых проектов для студентов выпускных курсов (другим проектом
может быть трехмерный манипулятор (спецификация 3-1)). Студенты старших
курсов могут выполнить подобную разработку примерно в течение трех недель.
Вторая спецификация — это трехмерный манипулятор (спецификация 3-1).
Трехмерный манипулятор позволяет изображать и совершать различные
преобразования (вращение, перемещение, масштабирование, проецирование и т.д.)
над трехмерными объектами. Трехмерный манипулятор значительно облегчает
задачу визуализации объектов. Кроме того, он улучшает возможности
визуализации в трех измерениях. В довершение всего, он полезен для лучшего усвоения
материала по трехмерным кривым и поверхностям (гл. 5 и 6). Для студентов
старших курсов он может служить вторым из двух курсовых проектов. Дипломник
должен справиться с этой работой в течение примерно трех недель.
При проектировании и реализации этих программ особое внимание должно
уделяться концепциям структурного программирования и особенно модуляриза-
ции программ. Каждая из предложенных спецификаций достаточно ясно
распадается на умеренное количество графических инструментальных модулей.
Например, большинство графических инструментов для трехмерного
манипулятора даны в виде псевдокода в приложении G. Язык реализации несуществен. К
настоящему времени все спецификации реализованы студентами на различных
вычислительных машинах и различных языках программирования.
Необходима хорошая документация. Пример хорошего документирующего
заголовка показан в табл. F-1. Необходимо также подробное документирование
внутри программы.
Таблица F-1 Заголовок документации
программы
имя:
программист:
дата:
история:
назначение:
метод:
система:
язык:
вызываемые подпрограммы:
файлы ввода:
команда компилятора:
команда компоновщика:
аргументы вызова:
список переменных:
Так как ряд спецификаций задуман для работы в интерактивном режиме,
уместно сказать несколько слов об интерфейсе пользователя. В графической
среде, не рассчитанной на работу в реальном времени, в качестве интерактивного
устройства наиболее часто используется обычная алфавитно- цифровая
клавиатура. Для такой среды простым в изучении, быстрым и эффективным является
хорошо разработанный интерфейс клавиатуры.
Если не требуется специфический числовой ввод, интерфейс клавиатуры
принимает для ввода буквенные слова. Цифровые списки ответов неприемлемы
вследствие того, что пользователь мыслит в терминах слов и фраз, а не цифровых
элементов или списков. Например, если желаемое действие — это поворот объекта,
то пользователь думает о повороте, а не об элементе 3 из списка опций.
Далеко не все пользователи хорошо печатают на машинке. Поэтому число
символов, необходимое для ввода команды, должно быть сведено к минимуму.
Однако те, которые хорошо печатают, не должны быть поставлены в неудобное
положение, раздражены использованием странных последовательностей
символов. Одно из возможных решений состоит в том, чтобы допустить полное слово
в качестве ввода и затем усечь его до минимального количества символов,
необходимого для уникального определения команды. Например команда rotate
(поворот) усекается до первых двух символов, т. е. го. Допустимое усечение, которое
дает уникальную последовательность символов, выделяется скобками, например
(ro)tate. Численный ввод должен допускаться в свободном формате. Например, в
числах с плавающей точкой не обязательно присутствие десятичной точки, т. е.
числа 30 и 30. эквивалентны.
Следовало бы обеспечить командное меню. Важный вопрос —как и когда оно
поддерживается. Его следовало бы высвечивать один раз при инициировании
выполнения программы и затем по запросу. Нецелесообразно высвечивать
меню после приема каждой очередной команды, так как это раздражает и к тому
же поглощает много времени. Полезно, чтобы командное меню полностью
помещалось на экране. На каждом уровне программы, обрабатывающей командьг,
должно быть обеспечено соответствующее командное меню. Требуется, чтобы для
высвечивания командного меню использовалась единственная командная строка.
Такая командная строка состоит из единственного слова или символа. Например
«?» или «Option?» или «Command?».
Существует столько же способов запроса командного меню или меню
(экрана) помощи, сколько существует программистов. Например, можно набрать h или
help или ? или ?? или все, что угодно. Подбор подходящей команды часто
оказывается довольно интересным занятием. Простое решение — принимать любой
из этих запросов или возвращать простой carriage (символ возврата каретки).
Инструментарий прост. Если при разборе командного ввода не обнаруживается
допустимой команды, то высвечивается подходящее для этого уровня командное
меню (экран подсказки).
При использовании концепции, называемой «командный стек»,
эффективность интерфейса значительно возрастает. Лучше всего ее смысл проясняется из
примера. В спецификации трехмерного манипулятора (спецификация 3-1)
команда поворота запрашивает описание оси поворота (ось х, у, z или произвольная) и
угла поворота в градусах. Процессор команд верхнего уровня принимает команду
rotate (поворот) и вызывает процессор команд нижнего уровня, который
запрашивает и вводит оси и угол. Командный стек позволяет опытному пользователю
набрать команду в виде
го х 30.
Здесь параметры выделены пробелами. Командный процессор верхнего уровня
разбирает строку ввода, определяет, является ли первая команда го допустимой,
и, если это так, передает оставшиеся команды командному процессору
нижнего уровня. Командный стек позволяет опытному пользователю выполнять серии
манипуляций, минимизируя ввод и время ожидания. Начинающий пользователь
имеет доступ к таким же возможностям. Например, с помощью командного стека
sc о 2
го х 30
го у —45
dr
объект масштабируется по всем координатам с коэффициентом 2, поворачивается
вокруг оси х на 30°, поворачивается вокруг оси у на 45°, а результат отображается
в плоскости z = 0 с использованием ортографической проекции.
В завершение отметим, что интерфейс пользователя должен быть согласован
на всех уровнях. Следует придерживаться «принципа наименьшего удивления».
Иначе говоря, при наличии множества ответов на команду выбор должен
основываться на том, «какой ответ вызовет наименьшее удивление пользователя».
ГЛАВА 2
Первые две спецификации были разработаны для того, чтобы ознакомить
студентов с локальным графическим пакетом и заложить основу базисного
инструментария графических модулей. Третья спецификация служит для приобретения
опыта работы с оконной техникой на графическом устройстве и является основой
для разного рода управляющих преобразований. Четвертая относится к развитию
программы визуализации научных результатов.
2-1. Разработать и реализовать программу рисования замкнутого
многоугольника с вершинами Pi [О 0],Р2[2 -2],Р3[2 1],Р4[0 3],Р5[-2 1],Р6[-2 -2],
выбрав направление обхода против часовой стрелки. Использовать команды окна
и/или области вывода графического устройства, чтобы многоугольник заполнял
все пространство экрана. Будьте внимательны при построении геометрических
отношений, одна единица по оси х должна быть равна одной единице по оси у.
Включить оси, проходящие через начало координат. Разбить оси на единичные
интервалы, расставить маркировку на осях.
Разработать и включить в программу инструментальные модули для:
Рисования осей через точку хО, уО, от i-min до я-тах и от y-min до у-тах.
Размещения левых, правых или центральных осевых маркеров на осях а; и у,
определенной длины, расположенных через определенный интервал, начиная
от определенной точки.
Разметки осевых маркеров подходящими значениями.
Рисования произвольного многоугольника. (Приложение А-7.)
2-2. Разработать и усовершенствовать программу генерации и отображения
кривых, описанных параметрическими уравнениями
а.х = {2 + 7cos(sin(0) + sin(1210))} cos(0) 7г/2500 < 0 < 2тг
у = {2 + 7cos(sin(0) + sin(1210))}sin(0)
Ъ.х = {11/10 + cos(80)19} cos(0) тг/2000 < 0 < 2тг
y={l.l + cos(80)19}sin(0)
с.х = {1 + 2sin(170/4)} cos(0) тг/500 < 0 < 8тг
y = {l + 2sm(170/4)}sin(0)
d.x = {-в sin(7T0)/8} cos(0) 9тг/1000 < 0 < Збтг
у = {-0sin(7r0)/8}sin(0)
е.х = {sin(130/4)} cos(0) тг/100 < 0 < ЮОтг
y = {sin(130/4)}sin(0)
Используя команды работы с окнами и/или управления областями вывода,
увеличить эти фигуры до размеров экрана. Будьте внимательны при построении
геометрических отношений, одна единица по оси х должна быть равна одной
единице по оси у. Включить оси, проходящие через начало координат. Разбить
оси на единичные интервалы, расставить маркировку на осях.
Разработать и включить в программу инструментальные модули для:
Рисования осей через точку хО, уО, от i-min до х-тах и от y-min до у-тах.
Размещения левых, правых или центральных осевых маркеров на осях а; и у,
определенной длины, расположенных через определенный интервал, начиная
от определенной точки.
Разметки осевых маркеров подходящими значениями.
Рисования фигуры. (Приложение А-7.)
После преобразования
Н-НН-Н- -Н-Н--Н-+- -Н-+-Н-Н- -Н-НН-К- -Н-НН-Н- -H-hH-K
■Н-Ы-Н- -+-Н--Н-Н -НИ—Ш- -Н-Н-Н-Н -Н-Ы-Н- -Н-Ы-Н
la lb Ic Па ПЪ Пс
До преобразования
Рис. F-1
2-3. Выполнить следующие преобразования для двух прямых Р\Р2 и Р3Р41
заданных Pi[-2 - 1], Р2[1 2], Р3[-1 - 1], Р4[-1 2]:
a) поворот на —60°;
b) зеркальное отражение относительно прямой у = х;
c) масштабирование с коэффициентом 2.
Выполнить следующие преобразования для второй пары прямых РьРъ и Р7Ръ,
определенных через Р5[-1 - 1], Р6[2 2], Р7[-3 - 1], Р8[0 2]:
a) поворот на 60°, а затем зеркальное отражение относительно оси х;
b) зеркальное отражение, относительно оси х, после поворота на 60°;
c) преобразования [ ~\ \ .
Получить указанные результаты с помощью вычислений вручную.
Разработать и реализовать программу отображения результатов на один экран
в формате, показанном на рис. F-1. Три левые клетки в нижнем ряду содержат
первую пару прямых до преобразования. Три правых клетки содержат вторую
пару прямых до преобразования. В верхнем ряду находятся соответствующие
преобразованные прямые. Каждая клетка содержит оси с разметкой. Так как
пространство ограничено, может оказаться желательным не наносить метки
значений маркеров. Однако необходимо указать значение каждого маркера в каждой
клетке. Соответствующее изображение должно быть помечено как индикатор.
При разработке и реализации этих программ добросовестный пользователь
обратится к концепции окон и областей вывода графического устройства (разд.
1-4 и приложение А-4). Если абстрагироваться от размера окна, размещения
клеток на экране и конкретных операций преобразования, то действия, требуемые
для генерации каждого бокса, представляются идентичными. Таким образом,
главная программа выглядит так:
for i = 1 to 6
применить преобразование, если надо
определить размер окна
call window
for j = 1 to 2
call viewport (j)
call box
call axes
call tick
call label
call drawlines(j)
next j
next i
Разработать и включить в программу инструментальные модули для
a) определения требуемого размера окна;
b) рисования клетки вокруг окна;
c) рисования осей через точку хО, уО, от i-min до я-max и от у- min до у-тах;
d) размещения левых, правых или центральных осевых маркеров на осях х и у
определенной длины, расположенных через определенный интервал, начиная
от определенной точки;
e) разметки осевых маркеров подходящими значениями;
f) рисования прямых.
Позаботьтесь также о включении общепринятых модулей двумерного поворота,
отражения и масштабирования на плоскости (приложение G). Используйте эти
модули в программах для генерации матриц необходимых преобразований. Когда
требуются комбинированные преобразования (задания а и b для второй пары
линий), нужно перемножить матрицы перед применением их к исходной паре
прямых.
2-4. Разработать и реализовать программу визуализации научных данных,
которая принимает входной поток данных в форме двумерного файла .sgf (табл. А-2
из приложения А-6). При решении данной задачи воспользуйтесь
комментариями относительно интерфейса пользователя, данными в начале этого приложения.
Программа должна удовлетворять следующим характеристикам и условиям:
ввод Ввод данных из двумерного файла .sgf.
черчение Отображение графиков в соответствии с пределами, метками,
аннотациями и другими спецификациями. По умолчанию применяется
автоматическая установка пределов, данные присоединяются в виде
единой линии, нет меток, клетка без сетки и аннотация отсутствуют. (См.
ниже.)
метки Помечаются график, ось х и ось у.
оси Обе оси линейные, одна или обе оси логарифмические. Требуются
точные значения пределов по осям. Допустимые пределы по осям
начинаются или заканчиваются в 0, ±1, ±2, ±5. Таким образом, оси могут
иметь пределы 0 —У 1, 0 —> 2, 0 -» 5, — 1 -4 1, — 1 -4 5, — 2 -4 5 и т.д.
Случайные пределы, например 0 —>• 1.736, не допускаются, за
исключением специально установленных командой range (пределы). Оси
помечаются в соответствии с порядком значения 1. Величина метки ука-
зывается как множитель, расположенный следом за последней меткой
оси, который задается в форме х102. Логарифмические оси
размечаются только в интервалах, соответствующих 1, 5 и 10.
диапазон Изменение пределов графика. Запрашиваются минимальное и
максимальное значения х и у.
автодиапазон Автоматически определяются приближенные значения пределов по
осям х и у. (См. оси.)
тип линии Выбирается тип линий для определяемой кривой. Представлено меню
допустимых типов. Минимально необходимое множество — это
штриховая линия, непрерывная линия, точка в каждой позиции графика,
звездочка в каждой позиции графика, плюс в каждой позиции
графика или х в каждой позиции графика. Допустимы комбинации позиций
графика и типов линий.
пометки Выбор типа маркера пометки. Представлено меню возможных типов.
Минимально необходимое множество — это пометки на левой или
правой стороне осей, если смотреть из начала координат в положительном
направлении осей, пометки на обеих сторонах осей, длинные пометки
в более важных точках деления и короткие в менее важных.
у-метка Способ высвечивания метки оси у: метка расположена по вертикали
так, что читается сбоку, или так, что читается сверху вниз.
сетка Включение/выключение сетки.
квадрат Построение графического квадрата, сохраняющего геометрические
отношения, т.е. единица по оси х равна единице по оси у.
клетка Переключение способа отображения графика на экране: график
отображается в клетке с разметкой по всем четырем сторонам или график
отображается только с двумя координатными осями.
масштаб Изменение размеров графика путем указания масштабных
множителей по осям х и у.
цвет Задает цвет отдельно каждой кривой графика из смешанной палитры
красного, зеленого и синего цвета. Значения цвета задаются из
интервала 0 < г, д, Ь < 1, где 0 — отсутствие данного цветового компонента,
1 — максимальный вклад.
аннотация Размещает соответствующую текстовую аннотацию в произвольной
позиции графика. Возможно как автоматическое, так и
интерактивное размещение аннотации. Опция автоматического размещения
служит для ввода строк и отображения их в левом верхнем углу графика.
Опция интерактивного размещения позволяет позиционировать
каждую введенную строку аннотации запросом координат х, у для левого
нижнего угла строки. Представлено меню возможных шрифтов для
вывода аннотации. (См. шрифты)
отмена Позволяет отменить некоторые предыдущие команды, например
метка, аннотация, пределы и т. д., в частности ввод последней команды.
переустановить Перезадает всем опциям значения по умолчанию. (См. черчение.)
шрифт Выбор одного из типов шрифта. Представлено меню возможных
шрифтов.
твердая Делает твердую копию изображения графика.
копия Представлено меню доступных опций, включающее вывод в файл в
формате .sdf (табл. А-1 из приложения А-5).
сохранить Сохраняет текущий график в файле.
восстановить Загружает из файла ранее сохраненный график. После этого
возможны любые модификации этого графика.
округлить Генерирует кривую, проходящую через заданные точки кривой.
Представлено меню возможных методов построения таких кривых, которое
должно включать следующие методы: полиномов, степенной и экспо-
выход
ненциальный наименьших квадратов, кубический сплайн, сплайн Бе-
зье и В-сплайн.
Прекращает работу программы и возвращает управление
операционной системе.
ГЛАВА 3
Здесь приведена единственная спецификация — разработка и развитие
трехмерного манипулятора. Предполагается, что объекты отображаются с
использованием каркасного представления. Разрешен ввод множественных (составных)
объектов. Для успешного вьшолнения задания требуется разработка необходимых
модулей для трехмерного поворота, переноса, масштабирования и т. д., а также
для получения ортографической, косоугольной, перспективной проекций и т. д.
3-1. Разработать и реализовать программу трехмерного манипулятора,
который вводит данные из файла как в формате .sgf, так и в формате .spf, описанных
в табл. А-2 и А-3 из приложения А-6. Комментарии по поводу интерфейса
пользователя, приведенные в начале этого приложения, справедливы и при разработке
этой программы. Программа должна удовлетворять следующим
характеристикам и условиям:
ввод Ввод данных из файла как в формате .sgf, так и в формате .spf.
разделитель Спецификации объектов разделяются с помощью знака ф.
поворот Поворот объектов относительно координатных осей х, у, z или
относительно произвольной оси вращения. Произвольная ось вращения
определяется как с помощью точки и трех направляющих косинусов, так
и двумя точками на осях координат. Произвольный поворот
получается из поворотов относительно координатных осей. Поворот может
задаваться как относительно мировых координатных осей, так и
относительно локальных осей тела.
перенос Параллельный перенос объектов в направлении х, у или z.
отражение Зеркальное отражение объектов относительно плоскостей х = 0, у = О
или z = 0.
масштаб Масштабирование объектов локально, т.е. отдельно в направлении х,
у или z, или глобально, т. е. одинаково по всем направлениям.
оси Определены два типа трехмерных осей: оси тела и фиксированные
оси. В любой момент времени могут отображаться как одни из них,
так и те, и другие сразу. Размеры переменные. Маркеры разметки
могут быть включены или выключены. Оси тела фиксированы в центре
объекта или группы объектов. Они перемещаются, т. е. вращаются,
переносятся, отражаются вместе с объектом. Фиксированные оси
располагаются в точке начала мировой системы координат. Они являются
субъектом преобразования кадра, т. е. изометрической, диметрической,
косоугольной или перспективной проекции.
проекция Проекция объектов на плоскость z = 0 — изометрическая, диметриче-
ская, косоугольная, кабине, кавалье или центральная перспективная
проекция. Изометрические и диметрические преобразования
поддерживают выбор положительного или отрицательного поворота
относительно осей х, у. Диметрическая и косоугольная проекции допускают
переменный множитель искажения. Косоугольная, а также проекции
кабине и кавалье допускают переменный угол наклона относительно
горизонтали. Центральная перспективная проекция на плоскость z = 0
с переменным центром выполняется только для центров,
расположенных на оси z.
трансфокация Трансфокация (наезд) камеры относительно кадра изображения.
Замечание: это не масштабирование объектов.
исходный Восстанавливает исходные данные объекта.
рисовать Рисует преобразованные объекты, используя ортографическую
проекцию на плоскость z = 0.
вывод Сохраняет текущие преобразованные данные точек в файле формата
.sgf или .spf.
сохрматр Сохранить текущую матрицу преобразования в файле.
тень Создать изображение с тенями.1 Требуется, чтобы данные вводились
в формат .spf.
невидимые Создать изображение с невидимыми линиями/поверхностями.2
Требуется, чтобы данные вводились в формате .spf.
твердая копия Делает твердую копию изображения. Представлено меню доступных
устройств вывода. Требуется возможность вывода в файл формата
.sdf. (Табл. А-1 из приложения А-5.)
центр Изображение объектов центрируется относительно геометрического
центра данных.
объект ф Включает/выключает отдельный объект или группу объектов,
задаваемую как ф.
4 вида Создает четыре вида объектов: ортографические фронтальные
проекции, виды сбоку и сверху в нижнем левом, нижнем правом и верхнем
левом квадрантах соответственно, плюс текущую проекцию в верхнем
правом квадранте.
окружение Удаляет с экрана любые элементы окружения, например меню.
выход Прекращает работу программы и возвращает управление
операционной системе.
Программа структурирована так, чтобы все матрицы преобразований
применялись до выполнения команды рисования или какой-либо команды
проецирования. Перед вьшолнением любой из этих команд комбинированная матрица
преобразования применяется к базе данных, а результирующие
преобразованные двумерные координатные векторы рисуются на устройстве вывода. Исходная
трехмерная база данных не модифицируется командами рисования или проекции.
Главная программа состоит из условного цикла в виде:
Выход = произвольная строка
while Выход О q then
print Опцию ? на экран
input Ответ от клавиатуры
truncate Ответ до первых двух символов
convert Ответ в регистр строчных букв
if Ответ = го then call подменю поворота
if Ответ = re then call подменю отражения
if Ответ = рг then call подменю проекции
print главный экран помощи
end while
1 См. Д. Роджерс, Алгоритмические основы машинной графики. — М.: Мир, 1989.
2 См. предыдущую ссылку.
Типичная программа подменю могла бы выглядеть так:
Выход = произвольная строка
while Выход О q then
print Вращение относительно какой оси?
input Ответ от клавиатуры
truncate Ответ до первых двух символов
convert Ответ в регистр строчных букв
if Ответ = х then call программу х-поворота
if Ответ = у then call программу у-поворота
if Ответ = z then call программу z-поворота
if Ответ = g then call программу произвольного поворота
print локальный экран помощи
end while
Опираясь на эту базовую концепцию, легко понять, что программа имеет по
крайней мере три уровня действий. Первый —выбор основной операции,
например поворот, второй —выбор ее параметров, например ось поворота, третий —
выполнение операции.
При необходимости возможности, описанные в спецификации, можно
сократить путем удаления требований к программе.
В качестве примера рассмотрим Т-блок, определенный ниже
' 0
4
4
3
3
1
1
0
0
4
4
3
3
1
1
0
0
0
2
2
4
4
2
2
0
0
2
2
4
4
2
2
4 ■
4
4
4
4
4
4
4
0
0
0
0
0
0
0
0
А
В
С
С
Е
F
G
Н
I
J
К
L
М
N
0
Р
Разработать единую матрицу преобразования, которая:
a) сокращает размер на 1/2;
b) поворачивает относительно оси х на 30°;
c) поворачивает относительно оси у на —30°;
d) переносит на —2 единицы в направлении у;
e) выполняет центральную перспективную проекцию на плоскость z = 0 с
центром проекции z = 10.
Сначала разработать, потом применить комбинированную матрицу
преобразования для этих операций к базе данных путем вычисления вручную. Построить
результат на графической бумаге. Вычислить и построить некоторые невидимые
точки. Использовать результаты этих ручных вычислений для проверки
операций трехмерного манипулятора.
ГЛАВА 4
Единственная приведенная здесь спецификация основывается на расширении
материала разд. 4-9. Предлагаемое расширение дано в задачах с 4-6 по 4-10.
Подобные конструкции требуются в системах компьютерной поддержки черчения и
во многих управляющих приложениях.
4-1. Разработать и реализовать программу интерактивного задания
геометрии, определенной в разд. 4-9, и/или ее расширения, определенного в задачах с
4-6 по 4-10. Будьте внимательны при построении корректных геометрических
отношений для отображения результатов; например, окружность должна выглядеть
как окружность, а не как эллипс. Комментарии по поводу интерфейса
пользователя, приведенные в начале этого приложения, справедливы и при разработке
этой программы. Программа должна удовлетворять следующим
характеристикам и условиям:
line Определяет отрезок по его двум конечным точкам.
circle Определяет окружность по ее центру и радиусу (Л, к).
add Добавляет окружность или отрезок к геометрии.
delete Удаляет окружность или отрезок из геометрии.
move Перемещает ранее определенные окружность или отрезок.
oxes Включает/выключает оси.
ticks Включает/выключает маркеры разметки осей.
tab els Включает/выключает метки маркеров разметки осей.
solution Выбирает подходящее из возможных решений, используя такие
концепции, как левый, правый, ближний, дальний, внутри, вне, см.
разд. 4-9.
В качестве частей программы разработать и включить инструментальные
модули для
a) рисования осей, проходящих через точку хО, уО, от i-min до х- max и от y-min
до у-тах;
b) левого, правого или центрального расположения маркеров разметки осей хиу,
определенной длины, начиная с заданной позиции через заданный интервал;
— нанесения на маркеры разметки подходящих значений;
— генерациии и рисования окружности и дуги окружности.
Обязательно также разработайте модули необходимых двумерных
преобразований, например поворота, переноса, зеркального отражения и т.д., необходимых
для размещений в стандартной ориентации. Когда требуются множественные
преобразования, перемножайте матрицы перед их применением к геометрической
базе данных. Разработайте необходимые модули для поддержки движения по дереву
решений, для выбора необходимого решения, для определения, является ли
выбранное решение физически возможным, и выполнения необходимых вычислений
для поиска некоторых неизвестных геометрических величин.
ГЛАВА 5
Здесь приведена спецификация программы генерации и манипуляции с
кривыми. Каждая из этих кривых обсуждалась в гл. 5. В частности, речь шла о
кубическом сплайне, параболически смешанном, сплайне Безье и В-сплайне как
рациональных, так и нерациональных. Они используются в качестве базиса
программы. Включение возможностей генерации составной кривой нескольких типов
делает особенно удобным сравнение.
5-1. Разработать и реализовать программу генерации и манипуляции
трехмерными кривыми, которая принимает входные данные в формате трехмерного
файла .sgf (табл. А-2 из приложения А-6). Сгенерированная трехмерная кривая
строится с использованием ортографической проекции на плоскость z = 0.
Комментарии по поводу интерфейса пользователя, приведенные в начале этого
приложения, справедливы и при разработке этой программы. Программа должна
удовлетворять следующим характеристикам и условиям:
ввод
тип
многоугольник
метка
добавить
удалить
переместить
очистить
оси
диапазон
автодиапазон
тип линии
кривая #
восстановить
#
исходные
печать
Ввод данных из файла в трехмерном формате .sgf.
Выбор типа кривой. Представлено меню возможных типов кривых,
например кубический сплайн, параболически смешанный, сплайн
Безье, В-сплайн. Для кубического сплайна реализованы как
нормализованная, так и хордовая аппроксимации и, по крайней мере, условия
жесткого и свободного конца. Для параболически смешанной кривой
реализована аппроксимация для а и /3 с переменным значением а,
а = 0.5 по умолчанию. Для кривых Безье и В-снлайна реализованы
рациональный и нерациональный варианты, а также возможности
повышения степени и подразбиения.
Рисует прямые линии между введенными точками данных. Для
кривых Безье и В-сплайна это задание определяющего многоугольника.
Отображает метки следом за отдельными точками входных данных,
например Pi, Рг, Рг и т.д.
Добавляет точку данных. Обязательна возможность добавить точку
перед первой точкой данных.
Удаляет точку данных.
Перемещает точку данных.
Определяет, будет или нет экран очищаться перед рисованием первой
кривой.
Включает/выключает графические оси. Оси включают подходящие
маркеры разметки и метки.
Изменяет пределы графика. Запрашиваются минимальное и
максимальное значения для хну.
Автоматически определяет подходящие пределы для хну.
Выбор типа линии для заданной кривой. Представлено меню
возможных типов. Как минимум, оно должно включать штриховую и
сплошную линии.
Включает/выключает отдельную кривую или группу кривых,
определенных как #.
Восстанавливает кривые, определяемые как #, из базы данных
программы.
Восстанавливает исходные данные кривой.
Печатает на экране конструктивные данные кривой, например
определяющий многоугольник для кривой Безье или В-сплайна.
твердая Делает твердую копию текущего изображения.
копия Представлено меню доступных устройств вывода. Необходима
возможность вывода в файл в формате .self. (Табл. А-1 из приложения А-5.)
вывод Сохраняет трехмерные точки данных сгенерированной кривой в файле
формата .sgf для последующего отображения на экран и
преобразований с помощью трехмерного манипулятора. (Спецификация 3-1.)
выход Прекращает работу программы и возвращает управление
операционной системе.
При необходимости возможности, описанные в спецификации, можно сократить
путем удаления требований к программе.
Используйте вычисления из примера 5-2 и задач 5-2, 5-5, 5-7, 5-9, 5-10, 5-12,
5-20 и 5-21 для проверки работы программы генерации и преобразований
трехмерных кривых.
5-2. Добавить к спецификации 5-1 возможности для кривых Безье и В-
сплайна, как нерациональных, так и рациональных. Данные вводятся из файла
в формате .sgf.
ГЛАВА 6
Здесь приведена спецификация программы генерации и манипуляции для
поверхности. Она очень похожа на программу генерации и преобразований для
кривой из гл. 5 и обладает многими аналогичными характеристиками. Она также
может быть построена как расширение программы трехмерного манипулятора
(спецификация 3-1). В этом случае генерация и манипуляция поверхностью является
просто дополнительной функцией.
Поверхности, обсуждавшиеся в гл. 6, например билинейные, правильные,
линейные или бикубические поверхности Кунса, поверхности Безье или В-сплайны,
как нерациональные, так и рациональные, используются в качестве базиса
программы. Включение возможностей генерации и отображения составных
поверхностей делает особенно удобным исследование эффектов воздействия различных
вариантов входных данных.
6-1. Разработать и реализовать программу генерации и манипуляции
трехмерными поверхностями, которая получает входные данные в формате трехмерного
файла .sgf, описанного в табл. А-2 приложения А-6 или точки многоугольной
сетки в форме файла .рпр для поверхности Безье или В-сплайна (табл. D-1
приложения D). Сгенерированная поверхность строится с использованием подходящей
проекции на плоскости z = 0, например изометрической, диметрической, кабине
или кавалье. Результаты выводятся в формате .sgf или в формате .spf и могут
быть использованы впоследствии. Комментарии по поводу интерфейса
пользователя, приведенные в начале этого приложения, справедливы и при разработке
данной программы. Программа должна удовлетворять следующим
характеристикам и условиям:
ввод Ввод данных из файла в трехмерном формате .sgf.
поверхность Генерирует поверхность. Для поверхностей Безье и В-сплайна
реализованы как нерациональный, так и рациональный варианты, а также
возможности увеличения порядка и степени разбиения. (Задачи 6-17
и 6-28 предлагаются в качестве тестовых поверхностей.)
границы
диагонали
параметризация
рисовать
многоугольник
оси
метка
модифицировать
тр ансфокация
очистить
исходные
печать
твердая
копия
вывод
выход
Вычисляет и отображает четыре граничные кривые поверхности.
Вычисляет и отображает две диагональные кривые поверхности.
Вычисляет и отображает ортогональную сетку изопараметрических
линий на поверхности. Запрашивает число линий в каждом
параметрическом направлении.
Отображает поверхность с использованием подходящей проекции,
например изометрической, диметрической, кабине или кавалье.
Рисует прямые линии между точками входных данных. Применяется
для поверхностей Безье и В-сплайна, чтобы показать определяющий
многоугольник.
Определены два типа трехмерных осей: оси тела и фиксированные
оси. В любой момент времени могут отображаться как одни из них,
так и те и другие сразу. Размеры переменные. Маркеры разметки
могут быть включены или выключены. Оси тела фиксированы в
центре объекта или группы объектов. Они перемещаются, т. е.
вращаются, переносятся, отражаются вместе с объектом. Фиксированные
оси располагаются в точке начала мировой системы координат. Они
являются субъектом преобразования кадра, т. е. изометрической,
диметрической, косоугольной или перспективной проекции.
Отображает метки вслед за отдельными точками входных данных,
например Pi, Р2, Рз и т.д.
Модифицирует характеристики поверхности. Представлено меню
возможных модификаций, одной из которых является перемещение
координатных векторов. Для бикубической поверхности Кунса также
включены модификации касательных векторов и векторов вращения.
Трансфокация камеры относительно кадра изображения. Замечание:
это не масштабирование поверхности.
Определяет, будет ли очищаться экран перед рисованием текущей
поверхности.
Восстанавливает исходные данные поверхности.
Печатает на экране конструктивные данные поверхности, например
определяющий многоугольник для поверхности Безье и В-сплайна.
Делает твердую копию текущего изображения.
Представлено меню доступных устройств вывода. Необходима
возможность вывода в файл в формате .sdf. (Табл. А-1 из приложения
А-5.)
Сохраняет трехмерные точки данных сгенерированной поверхности
в файле в трехмерном формате .sgf для последующего отображения
на экран и манипулирования с помощью трехмерного манипулятора.
Прекращает работу программы и возвращает управление
операционной системе.
При необходимости возможности, описанные в спецификации, можно
сократить путем удаления требований к программе.
Использовать вычисления из примеров 6-9, 6-10, с 6-12 по 6-15 и 6-18 и
задач с 6-9 по 6-11 для проверки операций программы генерации и манипуляций
с поверхностями.
6-2. Добавить к спецификации 5-1 возможности для трехмерных
поверхностей. Данные вводятся из файла в формате .sgf. (Табл. А-2 из приложения А-6.)
Приложение G
Алгоритмы
В этом приложении приведено несколько полезных алгоритмов. Все они
представлены с помощью псевдокода, описанного в приложении С. Выбрать язык для
представления алгоритмов было непросто. Перспективными кандидатами
выглядели Паскаль, Фортран, Си и ANSI Бейсик. С точки зрения машинной графики
каждый из этих языков имеет сильные и слабые стороны. Окончательное
решение выбрано на основе педагогических соображений. Представление с помощью
псевдокода требует, чтобы алгоритмы были переведены на «реальный» язык
программирования. Есть надежда, что этот процесс улучшит понимание алгоритмов,
а следовательно, и лежащей в их основе математики.
Версии алгоритмов на псевдокоде алгоритмически построены на основе
работающих программ. Мы надеемся, что такой способ привел к получению более
точных алгоритмов. Однако в процессе печати могли быть внесены отдельные
ошибки. Поэтому при реализации следует еще раз внимательно сверить
алгоритмы с математическим представлением в тексте.
Алгоритмы разрабатывались для обучения, т. е. они задуманы в качестве
иллюстраций математических методов, обсуждавшихся в книге, но не как
эффективно работающие программы для промышленной эксплуатации. Во многих
случаях признавалась приемлемой вычислительная неэффективность, если она
окупается тем, что алгоритм более полно соответствует основному тексту книги.
Вычислительная неэффективность допускалась и для сокращения требуемой
памяти. Таким образом, программы, разработанные в соответствии с предложенными
алгоритмами, применимы для микрокомпьютерных операционных систем в
условиях ограниченной доступной оперативной памяти. Примером служит алгоритм
bsplsurf построения поверхности В-сплайна. В предложенном ниже алгоритме
на псевдокоде все базовые функции для каждого значения параметра
вычисляются вне главного цикла. Это сокращает требования к размерам памяти. Однако
с точки зрения минимизации времени выполнения было бы более эффективно
вычислять все базовые функции в главном цикле, получать результаты и запоминать
их в большом массиве. Элементы этого массива используются затем в основном
цикле для вычисления координатных векторов на поверхности. Через несколько
минут работы становится ясно, что для достаточно сложных поверхностей
размеры массива получаются довольно большими. Однако алгоритм выполняется в
несколько раз быстрее, чем представленный алгоритм на псевдокоде. При
реализации алгоритмов предполагается, что первоначально они будут реализованы
в том виде, в котором они даны в книге. Сначала надо удостовериться в
правильности программы, а уже затем следует заниматься исследованием алгоритма
и его математического обоснования с целью обнаружения методов повьппения
эффективности.
Алгоритмы сгруппированы по главам книги и расположены в алфавитном
порядке для каждой главы.
ГЛАВА 2
Здесь приведены алгоритмы, выполняющие базовые двумерные манипуляции.
Вот они в алфавитном порядке: reflt2d, rot2d, scale2d, tran2d.
reflt2d
Подпрограмма формирования и конкатенации матрицы отражения в
плоскости к текущей преобразующей матрице (уравнения 2-34-2-36).
re/ft(,) = матрица отражения
refltcode = код отражения
1 = относительно оси х
2 = относительно оси у
i(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица отражения
subroutine refit2d (rfltcode; t(,))
dimension reflt(3,3)
Mat refit = Idn
if rflcode = 1 then reflt(2,2)
if rflcode = 2 then reflt(l,l)
Mat t = Ureflt
return
rot2d
Подпрограмма формирует матрицу поворота в плоскости и конкатенирует ее
с текущей матрицей преобразования (уравнение (2-29)).
rot(,) = матрица поворота
theta = угол поворота в градусах
i(,) = матрица, с которой будет конкатенирована матрица поворота
subroutine rot2d (theta; t(,))
option angle degrees
dimension rot(3,3)
Mat rot = Idn
rot(l,l) = Cos(theta) установка значений матрицы поворота
rot(l,2) = Sin(theta)
rot(2,2) = rot(l,l)
rot(2,l) = -rot(l,2)
—1 установить соответствующий элемент равным —1
-1
конкатенировать матрицы
Mat t = t*rot конкатенация матриц
return
scale2d
Подпрограмма формирует матрицу масштабирования в плоскости и
конкатенирует ее с текущей матрицей преобразования (уравнения (2-37)-(2-58)).
a,d = масштабирующие множители в направлениях х и у;
a,d> 1 — растяжение; a,d < 1 — сжатие
s = общий масштабирующий множитель; s > 1 — увеличение;
s < 1 — сокращение
Scale(,) = матрица масштабирования
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица масштабирования
subroutine scale2d (a, d, s; t(,))
dimension scale(3,3)
Mat scale = Idn
scale(l,l) = a
scale(2,2) = d
scale(3,3) = 1/s
Mat t = t*scale
return
tran2d
Подпрограмма формирует матрицу параллельного переноса в плоскости и
конкатенирует ее с текущей матрицей преобразования (уравнение (2-50)).
т, п = множитель переноса в направлениях х и у, соответственно
£(,) = матрица, с которой будет конкатенирована
матрица переноса
tran(,) = матрица переноса
subroutine tran2d (m, n; t(,))
dimension tran(3,3)
Mat tran = Idn
tran(3,l) = m
tran(3,2) = n
Mat t = t*tran
return
ГЛАВА 3
Здесь приведены алгоритмы, выполняющие базовые трехмерные
манипуляции. Также предлагается ряд алгоритмов для проецирования на плоскость. В
алфавитном порядке это: cabinet, cavalier, dimetric, genrot, isometric, oblique,
perspective, project, reflt3d, scale3d, tran3d, xrot, yrot, zrot.
установка значений матрицы масштабирования
конкатенация матриц
установка значений матрицы переноса
конкатенация матриц
cabinet
Подпрограмма формирует матрицу проекции кабине и конкатенирует ее с
текущей матрицей преобразования (с. 187 и пример 3-16).
alpha = угол между горизонталью и осью проекции z
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица проекции кабине
subroutine cabinet (alpha; t(,))
option single degrees
выполнить проекцию кабине, вызвав oblique при f = 0.5
call oblique(alpba,0.5; t(,))
return
cavalier
Подпрограмма формирует матрицу проекции кавалье и конкатенирует ее с
текущей матрицей преобразования (с. 187 и пример 3-16).
alpha = угол между горизонталью и осью проекции z
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица проекции кавалье
subroutine cavalier (alpha; t(,))
option single degrees
выполнить проекцию кавалье, вызвав oblique при f = 1
call oblique(alpha,l; t(,))
return
dimetric
Подпрограмма формирует матрицу диметрической проекции и конкатенирует
ее с текущей матрицей преобразования (уравнения (3-32), (3-39), (3-40) и пример
3-14).
/ = коэффициент искажения в направлении z
t(,) = текущая преобразующая матрица, с которой будет
контаненирована матрица диметрической проекции
xcode = код х поворота
0 = отрицательный угол поворота
1 = положительный угол поворота
ycode = код у поворота
0 = отрицательный угол поворота
1 = положительный угол поворота
subroutine dimetric (ycode,xcode,f; t(,))
option angle degrees
найти углы поворота
phi = Arcsin(f/(Sqrt(2 - f*f)))
theta = Arcsin(f/Sqrt(2))
установить значения направлений поворота
if ycode = 0 then phi = —phi
if xcode = 0 then theta = —theta
выполнить диметрические преобразования, вызвав yrot, xrot u project
call yrot (phi; t)
call xrot (theta; t)
call project (3, t)
return
genrot
Подпрограмма формирует матрицу трехмерного поворота относительно
произвольной оси в пространстве и конкатенирует ее с текущей матрицей
преобразования методом совмещения оси поворота с осью z (уравнения (3-21) и (3-23)-
(3-26)).
а(,) = массив, содержащий две точки оси поворота
delta = угол поворота относительно произвольной оси в градусах
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица поворота
subroutine genrot (a(,),delta; t(,))
option angle degrees
dimension rx(4,4) ,ry(4,4) ,rdelta(4,4) ,rxmv(4,4) ,ryinv(4,4)
dimension tran(4)4),traninv(4,4)
dimension m(4,4),minv(4,4)
dimension templ(4,4),temp2(4,4)
Mat rx = Idn
Mat ry = Idn
Mat rdelta = Idn
Mat tran = Idn
Mat rxinv = Idn
Mat ryinv = Idn
Mat traninv = Idn
вычислить направляющие косинусы
ex = a(2,l) - a(l,l)
cy = a(2,2) - a(l,2)
cz = a(2,3) - a(l,3)
nfactor = Sqrt(cx*cx + cy*cy + cz*cz)
ex = cx/nfactor
cy = cy/nfactor
cz = cz/nfactor
d = Sqrt(cy*cy + cz*cz)
установить значения переменных матриц
заметим, что, так как гх и ту — абсолютные повороты, обращение
является транспонированием
tran(4,l) = -a(l,l)
tran(4,2) = -a(l,2)
tran(4,3) = -a(l,3)
traninv(4,l) = a(l,l)
traninv(4,2) = a(l,2)
traninv(4,3) = a(l,3)
гх(2,2) = cz/d
гх(2,3) = cy/d
rx(3,2) = -гх(2,3)
rx(3,3) = гх(2,2)
Mat rxinv = ТУп(гх)
ry(l,l)=d
ry(l,3)=cx
ry(3,l)=-cx
ry(3,3)=d
Mat ryinv = ТУп(гу)
rdelta(l,l)=Cos(delta)
rdelta(2,2)=rdelta(l,l)
rdelta(l,2)=Sin(delta)
rdelta(2,l)=-rdelta(l,2)
конкатенировать переменные матрицы
Mat tempi = rx*ry
Mat m = tran*tempi
Mat temp2 = rxinv*traninv
Mat minv = ryinv*temp2
Mat tempi = rdelta*minv
Mat temp2 = m*templ
Mat t = t*temp2
return
imsometric
Подпрограмма формирует матрицу изометрической проекции и
конкатенирует ее с текущей матрицей преобразования (уравнения (3-32), (3-41) и пример
3-15).
4(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица изометрической проекции
xcode = код х поворота
О = отрицательный угол поворота
1= положительный угол поворота
ycode = код у поворота
О = отрицательный угол поворота
1= положительный угол поворота
subroutine isometric (ycode,xcode; t(,))
option angle degrees
установить значения направлений поворота
if ycode = 0 then phi = —45
if ycode = 1 then phi = 45
if xcode = 0 then pheta = -35.26439
if xcode = 1 then pheta = 35.26439
выполнить изометрические преобразования, вызвав yrot, xrot u project
call yrot(phi; t)
call xrot(pheta; t)
call project(3; t)
return
oblique
Подпрограмма формирует матрицу косоугольной проекции и конкатенирует
ее с текущей матрицей преобразования (уравнение (3-44)).
alpha = угол между горизонталью и осью проекции z
f = коэффициент искажения в направлении z
4(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица косоугольной проекции
subroutine oblique (alpha,f; t(,))
option angle degrees
dimension oblique(4,4)
Mat oblique = Idn
oblique(3,3) = 0
oblique(3,l) = —f*Cos(alpha)
oblique(3,2) = —f*Sin(alpha)
Mat t = t*oblique
return
perspecitve
Подпрограмма формирует матрицу центральной перспективной проекции на
плоскость z = 0 и конкатенирует ее с текущей матрицей преобразования
(уравнение (3-47)).
ср = центр проекции на оси z
f(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица перспективной проекции
subroutine perspective (cp; t(,))
option angle degrees
dimension perspective(4,4)
Mat perspective = Idn
perspective(3,3) = 0
perspective(3,4) = — 1/cp
Mat t = t*perspective
return
project
Подпрограмма формирует матрицу простой ортографической проекции на
одну из координатных плоскостей и конкатенирует ее с текущей матрицей
преобразования (уравнения (3-27)-(3-29)).
PT0J(>) = матрица проекции
projcode = код проекции
1 = на плоскость х = О
2 = на плоскость у = О
3 = на плоскость z = О
4(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица проекции
установить значения преобразующей матрицы
конкатенировать матрицы
установить значения матрицы центральной
перспективной проекции
конкатенировать матрицы
subroutine project (projcode; t(,))
dimension proj(4,4)
Mat proj = Idn
if projcode = 1 then proj(l,l) = 0 установить соответствующий элемент
матрицы равным О
if projcode = 2 then proj(2,2) = О
if projcode = 3 then proj(3,3) = 0
Mat t = t*proj конкатенировать матрицы
return
reflt3d
Подпрограмма формирует матрицу зеркального отражения в пространстве и
конкатенирует ее с текущей матрицей преобразования (уравнения (3-11)—(3-13)).
refltcode = код отражения
1 = относительно плоскости х — О
2 = относительно плоскости у = О
3 = относительно плоскости z = О
re/^G) = матрица отражения
£(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица отражения
subroutine reflt3d (frltcode; t(,))
dimension reflt(4,4)
Mat refit = Idn
if rfltcode = 1 then reflt(l,l) = -1
if rfltcode = 2 then reflt(2,2) = -1
if rfltcode = 3 then reflt(3,3) = -1
Mat t = Ureflt
return
scale3d
Подпрограмма формирует матрицу масштабирования в пространстве и
конкатенирует ее с текущей матрицей преобразования (уравнения (3-3) и (3-4)).
а = масштабирующий множитель в направлении х а > 1 —
растяжение; о < 1 — сжатие
е = масштабирующий множитель в направлении у е > 1 —
растяжение; е < 1 — сжатие
j = масштабирующий множитель в направлении z j > 1 —
растяжение; j < 1 — сжатие
s — общий масштабирующий множитель s > 1 — увеличение;
s < 1 — сокращение
scale = масштабирующая матрица
£(,) = текущая преобразующая матрица, с которой будет
конкатенирована масштабирующая матрица
установить соответствующий терм
в матрице отражения равным —1
конкатенировать матрицы
subroutine scale3d (a,ej,s; t(,))
option angle degrees
dimension scale(4,4)
Mat scale = Zer
scale(l,l) = а установить значения масштабирующей матрицы
scale(2,2) = е
scale(3,3) = j
scale(4,4) = 1/s
Mat t = t*scale конкатенировать матрицы
return
tran3d
Подпрограмма формирует матрицу параллельного переноса в пространстве и
конкатенирует ее с текущей матрицей преобразования (уравнение (3-14)).
/ = множитель переноса в направлении х
т = множитель переноса в направлении у
п = множитель переноса в направлении z
tran(,) = матрица переноса
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица переноса
subroutine tran3d(l,m,n; t(,))
dimension tran(4,4)
Mat trail = Idn
tran(4,l) = 1
tran(4,2) = m
tran(4,3) = n
Mat t = t*tran
return
xrot
Подпрограмма формирует матрицу поворота в пространстве относительно оси
х и конкатенирует ее текущей матрицей преобразования (уравнение (3-6)).
rot(,) = матрица поворота
theta = угол поворота в градусах
*(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица поворота
subroutine xrot (theta; t(,))
option angle degrees
dimension rot(4,4)
Mat rot = Idn
rot(2,2) = Cos(theta)
rot(2,3) = Sin(theta)
rot(3,3) = rot(2,2)
rot(3,2) = -rot(2,3)
Mat t = t*rot
return
установка значений матрицы поворота
конкатенировать матрицы
установка матрицы поворота
конкатенировать матрицы
yrot
Подпрограмма формирует матрицу поворота в пространстве относительно оси
у и конкатенирует ее с прикладной матрицей преобразования (уравнение (3-8)).
phi = угол поворота в градусах
rot(,) = матрица поворота
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица поворота
subroutine yrot (phi; t(,))
option angle degrees
dimension rot (4,4)
Mat rot = Idn
rot(l,l) = Cos(phi)
rot(3,l) = Sin(phi)
rot(3,3) = rot(l,l)
rot(l,3) = -rot(3,l)
Mat t = t*rot
return
zrot
Подпрограмма формирует матрицу поворота в пространстве относительно оси
z и конкатенирует ее с текущей матрицей преобразования (уравнение (3-7)).
rot(,) = матрица поворота
theta = угол поворота в градусах
t(,) = текущая преобразующая матрица, с которой будет
конкатенирована матрица поворота
subroutine zrot (theta; t(,))
option angle degrees
dimension rot(4,4)
Mat rot = Idn
rot(l,l) = Cos(theta)
rot(l,2) = Sin(theta)
rot(2,2) = rot(l,l)
rot(2,l) = -rot(l,2)
Mat t = t*rot
return
ГЛАВА 4
Здесь даны алгоритмы, которые генерируют точки на периметре конического
сектора. В алфавитном порядке это circle, ellipse, hyper 1, hyper 2, parabola.
Каждый из этих алгоритмов легко модифицируется для генерации точек на
отдельной части конического сектора.
установка матрицы поворота
конкатенировать матрицы
установка матрицы поворота
конкатенировать матрицы
circle
Подпрограмма генерирует точки на внешней окружности круга (уравнение
(4-5)).
cdtheta = cos (dtheta)
circ(,) = массив, содержащий точки плоскости
сггс(Д) = координата х
сггс(,2) = координата у
dtheta = приращение theta
h = координата х центра окружности
к = координата у центра окружности
п = число точек на окружности
г = радиус
sdtheta = sin (dtheta)
tcirc(,) = массив, содержащий точки плоскости
tcirc(,l) = координата х
tcirc(,2) = координата у
tcirc(,Z) = 1, однородная координата
t(,) = матрица переноса в плоскости 3x3
subroutine circle (h,k,r,n; circ(,))
option angle degrees
dimension t(3,3),tcirc(256,3)
изменение размера, заполнение преобразования и массива tcirc
Mat rot = Idn
Mat tcirc = Zer(n,3)
Mat tcirc = Con(n,3)
определение констант
dtheta = 360/(n - 1)
cdtheta = Cos(dtheta)
sdtheta = Sin(dtheta)
определение начальной точки
tcirc(l,l) = г
tcirc(l,2) = 0
вычисление точек на исходной центрированной окружности,
for i = 2 to n
tcirc(i,l) = cdtheta*tcirc(i — 1,1) — sdtheta*tcirc(i —1,2)
tcirc(i,2) = sdtheta*tcirc(i — 1,1) + cdtheta*tcirc(i —1,2)
next i
перенос результатов в h, k
call tran2d(h,k; t)
Mat tcirc = tcirc*t
приписывание перенесенных значений в массив 2D
for i = 1 to n
circ(i,l) — tcirc(i,l)
circ(i,2) = tcirc(i,2)
next i
return
ellipse
Подпрограмма генерирует точки на периметре эллипса (уравнение (4-8)).
о = длина большой полуоси
Ъ = длина малой полуоси
с\ = константа —(а/Ъ)* cdtheta
cl = константа — (Ъ/a)* sdtheta
cdtheta = константа — cos (dtheta)
dtheta = приращение параметра
ellip(,) = массив, содержащий точки эллипса
ellip(,l) = компонента х
ellip(,2) = компонента у
h = х координата центра эллипса
inclin = угол наклона большой оси в градусах
к = у координата центра эллипса
п = число точек на эллипсе
sdtheta = константа — sin (dtheta)
tellip(,) = 1,массив, содержащий однородные точки пространства
tellip(,l) = x координата
tellip(,2) = у координата
tellip(,Z) = 1, однородная координата
t(,) = матрица преобразования в плоскости 3x3
subroutine ellipse (h.k.a^inclinjii; ellip(,))
option angle degrees
dimension t(3,3),tellip(256,3)
изменение размера, заполнение преобразования и массива tellip
Mat t = Idn
Mat tellip = Zer(n,3)
Mat tellip = Con(n,3)
определение констант
dtheta = 360/(n - 1)
cdtheta = Cos (dtheta)
sdtheta = Sin(dtheta)
cl = (a/b)*sdtheta
c2 = (b/a)*sdtheta
определение начальной точки
tellip(l,l) = a
tellip(l,2) = 0
вычисление точек на исходном центрированном эллипсе
for i = 2 to n
tellip(i,l) = tellip(i - l,l)*cdtheta - cl*tellip(i -1,2)
tellip(i,2) = c2*tellip(i - 1,1) + tellip(i -l,2)*cdtheta
next i
поворот на i и перенос результатов в h, k
call rot2d(inclin; t)
call tran2d(h,k; t)
Mat tellip = tellip*t
приписывание перенесенных значений в массив 2D
for i = 1 to n
ellip(i.l) = tellip(i,l)
ellip(i,2) = tellip(i,2)
next i
return
hyper 1
Подпрограмма генерирует точки на гиперболе (уравнение (4-15)).
Генерирует только гипербола в первом квадранте, открытая вправо, с осью х в качестве
оси симметрии. Полная гипербола может быть получена зеркальным отражением
сначала относительно оси х, затем относительно оси у. Произвольные ориентация
и центральные позиции могут быть получены соответствующими поворотами и
переносами.
о = расстояние от центра гиперболы до вертикали
Ь = определяет наклон асимптот = ±Ь/о
cl = константа — (b)*tdtheta
с2 = константа — (a)*cdtheta
cdtheta = константа — cos (dtheta)
dtheta = приращение параметра
hyper (,) = массив, содержащий точки параболы
hyper(,1) = х компонента
hyper(,2) = у компонента
п = число точек на гиперболе
tdtheta = константа — ton (dtheta)
sdtheta(,) = 1, константа — sin (dtheta)
subroutine hyperl (a,b,n; hyper(,))
изменение размера и заполнение массива hyper нулями
Mat hyper = Zer(n,2)
определение констант
dtheta = (Pi/2)(n - 1)
cdtheta = Cos(dtheta)
sdtheta = Sin(dtheta)
tdtheta = Tan(dtheta)
cl = (b)*tdtheta
c2 = (b)*cdtheta
определение начальной точки
hyper(l,l) = a
hyper(l,2) = 0
вычисление точек на исходной центрированной гиперболе
for i = 2 to n
hyper(i,l) = b*hyper(i — l,l)/(c2 — sdtheta*hyper(i —1,2)
hyper(i,2) = b*(hyper(i - 1,2) + cl)/(b - hyper(i -l,2)*tdtheta)
next i
return
hyper 2
Подпрограмма генерирует точки на гиперболе с использованием
гиперболических функций (уравнение (4-17)). Генерируется только гипербола в первом
квадранте, открытая вправо, с осью х в качестве оси симметрии. Полная гипербола
может быть получена зеркальным отражением сначала относительно оси х,
потом относительно оси у. Произвольные ориентация и центральные позиции могут
быть получены соответствующими поворотами и переносами.
а
Ь
с\
с2
cdtheta
dtheta
hyper(,)
п
s dtheta
thetamax(,)
= расстояние от центра гиперболы до вертикали
= определяет наклон асимптот = ±Ь/а
= константа — (a/b)*sdtheta
= константа — (b/a)*sdtheta
= константа — cosh (dtheta)
= приращение параметра
= массив, содержащий точки параболы
hyper(,l) — х компонента
hyper(,2) = у компонента
= число точек на гиперболе
= константа — sinh (dtheta)
= максимальное значение параметра
subroutine hyper2 (a,b,thetamax,n; hyper(,))
изменение размера и заполнение массива hyper нулями
Mat hyper = Zer(n,2)
определение констант
dtheta = thetamax(n — 1)
cdtheta = Cosh(dtheta)
sdtheta = Sinh(dtheta)
cl = (a/b)*sdtheta
c2 = (b/a)*sdtheta
определение начальной точки
hyper(l,l) = a
hyper(l,2) = 0
вычисление точек на исходной центрированной гиперболе
for i = 2 to n
hyper(i,l) = hyper(i — l,l)*cdtheta + cl*hyper(i — 1,2)
hyper(i,2) = c2*hyper(i — 1,1) + hyper(i — l,2)*cdtheta)
next i
return
parabola
Подпрограмма генерирует в первом квадранте точки на параболе,
симметричной относительной оси х, открытой вправо (уравнение (4-12)). Для генерации
полной параболы в пространстве, расположенной в произвольной позиции и
произвольной ориентации, применяют необходимые преобразования зеркального
отражения, поворота и параллельного переноса.
0 = расстояние от фокуса до вертикали параболы
01 = константа —■ a* dtheta* dtheta
Ы = константа 2 * a* dtheta
dtheta = приращение параметра
п = число точек на параболе
рага(,) = массив, содержащий точки параболы
рага(,1) = координата х
рага(,2) = координата у
thetamax = максимальное значение параметра
subroutine parabola (a,thetamax,n; para(,))
изменение размера и заполнение массива para нулями
Mat para = Zer(n,2)
определение констант
dtheta = thetamax/(n — 1)
al = a*dtheta*dtheta
Ы = 2*a*dtheta
определение начальной точки
рага(1,1) = О
рага(1,2) = О
вычисление точек на исходной параболе
for i = 2 to n
para(i,l) = para(i — 1,1) + dtheta*para(i — 1,2) + al
para(i,2) = para(i — 1,2) + Ы
next i
return
ГЛАВА 5
Здесь приведены алгоритмы реализации методов построения оболочек.
Алгоритмы даны для кубического сплайна, параболически смешанных кривых и
кривых В-сплайна. Алгоритмы каркасного представления кривых даны для кривых
Безье, для рациональных и нерациональных кривых В-сплайна, однородных и
неоднородных узловых векторов и для базисных функций В-сплайна: basis, bezier,
bsplfit, bspline, bsplineu, cblend, cspline, dbasis, dbasisu, dbezier, dbspline,
dbsplineu, knot, knotc, knotu, matpbspl, nmatrix, parabld, param, rbasis,
rbspline, rbsplinu.
basis
Подпрограмма генерирует базисные функции В-сплайна для открытых
неоднородных узловых векторов (уравнение (5-84)).
с = порядок базисной функции В-сплайна
d = первый терм рекурсивного отношения базисной функции
е = второй терм рекурсивного отношения базисной функции
npts = число вершин определяющего многоугольника
п(,) = массив, содержащий базисные функции
п(1,1) содержит базисную функцию, соответствующую В\ и т. д.
nplusc = константа — npts +c — максимальное
значение номера узла
t = значение параметра
tempQ = временный массив
х() = узловой вектор
subroutine basis (c,t,npts,x(); n(,))
dimension temp(20) допускает 20 вершин многоугольника
nplusc = npts + с
вычисление основных функций Ni,i (см. уравнения (5-84а))
for i = 1 to nplusc — 1
if t >= x(i) and t < x(i + 1) then
temp(i) = 1
else
temp(i) = 0
end if
next i
вычисление основных функций высшего порядка (см. уравнения (5-8$))
for к = 2 to с
for i = 1 to nplusc — к
if temp(i) ф 0 then если основная функция равна нулю, пропустите вычисление
d=((t-x(i))*temp(i))/(x(i+k-l)-x(i))
else
d=0
end if
if temp(i+l)^0 then если основная функция равна нулю, пропустите вычисление
е = ((x(i + к) - t)*temp(i + l))/(x(i + к) - x(i + 1))
else
е = 0
end if
tepm(i)=d+e
next i
next к
if t = x(nplusc) then temp(npts) = 1 начните с последней точки
вставить в массив
for i = 1 to npts
n(l,i) = temp(i)
next i
if t = x(nplusc) then n(l,npts) = 1 начните с последней точки
return
bezier
Подпрограмма вычисляет кривую Безье (уравнеие (5-62)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
Ь(,1) содержит компоненту х вершины
Ь(,2) содержит компоненту у вершины
Ь(,3) содержит компоненту z вершины
Basis = функция для вычисления базисного значения Бернштейна (уравнение (5-63))
cpts = число точек, которые будут вычислены на кривой
Factrl = функции для вычисления факториала числа
j(,) = базисная функция Бернштейна
Ni = функции факториала для базисной функции Бернштейна
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р(,1)содермсит компоненту х точки
р{,2) содержит компоненту у точки
р{,3) содержит компоненту z точки
t = значение параметра 0<t < 1
subroutine bezier (npts,b(,),cpts; p(,))
defNi(n,i)=Factrl(n)/Factrl(i)*Factrl(n— i)) функция факториал
def Basis(n,i,t) = Ni(n,i)*(tAi)*((l —t) Л(п — i)) базисная функция Вернштейна
dimension j(l,20) допускает 20 вершин многоугольника
dimension temp(l,3)
icount = 0
Mat j = Zer(l,npts)
for t = 0 to 1 step l/(cpts — 1)
icount = icount + 1
определение основной функции Вернштейна (см. уравнение (5-63))
for i = 1 to npts
j(l,i) = Basis(npts — l,i — l,t)
next i
определение точки на кривой
Mat temp = j*b
вставить в массив
for i = 1 to 3
p(icount,i) = temp(l,i)
next i
mext t
return
bsplfit
Подпрограмма выравнивает кривую В-сплайна, используя открытый
однородный узловой вектор (уравнение (5-117)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
Ь(,1) содержит компоненту х вершины
Ь(,2) содержит компоненту у вершины
Ь(,3) содержит компоненту z вершины
dpts = число точек данных
d(,) = массив, содержащий точки данных
d(,l) содержит х компоненту точки данных
d{,2) содержит у компоненту точки данных
d{,3) содержит z компоненту точки данных
к = порядок базисной функции В-сплайна
п = матрица базисной функции
nbasis = массив, содержащий базисные функции для единственного значения t
ninv = обращение trn(n)xn
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
ntemp = временная матрица для хранения trn(n)xn
ntmp = временная матрица для хранения обращения trn(n)xnxd
ntrn = транспонирование матрицы п
t = параметрическое значение 0 <t < 1
tpar§ = массив, содержащий аппроксимацию хордами для параметрических значений
я; () = массив, содержащий узловой вектор
subroutine bsplfit (dpts,d(,),npts,k; b(,))
dimension nbasis(l,20),x(30))n(20,20),temp(l,3) допускает данные о 20 точках
dimension tpar(20),ninv(20,20),ntrn(20,20),ntemp(20,20),ntmp(20,3)
изменение размера и заполнение матриц нулями
Mat nbasis = Zer(l,npts)
Mat x = Zer(npts + k)
Mat n = Zer(dpts,npts)
Mat ntrn = Zer(npts,dpts)
Mat ntemp = Zer(npts,npts)
Mat ntmp = Zer(npts,2)
Mat ninv = Zer(npts,npts)
Mat tpar = Zer(dpts)
call knot(npts,k; x())
call param(dpts,d; tpax)
nplusc = npts + к
генерация матрицы основных функций
for i = 1 to dpts
t = tpar(i)*x(nplusc) вычисление значения параметра для одной строки
call basis(k,t,npts,x; nbasis) вычисление основной функции для одной строки
for j = 1 to npts
n(i,j) = nbasis(lj) построение матрицы строка за строкой
next j
next i
генерация вершин определяющего многоугольника методом наименьших квадратов
Mat ntrn = trn(n) нахождение транспонированной матрицы основной функции
Mat ntemp = ntrn*n trn(n)xn
Mat ninv = Inv(ntemp) обращение матрицы tTn(n)xn
Mat ntmp = ntrn*d обращение матрицы tTn(n)xn x d
Mat b = ninv*ntmp вычисление вершин определяющего многоугольника
return
bspline
Подпрограмма генерирует кривую В-сплайна, используя открытый
однородный узловой вектор (уравнение (5-83)).
6(,) = массив, содержащий вершины определяющего многоугольника
Ь(,1) содержит компоненту х вершины
Ь(,2) содержит компоненту у вершины
Ь(,3) содержит компоненту z вершины
к = порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для единственного значения
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р(,1) содержит компоненту х точки
р(,2) содержит компоненту у точки
р(,3) содержит компоненту z точки
pi = число вычисляемых точек кривой
t = параметрическое значение 0 <t < 1
х() = массив, содержащий вектор
subroutine bspline (npts,k,pl,b(,); p(,))
dimension nbasis(l,20),x(30),temp(l,3)
nplusc = npts + k
допускает 20 вершин многоугольников
с базисной функцией порядка б
обнулить и изменить размерность узлового вектора и базисного массива
Mat nbasis = Zer(l,npts)
Mat x = Zer(nplusc)
генерация однородного открытого узлового вектора
call knot(npts,k; x)
icount = 0
вычисление точек на кривой В-сплайна
for t = 0 to x(npts + к) step x(npts + k)/(pl — 1)
icount = icount + 1
call basis(k,t,npts,x; nbasis) генерация базисной функции для этого значения t
Mat temp = nbasis*b генерация точки кривой
p(icount,l) = temp(l,l) приписывание текущего значения точки кривой
p(icount,2) = temp(l,2) массиву этой кривой
p(icount,3) = temp(l,3)
next t
return
bsplineu
Подпрограмма генерирует кривую В-сплайна, используя периодический
однородный узловой вектор (уравнение (5-83)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит, компоненту у вершины
Ь{ ,3) содержит компоненту z вершины
к = порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для
единственного значения t
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р( ,1) содержит компоненту х точки
р{ ,2) содержит, компоненту у точки
р( ,3) содержит, компоненту z точки
pi = число вычисляемых точек кривой
t = параметрическое значение 0 <t < 1
х() = массив, содержащий узловой вектор
subroutine bspline (npts,k,pl,b(,); p(,))
dimension nbasis(l,20),x(30),temp(l,3) допускает 20 вершин многоугольника
с базисной функцией порядка б
обнулить и изменить размерность узлового вектора и базисного массива
Mat nbasis = Zer(l,npts)
Mat x = Zer(npts + k)
nplusc = npts + k
генерация однородного периодического узлового вектора
call knotu(npts,k; x)
icount = О
вычисление точек на кривой В-сплайна
for t = (k - 1) to (npts -1 + 1) step (npts - 1 + 1) - (k - l)/(pl - 1)
icount = icount + 1
call basis(k,t,npts,x; nbasis)
Mat temp = nbasis*b
p(icount,l) = temp(l,l)
p(icount,2) = temp(l,2)
next t
return
cblend
Подпрограмма вычисляет нормализованные кубические смешанные функции
(уравнение (5-21)).
/(,) = массив 1 х 4у содержащий смешанные функции
f(l,l) содержит F\
f(l,2) содержит Fi
f(l,3) содержит F^
f(l,4) содержит, Fa
tau = значение нормализованного параметра 0 < tau < 1
subroutine cblend (tau; f(,))
f(l,l) = 2* (tau)A 3 - 3*(tau)A 2 + 1
f(l,2) = -2* (tau)A 3 + 3*(tau)A 2
f(l,3) = tau* ((tau)A 2 - 2*tau + 1)
f(l,4) = tau* ((tau)A 2 - tau)
return
cspline
Подпрограмма вычисляет кривую кубического сплайна (уравнение (5-1)).
bcflag = флаг граничного условия
bcflag = 1 — условия закрепленных концов
bcflag = 2 — условия свободных концов
d(,) = массив, содержащий подходящие точки данных
d ( ,1) содержит компоненту х точки данных
d ( ,2) содержит компоненту у точки данных
d ( ,3) содержит компоненту z точки данных
/(,) = массив 1 х 4, содержащий смешанные функции
f(l,l) содержит, F\
f(l,2) содержит Fi
f{l,3) содержит F^
f(l,4) содержит F4
g = геометрическая матрица
icount = счетчик числа точек на кривой
тп(,) = матрица коэффициентов [М] (уравнение (5-15))
minv(,) = обращение матрицы коэффициентов [М]
npts = число подходящих точек
р(,) = массив, содержащий точки кривой
р( ,1) содержит компоненту х точки
р( ,2) содержит компоненту у точки
р( ,3) содержит компоненту z точки
генерация базисной функции для этого значения t
генерация точки на кривой
приписывание текущего значения точки на кривой
массиву этой кривой
point(,) = единственная точка кривой
point(l,l) содержит компоненту х точки
point(l,2) содержит компоненту у точки
point(l,3) содержит компоненту z точки
pi = число точек, вычисляемых для каждого сегмента кривой
г(,) = матрица [R] для умножения справа (уравнение (5-15))
£(,) = матрица параметра, аппроксимированного хордами
tangent(,) = матрица касательного вектора (уравнение (5-15))
tau = значение нормализованного параметра 0 < tau < 1
subroutine cspline (npts,pl,d(,),bcflagl,icount,tangeiit(,); p(,))
dimension t(20),m(20,20),mmv(20,20),r(20,3) допускает данные для 20 точек
dimension g(4,3),point(l,3))f(l,4)
Mat m = Zer(npts,npts)
Mat minv = Zer(npts,npts)
Mat г = Zer(npts,3)
Mat t = Zer(npts)
определение значений параметра с использованием хордовой аппроксимации
(уравнение (5-2))
for i = 2 to npts
t(i) = Sqrt((d(i,l)-d(i - l,l))A2+(d(i,2)- d(i- 1,2))л 2)
next i
вставить коэффициенты матрицы [М] (уравнение (5-15))
for i = 2 to npts — 1
m(i,i - 1) = t(i + 1)
m(i,i) = 2*(t(i) + t(i + 1))
m(i,i + 1) = t(i)
next i
вставить первую строку матрицы [R] (уравнение (5-15))
for i = 2 to npts — 1
coeff = (3/(t(i)*t(i + 1)))
for j = 1 to 3
r(ij) = coeff*((t(i)A2)*(d(i + 1 j) - d(ij)) + (t(i + l)A2)*(d(ij) - d(i - IJ)))
next j
next i
добавить граничные условия в матрицы (табл. 5-3)
bcflag = 1 — зафиксировать концевые условия
bcflag = 2 — погасить концевые условия
циклические и антициклические граничные условия рассмотреть как упражнение
if bcflag = 1 then
m(l,l) = 1
m(npts,npts) = 1
for j = 1 to 3
r(l j) = tangent(l j)
r(nptsj) = tangent(nptsj)
next j
end if
if bcflag = 2 then
m(l,l) =1
01(1,2) = 1/2
m(npts,npts — 1) = 2
m(npts,npts) = 4
for j = 1 to 3
r(ij) = (3/2*t(2)))*(d(2j) - d(l,j))
r(nptsj) = (6/t(npts))*(d(nptsj) - d(npts - lj))
next j
end if
вставить коэффициенты матриц [М] (уравнение (5-16))
Mat minv = Inv(m)
вычислить внутренние касательные векторы для [М]_ [R]
Mat tangent = minv*r
генерировать точки на кубическом сплайне (уравнение (5-22))
ограничить интервал для предупреждения вычислений точки на конце интервала,
дважды убрать эту последнюю точку позже
icount = О
for i. = 2 to npts
for tau = 0 to 1 — (l/(pl — 1)) step l/(pl — 1) pl>l или ошибка в результате
icount = icount + 1
' установить матрицу смешанной функции (уравнение (5-21))
f(l,l) = -2*(tauA 3) + 3*(tau Л2)+1
f(l,2) = 2*(tauA3) - 3*(tau Л2)
f(l,3) = tau*(tauA2 — 2*tau + l)*t(i)
f(l,4) = tau*(tauA2 — tau)*t(i)
установить геометрическую матрицу (уравнение (5-20))
for j = 1 to 3
g(lj) = d(i - lj)
g(2,j) = d(i j)
g(3,j) = tangent(i - lj)
g(4j) = tangent(ij)
next j
вычислить единственную точку на кривой (уравнение (5-22))
Mat point = f*g
приписать векторную матрицу
for j = 1 to 3
p(icount j) = point(l j)
next j
next tau
next i
сохранить специально последнюю точку
icount = icount + 1
for j = 1 to 3
p(icount j) = d(nptsj)
next j
return
dbasis
Подпрограмма генерирует базисные функции В-сплайна и их производные для
однородных открытых узловых векторов (уравнения (5-84) и (5-97)—(5-100)).
Ы = первый терм базисной функции
Ъ2 = второй терм базисной функции
с = порядок базисной функции В-сплайна
dl (,) = массив, содержащий производную базисной функции
dl(l,l) содержит производную базисной функции для В\ и т.д.
d2(,) = массив, содержащий производную базисной функции
d2(l,l) содержит производную базисной функции для В\ и т.д.
f1 = первый терм первой производной базисной функции
f2 = второй терм первой производной базисной функции
f3 = третий терм первой производной базисной функции
f4 = четвертый терм первой производной базисной функции
npts = число вершин определяющего многоугольника
п(,) = массив, содержащий базисные функции
п(1,1) содержит базисную функцию для Вг и т. д.
nplusc — содержит максимальное узловое значение
si = первый терм второй производной базисной функции
s2 = второй терм второй производной базисной функции
33 = третий терм второй производной базисной функции
34 = четвертый терм второй производной базисной функции
t = параметрическое значение
tempQ = временный массив
х() = узловой вектор
subroutine dbasis (c,t,npts,x(); n(,),dl(,),d2(,))
dimension temp(20),templ(20),temp2(20) допускает 20 вершин многоугольника
nplusc = npts + с
заполнение нулями временных массивов
Mat temp = Zer(npts + с)
Mat tempi = Zer(npts + с)
Mat temp2 = Zer(npts + c)
вычислить базисные функции первого порядка n(i,j) (уравнения (5-84а))
for i = 1 to nplusc — 1
if t > x(i) and t < x(i + 1) then
temp(i) = 1
else
temp(i) = 0
end if
next i
if t = x(nplusc) then temp(npts) = 1 обработать конец специально
вычислить базисные функции высшего порядка и их производные
(уравнения (Б-ЦЪ) и (5-97)-(5-100))
for k = 2 to с
for i = 1 to nplusc — к
вычислить базисную функцию
if temp(i) ф 0 then если базисная функция равна нулю, прервать вычисление
Ы = ((t - x(i))*temp(i))/(x(i + к - 1) - x(i))
else
ы = о
end if
if temp(i +1)^0 then если базисная функция равна нулю, прервать вычисление
Ъ2 = ((x(i + к) - t)*temp(i + l))/(x(i + к) - x(i + 1))
else
Ь2 = 0
end if
вычислить первую производную
if temp(i) ф О then если базисная функция равна нулю, прервать вычисление
fl = temp(i)/(x(i + к - 1) - x(i))
else
fl = 0
end if
if temp(i + 1) ф 0 then если базисная функция равна нулю, прервать вычисление
f2 = -temp(i + l)/(x(i + к) - x(i))
else
f2 = 0
end if
if tempi (i) ф 0 then если базисная функция равна нулю, прервать вычиление
{3 = (t - x(i))*templ(i)/(x(i + к - 1) - x(i + 1))
else
Й = 0
end if
if tempi (i + 1) ф 0 then если базисная функция равна нулю, прервать вычисление
f4 = (x(i + к) - t)*templ(i + l)/(x(i + к) - x(i + 1))
else
f4 = 0
end if
вычислить вторую производную
if tempi (i) ф 0 then если базисная функция равна нулю, прервать вычисление
si = 2*templ(i)/(x(i + к - 1) - x(i))
else
si = О
end if
if tempi (i + 1)^0 then если базисная функция равна нулю, прервать вычисление
s2 = -2*templ(i + l)/(x(i + к) - x(i + 1))
else
s2 = О
end if
if temp2(i) ф 0 then если базисная функция равна нулю, прервать вычисление
s3 = (t - x(i))*temp2(i)/(x(i + к - 1) - x(i))
else
s3 = О
end if
if temp2(i + 1) ф 0 then если базисная функция равна нулю, прервать вычисление
s4 = (x(i + к) - t)*temp2(i + l)/(x(i + к) - x(i + 1))
else
s4 = 0
end if
temp(i) = bl + b2
templ(i) = fl+f2+f3+f4
temp2(i) = si + s2 + s3 + s4
next i
next к
вставьте в массив
for i = 1 to npts
n(l,i) = temp(i)
dl(l,i) = templ(i)
d2(l,i) = temp2(i)
next i
return
dbasisu
Подпрограмма генерирует базисные функции В-сплайна и их производные для
однородных периодических узловых векторов (уравнения (5-84) и (5-97)-(5-100)).
Ы = первый терм базисной функции
Ь2 = второй терм базисной функции
с = порядок базисной функции В-сплайна
dl(,) = массив, содержащий производную базисных функций
dl(l,l) содержит производную базисной функции для В\ и т.д.
d2(,) = массив, содержащий производную базисных функций
d2(l,l) содержит производную базисной функции для В\ и т. д.
fl = первый терм первой производной базисной функции
f2 = второй терм первой производной базисной функции
f3 = третий терм первой производной базисной функции
f4 = четвертый терм первой производной базисной функции
npts = число вершин определяющего многоугольника
п(,) = массив, содержащий базисные функции
п(1,1) содержит базисную функцию для Bi и т. д.
nplusc = содержит максимальное узловое значение
si = первый терм второй производной базисной функции
32 = второй терм второй производной базисной функции
33 = третий терм второй производной базисной функции
34 = четвертый терм второй производной базисной функции
t = параметрическое значение
tempQ = временный массив
i() = узловой вектор
subroutine dbasisu (c,t,npts,x(); n(,),dl(,),d2()))
dimension temp(20),templ(20),temp2(20) do 20 вершин определяющего многоугольника
nplusc = npts + с
заполняем нулями временный массив
Mat temp = Zer (nplusc)
Mat tempi = Zer(nplusc)
Mat temp2 = Zer(nplusc)
вычисляем базисные функции первого порядка Ni,i (уравнения (5-84а))
for i = 1 to nplusc — 1
if t > x(i) and t < x(i + 1) then
temp(i) = 1
else
temp(i) = 0
end if
next i
отдельно определяем конец путем перестановки
базисных функций первого порядка
if t = x(npts + 1) then
temp(npts) = 1
temp(npts + 1) 0
end if
вычисляем базисные функции высших порядков и их производные
уравнения (5-84Ь) и (5-97)-(5-100
for к = 2 to с
for i = 1 to nplusc — к
вычисляем базисную функцию
if teiup(i) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
Ы = ((t - x(i))*temp(i))/(x(i + к - 1) - x(i))
else
bl = О
end if
if temp(i +1)^0 then если базисная функция равна нулю,
пропускаем вычисления
Ъ2 = ((x(i + к) - t)*temp(i + l))/(x(i + к) - x(i + 1))
else
Ь2 = 0
end if
вычисляем первую производную
if temp(i) ф 0 then
fl = temp(i)/(x(i + к - 1) - x(i))
else
fl =0
end if
if temp(i + 1) ф 0 then
f2 = -temp(i + l)/(x(i + k) - x(i))
else
f2 = 0
end if
if templ(i) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
О = (t - x(i))*templ(i)/(x(i + к - 1) - x(i + 1))
else
ft = 0
end if
if templ(i + 1) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
f4 = (x(i + к) - t)*templ(i + l)/(x(i + к) - x(i + 1))
else
f4 = 0
end if
вычисляем вторую производную
if tempi(i) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
si = 2*templ(i)/(x(i + к - 1) - x(i))
else
si = 0
end if
если базисная функция равна нулю,
пропускаем вычисления
если базисная функция равна нулю,
пропускаем вычисления
if tempi(i + 1) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
s2 = -2*templ(i + l)/(x(i + к) - x(i + 1))
else
s2 = 0
end if
if temp2(i) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
s3 = (t - x(i))*temp2(i)/(x(i + к - 1) - x(i))
else
s3 = 0
end if
if temp2(i + 1) ф 0 then если базисная функция равна нулю,
пропускаем вычисления
s4 = (x(i + к) - t)*temp2(i + l)/(x(i + к) - x(i + 1))
else
s4 = 0
end if
temp(i) = bl + Ъ2
templ(i) = fl + f2+f3+f4
temp2(i) = si + s2 + s3 + s4
next i
next к
помещаем в массив
for i = 1 to npts
n(l,i) = temp(i)
dl(l,i) = templ(i)
d2(l,i) = temp2(i)
next i
return
dbezier
Подпрограмма вычисляет кривую Безье и ее первую и вторую производные
(уравнения (5-62), (5-72) и (5-73)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
Basis = функция для вычисления базисного значения Вернхитейна
cpts = число точек, которые будут вычислены на кривой
dl (,) = массив, содержащий первую производную кривой
dl{ ,1) содержит компоненту х производной
dl( ,2) содержит компоненту у производной
dl( ,3) содержит компоненту z производной
d2(,) = массив, содержащий вторую производную кривой
d2( ,1) содержит компоненту х производной
d2( ,2) содержит компоненту у производной
d2( ,3) содержит компоненту z производной
Factrl = функция для вычисления факториала числа
j(,) = базисная функция Вернхитейна
jl(,) = первая производная базисной функции Бернштейна
j2(,) = вторая производная базисной функции Бернштейна
Ni = функция факториала для базиса Бернштейна
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р( ,1) содержит компоненту х точки
р( ,2) содержит компоненту у точки
р( ,3) содержит компоненту z точки
t = значение параметра 0 < t < 1
subroutine dbezier (npts,b(,),cpts; p(,),dl(,),d2(,))
def Ni(n,i) = Factrl(n)/(Factrl(i)*Factrl(n — i)) функция факториала
def Basis(n,i,t) = Ni(n,i)*(tAi)*((l — t)A(n — i)) базисная функция Бернштейна
dimension j(l,20) jl(l,20) J2(l,20) допускает 20 вершин многоугольника
dimension temp( 1,3),templ (1,3) ,temp2(1,3)
определяем размерности и заполняем нулями матрицы
Mat j = Zer(l,npts)
Mat jl = Zer(l,npts)
Mat j2 = Zer(l.npts)
for t = 0 to 1 step l/(cpts — 1)
icount = icount + 1
if icount = cpts then t = 1 необходимо организовать вычисление приращения t
определяем базисную функцию Бернштейна и ее первую и вторую производные
(уравнения (5-63), (5-74), (5-75))
for i = 1 to npts
j(l,i) = Basis (npts — 1, i — l,t)
if t ф 0 and t ф 1 then специально устанавливаем конечные точки
jl(l,i) = (((i - 1) - (npts - l)*t)/(t*(l - t)))*j(l,i)
j2(l,i) = ((i - 1) - (npts - l)*t)A2 - (npts - l)*t*t - (i - 1)*(1 - 2*t)
j2(l,i) = j(l,i)*2(l,i)/(t*t*(l - t)*( - t))
end if
next i
определяем точку кривой
Mat temp — j*b
определяем производные кривой первого и второго порядков (уравнения (5-62), (5-72),
(5-73))
if t <> 0 and t ф 1 then специально устанавливаем концевые точки
Mat tempi = jl*b
Mat temp2 = j2*b
else
if t = 0 then
templ(l,l) = (npts - l)*(b(2,l) - b(l,l))
templ(l,2) = (npts - l)*(b(2,2) - b(l,2))
end if
if t = 0 then
temp2(l,l) = (npts - l)*(npts - 2)*(b(l,l) - 2*b(2,l) + b(3,l))
temp2(l,2) = (npts - l)*(npts - 2)*(b(l,2) - 2*b(2,2) + b(3,2))
end if
if t = 1 then
templ(l,l) = (npts - l)*(b(npts,l) - b(npts - 1,1))
templ(l,2) = (npts - l)*(b(npts,2) - b(npts - 1,2))
end if
if t = 1 then
temp2(l,l) = (b(npts,l) - 2*b(npts - 1,1) + b(npts - 2,1))
temp2(l,l) = (npts - l)*(npts - 2)*temp2(l,l)
temp2(l,2) = (b(npts,2) - 2*b(npts - 1,2) + b(npts - 2,2))
temp2(l,2) = (npts - l)*(npts - 2)*temp2(l,2)
end if
end if
помещаем в массив
for i = 1 to 3
p(icount,i) = temp(l,i)
dl(icount,i) = templ(l,i)
d2(icount,i) = temp(l,i)
next i
next t
return
dbspline
Подпрограмма генерирует кривую В-сплайна и ее производные, используя
открытый однородный узловой вектор (уравнения (5-83), (5-95) и (5-96)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
dl (,) = массив, содержащий первую производную кривой
dl( ,1) содержит компоненту х производной
dl( ,2) содержит компоненту у производной
dl( ,3) содержит компоненту z производной
d2(,) = массив, содержащий вторую производную кривой
d2( ,1) содержит компоненту х производной
d2( ,2) содержит компоненту у производной
d2( ,3) содержит компоненту z производной
dlnbasis(,) = первая производная базисной функции для единственного значения t
d2nbasis(,) = вторая производная базисной функции для единственного значения t
к — порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для единственного значения t
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р{ ,1) содержит компоненту х точки
р( ,2) содержит компоненту у точки
р( ,3) содержит компоненту z точки
pi = число вычисляемых точек кривой
t = параметрическое значение 0<t<l
х() — массив, содержащий узловой вектор
subroutine dbspline (npts,k,pl,b(,); p(,),dl(,),d2(,))
допускает 20 вершин многоугольника с базисной функцией порядка 5
dimension x(30),nbasis(l,20),dlnbasis(l,20),d2nbasis(l,20)
dimension temp(l,3),templ(1,3),temp2(l,3)
определяем размерности и заполняем нулями узловой вектор
и массивы базиса, кривой и производных
Mat р = Zer(pl,3)
Mat dl = Zer(pl,3)
Mat d2 = Zer(pl,3)
Mat nbasis = Zer(l,npts)
Mat dlnbasis = Zer(l,npts)
Mat d2nbasis = Zer(l,npts)
Mat x = Zer(npts + k)
nplusc = npts + к
генерация однородного открытого узлового вектора
call knot(npts,k; x)
icount =0
вычисляем точки на кривой В-сплайна и их первую и вторую производные
for t = 0 to x(nplusc) step x(nplusc)/(pl — 1)
icount = icount + 1
if icount = pi then t = x(nplusc) компенсация для вычисления приращения t
генерация базисной функции и ее производных для этого значения t
(уравнения (5-84) и (5-97)-(5-100))
call dbasis(k,t,npts,x; nbasis,dlnbasis,d2nbasis)
Mat temp = nbasis*b генерация точки на кривой
Mat temp 1 = dlnbasis*b первая производная в этой точке на кривой
Mat temp 2 = d2nbasis*b вторая производная в этой кривой
p(icount,l) = temp(l,l) сохраняем текущее значение точки на кривой
p(icount,2) = temp(l,2) в массиве этой кривой
dl(icount,l) = templ(l,l) сохраняем текущее значение производной в этой точке
dl(icount,2) = templ(l,2) на кривой в массиве производной
d2(icount,l) = temp2(l,l) сохраняем текущее значение производной в этой точке
d2(icount,2) = temp2(l,2) на кривой в массиве производной
next t
return
dbsplineu
Подпрограмма генерирует кривую В-сплайна и ее производные, используя
периодический однородный узловой вектор (уравнения (5^83), (5-95) и (5-96)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
dl (,) = массив, содержащий первую производную кривой
dl{ ,1) содержит компоненту х производной
dl( ,2) содержит компоненту у производной
dl{ ,3) содержит компоненту z производной
d2(,) = массив, содержащий вторую производную кривой
d2( ,1) содержит компоненту х производной
d2( ,2) содержит компоненту у производной
d2( ,3) содержит компоненту z производной
dlnbasis(y) = первая производная базисной функции для единственного значения t
d2nbasis(,) = вторая производная базисной функции для единственного значения t
к = порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для единственного значения t
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
p( ,1) содержит компоненту х точки
р( ,2) содержит компоненту у точки
р( ,3) содержит компоненту z точки
pi = число вычисляемых точек кривой
t = параметрическое значение 0 <t < 1
х0 = массив, содержащий узловой вектор
subroutine dbsplineu (npts,k,pl,b(,); p(>),dl(,),d2(,))
допускает 20 вершин многоугольника с базисной функцией порядка 5
dimension x(30),nbasis(l,20),dlnbasis(l,20),d2nbasis(l,20)
dimension temp(l,3),templ(l,3),temp2(l,3)
определяем размерности и заполняем нулями узловой вектор
и массивы базиса, кривой и производных массива
Mat р = Zer(pl,3)
Mat dl = Zer(pl,3)
Mat d2 = Zer(pl,3)
Mat nbasis = Zer(l,npts)
Mat dlnbasis = Zer(l,npts)
Mat d2nbasis = Zer(l,npts)
Mat x = Zer(npts + k)
nplusc = npts + к
генерация периодического однородного открытого узлового вектора
call knotu(npts,k; x)
icount =0
вычисляем точки на кривой В-сплайна и их первую и вторую производные
(уравнения (5-84), (5-93), (5-94))
for t = (к — 1) to npts step (npts — l))/(pl — 1)
icount = icount + 1
if icount = pi then t = npts компенсация для вычисления приращения t
генерация базисной функции и ее производных для этого значения t
call dbasisu(k,t,npts,x; nbasis,dlnbasis,d2nbasis)
Mat temp = nbasis+b генерация точки на кривой
Mat temp 1 = dl nbasis *b первая производная в этой точке на кривой
Mat temp 2 = d2nbasis*b вторая производная в этой точке на кривой
p(icount,l) = temp(l,l) сохраняем текущее значение точки на кривой
p(icount,2) = temp(l,2) в массиве кривой
dl(icount,l) = templ(l,l) сохраняем текущее значение производной в этой точке
dl(icount,2) = templ(l,2) на кривой в массиве производной
d2(icount,l) = temp2(l,l) сохраняем текущее значение производной в этой точке
d2(icount,2) = temp2(l,2) на кривой в массиве производной
next t
return
knot
Подпрограмма генерирует открытый узловой вектор В-сплайна с
коэффициентом на концах (с. 315).
с = порядок базисной функции
п = число вершин определяющего многоугольника
nplus2 = индекс массива х() для первого приближения
максимального значения узлового вектора
nplusc — максимальное значение узлового вектора — п + с
х() = массив, содержащий узловой вектор
subroutine knot (n>c; x())
nplusc = n + с
nplus2 = n + 2
x(l) = 0
for i = 2 to nplusc
if i > с and i < nplus2 then
x(i) = x(x - 1) + 1
else
x(i) = x(i -. 1)
end if
next i
return
knotc
Подпрограмма генерирует неоднородный открытый узловой вектор,
пропорциональный длинам хорд между вершинами определяющего многоугольника
(уравнение (5-86)).
Ь = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
с = порядок базисной функции
chord = хордовое расстояние между вершинами определяющего многоугольника
csum = накопитель суммы хордовых расстояний
maxchord = сумма хордовых расстояний между вершинами
определяющего многоугольника
npts = число вершин определяющего многоугольника
nplusc = максимальное значение узлового вектора — п + с
numerator = нумератор уравнения (5-86)
х() = массив, содержащий узловой вектор
xchord — компонента х расстояния между вершинами
определяющего многоугольника
ychord = компонента у расстояния между вершинами
определяющего многоугольника
subroutine knotc (npts,c,b(,); x())
dimension chord(20)
nplusc = npts + с
n = npts — 1
определяем размерности и заполняем нулями узловой вектор и значения хорд
Mat chord = Zer(n)
определение хордового расстояния между вершинами определяющего
многоугольника и их суммы
maxchord = О
for i = 2 to npts
xchord = b(i,l) - b(i - 1,1)
ychord = b(i,2) - b(i - 1,2)
chord(i — 1) = Sqrt(xchord*xchord + ychord+ychord)
maxchord = maxchord + chord(i — 1)
next i
заводим к нулей в начале открытого узлового вектора
for i = 1 to с
x(i) = О
next i
генерация внутренних узловых значений
for i = 1 to n — с + 1
csum = 0
for i = 1 to i
csum = csum + chord(j)
next j
numerator = (i/(n — с + 2))*chord(i + 1) + csum
x(c + i) = (numerator/maxchord)*(n — с + 2)
next i
заводим k нулей в конце открытого узлового вектора
for i = n + 2 to nplusc
x(i = n - с + 2
next i
return
knotu
Подпрограмма генерирует периодический однородный открытый узловой
вектор В-сплайна (с. 311).
с = порядок базисной функции
п = число вершин определяющего многоугольника
nplusc = максимальное значение узлового вектора — п + с
х() = массив, содержащий узловой вектор
subroutine knotu (n,c; x())
nplusc = n + с
for i = 1 to nplusc
x(i) = i - 1
next i
return
matpbspl
Подпрограмма генерирует кривую В-сплайна с использованием матричных
методов и периодических однородных узловых векторов (уравнение (5-93)).
Ь(,) = массив, содержащий вершины определяющего многоугольника
в скользящем окне
Ь( ,1) содержит компоненту х вершины в скользящем окне
Ь( ,2) содержит компоненту у вершины в скользящем окне
Ь( ,3) содержит компоненту z вершины в скользящем окне
d(,) = массив, содержащий вершины определяющего многоугольника
d( ,1) содержит компоненту х вершины
d( ,2) содержит компоненту у вершины
d{ ,3) содержит компоненту z вериьины
fcoeff = коэффициент для целочисленной матрицы
к = порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для единственного значения t
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р( ,1) содержит компоненту х точки
р( ,2) содержит компоненту у точки
р{ ,3) содержит компоненту z точки
pi = число вычисляемых точек кривой
ptemp(,) = временная матрица, содержащая единственную точку кривой —t*n*b
t(,) = параметрическая матрица
temp(t) = временная матрица — t * п
и = нормализованное параметрическое значение 0< и < 1
subroutine matpbspl (kjiiptSjpl.df,); p(,))
dimension t(l,9),b(913),n(919),temp(l,9),ptemp(lJ3) допускает 9-й порядок
определяем размерность и заполняем нулями матрицы
Mat Ъ = Zer(k,3)
Mat n = Zer(k,k)
Mat t = Zer(l,k)
Mat temp = Zer(l,k)
устанавливаем значения матрицы [N]
call nmatrix(k; fcoeff,n)
устанавливаем значения матрицы скользящих вершин многоугольника
и вычисляем точки
icount = О
for j = 0 to npts устанавливаем значения матрицы
скользящих вершин многоугольника
for 1 = 0 to к - 1
Ь(1 + 1,1) = d(mod(j + l.npts) + 1,1)
b(l + 1,2) = d(mod(j + l,npts) + 1,2)
b(l + 1,3) = d(mod(j + l.npts) + 1,3)
next 1
for u = 0 to 1 - (l/(pl - 1)) step l/(pl - 1)
icount = icount + 1
for i = 1 to к устанавливаем значения параметрической матрицы
t(l,i) = иЛ(к - i)
next i
Mat t = fcoeff*t вычисляем точки на этом сегменте
Mat temp = t*m
Mat ptemp = temp*b
p(icount.l) = ptemp(l,l) присваиваем текущее значение точки
p(icount,2) = ptemp(l,2) на кривой массиву кривой
p(icount,3) = ptemp(l,3)
next u
next j
return
nmatrix
Подпрограмма вычисляет общую матрицу периодического базиса В-сплайна
(уравнение (5-91)).
Factrl = функция, вычисляющая факториал числа
fcoeff = коэффициент целочисленной матрицы — l/(k — 1)!
А; = порядок периодической базисной функции
п(,) = целочисленная форма матрицы
Ni(n, г) = функция, вычисляющая (™)
subroutine nmatrix (k; fcoeff,n(,))
def Ni(n,i) = Factrl(n)/Factrl(i)*Factrl(n-i))
определяем размерность и заполняем нулями матрицу [N]
Mat n = Zer(k,k)
fcoeff = 1/Factrl(k — 1) вычисляем постоянный коэффициент
устанавливаем значения матрицы
for i = 0 to k - 1
temp = Ni(k - l,i)
for j = 0 to k - 1
sum = 0
for 1 = j to k — 1
suml = (k - (1 + l))Ai
sum2 = (-l)A(l - j)
sum3 = Ni(k,l - j)
sum = sum + suml*sum2*sum3
next 1
n(i + 1, j + 1) = temp*sum
next j
next i
return
parabld
Подпрограмма вьтолняет параболическое смешивание alpha ф beta, используя
аппроксимацию хордами (уравнения (5-44) и (5-6)).
Предполагается, что эта программа в каждый момент времени обеспечивается
четырьмя точками данных. Вычисляются точки, расположенные внутри
интервала вдоль параболически смешанной кривой.
а(,) — матрица 4 х 4 параболически смешанной функции
alpha = значение параметра г при Рг
beta = значение параметра s при Рз
с(,) = массив, содержащий точки смешанной кривой
с( ,1) содержит компоненту х точки на кривой
с( ,2) содержит компоненту у точки на кривой
с( ,3) содержит компоненту z точки на кривой
с12 = хордовое расстояние между точками 1 и 2
с23 = хордовое расстояние между точками 2 и 3
с34 = хордовое расстояние между точками 3 и 4
icount = счетчик числа точек на смешанной кривой
inter(,) = промежуточная матрица [A][G]
р(,) = массив, содержащий четыре точки данных
р( ,1) содержит компоненту х точки данных
р( ,2) содержит компоненту у точки данных
р( ,3) содержит компоненту z точки данных
point(,) = единственная точка смешанной кривой
point( ,1) содержит компоненту х точки
point( ,2) содержит компоненту у точки
point{ ,5) содержит компоненту z точки
pi = число точек, вычисляемых на этом интервале
((,) = кубическая параметрическая матрица
tl = параметрическое значение вдоль смешанной кривой
subroutine parabld (p(,); c{,),pl,icount)
dimension a(4)4))t(l,4),inter(4,3),point(l,3)
вычисляем длины хорд
с12 = Sqrt((p(2,l) - р(1,1))Л2 + (р(2,2) - р(1,2))Л2)
с23 = Sqrt((p(3,l) - р(2,1))Л2 + (р(3,2) - р(2,2))Л2)
с34 = Sqrt((p(4,l) - р(3,1))Л2 + (р(4,2) - р(3,2))Л2)
вычисляем alpha и beta
alpha = с12/(с23 + с12)
beta = с23/(с23 + с34)
вычисляем [А]
а(1,1) = -((1 - alpha)A2)/alpha
а(2,1) = 2*((1 - alpha)A2)/alpha
а(3,1) = а(1,1)
а(4,1) = О
а(1,2) = ((1 — alpha) + alpha+beta) /alpha
а(2,2) = -(2*(1 - alpha) + alpha*beta)/alpha
а(3,2) = (1 - 2*alpha)/alpha
а(4,2) = 1
а(1,3) = (-(1 - alpha) - alpha*beta)/(l - beta)
a(2,3) = (2*(1 - alpha) - beta*(l - 2*alpha))/(l -beta)
a(3,3) = alpha
a(4,3) = 0
a(l,4) = (betaA2)/(l - beta)
a(2,4) = -a(l,4)
a(3,4) = 0
a(4,4) = 0
вычисляем матрицу [A][G]
Mat inter = a*p
определяем точки на сегменте кривой
for tl = 0 to 1 - (l/(pl - 1)) step l/(pl - 1)
устанавливаем значения матрицы [Т]
t(l,l) = tlA3
t(l,2) = tlA2
t(l,3) = tl
t(l,4) = 1
вычисляем точки на смешанной кривой и запоминаем их в C(t)
Mat point = t*inter
icount = icount + 1
for i = 1 to 3
c(icount,i) = point(l,i)
next i
next tl
return
param
Подпрограмма вычисляет хордовые значения, базирующиеся на хордовых
расстояниях.
массив, содержащий точки данных
число точек данных
накопитель суммы хордовых расстояний
сумма хордовых расстояний
массив, содержащий параметрические значения
subroutine param (dpts,d(,); tpaxm())
sum = 0
isum = 0
tparm(l) = 0
вычисляем сумму хордовых расстояний для всех точек данных
for i = 2 to dpts
sum = sum + Sqrt((d(i,l) - d(i - 1,1))Л2 + (d(i,2) - d(i - 1,2))Л2)
next i
вычисляем параметрические значения
for i = 2 to dpts
isum = isum + Sqrt((d(i,l) - d(i - 1,1))Л2 + (d(i,2) - d(i - 1,2))Л2)
tparm(i) = isum/sum
next i
return
rbasis
Подпрограмма генерирует базисные функции рационального В-сплайна для
открытого узлового вектора (уравнение (5-123)).
с = порядок базисной функции В-сплайна
d = первый терм рекурсивного отношения базисной функции
е = второй терм рекурсивного отношения базисной функции
h() = массив, содержащий однородные координатные весовые множители
npts = число вершин определяющего многоугольника
nplusc = константа — npts + с — максимальное число узловых значений
г(,) = массив, содержащий производную базисных функций
г(1,1) содержит производную базисной функции для В\ и т. д.
sum = сумма произведений нерациональных базисных функций
и однородных координатных весовых множителей
t = параметрическое значение
tempQ = временный массив
х0 = узловой вектор
dpts
isum
sum
tparmCj
subroutine rbasis (c,t,npts,x(),h(); r(,))
dimension temp(20) допускает 20 вершин многоугольника
nplusc = npts + с
вычисляем нерациональные базисные функции первого порядка Ni,i (уравнение (5-84а))
for i = 1 to nplusc — 1
if t > x(i) and t < x(i + 1) then
temp(i) = 1
else
temp(i) = 0
end if
next i
вычисляем нерациональные базисные функции высшего порядка (уравнение (5-84Ь))
for к — 2 to с
for i = 1 to nplusc — к
if temp(k) ф 0 then если нуль, пропускаем вычисление
d = ((t - x(i))*temp(i))/(x(i + к - 1) - x(i))
else
d = 0
end if
if temp(i +1)^0 then если нуль, пропускаем вычисление
е = ((x(i + к) - t)*temp(i + l))/(x(i + к) - x(i + 1))
else
e = 0
end if
temp(i) = d + e
next i
next к
if t = x(nplusc) then temp(npts) = 1 добавляем последнюю точку
вычисляем сумму для знаменателя рациональных базисных функций (уравнение (5-123))
sum = 0
for i = 1 to npts
sum = sum + temp(i)*h(i)
next i
образуем рациональные базисные функции и помещаем их в вектор г (уравнение (5-123))
for i = 1 to npts
if sum / 0 then
r(l,i) = temp(i)*h(i)/sum
else
r(l,i) = 0
end if
next i
return
rbspline
Подпрограмма генерирует кривую рационального В-сплайна, используя
открытый однородный узловой вектор (уравнения (5-122) и (5-124)).
6(,) = массив, содержащий вершины определяющего многоугольника
Ъ{ ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
h(,) = массив, содержащий однородные координатные весовые множители
к = порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для единственного значения t
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р( ,1) содержит компоненту х тонки
р( ,2) содержит компоненту у точки
р{ ,3) содержит компоненту z точки
pi = число вычисляемых точек кривой
t — параметрическое значение 0 <t < 1
х() = массив, содержащий узловой вектор
subroutine rbspline (npts,k,pl,b(,),h(); p(,))
dimension nbasis(l,20),x(30),temp(l,3) допускает 20 заданных точек
с базисной функцией порядка 5
nplusc = npts + к
определяет размерность и заполняет нулями узловой вектор и базисный массив
Mat nbasis = Zer(l,npts)
Mat x = Zer(nplusc)
генерирует открытый однородный узловой вектор
call knot (npts,к; х)
icount = 0
вычисляем точки на кривой рационального В-сплайна
for t = 0 to x(npts + к) step x(npts + k)/(pl — 1)
icount = icount + 1
call rbasis(k,t,npts,x,h; nbasis) рациональные базисные функции
для этого значения t
Mat temp = nbasis*b генерируем точки на кривой
p(icount,l) = temp(l,l) присваиваем текущее значение точки на кривой
p(icount,2) = temp(l,2) массиву кривой
p(icount,3) = temp(l,3)
next t
return
rbsplinu
Подпрограмма генерирует кривую рационального В-сплайна, используя
периодический однородный узловой вектор (уравнения (5-122) и (5-124)).
6(,) = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту х вершины
6( ,2) содержит компоненту у вершины
6( ,3) содержит компоненту z вершины
h() = массив, содержащий однородные координатные весовые множители
к = порядок базисной функции В-сплайна
nbasis = массив, содержащий базисные функции для единственного значения t
nplusc = число узловых значений
npts = число вершин определяющего многоугольника
р(,) = массив, содержащий точки кривой
р{ ,1) содержит компоненту х точки
р( ,2) содержит компоненту у точки
р( ,3) содержит компоненту z точки
pi = число вычисляемых точек кривой
t = параметрическое значение
xQ = массив, содержащий узловой вектор
subroutine rbsplinu (npts,k,pl,b(,),h(); p(,))
dimension nbasis(l,20),x(30),temp(l,3) допускает 20 заданных точек
с базисной функцией порядка 5
nplusc = npts + к
определяем размерности и заполняем нулями узловой вектор и базисный массив
Mat nbasis = Zer(l,npts)
Mat x = Zer(nplusc)
генерируем открытый однородный вектор
call knotu(npts,k; x)
icount = О
вычисляем точки на кривой рационального В-сплайна
for t = (к - 1)) to (npts -1 + 1) step ((npts - 1 + 1) - (к - l))/(pl - 1)
icount = icount + 1
call rbasis(k,t,npts,x,h; nbasis) рациональные базисные функции
для этого значения t
Mat temp = nbasis*b генерируем точку на кривой
p(icount,l) = temp(l,l) присваиваем текущее значение точки на кривой
p(icount,2) = temp(l,2) массиву этой кривой
p(icount,3) = temp(l,3)
next t
return
ГЛАВА 6
Здесь представлены алгоритмы генерации трехмерных поверхностей.
Включены алгоритмы для билинейных, правильных поверхностей, линейных и
бикубических поверхностей Кунса, поверхностей Безье, рационального и нерационального
В-сплайна. В алфавитном порядке представлены следующие алгоритмы:
bezsurf
Подпрограмма вычисляет поверхность Безье (уравнение (6-58)).
6(,) = массив, содержащий вершины определяющего многоугольника
Ь( ,1) содержит компоненту! вершины
Ь( ,2) содержит компоненту у вершины
Ь{ ,3) содержит компоненту z вершины
Замечание: массив Bij = 6(,) имеет размерность п* т х 3, причем j
изменяется быстрее
Basis = функция для вычисления базисного значения Бернштейна
Factrl = функция для вычисления факториала числа
jin = базисная функция Бернштейна в направлении и (уравнение (5-63))
kjm = базисная функция Бернштейна в направлении w (уравнение (5-63))
т = число, на единицу меньше, чем число вершин многоугольника в направлении w
n = число, на единицу меньшее, чем число вершин многоугольника в направлении и
Ni = функции факториала для базисной функции Бернштейна
pi = число параметрических линий в направлении и
р2 = число параметрических линий в направлении w
q(,) = координатные векторы, для точек на поверхности
q{ ,1) содержит компоненту х вектора
q( ,2) содержит компоненту у вектора
q{ ,3) содержит компоненту z вектора
для фиксированного значения и следующие т элементов содержат
значения для кривой q(ui,w); q имеет размерность pl*p2 х 3
subroutine bezsurf (b(,),n1m,pl,p2; q(,))
def Ni(n,i) = Factrl(n)/(Factrl(i)*Factrl(n - i))
def Basis(n,i,t) = Ni(n,i)*(tAi)*((l - t)A(n - i))
icount = 0
for u = 0 to 1 step l/(pl — 1) для фиксированного и вычисляем различные w
for w = 0 to 1 step 1/(р2 - 1)
icount = icount + 1
for i = 0 to n
jin = Basis(n,i,u) базисная функция Бернштейна в направлении и
for j = 0 to m
jl = (m + l)*i + 0 + 1)
kjm = Basis(mj,w) базисная функция Бернштейна в направлении w
for к = 1 to 3
q(icount,k) = q(icount,k) + b(jl,k)*jin*kjm вычисляет точку поверхности
next к
next j
next i
next w
next u
return
bicubic
Подпрограмма генерирует бикубическую поверхность Кунса (уравнение (6-
51)).
п(,) = матрица смешанной функции 4*4 (уравнение (6-31))
р(,) = матрица граничных условий 4*4 (уравнение (6-36))
pi = число точек вдоль направления и
р2 = число точек вдоль направления w
q(,) = матрица, содержащая координатные векторы для бикубической поверхности,
имеет размерность pl*p2 x 3
первый столбец — компонента х
второй столбец — компонента у
третий столбец — компонента z
первые р2 элементов для и = О
вторые р2 элементов для и = 1/(р1-1) и т. д.
и(,) = кубический смешанный вектор 1x4 (уравнение (6-37))
w(,) = кубический смешанный вектор 4*1 (уравнение (6-37))
х(,) = массив 4 х 4> содержащий компоненты х матрицы
граничных условий р (уравнение (6-36))
t/(,) = массив 4 x 4> содержащий компоненты у матрицы
граничных условий р (уравнение (6-36))
z(,) = массив 4 х 4> содержащий компоненты z матрицы
граничных условий р (уравнение (6-36))
subroutine bicubic (pl,p2,x(,),y(,),z(,); q(,))
dimension p(4,4(,n(4,4),ntrn(4,4)Iu(l,4)iw(4,l)
dimension templ(4,4),temp2(4,4),temp3(l,4),temp4(l,l)
определяем размерности матриц и заполняем нулями эти матрицы
Mat р = Zer(4,4)
Mat n = Zer(4,4)
Mat u = Zer(l,4)
Mat w = Zer(4,l)
Mat q = Zer(pl*2,3)
Mat tempi = Zer(4,l)
Mat temp2 = Zer(4,l)
Mat temp3 = Zer(4,l)
Mat temp4 = Zer(l,l)
устанавливаем значения п-матрицы
n(l,l) = 2
n(l,2) = -2
n(l,3) = 1
n(l,4) = 1
n(2,l) = -3
n(2,2) = 3
n(2,3) = -2
11(2,4) = -1
n(3,3) = 1
n(4,l) = 1
транспонируем п-матрицу Mat ntrn = trn(n)
for к = 1 to 3
icount = 0
if к = 1 then Mat p = x
if к = 2 then Mat p = у
if к = 3 then Mat p = z
Mat tempi = p*ntrn вычисляем p * ntrn-константу для всех и, w
Mat temp2 = n*templ вычисляем п*р* ntrn-константу для всех и, w
for ul = 0 to 1 step l/(pl — 1) устанавливаем значения п-матрицы
u(l,l) = ul*ul*ul
u(l,2) = ul*ul
u(l,3) = ul
u(l,4) = 1
for wl = 0 to 1 step l/(p2 — 1) устанавливаем значения w-матриц
icount = icount + 1
w(l,l) = wl*wl*wl
w(2,l) = wl*wl
w(3,l) = wl
w(4,l) = 1
Mat temp3 = u*temp2 вычисляем и*п* ntrn
Mat temp4 = temp3*w вычисляем q(u, w)
q(icount,k) = temp4(l,l) запоминаем q(u,w)
next wl
next ul
next к
return
bilinear
Подпрограмма вычисляет билинейную поверхность (уравнение (6-41)).
п = число приращений в и
т = число приращений в w
р(,) = содержит координаты угловых точек
р имеет размерность 4 * 3. Первый столбец содержит
компоненты х, второй — компоненты у, а третий — компоненты z
координатных векторов углов.
д(,) = содержит координаты интерполируемой поверхности z
q имеет размерность т * пх 3
первые т координат соответствуют константе и = О
вторые т координат соответствуют константе и = 1 /(п —1)
третьи т координат соответствуют константе и = 2/(п —1) и т. д.
subroutine bilinear (n,m,p(,); q(,))
Mat q = Zer(n*m,3) определяем размерность массива q и заполняем его нулями
icount = О
вычисляем поверхность
for u = 0 to 1 step l/(n — 1) цикл установки константы и
for w = 0 to 1 step l/(m — 1) цикл цстановки константы w
icount = icount + 1 увеличиваем счетчик точек
q(icount,l) = р(1,1)*(1 - и)*(1 - w) + р(2,1)*(1 - u)*w + p(3,l)*u*(l - w)
q(icount,l) = q(icount,l) + p(4,l)*u*w
q(icount,2) = p(l,2)*(l - u)*(l - w) + p(2,2)*(l - u)*w + p(3,2)*u*(l - w)
q(icount,2) = q(icount,2) + p(4,2)*u*w
q(icount,3) = p(l,3)*(l - u)*(l - w) + p(2,3)*(l - u)*w + p(3,3)*u*(l - w)
q(icount,3) = q(icount,3) + p(4,3)*u*w
next w
next u
return
bsplsurf
Подпрограмма вычисляет декартово произведение В-сплайн поверхности,
используя открытые однородные узловые векторы (уравнение (6-58)).
6() = массив, содержащий точки сетки многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
Замечание: Bij = 6(,) имеет размерность п*т х 3,
причем j изменяется быстрее. Размер сетки многоугольника: п х т
к = порядок в направлении и
I = порядок в направлении w
mbasis(,) = нерациональные базисные функции для одного значения w (уравнение (5-84))
mpts = число вершин многоугольника в направлении w
нерациональные базисные функции для одного значения и (уравнение (5-84))
число вершин многоугольника в направлении и
число параметрических линий в направлении и
число параметрических линий в направлении w
массив, содержащий результирующую поверхность
q( ,1) содержит компоненту х вектора
q( ,2) содержит компоненту у вектора
q{ ,3) содержит компоненту z вектора
для фиксированного значения и следующие т элементов содержат
значения для кривой q(ui,w) q имеет размерность pl*p2 х 3.
Отображается поверхность размера pi х р2
subroutine bsplsurf (b(,),k,l,npts,mpts,pl,p2; q(,))
допускает 20 заданных точек с базисной функцией порядка 5
dimension x(30),y(30),nbasis(l,20),mbasis(l,20)
определяем размерности и заполняем массивы нулями
Mat х = Zer(npts + к)
Mat у = Zer(mpts + 1)
Mat nbasis = Zer(l,npts)
Mat mbasis = Zer(l,mpts)
Mat q = Zer(pl*p2,3)
генерируем открытые однородные узловые векторы
call knot(npts,k; x()) вычисляем угловой вектор и
call knot(mpts,l; y()) вычисляем угловой вектор и>
nplusc = npts + к
mplusc = mpts + 1
icount = О
вычисляем точки на В-сплайн поверхности
for u = 0 to x(nplusc) step x(nplusc)/(pl — 1)
call basis(k,u,npts,x; nbasis) базисная функция для этого значения и
for w = 0 to y(mplusc) step y(mplusc)/(p2 — 1)
call basis(l,w,mpts,y; mbasis) базисная функция для этого значения w
icount = icount + 1
for i = 1 to npts
for j = 1 to mpts
jl = mpts*(i — 1) + j
for s = 1 to 3
q(icount,s) = q(icount,s) + b(jl,s)*nbasis(l,i)*mbasis(l j)
next s
next j
next i
next w
next u
return
bspsurfu
Подпрограмма вычисляет декартово произведение для В-сплайн поверхности,
используя периодические однородные узловые векторы (уравнения (6-58)).
6() = массив, содержащий точки сетки многоугольника
nbasis
npts
pi
Р2
ff()
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины,
Замечание: Bij = b(,) имеет размерность п* т х 3, причем j
изменяется быстрее. Размер сетки многоугольника: п х т
q() = массив, содержащий результирующую поверхность
q{ ,1) содержит компоненту х вектора
q( ,2) содержит компоненту у вектора
q( ,3) codepoicum компоненту z вектора
для фиксированного значения и следующие т элементов содержат
значения для кривой q(ui,w); q имеет размерность pl*p2 x 3.
Отображается поверхность размера pi x р2
к = порядок в направлении и
I = порядок в направлении w
mbasis(,) = нерациональные базисные функции для одного значения w (уравнение (5-84))
mpts = число вершин многоугольника в направлении значения w
nbasis(,) = нерациональные базисные функции для одного значения и (уравнение (5-84))
npts = число вершин многоугольника в направлении и
pi = число параметрических линий в направлении и
р2 = число параметрических линий в направлении и
subroutine bspsurfu (b(,),k,l,npts,mpts,pl,p2; q(,))
допускает 20 заданных точек с базисной функцией порядка 5
dimension x(30),у(30),nbasis(l,20),mbasis(l,20)
определяем размерности и заполняем массивы, нулями
Mat х = Zer(npts + к)
Mat у — Zer(mpts + 1)
Mat nbasis = Zer(l,npts)
Mat mbasis = Zer(l,mpts)
Mat q = Zer(pl*p2,3)
генерируем периодические однородные узловые векторы
call knotu(npts,k; x()) вычисляем узловой вектор и
call knotu(mpts,l; y()) вычисляем узловой вектор w
nplusc = npts + к
mplusc = mpts + 1
icount = 0
вычисляем точки на В-сплайн поверхности
for u = (к - 1) to (npts -1 + 1) step ((npts - 1 + 1) - (к - l))/(pl - 1)
call basis (k,u,npts,x; nbasis) базисная функция для этого значения и
for w = (1 - 1) to (mpts -1 + 1) step (mpts - 1 + 1) - (1 - 1)/(р2 - 1)
call basis(l,w,mpts,y; mbasis) базисная функция для этого значения w
icount = icount + 1
for i = 1 to npts
for j = 1 to mpts
for s = 1 to 3
jl = mpts*(i — 1) + j
q(icount,s) = q(icount,s) + b(jl,s)*nbasis(l,i)*mbasis(l j)
next s
next j
next i
next w
next u
return
coonslin
Подпрограмма вычисляет линейную поверхность Кунса (уравнение (6-49)).
а(,) = массив размера р(и, 0), содержащий точки на кривой п х 3
Ь(,) = массив размера р(и, 1), содержащий точки на кривой п х 3
с(,) = массив размера p(0,w), содержащий точки на кривой т х 3
d(,) = массив размера р{1, w), содержащий точки на кривой т х 3
п = число точек на граничных кривых р(и, 0) и р(и, 1)
т = число точек на граничных кривых р(0, w) up(l,w)
g(,) = массив размера , содержащий кривые, которые описывают поверхность
71 * 7пх 3. Формат дан для фиксированного значения и, каждые следующие
т строк матрицы q содержат значения для переменного и>.
subroutine coonslin (n,m,a(,),b(,),c(,),d(,); q(,))
Mat q = Zer(n*m,3) определяем размерность матрицы q
и заполняем нулями эту матрицу
вычисляем поверхность
for u = 0 to 1 step l/(m — 1)
for w = 0 to 1 step l/(n — 1)
icount = icount + 1
for 1 = 1 to 3
q(icount,l) = a(k,l)*(l - w) + b(k,l)*w + c(j,l)*(l - u) + d(j,I)*u
q(icount,l) = q(icount,l) — a(l,l)*(l — u)*(l — w) — b(l,l)*(l — u)*w
q(icount,l) = q(icount,l) — a(n,l)*u*(l — w) — b(n,l)*u*w
next 1
next w
next u
return
dbicubic
Подпрограмма вычисляет бикубическую поверхность Кунса и ее производные
(уравнения (6-51) и (6-53)-(6-57)).
du(,) = смешанный вектор производной размера 1x4 (уравнение (6-53))
dw(,) = смешанный вектор производной размера 4 х 1 (уравнение (6-54))
п(,) = матрица смешанной функции размера 4 х 4 (уравнение (6-26))
р(,) = матрица граничных условий размера 4*4 (уравнение (6-51))
pi = число точек вдоль направления и
р2 = число точек вдоль направления w
q(,) = матрица размера pl*p2 x 3, содержащая
координатные векторы для бикубической поверхности
первый столбец — компонента х
второй столбец — компонента у
третий столбец — компонента z
первые р2 элементов для и = О
вторые р2 элементов для и = 1/{р1— 1)
все производные размещаются подобным образом
du(,) = матрица размера pi *p2 х 3,
содержащая векторы производной и для бикубической поверхности
dw(,) = матрица размера pi * р2х 3,
содержащая векторы производной w для бикубической поверхности
duu(,) = матрица размера pi * р2 х 3,
содержащая векторы производной ии для бикубической поверхности
duw(,) = матрица размера pi * р2х 3,
содержащая векторы производной uw для бикубической поверхности
dww(,) — матрица размера pi * р2 х 3,
содержащая векторы производной ww для бикубической поверхности
u(j) = кубический смешанный вектор размера 1 х4 (уравнение (5-26))
w(,) = кубический смешанный вектор размера 4 х 1 (уравнение (5-26))
х(,) = массив 4 х 4> содержащий х компоненты матрицы
граничных условий р (уравнение (6-36))
у(,) = массив 4x4j содержащий у компоненты матрицы
граничных условий р (уравнение (6-36))
z(,) = массив 4 х 4> содержащий z компоненты матрицы
граничных условий р (уравнение (6-36))
subroutine dbicubic (pl,p2,x(,),y(,),z(,); q(,),qu(,),qw(,),quu(,),quw(,),qww(,))
dimension p(4,4),n(4,4),ntrn(4,4),u(l,4),w(4,l)
dimension du(l,4),dw(4,l),duu(,l,4),dww(l,4)
dimension templ(4,4),temp2(4,4),temp3(l,4),temp4(4,l)
dimension temp5(4,l),temp6(4,l),temp7(4,l)
dimensiondtempl(l,l),dtemp2(l,l))dtemp3(l,l))dtemp4(l,l))dtemp5(l,l)
определяем размерность матриц и заполняем их нулями
Mat р = Zer(4,4)
Mat n = Zer(4,4)
Mat u = Zer(l,4)
Mat w = Zer(4,l)
Mat q = Zer(pl*p2,3)
Mat qu = Zer(pl*p2,3)
Mat qw = Zer(pl*p2,3)
Mat quu = Zer(pl*p2,3)
Mat quw = Zer(pl*p2,3)
Mat qww = Zer(pl*p2,3)
Mat tempi = Zer(4,4)
Mat temp2 = Zer(4,4)
Mat temp3 = Zer(l,4)
Mat temp4 - Zer(4,l)
Mat temp = Zer(l,l)
Mat dtempl = Zer(l.l)
Mat dtemp2 = Zer(l.l)
устанавливаем значения п-матрицы
n(l,l) = 2
11(1,2) = -2
11(1,3) = 1
n(l,4) = 1
n(2,l) = -3
n(2,2) = 3
n(2,3) = -2
n(2,4) = -1
n(3,3) = 1
11(4,1) = 1
транспонируем п-матрицу
Mat ntrn = Trn(n)
for к = 1 to 3
icount = 0
if к = 1 then Mat p = x
if к = 2 then Mat p = у
if к = 3 then Mat p = z
Mat tempi = p*ntrn
Mat temp2 = n*templ
for ul = 0 to 1 step l/(pl - 1)
u(l,l) = ul*ul*ul
u(l,2) = ul*ul
u(l,3) = ul
u(l,4) = 1
du(l,l) = 3*ul*ul
du(l,2) = 2*ul
du(l,3) = 1
du(l,4) = 0
duu(l,l) = 6*ul
duu(l,2) = 2
duu(l,3) = 0
duu(l,4) = 0
for wl = 0 to 1 step l/(p2 - 1)
icount = icount + 1
w(l,l) = sl*sl*sl
w(2,l) = sl*sl
w(3,l) = wl
w(4,l) = 1
dw(l,l) = 3*wl*wl
dw(2,l) = 2*wl
dw(3,l) = 1
dw(4,l) = 0
dw(l,l) = 6*wl
dw(2,l) = 2
dw(3,l) = 0
dw(4,l) = 0
Mat temp3 = u*temp2
Mat temp4 = temp2*w
Mat temp5 = du*temp2
Mat temp6 = temp2*dw
Mat temp7 = temp3*w
Mat dtempl = du*temp4
Mat dtemp2 = temp3*dw
Mat dtemp3 = temp5*dw
Mat dtemp4 = duu*temp4
Mat dtemp5 = temp3*dww
q(icount,k) = temp7(l,l)
qu(icount,k) = dtempl(l,l)
qw(icount,k) = dtemp2(l,l)
quw(icount,k) = dtemp3(l,l)
quu(icount,k) = dtemp4(l,l)
вычисляем p * ntrn-константу для всех и, w
вычисляем п*р* ntrn-константу для всех и, w
устанавливаем значения и-матрицы
устанавливаем значения du-матрицы
устанавливаем значения duu-матрицы
устанавливаем значения w-матрицы
устанавливаем значения dw-матрицы
устанавливаем значения dww-матрицы
вычисляем и* п *р * ntrn
вычисляем п*р* ntrn * w
вычисляем du * п * р * ntrn
вычисляем п* р* ntrn * dw
вычисляем q(u, w)
вычисляем qu(u, ui)
вычисляем qw(u, w)
вычисляем quw(u, ui)
вычисляем quu{u, ui)
вычисляем qww(u, ui)
запоминаем точку поверхности q
запоминаем производную поверхности qu
запоминаем производную поверхности qw
запоминаем производную поверхности quw
запоминаем производную поверхности quu
qww(icount,k) = dtemp5(l,l) запоминаем производную поверхности qww
next wl
next ul
next к
return
dbsurf
Подпрограмма вычисляет декартово произведение для. поверхности В-сплайна
и его производные, используя открытые однородные узловые векторы (уравнения
(6-58) и (6-62)-(6-66)).
Ь() = массив, содержащий точки сетки многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь{ ,3) содержит компоненту z вершины
Замечание. Bi,j = Ь(,) имеет размерность п*т х 3, причем j
изменяется быстрее. Размер сетки многоугольника п х т
dlmbasis(,) = первая производная базисных функций для w (уравнение (5-74))
dlnbasis(,) = первая производная базисных функций для и (уравнение (5-74))
d2mbasis{,) = вторая производная базисных функций для w (уравнение (5-75))
d2nbasis{,) = вторая производная базисных функций для и (уравнение (5-75))
к = порядок в направлении и
I = порядок в направлении w
mbasis(,) = базисные функции для w (уравнение (5-63))
mpts = число вершин многоугольника в направлении ,w
nbasis(,) = базисные функции и (уравнение (5-84))
nptw = число вершин многоугольника в направлении и
pi = число параметрических линий в направлении и
р2 = число параметрических линий в направлении w
50 = массив, содержащий результирующую поверхность
q(, 1) содержит компоненту х вектора
q(, 2) содержит компоненту у вектора
q(, 3) содержит компоненту z вектора
для фиксированного значения и следующие т элементов содержат
значения для кривой q(u(subi), w); q имеет размеры
pi * р2х 3- Отображается поверхность размера pi x р2
qu(,) = производная векторов и для В-сплайн поверхности;
имеет размеры pi *p2 x 3 (уравнение (6-62))
qw(,) = производная векторов w для В-сплайн поверхности;
имеет размеры pi *р2х 3 (уравнение (6-63))
quu(,) = производная векторов гш для В-сплайн поверхности;
имеет размеры pi * р2х 3 (уравнение (6-64))
quw{,) = производная векторов кш для В-сплайн поверхности;
имеет размеры pi * р2х 3 (уравнение (6-65))
qww(,) = производная векторов шш для В-сплайн поверхности;
имеет размеры pi * р2х. 3 (уравнение (6-66))
subroutine dbsurf (b(,)!k,l,npts,mpts,pl,p2; q(,),qu(,),qw(,),quw(,),quu(,),qww(,))
допускает 20 заданных точек с базисной функцией порядка 5
dimension x(30),y(30)
dimension nbasis(l,20),mbasis(l,20)
dimension dlnbasis(l,20),dlmbasis(l,20)
dimension d2nbasis(l,20),d2mbasis(l,20)
определяем размерности и заполняем массивы нулями
Mat х = Zer(npts + к)
Mat у = Zer(mpts + 1)
Mat nbasis = Zer(l,npts)
Mat mbasis = Zer(l,mpts)
Mat dlnbasis = Zer(l,npts)
Mat dlmbasis = Zer(l,mpts)
Mat d2nbasis = Zer(l,npts)
Mat d2mbasis = Zer(l,mpts)
Mat q = Zer(pl*2,3)
Mat qu = Zer(pl*2,3)
Mat qw = Zer(pl*2,3)
Mat quw = Zer(pl*2,3)
Mat quu = Zer(pl*2,3)
Mat qw = Zer(pl*2,3)
генерируем открытые однородные узловые векторы
call knot(npts,k; x()) вычисляем узловой вектор и
call knot(mpts,l; y()) вычисляем узловой вектор w
nplusc = npts + к
mplusc = mpts + 1
icount = 0
вычисляем точки на В-сплайн поверхности
for u = 0 to x(nphisc) step x(nplusc)/(pi — 1)
call dbasis(k,u,npts,x; nbasis(dlnbasis,d2nbasis) базовые функции и поверхности
for w = 0 to y(mplusc) step y(mplusc)/(p2 — 1)
call dbasis(l,w,mpts,y; mbasis(dlmbasis,d2mbasis)
icount = icount + 1
for i = 1 to npts
for j = 1 to mpts
for s = 1 to 3
jl = mpts*(i - 1) + j
q(icount,s) = q(icount,s) + b(jl,s)*nbasis(l,i)*mbasis(l j)
qu(icount,s) = qu(icount,s) + b(jl,s)*dlnbasis(l,i)*mbasis(l j)
qw(icount,s) = qw(icount,s) + b(jl,s)*nbasis(l,i)*dlmbasis(l j)
quw(icount,s) = quw(icount,s) + b(jl,s)*dlnbasis(l,i)*dlmbasis(l j)
quu(icount,s) = quu(icount,s) + b(jl,s)*d2nbasis(l,i)*mbasis(l j)
qww(icount,s) = qww(icount,s) + b(jl,s)*nbasis(l,i)*d2mbasis(l j)
next s
next j
next i
next w
next u
return
loftlinu
Подпрограмма вычисляет правильную поверхность в направлении и
(уравнение (6-43)).
a(,) = массив размера п х 3, содержащий точки на кривой р(и, 0)
Ь(,) = массив размера п х 3, содержащий точки на кривой р(и, 1)
гпит = число точек на каждой правильной ликгш
п = число точек на граничных кривых
q(,) = массив размера п * гпит х 3, содержащий точки на промежуточных кривых
subroutine loftlinu (n,a(,),b(,),inum; q(,))
icount = 0
вычисляем поверхность
for w = 0 to 1 step l/(inum
for 1 = 1 to n
icount = icount + 1
for k = 1 to 3
q(icount,k) = a(l,k)*(l
next k
next 1
next w
return
loftlinw
Подпрограмма вычисляет правильную поверхность в направлении w
(уравнение (6-44)).
а(,) = массив размера п х 3, содержащий точки на кривой p(0,w)
b(,) = массив размера п х 3, содержащий точки на кривой p{l,w)
mum = число точек на правильной линии
п = число точек на граничных кривых
р(,) = массив размера п * гпит х 3, содержащий точки на правильных линиях
subroutine loftlinw (n,a(,),b(,),inum; q(,))
вычисляем поверхность
for u = 0 to 1 step l/(inum — 1)
for 1 = 1 to n
icount = icount + 1
for k = 1 to 3
p(icount,k) = a(l,k)*(l — u) + b(l,k)*u вычисляем поверхность (уравнение (6-44))
next k
next 1
next u
return
-1)
— w) + b(l,k)*w вычисляем поверхность (уравнение (6-43))
mbezsurf
Подпрограмма вычисляет поверхность Безье, используя матричные методы
(уравнение (6-59)).
Ь(,) = массив, содержащий вершимы многоугольника
Ь{ ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь{ ,3) содержит компоненту z вершины
Замечание: Bij = b(,) имеет размерность п* т х 3, причем j
изменяется быстрее
jin = базисная функция Бернштейна в направлении и (уравнение (5-63))
kjm = базисная функция Бернштейна в направлении w (уравнение (5-63))
т(,) = матрица [М] (уравнение (6-59))
ml = число, на единицу меньшее числа вершин многоугольника в направлении w
nl = число, на единицу меньшее числа вергиин многоугольника в направлении и
Factrl = функция для вычисления факториала числа
п(,) = матрица [N] (уравнение (6-59))
Ni{n,i) = функция, вычисляющая (™) (уравнение (5-64))
pi = число параметрических линий в направлении и
р2 = число параметрических линий в направлении w
q{,) = координатные векторы для точек на поверхности
q( ,1) содержит компоненту х вектора
q( ,2) содержит компоненту у вектора
q( ,3) содержит компоненту z вектора
для фиксированного значения и следующие т элементов содержат
значения для кривой q(ui,w); q имеет размерность р1*р2У. 3
и(>) = [U] параметрическая матрица (уравнение (6-59))
ш(>) = [W] параметрическая матрица (уравнение (6-59))
subroutine mbezsurf (b(,),nlIml,pl,p2; q(,))
допустимая сетка Безье 10x10
dimension x(10,10),y(10,10),z(10,10),g(10,10)
dimension n(10,10),m(10110),u(l,10),w(10>l)
dimension templ(10,10),temp2(10,10),temp3(l,10),temp4(l,l)
def Ni(n,i) = Factrl(n)/(Factrl(i)*Factrl(n - i))
определяем размерности матриц и заполняем нулями эти матрицы
Mat n = Zer(nl + l,nl + 1)
Mat m = Zer(ml + l,ml + 1)
Mat x = Zer(nl + l,ml + 1)
Mat у = Zer(nl + l,ml + 1)
Mat z = Zer(nl + l,ml + 1)
Mat g = Zer(nl + l,ml + 1)
Mat и = Zer(l,nl + 1)
Mat w = Zer(ml + 1,1)
Mat tempi = Zer(nl + l,ml + 1)
Mat temp2 = Zer(nl + l,ml + 1)
Mat temp3 = Zer(l,ml + 1)
Mat temp4 = Zer(l.l)
устанавливаем значения для матриц х, у, z, т. е. компоненты матрицы [В]
for i = 1 to nl + 1
for j = 1 to ml + 1
ij = (ml + l)*(i - 1) + j
x(i,j) = b(ij,l)
y(ij) = b(ij,2)
z(ij) = b(ij,3)
next j
next i
устанавливаем значения для матриц [N] и [М]
for i = 0 to nl
for j = 0 to nl
if i + j <= nl then
n(i + 1 j + 1) = Ni(nl j)*Ni(nl - j,nl - i - j)*(-l)A(nl - i - j)
else
n(i + 1 j + 1) = 0
end if
next j
next i
for i = 0 to ml
for j = 0 to ml
if i + j <= ml then
m(i + lj + 1) = Ni(mlj)*Ni(ml - j,ml - i - j)*(-l)A(ml - i - j)
else
m(i + l,j + 1) = 0
end if
next j
next i
Mat m = Trn(m) транспонируем матрицу [М] для последующего использования
for к = 1 to 3
icount = 0 переустанавливаем счетчик точек поверхности
if к = 1 then Mat g = х присваиваем значение каждой компоненты
матрицы [В] матрице [G]
if к = 2 then Mat g = у
if к = 3 then Mat g = z
устанавливаем значения для постоянной матрицы [N][B][M]
(напомним, что [М]=[М]Т)
Mat tempi = g*m [B][M]r
Mat temp2 = n*templ [N][B][M]T
for t = 0 to 1 step l/(pl — 1) устанавливаем значения матрицы и
for i = 0 to nl
u(l,i + 1) = tA(nl - i)
next i
Mat temp3 = u*temp2 [U][N][B][M]T — константа для каждого значения и
for s = 0 to 1 step 1/(р2 — 1) устанавливаем значения матрицы w
icount = icount + 1
for i = 0 to ml
w(i + 1,1) = sA(ml - i)
next i
Mat temp4 = temp3*w вычисляем точку поверхности
q(icount,k) = temp4(l,l) запоминаем точку в массиве q
next s
next t
next к
return
rbspsurf
Подпрограмма вычисляет декартово произведение поверхности рационального
В-сплайна, используя открытые однородные узловые вектора (уравнение (6-85)).
Ь() = массив, содержащий точки сетки многоугольника
Ь{ ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь( ,3) содержит компоненту z вершины
Ь( ,4) содержит однородную координату нормирующего множества
Замечание: Bij — b(,) имеет размерность п*т х \, причем j изменяется
быстрее. Размер сетки многоугольника п х т
к = порядок в направлении и
I = порядок в направлении w
mbasis = массив, содержащий нерациональные базисные функции для w
(уравнение (5-84))
mpts = число вершин многоугольника в направлении w
nbasis = массив, содержащий нерациональные базисные функции для w
(уравнение (5-84))
npts = число вершин многоугольника в направлении и
pi = число параметрических линий в направлении и
р2 = число параметрических линий в направлении w
q() = массив, содержащий результирующую поверхность
q( ,1) содержит компоненту х вектора
q( ,2) содержит компоненту у вектора
q( ,3) содержит компоненту z вектора
для фиксированного значения и следующие т элементов содержат
значения для кривой q(ui,w); q имеет размерность pl*p2x 3.
Отображается поверхность размера pi x р2
sum = сумма рациональных базисных функций поверхности
subroutine rbspsurf (b(,),k,l1npts,mpts1pl,p2; q(,))
допускает 20 заданных точек с базисной функцией порядка 5
dimension x(30),y(30),nbasis(l,20),mbasis(l,20)
определяем размерности и заполняем массивы нулями
Mat х = Zer(npts + k)
Mat у = Zer(mpts + 1)
Mat nbasis = Zer(l,npts)
Mat mbasis = Zer(l,mpts)
Mat q = Zer(pl*p2,3)
генерируем открытые однородные узловые векторы
call knot(npts,k; x()) вычисляем узловой вектор и
call knot(mpts,l; y()) вычисляем узловой вектор w
nplusc = npts 4- k
mplusc = mpts + 1
icount = 0
вычисляем точки на В-сплайн поверхности
for и = 0 to x(nplusc) step x(nplusc)/(pl — 1)
call basis(k,u,npts,x; nbasis) нерациональная базисная функция для и
for w = 0 to y(mplusc) step y(mphisc)/(p2 — 1)
call basis(l,w,mpts,y; mbasis) нерациональная базисная функция для w
call sumrbas(b,nbasis,mbasis,npts,mpts; sum) суммируем базисные функции
icount = icount + 1
for i = 1 to npts
for j = 1 to mpts
for s = 1 to 3
jl = inpts*(i - 1) + j
qtemp = Ь(]1,4)*Ь01,з)*пЬаа18(1Д)*тЬаа1з(1 j)/sum точка поверхности
q(icount,s) = q(icount,s) + qtemp сохраняем в массиве поверхности
next s
next j
next i
next w
next u
return
sumrbas
Подпрограмма вычисляет сумму нерациональных базисных функций
(уравнение (6-87)).
Ь() = массив, содержащий точки сетки многоугольника
Ь( ,1) содержит компоненту х вершины
Ь( ,2) содержит компоненту у вершины
Ь{ ,3) содержит компоненту z вершины
Ь( ,4) содержит однородную координату нормирующего множителя
Замечание: Bij = b(,) имеет размерность п*т х 4> причем j изменяется
быстрее. Размер сетки многоугольника п х т
mbasis = массив, содержащий нерациональные базисные функции для w (ур. 5-84)
mpts = число вершин многоугольника в направлении w
nbasis = массив, содержащий нерациональные базисные функции для и (ур. 5-84)
npts = число вершин многоугольника в направлении и
sum = сумма базисных функций
subroutine sumrbas (b(,),nbasis(,),mbasis(,),npts,mpts; sum)
sum = 0
for i 1 to npts
for j 1 to mpts
jl = mpts*(i - 1) + j
sum = sum + b(jl,4)*nbasis(l,i)*mbasis(i,j) вычисляем сумму
next j
next i
return