Похожие
Текст
Н. ИДЕЛЬСОН
СПОСОБ
НАИМЕНЬШИХ
КВАДРАТОВ
I
ВТОРОЕ ИЗДАНИЕ,
ПРОСМОТРЕННОЕ И ДОПОЛНЕННОЕ
Н. ИДЕЛЬСОН
СПОСОБ НАИМЕНЬШИХ
КВАДРАТОВ
ВТОРОЕ ИЗДАНИЕ,
ПРОСМОТРЕННОЕ И ДОПОЛНЕННОЕ
ЛЕНИНГРАД
19 3 2
Типография им. Волокарского. Ленинград. Фонтанка, Б7.
Ответ, редактор: Н. Идельсон Технич. редактор: JI. А. Хомутовокий.
ЛОИЗ № 360. Бумага 72 X НО — 127а печ. листов. — Колич. знаков в листе 89.600.
Сдано в набор 14/XI — 31 г. Подписано к печати 3/XII — 31 г.
Ленинградский Областлит № 22661. Заказ № 2406. Тираж 10.000.
Оглавление.
Стр.
Предисловие . 7
Отдел I.
Системы с недостаточным числом уравнений.
1. Вводные замечания: обозначение сумм; формулы, относящиеся к среднему
арифметическому 9
2. Постановка задачи уравнивания 14
3. Простейшие примеры. Принцип Лежандра 15
4. Общий случай одного условного уравнения со многими неизвестными.
Решение Лежандра. Введение неопределенного множителя; понятие
о коррелате. Примеры 20
5. Уравнение полюса 24
6. Уравнивание при задании системы условных уравнений. Выражение попра¬
вок через коррелаты; нормальные уравнения для коррелат ...... 26
7. Практические указания; схема; примеры 31
8. Уравнивание четыреугольника 33
9. Поправки к наблюдениям различного веса. Обобщенный принцип
Лежандра 36
10. То же — в случае системы условных уравнений; введение множителей,
обратных весам; вид нормальных уравнений в этом случае. Пример:
уравнивание высот 40
11. Составление нормальных уравнений. Таблицы. Арифмометр. Контроли . . 43
12. Решение нормальных уравнений. Схема 47
13. Сокращенная схема . 49
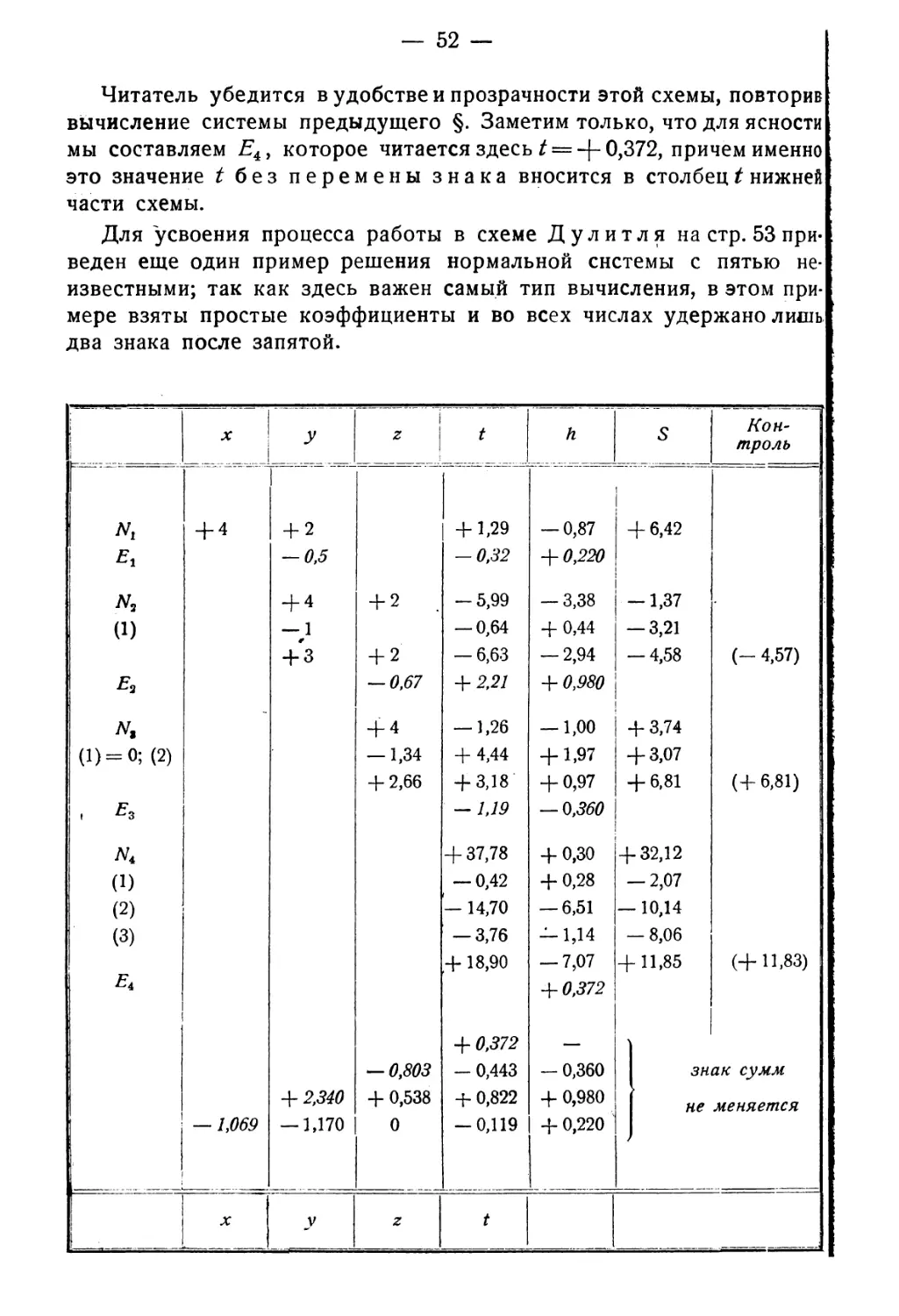
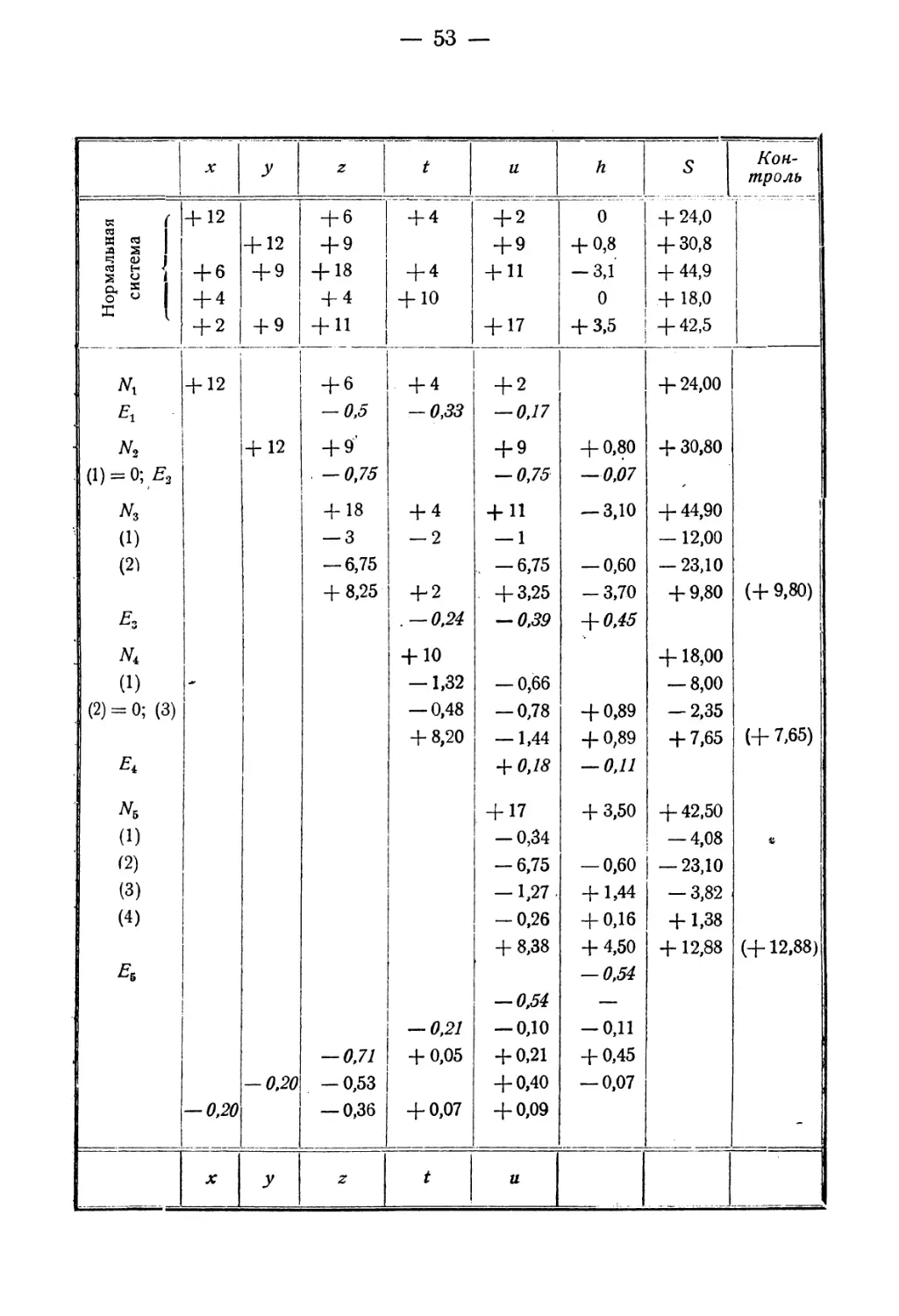
14. Схема Дулитл я 51
Отдел II.
Обработка рядов наблюдений одной величины.
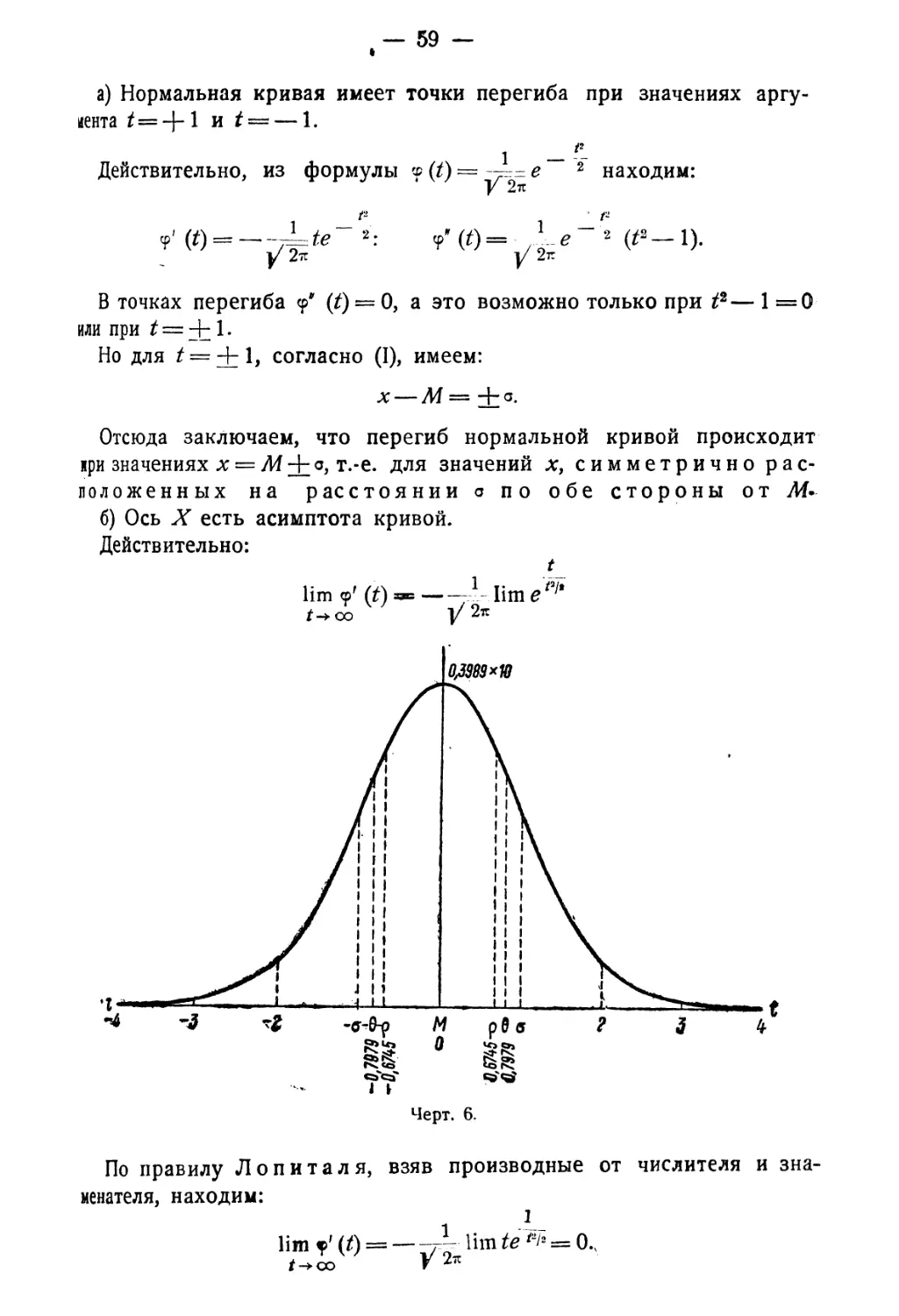
§ 1. Нормальное статистическое распределение. Понятие о кривых распределе¬
ния; частоты; среднее значение характеризующего признака; среднее
квадратичное уклонение (дисперсия). Формула Гаусса. Свойства
нормального распределения. График нормальной кривой 55
— 4 —
Стр.
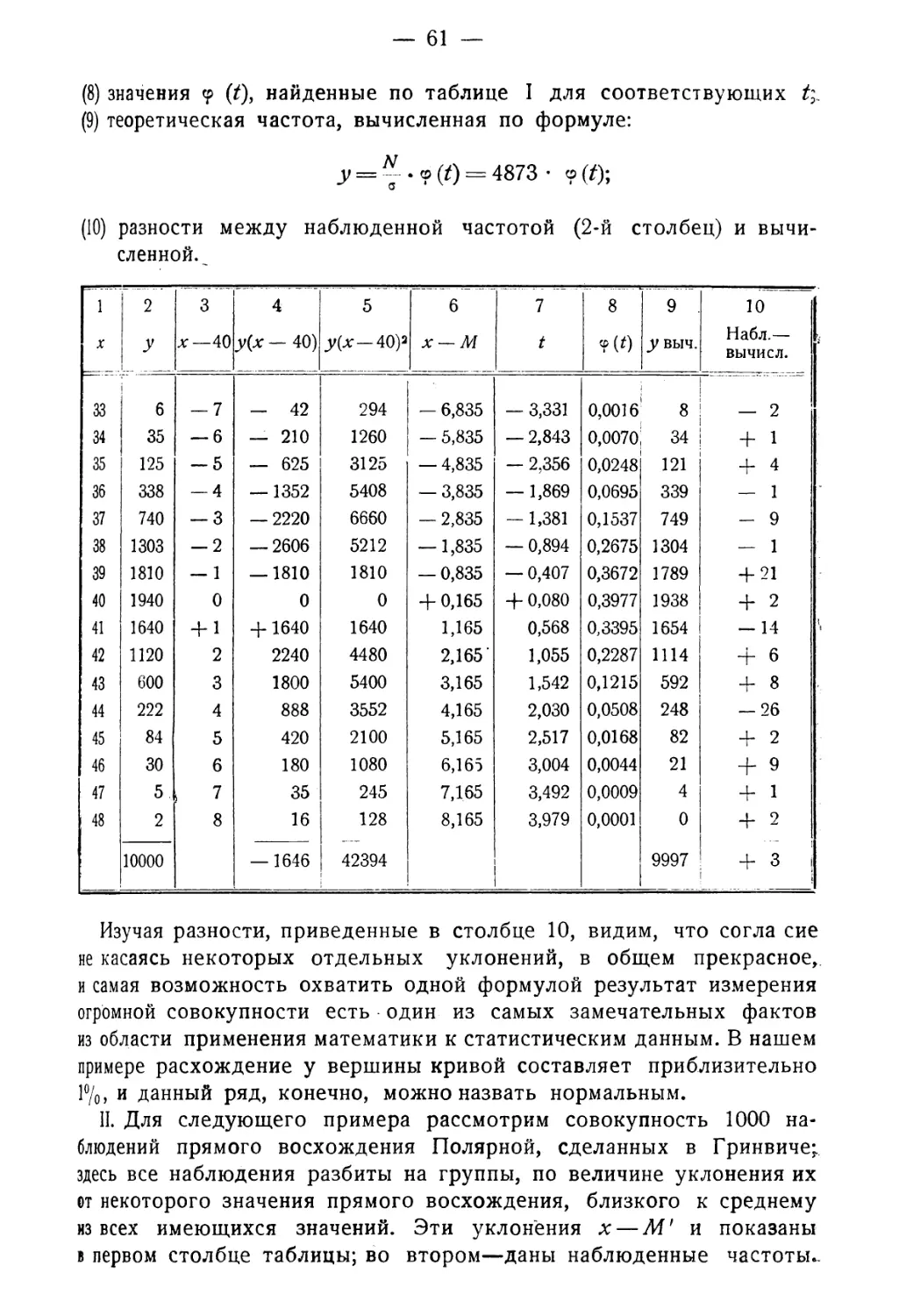
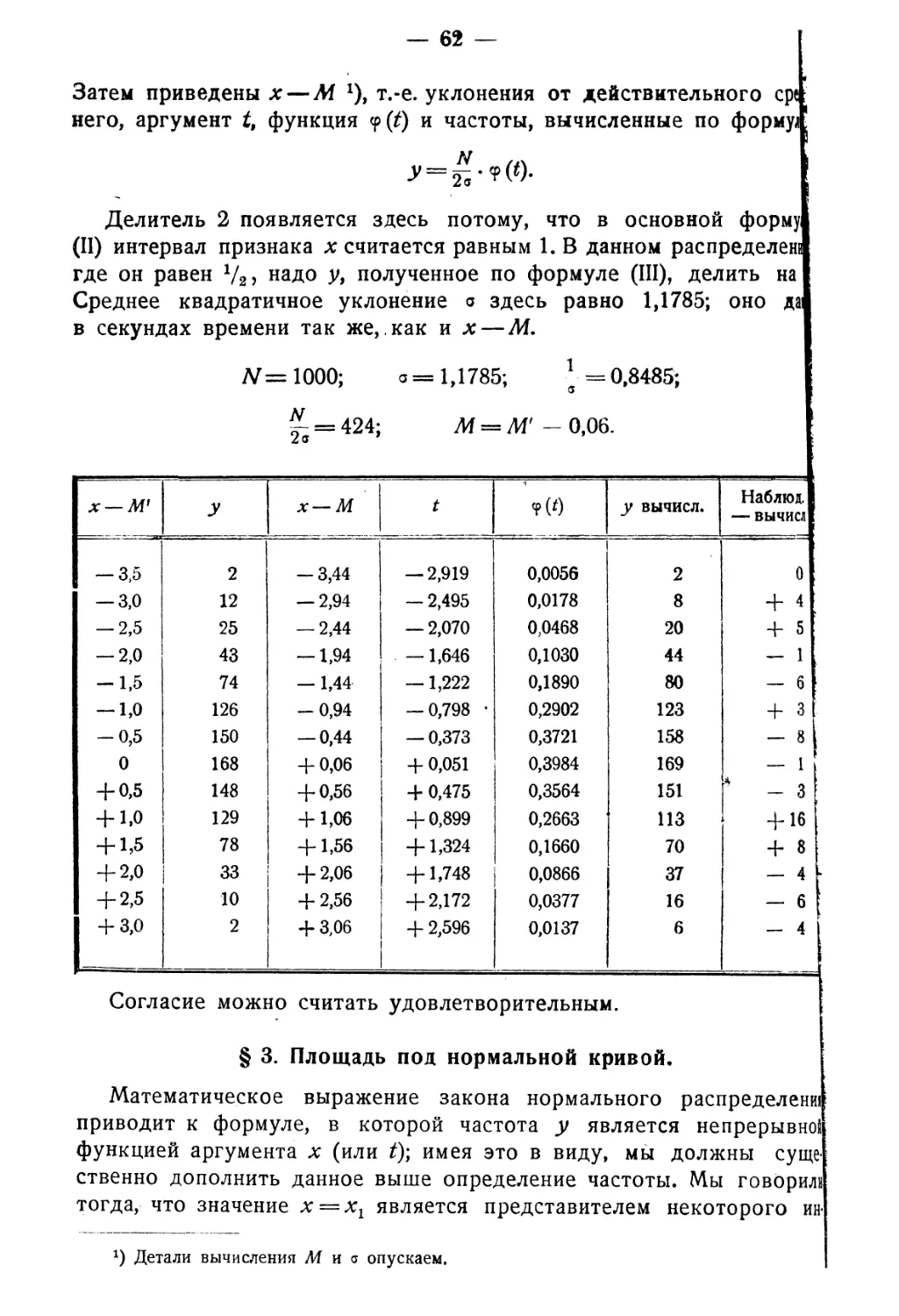
§ 2. Примеры обработки статистических рядов . . . . 60
§ 3. Площадь под нормальной кривой Формула для числа объектов, характери¬
зуемых заданными предельными значениями признака. Ординаты, между
которы и заключена половина площади под нормальной кривой. Инте¬
гральные кривые распределения. Теорема Чебышева 62
§ 4. Теория ошибок. Предположения, лежащие в ее основе. Применение к ней
- выведенных формул. Мера точности. Вероятная ошибка и срединная
ошибка 72
§ 5. Закон распространения средней ошибки. Примеры 80
§ 6.* Правило наибольшего веса и способ наименьших квадратов. Формула для
взвешенного среднего. Начало арифметического среднего как частный
случа \ правила наиСо 1ьшего веса 85
§ 7. Формулы Бесселя и Петерса. Средняя ошибка единицы веса;
средняя ошибка результата 89
§ 8. Обработка ряда наблюдений одинакового веса. Критерий Аббе. Числен¬
ный пример 94
§ 9. Уравнивание рядов наблюдений. Средние ошибки до и после уравнивания. 97
Пример 100
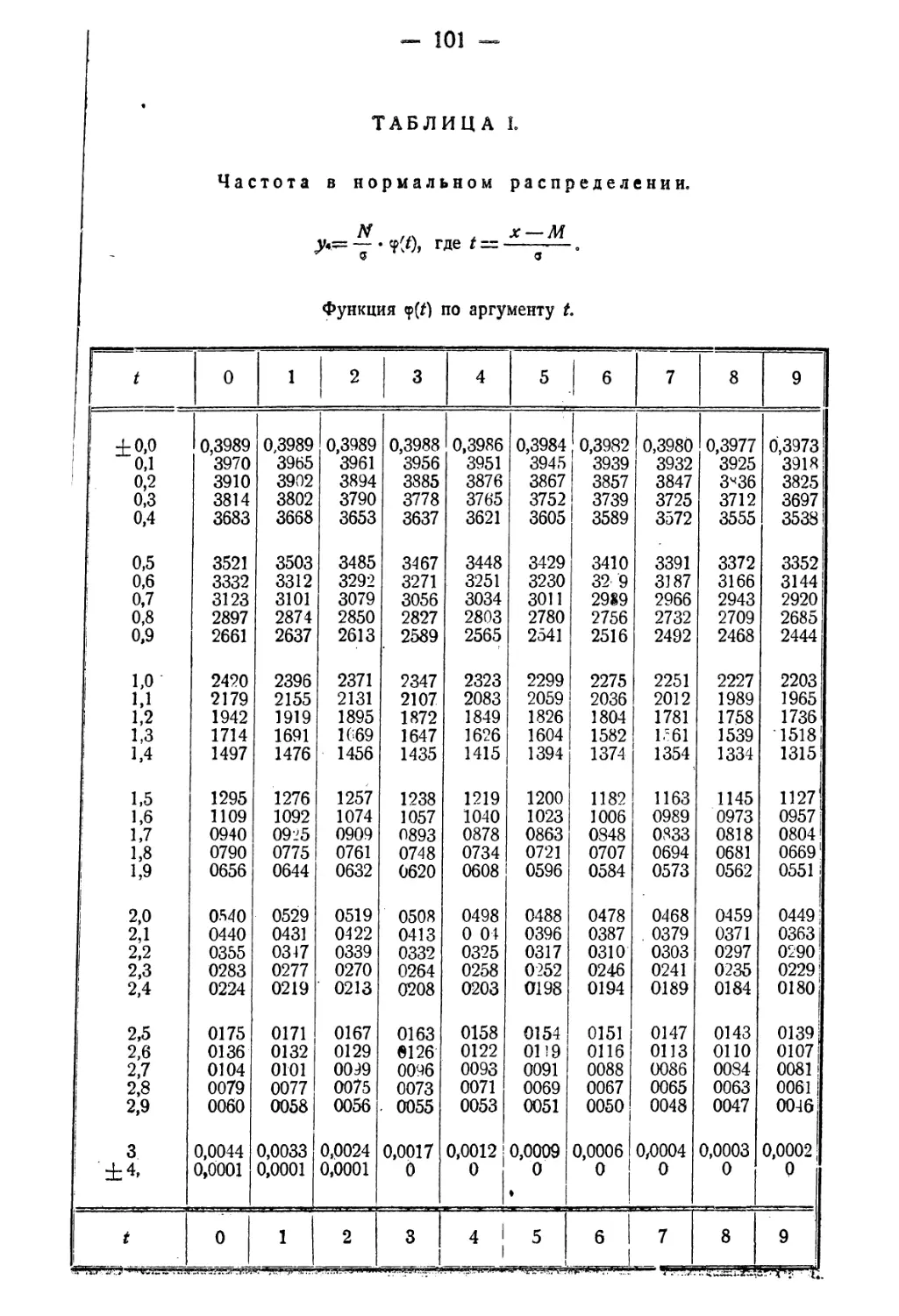
Таблица I. Частота в нормальном распределении 101
w II. Площадь под нормальной кривой 102
, III. Число случайных погрешностей, не превосходящих дан¬
ной кратности вероятной ошибки ...... в .... . 103
Отдел III.
Системы с избыточным числом уравнений.
§ 1. Применение принципа Лежандра. Основные уравнения д'тя остаю¬
щихся погрешностей, сумма квадратов которых имеет минимальное зна¬
чение 104
§ 2. Нормальные уравнения для неизвестных; выражение для минимальной
суммы квадратов остающихся погрешностей. Приведение условных
уравнений к одинакозому весу 107
§ 3. Приведение условных уравнений к линейному виду. Улучшение решения.
Примеры 110
§ 4. Системы с одним и двумя неизвестными. Вычисление весов и средних
ошибок неизвестных. Численный пример ....... ...... 114
§ 5. Взвешенное уравнивание треугольника; вычисление средних ошибок . . 120
§ 6. Случай упрощения: понижение числа нормальных уравнений, когда коэф-
ф циент при одной из неизвестных равен 1 122
§ 7. Примеры. Вычисление хода хронометра; два способа обработки. Эксцен¬
триситет алидады. Измерение горизонтальных углов; способ Шрей¬
бера 125
§ 8. Нормальные коррелатные системы для величин, обратных весам неизвест¬
ных. Коэффициент при неизвестной и ее вес. Теорема Г а у с с а о мак¬
симальных весах неизвестных, определяемых по спосо (* наименьших
Стр.
§ 9. Вычисление весов; применение определителей в системах с тремя неиз¬
вестными; схемы для вспомогательных коррелатных систем. Пример.
Средние ошибки • 142
§ 10. Обозначения Гаусса и формула для суммы квадратов остающихся
погрешностей ' ..... . 147
§ 11. Приведен «е квадратичной формы для суммы квадратов остающихся
~ погрешностей к каноническому виду 151
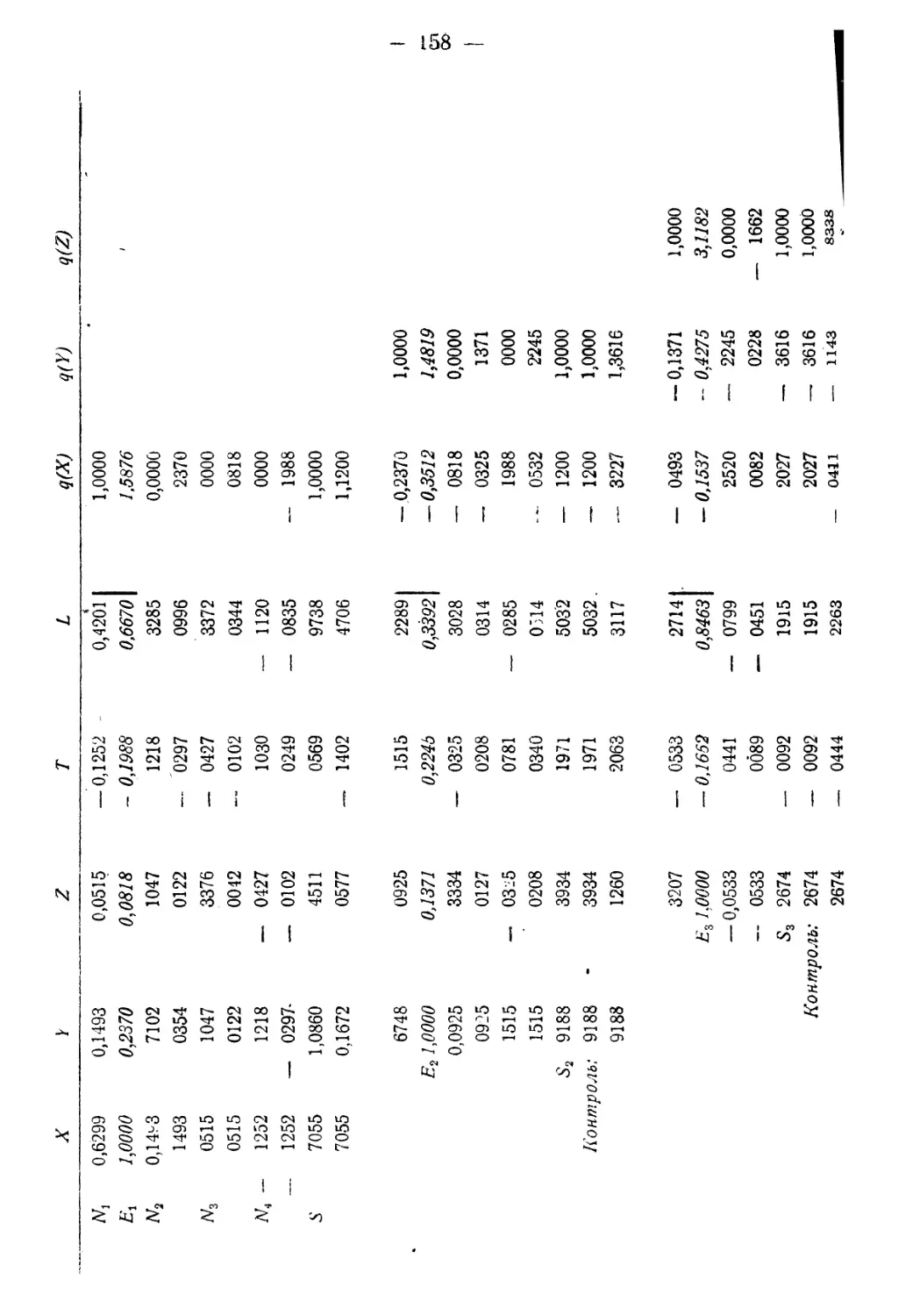
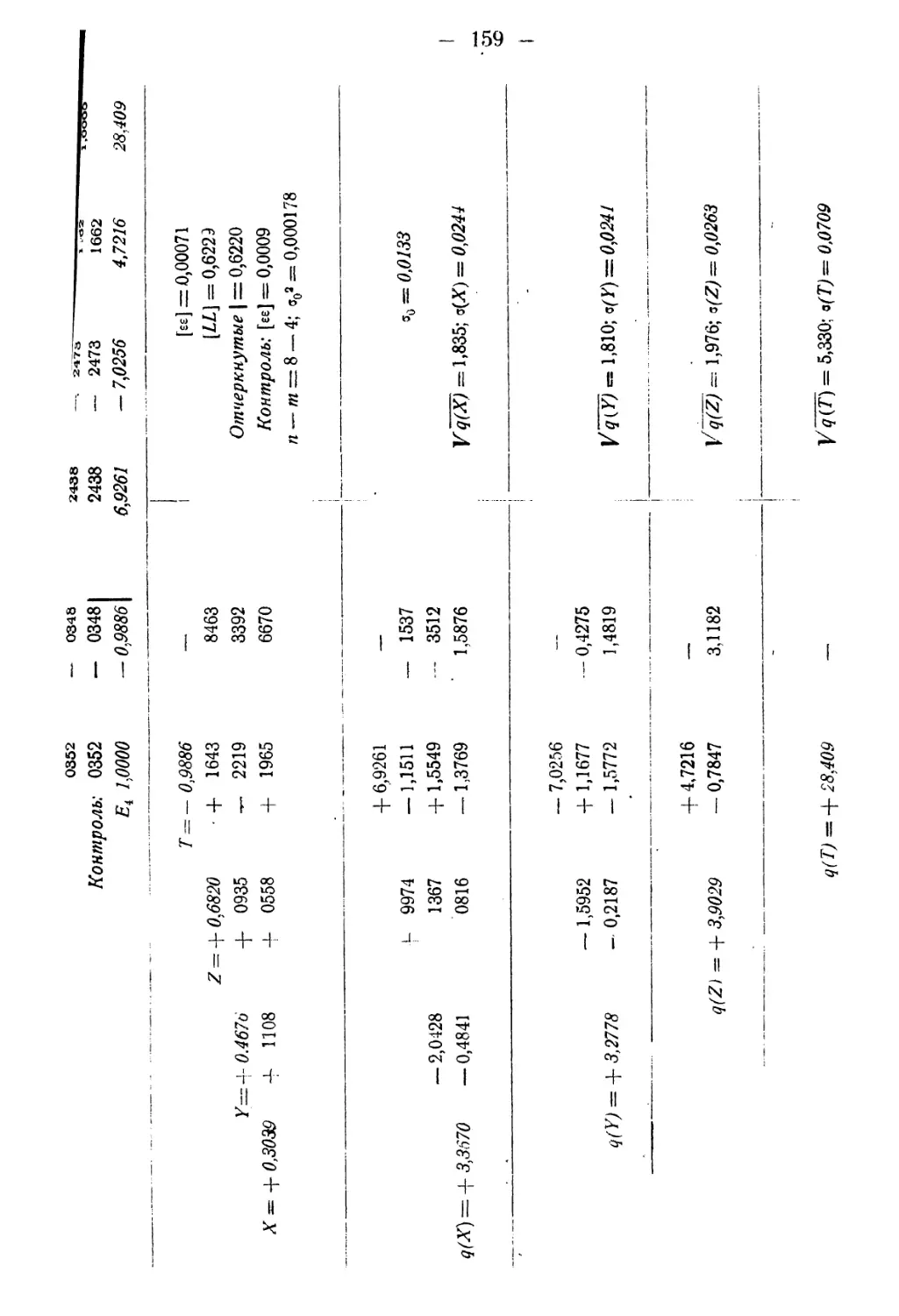
§ 12. Заключительный пример и схема ....... 154
Отдел IV.
Интерполирование по способу наименьших квадратов.
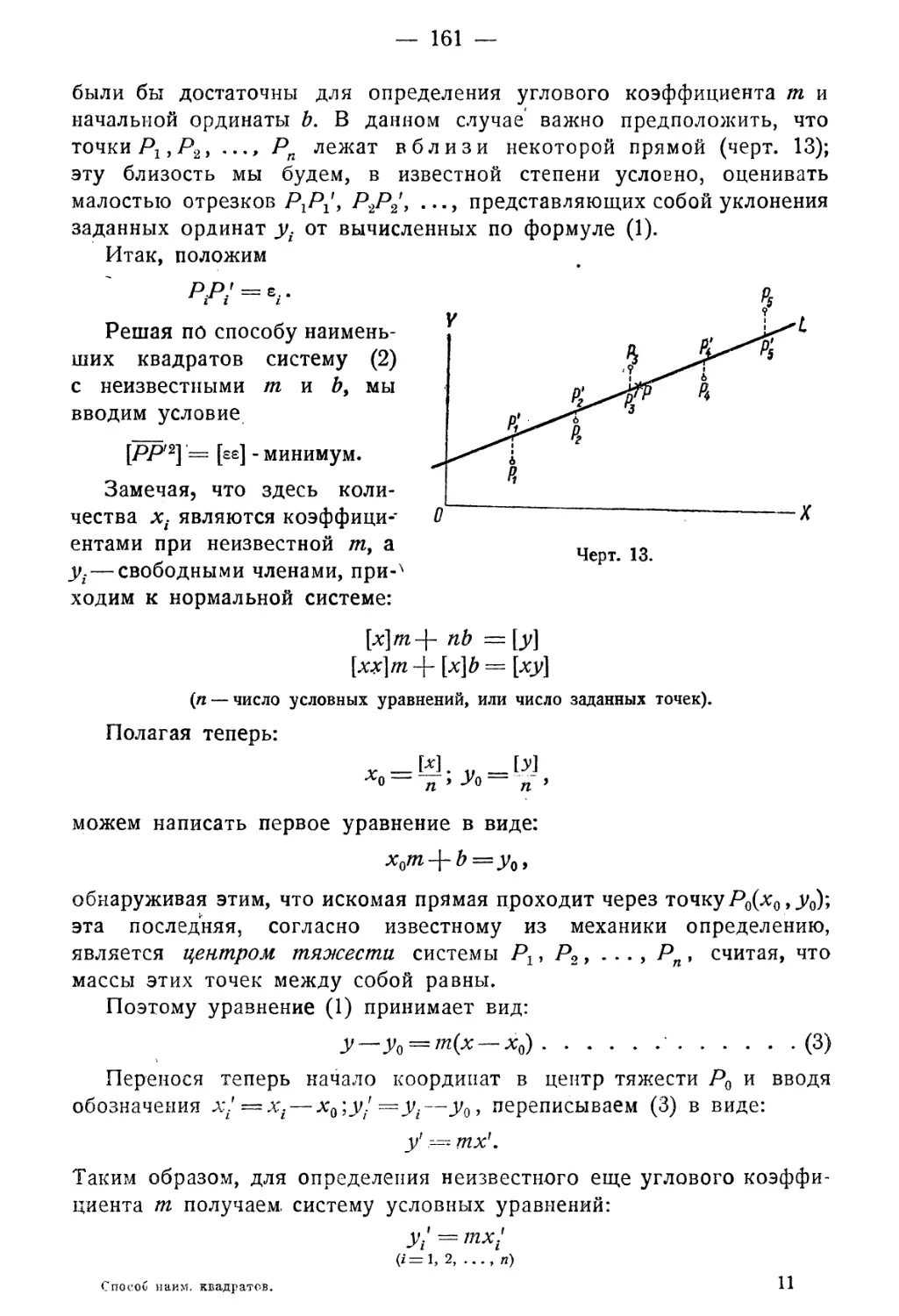
§ 1. Линей ое интерполирование. Линии регрессии . 160
§ 2. Вероятнейшая прямая 164
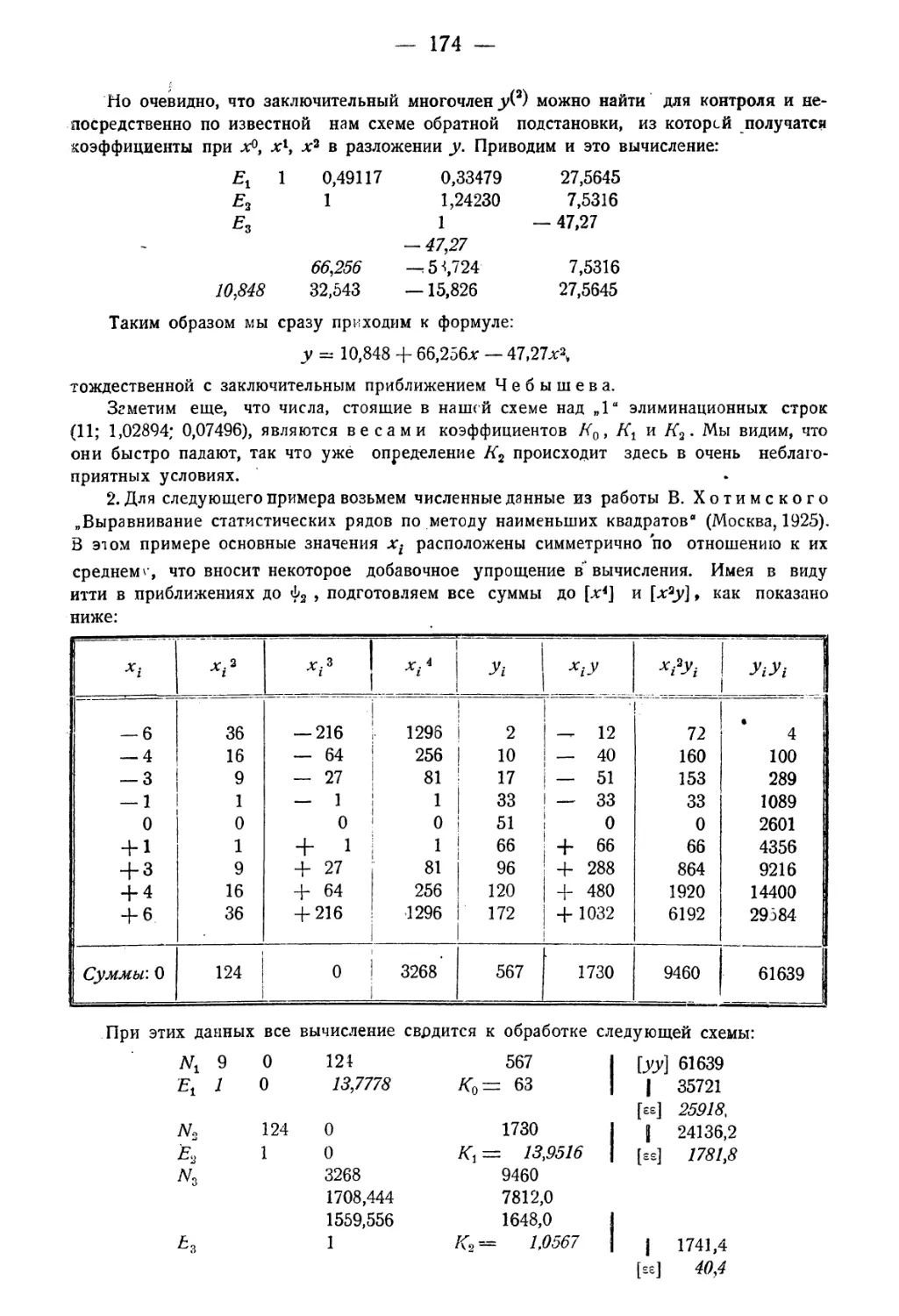
§ 3. Параболическое интерполирование (способ Чебышева) ....... 166
§ 4. Примеры 172
§ 5. Интерполяционный ряд Чебышева 175
§ 6. Разложения по ортогональным функциям; их связь со способом наимень¬
ших квадратов 180
§ 7. Основы гармонического анализа 184
§ 8» Разложения по полиномам Лежандра 191
Литература • 199
, Предисловие.
Настоящий курс имеет назначением прежде всего раскрыть перед
Ьучающим всю вычислительную технику способа наименьших квадра¬
тов, как основной методы обработки наблюдений, рассматриваемой здесь
в ее разнообразных применениях. Это задача чисто практическая;
к ней постоянно обращается геодезист, астроном, физик, статистик;
поэтому ни одна деталь, которая могла бы облегчить эту работу
практика, не должна быть опущена. Имея это в виду, я стремился
расположить материал концентрически, начиная с вопросов простей¬
ших и кончая более сложными; как всегда, при таком методе изло¬
жения оказались неизбежными повторения. Это изложение начинается
здесь со способа неопределенных множителей, называемого в геодезии
методой коррелат; оно переходит к обработке рядов наблюдений
одной величины, изучаемой на основе понятий статистических, и обра¬
щается затем к системам с избыточным числом уравнений. Такое рас¬
пределение материала, несколько необычное в курсе способа наимень¬
ших квадратов, объясняется тем, что способ коррелат, представляю¬
щий собой решение ясно поставленной задачи на максима и минима,
является теоретически наиболее простым применением данной методы;
он довольно далек от теории ошибок со всеми ее своеобразными
трудностями; наконец, владея формулами этого отдела, можно суще¬
ственно упростить доказательство основной теоремы Гаусса
о весах неизвестных, служащей простым и рациональным обосно¬
ванием всей методы наименьших квадратов. Связь же ее с тео¬
рией вероятностей в настоящем курсе не рассматривается; мне каза¬
лось нецелесообразным входить в эту сторону вопроса, при наличии
классического трактата А. А. Маркова или курса „Теории вероят¬
ностей" акад. С. Н. Бернштейна, имея к тому же в виду и некото¬
рую условность такого обоснования.
Но свести изложение способа наименьших квадратов к нескольким
схемам и вычислительным правилам—все-таки значило бы взять вопрос
с его узкой стороны. В математическом смысле этот способ приобре¬
тает свою полнуй ценность только после появления мемуаров П. Л. Ч е-
бышева об интерполировании по способу наименьших квадратов,
т.-е. о построении функции, которая приближалась бы к заданной
совокупности ее отдельных значений в наилучшем, с точки зрения
способа наименьших квадратов, смысле. К сожалению, метод Чебы¬
шева довольно редко применялся на практике, быть может из-за
некоторой сложности не только выводов, но и заключительных фор¬
мул, предназначенных для вычислителя. В последнем отделе книги
дано строгое и вместе с тем элементарное изложение этого способа,
органически связанное с предыдущими частями курса, причем пока¬
зано, что все нужное для его применения удобно укладывается в обыч¬
ные формулы и схемы способа наименьших квадратов; первое указа¬
ние на возможность такого упрощения встречается, насколько мне
известно, в работе проф. А. Я. Орлова, в Изв. Русск. Астроном.
Общества за 1918 г. Но если из этих формул и схем легко строятся
ортогональные полиномы Чебышева, то естественно выяснить и
общую связь способа наименьших квадратов с разложениями по орто¬
гональным функциям, получившим теперь столь обширное примене¬
ние в различных отделах анализа. Этому вопросу посвящены послед¬
ние страницы курса.
Ленинград,
Декабрь 1931 г.
ОТДЕЛ I.
СИСТЕМЫ С НЕДОСТАТОЧНЫМ ЧИСЛОМ УРАВНЕНИЙ.
§ 1. Вводные замечания.
1. Обозначение сумм. Нам придется в дальнейшем систе¬
матически пользоваться специальным обозначением сумм, введенным
Гауссом; с пояснения его мы и начнем.
Имея ряд количеств:
» ал»* * *»%
мы будем алгебраическую сумму всех этих количеств обозначать зна¬
ком [а], т.-е. писать:
а\ + а2 + аг + •' * + ап — И ■•
Точно так же, имея два ряда количеств, по одинаковому
числу в каждом, например:
t ^а > ' * * &п
ьг, ь2, ьй, •••*„,
будем сокращенно обозначать знаком [ab] алгебраическую сумму
произведений каждого из чисел верхнего ряда на соответствующее ему
число нижнего ряда, т.-е. положим:
[а*] = аА + аАН НА'-
аналогично этому весьма часто пишут [аа] для обозначения суммы
квадратов всех а, так что:
[аа] = ах* -{- а23 -| f-ana.
Далее, имея три ряда чисел:
&1 , , &Q f • * * , Un
ьх, ь2, Ьй> ьп
Рх> Рз>Рз> ", Р„
вводят обозначения:
[abp] — a1b1p1 -f- asb2p2 -f.,,, -j- aJ>j)n,
— 10 —
или
точно так же:
[раа] =р1а12+р2а2*+ ... +рнап*.
Основное свойство написанных сумм то, что все множители каж¬
дого из слагаемых имеют один и тот же значок; поэтому суммы
произведений вида аф2 -f- афх -f-... в обозначении Гаусса записаны
быть не могут.
Знак [ ] позволяет обозначать сокращенно результаты целой сово¬
купности алгебраических операций. Пусть, например, дан ряд равенств
вида:
1.= и. + а.
(/ = 1, 2, 3, п).
Возводя каждое из этих равенств в квадрат и складывая, полу¬
чаем:
[Щ = [ии] + 2 [т] + [«а].
Точно так же, умножая каждое из тех же равенств на соответствую¬
щее I. (т.-е. первое равенство на /х, второе на /2 и т. д.) и складывая,
находим:
[//] = И + Н.
В частности, когда а. равны между собою, т.-е. когда
а1=а2 = а3= ... =oc„ = a,
будем иметь:
[//] = [ии] 2а [и] 4- «а2,
а во втором случае:
[//] = [/«] 4-«[/].
Допустим теперь, что, возведя те же равенства в квадрат, мы
после этого каждую из строк: 1{1. = и1и1-\-2ир1-\-ар.} помножим на
соответствующий множитель р. и результаты сложим. Тогда придем
к равенству:
[рЩ = [рии] 4- 2\рт) 4- [раса].
Заметим, наконец, что при суммировании ряда выражений, в каж¬
дое из которых входит множитель [/], эта сумма выносится за скобки,
как всякий общий коэффициент.
Напр.:
т+кщ+.--+1пщ=щ-щ=щ*
2. Формулы, относящиеся к среднему арифм етиче-
с к о м у. Весьма часто в течение курса придется ссылаться на две
теоремы, касающиеся среднего арифметического из данных величии
— 11 —
4,... I . По определению среднее арифметическое равно алгебрам*
ческой сумме данных величин, деленной на их число. Обозначая это
среднее через L, имеем:
lt + lQ+.
L-
п
или:
1 = ^, ............ .(1)
откуда
ttL — Щ — О (*)
Пусть Хх, \,... Хя обозначают уклонения данных величин l.t от их
среднего в смысле „данное минус среднее" т.-е.:
X, = . (2)
просуммировав все эти равенства, получаем:
[X] = [/]-«£;
но в силу (*) правая часть равна нулю, так что:
N = 0 . . .(3)
т.-е. алгебраическая сумма уклонений данных величин от их среднего
арифметического равна нулю.
Выведем теперь весьма важную формулу для суммы квадратов
тех же уклонений \. Чтобы получить ее, возводим все равенства (2)
в квадрат и суммируем. Согласно сделанным выше указаниям это
дает:
[XX] = [//] —2Z.[/] + wI2.
Но
Ь = [-й-
п •’
поэтому:
м-и-ам+ад:
или, после очевидных преобразований:
[XX] =[//]-!£ (4)
т.-е. сумма квадратов уклонений любых величин от их арифметиче¬
ского среднего равна сумме квадратов этих величин, без квадрата их
суммы, деленного на их число.
Г/13
Так как величина при любых значениях lt не может иметь от¬
рицательного значения, то из (4) выводим:
[XX] £[//],
- 12
т.-е. сумма квадратов уклонений любых величин от их среднего не
больше суммы квадратов тех же величин. Нгконец, заметим, что [U],
как сумма положительных величин, может обратиться в нуль только
тогда, когда каждое из слагаемых А,2 равно нулю, следовательно,
когда lt—L— 0, т.-е. только в том случае, когда все lt равны между
собой.
Нетрудно вывести и для суммы произведений типа [ab] формулу,
аналогичную (4).
Пусть даны два ряда величин:
> ^2 > * • • >
« ^2 » • • • > *
Обозначим через а0 и Ь0 средние арифметические из этих рядов,
и через а! и Ь! уклонения данных величин от соответствующих сред¬
них. По доказанному
[а'] = [&']=0.
При этих обозначениях имеем:
[а'Ь'] = [а!ф-Ьй)\ = [а'Ь] - Ьй[а'}.
Но второй член справа равен нулю; преобразовывая же первый
член, находим:
[a!b] = [(а, — а0)Ь] = [ab] — а0[Ь\. _
Подставляя сюда а0 — ~ > получаем:
[a!b’] = \ab)-{^P-. (5)
Полагая здесь
возвращаемся к формуле (4).
3. Практика вычисления среднего. Если число дан¬
ных величин lt значительно, то находить их среднее L путем сум¬
мирования по формуле (1) довольно затруднительно. Для облегчения
этой операции выбирают на глаз приближенное (круглое) значение
L!, близко к среднему из всех lt и полагают:
^ ^ Vp I — 1* 2,.. . . я;
Складывая атц равенства, имеем:
[/]-.«£'= м,
откуда
« «
ГЛ г
но ^ = L, и потому
L-V + Ы
(!)
Итак, для нахождения точного среднего нужно к произвольно
выбранному L' придать среднее из уклонений от него данных lv
Из (7) получаем:
>. = /,— L = /, - V' —И-' = v - М
I 1 1 п 1 п
(8)
Таким образом \ суть не что иное, как уклонения величин v. от
их среднего. Поэтому, применяя (4), находим:
(9)
Формулы (7), (8) и (9) имеют постоянное применение при обра¬
ботке рядов наблюдений. — Контролем (9) служит формула:
[XX] = [XV] .
(10)
Для вывода этой формулы множим уравнения (8) соответственно
на X,- и складываем, что дает:
но [X] =0, чем и доказывается (10).
Найти среднее арифметическое из данных восьми
величин
1
V
X
XX
Ь
1.
11,732
— 18
— 21
441
378
2.
11,753
+ 3
0
0
0
3.
11,765
-{- 15
+ 12
144
180
4.
11,731
— 19
— 22
484
418
5.
11,745
— 5
— 8
64
40
6.
11,760
+ ю
+ 7
49
70
7.
11,766
+ 16
+ 13
169
208
8.
11,772
+ 22
+ 19
361
418
Суммы:
+ 24
0
1712
1712
кенное среднее U было взято 11,750; поэтому
24
L = 11,750 +-q- единиц 3-го знака = 11,753
Сумма квадратов уклонений X равна 1712 единиц шестого знака, т.-е. 0,001712
~ 14
4. Основное свойство арифметического среднего
Вернемся к ф-е (9), которую перепишем в виде: \
[vv] = [xx]+M-\
- Но, в виду (7), [v] = п (L — L'), и потому
И = [ХХ]+л(£-//)*
Так как при L' неравном L второй член справа есть величина су
щественно положительная, то
и>т
так что сумма квадратов уклонений данных величин U от любо\
величины L' всегда больше суммы квадратов их уклонений он
арифметического среднего L.
В примере, рассмотренном выше L — V — 3 (в единицах третьего знака),
потому:
[w] = 1712 + 8. 9 = 1784 ед. б-го знака,
что и предлагается проверить непосредственным вычислением,
§ 2. Постановка задачи.
Сущность уравнительных вычислений, к которым мы переходим
состоит в следующем. Отыскиваются значения нескольких неизвеп
ных величин: х1г х2,..., хп. Эти величины по предположению н
являются друг от друга независимыми, но связаны между собой не
которыми уравнениями, вытекающими из общих условий дашш
задачи. Далее предполагается, что все значения xt получаются в ре
зультате физического измерения, так что это могут быть длины, углк
веса и т. п. Значения xlf х2,..., хп, найденные в результате соответ
ствующих определений, будем обозначать:
^11 ^2 » • • • > °
Но наблюдения показывают, что если полученные числа I. подста
вить в упомянутые выше уравнения—так назыв. условные уравне
ния,—то эти последние не удовлетворятся в полной точности и в ка»
дом из них обнаружится некоторая невязка. Считая, что у нас
условных уравнений, мы будем соответствующие невязки называть:
> ^2 » • • •» •
- 15 —
В виду этого ставится задача: найти к наблюденным величинам
такие поправки *): Хх, Х2,..„, Хя, чтобы исправленные значения 1{, т.-е,
величины
;i+xi;
строго удовлетворяли имеющейся совокупности условных уравнений.
Задача эта, если число уравнений меньше числа искомых величин—
как это обычно бывает на практике — является неопределенной, и
сущность методы, предложенной Лежандром в 1806г.2), сводится
к тому, чтобы подчинить всю систему поправок еще одному до¬
бавочному условию, при наличии которого каждая из Х; полу¬
чит совершенно определенное и единственно возможное значение.
Найдя такую систему \ и следовательно решив поставленную задачу,
мы, однако, отнюдь не можем говорить, что совокупность величин /i+Xf
даст нам „истинные" значения искомых количеств х; мы должны огра¬
ничиться утверждением, что эти исправленные величины наилучшим
образом, в смысле принципа Лежандра, удовлетворяют всей сово¬
купности имеющихся в данном случае наблюдений и условных урав¬
нений.
§ 3. Простейшие примеры. Принцип Лежандра.
Допустим, что в результате измерений трех углов плоского тре¬
угольника получены значения:
= 53°,5; /2 = 49°, 1; /3 = 78°,6.
В сумме они дают: lx —f— /3 = 181 °,2; между тем истинные значения
искомых углов удовлетворяют, по геометрической природе задачи,
уравнению: хх 180°; таким образом у нас обнаруживается
невязка8)
h— 181°,2—180° = 1°,2.
Какие дать поправки искомым углам? Это вопрос достаточно про¬
извольный. Если бы в результате измерений сумма трех углов вышла
равной 190°,,то можно было бы только сказать, что эти измерения грубо
:) Полезно условиться называть поправкой (в отличие от ошибки) количество, которое
придается с его знаком к приближенной величине для получения исправленного ее
значения.
а) Г а у с с, в „Теории движения небесных тел, обращающихся вокруг солнца по
коническим сечениям' (1809), говорит: „Впрочем это правило, которым мы поль¬
зуемся уже с 1795 г., недавно появилось в сочинении Л е ж а н д р а'... (рус. пер.,
стр. 285). См. также письмо Гаусса к Лапласу от 30 января 1812 г. (Gauss,
Werke, Bd. X, S. 371).
s) Невязку мы будем всегда считать в смысле: „есть минус должно быть".
— 16 —
ошибочны и не могут быть сделаны годными путем каких бы то нн
было поправок. Но считая в данном случае (совершенно условно)
невязку в 1°,2 достаточно малой, мы поступим наиболее рационально
если каждую из измеренных величин уменьшим на одну треть
невязки, т.-е. на 0°,4 и примем соответственно:
хг = 53°, 1; х2 = 48°,7; лг3£й78°,2 [х] = 180°
(знак = означает приближенное равенство); такое решение оставляет
совершенно открытым вопрос, чему „фактически* равны величины xv
х2, х3; мы устанавливаем только, что написанные исправленные зна¬
чения удовлетворяют имеющемуся геометрическому у ловию.
Алгебраически имеем здесь следующее: к величинам /х, /2, /3 при¬
даны равные между собою поправки Хх = Х2 — Х3 = — , так что:
[X] А.
Весьма важно отметить теперь, что при всей своей очевидности
это решение обладает замечательным алгебраическим свойством,
именно: сумма квадратов поправок Хх, Х2, Ха имеет значение наимень¬
шее по сравнению с суммой квадратов всяких других поправок, допу¬
стимых при условиях данной задачи..
Доказательство. Допустим, что вместо прежних поправок \
мы взяли бы новые поправки X/, положив:
V = ^1 4"а1 > Ц,==^2~Ьа2> Х3' == Xg«3 , ....(*)
где fltj, <*2, а3 некоторые произвольные, положительные или отрица¬
тельные числа. Покажем, однако, что эти числа должны быть свя¬
заны здесь уравнением:
*1 “Ьа2Н"аЗ — 0-
Действительно, система поправок будет только тогда соответство¬
вать данной задаче, если сумма их равна — А; иначе введением такой
системы поправок уравнивание, т.-е. уничтожение невязки, не
будет достигнуто. Сложив теперь равенства (*), имеем:
М = [х] + №
но, как сейчас отмечено:
М=[Х] = ~ А;
следовательно
[«] - 0.
Возведем теперь каждое из равенств (*) в квадрат и сложим их,
припоминая, что \ = Х2 — Х3 =—В результате находим:
— 1? —
Р'У1 = [Ц-^и+м.
Но H*=0, и у нас остается:
[XT] = [XX]+ [*«).
Так как при любых значениях а, неравных нулю, вторая сумма
справа, как сумма квадратов, есть число положительное, то'
[XT] > [XX],
т.-е. сумма квадратов новых поправок больше суммы квадратов X, что
и требовалось доказать.
В нашем примере, вместо—0°,4, мы могли бы взять для новых
поправок значения: — 0°,38, — 0С39, — 0°,43; в сумме они дают—1°,20,
как и должно быть; но сумма их квадратов равна 0,4814, тогда как
сумма квадратов трех исходных поправок есть 0,4800.
В этом совершенно элементарном математическом факте и заклю¬
чается основа способа уравнивания, известного под названием способа
наименьших квадратов.
Пример. Взвешивание одного груза дало 7,23 кг, взвешивание второго —
5,28 кг, но взвешивание обоих вместе дало 12,66 кг.
Здесь должно было бы быть:
*i + х2 — х3 = 0;
но у нас получилось:
/1 + /а-/3 = --0,15,
так что:
h = — 0,15.
Аналогично тому, что было в первой задаче, здесь можно взять:
Х = + 0,05, Ха = + 0,05 Х3 = — 0,05,
и соответственно этому положить:
7,28; х2 & 5,33; лг3 12,61,
так что действительно будет:
xl -f- х2 — х3 0с
Мы покажем сейчас, что именно эта система X обладает тем свойством, что для нее
[XX] меньше, чем для любой другой системы поправок, допустимых по условиям дан¬
ной задачи.
Действительно, поправки \, Х2, Х3, как убеждаемся непосредственной проверкой,
связаны соотношением:
Xi + Х3 — Х3 = + 0,15;
то же самое соотношение должно очевидно иметь место и для всякой другой системы
поправок X/, Ла', Х3', так что, если
X i = Xt + 04; Х'2 = Ха -{- а2; Х'3 = Х3 + а3, . . . . (*)
то 04, а2, az должны быть подчинены условию:
ai + — аз — 9.
Споооб нанм. вводраздв. 2
Возводя в квадрат и суммируя равенства (’), имеем:
[Х'Х'] = [ХХ] + [аа] + 2[Х*].
при чем здесь:
[Ха] = 4- 0,05aj -f- 0,05as — 0,053 = 0,05(a, -}- в* — о3) ~ О,
и мы снова приходим к выводу:
[Х'Х']>[ХХ].
Положим теперь, что в результате повторных наблюдений одно!
и той же величины получились значения:
• • • j ^я*
Мы предполагаем, что все наблюдения произведены с одинаково!
точностью и не подвержены так называемым систематически!
ошибкам инструментального или личного характера. Опыт показы
вает, что благодаря случайным погрешностям наблюдений данньи
измерения 1и /3, будут несколько отличаться друг от другз
колеблясь в ту и другую сторону от некоторого среднего значения
Мы учтем простейшим образом все эти случайные уклонения*) если а
наилучшее определение измеряемой величины х на основании дав
ного ряда примем среднее арифметическое из всех полученных I., т.-«
положим:
дг^£ = Ш.
П
Такую замену каждого из на общее L можно представить себе так
что к каждому из I. мы придаем поправку, равную здесь \ — L — 1р иб(
тогда //—|— = L.
Покажем теперь, что именно такой выбор системы поправок и со
ответствует принципу наименьших квадратов, т.-е. что для любо1
другой системы Xf' будет
[ХТ]>[ХХ].
Доказательств о. Возьмем для приближенного значения ;
какую-нибудь величину L', неравную L; тем самым мы вводим новук
систему поправок:
но мы имели:
или, вычитая почленно,
X.' —Х.= Г —Z = a,
где а произвольное число, поскольку произвольна величина V.
>) Более подробно об этом см. в отделе II.
— 19 —
Последнее равенство дает:
V. = Х^ а.
Возводя в квадрат и суммируя находим:
[Х'Х']=[ХХ]+2а[Х]+яа2;
но на основании теоремы, доказанной на стр. (11), [X] = О,
следовательно:
[Х'Х'] = [ХХ] + /ю3,
и потому действительно:
[XT ] > [XX].
Мы пришли таким образом к той же основной теореме, которую
вывели несколько иначе на стр. 14 непосредственным вычислением.
На предыдущих примерах мы могли убедиться в том, что правило
наименьших квадратов действительно дает единственную в каж¬
дом данном случае систему поправок* удовлетворяющую и условиям
задачи и условию [ХХ]-минимум; вместе с тем мы видим, что в этих
задачах оно приводит к весьма простому и естественному решению.
Это именно правило, т.-е. определение совокупности поправок при
условии, чтобы сумма их квадратов имела значение наименьшее по
сравнению с другими допустимыми системами поправок, и составляет
правило Лежандра, полное обоснование которого было бы несколько
затруднительно без изложения начал теории вероятностей. Заметим
только следующее: совокупностью значений поправок Xf, требуемых
для уравнивания, характеризуется в известном смысле самое достоин¬
ство полученной из наблюдений системы величин 1К. Но очевидно, что
для этой характеристики нельзя было бы пользоваться ни алгебраи¬
ческой суммой X,, ни вообще суммой их нечетных степеней, ибо в этом
случае, даже при поправках очень больших, указанная сумма, в силу
компенсации положительных и отрицательных \ или X,-2ft+1 могла бы
выйти близкой к нулю; естественно принять за эту характеристику
сумму четных степеней Х;, и проще всего, конечно, сумму их квадра¬
тов. Но остается открытым вопрос, почему не взять за нее сумму
численных значений X., т.-е. [|Х|]*), ибо она свободна от недостатка,
указанного для нечетных степеней. Такая попытка фактически и была
сделана Лапласом, который имел в виду обосновать всю теорию
ошибок и уравнительных вычислений на принципе:
[|Х|]-минимум.
1) Знаком |а| принято обозначать численное значение а.
2*
— 20 —
Однако, предложение Лапласа не получило распространения на
практике; оно „приводило к весьма сложным вычислениям. Между тем
принцип Лежандра-Гаусса, т.-е. подыскание такого решения,
при котором сумма квадратов уклонений определяемых чисел xt
от совокупности заданных чисел 1{ была бы минимум, при всей
его простоте и элементарности, оказался одним из наиболее суще¬
ственных для современной математики. От простых уравнительных
вычислений он проникает до весьма сложных построений теории, при¬
водя к глубоким и важным результатам. В этих вопросах особенное
значение имеют труды акад. П. Л. Чебышева (1821—1894) и акад.
А. А. Маркова (1856—1922).
§ 4. Общий случай одного условного уравнения со многими
неизвестными. Понятие о коррелате.
Перейдем к условному уравнению более сложного типа, чем только-
что рассмотренные. Положим, что искомые величины хи х2 и дг3
должны удовлетворять уравнению:
<*1*! + а2х2 + айха = А, (1)
где ах, а2, аа и А заданные числа.
Допустим, что в результате измерений для xv х2 и ха найдены
значения llt 12, 1я и что по подстановке их в (i) получается:
Qih “Ь a2.h Ч" aJs ~ А 4" * - - - (2)
Положим далее, что если к 1{ придать поправки:
Xj , Х2 , Хд ,
то уравнение удовлетворится в точности, т.-е. получится:
ai (А + К)+а2(к + Х2) -f- а&(1& -f- Х3) == А (3)
Раскрывая здесь скобки и вычитая из полученного уравнения по¬
членно уравнение (2), приходим к основному уравнению поправок *):
fljXj -f- а,^-2 -f- ЯдХд —A = 0 (4)
Очевидно, что это уравнение не определяет всех трех X: задав две
из них по произволу, получим третью. Но при условии [XX]-минимум,
для каждой из X* получается одно и только одно определенное зна-
>) Полезно заметить, что в уравнении пправок в леЕОЙ части вместо хх при
тех же коэффициентах щ стоят Х<; невязка с ее знаком стоит слева; сво¬
бодный член А исчезает.
— 21 —
чение, которое мы тотчас же и выпишем, откладывая несколько его
вывод. Решение это имеет вид:
1 a\h \ ct3h # . a3h .с\
А1 — af + aj + af' + + + а3’+ а3* W
Легко убедиться в том, что оно действительно удовлетворяет обоим
поставленным условиям:
(О- Уравнение (4) обращается в тождество. Действи»
тельно, подстановкой в (4) находим:
+ или -Л+А- 0.
(2). Условие [ХХ]-минимум удовлетворяется. Возьмем
для доказательства новую систему поправок:
V = "Ь®i5 V = ^2+a2» (*)
Тогда, в силу уравнения (4), которое должно иметь место для
любой системы поправок,
ai(^i + ®i) + аг(^2 ~Ь ®г) + аз(^з ~Ь ®з) “Ь ^ — 0»
ИЛИ
[аХ] [па] -J-A = 0.
Но так как и для исходных X, по уравнению (4) имеем:
[аХ]+А = 0,
то, вычитая почленно, получаем:
[т] = 0.
Возводя в квадрат и суммируя равенства (*), находим:
[XT] = [XX]+2[Х«]+ [««].
Но средний член справа равен нулю, ибо
М = + v + (aiai + «2*2 + «а«а) = — • М - °-
Таким образом, как и в прежних примерах, при любых а, неравных
нулю, т.-е. для всякой системы X', отличной от X, имеем:
[Х'Х']>[ХХ],
следовательно [XX] есть минимум.
Остается определить, чему же фактически равна эта минимальная
сумма [XX]. Возводя в квадрат равенства (5) и складывая получаем:
[XX] = (aj2 п82 -f- a32) • (в1» + ваа+в42)2= а,» + о3а + а/ ' ' ' №
— 22 —
Сопоставим окончательно группу формул (4), (5) и (6).
И1+*=0; M-rsj-
Едва ли стоит упоминать, что эта группа формул применима и
к общему случаю одного уравнения с любым числом неизвестных xv
Х2> Хя.
Переходим теперь к выводу решения, данного выше в формуле (5)
и для этого воспользуемся приемом введения так называемого
неопределенного множителя.
Мы имеем уравнение:
П,Х, -|— ^3^3 “Ь* ^ ==z ^ • • •••••••• (п)
и условие:
Х!2-}-Х22-}-Х23-минимум (b)
Умножим левую часть (а) на неопределенный пока множитель х)
2у и вычтем произведение из функции в левой части (Ъ).
Получаем выражение:
V ~Ь ^г2 “Ь V — 2у(а1Х1 -f- а2Х2 -f- а3Х3 -\-Щ (г)
Так как сумма, заключенная в скобки, при всех значениях пере¬
менных X,, подчиненных условию (а), равна нулю, то минимум функ¬
ции (с) при всех допустимых значениях X совпадает с мини¬
мумом функции X,2 Х22 —)- Х23.
По правилам дифференциального исчисления, предельные значения
(максима и минима) этой функции мы найдем, взяв частные производ¬
ные от (с) по'каждой из приравняв эти производные нулю и опре¬
делив значения \ из полученных таким путем уравнений 2). К тому
же заметим, что в данном случае предельные значения могут быть
то-ько минима функции X,2 -f-Х22-f-X2S, ибо эта сумма величина суще¬
ственно положительная и может возрастать беспредельно с возрастанием
переменных X!, Х2 ri Х3. Итак, по приведенному правилу, находим:
2Х, — 2 уа, = 0; 2Х2 — 2уа2 = 0; 2Х3 — 2уа3 == О,
т.-е. совокупность трех уравнений с четырьмя неизвестными,
именно Xj, Х2, Х3 и у. Из них получаем:
\ = Yai
а 1
Х2= уа2
а2
Х3 = у а-
(d)
*) Коэффициент ,2е вводится для удобства дальнейших вычислений.
3) Подробную теорию этих так навыв. условных максима и минима см., напр,,
у Смирнова, Курс высшей математики, т. I, стр. 458 и сц9
— 23 —
Помножив каждое из этих уравнений на поставленный сбоку коэффи¬
циент и сложив, получаем:
а1^1 Н- а-2^2 "Ь azh — Y(«!2 а2 ~Ь ай)-
Но в силу основного уравнения (4):
Н- я2^2 ~j~ #3Х8 “ — h\
поэтому
Y == — h: (ax2 + a2z -f- ай2); (7)
с этим значением у из уравнений (d) находим:
_ - ath . . _ аф. . } _ - и
А1 2 'лаХл.ИХл!' 8
О? + в,* + «за ’ 2 в1а + йа2+ а3а ’ ' » — а? + в22 + й32 »
что и соответствует формулам (5).
Помножим теперь уравнения системы (d) на Хх, Х2 и Х3 и сложим.
Имеем:
[X*]=Y[aX]= (8)
что соответствует уравнению (6).
Остановимся на идее этого замечательного решения. Она состоит
в том, что условие минимума дает нам три уравнения (d), которые
вместе с основным условным уравнением (4) составляют в совокуп¬
ности четыре уравнения, достаточные для нахождения четырех величин,
именно, трех X и неопределенного множителя у. Эта идея допускает
широкие обобщения на случай задания системы условных уравне¬
ний для неизвестных величин. Как мы увидим, в этом случае каждому
из уравнений будет принадлежать свой неопределенный множитель уJ).
Гаусс называет их коррелатами, т.-е. множителями, соответствую¬
щими данным условным уравнениям, или как говорили у нас раньше,
,соответствователями“ условных уравнений.
Сопоставляя теперь (5) и (7), имеем:
Xi I,
' [аа] ~ Т’
так что все поправки пропорциональны коэффициентам,
с которыми соответствующие а входят в условные уравнения, а кор¬
релята у есть общий коэффициент пропорциональности в этих отно¬
шениях.
Желательно, чтобы изучающий сразу уяснил себе исключительную
простоту применения правила Лежандра на примерах.
1) Эти множители обычно называются множителями Лагранжа; они имеют при¬
ведение в задачах механики.
— 24 —
(1). Пусть величины х1г х2, х3, х4 связаны уравнением:
2xt + Зх2 — 4х3 + х4 = 10,00.
Измеренные же величины дают:
21Х + 3/2 - 4/3 + /4 = 10,90; Л = + 0,90.
Требуется найти поправки. Здесь
[дя]=4 +9+16 + 1=30,
2-0,90
Х9 = -
30
3-0,90
30
•0,00;
= — 0,09;
=+~+0,12;
х*=-
0,90
30
■ 0,03.
Контроль:
[XX] = 0,0270
(0,90)2
30
(2). По измерении углов (1), (2), (3), и (4)
(см. черт. 1) получено:
/i + /2 + /3-/* = + 2",40;
/г = + 2",40; [аа]= 4.
Найти X.
i
2",40
Л1 = ^— = — 0",60; Х2 = — 0Т,60;
Х3 = — 0",60; Л4= + 0',60. *
Заметим, что поправки не зависят от величины
углов.
(3). Измерение сопротивления на трех частях нейзильберовой проволоки дало:
на АВ: 1Х = 1345* 10 ®. ом; на ВС: 12 = 846-10 ' 6 ом; на АС: /3 = 2212-10-® ом.
Найти наилучшую систему значений х19 х2, х3.
Здесь
xi + *2 — *3 = °; [аа] = 3; 1Х + /2 — /3 = — 21; h = — 21.
Х,=+у = 7; Х3 = + ^ = 7; Х, = -^ = -7.
х1 s* 1352; х3 3Z 853; xa е* 2205 (в 10-в ом); [XX] = 147-10-12.
Заметим, что и здесь решение не зависит от длин АВ, ВС и АС.
§ 5. Уравнение полюса.
Применим правило Лежандра к уравнению несколько более
сложного вида и выберем для этого из курса геодезии так называемое
уравнение полюса. Если в треугольнике ABC, с внутренней точкой Di
измерены всего лишь пять углов, например, показанные на черт. 2
углы 1, 2,..5, то очевидно, что нельзя будет составить таких со¬
отношений между измеренными углами, суммы которых равнялись бы
0°, 180° или 360°.
— 25 —
Поэтому, выбрав точку D за полюс, образуют произведения длин
трех лучей, из нее исходящих, и пишут тождество:
DA-DB-DC
DB-DC-DA
= 1.
Заменяя здесь отношения сторон синусами противолежащих углов
и замечая, что против DB лежит угол: 180°—1—2— 3 — 4—5, при¬
ходим к уравнению:
sin 2 sin 5 sin 4
sin 3 sin 1 sin 5
l.
8
где S= 180°—1—2 —3 — 4 —5.
Взяв логарифмы обеих частей, мы должны были бы получить нуль;
но, в виду неточности наблюдений, слева обнаружится логарифми¬
ческая невязка (так называемая ошибка
смыкания), которую и нужно унич¬
тожить уравнительным вычислением.
Допустим, что требуемые для этого по¬
правки углов 1, 2, 3, 4 и 5 настолько
малы, что при изменении каждого из
этих углов на \ и сообразно этому
угла S на минус [X], — изменения ло¬
гарифмов синусов достаточно положить
равными d.\, гдed. табличные разности
логарифмов синусов, отнесенные к 1". Итак, вводя коэффициенты dx
di> d&, dit d6 и ds (табличная разность при логарифме синуса 5), обра¬
зуем, логарифмируя (1), условное уравнение поправок:
d2\ — ~Ь — d^ — d5X6 -}- h = 0 (2)
или раскрывая скобки и сделав приведения:
(—ds — d{) -f- Х2 (— ds -f- d2) -f - X3 (— ds—dz) -)- X4 (— ds -f- dt) -j-
-{-X5(—ds — rfs)-f-A = 0
что можно записать:
atXx -{- a2X2 -{- a3X3 -|- a4X4 -{- ab\5 -\-h = 0,
где положено
— d^ d\y (t2 — d^ —J— rfgj ай — — d^ rfg и т. д.
(*)
(
Решая это уравнение по правилу Лежандра, мы и получим
искомые поправки в секундах дуги, по формулам:
' cifl, где у! ~Н
i
, [XX] = —
- 26 —
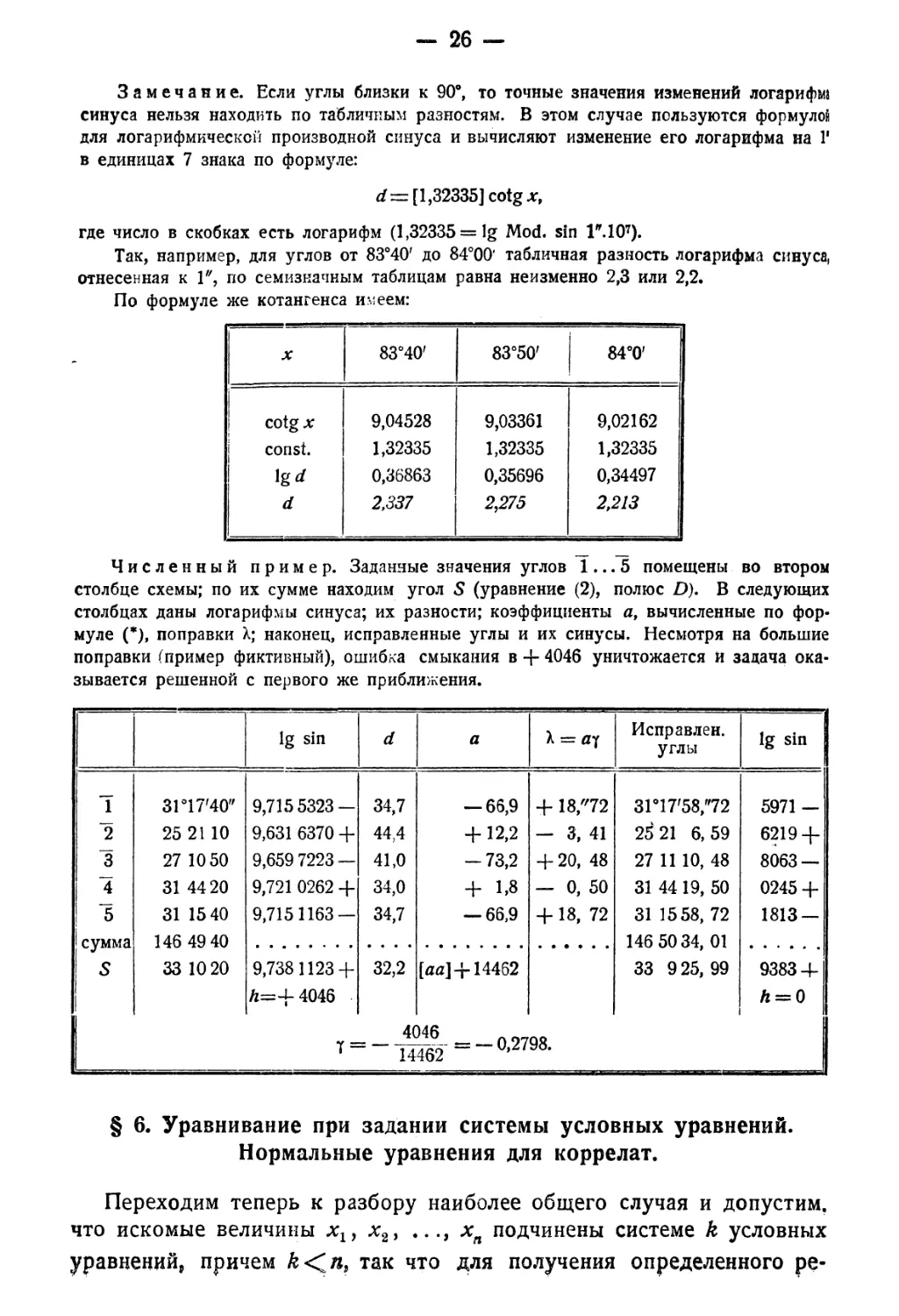
Замечание. Если углы близки к 90°, то точные значения изменений логарифма
синуса нельзя находить по табличным разностям. В этом случае пользуются формулой
для логарифмической производной синуса и вычисляют изменение его логарифма на 1'
в единицах 7 знака по формуле:
^Г= [1,32335] cotgjc,
где число в скобках есть логарифм (1,32335 = lg Mod. sin 1М07).
Так, например, для углов от 83°40' до 84°00' табличная разность логарифма синуса,
отнесенная к 1", по семизначным таблицам равна неизменно 2,3 или 2,2.
По формуле же котангенса имеем:
X
83°40'
83°50'
84°0'
COtgJC
const,
lg d
d
9,04528
1,32335
0,36863
2,337
9,03361
1,32335
0,35696
2,275
9,02162
1,32335
0,34497
2,213
Численный пример. Заданные значения углов 1... 5 помещены во втором
столбце схемы; по их сумме находим угол 5 (уравнение (2), полюс D). В следующих
столбцах даны логарифмы синуса; их разности; коэффициенты а, вычисленные по фор¬
муле (*), поправки X; наконец, исправленные углы и их синусы. Несмотря на большие
поправки (пример фиктивный), ошибка смыкания в + 4046 уничтожается и задача ока¬
зывается решенной с первого же приближения.
lg sin
d
a
X = fly
Исправлен.
углы
lg sin
1
2
3
4
5
сумма
5
31°17'40"
25 21 10
27 10 50
31 44 20
31 15 40
146 49 40
33 10 20
9.715 5323-
9,631 6370 +
9,659 7223 —
9,721 0262 +
9.715 1163 —
34.7
44,4
41.0
34.0
34.7
— 66,9
+ 12,2
-73,2
+ 1.8
— 66,9
+ 18,"72
— 3, 41
+ 20, 48
— 0, 50
+ 18, 72
31°17'58,"72
25 21 6,59
27 11 10, 48
31 44 19, 50
31 1558, 72
146 50 34, 01
33 9 25,99
5971 —
6219 +
8063 —
0245 +
1813 —
9383-4-
6 = 0
9,738 1123 +
6=4-4046
T =
32,2
4(
14
[aa]+14462
--0,27
98.
§ 6. Уравнивание при задании системы условных уравнений.
Нормальные уравнения для коррелат.
Переходим теперь к разбору наиболее общего случая и допустим,
что искомые величины xlt х2, хп подчинены системе k условных
уравнений, причем &<л, так что для получения определенного ре¬
— 27 —
шения данная система недостаточна. Мы покажем сейчас, что и в этом
случае, подобно тому, как и при одном уравнении, вводя условие
минимума [XX], мы приведем систему к полной определенности и по¬
лучим из нее одно и только одно решение для каждой из искомых
поправок X,. Последующие раосуждения принципиально не -будут
отличаться от выводов § 4.
Пусть дана система k уравнений {k < п):
«Л + а,х, +...+ апхп = А
&1Х1 4“ Ь'ЛХ2 4"
Сххг 4- С2Х2 4-
t\Xl “Г ^2Х2 +
•■ + ЬпХп=В
..-\-спхп — С
I п п
Допустим, что полученные из наблюдений для xt значения 11г12,..., с п
по подстановке их в данные уравнения, не обращают их в тождества,
а оставляют невязки hx, h2, ... hk, так что:
а1-'1 4~ а2^2 4* • • •+ aJn = A-\-hl
bxlx-^bj,.^.. bnln = B-\-h2
cih 4~ c2^2~\~- ■ •+ cJn = С4" (*)
tA+hh+-'-+ijn = T+iik.
Допустим далее, что, придав к величинам 11г 12 ..., 1п поправки
Х[, Х2, ..., хл, мы приведем эти уравнения к тождеству, так что полу¬
чится:
ai(h 4-х,) 4- a4-h 4-Хо)4-- • -4- аг№п 4- х„) = а
ь$14” Xj) 4- b2(i2 4~ х2) 4~ • • + Ьп (/„ + Хп) = в
и т. д.
Раскроем скобки в тольхо-что написанных уравнениях и вычтем
из них почленно уравнения (*) с невязками h. в правых частях. Мы
получим тогда основную систему уравнений для поправок (система А),
к которым присоединим еще условие минимума [XX].
Система эта напишется так *);
а\К 4" ^3X2 4“- • •4-яЛ4-А1= О
Ь{кх 4-6Л4--. .-\-b\n-\-h2—0
(А)
/jXj -f-t2i2 4" • • • 4~ tnK 4-^ = 0
Xi24"X224- Х32 -f...4-Х/-минимум.
А) При X те же коэффициенты, что и при х в условных уравнениях, невязки с их
знаком слева, свободные члены А, В... не фигурируют.
— 28 —
Умножая левые части уравнений (А) на неопределенные пою
множители 2уг, 2y2...., 2у*; вычитая результат из функции V + V'l
и вынося при этом за скобки у1} составляем функции
V — 2Хх (fljYj -f- ftjY2 -j- • • • 4"
+ К2 — 2^ («2Т1 + К т2 + ... 4y*) +
+ Xn2 — 2X„ (a«Tx + b„ y2 + ... /‘„y*) +
— 2 (Yi^ 4“
Рассматривая это выражение как функцию всех X,-, видим, что онс
может иметь минимальное значение для тех же самых значений X, дл!
которых и сумма [XX] будет минимум; ибо прибавленная к [XX] часть
при всех системах поправок X,-, допустимых по условия!
задачи, т.-е, удовлетворяющих уравнениям (А), есть нуль.
Следовательно, минимум [XX] (максимум здесь исключается, см
стр. 22) мы найдем, взяв производные по X/ от только-что написанно(
функции и приравняв их нулю. Легко видеть, что каждая строк
(кроме последней) даст одно уравнение подобного рода; по сокраще
нии на 2 эти уравнения принимают вид:
*1= aiTi + 4“ • • • + *iT*
Х2 = <*2Yl 4- b2b + • • • 4- *2Tft
хз = aaTi 4" ^Vf2 4“ • • • 4" ^зТ*
(в;
X/t = anYi 4“ 4~ • • • 4An* ■
Система (В) даст нам решение нашей задачи, как только мы сумеен
определить y: действительно, подставив y в уравнения (В), получае»
значения искомых поправок Х2,...,Х„. Весьма важно обратить вни
мание на то, что система (В) по отношению к системе (А) является
как говорят, транспонированной—ее коэффициенты по строка»
(а‘, bi, Ci,...ti) соответствуют коэффициентам (А) по столбцам
Составив одну из этих систем, мы тем самым имеем и все данньн
для написания другой.
Переходим к составлению уравнений для коррелат. Для этого,
множим уравнения (В) соответственно на а1г а2,..., а„ и складываем,
Это дает:
aА 4- °2Х2 4~ • • • 4~ Я/А = [аа\ Y! 4“ [аЬ\ Тг 4~ • • • 4~ [a^] Т/ь
но по первому уравнению системы (А) сумма, написанная справа
равна—hlt и потому полученное сейчас уравнение приводится квиду;
[аа] Yi 4~ И Y2 4* • • *4“ И Y* 4“ Ai =* О*
— 29 -
Таким же образом, умножая уравнения (В) соответственно на Ьи... Ь„
и обращаясь для исключения неизвестных X ко второму уравнению
системы (А), приходим к уравнению:
[яА]ух + [bb\ у2 + • • • + [Щ^к + А2= 0.
Повторив эту операцию умножения на ct,...,ti, получим последо¬
вательно систему k уравнений для k коррелатух,. у; она называется
нормальной системой, соответствующей системе (А) к.
[««]■),! + [ab] y2-f-.. ~0
[ab] Yi + [^]T2+- у* + й2 = 0
И Yi 4" [be] Ъ “К • -+И Y* + = 0
(С)
[at] yi -\-[bt] у2 +. • •4'[^]
Полученная система допускает, вообще говоря, одно и только одно
решение для каждой из коррелат у,, у2,..., у*. Найдя их значения
и поде I авив их в систему (В), получим ту единственную систему
поправок X, которые yдoвлefворяют уравнениям системы (А) и вместе
с тем соответствуют условию минимума [XX].
Следует обратить внимание на замечательную структуру нормаль¬
ной системы (С): коэффициенты, стоящие по главной диагонали, суть
суммы квадратов коэффициентов системы (А); это числа положи¬
тельные и обычно численно превышающие все прочие суммы
на той же строке, т.-е. [ab], [ас], [be],..., [dt].. .и т. п.; коэффициенты же,
стоящие по обе стороны от диагонали, между собой равны. Такая
система, у которой коэффициенты по столбцам повторяются в стро¬
ках, носит название симметрической-, этим свойством симметрии поль¬
зуются для сокращенной записи нормальной системы, выписывая
только члены, стоящие по диагонали и над ней; например, для 4 кор¬
релат имеем такую форму:
Yi Ъ 1 Ъ Ъ h
[iаа] [ab\ [ас] [ad] hx
[bb] [be] [bd\ h2
[cc] [cd] A3
[dd] h^~
При такой записи каждое уравнение читается по столбцу до его
конца и затем по строке направо до конца строки, как здесь отмечено
для третьего уравнения.
Замечание 1-е. Легко показать, не прибегая к правилам дифференциального
исчисления, что система поправок X, определяемая уравнениями (В) и удовлетворяющая
уравнениям (А), действительно соответствует условию [XX] • минимум.
30 -
Доказательство. Пусть некоторая совокупность поправок X' удовлетвор!
уравнениям (А), которые запишем сокращенно:
[аЩ +Нг = 0; |>Х'] + h2 = 0 . . . и т. д !
Положим, что поправки эти связаны с поправками X такими соотношениями:
V = \ + av V = *2 + *2 • * * И Т* Д С
Тогда уравнения (*) перепишутся так:
[вХ] + [ал] + h,= 0; [Ы] + [ba] + h2 = 0 (*j
Но X, по предположению, удовлетворяют системе (А), т.-е.
' [аХ] + Л1 = 0; [АХ] + А* = 0. . • •
Вычитая эти равенства из (***), получаем: ;
[ad] = 0; [6а] = 0 и т. д. |
Из (**), возводя в квадрат и суммируя, находим:
[Х'Х'] = [ХХ] + 2[Ха] + [аа].
Повторяя уже много раз примененное рассуждение, нам остается только показа!
что [Ха] = 0. Но гак как, по предположению, X задаются через систему (В), то для пд
чения [Ха] множим уравнения (В) последовательно на alt а2, . . ., ьп и суммируем, выно
за скобки множители ?; таким образом находим:
[XX] = Yi [аа] + Ya [М + ТзГ^а] + • • •
Но каждая из сумм справа равна нулю в силу (а), следовательно [Ха] = 0, и потои
[Х'Х'] > [XX].
Читатель заметит полную аналогию с доказательствами в §§ 3 и 4.
Замечание 2-е. В случае одного уравнения (§ 4) коррелата y определяла
равенством:
[<аа] y -f- h = 0.
Нетрудно видеть, что к такому именно уравнению сведется нормальная система (
если система условных уравнений состоит из одного уравнения вида (А). Таким об]
зом, можем сказать, что коррелаты во всех случаях определяются из уравнений hi
мального типа.
Формула для [XX]. Найдем теперь, чему равна минимальная [).
полученная из систем (А), (В) и (С). Для этого множим уравнения (
соответственно на Х1} Х2,.,., Х„ и складываем, вынося за скоб
Yi> Ъ>- ■ •’ Y*• Получаем:
[XX] = у! [яХ] -Руг + • • • + у*[^Ь
Но в виду системы (А) первая скобка справа равна—hx, вторая—I
последняя — hk. Поэтому:
[XX] =5 Yi^i Y-^2 • • • ykh/t,
или сокращенно *):
м—т (
‘) Слева и, справа # слагаемых.
- 31 -
т.-е. минимальная сумма квадратов поправок равна сумме произве¬
дений коррелат на невязки соответствующих уравнений, взятой
с обратным знаком.
Эта формула применяется как контрольная в вычислениях.
§ 7. Практические указания. Примеры.
Применение методы коррелат приводит на практике к очень неслож¬
ным вычислениям, если только число условных уравнений (а следо¬
вательно и коррелат) невелико. В этих случаях не следует прибегать
к особым схемам решения нормальных систем (§§ 12, 13 и 14) и можно
воспользоваться любым приемом элементарной алгебры. Порядок
работы сводится к следующему: 1) определение по данным значе¬
ниям невязок hi\ 2) составление уравнений (А). Эти уравнения
записываются обыкновенно столбиком, причем искомые Хх,...,Хя
выписываются во входе таблицы, а внутрь ее пишутся одни коэффи¬
циенты в условных уравнениях при хх> х2,...хп; на последней строке
пишутся невязки А*; 3) образование нормальных уравнений
производится в таком случае по правилу: столбец сам на себя
ина все следующие; так составляются суммы [аа], [ab],..., [bb\,
[Ьс],..., [сс\, [cd]..., которые и вносятся в схему нормальной системы,
отступая с каждой строкой на одно место влево; в конце строк при¬
писываются Ах, h2,..., hk с их знаками. В случаях несложных можно
заполнить всю схему книзу от диагонали, пользуясь симметрией
системы; 4) решение нормальной системы, как уже сказано, произво¬
дится любым из известных способов; 5) определение X через у (система В)
не требует дополнительной схемы: так как система (В) транспониро¬
вана в отношении (А), то достаточно надписать над столбцами (А)
значения у и образовать произведения у на коэффициенты строки;
суммы этих произведений и дадут Хг, Х2,..., Хя; 6) сумма произведе¬
ний уh (последняя строка схемы) дает—[XX], чем можно воспользо¬
ваться для контроля, вычислив [XX] непосредственно.
Кроме того, очевидный контроль решения цолучится, если числа
каждого столбца помножим на найденные X. Прибавив еще h, должны
получить нуль.
При трех уравнениях для 5 неизвестных все схемы имеют такой
вид:
а111 +•••-{-■ аь1ъ — A -J- Ах
bih "Ь • • • ~Ь &bh — B-\-h2
cih + ''' *Ь cbh — С К
— 32 -
Система (А) Нормальная система:
Ti
Тз
Тз
Ti Тз Тз
X*
Х3
«1
«2
*1
^2
ci
С3
К
х3 j
[дд] [д£] [дс] + ht = 0
[д&] [66] [6с] + h2 = 0
^3
fl3
*3
*3
*3 |
[дс] [fa] [сс] + hz = 0
х4
«4
*4
^4
*4 !
Найденные т2, у3 впи¬
*5
«5
*5
С5
*5
сываются над столбцами (А),
/г
h,
h2
/г3
[Щ
после чего образуют суммы:
\ = Wt + Ъ&1 + bci
Х3 rr 7jfl3 + ~!«Ь„ -f- Y3C3
h = Ti«s + ГА + ТгА
Контроль:
тЛ + iA + tA = — [XX]
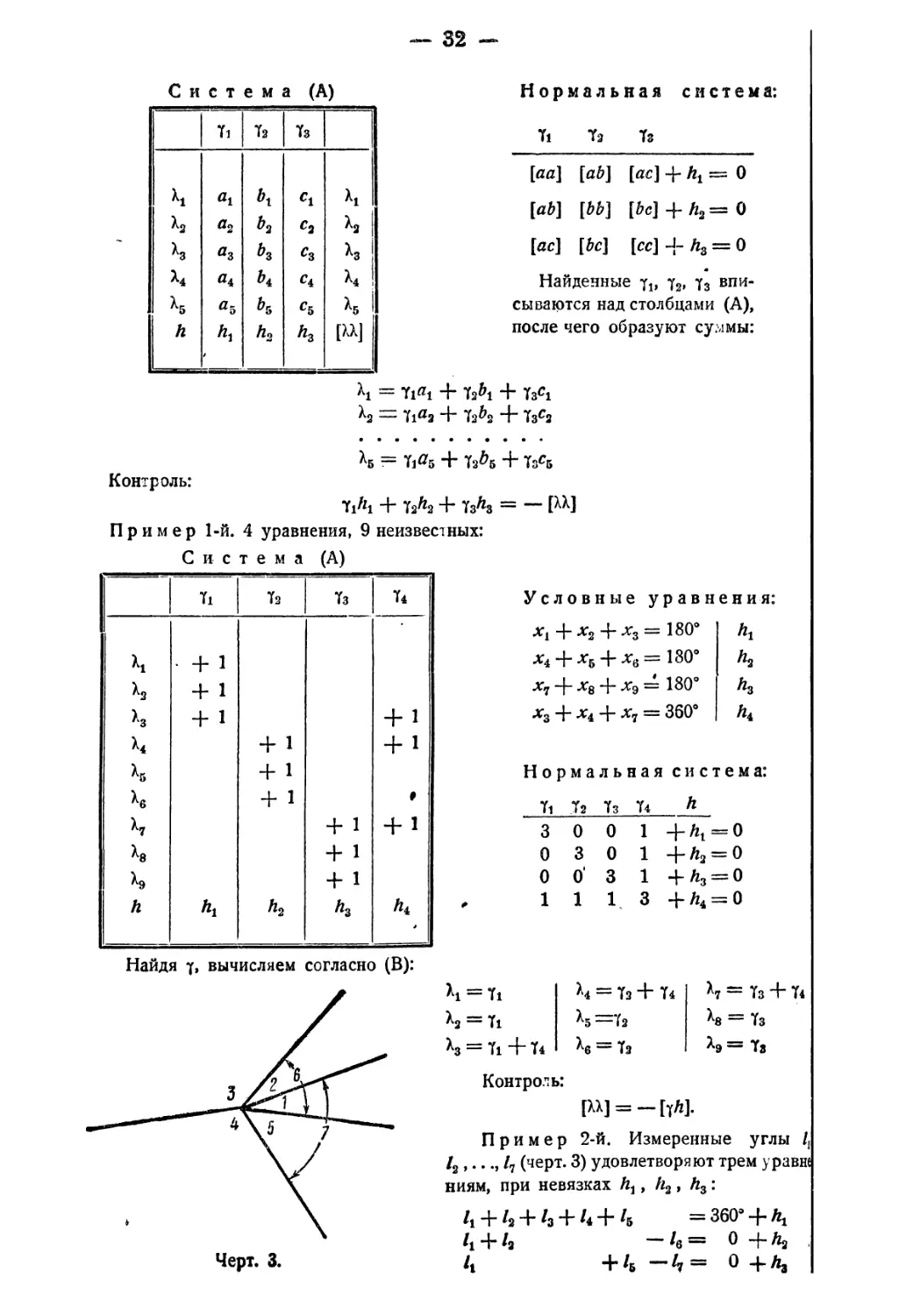
Пример 1-й. 4 уравнения, 9 неизвестных:
Система (А)
Ti
Тз
Тз
Т 4
Условные уравнения:
Xi + Jfj + *3 = 180°
К
*1
+ 1
*4 + *6 + *6 = 180°
h2
^2
+ 1
х-1 + ХВ + ха = 180°
^3
+ 1
+ 1
-f" лг4 -{" Хц = 360°
h,
Х4
+ 1
+ 1
Х5
+ 1
Нормальная система:
\
+ 1
*
Ti Тз Тз Т4 h
Х7
+ 1
+ 1
3 0 0 1 + /*t =
= 0
Хв
+ 1
0 3 0 1 +Л2 =
= 0
х»
+ 1
0 0 3 1 +Л3 =
= 0
h
h2
h3
Й4
1 1 1 3 +Л4 =
= 0
Найдя y, вычисляем согласно (В):
*1 == Tl *4 = Т2 + Т4 *7 ~ Тз + Т4
^2 = Tl ^5 — Тз ^8 = Тз
= Ti ~Ь Т4 ^6 “ Тз Х9 = Тз
Контроль:
[ХХ] = -[ТЛ].
Пример 2-й. Измеренные углы 1{
/2,..., /7 (черт. 3) удовлетворяют трем уравне
ниям, при невязках , h2, Л3:
Л + + h + h + h = 360° + hx
lt + /9 — /б = 0 -f- Лз
Л 4" и """ ^7 ^ 0 -f- /и
- 33 -
Система (А):
Yi
ь j
ъ
К
+ 1
+1
+1
^2
+ 1
+1
- ^3
+ 1
Х4
+ 1
^5
+ 1
+1
— 1
— 1
л,
л3
Л3
Нормальная система:
5?i + 2уа + 2?3 + 6j = О
2Ti + 3y2 + Тз + 63 = О
2?1 + Тз + ^73 + 63 = О
Найдя 7t, y3 , Y3, получаем:
*4 = Т,
*5 = Ti + Тз
Хб = —ь
>7= “Тз
Л = Ti + Тз + Тз
*2 = Tl + Тз
= Ti
Пример 3-й. Углы /м..., Iq
связпны тремя уравнениями, в кото¬
рых получаются невязки hlf h2, 63:
/± + /2 — /7 = —1/'52
/4 + /5-/8=+1.71
/з + /а + /7 + ^8 = -0,14
+ 0,514
+ 0,562
+ 0,023
X
XX
+ 1
+ 0/514
0,264
1,
+ 1
+ 0, 514
0,264
^3
+ 1
+ 0, 0 3
0,001
+ 1
— 0, 562
0,316
*5
+ 1
— 0, 562
0,316
+ 1
+ 0, 023
0,001
Х7
— 1
+ 1
— 0, 491
0,241
— 1
+ 1
+ 0, 551
0,342
h
— 1,52
+ 1,71
— 0,14
1,745
Нормальная система:
+ 3Ti - Тз-Ь#52 = 0
+ 3?2— 73+1,71=0
- Ti— Т* + 4Тз— 0, 14 = 0
Найдя коррелаты (их значения вписаны в первую строку схемы), образуем X по фор¬
мулам В; в последнем столбце даны их квадраты, откуда контроль:
[XX] = 1,74 = — 7^ — 726з — 73Л3.
§ 8. Уравнивание четыреугольника.
Для примера более сложной системы решим ?адачу уравнивания
четы; еугольника, в котором измерены восемь углов (1, 2, . . 8 на
черт. 4). Легко видеть, что из этих восьми углов только четыре являются:
Мяеаеб маям- квадратов. 3
— 34 -
i
^независимыми, ост^ьные же определяются через них по сумме углов!
треугольника. Но если возьмем, напр., 1, 2, 5, 6, за независимые (так
что 2 + 5; 6 + 5, 1+2 определят соответственно: 3 + 4; 7 + 4; 7-\-1,
8 + 4), то комбинируя эти условия, мы не получим 3, 4, 7, 8 через 1, 2,
-5 и 6л вот почему: из числа весьми углов имеется четыре зависимых,
и нужно составить четыре уравнения, которые и явятся условными
уравнениями задачи. Однако, если написать—-что было бы проще
всего — уравнения сумм углов для каждого из четырех треугольников,
на которые ABCD разбивается диагоналями:
2 + 3 + 4 + 5=180° :
1+6 + 7 + 8=180° - ' ‘ ‘ (а|
то эти уравнения не незави¬
симы: складывая первое со вто¬
рым и вычитая третье (или чет-|
вертое), получаем четвертое (или|
третье). Поэтому из уравнений!
(а) можно взять только три;
четвертое же независимое урав¬
нение следует искать из отноше!
ния сторон.
Возьмем, например, обе диагонали и напишем тождества:
АС АС АК АС АС СВ
BD~ AB ' BD и BD ~ СВ ‘ BD
шли, переходя к синусам противолежащих углов:
sin (3 + 4) sin 8 sin (3+4) sin 7
sin 5 sin (1+2) sin 2 sin (5 + 6) ’
откуда:
sin 2 . sin (5 + 6) . sin 8
— 1 ...... . .101
sin 5 . sin (1 -f- 2) . sin 7
Обозначая, как показано на стр. 25, перемены логарифмов сину¬
сов на 1' через d2, d5+e, db... и т. д., получим из (б) уравнение для
поправок Xj, Х2,..., Х8, именно:
а+ + а2к2 + аьК + +'•« + а?1 + Д+ + = 0, (в)
где положено:
ai— ^1+2 a5 = ^5-t-e ач = — d.
ai = di dx f K -- + = + +
34 h±— ошибка смыкания уравнения (б).
1 + 2 + 3+ 8- • 180е
4 + 5 + 6 + 7 = 180
— 35 —
Уравнение (в) присоединяем к трем условиям для поправок, кото¬
рые доставляют любые три уравнения из группы (а) — например, три
первые — и получаем систему (А) и соответствующую ей нормальную
систему для четырех коррелат в таком виде:
Нормальная система:
4у, -{- 2у3 («1 + а2 -(- а8) у4 -|- hY = О
+ 2у3 -j- (а5 + й6 -f- а7) у4 -f- Л» = О
2yi + 2уз -f - 4у3 -+- (а2 + аь) Y* + К = О
(ai ~Ь Н- ae) Yi “Ь (а5 Н~ аъ + ai) Уг ~Ь
~Ь (а2 -j- а5) у» + [аа) Y4 + ^4 — О
Решение этой системы будет
сложнее, чем в примерах § 7, так
как а. и [аа], фигурирующие в послед¬
нем уравнении (аналогичном уравненю
полюса и называемом уравнением
сторон), не являются уже неболь¬
шими целыми числами.
Однако, и в этом случае нет еще небходимости переходить к общей
схеме решеня нормальных систем (см. ниж’ё), а рекомендуется, поль¬
зуясь первыми тремя нормальными уравнениями, выразить Yi > Ya и Y»
через все h и через у4» подставить эти значения первых
трех коррелат в четвертое нормальное уравнение, из
него получить у4» затем определить и первые три коррелаты. После
этого поправки klt..., а.8 , найдутся, как обычно, по схеме (В).
Численный пример. Уравнивгя четыреугольник, В. В. В и т к о в с к и й 1) при¬
ходит к таким четырем нормальным уравнениям:
ь
Тз
и
Н
2
0
-f-1,29
— 0,87
4
2
- 5,99
— 3,38
•
4
— 1,26
— 1,00
37,78
4-0,30
Для решения перепишем систему н ее дополненном вйде, начав с четвертого урав¬
нения; затем из уравнений 1, 2 и 3 будем исключать последовательно и затем
X, и , наконец, Xi и х3; для этого множим их на легко подбираемые множители
+ 3,-2, +1; + 1, —2, -f-1; -f-l, —2, 4-3 и складываем; в результате получаются
строки, подписанные слева, которые читаются:
8?! 4-14,59 Xi-f 3,15=0
н Т. д.
Из них для , 7l, и y3 получаются выражения, выписанные справа; достаточно
помножить эти выражения на коэффициенты при Yi» Тз и Уз в четвертом уравнении
(1,29; — 5,99; — 1,26) и прибавить к сумме этих произведений 37,780 Xt 4- 0,30, чтобы
получить уравнение для ?4, именно: 18,94 у* - 7,072 — 0, откуда х* = + 0,373. Подставляя
Tt
Ъ
Тз
T4
4“ l
h
4-1
4-1
a*
ч
■! 1
+ 1
и 1
4-1
+ 1
** !
+ 1
4-1
аь
/v i
4 1
Ч
4 1
h
■f i
*8
h ,l
i
h{
h.2
L _
. ‘h
\
h,
I *) Практическая геодезия, § 123.
— 36 —
это значение в выражении для , 7з > 7з * находим и эти три коррелаты (ср. пример!
в §§ 12, 13 и 14): ;
Ti __„л?
+ 1,29 — 5,99
4 2
2 4
О 2
873
1 Т*._
h
26 + 37,78
+ 0,30
0+1,29
— 0,87
+ 3 +1
+ 1
2 — 5,99
— 3,38
— 2 —2
— 2
4 — 1,26
— 1,00
+ 1 +1
+ 3
+ 14,59 74
+ 3,15
7i
= - 1,824 74-
0,393
+ 1,29
+12,01 74
+ 4,89
Ь
= + 3,002 74 +
1,222
— 5,99
, + 9,49 74
+ 2,89
7з
= — 1J 86 74-
0,361
- 1,26
— 2,353 74 —
0,507
— 17,982т4 —7,320
+ 1,494 74 +0,455
+ 37,780 74 +0,300
18,9474 - 7,072 = 0
7i:
7з :
73 :
74 :
: — 1,07|.
= + 2,34
: — 0,8(|
: + 0,37г.
§ 9. Поправки к наблюдениям различного веса. Обобщенный
принцип Лежандра.
При изучении теории ошибок мы остановимся более подробно
на понятиях меры точности и веса рядов наблюдений одной и той ш
величины. Пока достаточно указать, что веса определений каждой
из величин 1Г, назначаются, вообще говоря, пропорционально
числу отдельных наблюдений, из которых данное U получено кап
арифметическое среднее *). Поэтому, зная', например, что lv /2 и /3 полу
чены как средние из пх, п2 и я3 наблюдений, мы введем веса этш
определений рх, рг и рй путем пропорции:
рх:р2:р3 = пх:п2: п^.
При решении задачи об уравнивании* разновесных наблюдений
будем исходить из следующего простого правила:
Поправки X/ разновесных наблюдений h должны быть обратт
пропорциональны соответствующим весам pi.
Расмотрим с этой точки зрения задачу „взвешенного уравнивании
треугольника*.Допустим, что углы и /3, определенные свесам»
Ри Р% и Рз> оставляют в условном уравнении невязку А, так что
поправки X,, Х2 и Х3, вводимые для уничтожения этой невязки, должны
удовлетворять уравнению
“Ь *2 + *а “Ь А = 0 . . . (1)
*)В геодезических вычислениях, веса вводятся иногда на основании иных, более или
менее условных принципов.
— 37 —
Применяя только-что установленное правило, вводим неопределен¬
ный пока множитель у и полагаем
*i = —; *2 = —■; кл — -
А Рг Pi
По ^подстановке в (1), находим:
откуда *):
\А Pi pj
T=,_ h
ш
л следовательно:
h h
) Р_\ Р*Ь \ Ръ /94
"lil Ш ’"Ш
Эти формулы и решают поставленную нами задачу. Действительно,
[Х] =
Т.-е.:
[Х]+Л = 0;
из них же мы видим, что при рх очень большом сравнительно с р2
и Х^О, т.-е. наблюдение очень большого веса не получит замет¬
ной поправки при уравнивании; наоборот, при рх очень малом, знамена¬
тели у X, и Х3 (куда входит —) будут очень велики и следовательно,
вся поправка ляжет на наблюдение наименьшего веса2).
Докажем теперь, что полученное решение соответствует следую¬
щему условию:
[рМ] для системы (2) есть минимум, по сравнению с любыми систе¬
мами поправок, удовлетворяющими уравнению (1), при тех же весах
Л.АИА*
Доказательство. Введем новую систему поправок X', положив:
V — ^1 “Ь V = ^2 а2» V + а3 (3)
*) £ читается: сумма обратных весов; появление обратных весов характерно доя
«оррелатного уравнивания.
*) Легко видеть, что при рх 0, «
- 38 -
по условию.
[X'] = - h,
но так как и [X] = —А, то должно иметь место уравнение:
[«] = 0.
Возводя в квадрат равенства (3), умножая их после этого на f
и суммируя, получаем:
fcA'V] = [рХХ] + 2[рХсс] + [/Н; (»
/»[«] .
[/>Хос] = 0.
Таким образом, средний член справа в формуле (*) обращаете
в нуль, и мы имеем:
ОХ'Х'] = [рХХ] -ф [роса].
Так как вторая скобка справа есть сумма квадратов в, умножен
ных на всегда положительные числа то заключаем, что для все)
а ф 0, т.-е. для всех X', отличных от X, найденных по системе (2), вый
дет [рХ'Х']>[рХХ], что и требовалось доказать. !
Таким образом, решение (2) удовлетворяет условию: |
[/?ХХ] - минимум, !
что можно назвать принципом Лежандра, обобщенным на случё
определений различного веса. ;
И подобно тому, как уравнивание наблюдений одинакового вес)
было построено на начале [XX] - минимум, так вся обработка наблц
дений разного веса производится в уравнительных вычислениях согласй
правилу: сумма квадратов поправок, умноженных на веса определен»)
уравниваемых величин, должна иметь минимальное значение по сравне
нию со всеми системами поправок, удовлетворяющих той же совоку!
ности уравнений и при тех же весах.
На практике применение формул (2) весьма облегчается тем, чя
все выражения для X однородны в весах, так что, введя вместо р1,1
и pR количества:
но из уравнений (2) находим:
— )тх — koi.j — ha3
ш
отсюда, в виду [а] == 0, заключаем:
где К произвольное положительное число, можем написать формулы
(2) в виде:
^ = ~ » }'2 == ~ [q]'^2 ’ f"i ^
которые более удобны для вычисления, чем (2), так как дроби в них;
больше не входят. Наконец, нетрудно показать, что выражение для
1/>ХХ] приводится здесь к виду:
Г 1 м К ft2
[^ХХ] — .
Численный пример1): По измерении трех углов треугольника, с весами
5, 2 и 8 обнаружена невязка h = 10". Найти поправки углов.
Положив К ~ 40, вычисляем:
р
Я
л = —о,зоз-?
h
Здесь = 0,303; с по¬
]
i
\
1
мощью этой величины опреде¬
5
8
— 2",42 1
ляются \ и Х2 и Х3.
2
20
- 6,06 1
Для контроля имеем:
40-102
8
5
- 1.52 I
[рЩ = 23 — 121,2 что
можно проверить и непосред¬
33
— 10",00 1
ственным вычислением.
Формулы (2) и (5) легко обобщаются на случай одного уравнения
с любым числом неизвестных вида:
a\h + — + aJn = A-\-h.
В этом случае мы приходим к формулам, совершенно аналогичным
формулам § 4. Вывод их предоставляем читателю и напишем окон¬
чательный результат.
Уравнение поправок: а2К -|-... + ап1пh == 0.
Веса определений 1Х, /2,...,/г принимаем равными: —» Рп* Вводя
к
количества q. обратно пропорциональные весам, т.-е, положив, q.= ---t
> Pi
при произвольном К, находим коррелату у по формуле: у = — \aaqy
тогда
X,- = -f a.q.y, [р)11 = — Khy.
J) К взвешенному уравниванию треугольника мы еще вернемся для определения?
средних ошибок неизвестных (см. стр. 120).
— 40 —
Пример. При измерении отрезков АВ, ВС, АС с весами 1, 3, 6 обнаружен!'
аевязка Л=-(-9m. Уравнять отрезки. '
\ 4- X, — Х3 + 9 = 0
при К= 6, ^ = 6, q2 = 2, qs = 1; [aaq] = 6 + 2 + 1 == 9;
•V :=— 1; X, = — 6; Х3 = —2; X3 = + 1; [/jXX] = 6-9 = 54 = 36+ 12 + 6 (контроль). !
”§ 10. Поправки к неравновесным наблюдениям в случае системы!
условных уравнений. Уравнивание высот.
Обобщенный принцип Лежандра, т.*е. правило отыскания nonpaj
вок при'условии [рХХ]-минимум, легко распространяется на системы!
условных уравнений, причем все выводы являются повторением pac-j
суждений § 6. i
Итак, положим, что искомые поправки должны удовлетворять!
•системе уравнений: j
ахХх -|-... + а\п hx = 0
bx\ 4- — 4~ Ь1п 4- А2 = 0
(А')
txk 14-... 4- tn\ -{-hk=o
и кроме того условию:
/>Л*'4-/»Л* + -+/,Л*’МИНИМУМ • (*)
Умножая левые части уравнений (А') на неопределенные пока мно¬
жители 2А+ , 2Ку2,...., 2Kyk х), вычитая эти произведения из (*) и со¬
бирая при этом в разности члены, содержащие \, Х2,... ,Хя, приравняв
«улю произзодные от полученной функции по X,, Х2, ...,Хя, получаем
транспонированную систему:
рх\ = К(а,гх 4- bxf ., -f-... 4~ tx'(k)
Введя числа q.t обратно пропорциональные весам, именно:
К К К
переписываем эту систему в более удобном для вычислений виде:
Xi — 4” Ь\Ч-2 4- — 4- Ат*)
Ха = 4“ b-fiz 4“ — 4- 4у*) (В')
\ = 4n(an\i 4- ьп у2 4- - -Ь tn4k)
^Коэффициент 2К введен для удобства дальнейших вычислений.
- 41 -
Мы замечаем, что поправки Х;, согласно данному на стр. 36 пра¬
вилу, оказываются прямо пропорциональными числами qn или обратно
пропорциональными весам рг
Для получения нормальной системы для коррелат множим уравне¬
ния (В') последовательно на коэффициенты ап затем bt и т. д., и после
сложения исключаем X из левой части, заменяяa,Xt + ...ап\ на — hx
и т. д.,' в силу уравнений (А'). Это приведет нас к нормальной
системе такого вида:
[abq]'( 1 + \bbq\fz +... + \btqY(k -f- ht — О
[acq]^x -f- [bcq\^z -(-... -)- [ctq]yk -f- hb = 0 . (C )
\atqy(x + [btq]ft +... -f [ttqk-(\ -f- hk = 0
Решив (С') и подставив Yi > Y* > • • • > Y* в (^ )» находим систему попра¬
вок X,, удовлетворяющих системе (А'), а вместе с тем и условию
I/MJ минимум.
Введением неопределенного множителя типа 2Ку, где К произ¬
вольное положительное число, достигаем того, что в наши вычисле¬
ния вместо весов pt можно вводить любую систему чисел <7,,обратно
пропорциональных весам (q.=—\, что представляет вычислительные
V Pi /
преимущества.
Остается вывести формулу [рМ]. Для этого множим уравнения
(В') соответственно на /?1Х1, /?2Х2,,.. и замечаем, что в правых частях
появляются произведения:
РхЯх = Р-гЯ* = - =РЯЧШ = К-,
по сложении получаем:
\рЩ = K(Yl[aX] + Y #Х] 4-... +Т*[А])
.или, пользуясь системой (А'),
f/?xx] = — K(rA -Ь уЛ-2+•••■+■ yA);
•окончательно можем написать: [рХХ] =— (D')
, ft
Таким образом, задача решается совокупностью формул: ^ = —,
системы (С'), группы (В') и заключительной формулы (D').
- 42 -
Черт. 5.
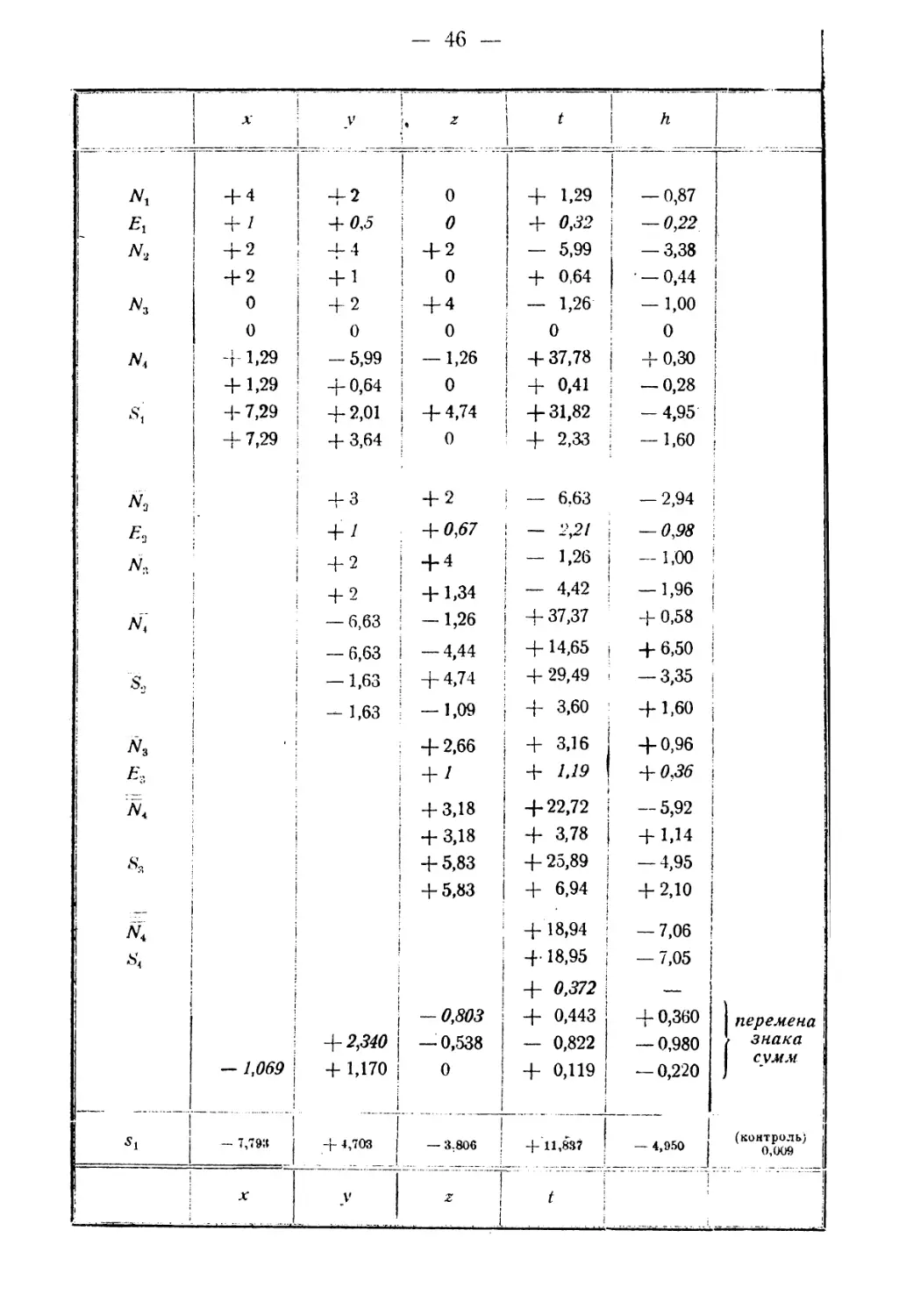
Численный пример. Уравнивание высот. При уравнивании три]
нометрического нивелирования и нивелир-теодолитных рядов применяется обычно вз!
шенное уравнива !ие. Вычисления от этого почти i
усложняются, если вместо весов pt, путем подходяще!
выбора числа К> вводить сразу удобные в данной а
даче qt. Напр., при уравнивании высот, веса наблюдет
принимаются обратно пропорциональными квадратг
расстояния s2 между вершинами. В виду совершенна
^произвольности числа К, мы можем заменить s2 л||
быми числами, им пропорциональными, оставляя оди;
два знака после запятой. Говорить здесь о больш
точности, при очевидной условности самого назначен!
весов, не приходится.
Допустим, что в четыреугольнике измерены ра
ности высот между вершинами по сторонам и диагош
лям; обозначая через 1, 2. . . .6 указанные раэност
должны бы ли бы иметь согласно чертежу (скаты показаны стрелками), следующи
соотношения:
2 4-1 — 4=0 6 — 3 — 2 = 0 Г+5 — 3 = 0.
Но подстановка наблюденных определений х) дает невязки
4 0,63; —0,29; 4-0,03.
Веса определений принимаются, согласно сказанному, обратно пропорциональны!
s2; в данном случае было:
— =л,3 =171; — = s.,1 = 682; -- = s,3 = 303;
Ру 1 Рз Рз J
— = s43 = 512; — = s53 = 622; — = se3 = 387.
Pi Рз Рз
Для упрощения вычислений делим все эти числа на 682 и частные q проставляв
в первом столбце известной нам схемы. |
Я
— 0,338
- 0,033
+ 0,043
X
!
Р'
>0
0,25
+ 1
+ 1
- 0,073
4,00
j >«2
1,00
+ 1
— 1
— 0,305
1,00
h
0,44
— 1
— 1
— 0.004
2,28
h
0,75
— 1
+ 0,253
1,33
АГ(
0,91
'+1
+ 0,039
1,11
К
0,57
+ 1
— 0,019
1,76
h
+ 0,63
— 0,29
+ 0 03
2) Данные взяты из „Практической геодезии® В. Витковского, § 160.
43 —
При составлении нормальных уравнений по правилу „столбец сам на себя и на'
следующие*, при каждом произведении двух множителей нужно брать третьим мно¬
жителем число q на той же строке.
Так получается нормальная система:
+ 2,00 Yi — 1,00'Тз + 0,25 у3 + 0 63 = О
— 1,00 Ti + 2,01 fo + 0,44 73 — 0,29 = 0
+ 0,25 ь + 0,44 v2 + 1,60 у3 + 0,03 - 0
Решая ее исключением и из первых двух уравнении, находим:
Ti = — 0,338; Та — 0,033; у3 = + 0,043.
После этого поправки X по системе (В') определяются по строкам системы
(А'), причем q, стоящее в первом столбце, будет и здесь фигурировать третьим мно¬
жителем, напр.:
\ = 0,25 •(— 0,338 + 0,043); Х3 = 1,00-(— 0,338 + 0,033),
и т. д., см. предпоследний столбец схемы.
Наконец [рЩ, где р первоначальные веса, получается по формуле»
1рАХ]=— KVih]\ здесь К — множитель, введенный в начале вычислений, т.-е. ; в дан-
OOZ
ном случае будет:
О 202
\рЩ ■= + - =. 0,000296.
Но контроль по этой формуле нецелесообразен; удобнее ввести новые веса р( (см.
/ РЛ
последний столбец схемы), обратные числам <7 первого столбца (т.-е. положить
убедиться в том, что имеет место равенство:
[р>щ — — [у/г] — 0,202.
§ 11. Составление нормальных уравнений. Таблицы. Арифмометр.
Контроли.
Составление и решение нормальных уравнений является главною
частью работы в практическом применении методы наименьших ква¬
дратов, и на ней должно сосредоточиться все внимание вычислителя.
Гаусс облек всю схему решения в особые формулы, предложив обо¬
значения для коэффициентов, получаемых на каждой ступени, по исклю¬
чении одной, двух и т. д. неизвестных х). Но опыт показывает, что
усвоение этих формул имеет для вычислителя сравнительно малое
значение, ибо все дело для него сводится к работе по определенной
схеме, в которой методически и планомерно проходит совершенно
элементарный процесс последовательного исключения неизвестных.
Из таких схем мы изучим обычную схему, всегда применяемую в астро¬
номии (где принято находить и веса неизвестных), затем ее упро
1 См. Отд. ш, § ю *
— 44 —
щенный вариант, применяемый в геодезических вычислениях, а затеь
и еще дальнейшее упрощение, так назыв. схему Дулитля, река
мендованную Геодезическим управлением С.-А. Соединенных Штатов
Но прежде всего нужно коснуться сам^й техники вычисленш
Составление и решение нормальных систем требует умножения и де
ления трехзначных и четырехзначных чисел, и эти действия следуе
производить либо по особым таблицам умножения, либо на арифмо
метре. Пользование логарифмами решительно не рекомендуется, not
скольку ими загромождается схема и требуется производство целоп
.ряда действий „в уме". Логарифмическая линейка, вообще говоря,
не обладает достаточной точностью и кроме того требует слишког
напряженного внимания в отношении места запятой. Из численны!
таблиц наиболее подходящими являются известные таблицы Crelle
или ZimmermanrTa, или О'Рурка. Но неоспоримое преимущество
в этой работе принадлежит арифмометру, благодаря возможности
производить на нем последовательно ряд арифметических действий,;
не останавливаясь на результате каждого из них в отдельности.
Иллюстрируем процесс такой работы на примере.
Пусть задано вычислить с точностью до четырех знаков выражение:
+ 0,3732 . 0,4813 + 1,5613 • 0,2243 — 2,1873 . 0,5234.
Арифмометр дает ответ на всю эту строку сразу, без малейшей возможности оши¬
биться в месте запятой. Действительно, каждое из полных произведений будет иметь
8 знаков после запятой. Так как их здегь требуется только 4, то мы отделим путем
указателя над ответный рядом четыре знака от правого края и затем будем ставить
один из множ..телей на последних справа спицах и множить на крайних
местах справа в счетном ряду. Итак, поставив на спицы 3732, множим
на 4813 и затем, на ооращ)я внимания на результат и не снимая произведения
в ответном ряду, но сняв только сомножителей, ставим на спицы 15613, множим
на 2243 и снова оставляем результат. Затем ставим 21873 и — так как требуется вычи¬
тание— множим в обратную сторону на 5234 (в счетном ряду красные цифры 5 2 3 4).
В определенном момеше этого последнего умножения арифмометр, дав звонок, пройдет
через’девятки. Но это отнюдь не останавливает работы, ибо дойдя до конца, наводим
в ответном ряду перед поставленной заранее запятой 999993849,87..., что есть не что
иное как дополнение отрицательного числа — 0,6150, которое и является ответом.
Такое комбинированное умножение и сложение (или вычитание)
чрезвычайно облегчает составление сумм квадратов, или соотвётствую-
щих произведений, т.-е. коэффициентов нормальной системы. Тем не
менее, существенной частью работы является применение контроль¬
ных формул, обеспечивающих безошибочность работы на каждом ее
этапе. Эти формулы вытекают из самого способа составления нор¬
мальной системы и ее симметрии по строкам и столбцам.
Действительно, пусть условные уравнения поправок суть:
— 45 —
«А + «2^2 + — “Ь ап “Ь К — О
Ь{кх 4- ь2\2 -(-... 4~ bn \ 4- ь2 = о
*А + 4^2 + — t„K 4- hk = о.
S1 S2 sn
Обозначим через sx, s2,...,s„ суммы коэффициентов при каждой?
из неизвестных и составим новую сумму типа:
«1*1 + «2*2 + - + «А = [as].
Не трудно видеть, что сумма эта приводится к сумме:
[аа\ -|- [ab~\ -J-... -{- [аЦ>
т.-е. сумме коэффициентов первого нормального уравнения. Таким же
образом
[bs] = [ab] + [bb] 4-... 4- [«1 и Т. д.
Итак, составив нормальные уравнения, можем их проконтролиро¬
вать, убедившись в том, 410 сумма коэффициентов каждого из них
(читая, как условлено выше, по столбцу и строке) равна [as], [&s]
И т. д.
Остается указать еще на прием приведения условных уравне¬
ний к однородному виду в смысле величины коэффициентов при
отдельных неизвестных. Например, если все коэффициенты при хх
приблизительно в а раз более коэффициентов при остальных х, то
делят коэффициенты при хх на а, затем составляют нормальную си¬
стему и решают ее. После этого надо хх снова разделить (не умно¬
жить!) на а, чтобы получить значение исходной неизвестной. Далее,
иногда делят только свободные ччены (невязки) на подходящее
число d. Очевидно, что после решения надо все х умножить на d.
В более сложных системах (см. отд. III) принято все коэффициенты
при каждой из неизвестных делить на наибольший из них, и точно-
так же все свободные члены на наибольший из них. Тогда переход
к значениям основных неизвестных получаем, умножая найденные зна¬
чения-на ^,...и т. д., где D есть численно наибольший из сво¬
бодных членов, А — наибольший из коэффициентов первой неиз¬
вестной, В—второй неизвестной и т. д.
>) При написании уравнений столбиком я будут суммы коэффициентов на каждой;
строке схемы; [as] и т. д. получается, перемножая столбцы а и s и складывая.
- 46 —
+ 4
+ 1
+ 2
+ 2
О
О
+ 1,29
+ 1,29
+ 7,29
+ 7,29
- 1,069
— 7,793
+ 2
+ 0,5
+ 4
+ 1
+ 2
О
-5,99
+ 0,64
+ 2,01
+ 3,64
+ 3
+ 1
+ 2
+ 2
— 6,63
— 6,63
— 1,63
— 1,63
+ 2,340
+ 1,170
- 4,703
Z
!
1
i t
i
i
Г
I h
i
i
0
+ 1,29
i
I
; -0,87
0
+ 0,32
j — 0,22
+ 2
— 5,99
| — 3,38
0
+ 0,64
1 ' — 0,44 |
+ 4
— 1,26
! —1,00 1
0
0
! 0
— 1,26
+ 37,78
i + 0,30 j
0
+ 0,41
— 0,28 I
+ 4,74
I +31,82
i — 4,95 j
0
1 + 2,33
! —1.60 j
+ 2
i — 6.63
— 2,94 |
+ 0,67
- 2,21
1 — 0,98 |
+ 4
— 1,26
j —1,00 !
+ 1,34
— 4,42
j —1,96 j
— 1,26
+ 37,37
j
+ 0,58 ;
— 4,44
+ 14,65
i + 6,50 |
+ 4,74
+ 29,49
i
CO
Co
Сл
— 1,09
+ 3,60
: +1.60 j
+ 2,66
+ 3,16
j +0,96 |
+ 1
+ 1Л9
I +0.36 i
+ 3,18
+ 22,72
j —5,92 j
+ 3,18
+ 3,78
| +1,14
+ 5,83
+ 25,89
— 4,95
+ 5,83
+ 6,94
+ 2,10
+ 18,94
— 7,06 !
i
1
+ 18,95 j
1 — 7,05
1
j
1
+ 0,372
—
- 0,803
+ 0,443
+ 0,360
— 0,538
— 0,822
— 0,980
0
+ 0,119
i
— 0,220
— 3:806
-j- 11,837 J
— 4,950
* I
i
t |
перемена
знака
С VMM
(контроль)
0,009
§ 12. Решение нормальных уравнений.
Переходя к изучению схем, начнем с наиболее простой из них,
именно полной (астрономической) 1). Для примера берем уже решен¬
ную на стр. 36 упрощенным приемом систему нормальных уравнений
с четырьмя неизвестными (коюрые вместо у обозначим здесь через
х, у, z, t) и перепишем ее в полном виде:
х
У
Z
t
h
+ 4
+ 2
0
+ 1,29
— 0,87
+ 2
4" 4
+ 2
— 5,99
— 3,38
0
+ 2
+ 4
— 1,26
— 1,00
+ 1,29 1
— 5,99
— 1,26
+ 37,78
+ 0,30.
Решение проводится в четырех последовательных стадиях исклю¬
чения неизвестных (четыре ступени) и подстановке каждой из най¬
денных неизвестных в предыдущие уравнения. Оно располагается,
как показано в схеме (стр. 46), которую мы сейчас и выясним
подробно. Обращаем внимание на то, что известные члены стоят
в левых частях уравнений.
Пояснение. 1) Исключение неизвестных. Переписав
все четыре нормальные уравнения (назовем их Nlt N2, Ns, Af4) через
строчку, выписываем на пятой строке алгебраические суммы чисел по
столбцам; эта строка составит так называемое первое суммовое урав¬
нение . После этого делим Л7, (т.-е. все числа этой строки) на его
первый коэффициент (здесь 4) и частные подписываем под Ny более
заметным шрифтом (красными чернилами). Эта красная строка назы¬
вается первым элиминационным уравнением Ь\ (она послужит к опре¬
делению х). Все числа Ех последовательно множатся на первые коэф¬
фициенты N2 (здесь 2), потом Ыя (0), Nt (1,29) и 5Х (7,29) и прои-ве¬
дения подписываются под N2, Af3, Nt и St.
На этом первая ступень работы кончается, ибо, вычитая подписан¬
ные только-что строки из первоначальных уравнений N и 5, мы оче¬
видно приведем к нулю все коэффициенты при х, т.-е. исключим
*) Эта классическая схема не заключает в себе ничего характерного для решения
нормальных уравнений, так как мы не пользуемся здесь их симметрией; она применима
поэтому к решению любых систем линейных уравнений. Но важность самого приема
последовательного исключения неизвестных именно для способа наименьших квадратов
«няснится далее, при доказательстве теоремы Гаусс* о весах неизвестных (стр.
137 я след.)
_ 48 -
неизвестную х. В результате этого вычитания образуется втора
группа схемы (уравнения N2, ЛЛ, и S2), причем, составив ее, имеа
важный контроль: коэффициенты S2 должны фактически рав
няться сумме чисел, написанных в столбцах над ними (здесь—1,63 =
= 3 —{— 2 — 6,63; 4,74 = 2 —[— 4 — 1,26 и т. д.). После этого во втор01
квадрате действуем как в первом: первое из N делим на его первьи
коэффициент (здесь 3). Это дает красную строку, т.-е. второе элими
национное уравнение Е2\ Е2 множится последовательно на первш
коэффициенты остальных N и S2 (в данном случае на 2; на — 6,63
на —1,63) и результаты подписываются под строками N и S2.
Вычитание дает третий квадрат (у исключено), в нем контрольно!
явится строка S2 (напр., 2,66-(-3,18 и 5,83, допустимая погрешность)
Первая строка группы N, деленная на ее первый коэффициент (здесг
2,66), дает красную строку Ей; £3 множится на 3,18 и 5,83; в четверто!
квадрате остается только одно уравнение Niи суммовоеS4; очевидно,
эти строки должны в пределах точности вычисления между собой
совпадать.
2) Обратная подстановка. Эту часть работы рекомендуете!
производить в той же схеме, располагая вычисления „горкой". Здесь
контроли отсутствуют и требуется внимание.
Из последнего нормального уравнения, т.-е. 18,94 7— 7,С6 = 0 вы¬
водим 7 = 0,372 и это значение 7 вписываем красными чернилами
в его столбец. После этого множим на 0,372 все курсивные числа
в этом же столбце 7 и вписываем их под 0,372; это дает столбик:
0,433 = 0,372 X 1,19; —0,822 = 0,372-—2,21; 0,119 = 0,372-0,32; рядом
с ними выписываем свободные члены элиминационных строк, т.-е.
+ 0,360; — 0,980; — 0,220.
Так как Ей гласит: z+1,19 7 + 0,360 = 0, и так как мы уже полу¬
чили произведение 1,19-0,372 = 0,443, то очевидно, что, сложив 0,443
и 0,360 и переменив знак суммы, мы найдем z ——0,803, ко¬
торый и подписывается красными чернилами слева от 0,423 в своем
столбце z. Помножая — 0,803 на все курсивные числа над ними (0,67
и 0), подписывая их под — 0,803, складывая по строке—0,538 — 0,822
— 0,980 и переменив знак суммы, находим _у = + 2,340, который и
вписываем в его столбце. Помножив у на 0,5, сложив это произ¬
ведение со всеми числами, уже приготовленными на последней строке,
и переменив знак суммы, имеем л; = —1,069, на чем и заканчивается
вся работа; для заключительного её контроля необходимо подставить
найденные значения х, у, z, 7 в одно из нормальных уравнений или,
лучше, в первое суммовое уравнение 5,; «это и сделано на последней
строке нашей схемы, где проставлены произведения х-7,29: 2,01
и т. д., и к сумме этих произведений придан свободный член 51:
именно — 4,95.
- 49 —
Применение описанной полной схемы рекомендуется в тех случаях*
когда требуется найти так называемые веса неизвестных х, у,...,
как обычно принято в астрономических вычислениях; ею же удобно
пользоваться, если вести исключение неизвестных не в том именно
порядке, в котором написаны нормальные уравнения, а начиная на
каждой ступени исключение с той неизвестной, у которой наибо¬
лее сильный коэффициент—что теоретически правильнее;
практически же вся разница Ьыйдет только в том, что красные строки Е
не будут уже обязательно стоять под первыми N своих групп.
§ 13. Сокращенная схема.
В сокращенной схеме мы будем иметь в виду симметрию
нормальной системы, что позволяет выписывать в схеме только
члены, стоящие по диагонали и справа от нее. Кроме того, мы не
будем отделять все ступени исключения одну от другой, а будем
последовательно вычитать из каждого нормального уравнения все те
строки, которые получаются уможением всех предшествующих
элиминационных строк на соответствующие множители. С этой
целью, подготовляя схему, оставляем для Nx три строки, для Nz пять,
для N5 семь и т. д. и вписываем, эти уравнения на их места, ведя
рядом контрольный суммовой столбец (S равно сумме всех коэф¬
фициентов данного нормального уравнения плюс А; все уравнения
читаются, как уже сказано, по столбцу до его конца и затем по
строке). Из Nx немедленно образуем Е{ (первый коэффициент ' его*
единицу, писать не требуется; равным образом, число в 5 столбце
на строке Е не нужно). После этого множим Nx последовательно на
второй коэффициент Е1 (0,5), на третий (0), на четвертый 2)(0,32) и эти
произведения (они обозначены „от Ег“) подписываем под N2, N* и TV4.
Вычитаем эти строки из N2, jV3 и Af4 (N, остается без изменения,
ибо третий коэффициент в Ег равен нулю). Соответствующие строки
в схеме помечены „ост.“. Теперь из остатка от N2 делением на 3
образуем Е2\ множим строку „ост.“ сперва на 0,67, затем на — 2,21
и подписываем результаты под остатками у iV8 и N± (строки „от Е2и).
После этой операции и вычитания получается ост. у N2 (в сущности
это второй остаток), из которого образуем Е%; умножаем этот послед¬
ний остаток на 1,19 и результат подписываем под последним остатком
у jV4 (строка „от /Г3“). Вычитая, находим заключительный остаток
18,90 /—7,07 = 0, откуда получаем t и затем подстановкой, как по¬
казано выше, определяем z, у, х.
, Резюмируя, можем сказать, что каждая ступень работы состоит
из следующих операций: получения элиминационного уравнения,
*) Все эти умножения начинаем с того числа строки , которое стоит над дан¬
ным множителем.
СвосоС найм, квадратов. 4
— 50 —
умножения на каждый из его коэффициентов всех чисел, стоящ
в предыдущей строке над ним и направо; вычитания уравнен»
получаемых путем этих умножений, из стоящих над ними во вс
группах и образования следующего уравнения Е.
Необходимо отметить, что числа в столбце h в элиминационш
строках (здесь —0,22, —0,98, +0,36) подготовляются только д
второй части вычисления („горка”) и в качестве множителей
X
У
z
t
h
5
Кон¬
троль
Nx
+ 4
+ 2
+ 1,29
— 0,87
+ 6,42
Ei
+0,5
+ 0,32
-0,22
+ 4
+ 2
-5,99
— 3,38
-1,37
от Ei
+ 1
+ 0,64
— 0,44
+ 3,21
ост.
+ з
+ 2
— 6,63
— 2,94
-4,58
(-4.57)
Ег
+0,67
— 2,21
— 0,98
N*
+ 4
— 1,26
— 1,00
+ 3,74
от E2
+ 1,34
— 4,44
— 1,97
-3,07
ост.
+ 2,66
+ 3,18
+ 0,97
+ 6,81
(+6,81)
E,
+ 1,19
+ 0,36
Nt
+ 37,78
+ 0,30
+ 32,12
от Ex
+ 0,42
— 0,28
+ 2,07
OCT.
+ 37,36
+ 0,58
+ 30,05
(*)
от E2
+14,70
+ 6,51
+ 10,14
OCT.
+ 22,66
-5,93
+19,91
(*)
от Ег
+ 3,76
+ 1,14
+ 8,06
OCT.
4- 18,90
— 7,07
+ 11,85
(+11,83)
+ 0,372
-0,803
+ 0,443
+ 0,360
Перемена знака
+ 2,340
— 0,538
- 0,822
- 0,980
сумм
— 1,069
+ 1,170
0
+ 0,119
— 0,220
1 *
у
2
t
участвуют. Наконец, контрольные числа в столбце S должны coi
падать, в пределах точности вычисления, с суммами чисел на каждо
из заключительных остаточных строк; для сравнени:
в нашем примере (уже решенном по полной схеме в § 12) эти сумм
.поставлены в скобках рядом с соответствующими числами столбца .
— 51 —
§ 14. Схема Дулитл я.
Схема, принятая Американским Геодезическим Управлением,
имеет несомненное преимущество над только-что разобранной, в том
случае, когда число неизвестных (коррелат) значительно. Чтобы выяс¬
нить ее,- обратимся к приведенному сейчас примеру, именно, к группе,
подписанной под Л74. Из этого уравнения мы вычитаем уравнение,
полученное от Ех [условимся писать вместо этого (1)]; из первого
остатка вычитаем (2) — т.-е. уравнение, полученное от Еа; из второго
остатка вычитаем (3). Ясно, что все эти последовательные вычи¬
тания излишни, ибо достаточно под А74 подписать строки (1), (2), (3)
с обратными знаками и сложить их все алгебраически с N± —
мы получим сразу заключительную остаточную
строку. Поэтому делаются ненужными те строки схемы, при
которых у нас поставлена (*). Точно таким образом, в общем
случае, мы под N5 подписали бы с обратными знаками строки
от (1), (2), (3), (4) и, взяв алгебраическую сумму, нашли бы сразу
тот последний остаток, из которого образуется Еъ, сократив эту
часть схемы на т р и строки; очевидно, что при большом числе кор¬
релат эти сокращения дают значительную экономию во всей работе
Применяя эту схему, было бы нецелесообразно высчитывать
наперед, на каких именно строках ее придутся нормальные уравнения
Nlt Nz, Na, Они вписываются в схему по мере хода работы, от¬
ступая всегда вправо на один столбец; тогда все числа, стоящие
в курсивных строках над первым коэффициентом вписанного уравнения
и являются множителями для заключительных остаточных строк.
Так, например, положим, что в приведенной ниже схеме мы дошли
до Л74; следовательно, мы вписываем в схему (-{-37,78; —{— 0,30; 4-32,12)
тогда видим, что числа — 1,19; -[-2,21; —0,32, т.-е. все курсивные числа
над 37,78, и будут соответственно множителями строк (3,18; +0,97
+ 6,81); (—6,63; —2,94; —’4,58); (-+1,29; —0,87; +6,42). Произведения
вписываем последовательно' под TV4, образуем алгебраическую сумму,
делим ее на первый коэффициент +18,90, при этом меняем знаки'.
это и будет Et. После этого надлежало бы, в общем случае, вписать
в схему N5 и повторить описанную последовательность операций.
Разумеется, если бы в данном примере одно из курсивных чисел над
37,78 было равно нулю, то соответствующая строка под TV4 выпала
бы совершенно, — обстоятельство, которое приводит иногда к зна¬
чительному сокращению схемы.
Остается обратить внимание на то, что в виду перемены знака на
строках/: не следует менять знака в тех суммах, которые на
последней части схемы горкой дают значения неизвестных.
4*
— 52 —
Читатель убедится в удобстве и прозрачности этой схемы, повторив
вычисление системы предыдущего §. Заметим только, что для ясности
мы составляем Eiy которое читается здесь / = —f- 0,372, причем именно
это значение t без перемены знака вносится в столбец t нижней
части схемы.
Для усвоения процесса работы в схеме Дулитл я на стр. 53 при¬
веден еще один пример решения нормальной системы с пятью не¬
известными; так как здесь важен самый тип вычисления, в этом при¬
мере взяты простые коэффициенты и во всех числах удержано лишь
два знака после запятой.
X
у
\
z
t
h
5
Кон- 1
тролъ
Ну
+ 4
+ 2
+ 1,29
— 0,87
i
!
+ 6,42
Еу
— 0,5
— 0,32
+ 0,220
N,
+ 4
+ 2
-5,99
— 3,38
-1,37
(1)
— 1
— 0,64
+ 0,44
-3,21
+ з
+ 2
— 6,63
— 2,94
-4,58
(-4,57)
Е3
— 0,67
+ 2,21
+ 0,980
Н,
+ 4
— 1,26
— 1,00
+ 3,74
(1) = 0; (2)
— 1,34
+ 4,44
+ 1,97
+ 3,07
+ 2,66
+ 3,18
+ 0,97
+ 6,81
(+6,81)
, Es
— 1,19
— 0,360
N<
+ 37,78
+ 0,30
+ 32,12
0)
— 0,42
+ 0,28
-2,07
(2)
— 14,70
— 6,51
-10,14
(3)
— 3,76
-1,14
-8,06
+ 18,90
— 7,07
+ 11,85
(+11,83)
^4
+ 0,372
1
+ 0,372
—
— 0,803
— 0,443
- 0,360
знак сумм
+ 2,340
+ 0,538
+ 0,822
+ 0,980
не
меняется
—1,069
— 1,170
0
— 0,119
+ 0,220
-
X
у
Z
t
— 53 —
X
У
Z
t
и
h
5
Кон¬
троль
К
+ 12
+ 6
+ 4
+ 2
0
+ 24,0
X
л S
+ 12
+ 9
+ 9
+ 0,8
+ 30,8
tj <1>
03 н
X и
+ 6
+ 9
+ 18
+ 4
+ П
— 3,1
+ 44,9
CL ®
О «
X
+ 4
+ 4
+ 10
0
+ 18,0
+ 2
+ 9
+ П
+ 17
+ 3,5
+ 42,5
г*х
+ 12
+ 6
+ 4
+ 2
+ 24,00
Ех
-0,5
-0,33
— 0,17
N,
+ 12
+ 9’
+ 9
+ 0,80
+ 30,80
(1) = 0 \Е
2
— 0,75
— 0,75
—0,07
N3
+ 18
+ 4
+ 11
— 3,10
+ 44,90
(1)
— 3
— 2
— 1
— 12,00
(2)
— 6,75
. —6,75
— 0,60
— 23,10
+ 8,25
+ 2
+ 3,25
-3,70
+ 9,80
(+ 9.80)
Е3
— 0,24
— 0,39
+ 0,45
\ лг4
+ 10
+18,00
(1)
-
— 1,32
— 0,66
— 8,00
(2) = 0; (3)
— 0,48
— 0,78
+ 0,89
— 2,35
+ 8,20
— 1,44
+ 0,89
+ 7,65
(+7,65)
Е*
+ 0,18
— 0,11
Nb
+ 17
+ 3,50
+ 42,50
(1)
— 0,34
— 4,08
(2)
— 6,75
— 0,60
— 23,10
(3)
—1,27
+ 1,44
— 3,82
(4)
-0,26
+ 0,16
+ 1,38
+ 8,38
+ 4,50
+12,88
(+12,88)
Е,
— 0,54
!
— 0,54
—
— 0,21
— 0,10
-0,11
— 0,71
+ 0,05
+ 0,21
+ 0,45
-0,20
-0,53
+ 0,40
— 0,07
— 0,20
— 0,36
+ 0,07
+ 0,09
-
X
У
Z
t
и
ОТДЕЛ II.
ОБРАБОТКА РЯДОВ НАБЛЮДЕНИЙ ОДНОЙ ВЕЛИЧИНЫ.
В предыдущем изложении, говоря о способе получения наилучшего
значения одной или нескольких величин по данным непосредственных
наблюдений, мы совершенно отвлекались от понятия действитель¬
ного или „истинного" значения тех величин, которые являются
предметом этих наблюдений.
Теперь нашей задачей явится перейти от наблюденных величин k
к действительному значению X, или, по крайней мере, указать те
пределы, в которые имеется основание заключить X согласно данному
ряду наблюдений. Не трудно видеть, что в этом вопросе весьма
важную роль будет играть понятие точности наблюдений, ибо чем
точнее наблюдения, тем теснее пределы, которые мы в праве назна¬
чить для X. С другой стороны, суждение о точности данного ряда мы
можем почерпнуть только из самого этого ряда, ибо, вообще говоря,
предполагается, что величина X определяется впервые и мы с дру¬
гими рядами ее наблюдений связаться не можем. Таким образом
здесь возникает своеобразное затруднение, которое устраняется
только некоторым обходным путем: мы делаем основное предполо¬
жение, что те случайные погрешности, с которыми сопряжено каждое
из наблюдений, группируются по своей величине согласно некото¬
рому определенному закону, общему для всех и всяких рядов на¬
блюдений, если только эти наблюдения не искажены постоянными
и систематическими ошибками. Этот закон носит название закона
нормального (гауссова) распределения, и сущность его применения
сводится к тому, что мы по распределению погрешностей определяем
меру точности ряда наблюдений, затем выводим среднюю и веро¬
ятную ошибки определения X на основании этого ряда и, наконец,
получаем правила комбинации результатов нескольких рядов наблю¬
дений того же X, характеризуемых различной мерой точности. Тот
факт, что формула, выражающая этот закон, может быть получена
из основных положений теории вероятностей и некоторых предель¬
ных переходов, имеет здесь сравнительно меньшее значение; для
практика важнее подчеркнуть, что область применения закона Гаусса
не ограничивается одной теорией ошибок: он находит приложение
— 55 —
в разнообразных задачах математической статистики, затем в про¬
блемах молекулярной физики — вообще, в целом ряде случаев, где
происходит статистическое изучение совокупности объектов по какому-
либо характерному для них признаку, при условии, что число этих
объектов достаточно значительно. Поэтому кажется естественным
предпослать изложению непосредственно интересующего нас вопроса
самые'краткие сведения о законе нормального распределения, иллю¬
стрировав их некоторыми примерами, на которых будут выяснены
и вычислительные приемы, необходимые при обработке рядоа
наблюдений.
§ 1. Нормальное статистическое распределение.
Допустим, что изучению подлежит совокупность, состоящая из ЛГ
объектов, из которых каждый характеризуется определенным числен¬
ным значением какого-либо признака (например, у каждого из ЛЛ
человек, совокупность которых мы будем исследовать как статисти¬
ческое целое, можно измерить высоту роста или ширину грудной
клетки и т. п.). Обозначим через х1г х2, х3, ..., Xk ряд значений харак¬
теризующего признака, причем для удобства возьмем эти значения
через равные интервалы (например, высоту роста — через один санти¬
метр), и произведем классификацию данной совокупности, подсчитав,,
у скольких объектов значение признака равно хх, у скольких оно
равно х2 и т. д. Практически, конечно, может и не быть ни одного
объекта, у которого признак х равен в точности хх, или х2 и т. д.,
и потому естественно каждое из этих чисел считать представителем
интервала, распространяющегося по обе стороны от данного значения
на половину деления; например, под „ширина грудной клетки
в 86 сми подойдут все объекты, у которых этот признак имеет
значения от 85,5 (исключительно) до 86,5 (включительно).
Произведя такую классификацию и установив число объектов со
значением признака хх, затем л;2 и т. д., мы получаем ряд чисел:
Л» Уа>' из которых каждое показывает, у скольких объектов
из общего числа N величина признака равна atx , затем х2 и т. д. Эти
числа носят название частот появления данного значения л: в изу¬
чаемой совокупности. Очевидно, мы имеем:
Уг ~\гУ2 + • • • + У* = N
Всякий закон статистического распределения дает выражение у
(частоты) как функцию х (величины характеризующего признака);
иными словами такой закон представляется зависимостью вида:у =f(x).
Графическое изображение этой зависимости носит название кривой
распределения', ординаты кривой суть частоты, абсциссы — значения
признака.
— 56 —
В формулу для у должны очевидно входить как параметры не-
которые постоянные, получаемые при численной обработке данной
совокупности. Из этих параметров нам понадобятся в дальнейшем для
изучения простейших (так назыв. нормальных) совокупностей
только три, именно:
1) N—общее число объектов (называемое объемом совокупности);
2) М — среднее арифметическое из всех значений характеризующего
признака;
3) о —среднее квадратичное уклонение признака, называемое также
его дисперсией, (рассеяние); смысл этого термина выяснится не
сколько далее.
Для определения этих основных постоянных служат формулы:
М=Л+Л + ”-+.У* (1)
_ + • • • + **У* _ [ху] .
J1 ~ N ~~ [у] w
Применяя последнюю формулу, мы считаем, что у всех уг объектов
первой категории (первого класса) величина признака одинакова
и равна л^; у всех у2 объектов второй она одинакова и равна х2 и т. д.;
с этим упрощением образуем сумму произведений: частота на зна¬
чение презнака и делим ее на число объектов.
Для определения третьей постоянной, а, имеем:
/(*, — Myy't + М)*у3 + .т: -I- (xk~^M)*yk _ Г[у(х—М)Ц
N ~у [у] • * (3)
Здесь мы полагаем, что у всех объектов первого класса уклонение
от среднего равно хх — М; у всех объектов второго лг2 — М и т. д.;
образуем квадраты этих уклонений и сумму их произведений на
частоты у делим на N.
у Для практического вычисления М и о полезно выбрать „на-глаз"
из заданных значений признака некоторое приближенное его значение
М', близкое к среднему; тогда имеем:
M = Wx~m + M' . . (4)
02 в [у(х -М')*] _ цц, _ (5)
Для доказательства этих формул, заметим, что при любом значении М',
= [у (х-М' + М')) = [у(х - т1 'М,[у).
N N ' N ’
яо [у] = N; подставляя, иолучаем из написанной строки ф-лу (4).
Далее,
_ [у (х — М'+М' — М)Ц =
= [У (х~ уИ')2]'+ 2 (М' — М) У(Х~МЧ± M'f
— 57 —
Последние два члена справа, в виду (4) дают:
— 2 (М — МУ + (М — М')а = — (М — Л4')з,
чем и доказывается ф-ла (5),
Допустим теперь, что для данной совокупности основные посто¬
янные N, М и о вычислены; как сказано, только они и войдут в урав¬
нение, y—fi*), если распределение следует нормальному закону.
Наконец, следует сразу заметить, в какой форме войдет в него аргу¬
мент х; именно, мы будем отсчитывать его значения не в той произ¬
вольной и случайной мере, в которой он задан (сантиметры, секунды
и т. п.), а особым образом: значения признака отсчитываются от его
среднего значения М и выражаются в частях среднего квадратичного
уклонения о. Иными словами, вместо х мы вводим новый аргумент t,
лолагая:
0)
Из приведенных выше выражений для М и о видно, что обе эти
величины получаются в единицах того же наименования, как и х.
Поэтому t, которое будет входить во все дальнейшие формулы, есть
число отвлеченное; оно получает название нормированного укло¬
нения.
После этих замечаний приведем, наконец, и самую формулунор¬
мального распределения (закон Гаусса); она гласит:
" N 1
v = - ~е ~ ™ (II)
0 ]/2в 4 '
(«—основание натуральных логарифмов).
Пользуясь сделанным только-что замечанием относительно правила
отсчета х, т.-е. заменяя в показателе (х — Л4)2:о2 на t'3, перепишем
формулу II в виде:
у- N ■ Д (1Г)
^ а j/2tt
/*
Для функции --! « 2 составлена таблица2)по аргументуt; обо-
у2п
значая через <p(f) число, полученное по этой таблице для данного t,
имеем окончательно:
У--Т -fit) (III)
2)Обоснование этой формулы,—на которую читатель может смотреть здесь как на
эмпирический закон, приложимый к обширным классам статистической действительности,—
лежит вне задач этого курса.
3) Таблица I, стр. 101.
- 58 —
Применяя эту простую формулу к обработке совокупностей, следу
иметь в виду, что она доставляет частоту объектов, характеризуем!
значением признака x = x1 (или аргумента t=t^), причем частота э
всегда расчитана на единицу интервала для признака х или же
интервал равный -у- для аргумента t.
_ Обращаемся теперь к изучению основных свойств нормально!
распределения, вытекающих из формулы (И).
р
1. Так как показатель—^ ПРИ всех значениях ^есть величина отр
дательная и е>1, то с увеличением х — М частота у убывае
максимальная частота приходится для показателя, равного нули
но t== 0, по формуле (1), соответствует х = М', поэтому в нормальн!
распределении наиболее часто появляются объекты, у котор!
значение признака близко к среднему из всех значени
его в данном ряду.
Подставляя х = М или t = 0 в формулу (II), находим:
Утах = 4---7==0>3989-Т--
0 ]/2ir 0
Следует заметить, что, с возрастанием t, ® (t) падает весьма быст
и в четырехзначной таблице достаточно ограничиться значения!
аргумента t от 0 до 4. Для t — 5 имеем:
?(5;= }-е -35/з = 1,5.10-*
TW у 2г
т.-е. практически ничтожно.
2. Для значений х, одинаково уклоняющихся от среднего М в oi
стороны, у имеет одинаковое значение, ибо (х — М) входит в квау
рате в показатель при е.
Это обнаруживает, что нормальное распределение симметричн
в отношении среднего значения признака.
3. Падение у происходит тем быстрее, чем меньше о, иб
с уменьшением а численно увеличивается показатель при е. Поэток
можно сказать, что скученность объектов данной совокупности завис»
именно от о; при малых о они почти все должны иметь значенш
близкие к М; наоборот, при больших о ряд их, как говорят,рассеивает
т.-е. значительно протягивается по обе стороны от М. По этой причин
среднее квадратичное уклонение о и носит в статистике 'названи
дисперсии (рассеяния) данной совокупности.
Кривая, изображающая функцию
-У = <Р (Й,
носит название основной кривой нормального распределения (ил
гауссовой кривой вероятности). Отметим два геометрические cboi
ства этой кривой:
— 59 —
I
а) Нормальная кривая имеет точки перегиба при значениях аргу-
иента t = и t = — 1.
Действительно, из формулы ® (t) = —==. е 2
находим:
(0 = -^
(О-
В точках перегиба <р' (£) = 0, а это возможно только при t2— 1 =0
или при f = + 1.
Но для / = + 1, согласно (I), имеем:
х — М = +о.
Отсюда заключаем, что перегиб нормальной кривой происходит
жри значениях х — М + о, т.-е. для значений х, симметрично рас¬
положенных на расстоянии а по обе стороны от М•
б) Ось X есть асимптота кривой.
Действительно:
t
lim *'(*) — Пш ер>*
t-+ 00 l/2it
Черт. 6.
По правилу Лопиталя, взяв производные от числителя и зна¬
менателя, находим:
1
1 lim te ‘2i2 = 0..
lim f1 (t) ■■
t~* 00
У 2я
— 60 —
Так как + (t) есть тангенс угла касательный с осью X, то заю
чаем, что касательная на бесконечности параллельна этой оси; но
как при t—»-оо ординаты кривой стремятся к нулю, мы видим, 1
касательная на бесконечности не только параллельна, но и сливае
с осью X, т.-е. является ее ассимптотой.
Все выведенные свойства нормального распределения иллюст
руются графиком нормальной кривой (черт. 6), в котором для
четливости масштаб ординат взят в 10 раз больше масштаба абсцв
На графике отмечены ординаты при следующих значениях ар
мента: 1
I. t— 0 (или л; — М = 0 — вершина кривой)
И. £ = + 0,6745 ( х — М = ± р)
III. *=± 0,7979 ( х — М = ±Ъ)
IV. £ = + 1 ( х — М = ^=з — точки перегиба)
О точках II и III будет сказано ниже.
§ 2. Примеры.
Для примера полной обработки статистического ряда выбира!
данные относительно совокупности в N—10000 человек, у котор|
была измерена ширина грудной клетки х). Все вычисление удобно pi
полагается в приведенной ниже схеме, отдельные столбцы котор
имеют следующие значения:
(1) величина признака х (в дюймах);
(2) соответствующие наблюденные частоты у,
(3) х — 40; это последнее число выбрано как приближенное среда
значение признака х (см. стр. 56);
(4) у(х — 40); с помощью суммы чисел этого столбца наход
среднее М:
714 = 40 — ^ = 40 — 0,165 = 39,835;
(5) произведения у (х — 40)2; найдя их сумму, долучаем среднее кв;
ратичное уклонение (дисперсию) о по формуле
с2 = Ш00 ~ (М'-МУ = 4-239 - (°>165)2 = 4,212,
откуда:
в = 2,052; 1 =0,4873; N = 4873;
99 с а ■ 9
(6) х — М = х — 39,835;
(7) аргумент t=(x — М) . ^ = (х — М) . 0,4873;
0 Данные из английской статистики.
— 61 —
(8) значения <? (t), найденные по таблице I для соответствующих t;.
(9) теоретическая частота, вычисленная по формуле:
=-.9(0 = 4873- <?(/);
(10) разности между наблюденной частотой (2-й столбец) и вычи¬
сленной.
1
X
2
У
3
х —40
4
у{х — 40)
5
у(х — 40)з
6
х — М
7
t
8
9
у выч.
10
Набл.—
вычисл.
33
6
— 7
— 42
294
— 6,835
— 3,331
0,0016
! 8
! — 2
I
34
35
— 6
— 210
1260
- 5,835
— 2,843
0,0070
34
+ 1
35
125
-5
— 625
3125
— 4,835
— 2,356
0,0248
121
+ 4
36
338
— 4
— 1352
5408
— 3,835
— 1,869
0,0695
339
— 1
37
740
— 3
— 2220
6660
— 2,835
-1,381
0,1537
749
- 9
38
1303
-2
— 2606
5212
— 1,835
— 0,894
0,2675
1304
— 1
39
1810
— 1
— 1810
1810
— 0,835
— 0,407
0,3672
1789
+ 21
40
1940
0
0
0
+ 0,165
+ 0,080
0,3977
1938
+ 2
41
1640
+ 1
+ 1640
1640
1,165
0,568
0,3395
1654
— 14
42
1120
2
2240
4480
2,165'
1,055
0,2287
1114
+ 6
43
600
3
1800
5400
3,165
1,542
0,1215
592
+ 8
44
222
4
888
3552
4,165
2,030
0,0508
248
-26
45
84
5
420
2100
5,165
2,517
0,0168
82
+ 2
46
30
6
180
1080
6,165
3,004
0,0044
21
+ 9
47
5
, 7
35
245
7,165
3,492
0,0009
4
+ 1
| 48
2
8
16
128
8,165
3,979
0,0001
0
+ 2
10000
— 1646
42394
9997
+ 3 |
1 i
Изучая разности, приведенные в столбце 10, видим, что согла сие
не касаясь некоторых отдельных уклонений, в общем прекрасное,,
и самая возможность охватить одной формулой результат измерения
огромной совокупности есть один из самых замечательных фактов
из области применения математики к статистическим данным. В нашем
примере расхождение у вершины кривой составляет приблизительно
1%, и данный ряд, конечно, можно назвать нормальным.
II. Для следующего примера рассмотрим совокупность 1000 на¬
блюдений прямого восхождения Полярной, сделанных в Гринвиче;,
здесь все наблюдения разбиты на группы, по величине уклонения их
от некоторого значения прямого восхождения, близкого к среднему
из всех имеющихся значений. Эти уклонения д: — М' и показаны
в первом столбце таблицы; во втором—даны наблюденные частоты-
— 62 —
Затем приведены х—М *), т.-е. уклонения от действительного cpt
него, аргумент t, функция <?{t) и частоты, вычисленные по формул
= 55’*(*)•
Делитель 2 появляется здесь потому, что в основной форму
(II) интервал признака х считается равным 1. В данном распределен!
где он равен х/2, надо у, полученное по формуле (III), делить на
Среднее квадратичное уклонение о здесь равно 1,1785; оно да1
в секундах времени так же, как и х—М.
N— 1000; а = 1,1785; \ = 0,8485;
- = 424; М = М' — 0,06.
2 а 9
х — М1
У
х — М
t
у вычисл.
Наблюд.
— вычисл
— 3,5
2
— 3,44
— 2,919
0,0056
2
0 :
— 3,0
12
— 2,94
— 2,495
0,0178
8
+4;
— 2,5
25
— 2,44
— 2,070
0,0468
20
+ 5
— 2,0
43
— 1,94
—1,646
0,1030
44
— 1 f
-1,5
74
—1,44
— 1,222
0,1890
80
- б |
-1,0
126
- 0,94
— 0,798 •
0,2902
123
+ з
-0,5
150
— 0,44
— 0,373
0,3721
158
- 8 ;
0
168
+ 0,06
+ 0,051
0,3984
169
— 1
+ 0,5
148
+ 0,56
+ 0,475
0,3564
151
* - 3
+ 1,0
129
+ 1,06
+ 0,899
0,2663
ИЗ
+ 16
+1,5
78
+ 1,56
+ 1,324
0,1660
70
+ 8
+ 2,0
33
+ 2,06
+ 1,748
0,0866
37
— 4 »
+ 2,5
ю
+ 2,56
+ 2,172
0,0377
16
— 6
+ 3,0
2
+ 3,06
+ 2,596
0,0137
6
— 4
Согласие можно считать удовлетворительным.
§ 3. Площадь под нормальной кривой.
Математическое выражение закона нормального распределенш
приводит к формуле, в которой частота у является непрерывной
функцией аргумента д: (или t); имея это в виду, мы должны суще¬
ственно дополнить данное выше определение частоты. Мы говорил»
тогда, что значение х — хг является представителем некоторого ин¬
1) Детали вычисления М из опускаем.
— 63
тервала, принимаемого за единицу (например, от 85,5 до 86,5), и под¬
считывали число объектов, для которых признак х имеет значения
между указанными пределами. Условимся это определение частоты
называть статистическим. Но математически, имея дело с непрерыв¬
ной функцией у, мы должны не только утверждать, что всякому
данному значению х соответствует своя частота у, но более того —
что бесконечно малому изменению х соответствует и бесконечно
малое изменение у; поэтому понятие частоты, соответствующей целому
интервалу х, математически недостаточно. К более строгому
определению у мы придем, если, переходя от данного значения х
к значению сколь угодно к нему близкому, будем изучать меру на¬
растания числа объектов при этом значении х.
С этой целью мы введем еще одну новую функцию; именно, будем
рассматривать число объектов, у которых признак имеет все воз¬
можные значения, не превышающие данного х, как функцию этого х,
и найдем меру или скорость возрастания этой функции. Называя ее
п(х) и обозначая через h приращение значения признака х, мы опре¬
делим частоту при данном значении аргумента формулой:
Иными словами, мы вводим здесь частоту у как производную от
числа объектов п(х) по признаку х, т.-е. полагаем:
Эта формула, в связи с законом нормального распределения,
и является основой всех дальнейших выводов.
Прежде всего из нее выводим:
Но, как известно из курса анализа, интегралом (*) выражается
величина площади, ограниченной кривой у =/(х), осью абсцисс, пре¬
дельной ординатой и неопределенной пока еще начальной ординатой,
от которой начинается счет площадей.
Чтобы освободиться от произвольной постоянной С, фигурирую¬
щей в (*), условимся считать площади от «крайней" слева ординаты,
соответствующей л: = — с°; тогда площади между ординатами, соответ¬
ствующими х = —°° и x = xlt будет отвечать, очевидно, число объ¬
ектов, у которых признак имеет все возможные значения от
крайних отрицательных и до данного х — х1. При этом условии С— О
и мы можем написать *):
у = Уш
^ А-0 h
X
(*)
Нам остается теперь только подставить вместо у его выражега
по закону Г а у с с а. Это приводит к формуле:
. - х, — (х — ЛГ)2
«(*)= "-.* [е ™ dx.
У 1 5 ]/ 2^ J
— оо
Введем теперь вместо х основной аргумент t. Мы имели t— х~ М, от
куда следует dx — idt. Положим еще, что верхнему пределу х=\
соответствует значение t = t1. Подставляя, находим:
п(х\) — N • fe 2 dt (II
ОО
Формулой (II) определяется число объектов совокупности (и
общего ее объема N), для которых аргумент t имеет все значения о
t = — оо до t = t1; мы напишем ее в виде:
n(x)^N-S(t), (Ill
где положено:
ЭД-те/»"2*
— ОО
Получив таким образом формулу для числа объектов, т.-е. выра¬
жение для первичного статистического понятия, мы можем рассма¬
тривать теперь S(t) как исходную статистическую функцию, произ¬
водная от которой и служит к определению „частоты при данном t\
Замечая, что производная от S(t) есть основная гауссова функция ф (t)
и возвращаясь к формуле (И), стр. 57, имеем:
v(x) = N -у5'(0 dll')
Геометрически, S(t) дает величину площади, ограниченной нор¬
мальной кривой, как,она изображена на графике стр. 59, считая от
„крайних- ординат слева и до данного t; площадь эта есть, разумеется,
функция аргумента t (т.-е. правой предельной ординаты); численное
значение ее получается по аргументу t из таблицы II, приведенной
существует. В данной случае, когда у — нормальная кривая, этот предел легко вычис*
кяется; мало того, быстрота приближения нормальной кривой к ее асимптоте, оси
абсцисс, практически позволяет положить вместо / =— с», например, t — — 5, т.-е
лс= — оо заменить на х = М — 5а (см. стр. 58).
— 65 —
на стр. 102. С помощью этой таблйцы легко решается следующая
основная задача математической статистики и теории ошибок:
Найти число объектов данной нормальной совокупности, для кото¬
рых характеризующий признак принимает значения от х = хх до
х=х2.
Для решения этой задачи находим значения tx и t2, соответствую¬
щие заданным хх и х2, и вычисляем:
n(x^=N-S{t2) и п(хх) = N • S(txy,
нз этих равенств для искомого числа объектов получаем:
п(х2) — п(хх) = N • [5(Q — 5(^)] (IV)
Геометрически очевидно, что это число объектов пропорционально
площади, ограниченной кривой нашего графика, осью абсцисс и обеими
ординатами при tx и t2.
Из формул (I) —(III) выведем теперь некоторые следствия:
(1). Число всех объектов совокупности равно N; поэтому мы
должны получить п(х) = N, если для верхнего предела t в формуле
(II) возьмем t = -\-oo, иными словами, если примем в рассмотрение
объекты, у которых признак принимает все значения от наименьших
до наибольших, вообще возможных для данной совокупности.
Итак:
л(+ оо) = ЛЛ5(+ оо)1== М
это равенство может иметь место, если только
+ СО р
5(+°°)в7^Г f e~*dt==l-
—оо
Но эта формула и выводится в теории определенных интегра¬
лов, так что мы можем сказать: величина всей площади, ограни¬
ченной основной нормальной кривой у = <р (t), равна единице1).
Соответственно этому, оставаясь при переменной х и пользуясь
формулой (III') имеем:
оо +оо +оо
f ydx = N- S'(t)dx =N- f S'(t)dt = N.
— OO OO OO
(2). По симметрии нормальной кривой непосредственно видно, что
площадь от £ = — оо до £ = 0 (так же, как и симметричная ей пло-
г) Это надо понимать, конечно, так: предел, к которому стремится площадь, когда
крайние ординаты стремятся к бесконечности, равен единице. Заметим, что мно¬
житель 1 : \/ 2п и появляется в наших формулах для того, чтобы притти к простому
.равенству S (+ оо) = 1.
Способ нанм. квадратов. 5
— 66 —
щадь от t = 0 до * = + oo), равна половине всей площади от —i
до +оо; поэтому:
5(0) = 4;
но так как значению £ = 0 соответствует значение признака дс = |
то заключаем:
п(М) — N - S(0) — -j
иными словами: в нормальном распределении число объектов, у к(
торых величина признака не меньше (или не больше) среднего зна
чения М, равно половине всего объема совокупности.
(3). Часть площади, ограниченная двумя* симметричными otiioci
тельно начала ординатами при £ = — tx и (гАе 0), равн
2S(tx) - 1.
Доказательство: очевидно, что часть площади от t = 0 до tM
составляет:
ад - 5(0)-ад-»/*.
В виду симметрии такое же значение должна иметь величина пло
щади от £ — — tx до ^ .0; поэтому, удваивая только-что написанно!
выражение, находим для искомой площади: 2S(t:) — 1.
(4). Часть площади, лежащая вне обеих указанных симметричны]
ординат (т.-е. сумма площадей от —<х> до —tx и от -\-tx до -j-oo)
равна 2—2 S(tx).
Чтобы получить последнее выражение, достаточно из величины
всей площади, равной 1, вычесть выражение, найденное сейчас для
внутреннего участка, что и дает:
1-{2ЗД-1| = 2-2ЭД.
Последние результаты можно высказать и в такой форме:
Число объектов совокупности, для которых нормированное укло
нение t имеет значения от —t, до -\-tu равно N • {25(/х) — 1); числе
объектов, для которых оно имеет значения, лежащие вне этих пре
делов, равно N • {2 — 25;^ }; иными словами, имея в виду, что все
значения t от —tx до численно меньше или равны tx, можеи
сказать:
Число объектов совокупности, дт которых |£|<£х равт
N- {25(7j) — 1} х); кисло объектов, для которых \t\+>tu равт
') По этой формуле и пользуясь табл. II, находим, напр., что число объектов, м
которых |71<1, т. е. — в, составляет 0,68 7V, или приблизительно g N (т. i
правило .двух третей* в статистике).
— 67 —
(5). Так как площадь обоих внешних участков, как показано сей¬
час, равна 2 — 25(0), то площадь каждого из них составляет 1 — 5(0).
Но площадь левой части от — оо до — О мы можем обозначить через
S(—0); отсюда приходим к равенству:
5(-0) = 1 —Sit,). (V)
Отсюда видно, что нет необходимости строить таблицу для отри¬
цательных значений аргумента, ибо 5(—t) является дополнением
S(-)-0 до единицы. Так, найдя по таблице II, что 5(0,25) = 0,5987,
заключаем, что 5(—0,25), т.-е. площадь участка от —оо, до —0,25,
равна 0,4013.
Для ясности на черт. 7 изображена схематически относительная
величина тех четырех участков, на которые вся площадь от — со
до -f-oo разбивается двумя симметричными ординатами при —tv
-\-t и осью Y.
Черт. 7.
Формула V позволяет'распространить формулу (IV) для п(х2)—«(xx)
на те случаи, когда оно из чисел 0 или t2, или когда оба эти значе¬
ния t отрицательны.
Допустим, что t,<t2 и 0 < 0, но t2 > 0; тогда:
й(х2)-л(х1) = ^[ЭД-5(^)]=^[ад + 5(|^|)-1]. . . (V)
Если же 0 <0 и притом ^<0 и то
п(х2) - п(х,) = N [S(t2) - Sit,)] = N [5(|01) - 5(1121)].
Решим теперь следующую, весьма важную для дальнейшего,
задачу:
Определить, при каком значении нормированного уклонения t часть
площади, заключенная между ординатами при -j-1 и — t, равняется
сумме площадей, лежащих вне этих ординат.
В п. 3 мы нашли для внутренней площади значение: 2S(t) — 1;
для внешней 2 — 25(0. По условию задачи эти два выражения должны
быть равны, т.-е.
25(0 —1=2 — 25(0,
5*
— 68 —
откуда
5(0 = 0,75.
Остается приискать по таблице II значение t, для которого знач
ние функции 5(0 равнялось бы 0,75. Интерполирование дает:
* = 0,6745.
Отсюда заключаем, что обе ординаты при t = + 0,6745 вмес
с осью У делят всю площадь на четыре равных между сой
участка, так что площадь каждого из них равна (сумма внутре
них = сумме внешних = V2)>
Переходя теперь от аргумента t к величине признака х, мы за»
чаем, что значениям +£ соответствуют значения х — М, равные 4
так что в данном случае:
х — М = ±0,6745 а.
Положив теперь:
0,6745 а = р,
мы можем сказать, что двум симметричным ординатам при t = ± 0,67(
соответствуют два значения признака х, именно:
хх — М — р и х2 — М -f- р,
в отношении которых имеет место следующее положение:
число объектов совокупности, для которых признак х принимай
значения от М — р до М-\-р, равно половине всего объема совощъ
ности.
Примеры. Для иллюстрации выводов настоящего § вернемс
к примеру I § 2. Мы имели N=10000; о = 2,052; Ж = 39,835; найда
теперь по выведенным формулам число объектов для значений!
от 37 до 42; имея в виду, что к * = 37 отнесены объекты с *«
36,5, а к * = 42 — объекты с * до 42,5, будем вычислять значем
аргумента t по формулам:
, _ 36,5 — М. + _ 42,5 — М.
li— о > h— з ’
так что
— —1,625; и = + 1,299.
По таблице II находим:
5 (tj) — 1 — 5 (1,625) = 1 — 0,9479 = 0,0521
5 (*,) = 5 (1,299) = 0,9030.
Применяя формулу (V), находим для искомого числа объектов:
п = N • (0,9030 — 0,0521) = N • 0,8509 = 8509.
Непосредственный подсчет, согласно данным стр. 61, дает:
740 +1303 -f-1810 + 1940 +1640 +1120 = 8553.
— 69 -
Расхождение составляет 72% •
Точно также, задав пределы = 35; х2 = 44, нашли бы:
4 = 34,5 = — 2,600; S (4) = 1 — 0,9953 = 0,0047;
4 — = + 2,273; S (4) = 0,9883.
Отсюда
п = 10000 • (0,9883 — 0,0047) = 9836.
Подсчет дает л = 9838.
Перейдем теперь к примеру II § 2 и вычислим число объектов
(здесь число уклонений от приближенного среднего М'), в пределах
от —2,0 до + 1,5. Уклонения от действительного среднего М равны
(столбец 3): —1,94 и +1,56; помня, что эти пределы мы должны
увеличить на 7г интервала вверх и вниз, и что в примере II интервал
равен 72, вычисляем 4 и 4 по формулам:
^ — 2.19. ,+1,81.
С1— с > 1'2~ а >
но о=1,1785 и мы находим:
4 = —1,858; 5 (4) = 1 — 0,9684 = 0,0316
4 = +1,536; 5 (4) = 0,9377
Искомое число объектов равно:
п = N • (0,9377 — 0,0316) = 1000 . 0,9061 = 906.
Непосредственный подсчет дает 916, так что расхождение соста¬
вляет ТОЛЬКО 1%.
Интегральные кривые распределения. До сих пор мы
пользовались для графического изображения закона нормального
распределения основной гауссовой кривой (черт. 6), ординаты кото¬
рой дают для данного значения нормированного уклонения t соот¬
ветствующую ему частоту появления признака. Однако, не менее
характерный график получится, если построить кривую у = S (t), орди¬
наты которой (по умножении на Л/), представят число объектов,
обладающих значениями признака от — оо до данного t.
Для построения кривой служит таблица II, которая для отрица¬
тельных значений t дополняется по правилу:
S(— 0 = 1— S(t).
Эта кривая дана на черт. 8 (стр. 70). Мы видим, что для t-*oо,
1; при этом, так как производная от S(t) есть гауссова функ¬
ция остающаяся положительной для всех 4 то кривая S (t) моно¬
тонно возрастает от 0 до 1; точка £ = 0; З'==у является точкой ее
— 70 —
симметрии. Эта кривая носит название интегральной кривой нормаль
ного распределения; соответственно этому основная кривая Гаусо
(черт. 6) получает название ее дифференциальной кривой. Построен»
интегральной кривой по ее дифференциальной представляет собо]
задачу графического интегрирования, в детали которой мы здесь не
входим J).
Помимо интегральной кривой черт. 8, можно построить еще крю
вую, ординаты которой (по умножении их на N) представят число
объектов совокупно'
сти, у которых норм»'
рованное уклонение по
численной вели
чине не превосходит
данного значения t\ со¬
гласно сказанному вы¬
ше для этого нужно,
пользуясь табл. II,
строить при данном
1 ординату, равную
2 S(t) — 1; получается
кривая, показанная на
черт. 9.
Кривые на черт. (8) и (9) соответствуют специально закону нор¬
мального распределения; но очевидно, что какое бы распределение
мы не взяли, его интегральные кривые будут всегда монотонно воз¬
растающие, так как, увеличивая значения нормированного уклонения /,
мы тем самым расширяем пределы значений признака, для которых
Черт. 9.
1 См. Бернштейн, „Теория Вероятностей", стр. 115 и след.
- 71 —
«едем подсчет объектов совокупности; при этом, число их может,
конечно, только возрастать (во всяком случае'не убывать).
Помимо этого имеется замечательная теорема, указывающая ниж¬
ний предел ординат кривой типа черт. 9, годный для всевозможных
законов распределений; эта теорема, принадлежащая Чебышеву, гласит:
Число объектов совокупности, у которых нормированное уклонение
но численной величине не превосходит любого положительного и боль¬
шего единицы числа а, больше чем Л/^1—
Для доказательства, будем исходить из основного определения
дисперсии данной совокупности, именно
._[(х-мру]и
N ’
отсюда'
Г (х-MM.
но
х{ — М = otj
так что
N = t12y1 -f- t/y, t2yk
Возьмем теперь любое положительное число а, большее 1; мы
имеем
N Г}3 | г23 , /*\
"а3 ~1ау^ + ~ЖУ* ' '
Допустим, что нормированные уклонения
/|, t2, .. •. tm
по численной величине больше а, а нормированные уклонения
С + 1, +2 ' * * *
по численной величине меньше или равны а. Тогда, во всяком случае
А •> . и 4- 1
а3 ^ а 3 У1 ^ а3 У/*
(ибо в правой части равенства (*) мы отбросили ряд положительных
членов); но в правой части только - что написанного неравенства
каждый из коэффициентов при у больше 1, и потому во всяком
случае будет:
N - | ,
~а3 У1 +-^2 + • • • Ут
Здесь справа получилось число объектов совокупности, у кото¬
рых |^Г>а и оно оказывается меньшим чем отсюда мы заключаем,
- 72 —
что число объектов, у которых Щ^а, будет больше чем N—-3, т.-е.
Л^1—что и требовалось доказать.
Если вместо а писать снова t (предполагая 111 > 1), то мы можем
сказать, что число объектов совокупности, у которых нормированное
уклонение по численной величине не превосходит t, должно быть
больше чем N ^1 —^; таким образом на черт. 9 кривая, у которой
ординаты равны 1—есть та „нижняя граница" Чебышева, ниже
кот'орой не могут опуститься ординаты интегральной кривой ни
у какого статистического распределения; и мы видим, действительно,
на черт. 9, что для нормальных распределений эта кривая про¬
ходит значительно - выше кривой Чебышева; но это сопоставление
возможно только для |/|>1.
§ 4. Теория ошибок.
К вопросу об обработке рядов наблюдений одной и той же вели¬
чины X мы подойдем с помощью общих положений, установленных
в предыдущих §§.
Допустим, что при измерении величины X получено N значейий:
^1 у 4 1 • • • > •
Если имеется основание утверждать, что все измерения данного
ряда свободны от постоянной или систематической, т.-е. изменяющейся
по определенному, хотя бы и неизвестному нам закону, погрешности,
то разногласия между результатами отдельных наблюдений можно
объяснить только влиянием случайных погрешностей, которые мы
обозначаем:
°1 ) » * •- • > ®‘
Сообразно этому мы должны положить:
Xl = l1 — 5j, X —1% — 82, . . . , X—lN—&N.
По сделанному сейчас предположению в группе величины St. нельзя
обнаружить такой части Д, которая была бы общей для всех Ь. или
изменилась бы от одной из них к другой по определенному закону,
ибо в этих случаях нельзя было бы говорить о .случайности* всех
Но равенства типа Х=1. — Ь. имеют ту особенность, что каждое
из 8. нам, вообще говоря, столь же мало известно, как и само действи¬
тельное значение X *). Поэтому мы можем приступить к дальнейшим
9 Можно представить себе и исключения из этого правила: например, исследуя
точность логарифмической линейки, мы можем отсчитанные по ней произведения срав¬
нить с их истинными значениями; разности и выразят случайные погрешности
отсчета.
_ 73 -
выводам не иначе, как сделав некоторые допущения относительно
всей совокупности 8.. Эти допущения состоят в следующем:
1. При увеличении числа наблюдений, т.-е. при N-*-oо, [8] остается
величиной ограниченной; иными словами, сумма погрешностей поло¬
жительных, при достаточном возрастании числа наблюдений, уравно¬
вешивает сумму погрешностей отрицательных; действительно, в про¬
тивном случае мы могли бы считать, что во всех 8г содержится,
вопреки условию „случайности", некоторая постоянная или система¬
тическая часть А.
Отсюда следует, что
т.-е. среднее арифметическое из 8;. приближается к нулю при N-► оо.
2. Распределив все случайные погрешности по их величине, мы
могли бы изучать их совокупность как статистическое целое, если бы
все 8,. нам были известны; но в данном случае, не зная этих 8(. в отдель¬
ности, мы ограничимся допущением, что их распределение подчи¬
нено простейшему из законов распределения, именно нормальному.
Согласно этому последнему предположению мы будем применять
к совокупности случайных погрешностей закон Г а у с с а; для этого
нужно выяснить значение обоих входящих в него параметров, именно
М и о. Заметим, что здесь характеризующим признаком х является
сама величина случайных погрешностей, которую мы и будем
обозначать через 8. По определению, параметр М, т.-е. среднее из
всех значений 8, есть
Но в виду сказанного выше, М в пределе не может быть отлично
от 0. Поэтому, применяя формулу Гаусса, мы положим в ней М = О,
т.-е. для величины М возьмем ее предельное значение, как будто бы
число наблюдений фактически было бесконечно велико, а данные
82, . ..., ZN являлись бы только отдельными и случайно взятыми
из всей бесконечной совокупности погрешностями.
Из условия М = 0 мы видим, что уклонения 8. —М здесь сводятся
к 8,-, в виду чего формула для среднего квадратичного уклонения
(дисперсии) о принимает вид х):
(*>
’) Мы не разбиваем погрешностей на классы по их величине, как было в обще.?-
формуле § 1, а каждую из них считаем отдельно, что не вносит никакого принципиаль¬
ного отличия.
74 —
Величина о носит в тероии ошибок название средней квадратичной
погрешности или, просто, средней ошибки; в дальнейшем мы научимся
выражать ее не через неизвестные нам 8., а через уклонения lt от ия
среднего арифметического L,
Установив таким образом значения параметров М и о для сово¬
купности случайных погрешностей, получаем без труда, повторяя
дословно рассуждения §§ 1 и 3, следующие основные положения
теории ошибок:
1. Нормированное уклонение t. Так как х = 8 и М = 0, то
1 о *
иными слрвами, t есть величина случайной погрешности, выражек
н а я в частях средней ошибки данного ряда.
2. Частота появления случайной погрешности +8, расчитанная
на единицу интервала, выражается формулой:
N 1 _ -s’- N ,,ч
V = — • ---Г- е 2а» = — -
* о К2* * YV '*
она вычисляется с помощью таблицы I.
3. Число погрешностей, величина которых имеет значения от
крайних возможных отрицательных до данного 8и определяется фор
мулой:
n(b1)^N^S^) = N.S(tiy,
оно вычисляется по таблице И.
4. Число случайных погрешностей, величина которых может иметь
все значения от -f-&i до -}-82, равно
л(32) ~ «(*,) = W [S &) - ЗД],
то же число в случае, если 8t < 0:
п(8*) - п(8,) = N[S (t,) -f 5(|tx I) -1 ] .
5. Число случайных погрешностей, абсолютная величина которых
:зе превосходит 181, выражается формулой:
л(|8|) = ^[25(/)-1],
а число погрешностей, численно превосходящих |8|, составляет:
ЛГ —л(|г|) = 2Лф — S(t)].
Таковы основные формулы теории ошибок. Еще раз обращаем внима¬
ние на то, что они вытекают как следствие из самого определения „слу¬
чайного* распределении, находящего свое математическое выражение
в законе Гау с с а. Можно сказать, чго теория ошибок признает за
случайные только те ряды погрешностей, к распределению которых
применим закон Г а у с с а; если же в отношении данного ряда можно
установить заметное уклонение его от этого закона, мы не будем уже
считать такой ряд свободным от постоянной или систематической
погрешности. Практика показывает, что, вообще говоря, ряды наблю¬
дений вполне удовлетворительно укладываются в нормальный закон
(ср. ^ 2, пример II). Правда, имеются указания, что большие погреш¬
ности появляются иногда чаще, чем того требует формула Гаусса;
тем не менее, пока еще не встретилось необходимости менять этот
закон на более сложный (скошенное распределение),—хотя отдельные
работы в этом направлении и имеются.
Весьма важно выяснить особое значение средней ошибки, или дис¬
персии о совокупности случайных погрешностей. Основная идея теории
ошибок состоит в том, что ряд наблюдений является тем более
точным, чем меньше эта величина. Действительно, мы видели, что
при малых о кривая распределения круто опускается по обе стороны
от ее вершины, так что все о. группируются вокруг их среднего зна¬
чения, равного нулю; поэтому значительное число наблюдений дают
значения близкие к действительной величине Х\ обратно, при
больших о, сравнительно большое число погрешностей будут иметь
значения, сильно уклоняющиеся от нуля, значит полученные lt плохо
определяют X и ряд наблюдений оказывается менее точным.
Имея это в виду, вводят, согласно Гауссу, новое понятие: меры
точности ряда наблюдений, определяя ее, как величину обратно про¬
порциональную его дисперсии (или средней ошибке) о.
Обозначая меру точности через k, полагают:
откуда
1
а = —— .
kV 2
Подставляя это выражение о в формулу п. (2), можем переписать
основное выражение для частоты у в виде:
' ^ У ТС
Таким образом у нас появляется новый аргумент:
f = kb = 4= ■ - = 4^1 = 0,707U.
у/2 0 у/2
Очевидно, основные таблицы I и II можно было бы привести к этому
аргументу, перевычислив их для f = 0 1; 0,2 ... и т. д. Но с практи¬
ческой точки зрения введение величины k является бесцельным, ибо
— 76 —
из наблюдательного материала получается непосредственно о, а с нею
' §
и аргумент t = — таблиц I и II *).
Вероятная ошибка. В § 3 решена задача: найти такую
ординату нормальной кривой, чтобы площадь, лежащая под нормаль¬
ной кривой между этой ординатой и ей симметричной относительно
начала, равнялась половине всей площади, ограниченной нормальной
кривой. Мы нащли для этой ординаты:
t — 0,6745,
откуда:
х — М = о • ^ = 0,6745 о
и произведение 0,6745 о обозначили через р.
В теории ошибок, где х = 3 и М = 0, соответствующее значение «
определяется равенством:
8 = 0,6745 о = р.
Случайная погрешность, величина которой составляет 0,6745 сред¬
ней ошибки, имеет важное значение в изучаемой теории. Так как
часть площади от 8 = — р до 8==-|-р равная площади, лежащей вне
этих ординат, то мы можем утверждать, что при нормальном распре¬
делении погрешностей половина всего их числа будет иметь значения
от —р до -j-p (т.-е. численно не превосходить р), а половина будет
иметь значения, лежащие вне этих пределов (т.-е. будет численно
больше р). Поэтому величину р называют вероятной погрешностью
данного ряда, имея в виду, что из всех N объектов этой совокупности
одинаково часто должны встречаться как погрешности |8|sgp, так
и погрешности |8|^>р.
При обработке рядов наблюдений вероятная ошибка р весьма
часто заменяет среднюю ошибку о. Действительно, выражая случайные
погрешности в долях р, мы можем ввести новый аргумент:
ГЧ
О
— р
*) В сборниках математических таблиц обычно приводится, под названием таблицы
интеграла вероятности, некоторое видоизменение таблицы II, а именно, таблица функции
2S(t)—1, расположенная по аргументу t'. По этой таблице вычисляется непосредственно
число погрешностей, численная величина которых меньше | 8 | (см. стр. 74, п. 5), но для
о
входа в нее, по данным о и а, нужно найти аргумент *' = 0,7071 —. Так, например, при
Ь = 1/ЧЮ и а = 2,"5, t = 0,4; S(t) = 0,6554; 2S(t) — 1 = 0,3108; если же образовать аргу¬
мент ^ = 0,4 X 0,7071 — 0,2828, то по таблице интеграла вероятности с аргументом
0,2828 находим непосредственно 0,3108, как выше. Считая таблицу интеграла вероят¬
ности менее удобной для пользования, чем таблицу II, мы не прилагаем ее к этому
курсу.
— 77 —
Так как Р = 0,6745*, то (*)
Введем этот аргумент в формулу, которой определяется число
случайных погрешностей, численно не превышающих | S |, именно:
. л(|8|) = ЛГ[25(*)-1]
поставляя сюда t — 0,6745 т, имеем:
л(| 81) = N [2 5(0,6745 т) — 1 ].
Для функции, стоящей в квадратных скобках, составлена удобная
таблица по аргументу т (так называемая таблица Энке, стр. 103).
Обозначая эту функцию через Ф(т), имеем:
л(|8|) = ЛГ.ф(т), где т =
Р
В виду того, что N (число наблюдений) редко доходит до 1000,
в таблице Ф(т) достаточно ограничиться, как мы и сделали, тремя
знаками после запятой.
Желательно, чтобы читатель убедился в соответствии между таблицами 111 и И.
Напр., для т = 0,5 табл. III дает Ф(т) = 0,264; но при т = 0,5, 1=0,5 X 0,6745 = 0,3372
и по таблице II находим: S (0,3372) = 0,6320, так что 2S — 1 — 0,264 = Ф (0,5).
Итак, таблица III дает непосредствен¬
ный ответ на вопрос: сколько погрешно¬
стей, при условии нормального распреде¬
ления, по численной величине не превы¬
шают заданного значения |&|. Пользование
этой таблицей настолько просто, что можно
считать обязательным всякий ряд наблю¬
дений исследовать „на нормальное распре¬
деление". Кроме того, полезно заметить
себе краткое извлечение из той же таб¬
лицы III, показывающее, какая часть всех
погрешностей в нормальном ряду должна
лежать между данными, сравнительно широкими пределами.
Таким образом, следует запомнить, что при нормальном распре¬
делении из 1000 погрешностей только семь могут иметь величину,
в четыре раза превышающую вероятную. Поэтому, практически, вся¬
кая погрешность, превышающая 4р, заставляет отнестись с осторож¬
ностью к соответствующему наблюдению.
Наконец, с помощью той же таблицы III можно решить и следую¬
щую любопытную задачу: найти такое значение 8 —8t, чтобы только
одна погрешность из общего числа N могла численно превышать
Так как число погрешностей, не превышающих численно 8,, равно
А^-Ф(тх), где = то число погрешностей, превышающих 8Х, выра¬
жается через:
/V—N • Ф(тх) = Лф — ФСО].
Предельное
значение Д
Со от в. число
погрешностей
± 0,5 р
26°/о
Р
50
1,5 р
69
2р
82
3Р
96
± 4Р
99,3
— 78 —
По условию задачи, это число погрешностей должно равняться 1
таким образом, должно быть:
А^[1_ф(х1)] = 1,
откуда
Из этого равенства, при заданном N, находим величину Ф(тх), затеи
по таблице III определяем соответствующее значение аргумента \
и получаем искомое предельное значение по формуле: = pxj.
Если бы мы нашли, что за указанным пределом лежит не одна погреш¬
ность, а больше, то это показало бы, что эти крайние погрешности
не удовлетворяют условиям нормального распределения, и соответ¬
ствующие наблюдения нецелесообразно принимать в расчет с полным
весом при обработке ряда.
Пример. В ряде из 100 наблюдений о = 2,25. Отсюда р = 1,52;
для предельного значения аргумента т = тх имеем:
Ф^) = 1-Ш=°>990-
По таблице III этому значению функции соответствует Tt=3,8;
следовательно, искомое значение St = 1,52-3 8 = 5,78, и потому можно
предполагать, что только одна случайная погрешность данного
ряда выйдет за пределы + 5,78, если, конечно, к этому ряду закон
Гаусса применим во всей точности (заметим, что здесь 4р=6,08).
Для иллюстрации теории приведем теперь классический пример,
именно ряд в 470 наблюдений прямого восхождения Сириуса, произ¬
веденных в Гринвиче Брадлеем и обработанных затем Бесселем.
Вероятная ошибка 1) получилась здесь равной р = 0/264. Полагая
последовательно Х = 0/1; 0/2 и т. д., мы найдем по формуле
^где N = 470; -с —сколько уклонений X, из числа 470, должны
по абсолютной величине не превышать 0/1; затем 0/2 и т. т. Срав¬
нение результатов этого вычисления (4-й столбец) с числами, приводи¬
мыми Бесселем по данным наблюдений, показывает, что в общем
этот ряд удовлетворительно согласуется ,с законом нормального
распределения.
*) Формула для вычисления р через т.-е. через уклонения 1( от их арифметиче¬
ского среднего, дана ниже, в § 7.
— 79 —
X
| О-
II
Ф(т)
ЛЛФ(т)
Наблюден.
На блюд. —
вьписл.
0/1
0,38
0,202
95
94
— 1
0, 2
0,76
0,392
184
182
— 2
0, 3
1,14
0,558
262
260
— 2
0, 4
1,52
0,695
327
318
— 8
0, 5
1,90
0,800
376
369
— 7
0, 6
2/28
0,875
411
405
— 6
0, 7
2,65
0,927
436
431
— 5
0, 8
3,03
0,959
451
445
-6
0, 9
3,41
0,979
460
455
— 5
1, о
3,79
0,989
465
452
— 3
14
5,3
1,000
470
470
0
Срединная ошибка. В теории ошибок, наряду с си р, рас¬
сматривается еще среднее арифметическое из численных значе¬
ний случайных погрешностей, именно, величина:
Формулы интегрального исчисления, на которых мы не останав¬
ливаемся, показывают, что в нормальном ряду срединная ошибка 6
связана со средней квадратичной ошибкой о, при N—»-оо,следующим
предельным соотношением:
8=j/-~.o, 6 = 0,7979 а,
откуда обратно:
0= 1,2533 6.
В статистике 6 определяется равенством:
я _ [\х — М\ у] . lim ,6 = у ~~'
N ‘ ’ N-*со г
0
При х—М = Ъ аргумент t равен —, или 0,7979; ордината при;
t — 0,7979 показана на графике стр. 59.
В нормальном ряду значения о, вычисленные по основной формуле
(стр. 56) и через 6, т.-е. через среднее из численных значений \х—М\,.
должны совпадать. Следует проверить, насколько это условие выпол¬
няется на примерах § 2.
- 80 —
Владея формулами нестоящего отдела, мы, казалось бы, могли й
уже приступить к сводке всех правил для обработки рядов набли
дений. На самом же деле это не так, ибо нам нужно еще вывеа
весьма важную формулу, выражающую о через уклонения наблюда
ных /. от их среднего, т.-е. через (так называемая классическая фор
мула или формула Бесселя). Но здесь мы встречаемся со следующи
обстоятельством. Понятие средней ошибки о (среднего квадратичног
уклонения) нами получено из изучения ряда наблюдений, рассма!
риваемого как статистическая совокупность; иначе оно и не може
быть обосновано. Но на практике часто говорят о «средней ошибк
одного наблюдения», о „средней ошибке арифметического среднего
и т. п. Эти выражения, понимаемые буквально, не имеют решительн
никакого смысла и вводить их в таком виде в изложение предмет
невозможно. Но чтобы выяснить то содержание, которое надо придо
вать, в известной мере условно, подобным терминам, мы должш
пройти довольно длинный путь; для этой цели следует ;обратитьо
к изучению не одного ряда наблюдений, а целой совокупности по
добных рядов^ и установить при этом два важных положения, именно
1) Закон распространения средней ошибки и
2) Правило комбинации рядов по принципу наибольшего веса им
по способу наименьших квадратов.
После этого мы снова вернемся к задаче обработки одного ряд
наблюдений, придадим известный смысл указанным выше терминам!
выведем формулы, нужные для практической обработки наблюдений.
§ 5. Закон распространения средней ошибки.
Допустим, что имеются два ряда наблюдений: один для определе^
ния величины X и другой — для определения величины Y, независи
мой от X; положим, что получены значения:
/2, /2, ... для X и т1г т2,... для Y.
Будем теперь комбинировать любое из / с любым из т, т.-е. введе»
числа:
ry. = /.+ mft,
и будем каждое из этих чисел считать за определение действительной,
т.-е. имеющей физический смысл, но неизвестной нам величины:
Z=X+ Y.
Таким образом, каждое из г. доставит нам значение величины I
т в каждом из них будет своя случайная погрешность равная сумме
*) Такие задачи называются задачами второго порядка — в них каждый ряд стано¬
вится одним из объектов совокупности рядов.
- 81 —
погрешностей соответствующих / и т. Какому закону подчинено
распределение этих погрешностей?
Теорема, которую мы имеем в виду, дает ответ на этот вопрос-
Ею устанавливается следующее:
Если погрешности в ряде /ив ряде т подчинены закону нормаль¬
ного распределения, и если и о2 суть средние ошибки этих рядов,
то случайные погрешности в ряде сумм этих величин, считая каждую
из них за определение Х-\-У, тоже подчинены нормаль¬
ному закону, причем средняя ошибка <з этого комбинированного
ряда определяется формулой:
О2—Ох2 + °8*,
т.-е. квадрат средней ошибки ряда сумм равен сумме квадратов сред¬
них ошибок обоих комбинируемых рядов.
Этой теоремой характеризуется основное и весьма важное свойство
нормального распределения. Вывод ее основан на предложениях
теории вероятностей и здесь не приводится: что же касается формулы
для о2, которая получается весьма просто при этом выводе, то она
может быть „приблизительно" доказана следующими элементарными
соображениями.
Обозначим через Sj, S2... случайные ошибки ряда /
в в ^2 • • • п в и ^
» в ^1» ^2 • • • в в в Г
Мы имеем очевидно:
возводя в квадрат и суммируя, находим:
p]=[S8]-f[S'8']-p2'-:S.5'A,
где последняя сумма распространяется на все возможные произведе¬
ния каждой из о. на каждую из 8'й.
Но так как, в предположении, что 3 и 8' распределены по нормаль¬
ному закону, на каждое -(- 8 имеется численно равное и обратное
ему по знаку—8, а на каждое -f- 8' равное и противоположное ему
— 8', то вероятное значение £83' мы можем считать равным нулю,—
очевидно с тем большим правом, чем больше число наблюдений и
чем строже выражена в их распределении симметрия нормального
закона. Считая, что все это имеет место, полагаем £63'= 0, а потому
находим:
[П] = [8 8] + [8' 8']
Способ вавн. квадратов.
s
82 —
или l% припоминая выражение для о2,
Эта важная формула показывает, как распространяются средние
ошибки отдельных рядов на ряд комбинированных величин г =«/-{-т.
Она допускает целый ряд обобщений, именно:
1) число радов может быть и больше двух; тогда:
02 = 0i24-022 + 032...,
где Oj, о2... средние ошибки каждого из рядов, отдельные наблюде¬
ния которых мы комбинируем для получения приближенного значения
неизвестной X -{- F-f- Z :
2) вместо суммы можно рассматривать и общую линейную
комбинацию независимых величин X, Y, Z
Напр., можно взять функцию:
V=*lX+atY+aiZ + ...,
где —произвольные постоянные коэффициенты, и за приближенное
ее определение рассматривать каждую из величин вида
Г=а11-\- а2т -f- айП ,
где /, т и п любые отдельные наблюденные значения величин X, Y, Z.
В таком случае для определения средней ошибки ряда г служит
формула
о2 = CLx\z + a2V + ar,V, ........ (а)
где <>j, о2, о3 — средние ошибки в рядах X, Y, Z.
Действительно, если средняя ошибка в ряде измерений X есть о,
то в ряде измерений величины аХ та же ошибка, по самому опреде¬
лению о, стр. 56, равна ао, откуда, применяя правило п. 1, и выво¬
дим формулу (а).
3. Если функция V не представляет собой линейной комбинации X,
Y, Z, то применить к ней правило распространения средней ошибки
нельзя. Но если V=f(X, Y, Z) разложить в строку Маклорэна и
ограничиться первыми степенями X, Y, Z, считая их малыми величи¬
нами, положив:
^ — °0 “Ь а1-^ +а2^ + V?
[где «о = /(0, 0, 0); а,, а2, а3 — частные производные V по X, Y и Z,
в которые вместо этих переменных поставлены их значения 0, 0, 0],
то получим:
о2 = aiV + «2 V + aVs2
(так как средняя ошибка постоянной а0 очевидно равна нулю).
х) Мы ограничиваемся здесь случаем, когда в обоих рядах одинаковое число членов’
При строгом выводе это отпадает.
— 83 —
Из формулы (а) вытекает весьма важное следствие; предположим,
что имеется п рядов наблюдений одной и той же величины X,
так что:
Y = Z = ... — X,
причем средние ошибки этих рядов равны (т.-е. все ряды обладают
одной и той же степенью точности), т.-е.:
°1 = °2 = • • • = °л = °0
Составим функцию:
t/ X+Y + Z + ---
Очевидно, что каждая из комбинаций типа V даст нам арифме¬
тическое среднее из некоторых отдельных наблюдений, взятых по
одному в каждом из данных рядов. В этом случае все коэффициенты
«. между собой равны, причем:
1
в, = 0U =»• • = а =. — •
1 2 — п п
Применяя формулу (а), выводим для средней ошибки ряда V:
•*= f.O’.'-KM- • • +”’•)=•
откуда:
Иными словами: средняя ошибка в ряде, составленном из средних
арифметических из наблюдений, произведенных в п одинаково to4i ых
рядах, равна—, т.-е. она обратно пропорциональна корню квадрат-
V п
ному из числа рядов.
Для иллюстрации теории приведем несколько примеров.
Пример 1-й. Найти среднюю ошибку измерения 150 tn длины 5 т
жезлом, если длина последнего определена со средней ошибкой
»i = + l тт., а средняя ошибка приложения о2 составляет +2 тт.
Жезл умещается в данной длине 30 раз, приложений конца к
концу 29. По первой причине происходит средняя ошибка измерения,
квадрат который равен 302Oj2; так как в формулу для длины 29 раз
войдет со знаком + ошибка приложения, то от второй причины
к этому же квадрату 29 раз прибавится о22. Таким образом,
«!=900sj2-(-29о22= 1016; о = +32 тт.
Пример 2-й. Найти среднюю ошибку определения стороны
треугольника АВ, если измерения дали:
АС= 106от,00+0,06
/Я = 29°39' + 1'
1_С —120°07' + 2'.
_ 84 —
Мы имеем здесь:
(*)
прологарифмировав зго равенство, находим:
\gAB = IgAC -j- lg sinC—IgsinZJ;
следовательно, по формуле (a)
<32(lgAB)=o‘!(]gAC) -|-os(lg sinQ+o2(lg sinfi).
Теперь применим такой вычислительный прием: чтобы найти
средние ошибки логарифмов по заданным значениям ошибок их ар¬
гументов, найдем по таблице, на сколько единиц последнего знака
изменяются соответствующие lg при переходе от 106,00 к 106,06, от
sin 29с39' к sin 29°40' и or sin 12СГ07' к sin 120°09'; по пятизначной
таблице получаем:
Затем, произведя вычисление стороны АВ по (*), имеем: lg АВ =
= 2,26799; после этого ищем на соответствующем месте таблицы из¬
менение числа, происходящее от изменения lg на 36 единиц послед¬
него знака; при табличной разности 23 видим, что для этого надо
изменить число на +17 единиц пятого знака.
АВ= 185* 35 + 0,17.
Такой же прием рекомендуется применять при вычислении сред¬
ней ошибки выражений /sina или /cosa, если заданы средние ошибки
определения длины I и угла а.
венно отличным от нуля. Полагая х = х0-\-Ьх, у=Уо-\-&У имеем:
отсюда, отбрасывая квадраты и произведения Дд: и Ьу, и полагая
^°=£/0, находим:
о (lg АВ) = (24,6)2 + 222~f 152=1314;
следовательно:
з(1дЛ£?) = + 36 ед. пятого знака.
Итак:
Пример 3-й. Пусть £У = у, причем мы предполагаем у сущест-
и поэтому:
85
Допустим, для примера, что измерения веса тела дали
16,364 г+ 7 мг, а измерения его объема 3,219 5 мм*. Тре¬
буется определить плотность D и ее среднюю ошибку. Полагая
*,= 13,364; j/0 = 3,219, имеем:
£>0 = 5,084;
<.(£>)=5,1-]/(в-)!+(з|)!- ^-±8,1.10-*
Пример 4 й. Пусть U — xy; полагая х — х0-J-Д*; у0-{-Ду и огра¬
ничиваясь в разложении U первыми степенями Ах и Ду, имеем:
U = ХоУ0 -f-Ах-у0 -f Ау-х0,
откуда
так что:
§ 6. Правило наибольшего веса и способ наименьших квадратов.
Выводы предыдущего § позволяют нам подойти к основной задаче
уравнивания. Допустим, что для определения величины Xпроизведено
п рядов наблюдений, и что из них получены, как средние из отдель*
ных определений, такие приближенные значения X:
Обозначим через ах, о2,..оп средние ошибки этих рядов.
Какая комбинация из Lt будет в данном случае наиболее приемле¬
мой?— вот центральный вопрос настоящего отдела.
Обозначим через L искомую комбинацию. Мы утверждаем прежде
всего, что L должно выражаться через Lt следующим образом *):
1. — “j- ^1^3 I •*•••••• (1)
где а,, а2 и-а3 — некоторые постоянные коэффициенты, подчиненные
условию:
®i “Ь в2_Ьаа= 1*
Действительно, если бы оказалось, что £1 = £2 = £3 = 0, то и для
L мы могли бы взять только значение, равное нулю; поэтому в фор¬
муле (1) не может быть свободного члена, не зависящего от Lv L2 и £а;
далее, если все Lt увеличить в т раз, то во столько же раз надо уве-
1) Для простоты письма положено п 3.
— 86 —
личить и Z.; следовательно, Lt должны входить в нашу формулу ли
нейно; наконец, положим, что Lx = L2 — Lz\ тогда L => («х-|-а2 -J-а3)
но, очевидно, мы в этом случае должны положить L — Lv откуда
следует:
®1 “f" *2 -f- ®3 ==
Какая же система коэффициентов а будет наилучшей для искомо!
комбинации Lx, L2 и £3? Этот вопрос мы решим, введя следующее
новое условие уравнивания:
Коэффициенты a.v а2 и ог3 должны быть выбраны под условием,
чтобы средняя ошибка комбинированного ряда L имела минимальное
значение.
Но в виду основной формулы (а) § 5 средняя ошибка а этого ком¬
бинированного ряда определяется формулой:
о2 = -)- a22o22 -(- «32о32 (2)
Поэтому поставленное сейчас условие проводит к такой задаче:
Определить неизвестные коэффициенты а, из уравнения:
*1 + «2 + «з — 1 = 0 • • О
при условии, чтобы выражение:
«12<,12 + а22°22 + «зЧ2 О
(где а,, а2 и о3 — заданные числа) имело минимальное значение.
Эта задача коррелатного типа, и мы решим ее, повторив дословно
рассуждения стр. 22—23, именно: умножив левую часть (*) на неопре¬
деленный пока множитель у» вычитаем произведение из функци (**),
что дает:
ai42 + «* V+а22<5з2 — 2y(ai + а2 + аз—1)-
Минимум этого выражения, рассматриваемого как функция а1, а2 и а3)
получим, взяв производные по a,, а2 и а3 и приравняв их нулю;
таким образом находим:
®1°12 = Г. a2°22 = Y. «3632 = Y-
Отсюда заключаем, что
= ’ 012 = ~ef ’ а* = @)
т.-е., что искомые коэффициенты обратно пропорциональны квадратам
средних ошибок соответствующих рядов.
Подставляя эти значения л1 в (*), получаем
— 87 —
или:
Y=1:(^ + ^ + i); * • (4)
следовательно, окончательно
*« = (5)
Подставив эти выражения а в (2), находим, наконец, и искомую
минимальную среднюю ошибку комбинированного ряда L. После упро¬
щений ее выражение приводится к виду
(6)
Введем теперь систему чисел р, обратно пропорциональных ква¬
дратам средних ошибок всех рядов, т.-е. положим:
_А_ _ А _ А
Pi ota Р*~ Pz— оза >
где А — произвольное положительное число; аналогично этому положим:
Р = — .
в»
Сравнивая (4) и (6), находим:
о» = у; Р=Т'
Подставляя теперь числа р{ в (5) получаем:
в = Р*1л = Pi
1 Pi/a + pJa+pJa Pi + Рз+Рз
и подобно этому:
а = и а„ = Р*
2 Pi+Рз+Рз Pt + Рз+Рз
так что, действительно, аа =* 1.
Далее, для Р, применяя (6), получаем:
Р==Л(л• (7)
Внося найденные значения аг в формулу (1), находим:
~f P\L\ + Ра^а 4~ P3L3 \pL\ t /т
Pi + Рз+Рз IpI
Называя теперь систему чисел р0 обратно пропорциональных квад¬
ратам средних ошибок о., весами этих рядов, а величину Р=~весам
— 88 —
комбинировано™ ряда L, и замечая, что минимуму о с о ответ-
ствует максимум Р, мы приходим к следующим важным положения!
1. Если веса рядов Llt L2 и Z.8 соответственны равны р1У р,
и рй, то наилучшее определение L есть ^ (называемое взвешеннт
средним из Lt) и
2. Вес Р взвешенного среднего L получает при такой комбинации
рядов его наибольшее возможное значение, равное сумме весов вт
отдельных рядов.
В виду последнего результата введенный выше принцип комби¬
нации рядов можно назвать „правилом наибольшего весаи. Как сейчас
увидим, он тесно связан со способом наименьших квадратов.
Действительно, возьмем уклонения X,-отдельных Li от произвольной
величины L, т.-е. положим:
Х^ z>.
Мы покажем сейчас, что выбранному при условии наибольшего
веса значению L — L соотвествует минимум суммы:
[рХХ] ^\p{Lt-Lf\,
Действительно, рассматривая это выражение, как функцию L (ибо
величины Lt заданы), найдем его минимум, взяв производную по L
и приравняв ее нулю; это дает:
[/>(£,-£]= 0. ^
или, раскрывая скобки,
{p]L = u>q,
таким образом, определяя \ как уклонения от взвешенного сред¬
него, мы действительно достигаем минимума выражения [/?ХХ] и воз¬
вращаемся к принципу Лежандра, т.-е. к правилу наименьших
квадратов.
Рассмотрим теперь случай, когда все ряды обладают одинаковой
точностью, а следовательно, и одинаковым весом; здесь мы можем
положить:
Р1=р2 = ..-=Рп = 1 и [р]=п,
где п число рядов. -
В этом случае формула взвешенно» о среднего упрощается, и мы
получаем формулу среднего арифметического
l_Li+i3+. • _[I]
n n
89
Таким образом, приходим к выходу, что „начало среднего арифме¬
тического* совпадает, в случае задания рядов одинаковой точности,
с началом наибольшего веса, а следовательно, и со способом наимень¬
ших квадратов; но вместе с тем, как и само правило наибольшего
веса, оно имеет в своей основе закон распространения средней ошибки,
вытекающий из свойств нормального распределения. Этим и объ¬
ясняется, что к правилу арифметической середины можно подходить
при изложении теории ошибок с нескольких различных точек зрения.
Замечания: 1. В отделе III будет показано, что в методе наименьших квадратов
весом неизвестной называется коэффициент, с которым эта неизвестная входит в опре¬
деляющее только ее уравнение. Считая здесь Llt L2 и Z,3 данными величенами, a L иско¬
мой, и обозначая ее через х, имеем для х, по формуле взвешенного среднего, следую¬
щее уравнение:
(Pi + Р2 + Рз)Х = Pl^l + Рч^Ч + Рз^З *
Таким образом pt -f рм + р3 = Р, в смысле этого нового определения, является весом
Неизвестной х, и мы видим, что комбинирование рядов по способу наименьших квадра¬
тов обеспечивает неизвестной наибольший вес, т.-е. наиболее сильный коэффициент.
2. Для дальнейшего полезно иметь выражение для [рЩ через заданные вели¬
чины Lr С той целью обращаемся к равенствам Хх. = (Li — L), из которых выводим:
[рЩ = [рЩ-ЩрЦ+Ъ[р],
или подставляя сюда L — [pL]: [р],
[рЩ^\рЩ-Ш. (9)
(сравнить с формулой (4) стр. И).
3. Вес функции нескольких независимых переменных.
Возвращаясь к формулам § 5, найдем вес выражения:
V= ax-\-by -\-czt
если известно, что средние ошибки х, у, z соответственно равны о„ о3 и а3. Исходя из
закона распространения средней ошибки и вводя веса х, у, z и функции V:
р{х) = А; р(у) = А; P(z)=—2‘,P(V) = A
®i °з 6
нолучаем:
p(V) p(x)~r p{y)~r p(z)'
В частности, при а = Ь~с~1, имеем: -J— — —}— jl—}—. Следует обра-
Р(У) Р{х) +'Р(У) + Р{г)
тить внимание на то, что при определении веса V никакой задачи уравнивания не воз¬
никает, так что полученная сейчас формула [ср. ее с формулой (7), стр. 87] вовсе
не стоит в связи с правилом наибольшего веса или способом наименьших квадратов.
§ 7. Формулы Бесселя и Петерса. Средние ошибки.
Обращаясь теперь к случаю одного ряда наблюдений и имея
в виду воспользоваться предыдущими результатами, мы можем,
конечно, условиться считать каждое из входящих в него наблюдений
— 90 —
как бы представителем целого ряда и поэтому каждому из отда
ных результатов приписать свой вес *). Этот вес можно назнаи
пропорционально числу тех отдельных определений, из которых д
ное lt получено как среднее (см. стр. 36), или же по некоторым д
гим признакам, правилам и внешним условиям — все это вопр®
целесообразности, стоящие в стороне от математического исследт
ния. Но если таким образом наблюдатель каждое отдельное набл
дение понимает как ряд, т.-е., если он превращает задачу перво
порядка в задачу второго порядка, то можно вывести и соответств;
щие такому предположению формулы. Мы ограничимся здесьч проси
шими из них.
1. Выражение о для данного ряда через квадраты уклонеш
отдельных наблюдений от их среднего арифметического.
Пусть /х, /2,..., I.—данные отдельных наблюдений; L =
/,—L — \
Выражая действительное значение X через lt и истинные погрев
ности S., мы полагали (см. стр. 72):
Х—1,—Ьр
ц = 1,г.. . .,л).
Суммируя эти последние равенста, находим:
пХ=Щ — [8]
или,
Ar==m_[U==i_ti]
п п П 9
так что
L-X+Щ.
Возьмем первое из равенств (*), именно — Z. = Xx, и подставив
в него найденное значение L \ это дает, в виду (**):
Х1 = /1_ЛГ-®~81-И = 81_!
II И ‘ п I
Ьп
п * ’' п
или:
1-8,— -8, —...— (*«)
1 п 1 п J п 4 1
Теперь представим себе, что нам дано п рядов, именно ряд величин
8Х, затем ряд величин 82 и, наконец, ряд 8л. По определению, средняя
ошибка каждого из рядов 8Х, 82,...8я равна о (по существу это один
и тот же ряд, п раз повторенный, и средняя ошибка остается о).
Точно также, в виду (***), мы можем представить себе, что п рядов
*) Иными словами свою среднюю ошибку, или свою меру точности.
— 91 —
8я мы скомбинировали в ряд Хх. Называя теперь через ох
среднюю ошибку ряда Хх на основании закона распространения сред¬
них ошибок (формула (а) § 5) находим из уравнения (***):
в (я- IP а2 П о8 , , 1Л _Г(п_-О» , п-1)2 я л-1 о2
1 ' \/22 * ‘ ’ * П2 ) \ V? ‘ П2 ) П
(п— 1) слагаемое
Но похамому определению средней ошибки, для о, ряда X непосред¬
ственно имеем (учитывая, что среднее из \ равно нулю):
в з РЧ.
итак,
_ 2 РЧ п — ^ „2
ИЛИ
?2_ [XX]
п — 1
(1)
Эта важная формула и носит название классической формулы, или
формулы Бесселя. Она дает возможность определять о через X,
не зная ни X, ни о, и создает, таким образом, основу для практического
применения теории ошибок.
Из формулы ог2 = ■■ п о2 следует, что при п достаточно большом
при >0.
2. Выражение о для данного ряда через численные значения укло¬
нений отдельных наблюдений от их среднею.
Обозначим через 0х срединную ошибку ряда X
е. = N4J.
1 п
Для бх имеется, как указано на стр. 79, предельное равенство:
где ох — средняя ошибка ряда X.
Но мы только что нашли:
поэтому:
"=/1 • /S°.=/! • VS 4™=/! • тгЬпчь
или, замечая, что при п достаточно большем:
п(п— 1) ш п? — п+\ = (я — у)2,
]=Ь^з_[|Х1] . ....... .(2)
У 1 п — 4- п— 4-
92 —
этсюда:
р = 0,6745 в == ?’8454 [| X []
П ~2
Эти формулы предложены Петерсом.
3. Средняя ошибка единицы веса и средняя ошибка определенij
имеющего вес р.
Продолжая считать каждое из наблюдений за самостоятелыл|
ряд вернемся к равенствам
— А. » — А . _А.
р 1 — 0t3; Рз — 0аз; • • -Рп — „пз;
А
и к формуле Р—-^ — \р], которую мы вывели из правила наибо^
шего веса (стр. 87). ■
Положим здесь А = о02, гда о0 есть произвольная постоянная: i
можем назвать ее средней ошибкой единицы веса-, действительно, пр)
няв, напр., o0=°i, находим рх — 1, так что в этом случае о0 будет соя
ветствовать ряду (или наблюдению), вес которого рх равен 1. Ип|
полагая А = а02, имеем:
р Ъ?.
Г~~ а*~ а*»
откуда
■о =—А — _А
V р V т
иными словами: средняя ошибка ряда с весом р равна средней ошщ
единицы веса, деленной на корень из р (или, для комбинированно^
ряда — на корень из [/>]); очевидно, такое же значение имеет среди
ошибка взвешенного среднего L.
Наконец, в случае п наблюдений одинакового веса средняя ошпк1
результата, т.-е. среднего арифметического L = ^, выражается черея
в« А»_
уЛГ’
что Является повторением формулы, уже выведенной на стр. 83,
Возвращаясь теперь к понятию меры точности ряда, обратно пр<
порциональной о, мы из последней формулы заключаем, что с уве|
личением числа наблюдений в ряде в п раз точность его увемш
вается в >/ п раз, что составляет одно из важных следствий заш|
нормального распределения.
Остается сказать, как определяется средняя ошибка единицы веа
При комбинации рядов можно задать эту величину совершенно прою
- 93
вольно, сообразуясь только с общими условиями задачи, как мы
и увидим в соответствующем месте. Но, имея ряд наблюдений оди¬
наковой точности, мы, очевидно, можем принять за нее величину о
выведенную для этого ряда по выведенным выше правилам.
Таким образом, по формуле Бесселя:
0, = ./Ж
• V Пг- 1 >
и средняя ошибка результата
0(i) = /^S-VH (5)
п~ 2
по формулам Петерса:
«.= —JI41; о(1) = .^-[|х|]. ...... .(6)
п-± V п гг—4-
2 2
Таким образом, для о получены два выражения, (5) и (6); первое
нз них дает о через [XX], второе через [| X |]; закон нормального рас¬
пределения требует, чтобы оба эти выражения при я —■> оо, были
равны между собой. Поэтому, если при обработке ряда наблюдений
обнаруживается, что формулы (5) и (6) приводят к несогласным между
собой результатам, то это послужит указанием на то, что данное рас¬
пределение погрешностей не подчиняется закону нормального
распределения и поэтому можно предположить в наблюдениях дей¬
ствие систематической погрешности (все это с оговоркой, что я
достаточно велико).
Допуская же, что обработка ряда набюдений величины X дает
основание считать, что ошибки наблюдений носят характер случай¬
ных погрешностей, мы можем выразить результат обработки фор¬
мулой:
X=L + *(L) (7)
Такая запись имеет, в сущности, только тот смысл, что из всех я
наблюдений у 0,68л погрешности лежат в пределах+ е(/,).|/я; у
0.95/г они заключены в пределах ziz 2а(£). ]/«; и т. д.
Аналогично этому, переходя к вероятной ошибке р, можем резю¬
мировать результат обработки данного ряда формулой:
X = L±?(L), ............... .(8)
где p(Z.) = 0,6745 • а(Д);
этой записью мы отмечаем, что у 0,50л наблюдений ошибки лежат
в пределах + p(L)-Vn'>y 0,82л в пределах ±2р(£).)/я и т. д.
94 —
§ 8. Обработка ряда наблюдений одинакового веса.
Соберем все формулы, нужные для этой работы:
Вычисление о и р.
v«=/x —Z,', где L' приближенное среднее [см. стр. 13, (7) и (8)].
fv 1
L=L'-\-JL\ п число наблюдений;
п
X. — I. — L = V. — И. контроль [X] = 0.
[XX] = [w] — контроль: [XX] = [Xv]
с0 = ./IE ; a(L) = ,/. R_
V п — 1 У п{п — 1)
Р = 0,6745 О
II. Поверка условий нормального распределения:
1. [Х]^4Р.
2. Только одно X численно больше тхр, где тх определяется из
уравнения: Ф(тх) = 1 —
1 253
3. Формула Петерса: о0 = ——fj X |] должна дать значение о,
л_~2
близкое к полученному выше.
III. Распределение по нормальной кривой.
Взяв положительные значения X через равные промежутки X',V,...
л; X"
находим соответствующие т(т' = -; В нормальном ряду число
Р‘ Р
уклонений, не превышающих численно X', должно быть равно яФ(т)
и т. д.
В случае достаточно длинного ряда можно испытать его и через S(t),
назначая произвольные пределы Для Хх и Х2 и находя
я(Х2) — n(X1) = n{St2)—S(*х)} .
Для примера обработки я выбираю небольшой ряд из 22 наблю*
дений зенитных расстояний a Orionis х). В 1-м столбце дан текущий
номер, во 2-м — секунды зенитных расстояний (которые освобождены
от всех известных наблюдателю погрешностей систематического и
инструментального характера). В 3-м столбце даны уклонения от при¬
ближенного среднего, за которое принято:
L' — 52°22'49,"50.
’) Пулковский каталог склонений 1915 г.
— 95 —
1
| 2 = 52=22'
V
X
^ = 52°22'
V
X
1
48,"90
— 60
— 40
п
49,"65
+15
+ 35
2
49, 47
— 3
+ 17
13
48, 69
— 81
— 61
3
48, 43
— 107
— 87
14
49, 37
— 13
+ 7
4
497 П
— 39
—19
15
49, 67
+ 17
+ 37
5
49, 91
+ 41
+ 61
16
49, 02
48
— 28
6
49, 05
— 45
- 25
17
48, 85
-65
— 45
7
49, 77
+ 27
+ 47
18
49, 61
+ 11
+ 31
8
49, 54
+ 4
+ 24
19
48, 84
— 66
— 46
9
49, 26
— 24
— 4
20
49, 26
— 24
— 4
10
49, 68
+ 18
+ 38
21
49, 65
+ 15
+ 35
11
49, 72
+ 22
+ 42
22
49, 22
— 28
— 8
Так как [v] = — 4/33, то L = 52°22'49,"50 — ^ = 52°22'49,"30.
В четвертом столбце—уклонения X (получаемые путем вычитания
М
взу; величины здесь—0,"20). Через квадраты X находим:
,.= /JML=/»f* = ±0'401.
Следовательно, р = 0/401‘0,6745 = 0/270. Отсюда для „предельной
погрешности" (4р), находим значение 1 ,"08; и действительно, среди
данных X столь больших уклонений не имеется. Найдем теперь то
значение X, численно больше которого может быть только одно из
уклонений данного ряда. Для этого вычисляем: Ф(т/ = 1—^ = 0,955;
по таблице III подыскиваем соответствующее = 2,97. Следовательно,
1,=2,97* 0,270 = 0/80. Фактически только одно из данных X (под
номером 3) численно превышает 0/80. Наконец, контролируем с0 по
1 25
формуле Петерса. Здесь [| X |] = 7,41 и надо вычислить: —!—г • 7,41
22 —j
но дает 0/431 вместо прежнего 0/401; это небольшое расхождение
ножно объяснить тем, что п (здесь 22) слишком мало для статисти-
ческих обобщений.
Переходим к распределению по нормальной кривой; назначая
здесь X через 0/1 и деля 0/1; 0/2 и т. д. на р = 0/27, получаем соот¬
ветствующие т, по ним (табл. III) Ф(т), затем теоретические частоты
лФ(т); подсчитывая затем число погрешностей, не выходящих из пре¬
делов + 0/1; +0/2 и т. д., сравниваем эти наблюденные данные
с вычисленными. Расхождение не превышает трех единиц и этот ряд
пожно считать весьма близким к нормальному.
! 1
__ X
~ р
Ф( т)
ПФ( т)
Наблюден.
Наблюл. -
вычисл.
0,"1
0,37
0,197 .
4
4
0
L 2
0,74
382
8
6
— 2
3
1,11
546
12
9
— 3
' 4
1,48
682
15
14’
— 1
5
1,85
788
17
19
+ 2
6
2,22
865
19
19
0
7
2,59
919
20
21
+1
8
2,96
954
21
21
0
0, 9
3,33
975
21
22
— 1
После всего этого можно вычислить „среднюю ошибку результата'
*(1)=-^ = 0/086
и написать:
z = 52°22'49,"30 + 0,"086 (ср. ошибка), или
+ 0,058 (вер. „ ).
Критерий Аббе. Вычисляя о и б мы пользуемся только квадратам
и численными значениями уклонений от среднего; ни их знаки, ни в
последовательность не учитываются; поэтому если желательно удосто
вериться в случайности их распределения, то можно прибегнуть к дру¬
гим критериям, в которых эти условия принимаются во внимание;
в этом направлении было предложено несколько признаков, ю
которых мы отметим здесь только т. н. критерий Аббе.
Пусть я наблюдений, произведенные в определенной последова
тельности во времени, отягчены ошибками:
^1 > ^2 > •
Если с течением времени наблюдаемая величина подвержена систе¬
матическим изменениям, то можно предполагать, что её влияние
исключится, по крайней мере частично, в разностях:
^1 ®2 > ^2 h', • • • • у
Вычислим две суммы квадратов:
i4 = v+V+- • .+V
B = (*1-h)2 + (h-hY + • +(8n-1-8„)2 + (8n~8i)2-
Если бы все ошибки были совершенно случайны, то в пределе,
при я —> оо, мы должны были бы иметь:
£ = 2А;
2/4
при конечных значениях п, отношение -g- , при условии случайности
ошибок 8, должно лежать, как можно показать, в пределах:
2А
Если же отношение -g- выходит за указанные пределы, то это
I должно провести к предположению, что измеряемая величина подвер-
1 галась систематическим изменениям во время данного ряда наблю-
! дений.
Заметим еще, что в нашем распоряжении имеются не истинные
ошибки 8^ а уклонения от среднего X.; но если критерий Аббе дает
отрицательный результат на X то тем больше оснований утверждать,
что ему не удовлетворят и В.
В примере разобранного выше ряда из 22 наблюдений должно
быть:
Ц= 1+0,21;
но здесь получается А = [XX] = 3,37; В — 7,90; поэтому отношение
\к
j=0,85; оно лежит внутри границ критерия Аббе.
§ 9. Уравнивание рядов наблюдений.
Под вычисления этого типа подойдет как уравнивание нескольких
рядов наблюдений одной и той же величины, так и обработка одного
ряда разновесных ее наблюдений. Мы имеем совокупность величин
4> • • • > Ln и соответствующие им средние ошибки: Oj, о2, ..., ап,
В этом случае работа идет в такой последовательности.
1. Выбрав произвольную среднюю ошибку единицы веса о0
(которую называем средней ошибкой единицы веса до уравнива¬
ния), вычисляем веса pt через заданные с. (так назыв. средние ошибки
до уравнивания) по формулам:
0,2 Оп2 - О, ,2
2. Определив веса, находим взвешенное среднее:
1 = —• ’ 61)
L 1рГ
Для упрощения вычисления принимаем за приближенное значение
взвешенного среднего „на-глаз“ подходящую величину И и полагаем:
Способ ааны: квадратор
?
- 98 —
тогда:
так что:
[!»\ = \pl]-L'[p] = [p]L-L'[p],
IН
[р]
3. Следующей задачей является вычисление „средней ошиби|
результата". По формуле (4), стр. 92, имеем
т
Эта величина носит название „средней ошибки результата до урав1
нивания". Вычисление ее, как видим, очень просто. Гораздо болыш
работы требует определение средней ошибки результата через уклоГ
нения X данных величин от взвешенного среднего, к чему мы тепер|
переходим. _ _
4. Образуем [Дх], где xf = I.—ц
так как _
Ху = vi -J- L' — L,
то _
[Дх~] = М + 2(Г - L)[p.] + [p\{L< - Lf =
2|)*р . f/w]*
[pvv]
[p]
[Pi ’
так что:
5. Контролем произведенных вычислений служат формулы:
И] = 0; [>vX] = [ДХ];
они легко получаются из (2) и (3). — Вторая из них удобна и для
вычисления [Дх]
6. Средняя ошибка единицы веса, называемая тут средней ошибкой
единицы веса после уравнивания, получается по формуле, анало¬
гичной формуле Бесселя
7. Средняя ошибка каждого из lt после уравнивания полу¬
чается из о0, по формулам:
°0 . ~ °0
2~у/Д •••
8. Средняя ошибка результата после уравнивания (т.-е. взвешен¬
ного среднего):
<£>
ЛрУ
вес результата p(L) — [р].
_ 9§ -
9. Если ряд достаточно велик, то изучаем распределение уклоне¬
ний X от взвешенного среднего, пользуясь функцией Ф(х) и полагая
здесь р = 0,6745 а0 и т = -4. Впрочем, в данном случае можно вос-
р _
пользоваться и более простым критерием; если а0 после уравнивания
значительно разойдется с а0, произвольно выбранной нами до уравни¬
вания, то это покажет, что данные ряды не могут быть друг с дру¬
гом согласованы; если же одна из а., или некоторые из них после
уравнивания окажутся существенно отличными от соответствующих о/
до уравнивания, т.-е. заданных, то это будет служить признаком, что
в определении этих I. скрыты постоянные или систематические по¬
грешности.
Пример 1. Даны (стр. 100) семь определений постоянной солнеч¬
ного параллакса, произведенных разными наблюдателями и разными
методами. Эти значения даны вместе с их средними ошибками (а до
уравнивания, столбец 2-й). Приняв за среднюю ошибку единицы веса
до уравнивания а0 = 0/020 (произвольно), находим веса (3-й столбец).
Для вычисления взвешенного среднего принимаем за приближенное
среднее V = 8/800; в 4, 5 и 6-м столбцах даны v^/.— 8/800,/w
и /ш; взвешенное среднее получается равным:
L = 8,"800 -f ^ = 8,"800 + ^ = 8/8059.
Найдя затем
[рЩ = [/Н - = 4693 -= 3029,
определяем среднюю ошибку единицы веса после уравнивания:
о0 = j/1>>~1 = |/~9 = 22,5 (ед. 3 знака) = 0/0225
(в достаточном согласии с взятым первоначально 0/020).
Деля о0 на корни квадратные из весов, находим средние ошибки
после уравнивания; как видим, они достаточно хорошо — но все-таки
не вполце — согласуются с исходными (2-й столбец). Наконец,
0,0225 л #ллол
о результата = = -^==- = 0, 0032.
Итак, в результате уравнивания данных семи рядов находим:
я0 = 8/8059 + 0,'*0032 (средняя ошибка).
Г
4- 100 -
/
а
Р
V
рч
pvv
а
3/780
0/'020
1,0
— 20
- 20,0
400
0,"022
8, 794
022
0,8
— 6
- 4,8
29
025
8, 857
023
0,8
+ 57
+ 45.6
2599
025
8, -802
007
8,2
+ 2
+ 16,4
33
008
8, 806
044
0,2
+ 6
+ 1,2
7
050
8, 806
006
11,1
+ 6
+ 66,6
400
007
8, 807
0, 004
25,0
+ 7
+ 175,0
1225 .
0,004
[ ] = 47,1
+ 280,0
4693
Найденная здесь величина о есть средняя ошибка результата поел
уравнивания. Та же величина, но до уравнивания, получается по про
стой формуле:
0",020
= 0",0029;
у/\р\ /47,1
это довольно близко подходит к найденной выше о = 0,0032.—
При обработке длинных рядов величене о отдается предпочтенш
перед о.
Пример 2. Даны пять измерений высоты h с их средними ошиб
ками. Найти взвешенное среднее и среднюю ошибку результата.
За приближенное среднее принимаем /,' = 12350 мм, за среднюю
ошибку единицы веса (произвольно) о0 = 4,3 мм; найдя веса и взвешею
ное среднее вычисляем ошибку результата по двум формулам:
' (п —
о =
И О:
(Л-1) [р]
h мм
<5 ММ
Р
V мм
рч
X
р\
pvk
12 356
2,1
4,2
+ 6,0
25,2
-0,5
— 2,1
-12,6
12 361
3,4
1,2
+ 11,0
13,2
+ 4,5
+ 5,4
+ 59,4 ;
12 357
1,2
12,8
+ 7,0
89,6
+ 0.5
+ 6,4
+ 44,8
12 355
4,3
1,0 ♦
+ 5,0
5,0
—1,5
— 1,5
— 7,5 ;
12 352
3,2
1,8
+ 2,0
3,6
— 4,5
— 8,1
-16,2
21,0
136,6
0,1
,+ 67,9
Здесь L = 12350 + -^= 12356,5
4 3 *
= 0,94 мм („до уравнивания"),
о = \/-4^-~0,9Э мм („после уравнивания").
4,3
а =
или же
- 101 —
ТАБЛИЦА 1.
Частота в нормальном распределении.
N ,.ч 4 х — М
>= — • <t'A где t = —.
Функция (p(f) по аргументу t
‘
0
1
2
3
4
5
6
7
8
9
I 1 ± 0,0
0,3989
0,3989
0,3989
0,3988
0,3986
0,3984
0,3982
0,3980
0,3977
0,3973
1 0,1
3970
3965
3961
3956
3951
3945
3939
3932
3925
3918
1 ' 0,2
3910
3902
3894
3885
3876
3867
3857
3847
3^36
3825
0,3
3814
3802
3790
3778
3765
3752
3739
3725
3712
3697
0,4
3683
3668
3653
3637
3621
3605
3589
3572
3555
3538
i 0,5
3521
3503
3485
3467
3448
3429
3410
3391
3372
3352
; 0,6
3332
3312
3292
3271
3251
3230
32 9
3187
3166
3144
! 0,7
3123
3101
3079
3056
3034
зон
2989
2966
2943
2920
0,8
2897
2874
2850
2827
2803
2780
2756
2732
2709
2685
| 0,9
2661
2637
2613
2589
2565
2541
2516
2492
2468
2444
| 1,0
2420
2396
2371
2347
2323
2299
2275
2251
2227
2203
1,1
2179
2155
2131
2107
2083
2059
2036
2012
1989
1965
1 1,2
1942
1919
1895
1872
1849
1826
1804
1781
1758
17361
1,3
1714
1691
1669
1647
1626
1604
1582
1561
1539
1518!
1 1,4
1497
1476
1456
1435
1415
1394
1374
1354
1334
1315
1,5
1295
1276
1257
1238
1219
1200
1182
1163
1145
1127
! 1,6
1109
1092
1074
1057
1040
1023
1006
0989
0973
0957
1,7
0940
0925
0909
0893
0878
0863
0848
0833
0818
08041
! ]>8
0790
0775
0761
0748
0734
0721
0707
0694
0681
0669'
| 1,9
0656
0644
0632
0620
0608
0596
0584
0573
0562
0551
2,0
0540
0529
0519
0508
0498
0488
0478
0468
0459
0449!
2,1
0440
0431
0422
0413
0 04
0396
0387
. 0379
0371
0363
2,2
0355
0347
0339
0332
0325
0317
0310
0303
0297
0290
2,3
0283
0277
0270
0264
0258
0252
0246
0241
0235
0229!
; 2,4
0224
0219
0213
0208
0203
0198
0194
0189
0184
0180
1 2,5
0175
0171
0167
0163
0158
0154
0151
0147
0143
0139
2,6
0136
0132
0129
0126
0122
0119
0116
0113
0110
0107
1 2,7
0104
0101
0099
0096
0093
0091
0088
0086
0084
0081
! 2,8
0079
0077
0075
0073
0071
0069
0067
0065
0063
0061 j
2,9
0060
0058
0056
. 0055
0053
0051
0050
0048
0047
0046
3
0,0044
0,0033
0,0024
0,0017
0,0012
0,0009
0,0006
0,0004
0,0003
0,0002
! '±4,
0,0001
0,0001
0,0001
6
0
0
•
0
0
0
0 1
0
1
2
3
4 1
1
5
1
6 1
7
8
9
— 102 —
ТАБЛИЦА И.
S(t)t площадь под нормальной кривой,
от —со до L
Функция 5(0 по аргументу t.
1 t
0
1
2
3
4
5
6
7
1 8
9
I + 0,0
0,5000
0,5040
0,5080
0,5120
0,5160
0,5199
0,5239
0,5279
0,5319
0,5359
0,1
5398
5438
5478
5517
5557
5596
5636
5675
5714
5753
0,2
5793
5832
5871
5910
5948
5987
6026
6064
6103
6141
0,3
6179
6217
6255
6293
6331
6368
6406
6443
6480
6517
0,4
6554
6591
6628
6664
6700
6736
6772
6808
6844
6879
0,5
6915
6950
6985
7019
7054
7088
7123
7157
7190
7224
0,6
7257
7291
7324
7357
7389
7422
7454
7486
7517
7549
0,7
7580
7611
7642
7673
7704
7734
7764
7794
7823
7852
0,8
7881
7910
7939
7967
7995
8023
8051
8078
8106
8133
0,9
8159
8186
8212
8238
8264
8289
8315
8340
8365
8389
1,0
8413
8438
8461
8485
8508
8531
8554
8577
8599
8621
1,1
8643
8665
8686
8708
8729
8749
8770
8790
8810
8830
1,2
8849
8869
8888
8907
8925
8944
8962
8980
8997
9015
1,3 '
9032
9049
9066
9082
9099
9115
9131
9147
9162
9177!
1,4
9192
9207
9222
9236
9251
9265
9279
9292
9306
9319
1,5
9332
9345
9357
9370
9382
9394
9406
9418
9429
9441
1,6
9452
9463
9474
9484
9495
9505
9515
9525
9535
9545
1,7
9554
9564
9573
9582
9591
9599
9608
9616
9625
9633
1,8
9641
9649
9656
9664
9671
9678
9686
9693
9699
9706!
1,9
9713
9719
9726
9732
9738
9744
9750
9756
9761
9767
+ 2,
0,9772
0,9821
i
0,9861
0,9893
0,9918
0,9937
0,9953
0,9965
0,9974 :
0,99811
t
'
0
l
2
3
4
5
6
7
8
9
юз -
ТАБЛИЦА IIL
Число случайных погрешностей, не превышающих
численно т•р
Функция Ф (т) по аргументу х.
т
0
1
2
3
4
5
6
7
8
9
; +0.0
0,000
0,005
0,011
0,016
0,022
0,027
0,032
0,038
0,043
0,048
0,1
054
059
065
070
075
081
086
091
097
102
0,2
107
113
118
123
129
134
139
145
150
155
0,3' 1
160
166
171
176
181
187
192
197
202
207
0,4
213
218
223
228
233
239
244
249
254
259
0,5
264
269
274
279
284
289
294
299
304
309
0,6
314
319
324
329
334
339
344
349
354
358
0,7
363
368
373
378
382
387
392
396
401
406
0,8
411
415
420
.424
429
434
438
443
447
452
0,9
456
461
465
470
474
478
483
487
491
496
1,0
500
504
509
513
517
521
525
530
534
538
1,1
542
546
550
554
558
562
566
570
574
578
1,2
582
586
589
593
597
601
605
608
612
616
1,3
619
623
627
630
634
637
641
645
648
652
1,4
655
658
662
665
669
672
675
679
682
685
1,5
688
692
695
698
701
704
707
710
713
716
1,6
719
722
725
728
731
734
737
740
743
746
1,7
748
751
754
757
759
762
765
767
770
773
! 1,8
775
778
780
783
785
788
790
793
795
798
1,9
800
802
805
807
809
812
814
816
818
820
2,
823
843
862
879
894
908
921
931
941
950
! з,
957
963
969
974
978
982
985
987
990
991
+ 4,
0,993
0,994
0,995
0,996
0,997
' 0,998
0,998
0,998
0,999
0,999
Т
0
1
2
3
4
I 5
6
7
8
ОТДЕЛ III.
СИСТЕМЫ С ИЗБЫТОЧНЫМ ЧИСЛОМ УРАВНЕНИЙ.
§ 1. Применение принципа Лежандра. Основная теорема.
В тех уравнительных вычислениях, к которым мы теперь обр*
щаемся, особенность задачи сводится к тому, что искомые величина
х, у, г, ... не подлежат, вообще говоря, непосредственному наблю
дению; это будут, например, разного рода инструментальные постоян
ные, ходы хронометров, коэффициенты расширения и т. п.; но те вь
личины /, которые при данных измерениях определяются, — напри
мер, длины стержней, показания хронометров и т. п. — являются!
функциями неизвестных х, у, z, ... и связаны с ними зависимостью:
l=f(x, у, z ...), где / есть известная из теории данного вопроса
функция. Как увидим ниже, эту зависимость всегда можно свести
к простейшей, именно линейной, так что наши уравнения приню
мают вид: |
/ = ах ■+• by -j- cz+...
где а, Ь, с суть заданные постоянные коэффициенты.
Таких уравнений можно, очевидно, составить столько, сколько
имеется наблюдений, а число последних может быть и значительно
больше числа неизвестных х, у, z ... Таким образом, мы приходим
к избыточной системе уравнений, которые будем называть здесь
условными уравнениями для неизвестных х, у, z *):
ахх -f- bx у cxz = lx
a%x -j- b2y -j- c2z — L
anx + bny + cnz = ln (1)
l) В настоящем отделе, для сокращения письма, мы считаем число неизвестных
равным трем, но все результаты будут иметь, конечно, общее значение. Следует заме¬
тить существенную разницу между условными уравнениями (1) й условными уравне¬
ниями для поправок в методе коррелат, где эти уравнения, числом менее числа иско¬
мых поправок X, должны были удовлетворяться в совершенной точности. По поводу
Терминологии, см» ниже, стр. 134.
— 105 —
Нетрудно видеть, что эта система не допускает точного реше¬
ния для неизвестных х, у, z; прежде всего потому, что все lt отяго¬
щены случайными погрешностями наблюдений и, следовательно,
в известной мере друг другу противоречат; затем, в силу того обстоя¬
тельства, что, определив х, у, z из любых трех уравнений, мы могли бы
удовлетворить этими значениями остальным («— 3)-м уравнениям,
если бы они являлись простым следствием первых трех — чего, вообще
говоря, мьг не предполагаем. Поэтому при всякой системе значе¬
ний х, у, z в правых частях (1) мы получим не числа lt, а некоторую
отличную от них систему величин -f-Cjj l2-\-е2 числа е, мы
называем остающимися погрешностями условных уравнений; согласно
сказанному, мы предполагаем, что все s; не могут быть одновременно
равны нулю, ибо это соответствовало бы случаю точного решения
системы при заданных 1Х, /2, ..., 1п. Итак, подставляя в (1) любую
совокупность значений х, у, z, мы приходим к равенствам вида:
aix ср — lt -}- . . . (1')
(/=1, 2, . . п)
Варьируя в известных пределах систему х, у, z, мы будем варьи¬
ровать и систему остающихся погрешностей е.. Спрашивается, какую же
из возможных систем х, у, z признать за наилучшую? Это задача
уравнивания и она решается (также, как и задачи отдела I) примене¬
нием принципа Лежандра: наилучшей системой значений неизвест¬
ных х, у, z признается та, для которой сумма квадратов остающихся
погрешностей принимает минимальное значение. Итак, решая систе¬
му (1), мы будем искать систему значений х, у, z, приближенно удо¬
влетворяющих уравнениям (1), при условии [ег]-минимум.
Все дальнейшее основано на следующей теореме (лемма Г а у с с а):
Совокупность погрешностей ех,. . ., ед, остающихся при уравнива¬
нии системы (1), может соответствовать условию [$г] - минимум
только в том случае, если эти значения ех, . . . ., ед удовлетворяют
уравнениям:
а\Ч 4~ a2s2 4- • • • 4~ о„е„ = 0
£>isi -j- Ь2е2 4- Ьпгп — 0
с1®1 4" с2®2 + • • • + сп~п = 0
Доказательство. Допустим, что системе значений х, у, z
соответствует определенная совокупность остающихся погрешностей
61> • • •» V Изменим теперь эту систему х, у, z и возьмем другое,
близкое к ней решение, положив:
•*' = *4-^; У=уz' = z+cc3>
где аи а2, а3 — произвольные приращения исходных х, у, z. Подставив
эти значения в дюбое из Я^внений (1), мы получим:
ajt -Н +ср' = /;4- •/ . . . ....(*)
— 106 —
Здесь е/, отличны от исходных е., так что можно положить:
*/ = е/ + ^
(<=1. 2 Я)
Внося эти значения еД равно как и х\ у', z\ в (*), имеем:
at{x -j- «j) + bfy -(- a2) -j- cfz -f- a3) = I, -f- e,-f- P/
ИЛИ I
aix + bly-\-a.z + a a, -fft л2 + ci4 = /,. + e, -f p.;
но подчеркнутые члены равны друг другу в виду сисемы (Г) и сле¬
довательно остается:
a.ai + ft.a2 + c.a3 = pf (**)
(/ = 1, 2, . . . , п)
Далее, возводя в квадрат и суммируя равенства
е/ +
имеем:
[г'е'] = И+2[И + [Р,3].
Первый и третий члены справа, как суммы квадратов, суть вели¬
чины существенно положительные; что же касается [ре], то она, путем
надлежащего выбора р;, может быть сделана и отрицательной. Но
если мы подчиним величины рх условию:
[j3e]=0,
то при всех системах р;, отличных от нуля, т.-е. при всех а, неравных
нулю, или же-при х', у', z' отличных от х, у, z, будет:
^ М + №М.
и потому:
[eV]>[ee],
а следовательно [ее], как требует принцип Лежандра, будет иметь
минимальное значение. Посмотрим поэтому, что нам дает условие
[Ре] = 0. Для этого умножим каждое из уравнений (**), определяю¬
щих р,, на соответствующее в. и сложим, вынося за скобии ах, а2 и а3.
Это приводит к уравнению:
«1N + 32[fte] 4- «3[се] = [ре] (***)
Но приращения ах, а2 и а3 взяты нами совершенно произвольно
и независимо от стоящих внутри сумм *х, е2, . , ея ; поэтому левая
часть уравнения (***) приведется к нулю при любых значениях
107 —
*i, <х2 и а3 только в том случае, если каждый из коэффициентов при
этих величинах порознь равен нулю, т.-е., если соблюдены условия:
И = 0 [Ьг] = 0 [се] = 0 (2)
Таковы основные уравнения, которым должны удовлетворять
остающиеся погрешности е,, е2, ..., ел, соответствующие условию
[ее]-минимум; число уравнений (2) всегда равно числу неизвестных
х, у, z и поэтому для определения значений каждой из е,, ..., ел
в отдельности уравнения эти недостаточны. Но условие [ее] - минимум
делает нашу задачу определенной в том смысле, что исходя из урав¬
нений [ае] = 0, [be] = 0, и т. д., мы найдем ту систему значений
х, у, z, при которой соответствующая совокупность остающихся
погрешностей действительно обращает в минимум сумму [ее].
§ 2. Нормальные уравнения для неизвестных и выражение для
минимальной суммы квадратов остающихся погрешностей.
Возвращаемся к системе (Г) § 1:
ахх -j— “I- cxz = 1Х —|— бу
a2x + b2y + c2z = l2 + е2
апХ + ЬпУ + СпZ = *я+ еп
Помножим каждое из этих'равенств соответственно на alt а2,..., ап
и сложим, вынося за скобки х, у, z; это дает:
[аа]х-\-[аЬ]у-\- [ас]г=[а1\-\-[аг] . (*)
Но, в виду условия [ее] - минимум, подчеркнутая сумма справа
должна быть равна нулю, и уравнение (*) приводится к виду:
[aa]х-\- [ab]y -\-\ac]z = [я/].
Точно так же,умножая эти уравнения на коэффициенты blf ..., bn,
затем на сх, ..., сп и замечая, что появляющиеся в правых частях
суммы [Ы] и [се] равны нулю, мы получаем для значений неизвестных
х, у, z, соответствующих поставленному условию уравнивания, сле¬
дующую систему нормальных уравнений:
. \аа]х \ab]y rf- [ас] z — [at]
[ab]x -j- [bb]y -j- [bc]z = [bl] (1)
\ac\x -j- [bc]y -f- \cc\z — [cl]
Число этих уравнений равно числу неизвестных х, у, z, и они
допускают, вообще говоря, одно и только одно решение; следова¬
тельно, для каждой из искомых величин х, v, z мы найдем вполне
- 108 -
определенное значение; если эти значения подставить в левые части
условных уравнений (1) § 1, то в правах их частях обнаружатся те
именно остающиеся погрешности t{, сумма квадратов которых имеет
минимальное значение.
Но это значение суммы [ss] может быть помимо указанной под¬
становки найдено и непосредственно. Действительно, помножим равен¬
ства (Г) последовательно на ..., ея, и сложим,вынося за скобки
х, у, Z-, это приводит к уравнению:
х[аг\+у[Ы\+г[сг\ = Щ+ [ее].
Но в силу леммы Гаусса, [яг] = [Ы\ — [«] = 0, и следовательно:
Ы= № (2)
Эта формула показывает, что минимальная сумма [ге] равна сумме
свободных членов /, помноженных на соответствующие погрешности е,
взятой с обратным знако i (последнее — в том случае, когда свобод¬
ные члены I стоят в правых частях).
В формуле (2) нетрудно из [г] исключить неизвестные нам elt ...,ея
Для этого множим каждое из уравнений (1') на 1и /2, ..., 1„ и скла¬
дываем; находим:
x[al\ 4-у[Ы\ + гЩ = [//] + 1ц
заменяя здесь, в виду (2), [/е] на — [ее], имеем:
[al)x + [Ы\у+Щг — [//] — [ее] . (3)
Уравнение (3) служит для определения [ее] после того как наилуч¬
шая система х, у, z найдена из нормальной системы (1); мы видим,
что для него нужно составить только одну новую сумму, [Щ, ибо
коэффициенты [я/], [Ы\, [cl\ уже найдены при составлении нормальных
уравнений. Уравнение (3) дополняет в известном смысле нормальную
систему (1) и обнаруживает с ней своеобразную симметрию: в нем
коэффициенты при х, у, z равны свободным членам в правых частях
нормальных уравнений (1).
Переписав (1) и (3) вместе, имеем окончательно:
[аа]х 4- \ab\y-\- [ac]z = [а/]
\ab\x -j- [bb]y -+■ \bc\z = [Ы\
[ас]х [Ьс]у 4- [cc]z = [cl] (4)
[al]x + [bl)y 4- [cl\z = [#] — N
Исходя из (4), можем уже наметить следующий порядок работы
в уравнительных вычислениях изучаемого типа: а) составление нор¬
мальных уравнений; б) решение их; в) контроли: формальный — под¬
становкой х, у, z в нормальные уравнения, которые, конечно,
должны быть удовлетворены в точности; затем более глубокий ион-
~ 109 —
троль: подстановка х, у, z в условные уравнения § 1, нахожде¬
ние е, и образование [ее]; контроль этой суммы по последней строке
только-что написанной системы:
[ее] = [Щ — \al\x — [Ы]у — [cl\z,
где вместо х, у, z поставлены их значения, полученные при решении
нормальных уравнений. Отдельно стоит задача определения весов
неизвестных и их средних ошибок, к которой мы обратимся несколько
ниже. Здесь коснемся только пунктов а) и б).
а) Составление нормальных уравнений производится
по правилу „столбец сам на себя и на все следующие", напр.:
[ab\ = albl -f- a.2b.2 -]-....-]- anbn,
и т. д. Для контроля применяются суммы:
[aa] [аЪ] + [ас] = [as] s2 = аг + Ьг -f сх
[ab] + [bb\ + [be] = [6s] s2 = a2 + b2 + с2
[ac] -|- [be] -f- [сс] — [cs]
[a/] -f- [^] + № — [&] sn~ an~k'bn -\-cn
Меньше работы требует следующая контрольная формула:
[ab] “I- [ас] -]— [а/]
2 X ^ ~1“ [be] -j- [bl]
+ Й]
где s'. = at-\- bt -f с •+h-
+ М + \bb] + [сс] + [Щ = [s's'], ... (5)
б) Решение нормальных уравнений производится по тем
правилам, которые уже разобраны в отд. I курса. Но здесь надо
иметь в виду весьма важное обстоятельство: если помимо х, у, z
требуется найти веса этих неизвестных, то нормальные уравнения, как
будет показано ниже, нельзя ни множйть, ни делить ни на какие
числа, и можно применять только последовательное исключение неиз¬
вестных, вычисляя по одной из схем, указанных в отд. I, предпочти¬
тельнее всего по полной (стр. 46).
Приведение условных уравнений к одинаковому
весу. В некоторых случаях каждой из наблюденных величин 1{ при¬
писывается ее особый вес р{ и тогда уравнивание производится по
обобщенному принципу Лежандра, именно под условием, чтобы
сумма квадратов остающихся погрешностей е,, умноженных на-веса
соответствующих величин 1{, т.-е. сумма [^ее], приводилась к минимуму.
Переписав это условие в виде:
(j//W2 + (]/Р^ +• • (V4e„)2-M инимум.
- по —
замечаем, что мы можем притти к нему, исходя из основного прин¬
ципа [ег]-минимум, если заданные условные уравнения умножим соот¬
ветственно на Уpt. Действительно, после этого умножения система (1')
§ 1 принимает вид:
1/Л¥+1/А^+1/тг =j/M + l/Aei
У~р2а.,х + yj,b,y -f -\/У,с.,г = j/M + У~Р*Ч
YPnanX + 1/>АЛ + ]/PnCnZ = VPjn + VPn-n
Остающиеся погрешности этих уравнений суть У, .. •, УРп%
и приведение к минимуму суммы их квадратов, т.-е. суммы [д«]
соответствует обобщенному принципу Лежандра.
Нормальные уравнения и уравнение для [рее] в такой системе
будут:
\paa\x -f- \pab\y -f- \pac\z = [pa/]
[pab]x + [pbb]y -j- \pbc\z = \pbl\ „
[pac\x-\- \pbc\y-\- \pcc\z— [pci]
[pal\x-{- [pbl]y-\- [pcl]z — [pll] — [pee].
Таким образом, практически Все сводится к тому, что образовывая
произведения по правилу „столбец на столбец*, мы к каждому про¬
изведению вида a, bt присоединяем в качестве третьего множителя
вес соответствующего уравнения. (Заметить, что здесь входят самые
веса, а не их обратные величины q., как было в нормальных уравне¬
ниях для коррелат, стр. 43).
§ 3. Приведение условных уравнений ы линейному виду. Примеры.
Предположим, что наблюденные величины /х, /2, ..., /п связаны
с искомыми х, у, z зависимостями общего вида:
k =/iО. У, z)vk=fi(*> у, z); ln=fn(x, у, z), . . . (*)
причем функции fx, f2, считаются данными.
Допустим далее, что нам известны приближенные значения неиз¬
вестных х, у, z, именно х = х0-, у=у0; z — z0, так что, подставив
хо> Уоу z0 в функции /х, .... /п, мы получим величины 1и /2, ..., 7Я,
близкие к заданным 11г 12,..., 1п\ таким образом, имеем:
A=/i<Xi> Уо, z0); k=f2(x0,y0, z0); ... 7n = fn(x0, y0, z0) .-. (**)
Допуская, что предварительные значения х0, у0, z0 достаточно
близки к системе наилучших значений х, у, z, можеад положить:
х = ха-\-1\ У=Уо-\-'П; z — z0-j-:; таким образом, £, и С являются
искомыми, поправками к ха, ув, z0 и наша задача сводится к соста-
- Ill -
влению и решению условных уравнений для этих новых неизвестных.
С этой целью возьмем одно из уравнений (*), напр., l.—f.{x, у, z),
и разложим /Дл:, у, z) по степеням приращений £, т), С, считая эти
величины настолько малыми, что их квадратами и произведениями
можно пренебречь; тогда находим:
h—ft (хо > -Vo > 2о) + аг ~~Ь М “Ь сг (***)
Здесь первый член справа, согласно (**) есть ip, коэффициенты
й;, Ьп с{ суть производные от f. по х, у и z, в которые вместо х, у, z
подставлены их исходные значения хд, у0, z0.
Перенесем lt в правую часть (***) и обозначим l{ — li = hi', мы мо¬
жем назвать ht невязками условных уравнений (*), когда вместо наи¬
лучшей системы х, у, z в них подставлены приближенные значения
хт Уч> 2о • Таким образом, уравнение (***) приводится к виду:
^ + +^ =
Произведя такое же разложение для всех функций/^, /2,... ,/Л, нахо¬
дим систему линейных условных уравнений для поправок к исход¬
ным значениям х0, у0, z0:
+ К
а2Ъ -j- b%i\ -}- с2С == h2
ап ^ + V) + Сп- = hn
Соответствующая ей нормальная система будет:
[aa]%-\- [аЬ]г[-\- [ac]Z = [ah]
[ab]\+[ЬЬ\п + [Ьсу, = [ЬИ\
[йг]?-)- [^г]т)-j- [сс]£ — [ch\
Наконец, уравнение для [ее] принимает вид [см. стр. 108, (4)].
[ее] = [АА] -МЩМЬ+ИА
Для уяснения значения отчеркнутой части заметим, что при
х = х0 ;у=у0; z = z0, 5 = т) = С = 0; следовательно, вся эта часть равна
нулю и поэтому [ее] = [hh\, т. - е. [ее] равна сумме квадратов невя¬
зок h., полученных при подстановке хс, у0, z0 в условные уравне¬
ния (*); поэтому отчеркнутая часть представляет так называемое.у./гу'ше-
нае решения; она показывает, насколько уменьшается [hh] введением
приращений 5, т), С; следовательно, окончательная система поправок будет
та, которая даст наибольшее улучшение решения. На этом основан
особый способ решения нормальных систем по методу последова¬
тельных приближений; образовав [hh], мы подбираем ;, -q, С так,
чтобы последовательно ослаблять [ее], и решение считается закончен¬
ным, когда дальнейшие поправки по своей малости оставляют [ее] без
изменения. К сожалению, недостаток места не позволяет привести
~ 112
здесь соответствующую схему (схема Рунге). Однако, можно пред¬
ставить себе случаи, когда любая система поправок даст весьма мглое
улучшение решения. Это покажет, что наблюденные величины llt /2,
1п столь неточны и противоречат друг другу, что способ наименьших
квадратов не может внести в дело заметного улучшения.
Пример 1-й. Найти наилучшую систему значений прямоугольных
координат точки Р (л:, у), если для расстояний ее от точек (0, 0),
(7, 0) и (0, 6) получены значения: 6,40; 4,47 и 5,38.
Выведем формулу для расстояния lt между точками Р(х, у) и
М(а, Ь), предполагая, что нам известны приближенные координаты Pt
именно хй, у0\ для искомых координат точки Р положим:
= у = у0-j-Tj;
мы имеем здесь:
РМ2 = 12 — (х — a)2 -j- (у — Ь)2;
взяв частные производные от I2 по х и у, находим:
откуда:
31 х—а
дх ~" Т~;
— а (Н у — Ь
I ’ ду I °
Разлагая функцию / по степеням
М(а,Ь) приращений 5 и i\, мы должны в толь-
ко-что написанных производных по¬
ложить х = х0 и у—у0. Обозначив
через / расстояние Р0М, можем напи-
Р(ку)
сать:
Х — Хц У —Уа
В(ХъХ)
подставляя значения производных,
имеем:
Черт. Ю.
или, окончательно:
Можно заметить еще, что
*°_ - = cos (IX) — cos <f; ——- = cos (IY) = sin <p.
- 113
ик что полученное сейчас уравнение принимает вид:
Scos «-f-K)sin<p = h.
В условиях написанного выше численного примера можно найтй
по чертежу приближенные значения искомых координат, именно,
*0 = 5 а у0 = 4; тогда каждое из заданных расстояний доставит одно
уравнение для определения поправок 1 ит]; в данном случае их три,
именно:
, а==0;6=0; 7= |/52 -f 42 =>/41
5 , 4
ЕЙ+’1дт-6-40-,/41 =
0,0031 (1)
а=7; 6 = 0;
/ = j/(— 2)2 -J- 42 = ]/ 20
— 5^ + -1-7^ = 4,47 —V/20 —•
0,0021
й=0; 6 = 6;
/ = l/524-(—2)2 = V29
5 L — TJ -L = 5,38 — т/29 = — 0,0052
v/29 \/29
(2)
(3)
Эти уравнения линейны в отношении £ и т) и обрабатываются как
обычные условные сравнения по. правилам § 2.
Пример 2-й. Из точек Мх, Ж2, . . .
определены направления на точку Р(х,у)\
считая координаты точек заданными,
найти положение Р.
Пусть av 6/, а2, 62; as
координа-
Мг
ты М,, а <?!, <?2, <р3 — наблюденные азиму¬
ты (углы PMV X).
На чертеже прямые Мр в одной точке
не пересекутся и образуют многоугольник,
внутри или вблизи сторон которого нахо¬
дится искомая точка Р. Для определения
ее кординат х и у примем за приближенное ее положение точку
Ро(хоУо) и введем обозначения: х = *0 + '; У = Уо -Ьтй проведем вспо¬
могательные прямые Мрй, ... и азимуты их обозначим через <fu
?2 И т- д-
Мы имеем- здесь: .
* tg?i = JeI1 ;
х0— а}
найдя отсюда 7f1, образуем невязку hx =ог — <j>j. Задача состоит в том,
чтобы эти невязки h между измеренными азимутами <р и приближен¬
ными <р разложить по степеням \ и ttj, ограничиваясь первыми степе¬
нями этих поправок, которые мы считаем величинами малыми.
Способ найм. квадратов. 8
- 114
Положим для этого: tg<p; <р— arctg^- и найдем частные про¬
изводные этой функции по а: и по у:
/arctr у)' — 1 . у = — у = _ — !il?
^ х '* 1 л. ** х* т У* р 1
■+• х3
Гa x)y 1 + i^_ X ^x* + y* ^ P T
Чтобы разложить arctg ^ по степеням S и •*), мы должны в этих
производных взять х — х0 и у=у0, т.-е. принять:
?==- 1==1=ром. = (*0 - я.)2 + (у0 ~ ьу;
таким образом находим:
— sin <р t , coscp
=2. g-J =2-ч,
или окончательно
•sinш f ■ cos® , —
=?- i Ч =i- ri — h = rf — 9 •
/ 1 /
Таким образом, в коэффициенты при i Hi] входят только рас¬
стояния от приближенной точки Р0 до М. и соответствующие на¬
правления, т.-е. величины известные. Таких уравнений составится
столько, сколько измерено направлений, и обработка их по правилам
§ 2 не представит труда.
§ 4. Системы с одним и двумя неизвестными.' Веса и средние
ошибки.
Применение методы § 2 поясним на простейших случаях.
1. Одно неизвестное. Задается система условных уравне¬
ний:
aijX = /х; вес рх
а2х = /у, вес р2
ах — вес р„
п п* г п
Для составления нормального уравнения множим все условные
уравнения на ах, а2, ..., ап, затем на рх, р2,.. 1, рп и складываем;
это приводит к уравнению:
\раа\ х= Ipal\.
Для минимальной суммы [/?ее] по формуле (6), стр. 110, имеем:
\pal\x = \pll] — [рее] (*)
Из нормального уравнения находим:
Н-3 о)
подставляя это значение в (*), получаем:
[/*•] = И] (П
Рассмотрим тот частный случай, когда все at равны единице.
Здесь мы имеем:
х — — . (2)
* 1р) • { }
т.-е. снова приходим к формуле для взвешенного среднего.
Уравнение (1') принимает вид:
\М = [рЩ- Lgf (2')
Вернемся теперь к уклонениям заданных величин lt от их взве¬
шенного среднего, которые мы обозначали через X; для суммы [рХХ]
на стр. 89 была выведена формула (9), тождественная с полученной
сейчас (2'); итак,
[рк = [р£е]
и следовательно уклонения от взвешенного среднего X обладают тем
свойством, что для них [рХХ] имеет минимальное значение: результат,
уже полученный другим путем на стр. 88; таким образом, будем ли
мы рассматривать группу уравнений вида х==1(; (г = 1, 2, ..., я),
как задачу обработки ряда наблюдений, или же как уравнивание
системы из я уравнений с одной неизвестной — результат получается
одинаковый.
Допустим теперь, что все веса р. между собой равны; не ограни¬
чивая общности, можем считать их равными единице; тогда из ($)
имеем:
*=т n=M-g <3>
и наконец, если все af равны единице:
* = ” [•*] = [«]-? И)
Г/13
Но, в виду теоремы на стр. 11, [//] — U-=[XX], где X суть уклонения
данных /. от их среднего; следовательно, здесь [гг] = [XX]; мы заме¬
чаем, что в рассматриваемом простейшем случае х определяется как
арифметическое среднее из 1п согласно с тем, что мы имели уже
в предыдущих частях курса.
Уже упоминалось, что коэффициент при х в нормальном уравне¬
нии, из которого определяется неизвестная, называется весом х. Это
своеобразное понятие, и\еющее чисто теоретическое обоснование,
отличное от понятия весов наблюденных величин I. (котсрые могут
быть оценены наблюдателем по произволу). Вес х, для которого вве¬
дем обозначение р(х), есть Еполне определенная функция коэффи¬
циентов a., br ct и весов р.; но он не зависит от I.. Возвращаясь
к различным разобранным здесь случаям и ра прост; аняя на уравне¬
ния (1) и (3). то определен е веса неизвестной, которое было
дано в отд. II, стр. 87 — 88, для уравнений типа (2) и (4), находил;:
Система ах = L; в:с 1Г р.; р(х) = [раа]
axi = ll; „ L..A; р{х) = [аа]
х = . 1г-ра р(х) = [р\
х „ /г.. 1; р(х) = п.
Остается ввести среднюю ошибку о(лг); по общему правилу имеем
в(х) = —='==, и задача состоит в определении а0; но здесь мы можем
V р(х)
воспользоваться формулой Бесселя или ей аналогичным, полагая
o0 = j/ > так как> п0 доказанному выше \ргг] •= таким обра¬
зом, приходим к формулам:
(1) система а,х. = /; вес pt; о(х) = }Г
(2) » Х=1А » РА =
Пример. Система из восьми уравнений: apc = lt (вес р.)
а
/
Р
ра
раа
pal
/
Б
0,425
0,750
0,5
0,2125
0,0903
ОД 594
0,764
+
14
0,731
1,250
1,0
0,7310
0,5344
0,9138
1,315
+
65
Ю,082
0,070
1,0
0,0820
0,0067
0,0057
0,147
+
77
0,143
0,312
0,75
0,1072
0,0153
0,0334
0,257
—
55
0,168
0,289
1,0
0,1680
0,0282
0,0486
0,302
+
13
0,565
1,045
1,0
0,5650
0,3192
0,5904
1,016
—
29
0,676
1,310
0,8
0,5408
0,3656
0,7084
1,216
—
94
0,834
1,472
0,6
0,5004
0,4173
1,7770
0,7366
3,1963 ,
1,500
+
28
Найдя для этой системы решение по ф-ле (2), подставляем полу¬
ченное х во все условные уравнения; результат подстановок обозна¬
117
чаем через остающиеся погрешнбсти е. получаются как разности
l{—lv Мы имеем здесь:
*==1>7987; = № ~ и=5)7701 “5,7492=°'0209;
непосредственный подсчет дает \р&г]~ 0,0211.
°(*) = У== ± °'041 •
2. Система с двумя неизвестными. Не нарушая общности,
здесь можно допустить, что все уравнения приведены к одинаковому
весу умножении на ]//?,..
• Условные уравнения:
аус -\-by = l1
a2x-\-b.iy = l2
а хЛ-b v — l .
п I ПУ п9
Нормальная система:
[аа] х -{- [ab]y = [atJ
■[аЬ\х+[ЬЬ\у=*[Ы\
[al)x + [Ы]у = [//] - [ее] .
Переходим к вопросу о весах р{х) и р'у). Для сокращения письма
введем обозначения:
А — [аа\\ В=[аЬ]-, D=[bb]-, L = [al\-, М=[Ы\.
Нормальная система принимает вид:
Ах-\-Ву = L
Bx-\-Dy — M.
Чтобы найти вес дг, т.-е. тот коэф [жциент, с которым х войдет
в уравнение, его одно содержащее, условимся поступать так •): оста¬
вим первое уравнение как оно есть и подставим в него у из
второго:
в , м
У ~ ~о х ~jp»
подстановка дает:
(A-§)x = L-M^; («)
поэтому:
/>(*)=л
1) Смысл этих правил выяснится в § 8, стр. 140,
— 118 —
Чтобы найти вес у, оставим второе уравнение, как оно есть,
и подставим х из первого: *
в * V L
-Н-т;
отсюда:
[D-^)y = M-L £, П
так что:
p(y) = D — ~=p(x) - ~
Однако, столь простые формулы для выражения весов через коэф¬
фициенты faa], [ab] и [bb] в системах с тремя и большим числом
неизвестных не имеют места. Поэтому, для дальнейшего, заметим
следующее:
[ Ах -{- By = L
Если одновременно с нормальной системой | gx _j_ _ ^решать
вспомогательную систему с теми же коэффициентами, но другими
( Ayt -f- Ву2 = 1
свободными членами, именно | g _j_ р _ q , то вспомогательная
неизвестная у, даст обратную величину веса х; если же ре-
i + By2' = О
шить еще вторую вспомогательную, систему | Byy-\-Dy2— 1’ то не¬
известная у2', даст обратную величину веса у.
Доказательство этой теоремы получается непосредственно из фор¬
мул (*) и (**). Действительно, положим в (*) х = у1\ L = \\ M = Q]
тогда
Yj =——^ = -У; обратимся теперь к (**) и положим у = у2'; L = О
a~~d
и М= 1; тогда у2' = —~ 4X0 и требовалось доказать.
°~~А
Переходим теперь к средним ошибкам по общим формулам:
о(л:) = —т~=.; о(у) = ^=.
v Ур(х) и/ V Р(У)
Для вычисления средней ошибки единицы веса, а0, в данном слу¬
чае применяется формула, аналогичная формуле Бесселя, вывод
которой мы опускаем:
--l/M -
, ул_2.
здесь в числителе минимальная сумма квадратов остающихся погреш¬
ностей:
N = Ш — И* “
— 119 —
в знаменателе-
таким образом:
число условных уравнений без числа неизвестных;
з(*)=У
[«]
р(х) (п — 2)
3(у) = У
Р(У) (л-2)
Численный при¬
мер.
Решить систему:
*+ _У = + 5,95
2х — у = -j- 0,16
х -j- 3у = —]—14,12
3* + у = -J— 9,85
х— у = — 2,06
Нормальная
система:
[ая]= 16
[ab] = 4
[bb]= 13
[а/] = 4,880
[Ы\ = 60,060
[//] =336,069
Вычисления расположим по известной уже из отд. I схеме (стр.*46):
16*+ 4у = 47,880
Ах + 13_у = 60,060
47,800* +60,060у =
= 336,069 —И.
I.
*
У
II.
У
X
Nx
16
4
47,880
13
4
60,060
Ег
1
0,25
2,992
Ег
1
0,308
4,620
к2
4
13
60,060
4
16
47,800
4
1
11,970
4
1,232
18,480
ЛГ2
12
48,090
М2
14,768
29,400
Е2
1
4,008
Е2
1
1,990
4,008
—
1,990
—
1,990
1,002
2,992
4,007
0,613
4,620
X
У
У
*
Вычисление проведено здесь два раза и вот почему: в I исклю¬
чаем* и приходим к уравнению 12 у = 48,090, откуда выводим у — 4,008
и Ху) = 12; затем'получаем *=1,990; но из I мы никоим образом не
могли бы получить р(х). Чтобы найти /?(*), переписываем нормаль¬
ную систему в виде:
13 _у+ 4 * = 60,060
4 у +16 * = 47,880
и в решении II исключаем у; тогда приходим к уравнению
14,768* = 29,400, откуда * = 1,990 и, кроме того, р(х) — 14,778; затем
из II снова можем найти у = 4,007 (как раньше); однако, из II нельзя
никак найти р(у). Таким образом, только коэффициент последней
неизвестной, т.-е. оставшейся после исключения остальных, даст ее
вес. Следовательно, вообще говоря, систему надо было бы п рере-
шать несколько раз, чтобы получить все веса. Но, как мы увидим,
к этому приему на практике не прибегают, в виду наличия более
удобных способов.
— 120 —
В настоящем случае (при двух неизвестных) можно найти веса и
по формулам (*) и (**); действительно:
Наконец, для той же цели можно решить и обе вспомогательны!
системы:
Заметим, что в каждой из этих систем нужно найти только одну
неизвестную (ух или у2'); вторая неизвестная (т.-е. у2 и у/) здесь ни¬
какой роли не играет и потому не определяется.
Переходим к средним ошибкам и вычисляем [ее]; для этого под¬
ставляя х= 1,990 и .у = 4,008 в данные условные уравнения, находим
остающиеся погрешности е: 0,048; —0,188; —0,106; —j— 0,128; -{-0,042;
откуда [ее] = 0,067. Для контроля воспользуемся формулой:
[ее] = [//] — [al\x — [bl]y = 336,069 — 47,880 • 1,990 — 60,060 • 4,008 =
в полном согласии с предыдущим.
Отсюда, имея в виду, что л = 5 и что число неизвестных равно
двум, находим:
Формулы для весов и средних ошибок позволяют довести до конца
задачу о взвешенном уравнивании треугольника (стр. 39). Допустим,
что для трех его углов х, у, z получены значения 1Х, /2, /3 с весами
Pi > Рг» Рз • Особенность задачи состоит в том, что х, у и z связаны
соотношением: x-\-y-\-z— 180°, которому наилучшие значения углов
должны удовлетворять в точности.
Итак, имеем уравнения:
х = 1г (вес рг); у = 12 (вес р2); г — 1й (вес р3); x-\-y-\-z= 180°.
Введем новые неизвестные х' и у', положив:
16 Tl-j- 4 у2 = 1
4 у, + 13 у2 = 0,
16 у/+ 4 у2' — О
4 Tl' + 14 у2' = 1,
откуда
откуда
/>(*) = 9 = И,769-
К* — 192
= 0,067,
Итак: х= 1,990 + 0,039
у = 4,008+ 0,043
(средние ошибки).
§ 5. Взвешенное уравнивание треугольника.
121 -
так что х' и у соответствуют прежним поправкам Xt и Х2. После такой
подстановки первые два условные уравнения принимают вид: х' — О
(вес/^и^^О (вес р2). Для получения третьего уравнения поль¬
зуемся точным соотношениех: z=180°— х—у, откуда
2 = 180° — 1Х — х' — /2 —у = /3
или х' +у = 180° — lx —/2 —13 — — h (невязка).
Таким образом мы имеем три уравнения для двух неизвестных х’
и У, именно:
х' = 0 (вес рг)
У = 0 ( „ р2)
*'+У= — h{ „ рй).
Вычисляем коэффициенты нормальной системы:
\раа] =ргЛ +А-0 + Л-1 =Pi+P*
[pab]=pS‘l =р&
[pbb] =/V 1 “Ь/’з"! —Pz+Ps
[pal] = —p.Ah
[pbl] =—pji
[рЩ = -\~PA2 1
Следовательно, нормальная система и уравнение для [ргг] прини¬
мают здесь вид:
(Pi +Ръ)х' +рйу' = - РА
РА + (р2-\-Рг)У' = —рА'
[ргг] =рА +рА*’ +рАУ‘
Для решения нормальной системы вычитаем из первого уравнения
второе, выражаем у через х'; делим первое уравнение на р^рх и под-
У
ставляем в него что дает:
р 1
А А
w _ Pi . „г _ Ря
1 1 1’ У = --1—Г—Г (!)
— +■—+— — + -+—
Pi Pi Рз Pi Pi Рз
Эти формулы, как и должно быть, тождественны с формулами,
выведенными на стр. 37 для Xt = х' и Х2 =у'. Очевидно, если бы мы
исключали из уравнения x-[-yAz —180° неизвестную л: или у, то
нашли бы аналогичное выражение для z
л
z' = X,
Рз
1+1 + 1'
Pi Pi Рз
Переходим теперь к средним ошибкам; подставляя значения У и У
в формулу:
[ptt] =pA-\rPjix' +рАу\
находим:
1Н“Л* [£ + £+'] -**= £-4 + #-
— 122 —
Для определения весов пользуемся формулами (*) и (**)
здесь:
Л“Л+/У В=ра) D=p2+p3-,
поэтому:
n(x'\-A — ^ — D = PtP*+P*P* + W* „
D ' Л Л+Л л+л
_ Р1Р2Р3 /1.1 J j L\
(Pi + />з) \/»1 Рз Рз) "
Наконец, при трех условных уравнениях и двух неизвестно
имеем:
_ / И (__ / ' Щрз + Рз) _
V «т-» ¥(+++*«
= ±1+1+1|/ л (л+л) •
Л Л Рз*
Вводя для удобства письма числа qx = —; <7» = ^-; q$= и поль-|
Pi Pi Рз I
зуясь симметрией задачи в отношении углов х, у, z, можем написатн|
+) д(р) _ Ф) _ _] h
V 4i (4i + Чз) V 4i (?1 +~<h) УчАяГ+Я^) ~Уч1+Чз+Чз '
Положим теперь, что все веса pt между собой равны, т.-е 1
pi = qi = 1. В этом случае (1) и (2) дают:
*' = у' = 2' = —~ и o(x) = o(y) = a(z) = ±^h = ±0,mh. I
Для численного примера вернемся к задаче стр. 39, где
было h = 10"; рх — 5; р2 = 2; рй = 8; таким образом ^ = 0,2; #2 = 0,5;
#3 = 0,12; общий множитель пропорциональности здесь равен
10' 10'
/,=12/20.
0,2 -(- 0,5 —0,12 0,82
Поэтому
а(х) = + 12/201/0,2 • 0,62 = +4/29
o/W = ± 12/201/0,5-0,32 =+4/88
= + 12/20/0,12-0,7 = +3,"54
§ 6. Случай упрощения.
Во многих практических вопросах, напр., при определении постоян¬
ных инструментов, встречаются системы условных уравнений, в кото¬
рых все коэффициенты при одной из неизвестных, напр., все at, равны
единице. Решение таких систем допускает существенное упрощение,
которое необходимо применять в вычислениях.
— 123 —
Положим, что дана система я уравнений:
•к + ^У-К-2^; (*)
(* = 1, 2 It)
Сложив все эти уравнения, находим:
“ + [%+[Ф=
или, деля на п,
* + — — (**)
1 п 1 п п ' '
Здесь, очевидно, коэффициенты и свободный член суть средние
арифметические из заданных чисел Ьг с., I..
Если теперь строку (**) вычитать последовательно из строк (*), то х
исключится, а вместо bt, с., 1{ появятся числа:
— с! = с — [-1; // = /—И,
I I п I I I п > I I п ’
где буквами со штрихом обозначено, что значения Ь., с., lt отсчиты¬
ваются от их арифметического среднего (в смысле данное минус
среднее).
Таким образом, мы приходим к системе:
b.'y -f- cjz = //, (***).
(/ = 1, 2,. . п)
в которой число неизвестных на единицу меньше, чем в исходной
системе, и у которой коэффициенты Ь', с' и свободные члены /', на
основании теоремы об уклонениях от среднего (стр. И) удовлетво¬
ряют условию:
[Ь'] = 0; [с'\ = 0; [/']=0.
Нормальная система, соответствующая (***), принимает вид *):
[Ъ'Ь']у+[Ь'с']г=[Ь'1'\
[b'f]y+[c'c\zJ[c'l\ ; [Ь'1>]х=[с'1']у+[1'Г}-М.
Решив ее. можем вычислить, как показано выше, веса и средние
ошибки у и z; затем находим и ж из уравнения (**), именно:
п п ^ п
*) Заметим, что в виду формул для средних арифметических, стр. 12, формула (5),
коэффициенты нормальной системы имеют здесь следующие значения:
[Ь'Ь’\ = [ЬЬ] —; [Ь'С] — [Ьс]— ШМ и I. д.
Это обнаруживает, — в чем предлагаем убедиться читателю, — что написанные
сейчас нормальные уравнения соответствуют нормальным уравнениям второй сту¬
пе ни в общем случае решения, при условии = 1,
— 124 —
Но для получения веса х следует обратиться к общим прави
которые будут объяснены ниже (§§ 8 и 9).
Отметим еще, что для этих систем имеется простой способ
троля вычислений: подставив найденные значения х,у, z в yc.il
н ы е уравнения и образовав остающиеся погрешности е, мы дсш[
иметь:
[е]=0.
Действительно, здесь а.= 1, и поэтому из основного уравна
[ае]=0 следует только-что написанное равенство.
Переходим теперь к системам подобного рода с двумя не|
вестными и приведем несколько иной способ решения, котор|
даст нам возможность получить средние ошибки как у, так и х.
Задана система:
x’\~biy = li
(« = 1,2,. . ., я)
Обозначим через Ь0 и /0 арифметические средние из Ь. и и по]
жим:
b! = b. Ьй, L^ I. ,
так что:
[5'] = 0 и [/']=<).
Переписав строку (1) в виде:
x + hy+b.y- b0y = lit
введем новую неизвестную положив:
х' — х-{-Ь0у
С этой подстановкой (1) принимает вид:
x'+y(bi-b0) = ll
или
х' ~\~bly = li •
Системе (3) соответствует такая нормальная система:
пх'+ W] у=Щ
\Ь') х'+[Ь’Ь]у=[ЬЧ]
Щх' + [ЬЧ]у=[11]-[гг\
Заметим теперь, что [ЬЧ] — [V (/0 + Л] = 10 [Ь ] + [ЬЧ] *= [ЬЧ], и
[&']=0; поэтому нормальные уравнения существенно упрощаются:
пх' = [/]
[Ь'Ь']у=[ЬЧ'] (4)
Щх' + [ЬЧ]у=[Щ-[гг]
В первых двух уравнениях неизвестные отделены, и мы без вся-
й подстановки находим:
У I hi у
Гb’l']
Ib'b'i
р(х') = П
........ (5)
p{y)=[b'b]
Внося найденное значение у в формулу х'=х-\-Ьйу, где
[Ь]
= —. имеем:
п ’
... .(6)
п п 4 у
I, кроме т:го, по теореме о распространении средней ошибки легко
каходим:
р(Х) р(х')' п'1 р(у n'[b'b'\ ' ’ ’ ' '
Переходим к формуле дтя [ г]; по последнему из уравнений (4)
N = т -V\x'-[Ь'Г]у =[//]-^ - [Ь'Г]у
ни, в виду-теоремы стр. 11,
Ы = [ГГ]-[Ь'1’]У (8)
Сумма [ег] контролируется непосредственным вычислением оста-,
мцихся погрешностей, причем последние, как указано выше, должны
■довлетворять еще условию: Н=0.
Соберем вместо формулы этого последнего отдела; ими весьма
часто приходится пользоваться на практике.
Система условных уравнений:
х ~Ь bty —
(i = 1, 2,. . ., п)
= = ¥ b't = bt-b0 l! = l-l0 [b’\ = [/'] = О
У = 1т х~ lo b0_
• N = т-[Ь'Цу W=0
■••и-Ж «(^VF14
]1У = Ш x = lo-hy, р{у) = [Ь'Ь') = ! + _*£.
IV,
(я - 2) [b’b']
§ 7. Примеры.
I. Ход хронометра. Из сравнения показаний хронометра с
астрономическими часами, или же непосредственно из наблюдений,
определяются поправки хронометра, т.-е. те величины, которые
надо придать с их знаком к его показанию для получения верного
йремени. Пусть в моменты tlt 4 • • • > tn определены поправки
«!, м2 ия. Так как поправка с течением времени меняется, то
полагают:
u = u0-{-g(t—t0),
считая, что изменение поправки происходит пропорционально вре¬
мени; за 4 можно принять любой момент; для t = t0 получается а = и0,
так что и0 есть неизвестная нам поправка в начальный момент вре¬
мени. Если интервалы 4 —4 выражены в днях, то величина g, вторая
неизвестная нашей задачи, называется суточным ходом хронометра.
Таким образом для определения и0 и g имеем систему п условных
уравнений:
^ = «0+g(ti — t0)
(/=1,2 л)
Для упрощения обработки примем за 4 арифметическое среднее из
всех заданных моментов tlt 4» ..., tn, т.-е. положим: 4 = ^> и будем
вести счет времени от этого среднего момента, обозначив tt — 4 = t'.\ по
свойству уклонений от среднего [t'\ = 0.
Таким образом приходим к системе:
'= Щ, О)
которая совершенно тождественна с рассмотренной в предыдущем §
системой вида х-\-Ь.у = 1., при добавочном условии
ДО = [*'] = о, *о = °-
Остается привести в соответствие обозначения, именно положить:
х = и0; bt — Ц\ g=y\ 4 = Up b0=O,
чтобы дать решение нашей задачи по формулам I—IV, стр. 125.
«о = ^ р(«о) = я
s=m <g)=\Z[ttV- 2)
[es] = [и!и!] — [и’?] • g Контроль: [е] = 0
Численный пример. Поправка хронометра определялась еже¬
дневно, в 0 часов с 20 по 29 января 1926 года (я = 10).
Соответствующие даты tt приведены в первом столбце схемы, на¬
блюденные и{ — во втором. С этими данными образуем:
j ‘ п, г 315,98 п, rrto
4 = 24,5, ив = —— = 31,593.
- 127
1
2
3
4
5
6
t
Ui
tf
i
uf
и вычисл.
e(набл.—
вычисл.)
20-0 ^
20*,23
— 4,5
— 11*368
20*,22
+ 1
21,0
22 ,78
— 3,5
- 8,818
22 ,75
+ з
22,0
25 ,42
— 2,5
— 6,178
25 ,28
+ И
23,0
27 ,83
— 1,5
— 3,768
27 ,81
+ 2
24,0
30 ,27
— 0,5
— 1 ,328
30 ,33
— 6
25,0
32 ,74
+ 0,5
+ 1,142
32 ,86
— 12
26,0
35 ,20
+ 1,5
+ 3,602
35 ,39
— 19
27,0
37 ,80
+ 2,5
+ 6,202
37 ,92
- 12
28,0
40 ,59
+ 3,5
+ 8,992
40 ,45
+ 14
29,0
43,12
• +4,5
+ 11 ,522
42 ,97
+ 15
315,98
0
0
0
В 3-м столбце даны уклонения ? от среднего, в 4-м уклонения
г',, (контроля [7']= 0 и [и']=0). Затем образованы (непрерывным сче¬
том на арифмометре) суммы = 208,58 и [tt'\ = 82,50.
Отсюда:
208,58
g-
82,50
: 2*,5282.
Для весов имеем:
р(и0) = 10; p(g) = 82,50.
В 5-м столбце даны поправки, вычисленные на моменты наблю¬
дай по формуле: и = 31,598 2,5282 (подобные суммы то'же вы-
шяются на арифмометре непрерывным действием); наконец, в б-м
столбце, е = наблюд. — вычислен., в единицах 2 знака (контроль
:0). С этими значениями имеем [ее] = 0^,132. Для окончательного
контроля находим ту же величину по формуле:
[ег] = [и'и'] — {u!t']g = 527,4736 — 208,58 • 2,5282 = 0,142;
согласие достаточно хорошее, в виду неизбежной здесь неточности
последних знаков.
Наконец:
=/]mrhr ± °'0414; =/Шг ” ± °'0144-
Итак:
и = ЗР,598 4- 2s,5282 (t — 24,5),
±41 ±144
128
Однако, представление заданных величин щ этой формулой, в виду
значительности нельзя назвать вполне удовлетворительным.
Замечание. До сих пор предполагалось, что ход хронометра
является величиной постоянной; но наблюдения показывают, что у
всякого хронометра ход подвержен систематическим измениям, зави-
сящим-и от времени и от температуры. Характер этих изменений
обычно выражают следующей формулой Льессу:
g=go+at + c{T-T0)\
где t—время, Т—температура; g0, а, с и Го—четыре подлежащие
определению постоянные (g0 ход при ^ = 0 и Т = Т.о; а—коэффициент
ускорения; с температурный коэффициент; Г0 — температура ком¬
пенсации); получив несколько определений хода (во всяком случае
больше четырех) в различные моменты t и при разных 7', состав¬
ляют соответствующие уравнения и обрабатывают их по способу наи¬
меньших квадратов *).
Другой способ обработки. Рассматривая схему предыду¬
щего вычисления, можно заметить, что в ней является необходимость
в образовании суммы u't', а эги произведения, вообще говоря, могут
быть довольно значительными числами. Поэтому иногда целесообразно
вести обработку несколько иным способом, который поясним на том
же примере.
Имея ряд уравнений вида:
«о+g(t — t0) = u.,
оставим как раньше,
но для второй неизвестной g найдем ее предварительное значение
(т.-е. разность крайних поправок, деленная на весь интервал). Если
с этим предварительным ходом g0 вычислить поправки на моменты
наблюдения, то получатся предварительные значения щ\ разно¬
сти значений данных и предварительных обозначим через hp так что
ui — ui= К • Пусть теперь поправка предварительного хода gQ равна 5,
так что
^Поэтому вопросу см, статью П. Шпгулькерца, в Записках по Гидрографии, 1930,
— 129 —
Итак, мы имеем два ряда уравнений:
и. = и0 -\~gt' = Й„ -)- (^0 -f- ?)£.'
=«0+М'-
Вычитая находим:
и, —и,= А.==й/.
Таким образом получаем систему условных уравнений:
решая ее по формуле (3), стр. 115, имеем:
« — [«Ч
5—[«Г
и, кроме того, контрольную формулу:
[А] = 5Р'] = о.
Наконец, нетрудно видеть, что
г.— h. — М\
I I I >
поэтому
[е]=0 и =
Выпишем все формулы, нужные при этом способе обработки:
Ио+йЧ* —
(i = 1, 2, . . . , п)
(1) “о tj — t.t —10 p(u0) = ft
и — и,
(2) So = t—_-r = u—Ui = h.\ контроль [k] = 0
n
(3)S *£) = [*'*'];
(4) г. = A. — E£'e.; контроль [e] = 0; [ее] = [hh] — t[ht1].
Применим эти формулы к только-что рассмотренному примеру.
Значения t и и переписаны снова в первых двух столбцах схемы
и дают, как выше, t0 = 24,5; и0 — 31,598.
*) Второй член справа представляет собой улучшение предварительного реше¬
ния, см. стр. 111.
Способ нанм. квадратов. 9
— 130 —
1
2
3
4
5
6
7 1
t
и
V
и
h
£
' 20,0
20^,23
— 4,5
20*153
+ 8
— 7
+ 1 1
21,0
22 ,78
— 3,5
22 ,696
+ 8
» — 5
+ з
22,0
25 ,42
— 2,5
25 ,240
! + 18
— 4
+ И
23,0
27 ,83
-1,5
27 ,783
+ 5
— 2
+ з
24,0
30 ,27
— 0,5
| - 30 ,326
— 6
— 1
— 7
25,0
32 ,74
-Ь 0,5
, 32,870
— 13
+ 1
— 12
26,0
35 ,20
+ 1,5
35 ,413
— 21
+ 2
— 19
27,0
37 ,30
+ 2,5
37 ,956
- 16
+ 4
— 12
28,0
40 ,59
+ 3,5
40 ,500
+ 9
+ 5
+ И
29,0
j 43,12
+ 4,5
43 ,043
+ 8
+ 7
+ 15
i
i
1
! о
j
4 5
0
0
Предварительный ход здесь равен:
43,12 — 20,23
£о =
29 — 20
= 2,5433;
с этим ходом вычислены (столбец 4) предварительные поправки и по
формуле:
и = 31,598 + 2,5433 (t — 24,5).
Вычитая полученные и из данных и, находим невязки h, в ед. 2
знака (столбец 5); контроль [Л] = 0; затем образуем [ht] = —124,0
(ед. 2 знака); \t’t'] = 82,5; следовательно, поправка хода равна:
£ = —= — 1»50 ед. 2 знака,
oZfO
так что:
g = go -f $ = 2,5433 — 0,0150 = 2,5283,
как было найдено выше, стр. 127.
В 6-м столбце даны величины — U.; в последнем, еi = hi — U/ (сра¬
внить их с числами 5-го столбца предыдущей схемы). Контроль: [s] =0.
Наконец, вычисляем:
И = [Щ — ] = 0,1524 - 0,0150 . 1,240 = 0,134;
непосредственный подсчет дает
И =0,133.
— 131 —
II. Эксцентриситет алидады. Нормальные уравнения преды¬
дущего примера имеют ту особенность, что неизвестные х и у в них
отделяются, так что для определения их не требуется производить
подстановки одной из неизвестных в другое уравнение. Пример такой
же системы с тремя отделяющимися неизвестными дает теория угло¬
мерных инструментов. Как известно, в каждом таком инструменте су¬
ществует неизбежная погрешность, происходящая от несовпадения
центра вращения алидады с центром круга делений; в соответствую¬
щих курсах показано, что каждый отсчет по двум противоположным
верньерам приводит к уравнению вида:
a -f- Р sin М Т cos М — /,
где / суть наблюденные разности отсчетов по обоим вергньерам, всегда
близкие к 180°; М — углы отсчета по кругу, и наконец а, р и у — иско¬
мые постоянные, через которые и определяется эксцентриситет али¬
дады.
Предположим, что сделано всего п отсчетов через равные углы
360°
—, так что угол М последовательно принимает значения:
зет. 3601. .
’ п ’ п ’ " ’ ’ ■ ' п
Таким образом, можно составить п условных уравнений вида:
ос -J- р sin Mt -(- у cos — L,
где sin vVf. ,cos М. и lt суть известные числа.
Для образования нормальной системы примем во внимание, чтэ
здесь a.t = 1; bt — sin М., с. = с os М., так что:
[аа\ — щ [a sin М) = [sin М] и т. д.
В виду этого, нормальные уравнения принимают вид:
лос —1— р [sinM] -(-у [cos М] — Щ
a [sin М] -f Р [sinW] ' -фу [sin Ж • cos Ж] = [/sin/И] . (1)
a [cos М] -f- Р [sin М cos М] -}- у [c°s2 Щ — Г cos Щ
« М + Р I1 sin Щ + т [I cos М] = [//] — [и]
Но из формул тригонометрии выводится следующее предложение:
если угол М, возрастая в арифметической прогрессии, один или не¬
сколько раз обходит окружность, то
[sin М] = [cos М] = [sin М • cos М] = 0,
между тем как
[sin2M] = [cos2М] = ” ,
где и число точек деления круга.
— 132 —
Таким образом, в нормальных уравнениях остаются только члены:
т — [/]; ~ р = [/ sin М]; ~ у = [/ cos Л4] .
Отсюда имеем:
а = W о(а) = п
?=-* [/sinЖ] р(3)= "
2
Y= -J [/созЖ] /*т)=+
Подставляя теперь в четвертое из уравнений (1)
[/] = ш\ [/ sin М] = -у и [/ cos М] — ~ ,
приходим к следующей важной формуле, типичной для разнообраз¬
ных вопросов тригонометрического и более сложного уравнивания
(см. отд. IV):
[ее] = [Щ — -J { 2а2 + р2 -f Y2'
Численный пример. При углах М = 0°, 30°..., 330°, изме¬
рены показанные во 2-м столбце разности отсчетов по обоим вернье¬
рам (уменьшенные на 180°).
1
2 ,
3
4
5
6
М1
h
sin Mt
cos Mt
h
zi |
0°
+
2,/,6
0,00
1,00
+
1",4
— 1'
',2
30
+
6 ,2
0,50
0,87
+
5 ,7
— 0
,5
60
+
11 ,0
0,87
0,50
+
11 ,4
+ 0
,4
90
+
16 ,4
1,00
0,00
+
17 ,0
+ 0
>б 1
120
' +
21 ,4
0,87
— 0,50
+
20 ,9
-0
,5 :
150
+
22 ,8
0,50
— 0,87
+
22 ,2
! —о
1
,6
180
+
18 ,8
0,00
— 1,00
+
20 ,4
_L 1
! i 1
,6 i
210
+
16 ,4
— 0,50
— 0,87
+
16 ,1
— o.
,.3 !
240
+
10 ,8
-0,87
— 0,50
+
10 ,3
— 0
,5
270
+
,8
— 1,00
0,00
+
4 ,8
— 1
,0
300
0 ,0
— 0,87
+ 0,50
+
0 ,8
+ 0
,8
330
—
1 ,6
— 0,50
+ 0,87
—
0 ,4
+ 1
,2
Составляя [/] и сумму произведений L sin и L cos М., находим:
[/] = 130,6; [/ sin М] = 36,49; [/ cos М] = — 56,90.
— 133 —
Отсюда:
* = =М0,"88; р = • 36,49 = 6,"08; у = —^-56,90 = —9,''48.
Подставляя найденные а, р и у в формулу для /, находим „вычис¬
ленные" значения этой величины, 7 (столбец 5) и образуем разности
Для контроля решения можем применить формулы, выте¬
кающие из леммы Г а у с с а:
[е] = 0; [в sin М] =0; [scosM]=0.
Как показано в теории инструментов, а есть угол между обоими
противоположными верньерами. Через р и у получаются: эксцентри¬
ситет алидады (где R радиус круга) и угол положения линии
центров Е, для чего служат формулы:
2 ^ • sin Е = — у 2 ~ • cos Е = £
В нашем примере находим:
Е = 57°; ~ = 5",63 или е = 0,0000273 R.
Средние ошибки величин а, "Р и т вычисляются по формулам (см:
стр. 119):
з = у р ; «о = \/л'Ц]з; />(«) = щ />(Р) - k'i) = у; (л =»12).
[ев] = [//] — ~ [2а2 + р2 + f] = 2188 — 2181=7
о0 == + 0,"88; <«) = ± 0,"26; о(р) = о(т) = ± 0,"36.
III. И змерение горизонтальных углов. Одним из спо¬
собов определения величины углов, образуемых прямыми, направлен¬
ными из точки стояния Р на предметы
О, X, Y, Z..., в геодезии служит метод ^ t %
измерения углов „во всех комбинациях", * 1 / 9
предложенный Гауссом и практически \ \ if
разработанный Шрейбером. Он состоит \ \ / 'S'
в том, что сначала измеряют все углы, \ г*—yl
образуемые первой из прямых, РО, со все- \-Д-г-~/ /
ми последующими, т.-е. с РХ, PY, PZ...; \ \ ГУ
затем углы между вторым направлением, \\ //
РХ, и всеми остальными; потом углы меж-
ду PY и следующими, и т. д.; очевидно, о
что при п направлениях способ Г а у с с а Черт. 12.
предписывает измерить в общей сложно¬
сти i&pAL углов. Положим, для простоты письма, что данных на¬
— 134 —
правлений имеется 4. Взаимное расположение четырех прямых РО
РХ, PY, PZ определяется тремя независимыми углами, так что за
подлежащие определению величины мы можем принять здесь углы:
(РО, РХ) = х; (РО, РГ)=у; (РО, PZ) = г.
Пусть в результате измерений для этих углов получены знамени»
4 > 4 > 4; следуя правилу Гаусса на практике не огр^ничиваютс»
этими непосредственными определениями искомых углов, а измеряют
сверх того углы:
(РХ, РГ)=у — х; (РХ, PZ) = z — x; (PY,PZ) = z—y.
Допустим, что для этих последних получены значения /4, 4>4
При этих данных мы приходим к следующей избыточной системе
б условных уравнений *) для неизвестных х, у, z:
х = 1г у — х = 14
У= 4 z х = /5 . (1)
Z = /д Z У = /g
Для упрощения решения положим х = х0-{-£, где хя есть прибли¬
женное значение угла х, а \ искомая к нему поправка, и примем за
приближенное значение х0 именно величину 1Х, найденную из непо¬
средственного измерения угла х. Очевидно, что первое условное
уравнение примет тогда вид & = 0; поступая аналогично для у и г,
приходим к следующей системе:
£ = 0 Т] 1'2 —j“
7) = о с— 1 = 4—4 + 4 = ^2 (2)
с = о с—tj=4—/а+4 = А»
В правых частях уравнений второй группы величины , Л2 и kt
являются невязками, обнаруживающимися здесь в виду неточност»
измерений углов /х, /2...,/6. Алгебраически мы имеем здесь своеоб¬
разный „случай упрощения*: коэффициенты при всех неизвестных
равны+ 1. Для составления нормальной системы, соответствую¬
щей (2), поступаем так: отбираем те из уравнений, в которые входит
меняем знаки в тех из них, куда £ входит со знаком —, и эти уравне-
’) Здесь умгстно остановиться на терминологии. В астрономической и физической
литературе избыточные уравнения вида ax + by + ... = / всегда называются .услов¬
ными уравнениями для неизвестных х, у,...’. В геодезии, где величины х, у... сам*
обычно подлежат непосредственному наблюдению, уравнение рассматриваемого типа
получают название „уравнений ошибок", подразумевая под этим ошибки в наблюденных
величинах /; термин .„условные уравнения" сохраняется в геодезии только для тех
уравнений с поправками X, которым эти последние дэлжны удовлетворять точно. Каза¬
лось бы целесообразным сохранить название .услов;ых уравнений" для всех избыточ¬
ных систем, а к недостаточным системам коррелатного типа применять принятое в меха¬
нике название .уравнений связи".
— 135 —
яия складываем; также для т] и для С. Это приводит к следующей
нормальной системе, под которой написана ее суммовая строка:
35— т)— С =— hx — h2
—5 + 3'/]— С= hx — hi
—5— ^ + ЗС= /z2 + A3 . . (3)
6+ 7]+ с= О
Складывая суммозую строку с каждой из строк (3), получаем зна¬
чения искомых поправок:
S (- К - КУ- \ = 4 (К - А3); с = 4 (Аз + А3) • • • • (4)
ч
Отсюда, по уравнениям х =/, -j- £; y — la-f- т); д = /3 -|- С, найдем
и значения определяемых углов. Мы получаем по формулам (2):
£ = — '211 -j- 4 —4 -J- 4 — 4
Т1 — — 2/2 -f- 4 “Ь 4 4" 4 — 4
£ = — 2/а -j- /, -j-4 -f- /2 -}- Z6,
и затем:
' ■* — 4 (2/j ~т~ 1-2 — 4 “b 4 — 4)
у — ^ (2/2 -j- /, -p 4 -)- 4 — 4)
= 4 (24 -f- A+4 + 44-4)'
Дия придания этим формулам большей наглядности положим:
4 = (1,2) 4 = (2,3)
4 = (1,3) 4 = (2,4)
4 = (1,4) 4-=(3,4)
Здесь через 1, 2, 3, 4 мы обозначаем направления РО, РХ, PY, PZ;
тогда:
х = [ {2(1,2) Ч- [(1,3) - (2,3)] + [(1,4) - (2,4)]}
V = I {2(1,3) + [(1,2) + (2,3)] + [(1,4) - (3,4)]}
\ {2(1,4) + [(1,2) + (2,4)] + [(1,3) + (3,4)]}.
Обобщая эти формулы г) на случай, когда имеется п направлений
РО, РХ, PY , видим, что наилучшее значение каждого из углов
(РО, РХ) = х; (РО, PY)=y; (РО, PZ) = z и т. д. получается как
*) Подробнее об этом см. Ф. Красовскши Руководство по высшей геодезии,
ч. 1, стр. 235. (Москва, 1926).
— 136 —
взвешенное среднее, с весом п, из всех измерений данного угла, при¬
чем в него входят: с двойным весом непосредственное измерение
этого угла и с весом 1 все те его определения, которые получаются
как суммы или разности других непосредственно измеренных углов.
Напр. (1,3), измеренный непосредственно, получается также как сумма
(1,2) (2,3) и как разность (1,4) — (3,4).
Теперь важно показать, что то же самое решение может быть
легко получено и по правилам коррелатного уравнивания. Действи¬
тельно, все 6 найденных величин , /2,..., /6 должны удовлетворять
здесь трем геметрически-очевидным условиям: /4 = /2 — А А —
4 — А — А- Между тем, по правым частям уравнений второй группы
(2) мы видим, что именно эти уравнения обременены невязками hx, h2
и А,. Обозначая поэтому через Ах, 12,..., Ав поправки всех измерен¬
ных углов, получаем три „условных уравнения поправок":
А — 4 4* А + А] = о
А — А Н- А А=о •
• (5)
Записывая их столбиком, образуем по правилам отдела I нормаль¬
ную систему для трех коррелат у1( у3 и у8.
Ti
Та
Тз
А
+1
+ 1
4
— 1
А- 1
4
— 1
— 1
4
+1
Хг
Г)
+ 1
4- 1
А
А!
к2
А
Нормальная система:
3Ti 4~ Т2— Тз + А — О
Т1 "4“ Зуа —I- Тз4~А —О- • • (6)
— Тх 4" Та 4~ ЗТз “Г А,= о
Вычитая второе из уравнений (6) из суммы двух других и комби¬
нируя полученную строку с каждой из трех данных находим:
Тх — 4“ (— 2Aj -\-к2 — А3)
Та= 4 (4~ А 2А2 4- Ай)
Тз = 4 (— АН-А — 2А3).
Отсюда, по основным правилам методы коррелат:
A = +Ti+Ta— "4"(— А — А)
А ~—'и А 7з= 4 (А — А)
А = — Та — Тз = х( А + Ах)
А = Тх
А — Та
4 = Тз
(А
— 137 —
Замечая, что поправки ?, ч\, С по формулам (4) совпадают с по*
правками /ч, Х2, Х3 по формулам (7), мы убеждаемся в тождестве
решений, доставляемых обеими методами; способ коррелат дает
к тому же еще поправки )ч, , Х6, не имеющие' здесь геоде¬
зического значения. ‘
Этот пример обнаруживает, что в тех случаях, когда условные
уравнения для неизвестных не все между собою независимы, имеется
возможность' решать задачи уравнивания как через избыточные
системы, так и через коррелаты; выбор методы обусловливается здесь
только сравнительным удобством применения той или другой. Допу¬
стим, например, что между я наблюденными величинами д. имеется
всего /я независимых, так что могут быть выражены через т неза¬
висимых неизвестных х, у, zтогда, решая соответствующие услов¬
ные уравнения, как избыточную систему, мы приходим к системе т
нормальных уравнений для этих неизвестных х, у, z.... С другой
стороны, в подобной задаче должно бытья — т — к условий (уравне¬
ний связи) между величинами /,, /2,..., 1п и мы можем решать систему к
условных уравнений для поправок Х2,..., Ал, что приводит к нор¬
мальной системе из к уравнений для коррелат т2» • • • > Y*- Так как
вся трудность вычислительной работы состоит в решении нормальных
систем, то коррелатное уравнивание выгоднее, если й < /я (т.-е.
п — т < т, или я •< 2/я); если же к > т (т.-е. п > 2/я), то проще итти
через избыточные системы. В примере, разобранном выше, я = 6 и
т — 3, так что обе методы одинаково приемлемы.
§ 8. Теорема Гаусса о весах неизвестных.
Переходим теперь к общей задаче определения весов неизвестных
она составляет важнейшую часть способа наименьших квадратов, и'
относящаяся к ней теорема Гаусса служит теоретическим обоснова¬
нием всей методы. Доказательство ее — вообще говоря, не слишком
короткое — мы проведем по частям и для упрощения воспользуемся
формулами теории коррелат.
I. Предложена система условных уравнений:
avx -f- bxy -j-CjZ — lx
a.,x -f • b^y -f- c„z — L
• • • (1)
anx -r bny-\-c„z = ln
He ограничивая общности, можно допустить, что эти уравнения
уже приведены к одинаковому весу умножением на ]///,. и, следова-
зательно, предположить, что все L получены в результате наблюде-
— 138 —
ний одинаковой точности и задаются с одинаковой средней ошибкой,
которую мы примем за среднюю ошибку единицы веса о0.
Для решения этой системы мы должны определить х, у, z, из
системы нормальных уравнений:
[aa] х -j- [ab]y~\- [ас] z — [al]
[ab]x-\-\bb]'y-±[bc]z = \bl] (l'|
[ac] х -j-\bc\ у -J- [сс] z = [с/]
Допустим теперь, что в результате некоторых алгебраических дей¬
ствий нам удалось бы представить х в виде'линейной функции всег
заданных 1п т.-е. выражением вида:
х = ofj/j -j- а2/2 4- • • • + ая/„ , (2]
где <*i, а2,..., ая — пока неопределенные коэффициенты, зависящие
только от а., Ь. и с.. В таком случае (см. стр. 82 и след.) мы могли бы
рассматривать х как результат комбинации рядов /х, /2,.. .,1п,'и,сле¬
довательно, по закону распространения средней ошибки, имели бы:
а\х) = GCjV 4- аро 02 ‘4-... 4- an2a02 = оДо^2 4~a22 4~.. .-]- осД = аДвд].
Для веса х получилось бы значение:
Р(х) — — а0фа] = [aaj
Назовем теперь наилучшим решением системы условных уравне¬
ний (1) то решение, при котором р(х) достигает максимума; так как
но формуле (3) максимуму р{х) соответствует минимум знаменателя
[aa], то наилучшим решением системы (1), приведенным к виду
x — all1-\-...-\-anln, будет то, для которого коэффициенты ^.подчи¬
нены условию: [оса]-минимум.
II. Найдем те уравнения, которым должны удовлетворять коэффи¬
циенты «j, а2,...,ад для того, чтобы формула (2) могла служить реше¬
нием системы (1). Для этой цели множим уравнения (1) соответ¬
ственно на ax, a2,..., an и суммируем, вынося за скобки х, у я z. Это
нриводит к уравнению:
х[а,а, 4- й2а2 ~Ь — + ап +J/[^iai + — + ~Ь 2[ciai -ф- ciH + — + с„ая]
— аЛ Н~ *2^2 4- -• + «Л •
Если теперь в цаписанной суз^ме мы приравняем первую квадрат¬
ную скобку единице, вторую и третью нулю, то и получим требуемое
выражение для х, именно:
X — aj/j 4- a2/2 4-... 4" ajn.
— 139 —
Иными словами: если коэффициенты ах, а2,..., ап подчинить трем
уравнениям:
й1а1 4~ а2а2 4" • • • 4" апап ~ *
^iai 4" ^за2 ~Ь • • • 4~ ь«п=о ........ . (4)
ciai 4“ с2а2 4“ • • • + спап = О,
то выражение х — ах1х 4- 4" • • • 4~ aJn будет решением системы (1).
Если к тому же а. будут удовлетворять еще и условию [аа]-минимум,
то это решение (2) будет и * наилучшим решением системы (1).
Так как для определения ах, а2,...,ая мы получили всего три урав¬
нения (по числу неизвестных х, у, z г) и должны подчинить их усло¬
вию [аа]-минимум, то очевидно, что перед нами задача коррелатного
типа; действительно, нетрудно заметить, что уравнения (4) — не что
иное, как „условные уравнения для поправок", система А, стр. 27,
в которых буква X заменена на букву айв которых невязки h имеют
следующие частные значения: hx~—1, h.2 — 0, /г3 = 0. Поэтому для
решения данной задачи строим нормальную систему для коррелат,
которых здесь три [по числ}Эусловных уравнений (4)]; при указанных
значениях невязок h эта система принимает вид (ср. с системой С,
стр. 29):
[aa\ix 4- [а.ЬУ(.2 -f [яф8— 1 = О
[аЬ}1х+[ЬЬ}ь + [Ьс]ъ =0 . . . . .(5)
[яфч + [bch2 4- [сс] тя = о
Здесь мы отмечаем следующее важное обстоятельство: коэффи¬
циенты коррелатной системы (5) совпадают с коэффициентами нор¬
мальной системы (1') стр. 138, соответствующей заданным условным
уравнениям (1); но свободные члены нормальной системы для х, у, z
'(именно [а/], [Ы\ и [с/]) здесь заменены на 1,0, 0.
Допустим теперь, что решая нормальную систему (5) мы нашли бы
только ее первую неизвестную Yi. Легко показать, что в этом случае
задача определения ,веса х была бы решена; именно мы имели бы:
Р(х) = } (6)
11
Действительно, в виду (3), /»(лг) = . Но по „контрольной фор¬
муле* D, стр. 30, для минимальной суммы квадратов величин а (ко¬
торые там назывались X), мы имеем:
[XX] = [«а] = — [ф] = — -hhx — т2/г2 — у А
мо здесь
К = 1, h% = = 0,
*) В случае одного неизвестного, стр. 86, у нас было только одно аналогичное
уравнение: at -|- аз + аз + • • • = * •
— 140 —
следовательно:
М = ?i; I
но как показано выше:
№ = R
поэтому р(х) = -1-, что и требовалось доказать.
Ti
HI. Отмеченный только-что параллелизм между нормальной систе¬
мой (Г) для х, у, z и нормальной коррелатной системой (5) приво¬
дит к следующей алгебраической теореме:
Если, имея в виду найти вес х, мы будем нормальную систему для
х, у, z решать так, чтобы не множить и не делить при этом ее пер.
вое уравнение ни на какое число, а ограничимся исключением из
него у и z при помощи прочих уравнений нормальной системы, то
в результате этих подстановок коэффициент при х окажется равным
у- ; иными словами и в виду (6), этот коэффициент при х будет
равен весу х.
В справедливости этого положения уже убедились для систем
с двумя неизвестными (стр. 117); мы решали там вспомогательную
нормальную систему:
Aji +Вуа — 1 -f- Dy2 — 0
и нашли, что
ры=•
Для систем с тремя и большим числом неизвестных эта теорема
легко доказывается с помощью основных положений теории опреде¬
лителей *).
Действительно, для решения системы п линейных уравнений с п
неизвестными, вида
Aix + Biy + Ciz + ...=Li
/ = 1,2, . . . , п
служат формулы:
xD = L1Dn -f- L2Di2 +... + LnDln (*)
где D — определитель системы: Dn , D12,..., DXn — миноры элементов
ее первого столбца. Для коррелатной системы (5) Ll==\\ L2 = LZ = 0
и первой неизвестной л; является коррелата Yi • Поэтому согласно (*):
*) Читатель, незнакомый с этой теорией, пропустит доказательство. В § 9 даны
все указания для применения ее к системам с тремя неизвестными, где таким путем
достигается существенное вычислительное упрощение.
— 141 —
где Dn минор элемента \аа\. Далее, мы условились решать нормаль¬
ную систему для х, у, z „без умножений и делений" ее первого урав¬
нения и в левой части (*) должны получить Lx без всякого посторон¬
него множителя. Следовательно, уравнение (*) должно привестись
к виду:
так что коэффициент при х равен Но как сейчас показано,
и поэтому коэффициент при х равен -или, в виду (6), он равенр(х),.
Ti
что и требовалось доказать.
IV. Остается сказать о неизвестных у и z. Для определения их
весов мы представим их в виде:
У — *1^1 "Ь *2^2 + • • • + «Л; 2 = ai'h + а2% +-••-+- ’
и без труда найдем, что коэффициенты а.' и а." будут удовлетворять
системам трех уравнений, аналогичным (4) с невязками, для у. О, —1,0
и для 2:0,0,— 1. Поэтому, составляя нормальнь/е системы (5) для
коррелат -.у', у2', у8' и ух", ';2", у3", мы в левых частях соответственно
получим 0, — 1, 0 и 0, 0, — 1. Затем точно так же, как выше, дока¬
жем, что
Р(У) ~ [a'a'j ~ у~' P(Z) = [а"а"] = 77"
и найдем что р(у) равен коэффициенту при у во втором нормальном
уравнении, когда из него исключим х и z; аналогично этому p(z) будет
получен как коэффициент при z в третьем нормальном уравнении, когда
исключим из него х и у.
Наконец, пользуясь определителями, найдем, как выше:
Р(*)= тг> Р(У) = £~> P(z) = ~,
Uli U22
где в знахменателях стоят миноры диагональных элементов нормаль¬
ной системы, т.-е. элементов [аа\у [bb\ и [сс\, — что можно в общем
виде формулировать так: веса неизвестных равны отношениям опре¬
делителя нормальной системы к его главным минорам.
V. В п. II было показано, что — представляет собой тот наи-
TL
больший вес, который неизвестная д: может получить в результате
комбинации заданных L в виде линейного выражения (2). Сопоставляя
это с п. III, видим, что решение нормальной системы (Г) для неизвест¬
ных приводит к уравнению для х, в котором коэффициент при неиз¬
— 142 —
вестной равен именно этому максимальному ее весу *). Таким образом
мы приходим к теореме Гаусса:
Решение избыточной системы условных уравнений по способу наи¬
меньших квадратов, т.-е. через посредство системы нормальных
\равненийу обеспечивает неизвестным наибольший коэффициент и,
следовательно, наименьшую среднюю ошибку или наибольший вес.
Таким образом, наилучшее решение в смысле „[ае]-минимума есть
в то же время наилучшее решение в смысле „вес неизвестных мак¬
симум “, и в этом обстоятельстве заключается обоснование способа
наименьших квадратов, как общей методы уравнивания 2).
§ 9. Вычисление весов и средних ошибок. Пример.
Применим выведенные правила к решению практических задач,
Начнем с системы с тремя неизвестными. Здесь наиболее простым
является способ определителей и для пользования им достаточно
иметь в виду следующие положения:
1. Из 9 заданных коэффициентов трех уравнений
А^х —[“ Р\У ~|“ CyZ ==
А2х —J— В?У “f" £*2^ === -^2
А$х -j- Bvy -|- С3£ = Z,3
составляется определитель третьего порядка:
D =
A'i ВД
А2В2С2
А,В,С,
= А1т
В2С2
В,С,
-вг.
а2с2
а,а
+Q-
а2в2
AqBs
где множители при А1У В1 и С± — определители второго порядка, рав¬
ные разностям произведенйй их элементов, взятых крест-на-крест
Таким образом:
В2С2
В%Сй
А2С2
AqCq
— А2Сл С2А% ,
а2в2
A*BZ
*) Алгебраически доказывается еще следующее: выражение для х вида
х = + a,J2 +... + ап1п, при условии [асх]-минимум, удовлетворяющее заданной системе
уравнений (1), тождественно со значением х, получаемым при решении нормальной
системы, а именно:
*=т %+[Ы] +щ -g.
2) Следует отметить полную аналогию между проведенным здесь доказательством
и выводами в § 5, отд. II, где условием уравнивания было поставлено начало комби¬
нации ряд ,в по правилу наибольшего веса, и обнаружено тождество этого правила
со способом наименьших квадратов: (См. стр. 86—87).
— 143
2. Минор, соответствующий данному элементу, есть определитель
второго порядка, который получается из В, если в нем вычеркнуть ту
строку и тот столбец, на пересечении которых стоит данный элемент.
Написанное выше выражение для D есть разложение его по ми¬
норам первой строки.
Согласно этому определению миноры диагональных элементов (глав¬
ные миноры) суть:
Du —
в„с2
в1а
£>22 =
•AiCi
А»Са
D.
за-
А,В,
А&
С помощью этих простых формул и вычисляются веса не¬
известных:
р(х) р(у) = 7Г ; /»(*) = 7? •
Пример. Дана нормальная система:
12,0 х- ЬАу— 1,8 z — 18,57
— 5,4* +21,6у —13,1* = 46,45
— 1,8 х — 13,1 v + 28,9 = 199,94
Здесь мы имеем:
£>=12,0 { 21,6-28,9—13;ЫЗ,1 }+5,4 { —5,4-28,9 +
— 13,1-1,8 } — 1,8 {5,4-13,1 +21,6-1,8 } =4265,2.
£>„ = 452,6;
£>22 = 343,6 Dj.
: 230,0.
Таким образом;
. . 4265 .. , . 4265
^)= 453 =9'4; Р{У)=Ш-
■ 12,4; p(z) =
4265
230
: 18,5.
Заметим, что точность до 0,1 в этих вычислениях обычно вполне достаточна.
Переходим теперь к другим вычислительным способам и обратимся
к схеме решения нормальных уравнений на стр. 46. Нетрудно видеть»
что в ней заключительное уравнение для последней неизвестной t
(именно уравнение 18,94 t — 7,06 = 0) получено в полном соответствии
с условием „не множить и не делить" — ибо мы исключали на пре¬
дыдущих ступенях л;, потом у и 2, но оставляли последнее нор¬
мальное уравнение, каким оно было дано. Поэтому коэффициент
неизвестной в уравнении, получаемом на последней ступени, или, как
говорят, коэффициент последней неизвестной равен ее весу. В этом
примере p(t)— 18,94.
Чтобы получить веса других неизвестных, можно было бы пере¬
страивать систему так, чтобы на последнем месте оказалась любая
из неизвестных. Тогда ее заключительный коэффициент и будет
равен ее весу 1). Но этот прием, требующий повторной работы
*) Ср. также примеры, стр. 319.
- 144 —
исключения, не рекомендуется; вместо него, пользуясь теорией пре¬
дыдущего §, мы введем в схему наряду со столбцом свободных
членов — [al], — [bl], — [cl] новый столбец со свободными членами
нормальных уравнениях—1, 0, 0, 0, .... Этот столбец мы будем
вести совершенно так же, как столбец — [al], — [bl], вписывая
в него числа элиминационных строк, контролируя через .S, причем
5Х = — 1 —f- 0 —[— 0 —j— = — 1 и т. д., и когда дойдем до конца, построим
новую схему „горкой"; крайняя неизвестная этой горки влево, т.-е.
соответствующая х, даст утиными словами величину обратную
р(х). Чтобы найти р(у), мы заведем еще один столбец, начиная со
второй ступени, в которой х уже исключено, со свободными чле¬
нами—1,0,0, 0,..., и доведем его до конца; затем составим новую
„горку", крайняя неизвестная которой, соответствующая у, даст
величину обратную р(у). Таким же образом для третьей
неизвестной мы повели бы еще один дополнительный столбец,
начиная с третьего квадрата, составили бы еще одну схему горкой
и нашли бы величину,, обратную p(z). Но если г — последняя неиз¬
вестная, то эта часть работы отпадает, ибо коэффициент при z, как
уже сказано, равен p(z).
Все это иллюстрируем на примере, который читатель повторит
за нами, чтобы раз навсегда уяснить себе ход работы.
Задана система из 4 условных уравнений для 3 неизвестных х):
х— .у + 2 z = 3 [аа] = 27 [ab] = 6 [ас] — 0
3x + 2j; __5z= 5 [bb] =15 [be] = 1 [cc] = 53
4-*+ У + 4^=21 [al] =88 [bl] =70 [c/] =107
— * + 3.y + 3z=14 [ZZ] = 671
Нормальная система для x, у, z имеет вид:
27*+ 6у — 88 = 0
6* + 15.У+ z — 70 = 0
+ у +54 z — 107 = 0.
Пояснение схемы (стр. 147). Обозначения q(x), q(y), q(z) введены
для величин, обратных весам: q(x) — и т. д. Вычисление
х, у, z производится совершенно так же, как в основном примере
стр. 46; свободные члены условных уравнений, для удобства обрат¬
ной подстановки, перенесены в левую часть. В столбце
q(x) на строках Nlt N2, N& поставлено — 1, 0, 0, так что свободные
члены и здесь перенесены налево; поэтому в строке 5 имеем
51==— 1+0 + 0 = — 1; в строке стоит — А — — 0,0370. Это число
мы множим на 6, на 33 и т. д., параллельно с умножением на них
1) Пример Гаусса из „Теории движения небесных тел"
— 145 —
чисел —[а/], —[Ы]... Таким образом, весь этот столбец доводится
до конца. После этого оба „курсивные числа“ этого столбца,
именно -{-0,0163 и —0,0370, переносим в столбец —/и производим
подстановку с теми самыми множителями, которые уже имеются в
столбцах х, у, z.
Первая неизвестная вспомогательной системы равна здесь:
Эту величину множим на курсивные числа в столбце
z (т.-е. 0,0732 и 0); придав произведение к-{-0,0163, получаем, после пе¬
ремены знака вторую неизвестную в столбце^, именно —0,0163; помно¬
жив ее на курсивное число из столбца у, т.-е. на 0,2222, и придав про¬
изведение к—0,0370, находим, после перемены знака, „крайнюю" неиз¬
вестную первой системы, которая и есть q(x) — = 0,0406. Такая же
обработка второго столбца для q(y) приводит еще к одной схеме
горкой, причем из столбца q(y) в столбец —/ переписывается
ЛЛ7пл 0,0735 л г\г\ 1 о
0,0732; первая неизвестная здесь равна—5393” —~0,0013; она мно¬
жится на 0,0732 и произведение прилагается к —0,0732, что дает
после перемены знака крайнюю левую неизвестную этой вспомога¬
тельной системы, в данном случае:
q(y) = ^ = + 0,0733.
Наконец, для p(z) особого вычисления не требуется; он равен
коэффициенту при z, т.-е. 53,93, и поэтому для симметрии приписано
q(z) = 1 : 53,93.
Таким образом находим:
Р(х) - 0^06 = 24’63; р{^ =■ 0,0733 = 13>65’ № = 53-93-
Вычислим те же веса с помощью определителей. Здесь
| 27 6 0
D=] 6 15 1
i 0 1 54
27 . (15-54— 1)- 6.(6.54) + 0=19899
Du = 15.54 — 1 = 809; D,, =27.54 = 1,458; 2>яя = 27 .15 — 6. 6 = 369
Таким образом значения весов следующие:
**)="w=24>597; м ~w »13>648; № - -ж?=53’926-
Веса, найденные выше по схеме, совпадают с этими значениями
в пределах точности вычисления.
Но наша схема может, конечно, служить для самой об!цей системы
п нормальных уравнений; в ней появятся п—1 вспомогательных
столбцов для величин обратных весам q(x), q(y) .. .; столбцы эти
спускаются лестницей в правой части схемы. Числа из этих столб-
СпосоС найм, квадратов. ^
- (46
цов, стоящие в элиминационных строках, переносятся последова
тельно в столбец —/. Затем образуются я—1 вспомогательные
схемы „горкой”; в первой из них я строк, во второй я— 1, затем
я— 2 наконец, 2 строки. Крайние слева неизвестные этих схем
и дают искомые величины q(x), q(y), q{z) ..., обратные весам р(х),
р(у), p(z)... Остается упомянуть еще про средние ошибки неизвестных;
по общему правилу:
<*) = -+,; е(у) = *(*) =
VЫх) \/р(У)
Для о0 Гауссом дана формула:
V
}
т
где я число условных уравнений, tn число неизвестных. ,
(Вывода этой формулы, который в основе соответствует выводу
формулы Бесселя, стр. 91, но алгебраически значительно более
сложен, мы не приводим).
Стоящая в числителе [ее] определяется непосредственной подста¬
новкой найденных х, у, z в условные уравнения и контролируется
по формуле *):
[ее] = [//] — \al\x— \Ы]у — [cl\z
(знаки соответствуют случаю, когда свободные члены справа).
Для примера Гаусса [//] = 671 и поэтому;
[ее] = 671 —88*2,4702 — 70-3,5508 — 107* 1,9157 = 0,0865.
Непосредственная же подстановка дает для г.:
— 0 2492; -0,0663; +0,0944; —0,0707.
отсюда [ее] = +0,0804; большее согласие здесь недостижимо.
Таким образом (при я = 4 и т. — 3) имеем:
-Ах) = ]/°’°860 = + 0,057; а(у) = |/°’°80 -= ± 0,077;
, . т f 0,
Az) — У 53 '
°f = + 0,039.
§ 10. Обозначения Гаусса и формула для суммы квадратов
остающихся погрешностей.
' Для выделения последовательных стадий исключения неизвестных
при решении нормальных систем Гаусс ввел особое знакоположе-
кие. Взятое само по себе, оно не имеет большого практического зна¬
чения, и мы приводим его только с целью облегчения вывода еще
J) Еще один способ вычисления [ее] будет показан ниже, см. стр. 150.
— 147 -
£
ГМ CM
N. CM CM
<*> CM CM
^ CM CM
« <^To сГ о
i I ! I
cm cm
£0 со
N I—
Q> о
CM CM CM Co
00 00 00 ^
N-. t— ^
о о o^>
<^> О О —ч—
I I
О О C^
+++
О» CVj
CM 4>
CM ^
CM <2>
00 CM CM Ю
to o- CMOO
r-. CM CM 00
О CM CM CM
^ О Tt* ^ f-
Tf *"4 r—t Tf Ю
Ch OlTTTfCO
o'co t—con'nTt^
ю о ЮЮЮ
£м
R
см
СО
СОч
N-
N- t—
см
СО
со
CD
СО СО
СМ
со
со
СО
со со
СМ
со
со
со^
со со
О 45 Ю т—< гН
см |>Г
СО**ч т—*
*—*
СМ
т—<
Т— 1—1
I - *nCD to CO CO
CM CO oo
Ssute; 5: со"
l^aTISs"
Co
oo oo oo
to CO C2>
T—1 Г—I ^5
о о ^
ootf
-I—1_ _l—j—I—1_ I I I
N N.
OO lo
о ^
COO^
oo' "-Г
о
см
см
оо
со
со
со
N»
N
<м
о
ож
о
о'юю
•r-J4
со
ю ю
ю
l£§^-
S
e§
*
I
C3
ж
05
<3
<ъ
8*
«
о oo
—• ©
CD Ю
CCCN
od od
N. CM
*o о
’*•4
<o“
OOr-t
45 CD
oo
to N-
СУЭ ©
см
R
Cm
+
C'O
45
CM
г*.
4>
<*d
a
8f
к
$
«а.
00 о
to N-
— 00
о о
+
см
00
N-
о
o'
00 о
о о
О Г->
о о
сГо“
+
СО*-«
«-Н О
о о
о о
3}
$
ч!
О
оо со
СО СО
- о
о о
45
оГ
22
R
4>ч
+
>5
Cj«
+
42.
CJ1
10*
— 148 -
одной формулы для [гг], имеющей первостепенную важность для спо¬
соба наименьших квадратов.
Пусть дана нормальная система с четырьмя неизвестными х, у, г
и t; запишем ее в сокращенном виде, поместив на (л-|-1)-ю — здесь
пятую строку член [//], необходимый для вычисления [гг] по фор¬
муле;
M = [ll)-\{al]x-\-[bl\y+[cl]z+\dl}t) (а)
Итак, имеем:
у
Z
t
1
I-
[аЬ]
[ас].
]ad]
[al]
[ЬЬ]
[Ьс]
[bd]
[bl]
[сс]
[cd]
[d]
[dd]
[dl]
[11]
Для исключения х нам надо будет под первой строчкой подпи¬
сать первую элиминационную строку Еи именно:
j \аЬ] \ас} \ad] [al]
[аа] [аа\ \аа]
Путем уже известного нам процесса умножений и вычитаний
(стр. 46) мы к следующей ступени схемы освободимся от неизвест¬
ной л*; это обстоятельство, т.-е. факт исключения одной неизвестной,
по Гауссу обозначается приписывая „1“ внутрь коэффициентов,
общие обозначения которых берутся со второй и следующих строк
написанной выше сх^мы. Поэтому уравнения второй ступени записы¬
ваются следующим образом:
у z t I
~[bbl] [bcl] [bdl] [bl\]
[ccl] [cdl] [c/1]
[ddl] [dll]
[III]
Здесь каждое число получается из соответствующего числа первой
схемы, притом так, что если это последнее находится в её 6-й строке,
то из него вычитается произведение 6-го члена ее элиминационной
строки на член первой строки, стоящий в ее 6-м столбце.
Так, например, имеем:
[bbl] = [ЬЬ] --И]; [а/1] = [cd] -[ad]
и т. п.
При этом, под [III] мы понимаем аналогично образованное выра¬
жение:
1"Ч = М-Й.М = [Щ-Й <■>
— 149 —
Переходим к третьей ступени; тут будут уже исключены две не¬
известные, и обозначения примут следующий вид:
z t I
[сс2] \ссЩ [с/2]
[dd2] [dl2]
[112]
Здесь, аналогично предыдущему, имеем, например:
[сс2] = [сс\\-Щ±.[Ьс\\, {dl2} = [dl\]-[^.[bl\\.
Заметим, что и здесь положено:
[112] = [//1] - Ц1Ь\\ [Ы1] = [//1] - М]2 (2)
Наконец, на последней ступени, из которой определится неизвест¬
ная t бу^ем иметь:
t I
[dd‘3] [dl3]
[ИЗ]
Согласно предыдущему, здесь введено обозначение:
[ИЗ] = [U2] - '^{-И2] - [112] - [Ц* (3)
После этой стадии вычислений начинается обратная подстановка,
т.-е. нахождение z, у, х; но мы можем, пользуясь числами последней
схемы составить еще выражение:
\1Щ = [ИЗ] - ,gj ■ \4Щ = [ИЗ] -Щ. (4)
Внося в (4) полученные выше значения для [//3], [112], [III], из (3),
(2), (1), выводим:
т=т-{т+^+Ш&Ш ©
Покажем теперь, что часть выражения (5), заключенная в фигур¬
ные скобки, равна [а/]л:-|- [Ы]у-\- [cl]z-\- [dl]t.
Для этой цели выпишем все четыре элиминационные строки, со¬
ответствующие данной нормальной системе, и сложим их, предвари¬
тельно умножив на [al], [bll], [с/2] и [dl3\. Мы имеем:
v _ц И] ,, I Гас1 ~ I ИП + _ И].
[аа]у Г [ал] ^ “I [аа] L ~ [аа]
, [bc\] \[bdl] ,\ЬП]
у 1 [ЬЬЦ ' [ЬЬЦ [ЬЬЦ
, [cd2] . _ [сЩ
* 1 [сс2] ~~ [сс2]
f —
~~ [ddi]
[al]
^ (б)
[с/2]
[dl3]
- 150 —
После простых приведений слева получится сумма [at\x-\-[bl\y-f
-\-[ct\z-\-[dI]t-, а справа — сумма заключенная в фигурные скобки!
в формуле (5). Имея это в виду и сравнивая формулу (а) с форму¬
лой (5), приходим к равенству:
Это и есть окончательная формула Гаусса для суммы квадратов
остающихся погрешностей. Очевидно, что она применима к любому
числу т неизвестных и в общем случае напишется:
м-[/'.«ч-и-Н-Ц- - • •«
Приняв во внимание взаимное расположение величин и [а/]?
|Ш\ и и Тв А* в предыдущих схемах, мы можем найденную фор¬
мулу высказать в следующем виде: сумма квадратов остающихся
погрешностей равна сумме квадратов свободных членов I без суммы
произведений чисел, находящихся в столбцах свободных членов в эли-
минационных строках, на числа, стоящие непосредственно над ними.
В таком виде формулой (Ь) и пользуются для нахождения [зе] не¬
посредственно из схемы нормальных уравнений; так, обращаясь к при¬
меру стр. 147 и перемножая числа, отчеркнутые сбоку в столбце /,
имеем:
[ее] = 671 — 88-3,2593 — 50,443-3,6910 — 103,3090-1,9157 = 0,0837
На стр. 146 по другой формуле мы нашли [зе] = 0,0865; схождение
достаточное в виду неизбежной игры последних знаков.
Но формула (Ь) имеет и более глубокое значение. Сопоставляя ее
с формулой для [ег] на стр. 111, находим, что сумма, заключенная
в (Ь) в фигурные скобки, представляет собой улучшение реше¬
ния в том случае, когда I. являются невязками, получаемыми в ре¬
зультате подстановки в условные уравнения приближенных значений
неизвестных. Поэтому важно убедиться, что каждый из членов внутри
фигурных скобок есть величина существенно положительная, так что
от вычитания его из [//], [ез] уменьшается и, следовательно, происхо¬
дит улучшение решения. Чтобы доказать это, достаточно выяснить,
* „ [л/р [Ы\ р
что знаменатели дробей ^^ и т. д. суть величины положитель¬
ные. Это свойство очевидно для [аа}\ для [bb\\ оно доказывается,
исходя из формулы:
[ЬЫ) = [bb\ - .[ab] _ \ЬЬ\-\а«]--\аЬ]*
Применяя к числителю известное тождество Лагранжа:
А2 4- *22 4- • • 4-о • А2 4- ьг +... ■+ V) - («А +•»• • + 4А)2 =
= (алЬ2 — афгу 4- ... 4- (апьп_ 1 — an_tbn)\
мы видим, что \bb\] распадается на сумму квадратов, деленных на
всегда положительное \аа\, и потому является величиной существенно
положительной. Точно также докажется это свойство для \сс2], \ddS>\
и прочих знаменателей формулы (Ь). Но это и обнаруживает, что
после решения системы по способу наименьших квадратов, [гг] должна
всегда -уменьшаться по сравнению с [//]; а так как вся величина [se]
должна привестись к минимуму, то сумма, заключенная в фигурные
скобки в формуле (Ь) и представляет собой максимальное улуч¬
шение, возможное для данной системы условных уравнений при ре¬
шении её по методе наименьших квадратов.
Формула (с) лежит в основе применения методы наименьших ква¬
дратов к весьма важным вопросам, с которыми мы познакомимся
в следующем отделе курса.
§ 11. Приведение квадратичной формы для суммы квадратов
остающихся погрешностей к каноническому виду.
Только на данной ступени изложения оказывается возможным при¬
вести некоторую заключительную формулировку всей изучаемой ме¬
тоды уравнивания. С этой целью мы выразим сумму квадратов остаю¬
щихся погрешностей в функции неизвестных х, у, z и будем отыскивать
минимум этой суммы, рассматривая теперь х, у, z как независимые
переменные. Условные уравнения стр. 104 показывают, что каждой
совокупности значений этих переменных соответствует определенная
совокупность значений остающихся погрешностей е.,. определяемых
равенствами:
*t = atx + bly-\-c? — lt
U 1, 2, . . п)
Отсюда находим:
[ег] = [(«!■*; -}- Ъ.у -|- cz — /,)2]
Обозначая функцию, стоящую в правой части, через 2 (х, у, z)
раскрывая скобки и делая приведения, имеем:
2 (х, у, z) — [аа)х2 -f- [bb]y2 -f- [cc\z2 -j- 2\ab\xy 2\ac\xz -f-
-f- 2 \bc\yz — 2\al\x — 2 [bl\y — 2 \cl\z + [//] (1)
Выражение подобного рода носит название квадратичной
формы в переменных х, у, z\ в данном случае, происходя из суммы
квадратов, эта форма может принимать только положительные
значения при любых значениях этих величин *). Поэтому форма
2 (д;, у, z) допускает определенный минимум, и на основании теоремы
') Мы предполагаем, что все г- не могут быть равны нулю, следовательно, и
Щх, у, г) не может обратиться в нуль ни при каких значениях переменных.
— 152 —
предыдущего § мы знаем, что этот минимум равен [//,3]. Наша задача
сводится теперь к тому, чтобы путем введения новых переменных
5 преобразовать форму (1) к такому виду, при котором именно это
значение ее минимума и будет очевидным. С этой целью вводим
функции*):•
Afj = [аа\х -|- [ab]y -\- [ac]z — [al]
N.,= [ab]x+[bb]y + [bc}z — [bl)
N3 — [ас] х -)- [be] у -f- [сс\ z — [cl]
L' = [al] x + [bl] у + [cl] z — [11]
Как легко убедиться, при этих обозначениях имеем тождественно:
2(х, у, z) = xN1-\-yN.i-\-zN.i — L (3)
Обратимся теперь к схеме элиминационных уравнений (6) стр. 149
и будем рассматривать левые их части (куда перенесем и свободные
члены) как функции х, у, z, которые обозначим через Ех, Е2 и Е3,
т.-е. положим:
р I [аЬ] | [ас] [al]
Zi—x-f-^у -f- г ^
в — v + шг-т. • (4)
Ci~ V^[bb\] [ЬЬЦ w
F- z-[cl2]
\сс2]
Из самой схемы решения нормальных уравнений, т.-е. из процесса
получения элиминационных уравнений £\ = 0 из нормальных уравне¬
ний АЛ = 0, не трудно установить, что между функциями Е. и функ¬
циями АЛ существует следующая зависимость:
Е> = Г«2]'' N‘ ~ ^'Е'- ~ ^
Из этих уравнений, обратно, выводим:
Nx = [аа] Ех
N, == [ab] Ег + [ЬЬ 1] Е,
ЛЛ, = [ас] Ел + [Ьс\] Е., + [сс2] Е3,
Поэтому выражение xNl-\-yN.,-\-zN.i, входящее в правую часть (3),
нринимает вид:
xN1 -\-yN2 zN.a = Ех {[дя]л; -f- [ab]y -j- [ac]z j -f-
+ Ей{[ЬЬ\]у+[Ьс\]г} +
+ E3-[cc2]z
*) Следует заметить, что, полагая N] — N2 = N3 = 0, мы получаем систему нормаль¬
ных уравнений для неизвестных; Nt, N2, N3 суть частные производные £2 по х, по у
и по z (деленные на два). Таким образом, нормальные уравнения могут быть получены
из Q по правилам дифференциального исчисления для нахождения минимума функций
многих переменных.
- 153 —
В силу уравнейий (4) первая фигурная скобка равна [aa]Ex-\-[al]\
вторая скобка равна [bbl] Е2-\-[bll]; наконец, множитель при Е« равен
[сс2]Ео-\-[с12\\ подставляя эти выражения в только-что написанное
равенство имеем:
xh\ + yN, + zNn = [аа] Е2 + [bb\] Е2 + [сс2\ Е* +
+ [al] Ег + [ЫЛ] Е, + [с/2] Е, (5)
Для преобразования последних трех членов в правой части множим
уравнения (4) соответственно на [а/], [Ы\] и [с/2]; после простых пре¬
образований (ф-лы стр. 148—149) эти члены приводятся к виду:
[al] Ех + [bll] Е2 + [с/2] Е, = \al\x + [Ы\у -f [cl\z +
_ [aiy [bllf _ Icl2]a
~[aa\ [bbl] [cc2] * ’
В виду последней из формул (2) первые три члена в правой части
могут быть заменены выражением L [//], и поэтому, подставляя все
в (5), находим:
хМг +yN2 + zN2 = [аа] Е2 -f [bbl] Е2 -f [сс2] Е 2 + L +
, г//1 _ М2 _ № I3 _
. ' 1 J [аа] [bbl] [сс2] '
Но при обозначениях, принятых при доказательстве теоремы пре¬
дыдущего §, совокупность членов во второй строке справа есть [//3].
В В1$ду этого, комбинируя (3) с полученным сейчас равенством, при¬
ходим к окончательному выражению для формы Q (х, у, z):
Q (*, у, z) = [аа] Е2 + [bbl] Е2 + [сс2] Е2 + [//3] .... (6)
Рассматривая в этой формуле Е19 Е29 Еп как новые переменные
введенные вместо х, у, z по формулам (4), мы заключаем, что квадра¬
тичная форма (1) преобразована здесь к такому виду, в котором эти
новые переменные входят только в квадратах (произведения и первые
степени их отсутствуют). Подобный вид формы носит название кано¬
нического; в данном случае, он имеет еще ту особенность, что
все коэффициенты при квадратах новых переменных Ег, Е2 и Е.л, т.-е.
величины [аа], [bb\] и [сс2], по доказанному раньше, суть числа по¬
ложительные. Но именно из этого обстоятельства обнаружи¬
вается, что форма Q (х, у, z) достигает минимума тогда и только
тогда, когда Ех = Е2 = Е?) = 0.
При этом условии мы имеем:
2„,„ = М = [ЙЗ] т
что и соответствует теореме § 10-го.
Формула (6) распространяется, очевидно, и на избыточные системы
с любым числом т неизвестных; исходя из нее, мы можем резюми-
— 154 -
ровать алгебраическую сущность способа наименьших квадратов сле¬
дующим образом:
Квадратичная форма, выражающая сумму квадратов остающихся
погрешностей в функции независимых переменных х, у, z...,npu
любых значениях этих переменных может быть преобразована
к каноническому виду, с положительными коэффициентами [аа\,
\ЬЬЦ, [сс2]... при квадратах новых переменных, Ех, Е2, Ея..Ет; эта
форма принимает ее наименьшее значение при условии определения
х, у, z... из системы уравнений Ех— 0; Е, = 0;... Ет — 0, соответ¬
ствующих системе элиминационных уравнений схемы Гаусса; при
этом минимум ее равен свободному члену преобразованной формы
и определяется выражением:
I// т\г/л _ w _ lwl l2 _ Гс/2р
\ll,m\ [ll\ jcc2j
Указанные сейчас преобразования имеют фундаментальное значение
при изложении методы наименьших квадратов в связи с положениями
теории вероятностей *).
§ 12. Заключительный пример и схема 2).
Для пояснения всех деталей вычислительного процесса рассмотрим
решение системы из 8 условных уравнений с 4 неизвестными:
cix-irbiy^ciz^dit = li *
(/^1, 2, . . 8)
1
° !
b
I
С ]
d
/
1
— 4,958
-1,629
— 2,634
+ 2358,0
- 0,006387
2
-f 0,988
- 5,299
+ 2,608
-1156,0
+ 0,000741
3
— 5,409
- 0,457
+ 2,710
+ ■ 77,0
— 0,000085 ;
4
- 1,317
- 6,300
— 3,310
—1651,0
— 0,003969
5
—1,711
— 0,579 %
— 0,912
+ 819,0
— 0,002255
6
— 0,075
— 0,073
+ 0,032
+ 2,0
+ 0,000168
7
-1,869
-0,164
+ 0,937
+ 26,0
— 0,000025 1
8
— 0,124 .
— 0,127
!
1
— 0,079
— 56,0
— 0,000263
Свободные члены / выражены здесь в радианах; в той же мере
получатся и неизвестные' х, у, z, t.
5) Ср. Лахтин. Курс теории вероятностей, ГИЗ. 1926, стр. 165 и след.
2) Пример сообщен Н. В. Комендантов ым; данные относятся к исправлению
элементов планетной орбиты.
— 155 —
Для приведения уравнений к однородности вводим новые неиз¬
вестные, так чтобы коэффициенты при них выражались в единицах
4 знака; вместе с тем умножим свободные члены на 100, чтобы
иметь и в них четыре знака после запятой.
Таким образом приходим к системе:
где:
1
10
А.Х+ ВSY -f CZ -|- D,T= Z, ,
ai; В, — 10 6,; С. = 10 с.; — ]0000 dt \L.— \00 L.
Пусть X, Y, Z и T - решения соответствующей нормальной
системы, и о(Х), о(К) и т. д. их средние ошибки. Тогда исходные
неизвестные с их средними ошибками получатся по формулам
(см. стр. 45):
Х ” l OOO Х',У = -Що 2 ~ 1006 ^ ^ ~ 1666666 7
Ю00°(П <V) ню0 °(}/)> a(z)= 1666 Гообооо °CD •■•(*)'
Переписывая систему условных уравнений в ее однородном виде,
составляем по строкам суммы S’, включая в них и свободные
члены L. Столбцы L.t и е. заполняются после решения нормальной
системы и подстановки X, Y^Z, Т в условные уравнения.
А
В
С
D
L
L
£
5'
1
0,4958
-0,1629
0,2634
+ 0,2358
I
0,6387
- 0,6396
_
9
.
1,3250
2
+
988
- 5299
+
2608
—
1156; +
741
+ 744
+
3
2118
3
—
5409
- 457
+
2710
+
77
—
85
— 85
0
—
3164
4
—
1317
- 6300
—
3310
—
1651
—
3969
— 3971
—
2
—
1,6547
1 5
—
1711
- 579
—
912
+
819
—
2255
— 2222
+
33
—
46381
6
—
75
73
+
32
+
’ 2
+
168
— 37
—
205
+
54
7
1869
— 164
+
937
_j_.
26
—
25
- < 31
—
6
1
1095
Г
—
124
— 127
—
79
—
56
L
263
— 96
+ 167
1
649
I 2
—
1,4475
—1,4628
—
0,0648
+ 0,0419
i
1,2075
(= — 4,1407)
! _ _
s —
4,1407
Правильность вычисления 5' контролируется тем, что сумма чисел
в столбце S’ составляет — 4,1407, в согласии с суммой чисел в стоке
Коэффициенты нормальных уравнений образуем путем непрерыв¬
ного действия на арифмометре, последовательно умножая столбец на
самого себя и на все следующие. Это приводит к системе:
156 —
X
Y
Z
г !
j
I 1
L !
+ 0,6299
+ 0,1493
+ 0,0515
— 0,1252
+ 0,4201
+ 7102
+ 1047
+ 1218
+ 3285
+ 3376
- 0427
■ + ‘3372 |
'
+ 1030
— 1120
+ 0,7055
+ 1,0860
+ 0,4511
• +0,0569
+ 0,9738
Для, контроля составления нормальной системы образуем ее сум¬
мовую строку Sx (читая каждый столбец до его конца и продолжая
затем направо до столбца Т). Тогда сумма чисел суммовой
строки, считая в ней свободный член дважды, должна
равняться сумме квадратов S' без суммы квадратов
свободных членов L (что легко выводится из формулы (5),
стр. 109). Обе последние суммы составляются особо. В данном случае:
[S'S'] = 4,8700; [LL] = 0,6229; [S'S'] — [LL] = 4,2471.
Сумма всех чисел на суммовой строке Sv включая член L, равна
3,2733; прибавляя к ней еще раз, свободный член 0,9738, получаем
4,2471, как и выше.
После этого контроля переходим к самому решению нормальной
системы для X, Y, Z, Т и их весов, по правилам и схемам стр. 144
и сл. Заметим только, что здесь свободные члены стоят в правых
частях; поэтому, дойдя до последнего остаточного уравнения, 0,0352Г=
= — 0,0348, получаем Т= — 0,9886 (без перемены знака). Помножая
эту величину на числа, стоящие над ней в элиминационных строках,
мы должны придать произведения к свободному члену, но с пере¬
меной знака. Так, имеем: Z +0,1643 = 0,8463, откуда Z = + 0,6820
и т. д.; то же и при решении вспомогательных систем для величин
q(X), q{Y), q(Z) и q{7), обратных весам р(Х), p(Y), p(Z) и р(Т). Схемы
этих решений, напомним еще раз, получаются из основной, последова¬
тельно внося в столбец L „курсивные числа" из столбцов q(X), затем
q{Y) и т. д. и принимая за первые неизвестные, с которых начинается
подстановка в схемах „горкойа, числа строки Z4, т.-е. -(-6,9261;
— 7,0256; +4,7216.
Найдя значения X, Y, Z, Т, мы должны были бы подставить их
для формального контроля в нормальные уравнения Nly N2y
N% и Л+ Вместо этого можно ограничиться подстановкой их в пер¬
вую суммовую строку S1. Это дает здесь 0,9736, в то время как сво¬
бодный член этой строки равен 0,9738.
Для более полной проверки всего решения нужно обратиться к [ге].
Прежде всего, подставляя Ar, Y, Z, m в условные уравнения, обра-
- 157 —
зуем числа Z; с ними составляем s. — Li — L. и находим [гг] ~ 0,00071.
С другой стороны по формуле Гаусса [гг] равно [LL\, здесь 0,6229,
без суммы произведений чисел, отчеркнутых в схеме в столбце L-,
эта сумма составляет 0,62196, так что [гг] = 0,00094, в достаточном
согласии с непосредственным ее определением.
'Имея [гг], находим о02 — — 0,000178, так что
о0 = zi= 0,0133.
Отсюда выводим средние ошибки неизвестных X, Y, Z, Т (помня,,
что q(X), . . . суть величины обратные весам):
<Х) = Яу^ху, С (Г) = а0 \/q(Y) ... И Т. д.
Значения Уq и произведения их на о0 даны в правом нижнем
углу схемы. Таким образом получаем: ,
^= + 0,3039 + 0,0244 Z =+ 0,6820 + 0,0263
Y = + 0,4676 + 0,0241 Т = — 0,9886 + 0,0709
После этого остается перейти к исходным неизвестным х, у,- z
и t их средним ошибкам; по формулам (*) получаем:
х = + 0,0003039 + 0,0000244; 2 = + 0,0006820 + 0,0000263
у = + 0,0004676 + 0,0000241; t = — 0,0000009886 + 0,0000000709
Все эти значения выражены в радианах; по условиям задачи их
нужно превратить еще в секунды дуги, умножая на 206264",8, что
и дает окончательно:
х = + 62",68 + 5",03 г = + 140",67 + 5",42
V = + 96",45 + 4",97 t = — 0",2039 ±0",0146 (средн. ошибки)..
0,6299 0,1493 0,0515 —0,1252 - 0,42011 1,0000
1,0000 0,2370 0,0818 - 0,1988 0,6670 \ 1.5876
0,14v3 7102 1047 1218 3285 0,0000
1493 0354 0122 — 0297 0996 2370
0515 1047 3376 - 0427 3372 0000
- 158
О С\* О СМ
О Оо о CD
О О
О *ч О
—~ «о4 о
О 0Q
СО О S со i
i-и О О 00
2s
ОО^Ог-»ОЮООСО
О^ОГ^О^ООг-.
ООООСООСЧООСО
Ч ^ О ~ О СМ 0^0^ со
•—* о I—I 4-1 1—<
М to Ю ао (О Ю р)
N К (N н г-, 1
СО <N (N м (О 0 н
^ (М о М со н
о" сГ
00
о
оо
о
о
о
ОО
о
о
00
о
о>
о
см
о
о
о
г-н
1—^
ч-Н
О СМ
N **ч
со &
СМ СУЭ
о"
ю
оо
см
о
о
Г—
со
см
оо
00
о
о
см
05
оо
05
to
см
см
см
о
'—t
о
«—*
со
о
о CM
‘О ю
*ч (М
I I
Tt4
о
ю
00
CD
05
CM
CO
to
CM
CM
c—
CO
05
pH
to
Ю
CO
см
со
со
о
00
05
CM
GO
CO
CO
<o
05
Ю
-H
CO
со
оо
IT-
t—
CM
4
о
CO
CM
о
о
1—*
C--
t—
s
05
05
CM
о
о
05
■^l4
CM
CO
о
о
о
Ю
Ю
CO
CM
Co
о
r—«
1—H
CM
CM
о
05
05
см
ю
•о
ю
00
pH
о
PH
pH
со
СО
См
PH
О)
см
см
о
СО
CD
о
V—Н
мь
ГМ
о
оо
г-
IT-
со
со
00
05
05
о
CM
ю
ю
См
со
см
г—
СО
05
05
о
to
<о
•о
о
о
о
'—'
о
о
*—*
См
о
о
о
о
г—I
г-н
см
о
v—н
о
о
о
о
тг
о
I I
I I I
см
см
pH
С—
ю
Г1
со
о»
to
00
4J4
П4
о
г-
05
со
со
мг
см
о
IT—
см
к.
см
о
со
оо
СО
о
<^5
со
СО
1--
t4-
о
т-н
ю
ю
05
со
со
со
см
05
05
см
см
ю
ю
40
со
о
о
о
Tt4
о
о
I
со
о
о
о
со
О0
со
о
о
см
см
см
со
о
см
ОО
<г>
ю
ю
ю
ю
оо
ОО
оо
см
т—1
05
со
г-
П4
см
оо
оо
оо
см
см
00
со
t-
о
05
05
ю
ю
г А
о
о
о
1-^
о"
со
—-г
о
o'
о
Г-Н
'~~1
05
05
СГ5
to
05
см
ю
to
ю
to
ю
ю
ю
см
см
о
о
о
1
♦—4
t-
t-
ty
05
ж
о
I СО
о
I-
ж
- 159 -
£>"
N <М <©
о со ^
• CD <N
—| к
л со £
r« г- *0
k ^ £•
N <N ^
1чГ
3 3 §
N М О)
'О
Й оо
1* 't Оо
8 8 §?
<^г
2> о
о о
*-« гп О
£Г СМ СМ
g (N N
о СО СО
я. сГ o' о
и Л!Л
*■4
3-
*S
* £
£ |
СМ СМ
Ю to
й 22
о о
о
а,
SS:
ж
§
§
§
оо см о
со 03 Ь-
^ СО со
м со со
'О со О) Ю
Оо ^ *ч CD
Оо со см сг»
0> Г-н CS Г—«
<5?
Ю оо
c\i со ю
ро с ю
Со о о
4- +
N
'О оо
К, о
Со т-ч
^ .-ч
СО
+ +
1
Оо
<о
+
22
Оз
<г>
8
IO
со
оо
С\*
СО
о
гН
00
в
15
1 ^
I
§
<о
II
R
со
о-
03
IR
СМ со
r-i
_ Ю оо
1-1 со ю
8
СО
03 о>
тг со
Ю Ю t^-
О »-ч iO СО
СО »—1 »-• г—(
+ 1 + 1
гг С- СО
СО 1—1
03 со оо
оз о
J-
00 —»
CM
+- оо
со тг
см о
со
CV3
+
II
С>
to оз
t— '
CM оо
CD N CM
»C N t>-
CM CO O-
О гч Ю
+
Ю 00
03 t—(
Ю CM
—г o“
I i
ss
C\J
c6
+
CO C-
r-t
CM oo
c-
^ o'
+ I
s>
<>M
03
съ
+
II
£
+
N
>£
о
28,409 - V Я (T) = 5,330; в(Т) = 0,0709
ОТДЕЛ IV.
ИНТЕРПОЛИРОВАНИЕ ПО СПОСОБУ НАИМЕНЬШИХ
Под термином интерполирование мы понимаем здесь задачу оты¬
скания функции, принимающей заданные численные значения при
заданных значениях ее аргумента; с простейшим вопросом этого рода
мы уже встретились в одном из примеров предыдущего отдела (§ 7),
где требовалось, например, по заданным’значениям независимой пере¬
менной— времени t — и соответствующим им значениям наблюденной
величины и составить функцию первой степени вида:
которая для i~tx, t\>, ..., tn принимала бы заданные значения
их , и21...у ип. Так как для отыскания двух неизвестных коэффициентов
g и а достаточно двух условных уравнений, то при п >2 мы имеем
дело с избыточной систехмой, которую решаехм под условием, чтобы
сумма квадратов уклонений величин ип вычисленных по формуле (*),
от наблюденных значений и. имела минимальное значение; отсюда
происходит термин линейное интерполирование по способу наимень¬
ших квадратов. Формулы, выведенные в конце § 6, стр. 125, решают
эту задачу и мы возвращаемся к ней только в виду некоторого
обобщения.
Пусть х1У х2У...ухп представляют данные значения независимой
переменной, ау1 ,у2,. . ., уп — соответствующие значения наблюденной
величины уу для которой мы ищем общее выражение вида:
Возьмем на плоскости систему прямоугольных координат и будем
рассматривать заданные числа (х1У уг), (х2Уу2)у . . ., (,хп>уп)9 как коор¬
динаты точек Рх, Р2У . . ., Рп. Тот случай, когда все эти точки лежат
на одной прямой, здесь не представляет интереса; ибо тогда каждые
два условные уравнения из совокупности:
КВАДРАТОВ.
§ 1. Линейное интерполирование. Линии регрессии.
о
у = тх -f- b
(Н
V. = тх. -{- b i = 1, 2,..., п (2)
— 161 —
были бы достаточны для определения углового коэффициента т и
начальной ординаты Ь. В данном случае важно предположить, что
точки Р1,Р2, Рп лежат вблизи некоторой прямой (черт. 13);
эту близость мы будем, в известной степени условно, оценивать
малостью отрезков /W, Р2Я2', представляющих собой уклонения
заданных ординат yt от вычисленных по формуле (1).
Итак, положим
ЯЯ.' = е..
I t 1
Решая по способу наимень¬
ших квадратов систему (2)
с неизвестными т и Ь, мы
вводим условие
[ЯР'2] = [ее] - минимум.
Замечая, что здесь коли¬
чества хг являются коэффици¬
ентами при неизвестной т, а
у. — свободными членами, при-х
ходим к нормальной системе:
[.х]т-\- nb = [у]
[хх\т -| [х]Ь = [ху\
(п — число условных уравнений, или число заданных точек).
Полагая теперь:
* _W. v _[>■]
*0 — „ > У о — п ,
можем написать первое уравнение в виде:
лугс-f Ь=у0,
обнаруживая этим, что искомая прямая проходит через точкуР0(х0,у0);
эта последняя, согласно известному из механики определению,
является центром тяжести системы Рх, Я2, ..., Рп, считая, что
массы этих точек между собой равны.
Поэтому уравнение (1) принимает вид:
У—Уо = т{х — хо) ■ (3)
Перенося теперь качало координат в центр тяжести Я0 и вводя
обозначения x!=xt—х0;у/ =yt—у0, переписываем (3) в виде:
Утх'.
Таким образом, для определения неизвестного еще углового коэффи¬
циента т получаем, систему условных уравнений:
у! = тх!
(1=1,2 я)
Способ найм, квадратов.
11
- 162 -
Решая ее по формуле 3, стр. 115, находим:
НЙ'1 (4>
Полученное сейчас выражение для углового коэффициента мы пре¬
образуем, рассматривая оба ряда заданных величин, именно абсциссы
хх, х2,..., хп и ординаты уг, у.,,..., уп, как некоторые статистические
совокупности.
Введем б рассмотрение дисперсии ряда х и ряда у. По определе¬
нию имеем:
, [(*;-*о)3] Г*'*']
з-(лО = =
v J 11 п
2/ ч [(Л-Д'о)3] Г//]
° (у) = = —- •
11 п
Условимся еще выражать заданные координаты х! и у! (т.-е. коор¬
динаты точек Р. относительно начала Я0) в частях дисперсий соответ¬
ствующих рядов, т.-е. введем параметры:
JL • - — Z_
g(T)’ — а (у)'
Таким образом, получаем два ряда величин (нормированные коор¬
динаты точек Р.):
£ * 5
Ч1 1 > ■ • ’ > ~п
6i, 62»• • •. V
Составляя сумму соответствующих произведений получаем-
rtri — _.1УУ1_
L lJ *(х) • Чу)
Отсюда для углового коэффициента т находим:
_ \х'у'\ _ [-Ч • <х) • о(у)
[х’х'\ ~ [х'х1]
Но [Л'] = /г-а2(х), и потому окончательно:
где положено
т _ ЧУ . И _ <У ,
а{х) П ~ а(х)' :
Г = ^ . (5)
п 7
Подставляя это выражение в (3), приводим уравнен^ искомой
прямой к виду:
У~Уо = — *о) (3')
Для более удобного вычисления г преобразуем выражение (5):
г_т = гея = [^/] (бч
Я Ч-*)-о(у)"Я *
— 163 —
Из этой формулы, имея в виду тождество Лагранжа, легко
заключить, что по численному значению г не может быть больше
единицы *). В математической статистике величине г дается название
коэффициента корреляции между совокупностями хиу, а прямая (3')
называется „линией регрессии у по х“. Ее назначение — доставлять
наилучшие значения у, соответствующие заданным х, оценивая бли¬
зость приближения малостью суммы квадратов отрезков, параллель¬
ных оси Y. Но важно обратить внимание на то, что уравнение най¬
денной прямой отнюдь не может служить к решению обратной
задачи, именно к определению наилучших х, соответствующих задан¬
ным у, так что для ответа на этот новый вопрос недостаточно про¬
сто решить уравнение (3') в отношении (х—х0). Действительно, для
этой цели мы должны были бы в предыдущем рассуждении переста¬
вить координаты X и Y и оценивать качество приближения малостью
суммы квадратов отрезков, проведенных из точек Р. на искомую
прямую, яоЩже параллельно, оси X’. Как нетрудно видеть,
коэффициент корреляции г сохранит в этом случае свое значение,
но уравнение „линии регрессии л; по у“ примет вид:
Прямая эта, при гф 1, будет отлична от (3') и пересечется с ней
в центре тяжести Я0.
В обоих случаях отрезки г. = Р.Рч будут удовлетворять условию:
как это вытекает из леммы Гаусса.
Переходя к параметрам 5 и к), можем переписать (3') и (3") в сле¬
дующей любопытной форме:
Каждое из этих уравнений выражает определенное статистическое
свойство совокупностей х и у, а потому первое не решается для Е,
второе для yj.
Пример. Положим, что дано п = 310 значений х, причем сред¬
нее х0 = 80,76 и столько же значений у со средним у0 = 81,00. С по¬
мощью уклонений л; и у от их средних (х — х0 = х' и у—\у0=у)
получено:
(3")
(4)
т( = г\
Ь = Г1\.
[х’х1] = 2451,14; [УУ] = 1394,78; [л'у']= 1280,43.
*) Из этого тождества (стр. 150) следует, что только при
■V _ х_%_
У1Г~У2 ~ у'п ’
т.-е., когда точки Ph лежат на одной прямой, [г] =. 1.
- 164 —
Требуется найти линии регрессии у по х и х по у.
Здесь
о»(*).= 24з1014 = 7,907; о(*) = 2,812;
13!1<г=4>499’ °0) = 2,i2i;
1280,43
"20) =
л/2451,1-1394,8
■ 0,6925.
Поэтому:
У-
•81,00:
<у)
<**)'
Г‘(х — 80,76) = 0,5223 (х — 80,76)
или
Затем:
или
у= 0,5223л: + 38,81 (1)
х — 80,76 = ^ • г • (у — 81,00) = 0,91800— 81,00)
* = 0,9180j/4-6,40 (2)
Уравнение (2) отнюдь не может быть получено обращением урав¬
нения (1).
§ 2. Вероятнейшая прямая.
В предыдущем параграфе интерполирующие прямые проводились
так, чтобы сумма квадратов отрезков, проведенных от заданных
точек до искомой прямой параллельно одной из осей, имела
минимальное значение. Но мы можем также поставить условием,
чтобы в минимум обращалась сумма квадратов расстояний заданных
точек до искомой прямой^
ПустьЯг,Р2,* • «,Яя за¬
данные точки; PJP\\
P‘iP%' " > Рп Рп — перпен¬
дикуляры, опущенные из
них на прямую L. Тре¬
буется определить поло¬
жение последней так, что¬
бы [РР*\ сводилась к ми¬
нимуму.
Согласно известному
из механики определе-
; нию, сумма квадратов
расстояний Р. до прямой L, умноженных на массы точек mi является
моментом инерции системы точек Р. относительно прямой L. Пред¬
Черт. 14.
— 165 —
полагая, что массы всех данных точек Р. между собой равны, мы ви¬
дим, что искомая — так называемая вероятнейшая — прямая является
вместе с тем прямой, в отношении которой момент инерции системы
имеет наименьшее значение. Легко показать, что вероятнейшая пря¬
мая, подобно прямым регрессии, проходит через центр тяжести
системы Р0, координаты которого (при равных массах точек Р.) опре¬
деляются равенствами:
X —И- V - И
П ’ У°~ п '
Таким образом, для определения положения прямой L достаточно
найти угол а, образуемый ею с осью X. Положим для решения за¬
дачи, что L и есть искомая прямая. Примем ее за ось X' новой
системы координат, проведя вторую ось Y1 перпендикулярно к L
через, точку Р0, в которую перенесем новое начало координат.
Пусть х! и у! означают координаты точек Р. в старой системе
относительно начала Р0, так что:
х/ = х. —хп; у! =_у —j/0 •
Обозначим еще через и ч\. координаты тех же точек в системе
XY', повернутой на угол а относительно XY. По формулам пово¬
рота осей имеем:
£г = + х! COS a -f-у. 'sin а ^
т)г. = — X.' $in а + у. 'COS а
Взяв во втором уравнении производную по «, находим:
5?=-?, .о)
Заметим теперь, что в новой системе осей расстояния точек Р.
от прямой L выражаются их ординатами, т.-е. величинами тг)г. Поэтому
вероятнейшая прямая должна удовлетворять условию:
[irpj]-минимум.
Рассматривая написанную сейчас сумму как функцию угла а,
берем от нее производную по а и приравниваем ее нулю, что дает:
Ь£]-°
или, в виду (1),
м=0 (2)
Иными словами: сумма произведений расстояний точек Р( от пря¬
мой i и от второй прямой, перпендикулярной к L, должна приво¬
диться к нулю. Системы осей, удовлетворяющих такому условию,
— 166 —
носят в механике название главных осей инерции и, следовательно, мы
приходим к теореме: вероятнейшая прямая есть одна из главных
осей инерции, именно та, в отношении которой момент инерции
имеет минимальное значение 1).
Подставляя теперь выражения (*) в формулу (2), находим:
[ж'2—У2] sin a-cos а — [УУ] (sin2 а — cos2 а) = О,
откуда окончательно:
№ = О»
По этой формуле находим два значения: ах и Oj-f-900, соответ¬
ствующие осям L и V; выбор между ними в условиях данной задачи
не представляет труда и таким образом, имея угол наклона L к оси
X и зная, что она проходит через центр тяжести Р0, можем считать
нашу задачу решенной.
Заметим еще, что соответствующая задача ставится и для про¬
странства, когда требуется найти плоскость, по отношению к которой
сумма квадратов расстояний заданных точек имеет минимальное зна¬
чение. Решение этой задачи любопытно ее механическими аналогиями.
§ 3. Параболическое интерполирование (способ Чебышева).
Во многих практических вопросах может обнаружиться, что пред¬
ставление искомой зависимости в виде линейной функции у = ах -f- b
является недостаточным, в силу слишком значительных уклонений
вычисленных ординат от заданных значений уг В этих случаях бывает
целесообразно искать для у выражение . в виде квадратичной функ¬
ции х, или же, в наиболее общем случае, в виде некоторого много¬
члена, расположенного по степеням х. Пусть выражение такого много¬
члена есть
У — Ро +Pix + р2х2 Н \-Ртхт (1)
Кривые, соответствующие форме (1), носят название парабол выс¬
ших порядков, откуда и происходит термин параболическое интерпо¬
лирование.
Подставляя в (1) вместо х его заданные значения х., а вместо у—
соответствующие заданные значения у., мы получаем для определе¬
ния неизвестных коэффициентов
Ро> Pi. Р*> ■■•>Рт
систему условных уравненцй вида:
У; — Ро + P\xi ~\~P-2Xi~ ~Ь’ : • + РтХГ (* = 1-2> •••>«)• • • • (2)
*) Предоставляем читателю доказать, что момент инерции относительно оси У' имеет
максимальное значение.
- 167 —
Полагая, что число данных уравнений п больше числа искомых
коэффициентов, т.-е. больше т-\-1, мы приходим к случаю избыточ¬
ной системы, подлежащей решению по способу наименьших квадра¬
тов. Однако, обычное применение этого способа встречается здесь
-С некоторыми затруднениями. В самом деле, для практики важно,
не назначая наперед степени интерполирующего
многочлена, искать для у выражения типа (1) в процессе после¬
довательных приближений, т.-е. исходить сперва из линейной функции:
y=Po + Pix>
затем, если оказывается нужным, переходить к функции:
У=Р0+Р1Х + Р2**> \
и повышать таким образом степень многочлена, пока по малости
суммы квадратов остающихся погрешностей _рвыч —_уна6л_ процесс
интерполяции не будет признан законченным. Между тем, применяя
способ наименьших квадратов к системам (2), мы убедимся, что
с каждым следующим приближением все коэффициенты при низших
степенях х приобретают новые значения, так что работа, выполнен¬
ная в предыдущих приближениях, теряет свое значение при переходе
к последующим.
Однако, эти неудобства устраняются, если к интересующей нас за¬
даче применить замечательный метод интерполирования по наимень¬
шим квадратам, предложенный П. Л. Чебышевым и выведенный
им из теории алгебраических непрерывных дробей.
К изучению этого способа мы и переходим, имея в виду связать
его с прежними отделами курса, в частности с формулами и схемами
Гаусса. '
Для удобства изложения условимся в некоторых терминах и обо¬
значениях. Пусть хх, х2,'--,хп суть заданные значения независимой
переменной х; эти числа назовем основной системой значений х1%
Нам придется составлять различные функции б(д:), в которые
данные х. будут входить как параметры. Такие функции будем назы¬
вать построенными для основной системы значений хр, наконец, при¬
дется, подставив в функцию ф(лг) заданные значения х, образовывать
суммы полученных значений ф(лгг); такую операцию будем называть
суммированием по основной системе xl> обозначая ее так:
'K*i) + 'Кхг) + • • • ~Ь 'К'О = ['Не¬
подобно этому для суммы квадратов значений функций <!> будем
писать:
ф*(*1)+«*,)+ И2Ю= [УШ
— 168 —
Нам необходимо теперь выяснить аналогию между решением си¬
стемы условных уравнений типа (2) с изученными ранее системами
вида:
арс -]- Ъ.у -f cLz 4- dt — lt (3)
С этой целью мы будем предполагать здесь, что а, Ь, с являются
некоторыми известными функциями х, которые для частных значений
•х1(л:2, • • ,хп принимают значения: ах, • • •ап;Ь1, • •bn\cx• • -с„ит. д.
Количества х, у, z, которые в системе (3) являются неизвестными,
здесь будут рассматриваться как искомые коэффициенты при'функ¬
циях а, Ъ, с; мы обозначим их через X, У, Z, Т; наконец, вместо /
будем писать у., полагая, что у. есть частное значение функции у при
х = х..
Таким образом, мы можем написать формулу:-*
у = аХ -\-bY-\-cZ-\-dT, (4
которая выражает неизвестную еще нам (поскольку неизвестны коэф¬
фициенты X, У, Z, Т) зависимость у от х, через посредство заданных
функций а, Ь, с\ поэтому для определения неизвестных коэффициен¬
тов X, У, Z, Т, необходимо решить систему условных уравнений:
y. = a.X + biY+c.Z + d.T, (i = i, % . .(4')
где^г, а.,Ь. и d. — величины известные.
Вместо формулы (4) или, как говорят, разложения у по функциям
а, b, с, d, будем искать, по Чебышеву, представления у в виде
некоторого особого ряда, положив:
У = •K’o'i'oC*) + “Г у • Л~К^т{х) . - . . . . (5)
В этом разложении коэффициенты Кх и функции Л.(х) подчинены
следующим условиям:
1) К0 есть число, зависящее только от заданных у. и аг
К\ » п а и п „ У 11 пс и Ь, ~
К, „ „ „ _ „ „ ур аР bt и г..
Кя „ „ „ ,,v ‘ „ „ ур ар Ьр с. и dr
2) 40(.к) есть функция х, зависящая от функции а и от параметров аг
t^i(x) „ „ „ „ а, b и от парамет¬
ров at, bt.
<]>2(х) есть функция х, зависящая от функций а, Ь, с и от пара¬
метров а., Ьп с..
— 169 —
Резюмируя, можем написать:
У == , at) ■ %(а; at) + Кх(yt, а., Ь:) • 'Ьх(а, Ь\ at, bt) +
I Къ[уi f ci., b .L, ф)*У2(//, by с у ci., b^y c?) —[~ * * - . . . . (6r)
Чтобы получить простейшим способом коэффициенты К и функ¬
ции $(х), напишем, по ф'-ле (6) стр. 149, элиминлционные уравнения,
соответствующие системе условных уравнений (4').-
Эти уравнения имеют здесь вид:
у I lab] у_\_ [®f_] 7 [a<f] у \аУ'\
laal f >«1 ^ [аа\ \аа\
У [bc\] 7. [Ml] т [ЬуЦ
"г- [ЬЬЦ [ЬЬЦ [ЬЬЦ
У , [ссЩ т [с>2]
1 \сс2] [сс2\
= Ко)
ФоС*)
= КХ)
=*«)
= КЯ)
'Мх)
(б)
T==w*\ (
[ddZ] v
Докажем теперь, что коэффициенты Чебышева Ко, Кх, К2 • • •
суть свободные члены элиминацио’нных строк, т.-е.:
17 [аУ] . 17 [АУЛ . 17 [£у21 . у __ [dyZ] ...
А° [ад] ’ А' [ЬЬЦ > А2 — [сс2] ’ А» ~ [Л/3] *• '
Действительно, по составлению этих чисел легко видеть, что они
соответственно зависят: Ко от аг, у.; Кх от а., bt, у. и т. д., т.-е. удо¬
влетворяют поставленному выше условию. Далее, можно составить
и систему функций ф(лт), соответствующих этим коэффициентам,
если помножить все строки (6) справа и слева на неопределенные еще
пока множители '{'оМ; <К(Л:); туМ и W*) и сложить, взяв за скобки
коэффициенты X, Y, Z, Т. Это приводит к уравнению:
X' '1>о(х) -J- ■
+ г-{ «*) + [£{ *,(*)}+
+z- { fe W + feM+\z\ few} +
+ г. ( ш + fe»+!"{]’few + gjfew}-
— K0'bQ(x) -f- KMx) + ~t~ =У-
Но по определению, для у имеется исходное разложение (4):
y = aX+bY-\-cZ + dT.
Таким образом мы получили два разложения -для функции у: пер¬
вое по функциям а, Ь, с, d, второе — по функциям tyoC*)» 'КС*)* • •<Ь(-*Г);
в обоих случаях коэффициентами являются X, Y, Z и Т; разумеется,
мы можем теперь определить функции «Ц*)» • • -^(х) из условия,
чтобы эти разложения были тождественны, т.-е., чтобы множители
- 170 —
при X, У, Z, Т были равны. Таким образом, приходим к. системе
формул, выражающих связь функций ф.(л:) с функциями а, Ь, с, d,
именно:
Фо (х) = а
i'l (•*■)■ + [ад] 't'oW = Ь
+ = ^ (,)
«*) + Ш + [Ifrj V*) + «*) “ d S
Из этих соотношений мы видим, что каждая из функций ф(*)
является некоторой комбинацией функций ^(х), ей предшествующих,
и кроме того, что все они зависят от данных а, Ь, с и а., b., c.t именно
в той последовательности, которая была обусловлена выше на стр. 168,
т.-е., что ф0 = ф0(а; а.); ф^фДа, Ь\ а.,Ь.), и т. д.
От этих общих выражений для функций ФДх) нам важно перейти
теперь к частному случаю многочленов Чебышева; они получаются
нз предыдущей системы (*) в том случае, когда
а= 1; b = х; с, = х2; d = Xя,
т.-е., когда разложение (4) для у есть разложение по степеням пере¬
менной х. — Однако, при этом переходе, имея в виду удоб¬
ство обозначений типа [bbl\, [сс2\ и им подобных, мы сохраним их
в формулах, помня, что они являются теперь обозначениями для
комбинаций сумм ступеней и произведений заданных чисел xt, соста¬
вляющих основную систему значений х. Таким образом, выводим
систему многочленов Чебышева:
Ь (*) = - 1
'Ы*) = — [^а]'^(х) + х
* (В)
w*) = - Ш 1[Ш] ЬМ- S +**
Весьма замечательно то обстоятельство, что эти формулы скрыты
в самой схеме элиминационных уравнений (6). Действительно, доста¬
точно последовательно помножить числа (k-f- 1-го) столбца этой
схемы на — -ФоМ;—ФгС*)»—и т* Д-> и к сумме придать -f- х*>
где k соответствует значку при ^(х), чтобы .получить выражение
для й-го многочлена Чебышева. Так, например, в 4-м столбце стоят
коэффициенты:
[ad] [М] [cd2] 1
[аа] [ЪЪ\] \сс2]
— 171 —
Помножая их на функции:
— ФоС*)» — 'ф8(#;, л3
и сделав приведения по х (ибо ф0М» W*) и ФзС*) известны из пре¬
дыдущих стадий работы), мы находим многочлен Чебышева ш
построенный для основной системы значений х.. Наконец, коэффициент
К3 с которым этот многочлен входит в искомое разложение для у.
равен свободному члену последней элиминационной строки, располо¬
женному в схеме на уровне члена Xs. Отсюда легко понять, что
каждое приближение Чебышева соответствует одному столбцу в
схеме решения нормальной системы. Поэтому, ограничивая эту схему
одним, двумя и т. д. столбцами (не считая, конечно, столбца свобод¬
ных членов), мы последовательно находим приближенные разложения
для у, именно:
У — Кп (Фо = 1)
у = К0 -(-
у — Л’о 4- к г ух) 4- (•*)>
Таким образом, каждое новое приближение в данной методе све¬
дется к вычислению нового члена типа К$.(х), причем все преды¬
дущие коэффициенты К и функции <[* остаются без изменения. В этом
я состоит значительное практическое преимущество методы Чебы¬
шева перед применением обычной схемы способа наименьших ква¬
дратов при параболическом интерполировании.
Остается вывести еще формулу для суммы квадратов погрешностей
остающихся после каждого приближения. С этой целью достаточно
применить формулу Гаусса [стр. 150 (с)]:
г„1 _ г/л _ И2_[ЬП?т
tccj _ [W1] [сс2] [<Ш] ‘ * •
Заменяя здесь L на yt и вводя коэффициенты К0, Кх,... по формулам
(А), приходим к весьма важному равенству:
[ее] = \уу] - [аа] К0^ -[ЬЬ\] К* - [сс2] К*- (С)
Ч
Из формулы (С) видно, что с каждым приближением [ев] умень¬
шается на величину, пропорциональную квадрату
соответствующего коэффициента Чебышева. -(Заметим,
что [аа], [bb\] и т. д., как показано выше, суть числа всегда поло¬
жительные). Поэтому оказывается возможным на каждой ступени
вычисления определять [ее] и, следовательно, выяснять, является ли
данное приближение достаточным, или же желательно вести разло¬
жение еще на одну степень выше, с целью уменьшения суммы ква¬
дратов остающихся погрешностей.
— 172 —
!
§ 4. Примеры.
Из сказанного в предыдущем § видно, что все вычисления при
интерполировании по способу Чебышева удобно укладываются в
схему решения нормальных уравнений; остается только отметить
некоторые особенности их составления. Согласно нашим обозначениям
здесь имеем:
а — 1; [а) — п, где я— число условных уравнений
6 = x; [b] = [х]; [ab]= [х]; [ЬЬ] = [&]
' с =-- х3; [с] = [х2]; [ас] = [х2]; [Ьс] = [X3]
1=У; [al] = \у]; \Ы\ = [ху]; [cl\ = [л^у] • • •
Поэтому нормальная система принимает здесь вид:
п [X] [х2] [X3] ... [у]
[Х2] [Xй] [х*] . . . [ху]
[х4] [х5] . . . [х2у]
[*6] • •• Wy\
Составив соответствующую ей элими-н а ц ионную систему, мы
строим, как было показано, функции Чебышева: фг(дс), ty2(x), ^Г((х)
и т. д. при помощи чисел, которые получатся в столбцах этой системы.
Таким образом, чтобы дойти, напр., в приближениях до много¬
члена третьей степени 63fx), надо иметь подготовленными суммы
степеней основных значений х. до шестой включительно и суммы
произведений заданных у. на х.,х.2 и х?1). Если бы после л энного
приближения было признано необходимым перейти к многочлену ^4(х),
то потребовалось бы составить: [х7], [х8] и [х4у]. Точно также, переход
от многочлена <ЬА(х) к многочлену бА+1(х) потребует составления т р е х
новых сумм, именно [х2*+7] , [х2*+2] и [х*+1_у].
На практике, в приложениях к физике и статистике, редко идут
выше <!»<)(х), так как вычисление седьмых и восьмых степеней задан¬
ных х; является уже довольно затруднительным.
1. Для первого числового примера заимствуем данные из сочинений Чебышева
(т. I, стр. 493). Задав 11 значений xi и соответствующие им значения^- которых мы
здесь переписывать не будем, Чебышев находит в различных стадиях вычисления
следующие суммы:
[п = 11; [х]= 5,40292; [*2]= 3 68269; [х*] = 3,08709; [*<] = 2,89586
Q/] = 303,2100; [ху] = 156,67832; [х*у] = 107,59549 '
[уу] = 8590,8
С этими данными произведена обработка по схеме нормальных уравнений.
Эти суммы носят название моментов у первой, второй и третьей степени.
— 173 —
1 прибл.
2 прибл.
3 прибл,
4 прибл.
+ п
+ 5,40292
+ 3,68269
+ 3,08709
+ 303,21 ('0 |
[уу] 8590,8
Е,
1
+ 0,49117
+ 0,33479
К0 + 27,5645 1
| 8357,8
[ее] 233,0
N*
+ 3,68269
+ 3,08709
+ 2,89586
+ 156,67832 1
I
— 2,65375
— 1,80884
— 148,92879
+ 1,028j4
+ 1,27825
+ 7,74953 I
1 58,4
Е,.
1
+1,24230
К± + 7,5316 1
[ее] 174,6
+ 2,89586
+ 107,59549
— 1,23293
— 103,51168
— 1,58797
— 9,62721
+ 0,07496
— 3,54340 I
1 167,5
*
1
•,
Л*2 — 47,27 1
М 7,1
В этом вычислении, к которому мы применили весьма удобную схему Д у л и т л я
(см. стр. 53), работа велась последовательными столбцами, из которых каждый, как
мы знаем, соответствует одному приближению Чебышева; при этом одновременно
с данным столбцом заполняется и соответствующий ему отрезок столбца свободных
членов; тогда в этом последнем* столбце, в э шминационных (обозначенных курсивным
шрифтом) строках, на уровне в1появляются коэффициенты Чебышева К0, Кj
и т. д. Возводя их в квадрат, умножая на [аа], [ЬЬ\] и т. д., т.-е. на числа, стоящие
непосредственно над „Г1, + и вычитая произведения сперва из [уу], потом из первого
остатка и*т. д., получаем [ее], соответствующее каждому приближению. Оно кончается
здесь на <Ь2(.к); но для большой ясности схемы в ней оставлен свободным 4-й столбец,
в который вписаны [а:3], [а4] и в который пришлось бы включить [*5] и [л:6], если бы
потребовалось перейти к 4+лг).
На каждом этапе работы, руководясь правилом стр. 170, составляем многочлены
Чебышева и их произведения на коэффициенты К.
Таким образом здесь находим:
ФоМ = 1
ф,(х)~- 0,49117 % + х
ф2(ж) = —0,33479 — 1,24230 bt(x) + x*
= + 0,27540 — 1,24233 х + х»
Поэтому система последовательных приближений для функции у будет:
уф) = КЦ'Ь0 = 27,56 4 ! [^] = 233,0
y(i> = К0% + К^х) = 23,865 + 7,532 х • J 174,6
у( 2) = + К^х) + К3-Ь3(х) = 10,817 + 66,25 5х — 47;27х» ! 7,0
Каждая из этих формул дает наилучшее выражение для у в виде многочлена
нулевой, первой и т. д. степени в х, причем каждой из них соответствует приписан¬
ная сбоку №
4 Вместо этого мы множили К на число, стоящее непосредственно над ним, как к
примере стр. 158 — 159.
К0% = 27,564
К,ф, = — 3,699 + 7,532 х
К2'Ь3 = — 13,018 + 58,724 х — 47,27 х*
— 174 —
Но очевидно, что заключительный многочлен jy(2) можно найти для контроля и не¬
посредственно по известной нам схеме обратной подстановки, из которей получатся
коэффициенты при *°, х1, х2 в разложении у. Приводим и это вычисление:
1 0,49117 0,33479 27,5645
Е2 1 1,24230 7,5316
Е3 1 — 47,27
- 47,27
66,256 -.5V/24 7,5316
10,848 32,543 —15,826 27,5645
Таким образом мы сразу приходим к формуле:
у = 10,848 + 66,256* — 47,27*2*
тождественной с заключительным приближением Чебышева.
Заметим еще, что числа, стоящие в нашей схеме над „1“ элиминационных строк
(11; 1,02894; 0,07496), являются весами коэффициентов К0, Кх и К2. Мы видим, что
они быстро падают, так что уже определение К2 происходит здесь в очень неблаго¬
приятных условиях.
2. Для следующего примера возьмем численные данные из работы В. Хотимского
„Выравнивание статистических рядов по методу наименьших квадратов*1 (Москва, 1925).
В этом примере основные значения xi расположены симметрично по отношению к их
среднем^, что вносит некоторое добавочное упрощение в’вычисления. Имея в виду
итти в приближениях до <Ь3 , подготовляем все суммы до [**] и [х2у], как показано
ниже:
xi
V
V
1
V
У1
*ьУ
лл-
— 6
36
— 216
i
! 1296
\
1 2
— 12
72
•
4
— 4
16
— 64
256
10
— 40
160
100
— 3
9
— 27
81
17
— 51
153
289
— 1
1
— 1
1
33
I — 33
33
1089
0
0
0
0
51
I 0
0
2601
+ 1
1
+ 1
1
! 66
| + 66
66
4356
+ 3
9
+ 27
81
96
! + 288
864
9216
+ 4
16
+ 64
256
120
+ 480
1920
14400
+ 6
36
+ 216
I
1296
I
172
| +1032
j
6192
29584
Суммы: 0
124
о !
! 3268
567
1730
9460
61639
При этих данных все вычисление сводится к обработке следующей схемы:
N± 9
0
121
567
I [yy\ 61639
Et 1
0
13,7778
K0- 63
I 1
35721
N
25918,
No
124
0
1730
I I
24136,2
E8
1
0
Ki = 13,9516
1 M
1781,8
3268
9460
1708,444
7812,0
1559,556
1648,0
£3
1
K2 = 1,0567
1 1
1741,4
И
40,4
— 175 —
Отсюда по правилам стр. 170 находим:
/с0ф0 =4-63; К^(х) = + 13,95*
КМ*) = + 1,0567 . (- 13,778 +х*) = - 14,559 + 1,057x2
следовательно, приближения для у здесь будут:
У°> = 63; д*1) = 63 + 13,952 х; у{2) = 48,44 + 13,952 х + 1,06 х\
которым соотвзтствуют [ее], равные 25918; 1781,8 и 40,4.
По условиям задачи последняя из них представляется достаточно малой, почему
приближение на ^2(х) и заканчивается.
§ 5. Интерполяционный ряд Чебышева.
Пусть <Ь0(лг), <К(Х), ф2(^)... составляют последовательность много¬
членов Чебышева, построенных для одной и той же основной
системы значений х1У х2,..., хп. Обозначим через (х) и ^(х) два
многочлена из этого ряда, соответственно степеней k и у, и образуем
сумму произведений вида:
Ыъ)-
взяв эту сумму по основной системе значений х= хХ) х2,... ,хп
Основное свойство многочленов Чебышева состоит в том, что
сумма этих произведений приводится к нулю, так что:
№/*№,(■*)] ==°
(при k не равном j)
Для доказательства этой важной формулы допустим, что решая
систему условных уравнений вида:
-У,- = К+ • • • +
(i — X, 2 ... п)
мы остановились на 1) -м приближении, причем после решения у нас
образовалась совокупность остающихся погрешностей е2, е2, ел;
по свойству самого решения, эта совокупность отвечает условию
[esj-минимум, по сравнению с любыми другими представлениями у
в виде многочлена т-й степени со старшим коэффициентом, равным 1.
Таким образом после решения системы мы приходим к совокуп¬
ности равенств:
+ ■■■ + =у. + е.,
(i ~ 1, 2 . .. , п)
где у.—заданные величины.
Возводя каждое из этих равенств в квадрат и складывая все
вместе, находим:
tfoWC*)] + • • -+KJ[bJ(x)} + 2ВД[ф0(*Ж(*)] +.:.
4 ■ • • -f жт_,кту<т_л{ху<т{х)\ = Ш + 2Lye] + N • .(*)
— 176 —
В этой формуле все суммы, как обычно, в^яты по основной
системе значений лг(..
Заметим теперь, что по формуле (2), стр. 108, для погрешностей si,
удовлетворяющих условию [ssj-минимум, имеет место соотношение;
[ее] = \уу\ — [aa\KQ2 — [bb 1 )К* — [сс2]К* — \dd5\Kf — (Ь)
В уравнене (**) погрешности е. больше не входят; вместе с тем,
оно должно удовлетворяться при любых значениях величин у., вхо¬
дящих в коэффициенты К., но не. входящих в функции и их суммы.
При этих условиях левая часть (**) только тогда может привестись
к нулю, когда каждый из ее членов порознь равен нулю, а для этого,—
имея в виду, что числа К отличны от нуля, — должны иметь место
соотношения:
Равенства второй группы содержат доказательства основного
свойства многочленов Чебышева, которое можно резюмировать
Замечая к тому же, что ty0 —и полагая в только-что написан¬
ной сумме fy=60, можем дополнить систему (D) также и следующими
формулами:
(а)
Подставляя (а) и (Ь) в (*) и делая приведения, получаем:
+ 2К0КШх)Ч*)\ Л- • • • + ЩКЩхЩх)] + - • •
••• + 2/WUW*>U*)]==o . ,
(**)
ИД*)] = [аа]
[«№)] = т\
['№)] = [сс 2]
[ФА*)] = [АЙ]
[Фо(*Ж (*)] = 0
[Фо(*)Фа(*)] = 0
(D)
(КОЖО)] = о
формулой:
['КО)'!'/*)] = о
(при к не равном j)
[Ф*0)1 = °>
(D-)
(£ = 1, 2, . .. , пг)
— 177
Свойство многочленов Чебышева, выражаемое формулами
групп (D) и (D'), носит название их ортогональности по отношению
к основной системе значений х{ х). В следующем § будет выяснена
общая зависимость между способом наименьших квадратов и разло¬
жениями по ортогональным функциям (частным случаем которыд
являются многочлены Чебышева); теперь же мы воспользуемся
этим свойством, чтобы привести ряд Чебышева к его окончатель¬
ному виду.
Для этой цели положим снова, что после разложения до т-й
степени включительно и сравнения заданных ординат у;. с вычислен¬
ными, мы пришли к п равенствам вида:
ЛАС*!) + • • • Т Kfifx l) + • • • + — ^1 + ®1
Л’о^оС-^г) + • • • + + • • • + =Л + е2 • • (***)
*А(*л) + • • • + + • • + Кп$т(Хп) ==Л + ел
% Прежде всего установим лемму:
Для каждого из многочленов ^(х),
ei<!'*(-vi) + 4^kix^ + • • • + VW-O= О-
Для доказательства обращаемся к системе уравнений (*), стр. 170.
Полагая в первом из них л: = , х2,...,хп, имеем: <
'М’Ч) = а1 > — а2> " • ^о(-^л) = ап ’
Умножая эти равенства на ej... ел, складывая и применяя лемму
Гаусса, найдем:
КоС*)1 = [«] = 0.
Поступая точно так же со вторым уравнением, получим:
Hi(*)] + [^{ Шх)] = N = °. откуда ИД*)] = 0.
Таким же образом, последовательно установим:
И*(*)] = 0; [®Фз(-^)] = 0; ••• Ит(*)] = о.
Имея это, помножим равенства (***) соответственно на фуС-Vi),
’J'y(x2),...,fy(*n) и сложим все вместе. Тогда в левой части, по свой¬
ству ортогональности, уничтожатся все суммы вида [фА(лг) фу(л:)]> при /е
неравном /, и здесь останется только А’ДфД*)].
г) Название дается по аналогии с формулами аналитической геометрии в простран¬
стве, выражающими условие перпендикулярности двух направлений.
Способ ванмо квадратов* 12
— 178 —
Справа же сумма [г fy(jc)], по доказанному сейчас, приведется
к нулю, так что тут останется лишь [.yfy(.v)]; в виду этого, мы при¬
ходим к формуле:
К = (Е)
А' №/(*)]
Таким образом, каждый из коэффициентов Kj выражается через
сумму произведений заданных у. на значения соответственной fyO*,),
деленную на сумму квадратов значений <У{х).
Формулы типа (Е) имеют обширные применения в Анализе, где они
известны под названием формул Фурье.
Подставляя полученные значения коэффициентов в общую фор¬
мулу разложения:
У — КоШ КМ*) 4~ *{■•••>
приходим к окончательной формуле, носящей название интерполя¬
ционного ряда Чебышева:
»м*м+Ш*м+Ш**/>+ (О
Заметим, что в этом ряде разложение производится по многочле¬
нам Чебышева, построенным для основной системы значений х.\
коэффициенты этого ряда составляются из сумм, взятых по этой именно
системе значений, причем в эти суммы входят множителями заданные
значения у., соответствующие основным xt; все многочлены и коэффи¬
циенты при них образованы по одному и тому же весьма простому
закону. Отметим еще, что в виду условия <Ь0 = 1, первый член этого
ряда во всех случаях сводится к т.-е. к среднему арифметиче¬
скому из заданных значений у. — что соответствует началу среднего
арифметического, столь тесно связанному со способом наименьших
квадратов.
Обращаемся, наконец, к формуле для [ее]. Согласно формуле (С),
стр. 171, имеем:
[ее] = [уу] - [аа}К? - [ЬЬЦК?- [сс2]К.? - [йШ]АГ32 -...
Заменяя здесь [аа], [bb\], и т. д., по первой группе соотношений
(D), на [-У(-к)], [4x2(a:)] и т. д., находим:
N = [уу] - ['УМКо2 - [«K’WKx2 - [<№№,*
или, наконец, приняв во внимание выражение коэффициентов через
суммы (формулы Е):
feel = Г V Vi — [-v6"(-r)]3 _ М(*)]3 _ [AWP _ CG1
I J 1УУ1 {,ьЛх)] (VWJ *\У)
— 179
Это замечательное равенство и является как бы последним обоб¬
щением формулы Гаусса [стр. 150, (с)]; оно обнаруживает, что
с включением в разложение Чебышева каждого нового ч ;ена типа
[yl.(jc)J э
М уменьшается на -цкщ-; таким образом, то улучшение ре¬
шения, о котором мы говорили, изучая формулу Гаусса, здесь рас¬
членяется на отдельные слагаемые, из которых каждое соответствует
отдельному приближению Чебышева.
Заметим еще, что в #иду ^0(лг) = 1 совокупность первых двух
членов в правой части (G) всегда приводится к виду:
[УУ]
\у]3
= [У/]>
> Гу1
где у(. —уклонения заданных у. от их среднего значения —; поэтому:
N = 1уУ)~Щ
ЬА.МР [У'Ш?
Л*)] МШ (Н)
Не расширяя пределов курса, мы не можем остановиться на вы¬
воде важных свойств многочленов Чебышева, вытекающих из усло¬
вия ортогональности. Приведем лишь без доказательства следующие
положения:
1) Сумма квадратов значений многочлена '\к{х), взятая по основной
системе х., меньше суммы квадратов значений любого другого много¬
члена fk(x) той же степени k,
со старшим коэффициен¬
том равным 1, взятой по
той же системе чисел х..
2) Многочлен фА(лг), по¬
строенный для основной
системы значений хи х2,
хп, имеет k неравных веще¬
ственных корней, заклю¬
ченных в пределах от хх
до хп.
3) Между двумя корня¬
ми многочлена '\{х) содер¬
жится один и только один
корень многочлена ФА_1(лг). Черт. 15.
Эти свойства иллюстри¬
руются графиком первых четырех многочленов Чебышева '^(х), ...
'^(х), построенных для основной системы десяти значений:
\ ftW
Мх) / ft
Г \ \ 1 / 1 / /1
\ \ / ' //?
(}
•Jf3(x) -л'5- 0,7375х
- ШдЗг^Ш
у. _ _ 1 _ 3 _1 __1_ 0 /1 , А , 3
X — * у д » 9 9 д > V, ^ у ” ‘2 ’ 4 ’
1.
12*
— 180 -
Из черт. 15 видно, что совокупность многочленов ^(х), ^(х)
представляет собой систему кривых, колеблющихся в основном
интервале от хг до хп, со взаимно отделяющимися точками пересе¬
чения на оси X *).
§ 6. Разложения по ортогональным функциям и их связь
со способом наименьших квадратов.
Обобщая понятия, установленные в ^федыдущем §, мы можем
допустить, что для основной системы значений х., именно: xlt х2,
..., хп, построена система ортогональных функций
?о(*)» ?i(*). •••• 9т(х) (1)
Иными словами, мы предполагаем, что для каждых двух различ¬
ных функций ^(х) и ®у(х) из этой совокупности имеют место соотно¬
шения:
[?*(*) ?/(*)] =0, при k фу, . (а)
где суммирование произведено по основной системе значений х..
Не нарушая общности, можем положить, что <р0(х) —так как
в противном случае было бы достаточно разделить все функции (1)
на «pcW- В виду этого, заменяя в (а) <р7 (х) на приходим к ра¬
венствам:
[?*(х)] = 0, при k—1,2т. . . . . . . .(b)
Число функций <f(x) мы будем считать меньшим числа основных
значений хР т.-е. п.
Положим теперь, что для той же системы значений хх, х2,... хп
задано п соответствующих значений величины у, именно ух, у2,..., уп
причем зависимость у от х дана разложением вида:
У = ■'V?о(*) + -^i?iW + • • • + - .... (с)
Коэффициенты этого разложения, А0, А1г ... Ат нам нужно опре¬
делить из условия, чтоу принимает значения ух, у2, ... уп npHX = xx,
х2,..., хп. Исходя из ортогональности функций <рА(х), мы покажем
сейчас, что каждый из коэффициентов Ak вполне определяется сово¬
купностью всех заданных значений у. и частных значений соответ¬
ствующей функции <р*(х) для х — х1г х2,...,хя; при этом зави¬
симость Ак от указанных величин выражается формулами Чебышева-
Фурье [стр. 178, (Е)].
*) Общее учение о кривых этого рода принадлежит теории линейных дифферен¬
циальных уравнений второго порядка и соответствует так называемой проблеме
Штурма-Лиувилля.
— 181 —
Для доказательства выпишем все уравнения, получаемые из (с)
при замене в них х на хх, х2, • т.-е.:
Ух — А<фх) -{-... -f- Ак'£>к(х^) -)- ,.. -[-
Уч. =■ Л?0(xi) + • • • + Atfk(Xi) Ч* • • • + АпРт(Хч)
**(*«)
(2)
- v„=A?o(*„)+ • •• +^aW+ •••
Помножая все строки на приписанные сбоку величины <?к(х^),...,
срА(лгл) и складывая их вместе, мы замечаем, что все суммы вида
Ajbk{x)’^j{x)] приведутся к нулю по свойству ортогональности, и у нас
остается только:
ОрА(*)] =Ak[?k\x)\,
откуда:
_1уъМ)]
* * *{ )
Эти выражения соответствуют формулам, выведенным на стр. 178
для коэффициентов Чебышева К0, Кх,. • •, Кт.
Но с другой стороны, мы можем рассматривать систему (2) как
систему условных уравнений, для неизвестных Ak при произвольных
у.; эта система избыточная (m-f-l<«), и для решения ее мы при¬
меним способ наименьших квадратов. Для этого надо составить
систему из (m-f-1) го нормального уравнения для А0, Ах,..., Ат; как
известно, первое из этих уравнений получится, если условные урав¬
нения (2) помножим на коэффициенты при Л0, т.-е. на 'f0(*i)> ...,
?о(хп); второе — помножая их на ..., ?х(-хп), т.-е. на коэффи¬
циенты при Ах и т. д. и складывая все строки вместе. Мы снова за¬
мечаем, что произведения типа Aj\st{x)rf^x)\ обращаются в нуль, так
что нормальная система гриводится к ее простейшему виду, когда
в каждом уравнении содержится только одна неиз¬
вестная. ^
Таким образом, получаем нормальные уравнения:
[У? о(*)]=Л>[?<Д*)]
Lm(*)] =АхЬЛх)\
iyux)\=кълх))
Из этой системы опять выводим, что
, _b«p*WI
*“ ЪА*) ’
Таким образом, решая условные уравнения (2) по способу наимень¬
ших квадратов, мы находим для Аь те же значения, которые получены
— 182 —
выше из одного условия ортогональности функций <?0(х), уфх),..., ®w0c).
Это приводит к весьма важному положению: если общее выражение^
в функции х получается в виде разложения у по ортогональным
функциям *р0(х), ..., то результат во всех случаях соответствует
способу наименьших квадратов; вычисление коэффициентов по фор¬
мулам Чебышева - Фурье само по себе обеспечивает минимум суммы-
квадратов уклонений вычисленных ординат у. от заданных произ¬
вольных значений у.. Отсюда следует, что разложение (с) характе¬
ризуется всеми свойствами, соответствующими теории наименьших
квадр.-тов. Мы отметим сейчас важнейшие из них.
Петь ех, е2 ..., &п означают уклонения данных у{ от вычислен¬
ных у..
Тогда, в силу леммы Гаусса (стр. 105), можем написать:
ei?o(*i) + -f • • • -f V?«K) =0
sr?l(*l) ~\~s2?l(Xl) • ■ • ■fyiW =0
... +VPj*a) = 0
или, сокращенно,
[«?*(*)] =0 (4)
при k — 0, 1, 2, ..m
Это условие выражают словами: остающиеся погрешности г. орто¬
гональны к каждой из функций ®А(х).
Составим теперь выражение для [ег]. Для этой цели применим
формулу (стр. 108):
[ее] = [//] — \at\x — [Ы]у — \cl\z —...
В условиях настоящей задачи х,у, z ... заменяется на А0, Alt А2 ...
/'■ на ур, а., Ь., с. на ®0(х.), ^(х.), ®2(х.),..., так что [а/], [Ы\,...
переходят в [yfopc)], [ууфх)], ..., и мы получаем:
N = [УУ\ — ЛЬ?оМ] — Ai[y?i(x)] —А [у?8Р0] — • • •
Так как, по (3), [y?k(x)] = Ak['?kz(x)], то последнее уравнение при¬
нимает вид:
[ее] = [уу] - Л02[?Дх)] - Л Д?Дх.] - Л Д® Дх)] - .... . . (5)
Наконец, еще раз прилагая к (5) формулы Фурье, находим:
г-l _ Г шЛ _ Г-У'-РоМ]3 _ [У'Ь(Х)\2 _ [у-РаМР _ (Q)
[°°] “ j [?o3WI IfiHx)) [<ра3(х)] (bj
Группа формул (3 — 5) обобщает результаты, полученные в преды¬
дущем § для частного случая ортогональных разложений по много¬
— 183 —
членам Чебышева; она имеет фундаментальное значение в различ¬
ных отделах Анализа.
Не входя в подробности, допустим лишь, что при достаточном
продолжении разложения (с), все е.—»-0. Тогда формула (6) перехо¬
дит, при п—*оо, в предельное соотношение (так называемая фор¬
мула Парсеваля):
Г 1,1,1 — П'?о(*)Р I [У-PiWP I [-ГУз(-у)]3 I /7\
1УЛ №)] ^ f'Vto] ^ t?33W] ^ к '
В Анализе система формул (3) — (6) развивается для случая, когда
подлежащая разложению функция у=/(х) задается не для отдельных
значений х1,х.,, хп, а для всех точек интервала от х = а до
х — Ь, так чтр основная система чисел х. переходит в непрерывную
совокупность значений х, лежащих между указанными пределами.
Иными словами, здесь ставится задача: представить f(x) под видом:
(8) Я*) = ?(*) + *(*)
где <?(х) представляет собой ряд, расположенный по заданным
функциям <р0(л:)> ®г(лг), — 9т(х), а &(х) есть погрешность разложения
(в данном случае это будет уже не постоянная величина, а функция х).
Для решения этой задачи требуется найти коэффициенты разло¬
жения А0, Аг Ат, которые войдут в выражение <р(л:), именно:
?(•*) = Л?о(-*0 -Ь А1?1С*) + ' + Л,п?т(х)’
причем отыскание их подчиняется условию наименьших квадратов;
иными словами, здесь требуется, чтобы средняя квадратичная погреш¬
ность разложения, определяемая равенством
ъ ь
<х) = ~-f*\x)dx = [/(*) - '{(х)}Чх,
а а
имела бы минимальное значение.
Функций OoW) TffiW предполагаются ортогональными на участке
а ... Ь, т.-е. удовлетворяющими условиям:
/ ? к(х)ъ(х)йх=° ?=о!’ I:::«k =£1 • ■ • • • * о7)
а г * >
В курсах Анализа выводятся следующие формулы, которые мы
получим непосредственно из (3) — (6), заменяя в них суммы инте¬
гралами J):
1) Нормальные уравнения для коэффициентов Ak:
Akj?k\x)dx = jf (xy>k(x)dx ....... ( 3 )
1) Все интегралы берутся в пределах от а т Ь
184 —
из них определяются коэффициенты Фурье:
ff(x)fk(x)dx
* / 4k^x)dx
2) Обобщенные формулы Гаусса:
f z{x)vk{x)dx = О Л = 0,1, 2, .... т . . . . (4')
3) Обобщенная формула Чебышева для средней квадратичной
погрешности разложения:
(Ь — а) с2(х) = /e?(x)dx — / f2(x)dx — A^f y02(x)dx —
— A2f?2{x)dx — A2f'*2{x)dx — .(5')
-
Более подробное изучение относящихся сюда вопросов является
предметом курсов Анализах); нам было лишь важно отметить, как
тесно связаны они с основными положениями и формулами способа
наименьших квадратов.
§ 7. Основы гармонического анализа.
Применим результаты предыдущего § к разложению периодических
функций в тригонометрические ряды. Если подлежащая разложению
функция предполагается заданной на всех точках какого-либо интер¬
вала независимой переменной х (напр, от 0 до 2я), то вопрос о раз¬
ложении ее по sin’aM .H cos’aM дуг, кратных х, приводит к так назыв.
рядам Фурье, в теорию которых мы здесь входить не будем2). Если же
периодическая функция х, с периодом 2п, задается на п отдельных
точках (обычно равноотстоящих), то представление ее под видом
суммы периодических членов вида Akcoskx и Bksmkx является пред¬
метом гармонического анализа, о котором сообщим здесь краткие
сведения.
Положим, что для п значений х, равных
Л 2тс n 2iz , 2it . .. 2r. ...
’"л"’ ~п ~п (я — l)*7jr 0)
задано п значений периодической (с периодом 2*) функции у, именно:
Ус> Л. Л* Л> ••••-Л-i- • (2)
По этим данным требуется найти общую зависимость у от х через
sin’bi и cos’bi дуги х и ее кратных, до некоторой кратности т вклю¬
чительно. Такая зависимость выражается тригонометрическим много¬
членом вида:
у = ао-\-А1 cosх-[-А2cos2хАтcosтх-\- . . . . (3)
-j-5j sinx -f- В2 sin 2х-(- Вт sin тх.
1) См. Смирнов, Курс высшей математики, т. ТТ (1931), стр. 410 и след.
9) См. Привалов, Ряды Фурье (1930)*
— 185 —
Число неизвестных коэффициентов составляет 2/ге-}-1; очевидно,
что если п = 2т-\-\, то мы сможем определить все эти коэффи¬
циенты, так что кривая, выражаемая формулой (3) пройдет в точ¬
ности через ординаты:
У о у У1 У У2 Л-1
Но если /1>2от-{-1, то коэффициенты Ак и Вк придется находить
из избыточной системы уравнений, подчинив их определение условию,
чтобы сумма квадратов уклонений вычисленных ординат от значений
(2) имела наименьшее значение.
Для вычисления искомых коэффициентов будем исходить из фор¬
мул х):
[sin kx] = [cos kx] = [sin kx sin/*] = 0 \
[cos kx cos/x] = [sin kx cos/*] = 0 J ^ ^
[sin2 kx] = [cos2 kx] — ~.
Во всех этих~суммах * принимает последовательно всю совокуп¬
ность значений ряда (1); k и / означают любую целую кратность этих
значений, не большую чем
Из (4) мы заключаем, что функции 1, cos *, cos 2*, ... cos тх
sin*, sin2*, sin tnx (где составляют систему функций
ортогональных по отношению к системе п равноотстоящих значений
*г из ряда (1). Но этого замечания достаточно для определения коэф¬
фициентов разложения по формулам Фурье, а следовательно, и для
получения разложения у, соответствующего методе наименьших ква¬
дратов.
Применяя к настоящему случаю формулы (3), (4) и (5) § 6 и поль¬
зуясь соотношениями (4), немедленно получаем:
(А) Формулы для коэффициентов:
Л = А = -^ [.У cos*]; А2 = ~[у соь2х\,.... Ат = ~\у cos тх]
Вх = ~\уsin*]; = ~[^sin2*];... Bm = ~[yiinтх].
*) Первые две формулы (4) выводятся, выражая sin kx и cos kx через е*1 п е~*1 по
формулам Эйлера, после чего суммы sin’oe и cos’ob превращаются в геометрические
прогрессии, суммы которых равны нулю; остальные получаются из обоих первых три-
гонометрическими преобразованиями, предполагая что (£+./)<£**«
— 186 —
(B) Формулы для остающихся погрешностей:
[г] = 0; [г COS х] = 0; [е COS 2х] =0; .... [г COS тх] = 0
[$ sin л;] = 0; [г sin 2х] = 0; [г sin mx] = 0.
Любая из этих формул может служить как контрольная в вычис¬
лениях, когда, получив коэффициенты А. и В., мы вычислим зна¬
чения yt для х = х. v образуем е. =улшиов —Лычйсл.
(C) Формула для [ге]:
И = [уу] _ пА* - JL (Л +....+ AJ _|_ в» +...+ BJ)
Замечая теперь, что
[уу] - пА0* = [уу] - И-3 = [УУ ],
где у. означают уклонения заданных у. от их арифметического сред¬
него, приводим последнюю формулу к виду:
N = [у'у'1 - -у 0V+В*+А/+В* +... AJ + /у).
Положим теперь
'Up-«я
Мы имеем тогда:
' i [“] = 2^2(У - (А*+В* 4- Л2»+В*+... AJ+BJ)
Так как [ае]>0, то
W + S12 + A* + Si2 + .... Ая* + Вя*)*=.Ъ*{у). . . .(5)
Но каждые два члена вида
Ak cos kx Bk sin kx
можно привести к одному, называемому гармоникой k - ого порядка
в данном разложении, именно:
* С* sin (&* + «*);
для этого достаточно положить:
Аъ = Су sin а.
Bk = Ckcosak>
Ak
так что
"ск = А1 + вк ; = arcts щ;
Ck есть амплитуда гармоники; «4— ее фаза; период ее равен
— 187 —
Заменяя теперь в формуле (5) члены на Ct2, имеем:
СА + С/ + ... Ся*<23*00 (7)
иными словами: сумма квадратов амплитуд периодических членов
разложения (3) не больше удвоенного квадрата дисперсии заданных
ординат (теорема Бесселя).
Заметим теперь, что если п = 2т-\-\, то кривая, выражаемая фор¬
мулой (3), проходит в точности через заданные точки, так что все
е. = 0; в этом случае в формулах (5) и (7) остается только знак ра
венства, так что
C* + Cf + ... С*я = 2**00 (8)
Приведенными формулами решаются важнейшие вопросы, относя¬
щиеся к представлению периодических функций в виде тригонометри¬
ческих полиномов. С простейшим примером подобного рода мы уже
познакомились, решая задачу об эксцентриситете алидады (стр. 131),
где, имея 12 ординат, мы ограничились членами
А0 Al cos sin х.
Но существенно отметить, что мы могли бы включить в это раз¬
ложение и члены следующих кратностей, напр. i42cos2.x: и В2 sin 2*;
при этом найденные раньше коэффициенты Л0, Аг и Вг остались бы
без изменений, что соответствует общим свойствам разложений по
ортогональным функциям; но при этом сумма [гг] уменьшилась бы
а А* + В*.
Вернемся теперь к формуле (8); исходя из нее мы можем ввести
понятие „средней квадратичной амплитуды“ разложения у; именно
если положим:
то в виду (8) будет:
С=ЧУ)У 1 (9)
Заметим, что формула (9) дает во всех случаях полный контроль.
разложения (3).
Допустим теперь, что задано п наблюдений какой-либо вели¬
чины у, расположенных последовательно по времени t и отделенных
друг от друга равными промежутками Т. Введем вместо х переменную
тогда значениям t, равным
О, Т, 2Г .... (я— 1)Г
— 188 —
будут соответствовать значения в, данные выше в ряде (1). В виду
этого мы можем всегда найти для у разложение вида:
у = Уд -J- Cj sin (0 -{- flCj) -j- C3 sin (20 -j- oc2) -j-.... Cm sin (rat0 -J- ctm), (10)
где
Обратим внимание, что при га четном высшая кратность т будет
равна п1%; но в этом случае -2- 0 = тг и потому Вп/3 = 0, так что
_ . я—1
Сп/г = Ani3) при га нечетном высшая кратность т равна -у-*
Найдя для у разложение (10) мы можем поставить вопрос: указы¬
вает ли это разложение на то, что у действительно является периоди¬
ческой функцией t? Допустим, например, что.у фактически обладает
_ пТ
периодичностью внутри интервала га/; пусть период ее есть где
k— 1, 2 ... /га.
Мы имели бы тогда
У — У о ~Н sin(^® “Ъ °0-
Написав га таких равенств для У=У0,У, • • • • Уп-t, возводя их
в квадрат и суммируя находим:
или:
Ск = °(у)]/2. (11)
Эта важная формула обнаруживает, что если у внутри заданного
интервала пТ ведет себя как любая из гармоник разложения (10),
то ее амплитуда равна дисперсии заданных ординат, умноженной
на "|/2 .
Допустим теперь — в виде другой крайности, — что все последо¬
вательные значения у представляют собой только неизбежные коле¬
бания наблюденных y.t вокруг их среднего значения у0; в этом слу¬
чае мы вправе ожидать только, что все амплитуды С{ равны их
средней квадратичной величине о (у) J/ т.-е. в j/гаг раз меньше
величины (11). — Исходя из этого обыкновенно считают, что те
члены разложения (10), амплитуда которых близка к «(у)/2» указы¬
вают на действительную периодическую зависимость у от t; напро¬
тив, разложение, у которого все ампитуды близки к о(у) ]/Ь За¬
зывает на отсутствие такой зависимости. Более подробное развитие
— 189 —
этих вопросов относится к так называемому приодограмному анализу
и выходит из рамок настоящего курса *).
Для облегчения вычислений, применяемых в гармоническом ана¬
лиз , разработаны специальные схемы, таблицы и шаблоны 2).
Мы ограничимся здесь формулами для л =12. Определению под¬
лежат коэффициенты А0, Ах А3, В1У В2 В&. Схема состоит
в том, что ряд заданных ординат записывается в яперегнутом" виде,
так что друг под другом приходятся ординаты у, значки которых
дополняют друг друга до 12. От полученных рядов чисел берутся
суммы s и разности d; затем ряды 5 и d в свою очередь переги¬
баю, ся и вписываются в схему так, чтобы значки дополняли друг
друга до 6; после этого вторично берутся суммы и разности.
Уо
Ух
У2
Уо Ух
Уь
Л
Ухх
Ухо
У9 Ув
Ух
Суммы s0
Н
s*
s3 st
sb
Разности
d1
d*
d3 dk
d5
$о
Si
S2
Ss 1 dx
d2
d3
s*
Ss
Si
! d5
dx
Суммы р0
Pi
P2
Po 1 h
Jj
Го
Разности q0
Ях_
Яо
1 tl
£2
Величины qx, г2, tx и t2 множатся на cos 30° = 0,866.
Для вычисления искомых коэффициентов служат формулы:
6(Л0-}-Лв) ~Ро~^~р2 В, — 0
6(Л — Лв) = А+Л> 56=о
3 (Ax
+ Л6) =
= + y Я2
3 (5,
+ 56) =
1
2
''i + 's
3 (Л,
-Л5Ь
= qx cos 30°
3(5,
— 56) =
Г2
cos 30°
3 (A2
+ •^4) =
1
~Po 2 B2
3(5,
+ 54) =
■ tx
cos 30°
3 (A2
-Ax)=
= \px—Po
3(5,
— 54) =
to
cos 30°
6Л3 — <7 о Яо 6Д3 — тх гй
Складывая и вычитая написанные друг под другом строки полу¬
чаем 12 Л0 и 12 Л„; затем 6Л4 и 6 Л6 и т. д.; отсюда находим и иско¬
мые коэффициенты Ак и Вк.
>) Подробности см. в указанной в литературе статье К. Mader а в Ill-м томе
Handbuch der Physik.
а) Из них особенно удобны таблицы L. Poliak, Rechentafeln zur harraonischen
Analyse, Leipzig, 1926. См. также В. Смирнов, Курс высш. матем., т. И, стр. 392 и сл.
— 190
Пример. Произвести разложение по следующим двенадцати
заданным значениям у.
у 25.3 35.4 26.0 14.7 25.0 34.0 25.2 15.0 24.7 35.9 25.0 14.7
у' +0.2 +10.3 +0.9 —10.4 -0.1 +8.9 +0.1 —10.1 —0.4 +10.8 —0.1 -10.4
На второй строке даны уклонения у от их среднего у0 = 25.1.
Для вычисления коэффициентов применяем данную выше схему.
s
d
Р
Я
6(4, +А) =+151.2
6(А —А) —+149;7
3!А+А)*=+ 07 3(4 + 4) =-1.4
3(4 — А) =+ 1-0 3(4-4) =+l.i
3(4 + 4)=+ 0.1 3(4 + 4) =+1.5
3(4-4)=— 1.0 3(4 — 4) =+о.б
64=— 1.2 64=+60.9
Отсюда находим коэффициенты Ak и Вк, амплитуды Ck и фазы лк\
25.3
35.4
26.0
14.7
25.0
34.0
25.2
14.7
25.0
35.9
24.7
15.0
25.3
50.1
51.0
50.6
49.7
49.0
25.2
20.7
1.0
—21.2
0.3
19.0
25.3
50.1
51.0
50.6
20.7
1.0
—21.2
25.2
49.0
49.7
19.0
0.3
50.5
99.1
100.7
50.6
Г
39.7
1.3
—21.2
0.1
1Л
1.3
t
1.7
07
А
С 2
С*
«А
0
+25.07
1
+ 0.28
- 0.05
0.0809
0.28
100°.1
2
— 0.15
+ 0.35
0.1450
0.38
336.8
3
— 0.20
+10.15
103.0625
10.15
358.9
4
+ 0.18 ,
+ 0.15
0.0549
0.23
50.2
5
— 0.05
— 0.42
0.1789
0.42
186.8
6
+ 0.12
0.0144
0.12
90.0
103.52
Таким образом разложение для у есть:
у = 25.07 + 0.28 sinfx + 100°.1) + 0.38 sin(2x + 336п.8) + 10.15 sin(3x + 358°.9)
+ 0.23 sin(4jc + 50°.2) + 0.42 sin(5x + 186°.8) + 0.12 sin(6x + 90°).
Для контроля подставляем х = 0°, 30°, .... 330° и убеждаемся,
что для у получаются в точности заданные его значения.
Средняя квадратичная амплитуда равна здесь:
10|—= 4,154.
Вычислим теперь дисперсию заданных ординат; найдя [у’у1], рав¬
ную здесь 621,31, получаем
«СУ)=/^Г = 7,196.
191 —
Отсюда: _
/2 7,196 ..г, 7=;
м = рт
Полученный результат дает полный контроль всего вычисления.
Вместе с тем мы замечаем, что амплитуды С19 С2 ... . Сб найден¬
ного выше разложения для у весьма далеки от полученного значе¬
ния С. Поэтому мы можем поставить вопрос: не проявляет ли
заданная совокупность у действительной периодической зависимости
от х\ с этой целью мы должны убедиться, нет ли в разложении у
амплитуд, близких к о(у) ]/~2, что в данном случае равно 7,196|/ 2= 10,17;
но мы имеем в разложении член
10,15sin(3;t + 3580,9)
и поэтому заключаем, что данная совокупность значений у действи¬
тельно указывает на периодическую зависимость от х, с периодом
2ir
в з-
§ 8. Разложения по полиномам Лежандра.
Для второго примера разложений по ортогональным функциям
рассмотрим систему многочленов, которые получаются из многочленов
Чебышева в том предельном случае, когда число основных зна¬
чении хг заданных в конечном интервале от хг до хп , стремится
к бесконечности, причем
•*7+i xi
Прежде всего заметим, что этот основной интервал путем надле¬
жащего изменения масштаба по оси абсцисс и переноса начала
координат всегда можно свести к интервалу от—1 до--(-I1); таким
образом, основная система значений хп для которой строились много¬
члены Чебышева, превращается здесь в непрерывную совокупность
всех вещественных чисел от — 1 до-j-l.
Для решения поставленной задачи обращаемся к системе тех нор¬
мальных уравнений, из которых были выведены многочлены Чебы¬
шева (стр. 172); переписывая левые части нормальных строк в допол-
неном виде и деля все эти строки на п, получаем систему:
1 м и —
п п
[*2] м...
п п
J) Для этого достаточно вместо х ввести новую переменную t~—————; тогда
при х = хг, t = — 1; при х = хп, t = + 1; в дальнейшем мы пишем снова х вместо U
— 192 —
Теперь нужно найти пределы всех написанных сумм при п—► со.
Замечая, что длина всего интервала равна здесь 2, и что в этом
интервале дано п значений каждой из функции хк, находим:
- f -— при k четном
+ 1 Г 2
[xk] — fxkdx = |2ft +1
п-*- со —1 10
-со —1 10 при нечетном
следовательно:
п |2А +
/>-*• со I О
НтЦг* = Ц+1- при k четном
при k нечетном
Таким образом, нормальная система стр. 172 принимает здесь
следующий предельный вид:
1
0
1
3
0
1
5
0
1
7
1
3
0
1
5
0
1
7
0 ввя
1
5
0
1
7
0
1
9 воя
Эту систему мы будем обрабатывать теперь по обычным прави¬
лам решения нормальных уравнений, т.-е. будем последовательно
составлять элиминационные строки ЕХ,Е2, Ей,... (см. стр. 52). В резуль¬
тате этого процесса приходим к схеме, приведенной на стр. 193.
Обозначим теперь через Хй(х), Хх{х),... Хк{х) те многочлены, в кото¬
рые в рассматриваемом случае, т.-е. при я—*■ оо, соответственно пере¬
ходят многочлены Чебышева ф0(я:), Фх(.а:), ..., Цк(х). Очевидно, что
коэффициенты многочленов Хк(х) будут получены из только-что напи¬
санной схемы по тому же самому правилу, которое дано для образо¬
вания многочленов $к(х) из схемы на стр. 170. Поэтому, чтобы выра¬
зить зависимость Хк(х) от всех предшествующих ему A"0(x:), ^(л:),...,
и от х\ мы должны числа стоящие в элиминационных строках
B(fc-f-l)*M столбце полученной сейчас схемы множить последова¬
тельно на—Х0,—Х1,—Х2, — Xt_lt и заключительную единицу
этого столбца на хк. Сумма этих произведений после приведения
по х и составит многочлен fc-й степени Хк(х). Таким образом, из
одной только гауссовой схемы решения нормальных уравнений
мы получаем здесь всю цепь многочленов Хк(х), имеющих весьма
важные приложения в Анализе; они носят название многочленов
Лежандра.
— 193 —
Nx 1 О
£, / О
К, з
£, 1
N..
£<
ЛЛ,
1
'6
!; о
1
5
0
1
7 '
1
3
1
0
1
5
0
У
7 '
0
1
5
0
1
7
0 .
0
3
, 5
(7
5
7
0 .
1
5
0
1
7
0
1
9 *
1
9
0
1
15
0.
1
2! ‘
■I-
45
0
8
105
0
12
189 *
Г
0
в
/
0
/
1
7
0
1
9
0 .
3
25
о
3
35
0 .
4
175
0
8
315
0 .
/
0
10
9
0 .
1
9
0
1
11 *
1
25
0
1
35 * '
43
735
0
72
1323*
64
0
0
64
11025
7
8085*
15
11 ’
£5
Написанных выше пяти элиминадионных строк достаточно для
составления многочленов .А^, Хх,..., Х6. По приведенному сейчас пра¬
вилу находим:
Л(*)= =1
Хх(х) = = х
ад = -|-^1+^ =x*~ix
Х,(х) = х3 + х* = ** - +15
ВД = - i ХХ - ^ X, + Xй =^5- ^
Х9(х) = — )х0 — )Х, -^..V = *•- !J^ + n^2-.|T-
Способ найм. квадратов.
13
— 194 -
Из полученных выражений для Хк{х) легко убедиться, что каждый
из них, начиная с Х.2(х), связан с двумя предшествующими ему сле¬
дующей зависимостью (доказательство которой для общего случая
здесь не приводится):
\ №
Xk+\ — x • Xk~ (2k—1)12А+1) • Xb-i-
Многочлены Лежандра характеризуются теми же свойствами,
которыми отличаются, многочлены Чебышева, при условии
замены в соответствующих теоремах сумм на определенные интегралы,
взятые в пределах от—1 до-f 1. Таким образом:
1) Многочлены Х0(х), Х^х),..., Xk{x) ортогональны
на основном интервале от—1 до-}- 1, т.-е.
-М
j‘ XJx) Xt(x)dx — 0, при т ф I]
— 1
в частности, в виду Л”0(л;) = 1;
-Г 1
у*Xm{x)dx — 0, при любом т, неравном нулю.
— 1
2) Интеграл от квадрата многочлена Ленжандра
Хк(х), взятый в пределах от —1 до -J— 1, меньше интеграла,
взятого в тех же пределах от квадрата любого дру¬
гого многочлена той же степени k, со старшим
коэффициентом равным 1.
Замечательно, что значения этих интегралов от Хк2(х) могут быть
непосредственно найдены, из приведенной на стр. 193 схемы нормаль¬
ных строк. Действительно, по формулам первой группы (D), стр. 176
мы 'имели:
Ы*)] = И]; [<№)] = [Mi]; [№)]; = М;...
Числа [аа], [bb\], сс2] и т. д. стоят в нашей схеме непосредственно
14 4
над единицами элиминационных строк; это суть числа: 1, у, ^ , щ,
64 „
П025 с ДРУГ0® стороны, аналогично предыдущему, здесь имеем:
—1
lim ['К(х)] — -Г f Xk\x)dx.
п+со фх
Таким образом, непосредственно находим:
— 195 —
i V i
j J Xf(x)dx = [bb\] = \
— 1
— t
\f x^ytx = ИЗ] - j|s - (fckir ■ ‘
— 1
+ 1
1 /’v,, ч , r И1 64 /1.2 3 4\2 1
2 j Xt{x)dx — [ee4] — по2^ — (j e 3 _ 5 j) • 9
— 1
Отсюда (не останавливаясь на подробном доказательстве) заклю¬
чаем:
7 -гд*н - (В: I; а - У ■ агт? • • <»
— 1
Введем теперь в рассмотрение вместо Xk(x) ряд многочленов Pk(x),
отличающихся от Xk(x) постоянными множителями, именно положим:
од=( Н--Й-.----Л1) • /Щ1 ■ w *2)
Очевидно, что свойство ортогональности сохранится и для много¬
членов Рк(х), так что:
f PH PJx)dx = 0, при тф1 (3)
— 1
Кроме того, в виду (1), полагая еще Р0(х) = получим *):
у 2
-L- 1
Jp*(x)dx= 1 (4)
— 1
Построив таким образом систему многочленов Р0(х), Рг(х),
Р»(х),..., мы можем воспользоваться ею для разложения всякой
непрерывной функции, заданной на интервале от — 1 до +1 в ряд,
расположенный по этим многочленам (подобно тому как фунция, зна¬
чения которой были даны для точек xlf х*,..., хп, разлагалась в ряд
Чебышева), причем и это новое разложение точно так же как
и ряд Чебышева будет соответствовать основам способа
наименьших квадратов. Отличие этого ряда от прежнего выразится
>) Система функций, удовлетворяющих равенствам (3) и (4), носит название нор¬
мальной ортогональной системы.
13*
— 196 -
лишь в том, что остающаяся погрешность е будет здесь в свою оче¬
редь непрерывной функцией г(х), так что условие минимума [гг]
заменится условием минимума Je%x)dx. Но все формулы предыду-
— 1
щега § найдут здесь непосредственное применение, с заменой вхо¬
дящих в них сумм на определенные интегралы, взятые в пределах
от — 1 до + 1.
Таким образом, мы приходим к задаче разложения непрерывной
функции у —fix), значения которой заданы для — 1 sS-tsS 1 по орто¬
гональной и нормальной системе полиномов Рк(х).
Положим, что А0, А,Ак суть искомые коэффициенты разло¬
жения, так что:
у=/х) = А0Р0<х) + А1Р1(х) + АлРг(х) + . . . +А,Р-х) (5)
и соответственно с этим:
e(x)=f(x) — A0P0(x) — A2P2(x) — . . .—AkPt<x).
Применяя к этому ряду формулы (3'), (4') и (5') § 6, стр. 183— 184,
и пользуясь равенством (4), приходим к следующим зависимостям,
одинаково характерным и для методы наименьших квадратов, и для раз¬
ложений по ортогональным функциям вообще:
Ak — f fix) P.(x)dx (а)
— 1
+ 1
/•<*> Pm(x)dx = 0, при т = 0, 1,, . . . , k . . .(b)
— 1
-И +i
js2(x)dx = ff(x)dx~A02-A,2 - . . . - -А*. . . .(с)
- I — 1
Так как интеграл в левой части (с) есть величина не отрицатель¬
ная, то.
* . '7
2 А2т < I f\x)dx, при любом k .(d)
о
— 1
Отсюда заключаем (если только интеграл от f2(x) существует),
что ряд есть ряд сходящийся, и следовательно: \\т]/И Ak = 0\
* k ► ОС
кроме того, из сходимости ряда 2А 2 легко выводится сходимость
’vHit
ряда 2и-~г ■
— 197 - '
Наконец, для разложений по полиномам Лежандра доказывается,
что сумма этого ряда при k—»эс имеет пределом именно интеграл,
стоящий справа, так что:
Заметим еще,; что для вычисления коэффициентов А\ по фор¬
мулам {а) нужно пользоваться, когда аналитическое выражение у =Дх)
не дано, приемами численного интегрирования. Внося полученные
значения Ак в (5) и делая приведение по х, мы последовательно
получаем для у=Дх) выражения в виде полиномов первой, второй
и т. д. степени, причем каждый из них представляет ход функции
Дх) на всем данном интервале с меньшей средн й квадратичной по¬
грешностью, чем любой другой многочлен одинаковой с ним степени.
Пример. Найти для функции у = sin* выражение в виде много¬
члена не выше четвертой степени, который представлял бы эту
функцию в интервале от — тс до-)-71 с наименьшей средней квадра¬
тичной погрешностью.
Начнем с разложения .функции sin-*1 для — положив:
Из формул для Pk и Xk видно, что все многочлены с четными
значками содержат только четные степени переменной.
Поэтому I ьт(к£)Р$)(И = 0, при k = 0,2,4. . . . и следовательно,
вычисляем по формулам (a): AY — 0,779697; А* = —0,619104.
Таким образом:
sin (тЛ) ^ A.P^t) -f A,P:](t) = 2,692301 — 2,89559
Переходя теперь обратно к переменной х, т.-е. полагая t на¬
ходим окончательно:
1
sin («*) = Л0 + ЛхЛ(0 + АР St) + AP,(t) + A.PSt).
по формулам (а), А0 = A2 = Ai = 0. Далее, из (2) находим:
Р&) = 1,224745 t
P,(t) = 4,6770721* — 2,806243 t.
Замечая теперь, что
— 1
— 1
sin* eg 0,856982 x — 0,093387 xs.
— 198 —
Для квадрата средней квадратичной погрешности этого разло¬
жения на интервале от—1 до-f-l по формуле (с) имеем:
J e2(z‘)dt = J sin2 (rd) dt—A^—Л32 —1 — 0,607928—0,383290=0,008782,
Полученный таким образом многочлен представляет функцию sin.*
на всем интервале от — я до-(-я с наименьшей средней квадратичной
погрешностью, возможной для многочлена не выше четвертой степени
вообще, и в этом смысле данное приближение лучше, чем первые
два члена соответствующего разложения в ряд Тэйлора, именно:
Такое различие между обоими разложениями становится очевидным,
если иметь в виду, что первые члены ряда Тэйлора приближаются
к данной функции тем лучше, чем меньше х; следовательно, они
дают представление о ее ходе в непосредственной смежности с х = 0,
а отнюдь не на всем интервале от —it до -|-ir.
— 1
и потому при длине интервала, равной 2,
sin х — х— -g-
ЛИТЕРАТУРА.
Основные мемуары Гаусса по сп. н. кв.: „Theoria Combinationis Observationum
etc.* и Supplementum, в IV томе поли. собр. соч.; см. также .Теория движения небесных
тел“ (русск. пер. М. 1861), кн. II, ч. III; мемуары Гаусса переизданы на фр. языке
в переводе J. Bertrand.
Из более детальных изложений предмета в русской литературе упомянем книги:
Савич, „Приложение теории вероятн. квычисл. наблюдений" (1857) и Майевский,
,, Изложение сп. н’ кв. и применения его преимущественно к. исследованию результатов
стрельбы" (Спб. 1881). Соответствующие главы из трактата акад. А. Маркова („Исчис¬
ление вероятностей", ГИЗ 1924) имеют чрезвычайно большую теоретическую важность;
в частности, методическое сведение сп. н. кв. к „правилу наибольшего веса* особенно
рельефно выражено у Маркова; но эти главы мало расчитаны на вычислителя-
практика.
В книге акад. С. Н. Бернштейна „Теория Вероятное гей* (ГИЗ 1927) содержится
глубокий анализ закона нормального распределения й условий его применимости
к статистическим явлениям.
Из современных иностранных руководств можно указать: Brunt, „The Combination
of Observations" (Cambr. 1917), и Whittaker and Robinson, „Calculus of Observa¬
tions", London 1921, ch. IX; свежо и интересно все написанное по уравниванию в книгах
Runge: „Praxis der Gleichungen" (Lpz. 1921); „Theorie und Praxis der Reihen, §§14, 16
(Lpz. 1904), а также Runge und К 6 n i g, „Numerisches Rechnen" (B. 1924).
В 1930 г. вышла книга Deltheil. Erreurs. Moindres Саггёэ. (Gauthiers—Villars).
Из числа кратких пособий отметим: Weitbrecht, „Ausgleichungsrechnung"
Gtischen, №№ 302 и 641).
Весьма интересна статья поуравниванию К. М a de r’a, Ausgleichungsrechnung в III томе
Handbuch der Physik (Springer, 1928); в ней даны и обильные литературные указания.
Для приложений к геодезии — подробное, но исключительно тяжелое изложение
у Helmert’a, „Ausgleichungsrechnung nach der Meth. der kl. Quadrate" (3. Aufl. 1924);
первая часть имеется в русском переводе Сопоцько (Москва, 1914). В заключитель¬
ных главах (разложение функций) это сочинение совершенно устарело. Схему D о о 1 i t-
Пе’я и т. п. я излагал по Adams, „Application of least squares to triangulation", Coast
and Geodetic Survey, Spec. Public. № 28, Wash. (Depart, of Commerce, 1915); очень
полезен для геодезиста сборник упражнений: Hegemann, „Uebungsbuch fur die An-
wendung der Ausgleichungsrechnung" (3. Aufl., B. 1925).
Вопросы математической статистики здесь затронуты, так как излагать теперь
теорию ошибок вне основных статистических понятий кажется невозможным. По этому
отделу см. Charlier, „Vorlesungen iiber die Grundsatze der mathem. Statistik" (Lund,
1920), откуда взяты обе таблицы, стр. 101 и 102; Митропольский, „Основы стати¬
стики*, ГИЗ 1925; Rietz, „Handbook of mathem. Statistics* (Boston, 1924). Но изучение
предложенных за последние годы в теории ошибок видоизменений закона Г аусса
(С h а г 1 i е г, М. Субботин) осталось за пределами этой книги.
Способ Чебышева представляет собой как бы связующее звено между старым
сп. н. кв. и обширным полем современного анализа, относящимся к разложениям по
— 200 —
ортогональным функциям. Кроме основных мемуаров Чебышева („Об интерполиро¬
вании по способу н. кв.* и „О разложении функций одной переменной"), см. А. Мар¬
ков, „Исчисл. вер.", стр. 427; Н. Poincar£, „Calcul des probabilitds" (1912), ch. XX;
затем работы А. Саткевича (Изв. Гидрологического Института, 1920) и Хотим-
ского, „Выравнивание статистических рядов по сп. н. кв.“ (ВСНХ. 1925). Изложение,
данное здесь, обнаружит, я надеюсь, что подход к способу Чебышева со стороны
нормальных уравнений Гаусса не является ни трудным, ни неудобным. — Ср. А. Ор л о в,
„Интерп. по способу Чебышева" (Изв. Русск. Астрон. Об-ва, 1919); N. Idelson.
„Sitr l’interp. par la methode de Tchebycheff" (Bull. Inst. Astron. № 14, Lgr. 1926).
Желающие ознакомиться подробнее с проблемами ортогональных разложений
обратятся к „Курсу высшей математики" В. И. Смирнова, т. II (ГИЗ, 1931) и к первым
главам „Основных задач математической физики* В. А. Стек лова (Птг. 1922). Для
статистических приложений особенно важны многочлены Чебышева-Эрмита: см. Лах-
т и н, „Кривые распределения*, ГИЗ, 1921, и Rieina'nn-Weber, „Different, und
Integral Gleicli. d. math. Pliysik", 1925, Кар. VIII and IX (ряд В r u n s’a).
Для разложений в ряды Фурье см. И. Привалов, „Ряды Фурье", (ГИЗ 1930);
полезные указания имеются в „Справочной книге для электротехников" (СЭТ), т. I,
(Кубуч, 1930).
По этим вопросам следует иметь в виду работу М. Н. Сергеева, „О построении
многочленов, приближенно изображающих на конечном отрезке данную непрерывную
функцию" (Трзпш Моск. Меж. И-та, 1927).
Последним обобщением сп. н. кв., вопросов математической статистики и разло¬
жений по ортогональным системам является трудная и глубокая „проблема моментов";
подготовленный читатель ознакомится с ней по В о г е I, „Les principes dc la theorie
des probabilites" (P. 1925), ch. VI, и затем’уже перейдет к заключительным главам трак¬
тата А. Маркова (см. также Введение к нему А. С. Б е з и к о в и ч а) и к мемуарам
Ч е б ы ш е в а. у
СКЛАД ИЗДАНИЯ:
Ленинград, Мойка, 53
Издательство „КУБУЧ44