Автор: Горячева И.Г.
Теги: механика деформируемых тел упругость деформация механика физика
ISBN: 5-02-002567-4
Год: 2001
Текст
РОССИЙСКАЯ АКАДЕМИЯ НАУК
ИНСТИТУТ ПРОБЛЕМ МЕХАНИКИ
И. Г. ГОРЯЧЕВА
ЕХАНИКА
ФРИКЦИОННОГО
ВЗАИМОДЕЙСТВИЯ
МОСКВА «НАУКА» 2001
УДК 539.3, 621.891
ББК 22.251
Г 67
Ответственный редактор:
академик А.Ю. Ишлинский
Рецензенты:
доктор физико-математических наук, профессор В.М. Александров
доктор физико-математических наук, профессор А.С. Кравчук
Горячева И.Г.
Механика фрикционного взаимодействия. - М.: Наука, 2001. - 478 с.
ISBN 5-02-002567-4
В монографии методами механики контактного взаимодействия и механики
разрушения исследуются процессы и явления, имеющие место при контактирова-
контактировании подвижных элементов машин, в технологических операциях и определяющие
потери энергии и материалов при трении. Изучаются напряжённое состояние и
разрушение поверхностей (изнашивание) при взаимодействии деформируемых тел
с учётом геометрической и механической неоднородностей их поверхностных слоев
(являющихся следствием применения к ним различных видов обработки, в том чис-
числе нанесения покрытий, упрочнения), адгезионного взаимодействия поверхностей,
свойств промежуточной среды и условий контактирования (трение скольжения, ка-
качения и др.).
Для специалистов в области механики контактного взаимодействия и трибо-
трибологии, а также студентов и аспирантов технических университетов.
ТП-2001-I-N 166
Goryacheva I.G.
Mechanics of friction interaction. - Moscow: Nauka, 2001. - 478p.
ISBN 5-02-002567-4
In the monograph the methods of contact and fracture mechanics are used to
investigate the processes and phenomena which occur in friction interaction of mov-
moving components resulting in the energy and material losses in machines and during
technological processes. Stresses and surface fracture (wear) in contact of deformable
bodies are studied taking into account the geometric and mechanical surface inhomo-
geneities (due to different kinds of surface treatment including application of coatings
and hardening), adhesion, properties of an intermediate medium and friction conditions
(sliding/rolling contact, etc.).
The monograph can be helpful for engineers and researchers in the field of contact
mechanics and tribology, for graduate and postgraduate students.
ISBN5-02-002567-4 ©Издательство "Наука", 2001
ПРЕДИСЛОВИЕ
Механика фрикционного взаимодействия (трибомеханика) явля-
является направлением исследований одной из фундаментальных
наук - механики, в частности её разделов - механики контакт-
контактного взаимодействия и механики разрушения, и прикладной на-
науки - трибологии. Благодаря совместным усилиям механиков и
трибологов, а также специалистов в области химии и физики
удаётся всё глубже проникнуть в тайны трения и разрушения
поверхностей и создать способы управления этими процессами.
Эта книга родилась в стенах Института проблем механики
Российской академии наук и посвящена изучению методами ма-
математического моделирования напряженного состояния и харак-
характера разрушения поверхностей при фрикционном взаимодейст-
взаимодействии. Автор, не претендуя на полноту исследования всей пробле-
проблемы, основное внимание уделил анализу влияния микрогеометрии
поверхности (её шероховатости), неоднородности механических
свойств поверхностных слоев, а также свойств поверхности и
покрывающих её плёнок на характеристики контактного взаи-
взаимодействия, силу трения и распределение напряжений в припо-
приповерхностных слоях при разных условиях контактирования.
Поскольку механические и геометрические свойства контак-
контактирующих тел меняются в процессе трения, в книге также рас-
рассматриваются вопросы моделирования накопления поврежден-
ности в поверхностном слое, усталостного разрушения поверх-
поверхностей, изменения их макро- и микрогеометрии при изнашива-
изнашивании; обсуждаются общие методы решения износоконтактных за-
задач, в которых все контактные характеристики (распределение
напряжений, форма тел, их сближение и т.д.) являются функ-
функциями времени. Решения этих задач используются для анали-
анализа изнашивания поверхностей, предсказания характера протека-
протекания этого процесса в зависимости от свойств взаимодействую-
взаимодействующих тел, промежуточной среды и условий нагружения, для вы-
бора оптимальных параметров технологической обработки по-
поверхностей с целью повышения износостойкости и долговечнос-
долговечности трущихся сопряжений.
Для решения рассматриваемых в книге задач применяются
аналитические и численные методы, при этом ряд результатов
получен в аналитическом виде.
В большой степени исследования, результаты которых из-
изложены в книге, являются развитием идей выдающегося учё-
учёного в области механики Л.А. Галина, под руководством ко-
которого автору посчастливилось сделать первые шаги в нау-
науке. Часть исследований выполнена автором со своими ученика-
учениками и коллегами - сотрудниками лаборатории трения и износа
ИПМ РАН к.т.н. М.Н. Добычиным, к.ф.-м.н. Ю.Ю.Маховской,
д.ф.-м.н. И.А. Солдатенковым, к.ф.-м.н. Е.В.Торской, к.ф.-м.н.
О.Г. Чекиной, а также с профессорами Ф. Садеги и Т. Фаррисом
(США). Автор выражает всем им свою глубокую благодарность.
Работы последних лет, вошедшие в книгу, выполнялись в
рамках финансируемых проектов Российского фонда фундамен-
фундаментальных исследований (проекты 98-01-00901, 01-01-00034) и фон-
фонда ИНТАС (проект 99-0675).
Автор надеется, что книга будет полезна широкому кругу
специалистов, работающих в области механики фрикционного
взаимодействия, и будет способствовать новым исследованиям в
этом направлении.
ВВЕДЕНИЕ
Процессы и явления, происходящие при фрикционном взаимо-
взаимодействии (трении), имеют механическую, электрическую, маг-
магнитную, тепловую и химическую природу и являются предме-
предметом изучения трибологии - области знаний, ставящей своей за-
задачей как выявление и объяснение механизмов взаимодействия
поверхностей и природы трения, так и решение ряда приклад-
прикладных задач, связанных с увеличением срока службы сопряжений
и уменьшением энергетических потерь на трение.
Механика вносит существенный вклад в изучение трения и
разрушения поверхностей. Действительно, на все процессы раз-
различной природы, протекающие в области контакта и его окрест-
окрестности, большое влияние оказывает величина действующих там
напряжений. Высокие фактические давления и скорости сколь-
скольжения обусловливают значительные температуры в областях
взаимодействия, приводят к существенным изменениям свойств
поверхностных слоев, вызывают в них механические и темпера-
температурные напряжения, способствуют протеканию химических ре-
реакций, активизируют взаимную диффузию [109]. В поверхност-
поверхностном слое, испытывающем большие деформации, происходит за-
зарождение и рост трещин, накопление повреждённости, что в ко-
конечном счёте приводит к его разрушению.
На базе механики фрикционного взаимодействия (трибоме-
ханики)
• строятся модели трения и изнашивания поверхностей;
• анализируется напряженное состояние и характер разру-
разрушения поверхностных слоев;
• оценивается долговечность работы сопряжения и определя-
определяются критические условия, приводящие к нарушению его
нормального функционирования;
• разрабатываются способы управления процессами трения
и изнашивания.
Методы механики деформируемого тела, в частности меха-
механики контактного взаимодействия и механики разрушения, явля-
являются мощным средством аналитического исследования проблем
трибологии.
В трибологии, например, уже давно используется задача те-
теории упругости о локальном сжатии тел (задача Герца). Она
позволила создать метод расчёта фактических площадей кон-
контакта шероховатых тел и контактной жёсткости сопряжений,
исследовать некоторые вопросы теории скольжения и качения,
разработать инженерные методики оценки предельных нагрузок
в опорах качения, износа кулачковых механизмов и зубчатых пе-
передач и т.д.
Между тем известно, что теория Герца построена на ряде
допущений, суть которых состоит в идеализации свойств реаль-
реальных тел и условий их взаимодействия. Так, например, считается,
что контактирующие тела являются упругими, однородными и
изотропными, их поверхности принимаются идеально гладкими,
не учитываются силы трения и адгезионное взаимодействие, а
форма контактирующих тел предполагается заданной и не ме-
меняющейся во времени.
В большинстве своём эти допущения касаются именно тех
свойств, которые оказывают существенное влияние на процессы,
имеющие место при фрикционном взаимодействии поверхностей.
Прежде всего следует упомянуть, что эти процессы протекают
в тонком поверхностном слое, который неоднороден по механи-
механическим характеристикам и имеет сложную структуру. Неодно-
Неоднородности поверхностных слоев, возникающие в силу применения
различных видов технологии обработки поверхности, нанесения
износостойких и твёрдых смазочных покрытий, а также в про-
процессе эксплуатации, влияют на характер напряжённого состоя-
состояния и разрушения поверхностных слоев при контактном взаимо-
взаимодействии двух тел. К этим неоднородностям относятся, прежде
всего, геометрическая и механическая неоднородности, схемати-
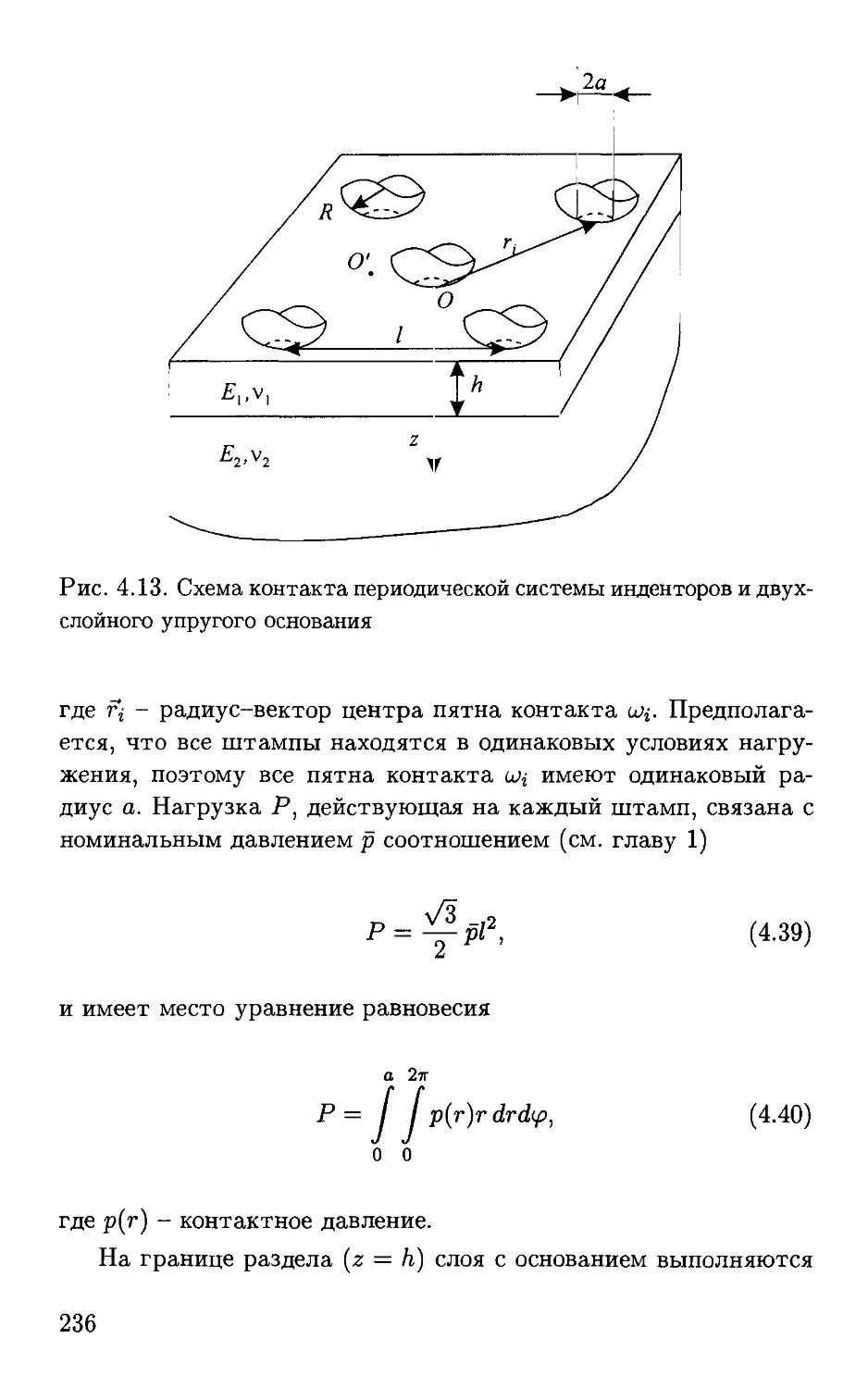
схематически изображенные на рисунке.
Геометрическая неоднородность, т.е. наличие поверхност-
ного микрорельефа в виде волнистости или шероховатости, при-
приводит к дискретному характеру взаимодействия. В результа-
результате на пятнах фактического контакта возникают высокие давле-
давления, приводящие к концентрации напряжений в тонком поверх-
поверхностном слое, толщина которого соизмерима с характерным раз-
размером пятна контакта. Распределение напряжений в этом слое
определяет во многом характер его разрушения.
Геометры ческая
неоднородность
Механыческая
неоднородность
Промежуточная
среда
Схема контакта
Механическая неоднородность материалов взаимодействую-
взаимодействующих тел проявляется, в частности, в отличии механических ха-
характеристик поверхностного слоя от характеристик основного
материала. Несмотря на малость толщины этого слоя, его меха-
механические характеристики оказывают существенное влияние на
трение и характер поверхностного разрушения.
Промежуточная среда также существенно влияет на рас-
распределение напряжений вблизи области взаимодействия. Тонкий
слой жидкости (смазочного материала) между контактирующи-
контактирующими поверхностями значительно уменьшает трение и изнашива-
изнашивание поверхностей. При некоторых условиях взаимодействия эта
жидкость образует мениски вокруг пятен фактического контак-
контакта, порождая силы адгезии между поверхностями.
Кроме того необходимо подчеркнуть, что в процессе трения
7
механические и геометрические свойства поверхностных слоев
меняются вследствие их нагрева, разрушения, накопления уста-
усталости, изменения структуры, что, в свою очередь, влияет на на-
напряженное состояние и характер последующего разрушения.
Наличие только уже перечисленных свойств фрикционного
контакта требует специальных постановок задач механики кон-
контактного взаимодействия (контактных задач) с усложнёнными
граничными условиями, с учётом существования промежуточ-
промежуточной среды, неоднородности взаимодействующих тел, формоиз-
формоизменения поверхностей при трении.
В последнее время наблюдается всё более тесное сближение
механики контактного взаимодействия и трибологии, поскольку
предметом исследования как одной, так и другой науки является
фрикционный контакт. Постановки контактных задач включа-
включают в себя такие специфические свойства фрикционного контакта
как поверхностная микроструктура, трение и адгезия, тепловы-
тепловыделение при трении и т.д. [102]. Решение этих задач позволяет
определить напряжения в области контакта, а также в тонких
приповерхностных слоях, что очень важно с точки зрения про-
прогнозирования характера их разрушения при трении (изнашива-
(изнашивания).
Таким образом, благодаря тесному взаимному контакту три-
трибологии и механики возникают новые направления исследова-
исследований, являющиеся фундаментом для анализа явлений, имеющих
место при фрикционном взаимодействии. Некоторые из них об-
обсуждаются в последующих главах книги.
Глава 1
МЕХАНИКА ДИСКРЕТНОГО
КОНТАКТА
Контактная задача в классической постановке предполагает иде-
идеальную гладкость поверхностей и связность области контакт-
контактного взаимодействия. Однако на практике область контактного
взаимодействия, как правило, дискретна, т. е. состоит из сово-
совокупности пятен контакта.
В этой главе даются постановка задачи дискретного контак-
контакта и метод её анализа, который позволяет рассчитать как фак-
фактические давления на пятнах контакта, так и распределение но-
номинальных давлений в области контактного взаимодействия с
учётом параметров макро- и микрогеометрии поверхностей.
1.1. ЗАДАЧА ДИСКРЕТНОГО КОНТАКТА
1.1.1. ПОВЕРХНОСТНЫЙ МИКРОРЕЛЬЕФ
Самой распространённой причиной возникновения дискретности
контакта является шероховатость контактирующих поверхнос-
поверхностей. Совокупность пятен контакта щ составляет область фак-
фактического контакта ш (рис. 1.1). Площадь этой области для
реальных сопряжений может составлять десятые или сотые до-
доли номинальной области контакта П, которая, как правило,
является односвязной и включает в себя все пятна фактического
контакта. Размеры и положение пятен фактического контакта
зависят от условий контактного взаимодействия, механических
характеристик, а также макроформы поверхности и отклонений
от неё, которые образуют поверхностный рельеф. Рельеф поверх-
поверхностей может быть весьма различен как по способу возникнове-
возникновения, так и по масштабу. Так, рельеф протекторов шин имеет
характерные размеры порядка нескольких сантиметров. На по-
z = -F(x,y)
Рис. 1.1. Номинальная и фактическая области контакта при взаимо-
взаимодействии деформируемых тел с шероховатыми поверхностями
верхностях тонкоплёночных магнитных дисков микрорельеф об-
обнаружен как в миллиметровом, так и в нанометровом масшта-
масштабе [207]. В зависимости от масштаба отклонения от макроформы
называются макроотклонениями, волнистостями или шерохова-
шероховатостями. Для макроотклонений характерны небольшая высота
и малый наклон неровностей; они возникают вследствие несовер-
несовершенной калибровки обрабатывающего инструмента, его износа
и т. д. Волнистость занимает промежуточное положение между
макроотклонениями и шероховатостями. Характерное отноше-
отношение расстояния между неровностями к их высоте для волнистой
поверхности равно 40 [127]. Шероховатость определяется как
совокупность неровностей, расстояние между которыми много
меньше базовой длины, на которой изучаются свойства поверх-
поверхности. Шероховатость образует микрорельеф (микрогеометрию)
поверхности, который, как правило, имеет сложный статисти-
10
ческий характер. Микрорельеф может наноситься искусственно
или получаться в результате различных видов обработки по-
поверхностей. В настоящее время широко используются поверхнос-
поверхности с регулярным микрорельефом, параметры которого выбира-
выбираются из соображения оптимальной работы узла трения. Особен-
Особенно это имеет место в устройствах для обработки и накопления
информации [126].
Для получения информации о рельефе поверхности использу-
используются различного вида щуповые приборы (профилометры, профи-
лографы), оптические интерферометры, туннельные и сканиру-
сканирующие атомно-силовые микроскопы и т. д. Они позволяют с той
или иной степенью точности воссоздать микрорельеф поверх-
поверхности на заданном ее элементе, а также определить некоторые
её характеристики (осреднённый высотный и шаговый парамет-
параметры, средний наклон и радиус кривизны в вершине неровности,
среднее количество неровностей на единицу площади и т.д.).
Развитие измерительной техники приводит к изменению пред-
представлений о топографии, что стимулирует возникновение новых
математических моделей, используемых для описания топогра-
топографии поверхности. С другой стороны, при создании приборов для
исследования топографии в конструкцию и программное обеспе-
обеспечение закладывается возможность измерения и расчёта харак-
характеристик, наиболее широко используемых при моделировании.
Обзор экспериментальных методов исследования топографии по-
поверхностей содержится в [59, 235].
Для изучения влияния топографии поверхности на напряжён-
напряжённо-деформированное состояние приповерхностных слоев тел, на-
находящихся в условиях контактного взаимодействия, необходимо
решать задачу дискретного контакта, т.е. смешанную зада-
задачу механики деформируемого твёрдого тела для системы пятен
контакта. Следует отметить, что задача дискретного контакта
возникает также при исследовании контактного взаимодействия
неоднородных тел, имеющих различного рода включения [55],
композиционных материалов, тел сложной конфигурации, систе-
системы тел, близко расположенных друг к другу (например, роли-
роликовые и шариковые подшипники, система резцов в инструмен-
инструменте [45]) и т.д.
11
1.1.2. ПОСТАНОВКА ЗАДАЧИ
В достаточно общем виде задача дискретного контакта может
быть сформулирована в следующем виде. Рассмотрим контакт-
контактное взаимодействие двух тел (см. рис. 1.1), одно из которых опи-
описывается функцией z = —F(x,y) в системе координат, связан-
связанной с полупространством (плоскость Оху совпадает с границей
полупространства, а ось Oz направлена в глубь полупростран-
полупространства). Функция F(x,y) такова, что при сближении тел на ве-
величину D номинальная область контактного взаимодействия fi
включает в себя конечное N или бесконечное число пятен кон-
контакта U>i-
В пределах каждого пятна контакта действует фактическое
давление pi(x,y), где (х,у) € щ. Тангенциальные напряжения в
областях контакта будем считать пренебрежимо малыми. Под
действием давлений р^(х,у) граница полупространства дефор-
деформируется, при этом перемещения uz(x,y) границы в направле-
направлении оси Oz связаны с контактными давлениями pi(x,y) соотно-
соотношением
uz = A\p1,p2,...,PN,---]- A-1)
Оператор А зависит от выбранной модели деформируемого тела.
Так, для упругого полупространства соотношение A.1) прини-
принимает вид
ц
- X? + („< - yf
В каждой области Ш{ должно выполняться условие контакта
uz(x,y) = D - F(x,y). A.3)
Если величина сближения D неизвестна, а задана суммарная на-
нагрузка Р, действующая вдоль оси Oz, к уравнениям A.2) и A.3)
следует добавить уравнение равновесия
N
J2JJ Pi(x,y)dxdy = P. A.4)
b>i
12
Система уравнений A.2), A.3) и A.4) может быть использована
для определения неизвестных функций распределения фактичес-
фактических давлений pi(x,y) внутри единичных пятен контакта a»j.
При заданной области фактического контакта (какой бы
сложной она ни была) и заданном внедрении D задача опреде-
определения контактного давления сводится к решению интегрального
уравнения, вытекающего из A.2) и A.3):
'-Е// ."fr1""*1*1 .-д-n*.»). A.Ч
ЖЕ
При заданной нагрузке Р уравнение A.5) решается совместно
с A.4). Если же область контакта неизвестна, для её определения
необходимо осуществлять итерационную процедуру и решать
интегральное уравнение A.5) на каждом шаге. В случае глад-
гладкой функции F(x, у) для определения областей щ используется
условие равенства нулю фактических давлений на их границе.
Задача с неизвестной площадкой контакта является нелинейной,
что не позволяет применять для её решения принцип суперпо-
суперпозиции.
1.1.3. ПОДХОДЫ К ОПРЕДЕЛЕНИЮ ХАРАКТЕРИСТИК
ДИСКРЕТНОГО КОНТАКТА
Решение сформулированной выше задачи дискретного контак-
контакта может быть получено численными методами, при этом по-
погрешность определения напряжённо-деформированного состоя-
состояния тел определяется точностью задания функции F(x,y), опи-
описывающей геометрию поверхностей контактирующих тел, и
точностью применяемых вычислительных алгоритмов. В [226]
проведён численный расчёт фактических контактных давле-
давлений pi(x,y) и областей фактического контакта щ в простран-
пространственной контактной задаче при описании микрогеометрии по-
поверхностей на основе данных профилометрирования. Известны
также численные решения ряда контактных задач в плоской по-
постановке для однородных тел и тел с покрытиями, в которых
профиль поверхности задаётся в виде профилограммы (см., на-
например, [158, 224]).
13
В последнее время наблюдается тенденция к проведению рас-
расчётов контактных характеристик шероховатых тел на основа-
основании прямого численного моделирования. При этом отпадает не-
необходимость модельного описания поверхностей - определения
их статистических характеристик, введения понятия неровности
и т. д. Такие подходы стали реальностью в связи с возможнос-
возможностью получения данных о трёхмерной топографии поверхностей,
в частности с помощью сканирующего атомно-силового микро-
микроскопа, и развитием вычислительной техники.
Увеличение точности описания поверхности требует разра-
разработки специальных численных методов при решении контакт-
контактных задач, позволяющих работать с большими массивами дан-
данных [153, 205, 238]. В большинстве случаев определение контакт-
контактных характеристик сводится к решению интегрального урав-
уравнения A.5). Алгоритм расчёта контактных характеристик, не-
непосредственно использующий данные о топографии шерохова-
шероховатой поверхности и основанный на обратных соотношениях, опи-
описан в [156]. Перспективным при численном решении задач дис-
дискретного контакта является использование методов, основанных
на быстром преобразовании Фурье. Использование этих методов
практически позволяет нивелировать различия при проведении
расчётов для однородных тел и тел с покрытиями [209, 221, 229].
Следует отметить, что строгое решение задачи дискретного
контакта, сформулированной в 1.1.2, вряд ли является необхо-
необходимым, поскольку сама функция F(x,y) задаётся, как правило,
приближённо на основе исследования некоторого участка поверх-
поверхности до деформации. Существуют некоторые принципиальные
ограничения на точность её определения с помощью различных
приборов. Она не является, кроме того, стабильной, так как мо-
может быть различной на разных участках поверхности. При этом
эта функция может измениться в результате контактного взаи-
взаимодействия (например, при изнашивании поверхности). Решение
задачи контактного взаимодействия, полученное для одной пары
поверхностей и требующее трудоёмких вычислительных опера-
операций, не может быть непосредственно использовано для анали-
анализа характеристик другой пары трения, работающей при других
условиях контактирования.
14
В силу указанных причин задача дискретного контакта для
шероховатых поверхностей, как правило, решается в прибли-
приближённой постановке. Это прежде всего относится к способу описа-
описания микрорельефа поверхности. Реальной поверхности ставится
в соответствие модельная поверхность, характеристики кото-
которой совпадают с некоторыми наперёд выбранными характерис-
характеристиками реальной поверхности.
Для описания шероховатой поверхности широко использует-
используется теория случайного поля [127], в которой форма поверхнос-
поверхности представляется скалярной случайной функцией, На основе её
анализа определяются параметры поверхности, необходимые для
расчёта контактных характеристик. Для изотропных поверхнос-
поверхностей такой анализ осуществлён в [220], для анизотропных поверх-
поверхностей - в работах [128, 129]. Использование теории случайного
поля при решении контактных задач и статистические вопросы,
связанные с описанием топографии поверхностей, обсуждаются
также в [178].
Свойства самоподобия делают шероховатую поверхность
перспективным объектом для описания с помощью фрактальной
геометрии. В [206, 207] показано, что многие шероховатые по-
поверхности являются фрактальными и приведены методики опре-
определения их фрактальных размерностей, а также подходы к мо-
моделированию контактного взаимодействия поверхностей. Однако
использование фрактальных моделей для определения контакт-
контактных характеристик наталкивается на ряд трудностей. В част-
частности, при контактировании со сплошной средой тела с само-
самоподобным профилем расположение пятен контакта не является
самоподобным и, следовательно, к описанию геометрии области
фактического контакта методы фрактальной геометрии в общем
случае не могут быть применены. Судя по всему, именно по этой
причине в [16] для изучения контактирования деформируемых
шероховатых тел использовалась модель Винклера или модель
локально пластически деформируемого тела (решение Хилла). В
этом случае определение геометрических характеристик области
контакта (например, площади контакта) сводится к анализу гео-
геометрических характеристик самого контактирующего тела. Для
моделей такого рода удалось получить зависимости, связываю-
15
щие параметры построенной модели с используемой инженерной
характеристикой - опорной кривой, а также провести расчёты
зависимости внедрения от нагрузки.
Традиционным в трибологии является модельное описание
поверхности в виде набора неровностей правильной геометри-
геометрической формы, пространственное расположение которых моде-
моделирует распределение материала в поверхностном шероховатом
слое. Выбор конкретной формы выступа достаточно произволен.
При этом исследователи руководствуются самыми различными
соображениями, в том числе и ассоциативного характера. До-
Достаточно полный перечень используемых форм выступов, сопро-
сопровождаемый анализом их преимуществ и недостатков, приведён
в [91]. Форма выступа определяется некоторым набором пара-
параметров (например, для сферической формы - радиусом сферы,
для эллипсоидальной формы - размерами его полуосей), кото-
которые рассчитываются на основе обработки результатов измере-
измерения рельефа исходной поверхности. Затем выбирается закон рас-
распределения выступов по высоте, исходя из условия, что модель
и натура считаются адекватными, если у них совпадают пара-
параметры распределения материала в шероховатом слое [65].
Помимо приближённого описания микрорельефа поверхнос-
поверхности при исследовании задачи дискретного контакта используют-
используются различные приближённые методы решения системы уравне-
уравнений A.1), A-3) и A.4). В первых исследованиях в области ме-
механики дискретного контакта не учитывалось взаимное влия-
влияние микроконтактов, т. е. напряжённо-деформированное состоя-
состояние материала в области пятна контакта полностью определя-
определялось нагрузкой, воспринимаемой этим контактом. Эта гипоте-
гипотеза обеспечивает хорошее соответствие между теорией и экспе-
экспериментом при малой плотности пятен контакта. Однако в тех
случаях, когда это требование не соблюдается, такое допущение
приводит к ошибочным результатам.
Наглядным примером ограниченности такой модели являет-
является эффект насыщения площади контакта, экспериментально об-
обнаруженный на полимерных материалах и резинах [13]. В част-
частности, установлено, что при больших отношениях номинального
давления р к модулю упругости Е полимера приращение площа-
16
ди фактического контакта с ростом нагрузки тем меньше, чем
больше величина фактической площади контакта. Полученная
в [13] для ряда полимеров и резин экспериментальная зависи-
зависимость фактической площади контакта от давления имеет вид:
Л = 1 - еМ-Рр/Е), A.6)
1»де А = Аг/Аа - относительная величина фактической площади
контакта, 0 - параметр, зависящий от шероховатости поверх-
поверхности. В соответствии с зависимостью A.6) полный контакт
шероховатых поверхностей (А = 1) невозможен при конечных
значениях давления (эффект насыщения), что не вытекает на
основании расчётов по приближённой модели дискретного кон-
контакта, не учитывающей взаимного влияния между отдельными
пятнами контакта. Например, для волнистой поверхности, мо-
моделируемой цилиндрическими индснторами радиуса R с осями,
параллельными границе полупространства, и расположенными
на расстоянии / друг от друга, А = 1 при величине нагруз-
нагрузки Р = тгЕ*12 /A6R), действующей на единицу длины цилиндра.
Здесь
где Ei, v\ и Ei, V2 - модули упругости инденторов и полупро-
полупространства соответственно.
В механике контактного взаимодействия шероховатых тел
для расчёта характеристик дискретного контакта широко ис-
используется модель Гринвуда и Вильямсона [182] (см. так-
также [66, 181]). Шероховатость в ней моделируется системой сфе-
сферических сегментов одинакового радиуса (неровности), высота
которых является случайной величиной, подчиняющейся неко-
некоторому закону распределения. Предполагается, что каждая не-
неровность деформируется упруго в соответствии с теорией Гер-
Герца. Влияние же других неровностей оценивается осреднённым
(номинальным) давлением. Были разработаны многочисленные
модификации данной модели, анализу которых посвящена рабо-
работа [213]. Как будет показано ниже (см. 1.2), такой подход может
привести к погрешности в расчётах при высоких плотностях
17
контакта, когда внедрение отдельной неровности существенно
зависит от распределения фактических давлений на соседних к
ней пятнах контакта, что требует постановки и решения задачи
дискретного контакта с учётом взаимного влияния пятен кон-
контакта.
1.2. ПЕРИОДИЧЕСКИЕ КОНТАКТНЫЕ
ЗАДАЧИ И МЕТОД ЛОКАЛИЗАЦИИ
1.2.1. ПРЕДЫДУЩИЕ ИССЛЕДОВАНИЯ
Для поверхностей с регулярным рельефом (например, волнистая
поверхность) для исследования системы уравнений A.4) и A.5)
могут быть применены методы решения периодических контакт-
контактных задач. В плоской постановке периодические контактные за-
задачи для упругих тел при отсутствии сил трения рассматрива-
рассматривались в [146] и [239]. В [93, 94] дано решение плоской периодичес-
периодической контактной задачи с учётом сил трения, полученное с помо-
помощью формул Колосова-Мусхелишвили и аппарата автоморфных
функций. Для периодического штампа, профиль которого описы-
описывается функцией
где / - период, R - радиус кривизны в точке касания, 7 ~
расстояние между осью симметрии выступа и серединой пло-
площадки контакта, выражение для давления на площадке контак-
контакта (—о — 7, о — т) имеет вид [94]:
4G/cos7ra гтг
х sin1/2"" [y(a + х)\ sml'2+a [у(a - х)\ ,
где а - полуширина площадки контакта, Сих- упругие по-
постоянные материала основания (G - модуль сдвига, х - посто-
постоянная Мусхелишвили), a - параметр, определяемый из соотно-
соотношения:
tg(Tra) = ц ^-j-y ,
а jj, - коэффициент трения.
18
Смещение площадки контакта j определяется следующим
выражением:
4тгаа 2тга
> sin— h 2аsin——
7=^arctg ^Г
cos —- V cos
V cos г
I i
В [94] и [95] проведён анализ совместного влияния коэффициента
трения fi и параметра плотности контакта а/1 на распределение
давления под штампом и размер и положение контактных зон, а
также изучено напряжённо-деформированное состояние поверх-
поверхностных слоев при различных параметрах микрорельефа поверх-
поверхности.
Пространственная периодическая контактная задача для по-
поверхности, имеющей синусоидальную волнистость в двух вза-
взаимно перпендикулярных направлениях, рассматривалась Джон-
Джонсоном и др. [196]. На основе принципа суперпозиции в работе
показано, что для регулярного рельефа, описываемого функцией
27га; А 2тгу
f(x, у) = Аг + А2 - Ai cos Д2 cos -— ,
'i h
давление при полном контакте такой волнистой поверхности с
упругим полупространством определяется следующим выраже-
выражением:
/ ч _ * 27ПЕ 2пу
р(х, y)=p + pxcos-j-+ Ру cos — ,
гдер* = nE*Ai/h ир* = nE*A2/l2, E* - эквивалентный модуль
упругости (см. A.7)). Для осуществления полного контакта не-
необходимо выполнение неравенства р ^ р* + р* При меньших
значениях средних давлений р имеет место неполный контакт.
В [196] предложены асимптотические решения задачи в случае
малых значений р, основанные на теории Герца, и для значе-
значений р, близких к р* + р* но не превышающих эту величину.
В последнем случае малые области раздела моделировались эл-
эллиптической трещиной. Для промежуточных значений р реше-
решение строилось численно.
Ниже будут даны постановка и аналитический метод реше-
решения периодической контактной задачи для упругого полупро-
полупространства и системы выступов заданной геометрической формы,
19
позволяющие исследовать зависимость контактных характерис-
характеристик от номинального давления во всем диапазоне изменения ве-
величины р (см.также [42]).
1.2.2. ПОСТАНОВКА ПРОСТРАНСТВЕННОЙ
КОНТАКТНОЙ ЗАДАЧИ ДЛЯ ОДНОУРОВНЕВОЙ
СИСТЕМЫ ИНДЕНТОРОВ
Рассмотрим систему одинаковых осесимметричных упругих ин-
инденторов, форма контактирующих поверхностей которых описы-
описывается функцией z = /(г), взаимодействующих без сил трения с
упругим полупространством (рис. 1.2). Оси инденторов перпен-
перпендикулярны границе полупространства z = 0, а точки их пересе-
пересечения с границей равномерно распределены в плоскости z = О
и имеют полярные координаты (j"j,#jj)) где г — 1,2,...; j —
= 1,2, ...,rrii, гп{ - количество инденторов, расположенных на
окружности радиуса п, причём Г{ < rj+i.
Для определения распределения давления на произвольном
пятне контакта воспользуемся полученным Л.А. Галиным [25]
решением контактной задачи о внедрении в упругое полупро-
полупространство осесимметричного штампа (z = f{r)) при действии
на границе полупространства вне штампа заданной пригруз-
ки q(r,9). Выражение для давления р(г,в) внутри области кон-
контакта г ^ а, обобщённое на случай контакта двух упругих тел,
имеет вид:
+°о2тг A.8)
J f
J
а о
где
A.9)
20
Рис. 1.2. Схема контакта периодической системы инденторов и упру-
упругого полупространства (а) и представление области контакта, осно-
основанное на методе локализации (б)
21
а ядра интегральных операторов в A.9) и A.8), т.е. функ-
функции Н\{г,г') и Н2(т,9,г',в') определяются соотношениями
A-Ю)
Н2(г,в,г',в') =
в которых
Д (г, г', 0') = \/r2-2rr'cos6>' + r'2, A.11)
а величина i?* выражается (см. A.7)) через модули упругости Е\
и ??2 и коэффициенты Пуассона ь*1 и ^ материалов инденторов и
основания соответственно. Функция с(в) зависит от формы ин-
дентора f{r). Для гладкого индентора (функция /'(г) непрерыв-
непрерывна при г ^ а) в силу условия равенства нулю давлений на краю
области контакта, т. е. р(а, в) = 0, функция с[в) имеет вид:
+ ОО 27Г
с(в) = I f q(r',6')H2(a,e,r',6')r' dr'de1. A.12)
а 0
Первый член в правой части уравнения A.8) представляет со-
собой давление, возникающее под единичным осесимметричным
индентором, форма которого описывается функцией f(r), кото-
который внедряется в упругое полупространство. Другие два члена
представляют собой дополнительное контактное давление, воз-
возникающее в результате пригрузки, распределенной вне области
контакта.
Учитывая, что в рассматриваемом случае периодической за-
задачи пригрузка создаётся такими же инденторами, и предпола-
предполагая, что давление под каждым индентором распределено внут-
внутри круговой площадки контакта радиуса а, получим следую-
следующее интегральное уравнение для определения контактного дав-
давления р(г,в):
а 2ж
р(г, в)- j f К (г, в, г1, в') р(г', в'У dr'dB' = G(r), A.13)
о о
22
где функция G{r) определена соотношением A.9),
оо
{а,9,г',9')-Кц{г,9,г',9')]}
r,9,r',9') =L{ri,r',eij-e')\(r,6,r',e',ri,9ij), A.16)
L (ri, г', </?) = Jrf + г'2 + 2r,r' cos (/? — a2,
= \(r cos в — r'cos в'— x cos (p) + (r sin9—r' sm9' — x simp)
При выводе соотношения A.13) было предположено, что ин-
денторы имеют гладкую форму и, следовательно, р(а, 9) = 0 (ра-
(радиус а площадки контакта при этом заранее не известен).
Заметим, однако, что аналогичные рассуждения могут быть
проведены и для штампов с фиксированным размером площадки
контакта (например, цилиндров с плоским основанием). В ре-
результате будет получено уравнение, по своей структуре совпа-
совпадающее с уравнением A.13).
Ядро К (г, в, г',9') интегрального уравнения A.13) представ-
представлено в виде бесконечного ряда A-14). Общий член A-15) этого
ряда может быть преобразован к виду
Кг(г,9,г',9') =
+{а - г) [-а - г - 6r' cos {9ц - 9') cos {9ц -в) +
+2r'cos@' - 9)]rf + О (г;4)} .
Поскольку в случае периодической задачи для любого инденто-
ра, расположенного в точке {гг,9ц), существует симметричный
ему в точке (rj,7r + 9ц), то первое слагаемое в фигурных скоб-
скобках равно нулю. Так как т^ ~ т^, общий член ряда A.14) имеет
порядок г\ 2, и, следовательно, этот ряд сходится.
23
1.2.3. МЕТОД ЛОКАЛИЗАЦИИ
Наряду с интегральным уравнением A.13) рассмотрим уравне-
уравнение
о о -1 AЛ7)
= G(r) + NPQ(r,An),
где
A.18)
В этих формулах N - среднее количество пятен контакта на
единице площади, а Р - нагрузка, действующая на каждое пятно
контакта:
а 2тг
р= [ fP(r,e)rdrd9. A.19)
о о
Уравнение A.17) получено из уравнения A.13) путем заме-
замены суммирования при г > п в A.14) интегрированием по об-
области (О,п : п ^ Ап, 0 ^ 9ij ^ 2тг) с учётом того, что центры
контактных зон (п,6>.у) равномерно распределены в Qn.
вительно,
оо +оо 2тг
Jn =
x [Л (а, в, г', в', x,ip)-\ (г, в, г', в', х,<р)]х dxdip.
Произведя замену переменных
у cos ip = х cos ip + r' cos в',
у sin tp = ж sin ip + r' sin 6'
24
и принимая во внимание, что г' ^ a <S Ап, окончательно полу-
получим:
+оо 2тг
R2(r,y,p)
ydyd<p = NQ(r,An).
Здесь Ап - радиус круга, в котором расположено т\ + т,2 + ¦ ¦ ¦ +
+тп + 1 центральных инденторов, т. е.
Заметим, что за счёт выбора п решение уравнения A.17)
можно сколь угодно приблизить к решению исходного уравне-
уравнения A.13).
Рассмотрим более подробно структуру уравнения A.17). Ин-
Интегральный член в левой части уравнения A.17) учитывает вли-
влияние на распределение давления на фиксированном пятне кон-
контакта фактических давлений на близлежащих к нему пятнах
контакта (эффект близкодействия). Влияние же нагрузки, рас-
распределенной по удалённым пятнам контакта, учитывается вто-
вторым членом правой части, описывающим дополнительное дав-
давление, возникающее в круговой области (г ^ а) при действии
вне её (в области г > Ап) номинального давления р = PN
(см. рис. 1.2,6). Действительно, из соотношений A.8) и A.12)
следует, что если вне круга радиуса Ап давление распределено
равномерно, то есть q(r, в) = р, оно создаёт на площадке контак-
контакта (г ^ а) индентора с упругой полуплоскостью дополнительное
давление pa{r) = pQ(r,An), где Q(r,An) определено в A.18).
Таким образом, в периодических контактных задачах с опре-
определённой степенью точности влияние фактического давления на
удалённых от рассматриваемого пятнах контакта (в области пп)
может быть учтено путем рассмотрения в этой области номи-
номинального давления р.
25
Этот результат является частным случаем более общего
утверждения, которое назовем методом локализации: в условиях
множественного контакта напряжённо-деформированное состоя-
состояние взаимодействующих тел вблизи отдельного пятна контакта
с достаточной степенью точности может быть определено путём
учёта реальных условий контактирования на рассматриваемом и
близлежащих к нему пятнах контакта (в локальной окрестности
пятна) и осреднённого по поверхности (номинального) давления
на остальной части поверхности взаимодействия (номинальной
области контакта).
Справедливость этого утверждения подтверждена также при
изучении задачи множественного контакта с ограниченной но-
номинальной областью взаимодействия (см. 1.3).
Соотношения A.17) используются для определения давле-
давления р(г, 9) на каждом пятне контакта и радиуса а пятна контак-
контакта. Затем по известным давлениям на границе упругого полу-
полупространства определяется напряжённое состояние в приповерх-
приповерхностных слоях. Для определения напряжений в полупространст-
полупространстве в качестве функций Грина можно воспользоваться решением
Буссинеска (см., например, [96]).
Для упрощения численных расчётов при определении внут-
внутренних напряжений можно также, используя метод локализа-
локализации, заменить номинальными контактные давления, действую-
действующие на границе упругого полупространства на удалённых от
рассматриваемой областях взаимодействия. Для оценки их вкла-
вклада в напряжённое состояние полупространства на оси, проходя-
проходящей через центр отдельного пятна контакта, воспользуемся, на-
например, следующими аналитическими выражениями, получен-
полученными интегрированием внутренних напряжений от номиналь-
номинальных давлений р, равномерно распределённых в области ?7П =
= {г > Ап]. Тогда получим следующие выражения для величи-
величины максимальных касательных напряжений
pz
z
2 Al
2
A.21)
26
а также для компонент тензора напряжений
pz3
О, =
A.22)
= TQz = тгв = 0.
1.2.4. РАЗНОУРОВНЕВАЯ СИСТЕМА ИНДЕНТОРОВ
Предложенный выше метод решения периодических контактных
задач для упругого полупространства может быть использован
для исследования контактных характеристик при внедрении в
упругое полупространство инденторов, расположенных на раз-
разных уровнях. Пусть формы контактирующих поверхностей ин-
инденторов описываются гладкими функциями z = fm(r) + hm, где
величина hm (m = 1, 2,... , к) задаёт высоту каждого уровня сис-
системы инденторов, к - количество уровней. Будем считать, что
пятно контакта на rn-ы уровне - круг радиуса ат. Пример рас-
расположения в узлах гексагональной решетки инденторов каждого
уровня для к = 3 приведён на рис. 1.3,а.
Зафиксируем произвольное пятно контакта индентора т-го
уровня и поместим в его центре начало полярной системы ко-
координат (см. рис. 1.3,tf). Используя метод локализации, при-
примем во внимание распределение фактических давлений pj(r,9)
(j = l,2,...,fc) на всех пятнах контакта, находящихся внутри
круга (г < Ат), где
и TVj - плотность расположения инденторов j-ro уровня, опреде-
определяемая их количеством на единицу площади, kjm - количество
инденторов j-ro уровня внутри круга (г < Ат) (при j = m ко-
количество инденторов равно ктт + 1). Заменяя фактические дав-
давления на удалённых пятнах контакта (г{ > Ат) номинальным
27
Рис. 1.3. Расположение инденторов каждого уровня в модели
(к — 3) (о) и схема вычислений, основанная на решении уравне-
уравнений A.23)-A.25) при п = 1 (б)
давлением р, действующим в области г > Ат,
к
г-, в)г drdO,
о о
получим по аналогии с A.17) соотношение
27Г
рт(г,
^2jjK]m(am,r,9,r',e'
J=1 о о
= Gm(r) + — arctg
Ядро уравнения A.23) имеет вид:
(am, г, в, г',в') =^Кг (г, 0, /, в')
A.23)
28
Функции Ki (r, 9, г1,9') и Кц (г, 9, г', 9') определены соотношени-
соотношениями A.15) и A.16) , в которых нужно положить а = ат; rijm
- количество слоев инденторов j-ro уровня внутри круга ради-
радиуса Ат. Функция Gm определена соотношением A.9), в кото-
котором а = ат и /(г) = fm{r)-
Записывая соотношения A-23) для инденторов каждого т-
го уровня, получим систему интегральных уравнений для опре-
определения неизвестных давлений рт(г,9) внутри пятен контакта
(г < ат) каждого уровня (т = 1, 2,... , к).
Неизвестные радиусы ат пятен контакта определяются на
основании заданных высот инденторов hm по формуле:
~ пщ 27Г
hm = ^- f fpm(r,9)drd9 + 2np(AO0-Am) +
ъЬ* J J
A.24)
где (т-jj, ftjj) - координаты центров инденторов всех уровней, рас-
расположенных внутри области (ат < тц < Ат, 0 < 9%j < 2тг), а
функция R(r,r',e') определена в A.11). Для исключения посто-
постоянной Aqo система уравнений A.24) составляется для разностей
высот инденторов hi — hm, где hi - высота самого высокого ин-
дентора. Для замыкания системы уравнений A.23) и A.24) ис-
используется уравнение равновесия
к <Ч 2тг ат 2тг
jmj JPj(r,9)rdrde + J jPm(r,9)rdrd9. A.25)
•? = 1 0 0 0 0
Следует отметить, что при заданных hm все инденторы сис-
системы войдут в контакт лишь при определённом значении номи-
номинального давления р *. При р < р * в контакте будет находиться
меньшее число уровней системы инденторов.
1.2.5. АНАЛИЗ НАПРЯЖЁННОГО СОСТОЯНИЯ
Воспользуемся полученными выше соотношениями для анализа
контактных характеристик и напряжённого состояния упруго-
29
го полупространства, находящегося в условиях множественного
контакта. Особое внимание обратим на изучение влияния гео-
геометрического параметра, связанного с плотностью расположе-
расположения инденторов, на исследуемые характеристики, что позволит
оценить границы применимости упрощенных теорий, не учиты-
учитывающих взаимное влияние отдельных пятен контакта.
Численные расчёты проводились для системы сферических
инденторов (/(г) = r2/BR), R - радиус кривизны инденто-
ра), расположенных в узлах гексагональной решётки с шагом I.
Для разноуровневой системы инденторов принималось к = 3
(см. рис. 1.3,а).
Были введены следующие безразмерные параметры и функ-
функции:
_ г - _ Ап _ _ а ~ I
Р~ Д ' An~~R' п~ Д ' Д '
Системы уравнений A.17) и A.19) для одноуровневой моде-
модели и A.23)—A.25) для разноуровневой модели решались методом
итераций. Плотность расположения инденторов каждого уровня
вычислялась по формуле
2
Для одноуровневой модели N — 3Nj = г .
Для оценки точности метода локализации и выбора значе-
значения п, дающего погрешность в пределах заданной степени точ-
точности результатов, были проведены расчёты контактного дав-
давления р(р, в) для одноуровневой системы инденторов при раз-
разном значении п, характеризующем количество слоев инденторов,
близлежащих к рассматриваемому индентору, на пятнах контак-
контакта которых принимается во внимание фактическое распределе-
распределение давления. Так, при п = 0 интегральный член в левой час-
части уравнения A.17) равен нулю, влияние всех пятен контакта,
окружающих произвольное фиксированное пятно, оценивается
номинальным давлением, распределенным вне окружности ра-
радиуса Aq (второй член в правой части A.17)), где Aq определено
30
пр/BЕ")
0,2
0,1
0,0
0,0
0,5
г/а
1,0
Рис. 1.4. Распределение давлений на пятне контакта, рассчитанное по
формуле A.17) при a/R = 0,1, l/R = 0,2 для п = 0 A), п = 1 и п - 2 B)
(одноуровневая модель)
в A.20). При п — 1 принимаются во внимание фактические дав-
давления, распределённые на пятнах контакта, удалённых от рас-
рассматриваемого на расстояние / F пятен, один слой), при п — 2 -
уже 12 пятен, удалённых от рассматриваемого на расстояние /
(первый слой) и l\f'i (второй слой) и т.д. Результаты расчётов
для а = 0,1, I = 0,2 (а/1 — 0,5, что соответствует предельному
случаю плотного контакта) ип = 0,гг = 1ип = 2 представлены
на рис. 1.4. Результаты показывают, что максимальная погреш-
погрешность в определении давления при п = 0 не превышает 20%,
а распределения давлений, рассчитанные при п = 1 и п = 2,
различаются менее чем на 0,1%. При увеличении а/1 эта оценка
улучшается. Поэтому при дальнейших расчётах, как правило,
принимали п = 1.
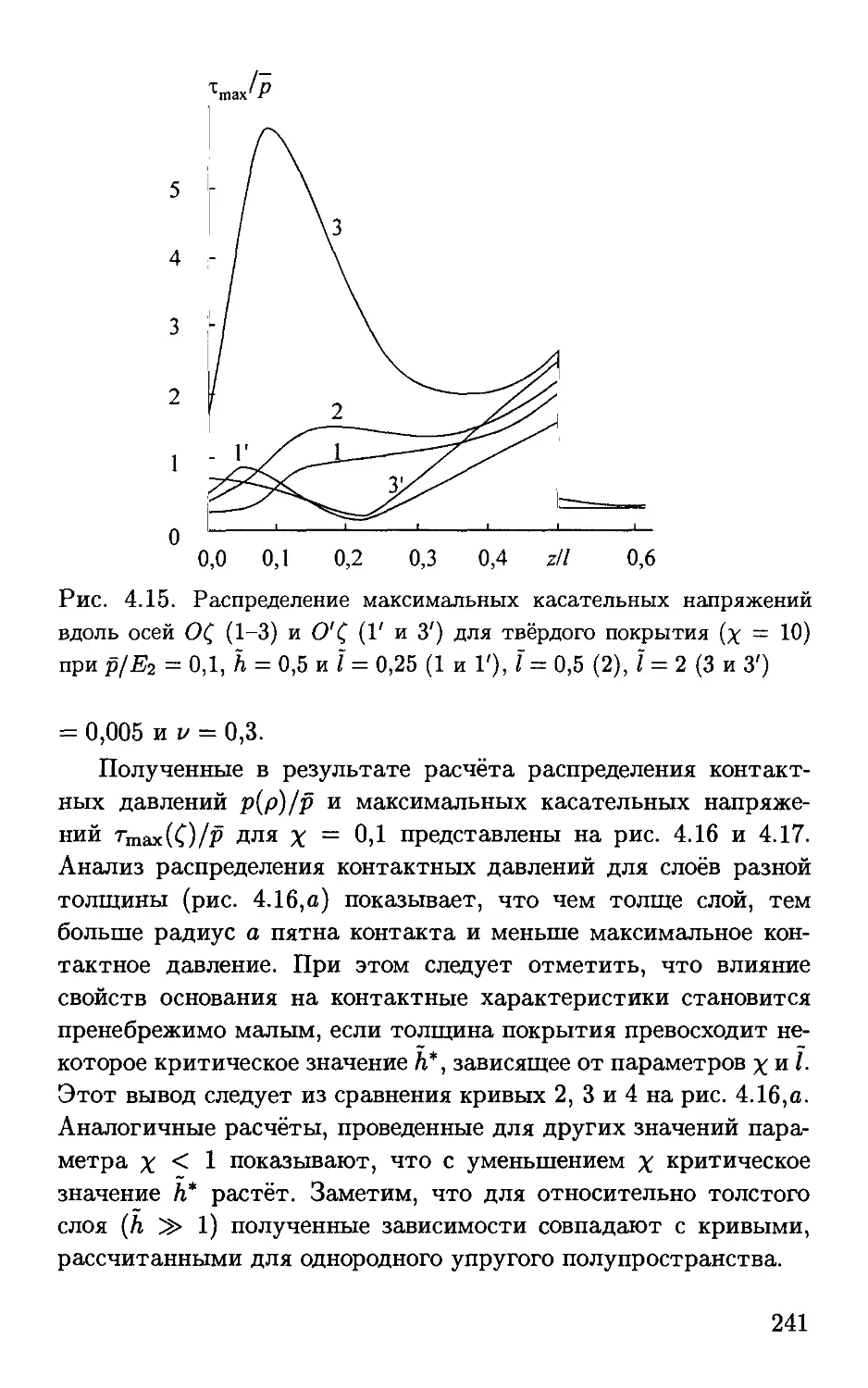
Рис. 1.5 иллюстрирует распределение фактического давле-
давления на единичном пятне контакта при различных значениях па-
параметра 1/R, характеризующего относительное расстояние меж-
31
%р/{2Е')
0,2
0,1
0,0
0,00
0,05
0,10
r/R
0,15
Рис. 1.5. Распределение давлений под индентором (одноуровневая
модель), к которому приложена безразмерная нагрузка Р = 0,0044,
при различных расстояниях между инденторами: 1/R = 1 A), 1/R =
= 0,25 B), l/R = 0,2 C)
ду инденторами одинаковой высоты (одноуровневая модель). Ре-
Результаты показывают, что с уменьшением расстояния / между
инденторами уменьшается радиус отдельного пятна контакта
и растут максимальные давления на пятне контакта, при этом
плотность контакта, характеризуемая параметром а/1, возрас-
возрастает (а/1 = 0,128 (кривая 1), а/1 = 0,45 (кривая 2), а/1 = 0,5
(кривая 3)). Кривая 1 практически совпадает с распределени-
распределением давления, рассчитанным по теории Герца, что позволяет за-
заключить, что при малых значениях параметра а/1 при расчётах
фактических давлений можно пренебречь взаимным влиянием
пятен контакта.
Зависимости радиуса пятна контакта от безразмерного номи-
номинального давления р = ртт/BЕ*), рассчитанные для различных
расстояний / между штампами (/ = IR), приведены на рис. 1.6.
Для сравнения штриховыми линиями показаны соответствую-
соответствующие кривые, построенные по теории Герца. Расчёты показыва-
32
0,4
0.2
0,0
0,00
0,06
пр/{2Е') о,12
Рис. 1.6. Зависимость радиуса пятна контакта от номинального дав-
давления для 1 = 1 A, 1'), I = 0,5 B, 2'), I = 0,2 C, 3'), рассчитанные по
уравнению A.17) A, 2, 3) и из теории Герца A', 2', 3')
ют, что при постоянном номинальном давлении р с уменьшением
относительного расстояния между инденторами 1/R уменьшает-
уменьшается радиус отдельного пятна контакта, и следовательно, факти-
фактическая площадь контакта. Сравнение с кривыми Герца даёт воз-
возможность заключить, что при а/1 < 0,25 расхождение в расчётах
фактической площади контакта по предлагаемому здесь методу
и по теории Герца не превышает 2,5%. При больших номиналь-
номинальных давлениях и, следовательно, высоких плотностях контакта
это различие становится весьма существенным. Так, при / = 0,5
(кривая 2) и а/1 = 0,44 погрешность при расчётах по теории
Герца составляет 15%.
Интерес представляет исследование контактных характерис-
характеристик для разноуровневой системы инденторов, поскольку в силу
эффекта взаимного влияния, учитываемого данной моделью, мо-
момент вступления в контакт каждого нового уровня инденторов
2. Горячева И.Г.
33
0,3
пр/BЕ")
0,2
ОД
0,0
0,0
0,1
0,2
rlR
0,3
Рис. 1.7. Распределение давления на пятнах контакта инденторов с
высотами h\ A, 1'), h2 B, 2'), /13 C, 3'), для трёхуровневой модели
((hi - h2)/R = 0,014, (hi - h3)/R = 0,037, P = 0,059), рассчитанное по
уравнениям A.23)-A.25) A, 2, 3) и из теории Герца A', 2', 3')
определяется не только номинальным давлением и высотой ин-
дентора, но и плотностью расположения пятен контакта, кото-
которая существенно влияет на кривизну границы полупространст-
полупространства между пятнами контакта. Были проведены расчёты для сис-
системы инденторов с фиксированной разницей высот различных
уровней: (hi - h2)/R = 0,014 и (hi - h3)/R = 0,037. На рис. 1.7
приведены графики распределения давления на пятнах контакта
каждого уровня при заданной общей нагрузке Р на три инден-
тора, т.е. Р — Р\ + Рг + Рз- Сплошные кривые 1, 2, 3 построе-
построены на основании решения периодической задачи для инденторов
каждого уровня с высотами hi, hi и h% соответственно, а штри-
штриховые кривые получены по теории Герца. Расчёты показывают,
что чем меньше высота индентора, тем больше радиус пятна
контакта и распределение давления на нём отличаются от соот-
соответствующих результатов теории Герца.
34
1,0
0,5
0,0
0,0
0,5
zIR
1,0
Рис. 1.8. Распределение максимальных касательных напряжений
вдоль осей Oz A, 2) и O'z A', 2') при р = 0,12 ш 1/R = 1 A, 1'),
l/R = 0,5 B, 2')
Исследование напряжённого состояния внутри упругого по-
полупространства при его взаимодействии с системой одноуров-
одноуровневых инденторов показало, что увеличение напряжений имеет
место в приповерхностном слое, толщина которого соизмерима
с половиной периода, причём распределение напряжений в этом
слое существенно зависит от параметра а/1. На рис. 1.8 приведе-
приведены зависимости максимальных касательных напряжений ттах/р
от глубины z/R, рассчитанные для одного и того же значения но-
номинального давления при различных величинах параметра I/R.
Кривые 1 и 2 характеризуют распределение ттах вдоль оси Oz,
проходящей через центр пятна контакта, а кривые 1' и 2' - вдоль
оси O'z (см. рис. 1.2), проходящей через центр ненагруженной
зоны. Расчёты показали, что зависимость внутренних напряже-
напряжений от параметра плотности контакта а/1 заметно проявляет-
проявляется лишь при достаточно больших относительных размерах пят-
пятна контакта 0,25 < а/1 ^ 0,5. С увеличением параметра а/1
2*
35
максимальные значения максимальных касательных напряже-
напряжений падают, а точка их достижения приближается к границе.
Так, при а/1 = 0,35 (см. рис. 1.8, кривая 1) максимальное зна-
значение функция rmax(r, z) имеет в точке г = 0, z/a = 0,43, а
при а/1 = 0,42 (кривая 2) - при г = 0, z/a = 0,38. При этом
перепад напряжений на фиксированной глубине уменьшается.
Предельные значения напряжений при z -> со определяются зна-
значениями номинальных контактных давлений р.
На рис. 1.9 приведены изолинии функции rmax/p в плоскос-
плоскости Оху, находящейся на глубине z/R = 0,08, где максимальные
касательные напряжения близки к своим наибольшим величи-
величинам. Изолинии построены на участке плоскости (—1/2 < х < I,
—[\/3/4 < у < Г\/3/2) для случая а = 0,2 и двух разных значений
плотности расположения штампов. Результаты показывают, что
при больших плотностях контакта значения максимальных ка-
касательных напряжений на фиксированной глубине изменяются
незначительно. Аналогичный вывод может быть сделан относи-
относительно всех компонент напряжений.
Таким образом, возрастание плотности контакта приводит к
возникновению на некоторой глубине напряжённого подповерх-
подповерхностного слоя. Концентрация напряжений в этом слое может
привести к развитию в нём пластических деформаций и зарож-
зарождению микротрещин. Полученные результаты качественно сов-
совпадают с выводами, сделанными в [95, 202] при исследовании
контактного взаимодействия синусоидального штампа с упругой
полуплоскостью.
1.3. ЗАДАЧА С ОГРАНИЧЕННОЙ
НОМИНАЛЬНОЙ ОБЛАСТЬЮ КОНТАКТА
Характерной особенностью периодических контактных задач яв-
является постоянство номинального давления; перераспределение
нагрузок между пятнами контакта может иметь место только
внутри одного периода за счёт разности высот контактирующих
инденторов.
В случае действия на упругое полупространство конечного
числа инденторов, связанных между собой (системы инденто-
36
0,8
..7
0,4-L
-0,4-L
0,07
0,07.
0,07
-0,4 0 0,4 0,8
-0,2 4
-0,2
0,4
Рис. 1.9. Изолинии функции rmax/p в плоскости z/R = 0,08 при о = 0,2
й/~=1 (а), [=0,44 (tf)
37
ров), области фактического и номинального давления являются
ограниченными. Имеющееся при этом неравномерное распреде-
распределение нагрузок между отдельными пятнами контакта определя-
определяется как высотными характеристиками контактирующих инден-
торов, так и местом расположения отдельного пятна контакта
в пределах номинальной области взаимодействия. Даже в слу-
случае равномерного распределения равновысоких инденторов по
номинальной области контакта, распределение нагрузок, дейст-
действующих на каждый из них, является неравномерным. Величины
нагрузки и фактического давления на отдельном пятне контак-
контакта существенно зависят от пространственного расположения ин-
инденторов в системе.
Ниже мы дадим метод решения задачи о внедрении ограни-
ограниченной (состоящей из конечного числа) системы штампов в уп-
упругое полупространство и исследуем зависимость контактных
характеристик от пространственного расположения штампов в
системе.
1.3.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим внедрение системы штампов в упругое полупро-
полупространство (рис. 1.10). Введём следующие величины, использу-
используемые для характеристики рассматриваемой модели рельефа по-
поверхности:
• количество штампов JV,
• форма контактирующей поверхности отдельного штампа
/г(г) (предполагается, что каждый штамп есть тело враще-
вращения, ось которого перпендикулярна недеформированной по-
поверхности полупространства, г - расстояние от оси враще-
вращения до рассматриваемой точки на границе полупростран-
полупространства),
• расстояние /^ между осями симметрии г'-го и j-то штампов,
• высотное распределение штампов /ij.
Область фактического контакта системы штампов с упру-
упругим полупространством представляет собой N подобластей щ
38
Рис. 1.10. Схема контакта системы штампов с упругим полупростран-
полупространством
(г = 1,2,... JV"), расположенных внутри номинальной области
контакта П, включающей в себя все подобласти Ш{. Остальная
граница полупространства свободна от усилий.
Введём систему координат Oxyz. Ось Oz совпадает с осью
вращения произвольного фиксированного г-го штампа, а плос-
плоскость Оху - с недеформированной поверхностью полупростран-
полупространства. Направления осей Ох и Оу выбираются совпадающими,
где это возможно, с осями симметрии системы штампов. -
Сформулируем граничные условия для г-го штампа и заме-
заменим действие других штампов на упругое полупространство
давлением, распределённым по всем пятнам контакта, т. е. внут-
N
ри области М u>j. Смещение границы упругого полупростран-
ства в направлении оси Oz внутри пятна контакта и>{, вызван-
вызванное приложенным давлением Pj(x, у), (ж, у) G u>j, (j = 1,2,..., N,
3 ф i) вычисляется по формуле, которая является обобщением
39
решения Буссинеска (см. [25]):
Pj(x',y')dx'dy
Давление pj(x,y), вообще говоря, заранее неизвестно. Чтобы
упростить задачу, мы аппроксимируем и\{х, у) следующей функ-
функцией:
U
- х? + (У, - У?
где Pj
j = / / pj(x,
y) dxdy - сосредоточенная сила, приложенная
к центральной точке (Xj,Yj) подобласти Шу Точность предлага-
предлагаемой замены может быть оценена в частном случае осесиммет-
ричной функции p(r) = Pj(x',y'), (r ^ а) следующим образом:
27Г а
//
О О
p(r)r drdO
P
+ /2 - 2W cos в I
а
где I = \МЛ,- -х) + (Yi -у) , f = 2тг I p(r)rdr, iS.(x) - эл-
эллиптический интеграл первого рода. При получении оценки бы-
40
ли использованы следующие соотношения [58]:
йв 2 ..
/
(L28)
На основании принципа суперпозиции, справедливого для ли-
линейной теории упругости, смещение границы упругого полупро-
полупространства вдоль оси Oz под г'-м штампом можно представить как
- »(!)/¦ ч iB)/ \ гB1/ ч
сумму смещении uz (х, у) и uz (z, у), где uz [х, у) - смещение,
обусловленное приложенным внутри рассматриваемого г-го пят-
пятна контакта (подобласти и>$) давлением Pi(x,y).
Таким образом, давление Pi(x, у) под произвольным фиксиро-
фиксированным штампом может быть определено из решения следующей
задачи теории упругости для полупространства со смешанными
граничными условиями:
Tzx = Tzy = О, (Ж, у) G Ш{, I19)
<7г = Tzx = Tzy = О, (X, у) ? Wi,
где Di - смещение г-го штампа вдоль оси Oz.
Для определения соотношения между смещениями штам-
штампов Di и силами Pi, действующими на них в направлении нор-
нормали, воспользуемся теоремой Бетти (см. [120]). Предположим,
что область контакта щ осесимметричного штампа с деформи-
деформированной поверхностью упругого полупространства есть круг
радиуса а,. Известно (см., например, [25]), что давление р*(г),
где г = у/х2 + у2, под осесимметричным штампом с плоским
основанием радиуса а^, внедрённым в упругое полупространст-
полупространство на глубину D*, определяется по формуле:
*, s ED*
Т) [7") —
тг A - и2) yja} - г2
41
Из теоремы Бетти следует
2п ас 2тт a.i
I IPi(r,e)D*rdrde= f I'p*{r)^2\r,e)rdrde, в = arctg - ,
0 0 0 0
или
27Г ui .,
7гA-^2O У . /я? _ r2
о о VaJ ~r
Для вычисления интеграла в правой части последнего соотноше-
соотношения подставим в него выражения A.26) и A.29) и воспользуемся
соотношениями A.27), A.28), а также значениями следующих
интегралов
i2
/
dx' 1 1 -f xsimp
=- In- г-^
1
тг/2
/1 1 + isini/j
In d^p = ix arcsin ж.
sin v? 1х sin y>
х sin y>
о
Тогда из соотношения A.30) получим
- /(г)) -^?= - - Е Pj arcsin fi , A.31)
Рассматривая соотношения A.31) для каждого штампа сис-
системы совместно с условиями контакта
Di = hi- Do, A.32)
где Dq - сближение тел под действием нагрузки Р (см. рис. 1.10),
получим 2N уравнений для определения величин Di и Р{ (г =
= 1,2,...,#).
42
Если сближение тел Dq неизвестно, а задана нагрузка Р, то
для определения Do к уравнениям A.31) и A.32) следует доба-
добавить условие равновесия
N
При исследовании контактного взаимодействия системы
гладких осесимметричных штампов с упругим полупростран-
полупространством радиус п{ каждого отдельного пятна контакта является
неизвестной величиной. Для его определения используется до-
дополнительное условие
Из последнего соотношения и уравнения равновесия
Ы = J jP(r,e)rdrde
о о
следует, что дР{/дсц — 0. Дифференцируя уравнение A.31) по щ,
получаем
A.34)
Уравнения A.34) вместе с A.31) и A.32) служат для определения
величин Di, Oj и Pi, необходимых для анализа внедрения системы
гладких штампов в упругое полупространство.
1.3.2. СИСТЕМА ЦИЛИНДРИЧЕСКИХ ШТАМПОВ
Рассмотрим внедрение системы цилиндрических штампов с
плоскими основаниями радиуса щ (f(r) = 0) в упругое полу-
полупространство. Область фактического контакта представляет со-
собой совокупность круговых подобластей wj (г < щ). Из уравне-
43
ний A.31) в рассматриваемом частном случае следует выраже-
выражение для внедрения г-го штампа:
(i-«)
Обратим внимание, что внедрение штампа зависит от суммар-
суммарной интенсивности сосредоточенных нагрузок Pi, расположен-
расположенных на некотором расстоянии I от его центра и не зависит от
характера их расположения на этой окружности.
Уравнение A.35) вместе с условием контакта A.32) и урав-
уравнением равновесия A.33) используется для расчёта распреде-
распределения усилий Pi между штампами. Затем распределение дав-
давления pi(x,y) на каждом г-м пятне контакта может быть при-
приближённо определено на основании формулы A.8), в которой до-
дополнительное давление, распределённое на пятнах фактического
контакта loj при j Ф г заменено сосредоточенными силами Pj,
приложенными в центрах подобласти u>j, т.е.:
7г2 у а2 — х2 — у2
Рассмотрим для определённости систему N цилиндрических
штампов с плоским основанием радиуса а, находящуюся под дей-
действием вертикальной силы Р. Введём следующие обозначения:
(
ij = \ 2 ¦ а •-/• (L36)
— arcsin —, ]ф%.
7Г Uj
Тогда система уравнений A.32), A.33) и A.35) примет вид:
ве = s, A.37)
где В - квадратная невырожденная матрица с элементами Ьц,
6 - вектор-столбец с элементами Sj > 0, в - вектор-столбец с
44
элементами Qj. Мы предполагаем, что все N штампов находятся
в контакте, т. е. Qj > 0 при j = 1, 2,..., N.
В силу невырожденности матрицы В из A-37) следует
9 = B~l8. A.38)
При сложении всех строк системы уравнений A.38) с учётом
уравнения равновесия A.33) получим
1 = 1 jzzl
где Ьц - компоненты обратной матрицы В. Это соотношение
позволяет определить связь между нагрузкой Р, действующей
на систему штампов, и сближением Do при различном распо-
расположении штампов внутри контурной области О, и их высотном
распределении hj.
Система уравнений A.37) и соотношение A.39) были исполь-
использованы для расчёта распределения нагрузок между штампами,
а также соотношения между нагрузкой и внедрением для систе-
системы TV цилиндрических штампов радиуса а, заделанных в жест-
жесткую плиту так, что их оси проходят через узлы гексагональной
решётки с межузловым расстоянием /, а основания лежат в одной
плоскости, т. е. hj = h для всех j = 1,2,... ,п. При этом штампы
располагались симметрично относительно центрального штам-
штампа так, чтобы контурная область контакта была близка к кру-
круговой. Схема расположения штампов приведена на рис. 1.11,а.
Плотность распределения штампов в системе определялась па-
параметром а/1.
Рис. 1.11,6" иллюстрирует характер распределения нагруз-
нагрузки между отдельными штампами системы, расположенными на
разных расстояниях hj/l от центрального штампа, при различ-
различной плотности расположения штампов. Так, для системы, состо-
состоящей из 91 штампа (N — 91) при а/1 = 0,5 (тёмные прямоуголь-
прямоугольники) периферийные штампы нагружены усилиями примерно
в 5 раз большими, чем центральный штамп, а при а/1 = 0,2
9то отношение равно 1,14 (светлые прямоугольники).
45
4-
3 -
2-
1 _
и 1 L i 4 ¦> 1 /1
V<
Рис. 1.11. Схема расположения штампов (а) и распределение нагрузки
между цилиндрическими штампами (<?), расположенными на разных
расстояниях от центрального штампа при а/1 = 0,5 (тёмные прямо-
прямоугольники), а/1 = 0,2 (светлые прямоугольники)
Как следует из соотношения A.39), для рассматриваемой сис-
системы одноуровневых штампов соотношение между нагрузкой Р
и внедрением D {D = h — Dq) имеет вид:
Р = jaPD, A.40)
где jo — 2аЕ/ (l — г/2) - отношение нагрузки, действующий на
уединенный штамп, к его внедрению (жёсткость уединенного ци-
N N
линдрического штампа), /3 = У^У^у- В работе [44] показано,
что величина C может быть аппроксимирована зависимостью:
f3 = kNa, 0,5<a^l, A.41)
где коэффициент к и показатель а зависят от параметра а/1.
При а/1 = 0,5, т. е. когда штампы расположены предельно плот-
плотно, а = 0,5. Этот вывод следует из простых рассуждений. При
плотном расположении штампов всю систему штампов мож-
можно отождествить с одним штампом, имеющим радиус гдг, при
этом 7ГГдг ~ na2N или радиус гдг пропорционален N1/2. Посколь-
Поскольку жёсткость уединенного цилиндрического штампа с плоским
основанием пропорциональна его радиусу, то и жёсткость сис-
системы пропорциональна N1!2. Напротив, если штампы располо-
расположить весьма редко [а/1 —> 0), то взаимное влияние их друг на
46
In
2,5
3,0
3,5
4,0
\nN
5,0
Рис. 1.12. Зависимость величины /3 от количества штампов N
при а/1 = 0 A), а/1 = 0,125 B), а/1 = 0,3 C), а/1 = 0,5 D)
друга очень мало, Pj = P/N и, как следует из A.40), C = N. За-
Зависимости /3 от N, полученные расчётным путем для различных
значений параметра а/1, представлены на рис. 1.12. Расчётные
значения группируются около прямых линий, что дает основа-
основание для выбора функции /3 в виде A.41).
Таким образом, численное исследование задачи показало су-
существенное влияние параметра плотности контактов на распре-
распределение усилий между штампами и жёсткость системы штам-
штампов. Если пренебречь взаимным влиянием микроконтактов (вто-
(второй член в A.35) равен нулю и, следовательно, Р = jqND), по-
получим завышенное значение жёсткости контакта P/D системы
Штампов, причём ошибка возрастает с увеличением числа штам-
штампов и плотности контакта.
Проведённое в [44] исследование влияния формы контурной
области контакта, занимаемой системой штампов, на жёсткость
такой системы позволило сделать вывод, что для моделей, рас-
рассчитанных при одинаковой плотности контакта и одинаковом
числе штампов, но при разных формах областей, занимаемых
Штампами (рассматривались формы в виде эллипсов с разны-
разными эксцентриситетами), жёсткость контакта примерно одина-
47
Таблица 1.1. Параметры модели с различным пространственным
расположением штампов
Номер
слоя
Число
штампов
в слое
A)
"¦max
А *- '
"¦max
1
1
0,9
0,9
2
•
0,7
0,7
3
6
0,5
0,5
А
6
0,3
0,3
5
12
1,0
0,4
6
6
0,6
0,6
7
6
0,8
0,8
8
12
0 4
1,0
кова. Интересно отметить, что аналогичный вывод был сделан
Л.А. Галиным [25] для штампов с плоским основанием эллипти-
эллиптической формы в плане.
Для анализа зависимости сближения и фактической площади
контакта тел, обладающих поверхностным рельефом, от условий
нагружения представляет интерес рассмотрение контактной за-
задачи для системы разновысоких штампов. Численные расчёты
были выполнены для системы 55 цилиндрических штампов с
плоскими основаниями, расположенных в узлах гексагональной
решётки (см. рис. 1.11,а). Рассмотрены различные варианты
пространственного расположения штампов. Два из них пред-
представлены в табл. 1.1. Штампы j-ro слоя расположены на рассто-
расстоянии l\j от центрального штампа системы. Все рассмотренные
варианты отвечали одному условию - число штампов, пересе-
пересекаемых плоскостью, расположенной на расстоянии х от торцов
самых высоких штампов, во всех вариантов было одним и тем
же (слои модели с заданными высотами штампов произволь-
48
ArIA\
1,0 -
J
s--
- - "* " Д
--'" 2
- ¦*?"
P' Д
1,0
PIP'
2,0
Рис. 1.13. Зависимость фактической площади контакта от нагруз-
нагрузки для системы цилиндрических штампов, распределённых по высоте
(см. табл. 1.1) при а/1 = 0 A) и а/1 = 0,45 B)
ным образом менялись местами при условии, что количество
штампов в слоях одинаково), т.е. рассматриваемые модели ха-
характеризовались одной и той же функцией распределения штам-
штампов по высоте. Результаты расчётов для различных вариантов
расположения штампов описаны подробно в [44]. Они позволя-
позволяют построить зависимость относительной фактической площа-
площади контакта Аг/А* (А* = 557га2) от безразмерной нагрузки Р/Р*
(Р* - наименьшая нагрузка, необходимая для вступления в кон-
контакт всех штампов системы в случае а/1 — 0, т. е. когда можно
пренебречь взаимным влиянием штампов в системе) для раз-
различных значений плотности расположения штампов в системе
(рис. 1.13). Следует заметить, что для рассматриваемых моде-
моделей эта зависимость описывается кусочно-постоянной функцией.
Штриховая линия получена в результате осреднения зависимос-
зависимостей для разных моделей, характеризуемых одной и той же плот-
плотностью расположения штампов {а/1 = 0,45). Расчётные значения
фактической площади контакта для моделей 1 и 2, представлен-
49
ных в табл. 1.1, обозначены треугольниками и квадратами со-
соответственно.
Результаты вычислений позволили установить, что по ме-
мере увеличения плотности пятен контакта, т.е. параметра а/1,
возрастают нагрузка и перемещения в направлении оси Oz мо-
модели, необходимые для вступления в контакт всех её штампов.
Это объясняется тем, что в рассматриваемом подходе учитыва-
учитывается искривление границы упругого полупространства вне пятен
контакта при последовательном внедрении штампов модели, т. е.
взаимное влияние пятен контакта при внедрении системы штам-
штампов.
Численный анализ решения задачи для системы цилиндри-
цилиндрических штампов показал существенное влияние параметра плот-
плотности контактов на распределение усилий между штампами,
жёсткость системы штампов, а также на зависимость фактичес-
фактической площади контакта от нагрузки при заданной функции рас-
распределения штампов по высоте [44]. Результаты дают возмож-
возможность оценить ошибку, возникающую при расчёте фактической
площади контакта по упрощённым инженерным формулам, не
учитывающим параметр плотности расположения штампов.
Для того чтобы оценить точность предложенного метода рас-
расчёта, содержащего ряд упрощающих предположений, были про-
проведены эксперименты на моделях. Модельный образец представ-
представлял собой стальную плиту, в которую запрессованы стальные
цилиндрические штыри диаметром 2о = 3 мм. Оси штырей об-
образуют гексагональную решётку с постоянным шагом /, а вер-
вершины штырей расположены в одной плоскости, равноудалённой
от поверхности плиты. В экспериментах использовали два об-
образца: один с плотностями расположения штырей а/1 = 0,125,
(образец А), а другой - с а/1 = 0,25 (образец Б). Количество
штырей ./V в каждом образце равнялось 55. Контртелом, имити-
имитирующим упругое полупространство, служил резиновый образец,
имеющий форму параллелепипеда.
Экспериментально полученные зависимости нагрузки от
внедрения представлены на рис. 1.14. Для сравнения сплошными
линиями на том же рисунке приведены теоретические зависимос-
зависимости, полученные из соотношения A.40). При расчётах использова-
50
Р, кН
0,00
0,0
0,2
0,4
0,6
D, мм
Рис. 1.14. Соотношение между нагрузкой и внедрением системы ци-
цилиндрических штампов при а/1 = 1/4 A), а/1 = 1/8 B), а/1 = 0 C);
(сплошные линии - теория, штриховые линии - эксперимент)
лось экспериментально определённое значение комплекса, харак-
характеризующего упругие свойства резинового образца: (l-^2) /E=
= 21,2 МПа. Экспериментальные кривые хорошо описываются
линейными зависимостями, что полностью согласуется с теоре-
теоретическими результатами. Угловые коэффициенты эксперимен-
экспериментальных кривых рассчитаны по методу наименьших квадратов
и равны: 1,44Н/м (образец А) и 0,93 Н/м (образец Б). Эти зна-
значения очень близки к расчётным, составляющим 1,37 Н/м для
образца А и 0,86 Н/м для образца Б. Небольшое различие тео-
теоретических и экспериментальных значений угловых коэффици-
коэффициентов может быть объяснено влиянием тангенциальных напря-
напряжений в области взаимодействия, которое не учитывалось в те-
теоретических расчётах, но не могло быть полностью исключено
при проведении экспериментов. Погрешность в расчётах связана
также с заменой реального распределения давлений на удалён-
удалённых штампах действием сосредоточенных сил. Оценка точности
такой замены приведена в [43].
51
Изложенный выше метод расчёта зависимости внедрения
системы штампов от действующей на неё нагрузки был исполь-
использован в [43] для обработки экспериментальных результатов, по-
полученных Кендаллом и Табором [200]. Хорошее соответствие те-
теоретических и экспериментальных зависимостей указывает на
возможность использования модели в практике расчётов кон-
контактных характеристик тел, имеющих поверхностный рельеф.
1.3.3. СИСТЕМА СФЕРИЧЕСКИХ ШТАМПОВ
Для сферических штампов радиуса R (/(г) = г2/BЛ)) при за-
заданном их пространственном расположении система уравне-
уравнений A.31)—A.34) имеет вид:
4Еа? 2
N
г~ЗЖ1-*/2) 7r^- J
N
- arcsin
A.42)
у
г=1
Система уравнений A-42) позволяет определить распределе-
распределения усилий Pi между N штампами, нагруженными суммарной
силой Р и взаимодействующими с упругим полупространством,
радиусы ai пятен контакта u>j, полную фактическую площадь
N
контакта Аг = ж VJ а^ и зависимость сближения от нагруз-
ки Dq{P).
Из второй группы уравнений A.42) следует, что радиус г'-го
пятна контакта может быть определён с точностью до членов
порядка (ai/lij) по формуле Герца
ai=
52
Тогда фактическая площадь контакта приближенно может быть
рассчитана по формуле:
N
г=1
3RPi A -
2/3
где Pi определяется из первой группы уравнений A.42).
А/А,.
0,5
0,4-
0,3-
На рис. 1.15 приведена
зависимость относитель-
относительной фактической площади
контакта Аг/Аа (Аа - но-
номинальная площадь кон-
контакта) от номинального
давления р = Р/Аа,
рассчитанная по уравне-
уравнениям A.42) (кривая 1) °>2[
для системы 52 сферичес-
сферических штампов радиуса R,
расположенных на одном
уровне в узлах квадрат-
квадратной сетки (/ - шаг сет-
сетки) для 1/R = 0,5. Схема
расположения штампов в
модели приведена в ниж-
нижнем правом углу рисунка.
Кривая 2 рассчитана по
* * * *
********
********
********
********
******
* * * *
0,00 0,01 0,02 0,03 0,04 /?(l-v2)/?
Рис. 1.15. Зависимость относитель-
относительной площади контакта от номинально-
номинального давления при 1/R = 0,5, рассчитан-
рассчитанная из системы A.42) A) и теории Гер-
Герца B)
приближённой теории, которая не учитывает перераспределения
нагрузок между штампами, обусловленного их взаимным влия-
влиянием друг на друга (при построении зависимости 2 считалось,
что Pi = P/N). Начиная с Ат/Аа = 0,3, ошибка в расчёте фак-
фактической площади контакта по приближённой теории превыша-
превышает 6%.
Зависимость глубины внедрения D от нагрузки Р для рас-
рассматриваемой системы сферических штампов (неровностей) при
разных расстояниях между штампами представлена на рис. 1.16.
Чем выше плотность контакта (меньше параметр 1/R), тем
Меньшая нагрузка требуется для достижения заданной глубины
53
DIR
0,04
0,00 i
0,0 0,2 0,4 0,6 0,8 1,0 P(l-v2)/(?tf2)
Рис. 1.16. Зависимость глубины внедрения системы штампов от на-
нагрузки для системы сферических штампов при 1/R = 0,5 A), 1/R =
внедрения. Аналогичные результаты были получены теорети-
теоретически и экспериментально при изучении взаимодействия систе-
системы цилиндрических штампов, расположенных на одном уровне,
с упругим полупространством (см. рис. 1.14).
На основании проведенного анализа можно заключить, что
приближённые методы расчёта, не учитывающие взаимного вли-
влияния пятен контакта, дают завышенные значения контактной
жёсткости dP/dD и фактической площади контакта Аг\ ошибка
возрастает с увеличением числа пятен контакта и их плотности.
Всевозможные отклонения от правильной геометрической
формы поверхностей, к которым в первую очередь следует от-
отнести волнистость, обеспечивают локализацию пятен контакта
внутри малых областей вблизи гребня волны в такой степени,
когда даже умеренные нагрузки приводят к высокой относитель-
относительной площади контакта в этих областях, при которой погреш-
погрешность расчётов по приближённым теориям может оказаться зна-
значительной.
54
Заметим, что постановка задачи множественного контакта,
описанная в 1.2 и в 1.3, требует задания дополнительного пара-
параметра, характеризующего плотность расположения контактных
зон. Эта информация может быть, в частности, получена из опи-
описания шероховатой поверхности с помощью случайных функций
и полей [127].
1.4. ФУНКЦИЯ ДОПОЛНИТЕЛЬНОГО
СМЕЩЕНИЯ
1.4.1. ОПРЕДЕЛЕНИЕ ФУНКЦИИ ДОПОЛНИТЕЛЬНОГО
СМЕЩЕНИЯ
Обратимся снова к уравнению A.2), определяющему смещение
границы упругого полупространства при действии на него внут-
внутри областей контакта Ш{ давлений pi(x,y), и заменим реальное
распределение давлений в областях щ € f2 \ Г2о> удалённых от
рассматриваемой точки (х,у), на номинальное давление р(х,у),
распределенное по области П \ По, т-е-
? K(x',y')dx'dy' +
+ pjx'^dx'dy1
Здесь По ~ круг с центром в точке (х,у), внутри которого учи-
учитывается фактическое распределение давлений на пятнах кон-
контакта щ.
Как следует из метода локализации (см. 1.2.3), такую замену
можно осуществить с любой наперёд заданной степенью точ-
точности. Радиус Rq области По может быть определен на основе
следующей предельной оценки. Предположим, что внутри коль-
кольца (Пд0 : Rq < г < Ri) действует N сосредоточенных сил интен-
интенсивности Pi (i = 1,2,... ,п), равномерно распределённых в этой
области так, что номинальное давление в ней можно считать по-
постоянным: р(х, у) = р. Этот случай в определённой степени яв-
является предельным случаем дискретного контакта. Определим
55
разность перемещений Auz в центре кольца от сосредоточенных
сил и номинального давления:
где т"г определяют расстояние от центра приложения сосредото-
сосредоточенной силы до точки (ж, у). Разобьём область ?1ц0 на п подо-
подобластей Qj так, чтобы в каждой подобласти находилась одна из
сил и выполнялось условие р = Р{/ mesfij. Тогда на основании
теоремы о среднем получим
pr drdip Pi
где г* есть расстояние до некоторой точки в области Г2;. Окон-
Окончательно имеем:
р N , 1 .ч N maxd(ui)
Д(„ g (I - i) fl « —^—
,
При равномерном распределении сосредоточенных сил одинако-
одинаковой интенсивности Pj = P/N эта оценка принимает простой вид:
пЕ .2PRI- R20
Запишем условие контакта A.3) в виде
иг{х,у) = D-f(x,y) + h(x,y), (х,у)еш0, A.44)
где f(x, у) - функция, описывающая макроформу тела, a h(x, у) -
его микрогеометрию в пределах пятна контакта щ.
Из соотношений A.43) и A.44) получим следующее интег-
интегральное уравнение
A.45)
56
в котором функция /3(х,у) зависит только от параметров нагру-
жения и микрогеометрии в окрестности рассматриваемой точ-
точки (х, у) и имеет вид:
х,у) = ~h(x,y) +
Pi(x',y')dx'dy'
i=i",.,f \f [x1 - хГ + [у1 - у)' A.46)
l
//
p(x',y')dx'dy
Имея в виду, что в данной задаче существует два масштаба
изменения исследуемых величин: на макроуровне, соизмеримом
с номинальной областью контакта и макроформой индентора,
и микроуровне, соизмеримом с размерами и пятнами фактичес-
фактического контакта, в дальнейшем будем считать, что все функции,
входящие в интегральное уравнение A.45) и относящиеся к мак-
макроуровню, т. е. р(х, у), f(x, у), [3(х, у), изменяются пренебрежимо
мало на расстояниях, соизмеримых с характерным расстоянием
между пятнами фактического контакта.
Покажем, что при сделанном предположении величи-
величина Р(х,у), которую мы будем называть дополнительным сме-
смещением, может быть представлена как функция номинального
давления С\р], и определим вид этой функции для некоторых
модельных описаний микрогеометрии поверхности.
1.4.2. ПОВЕРХНОСТЬ С РЕГУЛЯРНЫМ
МИКРОРЕЛЬЕФОМ
Рассмотрим выражение A.46) в точке (жо,Уо) ? <^о> в которой
располагается вершина высоты /io-
Предполагая на основании сказанного выше, что внутри кру-
круга Г^о радиуса Rq номинальное давление постоянно и равно дав-
57
лению р{хо,уо), преобразуем выражение A.46) к виду:
/3(хо,уо) = -h0 +
1-й2
пЕ
A.47)
Величина /3(хо,уо) является локальной характеристикой сближе-
сближения тел в подобласти Qq, находящейся под действием номиналь-
номинального давления р{хо,уо)- Поскольку подобласть По много мень-
меньше номинальной области контакта П, при определении Р(хо,уо)
можно пренебречь кривизной поверхности f(x, у) в точке (жо, уо)-
Указанные обстоятельства дают основание для использования
при определении дополнительного смещения @(хо,уо) решений
периодических контактных задач, в которых пространствен-
пространственное расположение инденторов моделирует параметры микро-
микрогеометрии поверхности в окрестности рассматриваемой точ-
точки (хо,уо), а уровень номинальных давлений определяется ве-
величиной р(хо, уо)- Как было показано в 1.2, при известных номи-
номинальном давлении и пространственном расположении инденто-
инденторов фактические давления pi{x, у) на пятнах контакта определя-
определяются однозначно, что дает возможность сделать вывод о пред-
представимости дополнительного смещения A-47) как функции но-
номинального давления С\р]. Эта функция может быть построена
на основании соотношения A.47), в котором фактические распре-
распределения давления на пятнах контакта определяются из решения
интегральных уравнений A.17) и A.23).
Если шероховатая поверхность однородна, вид функции С\р\
не зависит от координаты точки поверхности.
Заметим, что функция С\р) может быть представлена с до-
достаточной степенью точности аналитически для ряда поверхнос-
поверхностей с регулярным рельефом. Действительно, применяя в A.47)
для вычисления интегралов внутри областей u>i ? Г2о (*' =
= 1,2,..., к) теорему о среднем, преобразуем это выражение к
виду:
\v2 \ k Р
58
где
Po(x',y')dx'dy'
*Е it
it \l& - *оJ + (у' - j/oJ
Pi = JJpi(*',y')dx'dy',
a /oi ~ расстояние от точки (xq, yo) до некоторой внутренней точ-
точки области wj.
Пусть микрогеометрия поверхности моделируется системой
равновысоких цилиндрических выступов радиуса а, равноотсто-
равноотстоящих друг от друга на расстояние /. Как показывают исследова-
исследования, проведённые в 1.3, с достаточной степенью точности можно
положить к = 6 в формуле A.47). Тогда i?o = \/7/(тгп), где п -
количество выступов на единицу площади. Если выступы рас-
расположены в узлах гексагональной решётки с шагом I, то п =
= 2/ (/2\/3). Если все штампы находятся в одинаковых усло-
условиях, определим нагрузку Р, действующую на каждый штамп
как
PP(XQ,yQURl ^
( ть
Для цилиндрического выступа, как известно,
2аЕ
Подставляя полученные соотношения в формулу A.48), получим
вид функции дополнительного смещения в случае микрогеомет-
микрогеометрии, моделируемой цилиндрическими выступами, расположен-
расположенными в узлах гексагональной решётки,
jC\p(x,y)]=C(x,y) =
(L49)
Заметим, что в случае равновысоких выступов их высота h мо-
может быть внесена в правую часть уравнения A.45).
59
Для равновысоких выступов сферической формы радиуса R,
расположенных в узлах гексагональной решётки с шагом /, функ-
функция дополнительного смещения может быть получена аналогич-
аналогичным способом, опираясь на результаты 1.2. Опуская промежу-
промежуточные выкладки, запишем окончательный вид этой функции:
C\()]
(L50)
где
R I -
' ~ 8
B= — -hi r-
1.4.3. АНАЛИЗ ФУНКЦИИ ДОПОЛНИТЕЛЬНОГО
СМЕЩЕНИЯ
Уравнение вида A.45) впервые было предложено И.Я. Штаерма-
ном [146] для определения номинальных давлений и номиналь-
номинальной области контакта при взаимодействии шероховатых тел. Им
была выдвинута гипотеза, что при постановке контактной зада-
задачи для тел с поверхностной микроструктурой необходимо учи-
учитывать дополнительную податливость (аналог мягкой прослой-
прослойки), связанную со смятием микронеровностей. При расчётах кон-
контактных характеристик использовалась экспериментально опре-
определённая функция дополнительного смещения, которая, как пра-
правило, принималась в виде линейной или степенной функции но-
номинального давления
С\р(х, у)] = Вр*{х, у), 0 < х ^ 1. A.51)
60
0,032
OR
0,016
0,000
0,0
0,1
np/BE*)
0,2
Рис. 1.17. Функция дополнительного смещения для трёхуровневой мо-
модели A) и одноуровневых моделей, характеризующихся 1/R = 1 B, 2')
и 1/R = 0,5 C, 3'), рассчитанная по уравнениям A.17) и A.23)-A.25)
A, 2, 3) и по уравнению A.50) B', 3')
Следует отметить, что экспериментальное определение функ-
функции С\р(х, у)] и, в частности, коэффициента В и показателя х в
соотношении A.51) для заданной шероховатой поверхности яв-
является достаточно сложной и трудоёмкой задачей.
Предложенный выше метод определения функции дополни-
дополнительного смещения на базе модельных представлений о микро-
микрорельефе поверхности позволяет получить эту функцию расчёт-
расчётным путём. На рис. 1.17 приведены функции дополнительного
смещения, рассчитанные для трёхуровневой системы сферичес-
сферических инденторов, расположенных в узлах гексагональной решётки
с шагом 1/R = 1и характеризуемых относительными разницами
высот уровней (h0 - hi)/R = 0,01, (ho - /i2)/i? = 0,015 (кривая 1)
и для одноуровневой системы сферических инденторов, располо-
расположенных в узлах гексагональной решётки, с шагом 1/R = 1 (кри-
(кривая 2) и 1/R = 0,5 (кривая 3). Расчёты проведены по форму-
формуле A-47), где функции pi(x,y) получены из решения интеграль-
интегральных уравнений A.17) и A.23)—A.25). Расчёты показывают, что
с увеличением номинального давления и, следовательно, с рос-
61
том фактической площади контакта замедляется скорость изме-
изменения функции дополнительного смещения С\р]. Расчёты, вы-
выполненные при относительной фактической площади контакта,
близкой к единице (Аг/Аа « 1), для одноуровневой системы ин-
денторов B) и C), показывают, что функция дополнительного
смещения при больших площадях контакта близка к постоянно-
постоянному значению, что говорит об исчерпании дополнительной подат-
податливости шероховатого слоя, т. е. dC/dp = 0 при Аг/Аа яз 1.
Графики функции дополнительного смещения, рассчитанные
на основании соотношения A.50) для рассматриваемых моде-
моделей равновысоких выступов сферической формы, изображены на
рис. 1.17 (штриховые линии). Совпадение кривых 2 и 2', а так-
также 3 и 3' говорит о возможности использования приближённых
аналитических зависимостей при относительно невысоких плот-
плотностях контакта (а/1 < 0,2). Погрешность в результатах при
больших значениях параметра а/1 объясняется тем, что при вы-
выводе соотношения A.50) реальное распределение давления на со-
соседних к рассматриваемому пятнах контакта было заменено эк-
эквивалентными значениями сосредоточенных сил.
Таким образом, с ростом номинального давления величина
дополнительной податливости контакта dC/dp, связанная с на-
наличием микрорельефа, постепенно уменьшается и стремится к
нулю при переходе от дискретного контакта к непрерывному.
Отметим, что степенная функция A.51) не описывает этот
процесс, поэтому её можно использовать только при невысоких
значениях номинального давления, когда полный контакт не на-
наступает.
1.5. РАСЧЁТ КОНТАКТНЫХ
ХАРАКТЕРИСТИК С УЧЁТОМ
ПАРАМЕТРОВ МАКРО- И
МИКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ
1.5.1. ПОСТАНОВКА ЗАДАЧИ
При контактном взаимодействии деформируемых тел, обладаю-
обладающих поверхностным микрорельефом, существуют два масштаба
длины: первый из них связан с характерным размером Ra номи-
62
нальной области контакта ?1, а второй - с характерным размером
неровности и расстояний между ними 1а. Соотношение между Ra
и 1а может меняться в процессе контактирования. Так, при не-
незначительных нагрузках возможна ситуация, когда Ra ~ /0> в
контакте находится небольшое число выступов. В этом случае
для определения контактных характеристик может быть при-
применён метод, изложенный в 1.3.
При la <SC Ra Для определения номинальных (осреднённых)
давлений целесообразно использовать интегральное уравне-
уравнение A.45), в котором функция дополнительного смещения С\р]
может быть получена методом, изложенным в 1.4. При извест-
известной функции дополнительного смещения интегральное уравне-
уравнение A.45) полностью решает задачу определения номинально-
номинального давления р(х, у) при заданной области номинального контак-
контакта П, заданной макроформе взаимодействующих тел, описывае-
описываемой функцией f(x,y), и их сближении D. В случае, если номи-
номинальная область контакта заранее не известна, задача сводится
к определению области О с границей дп и номинального давле-
давления р{х, у) из следующих условий:
uz(x,y) = С\р(х,у)}+ // K(x,y,x',y')p(x'y')dx'dy',
п
р(х,у)>0, если uz(x,y) = D - f(x,y), (х,у)еп, A.52)
р(х,у) = 0, если (х,у) G дп,
р(х,у) = 0, если uz(x,y) > D-f(x,y), (х,у)$П.
Если величина D заранее неизвестна, то для её определения ис-
используется уравнение равновесия
Р= ffp(x'y')dx'dy'. A.53)
п
Исследованию и разработке методов решения интеграль-
интегральных уравнений A.45) или A.52) при различных видах функ-
функции С\р] и наиболее часто встречающихся в контактных зада-
задачах ядер К(х,у,х',у') интегральных операторов посвящены ра-
работы [8, 21, 37, 116, 123, 146] и др.
63
Рис. 1.18. Схема контакта индентора с упругим слоем
1.5.2. ПЛОСКАЯ КОНТАКТНАЯ ЗАДАЧА
Рассмотрим задачу о взаимодействии полосового штампа или
длинного упругого цилиндра с упругой шероховатой полосой
(рис. 1.18). Эта задача может рассматриваться в плоской по-
постановке. Индентор имеет форму /(ж) и вдавливается в упру-
упругую полосу {|ж| < +оо, 0 < z < h} силой Р, действующей вдоль
оси Oz. Предпологается, что тангенциальные силы на площад-
площадке контакта отсутствуют. Исследуются параллельно два случая
закрепления полосы (z = h):
1. Полоса лежит на жёстком основании без трения:
Txz(x,h) =0, uz(x,h) = 0, \х\ < +оо.
2. Полоса жёстко закреплена на основании:
ux{x,h) = uz(x,h) = 0.
Граничные условия на поверхности z = 0 в обоих случаях
имеют вид:
Txz(x,0) = 0, crz(x,0) = 0,
tXz{x,0) = 0, uz(x,0) = -f(x)
а < \х\ < +оо,
\x\ < а.
64
Основное интегральное уравнение A-52) для исследуемой за-
задачи в случае внедрения штампа с шероховатой поверхностью
может быть представлено в виде:
D-f(x,y) = C\p(x,y)] +
f A.54)
Как показано в [20], ядро интегрального оператора в сформули-
сформулированной контактной задаче для упругой полосы имеет вид:
+ ОО
k(t)= I -^-cosutdu. A.55)
J u
о
Конкретный вид функции L{u) зависит от граничных условий.
Для случая 1:
ch 2u — 1
L(u) = . A.56)
Для случая 2:
ВД = 5—i-^TTTXTTH» • ^. = 3-41/. A.57)
2х* ch 2и + Аи2 + 1 + к2
Запишем уравнение A.54) и условие равновесия в безразмерных
координатах. Для этого введём обозначения:
_х D а
a a h
F2) v - 2 A -
, , 2
«о =-
Тогда получим
1
fc(A(* - O)p(t) dt + С№)] = s ~ Ж), A-59)
3. Горячева И.Г. 00
1
[
p(x)dx = P. A.60)
-l
При известном размере площадки контакта а уравнения A.59)
и A.60) позволяют определить контактное давление и внедрение
штампа в упругую полосу.
Уравнение A.59) является уравнением типа Гаммерштейна,
которое может быть записано в виде:
1
J
k{\{t - о) (р№) - f(t) + 6}) г dt + xjj(o = о, (i.6i)
где
Ф(О = с\р(О]+ 1@-6. A.62)
Для решения уравнения A.61) можно применить метод последо-
последовательных приближений. Например, положить Vo(?) = 0> а все
последующие значения определять с помощью рекуррентного со-
соотношения:
1
= J
(( о) ([М) /() }) dt.
-1
Сходимость метода зависит от конкретного вида функции С\р].
Анализ этой функции, проведённый в 1.4, показывает, что для
относительно невысоких контактных давлений, когда фактичес-
фактическая площадь контакта ещё далека от насыщения, дополнитель-
дополнительное смещение может быть аппроксимировано степенной функци-
функцией A.51).
Как показано в [37], для степенной функции метод последова-
последовательных приближений сходится к единственному решению урав-
уравнения A.61), если параметры задачи удовлетворяют неравенст-
неравенству:
} 1
/ k2(\{t-x))dV dx < 1, A.63)
L-l
66
где
При других значениях параметров для решения уравнения A.61)
может быть применён метод Ньютона-Канторовича. Зная реше-
рие уравнения A.61), по формуле A-62) можно найти безразмер-
безразмерное давление при заданном внедрении D. Если внедрение штам-
штампа не задано, то для его определения используется дополнитель-
дополнительно уравнение A.60).
Покажем, что для функции С\р], заданной выражени-
выражением A.51), давление не может возрастать до бесконечности на
концах площадки контакта. Действительно, предполагая, что
давление имеет интегрируемую степенную особенность, т.е. осо-
особенность вида A — ?)~в @ < в < 1) в точке ? = 1, и учитывая, что
ядро интегрального уравнения имеет особенность вида 1пA — ?),
получим, что левая часть уравнения A.59) имеет особенность
порядка A — ?)"**> в правой же части особенности нет, что и до-
доказывает высказанное выше утверждение. Таким образом, учёт
дополнительной податливости за счёт смятия микронеровностей
Нриводит к исчезновению особенностей давления на краях облас-
области взаимодействия, имеющих место в случае постановки кон-
контактной задачи для гладких тел, макроформа которых такова,
Что имеет место разрыв производной функции смещения и'г(х)
на краях площадки контакта (например, для штампа с плоским
Основанием, т. е. f'(x) — 0 при \х\ < а).
В случае линейного контакта цилиндрических упругих тел с
шероховатыми поверхностями, используя условие равенства ну-
Яю давления на краях площадки контакта и то, что С@) = 0, ин-
интегральное уравнение A.59) для определения номинальных дав-
Дений может быть приведено к виду:
(L65)
Это уравнение также является уравнением типа Гаммерштейна,
Которое может быть решено методом последовательных прибли-
приближений или методом Ньютона-Канторовича.
3* 67
(k(\(t - 0) - H4t - mm dt +
Покажем, что решение уравнения A.65) для функции С\р] ви-
вида A.51) при показателях >с < 1 имеет производную р^ = dp/d?,
равную нулю на концах области интегрирования, т.е. р^(—1) =
= р^A) = 0. Продифференцируем уравнение A.65) по ? и рас-
рассмотрим его при ? = — 1 (случай ? = 1 может быть исследован
аналогично). Тогда мы имеем:
где Д = df/d?, а постоянная В\ определена в A.64). Поскольку
функция р(?) является непрерывно дифференцируемой и р(—1) =
= рA) = 0, а ядро &(?) (см. A.55)) представимо в виде [20]:
k(t) = -ln|i| + F{t),
где F(t) - аналитическая функция, интегральный член в ле-
левой части уравнения A.66) конечен. При ограниченной величи-
величине Д(—1) второе слагаемое в левой части A.66) также долж-
должно быть ограничено, что возможно лишь при Pf( — 1) = 0, ес-
ли 0 < х < 1.
Рассмотрим в качестве примера контактную задачу о вда-
вдавливании без трения штампа с плоским основанием f{x) = 0
в толстый шероховатый слой. Для определения давления в этом
случае имеем интегральное уравнение A.59), в котором /(?) = 0,
а ядро имеет вид k(t) — — In 11 \ + ао, где ао = —0,352 для зада-
задачи 1 и ао = —0,527 - для задачи 2 при v — 0,3 (см. [20]). Такое
асимптотическое представление ядра имеет место для достаточ-
достаточно толстых полос, для которых А ^ 1/2. Функцию С\р] зададим
в виде A.51).
При этих условиях, решая уравнение A.61) методом после-
последовательных приближений, получим для давления на площадке
контакта выражение
68
1,0
A 2(l-v2)p/(nE)
0,6 -
0,2
0,0
xl a
1,0
Рис. 1.19. Распределение давления в области контакта упругой полосы
и штампа с плоским основанием при разных значениях параметров
Шероховатости (сплошные линии) и в случае гладких поверхностей
(пунктирная линия)
ще ip(?) - предел последовательности функций {xjjn(^)}, причём
1
'¦' = В~1/к I(ln\ t - ?\ + co)[tl>n(t) + 5}1/x dt,
о
— Ш I — I — UQ.
со
Этот предел существует, если выполняется условие A-63), кото-
которое в данном случае принимает вид:
3,5)
< 1.
Рис. 1.19 иллюстрирует распределение давления под штам-
штамбом при х = 0,4, со = —3 и разных значениях нагрузки Р и па-
параметра шероховатости В\. Кривые 1 и 2 построены при В\ — 1
В РA) = 0,6 • 1СГ2 A) и РB) = 0,75 ¦ 10 B). Внедрения, соответ-
соответствующие нагрузкам Р^\ и РB), равны 5^ = 0,15 и 6/2\ = 0,17
69
соответственно. Расчёты показали что при одинаковых парамет-
параметрах шероховатости при действии большей нагрузки давление
возрастает, особенно на концах площадки контакта. При дей-
действии одинаковых нагрузок, равных 0,41 ¦ 10~2, внедрение штам-
штампа и давление под ним меняются в зависимости от параметра
шероховатости В\. При В\ = 0,75 штамп углубится на вели-
величину S = 0,1, а при В\ = 0,35 (более гладкая поверхность) -
на меньшую величину S = 0,06. Графики распределения давле-
давления в этих двух случаях показаны на рис. 1.19 кривыми 3 и 4
соответственно; пунктирная линия - график распределения дав-
давления без учёта шероховатости. Следует отметить удовлетво-
удовлетворительную сходимость метода последовательных приближений
и его эффективность. С точностью до 10~5 оказалось достаточ-
достаточным вычислить 15-20 приближений функции ф(х).
1.5.3. ОСЕСИММЕТРИЧНАЯ КОНТАКТНАЯ ЗАДАЧА
Рассмотрим взаимодействие штампа или упругого индентора,
форма контактирующей поверхности которых задана уравнени-
уравнением z = f(r) (/@) = 0), с упругим полупространством (z < 0).
Площадка контакта Q имеет форму круга радиуса а. На ос-
основании потенциала Буссинеска интегральный член в уравне-
уравнении A.52), имеющий смысл упругих перемещений и™ грани-
границы полупространства от действия номинального давления р(г)
внутри круга радиуса а, можно записать в виде [121]:
а 27г
ип' =
где
а
" «E* J
a K(t) - полный эллиптический интеграл первого рода.
70
Запишем основное уравнение задачи в безразмерном виде.
Для этого введём обозначения:
т л D
1
J
/¦
С\р(ра)}
Тогда в случае контакта штампа с упругим полупространством
при заданном радиусе а контактной области, который опреде-
определяется формой штампа, будем иметь следующее интегральное
уравнение для определения номинальных давлений
1
J Н(р, p')p(p')p' dp' + С\р(р)} = 6 - f(p). A.67)
о
При неизвестном радиусе области интегрирования, используя
дополнительные условия рA) = 0 и С@) = 0, получим для опре-
определения давлений следующее интегральное уравнение:
1
\н(Р,р1) - H(l,p')W)p'dp' + С\р(р)} = /A) - /(р). A.68)
о
Поскольку эллиптический интеграл К(?) при t2 « 1 имеет ло-
логарифмическую особенность вида In D/\/1 — t2), т.е. того же
|щда, что и главная часть ядра k(t) (см. A.55)), анализ уравне-
уравнений A.67) и A.68) может быть осуществлён при известной функ-
дии дополнительного смещения С\р) изложенными выше метода-
методами. При этом выводы, сделанные в 1.5.2 относительно поведения
функции номинального давления на краях площадки контакта
При С\р] вида A-51), сохраняются и в случае осесимметричной
постановки задачи, т. е. р(а) является всегда ограниченной ве-
величиной и р(а) = р'(а) = 0, если /'(р) непрерывна при р = а.
Рассмотрим в качестве примера численное решение задачи
ЩЯя штампа с плоским основанием, /(г) = 0, при С\р] = Врн и
|яедующих значениях безразмерных параметров: х = 0,4, В\ =
ш В(пЕ*)н/а = 0,9, 8 = 0,1. Полученный график функ-
ЙЗИи р(р), представляющий собой безразмерное давление, при-
приведён на рис. 1.20 сплошной линией, пунктирная линия - график
71
распределения давления под штампом без учёта шероховатости
основания. В обоих случаях на штамп действует безразмерная
нагрузка Р = 0,8625 • 1СГ2.
А
0,5 L
о,з -
0,1
0,0
о
г/а
1
Заметим, что в случае
линейной функции допол-
дополнительного смещения С =
= Вр интегральное уравне-
уравнение A.52) является интег-
интегральным уравнением Фред-
гольма и для его реше-
решения могут быть исполь-
использованы стандартные мето-
методы (например, сведения к
линейным алгебраическим
уравнениям). При линей-
линейной функции дополнитель-
дополнительного смещения соотношение
между внедрением штам-
штампа и приложенной к нему
нагрузкой в рассмотренном
выше примере будет также
линейным. Расчёты показа-
показали (см. [44]), что при одной и той же нагрузке с увеличением па-
параметра В возрастает внедрение штампа D, т. е. уменьшается
контактная жёсткость P/D, при этом происходит выравнивание
контактных давлений.
Рис. 1.20. Распределение давления
в контакте шероховатого (сплош-
(сплошная линия) и гладкого (пунктир-
(пунктирная линия) осесимметричного штам-
штампа с плоским основанием и упругого
полупространства
1.5.4. РАСЧЕТ ХАРАКТЕРИСТИК ДИСКРЕТНОГО
КОНТАКТА
Номинальные давления, полученные из решения уравне-
уравнения A.52) и его частных случаев - уравнений A.59) и A.67),
могут быть использованы далее для определения характеристик
дискретного контакта, которые необходимо знать при изучении
вопросов, трения и изнашивания взаимодействующих тел, расчё-
расчёте электро- и теплопроводности контактов, герметичности сты-
стыков и т. д.
72
0,3
0,2
0,1
0,0
0,0
0,2 %plBE*)
0,4
Рис. 1.21. Зависимость фактической площади контакта от номиналь-
номинального давления для различных моделей поверхностного микрорельефа
Обозначения кривых те же, что и на рис. 1.17
Мы дадим здесь алгоритм определения характеристик дис-
дискретного контакта на примере расчёта фактической площади
контакта. Как показано выше, при заданных параметрах микро-
микрогеометрии взаимодействующих поверхностей из решения задачи
множественного контакта по методу, изложенному в 1.2-1.4, мо-
могут быть рассчитаны функция дополнительного смещения С\р]
и функция А(р), описывающая зависимость относительной пло-
площади контакта от номинального давления р. Так, в случае мик-
микрогеометрии, моделируемой одноуровневой или многоуровневой
системой равномерно распределённых выступов, эти функции
могут быть определены из решения периодической контактной
задачи для системы инденторов и упругого полупространства.
Зависимости С\р] для некоторых конкретных значений парамет-
параметров микрогеометрии приведены на рис. 1.17. На рис. 1.21 по-
показаны зависимости значений А = 4.7Г [а\ + а^Л- а^) / (/2л/3) от
номинального давления, построенные для одноуровневой [а\ =
= й2 = аз) и трёхуровневой системы инденторов при том же со-
соотношении между высотами инденторов, что и для кривых на
рис. 1.17.
При заданной микрогеометрии поверхности и, следовательно,
73
заданной функции С\р] характеристики номинального контакта
рассчитываются затем из соотношений A.52) и A.53), если из-
известны макроформа взаимодействующих тел и приложенная к
ним нагрузка. Тогда окончательно фактическая площадь кон-
контакта Аг для заданных параметров, описывающих макроформу
и микрогеометрию поверхностей, определяется из соотношения
Аг = [\\р(х,у)] dxdy. A.69)
п
В качестве примера определим зависимость фактической
площади контакта Аг от нагрузки для цилиндра, форма контак-
контактирующей поверхности которого описывается функцией f(x) =
= x2/BRo) (До - радиус цилиндра), вдавливаемого в толстый
упругий слой (см. рис. 1.18). Микрогеометрия поверхности ци-
цилиндра моделируется по-прежнему системой сферических неров-
неровностей, расположенных на одном или трёх уровнях. Функция до-
дополнительного смещения С\р] и зависимости относительной фак-
фактической площади контакта от номинального давления \(р) для
этих видов микрогеометрии представлены на рис. 1.17 и 1.21. Ис-
Используя функцию С\р], определим номинальное давление р(х) и
полуширину площадки контакта а/До из уравнений A.60)
и A.65) при заданном значении безразмерной нагрузки Р =
= 2 (l — и2) Р/ (tyERq), приложенной к цилиндру.
Распределение номинальных давлений внутри номинальной
области контакта \х\ ^ а показано на рис. 1.22 для Р = 3.2 ¦ 10~3
и функций С\р], представленных на рис. 1.17. Кривые с одина-
одинаковыми номерами на рис. 1.17 и 1.22 соответствуют одинаковым
моделям микрогеометрии поверхности. Полуширина площадки
контакта для рассматриваемых случаев микрогеометрии рав-
равна а/До = 0,09 A), а/До = 0,08 B), а/Д0 = 0,065 C).
Тогда относительная фактическая площадь контакта Аг/Аа
может быть определена по формуле
1
-1
На рис. 1.23 построены зависимости относительной фактической
площади контакта от безразмерной нагрузки Р при различных
74
0,04
2р/(пЕ')
0,02
0,00
0,0
0,5
xla
1,0
Рис. 1.22. Номинальные давления в контакте шероховатого цилиндра
и толстого упругого слоя для различных моделей поверхностного мик-
микрорельефа
Обозначения кривых те же, что и на рис. 1.17
А./Аа
0,10 ^—а-
з/
0,08
0,06
0,04
0,02
0,00
0,000 0,002 0,004 0,006 0,008 Р 0,012
Рис. 1.23. Зависимость фактической площади контакта от нагрузки,
приложенной к цилиндру, для различных моделей поверхностного мик-
микрорельефа
Обозначения кривых те же, что и на рис. 1.17
75
параметрах микрогеометрии и фиксированной макрогеометрии
контакта (кривые с одинаковыми номерами на рис. 1.17, 1.21,
1.22 и 1.23 соответствуют одинаковым моделям микрогеометрии
поверхности).
Аналогичным способом можно рассчитать объём зазора меж-
между взаимодействующими телами в зависимости от их поверх-
поверхностной микрогеометрии, количество неровностей в контакте
и т.д.
Представляет значительный интерес оценка фактических
давлений и их максимальных значений в контакте упругих тел с
шероховатыми поверхностями. Значения фактических давлений
определяют степень концентрации напряжений в подповерхност-
подповерхностных слоях взаимодействующих тел и характер их изнашивания
(см. главу 6). Если параметры микрогеометрии взаимодействую-
взаимодействующих поверхностей не меняются по поверхности тел (однородная
шероховатость), максимальные значения фактических давлений
имеют место там, где номинальные давления достигают макси-
максимальных значений. Тогда уровень максимальных фактических
значений можно оценить из решения периодической контактной
задачи, в которой в качестве известного среднего давления на пе-
период взято максимальное номинальное давление в контакте тел
известной макроформы.
Таким образом, рассматривая контактирование деформиру-
деформируемых тел с шероховатыми поверхностями на двух масштабных
уровнях, можно рассчитать как характеристики дискретного
контакта (фактические давления, фактическую площадь контак-
контакта, зазор между телами и т. д.), так и номинальные давления, но-
номинальную площадь контакта и сближение тел под нагрузкой.
Существенно новым в предложенном алгоритме расчёта харак-
характеристик дискретного и номинального контактов является учёт
взаимного влияния пятен фактического контакта.
Общая схема расчёта контактных характеристик с учётом
макро- и микрогеометрии взаимодействующих тел представлена
на рис. 1.24.
76
Макроуровень
Микроуровень
Макроформа
нагрузка Р
Задача
непрерывного
контакта
(уравнение A.52))
Номинальные
контактные
характеристики:
область контакта Q,
внедрение D,
давление р (х, у)
С(р)
Р(х,у)
Характеристики
микрогеометрии
f,(r),h,,n,,
номинальное
давление р
Задача
дискретного
контакта
(уравнения
A.17) или A.23))
Характеристики
дискретного
контакта:
фактическая
площадь контакта,
фактические
давления, зазор
и т. д.
Рис. 1.24. Схема определения контактных характеристик с учётом
макро- и микрогеометрии взаимодействующих поверхностей
Глава 2
АДГЕЗИОННОЕ ВЗАИМОДЕЙСТВИЕ
УПРУГИХ ТЕЛ
При разработке и оценке работоспособности ряда сопряжений,
широко используемых в микроэлектронике, микромашинах, ме-
медицинской технике и других областях и характеризующихся вы-
высокой степенью гладкости взаимодействующих поверхностей и
малыми размерами, важную роль играет учёт тонких эффектов,
к которым, в частности, относится адгезионное взаимодействие
поверхностей.
В данной главе рассматриваются задачи о взаимодействии
упругих тел при наличии сил притяжения (адгезии) различной
природы, вызванной их поверхностной энергией или присутстви-
присутствием в зоне контакта менисков жидкости. Большое внимание уде-
уделяется анализу совместного влияния параметров микрогеомет-
микрогеометрии контактирующих поверхностей и свойств поверхности и по-
поверхностных плёнок на характеристики контактного взаимодей-
взаимодействия. Полученные зависимости используются, в частности, для
расчёта адгезионной составляющей сопротивления качению уп-
упругих тел. Глава составлена по работам [47, 48, 101, 208], вы-
выполненным совместно с Ю.Ю.Маховской.
2.1. ВИДЫ АДГЕЗИОННОГО
ВЗАИМОДЕЙСТВИЯ
В контактных задачах в классической постановке предполагает-
предполагается наличие сжимающих напряжений в области контакта и нуле-
нулевых - на свободной поверхности взаимодействующих тел. Одна-
Однако, реальные тела обладают поверхностной энергией, приводя-
приводящей к возникновению сил притяжения между взаимодействую-
взаимодействующими поверхностями. Если молекулы твёрдого тела взаимодей-
78
ствуют друг с другом в соответствии с потенциалом Леннарда-
Джонса, то сила взаимодействия между двумя параллельными
поверхностями, рассчитанная на единицу площади, может быть
Представлена в виде:
*-*(?)'[(?)'-']• <»>
где z - расстояние между поверхностями, zq - равновесное рас-
расстояние, на котором силы притяжения и отталкивания компен-
компенсируют друг друга, А - постоянная, определяемая поверхностной
энергией взаимодействующих тел.
Контактные задачи для упругих тел с учётом их поверхност-
поверхностной энергии рассматривались аналитическими методами в [63,
88, 197, 211] в приближённых постановках с использованием раз-
различных упрощённых форм потенциала взаимодействия. В [194,
195] проведено сравнение различных упрощённых моделей с ука-
указанием областей их применимости. Численное решение задачи с
использованием соотношения B.1) дано в [179, 219]. Результаты,
полученные при исследовании адгезионного взаимодействия как
численными, так и аналитическими методами показали, в част-
частности, что зависимость силы взаимодействия между телами от
расстояния между ними является неоднозначной. Это говорит о
возможности гистерезиса в цикле сближение - удаление тел.
Поверхностной энергией обладают не только твёрдые тела,
но и покрывающие их тонкие плёнки жидкости. При взаимодей-
взаимодействии тел это может приводить к образованию менисков в зазоре
между телами, которые вызывают притяжение поверхностей -
капиллярную адгезию.
Наличие водяных паров в атмосфере также приводит к обра-
образованию тонких плёнок жидкости на поверхности твёрдых тел.
При взаимодействии таких поверхностей капиллярные эффек-
эффекты играют значительную роль. Так, экспериментально показа-
показано [204, 236], что сила сцепления при взаимодействии магнитного
Диска с головкой существенно возрастает с увеличением влаж-
влажности окружающего воздуха, что может привести к поврежде-
повреждению поверхностей.
79
Для силы капиллярного притяжения между плоскостью и
жёстким полусферическим выступом радиуса R была получе-
получена [222] формула Ра = 47гЯа cos в (а - поверхностное натяжение
жидкости, в - угол смачивания), согласно которой сила адгезии
больше для более пологих выступов и не зависит от количества
жидкости.
При расчёте силы капиллярной адгезии между шероховаты-
шероховатыми поверхностями использовалась следующая формула для си-
силы, действующей на отдельный выступ [143]:
Ра = 4тгДстA + 8), B.2)
где 6 - величина, зависящая от толщины плёнки жидкости и
смятия выступа. При этом принималась во внимание упругость
выступов, но предполагалось, что давление жидкости не влия-
влияет на изменение их формы. Такой подход, однако, не позволяет
оценить влияние капиллярных эффектов на напряжённо-дефор-
напряжённо-деформированное состояние контактирующих тел.
В исследованиях, посвященных анализу роли адгезии при
взаимодействии шероховатых тел (см. [143, 168, 212]), показа-
показано, что адгезионные силы достигают заметных величин только
в контакте достаточно гладких поверхностей и существенно за-
зависят от формы зазора между поверхностями.
В дальнейших разделах этой главы предлагается метод ре-
решения задач о взаимодействии упругих тел с учётом адгезион-
адгезионных сил различной природы, приводятся аналитические выраже-
выражения для контактных давлений, величины зазора между поверх-
поверхностями, а также рассматривается вопрос, при каких значениях
механических и геометрических характеристик взаимодейству-
взаимодействующих тел, их поверхностной энергии или свойств промежуточ-
промежуточной среды зависимость нагрузки от величины, характеризующей
изменение расстояния между телами, является неоднозначной,
что приводит к потере энергии в цикле сближение - удаление
взаимодействующих поверхностей. Изучается зависимость вели-
величины потери энергии от механических характеристик и формы
тел, поверхностного натяжения жидкости и её объёма, а также
поверхностной энергии тел.
80
Рис. 2.1. Схема взаимодействия упругих тел при наличии мениска
между ними для случаев отсутствия контакта поверхностей (а) и при
наличии контакта (б)
2.2. КАПИЛЛЯРНАЯ АДГЕЗИЯ
2.2.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим взаимодействие двух упругих тел при наличии жид-
жидкости, образующей мениск в зазоре между контактирующими
телами. Полагаем, что тела осесимметричны и форма зазора
между поверхностями в недеформированном состоянии описы-
описывается степенной функцией /(г) = /i(r) + /г(г) = Сг2п, где /;(г)
(г = 1,2)- форма каждого из взаимодействующих тел. Тела при-
прижаты друг к другу внешней силой Р. Схема контакта для част-
частного случая жёсткого осесимметричного тела 1, форма которого
описывается функцией /(г), и упругого полупространства 2 при-
приведена на рис. 2.1.
Величина зазора h(r) между поверхностями в деформирован-
81
ном соотоянии определяется выражением
h(r) = f(r) + uz(r) + D, B.3)
где uz(r) = u\(r) + uz{r) - суммарное нормальное смещение
поверхностей взаимодействующих тел за счёт их деформиро-
деформирования, D - изменение при деформировании расстояния между
двумя фиксированными точками тел, расположенными на их об-
общей оси симметрии и удалёнными от контактной поверхности.
При h@) > 0 тела не соприкасаются и величина D положитель-
положительна (рис. 2.1,а). При h@) = 0 имеет место контакт поверхностей
внутри области па = {г ^ а} (рис. 2.1,6), включая точечный
контакт при а = 0, при этом величина D может быть как поло-
положительной, так и отрицательной.
Будем считать, что внутри области
Пь f<UrO, при МО) > О,
1 а < г < Ъ, при /i@) = О,
где Ь - некоторое расстояние, b ^ а, к взаимодействующим по-
поверхностям приложено равномерное давление, обусловленное на-
наличием жидкости в зазоре, которое, согласно формуле Лапласа,
меньше атмосферного на величину
B-5)
где а - поверхностное натяжение жидкости, R\, B.2 - радиусы
кривизны боковой поверхности мениска. Считая, что угол смачи-
смачивания жидкостью поверхностей взаимодействующих тел равен
нулю и штамп имеет пологую форму, т. е. выполняется усло-
условие /'F) <С 1, можно положить в B.5) Ri ~ h(b)/2, R2 ~ Ь.
Кроме того, предполагая, что h(b) <S b, из B.5) получим
Следует отметить, что на границе взаимодействующих тел
по окружности г = b действует также сила натяжения плёнки
82
жидкости fs = —2irba, которая при нулевом угле смачивания на-
направлена по касательной к границе тел. Простые оценки показы-
показывают, что эта сила много меньше силы fi, обусловленной давле-
давлением Лапласа. Если поверхности разделены мениском (/i@) > 0),
имеем fi = — тгЬ2р0) откуда следует оценка
В случае контакта поверхностей (h@) — 0) получаем, что си-
сила Д = —про (Ь2 — а2) и, следовательно,
В дальнейшем силой fs будем пренебрегать.
Полагая атмосферное давление равным нулю, получим сле-
следующие условия на границе тел:
• при отсутствии контакта (h@) > 0):
р(г) = 0, г>6, р(г) = -р0, гепь; B.7)
• в случае контакта поверхностей (Л@) = 0) к условиям B.7)
следует добавить соотношение:
h(r) = 0, re Ua. B.8)
В силу гладкости формы взаимодействующих тел давление р(г)
на границе области контакта Qa = {г ^ а} должно удовлетво-
удовлетворять условию
р(а) = -р0. B.9)
Условием для определения давления ро служит задание объёма v
жидкости в мениске, который связан с геометрией зазора соот-
соотношением
v= rh{r)drd<p. B.10)
83
Нормальные смещения uz(r) границы упругих тел от дейст-
действия нормальных давлений р(г) определяются известным выра-
выражением [25]:
uz(r) = A\p{r),b], О^г^б; B.11)
_l = l_^ + l^i, B.13)
где Ei и Vi (i = 1,2) - модули Юнга и коэффициенты Пуассона
взаимодействующих тел, К(х) - полный эллиптический интег-
интеграл первого рода.
И, наконец, из условия равновесия следует, что
ь
Р = 2тг / rp(r) dr. B.14)
о
Полученные соотношения B.3)—B.14) позволяют определить
неизвестные функции p(r}, uz{r) и величины a, b, D и р$.
2.2.2. МЕТОД РЕШЕНИЯ
Случай отсутствия контакта поверхностей (h@) > 0).
Адгезионное взаимодействие при отсутствии контакта описыва-
описывается уравнениями B.3)-B.14), исключая условие B.8). Величина
зазора h(r) определяется исходя из уравнений B.3), B.7) и B.11).
С учётом значения интеграла [66]:
, , /"_, B^\ r'dr'
Х(г) =
6EQ
84
где Е(х) - полный эллиптический интеграл второго рода, полу-
получим следующие выражения для упругих смещений uz(r) грани-
границы и величины зазора h(r):
^(r), B.16)
Cr^. B.17)
Подставляя соотношение B.17) в выражение B.6), получим
следующее уравнение:
Кроме того, из уравнения равновесия B.14) следует, что
Р = -пЪ2р0. B.19)
Для определения неизвестных величин давления ро жидкос-
жидкости в мениске, радиуса Ь области взаимодействия и расстояния D
к полученным соотношениям B.18) и B.19) следует добавить
условие постоянства объёма жидкости B.10), которое после под-
подстановки в него выражения B.17) примет вид:
v =nDb2 - jkpob3 + ^тт Cb2n+2- B-20)
Уравнения B.18), B.19) и B.20) справедливы при отсут-
отсутствии контакта, т.е. при Ь < Ь*. Для того чтобы определить
радиус 6*, соответствующий точечному контакту при заданном
объёме жидкости в мениске, подставим в соотношение B.17)
условие h@) = 0 и примем во внимание B.18). Тогда получим
уравнение
B.м)
ттЕ*
которое необходимо решить совместно с уравнением B.20)
при b = Ъ* относительно ро и Ь*.
85
Случай контакта поверхностей (h@) = 0). Для ре-
решения системы уравнений B.3)—B.14), имеющей место в случае
контакта поверхностей внутри области па = {г ^ а}, предста-
представим функцию р(г) в виде
p{r) = pi{r) -ро, rGQa. B.22)
При этом в точке г = а выполняется условие р\(а) = 0. Тогда
из B.11) с учётом B.7) и B.15) следует соотношение, справед-
справедливое для 0 ^ г ^ Ъ:
^Qr),a], B.23)
где Л[р(г),х] определено в B.12). Подставляя B.23) в условие
контакта B.8), получим интегральное уравнение для определе-
определения функции рг{г):
A\pi(r),a] = -f1(r)-D, r^a, B.24)
где
^0 B.25)
Из условия равновесия B.14) с учётом B.22) следует дополни-
дополнительное соотношение для определения величины D:
а
Р + ттр0Ь2 = 2тг / rpi{r) dr. B.26)
о
Полученное интегральное уравнение аналогично имеющему
место в задаче о внедрении в упругое полупространство осесим-
метричного гладкого штампа заданной формы /i(r) (см. B.25))
при действии на него силы, описываемой выражением в ле-
левой части соотношения B.26). При этом правая часть B.23)
при а < г ^Ь определяет смещения границы упругого полупро-
полупространства вне области контакта с таким штампом.
Воспользуемся решением этой задачи, полученным в [67], на
оснований которого и соотношений B.22)-B.24), найдём выра-
выражения для нормальных давлений р(г) при г^аи смещений uz(r)
86
границы тел при а < г ^ Ь:
p(r) = -Po
1 1
a?E* [ydy [ x
-r
2 2 2
а2 — г2
l
2a f ydy
— /
7Г J
0
х
д
— y2 J Vr2 — x2a2
а также условие для определения величины D:
1
У
о
-у2
—(yD + yh(ay))dy = O.
B.29)
Воспользовавшись формулой Л.А. Галина [25] для силы, при-
прижимающей осесимметричный штамп, и учитывая B.26), будем
иметь:
Р = 2Е*
а2 - г2 dr - тгр0Ъ2.
B.30)
Разлагая эллиптический интеграл в ряд и учитывая, что
функция /(г) = Сг2п, преобразуем выражение B.25) к виду:
r
\m=l
Bш-1)!!
-11.B.31)
Для определения искомых выражений для давления р(г) и
смещений uz(r), а также величин внедрения D и нагрузки Р, под-
подставим выражение B.31) в соотношения B.27)-B.30) и введём
87
безразмерные величины:
г _ v
Р= -, Р =
Р =
тгЕ*Ь2 '
и =
РО
B.32)
Окончательно получим:
uz
2 / ДГ/\
1 arctg 6\ , р ^ 1,
(р) = — (I) + (pWJn) arcsin - +
7Г V /О
7Г
fc=l
Е (<5р) — Е I arcsin -,6p
\ Р
г —F I arcsin <5, —
к \ РО
B.33)
B.34)
B.35)
2n)!! 4n(WJn+1
Bп + 1)!! 7г
—2роЬ2 (arccos <5 + 5у/1 — <52
B.36)
где F(x, ф), Е(х, ф) - неполные эллиптические интегралы перво-
первого и второго рода. Вывод соотношений B.33)-B.36) содержится
в [47]. Заметим, что выражения B.33), B.35) и B.36) при ро = О
совпадают с формулами, полученными в [146].
Для определения оставшихся неизвестных параметров <S, b
и ро воспользуемся соотношениями B.3), B.6) и B.10). Преобра-
Преобразуем формулу B.3) с учётом B.34) и B.35). Тогда получим для
безразмерной величины зазора h = h/L выражение:
2 1
h(p) = — arccos -
тг р
Bп- 1)!!
- B.37)
— Е I arcsin - , рб
V Р
Подставляя B.37) в B.6) и B.10), после преобразований (см. [47])
получим:
B.38)
Во-
2Bi
B.39)
где
fc — 1
<p = — arccos 6.
89
Подстановка B.39) в B.38) приводит к уравнению, содержа-
содержащему неизвестные b и 5. Это уравнение может быть решено чис-
численно относительно Ь при заданном 8, затем, согласно B.39),
определяется безразмерное давление в жидкости ро- После это-
этого остальные характеристики задачи находятся из соотноше-
соотношений B.33)—B.36). Выражение B.36) служит для определения на-
нагрузки Р, соответствующей выбранному значению 5. Если за-
задана величина нагрузки Р, неизвестные величины b и 8 мо-
могут быть определены на основании решения системы уравне-
уравнений B.36) и B.38).
Если пренебречь упругими деформациями полупространства
вне области контакта, т.е. считать, что \uz(r) — uz(a)\ <S \f{r) —
—f{a)\ для г ^ а, то условия B.6) и B.10) приводятся к простому
виду:
Г V{n + 1) VBn+2)
Ь= [ \
Полученные соотношения B.40), B.41) совместно с выраже-
выражениями B.33)-B.36) дают аналитическое решение задачи в пара-
параметрическом виде.
2.2.3. АНАЛИЗ КОНТАКТНЫХ ХАРАКТЕРИСТИК
Анализ полученной системы уравнений показывает, что ре-
решение задачи зависит от четырёх безразмерных параметров
(см. B.32)): параметра v, определяемого объёмом жидкости в
мениске и геометрией штампа; параметра Р, характеризующе-
характеризующего приложенную к штампу нагрузку; параметра а, зависящего
от поверхностного натяжения жидкости и упругих свойств по-
полупространства, и числа п, определяющего форму штампа.
Для реальных поверхностей со средним радиусом кри-
кривизны неровностей 0,12 мм и эффективным модулем упругос-
упругости 75,6 ГПа, покрытых плёнкой жидкости толщиной 1 -=- 10 нм с
поверхностным натяжением 0,07 Н/м (данные взяты из [236], где
90
р/(пЕ*)
-uz/BR)
-0,01
0,05 r/BR) 0,10
0,00
0,05 r/BR) 0,10
Рис. 2.2. Распределение давления (а) и форма деформированной по-
поверхности {б) при п = 1, а = 1(Г4, v = 10~4 и Р - 4,05 ¦ 10~5 A),
Р = -1,35 • Ю-5 B) Р = -3,21 • 1(Г5 C), Р = -4,74 • 1СГ5 D)
Р = -5,09 • 10~5 E) и Р = -5,23 • 10~5 F)
изучалось взаимодействие стеклянных дисков, на которые нане-
нанесено угольное покрытие, с головкой из окиси алюминия и кар-
карбида титана во влажной среде), безразмерный объём v мениска
меняется в пределах 10~6-j-10~5, параметр а имеет порядок 10~9.
Эти оценки получены в предположении параболической формы
неровностей (п = 1). Для более мягких тел (модуль упругос-
упругости порядка нескольких ГПа) с шероховатыми поверхностями,
средний радиус кривизны неровностей которых составляет не-
несколько микрон, параметр v меняется в пределах 10~4 -г 10~3, а
параметр и - в пределах 10~5 -=- 1СГ4. При численных расчётах
мы использовали значения параметров, лежащих в приведённых
здесь пределах.
На рис. 2.2-2.4 представлены результаты расчёта контакт-
контактных характеристик для случая, когда форма зазора в неде-
формированном состоянии описывается квадратичной функци-
функцией, т.е. /(г) = г2/BЯ) (п = 1, С = L~l = {2R)'1). Распре-
Распределение давления и упругих смещений приведены на рис. 2.2,а
и б соответственно, для разных значений нагрузок. Кривые 1-3
соответствуют случаю контакта поверхностей, в то время как
кривые 5 и 6 - случаю отсутствия контакта. Кривая 4 построе-
построена при /3 = /3*, т. е. при точечном контакте.
91
a/BR)
0,00 L
0,10
0,05
(b - a)/BR)
1:1 1 :
1 у i ;
I'M :-
6
^^
1
0,00
-0,5 0,0 P/DnE*R2) 1,0
-0,5 0,0 P/^nE'R2) 1,0
Рис. 2.З. Зависимости радиуса области контакта (а) и ширины коль-
кольцевой области, занятой жидкостью F), от нагрузки при п = 1 и ст =
= 2-10 A, 1'),а = 1(Г4 B,2')
Кривые 1 и 2 соответствуют значению V = 10~4, кривые 1' и 2' - значе-
значению V = 2 • 10~4, кривая 3 соответствует решению Герца
На основании полученных результатов можно заключить,
что давление отрицательно вблизи краёв области контакта
(рис. 2.2, кривые 1, 2). Это означает, что на указанных учас-
участках действуют давления, меньшие по величине атмосферных.
При уменьшении нагрузки Р область, внутри которой давления
отрицательны, растёт. Начиная с некоторого отрицательного
значения Р давление становится отрицательным во всех точках
площадки контакта (кривая 3). При дальнейшем уменьшении
нагрузки контактные давления, абсолютная величина давления
жидкости в мениске и радиус области контакта па уменьшают-
уменьшаются.
Графики формы деформированной границы тел, представ-
представленные на рис. 2.2,5, показывают, что при наличии мениска гра-
граница тел искривляется и при удалении тел кривизна поверхнос-
поверхности меняет знак. На внешней границе р = b области fij,, занятой
жидкостью, функция и'(р) не является непрерывной.
На рис. 2.3 приведены графики зависимости радиуса облас-
области контакта и ширины кольцевой области, занятой жидкостью
92
от нагрузки, построенные для различных безразмерных значе-
значений поверхностного натяжения Ъ и объёма v жидкости в зазоре.
Представленные зависимости позволяют заключить, что ради-
радиус области контакта отличен от нуля при некоторых отрица-
отрицательных нагрузках и превосходит по величине соответствующие
герцевские значения (кривая 3) при положительных нагрузках.
Этот эффект тем заметнее, чем больше параметр а. Увеличе-
Увеличение объёма жидкости приводит к уменьшению области контак-
контакта, при этом кольцо жидкости становится шире. Характерной
особенностью данных, а также представленных ниже графиков
является неоднозначная зависимость контактных характеристик
от нагрузки в некоторой области её отрицательных значений.
Графики зависимости безразмерных нагрузки Р, давления в
жидкости ро, радиуса b области Q& от безразмерного расстоя-
расстояния D, построенные для разных значений объёма v жидкости
и её поверхностного натяжения, характеризующегося парамет-
параметром <т, приведены на рис. 2Л,а-в. Здесь и в дальнейшем участ-
участки кривых, выделенные жирными линиями, соответствуют слу-
случаю контакта поверхностей, остальная часть приведённых кри-
кривых (тонкие линии) - отсутствию непосредственного контакта.
Для сравнения на рис. 2.4,а приведена зависимость нагрузки от
расстояния, соответствующая случаю отсутствия мениска (кри-
(кривая 0).
Результаты, представленные на рис. 2.4,а, показывают, что
зависимости нагрузки Р от расстояния D являются немонотон-
немонотонными и имеют точку минимума. На величину этого минимума
наиболее сильно оказывает влияние параметр <т, с ростом кото-
которого абсолютные значения минимальных нагрузок возрастают.
Увеличение параметра а, связанное либо с увеличением поверх-
поверхностного натяжения, либо с уменьшением эквивалентного мо-
модуля упругости взаимодействующих тел, приводит к росту аб-
абсолютного значения ро давления в жидкости (см. рис. 2.4,<?) и
радиуса 6 области О^, занятой жидкостью (см. рис. 2.4,е). При
увеличении объёма жидкости в мениске (увеличение парамет-
параметра v) наблюдаются увеличение радиуса b и уменьшение давле-
давления ро жидкости в мениске, особенно в случае, когда сохраняет-
сохраняется контакт поверхностей. На основании полученных результатов
93
-0,0005^
0,050
0,025
0,000
-0,01
Рис. 2.4. Зависимости нагрузки (а), давления в жидкости (б) и внеш-
внешнего радиуса области, занятой жидкостью (в), от изменения рассто-
расстояния между телами, построенные при п = 1 и v = 10~5 A, 2, 3),
v = 5- Ю-5 A', 2', 3') и а = Ю-5 A, 1'), а = 4 ¦ 10~5 B, 2'), сг = 8 • 10
C, 3')
94
-1,0 -0,5 0,0 0,5r/Z,l,0
-0,05
1,0 r/a, 1,5
Рис. 2.5. Профили штампа (а) и распределение давления в контакте
(б) для п = 1 (кривые 1, 1') и п = 2 (кривые 2, 2') Кривые 1', 2'
построены без учёта капиллярной адгезии
можно заключить, что как и зависимости контактных характе-
характеристик от нагрузки, так и зависимости нагрузки Р от изменения
расстояния D между телами вследствие их деформации в опре-
определённой области изменения значений D и параметров v и а име-
имеют неоднозначный характер: одному и тому же значению D со-
соответствуют два различных значения нагрузки (см., например,
точки Е и F на линии 3, рис. 2.4,а).
2.2.4. ВЛИЯНИЕ ФОРМЫ ШТАМПА
Описанные выше результаты относятся к случаю штампов в
форме параболоидов вращения. Такая форма штампов наиболее
часто используется для моделирования неровностей на поверх-
поверхности шероховатых тел. Однако полученные в 2.2.2 общие со-
соотношения применимы для изучения адгезионного взаимодейст-
взаимодействия осесимметричных выпуклых тел произвольной формы. Ни-
Ниже проведены сравнительные расчёты контактных характерис-
характеристик для штампов, форма контактирующих поверхностей кото-
которых описывается функциями /(г) = С г2 (п = 1, параболоид вра-
вращения) и /(г) = СУ4 (п = 2). Исследуемые профили штампов, в
безразмерном виде задаваемые функцией F(p) = р2п (р = r/L),
изображены на рис. 2.5,а кривыми 1 (п = 1) и 2 (п = 2).
95
На рис. 2.5,6 представлены графики функции безразмерного
давления в контакте для двух форм штампа: п — 1 (кривая 1)
и п = 2 (кривая 2), при Р = О, а = 10~4, v = 10~4. Кривые 1',
2' соответствуют распределениям давлений для тех же значе-
значений радиуса области контакта щ при отсутствии жидкости. На
приведённых графиках величина Si = bi/ai определяет внешний
радиус кольцевой области, занятой жидкостью, отнесённый к ра-
радиусу ai области контакта, соответствующей исследуемому слу-
случаю. Сравнение зависимостей свидетельствует о том, что при
одной и той же площади контакта давления под штампом при
наличии мениска меньше, чем при сухом контакте.
Форма штампа существенно влияет на эпюру распределения
давлений, а также ширину кольцевой области, занятой жидкос-
жидкостью. Результаты показывают, что чем более пологой является
форма вершины штампа, т. е. чем больше величина п, тем боль-
больше абсолютная величина капиллярного давления в жидкости ро
и меньше относительная ширина кольца b/а. Это объясняется
тем, что для штампов с более плоской вершиной величина зазо-
зазора h(r) меньше, а значит, согласно формуле B.6), капиллярное
давление в жидкости больше.
P/(EL2)
На рис. 2.6 при-
приведены зависимос-
зависимости безразмерной на-
нагрузки РI (E*L2)
от величины D / L
-0,5
В М:
-0,5
0,0
0,5 DIL 1,0
L = BС). 2"-
для штампа, форма
которого изобра-
изображена на рис. 2.5,а
(п = 2, кривая 2).
Как и в слу-
случае формы тел,
описываемой квад-
квадратичной функцией
(п = 1), кривые
имеют неоднозначный характер начиная с некоторого значения
безразмерного поверхностного натяжения 2a/(E*L).
Рис. 2.6. Зависимость нагрузки от сближения
тел при п = 2, v/L3 = 0,05 и 2a/(E*L) = 0,05
(кривая 1), 2a/{E*L) = 0,1 (кривая 2)
96
V
1
1
/
' а
г
1
Z
J
11
г
А
3
р
о -
Ра'
/
1/
\/
К
2
б
z
Рис. 2.7. Схема контакта с учётом сил молекулярного притяжения (а)
и зависимость сил притяжения от расстояния {б) в виде функции Лен-
нард а-Джонса A) и аппроксимирующей её кусочно-постоянной функ-
функции B)
2.3. АДГЕЗИЯ СУХИХ ПОВЕРХНОСТЕЙ
Рассмотрим теперь взаимодействие двух упругих тел, облада-
обладающих поверхностной энергией (рис. 2.7,а). Полагаем, что тела
осесимметричны и зазор в недеформированном состоянии опи-
описывается степенной функцией /(г) = /i(r) + /г(^) = Сг2п. Тела
прижаты друг к другу внешней силой Р.
При взаимодействии сухих поверхностей учтём возникающие
при этом силы молекулярного притяжения между поверхностя-
поверхностями. Для количественного описания этих сил воспользуемся за-
зависимостью Леннарда-Джонса B.1) (см. рис. 2.7,#, кривая 1).
Следуя известному методу [211], аппроксимируем эту зависи-
зависимость кусочно-постоянной функцией в форме ступеньки (кри-
(кривая 2). Тогда давление — ро имеет смысл высоты этой ступеньки,
а поверхностная энергия, рассчитываемая на единицу площади,
определяется соотношением
7
+ ОО
= / p
B.42)
Величина До имеет смысл максимального расстояния, на кото-
котором ещё проявляются силы молекулярного притяжения между
4. Горячева И.Г.
97
поверхностями. Параметры потенциала взаимодействия 7 и Ро
будем считать заданными величинами.
Как и в случае капиллярной адгезии, напряжённое состояние
взаимодействующих тел и величина зазора h(r) между поверх-
поверхностями в деформированном состоянии будет определяться
• при отсутствия контакта: распределением давления —ро
внутри круговой области Г2(,;
• в случае контакта поверхностей: распределением контакт-
контактных давлений р(г) в круговой области па и давлением — ро
внутри кольцевой области Г2ь.
Однако в отличие от задачи с учётом капиллярной адгезии,
давление — ро внутри области Пь является заданной величиной.
Для определения внешнего радиуса b области Qj, воспользуемся
соотношением B.42), из которого следует
h(b) = 1.. B.43)
Ро
Это соотношение совпадает с B.6), если положить 7 = 2<т.
Смещение uz{r) границы упругих тел от действия на неё
давления р(г) определяется, как и прежде, соотношением B.11).
Кроме того, выполняется условие равновесия B.12).
Таким образом, система уравнений и граничные условия в за-
задаче о взаимодействии упругих тел с учётом их поверхностной
энергии при сделанном предположении об аппроксимации функ-
функции Леннарда-Джонса кусочно-постоянной функцией является
частным случаем системы, полученной при изучении капилляр-
капиллярной адгезии. Следовательно, построенные в 2.2 решения могут
быть использованы и для анализа контактных характеристик
при взаимодействии упругих тел, характеризуемых поверхност-
поверхностной энергией j. При этом в полученных решениях следует поло-
положить а = 7/2.
При отсутствии контакта поверхностей неизвестные функ-
функции упругих смещений uz(r) границы тел и зазора h(r) опре-
определяются по формулам B.16) и B.17) соответственно. Величи-
Величины радиуса Ь области П& (Ь < Ь*) и сближения D тел находят-
находятся из соотношений B.18) и B.19), которые после подстановки в
98
них <т = 7/2 могут быть записаны в виде:
B.44)
B.45)
Заметим, что сила Р при отсутствии контакта является отри-
отрицательной величиной, т.е. Р < 0.
Величина Ь*, соответствующая состоянию, при котором по-
поверхности соприкасаются в одной точке (h@) = 0), находится из
уравнения B.21).
В случае контакта поверхностей неизвестные функции кон-
контактных давлений р(г), упругих смещений йг(г) границы тел
и зазора h(r) определяются по формулам B.33), B.34) и B.37)
соответственно. Радиус а области контакта па (о = a/L = bS),
внешний радиус b кольцевой области Qf,, а также изменение рас-
расстояния D находятся из системы уравнений B.35), B.36) и урав-
уравнения:
252"й) [Г BпI! 1
тг \[Bп-1)!! 6
\\ 2(п_к)
<р = arccos 5.
Заметим, что уравнение B.46) при 5 = 0 совпадает с уравнени-
уравнением B.21), которое служит для определения величины Ь*, соот-
соответствующей точечному контакту поверхностей.
Полученные соотношения были использованы для анализа
зависимости контактных характеристик от параметров Сип,
определяющих форму поверхностей, приведённого модуля упру-
упругости Е* взаимодействующих тел, характеристик потенциала
адгезионного взаимодействия поверхностей ро и 7> а также от
величины приложенной нагрузки Р.
4* 99
0,007
P/(nEL)
alL,blL
0,000
-0,007
\
! \
! A F
4) 1 if
i
-0,06
0,00 DIL 0,06
0,4
0,2
0,0 '
-0,003 0,000 P/(nE'L2) 0,006
Рис. 2.8. Зависимости безразмерных нагрузки от расстояния (а) и ра-
радиусов области контакта A) и области действия молекулярного при-
притяжения A') от нагрузки (б), построенные при п = 2, ро/(пЕ*) = 0,01
и -у/(ттЕ*Ь) = 0,0001 A, 1'), l/(irE*L) = 0,0005 B)
Результаты расчётов позволили установить, что наличие ад-
адгезии, связанной с молекулярным взаимодействием поверхнос-
поверхностей, приводит к эффектам, аналогичным имеющим место при ка-
капиллярной адгезии: наличие отрицательных давлений в контак-
контакте, увеличение размера области контакта, неоднозначность опре-
определения контактных характеристик при отрицательных значе-
значениях силы. Кроме того, зависимость нагрузки, действующей на
тела, от расстояния между ними является немонотонной и неод-
неоднозначной. Это иллюстрируется рис. 2.8,а, где приведены гра-
графики безразмерной нагрузки от безразмерной величины D/L, ха-
характеризующей изменение расстояния между телами при дефор-
деформировании (L = С1"") - характерный геометрический раз-
размер), построенные для случая контакта двух упругих тел, форма
зазора между которыми в недеформированном состоянии описы-
описывается функцией /(г) = Сг4 (см. рис. 2.5,а, кривая 2). Кривые 1
и 2 соответствуют двум разным значениям величины поверх-
поверхностной энергии 7- Участки непосредственного контактирова-
контактирования поверхностей выделены на кривых, как и прежде, толстыми
линиями. В отличие от случая капиллярной адгезии неоднознач-
неоднозначность зависимости нагрузки от расстояния имеет место при всех
значениях параметров.
Кривые, представленные на рис. 2.8,6', демонстрируют зави-
зависимости безразмерных радиуса а области контакта (кривая 1)
100
и внешнего радиуса b области, где проявляется действие моле-
молекулярных сил (кривая 1') от безразмерной силы Р. Из анализа
результатов следует, что в области отрицательных значений Р
каждому значению Р соответствуют две пары значений а и Ь.
При Р > 0 зависимости радиусов областей Ua и П^ от силы Р од-
однозначны, при этом ширина кольца, в котором действуют силы
молекулярного притяжения, постепенно уменьшается с ростом
нагрузки. Качественно аналогичные результаты наблюдались
при анализе контактных характеристик в случае капиллярной
адгезии (см. 2.2).
Заметим, что решение задачи об адгезии сухих поверхностей
в аналогичной постановке для частного случая взаимодействия
штампа в форме параболоида вращения (п = 1) с упругим по-
полупространством получено ранее методами механики разруше-
разрушения [211]. Это решение, полученное только для случая контак-
контакта поверхностей, также указывает на немонотонность и неодно-
неоднозначность зависимости нагрузки от расстояния между телами.
2.4. ДИССИПАЦИЯ ЭНЕРГИИ В ЦИКЛЕ
СБЛИЖЕНИЕ - УДАЛЕНИЕ
ПОВЕРХНОСТЕЙ
Полученные зависимости нагрузки Р от расстояния D между
телами позволяют рассчитать работу, производимую в процес-
процессе уменьшения и последующего увеличения расстояния между
телами при наличии адгезии. Рассмотрим кривые 2 на рис. 2.6
и 2.8,а, иллюстрирующих зависимость P(D) для случаев капил-
капиллярной адгезии и адгезии сухих поверхностей соответственно.
Если контакт осуществляется при контролируемой (монотонно
уменьшаемой) нагрузке Р, то при достижении этой нагрузкой
минимального значения Pmjn (точка М) произойдёт скачкооб-
скачкообразный отрыв поверхностей в случае как сухих поверхностей,
так и капиллярной адгезии при любых значениях параметров.
При этом в момент отрыва имеет место контакт поверхностей
по конечной области.
Если взаимодействие осуществляется при контролируемой
(монотонно увеличиваемой) величине D, то при достижении точ-
101
в
Рис. 2.9. Схема процесса сближения поверхностей, имеющего место
на участке А - В (см. рис. 2.6)
ки Е происходит скачкообразный переход в точку F. И обратно,
при уменьшении величины D имеет место скачок из точки А в
точку В. Заметим, что точки А и F всегда соответствуют от-
отсутствию контакта между поверхностями, в то время как точ-
точки В и Е могут соответствовать как контакту, так и отсутствию
контакта поверхностей. Следовательно, возможно скачкообраз-
скачкообразное разрушение контакта и вступление поверхностей в контакт.
Последний процесс иллюстрируется на рис. 2.9 для случая ка-
капиллярной адгезии при взаимодействии штампа с упругим по-
полупространством.
Таким образом, из рассмотрения цикла уменьшение-увеличе-
уменьшение-увеличение расстояния между телами следует, что работа, совершаемая
внешней силой при сближении поверхностей, не равна работе,
совершаемой телами при их удалении друг от друга. Соответ-
Соответствующая потеря энергии определяется площадью заштрихован-
заштрихованных областей на рис. 2.6 и 2.8,о и может быть рассчитана по
формуле:
Aw= IP(D)dD. B.47)
ABEF
Используя полученные зависимости нагрузки от изменения
расстояния между телами можно определить величины потери
энергии Aw и силы отрыва поверхностей Pmin как при капил-
капиллярной адгезии, так и для адгезии сухих поверхностей.
102
Aw/(p0L3)
10
5
о
y\
--___21__
2
0
2 y/(PoL) 4 0 1 y/(PoL) 2
Рис. 2.10. Зависимости безразмерных потери энергии (а) и силы от-
отрыва (б) от безразмерной поверхностной энергии для случая адге-
адгезии сухих поверхностей, построенные при п = 1 A, 2), п = 2 B')
и ?7ро = 1 A), Е*/Ро = 2 B, 2')
Зависимости безразмерной потери энергии Aw/ (po-^3) и си-
силы отрыва .Pmin/ (pqL2) от безразмерной поверхностной энер-
энергии j/(pqL), полученные для случая адгезии сухих поверхнос-
поверхностей, представлены на рис. 2.10,а и б соответственно. Зависимос-
Зависимости построены для двух различных форм штампов: параболои-
параболоида вращения (п = 1, сплошные линии) и описываемой функци-
функцией /(г) = Сг4 (п = 2, штриховые линии). Результаты показы-
показывают, что при увеличении поверхностной энергии тел значение
функции Aw/ (pqL3) растёт и при больших величинах *y/(poL)
выходит на постоянную. Потеря энергии Aw/ (pqL^ больше для
меньших значений Е*/ро, т. е. для более мягких тел. Сила отры-
ва Pmin/ {pqL2), напротив, увеличивается с увеличением Е*/р$.
Сравнение кривых 2 и 2' позволяет заключить, что форма штам-
штампа оказывает существенное влияние на величину силы отрыва
при больших значениях поверхностной энергии взаимодейству-
взаимодействующих тел.
На рис. 2.11 приведены зависимости безразмерной потери
энергии Aw/ (?^*L3) от безразмерного поверхностного натяже-
натяжения 2сг/ (E*L) в случае капиллярной адгезии для двух форм
103
1,0
0,5
0,0
0,0
0,2
0,4 2g/(E'L) 0,6
Рис. 2.11. Зависимости безразмерной потери энергии от безразмерной
величины поверхностного натяжения жидкости для случая капилляр-
капиллярной адгезии, построенные при п = 1 A, 2), п — 2 B') и v/L3 = 0,01 A),
v/L3 = 0,05 B, 2')
взаимодействующих тел (п = 1 - сплошные линии и п = 2 -
штриховая линия). Потеря энергии отлична от нуля только на-
начиная с некоторого значения безразмерного поверхностного на-
натяжения и возрастает неограниченно при увеличении этого па-
параметра. Кроме того, величина A.w/ (E*L3) тем больше, чем
меньше объём жидкости в мениске (см. кривые 1 и 2).
Случай параболических тел. Случай п = 1 соответ-
соответствует взаимодействию поверхностей сферической формы, при-
причём величина L = BС)~1'^п~1' имеет смысл их приведённого
радиуса:
L 1 N -1
Анализ полученного решения задачи об адгезионном взаи-
взаимодействии сухих поверхностей показывает, что в этом случае
зависимость между безразмерной нагрузкой Р и безразмерной
104
величиной D, определяемыми соотношениями
'г B 48)
описывается единственным параметром А:
1 /О
( 9Я
впервые введенным Табором [233]. Этот параметр использовался
также в [211] при анализе эффекта адгезии в контакте сухих
поверхностей.
Работа в цикле уменьшение-увеличение расстояния между
телами, представленная в безразмерном виде как
V3
¦ B-49)
при п = 1 является функцией одной переменной А.
Соотношения B.44), B.45) в случае отсутствия контакта по-
поверхностей и соотношения B.35), B.36) и B.46) в случае контак-
контакта поверхностей, определяющие решение задачи об адгезионном
Взаимодействии сухих поверхностей, при п — 1 упрощаются и
позволяют найти точное аналитическое выражение для функ-
функции АИ^(А) в области малых значений параметра А:
Анализ полученных соотношений позволяет также установить,
что при А—> + оо функция AW стремится к постоянному значе-
Йию AWoo, которое выражается в аналитической форме и при-
приближённо равно ДЖх> ~ 1,80. В работе [211] показано, что пре-
йельный случай А —> 0 соответствует теории адгезии Дерягина-
Мюллера-Торопова, а случай А —» +оо - теории Джонсона-Кен-
Налла-Робертса.
График функции AW(X), рассчитанный во всём диапазоне
Изменения параметра А, приведён на рис. 2.12,а(кривая 1).
105
AW,AWW
AW, AWW
0
2
/ a
0
1 К К 2
О
i
/
/
/л
б
1
Рис. 2.12. Зависимость диссипации энергии от параметра Л в случае
адгезии сухих поверхностей (а) и от параметра ц в случае капиллярной
адгезии (б), построенные при п = 1 с использованием модели упругих
тел A) и модели Винклера B)
Как и при адгезии сухих поверхностей, в случае капиллярной
адгезии для тел параболической формы зависимость безразмер-
безразмерной нагрузки Р от безразмерной величины D (выражения для Р
и D даны в B.48) с учётом замены 7 = 2сг) определяется одним
безразмерным параметром
Г} =
BаL/3 Д5/3
В этом случае безразмерная потеря энергии AW B.49) зависит
от одного параметра ц. График функции AW(t)) представлен
на рис. 2.12,5 (кривая 1). Результаты показывают, что величи-
величина ДИ^ отлична от нуля только начиная с некоторого значения г)
и неограниченно возрастает при увеличении г}.
Заметим, что для тел, форма поверхности которых описы-
описывается полиномом более высокой степени (n ^ 2), необходимо
использовать два безразмерных параметра для описания зависи-
зависимости нагрузки от изменения расстояния между телами (напри-
(например, параметры v/L3, 2a/{E*L) для случая капиллярной адгезии
и ро/(пЕ*), ^/{тхЕ*Ь) для случая адгезии сухих поверхностей,
использованные на рис. 2.6 и 2.8).
106
2.5. АНАЛИЗ УПРОЩЁННЫХ МОДЕЛЕЙ
Решение задачи об адгезионном взаимодействии поверхностей
можно существенно упростить, если считать, что упругие свой-
свойства взаимодействующих тел описываются моделью Винклера.
В этом случае нормальное смещение поверхностей uz(r) связано
с приложенным давлением р{г) соотношением
uz(r) = kp(r), к = к\ + &2, B.50)
где к\ и &2 ~ постоянные, описывающие упругие свойства вза-
взаимодействующих тел. Соотношение B.50) является приближён-
приближённым аналогом соотношения B.11).
Соотношение B.50) и уравнения B.3)—B.9), B.14) образуют
систему уравнений для определения всех контактных характе-
характеристик в случае адгезии сухих поверхностей, а совместно с урав-
уравнениями B.3)—B.10), B.14) - в случае капиллярной адгезии. Эти
системы уравнений допускают аналитическое решение. В част-
частности, в случае взаимодействия тел вращения параболической
формы (п = 1), т.е. когда /(г) = Сг2, где С = 1/BД), получим
следующие выражения для контактного давления р(г), упругих
смещений uz(r), радиусов а и b области взаимодействия, а так-
также соотношение между силой Р и расстоянием D, справедливые
как для сухой, так и для капиллярной адгезии:
• при контакте поверхностей (h@) = 0)
Р{г) = -- — + D , г < о;
К \2К )
uz{r) - -kp0, a <r ^b,
2R-y B-51)
a2 = 2R(kp0 - D), b2 - a2 -1 ,
Po
в отсутствие контакта (h@) > 0)
р
uz{r) = -kp0, O^r^b, b2 = ,
*Р B.52)
Р = -2tvRj + 2ttRpo(D - кр0).
107
При точечном контакте, полагая а = 0 в B.51), получаем
Р* = -2irRj, D* = кРо. B.53)
Соотношения B.51)—B.53) определяют решение задачи в слу-
случае адгезии сухих поверхностей. Для того чтобы получить реше-
решение в случае капиллярной адгезии, в этих соотношениях следует
положить 7 = 2G и дополнить их следующими выражениями для
давления в жидкости ро> полученными из соотношения B.10):
• при контакте поверхностей
ро = 2а ^™ J ; B.54)
• в отсутствие контакта
(Ж^) B-м)
Заметим, что уравнение B.50) при к — 0, имеющее
вид uz(r) = 0, соответствует случаю жёсткого полупростран-
полупространства. Полагая uz(r) = 0 в соотношениях B.3)-B.14), получим
решение
D = -Ъ2п + х,
рС1/Bп-1)
а
пЬ2п
УС=
описывающее взаимодействие жёстких штампа и полупростран-
полупространства при наличии капиллярной адгезии. При этом величина Ь,
соответствующая точечному контакту поверхностей, определя-
определяется выражением
Полученные решения позволяют построить зависимость
между нагрузкой Р и величиной D. Если ввести безразмерные
108
величины Р (первое соотношение B.48)) и Dw = D(kj) ll2, то
искомая зависимость будет содержать единственный безразмер-
безразмерный параметр.
Так, в задаче об адгезии сухих поверхностей, используя без-
безразмерный параметр
представим последние соотношения в B.51) и B.52) в виде:
{П2 - 2 - A2 D < А
1Jw L "ил •*-/u> ^ Лил
/ \ - B-56)
2 (Аш?»ш - Д2 - 1J , Dw > Xw.
Если ?)„, ^ Ац,, то имеет место контакт поверхностей, а ес-
если Dw > Аш, то отсутствие контакта. Случай D^, = Аш, Р* = — 2
соответствует точечному контакту.
В задаче о капиллярной адгезии, подставляя B.54) и B.55)
в последние соотношения B.51) и B.52) соответственно и вводя
безразмерный параметр
_ 2nRka
v
получим:
-
Dw>r)
T]WP P + 4
При Dw ^ r]w поверхности находятся в контакте, а при Dw > rjw
контакт отсутствует. Случай D^ = т/ш, Р* = —2 соответствует
точечному контакту поверхностей.
Из полученных соотношений B.56) и B.57) следует, что за-
зависимость нагрузки Р, приложенной к телам, от величины Dw
является немонотонной и однозначной в случае адгезии сухих
поверхностей, а в случае капиллярной адгезии - немонотонной и
неоднозначной в определённой области изменения параметров.
109
20
10
0
-10
-20
PI{oL) PI{qL
0
-40
-80
-0,1 0,0 DIL 0,1 -0,02 0,00 0,02 DIL 0,04
\
\
\
а
7
б
Рис. 2.13. Зависимость нагрузки от изменения расстояния между те-
телами при п = 1 (а) к п = 2 (б) в случае капиллярной адгезии
Кривые 1 соответствуют модели упругих тел, кривые 2 - модели Винклера,
кривые 3 - модели жёстких тел
Анализ зависимости B.56) для случая сухой адгезии да-
дает основание заключить, что эта зависимость качественно со-
соответствует точной, полученной с использованием соотноше-
соотношения B.11), только в случае контакта поверхностей.
На рис. 2.13 приведены зависимости нагрузки от сближения
тел для случая капиллярной адгезии, полученные с использова-
использованием точных соотношений B.11) для упругих тел (кривые 1),
упрощённых B.50), соответствующих модели Винклера (кри-
(кривые 2) и с использованием модели жёстких тел (кривые 3) для
двух различных форм штампов, т.е. для п = 1 (а) и п = 2 (б).
Сравнение кривых показывает, что только в случае учёта уп-
упругости тел можно получить немонотонные и неоднозначные за-
зависимости нагрузки от сближения тел. При этом зависимости,
построенные на основании модели Винклера, идентичны полу-
полученным с использованием точных соотношений. Такой же вывод
можно сделать из анализа соотношений, приведённых выше.
На основании полученных соотношений между нагрузкой Р
и величиной Dw (см. B.56) и B.57)) можно рассчитать зависи-
зависимости безразмерной потери энергии A.WW в цикле уменьшение-
увеличение расстояния между телами
1/2
тгВ.
ПО
от параметров Xw и 7]w для случаев адгезии сухих поверхнос-
поверхностей и капиллярной адгезии соответственно. Они представлены
кривыми 2 на рис. 2.12. В случае адгезии сухих поверхностей
функцию AWW(XW) можно представить в аналитическом виде:
{\3 \ <- 1
1 (М - 1) BXJ + Ъ\1 - 1) 1
з a» +a;' K>h
Эта функция близка к функции AW(X) (см. рис. 2.12,а, кри-
кривая 1), соответствующей точной постановке задачи, лишь при
малых значениях Xw.
В случае капиллярной адгезии зависимость &Ww(r]w) качест-
качественно напоминает кривую AW(rj), полученную при решении за-
задачи в точной постановке. При этом значение r]w, начиная с ко-
коли/
торого значение AWW становится отличным от нуля, равно
4
(см. рис. 2.12,6, кривая 2).
2.6. АДГЕЗИОННОЕ ВЗАИМОДЕЙСТВИЕ
ШЕРОХОВАТЫХ ТЕЛ
Шероховатость поверхностей существенно влияет на характе-
характеристики адгезионного взаимодействия. Контактирование шеро-
шероховатых упругих тел при наличии капиллярной адгезии, т. е.
стягивающих поверхности менисков жидкости, изучалось в [143,
210] в приближённой постановке. В этих работах не учитыва-
учитывалось влияние давления жидкости на геометрию зазора и взаим-
взаимное влияние неровностей.
Ниже исследуется роль поверхностной шероховатости при
взаимодействии упругих тел с учётом адгезии различной приро-
природы. В качестве модели шероховатой поверхности, как и в главе 1,
Используется периодическая система осесимметричных штам-
штампов.
2.6.1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается взаимодействие упругого полупространства с
периодической системой штампов, расположенных в узлах гек-
111
L/
Рис. 2.14. Схема адгезионного взаимодействия системы штампов с
упругим полупространством (о) и представление области нагружения,
основанное на принципе локализации (б)
сагональной решётки с шагом I (рис. 2.14,о). Пусть начало О ло-
локальной цилиндрической системы координат (г, z, ф) совпадает
с точкой, в которой недеформированное полупространство со-
соприкасается с одним из штампов. Ось Oz направлена в глубь
полупространства. В данной системе координат форма штампа
описывается функцией f(r) = Cr2n, где п - целое число.
К каждому штампу приложена нормальная сила Р. Будем
считать распределение давлений и упругих смещений полупро-
полупространства в окрестности каждого штампа осесимметричным.
Величину зазора между контактирующими поверхностями пред-
112
ставим в виде:
h(r) = /(г) - /(а) + uz(r) - щ(а), B.58)
где uz(r) - нормальное упругое смещение поверхности полупро-
полупространства, а - радиус области контакта.
Для того чтобы учесть адгезионное взаимодействие, введём
Отрицательное давление —ро, действующее на полупространство
в кольце а < г ^ 6 вокруг каждого штампа. Будем рассматри-
рассматривать два вида адгезионного взаимодействия.
Адгезия сухих поверхностей. Как и в 2.3, аппроксими-
аппроксимируем силу молекулярного притяжения поверхностей на единицу
площади кусочно-постоянной функцией (см. рис. 2.7). Считая,
как и прежде, заданными величины поверхностной энергии 7 и
давления ро, для определения внешнего радиуса b области Г2& ад-
адгезионного взаимодействия, возникающей вокруг площадки кон-
контакта произвольного фиксированного штампа (неровности), бу-
будем использовать выражение B.43).
Таким образом, в задаче об адгезии сухих поверхностей тре-
требуется по заданным значениям периода /, нагрузки Р, поверх-
поверхностной энергии 7, давления ро и функции /(г) определить дав-
давления в контакте р(г) (г ^. а), смещения границы упругого полу-
полупространства вне области контакта uz{r) и радиусы а и 6 еди-
единичного пятна контакта и зоны адгезионного взаимодействия со-
соответственно.
Капиллярная адгезия. Пусть поверхность полупро-
полупространства до взаимодействия покрыта тонким слоем жидкости
толщины h\. Предполагается, что при взаимодействии со штам-
штампами вся жидкость стягивается в мениски, окружающие области
контакта. Тогда объём жидкости в каждом мениске будет равен
В этом случае кольцевая область а < г ^ b вокруг каждого
штампа занята жидкостью. Равномерное давление —ро, дейст-
действующее на поверхность упругого полупространства в этой об-
области, представляет собой капиллярное давление под искрив-
113
ленной поверхностью жидкости, которое определяется выраже-
выражением B.6). Как уже отмечалось, выражения B.43) и B.6) сов-
совпадают, если в последнем положить а — у/2. Объём жидкос-
жидкости v в каждом мениске связан с формой зазора h(r) соотношени-
соотношением B.10).
Таким образом, в задаче о капиллярной адгезии по задан-
заданным величинам периода I, нагрузки Р, поверхностного натяже-
натяжения жидкости а, толщины плёнки жидкости hi и функции /(?"),
описывающей форму штампа, необходимо определить функции
контактных давлений р(г) (г ^ а) и упругих смещений иг(г)
(а < г ^ 6), размеры а и 6 кольцевых областей, занятых мениска-
менисками жидкости, и абсолютную величину давления в жидкости pq.
2.6.2. ПРИМЕНЕНИЕ МЕТОДА ЛОКАЛИЗАЦИИ
Для решения поставленных задач воспользуемся методом ло-
локализации, который изложен в 1.2.3. Согласно этому методу,
для определения напряжённо-деформированного состояния вбли-
вблизи отдельного пятна контакта учитываются реальные условия
контактирования на ближайших пятнах контакта, а влияние
остальных пятен заменяется действием осреднённого по поверх-
поверхности давления.
Рассмотрим простейший случай, в котором учитывается вза-
взаимодействие с полупространством одного штампа при наличии
пригрузки в виде равномерного давления р, действующего в об-
области г ^ Aq (см. рис. 2.Ы,б).
Давление р рассчитывается по формуле
р <259)
а радиус Aq определяется из условия равенства среднего дав-
давления в области г < Aq и вне её, т.е. р = P/(irA%), откуда с
учётом B.59) получаем
B.60)
114
В результате имеем задачу о нагружении упругого полупро-
полупространства со следующими граничными условиями:
uz(r) = -/(г) -D, г < а,
Р{г) = -Ро, а^г О, , .
р{г) = О, 6 < г < Ао, [ }
р(г) = р, г> Ао,
где D - постоянная, равная расстоянию между вершиной штам-
штампа и недеформированной поверхностью полупространства.
Упругие смещения uz(r) и давления р(г) на границе упругого
полупространства связаны соотношением [25]:
(,62,
где Ежу- модуль Юнга и коэффициент Пуассона для полу-
полупространства, К (ж) - полный эллиптический интеграл первого
рода.
Кроме того, выполняется условие равновесия B.14).
Таким образом, задача об адгезии при дискретном контакте
сухих поверхностей сводится к системе уравнений B.14), B.43),
B.58)—B.62), а задача о капиллярной адгезии в дискретном кон-
контакте - к системе B.10), B.14), B.43), B.58)-B.62).
2.6.3. ВЫВОД ОСНОВНЫХ СООТНОШЕНИЙ
Для решения полученных систем уравнений воспользуемся ме-
методом, изложенным в 2.2.2. Представляя функцию р(г) при зна-
значениях г € [0, а] как
р(г) = Pi(r) - ро B.63)
и используя условия B.61), преобразуем соотношение B.62) к
виду:
115
где
= /W-^T^|PobE(I)+MoE(-ojj, B.65)
B.66)
Заметим, что расстояние D бесконечно, так как полупростран-
полупространство нагружено по бесконечной области. Однако постоянная Da
является конечной величиной, поскольку она представляет со-
собой расстояние между вершиной штампа и границей полупро-
полупространства, всюду нагруженого равномерным давлением р. Ве-
Величину Da назовём дополнительным перемещением штампа.
Соотношение B.64) можно рассматривать как уравнение для
определения давления р\(г) под гладким штампом, форма по-
поверхности которого описывается функцией fi(r) B.65), при от-
отсутствии других нагрузок на упругое полупространство. Решая
эту задачу с помощью метода разложений в ряды, изложенного
в 2.2.2, получим для искомых давлений, дополнительного пере-
перемещения штампа и смещений границы упругого полупростран-
полупространства следующие выражения:
, ч СЕа2п~1
р(г) =
+ ^arCtg\/4^'
0
2п , 2A-г/2)Ро&
1 + Ё
B.68)
2A -v2) pA0 I (_a_\
E V Uo7
116
uz(r) = -- (Da + Cr2n)
7Г v
7Г
-Y-1 x
-E ( arcsin - , -7- ) I - D + Da -
in - , - 1 , a<r ^b,
B.69)
< E ( - 1 -
_ I , a
E I arcsm - , - I —
о r,
: F
Нагрузка Р, после подстановки в неё выражения B.59) для
номинального давления р, имеет вид:
Р=
B.70)
,2 / а а Г /ах2
-npob arccos т + r \/1 - ( т )
\ boy \b/
V
Полученные соотношения B.67)-B.70) совместно с выраже-
выражениями B.43), B.59), B.60) определяют решение задачи об адге-
адгезии сухих поверхностей. В случае капиллярной адгезии к этим
соотношениям добавляется условие B.10).
С целью определения неизвестных постоянных а и b пре-
преобразуем полученные соотношения. Подставляя смещения uz(r)
из B.69) в выражение B.58) для зазора между контактирующи-
117
ми поверхностями, будем иметь:
Лп
*«- ^-(sr^*-
2 . о ,
1 arcsm - ) 4-
7Г Г
+ "
^Ъ
W
B.71)
4A -y
тгЕ
^-E^arcsin-,-)!,
а < г ^Ь.
В случае капиллярной адгезии для объёма жидкости в мениске
получим:
^ BА)!! fb\2(n-k}
2n
n
а
arccos -
о
3a
) arccos6
B.72)
Это соотношения выведено из условия постоянства объёма жид-
жидкости B.10) с использованием выражения B.71). Система урав-
118
нений B.70) и B.71) (с учётом B.43)), B.72) служит для опре-
определения неизвестных величин а, Ь, и ро в случае капиллярной
адгезии.
В случае адгезии сухих поверхностей величины а и Ь нахо-
находятся из соотношения B.70) и уравнения, следующего из B.71)
при г = b с учётом условия B.43).
Случай отсутствия контакта. Решение значительно
упрощается в случае, когда полупространство не контактиру-
контактирует со штампами, но испытывает к ним адгезионное притяжение
(при капиллярной адгезии - связано со штампами менисками
жидкости). В этом случае на упругое полупространство дейст-
действует только отрицательное адгезионное давление —ро по пери-
периодически расположенным круговым областям радиуса Ь. Пола-
Полагая а = 0, из соотношений B.43), B.58)-B.62) после несложных
преобразований получим следующие выражения для нагрузки и
дополнительного перемещения при адгезии сухих поверхностей:
Р = -ттр0Ь2,
Da = -Cb2n + -
7
В случае капиллярной адгезии к этим соотношениям добавляет-
добавляется условие сохранения объёма жидкости, полученное из B.10):
В заключение заметим, что полученные соотношения могут
быть использованы и в случае шероховатого тела, неровности
которого деформируются упруго. Для этого в полученных соот-
соотношениях величину E/(l — v2), характеризующую упругие свой-
свойства полупространства, необходимо заменить на приведенный
модуль упругости Е* (см. B.13)) взаимодействующих тел.
119
2.6.4. РЕЗУЛЬТАТЫ РАСЧЁТОВ
При численном анализе полученных соотношений введём следу-
следующие безразмерные величины: контактные давления р = р/Е'
{Е' = 7г.Е/ (l — v2)), смещения границы упругого полупростран-
полупространства uz = uz/L (L = С^2"-1)), нагрузка на один штамп Р =
= Р/ (E'L2), дополнительное перемещение штампа Da = Da/L,
радиус области контакта а = a/L и внешний радиус Ъ =
= Ь/L области, в которой действует адгезионное давление.
При этом задаваемыми параметрами были число п, опреде-
определяющее форму штампов, безразмерное расстояние между ни-
ми Л = \/Ъ1/ [y/2nL) = Aq/L, а также параметры 7 = 7/ BE'L)
и ро = pq/E', зависящие от поверхностной энергии и модулей
упругости полупространства. В случае капиллярной адгезии ве-
величина ро представляет собой безразмерное давление в жидкос-
жидкости и определяется в ходе решения задачи. Параметр у в этом
случае характеризует поверхностное натяжение жидкости. При
этом ещё одним задаваемым параметром является безразмерная
толщина плёнки жидкости hi = hi/L.
Шероховатость поверхности в рассматриваемой модели ха-
характеризуется формой выступов и плотностью их расположения,
т. е. параметрами пи X. Все дальнейшее исследование посвящено
анализу влияния этих параметров на характеристики адгезион-
адгезионного взаимодействия поверхностей. Для оценки этого влияния
проведено сравнение полученных решений со случаем взаимо-
взаимодействия одной изолированной неровности (А —> +оо), рассмот-
рассмотренным в 2.2-2.5.
Адгезия сухих поверхностей. На рис. 2.15 представле-
представлены распределения контактных давлений р на единичном пятне
контакта при одной и той же нагрузке Р = 0,002, приложенной к
одному штампу, для различных форм штампа. Сравнение кри-
кривых 1, 2 и 1', 2', построенных с учётом взаимного влияния пятен
контакта и без него соответственно, позволяет заключить, что
учёт влияния других штампов приводит к уменьшению радиуса
области контакта а и внешнего радиуса Ь области, в которой дей-
действует адгезионное давление, при этом максимальное давление
в контакте увеличивается.
120
1
]'
2
: =
1
1
2
2'
р/Е'
0,08
0,06
0,04
0,02
0,00
-0,02
0,00 0,05 0,10 0,15 0,20 0,25 rIL 0,35
Рис. 2.15. Распределение давлений при j = 0,00005, ро = 0,02, и п = 1
A, 1'), п = 2 B, 2') для Л = 0,15 A), А = 0,35 B) и А 4 +оо A' и 2')
Адгезия сухих поверхностей
Графики зависимости uz(l) — uz(p) (р = г /а), приведённые на
рис. 2.16, иллюстрируют форму упругого полупространства вне
области контакта со штампом при тех же значениях 7, Po, Р, что
и на рис. 2.15. Результаты показывают, что по мере уменьшения
расстояния между штампами поверхность полупространства вне
штампов прогибается сильнее.
На рис. 2.17 представлены результаты расчёта контактных
характеристик при различных значениях безразмерного рассто-
расстояния Л между штампами. Кривые 3 описывают случай единич-
единичного штампа (А —> +оо). Зависимости безразмерного радиуса
области контакта а от нагрузки на один штамп Р, представ-
представленные на рис. 2.17,а, показывают, что при положительных на-
нагрузках уменьшение расстояния между штампами приводит к
уменьшению размера области контакта, как и в случае дискрет-
дискретного контакта без адгезии (см. главу 1). Однако в области отри-
отрицательных нагрузок, в которой контакт поверхностей ещё име-
имеет место, уменьшение расстояния между штампами приводит к
увеличению радиуса области контакта а.
На рис. 2.17,6 приведены зависимости нагрузки Р от допол-
дополнительного перемещения штампа Da. Толстые линии соответ-
соответствуют контакту поверхностей, т. е. рассчитаны по соотношени-
соотношениям B.67)-B.70). Тонкие линии соответствуют отсутствию кон-
121
0,004
u?\)-ulrla)
0,002
1,0
Ыа
1,1
1,2
г/а
1,3
Рис. 2.16. Форма упругого полупространства вне области контакта
при 7 = 0,00005, ро = 0,02 и п = 1 A, Г), п - 2 B') для Л = 0,2 A)
и А = 0,5 A', 2')
Адгезия сухих поверхностей
такта и соотношениям B.73). Результаты показывают, что зави-
зависимость дополнительного перемещения штампа от расстояния А
между штампами имеет вид, аналогичный зависимости радиуса
области контакта а: при Р > 0 с уменьшением А величина Da
уменьшается, а при Р < 0 - возрастает.
Представленные зависимости нагрузки, действующей на
один штамп, от дополнительного внедрения этого штампа яв-
являются неоднозначными. Как было показано в 2.4, неоднознач-
неоднозначность функции P{Da) приводит к гистерезису в процессе сбли-
сближения и удаления тел. Другими словами, работа, совершаемая
при сближении тел, не равна работе, необходимой для их разде-
разделения, т.е. происходит диссипация энергии. Например, для кри-
кривой 1 на рис. 2.17,tf величина потери энергии за цикл сближе-
сближения-удаления тел соответствует площади заштрихованной об-
области ABEF. Результаты расчётов показывают, что при умень-
уменьшении расстояния между штампами А величина потери энергии
122
all
0,10
0,05
0,00
2,5 10
0 P/(E'L2) 2,5-10"
-0,01
0,00 DJL 0,01
Рис. 2.17. Зависимости радиуса области контакта от нагрузки (а)
и нагрузки от дополнительного перемещения штампа (б) для j =
= 0,00005, р0 = 0,02, п = 1иА = 0,12 A), А = 0,15 B), А -» +оо C)
Адгезия сухих поверхностей
(рассчитанная на один штамп при фиксированной нагрузке, при-
приложенной к штампу) уменьшается. Заметим, что при этом по-
потеря энергии на единицу площади полупространства может воз-
возрастать вследствие увеличения количества штампов на единицу
площади.
Капиллярная адгезия. На рис. 2.18 представлены рас-
распределения давлений р в области взаимодействия произвольной
неровности (штампа) для различных расстояний между штам-
штампами. Вследствие постоянства количества жидкости в зазоре
между телами, уменьшение расстояния между штампами озна-
означает уменьшение объёма жидкости в мениске вокруг каждого
123
0,06
0,00
-0.06
PIE'
-0.12
V
1 \
1
2
0,00
0,05
0,10
rIL
0,20
Рис. 2.18. Распределение давлений в области взаимодействия неров-
неровности при п = 1, 7 = 0,00005, Ы = 0,0001, Р = 0,001 и Л = 0,2 A),
Л = 0,5 B), А = 1 C)
Капиллярная адгезия
штампа, что приводит к резкому возрастанию величины капил-
капиллярного давления в жидкости и уменьшению ширины b — а об-
области, занятой жидкостью. При этом контактные давления из-
изменяются незначительно.
Анализируя результаты, представленные на рис. 2.18, мож-
можно также заметить, что радиус области контакта а немонотонно
зависит от расстояния между неровностями А. Это подтвержда-
подтверждается полученными зависимостями а от А (рис. 2.19,а). Кривые 1
и 2 соответствуют тем же значениям п, у и Р, что и на рис. 2.18,
и построены для различных значений толщины плёнки жидкос-
жидкости.
Характер зависимостей радиуса области контакта от рассто-
расстояния между штампами /, представленных на рис. 2.19,а, объ-
объясняется наличием двух механизмов, приводящих к различным
эффектам при изменении расстояния /. Во-первых, это взаимное
влияние штампов через упругое полупространство. Оно прояв-
проявляется только при малых значениях /. В случае контакта без
адгезии при уменьшении расстояния между штампами взаим-
124
0,13
0,11
alL
0,00
0,2
0,4
0,6
0,8 X
1,0
Рис. 2.19. Зависимости радиуса площадки контакта (а) и давления
в жидкости (б) от плотности расположения штампов при п = 1,7 =
= 0,00005 и Р = 0,001 для 1ц = 0,0001 A), ht = 0,001 B), h, = 0 C);
линия 1' построена при hi = 0,0001 и Р = -0,0001
Капиллярная адгезия
ное влияние приводит к уменьшению размера области контакта
(кривая 3). При наличии капиллярной адгезии взаимное влия-
влияние штампов при положительных нагрузках приводит к умень-
уменьшению размера области контакта с уменьшением расстояния /
(кривые 1 и 2 при малых Л), а при отрицательных нагрузках - к
противоположному эффекту (кривая 1' при малых А). Этот меха-
механизм аналогичен взаимному влиянию выступов в случае адгезии
сухих поверхностей.
Второй механизм осуществляется только в случае капилляр-
капиллярной адгезии и связан с тем, что при заданной толщине плёнки hi
с уменьшением расстояния между штампами объём жидкости в
мениске вокруг каждого штампа уменьшается. Вследствие этого
размер а области контакта увеличивается с уменьшением рас-
расстояния Л независимо от знака нагрузки Р.
125
Таким образом, указанные два механизма оказывают проти-
противоположное влияние на размер области контакта при Р > О, что
объясняет немонотонный характер кривых 1 и 2 на рис. 2.19,а.
При Р < 0 эти эффекты усиливают друг друга (монотонная
зависимость 1'). Для сравнения на рис. 2.19,а приведена зави-
зависимость (кривая 3) для случая дискретного контакта без учёта
адгезии.
На рис. 2.19,6 приведены зависимости безразмерной величи-
величины давления в жидкости р$ от расстояния Л между штампами.
Кривые 1, 2, 1' построены при тех же значениях параметров, что
и соответствующие кривые на рис. 2.19,а. Видно, что при любых
нагрузках величина давления в жидкости ро растёт с уменьше-
уменьшением расстояния между штампами А. Результаты расчётов пока-
показали также, что внешний радиус Ь области, занятой жидкостью,
монотонно уменьшается с уменьшением А при любых значениях
нагрузки Р. Два последних результата связаны с уменьшением
количества жидкости в каждом мениске.
Сравнение кривых 1 и 2 на рис. 2.19 позволяет заключить,
что уменьшение толщины плёнки жидкости приводит к увели-
увеличению размера области контакта и величины давления в жид-
жидкости, а также к более быстрому росту этих величин при умень-
уменьшении А.
На рис. 2.20 представлены зависимость безразмерной нагруз-
нагрузки Р на один штамп от дополнительного перемещения штам-
штампа Da при различных расстояниях между штампами. Толстые
линии, как и прежде, соответствуют контакту поверхностей и
рассчитаны из соотношений B.67)—B.70), B.72). Тонкие линии
соответствуют отсутствию контакта и построены по соотно-
соотношениям B.73), B.74). Как и при адгезии сухих поверхностей,
полученные зависимости нагрузки от внедрения имеют неодно-
неоднозначный характер, однако не при всех значениях параметров.
В частности, как следует из представленных результатов, неод-
неоднозначность имеет место лишь при достаточно малых расстоя-
расстояниях А между штампами. В этом случае при сближении и уда-
удалении поверхностей происходит потеря энергии, величина кото-
которой для 'кривой 1 соответствует площади заштрихованной об-
области ABEF.
126
0,0003
P/(E'L2)
0,0000
-0,0003
-0,005
0,000
DJL
0,010
Рис. 2.20. Зависимость нагрузки, действующей на один штамп, от
дополнительного перемещения штампа при п — 1, j = 0,00005, hi —
= 0,00001 и А = 0,2 A), Л = 0,4 B), Л = 2 C)
Капиллярная адгезия
В заключение отметим, что, как показали проведённые рас-
расчёты, форма штампов, определяемая параметром п, оказывает
существенное влияние лишь на распределение контактных дав-
давлений (см. рис. 2.15). Характер остальных зависимостей при из-
изменении п качественно не меняется.
2.7. АДГЕЗИОННОЕ СОПРОТИВЛЕНИЕ ПРИ
КАЧЕНИИ
Проведённый анализ взаимодействия упругих тел с учётом их
поверхностной энергии или поверхностной энергии плёнок жид-
жидкости, покрывающих тела, показал, что зависимость нагрузки
от изменения расстояния между телами является неоднозначной
в случае адгезии сухих поверхностей при любых значениях опре-
определяющих параметров задачи, а в случае капиллярной адгезии -
в некотором интервале их изменения. В силу этой неоднознач-
127
ности в цикле уменьшение-увеличение расстояния между тела-
телами имеет место потеря энергии. Это явление при определённых
условиях взаимодействия может внести вклад в сопротивление
качению тел.
Рассмотрим простейшую схе-
схему качения жёсткого шероховато-
шероховатого цилиндра радиуса R по гра-
границе упругого полупространст-
полупространства (рис. 2.21). Цилиндр находит-
находится под действием нормальной си-
силы Р и катится с угловой ско-
скоростью и). Будем считать, что
на единице площади поверхности
Рис. 2.21. Схема качения находится N неровностей одина-
жёсткого шероховатого ци- ковой высоты h. Форма неровнос-
линдра по границе упругого Ти описывается функцией /(г) =
полупространства = CV2n.
При качении каждая неров-
неровность приближается к поверхности основания с некоторого рас-
расстояния Г>оо, при котором не проявляется действие адгезионных
сил притяжения, до минимального расстояния Dq, которое име-
имеет место в точке наибольшего нагружения области контакта. За-
Затем неровность начинает удаляться от поверхности основания до
значения D^. Как показано в 2.4, если значение Dq удовлетворя-
удовлетворяет условию Dq ^ Dc, в цикле сближение-удаление неровности,
который имеет место при прохождении единичной неровности
через контактную зону, происходит диссипация энергии, вели-
величину которой обозначим Aw. Величина Dc определяется рассто-
расстоянием, соответствующим точкам А на кривых, представленных
на рис. 2.4,о, 2.6, 2.8,а, 2.17,6, 2.20, которые рассчитаны для слу-
случаев капиллярной и сухой адгезии по моделям единичного или
дискретного контакта.
Тогда величину диссипации энергии за один оборот цилинд-
цилиндра можно рассчитать по формуле
Wo = 2ttRL0NAw,
B.75)
128
где Lq - единица длины цилиндра по его образующей. Принимая,
что диссипация энергии равна работе адгезионной силы трения
качения Fa на пути, пройденном за один оборот, получим сле-
следующее выражение для силы сопротивления, действующей на
единицу длины цилиндра:
^ - AwN. B.76)
Из соотношения B.76), а также из анализа величины диссипации
энергии в цикле сближения-удаления упругих тел с учётом адге-
адгезионных связей различной природы, изложенного в 2.4, следует,
что адгезионная составляющая Fa силы сопротивления при ка-
качении зависит от плотности и формы неровностей, а также от
величины поверхностной энергии и модуля упругости основания
в случае сухих поверхностей и от модуля упругости основания,
толщины пленки жидкости и её поверхностного натяжения - при
взаимодействии смоченных поверхностей, а также при взаимо-
взаимодействии во влажной среде. При этом значение Fa возрастает
с увеличением поверхностной энергии и уменьшением объёма
жидкости в мениске, а также при уменьшении модуля упругос-
упругости тел (для более мягких материалов). Кроме того, для смочен-
смоченных поверхностей в некоторых случаях (например, большой слой
жидкости на поверхности, малая величина поверностного натя-
натяжения, жёсткое основание) величина адгезионной составляющей
сопротивления качению равна нулю.
Если неровности имеют сферическую форму радиуса г, вы-
выражение B.76) может быть представлено в виде (см. 2.4):
• при качении сухих поверхностей
Fa ( 16Я*2 yll\ ( ( 9r y/3\
N) ^U
•
при качении смазанных поверхностей
Fa ( 16Д \
где вид функций <&i(?) и Ф2(?
5. Горячева И.Г. 129
Заметим, что выражения для адгезионной составляющей си-
силы трения, полученные из рассмотрения одномерной модели ше-
шероховатого тела (равновысокие неровности), явно не зависят от
нагрузки Р. Единственное условие, которое накладывается на
величину Р - выполнение неравенства Dq < Dc. Если же при
моделировании шероховатостей учесть их распределение по вы-
высоте, то количество неровностей iVi на единицу площади по-
поверхности, для которых имеет место диссипация энергии при
прохождении контактной зоны, существенно зависит от нагруз-
нагрузки Р, радиуса цилиндра R и функции (p(h) распределения не-
неровностей по высоте, т.е. JVi = Ni(P,R,(p(h)). В этом случае в
выражении B.76) следует положить N — N\. Метод построения
функции Ni(P,R,tp(h)) изложен в главе 1.
Глава 3
ТРЕНИЕ ПРИ КОНТАКТНОМ
ВЗАИМОДЕЙСТВИИ
В этой главе изучается роль касательных напряжений, возника-
возникающих в области контакта деформируемых тел (упругих и вязко-
упругих) при их относительном скольжении или качении, а так-
также в условиях предварительного смещения, когда внешняя тан-
тангенциальная сила не превосходит величины предельного трения,
соответствующей началу скольжения. Считается, что скорости
скольжения и качения тел много мриыпе скорости распростране-
распространения в них звука. Это даёт основание пренебречь динамическими
эффектами при постановке контактных задач.
Почти все изложенные ниже результаты могут быть приме-
применены для определения контактных характеристик взаимодейст-
взаимодействующих тел и силы сопротивления их относительному переме-
перемещению по крайней мере на двух масштабных уровнях. Макро-
Макромасштаб - это некоторая расчётная схема реального сопряжения.
На этом уровне изучается распределение номинальных напря-
напряжений внутри номинальной области контакта в зависимости от
макроформы и свойств контактирующих тел и условий взаимо-
взаимодействия. Микромасштаб - это модель элементарного (на дан-
данном структурном уровне) фрикционного контакта (например,
контакт двух неровностей). Это позволяет использовать полу-
полученные результаты для расчёта контурных и фактических пло-
площадей контакта, сближения тел под нагрузкой, распределения
контактных и внутренних напряжений при качении и скольже-
скольжении. Кроме того, представленные в этой главе результаты поз-
позволяют определить те области изменения параметров, при ко-
которых учёт трения и несовершенной упругости приводит к су-
существенному изменению конечных зависимостей по сравнению с
упрощёнными постановками.
5* 131
3.1. АДГЕЗИОННАЯ И МЕХАНИЧЕСКАЯ
СОСТАВЛЯЮЩИЕ СИЛЫ ТРЕНИЯ
Одной из главных задач трибологии является изучение меха-
механизмов диссипации энергии в подвижных сопряжениях машин
и механизмов. Согласно современным положениям трибологии
существует два основных источника диссипации энергии при
фрикционном взаимодействии.
Первый из них ассоциируется с созданием и разрывом ад-
адгезионных связей в точках контакта элементов подвижных со-
сопряжений. Сила, необходимая для разрыва связей, известна как
адгезионная (молекулярная) составляющая силы трения. Ме-
Механизм образования адгезионных связей зависит от свойств кон-
контактирующих тел и условий трения. При скользящем контак-
контакте металлических поверхностей он связан с разрушением мос-
мостиков сварки в области взаимодействия. Для резин и резинопо-
добных полимеров диссипация энергии имеет место в процессе
термического перехода молекулярных цепей от одного равновес-
равновесного состояния к другому. Адгезионная компонента силы трения
зависит также от свойств поверхности обоих контактирующих
тел. Интересный подход к моделированию адгезионного взаимо-
взаимодействия в скользящем контакте развит в работах [12, 171], в
которых рассмотрено движение третьего тела — среды между
взаимодействующими поверхностями, свойства которой зависят
от механических характеристик поверхностей контактирующих
тел, граничных пленок, свойств частиц, отделившихся с поверх-
поверхностей в процессе трения, и т. д. Метод расчёта адгезионной со-
составляющей силы трения при качении изложен в 2.7.
Другая причина диссипации энергии - это циклическое де-
деформирование контактирующих тел при скольжении. Сила со-
сопротивления, возникающая в этом процессе, называется меха-
механической (деформационной) составляющей силы трения. Она
зависит от механических характеристик тел, геометрии их по-
поверхностей, приложенных сил и т. д. Поскольку механическая
составляющая силы трения определяется, главным образом, ха-
характером деформирования тел, для её исследования привлека-
привлекаются методы механики контактного взаимодействия.
Известно, что при циклическом деформировании упругих тел
132
диссипации энергии не происходит и, следовательно, механичес-
механическая составляющая силы трения для упругих тел равна нулю.
Чтобы изучить механическую составляющую силы трения, не-
необходимо использовать более сложные модели несовершенно уп-
упругих тел. В этой главе для исследования зависимости механи-
механической составляющей силы трения от свойств взаимодействую-
взаимодействующих тел, условий нагружения, скорости скольжения использует-
используется модель вязкоупругого тела.
В трибологии адгезионная и механическая составляющие си-
силы трения считаются независимыми друг от друга. Однако ряд
экспериментальных результатов (см. [217]) показывает, что со-
соотношение между составляющими силы трения зависит от усло-
условий трения, механических свойств контактирующих тел и т. д.
Изучение трения в контакте скольжения вязкоупругих тел даёт
возможность проанализировать соотношение между механичес-
механической и адгезионной составляющими силы трения (см. 3.5).
Оба указанных выше источника диссипации энергии присут-
присутствуют также при качении тел. Было установлено теоретически
и экспериментально, что основными источниками сопротивле-
сопротивления качению являются:
• трение, обусловленное относительным проскальзыванием
поверхностей в пределах площадки контакта, возникаю-
возникающим вследствие разницы в кривизнах и механических свой-
свойствах контактирующих тел. Этот источник диссипации
энергии впервые был обнаружен О. Рейнольдсом [223], за-
затем изучался в экспериментальных работах [84, 112, 186]
и т.д.;
• несовершенная упругость реальных материалов (см. [165,
166, 231] и т.д.);
• силы молекулярного сцепления (см. [237]).
В большинстве исследований, посвященных анализу сопро-
сопротивления качению (см. [31, 32, 66, 71-73, 112, 140, 154, 198]) из-
изучается зависимость коэффициента трения качения от одного из
йеречисленных выше факторов: либо принимаются во внимание
№лы трения скольжения при качении идеально упругих мате-
материалов, либо учитывается несовершенная упругость материалов
133
в предположении отсутствия сил трения в области взаимодей-
взаимодействия. В этой главе трение качения рассматривается как сум-
суммарный результат проявления несовершенной упругости и дей-
действия сил трения скольжения на площадке контакта (см. 3.4),
что позволяет дать ответ на вопрос, каков же вклад каждого из
перечисленных механизмов в формирование силы сопротивления
качению при различных условиях взаимодействия.
При формулировке задач механики контактного взаимодей-
взаимодействия трение (сопротивление относительному перемещению кон-
контактирующих точек) учитывается феноменологически заданием
некоторого соотношения между нормальными р и тангенциаль-
тангенциальными г напряжениями, действующими в зоне контакта. Наибо-
Наиболее часто используется закон трения Амонтона вида г = /лр.
Методы исследования плоских контактных задач с трением, ос-
основанные на сведении их к решению смешанных задач теории
функций комплексного переменного, разработаны Н.И. Мусхели-
швили [107], Л.А. Галиным [23], А.И. Каландия [74]. Эти мето-
методы нашли применение при решении задач для тел с различ-
различной макроформой. Контактные задачи с законом трения в форме
Амонтона в пространственной постановке рассмотрены в рабо-
работах [29, 86, 87, 106] и т. д.
С точки зрения молекулярно-механической теории трения,
развитой в работах Ф. Боудена и Д. Табора [17], Б.В.Деря-
гина [62], И.В.Крагельского [89], более общим является дву-
двучленный закон трения, установленный экспериментально Куло-
Кулоном [160]:
т = то + цр, C.1)
где го и /х - параметры закона трения, зависящие от свойств
поверхности и поверхностных пленок, сил молекулярного взаи-
взаимодействия между телами и т.д. Уравнение C.1) используется
при постановке контактных задач с трением в 3.2.
В случае, когда касательная сила, приложенная к телу, мень-
меньше предельной силы трения, тело находится в состоянии пред-
предварительного смещения (трения покоя), при этом в области кон-
контакта возникают зоны сцепления поверхностей и относительного
проскальзывания. В результате сопротивление сдвигу и разме-
134
ры зон сцепления и проскальзывания зависят от коэффициен-
коэффициента трения между взаимодействующими поверхностями. Задачи
с частичным проскальзыванием поверхностей при их нагруже-
нии нормальной и касательной силами рассмотрены, например,
в работах [23, 33, 66]. На основании построенных решений пока-
показано, что по мере возрастания касательной силы зона сцепления
уменьшается и стягивается в точку при Т = fiP (переход к мак-
макросдвигу).
Для анализа контактного взаимодействия в условиях предва-
предварительного смещения в 3.6 даются постановка и решение задачи
о контакте с частичным проскальзыванием двух упругих тел,
нагруженных нормальными и тангенциальными силами и мо-
моментом.
3.2. ТРЕНИЕ ПРИ СКОЛЬЖЕНИИ УПРУГИХ
ТЕЛ
3.2.1. ПОСТАНОВКА ПЛОСКОЙ КОНТАКТНОЙ
ЗАДАЧИ
Рассмотрим контактную задачу о скольжении цилиндрического
штампа по границе упругого полупространства (рис. 3.1). Фор-
Форма штампа описывается функцией у = f(x). Предполагается,
что внешние силы также не зависят от координаты г, что поз-
позволяет рассматривать задачу в двумерной (плоской) постановке.
На всей площадке контакта (—а, Ь) выполняется двучленный за-
закон трения C.1), который может быть представлен в виде:
тху(х) = (т0 + цр(х)) sgn V, C.2)
где р(х) — —сгу(х) и тХу(х) - нормальные давления и касатель-
касательные напряжения на границе упругой полуплоскости (у = 0), V -
скорость цилиндра.
Действующие на штамп тангенциальные Т и нормальные Р
силы обеспечивают ему состояние предельного равновесия или
равномерного движения с малой скоростью, которая позволяет
пренебречь динамическими явлениями и рассматривать задачу
как квазистатическую.
135
> А
Рис. 3.1. Схема контакта штампа с упругой полуплоскостью
В системе координат, связанной со штампом, будут иметь
место следующие граничные условия (у = 0):
ау = 0, тху = 0, — со < х < —a, b < х < +оо,
иу(х) = f(x) - А тху = Ы +
C.3)
где иу - нормальная компонента смещений границы полуплос-
полуплоскости, D — сближение контактирующих тел.
На границе упругой полуплоскости выполняется соотноше-
соотношение [25]:
тгЕ ди,
2A -и2) дх
+00
диу _ f dt 1 -
UX J t X L
C.4)
Используя метод, предложенный Л.А. Галиным [25], введём в
нижней полуплоскости у ^ 0 следующую функцию w\(z) комп-
комплексного переменного z:
+00
1(г) = ^1-гУ1= J ay
dt
z z
C.5)
Принимая во внимание предельное значение интеграла ти-
типа Коши C.5) при z -» х — гО, а также C.3) и C.4), получим
136
граничные условия для определения функции w\ (z):
V\ = 0, —оо < х < —a, b < х < +00,
sgn V = ttF(x), -a^x^b,
где
(l-i/»)' * 2A-1/)'
Определение аналитической в нижней полуплоскости функ-
функции iv\{z) C.5) по заданным на границе соотношениям между
её действительной U\ и мнимой Vi частями является частным
случаем задачи Римана-Гильберта [25].
Решением задачи с граничными условиями C.6), имеющим
при z —У х — гО интегрируемые особенности вида z~a @ < а < 1)
и ведущим себя при z ->¦ 00 как P/z, является функция:
C'8)
где
г? = - arctg(/ztf) sgn F, |r/| < \ . C.9)
Функция C.8) позволяет по известным формулам [25] опреде-
определить напряжённо-деформированное состояние в упругом теле. В
Растности, из соотношения C.5) следует, что компонента напря-
Цений ау(х,0) представляет собой мнимую часть функции C.8)
Ври z —> х — г'О. Предельное значение интеграла типа Коши
+00
— z
137
при z —> х — гО может быть определено по формуле Племеля
(см. [107]):
+СО
*? I-*-1 — ~ г
!
—oo
Принимая во внимание предельное значение функции
при z —> х — iO, а именно:
1
(z + a
z-x-iO
1
-оо < х < —а,
sin тгт? + i cos тгг/
- , —о ^ х ^ о,
6 < ж < +оо,
получим для контактного давления
где 14(ж,0) - мнимая часть функции w\(z) при z -4 х — гО, сле-
следующее выражение:
р(х) = -F(x)gsmnr] +
—а < х < Ь.
3.2.2. ЗАДАЧА ДЛЯ ШТАМПА С ПАРАБОЛИЧЕСКИМ
ОСНОВАНИЕМ
Рассмотрим частный случай решения задачи для штампа, фор-
форма контактирующей поверхности которого описывается функци-
функцией f(x) = x2/BR). В этом случае функция F(x), определяемая
138
соотношением C.7), примет вид:
Е'х
C.11)
Подставив функцию C.11) в C.10) и вычислив значение ин-
интеграла (см. [44]), получим следующее выражение для давления
на площадке контакта (—а, Ь):
Р(х) = ^~
(a + bfll-v*
C.12)
Из условия ограниченности давления на концах площадки кон-
контакта гладкого штампа с упругой полуплоскостью и выраже-
выражения C.12) следует, что давление в этих точках обращается в
нуль. Из выражения C.12) с учётом того, что р(—а) = р(Ь) = 0,
можно получить систему уравнений для определения неизвест-
неизвестных концов площадки контакта —а и b (см. [44]):
а-Ь , 2tot3Rtt
Z + ^F C.14)
Соотношения C.13) и C.14) определяют длину и смещение пло-
площадки контакта относительно оси симметрии параболического
штампа. Используя эти выражения, приведем выражение C.12)
для контактного давления р(х) к виду:
C.15)
139
Из полученных соотношений следует, что величина tq в законе
трения C.2) оказывает влияние только на смещение площадки
контакта. Полученные соотношения при tq — 0 совпадают с вы-
выражениями для контактных давлений, площадки контакта и ее
смещения, полученными в [23], где рассматривалась контакт-
контактная задача в аналогичной постановке с законом трения в форме
Амонтона, т.е. тху = [мту.
Как следует из выражения C.15), давление р(х) распределено
несимметрично относительно оси симметрии штампа и создает
момент М:
М = Jp(x)xdx = -p(pr]+^^-sgnvY C.16)
где
ь
-I
Р — / р(х) dx.
Если к рассматриваемому штампу не приложен активный мо-
момент, момент сил давления М должен уравновешиваться момен-
моментом силы тяги Т:
Т= I rxydx = {то1 + цР) sgn V. C.17)
Из условия равновесия штампа (см. рис. 3.1), находящегося под
действием только касательной силы Т и нормальной нагрузки Р
следует, что точка приложения силы Т должна находиться на
расстоянии d от подошвы штампа, где d = \М/Т\.
Заметим, что в случаях, представляющих практический ин-
интерес, /и? < 1. По этой причине мы можем аппроксимировать
выражение C.9) как \т]\ ~ ц'д/тт <S 1. Исходя из этой оценки
и выражений C.13)—C.15) можно заключить, что коэффициент
трения \х не оказывает существенного влияния на контактные
давления, величину и смещение площадки контакта.
Анализ распределения внутренних напряжений позволил
установить, что влияние величины то на напряжённое состоя-
140
0,0
-1,5 -1,0 -0,5 0,0 0,5 1,0 1,5
Рис. 3.2. Линии уровня максимальных касательных напряже-
напряжений под параболическим штампом в случае предельного трения
(А* = 0, 7-0/ро = 0,1)
ние упругого полупространства подобно влиянию коэффициен-
коэффициента трения [г: увеличение значения то смещает точку максимума
максимальных касательных напряжений (ri)max ближе к поверх-
поверхности и увеличивает значение функции (ri)max (рис. 3.2).
Полученные соотношения могут быть также использованы
для определения контактных характеристик (контактные на-
напряжения, длина и смещение площадки контакта и т. д.) при
взаимодействии двух упругих тел, имеющих радиусы кривиз-
кривизны Ri и i?2- Действительно, поскольку длина площадки контак-
контакта I <С Щ, (i = 1,2), мы можем заменить взаимодействующие
тела полупространствами и использовать уравнение C.4) для
определения градиента нормальных смещений каждого из полу-
полупространств, принимая во внимание соотношение тху = —тХу. В
этом случае параметры Е', ¦&, R и т) (см. выражения C.7) и C.9))
в соотношениях C.13)—C.16) должны быть заменены параметра-
параметрами ттЕ*, г?*, R*, г]* соответственно:
• для плоского напряжённого состояния
Е* = ( - + —
E Е
„„ _ E* (l-v2 \-v\
C.18)
141
Рис. 3.3. Схема контакта штампа с упругой полуплоскостью в случае
предельного трения
• для плоской деформации
*._.¦'-•*
2
тр ' гр
1/2X1-21/2) A
и
Л.
Е2
1
C.19)
sgn V.
3.2.3. ЗАДАЧА ДЛЯ ШТАМПА С ПЛОСКИМ
ОСНОВАНИЕМ
Рассмотрим теперь внедрение в упругую полуплоскость штам-
штампа с плоским основанием, который под действием приложен-
приложенных к нему вертикальной Р и горизонтальной Г сил и момен-
момента М может поворачиваться на некоторый угол, тангенс кото-
которого определяется величиной 7 (рис. 3.3). Тогда уравнение осно-
основания штампа имеет вид: f(x) = —jx — D.
Функцию F(x) (см. C.7)) в этом случае можно записать сле-
следующим образом:
F(x) = TOtisgnV-
—a
x < b.
C.20)
142
Подставляя функцию F{x) C.20) в выражение для давле-
давления (см. C.10)), после преобразований получим (—а ^ х ^ Ъ):
где
J C.22)
Здесь b - полуширина основания штампа.
Функция р(х) (см. C.21)) вблизи концов площадки контак-
контакта {х -> +0) может быть представлена в виде
(а + Ь)
'"
2 7Г&
Рассмотрим прежде всего случай полного контакта штампа
с упругой полуплоскостью. Положив а = b в выражении C.21),
получим
_ Ре [Ъ - пя(х + 26т?)]
Поскольку давление на площадке контакта всюду неотрицатель-
неотрицательно (р(х) ^ 0 при —Ь < х < Ь), то отсюда следует, что
xi<x^x2, C.26)
143
где
^ C-27)
Давление р(х) (см. C.25)) стремится к бесконечности на краях
площадки контакта (при х = ±6), если х Е (xi, хг). При х = щ
или х = Х2 контактное давление равно нулю соответственно на
левом или правом конце площадки контакта.
Если параметр х ? [я\, хг], имеет место неполный контакт
штампа с упругим основанием. При х ^ xi < О отрыв штампа
от основания имеет место в левой части области контакта в точ-
точке х = —а, где \а\ < b (см. рис. 3.3). Длина площадки контакта
в этом случае определяется из выражения C.23):
а + Ь= у± г> C.28)
7ГХ [ - - 7?
а контактное давление - на основании соотношений C.21)
и C.28):
р(х) = Ц ¦ --Ц ^—М . C.29)
Если х > Х2 > 0, контактное давление равно нулю в правой
части контактной зоны в точке х = Ь, где |6| < а (величина а обо-
обозначает полуширину штампа в этом случае). Для контактного
давления имеем следующее выражение, полученное из соотно-
соотношений C.21) и C.24):
р(х) -
Из выражений C.21) и C.24) следует соотношение для опреде-
определения координаты х = Ь:
Ъ=-а+— Р . C.30)
144
р(х)ЫР
-1
О
xlb
1
Рис. 3.4. Контактное давление под штампом с плоским основанием,
скользящим по упругой полуплоскости (/л9 = 0,057); к = 0 A); х =
= xi = -0,33 B); я = -0,5 C); к = -0,75 D)
Распределения контактных давлений для случая \а\ ^ Ъ
(см. рис. 3.3) при разных значениях параметра >с приведены
на рис. 3.4. Кривая 1 соответствует случаю полного контакта
штампа с упругой полуплоскостью, когда давление стремится к
бесконечности на обоих концах площадки контакта, кривая 2 -
полному контакту прир(—Ь) = 0 [к = щ, см. соотношения C.25)
и C.27)). Кривые 3 и 4 построены для случаев неполного контак-
контакта штампа с упругой полуплоскостью. При вычислениях было
положено |/ztf| = 0,057 (ц = 0,2, v = 0,3).
Заметим, что приведенные здесь результаты совпадают с вы-
выводами, полученными Л.А. Галиным [23] при решении задачи в
аналогичной постановке в случае отсутствия сил трения (/i =
= 0, 7D = 0).
Параметр х связан с углом наклона штампа 7 (см- C-22)).
Рассмотрим для определённости движение штампа в направле-
направлении оси Ох (т.е. V > 0). Для определения величины -у воспользу-
воспользуемся условием равновесия штампа (см. рис. 3.3). Давление р(х)
и касательные напряжения тху(х) на площадке контакта оказы-
оказывают сопротивление движению штампа и удовлетворяют следу-
145
ющим уравнениям:
ь
P=fp{x)dx, Т = I тху(х) dx = то(а + Ъ) + цР, C.31)
b
(b- x)p{x) dx- Pb + Td- M = 0, C.32)
—a
где @, d) - координаты точки приложения силы Т, М - активный
момент, рассматриваемый по отношению к точке х = Ь.
С помощью соотношений C.21), C.31) уравнение C.32 может
быть преобразовано к виду
2 7 26 \А • J ' C.33)
+то(а + b)d + p,Pd - М = 0.
Соотношения C.22) и C.33) используются для определения угла
наклона штампа 7 в зависимости от значений d и М.
Рассмотрим частный случай отсутствия активного момен-
момента М (т. е. М = 0) и исследуем зависимость угла наклона штам-
штампа 7 от расстояния d. Из соотношений C.22), C.26) и C.33) сле-
следует, что полный контакт имеет место для значений d 6 @, d\),
где
"(И
<3-34>
Угол наклона j в этом случае определяется по формуле
2ЬРг] + B6гр + ,xP)d 2тО7п9
7 = у г + —^— . C.35)
Е'Ъ2 Q - / ^
При d € (di, ^2) имеет место неполный контакт штампа, при
этом точка отрыва х = — а (\а\ < Ь); величина d^ определяется из
146
5,0
nbE
P(]-v2)'
2,5
0,0
о
dlb
Рис. 3.5. Зависимость угла поворота штампа от положения точки
приложения тангенциальной силы Т (v = 0,3, tq = 0); /л = 0,1 A),
ц = 0,2 B), М = 0,3 C)
тёмные кружки означают точку перехода от полного контакта к неполному
условия —о = Ь, соответствующего случаю контакта штампа с
основанием в одной точке. Из уравнения C.33) следует, что cfo =
= b/ii. Угол наклона штампа 7 при d\ ^ d < d% можно найти,
используя соотношения C.22), C.28) и C.33):
7 =
*<5-
Е'
C.36)
Из выражения C.36) следует, что 7 —>• +оо (это означает, что
штамп опрокидывается) при d —» ^2 — 0. На рис. 3.5 приведены
зависимости угла наклона j от расстояния d e [0, с?г), построен-
построенные на основании соотношений C.35) и C.36) для разных значе-
значений /i и го = 0. Точки перехода от полного контакта к неполному
(тёмные кружки) рассчитаны на основании формулы C.34).
Полученные результаты могут быть использованы, в част-
частности, при конструировании машин для испытания триботех-
147
нических свойств материалов. Для обеспечения плотного приле-
прилегания плоских образцов друг к другу один из них закрепляют
в держателе с помощью шарнира. Результаты проведённого ис-
исследования показывают, что для обеспечения полного контак-
контакта между образцами шарнир должен быть закреплён на рас-
расстоянии d G @,<ii) от подошвы одного из образцов. Предельное
расстояние d\ существенно зависит от коэффициента трения /и.
При го = 0 из C.34) следует
x
d
~Ь '~ 2/х 2тгA - и) '
3.2.4. ПРОСТРАНСТВЕННАЯ ЗАДАЧА С
ПРЕДЕЛЬНЫМ ТРЕНИЕМ
Рассмотрим теперь пространственную контактную задачу о
движении штампа с постоянной скоростью по границе упругого
полупростанства (квазистатическая постановка). Будем предпо-
предполагать, что силы трения, действующие на площадке контакта,
коллинеарны направлению движения.
Этот случай возникает для поверхностей с анизотропным
трением, когда величина трения зависит от направления сколь-
скольжения (см. [19, 240]). В работе [227] показано, что коэффициент
трения двух алмазных образцов может меняться от 0,07 до 0,21
в зависимости от ориентации образцов. Подобное явление было
также обнаружено в экспериментах с полимерами, имеющими
заданную ориентацию молекулярных цепей [234]. Для произволь-
произвольных поверхностей сделанное предположение о коллинеарности
сил трения направлению движения выполняется приближённо.
Введём систему координат (x,y,z), связанную с движущимся
штампом (рис. 3.6). Тангенциальные напряжения txz в области
контакта п удовлетворяют соотношению C.1), т.е. тХ2 = то +
+/лр(х,у), где р(х,у) = —az(x,y,0) - неотрицательное контакт-
контактное давление (р(х,у) ^ 0). Граничные условия имеют вид:
uz(x,y)-f{x,y)-D, txz-t0 »az, ryz-0, [x,y) e П,
а =т. =tz=0 (x y) 4. Q,
где f{x,y) - форма штампа, D - его смещение вдоль оси Oz.
148
Рис. 3.6. Схема контакта в задаче о скольжении штампа по границе
упругого полупространства
Смещение uz границы упругого полупространства в направ-
направлении оси Oz может быть представлено как суперпозиция пере-
перемещений точек основания, вызванных действием давления р(х,у)
и тангенциального напряжения тхг в пределах площадки контак-
контакта Q. Из решения задачи о действии на упругое полупростран-
полупространство сосредоточенной силы, имеющей составляющие Тх и Tz по
осям Ох и Oz и приложенной в начале координат, следует, что
вертикальные перемещения uz точек граничной плоскости z = О
определяются по формуле [96]:
-
Uz~
тгЕ
- , г = Vz2 + У2 ¦ C.38)
На основании C.37) и C.38), переходя к распределённой по
области fi нагрузке, получим следующее интегральное уравне-
149
ние для определения контактных давлений р(х,у):
1
//
х — х')
р(х, у') dx'dy' +
^y' = E'iD~ /(*. у)]
C.39)
где величины Е' и д определены в C.7). Второй интеграл в левой
части уравнения C.39) можно вычислить, если известна форма
области контакта VI. Так, если VI - круг радиуса а, переходя к
полярным координатам, получим
а 27г
(х - х') dx'dy' f f (г cos в - г' cos в')г' dr'dO'
II
(х - х'J + (у-у
Принимая во внимание, что
J I I
х'2+у'2^а2 О О
r'2 -2rr' cos (в -в')
2тг
/
(г cos в-г' cos 9') d&
г2 + г'2 - 2rr' cos F> - в')
— cos в,
О,
/2тг
J v1
и результат интегрирования / — cos#r dr = nrcosO = тгж,
о
приведём уравнение C.39) к
JJp{x',y')
(У ~ У1)
--+
- х1)
C.40)
= E'[D-J{x,y)}-ivtiTux,
150
Заметим, что коэффициент д равен нулю при ^ = 0,5, т. е. ког-
когда упругое тело несжимаемо. В этом случае наличие сил трения
не оказывает влияния на распределение контактных давлений.
Для реальных материалов коэффициент Пуассона v принимает
значения 0 < v < 0,5, при этом коэффициент -в = A — 2и)/B — 2и)
изменяется в пределах от 0 до 0,5 (например, д = 0,286 для v =
= 0,3). Следует, кроме того, учесть, что коэффициент трения ц
также мал. При трении без смазочного материала стали по ста-
стали fi — 0,2. Полагая в этом случае v = 0,3, получим цд и 0,057.
Для смазанных поверхностей величина цф принимает ещё мень-
меньшие значения.
Мы будем решать уравнение C.40) в предположении, что па-
параметр fi'd = e мал и представим искомую функцию р(х, у) в
виде ряда
р{х,у) = ро{х,у) + epi{x,y) + ¦ ¦ ¦ + епрп(х,у) + --- . C.41)
Функция ро(х,у) есть решение интегрального уравнения C.40)
при /д? = 0. Подстановка ряда C.41) в интегральное уравне-
уравнение C.40) позволяет получить рекуррентную систему уравнений
для определения неизвестных функций рп(х,у)'-
= l,2,.... C.42)
Здесь введены следующие обозначения операторов:
',y')dx'dy'
JJ J(x - x'V
"М--//
у/{х - х'У + (у- у'?
C.43)
ш(х',у') (х — x')dx'dy'
(х - x'f + (у - у'J ¦
п
Сходимость ряда C.41) доказана в работе [29] для случая огра-
ограниченной функции ш(х, у.
Предложенным методом в [29] рассмотрена задача о движе-
движении гладкого осесимметричного штампа круговой формы в пла-
плане (например, шара) по границе упругого полупространства. По-
Показано, что если форма штампа описывается функцией /(г) —
151
= r2/BR) (R - радиус кривизны контактирующей поверхности
штампа) и tq = О, контактное давление может быть представле-
представлено в полярной системе координат в виде:
р(г, в) = ро(г) + eg(r) cos в + О (е2),
где
2.Е'
Po{r) =
а функция q(r) - решение следующего интегрального уравнения
(см. [29]:
о
а
Гк[1|-
где
а К(ж) и Е(ж) - полные эллиптические интегралы первого и
второго рода соответственно.
Таким образом, давление под штампом распределено несим-
несимметрично, вследствие чего возникает дополнительный момент
Му относительно оси Оу:
а 2тг а
Му= р(г, в)г2 cos 9dr d6 = en q(r)r2dr + О (е2).
0 0 0
Для анализа влияния параметра tq/E' на решение уравне-
уравнения C.40) рассмотрим сначала случай гладкого осесимметрич-
ного штампа, контактирующая поверхность которого описыва-
описывается функцией /(ж, у) = (ж2 + y2)/BR). Тогда правую часть
уравнения C.40) можно представить в виде:
Е' [D -f{x, у)] - тп?тож = Е' [а - (Ж + з
C-44)
152
где
Выражения C.45) определяют характер зависимости величины
смещения е области контакта и внедрения D штампа от пара-
параметра та/Е1.
Для штампа с плоским основанием круговой формы в плане,
т.е. f{x,y) = 0 при х2 + у2 ^ а2, правая часть уравнения C.40)
примет вид:
Е' [D - f(x, у)] - пдтох = E'D - пдтох.
Распределение давления в этом случае соответствует решению
уравнения C.40) при tq — 0 для штампа с плоским основанием,
наклонённого на угол тп9то.
Приведённые результаты качественно совпадают с вывода-
выводами, полученными при решении плоской контактной задачи с пре-
предельной силой трения (см. 3.2.2 и 3.2.3).
3.3. ТРЕНИЕ ПРИ СКОЛЬЖЕНИИ
ВЯЗКОУПРУГИХ ТЕЛ
Поскольку многие явления, имеющие место при фрикционном
взаимодействии тел, не могут быть объяснены с помощью мо-
модели идеально упругого материала, ниже мы исследуем задачу
о скольжении с постоянной скоростью V жёсткого цилиндра по
границе вязкоупругого основания (рис. 3.7). Задачу будем рас-
рассматривать в плоской квазистатической постановке, считая, что
скорость V много меньше скорости Vs распространения звука в
вязкоупругом теле. Заметим, что характерные значения скорос-
скорости Vs составляют: Vs « 5-103 м/с (для стали), Vs и 103 м/с (для
полимеров), Vs « 30 -f- 50 м/с (для мягких резин).
3.3.1. СООТНОШЕНИЯ МЕЖДУ НАПРЯЖЕНИЯМИ И
ДЕФОРМАЦИЯМИ ДЛЯ ВЯЗКОУПРУГОГО ТЕЛА
Соотношение между компонентами деформации и напряжения в
изотропном вязкоупругом теле примем в следующем виде (слу-
153
„о А
А
Vt
Рис. 3.7. Схема контакта при скольжении цилиндра по вязкоупругому
основанию
чай плоской деформации):
_ С/?~о 1 —
Е
de.fi 1 -
v
Е
е
да~о
да,,о
дауо
т~дТ
~ дал
C.46)
154
Здесь Те и Та характеризуют вязкие свойства среды, Ежу- мо-
модуль Юнга и коэффициент Пуассона соответственно. Заметим,
что случай плоского напряжённого состояния рассматривается
аналогично.
Уравнения C.46) являются двумерным аналогом модели
Максвелла-Томсона, для которой величина Н = Т?Е/Та есть
мгновенный модуль упругости, Т? > Та. Параметр а = Т?/Та
равен 105 -г- 107 для аморфных линейных полимеров, 10 Ч- 102 -
для полимеров с высокой степенью кристалличности, 1,1 -г 1,5 -
для чёрных металлов; 1/Те - коэффициент скорости последейст-
последействия.
При равномерном движении цилиндра 1 (см. рис. 3.7) дви-
движение среды можно считать установившимся по отношению к
системе координат (х, у), связанной с цилиндром: х = х° — Vt,
у = у0. В этой системе координат смещения их и иу, а также
напряжения не зависят явно от времени и являются функциями
координат {х,у), т.е. v%(x + Vt,t) = их(х), Uy(x + Vt,t) = иу(х)
и т. д. Дифференцируя первое тождество по времени t и по ко-
координате х, получим:
du°x(x°,t) ди°х dux(x°,t) дих(х)
dt '
дх° dt ' дх° дх '
или
dux(x°,t) = дих(х)
dt дх
Аналогичным образом выражаются производные по времени от
перемещения Uy(x°,t) и всех компонент напряжений и деформа-
деформаций в соотношениях C.46). Обозначим
о , т deij _ _ т ydfa _ *
дх
~д ~~ х" у
u и -TV^u
дх ~~ х" у дх ~ у'
Введённые функции е*, е*, *у*у, а*, а*, т*у удовлетворяют урав-
уравнениям, эквивалентным уравнениям равновесия, совместности
деформаций и закону Гука для изотропного упругого тела.
155
3.3.2. ПОСТАНОВКА ЗАДАЧИ
Вследствие малости деформаций уравнение контура цилиндра
приближённо заменим параболой f(x) = x2/BR), а граничные
условия на поверхности вязкоупругой полуплоскости отнесём к
недеформированной границе (у = 0). Из условия контакта сле-
следует, что для всех точек площадки контакта (—а, Ь) для переме-
перемещений иу по нормали к поверхности (у = 0) выполняется соот-
соотношение иу = f(x) + const, или
В предположении выполнения условий предельного трения, на
площадке контакта имеет место следующее соотношение между
нормальной оу и тангенциальной тху компонентами напряжений
(закон трения Амонтона):
тху = -цау sgn V, у = 0, C.49)
где /j, - коэффициент трения скольжения. Поверхность вне пло-
площадки контакта не нагружена, т. е.
&у — тху — 0 — оо < х < —а, Ь < х < +оо.
Используя обозначения C.47), запишем граничные усло-
условия C.48) и C.49) в виде (у = 0):
а* = т*у = 0, — оо < х < —a, b < х < +оо,
ди* x-TeV
^ тхУ
C-50)
xTeV
= ^ тхУ + M°V sgn F = 0, -а ^ х ^ 6.
3.3.3. АНАЛИЗ КОНТАКТНЫХ ХАРАКТЕРИСТИК
Сформулированная выше граничная задача для определения
функций е*, е*, -у* , ах, а*, т*у сводится к задаче Римана-Гиль-
берта методом, изложенным в [23] и использованным при реше-
решении плоской задачи с трением для упругих тел в 3.2. Затем ис-
истинные на'пряжения и перемещения в вязкоупругом теле опре-
определяются из решений дифференциальных уравнений C.47). Не
156
останавливаясь подробно на решении задачи (см. [34]), приведём
здесь лишь конечные результаты.
Для контактных давлений р(х) получено выражение:
р{х) =
E'gexp(x/(TaV)) j
2nTaVR J
—a
-<7y(x,
~(a + b
2
0) =
O2 /1
U
2\ 2PR
11 ) l E'
C.51)
-(аг'-ТеУКа + а:')
где Е', д и ц определены соотношениями C.7) и C.9), Р ~ вер-
вертикальная сила, действующая на цилиндр, т. е.
ь
Р
—а
о
= p(x)dx. C.52)
Тангенциальные напряжения тху на поверхности полуплоскости
определяются соотношением C.49).
Длина площадки контакта I — Ь + а определяется из решения
уравнения
1~{гЕ
где ( = l/BTeV) представляет собой отношение времени, за ко-
которое каждый элемент проходит расстояние, равное полушири-
полуширине 1/2 области контакта, ко времени последействия Т?, т. е. /# =
157
1 A — 4?72)] - длина площадки контакта при сколь-
скольжении цилиндра по упругой полуплоскости под действием вер-
вертикальной силы Р, если упругие свойства полуплоскости харак-
характеризуются параметрами Е' и д (см. соотношения C.7)), а =
= Т?/Та, Ф(/3,7;z) и Ф(/?,7;-г) - вырожденные гипергеометри-
гипергеометрические функции (см. [58, 148]):
!)(/? + 2)
3!
Г(/3-7
Как следует из уравнения C.53), длина I площадки контакта
в рассматриваемой задаче зависит не только от вязкоупругих
характеристик материала, вертикальной силы Р, приложенной
к цилиндру, его радиуса R, но и от коэффициента трения /х, с
которым связана величина г). Так как второе слагаемое в C.53)
отрицательно (а > 1, | г/ \ < 1/2), то первое должно быть поло-
положительным и, следовательно, I2 ^ l\.
Для смещения е площадки контакта относительно начала ко-
координат @,0) получено выражение:
Ь — а
е = = -2т? +
Ь + а
+ ¦
C.54)
Концы площадки контакта —а и b определяются из решения
уравнений C.53) и C.54).
158
Заметим, что соотношения C.51), C.53) и C.54) применимы
также для расчёта контактных характеристик в задаче о сколь-
скольжении вязкоупругого цилиндра с механическими характеристи-
характеристиками Ei,i>i,T?, Ta по вязкоупругому основанию с механическими
характеристиками 1?2, ^2, Те, Тст, если заменить в этих соотно-
соотношениях Е' и ¦# на параметры тгЕ* и ¦$*, определённые в C.18)
и 13.19).
Рассмотрим теперь равновесие сил и моментов, действующих
на цилиндр (см. рис. 3.7). Вертикальная компонента Pi силы
реакции не проходит через центр цилиндра и создаёт момент
ь ь
= I xp(x) dx = - I ха*у(х, 0) dx - TaVP. C.55)
n
—a
При вычисление момента М\ принято во внимание, что
о
fx
в силу непрерывности напряжений на границе зоны контакта и
уравнения равновесия C.52).
Подставив C.51) в формулу C.55) и вычислив интегралы,
получим следующее выражение для момента М\:
Мл A\2A е п\ /б 1
_ 1 _ 1 i
ОЛ О Q ] \ О
Касательная силы Т\ = \хР и Т (|Т| = |Ti|) создают мо-
момент М2 = pPd, где @, d) - точка приложения силы Г
(см. рис. 3.7). Чтобы обеспечить установившееся движение ци-
цилиндра, должно выполняться соотношение М\ = Мг, или d =
3.3.4. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ
Если положить в приведённых выше соотношениях ц = 0, то по-
получим решения задачи о скольжении без трения (/л = 0) цилинд-
цилиндра по границе вязкоупругого основания или контактной задачи
с трением для одинаковых вязкоупругих материалов (i9* = 0).
159
В том и другом случае будем иметь следующее выражение
для давления на площадке контакта, которое следует из C.51)
при г\ = 0:
Р{Х) - 2nTaVR
X
X
x L (
I Q
—а
Касательные напряжения в первом случае отсутствуют,
т.е. тху = 0, а во втором, т.е. при д* = 0 определяются соот-
соотношением C.49).
Положив г] = 0 в соотношениях C.53) и C.54), получим
C-58)
-Ш-Ш
где /о = y/lQRP/E' - длина площадки контакта в соответствую-
соответствующей контактной задаче для упругих тел, механические свойства
которых характеризуются параметром Е' (см. C.7)). При выво-
выводе C.58) и C.59) были использованы следующие соотношения
между гипергеометрическими функциями и модифицированны-
модифицированными функциями Бесселя 1и(х) и КДж) [58, 148]:
Ф (i + и, 1 + 2i/; 2x J = 2T(i/ + ljar" exp(x)Il/(x),
Ф ( \ + v, 1 + 2i/; 2x ) = 4= ехр(а;)Bа;)-'/К1/(а;).
V2 / V^r
На рис. 3.8 приведены зависимости безразмерных длины пло-
160
1,0
l0, e//B/0)
0,5
0,0
- - -*¦"
-3
-2
-1
lg(/0/BFTE))
1
Рис. 3.8. Длина площадки контакта (сплошные линии) и её смеще-
смещение (штриховые линии) при скольжении или качении {цд* = 0) ци-
цилиндра по вязкоупругому основанию для разных значений параметра
q = Т?/Та: а = 1,5 A, 1'), а = 5 B, 2'), а = 10 C, 3')
щадки контакта I/Iq и её смещения el/Blo) от параметра ?о =
= lo/BT?V), рассчитанные по формулам C.58) и C.59). Величи-
Величина ?о представляет собой отношение половины времени контакта
упругого цилиндра с упругим основанием в некоторой точке ко
времени Т? последействия материала. На основании результатов
расчётов можно заключить, что длина / площадки контакта из-
изменяется в пределах 1ц ^ / ^ Iq, где /я = y/l6RP/(E'a) - длина
площадки контакта в соответствующей задаче для упругих тел,
имеющих мгновенный модуль упругости Н = аЕ. Сдвиг е пло-
площадки контакта является немонотонной функцией параметра (о,
имеющей максимум между 0,1 и 1.
На рис. 3.9 показано распределение контактных давлений,
рассчитанных по формуле C.57) при различных значениях па-
параметра ?о = lo/BT?V). При малых значений этого парамет-
параметра (кривая 1) контактное давление распределено симметрично
6. Горячева И.Г.
161
np(x)lo/P
6 -
3 -
-0,6
-0,3
0,0
xlL
0,6
Рис. 3.9. Давление в контакте скольжения или качения (^¦в* = 0)
цилиндра по вязкоупругому основанию (а = 5) при Со = Ю~3 A),
Со = 0,4 B), Со = 1 C), Со = Ю4 D)
внутри области взаимодействия и соответствует решению зада-
задачи для упругих тел с модулем упругости Н. Для больших зна-
значений параметра (кривая 4) контактное давление соответствует
случаю упругих тел, имеющих модуль Е. Если Со ? (Ю~3> Ю4),
контактное давление распределено несимметрично по площадке
контакта (кривые 2 и 3). Максимальное значение контактного
давления уменьшается с ростом параметра Со-
Соотношения C.51), C.53), C.54) при ТЕ = Та дают реше-
решение контактной задачи с предельным трением для жёсткого ци-
цилиндра и упругого полупространства с модулем упругости Е или
для двух упругих тел, характеризующихся приведенным моду-
модулем упругости Е* и параметром •в* C.19).
В этом случае выражения для контактного давления, длины
площадки контакта и её смещения имеют вид
Р(х) =
C.60)
162
\-П^), e = -2V. C.61)
При выводе этих выражений принято во внимание соотношение,
справедливое для модифицированных функций Бесселя
и условие T?V ф 0.
Выражения C.60) и C.61) совпадают с полученными в 3.2, а
также в работах [25] и [66].
3.4. ТРЕНИЕ ПРИ КАЧЕНИИ УПРУГИХ И
ВЯЗКОУПРУГИХ ТЕЛ
Как уже отмечалось в 3.1, при качении деформируемых тел со-
сопротивление перекатыванию обусловлено, прежде всего, несовер-
несовершенной упругостью реальных материалов и проскальзыванием
поверхностей в пределах площадки контакта.
Ниже на примере задачи о качении цилиндра по вязкоупру-
гому основанию мы изучим совместное влияние этих двух ис-
источников диссипации энергии на распределение напряжений в
области контакта и коэффициент трения качения.
3.4.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим качение с постоянными линейной V и угловой ш
скоростями вязкоупругого цилиндра A) радиуса R по основа-
основанию B) из того же материала (см. рис. 3.7). Задачу будем ис-
исследовать в плоской квазистатической постановке. Как и в 3.3,
введём подвижную систему координат (х,у), связанную с дви-
движущимся цилиндром.
При качении вся область контактного взаимодействия состо-
состоит из зон сцепления и относительного проскальзывания. В слу-
случае качения тел из одинаковых материалов в работах [33, 35]
показано, что на площадке контакта (—а, Ь) имеет место только
два участка: зона сцепления (с, Ь) на стороне набегания цилиндра
б* 163
и зона (—а, с), где имеет место проскальзывание контактирую-
контактирующих поверхностей.
На участке сцепления (с, Ь) равны скорости тангенциальных
смещений точек цилиндра и основания, т. е.
at ot
В системе координат (х,у), связанной с цилиндром, это соотно-
соотношение может быть записано в виде (у = 0):
^^Е1=6, с<х<Ь, 6=^-^-. C.62)
ах ах V
Касательные и нормальные напряжения на этом участке связа-
связаны неравенством: \тху\ < цр{х).
На участке скольжения (—а, с) выполняется закон трения Ку-
лона-Амонтона:
тху = -^P{x)sga.sx, p{x) > 0.
Здесь \х - коэффициент трения скольжения, sx - разница скорос-
скоростей тангенциальных перемещений граничных точек цилиндра и
основания:
>"-ii 0Uxi it , t-> т, / r , aux\ аиХ2 \
Sx = ~^7 wr- -V + uR = V[S+ — — .
ot ot \ ax ax J
Граничное условие C.48) выполняется на всей площадке кон-
контакта (—а, 6). Поверхности взаимодействующих тел вне площад-
площадки контакта (—а,Ь) не нагружены.
Соотношения между напряжениями и деформациями в вяз-
коупругом теле примем в виде C.46).
3.4.2. МЕТОД РЕШЕНИЯ
В системе коодинат (х, у) перемещения и напряжения не зави-
зависят явно от времени, что позволяет ввести в рассмотрение, как
и в 3.3, функции е*, е*, уху, а*, а*, т*у C.47), которые удов-
удовлетворяют уравнениям, эквивалентным уравнениям равновесия,
164
совместности деформаций и закону Гука для изотропного упру-
упругого тела. Для определения этих функций используется метод,
изложенный в [25].
Введём в нижней полуплоскости две функции комплексного
переменного w\{z) и w2(z), которые являются интегралами типа
Коши (z = х + iy):
b
M*) = j*T*y(t,O)j^ = U2{x,y)-iV2(x,y).
—a
Выражая функции
определённые внутри каждого из контактирующих тел, через
действительные и мнимые части функций w\(z) и w2(z) (см. [25])
и подставляя их в граничные условия, преобразованные с помо-
помощью соотношений C.47), получим следующую задачу линейного
сопряжения: определить аналитические в нижней полуплоскости
функции wi(z) и w2(z), удовлетворяющие следующим условиям
на границе:
У\ — V2 = О, х ф (—а, 6),
(х-Т?У)Е'
it, ^z угу Л- II1/-1 ^ (J ij с О, С)
4Д к ' " C.63)
где Е' определено в C.7).
165
Решением этой задачи являются функции [34]:
ъ
{t-TeV)E'
7Г
ь
dt
C.64)
z-c
Здесь Сг - некоторая постоянная и
-6'
c-t
, te(-a,c),
, te(c,b),
b о b
p = f p(x)dx = - <jy(x,0)dx = - / a*y(x,Qi)dx.
—a —a — о
Последнее соотношение получено из C.47) при условии,
что ау(-а,0) = сгу(Ь,О) = 0.
Вычисляя действительные и мнимые части функций w\(z)
и W2{z) на действительной оси, определим а*(х, 0), г*^(а;, 0):
Затем истинные напряжения р(х) = -ау(х,0) и ^(а;) на пло-
площадке контакта находятся из решения дифференциальных урав-
уравнений C.47).
166
3.4.3. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЙ И
ТАНГЕНЦИАЛЬНЫХ КОНТАКТНЫХ
НАПРЯЖЕНИЙ
Из анализа функции w\{z) C.64) следует, что тангенциальные
напряжения не влияют на распределение давлений при контакт-
контактном взаимодействии тел из одинаковых материалов. Контакт-
Контактное давление в рассматриваемой задаче определяется выраже-
выражением C.57) и представляется кривыми на рис. 3.9.
Воспользовавшись следующим выражением для мнимой час-
части V\{x, 0) функции w\(z) при z -» х — г'0:
Vi(ar,O) =
F(x)
x)(b-x)
= , xe(-a,b),
где
F{x) = E'(a + b? + E'(x-TeV)(b-a-2x) + ^
32Д 8Л
и результатом интегрирования [58]:
C.65)
C.66)
/ 1Ь~Ь dt -
J У t-c't-x~
—7Г
C.67)
-7Г,
получим выражение для мнимой части Кг(а;,0) функции
(см. C.64)) при z -> х - гО:
V2(x, 0) = -цУ^х, 0), х е (-а, с),
Тогда тангенциальные напряжения тху(а;) находятся из решения
уравнения C.47) и имеют вид [34]:
167
• на участке проскальзывания (—а, с)
тху(х) = рр(х),
• на участке сцепления (с, Ъ)
тху{х) - ww
C.69)
Для определения постоянной Сч и точки с перехода от участка
проскальзывания к участку сцепления используются два усло-
условия. Первое из них - соотношение C.62), записанное при х — b в
виде:
+ОО
J С/2(х,0)ехР (-^7) dx = y&TeVexp ("^) ¦ C-70)
6
Здесь U2(x,0) - действительная часть функции w%(z)
при z —> х — г'0:
, ,€(Ь.+оо),
а функция F(x) определена в C.66).
Второе условие - это непрерывность напряжений на концах
площадки контакта, в частности, тху(Ь) = 0. Оно приводит к
следующему уравнению:
ь
F2(x,0)exp (-^7) dx = 0. C.71)
168
Используя соотношения C.68), C.70) и C.71), получим
»Е?{Ъ-с) Г 2Д*
г + с ~2TeV h
2R5\ l \2T?V
В [34] показано, что выражения для длины площадки кон-
контакта I = Ь + а и её смещения е = (Ь — а)/(Ь + а) совпадают с
выражениями C.58) и C.59), имеющими место в задаче о сколь-
скольжении вязкоупругого цилиндра по границе вязкоупругой полу-
полуплоскости из того же материала. Графики зависимости длины
площадки контакта и её смещения от скорости и механических
свойств взаимодействующих тел приведены на рис. 3.8.
На основании уравнений C.70) и C.71) можно вывести следу-
следующее уравнение для определения параметра /3 = F - с)/(Ь + а),
характеризующего относительную длину участка сцепления:
1+6-/3- ^p)]
C.72)
где ( = l/BTsV) - параметр, введённый в 3.3.3.
3.4.4. СОПРОТИВЛЕНИЕ КАЧЕНИЮ
Рассмотрим условия равновесия сил и моментов, приложенных
к цилиндру. Будем считать, что цилиндр - ведущий и нахо-
находится под действием активного момента М и вертикальной си-
силы Р (см. рис. 3.7). Со стороны основания на цилиндр действу-
действуют силы реакции Pi и Т\, являющиеся равнодействующими нор-
нормальных и тангенциальных напряжений, возникающих в облас-
зги контактного взаимодействия цилиндра с вязкоупругим телом.
Условие равенства моментов сил относительно центра цилиндра
169
имеет вид:
М + Mi + TiR = 0,
где
ь
Mi
—а
о
= I хр(х) dx,
= J rxydx = Jr*xydx = ^j V2{x, 0) dx,
—a —a —a
\тХу(-а) = rxy(b) = 0j.
Используя C.55), C.65) и C.68), выражения для Mi и Т\ можно
преобразовать к следующему виду:
4
к
Поскольку длина площадки контакта / изменяется в преде-
пределах /я ^ / ^ 1о, где /я = Iq/сх (а > 1), оба слагаемых
в C.73) неотрицательны и поэтому всегда Mi > 0. Сумма
моментов нормальных и тангенциальных напряжений относи-
относительно центра цилиндра создают момент сопротивления каче-
качению М* = Mi + TiR.
Характеристикой сопротивления качению является коэффи-
коэффициент трения качения, представляющий собой отношение момен-
момента трения качения М* к вертикальной нагрузке Р. Используя
170
выражения C.59), C.72), C.73) и C.74), запишем выражение для
коэффициента трения качения /хг в безразмерном виде как
М*
Ko
При свободном качении Т = 0 и, следовательно, М* = Mi. На
рис. 3.10 представлены зависимости коэффициента трения каче-
качения /лг от параметра Со = /o/BTeV) в случае свободного каче-
качения. Максимальное значение коэффициента трения качения цт
достигается при ?о ~ 1 и существенно зависит от параметра а,
характеризующего вязкие свойства контактирующих тел.
Анализ выражений C.73) и C.74) показывает, что при зна-
значениях М > М\ тангенциальные напряжения тху направлены в
сторону движения цилиндра (д > 0). При М < Mi тангенциаль-
тангенциальные напряжения имеют противоположное направление (д < 0),
в этом случае к оси цилиндра должна быть приложена ещё
сила тяги Т в направлении движения. Из соотношений C.72)
и C.74) следует, что размер зоны сцепления зависит от величи-
величины С = Ti/(/j,P). Уравнение C.72) было решено при различных
значениях С. Графики зависимости длины зоны сцепления от
параметра Со представлены на рис. 3.11. Длина зоны сцепления
возрастает с уменьшением величины С и приближается к длине
площадки контакта (кривая 5).
Величина относительного проскальзывания S может быть
определена из соотношения C.74). На рис. 3.12 приведены зави-
зависимости величины T/(fiP) от относительного проскальзывания
при различных значениях параметра Со = /o/2TeF. На основа-
основании результатов расчётов можно заключить, что при фиксиро-
фиксированном значении T/(fiP) величина относительного проскальзы-
проскальзывания уменьшается с уменьшением параметра Со (с ростом ско-
скорости V).
171
0,4
ц,Д//0
0,2
0,0
0
lo/BVTz)
10
Рис. 3.10. Коэффициент трения качения вязкоупругого цилиндра по
вязкоупругому основанию (одинаковые материалы, \х = 0) при разных
значениях параметра а = T€jTa: а = 1,5 A), а = 5 B), а = 10 C),
а = 100 D)
{Ь-сI10
1,0 -
0,5
0,0
-1
0
18(/0/B*Тв))
Рис. 3.11. Зависимость длины зоны сцепления от параметра ?о при
а — 10 и различных значениях величины С = Ti/цР: С = 0,9 A),
С = 0,6 B), С = 0,4 C), С = 0,2 D), С = 0 E)
172
0,9
0,6
0,3
0,0
A /
0,0
0,2
25Л/(ц/0)
0,6
Рис. 3.12. Кривые проскальзывания при качении вязкоупругого ци-
цилиндра по вязкоупругому основанию (одинаковые материалы, а = 10)
при различных значениях параметра Со = /o/BTEV): Со = Ю2 A),
Со = Ю-1 B), Со = Ю-4 C)
3.4.5. ИССЛЕДОВАНИЕ НЕКОТОРЫХ ПРЕДЕЛЬНЫХ
СЛУЧАЕВ
Из решения задачи о качении вязкоупругого цилиндра по вязко-
упругому основанию можно получить решение задачи о качении
упругого цилиндра по основанию из того же материала, меха-
механические свойства которого характеризуются модулем упругос-
упругости Е и коэффициентом Пуассона v. Для этого в полученных со-
соотношениях следует положить а = 1.
Тогда получим следующие выражения для нормальных и
тангенциальных напряжений на площадке контакта (—а, а), ко-
которая расположена симметрично относительно оси симметрии
цилиндра (е = 0):
р{х) =
4тгД
—а < х < а,
тху{х) =
4тгД
—а < х < с,
-—— у/а2 — х2 — у/(а — х)(х — с) , с < х < а.
173
Длина площадки контакта определяется по формуле I = 2а =
= \f%2RP/E', а длина зоны сцепления /3 = 1 — 8R/{^a). Кон-
Контактное давление распределено симметрично (Mi = 0). Танген-
Тангенциальная сила Т определяется выражением
JL - 5Л (о - —
/лР ца \ /ла
Заметим, что относительная длина зоны сцепления не зависит
от упругих свойств контактирующих материалов и вычисляется
по формуле:
При а ф 1 решение стремится к решению для упругих ма-
материалов с модулями упругости Е или Н — аЕ, если TEV —> 0
или TeV —>¦ +оо соответственно.
3.5. РАСЧЁТ МЕХАНИЧЕСКОЙ
СОСТАВЛЯЮЩЕЙ СИЛЫ ТРЕНИЯ
При исследовании задачи о скольжении цилиндра по границе
вязкоупругого основания в 3.3 установлено, что сопротивление
движению цилиндра существует даже при отсутствии танген-
тангенциальных напряжений в области контактного взаимодействия.
Для упругих тел при сохранении предположения об отсутствии
сил трения на площадке контакта, как известно, сопротивление
их относительному скольжению равно нулю (см. 3.2). Причина
этого явления заключается в обратимости упругих деформаций,
в силу чего область контакта и контактные давления для упру-
упругих тел распределены симметрично относительно оси симметрии
движущегося цилиндра. Не так обстоит дело при взаимодейст-
взаимодействии вязкоупругих тел. Как показано в 3.3, центр площадки кон-
контакта и точка, в которой контактные давления достигают своего
максимального значения, сдвинуты по направлению к переднему
краю области взаимодействия. Именно в силу такого характера
распределения напряжений и возникает сопротивление при от-
относительном скольжении вязкоупругих тел.
174
Рассчитаем тангенциальную силу Т, которую надо прило-
приложить к цилиндру, чтобы обеспечить его установившееся дви-
движение с постоянной скоростью по границе вязкоупругого полу-
полупространства (рис. 3.13). Предположим, что тангенциальные на-
напряжения на площадке контакта пренебрежимо малы (тху = 0).
Это позволяет изучить только механическую составляющую си-
силы трения. Поскольку нормальные напряжения направлены к
центру цилиндра, сила реакции F также направлена к центру
цилиндра (см. рис. 3.13,о). Вычислим компоненты Tj и Pi си-
силы реакции F в направлении осей Ох и Оу, соответственно.
Поскольку длина площадки контакта I = а + b много меньше
радиуса R цилиндра, справедливы соотношения
ь ь
Р\= / р(х) cos <p(x)dx « p(x)dx, C.75)
о
Г М
= P{x) sin <p(x) dx*^> C-76)
где
М
о
— I хр(х) dx.
-а
Из уравнений равновесия следует, что Т^ = Т и Pi = Р. Си-
Сила Т^ называется механической составляющей силы трения. Ме-
Механическая составляющая коэффициента трения \i^ может быть
определена на основании соотношений C.75) и C.76) как
» C77)
где М вычисляется из C.56) при условии ц = О и, следователь-
следовательно, 1е = /о- Окончательно выражение для /^ можно представить
в виде
О /о то\
Md = ah~5 ' (o.7cSJ
175
Рис. 3.13. Схема сил, действующих на цилиндр при его скольжении
по основанию: при отсутствии сил трения на площадке контакта (а),
контакт с трением (б)
176
где
Интересно отметить, что механическая составляющая fid C.78)
коэффициента трения скольжения совпадает с коэффициентом
трения качения при свободном качении вязкоупругого цилиндра
по вязкоупругому основанию. Это заключение следует из того,
что выражение C.79) подобно соотношению C.73), делённому
на /о//- Поэтому кривые на рис. 3.10 иллюстрируют также за-
зависимость механической составляющей коэффициента трения fid
от параметра Со • Эта зависимость не является монотонной и име-
имеет максимум при ?о ~ 1, т.е. когда время прохождения элемен-
элементом половины длины площадки контакта приблизительно равно
времени последействия. Механическая составляющая силы тре-
трения стремится к нулю при малых и больших значениях пара-
параметра ?о-
Первым, кто предложил определять механическую составля-
составляющую коэффициента трения скольжения в экспериментах с ка-
катящимися телами, был Д. Табор [231]. На рис. 3.14 представлены
экспериментальные результаты, полученные в [180], где изуча-
изучалось контактное взаимодействие стального шара с резиновыми
образцами в условиях качения и скольжения. Для уменьшения
адгезионной составляющей силы трения при скольжении в ка-
качестве смазки использовалось мыло. Как следует из результатов
измерений, представленных на рис. 3.14, коэффициенты трения в
контакте качения и скольжения мало отличаются друг от друга.
При номинальном давлении, меньшем, чем 3-Ю4 Па, эксперимен-
экспериментальные значения коэффициента трения близки к теоретической
кривой, рассчитанной по гистерезисной теории трения [232]. Со-
Согласно этой теории, построенной для исследования трения ка-
качения, коэффициент трения качения рассчитывается по форму-
формуле C.78). При этом предполагается, что коэффициент а^ зависит
от вязкоупругих свойств материала и скорости качения. Значе-
Значение коэффициента а^ определяется из экспериментов на цикли-
циклическое нагружение материала.
177
0,25
0,20
0,15
0,10
...А.^.
0,05
0,00 -^1
0,00
0,01
0,02
, МПа
0,04
Рис. 3.14. Коэффициент трения стальной сферы и хорошо смазанной
резины как функция номинального давления в контакте качения (свет-
(светлые треугольники) и в контакте скольжения (тёмные треугольники)
(экспериментальные результаты [180])
Штриховой линией обозначена теоретическая кривая, полученная на осно-
основании гистерезисной теории трения [231]
Полученные решения контактных задач для цилиндра и вяз-
коупругого полупространства (см. 3.3 и 3.4) позволяют постро-
построить теоретическую зависимость коэффициента ад C.79) в кон-
контакте скольжения (качения) от вязкоупругих характеристик ма-
материала (Е, v, Та, Те) и скорости скольжения (качения). Ана-
Анализ соотношения C.79) показывает, что величина а^ зависит
также от нормальной нагрузки Р, поскольку /о ~ у/Р. Разли-
Различие между теоретическими и экспериментальными результата-
результатами (см. рис. 3.14) может быть объяснено тем, что в теоретичес-
теоретических расчётах пренебрегалась зависимость ад от давления (тео-
(теоретическая кривая соответствует ад = 0,35).
В предыдущем анализе предполагалось, что единственной
причиной сопротивления скольжению является потеря энергии
178
за счёт необратимости деформаций. Принимая во внимание, что
в контакте скольжения имеют место обе составляющие дисси-
диссипации энергии (деформационная и адгезионная), представляет
интерес изучить их совместное влияние на силу трения. Возни-
Возникает также вопрос: существует ли взаимное влияние адгезионной
и механической составляющих силы трения? Некоторые резуль-
результаты, полученные в этой главе (см. 3.3) позволяют дать ответ
на этот вопрос.
Рассмотрим цилиндр радиуса R, скользящий с трени-
трением (тху(х) = цар(х)) по вязкоупругому основанию (рис. 3.13,6).
В этом случае существует составляющая силы трения Та, рас-
рассчитываемая по формуле
ь ь
Та= тху cosip(x) dx^ ца J p(x)dx = fiaP. C.80)
—о —а
Из уравнения равновесия следует
М
T = Ta+Td = HaP+—.
Поэтому полный коэффициент трения определяется выражением
Т М
+ C81)
Второй член в C.81) известен как коэффициент механичес-
механической составляющей силы трения. Момент М рассчитывается из
соотношения C.56). Поскольку момент М зависит от парамет-
параметра 7] (см. соотношения C.53), C.54) и C.56)), и т], в свою очередь,
является функцией коэффициента трения ца (см. C.9)), механи-
механическая составляющая зависит от ца. Напомним, что коэффици-
коэффициент трения /ia во многом определяется свойствами контактиру-
контактирующих поверхностей и поверхностных пленок. Таким образом, на
величину механической составляющей силы трения оказывают
влияние процессы взаимодействия поверхностей на более низком
масштабном уровне, включая и их молекулярное взаимодейст-
взаимодействие. На рис. 3.15 представлены зависимости безразмерного мо-
момента M/(PIq), пропорционального механической составляющей
179
M/(Pl0)
0,2
0,1
0,0
-0,1
-0,2
-3
_2
-1
0 lg(/0/BJTE))
Рис. 3.15. Механическая составляющая силы трения при а = 5 и
разных значениях коэффициента трения да: /ха = 0 A), /л0 = 0,3 B),
»а = 0,6 C)
силы трения, от параметра ?о при разных значениях коэффици-
коэффициента трения fia. Результаты показывают, что при увеличении
коэффициента ца механическая составляющая силы трения па-
падает. При малых и больших значениях параметра Со механичес-
механическая составляющая становится отрицательной для положитель-
положительных значений коэффициента /ха.
3.6. КОНТАКТ УПРУГИХ ТЕЛ В УСЛОВИЯХ
ЧАСТИЧНОГО ПРОСКАЛЬЗЫВАНИЯ
В тех случаях, когда тангенциальная нагрузка, приложенная к
взаимодействующим телам, меньше, чем предельная нагрузка,
способная вызвать полное скольжение в области контакта, воз-
возникает контакт с частичным проскальзыванием. Анализ рас-
распределения напряжений в условиях частичного проскальзыва-
180
ния является важным для предсказания характера разрушения
тел, подверженным слабым осциллирующим нагрузкам (явление
фреттинга).
Эта задача может
быть классифицирована
как одна из наиболее
сложных задач механики
контактного взаимодей-
взаимодействия, поскольку в
процессе её решения
необходимо определять
не только границы
области контакта, но
также и границы зон
сцепления и проскальзы-
проскальзывания. Обзор известных
решений контактных
задач с частичным
проскальзыванием для
тел различной формы
недавно был сделан в
работе [189].
Ниже рассмотрена
контактная задача с
частичным проскаль-
проскальзыванием для упругого
индентора с плоским
основанием и закруг-
закруглёнными кромками и
упругого основания
(рис. 3.16). Такая форма
индентора является более реалистичной, чем рассмотренная
в 3.2.3, где штамп имел острые углы, что порождало сингуляр-
сингулярные значения давления на одном или на обоих концах площадки
контакта. Под действием приложенных сил и момента индентор
может быть наклонён к границе упругого основания, при этом
область контакта, вообще говоря, расположена несимметрично
Рис. 3.16. Схема контакта индентора с
основанием при 7 < 7i (а)> 7i < 7 < 72
(б) и 72 < 7 (в)
181
по отношению к его оси симметрии (см. 3.2.3). Изучается рас-
распределение контактных напряжений, а также расположение зон
сцепления и проскальзывания в области контакта в зависимости
от формы индентора и действующих на него сил и моментов.
3.6.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим взаимодействие упругого индентора, имеющего
плоское основание длины 1с и скруглённые углы (R - ради-
радиус кривизны в точках ±(с + 0)), с упругим полупространством
(см. рис. 3.16). Задача рассматривается в плоской постановке.
Индентор находится под действием вертикальной Р и горизон-
горизонтальной Т сил и момента М. Сила Т приложена на некотором
расстоянии d от основания индентора и создаёт момент М' = Td,
который существует даже при отсутствии активного момента,
т.е. при М = 0. Под действием приложенных сил индентор,
вообще говоря, наклонён к границе упругой полуплоскости на
угол а. Обозначим tga = 7 G ^ 0)- Форма наклонённого штам-
штампа описывается функцией:
/(*) =
(х - сJ
— '¦ух, —а ^ х ^ —с,
—7Ж, — с < х < с, C.82)
— jx, с ^ х ^ Ь.
Условие контакта индентора с упругим основанием внутри об-
области [—а, Ъ] имеет вид:
где uyi - смещения границы упругой полуплоскости (г = 1) или
индентора (г = 2) вдоль оси Оу, которые считаются положитель-
положительными для каждого тела, штрих (') означает производную по х
от исследуемых функций.
Предположим, что тангенциальная сила Т удовлетворяет
условию:
182
где \i - коэффициент трения, т.е. взаимодействующие тела на-
находятся в условиях частичного проскальзывания (предваритель-
(предварительного смещения). Граничные условия в областях скольжения и
сцепления имеют вид:
• в области скольжения па выполняется закон трения Амон-
тона и направление касательных сил q(x) = тху(х) проти-
противоположно направлению проскальзывания, т. е.
, C.83)
где
s(x) = (uxi(x) - иХ2(х)) - 6Х, 5Х = const, C.84)
(uXi(x) - смещение границы каждого тела (г = 1, 2) вдоль
оси Ох, дх - относительное смещение в направлении оси Ох
фиксированных точек тел, расположенных на некотором
удалении от области контакта);
• в области сцепления Па относительное проскальзывание
равно нулю, т. е.
uxi{x) - их2(х) = 6Х, C.85)
и выполняется неравенство:
\q(x)\ ^ цр(х). C.86)
Контактные давления р(х) и касательные напряжения q(x)
удовлетворяют следующим уравнениям равновесия сил и момен-
моментов:
ь ь
I р(х) dx = P, I q(x) dx = Т, C.87)
о
/ хр(х) dx =
Td + M. C.88)
183
3.6.2. РАСПРЕДЕЛЕНИЕ КОНТАКТНЫХ ДАВЛЕНИИ
Для упрощения анализа задачи предположим, что материалы
контактирующих тел одинаковы. В этом случае касательные на-
напряжения на площадке контакта не влияют на распределение
контактных давлений (см., например, [66, 107]). Поэтому полу-
полученные ниже выражения для контактных давлений справедливы
и в случае взаимодействия тел, характеризуемых разными уп-
упругими постоянными, при отсутствии сил трения.
При построении решения будем использовать обычный в тео-
теории контактных задач прием замены контактирующих тел упру-
упругими полуплоскостями. Возможность такой замены в случае уп-
упругого индентора с плоским основанием и закруглёнными кром-
кромками изучена в [157].
С учётом сделанных замечаний давление р(х) в области кон-
контакта [—а, Ь] определяется из соотношения
х —
—а
где приведённый модуль упругости Е* (см. A.7)) в случае одина-
одинаковых материалов взаимодействующих тел вычисляется по фор-
формуле Е* = Е/ BA - и2)) и
C.90)
Решение уравнения C.89) с граничными условиями р(—а) =
= р(Ь) = 0 получено Н.И. Мусхелишвили [107] в виде:
h'(x) = <
X
X
+
R
—
D
С
С
1-7,
7,
1-7,
—с
с
<
X
X
<
с,
ь,
р{х) = _&j Г
h'(t)dt
C.91)
хе [-а,Ь],
184
где концы области контакта — а и Ь находятся из условий:
ь ь
= 0. C.92)
b b
f th'{t)dt _ IP Г V|
J J(t + a)(b~lS~~E^' J JUT
t)(b-t)
Область контакта может иметь различное положение по от-
нощению к плоскому участку |х| ^ с основания индентора в зави-
зависимости от его угла наклона к границе основания (см. рис. 3.16).
Ниже рассмотрены разные варианты расположения области кон-
контакта.
Случай —а ^ —с, с ^ Ъ (рис. 3.16,а). Вначале рассмот-
рассмотрим случай, когда область контакта включает плоский участок
индентора (см. рис. 3.16,а). Подставляя уравнение C.90) в C.91),
получим
6
-р*
-x) -7 / -—
dt
(t-x)J(t+a)(b-t)
X + С
J (t-x)
dt
+ ¦
R J {t-x)J{t + a){b-t)
dt
—a
b
X — С
J (t-
R J {t-x)J{t + a){b-t)
с
b
dt
a){b-t) R
dt
1
—а с
или, после вычисления интегралов,
a)(b-t)
+2arctgy2) + ^^^lln
-уу\)
A+У?)
In
yl)
У\~У
2/2 -У
УУ1-1
C.93)
C.94)
185
где
У = tg - arcsm
1 . 2х - b + а
2 a + b
2c-b +
оarcsm
2
a + о
1 . -2c -b + a
arcsm 6
При выводе выражения C.94) мы воспользовались значением
следующего интеграла:
XI 2/2
Г dt = 2A +у2) Г dr =
J it- x)J(t + a)(b-t) (a + b) J (r - y)(l - ту)
2A + И) ,n
(a + b)(l-f)
при вычислении которого применены подстановки:
__ Ь~а , У /- , м
Подставляя C.90) в соотношения C.92) и вычисляя соответ-
соответствующие интегралы, получим систему уравнений для определе-
определения концов площадки контакта —а и b при заданных величинах
нагрузки Р и наклона индентора *у'-
2PR (a + b)R _ 2c + 3a + b
-w = -^~t-+L2—i
L 3a + 6-2c + a + 6 F 3 4
(b3e + 4C
(Ы-2c - oH! - (a + 2c - 6N2 =
= тг(Ь - о - 27Д) - 2Li + 2L2, '
186
где
. 2c + b-a n . 2c-b + a
в\ = arcsm ;— , 62 = arcsin
a + b
;, 62 = arcsin,
a + b a + b C.1ОО)
Предельный наклон индентора ji, для которого возможен
рассмотренный здесь случай, определяется из уравнений C.98)
и C.99) при условии а = с.
Если наклон 7 неизвестен, для его определения использу-
используется дополнительно уравнение C.88). Подстановка соотноше-
соотношения C.91) в C.88) даёт:
b
M + Td
—a
о
= / xp(x) dx =
E* }. ГТ-.7UT-.-M ) h'(t)dt
—а
Ь
-x)y/(t+a)(b-t)
2" J Jlt + a)(b-t) J t-x
а а
Е* Г h'(t)dt ! [ п гтт г,
=--г- / v ' = \ \ J(x + a)(b-x)dx+
2тг J V(i + a)(b - t) \ V V Д ;
+t
о
I
x — t
—a
Соотношение C.101) с помощью уравнений C.92) может быть
преобразовано к виду:
^ '
2 J y/(t + a)(b - t) 2
—a
187
После подстановки выражения C.90) в C.102) и вычисления ин-
интегралов следует соотношение для определения у:
2R Г
-— \
M+Td
Р(Ь-а)
тг(Ь-а)Eа2
с(Ъ - a) (Lx + L2)
16
24
F - а)Eа2 + 2аЬ + 5b2)F>i + в2)
16
с (За2 - 2аЬ + ЗЬ2) (вг - в2)
(ЗЛ03)
Случай —с ^ —а ^ с < 6 (рис. 3.16,6). Аналогич-
Аналогичным образом с использованием C.96) и C.97) могут быть по-
получены выражение для определения контактных давлений и со-
соотношения для нахождения границ площадки контакта в слу-
случае —с ^ —о < с < Ь, т. е. когда наклон 7 удовлетворяет нера-
неравенству 7 > 7i- Приведем здесь лишь окончательное выражение
для давления:
A-у2)
In
У1-У
vvi
C.104)
(у и у! определены в C.95)) и уравнения для определения то-
точек —а и Ь:
2PR
2 + I
(а+ 6) F-За-4с) (п
C.105)
188
Система уравнений C.105) и C.106) совпадает с уравнения-
уравнениями C.98) и C.99) при а = с.
Подстановка —а = с в уравнения C.105) и C.106) даёт воз-
возможность определить предельный угол 72- Таким образом, соот-
соотношения C.105) и C.106) справедливы, если 7i < 7 < 72-
При неизвестном наклоне у индентора имеет место дополни-
дополнительное соотношение:
За2-2а6+362
+
-— [4с2 + 8c(b -a)- 15F - аJ - 16аб1 -
24 L J C.107)
-i [(Ь - а) Eа2 + 2а6 + 562) -
Случай с ^ —а < Ъ (рис. 3.16,в). В этом случае, как
следует из C.91), давление совпадает с известным решением для
параболического штампа:
р(х) = ^(х + а)(Ь-х). C.108)
Соотношения для определения концов площадки контакта имеют
вид (см. выражения C.92)):
7R = ^ - с, C.109)
C.110)
пЕ*(а + Ъ) ' ' 4 '
В частности, из последних соотношений следует:
Р =
16R
Эта формула совпадает с решением, полученным в [23].
189
Уравнения C.109) и C.110) можно использовать для вычис-
вычисления угла 72, соответствующего условию —а = с. В этом слу-
случае уравнения C.109) и C.110) совпадают с уравнениями C.105)
и C.106).
Заметим, что случай [—а, Ь] € {—с, с] невозможен. Такой вы-
вывод следует из соотношения C.91), которое после подстановки в
него функции h'(x) (см. C.90)) принимает вид
2тг J (t-x
—а
(t-x)y/(b-t)(t-
= 0,
т. е. давление в этом случае всюду равно нулю.
Из соотношений C.94), C.105) и C.108) следует, что без-
безразмерное контактное давление р — 2pR/(E*c) зависит от без-
безразмерной нормальной нагрузки Р = 2PR/(E*c2) и безразмер-
безразмерной величины наклона индентора 7 = jR/c. Распределение кон-
контактного давления при различных значениях 7 представлено на
рис. 3.17. Прежде всего, распределение давления несимметрич-
несимметрично по отношению к оси симметрии индентора. Если область
контакта включает плоское основание штампа, т.е. 7 < 7ь
(см. рис. 3.16,а), функция давления имеет два локальных мак-
максимума. При больших значениях угла наклона функция давле-
давления имеет только один максимум вблизи правого конца площад-
площадки контакта, причем его величина возрастает с увеличением 7-
Правый конец области контакта расположен на плоском осно-
основании индентора при 71 < 7 < 72 > и на правом скруглении
при 7 > 72- Зависимости ширины области контакта (Ь+а)/с и её
смещения (Ь — а)/(Ь + а) от угла у наклона индентора для двух
значений безразмерной нагрузки Р представлены на рис. 3.18.
Смещение площадки контакта возрастает, а её ширина умень-
уменьшается с ростом угла наклона.
Зависимости наклона индентора 7 от безразмерного момен-
момента М = 2(M + Td)R/(E*c3), построенные на основании получен-
полученных соотношений для двух значений нормальной нагрузки Р,
представлены на рис. 3.19. При 7 ^ 7i эти завимости близки к
линейным. На рисунках 3.18 и 3.19 обозначены точки, соответ-
соответствующие 7 = 71 (тёмные кружки) и 7 = 72 (светлые кружки).
190
2pR/(E*c)
0,5
0,4
0,3 -
0,2
0,1 -
0,0
-1,5 -1,0 -0,5 0,0 0,5 1,0 xlc 2,0
Рис. 3.17. Распределение контактных давлений при 7 = 0 A), у
= 0,05 B), 7 = 0,1C), 7 = 0,44 D)
3.6.3. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
Уравнение для определения касательных напряжений q(x) в слу-
случае взаимодействия тел из одинаковых упругих материалов име-
имеет вид [25]:
s'(x) = -
2 fq{t)dt
~пЁ* J x-t '
C.111)
где функция s(x) определена соотношением C.84).
Представим функцию q(x) в области сцепления С1а в виде
q{x) = np(x)-q*(x).
C.112)
Подставляя C.112) в C.111) и учитывая, что внутри области
191
b + a b-a
с ' Ь + а
0,0 0,1 0,2 0,3 у Rlc 0,5
Рис. 3.18. Зависимость ширины области контакта (сплошные линии)
и ее смещения (штриховые линии) от угла наклона индентора при
Р = 0,2 A) и Р = 0,4 B)
проскальзывания q(x) = цр(х), получим
ь
fip(t) dt 2
x-t nE*
-а П
Г q*{t)dt
J ~x-t
или, принимая во внимание соотношение C.89),
C.113)
C.114)
Поскольку s'(x) = 0 внутри области сцепления, из C.114)
следует уравнение для определения функции q*(x):
192
yR/c
0,0
0,0
0,1
0,2
0,3
M
0,5
Рис. 3.19. Зависимость наклона индентора от приложенного момента
при Р = 0,2 A) и Р = 0,3 B)
где функция h'(x) определена соотношением C.90).
Докажем, что при рассматриваемых условиях контактного
взаимодействия возможна только одна зона сцепления внутри
области контакта, т.е. Г20 = [di,^]. Предположим, что Qa =
= Ы №,сЫ и рассмотрим функции s'(x) и s"(x) внутри зоны
к
скольжения, расположенной между двумя областями сцепления,
т.е. при х е (с?2)^1+1 )• Поскольку функция q*(x) удовлетворяет
условиям q* (d?) = q* (g^) = 0, функция s'(x) непрерывна. Диф-
Дифференцируя соотношение C.114) внутри интервала
получим
Поскольку h"(x) ^ 0 (см. C.90)) и q*(x) ^ 0, можно заключить,
7. Горячева И.Г. 193
что s"(x) < 0. Тогда справедливо неравенство
s'(d^+1) - s\d\) = I s"(x)dx < 0. C.117)
С другой стороны, s' (di+1) = &' (d|) = 0- Полученное противо-
противоречие доказывает утверждение, что зона скольжения не может
существовать между двумя зонами сцепления, и, следовательно,
в области контакта существует только одна зона сцепления.
Решение уравнения C.115) внутри области сцепления fia =
= [di,e?2], удовлетворяющее условию
q*(d1)=q*(d2) = 0,
имеет вид [107]:
q*{x) = —
х
«2
Sir-
(t-x)y/(d2-t)(t-di)
При этом концы области контакта d\ и d2 определяются из
следующих условий:
1 mdt =0 C.119)
1
J
-t)(t-dX)
И
(ЗЛ2О)
Соотношение C.120) получено из уравнения равновесия C.87).
Проведём анализ возможных расположений зоны сцепления
внутри области контакта [—а, Ь].
194
Случай —о < d\ < —с, с < d2 ^ Ь. Подставляя C.90)
в C.118) и интегрируя полученные выражения с учётом C.96)
и C.97), найдём выражение для функции q*(x):
/j,E*(d2 -di)
2тгЯA + 772)
+ 2arctg772) +
G7 - 772) A - VV2)
In
772-77
77772 -1
C.121)
G7 - 771) A - 77771)
In
771-77
77771 -1
где
V = *6 о arcsi"
02 —
1 . 2cd2
771 =tg{ -arcsm ^_^
. .1 . -2c-d2-di
772 = tg(- arcsm ^ _ ^
C.122)
Уравнения для определения неизвестных концов di и d2 зоны
сцепления при заданных значениях 7, Р и Т следуют из соотно-
соотношений C.90), C.119) и C.120):
2Я(цР-Т) _ (d2-di)R s2Bc-Zdi+d2)
JlE~* ~ 77Г 2 4
siCdx-d2+2c) (d2-<
4 8
(d2-di)(d2 + 3d!+4c) /тг
8
d2)
- 2c
+ d2 + 2c
2
L2 — I<i,
4>i ~
C.124)
7*
195
где
= arcsin
d2-di
. 2c-di-d2
, </>2 = arcsin —
C.125)
si = y/(-c-di)(d2 + c), s2 = y/(c-di){d2 - c),
a L\ и L2 определены соотношениями C.100).
Случай —с ^ d\ < с < d2 < Ь. Функцию q*(x) в этом
случае можно получить из уравнений C.90) и C.118) в виде:
/j,E*(d2 -di) [1 -ту2 /тг
(
di) [1 -ту2 /тг \
-Г/7?х)
In
ГЦ-Т1
vm -i
C.126)
где ту и 7^1 определяются из соотношений C.122). Концы зоны
сцепления рассчитываются из системы уравнений:
+
-4с) /тг
C.128)
Случай с ^ di < d2 < 6. Из уравнений C.90) и C.118)
получаем:
C.129)
Уравнения для определения концов d\ и d2, выведенные из
соотношений C.90), C.119) и C.120), имеют вид:
*
C.130)
C.131)
196
Случай [di, <Лг] ? (~с?с] невозможен, поскольку, как сле-
следует из соотношений C.90) и C.118),
dt = = о.
d)
2
-zXx-b) f
J [t-x
Таким образом, касательные напряжения в области контак-
контакта (—а, 6) определяются соотношением
{(лр{х), -a^x^di, d2^x^b,
где выражения для функции q* (х) при различных положениях
зоны сцепления приведены в C.121), C.126) и C.129).
Так как функция q*(x) удовлетворяет соотношению
0 <~q*(x) < цр(х) при х € (di,d2),
то функция q(x) удовлетворяет условию C.86) внутри зоны сцеп-
сцепления.
Функция q(x) удовлетворяет также соотношению C.83). Что-
Чтобы проверить это утверждение, рассмотрим функцию s'(x) в зо-
зонах скольжения (—a, di) и (cfo, b). Из соотношений C.90) и C.114)
следует
• в зоне скольжения (—a,di), т.е. при х = d\ — е (е > 0):
в зоне скольжения (d2,b), т. е. при х = d2 + е (е > 0):
з'(х) = s'(d2 + e)- s'(d2) =
_?? _ JL J q^dt < о
R пЕ* J (d2 - t + )(d t)
t + e)(d2 - t)
197
2qRI{\iE*c)
2qR/(\iE'c)
1 xlc 2
Рис. 3.20. Распределение касательных напряжений при 7 = 0,12, Р =
= 1 и Т = 0 A), f = 0,42 B), Г = 0,75 C), Г = 0,9 D), f = 0,98 E)
(а) и при 7 = 0,2, Р = 0,5 и Г = О A), Г = 0,22 B), Г = 0,40 C) и
Г = 0,47 D) (б)
Принимая во внимание условие з(х) = s'(x) = 0 при х G [di,^],
можно заключить, что s(x) < 0 в зонах проскальзывания, т.е.
направление проскальзывания противоположно направлению
касательных напряжений, поскольку q(x) > 0.
Распределения касательных напряжений при различных зна-
значениях безразмерной тангенциальной силы
2{fiP-T)R
Г =
представлены на рис. 3.20,а для случая j — 0,12 (область контак-
контакта включает полностью плоскую часть основания индентора) и
на рис. 3.20,# для случая j = 0,2 (левый конец области контак-
контакта находится на плоском основании). Для обоих случаев шири-
ширина зоны сцепления зависит от величины тангенциальной силы.
Касательные напряжения имеют два или три максимума в за-
зависимости от расположения области контакта и зоны сцепления
на ней.
Функция s(x) в зонах проскальзывания определяется соотно-
соотношениями, следующими из уравнений C.84), C.85) и C.111):
198
в зоне проскальзывания (—a,d\):
Ь
х — х
dx'=
с') In
X — X
— x'
dx' +
C.133)
с') In
x — x
— x'
ds';
• в зоне проскальзывания (d,2,b):
ь
2 f
-^jp I q(x')
ln
x — x
dx' =
о
Jp(x')
In
x — x
C.134)
с')\п
ж —
Функция проскальзывания при разных углах наклона ¦у пред-
представлена на рис. 3.21. Величина проскальзывания на концах об-
области контакта растёт с увеличением угла наклона инденто-
ра. Размер зоны проскальзывания и величина проскальзывания
больше в левой части области контакта, где давление меньше.
3.6.4. РАСТЯГИВАЮЩИЕ НАПРЯЖЕНИЯ
Воспользуемся методом Н.И. Мусхелишвили [107] для расчёта
компоненты напряжений ах при у — 0. При известных нормаль-
нормальных и касательных контактных напряжениях функция Мусхели-
199
0,10
0,00
-1,5 -1,0 -0,5 0,0 0,5
1,0
xlc
2,0
Рис. 3.21. Функция проскальзывания при 7 = 0 A), у = 0,1 B)
и 7 = 0,25 C)
швили Ф(г), определяемая интегралом типа Коши
ь
^)=^ilpixl+-f)dx'-
C.135)
позволяет найти все компоненты напряжении в упругом теле.
В частности, справедливо соотношение:
ах + Оу = 2 [Ф{г) + Ф(г)] .
На границе у = 0 соотношение C.136) имеет вид:
К + <г»)у=0 = 2 [ф-(х)
C.136)
у ] , C.137)
где Ф~(х) - граничное значение функции Ф(г) при стремлении z
к а; из нижней полуплоскости, Ф+(ж) - граничное значение функ-
функции Ф(г), если z стремится к ж из верхней полуплоскости.
Из соотношения C.135) с использованием формул Сохоцкого-
Племеля следует
ь
ф-(*)г = -\ №) + «Ф)] + гЬ / Р(ж1+Л(ж/) da;/> C-138)
200
о
= \ [-Р(х) + Щ(х)} + ~J ~P{XyjfX>) dx>. C.139)
Так как ау{х) ¦— — р(х), из соотношений C.137)—C.139) оконча-
окончательно будем иметь:
ь
ах = -р[х) + - [ q{x')dX' , -оо < х < +оо. C.140)
7Г J X — X
Рассмотрим выражение C.140) при различных значениях х.
Если х G [di,d2]> TO из соотношений C.85) и C.111) следует
ах = -р(х), di < х ^ d2. C.141)
Если —а ^ ж < d\ или ^2 < ж ^ 6, то выражение C.140)
с учётом C.112) преобразуется к виду:
C.H2)
п J х' - х п J х1 - х
-a
откуда, используя C.89), получаем
ах = -р(х) + nE*h'(x) - - I q4f)dX' ¦ C-143)
7Г J X' ~ X
Интеграл в правой части соотношения C.143) не является син-
сингулярным и может быть вычислен для разных функций q*(x),
определённых выражениями C.121), C.126) и C.129).
Если х ф (—а,Ь), для вычисления функции ах при у = О
можно воспользоваться соотношением C.142), которое примет
вид:
,.=w**3*: _*???>*!:. (з.ш)
п J х' — х п J х — х
—a di
201
2ох ЩЕ'с)
-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 х/с 2,5
Рис. 3.22. Распределение напряжений ах(х,0) для упругой полуплос-
полуплоскости при 7 = 0 A), 7 = ОД B), 7 = 0,25 C) и j = 0,6 D)
2axR/(E'c)
-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 х/с 2,5
Рис. 3.23: Распределение напряжений ах(х, 0) для упругого индентора
при 7 = 0 A), 7 = 0,1 B), 7 = 0,25 C) и 7 = 0,6 D)
202
При этом функция р(х) определена соотношениями C.94), C.105)
или C.108). Оба интеграла в C.144) несингулярны.
На рис. 3.22 и 3.23 показано распределение напряжений ах
при у = 0 внутри основания (рис. 3.22) и индентора (рис. 3.23)
при разных значениях 7- Увеличение угла наклона уменьша-
уменьшает растягивающие напряжения внутри основания на левом кон-
конце площадки контакта. Максимальные значения растягивающих
напряжений внутри индентора имеют место на правом конце об-
области контакта и они возрастают с увеличением угла наклона
индентора.
Полученные аналитические выражения для напряжений поз-
позволяют оценить их величину при любых заданных внешних на-
нагрузках, а также подобрать такие нагрузки, которые бы обеспе-
обеспечивали оптимальное распределение напряжений вблизи области
контакта.
Глава 4
КОНТАКТ НЕОДНОРОДНЫХ ТЕЛ И
ТЕЛ С ПОКРЫТИЯМИ
Любой материал прежде чем стать элементом подвижного со-
сопряжения подвергается технологической обработке, которая из-
изменяет его свойства и в первую очередь свойства приповерхност-
приповерхностных слоев. Свойства материала меняются и в процессе трения
и изнашивания поверхностей. В силу даже только этих причин
возникает неоднородность механических характеристик матери-
материалов элементов сопряжений, что существенно влияет на все про-
процессы, протекающие при трении поверхностей.
Значение поверхностных слоев твёрдых тел при их фрик-
фрикционном взаимодействии наиболее полно проявилось при созда-
создании специальных материалов с покрытиями, имеющими высокие
триботехнические показатели (малый коэффициент трения, вы-
высокую износостойкость, стойкость к задирам и т. д.). В таких ма-
материалах наилучшим способом сочетаются высокие антифрик-
антифрикционные и прочностные характеристики, они имеют высокую
коррозионную стойкость, хорошую теплопроводность. В зависи-
зависимости от их функционального назначения различают антифрик-
антифрикционные покрытия, играющие роль твёрдой смазки, износостой-
износостойкие покрытия и т. д.
В этой главе изучаются два вида неоднородностей: наличие
пор и включений вблизи поверхности, а также существование
покрытий, механические свойства которых отличны от свойств
подложки. Для каждого из указанных видов неоднородностей
анализируется характер распределения напряжений вблизи по-
поверхности при контактном взаимодействии. Проведенное иссле-
исследование дает возможность ответить на очень важный для прак-
практики вопрос: "Как влияет толщина покрытия, его относитель-
относительные механические характеристики, а также степень сцепления
204
с подложкой на напряжённое состояние и характер разрушения
покрытий при разных условиях взаимодействия?"
4.1. МЕТОД АНАЛИЗА НАПРЯЖЕНИИ В
УПРУГИХ ТЕЛАХ, ИМЕЮЩИХ
ВНУТРЕННИЕ ДЕФЕКТЫ
При решении целого ряда прикладных задач требуется учиты-
учитывать влияние систем дефектов (типа микротрещин и микро-
микрополостей) на напряжённо-деформированное состояние упругих
тел. С точки зрения оценки поверхностной прочности тел при их
контактном взаимодействии особый интерес представляет изуче-
изучение полей напряжений в приповерхностных слоях, где, как пра-
правило, появление микротрещин и другого рода дефектов связано
с применением разных видов механической и термической обра-
обработки поверхностей (нанесение покрытий, упрочнение и т.д.).
Подобное исследование приводит к необходимости решения
краевой задачи теории упругости в сложной области, которое
может быть осуществлено в точной постановке лишь для неко-
некоторых идеализированных случаев. Одной из традиционных иде-
идеализации является предположение о неограниченности облас-
области, в которой расположены дефекты. Методы определения на-
напряжённого состояния упругих тел вблизи внутренних концен-
концентраторов напряжений в виде систем трещин, разрезов и тонких
включений изложены в монографиях Н.И. Мусхелишвили [107],
Г.Я. Попова [115], Т.Н. Савина [125]. Случаи, когда дефекты рас-
расположены вблизи границы упругого тела, не могут рассматри-
рассматриваться в рамках упомянутой выше идеализации. В.В. Можаров-
ским и В.Е. Старжинским [104] предложен метод решения плос-
плоской контактной задачи для полосы, дискретно спаянной с основа-
основанием (имеющей конечное число разрезов на границе их раздела).
Система круговых отверстий, расположенных вблизи границы
полуплоскости, рассмотрена в [125]. Однако алгоритмы решения
задач, развитые в [104, 125] и некоторых других работах, доста-
достаточно сложны для конкретных реализаций (особенно в случае
исследования смешанных задач теории упругости) и, кроме того,
205
предполагают наличие в области конечного числа внутренних
дефектов.
При решении контактных задач для областей, имеющих сис-
системы дефектов, близко расположенных к границе тел, важно оце-
оценить их влияние на напряжённое состояние тел вблизи границы.
Поскольку в точной постановке даже для регулярной системы
дефектов задача является сложной, возникает вопрос: "Каким
образом учесть влияние системы дефектов, не решая задачу в
точной постановке?"
Ниже предложен подход, основанный на теории дифференци-
дифференциальных операторов в областях с мелкозернистой границей, кото-
который позволяет ответить на поставленный вопрос. Рассмотрена
система дефектов, локализованная у некоторой внутренней по-
поверхности Г области fi, занимаемой упругим телом. Основной
идеей предлагаемого метода является введение характеристик
"дефектного слоя" (слоя, содержащего систему дефектов), кото-
которые в среднем отражают его поведение при деформировании.
Это позволяет свести исходную точную формулировку гранич-
граничных условий на поверхностях дефектов к условию сопряжения
на Г. Метод позволяет рассчитать осредненные значения напря-
напряжений на некотором удалении от системы дефектов.
4.1.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим упругое тело, занимающее область п С W1 (п = 2
или 3). В этой области находится система дефектов F^ =
с ^ (рис. 4.1). Все элементы F^ локализованы вбли-
i
зи некоторой внутренней поверхности Г (или около внутренней
кривой в двумерном случае).
Задача сводится к исследованию уравнений Ламе в облас-
области п \ F(s> (объёмными силами пренебрегаем):
(А + (i)ujtjk + /iAuk = 0, D.1)
где А и /1 - постоянные Ламе, uj - упругое смещение точки
вдоль j-й оси координат (j = 1,2,3 в трёхмерном случае при п =
= 3, или j = 1, 2 в двумерном случае при п = 2). Предположим,
206
Рис. 4.1. Расположение системы дефектов F^ в области
что граница dF^*> дефектов не нагружена, т. е.
= 0,
D.2)
где TV - вектор нагрузки, действующей на единицу площади
элемента границы dF^ с нормалью v. Заметим, что в уравне-
уравнениях D.1) и дальше, если индекс j повторяется два раза, то по
нему идет суммирование от j = 1 до j = п (свёртка тензора).
Условия на границе тела дп могут быть заданы в произволь-
произвольной форме (в напряжениях или смещениях, а также смешанные
условия).
Обозначим решение этой задачи вектором и^ с компонента-
компонентами и
(*)
4.1.2. ТЕНЗОР ВЛИЯНИЯ
Введём характеристики влияния системы дефектов F^s> на ре-
решение уравнений Ламе в области Q.
Пусть 7 - открытое связное множество на Г; 7+ и 7~ ~ по-
поверхности, образованные концами векторов длины 6, нормаль-
нормальных к 7 (см. рис. 4.1); H(y, S) - слой толщины 26 со срединной
207
поверхностью у, включающий в себя все дефекты, т. е. множес-
множество F^ С #G,<5)- Обозначим H(j,S,s) = H(y,S)\F^s\
Определим u? как решение краевой задачи для уравнений
Ламе D.1) в области H(y,6,s) со следующими граничными усло-
условиями:
7" : uf = О, 7+ : < = Sia, т*\арМ = °- D-3)
где индекс а означает, что отлично от нуля только смещение в
направлении оси а на 7+> (<х = 1,2, C)), Sia - символ Кронекера.
Влияние множества F^ характеризуется тензором второго
ранга P(j,S,s) с компонентами
Paf3A,S,s)= J a^dv, dv = f[dxu n = 2,C), D.4)
H(-y,6,s) г=1
где а^ - компоненты тензора напряжений, соответствующего
решению граничной задачи D.3):
ам(- решение граничной задачи D.3), в которой индекс а за-
заменен на /3, {Р = 1,2,C)).
Интегральный член в соотношении D.4) может быть пред-
представлен в виде:
4*>- f ofcu?kdv. D.5)
Второй интеграл в правой части соотношения D.5) равен нулю
в силу условий равновесия при отсутствии массовых сил и сил
инерции (сг?г- j = 0), а первый интеграл может быть преобразован
в поверхностный с использованием теоремы Остроградского-
208
Гаусса:
J
a,/3 = 1,2,C),
Таким образом, используя также граничные условия D.3), ком-
компоненты тензора влияния D.4) можно представить в виде:
,6, з) = У T?8kf) d ? = У Jf d S, D.6)
где Тд? = cr^i/j - fc-я компонента вектора нагрузки Т^ , действу-
действующая на единицу площади границы у+ области Н("у, S, s) в точке
с нормалью I/, имеющей компоненты щ, в задаче с граничными
условиями D.3). Таким образом, компонента PQ/3G) S, s) тензора
влияния РG) 8, з) равна работе, произведённой силой Т„ на /3-
смещениях границы -у+, удовлетворяющих граничным усло-
условиям D.3). Из теоремы Бетти (см. [169]) следует, что тен-
тензор РG,6, s) - симметричный.
4.1.3. ВСПОМОГАТЕЛЬНАЯ ЗАДАЧА
Наряду с основной граничной задачей, сформулированной
в 4.1.1, рассмотрим вспомогательную граничную задачу для
уравнений Ламе D.1) в области п \ Г. Обозначим её решение
вектором и с компонентами щ, i = 1,2,C). Функции щ удов-
удовлетворяют тем же условиям на внешней границе д?1 области П,
что и функции uf , и следующим условиям на поверхности Г:
Т
Г
= т
= k(x)(u+-u-)|r, D.7)
209
где Т+ и Т„ - векторы нагрузки, действующей на единицу эле-
элемента поверхности Г с нормалью v с различных сторон этой по-
поверхности, (и+ — и") - скачок вектора перемещений на Г, к(х) -
тензор с неотрицательными компонентами.
Соотношения между тензорами k(x), PG,^, s) и решения-
, (s)
ми основной и вспомогательной задач, т.е. функциями и\ и щ,
устанавливаются на основании теоремы:
Пусть при s —» +оо выполняются следующие условия.
1. Все элементы F^ находятся в сколь угодно малой окрест-
окрестности Г.
2. Для любого 7 С Г существуют следующие пределы и тен-
тензор к(х), что
Urn lim РG,<Ы = Нт Нт Р(-у,6,з)= /k(x)rfS, D.8)
где х =
Тогда последовательность u^s^ решений основной задачи, сфор-
сформулированной в 4.1.1, сходится к решению и вспомогательной
задачи вместе с первыми и вторыми производными.
Эта теорема является частным случаем более общей теоре-
теоремы, сформулированной и доказанной в [99]. Подробное изложение
решения поставленной выше задачи, основанное на применении
сформулированной выше теоремы, дано в [54]. Применение этой
теоремы позволяет провести асимптотический анализ напряже-
напряжений на некотором удалении от поверхности Г. Отметим, что идеи
метода осреднения, использованного в рассматриваемом подхо-
подходе, изложены также в работе [225].
Из сопоставления выражений D.6) и D.8) следует, что ком-
компоненты тензора к(х) численно равны предельным значениям
при S -> 0, s —> +оо компонент векторов усилий Т„ (а =
= 1,2, C)), действующих на единичную площадку границы -у+
(в пределе 7+ совпадает с 7) в задаче с граничными условия-
условиями D.3)).
Таким образом, тензор к(х), используемый при постановке
вспомогательной задачи, осреднённо отражает деформационные
свойства слоя, содержащего дефекты.
210
-CO:
У+
г
Y-
Рис. 4.2. Схема расположения системы дефектов
4.1.4. ОДИН ЧАСТНЫЙ ВИД СИСТЕМЫ ДЕФЕКТОВ
В качестве примера определим тензор к(х) в одном частном слу-
случае. Пусть область fl С I2, Г - линия, параллельная оси Ох,
F^ - множество прямоугольников со сторонами Ь и d, равно-
равномерно распределённых вдоль прямой Г (рис. 4.2). Выберем 7+
и 7~ так, чтобы слой H(j, 6) имел толщину 26, равную стороне
прямоугольника d.
Такой выбор основан на следующем соображении. Теорема
даёт метод анализа асимптотического поведения решения зада-
задачи D.1) и D.2). на расстояниях от Г тем больших, чем больше
толщина 11(^,6). Другой выбор 7+ и 7~ приведет к более от-
отдалённой асимптотике. Это можно проиллюстрировать предель-
предельным случаем: если 6 много больше характерного размера Fi ,
то решение вспомогательной задачи D.3) и компоненты РG> 8, s)
почти не "чувствуют" множество iy , что соответствует реше-
решению основной граничной задачи на бесконечности.
Рассмотрим элемент ш, представляющий собой прямоуголь-
прямоугольник со сторонами с — b и d, ограниченный 7+) 7~ и сторонами
двух соседних дефектов (см. рис. 4.2). Предположим, что дефор-
деформирование каждого элемента ш не зависит от деформирования
соседних элементов. Чтобы удовлетворить граничным услови-
условиям D.3) на 7+ и 7~> рассмотрим решение уравнений Ламе D.1)
в форме (х — Х\ и у =
D.9)
211
Смещения и1 (а = 1) и и2 (а = 2) дают однородное напряжённое
состояние в элементе ш:
<rl = -d, °Ъ = ^, о?2 = 0, (а = 2). D.11)
Граничные условия на сторонах х = Ъ и х = с прямоугольника
(ненагруженные стороны) при этом, вообще говоря, не удовле-
удовлетворяются.
В силу равномерного распределения дефектов F^ тен-
тензор РG) S, s) зависит только от длины -у. Обозначим через /
длину множества 7, включающего в себя N элементов ш, так
что N = 1/с, N » 1. Тогда из D.6) будем иметь:
'$dx. D.12)
ь
Компоненты Т% на границе 7+> имеющей вектор нормали и =
= {0; 1} имеют вид:
Т'1 1 /~i2 2 Т1^- гг\2> г\
1 ~" al2i 12 — CT22i 12 — ±\ —у}-
На основании выражений D.10), D.11) и D.12) получим
'/* 0 \
0 Х + 2и )'
Из D.8) с учётом равномерности распределения элементов и> сле-
следует:
k=^f Uf V D.1S)
(ic 1^0 A + 2/ij ^ 0 к2 )
На основании D.7) для рассмотренной системы дефектов, распо-
расположенных вдоль линии Г, параллельной оси Ох, должны выпол-
выполняться следующие соотношения:
г+у = т-у = кх (u+ - и"),
С7+ = ff" = к2 (u+ - U") ,
212
Рис. 4.3. Схема контакта штампа и упругой полуплоскости, ослаблен-
ослабленной системой дефектов, локализованных вдоль прямой Г
где т^у, а^, «? , и^ - тангенциальные и нормальные напряжения
и смещения на Г.
Заметим, что если форма дефектов близка к разре-
разрезам (d —> 0), то ki -» +оо. Для d ф 0 параметры ki ->• 0 при 6 —> с.
В этом случае верхний слой лежит на основании без трения.
4.1.5. ПОЛУПЛОСКОСТЬ, ОСЛАБЛЕННАЯ СИСТЕМОЙ
ДЕФЕКТОВ
Рассмотрим применение предложенного подхода к решению кон-
контактной задачи для упругого основания, ослабленного систе-
системой дефектов (двумерная постановка). Пусть штамп, форма кон-
контактирующей поверхности которого описывается функцией у =
= f(x), вдавливается без трения в упругую полуплоскость Q =
= {{х,у) : у > 0} силой Р (рис. 4.3). Условия на границе у = 0
имеют вид:
иу = D - /(ж),
ау = 0,
'ху
= 0,
\х\ > а,
—оо < х < +оо,
D.15)
где а - полуширина площадки контакта, D - внедрение штампа.
Система дефектов F^ равномерно расположена вдоль пря-
прямой Г : {у = h} (см. рис. 4.3). Предположим, что условия сопря-
213
жения на этой прямой имеют вид D.14), при этом значения &х
и &2 известны и, согласно D.13), связаны соотношением:
Л + 2, 2Щ^)
р, 1 — 2и
где v - коэффициент Пуассона для полуплоскости.
Задача решалась методом преобразований Фурье, применен-
примененном в [НО] при исследовании плоских контактных задач для мно-
многослойных упругих тел. Образы Фурье F\ и F2 функций Эйри,
являющихся бигармоническими в областях {(х,у) : 0 < у < h}
и {(х,у) : у > h}, имеют вид
Fi(w,y) = [Ах{ш) + В1{ш)у]ехр(уш) +
+ [Ci(w) + L>i(w)i/]expH/w), D.16)
F2(cv,y) = [А2{ш) + В2(ш)у]ехр(-у\ш\).
Образы Фурье йх(ш,у), йу(ш,у), <ту(ш,у), тху(ш,у) смещений и
напряжений выражаются через функцию F(co,y), которая сов-
совпадает с Fi(u),y) в области {{х,у) : 0 < у < h} и с F2(oj,y) в
области {(х,у) : у > h}, с помощью соотношений:
D.17)
D-18)
dF dF
= iu>3 — , тху(ш,у)=ш2 -^ . D.19)
dF
— ,
Коэффициенты А\{ш), В\{ш), С\(ш), Di(w), ^(w), ^(w) в D.16)
определяются из решения системы уравнений, полученной путём
подстановки D.17)—D.19) в граничные условия D.14) при у — h
и D.15) при у = 0, которые предварительно также подвергну-
подвергнуты преобразованию Фурье. Обратное преобразование Фурье осу-
осуществлялось численно.
214
0,06
0,04
0,02
0,00
plE
0,0 0,2 0,4 0,6 xla 1,0
Рис. 4.4. Контактные давления под штампом параболической формы
при h = 1, о = ОД и к =-0,1 A), к = 1,0 B), fc = 3,0 C)
штриховал линия соответствует решению Герца
4.1.6. ВЛИЯНИЕ ДЕФЕКТНОГО СЛОЯ НА
КОНТАКТНЫЕ ХАРАКТЕРИСТИКИ И
ВНУТРЕННИЕ НАПРЯЖЕНИЯ
Исследуем характер распределения контактных давлений и
внутренних напряжений в полуплоскости, ослабленной системой
дефектов, расположенных вдоль линии у == h и имеющих ха-
характеристики, описанные в рассмотренном в 4.1.4 примере. При
расчётах использовались следующие безразмерные параметры и
функции:
у
г h
h=a>
кха
Результаты расчёта контактных давлений р(х) для штампа
параболической формы (f(x) = x2/BR), R - радиус штампа)
представлены на рис. 4.4. Расчёты показали, что с увеличени-
215
ем дефектности слоя (уменьшением значения к) при заданной
полуширине а области контакта и фиксированной глубине h ло-
локализации дефектов максимальные значения контактных давле-
давлений р@) падают и уменьшается нагрузка, требуемая для дости-
достижения размера а площадки контакта (см. рис. 4.4). Для сравне-
сравнения на рис. 4.4 штриховой линией показано распределение дав-
давлений по теории Герца, соответствующее тому же значению па-
параметра а. На основании результатов расчётов (см. [54]) можно
также заключить, что при увеличении расстояния от площадки
контакта до дефектного слоя влияние дефектов на распределение
давлений под штампом снижается.
Распределение внутренних напряжений вдоль оси Оу при на-
гружении упругой полуплоскости давлением ро, равномерно рас-
распределённым по отрезку {—а ^ х ^ а, у = 0}, иллюстрируется
графиками, представленными на рис. 4.5. Построенные графи-
графики позволяют оценить характер влияния параметра к, харак-
характеризующего степень дефектности границы у = h, на харак-
характер распределения максимальных касательных напряжений rmax
(рис. 4.5,а) и компоненты ах напряжений (рис. 4.5,5). Для боль-
больших значений параметра к распределение максимальных каса-
касательных напряжений и компоненты ах подобно их распределе-
распределениям для случая однородного упругого полупространства (кри-
(кривые 1). Для малых значений к (кривые 2 и 3) напряжения име-
имеют скачок на Г (т.е. при у = h), причём скачок тем больше,
чем меньше значение к. Интересно отметить также, что ком-
компонента ах напряжений при малых значениях к становится от-
отрицательной вблизи линии дефектов Г при приближении к ней
со стороны границы упругой полуплоскости, т. е. в этом месте
возникают растягивающие напряжения, которые могут вызвать
возникновение трещин.
Результаты, представленные на рис. 4.4 и 4.5, получены при
значении и = 0,3.
Проведённое исследование показывает, что существуют гра-
границы изменения параметров, характеризующих степень дефект-
дефектности слоя и его удалённости от границы, в пределах которых
дефектный слой оказывает существенное влияние на контакт-
контактные характеристики. Предложенный подход позволяет учесть
216
0,2 0,4 0,6 0,8 1,0 1,2 1,4 y/h 1,8
0,2 0,4 0,6 0,8 1,0 1,2 1,4 y/h 1,8
Рис. 4.5. Распределение максимальных касательных напряжений
fmax (а) и компоненты ах (б) вдоль оси Оу при h = 2 и к = 5000 A),
А; = 0,5 B), Л = 0,05 C)
217
это влияние при решении контактных задач и исследовании на-
напряжённого состояния упругих тел, имеющих внутренние сис-
системы дефектов.
4.2. НАПРЯЖЁННОЕ СОСТОЯНИЕ УПРУГИХ
ТЕЛ С ПОКРЫТИЯМИ ПРИ РАЗНЫХ
ВИДАХ НАГРУЖЕНИЯ
Исследование напряжённого состояния тел с покрытиями явля-
является необходимым звеном при анализе характера их разрушения
и разработке способов создания износостойких покрытий.
Эта задача изучалась многими авторами с использованием
модели двухслойного упругого основания как в плоской, так и
в пространственной постановках. В плоской постановке зада-
задача решалась с использованием интегрального преобразования
Фурье, а в осесимметричном случае - преобразования Ханкеля
(см. [97, 98, 108, 201] и др.). Обзор исследований контактных
задач для упругого слоя, сцепленного с упругим или жёстким
основанием, содержится в монографиях [9, 20, 108].
Для тел с покрытиями возникает вопрос: "Как влияет дис-
дискретность контакта, имеющая место вследствие шероховатости
поверхностей, на напряженное состояние и характер разруше-
разрушения покрытий?" Ответ на этот вопрос особенно важен в связи
с широким применением тонких износостойких покрытий, тол-
толщина которых соизмерима с расстояниями между неровностями
и размерами единичного пятна контакта. Некоторые численные
результаты расчёта напряжённого состояния тел с покрытия-
покрытиями с учётом шероховатости поверхности обсуждаются в рабо-
работах [158, 224]. Однако эти результаты не могут быть использо-
использованы для анализа влияния параметров микрогеометрии на места
концентрации напряжений в телах с покрытиями, поскольку они
получены для одного частного вида поверхностного рельефа.
Как показывают эксперименты, характер напряжённого со-
состояния и разрушения тел с покрытиями существенно зависит от
степени сцепления покрытия с подложкой [122]. Поэтому другой
важной задачей является изучение влияния степени сцепления
покрытия с подложкой на распределение контактных давлений
218
и внутренних напряжений. Однако в большинстве теоретичес-
теоретических исследований напряжённого состояния двухслойных упру-
упругих тел делается предположение, что поверхностный слой либо
сцеплен с основанием, либо лежит на нём без сил трения. Мо-
Моделирование условий на границе раздела слоев, отражающих их
неполное сцепление, является непростой математической зада-
задачей.. Один из методов решения плоской контактной задачи для
полосы, дискретно спаянной с основанием (имеющей конечное
число разрезов на границе их раздела) предложен в [104].
Ниже рассмотрен ряд задач для двухслойного упругого по-
полупространства, решения которых дают возможность изучить
совместное влияние механических и геометрических свойств по-
покрытий, дискретности контакта, связанной с микрогеометрией
поверхности, а также степени сцепления покрытия с подложкой
на распределение контактных и внутренних напряжений.
4.2.1. ЗАДАЧА О НАГРУЖЕНИИ ДВУХСЛОЙНОГО
УПРУГОГО ОСНОВАНИЯ ПРИ НЕПОЛНОМ
СЦЕПЛЕНИИ СЛОЕВ
Постановка задачи. Рассматривается упругий слой толщи-
толщины h, лежащий на упругом полупространстве и нагруженный
давлением р(г) внутри круговой области радиуса а (рис. 4.6).
На границе раздела упругого слоя и упругого полупространст-
полупространства (z = 0) имеют место следующие граничные условия:
тЙ
Й> = т<? =
т<? = к („W - «?>) , D.20)
A) B) A) / . A)\ B) / , B)\
иу =иу, и\ ! [г + иУ) = иУ (г + и). ') ,
(г) (г) (г) i i i
где az , Trz , i~gz', игг, щ, и\ - компоненты тензора напряжении и
перемещений в слое (г = 1) и в полупространстве (г = 2).
Условия D.20) являются частным случаем соотноше-
соотношений D.14) при к\ = к и &2 —> +оо, т. е. когда дефектный слой на
границе раздела покрытия и основания обладает только сдвиго-
сдвиговой податливостью в радиальном направлении при бесконечной
219
Рис. 4.6. Схема нагружения двухслойного упругого полупространства
жёсткости в направлении оси Oz. Таким образом, в плоскос-
плоскости z = 0 допускается относительное проскальзывание в ради-
радиальном направлении точек слоя и полупространства. Поскольку
тангенциальные напряжения направлены против проскальзыва-
проскальзывания, коэффициент к > 0.
При к —> +оо соотношения D.20) совпадают с условиями пол-
полного сцепления слоя и основания:
(
A) _ _B) A) _ B) A) _ B)
z — Oz > T0Z — Tqz , Trz — TTZ ,
B) A) B) A)/ ч B)/ ч
D.21)
При к = 0 соотношения D.20) соответствуют случаю, когда слой
лежит без трения на упругом основании, и имеют вид:
D.22)
Заметим, что условия на нормальные перемещения слоя uz и
B)
основания щ записаны в соотношениях D.20) и D.22) в уточ-
уточнённой форме, учитывающей неравенство смещений в радиаль-
радиальном направлении граничных точек слоя щ и основания иг при
конечных значениях к.
220
Условия на верхней границе слоя z = h имеют вид:
а^ = -p{r), r^a, ai1} =0, г > а,
D.23)
тг1] = т?} = 0, 0 ^ г < +оо.
]у!етод решения. Преобразуем последнее соотношение в
граничных условиях D.20), разложив функции щ {г + Щ ) (i =
= 1,2) в ряд и отбрасывая члены, начиная со второго порядка
малости по щ . Тогда получим соотношение:
г$)(г)-и?Цг) = ф(г), D.24)
в котором
Я t1) Я B)
W = -t41)^- + 42)^- D-25)
Соотношение D.24) совпадает с последним соотношением в усло-
условиях D.21) при ф(г) = 0.
В общем случае функция ф{г) неизвестна, что не позволя-
позволяет применить для решения задачи прямую процедуру сведения
её к линейным системам функциональных уравнений, исполь-
используя преобразование Ханкеля [108]. Поэтому для решения задачи
применим итерационный процесс.
Рассмотрим некоторый j-й шаг, на котором известна функ-
функция ф]{г). Тогда для определения осесимметричных полей на-
напряжений и деформаций в двухслойном упругом теле имеем сле-
следующие соотношения при z = 0:
_A) _ _B) A) _ B) _ . / A) _ B)\
V ' D.26)
i1L2)
Условия на верхней границе слоя задаются в виде D.23).
Для решения сформулированной выше граничной задачи при-
применим интегральное преобразование Ханкеля. Для этого пред-
представим напряжения и перемещения внутри слоя (г = 1) и внутри
221
полупространства (i = 2) в форме Лява (см. [108]):
@ д i" (г) ЗУ°~
9г ar2 j
д г А ,,л 1 а^о"
СТо =
,@ -
dz2 '
D.27)
dz2
Здесь Ei я щ (г = 1,2)— модули упругости и коэффициенты Пу-
Пуассона материалов слоя и основания; <р^> (г, z) - бигармонические
функции, определённые в слое (г = 1) и основании (i = 2). Эти
функции могут быть представлены в виде:
+ОО
+ OO
'-0z/h)]Jo@r)d0, D-28)
-,z) = J (A2(C) + zB2(p))exp(-Cz/h)Jo(f3r)dC,
где Jo (x) - функция Бесселя нулевого порядка.
Соотношения D.23) и D.26), выраженные с помощью D.27)
через бигармонические функции D.28), позволяют свести задачу
к следующей системе шести линейных относительно коэффици-
коэффициентов Аг{]3), Вг{р), Ci{p), DM, A2(f3), B2(/3) уравнений:
M-^L = ~&, D.29)
222
где матрица ЛЛ шестого порядка имееет вид:
( P'x ^ 0
2и{)е-Р~х О
v\ I
= {P@),O,O,O,O,T№} >
v2) - h _
A 1^
Здесь р(/?) и ф](Р) - преобразования Ханкеля от функций р(р)
и V»j(p) (p = r/a), т.е.
Ж/?) = J pp(p)J0(pC)dp,
о
+00
W) = J рФМ
Система D.29) может быть решена в аналитическом виде,
после чего напряжения и перемещения в двухслойном основа-
основании рассчитываются с помощью соотношений D.27), используя
функции (fi(r,z) и <рг(г,z), определённые формулами D.28). На-
Например, перемещение щ (р) верхней границы слоя (z = h) в
направлении оси Oz определяется соотношением:
+00
^ D.30)
A
где
z L J
1/3) - (f3\ + 2?i)AX5)l exp(-/3A).
223
Интеграл в D.30) берется численно, используя алгоритм, разра-
разработанный в [108].
По найденным на j-м шаге значениям перемещений щ '(г),
щ (г), Uz(r) и щ (г) на границе (z = 0) слоя и основания по
формуле D.25) определялась функция ipj+i(r). Значение функ-
функции ipj+i(r) использовалось на следующем шаге итерационно-
итерационного процесса в качестве правой части в последнем соотноше-
соотношении D.26).
При заданной точности вычислений е итерационный процесс
заканчивался на j + 1-м шаге, если выполнялось следующее не-
неравенство:
max
г
< ?.
При численной реализации в качестве нулевого приближения
использовалась функция i/>o(r) = 0. Проведённые вычисления по-
показали хорошую сходимость итерационного процесса при раз-
различных значениях параметров задачи. Как правило, количество
итераций при е = 10~3 не превышало четырёх.
После окончания итерационной процедуры по форму-
формулам D.27) и D.28) вычислялись напряжения и перемещения
внутри слоя и полупространства.
Анализ влияния условий на границе раздела на на-
напряжённое состояние. Изложенный выше алгоритм был ис-
использован для анализа влияния условий на границе раздела слоя
и основания, отражающих неполное сцепление покрытия с ос-
основанием и учитывающих относительный сдвиг точек границы
вследствие деформаций тел, на напряжённое состояние основа-
основания и покрытия при действии на верхнюю границу покрытия
давления, равномерно распределённого внутри круга радиуса а,
т.е. р(г) =р0 (г < а).
Исследование уравнений задачи, полученных в 4.2.1, поз-
позволяет заключить, что распределение безразмерных напряже-
напряжений аг/ро, &в/ро, &z/PQ} Ttz/po и безразмерных перемещений иг/а
и uz/a в слое и основании зависит от следующих безразмерных
параметров:
Е\ - h _ ро г ка
h к
224
а также от коэффициентов Пуассона покрытия i/\ и основания i/2 •
Параметр к характеризует степень сцепления покрытия с осно-
основанием. Покрытие считается относительно твёрдым при х > 1 и
мягким при х < 1- Кроме того, покрытие классифицируется как
относительно тонкое, если h < 1, и как относительно толстое,
если h > 1.
Подробный анализ результатов расчётов содержится в ра-
работе [53]. На основании проведённого анализа можно сделать
вывод, что условие ul(r) = u^(r), которое обычно ставится на
границе слоя и основания, с достаточной точностью выполняет-
выполняется в случае относительно мягких покрытий. Для относительно
твёрдых и тонких покрытий, особенно в случае малых значе-
значений к, необходимо использовать уточнённые граничные условия,
сформулированные в D.20).
Относительное проскальзывание (?ij — v%) /а точек слоя и ос-
основания на границе раздела z = 0 для различных значений к, х
и h представлено на рис. 4.7. Знак этой функции положителен в
случае мягких покрытий (кривые 1-4) и отрицателен в случае
твёрдых покрытий (кривая 5), при этом абсолютная величина
относительного проскальзывания возрастает с уменьшением па-
параметра к. Результаты расчётов показали, что с увеличением
толщины покрытия h при % < 1 и постоянном к величина отно-
относительного проскальзывания в каждой точке сначала возрастает
до некоторого максимального значения, зависящего от величи-
величины к, а затем убывает до нуля. Этот вывод иллюстрируется
кривыми 1, 2 и 3 на рис. 4.7. Уменьшение проскальзывания при
очень малых толщинах слоя объясняется тем, что очень тонкие
мягкие покрытия, как показывают расчёты напряжённого состо-
состояния, ведут себя подобно основанию Винклера.
Анализ функции az (р) на границе раздела слоя с основанием
позволил установить, что в случае мягких (х < 1) покрытий по-
поведение функции практически не зависит от параметра к. В слу-
случае же относительно твёрдых (х > 1) покрытий при уменьшении
степени сцепления покрытия с основанием увеличиваются зна-
значения отрывающих нормальных напряжений az(r) < 0 на гра-
границе раздела относительно твёрдого тонкого покрытия и основа-
основания, что может привести к отслаиванию покрытия. Результаты
8. Горячева И.Г. 225
Рис. 4.7. Относительное проскальзывание точек слоя и основания на
границе раздела (z = 0) при х — 0H5, ро = 0,02, v\ = 0,45, щ = 0,33,
к = 0,01, h = 0,55 A); h = 0,15 B); К = 1,2 C); к = 0,5, h = 0,15 D);
X = ЮО, ро = 0,5, vx = 0,33, z/2 = 0,45, к = 0,01, Я = 0,15 E)
расчётов также показали, что при уменьшении степени сцепле-
сцепления покрытия с основанием абсолютные значения функции тгг
на границе раздела слоев также уменьшаются (см. [53]).
Характер разрушения покрытия во многом определяется рас-
распределением максимальных касательных напряжений ттах в
слое и основании. На рис. 4.8 представлены графики функ-
функции ттах(?), где С, = z/h, построенные на оси Oz, проходящей
через центр области нагружения, т.е. при г = 0, для относи-
относительно твёрдых и тонких покрытий. Сравнение кривых 1 и 1'
позволяет заключить, что при уменьшении степени сцепления
покрытия с основанием, т.е. с уменьшением параметра к уве-
увеличиваются значения максимальных касательных напряжений
в слое вблизи границы раздела. Увеличение толщины слоя при
постоянном значении к (кривые 1 и 2) приводит к уменьшению
значения rmax на границе раздела ? = 0. Результаты расчётов
226
12
Tmax'A>
\
1.1'
V
\\
\\
\\
\\
\\
A
ч г А
\ M
\ л
v д
\ \\
2\\
\\\
\\\
w
\
1
/'
'/
'/
;/
;/
1
., 1,1
Ij
i
ii
. /7 у
-1,0
-0,5
0,0
zlh
1,0
Рис. 4.8. Функция максимальных касательных напряжений при х =
= 100, г/i = 0,33, V2 = 0,45 и Л = 0,2, к = 0,01 A); к = 10 (I1); Л = 0,55,
? = 0,01 B)
позволили также установить, что для твёрдых и толстых по-
покрытий разница в значениях функции ттах(?) при изменениях
параметра к становится пренебрежимо малой. В случае мягких
покрытий параметр к оказывает слабое влияние на распределе-
распределение максимальных касательных напряжений в слое и основании.
Таким образом, можно сделать вывод, что условия на гра-
границе раздела покрытия и основания наиболее сильно влияют на
характер напряжённого состояния в двухслойном теле для от-
относительно тонких h < 1 покрытий, при этом использование
уточнённых граничных условий на нормальные перемещения то-
точек слоя и основания является необходимым в случае относи-
относительно твёрдых х > 1 и тонких покрытий при малой степени их
сцепления с основанием (малых значениях к).
4.2.2. ОСЕСИММЕТРИЧНАЯ КОНТАКТНАЯ ЗАДАЧА
ПРИ НАЛИЧИИ ПРИГРУЗКИ ВНЕ ШТАМПА
Изложенный выше метод был использован для решения кон-
контактной задачи о внедрении осесимметричного штампа (/(г) -
227
Рис. 4.9. Схема контакта штампа с двухслойным основанием при на-
наличии пригрузки
форма контактирующей поверхности штампа) в двухслойное
упругое полупространство при наличии пригрузки вне штам-
штампа (рис. 4.9). Граничные условия на верхней поверхности слоя
т. е. при z = h, имеют вид:
z = Рс(г),
$ = т?} = 0,
а <г < +оо,
0 < г < +оо,
D.31)
где а - радиус площадки контакта, D - смещение штампа вдоль
оси Oz, pc(r) - давление, приложенное к границе слоя вне пло-
площадки контакта. В частном случае, когда верхняя поверхность
слоя вне площадки контакта не нагружена, рс(г) — 0.
Условия на границе раздела слоя с основанием {z — 0) зада-
задаются формулами D.20), в которых последнее соотношение заме-
заменено на условие: u\(r) = u2z(r).
Кроме того, выполняется уравнение равновесия
а 27Г
= / /
о о
p(r)r drdip,
D.32)
228
где Р - нагрузка, действующая на штамп, р(г) - контактное
давление.
Решение контактной задачи состоит из двух этапов. Первый
этап - определение формы д(г) деформированной поверхности
свободной от нагрузки круговой области {0 ^ г ^ а} верхней
границы слоя при действии вне её в области {а ^ г < +оо}
давления рс{г) (рс{г) —> О при г —> +оо), т.е. решение задачи с
условиями на верхней границе слоя (z = h) вида:
41} = 0, 0 < г < а,
ail)=Pc(r), a<r<+oo, D.33)
туф = т$ = 0, 0 ^ г < +оо.
Решение этой задачи строится методом, изложенным в 4.2.1.
На втором этапе полученная функция д(г) используется при
формулировке условия сопряжения штампа с верхней границей
слоя (z = h). Распределение давления р(г) в области контак-
контакта г ^ а ищется в классе кусочно-постоянных функций. Для
этого область контакта разбивается на N колец толщины Аг,
в каждом из которых функция р(г) постоянна, т.е. p(r) = pj,
(rj-i < r < rj, го = 0, rj = jAr, j = 1,2, ...,N). Значения pj
находятся из решения следующей системы линейных уравне-
уравнений, полученной из граничных условий D.33) и условия равно-
равновесия D.32):
f ] ^] = Л (гг), i = 1,2,..., N - 1, D.34)
N
где /i(r) = (f{r) - f(a)j - (g(r) - g{a)j, причём представле-
представление правой части в виде разности функций исключает из рас-
рассмотрения неизвестную постоянную D в соотношениях D.31).
Коэффициенты х:- определяются из решения первой основной
задачи для двухслойного упругого полупространства (см. 4.2.1)
и представляют собой разницу нормальных смещений колец с
229
внешними радиусами г, и гм при действии единичного давления
внутри кольца с внешним радиусом rj.
Если /i(r) - гладкая функция, что имеет место, например,
когда форма штампа описывается гладкой функцией /(г), для
определения неизвестного радиуса а площадки контакта исполь-
используется дополнительное условие:
PN=Pc{a). D.36)
Неизвестный радиус а площадки контакта при заданной нагруз-
нагрузке Р, действующей на штамп, определяется методом итераций.
Точность полученного решения проверяется путем увеличения
количества разбиений N площадки контакта.
Заметим, что аналогичным образом рассчитываются давле-
давления и в задаче о внедрении в двухслойное упругое основание
упругого индентора. В этом случае в соотношениях D.34) ко-
коэффициенты >г- в качестве дополнительного слагаемого будут
содержать величины, описывающие смещения границы упругого
индентора.
После определения контактных давлений внутренние напря-
напряжения рассчитываются в соответствии с алгоритмом, изложен-
изложенным в 4.2.1.
Описанный выше метод был использован для анализа кон-
контактных давлений и внутренних напряжений при внедрении в
двухслойное упругое основание штампа в форме параболоида
вращения, а также штампа с плоским основанием и скруглён-
скруглёнными кромками (см. рис. 4.9). Форма штампа в общем случае
описывалась функцией:
Г 0, 0 < г ^ с,
/(г) = 4 (г_сJ D.37)
Эта функция соответствует штампу в форме параболоида вра-
вращения при с = 0 и штампу с плоским основанием при R —> 0. Ис-
Использование функции D.37) позволяет описать различные фор-
формы неровностей шероховатой поверхности.
Анализ уравнений задачи и граничных условий позволил за-
заключить, что решение зависит от следующих безразмерных па-
параметров:
230
1,0
0,5
0,0
0,0
0,4
0,8
rlc
1,6
Рис. 4.10. Распределение контактных давлений под штампом с плос-
плоским основанием и скруглёнными кромками при р* = 0,2Е2, х = 20,
Рс = о, vi = 0,3, v2 = 0,4, R = 0,4, и Л -> оо A), h = 1 B), h = 0,5 C,
3'); Jfe = 100 A, 2, 3), к = 0,05 C')
X = Е1/Е2 - отношения модулей упругости покрытия и
основания,
^1, ^2 ~ коэффициентов Пуассона покрытия и основания,
h = h/L - относительной толщины покрытия,
R = R/L - относительного радиуса скругления кромки,
к — kL/p* - параметра, характеризующего степень сцеп-
сцепления покрытия с подложкой,
р*/Е% - безразмерного характерного давления,
где р* = Р/ (тгЬ2), L = R для штампа в форме параболоида
вращения и L = с для штампа с плоским основанием и скруг-
скруглёнными кромками. Величина пригрузки рс определялась по от-
отношению к величине р*.
На рис. 4.10 и 4.11 приведены результаты расчёта контакт-
контактных и внутренних напряжений для штампа с плоским основани-
основанием и скруглёнными кромками при отсутствии пригрузки, т. е. в
случае рс(г) = 0 (г > а).
231
На рис. 4.10 показаны распределения контактных давлений
под штампом, внедряемым в относительно твёрдое покрытие
различной толщины. Для толстого покрытия (кривая 1) распре-
распределение давления подобно тому, которое имеет место при внедре-
внедрении штампа в упругое полупространство, характеризуемое мо-
модулем упругости Е\. Чем тоньше покрытие, тем выше давле-
давления на периферии зоны контакта и больше радиус а площадки
контакта; давление же в центральной части площадки контакта
уменьшается и становится равным нулю для относительно тон-
тонких покрытий. В этом случае контакт имеет место внутри коль-
кольцевой области (кривая 3). С увеличением значений х и Р*7-^2
кольцевая область контакта имеет место и для более толстых
покрытий. Заметим, что в случае относительно мягких покры-
покрытий (х < 1) область контакта при любой толщине слоя имеет
форму круга.
Сравнение кривых 3 и 3' на рис. 4.10 показывает, что с умень-
уменьшением параметра к, т.е. с уменьшением сцепления покрытия с
основанием, максимальное значение контактных давлений пада-
падает, а размер площадки контакта растёт. Чем толще покрытие,
тем меньше влияние параметра А; на контактные характеристики.
Изолинии максимальных касательных напряжений ттах(г, z)
и компоненты ar(r, z) напряжений внутри покрытия @ < z < h)
и основания [z < 0) для значений параметров, соответствующих
кривой 2 на рис. 4.10, приведены на рис. 4.11,а и # соответствен-
соответственно. Функция ттах(г,г) внутри покрытия имеет два локальных
максимума: ттах = 1Др*, {z = 0, г/с = 0,73) и ттах = 1,31р*
(z = h, г/с = 0,69); и локальный минимум rmax = 0,21p* (z =
= 0,45h, г = 0). Увеличение толщины покрытия приводит к
появлению локального максимума внутри покрытия на оси сим-
симметрии штампа (г = 0, 0 < z < h), величина которого превосхо-
превосходит максимумы на границах слоя z — 0 и z = h. При больших
значениях h (h —> +оо) значение этого максимума совпадает с
максимумом функции ттах(г, z) при внедрении штампа в одно-
однородное упругое полупространство.
Функция oT{r,z) внутри покрытия имеет локальный макси-
максимум оТ = 1,5р* (z = 0, г/с = 0,7) и минимум ar = -2,3p* (z = h,
г/с = 0,88). Это означает, что тонкое твёрдое покрытие при
232
б
Рис. 4.11. Изолинии функций ттах(г, z) (а) и ar(r,z) (б), построенные
при значениях параметров, соответствующих кривой 2 на рис. 4.10
233
1,0
0,5
0,0
pip'
2' ¦
3 л
1 i
1
/
0,0
0,4
0,8
rlc
1,6
Рис. 4.12. Распределение давления под штампом с плоским основани-
основанием и скруглёнными кромками при х = 0,05, v\ = 0,4,1/2 = 0,3, R = 2/3,
к = 100 и Рс = 0 A, 2, 3), рс = р, A', 2'), Л = 0,05 A, 1'), Л = 2 B, 2'),
Л = 10 C)
нагружении штампом подвержено изгибным деформациям. Для
более толстых покрытий эти деформации становятся незначи-
незначительными. Расчёты позволили также установить, что уменьше-
уменьшение сцепления покрытия с основанием, характеризуемое величи-
величиной параметра к, увеличивает изгибные напряжения на границе
раздела слоя и основания.
На рис. 4.12 показаны распределения давлений при внедрении
штампа в относительно мягкие покрытия различной толщины.
Сравнение кривых 1, 2 (рс = 0) и 1', 2' позволяет оценить влия-
влияние на контактные характеристики пригрузки вне штампа, ко-
которая рассматривалась равной р* и приложенной внутри кольца
Bс ^ г ^ 4с). Наличие пригрузки оказывает существенное вли-
влияние на характер распределения давлений и размер площадки
контакта, особенно в случае относительно толстого покрытия.
На основании результатов расчётов можно заключить, что для
относительно толстых покрытий (кривая 2) распределение дав-
давлений близко к тому, которое имеет место для однородного полу-
полупространства (кривая 3). Как уже отмечалось, подобный резуль-
результат имеет место и для относительно твёрдых покрытий (х > !)•
При уменьшении толщины слоя давления в центральной час-
234
ти области контакта, взаимодействующей с плоской поверхнос-
поверхностью индентора, становятся более равномерными. Этот резуль-
результат подтверждает применимость модели Винклера для анализа
контактных характеристик в случае относительно тонких мяг-
мягких покрытий.
Полученные результаты могут быть использованы для про-
прогнозирования характера разрушения покрытия. В частности,
концентрация растягивающих напряжений (оу < 0) на грани-
границе раздела относительно тонких твёрдых покрытий с основа-
основанием может вызвать зарождение вертикальных трещин. Высо-
Высокие амплитудные значения максимальных касательных напря-
напряжений ттах в поверхностном слое приводят к усталостному раз-
разрушению покрытий.
4.2.3. ЗАДАЧА ДИСКРЕТНОГО КОНТАКТА ДЛЯ
ДВУХСЛОЙНОГО УПРУГОГО ОСНОВАНИЯ
С целью анализа совместного влияния параметров рельефа по-
поверхности и характеристик покрытия на напряжённое состояние
взаимодействующих тел рассмотрим задачу дискретного кон-
контакта для двухслойного упругого полупространства.
Постановка задачи. Пусть периодическая система од-
одноуровневых взаимосвязанных штампов, форма контактирую-
контактирующих поверхностей которых описывается функцией z = /(г),
взаимодействует с двухслойным упругим полупространством
(рис. 4.13). Оси штампов перпендикулярны границе полупро-
полупространства, а точки их пересечения с границей расположены в
плоскости z = 0 в узлах гексагональной решётки с шагом /. По-
Поместим начало полярной системы координат в точку пересечения
оси симметрии произвольного штампа с плоскостью z = 0.
Условия на верхней границе слоя (z = 0) имеют вид:
ai1} =0, г$ши г = 1,2,3,..., D.38)
т!$ = 0, t^J =0, 0 < r < +00,
235
Рис. 4.13. Схема контакта периодической системы инденторов и двух-
двухслойного упругого основания
где fj - радиус-вектор центра пятна контакта щ. Предполага-
Предполагается, что все штампы находятся в одинаковых условиях нагру-
жения, поэтому все пятна контакта щ имеют одинаковый ра-
радиус а. Нагрузка Р, действующая на каждый штамп, связана с
номинальным давлением р соотношением (см. главу 1)
D.39)
и имеет место уравнение равновесия
а 27г
= p{r)r drdtp,
о о
D.40)
где р(г) - контактное давление.
На границе раздела (z = h) слоя с основанием выполняются
236
условия следующие условия:
тA) _ _B) _ к ( A) _ B)\ Г44П
A) _ B) A) _ B)
Ua — Uq , Uz ~~ 'U'Z j
представляющими собой соотношения D.20), в которых послед-
последнее условие заменено на uz = uz .
Вспомогательная задача. Воспользовавшись методом ло-
локализации, сформулированным в главе 1, сведём рассматривае-
рассматриваемую периодическую задачу к следующей осесимметричной зада-
задаче, для которой условия на верхней границе слоя (z = 0) имеют
вид:
«*(»•) = /W» 0 < г < а,
azl) = 0, а < г < До,
(D D-42)
<тГ=р, Ro<r <+oo,
Тг(г} = Т^ = 0, 0 < Г < +00,
т. е. рассматриваются реальные условия сопряжения для произ-
произвольного фиксированного пятна контакта с центром в точке О, а
действие остальных штампов заменяется номинальным давлени-
давлением р, распределенным равномерно в области г > i?o- Радиус До
выбирается таким образом, чтобы удовлетворить условиям рав-
равновесия внутри круга г < До, т. е. тгЩр = Р, или, принимая во
внимание соотношение D.39), получаем
D.43)
Метод решения вспомогательной задачи с граничными усло-
условиями D.41) и D.42) изложен выше. Заметим только, что при
определении деформированной формы д(г) верхней границы уп-
упругого слоя за счёт пригрузки р при г > До для исключения
237
интегрирования по бесконечной области вместо условий D.33)
рассматривались следующие граничные условия при z = 0:
A) (-р, 0<r<R0,
<7Г'.= S D.44)
| 0, Ro < г < +оо.
Решение д(г) задачи с граничными условиями D.44) связано с
функцией д(г) соотношением
д = д{г) + С, D.45)
где С - произвольная постоянная, не оказывающая влияния на
решение системы уравнений D.34).
В главе 1 показано, что точность решения задачи дискретно-
дискретного контакта, полученного с помощью метода локализации, повы-
повышается с увеличением числа слоев штампов, на которых условия
контакта формулируются точно. С целью оценки точности по-
полученного на основании рассмотрения вспомогательной задачи
решения мы сравнили его с решением, получающимся, если при
постановке задачи принять во внимание ещё один слой штам-
штампов (в рамках осесимметричной постановки последний модели-
моделировался кольцом радиуса / и ширины 2а, внутри которого при-
прикладывалось эквивалентное давление). Результаты расчётов для
системы сферических штампов показали (см. [52]), что разница
в рассчитанных двумя способами радиусах пятна контакта при
самом плотном расположении контактных зон не превышает 8%.
Полученное в результате решения контактной задачи распре-
распределение давления на каждом пятне контакта используется затем
для определения методом суперпозиции напряжённого состояния
внутри упругого слоя и упругого основания.
Анализ результатов. Численные расчёты проводились
для системы сферических штампов (/(г) = г2/BЛ), R - ради-
радиус кривизны штампа), расположенных в узлах гексагональной
решётки с шагом I. Установлено, что контактные характеристи-
характеристики и напряжённое состояние внутри тел зависят от следующих
безразмерных структурных параметров: относительного модуля
упругости поверхностного слоя \ = Е\/Е2, безразмерного рас-
расстояния между инденторами I = 1/R, относительной толщины
238
0,0 0,2 0,4 rll 0,0 0,4 0,8 zll
Рис. 4.14. Распределения контактных давлений (о) и максимальных
касательных напряжений вдоль оси Oz {б) в случае относительно
твёрдого покрытия (х = 10) при Р/Е2 = 0,1, v = 0,3,1 = 0,5 и h -> +00
A), Л = 1 B), Л = 0,5 C), h = 0,25 D), h = 0 E); E') соответству-
соответствует Л = 0 и Г-* +оо
слоя h = h/l, а также от безразмерного номинального давле-
давления Р/Е2 и коэффициента Пуассона и (в расчётах полагалось,
ЧТО V\ = V2 = v).
Для удобства анализа результатов оказалось целесообраз-
целесообразным выделить два типа упругих покрытий: относительно твёр-
твёрдые (х > 1) и относительно мягкие (х < 1)-
Твёрдые покрытия. Кривые распределения давле-
давления р{р), где р = г/1, на единичном пятне контакта при
различной толщине покрытия (кривая 5 иллюстрирует слу-
случай, когда покрытие отсутствует), и постоянной плотности
расположения штампов (/ = 0,5) представлены на рис. 4.14,а.
Результаты показывают, что с уменьшением толщины по-
покрытия максимальное контактное давление падает, а радиус
площадки контакта возрастает. Однако для каждой фикси-
фиксированной толщины слоя этот радиус меньше того, который
получается в расчётах без учёта влияния соседних штампов,
т. е. для уединенного единичного пятна контакта. Такой же
вывод следует и из анализа решения задачи для однородного
полупространства (кривые 5 и 5' на рис. 4.14,а).
239
Анализ влияния параметра х на контактные характеристики
показал (см. [52]), что с увеличением параметра х радиус а/1
площадки контакта уменьшается, а максимальное давление р@)
на ней возрастает.
Рассмотрим влияние параметров h (рис. 4.14,6') и / (рис. 4.15)
на распределение максимальных касательных напряже-
напряжений ттах(?) (? = z/l) вдоль осей Oz, проходящей через центр
пятна контакта, иО'г, проходящей через центр ненагруженной
зоны. Как показывают расчёты, общей для твёрдых покрытий
закономерностью является скачкообразное уменьшение значе-
значений ттах на границе раздела покрытия и основания (z = h), так
что T^ix - Tmlx > 0, где TiL - значения ттах на границе раздела
со стороны покрытия (г = 1) и основания (г = 2) соответствен-
соответственно. Функция ттах(?) имеет, как правило, два максимума: один
внутри упругого слоя или на поверхности z = О для очень
тонких покрытий (кривая 4 на рис. 4.14,tf), второй - на границе
раздела слоя и полупространства ? = h. При этом соотношение
между максимумами меняется при изменении толщины слоя
(см. рис. 4.14,б): для относительно толстых слоев (кривые 1
и 2) наибольшее значение ттах имеет место внутри слоя, для
более тонких (кривые 3 и 4) - на границе покрытие-основание.
На величину и положение наибольшего максимума функ-
функции ттах(?) на оси ОС, оказывает значительное влияние пара-
параметр I, характеризующий расстояние между пятнами контакта,
что иллюстрируется кривыми 1-3 на рис. 4.15. Там же приве-
приведены графики функции ттах(() вдоль оси О'С, (кривые 1' и 3',
рассчитанные для тех же значений параметров, что и кривые 1
и 3 на этом рисунке). Сопоставление графиков позволяет за-
заключить, что при фиксированной толщине слоя h с уменьше-
уменьшением параметра / (и, следовательно, а/К) максимальная раз-
разница Дттах(С) значений максимальных касательных напряже-
напряжений ттах(?) на фиксированной глубине С, уменьшается. Подобный
вывод был сделан для однородного упругого полупространства в
главе 1. При больших значениях параметра I функция &.ттж{(,)
близка к функции ттах(?).
Мягкие покрытия. Для относительно мягкого покры-
покрытия (х < 1) при расчётах полагалось, что отношение р/Е2 =
240
о
0,0 0,1 0,2 0,3 0,4 zll 0,6
Рис. 4.15. Распределение максимальных касательных напряжений
вдоль осей ОС A-3) и О'С, {V и 3') для твёрдого покрытия (х = 10)
при р/Е2 = ОД, h = 0,5 и I = 0,25 A и 1'), I = 0,5 B), Г = 2 C и 3')
= 0,005 и v = 0,3.
Полученные в результате расчёта распределения контакт-
контактных давлений р(р)/р и максимальных касательных напряже-
напряжений rmax(C)/p Для х — 0,1 представлены на рис. 4.16 и 4.17.
Анализ распределения контактных давлений для слоев разной
толщины (рис. 4.16,а) показывает, что чем толще слой, тем
больше радиус а пятна контакта и меньше максимальное кон-
контактное давление. При этом следует отметить, что влияние
свойств основания на контактные характеристики становится
пренебрежимо малым, если толщина покрытия превосходит не-
некоторое критическое значение h*, зависящее от параметров х и I-
Этот вывод следует из сравнения кривых 2, 3 и 4 на рис. 4.16,а.
Аналогичные расчёты, проведенные для других значений пара-
параметра х < 1 показывают, что с уменьшением х критическое
значение h* растёт. Заметим, что для относительно толстого
слоя (h 3> 1) полученные зависимости совпадают с кривыми,
рассчитанными для однородного упругого полупространства.
241
4 -
О
0,0 0,2 rll 0,4 0,0 0,5 1,0 zll
Рис. 4.16. Распределение контактных давлений (а) и максимальных
касательных напряжений вдоль оси ОС, (б) для мягкого покрытия (х =
= 0,1) при р/Е2 = 0,005, I = 0,5, к = 100 и h = 0,1 A), h = 0,5 B),
h = 1 C), Л -> +оо D)
Анализ распределение максимальных касательных напряже-
напряжений в слое и основании позволяет сделать вывод, что для отно-
относительно мягких слоев, как и для относительно твёрдых, функ-
функция ттах имеет скачок на границе раздела слоя с основанием.
Максимальные значения функции ттах достигаются внутри по-
покрытия или внутри основания, в зависимости от толщины по-
покрытия к. Для толстых покрытий функция ттах имеет максимум
внутри покрытия, а для более тонких (кривая 1) - внутри осно-
основания.
На рис. 4.17 представлены распределения максимальных ка-
касательных напряжений rmax(() вдоль осей ОС, (кривые 1-3) и О'С,
(кривые 1' и 3') при разных значениях параметра I. Так же, как
и в случае х > 1, перепад значений rmax(C) на фиксированной
глубине уменьшается при сближении штампов (уменьшении па-
параметра /).
Следует отметить, что распределение напряжений внутри
мягкого покрытия стремится к равномерному с уменьшением па-
параметра h/a.
Таким образом, характер напряжённого состояния внутри
242
о
0,0 0,2 0,4 zll
Рис. 4.17. Распределение максимальных касательных напряжений
вдоль осей ОС (кривые i-З) и O'z (кривые 1' и 3') для мягких покры-
покрытий (х = 0,1) при р/Е2 = 0,005, h = 0,5, к = 100 и I = 0,1 (кривые 1
и 1'), [=0,5 (кривая 2), / = 1 (кривые 3 и 3')
слоя и полупространства, а также контактные характеристики
(радиус пятна контакта и распределение контактных давлений)
существенно зависят от безразмерных параметров, связанных с
относительной нагрузкой, относительными механическими свой-
свойствами слоя и основания, с относительной толщиной покрытия
и степенью его сцепления с основанием, а также от параметров
рельефа поверхности.
Дискретность области контакта меняет картину на-
напряжённого состояния, особенно в случае тонких и относительно
твёрдых слоев. Поэтому обычно используемая классификация
покрытий по толщине - относительно тонкие (h/a < 1) и
толстые (h/a > 1) - не приемлема при анализе распределения
напряжений в контакте шероховатых поверхностей. В рассмот-
рассмотрение необходимо ввести ещё один геометрический параметр,
связанный с отношением расстояния между пятнами контакта
к толщине покрытия.
Полученные результаты могут быть использованы при про-
прогнозировании характера разрушения (поверхностный износ, от-
243
слаивание, подповерхностное разрушение) покрытия, а также
мест зарождения микротрещин, во многом определяемых мес-
местами и величиной концентрации напряжений в поверхностном
слое. Предсказываемое теорией отслаивание относительно тон-
тонких твердых покрытий вследствие возникновения отрицатель-
отрицательных нормальных напряжений на границе раздела наблюдалось
и в экспериментах [193].
При относительных перемещениях тел с покрытиями, име-
имеющих шероховатые поверхности, вследствие дискретности кон-
контакта внутри покрытия, основания и на границе раздела возни-
возникает циклически меняющееся поле напряжений. На основании
рассчитанных выше амплитудных значений напряжений в раз-
разных точках покрытия и основания методом, изложенному в гла-
главе 6, можно определить скорость накопления повреждённости
внутри контактирующих тел и изучить кинетику усталостно-
усталостного разрушения тел с покрытиями.
Возможно также применение результатов для выбора опти-
оптимальных по критериям долговечности механических и геомет-
геометрических параметров покрытий, наносимых на поверхности с
заданными свойствами и работающих при разных условиях на-
гружения.
Глава 5
РОЛЬ ТОНКИХ ПОВЕРХНОСТНЫХ
СЛОЕВ ПРИ ТРЕНИИ
В этой главе изучается роль тонких поверхностных слоев в кон-
контакте скольжения и качения в условиях граничной и гидроди-
гидродинамической смазки. Решение этих задач особенно важно для из-
изучения зависимости силы трения от скорости для сопряжений,
работающих в различных режимах смазки, или имеющих на по-
поверхности твёрдые смазочные покрытия.
5.1. КОНТАКТ КАЧЕНИЯ И СКОЛЬЖЕНИЯ
Взаимодействие поверхностей, покрытых тонкими твёрдыми
слоями или плёнками, исследуется путём анализа контактных
задач для слоистых сред. При этом важно отметить, что в кон-
контактах качения и скольжения реологические свойства поверх-
поверхностных слоев оказывают существенное влияние на контакт-
контактные характеристики взаимодействующих тел и силу трения, что
учитывается при постановке контактных задач путём моделиро-
моделирования поверхностного слоя вязкоупругой средой.
В работах [150, 203] рассмотрена задача в плоской постановке
о движении нагрузки по границе вязкоупругой полосы, сцеплен-
сцепленной с вязкоупругой полуплоскостью, и исследованы деформации
и напряжения сдвига в слое и основании. Контакт качения двух
цилиндров, покрытых вязкоупругими слоями, изучался теорети-
теоретически и экспериментально в [152, 199]. В этих работах развиты
численные методы определения напряжений в контактных зада-
задачах для слоистых упругих и вязкоупругих тел.
Ниже предлагается аналитический метод исследования роли
поверхностного вязкоупругого слоя при качении или скольжении
индентора по упругому основанию.
245
Рис. 5.1. Схема контакта цилиндра с вязкоупругим слоем, сцепленным
с упругим основанием
5.1.1. МОДЕЛЬ КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ
Рассмотрим контактную задачу в плоской постановке для упру-
упругого цилиндра и основания, состоящего из вязкоупругой поло-
полосы толщины h, сцепленной с упругой полуплоскостью (рис. 5.1).
Цилиндр катится или скользит по основанию с постоянной ли-
линейной скоростью V и угловой скоростью ш. Контактирующая
поверхность цилиндра описывается функцией f(x) = —x2/BR)
(R - радиус цилиндра).
Введём неподвижную (х',у') систему координат, связанную
с основанием, и подвижную {х,у), связанную с движущимся ци-
цилиндром. При этом
х' = х + Vt, у' =
E.1)
При равномерном движении цилиндра движение среды мож-
можно считать установившимся по отношению к системе коорди-
координат (х, у). В этой системе координат смещения и напряжения
246
не зависят явно от времени t и являются функциями коорди-
координат (х,у).
Граничные условия. Следуя Рейнольдсу [223], разобьём
область контакта (—а, Ь) на подобласти скольжения (S) и сцеп-
сцепления (А). В подобласти E) трение скольжения моделируется
законом Кулона-Амонтона
\т(х)\ = fip(x), y = 0,xeS, E.2)
где т(х) и р(х) - соответственно тангенциальные и нормальные
напряжения на площадке контакта, причем направление танген-
тангенциальных напряжений противоположно направлению скорости
проскальзывания.
В подобласти (А) равны скорости контактирующих точек
цилиндра и вязкоупругого слоя. Поэтому в системе коорди-
координат (х1, у') тангенциальные смещения щ и и соответственно то-
точек цилиндра и основания удовлетворяют соотношению:
E.3)
at at
Уравнение E.3) в системе координат (х, у) имеет вид:
du\ du л , .
~~dt + arx'= ' */ = 0'жеЛ' E-4)
где 5 - величина относительного проскальзывания:
^. E.5)
Кроме того, в подобласти (А) нормальные и тангенциальные на-
напряжения связаны неравенством:
\т(х)\^ю(х). E.6)
Заметим, что в случае полного скольжения закон Кулона-
Амонтона E.2) имеет место на всей площадке контакта (—а, 6).
247
Из условия контактирования следует соотношение, выполняю-
выполняющееся для всех точек х G (—а, 6):
х2
vi(x) + v2(x) + v3(x) = D-~, E.7)
где v\, V2 и vs - нормальные перемещения граничных точек ци-
цилиндра, упругой полуплоскости и слоя соответственно (счита-
(считающимися положительными для каждого тела), D - внедрение
цилиндра в основание.
Предполагается, что слой сцеплен с полуплоскостью и на гра-
границе раздела у = h имеют место следующие граничные условия:
u(x,h~) = u{x,h+), v(x,h~) = v(x,h+),
p(x,h~~) = p(x,h+), r(x,h~) = r(x,h+).
Модель вязкоупругого слоя. В предположении, что тол-
толщина h вязкоупругого слоя много меньше ширины (а 4- Ь) пло-
площадки контакта, будем моделировать его нормальную и танген-
тангенциальную податливость, используя одномерную модель Макс-
Максвелла, а именно:
'(И ?(Н (S9)
где из и из - касательные и нормальные смещения границы
слоя (у = 0) соответственно, (') обозначает производную по вре-
времени. Как известно, модель Максвелла представляет собой пру-
пружинку с модулем Еп (Ет), последовательно соединённую с дем-
демпфером вязкости ЕпТп (ЕТТТ). В этой модели Еп (Ет) и Тп (Тт) -
модуль упругости и время релаксации соответственно в направ-
направлении оси Оу (Ох).
В системе координат (ж, у) соотношения E.9) имеют вид:
du3 _ h Г т(х) dr(x)
[ +
dx ET [ V?T+ dx
dv3 _ h Г р(х) , dp(x)
248
В рассматриваемой модели предполагается, что нормальные и
тангенциальные напряжения на верхней границе слоя (у = 0) и
на границе между слоем и упругой полуплоскостью (у = h) име-
имеют одинаковые значения. Поэтому градиент смещений границы
упругих тел (цилиндра (г = 1) и упругой полуплоскости (г = 2))
определяется следующими соотношениями [107]:
йщ _ A - 2ц) A + щ) 2 A - vf) 'г ф>)
лГ-~ Ek p[x)" *% J ^^dx' EЛ2)
dvi_ _ A - 2vj) A + щ)
dx E;
Уравнения E.10)-E.13) вместе с граничными условиями E.2),
E.4) и E.7) используются для определения нормальных и тан-
тангенциальных напряжений в зоне контакта (—а, Ь).
5.1.2. РАСПРЕДЕЛЕНИЕ КОНТАКТНЫХ ДАВЛЕНИЙ
Для упрощения расчётов пренебрежём влиянием тангенциаль-
тангенциальных контактных напряжений на нормальные. Тогда, используя
соотношения E.7), E.11) и E.13) (последнее рассматривается
при т(х) = 0) и вводя новую переменную ?, связанную с х ра-
равенством
х=6-« + а+^ E14)
получим:
1
Рп ~чt\ _ г <¦, i е\
+ 0, E.15)
-1
где
E.16)
249
hirE* ЬжЕ* т a + b b-a
Принимая во внимание условие равенства нулю давления на
концах (х = —а и х = Ь) области контакта, т. е. р{—1) = рA) = О,
и используя следующие соотношения
-1 -1
1
преобразуем уравнение E.15) к уравнению Фредгольма второго
рода
E.19)
где
F(Z)=p'(Z). E.20)
Интегрируя уравнение E.19) по сегменту [—1,1], получим
E.21)
+A - ?') ln(l - ?') - an?' - 2] d? =
250
Соотношение E.21) позволяет исключить параметр е из уравне-
уравнения E.19) и преобразовать его к виду:
1
[in К - ? ?
L
Л L 2 2 E.22)
# - ^F@ = l-L.
Из условия равновесия нормальных сил, приложенных к цилинд-
цилиндру, следует, что искомая функция F(?) удовлетворяет также со-
соотношению
p=^&=-4tm<K, <5-23)
где Р - безразмерная вертикальная нагрузка, приложенная к ци-
цилиндру (см. рис. 5.1).
Уравнения E.20)-E.23) используются для определения без-
безразмерных величин контактного давления р(?), размера L и
смещения е области контакта, а также максимального внедре-
внедрения Атах цилиндра в вязкоупругий слой:
-1
— 1
? = _ * ..._ _ E-24)
-l
л уз(х) т
Дшах = max ——- = L ¦ max
-a<x<b К —Kf<l
251
где
Заметим, что если пренебречь упругостью цилиндра и ос-
основания и определить давление в области контакта из решения
уравнения E.11) с граничными условиями E.7), то получим сле-
следующее выражение для безразмерного контактного давления:
exp
shi
С i
E.25)
1,5
1,0
0,5
0,0
-1,0 -0,5 0,0 E, 1,0
Рис. 5.2. Распределение контактных дав-
давлений, рассчитанное из уравнений E.22)
и E.23) (сплошные линии), и выраже-
выражения E.25) (штриховые линии), при /Зп =
= 0,1, L = 0,1 и ап = 1 A и 1'), а„ = 10 B
и 2')
/
/
/
/
/
*¦ ч
' ; ч
/" : N
/¦ :
/ j
/ j
/ :
t '¦
¦¦¦'/ у i -¦-¦¦""
\
\
v
X
\
?•'
где ? - число Деборы,
представляющее собой
отношение времени
релаксации Тп матери-
материала слоя ко времени,
которое требуется для
прохождения элемен
том половины ширины
площадки контакта,
т.е. (а + Ь)/2 (см. [66]):
Выражение
a + b
E.25)
определяет распре-
деление контактных
давлений в случае,
когда податливость
слоя в нормальном направлении много больше податливостей
основания и цилиндра, т.е. Еп/Е* <SC 1.
На рис. 5.2 представлены графики функции контактного дав-
давления р(?)/ро, где ро — Е*L/2 - максимальное контактное дав-
давление Герца, построенные при разных значениях параметра ап.
252
Сплошные линии соответствуют общему случаю контактного
взаимодействия упругих тел при наличии между ними вязко-
упругого слоя, штриховые линии построены по формуле E.25)
в случае пренебрежения упругими свойствами индентора и ос-
основания. Расчёты проводились при постоянной ширине площад-
площадки контакта L = 0,1, при этом варьировалась нагрузка, дейст-
действующая на индентор. Результаты показывают, что с уменьше-
уменьшением скорости V перемещения индентора, т. е. с увеличением
параметра ап (см. E.17)), эпюра распределения давлений р(?)
становится более несимметричной. При фиксированном размере
площадки контакта и заданных вязкоупругих характеристиках
слоя контактные давления и их максимальные значения сущест-
существенно зависят от упругих свойств индентора и основания при
малых значениях параметра ап (больших скоростях V). Однако
при уменьшении скорости (ап = 10), различие между распре-
распределением давления в обоих случаях становится пренебрежимо
малым. Таким образом, вязкоупругий слой оказывает определя-
определяющее влияние на распределение контактных давлений при низ-
низких скоростях движения.
На рис. 5.3 представлены графики зависимостей безразмер-
безразмерной полуширины L/Lq области контакта (Lo - безразмерная
полуширина области контакта в задаче Герца, Lq = у2Р ), её
смещения е = (Ь — а)/(Ь + а) и максимального внедрения Атах
цилиндра в вязкоупругий слой от параметра Eп/ап = TnV/R,
зависящего от времени релаксации Тп и скорости V, при двух
различных значениях параметра (Зп. Заметим, что параметр /Зп
зависит от толщины слоя и относительных упругих характе-
характеристик слоя и основания. На основании результатов расчётов
можно сделать вывод, что с увеличением параметра TnV/R по-
полуширина площадки контакта уменьшается и стремится к по-
постоянному значению (L — l,49L0 и L = 2,71L0 при (Зп = 0,1
и /3„ — 1 соответственно). При малых значениях парамет-
параметра TnV/R длина площадки контакта возрастает существенно,
особенно с увеличением параметра Eп (см. рис. 5.3,а). С умень-
уменьшением времени релаксации Тп и уменьшением скорости V дви-
движения индентора возрастает смещение е площадки контакта
(см. рис. 5.3,6") и максимальное внедрение Атах цилиндра в вяз-
253
5,0
LILn
3,0
1,0
1,0
b-a
b + a
0,5
0,0
0,10
Amax
0,05
0,00
0,001
0,01
0,1
TnVIR
Рис. 5.3. Зависимости размера (а) и смещение (б) области контакта,
а также максимального внедрения цилиндра в вязкоупругий слой (в)
от параметра TnV/R при Р = 0,001 и [Зп = 1 A), (Зп = 0,1 B)
254
коупругий слой (см. рис. 5.3,в), что обусловлено проявлением
вязкоупругих свойств поверхностного слоя. При увеличении вре-
времени релаксации или скорости V смещение е площадки контакта
становится пренебрежимо малым для всех значений парамет-
параметра/3„.
Проведённый анализ распределения контактных давлений
справедлив как в случае скольжения, так и качения упругого
цилиндрического индентора по границе упругого основания, по-
покрытого тонким вязкоупругим слоем.
5.1.3. РАСПРЕДЕЛЕНИЕ ТАНГЕНЦИАЛЬНЫХ
НАПРЯЖЕНИЙ НА ПЛОЩАДКЕ КОНТАКТА
ПРИ КАЧЕНИИ
Как было отмечено, при скольжении цилиндра по границе тела
с покрытием тангенциальные контактные напряжения т(х) свя-
связаны с контактным давлением р(х) соотношением \т(х)\ — /^р(х).
В задаче о качении, если известно контактное давление, тан-
тангенциальные напряжения в области контакта могут быть полу-
получены на основании соотношений E.2), E.4), E.8), E.10) и E.12).
В области сцепления (А) имеет место следующее интегральное
уравнение для определения функции т(х):
2
2 / <х') dx< -
irE* J x - x' ~
VETTT v ' Er dx тгЕ*
E.26)
), x e A,
где
„ nE*
Для решения этого уравнения используем метод, изложенный
выше (см. 5.1.2) при анализе контактных давлений. Введём сле-
следующую безразмерную функцию переменной ? (см. E.14)) и
255
параметры:
' b — a a + b
hnE* hnE*
E.27)
ar ~ 2VETTT' ^т ШЁТ '
Тогда уравнение E.26) приводится к виду:
?>(?)= 0, ее^{, E-28)
где
-1
Кроме того, в области сцепления (А^) тангенциальные напря-
напряжения удовлетворяют неравенству |т(?)| < МР(О> следующему
из E.6).
Соотношение E.2) служит для определения тангенциальных
напряжений в областях проскальзывания (S). Учитывая также,
что в этих зонах тангенциальные напряжения противоположны
направлению проскальзывания, получим соотношение
i \ ( \ (du2 dui _l duz Л (к Qn^
r(x) = №{х) ^[-^~^ + ^-SJ. E.30)
Подставляя E.10) и E.12) в выражение E.30) и используя обо-
обозначения E.27) и E.29), придём к следующему соотношению в
области проскальзывания (S^):
r(?) = w@sgn </>(?), ^% E.31)
В точках & перехода из одной зоны в другую имеет место условие
непрерывности
, « = 1,2,...,*, E.32)
256
где (к +1) - общее количество зон сцепления и проскальзывания.
Уравнения E.28), E.31) и E.32) используются для определе-
определения тангенциальных напряжений в области контакта, а также
расположения и размеров зон сцепления и проскальзывания. Для
численного анализа полученных уравнений применялся итераци-
итерационный процесс.
Задача определения тангенциальных напряжений существен-
существенно упрощается в предположении, что цилиндр и основание име-
имеют одинаковые упругие постоянные ($ = 0) и что модуль упру-
упругости слоя много меньше модуля упругости цилиндра и основа-
основания, т.е. Ет/Е* «С 1. В этом случае уравнения E.28) и E.31)
сводятся к следующим:
r(O-Cr^ = -B, UAb E.33)
?е% E.34)
где
- =2VTL 28VETTT
^т а + Ь ' hnE* '
Решение дифференциального уравнения E.33) имеет вид
Ст
E.35)
где С - некоторая постоянная. В зонах сцепления (А^) функ-
функция f (?) удовлетворяет неравенству
НО < №(()¦ E-36)
Опишем процедуру определения расположения зон сцепления
и проскальзывания на площадке контакта. Предположим, что
начальная точка (х = 6) площадки контакта совпадает с правым
концом зоны сцепления. Тогда из соотношений E.34), E.35) и
условия непрерывности напряжений, т.е. тA) = 0, получим
[ и№, ее (-1,6),
Н0 = \ Г /?-1\1 E-37)
l-^i-exp^ijj, ее F,1), ;
9. Горячева И.Г. 257
где ?i - точка перехода зоны сцепления в зону скольжения. Эта
точка может быть найдена из соотношения:
E.38)
Тангенциальные напряжения т(?), определённые соотношения-
соотношениями E.37), удовлетворяют E.34) и E.36), если
Ст/ф'A - 0) - В < 0. E.39)
Неравенство E.39) является необходимым условием осуществи-
осуществимости контакта с одной зоной сцепления на входе в область кон-
контактирования, которая сменяется зоной проскальзывания. Если
условие E.39) не удовлетворяется, на входе в область контакта
находится зона проскальзывания (?г, 1) и выполняются соотно-
соотношения
6<?<1, E.40)
'(О-Я>0. E-41)
Заметим, что если
*(О = -/*Ж). 6<?<1, E-42)
выражение в скобках в E.34) становится неположительным, т. е.
UO, 6<?<1- E.43)
Неравенство E.43) не удовлетворяется на входе в область кон-
контакта (? —> 1 — 0). Поэтому соотношение E.42) невыполнимо.
В точке ?2 имеет место переход зоны проскальзывания в зону
сцепления. В зоне сцепления выполняется соотношение E.35),
поэтому
E.44)
Cr
258
Для того, чтобы удовлетворить неравенству E.36), необходимо
потребовать, чтобы в точке ?2 выполнялось следующее условие:
г'F - 0) ? f F + 0). E.45)
Подставляя E.40) и E.44) в E.45), получим
+ В2Ст№'(Ь)- E-46)
Из неравенств E.41) и E.46) следует уравнение для определения
точки 6:
МрF) + ??-мСтР'F) = 0. E.47)
Как следует из равенства E.44), значение 6 ф — 1, поэтому на
участке (—1,6) существует ещё одна зона проскальзывания, в
которой выполняются соотношения:
В + №(&) + В) ехр (^^О = Мб), E-48)
Ст
-В>0, E.49)
+ В] ехр {^j^j ¦ E-50)
Заметим, что соотношения E.48)—E.50) удовлетворяют E.34) и
условиям непрерывности напряжений.
Итак, в случае существования трёх зон тангенциальные на-
напряжения на площадке контакта (—1,1) определяются по фор-
формуле:
@ -
ее (-1,6)иF,1),
E.51)
Ст
где 6 и 6 - решения уравнений E.47) и E.48).
Таким образом, область контакта может иметь две (сцепле-
(сцепления и проскальзывания) или три (проскальзывания, сцепления,
9* 259
2т/(тс?*)
0,004
0,002
0,000
-1
0
1
Рис. 5.4. Тангенциальные контактные напряжения при /Зп = 0,1, а„ =
= 1, Р = 0,01, ц = 0,1, /Зт = 0,1 и Г = 0,6/zP, 0 = 0,1, 1? = -0,4 A);
Г = 0,8/iP, 0 = 1, 0 = -0,4 B); Г = 0,8/хР, 6» = 0,1, 0 = -0,4 C),
Г = 0,8/iP, 61 = 0,1, 0 = 0,4 D) и Г = цР E)
проскальзывания) зоны. При отсутствии вязкоупругого слоя, как
уже отмечалось в главе 3, существуют только две зоны (сцеп-
(сцепления и проскальзывания) на площадке контакта при качении
упругого цилиндра по основанию из того же материала (¦# = 0).
Результаты расчётов тангенциальных напряжений на пло-
площадке контакта катящегося цилиндра с основанием при нали-
наличии на нём поверхностного слоя, базирующиеся на анализе урав-
уравнений E.28), E.31) и E.32), представлены на рис. 5.4. Свой-
Свойства вязкоупругого слоя в этом анализе описываются парамет-
параметром в = Тт/Тп, представляющим собой отношение времён ре-
релаксации в тангенциальном и нормальном направлениях (в =
= (/3Tan')/(/3naT)), a также безразмерными параметрами ап, (Зп
и fa (см. E.17) и E.27)).
260
0,012 -
0,009
0,006 -
0,003 -
0,000
-1,0 ' -0,5 0,0 0,5 \ 1,0
Рис. 5.5. Тангенциальные контактные напряжения при д
Ет/Е* « 1, /Зп = ОД, а„ = 1, Р = 0,01, м = 0,3 и f =
f = 0,9/хР B), f = 0,75цР C), f = 0,55/хР D)
0 и
A),
Результаты показывают, что с увеличением параметра в воз-
возрастают значения максимальных тангенциальных напряжений
на площадке контакта и уменьшается размер зоны сцепления.
При тех же характеристиках слоя (/Зт = 0,1 и в — 0,1) измене-
изменение упругих характеристик цилиндра и основания от $ = —0,4
(кривая 3) к д = 0,4 (кривая 4) влечёт за собой переход от трёх-
зонного контакта к двухзонному. Кроме того, установлено, что
с уменьшением значения тангенциальной силы Т контакт пере-
переходит от полного скольжения (кривая 5) к трёхзонному, а затем
к двухзонному случаям.
Качественно те же результаты были получены в расчётах по
формулам E.37), E.51) для частного случая одинаковых упру-
упругих характеристик цилиндра и основания (д = 0) и Ет/Е* <С 1.
На рис. 5.5 показаны распределения тангенциальных напряже-
напряжений на площадке контакта при различных значениях Т для этого
частного случая. Из расчётов следует, что размер зоны сцепле-
сцепления возрастает при уменьшении тангенциальной силы.
261
5.1.4. АНАЛИЗ СОПРОТИВЛЕНИЯ КАЧЕНИЮ
Катящийся цилиндр находится под действием нормальной Р и
тангенциальной Т активных нагрузок, момента М, а также сил
реакции основания Р\ и Т\, возникающих в результате действия
нормальных и тангенциальных напряжений на площадке кон-
контакта (—о, Ь) (см. рис. 5.1). Из условия равновесия сил и момен-
моментов следует:
ъ
- fxp(x)
М — I xp(x) dx
-l
Используя введённые в 5.1.2 и 5.1.3 обозначения, получим выра-
выражения для безразмерных величин силы сопротивления Г
E.52)
-1
и момента трения качения М
1М Т f
] К + Ь?П0 « - Г. E.53)
-1
Уравнение E.52) (или уравнение E.53)) также может быть ис-
использовано для определения величины относительного проскаль-
проскальзывания 5 E.3), если величина тангенциальной силы Г (или мо-
момента М) известна.
При Т = цР скольжение имеет место на всей площадке кон-
контакта. Случай Т = 0 соответствует чистому качению.
Коэффициент трения качения определяется из соотношения
Mr = j , E.54)
где М и Р находятся по формуле в E.53) и формуле E.23) соот-
соответственно.
На рис. 5.6 представлены графики зависимости коэффици-
коэффициента трения качения цг, рассчитанного по формуле E.54), от
262
0,3 с
0,2
0,1 "
0,0
0,001 0,01 0,1 1
10 Т„ VIR
Рис. 5.6. Зависимость коэффициента трения качения от параметра
TnV/R при Р = 0,001, f = 0 и рп = 0,1 A), /3„ = 1 B)
безразмерного параметра f3n/(*n = TnV/R, построенные при раз-
различных значениях параметра (Зп (см. E.17)). Коэффициент тре-
трения качения для рассматриваемой модели вязкоупругого слоя
(тело Максвелла) монотонно убывает с ростом параметра TnV/R
и цг -> 0 при TnV/R ¦-* +оо.
Проведённый анализ показывает, что несовершенная упру-
упругость поверхностного слоя оказывает существенное влияние на
характер распределения контактных напряжений при скольже-
скольжении и качении упругих тел, особенно при малых значениях па-
параметра TnV/R.
5.2. СКОЛЬЖЕНИЕ ШЕРОХОВАТЫХ ТЕЛ
В 4.2.3 предложен метод анализа совместного влияния свойств
поверхностного слоя и рельефа поверхности на контактные ха-
характеристики при нормальном нагружении тел. В качестве мо-
модели основания рассматривалось двухслойное упругое полупро-
полупространство.
Как было установлено в 5.1, в контакте скольжения в опре-
определённом диапазоне изменения параметров несовершенная упру-
263
Рис. 5.7. Схема скольжения шероховатого индентора по границе слоя,
сцепленного с основанием
гость поверхностного слоя существенно влияет на характер на-
напряжённого состояния и зависимость коэффициента трения от
скорости. При скольжении шероховатых тел зависимость кон-
контактных характеристик и трения от скорости и свойств поверх-
поверхностного слоя имеет более сложный характер.
С целью исследования влияния микрогеометрии индентора
и несовершенной упругости поверхностного слоя на напряжён-
напряжённо-деформированное состояние тел при трении скольжения ни-
ниже рассмотрена периодическая контактная задача об установив-
установившемся движении упругого индентора по вязкоупругому слою,
сцепленному с упругим основанием (в плоской квазистатической
постановке).
5.2.1. ПОСТАНОВКА ЗАДАЧИ И МЕТОД ЕЁ РЕШЕНИЯ
Схема контакта шероховатого упругого индентора с упругой
полуплоскостью, имеющей на поверхности тонкий вязкоупру-
гий слой -толщины h, изображена на рис. 5.7. Форма инденто-
индентора описывается периодической (с периодом /) функцией f(x),
т. е. /(ж) = f(x +1) для всех х. Индентор скользит по основанию
264
с постоянной скоростью V и находится под действием нагрузки
на период Р.
Введём, как и в 5.1, неподвижную, связанную с основани-
основанием, систему координат (х',у') и подвижную - (ж, у), связанную
с движущимся индентором. Соотношение между подвижными и
неподвижными координатами дано в E.1). Считается, что дви-
движение установившееся, поэтому все напряжения и деформации
не зависят от времени в системе коодинат (х, у).
Рассмотрим одномерные модели поверхностного слоя, для ко-
которых давление не меняется по толщине слоя, т.е. р{х,у) =
= р(х, 0) = p(x,h) = р(х) для всех у е [0, h]. Для упрощения
анализа предположим также, что тангенциальные напряжения
не влияют на распределение давлений. Тогда справедливо сле-
следующее соотношение между нормальными упругими перемеще-
перемещениями Vi граничных точек индентора (г = 1) и полуплоскос-
полуплоскости (г = 2) и давлениями р(х), распределёнными периодичес-
периодически внутри площадок контакта [Bп + 1I/2 — а, Bп + 1I/2 + Ь],
(п = 0,±1,±2,...) (см. [146]):
г/2+6
vi(x) + v2(x) =—^ J p(x')\n 2 sin И* { Х>]
l/2-a
dx', E.55)
где Е* - эквивалентный модуль упругости (см. E.18)).
Для определённости положим, что функция f(x) имеет вид:
( 0 (о/) E.56)
Поэтому контактное давление р(х) на концах площадок контакта
удовлетворяет условию:
В силу периодичности функции р(х) имеем
р(х)=р{х + 1). E.58)
265
Кроме того, внутри площадок контакта выполняется условие
vi(x) + v2(x) + v3(x) = D-f(x), E.59)
где D - сближение тел за счёт деформирования, v% - смещение
по нормали границы слоя вследствие его деформирования. Ниже
мы рассмотрим две модели деформирования слоя.
Модель Максвелла. Для описания податливости слоя
при нагружении его давлением р(х) используем, как и в 5.1, мо-
модель Максвелла, для которой соотношение между производной
от нормальных смещений v% и давлением р{х) в системе коорди-
координат (х, у) имеет вид E.11).
Из соотношений E.11), E.55), E.57) и E.59) следует интег-
интегральное уравнение в области х € [1/2 — а, 1/2 + Ь] для определе-
определения контактного давления р(х):
г/2+6
o'(x') In
2 sin
h dp
. \тг(х'-х)
I
l/2-a
Вводя новые переменные f и ц:
b-a+l a+b
dx' = -f'(x).
E.60)
x =
а также безразмерную функцию
2 fb-a
a + b
E.61)
E.62)
и подставляя E.56), E.61) и E.62) в уравнение E.60), получим
следующее интегральное уравнение Фредгольма второго рода:
In
E.63)
266
где F(?) = p'{i), I = l/BR), а параметры ап, /3n, L и е опреде-
определены в E.17).
Уравнение E.63) решается совместно со следующими соот-
соотношениями
1
= 0, E.64)
-1
E.65)
-1
полученными из E.57) и условия равновесия. Здесь Р - безраз-
безразмерная нагрузка, действующая на период, т. е. Р = 2P/(irE*R).
Решение системы уравнений E.63), E.64) и E.65) даёт воз-
возможность определить безразмерные контактные давления
размер L и смещение е площадки контакта:
E.66)
-l
i
= -P j
-i
-l
E.67)
Г l l
е =
L-l -1
-l
E.68)
Заметим, что если размер площадки контакта мал по сравне-
сравнению с периодом, т.е. L/1 <С 1, уравнение E.63) преобразуется
к виду E.19), соответствующему случаю скольжения единично-
единичного индентора, форма которого описывается функцией E.56), по
поверхности вязкоупругого слоя (см. 5.1).
267
Модель Кельвина. Поскольку модель Максвелла, как из-
известно, обладает неограниченной ползучестью, с её помощью
нельзя описать восстановление формы поверхности слоя после
снятия нагрузки. Поэтому мы рассмотрим также в качестве од-
одномерной модели слоя тело Кельвина, обладающее ограниченной
ползучестью [119]. В рамках этой модели упругие перемещения
слоя уз в направлении оси Оу связаны с нормальным давлени-
давлением р(х) соотношением
где Те и Та - времена последействия и релаксации, El - дли-
длительный модуль упругости.
В подвижной системе координат (х, у) соотношение E.69)
имеет вид:
Заметим, что нормальные смещения слоя также удовлетворяют
условию периодичности:
vz(x) = v3(x + l). E.71)
Исключая из уравнений E.55), E.59), E.70) функции Vi(x),
где i — 1,2,3 и используя выражение E.56), получим соотно-
соотношение, выполняющееся для всех точек области контакта, т. е.
для х Е [1/2 -а, 1/2+ Ь}:
2
l/2+b
тгЕ*
l/2-a
In
2 sin
:_ *(х' ~ Х)
I
nT?V тг{х'-х)]^ h .. hTaV ,. . E.72)
]dx +— p(x)-—-p(x) =
1 / l\2 TeV ( I
+
2RV 2
268
Решением уравнения E.70) на ненагруженных участках, т.е.
при х G [—'/2 + Ь, 1/2 — а], где р(х) = 0, является функция
v3 = voexp(x/TEV).
E.73)
Эта функция должна удовлетворять условию контактирова-
контактирования1 E.59) при х = 1/2 — а и х = 1/2 + Ъ и условию периодич-
периодичности E.71), из которых следует:
Ь-
Ь2
2
'тгЁ*
l/2+b
J P(s')h
Z/2-а
7Г(Х'
2 sin——
exp
1/2 -а
TFV
l/2+b
l/2-a
с') In
2 sin
dx',
. n(x'-l/2 + a)
dx'.
E.74)
Исключая из соотношений E.72) и E.74) постоянные D и vo, a
также используя обозначения E.17), E.61) E.62) и следующие
безразмерные параметры
hirE*
а + Ъ - I
> l=2R>
получим уравнение для определения безразмерных контактных
давлений р(?) в виде:
E-76)
269
где ядро #(?,?') и функция G(?) имеют вид:
1-exp 2Co U-l
Co/ Co
1 — exp
Условие E.57) и уравнение равновесия в безразмерном виде за-
запишутся как
E.77)
-l
Линейное интегро-дифференциальное уравнение E.76) и со-
соотношение E.77) используются для определения распределения
безразмерного контактного давления р(?) (—1 ^ ? ^ 1) и без-
безразмерных ширины L и смещения е площадки контакта, для
слоя, деформационные свойства которого описываются соотно-
соотношением E.69). Численное решение уравнений осуществлялось
путём сведения их к линейной алгебраической системе, которая,
в свою очередь, решалась методом итераций [46].
270
Распределение тангенциальных напряжений при ? € [—1,1],
т.е. в области контакта, определяется соотношением
E-78)
где fj, - коэффициент трения.
5.2.2. АНАЛИЗ КОНТАКТНЫХ ХАРАКТЕРИСТИК
Соотношения, полученные в 5.2.1, были использованы для ана-
анализа совместного влияния свойств тонкого поверхностного слоя и
параметров микрогеометрии поверхности на распределение кон-
контактных давлений, размер и смещение зоны контакта.
Для модели Максвелла свойства слоя описывались парамет-
параметром рп = hnE*/BREn), зависящим от относительной толщины
слоя h/R и его относительного модуля упругости Еп/Е*, и пара-
параметром Рп/ап = TnV/R, пропорциональным скорости V сколь-
скольжения индентора и времени релаксации Тп вязкоупругого слоя.
При моделировании слоя телом Кельвина его свойства описы-
описывались параметрами ост, Со и /Зе (см. E.75). Параметр от пред-
представляет собой отношение времени запаздывания Те ко време-
времени релаксации Та материала поверхностного слоя, причём слу-
случай ат = 1 соответствует упругому слою с модулем упругос-
упругости, равным длительному модулю El- Параметр ?о зависит от
времени запаздывания Те и скорости V скольжения индентора
и представляет собой отношение времени, за которое элемент
проходит расстояние, равное полуширине (а + Ь)/2 области кон-
контакта, ко времени запаздывания вязкоупругого материала. Па-
Параметр /Зе характеризует относительную толщину и относитель-
относительный модуль упругости слоя и имеет такой же смысл, как и па-
параметр /Зп в модели Максвелла. Случай /Зе —> +оо соответству-
соответствует модели жёсткого индентора, скользящего по вязкоупругому
слою, сцепленному с жёстким основанием.
Рельеф поверхности (её шероховатость или волнистость) ха-
характеризуется плотностью контакта а или безразмерным рас-
расстоянием между неровностями /. Если неровности расположены
далеко друг от друга (параметр I - большой), значения пара-
параметра а малы.
271
-1,0 -0,5 0,0 0,5 § 1,0
Рис. 5.8. Распределение контактных давлений в случае модели Макс-
Максвелла при а = 0,5, Р = 0,01 и /3„ = 0,1, (Зп/ап - 0,1 A); /3„ = 0,01,
Рп/ап = ОД B); /Зп = 0,01, /Зп/а„ = 0,01 C)
На рис. 5.8 и 5.9 представлены результаты расчётов, по-
полученные с использованием модели Максвелла. Более подроб-
подробный анализ этой модели приведён в [176]. Результаты показы-
показывают, что наличие вязкоупругого поверхностного слоя приводит
к несимметричному распределению давлений на площадке кон-
контакта (см. рис. 5.8). Контактные давления отнесены к макси-
максимальному давлению, рассчитанному по теории Герца при отсут-
отсутствии вязкоупругого слоя, т.е. ро = v2P/n. Наибольшее вли-
влияние на распределение давлений (его несимметрию) оказывает
параметр /Зп/ап. Несимметрия возрастает при малых значени-
значениях этого параметра. Параметр /?п влияет, главным образом, на
значение максимальных контактных давлений.
Рис. 5.9 иллюстрирует изменение относительной ширины
площадки контакта L/Lq, где Lq - безразмерная ширина пло-
площадки контакта, рассчитанная по теории Герца, Lq — у 2Р, и
её смещения е в зависимости от безразмерного расстояния меж-
между неровностями I = l/BR) при различных значениях парамет-
параметров /Зп и /Зп/&п- Результаты показывают, что параметр I ока-
оказывает существенное влияние на контактные характеристики,
когда он мал (I ^ 0,6). В этом диапазоне при уменьшении пара-
272
LIL0
1,2 -
1,0
0,8
0,3
0,2
01
-
ауф н
ha)
1
4
б
0,4
1,0 l/BR)
0,4
1,0 l/BR)
Рис. 5.9. Зависимость ширины (а) и смещения (б) площадки контак-
контакта от безразмерного расстояния между неровностями в случае модели
Максвелла при Р = 0,01 и /3„ = ОД, 0п/ап = 0,1 A); /3„ = 0,05,
рп/ап = 0,1 B); /3„ - 0,01, /3„/а„ = 0,01 C); /Зп = 0,01, /Зп/ап = 0,1 D)
метра / ширина площадки контакта уменьшается, а её смещение
растёт. При больших значениях I контактные характеристики
совпадают с рассчитанными в задаче о скольжении единичной
неровности по границе вязкоупругого слоя (см. 5.1). Поэтому
при I ^ 0,6 контактные характеристики можно определять по
упрощённой модели, не учитывающей взаимное влияние неров-
неровностей. Из полученных результатов также следует, что ширина
площадки контакта и её смещение уменьшаются при увеличении
параметра /Зп/ап, а также при уменьшении (Зп.
Результаты расчётов, полученные с использованием модели
Кельвина, представлены на рис. 5.10-5.13. На рис. 5.10 приведе-
приведены графики зависимости безразмерного контактного давления р
при различных значениях параметров ат и [ = 1/{2R). Резуль-
Результаты показывают, что при увеличении ах распределение в кон-
контакте становится более несимметричным. Однако уменьшение
расстояния l/BR) между неровностями, т. е. увеличение плот-
плотности контакта, частично сглаживает эту несимметрию.
При малых значениях параметра l/BR) наблюдается разли-
различие в результатах, полученных с использованием моделей Макс-
Максвелла и Кельвина. Результаты, основанные на модели Кель-
Кельвина, предсказывают уменьшение ширины области контакта и
273
2р/(пЕ')
0,00
-1,0
-0,5
0,0
0,5
1,0
Рис. 5.10. Распределение контактных давлений в случае модели Кель-
Кельвина при Р = 1/15, Ье = 10, T?V/R = 1 и ат = 1 A, 1'), <*г = 5 B, 2'),
ат = 50 C, 3'); I = 5 A, 2, 3), [= 1 A', 2', 3')
её смещения при уменьшении расстояния между неровностями
(см. рис. 5.11). Этот эффект обусловлен влиянием друг на друга
соседних неровностей индентора и связан, в частности, с тем,
что в рассматриваемой модели вязкоупругого слоя учитывается
восстановление его формы после снятия нагрузки. Действитель-
Действительно, из соотношений E.73) и E.74) следует, что смещения гра-
граничных точек слоя на ненагруженном участке (—1/2 + Ь, 1/2 — а),
если пренебречь упругими свойствами индентора и основания,
удовлетворяют соотношению:
v3(l/2-a) fl-a-b
= exp
v3 (-1/2 + b)
TFV
Если длина (I — a — b) участка между площадками контакта до-
достаточно мала, слой не успевает восстановить свою форму за
время (I — a — b)/V, поскольку в этом случае (I — а — b)/V <g! T? и,
следовательно, г>з A/2 -а)«из (—1/2 + Ь); это приводит к умень-
уменьшению размера области контакта и её сдвига. Эффект уменьше-
уменьшения ширины области контакта при малых значениях l/BR) воз-
возникает также и за счёт упругих свойств основания, на котором
лежит вязкоупругий слой, и проявляется как в модели Кельвина,
так и в модели Максвелла (см. рис. 5.9,а). Заметное влияние рас-
расстояния м'ежду соседними неровностями индентора на контакт-
контактные характеристики начинает проявляться лишь при достаточ-
274
0,45
(b - a)l{b + a)
0,00
0,075
0,250
l/BR)
0,600
Рис. 5.11. Смещение области контакта как функция расстояния между
неровностями в случае модели Кельвина при ат = 50, Р = 1/15 и
TeV/R = 1 A, 1'), TEV/R = 10 B, 2'); & = 10 (сплошные линии) и
/Зс —> +оо (штриховые линии)
но малых значениях l/BR) (l/BR) < 0,2). Сравнение кривых 1,
2 и 1', 2' на рис. 5.11 (последняя пара построена для случая,
когда индентор и основания - жёсткие тела), показывает, что
учёт упругости индентора и основания приводит к уменьшению
смещения площадки контакта, что наиболее сильно проявляется
при больших значениях параметра T?V/R, т. е. при больших ско-
скоростях скольжения. При этом, как показывают расчёты, ширина
площадки контакта увеличивается.
На рис. 5.12 представлены графики зависимости безразмер-
безразмерной ширины области контакта L/Lo, её смещения е и максималь-
максимального внедрения Атах индентора в вязкоупругий слой от парамет-
параметра Со при различных ат и I. Для определения величины Дтах
использовалось выражение
= max
х6(-о,Ь) R
-1
2eL2
ехр I 2Со I ^ - 1 I 1-1
275
1,5
L/Lo
1,0
0,5
0,50
Лпах
0,20
0,05
в
-^-^~
~-7
0 In Со
Рис. 5.12. Зависимость ширины (а) и смещения (б) области контакта,
а также максимального внедрения в вязкоупругий слой (е) от парамет-
параметра Со в случае модели Кельвина при Р — 1/15, /3? = 10 и I = 5 A, 1'),
[= 1 B, 2'); ат = 50 A, 2), ат = 5 A', 2')
276
полученное на основании соотношений E.55), E.59) и E.74). Ре-
Результаты расчётов позволяют заключить, что ширина площадки
контакта и максимальное внедрение в вязкоупругий слой ограни-
ограничены предельными значениями, которые они имеют при ?о —> О
и ?о —> +оо. Случай ?о —* +оо, т. е. V —> 0, соответствует ре-
решению задачи о взаимодействии упругого индентора с упругим
слоем, характеризующимся модулем El, на упругом основании.
В случае ?о —> 0, т.е. V —> +оо, промежуточный слой ведёт
себя как упругая полоса с модулем атЕ^, называемым мгно-
мгновенным модулем упругости. Заметим, что увеличение скорости
скольжения V (уменьшение Со) приводит к уменьшению размера
площадки контакта и величины внедрения индентора (эффект
всплытия). Смещение площадки контакта достигает максимума
при некотором (о и стремится к нулю при (о —> 0 и ?о —>• +оо.
Более полный анализ контактных характеристик, полученных
в рассматриваемой задаче с использованием модели Кельвина,
изложен в [46].
5.2.3. ДЕФОРМАЦИОННАЯ СОСТАВЛЯЮЩАЯ
КОЭФФИЦИЕНТА ТРЕНИЯ
Смещение области контакта относительно оси симметрии неров-
неровности, а также несимметрия распределения контактных давле-
давлений приводят к тому, что на каждую неровность индентора дей-
действует тангенциальная сила в направлении, противоположном
направлению скольжения индентора, называемая деформацион-
деформационной (механической) составляющей силы трения. Безразмерная
величина этой силы может быть найдена из соотношения
гр
О
I xp(x) dx. E.79)
жВ?Е*
—а
Деформационная составляющая \i& коэффициента трения опре-
определяется с учётом соотношений E.17), E.61), E.62) и E.79) по
формуле
1
Т L f
f*d = — = — \ (е + 0Р{?) dZ- E-80)
— 1
277
0,045
0,030
0,015
0,000
0
6
8
Рис. 5.13. Деформационная составляющая коэффициента трения как
функция параметра Со для модели Кельвина при /Зе = 10, Р = 1/15
и I = 5 A, 1'), I = 1 B, 2'); ау = 50 (сплошные линии), ат = 5
(штриховые линии)
На рис. 5.13 представлены графики зависимостей величи-
величины ид, рассчитанной по формуле E.80), от параметра Со при
различных плотностях расположения неровностей. Результаты
показывают, что деформационная составляющая коэффициента
трения отлична от нуля в некотором диапазоне значений Со и
стремится к нулю при Со -> 0 и Со -+ +°о. Эти предельные слу-
случаи, как отмечалось, соответствуют решению задачи в упругой
постановке. С уменьшением параметра / = l/BR) коэффициент
трения уменьшается. Таким образом, увеличение плотности кон-
контакта (уменьшение /) можно считать эквивалентным уменьше-
уменьшению эффективной вязкости слоя.
5.2.4. РАСПРЕДЕЛЕНИЕ ВНУТРЕННИХ
НАПРЯЖЕНИЙ
Если известно распределение контактных напряжений
и q(?), бнутренние напряжения в некоторой точке (?, rj) упру-
упругой полуплоскости или индентора могут быть рассчитаны по
278
формулам (см., например, [66]):
2_
тг
+оо
E.81)
У
<Гп(?>П) =
E.82)
Гт+ 1
2n
- d
f+1
/
E.83)
где
Вводя новую переменную ?i = ?' — Bп/а), приведём выраже-
выражения E.81), E.82) и E.83) к виду:
x\(t,v), E-84)
2
7Г
279
где
_ Х„(?,т?), E-85)
7Г *—'
п=—оо
_ Х«(?^), E-86)
¦к t—1
П——СО
/ 74
|
-1
/•т?(е-^1-
/ д4
В силу периодичности задачи достаточно рассмотреть её реше-
решение в области
{ а а }
В этом случае |?i| <С |^ — 2п/а\ при п > N, поэтому бесконечные
ряды в соотношениях E.84)-E.86) могут быть аппроксимирова-
аппроксимированы как
2 N
*««,»?) = -- Е &t,i) + °< &V), E-87)
280
E Xn(^)+ <(?,*?), E-88)
n=-N
1
>4) = ~- E x2(?,»7) + rS^)' E-89)
п=-ЛГ
где cr^iCrf), сг^(^,т]), т^((,г]) - напряжения, вызванные в точ-
точке (?, г/) области По действием нормальных и касательных на-
напряжений
1
p(Odt, E.90)
1
1
q{?)d{, E.91)
на участке Ооо границы, причём
a
Полученные соотношения были использованы для ана-
анализа совместного влияния свойств поверхностного слоя, па-
параметров шероховатости и коэффициента трения на рас-
распределение внутренних напряжений в упругой полуплоскос-
полуплоскости. Результаты расчёта максимальных касательных напря-
напряжений ттах(?,7/) с использованием полученных выше соот-
соотношений приведены в табл. 5.1 и на рис. 5.14. Величина
напряжений представлена в безразмерном виде как отноше-
отношение fmax(?,77) = rmax(^,r?)/po, где р0 = л/2Р/тг - макси-
максимальное давление Герца. В таблице даны величина тшах =
= тахттах(?,т?) и положение (?т>т?т) точки внутри упругой
полуплоскости, в которой функция ттах(?, г/) достигает макси-
максимального значения. На рис. 5.14 представлены изолинии функ-
функции ттах(?,?7) для двух значений плотности расположения кон-
контактных зон при взаимодействии шероховатого индентора с вяз-
коупругим слоем, лежащим на упругом основании. Контактное
281
Таблица 5.1. Величина максимальных касательных напряжений в
точке их максимума при о = 0,1, Р = 0,01 для слоя,
моделируемого телом Максвелла
А» Г 0п/ап
.max
0,01
0,01
0,00
0,10
0,26
0,28
0,292
0,302
0,342
0,349
0,32
0,60
0,88
0,92
0,72
0,60
0,34
0,28
0,01
0,00
0,10
0,26
0,28
0,293
0,299
0,330
0,335
0,04
0,36
0,76
0,80
0,76
0,70
0,46
0,42
0,1
0,1
0,00
0,10
0,26
0,28
0,261
0,268
0,296
0,301
0,20
0,44
0,76
0,32
0,70
0,62
0,42
0,00
0,1
1
1
0,00
0,10
0,26
0,28
0,262
0,266
0,290
0,300
0,04
0,28
0,20
0,20
0,70
0,68
0,02
0,00
давление на периоде приложено внутри интервала (—1,1) на
оси О?.
Сравнение полученного распределения максимальных каса-
касательных напряжений для случая ц = 0 и малой плотности рас-
расположения контактных зон (см. рис. 5.14,а) с решением для уп-
упругой полуплоскости (задача Герца) позволяет заключить, что
наличие вязкоупругого слоя приводит к несимметричному по от-
отношению к оси симметрии контактной зоны распределению на-
напряжений ттах(?, ??). С увеличением значения /Зп (при сохранении
величины (Зп/ап) точка (?m,i]m) максимума функции rmax(?, rf)
приближается к границе (значение г]т уменьшается) и величи-
величина rmax уменьшается (см. табл. 5.1).
В присутствии вязкоупругого слоя максимальное значение
функции ттах(?, if) достигается на границе (т]т = 0) при более
282
-1.5-1.0-0.5 0.0 0.5 1.0 1.5 -1,5 -1.0 «0.5 0.0 0.5 1.0 1.5
а б
Рис. 5.14. Изолинии функции fmax(?, jf) при /Зп = 0,01, /?„/<*„ = 0,01,
ц = 0 и (а + Ъ)/1 = 0,1 (а), (а + Ь)Ц = 0,7 (б) для слоя, моделируемого
телом Максвелла
высоком значении коэффициента трения по сравнению со случа-
случаем контакта двух упругих тел. Заметим, что при этом вязко-
упругий слой оказывает существенное влияние на контактные
характеристики (см. рис. 5.8 и 5.9) и, следовательно, на внут-
внутренние напряжения.
При высокой плотности пятен контакта (см. рис. 5.14,5) ам-
амплитудные значения максимальных касательных напряжений на
фиксированной глубине под поверхностью близки друг к другу.
Подобный результат отмечался в главе 1 при исследовании рас-
распределения напряжений в упругом полупространстве для раз-
различной плотности пятен контакта.
На основании проведённого анализа можно заключить, что
несовершенная упругость поверхностного слоя и параметры ше-
шероховатости поверхности оказывают существенное влияние на
распределение контактных и внутренних напряжений при от-
относительном скольжении тел, при этом напряжённое состояние
меняется с изменением скорости скольжения.
Распределение максимальных касательных напряжений для
разных значений плотности контакта может быть использовано
для расчёта накопления повреждённости вблизи поверхности и
характера усталостного разрушения при скольжении шерохова-
шероховатых тел (см. главу 6).
283
5.3. КОНТАКТ КАЧЕНИЯ СО СМАЗКОЙ
В этом разделе изучается влияние свойств тонкого поверхност-
поверхностного слоя на характеристики контактного взаимодействия при
качении упругих тел, разделённых жидким смазочным матери-
материалом. Давление, возникающее в слое жидкости при относитель-
относительном движении поверхностей, и толщина плёнки смазки в этом
случае зависят от геометрии контакта и вязких свойств жид-
жидкости (гидродинамическая смазка), а также от упругих свойств
взаимодействующих тел (эластогидродинамическая смазка). Те-
Теории гидродинамической и эластогидродинамической смазки из-
изложены в монографиях [22, 60, 81, 162, 185]. Эти теории, базиру-
базирующиеся на ньютоновской модели жидкости, удовлетворительно
предсказывают толщину плёнки смазки в зазоре между тела-
телами. Однако при высоких давлениях и низких скоростях относи-
относительного проскальзывания наблюдается различие в предсказы-
предсказываемых теорией величинах силы трения и диссипации с наблю-
наблюдаемыми в экспериментах. Для получения более достоверных
результатов рассматривались модели, учитывающие эффект из-
изменения вязкости от температуры и неньютоновское поведение
жидкости при высоких давлениях (см. [190, 230]).
Ниже рассматривается контактное взаимодействие двух уп-
упругих цилиндров, содержащих на поверхности слои, моделируе-
моделируемые вязкоупругими телами, и разделённых слоем смазки. Такая
модель дает возможность изучить совместное влияние объём-
объёмных свойств жидкости, а также свойств тонких поверхностных
плёнок на характеристики контактного взаимодействия и коэф-
коэффициент трения при различных условиях взаимодействия (ско-
(скорость относительного проскальзывания, нагрузка и т.д.).
5.3.1. ПОСТАНОВКА ЗАДАЧИ
На рис. 5.15 показана схема контакта двух вращающихся ци-
цилиндров, разделённых тонким слоем смазочного материала. Сис-
Система координат (ri,6i) связана с каждым из цилиндров и вра-
вращается с угловой скоростью щ (г = 1, 2 для верхнего и нижнего
цилиндров соответственно). Система координат (х,у) фиксиро-
фиксирована в плоскости таким образом, что ось Оу совпадает с ли-
284
нией, соединяющей центры цилиндров. Форма взаимодействую-
взаимодействующих поверхностей цилиндров описывается функциями /,(ж) =
— щ ± х2/BЯг) (щ их2~ некоторые постоянные).
Соотношение между по-
подвижными (ri,6i) (i = 1, 2)
и фиксированной (х, у) сис-
системами координат имеет
следующий вид:
X=Ti COS
у=Г( sin (
E.92)
где 2/о,1 и 2/0,2 - ординаты
центров цилиндров.
Для описания податли-
податливости поверхностных сло-
слоев используется одномер-
одномерная модель Максвелла, для
которой справедливо сле-
следующее соотношение меж-
между нормальным давлени-
давлением р, которое предполагает-
предполагается распределенным равно-
равномерно вдоль координаты у
внутри слоя толщины hi, и
нормальным смещением vf:
Рис. 5.15. Схема контакта двух ци-
цилиндров, разделённых смазочным ма-
материалом и имеющих на поверхности
тонкую плёнку или покрытие
(
dt En \Tn dt
E.93)
где Еп жТп - модуль упругости и время релаксации материа-
материала слоя. Чтобы упростить анализ здесь сделано предположение,
что механические свойства материалов поверхностного слоя на
верхнем и нижнем цилиндре одинаковы. Однако описанный ниже
алгоритм может быть использован и для решения более общей
задачи, когда механические характеристики слоев различны.
285
На основании E.92) представим соотношение E.93) в системе
координат (х, у):
dx ~ Еп[ ViTn+ dx
где Vi и V2 - линейные скорости поверхностей верхнего и ниж-
нижнего цилиндров.
Для описания течения вязкой жидкости между поверхностя-
поверхностями, движущимися со скоростями V\ и V2, воспользуемся уравне-
уравнением Рейнольдса:
где Н(х) - толщина пленки жидкости. В этом уравнении зави-
зависимость вязкости г] от давления р(х) описывается соотношением
Баруса [151]:
V = Voeap, E.96)
где т)о - вязкость, соответствующая внешним давлению и тем-
температуре, а - пьезокоэффициент вязкости жидкости.
Для уравнения Рейнольдса E.95) имеют место следующие
граничные условия:
р(-оо)=рF) = 0, ^
= 0. E.97)
х=Ь
где b - точка выхода.
Для описания механических свойств материалов цилиндров
используется модель однородного изотропного линейно упруго-
упругого тела. Градиент нормальных перемещений Vi(x) поверхности
цилиндра определяется соотношением:
, ,, ь
nti- 2A — и* I Г т>1 т I пф
\JL\Ja & I ш1ь "л I I U\ vij I XJutAJ .
286
Внутри области взаимодействия толщина плёнки смазки
определяется выражением:
Н(х) = Н(Ь) + 4т^ + «(*) ~ v(b) + vL(x) - vL(b), E.99)
где
vL{x) = v[{x) + v%{x), E.100)
v(x)=v1(x) + v2{x), E.101)
Смещения vf'(x), Vi(x) определены соотношениями E.94) и E.98).
Из условия равновесия сил следует соотношение
ь
p(x)dx = P, E.102)
где Р - вертикальная сила, действующая на цилиндр. Уравне-
Уравнения E.94)—E.102) используются для определения давления р(х),
толщины плёнки смазки Н(х), а также упругих Uj(x) и вязкоуп-
ругих vf(x) смещений поверхностей взаимодействующих тел.
5.3.2. МЕТОД РЕШЕНИЯ
Рассмотрим полученную систему уравнений для случаев посто-
постоянной и переменной вязкости, описываемой соотношением E.96).
При постоянной вязкости г/о система уравнений E.94)—E.102)
может быть сведена к одному уравнению для определения тол-
толщины плёнки смазки. Интегрируя соотношения E.94) и E.98) и
используя граничные условия E.97), получим
ь
E.103)
287
E-Ю4)
Подставляя уравнения E.103) и E.104) в выражение E.99) и
используя проинтегрированную форму уравнения E.95), будем
иметь
ь
J к{х,х',Ь)Н{Хн]~х^ dx',
Н(х) = H(b) + ^^~ + / к(х,х',Ь) я3, л dx'> EЛ05)
— 00
где Н* - толщина плёнки смазки в точке, для которой dp/dx = 0.
Ядро уравнения E.105) имеет вид:
^ + |) [(,-,')- E.106)
Вводя безразмерные переменные, параметры и функции
х п(п яF° h b я -
E*R> Ь~ Р
EnR =Vi-V2
y 7 V + F
2/i ' " 2E*h
где h = (hi + /12) /2, представим E.105) и E.106) в безразмерном
виде:
ЗЪ2 , -_ . г, - . .,^ E ш)
яз у v<5'4' ^ яз
288
A.pq
*
Из соотношений E.95), E.97) и E.102), используя введённые без-
безразмерные переменные, параметры и функции E.107), получим
два дополнительных условия:
1 .
%?Ы E.111)
Система уравнений E.108), E.110) и E.111) используется для
определения функции Н(х) и двух неизвестных параметров Ь
и Н*. Безразмерное контактное давление р(х) = p(x)R/P затем
определяется путём интегрирования уравнения E.95), т.е.
665 \НШ-Л
*' щ J яз(е)
Для решения системы уравнений E.108), E.110) и E.111) ис-
использовался метод Ньютона-Канторовича [75]. При численном
анализе бесконечный интервал (—оо, 1) делится на две час-
части: (— oo,gM и Id, 1), на которых функция Hi(?) аппроксими-
аппроксимируется как
d < е < 1,
- - EЛ13)
, -оо <^< d,
а параметры 5 и d определяются из условий:
hU-o) =н(И+о\,
H'(d-0\ =H' (d + 0).
10. Горячева И.Г. 289
pRIP
HIH{b)
0 xlb 1
Рис. 5.16. Давление A и 2) и толщина плёнки смазки A' и 2') при
Р = Ю-4, /3=1,5 = 2. Ю-5 и fj/(l - 72) = 5 • КГ8 A, 1'), fj = 0B, 2')
Система уравнений сводится к линейным алгебраическим урав-
уравнениям, для решения которых используется метод Гаусса.
5.3.3. АНАЛИЗ КОНТАКТНЫХ ХАРАКТЕРИСТИК И
ТОЛЩИНЫ ПЛЁНКИ СМАЗКИ
Для простоты анализа положим, что толщина поверхностного
слоя на верхнем и нижнем цилиндре одинакова, т.е. hi = h^ — h.
Тогда контактные характеристики зависят от пяти безразмер-
безразмерных параметров (см. E.107)): параметра fj = 4r]h/(EnTnR), ха-
характеризующего относительную вязкость жидкости и поверх-
поверхностного слоя; параметра /3 = (EnR)/BE*h), описывающего от-
относительный модуль упругости слоя и основания и зависящего
также от толщины слоя h; числа Зоммерфельда S = 770(^1 +
+^г)/Р, пропорционального средней скорости движения поверх-
поверхностей и вязкости слоя и обратно пропорционального нагрузке;
параметра 7 = (Vi — ^2)/(Vi + V2), зависящего от разности ско-
скоростей; безразмерной нагрузки Р = P/(E*R).
Результаты расчётов, представленные на рис. 5.16, демонст-
демонстрируют влияние параметра относительной вязкости fj на распре-
распределение давления и толщину плёнки смазки. При fj = 0 поверх-
поверхностный слой упругий. При увеличении вязкости поверхностно-
290
го слоя распределение давления становится более несимметрич-
несимметричным, а толщина плёнки смазки выравнивается. При этом мак-
максимальное контактное давление меняется незначительно.
На рис. 5.17 приведены распределения давлений и толщи-
толщины плёнки смазки в зазоре между телами при различных зна-
значениях числа Зоммерфельда. Результаты расчётов дают осно-
основание заключить, что при малых числах Зоммерфельда (кри-
(кривая 1), т. е. малых скоростях качения, толщина плёнки смазки в
области контакта близка к постоянной, а распределение давле-
давления подобно тому, которое имеет место в несмазанном контакте
(см. результаты, представленные в 5.1). При увеличении скорос-
скорости (кривая 2) давление распределено по большей площади, при
этом максимальное давление уменьшается, а точка, в которой
оно достигается, приближается к точке выхода; профиль смазоч-
смазочного слоя в этом случае имеет черты, характерные для гидро-
гидродинамического режима. Положение точки выхода b существенно
зависит от скорости при малых значениях скорости. При этом с
увеличением значения fj точка выхода смещается к оси симмет-
симметрии цилиндра. При высоких скоростях качения положение точки
выхода практически не зависит от значения параметра fj.
Для оценки роли поверхностного слоя в контакте со смаз-
смазкой интересно также сопоставить величины деформаций слоя и
толщины плёнки смазки при различных числах Зоммерфельда
(рис. 5.18). Сравнение кривых 1, 2, 3 и 1', 2', 3' на этом рисунке
показывает, что при малых числах Зоммерфельда минимальная
толщина смазочного слоя Нт\п значительно меньше максималь-
максимального прогиба v^ax границы слоя. Однако с увеличением числа
Зоммерфельда толщина плёнки смазки растет, а перемещения
границы слоя за счёт его деформации падают, при этом мини-
минимальная толщина плёнки смазки становится значительно боль-
больше смещений границы слоя. Это даёт основание заключить, что
при малых числах Зоммерфельда свойства поверхностного слоя
оказывают определяющее влияние на контактные характеристи-
характеристики. При больших числах Зоммерфельда минимальная толщина
смазочного слоя практически не зависит от вязкости ЕпТп по-
поверхностного слоя. Минимальная толщина слоя смазки и макси-
максимальный прогиб слоя возрастают с уменьшением параметра C.
10* 291
pRIP
12
1,8
1,4
1,0
0,6
-1,5
-1,0
-0,5
0,0
xlb
1,0
Рис. 5.17. Давление (а) и толщина плёнки смазки (б) при Р — 10
/3 = 1, fj/(l - 72) = 5 • 10'8 и 5 = 10~5 A), 5 = 5- 1(Г5 B), 5 = 1(Г3
292
v'JR, HmJR
0,002
0,001
0,000
0
0,0001
0,001
Рис. 5.18. Максимальное смещение границы слоя вследствие его де-
деформации A, 2, 3) и минимальная толщина плёнки смазки (Г, 2', 3')
как функции числа Зоммерфельда при Р = 10~4 и /3 = 1, ц = 0 A, 1'),
/3 = 1, fj = 5 ¦ Ю-8 B, 2'), Р = 0,5, ?7 = 5 -10"8 C, 3')
Результаты, представленные на рис. 5.19, демонстрируют
влияние переменной вязкости (см. E.96)) на распределение дав-
давления и профиль смазочного слоя. Учёт зависимости вязкости
от давления приводит к увеличению толщины плёнки смазки по
сравнению со случаем постоянной вязкости, при этом появляет-
появляется незначительное уменьшение толщины плёнки вблизи точки
выхода. Максимальное давление, рассчитанное при переменной
вязкости, несколько выше максимального давления, рассчитан-
рассчитанного при т] = щ.
Проведённый анализ дает основание заключить, что при ма-
малых числах Зоммерфельда (малых скоростях качения) распреде-
распределение давлений и деформации тел в контакте определяются глав-
главным образом свойствами поверхностного слоя и основания, в то
время как при больших значениях числа Зоммерфельда наличие
поверхностного слоя практически не влияет на контактные ха-
характеристики, определяемые в основном объёмными свойствами
смазки.
293
pRIP
24 Г
Н/ЩЬ)
-\ 4
х1Ъ
Рис. 5.19. Распределение давления A, 2) и толщины плёнки смазки A',
2') при fj = КГ9, aP/R - 2 • КГ11 и 5 = 7- 1(Г6 для случая постоянной
вязкости A, 1') и с учётом зависимости вязкости от давления B, 2')
5.3.4. АНАЛИЗ СИЛ ТРЕНИЯ
В контакте со смазкой момент сопротивления качению М и тан-
тангенциальные силы сопротивления сдвигу для нижнего Т\ и верх-
верхнего Тг цилиндров определяется по формулам (см. [185]):
М
о
= I xp(x) dx,
E.114)
-оо
EД15)
EД16)
При этом коэффициенты трения качения и сопротивления сдвигу
имеют вид:
М Т
1Н = -р-
294
В безразмерном виде эти коэффициенты рассчитываются по фор-
формулам, полученным на основании приведенных выше соотноше-
соотношений:
ЗЬ35 } 2Н-1
_JbS }н-1 TbS }«
- Ж J ~W*+ н. J я'
— 00 —ОО
где /xf (/х^) - коэффициенты сопротивления сдвигу для верхнего
(нижнего) цилиндра.
Результаты расчёта коэффициентов трения качения и сопро-
сопротивления сдвигу при разных значениях безразмерных парамет-
параметров представлены на рис. 5.20 и 5.21.
На рис. 5.20 приведены зависимости коэффициентов трения
качения \iT и сопротивления сдвигу fif от числа Зоммерфель-
да при различных значениях параметра fj, характеризующе-
характеризующего вязкость поверхностного слоя. Как следует из расчётов, в
присутствии на поверхности вязкоупругого слоя (fj ф 0) зави-
зависимость fir(S) является немонотонной: с ростом числа Зоммер-
фельда значения /хг сначала уменьшаются, а потом растут (кри-
(кривые 2 и 3 на рис. 5.20). Она достигает минимума при некотором
значении 5 = 5*, зависящем от параметров fj и C. Объяснение
такого характера зависимости содержится в проведённом выше
анализе графиков распределения давления при разных числах
Зоммерфельда и fj/ (l — 72) = 5 • 10~8 (см. рис. 5.17). В случае
упругого поверхностного слоя (fj = 0) коэффициент трения каче-
качения монотонно растёт с ростом числа Зоммерфельда (кривая 1).
Коэффициент сопротивления сдвигу является монотонно возрас-
возрастающей функцией от числа Зоммерфельда, которая практически
не зависит от параметра fj. Величина этого коэффициента мень-
меньше величины коэффициента трения качения.
На рис. 5.21 представлены зависимости коэффициентов тре-
трения качения и сопротивления сдвигу от разницы -у скоростей
верхнего и нижнего цилиндров. Результаты показывают, что эти
коэффициенты слабо зависят от параметра 7 при малых значе-
295
0,0000
0,0001
0,0002
Рис. 5.20. Коэффициент трения качения \iT A, 2, 3) и коэффициент
сопротивления сдвигу nf A', 2', 3') как функция числа Зоммерфельда
при Р = Ю-4 и /3 = 1, г, = 0 A, 1'), /3=1, г) = 5- Ю-8 B, 2'), /3 = 0,5,
4 = 5- Ю-8 C, 3')
0,04
0,03
0,02 "
0,01
0,00
, 2'
0,001 0,01 0,1 у
Рис. 5.21. Коэффициент трения качения fir A, 2, 3) и коэффициент
сопротивления сдвигу д+ A', 2', 3') как функция скорости проскаль-
проскальзывания при Р = Ю-4, /3 = 1 и ?} = 5 • Ю-8 A, Г), fj = 10~8 B, 2'),
т? = 0 C, 3')
296
ниях этого параметра G ^ 0,1). При больших значениях -у коэф-
коэффициент /j,t = fif монотонно возрастает с ростом -у.
Таким образом, учёт специфических свойств тонких поверх-
поверхностных слоев в контакте со смазкой позволяет получить ка-
качественно новые зависимости коэффициента трения качения от
числа Зоммерфельда и, в частности, от скорости качения.
'Если рассматривать смазку между поверхностями как не-
неоднородную сплошную среду (тонкие слои смазки вблизи по-
поверхностей взаимодействующих тел подчиняются соотношени-
соотношениям, характерным для вязкоупругих материалов, в то время как
остальная её часть описывается уравнением вязкой несжимаемой
жидкости, т.е. уравнением Рейнольдса), то построенное решение
позволяет с единых позиций описать различные режимы тре-
трения, имеющие место в контакте реальных тел: при "малых чис-
числах Зоммерфельда вязкоупругий пограничный слой смазки игра-
играет определяющую роль в контакте (режим граничного трения),
в то время как при больших числах Зоммерфельда определяю-
определяющими являются объёмные свойства смазки (гидродинамическое
трение). Полученные аналитические зависимости хорошо опи-
описывают известные экспериментальные результаты (см. [217]).
5.4. КОНТАКТ КАЧЕНИЯ В УСЛОВИЯХ
ОГРАНИЧЕННОЙ СМАЗКИ
В этом разделе рассматривается модель, в которой поверхност-
поверхностный слой представляет собой композиционный материал, состо-
состоящий из матрицы и наполнителя (смазки). При нагружении слой
деформируется как упругое или вязкоупругое тело и смазка вы-
выдавливается на поверхность, обеспечивая режим гидродинами-
гидродинамического трения с ограниченным потоком смазки. Проведённый
Анализ позволяет установить особенности изменения контакт-
контактных характеристик (давления, размера области контакта, коэф-
коэффициента трения) со скоростью и нагрузкой при качении тел
в условиях ограниченной смазки (например, при использова-
йии пластичной смазки, пористых антифрикционных покрытий
fa т.д.).
297
5.4.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим контакт двух вращающихся упругих цилиндров
(см. рис. 5.15). Для упрощения выкладок в данном анализе пред-
предположим, что циилндры покрыты слоями одинаковой толщины,
т. е. h\ = hi = h. Как и в 5.3, задача рассматривается в плос-
плоской постановке и вводятся неподвижная и подвижная системы
координат, соотношения между которыми даны в E.92). Формы
контактирующих поверхностей цилиндров описываются функ-
функциями fi(x) = щ ± x2/BR{) (х\ и Х2 - некоторые постоянные),
при этом нижний цилиндр радиуса i?2 может иметь как поло-
положительную, так и отрицательную кривизну.
Рассмотрим две модели поверхностного слоя. В первой по-
поверхностный слой упругий и его перемещения vL в направле-
направлении нормали к поверхности описывается соотношением, соот-
соответствующим основанию Винкдера, т. е.
(
где р - контактное давление, Еп - модуль упругости.
Во втором случае слой моделируется вязкоупругим телом,
для которого соотношение между перемещением vL и контакт-
контактным давлением р в системе координат (г{,вг), связанной с вра-
вращающимся цилиндром, имеет вид:
р
dvL
dT
h
E.118)
PQ.
Эта модель аналогична модели Максвелла, которая обычно пред-
представляется упругой пружиной, имеющей модуль Еп, соединённой
последовательно с демпфером вязкости ЕпТп. Предполагается,
что при достижении критического давления ро работает только
демпфер, т. е. имеет место полное течение слоя.
При установившемся движении тел соотношение E.118) в
системе координат (х,у) может быть записано с учётом E.92)
298
в следующем виде:
(_h_
__t E~n
dx
p(x) dp(x)\
H :— I , P <Po,
dx
E.119)
(x),
где Vi = u>i\Ri\ - линейные скорости граничных точек цилиндров.
Для определённости положим, что V\ > ]/%.
Как уже отмечалось, слой представляет собой упругую или
вязкоупругую матрицу, наполненную жидкостью с вязкостью ц.
При нагружении жидкость выдавливается из слоя и попадает
в зону контакта. Количество жидкости Q, выдавленное в еди-
единицу времени, определяется деформациями слоев и может быть
рассчитано по формуле:
о
y. r
E.120)
J
где F + a)/Vi - время, которое произвольный элемент каждого
тела (г = 1,2) находится в контакте, (Ь + а) - ширина облас-
области контакта, к - коэффициент, характеризующий способность
жидкости выдавливаться из слоя @ ^ к ^ 1).
Для описания течения выдавленной жидкости между поверх-
поверхностями вращающихся цилиндров используется уравнение Рей-
нольдса E.95), в котором зависимость вязкости rj жидкости от
давления р(х) описывается соотношением Баруса E.96).
Граничные условия для уравнения Рейнольдса E.95) рас-
рассматриваются в виде:
р(-а) = р(Ъ) = 0, %¦
= 0,
E.121)
х=Ь
где —а и 6 - точка входа и выхода из области контакта соответ-
соответственно.
Скорость протекания объёма жидкости через произвольное
сечение определяется соотношением (см. [162]):
(Vi
E.122)
299
где Н* - толщина плёнки смазки в точке, где dp/dx = 0.
Предположим, что вся жидкость, выдавленная из слоя, попа-
попадает в зону контакта, т.е. Q = Q\. Тогда из E.120) и E.122)
получим:
E.123)
о
V2
Будем считать, что цилиндры являются упругими, изо-
изотропными и однородными, перемещения границы которых
подчиняются соотношениям E.98). Внутри области контак-
контакта (—а, Ь) толщина Н{х) плёнки смазки удовлетворяет уравне-
уравнениям E.99)-E.101).
Уравнения E.95), E.98), E.99), E.117), E.119) вместе с усло-
условиями E.121), E.123) и уравнением равновесия E.102) исполь-
используются для определения давления р(х), толщины плёнки смаз-
смазки Н(х), смещений границ слоя vL и основания Vi(x) внутри об-
области контакта (—а,Ь) в случае двух моделей деформирования
поверхностных слоев.
5.4.2. МЕТОД РЕШЕНИЯ И АНАЛИЗ РЕЗУЛЬТАТОВ
Запишем уравнения E.117) и E.119) в виде одного соотношения.
Проинтегрировав E.119) с учётом граничного условия v^(—a) =
= 0, получим:
E.124)
h En
где в случае упругого слоя ЕпТп -» +оо и ip(t) = 1 (см. E.117)), а
в случае вязкоупругого слоя ip(t) - кусочно-постоянная функция
вида:
ft '11 <
300
Интегрируя уравнение Рейнольдса E.95) и подставляя в выра-
выражение для толщины плёнки смазки E.99) соотношения E.98)
и E.124), а также принимая во внимание уравнение равнове-
равновесия E.102), получим следующую систему уравнений для опреде-
определения функций р(х) и Н{х):
р{х) = 6r/0(F1 + V2)
(x')) dx't E.126)
Po
E.127)
In
di.
С учётом E.124) преобразуем соотношение E.123) к виду:
Н*Еп(Ъ + а) 2
2hk
+
Ь
I P(x)tp
E.128)
Ро
dx.
Из соотношений E.121) и E.126) следует ещё одно условие для
определения неизвестных постоянных:
ь
I Я^3 ~5* exp (ap(x')) dx' = 0. E.129)
—а
Используя введённые ранее безразмерные параметры и функ-
функции (см. соотношения E.107)), а также обозначения
^
REn"
E.130)
Ь-о
б =
301
запишем систему уравнений E.126)—E.129) и условие равнове-
равновесия E.102) в безразмерном виде:
Н2М) + 6LSP I Н^}~ 1 ехр (ар(О) # = 0, E.
J ¦" (л ) ¦
'
|
131)
E.132)
-1
1 .
ехр
=0>
Eлзз)
-1
E.134)
-1
1
- §р /A -
-1
= 0. E.135)
Решение полученной системы позволяет определить функ-
функции р{?), Н{?) внутри области контакта (—1,1) и три безраз-
безразмерных параметра: Я*, L и е.
Заметим, что в случае упругого поверхностного слоя соотно-
соотношение E.135) принимает простой вид:
302
Для решения системы использовался метод Ньютона-Канторо-
Ньютона-Канторовича. Левая часть системы - нелинейный оператор в простран-
пространстве П, представляющем собой декартово произведение про-
пространства непрерывных функций Н(х) 6 С [—1,1], удовлетво-
удовлетворяющих условию НA) = 1, пространства непрерывных функ-
функций р(х) € С [—1,1], удовлетворяющих условиям р(-1) = рA) =
= 0, и пространства точек (е, L, ЙЛ € R3. Линеаризация этого
оператора позволяет свести задачу к системе линейных урав-
уравнений относительно поправок к решению на предыдущем шаге.
После выделения особенностей ядра последняя задача сводится
к системе линейных алгебраических уравнений, решаемых ме-
методом Гаусса.
В результате численного анализа получены распределения
давлений и толщины плёнки смазки в зависимости от относи-
относительных механических и геометрических параметров слоя (зна-
(значений h, /3, ро)) относительной вязкости жидкостного наполните-
наполнителя слоя (смазки) и его матрицы fj, коэффициента а, характеризу-
характеризующего зависимость вязкости смазки от давления, и коэффициен-
коэффициента к, характеризующего способность жидкости выдавливаться
из слоя.
Условия трения описываются в модели безразмерной нагруз-
нагрузкой Р, числом Зоммерфельда 5 и относительной скоростью про-
проскальзывания 7-
На рис. 5.22 и 5.23 приведены результаты, рассчитанные для
модели упругого поверхностного слоя, выделяющего смазку при
деформировании. Типичные кривые распределения давления и
толщины плёнки смазки внутри области контакта (—а, Ь) пред-
представлены на рис. 5.22. Сравнение кривых 1 и 2, рассчитанных без
учёта зависимости вязкости от давления, показывает, что с уве-
увеличением относительной податливости слоя (увеличением пара-
параметра C) контактное давление уменьшается, а толщина плёнки
смазки растёт.
Результаты расчётов дают основание заключить, что учёт
зависимости вязкости от давления приводит к существенно-
существенному изменению в характере распределения давления и толщины
плёнки смазки в зазоре. При а = 40 (кривая 3) толщина плён-
плёнки смазки остаётся приблизительно постоянной во всей области
303
0,0 xlb 1,0
0,008
0,006 \
0,004
0,002
-1,0 -0,5
0,0
0,5 xlb 1,0
Рис. 5.22. Распределение давления (а) и толщина плёнки смазки (б)
в модели с упругим слоем при 5 = 0,0005, Р = 0,1, h — 0,01, 7 = 0,1 и
а = 0, р = 4 A); a = 0, /3 = 0,4 B); a = 40, /3 = 0,4 C)
контакта за исключением малого участка вблизи выхода, где на-
наблюдается её сужение. Соответственно распределение контакт-
контактного давления близко к тому, которое имеет место в контакте
без смазки, при этом в точке, соответствующей сужению зазо-
зазора, имеет место скачок производной функции давления. Однако
в расчётах в указанном на графике диапазоне измененияпара-
метров не был обнаружен заострённый пик давления, имеющий
место в упругогидродинамическом контакте (при неограничен-
неограниченной смазке) с учётом зависимости вязкости от давления.
На рис. 5.23 приведены зависимости безразмерных ширины
площадки контакта F + a)/Bi?) и минимальной толщины плён-
плёнки Hmin/R от числа Зоммерфельда S, полученные без учёта
(кривые 1, 1') и с учётом (кривые 2, 2') зависимости вязкости от
304
(b + a)/BR), \OOHmJR
давления. С увеличением числа Зоммерфельда ширина площад-
площадки контакта уменьшается, а толщина плёнки смазки растёт. Об-
Общим свойством исследуемых зависимостей является стремление
к постоянной величине как минимальной толщины плёнки смаз-
смазки, так и размера области контакта при больших S (S —>¦ +оо),
причём асимптотические значения слабо зависят от парамет-
параметра <5.
Заметим, что
если известно асимп-
асимптотическое значение
размера L площадки
контакта, то можно
по формуле E.136)
рассчитать асимп-
асимптотическое значение
толщины плёнки
смазки на выхо-
выходе Й*, которое также
0,7
0,5
0,3
0,1
0,000 0,002
0,004 0,006 S 0,010
является ограничен- Рис. 5.23. Зависимость ширины площадки
ной величиной при контакта A и 2) и минимальной толщины
больших S. плёнки смазки A' и 2') от числа Зоммерфель-
Результаты рас- да в м°Депи с упругим слоем при Р = ОД;
считанные для моде- ~h = °>01! 7 = ОД, Р = 0,4 и а = 0 A, 1'),
ли вязкоупругого по- о; = 40 B, 2 )
верхностного слоя, выделяющего смазку при деформировании,
приведены на рис. 5.24 и 5.25. В дополнение к предыдущей моде-
модели в рассмотрение введены параметры fj и ро, характеризующие
вязкость слоя.
На рис. 5.24 приведены распределение давления и толщины
плёнки смазки при разных значениях числа Зоммерфельда (кри-
(кривые 1 и 4), параметра fj (кривые 1 и 3) и параметра ро (кривые 1
и 2). Кривые рассчитаны с учётом зависимости вязкости жид-
жидкости от давления (а = 40). В отличие от случая упругого слоя
для вязкоупругого слоя давление распределено несимметрично,
причем рост давления наблюдается вблизи точки входа (—о) в
область контакта. С увеличением вязкости слоя (уменьшением
параметра fj), уменьшением числа Зоммерфельда S и увеличени-
305
0,15
0,10
0,05
0,00
0,13
0,11
0,09
0,07
/
у
\
3/
/
V 1
4
\
/
/4
\
a ;
-8 -6 -4 -2
HIR
0 1
0,05
\
\2
\ v
3
N
ч4
! б
у
-8
-6
-4
-2 x/6 0 1
Рис. 5.24. Распределение давления (а) и толщина плёнки смазки (б)
в модели с вязкоупругим слоем при Р = 0,03, h = 0,1, 7 = 0Д> E = 40,
/3 = 0,4 и S = 0,1, т) = 0,008, ро = 0,1 A); 5 = 0,1, г) = 0,008, р0 =
= 0,02 B); 5 = 0,1, т? = 0,016, р0 = 0,1 C); 5 = 0,4, ту = 0,008, р0 =
= ОД D)
ем параметра ра точка максимума функции давления всё более
напоминает угловую точку (кривая 1). В этой же точке наблю-
наблюдается резкое утоныыение плёнки. Увеличение скорости (числа
Зоммерфельда S) приводит как к сглаживанию функции давле-
давления, так и к уменьшению максимального значения давления и
к более симметричному его распределению (кривая 4). Толщи-
Толщина плёнки смазки существенно зависит от параметров г) и S.
При увеличении этих параметров увеличивается толщина плён-
плёнки смазки. Влияние же параметра ро на толщину плёнки смазки
пренебрежимо мало.
306
0,2
Зависимости минимальной толщины плёнки смазки и шири-
ширины площадки контакта от числа Зоммерфельда S в случае по-
постоянной величины вязкости жидкости (а = 0) представлены на
рис. 5.25.
Сравнение полу- (b + a)/BR), Hmin/R
ченных зависимостей
с аналогичными за-
зависимостями, рассчи-
рассчитанными для упругого
слоя (см. рис. 5.23),
указывает на осо-
особенности поведения
вязкоупругого слоя.
Минимальная толщи-
толщина плёнки с ростом
величины о не воз- рИс. 5.25. Зависимость ширины площад-
растает, как в случае ки контакта A) и минимальной толщины
упругого слоя, а мед- ПЛёНКи смазки (Г) от числа Зоммерфельда
ленно уменьшается. в модели с вязкоупругим слоем при К = 0,1,
Это объясняется тем, 7 _ 01; р _ 04 и pQ _ 01] р _ 008) & _ 0
что в случае вязкоуп-
вязкоупругого слоя его деформации зависят от скорости. Поскольку
перемещения границы слоя уменьшаются с увеличением, в
частности скорости (величины S), это приводит к уменьшению
объёма Q выделяемой жидкости в единицу времени (см. E.120)).
5.4.3. АНАЛИЗ СИЛ ТРЕНИЯ
Используя соотношения E.114)—E.116), а также введённые без-
безразмерные параметры и функции, представим коэффициенты
трения качения \xr = M/(PR) и сопротивления сдвигу fit = Т%/Р
в виде:
E-137)
-l
307
^ = Чр
Я,
exp(ap(O)
df. E.138)
0,01
0,00
Результаты расчёта
коэффициента трения
качения для случаев
упругого и вязкоупру-
гого поверхностного
слоя приведены на
рис. 5.26 и 5.27 соот-
соответственно. Анализ
полученных зависи-
0,010 мостей показывает,
0,000 0,002 0,004 0,006 '5
Рис. 5.26. Зависимость коэффициента что ПРИ боль™ зна"
трения качения от числа Зоммерфельда
в модели с упругим слоем при Р — 0,1,
h = 0,01, 7 = 0,1, Р = 0,4 и a = 0 A),
a = 40 B)
чениях числа Зоммер-
Зоммерфельда 5 коэффициент
трения качения падает
с ростом S, т.е. с
увеличением скорости.
Это объясняется уменьшением ширины площадки контакта и
её смещения с ростом числа Зоммерфельда. Такая зависимость
коэффициента трения от скорости является характерной для
качения в условиях ограниченной смазки. Как было показано
в 5.3, в условиях эластогидродинамической смазки при наличии
поверхностного слоя, обладающего как упругими, так и вяз-
коупругими свойствами, коэффициент трения с ростом числа
Зоммерфельда S растёт при больших S. Сравнение кривых 1
и 2 на рис. 5.26 даёт основание заключить, что в тяжелонагру-
женных контактах увеличение пьезокоэффициента вязкости а
приводит к уменьшению коэффициента трения качения.
На рис. 5.27 для случая вязкоупругого слоя приведены за-
зависимости коэффициентов трения качения /ur и сопротивления
сдвигу /j,t от числа Зоммерфельда S. Как и в случае упругого
слоя, коэффициент трения качения уменьшается с увеличени-
увеличением 5. Зависимость же коэффициента /^ от числа Зоммерфельда
(кривая 1'), является немонотонной. Уменьшение функции Ht(S)
308
при малых значениях S объясняется быстрым уменьшением ши-
ширины площадки контакта в этом диапазоне значений парамет-
параметра S (см. рис. 5.25).
Представленные на
рис. 5.22-5.27 резуль-
результаты относятся к слу-
случаю к = 1. При умень-
уменьшении значений к
(О < к ^ 1) толщина
плёнки смазки умень-
уменьшается. При малых
значениях к распреде-
распределение давлений близко
к тому, которое имеет
место в случае ка-
качения упругих тел,
имеющих на поверх-
поверхности тонкий упругий
или вязкоупругий
слой (см. 5.1).
0,01 0,04 0,08 S 0,12
Рис. 5.27. Зависимость коэффициентов
трения качения A) и сопротивления сдви-
сдвигу B) от числа Зоммерфельда в модели с
вязкоупругим слоем при h = 0,1; 7 = 0,1,
/3 = 0,4, ро = 0,1; Р - 0,08, fj = 0,002, а - 0
Таким образом, контактные характеристики и коэффициент
трения в контакте двух вращающихся цилиндров в условиях
ограниченной смазки, выделяющейся в область взаимодействия
при деформировании поверхностного слоя, отличаются от тех,
которые были получены в 5.3. Эти характеристики становят-
становятся существенным образом зависящими от условий нагружения и
механических свойств поверхностного слоя, которые определяют
объём выделяющейся при деформировании жидкости (смазки).
Глава 6
МОДЕЛИ ИЗНАШИВАНИЯ
Исследование контактных задач с учётом микроструктуры и ха-
характера неоднородности поверхностных слоев, а также свойств
контакта и промежуточной среды позволяет определить напря-
напряжения в области контакта и в тонких приповерхностных слоях,
что очень важно с точки зрения прогнозирования характера их
разрушения при трении (изнашивания).
При моделировании разрушения поверхностных слоев ис-
используются методы и модели механики разрушения. Однако,
это моделирование не сводится только к применению резуль-
результатов, полученных в механике разрушения и теории контакт-
контактных задач. Изнашивание характеризуется рядом специфичес-
специфических свойств, выделяющих его в особый вид разрушения. От-
Отметим, что некоторые вопросы разрушения поверхностных сло-
слоев при контактном взаимлдействии обсуждаются в монографи-
монографиях [82, 100, 105, 188, 214].
В этой главе мы рассмотрим подходы к моделированию раз-
разрушения поверхности при трении, отметим специфические чер-
черты этого процесса и в качестве примера приведём две конкрет-
конкретные модели изнашивания поверхности.
6.1. ИЗНОС КАК СПЕЦИФИЧЕСКИЙ ВИД
РАЗРУШЕНИЯ
Изнашивание есть удаление материала с поверхности трения
вследствие её разрушения, проявляющееся в постепенном изме-
изменении формы и размеров взаимодействующих тел. Изнашивание
компонентов машин и механизмов приводит к ухудшению рабо-
работы сопряжений и выходу их из строя.
Каковы же механизмы изнашивания? Как показали исследо-
исследования, процесс разрушения поверхности происходит под дейст-
310
вием различных причин. Прежде всего, он может быть вызван
концентрацией напряжений в приповерхностных слоях материа-
материала при трении, приводящей к трещинообразованию и отделению
фрагментов материала (частиц износа) с поверхности трения.
Этот наиболее распространённый вид износа носит название ме-
механический износ, при этом часто слово "механический" опуска-
опускается. При ударном воздейстии на поверхность твёрдых частиц
или капель возникает эрозионный износ.
Среди других видов изнашивания следует отметить разру-
разрушение поверхности, вызванное протеканием химических и элек-
электрохимических реакций. Примером такого механизма изнашива-
изнашивания является коррозионный износ, обусловленный одновремен-
одновременным воздействием механических и электрохимических факто-
факторов. Этот механизм изнашивания преобладает в подвижных со-
сопряжениях, работающих в химически активной среде.
Некоторые физические процессы также могут вызвать изна-
изнашивание поверхности. Например, известно, что большая часть
энергии, затраченной на трение, превращается в тепло. Увели-
Увеличение температуры поверхностных слоев может вызвать измене-
изменение агрегатного состояния материала. В этом случае износ обу-
обусловлен расплавлением и вытеканием расплавленного материала
из зоны трения или его испарением (например, износ в тормозах,
высокоскоростных направляющих и т.д.). Высокая температу-
температура ускоряет также процессы диффузии, влияющие в некоторых
случаях на характер износа (например, в режущем инструмен-
инструменте). При этом износ имеет место на атомном и молекулярном
уровнях.
Следует отметить, что износ, имеющий место в подвижных
частях машин и механизмов, как правило, обусловлен одновре-
одновременным действием различных причин. Поэтому выделение и из-
изучение разных механизмов изнашивания по отдельности явля-
является в определённой степени идеализацией реальных процессов
различной природы, протекающих на поверхности трения и при-
приводящих к её формоизменению.
Поскольку механический износ двух тел при трении опре-
определяется напряжённо-деформированным состоянием их припо-
приповерхностных слоев, изучение процесса разрушения поверхности
311
в этом случае должно быть основано на методах механики кон-
контактного взаимодействия и механики разрушения.
6.1.1. АКТИВНЫЙ СЛОЙ
Механический износ тел в подвижных сопряжениях в свою оче-
очередь также протекает под действием различных механизмов.
Однако прежде чем остановиться на анализе этих механизмов,
выделим сначала ту область материала, которая подвержена
разрушению при трении. Проводя параллель между механикой
объёмного разрушения и механикой поверхностного разрушения,
сразу отметим, что если определение места зарождения трещи-
трещины в образце при его объёмном нагружении зачастую является
непростой задачей, при исследовании изнашивания поверхности
область возможного разрушения известна изначально.
Многочисленные исследования размеров и формы отделив-
отделившихся с поверхности трения частиц износа, а также микро-
микрогеометрии изношенной поверхности дают возможность оценить
толщину поверхностного слоя, подвергающегося разрушению
при трении [222]. Для того чтобы представить характерные раз-
размеры области взаимодействия и разрушения, рассмотрим кон-
контакт двух тел (рис. 6.1,а). В качестве масштаба рассмотрения
примем диаметр d пятна контакта, характерный размер которо-
которого находится в пределах от 1 до 10 мкм. Заметим, что высота hr
неровностей может принимать значения от 0,Ы до d. Размеры
частиц износа меняются в широких пределах, однако в среднем
они не превосходят одного-двух диаметров пятна контакта, что
позволяет оценить толщину приповерхностного слоя h^, в кото-
котором происходит разрушение при трении. Этот слой часто назы-
называют активным слоем.
Активный слой неоднороден по механическим характеристи-
характеристикам и имеет сложную структуру. Практически все поверхности,
участвующие в трении, загрязнены. На поверхности образуются
тонкие плёнки молекул, адсорбированных из атмосферы, а также
окисные и другие плёнки, возникающие в результате химичес-
химических реакций поверхности с окружающей средой (рис. 6.1,5).
Кроме- того, при разных видах технологической обработки
поверхности происходит изменение механических характерис-
312
Рис. 6.1. Схема контакта (а) и типичная структура поверхностного
слоя (б) при взаимодействии двух шероховатых поверхностей:
L\ - адсорбированный слой толщиной 10 нм; L,2 - окисная плёнка толщиной
10 -i-102 нм; Ьз - сильно деформированный слой толщиной 102 -т-103 нм
тик приповерхностных слоев по сравнению со свойствами ос-
основы. В этих слоях возникают дефекты различного масштаба и
природы, остаточные напряжения и т.д.
Свойства активного слоя не столь хорошо изучены по сравне-
сравнению со свойствами основного материала. Это объясняется тем,
что для исследования его свойств требуется применение специ-
специальных инструментов и методик вследствие его малой толщи-
толщины и значительного изменения свойств по толщине. Обычно для
исследования структуры и химического состава активного слоя
применяются методы электронной микроскопии, рентгенострук-
турного анализа, фотоэлектронной спектроскопии, дифракция
рентгеновских лучей и др. Метод нано-индентирования в соче-
сочетании с решением соответствующих контактных задач также
313
может быть использован для определения механических свойств
поверхностного слоя, т. е. его твёрдости и модулей упругости.
При контактном взаимодействии в активном слое возникают
высокие напряжения, неравномерно распределенные в силу дис-
дискретного характера контактирования тел с шероховатыми по-
поверхностями. Это утверждение может быть подтверждено сле-
следующими оценками. При взаимодействии шероховатых поверх-
поверхностей, как уже отмечалось в главе 1, фактическая площадь
контакта Ат составляет лишь малую долю номинальной (ка-
(кажущейся) площади контакта Аа, т.е. отношение Ат/Аа имеет
порядок 1СГ3 -г 10. Поэтому среднее фактическое давление рг
на пятнах контакта, определяемое как отношение общей нагруз-
нагрузки Р к фактической площади контакта Аг, т.е. рг = Р/Аг,
в 10 или 1000 раз превосходит номинальное контактное давле-
давление. При этом максимальные давления на пятнах контакта мо-
могут быть в несколько раз больше средних.
Интересно отметить, что многие экспериментальные и теоре-
теоретические исследования контактных характеристик шероховатых
поверхностей показывают, что среднее фактическое давление рг
мало меняется при изменении внешней нагрузки Р и зависит,
главным образом, от параметров шероховатости и механических
свойств взаимодействующих тел (см. [64, 90, 183, 191]). Оценка
средних значений фактического давления для разных материа-
материалов и свойств поверхности даёт основание заключить, что при
контактировании шероховатых поверхностей в поверхностных
слоях взаимодействующих тел напряжения могут достигать пре-
предела текучести, т. е. возникают условия пластического деформи-
деформирования материала.
Другой характерной особенностью напряжённого состояния
активного слоя является неравномерное распределение в нём
внутренних напряжений, возникающее вследствие дискретного
характера его нагружения по фактическим пятнам контакта ше-
шероховатых тел. Примеры распределения внутренних напряже-
напряжений в поверхностном слое для разных значений параметров мик-
микрогеометрии поверхности даны в главе 1.
При скольжении шероховатых тел возникает ещё одна осо-
особенность напряжённого состояния активного слоя. Вследствие
314
миграции пятен контакта, имеющей место при относительном
перемещении поверхностей, напряжения в некоторой фиксиро-
фиксированной точке поверхности меняются циклически и, следователь-
следовательно, циклически меняется поле внутренних напряжений в поверх-
поверхностном слое.
6.1.2. ВИДЫ ИЗНОСА ПРИ ТРЕНИИ ПОВЕРХНОСТЕЙ
Разрушение поверхности обычно возникает вблизи пятен кон-
контакта, на которых имеют место высокие значения нормальных
и касательных напряжений. При этом разрушение может наблю-
наблюдаться как после однократного, так и повторяющегося нагруже-
ния поверхности в рассматриваемой точке.
Разрушение при однократном нагружении возникает, если
внутренние напряжения, вызванные этим нагружением, столь
велики, что критерий разрушения выполняется в одной или не-
нескольких точках взаимодействующих тел. Этот тип разрушения
наблюдается при адгезионном износе, характеризуемом перено-
переносом материала с одной поверхности на другую. Высокая адгези-
адгезионная способность поверхностей взаимодействующих тел явля-
является необходимым условием для реализации этого вида износа.
Как правило, поверхностные загрязнения, такие как адсорбиро-
адсорбированные молекулы кислорода, водяной пар, плёнки окислов ме-
металлов и другие химические соединения, уменьшают адгезию.
Однако высокие контактные давления могут вызвать пластичес-
пластическое течение в поверхностных слоях и разрушение поверхностных
плёнок. При этом, если поверхностное течение, сопровождаемое
удалением окисных плёнок, имеет место в обоих телах (напри-
(например, их твёрдости мало отличаются друг от друга), адгезионный
износ протекает более интенсивно.
При фрикционном взаимодействии тел, .которые характери-
характеризуются существенно различной твёрдостью, часто реализуется
другой механизм разрушения поверхности, называемый абразив-
абразивным износом. При абразивном износе неровности более твёрдого
тела вытесняют мягкий материал из-под дорожки трения за счёт
его пластического деформирования (абразивное взаимодействие
двух тел). Кроме того, пластические деформации могут возни-
возникать и при наличии между телами в зоне трения твёрдых частиц
315
износа или абразива (абразивное взаимодействие трёх тел).
Абразивный износ может также возникнуть при однократном
нагружении пятна контакта, когда в активном слое возникают
высокие внутренние напряжения. В этом случае твёрдые неров-
неровности или частицы играют роль резца, удаляющего стружку с
поверхности мягкого тела. Такой вид абразивного изнашивания
известен как микрорезание. Микрорезание подобно таким тех-
технологическим операциям как обработка напильником или абра-
абразивной шкуркой (взаимодействие двух тел), а также обработка
поверхности путём притирки или полирования (взаимодействие
трёх тел). Оно характеризуется высокой скоростью изнашива-
изнашивания поверхностей.
В том случае, когда напряжения в активном слое не столь
велики (например, фактические давления не превышают предел
текучести) и нет сильной адгезии между поверхностями, раз-
разрушение при однократном нагружении не возникает. Однако,
вследствие циклического характера изменения напряжений при
относительных перемещениях поверхностей и их достаточно вы-
высоких амплитудных значений (среднее фактическое давление рт,
как правило, больше предела усталости) в активном слое проис-
происходит интенсивное накопление дефектов, приводящее к его уста-
усталостному разрушению. Усталостный износ практически всег-
всегда имеет место при фрикционном взаимодействии поверхностей.
Экспериментально установлено, что при усталостном изнаши-
изнашивании частицы отделяются с поверхности в дискретные момен-
моменты времени и размер частицы сравним с диаметром единичного
пятна контакта.
Усталостный износ преимущественно имеет место при уп-
упругом характере контактирования. В то же время он является
сопутствующим при других видах изнашивания (например, при
адгезионном и абразивном износе).
6.1.3. ОСОБЕННОСТИ ПРОЦЕССА ИЗНАШИВАНИЯ
Процесс изнашивания имеет ряд особенностей, которые выделя-
выделяют его как специфический вид разрушения. Специфика износа
заключается прежде всего в том, что сам факт протекания это-
этого процесса не является критическим для работы сопряжения.
316
Обычно допустимый износ [и>] (см. рис. 6.1) подвижных элемен-
элементов сопряжений намного больше характерного размера частицы
износа. Поэтому при работе сопряжений имеет место многократ-
многократно повторяющееся отделение частиц материала с поверхности
трения. Многократность элементарных актов разрушения яв-
является основной особенностью изнашивания, отличающего этот
процесс от разрушения материала в объёме. Если в классичес-
классической'механике разрушения требуется ответить на вопрос: "Ка-
"Какое время материал или конструкция будут функционировать
до разрушения?", то в трибологии важно знать ответ на иной
вопрос: "Как долго будет происходить процесс изнашивания,
т. е. отделения элементарных частиц износа и удаления их из
зоны трения, до достижения предельной величины износа?"
После удаления материала с поверхности в результате его
изнашивания вновь образованная поверхность снова вступает в
контакт. Её характеристики, включая те, которые определяют
скорость изнашивания, (микрогеометрия, степень поврежденнос-
ти и т.д.), зависят от истории процесса фрикционного взаимо-
взаимодействия. Таким образом, изнашивание можно рассматривать
как процесс наследственного типа.
Кроме того, изнашивание есть процесс с обратной связью.
Одной из характеристик, упрувляющих этим процессом, явля-
является микрогеометрия поверхности. С одной стороны, парамет-
параметры шероховатости влияют на напряжённое состояние и разру-
разрушение поверхности, а с другой - формирующийся при изнаши-
изнашивании рельеф поверхности определяется характером её разру-
разрушения. Процессы самоорганизации и формирования равновес-
равновесных структур при изнашивании как раз и являются проявле-
проявлением действия обратной связи. Как было показано многими ис-
исследователями (см. [91, 141, 147]), при изнашивании на поверх-
поверхности формируется равновесная шероховатость, являющаяся ти-
типичным примером формирования равновесной структуры в про-
процессе самоорганизации.
6.1.4. ЧАСТИЦЫ ИЗНОСА
Частицы материала, отделившиеся с поверхности при разруше-
разрушении, в будущем могут повести себя по-разному: они могут из-
317
менить форму и размер и сцепиться с одной из взаимодейству-
взаимодействующих поверхностей (адгезионный износ), или могут внедрить-
внедриться в поверхность более мягкого материала и затем выполнять
роль абразивной частицы по отношению к поверхности контрте-
контртела (абразивный износ). Наконец, отделившиеся частицы могут
покинуть зону контакта. Именно в этом случае они называются
частицами износа.
Заметим, что исследование поведения отделившихся при из-
износе частиц, а также инородных частиц, попавших в зону тре-
трения, является сложной задачей, которая до сих пор ещё мало
изучена. Эти частицы вместе со смазкой образуют между взаи-
взаимодействующими поверхностями особую промежуточную среду
(третье тело), свойства которой оказывают значительное влия-
влияние на характеристики контактного взаимодействия и изнаши-
изнашивание элементов трущейся пары. Знание свойств третьего тела
особенно важно при анализе таких видов разрушения, как фрет-
тинг (изнашивание при малых осциллирующих перемещениях
тел) и абразивный износ в присутствии третьего тела.
6.2. ПОДХОДЫ К МОДЕЛИРОВАНИЮ
ИЗНАШИВАНИЯ
Таким образом, при моделировании механического изнашивания
необходимо, прежде всего, определить напряжённое состояние и
поле температур, которые возникают в теле при заданных внеш-
внешних условиях взаимодействия, свойствах материалов контакти-
контактирующей пары и макро- и микрогеометрии поверхностей. На осно-
основании этого анализа устанавливаются наиболее вероятные меха-
механизмы разрушения поверхности, которые с использованием кри-
критериев разрушения позволяют определить момент разрушения
и форму поверхности после отделения частицы материала (или
её переноса на другую поверхность). Необходимость определе-
определения формы поверхности после элементарного акта разрушения
связана с тем обстоятельством, что вновь образованная поверх-
поверхность снова вступает в контакт и её форма влияет на после-
последующие акты разрушения. Изложенные этапы моделирования
схематично представлены на рис. 6.2. Понятие состояние кон-
318
Состояние
контакта на
макроуровне
Состояние
контакта на
микроуровне
Критерий
разрушения
Отделение
частицы
Изменение
макроформы
Изменение
формы на
микроуровне
Рис. 6.2. Основные этапы моделирования изнашивания и их взаимо-
взаимосвязь
такта включает в себя напряжённое состояние и распределение
температуры вблизи области контактного взаимодействия. На
макроуровне - это осреднённые (номинальные) характеристики,
определённые с учётом известных макроформы поверхностей и
условий взаимодействия. На микроуровне - это фактические дав-
давления, фактические поля внутренних напряжений и температур
в приповерхностных слоях, построенные с учётом микрогеомет-
микрогеометрии поверхностей.
Как видно из схемы, изнашивание - процесс с обратной свя-
связью, поскольку форма поверхности является как характеристи-
характеристикой, влияющей на износ, так и характеристикой, изменяющейся
в процессе износа. При изнашивании происходит своеобразное
приспосабливание формы поверхности к внешним условиям, ко-
которое может, в частности, приводить к возникновению стацио-
стационарных режимов изнашивания, описанных ниже.
Поскольку при анализе изнашивания в большинстве случаев
нас интересуют лишь глобальные характеристики процесса (из-
(изменение формы тела через промежутки времени, гораздо боль-
большие, чем интервал времени между отдельными актами разруше-
разрушения, максимум величины износа по поверхности и т. д.), измене-
изменение формы поверхности после элементарного акта разрушения,
форма отделяющейся при этом частицы, как и все характерис-
319
тики, связанные с расчётом полей напряжений и температур при
рассмотрении процессов на масштабах, соизмеримых с размером
единичного пятна контакта, в большинстве практических прило-
приложений являются внутренними параметрами модели. Фактически
в большинстве приложений задачей моделирования износа явля-
является прогнозирование перехода от одного макросостояния (мак-
(макроформы) к другому при заданных внешних условиях (нагрузки,
скорости).
Таким образом, моделирование изнашивания можно рассмат-
рассматривать на двух масштабных уровнях (см. рис. 6.2): макроуро-
макроуровень, определяющий кинетику изменения макроформы тел при
изнашивании, и микроуровень, описывающий каждый элемен-
элементарный акт отделения частицы с поверхности. Многократное
повторение расчётов на микроуровне позволяет оценить измене-
изменение характеристик сопряжения на макроуровне (изменение мак-
макроформы, сближение тел при изнашивании и т. д.) и рассчитать
долговечность сопряжения по критериям износостойкости. При-
Применение этого алгоритма к расчёту реальных сопряжений слож-
сложной конфигурации является чрезвычайно трудоёмким.
Часто анализ процессов, протекающих на микроуровне, поз-
позволяет разработать феноменологическую модель изнашивания
пары трения на макроуровне, в которой задается скорость из-
износа dw*/dt как функция макрохарактеристик сопряжения (дав-
(давления р, скорости V относительного перемещения поверхностей
и т.д.). Вид этой функции и её зависимость от процесса, проте-
протекающего на микроуровне, определяется на базе моделирования
элементарных актов разрушения поверхности.
6.2.1. ОСНОВНЫЕ ЭТАПЫ МОДЕЛИРОВАНИЯ ИЗНОСА
НА МИКРОУРОВНЕ
При моделировании износа на микроуровне объектом исследова-
исследования является активный слой. Моделирование износа включает в
себя определение момента зарождения трещины и траектории её
развития вплоть до отделения частицы материала, вынос отде-
отделившихся частиц из зоны трения, а также описание изменения
поверхностной микрогеометрии и свойств активного слоя при его
разрушении.
320
При построении модели изнашивания на микроуровне, схема
которой представлена в нижней части рис. 6.2, от состояния кон-
контакта на макроуровне необходимо перейти на более низкий мас-
масштабный уровень, на котором необходимо определить физичес-
физический механизм элементарного акта разрушения и выбрать кри-
критерий разрушения, соответствующий этому механизму; рассчи-
рассчитать напряжённо-деформированное состояние, температуру по-
поверхностного слоя и другие функции, входящие в критерий раз-
разрушения; построить модель отделения частицы; определить но-
новые характеристики поверхностного слоя после отделения части-
частицы (распределение контактных и внутренних напряжений, тем-
температуры и т.д.) и следующий момент разрушения.
Первый этап включает в себя анализ механизма изнашива-
изнашивания и определение критерия разрушения, соответствующего это-
этому механизму. Как правило, критерий разрушения зависит от
абсолютных или амплитудных значений напряжений, темпера-
температуры, механических характеристик материалов и т. д. Заметим,
что сам механизм разрушения во многом определяется уровнем
напряжений и температур в активном слое.
Следующий этап состоит в расчёте функции, входящей в кри-
критерий разрушения и в определении точки и момента зарожде-
зарождения трещины. С этой целью на базе решения соответствующей
задачи механики контактного взаимодействия для шерохова-
шероховатых поверхностей (см. главы 1-4) рассчитываются распределе-
распределения напряжений и температур в активном слое. Для решения
этой задачи могут также использоваться методы, изложенные в
монографиях [25, 66, 169] и др.
Для определения начала разрушения и моделирования отде-
отделения частицы с поверхности обычно применяются методы меха-
механики разрушения, позволяющие на основе выбора критерия раз-
разрушения и анализа состояния активного слоя рассчитать раз-
размеры и форму отделяющихся частиц. Как уже отмечалось, осо-
особенностью процесса изнашивания является его повторяющийся
характер. Поэтому чтобы построить модель этого процесса, пос-
после каждого отдельного акта разрушения необходимо определить
форму новой поверхности, вступившей в контакт, а также воз-
возникающее при этом напряженное состояние активного слоя и
11. Горячева И.Г. 321
распределение в нем температур, поскольку изменение микро-
микрогеометрии поверхности приводит к перераспределению факти-
фактических контактных давлений и внутренних напряжений.
Как отмечалось в 6.1.4, не все частицы, отделяющиеся с по-
поверхности, уносятся из зоны трения. Моделирование перемеще-
перемещений отделившихся частиц в зоне трения и их влияния на процесс
изнашивания на микроуровне является сложной задачей, кото-
которая здесь не будет рассматриваться.
Таким образом, моделирование процесса изнашивания на
микроуровне должно включать в себя решения задач механики
контактного взаимодействия, при постановке которых принима-
принимается во внимание макро- и микрогеометрия взаимодействующих
тел, неоднородность механических свойств поверхностных слоев,
а также неоднородность температурного поля, и задач механики
разрушения, используемых для описания отделения с поверхнос-
поверхности частиц материала.
На наш взгляд, наиболее трудным этапом моделирования яв-
является выбор критерия разрушения, поскольку процессы, вызы-
вызывающие отделение частицы, могут иметь различную природу.
Тип износа зависит от материалов пары трения, условий нагру-
жения, кинематики, наличия и природы смазки и других обстоя-
обстоятельств. Однако есть ряд общих свойств, которые отличают раз-
разрушение поверхности в условиях фрикционного взаимодействия.
Прежде всего, вблизи пятен фактического контакта шерохова-
шероховатых тел имеет место высокая концентрация напряжений, опреде-
определяемая характером нагружения, микрогеометрией тел, коэффи-
коэффициентом трения и т. д. Фрикционное тепловыделение на пятнах
фактического контакта приводит к значительному росту тем-
температуры в поверхностном слое. Наконец, вследствие миграции
пятен фактического контакта при относительных перемещениях
поверхностей происходит циклическое изменение полей напря-
напряжений и температур в приповерхностном слое.
Поскольку построение моделей изнашивания является непро-
непростой задачей, в трибологии обычно используются наиболее прос-
простые модели, учитывающие только основные факторы, влияющие
на процесс разрушения поверхности.
322
6.2.2. УСТАЛОСТНЫЙ ИЗНОС
Результаты многих экспериментальных исследований показы-
показывают, что наиболее часто поверхности разрушаются по уста-
усталостному механизму. При циклическом нагружении поверхнос-
поверхности, имеющем место при относительных перемещениях шерохо-
шероховатых тел, в активном слое возникает неоднородное циклическое
поле внутренних напряжений с высокими амплитудными значе-
значениями, что является причиной накопления в этом слое повреж-
повреждений.
Ниже мы используем макроскопический подход к построению
модели усталостного разрушения поверхности, который, как из-
известно (см. [70, 83]), состоит в построении положительной неубы-
неубывающей во времени функции Q(M,t), характеризующей меру по-
повреждения материала в точке М и зависящей от амплитудных
значений напряжений в данной точке. Разрушение наступает в
момент времени t*, когда эта функция достигнет заданного поро-
порогового значения. Такой подход применим к исследованию как по-
поверхностного разрушения, так и разрушения внутри тела. Кроме
того, в [91] показано, что параметры объёмного и поверхностного
усталостного разрушения для ряда материалов (например, для
некоторых видов резин) совпадают.
Специфика разрушения поверхности заключается в том, что
после акта разрушения, произошедшего в момент времени t*, и
удаления продуктов изнашивания оставшаяся часть материала,
характеризующаяся известной функцией распределения повреж-
повреждений Q(M,t*), вновь вступает в контакт, т.е. материал несёт
в себе следы истории процесса. Это обстоятельство обусловли-
обусловливает ряд характерных особенностей усталостного изнашивания
поверхностей, которые являются предметом обсуждения в после-
последующих разделах этой главы.
Существуют разные физические подходы к моделированию
поврежденности, в которых скорость накопления поврежденнос-
ти dQ(M, t)/dt рассматривается как функция напряжений в дан-
данной точке, температуры и других параметров, в зависимости от
механизма разрушения, вида материала и т. д.
Ниже приводятся примеры исследования усталостного изно-
износа на базе одномерной модели накопления поврежденности в no-
noil* 323
верхностном слое (модель отслаивания), а также на базе модели,
основанной на термокинетической теории прочности и позволяю-
позволяющей воспроизвести многократное отделение частиц износа и из-
изменение микрогеометрии поверхностей в зависимости от геомет-
геометрических характеристик контактирующих тел, механических и
теплофизических параметров материалов и условий нагружения.
6.3. МОДЕЛЬ ОТСЛАИВАНИЯ ПРИ
УСТАЛОСТНОМ ИЗНАШИВАНИИ
6.3.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим изнашивание упругого полупространства под дей-
действием распределённой по его поверхности нагрузки, цикличес-
циклически изменяющейся со временем. Возникающее внутри полупро-
полупространства поле напряжений вызывает накопление усталостных
повреждений в подповерхностных слоях. Будем считать, что ско-
скорость накопления повреждений q = dQ/dt ^ 0 есть функция ам-
амплитудного значения P(t) нагрузки и расстояния Az от рассмат-
рассматриваемой точки до поверхности полупространства. Поскольку
поле напряжений на бесконечности отсутствует, то
lim q(Az, P) = 0.
Дг-Ц-оо
Введём неподвижную систему координат Oxyz, связав плос-
плоскость Оху с поверхностью полупространства в начальный мо-
момент времени t = 0 и направив ось Oz в глубь полупространст-
полупространства.
Ниже мы покажем, что в процессе износа координата поверх-
поверхности вдоль оси Oz будет меняться. Координата поверхности в
неподвижной системе координат Oxyz будет описываться мо-
монотонно возрастающей кусочно-непрерывной функцией време-
времени Z(t), при этом Z@) = 0. Для каждого интервала [tn,tn+i]
(п = 0,1,2,...) функция Z(t) непрерывна. Поэтому определим
функцию накопления повреждений при z > Z(t) как
t
= Jq{z~ Z(t'), P(t')) dt' + Qn(z),
F.1)
324
где Qn(z) — Q(z, tn) - ловреждённость, имеющая место на глуби-
глубине z в момент времени tn, 0 < Qn(z) < Q*- Разрушение произой-
произойдет в точке z* промежутка [Z(t*), +oo), где впервые (в момент
времени t*) выполнится условие
Q(z*,t*) = Q*, F.2)
где Q* - некоторое критическое значение повреждённости, при
котором происходит элементарный акт разрушения.
Изучим процесс изнашивания с начального момента време-
времени to = 0. Из уравнений F.1) и F.2) следует, что процесс раз-
разрушения определяется функциями q(Az,P) и Qo{z), которые по
предположению являются непрерывными.
Исследуем особенности функции Q(z,T) и соответственно
процесса разрушения при разных видах функции q(z,P). Ес-
Если q(z — Z(t),P) и Qo(z) монотонно убывают по z, т. е. dq/dz < 0
и dQo/dz ^ 0, условие F.2) выполняется на границе z = Z(t) на-
начиная с момента времени t = t\, определяемого из соотношения
Jq{O,P(t'))dt' + Qo(O) = Q*, F.3)
о
и Z(t) = 0 при t ^t\. Возникающее непрерывное изменение ли-
линейного размера тела z = Z(t) будем называть поверхностным
износом.
Если одна из функций q(z — Z(t),P) или Qo(z) не являет-
является монотонно убывающей по z, а имеет, например, максимум на
некотором расстоянии от границы упругого полупространства,
условие F.2) может выполниться во внутренней точке z = Z\
полупространства в момент времени t\. В этом случае произой-
произойдет подповерхностное разрушение, заключающееся в отделении
слоя толщины AZ\ = Z\. В последующие моменты времени бу-
будет иметь место непрерывное изменение линейных размеров Z(t)
Для значений (t > t\) за счёт поверхностного износа. Для опреде-
определения дальнейшего протекания процесса, при t > t\, исследуем
функцию Q(z,?), определяемую соотношением F.1) при z > Z\,
Как и на предыдущем шаге и т. д. Если в некоторый момент
времени tn условие F.2) снова окажется выполненным внутри
325
тела в точке Zn = Z(tn + 0), (n = 2,3,...), то опять произойдёт
отделение слоя конечной толщины, которая определяется выра-
выражением
AZn = Z(tn + 0) - Z(tn - 0).
Следовательно, Z(t) в этом случае - кусочно-непрерывная функ-
функция.
6.3.2. СКОРОСТЬ ПОВЕРХНОСТНОГО ИЗНОСА
Мы можем определить скорость поверхностного износа dZ(t)/dt
в каждом интервале (tn,tn+i), в котором функция Z(t) непре-
непрерывна. Для этого получим уравнение для определения функ-
функции dt/dZ. Поскольку Q(Z(t),t) = Q*, то
= / F4)
dz dz/ at' [ '
Значения производных dQ/dZ и dQ/dt вдоль линии t = t(Z)
можно найти, дифференцируя выражение F.1):
dt , dQn(Z)
dZ ' dZ1 dZ
dQ_ =
dt
Из F.4) и F.5) получим следующее интегральное уравнение для
определения функции dt/dZ в интервале [tn,i
* 1 zfdq(z-z',P{z'))
L
L dZ dZ' F.6)
dZ
Уравнение F.6) при постоянной нагрузке Pq, т.е. при P(t) = Pq,
есть интегральное уравнение Вольтерра второго рода. Общее
326
решение этого уравнения, полученное с помощью преобразова-
преобразования Лапласа-Карсона, дано в [56]. Таким образом, если извест-
известны функции q(z,P) и Qn(z), мы можем аналитически описать
процесс поверхностного износа.
Рассмотрим в качестве примера процесс изнашивания, для
которого монотонно убывающая функция q(z, P) имеет вид
P\N 1
где Р» и Т* - характерная нагрузка и соответствующее ей вре-
время до первого разрушения; а(Р) > 0 - величина, имеющая раз-
размерность длины и зависящая от действующей нагрузки Р, N -
некоторая постоянная (N > 0).
Предположим также, что Qo{z) = 0 и что нагрузка P(t) яв-
является ступенчатой функцией, т. е.
t<tu
где ii = T» (P*/Pq)M. При t — t\ функция Q\{z) = Q(z,ti) может
быть определена из уравнения F.1):
Применяя преобразование Лапласа по переменной z, определим
скорость поверхностного износа при t > t\. Учитывая вид образа
функции q(z,P):
C[q(z,P);p] = [-) ^.—^jr, F.7)
где
C[f(z);p]= J exp(-pz)f(z)dz,
327
и используя F.6), получим
N
\dt I NT, (PA
N Р +
a (Pi))
Р V а(Р
Применяя затем обратное преобразование Лапласа, будем иметь
ей NT* (PAN\a(P0) fa(P0) \ ( N
dZ a{P0)
Интегрирование этого соотношения позволяет установить связь
между координатой Z поверхности и временем t:
Отсюда, в частности, следует, что скорость поверхностного из-
износа в рассматриваемом случае стремится к постоянному значе-
значению при t —>¦ +00, не зависящему от первоначального значения
нагрузки Pq, т.е.
dZ _ o(Px) fPi\N
t-F+oo ~di ~ NT*
Полученные результаты позволяют заключить, что при мо-
монотонно убывающей по z функции q(z,P) и начальной функ-
функции Qo(z) = 0 имеет место только поверхностный износ полу-
полупространства.
6.3.3. КИНЕТИКА ИЗНАШИВАНИЯ ПРИ
ПОСТОЯННОМ АМПЛИТУДНОМ ЗНАЧЕНИИ
НАГРУЗКИ
При изучении усталостного разрушения реальных тел в услови-
условиях сложного напряжённого состояния функцию интенсивности
328
накопления усталостных повреждений обычно связывают со зна-
значениями эквивалентных напряжений (максимальных касатель-
касательных, растягивающих и т.д.), ответственных за рассматривае-
рассматриваемый вид разрушения (83, 113].
В дальнейшем для определённости будем использовать в ка-
качестве критерия накопления усталостных повреждений величи-
величину максимальных касательных напряжений, а в качестве за-
закона, определяющего связь этой величины со значением функ-
функции q(z,P), - степенную зависимость, т.е.
^.. F.8)
где rmax(z, Р) - амплитудное значение максимальных касатель-
касательных напряжений на некоторой заданной глубине z. Значения г*,
Г* и N определяются экспериментально из испытаний на фрик-
фрикционную усталость (аналог параметров кривой Велера). Один
из возможных методов обработки результатов экспериментов с
целью определения значений г*, Т* и N изложен ниже в 6.3.6.
Предположим, что осциллирующее поле напряжений в уп-
упругом полупространстве вызвано скольжением по нему пери-
периодической системы инденторов (модель неровностей шерохова-
шероховатой поверхности). Анализ распределения внутренних напряже-
напряжений в периодических контактных задачах для упругого полупро-
полупространства при различных значениях параметров, характеризую-
характеризующих микрогеометрию поверхности (форма неровностей и их про-
пространственное расположение), выполненный в главе 1, а также
в работах [95, 202] и др. показывает, что случаи монотонного и
немонотонного изменения функции rmax(z) действительно име-
имеют место и, следовательно, выводы относительно особенностей
процесса усталостного изнашивания, сделанные в 6.3.1 на осно-
основании анализа уравнения F.1) для различных функций q(z,P),
являются реалистичными.
Ниже мы рассмотрим систему сферических инденторов,
скользящих без трения по поверхности упругого полупростран-
полупространства. Предполагая, что плотность пятен контакта невелика, пре-
пренебрежём их взаимным влиянием. Рассматриваемая модель мо-
может быть применена к анализу усталостного разрушения упру-
упругого полупространства штампом с шероховатой поверхностью,
329
скользящим без трения в разных направлениях по границе по-
полупространства. Считается, что характерные времена измене-
изменения нагрузки P(t), приложенной к штампу, таковы, что статис-
статистически можно считать все точки полупространства, лежащие
на определенной глубине, находящимися в равных условиях, что
даёт основание для построения одномерной модели изнашива-
изнашивания, все характеристики которой являются функциями рассто-
расстояния z от исходной (неизношенной) поверхности полупростран-
полупространства и времени t.
Подставляя в соотношение F.8) выражение для амплитуд-
амплитудных значений ттах на фиксированной глубине z (см. [184]), полу-
получим
N/3 1
где
N
91 (О =
С = 1 +1/,
ohi% у 4 ii* Hi* tj\ Л/2
Специфическим свойством функции q(z,P), определяющим ха-
характер процесса изнашивания, является её немонотонность (на-
(наличие максимума на глубине ? = z/a = 0,48). Эта функция удов-
удовлетворяет также условию lim q(z, P) = 0.
z-r+oo
В исследуемой модели повреждённость материала Q(z, P),
определяемая соотношением F.1), в каждый момент времени t
одинакова во всех точках полупространства, находящихся на
фиксированной глубине z. В силу этого обстоятельства разру-
разрушение полупространства происходит послойно и, следовательно,
геометрия контакта не меняется в процессе изнашивания.
Заметим, что разрушение наступает через некоторое время
после начала процесса, т. е. имеет место инкубационный период.
При постоянной нагрузке Р продолжительность инкубационного
периода Д? определяется из соотношения
330
IV
Рис. 6.3. Эволюция функции накопления повреждённости при изна-
изнашивании под действием постоянной нагрузки (N = 5)
Исследуем характер усталостного разрушения при постоян-
постоянной нагрузке Р. Нетрудно убедиться, что в безразмерных коор-
координатах
N
Z т. i f \
Т \ Р
функция Q(C, 0) не зависит от нагрузки. Следовательно, влия-
влияние нагрузки на процесс разрушения будет проявляться только
в изменении пространственного и временного масштаба в соот-
соответствии с приведённой заменой координат.
Для исследования процесса разрушения, описываемого урав-
уравнениями F.1), F.2) и F.9) применялся численный анализ. Функ-
Функция <5(С, в) в различные моменты времени при N = 5, Qo{z) = О
представлена на рис. 6.3. До момента в\ первого разрушения
кривая <5(С) 0) имеет характерный вид (I) с точкой подповерх-
подповерхностного максимума. После первого подповерхностного разру-
разрушения в точке ?i функция Q((,,9) имеет вид монотонной кри-
кривой (II) с максимумом на поверхности, характерной для про-
процесса поверхностного износа. Далее, вследствие немонотоннос-
немонотонности по z функции q(z,P), возникает перегиб функции Q((,6)
на некоторой глубине (III) (координата поверхности изменяется
в ходе изнашивания). В момент въ, когда величина подповерх-
331
ностного максимума станет равной критическому значению Q*,
т.е. Q(C2>#2) = Q*t происходит следующее подповерхностное
разрушение в точке ?г и т.д. Затем подповерхностное разру-
разрушение прекращается, а скорость поверхностного стремится к
постоянному значению. Кривая Q((,9) при этом приобретает
вид (IV), характерный для установившегося поверхностного из-
изнашивания.
Рис. 6.4, на котором представлена зависимость безразмер-
безразмерной координаты С = Z/a(P) поверхности от безразмерного вре-
времени в, иллюстрирует процесс разрушения в исследуемом слу-
случае. Момент подповерхностного разрушения обозначен точкой, а
цифры над графиком указывают глубину разрушения Д?п, т.е.
толщину отделившегося слоя.
Сравнение полученных зависимостей позволяет выявить
влияние показателя N в соотношении F.9) на кинетику изнаши-
изнашивания. При N = 3 преобладающим оказывается поверхностный
износ, переход к которому осуществляется после единственно-
единственного акта подповерхностного разрушения. При N = 5 происхо-
происходит 6 актов, а при N = 5,5 - 28 актов подповерхностного разру-
разрушения. В то же время можно указать на ряд характерных черт
процесса усталостного изнашивания при постоянной нагрузке:
монотонное уменьшение со временем толщины отделившегося
слоя, прекращение подповерхностного разрушения после конеч-
конечного числа актов, переход к установившемуся поверхностному
износу, характеризуемому постоянной скоростью.
Таким образом, весь процесс изнашивания можно разделить
на две стадии: начальный нестационарный режим (режим при-
приработки) и стационарный, при котором имеет место лишь по-
поверхностное изнашивание.
6.3.4. ВЛИЯНИЕ ХАРАКТЕРА ИЗМЕНЕНИЯ
НАГРУЗКИ НА КИНЕТИКУ ИЗНАШИВАНИЯ
При контактировании шероховатых тел амплитудные значения
нагрузки, действующей на неровность в рассматриваемой точ-
точке поверхности полупространства, меняются, что связано с вы-
высотным распределением неровностей, волнистостью поверхнос-
поверхности, переменным характером нагружения и т. д. Чтобы изучить
332
160 h
120
80
40 -
Zla
0
0
120
80 -
40
e
8 e 12
300 -
16 e 24
Рис. 6.4. Кинетика усталостного износа при постоянной нагрузке и
N = 3 (а), N = 5 (б) и N = 5.5 (б)
333
влияние переменного характера нагружения на характер изна-
изнашивания, рассмотрим процесс накопления повреждений, описы-
описываемый соотношениями F.1)иF.9),в которых амплитудное зна-
значение нагрузки P(t) является периодической функцией времени.
При численном анализе было положено N — 5, С = 1,25 и
введены следующие безразмерные функции и переменные:
w(t). 150V15E* - t
где величина износа w(t) в момент времени t совпадает по вели-
величине с координатой поверхности Z(t).
Сначала рассмотрим случай, когда P(t) - периодическая ку-
кусочно-постоянная функция с периодом ?q:
1-6, ч
= 0, ±1, ±2,... F.10)
/ i \ .
6, Ыо
Результаты расчётов, демонстрирующие влияние парамет-
параметров i и t"o на характер процесса разрушения, представлены
на рис. 6.5. Здесь и в дальнейшем на рисунках сверху для на-
наглядности изображена функция P(i). Кривые на рис. 6.5,а-в
иллюстрируют влияние амплитудных значений функции Р (?)
на характер процесса изнашивания. Несмотря на то, что период
и среднее значение функции Р (t) для всех трёх кривых оди-
одинаковы, они качественно отличаются друг от друга. При ма-
малых 6 процесс идет аналогично процессу при P(t) = const, т. е.
происходит несколько актов подповерхностного разрушения, а
затем идёт только поверхностный износ с периодически меня-
меняющейся скоростью. При увеличении значения 6 возникает неза-
незатухающее подповерхностное разрушение. В ходе подповерхност-
подповерхностного разрушения можно выделить две стадии: начальную, когда
возникновение разрушения не связано непосредственно с измене-
изменением Р (i); и стадию, когда подповерхностное разрушение воз-
возникает периодически с некоторым запаздыванием по отношению
к моменту увеличения функции Р (i), при этом число актов раз-
разрушения в периоде увеличивается при увеличении 6.
334
1,2 ._
0,8 '
1,7
0,3
! W
0,0 0,4 0,8 1,2 t
1,6 7
1,8 f
0,2
0,0 0,4 0,8 7 1,2
о
0,0 0,8 1,6 7
Рис. 6.5. Кинетика изнашивания в случае периодической функции
Р («) F.10) при N = 5: S = 0,2 (о), S = 0,5 (?), E = 0,8 (в), i0 = 0,4
(о-в); to = 1/20 (г), ?„ = 2/15 ((?), 10 = 2/5 (е), 5 = 0,7 (г-е)
335
Расчёты, проведенные для функции Р (I) (см. F.10)) при
фиксированном 6 и разных значениях периода ?о (см. рис. б.5,г-е,
позволили установить существенное влияние изменения периода
на ход процесса. Если период мал, система не реагирует на изме-
изменение величины Р (?) и подповерхностное разрушение прекра-
прекращается (см. рис. 6.5,г). При увеличении периода подповерхност-
подповерхностное разрушение не прекращается (см. рис. 6.5,д,е); при больших
периодах оно носит периодический характер и соответствует ха-
характеру изменения функции Р (i) (см. рис. 6.5,е).
Исследовалась также зависимость износа от времени в слу-
случаях, когда при одинаковых пределах изменения и характер-
характерных временах функции Р (?) имели различный вид (рис. 6.6).
Результаты расчётов показали, что в случае гладкой функ-
функции Р (i) = 1+6cos Bтг?/ to) подповерхностное разрушение пре-
прекращается (см. рис. 6.6,о), в то время как кусочно-постоянная
функция Р (i) приводит к установившемуся подповерхностно-
подповерхностному разрушению (см, рис. 6.6,tf).
Ближе к реальным условиям взаимодействия является рас-
рассмотрение в качестве Р (?) случайной функции. На рис. 6.6,в
представлена зависимость износа от времени, когда Р (?) - ку-
кусочно-постоянная случайная функция, значения которой равно-
равномерно распределены на отрезке [0,3; 1,7]. В этом случае подпо-
подповерхностное разрушение не прекращается, а моменты его воз-
возникновения связаны с большими скачками функции Р (i).
Из проведённого анализа следует, что если внешняя нагруз-
нагрузка зависит от времени, характер процесса определяется не самой
величиной нагрузки, увеличение которой, естественно, увеличи-
увеличивает среднюю скорость износа, а скоростью приращения нагруз-
нагрузки. На основании полученных результатов можно оценить час-
частоту актов разрушения и величину отделяющихся фрагментов
в зависимости от величины и характера приложения нагрузки.
Выводы о скачкообразном характере процесса усталостного
разрушения поверхностей качественно соответствуют результа-
результатам испытаний на фрикционную усталость по схеме "пальчик-
диск" полимерных материалов, используемых в искусственных
суставах [159], и некоторых видов резин [92]. Следует отметить,
что отделение фрагментов значительных размеров при работе
336
::; lywywy
140- w
70
0
1,7
0,3
L
0,0 _ 0,4 0,8 1,2
Рис. 6.6. Кинетика изнашивания при S = 0,7, i0 = 1/5, N — 5 для
различных видов функции P(i): синусоидальная функция (а), кусоч-
кусочно-постоянная функция (б), случайная функция (в)
337
сопряжения нежелательно, поскольку до момента выхода из кон-
контакта эти фрагменты могут вызвать существенные поврежде-
повреждения.
Таким образом, несмотря на значительные ограничения рас-
рассмотренная модель позволяет воспроизвести ряд особенностей
изнашивания, наблюдаемых на практике. В частности, описана
возможность одновременного протекания непрерывного (поверх-
(поверхностного) и дискретного (подповерхностного, возникающего на
конечной глубине) разрушения при едином механизме накопле-
накопления поврежденности. Знание конкретного вида функции q(z, Р)
позволяет определить кинетику процесса разрушения и его ко-
количественные характеристики (скорости поверхностного, подпо-
подповерхностного и полного износа, моменты отслаивания, толщину
отделяемого слоя и т.д.).
6.3.5. ХАРАКТЕРИСТИКИ УСТАНОВИВШЕГОСЯ
РЕЖИМА
Из рассмотренных выше примеров следует, что при периодичес-
периодическом изменении функции P(t) вслед за процессом неустановив-
неустановившегося разрушения (режим приработки), который имеет общие
черты при различном характере функции P(t), наступает уста-
установившийся режим разрушения. В этом режиме приобретают
конкретный смысл такие практически важные характеристики,
как средние скорости поверхностного Is, подповерхностного Iss
и полного Iw изнашивания, которые определяются как Aw До,
где Aw - изменение линейного размера тела в результате изно-
износа данного вида за период to-
В табл. 6.1 приведены скорости изнашивания, рассчи-
рассчитанные для периодической кусочно-постоянной функции Р( t)
(см. F.10)) F = 0,7). Результаты показывают, что хотя соотно-
соотношение скоростей Is и Iss в рассматриваемых случаях различно,
величины /„, отличаются незначительно (менее, чем на 10%);
минимум скорости полного износа достигается в случае, ког-
когда подповерхностного разрушения нет. Следующие рассуждения
показывают, что такие результаты вполне закономерны.
Определим полную повреждённость fi(?), накопленную мате-
338
Таблица 6.1. Скорости изнашивания для периодической
кусочно-постоянной функции P{i) E = 0,7)
1
0
0
0
о
«о
,00
,40
,20
,13
,04 |
Скорость
I. '
100,0
92,5
70,0
76,0
128,0
изнашивания
Iss
30,0
45,0
62,5
59,0
о
т
130
137
132
135
128
,0
,5
,5
,0
,0
риалом в момент времени t как
+ ОО
Z(t)
где Z(t)- текущая координата поверхности. Изменение значений
функции u(t) за время At происходит, с одной стороны, вслед-
вследствие отделения повреждённого материала: Afii = AZ ¦ Qav,
где Qav - средняя повреждённость отделённого за время At ма-
материала, AZ - его толщина. С другой стороны, П(?) возрастает
за время At вследствие накопления материалом повреждений
t+At+oo
= I [ q(z,P(t))dzdt.
Если P(t) - периодическая функция с периодом to, то в устано-
установившемся режиме
u(t +10) - u{t) = -АОх + Ап2 =
t+to +ОО
= -AZ-Qav+ j J q(z,P(t))
t 0
dzdt = O.
F.11)
339
Усредняя q(z,P(t)) по периоду, т.е. вычисляя
t+t0
9(*) = ^ J q(z,P(t))dt,
t
из соотношения F.11) получим
+00
= -?- fq(z)dz. F.12)
Wav J
*0
о
В случае, когда идёт только поверхностное изнашивание (напри-
(например, при постоянной нагрузке), то Qav = Q* и средняя скорость
полного изнашивания, определяемая соотношением F.12), дости-
достигает своего минимума. Если имеет место и подповерхностное
разрушение, то Qav < Q*, и средняя за период скорость полного
изнашивания выше, чем в случае только поверхностного изно-
износа. Как видно из рис. 6.3, отличие Qav от Q* в ходе процесса,
описываемого функцией F.9), незначительно. Следовательно, в
установившемся режиме скорости полного износа в присутствии
или отсутствии подповерхностного разрушения отличаются не-
незначительно. Все эти выводы согласуются с результатами, ко-
которые представлены в табл. 6.1.
Таким образом, если процесс разрушения выходит на устано-
установившийся режим, скорость полного изнашивания в этом режиме
можно оценить исходя из вида функции q(z, P(t)) на основании
соотношения F.12) без рассмотрения кинетики процесса. Заме-
Заметим, что при P(t) — Ро, q{z) = q(z,P0), Qav = Q* и уравне-
уравнение F.12) принимает вид:
+ОО
dZ 1 /•,_., ,с о,
7 = 7^7 / 4\z>Po)dz, F.13J
at Ц* J
О
т. е. стационарная скорость изнашивания dw/dt = dZ/dt в слу-
случае, когда разрушение имеет место только на поверхности, опре-
определяется величиной нагрузки Pq, критическим значением Q*
функции поврежденности и параметрами, входящими в функ-
функцию скорости накопления поврежденности q(z, P). На основании
340
соотношения F.13) можно определить скорость установившего-
установившегося поверхностного изнашивания для примера, рассмотренного
в 6.3.2.
Таким образом, если функция q(z, Р) известна, соотноше-
соотношение F.13) приближённо задает закон износа для стационарного
режима изнашивания и включает лишь параметры системы и
характеристики усталостного разрушения.
6.3.6. МЕТОДИКА ЭКСПЕРИМЕНТАЛЬНОГО
ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ИЗНОСА
Используя рассмотренную выше модель, можно предложить ме-
метод экспериментального определения параметров фрикционной
усталости в соотношении F.9).
Зависимость w(t), подобную изображенной на рис. 6.4, можно
получить экспериментально на установке "пальчик-диск" при
заданных величинах радиуса R пальчика и нагрузки Р. Если
полученная экспериментальная зависимость качественно подоб-
подобна модельной, т. е. модель адекватно описывает процесс изнаши-
изнашивания в экспериментальных условиях, величины N и (Р*)-^/3Т*
в соотношении F.9) могут быть определены из анализа харак-
характеристик установившегося режима изнашивания.
С этой целью рассмотрим скорость износа при постоянной
нагрузке Р. Как было показано в 6.3.3, в этом случае при уста-
установившемся режиме имеет место только поверхностный износ с
постоянной скоростью Z' = dZ/dt, которая определяется из со-
соотношений F.9) и F.13):
f Р\ ' 1 /3PR\
г'=Ч) ?.{Ж)
Измерим экспериментально скорости износа Z[ и Z'2 для двух
величин нагрузки Р\ и Pi соответственно. Тогда из соотноше-
соотношения F.14) получим:
\n(Z>/Z>)
6 "
341
Значение (Р*)^/3Т*, входящее в выражение F.9), может быть
рассчитано на основании соотношений F.9) и F.14).
Подобный метод может быть применён и для других функ-
функций q(z, P), используемых для описания процесса накопления по-
повреждений в экспериментах с различными материалами и усло-
условиями взаимодействия.
6.4. ИЗНАШИВАНИЕ ШЕРОХОВАТЫХ
ПОВЕРХНОСТЕЙ
Основным недостатком изложенной выше модели является её од-
одномерный характер. Поэтому с помощью этой модели можно опи-
описать только один частный вид поверхностного разрушения - от-
отслаивание поверхностных слоев в результате усталости.
Большой интерес представляет построение моделей уста-
усталостного разрушения поверхностей произвольной геометрии, в
которых не закладывается изначально предположение о форме
отделяющихся фрагментов. Одна из таких моделей [142], поз-
позволяющая исследовать эволюцию микрогеометрии поверхности
при изнашивании и размеров отделяющихся частиц, описана ни-
ниже.
6.4.1. РАСЧЁТ НАКОПЛЕНИЯ ПОВРЕЖДЕНИЙ
Используем подход к моделированию усталостного изнашива-
изнашивания, изложенный в 6.2.2. Первый этап моделирования состоит
в расчёте поврежденности тел как функции времени. Посколь-
Поскольку процессы, ведущие к усталостному износу, имеют место в
подповерхностных слоях, на их протекание существенное вли-
влияние оказывают напряжённое состояние поверхностного слоя и
его фрикционный разогрев. В свою очередь эти характеристи-
характеристики в значительной степени зависят от трения при контактном
взаимодействии поверхностей.
Рассмотрим процесс изнашивания при контактировании
двух шероховатых тел. Для описания процесса накопления по-
поврежденности используем термокинетическую модель [124], в ко-
342
торой скорость накопления повреждений задается соотношением
U--r*{x,ytzt)
dt т* \ kT(x,y,z,t)
где U - энергия активации, т* и j - характеристики материа-
материала, к - постоянная Больцмана, a(x,y,z,t) - характеристика по-
поля напряжений в точке (х, у, z) внутри деформируемого тела в
момент времени t. Используя в качестве а в F.15) различные
характеристики поля напряжений или их комбинации, в рамках
данного подхода можно воспроизвести различные типы разру-
разрушения.
Рассмотрение термокинетической модели накопления по-
вреждённости делает возможным исследование влияния темпе-
температурных эффектов на разрушение в явном виде. Поскольку поле
температур в подповерхностном слое Т(х, у, z, t) является весь-
весьма неоднородным, его расчёт должен проводиться с достаточно
высокой степенью точности. Рассмотрение осреднённых темпе-
температурных характеристик в данном случае недопустимо.
Для снижения вычислительных трудностей ограничимся
рассмотрением плоской задачи, однако аналогичный подход мо-
может быть использован и в пространственной постановке.
Рассмотрим периодическую контактную задачу для двух уп-
упругих тел, в которой тело 1 скользит с постоянной скоростью V
по поверхности тела 2 и находится под действием вертикальной
силы Р, приложенной к одному периоду (рис. 6.7). Система коор-
координат Oxz связана с одним из взаимодействующих тел и ось Oz
направлена вглубь тела. Форма контактирующих поверхностей
описывается периодическими функциями /i(x) и /2B;) (с одина-
одинаковым периодом I), которые представимы рядами Фурье, т.е.
п
fi(x, 0) = У2 Cij cos(ojjx + -0j), г = 1,2,
что позволяет воспроизводить как регулярные профили, так и
профили, характерные для реальных шероховатых поверхнос-
поверхностей.
Для того чтобы рассчитать внутренние напряжения и тем-
температуру, сначала определялись контактные давления для раз-
343
Рис. 6.7. Схема контакта двух шероховатых упругих тел
личных относительных положений двух тел (относительные пе-
перемещения поверхностей рассматривались пошаговым методом).
Для определения контактных давлений использовались реше-
решения периодических контактных задач для упругой полуплоскос-
полуплоскости [93, 146]. Использование модели полуплоскости допустимо,
поскольку реальные профили шероховатых поверхностей доста-
достаточно "пологие" (при расчётах предполагалось, что отношение
высоты неровности к периоду составляет 0,03). Выражение для
определения давления под упругим индентором, описываемым
периодической функцией, в случае полного контакта (все точки
взаимодействующих поверхностей находятся в контакте) имеет
вид [146]:
I
о sin
sin
fl-(e-g)
I
где E* - приведённый модуль упругости A.7),
рассчитываемая из условия равновесия, т. е.
р(х) dx — Р,
~ постоянная,
F.17)
344
функция /(ж) - эквивалентная форма контактирующих по-
поверхностей в произвольный фиксированный момент времени t,
т.е. /(*) = f2(x) - fx[x - Vt), f(x) = df(x)/dx.
Поскольку область контакта шероховатых тел не является
сплошной, будем определять давления в случае дискретного кон-
контакта из уравнения F.16), используя метод итераций. Давле-
Давление pj(x) на j-м шаге вычислим по формуле
Е* . /тгх\ [
о sin | — ) sm
i = 0,1,2,...,
где
(x) = f(x) если Pj(x) > 0,
/j+i(a;) = fj(x) + apj(x) если pj(x) < 0,
Ш = f(x),
а постоянная poj выбирается так, чтобы функция Pj{x) удовле-
удовлетворяла соотношению F.17). Расчёт считается законченным, ес-
если минимальное давление больше некоторой очень малой отри-
отрицательной величины. Эта процедура сходится к функции, пред-
представляющей собой давление р(х, t) внутри контактных зон и
равной нулю на свободных участках поверхности. Одновремен-
Одновременно fj(x) стремится к функции, описывающей упругие смещения
границы тел как внутри, так и вне области контакта. Сходи-
Сходимость процедуры обеспечивается надлежащим выбором пара-
параметра а. Касательные контактные напряжения затем определя-
определялись как rxz(x,t) = fip(x,t).
Внутренние напряжения рассчитывались на основании из-
известных соотношений для упругой полуплоскости, граница ко-
которой нагружена заданными нормальными и касательными на-
напряжениями (см., например, [25, 66]).
Для расчёта температурного поля использовались уравнения
теплопроводности в двумерной постановке [77] при следующих
граничных условиях на поверхности (z = 0):
345
• внутри области контакта
dT(x,z,t) _ т
~А — — q [x, с),
oz
• вне области контакта
—А тг—'— = О'
где А - коэффициент теплопроводности изнашиваемого тела.
Тепловой поток qT(x,t) в глубь рассматриваемого тела опреде-
определялся из соотношения qT(x,t) = Knp(x,t)V, где К - коэффици-
коэффициент разделения потоков, /х - коэффициент трения, р(х, t) - кон-
контактное давление в момент времени t. Предполагалось, что тем-
температура на некоторой глубине фиксирована T{z{) = Tq. Теп-
Тепловой поток на боковых границах х = 0 и х = I при рассмот-
рассмотрении периодической задачи определялся из условия периодич-
периодичности. Задача теплопроводности решалась численно, используя
пошаговую процедуру.
После произведённых расчётов полей напряжений и темпера-
температур функция повреждённости Q(x,z,t) определялась из соотно-
соотношений F.1) и F.15), в которых в качестве характеристики на-
напряженного состояния использовалась функция максимальных
касательных напряжений ттдх(х, z, t).
В целом процесс разрушения для данной модели описывается
следующей совокупностью параметров (индексы г = 1,2 соответ-
соответствуют двум контактирующим телам):
• исходная форма контактирующих поверхностей fi(x);
• зависимость внешней нагрузки от времени P(t);
• упругие характеристики тел Ei, щ {г = 1,2);
• параметры изнашиваемого тела: теплоёмкость С, тепло-
теплопроводность А, плотность р;
• характеристики, определяющие накопление повреждённос-
повреждённости: U, 7, г»;
346
• коэффициент разделения тепловых потоков К;
• коэффициент трения fj,;
• относительная скорость скольжения V;
• температура внешней среды То-
Для трибологии представляет интерес исследование влияния
коэффициента трения /i и коэффициента разделения тепловых
потоков К на повреждённость поверхностного слоя. На рис. 6.8
показано распределение повреждённости в поверхностном слое в
момент зарождения усталостной трещины (maxQ(x,z,t) — Q*)
при разных значениях /х и К. Линии уровня функции Q(x, z, t)
изображены сплошными линиями. Тёмными ромбами обозначе-
обозначены места зарождения усталостной трещины, т.е. точки (x*,z*),
где в момент времени 4* выполняется условие Q (x*,z*,t*) = Q*.
Результаты расчётов показывают, что при малых значениях fi
и К (см. рис. 6.8,а), критическое значение функции Q(x,z, t)
достигается под поверхностью. При увеличении коэффициента
трения (см. рис. 6.8,г) или коэффициента разделения тепловых
потоков (см. рис. 6.8,б) максимальная повреждённость достига-
достигается на поверхности. В этом случае имеет место поверхностный
износ, описанный в 6.3.1. Однако существует также локальный
максимум и под поверхностью, который может привести к подпо-
подповерхностному разрушению в последующие моменты времени. В
то же время, поскольку величина подповерхностного максимума
мала для случая, изображённого на рис. 6.8,г, можно заключить,
что подповерхностное разрушение для этого случая маловероят-
маловероятно.
Заметим, что если форма поверхности одного из тел плоская,
функция повреждённости в этом теле будет зависеть только от
координаты z. В этом случае процесс разрушения будет иметь
характер отслаивания подобно случаю, рассмотренному в 6.3.
Для того чтобы завершить построение модели усталостного
изнашивания, необходимо описать отделение частицы с поверх-
поверхности при неоднородном поле повреждений в подповерхностном
слое.
347
Рис. 6.8. Изолинии функции повреждённости и траектории распро-
распространения усталостной трещины в момент разрушения при следую-
следующих значениях параметров: ц = 0, К — 0 (a); /i = 0,2, К — 0 (б);
ц = 0,2, К =1 (в); ц = 0,5, К = 0 (г)
348
6.4.2. МОДЕЛИРОВАНИЕ ОТДЕЛЕНИЯ ЧАСТИЦЫ
ИЗНОСА
Наиболее существенным моментом, позволяющим построить за-
замкнутую модель процесса, является выбор механизма разруше-
разрушения. Предположим, что разрушение происходит за счёт распро-
распространения трещины, зарождающейся в момент времени t* в точ-
точке с'координатами (x*,z*), в которой выполнено условие разру-
разрушения Q(x*,z*,t*) = Q*.
Будем считать, что трещина распространяется мгновенно, а
направление её развития в каждой точке определяется направ-
направлением минимального убывания накопленной поврежденности.
Это предположение можно считать оправданным для таких ма-
материалов и условий работы, для которых мгновенное поле на-
напряжений оказывает меньшее влияние на траекторию развития
трещины, чем свойства повреждённого материала, а характер-
характерное время развития трещины существенно меньше характерного
времени накопления поврежденности.
Следует отметить, что предположение о направлении разви-
развития трещины, совпадающем с направлением минимума произ-
производной функции, описывающей критерий разрушения, использо-
использовалось ранее, например при моделировании хрупкого разруше-
разрушения упругих материалов [228].
Линиями уровня функции Q(x,z,t), построенной на основа-
основании соотношения F.15), в малой окрестности точки максиму-
максимума (x*,z*) являются кривые, мало отличающиеся от эллипса.
Если эксцентриситет эллипса не равен нулю, трещина, по пред-
предположению, будет распространяться в направлении её главной
оси. Направление в{ трещины в произвольной точке (ж,, -Zj) сетки
разбиения, находящейся на траектории распространения трещи-
трещины, определяется из условия (см. рис. 6.8):
maxQ(xi + е cos 0,2, + esin#) = Q(xi + ecosdi,Zi + esinflj),
в
где 0e(-7r/2 + 0i_i,7r/2 + 0i_i).
На рис. 6.8 показаны траектории распространения трещи-
трещины, рассчитанные на основании описанного подхода. Направле-
Направление распространения трещины от точки её зарождения изобра-
349
жено стрелками. В силу периодичности задачи распростране-
распространение трещины и отделение частицы одновременно происходит на
каждом периоде. Для функции повреждённости, изображённой
на рис. 6.8,а, разрушение имеет характер отслаивания.
Каждый акт разрушения ведёт к изменению микрогеомет-
микрогеометрии поверхности. Поверхность с изменённой микрогеометрией
вновь вступает в контакт. Её характеристики используются для
расчёта функции повреждённости и моделирования отделения
частиц на следующем шаге по времени.
6.4.3. АНАЛИЗ КИНЕТИКИ ИЗНАШИВАНИЯ
Предложенная модель позволяет описать кинетику процесса
усталостного изнашивания шероховатой поверхности и опреде-
определить его характеристики: скорость износа, размер и форму от-
отделившихся с поверхности частиц материала, изменение микро-
микрогеометрии поверхности, эволюцию контактных давлений.
Некоторые результаты проведённых расчётов представлены
на рис. 6.9 и 6.10. На рис. 6.9 показаны форма и размер час-
частиц износа, отделяющихся с поверхности в процессе её разруше-
разрушения, а также эволюция профиля изношенной поверхности. Рас-
Распределение повреждённости в момент первого разрушения для
рассматриваемого случая показано на рис. 6.7,в. Как следует
из расчётов, в процессе изнашивания происходит отделение как
очень мелких (поверхностный износ), так и крупных частиц
сложной формы (подповерхностное разрушение).
Зависимости среднеквадратичного отклонения а профиля и
полного износа W от времени t (выраженные в условных еди-
единицах) для двух различных значений коэффициента разделения
тепловых потоков приведены на рис. 6.10. В случае, когда тепло-
тепловые эффекты не учитываются (К = 0, кривые 2), продолжитель-
продолжительность инкубационного периода больше, износ несколько ниже,
однако он происходит за счёт отделения более крупных фраг-
фрагментов, что приводит к возникновению более шероховатой по-
поверхности, чем в случае, когда тепловые эффекты принимаются
во внимание (К — 1, кривые 1). Следует упомянуть, что для
сокращения времени расчётов определение контакного давления
производилось с использованием модели основания Винклера.
350
Рис. 6.9. Форма отделившихся с поверхности частиц (а) и изменение
профиля поверхности (б) при изнашивании (ц = 0,2, К = 1)
Таким образом, при изнашивании среднеквадратичное от-
отклонение профиля может увеличиваться или уменьшаться по
сравнению с начальным профилем (см. рис. 6.10,6). Обе эти тен-
тенденции наблюдались экспериментально [91].
Инкубационный период, измеряемый временным интервалом
от начала взаимодействия до первого разрушения, является ха-
характерной чертой усталостного изнашивания. Интенсивность
износа в течение этого периода равна нулю. Инкубационный пе-
период становится короче при возрастании скорости накоплений
повреждений, т.е. при росте температуры или напряжений в
подповерхностном слое. Этот рост может быть вызван увеличе-
увеличением нагрузки, коэффициента трения или увеличением потока
тепла в изнашиваемое тело. Заметим, что факторы, способству-
351
1000
2000
3000
1000
2000
3000
Рис. 6.10. Характеристики процесса изнашивания: полный износ (а)
и среднеквадратичное отклонение профиля (б) как функции времени
для р = 0,2 и К = 1 A), К = 0 B)
ющие сокращению инкубационного периода, приводят также к
увеличению скорости износа.
Существенно нелинейный характер данной модели, значи-
значительное влияние исходной микрогеометрии на ход процесса не
позволяют в данном случае провести интегральные оценки ин-
интенсивности изнашивания и вообще говорить об установившем-
установившемся режиме изнашивания в строгом смысле слова. Осреднённые
характеристики интенсивности изнашивания в зависимости от
параметров модели могут быть получены в результате прямого
численного эксперимента.
352
Анализ модели показывает, что размер отделившихся частиц
существенно зависит от коэффициента трения, оказывающего
влияние как на напряжённое состояние, так и на распределе-
распределение температуры. Увеличение коэффициента трения увеличива-
увеличивает фрикционный разогрев и смещает к поверхности точку мак-
максимума функции максимальных касательных напряжений. Оба
эти фактора ведут к уменьшению размера отделяемых частиц.
В пределе процесс изнашивания имеет характер поверхностного
износа, который аналогичен рассмотренному в 6.3.2 случаю.
Таким образом из анализа модели можно заключить, что:
• изнашивание может привести как к росту, так и к сни-
снижению шероховатости (за меру шероховатости было взято
среднеквадратичное отклонение профиля);
• увеличение коэффициента трения приводит к увеличению
интенсивности изнашивания и уменьшению размера отде-
отделяющихся фрагментов;
• увеличение нагрузки увеличивает интенсивность изнаши-
изнашивания, при этом размер частиц увеличивается, если тепло-
выдение отсутствует или его роль незначительна; в про-
противном случае размер частиц уменьшается за счёт интен-
интенсивного нагрева поверхностных слоев.
Некоторые выводы, следующие из анализа данной модели,
совпадают с результатами, полученными при исследовании од-
одномерной модели (см. 6.3), и по-видимому, могут быть отнесены
к общим закономерностям усталостного износа. К таким выво-
выводам относятся: существование инкубационного периода процес-
процесса; возможность одновременного протекания непрерывного по-
поверхностного изнашивания и отделения фрагментов конечных
размеров при одном заложенном в модель механизме, определя-
определяющем разрушение; наличие при определённых условиях стацио-
стационарного режима изнашивания.
12. Горячева И. Г.
Глава 7
ИЗНОСОКОНТАКТНЫЕ ЗАДАЧИ
Если отвлечься от дискретного характера изнашивания, имею-
имеющего место на микроуровне (масштаб отдельной неровности),
и перейти на макроуровень (масштаб области контакта макро-
макротел), изнашивание можно рассматривать как непрерывный во
времени процесс, приводящий к необратимому изменению мак-
макроформы взаимодействующих тел. Эти изменения соизмеримы с
деформациями тел и поэтому должны приниматься во внимание
при оценке эволюции контактных характеристик (распределе-
(распределения давлений, размера области контакта, сближения тел и т. д.)
и внутренних напряжений в подвижных сопряжениях при изна-
изнашивании.
В этой главе дается математическая постановка контактной
задачи с учётом изнашивания поверхностей взаимодействующих
тел, исследуется характер решения задачи для различных видов
сопряжений, анализируется кинетика изменения контактных ха-
характеристик при изнашивании для ряда конкретных пар трения.
7.1. УРАВНЕНИЕ ИЗНОСА
Как уже отмечалось в 6.1, для расчёта кинетики процесса изна-
изнашивания на макроуровне обычно используют феноменологичес-
феноменологические модели, в которых считается известным уравнение износа,
т.е. соотношение, устанавливающее связь между характеристи-
характеристиками износа поверхности и рядом параметров, характеризующих
свойства фрикционного контакта и условия взаимодействия.
7.1.1. СКОРОСТЬ И ИНТЕНСИВНОСТЬ ИЗНОСА
Наиболее распространенными характеристиками, используемы-
используемыми в трибологии для оценки износа поверхности, являются ско-
скорость износа и интенсивность износа.
354
Скорость износа определяется объёмом материала, изношен-
изношенного с единицы площади поверхности в единицу времени. В об-
общем случае скорость износа разных точек поверхности различна,
поэтому вводится понятие скорости износа в рассматриваемой
точке (х, у) поверхности, определяемой как
= lim Awf>y\ G.1)
At->0 At
где AA - элемент поверхности в окрестности рассматриваемой
точки (х,у), Avw(x,y) - объём материала, изношенного с эле-
элемента поверхности АА в течение интервала времени At (время
износа), Aw*(x,у) - линейный износ в точке (х,у), который ха-
характеризует глубину изношенного слоя в рассматриваемой точ-
точке за время At, т. е. изменение положения точки поверхности в
направлении, перпендикулярном границе тела.
Величина dw*/dt определяет скорость изменения положения
поверхности при износе. Если все точки поверхности находятся
в одинаковых условиях, так что скорость износа во всех точках
постоянна, величина Avw/AA равна отношению полного объёма
изношенного материала к площади поверхности трения.
Помимо скорости износа, часто используется также поня-
понятие интенсивности износа. Эта величина определяется объёмом
материала, изношенного с элемента трущейся поверхности при
прохождении единицы пути трения, т. е.
dw* Avw Aw* .
—=- = lim lim -——— = lim ——- , G.2)
dl Al->o aa^o AAAl Ai->o Al
где Al - длина пути скольжения.
Интенсивность износа - безразмерная величина. Обычно она
меняется в пределах от 10~3 до 1СГ13 в зависимости от свойств
материалов и условий взаимодействия. Заметим, что равенст-
равенство dw*/dl = 10~9 означает, что слой толщиной в 1 мкм изнаши-
изнашивается при скольжении на расстоянии в 1 км. Между скоростью
и интенсивностью изнашивания при постоянной скорости сколь-
скольжения V имеет место следующее соотношение:
? = "?• <«>
•2* 355
Характеристики износа, введенные выше, удобны для описания
процесса изнашивания на макроуровне, поскольку, во-первых,
они непосредственно характеризуют формоизменение поверхнос-
поверхности и, во-вторых, являются непрерывными или кусочно-непре-
кусочно-непрерывными функциями, т. е. относятся к классу функций, обычно
используемых при постановке контактных задач.
Таким образом, скорость изнашивания поверхности трения
оценивается с помощью соотношений G.1) или G.2). Характе-
Характеризуют ли при этом введённые величины только свойство мате-
материала тела, участвующего во фрикционном взаимодействии, или
они зависят также и от других факторов? Исследование этого во-
вопроса с использованием системного подхода (см. [68, 144, 216])
показало, что линейный износ го* является функцией структур-
структурных параметров {S} и внешних параметров {X}, т.е.
w. = F(S,X), G.4)
где {S} включает в себя структуру элементов (взаимодейству-
(взаимодействующих тел, промежуточной и окружающей среды), их свойст-
свойства (агрегатное состояние, геометрические характеристики, по-
поверхностные и объемные свойства) и взаимодействие элементов
структуры; {X} включает нагрузку, скорость, время, темпера-
температуру и т.д. Таким образом, скорость износа рассматриваемого
материала зависит как от свойств самого материала, так и от
свойств системы в целом.
7.1.2. ПОДХОДЫ К ПОСТРОЕНИЮ УРАВНЕНИЙ
ИЗНОСА
Соотношение вида G.4) представляет собой одну из возможных
записей уравнения износа. В исследованиях [89, 161, 215], по-
посвященных истории развития науки об изнашивании материа-
материалов, отмечалось, что существует порядка 200 соотношений, ко-
которые рассматриваются как уравнения износа. Такое многооб-
многообразие законов износа объясняется тем, что на скорость износа
при разных условиях может влиять до ста параметров.
Существуют два способа построения уравнения износа: эм-
эмпирический и основанный на математическом моделировании.
356
л
Приработка
Установившийся
износ
Катастрофический
износ
Время
Рис. 7.1. Типичная зависимость износа от времени испытания
Эмпирические уравнения износа базируются на эксперимен-
экспериментальных исследованиях. Перечислим здесь некоторые особеннос-
особенности трибологических испытаний на износ.
На рис. 7.1 изображена типичная зависимость линейно-
линейного износа от времени. Первый период процесса изнашива-
изнашивания @ < t < t\) называется приработкой. Это очень важная ста-
стадия процесса изнашивания. Во время приработки, как правило,
формируется равновесная (установившаяся) шероховатость по-
поверхности, её химический состав (проходят процессы окисления,
диффузии и т. д.), стабилизируется температурное поле во фрик-
фрикционной паре, т.е. протекает процесс самоорганизации систе-
системы [14, 18, 114]. Во время приработки скорость износа меняется
во времени; этот процесс может длиться продолжительное вре-
время.
После режима приработки обычно наступает установив-
установившийся износ. Во время этой стадии процесса изнашива-
изнашивания (t\ < t < ?2) износ является линейной функцией времени,
т. е. скорость (интенсивность) износа - постоянная величина.
357
Рис. 7.2. Схема испытательной установки на износ.
дорожка трения (след изношенной поверхности)
- кольцевая
Обычно именно на этой стадии процесса изнашивания строится
уравнение износа.
В ряде сопряжений после установившейся стадии изнашива-
изнашивания (t > ?2) наблюдается катастрофический износ, при котором
скорость износа растёт очень быстро. Такой вид износа, как пра-
правило, приводит к потере работоспособности сопряжения.
При оценке скорости износа следует принять во внимание,
что трущиеся поверхности взаимодействующих тел могут нахо-
находиться в различных условиях изнашивания. Рассмотрим наибо-
наиболее распространенный метод испытаний на трение и износ на
установке типа "пальчик-диск" (рис. 7.2). Когда пальчиковый
образец A) скользит по диску B), поверхность трения образ-
образца А\ совпадает с номинальной площадью контакта А\ = тга2;
для диска поверхность трения представляет собой кольцо пло-
площадью .At = 7г (Л| — Щ)- Время нахождения в контакте фикси-
фиксированных точек поверхности образца и диска также различны.
За время испытания At произвольная точка на поверхности об-
358
разца A) находится все время в контакте, т.е. её время нахож-
нахождения в контакте Ati равно At. За то же время At произвольная
точка поверхности диска находится в контакте с пальчиковым
образцов в течение времени Д?г = 2аAt/ (n(Ri + R2)). Таким об-
образом, скорости износа материалов тел A) и B) в испытаниях на
установке, изображённой на рис. 7.2, оцениваются по формулам:
fdwA _ A(^t[)I (dm A _ A(vwJ
{ ) )
fdwA _ A(^t[)I (dm A _ A(vwJ
{ dt )x~ па2 Ah ' \dt J~ icfiAh ' [ }
где А (г!шI и A (vwJ - измеренные в эксперименте объёмы из-
изношенного материала образца и диска соответственно.
Полученные экспериментальные зависимости скорости изно-
износа от условий трения и свойств материалов затем используются
для построения эмпирического уравнения износа. Заметим, что
при экспериментальном изучении зависимости скорости износа
от параметров трибосистемы (нагрузки, скорости скольжения,
температуры и т.д.) в ряде случаев наблюдается явление рез-
резкого изменения скорости износа при очень малых изменениях
значений параметров. Часто это связано с изменением механиз-
механизма изнашивания, что необходимо учитывать при испытаниях на
износ.
Уравнение износа может быть получено также методом ма-
математического моделирования. Наиболее простой подход к по-
построению этого уравнения базируется на идее, что скорость из-
износа пропорциональна площади фактического контакта шерохо-
шероховатых поверхностей [149, 192]. При этом коэффициент пропор-
пропорциональности определяется экспериментально.
Большое количество уравнений износа, базирующихся на
концепциях механики разрушения, предложено в последние де-
десятилетия. Уравнения включают характеристики усталостной
прочности материалов [89], предельные напряжения хрупкого
разрушения [163], критические значения энергии абсорбции [164]
и т. д. Эти теории значительно расширяют количество парамет-
параметров, влияющих на износ, включая параметры, характеризующие
свойства материалов.
Метод построения уравнения износа, исходя из исследования
процесса усталостного разрушения поверхности на микроуровне,
изложен в главе 6.
359
Таблица 7.1. Уравнения износа, полученные теоретически
Автор
Уравнение износа Механизм износа
Хольм A946)
Арчард A953)
dw* _ pV
dt ~ Н
Адгезионный
Крагельский
A965)
Рабинович
A965, 1971)
dw*
dt
¦ - KpaV
dw* v
dt
<« =
pV
H
>1)
Усталостный
Абразивный,
фреттинг
Харрикс A976)
dw*
~dt
= KpV
Фреттинг
В табл. 7.1 приведены некоторые уравнения износа, полу-
полученные теоретически при изучении различных механизмов из-
изнашивания. В этой таблице Н означает твёрдость материала, а
коэффициент К имеет определённое значение для каждого кон-
конкретного механизма изнашивания и модели, использованной для
его изучения. Как следует из приведённых уравнений, основны-
основными внешними характеристиками, влияющими на скорость из-
изнашивания, являются контактное давление р и относительная
скорость скольжения V.
Анализ большого количества уравнений износа, полученных
как теоретически, так и на основании обработки результатов
трибологических испытаний на износ, показывает, что во мно-
многих случаях зависимость скорости износа от давления и скорости
скольжения может быть представлена в виде
G.6)
где Kw - коэффициент износа, а и /3 - параметры. Величины Kw,
а т/1 E зависят от свойств материалов, фрикционных параметров
360
сопряжения, температуры и т.д. Их значения для конкретного
вида изнашивания могут быть определены на основании извест-
известных эмпирических и модельных уравнений износа (см. табл. 7.1).
7.2. ПОСТАНОВКА ИЗНОСОКОНТАКТНОЙ
ЗАДАЧИ
При математической постановке контактных задач с износом
принимают во внимание необратимое изменение формы контак-
контактирующих тел в направлении, перпендикулярном поверхности
трения. Это изменение оценивается величиной линейного изно-
износа го*, зависимость которой от давления и скорости скольжения
определяется уравнением износа. В общем случае износ распре-
распределяется по поверхности трения неравномерно и является функ-
функцией координат точек поверхности (х,у) и времени t, т.е. го* =
= ш* (ж, у, t). Контактные задачи, дополненные уравнением изно-
износа, составляют класс износоконтактных задач, математическая
постановка которых обсуждается ниже.
7.2.1. СООТНОШЕНИЕ МЕЖДУ УПРУГИМИ
СМЕЩЕНИЯМИ ПОВЕРХНОСТИ И
КОНТАКТНЫМИ ДАВЛЕНИЯМИ
Часто при постановке контактных задач с учётом формоизмене-
формоизменения поверхностей при изнашивании является допустимым пред-
соложение о малости необратимых перемещений го* (ж, у, t) по-
поверхности за счёт износа и их соизмеримости с упругими пе-
перемещениями uz(x,y, t). При определении напряжённо-деформи-
напряжённо-деформированного состояния тела в таких случаях граничные условия
Относят к недеформированной поверхности, пренебрегая как уп-
упругими перемещениями uz(x,y,t), так и формоизменением по-
поверхности за счёт износа w(x,y,t).
Тогда давления на площадке контакта р(х, у, t) связаны с уп-
упругими перемещениями uz(x,y,t) в произвольный момент вре-
времени с помощью оператора А, который аналогичен оператору,
Ввязывающему давление с упругими перемещениями в соответ-
соответствующей контактной задаче без учёта изнашивания поверхнос-
361
теи, т. е.
uz(x,y,t)=A\p{x,y,t)]. G.7)
Так, в случае контакта без трения осесимметричного штампа
с упругой полуплоскостью соотношение G.7) имеет вид:
ut(r,t) = A\p{r,t)] =
Ь G.8)
r + р \ г + р )
о ч '
О < г ^ a(t),
где К (ж) - полный эллиптический интеграл первого рода, г =
= (*2 + 2/2I/2.
В ряде исследований в качестве оператора А принимает-
принимается упрощённое соотношение между упругими перемещениями и
давлениями, соответствующее модели Винклера, используемой
для описания податливости упругого тела.
Как следует из соотношения G.8), оператор А зависит от раз-
размера площадки контакта a(t). Если в процессе изнашивания раз-
размер площадки контакта фиксирован, т. е. a(t) = а@), оператор А
в точности совпадает с оператором в начальный момент време-
времени t = 0. Такой случай имеет место, например, при изнашивании
упругого тела штампом с плоским основанием. В противном слу-
случае неизвестная граница сЮ области контакта fi(i) определяется
условием непрерывности перемещений границы упругого тела
при вдавливании в него гладкого штампа, которое обычно име-
имеет вид:
p(x,y,t) =0.
(х,у)едп
Заметим, что требование малости линейного износа w(x, у, t)
в ряде случаев диктуется самими функциональными свойства-
свойствами сопряжения, например, в прецизионных узлах трения. Од-
Однако в некоторых случаях изменение геометрии контактирую-
контактирующих поверхностей за счёт изнашивания соизмеримо с характер-
характерным размером тел. Тогда при определении упругих перемещений
уже нельзя пользоваться оператором соответствующей контакт-
контактной задачи без учёта изнашивания. Так обстоит дело, например,
362
при исследовании изнашивания тонкого упругого покрытия, ког-
когда перемещения за счёт износа могут оказаться соизмеримыми с
толщиной покрытия. В этом случае соотношение между упруги-
упругими перемещениями и давлением принимает более сложный вид
и зависит от геометрии изношенного контакта. Метод решения
задач такого класса будет изложен в 7.5 на примере задачи об из-
изнашивании штампом тонкого покрытия, сцепленного с упругим
основанием.
7.2.2. УСЛОВИЕ КОНТАКТА
При формулировке условия контакта принимаются во внимание
перемещения поверхности как за счёт упругих деформаций, так
и за счёт её износа. В общем случае условие контакта двух уп-
упругих тел в произвольный момент времени t имеет вид:
где uz(x,y,t) и w*(x,y,t) - соответственно суммарные упругие
и износные перемещения поверхностей взаимодействующих тел
в направлении оси Oz в точке (х,у), а Ф(х,у, t) - функция, за-
зависящая от формы контактирующих тел и характера их отно-
относительных перемещений. В начальный момент времени t = О,
когда w*(x,y,t) = О, функция Ф(ж,у,t) зависит только от на-
начальной формы fi(x,y) взаимодействующих тел (г = 1,2) и их
сближения -D(O) и имеет вид:
Ф(х,у,0) = D@) - (А(х,у) + h{x,y)).
Покажем, как зависит вид функции Ф(х,у,Ь) от характера
перемещений взаимодействующих тел. Рассмотрим, например,
плоскую контактную задачу о скольжении цилиндрического
штампа по упругому основанию (рис. 7.3). Пусть при этом осно-
основание изнашивается. Если движение происходит вдоль направ-
направляющей Оу цилиндра, то условие контакта в произвольный мо-
момент времени t имеет вид:
fi(x), \x\^a(t), G.9)
363
где функция /i (ж) описывает форму контактирующей поверхнос-
поверхности цилиндра в систе-
системе координат Oxyz, свя-
связанной с границей уп-
упругого полупространст-
полупространства. Ось Oz совпадает
с нормалью к границе
полупространства, про-
проходящей через точку О
начального касания тел,
D(t) - смещение ци-
цилиндра вдоль оси Oz
Рис. 7.3. Схема контакта цилиндричес- вследствие упругих де_
кого штампа с упругим основанием формацИЙ и ИЗНОса по-
верхности основания, a(t) - полуширина площадки контакта.
Заметим, что в правую часть уравнения G.9) функции времени
и координат входят аддитивно. Условия такого вида относят-
относятся к типу Л. Метод решения и некоторые задачи этого класса
изложены в 7.3 и 7.4.
Рассмотрим теперь движение со скоростью V цилиндра пер-
перпендикулярно его образующей, т. е. вдоль оси Ох. Для фиксиро-
фиксированной точки (х,у,0) границы упругого полупространства усло-
условия контакта изменяются при движении штампа и имеют вид:
uz(x,t)
U =
= D(t)-fi{x-Vt), -a{t)<x<b(t),
b(t) - a{t) GЛ°)
V
Здесь — a(t) и b(t) - точки, ограничивающие область контак-
контакта, t* - время контакта данной точки полупространства со
штампом за один проход. Подобные контактные задачи относят-
относятся к типу В. Примеры решения задач этого класса рассмотрены
в 7.6.
Следует отметить, что задача для одного и того же сопря-
сопряжения в зависимости от того, износ какого элемента изучается,
может относиться к типу Л или В. Так, задача об изнашива-
изнашивании цилиндра в предположении, что граница полупространства
не изнашивается, при любом характере его движения относится
364
к типу Л- Для уже обсуждавшегося в 7.1 сопряжения пальчи-
пальчиковый образец - диск (см. рис. 7.2), которое используется при
определении характеристик изнашивания материалов, контакт-
контактная задача об изнашивании образца относится к типу А, а об
изнашивании диска - к типу В.
При заданной нормальной нагрузке P(t), действующей на
штамп, и неизвестной величине смещения штампа D(t) к урав-
уравнению G.7) и условию контакта, которое в более общем случае
для задач типа Л имеет вид:
w*i(x,y,t) + uz2(x,y,t) + w*2(x,y,t) =
[h(y) + f(x)} { • j
(здесь «zj, w*i - упругие и износные перемещения взаимодей-
взаимодействующих тел (г = 1,2), имеющих начальную форму fi(x,y)),
следует добавить условие равновесия, связывающее контактные
напряжения с внешними нагрузками на взаимодействующие те-
тела. В случае, когда трение отсутствует и единственным кон-
контактным напряжением является контактное давление, уравно-
уравновешиваемое вертикальной силой P(t), условие равновесия имеет
вид:
JJp(x,y,t)dxdy = P(t). G.12)
п
Для замыкания системы уравнений износоконтактной зада-
задачи необходимо задать соотношение, связывающее линейный из-
износ w*(x,y,t) с контактным давлением p(x,y,t) и скоростью
скольжения V(x,y,t). В качестве такого соотношения может
быть использовано уравнение износа, виды которого для раз-
разных механизмов изнашивания приведены в 7.1. Используя соот-
соотношение G.6) как локальный закон изнашивания, справедливый
в каждой точке площадки контакта, получим
^ = Kwpa(x,y,t)V^x,y,t). G.13)
В общем виде соотношение G.13) представимо как
/Till
О- G-14)
365
Из G.13) следует выражение для линейного износа в точ-
точке (х,у):
t
w.(x,y,t) = Kw Jpa(x,y,t')V0(x,y,tl)dtl. G.15)
о
По своему физическому содержанию износ - это накопленные
за время t необратимые перемещения поверхности в точке (х, у),
обусловленные потоком разрушений, происходящих на малых
отрезках времени At. В более общем виде соотношение G.15)
может быть записано в виде:
t
w*{x,y,t) = JK{t,t')f {p(x,y,*'), V(x,y,t')) dt', G.16)
0
где K(t,t') и f(p, V) - заданные функции.
Соотношения G.7), G.11) (или G.10)), G.12) и G.13) пред-
представляют собой замкнутую систему уравнений для определения
контактных давлений p(x,y,t), формы изношенной поверхнос-
поверхности w*(x,y, t), упругих перемещений uz(x,y,t) и сближения D(t)
тел при изнашивании.
Следует отметить, что впервые задача о расчёте износа со-
сопряжений была поставлена А.С. Прониковым [117] в предполо-
предположении, что контактирующие тела абсолютно жёсткие. В этом
случае эволюция формы поверхности определяется главным об-
образом геометрией взаимодействующих тел и характером их от-
относительных перемещений. Эпюра давлений приближённо вы-
вычисляется с использованием уравнений износа G.13) и равнове-
равновесия G.12). Такой приближённый подход упрощает постановку
задачи и даёт возможность рассчитать эволюцию макроформы
тел и распределение износа по поверхности взаимодействующих
тел в различных сопряжениях [118]. Постановка задачи об износе
локального контакта упругих тел впервые изложена М.В. Коров-
чинским [85].
Наибольший вклад в теорию решения износоконтактных за-
задач внесён Л.А. Галиным [24-28], который был лидером этого на-
направления. Дальнейшее развитие это направление механики кон-
контактных взаимодействий получило, в частности, в работах [3-6,
366
15, 22, 36, 44, 79, 131, 135, 139], в которых рассмотрены различ-
различные формы контактирующих тел (полупространство, полуплос-
полуплоскость, полоса, области с круговыми границами, упругая балка),
разные физические модели деформируемых тел (упругие, линей-
линейно-деформируемые, вязкоупругие и т.д.), разные условия нагру-
жения и вида относительных перемещений поверхностей, случаи
постоянной и переменной площадки контакта. Подробный об-
обзор исследований в области износоконтактных задач содержится
в [102].
В последующих разделах этой главы, а также в главе 8 при-
приводятся общие методы решения износоконтактных задач, специ-
специфика их применения к исследованию изнашивания тонких покры-
покрытий, тел с переменным по поверхности коэффициентом износо-
износостойкости, изнашивания дискретного контакта и т. д. Получен-
Полученные решения могут быть использованы для исследования кине-
кинетики изнашивания некоторых широко используемых в практике
элементов машин, прогнозирования их работы на стадии проек-
проектирования, а также решения некоторых вопросов оптимизации
процесса изнашивания.
7.3. ИЗНОСОКОНТАКТНЫЕ ЗАДАЧИ ТИПА Л
7.3.1. УСТАНОВИВШИЙСЯ РЕЖИМ ИЗНАШИВАНИЯ
Рассмотрим полученную систему уравнений для задач типа Л и
предположим, что
V(x,y,t) = VOQ(x,y), ОД = Поо, ^р = Ах>, G.17)
т. е. скорость скольжения, область контакта и сближение тел под
нагрузкой не зависят от времени. Будем считать, что коэффи-
коэффициент износа Kw = Kw{x,y) в общем случае является функцией
координат. Это имеет место при изнашивании неоднородных,
а также упрочнённых поверхностей. Тогда исследуемая система
уравнений при степенном законе изнашивания G.13) может быть
записана в виде:
uz{x,y,t) = A\p(x,y,t)], G.18)
367
= Kw(x,y)pa(x,y,t)V?(x,y), G.19)
uz(x,у, t) + w*{x,у, t) =-- D(t) - f(x,y), G.20)
где
uz(x, y, t) = uzi(x, y, t) + uz2(x, y, t),
f(x,y) = fi(x,y) + f2{x,y),
ад*(ж, у, t) = wtl{x, y, t) + u\,2(z, y, t).
Если оператор А не зависит от времени, то система уравне-
уравнений G.18)-G.20) имеет стационарное решение, которое опреде-
определяет контактное давление Роо{х, у) = lim p(x, у, t) в установив-
установившемся режиме изнашивания:
G.21)
Из уравнения G.20) с учётом последнего равенства следует со-
соотношение, справедливое для установившегося режима изнаши-
изнашивания:
dw*(x,y,t) _dD{t) _
at ~ ~dT ~ °°'
т. е. в установившемся режиме изнашивания скорость износа в
каждой точке области контакта постоянна. Это, в свою очередь,
даёт основание заключить, что форма изношенной поверхнос-
поверхности при установившемся изнашивании не меняется и описывает-
описывается функцией fioo{x,y). Так, в рассмотренном выше примере об
изнашивании полуплоскости цилиндрическим штампом, движу-
движущимся вдоль своей образующей, установившаяся форма f2oo{x)
изношенной поверхности определяется функцией:
/2оо(ж) = lim [w*(x,t) - го*(х0,*)] =
*^+°° G.22)
= -fi(x) + fi(x0) - A [poo] (ж) + А \роо] (х0),
где точки х, xq е Поо, а А [роо] (х) (А [р,^] (жо)) - значение функ-
функции А\роо] в точке х (xq), причём функция Роо(я) определяется
соотноп1ением G.21). Соотношение G.22) следует непосредствен-
непосредственно из уравнений G.18), G.20) и G.21).
368
Подстановка G.21) в уравнение равновесия G.12) даёт вы-
выражение для определения значения нормальной нагрузки Р^ в
установившемся режиме изнашивания:
а?, у) К»' (яг, у)
Работа сопряжения в установившемся режиме изнашивания
является наиболее благоприятной, поскольку она характеризует-
характеризуется стабилизацией давления и, следовательно, всех характеристик
сопряжения (давление в данном случае является управляющим
параметром). Поэтому часто ставится задача оптимизации про-
процесса износа за счёт приближения его начальных характеристик
к стационарным. Некоторые задачи оптимизации изнашивания
поверхностей рассмотрены в 8.3 и в [55, 172].
7.3.2. УСЛОВИЯ АСИМПТОТИЧЕСКОЙ
УСТОЙЧИВОСТИ СТАЦИОНАРНОГО РЕШЕНИЯ
Рассмотренное выше стационарное решение Роо{х,у) системы
уравнений G.18)-G.20) является асимптотически устойчивым,
если общее решение представимо в виде
р(х, у, t) = роо(х, у) + <р(х, у, 0, G-24)
и выполняется условие
lim <p(x,y,t) = 0. G.25)
t—И-оо
При линейной форме уравнения износа (а = 1) можно указать
достаточные условия представимости решения в форме G.24)
и G.25). В предположении, что линейный оператор А не зависит
от времени, т. е. справедливо соотношение
из уравнений G.18)—G.21) и G.24) следует, что функция (р(х, у, t)
удовлетворяет уравнению
А [дФы'Ь)] - -Kw{x,yMXty,t)V?(x,y). G.27)
369
Будем искать решение этого уравнения методом разделения пе-
переменных, т.е. представим функцию (p(x,y,t) в виде
<р(х,у,Ь)=<ф(х,у)ТA). G.28)
Тогда получим:
T(t)A[iP(x,y)} = -Kw(x,y)V&(x,y)il>{x,y)T(t)
или
f{t) + XT{t) = 0, G.29)
q(x,y)-\A1[q(x,y)]=0, G.30)
где
q(x,y) = Kw(x,y)v?,(x,y)tp(x,y),
G.31)
= A
Kw(x,y)V&(x,y)
Обозначим систему собственных значений уравнения G.30) че-
через Л = {An}^L1. Из уравнения G.29) тогда получим
T(*) = T@)exp(-Ant). G.32)
Чтобы найти функцию гр(х,у), необходимо изучить спектр Л
оператора А\. Частные решения <p(x,y,t) уравнения G.27) удов-
удовлетворяют условию G.25), если все Ап > 0. Последнее неравен-
неравенство выполняется в случае, если А\ - непрерывный, самосопря-
самосопряжённый, положительно-определённый оператор [137].
В 7.4 мы исследуем некоторые износоконтактные задачи, в
которых оператор А\ удовлетворяет всем перечисленным выше
достаточным условиям существования асимптотически устойчи-
устойчивого установившегося режима изнашивания.
Достаточные условия существования асимптотически устой-
устойчивого установившегося решения системы уравнений в случае,
когда оператор А не зависит от времени, для нелинейного урав-
уравнения износа {аф \ в G.19)) обсуждаются в 8.1.
370
7.3.3. ОБЩИЙ ВИД РЕШЕНИЯ
Предположим, что А\ - непрерывный, самосопряжённый, поло-
положительно-определённый линейный оператор. В этом случае его
собственные функции {Un(x,y)} образуют полную ортонормиро-
ванную систему в пространстве непрерывных функций и все его
собственные значения {Ап} положительны.
Тогда, как следует из соотношений G.24), G.28), G.31)
и G.32), выражение для контактных давлений в произвольный
момент времени может быть представлено в виде ряда:
G 33)
Kw{x,y)V?>{x,y) n=1
Коэффициенты Ап находятся из разложения известной функции
давления в начальный момент времени t = 0 в ряд по полной
ортонормированной системе собственных функций Un(x,y):
1 оо
р(х, у, 0) = Роо{х, у) + —д- V AnUn{x, у). G.34)
Kw{x,y)V&{x,y) n=1
Форма изношенной поверхности в произвольный момент време-
времени находится из уравнения, полученного из G.19) для а = 1 и
выражения G.33):
оо
Пгг '~ -W1 --' \nt)). G.35)
n=i А"
Подобным методом рассмотрены задачи об изнашивании полу-
полуплоскости изогнутой балкой [24] и упругого кольца с разрезом
(модель поршневого кольца), вложенного в цилиндр [38, 39],
плоских направляющих скольжения [3, 4, 6], вращающегося осе-
симметричного тштампа, взаимодействующего с упругим полу-
полупространством (сопряжение пята-подпятник) [26, 27, 80].
Заметим, что если функции V(x,y,t), ?l{t), D(t) зависят
от времени, удовлетворяя условиям lim V(x, y,t) = Voo(x,y),
t>+oo
lim fi(t) = fioo и lim —-^ = D^ (или lim P(t) = Poo), то
t—>+oo t—>+oo at t—>+oo
371
решение системы уравнений G.6), G.7) и G.11) стремится к ре-
решению, определённому функциями G.33) и G.35) при t —> +оо.
Таким образом, необходимым условием существования устано-
установившегося режима изнашивания для контактных задач класса Л
является стабилизация во времени внешних параметров задачи
(скорости сближения D{t) взаимодействующих тел, нормальной
нагрузки P(t) и т.д.). Если Pqq = 0 или D^ = О, контактное
давление стремится к нулю, т.е. Роо(х,у) = 0.
Методы решения линейных износоконтактных задач для уп-
упругих тел изложены в монографиях [25, 44, 172], а также в рабо-
работах [4, 6, 80, 85] и т.д.
7.4. КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ УПРУГОГО
ПОЛУПРОСТРАНСТВА
В этом разделе излагается общий метод решения плоских и про-
пространственных линейных изноконтактных задач типа Л-, в ко-
которых предполагается постоянство области контакта при изна-
изнашивании (оператор А, определённый соотношением G.7), не за-
зависит от времени) и линейная зависимость скорости износа от
контактных давлений и скорости скольжения.
7.4.1. ПОСТАНОВКА ЗАДАЧИ
Пусть штамп, форма контактирующей поверхности которого
описывается функцией z = f(x,y), совершает вращательные или
возвратно-поступательные перемещения по границе упругого ос-
основания. В системе координат, связанной со штампом, соотно-
соотношение между упругими перемещениями uz(x, у, t) в направлении
оси Oz и давлением р(х, у, t) (см. G.7)) имеет форму интеграль-
интегрального уравнения
uz(x, у, t) = jj К(х, у, х', у')р(х', у', t) dx'dy', G.36)
п
где ядро К(х, у, х'', у'), известное в каждой конкретной задаче, не
зависит от времени. Как было отмечено в 7.2, это предположе-
предположение справедливо, если перемещения границы полупространства
372
в результате износа малы и соизмеримы с упругими перемеще-
перемещениями. Кроме того, ядро уравнения G.36) не изменяется в про-
процессе изнашивания, если изнашивается только штамп, а грани-
граница полупространства в недеформированном состоянии остаётся
плоской. В этом случае не ставятся ограничения на величину
линейного износа w*(x,y,t) штампа.
Ядра интегрального оператора G.36), используемого в кон-
контактных задачах для упругого полупространства (или полуплос-
полуплоскости), представляют собой функцию, описывающую перемеще-
перемещение границы полупространства в точке (х,у) в результате дей-
действия на границу полупространства в точке (х',у') нормаль-
нормальной силы p(x',y',t)dx'dy', т.е. зависящую от расстояния между
рассматриваемыми точками. Это обуславливает симметрию яд-
ядра К(х,у,х',у'). Чтобы установить положительную определён-
определённость ядра, рассмотрим функционал J[q\:
Г
J[q] = JJ q(x, у) JJ К(х, у, х', y')q(x', у') dx'dy'
dxdy,
где q(x, у) - произвольная непрерывная функция, не равная тож-
тождественно нулю внутри области О. На основании G.36) функци-
функционал J[q] можно представить в виде
=
q(x,y)wq(x,y)dxdy.
ft
Таким образом, функционал J[q] представляет собой суммарную
работу, производимую произвольными силами давления q(x,y)
на соответствующих перемещениях wq(x,y) точек площадки
контакта ((х,у) Е fi), которая для отличных от нуля давлений
положительна. Таким образом, интегральный оператор G.36)
является самосопряженным и положительно определённым.
Условие контакта G.11) штампа (uzi(x,y) = 0) и упругого
полупространства в произвольный момент времени имеет вид:
uz(x,у, t) + w*(x,у, t) = D{t) - f(x,у), G.37)
где износные перемещения ш*(х,у, t) удовлетворяют соотноше-
соотношению G.19).
373
Из уравнений G.19), G.36) и G.37) можно определить кон-
контактные давления р(х, у, ?), упругие смещения границы uz(x, у, t)
и перемещения w*(x,y,t) в результате износа, если известна
функция D(t), характеризующая сближение тел.
При заданной нормальной нагрузке P{t), приложенной к
штампу, для определения функции D(t) используется дополни-
дополнительно уравнение равновесия:
P(t) = JJp(x,y,t)dxdy. G.38)
n
Из анализа, проведённого в 7.3, следует, что для существо-
существования установившегося режима изнашивания, описываемого в
общем случае соотношениями G.21) и G.22), необходимо, что-
чтобы скорость сближения тел dD/dt и нормальная нагрузка P(t)
стремились к постоянным значениям, т. е.
dD(t) dw*(x,y,t)
lim = lim — = Doo, G.39)
>+oo dt ?->+oo dt
dP
lim -г- = Poo,
t->+oo dt
где Poo определяется выражением G.23):
'D
'oo
a ff dxdy
// тгР/а, ч '
JJ yZJ (х.у)
Если Pqo = 0 или ?>оо = 0, то контактное давление стремится к
нулю в процессе изнашивания, т.е. Роо{х,у) — 0.
Форма foo{x, у) изношенной поверхности штампа описывает-
описывается выражением, которое следует из соотношений G.22) и G.36):
= -JJ[K(x,y,x',y')-
-К(хо,у°,х',у')}
_KwV&(x>,y')\
374
dx'dy',
Pit)
2b
Рис. 7.4. Схема контакта кольцевого цилиндрического штампа с уп-
упругим полупространством
где (ж0, у0) € fi. В приведённых выше соотношениях положено,
что коэффициент износа Kw является постоянной величиной.
Как следует из G.40), установившаяся форма изношенной по-
поверхности, как и весь процесс изнашивания, существенно зави-
зависит от характера движения штампа.
7.4.2. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА
Рассмотрим осесимметричную контактную задачу о вдавлива-
вдавливании в упругое полупространство кольцевого штампа, уравне-
уравнение торцевой поверхности которого описывается функцией z =
= /(г), вращающегося вокруг своей оси с угловой скоростью ш
(см. рис. 7.4). Нормальная сила P(t) и момент M(t), приложен-
приложенные к штампу, являются функциями времени. Решение этой за-
задачи может быть использовано для расчёта износа таких сопря-
сопряжений, как осевой подшипник скольжения, торцевое уплотнение,
муфта сцепления, дисковый тормоз и др.
Предположим, что размер кольцевой площадки контак-
таа^г^бв процессе изнашивания не меняется. Такое предпо-
предположение оправдано для неизнашиваемого штампа с плоским ос-
основанием. В остальных случаях оно выполняется приближённо,
если при изнашивании изменение размеров площадки контакта
мало по сравнению с её шириной.
При вращении штампа на площадке контакта возникают ка-
касательные напряжения tz$, которые перпендикулярны радиусу
375
площадки контакта, и связаны с контактным давлением p(r, t)
законом Кулона-Амонтона
где ц - коэффициент трения.
Как показано Л.А. Галиным [23], касательные напряже-
напряжения Tzg(r, t) в осесимметричной контактной задаче с силами тре-
трения не оказывают влияния на распределение контактных дав-
давлений p(r, t). Контактные давления связаны с упругими пере-
перемещениями uz(r) следующим соотношением, справедливым для
контактной задачи при отсутствии сил трения:
и (r) = _±_ / / p{r\tydr'dy
КЕ* J J y/r2jrr,2_2rr, CQS ' K ¦ '
a 0 r
где E* = E/(l - v2).
Будем считать, что вращающийся штамп изнашивает по-
поверхность полупространства и воспользуемся уравнением изно-
износа в форме G.19), которое в случае а = /3 = 1 примет вид:
*аМ . К****). G.42)
Условие контакта штампа с полупространством в произволь-
произвольный момент времени имеет вид:
uz(r, t) + w*(r, t) = D(t) - /(г), G.43)
где D(t) - перемещения штампа вдоль оси Oz.
Подставляя в уравнение G.43) выражение G.41) и принимая
во внимание соотношение G.42), получим интегральное уравне-
уравнение для определения контактных давлений в задаче для упругого
полупространства с учётом его изнашивания:
/ p(r',t)r'dr'dy _
2 + г'2 - 2rr' cos ш
G.44)
кЕ* ] ]
= D(t) - f(r) - Kwur fp(r, t) dr.
376
Следуя общему методу решения линейных износоконтактных за-
задач, изложенному в 7.3, введём новую функцию q(r, t) = rp(r,t),
которую представим в виде:
оо
q{r, t) = qoo + ^2 9"(г)ехр (~Л«Ш*) • G-45)
п=1
Подставляя G.45) в G.44), получим уравнение
Kw . .
An
G.46)
Ь 2тг
K& j j yjr2+r"-2rr'cosy j
Рассмотрим разные возможные случаи постановки задачи. Если
штамп не перемещается вдоль своей оси, т.е. D(t) = D@), из
уравнения G.46) следует, что контактные давления в процессе
изнашивания стремятся к нулю (<7оо = 0). Для нахождения иско-
искомых функций qn(p) = qn(pb)/{bE*) и значений Лп имеем однород-
однородное интегральное уравнение Фредгольма второго рода (р = r/b):
1
Ш - Ап | H(p,p')qn(p')dp' = 0 G.47)
а/Ь
с симметричным положительным вещественным ядром
2тг
dip
VP2 + P'2 - 2pp' cos <p
где К(ж) - полный эллиптический интеграл первого рода. В
асимптотическом случае, когда площадка контакта представля-
представляет собой достаточно узкое кольцо, т. е. (b—a)/a <S 1, ядро #(р, р!)
377
принимает простой вид:
In
8а
' ttE*Kw \p - p'\ b "
Интегральный оператор в G.47) является самосопряжённым,
вполне непрерывным и положительным, в силу чего его харак-
характеристические числа Ап вещественны и положительны, а собст-
собственные функции образуют полную ортонормированную систему.
Контактное давление р(г, 0) в начальный момент времени мо-
может быть определено из решения осесимметричной контактной
задачи без сил трения для кольцевого штампа и упругого полу-
полупространства (см., например, [1, 61, 121, 170]. В частности, для
широкого кольцевого штампа ((Ь — а)/а >• 1) с плоским основа-
основанием, т. е. /(г) = Dq, выражение для давления имеет вид [61]:
р(г,0) =
2D0E
=+
G.49)
Раскладывая функцию q(p,O) = pp(pb,0)/E* в ряд по полной ор-
тонормированной системе собственных функций {Un(p)} уравне-
уравнения G.47), найдём коэффициенты Ап:
71 = 1
Тогда контактное давление p(p,t) = p(p,t)/E* в последующие
моменты времени вычисляется по формуле:
1
р(р, t) = -^T AnUn
G.50)
Случай линейного износа, когда D{t) — D{0) + Doot, также при-
приводит к необходимости решения интегрального уравнения G.47).
Решение задачи имеет вид:
nun(p) exp(-\nut)
n=l
G.51)
378
где Qoo = Dtx,/(KwujbE*). Из уравнения равновесия G.38) полу-
получим функцию P(t) изменения нагрузки во времени для случая
линейного износа
P(t) =Poo +
где
G.И)
J\WU>
1
J
1
un(p)dp.
a/b
В общем случае произвольно меняющихся функций D(t)
или P(t), удовлетворяющих условиям
D{t) = ?>@) + D^t + D*(t),
P(t) = ^oo + Р*{*),
где АиВ- некоторые постоянные, задача может быть решена
подобным методом (см. [36]), т.е. сведена к решению спектраль-
спектральных задач для интегральных уравнений Фредгольма второго ро-
рода.
Аналогичный подход используется и для исследования за-
задачи о вращении штампа круговой формы в плане (площадка
контакта представляет собой круг радиуса Ь) на границе упру-
упругого изнашиваемого полупространства. Однако в этом случае,
как следует из уравнения G.42), перемещения в центре площад-
площадки контакта, обусловленные износом, равны нулю, что должно
привести к росту давлений в этой точке. Этот процесс, в свою
очередь, приведёт к необратимым пластическим деформациям
в центре площадки контакта. Таким образом, для штампа кру-
круговой формы в плане решение задачи теории упругости будет
справедливо во всей зоне контакта, за исключением малой об-
области радиуса а вблизи центра площадки контакта. При этом
собственные функции Un(p) уравнения G.51) могут быть найде-
найдены из анализа уравнения G.47) с симметричным положительно
определённым ядром G.48) при а/Ь <?. 1.
379
Давление р(г, 0) в начальный момент времени определяется
по формуле [23]:
где
2тг
2г'
ж у г2 + г'2 — 2rr' cos (p
х arctg —, = dip,
by r2 + г' — 2rr' cos (p
_ i д д2
г' дг' дг'2
Для определения собственных функций Uk(r) и характерис-
характеристических значений Afc однородного интегрального уравнения
Фредгольма G.47) с вещественным, симметричным и положи-
положительно определённым ядром G.48) использовался метод Келлога
(см. [ЮЗ]). Последовательные приближения находились по фор-
формуле:
1
= J Щр,Р') [uin\P') - uin\P)} dP'
a/b
1
+uln)(p)jH(p,p')dp'.
a/b
Первое слагаемое этой суммы - интеграл, не имеющий особен-
особенности при р' = р, - вычислялся численно, другой же интеграл
вычислялся аналитически. Функция Щ \р) на к-ш шаге выби-
выбиралась из ортогонального дополнения к линейной оболочке, на-
натянутой на уже найденные на предыдущих шагах собственные
функции U\(p), Ui{p), ... , Uk-i(p), соответствующие характе-
характеристическим числам 0 < Ai < А2 < ¦ ¦ • < \k-i- Характеристи-
380
Таблица 7.2. Характеристические числа уравнения G.47)
10 1,39264
5,67423 21
8,06343
п
1
2
3
4
5
6
7
8
9
An
(| = 0,0005)
0,03643
0,06730
0,15221
0,29421
0,46936
0,63901
0,77450
0,99863
1,25300
An
A = °*)
0,18286
0,90155
1,57259
2,22609
2,79990
3,41897
3,83968
4,37473
5,06344
n
12
13
14
15
16
17
18
19
20
An
G = 0,0005)
1,91324
2,17578
2,42712
2,76887
2,91857
3,32462
3,75936
4,22465
4,80057
An
6,62237
7,48047
8,23339
8,46120
9,62898
11,06820
12,86998
15,48172
19,90402
30,73539
11
1,69633
6,18522
ческое число А*, вычислялось как
= lim Ai. =
lim
n—»oo
m
IL2
\L2
При a/b = 0,0005 и a/6 = 0,5 произведены расчёты, реали-
реализующие изложенный выше алгоритм. В каждом случае найде-
найдено 21 характеристическое число (табл. 7.2) и соответствующие
им собственные функции. Значения величин Ап = А„ /(nE*Kw)
быстро возрастают с увеличением п. Ввиду этого с достаточ-
достаточной степенью точности при больших временах в формуле G.45)
можно ограничиться рассмотрением лишь нескольких первых
членов ряда.
На рис. 7.5 приведены графики распределения давления под
кольцевым штампом с плоским основанием в начальный момент
381
времени и в установившемся режиме, т. е. при t —> +00. Заметим,
что особенности функции давления (р(г, 0) —>• +оо при г —> а + 0
иг —> Ь — 0), имеющие место в начальный момент времени ? = 0,
исчезают при t > 0.
Предложенный метод может быть использован для анали-
анализа изнашивания как упругого полупространства, так и штампа.
Форма изношенной поверхности штампа вычисляется по форму-
формуле, которая следует из выражения G.40):
г/Ь
/оо(г)-/оо(а)=
п2Е*{Ь-а)
, G.53)
а/г
а/Ь
где К(ж) - полный эллиптический интеграл первого рода.
Как уже отмечалось, ре-
8ДМ
2Kb
6,0-
4,0-
2,0-
шение задачи существенно
зависит от характера движе-
движения штампа. Если цилиндри-
цилиндрический штамп, контактирую-
контактирующий торцевой поверхностью с
упругим полупространством,
не вращается, а движется ха-
хаотически (|F| = const) по его
поверхности так, что послед-
' ' ' няя изнашивается равномер-
Рис. 7.5. Начальное A) и уста- н0) т. е. поверхность полупро-
новившееся B) давление в контак- странства остается плоской,
те вращающегося цилиндрического
кольцевого штампа с упругим по-
полупространством
пом при условии P(t) —> Poo {t
ному (см. G.21) и форма изношенной поверхности штампа пред-
ставима в виде G.40), т.е.
а форма штампа меняется
при изнашивании, то распре-
распределение давления под штам-
+оо) стремится к равномер-
G.54)
382
При выводе G.54) принято во внимание значение интеграла
27г а
pdpdtp
О О
Г2 + р2 — Irp COS if
= 4аЕ
(Т).
\а/
Заметим, что форма изношенной поверхности будет описывать-
описываться уравнением G.54) только в том случае, если сила Pqo обес-
обеспечивает полный контакт штампа с полупространством внутри
круга радиуса а.
7.4.3. ПЛОСКАЯ ЗАДАЧА
Рассмотрим теперь зада- дг
чу о взаимодействии поло-
полосового штампа C), скользя-
скользящего возвратно-поступатель-
возвратно-поступательно вдоль оси Оу по грани-
границе упругого слоя A), нахо-
находящегося на жёстком основа-
основании B) (рис. 7.6). Эта зада-
задача может быть исследована
в плоской (двумерной) поста-
Рис. 7.6. Схема контакта полосово-
полосового штампа с упругим слоем
новке. Её решение применимо
для изучения кинетики изнашивания направляющих скольже-
скольжения.
Из общей системы уравнений износоконтактной задачи, по-
полученной в 7.4.1, следует интегральное уравнение для рассмати-
ваемого вида контакта
' = D(t)-f(x)-KwV& jp(x,t')dt'.
ттЕ*
Здесь f(x) - форма контактирующей поверхности штампа,
D(t) - сближение тел при изнашивании, ho - толщина слоя, Vqo -
скорость скольжения штампа, p(x,t) - контактное давление Kw,
/3 - параметры уравнения износа, которое принято в виде
383
Ядро #i(y) представимо в виде [121]:
+00
нЛу)= / cos{uy)du,
J и
где
L(u) = ch2"~1
в задаче для упругого слоя A), лежащего на жёстком основа-
основании B) без сил трения;
2>csh2u — 4u
L() 34
в задаче для слоя, сцепленного с жёстким основанием.
Эта износоконтактная задача при фиксированной области
контакта также может быть сведена к исследованию интег-
интегрального уравнения Фредгольма методом, изложенным в 7.4.2.
(см. [41]). Приведём здесь лишь формулу для формы До изно-
изношенной поверхности штампа в установившемся режиме изнаши-
изнашивания, полученную из соотношения G.40):
/«,(*) - /оо(О) = ^-lW (^А - Я1 (f)] dx>. G.55)
Воспользовавшись разложением ядра Н\(у) в ряд (см. [2])
при ho/a > 1, из G.55) получим следующее выражение, справед-
справедливое при (a/hoL Cl (( = х/а):
/ool(f) = Б =
°°
= -A - 01пA - 0 + A + О ЬA + 0 + 1,432 (j?) .
Заметим, что если форма штампа в начальный момент времени
описывается функцией G.55) и область контакта не меняется в
процессе износа (например, ограничена формой боковой поверх-
поверхности штампа), то в этом случае форма начальной поверхности
384
остаётся неизменной в процессе изнашивания. Будет иметь мес-
место равномерный износ при равномерном распределении давлений
по площадке контакта. Этот вывод следует из анализа поцес-
са изнашивания, проведённого в 7.3. Использование образцов с
формой поверхности вида G.55) в испытаниях на изнашивание
по приведённой схеме позволит определить локальное (в каж-
каждой точке) уравнение износа на основании измерений суммарной
нагрузки и суммарного износа.
Подобное заключение можно сделать и относительно выра-
выражения G.53), описывающего установившуюся форму изношен-
изношенной поверхности цилиндрического штампа, взаимодействующе-
взаимодействующего с упругим полупространством.
7.5. ИЗНАШИВАНИЕ ТОНКОГО УПРУГОГО
СЛОЯ
Метод, изложенный в 7.3, применим для анализа кинетики из-
изнашивания толстого слоя, лежащего на упругом или жёстком
основании (см. 7.4.3). В этом случае перемещения за счёт изно-
износа, соизмеримые с упругими перемещениями, много меньше тол-
толщины слоя. Поэтому для определения упругих перемещений мы
можем использовать соотношение, имеющее место в контактных
задачах без учёта изнашивания слоя. При дополнительном пред-
предположении о неизменности размеров площадки контакта при из-
изнашивании оператор А в уравнении G.7) не зависит от времени.
Однако полученные решения непригодны, например, для ис-
исследования изнашивания тонких упругих покрытий, когда ве-
величина линейного износа может стать соизмеримой с толщиной
покрытия. Анализ долговечности покрытий требует рассмотре-
рассмотрения продолжительных процессов вплоть до полного износа по-
покрытия, при котором линейный износ в какой-либо точке равен
толщине покрытия. Точное решение такой задачи построить за-
затруднительно, поскольку не известен вид оператора А (см. G.7))
для области с произвольной формой границы (формой, приобре-
приобретаемой поверхностью в результате её изнашивания). Ниже изло-
изложено приближённое решение этой задачи, которое даёт возмож-
возможность изучить эволюцию контактных характеристик и толщины
покрытия в произвольной точке при его изнашивании.
13. Горячева И.Г. 385
7.5.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим контакт цилиндрического штампа с двухслойным
упругим основанием. Система координат Oxyz связана со штам-
штампом C) (см. рис. 7.6), форма контактирующей поверхности ко-
которого описывается чётной функцией z = f(x) (f(—x) = f(x)).
Задача рассматривается в плоской постановке.
Предположим, что модуль упругости покрытия A) меньше
основания B). Покрытие моделируется упругой полосой, лежа-
лежащей на упругой полуплоскости без трения (задача 1) или сцеп-
сцепленной с ней (задача 2).
Полоса изнашивается штампом, скользящим вдоль оси Оу.
Предположим, что скорость износа полосы dh(x, t)/dt связана с
величиной контактных давлений р(х, t) соотношением
ОТ/ j.\ Г/ i \ "I Ql
^ = -К» \Р-Щ . G-56)
от [ Р J
где Kw - коэффициент износа, зависящий от скорости, темпе-
температуры и условий взаимодействия, р* - некоторое характерное
давление. В начальный момент времени /i(x,0) = ho-
На штамп действует постоянная вертикальная нагрузка Р.
Касательные напряжения на площадке контакта действуют в
направлении движения штампа и отсутствуют в направлении
оси Ох, т. е. txz — 0. Компонента ryz тангенциальных напря-
напряжений не влияет на распределение контактных давлений, кото-
которые находятся из решения плоской контактной задачи. Однако
компонента туг оказывает влияние на скорость процесса изна-
изнашивания, что может быть учтено с помощью коэффициента Kw
в G.56).
В выбранной нами системе координат условие контакта
штампа с изношенной поверхностью полосы в произвольный мо-
момент времени t имеет вид:
h(x, t) - Л@, t) + (иг(х, t) - uz{0, t)) = /(ж),
/@) = 0, xe(-a,a),
где uz(x,t) - упругие смещения границы полосы в направление
оси Oz, a - полуширина площадки контакта, которая не меня-
меняется при изнашивании.
386
Градиент смещения u'z(x,O) = (duz/dx)\ границы упру-
гой полосы при её нагружении давлением р(х, 0) определяется
выражением (см. [10]):
а
f
p(x', 0) К l^Yl dx' = nh0Elu'z(x, 0), |z| ^ a, G.58)
-h
в котором ядро интегрального оператора имеет вид:
+ ОО
K(t)= f N(u)smtudu, G.59)
о
причём для задачи 1
ch2u
N{u)=-
а для задачи 2
M + 4uexp(—2u) — Lexp(—Аи)
^ = М - A + Аи2 + LM) exp(-2u) + Lexp(-4w) '
М = , L =
Здесь Ei, щ - модуль упругости и коэффициент Пуассона по-
полосы (г = 1) и полуплоскости (г = 2) соответственно, Е* =
— bi/ {/{1. -V{)),n — Ь1/Ь2.
Для тонкой полосы {h/a <C 1) воспользуемся асимпто-
асимптотическим представлением ядра K{t) при больших значени-
значениях t (см. [10]):
K{t)~--An8'{t), G.60)
ъ
где <5(г) - функция Дирака и
0,5 для задачи 1,
A-п)(ж-1)B-п + пж) о G.61)
; гт5 для задачи 2.
(х+1J
13* 387
В последнем соотношении принято, что v\ = V2 = v и, следо-
следовательно, х\ = Х2 = х. Подставляя G.60) в G.58), получим
уравнение
которое, как показано в [10], справедливо для тонкой полосы
при п ^ 2.
Интегрируя обе части уравнения G.62) по х, будем иметь
Ah0
G.63)
dx1 = uz(x,0) -иг@,0).
х1 — х
Первое слагаемое в левой части этого уравнения можно рассмат-
рассматривать как перемещение uz\(x,0) поверхности за счёт наличия
тонкой полосы, ведущей себя как основание Винклера с коэффи-
коэффициентом пропорциональности к = Aho/E^. Подобная интерпре-
интерпретация первого слагаемого в G.63) имеет смысл, если оно рас-
рассматривается в совокупности со вторым, представляющим пере-
перемещение упругого основания игз(х,0).
В [133] показано, что если изменение формы полосы при изна-
изнашивании удовлетворяет условию dh(x,t)/dx <S 1, первое слагае-
слагаемое в соотношении G.63) для произвольного момента времени t
приобретает вид:
иг1 (х, t) = -— [h(x,t)p(x, t) - fc@, t)p{0,1)]. G.64)
b
Уравнение G.63) с первым членом uz\{x,i) в форме G.64) яв-
является обобщением изложенной выше интерпретации соотноше-
соотношения G.63) на случай полосы переменной толщины h(x,t). Запи-
388
шем это соотношение в виде:
X — X
G.65)
dx' = uz(x,t) — uz@,t).
Подставляя G.65) в условие контакта G.57), получим уравнение
для определения контактных давлений в произвольный момент
времени t:
h(x, t) - Л@, t)- — [h(x, t)p(x, t) - h@, t)p(O, t)]
E-
- / р(х , t) In
X — X
X'
G.66)
dx' = f(x).
Толщина полосы в момент времени t определяется из уравнения
износа G.56):
t
h(x, t) = ho - Kw / '-— dt'.
J L У J
0
Кроме того, имеет место условие равновесия:
а
/ р(х, t) dx = P.
G.67)
G.68)
7.5.2. АНАЛИЗ КИНЕТИКИ ИЗМЕНЕНИЯ
КОНТАКТНЫХ ХАРАКТЕРИСТИК
Для решения уравнений G.66)-G.68) использовался пошаговый
метод. Шаг по времени Дт выбирался с таким расчётом, чтобы
в пределах каждого интервала (т^,г^+1), где Tk+\ = т^ + Ат,
го = 0, к = 0,1,..., можно было пренебречь перераспределением
389
давления на площадке контакта и износом поверхности. Если
ввести безразмерные координаты и функции:
? _.Kw_ р_ _Р_
* ~ а ' Г ~ а ' а?2* '
ho — — , /i(?, т) = — h I ?а, г -r^- I, А = — , G.69)
а а V л I» / п
то система уравнений G.66)—G.68) аппроксимируется следую-
следующими соотношениями, представленными в безразмерном виде:
= hit) - [^jr] Ar> hit) = h, G.70)
-А
G.71)
^' = fit),
-1
-- Р. G.72)
-1
При Дт —>• 0 полученные соотношения переходят в первоначаль-
первоначальную систему интегральных уравнений, записанную в безразмер-
безразмерном виде. После определения функции pkit) из уравнений G.71)
и G.72) находится функция h+iix) Для следующего шага по
времени из уравнения G.70) и т.д. В результате получаем рас-
распределение давления в различные моменты дискретного времени
при изнашивании поверхностного слоя.
На каждом шаге по времени для решения интегральных
уравнений G.71) и G.72) использовался метод замены их сис-
системой линейных алгебраических уравнений [75].
390
xla 1,0
Рис. 7.7. Профиль изношенной поверхности слоя (а) и распределение
контактных давлений F) в различные моменты процесса изнашива-
изнашивания: т = 0 A), г = 0,15 B), т = 0,64 C)
Численные расчёты проводились для случая жёсткого сцеп-
сцепления полосы с основанием (задача 2) в предположении, что
модуль упругости полосы меньше модуля упругости основания.
Этот случай наиболее интересен для практики, поскольку может
быть использован для анализа изнашивания твёрдых смазочных
покрытий.
На рис. 7.7 приведены графики распределения давления и
профиля изношенной поверхности покрытия в различные мо-
моменты времени в случае её изнашивания штампом с плоским
основанием (f'(x) = 0) ширины 2а. Были взяты следующие зна-
значения безразмерных параметров: а = 1,4, А = 3,8, р* = 0,26,
Ьо = 3 ¦ 10~2, Р = 9 • 10~3. В рассмотренном примере процесс из-
изнашивания условно можно разделить на две стадии. Начальная
стадия (стадия приработки) характеризуется значительной ско-
скоростью изменения формы и давлений. Давления на этой стадии
перераспределяются. По краям области контакта они снижают-
снижаются значительно, в то время как в центре площадки контакта не-
несколько возрастают и стремятся к равномерному по всей облас-
области контакта распределению. На стадии приработки наблюдает-
наблюдается также интенсивный износ полосы в угловых точках, где наи-
391
более высоки давления и, следовательно, скорость износа. Вто-
Вторая стадия характеризуется распределением давления, близким
к равномерному, и неизменной формой изношенной поверхности
(установившийся износ). Средняя скорость износа в этом режи-
режиме изнашивания минимальна, а работа пары трения в устано-
установившемся режиме является наиболее благоприятной. Снижение
давления в местах его концентрации приводит к более мягким
условиям работы. В ряде случаев это может привести и к смене
механизма износа, предотвратить катастрофический износ или
макроразрушение.
Следует отметить, что при изнашивании штампом тонкого
поверхностного слоя установившийся режим изнашивания мо-
может не наступить, если слой (покрытие) полностью износится
за время приработки. Анализ зависимости времени приработки
покрытия от его начальной толщины, относительных механичес-
механических свойств, коэффициента износа и других параметров задачи
содержится в [44, 49], где также даны оценки эффективной тол-
толщины покрытия после режима приработки и её соотношения с
начальной толщиной покрытия, а также долговечности покры-
покрытия в зависимости от всех исследуемых характеристик покрытия
и основания и геометрии взаимодействующих тел.
7.6. ИЗНОСОКОНТАКТНЫЕ ЗАДАЧИ ТИПА В
Математическая модель износоконтактных задач типа В вклю-
включает в себя уравнения G.7), G.10) и G.16). Из этой системы
уравнений следует, что условия контакта в произвольной точ-
точке границы упругого полупространства меняются во времени,
поэтому линейный износ в произвольной фиксированной точке
находится путём интегрирования функции давления по облас-
области взаимодействия, определяемой характером движения тел. За-
Заметим, что для некоторых задач этого класса изнашивание в
определённой точке тела имеет место только в течение ограни-
ограниченного промежутка времени.
Ниже рассмотрена одна частная задача, на примере которой
предлагается один из возможных методов решения задач этого
класса.
392
Пусть штамп прямоугольной формы в плане движется в на-
направлении оси Ох со скоростью V (рис. 7.8).
При движе-
движении штампа уп-
упругое полупрост-
полупространство изнаши-
изнашивается. Формоиз-
Формоизменение поверх-
поверхности полупрост-
полупространства опреде-
определяется из уравне-
уравнения износа G.13).
В системе коор-
координат (xi,?/i,zi),
связанной с упру-
упругим полупространством, представим его в виде:
Рис. 7.8. Схема взаимодействия штампа прямо-
прямоугольной формы в плане с упругим основанием
G.73)
Область контакта Г2 штампа с упругим полупространством
в системе координат Oxyz, связанной с движущимся штампом,
имеет форму вытянутого в направлении оси Ох прямоугольни-
прямоугольника, т.е. п = {{х,у) : х G (—а,а), у е (—b,b)}, a » b. Сечение
штампа плоскостью х = const также представляет собой прямо-
прямоугольник. В этом случае, как показано Л.А. Галиным [23], давле-
давление р(х, у) внутри области контакта п может быть представлено
в виде:
р(х,у) =
pi(x)
G.74)
где функция pi[x) линейно зависит от упругих смеще-
смещений uz(x,0) — w\{x) в направлении оси Oz. Таким образом,
где
к =
pi(x) - kwi(x),
¦кЕ
G.75)
393
Выражение G.75) аналогично модели основания Винклера.
Соотношение G.74) и характер движения штампа (в направ-
направлении оси Ох) дают основание для рассмотрения задачи в дву-
двумерной постановке в плоскости у = 0.
Исследуем установившийся процесс изнашивания и фикси-
фиксируем произвольную точку (xi,0) на границе полупространства.
Пусть в момент времени t = 0 точка (xi,0) входит в контакт,
т. е. Х\ = а. Обозначим через t(x) момент, в который точка (х\, 0)
имеет координату (х, 0) в системе координате Оху. Тогда полу-
получим
4.1 \ а~х
t(x) =
Введём следующие функции ТУ* (ж) и ps(x), не зависящие от вре-
времени в подвижной системе координат Oxz:
ТУ*(ж) — w*(a,0,t(x)), W*(x) = 0 если x > а,
Ps(a-Vt)=p{a,0,t).
Используя эти выражения и уравнение G.73), получим соотно-
соотношение между функциями ТУ*(ж) и ps{x):
t(x) a
W*(x) = KWV0 f pas{a - Vt')dt' = EnV0-1 Ipas{x')dx1. G.76)
0 x
Условие контакта штампа с изношенной поверхностью полупро-
полупространства в сечении у = 0 в подвижной системе координат Oxz
имеет вид:
W*{x) + Wl{x) = D-f(x), G.77)
где /(ж) - форма контактирующей поверхности штампа в плос-
плоскости у = 0, D - внедрение штампа.
Дифференцируя уравнения G.75), G.76) и G.77) и подстав-
подставляя G.75) и G.76) в соотношение G.77), получим
K*p?(x)-jp's(x) = f'(x), G.78)
где
K, = KWV0~\ G.79)
394
Из уравнения G.78) и условия равновесия
p8(x)dx = Ро
можно определить функцию рв(х). Величина Ро находится из со-
соотношения G.74) при известной нормальной нагрузке Р, прило-
приложенной к штампу.
Решение задачи для случая а = 1 может быть представлено
в аналитическом виде:
Ps(O = \С - J /[((') ехр (-*?') df I exp (хО , G.80)
-1
где
с- :
2shx
-1
x
ka ' s а' тгЬ
На рис. 7.9 приведены графики распределения безразмерного
давления ра(?) и формы W*(?) = W*/a изношенной поверхнос-
поверхности упругого полупространства в пределах области контакта (в
сечении у = 0) при движении по нему штампа с плоским осно-
основанием (f'(x) = 0). Функция W*(x), определённая из соотноше-
соотношений G.76) и G.80), имеет вид:
(ехр(х) -
Заметим, что уравнение G.78) также может быть использовано
для ответа на вопрос: какова должна быть форма /о (ж) штам-
штампа, чтобы при его установившемся движении по изнашиваемо-
изнашиваемому упругому основанию давление вдоль оси Ох было распре-
395
1,2
0,6
nbps/(ka)
W.I a
0,0
1,0
0,5
0,0
-1,0
0,0 xla 1,0
-1,0
0,0 xla 1,0
Рис. 7.9. Установившееся давление (а) и форма изношенной поверх-
поверхности упругого полупространства (б) при a = 1 и разных значениях
параметра х: х = 0,1 A), х = 0,5 B), к = 1 C)
делено равномерно, т.е. р\(х) = pq. Как следует из уравне-
уравнения G.78), функция, обеспечивающая выполнение этого условия,
имеет вид /о(х) = К*р%х + const, где К» определено в G.79).
Задача типа В об изнашивании упругого основания вращаю-
вращающимся диском, движущимся поступательно, рассмотрена в [132].
7.7. ЗАДАЧИ С ИЗМЕНЯЮЩЕЙСЯ
ПЛОЩАДКОЙ КОНТАКТА
В 7.3-7.5 рассмотрены контактные задачи при наличии износа
типа Л с фиксированным размером площадки контакта. Такая
постановка имеет место при контактировании штампа с упру-
упругим телом, когда размер площадки контакта определяется толь-
только конфигурацией штампа (например, случай штампа с плоским
основанием). В противном случае при малых изменениях разме-
размеров площадки контакта в результате износа взаимодействующих
тел это условие может быть выполнено только приближённо.
Если размер площадки контакта меняется при изнашивании,
т.е. а — q(t), оператор А в соотношении G.7) зависит от време-
времени. В таком виде задача усложняется и становится нелинейной
даже в случае, когда имеет место линейный закон изнашивания.
396
Рассмотрим общие закономерности изнашивания при изменяю-
изменяющейся площадке контакта на простейшей модели упругого тела -
основании Винклера.
7.7.1. АНАЛИЗ РАЗЛИЧНЫХ ПОСТАНОВОК ЗАДАЧИ
Пусть гладкий цилиндрический штамп, форма контактирующей
поверхности которого описывается дифференцируемой функци-
функцией z = f(x), вдавливается в упругое основание силой P(t) и
перемещается вдоль своей образующей (вдоль оси Оу) со ско-
скоростью V (см. рис. 7.3). Предположим, что упругие перемеще-
перемещения uz(x,t) границы основания в направлении оси Oz связаны с
контактным давлением p(x,t) соотношением
uz(x,t) = kp{x,t), G.81)
где к = h/K, а К - величина, характеризующая упругие свой-
свойства основания, которое представляет собой слой толщины h.
Поскольку износ штампа в процессе трения пренебрежимо
мал по сравнению с износом основания, будем считать, что из-
изнашивается только поверхность основания, и рассмотрим урав-
уравнение износа в виде
G-82)
где коэффициент износа Kw может зависеть от скорости V, тем-
температуры, коэффициента трения и т. д.
Запишем условие контакта штампа и упругого основания
внутри интервала (—a(t),a(t)) в произвольный момент време-
времени t:
uz(x,t)+w*(x,t) = D{t)-f(x), -a(t) ^ x < a{t). G.83)
где D{t) - перемещение штампа вдоль оси Oz.
Кроме того, из условия равновесия штампа следует
a(t
1
p(x,t)dx = P(t). G.84)
a(t)
397
Вследствие гладкости формы штампа на границе площадки кон-
контакта давление равно нулю, т. е.
p(±a(t),t) = O. G.85)
Уравнения G.81)-G.85) служат для определения неизвестных
функций p(x,t), uz{x,t), w*(x,t), a(t) и D(t).
Рассмотрим условие G.83) в точке х = a(t). Принимая во
внимание G.81) и G.85), получим
G.86)
Вычитая из соотношения G.83) соотношение G.86), будем иметь
uz(x,t) + w*{x,t) - w*(a(t),t) = f{a(t)) - f{x). G.87)
Продифференцировав полученное уравнение по t и воспользовав-
воспользовавшись соотношениями G.81) и G.82), получим
ot да at da at
Уравнение G.88) выполняется в каждой точке площадки контак-
контакта (—a(t), a(t)). Проинтегрировав его по длине площадки контак-
контакта и принимая во внимание G.85) и соотношение
а
d
dt
—а
получим
An Г Яо„ (п +\~\
G.89)
Используя уравнение G.89), получим условия, при которых пло-
площадка контакта в процессе изнашивания увеличивается, умень-
уменьшается или остаётся постоянной.
Прежде всего рассмотрим случай, когда площадка контакта
увеличивается в размерах, т. е. dajdt > 0, и определим, какие
это накладывает ограничения на характер изменения во времени
398
нагрузки Р(?), приложенной к штампу. Поскольку при растущей
площадке контакта износ на концах площадки контакта равен
нулю, справедливо соотношение w*(a(t),t) = 0. Дифференцируя
его по t, получим
dw*(a(t),t) dw*(a,t) da
dt d~a dt ~
Из соотношений G.82) и G.85) следует что dw*(a(t),t)/dt = 0.
Поэтому
дги* da
да dt
Из уравнения G.89) с учётом последнего соотношения получим
следующее выражение для скорости роста размера площадки
контакта:
da _ kP'jt) + KwP(t)
dt " 2a f (a) ' { ]
Считая /'(а) > О, получим необходимое условие роста площадки
контакта
P{t) к
В качестве примера рассмотрим случай постоянной нагруз-
нагрузки P(t) = Ро, действующей на штамп, форма поверхности кото-
которого описывается функцией f(x) = x2/BR). Условие G.91) при
этом, очевидно, выполнено. Для определения размера площадки
контакта в произвольный момент времени воспользуемся урав-
уравнением, следующим из G.90):
da _ KWPOR
dt ~ 2a2
Интегрируя его, будем иметь
a — uq = —PoRKwt, Яд = —PoRk,
L Z
или
з/, , Kw
а = а0 \11 + — t.
399
Определим теперь характер изменения внешней нагруз-
нагрузки P(t), приложенной к штампу, обеспечивающий постоянный
размер площадки контакта, т. е. a(t) — а§. Из соотношения G.89)
при da/dt = 0 следует
kP'{t) + KwP(t) = О,
что соответствует изменению нагрузки по экспоненциальному
закону
V
Дифференцируя G.86) по t, получим
dw*(a(t),t) fdw*(a{t),t)
dt ' V да ' J v V dt
откуда при da/dt = 0 с учётом G.82) и G.85) следует, что D'(t) =
= 0, т. е. в этом случае штамп не углубляется в основание в
процессе его изнашивания. Давление p(x,t) стремится к нулю
при t —> +оо как решение уравнения, полученного из G.88):
Как следует из соотношения G.83), форма изношенной поверх-
поверхности при t —> +оо будет повторять форму штампа, т. е. описы-
описываться функцией f(x).
Подобным же образом устанавливается необходимое условие
уменьшения размеров площадки контакта при изнашивании. По-
Полуширина площадки контакта уменьшается, т. е. da/dt < 0, если
нагрузка P(t) удовлетворяет условию
P'{t) Kw
P{t) k '
Следует отметить, что полученные выше соотношения, опреде-
определяющие размеры площадки контакта при изнашивании, спра-
справедливы только для рассматриваемой геометрии сопряжения в
случае простейшей модели упругого основания.
400
7.7.2. МЕТОДЫ РЕШЕНИЯ ИЗНОСОКОНТАКТНЫХ
ЗАДАЧ С ВОЗРАСТАЮЩЕЙ ВО ВРЕМЕНИ
ОБЛАСТЬЮ КОНТАКТА
Как уже отмечалось, задача с изменяющейся при изнашивании
областью контакта относится к классу нелинейных задач.
При решении нелинейных износоконтактных задач широко
используются численные подходы. Одним из наиболее широко
используемых является пошаговый метод, в основе которого ле-
лежит дискретизация времени и использование конечно-разност-
конечно-разностного представления дифференциального или интегрального опе-
оператора.
Один из подходов к решению износоконтактных задач с моно-
монотонно возрастающей областью контакта состоит в отображении
последней на область фиксированного размера [78, 130, 131, 139].
А именно, если х - координата, [—a(t),a(t)} - область контак-
контакта, v = da/dt - скорость возрастания области контакта, то опре-
определяя безразмерную координату X = х/а и соответствующие
распределения износа W(X,t) = W(x/a,t) — w*(x,t) и контакт-
контактного давления P(X,t) = P(x/a,t) = p(x,t), уравнение изно-
износа G.14) можно представить в виде:
Левая часть G.92) в отличие от исходного уравнения G.14) со-
содержит дополнительную производную по X. Однако, несмотря
на это, переход к фиксированной области контакта упрощает
процедуру численного решения износоконтактной задачи, так
как при этом возможно использование неизменной координатной
сетки узлов и отпадает необходимость в разработке алгоритма
учёта новых точек, входящих в контакт.
Ещё один прием, позволяющий упростить решение задач с
износом при растущей области контакта заключается в исполь-
использовании в качестве временного параметра размер а области кон-
контакта [7, 69, 130, 131, 138]. При подобной замене закон изнаши-
изнашивания G.14) принимает вид
401
Переход от переменной t к а позволяет избавиться в уравнениях
изнашивания от неизвестных пределов интегрирования a(t), что
упрощает их решение. Соотношение G.92) в этом случае прини-
принимает вид
Интегрирование полученного соотношения достаточно просто
осуществляется по известным характеристикам дифференци-
дифференциального оператора, стоящего в левой части [130].
Для анализа кинетики прицесса изнашивания при нелиней-
нелинейном уравнении износа и растущей области контакта использу-
используются также асимптотические методы [5, 79]. В частности, кон-
контактное давление представляется в виде
t). G.94)
k=i
Для нахождения неизвестных функций Рк(х, t) в разложе-
разложении G.94) используется рекуррентная процедура. В [79] с помо-
помощью разложения типа G.94) получено приближённое решение
износоконтактной задачи для подшипника скольжения при от-
относительно малых временах (t —>• 0).
В [134] решение задачи об изнашивании тонкой полосы свя-
связанной с упругой полуплоскостью при растущей области кон-
контакта строилось с помощью метода последовательных прибли-
приближений. Данный метод использовался как для решения линейного
уравнения с целью определения контактного давления, так и для
решения нелинейного уравнения относительно скорости роста
области контакта.
Другие постановки и методы решения нелинейных износокон-
тактных задач с изменяющейся во времени площадкой контакта
изложены в [102].
Глава 8
ИЗНАШИВАНИЕ НЕОДНОРОДНЫХ
ТЕЛ
В трибологии давно известно явление неравномерного изнашива-
изнашивания материалов с неоднородной структурой. Такими свойствами
обладают композиционные и неоднородные материалы, а так-
также материалы, поверхности которых подвергнуты локальному
упрочнению (лазерная обработка, ионная имплантация и т.д).
При изнашивании таких материалов наиболее интенсивному
разрушению подвергается менее прочная (чаще всего более мяг-
мягкая) структура, в результате чего первоначально ровная рабочая
поверхность становится волнистой.
Для исследования изнашивания неоднородных поверхностей
применимы те же математические постановки и методы решения
контактных задач, что и для однородных поверхностей (см. гла-
главу 7). В этой главе изучается кинетика формоизменения поверх-
поверхностей, характеризующихся коэффициентом износа, величина
которого зависит от координаты точки поверхности (например,
локально упрочнённой поверхности), а также решаются некото-
некоторые задачи изнашивания при дискретном характере контакти-
контактирования. На основе разработанных моделей исследуется обрат-
обратная задача - создания неоднородных поверхностей, удовлетво-
удовлетворяющих определенным требованиям относительно характера их
формоизменения при изнашивании.
8.1. ИЗНАШИВАНИЕ ТЕЛ С ПЕРЕМЕННЫМ
КОЭФФИЦИЕНТОМ ИЗНОСА
В этом разделе рассматриваются математические модели для
анализа перераспределения давлений и формоизменения поверх-
поверхностей, характеризуемых переменным по поверхности коэффи-
403
циентом износостойкости (неоднородных и локально упрочнён-
упрочнённых поверхностей). Исследуется зависимость контактных харак-
характеристик от геометрических и триботехнических параметров,
характеризующих неоднородность поверхности, и также обсуж-
обсуждается вопрос о возможности выбора этих параметров с целью
обеспечения заданных свойств изношенной поверхности.
8.1.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим задачу изнашивания упругого полупространства
бесконечным штампом с плоским основанием. Уравнение износа
имеет вид G.6), в котором коэффициент износа является функ-
функцией координат точки поверхности, т.е. Kw = Kw(x,y). Систе-
Система уравнений для анализа изменения контактных давлений во
времени и формоизменения поверхности полупространства име-
имеет вид G.18)-G.20).
При выполнении условий существования установившегося
режима изнашивания, сформулированных в 7.3.1 для задач ти-
типа Л, т. е. при условии, что скорость dD/dt сближения взаи-
взаимодействующих тел (или величина нормальной нагрузки P(t))
стремится к постоянному значению при t —> +оо:
dD dw(x,y,t)
hm —- = hm —y— = Doo,
t—H-oo at t-^+oo at
или
lim
установившееся распределение контактных давлений имеет вид:
D (V*)P 11/q
r4J • (8л)
где V(x, у) - установившееся распределение по поверхности от-
относительной скорости скольжения поверхностей, V* и р* - неко-
некоторые характерные значения скорости и давления.
При заданном асимптотическом значении Р^, нормальной на-
нагрузки величина D^ определяется из уравнения G.12):
—а
Г г г dxdy
¦II:
(8.2)
404
Установившаяся форма foo{x,y) изношенной поверхнос-
поверхности полупространства, соответствующая контактному давле-
давлению Роо{х, у) (см. (8.1)), имеет вид:
,у) =А\роо(х,у)} =
(р*)а(У*)РРоо
Kw(x,y)VP(x,y)
(8.3)
Таким образом, установившаяся форма зависит от коэффициен-
коэффициента износа Kw(x,y) и характера движения штампа, т.е. функ-
функции V(x, у).
В качестве оператора А рассмотрим следующие выражения,
соответствующие
плоской периодической контактной задаче [146]:
l
A\p(x,t)] = -
2A -v2
пЕ
Jp(x',t)
о
In 2
sin •
I
dx', (8.4)
где / - период; ~
• пространственной задаче:
А\р(х, у, t)] = I ' ffp{x', у', t)ip{x\ у', х, у) dx'dy1, (8.5)
п
где
(8.6)
Эти операторы являются вещественными, непрерывными, само-
самосопряжёнными и положительно-определёнными, что обеспечива-
обеспечивает асимптотическую устойчивость стационарного решения (8.1)
как в случае линейного (а = 1), так и нелинейного (а > 1) вида
уравнения износа G.6).
Таким образом, если выполнены условия существования
установившегося режима изнашивания, выражение для давле-
давления р(х, у) в произвольный момент времени может быть пред-
представлено в виде:
p(x,y,t)=poo(x,y)+pi(x,y,t),
405
где poo (#1 у) определено выражением (8.1) и
lim pi(x,y,t) = 0.
t—Ц-00
Процесс изнашивания в этом случае делится на две стадии: при-
приработка и установившийся режим, описываемым стационарным
решением (8.1), (8.2) и (8.3).
Отметим, что для неоднородных и неоднородно упрочнён-
упрочнённых поверхностей, как правило, функция Kw(x,y) принадлежит
к классу кусочно-постоянных функций и имеет вид:
(Kwl, (х,у)еп\и,
Kw(x,y) = { (8.7)
1^2, (х,у)еи>.
где си - совокупность упрочнённых зон, т. е. поверхность полу-
полупространства, характеризуемая коэффициентом износа KW2,
afl\u- неупрочнённая поверхность полупространства, харак-
характеризуемая коэффициентом износа Kw\ {Kw\ > Kwq).
Определим форму изношенной поверхности полупространст-
полупространства, распределение давления, скорость сближения тел за счёт их
износа и другие контактные характеристики в установившемся
режиме изнашивания в случае функции Kw(x,y), заданной соот-
соотношением (8.7), при различных конфигурациях и расположении
упрочнённых зон.
8.1.2. ИЗНАШИВАНИЕ ПОВЕРХНОСТИ,
УПРОЧНЁННОЙ ВНУТРИ ПОЛОС
Рассмотрим плоскую периодическую задачу для упругого полу-
полупространства II и штампа I с плоским основанием (рис. 8.1).
Штамп прижат к полупространству силой Р/1 (I - период) и со-
совершает возвратно-поступательные перемещения вдоль оси Оу
в плоскости z = 0, связанной с подошвой штампа. Упругое тело
внутри полос (nl + a 4;Х < (п + 1I, — оо < у < +оо) подвергнуто
локальному упрочнению, которое в первую очередь обусловлено
структурными эффектами. По этой причине можно считать, что
поверхность обладает переменным по координате х коэффициен-
коэффициентом износостойкости, в то время как упругие характеристики Е
406
Pll
ШШ11ГШШШ
Рис. 8.1. Схема контакта штампа с полупространством, упрочнённым
внутри полос
и v материала, являющиеся, как правило, структурно нечувст-
нечувствительными, можно положить постоянными.
Для определённости предположим, что в процессе трения из-
изнашивается только поверхность упругого полупространства. В
рассматриваемом случае уравнение износа G.19) примет вид:
8t
p(x,t)
где Kw(x) определяется выражением
ГKwi, х е [nl,a
[KW2, х ? [nl,a
(8.8)
(8.9)
a Kw\ и KW2 - коэффициенты износа поверхности вне и внутри
упрочнённых зон [nl + а,(п + 1I] соответственно {Kw\ > KW2).
Заметим, что показатель а в уравнении износа (8.8) мож-
можно считать не зависящим от координаты, поскольку в соответ-
соответствии с теорией усталостного изнашивания (см. [91]) а = 1 + *ст],
где х - параметр, зависящий от шероховатости поверхностей
407
трения (хг < 1); 77 - показатель кривой фрикционной усталости
материала, который для материалов одного класса (например,
сталей) имеет устойчивое значение.
Рассматриваемая задача является периодической с перио-
периодом / и относится к типу Л- Поскольку имеет место полный
контакт двух тел по плоскости z = 0, начальное давление рас-
распределено равномерно, т.е. р(х,0) = Р@)/1 (х 6 (—оо,+оо)).
При изнашивании имеет место формоизменение первоначаль-
первоначально плоской поверхности полупространства и перераспределение
контактного давления p{x,t). Так как движение происходит в
направлении, перпендикулярном плоскости Oxz, можно пренеб-
пренебречь влиянием сил трения на распределение контактных давле-
давлений и использовать оператор А в форме (8.4) для определения уп-
упругих перемещений границы полупространства. Упругие uz(x, t)
и износные w*(x,t) перемещения границы, а также контактное
давление р(х, t) являются периодическими функциями координа-
координаты х. Они могут быть определены из решения системы уравне-
уравнений G.18)—G.20), в которых оператор А имеет вид (8.4), уравне-
уравнение износа описывается соотношением (8.8), а условие контак-
контакта G.20) примет вид:
Из соотношений (8.1)—(8.3) получим следующие выражения для
давления Роо(х), скорости износа D^ и формы foo(x) изношенной
поверхности в установившемся режиме изнашивания:
D
9*Gw
, xe[nl,a
(8.10)
+ (I ~ a)K-wlla] J '
(8.11)
408
f (X)-
/oo( >
Dr
*-wl
I/a
\Kw2J
a
7-
0
H
. n(x' — x)
sin
(8.12)
7Г(Ж' - X)
sin
(fa'f,
где Pqo - постоянная нагрузка, действующая на период в уста-
установившемся режиме изнашивания.
Введём безразмерные параметры
a =
Kw2
Lwl
, (т
(8.13)
и выразим интегралы, входящие в выражение (8.12) с помощью
функции Лобачевского
у
Цу) = -
Incostdt,
Тогда соотношение (8.12) преобразуется к виду:
(8.14)
Для дальнейших вычислений удобно представить функцию L(y)
в виде ряда (см. [58]):
ОД = „Ш2-1
(8.15)
П=1
Воспользовавшись соотношениями (8.11), (8.14) и (8.15), запи-
запишем окончательно уравнение профиля изношенной поверхности
409
n2E
0,4 -
0,0
-0,4 -
Рис. 8.2. Установившаяся форма изношенной поверхности при т,\ =
= 0,5, а = 0,2 (сплошная линия) и mi = 0,3, а = 0,6 (штриховая линия)
в виде:
2х
где т\ = 1 - ml/a. Как следует из (8.16), функция foo(x) = 0
при а = 0 и а = 1. Это значит, что при отсутствии локаль-
локального упрочнения поверхность упругого тела остаётся при изна-
изнашивании плоской. При остальных значениях 5 функция foo(x) -
периодическая с периодом /.
Значения функции foo(x) в точках х = 0, х = а и х — I
совпадают и определяются по формуле
sin 2nna
(8-17)
На рис. 8.2 приведены графики функции foo(x) (8.16) при раз-
различных значениях параметров тпх и а. Эти графики показыва-
показывают, что поверхность полупространства в процессе изнашивания
становится волнистой, причём геометрические параметры изно-
изношенной поверхности определяются геометрическими и триботех-
ническими параметрами упрочнения.
410
Используя значение производной /^(ж), т.е.
4A — i/2)Poomi ^> вттгпа . / 2х
g ^ ™ V ~ Т
вычислим экстремальные значения функции foo(x), имеющие
место в точках х = a/2+kl и х = (а+1)/2+Ы, (к = 0, ±1, ±2,...),
где f^(x) = 0:
/ax
Joo\2J
2A — ^2
n2E(l-ami) 4i «2 '
1 (8-18)
2A - v2)P<x™>i v-^/ ,n
- ami) ^
Таким образом, перепад значений функций в точках экстемума
определяется величиной
Ф =
/ос (|) - /
/00
a
2
4A - u2)Poo пц ^ sinBn - 1)тга
^ Bп-1J '
Графики функции Ф(а)тг2Е/ DA — г/2)Роо) (сплошные линии)
при различных значениях параметра mi представлены на
рис. 8.3.
Объём впадин на поверхности является характеристикой её
маслоёмкости. Найдём величину площади S, заключённой меж-
между кривой z = foo{x) и прямой z = /оо (а + 1/2), на периоде /:
S = //ос (^) - У foo(x) dx. (8.20)
о
Поскольку интеграл в (8.20) равен нулю (см. (8.16)), то из (8.18)
и (8.20) следует, что объём S впадин на изношенной поверхности
на одном периоде может быть вычислен по формуле
с_ 2A - v2)Poomll ^ 1smmra
b ^A} (821)
411
0,0
0,2
0,4
0,6
all
1,0
Рис. 8.3. Зависимости амплитуды Ф волны (сплошные линии) и пло-
площади 5 впадин (штриховые линии) от параметра а/1 при т\ = 0,1 A'),
пц = 0,2 A), пц = 0,3 B'), пц = 0,5 C, 3'), пц = 0,7 D, 4'), пц = 0,9 E)
Зависимости безразмерной площади Sn2E/ BA — is2)Pool) от
параметра а при различных значениях mi приведены на рис. 8.3
(штриховые линии). Анализ результатов расчётов показывает,
что при изменении параметра а от 0 до 1, т.е. при умень-
уменьшении ширины полосы, подвергнутой локальному упрочнению,
от / (полная обработка поверхности) до 0 (необработанная по-
поверхность), объём впадин на изношенной поверхности сначала
увеличивается, а затем снижается до нуля. При а, равном не-
некоторому значению а*, имеет место максимальный объём впа-
впадин. Величина а* зависит от соотношения коэффициентов изно-
износа т упрочнённой и неупрочнённой зоны и находится в преде-
пределах 0,6 < а* < 1 при изменении т от 0 до 1. Значение а* возрас-
возрастает с уменьшением т. Таким образом, для достижения опре-
определённого объёма впадин на изношенной поверхности можно ли-
либо соответствующим образом подобрать соотношение коэффици-
коэффициентов износа т, либо при заданном т выбрать нужную шири-
ширину полосы, которую требуется подвергнуть локальному упроч-
упрочнению.
412
Зная объём впадин S на изношенной поверхности, можно оце-
оценить также минимальное количество материала, которое будет
изношено за время Т приработки, поскольку справедливо нера-
неравенство:
I
w*(x,T)dx.
о
Скорость изнашивания в установившемся режиме харак-
характеризуется эффективным коэффициентом изнашивания Dqo
(см. (8.11)), который для рассматриваемого случая имеет вид:
I р 1
Дэо = rnKwi
р*1 [1 - а A - mV«)] J
Зависимости безразмерного эффективного коэффициента износа
от параметров m и а представлены на рис. 8.4. Из проведён-
проведённых расчётов, в частности, следует, что повышение в полтора
раза эффективного коэффициента износа материала, характери-
характеризуемого в неупрочнённом состоянии величиной Kwi, может быть
получено путем выбора соответствующих значений параметров
упрочнения а и т, определяемых точками пересечения графиков
с пунктирной линией Kw = 2/3.
Основываясь на проведённом анализе, можно заключить, что
при изнашивании неоднородно упрочнённой поверхности возни-
возникает эксплуатационная волнистость, параметры которой зави-
зависят от соотношения коэффициентов износа упрочнённой и не-
упрочнённой зон и их характерных размеров. Объём впадин на
изношенной поверхности тем больше, чем больше отличаются
коэффициенты износа различных участков поверхности, а их
максимальные значения зависят от соотношения характерных
размеров упрочнённых и неупрочнённых зон. Образование та-
такой эксплуатационной волнистости при некоторых условиях тре-
трения способствует повышению триботехнических свойств сопря-
сопряжений. При несовершенном смазочном материале на поверхнос-
поверхности трения искусственно создают своеобразные карманы, увели-
413
чивая тем самым её маслоёмкость, что в свою очередь снижа-
снижает износ и опасность задира [30]. Наличие карманов позволяет
значительно ограничить присутствие продуктов изнашивания в
зоне трения, что повышает износостойкость сопряжения и обес-
обеспечивает стабильность его триботехнических характеристик.
Изложенный выше
подход и полученные
результаты примени-
применимы также к анализу
процесса изнашивания
бесконечным упругим
телом неоднородного
жёсткого основания, ко-
которое содержит участки
из различных мате-
материалов, обладающих
разными коэффициен-
коэффициентами износа. Использо-
Использование описанной выше
модели в работе [155]
для анализа процесса
химико - механического
полирования неодно-
неоднородной поверхности с
характерными размера-
0,0 0,2 0,4 0,6 т, а 1,0
Рис. 8.4. Зависимость эффективного ко-
коэффициента износа от параметра т при
а — 0,9 (штриховая линия) и от парамет-
параметра а (сплошные линии) при т = 0,2 A),
т = 0,4 B), т = 0,6 C); а = 1,5
ми включений порядка 1 мкм позволило изучить зависимость
стационарной формы обрабатываемой поверхности (её рельефа)
от величины нагрузки, упругих характеристик полироваль-
полировального круга, соотношения размеров участков из различных
материалов и их коэффициентов износостойкости.
8.1.3. ИЗНАШИВАНИЕ ПОВЕРХНОСТИ,
УПРОЧНЁННОЙ ПО КРУГОВЫМ ОБЛАСТЯМ
Рассмотрим теперь изнашивание упругого полупространства
бесконечным штампом с плоским основанием (/о(ж, у) = 0), дви-
движущимся поступательно в разных направлениях по поверхнос-
поверхности z = 0 полупространства. Поверхность полупространства, сов-
414
Рис. 8.5. Схема расположения упрочнённых областей на поверхнос-
поверхности полупространства (а) и форма изношенной поверхности на одном
периоде (б)
падающая с областью контакта Q, упрочнена внутри круговых
областей u>ij радиуса а, расположенных в узлах квадратной сет-
сетки с шагом I (рис. 8.5,а). Обозначим совокупность упрочнённых
оо
областей как ш — |J шц.
Предположим, что коэффициент износа Kw(x, у) можно пред-
представить в виде кусочно-постоянной функции (8.7). Введём без-
безразмерные параметры т = KW2/Kwi и а = а/1, характеризую-
характеризующие соответственно степень упрочнения и относительный ради-
радиус упрочнённой зоны и изменяющиеся в пределах: 0 < а ^ 0,5
и то ^ т < 1, где то - предельное минимальное значение т,
определяемое технологией упрочнения.
Определим зависимость скорости сближения тел в устано-
установившемся режиме изнашивания (эффективного коэффициента
износа) и геометрических характеристик изношенной поверхнос-
поверхности от параметров упрочнения т и а. Из соотношений (8.1), (8.2)
и (8.7) получим следующие выражения для установившегося
распределения давления Роо{х,у) и эффективного коэффициента
износа Kw:
Роо(х,у) )Р\,
(8.22)
к,„ =
К,,
*;2
р*1
у*
(8.23)
415
где
Р2=
\ш) Ы' (8.24)
т2 = т/01 - 1,
a Pqo - асимптотическое значение нагрузки на период.
Форма поверхности в установившемся режиме изнашивания
может быть получена из уравнений (8.3), (8.5) и (8.22):
foo(x,y) = ^j^- = \JjAp<p(x',y',x,y)dx'dy' + Cu (8.25)
где
Ар = ^-р*(Р2 - Pi) =
п
а функция if(x',y',x,y) определена в (8.6).
Запишем приближённо функцию fi(x,y) = }оо{х,у) — С\ в
следующем виде:
(x, у) = Е х // ^(а;/'у/> х>y)dx>dyl
(8.27)
% [(x - xyJ + B/ - ^
где ujki - упрочнённые области вблизи точки (х,у). Выраже-
Выражение (8.27) учитывает реальное распределение давления Ар в
областях шы] влияние же удалённых областей ш^ ф шы учте-
учтено путём замены распределенного давления сосредоточенными
силами Р — Артга2, приложенными в центрах (sijiJ/ij) облас-
областей uijj. Это даёт возможность заменить интегрирование сум-
суммированием (второе слагаемое в (8.27)). Такая замена основана
416
на анализе, проведённом в главе 1. Расчёты показывают, что
ошибка, возникающая в результате такой замены, имеет поря-
порядок О (а2/(ж2 + у2)). Например, при а = 0,5 ошибка составляет
менее 1% на расстоянии г = 1л/2 (г2 = х2 + у2).
Соотношение (8.27) для точек прямой х = у может быть пре-
преобразовано к виду:
(8-28)
+2Артга -
Здесь функция
14. Горячева И.Г. 417
функция
причём
s 2 12 Г V 2/
функции K(i) и E(?) - полные эллиптические интегралы пер-
первого и второго рода соответственно, а функция F(t) = Е(?) —
— (l — t2) K(t). Ряд (8.29) сходится, поскольку его общий член
имеет порядок 0A/ (А;2 + п2) ).
Выражение для формы поверхности в произвольной точ-
точке (х, у) здесь не приводится в силу его громоздкости. Гра-
График функции /i(x,y) внутри одного периода представлен на
рис. 8.5,6.
Амплитуда L = Ф\ A/2) и площадь диагонального сечения
1/2
S= I'ф1@# (8-30)
о
являются важными геометрическими характеристиками изно-
изношенной поверхности. Из выражений (8.26), (8.28) и (8.29) после
разложения эллиптических интегралов в ряды по малому пара-
параметру получим
L = Лат92 A - 1,1332а - 0,2285а3 + О(а5)) ,
1 + 7Га^ГП2
где
, _ 2A - ^2)Роо
ЕР
Простейший анализ зависимости амплитуды L от парамет-
параметров гп2 и а показывает, что
• при фиксированном значении а величина L достигает мак-
максимума при т = то;
418
LIX
0,3
0,2
0,1
0,0
0,0
0,1
0,2
0,3
0,4 all 0,5
Рис. 8.6. Зависимости амплитуды L (сплошные линии) и площади 5
диагонального сечения (штриховые линии) впадины изношенной по-
поверхности от параметров упрочнения: m2 = 0,1 A, 1'), тг = 0,5 B, 2'),
т2 = 1 C, 3'), т2 = 2 D, 4')
• для произвольного т существует значение а* 6 @; 0,5), при
котором амплитуда L максимальна.
Графики функции L(a) для различных значений параметра
m,2 представлены сплошными линиями на рис. 8.6. Штриховы-
Штриховыми линиями на рисунке показаны зависимости площади S диа-
диагонального сечения впадины изношенной поверхности от пара-
параметра а при различных значениях т?, полученные численно из
соотношений (8.28) и (8.30).
Анализ функции (8.23) показывает, что эффективный коэф-
коэффициент износа Kw в установившемся режиме равен 1 при а — 0
(неупрочнённая поверхность) и уменьшается с уменьшением ра-
радиуса а упрочнённой области или с ростом параметра т^ (умень-
(уменьшением параметра т).
Таким образом, варьирование параметрами т и а в преде-
пределах, допускаемых технологией упрочнения, позволяет управлять
14*
419
20
18
16
14
j
\ ,
0,4
I
/i
i
\
\
1
17
s ~ - -
0,6
1 \
1 (\
1 I1
1 1
1 ' ¦
\ ' 1 '
\J -
i
i
i OA
1
i ".
/ 1^
0,8
1,0
Рис. 8.7. Схема расположения упрочнённых зон (а) и профиль изно-
изношенной поверхности в радиальном поперечном сечении (б) при равно-
равномерном расположении упрочнённых зон (сплошная линия) и в случае
& = 0,35, & = 0,47, & = 0,78, ?4 = 0,925, & = 0,975 (штриховая
линия), р\г\ =0,2
трибологическими и геометрическими характеристиками волни-
волнистой поверхности, образуемой в результате изнашивания.
8.1.4. ИЗНАШИВАНИЕ ЛОКАЛЬНО УПРОЧНЁННОГО
КОЛЬЦЕВОГО ШТАМПА
Изнашивание локально упрочнённых поверхностей при ограни-
ограниченной области контактного взаимодействия обладает рядом до-
дополнительных особенностей. В качестве примера изучим фор-
форму изношенной поверхности цилиндрического штампа кольце-
кольцевой формы в плане, контактирующего с упругим полупростран-
полупространством, при различном характере движения штампа и располо-
расположении упрочнённых зон.
Рассмотрим сначала штамп с плоским основанием, упрочнён-
N
ный внутри области ш = (J щ (рис. 8.7,а). Подобласть щ есть
кольцо с внутренним радиусом Г{ и толщиной р, г\ и гдг + р -
внутренний и наружный радиусы цилиндрического штампа
кольцевой, формы в плане, N - количество упрочнённых зон.
Штамп нагружен вертикальной силой Р^ и движется поступа-
поступательно в различных направлениях по поверхности упругого по-
420
лупространства, при этом |F| = const. В процессе трения штамп
изнашивается, коэффициент износа Ки(х,у) задаётся кусочно-
постоянной функцией (8.7).
При установившемся режиме изнашивания давление рас-
распределяется в соответствии с соотношениями (8.22) и (8.24).
Из (8.24) получим
Pi/p2 = rn1/a, p2=pi + Ар,
где
Ар = р\ (т~1'а — 1J = р1Ш2-
Давление р\ находится из условия равновесия
N
(
P
\ i=l / р*
Выражение для формы изношенной поверхности может быть по-
получено из соотношений (8.3), (8.5) и (8.22):
TN+р , ч
*м = *?-*)?* [кЫгАг-^ +
J
4A - v2)p* _ Л V, (iy/r~r1\ r'dr'
Н — PlTTl2 > /К .
пЕ r^ J \r + r')r + r'
Это выражение упрощено и представлено с помощью эллипти-
эллиптических интегралов в [50].
На рис. 8.7,6^ показаны формы изношенной поверхности в ра-
радиальном сечении при различном расположении упрочнённых
зон. Сравнение функций
при равномерном и неравномерном расположении упрочнённых
зон (N = 5, ?i = 0,35), представляющих собой кольца одинаковой
толщины, даёт основание заключить, что расположение колец
оказывает существенное влияние на формируемый в процессе
421
Рис. 8.8. Схема расположения упрочнённых зон (а) и профиль изно-
изношенной поверхности в сечении г*/гг = 0,75 (б) при т3 = 2, в\ = 8° A),
т3 = 2,вг = 12° B), т3 = 3, вх = 8° C)
изнашивания рельеф поверхности. Вследствие ограниченности
области контакта равномерно расположенные упрочнённые зо-
зоны изнашиваются неравномерно (имеет место краевой эффект).
Варьируя параметры Г{, можно получить профиль поверхности,
удовлетворяющий, например, условию /(?j + р/2) = const. Этот
профиль показан штриховой линией на рис. 8.7,б.
Рассмотрим теперь другой вид упрочнения поверхности ци-
цилиндрического штампа кольцевой формы в плане. Пусть плоская
поверхность штампа упрочнена внутри N секторов
Г. . 2пк в\ 2тгк
Шк = \{г,в) : п < г < г2, -г=- - - < в < —-
У}'
как показано на рис. 8.8,а (заштрихованные области). Штамп
вращается вокруг своей оси, прижатый к упругому полупро-
полупространству силой Poq. Из выражений (8.1) и (8.7) получим уста-
установившееся распределение давления
р*
где
Pi (г) =
1/а
(г,в)еп\ш,
р2{г) =
(8.32)
1/а
422
область Q = {(р, в) : pi ^ p $s P2, 0 < # ^ 2тг}, множество ш =
= IJ Uk, а постоянная С определяется из уравнения равновесия:
роо = JJ Рос (г, 6)rdrde. (8.33)
п
Форма /оо(^) б) изношенной поверхности находится из соотноше-
соотношений (8.3), (8.5) и (8.32), на основании которых можно получить
выражения для расчёта установившегося профиля поверхности в
различных сечениях. На рис. 8.8,б представлены графики функ-
функции
С
рассчитанные при ri/гг = 0,5, г*/гг = 0,75, а = /?, N = 8 и
разных значениях параметров тпз = m1//Q и^ в [50]. Резуль-
Результаты показывают, что параметры упрочнения т w. в\ влияют
на геометрические характеристики профиля (высоту впадины,
угол наклона ф), что даёт возможность использовать локальное
упрочнение с последующим изнашиванием как один из способов
создания поверхности с заданным рельефом.
Таким образом, геометрические характеристики изношенной
поверхности существенно зависят от геометрии контактирую-
контактирующей пары, характера относительного движения, а также гео-
геометрических и триботехнических параметров упрочнения или
неоднородности поверхности.
8.2. ИЗНАШИВАНИЕ В ДИСКРЕТНОМ
КОНТАКТЕ
Дискретный характер контактного взаимодействия играет важ-
важную роль при изнашивании. В процессе изнашивания изменяется
макро- и микрогеометрия контакта, что, в свою очередь, влияет
на характер протекания самого процесса изнашивания.
Ниже предлагается математическая модель изнашивания
дискретного контакта, которая базируется на результатах, полу-
полученных в главе 1, где был предложен метод определения контакт-
423
ных характеристик с учётом макро- и микрогеометрии взаимо-
взаимодействующих тел. Модель изнашивания в дискретном контакте
применима как для анализа изменения микрогеометрии поверх-
поверхности в процессе приработки, так и для исследования кинетики
изнашивания неоднородных тел с жёсткими включениями.
8.2.1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Как было показано в 1.3, при взаимодействии жёсткого тела с
шероховатой поверхностью и упругого основания микронеров-
микронеровности можно моделировать системой штампов, контактирующих
с упругим полупространством. Для простоты положим, что каж-
каждый штамп имеет форму цилиндра и контактирует с упругим
полупространством своей плоской торцевой поверхностью, пред-
представляющей собой круг радиуса а.
Рассмотрим систему N цилиндрических штампов, находя-
находящихся под действием нагрузки P(t) (см. рис. 1.10). Штампы про-
произвольным образом расположены внутри номинальной области
взаимодействия П.
Будем считать, что в процессе трения поверхность полупро-
полупространства изнашивается, оставаясь плоской, а износ штампов
приводит к постепенному уменьшению их высоты. Скорость из-
изнашивания dwj/dt на каждом пятне контакта связана с действу-
действующей на него нагрузкой Р/и скоростью скольжения Vj степенной
зависимостью
где Wj - линейный износ j-ro штампа в центре площадки кон-
контакта (wj@) — 0), Р* и V* - некоторые характерные значения
нагрузки и скорости соответственно, Kw - коэффициент изно-
износа, численно равный скорости линейного износа при Pj = Р*,
Vj = V*.
Из условия контакта j-ro штампа системы с упругим полу-
полупространством следует, что
(8.35)
424
где uzj (t) - внедрение j-го штампа в произвольный момент вре-
времени t, hj - начальное распределение штампов по высоте, D(t) -
сближение тел под нагрузкой (см. рис. 1.10). Заметим, что в
начальный момент времени uZj(O) = Dj и D@) = Dq ф 0 в обо-
обозначениях, введённых на рис. 1.10 и в 1.3.
На основании соотношения A.35) выражение для определе-
определения .внедрения ,;-го штампа в упругое полупространство в про-
произвольный момент времени t:
1 _ 2 _ 2 N
Uzj{t) = ~^Pj{t) + ~^F ^ Pi(t) arcsin Г • (8l36)
где Е и v - модуль Юнга и коэффициент Пуассона упругого по-
полупространства, kj - расстояние от фиксированного j-ro штам-
штампа системы до i-го штампа. Следует заметить, что соотноше-
соотношение (8.36) в точности справедливо в начальный момент време-
времени t = 0, когда контактирующие поверхности каждого штампа
плоские. При изнашивании вследствие неравномерного распре-
распределения давления по площадке контакта имеет место формоиз-
формоизменение контактирующей поверхности каждого штампа в соот-
соответствии с его расположением внутри области Q. В дальнейшем
исследовании мы будем считать, что эти изменения пренебре-
пренебрежимо малы (главным образом они сводятся к скруглению угло-
угловых точек штампа, где в начальный момент времени давления
максимальны), что даёт возможность использовать соотноше-
соотношение (8.36) в произвольный момент времени.
Соотношения (8.34)-(8.36) вместе с условием равновесия
(8.37)
t=i
образуют замкнутую систему уравнений для изучения кинетики
изнашивания системы связанных между собой штампов, распо-
расположенных на произвольном расстоянии 1^ друг от друга.
8.2.2. АНАЛИЗ МОДЕЛИ
Преобразуем полученную систему уравнений. Для этого продиф-
продифференцируем соотношения (8.35) и (8.36) по t и примем во вни-
425
мание зависимость (8.34). В результате получим:
N
«(<> Е Mj® = -^1® " W*)' * = 1> 2, • • •, JV, (8.38)
Е*® = 2^ЁР®' (8-39)
где
a q(t) означает производную по t функции q(t).
При заданном начальном распределении штампов по вы-
высоте hi начальные значения qi{0) известны из соотноше-
соотношений (8.35)-(8.37) при t = 0.
Исследуем решение системы дифференциальных уравне-
уравнений (8.38) в соответствии с разными вариантами постановки
задачи.
Случай X>i (?) = — 6. Если система штампов при изна-
изнашивании перемещается по нормали к границе упругого полу-
полупространства с постоянной скоростью, т.е. D\ (?) = — St + 1, то
уравнения (8.38) принимают вид:
N
i=l
а соотношение (8.39) служит для определения характера изме-
изменения нагрузки P(t), действующей на систему штампов.
Представим решение системы уравнений (8.41) в виде
1/а
+ (Pi(i), i = l,2,...,N, (8.42)
426
где функции <pi (i) удовлетворяют следующей системе уравне-
уравнений:
N
фг (t) + Y^ bijVi (*) = ~CWi (*) + ° D>i (*)) ' (8-43)
i=l
В (8.43) введено обозначение
d = а6{а~^/аГ]/а (<ч>0). (8.44)
Поскольку последний член в (8.43) имеет порядок 0(||<р||2), где
система (8.43) имеет тривиальное решение щ (I) = 0, кото-
которое является асимптотически устойчивым, если таким свойст-
свойством обладает решение соответствующей линеаризованной систе-
системы, (см., например, [111]). Эта линеаризованная система в мат-
матричном форме может быть записана как
Вф - -С(р, (8.45)
где В - симметричная матрица с положительными элементами
(Ьц = 1 и bij (i ф j) определены в (8.40)), С - диагональная
матрица с элементами сц = Ci, определёнными в (8.44), и с^ = 0
при г ф j.
Покажем прежде всего, что матрица В положительно опре-
определена, т.е.
(Вх,х)>0 (8.46)
для всех х, удовлетворяющих условию ||ж|| Ф 0. Пусть х - век-
вектор, компонентами которого с точностью до множителя A —
—и2)/{2uDqE) являются силы Pj, действующие на штампы (j =
= 1,2,..., N). Тогда компоненты вектора Вх представляют со-
собой упругие перемещения uzj соответствующих штампов. Поэ-
Поэтому скалярное произведение (Вх, х) есть работа отличных от
нуля сил на соответствующих упругих перемещениях, которая
всегда положительна, что и доказывает неравенство (8.46).
427
В силу (8.46) матрица В невырожденная и для нее сущест-
существует обратная матрица В~1. Поэтому уравнение (8.45) эквива-
эквивалентно следующему:
ф = -В~хСч>. (8.47)
Рассмотрим функцию V = (Вх,х), которая является положи-
положительно определённой в силу (8.46) и непрерывно дифференциру-
дифференцируемой. Производная функции V в силу системы (8.47) имеет вид:
V = % = {-Сх, х) + {Вх, -В-гСх) = -2(х, Сх).
at
Здесь принято во внимание, что
{Вх, -В-гСх) = (х, -ВВ~1Сх) = ~{х, Сх),
так как В = Вт вследствие симметрии матрицы В. Таким об-
образом, можно указать непрерывную функцию W{x) = 2(x,Cx),
положительную для всех ненулевых векторов х и такую, что
производная функции Ляпунова V в силу системы (8.47) удов-
удовлетворяет условию V = —W. По лемме Ляпунова (см. [111])
решение tp = 0 системы (8.47) или равносильной ей системы
системы (8.45) асимптотически устойчиво.
На основании доказанного можно утверждать, что стацио-
стационарное решение системы (8.41):
«мо
является асимптотически устойчивым. Заметим, что частный
случай 6 = 0 соответствует решению задачи об изнашивании
системы штампов, расположенных на фиксированном расстоя-
расстоянии от полупространства.
Случай P(t) = Раз • Практически осуществима и дру-
другая постановка задачи, когда предполагается заданной нагруз-
нагрузка P(t), приложенная к системе штампов. Для определённости
положим P(t) = Poo. По-прежнему будем искать решение систе-
системы уравнений (8.38) и (8.39) в форме (8.42), где постоянная 6 на
428
основании соотношения (8.39) имеет вид:
N
(8.49)
з=1 1 '
а функции (fi (i) (i = 1,2,..., N) удовлетворяют системе урав-
уравнений
N
i = -a(Pi(i)-Di (i)+6+O(<p1(i)), (8.50)
ч-J N
Y^<Pi{i)=0, (8.51)
i=l
где коэффициенты Cj определены в (8.44). Разделим i-e уравнение
системы (8.50) на постоянную щ > 0 и сложим N полученных
уравнений. Тогда на оснований (8.51) получим
Е (\+Е *) ь $) = [-^ С")+s) Е т
\Ci c С
откуда следует •
S - Ь\ (i) = ]Р пгфг (i) + О(||<^||2), (8.52)
где
С учётом (8.52) система уравнений (8.50) примет вид
N N
()(")B) • (8-53)
Для доказательства асимптотической устойчивости нулевого ре-
решения системы (8.53) рассмотрим соответствующую ей линеа-
линеаризированную систему, имеющую в матричной форме следую-
следующий вид:
Вф - Аф + Ор = 0, (8.54)
429
и применим, как и прежде, метод Ляпунова. Рассмотрим про-
производную в силу системы (8.54) положительной (при ||ж|| ф 0)
непрерывно дифференцируемой функции Ляпунова V = (Вх,х).
Тогда получим
dV
V = -^ = (Ах,х) - {Сх,х) + (Вх,В~1Ах) +
at
+(Вх, -В~1Сх) = -2(х, Сх) + 2(Ах, х).
Поскольку (8.53) удовлетворяют соотношению (8.51), то скаляр-
скалярное произведение (Ах, х) = 0. Таким образом, V = —W, где W =
= 2(х, Сх) - непрерывная и положительная для всех ненулевых х
функция. По лемме Ляпунова решение </? = 0 системы (8.54), сле-
следовательно и системы (8.53), асимптотически устойчиво.
На основании (8.42) и (8.49) можно записать стационарное
решение системы (8.38) и (8.39) при P(t) = Р^ как
2aD0E j
которое является асимптотически устойчивым. Заметим, что в
случае P(t) ф const решение системы (8.38) и (8.39) стремится к
стационарному решению (8.55) при t —у +оо, если нагрузка P(t)
стремится к постоянной величине, т. е. P(t) —> Poo при t —> +оо.
Стационарное, или установившееся, решение qi^, как это
следует из (8.55), зависит от общей силы, действующей на сис-
систему штампов, скорости скольжения, характера расположения
и размеров штампов, упругих характеристик материала основа-
основания и не зависит от начальных значений qi@). Начальные значе-
значения влияют на время выхода системы на установившийся режим
изнашивания (время приработки).
8.2.3. РЕЖИМ ПРИРАБОТКИ
В качестве примера изучим кинетику изнашивания системы N
цилиндрических штампов радиуса а, расположенных внутри
круговой области Q в узлах гексагональной решётки с посто-
постоянным шагом I. Все штампы изначально расположены на од-
одном уровне, т. е. имеют одинаковую высоту. Эта модель описана
430
в 1.3, где изучалось внедрение такой системы штампов в упругое
полупространство. В данном случае предполагаем, что система
штампов совершает возвратно-поступательные перемещения по
границе упругого полупространства так, что средние скорости
скольжения для каждого штампа одинаковы, т. е. Vi = V2 = ¦ ¦ ¦ —
= Удг. На систему действует постоянная нагрузка Р^.
Степень перераспределения давления под штампами будем
оценивать отношением gmin/^max; где <7mjn соответствует мини-
минимальной нагрузке на штамп (для рассматриваемой модели ми-
минимальная нагрузка действует на центральный штамп), a qma.x -
максимальной нагрузке на штамп (в данном случае это нагруз-
нагрузка на штамп, лежащий вблизи контура области ?1). В устано-
установившемся режиме при возвратно-поступательных перемещениях
системы штампов, как следует из соотношений (8.40) и (8.42),
Отношение 9mm/<7max = 1-
Время Т выхода системы на установившийся режим, т. е. вре-
время приработки, оценивалось из условия
mini.-' J
где е - некоторая малая величина, задаваемая заранее (е < 1).
Рис. 8.9 иллюстрирует влияние плотности размещения
штампов на процесс приработки для модели, состоящей из 55
штампов (N = 55). В расчётах полагалось, что Г = 1\ = • • ¦ =
= Fjv, где Г; определено в (8.40). Как следует из решения сис-
системы уравнений (8.38), с уменьшением плотности (увеличением
расстояния I между штампами) требуется меньшее время для
достижения равновесного состояния. Это объясняется тем обсто-
обстоятельством, что при малой плотности расположения областей
контакта система штампов близка к равновесному состоянию
уже в начальный момент времени t — 0.
На рис. 8.10 приведены графики, показывающие влияние па-
параметра а на процесс приработки. Обращаясь к формуле (8.34),
отметим, что параметр а влияет на степень неравномерности
износа штампов: чем больше а, тем больше разница в скорости
износа штампов, нагруженных разными усилиями. Поскольку
для каждого рассматриваемого здесь случая начальное распре-
распределение нагрузок на каждый штамп одинаковое, а в процессе
431
0,4
10"
10"
10'
Рис. 8.9. Зависимость степени неравномерности распределения на-
нагрузок от времени изнашивания при а/1 = 0,355 A), а/1 = 0,2 B),
а/1 = 0,1 C) и а = 1, Г = 0,16; штриховая пиния соответствует уста-
установившемуся режиму
приработки давления выравниваются, то этот процесс заканчи-
заканчивается тем быстрее, чем больше а.
Представленные здесь аналитические результаты находятся
в хорошем соответствии с результатами модельного эксперимен-
эксперимента, описанными в [44].
В общем случае произвольной системы штампов время Т
приработки может быть оценено из условия
г
Тем же методом можно изучить кинетику изнашивания и оце-
оценить время приработки при другом характере движения штам-
штампов, например, при их вращении относительно фиксированной
оси. Экспериментальные и теоретические результаты показыва-
показывают, что время приработки составляет незначительную часть от
общего времени изнашивания штампов до определённого уров-
уровня. Большую часть времени имеет место установившийся режим
изнашивания.
432
1,0-
0,8-
Рис. 8.10. Кинетика изнашивания системы штампов при разных зна-
значениях параметра а: а = 2 A), а = 1,5 B), а = 1 C), а = 0,7 D),
а = 0,5 E) и а/1 = 0,2, Г = 0,16.
8.2.4. УСТАНОВИВШИЙСЯ РЕЖИМ ИЗНАШИВАНИЯ
Установившийся режим изнашивания характеризуется стацио-
стационарным распределением нагрузок между штампами, определяе-
определяемым соотношениями (8.48) или (8.55), и установившейся фор-
формой изношенной поверхности, характеризуемой соотношением
высот изношенных штампов, т.е. hi — Wioo(t). Стационарное
распределение нагрузок приводит к равенству скоростей изно-
износа dwioo/dt = SKW каждого штампа системы в соответствии с
уравнением (8.34). Поэтому мы можем определить высоту каж-
каждого штампа в установившемся режиме как hi^—SK^, где функ-
функция /ijoo описывает стационарную форму изношенной поверхнос-
поверхности системы штампов. Из соотношений (8.35), (8.36) и (8.48) по-
получим:
(l-V2)P*
2аЕ
1/а
1
V
¦0/а
9 N"
A v—v
- >
t=l
. a
arcsm —
, (8.56)
где постоянная 6 определяется либо заданной величиной ско-
скорости внедрения системы штампов в основание, либо задан-
заданным значением нагрузки Pqq, приложенной к системе штампов
433
Z{rlR)
(см. (8.49)). Поэтому соотношение между высотами штампов в
установившемся режиме зависит от их расположения внутри но-
номинальной области контакта Я и от характера движения сис-
системы штампов; в то же время это соотношение не зависит от
начального распределения штампов по высоте.
На рис. 8.11 пока-
показана сглаженная уста-
установившаяся форма из-
изношенной поверхнос-
поверхности системы штампов,
рассмотренной выше,
при её возвратно-по-
возвратно-поступательных переме-
перемещениях по границе уп-
упругого полупростран-
полупространства (Rq - радиус об-
области п, в которой на-
находятся все штампы).
Кривые 1-3 рассчита-
рассчитаны при разных значе-
значениях плотности кон-
0,0 0,5 Rj/Rn 1,0 rlR
Рис. 8.11. Зависимость установившегося
распределения выступов по высоте от
плотности их расположения при возвратно-
поступательных перемещениях системы
штампов: а/1 - 0,05 A), а/1 - 0,25 B),
а/1 = 0,45 C), гладкий цилиндрический
штамп радиуса R D)
такта, т. е. при раз-
разных значениях пара-
параметра а/1. Кривая 4
построена для гладко-
гладкого осесимметричного
штампа с равномерным распределением контактного давления,
форма торцевой поверхности которого в пределах площадки кон-
контакта радиуса R описывается функцией:
где Е(ж) - полный эллиптический интеграл второго рода. Та-
Такой штамп является предельным случаем рассмотренной выше
модели, у которой размер каждого штампа стремится к нулю, а
их плотность а/1 к 0,5 при условии равенства площадей контак-
контакта. Результаты расчётов показали, что с увеличением плотности
434
расположения штампов возрастает разница высот изношенных
штампов, расположенных на разном расстоянии от центрально-
центрального штампа модели.
Поскольку скорость износа зависит не только от нагрузки,
но и от скорости скольжения (см. (8.34)), на стационарную фор-
форму, описываемую соотношением (8.56), оказывает существенное
влияние характер движения системы штампов.
Рассмотрим такое движение системы штампов, при кото-
котором путь трения для разных штампов различен. Этому условию
отвечает, например, вращательное движение системы штам-
штампов вокруг некоторой фиксированной оси. В качестве иллюст-
иллюстрации определим распределение выступов по высоте в устано-
установившемся режиме изнашивания для системы цилиндрических
штампов, равномерно расположенных внутри кольцевой облас-
области (Ri ^ г ^ Д2) при вращении системы с постоянной угло-
угловой скоростью вокруг вертикальной оси, проходящей через цен-
центральную точку О. На рис. 8.12 показаны схема контакта и сгла-
сглаженная форма изношенной поверхности системы штампов. Кри-
Кривые 1 и 3 построены при одинаковых значениях относительной
площади контакта Л (Л = Na?/(Щ — Щ)) и различных значе-
значениях безразмерного радиуса пятна контакта а\ = a/i?2- Кри-
Кривые 1, 4 и 2, 3 построены для штампов одного размера, но при
разных значениях Л. Расчёты показывают, что при неизмен-
неизменном значении а\ чем выше относительная площадь контакта Л,
тем больше отличие графика функции hO0(p)/hoo(pi) (р = r/R.2,
р\ = R1/R2) от функции pi/p, соответствующей высотному рас-
распределению штампов без учёта их взаимного влияния друг на
друга. При одинаковых значениях относительной площади кон-
контакта Л взаимное влияние возрастает с уменьшением размера
штампов и, следовательно, с ростом их числа N, которое про-
пропорционально величине К/а\.
Таким образом, результаты показывают, что штампы изна-
изнашиваются неравномерно. Наиболее сильно изнашиваются штам-
штампы, расположенные близко к наружному радиусу кольца. Фор-
Форма изношенной поверхности системы штампов в установившемся
режиме существенно зависит от плотности расположения штам-
штампов и от характера движения системы штампов.
435
1,0
0,8
0,6
0,4
0,3
0,5
0,7
0,9
Рис. 8.12. Установившееся распределение выступов по высоте для
кольцевого образца при его вращательном движении вокруг оси ОО\
(см. схему) при Ri/R2 = 0,3 и Л = 0,05, аг = 0,001 A); Л = 0,1,
ai = 0,01 B); Л = 0,05, ах = 0,01 C); Л = 0,001, аг = 0,001 D)
8.2.5. МОДЕЛЬ ФОРМИРОВАНИЯ РАВНОВЕСНОЙ
ШЕРОХОВАТОСТИ
Анализ микрогеометрии реальных поверхностей на различных
стадиях процесса изнашивания позволяет сделать следующие ос-
основные выводы:
• в процессе приработки вне зависимости от первоначаль-
первоначальной топографии поверхностей формируется стационарная
микрогеометрия, которая воспроизводится при установив-
установившемся режиме изнашивания;
• параметры стационарной микрогеометрии существенно за-
зависят от условий трения (нагрузки, характера движения
и т.д.);
436
• качество поверхности трения в процессе приработки может
как улучшаться, так и ухудшаться.
Такая стационарная микрогеометрия обычно называется равно-
равновесной или оптимальной шероховатостью. Именно эта, а не ис-
исходная технологическая шероховатость в совокупности с други-
другими свойствами поверхностных слоев определяет скорость изна-
изнашивания и силу трения в установившемся режиме изнашивания.
Система штампов, рассмотренная выше, может быть ис-
использована как простейшая механическая модель шероховатой
поверхности. Использование её позволяет объяснить механизм
формирования равновесной шероховатости. Кинетика изнаши-
изнашивания системы штампов при её взаимодействии с упругим полу-
полупространством описывается системой уравнений (8.38). Началь-
Начальными условиями для этой системы уравнений являются пара-
параметры исходной шероховатой поверхности, которые определяют
начальное распределение нагрузок Pj(O) между неровностями.
Метод расчёта значений Р{@) описан в 1.3.
Параметры начальной шероховатости поверхности определя-
определяют также число N контактирующих неровностей и их распо-
расположение (значения /у) внутри номинальной области Q. Число
контактирующих неровностей, вообще говоря, может меняться
с течением времени, так как в процессе приработки в контакт
вступают новые неровности (штампы). Для учёта этого обсто-
обстоятельства следует разбить всё время приработки на временные
интервалы, считая, что внутри каждого интервала число кон-
контактирующих штампов остается постоянным.
Из анализа решения системы уравнений (8.38) можно сделать
следующие выводы относительно изменения параметров микро-
микрогеометрии при изнашивании:
• при заданных условиях нагружения (нагрузка в процес-
процессе изнашивания стремится к постоянному значению) весь
процесс изнашивания состоит из приработки и установив-
установившегося режима;
• параметры стационарной микрогеометрии, соответствую-
соответствующие установившемуся режиму изнашивания, зависят от
асимптотического значения общей нагрузки, действующей
437
на систему штампов, характера движения тел, размеров
и расположения неровностей внутри номинальной области
контакта Q, механических свойств контактирующих тел
и т.д. и не зависят от начального распределения неровнос-
неровностей по высоте; параметры начальной микрогеометрии вли-
влияют на время приработки и объём изношенного в процессе
приработки материала;
• в установившемся режиме изнашивания имеет место по-
постоянство скоростей износа на всех пятнах контакта, т. е.
воспроизводится микрогеометрия поверхности.
Эти выводы находятся в хорошем соответствии с описанны-
описанными выше результатами экспериментальных наблюдений.
Рассматриваемая модель предсказывает также снижение ин-
интенсивности изнашивания поверхностей в процессе приработки
при а > 1, что согласуется с рядом экспериментальных дан-
данных (см., например, [76]). Чтобы проиллюстрировать этот вы-
вывод, рассмотрим систему штампов, описанную в 8.2.3, которая
совершает возвратно-поступательные движения по границе уп-
упругого полупространства, так что V\ = V2 = • ¦ ¦ = Vn — V. В
соответствии с уравнением износа (8.34) объём Avi материала,
отделяемого с каждого пятна контакта за интервал времени At
за счёт износа, пропорционален Pf, т.е.
где К - величина, зависящая от коэффициента износа Kw, ско-
скорости скольжения V и т. д. Тогда объём материала, отделивше-
отделившегося на всех пятнах контакта за время At, определяется как
N
Av = K^P?At. (8.57)
г=1
Исследование функции (8.57) на экстремум, с использование ес-
естественного дополнительного условия
г=1
438
где Pqo - общая нагрузка, действующая на систему штампов, мо-
может быть проведено с помощью метода неопределённых множи-
множителей Лагранжа. Этот анализ показывает, функция (8.57) имеет
экстремум при равномерном распределении нагрузки, т.е.
Pi = Poo/'N, i = l,2,...,N, (8.58)
которое соответствует установившемуся режиму изнашивания,
причём при а > 1 - строгий минимум. Поэтому в установившем-
установившемся режиме при условии а > 1 скорость износа dv/dt минимальна.
Таким образом, используя простейшую модель шероховатой
поверхности в виде системы штампов и принимая во внимание
их взаимное влияние при контактировании с упругим полупро-
полупространством, можно объяснить существование равновесной шеро-
шероховатости, определить её параметры в зависимости от условий
трения, а также объяснить ряд других экспериментально наблю-
наблюдаемых закономерностей (снижение скорости износа в процессе
приработки и т.д.).
Заметим, что метод, описанный в этой главе, может быть
применен к исследованию изнашивания упругого шероховатого
тела, находящегося в контакте с гладкой неизнашиваемой по-
поверхностью. Такая (обратная) модель изучена в [44] для упругих
неровностей цилиндрической формы. Из сопоставления резуль-
результатов следует, что
¦"ioo ~ -"joo = (.^ioo ~ "¦jooj 7)
где hioo — hjoo - разница высот штампов в установившемся ре-
режиме изнашивания, ffjoo — -Hjoo ~ разница высот неровностей
упругого тела в установившемся режиме для обратной модели
(характер движения, распределения неровностей в поверхности и
другие условия предполагались идентичными). Коэффициент 7
определяется соотношением:
7 = 1 Р L
Таким образом, из модели следует, что при одинаковой плот-
плотности микроконтактов и одинаковых условиях трения разница
439
высот микронеровностей в установившемся режиме изнашива-
изнашивания для жёсткого тела будет меньше, чем для упругого. Как
показано в 8.1.4, эта разница для жёсткого тела пропорциональ-
пропорциональна нагрузке Pqq. Для шероховатого упругого тела она пропор-
пропорциональна величине РооТ- Однако величина 7 в пределах малых
упругих деформаций близка к 1.
Другая модель изнашивания дискретного контакта, включа-
включающая также механизм разрушения элементарных контактов за
счёт накопления усталости в подповерхностных слоях взаимо-
взаимодействующих тел, сформулирована и исследована в [11].
8.3. ЗАДАЧИ УПРАВЛЕНИЯ ПРОЦЕССОМ
ИЗНАШИВАНИЯ
В 8.1 и 8.2 мы показали, что параметры, характеризующие неод-
неоднородность свойств поверхности (относительный размер и коэф-
коэффициенты износа упрочнённых и неупрочнённых зон, плотность
расположения включений), оказывают существенное влияние на
формоизменение поверхности в процессе изнашивания. Исполь-
Используя полученные решения, можно прогнозироваить износ поверх-
поверхности по известным механическим и триботехническим характе-
характеристикам контактирующих тел. Однако на основе разработан-
разработанных моделей можно поставить и решить обратную задачу - "соз-
"создания" поверхностей (определения параметров их структуры),
износ которых оптимален с точки зрения критериев, сформули-
сформулированных на основе предъявляемых к сопряжению требований
практического характера.
8.3.1. ПОСТАНОВКА ЗАДАЧИ
В процессе изнашивания меняется форма f(x,y,t) поверхности
контактирующих тел. Для большого класса сопряжений при по-
постоянстве внешних условий (нагрузка, скорость и т. д.) вслед за
нестационарным периодом изнашивания (приработкой) наступа-
наступает стационарный период, отличающийся стабильностью всех ха-
характеристик, в частности установившейся формой fca(x,y) из-
изнашиваемой поверхности. Поскольку эксплуатация сопряжения
в режиме стационарного изнашивания является наиболее бла-
440
гоприятной, возникает задача минимизации времени приработ-
приработки за счёт приближения начальной формы fo(x,y) = f(x,y,0) к
установившейся foo(x,y) (задача 1).
В ряде случаев к форме изношенной поверхности предъяв-
предъявляются определённые требования. Назовём оптимальной фор-
МУ fs(x,y), удовлетворяющую им наиболее полно. Для того что-
чтобы оптимальная форма сохранялась длительное время, необхо-
необходимо, чтобы установившаяся форма foo{x,y) поверхности, со-
оветствующая заданным условиям изнашивания, совпадала (или
была близка) к оптимальной форме fs{x,y) (задача 2).
Ниже изложены математические постановки и методы реше-
решения задач 1 и 2 для ряда характерных сопряжений.
Рассмотрим контакт жёсткого тела (штампа) с упругим по-
полупространством. Будем считать, что скорость V{x,y) относи-
относительного скольжения известна и не зависит от времени, а форма
и размеры области контакта fi постоянны. Для определённости
положим, что изнашиваемым телом является штамп. Эта за-
задача исследовалась в главе 7, а также в 8.1 и 8.2. Было уста-
установлено, что процесс изнашивания выходит на установившийся
режим, если нагрузка, приложенная к штампу, и следовательно,
скорость сближения тел за счёт износа поверхности стремятся к
постоянному значению при t —> +оо.
В установившемся режиме уравнение foo(x,y) изношенной
поверхности штампа с точностью до не зависящего от координат
слагаемого имеет вид:
/11* ill — Тг\It ¦?# 1 I lim 1/пт* it V"l —
oo\x) У) — JO\xj У) i iim w\x, y, i) —
I/a"! (8.59)
где Kw(x, у) > О - коэффициент износа, а и C - параметры урав-
уравнения износа (8.34); А - оператор, вид которого зависит от харак-
характеристик контактирующих тел, формы области контакта и гео-
геометрии тел, параметров неоднородности и т.д. Постоянная D^
определяется либо значением заданной скорости износа в уста-
установившемся режиме ( lim D(t) = Дх,), либо асимптотическим
\ <->+оо /
значением нагрузки Роо = lim P(t) в соответствии с уравнени-
t-^+oo
ем (8.2).
441
Как следует из соотношения (8.59), на установившуюся фор-
форму foo{x,y) изношенной поверхности оказывают влияние коэф-
коэффициент износа Kw(x,y), скорость скольжения V(x,y), величи-
величина .Doo> а также вид оператора А со всеми входящими в него
параметрами. Обозначим совокупность всех параметров ji(x, у),
влияющих на функцию f<x>(x,y), через Т.
Будем решать сформулированные выше задачи 1 и 2 путём
вариации параметров ji ET (i = 1,2,... ,к).
Когда наложены жёсткие условия на конфигурацию, свой-
свойства материалов сопряжения и условия изнашивания, то, как
правило, все параметры в (8.59) заданы и тем самым полнос-
полностью определена установившаяся форма foo(x,y). При условии,
что функция fcxj(x,y) является допустимой с точки зрения ра-
работоспособности сопряжения, можно ставить и решать задачу
минимизации времени приработки за счёт приближения началь-
начальной формы fo(x,y) к foo(x,y) (задача 1). Если оказывается воз-
возможным создать поверхность с начальной формой fo{x,y) —
— foo(x,y), то время приработки равно нулю и установившийся
режим имеет место в течение всего процесса изнашивания.
Задача 2 также может быть решена на основании уравне-
уравнения (8.59), если положить foo{x,y) = fs(x,y) и рассмотреть пра-
правую часть соотношения как функцию подлежащих определению
параметров 7г- Следует отметить, что обычно на параметры л
накладываются некоторые ограничения, обусловленные реаль-
реальными возможностями технологии создания неоднородных по-
поверхностей, например, особенностями лазерного упрочнения, при
котором обработка ведётся импульсами (поточечно) или полоса-
полосами. Поэтому параметры 7г принадлежат к определённому клас-
классу функций S, т. е. Т Е S и задачу 2 можно сформулировать как
задачу отыскания одной или нескольких функций -yi(x,y) Е S,
минимизирующих функционал F, связанный с метрикой в неко-
некотором пространстве, например,
^^JJ dxdy, (8.60)
n \ I
где /а(х,у) = foo(x,y) — Л(#,?/), a mesfi - площадь области О.
442
В качестве S, в частности, можно рассматривать класс кусоч-
кусочно-постоянных функций. Если ограничения на Т отсутствуют,
то min F = 0.
Заметим, что функция fs(x,y) может быть настолько слож-
сложной, что единственным возможным путём её реализации являет-
является изнашивание изначально плоской локально упрочнённой по-
верхнрсти, как, например, в задаче получения волнистой поверх-
поверхности с максимальной маслоёмкостью, рассмотренной в 8.1.2
и 8.1.3.
Таким образом, мы поставили две задачи оптимизации про-
процесса изнашивания.
Задача 1. Сокращение времени приработки за счёт приближе-
приближения начальной формы /о(ж, у) поверхности к установив-
установившейся /оо(х, у).
Задача 2. Стабилизация оптимальной формы fs(x, у) изнашива-
изнашиваемой поверхности. Эта задача может быть поставлена, если
существуют некоторые параметры "^{х,у), характеризую-
характеризующие свойства сопряжения, которые допускают варьирова-
варьирование внутри определённого класса функций §.
Рассмотрим решения задач 1 и 2 для некоторых частных слу-
случаев.
8.3.2. УПРОЧНЁННАЯ ПОВЕРХНОСТЬ С
ПЕРЕМЕННЫМ КОЭФФИЦИЕНТОМ ИЗНОСА
Пусть изнашиваемым телом является штамп, представляющий
собой круговой цилиндр радиуса R, находящийся под действием
постоянной нагрузки Р (см. рис. 3.6). Штамп движется поступа-
поступательно в разных направлениях с постоянной скоростью V по по-
поверхности упругого полупространства, изнашивая его равномер-
равномерно. При этом поверхность полупространства остается плоской.
Предположим, что коэффициент износа Kw(r) является функци-
функцией радиуса г @ ^ г ^ R). Из (8.59) следует установившаяся
форма изношенной поверхности штампа:
443
Kw (r)/Kw @)
1,0 -^^ б
0,5 -
0,0
r/R
0,0
0,5 r/R 1,0
Рис. 8.13. Установившаяся форма изношенной поверхности при
Kw{r) = const (а) и коэффициент износа Kw(r) при а = 1 A), а = 2 B)
и а = 3 C) для случая /oo(r) = const E)
в = ]-?*-,
О f \ /
а К(?) - эллиптический интеграл первого рода.
При отсутствии ограничений на форму изнашиваемого тела
решением задачи 1 является функция /о(г) = foo(r), где foo{f)
определена соотношением (8.61). Если коэффициент износа яв-
является постоянной величиной, т. е. Kw(r) = Kw, форма /о(г), ко-
которую надо придать штампу, чтобы обеспечить стационарный
износ в течение всего времени работы, определяется соотноше-
соотношением
4 A - и2) Р
/о(г) =
[Е (?)-!]. (8-62)
где Е(?) - полный эллиптический интеграл второго рода. График
функции /о(р)//о@) представлен на рис. 8.13,а.
Рассмотрим теперь решение задачи 2 для рассматриваемо-
рассматриваемого сопряжения, когда оптимальная форма поверхности плоская,
т.е. /«(г) = const, а коэффициент износа Kw(r) допускает варь-
варьирование. Тогда соотношение (8.61) является интегральным
уравнением для определения функции Kw(r) при /оо(т") = const,
решение которого имеет вид [23]:
Kw(r)
444
Графики функции Kw(r)/Kw(O) при различных значениях а при-
приведены на рис. 8.13,5.
Решая задачу 2, мы не накладывали никаких ограничений на
характер изменения коэффициента износа. Как было отмечено
в 8.2, функция Kw(r) часто принадлежит к классу кусочно-по-
кусочно-постоянных функций. Пример, рассмотренный в 8.1.4, иллюстри-
иллюстрирует решение задачи в этом случае. Изменяя расположение уп-
упрочнённых зон, представляющих собой кольца постоянной тол-
толщины, можно удовлетворить условию, состоящему в том, что
значения f(ri + p/2) не зависят от г. Это условие можно рассмат-
рассматривать в качестве критерия оптимальности формы поверхности.
Аналогичным образом аналитически или численно на основе
анализа контактных задач теории упругости могут быть полу-
получены решения задач 1 и 2 для поверхностей и областей другой
формы при различном характере относительного движения тел.
8.3.3. ПОВЕРХНОСТЬ АБРАЗИВНОГО ИНСТРУМЕНТА
С ПЕРЕМЕННОЙ ПЛОТНОСТЬЮ ВКЛЮЧЕНИЙ
Коэффициент износа - не единственный параметр, влияющий
на установившуюся форму изнашиваемой поверхности. В слу-
случае дискретного контакта, как показано в 8.2, на установившу-
установившуюся форму существенно влияет взаимное расположение отдель-
отдельных пятен контакта. В качестве примера решения задачи оп-
оптимизации изнашивания дискретного контакта рассмотрим ре-
решение задачи 2 для абразивного инструмента и предложим ме-
метод рационального расположения включений на рабочей поверх-
поверхности инструмента, обеспечивающего равномерное изнашивание
поверхности инструмента.
Абразивный инструмент представляет собой матрицу, содер-
содержащую твёрдые режущие включения. Поскольку матрица изна-
изнашивается значительно быстрее включений, именно включения
являются выступающими элементами, находящимися в контак-
контакте с обрабатываемой поверхностью. Это даёт основание моде-
моделировать поверхность инструмента системой штампов (вклю-
(включений), связанных между собой (заключенных в матрицу). Об-
Обрабатываемую поверхность будем моделировать упругим полу-
полупространством, поверхность которого остаётся плоской в про-
445
цессе изнашивания. Каждое включение моделируется жёстким
цилиндром радиуса а.
Износ такой системы штампов изучался в 8.2. Было уста-
установлено, что штампы изнашиваются неравномерно в процессе
приработки, поэтому форма изношенной поверхности системы
штампов (определяемая распределением штампов по высоте) от-
отличается от исходной и существенно зависит от расположения
штампов внутри номинальной области контакта П. Выражение
для установившейся формы поверхности дано в (8.56).
Анализ частного случая равномерного распределения штам-
штампов внутри круговой области показал, что штампы, первона-
первоначально расположенные на одном уровне (имеющие одинаковую
высоту), изнашиваются неравномерно; штампы, расположенные
на периферии области fi изнашиваются сильнее, чем централь-
центральные. Подобное явление наблюдается при работе абразивного ин-
инструмента, когда первоначально плоская поверхность инстру-
инструмента становится искривленной в результате его неравномер-
неравномерного изнашивания. Приходится вводить дополнительную техно-
технологическую операцию с целью восстановления плоской формы
поверхности инструмента.
Рассмотрим рабочую поверхность инструмента в виде коль-
кольцевой области с внутренним радиусом R\ и внешним R%
(рис. 8.14,о). Инструмент находится под действием постоянной
нормальной силы Р и вращается с постоянной угловой скорос-
скоростью ш на поверхности упругого полупространства.
Если размер включений мал, а количество их велико, име-
имеет смысл говорить не о фиксированном их расположении, а
о функции к(х,у), характеризующей плотность расположения
включений в точке (х, у); при этом / / к(х,у) dxdy - суммарная
площадь контактирующих поверхностей включений в подоблас-
подобласти Аи. Будем считать, что плотность расположения включений
зависит только от радиуса г, т. е. к(х, у) в нашем случае есть
функция к(г). Для вывода установившейся формы foo(r) изно-
изношенной поверхности инструмента воспользуемся соотношени-
соотношением (8.56). При больших N заменим суммирование в (8.56) ин-
интегрированием, используя полученный в 1.4 вывод, что допол-
446
0,9 rlR2 1,0
Рис. 8.14. Поверхность абразивного инструмента с включениями (а)
и распределение плотности включений по поверхности инструмента,
обеспечивающее сохранение его плоской формы, т. е. fs(r) = const (б)
нительное внедрение некоторого фиксированного штампа (вклю-
(включения) от действия Nr сосредоточенных сил, расположенных на
расстоянии р (р ^ 4а) от фиксированного штампа, зависит от
общей интенсивности этих сил и не зависит от их расположения
на окружности радиуса р. Тогда для произвольного фиксиро-
фиксированного штампа, расположенного на расстоянии г от центра О
и имеющего линейную скорость V(r) = шг, получим на основа-
основании (8.56) соотношение
7Г Л2
-i- + -4-2 I I' <r')V(r,r'\(p)dr'
rP/a n a J J
d4>
0 Я1
4Е
я2
Pa(\-v2
r 'Qк(г')<1г'
(8.63)
где
il-в/а ¦ а . /
г arcsin -, 5 > s ,
s2 = г2 + г' - 2rr'cos </>, з' =
«(г)
447
Функция Ф(г, г',(р) исключает из области интегрирования круг
радиуса s' с центром в рассматриваемой точке г, внутри кото-
которого не находится других контактирующих включений кроме
рассматриваемого.
Соотношение (8.63) можно рассматривать как интегральное
уравнение для определения функции к(г), обеспечивающей оп-
оптимальную установившуюся форму fs(r) = foo(r) поверхности
инструмента. Поскольку на практике невозможно создать ин-
инструмент, у которого к(г) меняется непрерывно, будем искать
решение в классе кусочно-постоянных функций:
к(г) = Ki, Г Е (y*i_i,r;), г = 1,2,..., П.
Размер интервала не может быть меньше некоторой величины d,
определяемой возможностями технологии. Тогда задача оптими-
оптимизации может быть сформулирована как задача нахождения та-
таких ^ и г$, которые минимизируют функционал F (см. (8.60))
при условии \г{ — rj_i| ^ d.
Рассмотрим численный пример решения задачи при фикси-
фиксированном размере отрезков |п - r,-_i| = d в случае, когда оп-
оптимальная форма поверхности плоская (fs(r) = const). Расчёты
проводились при следующих значениях параметров:
Ri = 80 мм, R2 = 100 мм, а = 0,09 мм,
N = 10000, <* = 2мм, а/р = 1.
При этих параметрах среднее значение плотности к = 0,02,
где к = JVo2/(i?| — i?f). Это значение соответствует величи-
величинам, характерным для реальных абразивных инструментов при
условии, что в контакте находится 10% расположенных на по-
поверхности включений.
Задача построения приближённого решения интегрально-
интегрального уравнения первого рода (8.63) в классе кусочно-постоянных
функций Кп является корректной по Тихонову, поскольку Кп
компактно в пространстве L2 квадратично суммируемых функ-
функций, а интегральный оператор, стоящий в правой части уравне-
уравнения (8.63), непрерывен (см. [136]). Алгоритм численного решения
задачи описан в [40, 55].
448
Результат расчёта приведен на рис. 8.14,5. Функция к(г)
обеспечивает сохранение плоской формы рабочей поверхности
инструмента в процессе изнашивания. Эта функция состоит из
трёх участков, поскольку плотности, отличающиеся меньше чем
на 10%, считались неразличимыми из технологических сообра-
соображений.
Таким образом, при наличии параметров неоднородности
возможны постановка и решение более содержательных задач
оптимизации, чем в случае однородных поверхностей, учитывая
при этом ограничения практического характера на варьируемые
параметры неоднородности поверхностей.
15. Горячева И. Г.
ЗАКЛЮЧЕНИЕ
Рассмотренные в книге решения контактных задач с учётом
особенностей фрикционного взаимодействия поверхностей могут
быть использованы для изучения как фундаментальных, так и
прикладных вопросов науки о трении и изнашивании твёрдых
тел - трибологии.
К первым из них относятся задачи механики дискретного
контакта (глава 1) и моделирования взаимодействия поверхнос-
поверхностей с учётом адгезии (глава 2); задачи о скольжении единичного
(глава 3) и периодического (глава 5) инденторов по границе уп-
упругого или вязкоупругого основания, а также упругого основа-
основания с покрытием; модели усталостного разрушения поверхнос-
поверхностей, имеющего вид отслаивания или отделения частиц износа
(глава 6); модель изнашивания дискретного контакта (глава 8).
Основная идея подхода, лежащего в основе исследования дис-
дискретного контакта, состояла в рассмотрении фактического кон-
контакта поверхностей, обладающих микрорельефом, и процессов,
протекающих в нём при фрикционном взаимодействии, с учё-
учётом взаимного влияния пятен контакта. Этот подход позво-
позволил выявить ряд нетривиальных аспектов коллективного пове-
поведения микроконтактов, в частности объяснить явления насыще-
насыщения фактической области контакта, существования равновесной
шероховатости и т.д. Учёт в модели одновременно дискретнос-
дискретности контакта и неоднородности механических характеристик по-
поверхностного слоя (глава 4) позволил установить места концент-
концентрации напряжений и характер разрушения покрытий, толщи-
толщина которых соизмерима с характерными параметрами микроне-
микронеровностей поверхности (высота, радиус закругления, расстояние
между неровностями), при различном характере их нагружения,
установить роль тонких поверхностных плёнок в условиях гид-
гидродинамического и граничного трения и т.д. Все эти резуль-
результаты служат для объяснения процессов трения и изнашивания
450
поверхностей, т. е. решают фундаментальные вопросы триболо-
трибологии.
Вопросы, изложенные в главах 7 и 8, а также, частично, в
главе 3, больше относятся к решению прикладной задачи расчё-
расчёта контактных характеристик сопряжений с учётом трения
и изнашивания поверхностей.
Следует отметить, что нельзя провести чёткую границу по
характеру использования построенных моделей. Например, мо-
модель изнашивания системы штампов использована для изучения
фундаментального вопроса разрушения шероховатых поверхнос-
поверхностей, а также прикладного вопроса, связанного с формоизменени-
формоизменением поверхности абразивного инструмента (глава 8).
Многие из предложенных моделей могут быть применены
для анализа контактных характеристик на разных масштабных
уровнях. Так, задача о скольжении индентора по поверхности
вязкоупругого полупространства моделирует условия как мак-
макроконтакта, так и контакта единичного выступа, что и было ис-
использовано для расчёта механической составляющей силы тре-
трения.
Однако этим не исчерпывается роль построенных моделей.
С их помощью можно также предсказать поведение процес-
процесса в зависимости от заданных условий трения. Этим свойст-
свойством в большой мере обладают модели, учитывающие эволюцию
формоизменения поверхностей в процессе трения. Они позволя-
позволяют определить условия существования установившегося режи-
режима изнашивания, распределение давления и форму поверхности
в установившемся режиме, время приработки, долговечность со-
сопряжения и т.д. (главы 7 и 8).
Модели, рассмотренные в главах 3 и 5, могут быть исполь-
использованы для расчёта на стадии проектирования силы и момента
трения сопряжений в зависимости от условий контактирования
и свойств пары трения.
Но есть и ещё одно важное свойство разработанных моделей.
Они могут быть положены в основу создания способов управле-
управления процессами трения и изнашивания поверхностей, например
за счёт выбора оптимальных характеристик покрытий (глава 4),
параметров локального упрочнения и плотности расположения
15* 451
включений в неоднородном материале (глава 8) и т. д.
Наконец, рассмотренные задачи дают возможность оценить
границы применимости упрощённых подходов, которые уже ис-
используются в трибологии для анализа напряжённого состояния
поверхностей и расчёта контактных характеристик. Например,
ответить на вопросы: "При каких параметрах шероховатости и
условиях нагружения можно без большой погрешности рассчи-
рассчитывать фактические давления и фактическую площадь контакта
методами, базирующимися на теории Герца и не учитывающи-
учитывающими взаимное влияние пятен контакта? В каких случаях мож-
можно пренебречь свойствами тонких поверхностных плёнок, про-
промежуточной среды, а также поверхностной энергией при анали-
анализе напряжённого состояния взаимодействующих тел? При каких
механических характеристиках покрытия и его толщине можно
пренебречь упругостью подложки, считая её жёсткой?"
Безусловно, модели, рассмотренные в книге, являются идеа-
идеализацией реальных процессов и не включают все механизмы яв-
явлений, протекающих на фрикционном контакте. Совпадение ре-
результатов, полученных на моделях, с экспериментальными фак-
фактами служит подтверждением того обстоятельства, что зало-
заложенные в моделях механизмы являются определяющими для рас-
рассматриваемых условий взаимодействия.
За пределами книги остались очень важные вопросы о ро-
роли остаточных напряжений и пластических деформаций по-
поверхностных слоев, их разогрева при трении, а также измене-
изменения структуры и, следовательно, механических характеристик
в процессах трения и изнашивания шероховатых тел. Эти проб-
проблемы ставят новые постановки контактных задач, которые уже
решаются или будут решены в будущем.
Надеемся, что эта книга будет полезна как специалистам в
области механики контактных взаимодействий, так и триболо-
гам, помогая разобраться в сложных механизмах явлений, име-
имеющих место при фрикционном взаимодействии.
SUMMARY
This book suggests new formulations and methods for solution of
contact problems describing specific features of friction interaction
essential for tribology. These problems take into account the dis-
discreteness of contact between rough surfaces, surface inhomogeneity,
properties of intermediate medium, complicated boundary condi-
conditions, adhesion of contacting surfaces, surface fracture, and shape
variation of surfaces in the wear process.
The main idea of the approach used in the book for investigating
the discrete contact of rough surfaces is to take into account the in-
interaction between contact spots. This approach is the basis for the
analysis of the discrete contact characteristics (real contact pressure
and contact area, gap between the contacting bodies) and internal
stresses, and for modelling the wear process of rough surfaces. It
allows us to explain some important features of friction interaction
known from experiments, such as the fact that the process of surface
fracture can have a stationary, a periodic, or a catastrophic charac-
character; the effect of saturation of the real contact area; the equilibrium
roughness formation, and so on.
The method of calculation of the nominal contact pressure and
the nominal contact area taking into account the parameters of
macro- and microgeometry of contacting bodies is based on the
principle of localization which is formulated and supported by the
results of investigation of the periodic contact problem for an elastic
half-space and the problem for a system of indenters with bounded
nominal contact region.
In some models, the effects of contact discreteness and mechani-
mechanical inhomogeneity of contacting bodies are taken into account simul-
simultaneously. This allows us to analyze the stresses within the coatings,
the thickness of which is commensurable with the typical size of as-
asperities and distance between them, and to determine the type of
the coating fracture for different loading conditions.
453
Adhesion between contacting surfaces in contact interaction of
elastic bodies is also studied. The adhesion forces caused by molec-
molecular interaction or by menisci of fluid formed near contacting tips
of asperities are taken into account. The method is presented to
analyze the influence of the surface microgeometry parameters, sur-
surface energy, properties of thin surface films, and elastic moduli of
contacting bodies on the contact pressure distribution, real contact
area, gap between the surfaces and so on. It is shown that the de-
dependence of the normal load on the distance between the interacting
bodies is nonmonotone and ambiguous due to the combined effect
of elasticity and adhesion. Therefore the energy dissipation occurs
in the cycle of approach and separation of interacting bodies. The
lost of energy in the cycle vs. the basic parameters of the problem
is studied analytically and numerically. The results obtained are
used to calculate the adhesion component of friction force in rolling
contact of elastic bodies.
Contact problems with complete sliding for elastic and viscoelas-
tic bodies are considered in 2-D and 3-D formulations. The solu-
solutions are used to analyze the influence of the mechanical properties
of contacting bodies and friction coefficient on the contact pressure
distribution, and also size and position of the contact region, and
to calculate the mechanical component of the friction force and its
dependence on the sliding velocity.
Contact with partial slip arises if the tangential load applied to
the bodies is less than the force necessary to cause complete sliding
of the contacting bodies. The 2-D contact of an inclined indenter,
which has a flat base and rounded edges, and a half-space is consid-
considered. The contact stress distribution, location of the contact region,
and the size of stick and slip zones are analyzed for various external
conditions.
Some models presented in the book are used to analyze the effect
of thin surface films in sliding and rolling contact in the regimes of
elasto-hydrodynamic or boundary lubrication. On the basis of these
models, the dependence of the friction coefficient on the speed for
variable mechanical and geometrical characteristics of a surface layer
is studied.
Models of surface fracture (wear) process are based on the theory
454
of fatigue damage accumulation in cycling loading. The basic steps
in wear modelling include the evaluation of the internal stresses
and temperature distribution in subsurface layers, determination of
the onset of failure based on the fracture criterion, and modelling
of the particle detachment. This approach is used to describe the
delamination in the fatigue wear and to analyze the microgeometry
change in the wear process.
Time dependent contact problems which take into account the
surface shape variation during the wear process are also considered
in the book. General formulations of the wear contact problems and
methods of their solutions as well as the analysis of some particular
problems (wear of thin coatings, wear of bodies with variable wear
coefficient, wear of discrete contact, etc.) are presented. The evolu-
evolution in time of the pressure distribution, shape of the worn surface,
duration of the running-in stage, and the life time of junctions are
predicted from the wear contact problem solution.
The approaches developed in the book are also used to optimize
friction and wear process. Among the optimization parameters un-
under consideration, there are the thickness and mechanical properties
of coatings, parameters of local hardening of surfaces, etc. In the
last chapter, we formulate some problems of optimization of the
wear process and give their solutions.
All the problems are studied on the basis of the approaches of
contact mechanics and fracture mechanics. Both analytical and nu-
numerical methods are used to solve the problems. Some results are
expressed in the closed form.
Author: Irina G.Goryacheva, Ph.D., D.Sci., Corresponding
member of the Russian Academy of Sciences (RAS), Head of the
Tribology Laboratory of the Institute for Problems in Mechanics of
RAS, Professor of the Moscow University of Physics and Technology.
ЛИТЕРАТУРА
1. Александров В.М. Осесимметричная задача о действии кольце-
кольцевого штампа на упругое полупространство // Изв. АН СССР.
МТТ. 1967. №4. С. 108-116.
2. Александров В.М. Асимптотические методы в контактных зада-
задачах теории упругости // ПММ. 1968. Т. 32, №4. С. 672-683.
3. Александров В.М., Галин Л.А., Пириев Н.П. Плоская контакт-
контактная задача при наличии износа для упругого слоя большой тол-
толщины // Изв. АН СССР. МТТ. 1978. №4. С. 60-67.
4. Александров В.М., Коваленко Е.В. Плоские контактные задачи
теории упругости для неклассических областей при наличии из-
износа // ЖПМТФ. 1980. №3. С. 163-172.
5. Александров В.М., Коваленко Е.В. К теории контактных задач
при наличии нелинейного износа // Изв. АН СССР. МТТ. 1982.
№4. С. 98-108.
6. Александров В.М., Коваленко Е.В. Математические методы в
контактных задачах с износом // Нелинейные модели и зада-
задачи механики деформируемого твёрдого тела. М.: Наука. 1984.
С. 77-89.
7. Александров В.М., Коваленко Е.В. Аналитическое решение кон-
контактной задачи об изнашивании сопряжения вал-втулка // Тре-
Трение и износ. 1987. Т. 8, №6. С. 985-995.
8. Александров В.М., Кудиш И.И. Асимптотический анализ плос-
плоской и осесимметричной контактной задачи при учёте поверхност-
поверхностной структуры взаимодействующих тел // Изв. АН СССР. МТТ.
1979. №1. С. 58-70.
9. Александров В.М., Мхитарян СМ. Контактные задачи для тел
с тонкими покрытиями и прослойками. М.: Наука, 1983. 488 с.
10. Александрова Г.П. Контактные задачи изгиба плит, лежащих на
упругом основании // Изв. АН СССР. МТТ. 1979. № 1. С. 97-106.
456
11. Алексеев Н.М., Горячева И.Г., Чекина О.Г. Контактное взаи-
взаимодействие шероховатых тел с учётом процессов фрикционного
разрушения // Трение и износ. 1987. Т. 8, №6. С. 977-984.
12. Алексеев Н.М., Добычин М.Н. Модели изнашивания // Триболо-
Трибология: Исследования и приложения: Опыт США и стран СНГ / Под
ред. В.А. Белого, К.Лудемы, Н.К.Мышкина. М.: Машинострое-
Машиностроение; Нью-Йорк: Аллертон пресс, 1993. С. 66-87.
13. Бартенев Г.М., Лаврентьев В.В. Трение и износ полимеров.
М.: Химия, 1972.240 с.
14. Бершадский Л.И. Самоорганизация и надёжность трибосистем.
Киев: Знание, 1981. 35 с.
15. Богатин О.Б., Моров В.А., Черский И.Н. Основы расчёта поли-
полимерных узлов трения. Новосибирск: Наука, 1983. 214 с.
16. Бородич Ф.М., Мосолов А.Б. Фрактальная шероховатость в кон-
контактных задачах // ПММ. 1992. Т. 56, №5. С. 786-795.
17. Боуден Ф., Табор Д. Трение и смазка твёрдых тел. М.: Маши-
Машиностроение, 1968. 544 с.
18. Буше Н.А. Оценка роли металлических материалов в совмес-
совместимости трибосистем // Трибология: Исследования и приложе-
приложения: Опыт США и стран СНГ / Под ред. В.А.Белого, К.Луде-
К.Лудемы, Н.К. Мышкина. М.: Машиностроение; Нью-Йорк: Аллертон
пресс, 1993. С. 139-155.
19. Ванторин В.Д. Движение по плоскости с анизотропным трени-
трением // Трение и износ в машинах. М.: Изд-во АН СССР, 1962.
Т. 16. С. 210-219.
20. Ворович И.И., Александров В.М., Бабешко В.А. Неклассические
смешанные задачи теории упругости. М.: Наука, 1974. 456 с.
21. Галанов Б. А. Пространственные контактные задачи для упругих
шероховатых тел при упруго-пластических деформациях неров-
неровностей // ПММ. 1984. Т. 48, №6. С. 1020-1029.
22. Галахов М.А., Усов П.П. Дифференциальные и интегральные
уравнения математической теории трения. М.: Наука, 1990. 277 с.
23. Галин Л.А. Контактные задачи теории упругости. М.: Гостехте-
оретиздат, 1953. 264 с.
457
24. Галин Л.А. Контактные задачи теории упругости при наличии
износа // ПММ. 1976. Т. 40, №6. С. 981-989.
25. Галин Л.А. Контактные задачи теории упругости и вязкоупру-
гости. М.: Наука, 1980. 304 с.
26. Галин Л.А., Горячева И.Г. Осесимметричная контактная задача
теории упругости при наличии износа // ПММ. 1977. Т. 41, №5.
С.807-812.
27. Галин Л.А., Горячева И.Г. Контактные задачи теории упругос-
упругости при наличии износа // Теория трения, износа и проблемы
стандартизации. Брянск: Приок. кн. изд-во, 1978. С. 251-265.
28. Галин Л.А., Горячева И.Г. Контактные задачи и их приложе-
приложения к теории трения и износа // Трение и износ. 1980. Т. 1, № 1,
С. 105-119.
29. Галин Л.А., Горячева И.Г. Пространственная контактная зада-
задача о движении штампа с трением // ПММ. 1982. Т. 46, №6.
С.819-824.
30. Гаркунов Д.П. Триботехника. М.: Машиностроение, 1985. 424 с.
31. Глаголев Н.И. Сопротивление перекатыванию цилиндрических
тел // ПММ. 1945. Т. 9, №4. С. 318-333.
32. Голъдштейн Р.В., Зазовский А.Ф., Спектор А.А., Федорен-
ко Р. П. Решение вариационными методами пространственных
контактных задач качения с проскальзыванием и сцеплением //
Успехи механики. 1982. Т. 5, № 3/4. С. 61-102.
33. Голъдштейн Р.В., Спектор А.А. Вариационные методы реше-
решения и исследования пространственных контактных и смешанных
задач с трением // Механика деформируемого тела. М.: Наука,
1986. С. 52-73.
34. Горячева И.Г. Контактная задача качения вязкоупругого ци-
цилиндра по основанию из того же материала // ПММ. 1973. Т. 37,
№5. С. 877-885.
35. Горячева И.Г. Исследование трения качения при учёте про-
проскальзывания и вязкоупругости: Дис. ... канд. физ.-матем. наук.
М., 1973.
458
36. Горячева И.Г. Об одном методе решения контактных задач
теории упругости при наличии износа // Актуальные пробле-
проблемы механики деформируемых сред. Днепропетровск: ДГУ, 1979.
С.79-84.
37. Горячева И.Г. Плоские и осесимметричные контактные зада-
задачи для шероховатых упругих тел // ПММ. 1979. Т. 43, №1.
С.99-105.
38. Горячева И.Г. Контактная задача при наличии износа для коль-
кольца, вложенного в цилиндр // Там же. 1980. Т. 44, №2. С. 363-367.
39. Горячева И.Г. Расчётная оценка износа поршневых колец дви-
двигателей внутреннего сгорания // Теория и практика расчётов
деталей машин на износ. М.: Наука, 1983. С. 123-128.
40. Горячева И.Г. Контактные задачи теории упругости для систе-
системы изнашиваемых штампов // Изв. АН СССР. МТТ. 1987. №6.
С. 62-68.
41. Горячева И.Г. Контактные задачи в трибологии: Дис. ... д-ра
физ.-матем. наук. М., 1987.
42. Горячева И.Г. Периодическая контактная задача для упругого
полупространства // ПММ. 1998. Т. 62, №6. С. 1036-1044.
43. Горячева И.Г., Добычин М.Н. Оценка точности метода расчёта
жёсткости стыка шероховатых тел с учётом взаимного влияния
микроконтактов // Машиноведение. 1980. № 1. С. 70-77.
44. Горячева И.Г., Добычин М.Н. Контактные задачи в трибологии.
М.: Машиностроение, 1988. 254 с.
45. Горячева И.Г., Красник В.Г., Чекина О.Г. Сопротивление
породы проникновению штампа вблизи стенки скважины //
Физ.-техн. пробл. разраб. полез, ископаемых. 1992. №1. С. 39-44.
46. Горячева И.Г., Шаховская Ю.Ю. Влияние несовершенной упру-
упругости поверхностного слоя на контактные характеристики при
скольжении шероховатых упругих тел // Трение и износ. 1997.
Т. 18, № 1. С. 5-12.
47. Горячева И.Г., Маховская Ю.Ю. Контактирование упругих тел
при наличии капиллярной адгезии // ПММ. 1999. Т. 63, №1.
С. 128-137.
459
48. Горячева И.Г., Маховская Ю.Ю. Адгезионное взаимодействие
упругих тел // Там же. 2001. Т. 65, №2. С. 279-289.
49. Горячева И.Г., Солдатенков И.А. Теоретическое исследова-
исследование приработки и установившегося режима изнашивания твёр-
твёрдых смазочных покрытий // Трение и износ. 1983. Т. 4, №3.
С.420-431.
50. Горячева И.Г., Торская Е.В. Контактные задачи при наличии
износа для тел с переменным по поверхности коэффициентом из-
износостойкости // Там же. 1992. Т. 13, №1. С. 185-194.
51. Горячева И.Г., Торская Е.В. Анализ напряжённого состояния
тел с покрытиями при множественном характере нагружения //
Там же. 1994. Т. 16, №3. С. 349-357.
52. Горячева И.Г., Торская Е.В. Периодическая контактная задача
для системы штампов и упругого слоя, сцепленного с упругим
основанием // Там же. 1995. Т. 17, №4. С. 642-652.
53. Горячева И.Г., Торская Е.В. Напряжённое состояние двух-
двухслойного упругого основания при неполном сцеплении слоев //
Там же. 1998. Т. 19, №3. С. 289-296.
54. Горячева И.Г., Фельдштпейн И.В. Анализ влияния внутренней
системы дефектов на напряжённое состояние упругих тел //
Изв. РАН. МТТ. 1996. №5. С. 55-61.
55. Горячева И.Г., Чекина О.Г. Управление формоизменением по-
поверхностей при изнашивании // Трение и износ. 1989. Т. 10, № 1.
С. 5-12.
56. Горячева И.Г., Чекина О.Г. Модель усталостного разрушения
поверхностей // Там же. 1990. Т. 11, №3. С. 1-11.
57. Горячева И.Г., Чекина О.Г. Изнашивание поверхностей: от мо-
моделирования микроразрушения к анализу формоизменения //
Изв. РАН. МТТ. 1999. №5. С. 131-147.
58. Градштпейн И. С, Рыжик И.М. Таблицы интегралов, сумм, рядов
и произведений. 5-е изд. М.: Наука, 1971. 1108 с.
59. Григорьев А.Я., Мышкин Н.К., Холодилов О.В. Методы анализа
микрогеометрии поверхностей // Трение и износ. 1989. Т. 10, № 1.
С. 138-155.
460
60. ГрубинА.Н. Основы гидродинамической теории смазки тяжело-
нагруженных криволинейных поверхностей // Тр. ЦНИИТМАШ.
1949. №30. С. 126-184.
61. Губенко B.C., Моссаковский В.И. Давление осесимметричного
кольцевого штампа на упругое полупространство // ПММ. 1960.
Т24, №2. С. 334-340.
62. Дерягин Б. В. Молекулярная теория трения и скольжения //
Журн. физ. химии, 1934. Т. 5. С. 1165-1172.
63. Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы.
М.: Наука, 1985. 398 с.
64. Дёмкин Н.Б. Фактическая площадь касания твёрдых поверхнос-
поверхностей. М.: Изд-во АН СССР, 1962. 112 с.
65. Дёмкин Н.Б. Контактирование шероховатых поверхностей. М.:
Наука, 1970. 228 с.
66. Джонсон К. Механика контактного взаимодействия. М.: Мир,
1989.510 с.
67. Довнорович В.И., Яшин В.Ф. Некоторые пространственные за-
задачи теории упругости. Гомель: БИИЖТ, 1961. 55 с.
68. Захаров СМ., Жаров И.А. Методология моделирования слож-
сложных трибосистем // Трение и износ. 1988. Т. 9, № 5. С. 825-833.
69. Иваночкин П.Г., Коваленко Е.В. Расчёт изнашивания двухслой-
двухслойного вкладыша радиального подшипника скольжения // Там же.
1990. Т. 11, №4. С. 622-629.
70. Ионов В.Н., Огибалов П.М. Прочность пространственных эле-
элементов конструкций. М.: Высш. шк., 1972. 752 с.
71. Ишлинский А.Ю. Трение качения // ПММ. 1938. Т. 2, №2.
С.245-260.
72. Ишлинский А.Ю. Теория сопротивления перекатыванию (тре-
(трение качения) и смежных явлений // Трение и износ в машинах.
М.,Л.: Изд-во АН СССР, 1940. С. 255-264.
73. Ишлинский А.Ю. О проскальзывании в области контакта при
трении качения // Изв. АН СССР. ОТН. 1956. №6. С. 3-15.
461
74. Каландия А.И. Математические методы двумерной теории упру-
упругости. М.: Наука, 1973. 304 с.
75. Канторович Л.В., Крылов В.И. Приближённые методы высшего
анализа. М.,Л.: Физматгиз, 1962. 708 с.
76. Карасик И.И. Прирабатываемость материалов для подшипников
скольжения. М.: Наука, 1978. 136 с.
77. Карслоу Г., Егер Д. Теплопроводность твёрдых тел. М.: Наука,
1964.487 с.
78. Качалкин А.Ю., Мазинг Р.И. Контактная задача для цилинд-
цилиндрического тела с учётом износа // Машиноведение. 1988. №3.
С.49-51.
79. Коваленко Е.В. К расчёту изнашивания сопряжения вал-втул-
вал-втулка // Изв. АН СССР. МТТ. 1982. №6. С.66-72.
80. Коваленко Е.В. Исследование осесимметричных контактных за-
задач об изнашивании пары кольцевой штамп - упругое шерохова-
шероховатое полупространство // ПММ. 1985. Т. 49, №5. С. 836-843.
81. Коднир Д. С. Контактная гидродинамика смазки деталей машин.
М.: Машиностроение, 1976. 304 с.
82. Колесников Ю.В., Морозов ЕМ. Механика контактного разру-
разрушения. М.: Наука, 1989. 224 с.
83. Коллинз Д. Повреждения материалов в конструкциях: Анализ,
предсказание, предотвращение. М.: Мир, 1984. 624 с.
84. Конвисаров Д.В., Покровская А.А. Влияние радиусов кривизны
цилиндрических тел на их сопротивление перекатыванию при
различных нагрузках // Тр. Сиб. физ.-техн. ин-та. 1955. Т34.
С. 62-79.
85. Коровчинский М.В. Локальный контакт упругих тел при изна-
изнашивании их поверхностей // Контактное взаимодействие твёр-
твёрдых тел и расчёт сил трения и износа. М.: Наука, 1971.
С.130-140.
86. Кравчук А. С. К теории контактных задач с учётом трения на по-
поверхности соприкосновения // ПММ. 1980. Т. 44, № 1. С. 122-129.
462
87. Кравчук А.С. Решение некоторых пространственных контакт-
контактных задач с учётом трения на поверхности соприкосновения //
Трение и износ. 1981. Т. 2, №4. С. 589-595.
88. Кравчук А. С. Вариационные и квазивариационные неравенства
в механике. М.: МГАПИ, 1997. 339 с.
89. Крагельский И.В. Трение и износ. М.: Машиностроение, 1968.
480 с.
90. Крагельский И.В., Бессонов Л.Ф., Швецова Е.М. Контакт шеро-
шероховатых поверхностей // ДАН СССР. 1953. Т. 93, №1. С. 43-46.
91. Крагельский И.В., Добычин М.Н., Комбалов B.C. Основы расчё-
расчётов на трение и износ. М.: Машиностроение, 1977. 576 с.
92. Крагельский И.В., Непомнящий Е.Ф. Теория износа высокоэлас-
высокоэластичных материалов // Пластмассы в подшипниках скольжения:
(Исследования и опыт применения). М.: Наука, 1965. С. 49-56.
93. Кузнецов Е.А. Периодическая контактная задача для полуплос-
полуплоскости с учётом сил трения // Прикл. механика. 1976. Т. 12, № 10.
С.37-44.
94. Кузнецов Е.А., Гороховский Г.А. О фактическом контактном
давлении // Пробл. трения и изнашивания. 1977. № 12. С. 10-13.
95. Кузнецов Е.А., Гороховский Г.А. Влияние шероховатости на на-
напряжённое состояние тел при фрикционном взаимодействии //
Прикл. механика. 1978. Т. 14, №9. С. 62-68.
96. Лурье А.И. Пространственные задачи теории упругости. М.: Гос-
техтеоретиздат, 1955. 492 с.
97. Макушкин А.П. Напряжённо-деформированное состояние упру-
упругого слоя при внедрении в него сферического индентора. Опреде-
Определение контактного давления // Трение и износ. 1990. Т. 11, №3.
С.423-434.
98. Макушкин А.П. Напряжённо-деформированное состояние упру-
упругого слоя при внедрении в него сферического индентора. Опре-
Определение контактного давления // Там же. 1990. Т. 11, №4.
С.602-608.
99. Марченко В.А., Хруслов Е.Я. Краевые задачи в областях с мел-
мелкозернистой границей. Киев: Наук, думка, 1974. 280 с.
463
100. Марченко Е.А. О природе разрушения поверхностей металлов
при трении. М.: Наука, 1979. 118 с.
101. Маховская Ю.Ю. Дискретный контакт упругих тел при наличии
адгезии // Изв. РАН. МТТ. 2002. Вып. 6.
102. Механика контактных взаимодействий / Под ред. И.И. Воровича
и В.М.Александрова. М.: Физматлит, 2001. 672с.
103. Михлин С.Г., Смолицкий Х.Л. Приближённые методы решения
дифференциальных и интегральных уравнений. М.: Наука, 1965.
250 с.
104. Можаровский В.В., Старжинский В.Е. Прикладная механика
слоистых тел из композитов. Минск: Наука и техника, 1988. 271 с.
105. Морозов Е.М., Зернин М.В. Контактные задачи механики раз-
разрушения. М.: Машиностроение, 1998. 544 с.
106. Моссаковский В.И., Качаловская Н.Е., Голикова С.С. Контакт-
Контактные задачи математической теории упругости. Киев: Наук, дум-
думка, 1985. 176 с.
107. Мусхелишвили Н.И. Некоторые основные задачи математической
теории упругости. М.: Наука, 1966. 708 с.
108. Никишин B.C., Шапиро, Г.С. Пространственные задачи теории
упругости для многослойных сред. М.: Изд-во ВЦ АН СССР,
1970. 260 с.
109. Основы трибологии (трение, износ, смазка) / Под ред. А.В.Чи-
чинадзе. М.: Машиностроение, 2001. 664 с.
ПО. Петришин В.И., Приварников А.К., Шевеляков Ю.А. К реше-
решению задач для многослойных оснований // Изв. АН СССР. МТТ.
1965. №3. С. 138-143.
111. Петровский И.Г. Лекции по теории обыкновенных дифференци-
дифференциальных уравнений. М.: Наука, 1970. 280 с.
112. Пинегин СВ., Орлов А.В. Сопротивление движению при некото-
некоторых видах свободного качения // Изв. АН СССР. ОТН. Механика
и машиностроение. 1961. №3. С. 91-97.
113. Писаренко Г.С, Лебедев А.А. Деформирование и прочность ма-
материалов при сложном напряжённом состоянии. Киев: Наук, дум-
думка, 1976.415 с.
464
114. Польцер Г., Эбелинг В., Фирковский А. Внешнее трение твёрдых
тел, диссипативные структуры и самоорганизация // Трение и
износ. 1988. Т. 9, №1. С. 12-18.
115. Попов Г.Я. Концентрация упругих напряжений возле штампов,
разрезов, тонких включений и подкреплений. М.: Наука, 1982.
344 с.
116. Попов Г.Я., Савчук В.В. Контактная задача теории упругости
при наличии круговой области контакта с учётом поверхностной
структуры контактирующих тел // Изв. АН СССР. МТТ. 1971.
№3. С. 80-87.
117. Проников А.С. Надёжность машин. М.: Машиностроение, 1978.
592 с.
118. Проников А.С. Макротрибология и её задачи // Трение и износ.
1998. Т. 19, №2. С. 155-164.
119. Работное Ю.Н. Ползучесть элементов конструкций. М.: Наука,
1966. 752 с.
120. Работное Ю.Н. Элементы наследственной механики твёрдых
тел. М.: Наука, 1977. 384 с.
121. Развитие теории контактных задач в СССР / Под ред. Л.А. Га-
Галина. М.: Наука, 1976. 496 с.
122. Рафф А.В. Модифицированные поверхностные слои и покры-
покрытия // Трибология: Исследования и приложения: Опыт США
и стран СНГ / Под ред. В.А. Белого, К.Лудемы, Н.К.Мыш-
кина. М.: Машиностроение; Нью-Йорк: Аллертон пресс, 1993.
С.190-201.
123. Рвачёв В.Л., Проценко B.C. Контактные задачи теории упругос-
упругости для неклассических областей. Киев: Наук, думка, 1977. 236 с.
124. Регель Р.В., Слуцкер А.И., Томашевский Э.Е. Кинетическая
природа прочности твёрдых тел. М.: Наука, 1974. 560 с.
125. Савин Т.Н. Распределение напряжений около отверстий. Ки-
Киев: Наук, думка, 1968. 887 с.
126. Свириденок А.И., Чижик С.А. Контактное взаимодействие глад-
гладких поверхностей // Трение и износ. 1992. Т. 13, № 1. С. 130-137.
465
127. Свириденок А.И., Чижик С. А., Петроковец М.И. Механика дис-
дискретного фрикционного контакта. Минск: Навука i тэхшка, 1990.
272 с.
128. Семенюк Н.Ф. Средняя высота микровыступов шероховатой по-
поверхности и плотность пятен контакта при контактировании ше-
шероховатой поверхности с гладкой // Трение и износ. 1986. Т. 7,
№ 1.С. 85-91.
129. Семенюк Н.Ф., Сиренко Г.А. Описание топографии анизотроп-
анизотропных шероховатых поверхностей с помощью модели случайного
поля // Там же. 1980. Т. 1, №3. С. 465-471. №5. С. 815-823. №6.
С.1010-1020.
130. Солдатенков И.А. Изнашивание тонкого упругого покрытия при
изменяющейся площадке контакта // Там же. 1985. Т. 6, №2.
С.247-254.
131. Солдатенков И.А. Изнашивание покрытий в упругих сопряже-
сопряжениях при изменяющейся площадке контакта // Там же. 1987. Т. 8,
№2. С. 206-213.
132. Солдатенков И.А. Задача об изнашивании полуплоскости дис-
дисковым контртелом // Изв. АН СССР. МТТ. 1989. Т. 24, №6.
С. 107-110.
133. Солдатенков И.А. Асимптотический анализ решения задачи те-
теории упругости для полосы переменной толщины // Изв. РАН.
МТТ. 1994. Т. 29, №6. С. 57-73.
134. Солдатенков И.А. Решение контактной задачи для композиции
полоса-полуплоскость при наличии изнашивания с изменяющей-
изменяющейся областью контакта // Там же. 1998. № 2. С. 78-88.
135. Тёплый М.И. Контактные задачи для областей с круговыми гра-
границами. Львов: Вища шк., 1983. 176 с.
136. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных за-
задач. М.: Наука, 1974. 286 с.
137. Трикоми Ф. Дифференциальные уравнения. М.: Изд-во иностр.
лит., 1962. 352 с.
138. Усов П.П. Внутренний контакт цилиндрических тел близких ра-
радиусов при изнашивании их поверхностей // Трение и износ.
1985. Т. 6, №3. С. 404-414.
466
139. Усов П.П., Дроздов Ю.Н., Николашев Ю.Н. Теоретическое ис-
исследование напряжённого состояния пары вал-втулка с учётом
износа // Машиноведение. 1979. №2. С. 80-87.
140. Хантер С.К. Контактная задача качения жёсткого цилиндра
по вязкоупругому полупространству // Прикл. механика. 1961.
Т. 28, №4. С. 146-153.
141. Хрущов М.М. Исследование приработки подшипниковых сплавов
и цапф. М.,Л.: Наука, 1946. 146 с.
142. Чекина О.Г. Моделирование разрушения приповерхностных сло-
слоев при контактировании шероховатых тел // Прочность и плас-
пластичность. М.: Наука, 1996. Т. 1. С. 186-191.
143. Чижик С.А. Капиллярный механизм адгезии и трения шерохова-
шероховатых поверхностей, разделённых тонким слоем жидкости // Тре-
Трение и износ. 1994. Т. 15, № 1. С. 11-26.
144. Чихос X. Системный анализ в триботехнике // М.: Мир, 1982.
352 с.
145. Чичинадзе А.В., Матвеевский P.M., Браун Э.Д. Материалы
в триботехнике нестационарных процессов // М.: Наука, 1986.
248 с.
146. Штаерман И.Я. Контактная задача теории упругости. М.: Гос-
техтеоретиздат, 1949. 270 с.
147. Щедрое B.C. Анализ экспериментальных закономерностей при-
приработки на основе общих уравнений теории изнашивания // Тре-
Трение и износ в машинах. 1950. Т. 6. С. 3-12.
148. Янке Е., Эмде Ф., Лёш Ф. Специальные функции. Формулы, гра-
графики, таблицы. 2-е изд. М.: Наука, 1968. 344 с.
149. Archard J.F. Contact and rubbing of flat surfaces // J. Appl. Phys.
1953. N24. P. 981-988.
150. Batra S.K., Ling F.F. On deformation friction and interface shear
stress in viscoelastic elastic layered system under a moving load //
Amer. Soc. Lubr. Eng. Trans. 1967. N10. P. 294-301.
151. Barus C. Isothermal, isopiestics, and isometrics relative viscosity //
Amer. J. Sci. 1893. Vol.45. P.87-96.
467
152. Braat G.F.M., Kalker J.J. Theoretical and experimental analysis
of the rolling contact between two cylinders coated with multilay-
ered viscoelastic rubber // Contact mechanics, computational tech-
techniques / Ed. M.H. Aliabadi and C.A. Brebbia.: Contact Mechanics
publ., 1993. P. 119-126.
153. Brandt A., Lubrecht A.A. Multilevel matrix multiplication ans fast
solution of integral equations //J. Comput. Phys. 1990. P. 348-370.
154. Carter F. W. On the action of a locomotive driving wheel // Proc.
Roy. Soc. London A. Vol. 112. P. 151.
155. Chekina O.G., Keer L.M. Wear-contact problems and modeling
of chemical mechanical polishing // J. Electrochem. Soc. 1998.
Vol.145, N6. P. 2100-2106.
156. Chekina O.G., Keer L.M. A new approach to calculation of contact
characteristics // ASME. J. Tribol. 1999. Vol.121. P. 20-27.
157. Ciavarella M., Hills D.A., Monno G. The influence of rounded edges
on indentation by a flat punch // Proc. Inst. Mech. Eng. J. Mech.
Eng. Sci. 1998. Vol.212, N4. P.319-328.
158. Cole S.J., Sayles R.S. A numerical model for the contact of layered
elastic bodies with real rough surfaces // ASME. J. Tribol. 1991.
Vol.113, N2. P. 334-340.
159. Cooper J.R., Dowson D., Fisher J. Birefringent studies of polyethy-
polyethylene wear specimens and acetabularcups // Wear. 1991. Vol. 151.
P. 391-401.
160. Coulomb Ch.A. Theorie des machines simples // Memoire de Mathe-
matiques et de Physique de l'Academie Royale. P., 1785. P. 161-331.
161. Dowson D. History of tribology. L.: Longman, 1978.
162. Dowson D., Higginson G.R. Elastohydrodynamic lubrication: The
fundamentals of roller and gear lubrication. Oxford: Pergamon,
1966. 207 p.
163. Evans A.G., Marshall D.B. Fundamentals of friction and wear ma-
materials. Metals Park, Ohio: Am. Soc. for Metals, 1981. 439 p.
164. Fleischer G. Energetische Methode der Bestimnung des VerschleiB-
es // Schmierungstechnik. 1973. N4. S.9-16.
468
165. Flom D.G. Dynamic mechanical losses in rolling contacts // Rolling
contact phenomena. L.: Bidwell; Elsevier, 1962. P. 97-112.
166. Flom D.G., Bueche A.M. Theory of rolling friction for spheres //
J. Appl. Phys. 1959. Vol.30, N11. P. 1725-1730.
167. Fromm H. Berechnung des Schlupfes beim Rollen deformierbaren
Scheiben // ZAMM. 1927. N 7. S. 27-58.
168. Fuller K.N. G., Tabor D. The effect of surface roughness of the adhe-
adhesion of elastic solids // Proc. Roy. Soc. London A. 1975. Vol. 324.
P. 327-342.
169. Gladwell G.M.L. Contact problems in the classical theory of elastic-
elasticity. Alphen aan den Rijn: Sijthoff and Noordhoff, 1980. 716 p.
170. Gladwell G.M.L., Gupta O.P. On the approximate solution of elastic
contact problems for a circular annulus // J. Elast. 1979. N9.
P. 335-348.
171. Godet M. The third-body approach: A mechanical view of wear //
Wear. 1984. Vol. 100. P. 437-452.
172. Goryacheva I.G. Contact mechanics in tribology. Dordrecht etc.:
Kluwer, 1998. 344 p.
173. Goryacheva I.G., Goryachev A.P., Sadeghi F. The effect of surface
layer with bleeding properties in rolling/sliding contact // STLE.
Tribol. Trans. 2000. Vol.43, N1. P. 123-129.
174. Goryacheva I.G., Dobychin M.N. Multiple contact model in the
problems of tribomechanics//Tribology International. 1991. V. 24,
N1. P. 29-35.
175. Goryacheva I.G., Sadeghi F. Contact characteristics of
rolling/sliding cylinder and a viscoelastic layer bonded to an
elastic substrate // Wear. 1995. Vol. 184. P. 125-132.
176. Goryacheva I. G., Sadeghi F., Nickel D. Internal stresses in contact of
a rough body and a viscoelastic layered semi-infinite plane // ASME.
J. Tribol. 1996. Vol. 118, N1. P. 131-136.
177. Goryacheva I.G., Sadeghi F., Xu C. Viscoelastic effects in lubricated
contacts // Wear. 1996. Vol. 198, N1. P. 307-312.
469
178. Greenwood J.A. Contact of rough surfaces // Fundamentals of fric-
friction: Macroscopic and microscopic processes / Ed. I.L. Singer and
H.M.Pollok. Dordrecht etc.: Kluwer, 1992. P. 37-56.
179. Greenwood J.A. Adhesion of elastic spheres // Proc. Roy. Soc. Lon-
London A. 1997. Vol.453, N1961. P. 1277-1297.
180. Greenwood J.A., Tabor D. The friction of hard sliders on lubricated
rubber: The importance of deformation losses // Proc. Phys. Soc.
1958. Vol.71. P.989.
181. Greenwood J.A., Tripp J.H. The elastic contact of rough spheres //
ASME. J. Appl. Mech. E. 1967. Vol.34, N1. P. 153-159.
182. Greenwood J.A., Williamson J.B.P. Contact of nominally flat sur-
surfaces // Proc. Roy. Soc. London A. 1966. Vol.295, N1442.
P. 300-319.
183. Gupta P.K, Cook N.M. Statistical analysis of mechanical interaction
of rough surfaces // ASME, J. Lubr. Techn. F. 1972. Vol.94, N1.
P. 14-23.
184. Hamilton G.N., Goodman L.E. The stress field created by a circu-
circular sliding contact // ASME. J. Appl. Mech. E. 1966. V.33, N2.
P. 371-376.
185. Hamrock B.J. Fundamentals of fluid film lubrication. N. Y.:
McGraw-Hill, 1994.
186. Heathcote H.L. The ball bearing: in the making, under test on ser-
service // Proc. Inst. Auto. Eng. 1921. Vol.15. P. 569-622.
187. Hertz H. Uber die Beriihrung fester elastische Korper // J. Reine
und angew. Mathematik. 1882. N92. S. 156-171.
188. Hills D.A., Nowell D. Mechanics of fretting fatigue. Dordrecht etc.:
Kluwer, 1994. 236 p.
189. Hills D.A. Sosa G. Origins of partial slip in fretting - a review of
known and potential solutions // J. Strain Anal. 1999. Vol. 34, N 3.
P. 175-181.
190. Hirst W., Moore A.J. Non-Newtonian behavior in elastohydrody-
namics lubrication // Proc. Roy. Soc. London A. 1974. Vol.33.
P. 101-113.
470
191. Hisakado T. On the mechanism of contact between solid surfaces //
Bull. ASME. 1969. Vol. 12, N 54. P. 1528-1549.
192. Holm R. Electric contacts. Stockholm: Almquist and Wiksells, 1946.
193. Holmberg K., Matthews A. Coating tribology. Amsterdam: Elsevier,
1994.
194. Johnson K.L. Mechanics of adhesion //Tribol. Intern. 1998. Vol.31,
N8. P. 413-418.
195. Johnson K.L., Greenwood J.A. An adhesian map for the contact
or elastic spheres // J. Colloid and Interface Sci. 1997. Vol. 192.
P. 326-333.
196. Johnson K.L., Greenwood J.A., Higginson J. G. The contact of elastic
wavy surfaces // Intern. J. Mech. Sci. 1985. Vol.27, N6. P. 383-
396.
197. Johnson K.L., Kendall K., Roberts A.D. Surface energy and the
contact of elastic solids//Proc. Roy. Soc. London A. 1971. Vol.324.
P. 301-313.
198. Kalker J.J. Three-dimensional elastic bodies in rolling contact. Dor-
Dordrecht etc.: Kluwer, 1990. 314 p.
199. Kalker J.J. Viscoelastic multilayered cylinders rolling with dry fric-
friction // ASME. J. Appl. Mech. 1991. Vol58. P. 666-679.
200. Kendall K., Tabor D. An ultrasonic study of the area of contact be-
between stationary and sliding surfaces // Proc. Roy. Soc, London A.
1971. Vol.323. P.321-340.
201. Кио С.Н., Keer L.M. Contact stress analysis of a layered transversely
isotropic half-space // ASME. J. Tribol. Vol.114, N2. P. 253-262.
202. Kuznetsov Ye.A., Gorokhovsky G.A. Stress distribution in a poly-
polymeric material subjected to the action of a rough-surface indenter //
Wear. 1978. Vol.51. P.299-308.
203. Ling F.F., Lai W.M. Surface mechanics of layered media // Solid
contact and lubrication / Ed. H.S.Cheng and L.M.Keer. N. Y.:
ASME, 1980. N39. P. 27-50.
204. Liu C.C., Met P.B. Stiction at the Winchester head-disk interface //
IEEE Trans. Magnetics. 1983. Vol.19, N5. P. 1659-1661.
471
205. Lubrecht A.A. Ioannides E. A fast solution of dry contact prob-
problem and the associated subsurface stress field, using multilevel tech-
techniques // ASME. J. Tribol. 1991. Vol. 113. P. 128-133.
206. Majumdar A., Bhushan B. Role of fractal geometry in characteri-
characterization and contact mechanics of surfaces // Ibid. 1990. Vol. 112.
P. 205-216.
207. Majumdar A., Bhushan B. Fractal model of elasto-plastic contact
between rough surfaces // Ibid. 1991. Vol. 113. P. 1-11.
208. Makhovskaya Yu.Yu., Goryacheva I.G. The combined effect of cap-
capillarity and elasticity in contact interaction // Tribol. Intern. 1999.
V.32. P. 507-515.
209. Mao K., Bell Т., Sun Y. Effect of sliding friction on contact stresses
for multi-layered elastic bodies with rough surfaces // ASME. J. Tri-
Tribol. 1997. Vol.119, P. 476-480.
210. Matthewson M.J., Mamin H.J. Liquid mediated adhesion of ultra-
flat solid surfaces // Mater. Res. Soc. Symp. Proc. 1988. Vol.119.
P. 87-92.
211. Maugis D. Adhesion of spheres: The JKR-DMT transition using
a Dugdale model // J. Colloid and Interface Sci. 1991. Vol. 150.
P. 243-269.
212. Maugis D. On the contact and adhesion of rough surface // J. Ad-
Adhesion Sci. and Technol. 1996. Vol. 10. P. 161-175.
213. McCool J.I. Comparison of models for the contact of rough sur-
surfaces // Wear. 1986. Vol. 107. P. 37-60.
214. Mencik J. Mechanics of components with treated or coated surfaces.
Dordrecht etc.: Kluwer, 1996. 360 p.
215. Meng H.C., Ludema K.C. Wear models and predictive equations:
their form and content // Wear. 1995. Vol. 181/183. P. 443-457.
216. Molgaard J., Czichos H. The application of systems techniques tc
the study of wear // ASME. Wear of Materials. 1977. P. 30-35.
217. Moore D.F. Principles and applications of tribology. L.: Pergamon
1975.
472
218. Morland L. W. A plane problem of rolling contact in linear viscoelas-
ticity theory // ASME, J. Appl. Mech. E. 1962. Vol.29, N2.
P. 345-352.
219. Muller V.M., Yushchenko V.S., Derjagin B.V. On the influence of
molecular forces on the deformation of an elastic sphere and its stick-
sticking to a rigid plane // J. Colloid and Interface Sci. 1980. Vol. 77,
N11. P. 91-101.
220. Nayak P.R. Random process model of rough surfaces // ASME.
J. Lubr. Techn. Trans. F. 1971. Vol. 93. P. 398.
221. Nogi Т., Koto T. Influence of a hard surface layer on the limit of
elastic contact. 1. Analysis using a real surface model // ASME.
J. Tribol. 1997. Vol.119. P. 493-500.
222. Rabinowicz E. Friction and wear of materials. N. Y.: Wiley, 1965.
244 p.
223. Reynolds 0. On rolling friction // Philos. Trans. Roy. Soc. Lon-
London A. 1875. Vol. 166. P. 155-175.
224. Sainsot Ph., Leroy J.M., Villechase B. Effect of surface coating in
a rough normally loaded contact // Mech. Coating. Tribology Ser.
1990. N17. P. 151-156.
225. Sanchez-Palensia E. Non-homogeneous media and vibration theory.
N. Y.: Springer, 1980.
226. Seabra J., Berthe D. Influence of surface waviness and roughness on
the normal pressure distribution in the Hertzian contact // ASME.
J. Tribol. 1987. Vol.109, N3. p. 462-470.
227. Seal M. Friction and wear of diamond // Conf. Lubr. and Wear.
1957. N12. P. 252-256.
228. Sikarskie D.L., Altiero N.J. The formation of chips in the penetration
of elastic-brittle materials (rock) // J. Appl. Mech. E. 1973. Vol.40,
N3. P. 791-798.
229. Stanley H.M., Kato T. An FTT-based method for rough surface
contact // ASME. J. Tribol. 1997. Vol. 119. P. 481-485.
230. Sui P.C., Sadeghi F. Non-Newtonian thermal elastohydrodynamic
lubrication // Ibid. 1991. Vol.113. P. 390-397.
473
231. Tabor D. The mechanism of rolling friction // Philos. Mag. Ser. 7.
1952. Vol.43, P.345.
232. Tabor D. The mechanism of rolling friction: the elastic range //
Proc. Roy. Soc. London A. 1955. Vol. 229. P. 198.
233. Tabor D. Surface forces and surface interactions // J. Colloid and
Interface Sci. 1977. Vol.58, N1. P.2-13.
234. Tabor D., Wynne W. The effect of orientation on friction of polyte-
trafiuoroethylene // Wear. 1961. Vol.4, N5. P.391-400.
235. Thomas T. Rough surfaces. 2-nd ed. London: Imperial College press.
1999. 296 p.
236. Tian H., Matsudaira T. Effect of relative humidity on friction be-
behavior of the head/disk interface // IEEE Trans. Magnetics. 1992.
Vol. 28, N 5, pt 2. P. 2530-2532.
237. Tomlinson J.A. A molecular theory of friction // Philos. Mag. Ser. 7.
1929. Vol. 46. P. 905-939.
238. Venner C.H., Lubrecht A.A. Numerical analysis of the influence of
waviness on the flat thickness of a circular EHL contact // ASME.
J. Tribol. 1996. Vol. 118.. P. 153-161.
239. Westergaard EM. Bearing pressure and cracks // ASME. J. Appl.
Mech. E. 1939. Vol.6, N1. P.49-53.
240. Zmitrovicz A. Liniowe i nieliniove rownania konstytutywne tarcia
anizotropowego // Zesz. Nauk. Akad. Gorniczo-Hutniczei. Me-
chanica. 1990. T.9, N2. S. 141-154.
ОГЛАВЛЕНИЕ
Предисловие 3
Введение 5
1. Механика дискретного контакта 9
1.1. Задача дискретного контакта 9
1.2. Периодические контактные задачи и метод лока-
локализации 18
1.3. Задача с ограниченной номинальной областью
контакта 36
1.4. Функция дополнительного смещения 55
1.5. Расчёт контактных характеристик с учётом пара-
параметров макро- и микрогеометрии поверхностей . . 62
2. Адгезионное взаимодействие упругих тел 78
2.1. Виды адгезионного взаимодействия 78
2.2. Капиллярная адгезия 81
2.3. Адгезия сухих поверхностей 97
2.4. Диссипация энергии в цикле сближение - удаление
поверхностей 101
2.5. Анализ упрощённых моделей 107
2.6. Адгезионное взаимодействие шероховатых тел . . 111
2.7. Адгезионное сопротивление при качении 127
3. Трение при контактном взаимодействии 131
3.1. Адгезионная и механическая составляющие силы
трения 132
3.2. Трение при скольжении упругих тел 135
3.3. Трение при скольжении вязкоупругих тел 153
3.4. Трение при качении упругих и вязкоупругих тел . 163
3.5. Расчёт механической составляющей силы трения 174
475
3.6. Контакт упругих тел в условиях частичного про-
проскальзывания 180
4. Контакт неоднородных тел и тел с покрытиями 204
4.1. Метод анализа напряжений в упругих телах, име-
имеющих внутренние дефекты 205
4.2. Напряжённое состояние упругих тел с покрытия-
покрытиями при разных видах нагружения 218
5. Роль тонких поверхностных слоев при трении . 245
5.1. Контакт качения и скольжения 245
5.2. Скольжение шероховатых тел 263
5.3. Контакт качения со смазкой 284
5.4. Контакт качения в условиях ограниченной смазки 297
6. Модели изнашивания 310
6.1. Износ как специфический вид разрушения 310
6.2. Подходы к моделированию изнашивания 318
6.3. Модель отслаивания при усталостном изнашивании 324
6.4. Изнашивание шероховатых поверхностей 342
7. Износоконтактные задачи 354
7.1. Уравнение износа 354
7.2. Постановка износоконтактной задачи 361
7.3. Износоконтактные задачи типа Л 367
7.4. Контактные задачи для упругого полупространства372
7.5. Изнашивание тонкого упругого слоя 385
7.6. Износоконтактные задачи типа В 392
7.7. Задачи с изменяющейся площадкой контакта . . . 396
8. Изнашивание неоднородных тел 403
8.1. Изнашивание тел с переменным коэффициентом
износа 403
8.2. Изнашивание в дискретном контакте 423
8.3. Задачи управления процессом изнашивания .... 440
Заключение 450
Summary 453
Литература 456
CONTENTS
Preface 3
Introduction 5
1. Mechanics of Discrete Contact 9
1.1. Discrete contact problem 9
1.2. Periodic contact problem and principle of localization 18
1.3. Problem with a bounded nominal contact region . . 36
1.4. The additional displacement function 55
1.5. Calculation of contact characteristics taking into ac-
account surface macro- and microgeometry parameters 62
2. Adhesion of Elastic Bodies 78
2.1. Nature of adhesion 78
2.2. Capillary adhesion 81
2.3. Adhesion of dry surfaces 97
2.4. Energy dissipation in the approach - separation cycle 101
2.5. Analysis of simplified models 107
2.6. Adhesion of rough surfaces Ill
2.7. Adhesion resistance in rolling contact 127
3. Friction in Contact Interaction 131
3.1. Adhesive and mechanical components of friction force 132
3.2. Friction in sliding contact of elastic bodies 135
3.3. Friction in sliding contact of viscoelastic bodies . . . 153
3.4. Friction in rolling contact of elastic and viscoelastic
bodies 163
3.5. Calculation of the mechanical component of friction
force 174
3.6. Contact of elastic bodies under partial slip conditions 180
477
4. Contact of Inhomogeneous and Coated Bodies . . . 204
4.1. Method of the analysis of stresses in elastic bodies
with internal defects 205
4.2. Stress state of coated elastic bodies under various
loading conditions 218
5. Effect of Thin Surface Layers in Friction Interaction245
5.1. Sliding/rolling contact 245
5.2. Sliding contact of rough bodies 263
5.3. Lubricated rolling contact 284
5.4. Lubricated rolling contact under the condition of lim-
limited flow rate 297
6. Wear Models 310
6.1. Wear as a special form of fracture 310
6.2. Approaches to wear modelling 318
6.3. The model of delamination in fatigue wear 324
6.4. Wear of rough surfaces 342
7. Wear Contact Problems 354
7.1. Wear equation 354
7.2. Formulation of the wear contact problem 361
7.3. Wear contact problems of type Л 367
7.4. Contact problems for an elastic half-space 372
7.5. Wear of a thin elastic layer 385
7.6. Wear contact problems of type В 392
7.7. Problems with a time-dependent contact region . . . 396
8. Wear of Inhomogeneous Bodies 403
8.1. Wear of bodies with variable wear coefficient .... 403
8.2. Wear in discrete contact 423
8.3. Control of the wear process 440
Conclusion 450
Summary 453
Bibliography 456
Горячева Ирина Георгиевна
МЕХАНИКА ФРИКЦИОННОГО
ВЗАИМОДЕЙСТВИЯ
Зав. редакцией Р.С. Головина
Редактор Г.П. Панова
Художник Е.А. Быкова
Художественный редактор Т.В. Болотина
Оригинал-макет подготовлен А.П. Горячевым
ЛР № 020297 от 23.06.1997
Налоговая льгота -
общероссийский классификатор продукции
ОК-005-93, том 2; 953000 - книги, брошюры
Подписано к печати 19.11.2001
Формат 60 х 90'/]б- Гарнитура Тайме
Печать офсетная
Усл.печ.л. 30,0. Усл.кр.-отт. 30,0. Уч.-изд.л. 26,7
Тип. зак. 4470
Издательство "Наука"
117997 ГСП-7, Москва В-485, Профсоюзная ул., 90
E-mail:secret@naukar an.ru
Internet: www.naukaran.ru
Санкт-Петербургская типография "Наука"
199034, Санкт-Петербург В-34,9-я линия, 12
ISBN 5-02-002567-4
III
785020»025677