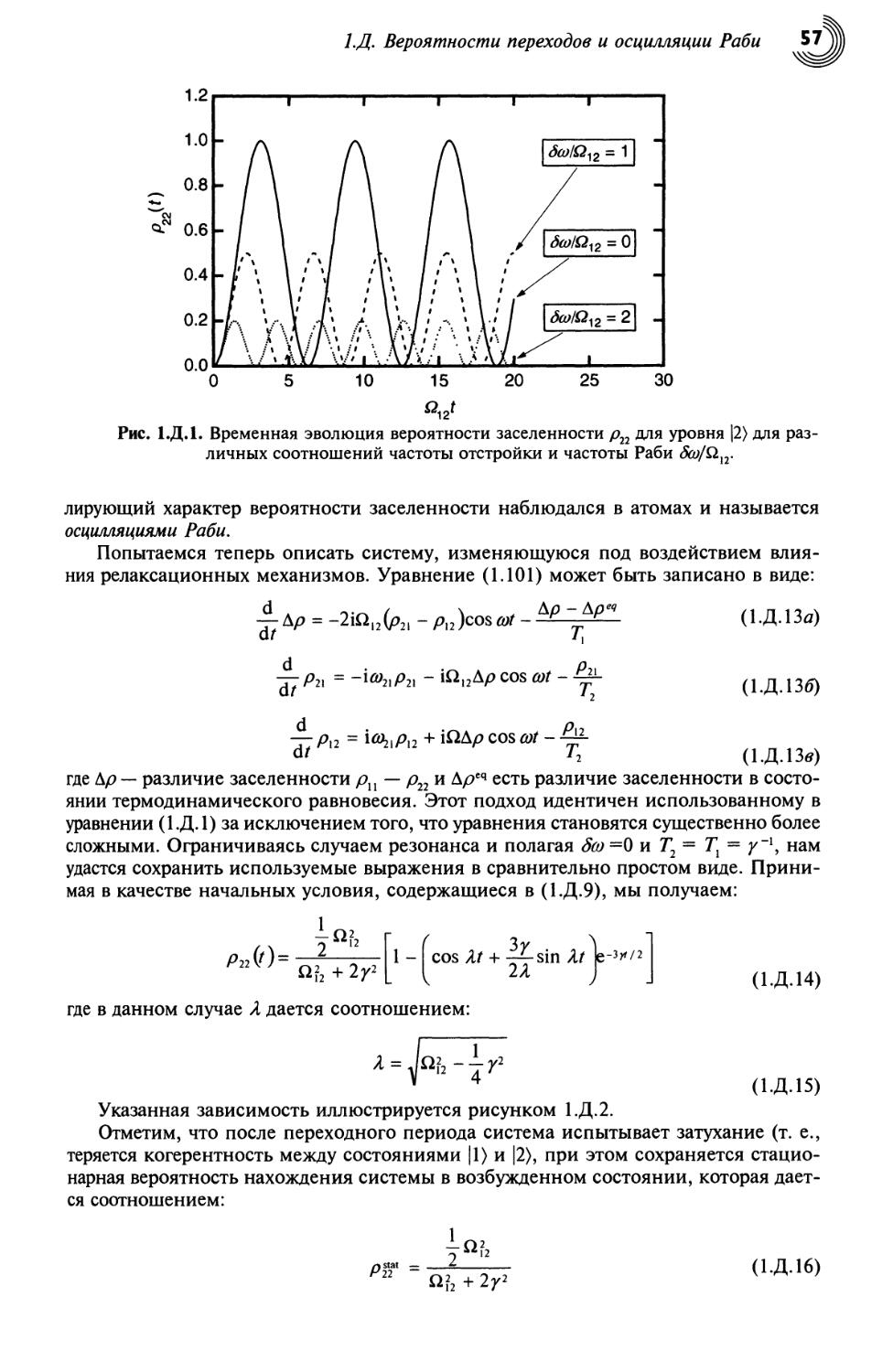
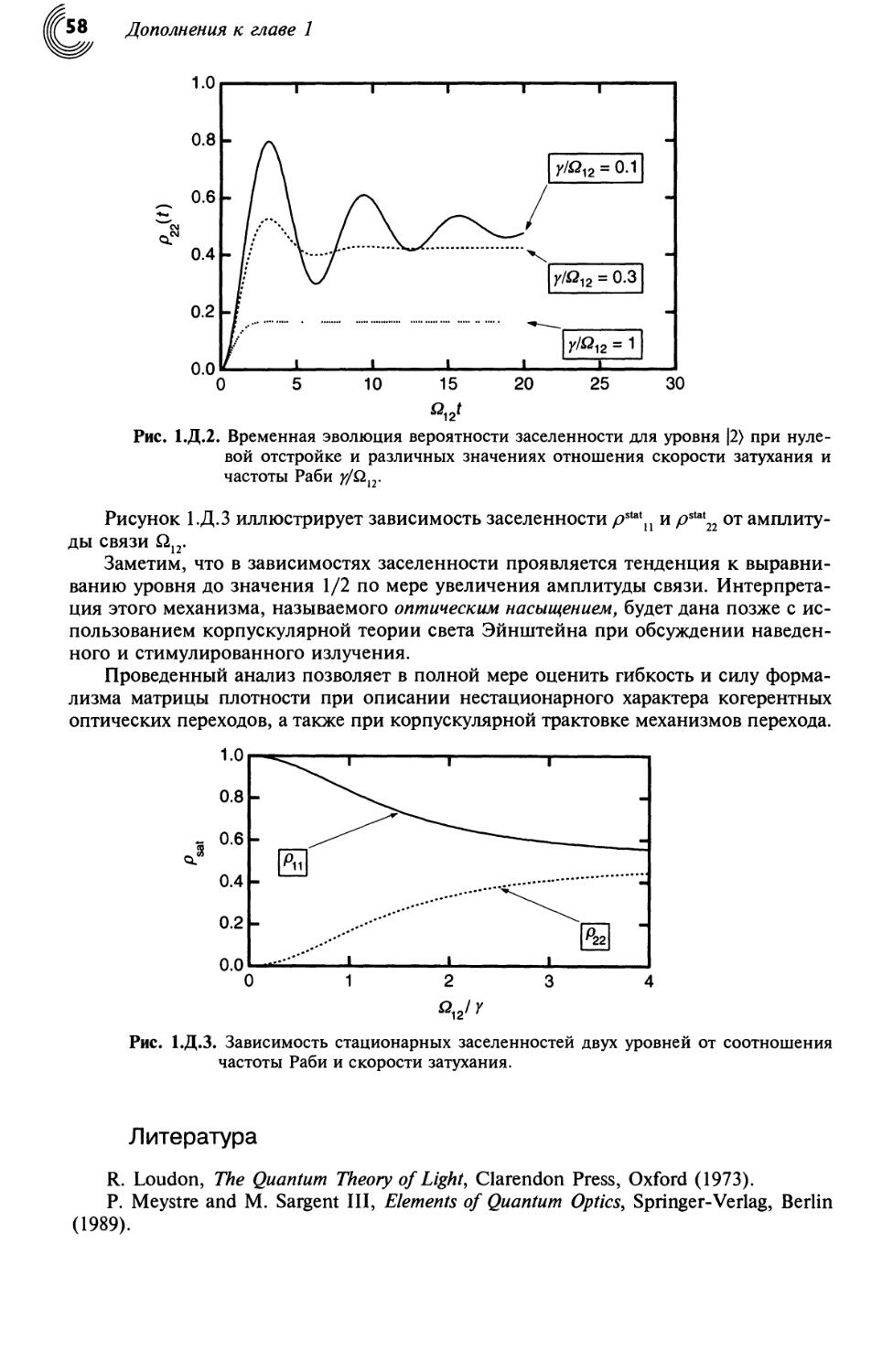
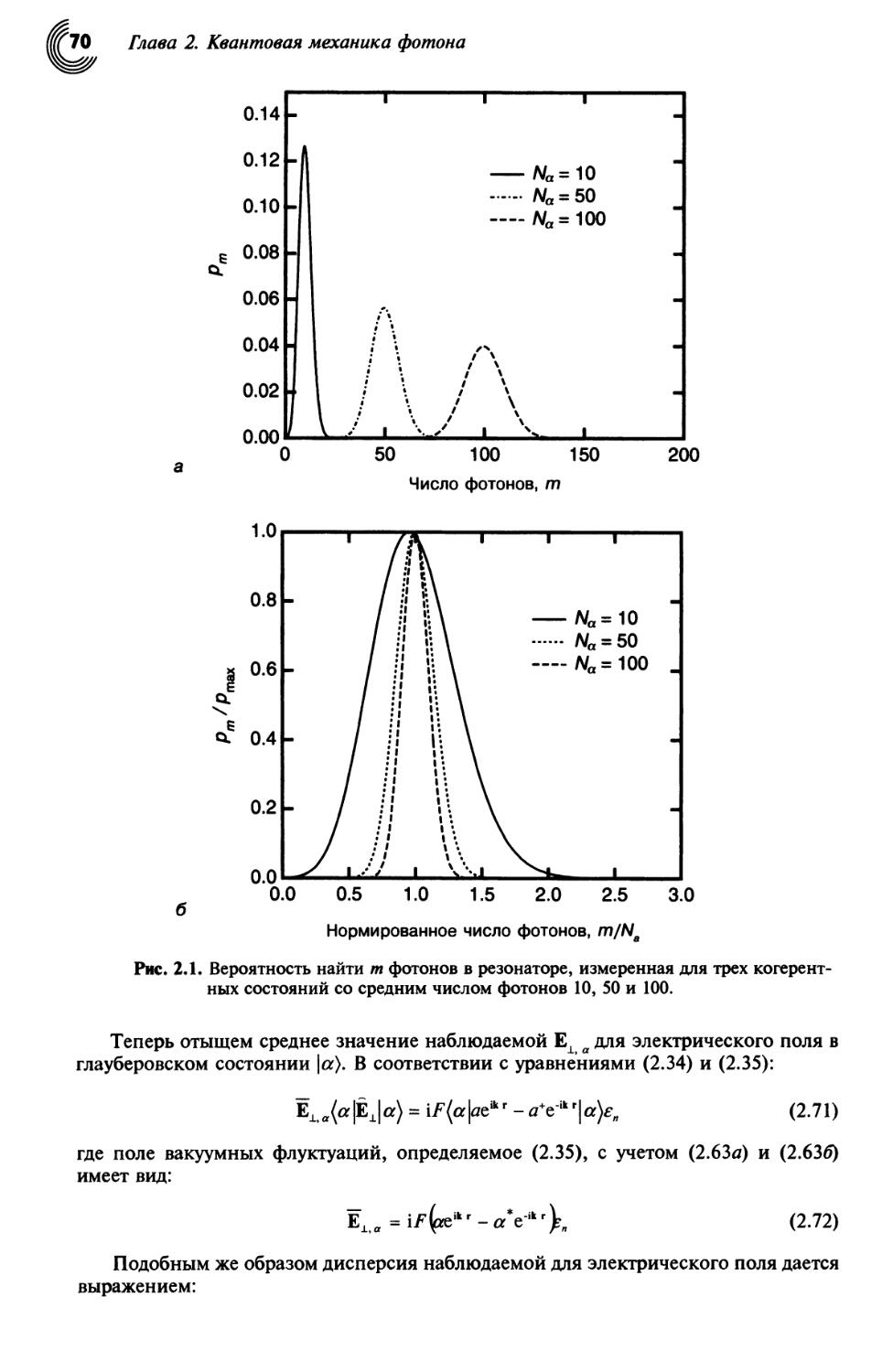
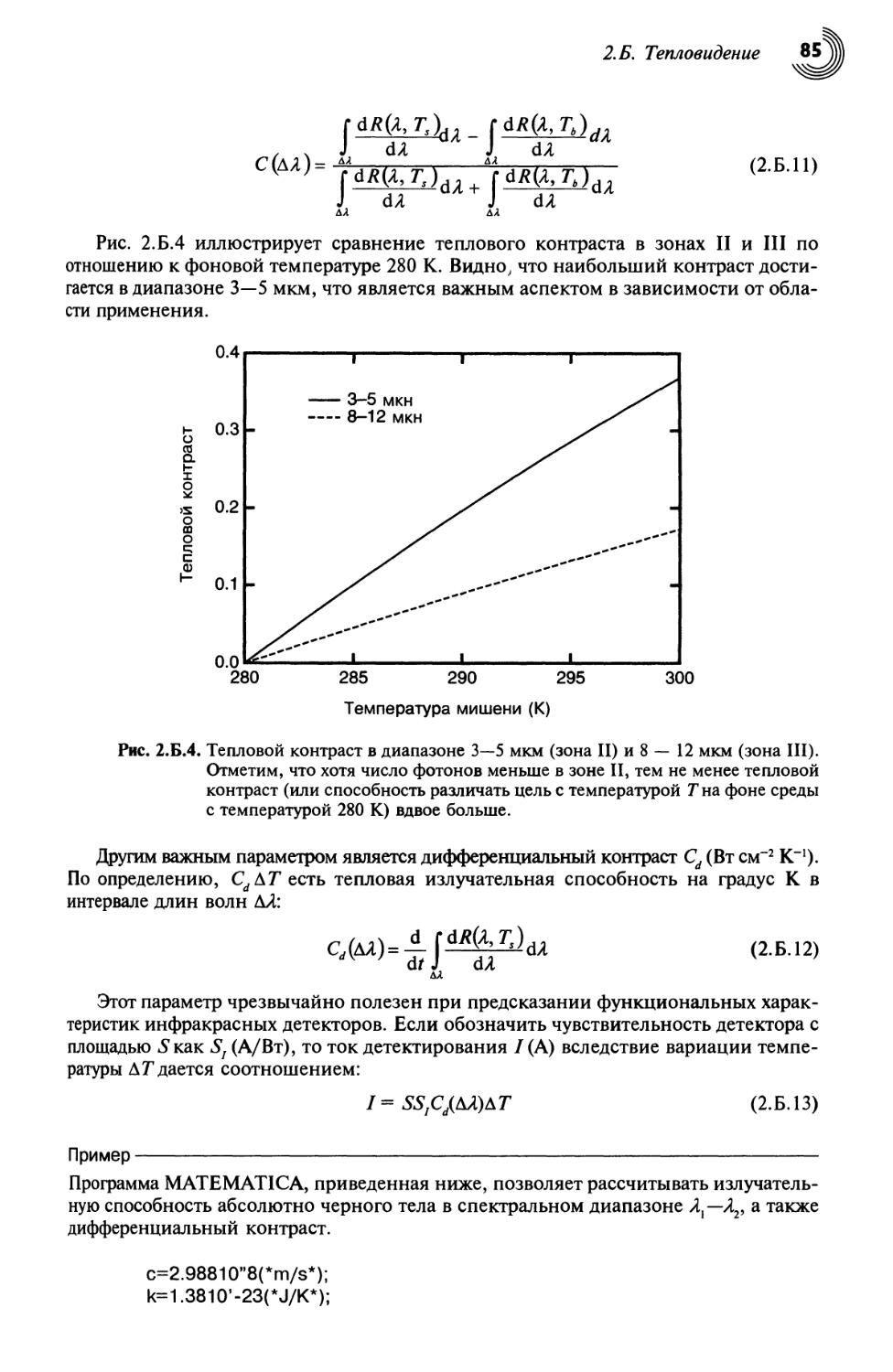
Текст
МИР
электроники
Э. РОЗЕНШЕР, Б. ВИНТЕР
Оптоэлектроника
Перевод с французского
под редакцией О.Н. Ермакова
ТЕХНОСФЕРА
Москва
2004
Э. Розеншер, Б. Винтер
Оптоэлектроника
Москва:
Техносфера, 2004. - 592 с. ISBN 5-94836-031-8
Перевод 2-го издания наиболее полной монографии по физическим
основам оптоэлектроники и ее применениям. Описаны принципы
функционирования основных оптоэлектронных приборов (свето-
излучающие диоды, квантово-размерные лазеры, фотоприемники,
устройства нелинейной оптики и т.д.). Рассмотрены такие
фундаментальные для понимания физики работы приборов темы, как квантовая
механика электрон-фотонного взаимодействия, квантование
электромагнитного поля, особенности электрон-фононного взаимодействия,
квантовая теория гетероструктур, нелинейная оптика и др. Все это делает
книгу незаменимым пособием для аспирантов, научных работников,
инженеров-разработчиков.
OPTOELECTRONIQUE
Cours et exercices corriges
Emmanuel Rosenctur
Oir«ctrtut dt rechtrch»» t rONERA.
Pfo(«««ui к rtcot» Potytichnqut
BorgeVmtv
Ingirucur ie rechtrchM chw THAUS
EnfegiwntKunivwut»
it У»г«.Ш« Stnt-Qutotin en Yvthnet
2* edition revue et corngee
DUNOD
© 2002, Dunod, Paris
© Masson, 1998 pour la premiere edition
© 2004, ЗАО «РИЦ «Техносфера»
перевод на русский язык, оригинал-
макет, оформление.
ISBN 5-94836-031-8
ISBN 2 10 005453 8 (франц.)
Содержание
Предисловие редактора 10
ГЛАВА 1. КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОНА 14
1.1. Введение 14
1.2. Постулаты квантовой механики 14
1.3. Стационарное уравнение Шредингера 18
1.3.1. Стационарные состояния 18
1.3.2. Расчет стационарных состояний для одномерного потенциала 19
1.4. Квантовая яма 20
1.4.1. Общий случай 20
1.4.2. Бесконечная потенциальная яма квадратного профиля 25
1.5. Стационарная теория возмущений 26
1.6. Нестационарные возмущения и вероятности переходов 28
1.6.1. Общий случай 28
1.6.2. Синусоидальное возмущение 30
1.7. Матрица плотности 33
1.7.1. Чисто квантовые ансамбли 33
1.7.2. Смешанные квантовые ансамбли 34
1.7.3. Матрица плотности и время релаксации для двухуровневой системы 35
ДОПОЛНЕНИЯ К ГЛАВЕ 1 37
1.А. Проблемы, накладываемые континуумом: виртуальный квантовый
ящик и плотность состояний 37
1.Б. Возмущение вырожденного состояния 40
1.8. Квантово-размерный эффект Штарка 44
1.Г. Гармонический осциллятор 47
1.Д. Вероятности переходов и осцилляции Раби 55
ГЛАВА 2. КВАНТОВАЯ МЕХАНИКА ФОТОНА 59
2.1. Введение , 59
2.2. Уравнения Максвелла в обратном пространстве 59
2.3. Свойства преобразования Фурье 60
2.4. Квантование электромагнитных волн 63
2.5. Фотон 65
2.6. Когерентное состояние 68
2.7. Излучение черного тела 72
Оптоэлектроника
ДОПОЛНЕНИЯ К ГЛАВЕ 2 75
2.А. Поле излучения осциллирующего заряда: калибровка Лоренца 75
2.Б. Тепловидение 81
ГЛАВА 3. КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОН-ФОТОННОГО
ВЗАИМОДЕЙСТВИЯ 87
3.1. Введение 87
3.2. Гамильтониан дипольного взаимодействия для электронов и дырок 87
3.3. Линейная оптическая восприимчивость в приближении матрицы
плотности 89
3.4. Линейная оптическая восприимчивость: поглощение и оптическое
усиление 91
3.5. Скоростные уравнения 94
3.5.1. Адиабатическая аппроксимация и корпускулярная интерпретация 94
3.5.2. Стимулированное излучение 95
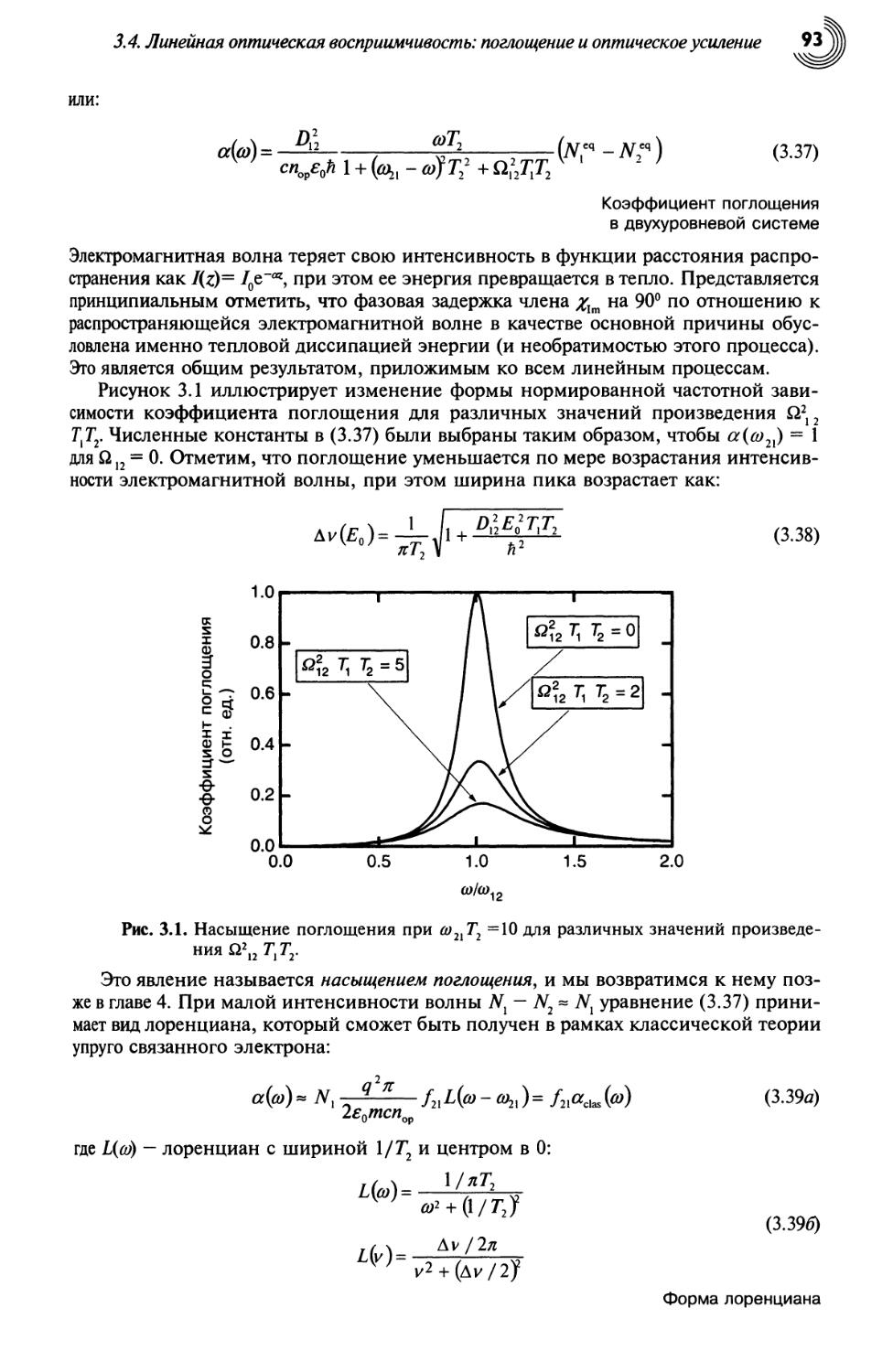
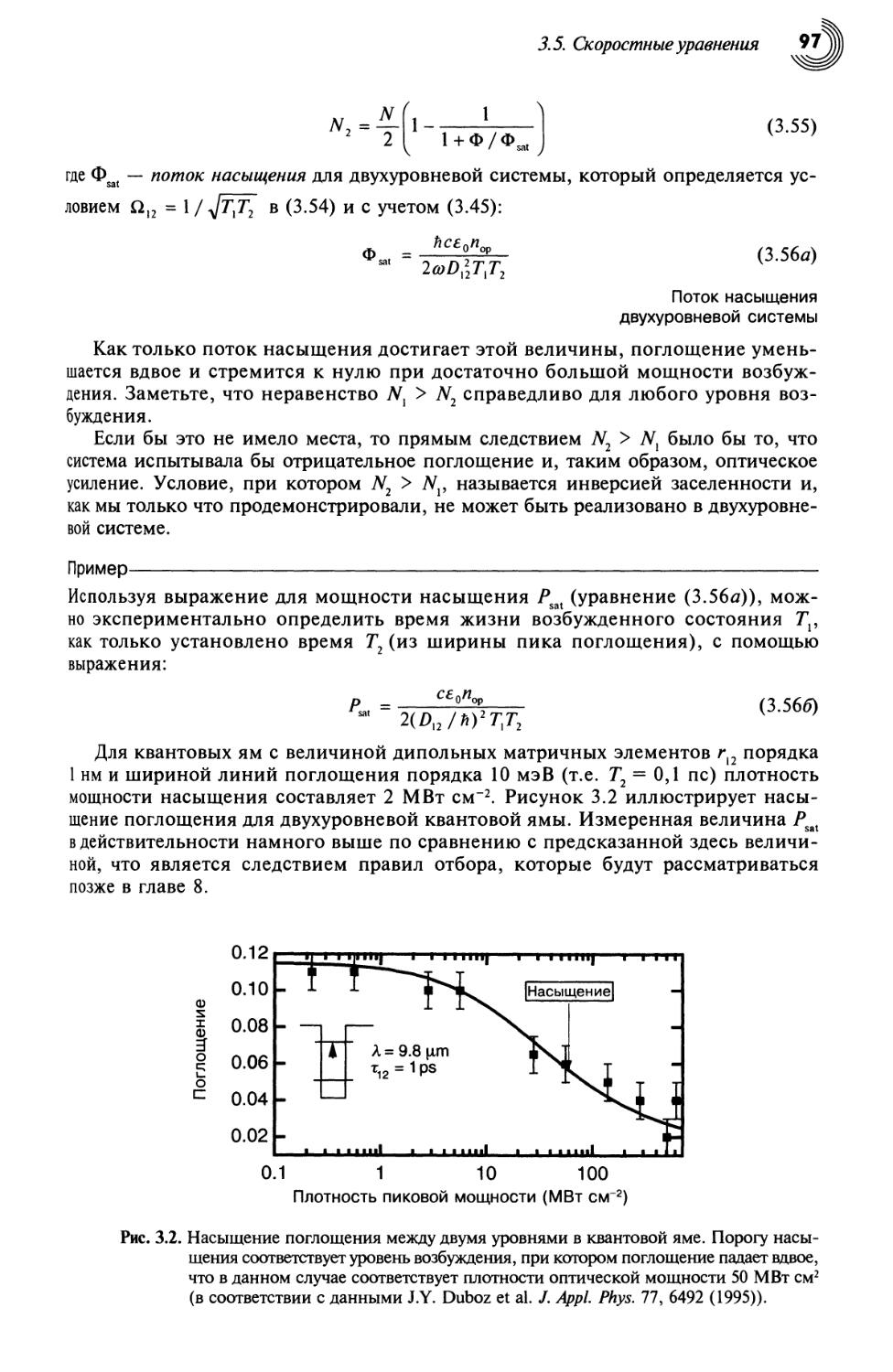
3.5.3. Насыщение поглощения 96
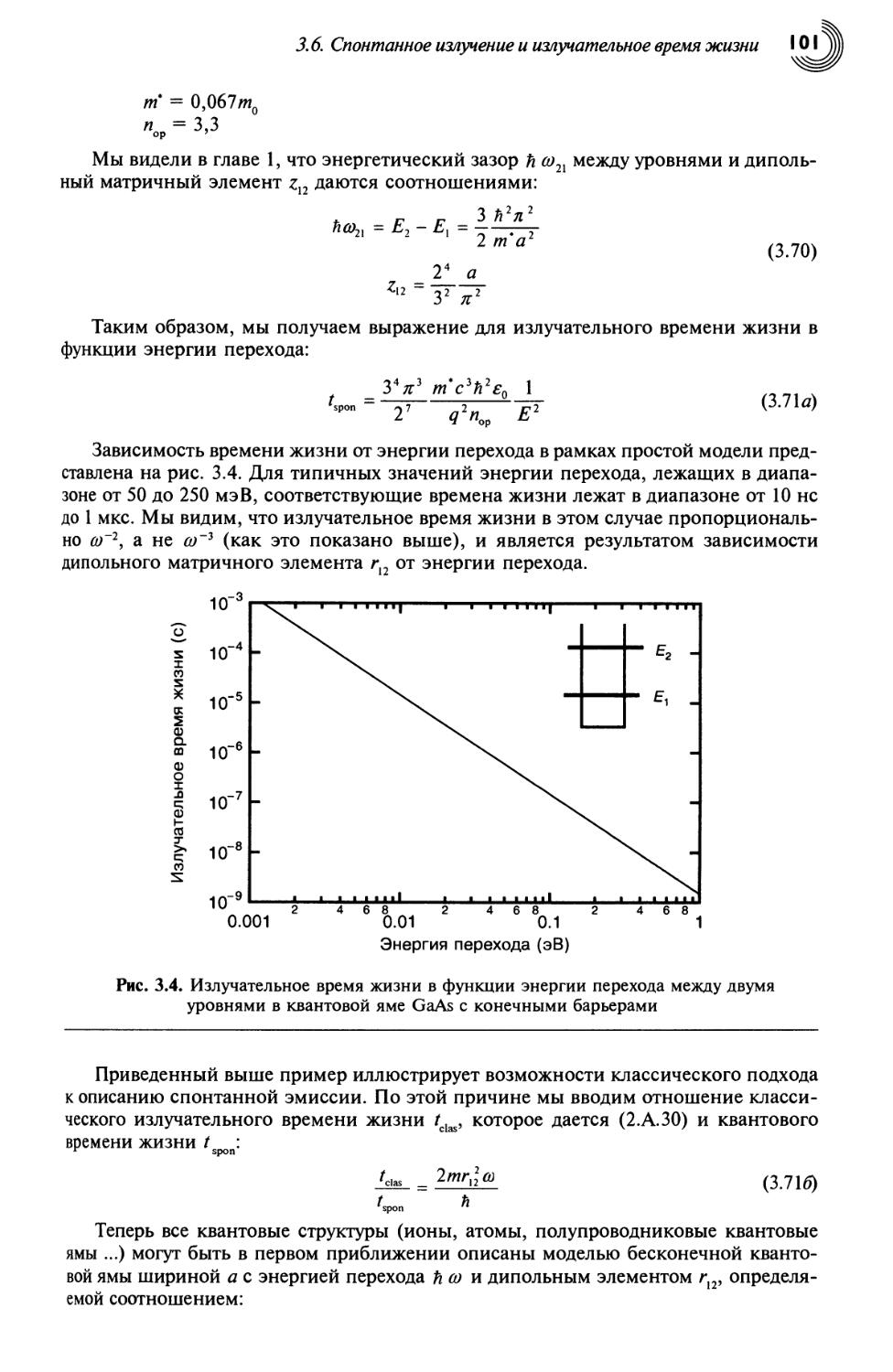
3.6. Спонтанное излучение и излучательное время жизни 98
3.6.1. Спонтанное излучение 98
3.6.2. Скоростные уравнения с учетом спонтанного излучения 102
3.7. Полихроматические переходы 103
3.8. Повторное рассмотрение скоростных уравнений 104
3.8.1. Монохроматические одномодовые волны 104
3.8.2. Многомодовые монохроматические волны 105
3.8.3. Полихроматические волны 105
ДОПОЛНЕНИЯ К ГЛАВЕ 3 107
З.А. Однородное и неоднородное уширение: когерентность света 107
З.А.1. Однородное уширение 107
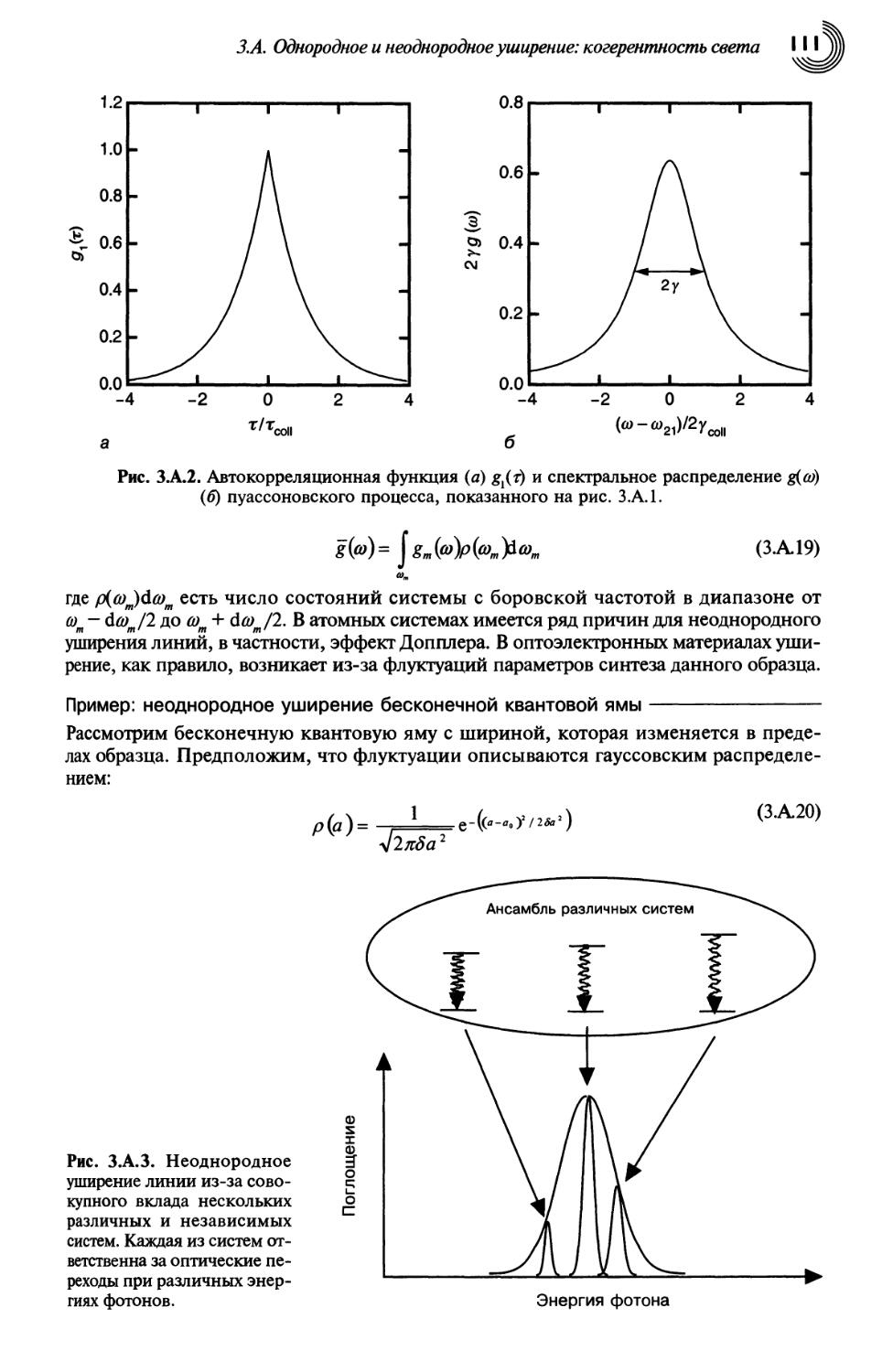
З.А.2. Неоднородное уширение НО
З.Б. Нестационарные возмущения второго порядка ИЗ
З.В. Коэффициенты Эйнштейна для двух предельных случаев:
квазимонохроматических и широкополосных оптических переходов 119
З.Г. Эквивалентность Ар- и DA- гамильтонианов и правило
Томаса—Райха—Куна 121
ГЛАВА 4. ЛАЗЕРНЫЕ КОЛЕБАНИЯ 125
4.1. Введение 125
4.2. Инверсия заселенности и оптическое усиление 125
4.2.1. Инверсия заселенности 125
4.2.2. Оптическое усиление и насыщение усиления 126
4.3. Трех-четырехуровневые системы 129
4.4. Оптические резонаторы и порог лазерной генерации 131
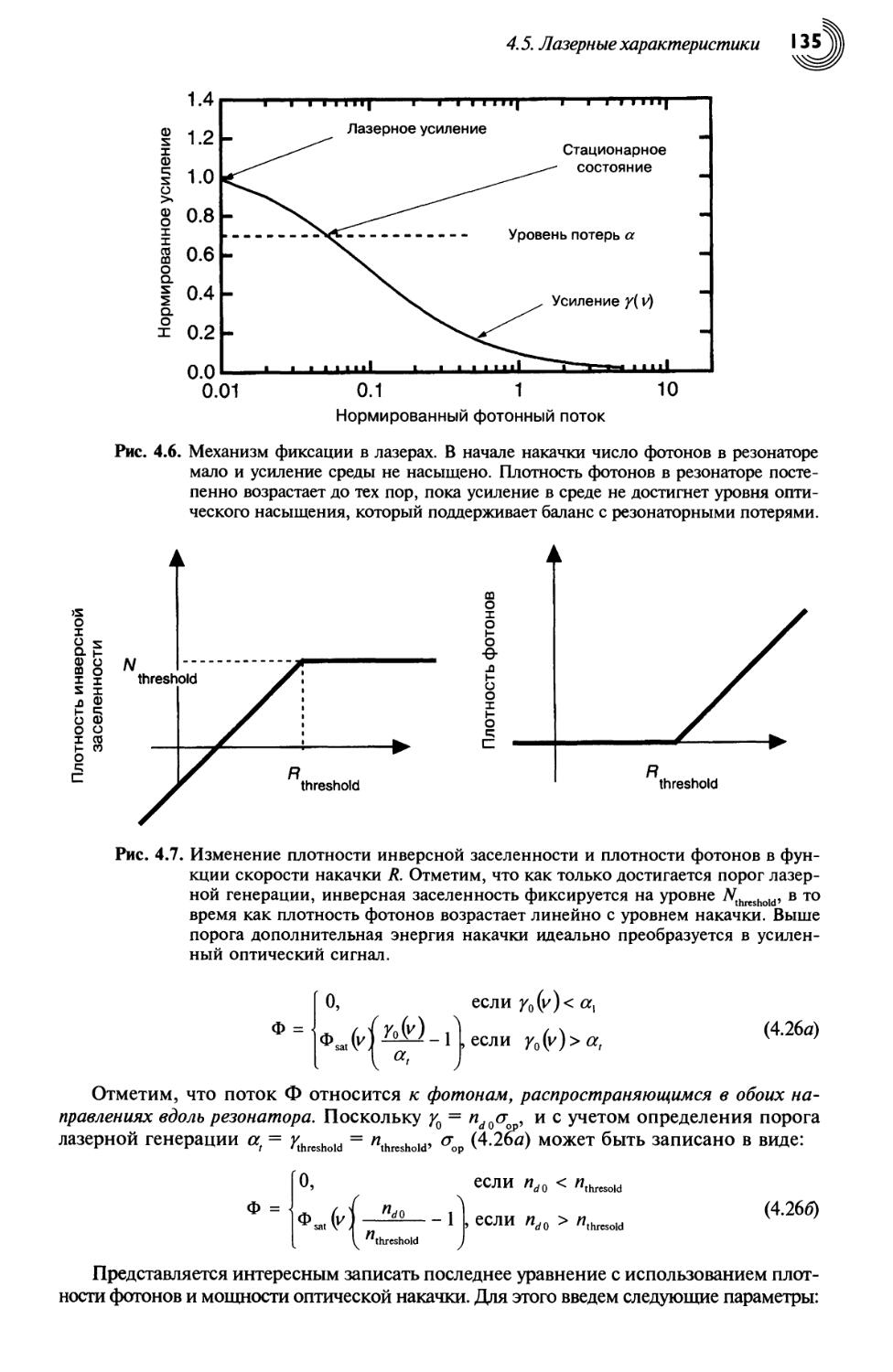
4.5. Лазерные характеристики 134
4.5.1. Внутренние лазерные характеристики и фиксация усиления 134
4.5.2. Выходная мощность 136
4.5.3. Спектральные характеристики 137
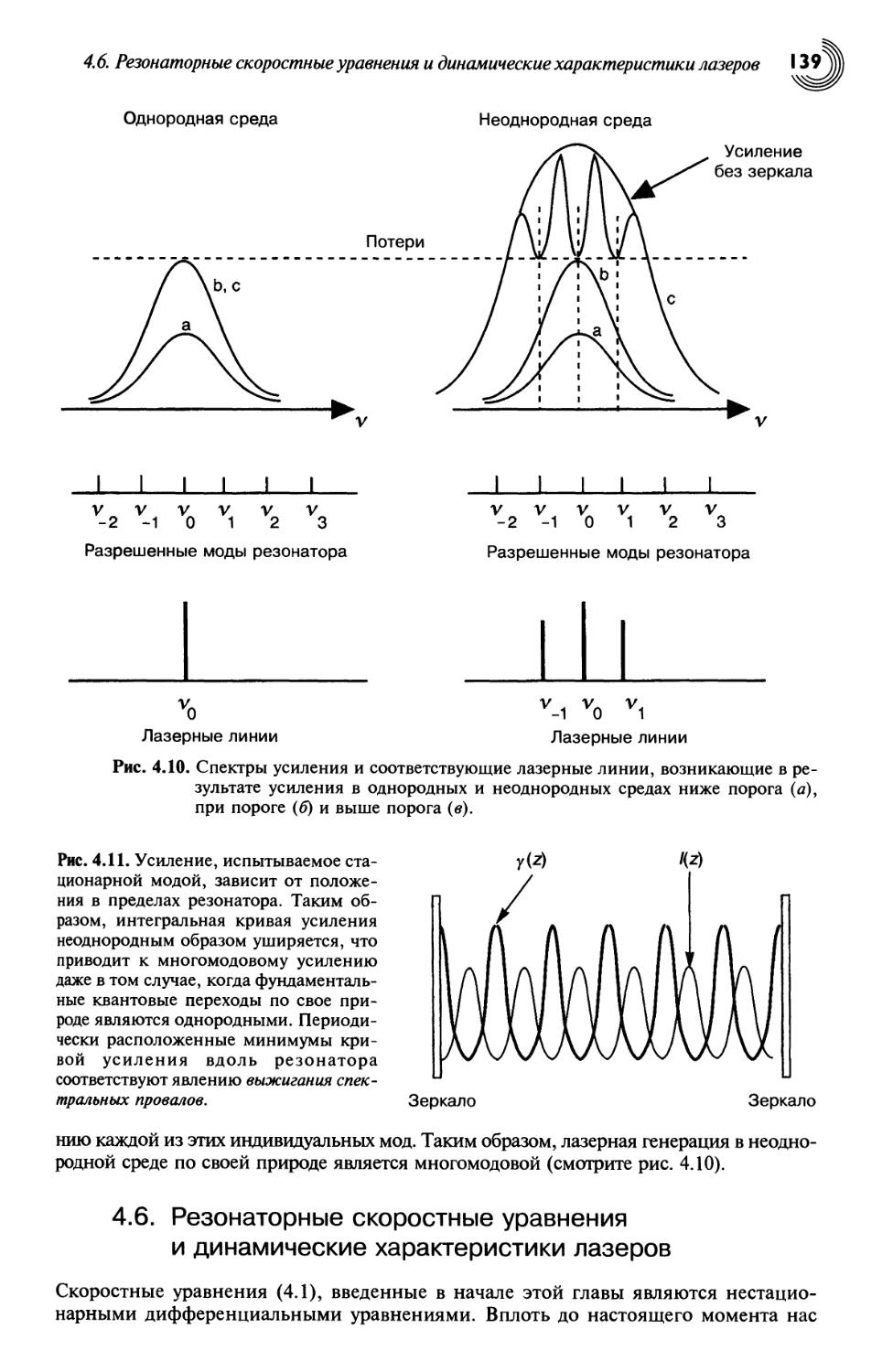
4.6. Резонаторные скоростные уравнения и динамические характеристики
лазеров 139
Оптоэлектроника
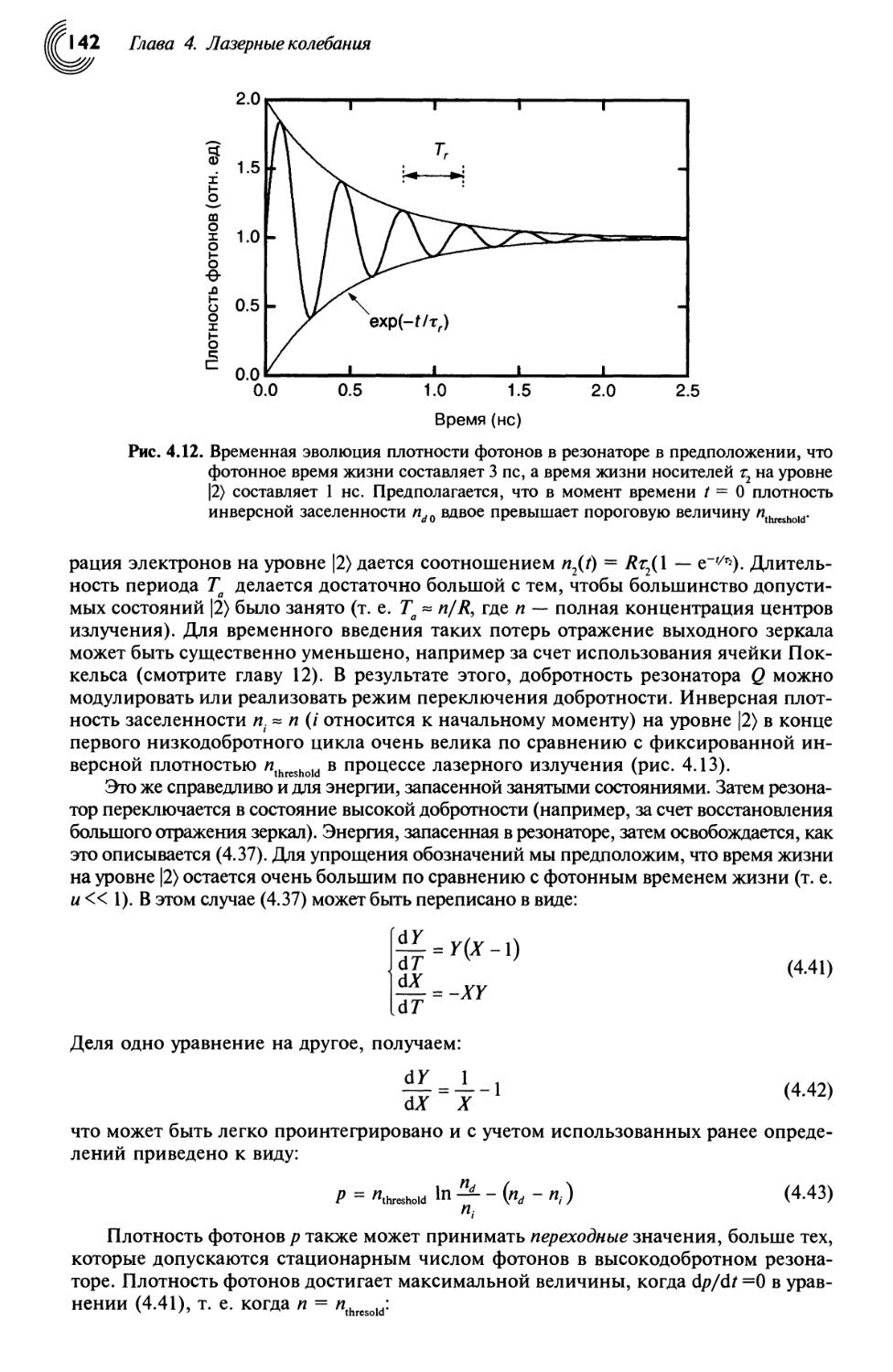
4.6.1. Демпфированные колебания 140
4.6.2. Демпфирование лазерного резонатора модуляцией потерь (переключение
добротности) 141
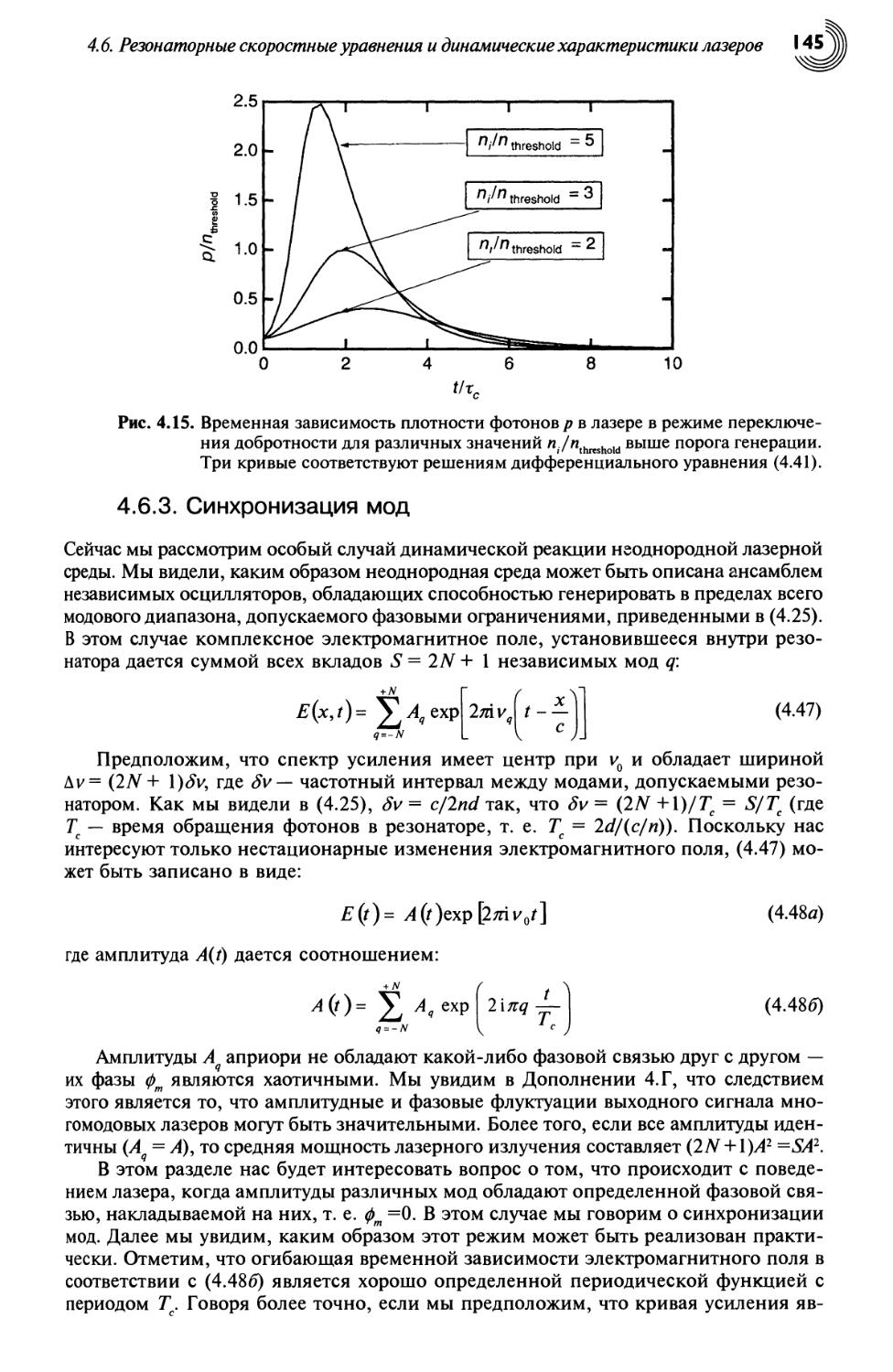
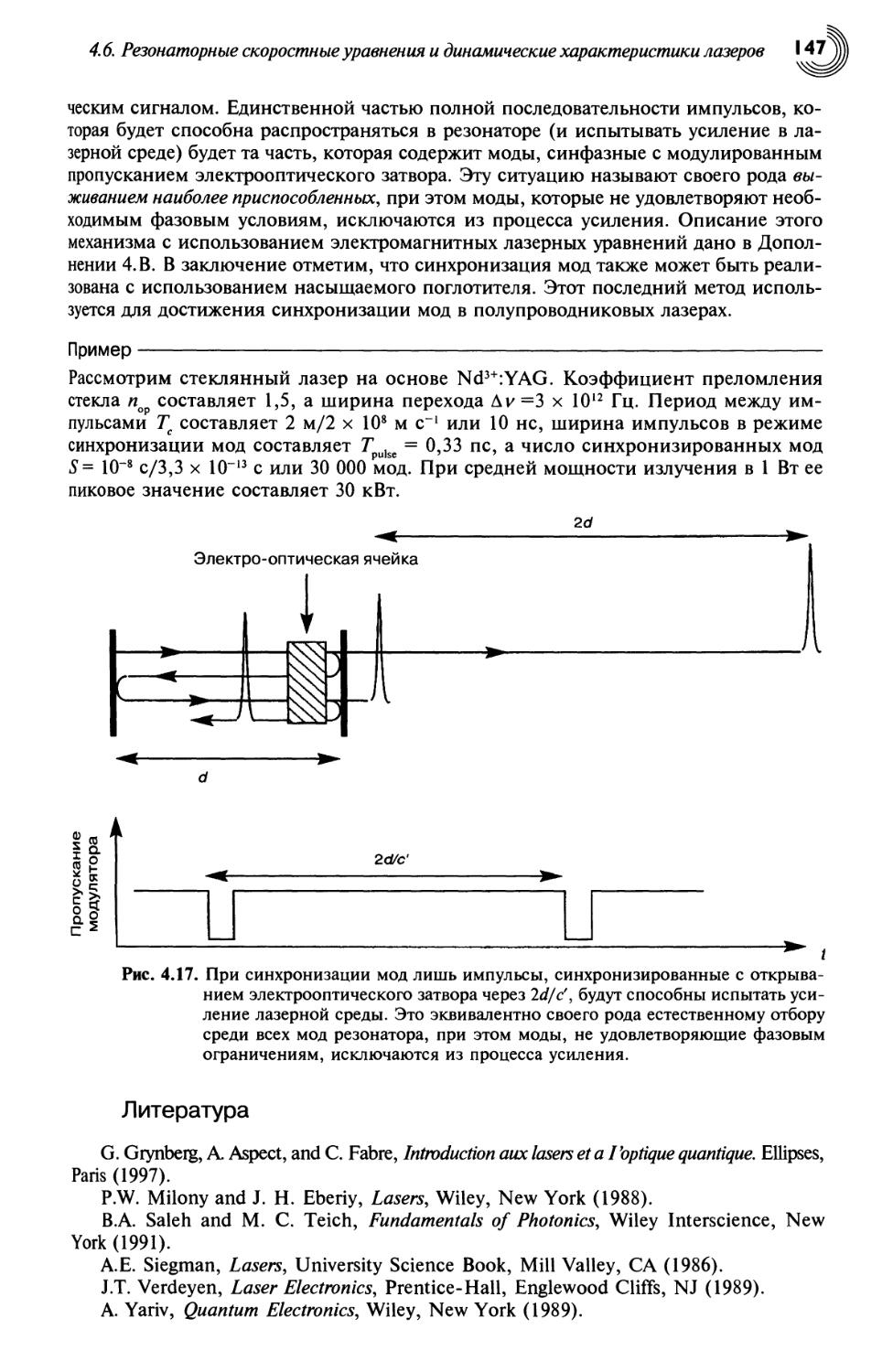
4.6.3. Синхронизация мод 145
ДОПОЛНЕНИЯ К ГЛАВЕ 4 148
4.А. Эффект спонтанной эмиссии и фотонная конденсация 148
4.Б. Насыщение в лазерных усилителях 151
4.В. Электродинамические лазерные уравнения: электромагнитные основы
синхронизации мод 157
4. Г. Предел Шавлова—Таунса и сила ланжевеновского шума 162
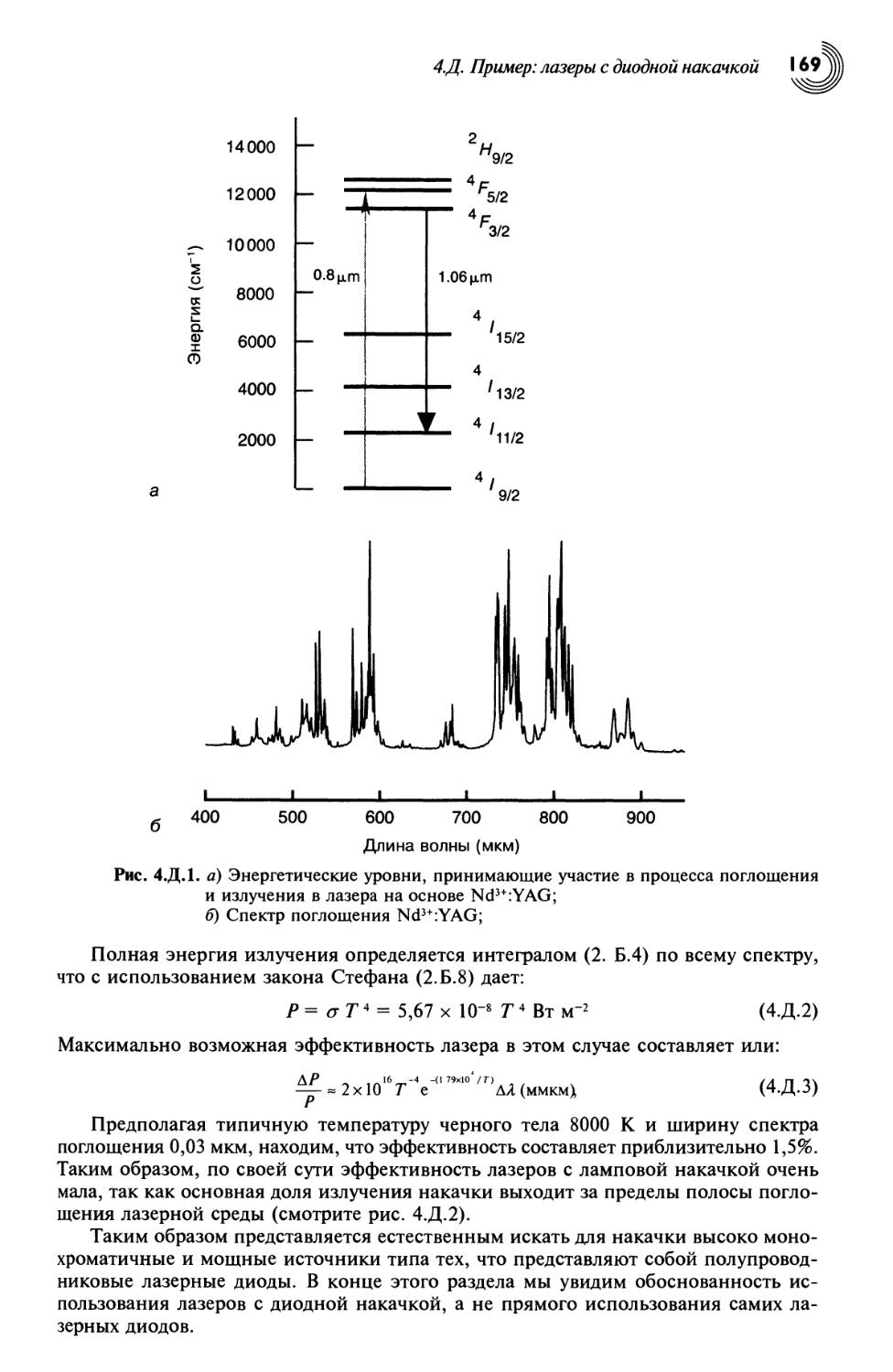
4.Д. Пример: лазеры с диодной накачкой 168
ГЛАВА 5. ЗОННАЯ СТРУКТУРА ПОЛУПРОВОДНИКОВ 173
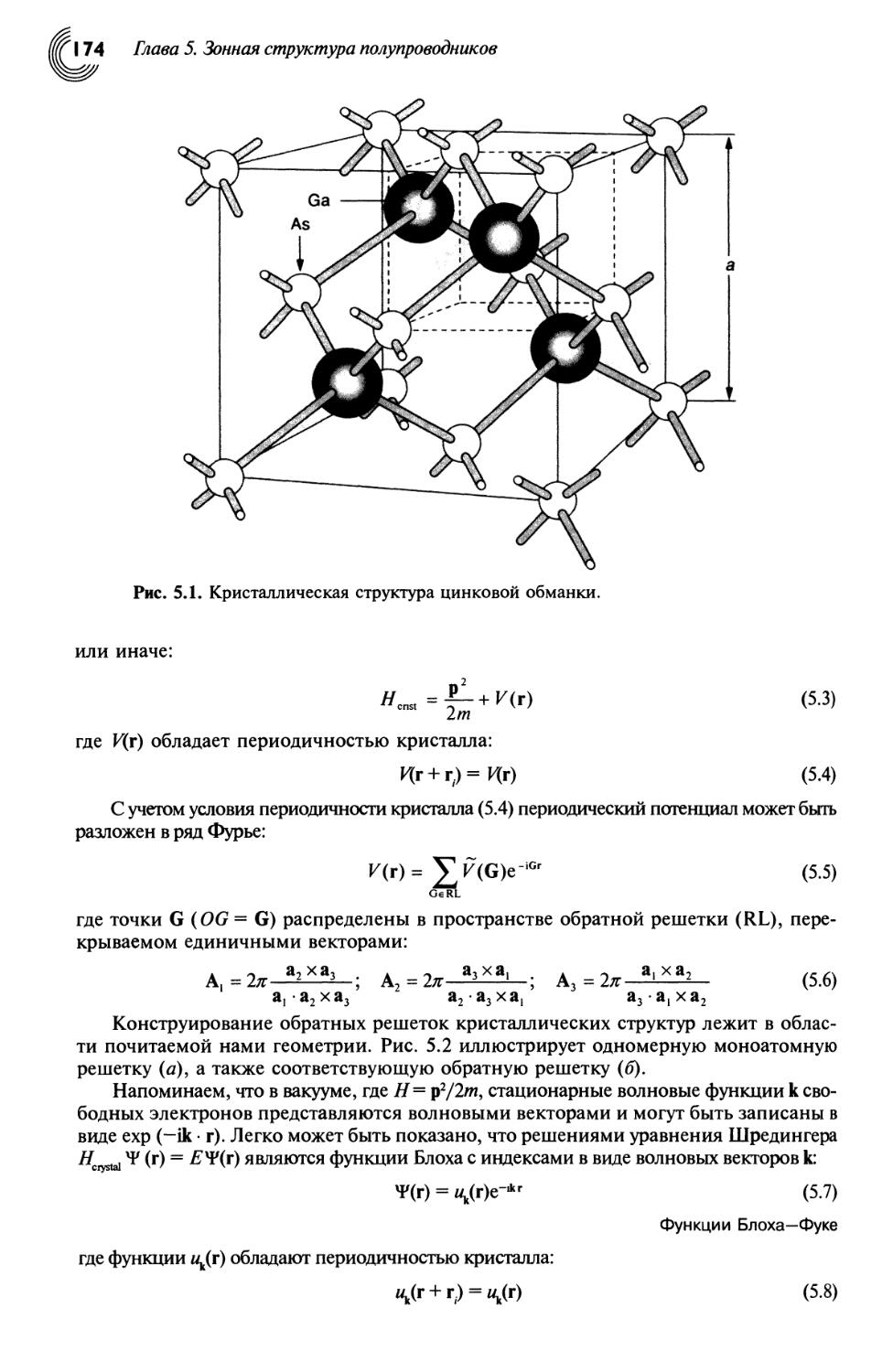
5.1. Введение 173
5.2. Кристаллические структуры, блоховские функции и зона Бриллюэна 173
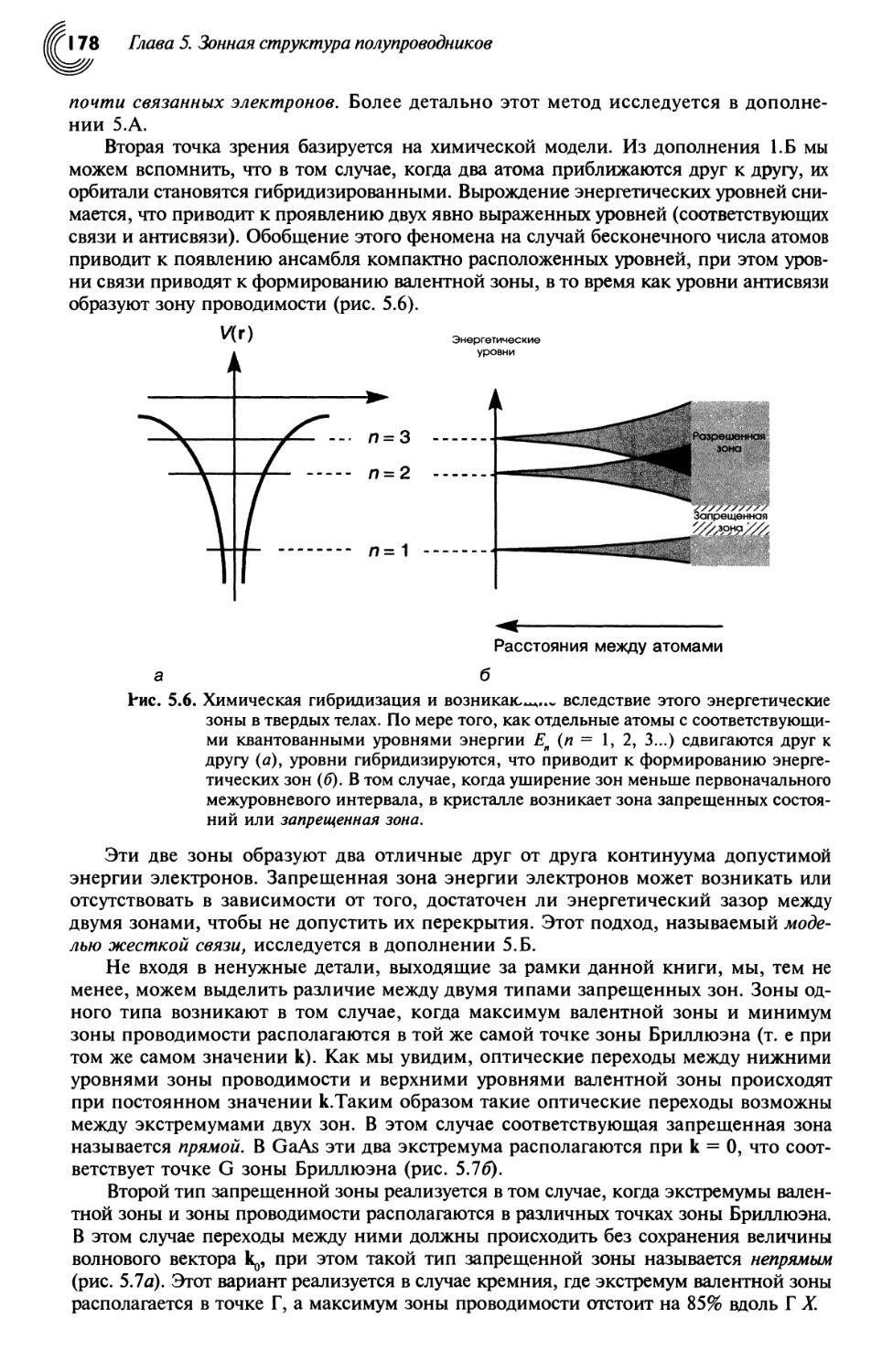
5.3. Энергетические зоны 177
5.4. Эффективная масса и плотность состояний 179
5.5. Динамическая интерпретация эффективной массы и концепции дырок 182
5.6. Статистика носителей заряда в полупроводниках 186
5.6.1. Статистика Ферми и уровень Ферми 186
5.6.2. Собственные полупроводники 190
5.6.3. Легированные полупроводники 191
5.6.4. Квазиуровень Ферми в неравновесной системе 193
ДОПОЛНЕНИЯ К ГЛАВЕ 5 L95
5.А. Модель почти свободных электронов 195
5.Б. Линейная комбинация атомных орбиталей: модель жесткой связи 198
5.В. к /ьметод Кейна 201
5.Г. Глубокие центры в полупроводниках 207
ГЛАВА 6. ЭЛЕКТРОННЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ 210
6.1. Введение 210
6.2. Уравнение Больцмана 210
6.3. Механизмы рассеяния 215
6.4. Горячие электроны 219
6.4.1. Теплые электроны 220
6.4.2. Горячие электроны: насыщение скорости 220
6.4.3. Горячие электроны: отрицательная дифференциальная скорость 222
6.5. Рекомбинация 223
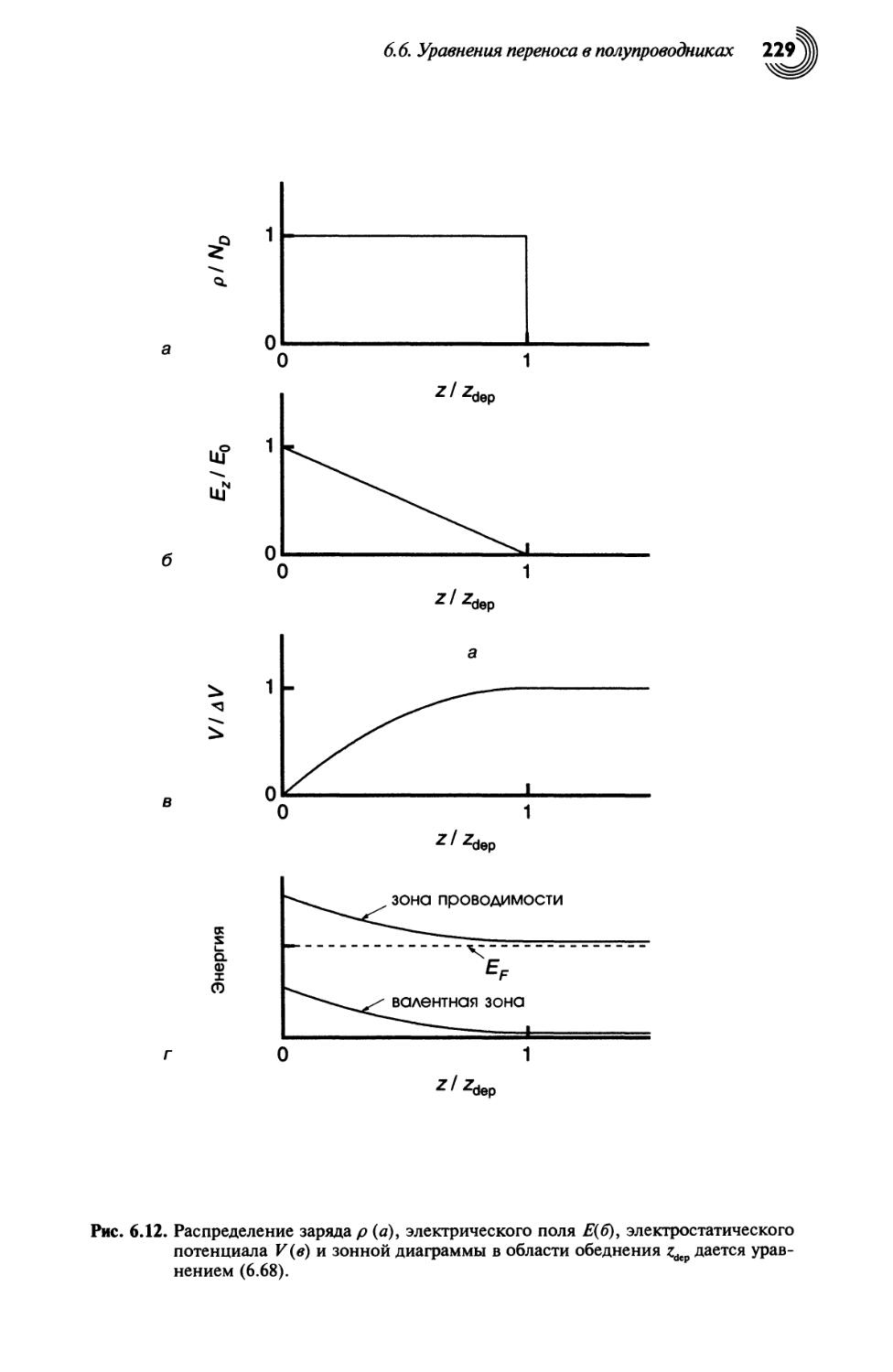
6.6. Уравнения переноса в полупроводниках 227
ДОПОЛНЕНИЯ К ГЛАВЕ 6 231
6.А. Эффект Холла 231
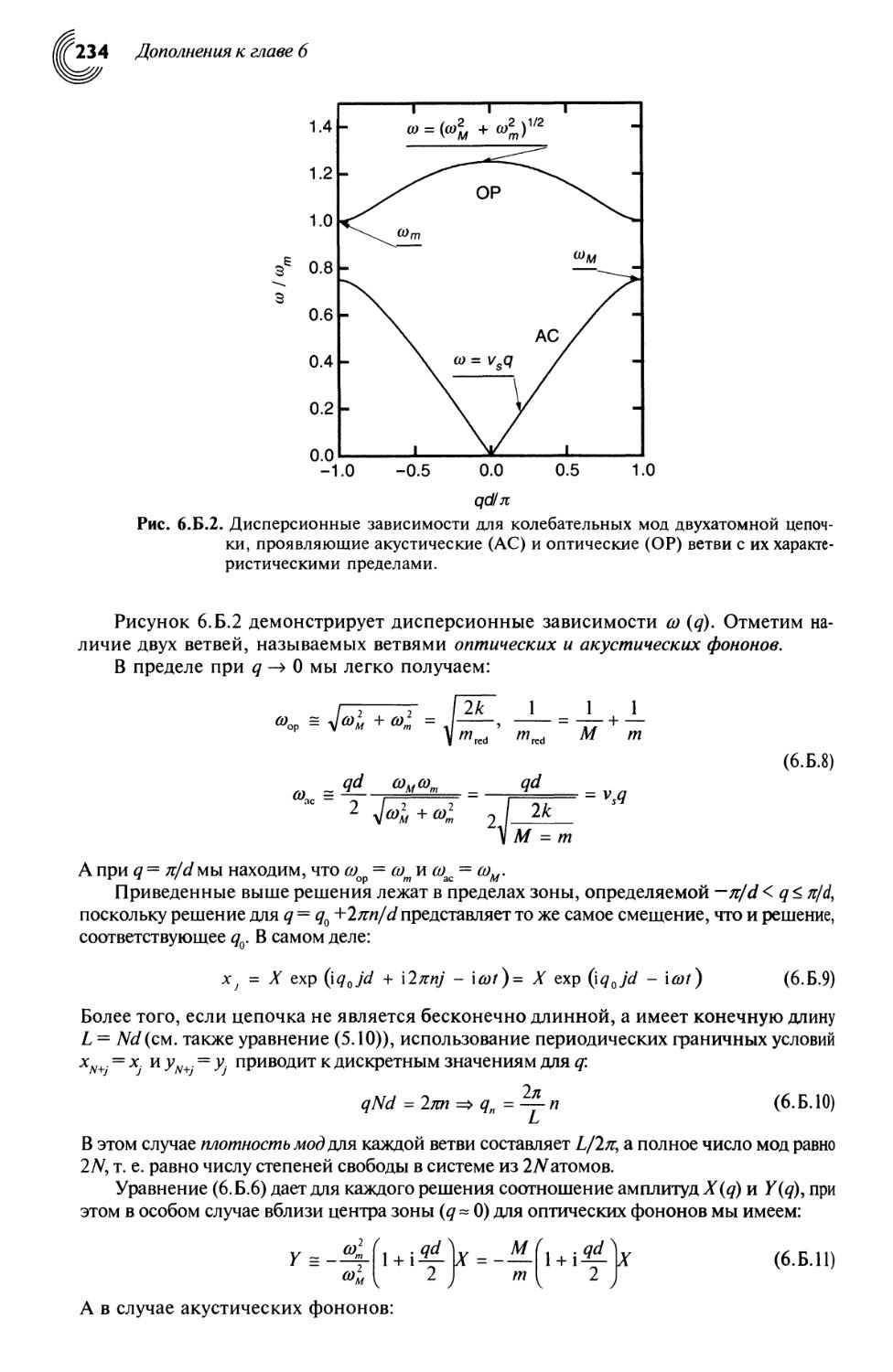
6.Б. Оптические фононы и фрелиховское взаимодействие 232
6.Б.1. Фононы 232
6.Б.2. Фрелиховское взаимодействие 238
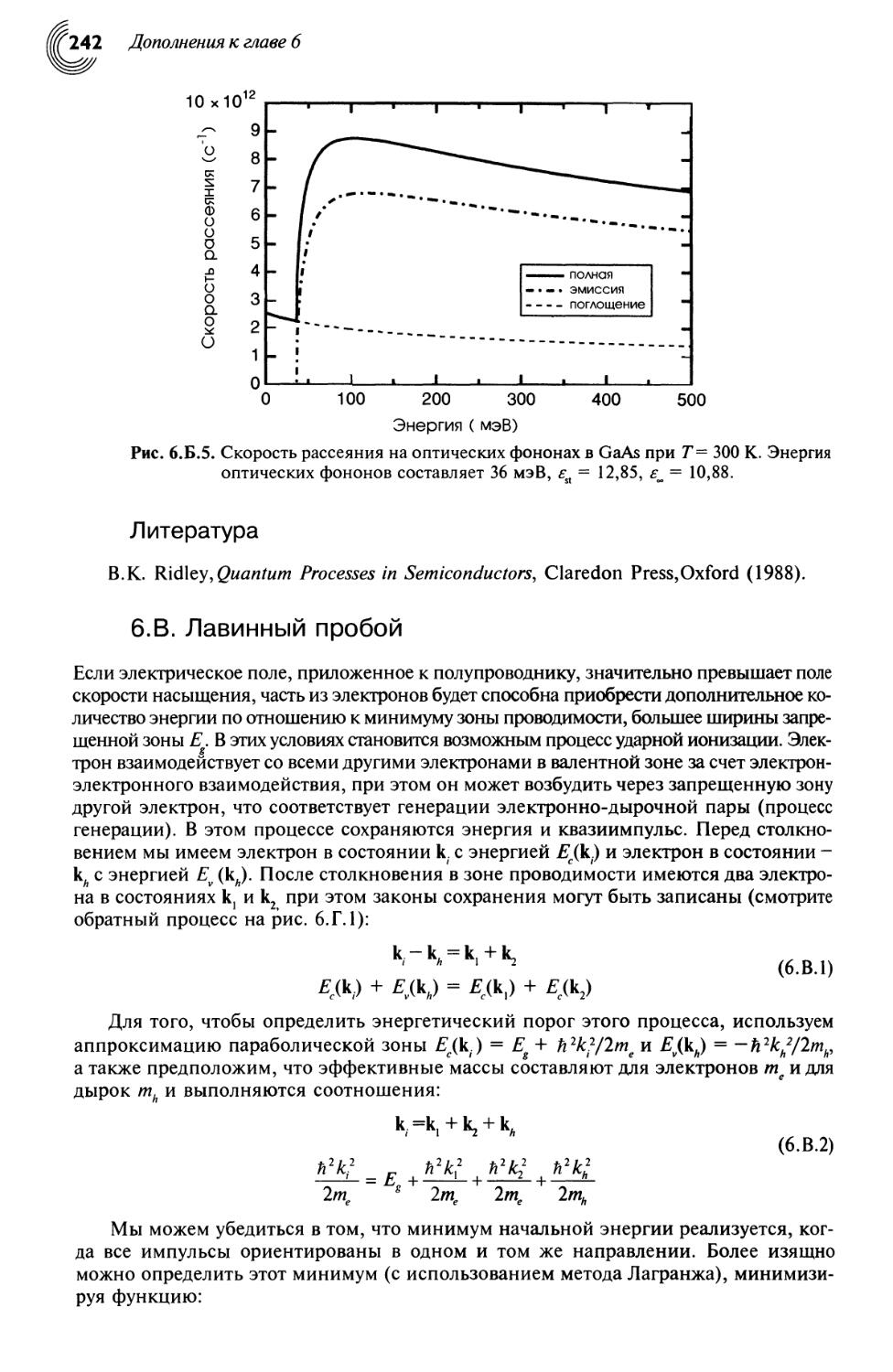
6.В. Лавинный пробой 242
6.Г. Оже-рекомбинация 246
Оптоэлектроника
ГЛАВА 7. ОПТИЧЕСКИЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ 251
7.1. Введение 251
7.2. Дипольные моменты в прямозонных полупроводниках 251
7.3. Оптическая восприимчивость полупроводника 255
7.4. Поглощение и спонтанное излучение 259
7.5. Коэффициент бимолекулярной рекомбинации 264
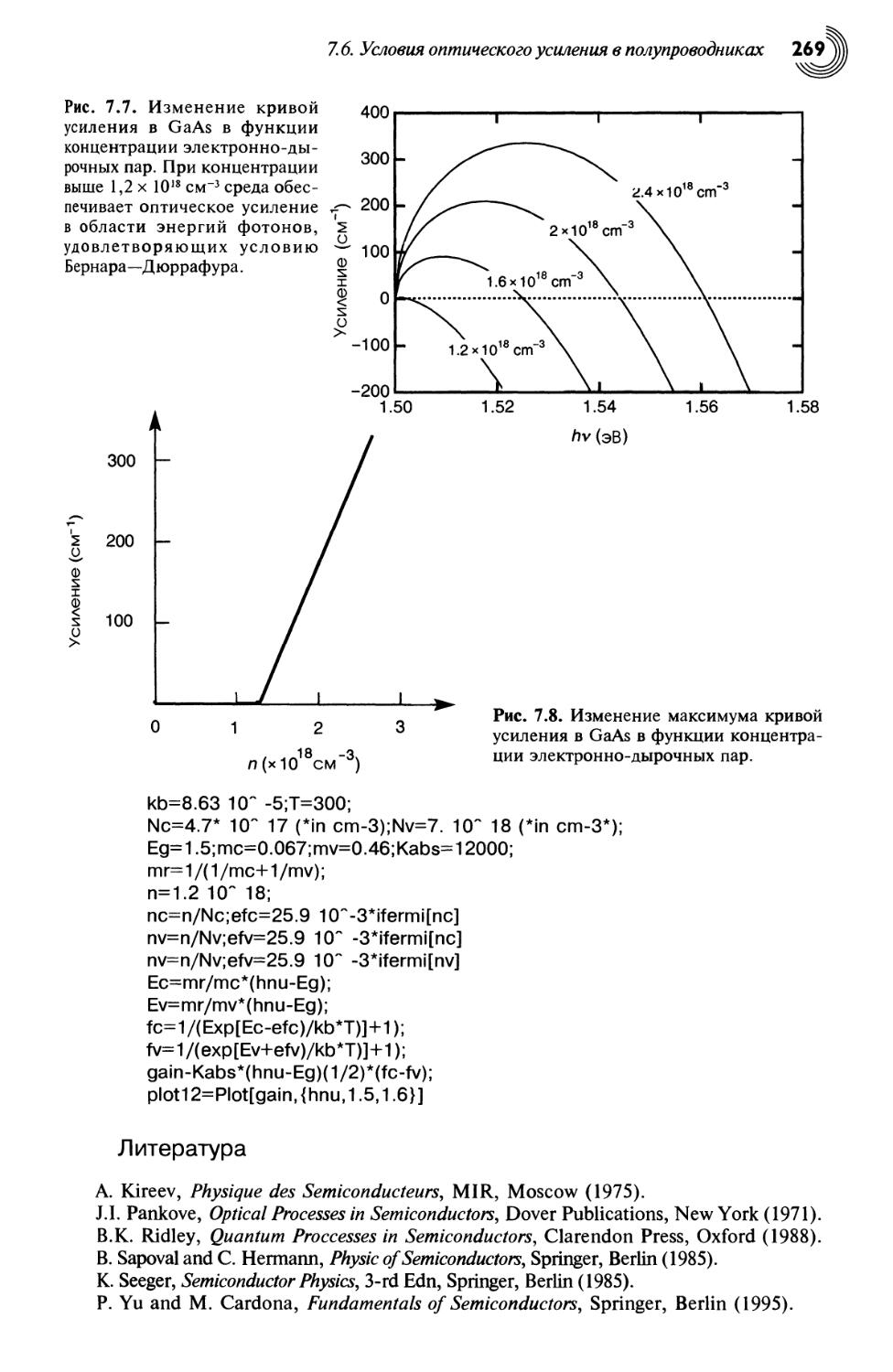
7.6. Условия оптического усиления в полупроводниках 267
ДОПОЛНЕНИЯ К ГЛАВЕ 7 270
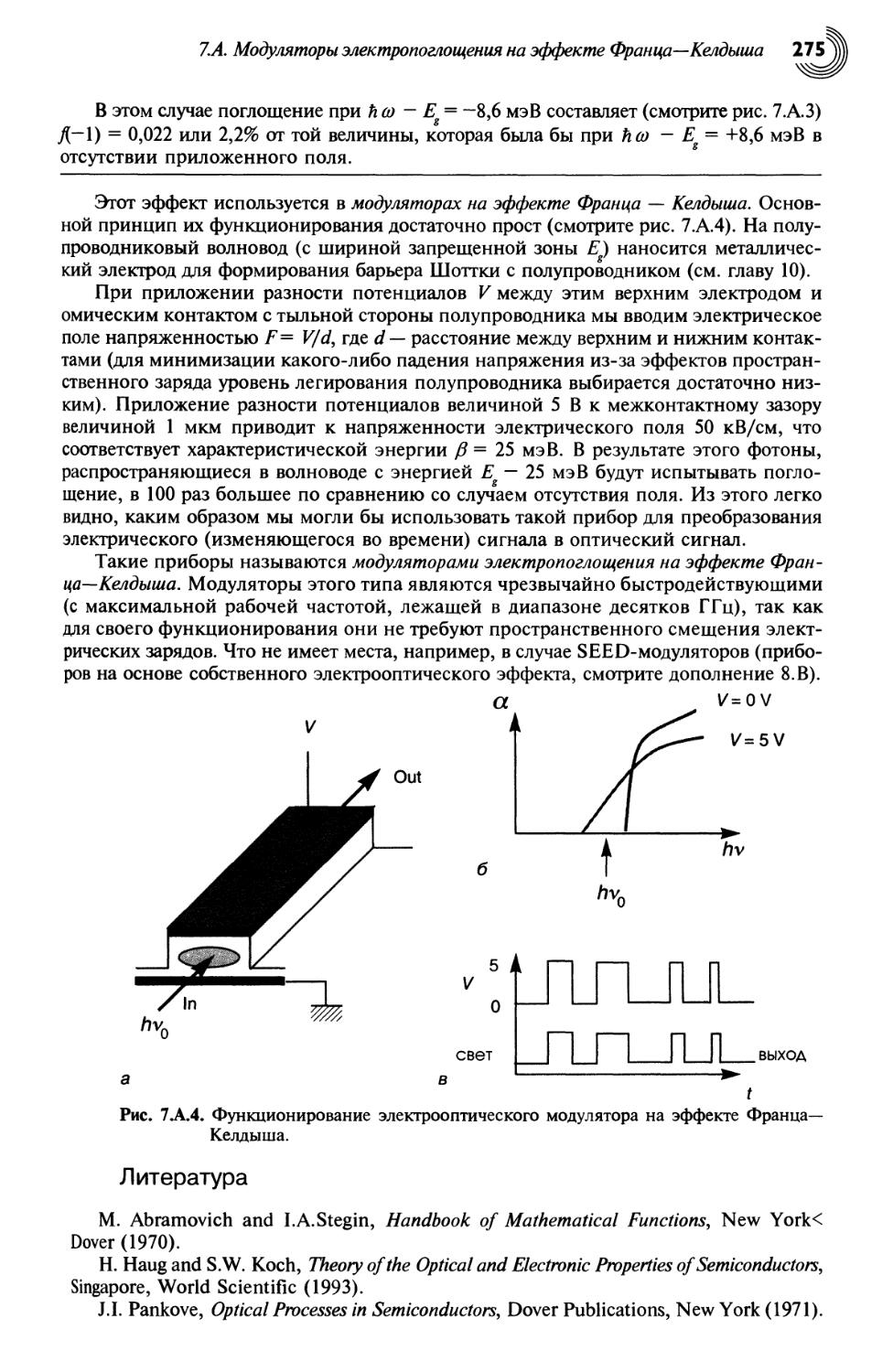
7.А. Модуляторы электропоглощения на эффекте Франца—Келдыша 270
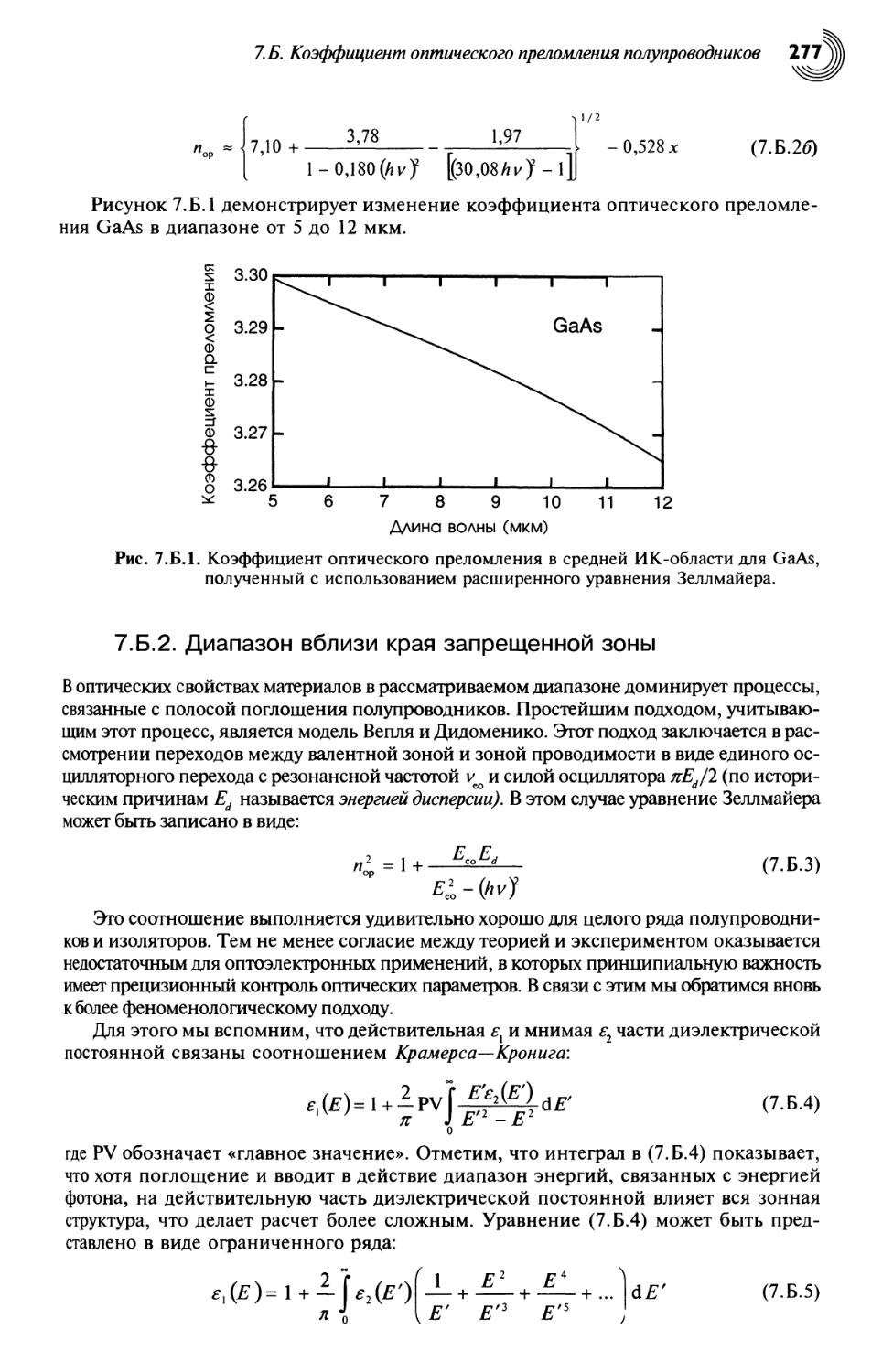
7.Б. Коэффициент оптического преломления полупроводников 276
7.Б.1. Средний и дальний ИК-диапазоны 276
7.Б.2. Диапазон вблизи края запрещенной зоны 277
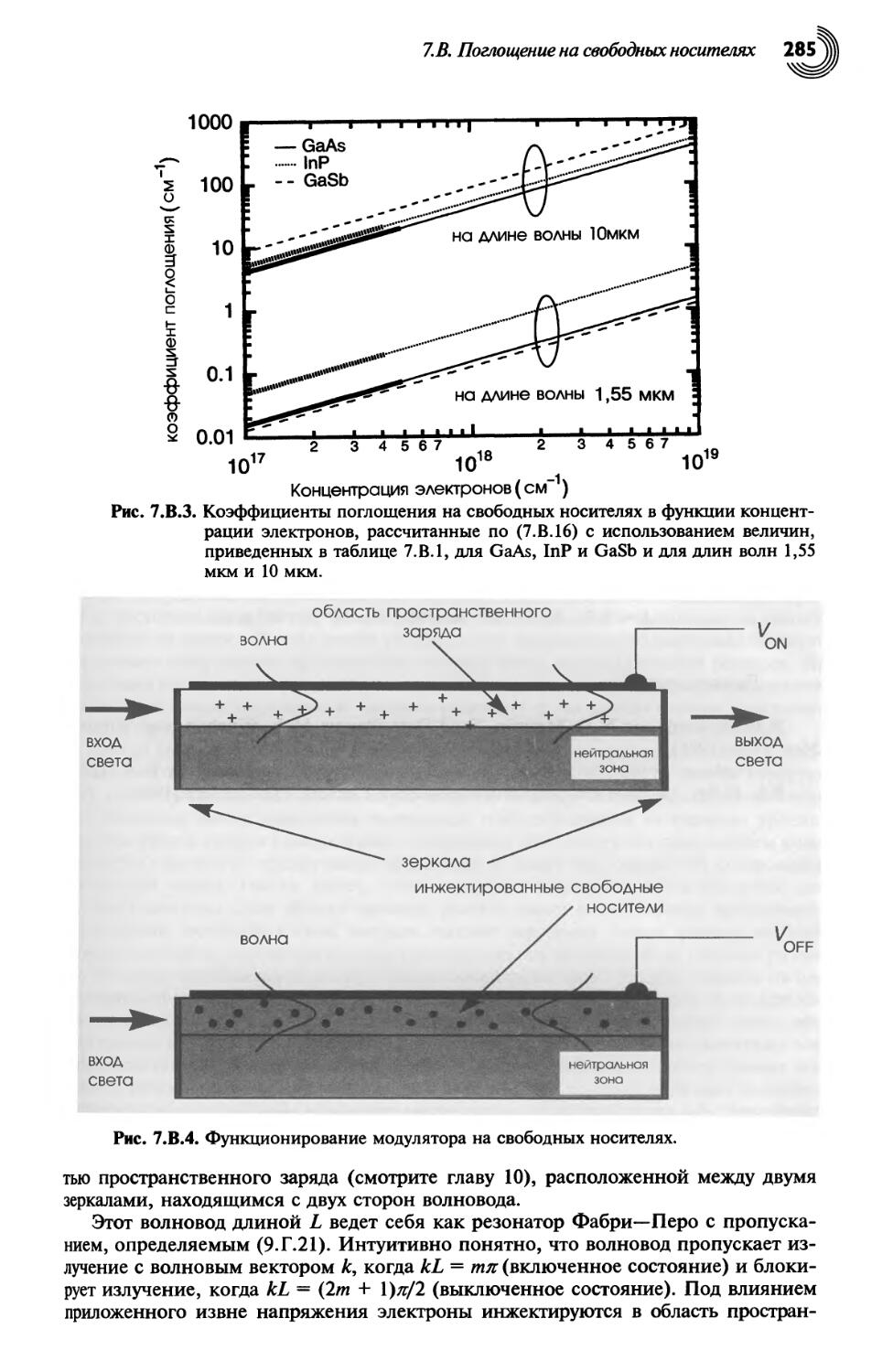
7.В. Поглощение на свободных носителях 280
ГЛАВА 8. ПОЛУПРОВОДНИКОВЫЕ ГЕТЕРОСТРУКТУРЫ
И КВАНТОВЫЕ ЯМЫ 287
8.1. Введение 287
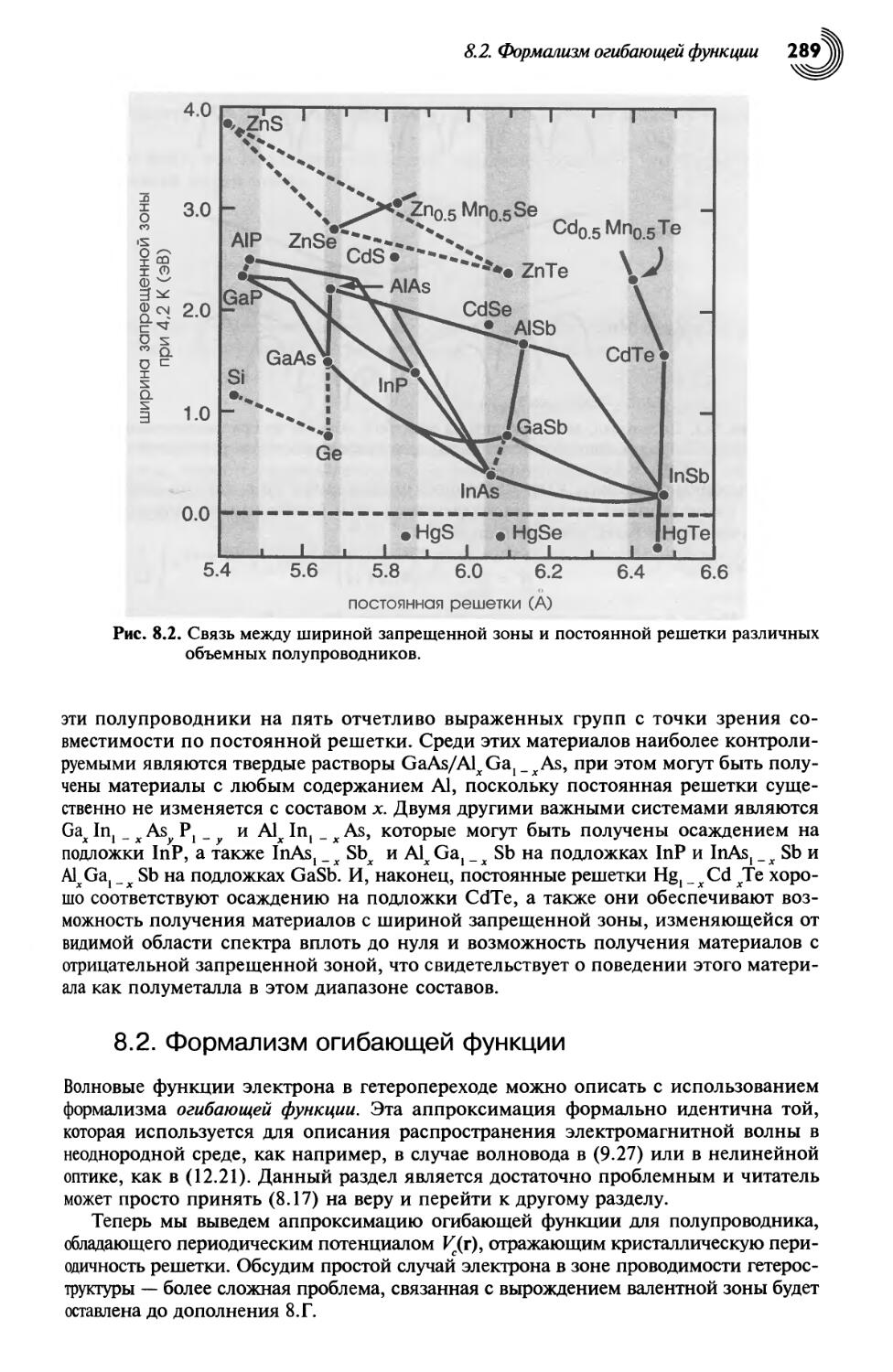
8.2. Формализм огибающей функции 289
8.3. Квантовая яма 293
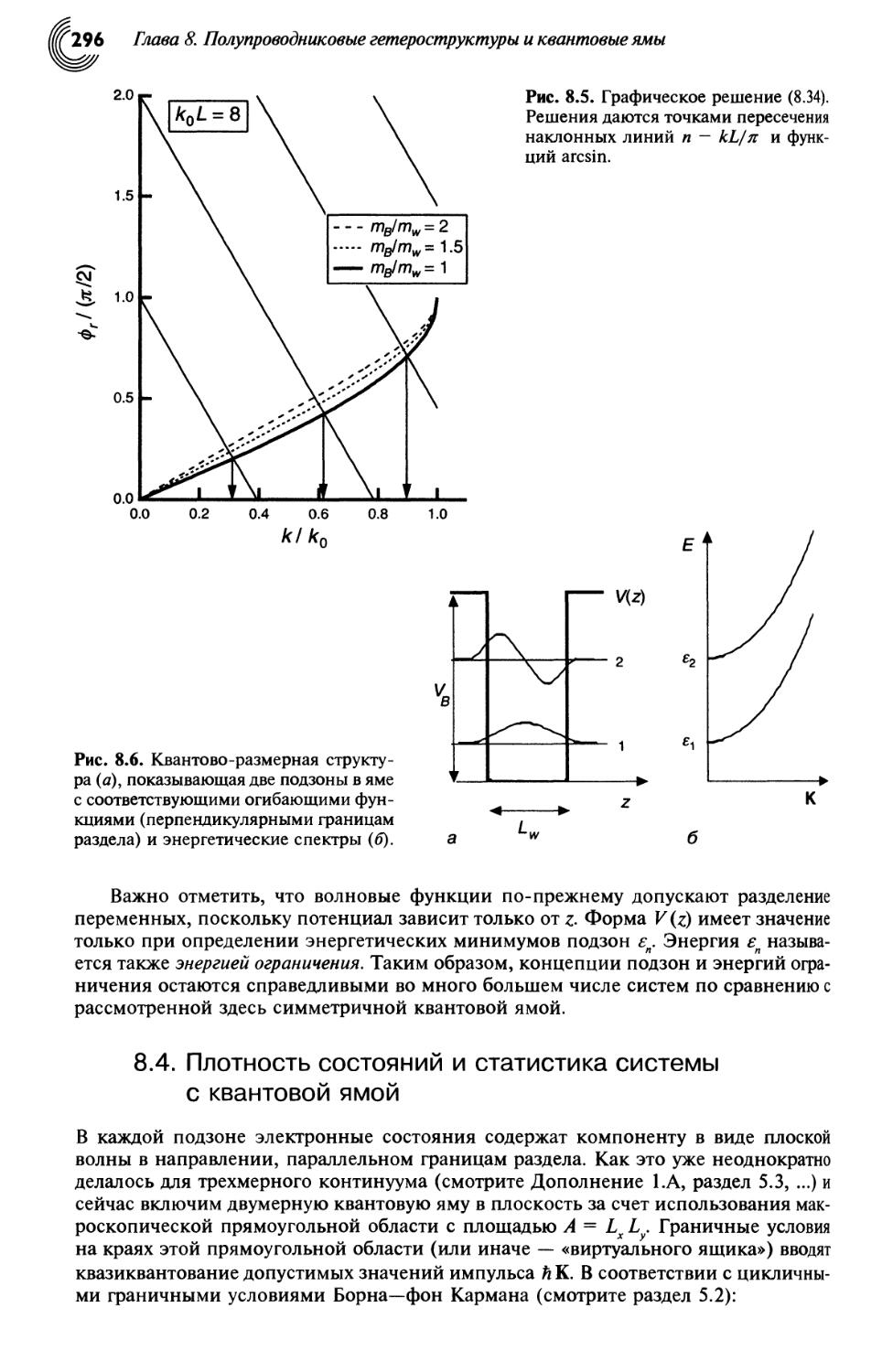
8.4. Плотность состояний и статистика системы с квантовой ямой 296
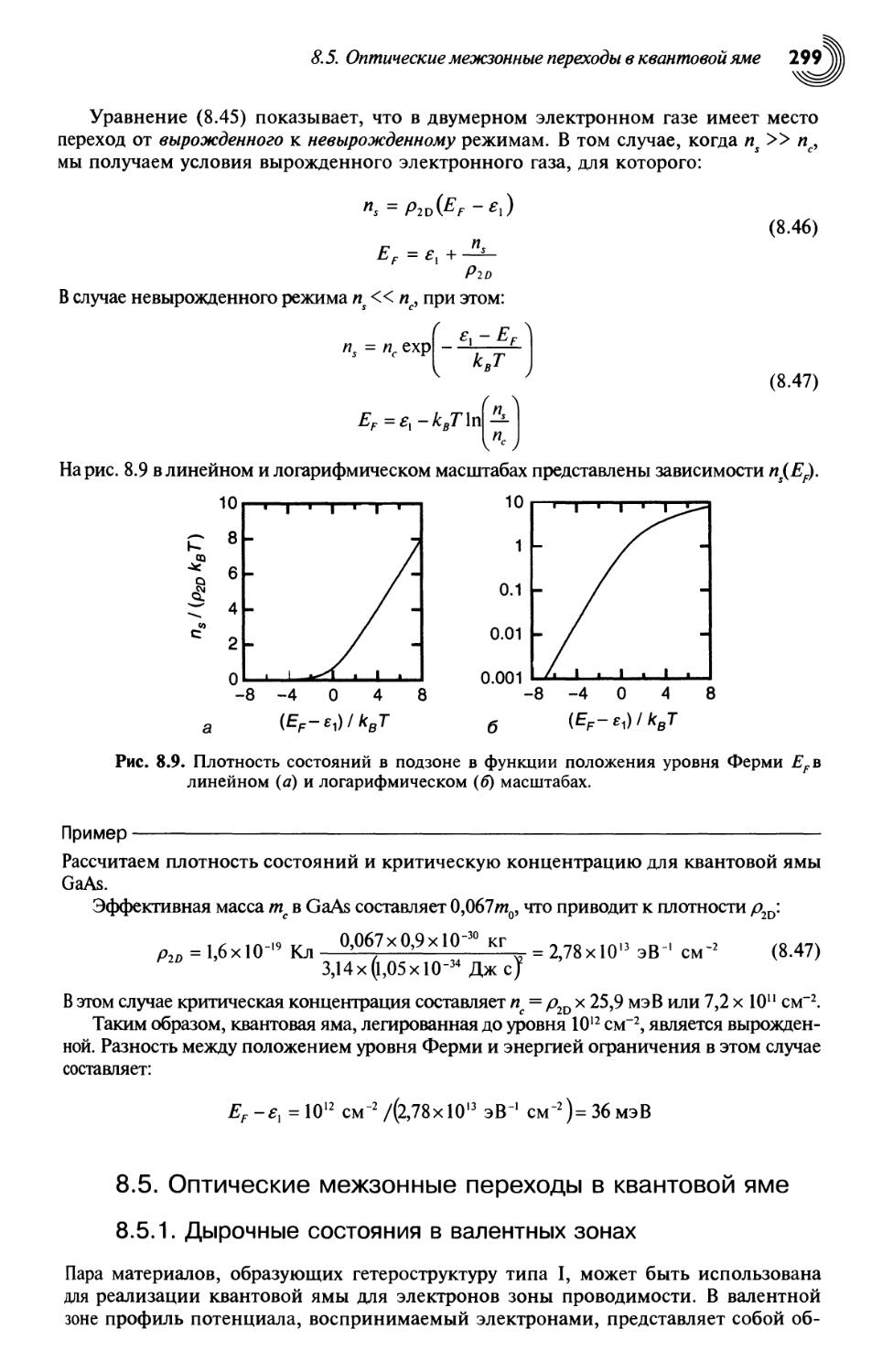
8.5. Оптические межзонные переходы в квантовой яме 299
8.5.1. Дырочные состояния в валентных зонах 299
8.5.2. Оптические переходы между валентной зоной и зоной проводимости 301
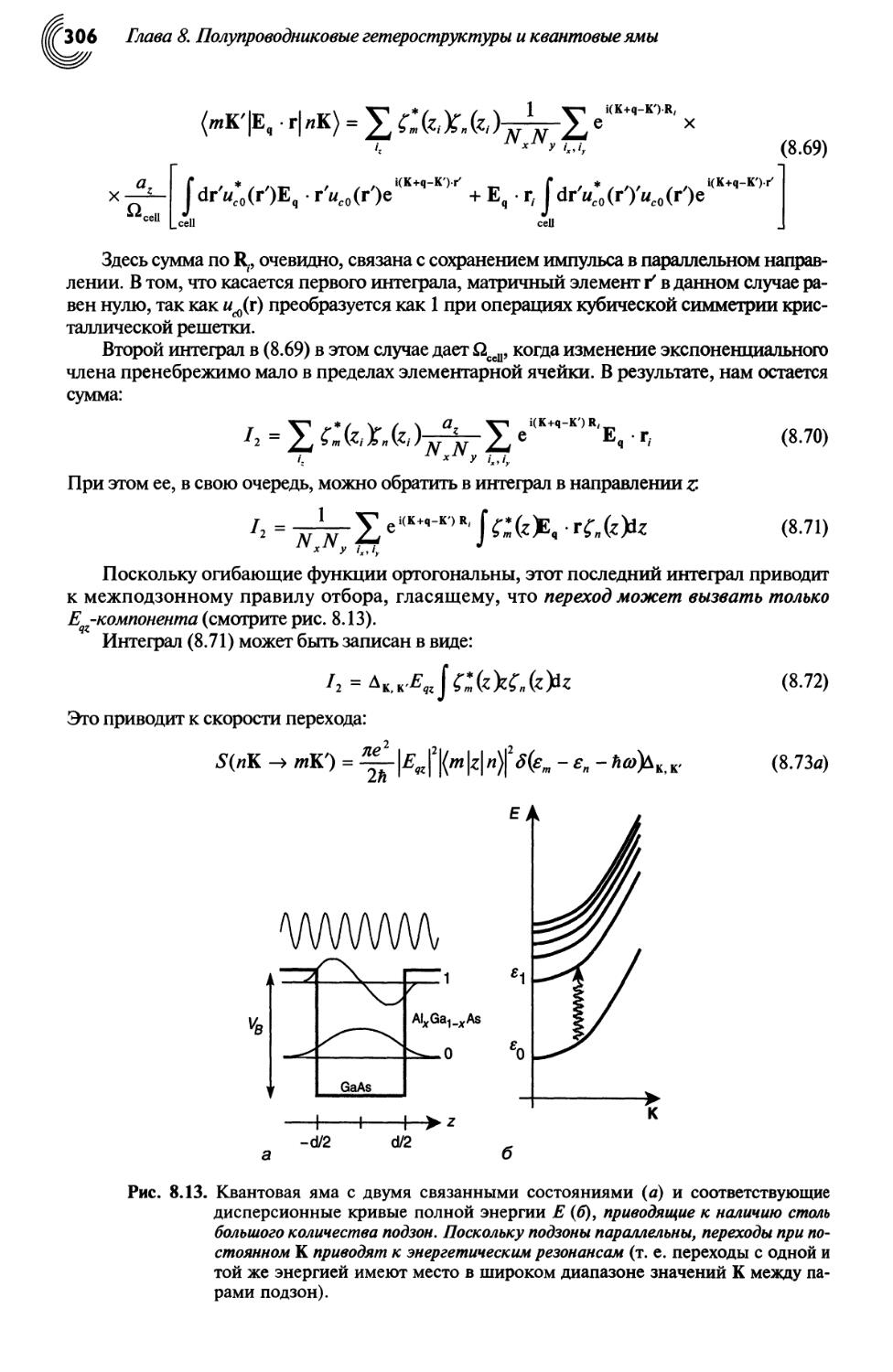
8.6. Оптические межподзонные переходы в квантовой яме 305
8.7. Оптическое поглощение и угол падения 308
8.7.1. Сводка по скоростям межзонных и межподзонных переходов 308
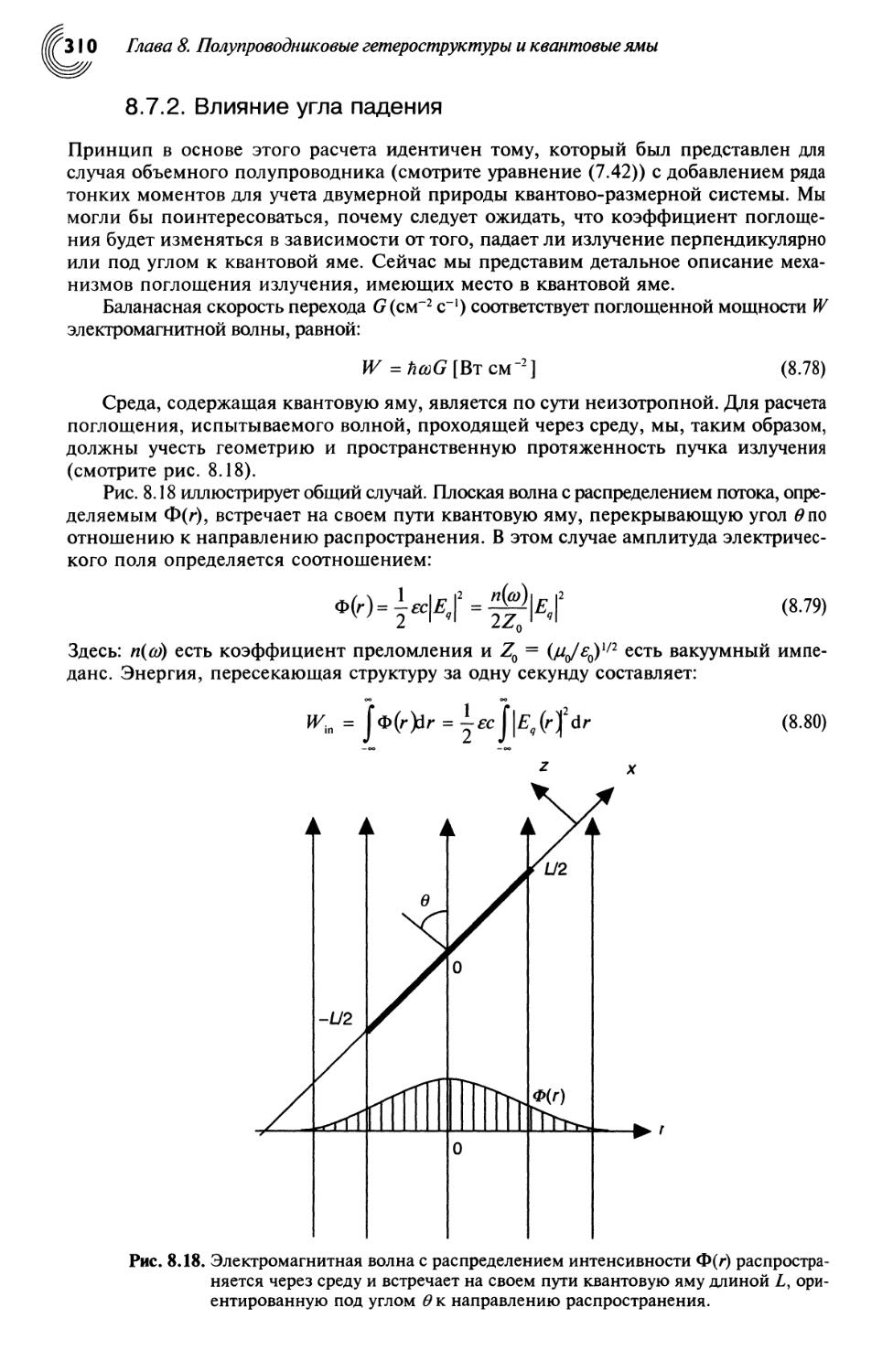
8.7.2. Влияние угла падения 310
ДОПОЛНЕНИЯ К ГЛАВЕ 8 314
8.А. Квантовые нити и ящики 314
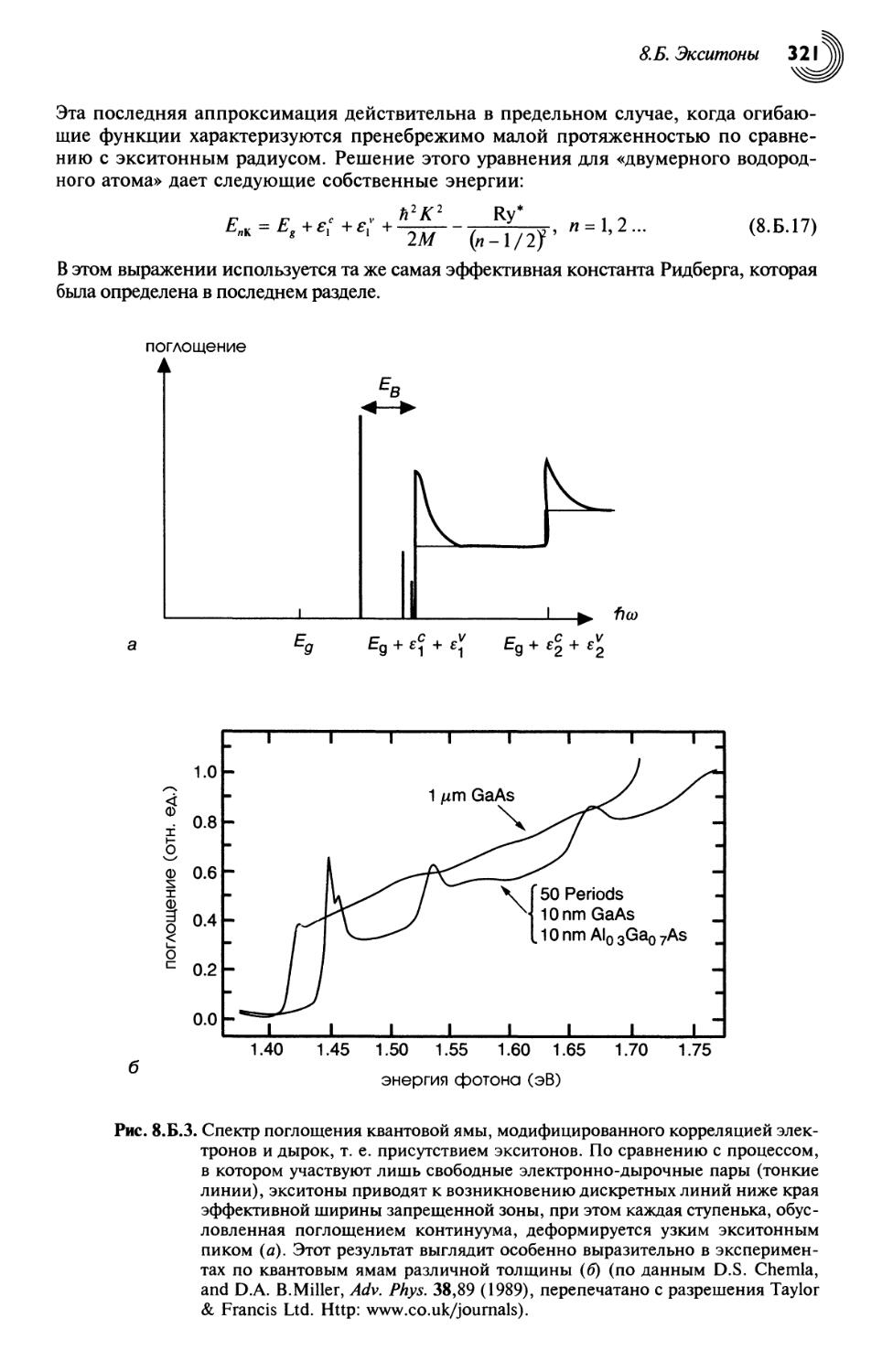
8.Б. Экситоны 316
8.Б.1. Трехмерные экситоны 317
8.Б.2. Двумерные экситоны 320
8.В. Квантово-размерный эффект Штарка и модуляторы с собственным
электрооптическим эффектом 322
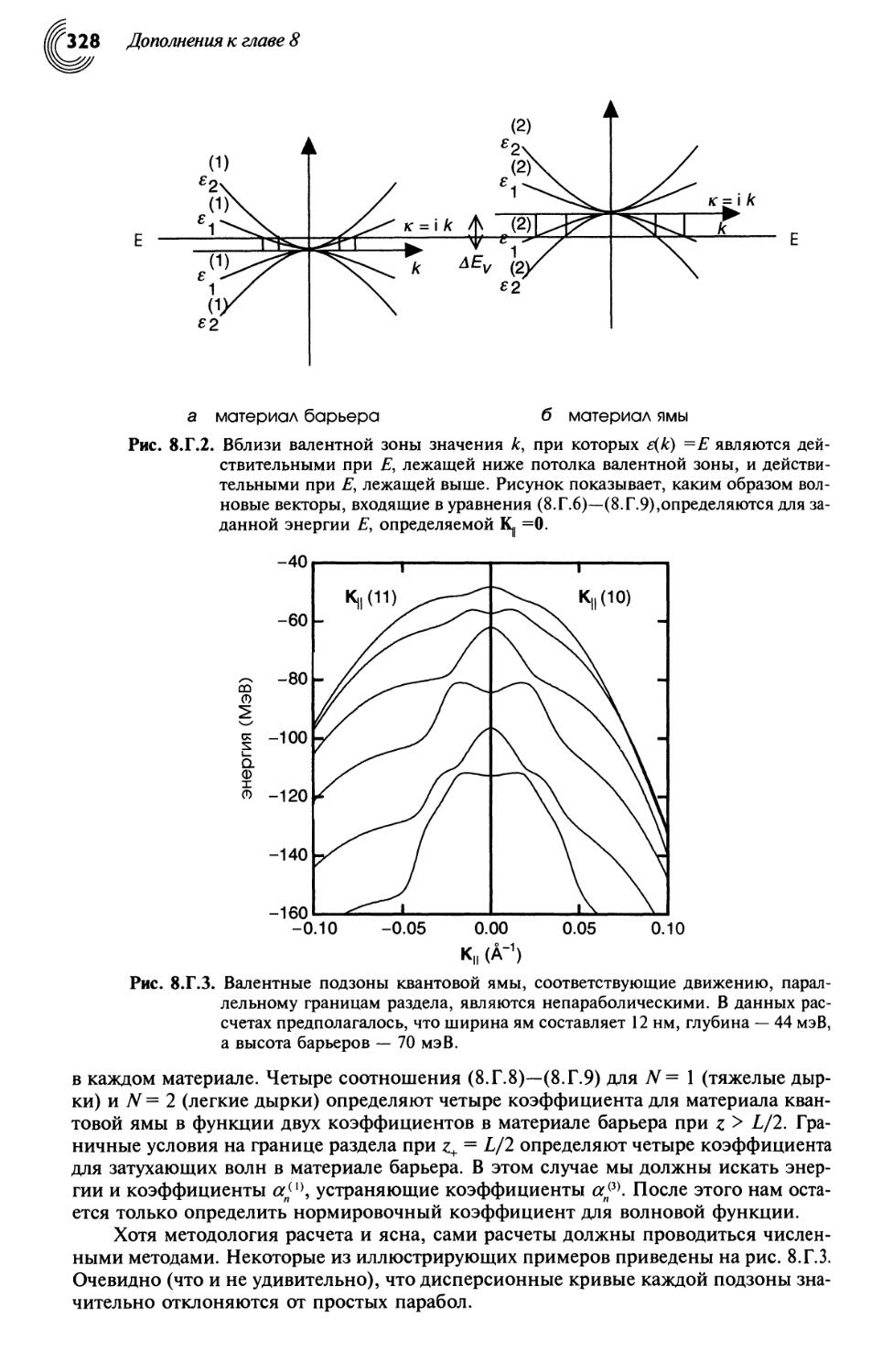
8.Г. Валентные подзоны 325
ГЛАВА 9. ВОЛНОВОДЫ 329
9.1. Введение 329
9.2. Геометрический подход к волноводам 329
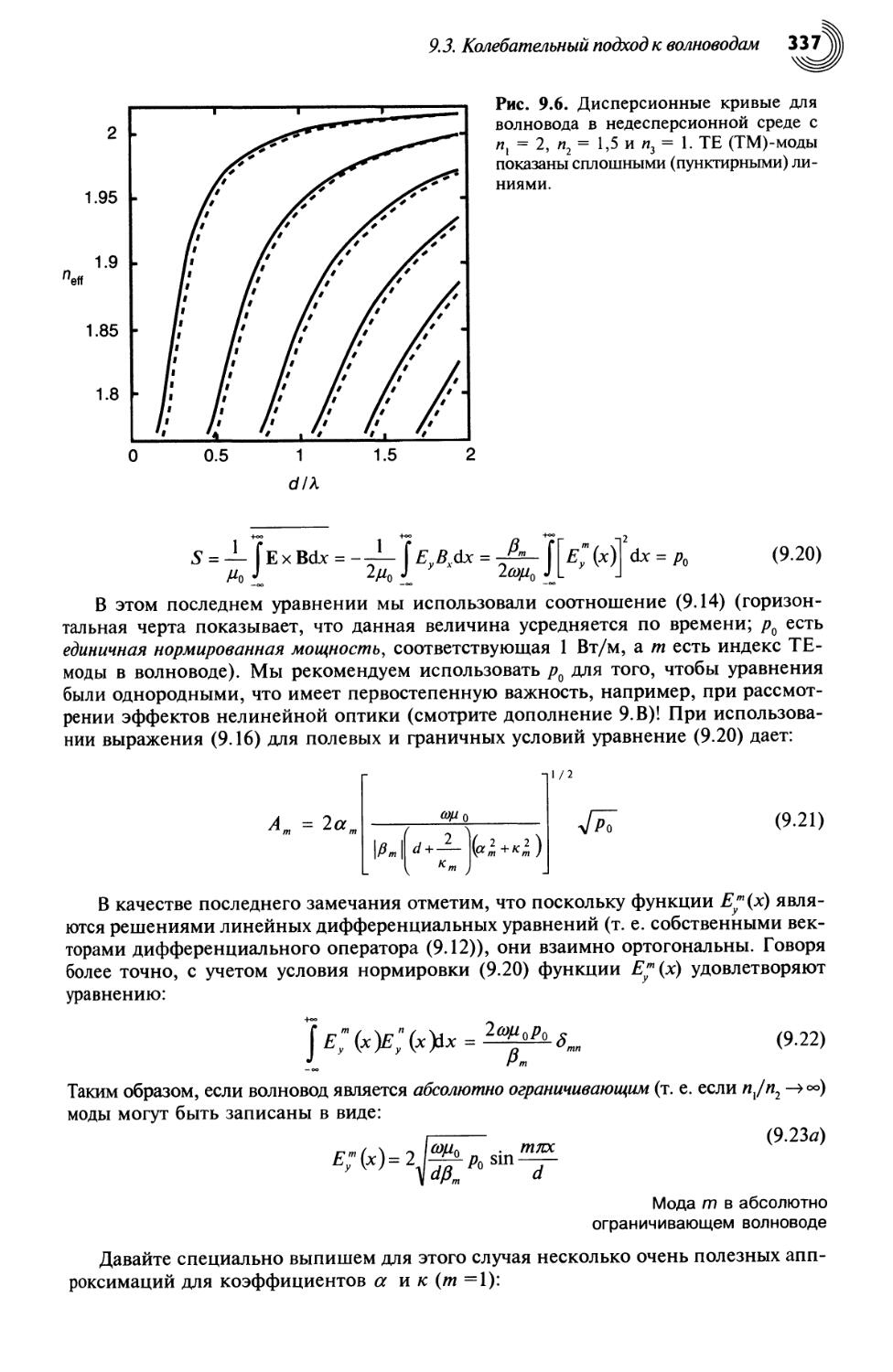
9.3. Колебательный подход к волноводам 332
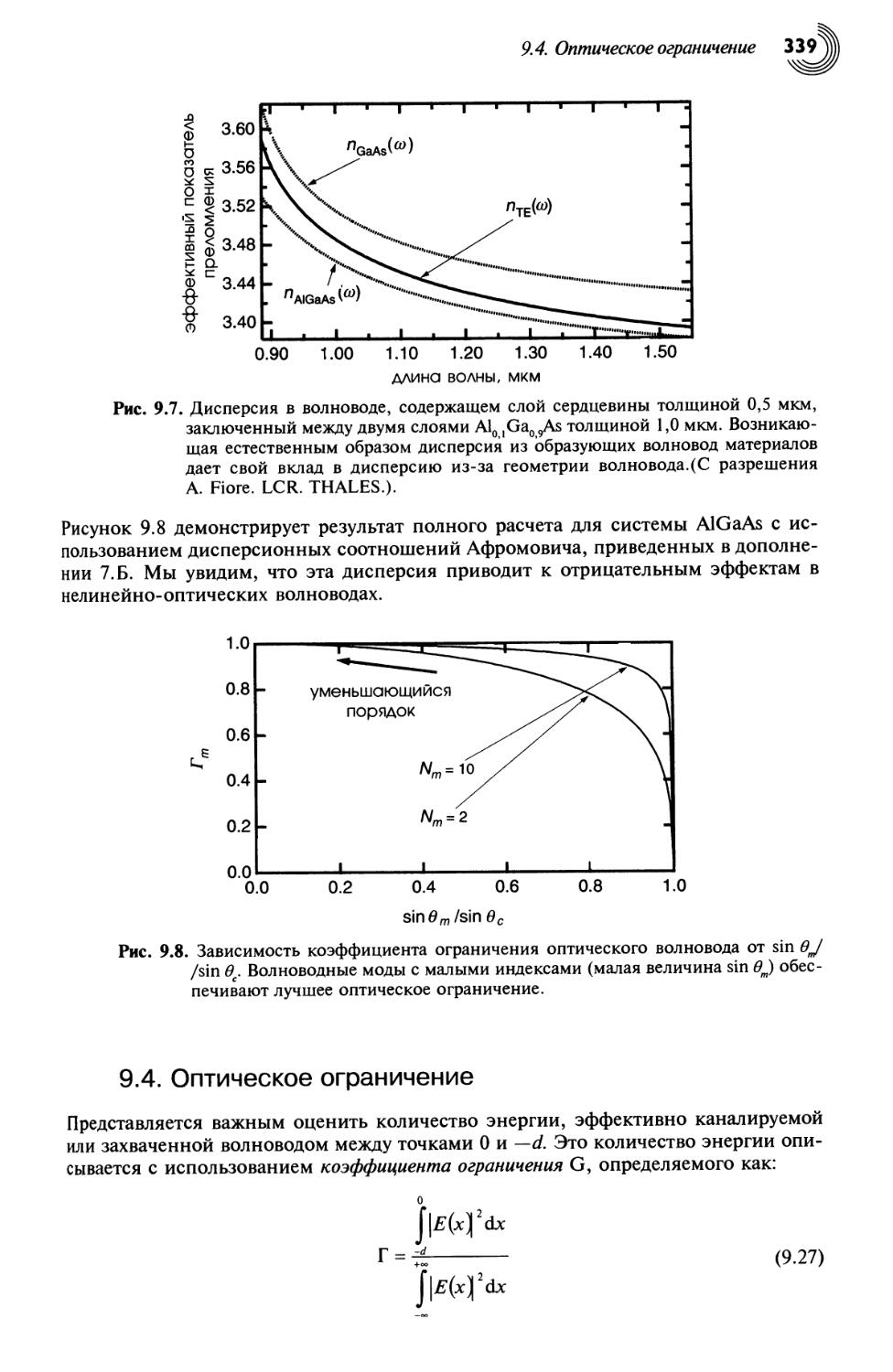
9.4. Оптическое ограничение 339
9.5. Взаимодействие между волноводными модами: теория
связанных мод 341
Содержание
ДОПОЛНЕНИЯ К ГЛАВЕ 9 344
9.А. Оптическое взаимодействие между волноводами: электрооптические
переключатели 344
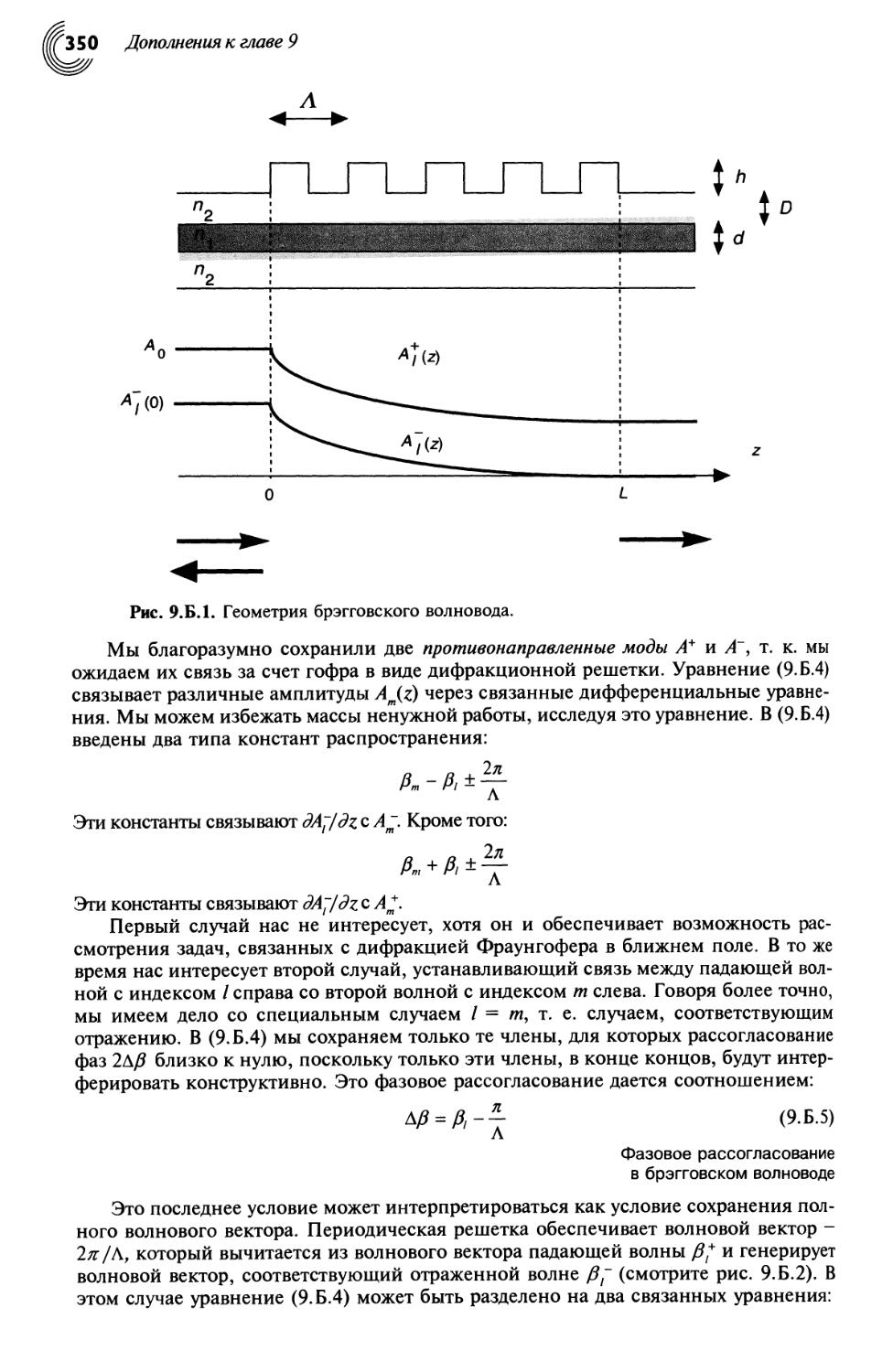
9.Б. Брэгговские волноводы 349
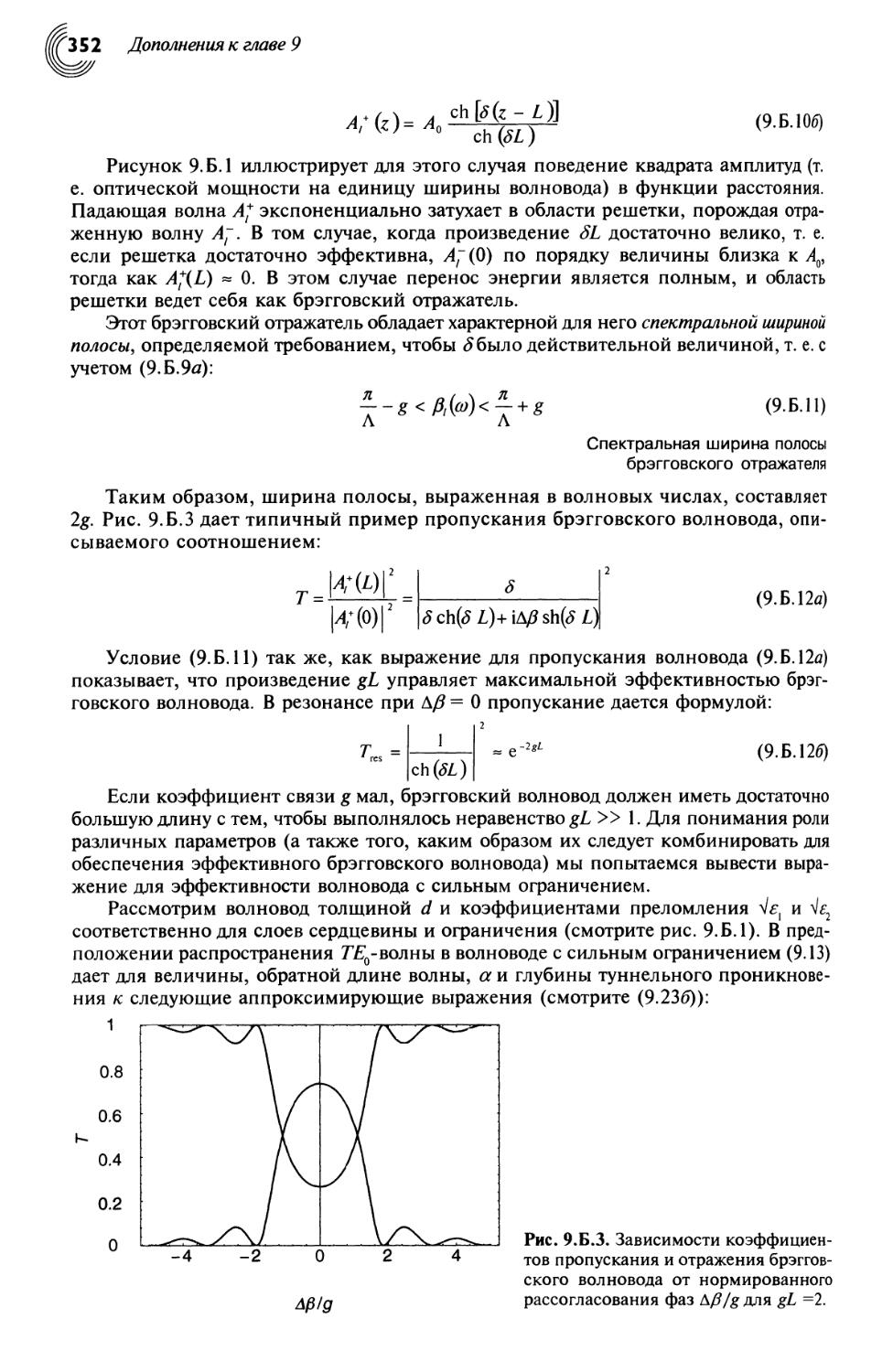
9.В. Преобразование частоты в нелинейных волноводах 353
9.8.1. Режим с входящей ТЕ-модой и выходящей ТЕ-модой 354
8.В.2. Режим с входящей ТЕ-модой и выходящей ТМ-модой 358
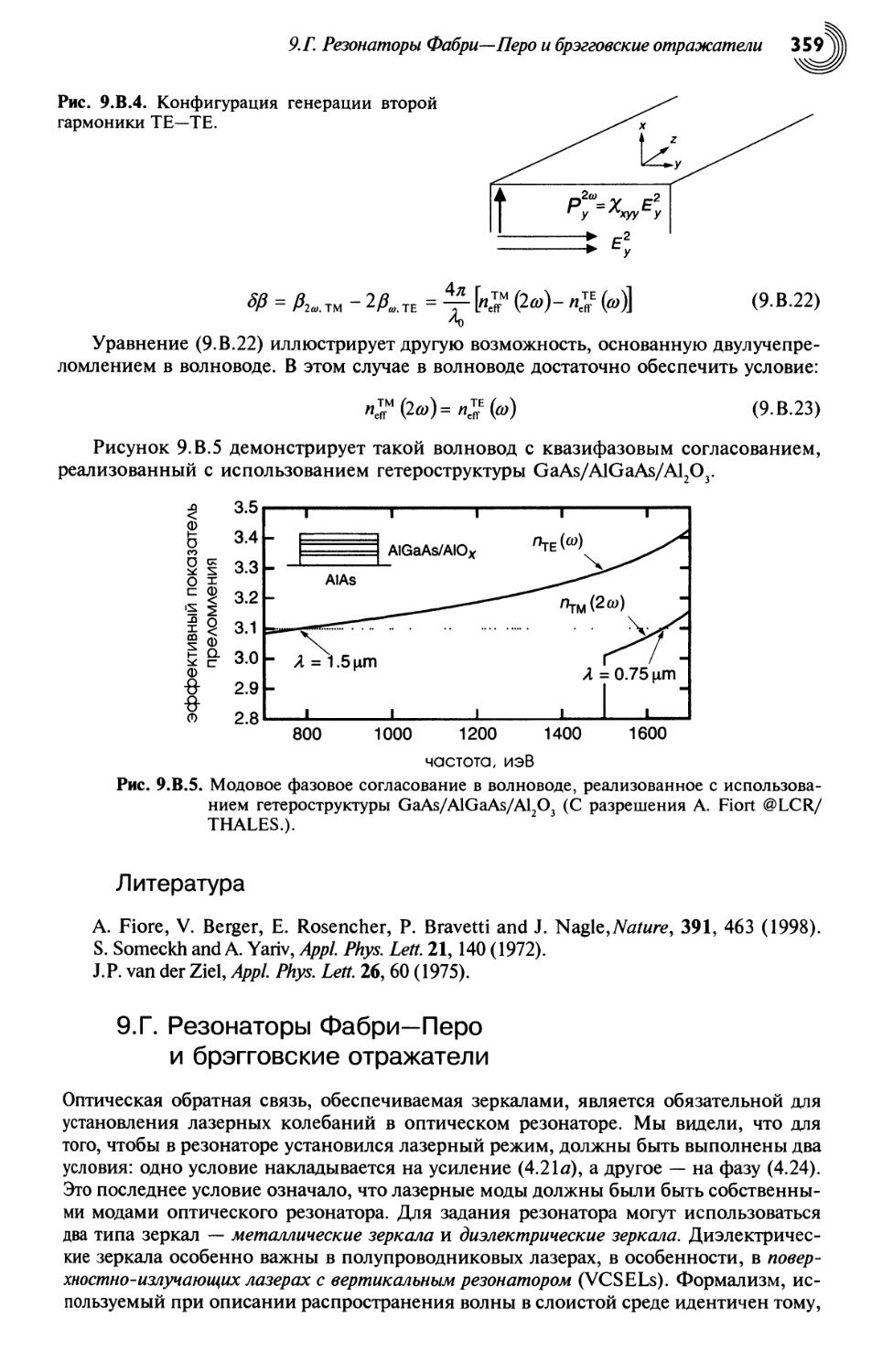
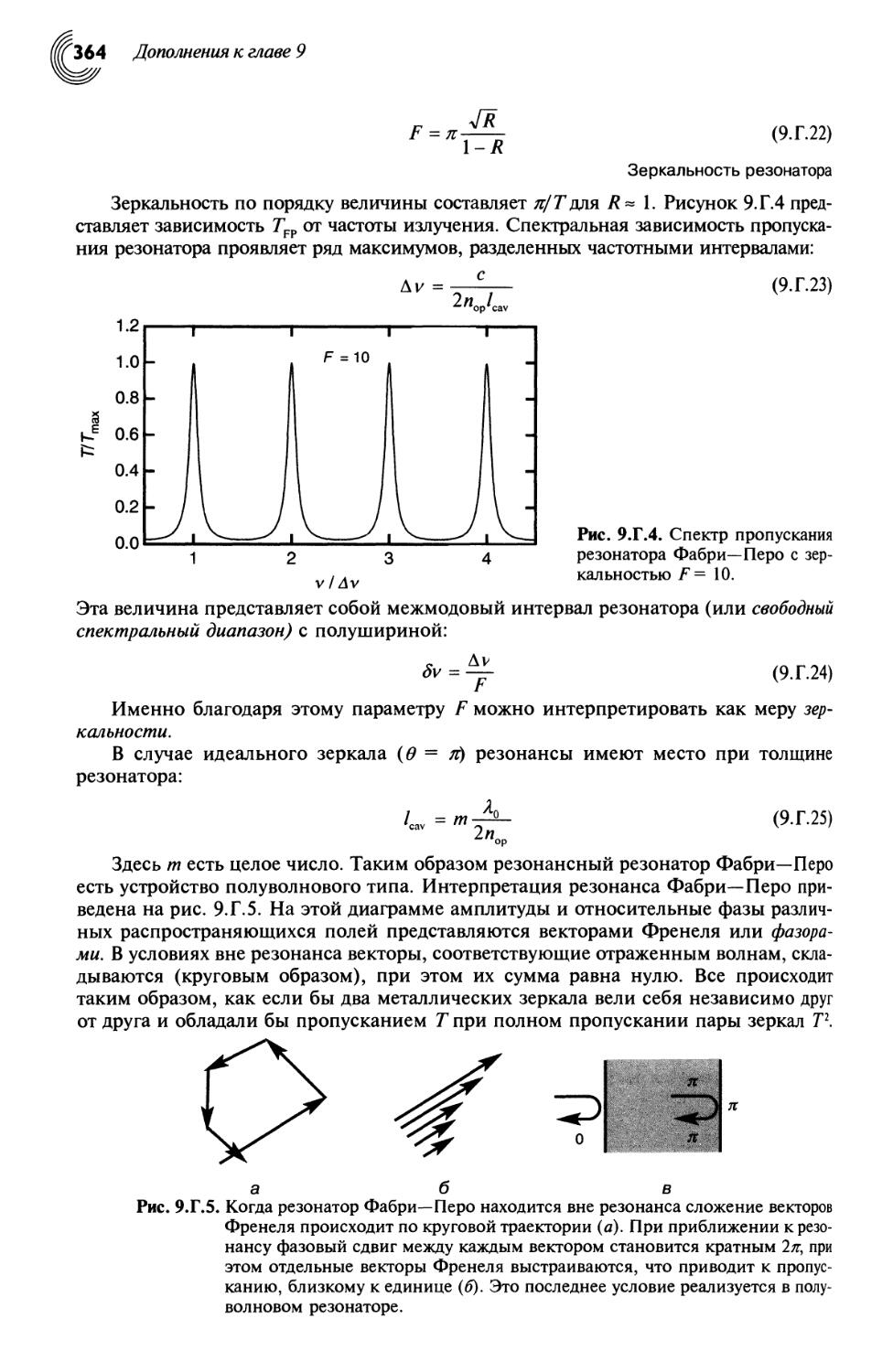
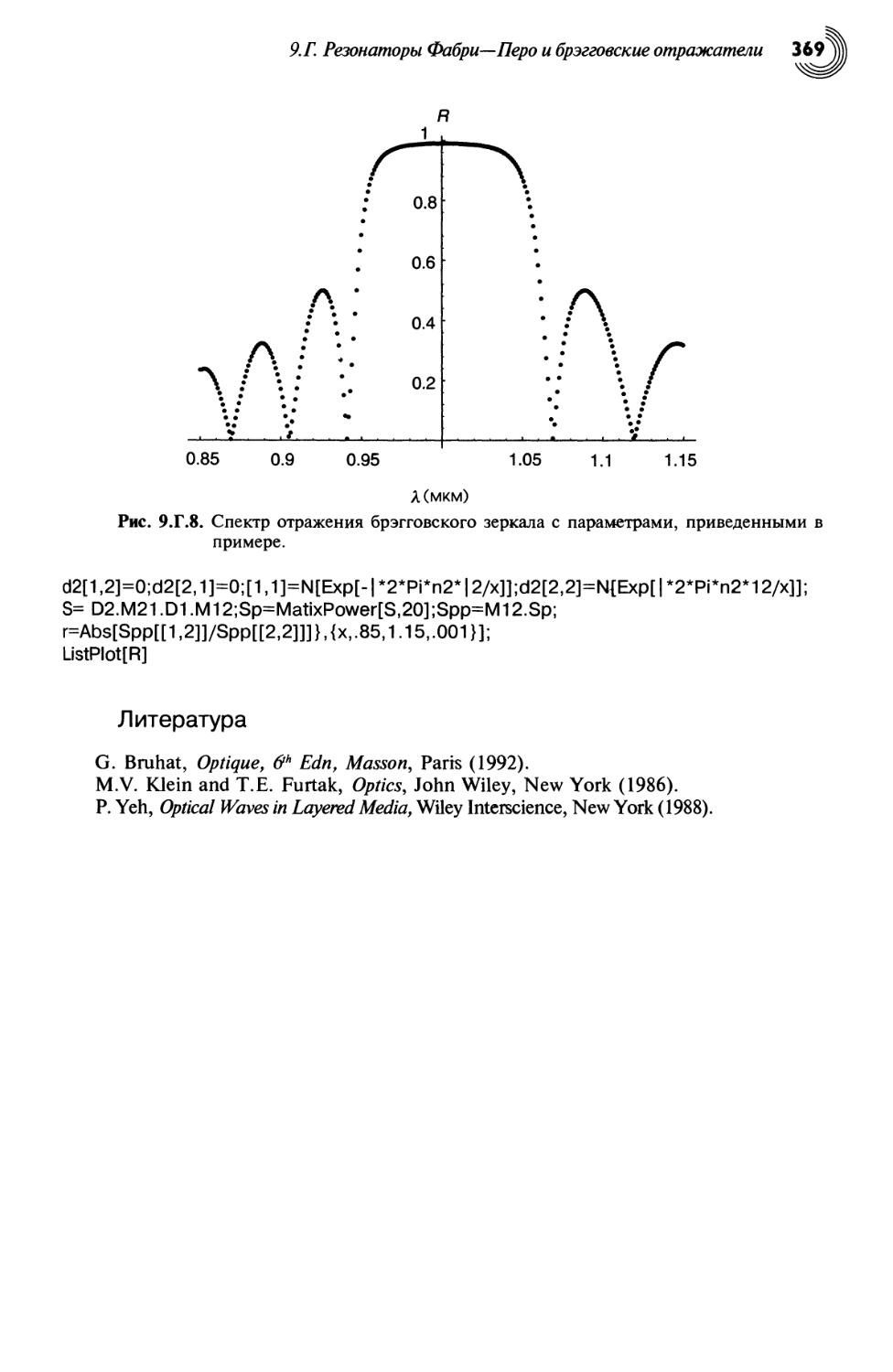
9.Г. Резонаторы Фабри—Перо и брэгговские отражатели 359
9.ГЛ. Резонатор Фабри—Перо 362
9.Г.2. Брэгговские зеркала 366
ГЛАВА 10. ОСНОВЫ ФИЗИКИ ПРИБОРОВ 370
10.1. Введение 370
10.2. Поверхностные явления 370
10.3. Переход с барьером Шотки 373
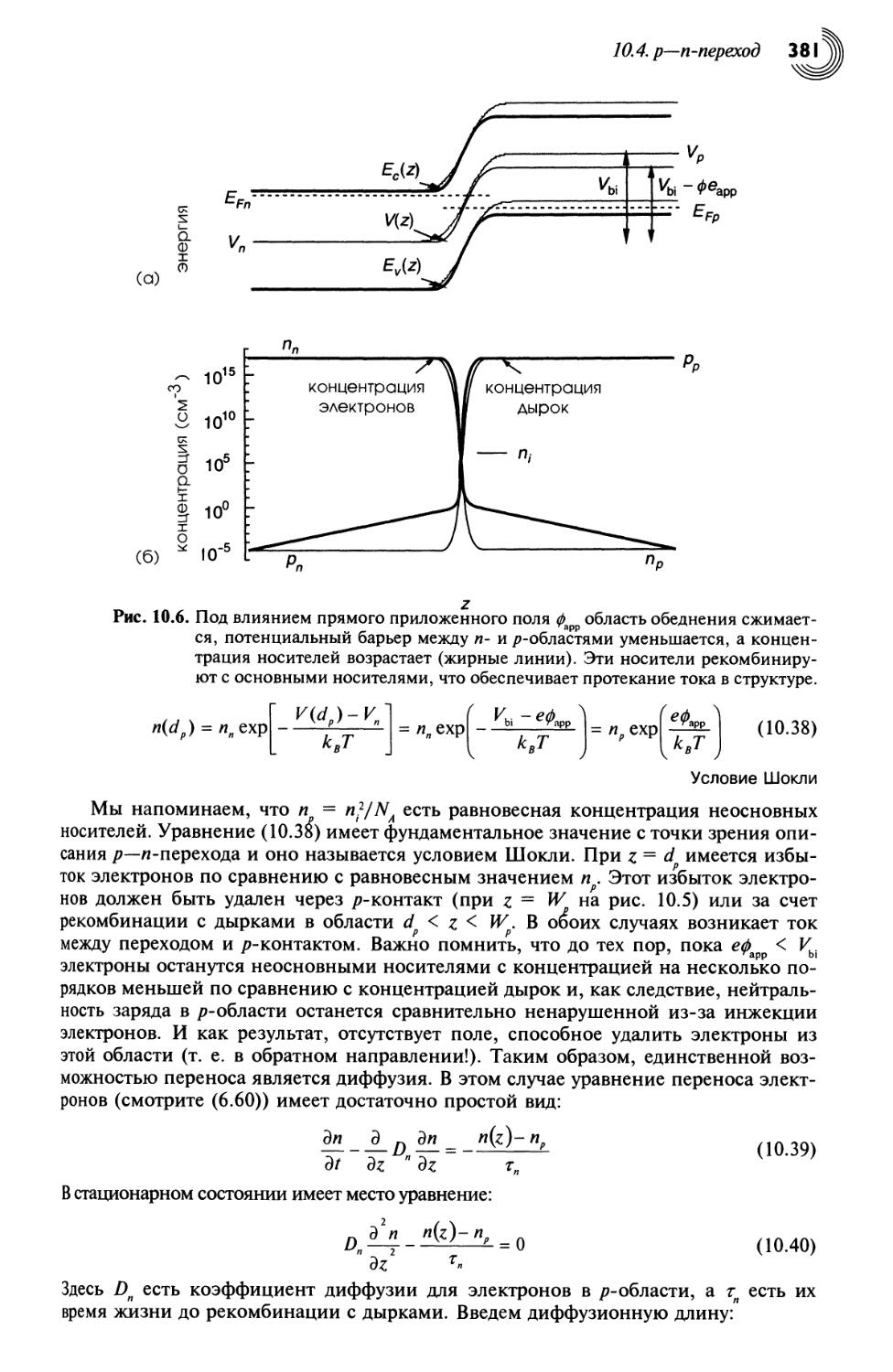
10.4. р—«-переход 377
ДОПОЛНЕНИЯ К ГЛАВЕ 10 385
10.А. Несколько вариантов диодов 385
10.А.1. Диод с р—n-гетеропереходом 385
10.А.2. р—i— л-диод 386
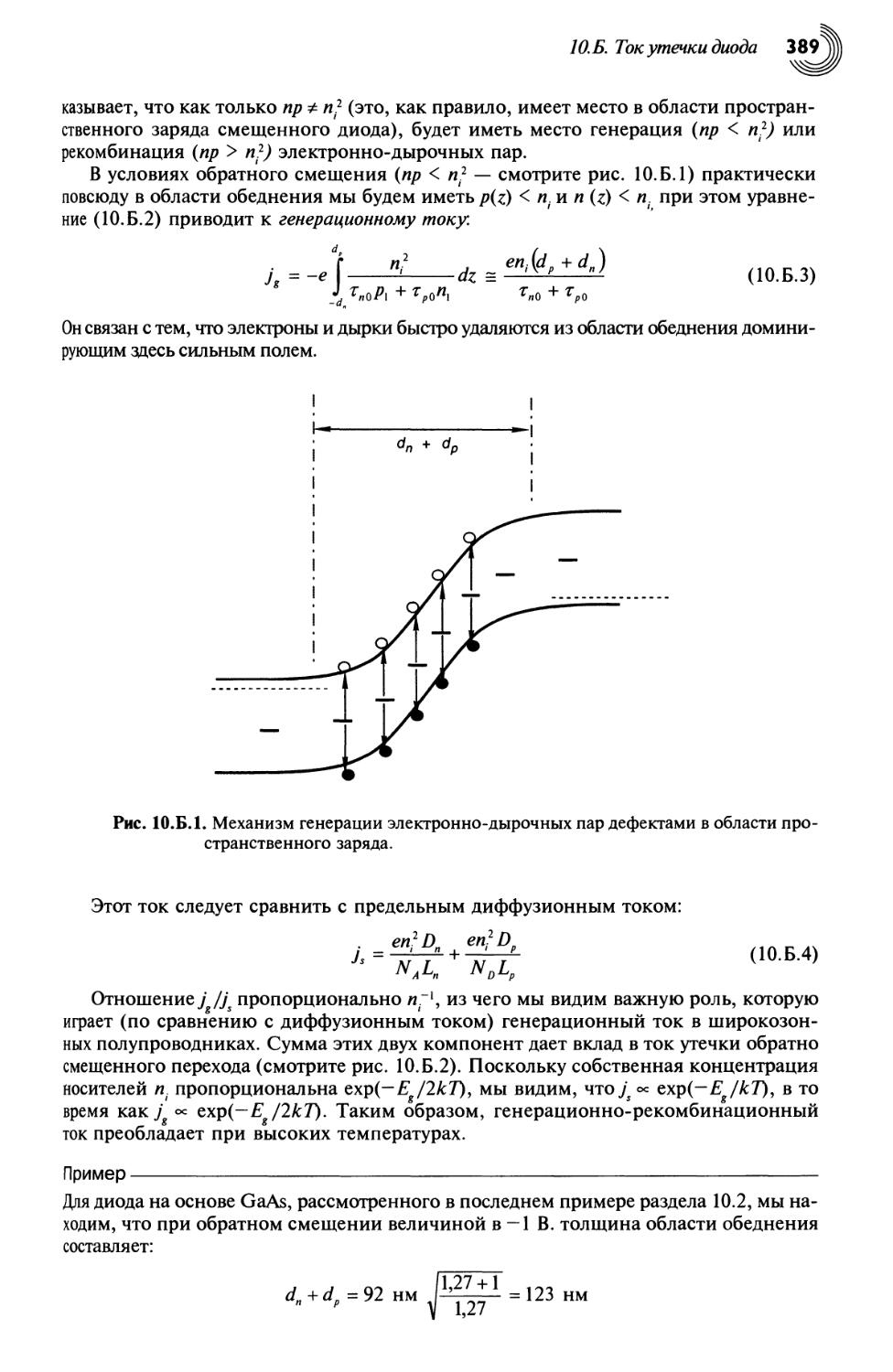
10.Б. Ток утечки диода 388
ГЛАВА 11. ПОЛУПРОВОДНИКОВЫЕ ФОТОПРИЕМНИКИ 392
11.1. Введение 392
11.2. Распределение носителей в фотовозбужденном полупроводнике 393
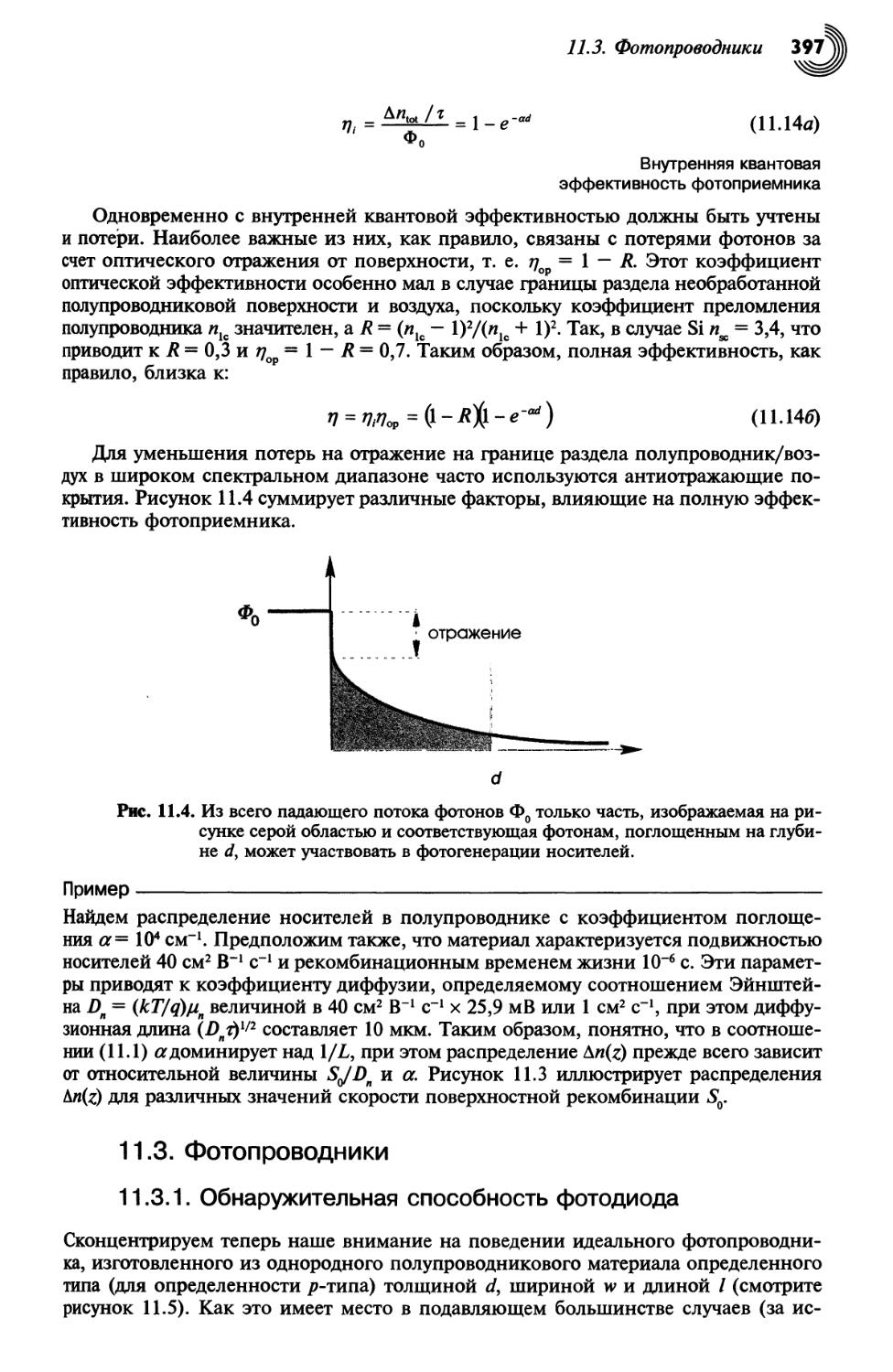
11.3. Фотопроводники 397
11.3.1. Обнаружительная способность фотодиода 397
11.3.2. Обнаружительная способность фотопроводника 400
11.3.3. Время отклика фотопроводника 402
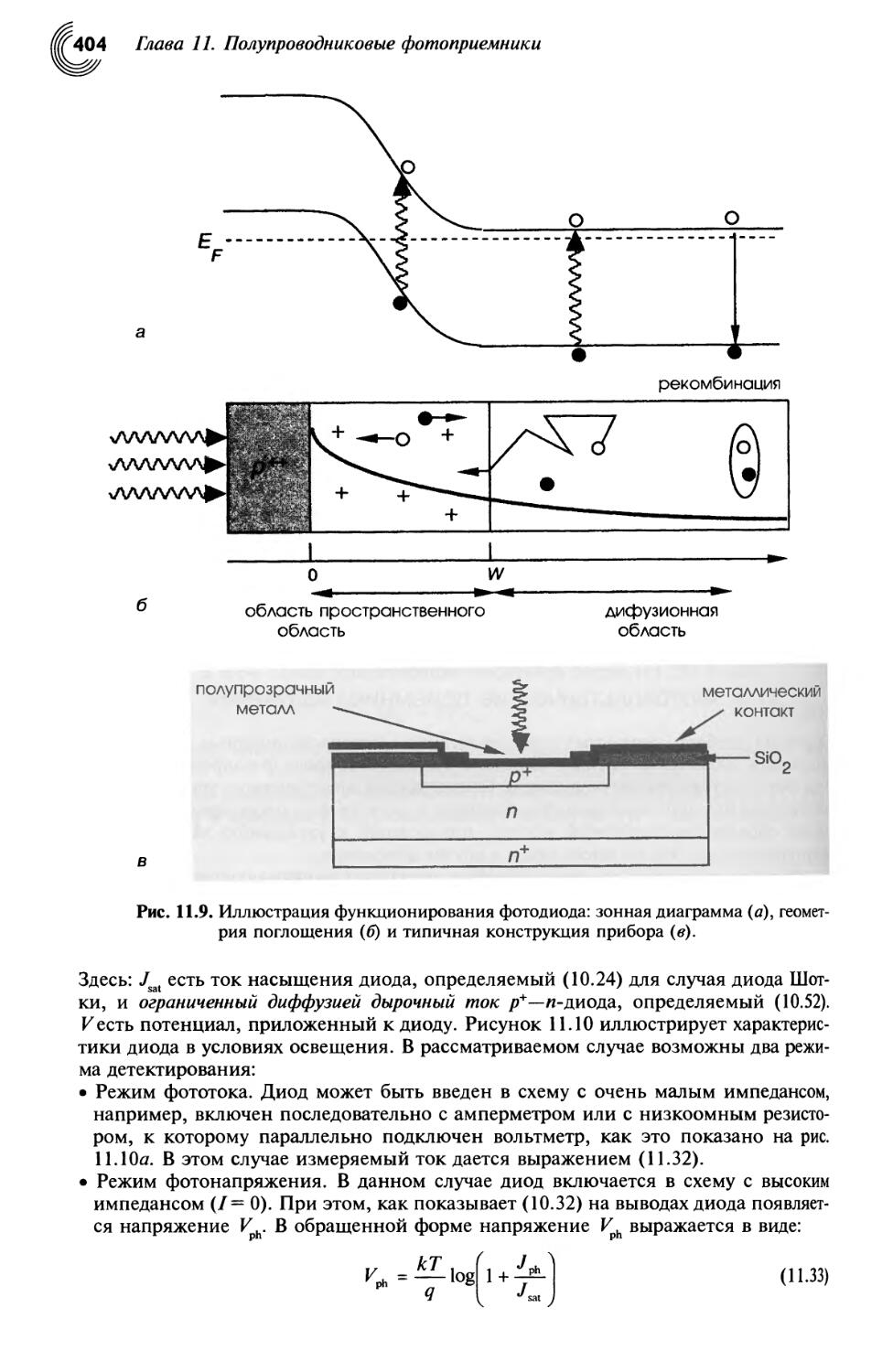
11.4. Фотовольтаические приемники излучения 403
11.4.1. Обнаружительная способность фотодиода 406
11.4.2. Время отклика фотодиода 408
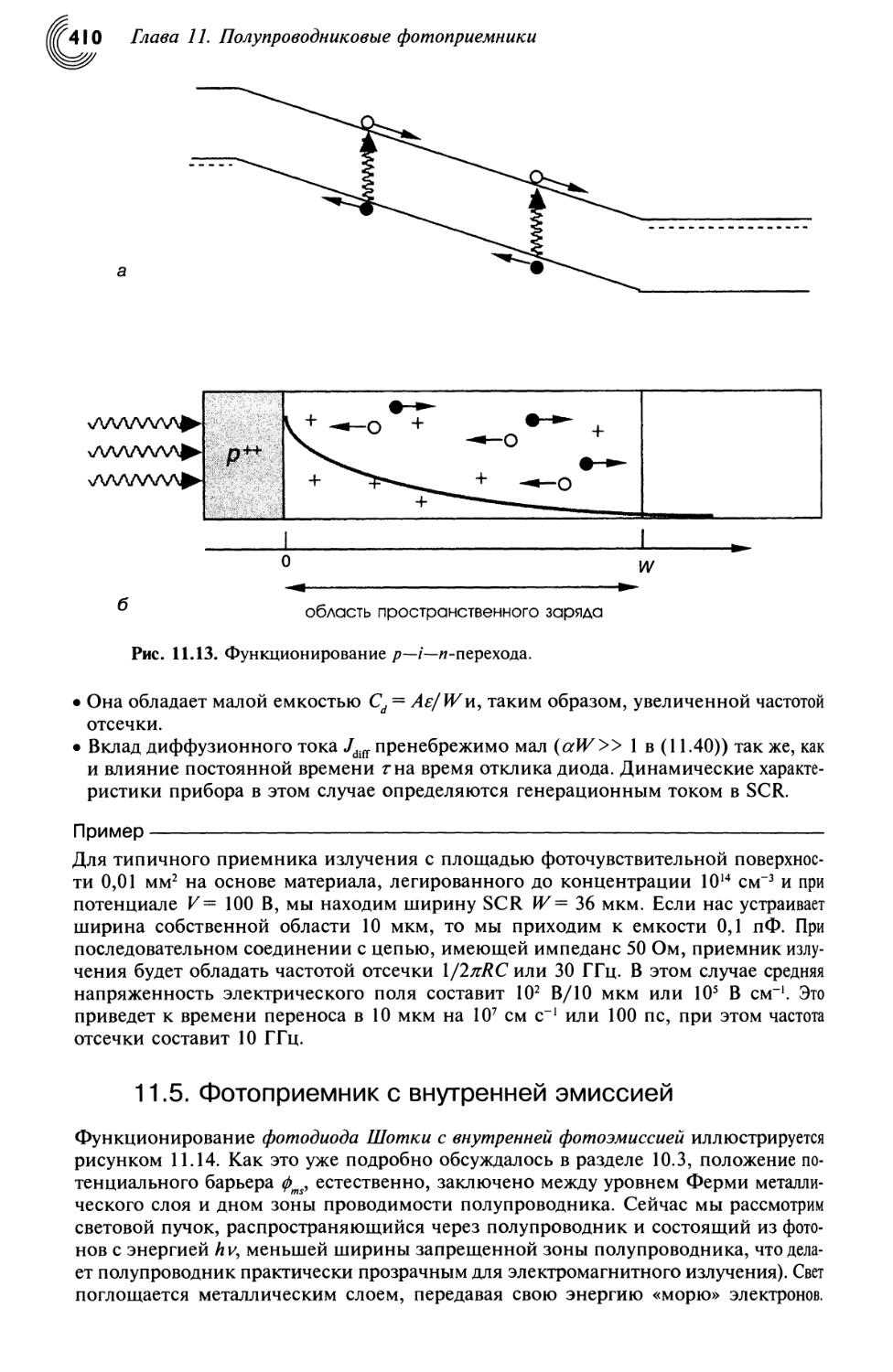
11.5. Фотоприемник с внутренней эмиссией 410
11.6. Квантово-размерные фотоприемники 413
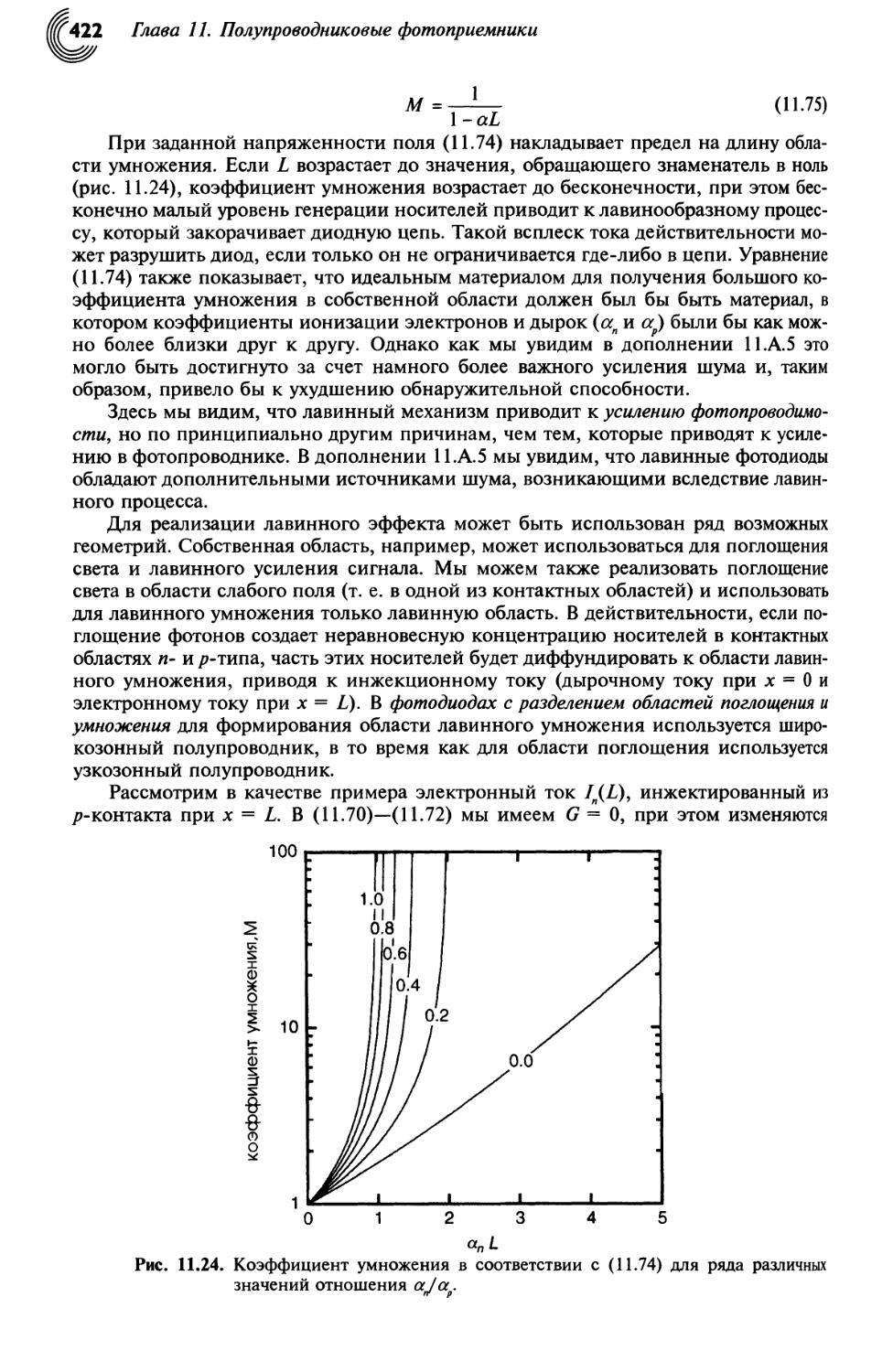
11.7. Лавинные фотоприемники 420
ДОПОЛНЕНИЯ К ГЛАВЕ И 424
11.А. Шум фотоприемника 424
\\АЛ. Флуктуации 425
11.А.2. Физическая природа шума 427
11.А.З. Тепловой шум 428
11.А.4. Генерационно-рекомбинационный шум 430
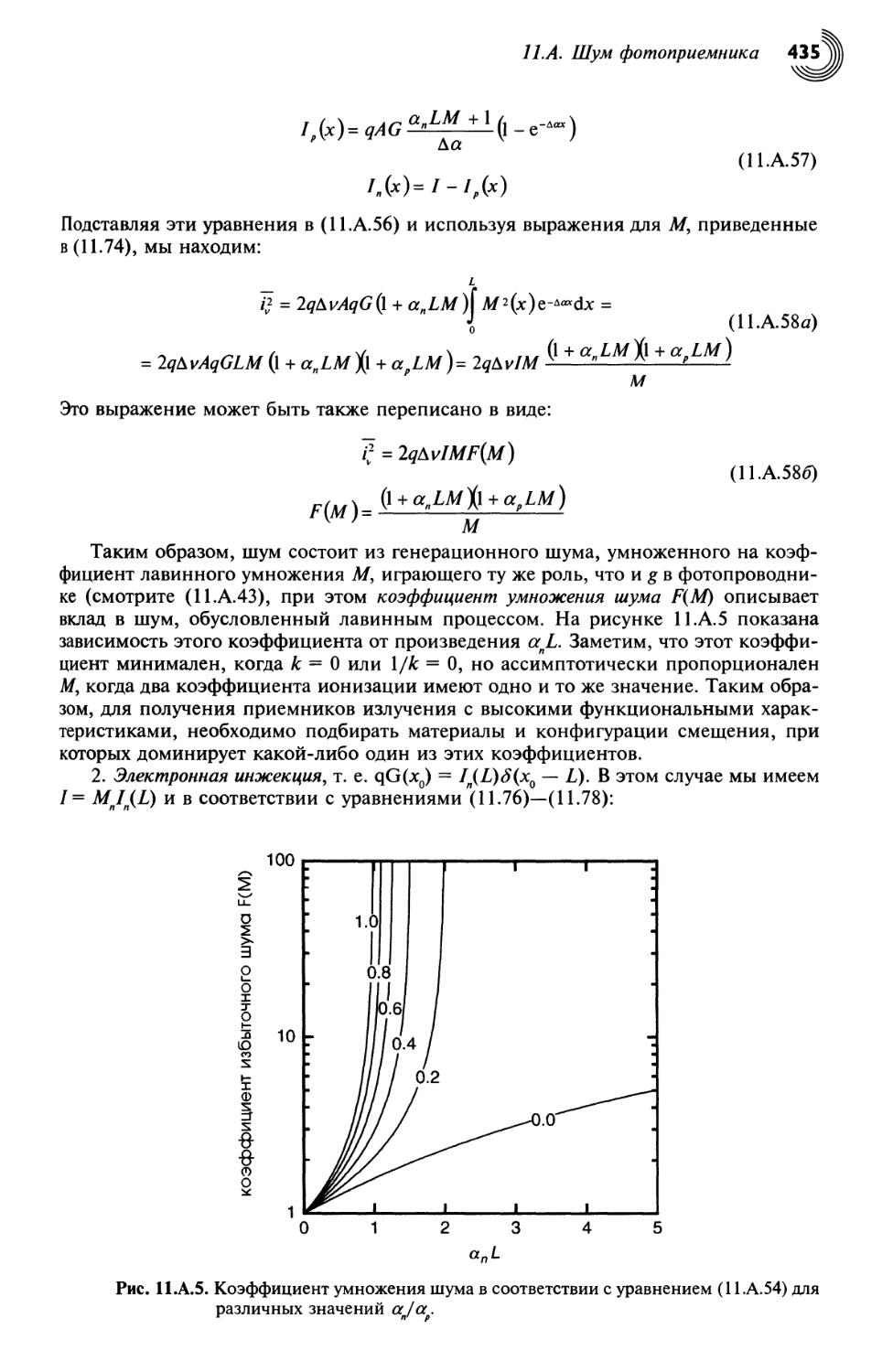
11 А.5. Шум умножения 433
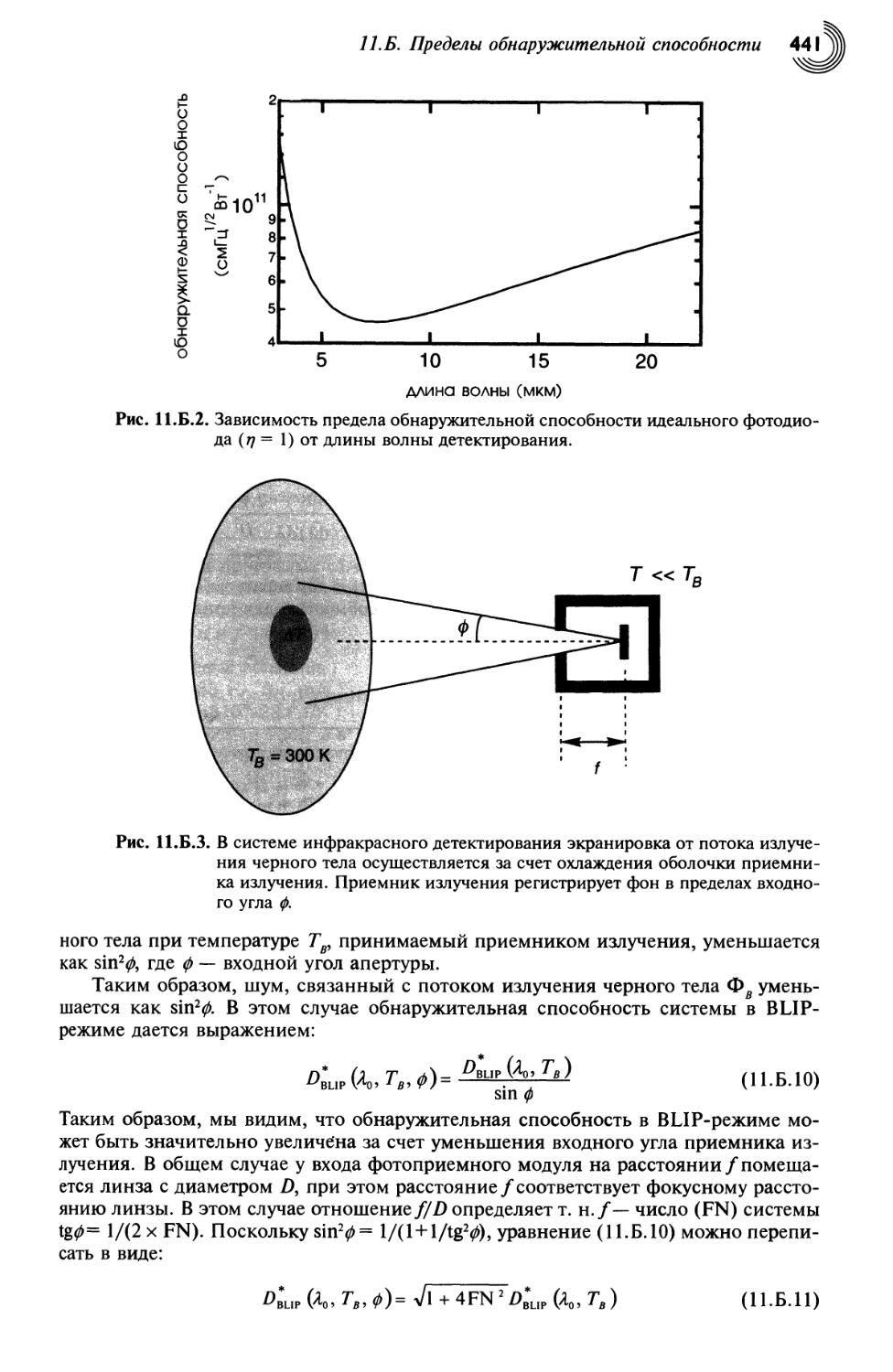
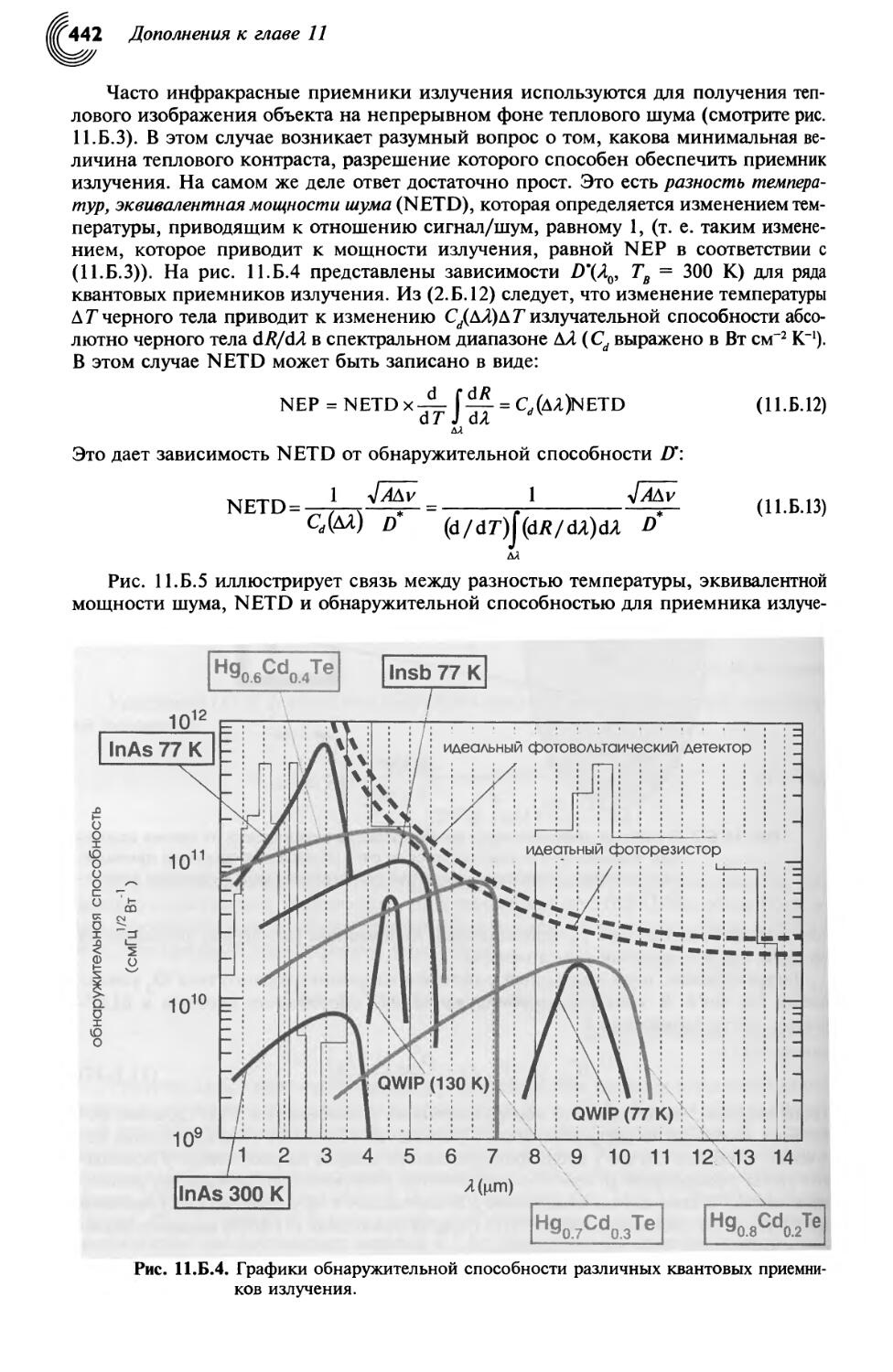
11. Б. Пределы обнаружительной способности: функциональные
характеристики, ограниченные фоном (BLIP) 438
Оптоэлектроника
ГЛАВА 12. ПРЕОБРАЗОВАНИЕ ОПТИЧЕСКОЙ ЧАСТОТЫ 444
12.1. Введение 444
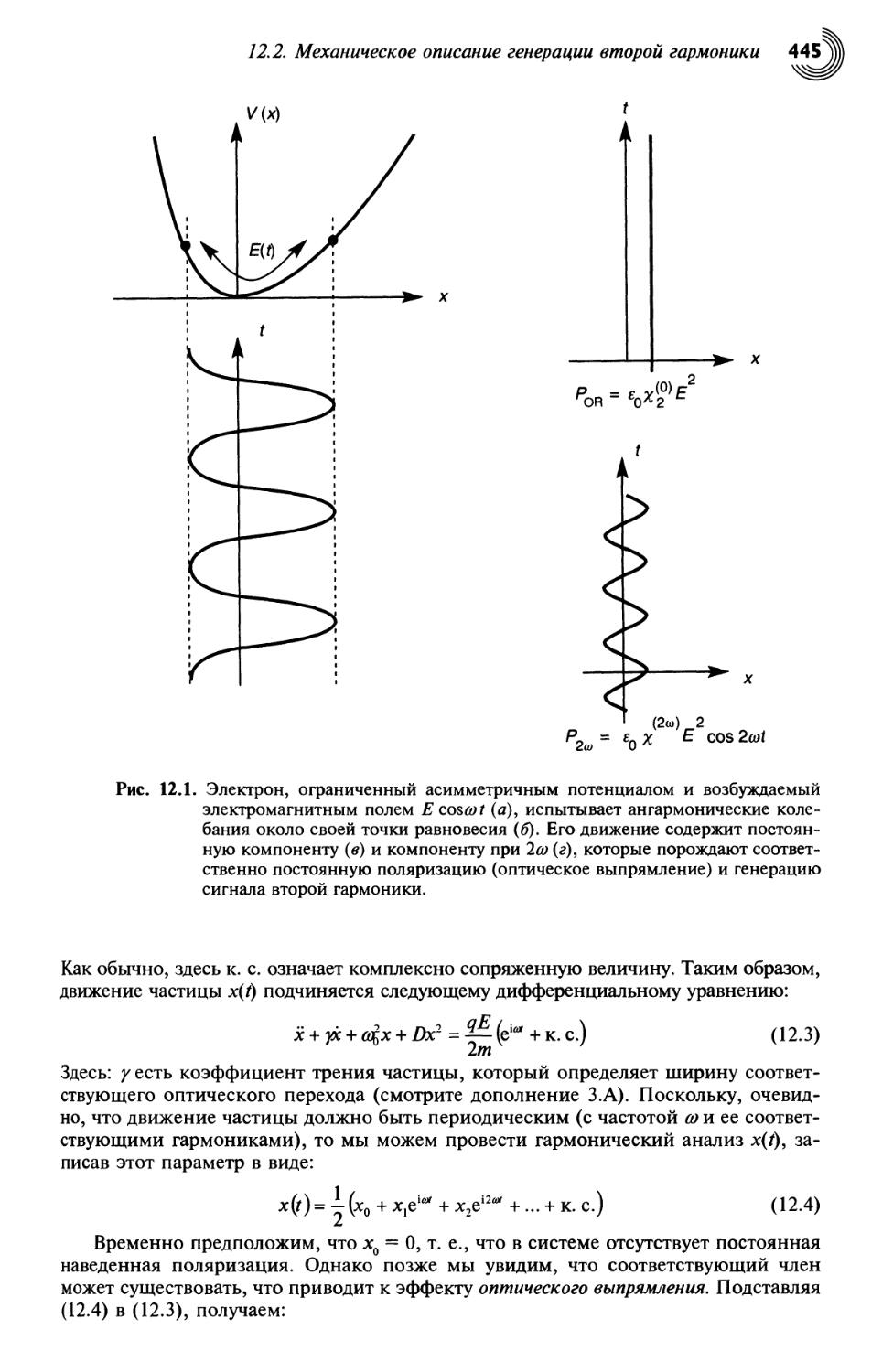
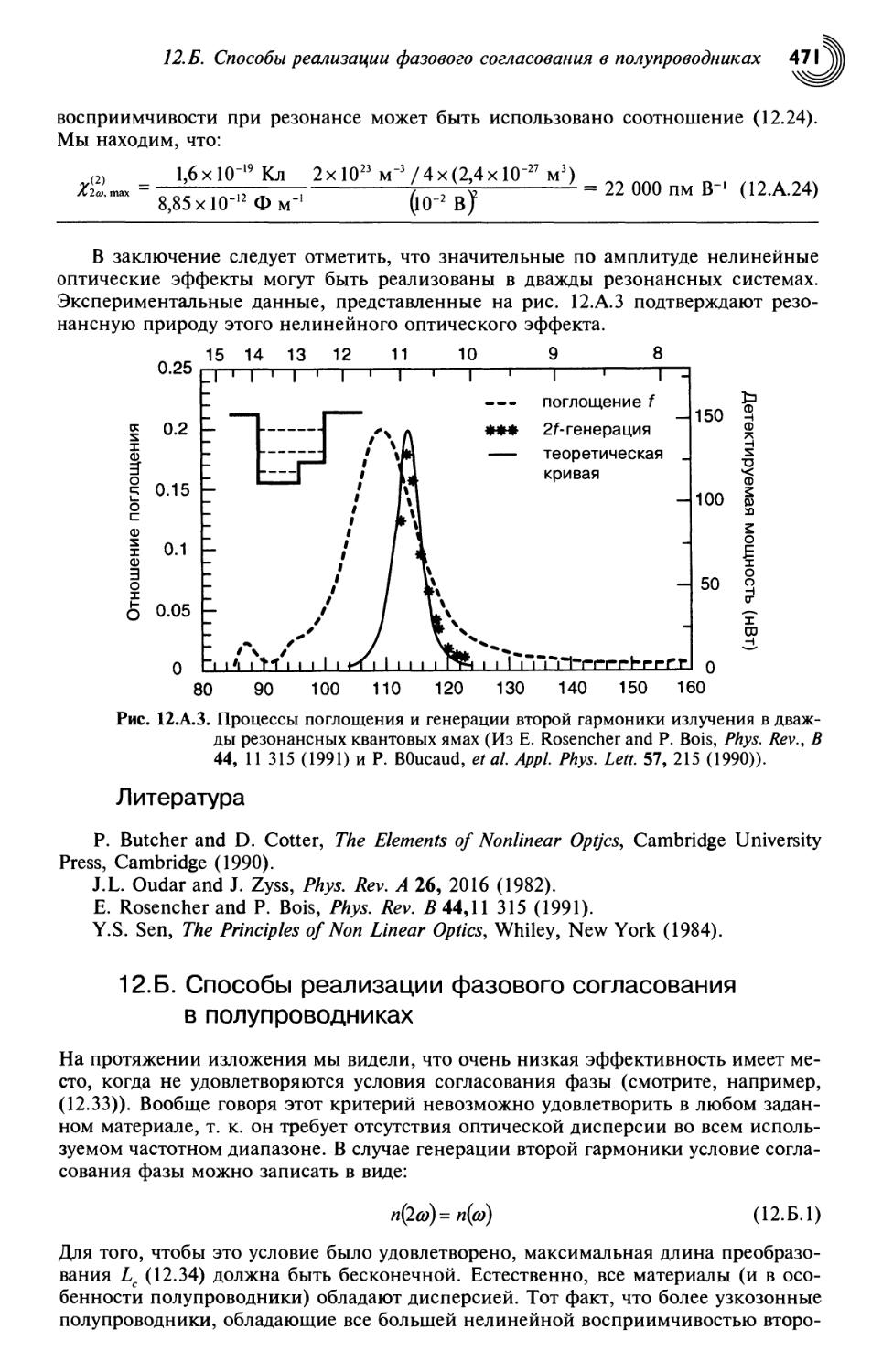
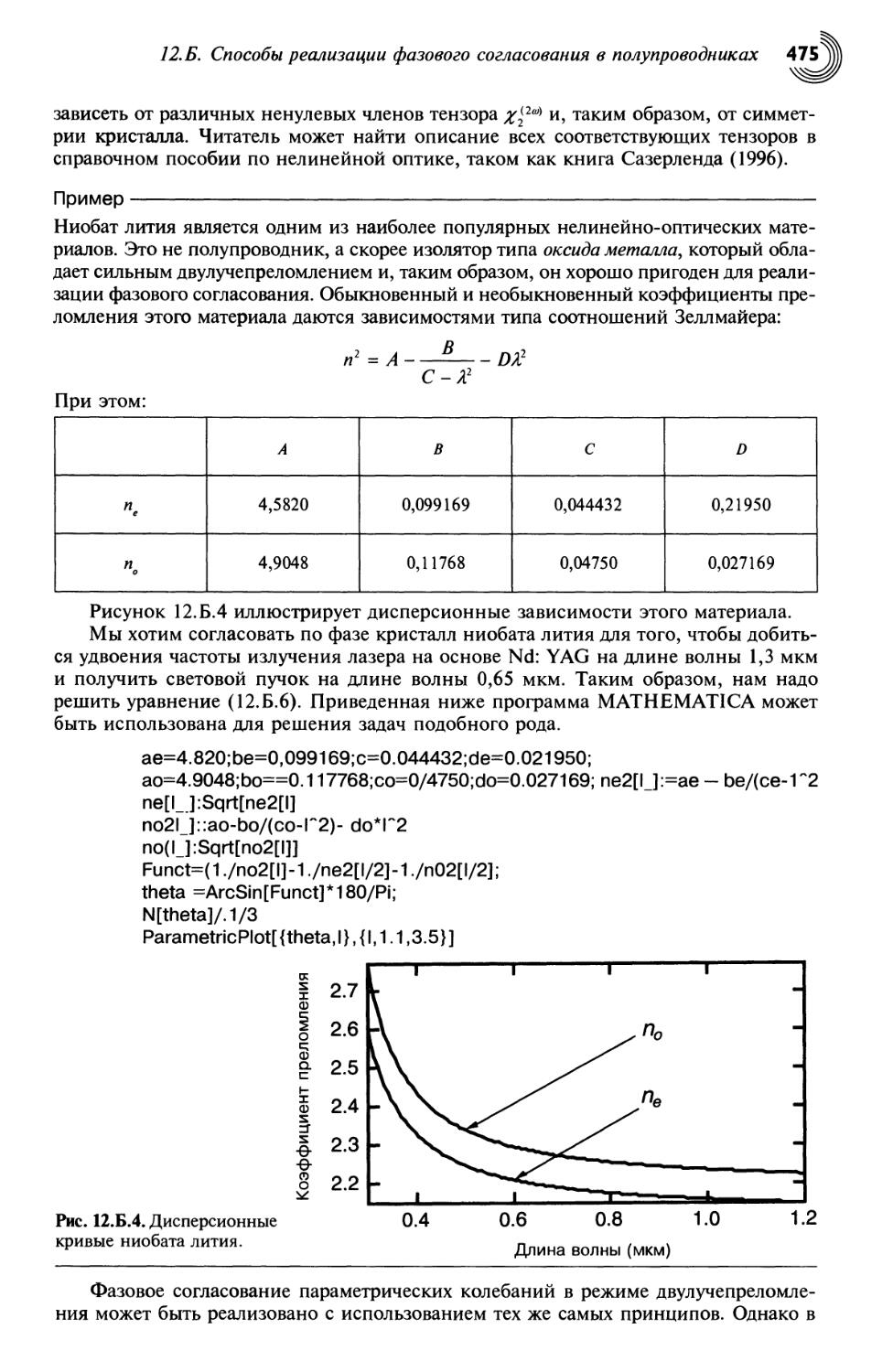
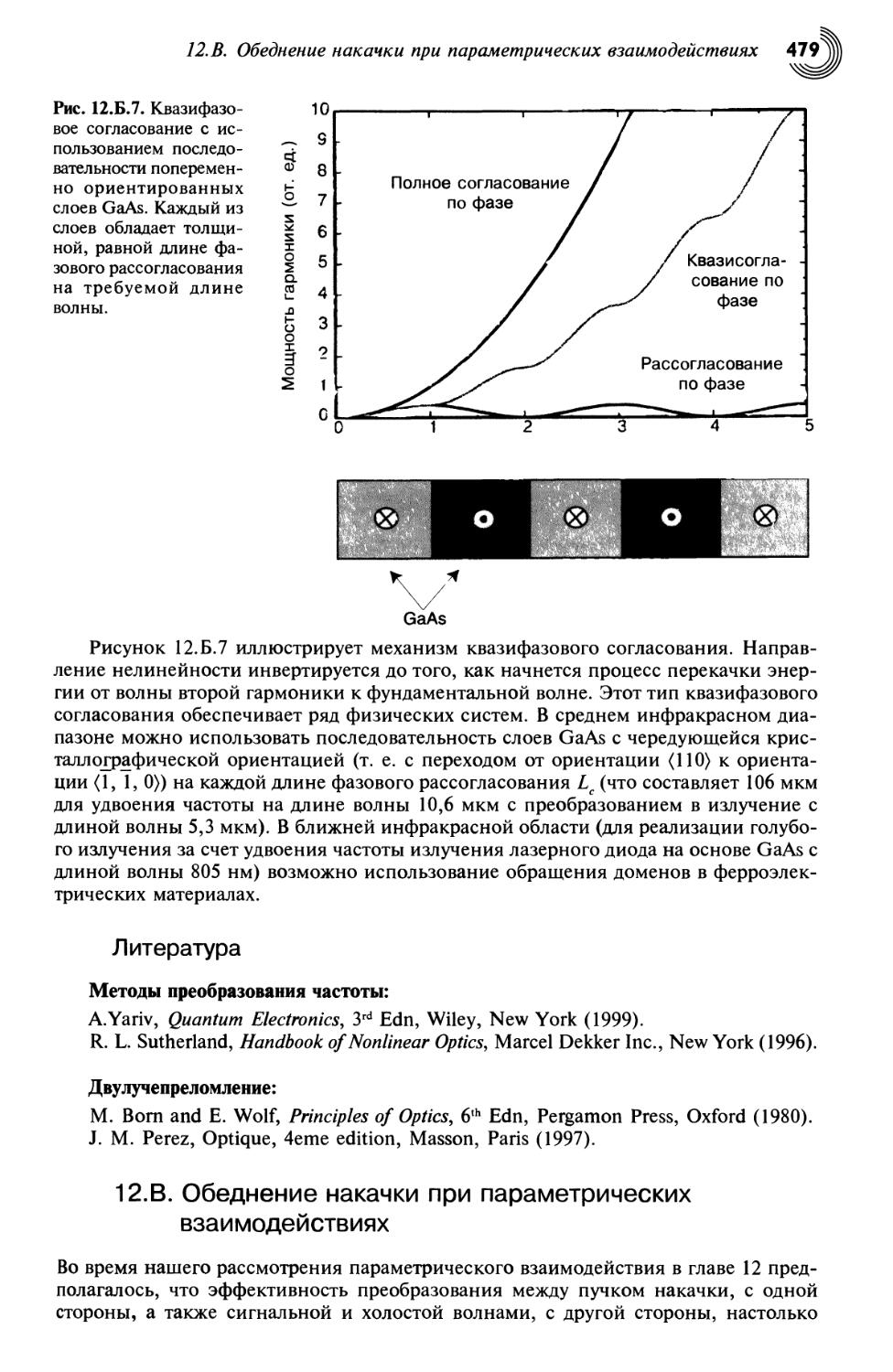
12.2. Механическое описание генерации второй гармоники 444
12.3. Электромагнитное описание нелинейной квадратичной оптической
восприимчивости 448
12.4. Оптическая генерация второй гармоники 450
12.5. Соотношения Мэнли—Роу 453
12.6. Параметрическое усиление 455
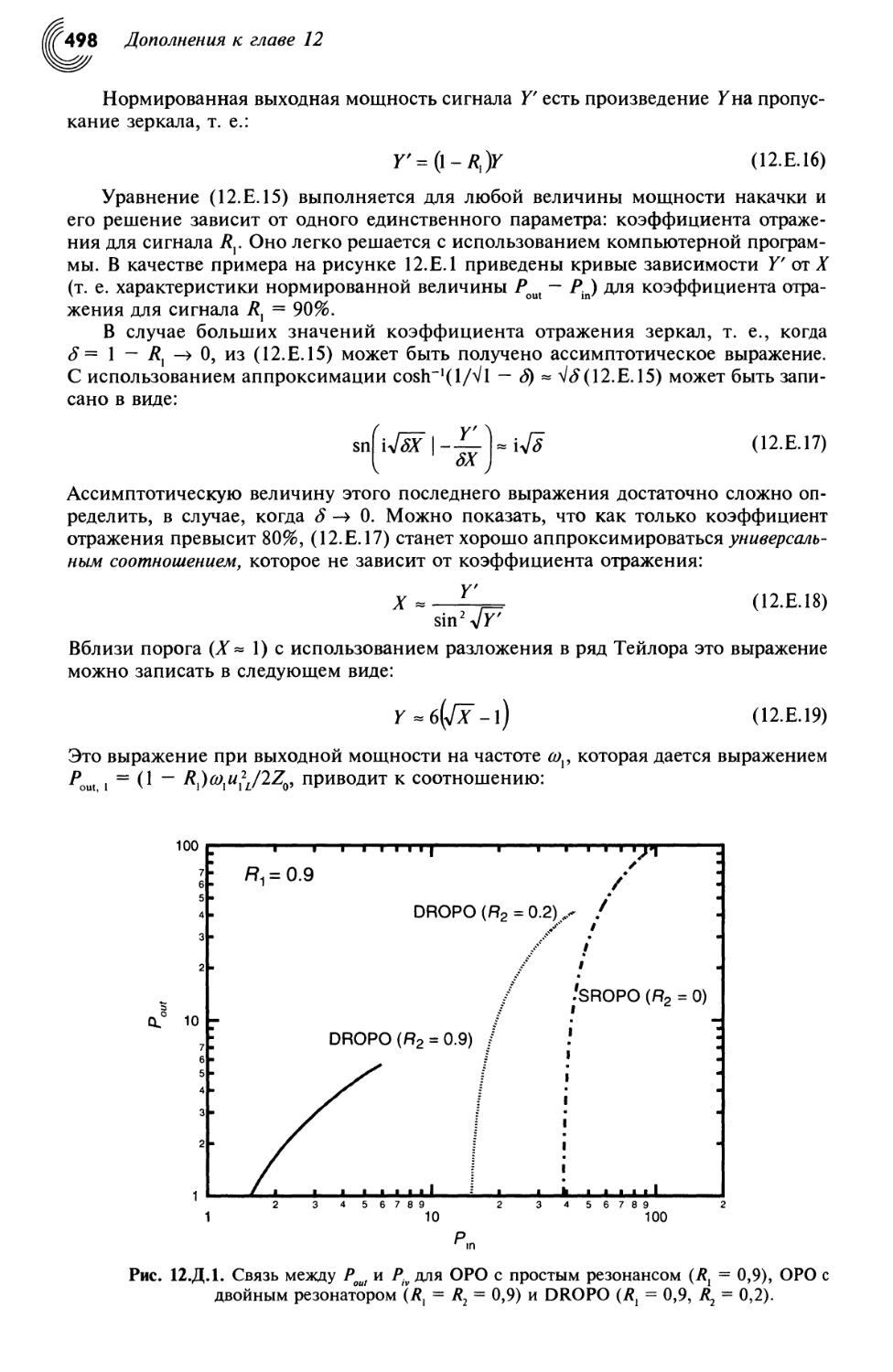
12.7. Оптические параметрические генераторы 457
12.7.1. Оптические параметрические генераторы с простым резонансом (SROPO) .... 458
12.7.2. Оптические параметрические генераторы с двойным резонансом (DROPO)... 459
12.8. Суммарная частота, разностная частота и параметрическое усиление 461
ДОПОЛНЕНИЯ К ГЛАВЕ 12 466
12.А. Квантовая модель квадратичной нелинейной восприимчивости 466
12.Б. Способы реализации фазового согласования в полупроводниках 471
12.Б.1. Согласование фаз в режиме двулучепреломления 472
12.Б.2. Квазифазовое согласование 477
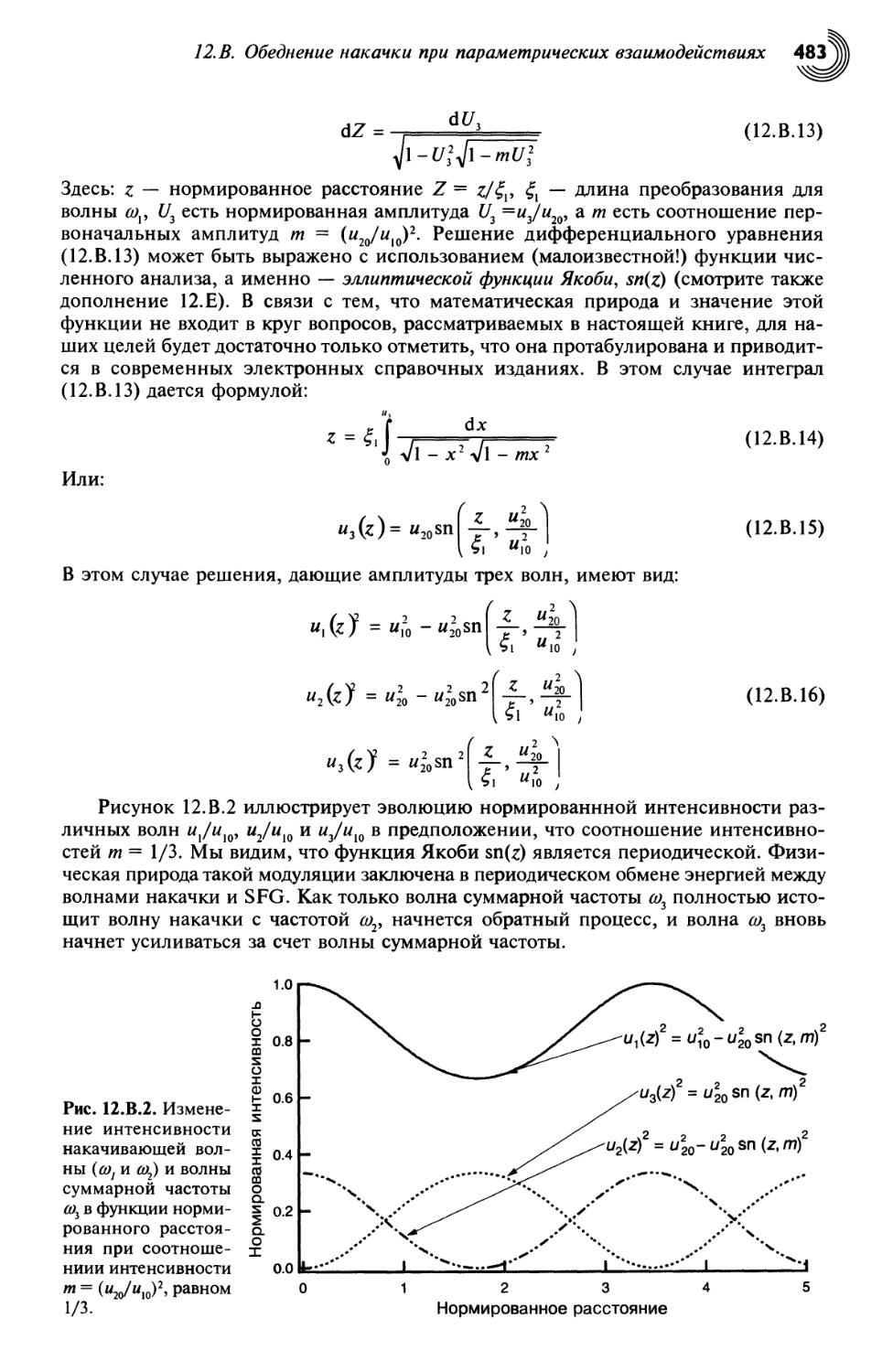
12.В. Обеднение накачки при параметрических взаимодействиях 479
12.Г. Спектральные и временные характеристики оптических
параметрических генераторов 484
12.Д. Параметрические взаимодействия в лазерных резонаторах 490
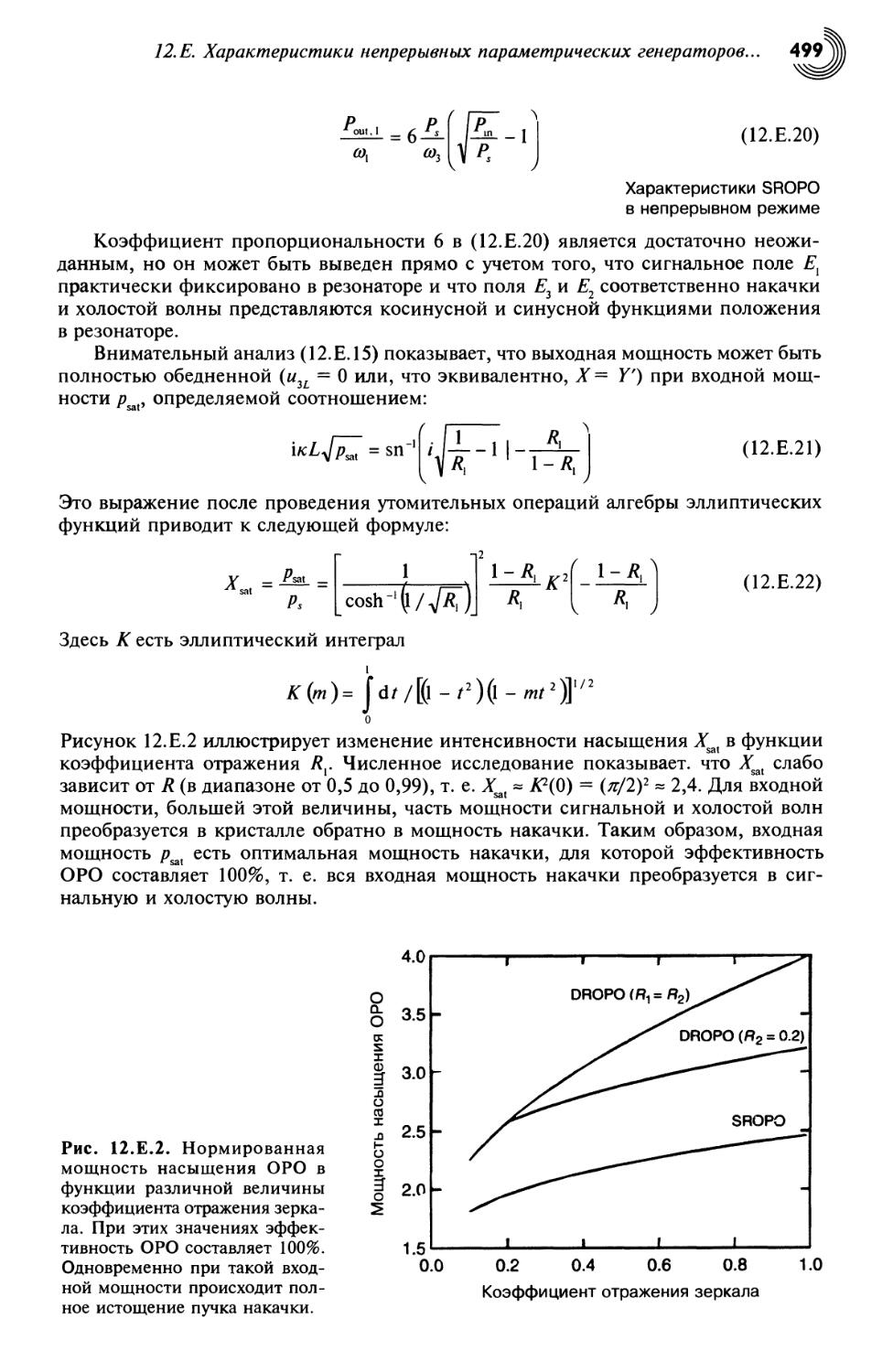
12.Е. Характеристики непрерывных параметрических генераторов
в непрерывном режиме 495
12.ЕЛ. ОРО с одиночным резонансном 496
12.Е.2. ОРО с двойным резонансом: сбалансированный DROPO 500
12.Е.З. Оптический параметрический генератор (ОРО) с двойным резонансом:
общий случай 502
ГЛАВА 13. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ И ЛАЗЕРНЫЕ ДИОДЫ 504
13.1. Введение 504
13.2. Электрическая инжекция и неравновесная концентрация носителей 504
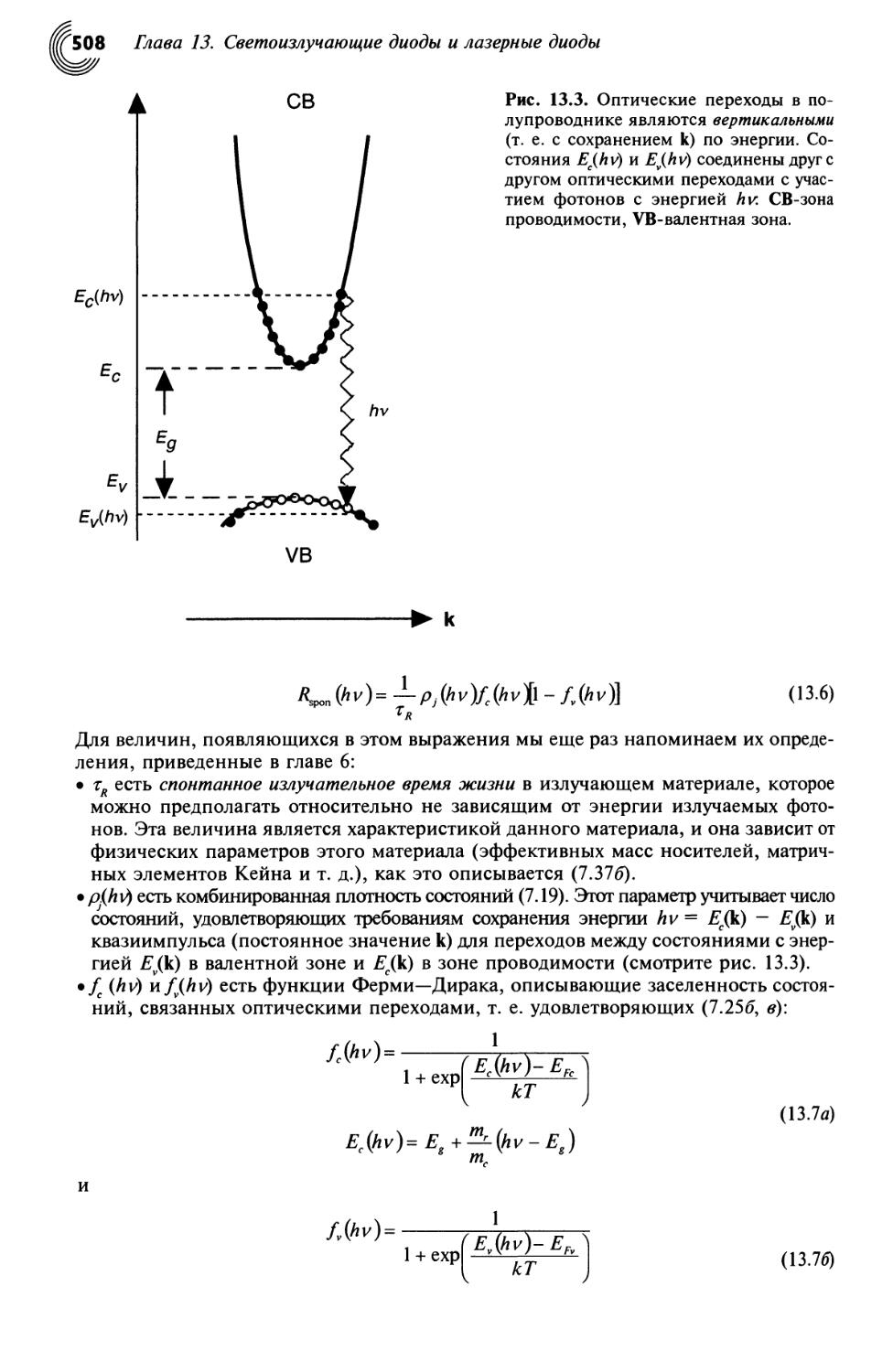
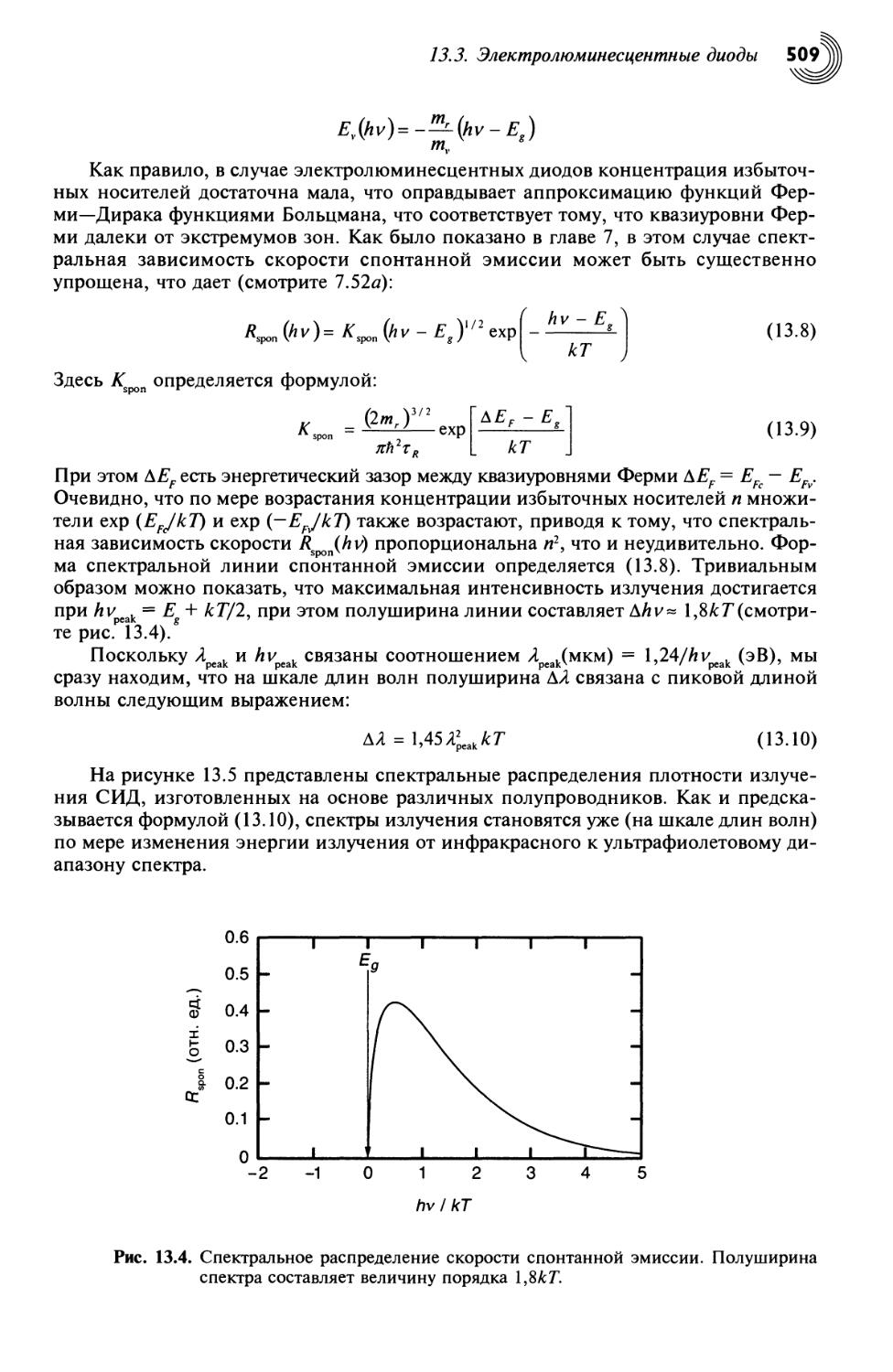
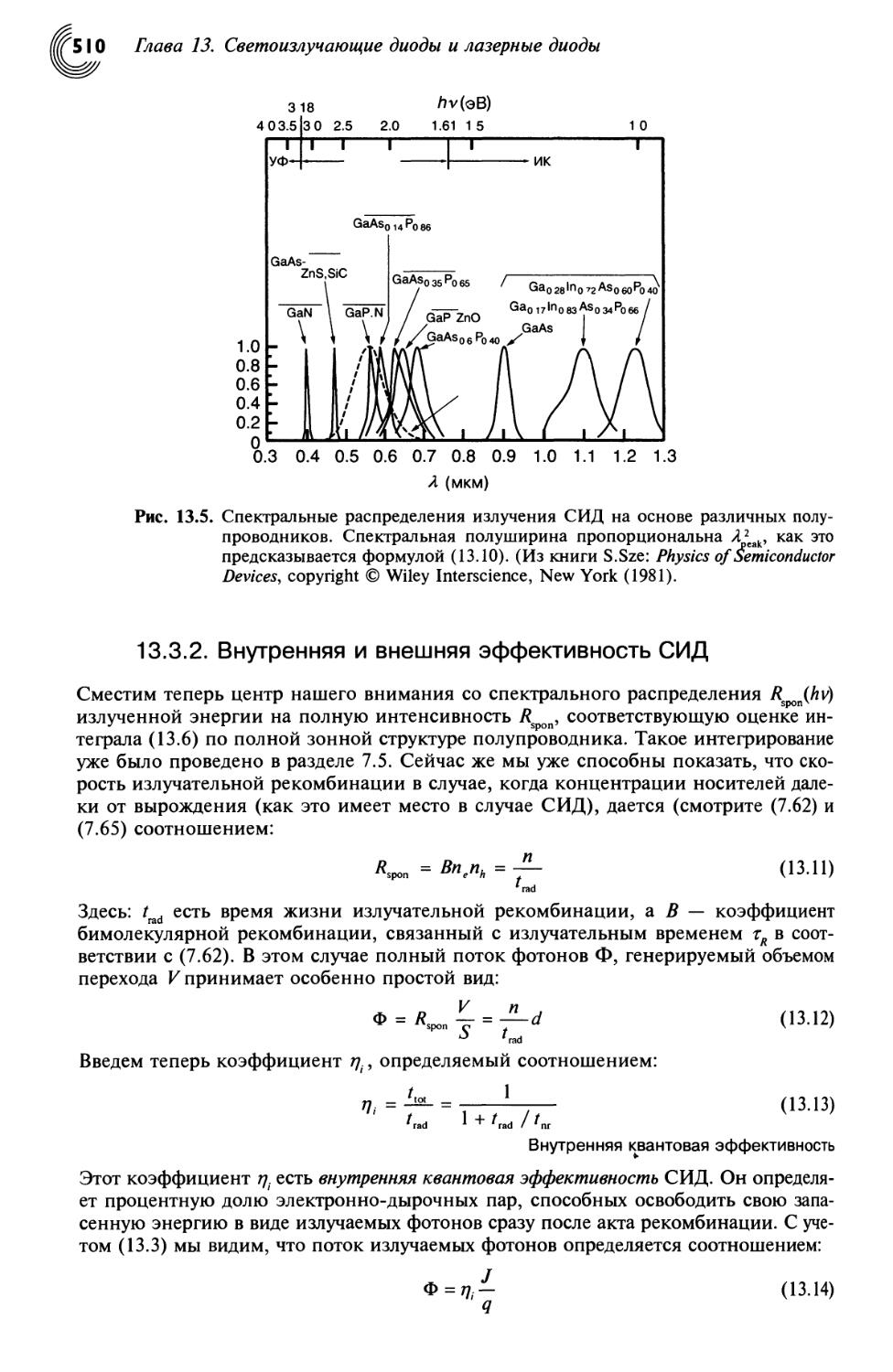
13.3. Электролюминесцентные диоды 507
13.3.1. Электролюминесценция 507
13.3.2. Внутренняя и внешняя эффективность СИД 510
13.3.3. Несколько приборных вопросов 512
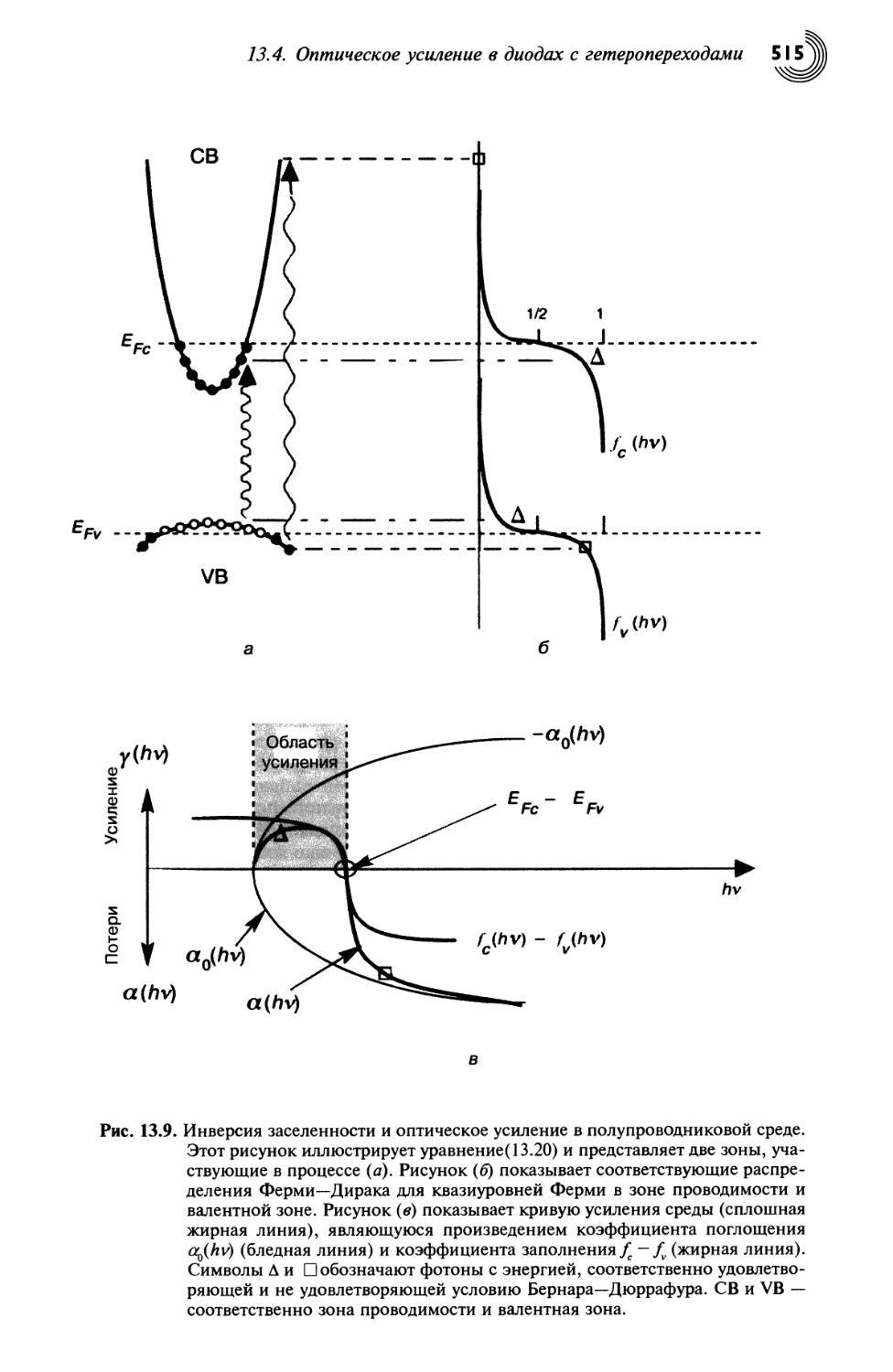
13.4. Оптическое усиление в диодах с гетеропереходами 514
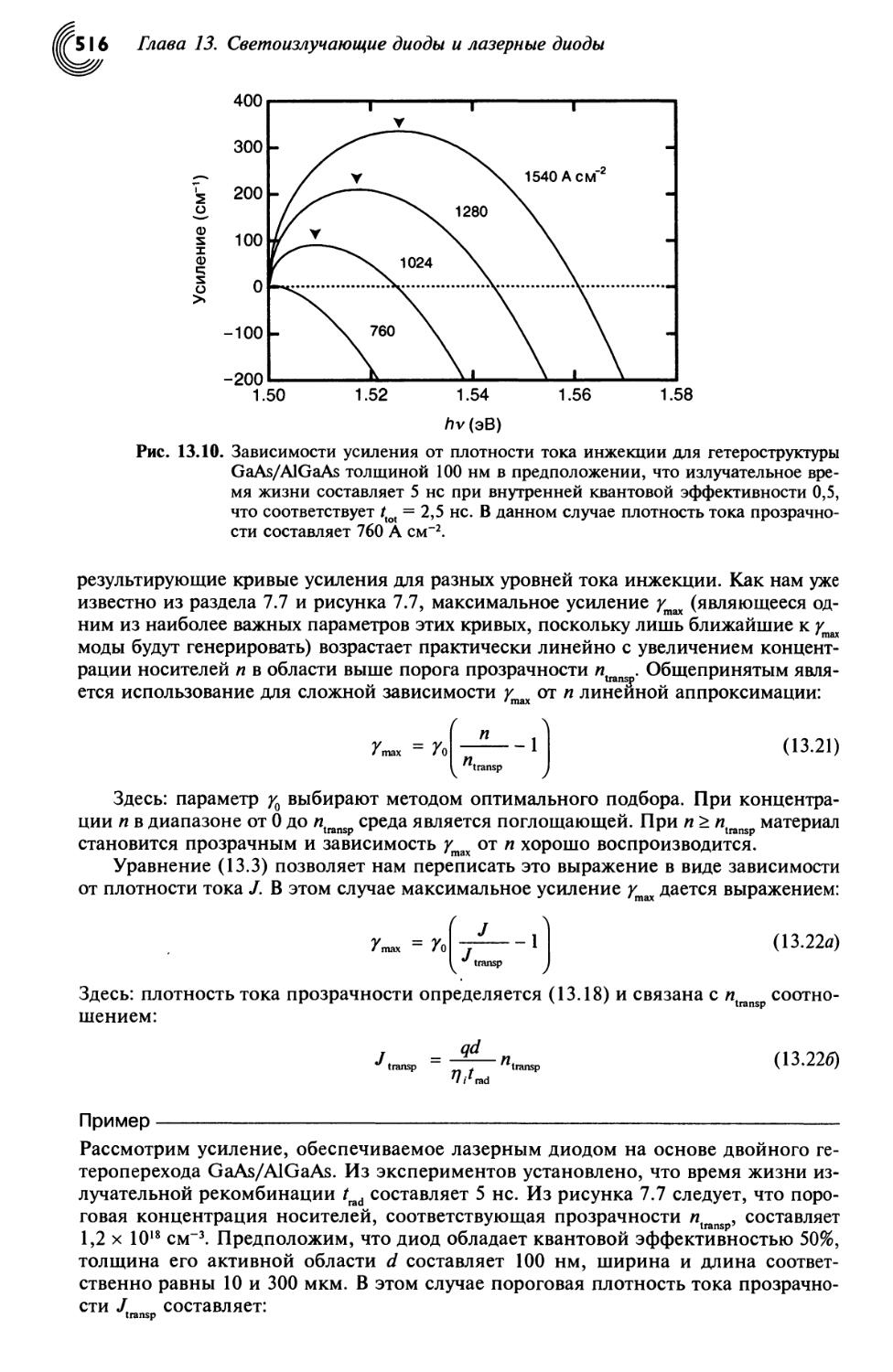
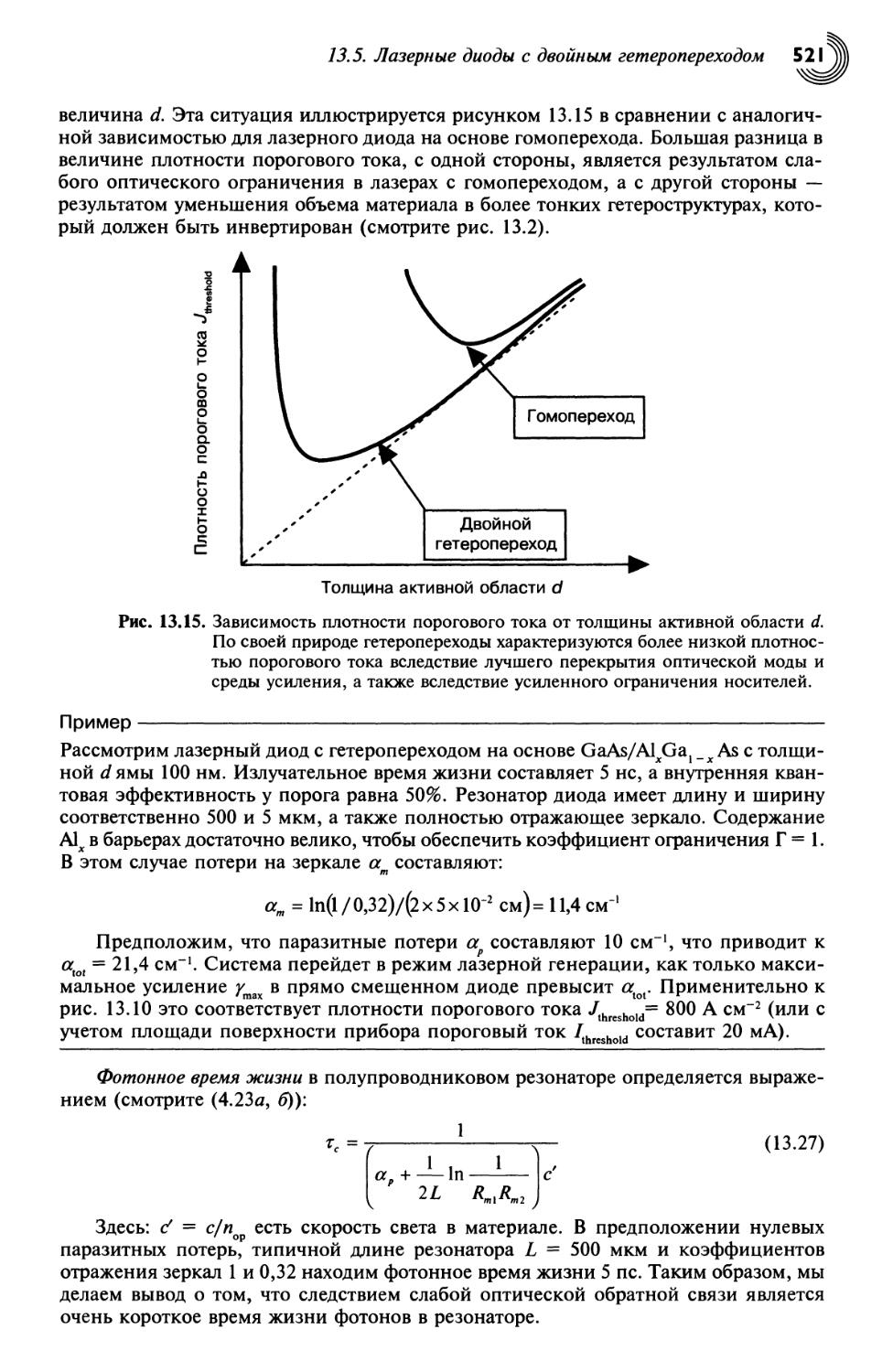
13.5. Лазерные диоды с двойным гетеропереходом 517
13.5.1. Лазерный порог 517
13.5.2. Выходная мощность 522
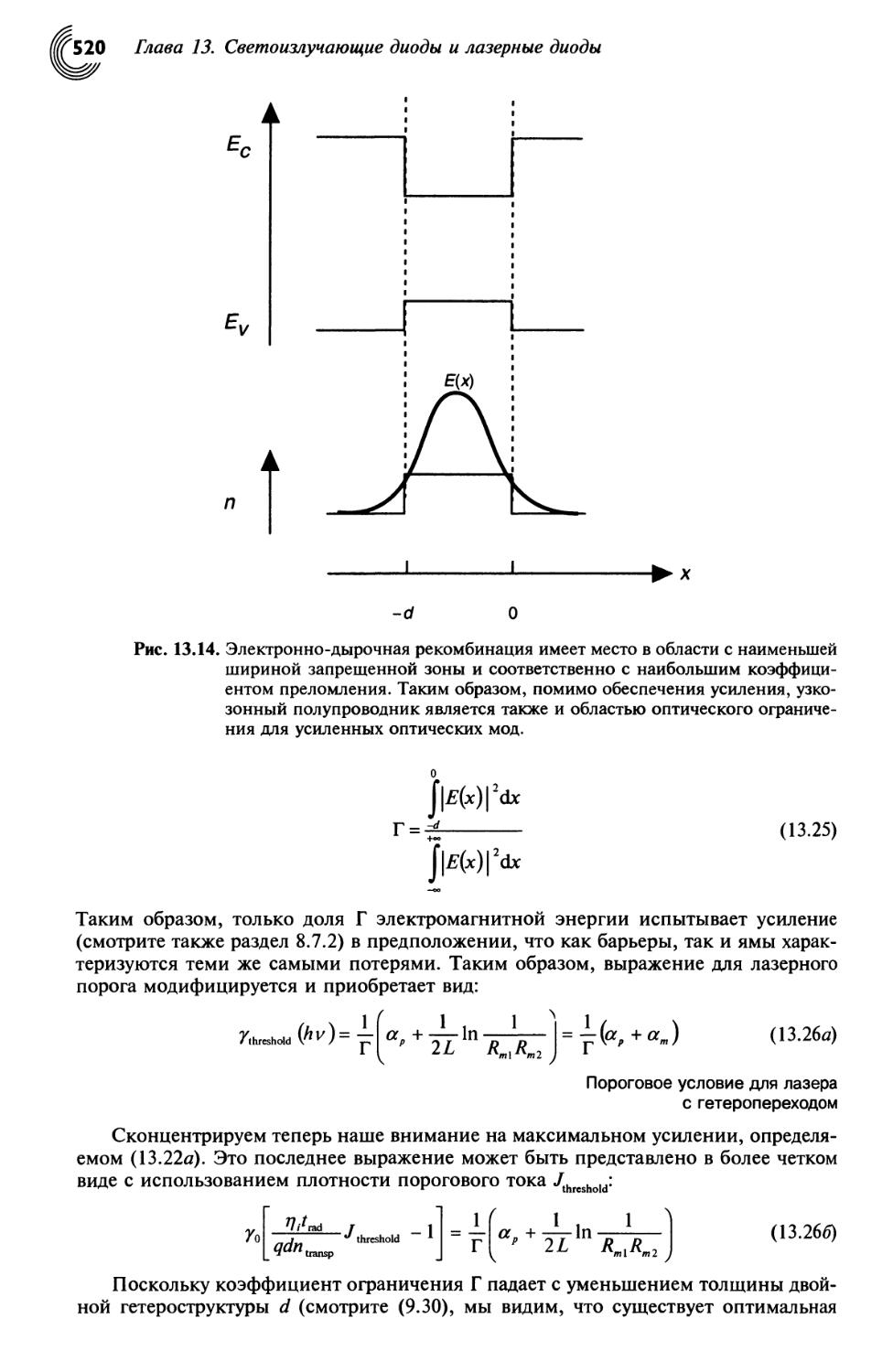
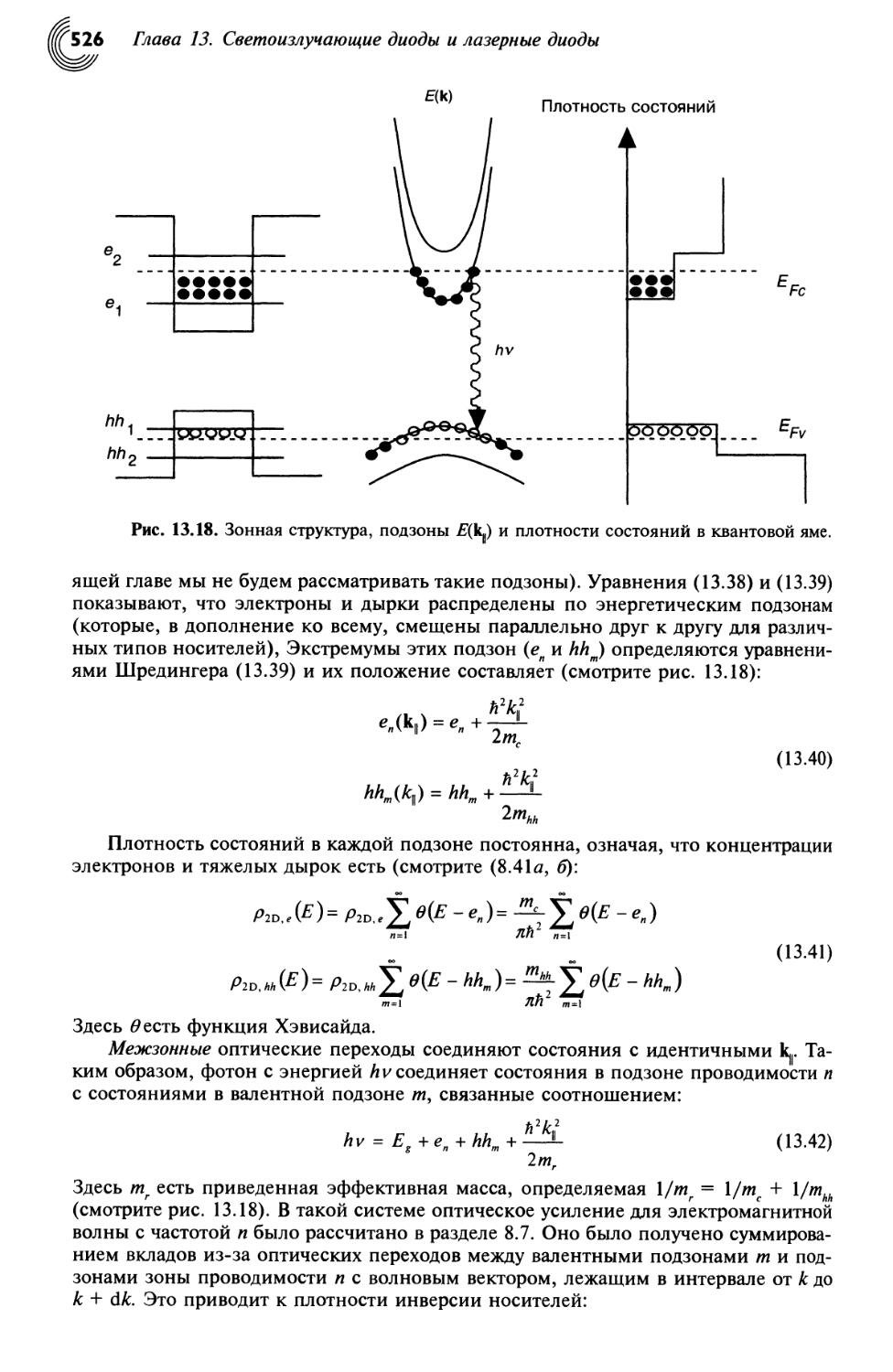
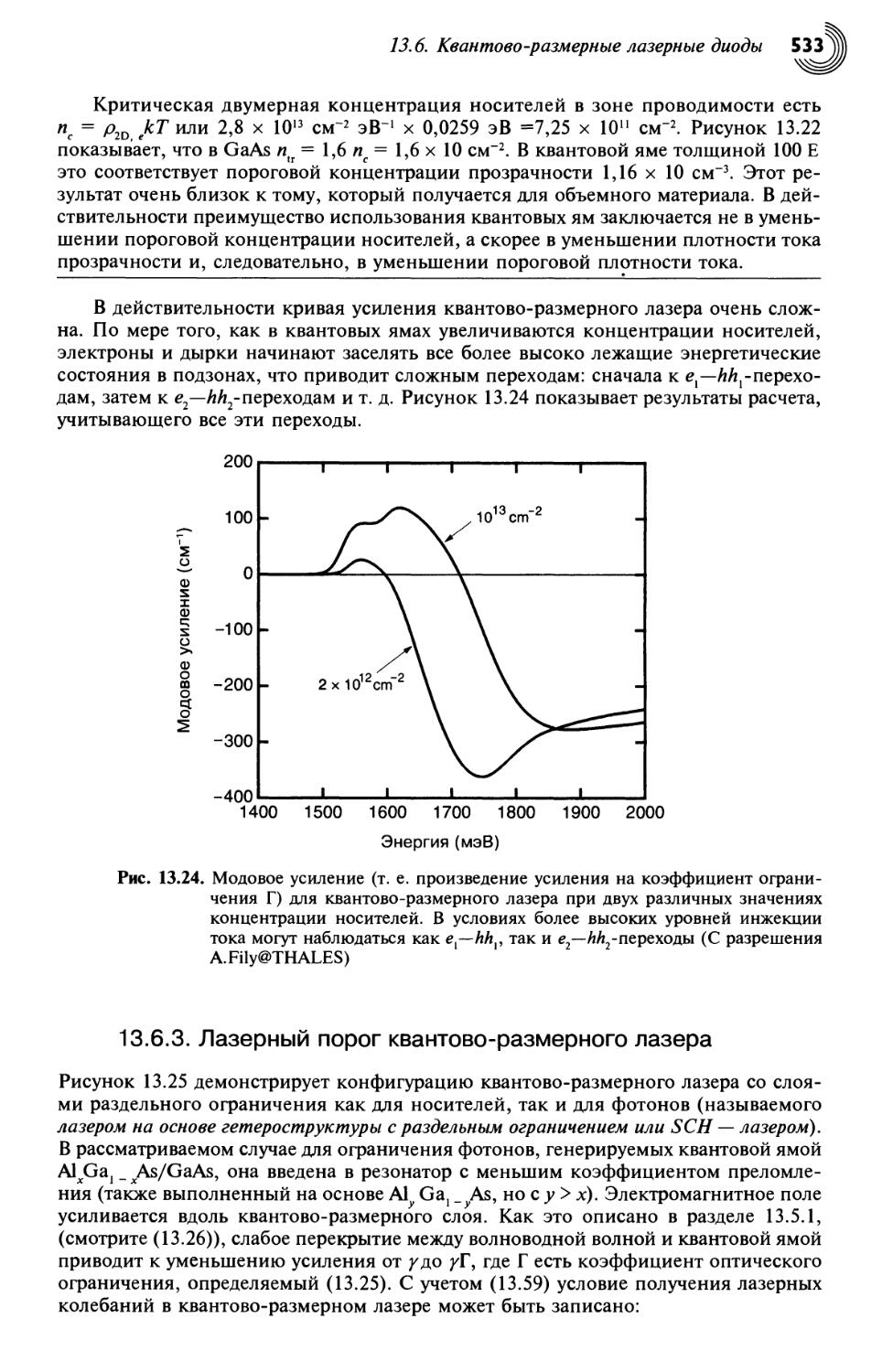
13.6. Квантово-размерные лазерные диоды 525
13.6.1. Оптическое усиление в квантово-размерной структуре: общий случай 525
13.6.2. Порог прозрачности 528
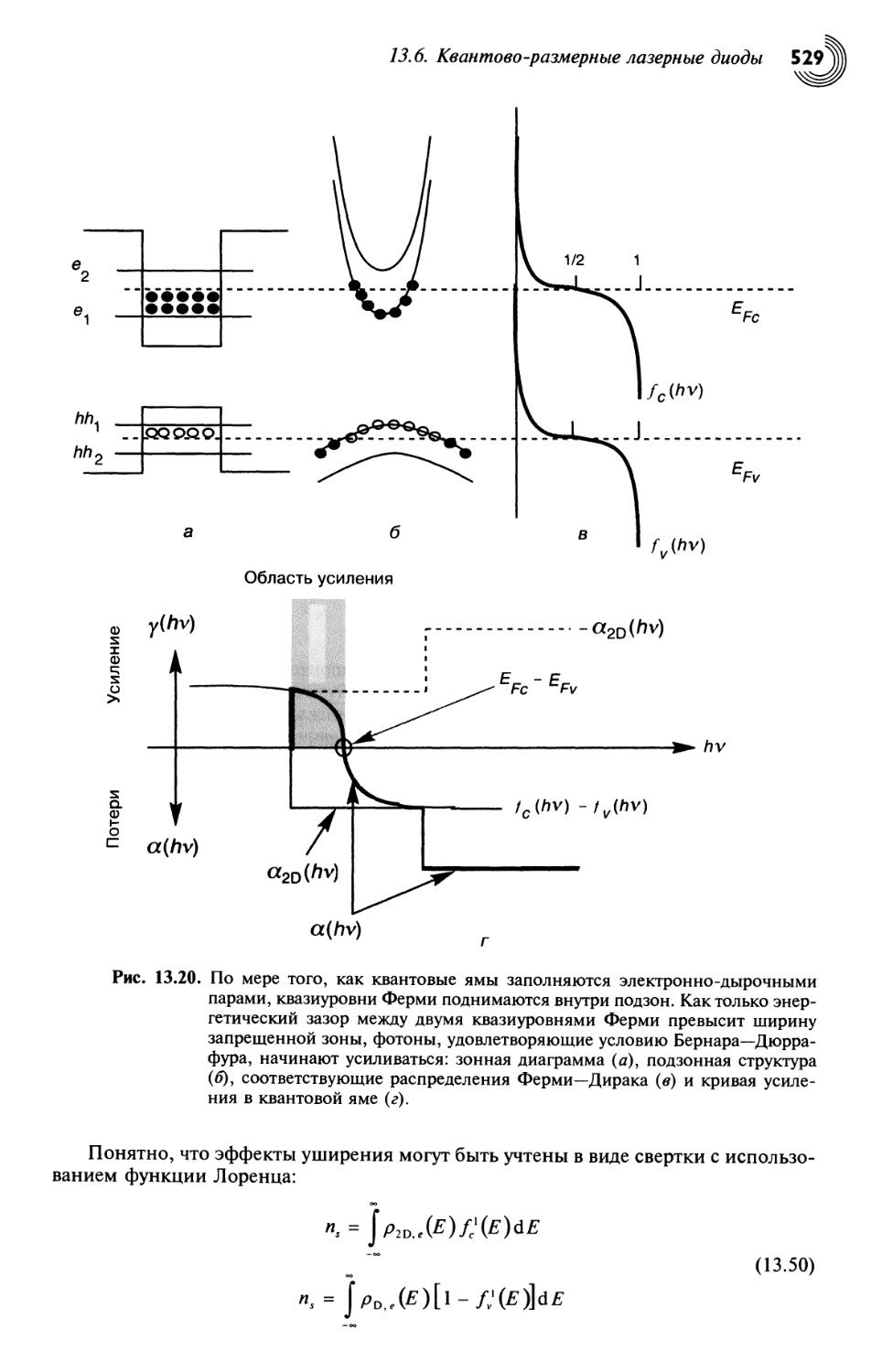
13.6.3. Лазерный порог квантово-размерного лазера 533
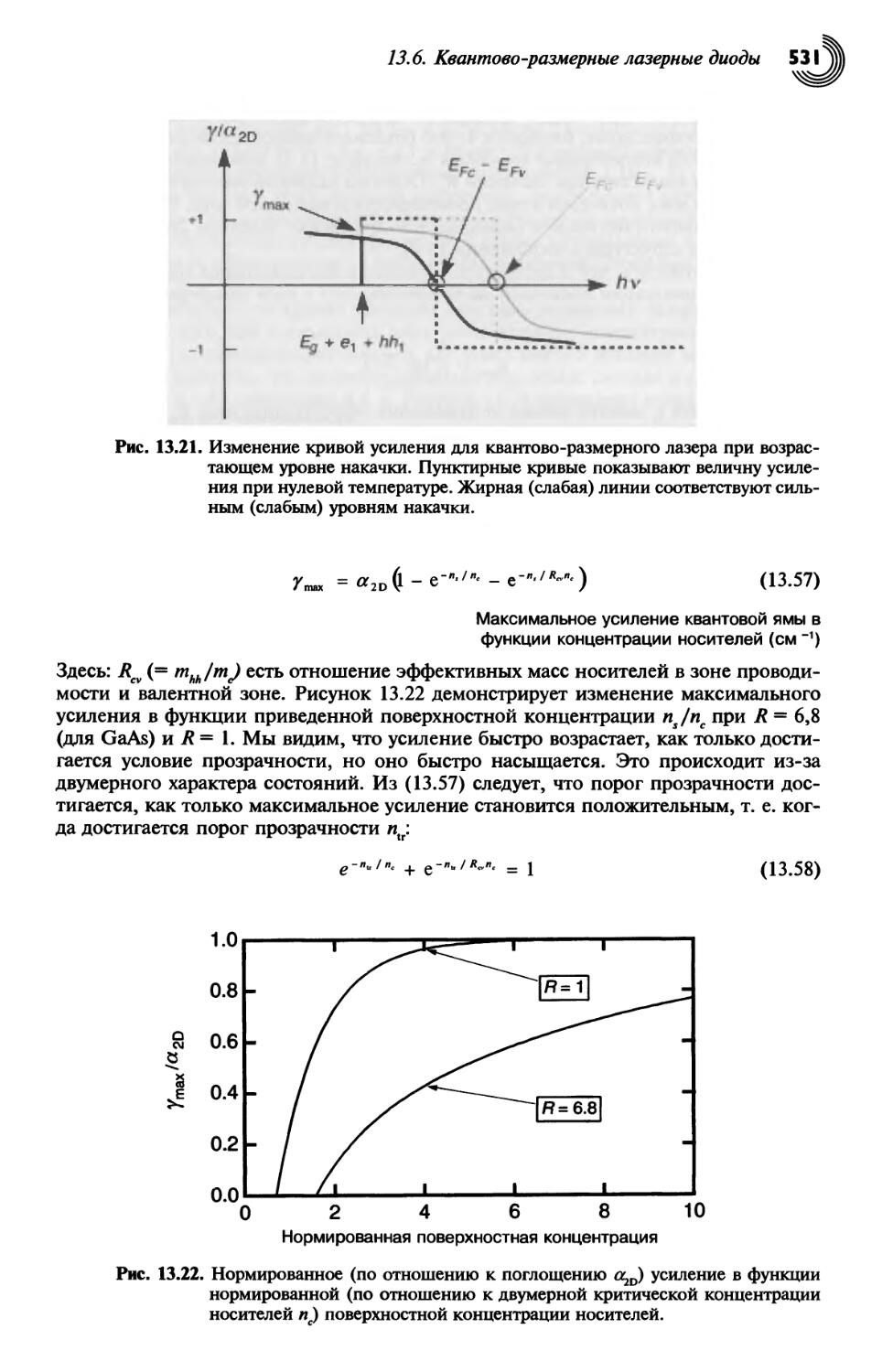
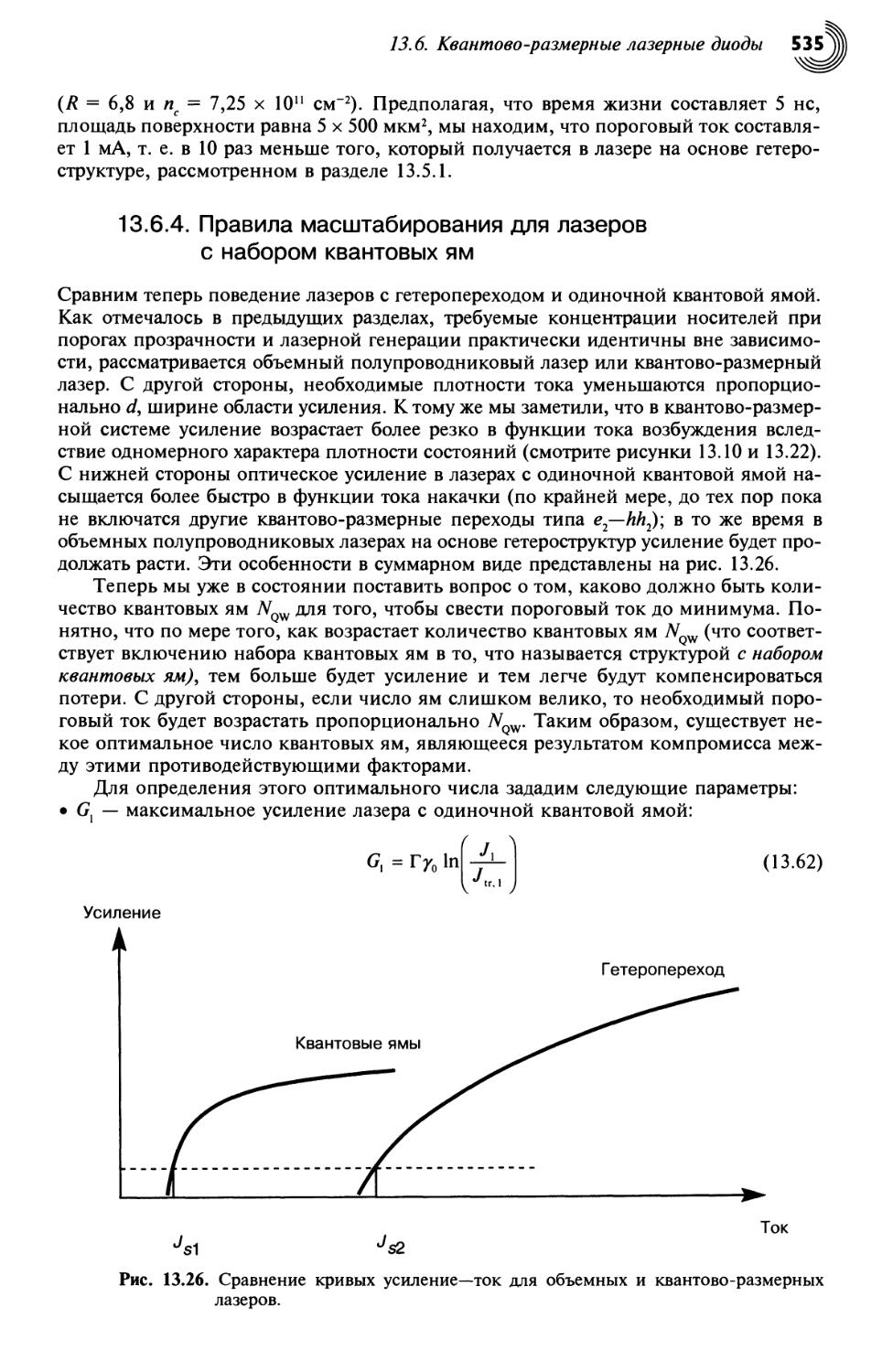
13.6.4. Правила масштабирования для лазеров с набором квантовых ям 535
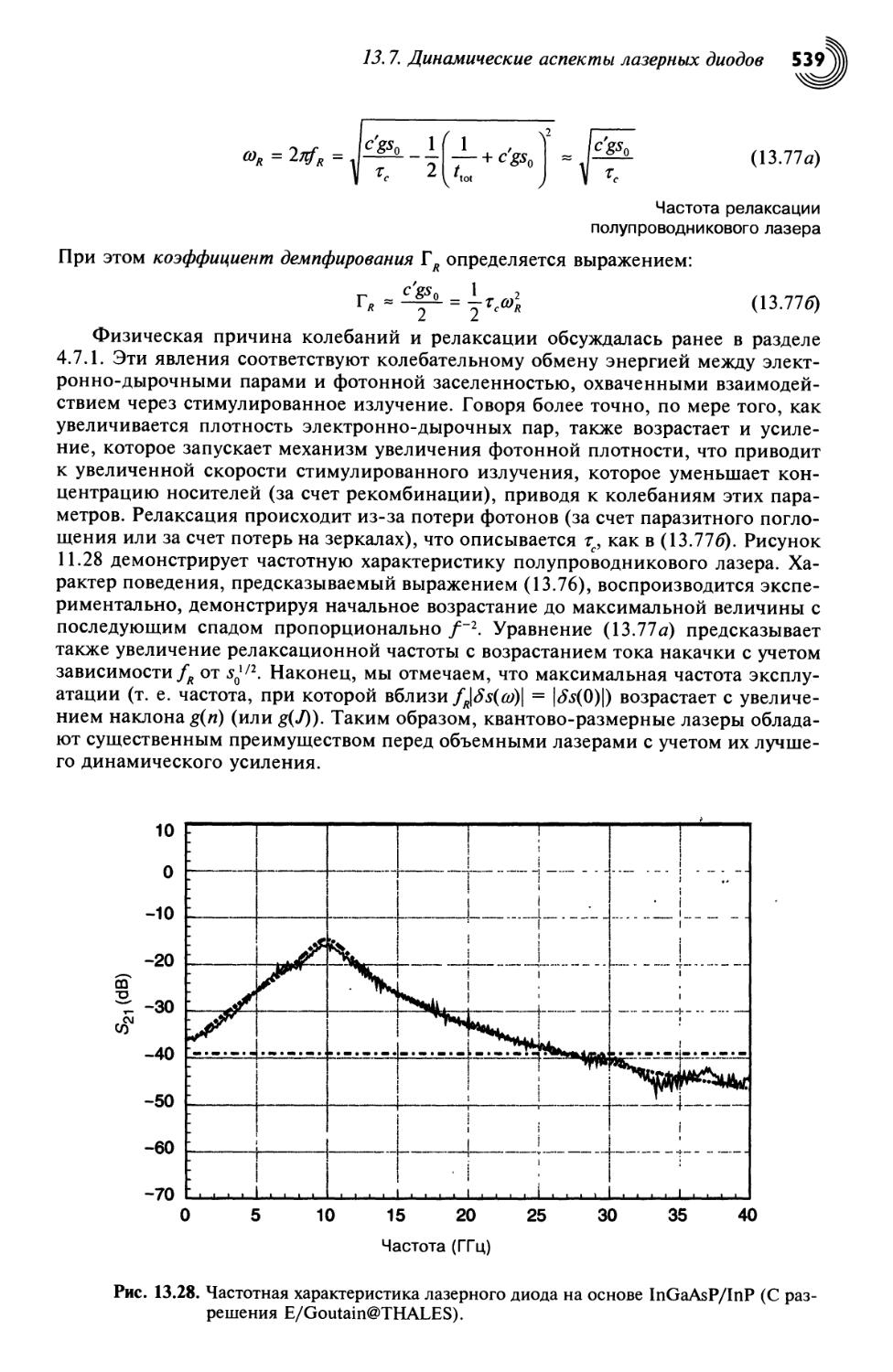
13.7. Динамические аспекты лазерных диодов 537
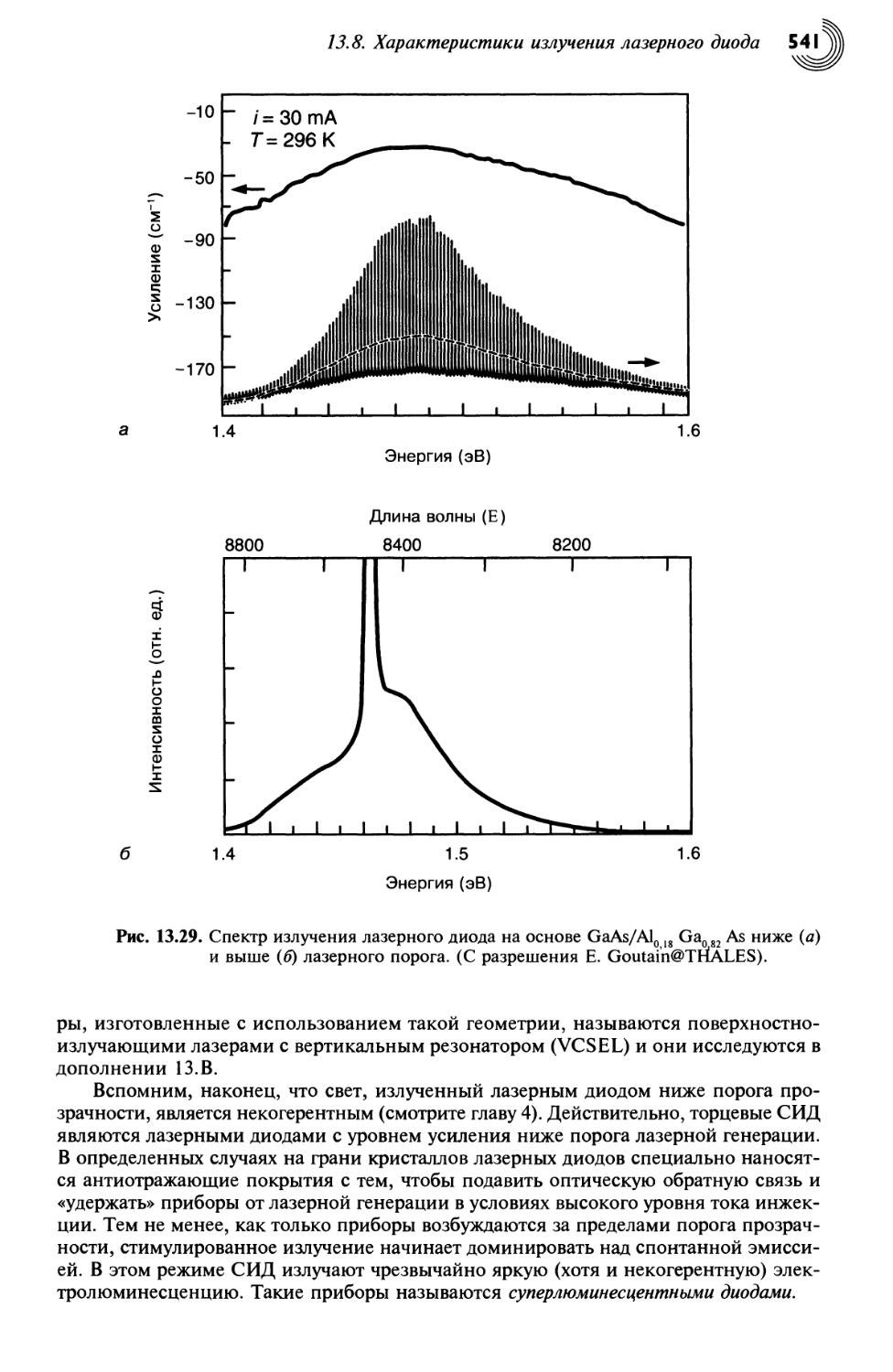
13.8. Характеристики излучения лазерного диода 540
Содержание
13.8.1. Спектральное распределение 540
13.8.2. Пространственное распределение 542
ДОПОЛНЕНИЯ К ГЛАВЕ 13 544
13.А. Лазеры с распределенной обратной связью (DFB-лазеры) 544
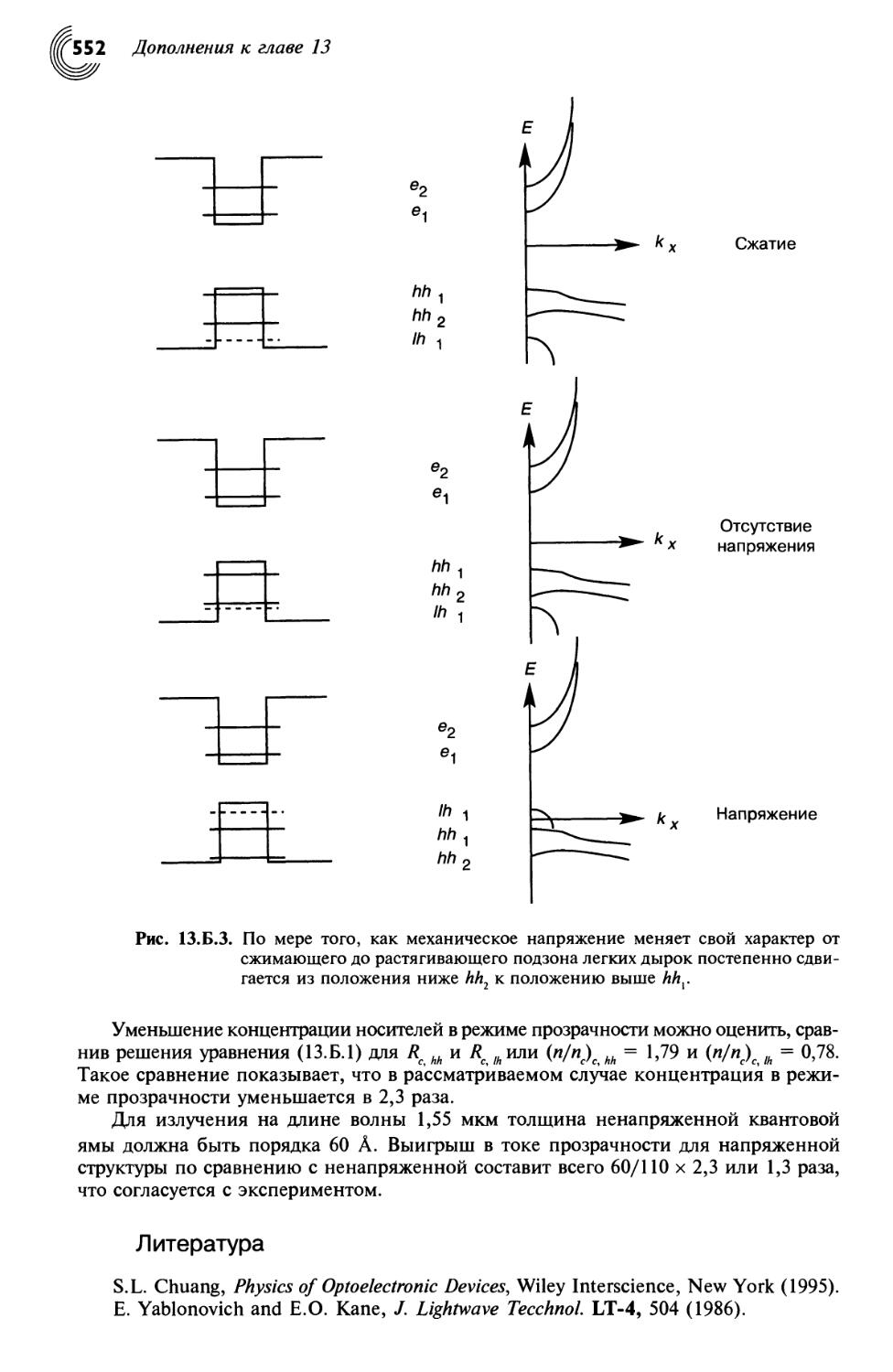
13.Б. Лазеры с напряженными квантовыми ямами 548
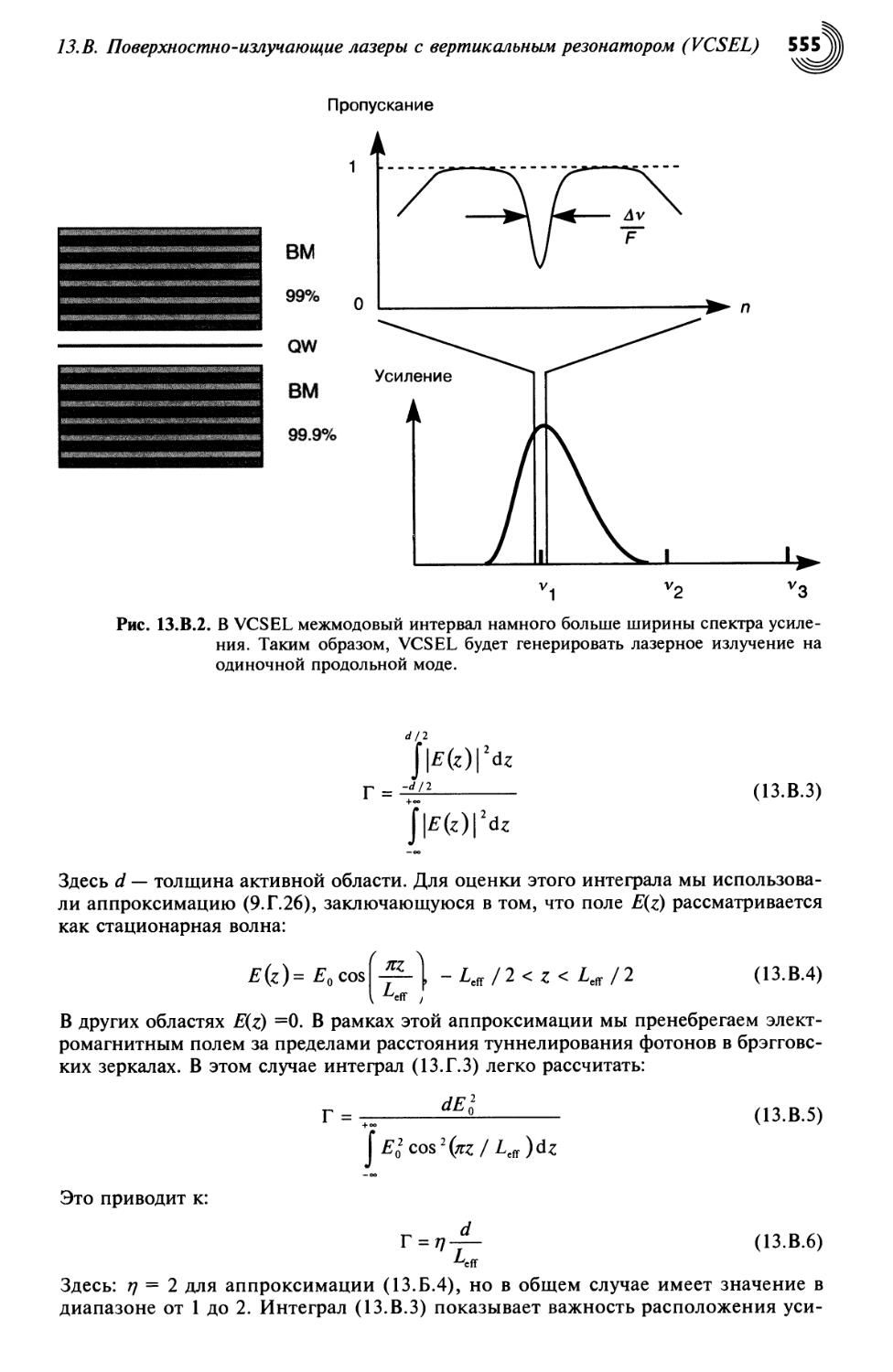
13.В. Поверхностно-излучающие лазеры с вертикальным резонатором
(VCSEL) 553
83.В.1. Условия достижения порога в VCSEL 553
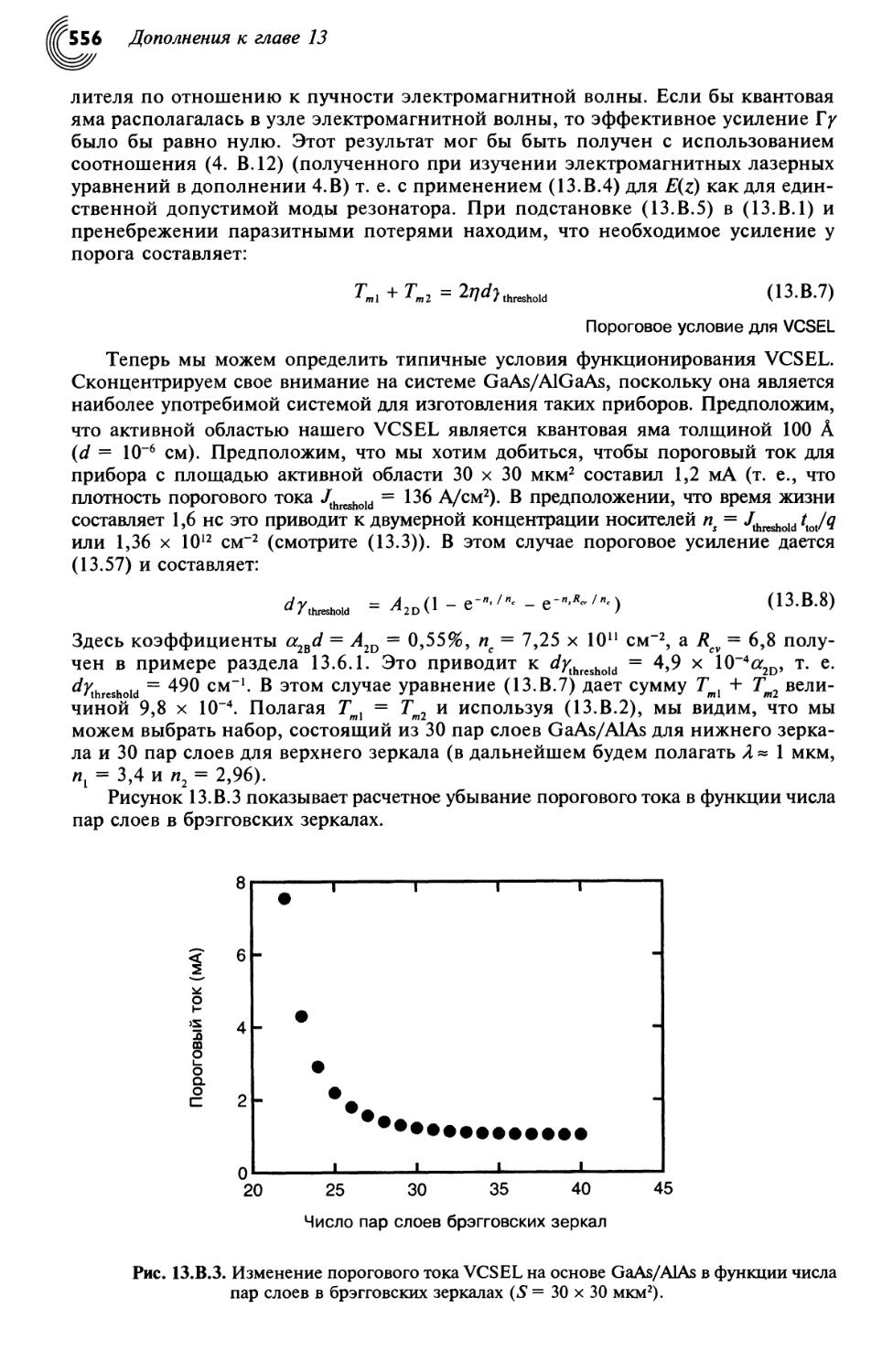
13.8.2. Функционирование VCSEL 557
13.Г. Тепловые аспекты лазерных диодов и мощных приборов 557
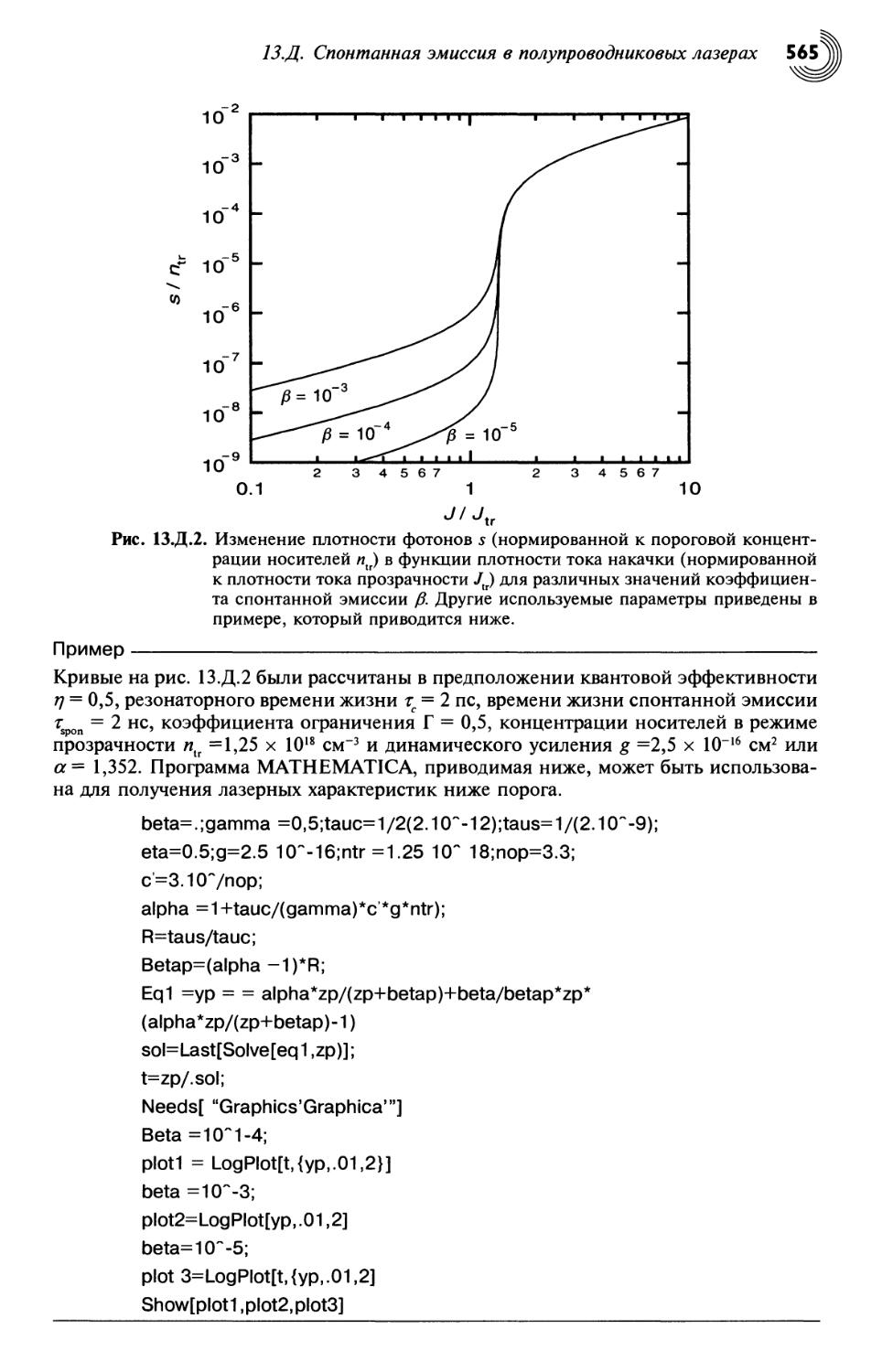
13.Д. Спонтанная эмиссия в полупроводниковых лазерах 563
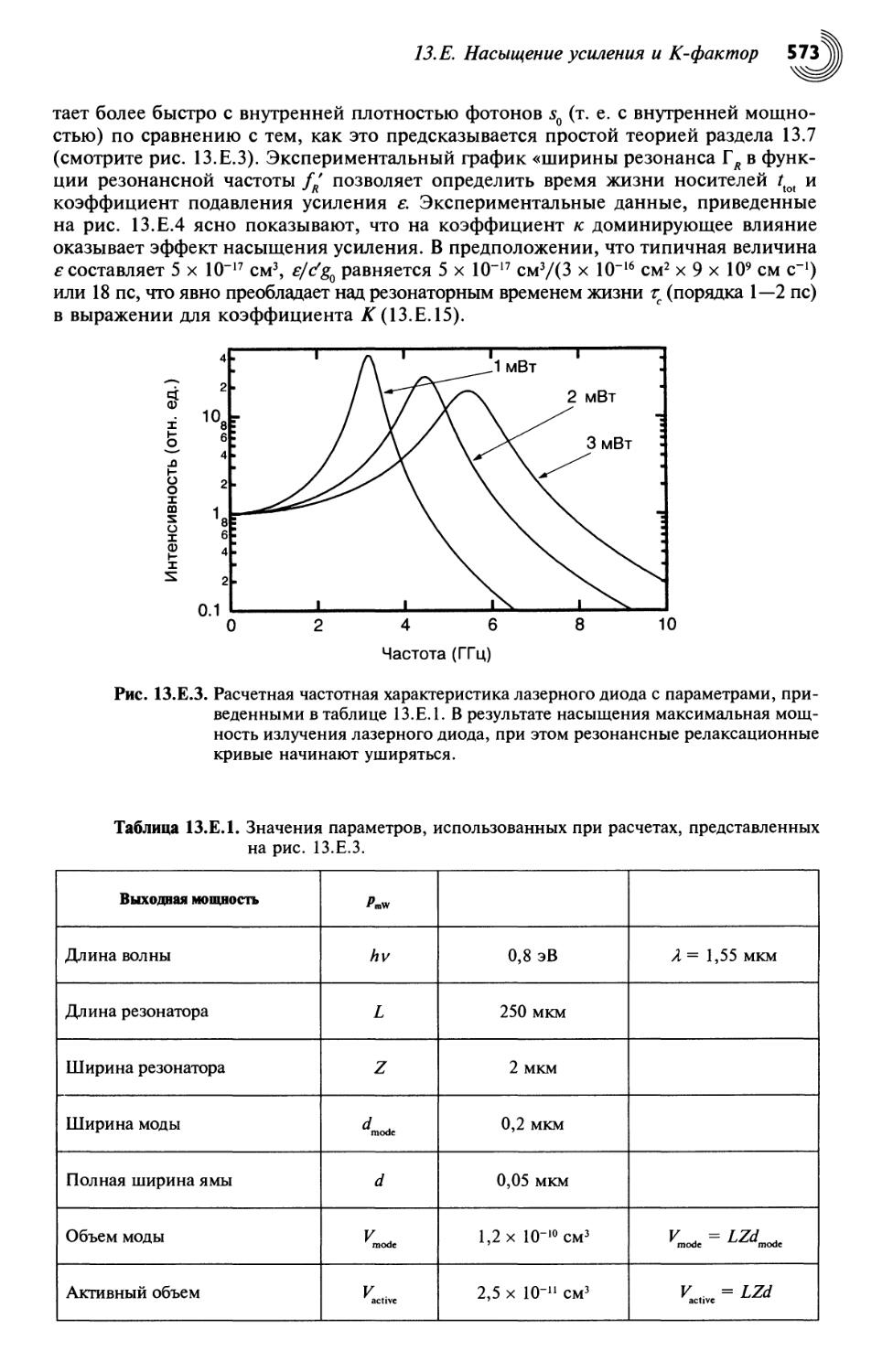
13.Е. Насыщение усиления и А'-фактор 569
13.Ж. Шум и ширина полосы лазерного диода 575
13.Ж.1. Уширение линии излучения 578
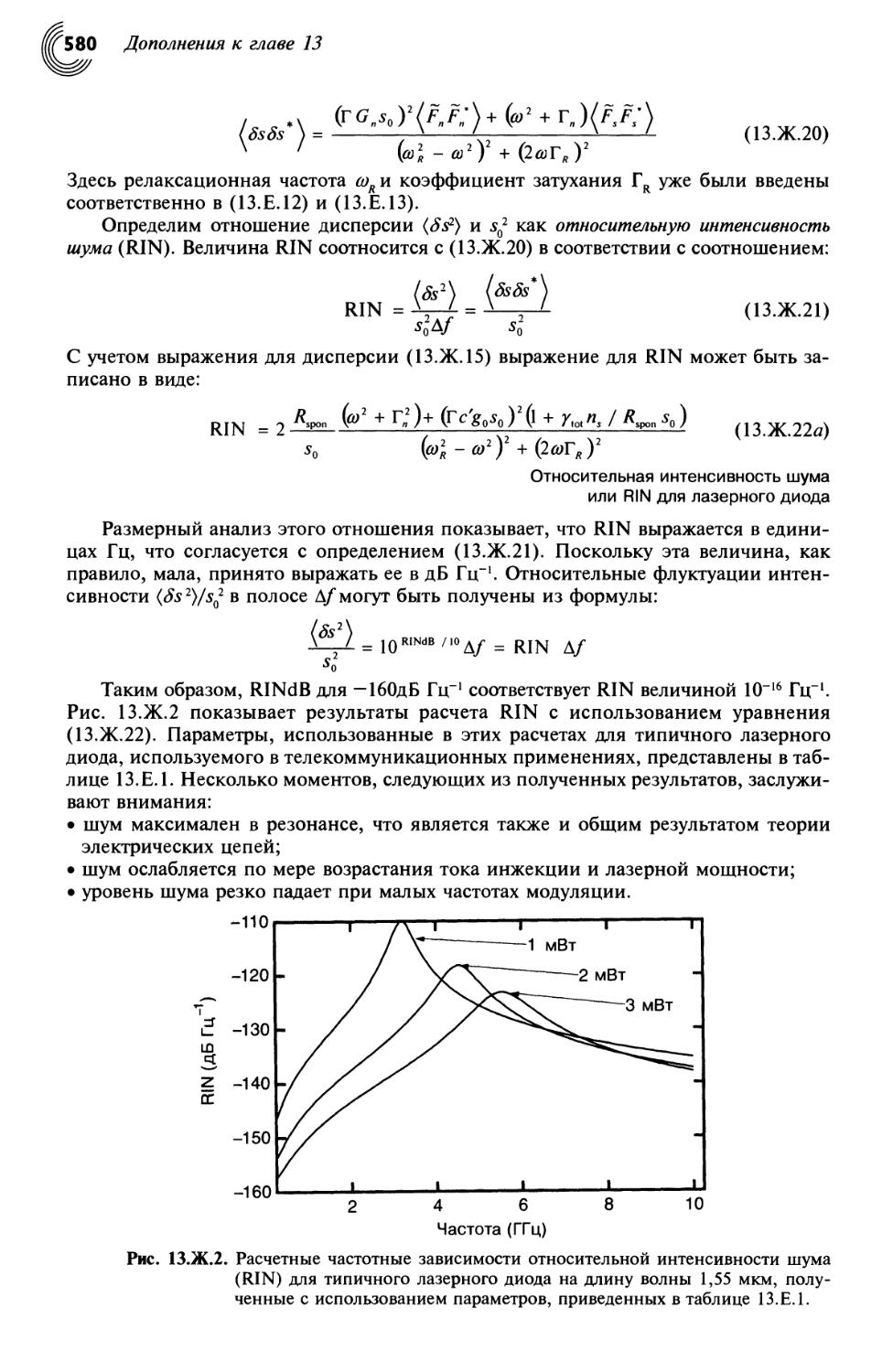
13.Ж.2. Относительная интенсивность шума (RIN) и баланс оптической связи 579
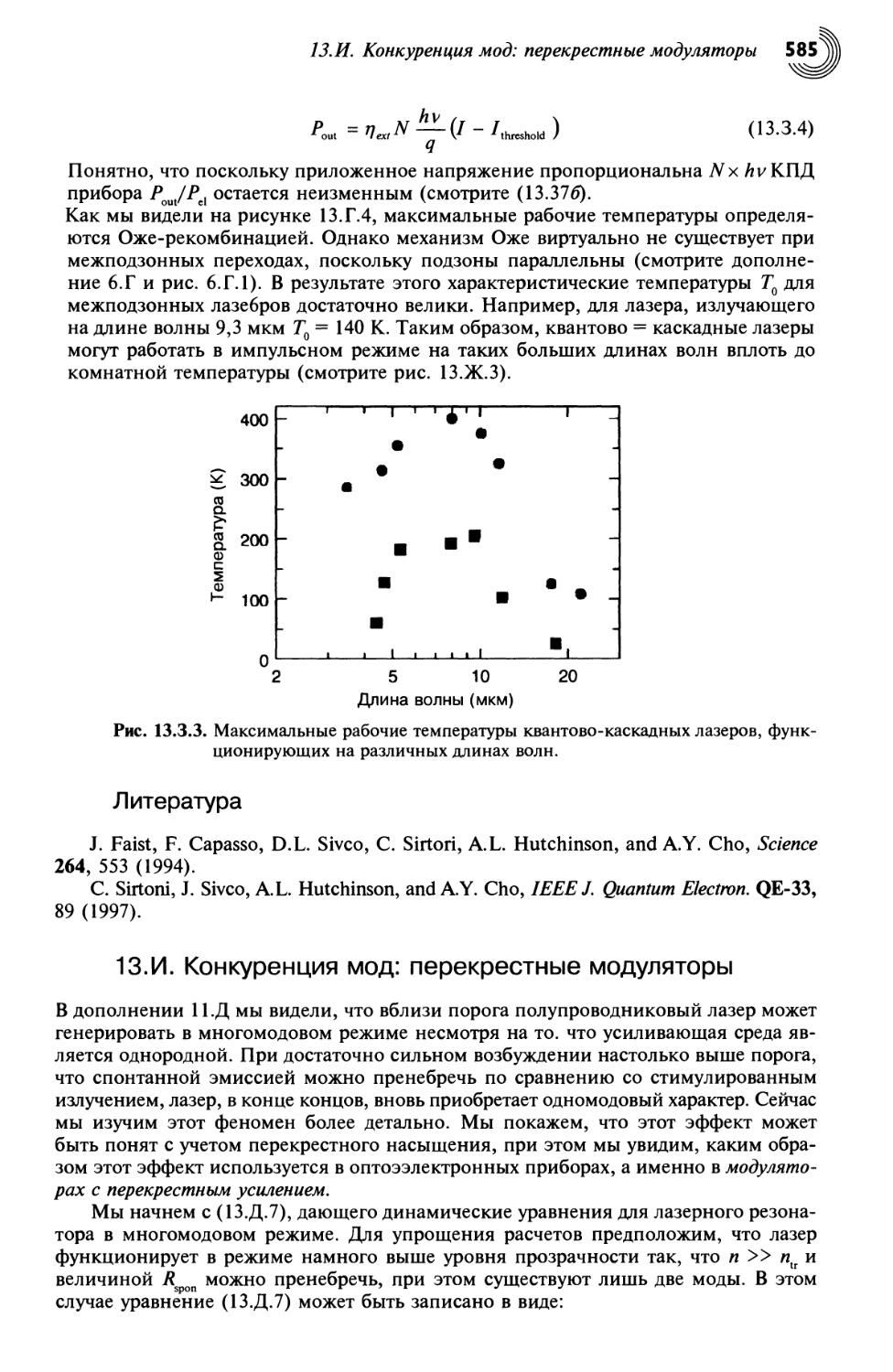
13.3. Униполярные квантово-каскадные лазеры 582
13.И. Конкуренция мод: перекрестные модуляторы 585
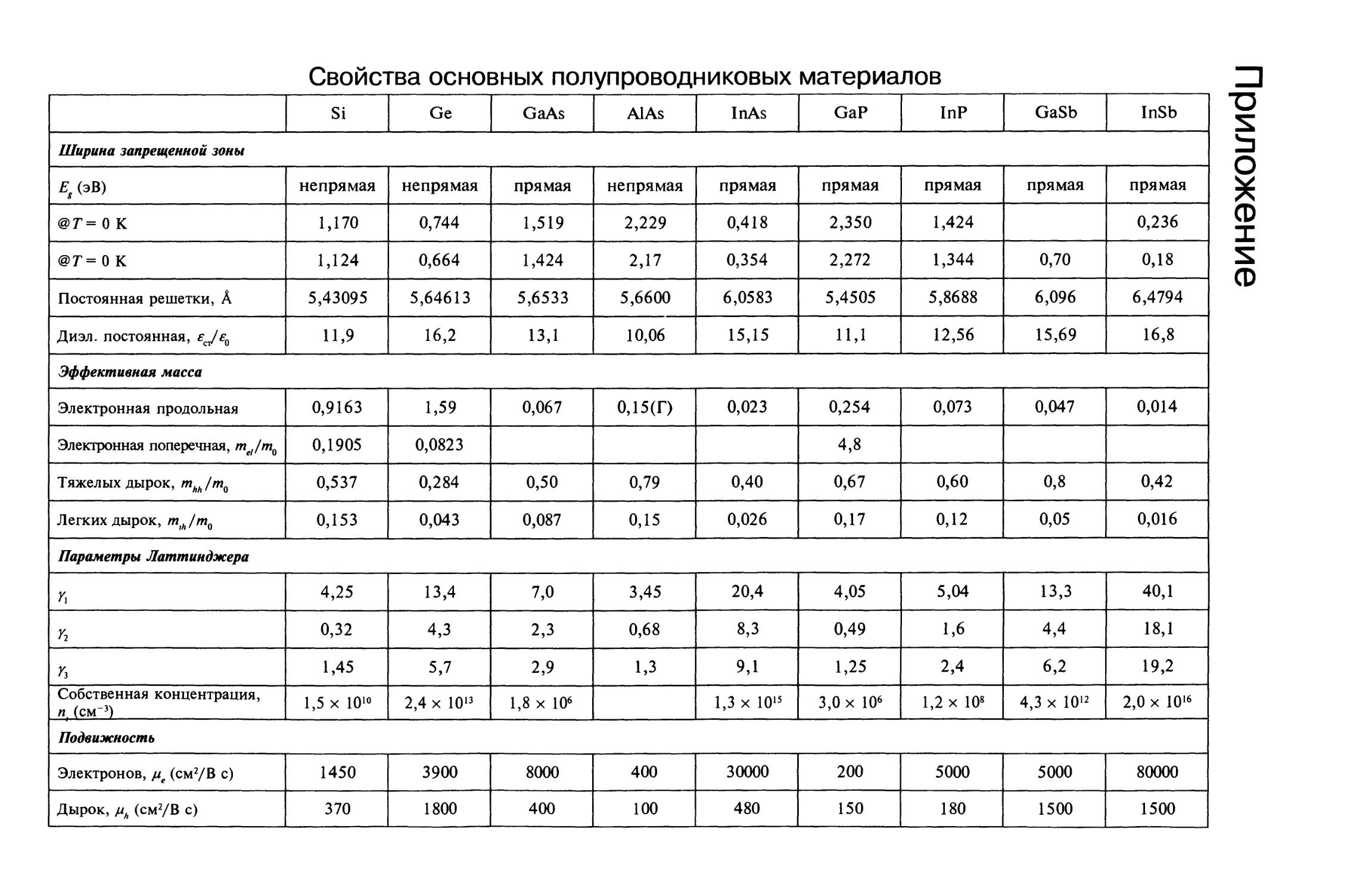
Приложение. Свойства основных полупроводниковых материалов 589
Предисловие редактора
Появление представляемой российскому читателю книги «Оптоэлектроника»
является в определенном смысле закономерным и долгожданным событием. Подобно
тому, как изобретение транзистора в 1947 г. привело к вычислительному изобилию
наших дней, оптоэлектроника как научно-техническое направление, стартовав с
открытия на заре прошлого века О.В. Лосевым явления электролюминесценции в
кристаллах карбида кремния, приобрела такую динамику своего развития, что
становится правомерным сравнение развития оптоэлектроники с очередной научно-
технической революцией. При попытке проанализировать феномен
оптоэлектроники прежде всего бросается в глаза широкий диапазон ее областей применения:
обширный круг волоконно-оптических датчиков, жидкокристаллические приборы,
лазерные принтеры, СД плоские цветные электролюминесцентные панели,
декодеры штрих-кодов, новое поколение эндоскопических медицинских инструментов
и т. д. Успехи, проблемы и перспективы оптоэлектроники освещены во многих
тысячах публикаций, которые появляются каждый год, а также в трудах
многочисленных конференций, проводящихся ежегодно.
Отечественному читателю знакомы как переводные [1], так и отечественные [2, 3]
книги по указанной тематике. Однако темпы появления новой информации о
принципиально новых оптоэлектронных приборов таковы, что постоянно имеется
потребность во все новых и новых книгах по оптоэлектронике.
Есть и еще одна «изюминка», выделяющая представляемую книгу из других
печатных изданий подобного рода. В ней предпринята попытка осмыслить оптоэ-
лектронику как самостоятельную науку. По своему жанру — это не монография, а
учебное пособие. Авторы избрали непростой путь — в рамках одной книги
изложить необходимые сведения из целого ряда самостоятельных дисциплин (физики
полупроводников и полупроводниковых приборов, физики твердого тела,
квантовой механики, статистической физики), при этом изложить ab initio, по
возможности, ясно и непротиворечиво.
Структурно, книга из 13 глав с многочисленными дополнениями условно
делится на две примерно равные части. В первой части подробно изложены
физические основы явлений, лежащих в основе оптоэлектроники (квантовая механика
электрона, фотона, электрон-фотонного взаимодействия, спонтанное и вынужденное
излучение и т. д.). С учетом того, что оптоэлектроника приобретает все более
отчетливый квантово-механический характер, представляется разумным, такое
внимание авторов к выводу основных соотношений из фундаментальных основ.
Методически ценным является то, что студентам прививаются навыки работы с
достаточно сложным расчетным инструментарием (формализмом матрицы плотности,
формализмом квантования электромагнитного поля, фейнмановскими
диаграммами), что, в свою очередь, является подготовительной стадией к формализму
функций Грина [4] и уравнений Дайсона, наиболее адекватно пригодным для
рассмотрения проблемных вопросов оптоэлектроники с учетом многочастных эффектов.
Естественно, что в силу ограниченного (хотя и достаточно большого) объема,
представляемая книга не является всеобъемлющим компендиумом по
оптоэлектронике: вторая часть книги посвящена достаточно подробному рассмотрению
основных классообразующих приборов (электрооптических модуляторов,
фотоприемников (включая тепловизионные приемники излучения), оптических
параметрических генераторов, светоизлучающих и лазерных диодов (включая квантово-каскадные
и поверхностно-излучающие лазерные диоды)).
Предисловие редактора
Особую ценность книге как учебнику придают многочисленные примеры
расчетов, а также компьютерные программы, приведенные в ней. Методически
ценным является использование в книге метода аналогии, когда для описания внешне
непохожих и несвязанных явлений используется один и тот же формализм.
Поучительными являются и многочисленные факты из истории науки с ее кризисами и
взлетами.
Вместе с тем (что, впрочем, естественно) книга не лишена определенных
недостатков, связанных с реальной «фактурой» и технологией оптоэлектроники.
Оптоэлектронные материалы представлены несколько эклектично и однобоко.
Авторы сконцентрировали свое внимание исключительно на «идеальных»
монокристаллических структурах, в то время как современной оптоэлектроникой
задействованы не только монокристаллические материалы, но и поликристаллические,
аморфные и даже полимерные среды. Строго говоря, даже приводимые в книге
материалы (в особенности твердые растворы) следует рассматривать как частично
неупорядоченные среды, характеризуемые определенной величиной дальнего и
ближнего порядка, а также определенной амплитудой флуктуации как состава, так и
связанных с ним параметров.
При рассмотрении физических аспектов оптоэлектроники опущены такие
важные явления, как эффекты зонной структуры, и очень схематично рассмотрены
экситонные эффекты, в то время как современная оптоэлектроника использует
явления связанные как с экситонами Ванье—Мота, так и с экситонами Френкеля.
В приборной части незаслуженно «обойденным» оказался такой важный класс
приборов, как оптроны.
И наконец, как справедливо отмечают авторы, оптоэлектроника сегодня
привлекает в свои учебные аудитории не только студентов, специализирующихся в
области научных исследований, но также и студентов инженерно-технических
специальностей, а сам предмет очень интересует инженеров-практиков. И в этом смысле
книга страдает определенной академичностью. За пределами рассмотрения остался
широкий круг вопросов, связанных с особенностями применения и схемотехникой
оптоэлектронных приборов.
В заключение следует подчеркнуть, что одним из важных аспектов
современной оптоэлектроники является многоуровневое проектирование:
• проектирование и реализация оптоэлектронных сред с необходимым набором
физических свойств;
• проектирование и реализация приборных структур, способных обеспечить
необходимые технические характеристики оптоэлектронных приборов;
• проектирование оптических микросистем;
• схемотехника применения оптоэлектронных приборов в сложных системах.
Другим, не менее важным аспектом современной оптоэлектроники является ее
устремленность в будущее и по-хорошему «амбициозные» планы реализации
оптоэлектронных интегральных схем, оптических процессоров и, в конечном счете,
оптоэлектронных компьютеров.
Литература
1. Т. Мосс, Г. Баррел, Б. Эллис. Полупроводниковая оптоэлектроника. (пер. с
англ. Под ред. С.А. Медведева). Москва, «Мир», 1976.
2. Ю.Р. Носов. Оптоэлектроника. Москва, «Радио и связь», 1989.
3. А.Н. Пихтин. Физические основы квантовой электроники и оптоэлектроники.
Москва, «Высшая школа», 1983.
4. В.Л. Бонч-Бруевич. СВ. Тябликов. Метод функций Грина в статистической
механике. Москва. ФИЗМАТГИЗ, 1961.
О.Н. Ермаков
ГЛАВА 1
КВАНТОВАЯ МЕХАНИКА
ЭЛЕКТРОНА
1.1. Введение
В этой главе приводится обзор фундаментальных принципов и методов квантовой
механики, необходимых для понимания оптоэлектроники как предмета изучения.
Часто по ходу книги рассматриваемые концепции не будут представлены во всей их
глубине, так как основной целью является скорее предоставление инструментария
и понятийного аппарата, необходимых для проработки всего материала,
изложенного в книге. Так, например, несмотря на огромное значение в других областях
физики, мы практически не скажем ни слова по поводу принципа
неопределенности Гейзенберга, сферических гармониках, спине электрона и т. д. Читателю,
желающему углубить свои представления по этим вопросам, можно рекомендовать
прекрасную работу К. Коэна—Таннуджи.
1.2. Постулаты квантовой механики
Рассмотрим электрон с зарядом q и массой те в поле обобщенного потенциала вида
V(r, t)9 изменяющегося в трехмерном пространстве г и времени /. Квантовая
механика утверждает, что понятие классической траектории теряет свой смысл в том
случае, когда интервал изменения потенциала имеет тот же порядок величины, что
и длина волны де Бройля (Лов), которая дается соотношением:
2лП ^ 1,23 (нм ) (
где h — постоянная Планка A,04 х 10~34 Дж с), V— средний потенциал,
воздействующий на частицу, а Е — энергия частицы. В дальнейшем мы увидим, что в
кристаллическом твердом теле, где электроны находятся под воздействием пространственно
изменяющихся потенциалов амплитудой порядка 5эВAэВ=1,6х10~19 Дж), их
длина волны де Бройля оказывается порядка 0,5 нм. Так как эта величина
соответствует межатомному расстоянию между атомами кристаллической решетки,
можно ожидать, что электроны проводимости в такой среде будут проявлять
интерференционные эффекты, характерные для механики волнового движения. Эти
эффекты (рассматриваемые в главе 5) являются фактором, приводящим к
возникновению запрещенных зон в полупроводниках, и их трудно рассмотреть,
используя классические теории, основанные на понятии строго заданных траекторий.
Квантовая механика утверждает, что от идеи траектории мы должны перейти к
более тонкому описанию с использованием понятий квантовых состояний и
волновых функций, В этом случае состояние электрона представляется вектором
состояния, изменяющимся во времени /. Один из наиболее сильных постулатов
квантовой механики заключается в том, что все эти векторы состояния перекрывает
гильбертово пространство. Например, существование линейных комбинаций состояний
(что приводит к таким важнейшим следствиям, как молекулярная стабильность,
запрещенные зоны и т. д.) является прямым следствием этого постулата. Это век-
1.2. Постулаты квантовой механики
торное пространство обладает характеристиками эрмитового скалярного
произведения, физическое значение которого будет раскрыто позже. Используем дираков-
ские обозначения для представления скалярного произведения двух векторных
состояний |^>и |^2>в виде {Щу/). Теперь вспомним свойства эрмитового скалярного
произведения:
(ф\ацг1 + Ру/2) = а{ф\у/{) + Р(ф\цг2) A.2)
(аф, + 0ф2\г) = а * {ф{ \у) + р * (ф2 \у/)
где {у/\у/) являются действительными, положительными числами, равными нулю
только, если \у/) =0, а звездочка обозначает операцию комплексного сопряжения.
По определению физическое состояние нормируется на единицу, что означает \уг^
описывает физическое состояние, если:
В гильбертовом пространстве действует ряд линейных операторов. Второй
постулат квантовой механики заключается в том, что классически измеряемые
величины такие, как положение, энергия и т. п. представляются эрмитовыми
операторами А (т. е. операторами, для которых справедливо соотношение Л* = А, где
символ * означает эрмитово сопряжение), которые называются наблюдаемыми, при этом
результатом измерения такой наблюдаемой может быть только одно из
собственных значений, связанных с этой наблюдаемой. Если ансамбль собственных
значений наблюдаемой А образует дискретный набор, в этом случае набор всех
возможных измерений системы дается ап решениями уравнения на собственные значения:
аЮ A-4)
Поскольку операторы наблюдаемых величин являются эрмитовыми, из этого
следует, что их собственные значения являются обязательно реальными числами в
соответствии с таким общеизвестным фактом, что результатом физического
измерения является реальное число. Определим также коммутатор двух операторов А и
В в соответствии с соотношением:
[А,В] =АВ-ВА A.5)
Можно показать, что если два оператора коммутируют (т. е. если их
коммутатор равен нулю), то они одновременно обладают полным набором собственных
векторов. Заслуживающим внимания следствием этого является то, что
существуют физические состояния, для которых результаты измерения обоих этих
наблюдаемых (А и В) могут быть наверняка получены одновременно, так как они
представляют их общие собственные состояния.
Если базис ортонормированных собственных векторов наблюдаемой А является
полным, то любое физическое состояние \y/(t)) электрона может быть описано в
виде линейной комбинации собственных векторов следующим образом:
где коэффициенты сп даются соотношением:
(} A-7)
Вероятностная интерпретация квантовой механики утверждает, что квадрат
модуля этих коэффициентов |сл(/)|2 дает вероятность нахождения электрона в состоянии \у/п)
в момент времени /, означая, что измерение наблюдаемой А в этот момент даст вели-
Глава 1. Квантовая механика электрона
чину ап с вероятностью |сл(/)|2. Следующий постулат заключается в том, что
непосредственно после осуществления измерения наблюдаемой Л функция состояния
определяется полностью одним из собственных состояний наблюдаемой Л (т. е. cn(t) = 1 или
М "l^,))- В том случае, когда собственная величина является вырожденной, функция
состояния после измерения ограничена подпространством, задаваемым
вырожденными собственными значениями. Последний постулат, который еще является предметом
интенсивных исследований, необходим для когерентности квантовой механики.
Таким образом, из вероятностной интерпретации следует, что в общем случае
мы не можем знать наверняка результат измерения. В то же время мы можем
получить информацию по средней величине наблюдаемой А по результатам статически
значительной выборки независимых измерений. Эта величина будет
соответствовать средней величине всех возможных результатов измерений ап наблюдаемой,
при этом каждый результат берется с весовым множителем, равным
соответствующей вероятности \cn(t)\2 нахождения системы в собственном состоянии |^Л),
связанном с собственной величиной ап:
^n\cn(tf 0-8)
Эта средняя величина может быть легко найдена из соотношения:
{A)(t) = <И0М|И0> A-9)
Некоторые из наблюдаемых могут быть векторными, как например, операторы
положения в пространстве координат г = (х, у, z) и импульса р. Для этих операторов
собственные значения принадлежат континууму величин. Таким образом,
собственный вектор |г) оператора положения г интерпретируется как вектор, описывающий
состояние системы как только измерение положения привело к конкретной
величине г. В этом случае мы можем сказать, что частица с определенностью может
быть найдена в точке г. Разложение вектора состояния по конкретному базису
собственных векторов называется представлением. Одним из важных представлений
является проецирование вектора состояния на собственные состояния оператора
положения г. Каждая компонента такого проецирования является волновой
функцией у (г, t), даваемой соотношением:
Возвращаясь назад к вероятностной интерпретации квантовой механики, мы
видим, что квадрат модуля волновой функции |#/(г, /)|2 дает вероятность нахождения
электрона в точке г в момент времени /. Более того, в координатном представлении
внутреннее произведение 2 состояний |^> и \ц/2) может быть записано в виде:
где интеграл берется по всему пространству. Наконец, эволюция состояния
системы со временем дается уравнением Шредингера:
i%j-\v(f)) = H(t)\W(t)) A.12)
Уравнение Шредингера
где Н @ — гамильтониан системы, который при его интерпретации как
наблюдаемой соответствует энергии1 системы. Общее выражение этого оператора имеет
вид:
1 Символ Л обычно используется тогда, когда может возникнуть путаница в различии между
физической величиной ( например положением г) и соответствующей ей квантовой наблюдаемой (f).
1.2. Постулаты квантовой механики
) A.13)
Гамильтониан частицы массой т
в поле потенциала V
где р — оператор импульса. В координатном представлении (т. е. при
проецировании на собственные векторы оператора положения |г)) принцип соответствия
приводит к следующему выражению для оператора р:
Л *Г7 Й
p=-V=-
Эх
A.14)
При этом в координатном представлении результат его действия на волновую
функцию ^(г, /):
V(г,t)
ду
A.15)
Это соответствие является следствием требования, чтобы оператор р\ действующий
на материальные волны де Бройля ( elkr) приводил к соответствующей собственной
величине импульса р = йк , то есть удовлетворяющей соотношению де Бройля.
Таким образом оператор р принимает вид (ft/i)V.
Операторы положения и импульса связаны друг с другом важными
коммутационными соотношениями:
Эх
dz
A.16)
|[v<] |
1 [Эх ду
из которых мы получаем соотношение коммутации:
A17)
A.18)
Антикоммутация наблюдаемых положения и
импульса, приводящая к первому из
соотношений неопределенности Гейзенберга
Глава 1. Квантовая механика электрона
Основной вывод из отмеченных выше свойств коммутирующих наблюдаемых
заключается в том, что некоммутирующие наблюдаемые не могут обладать общим
базисом из набора собственных векторов. Таким образом, ни наблюдаемая
положения, ни наблюдаемая импульса не могут быть известны одновременно с
произвольной точностью. Это — первый принцип неопределенности Гейзенберга, который,
как может быть показано, приводит к следующим соотношениям между
неопределенностью импульса и положения:
АхАрх > h I 2
АуАру >h/2
z >h/2
A.19)
Возвращаясь к уравнению Шредингера в координатном представлении, теперь мы
можем записать:
ih^-y,(r,t) = --^-Ay(r,t) + V(r,t)y,(r9t) A.20)
dt 2me
где А — оператор Лапласа ((Э2/Эх2) -I- (Э2/ЭУ) + (Э2/Э^2)). Как только заданными
являются временная и пространственная эволюция потенциала, становится
возможным, в принципе, рассчитать эволюцию вероятности в структуре. Отметим, что это
уравнение сохраняет нормировку функции, что согласуется с тем фактом, что
каждое физическое состояние переходит в пространстве и времени к некоторому
другому физическому состоянию.
1.3. Стационарное уравнение Шредингера
1.3.1. Стационарные состояния
В этом разделе нас будет интересовать описание физического состояния электрона,
подверженного воздействию независящего от времени потенциала (т. е. описание
т. н. консервативной системы). Этой системой может быть атом водорода, в котором
потенциал V(r) представляет собой кулоновское поле, локализованное в
пространстве, или кристалл, где потенциал V(r) является периодическим (соответствующим
регулярному расположению образующих кристалл атомов). Уравнение Шредингера
может быть записано следующим образом:
Э
2 т о
V(r)
И')) A.21)
Начнем с рассмотрения собственных состояний гамильтониана:
#к„(>)) = £>„(')> A.22)
Стационарное уравнение Шредингера
На некоторое время предположим, что такими состояниями являются:
• дискретные состояния, т. е. они обозначаются целыми числами;
• невырожденные состояния, т. е. два или большее число состояний не могут
иметь ту же самую энергию;
• полные состояния, т. е. любое физическое состояние может проецироваться
однозначным образом на базисный набор, сформированный из собственных
функций Я типа A.6).
1.3. Стационарное уравнение Шредингера
Подстановка уравнения A.22) в A.21) дает временную эволюцию собственного
состояния \у/)
k> k)e-^ A.23)
где
En=hcon A.24)
и соп — боровская частота колебаний, связанная с состоянием \у/). Уравнение A.23)
заслуживает внимание и позволяет сделать важное предсказание. Предположим,
что система находится в собственном состоянии | у/п), и мы ищем среднюю величину
наблюдаемой А:
(A)(t) = (г.«-""•' | A\¥lfi-^) = (¥к \А\ ¥я) A.25)
Таким образом, эта средняя величина не изменяется во времени, т. е.
собственные состояния являются стационарными для всех наблюдаемых. Эти стационарные
состояния являются особенно важными, так как они образуют состояния, дающие
неизменяющиеся величины наблюдаемых. В дополнение к этому они делают
возможным описание временной эволюции нестационарного состояния.
Предположим произвольное состояние \y/{t))> для которого мы знаем его проекцию (при / = 0)
на базис стационарных состояний \у/)\
5И A.26)
Определим теперь временную эволюцию коэффициентов cn(t). Для этого
подставим разложение стационарного состояния \y/(f))в стационарное уравнение
Шредингера A.21), что дает:
^) (L27)
Проецируя это уравнение на каждый собственный вектор \у/)> находим, что:
сп@ = спс-щ< A.28)
Таким образом, если мы знаем разложение функции состояния в момент времени
t = 0, то мы будем знать функцию состояния в любой последующий момент времени t
Такого типа разложение может быть обобщено на случай базиса с набором из
вырожденных собственных состояний и, или состояний, образующих континуум.
Такое обобщение достигается однако за счет большего усложнения, поэтому на
некоторое время мы ограничимся его использованием только в тех случаях, когда
без него нельзя обойтись.
1.3.2. Расчет стационарных состояний
для одномерного потенциала
Рассмотрим одномерное пространство с координатой х и предположим, что
ограничивающий потенциал V (х) таков, что V(x) > 0 во всем пространстве и V (х) -> 0
Глава 1. Квантовая механика электрона
при л: -> ±оо. В координатном представлении стационарное одномерное уравнение
Шредингера для стационарных состояний может быть записано в виде:
- — ^-гу/ (х) + [V(x) -Е]цг(х) = 0 A.30)
2те dx
Стационарное уравнение Шредингера
в координатном представлении
Напомним, что неизвестными являются собственные значения Еп и волновые
функции стационарного состояния у/п. Для каждой величины Еп уравнение A.30)
является дифференциальным уравнением второго порядка. Мы можем показать,
что решения этого уравнения являются непрерывными во всем пространстве
равно, как и их первые производные. Эти два условия с учетом требования
нормировки всех физических состояний приводят к квантованию энергии, т. е к
существованию дискретных энергетических уровней. Таким образом именно волновая природа
волновых функций в сочетании с требованиями по интегрируемости и непрерывности
приводят к квантовой природе энергетических уровней. Проиллюстрируем это
утверждение конкретным примером, который играет принципиальную роль в остальной
части книги, а именно — примером квантовой ямы.
1.4. Квантовая яма
1.4.1. Общий случай
Рассмотрим теперь электрон в поле потенциала, изображенного на рис. 1.1, а именно
потенциала, задаваемого соотношениями:
V(x) =0, если
| > у
A.31)
= -К0, если Н<|
500 г
СО
-20-10 0 10 20
-а/2 а/2
Положение (нм)
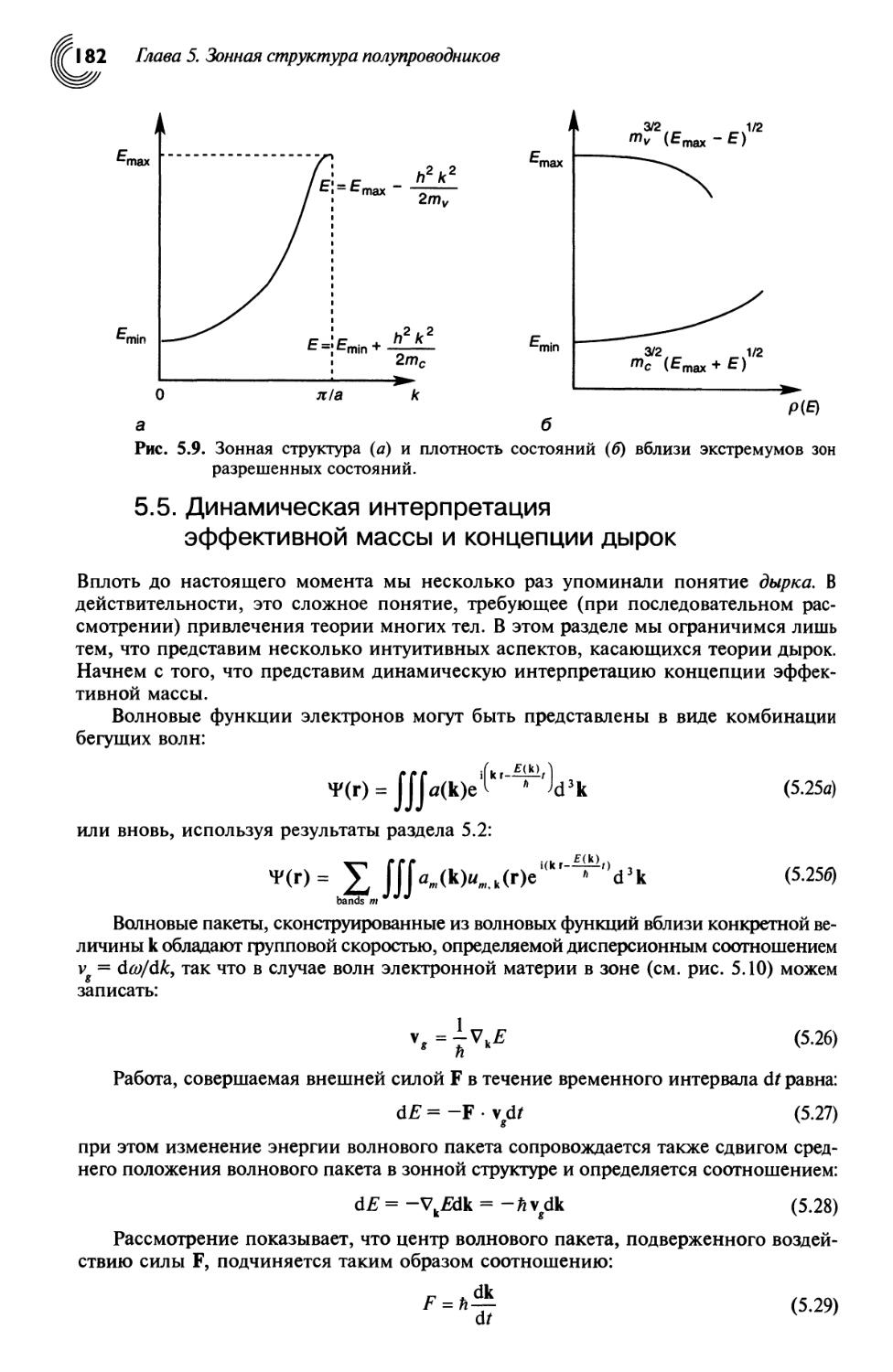
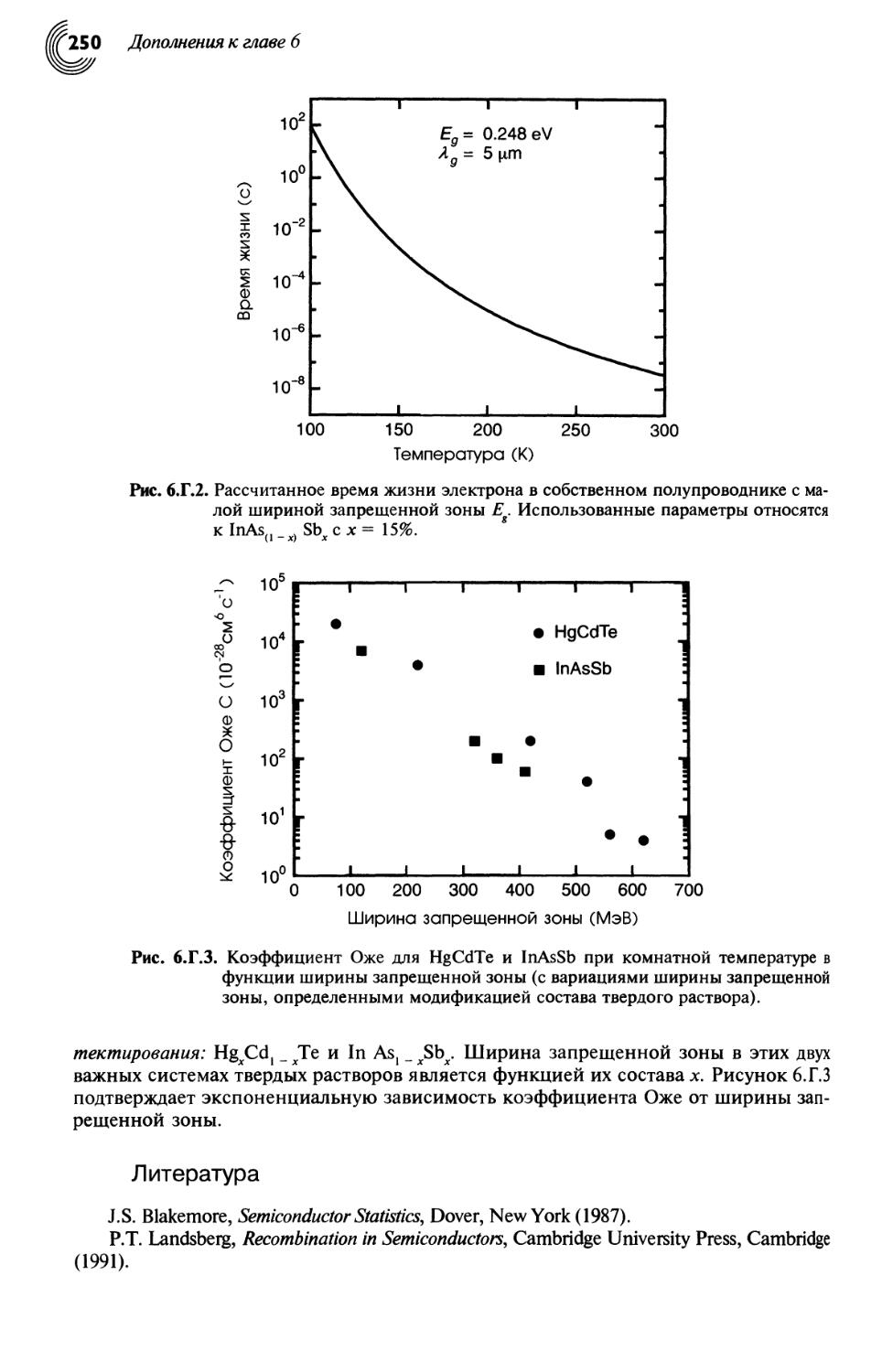
Рис. 1.1. Одномерная квантовая яма. Представлены собственные энергии и волновые
функции для трех связанных состояний системы. Такие квантовые ямы,
реализуемые в системе GaAs/Al0 45Ga0 55As. Интервал между первыми двумя
энергетическими уровнями составляет 104 МэВ, что приводит к поглощению
фотонов на длине волны 11,9 мкм.
1.4. Квантовая яма
Первая область (|jc| > а/2) задает потенциальный барьер, тогда как вторая
область (|jc| < а/2) определяет яму. Уравнение Шредингера, определяющее поведение
электрона в этой структуре, записывается в виде:
Ше " A.32)
П2 d2 ' ч "' ^ М = 0, для Ы < %
Сначала мы ищем решения этого уравнения с энергиями менее высоты
потенциального барьера, т. е. Е < 0. Для этого мы вводим три величины к, к и
к0 с размерностью обратной длины, т. е. имеющие размерность волнового
вектора (число пространственных периодов в 2 я), определяемые следующим
образом:
Е = -
Vo + E = --^- A.33)
2те
у - о
0 " 1т.
Отметим, что величина 2/г/к0 есть длина волны де Бройля, связанная с энергией
VQ ограничивающего потенциала. С использованием этого обозначения можем
записать решения уравнения A.32) в общем виде как:
¥с(х) = Асе[кх + Всс-[кх, ДЛЯ |х| < |
у/i(x) = AitKX + Biq~kx , для х<— A-34)
2
у/г{х) = ArtKX + BrQ~KX , для х > —
где символы с, I и г обозначают соответственно центральную, левую и правую
области. Теперь проиллюстрируем процесс квантования, распространяя условия
непрерывности волновой функции и ее первой производной (называемые также
граничными условиями) от —оо до +°о и, более того, требуя выполнения условий
нормировки результатов.
Поскольку волновая функция должна быть нормирована, ее величина не
должна расходиться при х -* —оо. Таким образом В{ = 0. В дополнение к этому граничные
условия при х = а/2 приводят к:
А /С + \К , ..,,.,_,-, А
™г —
:еЛ/
A.35)
Величины Ас и Вс связаны следующим соотношением:
A K+jk A36)
Вс к -\к
WTL Глава 1. Квантовая механика электрона
Граничные условия при х = а/2 дают:
А,ека'2 + Brz-KQi2 = Ac&ika/2 + Bce-ika/2
A.37)
\k , А .
Подстановка A.37) в A.35) дает:
A.38)
Вг = sin kaA,
2кк
Так как волновая функция должна оставаться конечной при х -> оо? это требует,
чтобы Аг = 0 или, чтобы выполнялось соотношение:
A.39)
к + \ка \
что может быть выражено в виде:
■^■ = tan(-y] (L4°)
или
-(f)-(ij
Имеется два типа решений, которые выражаются последующими
трансцендентными уравнениями.
A) Четные решения
-е^ A.42)
ч к + \ка
или
'ка
:os| 2
Из уравнения A.36) следует, что Ас = Вс или что решения являются четными.
Энергетические уровни решения уравнения Шредингера могут быть определены из
рис. 1.2. Они представляются точками пересечения прямых линий с наклоном
\/к0 и синусоидальных полуволн (штриховые линии). Таким образом, область
допустимых энергий электрона с полной энергией менее высоты потенциального
барьера образует дискретный спектр (означая, что энергетические уровни квантуются).
В этом случае волновые функции имеют вид:
¥пЛх) = Л cos Кх> А™ И < \
у/п1(х) = Де«, для х < ~| A.44л)
угя%г(х) = 2?яе-«, для х > ^
1.4. Квантовая яма
2.5 3.0
коа/я
Рис. 1.2. Графическое определение квантованных состояний для симметричной
квантовой ямы шириной a = 10 нм (см. пример) с использованием уравнений
A.43) и A.46) при к0 = 0,78 нм1.
где п обозначает я-ное решение уравнения. Величины Ап и Вп получаются, если
обратить внимание на то, что интеграл от квадрата у/п(х) в интервале от —«> до +°°
равен 1. Для основного состояния (п = 1) мы получаем:
a + 2 / к
A.446)
a + 2/ к
1/2
-/со/2
где кх — волновой вектор основного состояния, определяемый A.43). Уравнение
A.44) показывает, что электронная волновая функция проникает в барьер на
глубину, задаваемую величиной \/к. Это означает, что вероятность найти электрон в
барьерной области отлична от нуля (см. рис. 1.1). Это явление, известное как тун-
нелирование, не имеет классического эквивалента, в основе своей происходит из
волновой природы электрона и напоминает аналогичное поведение света. Теперь
вспомним уравнение, связывающее энергию собственного состояния и глубину
проникновения в барьерную область:
^tunnel "" ~
к J2me{-E)
A.45)
B) Нечетные решения
Этот случай соответствует альтернативному решению уравнения A.39):
к - \к
А именно:
\к
~\ = {, tanf^|<0
A.46)
В этом случае уравнение A.36) говорит нам о том, что Ап = ~Вп, т. е. решения
являются нечетными. В этом случае энергетические уровни даются пересечением
прямых линий с наклоном 1/к0 и другой серии синусоидальных полуволн
(сплошные линии на рис. 1.2).
Представляет интерес рассчитать число квантовых уровней в яме. Анализ рис. 1.2
дает:
Глава 1. Квантовая механика электрона
N = 1 + Int
A.47)
где символ Int означает «функцию целого числа».
К тому же, сколько бы мелкой ни была яма, в ней всегда имеется, по крайней
мере, одно квантовое состояние. В то время как это замечание имеет общий
характер и относится ко всем одномерным ямам, это может быть несправедливо в
отношении трехмерных систем. Квантовые уровни называются также и
локализованными, поскольку волновые функции имеют непренебрежимую величину только в
окрестности ямы; они называются также и связанными, так как вероятность найти
электрон значительна только поблизости от ямы (электроны не являются
подвижными и не могут участвовать в переносе тока). Энергетические уровни над
барьером (Е > 0) называются делокализованными или свободными (для получения
дополнительной информации ознакомьтесь с дополнением 1.А).
Важно отметить, что приведенный ход рассуждений может быть обобщен на
случай любого потенциала: т. е. квантование энергетических уровней следует из
распространения граничных условий в интервале от — «> до +оо, а также из
требования, чтобы амплитуды волновых функций исчезали на бесконечности.
Пример
Позже в главе 8 мы увидим, что электрон в полупроводниковой гетероструктуре,
изготовленной на основе GaAs/Al045 GaO55 As, находится в условиях потенциальной
ямы глубиной 360 мэВ. Более того, взаимодействие электрона с периодическим
потенциалом кристаллической матрицы GaAs учитывается умножением массы
электрона на коэффициент 0,067, при этом такое произведение соответствует
эффективной массе электрона т* = 0,067 те. Использование уравнения A.33) позволяет
нам получить выражение для волнового вектора к0 в виде:
Ко = -7Bx0,067 х 0,9 хЮ-30(кг)х 0,36 (эВ)х 1,6 х 1019(Лл) / 1,05 х10-34(Дж с)
или к0 = 0,78 нм, что соответствует длине волны 8,05 нм.
Теперь рассмотрим квантовую яму шириной 10 нм. Поскольку ширина ямы
сравнима с длиной волны де Бройля /0, связанной с потенциалом Ко = 360 нм, мы
можем ожидать, что система будет проявлять эффект квантования. Используя
уравнение A.47), мы видим, что в рассматриваемом случае мы можем ожидать
присутствие трех связанных состояний в этой конкретной системе (т. е. 1 + Int@,78 x 10/3,14)).
Волновые функции, соответствующие каждому из этих состояний, показаны на
рис. 1.1.
Приведенная ниже программа MATEMATICA очень полезна при решении
задач на ограничивающие потенциалы.
m0=0.911CT-30 (*kg*);hbar=1.0510"-34 (*J.s*);
q=1.610'-19(*C*);
meff=0.067 (* effective electron mass In GaAs*);
V0=.36 (*well depth in eV*);
a=10.(*well width in nm*);
kO=Sqrt[2*meff*mO*q*VO]*10"-9/hbar (*in nm-1*)
eq1=Cos[k*a/2];
eq2=Sin[k*a/2];
eq3=k/kO;
plot1=Plot[Abs[eq1],{k,0,kO}]
plot2=Plot[Abs[eq2],{k,0,kO}]
plot3=Plot[Abs[eq3],{k,0,kO}]
1.4. Квантовая яма
Show[plot1fplot2,plot3]
FindRoot[eq1==eq3,{k,0.2}]
Е1 =hbar»2*(k*10"9)>>2/B*meff*m0*q)/.S
FindRoot[eq2==eq3, {k,0.5}]
E2 =hbar»2*(k*10"9)/B*meff*m0*q)/.%
hnu=E2-E1 (*optical transition energy in eV)
1.4.2. Бесконечная потенциальная яма
квадратного профиля
Особо важным случаем, заслуживающим исследования, является бесконечная
потенциальная яма квадратного профиля (рис. 1.3).
В этом случае решения уравнения Шредингера получаются сразу:
ка = п (нечетные) ^
ка = п (четные) У„\
и в обоих случаях:
J= J— cos ял- —
а
[2 х
- sin юг-.
A.48)
Ъпд2
A.49)
Энергетические уровни
бесконечной квадратной ямы
Е- энергия ограничения.
Этим мы даем альтернативную интерпретацию волны
де Бройля, задаваемой соотношением A.1), а именно: это ширина бесконечной
квадратной ямы, необходимая для обеспечения энергии ограничения Ео, равной
энергии частицы. Важным понятием является тепловая волна де Бройля ADB th. Это —
ширина бесконечной квадратной ямы, необходимая для обеспечения энергии
ограничения, равной тепловой энергии кТ.
. 2жП A 50)
DB 'h J^Jf-
Таким образом, в потенциальных ямах шириной менее чем ADBth при Т= 300 К
квантовые эффекты будут проявляться без влияния тепловых колебаний. Только в
этих случаях мы можем говорить о квантовых ямах при комнатной температуре.
600
m 400
со
200
-8-4 0 4 8
Положение (нм)
Рис. 1.3. Бесконечная квантовая яма шириной 10 нм.
В отличие от решений для конечной ямы,
иллюстрируемых рис. 1.1, в рассматриваемом случае волновые
функции не проникают в барьеры, а энергетические
уровни смещены вверх по отношению к дну ямы.
Глава 1. Квантовая механика электрона
Пример
Предполагая бесконечную (хотя и нереализуемую на практике) квадратную яму на
основе GaAs при 300 К можем рассчитать, что
6,28 х 1,05 х10-*(Дж) . р
/t IZ НМ.
/tpg h
V2 х °>067 х °>9 х Ю-30(кг) х 0,0259 (эВ) х 1,6 х 1019(°С)
Таким образом, квантовые эффекты могут быть выявлены в слоях GaAs с
толщиной менее указанной выше величины, и только в этом случае мы можем
говорить о квантовых ямах GaAs при комнатной температуре.
1.5. Стационарная теория возмущений
Очень ограниченное число физических систем дают простые решения, подобные
тем, которые предоставляют квантовые ямы. Среди таких систем, допускающих
аналитическую трактовку, следует упомянуть атом водорода (который не
рассматривается в данной книге), а также гармонический осциллятор (рассматриваемый в
Дополнении 1.Г). Более общие системы редко дают аналитические решения. В то
же время, используя более простые системы, обеспечивающие более известные
решения, мы попытаемся распространить их на более сложные системы. Наиболее
известной (и возможно наиболее плодотворной с точки зрения успешности
расширения нашего концептуального понимания многих физических систем) является
стационарная теория возмущений.
Рассмотрим электрон в системе, описываемой стационарным гамильтонианом
Яо, базисный набор стационарных состояний {\у/)} которого состоит из решений
уравнения Шредингера:
Нй\¥п) = Е„\¥п) A.51)
(Заметьте, что начиная с этого момента для упрощения системы обозначений мы
будем опускать символ оператора «Л», так как мы предполагаем, что на этой стадии
читатель способен отличить оператор от переменной величины). На некоторое
время предположим, что состояния являются дискретными и невырожденными.
Важный случай распространения теории возмущений на вырожденные системы
приведен в приложении 1.Б. Теперь подвергнем систему небольшому дополнительному
возмущению W — ail, которое может быть реализовано, например, за счет
приложения электрического поля к квантовой яме. Под понятием «малое» мы понимаем
то, что а« \ и что собственные значения {/имеют величину порядка Еп (т. е., что
U~HQ или что собственные энергии в первом приближении имеют ту же величину,
что и для невозмущенного гамильтониана Но) Собственные значения нового
гамильтониана Н = Но + W представляют собой:
(Яо + av)M«)) = £»|у») A.52)
Затем, примем важную гипотезу, заключающуюся в том, что достаточно малые
возмущения позволят рассматривать нам решения модифицированной системы с
использованием первоначальных уровней невозмущенной системы (т. е., что такие
малые возмущения не искажают сильно первоначальный энергетический спектр
системы). В этом случае новые собственные значения и собственные векторы
возмущенной системы могут быть выражены через первоначальные собственные энергии
и собственные векторы с использованием коэффициента возмущения а.
Еп(а)= е0 + осе, + а2е2 + ... A.53)
1.5. Стационарная теория возмущений
Подстановка A.53) в A.52), группировка всех членов по степеням параметра а
дает:
Нулевой порядок: #0|0) = £0|0) A.54д)
Первый порядок: (Яо -£0)\l) + (U-е^О) = 0 A.546)
Второй порядок: (Яо - ео)\2) + (U - e^l) - е^О) A.54<?)
Нулевой порядок
Как мы и предполагали, что уровни являются невырожденными, уравнение A.54)
дает, что |0) является собственным состоянием Но. Из непрерывности при а —> «>
мы находим, что |0) = \у/). Это несправедливо, если уровни являются
вырожденными, т. к. в этом случае уравнение A.54а) более не соответствует одиночному
квантовому уровню.
Первый порядок
Спроецируем A.54) на |0) = \у/п) и используем тождество:
<0|Я,-£0|1) = 0 A.55)
для того, чтобы найти поправку первого порядка:
e,={wn\U\¥n) A.56)
или с использованием более ранних определений:
E' = En+(Wn\lV\¥n) A.57)
Возмущение энергии первого порядка
где энергия с учетом возмущения Е'п выражена без использования а.
Для того, чтобы найти ограниченный ряд для собственного вектора, нам
необходимо только спроецировать A.546) на другие состояния \у/) при р ф п:
(Ер-Еп)(у,р\1) + (¥р\и\у,п) = 0 A.58)
В этом случае получаем для возмущенных собственных векторов следующее
выражение первого порядка:
(L59)
Возмущение собственных
состояний первого порядка
Отметим, что к невозмущенному стационарному состоянию \ц/п) в этом случае
примешиваются другие состояния \i//p), при этом наибольший вклад дают состояния,
ближайшие к \у/) по энергии. Таким образом, при описании эффекта возмущения
нам будет достаточно при описании ограничиваться членами, ближайшими по
энергии (например, рассмотрение эффекта Штарка в дополнении 1.В).
Глава 1. Квантовая механика электрона
Второй порядок
В ряде случае первый порядок дает нулевой вклад, когда:
(¥„\Щ¥„) = 0 A.60)
Это происходит с учетом соображений симметрии (как, например, в случае
возмущения потенциала ограничения электрическим полем). В результате часто
является необходимым продолжить разложение с учетом более высоких порядков
возмущения. Проецируя A.54<?) на \ц/п), находим:
*2=(У„М1) A-61)
С использованием A.59) можем записать выражение с учетом поправки второго
порядка:
При этом опять мы отмечаем, что величина вклада любого состояния
увеличивается для ближайших по энергии состояний.
1.6. Нестационарные возмущения
и вероятности переходов
1.6.1. Общий случай
Ситуации, при которых точные решения нестационарного уравнения Шредингера
A.12), к сожалению, встречаются нечасто. Нестационарное поведение электрона в
квантовой яме достойно специального рассмотрения: оно может быть
проанализировано в качестве примера. В общем случае используем подход с использованием
теории возмущений, который дает нам возможность определить скорость переходов.
Рассмотрим систему, описываемую гамильтонианом Яо с начальным состоянием \у/.)
в момент времени 0. В момент времени 0 мы включаем возмущение W(t) = aU(f), при
этом на а и U (t) накладываются те же условия, что и в предыдущем разделе,
а именно а « 1 и U ~ Но. Для решения уравнения Шредингера:
1й|гИ>)> = [Я. + W(f)]\w(?} A.63)
и описания эволюции системы, мы можем разложить \y/(t)) по базису
стационарных состояний, как это дается уравнением A.6):
l^) (L64)
Подстановка A.64) в A.63) и перегруппировка подобных членов дает систему
связанных дифференциальных уравнений, связывающих коэффициенты cn(t) друг с
другом:
lfiTtCn{t)=£л(/)+Ха£^(/)с'(/) (L65)
р
где U — элементы матрицы:
1.6. Нестационарные возмущения и вероятности переходов
Предположим, что из соображений симметрии Umn = О для любого заданного
уровня п. Теперь сделаем следующее изменение переменных:
bn(t) = cn(t)eiE-"" A.67)
Это приводит к следующей записи уравнения:
f) A.68)
где сопр = (Еп — Ер)/П — блоховская частота колебаний для перехода п --> р. Как и в
разделе 1.5, осуществим ограниченное разложение:
*„(') = **0)@+ fl*J!)@+ <*2*<2)@+ - A.69)
позволяющее сгруппировать подобные по степеням а члены после подстановки
A.69) в A.68).
Нулевой порядок
Находим, что Ьп @) является константой. Это соответствует решениям для
стационарных состояний, даваемых A.29).
Вклад 4-го порядка
Мы получаем:
|()Х')(О A-70)
Таким образом, как только найдено решение нулевого порядка, мы можем
рассчитать решение первого порядка и затем последовательно решения других
порядков. На протяжении оставшейся части главы нас будут интересовать возмущения
нулевого порядка. Подход с использованием возмущений второго порядка будет
развит в главе 12 в связи с нелинейной оптикой.
При / =0 система находится в состоянии \у/) с начальными условиями:
bp(t = 0)=1
/V ) A.71)
£о(, = О)=О , ДЛЯ 1ФП
В нулевом порядке эти величины остаются неизменными во времени.
Подстановка этих величин в A.70) дает уравнение временной эволюции:
которое приобретает интегральную форму:
/><'>(/)= Lje<->.'unl(t')it' A.73)
0
Теперь мы уже в состоянии рассчитать вероятность Ptf(t) обнаружения системы
в конечном стационарном состоянии \y/f) в момент времени t. Следуя
вероятностной интерпретации квантовой механики, это может быть получено с
использованием оценки I^Ol2 или выражения:
Глава 1. Квантовая механика электрона
где
A.74а)
Вероятность перехода между
уровнями / и f под воздействием
нестационарного возмущения
A.746)
Эта формула является одной из наиболее важных в квантовой механике, и она
будет использоваться на протяжении всей книги. Сейчас же мы используем ее для
рассмотрения особенно важной и интересной задачи с изменяющимся во времени
синусоидальным возмущением.
1.6.2. Синусоидальное возмущение
В рассматриваемом случае потенциал возмущения может быть записан в виде:
W(r,/) = Ж (г, 0 sincot A.75)
Уравнение A.74) сразу приводит к нестационарной вероятности перехода Pif(t)
между начальным и конечным состояниями:
\ _ ei(a7?+<w)r
A.76)
В данном случае мы выполняем процедуру, которая классически называется
аппроксимацией фазы вращения или квазирезонанса, при которой пренебрегается
вклад члена с большим знаменателем cofi + со по сравнению с членом, имеющим
меньший знаменатель cofi — со. Таким образом, сохраняя второй член в выражении
A.76) мы приходим к выражению:
,Й
4/г2
, _ «,■(•,->
со„-а
4/г2
,„ К-®)'
sin
A-77)
Рисунок 1.4 иллюстрирует эволюцию этой вероятности в функции времени для
различных частот (или отстройки) между возбуждающим полем и резонансной
частотой перехода со— cofi. Отметим, что по мере того, как частота возмущающего поля
приближается к боровской частоте колебаний (т. е. со —> cof), временная
зависимость амплитуды перехода изменяет свой характер: от синусоидальной к
параболической зависимости от t. Дополнительно на рис. 1.5 показано спектральное
распределение вероятности перехода в функции отстройки для различных значений
времени t. Эта функция представляет собой произведение синусоиды на временную
параболу, которая стремится к 8 — функции Дирака при /-><». Таким образом
перепишем A.77) в виде:
4П2
|2
Г sin с-
A.78)
где sin с (х) есть sin х/х. Уравнение A. 78) при внешней простоте трудно охватить
сразу во всей его полноте, так как оно является функцией двух внутренне
связанных величин, а именно времени и частоты. Для лучшего понимания его характера
рассмотрим три различных случая.
1.6. Нестационарные возмущения и вероятности переходов 31
Рис. 1.4. Временная эволюция вероятности перехода между уровнями / и /для
различных величин частотной отстройки co.f — со. В условиях вне резонанса
электроны осциллируют между двумя уровнями.
40
-30
о?
10
0
= 7 отн.ед. |
5 отн.ед.
= 3 отн.ед.
-4
-2
Рис. 1.5. Вероятность перехода между двумя уровнями / и/в функции частоты
отстройки для различных моментов времени наблюдения / (в произвольных
единицах). При большем значении времени возможны лишь переходы между
состояниями, удовлетворяющие требованиям сохранения энергии. Это
согласуется со вторым принципом неопределенности Гейзенберга.
Случай 1: переходы между дискретными уровнями,
обусловленные одночастотным возбуждением
В этом случае в процессе доминирует резонансный переход, при этом:
A.79)
Поскольку вероятность указанного перехода возрастает квадратично со
временем, предлагаемое описание носит аппроксимационный характер, так как
параметр не может превысить единицу. В дополнении 1. Д мы увидим, что эта апрокси-
мация действительна только для очень коротких промежутков времени, в течение
которых разложение нулевого порядка A.69) может считаться действительным.
Отметим, что резонансное условие co=cofi альтернативно может записано в виде:
Глава 1. Квантовая механика электрона
Псо = Е/-Е1. =Пй)л A.80)
Боровская частота
Это уравнение описывает закон сохранения энергии с учетом энергии,
переданной системе, и различием энергии системы между начальным и конечным
состояниями АЕ — Ef— Er С технической точки зрения, касающейся расчета этих
величин, отметим только, что упорядочение в расположении индексов в этих
уравнениях (\lVjf\ = |WyJ) не играет какой-либо определенной роли из-за свойств
эрмитовых произведений. В то же время сказанное не относится к боровской частоте
колебаний 0)^= ~~cofl\
В дополнение к сказанному, рис. 1.5. иллюстрирует тот факт, что вероятность
перехода становится пренебрежимо малой, как только
AEt>h A.81)
Это последнее условие известно также и как второе соотношение
неопределенности Гейзенберга. Оно обеспечивает возможность снятия ограничений на
сохранение энергии при возбуждении, действующем в течение коротких периодов времени.
Случай 2: переходы между дискретным уровнем и континуумом,
обусловленные одночастотным возбуждением
В этом случае конечные состояния образуют континуум, описываемый непрерывной
переменной (Ор и вероятность перехода между дискретным уровнем и континуумом Р.с (/)
рассчитывается суммированием вероятностей по плотности конечных состояний p(cof):
+оо г- -|2
P*if) = i'2 f KM] SinC(^:^4 P(O)fi)dO)fl
4n i L 2 J A.82)
Теория распределений показывает, что если функция | WJ<cof)\2p{cof) обладает
нормальным характером (т. е. способностью нормировки и слабой скоростью
изменения), то:
limjsin c[i(^ - со)Л =2y8{cof, - со) A.83)
где 8 — есть ^-функция Дирака. Таким образом при больших значениях времени
уравнение A.82) принимает вид:
Pic@ = ^\^(а)л)\2 p(G) = cofl)t A.84)
Приведенное выше уравнение свидетельствует о том, что, если переход
происходит из дискретного состояния в континуум, то скорость перехода G.c = dPic /d/
является постоянной по времени и имеет величину, задаваемую соотношением:
G» = «,) <L85a>
Частотное выражение
золотого правила Ферми
или
^\j({Ef-E) A.856)
Энергетическое выражение
золотого правила Ферми
1.7. Матрица плотности
Это важное уравнение называется золотым правилом Ферми. Оно утверждает,
что в условиях монохроматического возбуждения со только уровни континуума с
энергией Ef— ЕЛ h со будут заселенными под воздействием оптического
возбуждения, при этом скорость оптических переходов будет даваться приведенным выше
уравнением.
Случай 3: переходы между двумя дискретными уровнями
при многочастотном возбуждении
В этом случае используется возбуждение, содержащее континуум возбуждающих
частот:
Wfi(t)[ g(a))Wfi(a))sin(u)t)dco A.86)
о
где g(co) — спектр возбуждения и Wfi матричный элемент гамильтониана
взаимодействия для каждой конкретной длины волны. Рассуждения, строго соответствующие
приведенным выше, дают скорость переходов в соответствии с соотношением:
Gif(hco) = ^-\Wif\2g(hcQ = Ef - Е,) A.87)
Скорость переходов при
широкополосном возбуждении
1.7. Матрица плотности
При описании физической системы встречаются два типа неопределенности.
Имеется чисто квантовая неопределенность, связанная с вероятностной
интерпретацией алгебры операторов, примененной к системе. Кроме того, имеется
неопределенность, возникающая из-за теплового возбуждения образующих систему частей, что
описывается статистической механикой. Формализм матрицы плотности
проявляет себя как очень мощный и одновременно элегантный инструментарий, в рамках
которого в едином математическом описании интегрируются оба эти понятия.
1.7.1. Чисто квантовые ансамбли
Рассмотрим квантовую систему в состоянии \y/(t)), описываемую A.64). Нам
хотелось бы знать среднюю величину оператора А. В соответствии с уравнением A.8)
эта средняя величина (А) может быть записана в определенном базисе \у/к)
следующим образом:
{) ^mncl(t)cn(t) A.88)
п, т
где Атп — элемент матрицы:
Лтп =КИЮ A.89)
Уравнение A.88) может привести к ложным заключениям, так как, кажется, что
существует особый базис, в рамках которого лучше всего проводить разложение. В то
же время, если мы изменим базис, то коэффициенты Атп, cm(t) и cn(t) изменятся
таким образом, который оставит A.88) инвариантным уравнением. Это неудобство
устраняется введением матрицы плотности, элементами которой являются:
РтЛ*)= <Ш0 A90)
Глава 1. Квантовая механика электрона
Фактически же матрица p(t) может быть записана также в виде:
С учетом этого определения уравнение A.88) приобретает вид:
A.92)
который инвариантен от базиса разложения р = 1^@X^@1» и след этой матрицы
является линейным оператором, чья величина не зависит от базиса, в котором он
оценивается. Более того, используя A.91), мы сразу видим, что временная
эволюция /ХО дается соотношением:
\hj-tp(t)=[H{t\p{t)]=H{t)p{t)-p{t)H{t) A.93)
Уравнение Шредингера
в формализме матрицы
плотности
1.7.2. Смешанные квантовые ансамбли
Рассмотрим теперь систему, состоящую из статистически распределенной смеси
состояний {\ф.)}. Эта система характеризуется термодинамической вероятностью р.
пребывания в состоянии \ф).
В пренебрежении квантовой интерференцией между термодинамически
размазанными состояниями представляется естественным определить среднюю
величину наблюдаемой А как:
где {А)ф. — средняя величина наблюдаемой А, когда система находится в состоянии
\ф). Следуя уравнению A.92), это может быть записано следующим образом:
Ц) = 2 PiTr(p,A)= Тг(дА) A.95)
где р — это матрица плотности смешанного ансамбля:
1 (L96)
Из уравнения A.96) видно преимущество введения матрицы плотности. Это —
линейная зависимость (А) от матрицы плотности р, что позволяет ввести оператор
плотности или усреднения р.
Так как любая матрица р обеспечивает ту же самую временную эволюцию в
соответствии с уравнением A.93), матрица плотности для смешанного ансамбля
может быть записана в виде:
Ь-^Р(О =№>?(*)] A97)
Уравнение Шредингера для
смешанного ансамбля
Фундаментальными для матрицы плотности являются уравнения A.95) — A.97).
В рамках концепции матрицы плотности мы можем провести различие между
двумя типами ее элементов.
1.7. Матрица плотности
(А) Диагональные элементы
Из уравнений A.90) — A.96) следует, что диагональные члены могут быть
выражены в стационарном базисе следующим образом:
где ск — это \ф') компонента в базисе \у/к). Непосредственной физической
интерпретацией диагональных элементов в виде ркк является то, что они представляют
вероятность нахождения системы после измерения в стационарном состоянии \у/к) с
учетом как квантовой, так и статистической неопределенности. Таким образом pkk
представляет заселенность состояния \у/к). Так как эти элементы возникают в
результате суммирования положительных членов, они не могут быть равными нулю,
если только величина каждого из этих членов не равна нулю (т. е. заселенность
каждого состояния — нулевая).
(Б) Недиагональные элементы
Имеются определенные трудности в осознании значения этих членов. Их иногда
называют элементами когерентности: они описывают квантовое поведение
системы. Когда тепловые колебания полностью размазывают квантовые
интерференционные эффекты, эти члены становятся равными нулю.
В разделе 1.7.3 будет дан пример двухуровневой системы, который позволит
нам лучше понять полезность этого мощного и изящного формализма. В
заключение отметим, что различие между заселенностью и когерентностью зависит от
базиса разложения (\у/)}.
1.7.3. Матрица плотности и время релаксации
для двухуровневой системы
Рассмотрим двухуровневую систему с гамильтонианом Но, обладающим
собственными энергиями Ех и Е2 и стационарными состояниями |1) и |2) (т. е. #0|/> = 2£|/>).
В базисе стационарных состояний гамильтониан Но может быть записан в виде:
£, О
О Е
A.98)
В момент t = t0 мы подвергаем систему синусоидальному возбуждению W(t)9
которое в базисе |1) и |2) может быть записано следующим образом:
lV=\m" "Hcosarf л 99)
[m2l т22\ V'yy>
где т.. — (i\W\j). Мы можем предположить из соображений симметрии, что
элементы тп, т22 нулевые и что члены тп и т21 являются действительными и равными.
Общий случай может быть рассмотрен как упражнение. В этом случае уравнение
A.97) может быть записано следующим образом:
0 A.100)
= ~Ш21р21 +i-j2-(p22-pn )COS O)t
Глава 1. Квантовая механика электрона
Второе уравнение системы A.100) означает, что полная заселенность
сохраняется (т. е. рп + р22 = 1). Решения этой очень важной системы связанных
дифференциальных уравнений даны в дополнении 1. Д. Тем не менее, уже сейчас мы можем
исследовать временную эволюцию системы. Например, ясно, что члены при cos cot
будут вести себя таким образом, чтобы ввести систему в колебательный режим.
Если возбуждение прекращается (т. е. предполагая, что приравниваем тп нулю)
диагональные элементы останутся постоянными, а недиагональные элементы
будут продолжать осциллировать с частотой со21.
Интуитивно мы могли бы ожидать, что как только возбуждение прекратится,
уровни заселенности р.. будут стремиться к уровням термодинамического равновесия p.*q с
определенной постоянной времени, определяемой стохастическими
взаимодействиями. Эту постоянную времени часто называют временем диагональной релаксации или
временем заселенности, не говоря о других названиях. Обозначается оно обычно как Тх,
когда его величина не зависит от / в р.., т. е. не зависит от уровня. В другихх ситуациях
принято использовать скорость релаксации Г.. Аналогичным образом мы можем
ожидать, что недиагональные элементы теряют когерентность с постоянной времени Г..
или Т2, если эта постоянная не зависит ij. При введении этих различных времен
релаксации уравнения для матриц плотности приобретают вид:
^ ^»-pn)coscot-<±jA- A.101a)
-тг =-'®2iP2i +i^r~fc» - Pu )cos a>/--^-
at n 12
Временная эволюция элементов матрицы
плотности для двухуровневой системы
или
At П ™
22 = i—-(/?2i ~ /?12)cos6rf - Tx[pu - Pu) A.1016)
dp91 ./ ._ \ . mn / \
at ~ ' n
Временная эволюция элементов матрицы
плотности для двухуровневой системы
Последние два выражения представляют собой два наиболее важных
заключения этой первой главы, и они будут интенсивно использоваться на протяжении
всей книги. Дополнение 1. Д дает пример применения полученных результатов,
трактовка которых подводит нас к оптическим блоховским уравнениям.
Литература
С. Cohen-Tannoudji, В. Diu, and F. Laloe, Quantum Mechanics, Wiley, New York A992).
С Cohen-Tannoudji, J. Dupont-Roc, and G. Grynberg, Atom-Photon Interactions: Basic
Processes and Applications, Wiley, New York A998).
R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol
HI: Quantum Mechanics, Addison-Wesley, Reading, Mass. A966).
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
E. Merzbacher, Quantum Mechanics, Wiley, New York A970).
A. Messiah, Quantum Mechanics, vols 1 and 2, Wiley, New York A966).
L. I. Scruff, Quantum Mechanics, 2nd edn, McGraw-Hill, New York A955).
ДОПОЛНЕНИЯ
К ГЛАВЕ 1
1.А. Проблемы, накладываемые континуумом:
виртуальный квантовый ящик и плотность состояний
Квантовое описание делокализованных состояний, принадлежащих континууму,
использует теорию распределений. Это описание пытается дать трактовку сложных
проблем, таких как нормировка волновых функций в нулевом потенциале в
интервале от —оо до +°о. В этой книге систематически используется прием, основанный на
введении понятия виртуальной бесконечной квадратной ямы шириной L, в которой
движение электронов континуума, как мы увидиим дальше, является квази-кванто-
ванным. Более того, когда мы принимаем L, стремящимся к бесконечности в
полученных выражениях, зависимость от L удобным образом исчезает из наших
физических предсказаний. В этих рассуждениях нет никакого дополнительного поучения;
разве что педагогическая защита теории распределений! Далее рассмотрим
иллюстрирующий пример: фотоэмиссию из одномерной ямы.
Рассмотрим квантовую яму шириной L, как это представлено на рис. 1.А.1.
^ L ►
QQ
Положение (нм)
Рис. 1.А.1. Процедура квази-квантования состояний потенциального барьера.
Ширина L бесконечной квадратной ямы имеет произвольную величину.
Эта квантовая яма допускает существование квантового уровня |/),
описываемого квадратично интегрируемой волновой функцией y/.(z) и квантовым
энергетическим уровнем — Ej (где индекс / соответствует (по причинам, которые будут
понятны позже) ионизации). Далее мы предположим, что яма достаточно глубока
для i/s.(z), чтобы рассматривать в качестве волновой функции основного состояния
функцию вида:
к
A.А.1)
Эта яма допускает существование делокализованных состояний, в которых
электроны могут иметь любую положительную величину энергии. Мы будем
пренебрегать влиянием ямы на свободные электроны, т. е. будем предполагать, что
свободные электроны подвержены воздействию нулевого потенциала, как только они
оказались в области континуума. Во избежание проблем, связанных с нормировкой
этих волновых функций, мы вводим виртуальную квадратную яму шириной L, внутри
которой электроны континуума являются захваченными. Соответствующие
собственные энергии и собственные функции несвязанных состояний имеют вид:
ополнения к главе 1
еп = п2е0
Vn(z)= J— sin nkLz , если п является четным A.А.2)
Vn&)- \\— cosnkLz, если п является нечетным
где е0 — энергия ограничения виртуальной ямы:
с волновым вектором kL:
Если L имеет сантиметровые размеры, то е0 имеет величину порядка 10~и эВ.
В этом смысле такой ящик был бы виртуальным, так как энергетический интервал
между уровнями был исчезающе мал по сравнению энергией тепловых
взаимодействий (порядка мэВ). Энергетические уровни в соответствии с A.А.2) настолько близки
друг к другу, что вместо того, чтобы пытаться рассматривать их по отдельности,
сгруппируем их вместе с помощью бесконечно малых секторов плотности состояний.
Рассмотрим некий интервал волнового вектора dk. В пределах этого интервала
отдельные состояния виртуального ящика разделены по волновому вектору на p/L.
Очевидно, что без учета электронного спина число состояний в пределах этого
интервала составляет:
dn = -dk A.A.5)
я
В этом случае плотность состояний dn/dk дается соотношением:
dk n
Дифференцированием A.А.З) получаем, что в том же интервале
соответствующее изменение энергии связано с dk соотношением:
dtai^? A-A.7)
В результате энергетическая плотность состояний принимает вид:
iV^l 1
Одномерная плотность состояний
без учета спина
Отметим, что при стремлении L к бесконечности, р (Е) также будет
возрастать без ограничений. Этого и следовало ожидать, так как все большее число
состояний будет находиться в пределах одного энергетического интервала, когда
энергетический интервал между состояниями уменьшается.
Теперь рассчитаем вероятность перехода между начальным квантовым
состоянием |/) и континуумом в условиях синусоидально изменяющегося дипольного
возмущения:
W{z9t)= -gfzcos(wt) A.A.9)
В соответствии с золотым правилом Ферми A.856) вероятность перехода может
быть записана в виде:
1.Л. Проблемы, накладываемые континуумом
Gic(hco) =
p(fico = Ef - Ei)
A.A.10)
Матричный элемент перехода zif отличен от нуля только для нечетных
конечных состояний и дается выражением:
или
A.А.11)
d/2 ,
\ cos( J
л d3
=4 —
A.А.12)
представляет собой одномерный интефал в уравнении A.А.11),
выражающийся соотношением:
ж2 - d2kj
sin
kfd
4kfd
1 -d2k}
-cos
kfd
и kf — волновой вектор соответствующего состояния с энергией Ej.
fi2k2
Ef = fico - E, —
2m*
A.A.13)
A.A.14)
Теперь подставим выражение для \zif\ в A.А.10). Заметьте, что, как и
предсказывалось, ширина виртуального ящика L, которая фигурирует в знаменателе
матричного элемента перехода и числителе плотности состояний, в этом случае
устраняется. С физической точки зрения, чем больше ширина квази-ямы, тем больше
должна быть плотность конечных состояний. Однако влияние этого фактора на
вероятность перехода устраняется, так как увеличивающаяся ширина приводит также
и к уменьшению плотности вероятности электронных состояний над квантовой
ямой (шириной L) на подобную же величину.
Учитывая, что плотность конечных состояний составляет лишь половину
выражения, представленного в виде A.А.8) (вследствие спина электронов,
сохраняющегося в процессе переходов), мы находим таким образом, что вероятность
перехода из начального квантового состояния в континуум может быть записана
в виде:
A.A.15)
Таким образом, мы обнаружили, что поведение системы не зависит от размера
виртуального ящика, введенного нами первоначально. Этот метод называется
методом квази-квантования, и он оказывается мощным инструментом несмотря на
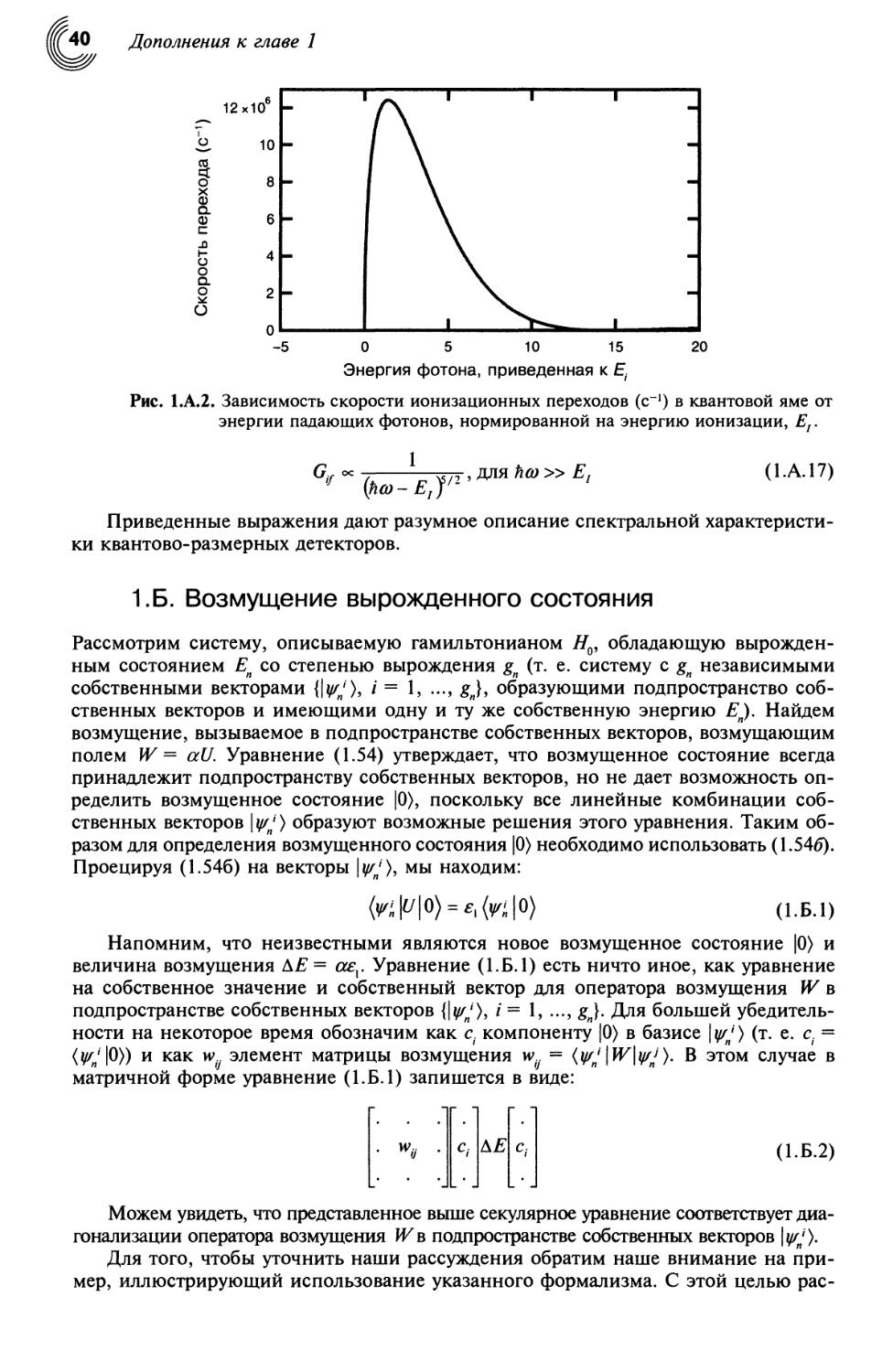
свою кажущуюся простоту. Рисунок 1.А.2 иллюстрирует зависимость скорости
перехода от частоты возбуждения со.
Обратите внимание на наличие порога ионизации для вероятности перехода.
Энергия среза для детектируемых фотонов соответствует энергии ионизации. Более
того, поглощение вблизи порога детектирования, т. е. для фотонов с h со ~ Ер
дается соотношением:
Gif ©с ^%со- Ej, для hco ~ Ej A.A.16)
Второй особенностью является квази-резонансная природа вероятности
перехода вблизи энергетического порога фотоионизации. Этот квази-резонанс
возникает как следствие уменьшения плотности состояний (как k~l) также и дипольного
момента (как k.f~2), что приводит к:
Дополнения к главе 1
О 5 10 15 20
Энергия фотона, приведенная к Еу
Рис. 1.А.2. Зависимость скорости ионизационных переходов (с) в квантовой яме от
энергии падающих фотонов, нормированной на энергию ионизации, Ег
1
(hco-Ej
/2
, для hco»
A.А.17)
Приведенные выражения дают разумное описание спектральной
характеристики квантово-размерных детекторов.
1.Б. Возмущение вырожденного состояния
Рассмотрим систему, описываемую гамильтонианом #0, обладающую
вырожденным состоянием Еп со степенью вырождения gn (т. е. систему с gn независимыми
собственными векторами {\фп')9 i = 1, .., gj, образующими подпространство
собственных векторов и имеющими одну и ту же собственную энергию Еп). Найдем
возмущение, вызываемое в подпространстве собственных векторов, возмущающим
полем W= aU. Уравнение A.54) утверждает, что возмущенное состояние всегда
принадлежит подпространству собственных векторов, но не дает возможность
определить возмущенное состояние |0), поскольку все линейные комбинации
собственных векторов \i//J) образуют возможные решения этого уравнения. Таким
образом для определения возмущенного состояния |0) необходимо использовать A.546).
Проецируя A.546) на векторы \tffj), мы находим:
Напомним, что неизвестными являются новое возмущенное состояние |0) и
величина возмущения АЕ = аех. Уравнение A.Б.1) есть ничто иное, как уравнение
на собственное значение и собственный вектор для оператора возмущения W в
подпространстве собственных векторов {\wj), i = 1, ..., gn}. Для большей
убедительности на некоторое время обозначим как с. компоненту |0) в базисе \if/f) (т. е. с. =
Aуп'\0)) и как w.j элемент матрицы возмущения w.. = (y/J\W\y/J). В этом случае в
матричной форме уравнение A.Б.1) запишется в виде:
АЕ
A.Б.2)
Можем увидеть, что представленное выше секулярное уравнение соответствует диа-
гонализации оператора возмущения W в подпространстве собственных векторов l^')-
Для того, чтобы уточнить наши рассуждения обратим наше внимание на
пример, иллюстрирующий использование указанного формализма. С этой целью рас-
1.Б. Возмущение вырожденного состояния 41
Рис. 1.Б.1. Вырожденная система из двух идентичных атомов, пространственно
разнесенных на расстояние L.
смотрим две идентичные физические системы, далеко расположенные друг от
друга (рисунок 1.Б.1).
Система слева центрирована при гр в то время как система справа
центрирована при г.. Соответствующие гамильтонианы обеих систем имеют вид:
*.-£♦"«
A.Б.З)
Обе системы обладают подобными гамильтонианами и таким образом имеют
идентичные собственные энергии. Например, |/) и \г) обладают одной и той же
энергией основного состояния:
A.Б.4)
Нг\г) =
Теперь плотно сблизим обе системы таким образом, чтобы каждая из них
оказывала возмущающее действие на другую систему. Теперь мы можем представить
это влияние в виде гамильтониана возмущения. В этом случае уравнение A.Б.2)
примет вид:
w.
= АЕ
A.Б.5)
Без ущерба для общности мы можем предположить, что wn = wtl = 0 и что wri
являются действительными и равными А. Тогда уравнение A.Б.5) может быть
переписано в виде:
A.Б.6)
Из этого следует, что система обладает собственными энергиями и
собственными векторами вида:
Е--Е-Л |-) = -^(
A.Б.7)
Дополнения к главе 1
В этом случае основное состояние Е более не является собственной энергией
состояний |/) и \г). Можем сказать, что взаимодействие между системами снимает
вырождение и что состояния |/) и \г) являются гибридизированными. Схематически
этот механизм иллюстрируется рисунком 1.Б.2.
Рис. 1.Б.2. Когда два состояния |/> и \г) плотно сближаются, они гибридизируются,
снимая вырождение системы.
Этот механизм образует основу химической связи. Рассмотрим в качестве
примера два атома водорода. При большом удалении друг от друга энергия их двух
электронов составляет 2Е (где Е представляет энергию основного состояния
каждого электрона). По мере сближения сила их взаимодействия W увеличивается,
приводя к снятию вырождения, при этом два электрона на уровне |—) теперь имеют
полную энергию 2(Е— А) (из-за вырождения по спину). Продолжим наше
рассмотрение, иллюстрируя его особенно наглядным примером.
Пример: связанные квантовые ямы ——
Прогресс в области синтеза высококачественных кристаллических
полупроводниковых гетероструктур обеспечил возможность выращивания квантовых ям,
разделенных барьерами толщиной порядка нескольких постоянных решетки (несколько
нанометров или несколько больше). Рассмотрим две такие квантовые ямы
шириной а, центрированные при +Ь и — Ъ соответственно (рисунок 1.Б.З).
Примем энергетическую глубину квантовых ям, равной Vo. Полный
гамильтониан электрона в рассматриваемой системе дается соотношением:
-10 0
Положение (нм)
10
Рис. 1.Б.З. Снятие вырождения в системе из двух связаннанных квантовых ям за
счет электронного туннелирования.
1.Б. Возмущение вырожденного состояния
где V — ступенчатая функция, равная — Ко в интервале между и —а/2, а/2 и 0 в
других областях. Мы уже видели, что можно записать полный гамильтониан в виде
суммы невозмущенных гамильтонианов и добавки, связанной с возмущением из-за
взаимодействия:
Я = Hr + V(x + b) = Я, + V(x - Ь) A.Б.9)
Каждая яма обладает одной и той же энергией основного состояния Ev
определяемой решением уравнения Шредингера. Если глубина квантовых ям Ко
достаточна. Волновые функции стационарных состояний в каждой из них приближенно
могут быть записаны с использованием A.446) в виде:
(x)~ J— cosifc(x + b\ для - {L/2 + b)< x < -L/2
V" A.Б.10)
-—z-<x+L/2\ для jc> -L/2
а ка
Фг(х)~ J— cosk{x ~ b\ Для L/2 < x < L/2 + a
A.Б.11)
e-*(*-L/2), для x < L / 2
а ка
где кик являются соответственно электронной длиной волны и глубиной
проникновения, описываемой A.33) при L = 2Ь — а. Таким образом, матричные элементы
A.Б.5) легко сосчитать. При этом недиагональные элементы имеют вид:
L/2+a а
wir =-V0 [фг{х)ф,{х)ах =--=^TV0U-KU cos k{u-a/2)du A.Б.12)
J ка J
L/2 0
что дает после несложных преобразований:
lr ()
ка
Аналогичный расчет позволяет определить величину диагональных элементов. Они
пропорциональны c~2lcL и ими можно пренебречь по сравнению с недиагональными
элементами. Связь между двумя квантовыми ямами за счет туннелирования снимает
таким образом вырождение системы, приводя к расщеплению величиной 2wlr или:
%p-kL
АЕ~— Е. A.Б.14)
ка
Снятие вырождения системы
из двух квантовых ям
Для двух квантовых ям шириной 4 нм с потенциальной глубиной 250 мэВ
соотношение A.43) дает энергию ограничения Ех величиной 106 мэВ и коэффициент
туннельного ослабления 0,502 нм. Если две квантовые ямы разделены интервалом
в 5 нм амплитуда снятия вырождения составит 34 мэВ. Рисунок иллюстрирует
результаты точных расчетов, показывающих, что на самом деле действительная
величина расщепления составляет 10 мэВ. Противоречие между двумя величинами
происходит из-за того, что аппроксимация бесконечной квадратной ямы
недействительна для конечных квадратных ям.
Дополнения к главе 1
Литература
С. Cohen-Tannoudji, В. Diu, and F. Laloe, Quantum Mechanics, Wiley, New York A992).
C. Weisbuch and B. Vinter, Quantum Semiconductor Structures, Academic Press, Boston
A991).
1.B. Квантово-размерный эффект Штарка
Рассмотрим квантовую яму GaAs/AlGaAs, в которой ось роста задана вдоль
направления Oz (смотрите главу 8). Электроны, захваченные зонами проводимости
квантовой ямы, описываются делокализованными волновыми функциями |/> и
энергией квантования Е. (рис. 1.1). В данном случае нас интересует влияние
электрического поля F, приложенного поперёк структуры, на энергетические уровни в квантовой
яме. Используем гамильтониан дипольного возмущения вида:
W=-qFz A.B.1)
Если квантовая яма симметрична, то в первом порядке возмущение дает
нулевой вклад. В пренебрежении вкладом состояний с высокими энергетическими
номерами (/ > 2) соотношение A.62) дает поправку второго порядка в величину Е. из-
за электрического поля:
АЕ, =Е']-Е1 =-АЕ2 =Ы
A.В.2)
Е\ ~ Ег
где zn — элемент матрицы дипольных переходов. Расчет может быть проведен
достаточно просто, если используется аппроксимация бесконечной квадратной ямы.
Уравнение A.49) дает выражения для энергетических уровней Ех и Е2, а A.48) —
соответствующие выражения для волновых функций. Интегрирование по ширине
ям приводит к выражению для элемента дипольного перехода:
Ы-~ A-в.з)
По мере того, как возрастает напряженность электрического поля зазор между
энергетическими уровнями увеличивается (смотрите рис. 1.В.1).
Со спектроскопической точки зрения мы можем сказать, что резонансный
оптический переход, связывающий эти два уровня, претерпевает голубой сдвиг по
энергии на величину:
, , 210 a2F2a4m*
АЕ = 2 Д£, = ——q Г т A.В.4)
1 И З^л:6 Й2
или после некоторых упрощений:
qFa A.B.5)
3**4 I Eo
где Ео — энергия ограничения из A.49). Напоминаем, что т* — это эффективная
масса электрона, которая в GaAs равна 0,067/яе. Таким образом, мы видим, что
эффект становится более значимым, когда перепад потенциала в квантовой яме qFa
становится непренебрежимым по сравнению с энергией квантового ограничения
Ео. Теория возмущений явно не срабатывает, когда волновые функции электронов
не затухают вне квантовых ям (смотрите рис. 1.В.1). В этом случае электроны в
основном состоянии могут туннелировать через треугольный барьер, что приводит
к ионизации квантовой ямы электрическим полем.
I.E. Квантово-размерный эффект Штарка
(мэВ)
Q.
0)
СО
эии
400
300
200
100
0
-
-
1 . 1
-20 -10 0
Положение (нм)
10
20
Рис. 1.В.1. Квантовая яма, аналогичная представленной на рис. 1.1, в условиях
статического электрического поля. Энергетический зазор между двумя
энергетическими уровнями возрастает в результате действия приложенного
электрического поля. Это приводит к голубому сдвигу из-за эффекта Штарка.
Пример
В квантовой яме GaAs толщиной 12 нм и эффективной массой электронов гп = 0,067 те
штарковский сдвиг &Е = 29/C х /г4) х A05 х В/см х 106 смJ/0,115 эВ или 2 мэВ
ожидается для напряженности электрического поля 10 В мкм. Этот сдвиг огромен в
сравнении с тем, что может быть индуцировано в атомах. Это же является прямым
следствием малой эффективной массы электронов в GaAs, а также значительно
больших напряженностей электрических полей, которые могут быть индуцированы в
структурах на основе конденсированных сред, сформированных с использованием
традиционных методов изготовления микроструктур (A. Harwit and J.J. Harris, Appl. Phys.
Lett. 50,685A987)).
Отмеченный сдвиг имеет важное значение, так как его величина может
превышать ширину линии для перехода Е{ -> Е2 (с типичной величиной 5 мэВ) и он
впервые наблюдался Харвисом и Томсоном A987). Рисунок 1.В.2 иллюстрирует
сравнение их экспериментальных результатов с теоретическими данными.
160
о:
h.
$
го
100
80
□ Асимметричная квантовая яма
ф Симметричная квантовая яма
20 40 60
Напряженность поля, кВ/см
80
Рис. 1.В.2. Наведенный эффект Штарка в оптических переходах симметричных и
асимметричных квантовых ям. Различный характер процессов в этих квантовых
ямах обсуждается в двух примерах, рассмотренных ранее.
Дополнения к главе 1
Как видно, полученные экспериментальные результаты для симметричной
квантовой ямы согласуются с параболической зависимостью штарковского сдвига от
напряженности электрического поля.
Если квантовая яма асимметрична (смотрите рис. 1.В.З), то возмущение
первого порядка не равно нулю и составляет:
АЕ = qFSn
A.В.6)
где дп =
— B|z|2) и представляет собой смещение среднего положения
электп
рона из состояния |1) в состояние |2).
Пример
Для квантовой ямы, представленной на рис. 1.В.2, решение уравнения Шредингера
дает дипольное смещение амплитудой 4,2 нм. При этом штарковское смещение для
перехода Е1 -» Е2 составляет 42 мэВ при напряженности поля 10 В/мкм. Таким
образом этот эффект в первом порядке играет существенно более важную роль, чем в
предыдущем примере для симметричной квантовой ямы (Е. Martinet, F. Luc, E. Rosen-
cher, P. Bois, E. Costard, S. Delaitre and Bockenhoff, in Intersuddand Transitions in Quantum
Wells, edited by E. Rosencher, B. Vinter, and B.Levine, Plenum, London A992) p.299).
Этот эксперимент был осуществлен с использованием асимметричных структур
GaAs /GaAlAs. На рис. 1.В.З представлены экспериментальные результаты для
величины штарковского сдвига в функции напряженности приложенного
электрического поля. В представленных данных четко прослеживается линейная
зависимость сдвига резонансного перехода от напряженности электрического поля, кото-
-20
-10 0 10
Положение (нм)
-20
-10 0 10
Положение (нм)
Рис. 1.В.З. Асимметричная квантовая яма в условиях воздействия электрического поля.
I. Г. Гармонический осциллятор
рая согласуется с предсказаниями A.В.6) для параметров, использованных в
приведенном выше примере. Указанный пример был использован в новом поколении
инфракрасных детекторов и будет более углубленно рассмотрен в главе 11.
Литература
G. Bastard, Wave Mechanics Applied to Semiconductor Heterostructures, Wiley, New
York A991).
E. Rosencher, B. Vinter, and B. Levine, Eds, Intersubband Transitions in Quantum
Wells, Plenum Press, New York A992).
С Weisbuch and B. Vinter, Quantum Semiconductor Structures, Academic Press, Boston A991).
1.Г. Гармонический осциллятор
Исследование гармонического осциллятора в квантовой механике обеспечивает
широкое поле для чисто физических ассоциаций. Поэтому мы дадим квантово-
механическое описание электрона, упруго связанного с притягивающим центром.
Эта система одинакова пригодна для описания поведения электрона в поле ядра,
колебаний атомов в кристалле или даже, как мы увидим далее в главе 2, для
описания специфических электромагнитных волн, которые иначе называются фотонами.
Теперь мы рассмотрим частицу массой т в условиях воздействия
притягивающего одномерного параболического потенциала:
V(x)=^kx> A.Г.1)
где к — коэффициент упругости квантово-механической пружины (смотрите
рисунок 1.Г.1).
Следует отметить, что обобщение этой задачи на трехмерный случай не
представляет особых теоретических трудностей. Однако одновременно с этим обилие
необходимых индексов усложняет описание, не очень расширяя его содержание.
В рассматриваемом случае гамильтониан частицы может быть записан в виде:
Я = ^— + —тсо$х2
2т 2
A.Г.2)
Классический гамильтониан
гармонического осциллятора
где со0 — резонансная частота системы:
10001-
-15 -10
-5 0 5
Положение (нм)
Рис. 1.Г.1. Потенциал гармонического осциллятора с локализованными
энергетическими уровнями и волновыми функциями для соответствующих
собственных состояний.
Дополнения к главе 1
<»„=,- A-Г.З)
V т
Классическое поведение системы в рассматриваемом случае хорошо известно:
система колеблется, при этом положение частицы дается соотношением:
где х0 — амплитуда колебаний, а ф — их фаза. Для квантово-механического описания
частицы и нахождения стационарных состояний необходимо решить уравнение:
y,)= E\W) A.Г.5)
Принцип соответствия дает нам форму уравнения Шредингера в координатном
t (Р = — \h (d/dx)) представлении:
-^-^-W{x)+\m<o^w{x)= EV{x) A.Г.6)
2т их 2
Уравнение Шредингера для
стационарного одномерного
гармонического осциллятора
Наша задача заключается в нахождении физически допустимых решений этого
уравнения (т. е. квадратично интегрируемых решений). Это дифференциальное
уравнение может быть решено многими различными способами (например с
использованием полиномов). Однако намного более эффективно решить эту задачу с
использованием алгебры операторов, впервые разработанной П.A.M. Дираком.
Начнем с того, что введем безразмерные операторы:
A.Г.7)
В этом случае гамильтониан может быть записан в виде:
Н=ПаHН (
где безразмерный оператор Й дается соотношением:
й = 1[х2 + рг] (
Вспомним соотношения антикоммутации между операторами координаты и
импульса, которые записываются в виде:
[x,p]=xp-px = ih A.Г.10)
где для безразмерных операторов справедливо соотношение:
[*,?]= i A.Г.11)
Теперь мы покажем, что это соотношение антикоммутации (которое просто
представляет собой переформулировку первого принципа неопределенности Гей-
зенберга) также приводит к квантованию энергии. Таким образом, мы ищем
решение системы:
1.Г. Гармонический осциллятор
Для этого нам необходимы два новых оператора:
V2V " V2
A.Г.13)
Определение операторов
рождения и уничтожения
Операторы координаты и импульса даются соотношениями:
~h
A.Г.14)
По причинам, которые вскоре станут понятными, а мы будем называть
оператором уничтожения, а а+ оператором рождения. Рассчитаем теперь произведение а+ а:
или
Таким образом:
Теперь получим выражения для коммутатора операторов рождения и уничтожения:
ka+]= -[х + \р,х - i^]= у ( [x,-i?]- [x,+i?])= -[(- i)i - i (+ i)]
так что:
["•]-' A.Г.16)
Уравнение A.Г.16) является, таким образом, выражением принципа
неопределенности на языке операторов рождения и уничтожения. Введем далее оператор N:
N = a+a A.Г.17)
Оператор N называется оператором числа. Гамильтониан гармонического
осциллятора и оператор числа связаны соотношением:
Теперь мы покажем, что собственные значения N являются либо целыми
положительными числами или равны нулю. Для этого нам необходимо доказать три
теоремы. Пусть |v) будет собственным вектором Nc собственным значением уили:
N\v) = v\v) A.Г.19)
((E0 Дополнения к главе 1
Теорема 1: Собственные значения оператора N либо положительны, либо
равны нулю.
Переписывая A.Г.19) в виде:
Мы можем спроецировать это уравнение на \\) с тем, чтобы получить:
(v|tf+tf|v) = v(v\v) = v
Это может быть также записано в виде:
так что:
Из этого мы выводим, что v является неотрицательным и что:
v = 0, если только a\v) = 0. A.Г.20)
Теорема 2: Если | v) является собственным вектором Л/ с собственным
значением ц то a\v) тоже является собственным вектором Л/ с собственным
значением v- 1.
В самом деле,
Поскольку соотношение антикоммутации требует, чтобы аа+ — а+а= 1, это последнее
соотношение может быть записано в виде:
Na\v) = (aa+ -Aa\v) = a(a+ -\]\v) = a(N - \)\v) = (у - \) a\v)
что мы и хотели доказать.
Теорема 3: Если | v) является собственным вектором Л/ с собственным
значением v, то a+\v) также является собственным вектором N с собственным
значением v+ 1.
Аналогично тому, как этот было сделано выше, запишем:
Na+\v) = | a a \a\v) = a+laa+ ]|v)
= (у + \)а |v)
Теперь мы уже в состоянии найти собственные значения N Предположим, что
v, собственное значение N, является нецелым и неравным нулю с п = Int(v), где Int
означает целую часть числа. Тогда а\ v) есть собственный вектор N с собственным
1.Г. Гармонический осциллятор
значением v— I; a2\v) есть собственный вектор с собственным значением v— 2, ...;
an\v) есть собственный вектор с собственным значением v — n = v— Int (v), которое
должно лежать между 0 и 1 (смотрите рисунок 1.Г.2). Так как v является нецелым,
v- n должно быть отлично от 0, при этом an+l\v) должно иметь собственное
значение v — п — 1, которое должно быть отрицательным. Это однако невозможно по
теореме 1. Величина v должна быть такой, при которой вектор an+l\v) не может
существовать, т. е. ап\\) = 0. Таким образом, собственные значения vоператора N
являются либо положительными целыми числами или равны нулю. Поскольку мы
можем получить из собственного вектора \т) любой другой собственный вектор \п),
применяя т — п раз увеличивающий или уменьшающий операторы а+ или а,
собственными значениями оператора N является весь ансамбль положительных целых
чисел, т. е.:
N\n) = n\n), л = 0,1, 2,...
A.Г.21)
а
s
i
9
га
x
n
s
S (
Q.
С
Я
|
1
I, I
CVJ
n-1
Рис. 1.Г.2. Каждое действие оператора уничтожения приводит к уничтожению
одиночного кванта возбуждения.
Из соотношения A.Г.18) мы видим, что энергии стационарных состояний
гармонического осциллятора квантуются и даются соотношением:
Еп = (п + -\а>09 п = 0,1, 2,... A.Г.22)
Энергетические уровни
одномерного гармонического осциллятора
При этом стационарными состояниями являются собственные состояния |л)
оператора числа. В таком случае энергетический спектр гармонического осциллятора
состоит из серии эквидистантных уровней, разделенных по энергии интервалами h co0
(смотрите рисунок 1.Г.1).
Теперь попробуем выяснить, как действуют операторы а и а+. Из теоремы 2 нам
известно, что а\п) является собственным вектором N с собственными значениями
/i-l. Так как мы видим, что энергетические уровни одномерного осциллятора
являются невырожденными (что может быть легко доказано), это означает, что а\п)
пропорционально \п — 1). Таким образом:
a\ri) = c|/z-l), n = 1, 2,...
Но модуль а\п) дается соотношением:
|(а|«)J = {а\п)){а\п))= (п\а+а\п) = (n\N\n) = п
Так, что с2 = п, с помощью чего мы получаем:
Дополнения к главе 1
а|л) = 7л|л -1), л = 1, 2,... A.Г.23)
Совершенно аналогичным образом мы получаем для а+:
а + \п) = л/п + \\п + 1), л = О,1,... A.Г.24)
Теперь мы уже в состоянии лучше понять трактовку проблемы в рамках
операторной алгебры Дирака. Начать с того, что каждое индивидуальное квантовое
состояние обладает большей энергией по мере увеличения п. Уравнение A.Г.23)
показывает, что действие оператора а проявляется в инициации перехода между состоянием
с квантовым числом п и состоянием с квантовым числом п — 1. Таким образом,
оператор а удаляет из системы квант возбуждения, соответствующий h co0. Важно
помнить, что операторы а и а+ не являются эрмитовыми и не обладают
собственными значениями в виде действительных чисел. Уравнение A.Г.24) может быть
использовано как рекуррентное соотношение для генерации всех состояний \п) оператора Я:
) A.Г.25)
П1
Теперь обратим наше внимание на состояние |0). Оно является основным
состоянием системы и обладает минимальной возможной энергией:
E0=UoH A.Г.26)
В противоположность классическому осциллятору, у которого минимальное
энергетическое состояние является нулевым (или состоянием покоя),
минимальное энергетическое состояние квантового гармонического осциллятора —
ненулевое. Это удивительное наблюдение следует из соотношения антикоммутации A.Г.16),
которое представляет собой переформулировку первого соотношения
неопределенности Гейзенберга. Таким образом, мы могли бы попробовать вывести этот
результат непосредственно из применения принципа неопределенности, утверждающего,
что неопределенности по х и по р связаны соотношением:
AxAp~h A.Г.27)
В рамках классического подхода полная энергия основного состояния частицы
дается соотношением:
Е = ^- + ImatfAjc' A.Г.28)
2/72 2
Подставляя A.Г.27) в A.Г.28), получаем выражение для энергии в виде:
Характер изменения Е в зависимости от Ах иллюстрируется рисунком 1.Г.З.
Как видно из представленного рисунка, кривая достигает минимума при:
Ах =
что соответствует минимальной энергии £= hco0. Это совсем неплохо для
эвристического подхода !
Теперь нашей задачей является нахождение собственных состояний в
координатном представлении, т. е. нахождение волновых функций стационарных
состояний. Начнем с основного состояния и применим оператор уничтожения A.Г.20):
Рис. 1.Г.З. Зависимость приведенной
энергии гармонического
осциллятора от неопределенности параметра
приведенного положения в
соответствии с A.Г.29).
1.Г. Гармонический осциллятор 53
или
Возвращаясь к определению A.Г.7), находим, что в координатном представлении:
или вновь:
A.Г.ЗО)
Легко установить, что решением этого классического дифференциального
уравнения является функция Гаусса вида:
тсо0
1/4
A.Г.31)
Волновые функции с большими значениями индекса могут быть получены
рекуррентным образом. Теперь мы уже в состоянии сделать некоторые предсказания
по поводу измерения квантовых наблюдаемых. Например, средняя величина
положения частицы в состоянии \п) дается соотношением:
С учетом того, что а+\п) = ^п\п — 1), и поскольку \п) и \п — 1) являются
ортогональными собственными векторами N, обладающими различными собственными
значениями, средняя величина х является таким образом нулевой (что не
удивительно с учетом симметрии системы). Для расчета средне-квадратичного значения
положения перепишем оператор х2 с использованием операторов а и а+:
х2 =—— (ai+a+*+aa+ +а+а)=—— (а* + а+* + 1 + 2а+а)
2тоH v ' 2тсо0 v
Среднее значение квадрата наблюдаемое для данного состояния \п) в таком
случае есть:
= (п\х2\п) = (п\а2 +а+2 + 1 + 2а+а\п)
х ' ' ' 2тщ х ' ' '
Дополнения к главе 1
Поскольку операторы а2 и (а+J направляют \п) в состояния, которые
ортогональны (п\, вклад этих операторов нулевой, из чего следует:
F (л + il A.Г.ЗЗ)
F (л +
тоH [ 2
Таким образом, чем больше энергия моды квантового осциллятора, тем больше
и степень неопределенности в положении частицы.
Нас могло бы шокировать, обнаружив, что ожидаемая величина положения
частицы в индивидуальных собственных состояниях осциллятора не осциллирует в реальном
пространстве. Мы увидим, что создание состояний с изменяющимися во времени
ожидаемыми величинами, согласующееся с нашей классической физической
интуицией, потребует конструировать тщательно выбранные линейные комбинации
(состояния Глаубера) на основе этих более фундаментальных стационарных состояний.
Классический пример
Рассмотрим сферу массой в 1 г, подвешенную на пружинке т и имеющую
собственную частоту колебаний 1 кГц. Квантовая неопределенность положения в
основном состоянии дается соотношением A.Г.ЗЗ) при п = 0 и составляет Ах =10~17 м!
Очевидно, что квантовый характер такой системы пренбрежим.
Квантовый пример: фононы Эйнштейна
Рассмотрим теперь периодическую цепочку взаимодействующих атомов,
образующих кристаллическую среду. Потенциальные ямы, связывающие каждый из атомов
с соседними обладают минимумом энергии при относительном расстоянии между
атомами г0. Поблизости от положения равновесия гамильтониан любой пары
соседних атомов может быть аппроксимирован соотношением:
Н =IL+Lu* х} A.Г.34)
2т 2
где хг и рг соответствуют расстоянию и моменту каждого атома, a U" есть вторая
производная потенциала в минимуме распределения. Тогда каждая пара атомов
образует гармонический осциллятор с резонансной частотой:
со0 = К- A.Г.35)
V т
Мы можем аппроксимировать кристаллический потенциал периодическим
полем, обладающим типичной амплитудой модуляции 5 эВ с периодом 0,5 нм. В этом
случае потенциал может быть записан в виде:
0,5 нм
и вторая производная U" равна 5 эВ х 4/г2/@,5 нмJ или 126 кг с. Для атомов,
содержащих приблизительно 50 нуклеонов (т. е. имеющих массу 8,35 х 10 26 кг) собственная
частота колебаний атомов дается A.Г.35) составляет VA26 кг с~2/8,35 х 10~26 кг)/2я
или 6 х 1012 с. Эти решеточные колебания (называемые продольными фононами или
фононами Эйнштейна) по своему спектральному диапазону соответствуют
инфракрасному диапазону спектра, обладая энергией взаимодействия порядка 25 мэВ.
Литература
С. Cohen-Tannoudji, В. Diu, and F. Laloe, Quantum Mechanics, Wiley, New York A992).
1.Д. Вероятности переходов и осцилляции Раби
1 .Д. Вероятности переходов и осцилляции Раби
Как мы видели в разделе 1.6 в двухуровневой системе синусоидальное возмущение
с частотой со вызывает переходы между двумя уровнями с вероятностью:
• пропорциональной t2, если переход имеет монохроматический и резонансный
характер (т. е. если квант возбуждения h со равен энергетическому зазору между
двумя уровнями Е2 — Е{);
• пропорциональной t, если возбуждение носит полихроматический характер, или
если конечное состояние принадлежит континууму.
Эти результаты выглядят несколько абсурдными, так как они приводят к
расходимости в пределе при больших значениях t. Такое поведение естественно
недопустимо, так как величина вероятности не может превысить единицу. В дальнейшем
мы покажем, что матрица плотности предлагает другое модельное описание
системы, которое способно примирить эти трудности.
В первом приближении предположим, что времена релаксации заселенности и
фазы (соответственно Т{ и Т2) бесконечны, т. е. что системы не подвержены
случайным флуктуациям или демпфированию. В этом случае уравнение A.100) может
быть записано в виде:
d
— Ар =-2iQl2(p2l -pn)coscot A.Д.1я)
d
dt
— рп = ico2lpl2 + iQl2Ap cos cot A.Д.1*)
где Ар есть различие заселенности рп — р22, при этом частота £112 дается соотношением:
/я12=Ш12 A.Д.2)
Ожидая резонансный и колебательный характер вблизи co2V введем частотную
отстройку Sco:
Sco = со - со21 A.Д.З)
Кроме того, введем новые переменные:
оп =р12е-,' A.Д.46)
Подставляя эти новые переменные в A.Д.1) и оставляя только члены с Sco (ква-
зи-резонансное приближение), получаем:
-^-Ар = -iQ12(a21e^ - <т12е-**") A.Д.5д)
а/
^^' A.Д.56)
Оптические блоховские уравнения
Уравнения A.Д.5я) — A.Д.5в) называются блоховскими уравнениями. Они
могут быть решены с использованием пробных функций:
Ар = Др°е* A.Д.6я)
о21 = о&е-^е^ AД66)
оп = о&е+^'е^ AД.6в)
Дополнения к главе 1
Подставляя A.Д.6а) — A.Д.6#) в A.Д.5д)—A.Д.5#), легко получаем систему
уравнений в новой форме:
-\а1
A.Д.7)
Для получения нетривиальных решений детерминант уравнения A.Д.7) должен быть
равен нулю. Таким образом, мы имеем только три возможные значения:
Я = 0, Я = К2, Я = -Ш
где п — частота Раби, определяемая соотношением:
О. =
- 0J
A.Д.8)
Теперь, мы можем определить поведение элементов матрицы плотности в
функции времени. В главе 3 мы возвратимся к вопросу о значении недиагональных
элементов оп и <т21, обеспечивающих базис для описания эффектов поглощения. Сейчас
же нас интересуют вероятности переходов, т. е. диагональные элементы рп и р2Г
Предположим, что в момент времени / = 0 система находится в основном
состоянии |1>, т. е. что:
Рй = 1; />2°2 = 0
= 0
A.Д.9)
Вероятность того, что система занимает первое возбужденное состояние |2) в
функции времени дается соотношением:
Pn(t)=-
-sin2| -Ш
A.Д.10)
Рисунок 1.Д.1 иллюстрирует зависимость этой вероятности от соотношения Sco/Qir
Из представленного рисунка видно, что вероятность осциллирует с
частотой п и что амплитуда осцилляции достигает максимума и равна 1, когда Sco = 0
(т. е. когда возбуждение резонансно по отношению к энергетическому зазору
между двумя уровнями). В этом случае A.Д.10) дает:
A.Д.П)
Для коротких промежутков времени (£212 / < 1) вероятность заселенности
приобретает вид:
Pn(t)=-CltAti A.Д.12)
Это соотношение представляет из себя ничто другое, как уравнение A.79),
полученное с использованием зависящей от времени теории возмущений. Как это
можно увидеть из рисунка 1.Д.1 синусоидальная функция для коротких
промежутков времени обладает выраженным параболическим характером. Соответственно
формализм матрицы плотности отражает этот параболический характер для малых
значений /, накладывает предел применимости и предсказывает осциллирующий
характер в течение протяженных периодов времени. Такой долговременный осцил-
1.Д. Вероятности переходов и осцилляции Раби
о
10
15
Рис. 1.Д.1. Временная эволюция вероятности заселенности р22 для уровня |2> для
различных соотношений частоты отстройки и частоты Раби Sco/Q.n.
лирующий характер вероятности заселенности наблюдался в атомах и называется
осцилляциями Раби.
Попытаемся теперь описать систему, изменяющуюся под воздействием
влияния релаксационных механизмов. Уравнение A.101) может быть записано в виде:
~. / \ Ар - Ареч
Ар = -2iQ12(p21 - p,2)cos cot - н Т н
— р21 = -\co2lp2l - iQ12Ap cos cot-
A.Д.136)
d
~JlP\2 =
1^ДР cos cot -
где Ар — различие заселенности рп — р22 и Apcq есть различие заселенности в
состоянии термодинамического равновесия. Этот подход идентичен использованному в
уравнении A.Д.1) за исключением того, что уравнения становятся существенно более
сложными. Ограничиваясь случаем резонанса и полагая 8со =0 и Т2 = Тх = у~\ нам
удастся сохранить используемые выражения в сравнительно простом виде.
Принимая в качестве начальных условия, содержащиеся в A.Д.9), мы получаем:
-[-[«*» + %«*»}*"']
где в данном случае Я дается соотношением:
AД14)
4 AДЛ5)
Указанная зависимость иллюстрируется рисунком 1.Д.2.
Отметим, что после переходного периода система испытывает затухание (т. е.,
теряется когерентность между состояниями |1) и |2>, при этом сохраняется
стационарная вероятность нахождения системы в возбужденном состоянии, которая
дается соотношением:
A.Д.16)
|Г58 Дополнения к главе 1
1.0
0.8
0.6
0.4 -
0.2 -
0.0
" \ А А-/^
-/ _
у/О12 = 0.1
у/012 = 0.3
У
г I 1 1 |
у/О12 = 1
-
10
15
20
25
30
Рис. 1.Д.2. Временная эволюция вероятности заселенности для уровня |2) при
нулевой отстройке и различных значениях отношения скорости затухания и
частоты Раби у/£112.
Рисунок 1.Д.З иллюстрирует зависимость заселенности /?statH и /?stat22 от
амплитуды связи £212.
Заметим, что в зависимостях заселенности проявляется тенденция к
выравниванию уровня до значения 1/2 по мере увеличения амплитуды связи.
Интерпретация этого механизма, называемого оптическим насыщением, будет дана позже с
использованием корпускулярной теории света Эйнштейна при обсуждении
наведенного и стимулированного излучения.
Проведенный анализ позволяет в полной мере оценить гибкость и силу
формализма матрицы плотности при описании нестационарного характера когерентных
оптических переходов, а также при корпускулярной трактовке механизмов перехода.
Рис. 1.Д.З. Зависимость стационарных заселенностей двух уровней от соотношения
частоты Раби и скорости затухания.
Литература
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
P. Meystre and M. Sargent III, Elements of Quantum Optics, Springer-Verlag, Berlin
A989).
ГЛАВА 2
КВАНТОВАЯ МЕХАНИКА
ФОТОНА
2.1. Введение
Фотоэлектрическая ячейка, которая была одним из первых оптоэлектронных
приборов, привела Альберта Эйнштейна в 1905 году к мысли о квантовании
оптического излучения в виде того, что позже стало известно как фотоны. Таким образом,
представляется естественным повстречать теорию квантования энергии на нашем
пути исследования. Цель настоящей главы состоит в суммировании принципов
квантования электромагнитной энергии. Эти концепции необходимы нам для
объяснения спектрального состава излучения черного тела, явлений стимулированного и
спонтанного излучения, а также многих других базовых вопросов, необходимых
для основательного понимания принципов функционирования оптоэлектронных
приборов.
2.2. Уравнения Максвелла
в обратном пространстве
Мы знаем, что в вакууме электрическое Е (г, t) и магнитное В (г, t) поля
генерируются плотностью осциллирующего заряда p(r, t) и плотностью тока j(r, t). Как
отмечал Лоренц: «Нет ни одной гранулы света, которая не была бы результатом
колеблющегося заряда». Эти поля связаны уравнениями, выведенными в различных
областях электростатики и магнетизма и объединенными в рамках электромагнитной
теории. Это и есть система уравнений Максвелла:
VE(r,/) = — p(M) B.1я)
£0
VB(r,/) = 0 B.16)
VE(r,/) = -|-B(r,0 B.1*)
ot
V • B(r, t) = -!-J-E(r, t) + -Ц-J(r, t) B.1г)
с2 dt £oc2
Первое уравнение системы обычно называется законом Пуассона Гаусса,
третье — законом Ленца, в то время как в четвертое уравнение, выражающее закон
Фарадея—Ленца, Максвелл ввел член, соответствующий току смещения d(£0E)dt.
Второе уравнение системы отражает отсутствие в природе магнитных монополей.
Исходя из этих уравнений, мы можем сделать заключение о существовании
плоской бегущей волны типа:
Е(г, t) = Е0(е+ ^-^ + к.с.) B.2)
где волновой вектор к и радиальная частота со связаны вакуумным дисперсионным
соотношением:
Глава 2. Квантовая механика фотона
<у=с|к| B.3)
Мы знаем, что уравнения B.\а) и B.1 я) приводят к существованию векторного
и скалярного потенциалов А(г, /) и U(r, t), определяемых как:
B(r, 0 = VxA(r,0 B.4a)
| B.46)
При этом указанные потенциалы не задаются однозначно, а допускают
возможность произвольного выбора потенциала F(r, t) в соответствии с приведенными
ниже уравнениями калибровочного преобразования:
А'(г, /) = А(г, t) + S7F(r, t) B.5a)
U'(r,t) = U(r,t)-^F(r,t) B.56)
at
которые не выявляются уравнениями Максвелла.
Таким образом, электрические и магнитные поля являются четко заданными,
когда известны распределения зарядов и электрических токов:
г,.) B.6а)
r') B'6б)
где г. — положение заряда, a v. — его скорость в момент времени t. Эти поля, в свою
очередь, влияют на эти распределения силами Лоренца:
mi A v;. = *,[Е(г„ /) + v,. х В(г„ /)] B.7)
ш
Система уравнений BЛа)—BЛг) и B.6а)—B.7) представляет собой уравнения
Максвелла—Лоренца и позволяет дать описание поведения любой оптической
среды. Однако структура этих уравнений чрезвычайно сложна, поскольку они не
являются пространственно локализованными.
В действительности же линейная форма этих дифференциальных уравнений
Максвелла—Лоренца легко допускает возможность преобразований Фурье. Мы
покажем, каким образом, будучи представлены в пространстве Фурье, эти уравнения
существенно упрощаются и становятся локальными по своей природе. В связи с
этим рассмотрим кратко определение и свойства преобразования Фурье.
2.3. Свойства преобразования Фурье
Пусть F(r) будет квадратно интегрируемой векторной функцией г, заданной в
трехмерном пространстве. Эта функция может также изменяться и во времени (это будет
отмечаться всякий раз по мере необходимости). Во избежание проблем, связанных
со сходимостью определенных интегралов, введем виртуальный куб объемом V= L3,
в котором волны будут ограничены. Подобно методу, использованному в
Дополнении 1.А допустим, что L может быть произвольно большим. В этом случае Фурье-
образ этой функции будет функцией F(k), определяемой соотношением:
Поскольку амплитуды волны должны быть нулевыми на внутренних
поверхностях куба, получаем:
2.3. Свойства преобразования Фурье
где пх, пу, nz есть целые положительные числа. Переменные (к^, кпу, кп^ являются
компонентами вектора кя в обратном пространстве и таким образом имеют
размерность обратной длины. Численный коэффициент, появляющийся перед интегралом
B.8) различен у различных авторов. Мы будем использовать масштабный множитель
1/BяK/2, так как он обеспечивает большую симметрию обозначений в реальном и
обратном пространстве. Очевидно, что соотношение B.8) равным образом может
быть легко применено как к векторной F(r, t), так и к скалярной Дг, /) функциям.
Напомним теперь важные свойства преобразования Фурье:
Обратный Фурье-образ:
^r B.10)
BЛ1)
Влияние преобразования на дифференциальные операторы:
если Fскалярная функция, то VF<r^> &nFn B.12)
если F векторная функция, то V-F <-> ilin-Fn B.13)
VxFeikflxf B.14)
Тождество Планшереля—Парсеваля:
G(r, t)d* ~Y}Fn^ B.15)
Свойства Фурье-образа
Частный случай уравнения B.15) при F — G может быть интерпретирован как
выражение закона сохранения энергии:
L^n(tJ B.16)
Таким образом, пространственное распределение энергии приводит к
перераспределению спектрального распределения.
Кроме того, отметим, что в результате дифференциальные операторы
преобразовались в векторные алгебраические операторы, что является фундаментальной
причиной введения Фурье-образов. В этом случае уравнения Максвелла приобретают вид:
к„
В '
*' с*
п
в„
= -
э
dt
1
£о
= 0
-—в
Е + l I
ейс*
B.17а)
B.176)
B.17*)
B.17г)
Уравнения Максвелла
в обратном пространстве
Глава 2. Квантовая механика фотона
где, как очевидно, рп и \п представляют собой Фурье-образы плотности заряда и
тока. Уравнение B.176) показывает, каким образом в обратном пространстве
вектор Вп ортогонален вектору kw (т. е. магнитное поле имеет только одну компоненту,
перпендикулярную своему волновому вектору). Здесь представляется естественным
разложить электрическое поле в обратном пространстве на две компоненты, при
этом перпендикулярная компонента записывается в виде:
а параллельная компонента дается соотношением:
Можно показать, что параллельная компонента Ец (г, t) электрического поля
является полем, создаваемым зарядами мгновенно в точке г. Следовательно,
параллельное поле, создаваемое в точке г зарядом в точке г0 в момент времени t дается
выражением:
д гг(/) B.19)
|г-г0(О|
Фактически выражение B.19) является обычным выражением для
электрического поля (закон Кулона) без члена задержки / — |г — го|/с. Процесс происходит
таким образом, как если бы информация о положении заряда в точке г0 приходила
бы мгновенно в любую точку пространства г. Однако это не противоречит
теории относительности. Можно показать, что поле, измеренное в точке г и
являющееся суммой параллельной и перпендикулярной компонентам, обладает
задержкой |г — го|/с, как и предсказывается теорией (т. е. перпендикулярная компонента
вводит член, устраняющий мгновенный вклад в B.19).
Таким образом, мы в действительности заинтересованы в рассмотрении
перпендикулярной компоненты электрического поля, которое связано с магнитным
полем соотношениями:
-^Bn = iknxEln B.20а)
dt £0
при этом j± n является перпендикулярной компонентой плотности электрического
тока. Отметим, что в действительности введение этих перпендикулярных
компонент избавляет нас от необходимости введения двух дополнительных уравнений.
Интегрирование этих уравнений достаточно просто приводит нас к выражению для
потенциала задержки и позволяет найти поле излучения осциллирующего диполя.
Эта задача будет решена в дополнении 2А.
И, наконец, введем Фурье-образ векторного потенциала в обратном
пространстве. Уравнение B.4д) дает нам его связь с магнитным полем:
Bn = ikaxAn B.21)
или с использованием того же разложения, как и в B.186):
*„ = *„* 4. B.22)
Уравнение B.17#) устанавливает связь между Е1п и А1п:
Е,я = ~Л1я B.23)
2.4. Квантование электромагнитных волн
Достаточно легко мы можем также показать, что А1п — калибровочно-инвари-
антная величина, что делает этот параметр настолько же физически важным, как
электрическое и магнитное поля.
2.4. Квантование электромагнитных волн
Обратим теперь наше внимание на то, чтобы получить выражение для
электромагнитной энергии, заключенной в резонаторе объемом V. Классический
гамильтониан электромагнитного поля описывается выражением:
Я-Т J|J [
3r B24)
Классический гамильтониан
электромагнитного поля
в обратном пространстве
или с использованием тождества Планшереля—Парсеваля:
B-25)
После чего классический гамильтониан может быть разбит на сумму
параллельной и перпендикулярной компонент:
Н<т = HLtm + НЬт B.26)
при этом:
tfx,m = 2^]j>x,,f + K|] B.27)
Параллельная компонента в данном случае нас не интересует. С учетом уравнения
B.23), а также дисперсионного соотношения со = c|kj, перпендикулярная
компонента классического гамильтониана в этом случае дается соотношением:
I ^r-i.1 j B 28)
E^=~YtA^ B.29)
Классический гамильтониан
электромагнитного поля
в обратном пространстве
Уравнения B.28) и B.29) дают основу для квантования электромагнитного поля.
Заметим, что B.28) фактически эквивалентно уравнению для гармонического
осциллятора (Дополнение 1.Г) при следующей связи между обозначениями:
частота, соп
масса, т<г*-Ц-
1 _ B.30)
положение, х <-> А1п
импульс, р <->—уЁ1п
JL
Тем не менее отметим и различие между гамильтонианом гармонического
осциллятора, который включает в себя только действительные наблюдаемые, и гамиль-
Глава 2. Квантовая механика фотона
тонианом электромагнитного поля, который может включать мнимые члены, такие
как е-1кг. Это может приводить к определенным трудностям, на которых мы не будем
сейчас останавливаться. Введем теперь операторы рождения ап+ и уничтожения а:
B31а)
Связь между операторами поля и
операторами рождения и уничтожения
Эти операторы воздействуют на п электромагнитных мод. По аналогии с
результатами для гармонического осциллятора постулируем, что эти операторы
подчиняются соотношениям коммутации и антикоммутации, связанными с B.29):
к, <*;,]= smn B.32)
Как показано в Дополнении 1.Г, в этом случае гамильтониан
электромагнитного поля принимает вид:
£() <2-33>
Квантовый гамильтониан
электромагнитного поля
Таким образом, гамильтониан электромагнитного поля в резонаторе может быть
записан в виде суммы гамильтонианов независимых гармонических осцилляторов,
каждый из которых соответствует классической моде электромагнитной волны в
резонаторе с частотой колебаний соп. Это заключение является основным
результатом настоящей главы.
Здесь важно отметить, что в явном виде время не входит в выражение для
гамильтониана. Гамильтониан электромагнитной моды является стационарным даже в
том случае, когда он предназначен для описания осцилляционного поля. Это является
парадоксом, который будет разрешен введением когерентного состояния в разделе 2.5.
Обращенная форма B.31я) и B.316) позволит нам рассчитывать различные
операторы электромагнитного поля в функции операторов рождения и уничтожения.
Тем не менее, как мы уже отмечали, выражение для классического гамильтониана
электромагнитного поля содержит лишь модули этих операторов, а не их фазы.
Однако мы можем показать, что операторы электрического и магнитного полей, а также
векторного потенциала, связаны с операторами рождения и уничтожения моды п1:
x = i Y -^-(а„е*«' - д;е-'к» •)£„ B.346)
iie*. - - в;е-»- •)€. B.34*)
Операторы поля в функции
операторов рождения и уничтожения
внимание! Символ г, который появляется в е*1" B.34я)—B.34*) является переменной в
реальном пространстве, а не оператором!
2.5. Фотон
где еп — вектор поляризации электрического поля, a Fn представляет флуктуацию
вакуумного поля:
B.35)
Флуктуация вакуумного поля
К значению этого поля мы возвратимся несколько позже. Отметим, что оператор
электрического поля может быть представлен в виде суммы двух наблюдаемых, что,
как мы можем показать, соответствует отрицательным и положительным частотам:
Е±(г) = Е(±+)(г) + Е(±-Чг) B.36)
Например, электрическое поле с положительной частотой дается выражением:
*/** г B.37)
Эти два последних уравнения позволят нам перейти от классического описания
электромагнитного поля к квантово-механическому описанию.
2.5. Фотон
Рассмотрим оптический резонатор только с одной электромагнитной модой п.
Гамильтониан для моды п в этом случае может быть записан в виде:
B.38)
Собственные состояния с индексом / или стационарные состояния
электромагнитной моды п с частотой соп даются выражением:
10 = %7
B.39)
где состояние |0й) есть пустое состояние моды «.Энергия этого стационарного
состояния дается выражением:
f 1 Л
B.40)
И, наконец, операторы рождения и уничтожения а+ и ап обеспечивают
возможность переходов между состояниями |/я) и |/я — 1) или \in + 1):
an\in) = yfc\in-\), если in> 0 B.41а)
^|0я> = 0 B.416)
a-\in) = yjin + l\in +1) B.41^)
Уравнения B.41а)—B.41 в) могут быть интерпретированы в рамках
корпускулярного подхода. В этом случае электромагнитная мода рассматривается как
сформированная ансамблем элементарных возбуждений, называемых фотонами, а именно:
|/л) = |имеется in фотонов моды п в резонаторе), B.42)
где каждый фотон моды п обладает энергией Е:
Е = hco B.43)
Глава 2 Квантовая механика фотона
Предполагая, что в резонаторе присутствует in фотонов моды я, получаем
выражение для полной энергии:
Ki = *№ +\ь<»п = КЕп+\ьс>п B-44)
Отметим, что даже, если в резонаторе отсутствуют фотоны, энергия моды п не
равна нулю, но составляет величину Evac n, соответствующую вакуумной энергии
моды п (т. е. состояния |0я»:
Е^п=\ь<оп B.45)
Это основное состояние энергии вновь можно рассматривать как результат
первого принципа неопределенности Гейзенберга (приведенного в Дополнении 1.Г
для гармонического осциллятора). Операторы рождения и уничтожения создают
или уничтожают фотоны с импульсом ря = h kw, соответствующим собственным
состояниям наблюдаемых:
р„ = Пкпа;ап B.46)
Теперь возвратимся к оптическому резонатору с произвольным объемом К= Z,3,
заселенному произвольно большим количеством п электромагнитных мод.
Гамильтониан для перпендикулярных электромагнитных мод резонатора в этом случае
может быть представлен в виде:
2„ B-47)
Собственные состояния этого гамильтониана образуются из независимых мод
каждого гамильтониана в так называемом пространстве тензорного произведения:
\il9 /2, ..., /„, ...) - j— = \V) B.48)
где состояние |0) обозначает состояние пустого резонатора |0,, 02, ...), в котором нет
фотонов. Каждая мода п может быть заселена произвольным числом фотонов. Эти
частицы являются таким образом бозонами и на них не распространяются правила
исключения. Электромагнитная энергия резонатора является суммой двух членов.
Первый член соответствует сумме энергий in фотонов для каждой моды п:
B.49)
а второй член возникает из-за энергии вакуума £vac, связанной с каждой модой:
B.50)
Ясно, что последний член будет расходиться, так как число мод в резонаторе
бесконечно. Последнее замечание ставит нас перед физическим абсурдом. Эта
проблема была решена исключительно изящной теорией перенормировки Фейнмана,
Швингера и Томогавы. К сожалению, у нас нет возможности рассмотреть ее
сколько-нибудь подробно.
Теперь мы уже можем с использованием результатов дополнения 1.Г
рассчитать математическое ожидание и дисперсии наблюдаемых для электрического Е±(г),
магнитного В±(г) полей, поля векторного потенциала А±(г) для фотонного
состояния in моды п. Уравнения A.Г.32) и A.Г.ЗЗ) показывают, что:
2.5. Фотон
Таким образом:
(in\EL(r)\in) = (/л|Вх(г)|/я) = (/л|А±(г)|/л> = 0 B.516)
В выражении B.51а) мы оставили член eikr вне скобок при оценке величины
(/JtfJ/,), так как напоминаем, что г в данном случае является переменной, а не
наблюдаемой в этой теории. Следовательно, если число in фотонов моды п
известно точно, средняя величина электромагнитного поля будет равна нулю в любом
месте резонатора в любой момент времени. Это может показаться странным с
учетом нашей концепции «электромагнитной волны». Однако, как мы увидим в
следующем параграфе, этот парадокс разрешается введением понятия
когерентного состояния.
Дисперсия наблюдаемой для электрического поля в состоянии |/я) может быть
определена аналогично схеме рассуждений, приведенной в дополнении 1.Г:
,„ У = -г.2 (?УШ"' + «;2e-2ik-' - «„«; - а;ал) B.52)
или с учетом A.Г.32)—A.Г.ЗЗ):
KD\)^2in + l) B.53)
или вновь:
И) B.54)
Подобный же результат получается как для векторного потенциала, так и для
магнитного поля. Уравнение B.54) влечет за собой ряд следствий. Во-первых, даже
тогда, когда в резонаторе нет фотонов, электрическое поле обладает дисперсией,
отличной от нуля и определяемой соотношением:
2e0L
B.55)
Теперь нам становится понятной важность Fn, введенного как коэффициент
нормировки при определении операторов рождения и уничтожения в качестве поля
вакуумных флуктуации. В соответствии с B.40) уравнение B.54) может быть
записано следующим образом:
feN
B.56)
что представляет собой классическое соотношение между электрическим полем и
энергией электромагнитной моды в резонаторе.
Суммируя результаты этого довольно сложного раздела, мы могли бы
сказать, что фотоны представляют собственные состояния гамильтониана
электромагнитного поля в резонаторе. Таким образом, эти собственные состояния
также приводят к ряду парадоксов: A) средние величины электрического,
магнитного полей, поля векторного потенциала равны нулю повсюду внутри резонатора,
и они не осциллируют во времени; B) даже в отсутствие фотонов внутри
резонатора в нем присутствуют ненулевые флуктуации дисперсии электрического
поля в соответствии с уравнением B.55). Решение первого парадокса
приведено в разделе 2.6. В то же время со вторым парадоксом нам придется однако
смириться, так как он подтверждается экспериментом (например,
экспериментами по лэмбовскому сдвигу) и позволяет лучше понять феномен спонтанного
излучения.
Глава 2. Квантовая механика фотона
Пример
Средне-квадратичная амплитуда электромагнитных вакуумных флуктуации для
фотонов «зеленого света»1 (h con = 2 эВ) в резонаторе с объемом 1 см3 (L =1 см) равна:
Fn = A,6 х 10'19 Кл х 2 эВ/B х 8,85 х 102 Ф/м х 10'6 м3)I/2 » 0,13 В/м
Хотя эта величина очень мала по величине напряженности поля, его влияние
может быть, например, обнаружено в чрезвычайно малых смещениях энергий
атомных переходов.
2.6. Когерентное состояние
Глаубер был первым, кто представил физическое состояние, позволившее
примерить волновой и корпускулярный подходы к фотонным состояниям. Мы не будем
здесь детально обсуждать гипотезу Глаубера, хотя наше последующее объяснение
может показаться отчасти произвольным. Рассмотрим резонатор, обладающий
единственной одномерной модой с частотой со (обобщение на случай трех измерений и
многомодовые возбуждения могут быть осуществлены сразу, но это влечет за собой
определенные трудности с обозначениями). Состояние Глаубера или когерентное
состояние определяется следующим соотношением:
|) B.57)
Когерентное состояние Глаубера
Вероятностная интерпретация квантовой механики позволяет понять нам
значение этого состояния следующим образом: \d) есть состояние в резонаторе, для
которого имеется вероятность:
A.=e-WOr B.58)
ml
нахождения т фотонов в резонаторе. В выражении B.58) мы узнаем закон Пуассона
теории вероятности. Этот классический закон дает вероятность нахождения т
фотонов в резонаторе в процессе произвольной выборки при условии, что в среднем в
резонаторе имеется \а\2 фотонов.
Ясно, что \ot) есть нормированное физическое состояние:
1 B.59)
Попробуем оценить изменение такого состояния в течение времени.
Предположим, что в момент времени / = 0 резонатор находится в состоянии,
определяемом B.57), т. е., что состояние B.57) соответствует |а@)). В соответствии с
уравнением A.29) глауберовское состояние \a(t)) изменяется следующим образом:
\a(t)) = У e-k/2)-^lre-*^/»|w) = Y e-k/2)-^e--(*+i/2>U\ B.60)
Это выражение сразу принимает вид:
1 Примечание ред..: строго говоря энергии фотонов h соп = 2 эВ соответствует оранжевый цвет
свечения.
2.6. Когерентное состояние
Поскольку каждое физическое предсказание относительно состояния \a(t))
нечувствительно к фазе e~ie", видно, что временная эволюция глауберовского
состояния \a(t)) может быть представлена в виде:
|a(/)) = |ae-i<*) B.62)
Дадим теперь соотношение, образующее основу квантовых свойств
глауберовского состояния:
d[a) = c\a) B.63a)
или в сопряженной форме:
(а\а+=а*(а\ B.636)
В самом деле:
а\а) = J e-k/2)^La|w) = £ ^U'^-^Щт - 1) B.64)
В этой сумме мы перейдем от индекса суммирования т — 1 к п, так что:
а\а) = У e-k/0^p|/i) = aj e-te»)-ZLa\a) B.65)
что мы и хотели показать.
С другой стороны, следует заметить, что а+\а) не дает нам ничего полезного.
Уравнение B.63) позволит нам легко оценивать средние значения для
наблюдаемых. Сначала отыщем среднее число фотонов Na в глауберовском состоянии \а):
Na = (а\а+а\а) = а* а = \а\2 B.66)
Аналогично, средняя величина квадрата числа фотонов в этом состоянии есть:
7VJ = (а\а+аа+а\а) = |а|2(<фа + |а) = \af(a\a+a + l\a) = \af{a\2 = l) B.67)
так что стандартная дисперсия AJVa числа фотонов составляет:
А^« = №1-~п1 = И = V^T B.68)
Эти уравнения являются характеристиками распределения Пуассона и могли бы
быть получены непосредственным использованием теории вероятности. К тому же мы
видим, что среднее число фотонов и связанная с ним стандартная дисперсия не зависят
от времени. И, наконец, это состояние подчиняется закону больших чисел, а именно:
г
Это последнее уравнение может быть записано также в виде:
S IN = (сРеДняя величинаJ = N2a = — B.70)
(дисперсия ) A7VO2
где S/N обозначает отношение сигнал/шум, связанное с пуассоновскими флуктуа-
циями числа фотонов. Это последнее соотношение образует основу теории
детектирования, которая будет приведена в главе 11.
Рис. 2.1 иллюстрирует распределение Пуассона для трех значений среднего числа
фотонов Na. Отметим, что это распределение сужается по мере увеличения
среднего числа фотонов.
Глава 2. Квантовая механика фотона
50 100 150
Число фотонов, т
200
1 1 1 1
%
/V
.'! •'•
•'I '•
i
i i i
\ N„ = 10
\ N„ = 50
\ -—N„=100 _
1.0
0.8
0.6 -
0.4 -
0.2 -
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
б
Нормированное число фотонов, m/Na
Рис. 2.1. Вероятность найти т фотонов в резонаторе, измеренная для трех
когерентных состояний со средним числом фотонов 10, 50 и 100.
Теперь отыщем среднее значение наблюдаемой Е± а для электрического поля в
глауберовском состоянии \а). В соответствии с уравнениями B.34) и B.35):
Ё± а(а|Ё±|а) = \F(cc\ae*r -a+e'ikr\a)£n B.71)
где поле вакуумных флуктуации, определяемое B.35), с учетом B.63л) и B.636)
имеет вид:
B.72)
Подобным же образом дисперсия наблюдаемой для электрического поля дается
выражением:
2.6. Когерентное состояние
(a\fpLY\a) = -/-2(a|a2e2ikr + *+V2ikr - a+a - a+a\e) B.73)
или:
A£lt. = F2[^lkr - a*e ikrJ + П B.74)
Вводя вновь соотношение B.72), описывающее временную эволюцию, и
предполагая также без потери общности, что а есть действительное число, равное а09
мы, в конце концов, получаем выражение для временной зависимости среднего
электрического поля:
Ех,а@ = 2/а0 sin(k • г - о*)вп B.75)
что соответствует классическому электрическому полю:
, @ = ^о sin< k г - Ш)е„ B.76)
Используя B.35) и B.66), получаем выражение, связывающее амплитуду
классического электрического поля Ео электромагнитной волны с частотой со и средним
числом фотонов Nb резонаторе с энергией h со:
B.77)
Амплитуда электрического поля,
выраженная через среднее число
фотонов с энергией h со
Это последнее уравнение может быть интерпретировано с использованием
корпускулярной модели. Среднее число фотонов N в резонаторе дается
отношением электромагнитной энергии, запасенной в резонаторе £0, VE02/2, и энергии,
переносимой каждым фотоном h со. Мы также можем определить фотонный
поток входящий или выходящий из резонатора за единицу времени, через
единичную площадь, используя оптическую мощность, приходящуюся на единицу
площади Р:
Р = Па)Ф B.78)
Пример
Падающий поток «оранжевых» фотонов (hco=2 эВ) в пучке с плотностью энергии
1 мВт/см2 (Р = 10~3 Вт/см2) составляет:
Ф = 10 Вт/см2/A,6 х 10~19 Кл х 2 эВ) = 3 х 1015 фотононов см'2 с
Плотность падающих «оранжевых» фотонов с энергией hco=2 эВ,
соответствующей напряженности электрического поля 1 В/см (Ео= 100 В/м), составляет:
N/L =104 (В мJ х 8,85 х 10~12 Ф м/B х 1,6 х 10~19 Кл х 2 В) = 1,4 х 10й м
Таким образом, даже в случае очень умеренных уровней оптической мощности
и напряженности электрического поля, огромное значение числа участвующих
фотонов делает трудно наблюдаемой корпускулярную природу этих частиц. Тем не
менее, вскоре мы столкнемся с приборами, способными детектировать одиночные
фотоны. Поразительно, но человеческое зрение, при возможности адаптироваться
к темноте в течение нескольких минут, способно обнаруживать фотонные потоки
амплитудой в несколько фотонов в минуту.
Глава 2. Квантовая механика фотона
2.7. Излучение черного тела
Именно исследование спектрального распределения света, излучаемого нагретыми
объектами, позволило Планку ввести понятие дискретных квантов энергии, на
основании которого в дальнейшем Эйнштейн разработал концепцию фотона. Мы
можем определить черное тело как соответствующий резонатор, в котором
электромагнитные моды находятся в термодинамическом равновесии со стенками при
температуре Т. В этом случае излучение поглощается и переизлучается внутри
резонатора без обмена с внешней средой. Без введения фотона (т. е. без постулата квантов
минимальной энергии) Рэлеем и Джинсом было установлено, что энергия,
содержащаяся внутри такого резонатора, стремится к бесконечности. Этот знаменитый
теоретический «тупик» был назван «ультрафиолетовой катастрофой». Здесь мы не
будем воспроизводить эти расчеты. Отметим лишь значение, которое оказала эта
проблема на ранний период развития квантовой механики.
Рассмотрим резонатор с объемом L3 и попробуем найти плотность оптических
мод для каждой частоты v(t. e. число мод, содержащихся в частотном интервале dv):
pm(v)dv
B.79)
Внутри резонатора волны состоят из линейных комбинаций мод, описываемых
выражением (eikr ± e~ikr)- Требование в качестве граничных условий обращения в
ноль электромагнитных полей на стенках резонатора накладывает условия на
волновые векторы к = (кх, ку, kz):
kx=jn*> *>=7Л'; ^=f^ B.80)
где пх, пу, nz — положительные целые числа. Таким образом, мы можем связать с
каждой модой (кх, ку, kz) объемный элемент dkx, dky, dkz в обратном пространстве
(рис. 2.2).
Число мод, содержащихся в интервале между к и к + dfc, составляет одну восьмую
(пх, пу9 nz положительны!) сферического слоя объемом 4лк2с1к, умноженную на два с
учетом двух возможных поляризаций каждого волнового вектора. Следовательно
имеется:
k=2xv/c
Рис. 2.2. Разрешенные электромагнитные моды в резонаторе образуют решетку,
определяемую кх = nxn/L, ку = nyn/L, кг = nzn/L. Число разрешенных мод с
частотой менее v в резонаторе объемом D дается числом точек, содержащихся в
одной восьмой объема сферы радиуса к = 2лу/с.
2.7. Излучение черного тела
dN=HJ^dk B.81)
я
электромагнитных мод. Используя дисперсионное соотношение для излучения,
распространяющегося в вакууме:
v=ikk B-82)
получаем выражение для плотности мод черного тела рт на единицу частоты и объема:
р» = ^1 B.83)
Приведенное выше уравнение дает плотность электромагнитных (ЭМ) мод в
частотном интервале от vдо v + dv. Теперь ответим на вопрос, какова же
вероятность того, что этот частотный диапазон (v, v + dv) в действительности заполнен
колебательными модами в условиях теплового равновесия?
Вероятность нахождения ЭМ-осциллятора в энергетическом состоянии Еп
дается законом Больцмана:
рп ос е-Еп/кт B.84)
где к — постоянная Больцмана (к = 1,38 х 10~23 Дж/К или 8,62 х 10 эВ/К) и символ
ос в B.84) обозначает пропорциональность. Поскольку Еп = hv(n + 1/2), эта
вероятность дается выражением:
Рп = *(e-(
где к — коэффициент пропорциональности, определяемый условием нормировки:
так, что:
£ р„ = К£ И"">)" = к ' мг) = 1 B.86а)
0 0 l e
Рп = (j - е-(л^лг>)(е-<^/АГ>)я B.866)
Теперь представляет интерес определить среднее число nv фотонов с частотой v
в резонаторе при температуре Т:
£
я=0
К = £«/>„ = G - e-<»"tf >jg «(e-<-^r>)" = >— B.87)
Подставляя уравнение B.87) в условие B.866), получаем распределение Бозе—
Эйнштейна:
Р = —5—Г—S:—1 B.88)
Аналогичный расчет (оставляемый нами в качестве упражнения) позволяет найти
дисперсию <т числа фотонов:
<уп ъ nv + n; B.89)
Сравнивая приведенное выше выражение с B.70), полученным в подходе Гла-
убера, приходим к выводу о том, что распределение Бозе—Эйнштейна намного
шире распределения Пуассона. Рис. 2.3 иллюстрирует это распределение для
среднего числа фотонов в резонаторе, равного десяти (п = 10). Флуктуации числа
фотонов в излучении черного тела намного больше, чем в когерентном состоянии, что
Глава 2. Квантовая механика фотона
о.Е
0.04
0.02
0.00
Распределение Пуассона
Распределение
Бозе—Эйнштейна
Г -L.
10
40
50
20 30
Число фотонов
Рис. 2.3. Сравнение распределений Пуассона и Бозе—Эйнштейна для среднего числа
фотонов в резонаторе, равного десяти.
впрочем и не удивительно. Теперь мы уже можем найти спектральное
распределение излучения черного тела при температуре Т.
Средняя энергия, распределенная в моде с частотой v, дается средним числом
фотонов в этой моде, умноженным на энергию фотонов:
Е =
hv
Qhv/kT _
B.90)
СЪ Qhv/kT _
В результате плотность энергии ре( у) излучения в резонаторе в единичном
частотном и объемном интервале (в Дж с /м3) дается произведением B.83) и B.90):
1 B.91)
Закон Планка (спектр
излучения черного тела)
Эта формула для спектра излучения черного тела была открыта Планком в
1900 году. В дополнении 2.Б мы исследуем более детально особенности, связанные
с тепловым излучением, а также рассмотрим использование спектров излучения
черного тела в тепловидении.
Литература
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
W. H. Louisell, Quantum Statistical Properties of Radiation, Wiley, New York A973).
P. Meystre and M. Saigent III, Elements of Quantum Optics, Springer-Verlag, Berlin
A989).
A. Aspect, C. Fabre, and G. Grynberg, Introduction aux lasers et a Ibptique quantique,
Ellipses, Paris A997).
ДОПОЛНЕНИЯ
К ГЛАВЕ 2
2.А. Поле излучения осциллирующего заряда:
калибровка Лоренца
Покажем теперь, каким образом уравнения Максвелла—Лоренца позволяют
рассчитать мощность электромагнного поля, излучаемого осциллирующим зарядом.
Такой расчет важен по нескольким причинам. Во-первых, с точки зрения
исторической перспективы эта теория потерпела неудачу в попытке объяснить
стабильность атома водорода и проложила еще один путь к формированию квантовой
механики. Она продемонстрировала также внутреннюю связь между движением
заряженных частиц и светом, что помогло Лоренцу, Пуанкаре и Эйнштейну встать на путь,
ведущий к теории относительности. И наконец, зависимость мощности излучения от
длины волны имеет и технические следствия там, где диффузный характер процесса
имеет место, например в оптических волокнах, атмосферных процессах и т. д.
Рассмотрим заряженную частицу, расположенную в начале координат точке О
и подвергнутую малому смещению re(t) около точки О (см. рис. 2.А.1).
Вспомним уравнения Максвелла—Лоренца:
Рис. 2А.1. Расчет векторного .,, *
потенциала точечного заряда j* ' '
VE(r,/) = — p(r,0 BЛЛа)
VB(r,/) = 0 B.А.16)
VE(r,0 = -|-B(r,0 BЛЛв)
at
V В(г, t) = -7 J-E(r, /) + J- j(r, 0 B.А.1г)
С2 dt €0C2
При этом в случае осциллирующего заряда плотность тока и заряда определяются
соотношениями:
p(r, t) = qS[r - гДО1 B.А.2*)
Как мы уже видели B.А.1д) и B.А.1в) позволяют ввести векторный и
скалярный потенциалы А(г, /) и Щт, t), определенные с точностью до калибровочного
преобразования:
В(г, t) = V х А(г, t) B.А.Зд)
Е(г, /) = -А А(г, /) - V tf (г, /) B.А.36)
at
Дополнения к главе 2
Вместо того чтобы использовать Фуре-преобразование, которое наилучшим
образом подходит для рассмотрения плоских волн, мы попробуем отыскать
дифференциальные уравнения, которым должны удовлетворять скалярный и
векторный потенциалы. Для этого подставим B.А.36) в уравнение Пуассона B.А.1д), что
дает:
V2U + — (V. А) = --£- B.А.4)
dt e0
Подобным же образом, вводя B.А.Зя) и B.А.36) в уравнение Фарадея—Ампера
B.А.1г), получаем:
Теперь применим классическое векторное тождество к А и V:
а х (Ь х с) = (a c)b - (a b)c B.A.6)
что позволяет записать B.А.5) в виде:
_V2A + — iiA + vfvA + — i-#] = _!_ j B.A.7)
с2 dt2 [ с2 dt ) €0c2 v '
Поскольку векторный потенциал определен с точностью до градиента
потенциала, можно показать, что мы можем воспользоваться этой степенью
свободы для введения калибровки, называемой лоренцовской калибровкой, в рамках
которой векторный и скалярный потенциалы связаны друг с другом
соотношением:
V-A£+— 4-U £=0 B.A.8)
L с2 Э/ L
Лоренцовская калибровка
Эта калибровка особенно удобна для рассмотрения проблем излучения. В
самом деле, B.А.7) сильно упрощается, так как прямо связывает одиночный
векторный потенциал А с движением заряда, создавшего его:
Решения этого дифференциального уравнения известны, соответствуют
потенциалу задержки и могут быть записаны в виде:
а£(г, о=-J- fi[r^:(ir:,ri/cW B.А.Ю)
Апеос2\ |г-г'|
Сделаем теперь несколько упрощающих предположений:
• смещение re(t) частицы мало по сравнению с расстоянием наблюдения. Таким
образом, при оценке векторного потенциала объем интегрирования может
рассматриваться как точечный по отношению к расстоянию г.
• смещение источника мало в сравнении с длиной волны излучения, что является
другим выражением условия, когда движение частицы является нерелятивистским.
В этом случае уравнение B.А. 10) сразу упрощается:
А,(г, О = А 1 , f /г', / - -W B.А.Ш)
4ле0с2г I у с )
где г — амплитуда вектора г, что с учетом определения плотности тока точечного
заряда B.А.б) приводит к выражению:
2.А. Поле излучения осциллирующего заряда
At(r,r)-
г
Векторный потенциал,
генерируемый движущимся зарядом
где D(/) есть векторный диполь D(/) = qxe (f). Для полного определения
электромагнитного поля мы должны еще рассчитать скалярный потенциал, задаваемый
условием Лоренца B.А.8):
Теперь мы должны рассчитать дивергенцию t)(t — г/с)/г. С этой целью
используем соотношение:
B.А.12)
и
1
э
а?
1
г
1
г
1
7
3"
__у_
г3
г3
так как г2 = х2 + у2 + z2- Подобным же образом:
гс
Теперь мы уже можем рассчитать дивергенцию векторного потенциала для B.1
B.A.13)
Отношение первого члена в скобках B.А.13) к второму члену по порядку
величины составляет ге/г и им можно пренебречь. В этом случае уравнение B.А. 13)
легко интегрируется, что с точностью до константы приводит к соотношению:
У£(г,/)= Г tHf-r/c)
4тсе0г2с
B.А.14)
Используя эти выражения для векторного и скалярного потенциалов в лорен-
цовской калибровке, мы можем рассчитать электрическое и магнитное поля.
Магнитное поле дается ротором векторного потенциала:
= VxAL=-
1
Ь(^7£I 1 rm ,>(,_r/c)+I
г \ 47се0с>1 [г) г
= —-—["- —xD(/-r/c)—r—xb{t-r/c)\
-г/с) =
B.А.15)
где вновь первым членом можно пренебречь по сравнению со вторым, что
позволяет нам записать:
1
rxb(t-r /с)
B.А.16)
Магнитное поле движущегося заряда
Расчет электрического поля осуществляется аналогичным образом, но требует
несколько больших усилий:
Дополнения к главе 2
Kr,/)-i.A<r,/)-Vg(r,r) 1 Ц/-г/с) 1 Jr-frz-r/c)!
Э/ 4ле0с2 г 4яе0с L r J
_^й 1
сг3 J
1 D(>-r/c) + г
г 4яе0с cr3
что в конце концов дает:
4Л£ОС2
или, как это было получено Рэлеем:
Е(г,/) = - - гх[]Гх1)(/-/*/с)]
"^'-'"", B.А.180)
Электрическое поле
движущегося заряда
где D± — компонента вектора диполя, перпендикулярная направлению точечного
источника (рис. 2.А.2). Заметим, что амплитуда излучаемого электрического поля
совпадает с расстоянием 1/г, а не 1/г2, что характерно для статического поля
точечного заряда. По этой причине радиоволны обладают существенно большим
диапазоном распространения по сравнению с электростатическим полем — этот
результат восхитил Герца и привел, в конце концов, к развитию радиосвязи. К
следствиям этого мы возвратимся позже. Как известно, электрическое и магнитное поля
перпендикулярны друг другу и по отношению к вектору распространения г. Говоря
более точно, они связаны друг с другом соотношением:
В(г,0 = -ГхЕ(Г>/) B.А.19)
с г
Поток энергии, излучаемой точечным зарядом через единицу площади в
единицу времени, дается вектором Пойнтинга S:
S(r, /) = — ЕхВ = ^i-ExfrxE) = -i-[£2r-(E- r)E] B.A.20)
//0
Поскольку Е и г перпендикулярны друг другу, уравнение B.А.20) может быть
записано в виде:
В
Рис. 2.А.2. Электромагнитное поле,
излучаемое точечным зарядом
2.А. Поле излучения осциллирующего заряда
B.А.21)
Поток энергии через единицу
площади в единицу времени, излучаемой
движущимся точечным зарядом
где ur— единичный вектор в направлении точечного источника. Выражение B.А.21)
содержит обильную информацию. Можно представить себе поток излучаемой
энергии как будто истекающим из точечного источника со скоростью света при
сохранении полной величины, проинтегрированной по поверхности сферы радиусом г и
с центром в источнике.
Применим теперь этот общий результат к частному случаю заряда q9
движущегося синусоидально вдоль оси Oz. В этом случае вектор диполя дается выражением:
D±(r, t) = qa cos(ct)t)ez B.A.22)
при этом вектор Пойнтинга принимает вид:
%/)=I™w^i BA23)
Поток энергии, усредненный по нескольким периодам, дается соотношением:
-„ГГ.**:' BА.24)
У1л2£<£ъ Г2
Ансамбли этих точек постоянной энергии (таких, для которых sin 6 /г остается
неизменным) расположены вдоль окружностей, касающихся осциллирующего
диполя (см. рис. 2.А.З).
Из-за того, что излучение диполя является достаточно направленным,
интенсивность поля спадает как 1/г, а не как 1/г2.
Мощность, излучаемую через поверхность сферы с центром в осциллирующем
заряде, можно получить, оценивая интеграл по поверхности от B.А.24), что дает:
Г sm4^2 sin мв& B.A.25)
J r2
yin2e^
r= const
или после интегрирования:
B.А.26)
Полная мощность излучения
осциллирующего диполя
Рис. 2Л.З. Поверхности
постоянной энергии излучающего
диполя
(f 80 Дополнения к главе 2
Это выражение также содержит богатую информацию. Оно, например,
показывает, что мощность излучения осциллирующего диполя пропорциональна четвертой
степени частоты. Таким образом, голубой свет (Л « 0,4 мкм) рассеивается
атмосферными частицами примерно в шесть раз сильнее, чем красный свет (Я = 0,65 мкм).
Это объясняет, почему небо голубое, а закат кажется окрашенным в красный цвет,
а также почему голубая неоновая реклама формирует яркое гало туманными
вечерами. Говоря более прозаически, оно дает основу метода расчета времен жизни
электронов на атомных уровнях.
То, что B.26) говорит нам, заключается в следующем: электроны теряют свою
энергию из-за электромагнитного излучения, и их движение в конце концов должно
прекратиться. Природа этого эффекта заключается в работе, совершаемой
движущейся заряженной частицей в электромагнитном поле, которое она сама создала! Для
описания этого эффекта введем в выражение для диполя член трения yR (равный 1/гЛ, где
rR — излучательное время жизни), соответствующий радиационным потерям:
mZ + myRZ + moJz = 0 B.А.27)
Мы знаем, что если rR » l/co, решения для описания движения принимают вид
z =acoscot e~'/2r, при этом энергия частицы уменьшается как Ee~t/T*. В этом случае rR
дается соотношением:
— =/> = -— B.А.28)
где Сдается выражением B.А.26), а энергия частицы определяется из соотношения:
Е = mV т<оЧг - тОJа2 B.А.29)
Таким образом, мы получаем излучательное время жизни осциллирующего
электрона, окружающего атом:
£ _•»
B.А.30)
что, будучи выражено через длину волны, дает:
Г 3
Излучательное время жизни
электрона, осциллирующего с частотой со
1к q2
Излучательное время жизни
электрона, излучающего
электромагнитную волну с длиной волны Л
Выражение B.А.31) позволяет нам понять отчаяние физиков в конце
девятнадцатого века. Поскольку, как представлялось, электроны орбитально вращаются вокруг
атомных ядер с частотами порядка 1015 Гц, выражение B.31) показывает, что все
они должны тормозить до остановки и, в конце концов, разрушаться на ядрах
после нескольких наносекунд. Как мы увидим в главе 3, квантовая механика позволяет
нам разрешить этот исторический парадокс. Тем не менее, уравнение B.31)
оказывается достаточно надежным в предсказании времен жизни для излучательных
переходов в лазерах. Ниже приводятся два типичных примера:
Л = 1 мкм, т = 45 не
Л = 10 нм, г= 4,5 пс
Таким образом, намного легче аккумулировать электроны в возбужденных
состояниях, подверженных инфракрасным переходам, чем заселить уровни, веду-
2. Б. Тепловидение
щие к проявлению рентгеновского излучения. И в результате, как мы увидим
позже, реализация инфракрасных лазеров намного проще, чем в случае
рентгеновских лазеров.
Пример
Уравнение B.А.26) является очень ценным инструментом для расчета оптической
мощности, излучаемой точечным источником, т.е. в случае, когда эффекты
распространения не принимаются во внимание. В качестве приложения определим
полную мощность излучения с удвоением частоты Bсо) в нелинейно-оптическом
материале, освещаемом фотонами с частотой со.
Пусть р будет атомной плотностью нелинейно-оптических центров (м~3), d
—нелинейной восприимчивостью (м/В), а рш — плотностью мощности падающего
оптического излучения (Вт/м2). Нелинейный дипольный момент qa связан с
коэффициентом d (смотрите главу 12) соотношением:
qap = eodE* = IZ^dPa, B. А. 32)
Полная мощность Р2о) излучения с удвоением частоты Bсо), преобразуемого pV
рассеивающими центрами (К— объем, на который сфокусировано первичное
излучение), дается B.А.26), а именно:
^с- '*• BА'33)
так, что:
I B. А. 34)
В случае ниобата лития d = 17пм/В, р = 1022 см, длины волны Л = 1,06 мкм и
мощности первичного излучения 100 МВт/см можно найти, что мощность
излучения на длине волны 532 мкм, излучаемого по всем направлениям, составит 1,4 мкВт.
Литература
A. Aspect, С. Fabre, and G. Grynberg, Laser et Atomes, Ellipses, Paris A997).
J.D. Jackson, Classical Electrodynamics, Wiley, New York A975).
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
2.Б. Тепловидение
Уравнение B.91) дает точное выражение для спектрального распределения
излучения черного тела при температуре Т. Тем не менее, нам еще необходимо
определить мощность падающего оптического излучения на единицу площади и
единицу длины волны, называемую спектральной излучательной способностью (т.
е. измеряемую величину, лежащую в основе термографии или теплового
отображения).
Рассмотрим элемент поверхности dS резонатора в пределах черного тела (рис.
2.Б.1). В телесном углу dQ, опирающемся на этот элемент поверхности, мощность
оптического излучения dR, падающего на dS в спектральном интервале dve
течение времени dt, определяется произведением плотности мод p(v) и объема,
занимаемого модами (с/2 dt) (dS cos0) d£2/2p или:
L7t
Дополнения к главе 2
Рис. 2.Б.1. Поток теплового электромагнитного
излучения черного тела.
В последнем уравнении коэффициент 2 в с/2 появляется в следствие того, что
уравнение B.91) учитывает стоячие волны (включая как падающие, так и
отраженные) тогда как для данного рассмотрения нам нужны лишь волны, падающие на dS.
Коэффициент 6п/2я предполагает, что излучение изотропно, а множитель cos 0
учитывает проекцию падающего потока на элемент поверхности dS. Вспоминая,
что элемент телесного угла дается соотношением 6S1 = 2л sin 6 d0, мы можем
проинтегрировать уравнение B.91) и найти:
ж/2
cos в sin в
2n i
B.Б.2)
Спектральная излучательная способность черного тела может быть получена
подстановкой B.91) в B.Б.2), что дает:
2nh v3dv
B.Б.З)
Наиболее широко используемой формой записи спектральной излучательной
способности является ее выражение не через частоту, а через длину волны. С этой
целью заменим в B.Б.З) уна с/Л, что дает:
<\Л У' }~ Я5
1
B.Б.4)
Спектральная излучательная
способность в Вт м м~2
Различные спектры излучения черного тела представлены на рис. 2.Б.2.
При рассмотрении относительной энергии, связанной с фотоном длины волны
Л (he/Л), а также тепловой энергии кТ источника представляют физический интерес
два предельных случая:
1. Коротковолновые фотоны с энергией, намного превышающей тепловую
энергию источника кТ.
В этом случае уравнение B.Б.4) приобретает вид:
B.Б.5)
Это соотношение действительно для ЛТ< 5000 мкм К и соответствует режиму
квантования энергии фотонов, о чем свидетельствует наличие члена hv/кТв уравнении.
2. Длинноволновые фотоны, переносящие энергию, пренебрежимую по
сравнению с тепловой кТ: he/Л « кТ.
Член первого порядка в разложении уравнения B.Б.4) сразу дает:
4т
ал
B.Б.6)
2. Б. Тепловидение
1 10
Длина волны (мкм)
100
Рис. 2.Б.2. Спектральная излучательная способность черного тела (Вт м~2 мкм 1) при
различных температурах (окружающей, 300 К; «раскаленное железо», 1200 К;
поверхность солнца, 8000 К).
Отметим исчезновение постоянной Планка h в выражении для спектральной
излучательной способности. В этом режиме, называемом режимом Рэлея—Джинса,
квантовый аспект фотонов маскируется тепловыми возбуждениями системы. Это
выражение могло бы быть получено прямо (как это и было сделано Рэлеем и Джин-
сом), исходя из классического выражения B.24) для электромагнитной энергии в
резонаторе. Отметим также, что B.Б.6) расходится при Л -> 0, что в начале двадцатого
столетия получило образное название ультрафиолетовой катастрофы. Именно эта
неудача классической физики привела в конце концов к развитию теории квантов.
Интегрирование B.Б.4) по всему пространству длин волн приводит к
выражению для полной излучательной способности черного тела:
B.Б.7)
I
Использование интеграла Бернулли
применительно к B.Б.7) сразу дает:
Я(Л, Т) = аТ4
где а — постоянная Стефана:
15<г/г
К"
B.Б.8я)
Закон Стефана—Больцмана
для излучения черного тела
B.Б.86)
Пример ——
Рассчитаем полную мощность Р излучения человеческого тела с площадью
поверхности S = 2 м при температуре 300 К.
Эта величина дает ожидаемые потери энергии незащищенного тела в условиях
окружающей температуры 0 К, что встречается отнюдь не так часто!
Как можно увидеть из рис. 2.Б.2, спектры излучения черного тела имеют
максимум при определенной длине волны для заданной температуры. Положение это-
Дополнения к главе 2
го максимума может быть определено дифференцированием по Л уравнения B.Б.4),
что дает следующее точное уравнение:
6 - 5-{hc/XkT) { '
допускающее в качестве решения следующую зависимость:
- 2о9о /л г. 1ЛЧ
Лпах=-у-5ВМКМ B.Б.10)
Закон Вина
Таким образом, максимум излучения для тела при комнатной температуре
располагается на длине волны, примерно составляющей 2898/290 или 10 мкм.
Следовательно, тепловое отображение объекта при комнатной температуре возможно при
использовании детекторов, чувствительных к излучению на длинах волн в
окрестности 10 мкм.
Этот спектральный диапазон представляет интерес еще и потому, что земная
атмосфера обладает большой прозрачностью на этих длинах волн. На рисунке 2.Б.З
представлен график зависимости прозрачности атмосферы от длины волны.
Отметим в особенности наличие двух широких зон, расположенных в
диапазоне 3—5 мкм (зона II) и 8—12 мкм (зона III), в пределах которых земная атмосфера
особенно прозрачна.
У каждого из отмеченных окон прозрачности имеются свои особые области
применения. В выборе оптимального варианта для поставленной задачи нам может
помочь ряд перечисленных ниже соображений:
• климатические условия: влажные воздушные массы лучше сохраняют
прозрачность в зоне II, в то время как рассеивающие облака представляют меньшие
трудности при использовании зоны III;
• тепловой контраст: понятно, что большая часть излучения объектов при
температуре 300 К сосредоточена в диапазоне 8—12 мкм A2,2 мВт см —
смотрите приведенный ниже пример), а не в диапазоне 3—5 мкм @,6 мВт см). Тем
не менее, иногда нам надо уметь детектировать тепловой источник с
температурой Г на фоне окружающей среды с температурой Ть. Таким образом,
тепловой контраст является физически более уместной величиной,
соответствующей нормированному различию мощности излучения объекта и фона в
спектральном диапазоне АД или:
4 6 8 10
Длина волны (нм)
12
Рис. 2.Б.З. Спектральная зависимость пропускания атмосферы в типичных условиях
B км над уровнем моря, 20°С, влажность 40%).
2. Б. Тепловидение
с(дя)=
йЯ
B.Б.11)
(ХЯ
Рис. 2.Б.4 иллюстрирует сравнение теплового контраста в зонах II и III по
отношению к фоновой температуре 280 К. Видно, что наибольший контраст
достигается в диапазоне 3—5 мкм, что является важным аспектом в зависимости от
области применения.
I
о
с;
0.4
о.з
0.2
3-5 мкн
8-12 мкн
280 285 290 295
Температура мишени (К)
300
Рис. 2.Б.4. Тепловой контраст в диапазоне 3—5 мкм (зона II) и 8 — 12 мкм (зона III).
Отметим, что хотя число фотонов меньше в зоне II, тем не менее тепловой
контраст (или способность различать цель с температурой Т на фоне среды
с температурой 280 К) вдвое больше.
Другим важным параметром является дифференциальный контраст Cd (Вт см К)-
По определению, С, А Г есть тепловая излучательная способность на градус К в
интервале длин волн АД:
С(ДЛ)= —
B.Б.12)
Этот параметр чрезвычайно полезен при предсказании функциональных
характеристик инфракрасных детекторов. Если обозначить чувствительность детектора с
площадью £как Sf (А/Вт), то ток детектирования /(А) вследствие вариации
температуры А Г дается соотношением:
1=
B.Б.13)
Пример
Программа MATEMATICA, приведенная ниже, позволяет рассчитывать излучатель-
ную способность абсолютно черного тела в спектральном диапазоне Ax—A2, а также
дифференциальный контраст.
c=2.98810"8(*m/s*);
k=1.3810l-23(*J/K*);
Дополнения к главе 2
h=6.62510'-34(*J.s*);
hb=h/B*3.1416);
m0=0.9110'-30(*kg*);
(* Wavelength range in mm *) iambda1= 8;lambda2= 12;
(* Blackbody as a function of temperature*) temp=.; lambda=.;
emm:=2*3.1416*h*cl2*(lambda*10'-6)>-5/(Exp[hV((lambda*10>-
6)*k*temp)]-1) emm = emm * 1(Г-6 (* W/nT2/|im*);
contr=D[emm,temp];(*contrast used for the calculation of NETD*)
temp=300 (*temperature of the blackbody*);
Plot[emm,{lambda,. 1,20}, Frame- >True, RotateLabel- > False,
FrameLabel- > {«micron'Y'W/nrT»} ]
Plot[contr,{lambda,.1,20}, Frame- >True, RotateLabel- > False,
FrameLabel- > {«micron'Y'W/nrT/K»} ]
(* Blackbody power radiated over the spectral range*)
Nlntegrate[emm,{lambdaflambda1,lambda2}] (*W/nT2*);
pp=%*10'-4(*W/cm'2*)
(* differential contrast for the spectral range *)
Nlntegratefcontr,{Iambda,lambda1 ,lambda2}] (*W/m'2/K*);
cc=%*1(r-4(*W/cm'2/K*)
Эта программа дает для источника с температурой 300 К плотность мощности
излучения в спектральном диапазоне 8—12 мкм и 3—5 мкм соответственно 12,2 мВт см
и 0,6 мВт см. Таким образом, сигнал детектора будет существенно больше в зоне
Ш по сравнению с зоной II. С помощью программы мы определяем также
дифференциальный контраст в диапазонах 3—5 мкм и 8—12 мкм, составляющий
соответственно 2,1 х 10~5 Вт см К и 1,98 10 Вт см К. При использовании детектора
с площадью 10 см2 и чувствительностью 1 А/Вт вариация температуры источника
величиной 10 мК приведет к току датектирования величиной 20 и 200 пА
соответственно в диапазонах 3—5 мкм и 8—12 мкм. Такой уровень тока является достаточно
надежно измеряемым, что свидетельствует о практической важности инфракрасных
детекторов. Вновь к этим важным приборам мы возвратимся в главе 11.
В заключение следует подчеркнуть, что большинство обычных объектов в
действительности не являются черными телами. Они поглощают только часть
излучения еж(Л), при этом остающаяся часть излучения либо отражается, либо
переносится. Таким образом, спектральная излучательная способность dR/dA связана с
аналогичным параметром абсолютно черного тела dRBB /dA соотношением:
МЪ Т) e&yRjb T) B.Б.14)
Типичные значения поглощательной способности варьируются в диапазоне от
0,03 для полированного алюминия (который считается хорошим отражателем) до
0,95 в случае черной сажи (хороший поглотитель)
Литература
G. Gaussoigues and S. Chomet, Infrared Thermography, Kluwer, Boston A993).
RJ. Keyes, ed., Optical and Infrared Detectors, Topics In Applied Physics Vol. 19,
Springer Verlag, Berlin A980).
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
ГЛАВА 3
КВАНТОВАЯ МЕХАНИКА
ЭЛЕКТРОН-ФОТОННОГО
ВЗАИМОДЕЙСТВИЯ
3.1. Введение
Эту главу мы начнем с описания взаимодействия между квантовой системой и
электромагнитной волной в резонаторе. Во время взаимодействия
электромагнитное поле можно рассматривать как классическое поле, принимающее
произвольные значения в пределах резонатора или, в альтернативном варианте,
квантующееся в виде фотонов. Первый вариант описания позволяет нам описывать явления
поглощения и стимулированного излучения в квантовой системе. Второй же
вариант описания позволит нам рассмотреть спонтанное излучение с участием
возбужденных состояний — явление, которое трудно трактовать с использованием
классических представлений (см. дополнение 2.А). Затем мы обсудим скоростные
уравнения Эйнштейна для системы в условиях проявления всех перечисленных выше
процессов, что явится основой для описания лазерного эффекта.
3.2. Гамильтониан дипольного взаимодействия
для электронов и дырок
Рассмотрим теперь частицу с зарядом q и массой т, подвергнутую воздействию
статического потенциала К(г) атома, квантовой ямы и т. д. В рамках классического
подхода гамильтониан частицы дается соотношением:
#=ll + K(r) (ЗЛ)
1т
В присутствии классического электромагнитного поля не представляется особенно
трудным (хотя отчасти и утомительным) показать, что классический гамильтониан
частицы представляет собой:
я = [р-?А(г,02] + к(г) + (?£/(г,/), C.2)
2т
где А(г, t) и U(r, f) соответственно векторный и скалярный потенциалы электромагнитной
волны (смотрите раздел 2.2). Принцип соответствия, примененный к одной частице, дает
нам выражение квантового гамильтониана:
r ) C.3)
В этом первом подходе отметим, что А сам по себе не оператор, а векторная функция
оператора г. Перед тем, как идти дальше, целесообразно решить, какой калибровкой нам
воспользоваться (раздел 2.2). При данном рассмотрении воспользуемся кулоновс-
кой калибровкой, так как она приводится к особенно простым выражениям для
гамильтониана взаимодействия с планарной электромагнитной волной.
Глава 3. Квантовая механика электрон-фотонного взаимодействия
Кулоновская калибровка
В случае кулоновской калибровки предполагается, что векторный потенциал обладает
нулевой дивергенцией:
VACoulorab(r,0 = 0 C.4)
С учетом соотношения B.13) в обратном пространстве это означает, что векторный
потенциал не обладает параллельной компонентой и полностью определяется своей
перпендикулярной компонентой А±. Возьмем для примера монохроматическую
электромагнитную волну с электрическим полем, которое определяется соотношением:
Е = Ео cos(kr -cot) C.5a)
В = ^^ cos( k • г - cot) C.56)
со
Ео к = 0 C.5*)
Векторный потенциал дается формулой B.23) или:
A±=^sin(k r-a)t) C.6)
со
Используя выражения B.4 б) и B.12), находим, что скалярный потенциал равен нулю
(U(r, t) = 0) и в этом случае гамильтониан взаимодействия C.3) принимает простой вид:
у C>7)
Гамильтониан одной частицы в
условиях электромагнитного поля
который может быть представлен в виде разложения:
Я = £- + V(t) -■£-& • Ах(г, /) + Ах(г, /) • р| + £-АЦТ, t) C.8)
lm lm lm
Два важных момента позволяют упростить последнее выражение. Членом второго
порядка Ах2 можно пренебречь, так как можно показать, что он мал по сравнению с
линейным членом. Во-вторых, операторы р и А±(г) коммутируют. Оценивая влияние оператора
V на произведение A(r, t)i/Aj, t), мы сразу находим:
[iW,A1(r,0] = i^VA1(r,0 C.9)
и, с учетом определения перпендикулярной компоненты А± (смотрите выражение B.13),
этот последний член равен нулю. Наконец, благодаря использованию кулоновской
калибровки гамильтониан системы принимает следующий простой вид:
C.10)
А А
где Яо — гамильтониан невозмущенной системы, a W{t) — гамильтониан возмущения:
±h±(t,t)-9 C.11)
m
Гамильтониан Ар взаимодействия для
электрона в электромагнитном поле
Этот последний гамильтониан носит название Ар — гамильтониана. Этот
параграф мы закончим, отметив два важных момента. Во-первых, в общем случае
амплитуда смещения частицы намного меньше длины волны электромагнитного
возбуждения. Типичные квантовые системы, которые изучаются в этой книге,
имеют физические размеры в диапазоне от 0,1 до 10 нм, что и в действительности
3.3. Линейная оптическая восприимчивость в приближении матрицы плотности
очень мало по сравнению с длинами волн их резонансных переходов (в диапазоне
от 200 нм до 10 мкм). В результате этого пространственными вариациями
векторного потенциала мы будем пренебрегать, так что если система имеет центр в точке
г0, то гамильтониан возмущения имеет вид:
C.12)
1@,ОР
т
Вторым важным моментом, который следует отметить, является то, что имеется
эквивалентная запись для гамильтониана возмущения, которой также достаточно широко
пользуются (т.н. калибровка Гопперта—Мэйера):
C.13)
А
где D — дипольный оператор, при этом такой гамильтониан называют электрическим ди-
польным гамильтонианом или D • Е — гамильтонианаом. Вопрос об эквивалентности этих
двух гамильтонианов рассмотрен в Дополнении З.Г.
3.3. Линейная оптическая восприимчивость
в приближении матрицы плотности
Поинтересуемся теперь взаимодействием между двухуровневой квантовой системой и пла-
нарной электромагнитной волной. Эта двухуровневая система описывается гамильтонианом
Яо со стационарными состояниями |1> и |2> и собственными энергиями Ех и Е2 (т. е. #0|/) =£|/)).
С тем, чтобы более не беспокоиться о путанице между операторами и классически
измеряемыми величинами, мы (временно) позволим себе отбросить символ «л» в обозначении
операторов. В базисе стационарных состояний гамильтониан Яо может быть записан в виде:
е
В момент времени / = 0 система подвергается возмущению W(t) = — ex • Ео cos cot
(электрический дипольный гамильтониан). В базисе состояний |1) и |2> матричное
представление W имеет вид:
—•
где члены D.. представляют собой элементы дипольной матрицы:
Напомним, что в этом выражении е— вектор поляризации волны. Мы предположили, что
система симметрична относительно центра и, как результат этого, элементы Dn и D22
равны нулю. Кроме того, для упорядочения обозначений мы предположили, что Dn и
D2l действительны и таким образом равны. Как мы видели в разделе 1.9, система
может быть описана своей матрицей плотности и в этом случае уравнение Шре-
дингера (смотрите A.101) может быть записано в виде:
^ = -i^E0(pn - pn)cos cot - ф22 - р5) C17)
= -iK - 1Г2)р21 - i^E0(p22 - Al)cosa*,
Глава 3. Квантовая механика электрон-фотонного взаимодействия
где Гг (= 1/Т{) — скорость неупругой релаксации заселенности между двумя
уровнями, а Г2 (= 1/Т2) — скорость фазовой релаксации. Как описано в дополнении
1.Д, нам известно, что после переходного периода, длящегося несколько Tv pn
будет осциллировать как cos cot, в то время как члены р пи р22 будут стремиться к
своим стационарным величинам. Таким образом, целесообразно провести замену
переменных:
которые после введения в C.17) и после пренебрежения нерезонансными членами в
со + со21, приводят к системе уравнений:
— ст21 + 1 {аJ1 - со)-1 — \а21 = i-^
d . Ар - Ар . Д2
т
Будучи в стационарном состоянии, заселенности рп, р22 и таким образом Ар=рп— р22
являются постоянными так же, как и амплитуды а12 и ст21. В этом случае уравнения C.19)
приобретают вид:
р
Kty)i
=-2Q12Im(cx2I),
где, как мы напоминаем, Qn = д£|A|г • £\2)/h = EQDn/h — частота Раби (смотрите
дополнение 1.Д). Эта система может быть сразу решена, что дает:
/ \2 2
1 + {со-,, — со) 7\ м
АР = ; V 21Ч2 2 2
1 + (со21 - со)) Т2 + ппТхТ2
Im a2l = —^-2- : гг—1 2 Ар^4 C.216)
Re a21 = ^— V ? , АР8" C.21в)
2 1 + K -юJГ2 +П12Г,Г2
Для того, чтобы перекинуть мостик к макроскопической шкале, мы должны
вспомнить, что число частиц в состоянии |1) и |2> дается выражениями N{ = Npn и
N2= Np22, где N — полное число частиц. С другой стороны уравнение A.92) дает
нам среднее смещение частицы в двухуровневой квантовой системе:
(f) = Tr(pf) = r,2(A2+p2l) C.22)
С учетом C.16) и C.18) поляризация среды в направлении вектора
поляризации дается соотношением:
P = N(p-e) = NDn(antl(Ot + апе~Ш) C.23а)
или вновь:
3.4. Линейная оптическая восприимчивость: поглощение и оптическое у сипение
Р = 2NDn (Re cr2l cos cot + Im a2l sin cot) C.236)
Таким образом мы вводим линейную оптическую восприимчивость ^(йУ),
определяемую как:
Р(/) = Re[£Qz(co)ei0"] = £0E0CfRccos cot — \%lm sin cot) C.24)
Оптическая поляризация
и линейная восприимчивость
где
у (со) = ув (оА + ix (fid C.25)
В атомной физике величина €^(со) является поляризуемостью квантовой
системы. Член ^Rc, который синфазен с волной £0cos cot, описывает мгновенную
реакцию среды и приводит к росту коэффициента преломления. С другой стороны,
член Х\т отстает по фазе на 90° от возбуждающей волны и, как мы увидим в
следующем параграфе, описывает поглощение (или диссипацию, имеющую место в
среде). Проводя идентификацию члена за членом, мы можем обнаружить три
макроскопические величины, которые описывают взаимодействие двухуровневой
системы с электромагнитной волной, а именно: различие заселенностей, действительную
и мнимую части линейной оптической восприимчивости:
"■-"'- ,+( У'1.1 »Г - N, | C.26.)
1 + (ю2, - со) Т2 + п12Т^
C.26*)
Эти уравнения иногда записывают в более компактном виде:
w*N C27«>
Теперь мы опишем связь между этими величинами и макроскопическими
свойствами, такими как поглощение и усиление квантовой системы.
3.4. Линейная оптическая восприимчивость:
поглощение и оптическое усиление
Материя состоит из отрицательно заряженных частиц (электронов), которые
экранируют фон положительно заряженных ядер. Когда электромагнитная (ЭМ) волна
воздействует на материю, движение электронов (легких частиц) относительно ядер
(тяжелые частицы) вызывает эффект осциллирующего диполя, который излучает
синхронно с полем. Это и есть атомная поляризация. Излучаемое поле
взаимодействует с первичным приложенным полем, что и приводит к уменьшению скорости
света в среде. Этот эффект может быть учтен с использованием микроскопического
Глава 3. Квантовая механика электрон-фотонного взаимодействия
подхода, основанного на использовании выражения для осциллирующего диполя
(уравнение B.А.18)). Рекомендуем читателю углубить свои знания по этому
поучительному аспекту преломления, прочитав легендарные Фейнмановские лекции.
В то же время, будучи менее проясняющими, уравнения Максвелла
предоставляют намного более эффективный инструментарий для учета этого эффекта без
необходимости прибегать к сложным выражениям. С этой целью в уравнение Фарадея—
Ампера вводится ток смещения из-за движения связанных зарядов. Это приводит к
уравнениям Максвелла для незаряженной, немагнитной и поляризуемой среды:
|r,0 C.28)
(r,/) C.29)
y|(,)
€0С2 dt
где D — вектор смещения, который дается выражением:
C.30)
и Р^ — вектор поляризации системы вблизи резонанса, а Р — вектор поляризации,
соответствующий всем нерезонансным вкладам (т. е. вкладам, возникающим из-за
материала среды, в которую помещена двухуровневая система). Член е0Е + Р
является, по определению, диэлектрической константой, заменяемой на dL Подобным
же образом, следуя определению линейной оптической восприимчивости C.246),
выражение C.30) может быть переписано в виде:
D =£^ + ^-;г(а>)]Е C-31)
В качестве решений уравнения Максвелла C.28) и C.29) допускают бегущие волны
вида:
Е(г, t) = ЕуОДе-^- *>] C.32)
где на этот раз волновой вектор к и радиальная частота *у связаны соотношением:
к = к = 22.
1 ' с
1/2
C.33)
где пор — коэффициент оптического преломления равный ^е / е0 . Так как
восприимчивость может и не быть большой величиной по сравнению с единицей, то:
Действительная часть последнего выражения свидетельствует о том, что скорость света
уменьшается на коэффициент п^ в среде. И вновь читателю рекомендуется углубить свои
представления по этому аспекту, читая Фейнмановские лекции. Подставляя C.34) в C.32), мы
видим, что амплитуда электромагнитной волны экспоненциально ослабляется с расстоянием:
Е(г, /) = E0c'a/2z Re[eD 'Л, C.35)
где kR дается действительной частью C.34), а коэффициент а представляет собой
коэффициент поглощения, определяемый как:
«И=—*,
Коэффициент поглощения
и линейная восприимчивость
3.4. Линейная оптическая восприимчивость: поглощение и оптическое усиление
aifo) = _Jil |ZL (# «. _ N«) (s.sy)
^ 7 лм л *. i . /-. _Vt2 . s-\2 тип \ 1 2 / \ /
или:
Коэффициент поглощения
в двухуровневой системе
Электромагнитная волна теряет свою интенсивность в функции расстояния
распространения как /(z)= /оеаг> ПРИ этом ее энеРгия превращается в тепло. Представляется
принципиальным отметить, что фазовая задержка члена %lm на 90° по отношению к
распространяющейся электромагнитной волне в качестве основной причины
обусловлена именно тепловой диссипацией энергии (и необратимостью этого процесса).
Это является общим результатом, приложимым ко всем линейным процессам.
Рисунок 3.1 иллюстрирует изменение формы нормированной частотной
зависимости коэффициента поглощения для различных значений произведения Q\2
Т{Т2. Численные константы в C.37) были выбраны таким образом, чтобы а(со21) = 1
для п 12 = 0. Отметим, что поглощение уменьшается по мере возрастания
интенсивности электромагнитной волны, при этом ширина пика возрастает как:
C.38)
Рис. 3.1. Насыщение поглощения при QJlT2 =10 для различных значений
произведения п\2Т1Тг
Это явление называется насыщением поглощения, и мы возвратимся к нему
позже в главе 4. При малой интенсивности волны Л^ — N2 ~ N{ уравнение C.37)
принимает вид лоренциана, который сможет быть получен в рамках классической теории
упруго связанного электрона:
а{со)- Nx q K f2lL(o)-oJl)= /21orclas(со)
2e0mcnop
где L(a>) - лоренциан с шириной \/Т2 и центром в 0:
C39а)
Ду/2л
C.396)
Форма лоренциана
Глава 3. Квантовая механика электрон-фотонного взаимодействия
где Av — полуширина (FWHM) лоренциана (Av = 2/Т2 =2Г2). aclas есть результат
классической теории Лоренца, af2l — безразмерная физическая величина,
называемая силой осциллятора, которая описывает интенсивность квантового
взаимодействия между двумя уровнями |1> и |2>:
f2l=^-E2l\(l\r-e\2)f C.40а)
Сила осциллятора
для перехода |1>-> |2)
Для системы с несколькими уровнями мы можем показать справедливость
правила Томаса—Райха—Куна (Дополнение З.Г):
/ = 1 C.406)
Это правило утверждает, что хотя квантовая механика распределяет силы
осцилляторов между несколькими уровнями, сумма этих вкладов поглощения должна быть равна
классически определенной величине. Поглощение в системе из-за оптических переходов
между основным уровнем |1) и произвольным числом уровней [/') дается обобщением C.39I:
3.5. Скоростные уравнения
3.5.1. Адиабатическая аппроксимация
и корпускулярная интерпретация
Теперь мы можем дать корпускулярную трактовку уравнений поглощения. Для
начала введем адиабатическую аппроксимацию, предполагающую, что время фазовой
релаксации Т2 очень мало по сравнению с временем релаксации заселенности 7j. В
пользу этой гипотезы говорит тот факт, что упругие механизмы, доминирующие в
Т2, намного более многочисленны по сравнению с неупругими процессами (также
включенными в 72), которые контролируют Тх. Таким образом, для стп мы
используем выражение C.20), связывающее мгновенную величину рп с Ар. Введем это
выражение во второе дифференциальное уравнение C.19), предполагая, что в
течение нескольких моментов времени время жизни заселенности Тх очень велико и
практически бесконечно (Г2 = 0). В этом случае мы можем записать изменение
заселенности уровня |1) как:
#, = RI2N2 - RnNt C.42)
где члены Rl2 и /{^ представляют скорости оптических переходов (с) и даются
выражением:
р - р -
■«42 "" ^21 "~
hiJb
2П2 (о)п - со) + A / TJ
В этом случае мы получаем тот же результат, что и полученный с
использованием стационарной теории возмущений (уравнение A.85)). Будучи подвержены воз-
1В контексте этого раздела поглощение не может быть отрицательным. Единственным
случаем, когда сила осциллятора отрицательна, является ситуация, при которой (/Д)не является
основным уровнем (т. е., если Ef < £,), в случае чего уравнение C.44) должно отслеживать
величины заселенности Nf.
3.5. Скоростные уравнения
действию фотонов, электроны на начальном уровне стремятся на второй уровень
со скоростью, которая определяется соотношением C.43). Равенство Rn = ^
является демонстрацией принципа микрообратимости. Мы можем переписать C.43) в
более узнаваемой форме:
*12 = о;рФ C.44)
Скорость перехода и
оптическое поперечное сечение
где Ф есть поток фотонов (фотон/с м2), связанный с напряженностью
электрического поля соотношением:
Ф = i"opC£o£°2 C.45)
2 fico
Поток фотонов и
напряженность электрического поля
а бтор представляет собой оптическое поперечное сечение (обычно выражаемое в см):
а
Оптическое поперечное сечение
3.5.2. Стимулированное излучение
Уравнение C.42) может быть переписано в следующем виде:
C.47)
Это последнее уравнение мы можем выразить и через число фотонов. Число фотонов
п в резонаторе с объемом К, пересекаемом потоком фотонов Ф со скоростью света в этом
материале d = с/лор, тривиально дается соотношением:
В этом случае выражение C.42) принимает вид:
Каждый член C.49) можно легко интерпретировать. Электроны покидают уровень 11)
со скоростью пропорциональной потоку или плотности фотонов, что хорошо согласуется
с нашим пониманием поглощения. В альтернативном процессе электроны релаксируют с
уровня |2> на уровень |1), сопровождаемые эмиссией фотонов, пропорциональной потоку
фотонов — этот случай соответствует явлению стимулированного излучения фотонов в
резонаторе. Таким образом, мы можем сделать заключение, что при каждом акте
поглощения число фотонов в резонаторе уменьшается на единицу, но при этом
каждый из этих фотонов, в конце концов, переизлучается и появляется подобно
клону в процессе последующего стимулированного излучения фотонов в
резонаторе. Отталкиваясь от C.49), мы можем также найти и уравнение, описывающее
изменение числа фотонов в резонаторе. При каждом переходе с уровня |2> на уровень
|1) в резонаторе освобождается дополнительный фотон. И обратно, каждый
электронный переход с уровня |1) на уровень |2) приводит к удалению одного фотона из
резонатора. Следовательно, dn/dt = +dNJdt = —dNJdt
N2) C.50)
|f 96 Глава 3. Квантовая механика электрон-фотонного взаимодействия
Другое выражение для изменения числа фотонов в резонаторе, полезное для
квантовой оптики, может быть получено, исходя из C.19):
л а - а - еа г\
721-<712) C.51)
Отметим, что член с \/Тх является безызлучательным (т. е. он ни поглощает, ни
излучает фотоны). Таким образом, разница между скоростями изменения этих двух
заселенностей (Nx — N2), которая лежит в основе исчезновения фотонов из
резонатора, обусловлена только различием ап и a2V что может быть выражено в виде:
Л = -2О121ш(<т21) C.52)
Поглощение и недиагональные
элементы матрицы плотности
Используя выражения C.216) для сг21, мы вновь можем получить C.50).
Исследуем теперь поведение двухуровневой системы в условиях резонанса.
В условиях резонанса оптическое поперечное сечение максимально и может быть
записано в виде:
<7OD = -^- (о)Т2) -У-— 1 = 9,2 х 10 ~2 (й)Т2 )-^- C.53)
"ор {ПСЬ0 J Пор
Поскольку соТ2, как правило, лежит в диапазоне 10~2—102, длина диполя гп
составляет несколько ангстрем и мы можем ожидать, что типичные значения
поперечного сечения будут лежать в диапазоне от 10~20 до 104 см2.
Пример
Рассчитаем типичное оптическое поперечное сечение в резонансе для квантовой
ямы при следующих параметрах:
Т2 = 0,1 пс
со= 1014 с
Dn = q x 1 Кл нм
Получаем, что типичная величина аор составляет 3 х 10~15 см2.
3.5.3. Насыщение поглощения
Возвратимся теперь к выражениям C.26), определяющие различие заселенности
между двумя уровнями в функции частоты Раби пп, которая, в свою очередь, дает
связь с напряженностью электрического поля E0Ql2 =EQDn /h . Вспоминая, что число
частиц в системе постоянно, получаем следующую систему из двух уравнений:
N{+N2=N
C.54)
где N— полное число электронов в системе. Таким образом, мы видим, что уровни
заселенности каждого из двух уровней стремятся сравняться по мере увеличения
потока фотонов (Ц2 -> °°). Интуитивно это может быть понято следующим
образом: по мере увеличения потока фотонов процесс поглощения стремится заселить
верхний уровень вплоть до такого значения, при котором скорость
стимулированного излучения полностью не скомпенсирует скорость поглощения.
Говоря более точно, если мы рассмотрим два уровня, достаточно далеко
разнесенные по энергии, так что при термодинамическом равновесии все электроны
находятся на уровне |1> (А^4 = N), то число частиц на уровне |2> приобретает вид:
3.5. Скоростные уравнения
1
где Фа1 — поток насыщения для двухуровневой системы, который определяется
условием пп = \/y[fj\ в C.54) и с учетом C.45):
Поток насыщения
двухуровневой системы
Как только поток насыщения достигает этой величины, поглощение
уменьшается вдвое и стремится к нулю при достаточно большой мощности
возбуждения. Заметьте, что неравенство N{ > N2 справедливо для любого уровня
возбуждения.
Если бы это не имело места, то прямым следствием N2 > N{ было бы то, что
система испытывала бы отрицательное поглощение и, таким образом, оптическое
усиление. Условие, при котором N2 > Nr называется инверсией заселенности и,
как мы только что продемонстрировали, не может быть реализовано в
двухуровневой системе.
Пример
Используя выражение для мощности насыщения PsM (уравнение C.56я)),
можно экспериментально определить время жизни возбужденного состояния Гр
как только установлено время Т2 (из ширины пика поглощения), с помощью
выражения:
C.566)
- 2(Dn/hJT{T2
Для квантовых ям с величиной дипольных матричных элементов гп порядка
1 нм и шириной линий поглощения порядка 10 мэВ (т.е. Т2 = 0,1 пс) плотность
мощности насыщения составляет 2 МВт см. Рисунок 3.2 иллюстрирует
насыщение поглощения для двухуровневой квантовой ямы. Измеренная величина Ps&i
в действительности намного выше по сравнению с предсказанной здесь
величиной, что является следствием правил отбора, которые будут рассматриваться
позже в главе 8.
0.12
0)
I
О)
1
о
о
с
0.10
0.08
0.06
0.04
0.02
гтт
А= 9.8 jxm
1
0.1 1 10 100
Плотность пиковой мощности (МВт см~2)
Рис. 3.2. Насыщение поглощения между двумя уровнями в квантовой яме. Порогу
насыщения соответствует уровень возбуждения, при котором поглощение падает вдвое,
что в данном случае соответствует плотности оптической мощности 50 МВт см2
(в соответствии с данными J.Y. Duboz et al. /. Appl. Phys. 11, 6492 A995)).
Глава 3. Квантовая механика электрон-фотонного взаимодействия
3.6. Спонтанное излучение
и излучательное время жизни
3.6.1. Спонтанное излучение
В том случае, когда второй уровень заселен, он стремится срелаксировать под
воздействием потока фотонов, о чем свидетельствует член —aopc'nN2/Vb C.49). Таким
образом, если число фотонов в резонаторе равно нулю (т. е. в резонаторе
отсутствует излучение) скорость стимулированного излучения также равна нулю. В
результате этого в отсутствие упругих соударений (Г{ = 0) частица должна оставаться в
возбужденном состоянии сколь угодно долго. Это, однако, противоречит опыту.
Например, когда атомы возбуждаются электрическим разрядом в разряженной
атмосфере для того, чтобы свести к минимуму атомные столкновения (как это
специально делается в неоновых лампах), возбужденные атомы релаксируют в течение
нескольких микросекунд. Каким же образом можно примирить этот парадокс
между до сих пор безупречной теорией и этим бытовым наблюдением из области
каждодневной практики?
Ответ же заключается в том, что мы выполнили только половину задачи. В то
время, как мы допустили квантование поведения частицы, мы не сделали то же
самое в отношении света. Для завершения нашей работы мы должны ввести в
выражение для гамильтониана взаимодействия C.12) и C.13) квантовую форму
электрического поля, соответствующего моде /, которая дается уравнением C.34а):
-ik г
W=iqF,(a,e - а,е )srr C.57)
где а{и а* операторы рождения и уничтожения фотонов моды /, a Ft —
интенсивность поля, связанного с квантовыми вакуумными флуктуациями той же самой
моды (уравнение B.35)). В этом случае гамильтониан действует в двух
гильбертовых пространствах (или более точно воздействует на тензорное произведение),
соответствующих пространству фотонов и заряженных частиц. Таким образом, в этом
случае мы должны говорить о состояниях, обозначаемых как |/, п), где / относится
к состоянию заряженной частицы (/' = 1,2 для двухуровневой системы), a nt
обозначает число фотонов моды / (смотрите рис. 3.3). Обобщение этой задачи на случай
произвольного числа мод следует прямо, но сопровождается усложнением
необходимых обозначений (например |/, яр ..., пр ...)). В связи с этим на время мы оставим
в стороне модовые индексы.
Оптические переходы могут иметь между состояниями \1,п)и\2,гГ),з. также в обратной
последовательности. Рассмотрим сейчас механизм поглощения. В этом случае начальным
уровнем является |1, п), а конечным —12, п — 1) (смотрите рис. 3.3), так как фотон в процессе
поглощения теряется. Из A.856) следует, что вероятность поглощения составляет:
Plt2 = ^|A, n\W\2, n - \)\28{ETm - Em) C.58)
где Ein = Е{ + h co(n + 1/2) и ЕГт = Е2 + h со((п — 1) + 1/2). Закон сохранения энергии
в данном случае соответствует условию h со = Е{ — Е2, что находится в согласии с
теорией главы 1(уравнение A.80)). В таком случае уравнение C.58) может быть
записано в виде:
Р12=^д2^2 \{\,п\(а^< -a;^r)err\2,n-\)\2 S(hco = E2-El) C.59)
Поскольку состояние частицы и фотона не зависят друг от друга, это выражение может
быть разделено следующим образом:
^2 l(«l|(«e»"ra;e-»'-)|«)|2|B|£f|l)l2 S{nm EE) C.60)
3.6. Спонтанное излучение и излучательное время жизни
i
i
- I1> —
a
г •
-*- I1> —I
6
j I2>
T и>
—I— io>
Б
Рис. 3.3. Взаимодействие между двухуровневой системой и квантованным
электромагнитным полем в виде гармонического осциллятора. Рисунок показывает
различные механизмы для следующих оптических переходов:
а — поглощение;
б — стимулированное, или индуцированное излучение,
в — спонтанное излучение.
С учетом свойств операторов рождения и уничтожения (A.Г.23) и A.Г.24)) можно
установить, что единственным ненулевым членом, связанным с фотоном, является:
(п-\\а\п) = 4~п
В этом случае вероятность поглощения в единицу времени приобретает вид:
•г|2)|2 S(hco= E2-Ex)
C.61)
C.62)
или вновь используя выражение B.77) для электрического поля в когерентном состоянии:
^s = - Ео |A \яе, • г12) Г 8(hco = E2-E{) C.63)
Таким образом, мы точно воспроизвели выражение A.856) для классического
электрического поля (испытав удовлетворение от полного согласия между теориями).
Теперь рассмотрим резонатор, содержащий п фотонов в моде /, но на этот раз
также и частицу, находящуюся изначально в состоянии |2>. Излучение в этом
случае соответствует переходу из состояния |2, п) в состояние |1, л) (рис. 3.3). В этом
случае вероятность перехода имеет вид:
C.64)
C.65)
C.66)
-a;^')\nf \{l\erf\2)\> 5(ho> = Ех - Ег)
При этом единственным ненулевым членом, связанным с фотонами, является:
и вероятность эмиссии в единицу времени приобретает вид:
Приведенное выше выражение показывает, что в излучении проявляются два
различных эффекта:
Глава 3. Квантовая механика электрон-фотонного взаимодействия
1. Механизм излучения, при котором скорость перехода пропорциональна
числу фотонов, уже присутствующих в резонаторе — это явление стимулированного
излучения, рассмотренное ранее.
2. Новый механизм излучения, проявляющийся даже тогда, когда в резонаторе
нет фотонов — называется спонтанным излучением. Скорость спонтанного
излучения дается выражением:
Ко, =-^1A №, ■ Г12) I2 *Ь» = ^ - я,) C-67)
Мы можем интерпретировать этот член как член, соответствующий скорости
эмиссии, стимулированной вакуумными флуктуациями Fr Под влиянием вакуумных
флуктуации частица может срелаксировать, освобождая фотон в моду п. Очевидно,
что частица может излучить этот фотон в любую из возможных резонаторных мод.
Полная скорость спонтанного излучения получается суммированием всех вкладов
C.67) для различных мод с частотой соп:
jond3k/ C.68)
Расчет этого интеграла использует выражение B.83) для плотности
электромагнитных мод в резонаторе и не представляет особых трудностей, так как мы можем расширить
область интегрирования по всему пространству, как это было оценено в B.А.25).
Таким образом, мы получаем скорость спонтанного излучения по всем
пространственным направлениям для квантового перехода с энергией h co0 в оптической
среде с коэффициентом преломления пор:
Скорость спонтанного излучения и излучатель-
ное время жизни для двухуровневой системы
где:
Л22 =Ы2 + М2 + Ы2 C-696)
Напоминаем, что это выражение действительно только в том случае, когда
фотоны излучаются изотропно.
Следует отметить несколько моментов:
1. Если частица находится на своем основном уровне |1), скорость спонтанного
перехода равна нулю, т. е. время жизни электрона на основном уровне бесконечно.
Таким образом мы разрешаем одну из величайших головоломок теоретиков в начале
столетия, а именно выясняем причину, почему все электроны на всех атомных орбитах
во вселенной просто не разрушаются на своих ядрах в течение наносекунд,
излучая при этом фотоны.
2. Степенная зависимость (со3) скорости спонтанной эмиссии предсказана
классической теорией Рэлея. Предполагая постоянным дипольный элемент, находим,
что время жизни спонтанной эмиссии становится меньше по мере возрастания
энергии перехода. Это является одной из причин, почему рентгеновские лазеры
труднее создать, чем инфракрасные лазеры. Безусловно, дипольный матричный
элемент также будет зависеть от энергии перехода, как это будет
проиллюстрировано примером, приведенным ниже.
3. Отсутствие постоянной Планка h в уравнении C.67) показывает, почему
классический подход, использованный в Дополнении 2.А мог бы быть успешно
применен в некоторых случаях.
Пример: излучательное время жизни в бесконечной квантовой яме
Рассмотрим квантовую яму на основе GaAs шириной а с бесконечными барьерами,
в которой:
3.6. Спонтанное излучение и излучателъное время жизни
т = 0,067т0
33
Мы видели в главе 1, что энергетический зазор ft co2l между уровнями и диполь-
ный матричный элемент zn даются соотношениями:
1 fc2 _ 2
. г-, г~. J ft 71
_ 24 a
C.70)
Таким образом, мы получаем выражение для излучательного времени жизни в
функции энергии перехода:
Уж1 т'с'Пге0
27 2
C.71а)
Зависимость времени жизни от энергии перехода в рамках простой модели
представлена на рис. 3.4. Для типичных значений энергии перехода, лежащих в
диапазоне от 50 до 250 мэВ, соответствующие времена жизни лежат в диапазоне от 10 не
до 1 мкс. Мы видим, что излучательное время жизни в этом случае
пропорционально со~2, а не <у~3 (как это показано выше), и является результатом зависимости
дипольного матричного элемента гп от энергии перехода.
со
ш
Q.
00
10"° -
10
0.001
3.01 0.1
Энергия перехода (эВ)
6 8
Рис. 3.4. Излучательное время жизни в функции энергии перехода между двумя
уровнями в квантовой яме GaAs с конечными барьерами
Приведенный выше пример иллюстрирует возможности классического подхода
к описанию спонтанной эмиссии. По этой причине мы вводим отношение
классического излучательного времени жизни /clas, которое дается B.А. 30) и квантового
времени жизни / :
2тг122а)
C.716)
Теперь все квантовые структуры (ионы, атомы, полупроводниковые квантовые
ямы ...) могут быть в первом приближении описаны моделью бесконечной
квантовой ямы шириной а с энергией перехода ft со и дипольным элементом г12,
определяемой соотношением:
Глава 3. Квантовая механика электрон-фотонного взаимодействия
fico = E2- El = N
и г12 = аа,
где N — целое число в диапазоне от 1 до 10, а а— действительное число порядка 10.
Следовательно, отношение (.lasAspon, таким образом, может быть записано в виде:
I^- = a2N27r2 -1
spon
Классическое выражение для излучательного времени жизни имеет, таким образом,
смысл, но с его помощью не удается описать такие эффекты, как стабильность
основного состояния квантовых структур, переходы, запрещенные правилами симметрии и т. д.
3.6.2. Скоростные уравнения с учетом спонтанного излучения
Теперь мы включим спонтанную эмиссию в скоростные уравнения в C.49) и C.50).
Для временного упрощения необходимых обозначений предположим до явного
упоминания, что в резонаторе существует лишь одна мода. Спонтанную эмиссию
и время жизни на уровне Г, будем учитывать введением членов ±N2/tspon ±NJTX и
+N2/T{ в скоростные уравнения для электронов C.49). В том, что касается C.50)
только доля Р спонтанно излученных фотонов будет переходить в резонаторную
моду. Соответственно, мы добавляем член /3N2 //spon в скоростное уравнение для
фотонов C.50), что дает:
N,=-
Я, = £^»/V, - £^»ЛГ, - ("■-*") C.72.)
V V т
spon
Скоростные уравнения
для резонатора
где / — время жизни в состоянии |2), что с учетом спонтанного излучения
принимает вид:
\ = J- + J— C.726)
/?называется коэффициентом спонтанной эмиссии. Введение членов 7Veq в C.72я)
гарантирует, что система возвращается в состояние термодинамического
равновесия, как только прекращается возбуждение.
Теперь нам остается только связать выражение для излучательного времени жизни с
оптическим поперечным сечением, что окажет нам помощь в ряде предстоящих
рассмотрений. В предположении, что спонтанное излучение изотропно (х12 = уп = zn), C.46) и
C.69) приводят нас к следующим известным уравнениям:
-*»»■)= о Д^ Mv-v2l) C.73)
Оптическое поперечное сечение
и излучательное время жизни
3.7. Полихроматические переходы
а(у)= -2 L(v -v2l)(Nl - N2) C.74)
8>™op'spon
Коэффициент поглощения
и излучательное время жизни
где Л — вакуумная длина волны, a L, как мы напоминаем, — функция Лоренца.
3.7. Полихроматические переходы
Уравнение C.63) дает нам вероятность поглощения для электромагнитной волны в
двухуровневой системе. Это уравнение может быть легко получено в рамках нестационарной
теории возмущений так же, как в рамках теории квантования электромагнитного поля.
Замена функции Дирака на функцию Лоренца возвращает нас обратно к соотношению
C.37), полученному с использованием формализма матрицы плотности. Другое
использование C.63) относится к случаю, когда переход происходит вследствие
произвольного распределения энергии pe(v). Эта ситуация имеет особе значение в
твердых телах, где оптические переходы происходят между энергетическими зонами.
Таким образом, рассмотрим объем F, в котором спектральное распределение
энергии pe(v) определено (предполагается, что ширина распределения больше, чем в
случае изолированных атомных переходов). В диапазоне от v до v + dv имеется
pe(v)Vdv/hv фотонов (где ре выражено в единицах энергии на единицу частоты и
единицу объема). Каждый фотон характеризуется вероятностью cropc/Vnop (смотрите
C.49)) индуцировать переход (либо за счет поглощения, либо за счет
стимулированного излучения). В этом случае полные скорости поглощения и
стимулированного излучения составляют:
}4^
о ор
C751
С использованием C.73) это уравнение может быть сразу проинтегрировано, чтобы
найти:
Р*. = Р«* = BaPt(vn) C.76)
где коэффициент Эйнштейна Вп дается соотношением:
Вп = - C.77я)
12 8*/<>spon
Коэффициент Эйнштейна для
поглощения и стимулированного излучения
Другим коэффициентом, введенным Эйнштейном, является скорость
спонтанного излучения:
Ап = — C.776)
spon
Коэффициент Эйнштейна для спонтанной эмиссии
Теперь скоростные уравнения могут быть обобщены с тем, чтобы описывать
полихроматические переходы между зонами шириной dv:
dtf, = -dN2 = AndN2 + (dW2 - dNx)Bnpe(y) C.78)
Скоростное уравнение Эйнштейна
где dNx и dN2 теперь обозначают дифференциальные величины dN{ = px(v) и
dN2 — px(v) dv и где p.s соответствует плотности заселенности на единичный частот-
Глава 3. Квантовая механика электрон-фотонного взаимодействия
ный диапазон переходов (в с см 3). В распоряжении Эйнштейна не было концепции
квантованного электромагнитного поля, с помощью которого можно было бы
установить соотношение C.78). Скорее он действовал эвристически, исходя из скоростных
уравнений C.49), которые позволили ему получить распределение Планка для pe(v)
при тепловом равновесии. Этот подход более детально исследован в дополнении З.В.
3.8. Повторное рассмотрение скоростных уравнений
Как можно легко заключить из проделанной до сих пор работы, физика электрон-
фотонного взаимодействия настолько же богата концепциями, как и
определениями. Таким образом, в этой секции целесообразно суммировать некоторые
принципиальные концепции, которые мы уже ввели, попутно указывая на их внутреннюю
связь. Все эти концепции возникают из переплетения подхода матрицы плотности,
нестационарной теории возмущений, а также квантования электромагнитного поля.
Мы рассмотрим резонатор объемом V, содержащий ансамбль двухуровневых
(|1) и |2» систем с плотностью N на см с энергией перехода h col2, дипольным
моментом Z>12, безызлучательным временем жизни Тх и шириной линии \/рТг
Взаимодействие такой системы с электромагнитной волной будет описано ниже.
3.8.1. Монохроматические одномодовые волны
Предположим, что электромагнитная волна является монохроматичной (т.е.
обладающей только одной частотой со). Скорость изменения числа частиц на уровнях |1)
и |2) дается соотношениями:
C.79)
где Ф — поток фотонов моды / (см 2 с 1). Время жизни т определяется как неупругой
безызлучательной рекомбинацией A/7^), так и излучательной рекомбинацией A/^):
- = — + — C.80)
Эти различные механизмы переходов схематически представлены на рис. 3.5.
Поперечное оптическое сечение стор дается выражением:
<ТорФ
и>
Рис. 3.5. Различные скорости переходов в двумерной системе, взаимодействующей с
оптическим полем. Механизмы релаксации показаны схематично в виде
взаимодействия с тепловым резервуаром
3.8. Повторное рассмотрение скоростных уравнений 10 5
а = Рпсо \/Т2
£о^"оР (оJ] - О)J + A / Т2J
или же опять в виде:
spon C.816)
где /spon — излучательное время жизни. Это время жизни представляет собой
вероят/spon
spon
ность в единицу времени испустить фотон в любую моду и дается выражением:
г = зЧ^Чр = 1
-~ 3*с>пео ~tspon C82)
Это приводит к поглощению (см):
а(со) = vJcoWt - N2)
Скоростные уравнения могут быть записаны также в виде: ' ' *
C.84а)
где п — число фотонов в резонаторной моде /, a d — скорость света в среде (= с/пор). Ъ есть
доля спонтанно излученных фотонов в моде /. Эти связанные дифференциальные
уравнения по Nl9 N2 и п являются сильно нелинейными и обусловливают многогранное
поведение лазерного излучения, исследованное в следующей главе.
3.8.2. Многомодовые монохроматические волны
Этот случай является простым обобщением C.84а) на все допустимые / мод резонатора:
C.846)
' ^spon
где, естественно, мы отметили, что поперечные сечения и коэффициенты
спонтанной эмиссии зависят от моды /.
3.8.3. Полихроматические волны
Если электромагнитная волна обладает спектральной плотностью энергии, которая
намного шире, чем спектральная ширина межуровневого перехода, то плотность
вероятности для стимулированного излучения или поглощения составляет:
((( 106 Глава 3. Квантовая механика электрон-фотонного взаимодействия
Щ
где Вп есть коэффициент Эйнштейна:
В этом случае скоростное уравнение может быть записано для каждой зоны частот
dv:
dTV, = -dN2 = AndN2 + (dN2 - &Nx)Bnpe{v) C.87)
(смотрите рисунок 3.6), где &N l и &N2 бесконечно малые уровни заселенности,
участвующие в оптических переходах мод pe(v)dv.
6,2 Ре М
Рис. 3.6. Оптические переходы, отражающие
скоростное уравнение Эйнштейна
Литература
A. Aspect, С. Fabre, and G. Grynbeig, Introduction aux lasers et a Foptique quantique, Ellipses,
Paris A997).
C. Cohen-Tannoudji, J. Dupont-Roc, and G. Grynberg, Atom-Photon Interactions:
Basic Processes and Applications, Wiley, New York A998).
R.P. Feynman, R.B. Leighton, and M. Sands, The Feynman Lectures on Physics,
AddisonWesley, Mass A964).
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
W.H. Louisell, Quantum Statistical Properties of Radiation, Wiley, New York A973).
P. Meystre and M. Saigent III, Elements of Quantum Optics, Springer- Verlag, Berlin A989).
ДОПОЛНЕНИЯ
К ГЛАВЕ 3
З.А. Однородное и неоднородное уширение:
когерентность света
В ряде мест мы видели, что два подхода могут быть использованы для описания
оптических переходов в двухуровневой квантовой системе. Один подход основан на
нестационарной теории возмущений (раздел 1.6), в то время как другой использует матрицу плотности
для того, чтобы учесть конечные времена жизни (уравнение C.43)). Заполним пробел между
двумя подходами, расширив функцию Дирака, использованную в первом из
перечисленных подходов, придав ей вид функции Лоренца L(v):
Нестационарное возмущение:
Рп=(а)=^тК\23(а>-а>21) (ЗАЛ)
Матрица плотности:
В рамках подхода с использованием D • Е гамильтониана возмущения | Wj2|= qE0rl2.
В самом деле, можно переписать (З.А. 1) в более общем виде:
Pn(co)=^Y\lVn\2g(co-co2]) CA.2a)
где#— функция формы линии, описывающая уширение перехода и подчиняющаяся
условию нормировки:
J g(co)dco = 1 (З.А.26)
Это уширение может быть обусловлено рядом причин, которые будут
исследованы ниже. Эти механизмы могут быть сгруппированы по двум различным
категориям — однородное и неоднородное уширение. В обоих случаях мы далее должны
рассматривать не единственную двухуровневую систему, а ансамбль таких систем.
З.А.1. Однородное уширение
В этом случае каждая из систем, образующих ансамбль, является идентичной. Все они
обладают той же самой боровской частотой колебаний и подвергаются тем же самым
механизмам уширения. Для такого уширения могут быть две причины.
1А. Уширение из-за конечного времени жизни (неупругие соударения)
Особенно изящный метод, позволяющий учесть конечное время жизни
заселенности каждого из уровней |1) и |2), заключается в том, чтобы считать, что каждая из
собственных энергий обладает мнимой частью:
Еп=псо + — (З.А.Зя)
В этом случае вероятность нахождения частицу на уровне \п) равна:
108 Дополнения к главе 3
Форма линии перехода пропорциональна амплитуде Фурье-образа волновой
функции, описывающей состоянии частицы |л). В этом случае функция формы линии
может быть легко найдена:
Av /2л:
(З.А.4)
где полуширина составляет:
+
2лг г, т7
(ЗА5)
1Б. Уширение из-за упругих соударений: временная когерентность
В этом случае мы рассматриваем каждую квантовую систему как подвергающуюся
хаотичным толчкам, которые приводят к потере ее фазы. Таким образом,
электромагнитное поле системы т может быть представлено в виде:
01 (ЗА6)
где фт(() есть результат стохастических процессов. Рисунок ЗА. 1 иллюстрирует такой
процесс. Результирующее электрическое поле, возникающее из вклада каждой из этих
идентичных систем, не имеющих какую-либо особую связь друг с другом, представляет собой:
E(t) = £ Em(t) =
(ЗА7)
Из теории стохастических процессов известно, что частотный спектр для данных
процессов, получаемый из оценки Фурье-образа электрического поля, есть:
(З.А.8)
-2л -
>► I
"coll
Рис. З.А.1. Амплитуда и фаза электрического поля, излучаемого квантовой системой
т, подвергнутой воздействию хаотичных «Пуассоновских» толчков.
Среднее время между толчками (или же время дефазировки) есть тсо]1.
ЗА. Однородное и неоднородное уширение: когерентность света
Он не имеет особого значения. Вместо этого понятия следует ввести концепцию
спектра автокорреляции:
с(*0=т- f |V(>)£(>'> 'W=-L f \E*(t)E(t + TymdtdT CA9)
где мы допустили возможность того, что электрическое поле имеет комплексную
компоненту. Таким образом, мы вводим автокорреляционную функцию первого порядка
которая дается соотношением:
) T) (ЗЛЛОа)
-Т/2
Корреляционная функция
первого порядка
Эта формула применима для достаточно больших значений Г, которые
обеспечивают сходимость статистической суммы. Существование такого предела (что мы не
будем демонстрировать) является одним из основных вопросов исследования
стохастических процессов, который называется эргодическим принципом. Этот принцип
утверждает, что существует эквивалентность между статистическим и временным
усреднением. Знак верхней черты означает статистическое усреднение случайного процесса.
Спектр автокорреляции G{co) и автокорреляционная функция связаны таким
образом соотношением:
)= — f
(З.АЛ06)
Таким образом, спектр автокорреляции имеет форму, близкую к форме Фуре-образа
автокорреляционной функции. Для обеспечения нормировки (ЗА 106) заметим, что для
г= 0 уравнение C.10а) дает:
Т/2
M)'y JE*(t)E(t)dt=\E(t]2
Т
-Т/2
что представляет собой среднюю интенсивность. В дополнение к этому, интегрируя
(ЗА 106), мы находим, что
^jAjm J (ЗА12)
Введем функцию формы линии g (со) как нормированный вариант C.10.6) (т. е.
без упоминания точного времени усреднения Т):
[G(o))d
что может быть записано с учетом (ЗА 12) и (ЗА 11) в следующем виде:
CA13e)
Форма линии и когерентность
первого порядка
где g^t) представляет собой временную когерентность излучения первого порядка:
W110 Дополнения к главе 3
©IV/- +Т/2
JE\t)E(t)dt
-Т/2
Уравнение (ЗА. 13а) представляет собой основной результат статистической
теории излучения. Форма линии спектрального распределения излучения является
Фурье-образом когерентности электрического поля первого порядка2. Это
положение известно под именем теоремы Винера—Хинчина.
Нам все еще необходимо уточнить процесс, описывающий толчки частиц со средним
временем между импульсами гсо11. Наиболее общим является процесс Пуассона с
вероятностью р(т)йт того, что атом не испытает соударение в течение времени г, определяемого:
p(T)dr = — e~'/Tco"dr CA14)
В этом случае автокорреляционная функция поля, излучаемого гп, приобретает вид:
(/||т j= xSq e e rm\// yj./\.Lj)
В этом уравнении единственный ненулевой вклад обусловлен атомами, имеющими
период между столкновениями, больший г, для которого 0m(t + т) = </>m(t), при этом другие
члены обладают нулевой средней величиной при оценке с суммированием по т9 так что:
£,(*•)= Е02е ~Ш»Т — (e-//T-d/ = £02е-!-'-г/т- (ЗА16)
В этом случае форма линии, показанная на рис. ЗА 12, дается Фурье-образом (ЗА 13а)
приведенной выше автокорреляционной функции:
T^J (ЗА17)
Возвращаясь к выражению, полученному с использованием матрицы плотности, мы
видим согласованность между формализмом матрицы плотности и статистической
теорией света (сравните уравнения C.43) и (ЗА 17)).
С учетом уширения из-за конечного времени жизни C А.5) и упругих соударений
(ЗА17), однородное уширение A v в этом случае дается соотношением:
Av=— (— + — + — I CA18)
З.А.2. Неоднородное уширение
В этом случае рассматриваемая среда состоит из ансамбля m различных систем,
обладающих различными боровскими частотами осцилляции of1... Интегральная форма линии в
этом случае представляет собой среднее по всем индивидуальным формам линии
(смотрите рисунок 3 A3):
2 По-видимому, существует столько же вариантов нормировки Фурье-образа, сколько
существует и авторов. Некоторые из них используют коэффициент 1/V2;r, другие 1/2ядля перехода
от со к t Третьи же авторы используют эти коэффициенты для перехода от t к со\
ЗА. Однородное и неоднородное уширение: когерентность света
-2 0 2
(<»-а>21)/2усо||
Рис. З.А.2. Автокорреляционная функция (a) gv(f) и спектральное распределение g(co)
(б) пуассоновского процесса, показанного на рис. З.А.1.
(ЗА 19)
где p(a)m)dcom есть число состояний системы с боровской частотой в диапазоне от
(от - dcom/2 до сот + da)m/2. В атомных системах имеется ряд причин для неоднородного
уширения линий, в частности, эффект Допплера. В оптоэлектронных материалах
уширение, как правило, возникает из-за флуктуации параметров синтеза данного образца.
Пример: неоднородное уширение бесконечной квантовой ямы
Рассмотрим бесконечную квантовую яму с шириной, которая изменяется в
пределах образца. Предположим, что флуктуации описываются гауссовским
распределением:
(З.А.20)
Рис. З.А.З. Неоднородное
уширение линии из-за
совокупного вклада нескольких
различных и независимых
систем. Каждая из систем
ответственна за оптические
переходы при различных
энергиях фотонов.
Ансамбль различных систем
Энергия фотона
Дополнения к главе 3
Здесь 6а является стандартной девиацией распределения ширины ямы. Как можно было
бы ожидать, это распределение должно приводить к подобному гауссовскому
распределению соответствующих боровских частот, которое может быть записано в виде:
-\(a>m-a>0f/2&o}
(ЗА21)
Уравнение A.49) позволяет нам рассчитать ширину результирующего распределения
боровских частот:
дсо
(О1Х
26а
(З.А.22)
В предположении, что ширина квантовой ямы и амплитуда флуктуации составляют
соответственно 6 и 0,5 нм,энергия перехода Е21 составляет 300 мэВ, флуктуация
энергии равна 8Е21 — 300 мэВ/6 или 50 мэВ. Эта величина меньше, чем для
конечной квантовой ямы, но тем не менее для того, чтобы этот фактор не превышал
влияние однородного уширения (с типичным значением 10 мэВ), следует
стремиться уменьшать амплитуду флуктуации вплоть до размеров монослоя.
Простым способом выявить, какой из механизмов однородного или
неоднородного уширения обусловливает характеристики системы, является
использование метода т. н. выжигания спектрального провала. В этом случае мощное
монохроматическое излучение (называемое накачивающим пучком) с частотой v0,
лежащей в пределах пика поглощения образца, смешивается со слабым излучением
широкополосного или перестраиваемого источника (зондирующий пучок) и
направляется на образец (смотрите рис. З.А.4). В том случае, когда уширение являет-
I
о
Энергия фотона
Рис. ЗЛА. Освещение неоднородной квантовой системы интенсивным
монохроматическим пучком излучения, которое насыщает поглощение подсистемы с
энергией перехода, равной энергии фотонов накачивающего пучка. Это
приводит к выжиганию спектрального провала в спектре поглощения
неоднородной системы при измерении вторичным зондирующим пучком меньшей
интенсивности. Указанный эксперимент называется выжиганием
спектрального провала, и он позволяет выявить природу (однородного или
неоднородного) уширения системы.
З.Б. Нестационарные возмущения второго порядка
ся неоднородным, единственным элементом, который будет оптически
насыщаться накачивающим пучком, является элемент т ансамбля, такой что v0 = vm2l. В
результате в спектре поглощения зондирующего пучка будет проявляться
дискретный провал на частоте v0. Если же однако уширение носит чисто однородный
характер, тогда все элементы системы будут насыщаться накачивающим пучком, и
полный спектр поглощения испытает ослабление по амплитуде.
Литература
М. Born and E. Wolf, Principles of Optics, 6th End, Pergamon Press, New York A980).
R. Loudon, The Quantum Theory of Light, Clarendon Press, Oxford A973).
A. Papoulis, Probability, Random Variables and Stochastic Processes, 4th Edn, Mc-Graw Hill,
New York A984).
З.Б. Нестационарные возмущения второго порядка
В главе 1 мы видели, каким образом нестационарный гамильтониан может
обусловить переходы между различными состояниями квантовой системы. Чтобы
показать это, мы записывали нестационарное уравнение Шредингера в базисе,
сформированном собственными состояниями системы и анализировали член за членом
все элементы дифференциального уравнения (уравнение A.70)). Сейчас же мы
представим альтернативный и более эффективный подход, обеспечивающий
графическую интерпретацию временной эволюции квантовой системы в условиях внешних
возмущений. Это позволит нам обобщить результаты на случай квантовых
переходов более высокого порядка, таких как двухфотонное поглощение свободными
носителями.
Начнем с нестационарного уравнения Шредингера, описывающего эволюцию
состояния |*F@) системы под влиянием нестационарного гамильтониана H(t):
Поскольку последнее уравнение является линейным, состояние системы в момент
времени tb связано с состоянием системы в момент времени ta линейным оператором
u(tb, ta), определяемым соотношением:
Этот оператор распространения должен удовлетворять уравнению:
H(tb)u(tb,tJ=ihj-u(tb,ta) (З.Б.З)
b
Если гамильтониан Яне зависит от времени (H(t) = #0), то в этом случае последнее
уравнение может быть легко проинтегрировано, что дает:
«(/„/в)=е-1(я-/йХ/*-'-) (З.Б.4)
(в этом уравнении экспоненциальный оператор ея соответствует ЪНп/п!).
Введем базис, сформированный собственными состояниями \т) оператора Но,
определяемыми Н0\т) = Ejm). Используя соотношение свертки:
i)(m\ (З.Б.5)
где / — оператор идентичности, оператор и может быть записан в виде:
«('.. О= 1«Ь, О = У \т)(т у^-° (З.Б.6)
Дополнения к главе 3
при этом сот соответствует боровской частоте Em/h.
Теперь мы предположим, что гамильтониан системы Но возмущен нестационарным
взаимодействием V(t) так, что Н= Но + V(t). В этом случае оператор распространения
является решением дифференциального уравнения:
[Щ + V{tb)]u (ta, 0= i*^-« (>*> О (З.Б.7)
ь
Беря в качестве образца для подражания замену переменных, которую мы
осуществили уже ранее в A.67), введем оператор С/в соответствии с соотношением:
«fc.O-e-'^'^H,/.) (З.Б.8)
Иногда такую замену переменных называют картиной взаимодействия. Подставляя
(З.Б.8) в (З.Б.7), получаем:
ihl/(tb, O= е-^°/Л*>-'«У(/>(О (З.Б.9)
Это уравнение может быть формально проинтегрировано, что дает:
U(t>, 0= I -±)с(НМН)и (t, tMt (З.Б.10)
ta
или в другом виде:
u(tb, ta)= u°(tb, О-1J u°(tb9 t)V{t)u (/, tjdt (З.Б.11)
Уравнение Шредингера для
оператора распространения
Где оператор и@) есть оператор распространения невозмущенной системы,
определяемый (З.Б.6). Уравнение (З.Б.11) не имеет практической пользы в том
смысле, что это просто интегральная форма дифференциального уравнения
Шредингера. В то же время оно предоставляет возможность графической интерпретации и
создает основу для итерационных вычислений, которые мы теперь и опишем.
Уравнение (З.Б. 11) может интерпретировано как ограниченный ряд по возмущениям
возрастающего порядка, при этом м@) соответствует первому члену этого многочлена.
В этом случае оператор распространения может быть записан в виде:
u(tb,O=u«%,O+uV(tb,ta)+uU(tb,O+... (З.Б.12)
где:
«@)('t.'«)=e-i("'/'x''-0 (З.Б.Ш)
»\, О= -{ J uu\tb,
(З.Б.136)
(З.Б.13*)
Сейчас мы уже можем интерпретировать графически эти уравнения:
а) В первом порядке wA): система изменяется с момента времени ta до момента
времени tx без взаимодействия (член м@)(^, О), взаимодействует с возмущением в
момент времени tx (член V(tx)) и продолжает эволюционировать без
взаимодействия вплоть до конечного момента времени tb (член ui0)(tbi t{)). Рисунок З.Б.1
дает графическую интерпретацию этой эволюции, известную как Фейнмановская
З.Б. Нестационарные возмущения второго порядка I15
Рис. З.Б.1. Фейнмановская
диаграмма возмущения первого порядка.
со
u{0)(tvta)
диаграмма. Поправка первого порядка к оператору распространения в этом
случае представляет собой интеграл всех этих элементарных вкладов по всем
промежуточным значениям времени tv Для детального и более углубленного
рассмотрения этого вопроса читателю рекомендуется ознакомиться с шедевром Ричарда
Фейнмана: The strange Nheory of Light and Matter A985).
Исходя из (З.Б.136) мы можем рассчитать поправку первого порядка к
состоянию системы:
где \f) = |*F@)(f = 0)) есть начальное состояние системы, а также рассчитать
скорость переходов между состояниями |/) и \f). Затем мы могли бы возвратиться к
более ранним результатам раздела 1.6, но оставляем это в качестве упражнения
читателю. Теперь мы обратим наше внимание на члены разложения второго
порядка. Взаимодействие второго порядка играет принципиально важную роль, когда
взаимодействие первого порядка дает нулевую скорость перехода (как это имеет
место в случае запрещенных переходов).
б) Во втором порядке: интеграл (З.Б. 13 в) может быть интерпретирован следующим
образом. Система переходит от ta к tv взаимодействует в момент времени tx затем
переходит от tx к tv вновь взаимодействует в момент времени t2 и переходит к tb
без взаимодействия (рис. З.Б.2).
В (З.Б. 13 в) мы заменяем выражение для невозмущенного оператора м@) на его точное
определение в соответствии с (З.Б.6), что дает:
о)=
(З.Б. 14)
CD
Q.
00
Рис. З.Б.2. Фейнмановская
диаграмма для
возмущения второго порядка.
(((Мб Дополнения к главе 3
Поправка второго порядка к начальному состоянию |/) = |*Р@)(/ = 0)) есть
или:
П '-0 '>=0 ' " (З.Б.15)
что после перегруппировки членов может быть записано следующим образом:
= ^21^)е""" =7 /ТХ^^^Ь)^^" <«|^('^'>^ kd/2 (З.Б.16)
/ 0 OL " J
В последнем выражении мы узнаем разложение состояния |^2)@)по всем возможным
конечным состояниям ]/), т. е.:
(З.Б.17)
Сейчас самое время детализировать потенциал взаимодействия V(t). Предположим,
что V(t) обусловлен вкладом двух осциллирующих источников:
K.c. (З.Б.18)
Подставляя вьфажение для V(t) в (З.Б. 17), замечаем, что cf(t) будет суммой различных
вкладов la)v 2со2, со{ + со2, сох — со2.
Сначала поинтересуемся суммой частот сох + со2 (что соответствует двухфотонному
переходу). Вьфажение (З.Б. 17) в этом случае приобретает отчасти неудобный вид:
% % Xе'- (ЗБ19)
где каждый элемент С7 j n получается интефированием (З.Б.17) или:
K)
Мы предположим, что однофотонные переходы являются нерезонансными (сотф cofn
cofn ф C0j), в то время как двухфотонные переходы близки к резонансу, т. е.:
Ef-E, =ha)]+hco2 (З.Б.21)
В этом случае в выражении (З.Б.20) доминирует первый член в скобках. Конечная
амплитуда cf(t) принимает вид:
В этом выражении мы узнаем вопросы, обсуждавшиеся в разделе 1.6. Для больших
промежутков времени вероятность \cAt)\2 нахождения системы, изначально
находящейся в состоянии |/), в состоянии \f) стремится к (смотрите A.77) и A.78)):
Ш-jr
Ея-Е,-Е,
27tiS{a>fi = o),+eOj) (З.Б.23)
З.Б. Нестационарные возмущения второго порядка
Как и в случае нестационарного возмущения первого порядка, мы узнаем, что
возмущение второго порядка обус/увливает постоянную скорость перехода Gfi,
которая в этом случае определяется соотношением:
6(Efi = ficOj + ficOj) (З.Б.24)
Второе золотое правило Ферми
Последнее выражение называется вторым золотым правилом Ферми. Каждый
член в сумме (З.Б.24) интерпретируется следующим образом: под влиянием
колебаний с частотой #>7система переходит из состояния |/) в состояние \п) с вероятностью
перехода, пропорциональной (л|К7|/). Поскольку энергия при этом не сохраняется,
переход может иметь место только в пределах временного интервала Af,
устанавливаемого вторым соотношением неопределенности (А/1 ~ й/Д^или h/(Eni — Ef)), и
который проявляется как весовой коэффициент в (З.Б.24). Рисунок З.Б.За
иллюстрирует двухфотонный процесс поглощения.
Рис. З.Б.З. Члены, дающие вклад в скорость двухфотонного перехода. Только
механизм, показанный на рисунке (д), является резонансным по отношению к
этому процессу и дает вклад в двухфотонное поглощение.
Теперь мы применим второе золотое правило Ферми к проблеме двухфотонного
B(о) поглощения. Рассмотрим двухуровневую систему (|1) и |2> с межуровневым
энергетическим интервалом h co2V Эта система подвергается воздействию
электромагнитной волны с частотой со. В этом случае гамильтониан возмущения имеет вид:
ш + к. с. (З.Б.25)
z
С учетом того, что в приведенном выражении отсутствует суммирование по
индексам /и /, скорость двухфотонного поглощения, определяемая (З.Б.24), дается
соотношением:
2/г
^ з
= 7со)
(З.Б.26)
Е„- Е, - Псо
Поскольку промежуточными состояниями могут быть только |1) или |2), получаем:
BИ2Х2И1) {
^2 - Ех - fico
-flQ)
и так как со21 ~ 2со\
2ж
(B\V\2)-(l\V\l)\2\V\l)
-О)
д(со21 = 2со)
l - 2со)
(З.Б.27)
(З.Б.28)
((A18 Дополнения к главе 3
и полагая:
(З.Б.29)
находим, что скорость перехода между двумя состояниями системы составляет:
(<у21 -со)
Таким образом, даже если переход |1>—> |2>не разрешен в первом порядке, двухфотон-
ный переход разрешен до тех пор, пока элемент Sl2 не равен нулю (т. е. до тех пор, пока
система асимметрична). Осциллирующая волна с частотой со испытывает
ослабление интенсивности /; (= есЕ2/2пор) во время распространения, равное:
(З.Б.31)
где Nx и N2 соответствуют плотности заселенности своих соответствующих уровней.
Подставляя (З.Б.ЗО) в (З.Б.31), мы видим, что поглощение может быть записано в виде:
£'---"■
(З.Б.32)
где /? представляет собой коэффициент двухфотонного поглощения, определяемый
соотношением:
2 2 Т~, ^ и VW21 ~ ^w/ (З.Б.ЗЗ)
€ С П \С02Х -СО)
Коэффициент двухфотонного
поглощения
Эта теория без труда может быть обобщена для трактовки двухфотонных
переходов в полупроводниках. В этом случае (З.Б.ЗЗ) должно быть проинтегрировано
по всей зонной структуре с использованием процедуры, изложенной в другом
контексте в главе 5. В таблице З.Б.1 представлены коэффициенты двухфотонного
поглощения в различных материалах. Двухфотонное поглощение имеет очень важное
значение, так как оно ограничивает плотность оптической мощности излучения,
которое может распространяться в оптоэлектронных компонентах (например в
лазерах, модуляторах и т. д.). Двухфотонное поглощение может использоваться также
и для оптической защиты от избыточных лазерных пучков.
Табл. 3.1. Коэффициенты двухфотонного поглощения для различных
полупроводниковых материалов. Показанный разброс по величине /? обусловлен большими
экспериментальными трудностями, связанными с измерением этого параметра
Материал
ZnSe
GaAs
CdTe
ZnTe
InSb
Длина волны (мкм)
0,532
1,064
1,064
1,064
10,6
Р (см/ГВт)
5-6
23-26
15-25
4-5
5000
З.В. Коэффициенты Эйнштейна для двух предельных случаев
Пример
а) Рассмотрим лазер на основе GaAs с волноводным слоем с толщиной 0,1 мкм и с
шириной 5 мкм. При внутренней мощности излучения 500 мВт плотность
мощности /0 излучения составляет 107 Вт см, что приводит к двухфотонному
поглощению /?/0 (/?= 25 см ГВт) или к паразитным потерям амплитудой 0,25 см. Это не
является пренебрежимо малой величиной, при этом двухфотонное поглощение
ограничивает уровни мощности излучения, которое может легко распространяться
в волноводах на основе GaAs.
б) Брусок InSb толщиной 1 мм помещен перед фокальной точкой линзы, что обеспечивает
диаметр световой точки 0,5 мм или площадь освещенной поверхности 2 х 10 см2.
Мощность выходного излучения на выходе бруска дается в этом случае интегралом
дифференциального уравнения (З.Б.32):
-j—)- = /*/ (З.Б.34)
где /0 — мощность излучения на входе. При мощности 2 МВт (или плотности
мощности 1 х 109 Вт см) плотность мощности на выходе равна fi/d или 1/E х 103 см ГВт х
х 10 см), что равно 2 х 10 ГВт см~2. Это соответствует коэффициенту ослабления
///0 = 2 х Ю-3.
Литература
L. I. Schiff, Quantum Mechanics, 2nd Edn, Mc-Graw Hill, New York A955).
A. Yariv, Quantum Electronics, Wiley, New York A989).
An illuminating explanation of Feynman diagrams may be found in:
R. P. Feynman, QED: TheStnmge Theory of Light and Matter, Princeton University Press, NJ A985).
З.В. Коэффициенты Эйнштейна для двух
предельных случаев: квазимонохроматических
и широкополосных оптических переходов
Сейчас мы представим трактовку индуцированной и спонтанной эмиссии, которая
была дана Эйнштейном в 1905 году. Этот подход представляет значительный
исторический интерес, так как он демонстрирует силу направленного эвристического
рассуждения.
Рассмотрим двухуровневую систему в состоянии термодинамического
равновесия с резонатором, образующим черное тело. Энергия электромагнитных мод в
резонаторе характеризуется распределением спектральной плотности pe(v) (Дж см).
Поскольку фотоны в резонаторе находятся в состоянии термодинамического
равновесия, плотность их энергии дается распределением Планка B.79). Обозначим
через Gl2d v скорость перехода с уровня |1) на уровень |2) благодаря
электромагнитной энергии, заключенной в интервале dv, а через G2ldv — скорость обратного
перехода. Скоростные уравнения перехода A.85) показывают, что в интервале dv
заключена энергия pe(v)dv, которая должна приводить к скорости перехода Gndv
(напоминаем, что в Gn член |И^22| пропорционален Е2, что, в свою очередь,
пропорционально энергии электромагнитного поля). По определению коэффициенты
Эйнштейна В2Х и Вп являются таким образом коэффициентами
пропорциональности между скоростями переходов и плотностью энергии pe(v):
120 Дополнения к главе 3
В действительности система (З.В.1) является неполной. Мы должны добавить в
нее член, который фигурирует в спонтанной эмиссии:
G" = B"PXV) C.B.2)
G21 = B2lpe(v)+ Лп
При термодинамическом равновесии плотности заселенности уровней остаются
постоянными, а переходы от 11) к |2) должны быть равными переходам от |2) к 11) или:
N,BnPe<y)= N2{B2lPe{v)+ Ап) (З.В.З)
Как уже отмечалось, плотность энергии для мод в резонаторе при
термодинамическом равновесии ре( v) дается законом Планка B.91), так что приведенное выше уравнение
приобретает вид:
C.B.4)
(где мы ввели коэффициент преломления лор, чтобы учесть оптическую дисперсию среды
резонатора). Теперь при термодинамическом равновесии отношение уровней
заселенности для каждого из уровней дается соотношением:
где мы временно ввели вероятность того, что степень вырождения двух уровней g{ и
g2 может быть отлична от единицы. Подставляя (З.В.5я) в (З.В.4), получаем
самосогласованное условие:
hv> Al2(g2/gl)
r-f) CB56)
Это уравнение должно выполняться при любой температуре. Это возможно, если имеют
место следующие соотношения:
(З.В.6)
Вп с3
Из этих соотношений мы вновь получаем уравнение C.77), полученное в рамках
квантования электромагнитного поля так же, как выражение для спонтанной
эмиссии. Уникальная проницательность Эйнштейна (или гениальность) позволила ему
вывести соотношение между Aw В с использованием условий, накладываемых
частным случаем термодинамического равновесия черного тела, но характеризуемое
универсальной применимостью даже вне равновесия и являющееся
характеристикой самой квантовой системы. В этом случае скорости переходов (З.В.2)
приобретают вид:
Скорость переходов (в секунду) между двумя
уровнями, обусловленных электромагнитной волной
с широким спектральным распределением pe(v)
где ре( v) есть спектральное распределение энергии падающей электромагнитной волны.
Рассмотренный выше подход трактует полностью монохроматические
переходы, т. е. одночастотные переходы, наведенные электромагнитной волной с широ-
З.Г. Эквивалентность Ар- и DA-гамильтонианов и правило Томаса—Райха—Куна
ким спектральным распределением. Нам было бы интересно узнать: позволит ли
этот подход получить результаты, которые даются соотношениями C.73) и C.74)
описывающими поглощение и оптическое поперечное сечение в связи с
переходами между уровнями, обусловленными квазимонохроматической волной и
представленные лоренцовской функцией формы линии L{v). Для того, чтобы
выяснить это, нам необходимо лишь использовать тот же самый аргумент, который
позволил нам перейти от C.75) к C.76), т. е. ввести спектральную зависимость
скорости перехода Gf.j.
"■■■sssSf** <ЗВ8)
Спектральная зависимость скорости переходов
(безразмерной) между двумя уровнями из-за
воздействия квазимонохроматической волны с
плотностью энергии pv. Переход уширен лоренцианом L(v).
где pv (Дж/м3) есть плотность энергии фотонов с частотой v, которая дается
соотношением Iv= cpv/nop (Вт/м2). Уравнение получается интегрированием (З.В.8) по
широкополосному спектру, т. е.:
]'Л> (ЗВ.9)
Таким образом (З.В.7) и (З.В.8) представляют два крайних случая, которые
могут возникнуть при использовании скоростных уравнений.
З.Г. Эквивалентность Ар- и DA-гамильтонианов
и правило Томаса—Райха—Куна
Определенный ряд общих заключений по поводу различных величин, влияющих на
оптические свойства (силы осцилляторов, ...), может быть извлечен из
коммутационных свойств наблюдаемых р и г. В этом разделе мы будем обращаться только к
операторам, и это позволит отбросить символ «А», который в других случаях
позволял отличать операторы от наблюдаемых. Начнем мы с того, что покажем
эквивалентность Ар- и Dp-гамильтонианов.
Мы напоминаем, что два типа гамильтонианов могут использоваться для
описания взаимодействия между квантовой системой (описываемого гамильтонианом Но
= p2/2w + F(r)) и электромагнитной волной (смотрите C.12) и C.13)):
Гамильтониан Ар: W^(i) = - — A1(r0, OP
т (З.Г.1)
Гамильтониан D E: WDlft) = — #E(r0, t)
Для плоских волн векторный потенциал и электрическое поле даются
соотношениями C.5а) и C.6):
E(r0,0 = E0cos(kr0-u>0
Е (З.Г.2)
A±(r0,t) = -±sin(k го-Ш)
со
Напомним, что г0 обозначает положение квантовой системы, и оно может быть
принято за начало отсчета. Для того, чтобы упростить обозначения, мы можем
предположить, что А± и Е ориентированы вдоль оси Oz- В этом случае уравнения (З.Г.1)
могут быть записаны в виде:
WAp(t)= WAp cosat = —2—±pz coswt
m со
wde @ = wde sin cot = -qEoz sin cot
m со C r 3)
((A22 Дополнения к главе 3
Мы видели, что скорости переходов, которые входят в выражения для
поглощения, используют элементы типа (/ \z\i) или (/\р |/) Таким образом мы будем
искать связь между этими двумя членами. Для этого используем коммутатор z и Щ
2т т (З.Г.4)
Будучи спроектированным на состояния |/) и |/) уравнение (З.Г.4) приобретает вид:
Из этого соотношения может быть установлена связь между двумя матричными элементами:
Связь между матричными
элементами z и pz
Подстановка (З.Г.6) в (З.Г.З) дает:
f \i) CXJ)
Это соотношение устанавливает эквивалентность двух гамильтонианов только в
условиях резонанса. Сила осциллятора в рамках Ар — подхода записывается в виде:
Сила осциллятора для перехода 1 -> 2
с использованием Ар-гамильтониана
Предпочтительное использование матричных элементов гамильтониана DE C.40)
или Ар (З.Г.8) прежде всего зависит от контекста самого использования. В общем
случае мы можем сказать, что Ар-гамильтониан лучше подходит для рассмотрения
переходов, связанных с делокализованными состояниями (т.е. состояниями
импульса), что встречается при описании межзонного поглощения в полупроводниках. В то
же время DE-гамильтониан больше подходит для описания переходов между
локализованными состояниями (глубокие дефектные состояния, квантовые ямы и т. д.)
Теперь продемонстрируем еще другое следствие этих правил коммутации.
Рассчитаем сумму сил осцилляторов для переходов между |/) и всеми возможными
конечными состояниями |/):
(З.Г.9)
Это последнее уравнение может быть существенно упрощено. С одной стороны:
Предположим, что базис собственных векторов |/) является полным. Это означает,
что любое состояние системы \п) может быть разложено однозначно в этом базисе:
Выражение для гамильтониана через
собственные энергии и состояния
З.Г. Эквивалентность Ар- и D А-гамильтонианов и правило Томаса—Райха—Куна 123
Это последнее уравнение может быть объяснено с учетом того, что, если (З.Г.11)
выполняется для всех собственных состояний |/), оно также должно выполняться
для любого произвольного состояния \п). В этом случае мы имеем:
(З.Г. 12)
Второй член правой стороны (З.Г.9) может быть записан в виде:
1 \
(З.Г.13)
• -J /
Легко может быть доказано следующее соотношение свертки:
(З.Г.14)
Соотношение свертки для полного базиса
собственных векторов и наблюдаемых
где 1 есть оператор тождества. Таким образом мы имеем:
При использовании (З.Г. 12) и (З.Г. 15) уравнение (З.Г.9) приобретает вид:
7 = Щ.(/\zhoz -Hoz2\i) (З.Г. 16)
Теперь, исходя из (З.Г.4) можно записать:
lz,H0\z]=^bz>z]=^ (З.Г.17)
а также:
(>\lz,H0]z]i) = (i\{2zHoz - Hoz2 -z2H0)i) = 2(i\ZH0z - Hoz2\i) (З.Г.18)
поскольку (/|#0z2|i) и (i\z2H0\i) оба равны E.(i\z2\i). Подставляя (З.Г.17) и (З.Г.18) в
(З.Г.16), мы получаем:
Правило суммы
Томаса—Райха—Куна
В сочетании с формулой для поглощения в многоуровневой системе C.41) дает:
-^/^-*>,,) (З.Г.20)
Tf 2e0mcn
Правило суммы (З.Г. 19) может быть интерпретировано следующим образом:
классическое выражение для поглощения а= Nxq2n/B£Qmcri)L(v), которое может быть
получено в контексте модели упруго связанного электрона, остается действенным
в квантовой механике. Единственно, это поглощение распределено между
различными осцилляторами, а также переходам между разлными осцилляторами,
соответствующими переходам между различными квантовыми уровнями системы.
При этом в указанное распределение в качестве весовых множителей входят силы
осциллятора, калибрующие интенсивность каждого их переходов. Несмотря на
это, сумма этих сил осциллятора равна единице. Выражаясь более эмпирическими
терминами, если мы рассмотрим полную кривую поглощения для квантовой
системы, отношение интегрального поглощения к заселенности основного уровня Nx
составляет:
W124 Дополнения к главе 3
I a(co)d(o
Nx 2e0mcn
Оно то же самое для всех систем. Эта концепция раскрывает свою полную силу при
осознании того, что сила осциллятора может быть отрицательной (смотрите сноску
к C.41)). Мы возвратимся к этому аспекту позже при рассмотрении межподзонных
переходов в квантовых ямах.
Пример: силы осциллятора в бесконечной квантовой яме
Проиллюстрируем концепцию силы осциллятора на примере достаточно простого
случая бесконечной прямоугольной ямы. Мы видели в разделе 1.4.2, что
собственные энергии и собственные функции стационарных состояний для квадратной
потенциальной ямы шириной а с бесконечно высокими потенциальными барьерами в
О и ©о даются соотношениями:
(З.Г.22)
В этом случае матричные элементы </\z\j)даются интегралами:
а Г
/•I I а 2 Г . . к . . к , а \ 1 1 г /. .\ л
/Ш) = — Z Sin/ — г Sin у — Zdz - —Т\- 7Т--, ZT LCOSV — У>Г —1
(З.Г.23)
■■ ' ' ai a a *"Ll/-'T U + 'TJ
и:
(З.Г.24)
• (/-,■)'
где Д / —у) равно 0, если (/ —у) четное число и 1, если (/ —у) — нечетное число. В этом случае
сила осциллятора для перехода / -^у дается соотношением:
(З.Г.25)
- /1- |_ /ш" j|_ л: у _j') J
Таким образом:
Сила осциллятора для перехода
/ —> у в бесконечной квантовой яме
Мы можем проверить правило суммы, используя разложение в ряд для к1. Заметим,
что сила осциллятора сконцентрирована на переходах между наиболее низкими
энергетическими уровнями. Говоря более точно, сила осциллятора/р начиная с
основного уровня |1) уменьшается как 1/у4, при этом первые два последовательные
члена имеют вид:
/21=-Йг = 0,960
71 J (З.Г.27)
/41= .2^ = 0,030
ГЛАВА 4
ЛАЗЕРНЫЕ КОЛЕБАНИЯ
4.1. Введение
В главе 3 мы сумели показать, что среда, в которой мы можем достичь инверсии
заселенности (т. е. реализуется ситуация, когда плотность заселенности в
возбужденном состоянии превышает аналогичную величину для основного уровня),
обеспечивает оптическое усиление электромагнитной волны вблизи резонансной
частоты системы. В случае обратной связи при введении усиленного сигнала в среду
система естественно может быть переведена в режим генерации, что приводит к
лазерным колебаниям. Для получения инверсии заселенности мы должны ввести в
систему, по крайней мере, третий (и возможно четвертый) энергетический уровень.
(Как мы уже видели, под влиянием интенсивного накачивающего пучка
двухуровневая система будет насыщаться, не достигая инверсии заселенности). Таким
образом, цель этой главы заключается во введении концепций, необходимых для
расширения двухуровневой системы до работоспособной модели, способной описать
феномен лазерной генерации. При этом мы не будем тратить много времени на
обсуждение лазеров с атомными переходами, так как они в явном виде не
используются в нашей трактовке квантовых электронных свойств полупроводников. В то
же время будут сделаны два исключения, когда мы обратимся в дополнении 4.Д к
частным вопросам, связанным с лазерами с диодной накачкой, а также в
дополнении 13.Ж при рассмотрении квантово-каскадных лазеров.
4.2. Инверсия заселенности и оптическое усиление
4.2.1. Инверсия заселенности
Покажем, каким образом инверсия заселенности может быть достигнута за счет
переноса носителей заряда с более высоко лежащих уровней на верхний уровень
интересующей нас подсистемы. Для этого рассмотрим резонатор с объемом V,
заполненный идентичными квантовыми системами с плотностью п (см), каждая из
которых обладает произвольным числом уровней Е. (/ = 0, 1, 2 и т. д.). Нас будут
интересовать эффекты, связанные с поглощением и излучением вблизи резонанса
|1) —> |2) (т. е. переходы с энергиями фотонов hv ~ E2l = hv2l). Предположим, что
второй уровень заполняется каким-то (пока неидентифицированным механизмом)
со скоростью заполнения R^ (см~3 с). Это заполнение происходит либо за счет
возбуждения электронов непосредственно на уровень |2) или за счет рекомбинации из
более высоко лежащих уровней (смотрите рис. 4.1). В свою очередь, электроны
уровня |1) переходят на более низко лежащие уровни с временем жизни г1? а электроны
уровня |2) — на уровень |1) за счет спонтанной эмиссии (с скоростью = l/^spon), за счет
безызлучательной рекомбинации (со скоростью = 1/г21), а также они могут
переходить на другие более низко лежащие уровни (со скоростью = 1/ т20). На время
предположим, что ts n» г21. Скоростные уравнения, описывающие плотность
заселенности пх =NX/Vn n2 = NJV приведены ранее C.84):
((A26 Глава 4. Лазерные колебания
spon
1
И>
Рис. 4.1. Различные динамические механизмы для двухуровневой системы,
взаимодействующей с другими уровнями.
dt
«1 ~ — + R2
D.1)
Тем не менее, мы видим определенные различия между C.84) и D.1).
Во-первых, уравнение C.84) было получено в рамках модели исключительно
двухуровневой системы. В этом случае пх и п2 будут стремиться лишь к значениям,
определяемым термодинамическим равновесием между двумя уровнями. В D.1) не
проявляются подобные ограничения, так как введение дополнительных уровней снимает
указанное ограничение. Напомним далее, что сгор есть оптическое поперечное
сечение (см2), определяемое C.81а) или C.816) и связанное с коэффициентом
поглощения а (см) соотношением а= <тор (п{ — п2) и с усилением у соотношением
у= сгор(п2 — п{) где Ф — поток фотонов (см^с), при этом т2 — результирующее
время жизни на уровне |2>, определяемое соотношением:
1111 ,А„
— = — + — + D.2)
Т2 Т2\ Т20 'spon
Как уже отмечалось ранее, мы предполагаем, что уровни |1) и |2) отстоят
достаточно далеко по энергии от более низко лежащих уровней с тем, чтобы можно
было пренебречь тепловым заселением этих уровней в условиях отсутствия
накачки (т. е. n{q = я2еч = 0). В отсутствие любого фотонного потока hv2l (Ф = 0, что
позволяет нам говорить о холодном резонаторе), полагая dn{/dt =dn2 /dt = 0,
получаем стационарное решение уравнения D.1). Определим теперь различие
заселенности верхнего и нижнего уровней nd0 в отсутствие фотонного потока:
= п, -п, = Ял Л 1 -
D.3)
Из этого соотношения видно, что в том случае, когда время жизни на более низком
уровне Tj короче рекомбинационного времени жизни г21, мы можем достичь инверсии
заселенности. Присутствие этого члена означает, что в этом случае ситуация далека от
допускаемой термодинамическим равновесием, когда п2/пх = ехр(—Еп/к7) < 1.
Некоторые авторы говорят об отрицательной температуре. Однако следует
подчеркнуть, что в этой концепции мало практической пользы. Дополнительно мы
можем отметить, что чем короче становится г, по сравнению с г21, тем больше будет
плотность инвертированных носителей. Соответственно, в этом случае можно
достичь большей степени оптического усиления с меньшими усилиями.
4.2.2. Оптическое усиление и насыщение усиления
Как видно из уравнений C.50) и C.74), в условиях инверсии заселенности
происходит усиление оптического сигнала вблизи резонанса. В этом случае происходит
усиление интенсивности по мере прохождения пучка через среду в соответствии с
соотношением:
4.2. Инверсия заселенности и оптическое усиление 127
l(z)= Ioey{v)z D.4)
где y(v) — коэффициент усиления(см~1), определяемый уравнением C.74):
Оптическое усиление
и инверсия заселенности
где nd = п2 — пх в рассматриваемом случае есть различие заселенности в условиях
фотонного потока, a g( v) — функция формы линии, описанная в Дополнении ЗА. Напомним, что
eR = rPop есть относительная проницаемость среды, Я — длина волны в вакууме и tspon — время
жизни спонтанной эмиссии, определяемое C.82). Уравнение D.4) действительно только,
если коэффициент усиления у не зависит от положения (это, как правило, не имеет места,
что обсуждается далее в Дополнении 4. Б). Стационарное значение nd мы получаем из D.1)
с учетом того, что в данном случае Ф ф 0. При этом уровень инверсии заселенности
определяется соотношением:
где т^ — постоянная времени оптического насыщения, определяемая соотношением:
D.7)
Уравнение D.7) может быть также записано в виде:
nd = ^ D.8)
Инверсия заселенности
и поток насыщения
где Фл1 — поток насыщения, определяемый соотношением:
Ф 1 %7teR tspon l
sat 7^ л 1 Т^\ У*'-7)
Поток насыщения лазерной среды
Этот параметр во многих отношениях подобен параметру, введенному в C.56). Таким
образом, мы сразу получаем выражение для изменения усиления среды в функции
фотонного потока:
) D10)
Насыщение лазерного усиления
где у0 — усиление в условиях слабого потока или холодного резонатора, которое дается
соотношением:
Уо(у)= ndo°oP(v)= ndo-^~f—g(v) D.11)
Усиление лазерной среды
в условиях холодного резонатора
На рисунке 4.2. показано относительное изменение коэффициента усиления
среды у/у0 в функции нормированного оптического потока Ф/Фм1. Отметим
уменьшение усиления по мере возрастания оптического потока. Этот механизм по
очевидным причинам называется насыщением оптического усиления, при этом в его
((A28 Глава 4. Лазерные колебания
0 12 3 4
Нормированный фотонный поток
Рис. 4.2. Насыщение оптического усиления в двухуровневой системе в функции
нормированного фотонного потока Ф/Ф^,.
основе лежит выравнивание заселенности между уровнями, обеспечивающими
усиление, как только поглощение и стимулированная эмиссия начинают
доминировать над другими механизмами.
Пример
В таблице 4.1 приведены характеристики основных переходов, используемых в
твердотельных лазерах. Лазер на основе алюмо-иттриевого граната (YAG),
активированного неодимом, работает в основном на переходе,обеспечивающем длину
волны 1,064 мкм.
Табл. 4.1. Длина волны излучения (Лст), оптическое поперечное сечение (<хор), время
жизни спонтанной эмиссии (fspon), ширина линии (Av) и коэффициент
оптического преломления (vop) основных лазерных сред, имеющих
технологическое значение
Лазерная
среда
Nd3+:YAG
Er3+:Si02
Ti3+:A12O3
Аг+
Лет (мкм)
1,064
1,55
0,66-1,88
0,515
OopCCM2)
4 х10-19
5 хЮ1
3 хЮ9
3 хЮ2
'spon
1,2 мс
Юме
3 мке
10 нс
А|/
120 ГГц
4ТГц
100 ТГц
3,5 ГГц
Vop
1,82
1,45
1,8
1
Измеренное время спонтанной эмиссии /spon = 1,2 мс, а ширина перехода
составляет 120 ГГц. В резонансе оптическое поперечное сечение дается
соотношением C.73):
Л2 1
— = 4хЮ9 см:
Если мы предположим, что плотность инверсной заселенности п^ при малом
фотонном потоке по порядку величины составляет 1016 см, получаем, что лазерное усиление yQ
составляет:
Го ="</о0"ор =4х10 см
4.3. Трех-четырехуровневые системы
Соответствующее усиление при одном проходе в стержне длиной 20 см будет
пренебрежимо малым @,08). Тем не менее многократный проход усиленного
излучения через ту же самую среду способен обеспечить значительный
результирующий уровень усиления. В предположении, что т{ = 30 не, т2 = /spon и г
использованием D.9) мы получаем поток насыщения:
'spon C
пт = 2,1хЮ21 см21 с
Л
Эта величина соответствует плотности оптической мощности 390 Вт см~2. Для такого
уровня потока фотонов (сравнительно низкого) усиление уменьшается вдвое.
4.3. Трех-четырехуровневые системы
Перейдем теперь к более углубленному (по сравнению с рассмотрением в разделе
4.2) обсуждению механизмов накачки с тем, чтобы получить усиление между двумя
уровнями. А именно: рассмотрим системы с тремя или четырьмя уровнями. В связи
с этим уравнение D.1) нуждается в некоторой модификации для учета различных
механизмов рекомбинации, проявляющихся в таких системах. В этих двух случаях
мы будем искать выражения для инверсии заселенности холодного резонатора,
когда плотность потока усиленных фотонов hvn в резонаторе равна нулю (Ф12 = 0).
В этом случае выражения D.7) и D.10) будут действительны, как только уровни
инверсии заселенности nd0 будут известны.
На рис. 4.3 схематически показан эффект накачки и механизмы последующего
поглощения носителей и их релаксации, проявляющиеся в четырехуровневой
системе. Уровень |3) заселяется электронами, возбуждаемыми из уровня |0), и именно
процесс релаксации носителей |3) —> |2) ответственен за обеспечения инверсии
заселенности уровня |2). Заселенность уровня |3) дается соотношением:
где /^ является результатом оптической накачки носителей с уровня |0):
D.12)
/j3 _ W03(n0 - пЛ= сго03Ф03(«0 - пъ) D.13)
Фоз представляет собой поток фотонов, связанный с накачивающим пучком. В
стационарном состоянии плотность носителей на уровне |3) есть:
i
т32 « т21
f
f ^ ▼
f Т1 « Т21
И>
Ю>
т32 « т21
1
б
Рис. 4.3. Динамические процессы заселенности в трехуровневой (а) и
четырехуровневой (б) системах.
Глава 4. Лазерные колебания
Поскольку г32 очень мало, мы ожидаем проявление насыщения поглощения только
в условиях очень сильной накачки. Стационарная заселенность состояний |2) и |1)
дается соотношениями:
D.15в)
где мы пренебрегли переходами типа |3> ->11> или |2> -> |1) (вклады этих процессов могут
быть четко учтены, но это приведет к меньшей четкости общей физической картины
интересующих нас физических концепций). К этим трем уравнениям (т. е. к D.14) и D. \5а))
мы добавим еще закон сохранения полного числа частиц:
Это очень просто приводит нас к выражению для инверсной заселенности:
D.156)
D.16)
в предположении, что механизм опустошения уровня |1) очень быстр по сравнению с
другими механизмами. Заметим, что как и ожидалось, по мере того, как поток фотонов
увеличивается, инверсия насыщается вблизи г21/(г21 + 2г32), что близко к полной
заселенности п системы (г32 << г21).
На рис. 4.36 представлена также трехуровневая система. В этом случае
основное состояние системы также соответствует более низкому уровню, связанному с
механизмом усиления. Действуя аналогично приведенным выше рассуждениям в
этом случае мы получаем:
<Ф13г21
D.17)
где Ф13 относится теперь к накачивающему пучку фотонов. Сравнивая D.16) и D.17) мы
замечаем, что в трехуровневых системах существенно труднее добиться инверсии
заселенности по сравнению с четырехуровневыми. Это связано с тем, что в трехуровневой
системе уровень |1> не может опустошаться за счет спонтанных переходов носителей на более
низко лежащий энергетический уровень, и это в основном обусловлено
поглощением из-за пучка накачки. Рис. 4.4 иллюстрирует достигаемые плотности
инверсной заселенности в трех- и четырехуровневых системах в функции нормированного
потока фотонов Ф/Ф^, где Фм1 относится к фотонному потоку насыщения \/а rMt
для переходов между основным уровнем |0) или |1> или возбужденным уровнем |5».
0.5
1.0 1.5 2.0
Фотонный поток накачки
2.5
3.0
Рис. 4.4. Сравнение
плотности наведенной инверсной
заселенности в функции
накачивающего потока фотонов
для трехуровневой и
четырехуровневой систем.
4.4. Оптические резонаторы и порог лазерной генерации
Рис. 4.4 иллюстрирует также, каким образом в четырехуровневой системе
достигается инверсия заселенности для всех значений потока фотонов. В то же время в
случае трехуровневой системы инверсия реализуется лишь за пределами
определенного порогового значения накачивающего пучка фотонов, соответствующего
условию прозрачности.
Пример
Особое значение с точки зрения телекоммуникационных технологий,
заинтересованных в передаче оптических сигналов на длине волны 1,55 мкм, представляют
волоконные лазеры, легированные эрбием. В этом случае атомы эрбия вводятся в
волокно на основе двуокиси кремния (Er3+:Si02), что приводит к образованию
трехуровневой лазерной усиливающей среды. Характеристики системы Er3+:SiO2
представлены в таблице 4.1. К ним следует добавить оптическое поперечное сечение
для оптических переходов накачки <т13о =2 10~21 см2 и длину волны накачки при
hcou = 1,26 эВ (Лритр = 0,98 мкм). Условие прозрачности, которое должно быть
выполнено перед достижением оптического усиления, выполняется при:
O13sat = 1/B х 10~21 см3 х Ю-2 с =5 х 1022 см2 с
или
transparency = 5 Х 1(Р СМ' С~' Х ^26 ЭВ Х *>6 X 1019 « 104 Вт/СМ2
При использовании волокна с диаметром сердцевины 10 мкм приведенная выше
величина соответствует входной мощности 8 мВт, необходимой для обеспечения
инверсии заселенности и выполнения условия прозрачности.
4.4. Оптические резонаторы и порог лазерной генерации
Лазерная среда в условиях инверсии заселенности может проявлять себя как
усилитель. Таким образом, для реализации лазерной генерации нам необходимо лишь
вновь ввести усиленный оптический сигнал (то, что называется оптической
обратной связью). Опишем теперь условия, выполнение которых необходимо для
получения лазерной генерации. Рассмотрим лазерную среду протяженностью d с
входной и выходной поверхностью соответственно Ме и Ms, покрытую отражающими
зеркальными поверхностями с коэффициентами пропускания и отражения te и ге
для входного зеркала ts и г для выходного зеркала (смотрите рис. 4.5). Заметим, что
все коэффициенты отражения г могут быть записаны в виде V/te'*, где R —
отражение, а ф — оптический фазовый сдвиг, вводимый зеркалом. Дополнительно мы
можем предположить, что эта среда «теряет» фотоны за счет паразитного
поглощения, диффузного рассеяния, дифракции и т. п. Перечисленные механизмы
учитываются ведением единого коэффициента ослабления ар (см) и действуют против
оптического усиления. Рассмотрим путь электромагнитной волны Е = Еосхр i(cot —
he), покидающей зеркало Ме и направляющейся по направлению к выходному
зеркалу М$. На выходе из Ме волна описывается выражением:
Ех = E0teeio* D.18в)
Когда волна приходит к зеркалу Ms, мощность сигнала усиливается в ехр(^— ар)d
раз, в то время как ее интенсивность возрастает в ехр (у — ap)d/2 раз, при этом
она умножается на коэффициент фазового сдвига ехр (ikd). Часть волны (г)
отражается и передается через среду, получая при этом дополнительное усиление ехр
(у- ap)d/2 и фазовый сдвиг exp(ikd), при этом еще одна часть ге волны повторно
отражается входным зеркалом. Компонента электромагнитного поля после
кругового прохода между зеркалами может быть записана в виде:
132 Глава 4. Лазерные колебания
I
rs t,
1
Рис. 4.5. Механизм установления лазерной генерации в резонаторе. Электрическое поле у
входного зеркала, соответствующее волне, идущей направо, есть сумма
компонент электромагнитного поля, показанных в кадре рисунка. Понятно, что для
лазерной генерации необходимо выполнение условий по фазе и амплитуде.
Е2 = Eotererse e
е D.186)
Сигнал у входного зеркала является суперпозицией полей всех полей,
распространяющихся вперед и назад. Таким образом, он дается суммой Е= Е{ + Е2 + Е3 + — или:
Е = E0teei(Ot[\
■<w(
V2
Это суммирование является тривиальным и оно приводит к:
Е =
D.19)
D.20)
Выражение для электромагнитного поля расходится, когда знаменатель в D.20)
стремится к нулю. Условие достижения нуля есть условие феномена лазерной
генерации. Это условие могло бы быть получено исходя из требования, чтобы в
стационарном состоянии два выражения для поля при х = 0 (Eote и E0t/reeBik + r~ a)d) были
эквивалентными.
Таким образом, мы видим, что до установления режима лазерной генерации в резонаторе
должны быть удовлетворены два условия.
Условие усиления
Усиление в усиливающей среде должно превысить уровень различных потерь (а именно:
пропускание зеркал, диффузное рассеяние и т. д.) Это условие может быть представлено в
виде следующего неравенства:
|v,|e > 1
Таким образом, существует соответствующий порог, выше которого среда начинает
спонтанно генерировать. Этот порог дается выражением:
^threshold = ар ~ ~7 {ПШ = «г D'21Я)
4.4. Оптические резонаторы и порог лазерной генерации
где at — полный коэффициент ослабления. Другим образом выражение D.21а)
может быть записано в виде:
yftK-M=S-^»nM. D-216)
Оптическое усиление и порог
лазерной генерации
где Re и Rs — коэффициенты отражения зеркал. Отметим, что усиление фиксируется на
этом уровне, так как в соответствии с D.20) эта величина не может быть превзойдена.
Уравнение D.216) может быть переформулировано с использованием плотности инверсной
заселенности и D.11):
п =^nLpllnReR) D.22a)
threshold A2g(y) [ р Id e s)
или в максимуме лоренциана:
Это уравнение может быть записано в более выразительном виде с использованием
концепции фотонного времени жизни. Представим себе фотон, перемещающийся
вперед и назад по резонатору со скоростью с' = с/пор. Вероятность выхода фотона во
время определенного цикла обращения через резонатор в этом случае дается
выражением dap — In (r r). Эту вероятность можно также рассматривать как
соотношение между длиной резонатора d средней длины прохода и Л фотона перед выходом из
резонатора. Эта средняя длина является произведением скорости распространения
фотона с' = с/пор и его времени жизни в резонаторе г, которая дается выражением:
г =7 г-1 л- D.23в)
Время жизни фотона в резонаторе
Или, вновь предполагая малую величину паразитного поглощения ар, Re = 1 и Rs =1 - Ts
при пропускании выходного зеркала Г « 1:
*.~- тх~ D23б)
TsC Ts
rhght~~ вРемя> необходимое для того, чтобы фотон прошел расстояние между двумя
зеркалами. Уравнение D.236) является очень показательным и полезным соотношением для
инженеров, специализирующихся на лазерной технике. Оно непосредственно
показывает, каким образом время обращения фотона в резонаторе 2^t усиливается в случае
слабого пропускания зеркал 7\ В этом случае уравнение D.22) может быть записано в виде:
Плотность инверсной заселенности
при пороге лазерной генерации
В случае оптической накачки необходимая пороговая мощность является тем, что
необходимо для достижения инверсии заселенности (уравнения D.16) и D.17)).
Фазовое условие
Фазовое условие, которое приводит к нулевому значению знаменателя D.20)
представляет собой:
Глава 4. Лазерные колебания
kd + ф = qn, q= 1, 2, ... D.25а)
где ф — средняя величина фазовых сдвигов, вводимых зеркалами. Если мы
предположим, что оба зеркала металлические (ф = я), усиленными будут моды:
которые попадают в спектр усиления усиливающей среды (смотрите рис. 4.9). Мы
возвратимся к этому вопросу в разделе 4.6.
Пример
1. В случае лазера на основе Nd3+: YAG длина волны излучения составляет
1,064 мкм, ширина спектра усиления равна 120 ГГц. Коэффициент преломления
равен 1,82, время жизни спонтанной эмиссии есть 1,2 мс и мы будем считать
время жизни фотона в резонаторе равным 1 не (таблица 4.1). В этом случае
плотность инверсной заселенности при пороге генерации дается D.24) и составляет
«threshold = VD х 109 см2 х 10"9 с х 1,65 х 1010 см с) или 1,5 х 1017 см.
2. Рассмотрим секцию волокна, легированного эрбием, длиной 10 м и с
зеркалами на обоих торцах. Одно из зеркал имеет нулевое пропускание, в то время как у
другого пропускание составляет 1%. Время жизни фотона в пренебрежении
паразитным поглощением составляет г = 2 х 10 м/A0~2 х 3 х 108 м с~У1,45) или 9,6 мкс.
В этом случае плотность инверсной заселенности получается с использованием
оптического поперечного сечения, приведенного в таблице 4.1 (<тор = 5 х 10~21 см2):
"th^id= V[C х 1010 см c-yi,45) х 5 х 101 см2 х 9,6 х 10 с ]
или:
= 1,0х1015см.
4.5. Лазерные характеристики
4.5.1. Внутренние лазерные характеристики
и фиксация усиления
Рассмотрим лазерную систему в условиях оптической накачки с возрастающей
скоростью (т. е. скорость накачки R^ возрастает). В стационарном состоянии (т. е.
перед началом лазерной генерации) плотность инверсной заселенности холодного
резонатора дается nd0 уравнениями D.16) или D.17) в зависимости от того имеем ли
мы дело с трех- или четырехуровневыми системами. Усиление yo(v) среды дается
соотношением D.11). До тех пор, пока система остается ниже порога генерации,
плотность инверсной заселенности пропорциональна скорости накачки Я^, как это
следует из D.3). Теперь предположим, что уровень накачки системы превышает
порог лазерной генерации. В этом случае система начинает генерировать и поток
фотонов в резонаторе усиливается, насыщая плотность инверсной заселенности и
уменьшая усиление (смотрите раздел 4.1 и рис. 4.2). Рисунок 4.6 иллюстрирует
эволюцию этого эффекта. Уменьшение усиления прекращается, как только
усиление среды y(v) начинает находиться в точном балансе с резонаторными потерями
at возникающими из-за паразитных потерь (уравнение D.22)). В этом случае
стационарное состояние резонатора определяется фиксированным усилением, т. е.
условием, при котором y(v) = ar В результате плотность инверсной заселенности
также фиксируется на своей пороговой величине «threshold. Эволюция плотности
инверсной заселенности в функции скорости накачки представлена на рис. 4.7.
Используя выражение для насыщенного усиления j'(v) = ^(v)/(l 4- Ф/Ф^), мы
получаем выражение для лазерного потока фотонов в резонаторе в стационарных условиях:
4.5. Лазерные характеристики
0.01
0.1 1
Нормированный фотонный поток
10
Рис. 4.6. Механизм фиксации в лазерах. В начале накачки число фотонов в резонаторе
мало и усиление среды не насыщено. Плотность фотонов в резонаторе
постепенно возрастает до тех пор, пока усиление в среде не достигнет уровня
оптического насыщения, который поддерживает баланс с резонаторными потерями.
00
о
I
о
I
I
threshold
threshold
Рис. 4.7. Изменение плотности инверсной заселенности и плотности фотонов в
функции скорости накачки R. Отметим, что как только достигается порог
лазерной генерации, инверсная заселенность фиксируется на уровне Nthreshold, в то
время как плотность фотонов возрастает линейно с уровнем накачки ° Выше
порога дополнительная энергия накачки идеально преобразуется в
усиленный оптический сигнал.
Ф = \
О,
если
yo(v)>at
D.26а)
Отметим, что поток Ф относится к фотонам, распространяющимся в обоих
направлениях вдоль резонатора. Поскольку у0 = ndQo• и с учетом определения порога
лазерной генерации at = rthrcshoid = "threshoid' % D.2fo) может быть записано в виде:
[О,
если nd0 < п{
Ф =
ld0 ^ "thresold
- 1 I, если n
d0 > wthresold
D.266)
Представляется интересным записать последнее уравнение с использованием
плотности фотонов и мощности оптической накачки. Для этого введем следующие параметры:
^-
{136 Глава 4. Лазерные колебания
1
D.27)
которые помогают нам переписать D.26) в виде:
если R2 < Rthrtshold
Р =
531 /?
I ^threshold
Плотность фотонов
в функции скорости накачки
Изменение потока фотонов в функции скорости накачки также схематически
показано на рис. 4.7. Этот последний рисунок иллюстрирует несколько
особенностей лазерного излучения: существование порога, фиксации плотности инверсной
заселенности, усиления и линейное увеличение плотности фотонов выше порога.
Предложенный подход является сильно упрощенным, так как мы явно пренебрегли
спонтанной эмиссией. Более полный подход будет представлен в дополнении 4.А.
Наконец, отметим, что намного выше порога число фотонов в резонаторе
дается соотношением:
Р s Рш "'° =z£-"do= T~"do = *г*с D.286)
''threshold ^sat T2
Это последнее уравнение ясно иллюстрирует роль, которую играет резонатор.
Благодаря наличию оптического резонатора он способен хранить электроны в
возбужденных состояниях, что в конце концов приводит к генерации фотонов на один
электрон в количестве tJt2. Эти различные концепции повторно рассматриваются
в дополнении 4.Д при обсуждении работы лазеров с диодной накачкой.
4.5.2. Выходная мощность
Сейчас нас интересуют внутренняя плотность и потоки фотонов в лазерной среде.
Выходной поток представляет собой излучение, вышедшее через выходное зеркало
Л/ с пропусканием 7\ Чем меньше величина Г, тем больше отражение (Rs« 1 — Т)
и меньше лазерный порог. С другой стороны, если пропускание равно нулю, свет
вообще не может выйти из резонатора! Таким образом, с учетом обоих этих
обстоятельств существует оптимальная величина отражения. Выходной поток из лазера
Фех1 определяется просто, беря половину от внутреннего потока D.26) (с у четом
того, что поток мгновенно распространяется в направлении выходного зеркала),
умноженную на пропускание зеркала, что дает:
ф = ф
^ext 2 sat
Рисунок 4.8 показывает изменение выходного потока Фсх1 в функции 7\ Этот
график принимает максимальное значение для Тор, определяемое соотношением
Т3 = ^2y^d^2apd-\nRe - Bad -\nRe) D.296)
Другим полезным результатом является соотношение между числом фотонов в
резонаторе Р и мощностью внешнего излучения Ptxi для случая, когда применимо
D.236) (Re =1, Ts « 1, ар = 0). Для этого рассмотрим временной интервал АЛ В
течение этого времени доля dtsijd от полногр числа фотонов Р в резонаторе падает
на выходное зеркало (d есть длина резонатора), При этом лишь половина этих
фотонов имеет правильное направление распространения. Более того, лишь доля Г
4.5. Лазерные характеристики
Рис. 4.8. Внешний поток фотонов в
функции пропускания выходного зеркала
лазерного резонатора с полным
усилением 2yd величиной 0,5 и потерями lad
величиной 0,05. Обращаем внимание на
существование оптимальной величины
пропускания зеркала.
0.1
5 С
ц
1
|
а.
о
00
I ' '
1
2yd=05
2ad=0.05
\
0.0 0.1 0.2 0.3 0.4
Нормированное пропускание
выходного зеркала Г
этих фотонов, каждый из которых обладает энергией h со, сможет покинуть
резонатор, излучая при этом лазерную энергию Pcxtht величиной:
PThco
или:
, Р
С
hco
D.30а)
D306)
Мощность выходного излучения
и число фотонов в лазерном резонаторе
Пример
1. При полном усилении среды 2yd, равном 0,5, пренебрегая пропусканием
входного зеркала (Яе = 1), пред полагая, что полные паразитные потери 2 ad составляют
0,05 см, а также используя D.296), находим, что оптимальное пропускание
составляет 10%.
2. Рассмотрим лазер с газовым резонатором длиной в 1 м, снабженным
выходным зеркалом с пропусканием 0,5%.. Фотонное время жизни, определяемое D.236)
составляет те = 2 х 102 см/E х 10~3х 3 х 1010 см с) = 1,3 мкс. Число фотонов с
энергией 1 эВ в этом резона-торе, соответствующее мощности излучения в 1 Вт,
дается D.30) или Р = 1 Вт х 1,3 х 10~6 с/ 1,6 х 10~19 Дж = 8 х 1012 фотонов.
4.5.3. Спектральные характеристики
Генерируют только те собственные моды резонатора, которые удовлетворяют
фазовому условию D.25) и которые обладают усилением холодного резонатора yo(vq),
большим порогового усиления (yo(vg) > ?;hrcshold). Рисунок 4.9 иллюстрирует
допустимые генерирующие моды резонатора.
Поскольку межмодовый частотный интервал составляет c/2nd, максимальное
число мод дается отношением ширины полосы и межмодового интервала
(смотрите рис. 4.9) и определяется соотношением:
В
D.31)
c/2nd
Кроме того, действительное число мод зависит от природы механизма ушире-
ния формы линии перехода, ответственного за поглощение в любой данной среде
(смотрите дополнение З.А).
((Г 138 Глава 4. Лазерные колебания
Полоса пропускания, В
I
Частота
d2nd
Рис. 4.9. Максимальное число мод, усиливаемых резонатором, дается отношением
спектральной ширины и частотным межмодовым интервалом.
Однородное уширение спектра (смотрите дополнение З.А)
В этом случае уширение обусловлено механизмами фазовой релаксации,
представляемой коэффициентом A v в лоренциане. О форме линии можно сказать, что она
«монолитна» так как механизмы насыщения действуют на весь спектр поглощения,
что может быть записано соотношением:
1
Av /2/r
D.32)
Спектральная характеристика лазерного усиления представлена на рис. 4.10.
Предполагается, что в момент времени t = 0 система накачивается до уровня,
намного превышающего порог. При этом все допустимые моды vq с усилением,
выше порогового, начинают генерировать. Как только все моды начинают
усиливаться, эффект насыщения начинает стремиться уменьшить возможное
усиление каждой моды; огибающая усиления однородно ослабляется по амплитуде,
сохраняя при этом свое первоначальное спектральное распределение.
Интегральное ослабление амплитуды сохраняется до тех пор, пока единственная мода,
расположенная в непосредственной близости от максимума усиления, будет
способна выдержать режим усиления. Таким образом, лазерные колебания,
установившиеся в однородной среде, будут стремиться к одномодовому лазерному
функционированию.
На практике однородные среды могут проявлять многомодовое лазерное усиление.
За это может быть ответственен ряд сопутствующих эффектов. Наиболее частой
является ситуация, когда амплитуды стационарных волн в резонаторе варьируются
от точки к точке (как cos kz или sin kz). Таким образом, даже одиночная мода
испытывает различные уровни усиления в пределах резонатора даже в том случае, когда
спектр усиления однороден по своей природе (смотрите рис. 4.11). Описанная выше
ситуация называется явлением выжигания спектральных провалов.
Неоднородный спектр усиления (смотрите дополнение З.А)
Эту ситуацию понять сравнительно просто (рис. 4.10). В этом случае система состоит из
ансамбля независимых подсистем, при этом каждая подсистема характеризуется своей
собственной системой скоростных уравнений и своими характеристиками насыщения.
В этом случае каждая мода, допускаемая D.25), будет соответствовать максимуму в
спектре усиления в этом частотном диапазоне, что будет приводить к независимому усиле-
4.6. Резонаторные скоростные уравнения и динамические характеристики лазеров 13 9
Однородная среда
Неоднородная среда
Усиление
без зеркала
J I
J I
V-2 V-1
vo
J_
I
1 2 3
Разрешенные моды резонатора
I
J I
V-2
vo
I
I
1 2 3
Разрешенные моды резонатора
v
Лазерные линии
-10 1
Лазерные линии
Рис. 4.10. Спектры усиления и соответствующие лазерные линии, возникающие в
результате усиления в однородных и неоднородных средах ниже порога (а),
при пороге (б) и выше порога (в).
Рис. 4.11. Усиление, испытываемое
стационарной модой, зависит от
положения в пределах резонатора. Таким
образом, интегральная кривая усиления
неоднородным образом уширяется, что
приводит к многомодовому усилению
даже в том случае, когда
фундаментальные квантовые переходы по свое
природе являются однородными.
Периодически расположенные минимумы
кривой усиления вдоль резонатора
соответствуют явлению выжигания
спектральных провалов.
Зеркало
Зеркало
нию каждой из этих индивидуальных мод. Таким образом, лазерная генерация в
неоднородной среде по своей природе является многомодовой (смотрите рис. 4.10).
4.6. Резонаторные скоростные уравнения
и динамические характеристики лазеров
Скоростные уравнения D.1), введенные в начале этой главы являются
нестационарными дифференциальными уравнениями. Вплоть до настоящего момента нас
Глава 4. Лазерные колебания
интересовало стационарное поведение лазерного излучения. Теперь же обратим
наше внимание на динамические характеристики лазеров. Держа эту цель в уме,
возвратимся к четырехуровневой системе, иллюстрируемой рис. 4.3. Напомним,
что уровень |2) находится в состоянии инверсной заселенности за счет накачки
носителей с уровня |0) на уровень |3). Предполагалось, что рекомбинация
электронов с уровня |3) на уровень |2) является мгновенной и такой, что скорость
«подпитки» уровня |2> определялась скоростью накачки уровня |3>. Динамическое
уравнение, описывающее заселенность уровня |2) в этом случае дается соотношением:
^ = Л-^-аорФ(«2-«,) D.33)
Предположим, что время жизни носителей на уровне |1> достаточно мало так, чтобы
уровень |1> был практически незанятым в любой момент времени, т. е. nd = n2 — пу~ п2.
Уравнение D.33) может быть записано более выразительным образом за счет введения
инверсной плотности холодного резонатора (Ф = 0), определяемой выражением
nd0 = Rrr Плотность фотонов р связана с потоком Ф соотношением р = Ф/cf, а
оптическое поперечное сечение дается соотношением D.24), т. е. <тр ==l/c/wthreshoId7 так, что:
D.34)
Динамика плотности фотонов р определяется вкладами стимулированного
излучения в системе (+пасго]Ф) и потерями фотонов (диффузное рассеяние, остаточное
поглощение, потери на зеркалах, ...), что описывается временем жизни фотонов (тс/т).
Таким образом, с учетом той же замены переменных, что и в D.34) получаем:
dt Tc Tc "^«hoid D.35а)
Уравнения D.34) и D.35) образуют систему связанных (за счет произведения pnd в
D.34) и D.35)) нелинейных дифференциальных уравнений. Хотя эти уравнения и
не учитывают спонтанное излучение (смотрите Дополнение 4.А), они имеют такое
значение, что мы перепишем их вновь одно за другим:
сЦ
dt
dp
dt
nd
P
T
nd
p
T
p
n,
"d
"threshold
nd
D.356)
Связанные динамические
уравнения лазерного резонатора
Этот тип нелинейных уравнений приводит к чрезвычайно сложному и
хаотичному протеканию процесса. В связи с этим ограничимся исследованием некоторых
из наиболее простых случаев.
Во-первых, стационарные решения этих уравнений имеют место в случае:
• либо р = 0 и nd = nd 0, что соответствует подпороговому режиму;
• либоp*0,nd= "threShOld ир = (ndQ- A2threshold) т2/тс, что соответствует надпороговому
режиму с фиксацией.
4.6.1. Демпфированные колебания
Предположим, что в момент времени / = 0 система находится в состоянии
инверсной заселенности, при этом ndQ превышает «threshold (т. е. еще перед началом режима
фиксации — в следующем разделе мы увидим, как все это точно происходит).
Перепишем D.34) и D.35я) и введем следующие безразмерные константы:
4.6. Резонаторные скоростные уравнения и динамические характеристики лазеров
X = "" , Y = —£—, Хо = П"° , Т = —, и = Ь. D.36)
^threshold ^threshold ^threshold Tc T2
В этом случае уравнения приобретают вид:
D.37)
Для того, чтобы описать поведение лазера вблизи равновесия, определим
переменные хиу, описывающие выход системы из стационарного режима:
Y = и{Х0 -1)+ у
Пренебрегая членами второго порядка в ху, приходим к другой записи D.37):
'&-«(*.-о
% „ <439>
Эта система связанных линейных дифференциальных уравнений может быть легко
проинтегрирована. В этом случае система ведет себя как демпфированный
осциллятор с собственной частотой сог = 2я/Тг и временем релаксации г, определяемыми:
D.40)
I "threshold ) ~
Время релаксации и период
генерации в лазерном резонаторе
Рис. 4.12 иллюстрирует демпфированные колебания с начальной плотностью
носителей, вдвое превышающей пороговую величину, т. е. nd /«threshold = 2.
Указанные колебания являются результатом попеременного обмена энергией между резо-
наторными фотонами и носителями в двухуровневой системе.
Пример
Рассмотрим полупроводниковый лазер с типичным значением г2 на уровне 1 не
и фотонным временем жизни 3 пс. Предполагая, что первоначальная
плотность инверсной заселенности составляет nd0 = 2«threshold, находим период
генерации Тг = 2я>/C х 10~12 х 1 х 10"9)/B — 1) или 0,34 не. В этом случае время
релаксации составляет тг = 2 х 10~9/2 или 1 не, как это показано на рис. 4.12.
4.6.2. Демпфирование лазерного резонатора
модуляцией потерь (переключение добротности)
Опишем теперь метод, позволяющий превысить пороговую концентрацию
носителей в лазере (позволяющую добиться nd0 » flthreshold). С этой целью в начальный
период времени резонаторные потери искусственно увеличиваются до уровня,
обеспечивающего выполнение условий холодного резонатора. В этом случае концент-
|Tl42 Глава 4. Лазерные колебания
2.0
0.0
0.5
1.0 1.5
Время (не)
2.5
Рис. 4.12. Временная эволюция плотности фотонов в резонаторе в предположении, что
фотонное время жизни составляет 3 пс, а время жизни носителей г2 на уровне
|2) составляет 1 не. Предполагается, что в момент времени / = 0 плотность
инверсной заселенности ndQ вдвое превышает пороговую величину «threshold.
рация электронов на уровне |2) дается соотношением n2(t) = Rr2(l — е~'/Т2).
Длительность периода Та делается достаточно большой с тем, чтобы большинство
допустимых состояний |2) было занято (т. е. Та « п/R, где п — полная концентрация центров
излучения). Для временного введения таких потерь отражение выходного зеркала
может быть существенно уменьшено, например за счет использования ячейки Пок-
кельса (смотрите главу 12). В результате этого, добротность резонатора Q можно
модулировать или реализовать режим переключения добротности. Инверсная
плотность заселенности п. ~ п (/ относится к начальному моменту) на уровне |2) в конце
первого низкодобротного цикла очень велика по сравнению с фиксированной
инверсной плотностью wthreshold в процессе лазерного излучения (рис. 4.13).
Это же справедливо и для энергии, запасенной занятыми состояниями. Затем
резонатор переключается в состояние высокой добротности (например, за счет восстановления
большого отражения зеркал). Энергия, запасенная в резонаторе, затем освобождается, как
это описывается D.37). Для упрощения обозначений мы предположим, что время жизни
на уровне |2) остается очень большим по сравнению с фотонным временем жизни (т. е.
и « 1). В этом случае D.37) может быть переписано в виде:
D.41)
D.42)
Деля одно уравнение на другое, получаем:
*!-!--1
АХ X
что может быть легко проинтегрировано и с учетом использованных ранее
определений приведено к виду:
Р = «threshold ^ — -
11;
D.43)
Плотность фотонов р также может принимать переходные значения, больше тех,
которые допускаются стационарным числом фотонов в высокодобротном
резонаторе. Плотность фотонов достигает максимальной величины, когда dp/dt =0 в
уравнении D.41), т. е. когда п = «thresold:
4.6. Резонаторные скоростные уравнения и динамические характеристики лазеров
Лазер Акустико-оптическая
ячейка
■е
Q
t
3s* ^ t
threshold
w t
Рис. 4.13. Принцип демпфирования лазерного резонатора за счет модуляции потерь
(переключение добротности). В промежутке времени между 0 и Та за счет
ухудшения добротности вводятся значительные резонаторные потери(нап-
ример, с использованием акустооптического модулятора). В то время как
добротность резонатора Q искусственно поддерживается на уровне 2low,
уровень инверсной заселенности имеет возможность возрасти до значения л.,
превышающего wthreshold для резонатора, который в других условиях является
высокодобротным. После чего добротность восстанавливает свое прежнее
значение 0^» а энергия, запасенная во время фазы низкодобротной
подзарядки, выделяется в виде гигантского импульса.
/>тах = Щ 1 +
п,
-In
D.44)
когда «threshold << п., что часто имеет место. Теперь мы уже в состоянии рассчитать
максимальную мощность лазера по сравнению со стационарным режимом. Без
переключения добротности число имеющихся фотонов (/>cw где индекс CW относится
к непрерывному режиму) в резонаторе дается соотношением D.44) или />cw = Ятс,
где, как мы напоминаем, R есть скорость накачки, а г время жизни фотонов в
резонаторе с высокой добротностью. Максимальная плотность фотонов (pQS),
реализуемая при переключении добротности, дается D.44) или pQS = п. = RTa, когда,
как мы напоминаем, п. « п есть полная концентрация излучательных центров. В
общем случае время Та достаточно близко к времени жизни г. В результате этого
отношение выходной мощности в непрерывном режиме к мощности в режиме с
переключением добротности (смотрите рис. 4.14) составляет:
'QS _
• - -ii-» 1
г.
D.45)
-■ CW "threshold
Поскольку, как правило, времена жизни т2 и г имеют величину соответственно
1 мс и 1 не, то отношение D.45) может быть значительным. Следуя той же схеме
рассуждений, что и при выводе D-30), мы видим, что пиковая выходная мощность
импульса точно дается произведением полной плотности фотонов (которую мы
делим надвое, так как следует рассматривать только фотоны, двигающиеся в
направлении выходного зеркала), пропускания выходного зеркала Ts и площади
поперечного сечения лазерного резонатора:
|Г144 Глава 4. Лазерные колебания
I- t
п2 = Rtc •••••»•• п2 = Ят2
Непрерывный режим Триггерный режим
а о
Рис. 4.14. В лазере, работающем в непрерывном режиме, максимальная заселенность
электронами возбужденного уровня определяется временем жизни фотонов
в резонаторе г. В режиме с модулированной добротностью максимальная
заселенность определяется временем жизни электронов на втором уровне
т2, которое может быть намного больше те.
P^=t*v^T,An, D.46)
Пиковая выходная мощность лазера
с переключением добротности
Наконец, длительность лазерного импульса может быть получена численным
интегрированием нелинейного дифференциального уравнения D.41). В следующем примере мы
дадим короткую программу MATEMATICA, позволяющую рассчитать динамику
лазера с переключением добротности.
Рисунок 4.15 дает несколько примеров, из которых мы заключаем, что
типичная длительность импульса составляет величину порядка нескольких г s (времен
жизни фотонов), т. е. десятки наносекунд для лазерных резонаторов с длиной в
несколько сантиметров. Отметим, что модуляция потерь в резонаторе может быть
осуществлена пассивно (т. е., например, без внешнего приложения напряжения к
оптическому затвору). Это может быть осуществлено за счет размещения в
лазерном резонаторе насыщаемого поглотителя. Этот материал поглощает
электромагнитное излучение вплоть до определенного уровня интенсивности, за пределами
которого среда становится прозрачной. Таким образом, введение такого
пассивного элемента приведет к самопроизвольному переключению добротности
резонатора. В начале цикла характеристики поглощения в этом материале понижают
добротность резонатора, при этом в течение этого времени электрическая энергия
хранится в резонаторе, увеличивая плотность электронной заселенности
возбужденного уровня. Как только среда насыщается, резонаторные потери уменьшаются,
и стимулированное излучение начинает освобождать накопленную носителями
энергию в виде мощного оптического импульса.
Пример
Поскольку D.41) характеризуется нулевой плотностью фотонов в начальном
состоянии (У@) = 0), оно допускает в качестве решений стационарные уровни
инверсной заселенности X(Т) = 0 и нулевую плотность фотонов YG). Как показано на
рисунке 4.15, для моделирования эффекта переключения добротности мы должны
были бы ввести искусственные начальные условия (Y@) = 0,1).
Это обстоятельство подчеркивает физическую необходимость спонтанной
эмиссии для запуска механизма лазерной генерации. Программа MATEMATICA,
приведенная ниже, позволяет нам рассчитывать временные характеристики лазера с
модуляцией потерь. Она написана в предположении, что начальное условие X @) =2.
condition of Д0)= 2.
eq1=y'[t]==y[t]*(x[t]-1)
eq2=x'[t]==-x[t]*y[t]
sol=NDSolve[{eq 1 leq2,x[0]==2>y[0]==0.1}, {x[t] ,y[t]}, {t,0,10}]
plot=Plot[Evaluate[y[t]/.sol,{t,0,10}]]
4.6. Резонаторные скоростные уравнения и динамические характеристики лазеров
2.5
2.0
1.5
1.0 -
0.5 -
0.0
А' '
/ \
/ \
/ \^^
1 х
nJn threshold 5
niln threshold =3
niln threshold = 2
•
-
10
Рис. 4.15. Временная зависимость плотности фотонов р в лазере в режиме
переключения добротности для различных значений n./nthicshold выше порога генерации.
Три кривые соответствуют решениям дифференциального уравнения D.41).
4.6.3. Синхронизация мод
Сейчас мы рассмотрим особый случай динамической реакции неоднородной лазерной
среды. Мы видели, каким образом неоднородная среда может быть описана ансамблем
независимых осцилляторов, обладающих способностью генерировать в пределах всего
модового диапазона, допускаемого фазовыми ограничениями, приведенными в D.25).
В этом случае комплексное электромагнитное поле, установившееся внутри
резонатора дается суммой всех вкладов S = 2N + 1 независимых мод q:
E(x,t)=
q=-N
D.47)
Предположим, что спектр усиления имеет центр при v0 и обладает шириной
Av= BN + l)Sv, где Sv — частотный интервал между модами, допускаемыми
резонатором. Как мы видели в D.25), Sv = c/2nd так, что Sv = BN +l)/Tc = S/Tc (где
Г — время обращения фотонов в резонаторе, т. е. Тс = 2d/(c/n)). Поскольку нас
интересуют только нестационарные изменения электромагнитного поля, D.47)
может быть записано в виде:
E(t)= A(t)exp[2mvQt]
где амплитуда A(t) дается соотношением:
D.48fl)
D.486)
Амплитуды Aq априори не обладают какой-либо фазовой связью друг с другом —
их фазы фт являются хаотичными. Мы увидим в Дополнении 4.Г, что следствием
этого является то, что амплитудные и фазовые флуктуации выходного сигнала мно-
гомодовых лазеров могут быть значительными. Более того, если все амплитуды
идентичны (Aq = А), то средняя мощность лазерного излучения составляет BЛг + 1)у42 =SA2.
В этом разделе нас будет интересовать вопрос о том, что происходит с
поведением лазера, когда амплитуды различных мод обладают определенной фазовой
связью, накладываемой на них, т. е. фт =0. В этом случае мы говорим о синхронизации
мод. Далее мы увидим, каким образом этот режим может быть реализован
практически. Отметим, что огибающая временной зависимости электромагнитного поля в
соответствии с D.486) является хорошо определенной периодической функцией с
периодом Г. Говоря более точно, если мы предположим, что кривая усиления яв-
Глава 4. Лазерные колебания
ляется константой в пределах интервала Av (т. е. если Aq = А), то в этом случае
интенсивность волны дается выражением:
sinBN + \}rt/Tc
sin nt/Te
D.49)
Оптический сигнал лазера с синхронизацией мод содержит последовательность
(пачку) импульсов с интенсивностью 2(+1JА2, разделенных временными
периодами Тс, при этом ширина импульсов Грике дается соотношением:
Т 1
D.50)
pulse 2N + j
(смотрите рисунок 4.16). Таким образом, чем шире спектр лазерного усиления, тем
больше число мод, испытывающих усиление, и тем меньше длительность
генерируемых импульсов. Для получения ультракоротких импульсов используются
кристаллы сапфира, легированного титаном, обладающие шириной полосы усиления
500 мэВ и позволяющие генерировать импульсы длительностью 10 фс. Как мы
увидим, полупроводники с шириной полосы усиления в несколько сотен мэВ
также являются хорошими кандидатами для реализации лазеров с синхронизацией
мод. В таблице 4.2 обобщены ключевые характеристики выходного сигнала лазеров
с синхронизацией мод.
На практике (смотрите рисунок 4.17) синхронизация мод может быть
осуществлена за счет введения быстродействующего электрооптического затвора между
двумя резонаторными зеркалами.
Таким образом, пропускание света между двумя зеркалами возможно только в
течение коротких периодов времени, определяемых приложенным извне электри-
Табл. 4.2. Ключевые характеристики выходного оптического сигнала лазеров с
синхронизацией мод
Период
Ширина импульса
Средняя интенсивность
Пиковая интенсивность
с с'
т _ Т< - !
"- S Av
Т = SA2
/,ak =S2A2 =ST
S-/
/
Интенсивность
Рис. 4.16. Временная зависимость суммы S синусоидальных вкладов, разделенных по
частоте интервалом 1/7\ Результат представляет собой последовательность
импульсов шириной TJS, разделенных во времени интервалами Тс и имеющих
пиковую интенсивность в S раз больше усредненного по времени уровня.
4.6. Резонаторные скоростные уравнения и динамические характеристики лазеров
ческим сигналом. Единственной частью полной последовательности импульсов,
которая будет способна распространяться в резонаторе (и испытывать усиление в
лазерной среде) будет та часть, которая содержит моды, синфазные с модулированным
пропусканием электрооптического затвора. Эту ситуацию называют своего рода
выживанием наиболее приспособленных, при этом моды, которые не удовлетворяют
необходимым фазовым условиям, исключаются из процесса усиления. Описание этого
механизма с использованием электромагнитных лазерных уравнений дано в
Дополнении 4. В. В заключение отметим, что синхронизация мод также может быть
реализована с использованием насыщаемого поглотителя. Этот последний метод
используется для достижения синхронизации мод в полупроводниковых лазерах.
Пример
Рассмотрим стеклянный лазер на основе Nd3+:YAG. Коэффициент преломления
стекла пор составляет 1,5, а ширина перехода Av =3 х 1012 Гц. Период между
импульсами Тс составляет 2 м/2 х 108 м с или 10 не, ширина импульсов в режиме
синхронизации мод составляет Гри1$е = 0,33 пс, а число синхронизированных мод
S= 10~8 с/3,3 х 10~13 с или 30 000 мод. При средней мощности излучения в 1 Вт ее
пиковое значение составляет 30 кВт.
Электро-оптическая ячейка
и
2d/C
U
Рис. 4.17. При синхронизации мод лишь импульсы, синхронизированные с
открыванием электрооптического затвора через 2d/c\ будут способны испытать
усиление лазерной среды. Это эквивалентно своего рода естественному отбору
среди всех мод резонатора, при этом моды, не удовлетворяющие фазовым
ограничениям, исключаются из процесса усиления.
Литература
G. Grynbeig, A. Aspect, and С. Fabre, Introduction aux lasers et a I'optique quantique. Ellipses,
Paris A997).
P.W. Milony and J. H. Eberiy, Lasers, Wiley, New York A988).
B.A. Saleh and M. C. Teich, Fundamentals of Photonics, Wiley Interscience, New
York A991).
A.E. Siegman, Lasers, University Science Book, Mill Valley, CA A986).
J.T. Verdeyen, Laser Electronics, Prentice-Hall, Englewood Cliffs, NJ A989).
A. Yariv, Quantum Electronics, Wiley, New York A989).
ДОПОЛНЕНИЯ
К ГЛАВЕ 4
4.А. Эффект спонтанной эмиссии
и фотонная конденсация
Как упоминалось ранее в главе 4, мы пренебрегли влиянием спонтанной эмиссии
на лазерный эффект. Одним из следствий этого упущения, которое мы специально
отметили в разделе 4.6, является то, что стимулированное излучение не может
начаться, если первоначальное число фотонов в резонаторе равно нулю. Другими словами,
число фотонов р = 0 в моде 1 при плотности инверсной заселенности п = nd = const
дает допустимое решение D.34) и D.35). Теперь мы покажем, каким образом
спонтанная эмиссия может быть включена в лазерные уравнения и обсудим влияние
этих эффектов на лазерные характеристики. Для начала возвратимся к двум
связанным уравнениям D.34) и D.35), описывающим динамическую связь между числом
фотонов р в данной моде 1 и плотностью инверсной заселенности nd =п2 — п{ для
четырехуровневой системы в резонаторе:
D.А.1)
dt -R- т2
Ар р
At т
, Р
X
Р
п,
"d
^thresshold
nd
D.A.2)
Напоминаем, что R есть скорость накачки уровня |2), г есть фотонное время
жизни в резонаторе и «threshold = 1/с'гсгор — плотность инверсной заселенности,
необходимая для достижения лазерного порога. Предположим также, что время жизни
тх на уровне |1) достаточно мало для того, чтобы позволить нам пренебречь
плотностью заселенности пх (где nd ~ п2), и следовательно rMt = т2 (уравнение D.6)).
Спонтанная эмиссия вводится в D.А.1) включением l/fspon при расчете 1/г2, как это
можно увидеть в уравнении D.2). С другой стороны, в D.А.2) мы должны отразить тот
факт, что даже в отсутствии каких-либо фотонов в резонаторе (р = 0) фотоны могут
освобождаться через спонтанную эмиссию. В главе 3 мы видели, что скорость
эмиссии в двухуровневой системе может быть записана в виде W(P + 1), где Р
есть число фотонов (а не плотность фотонов), WP есть стимулированное
излучение и W — спонтанное излучение (уравнение C.66)). Таким образом, для
включения эффектов спонтанной эмиссии достаточно выразить D.А.1) и D.А.2) через
число, а не плотность (умножая на объем резонатора), и заменить Рна. Р + 1 в D.А.2),
при этом мы получаем систему связанных уравнений:
D.А.З)
Nd
threshold
Динамические уравнения лазера
с учетом спонтанной эмиссии
В D.А.З): Nd = ndV и Р = pV. Более того, эти уравнения предполагают, что
существует единственная мода в резонаторе, в которую переходят все спонтанно
излученные фотоны (т.е. коэффициент спонтанной эмиссии Д введенный в C.72),
равен 1). Теперь введем безразмерную переменную:
4.А. Эффект спонтанной эмиссии и фотонная конденсация 149
v threshold
и напомним, что:
г = R D.A.4)
D _ ^threshold . „ ____L_. P ^ у - "d (Л А 5)
Athreshold ~ > "threshold ~ ~ J ■'sat ~ ~ 5 Л ~ y-r.rb.^j
~2 С &орТс С ОорТ2 "threshold
При всех изменениях переменных для стационарного состояния D.А.З) может
быть записано в виде:
Из решения результирующего квадратного уравнения тривиально находится число
фотонов Р:
- D.A.7)
Число фотонов в резонаторе
в функции скорости
(безразмерной) накачки
Это внешне невинное уравнение в действительности подразумевает
существование достаточно любопытного физического эффекта, который мы теперь и
исследуем. Начнем с того, что отметим Р^ — очень большое число, как правило ~1010,
что придает уравнению достаточно необычный характер.
При уровне накачки, слегка большем порогового (г = 1 + S), член 4г/Ра1 под
знаком радикала мгновенно становится пренебрежимо малым по сравнению с d,
что приводит к Р = Рш{—1), а это как раз то, что описывается D.28). В случае
уровня накачки слегка выше порога (г = 1 — S) D.А.7) приобретает вид:
D.A.8)
/».-* +Л 1 + 2^ U-Hf^-^ D-A.9)
ИЛИ
Другими словами, если система находится в состоянии настолько ниже порога, то
число фотонов хорошо аппроксимируется соотношением:
Р = -^— D.А.10)
\-г
Таким образом, при переходе от накачки с уровнем на 1% ниже порога к
накачке с порогом на 1% выше порога число фотонов в резонаторе изменяется от 102 до
jPMt х 10 ~ 108. Это соответствует подлинной фазовой конденсации, что является
следствием бозонной природы света, если принять во внимание наличие члена Р + 1
в D.А.З). Рисунок 4.А.1 иллюстрирует поведение числа фотонов в резонаторе как
функцию приведенной скорости накачки г при Р^х = 108 фотонов.
Подчеркнем теперь важное следствие спонтанной эмиссии для динамики
лазерного резонатора, которое мы используем в дополнении 4.Г. Второе
динамическое уравнение в D.А.З) может быть переписано в виде:
Дополнения к главе 4
Рис. 4.А.1. Зависимость
числа фотонов в резонаторе от
уровня накачки при уровне
потока насыщения Рм1 = 108
фотонов.
ю9
10е
ю7
10е
105 -
1<Г
ю2
ю1
10°
0.0
1
III
1 1 1
0.5
1.0 1.5
Накачка
2.0
2.5
3.0
Или, вновь учитывая определения в D.А. 5):
D.A.11)
D.A.12)
где G — оптическое усиление при одном проходе света по длине резонатора (G~gd),
g — усиление на единицу длины (см), определяемое соотношением g = ndcrop,
а тХфх — время прохода света между двумя резонаторными зеркалами. Уравнение
D.А.12) можно легко решить, что дает:
Р =
D. А. 13)
Таким образом, даже в том случае, когда в резонаторе нет фотонов в момент
времени t - 0, механизм лазерной эмиссии будет запускаться спонтанной эмиссией
одного фотона в моду до тех пор, пока будет справедливо условие G > TUght/rc = 27
(усиление превышает потери на зеркалах).
Более того, уравнение D.А. 13) показывает, что фотонная заселенность
формируется шумом с характерным временем формирования ть, которое может быть
легко рассчитано в предположении, что Go » \/тс (Go есть первоначальное
ненасыщенное усиление), т. е. когда пропускание зеркала мало. В самом деле, в этом
случае D.А. 13) может быть записано в виде:
/> = е'/г*
D.А.14)
с характеристическим временем формирования лазерного процесса ть, определяемым:
Г4=^ = А^ = _1_ DА15)
^о /о -^ То**
Характеристическое время
формирования лазерного процесса
Теперь вспомним, что у0 есть ненасыщенное усиление лазерной среды.
Многими авторами вводятся другие параметры (и даже в большей степени
произвольно) для того, что мы называем временем формирования лазерного процесса. Это
есть время tb, необходимое, чтобы лазер смог генерировать излучение с измеримой
мощностью Рт, беря в качестве исходной точки мощность шума Ро. В соответствии
с D.А.14) это время формирования дается соотношением:
4. Б. Насыщение в лазерных усилителях
h = log(^m / Ро)tb = log(Pm / Ро)-Ц D.А. 16)
Время формирования
лазерного процесса
Обычно величиной, принимаемой для log (PJP0), является 30, что соответствует
пороговой мощности детектирования 1 мВт и мощности фотонного шума 10~16 Вт.
Пример
В том случае, когда лазерное усиление мало, время формирования может быть
достаточно большим по сравнению с другими характеристическими временами в
резонаторе. Если мы предположим, что лазерная среда характеризуется
ненасыщенным усилением величиной 0,01 см, а скорость света составляет с' = 2 х 1010 см/с,
то характеристическое время формирования ть = 5 не, а время формирования tb
составляет 30 ть, т. е. 150 не.
4.Б. Насыщение в лазерных усилителях
В главе 3, а потом вновь в главе 4 мы видели, каким образом оптическое усиление,
возникающее из стимулированной эмиссии, быстро насыщается. Это насыщение
описывалось D.10), и выражение для него вновь будет выведено в этом разделе.
Рассмотрим четырехуровневую систему (рис. 4.3), в которой носители в основном
состоянии |0) переводятся оптической накачкой (R) в возбужденное состояние |3).
Предполагается, что носители с уровня |3) мгновенно релаксируют на уровень |2),
который, в свою очередь, характеризуется большим временем жизни. После чего
начинает развиваться процесс стимулированного излучения, включающий излуча-
тельную релаксацию носителей с уровня |2) на уровень |1) с характеристическим
временем т2. И,наконец, предполагается, что последующий процесс релаксации
между уровнями |1> и |0> протекает мгновенно. Эта ситуация описывается
следующей системой дифференциальных уравнений:
D.Б.1)
где Ф — фотонный поток, а <тор — оптическое поперечное сечение для перехода
|2) -> |1). Стационарная плотность электронов N2 на уровне |2) в этом случае дается
соотношением:
N2 = ^ = ^ D.Б.2)
1 + Ф/Ф^ 1 + Ф/Фз*
где Л^о — малосигнальная плотность инверсной заселенности, a Osat — поток
насыщения \/аорт2. Усиление усиливающей среды в этом случае определяется
У = ^(^2 " ^Гили:
у = — D Б 3)
где у0 = сгорЛт2 является усилением холодного резонатора для среды, а
интенсивность насыщения определяется соотношением:
/«=— D-Б.4)
|f 15 2 Дополнения к главе 4
Напомним, что, как правило, эта величина достаточно мала. Например, при
поперечном оптическом сечении 4 х 10~19 см, времени жизни 1,2 мс и энергии перехода
h со = 1,16 эВ, /^ ~ 500 Вт/см2, что соответствует достаточно малой плотности
оптической мощности.
Рассмотрим теперь область лазерной среды длиной L и площадью поверхности
А, которую мы используем в качестве усилителя. С одной стороны мы введем
световой пучок с интенсивностью / и будем искать интенсивность пучка / на выходе
каскада усиления. В этом усилителе отсутствуют зеркала, которые могли бы
обеспечить оптическую обратную связь. Напомним, что если усиление в среде
распространения составляет у, то напряженность электрического поля пропорциональна
е^2, а его интенсивность е*. Поскольку усиление обладает зависимостью от
интенсивности вследствие эффектов насыщения (уравнение D.3.Б)) и поскольку
интенсивность есть функция координаты z, интенсивность света в среде является, таким
образом, решением дифференциального уравнения:
D.Б.5)
Это уравнение может быть легко проинтегрировано с тем, чтобы получить
зависимость интенсивности / от координаты z в среде в виде выражения:
J
D.Б.6)
На рисунке 4. Б. 1 представлено изменение интенсивности в функции координаты Z-
Заметим, что по мере того, как интенсивность возрастает, в функции
координаты, наряду с усилением, наблюдается насыщение среды. Принимая G в качестве
полного усиления усилителя, a (G =/ //) как малосигнальное усиление (Go = e*>L),
можем переписать уравнение D. Б.6) в виде:
D.Б.7)
Из этого последнего уравнения видно, что G быстро стремится к 1, когда
интенсивность света превышает его пороговую величину в среде. Приведенный ниже
пример проиллюстрирует изменение усиления G лазерной среды с
малосигнальным усилением 800. Заметим, что доступная величина усиления быстро
уменьшается с /. Так при плотности мощности оптического излучения на входе 882 Вт/см2
усиление составляет всего 4, а выходная плотность мощности равна 3530 Вт/см2.
Таким образом, насыщение является негативным и неустранимым эффектом, как
это сейчас мы постараемся объяснить.
Обозначим через /^ оптическую мощность, потребляемую усиливающей средой, т. е.
/disp = / — /. В этом случае выражение D.Б.7) дает:
Рис. 4.Б.1. Изменение
интенсивности / в функции
координаты z в лазерной среде.
Величина интенсивности
нормирована к значению интенсивности
света на входе усилителя Ie, yQ
есть усиление холодного
резонатора для данной системы, и
предполагается, что отношение
/у/м1 составляет 0,1
4. Б. Насыщение в лазерных усилителях
D.Б.8д)
Если пренебречь логарифмическим членом перед линейным членом в D.Б.6),
то в этом случае D. Б.6) может быть записано в виде:
D.Б.86)
D.Б.9)
или, вновь используя другой набор параметров, получаем:
N.JlQ)
= Nd0
Максимально достижимая мощность
излучения оптического усилителя,
ограниченная оптическим насыщением
Это последнее уравнение устанавливает тот факт, что максимальная мощность,
которую способен передать усилитель падающему световому пучку, дается
энергией ft со, запасенной каждым атомом в состоянии инверсной заселенности (с
плотностью NdQ) в течение времени т2.
Пример
При использовании в качестве усиливающей среды Nd:YAG с уровнем
легирования 1019 см максимальная плотность накопленной энергии в этом случае дается
1019 см х 1,16 х 1,6 х 10~19 Дж или 1,85 Дж см~3. Максимальная плотность
мощности, которая может быть передана падающему пучку составляет в этом случае
1,85 Дж см~3/1,2 мс или 1,54 кВт см3. В случае усилительного каскада длиной в 1 м мы
получаем таким образом максимальную плотность мощности в 154 кВт см~2.
Малосигнальное усиление составляет у0 = аор = 4 х 10~19 см2 х 1019 см3 = 4 см. Усиление
усилителя в функции уровней входной и выходной мощности, определяемой D.Б.7)
(при Go = 2 х 1 м х 4 см = 800), иллюстрируется рис. 4.Б.2.
Другим аспектом насыщения усиления в лазерных усилителях является
искажение формы импульса. Естественно, поскольку амплитуда импульса нелинейно влияет
на коэффициент усиления, различные части оптических импульсов будут
подвержены различному уровню усиления, что приводит к сильным искажениям импульса.
Этот эффект имеет большое значение в оптических волоконных усилителях и очень
важен для широкой гаммы практических применений в телекоммуникационных
технологиях — сейчас мы обсудим это.
Рассмотрим оптический импульс потока Ф1п@» входящего в волоконный
усилитель. Заселенность усилителя инвертирована до момента отсчета t = 0 так, что
скорость накачки R равна нулю во время усиления импульса в волокне. Более того,
Рис. 4.Б.2. Мощность,
передаваемая усиливающей средой, в
функции входной мощности /,,
нормированной по уровню
мощности насыщения.
Усиление холодного резонатора Go
составляет 800.
нГ 15 4 Дополнения к главе 4
мы пренебрегаем спонтанной эмиссией (слишком медленной) в течение
длительности импульса. Теперь обратим наше внимание на отрезок волокна между хих + Ах
в течение временного интервала между / и / + d/. Уменьшение скорости
заселенности N2(x, t) за счет стимулированной эмиссии под воздействием фотонного потока
Ф(х, t) дается D.Б.1), т. е. с учетом приведенных выше допущений:
^N2(x, t)= -о^Мг{х, гЩх, t) D.Б.10)
Пространственно-временная эволюция фотонного потока описывается
уравнением непрерывности. Сейчас мы повторно выведем его, поскольку это всегда очень
стимулирующее упражнение! В интервале Ах поверхностная плотность фотонов pph
связана с фотонным потоком соотношением Ф(х, t) = c'p(x, t), где d — скорость
света в волокне. Скорость изменения числа фотонов в интервале Ах дается суммой
потока фотонов на входе и скорости стимулированной эмиссии в интервале Ах за
вычетом фотонного потока на выходе, т. е.:
|гр р)рх,/) D.Б.Ш)
что приводит к уравнению непрерывности:
|-Ф(х, /)+ с'^-Ф(х, t)= <7opJV2(x, ф(к, /) D.
D.Б.Ш)
Уравнения распространения
импульса в лазерном усилителе
Выше мы повторно записали уравнение D.Б. 10), поскольку все, что нам
необходимо сделать для решения вопроса об искажении формы импульса из-за
насыщения в усиливающих волокнах, так это решить два последние связанные
нелинейные уравнения.
Подобно всем уравнениям распространения D.Б.11) могут быть решены в
системе эйлеровых координат. Это означает, что мы должны следовать за
распространением импульса «верхом» на фотонах, иначе говоря, вводя новую систему координат:
D.Б.12д)
X = X + c't
По определению плотность фотонов и инверсная заселенность в этих новых
координатах представляют собой:
ф(х,Г)=Ф(х,/)
D. Б. 126)
N2(x, 7) = N2(x, t)
Величина Ф (константа, /) «разделяет судьбу» импульса в процессе его
распространения в волокне. Якобиан трансформации системы координат может быть
предоставлен в виде:
д_=Ь_
dt " Э/
D.Б.12*)
dt ~ Эх Эх dt х ~ Эх Э/
Таким образом, новая система координат D.Б. 10) и D.Б.11) принимает вид:
4. Б. Насыщение в лазерных усилителях
D.Б.13)
Г) D.Б.14)
Распространение импульса
в лазерном усилителе в
движущейся системе координат
Уравнения D.Б.13) и D.Б.14) выглядят симпатичнее, чем аналогичные
уравнения в системе координат Лагранжа. В действительности же это обман зрения: все
сложности теперь переносятся на граничные условия, которые теперь становятся
комплексными, но в оставшейся части распространения мы пренебрежем этим
аспектом. Дадим им теперь интегральную формулировку D.Б.13) и D.Б.14), что в
действительности известно как модель Франца—Нордвика. С этой целью мы
интегрируем D. Б. 13) по длине волокна с маленькой хитростью использования
граничных условий при х = 0 и Зс = L (оставляя читателю задачу определения критериев
справедливости этих граничных условий):
где, по определению, N^t) есть интегральная инверсная заселенность по длине
волокна (см~2). Из D.Б.15) сразу получаем:
ФоиД/)= Фш(^)е = G[t)<&m\f) D.Б.16)
где G(t) — мгновенное усиление лазерного усилителя. Теперь D.Б.13) и D.Б14)
можно «слить» с тем, чтобы получить второе интегральное уравнение:
x=L x=L
£ f N2{x,7)ix=-\ -^Цх,7)dx = -\ФОШ -Ф,М D.Б.17*)
at J J ax
x=0 x=0
так, что:
ДгУУг@=-[Фош@-Фш@] D.Б.176)
dt
Последнее уравнение утверждает, что усиление потока в волоконном усилителе
равно уменьшению интегральной инверсной заселенности, что само по себе имеет
смысл. Теперь мы можем решить систему, образованную D.Б.16) и D.Б.176) с тем,
чтобы в первую очередь описать временную эволюцию интегральной инверсной
заселенности:
D.Б.18)
Вводя фотонный флюенс как временной интеграл фотонного потока:
D.Б.19)
п
мы получаем уравнения для описания временной эволюции интегральной
инверсной заселенности, мгновенного усиления и выходного фотонного потока:
#г@= N^ log G° _Y it) D.Б.20)
/(A56 Дополнения к главе 4
D.Б.21)
G0-(G0-l)e"
D.Б.22)
Уравнения Франца—Нордвика
где N^ есть флюенс насыщения, Go — ненасыщенное усиление усилителя (Go = <JopNTQ)
и NT0 — начальная интефальная инверсная заселенность или полный флюенс в
волокне (см). Эти три уравнения описывают искажение формы импульса в
лазерном усилителе. Например, если на входе в волокно вводится импульс
прямоугольной формы Фт@ = Фш, то, как показывает уравнение D.Б.22), выходной импульс
будет затянут с экспоненциальной постоянной времени е~^рф«1. В другом случае
(гауссовский импульс на входе) анализируется в качестве примера, который
приводится ниже, а результаты этого анализа иллюстрируются рис. 4.Б.З. На
представленном рисунке явно видно проявление эффекта искажения формы импульса.
^ 15х103 -
со
о
10-
5-
Выход
Вход (х1000)
I
-40
-20 0 20
Время, нс
40
Рис. 4.Б.З. Искажение формы
импульса в волоконном усилителе из-
за насыщения (смотрите пример).
Наконец, как в случае непрерывного (CW) режима, рассмотренного в начале
этого раздела, легко определить максимально достижимую энергию £disp, которую
можно извлечь из волоконного усилителя:
D.Б.23)
Этот расчет мы оставляем читателю в качестве упражнения.
Пример
Исследуем поведение волокна, легированного эрбием, длиной 2 м с внутренним
диаметром 8 мкм и уровнем легирования 7 х 1019 см~3. Длина волны излучаемых
фотонов составляет 1,55 мкм @,8 эВ), а оптическое поперечное сечение Ег3+ в
кварцевом волокне принимается равным 10~21 см. В этом случае флюенс
насыщения составляет:
Nm = 1/A0~21 см) = 1021 см.
Полный флюенс NT0, который можно извлечь из волокна, в соответствии с
D. Б. 15) составляет:
NT0 = 7 х 1019 см х 2 х 102 см = 1,4 х 1022 см
т. е. он в 14 раз превышает флюенс насыщения. Таким образом, следует ожидать
сильного искажения импульса. Полная энергия, извлекаемая из волокна D.Б.23)
составляет:
Edisp = 1,4 х 1022 см х 1,6 х 109 Дж х 0,8 эВ [3,14 х (8 х 10J см2/4] = 0,9 мДж
4. В. Электродинамические лазерные уравнения I5 7
Приведенная ниже программа MATEMATICA дает пример искажения гауссов-
ского импульса.
NO = 7.1019(*cm-3*); (<т=1.1021 (*cm-2*); hv = —1.6109;
Usat = — (*J/cm2'); Dfibre = 810~4 (* Sju m *) S = N^r Dfibre 2/4] r = 10(* ns *)
о
Ifibre = 200(* 2m *) GO = Exp[a NOIfibre] 10 = -(* IWinput *)
lin[t_]:=10Exp -[-] (*W/cm 2*)llin = 1O"9lojExp -[-
dt(* J/cm 2 *)
t_]: -^ flin[t]dt;Nrel = K /* Log|-
Usat £ a NO Ifibre |_(
GO
G0-(G0-i)ExpL-(9(t)JJ'
) = S10
GO-(GO-i)Expl-^(t)J
[linp,{t,-50,50}
PlotRange-» All, PlotStyle -> RGBColorfl, 0,0] DisplayFuction -> Identity];
p2 = Plot[lout,{t,-50,50}
PlotRange-> All, PlotStyle -> RGBColor[o, 1,0] DisplayFuction -> Identity];
Show[p1, p2, DisplayFunction -> $DisplayFu notion, AxesLabel ->
-> rt(ns)#,#Pout(wr}]
Литература
L. M. Frantz and J. S. Nodvik, /. App. Phys. 24, 2346 A963).
4.B. Электродинамические лазерные уравнения:
электромагнитные основы синхронизации мод
Вплоть до настоящего момента нас, в основном, интересовала плотность фотонов,
содержащихся в лазерном резонаторе, при этом мы мало внимания уделяли
волновой (электромагнитной) природе лазерного излучения. Напомним, что фотон есть
результат квантования электромагнитной моды в резонаторе. Однако, это не
освобождает нас от необходимости наложения на фотоны соответствующего набора
граничных условий, связанных непосредственно с самим резонатором. Таким
образом, точное описание лазерного резонатора требует решения уравнений
Максвелла, модифицированных таким образом, чтобы включить в них лазерный
эффект. В этом разделе мы представим элементы теории мод Слэтера, что позволит
нам понять расчетный метод и его приложение к синхронизации мод. Рассмотрим
резонатор произвольной формы и на время будем считать его полностью пустым.
Слэтеру удалось показать, что уравнения Максвелла для такого полого резонатора
допускают набор решений, которые образуют полный и ортонормированный
базис. Более того, эти решения {Ео, Нд} не зависят от времени и должны подчиняться
любым другим граничным условиям, накладываемым резонатором (например, в
случае граничных условий для металлических стенок, Ед должно быть
перпендикулярно их поверхности, тогда как На имеет только параллельную компоненту).
Безусловно, понятие ортонормированности следует понимать в терминах распределе-
(f 15 8 Дополнения к главе 4
ний, т. е. JpEe(r)EA(r)d3r = 5ab символы Кронеккера. Более того, элементы,
образующие двойной базис Слэтера, должны удовлетворять следующим соотношениям:
к Е (г) = V х Н (г)
а а а DВ1)
(Напомним, что Н — вектор напряженности магнитного поля, связанный с
магнитной индукцией соотношением Н = B/ju0. Заметим, что при таком определении
векторы Еа и На автоматически удовлетворяют уравнениям Максвелла в вакууме, т. е.
Еа = 0 и divHo = 0. В дополнение к этому напряженность электрического поля Еа(г)
должна удовлетворять граничному условию на поверхности:
п х Еа = 0 D.В.2)
где п — вектор нормали к поверхности. Легко показать, что условие D.В.2) и
определение Но в соответствии с D.В.1), в свою очередь, требуют
удовлетворения граничного условия:
п Н = 0 D.В.З)
Вспоминая, что VxVxA=V(VA) — V2A и используя D.В.1), находим:
УЕ.(г) + *.'Е.(г) = 0 DВ4)
V*H.(r) + */Н.(г) = 0
Таким образом, любая электромагнитная волна при анализе в рамках максвел-
ловских уравнений в любом резонаторе произвольной формы может быть
разложена по базису Слэтера, что автоматически приводит к удовлетворению граничных
условий. Таким образом базис Слэтера является более общим инструментарием для
описания фотонов в резонаторах сложной геометрии, для которых плоские волны
могут уже не являться правильными решениями для резонатора (и таким образом
не дают возможность построить базис собственных функций). Следуя Слэтеру
разложение по базису можно записать в виде:
Е(г, /) =
-4_/,в(/)Е,(г)
D.В.5)
где соа = kad. Последние два из уравнений Максвелла действуют на разложение,
приведенное в D.В.5), и их результат может быть суммирован в виде:
Ра =Яа
D.В.6*)
Ра = ~®аЯа
что является очень компактной записью с учетом экономии обозначений!
Исключая qa из этих двух уравнений, мы находим:
А+яв2А=0 D.B.66)
Последняя запись говорит нам о том, что временная зависимость конструируется
из функций, осциллирующих с частотами, которые удовлетворяют требованию:
в)а = к с'. К тому же, D.В.5) напоминает нам о том, что ра и qa являются
сопряженными переменными и их квантование приведет к появлению наблюдаемых,
которые не будут коммутировать. Базис Слэтера приводит к очень компактной
формулировке уравнений Максвелла для пустого резонатора произвольной формы. В то
же время остается еще проделать значительную работу по нахождению базиса {Efl5 HJ.
Но несмотря на этот недостаток, предлагаемый подход значительно упрощает
трактовку проблем, связанных с колебаниями в резонаторах.
4. В. Электродинамические лазерные уравнения
Теперь обратим наше внимание на электромагнитные поля в резонаторе,
заполненном лазерной средой с восприимчивостью % = %к + \%1т. Электромагнитные
волны в этом лазерном резонаторе являются решениями уравнений Максвелла:
VxE(r,/) = -|-B(r,/)
э/ D.В.7я)
Mo
где плотность тока свободных носителей заряда i(r, t) дается законом Ома:
Кг,/) = <тЕ(г,>) D.В.76)
Обратите внимание: здесь а— электропроводность, а не поперечное сечение! Ток
смещения D(r, t) дается выражением:
D(r, /) = J-[*E(r, /) + Plaser(r, t) D.В.7*)
at
В последнем уравнении Plaser есть вектор поляризации, связанный с резонансной
восприимчивостью лазерной среды, тогда как поляризация основной матрицы
(например, кристалл YAG в лазере на основе Nd:YAG) включена в проницаемость е.
Подставляя D.В.76) и D.В.7в) в D.В.7я) и проецируя уравнение D.В.7я) на базис Слэ-
тера, мы сразу находим:
yle dt J
D.В.8)
Таким образом, любая мода Слэтера не связана с другими. Затем мы продифференцируем
D.В.8) и используем соотношение сопряжения D.В.6), что приводит нас к уравнению:
^ ^^ [ D.В.9)
Если а = 0 и PIaser = 0, мы вновь получаем дисперсионное соотношение соа = kad с
новой групповой скоростью, определяемой d — с/пор. При этом член в dpa/dt
является членом демпфирования. Фотоны покидают резонатор с постоянной времени,
которая является ни чем иным, как временем жизни фотонов в резонаторе:
гс=- = -^ D.В.10)
е (оа
где, по определению, Q есть добротность резонатора. В дополнение к омическим потерям
D.В.76) мы можем включить в а также и другие эффекты, механизмы диссипации,
такие как пропускание зеркал. В этом случае необходимо, чтобы потери в
оконечных областях были усреднены по всему объему среды.
Предположим, что фотонное время жизни велико по сравнению с модовой
частотой соа или вновь допустим, что добротность резонатора Q очень велика.
Решениями D.В.9) без членов источника, очевидно, являются синусоидальные
функции с частотами о)а, которые медленно демпфируются членами типа e~t/r. Таким
образом, соблазнительно выразить решения D.В.9) в виде:
Ра(*)= р:1°Ч*Уш D.В.11)
где соа ~ а)ира*™($ являются слабо изменяющимися функциями (т. е., что 6pfow(i)/6t« co^f^ii)).
В этом случае мы подставляем D. В. 11) в D.В.9) с тем, чтобы получить дифференциальное
уравнение относительно pauov/(t):
^ |j ^|Lj3r D.B.12)
uf 160 Дополнения к главе 4
Уравнение D.В. 12) является наиболее общим уравнением для расчета
реального лазерного резонатора произвольной формы и с произвольным распределением.
Для облегчения нашей физической интерпретации этого результата временно
предположим, что в резонаторе существует единственная мода l.B D.B.12)
поляризация поля в лазере дается выражением:
D.В.Ш)
далее, учет D.В.5) и D.В.11) приводит к:
Р,азеГ(г, О = -t4*r + ^^Ге'-'ЕДг) D.В.136)
где x]aset — восприимчивость лазерной среды, введенная в разделе 3.3. Подставляя
D.136) в D.В. 12) и предполагая, что лазер находится в стационарном состоянии,
находим самосогласованное решение относительно j и со:
{(О2_ОJ) + {^_ = ^(Z* + fciJ D.B.14)
Условие D.В.14) является ничем другим, как условием лазерной генерации, при
этом действительная часть устанавливает условие для фазы, а мнимая часть
определяет условие для усиления. Например, последнее условие может быть записано в
виде а— (ое^с1т. Напомним, что C.36) связывает мнимую часть оптической
восприимчивости с усилением в виде:
Хы =2J~ D.В.15я)
где п — коэффициент преломления, а к —волновое число. Условие для мнимой
части D.В. 14) в этом случае может быть записано в виде:
У = — D.В.156)
стс
что является ничем другим, как условием генерации D.216). Мы можем подобным
же образом определить условие и для действительной части D.В.14). Мы находим,
что резонансная частота резонатора не является его собственным значением, но
скорее она слегка смещена дефазировкой, возникающей из-за дисперсии лазерной
среды. Это явление называется подтягиванием частоты.
Теперь мы используем базис Слэтера для более детального исследования
механизма синхронизации мод в лазерном резонаторе. Предположим, что в резонаторе
имеется устройство, позволяющее модулировать резонаторные потери (например
акустооптическая ячейка, ячейка Поккельса и т. п., ...), как это показано на рис.
4.17. Механизм описывается модулированными потерями сг(г, t), определяемыми:
а (г, t) = amfos{(omXt)AT) D.B.16)
Функция/(г) является произвольной, она может быть функцией вида/(г)= S(z — z<),
которая могла бы представлять затвор, помещенный в плоскости z = z^- Для
упрощения анализа исследуем отклик резонатора без учета лазерного усиления, т.е. без
члена источника Plaser. Включение этого эффекта усложнило бы необходимые
обозначения без особой надобности и немного дало бы взамен в том, что касается
дополнительной информации по интересующей нас проблеме. Сконцентрируем наше внимание
на механизме синхронизации мод, который не связан с лазерной генерацией. Само
собой разумеется, что в дальнейшем член Plaser надо будет вновь ввести для полного
описания синхронизации мод.
Уравнения, описывающие резонатор, в этом случае даются уравнениями Максвелла:
1 а D'ВЛ7)
— V х В(г, /) = а(г, /)Е(г, 0 + е-Е(г, /)
4. В. Электродинамические лазерные уравнения
Вновь используя тот факт, что VxVxA=V(VA) — V2A и предполагая, что Е
da/dt « дсгЕ/dt (что вполне разумно с практической точки зрения), приходим к
записи D.17):
V2E-/v7(r,/) — E-/iof^-yE = O D.B.18)
Используем теперь базис Слэтера, учитывая в D.В. 11) вьфажение дляpa(t), т. е.:
Е(г, /) = XT'А~ (ОеЧ'Еа(г) D.В.19)
Выражение D. В. 18) в базисе Слэтера дает:
^Г-1 I slow 2 2 # slow # slow ..slow j icuj
D.В.20д)
Использование D.В.З), предположение большой величины добротности б для
резонатора (а/е « со) и слабого изменения /?dow (dtu™/dt« соарйол") позволяют нам пренебречь
членом pfow. В этом случае уравнение D.В.20я) приобретает вид:
D.В.206)
Затем мы можем использовать выражение D. В. 16) для модуляции потерь и
спроецировать полученное уравнение на моду Слэтера Е (г), что дает:
?(
D.B.21)
где S — интеграл перекрытия:
aq
Зщ = — [/(r)E0(r)E9(r)d3r D.B.22)
я v
Хотя внешне это и не совсем очевидно, но уравнение D.В.21) фактически
является тем уравнением, которое мы ищем. Оно показывает, каким образом
возмущение стт1 связывает изначально независимые моды одну с другой. Поскольку
интегрирование D.В.21) приводит к членам вида \/(соа ± сот1), ощутимые вклады будут
возникать только при coq « соа ± сотГ Таким образом, единственными модами,
предназначенными для «выживания» (по аналогии с механизмом «выживания
наиболее пригодного», упомянутого ранее) будут те моды, для которых частотный
интервал близок к частоте модуляции сот1, т. е.:
S=coq-coq±l±com^0 D.B.23)
Как и в резонаторе, частотный интервал между двумя прилегающими модами
является просто величиной, обратной времени обращения в резонаторе D.25), при
этом уравнение D.23) дает условие синхронизации мод, определенное ранее в
разделе 4.7.3. С учетом D.В.23) выражение D.В.21) принимает вид:
K°w = <°Г е* + <+Т е* D.В.24я)
где константа связи /сдается выражением:
к = Swi°°* e ^.J/(r)E9(r)E9±1(r)d3r D.B.246)
Для решения этой системы уравнений D.В.24) запишем коэффициентыр*1™ в виде:
p^(t)=icqQigSt D.B.25)
В этом случае подстановка в D.В.24) дает:
|Г 16 2 Дополнения к главе 4
-qCq =^Cq+l+jCg_l D.B.26)
Это рекуррентное соотношение допускает в качестве решения:
D.В.27)
где / — модифицированная функция Бесселя порядка q. И наконец, электромагнитное
поле в резонаторе дается D.В. 19), что приводит к:
Е(г, /) = 2 li^Y^\(r) , X 1 е^У— \(г) D.В.28)
где в качестве центральной частоты генерации лазерной среды мы ввели со0 (что отчасти
является достаточно произвольным в контексте приведенного вывода). Уравнение D.В.28)
показывает, каким образом фазы, частоты и амплитуды различных мод жестко
переплетены модуляционными потерями.
Таким образом, формализм мод Слэтера позволил нам показать, что модуляция
потерь в резонаторе будет приводить к синхронизации мод с частотным интервалом,
приближающимся к частоте модуляции. Уравнение D.В.24) показывает также, что если
потери распределены однородно по всему резонатору (/(г) = const), то
синхронизация мод становится неэффективной. Этот механизм приложим к многим
ситуациям и остается безошибочным подходом для решения любой проблемы, связанной с
лазерами. Наиболее общепринятый базис Слэтера, использованный до сих пор,
основан на функциях Гаусса.
И наконец, следует отметить, что этот формализм описывает только среду,
подверженную неоднородному уширению, где каждая мода может осциллировать
независимо от других мод. В среде с однородным уширением синхронизация мод все
еще возможна. В этом случае, боковые моды со0 ± qcom{ создаются за счет
нелинейного взаимодействия между лазерной средой и колебаниями модулятора comV В этом
случае формализм, необходимый для описания возникающей синхронизации мод в
резонаторе, становится существенно отличным от развитого в этом разделе.
Литература
W.H. Louisell, Quantum Statistical Properties of Radiation, Wiley, New York A973).
A.E. Siegman, Lasers, University Science Book, Mill Valley, CA A986).
J.C. Slater, Microwave Electronics, Van Nostrand, Princeton, NJ A964).
A Yariv, Quantum Electronics, Wiley, New York A989).
4.Г. Предел Шавлова—Таунса
и сила ланжевеновского шума
Одной из наиболее упоминаемой особенностей лазерного излучения (помимо его
яркости) является его высоко монохроматический характер. Может возникнуть
вопрос: «Что же ограничивает спектральную ширину лазерного излучения?» В качестве
причин мы могли бы подумать с достаточной долей основательности о
зеркальности резонатора или ширине атомных переходов, участвующих в стимулированном
излучении. Однако оба эти предположения в действительности неправильны! В
действительности, учет этих факторов приводит к выражениям на несколько
порядков величины большим того, что наблюдается! Например, для резонатора
Фабри—Перо (с длиной d и коэффициентом отражения зеркал г, смотрите рис. 4.Г.1)
зеркальность резонатора Ей ширина резонанса Фабри—Перо Av даются
выражениями (прочитайте дополнение 9.Г):
4. Г. Предел Шавлова—Таунса и силаланжевеновского шума
Ау = d/2d
Рис. 4.Г.1. Ширина полосы пиков пропускания в резонаторе Фабри—Перо равна меж-
модовому интервалу Av = с /Id, деленному на зеркальность резонатора.
2лг
D.Г.1)
F Id 2лт„
где г — время жизни фотонов в резонаторе, определяемое D.246). Для резонатора
длиной 10 см и коэффициентом пропускания 10~2 мы получаем зеркальность 628 и
ширину полосы 2,4 х 106 Гц, что ярко контрастирует с экспериментальными
значениями ширины полосы лазерного излучения порядка 1 Гц для определенных лазеров.
Возможные вклады из-за ширины атомных переходов, а также их частот, имеют
порядок ГГц (смотрите таблицу 4.1). Для понимания чрезвычайно малых значений
ширины полосы, связанной с лазерным излучением, нам необходимо возвратиться назад и
до определенной степени модифицировать динамические уравнения, приведенные для
фотонов в резонаторе D.А. 12). Для начала напомним, что электрическое поле Е(х, t) в
любой точке лазера дается выражением Е(х, t) = Kc(E(x, /)e~iutf), где временная
зависимость огибающей функции Е(х, t) описывает временную эволюцию
электромагнитного поля вследствие лазерного усиления. Эта зависимость намного слабее, чем
колебания электромагнитного поля, даваемые e~ifi". Заменим в D.А. 12) число фотонов в
резонаторе Р на огибающую функцию электрического поля E(t), определенную в
любой точке резонатора, предполагая, что входное зеркало находится в точке х = 0,
и напомним, что связь между двумя величинами дается соотношением (см. B.77):
D.Г.2)
2Псо
где е —диэлектрическая постоянная среды (я= £0п2ор). Отметим, что член
спонтанной эмиссии (член + 1 в D.А. 12)) ничего не говорит нам о моменте спонтанного
освобождения фотона. Таким образом, заменим его силой F(t), которая будет
использоваться для описания хаотического характера этого излучения. В этом случае
мы получаем:
А С 1/1 Г< \
D.Г.З)
Уравнение Ланжевена
где F{t) — сила Ланжевена, которая обладает следующими характеристиками:
• F(t) является стохастическим процессом случайной переменной с
нестационарным характером. Рис. 4.Г.2 описывает такой стохастический процесс. Функция
F(t, в) случайно выбирается в момент / = — °°, а в — событие, принадлежащее
\f( 164 Дополнения к главе 4
ящ
Рис. 4.Г.2. Стохастический процесс
является стохастической функцией f(t, в),
каждая реализация 0 которой приводит к
функции /(t). При заданном времени //(/, в)
есть произвольная переменная.
ансамблю возможных результатов Q. Для каждого толчка (т. е. для каждой
величины в) F(t, в) является функцией времени t и для каждого значения времени /
F(t, в) является случайной переменной.
• F{t) является эргодическим процессом (смотрите дополнение ЗА), что означает
идентичность временных и статистических средних в любой момент времени t
т/2
I T J/2
D.Г.4)
• Процесс не обладает памятью, т. е. случайные переменные F(t) и F*(t + /) не
скоррелированы для любого тф 0:
D.Г.5в)
где А — константа, которую еще надо определить. Далее предположим, что:
F(t]F(t + r)=0. D.Г.56)
Это не является абсолютно необходимым (это может быть записано в виде BS(t)),
но это сильно упрощает расчеты.
• Наконец, F(t) — процесс с нулевым средним:
F(t) = 0.
D.Г.6)
Запишем теперь решение D.Г.З). Можно легко показать, что решение дается
выражением:
где мы временно положили, что:
J J
* light
D.Г.7)
D.Г.8)
Решение D.Г.7) может быть интерпретировано как отклик системы с линейным
усилением (когда отклик на импульс изменяется как е"') на случайное возбуждение
вида F(t). Это является классической проблемой электроники (смотрите рис. 4.Г.З).
Сначала мы рассчитаем среднюю величину электрического поля E(t) из D.Г.6):
D.Г.9)
Дисперсия поля E(t) дается выражением:
\E(tf = [F{t'y{ll)dt'\F*{fy^
D.Г.10)
4. Г. Предел Шавлова— Таунса и сила ланжевеновского шума 165
S(<o)
ge(o>)
Рис. 4.Г.З. Система с линейным усилением S(co) преобразует стохастический процесс
со спектром gc(co) в стохастиченский процесс с gs(co) = \S(co)\2gc(co).
С учетом того факта, что система не обладает памятью D. Г.5) это последнее
выражение принимает вид:
\E(tf = A\dt'\ dfd{t' = ry{2'-r~r) =
или, заменяя v на ее величину в виде D.Г.8):
А
W2 =
или вновь, вводя число фотонов и с помощью D. Г. 2):
= eVA I \ (G/rmi-i/rcy Л
2ha>{G/Tlight-\/Tcf J
D.Г.11)
DSA2a)
D.Г.126)
Сравнивая этот результат с аналогичным результатом, полученным в рамках
Дополнения 4.А (смотрите D.А.13)), мы видим, что два подхода приводят к
идентичному результату при идентификации А в виде:
А =
2Gb со
D.Г.13)
Подход, основанный на уравнении Ланжевена лучше, чем подход «избыточного
фотона», введенный в дополнении 4.А., в том смысле, что он описывает хаотичную
динамику, связанную с лазерным излучением. Теперь мы введем амплитуду I(f) и
фазу </f(t) электрического поля (смотрите рис. 4.Г.4):
E(t) =
D.Г.14)
Очевидно, что /(/) и f{t) представляют стохатические процессы. Подставляя
D.Г.14) в D.Г.З), получаем следующую систему дифференциальных уравнений:
dL/_
d/
2vl =
D.Г.15д)
D.Г.156)
flm(E(f))
Рис. 4.Г.4. Френелевское представление
амплитуды и фазы электрического поля. Под
влиянием силы Ланжевена вектор E(t) вращается
в плоскости (говорят, что фаза имеет
диффузный характер), в то время как амплитудуа
остается, в основном, неизменной.
Re(E(/))
((Г 166 Дополнения к главе 4
Мы видим, что в D.Г. 15л) /демпфируется членом 2vl. Как следствие,
амплитудные флуктуации лазеров очень малы и ими часто пренебрегают. Мы проведем
этот расчет в дополнении 13.Г применительно к полупроводниковым лазерам.
Однако, уравнение D.Г. 156) не содержит такого демпфирующего члена по фазе.
Таким образом, фазовые флуктуации будут значительны. Этот эффект возникает из-
за хаотичных временных характеристик, связанных со спонтанным излучением.
Мы перепишем D.Г.156) в следующем виде:
-F*№1'] D.Г.16)
2W/
где с учетом слабых флуктуации по амплитуде / мы заменили / на ее среднюю
величину. Уравнение D. Г. 16) формально может быть проинтегрировано
следующим образом:
t
)(О1 !>(>-* -Р*($'У»Ъ? D.Г.17)
2iV/ {
Ясно, что средняя величина ф равна нулю. В то же время ее дисперсия дается
выражением:
Аф =Ш-40J =-Ljdfjd^F(f)^ -/(С)е*][^)е" -F<T)e*] D.Г.Ш)
Это последнее выражение может быть существенно упрощено, если мы используем
D. Г.5) и, кроме того, предположим, что:
D. Г. 186)
Это последнее выражение обычно выполняется несмотря на то, что процессы F и ф
являются явно коррелированными. В этом случае уравнение D. Г. 18) принимает вид:
41«
'° '° D.Г.19)
=л'
/.
В этом выражении мы видим, что стандартная дисперсия фазы изменяется со
временем в соответствии с соотношением:
(>-'o) D.Г.20)
Мы видим, что уравнение D.Г.20) принимает вид диффузионного уравнения, где
константа диффузии D дается D = А /21 или выражением для А в D.Г. 13) и для /в
D.Г.2) и D.Г.24д):
А^ = 1 2ficoG еУ_ = J_J?_ J_
2/ 2ет^У2Ьа>Р 2 тш Р К
Выше лазерного порога усиление G фиксируется на своем пороговом значении,
определяемом G/^ight = 1/г. Более того, D.Г.1) устанавливает, что ширина полосы
холодного резонатора (т. е. ширина полосы резонанса Фабри—Перо) дается
соотношением: Avc = 1/2ят. В окончательном виде коэффициент диффузии для фазы
записывается в виде:
4.Г. Предел Шавлова—Таунса и силаланжевеновскоео шума
D.Г.22)
Коэффициент диффузии по фазе
Теперь нам остается только рассчитать ширину полосы излучения лазера. Для
этого запишем электрическое поле, соответствующее лазерному излучению, в
каноническом виде, описанном в начале этого раздела:
Ё(<)= Re[£(,)f'*'] = 1[^)е-* + E\t)^] D.Г.23)
где со0 — частота излучения лазера. Из дополнения З.А мы знаем, что спектральное
распределение сигнала дается Фурье-образом автокорреляционной функции
(уравнение (З.А. 13)). Это есть теорема Винера—Хинчина (смотрите рис. 4.Г.З). Эта
автокорреляционная функция может быть рассчитана с использованием записи:
D.Г.24д)
tL J L J
или вновь:
E{t + r)E{t)=±[E(t + r)E*{ty14 +K.cJ D.Г.246)
Заменим электрическое поле E(t) на его выражение в D.Г.14) и вспомним, что
амплитуда флуктуации / достаточно мала, чтобы гарантировать нам ее замену на
среднее значение:
E{t)E(t + т)= ^I{t + r)l{ty^t+rym D.Г.25)
Мы уже встречали среднюю величину е1^"'** ~ *0) в (З.А. 16) в предположении,
что процесс имеет пуассоновский вид. Делая то же самое допущение в отношении
<j{t), находим:
ei¥(>+rF0{rD = e-2«*- = е-2 D.Г.26)
где 8ф2 есть дисперсия фазовых флуктуации. И, как следствие, выражение для
автокорреляционной функции D. Г.24) принимает вид:
GXr)= E(t)E(t + т) =i|7e"^re-iu)»T + к. с. |= уе"^' cos(co0r) D.Г.27)
Спектральное распределение для Е(со) в этом случае дается теоремой Винера—
Хинчина (З.А. 13), т. е. с использованием Фурье-образа D.Г.27) или:
DГ28)
1 л к {о)-оHУ + D2 /4
Используя выражение для коэффициента диффузии в D.Г.22), мы находим, что
ширина полосы спектрального распределения лазерного излучения (которая может
быть измерена, например, с использованием дисперсионного спектрометра) дается
выражением:
Д„8Т=£^ D.Г.29)
Ширина линии Шавлова—Таунса
Таким образом, мы заключаем, что ширина линии лазерного излучения есть
ширина полосы резонатора Av, деленная на число фотонов в резонаторе (довольно
значительное число). Таким образом, теоретически ширина полосы лазерного из-
(к 168 Дополнения к главе 4
лучения может быть крайне малой. Уравнение D.29) может быть представлено в
более доступном для расчетов виде за счет использования D.Г.1) для Av, а также
соотношения D.30), связывающего число фотонов в резонаторе Р с мощностью
лазерного излучения Pcxt:
Р*«=Р— D.Г.30)
В этом случае уравнение Шавлова—Таунса принимает вид:
hv
** к: <4Г31>
Уравнение Шавлова—Таунса
Пример
а) Ширина линии излучения лазерного резонатора на основе Nd3+:YAG (hv= 1,17 эВ,
пор = 1,82) длиной 1 см, с прозрачностью зеркала 0,5% (или фотонным
временем жизни 24 не) и мощностью излучения 1мВт составляет AvST = 1,17 х
х 1,6 х 109 Дж/Bятх B4 xlO"9 sJ х 10 Вт) или 5 х 10 Гц.
б) Ширина линии излучения полупроводникового лазера (hv = 1,4 эВ, пор = 3) длиной
100 мкм, имеющего зеркала с прозрачностью 30% (что соответствует
фотонному времени жизни 6 пс), а также мощность излучения 1 мВт составляет
AvST = 1,4 х 1,6 х 109 Дж/Bях F х 102 s) x 10 Вт) или 1 М Гц.
Литература
G. Grynberg, A. Aspect, and С. Fabre, Introduction aux lasers et a Foptique quantique,
Ellipses, Paris A997).
A.E. Siegman, Lasers, University Science Book, Mill Valley, CA A986).
4.Д. Пример: лазеры с диодной накачкой
В этом разделе нас будет интересовать аспект, имеющий существенное значение с
точки зрения технологического применения лазеров, а именно — лазерная
эффективность. Этот параметр определяется как отношение выходной мощности
излучения лазера к мощности оптической накачки. В качестве примера используем
достаточно распространенный лазер, используемый в промышленности — лазер
на основе алюмо-иттриевого граната, легированного неодимом (или Nd3+:YAG).
Диаграмма энергетических уровней, принимающих участие в функционировании
лазера YAG схематически представлена на рис. 4.Д.1я. Как можно заметить по
спектру поглощения этой ионной системы (рис. 4.Д.16) длина волны фотонных
переходов накачки составляет 0,81 мкм, при этом соответствующая ширина
полосы примерно составляет АЛ = 30 нм. Начнем с расчета эффективности этого
лазера, используемого в сочетании с ксеноновой лампой накачки. Ксеноновую лампу
можно рассматривать как черное тело с температурой Т; в этом случае
спектральная излучательная способность дается уравнением B.Б.4). В наиболее
благоприятном случае поглощенная мощность накачки дается интегралом перекрытия
спектральной излучательной способности B.Б.4) и окна поглощения АД лазерного
материала (смотрите рис. 4.Д.2) или:
АР=^-Л{Л,Т)АА=^ (hc/;kT) АЛ D.Д.1в)
ил л е — 1
или:
АР= 1,14 х 109е -O.79X10000/D дд Вт мкм м D.Д.16)
14000
12000
~ 10000
~ 8000
$ 6000
о
4000
2000
0.8 ц,т
4.Д. Пример: лазеры с диодной накачкой 169
^9/2
г5/2
F3/2
1.06(хт
4 .
15/2
'13/2
'11/2
9/2
б
400 500 600 700 800
Длина волны (мкм)
900
Рис. 4.Д.1. а) Энергетические уровни, принимающие участие в процесса поглощения
и излучения в лазера на основе Nd3+:YAG;
б) Спектр поглощения Nd3+:YAG;
Полная энергия излучения определяется интегралом B. Б.4) по всему спектру,
что с использованием закона Стефана B.Б.8) дает:
Р= <тТ4 = 5,67 х 10"8 Т4 Вт м D.Д.2)
Максимально возможная эффективность лазера в этом случае составляет или:
^^2xlOlV-4e-(lW/nAA(MMKMi D.Д.З)
Предполагая типичную температуру черного тела 8000 К и ширину спектра
поглощения 0,03 мкм, находим, что эффективность составляет приблизительно 1,5%.
Таким образом, по своей сути эффективность лазеров с ламповой накачкой очень
мала, так как основная доля излучения накачки выходит за пределы полосы
поглощения лазерной среды (смотрите рис. 4.Д.2).
Таким образом представляется естественным искать для накачки высоко моно-
хроматичные и мощные источники типа тех, что представляют собой
полупроводниковые лазерные диоды. В конце этого раздела мы увидим обоснованность
использования лазеров с диодной накачкой, а не прямого использования самих
лазерных диодов.
W170 Дополнения к главе 4
Nd3+: YAG
Рис. 4.Д.2. В лазере с накачкой от лампы (а) перекрытие спектрального распределения
излучения черного тела (очень широкого)и лазерного поглощения (очень
узкого) приводит к малой эффективности преобразования (б).
На рис. 4.Д.З представлена конфигурация лазера на основе Nd3+:YAG, как она
представлялась Роберту Байеру и его исследовательской команде в Стэнфорде.
В представленной конфигурации используется линза для ввода в лазерный
стержень расходящегося излучения лазерного диода на основе GaAs, при этом
лазерному стержню придается форма гауссовского резонатора с длиной d — 2L — 0,5 см.
Напомним, что гауссовский пучок идеально описывает распространение
электромагнитных волн, ограниченных дифракцией. Если гауссовская волна
распространяется вдоль оси Oz, амплитуда электромагнитного поля U(p, z) в функции
расстояния р от оси Oz дается выражением (смотрите рис. 4.Д.4):
D.Д.4)
где различные интересующие нас параметры представляют собой:
Радиус кривизны
)= Z
W(z)=lVQ
1 + 1-*-
Zo
1/2
*W.4
D.Д.5)
Пространственное отклонение
Рэлеевская длина
Фаза Гюйо
Расходимость
Для минимизации мощности накачки мы, в общем случае, заинтересованы в
уменьшении общего объема, занимаемого лазерной модой. Предположим, что
Лазер
GaAs
Nd:YAG
Линза
Рис. 4.Д.З. Схематическое представление лазера на основе Nd3+:YAG с накачкой от
лазерного диода.
4.Д. Пример: лазеры с диодной накачкой 17ljj)
Р
R(z)
Интенсивность
Рис. 4.Д.4. Геометрия гауссовского пучка
мы имеем пучок с шириной Wo порядка 40 мкм (этого достаточно сложно
добиться с использованием лазерного диода). Поскольку Л= 1,06 мкм и пор =1,82,
третье уравнение в D.Д.5) дает нам рэлеевскую длину пучка, т. е. z0 = 8,6 мм.
Радиус кривизны входного зеркала дается первым уравнением в D.Д.5), т. е.
Ro = 3,2 см. Поскольку ^ >> d/2, мы можем считать W(z)= const, так что объем,
занимаемый гауссовской модой в этом случае составляет 7tdW£ или 2 х 10~5 см.
Теперь нас будет интересовать время жизни фотона в резонпаторе в
пренебрежении паразитным поглощением ар. Входное зеркало обладает отражением Rs = 99,7%,
что дает фотонное время жизни (смотрите D.246)):
г, =
2x0,5 см
Tsc/nop 3xl0-3x3xl010 смс-4,82
= 20 не
Пороговая плотность заселенности в этом случае (смотрите таблицу 4.1 и
уравнение D.23#) дается выражением:
1
1,82
<Vc<7"op 4хЮ-19см2 х20 нсхЗх1010см с
и плотность пороговой мощности дается выражением:
— = 7,5хЮ15
А*
7,5х1015см-3х1,5Вх1,6х1019 С
- 1,2 х Ю-3 с
В этом случае пороговая мощность дается выражением:
= 0,03 мВт
Пороговая мощность, необходимая для накачки, мала по двум причинам:
• объем Кочень мал (поскольку он усилен гауссовским резонатором);
• все фотоны накачки обладают энергией, резонансной с переходом накачки в
лазерной среде (т. е. все фотоны участвуют в накачке лазерной среды).
Понятно, что паразитные механизмы потерь (поглощение примесями, ...) будут
стремиться ужесточить требования по мощности накачки. Тем не менее, лазеры с
диодной накачкой обладают чрезвычайно малыми порогами накачки.
Выходная мощность Ps в режиме намного выше порога дается соотношениями
D.286), D.29) и D.246) или в нашем случае (ар = 0, Re = 1, Г « 1):
Ps ~ — R2tcc / nopTshcolaseT = dR2hcola^r D.Д.6)
Напомним, что скорость накачки Л, дается в см с. В предположении, что все
фотоны накачки поглощаются на полной длине d лазерного стержня, скорость
накачки связана с мощностью накачки соотношением:
((A72 Дополнения к главе 4
В этом случае эффективность определяется соотношением:
Р. ^,„ 1
D.Д.7)
D.Д.8)
что концептуально легко понять: rjq есть лазерный квантовый дефект. В этом случае
избыточная энергия фотонов накачки (т.е. квантовый дефект) преобразуется в тепло.
Следует отметить, что по сравнению с прямым использованием лазерных
диодов в рассматриваемом случае имеются три преимущества. Во-первых, гауссовский
резонатор на основе стержня YAG выполняет роль преобразователя мод. В
результате этого оптическая мощность нескольких лазерных диодов на основе GaAs,
обладающих сравнительно посредственными характеристиками, может быть
эффективно преобразована резонатором в единый пучок с характеристиками,
ограниченными дифракцией. К тому же, как это разъясняется в дополнении 4.Г, ширина
линии лазера на основе Nd:YAG существенно меньше по сравнению с
аналогичным параметром полупроводникового лазера (основной причиной этого является
большое различие фотонных времен жизни в двух средах). И наконец, благодаря
большому времени жизни возбужденного состояния (т2 =1,2 мс) лазеры на основе
Nd:YAG обеспечивают возможность работы в режиме переключения добротности,
что позволяет генерировать импульсы с пиковой мощностью в 104 раз большей по
сравнению со средним уровнем мощности излучения, генерируемого
непосредственно диодами на основе GaAs. Рис. 4.Д.5 иллюстрирует реальную конфигурацию
реального лазера на основе Nd:YAG с диодной накачкой.
Ячейка
Лазерные модули
4 * 15 Вт
YAQ:Nd
35 см
Рис. 4.Д.5. Экспериментальная конфигурация лазера на основе Nd:YAG с накачкой от ЛД.
Литература
W. Koechner, Solid-State Laser Engineering, 4th Edn, Springer, Berlin A996).
T. Y. Pan and R. L. Byer, IEEEJ. Quantum Electron QE 24, 895 A988).
ГЛАВА 5
ЗОННАЯ СТРУКТУРА
ПОЛУПРОВОДНИКОВ
5.1. Введение
В этой главе мы впервые коснемся вопросов, связанных с физикой
конденсированного состояния как таковой. До настоящего момента мы изучали квантовые
системы, содержащие один, два и вплоть до четырех квантовых уровней в вакууме или в
среде, характеризуемой определенным коэффициентом преломления. Однако, мы
не рассматривали проблему взаимодействия многих таких систем с повышенной
концентрацией, что приводит к их химической связи в макрообъеме. Эта проблема,
априори неразрешимая в случае необходимости решения такого большого числа
связанных уравнений, сколь велико и число электронов в среде (порядка 1023 см~3),
значительно упрощается в кристаллических и поликристаллических материалах.
5.2. Кристаллические структуры, блоховские функции
и зона Бриллюэна
Наиболее устойчивая структура материи при температуре абсолютного нуля
реализуется в виде периодического расположения атома в кристаллической структуре.
Число возможных кристаллических структур огромно и является проблемой
особой науки как таковой, а именно — кристаллографии. Кристаллическая структура
характеризуется периодическим повторением (до бесконечности или практически
до бесконечности) от точки к точке (при этом возникающая конфигурация
называется кристаллической решеткой), базисом которой являются один или несколько
атомов. Термин «моноатомная решетка» используется для описания решетки,
возникающей в том случае, когда для заполнения решетки необходим базис,
включающий единственный тип атомов. Наиболее типичным типом структуры решетки
для кристаллов элементарных полупроводников (Si, Ge, С) является структура
алмаза. В случае бинарных полупроводников, таких как GaAs, наиболее типичной
является структура цинковой обманки, показанная на рис. 5.1.
В первую очередь, следует отметить тот факт, что кристаллическая решетка в этом
случае может быть представлена линейной комбинацией трех базисных векторов ар а2 и а3,
т. е. кристаллические узлы распределены по точкам г таким образом, что:
где п. соответствует произвольным целым числам. Гамильтониан, описывающий
взаимодействие между электронами и атомами в кристалле, является чрезвычайно
сложным, и он должен учитывать взаимодействие между всеми электронами,
движения ядер и т. д. Таким образом первая цель физики твердого тела заключается в
том, чтобы показать, что многие из этих взаимодействий по кристаллу могут быть
учтены с использованием эффективного потенциала U(r) таким образом, что
гамильтониан, используемый для описания электрона в кристалле, принимает вид:
+ Хи(гГ) E2)
uf 174 Глава 5. Зонная структура полупроводников
Рис. 5.1. Кристаллическая структура цинковой обманки.
или иначе:
где К(г) обладает периодичностью кристалла:
E.3)
) = Кг) E.4)
С учетом условия периодичности кристалла E.4) периодический потенциал может быть
разложен в ряд Фурье:
К(г)= У K(G)eiGr
GeRL
E.5)
где точки G (OG = G) распределены в пространстве обратной решетки (RL),
перекрываемом единичными векторами:
а,ха,
А,=2лг
А2 = 2л:-
А,=2тг-
E.6)
а, а2ха3 " а2 а3ха, а3 а,ха2
Конструирование обратных решеток кристаллических структур лежит в
области почитаемой нами геометрии. Рис. 5.2 иллюстрирует одномерную моноатомную
решетку (а), а также соответствующую обратную решетку (б).
Напоминаем, что в вакууме, где #= р2/2т, стационарные волновые функции к
свободных электронов представляются волновыми векторами и могут быть записаны в
виде ехр (—ik • г). Легко может быть показано, что решениями уравнения Шредингера
//crystal *F (г) = £*Т(г) являются функции Блоха с индексами в виде волновых векторов к:
E.7)
Функции Блоха—Фуке
где функции ^(г) обладают периодичностью кристалла:
E.8)
5.2. Кристаллические структуры, блоховские функции и зона Бриллюэна 175 Jn
Кристаллическая решетка Обратная решетка
-А
к=-я/а
/с= л/а
б
Первая зона
Бриллюэна
Рис. 5.2. Кристаллическая (а) и связанная с ней обратная (б) решетки. Вектор трансляции
для обратной решетки есть вектор А, расположенный при 2я/а. Два
перпендикуляра, проведенные из середины ОАи-ОА определяют первую зону Бриллюэна
обратной решетки.
Действительная (или мнимая) часть функции Блоха—Фуке показана на рис.
5.3. Отметим общую форму этих функций, характеризуемую быстро изменяющимися
атомными волновыми компонентами, медленно модулируемыми огибающей
функцией вида ехр(—ik • г). Именно эта модуляция переносится по кристаллу и лежит в
основе феномена эффективной массы, рассматриваемого в дальнейшем.
Как обычно при трактовке бесконечной среды, волновые векторы к из
соображений удобства представляются псевдо-квантованными (смотрите Дополнение 1 А).
Этого можно добиться, вводя бесконечные потенциальные барьеры вдоль шести
плоскостей, определяемых:
E.9)
В этом случае псевдо-квантование привело бы к положительным дискретным
волновым векторам к. Волновые функции Блоха были бы таким образом
стационарными, так как они были бы результатом наложения волн, распространяющихся
вперед и назад в обоих направлениях между ограничивающими поверхностями.
Традиционным в физике твердого тела является также и использование другой
процедуры: цикличных граничных условий Борна—фон Кармана. С этой целью
предположим, что при всех значениях L. = Na.(/ = 1, 2, 3) кристалл идентично
воспроизводит себя в пределах каждого из этих «ящиков», т. е., иначе говоря, все пространство
внутри кристалла полностью заполнено прилегающими друг к другу ящиками с
размерами L{x L2x Ly Циклические граничные условия Борна—фон Кармана
требуют, чтобы волновая функция Ч^г) была той же самой в каждом из этих ящиков,
т. е. чтобы \у (г + «jLj + n2L2 + я3Ь3) = Ч'(г) Волновые векторы к, в этом случае
принадлежат обратному пространству, описываемому точками:
е"
«кЮ •'
-ikr
Рис. 5.3. Функции Блоха—Фуке (стационарные электронные состояния в
периодически изменяющемся потенциале атомов, распределенном в пределах
кристаллической решетки) представляют собой периодическую модуляцию атомных
волновых функций бегущей волной вида е~*г.
Глава 5. Зонная структура полупроводников
, 2л , 2л , 2л
EЛ0)
где nv nv пъ в данном случае представляют собой положительные или
отрицательные целые числа. Понятно, что величина 7V может быть сделана сколь угодно
большой таким образом, чтобы сделать незаметным какое-либо влияние процедуры
псевдо- квантования.
В совокупности с граничными условиями Борна—фон Кармена уравнение Шре-
дингера E.3) имеет решения в виде функций Блоха E.7) или ^.(г) Для каждого к
имеется целый набор решений, собственные энергии которых мы обозначаем как
Ет(к), при этом т являются целыми. Мы можем представить, что эти наборы
решений образуют непрерывные зоны в том смысле, что при к',близких к k, EJ}l') будут
также близки к Ет(к). Вследствие этого т называют индексом зоны.
Мы должны также понимать, что в большем масштабе собственные состояния
блоховского вида E.7), соответствующие зоне т, с вектором обратного
пространства G могут быть также записаны в виде:
y/mk(v) = ит*(г)енк r = [w^(r)e"IG r]e -w-w r E.11)
что опять имеет блоховский вид, поскольку e~iG r является периодической
функцией кристаллической решетки. Таким образом, это выражение идентично одному из
решений уравнения Шредингера для волнового вектора k — G. Применительно к
собственным энергиям мы получаем:
EJk - G) = £,(k) E.12)
Следовательно, энергетические зоны периодичны по т\ при этом период
определяется обратной решеткой.
Следующим следствием того, что у/^ k _ G (г) идентична тому же самому решению
у/т k_G(r), является то, что для представления всех решений у нас нет
необходимости в обратном пространстве.
Принято (как это объясняется в дополнении 5.А) ограничивать целые значения п.
в E.10) интервалом — N/2 < п.< N/2 (т. е. пх 2 3= 0, ±1, ±2, ..., ±N/2). Таким образом,'
волновые векторы, принадлежащие той же самой зоне, определяются выражениями:
Я ^ 1 ^ Л Л ^ . . Л Л ^ , ^ Л /г лъ\
<кх<—\ <к2<—; ^^з^— E.13)
а, а, а2 а2 а3 а3
Эта зона задается набором перпендикулярно пересекающихся плоскостей,
которые пересекают посередине трансляционные векторы обратной решетки (RL)
(соединяющие ближайшие соседние точки RL). Область пространства в RL,
определенную таким образом, называют зоной Бриллюэна. На рис. 5.2 представлена
первая зоны Бриллюэна для одномерной структуры. Рис. 5Аа и 5.46 показывают
первую зону Бриллюэна для двумерной квадратной решетки, а также для
трехмерной структуры цинковой обманки. Наиболее важные точки (и соответствующие
направления) в последнем случае имеют общепринятые обозначения.
В ряде случаев при отсчете зон более удобно использовать периодичность,
связывая собственную энергию с каждой точкой обратного пространства. Примером
тому является модель почти свободных электронов, исследованная в дополнении
5.А. Для того, чтобы возвратиться к стандартной зонной структуре первой зоны
Бриллюэна в таком представлении решений, необходимо осуществить трансляцию
зоны (подобно уравнению E.12)) на вектор обратной решетки G, приводящую к
тому, что вектор k—G будет лежать в первой зоне Бриллюэна. Такая процедура,
обычно называемая приведением зон, иллюстрируется рис. 5.А.2.
Одной из главных проблем физики твердого тела является решение уравнения
Шредингера, получаемого подстановкой E.11) в E.12). Обычно это
осуществляется с использованием достаточно трудоемких численных методов, что позволяет
получить зависимость Ет(к), связывающую энергию электронов в структуре с соот-
5.3. Энергетические зоны 177
^Р:Ш Первая зона Бриллюэна
ИИ Вторая зона Бриллюэна
а б
Рис. 5.4. Первая и вторая зоны Бриллюэна двумерной квадратной решетки (а) и
первая зона Бриллюэна трехмерной структуры цинковой обманки (б). В
последнем случае приведены общепринятые обозначения для наиболее важных
точек симметрии.
ветствующими значениями волнового вектора к в первой зоне Бриллюэна для
заданного индекса т.Совокупность получаемых кривых Ет(к) определяет зонную
структуру материала. На время удовлетворимся суммированием основных аспектов этой
важной области физики твердого тела.
5.3. Энергетические зоны
Одним из наиболее важных следствий взаимодействия между электронами в
кристаллической решетке и периодически изменяющимся кристаллическим
потенциалом является существование запрещенных энергетических зон для электронов. Есть
несколько способов понять причину происхождения таких зон, при этом они,
безусловно, внутренне связаны друг с другом.
С точки зрения изложения в главе 1 длина волны электронов с энергией Е в
вакууме дается Л =2яН /^12тЕ. Типичная энергия ионизации электронов в атоме
составляет ~5 эВ, что соответствует длине волны 5 А.
Поскольку типичное расстояние между атомами в
кристалле составляет 3—5 А, материальные электронные
волны будут дифрагировать на периодическом
кристаллическом потенциале (см. рис. 5.5). Говоря более
точно, те электронные волны, для которых 2л;/Л = к = я/а.,
т. е., которые соответствуют краям зоны
Бриллюэна, дифрагируют и не могут распространяться через
кристалл, образуя таким образом зону запрещенных
энергий. Теоретический подход, основанный на этом
концептуальном представлении, соответствует модели
Рис. 5.5. Блоховские волны, период которых равен периоду
кристаллической решетки, не распространяются в
кристалле: это и есть причина возникновения запрещенных зон.
Поэтому внешняя электронная волна не может проникнуть в
кристалл.
Энергия, Е
Глава 5. Зонная структура полупроводников
почти связанных электронов. Более детально этот метод исследуется в
дополнении 5.А.
Вторая точка зрения базируется на химической модели. Из дополнения 1.Б мы
можем вспомнить, что в том случае, когда два атома приближаются друг к другу, их
орбитали становятся гибридизированными. Вырождение энергетических уровней
снимается, что приводит к проявлению двух явно выраженных уровней (соответствующих
связи и антисвязи). Обобщение этого феномена на случай бесконечного числа атомов
приводит к появлению ансамбля компактно расположенных уровней, при этом
уровни связи приводят к формированию валентной зоны, в то время как уровни антисвязи
образуют зону проводимости (рис. 5.6).
Энергетические
уровни
Разрешенная
зона
Расстояния между атомами
а б
Рис. 5.6. Химическая гибридизация и возникаю^^ вследствие этого энергетические
зоны в твердых телах. По мере того, как отдельные атомы с
соответствующими квантованными уровнями энергии £"я (л = 1, 2, 3...) сдвигаются друг к
другу (д), уровни гибридизируются, что приводит к формированию
энергетических зон (б). В том случае, когда уширение зон меньше первоначального
межуровневого интервала, в кристалле возникает зона запрещенных
состояний или запрещенная зона.
Эти две зоны образуют два отличные друг от друга континуума допустимой
энергии электронов. Запрещенная зона энергии электронов может возникать или
отсутствовать в зависимости от того, достаточен ли энергетический зазор между
двумя зонами, чтобы не допустить их перекрытия. Этот подход, называемый
моделью жесткой связи, исследуется в дополнении 5.Б.
Не входя в ненужные детали, выходящие за рамки данной книги, мы, тем не
менее, можем выделить различие между двумя типами запрещенных зон. Зоны
одного типа возникают в том случае, когда максимум валентной зоны и минимум
зоны проводимости располагаются в той же самой точке зоны Бриллюэна (т. е при
том же самом значении к). Как мы увидим, оптические переходы между нижними
уровнями зоны проводимости и верхними уровнями валентной зоны происходят
при постоянном значении к.Таким образом такие оптические переходы возможны
между экстремумами двух зон. В этом случае соответствующая запрещенная зона
называется прямой. В GaAs эти два экстремума располагаются при к = 0, что
соответствует точке G зоны Бриллюэна (рис. 5.16).
Второй тип запрещенной зоны реализуется в том случае, когда экстремумы
валентной зоны и зоны проводимости располагаются в различных точках зоны Бриллюэна.
В этом случае переходы между ними должны происходить без сохранения величины
волнового вектора Ц>, при этом такой тип запрещенной зоны называется непрямым
(рис. 5.1а). Этот вариант реализуется в случае кремния, где экстремум валентной зоны
располагается в точке Г, а максимум зоны проводимости отстоит на 85% вдоль Г X.
5.4. Эффективная масса и плотность состояний 179
[111] Г [100]
Волновой вектор
[111] Г [100]
Волновой вектор
Рис. 5.7. Два типа запрещенных зон: непрямая запрещенная зона в Si(fl) и прямая
запрещенная зона в GaAs (б).
5.4. Эффективная масса и плотность состояний
Обе модели (жесткой связи или почти связанных электронов) приводят к одному и
тому же результату в том, что касается дисперсии энергии Е (к) вблизи
экстремумов валентной зоны и зоны проводимости kext (смотрите дополнения 5.А и 5.Б). В
обоих случаях мы приходим к квадратичной зависимости Е от к, представляемой
матричным произведением:
^-(k-kext)'M4k-kext)
E.14)
где А — транспонированный вектор Аи М — действительная симметричная
матрица, называемая матрицей эффективной массы по причинам, которые будут
разъяснены позже. После диагонализации матрицы М~1 мы видим, что зонная структура
может быть записана в виде:
E.15)
/И,
АИ,
где к. и kcxt . являются компонентами к и kext так же, как собственные векторы М~1.
Мы узнаем выражение, связывающее энергию и волновой вектор свободных
электронов (Е = h 2k2/2m), но с другой массой. Это и есть эффективная масса,
обусловленная взаимодействием электронов с периодическим потенциалом
кристалла. Эффективная масса положительна, когда кривизна такова, что направляет
дисперсионную зависимость вверх, и отрицательна, когда дисперсионная
зависимость направлена вниз. Значение этой отрицательной эффективной массы мы
рассмотрим позже. Поверхности постоянной энергии, получаемые при Е= const
образуют эллипсоиды, центрированные вблизи экстремумов зоны Бриллюэна. Рисунок
Глава 5. Зонная структура полупроводников
Si GaAs
Рис. 5.8. Эллипсоиды постоянной энергии в Si и GaAs.
5.8 иллюстрирует такие эллипсоиды постоянной энергии вблизи экстремумов зоны
проводимости и валентной зоны кремния. Как следует из таблицы приложения
(стр. 588) кремний характеризуется двумя эффективными массами — одной в
поперечном направлении /wet и другой — в продольном направлении те1.
Для большинства полупроводников валентные зоны вырождены при к = 0.
Причиной этого является преимущественно триплетная природа 8р3-орбиталей,
формирующих валентную зону. Однако вырождение снимается при к ф 0, что приводит к
подзонам с различной кривизной. При этом подзоны с малой кривизной обладают
большей эффективной массой. Такие подзоны называются подзонами тяжелых дырок
(позже мы объясним, что мы подразумеваем под понятием дырка). И напротив,
подзоны с большей кривизной называются подзонами легких дырок. В таблице
приложения (стр. 588) представлены различные эффективные массы в Si и Ge.
Теперь нам предстоит рассчитать плотность состояний в различных
разрешенных зонах. Этот параметр имеет фундаментальное значение во всех расчетах,
связанных с переходами между зонами. Для того, чтобы без необходимости не
перегружать систему обозначений, временно сконцентрируем свое внимание на
простом примере, связанном с зоной проводимости GaAs, где эффективная масса
является изотропной. В этом случае зонная структура дается выражением:
h2k2
E.16)
где к есть модуль волнового вектора к, а Ес — энергия минимума зоны
проводимости. Мы можем легко рассчитать плотность состояний в к-пространстве. Уравнение
E.10) показывает, что в объеме d3k = dkxdkydkz в предположении цикличных
граничных условий Борна—фон Кармана имеется (Nax)(Na)(Na^/Sn3 =V/Sn3
состояний. Если бы мы использовали граничные условия в (э.9), плотность состояний
составила бы V/Sn39 но объем интегрирования в этом случае (при положительной
величине п{, п2, п3) был бы в восемь раз меньше. Плотность состояний в &-про-
странстве есть бесконечно малое число состояний d3N = p(k)d3k, расположенных в
элементарном объеме d3k:
EЛ7)
Плотность состояний в /с-пространстве
с учетом периодических граничных условий
и в пренебрежении спином электрона
5.4. Эффективная масса и плотность состояний
Число состояний dN в объеме между двумя сферическими поверхностями
радиуса к и к + dk вблизи экстремумов зон в этом случае дается выражением:
dN = -^T4nk2dk = ^-rk'dk E.18)
Этот объем k2dk в /:-пространстве соответствует эквивалентному объему в
энергетическом пространстве, получаемом дифференцированием E.16):
^\ (E-Ec)l/2dE E.19)
й )
Энергетическая плотность состояний рс(Е) в зоне проводимости GaAs есть
число состояний, расположенных между значениями энергии Е и Е + dE. Для
того, чтобы найти число состояний, нам необходимо только подставить E.19) в
E.18), не забывая учитывать вклад из-за вырождения электронов по спину (это
позволяет двум электронам с противоположно направленными спинами
занимать тот же самый энергетический уровень). Соответственно, окончательное
выражение должно быть умножено надвое, что дает:
\e-E<Y'2 E-20)
Плотность состояний для
изотропной зонной структуры
Обобщение этого результата на случай эллипсоидов произвольной формы
приводит нас к теории конических сечений и в данном случае не представляет особого
интереса. Мы находим, что для непрямых зон проводимости, в случае кремния и
германия имеет место:
(Е-ЕсУ<> E.21)
где т* — средняя эффективная масса зоны проводимости, которая определяется
соотношением:
т*е = (пт¥2тЛJ'3 E.22)
и где п — число эквивалентных долин (п = 6 в Si и 4 в GaAs). Эти величины также
приведены в таблице приложения (стр. 588). Аналогично плотность состояний
валентной зоны определяется соотношением:
(Е„-ЕУ<> E.23)
где Ev есть максимум валентной зоны, при этом эффективная масса для
эффективной плотности состояний валентной зоны есть:
т:={пти2тГУ/ъ E.24)
Важно помнить, что плотность состояний в трехмерном кристалле
возрастает как Е?/2 и ту2. Рис. 5.9. схематически показывает зонную структуру и
плотность состояний, полученные с использованием квадратичной аппроксимации
вблизи экстремумов зон.
Эта модель не позволяет сделать никакие общие заключения о характере
посередине зоны, где квадратичная аппроксимация явно нарушается.
W182 Глава 5. Зонная структура полупроводников
3/2 1/2
mv (Emax-E)
cmin
а б
Рис. 5.9. Зонная структура (а) и плотность состояний (б) вблизи экстремумов зон
разрешенных состояний.
5.5. Динамическая интерпретация
эффективной массы и концепции дырок
Вплоть до настоящего момента мы несколько раз упоминали понятие дырка. В
действительности, это сложное понятие, требующее (при последовательном
рассмотрении) привлечения теории многих тел. В этом разделе мы ограничимся лишь
тем, что представим несколько интуитивных аспектов, касающихся теории дырок.
Начнем с того, что представим динамическую интерпретацию концепции
эффективной массы.
Волновые функции электронов могут быть представлены в виде комбинации
бегущих волн:
E.25я)
E.256)
Волновые пакеты, сконструированные из волновых функций вблизи конкретной
величины к обладают групповой скоростью, определяемой дисперсионным соотношением
v = dco/dk, так что в случае волн электронной материи в зоне (см. рис. 5.10) можем
записать:
yg=^VkE E.26)
Работа, совершаемая внешней силой F в течение временного интервала dt равна:
E.27)
а{Ъ)Л п М3
или вновь, используя результаты раздела 5.2:
при этом изменение энергии волнового пакета сопровождается также сдвигом
среднего положения волнового пакета в зонной структуре и определяется соотношением:
dE = -Vk^dk = -h vdk E.28)
Рассмотрение показывает, что центр волнового пакета, подверженного
воздействию силы F, подчиняется таким образом соотношению:
E.29)
5.5. Динамическая интерпретация эффективной массы и концепции дырок
Рис. 5.10. Связь между зонной
структурой, групповой скоростью и
эффективной массой.
Отметим, что, если никакой
механизм диссипиации энергии
не противодействует воздействию
этой силы F, волновой пакет
будет двигаться или циркулировать
по зонной структуре (см. рис.
5.11). Колебания, возникающие
при циклическом обращении
носителей по редуцированной зоне
Бриллюэна, называются блохов-
скими осцилляциями.
Пример
Время релаксации г между
последовательными столкновениями
в твердых телах составляет
величину порядка 0,1 пс.
Предполагая, что напряженность
электрического поля Е составляет
приблизительно 104 В см, находим,
что волновой пакет получит смещение на dk =gEr/h
-ж/a
106 см. Эта величина
намного меньше типичного размера зоны Бриллюэна (п/а « 108 см). Как следствие
этого, блоховские осцилляции до сих пор не наблюдались в объемных материалах.
В том случае, когда диссипативные процессы полностью отсутствуют,
электрон, подверженный воздействию однородной силы F, будет однородно двигаться в
к-пространстве и испытает соответствующее ускорение в реальном пространстве.
Это ускорение определяется соотношением:
dvg
dt
d
или, учитывая E.29):
d\g
~df
E.30)
E.31)
Матрица [VkVk£"] не представляет из
себя ничего другого как h2M~l, где М есть
матрица эффективной массы в E.14).
Таким образом, реакция волнового пакета
может быть описана ньютоновской
динамикой с заменой массы частицы на ее
эффективную массу mcfr
Под влиянием электрического поля Е
каждый элемент d3k зонной структуры дает
Рис. 5.11. В отсутствие столкновений
электроны под воздействием электрического поля
будут циклично обращаться по зоне Бриллюэна
периодическим образом. Это приводит к
явлению, известному как блоховские осцилляции.
-л/а
Глава 5. Зонная структура полупроводников
вклад в элементарный объем d3k/8;r3, движущийся со скоростью vg(k) Таким
образом, электрический ток, проходящий через среду, составляет:
J = -
--2,
да
Bnllouin zone
E.32а)
или:
J =
^d'k E.326)
JJJ
Bnllouin zone
где мы учли дополнительный множитель 2 из-за электронного вырождения по спину. Если
энергетическая зона полностью занята (смотрите рис. 5.12), все возможные
движения в k-пространстве будут включать в себя только перестановки.
Поскольку Е(к) является симметричной относительно к, объемные элементы с
противоположными значениями к будут компенсироваться, т. е деструктивно
интерферировать (рис. 5.12). Таким образом, полностью заполненная зона не будет
проводящей, т. е.:
J (заполненная зона) = 0
E.33)
Материал, в котором последняя зона полностью заполнена электронами и
отделена запрещенной зоной от соседней близлежащей пустой зоны, не может
проводить электрический ток и называется изолятором.
Если эта зона, которую мы обычно называем зоной проводимости, частично
заполнена (вплоть до максимальной энергии = Етах), электроны смогут приобрести
скорость в к-пространстве, определяемую E.31), и двигаться в направлении силы.
Ток, возникающий из-за этих электронов не компенсируется из-за отсутствия
симметрии (рис. 5.12). Такие электроны проводимости могут быть обеспечены как
самим материалом (как это имеет место в случае металлов), так и быть добавлены в
изолятор (как этот имеет место в случае полупроводников). Говоря конкретнее,
в том случае, когда электрическое поле приложено вдоль оси Ох, электроны
переносятся из состояний с кх < О в область с состояниями кх > О, при этом через
кристалл потечет ток, определяемый в момент времени / =0 (см. E.32)):
• <? Г dE_
Jx~ An'h) dk/
-dk
E.34)
Этот ток будет монотонно возрастать со временем, поскольку Етах будет
постепенно смещаться в направлении электрического поля. Понятно, что в течение пе-
J = 0
(а) (б)
Рис. 5.12. В полностью заполненной зоне электрические токи, возникающие с
участием заполненных состояний при к и —к будут компенсироваться (а). В
частично незаполненной зоне (б) электроны под воздействием силы F,
определяемой E.26—5.29), приобретают скорость yg. Таким образом, электроны
переносятся вдоль оси симметрии, при этом полный баланс скоростей является
ненулевым. Таким образом, такая неполная зона может быть проводящей.
5.5. Динамическая интерпретация эффективной массы и концепции дырок
реходного периода, длящегося несколько десятков пикосекунд, столкновения
приведут к стабилизации тока. В стационарных условиях этот процесс описывается
уравнениями Больцмана, которые мы рассмотрим позже в главе 6.
Аналогичным образом, если нам каким-либо образом освободить электроны из
заполненной зоны (валентной зоны) и придать им энергию £min, возникающий при
этом ток составит:
Г dE л. а Г dE А1 \ q f dE ,. |
Occupied states x Ч" n Bnllouin zone х \ ^П П Unoccupied states x ,
E.35)
или с учетом E.33):
dE
л =+■
J £*. E.36,
где пределы интегрирования изменяются от Emin до вершины валентной зоны (рис.
5.13). Таким образом, мы видим, что ток, переносимый практически заполненной
зоной, может быть интерпретирован как поток положительно заряженных
квазичастиц, таких как дырки. Рассмотрение, аналогичное проведенному ранее, показывает,
что масса этих частиц положительна и определяется соотношением:
М'1 =—L[vkVk£] E.37)
h
поскольку кривизна вблизи максимума валентной зоны отрицательна. Рис. 5.13я
показывает нам, каким образом «дырку» (т. е. незанятое электронное состояние в
валентной зоне) можно рассматривать как несущую положительный заряд.
Отсутствие электрона при к <=> Присутствие дырки при —к
d/ d/
cl 1 Л 1
Л/е1 < 0 <=> Mh > О
заряд — е <=> заряд е
j =
к осе к осе
electrons holes
Читателю, впервые сталкивающемуся с такой концепцией может помочь аналогия
с простой гидродинамикой. В этом случае электроны можно рассматривать как
будто «падающими» на дно зоны проводимости подобно воде, стремящейся к дну
стакана, в то время как дырки «поднимаются» к вершине валентной зоны подобно
пузырькам (дыркам в жидкости) в стакане с шампанским.
Для завершения этого раздела нам остается добавить, что полная волновая функция
дырки определяется переплетением собственных состояний всей валентной зоны (сим-
метризованных в виде детерминанта Слэтера), из которых был удален один электрон. Этот
тип функций является не очень востребованным на практике, но иногда используется,
как, например, в теории экситонов.
W186 Глава 5. Зонная структура полупроводников
Энергия электронов
F
Энергия дырок
а б
Рис. 5.13. Рисунок слева представляет электроны в валентной зоне как частицы с
отрицательным зарядом и эффективной массой. Под влиянием
электрического поля электроны переносятся в направлении состояний с
отрицательными значениями к. При определении дырки при -к может
рассматриваться как отсутствие электрона, при к дырка может рассматриваться как
квазичастица с положительными зарядом и массой (д = ё).
5.6. Статистика носителей заряда в полупроводниках
5.6.1. Статистика Ферми и уровень Ферми
Электроны и дырки в полупроводниках подчиняются, как и все частицы со спином 1/2,
статистике Ферми—Дирака. Таким образом, вероятность того, что при температуре Гсо-
стояние с энергией Е будет занято, дается функцией распределения Ферми—Дирака
/(£). При температуре Г функция распределения по энергии имеет вид:
1
так, что концентрация носителей, например, в зоне проводимости полупроводника
определяется соотношением:
«= \pc{E)f(E)lE
E.39л)
Безусловно, ниже Ес не имеется разрешенных состояний. С учетом выражения
для плотности состояний в зоне проводимости (смотрите E.20)) это последнее
уравнение может быть записано в общем виде:
E.396)
где Fl/2 есть интеграл Ферми и Nc — эффективная плотность состояний в зоне проводимости.
5.6. Статистика носителей заряда в полупроводниках
1.0
0.5 -
0.0
-0.4
1
1
1 1 1 1
Г=600К
г=ок ►
1 1 j
0.1
0.2
Рис. 5.14 иллюстрирует
распределения Ферми—Дирака при нулевой и
ненулевой температурах. Мы
должны напомнить, что при температуре
Т= О К энергия Ферми есть энергия
последнего занятого состояния. По
определению, уровень Ферми есть
химический потенциал частиц в
системе. Он описывает количество
энергии, которое должно быть потрачено
для того, чтобы добавить одну
частицу (расположенную изначально
далеко) в систему. При
термодинамическом равновесии этот химический по-
тенциал одинаков для всех частиц и идентичен по всей структуре. К этому очень
важному моменту мы возвратимся позже во время нашего изучения диффузии.
При расчете положения уровня Ферми в полупроводнике в функции числа
электронов возникают две различные ситуации в зависимости от того, расположен ли
уровень Ферми в запрещенной зоне или зоне разрешенных состояний зонной
структуры материала.
-0.3 -0.2 -0.1 0.0
E-£FF(eV)
Рис. 5.14. Распределения Ферми—Дирака при
различных температурах.
Занятый уровень Ферми: вырожденная система (рис. 5.15)
В этом случае функция Ферми—Дирака может быть аппроксимирована
ступенчатой функцией:
/(£) = 1, если Е< EF
f(E) = 0, если Е > EF
В этом случае объемная плотность электронов дается перекрытием функцией
Ферми и энергетической плотностью состояний на единицу объема в зоне
проводимости, т. е.:
или иначе:
Отметим, что в этом выражении число носителей
не является функцией температуры. Этот момент
характерен для вырожденных систем таких, например, как
металлы или сильно легированные полупроводники.
Пример
Попробуем найти число носителей, соответствующих
положению уровня Ферми, отстоящему на 30 мэВ вглубь
зоны проводимости GaAs. Для GaAs mc = 0,067/тк
«=Bх 0,067 х 0,91 х 100 кг/1,1 х 108 Дж2 с2I5 х
х@,03эВх 1,6 х 109
Рис. 5.15. Способ расчета положения уровня Ферми, когда
он расположен в зоне разрешенных состояний.
'dE
E.40)
E.41)
Энергия, Е
188 Глава 5. Зонная структура полупроводников
или:
п = 4,4 х 1017 см
Таким образом, при концентрации электронов выше 1017 см GaAs ведет себя
как металл и его уровень Ферми заполнен даже при температуре абсолютного нуля.
Незанятый уровень Ферми (рис. 5.16)
В этом случае уровень Ферми располагается в запрещенной зоне полупроводника. Число
электронов вновь дается перекрытием функций распределения Ферми—Дирака для элек-
троновД^) = 1/A — ехр ((Е— Е)/кТ) и плотности состояний в зоне проводимости. В этом
случае требуется другая аппроксимация для функции Ферми. Сейчас мы предположим,
что уровень Ферми располагается достаточно глубоко в запрещенной зоне по сравнению с
кТ, так что Е— EF » кТ. В этом случае функция Ферми — Дирака может быть
аппроксимирована распределением Больцмана е ~(Е~ Efr)/kT (неквантовый режим):
■-J
= \р{ЕУЕ-Е>)/кЧЕ =
1 Bт*
2л-2 *
,3/2
E.42а)
т. е.:
п = N
«-£'>/*г E.426)
Концентрация электронов
и уровень Ферми
где, как мы напоминаем, т*есть эффективная масса для плотности состояний в
зоне проводимости, определяемой E.22). Nc есть эффективная плотность
состояний в зоне проводимости:
\
3/2
E.43)
В том, что касается дырок, вероятность заполнения fv(E) дыркой равна вероятности
того, что это состояние не занято электроном. Это приводит к:
1
1
-(Е-Е,)/кТ
E.44)
Статистика Ферми—Дирака
для дырок
Рис. 5.16. Способ расчета концентрации носителей в полупроводниковых зонах в
функции положения уровня Ферми.
5.6. Статистика носителей заряда в полупроводниках 189
Таким образом, в больцмановском режиме концентрация дырок в валентной
зоне связана с уровнем Ферми соотношением:
р =
Концентрация дырок
и уровень Ферми
где Nv — эффективная плотность состояний в валентной зоне, определяемая
соотношением:
Термин «эффективная плотность состояний» приобретает свой смысл при учете
уравнений E.42) и E.45). Статистика заселенности в полупроводниках имеет тот же
характер, что статистика двухуровневой системы с энергиями Ev и Ес при
энергетическом зазоре Ес — Ev = Eg, определяемом запрещенной зоной, и плотностями состояний,
определяемыми Nv и Nc соответственно (смотрите рис. 5.18). Вводя значения
соответствующих физических констант, указанные эффективные плотности принимают вид:
3/2
(
E.46)
\3/2
Эффективные плотности
состояний в полупроводниках
Пример
В случае GaAs при 300 К mj = 0,067 и т* = 0,64, что приводит к:
При условии, что концентрации электронов и дырок известны, для расчета
положения уровня Ферми полезны также уравнения E.42) и E.44):
EF = Ec-kT\n^ = Ev + JcT\n^L E.47)
п р
Уровень Ферми
и концентрация носителей
Таким образом, мы видим, что уровень Ферми проникает в зоны, т. е.
полупроводник становится вырожденным, как только концентрация электронов (или
дырок) превысит эффективную плотность состояний (смотрите рис. 5.17).
Уравнение E.47) интересно тем, что оно показывает, что уровень Ферми не
представляет собой ничто другое, как изменение переменных без непосредственно
физически добавленной величины. Это всего лишь мера плотности заселенности
на энергетической шкале. В то же время эта концепция проявит всю свою силу в
гетерогенных системах, являющихся основой физики приборов. В самом деле,
постоянство уровня Ферми во всех областях, где превалирует термодинамическое
равновесие, является одним из основных инструментов физики приборов.
И, наконец, если мы предположим, что электроны и дырки находятся в
термодинамическом равновесии, то они обладают также одним и тем же химическим
W190 Глава 5. Зонная структура полупроводников
зона проводимости
«2/3
In п
Рис. 5.17. Поведение уровня Ферми в функции концентрации свободных носителей п.
При концентрации носителей, превышающей эффективную плотность
состояний Ne, полупроводник становится вырожденным, при этом его
положение, как и в металлах, изменяется как п2/3.
потенциалом (т. е. химический потенциал имеет одно и то же значение там, где
выполняются условия термодинамического равновесия). В большей степени мощь
этой концепции мы оценим при исследовании аспектов физики приборов в главе
10. В соответствии с уравнениями E.42) и E.44) как их следствие мы находим, что
произведение пр не зависит от положения уровня Ферми и составляет:
пр = NcNvc-E'/kT E.48)
Закон действующих масс
для полупроводников
где Eg = Ec — Ev есть ширина запрещенной зоны. Выражение E.48) устанавливает
связь между концентрациями электронов и дырок в равновесных условиях и
известно, как закон действующих масс.
5.6.2. Собственные полупроводники
Говорят, что полупроводник является собственным, когда источником появления как
электронов, так и дырок является сам материал. В этом случае наличие дырок в валентной зоне
является следствием того, что электроны термически возбуждаются в зону проводимости
(рис. 5.18). В этом случае концентрации электронов и дырок (соответственно пир)
равны собственной концентрации носителей:
~ E.49)
Собственная концентрация
носителей
Рис. 5.18. В слаболегированном полупроводнике
термодинамическое состояние зон подобно состоянию двух уровней с
концентрацией Ncn Nv.
А
1
1
1
п
р
\
1
t
1
• СВ
Фононы
- VB
Пример
В GaAs, где ширина запрещенной зоны составляет Eg = 1,42 эВ, концентрация
носителей п. при Т = 300 К составляет п. =3 х 106 см. Понятно, что это делает
GaAs плохим изолятором при комнатной температуре. К тому же остаточные при-
5.6. Статистика носителей заряда в полупроводниках
меси, присутствующие в GaAs дают вклад в концентрацию носителей, существенно
увеличивая ее по сравнению с приведенным выше уровнем.
В случае HgCdTe малая ширина запрещенной зоны этого материала
(используемого для инфракрасного детектирования — смотрите главу 11) Eg = 0,116 эВ
приводит к собственной концентрации носителей п. = 1,0 х 1016 см. Таким образом,
такой материал обладает электропроводностью при комнатной температуре без
дополнительного легирования.
5.6.3. Легированные полупроводники
Собственный полупроводник сам по себе сравнительно бесполезен. Одновременно
он является плохим проводником и плохим изолятором. В то же время в
альтернативном варианте он становится фантастическим (и полезным!) материалом при его
легировании. В действительности, при введении в полупроводник малого уровня
определенных химических примесей, они могут эффективно занимать
кристаллические узлы в материале матрицы. В этом случае волновые функции гибридизиру-
ются с атомами основной матрицы и предоставляют избыточные электроны в зону
проводимости. Так происходит, например, с пятивалентным фосфором в кремнии
(рис. 5.19) или, когда кремний вводится как примесь в GaAs. Такие примеси
называются донорами, а легированный такими примесями полупроводник называется
полупроводником п- типа. Примеси другого типа могут захватывать электроны из
кристаллической матрицы (при этом захваченный электрон становится связанным
с примесью). Это происходит, например, с бором в кремнии (рис. 5.20). Такие
примеси (или акцепторы) таким образом освобождают дырки в валентную зону
полупроводника, обращая кристалл в материал /ьтипа.
Можно показать, что эти типы примесей (доноры и акцепторы) ведут себя как
водородоподобные примесные центры, связывающие электроны и дырки кулонов-
ским потенциалом с характеристической энергией ионизации:
87W^B E50)
6£R£0 П me£R
где /и* — эффективная масса и^- относительная диэлектрическая проницаемость
полупроводника. Это приводит к энергии ионизации, варьирующейся в диапазоне
между 5 и 25 мэВ. Как следствие, эти примеси, по большей части ионизируются
при комнатной температуре. В то же время это не имеет места в широкозонных
полупроводниках типа GaN, где энергии ионизации водородоподобных примесей
могут достигать 200 мэВ.
св
Si Si
\ /. \
Р+ Si
Рис. 5.19. Пятивалентная примесь такая, как фосфор, введенная механизмом
замещения в решетку кремния, гибридизируется с тетрагонально расположенными
соседними атомами и высвобождает избыточный электрон в решетку как
свободную частицу (а). Это состояние приводит к возникновению донорно-
го состояния, расположенного в нескольких десятках мэВ ниже зоны
проводимости (б). При комнатной температуре все эти центры ионизированы и
предоставляют свои электроны зоне проводимости материала матрицы.
Глава 5. Зонная структура полупроводников
Si
Si
Si
Si
Si
Si
e—e
а б в
Рис. 5.20. Трехвалентная примесь, подобная бору и введенная в кремний, гибридизи-
руется с соседними атомами в тетрагональной конфигурации, принимая
электрон для ковалентной связи с соседним атомом, при этом нехватка
электрона и есть дырка (а). В действительности эта примесь вводит акцепторное
состояние, расположенное в нескольких десятках мэВ над валентной зоной
(б). При комнатной температуре все эти центры заняты электронами
валентной зоны, в то время, как дырки «заселяют» валентную зону кристалла.
В последующем мы будем предполагать, что концентрация введенных доноров
составляет ND, а также то, что в рассматриваемом диапазоне температур все доноры
ионизированы. Если ND » п., мы можем легко показать, все носители заряда в
зоне проводимости термически возбуждаются из донорных уровней, при этом:
n = ND E.51)
Следовательно, положение уровня Ферми составляет:
E.52)
Аналогичным образом, если акцепторная примесь вводится в полупроводник в
концентрации NA, то концентрация дырок в валентной зоне, возникающая из-за
захвата электронов из вершины валентной зоны, составляет:
P = N, E.53)
при этом положение уровня Ферми определяется соотношением:
EF = Ev+kT\n^f-
E.54)
Уравнения E.52) и E.54) показывают, что до тех пор, пока уровень
легирования не превышает эффективную плотность состояний в зонах, полупроводник
будет оставаться невырожденным. Рисунок 5.21 показывает положение уровня
Ферми в GaAs в функции уровня легирования.
со
о
10
10
17
10
18
Уровень легирования (см ')
Рис. 5.21. Положение уровня
Ферми в функции уровня
легирования. Полупроводник
становится вырожденным при
уровне легирования, большем
эффективной плотности
состояний.
5.6. Статистика носителей заряда в полупроводниках
5.6.4. Квазиуровень Ферми в неравновесной системе
Вплоть до настоящего момента мы рассматривали различные случаи, приводящие
к уровням заселенности электронов и дырок в состоянии термодинамического
равновесия. Вместе с тем во многих случаях уровни заселенности определяются
неравновесными процессами. В самом деле, функционирование всех полупроводниковых
приборов происходит в неравновесных условиях, являющихся следствием
приложения либо электрического поля, либо засветки структуры. В этих случаях электроны
и дырки более не находятся в состоянии термодинамического равновесия друг с
другом, а также с кристаллом матрицы. Таким образом, мы можем рассматривать
внешний процесс, генерирующий электроны и дырки в полупроводнике со
скоростью Gn и Gp (см с) соответственно для электронов и дырок. Одновременно с
этим предусмотрим существование рекомбинационного процесса,
характеризуемого постоянными времени гиги приводящего к стабилизации заселенности
электронами и дырками до уровня, когда достигается баланс скоростей генерации и
рекомбинации, т. е. Gn = п/тп и Gp = р/тр.
В этом случае стационарная концентрация электронов и дырок определяется
соотношениями:
П =_ Gjn E.55)
р — G т
В последней формуле мы предположили, что возникающие концентрации
носителей превышают уровни тепловой генерации, т. е., что п » п0. Исключительно
плодотворным оказалось предложение Шокли считать, что эти уровни
заселенности по-прежнему можно описывать с использованием квазиуровня Ферми (шутливо
названного Имреф, что произносится как Ферми, прочитанное в обратном
порядке!) Если система является невырожденной, исходя из E.52) и E.54) эти уровни
определяются соотношениями:
E.56а)
N. "
Невырожденный квазиуровень Ферми
В том случае, когда система становится вырожденной, положение
квазиуровней Ферми можно определить из E.41) или:
E.566)
Вырожденный квазиуровень Ферми
Понятно, что при Gnrn » nQ и Gprp» p0 квазиуровни Ферми не совпадают
(смотрите рис. 5.22) и на самом деле отделены от уровня Ферми на величину:
Это последнее соотношение позволяет нам рассчитать смещение квазиуровня
Ферми в функции скорости накачки и различных рекомбинационных времен. Это
уравнение занимает центральное положение в физике полупроводниковых лазеров,
тему которых мы рассмотрим позже в главе 15.
W194 Глава 5. Зонная структура полупроводников
EFn
О О О О О О < Gp
(а) (б)
Рис. 5.22. В условиях теплового равновесия электроны и дырки характеризуются одним
и тем же положением уровня Ферми (а). При отклонении от
термодинамического равновесия (т. е. в случае, когда зоны заселены фотогенерированны-
ми или электрически инжектированными носителями) каждый из уровней
заселенности электронами и дырками описываются своими собственными
уровнями Ферми (или квазиуровнями Ферми), которые более не совпадают
друг с другом (б).
Литература
Физика твердого тела
N.W. Ashcroft and N.D. Mermin,5o//V/ State Physics, Holt,Reinhart and Winston,
New York A976).
С Kittel.Introduction to Solid State Physics, 5th Edn,Wiley, New York A976).
Физика полупроводников
A. Kireev, Phusique des demiconducteurs, MIR, Moscou A975).
F. Levy, Physique et techjnologie des semiconducteurs, Presses Polytechniques et
Universitaires Romandes, lausanne A993).
B. Sapoval and C.Hermann, 3rd Edn, Springer, Berlin A985).
S.M. Sze, Physics of Semiconductor Devices, 2nd Edn., Wiley Interscience, New York
A981).
ДОПОЛНЕНИЯ
К ГЛАВЕ 5
5.А. Модель почти свободных электронов
В этом разделе мы представляем первый подход к теории зонной структуры,
основанный на возмущении модели свободных электронов и называемый моделью
почти свободных электронов. Используем уравнение Шредингера для электронов в
периодическом одномерном кристалле с периодом решетки а (держа в уме, что
обобщение этого рассмотрения потребует лишь мужественного привлечения
соответствующих индексов). Периодичность кристаллического потенциала в этом
случае делает его пригодным для Фурье-анализа:
Reciprocal
lattice
где, как мы напоминаем, векторы G принадлежат обратной решетке, т. е. они
имеют вид G = (целое число) х 2п/а. С использованием этих параметров уравнение
Шредингера для потенциала приобретает вид:
2 >
Ну/{х)= I-+yVGeGx L(x)=£y(jt) E.A.2)
Волновая функция \|/ (х) может быть также представлена в виде ряда Фурье за счет
использования цикличных граничных условий Борна—фон Кармана —К = n2n/(Na),
где Na относится к полной протяженности кристалла и п положительное (или
нулевое) целое число — так что:
^(х)=^С(АГ)е"'Л E.А.З)
к
Подставляя E.А.З) в E.А.2), мы находим:
-1<М)* ' = О E.А.4)
Теперь давайте умножим это уравнение на t~{kx и проинтегрируем по всему объему
кристалла. Единственными ненулевыми членами будут те члены, для которых G —
К = к. Это означает, что если в сумме появляется член к, то появятся и все другие
векторы, являющиеся результатом прибавления к нему одного или нескольких векторов
обратной решетки G (смотрите рис. 5.А.1). Таким образом, в качестве индекса
волновых функций мы можем использовать волновые векторы к, выбираемые
произвольно в пределах первой зоны Бриллюэна, что позволяет записать собственные
функции в виде:
и/, iл I — у v^s \/с — kj ус уJ./л..*j)
G
Это есть ничто иное, как теорема Блоха—Флоке. В этом случае применение
уравнения Шредингера E.А.2) к блоховским функциям у/к приводит его к виду:
Ek-^-\:(k)+^VGC(k-G)=0 E.A.6)
) G
Это есть секулярное уравнение по С(к — G), обладающее нетривиальными
решениями (т. е. ненулевыми решениями) только в том случае, когда детерминанат
W196 Дополнения к главе 5
к
I
к + 2я/а
4
»•••♦••••
я/а
я/а
2л/а
Первая Бриллюновская зона
Рис. 5.А.1. Точки, показанные на этом рисунке, представляют волновые векторы к,
допускаемые цикличными граничными условиями Борна — фон Кармана
для кристалла длиной L = 20 я, где a — постоянная решетки. Если член
(к = —8 на этом рисунке) появляется в сумме E.А.4), все остальные члены
к + 2 л я/я также будут включены.
этой линейной системы равен нулю. Ранг этого детерминаната равен числу точек в
обратном пространстве. Могло бы показаться, что мы мало продвинулись по
сравнению с исходным видом уравнения Шредингера, если бы мы просто заменили
дифференциальное выражение на алгебраическое. Теперь примем гипотезу, что
функция является сильно периодической, т. е., что она обладает таким малым числом
Фурье-компонент, что мы можем рассмотреть единственную компоненту, что
имело бы место для чисто синусоидального потенциала. Часть секулярного уравнения
в E.А.6) в этом случае может быть записана в виде:
h2(k-Gj
2m
V
0
0
Е{к)-
h2k2
2m
о
V
0
0
0
etc
= 0
E.А.7)
Для каждого волнового числа к секулярное уравнение является полиномом Е
(к) одного порядка с матрицей (таким образом имеется столько возможных
решений, сколько рядов содержит матрица). Эти решения непрерывны по к и таким
образом образуют энергетические зоны. Особенно интересный случай имеет место, когда
к располагается вблизи границы зоны Бриллюэна, т. е. при к « G/2 = п/а. В этом
случае G — к и к имеют одну и ту же величину, при этом диагональные элементы
подматрицы форматом 2x2:
Е{к)-
ft2G2
8т
Е(к)-
h2G2
идентичны. Взаимодействие с ближайшим членом V снимает вырождение двух
невозмущенных уровней Е(к) — h2G1/Sm. Это означает, что энергетические зоны,
которые в другом случае обладали бы той же самой энергией при к = G/2,
становятся невырожденными — теперь исследуем этот эффект более детально.
Поблизости от к = G/2 в детерминанте E.А.7) доминирует подматрица формата 2x2
вблизи к = G/2, при этом уравнение для снятия вырождения приобретает вид:
(ff 198 Дополнения к главе 5
±те— E.А.11)
Таким образом мы видим, что чем меньше ширина запрещенной зоны 2 V, тем
меньше и эффективные массы. Такая же связь устанавливается и в рамках других
моделей. Узкозонные полупроводники (исключительно пригодные для
детектирования инфракрасного излучения), как правило, характеризуются малыми
эффективными массами электронов и дырок.
Литература
N.W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston,
New York A976).
C. Kittel, Inroduction to Solid State Phisics, 5th End, Wiley, New York A976).
5.Б. Линейная комбинация атомных орбиталей:
модель жесткой связи
В главе 1 мы видели, что собственные состояния двух идентичных, атомов,
обладающих идентичными энергетическими уровнями, гибридизируются, когда они
сводятся вместе, порождая уровни связи и антисвязи с отличными собственными
энергиями. Эти уровни разнесены на энергетической шкале на величину, связанную со
степенью перекрытия (в данном случае обратно скоррелированную с физической
величиной перекрытия) между собственными состояниями атомов. Теперь мы
покажем, каким образом можно распространить эту процедуру на описание всего
кристалла и каким образом с использованием данной модели можно подойти к
понятию разрешенной и запрещенной энергетических зон. Этот подход
полупроводниковой зонной структуры основан на значимости полупроводниковой зонной
структуры и называется моделью жесткой связи (рис. 5.Б.1). Целью этой модели
является отыскание кристаллических состояний с использованием линейных
комбинаций образующих систему атомных орбиталей. Рассмотрим одномерную
периодическую последовательность идентичных атомов. Начнем с предположения, что
атомы достаточно отдалены друг от друга, чтобы пренебречь влиянием потенциала
любого близлежащего атома на соседний атом.
Гамильтониан электрона в поле потенциала атома /, расположенного в решетке
при ia есть:
И, =lL+v(x-ia) E.Б.1)
Z.YYI
m-1 m
о 9 е g
V (г) V (г) V (г)
m-V ' /77 Х П7+1
Рис. 5.Б.1. Одномерная модель кристаллического потенциала. Орбитали каждого
атома кристалла связаны с соседним интегралом перекрытия, что позволяет
электронам переходить от атома к атому за счет туннелирования.
5.А. Модель почти свободных электронов
Е{к)-
П2к2
2т
Е(к)-
fi2{k-GJ
2т
= 0
E.А.8)
Это уравнение допускает два набора решений секулярного уравнения, которые с
небольшими усилиями можно получить в виде:
\2G2 h2g2
2m 2m
E.А.9)
где q = к — G/2. Мы вводим еф что представляет собой энергию, которой обладал бы
свободный электрон при к = G/2, т. е. eG — n\G/2J/2m. Для малых значений q уравнение
EА9) принимает вид:
E.А.10)
Рисунок 5.А.2 описывает решения уравнения Шредингера в виде E.А.7). Мы
видим, что можем выбрать по нашему желанию либо описание зонной структуры
по всем зонам Бриллюэна, либо привести всю зонную структуру в первую зону
Бриллюэна с соответствующим индексированием зон. Последний из подходов
получил название схемы редуцированных зон, и он используется наиболее часто. На
этом рисунке особо следует выделить ряд существенных моментов. Во-первых,
вдали от границ зоны Бриллюэна зонная структура приобретает вид, характерный для
энергетической дисперсии свободных электронов (что может быть показано). Во-
вторых, ширина запрещенной зоны величиной приблизительно 2 К обусловлена
снятием вырождения между волнами eikr и eI(*~G)r. Отметим также, что дисперсионное
соотношение E(q) является параболическим по q(~q2), что позволяет найти в
рамках этой модели величину эффективной массы в виде:
Свободный
электрон
Первая зона
Рис. 5.А.2. Существенные особенности модели почти свободных электронов.
Периодическое возмущение кристаллическим потенциалом снимает вырождение
вблизи краев зоны Бриллюэна (G/2 = я/а), что приводит к возникновению
запрещенной зоны. Полутоновые кривые получены приведением
энергетических кривых Е(к) в первую зону Бриллюэна — это называется схемой
зонного редуцирования.
5. Б. Линейная комбинация атомных орбиталей: модель жесткой связи
Таким образом все атомы обладают теми же самыми энергетическими уровнями Еп
и теми же самыми смещенными собственными функциями:
\n,i) = у/п f(x) = у/п(х - ia)
E.Б.2)
Теперь сблизим атомы и попробуем найти стационарные состояния и
собственные энергии Е для гамильтониана электрона в кристалле:
Н =-^- + У V(x-ia) E.Б.З)
2т ^
Поскольку базис волновых функций у/п .является полным, мы можем выразить
гамильтониан E.Б.З) в виде матрицы. Для этого внимательно посмотрим на различные
члены — диагональные члены </, n\H\i, n) даются выражением:
(п, i\H\n, /) = Еп + ^ (л, i\v(x - Xj)n, i) E.Б.4)
Член в сумме не зависит от / и приводит к сдвигу энергии. Таким образом этот член не
имеет особого физического значения и им можно пренебречь.
В том, что касается недиагональных членов, нас интересуют только те члены,
которые соответствуют ближайшему соседу:
(л, i\H\п, / ± 1) = Е„(п, /1 п, / ± 1) + ^ (л, i\v(x - Xj) n, / ± 1) = (л, i\V(x - х,] п, / ± 1) = -Ап
E.Б.5)
В вьфажении E.Б.5) мы пренебрегли перекрытием между орбиталями вида (л, /|л, / ± 1)
и оставили в сумме только члены Ап, соответствующие туннелированию между
ближайшими соседями. С учетом этого предположения гамильтониан, описывающий электроны
в кристалле, может быть разбит на независимые гамильтонианы для каждого
невозмущенного энергетического уровня Е:
Н =
В этом случае стационарные волновые функции даются выражением:
А
0
0
-лп
Еп
-А»
0
0
~Ап
Е„
-А..
0
0
-А
E.Б.6)
E.Б.7)
При этом коэффициенты Сп . даются уравнением Шредингера, т. е. решениями
системы уравнений:
E.Б.8)
bnCnj+l — АпСп l+2 =
где £есть энергия новых стационарных состояний. В уравнении E.Б.8) мы узнаем
рекуррентные соотношения для ряда Фибоначчи, которые допускают решения в
виде:
С ; =
E.Б.9)
где х. = ia. Таким образом, мы можем обозначать новые собственные состояния
кристаллического гамильтониана как y/k n. Легко показать, что эти функции экви-
ff 200 Дополнения к главе 5
W
валентны функциям Блоха—Фуке, полученным в E.Б.8) (смотрите рис. 5.Б.2).
Подставляя E.Б.9) в E.Б8) мы находим энергии для блоховских функций у/к п:
Еп(к) = Еп - 2Acos(ka) E.Б.10)
Таким образом, стационарные состояния располагаются в энергетических
зонах и синусоидально зависят от к. Схематически эти зоны изображены на рис.
5.Б.З. По сравнению с другими моделями эта модель дает ряд преимуществ, а именно
большую степень предсказуемости.
^л(х)
Jkx
\кх
V(X)
Рис. 5.Б.2. Функции Блоха—Флоке, описывающие стационарные состояния
электронов в условиях периодического потенциала, представляют собой линейные
комбинации изолированных атомных орбиталей (а), взвешенных на
коэффициенты, представляющие бегущую волну в кристалле (б).
Е(к)
-п1а
-ж! а
Рис. 5.Б.З. Разрешенные синусоидальные запрещенные зоны, полученные в рамках
модели жесткой связи. Наличие запрещенных зон подтверждает тот факт,
что разрешенные зоны не перекрываются.
5.В.кр метод Кейна
Зоны имеют химическую природу и возникают вследствие гибридизации
уровней, расширенных в зоны за счет туннельных эффектов между соседними атомами.
Эта картина нас более удовлетворяет (и она ближе к действительности!) по
сравнению с использованной в модели почти свободных электронов. Мы более ясно
понимаем, почему зона проводимости в кремнии характеризуется синглетными
состояниями sp3 и почему валентная зона обладает свойствами гибридизированных
триплетных состояний. К тому же мы лучше понимаем природу вырождения
валентной зоны.
Причиной возникновения запрещенных зон является незаполненная область
между состояниями Еп, возникающая после снятия вырождения. Если уширение
зон превышает энергетический интервал между уровнями Еп, зоны соприкасаются
и при этом запрещенные энергетические зазоры не возникают.
Чем более глубоки энергетические состояния (малые п), тем больше
потенциальные (или туннельные) барьеры, которые разделяют состояния близлежащих
атомов, и тем меньше величина Ап, что следует из интегралов туннелирования. В
результате этого более глубоко лежащие энергетические зоны существенно уже (имея
ширину 2Ап) по сравнению с более высоко лежащими зонами.
Вблизи экстремумов зон дисперсионные соотношения Е(к) являются
параболическими, и они приводят к эффективной массе:
И вновь мы обнаруживаем, что эффективная масса mcff обратно пропорциональна
ширине разрешенной зоны.
Литература
N.W. Ashcroft and N.D. Mermin, Solid State Physics, Holt, Rinehart, and Winston,
New York A976).
5.B. k • p метод Кейна
Модели почти свободных электронов и жесткой связи очень полезны в дидактических
целях, но одновременно они обладают существенным недостатком. На практике
чрезвычайно трудно, отправляясь от экспериментально определяемых параметров
(например, кристаллическая структура, электронная структура образующих материал
атомов, ...), предсказать, какова будет ширина запрещенной зоны, например, в GaAs и
т. д. Эта трудность возникает из-за сильно упрощенной природы аппроксимаций,
использованных при получении результатов дополнений 5.А и 5.Б. Введение
малейших усложнений приводит к необходимости чрезвычайно трудных вычислений.
Рассматриваемый к • р-метод представляет собой полуэмпирический подход,
использованный Кейном при расчете зонной структуры и использующий
экспериментально доступные данные (полученные из оптических измерений и т. д.)
"л \2т
где у/п k есть блоховские функции:
¥njj) = i/|fik(r)e4r E.B.2)
Мы видим, что оператор р = — i/jV действует на волновые функции Блоха-
Фуке следующим образом:
йк)\ь(г)]
E.B.3)
^202 Дополнения к главе 5
В результате, периодическая часть блоховских функций ип k является решением
уравнений шредингеровского типа:
+^ + к р + к(гI|/я k(r) = En kun k(r) E.B.4)
lm lm m J
Отметим, что при к = 0 это уравнение полностью эквивалентно уравнению Шредин-
гера для периодической части функций Блоха—Фуке ип 0:
0(г) = £я<01/я<0(г) E.В.5)
В качестве полного базиса для ип k k • р-теория использует ип 0:
При этом уравнение Шредингера E.В.4) преобразуется в:
— k-p+K(r)V'4kK0«^ E.B.7)
т0 I'm
Таким образом, используя проекцию на имо, находим:
^k-(^-°HM'».oK")(k) E.B.8)
Это уравнение представляет обычную проблему диагонализации матрицы
эффективного гамильтониана. Если все элементы (им 0\р\ит 0> известны, мы можем непосредственно
диагонализировать матрицу. Однако, это не всегда возможно. К тому же
действительный интерес представляют только области зон вблизи запрещенной зоны. Для
к вблизи 0 члены, обусловленные оператором к • р, можно рассматривать как
возмущения. Если мы определим:
НЦ. =— Мм«.о|рКо) E-В.9)
т0
то E.В.8) можно записать в виде:
к £ /У *,ci"(k) = 0 E.В.10)
В последнем уравнении мы использовали верхний индекс (п) для обозначения одного
из решений (обратите внимание на вырождение!), для которого Е{п)(к) стремится к Еп 0 по
мере того, как к стремится к 0. Упрощение задачи достигается разделением зон на
интересующую нас группу М{ (которая сильно связана с зоной я), а также на вторую группу М2
остальных зон. В этом случае мы имеем:
Я<"><к)к"ЧЮ + У Н2*\Ъ) + У НЩ^Нк) = 0
У Н2тс*
Для п е M{w Me M2 последняя сумма намного меньше первой. Это дает:
we A/, £ VU/~ E M 0
При п е Мх и Me Мх мы подставляем этот результат и находим:
2/и0
E.В.13)
5.В. к-рметодКейна
После переобозначения т' —> т, т —> т' в двойной сумме уравнение
приобретает характер задачи диагонализации только в базисе функций, принадлежащих
соответствующим зонам М е М{\
h2k:
= О
E.В.14)
где мы устранили аргумент к в коэффициентах ст. Таким образом, следуя подходу
возмущений мы ввели влияние не интересующих нас зон в эффективный гамильтониан,
который действует на интересующие нас зоны. Используя этот метод (называемый
методом Левдина), мы редуцировали объем нашей задачи за счет ограничения
диапазона справедливости подхода до области вблизи к = 0. При концентрации нашего
внимания на зонах, ближайших по энергии к Ем 0, этот метод становится
эквивалентным стационарным возмущениям — возмущению вырожденного уровня, если
Ем 0 вырожден или простому возмущению в противном случае.
В полупроводниках III—V кристаллическая структура реализуется в виде кубической
структуры цинковой обманки. В этом случае зона проводимости является
невырожденной (если учитывать спин, то дважды вырожденной) и имеет минимум вблизи центра зоны
Бриллюэна. Вблизи к = 0 дисперсия в этой зоне определяется E. В. 14) в простейшем виде,
когда группа Л/, содержит только одну зону (с):
2тп
сУ] = О
E.В.15)
Следовательно:
П2к2 [ П2к2
E.В.16)
Естественно, что самый важный вклад обусловлен состояниями, ближайшими по
энергии — состояниями валентной зоны. Если мы пренебрежем другими членами суммы, то
найдем:
Ь2к2 П2к2 Р2
2т0 2т0 Eg
где:
р2 =
E.В.17)
E.В.18)
есть матричный элемент Кейна, a Eg — ширина запрещенной зоны.
Из дисперсионного соотношения Е(с)(к) мы можем определить эффективную массу:
т,
E.В.19)
Оказывается, что Р2 можно определить из оптических измерений, при этом
этот параметр изменяется сравнительно слабо (-20—25 эВ) от одного соединения
III—V к другому. Таким образом, эта простая формула предсказывает, что, чем
меньше ширина запрещенной зоны полупроводника, тем меньше эффективная масса
iff 204 Дополнения к главе 5
в зоне проводимости. Это предсказание экспериментально подтверждается, и тот
факт, что тс/т0 «1 обусловлен сильной связью P2/Eg » 1 между зоной
проводимости и валентной зоной.
Тот же самый метод легко применить и к валентной зоне (которая предполагается
невырожденной), при этом в данном случае мы получаем:
:-^Е- E.В.20)
Это свидетельствует о том, что эффективная масса дырок должна быть приблизительно
равной эффективной массе электронов. К сожалению, ситуация с валентной зоной более
сложная, поскольку эта зона вырождена в максимуме.
К сожалению, мы не можем приводить детальные расчеты для валентной зоны,
поэтому мы ограничимся качественным описанием результатов.
Кристаллический потенциал V(r) обладает симметрией структуры цинковой
обманки. Это означает, что его величина является неизменной при применении операций
симметрии по г. С учетом аспектов симметрии можно показать, что такой потенциал
приводит к трехкратно вырожденным собственным состояниям в центре зоны Бриллюэна, при
этом вырождение не зависит от амплитуды потенциала. Валентная зона как раз и
обусловлена такими состояниями.
Три базисные функции могут быть обозначены как |Х>, |Y), |Z), где буквы
обозначают свойства симметрии этих волновых функций. Результат действия
операций симметрии на любую из этих функций сводится к их отражению в базисе двух
других (или обратно самой на себя). Возьмем, например, зеркальное отражение в
плоскости A11) (смотрите рис. 5.1), что соответствует изменению координат х —> у,
у -» х, z -> ь Базисные функции обладают свойствами:
\Y) = uY(y,x,z)=ux(x,y,z) E.B.21)
\Z) = uz(y, x, z)=uz(x, у, z)
Скажем, что эти функции преобразуются между собой как х, у и z. С учетом
таких свойств симметрии легко показать, что оператор импульса р = h / iV дает
нулевой матричный элемент по этим двум функциям. Возьмем, например, (Z\pz\X >.
Вращение на к вокруг оси z преобразует \Z) в \Z ), pz в pz и \Х) в —\Х). Таким
образом, (Z\pz\X) = —(Z\pz\X) = 0. Снятие вырождения при к ф 0 за счет к • р
взаимодействия не может произойти из-за связи между другими функциями
валентной зоны, но в обязательном порядке происходит из-за взаимодействия с
другими зонами. С учетом ограниченного базиса, сформированного тремя
функциями валентной зоны, кубическая симметрия приводит (смотрите E.В. 14)) к
эффективному взаимодействию в виде:
\У) \Z)
(Y\
(Z\
+M(k2+k2) Nkky Nkxkz
Nkkx Lk2+M(k2+k2) Nkykz (
Nkkx Nkky Lk2 + M (k2 +k2)
с тремя различными константами L, M, N. Теперь мы уже можем диагонализиро-
вать эффективный гамильтониан с тем, чтобы получить вид трех валентных подзон
для к ф 0 и с учетом этих трех параметров. К сожалению, наши трудности на этом
не кончаются, так мы должны все еще учесть спиновое и спин-орбитальное
взаимодействие. Если не учитывать последний вид взаимодействия, то влияние спина
5.В. к-рметодКейна
привело бы к удвоению числа возможных состояний в каждой валентной подзоне с
полным вырождением 3x2 при к = 0.
Спин-орбитальное взаимодействие обусловлено релятивистским эффектом,
который качественно может быть объяснен следующим образом: электрон пересекает
электростатический потенциал на огромной скорости. В системе отсчета электрона
электрическое поле, связанное с этим потенциалом, преобразуется в магнитную
компоненту, которая, в свою очередь, взаимодействует со спином электрона. В
результате этого движение электрона и его спин оказываются связанными. Это
приводит к тому, что оператор спина более не коммутирует с гамильтонианом. При
этом изначально 3x2 — вырожденные уровни расщепляются на два уровня, один
из которых четырехкратно вырожден, в то время как второй вырожден двукратно и
располагается на Ао ниже первого уровня. Снятие этого вырождения происходит в
полной аналогии с орбиталями рх, ру, pz в атоме под влиянием спин-орбитального
взаимодействия. В результате этого угловой момент / = 1 и спин s =1/2 более не
являются хорошими квантовыми числами. С другой стороны, новыми
стационарными состояниями системы являются собственные векторы наблюдаемых J2 и /,
где J = L + S. Наблюдаемая J2 имеет собственные значения J2 =у(у + 1) су = 3/2
и 1/2. Состояние у = 3/2 является четырежды вырожденным с 11 = ±3/2, 11 = ±1/2,
а состояние 11 = 1/2 является дважды вырожденным о, jz = ±1/2. Новые
стационарные состояния являются теперь линейными комбинациями базисных функций рГГ),
\Xl), |УТ), \Yi)9 |ZT), \Zi), а новые состояния обозначаются как \j,jz), что является
общепринятым в атомной физике. Это усложняет вид к • р-матрицы с малой
компенсацией, как можно заметить, вблизи к = 0 мы можем ограничиться уровнем у =
3/2, применяя метод Левдина к возникающим матрицам формата 4x4. Тот факт,
что здесь имеется всего три параметра, обусловлен влиянием кубической
симметрии. Достаточно кропотливые расчеты приводят нас к следующему виду
эффективного гамильтониана в базисе |3/2, ±3/2) и |3/2, ±1/2):
3 3
2
3
2
3\
2/
3 1\
2 2
3
2
1\
1
Hh с Ь 0
с* Н, 0 -Ъ
Ь* 0 Н, с
0 -Ъ* с* Hh
1 _!
2'~2
3 1
E.В.22)
с элементами:
2п%
2/w0
2mQ
2т0
E.B.23)
^206 Дополнения к главе 5
где три параметра Латтинджера yv yv уъ связаны с параметрами L, М, и N
соотношениями у{ = 2mQ(L + 2Л/)/3, у2 = 2mo(L — М)/ 6, у3 = 2m0N/6. Эти параметры для
GaAs и InP приведены в таблице 5.В.1.
Табл 5.В.1. Значения различных параметров Кейна—Кона—Латтинджера,
используемые при расчете зоной структуры GaAs и InP
Параметры
а(Е)
Eg (эВ)
Ао (эВ)
Уг
Уз
GaAs
5,6533
1,42
0,341
7,0
2,25
2,9
InP
5,8688
1,35
0,11
5,04
1,55
2,4
Диагонализация эффективного гамильтониана E.В. 14) приводит к дважды
вырожденным энергиям:
Е=ЕГ
н„ + н,^ 1(н„~н,у
- + Ь2+с2 =
E.B.25)
Если мы введем вклад свободных электронов в константу у{9 мы увидим, что
знак ± перед квадратным корнем соответствует массе тяжелой дырки (+) и легкой
дырки (—). В любом из этих двух случаев имеется зависимость от направления к. В
направлении A00) и эквивалентных направлений мы имеем:
А в направлении A11):
—°- = -у{ +2у2, —2- = -/1 -2у2
—- = -Г. + 2/3, —- = ~Ух ~ 2/з
E.В.26)
E.В.27)
Из этого мы можем заключить, что эквипотенциальные поверхности являются
сферическими только, если у2 = уу
Наконец, нам необходимо экспериментально определить параметры
Латтинджера для данного полупроводника. На практике измерения с использованием
циклотронного резонанса используются для определения формы дырочных
эквипотенциальных поверхностей, по которым методом наилучшего подбора варьируемых
параметров E.В25) до наилучшего совпадения с экспериментальными
зависимостями и определяются параметры Латтинджера.
Рисунок 5.В. 1 иллюстрирует зонную структуру GaAs, рассчитанную к • р-методом с
учетом 9x2 зон в E. В. 10).
Вблизи к = 0 мы видим, что зависимость от к для зон тяжелых и легких дырок
близка к E.В.25), но по мере того, как мы перемещаемся от центра зоны Бриллю-
эна, тем менее аппроксимация эффективной массы становится справедливой.
5. Г. Глубокие центры в полупроводниках 20 7
GaAslOO
Зпин-орбитально
отщепленная зона
0.0
0.5 1.0
к (нм })
1 5
Рис. 5.В.1. Зонная структура GaAs, рассчитанная с использованием к • р-метода и с
учетом 9x2 зон в E.В. 10). Вблизи к = 0 зоны тяжелых и легких дырок
изменяются в соответствии с E.В.25). Однако по мере удаления от центра
зоны аппроксимация эффективной массы становится все более
неудовлетворительной.
Литература
P. Yu and Cardona, Fundamentals of Semiconductors, Springer, Berlin A995).
5.Г. Глубокие центры в полупроводниках
Как мы показали ранее, возникновение запрещенных энергетических зон
обусловлено периодичностью кристаллического потенциала. Любое отклонение от этой
периодичности будет приводить к введению дополнительных разрешенных
энергетических уровней для электронов в запрещенной зоне. Для концептуального описания
этого явления мы можем использовать химическую модель (смотрите рис. 5.6). В
этом случае атом, не участвующий в формировании — связи, обладает
энергетическим уровнем прямо между энергетическими уровнями связи и антисвязи. Уровень
такого типа, расположенный, по своей природе, глубоко в запрещенной зоне (по
сравнению с мелкими водородоподобными состояниями донорных и акцепторных
атомов), называется глубоким центром, и он, как правило, негативно влияет на
характеристики основной матрицы. В главах 6, 11 и 13 мы увидим, что такие дефекты
ведут себя как центры безызлучательной рекомбинации. Сейчас же с
использованием модели жесткой связи мы дадим краткое теоретическое описание, которое
поможет добиться определенной степени понимания природы таких дефектов.
Возвратимся к нашему одномерному кристаллу, как это использовалось выше
в разделе 5.Б. В этом случае наша решетка состояла из периодической
последовательности изолированных атомных потенциалов, связанных через туннельный
интеграл А (идентичный для всех ближайших соседних атомов). Теперь мы
предположим, что дефект какой-либо природы (примесь, вакансия и т. д.) располагается
при т = 0. Будем предполагать, что эта примесь обладает отличной от атомов
матрицы энергией при т = 0, но для простоты туннельный интеграл Л для
ближайших соседей будем полагать тем же. В таком случае секулярные уравнения E.Б.8)
останутся неизменными:
208 Дополнения к главе 5
E.Г.1)
-ACm + E0Cm+l-ACm+2 = ECm+l
за исключением случая при т = О, где они будут иметь вид:
— АС_2 + EqC_x — АС0 = ЕС_{
л с 4- F'c —АС — fc
E.Г.2)
Можно показать, что при этом разрешенные зоны существенно не изменятся.
Сфокусируем наше внимание на том факте, что в данном случае имеются
пространственно локализованные состояния при т = 0, т. е. типа етка для т < 0 и с~ша
для т > 0, где к есть действительное число.
Функции:
Ст = е±тка, при т ф 0 E.Г.З)
по-прежнему останутся решениями E.Г. 1) до тех пор, пока будет выполняться соотношение:
Е{к)- Ео = -А(ека + е"™ )= -2А cosh(/az) E.Г.4)
При отсутствии среднего уравнения в E.Г.2) это есть просто равенство k = i&,
обусловленное цикличными граничными условиями Борна—фон Кармена,
которые и приводят к возникновению зон. И наоборот, уравнение при т = 0 E.Г.2)
приобретает другой характер на границах, который с учетом приведенного выше
уравнения и может быть записано в виде:
+ Сп = е + е
- At + E'0C0 -At = | En - A\ e + e
Со + е = е + е
E.Г.5)
Ясно, что верхнее (т = — 1) и нижнее (/я = +1) уравнения допускают в качестве
решения Со = 1, что приводит к записи для среднего уравнения (при т =0) в виде:
Е'о- Ео = -2 A sinh(/ctf)
E.Г.6)
Отметим, что поскольку к положительно, то будет только одно решение, если Е'о < EQi
т.е. примесь не может локализовать электронный уровень, если только энергия ее
основного уровня не глубже по сравнению с атомами основного материала. После чего
мы устраняем к из E.Г.4) и E.Г.6) с тем, чтобы получить энергетическое
положение примесного уровня Е(к), которое мы обозначим через Edcf:
П7-1 Л? /7) + 1
-e e • e e-
t
Рис. 5.Г.1. Дефекты в одномерном периодическом потенциале.
Рис. 5.Г.2. Зависимость положения
глубокого уровня в запрещенной зоне от
(£0 -
5. Г. Глубокие центры в полупроводниках
-Ej + AA* E.Г.7)
Этот уровень располагается под минимумом зоны проводимости Ео — 2А и,
таким образом, в запрещенной зоне полупроводника (смотрите рис. 5.Г.1 и 5.Г.2).
С этим глубоким уровнем связана локализованная волновая функция с параметром
затухания к, определяемым соотношением:
1
tdef = — arg cosh
а
гл
E.Г.8)
Чем глубже уровень располагается в запрещенной зоне, тем более
пространственно локализованным будет состояние. Таким образом, следствием присутствия
примесей в полупроводниках обычно является введение разрешенных
энергетических состояний в запрещенную зону, которые локализуют или захватывают
носители. Влияние таких центров нежелательно по ряду причин. Во-первых, эти центры
захватывают носители заряда, что снижает проводимость полупроводников. К тому
же эти уровни ведут себя как центры безызлучательной генерации и рекомбинации
носителей для электронов и дырок, что приводит к токам утечки через переходы, а
также к безызлучательной рекомбинации в лазерах. В результате этого новые
полупроводниковые материалы для приборных применений часто проходят
чрезвычайно объемную технологическую стадию, в процессе которой помимо других задач
решается проблема устранения (или уменьшения до некоторого критического уровня)
концентрации глубоких центров в объеме материала.
Литература
J.S. Blakemore, Semiconductor statisyics, Dover, New York A987).
S.T. Pantelides, Ed. Deep Centers in semiconductors, 2nd Edn, Gordon and Breach, New York
A992).
ГЛАВА 6
ЭЛЕКТРОННЫЕ СВОЙСТВА
ПОЛУПРОВОДНИКОВ
6.1 Введение
В главе 5 мы видели, что электроны в кристаллической среде распределены по зонам
разрешенных энергий (валентным зонам и зонам проводимости) и что
относительное положение уровня Ферми по отношению к экстремумам зон позволяет
объяснить тип (изолятор, металл или полупроводник) характеристик данного материала. С
использованием квантовой теории твердых тел мы также увидели, что приложенное
извне электрическое поле заставляет электроны кристалла циркулировать
периодическим образом по зоне Бриллюэна {Елоховские осцилляции)>, что является
предсказанием, которое еще только предстоит продемонстрировать экспериментально в
кристаллах (впрочем недавно этот эффект уже наблюдался в сверхрешетках). В этой главе
мы проработаем несколько теоретических вопросов, что позволит нам найти
корреляцию между квантовыми и классическими аспектами поведения электронов в
среде. В частности, мы обсудим, каким образом механизмы рассеяния между различными
состояниями в зонной структуре позволяют объяснить различные макроскопические
электронные свойства полупроводников, например, законами Ома, Фика и т. д. В
конце главы мы уже сможем представить систему уравнений, позволяющих
понимать доминирующие механизмы переноса в полупроводниках.
6.2. Уравнение Болыдмана
В главе 5 мы видели, что движение электронов в пределах полупроводниковой зоны под
воздействием электрического поля F можно представить как изменение состояний в зоне,
которое определяется выражением:
— ,0| F.1)
П )\
Это означает, что, если в момент времени t — О электрон находится в состоянии
к, то затем в момент времени / он будет находиться в состоянии к + qFt/h.
Напомним, что это обстоятельство лежит в основе феномена блоховских осцилляции.
Другим образом влияние электрического поля может быть описано уравнением:
Ь— = q¥ F.2)
dr
Эта формула аналогична закону Ньютона, если рассматривать h k как квазиимпульс. В
реальном пространстве скорость электрона в состоянии к определяется групповой скоростью:
v(k) = |vk£(k) F.3)
и, таким образом:
М"' qF F.4)
d,
dk d/
6.2. Уравнение Больцмана
где мы можем предположить, что обратная матрица Л/ для эффективной массы не
зависит от к вблизи энергетических экстремумов в обратном пространстве. Такой
подход справедлив в случае идеального полупроводника (как и для других
кристаллических твердых тел) с тем ограничением, что электрическое поле достаточно
слабо, чтобы вызвать межзонные переходы, а также что рассеянием на
несовершенствах (фононы, примеси и т. д.), приводящим к переходам между различными
k-состояниями, можно пренебречь (последнее требование в общем случае не
выполняется, и оно жестко ограничивает реализуемость этого подхода на практике).
С другой стороны, такое описание формирует основу полуклассической
аппроксимации явлений переноса. В этом случае реакция электрона (расположенного в
момент t в точке г полупроводника и в состоянии к зоны п) на воздействие
локального поля F(r) определяется соотношениями F.1)—F.4). Отклонения от
идеального случая (из-за примесей, колебаний решетки, дефектов...) вызывают переходы
между к и к' и не сопровождаются изменением положения частицы. Понятно, что
такой подход является всего лишь аппроксимацией, так как в квантовой механике
невозможно одновременное задание скорости и положения электрона (с любой
точностью), а также вследствие того, что само понятие состояния к не имеет
точного смысла за исключением бесконечно протяженного полупроводника. Несмотря
на эти ограничения, указанный подход достаточно корректен до тех пор, пока
изменениями интересующих нас параметров (например, напряженности поля, ...) на
длине, равной или большей среднего расстояния между двумя событиями
рассеяния, которое испытывает электрон, можно пренебречь. Ограничимся этим и не
будем приводить здесь более детальное обоснование справедливости
полуклассического подхода. Очевидно, что в случае квантовой ямы полуклассическое
приближение не является допустимым при рассмотрении движения электрона
перпендикулярно границам раздела. В самом деле, основной отличительной особенностью
полуклассической аппроксимации является то, что волновая природа электрона
учитывается лишь косвенно через зонную структуру в виде Е(к) и через процессы
рассеяния, которые рассчитываются как вероятности переходов в единицу времени
(определяемые золотым правилом Ферми) с использованием волновых функций в
начальном к и конечном к' состояниях. В этом случае ансамбль электронов в зоне
может быть описан функцией распределения /(г, k, t), описывающей либо
вероятность найти электрон в момент времени / в положении г и состоянии к, либо число
электронов в объемном элементе d3rd3k фазового пространства. Эти две
возможные интерпретации связаны друг с другом плотностью состояний gd3r/Bn)\ где
gs = 2 — вырождение электронов по спину.
Характер изменения Дг, к, /) в промежуток времени от / до / + dt и в отсутствие
каких-либо столкновений можно описать, рассматривая объем фазового
пространства в момент времени t + dt (рис. 6.1).
Теперь частицы, которые находятся в точке (г, к), изначально в момент
времени t находились в точке (г — vd/, k — (dk/d/)d/) и, таким образом, испытали дрейф:
Рис. 6.1. Орбиты группы частиц в фазовом
пространстве между моментами времени t0 и tx и в
отсутствие столкновений.
Глава 6. Электронные свойства полупроводников
Э/
dt dt d/ F.5)
= -v(k) • Vr/(r, Kt)~- Vk/(r, k, t)
at
К частицам, продрейфовавшим к точке (г, к) мы должны прибавить чистое
число частиц, введенных в эту область фазового пространства из-за столкновений
из состояний к':
Э/ ^о11 к'
где S(k? —> к) есть вероятность в единицу времени того, что переход происходит между
состояниями к' и к.
Уравнение, описывающее изменение /, под комбинированным воздействием
электрического поля и столкновений дается, таким образом, соотношением:
()r/ k/ F.7)
Э/ Л [dt )соП
Уравнение Больцмана
Это уравнение, называемое уравнением Больцмана является очень важным, так
как устанавливает взаимосвязь квантовых и классических аспектов поведения
электронов в твердых телах. Как только становится известным решение /(г, k, t) этого
уравнения, мы можем рассчитать такие средние макроскопические параметры, как
концентрацию носителей:
f4 F.8)
плотность тока:
J(r,O = J^^v(k)/(r,M) F.9)
среднюю кинетическую энергию частиц:
(Е(г, /)) = —l— f ^£(k)/(r, к, /) F.10)
A7(r'/)J Bя)
а также дисперсию скорости:
С7у2(Г,/) = —— Г^^Г2;2(к)-(уJ1/(Г,к,/) F.11)
«(r,0JB^)H N ' J
Уравнение F.7) в сочетании с членом столкновений F.6) обладает малым
практическим значением. Теперь попробуем получить несколько простых решений уравнений
Больцмана. Сначала предположим, что интеграл столкновений можно
аппроксимировать с использованием одного времени релаксации (зависящего только от энергии
состояния к), стремящейся привести распределение обратно к виду^ (г, k, t)
(смотрите рис. 6.2), т. с:
ЭЛ z /(r,k,Q-/cg(r,M)
Э/ L т(Е(к))
6.2. Уравнение Больцмана
Jeq
Рис. 6.2. Функции распределения в
состоянии равновесия 0^(к)) и под влиянием
электрического поля (Дк)).
Аппроксимация в виде F.12) имеет чрезвычайную физическую значимость. В то
время как все уравнения переноса, введенные нами до сих пор, инвариантны по
отношению к обращению времени, уравнение F.12) вводит предпочтительное направление
(«стрелу времени»). Многие связи между микроскопической теорией материи и
макроскопической термодинамикой скрыты в этом уравнении. Это последняя
аппроксимация означает, что как только возмущающее электрическое поле выключается,
функция будет экспоненциально по времени релаксировать к своей первоначальной
форме с временем релаксации т{Е). Отыскивая стационарное решение, близкое к функции
распределения, с помощью итераций мы находим функцию распределения:
/ = 4 - т(Е(к))[у(к) • Vr/ef + q¥ ■ Vk/J= /eg - r(£(k)jv(k) • Vr/ef + qy(k) • f||-J
F.13)
С использованием этого последнего выражения получаем для средней скорости:
F.14)
В случае простого невырожденного полупроводника при температуре Т или
/eqoc exp(—E/kBT), где кв — постоянная Больцмана и в предположении v(k)= hk/m*
можем переписать уравнение F.14) в виде:
juF-D^- F.15)
где ju — подвижность, определяемая соотношением:
q Jv2rexpH£(k)/*5r]}d3k
ЪкьТ Jexp{-[^(k)/^r]}d3k
a D — коэффициент диффузии:
F.16)
—f
jexp{-[E(k)/kBT}}d3k
F.17)
Сравнивая эти два последних уравнения, мы находим следующее отношение
Эйнштейна, связывающее подвижность и диффузионный перенос:
Я
Соотношение Эйнштейна
W2 14 Глава 6. Электронные свойства полупроводников
Возвращаясь к F.15), мы видим, что ток определяется суммой двух членов:
j(r) = ?/i(r)<v(r)> = qn(r);uF - qDVn(r) F.19e)
что может быть записано (смотрите рис. 6.3) в виде:
iO-)=ico»+Wr) F.196)
Рис. 6.3. В условиях комбинированного воздействия электрического поля и
соударений носители заряда увлекаются полем, но диффузионно рассеиваются
соударениями.
Ток проводимости jcond есть ток, описываемый законом Ома:
где а — есть электропроводность, которая связана с подвижностью соотношением:
а = nqju F.206)
Плотность диффузионного тока jd.ff связана с перемещением носителей в
области структуры с меньшей концентрацией носителей и дается законом Фика:
jdiff(r) = -qWn F.21)
Закон Фика
Замечание: С учетом q = — е в нашем определении электронной подвижности эта величина
является отрицательной. Более общепринятым однако является использование
абсолютных величин для q и //, что делает необходимым изменение знака перед // в
уравнении F.15).
Особо важный случай имеет место, когда занятыми являются только состояния
вблизи энергетического минимума, когда эффективная масса вблизи минимума
является изотропной (E(k) = h2k2/2m* + Е). В этом случае подвижность может быть
записана как функция определенной средней величины г для кинетической энергии:
JEi/2r(E)exp[-(E/kj)]iE
JEexp[-(E/kBT)}iE
Если время релаксации не зависит от энергии Е, это последнее выражение
сводится к простой модели Друде, при этом:
//=<?Л F.23а)
т
Подвижность (см2 В~1 с)
в модели Друде
В более общем случае, когда т(Е) = то(Е/Ео)а, уравнение F.22) принимает вид:
6.3. Механизмы рассеяния
и т* 3 гC/2)
где Г есть гамма-функция, ГA/2) = 4я, Г(х + 1) = хГ(х).
V ' ;
Пример —-
При температуре 300 К арсенид галлия, легированный до концентрации 1015 см
имеет время релаксации 0,3 пс. При использовании формулы Друде ожидаемая
подвижность электронов должна составлять 1,6 х 10~19 Кл х 3 х 10~13 с/@,067 х 0,9 х 10~30 кг)
или 8000 см2 В с.
6.3. Механизмы рассеяния
Механизмы рассеяния абсолютно необходимы для правильного описании электрических
свойств материалов. Более того, эти процессы объясняют пропорциональность между
индуцированным током и величиной приложенного электрического поля (закон
Ома). Среди этих механизмов наиболее важные вклады даются рассеянием
носителей заряженными примесями и фононами. Фононы (колебания решетки) и элект-
рон-фононное взаимодействие будут рассмотрены в дополнениях в конце этой
главы. Здесь же мы рассмотрим рассеяние носителей на примесях, процесс, в котором
доминируют остаточные ионы, используемые при легировании основного
полупроводникового материала.
С учетом длины волны электронов в зоне проводимости заряженную примесь
можно рассматривать как точечный заряд Ze. Поскольку этот заряд располагается в
кристалле, содержащем свободные электроны, мы можем ожидать, что концентрация
электронов вблизи примесей увеличивается, приводя к значительной экранировке
электрического поля дефекта. Наиболее простая возможная (и тем не менее очень
эффективная) трактовка этого явления, описываемая далее, приписывается Де-
баю. Мы знаем, что в невырожденном полупроводнике зона проводимости
характеризуется средней электронной плотностью п0 = Ncexp(—(Ec — Ef)/kBT) (смотрите
E.42) и E.43). Если мы добавим медленно изменяющийся (по сравнению с
постоянной решетки) электростатический потенциал К(г), каждый электрон будет
обладать в дополнение к своей решеточной энергии Е(к) еще и потенциальной
энергией — eV(r) (смотрите рис. 6.4). В этом случае мы можем отобразить полную
зону проводимости как будто смещенную вертикально на энергию — eV (г). При
термодинамическом равновесии энергия Ферми постоянна в пределах всей системы,
при этом концентрация электронов изменяется в соответствии с соотношением:
, ч л, [ [Ec-eV(r)~EF]\ \eV(r)] (, ~A ,
п(т) = Nc ехЫ - -^ -Y ^ \ = п0 ехр —^- F.24л)
{ Кв1 J L Кв1 J
В этом случае изменение, обусловленное потенциалом, составляет:
рм(т) = -е{п - «„) = -епАсхр I^jjA ~ П = ~^У^ = -*^K(r) F.246)
где линеаризация заряда определяется дебаевским волновым вектором qD или дебаев-
ской длиной AD = \/qD в соответствии с соотношением:
F.25)
Дебаевские волновой вектор и длина
216 Глава 6. Электронные свойства полупроводников
100
D
10
4 \
1
...1
^>ч
ч ^ \
4 ч
ч
\ \
7"
Т=
Г=
Г=
:300К
:200К
:100К
: 50К
-
10
15
10
16
ю1
10
18
10
19
Концентрация электронов (см'1)
Рис. 6.4. Электроны проводимости аккумулируются вблизи положительно заряженной
примеси, таким образом экранируя примесный потенциал на длине,
характеризуемой длиной волны Дебая (а). Дебаевская длина экранировки в функции
уровня легирования (б) для GaAs (eR = 12) при различных температурах.
Этот параметр важен, так как он описывает характерную длину в пределах
которой электронный газ может экранировать внешний потенциал. Этот момент лучше
иллюстрируется при рассмотрении электростатического потенциала из-за
плотности наведенного заряда /?ext(r). В этом случае такой потенциал определяется
уравнением Пуассона:
£ £ ~ £ °
где в есть проницаемость среды (е= £R£0). Этот уравнение может быть решено с
использованием Фурье-преобразования:
d3k к(ь)с»,
BлK )е е
К(г) = J
F.27)
V(k)=
Для точечного заряда p(r) = Ze8(i), такого, что Дк) = Ze, находим (после
отчасти длинного обратного преобразования) полный и внешний потенциалы:
6.3. Механизмы рассеяния
F(r) = ^-^—, Kcxt(r) = -^- F.28)
что, естественно, дает экранированный кулоновский потенциал на расстоянии
порядка дебаевской длины.
Пример
Для GaAs, легированного до уровня 1017 см~3, находим:
1е(квТ/е) ) 12х 8,8 х 10-12х 0,026
D \ еп0 \ l,6xl0"l9xl023
нм
Рассчитаем теперь вероятность рассеяния электрона, изначально находящегося в
кристалле в состоянии к и обладающего волновой функцией:
r F.29)
Распределение рассеивающих примесей, расположенных при г, дается выражением:
) F.30)
Возвращаясь к стационарной теории возмущений, рассмотренной в разделе 1.6.2, с
учетом стационарного потенциала, вводимого в момент времени / = 0, и с
использованием золотого правила Ферми находим вероятность скорости перехода в состояние к':
5(к -> к') = ^|(к'|Крег|к)|^[^(к') - Е(к)] F.31)
что с точностью до множителя представляет собой ту же самую формулу, которая дается
уравнениями A.78) и A.83) для со = 0. В данном случае множитель в четыре раза больше,
так как мы не выделили временную зависимость для положительных и отрицательных
частот. Закон сохранения энергии показывает, что такие столкновения являются упругими
(смотрите рис. 6.5).
Подставляя волновые функции для состояний кик', находим выражение для
матричного элемента:
^['^^ X F-32)
где в дополнение к периодичности волновых функций ик мы использовали
следующие аппроксимации:
• К^Дг) существенно не изменяется в пределах периода кристалла;
• интеграл перекрытия составляет:
f J<.(rK(r)e-^-^Kper(r)d3r - -у ^['^^ X е-""'"
■> ©
Рис. 6.5. Столкновение электрона с
примесью в реальном (а) и обратном
(б) пространстве.
Глава 6. Электронные свойства полупроводников
f
ll
= -1- f<(rK(r)
У
F.33)
При этом его часто аппроксимируют равным единице для близлежащих состояний,
расположенных в той же самой зоне.
Квадрат модуля матричного элемента будет содержать двойную сумму типа:
-i(k'-k)(ry-r/)
Априори, нам ничего неизвестно о положении г. примесей. Наиболее простой
подход — использовать этот недостаток информации — заключается в
предположении, что положение примесей хаотично таким образом, чтобы сделать вклады
различных примесей равными нулю поскольку фазы (к' — к) (г — г,) будут равным
образом хаотичны для у" —у'. В результате этого остается только сумма для у =у', что
определяет количество примесей, Nimp.
Наконец, можно найти, что скорость переходов равна:
') -
F.34)
где п.тр = N.mp/V есть концентрация примесей, a Ze заряд одиночной примеси.
Напоминаем, что 8 есть диэлектрическая проницаемость кристалла, однако без
учета вклада свободных носителей. Их поляризуемость учитывается qD. Отметим
также, что S(k -> k') = S(k -> к'), как это имеет место в процессах упругого рассеяния.
Если мы знаем 5(к -> к'), то мы можем рассчитать время релаксации т(к) для
простого случая электронов в изотропной параболической зоне, обладающих
эффективной массой т\ Уравнения F.6), F.12) и F.13) дают:
m
rn
k')
из чего мы заключаем, что:
F.35)
F-36)
Поскольку -^(к -» к') зависит от угла в между кик' скорость релаксации
отличается от средней скорости столкновений S^(k -» k'). Поскольку в выражения для
столкновений в качестве весового множителя входит изменение импульса,
сопровождающее рассеяние, этот процесс целесообразно характеризовать временем
релаксации импульса. Аппроксимируя I(k', k) единицей, мы, в конце концов, находим:
2к Z e
A - cos e)s[E(lc')- E(k)]
П
Ve
g 3?)
При этом интеграл может быть рассчитан с использованием сферических координат
(к?, в, ф) и соотношения S((h2/2m')(k"- - к2)) = (m'/h2k)S(k'- к):
1
W)
= п,„
ZV
m
е1 8лй3^3
In
Id
F.38)
Мы можем убедиться, что скорость переходов по порядку величины составляет
О(к), если к « qDw составляет величину порядка О(кЧп(к)), если к » qD.
Рисунок 6.6 демонстрирует численную величину 1/г для различных значений
п.тр при комнатной температуре для GaAs.
Представленные на рис. 6.7 значения подвижности получены численной
оценкой интеграла в F.16).
6.4. Горячие электроны
101'
|
X
с:
о 10
10
10
о
о
Q.
S
о
ю!
\ 1 I I 1 1 1
\ \% -^ -
\ *«ч. "— - ■
i 1 i
nimp
-- 10l6cm-3
—- 1015cm
--- 1014cm
10l3cm-3
-
-
I9 -
0 10 20 30 40 50 60 70 80 90 100
Энергия (МэВ)
Рис. 6.6. Величина \/т(Е) для рассеяния на заряженных примесях при Т= 300 К в GaAs
«-типа.
100
250
300
150 200
Температура (К)
Рис. 6.7. Подвижность, определяемая рассеянием на заряженных примесях.
В действительности, как мы увидим, что при комнатной температуре рассеяние
на фононах доминирует над примесным рассеянием во всех случаях за
исключением образцов, обладающих примесной концентрацией выше п.тр = 1017 см~3.
6.4. Горячие электроны
Решение уравнения Больцмана F.13) действительно только при том условии, что
напряженность электрического поля и градиент концентрации малы. В этом случае реализуется
линейный отклик, как этот имеет место в случае законов Ома и Фика. Для этого
режима мы легко можем показать, что кинетическая энергия электронов остается
равной равновесному значению C/2) кв Тп: если мы заменим к на -к в F.13), мы
увидим, что отклонение функции распределения от равновесной просто меняет
знак и таким образом не дает вклад в среднюю энергию.
С увеличением напряженности поля F уравнение Больцмана перестает
обладать общим аналитическим решением. Как следствие этого было разработано
большое количество численных методов для исследования различных частных случаев.
Эта достаточно техническая область анализа выходит за рамки настоящей книги,
поэтому мы ограничимся феноменологическим описанием некоторых из наиболее
важных эффектов, проявляющихся в рассматриваемых условиях.
Глава 6. Электронные свойства полупроводников
6.4.1. Теплые электроны
При превышении линейного режима электрическое поле поставляет энергию
электронному газу. Первичное влияние столкновений заключается в хаотизации скоростей частиц на
временной шкале, устанавливаемой временем релаксации импульса. Когда электроны
приобретают среднюю скорость (v) в направлении тока, энергетический вклад в энергию
электронов дается соотношением j • е¥ = etn^F. Сначала эта энергия «разогревает»
распределение электронов. Как только система приходит в стационарное состояние,
эта энергия начинает рассеиваться за счет неупругих процессов (преимущественно за
счет электрон-фонного взаимодействия, которое передает энергию колебаниям
решетки, т. е. преобразует энергию в нагрев материала матрицы). Такое
преобразование происходит в течение характеристического времени, которое называется
временем релаксации энергии. Это время, как правило, на несколько порядков величины
превышает время релаксации импульса. Такое описание означает, что электронный газ
приобретает среднюю кинетическую энергию, большую равновесного значения. При
этом температура электронного газа начинает превышать температуру
кристаллической решетки. Поскольку подвижность электронов зависит от температуры, мы
можем ожидать соответствующего изменения закона Ома в виде:
<v> = <jd+ aF 2)F F.39)
При этом член Р исключается симметрией (мы должны иметь (v) —> —(у)для
F -> — F, а а пропорционально dm/dT. Мы только что видели, каким образом
примесное рассеяние приводит к увеличению подвижности с повышением
температуры так, что а > 0. В дополнении 6.Б мы покажем, каким образом рассеяние на
фононах может приводить к а< 0 Таким образом, простое определение знака члена
коррекции закона Ома дает признак природы доминирующего процесса,
ограничивающего подвижность в полупроводнике.
Математическим выражением, соответствующим этой картине является
аппроксимация функции распределения, которая называется смещенной максвелловской
аппроксимацией:
В этом случае средняя скорость составляет < v > = АЦ/лГ, а средняя
кинетическая энергия на электрон равна (Ъ/2)квТе + (l/2)m*<v >2. Метод решения уравнения
Больцмана заключается в использовании этой аппроксимации для оценки
интеграла столкновений и времен релаксации в функции этих двух параметров и
процессов рассеяния. После чего сами параметры определяются из записи скоростных
уравнений для импульса и энергии, обусловленных полем, а также скоростей
релаксации из-за столкновений.
Мы не будем более касаться количественно этой темы, отметим лишь, что понятие
электронной температуры, которая может отличаться от температуры кристаллической
решетки, является достойным для упоминания. Оно полезно для того, чтобы провести
различие между двумя различными временными шкалами релаксации: одной, которая
отражает быструю термализацию самого электронного распределения, а также другой,
отражающей более медленный процесс, включающий передачу энергии решетке.
6.4.2. Горячие электроны: насыщение скорости
Под влиянием сильных электрических полей электронное распределение
становится сильно асимметричным. Средняя скорость, как правило, в этом случае
стремится к величине насыщения, когда скорость перестает зависеть от напряженности
поля. В полупроводниках этот параметр составляет величину порядка 107 см с.
Рисунок 6.8 показывает зависимость скорости от напряженности поля в Si и GaAs.
6.4. Горячие электроны
2.5x10'
I/C)
о
8
О
2.0
1.5
1.0
0.5
0.0
Напряженность поля (кВ*см )
Рис. 6.8. Зависимость скорости электронов от напряженности поля в слабо
легированных Si и GaAs я-типа проводимости.
Чрезвычайно упрощенная модель Шокли изящно объясняет эффект
насыщения скорости (рис. 6.9).
Предположим, что основной механизм неупругого рассеяния включает в себя
эмиссию (оптического) фонона с энергией h coop, а также то, что этот процесс
настолько эффективен, чтобы при приобретении электроном кинетической энергии,
соответствующей энергии фонона, он обеспечивал излучение фонона с потерей
всей энергии и скорости. После чего движение каждого электрона становится
строго детерминированным: сразу после излучения фонона электрон оказывается при
к = 0 и вновь начинает ускоряться, при этом величина к определяется:
Это ускорение продолжается вплоть до порога, определяемого энергией фонона:
h2k2 ж
2/и*
F.41)
F.42)
В результате этого распределение скоростей становится равномерным между
v = 0 и vmax в направлении, параллельном приложенному полю, при этом средняя
скорость составляет (v) = v /2, что явно не зависит от электрического поля F.
Зона проводимости
Рис. 6.9. Модель Шокли для насыщения скорости электронов.
Глава 6. Электронные свойства полупроводников
Пример
Подставляя соответствующие численные значения для GaAs, а именно h coop = 36 мэВ,
т* = 0,067 т, находим:
36x1,6x10 22 , ~ 1Л5 ,
М/С S 2X1° М/С
2x0,067x9,1x10
Этот результат является достаточно хорошим с учетом простоты модели.
В то же время модель обладает рядом недостатков. Во-первых, распределение
является полностью анизотропным и очень далеко от максвелловского
распределения. В связи с этим в данном случае не имело бы смысла вводить электронную
температуру. К тому же предположение о том, что фононная эмиссия возникает
как только она становится допустимой, исходя из закона сохранения энергии,
означает, что сама средняя энергия C/2) Ji соор не зависит от поля. Совершенно
понятно, что открыт широкий простор для улучшения этой модели.
6.4.3. Горячие электроны:
отрицательная дифференциальная скорость
В ряде полупроводников, как например в GaAs (смотрите рис. 6.8) и InP
зависимость средней скорости от напряженности поля проявляет максимум, за которым
следует режим уменьшения скорости. Объяснение этого явления может быть
найдено из рассмотрения зонной структуры этих полупроводников (рис. 5.7). Помимо
основного минимума в центре зоны Бриллюэна зона проводимости обладает
локальными минимумами (L- и ЛЧдолинами), лежащими на несколько сотен мэВ
выше Г-долины. В условиях теплового равновесия состояния в этих долинах
являются незанятыми. Однако, приложение достаточно сильного электрического поля
способно ускорить электроны Г-долины до энергии, приближающейся к энергии
состояний 1-долины, в которые они в конце концов и могут быть рассеяны. После
переброса в L-долину происходит резкое уменьшение скоростей электронов. Даже
несмотря на то, что электрическое поле будет способно вновь ускорить эти
электроны из состояний в этой долины, их скорости тем не менее останутся значительно
меньшими по сравнению с электронами в Г-долине с учетом того, что эффективная
масса mL значительно больше эффективной массы тг В стационарном состоянии
заполнение состояний с уменьшенной подвижностью продолжает усиливаться по
мере возрастания напряженности поля, что приводит к общему уменьшению
скорости электронов, как этот показано на рис. 6.10.
Этот эффект отрицательного дифференциального сопротивления (ОДС) не
является просто любопытным фактом, так как он способен приводить к
пространственным и/или временным нестабильностям. Например, представьте себе
полупроводник, легированный до среднего уровня концентрации п0 и поляризованный
напряженностью поля, обеспечивающей режим ОДС. Положительные флуктуации поля
в точке z в момент времени / приведут к уменьшению скорости в этой точке так, что
в направлении потока электронов плотность электронов будет меньше п0, а в
противоположном направлении выше п0. В результате возникнет заряженный диполь,
воздействие которого приведет к возрастанию поля (и следовательно,
неоднородности поля) в точке z. Этот процесс характеризуется собственной обратной связью,
что приводит к формированию дипольного домена, который движется со
скоростью, имеющей промежуточное значение между скоростью насыщения и
максимальной скоростью в кристалле. Такая дипольная структура исчезает, как только она
достигает анода, и вблизи катода возникает новый аналогичный домен. Из этого, мы
видим, что ток в цепи будет обладать колебательной компонентой с периодом порядка
L/v, где L есть длина активной зоны полупроводника. При L ~ 1 мкм и v ~ 105 м/с это
6.5. Рекомбинация
8
а
о
б
Электрическое поле
Рис. 6.10. Влияние электронного переброса между G- и L-долинами при
увеличивающейся напряженности поля. Электроны L-долины с малой скоростью
ответственны за область отрицательного дифференциального сопротивления в
зависимости от средней скорости напряженности поля.
соответствует частоте генерации 100 ГГц. Такие приборы (названные в честь
изобретателя диодами Ганна) обеспечивают возможность изготовления компактных
твердотельных СВЧ-источников и определяют важную сферу применения эффекта ОДС.
6.5. Рекомбинация
Именно возможность сосуществования одновременно электронов и дырок образует
основу для использования полупроводников в оптоэлектронике (и, в значительной
степени, электроники как таковой).
В главе 5 мы видели, что при термодинамическом равновесии концентрации
электронов п0 и дырок р0 связаны соотношением п0 р0 = п? G), где п. — собственная
концентрация носителей (уравнение E.49)). Концентрациями п0 и р0 можно
управлять легированием. Такое равновесие можно нарушить, создавая
электронно-дырочные пары, например, освещая образец (оптическая накачка) или инжектируя
носители с двух сторон границы раздела областей п- и />-типа проводимости (т. е.
рп- переход).
Природа консервативна в том, что она всегда обеспечивает проявление ряда
механизмов, способных привести систему обратно в состояние равновесия. В случае электронно-
дырочных пар такими механизмами являются генерационно-рекомбинационные
процессы. Каждый процесс нуждается в соответствующем взаимодействии.
Взаимодействие с электромагнитным полем приводит к излучательной рекомбинации, при
которой фотон излучается в то время, как поглощение фотона соответствует
процессу генерации электронно-дырочных пар. Два указанные процесса являются
основным предметом настоящей книги и они будут рассмотрены детально, в
особенности, в следующей главе.
Безызлучательные генерационно-рекомбинационные механизмы зачастую являются
раздражающим фактором в оптоэлектронике, так как они проявляются параллельно и
конкурируют с излучательными процессами. В связи с этим для оценки
функциональных возможностей и ограничений оптоэлектронных приборов важно понимать
эти процессы. Двумя доминирующими процессами этого рода являются:
1. Рекомбинация Шокли—Рида—Холла, при которой важную роль играют
примеси. В этом случае сначала электрон, а потом дырка захватываются той же самой
примесью, устраняя тем самым одну электронно-дырочную пару.
Глава 6. Электронные свойства полупроводников
2. Оже-рекомбинация, являющаяся результатом электрон-электронного
взаимодействия, при котором электрон рекомбинирует с дыркой и передает энергию,
выделяющуюся в процессе рекомбинации, другому электрону (или дырке) в виде
кинетической энергии. Этот процесс является собственным и не требует участия
дефектных или примесных центров. Соответствующим генерационным процессом
является ударная ионизация, при которой электрон с достаточной кинетической
энергией может создать электронно-дырочную пару за счет передачи своей энергии
электрону в валентной зоне, что вызывает его переход в зону проводимости.
Эффект Оже и ударная ионизация рассматриваются в дополнении 6. Г. Здесь же
мы опишем рекомбинацию Шокли—Рида—Холла (рис. 6.11).
СВ
ловушка
VB
— рекомбинация
СВ
ловушка — "t генерация
VB
Рис. 6.11. Рекомбинация Шокли—Рида—Холла и генерационные процессы (СВ-зона
проводимости, VB-валентная зона).
Для детализации картины предположим, что в материале имеются примеси с
концентрацией Nr вызывающие существование состояний с энергией ЕТ в
запрещенной зоне. В дополнении 5.Г. мы видели, что примесь может создать глубокий
электронный уровень (т. е. разрешенное состояние) в запрещенной зоне
полупроводника. Дополнительный электрон, предоставляемый донором может быть
ионизирован и он переходит в зону проводимости, оставляя положительно заряженный
донорный атом в соответствии с реакцией:
; +е
F.44)
Ионизированный донор может также захватить электрон из валентной зоны, что
соответствует созданию дырки в соответствии с реакцией:
дг;
F.45)
В первой реакции число электронов, создаваемых в секунду, пропорционально числу
нейтральных ловушек:
Ge = eeN? F.46)
щ& ее — коэффициент эмиссии (с)- Обратный процесс, описывающий
рекомбинацию при захвате, пропорционален числу электронов и ионизированных ловушек:
Re =
F.47)
6.5. Рекомбинация
При этом с, есть коэффициент захвата (см3 с).
При равновесии, что мы будем отмечать чертой над символом
соответствующей величины, скорости двух процессов равны:
Ge = Re^^ = ^£^ F.48)
се Nf
Такой тип рассуждений, при котором мы получаем выражение общего
характера, связывая излучение и рекомбинацию с использованием частного случая
равновесия, полностью аналогичен с ходом рассуждений Эйнштейна, представленным в
дополнении З.В (при установлении связи между коэффициентами
стимулированного и спонтанного излучения В и Л).
Уравнение F.47) называется принципом детального равновесия. В том, что касается
второй реакции F.44), мы подобным образом находим:
Gh = ehN;
Rh = chN?p F.49)
При отклонении от равновесия чистая скорость генерации электронов приобретает вид:
F.50)
Аналогичное выражение для дырок имеет вид:
dp (N° }
-£ = Gh-Rh= ch\ -=tP<>N; - pN? F.51)
С учетом распределения Ферми мы имеем:
В случае невырожденного полупроводника:
F.53)
Таким образом, выражения F.50) и F.51) приобретают вид:
F.54)
В стационарном состоянии (когда неравновесные условия поддерживаются,
например, непрерывной оптической накачкой), мы имеем dn/dt = dp/dt, так что мы
можем выразить это через число ионизированных и нейтральных ловушек с
использованием пир:
226 Глава 6. Электронные свойства полупроводников
F.55)
о ckN¥txp(-£r^\+c,n
Nt { M J F.56)
При этом скорость рекомбинации составляет:
&п _ пр - п}
F.57)
chNT\
Это формула может быть также выражена через время жизни -dn/dt = (п — по)/г.
J_ = (пр-п?)/(п-щ)
Т» \ л/ ( Ет~Е,
*по /> + Wt,exp - т
I { "в*
при этом r0 = \/ceNTw Tq = l/chNT.
Кажется, что представленное выражение имеет сложный вид. Тем не менее начнем
анализ с того, что выражения, зависящие от Ет, равны концентрациям электронов
и дырок, которые мы бы имели в случае, когда уровень Ферми совпадал бы с Ет.
Далее, два важных случая приводят к двум важным пределам:
1. В случае почти собственного полупроводника (п0 ~ р0 ~ я.), когда
ловушки располагаются вблизи центра запрещенной зоны и в случае сильной накач-
ки 8п = п — п0 = 8р = р — р0 » п.:
1 ОП I ОП 1 «т С С I, / s со\
— = '- = = NT —e-h— F.58)
тп тпо8п + тр08п тп0 + тро се + си
2. В случае полупроводника /ьтипа проводимости (п0 = п*/р0 « п) ловушки
располагаются вблизи центра запрещенной зоны и \8п\, \8р\ « р0:
у = ^- = — = NTce F.59)
В этих двух случаях время жизни не зависит от концентрации, и само понятие
«время жизни» теряет смысл.
Пример
Коэффициент захвата vth может быть записан в виде ce8vth, где £vlh соответствует
поперечному сечению захвата, a vth есть тепловая скорость vth2 = < v2 >. Для 8 ~ 1015 см и
vth ~ 107 см/с мы имеем с = 10~8 см/с. Коэффициент эмиссии определяется F.48) и
F.52), при этом:
квТ
При Nc = 5 х 1017 см~3 и в предположении, что дырки располагаются на 0,4 эВ
ниже зоны проводимости (кислород в GaAs) мы имеем ее = 560 с при комнатной
температуре.
6.6. Уравнения переноса в полупроводниках
6.6. Уравнения переноса в полупроводниках
В принципе, полуклассическое описание явлений переноса в полупроводниковом
приборе должно было бы иметь вид уравнения Больцмана, включающее все
электроны в зоне проводимости и валентной зоне. При этом в интеграле столкновений
следовало бы детализировать все соответствующие взаимодействия, включая те,
которые приводят к рассеянию электронов между зонами, что соответствует процессам
генерации и рекомбинации. К этому уравнению следовало бы еще добавить
уравнения Максвелла для полей, ответственных за силы, действующие на электроны.
Естественно, с такими уравнениями справиться очень сложно. К тому же
полученные результаты не носили бы детальный характер. Таким образом, более
предпочтительным является возврат к уравнениям, по своей природе более общего
характера и которые к тому же частично являются феноменологическими.
Первыми уравнениями являются уравнения непрерывности, получаемые из
уравнения Больцмана интегрированием функции распределения по всем состояниям к
и выделением электронной и дырочной составляющих:
Э/ е
F.60)
~dt + ~е ]п~
Полупроводниковое уравнение 1:
уравнение непрерывности
где G и R есть соответственно скорости генерации и рекомбинации, при этом
плотности электронного и дырочного тока составляют соответственно }п = —пе (уп)
и j, = ре (ур). Для плотностей тока мы используем уравнения:
]п = ejunnE + eDVn
\р = ejUppE — eDVp F.61)
J о d J J
Полупроводниковое уравнение 2:
законы Ома и Фика
Эти уравнения выведены под влиянием результатов, полученных в разделе 6.1
для слабых полей и малых градиентов, в то время как значения подвижности и
коэффициентов диффузии являются параметрами, полученными либо
экспериментально, либо численным решением уравнения Больцмана. Отметим также, что
напряженность электрического поля, обозначаемая в этих уравнениях как Е, не
следует путать с энергией. В зависимости от допустимой степени усложнения модели
мы можем также ввести в нее зависимости для /ап{Е) и т. д., а также учесть эффекты
с участием горячих электронов.
К уравнениям, описывающим реакцию частиц на воздействие полей, следует
добавить уравнения Максвелла, определяющие зависимость полей от параметров среды:
VD = p F.62)
VB=0 F.63)
V х Н = jcond + Щ- F.64)
***--* <«»
Полупроводниковое уравнение 3:
ураванения Максвелла
Глава 6. Электронные свойства полупроводников
Где для немагнитных полупроводников В = //0Н и D = £Е, а е есть проницаемость,
связанная с поляризацией локализованных зарядов.
В большинстве проблем переноса в полупроводниках значвения длин волн,
связанные с соответствующими частотами, намного больше размеров приборов,
где магнитные поля не играют особой роли. В этих случаях важными являются
уравнения Пуассона F.62) V • Е = р/е, а также тот факт, что полный ток j = jcond + Э D/dt
сохраняется при условии, что его дивергенция равна нулю в соответствии с F.64).
Плотность заряда определяется соотношением р= е(р — п + N+ — N~), где ND+
есть концентрация ионизированных доноров, a N~ — концентрация
ионизированных акцепторов.
Приведенные уравнения создают основу для описания классических
полупроводниковых приборов, (т. е. транзисторов, фотодиодов, фоторезисторов и т. д.).
Эффекты, проявляющиеся на шкале длин, соответствующей волновой природе
электронов, скрыты в параметрах этих уравнений или в членах — источниках,
подобных скоростям генерации носителей при поглощении фотонов и т. д.
Рассмотрим теперь важное применение этих уравнений. В разделе 6.3 мы
столкнулись с дебаевской длиной (уравнение F.24)), представляющих собой
характеристическую протяженность, в пределах которой свободные электроны могут
экранировать слабый возмущающий потенциал за счет обеднения, либо аккумуляции
электронов. Во многих приборах мы прикладываем достаточно сильные потенциалы (»
kB7), способные полностью привести электронный газ в режим обеднения в области
локализации потенциала (которая в этом случае характеризуется плотностью заряда,
связанного с ионизированными донорами). Оценка уравнения Пуассона для этого
случая приводит к другой длине экранировки, называемой длиной обеднения.
Представим себе легированный полупроводник с концентрацией доноров ND и
кроме того предположим, что при z = 0 электрическое поле «толкает» электроны в
направлении z > 0. В области 0 < z < zdep практически не будет электронов
(смотрите рис. 6.12). При этом уравнение Пуассона может быть записано в виде:
й£" eJy/n , 0<z<zdep F.66)
dz e
Оно может быть легко проинтегрировано, что дает:
Зона обеднения простирается вплоть до точки, где Е =0:
F.67)
{Ш)
При этом падение потенциала в этой области составляет:
v(zJ-V@)=^fzlp F.69)
Таким образом:
^-Ш F-70)
V е1У D
Глубина обеднения
Глубина обеднения является важным параметром, так как она определяет
протяженность области, в пределах которой падает потенциал в легированном
полупроводнике. Мы видим, что этот параметр принимает значение дебаевской длины,
если мы заменим 2ДКна квТ/е; предположение, что eAV» kBTозначает, что zdcp » Xff
В действительности, переход от области обеднения к нейтральному
полупроводнику не является резким, но простирается на длину порядка XD относительно zdcp.
Рисунок 6.13 демонстрирует толщину области обеднения для ряда случаев.
6.6. Уравнения переноса в полупроводниках 229j|
UiN
^
^
zlzt
dep
, зона проводимости
валентная зона
Рис. 6.12. Распределение заряда/? (а), электрического поля Е(б), электростатического
потенциала V (в) и зонной диаграммы в области обеднения zdcp дается
уравнением F.68).
](( 230 Глава 6. Электронные свойства полупроводников
0.01
ю
Уровень легирования (см )
Рис. 6.13. Протяженность области обеднения в GaAs (eR =12) для различных значений
высоты барьера А V.
Пример
Полагая, что АК = 1 В и ND= 1017 см, получаем для GaAs:
heAV _ /2x1
~\sND ~i l,i
2xl2x8,8xlO2xl
,6xl0-19xl023
м = 0,11 мкм
Литература
A.Kireev,Physique des semiconducteurs, MIR, Moscou A975).
B.Sapoval and C.Hermann, Physics of Semiconductors,Springer, Berlin A995).
K.Seeger, Semiconductor Physics, 3rd Edn,Springer, Berlin A995).
S.M.Sze, Physics of Semiconductor Devices, 2nd Edn, Wiley Interscience, New York A981).
ДОПОЛНЕНИЯ
К ГЛАВЕ 6
6.А. Эффект Холла
В этом дополнении нас интересует влияние приложенного магнитного поля на
полупроводниковый слой, в котором протекает ток. В рамках полуклассического описания можно
показать, что влияние магнитного поля В на электроны в полупроводнике приводит
просто к необходимости введения силы Лоренца в уравнение F.2):
h— = q[F + v(k) x В] F.А.1)
at
Если с целью упрощения ограничиться рассмотрением электронов, находящихся в тех
областях зонной структуры, где эффективная масса изотропна, v = hk/m\ движение
электронов является классическим и подобным тому, которое может быть получено в условиях
вакуума:
m*^ = ?(F + vxB) F.A.2)
d/
Идя дальше по пути упрощений, примем, что F лежит вдоль оси Ох, а В параллельна
оси Oz. Затем промоделируем влияние рассеяния, вводя член трения —/иЧ/г,
характеризуемый определенной постоянной времени релаксации. В этом случае уравнения движения
электрона могут быть записаны в виде:
dr A т
* dv7 m*v_
m -7s-=
<\t г
При этом стационарное состояние есть:
F m* 1 + (u)ctJ 1 + (a)crj
^- = -lL^_ = -^_ F.A.4)
Г ftl I + \CQCT J 1 + \COCT)
vz=0
При этом подвижность составляет ju = qr/m* (уравнение F.20)), а циклотронная
частота сос = qr/m\Mbi видим, что магнитное поле отклоняет ток от направления
электрического поля (смотрите рис. 6.А.1). Этот эффект известен как эффект
Холла. Измеряя плотность тока j = л^у,мы можем определить подвижность носителей
из соотношения \х = -jy/jxB, а также отдельно и концентрацию носителей из
соотношения п = j/juqF. Важно отметить, что знак подвижности отрицателен для
электронного газа и положителен для газа дырок. Таким образом, измеряя проводимость
и угол между направлением протекания тока и приложенным электрическим
полем, мы можем определить тип носителей, их концентрацию и подвижность.
На практике, мы обычно фиксируем направление протекания тока, изготовляя
образец в «холловской геометрии» (рис. 6.А.2). Наличие четырех контактов позволяет из-
/ft 23 2 Дополнения к главе 6
ТОК
. электрическое поле
Рис 6Л.1. Под влиянием магнитного поля (перпендикулярного странице) носители
отклоняются от траекторий между контактами, которые в отсутствие поля
были бы прямолинейными. Поскольку в этом случае между контактами
аккумулируется заряд, в образце возникает дополнительная компонента
электрического поля, направленная перпендикулярно току. Суммарное поле
направлено под углом по отношению к направлению тока, протекающего
между двумя контактами.
ток
Hall
Рис. 6.А.2. Принцип определения
концентрации и типа носителей с использованием
эффекта Холла.
мерять продольную и поперечную компоненты поля. Измерения такого рода являются
обыденной практикой при оценке характеристик полупроводниковых материалов.
6.Б. Оптические фононы и фрелиховское
взаимодействие
Рассмотрим теперь, каким образом фононы влияют в материале на динамику
носителей. Взаимодействия такого рода чрезвычайно важны как при рассмотрении
явлений переноса (т. к. электронная подвижность при комнатной температуре
определяется взаимодействием с фононами), так и при рассмотрении релаксационных
явлений с участием носителей, которые возбуждаются оптически или сильными
электрическими полями.
6.Б.1. Фононы
Фононы представляют собой колебательные волны атомов решетки. Для начала мы
начнем с изучения простой модели, представляющей собой линейную цепочку
двухатомных молекул. В качестве аппроксимации используем предположение о том, что
межатомные силы линейно возрастают с увеличением смещения от состояния равновесия,
при этом они направлены таким образом, чтобы возвращать атомы в положение
равновесия при d/2 (рис. 6.Б.1).
Такая двухатомная модель очень удачно описывает бинарные
полупроводниковые соединения, такие как GaAs или InP.
Предполагается, что смещение атома у по отношению к его равновесному
положению для тяжелых атомов (масса М) и легких атомов (масса т).
6.Б. Оптические фононы и фрелиховское взаимодействие 233 JJ)
М к гп к
ЛЛЛМОЛЛЛЛЛ^ЛЛ^^
xj У} ху41 УуЧ1 Ху+2 У/+2
Рис. 6.Б.1. Линейная цепочка из атомов с массами М и т. Межатомные силы
представлены на рисунке пружинками таким образом, что сила между
прилегающими атомами составляет kty - х). При этом х и у обозначают расстояния
смещения атомов от своих равновесных положений.
Классический гамильтониан такой системы представляет собой:
|^х} +!«# +±к(у,-х,) +!-<?„-у,} F.Б.1
При этом сопряженные переменные имеют вид:
О it шж . Oil . /г г* л\
Рх — —г" = М Xj, ру. = —— = ту j (o.b.2)
В этом случае динамическое поведение системы описывается уравнениями:
dXj ' ' F.Б.З)
-\ тт
Р — ffi у. — — ^\V- Jt-r-^lV- X )
У, J ^ J J J J + \
Таким образом:
M x, =к(у, + у, ,-2х7)
^J J J F.Б.4)
yj=k(xj+l+x.-2yj)
Приведенные выше вьфажения представляют собой уравнения Ньютона для
смещения каждого атома.
Будем искать решения в виде волн с частотами со (> 0):
jc, = X QxpCiqjd - icot)
F.Б.5)
ys = Y exp(iqjd -iat)
Подставляя F.Б.5) в F.Б.4) и полагая со* = 2к/Ми со* = 2к/т, получаем:
(югт - а>2)х - col 1 + e~"" Y = 0
F.Б.6)
Условие существования нетривиального решения дает частотные моды:
o
F.Б.7)
sit!
234 Дополнения к главе 6
1.4
1.2
1.0
0.8
0.6
0.4
0.2
0.0
-1.0
1
0) =
-
@
\
i
+ Ki
ОР
= vsq
\
V
1
I/2
-0.5
0.0
qd/я
0.5
1.0
Рис. 6.Б.2. Дисперсионные зависимости для колебательных мод двухатомной
цепочки, проявляющие акустические (АС) и оптические (ОР) ветви с их
характеристическими пределами.
Рисунок 6.Б.2 демонстрирует дисперсионные зависимости со (q). Отметим
наличие двух ветвей, называемых ветвями оптических и акустических фононов.
В пределе при q -^ 0 мы легко получаем:
1
=,31
~ 2
qd
— + —
М
т
F.Б.8)
= vsq
= т
А при q = n/d мы находим, что соор = соти соас = сом.
Приведенные выше решения лежат в пределах зоны, определяемой — я/d<q< n/d,
поскольку решение для q = q0 +2nn/d представляет то же самое смещение, что и решение,
соответствующее q0. В самом деле:
j = X exp (jqojd + \2nnj - \cot)= X exp (iqojd - [cot)
F.Б.9)
Более того, если цепочка не является бесконечно длинной, а имеет конечную длину
L = Nd (см. также уравнение E.10)), использование периодических граничных условий
xN+j — х. и yN+j = у. приводит к дискретным значениям для q:
qNd = 2тип => qn = — п
F.Б.10)
В этом случае плотность мод для каждой ветви составляет Ь/2л, а полное число мод равно
27V, т. е. равно числу степеней свободы в системе из 2N атомов.
Уравнение F.Б.6) дает для каждого решения соотношение амплитуд X(q) и Y(q), при
этом в особом случае вблизи центра зоны (q ~ 0) для оптических фононов мы имеем:
М
—
т
F.Б.11)
А в случае акустических фононов:
6. Б. Оптические фононы и фрелиховское взаимодействие
F.Б.12)
Таким образом, оптические фононы характеризуются противонаправленным
движением двух типов атомов, что и объясняет их высокие частоты. В то же время
акустические фононы не вызывают смещения пружинок при ^Ои таким образом
не обладают упругой энергией (что и объясняет, почему их частота стремится к
нулю в центре зоны).
Мы не будем изучать распространение модели нашей линейной цепочки на
случай трехмерной кристаллической решетки. Необходимый в этом случае
формализм потребовал бы внушительное число индексов для того, чтобы отследить
трехмерные смещения каждого из атомов и их волновые векторы в зоне Бриллюэна.
При этом сущность модели и в этом случае осталась бы неизменной. Для бинарной
системы типа GaAs полное число мод становится равным 6N (где 2N есть число
атомов в объеме V). Таким образом, решения распределены по трем акустическим
ветвям с co(q) —» 0 для q —> 0 и трем оптическим ветвям, для которых co(Q) ф 0.
Основным отличием одномерного и трехмерного случаев является
существование мод, для которых смешения не являются параллельными волновому
вектору q — это поперечные моды. Рис. 6.Б.З иллюстрирует различные варианты
смещений для волн, распространяющихся направо в симметричном случае (в любой
решетке в общем случае смещения, связанные с модами, не являются параллельными
или перпендикулярными волновому вектору).
Теперь возвратимся к одномерному случаю, который вплоть до настоящего времени
рассматривался чисто классически. Для получения картины, более близкой к реальности,
следует рассмотреть систему с точки зрения квантовой механики. Таким образом, мы
должны заменить наше выражение для гамильтониана в F.Б. 1) на оператор гамильтониана,
получаемый заменойp^^(Pt/i)d/dx. и т. д. и при использовании коммутаторов [х, />У.] =i h &M
и т. д. Однако более изящный путь заключается в трансформировании гамильтониана до
введения операторов.
С этой целью давайте введем нормальные координаты:
F.Б.13)
При этом обратное преобразование осуществляется с помощью соотношений:
F.Б.14)
При использовании переменных 1иК функция Гамильтона приобретает вид:
/ \qd -\qd
= NX У МХ<Х~< + Ут * \ ХЦ*
^2 2 q ~q у q q ~q q ~q 2 q 2
F.Б.15)
В этом случае сопряженными переменными являются:
F.Б.16)
(к 236 Дополнения к главе 6
Рис. б.Б.Зл. Картина смещения атомов в двумерной решетке, содержащей два типа
атомов. Поперечные акустические (ТА) и продольные акустические (LA)
фононы представлены соответственно в верхней и нижней части рисунка.
При этом динамические уравнения системы (введенные уже в виде F.Б.З)—F.Б.6))
принимают вид:
Рщх =
Р/ =
F.Б.17)
6.Б. Оптические фононы и фрелиховское взаимодействие 2371и
Рис. 6.Б.30. Картина смещения атомов в двумерной решетке, содержащей два типа
атомов. Поперечные оптические (ТО) и продольные оптические (LO)
фононы представлены соответственно в верхней и нижней части рисунка.
Собственные моды, обладающие временной зависимостью типа e~ifi", даются F.Б.7).
Для каждой моды амплитуды связаны соотношением:
@1
F.Б.18)
Это позволяет нам устранить Yq из функции Гамильтона, но приводит к
необходимости суммирования по всем модам:
238 Дополнения к главе 6
н =
F.Б.19)
Введение переменных Xq приводит нас к функции Гамильтона, представляющей
собой сумму независимых осцилляторных функций Гамильтона, обладающих собственными
частотами coq ±. Вместе с сопряженными переменными мы окончательно получаем:
" F.Б.20)
При использовании этого уравнения в качестве исходного пункта переход к квантовой
механике становится очевидным: каждый классический гармонический осциллятор
становится квантово-механическим осциллятором (смотрите Дополнение 1.Г) с собственными
энергиями:
к4) 7^ = о'1'2'- F-Б-21)
где «число фононов» nq ± в моде либо равно нулю, либо дается целым положительным числом.
Отметим сильное подобие квантования атомных перемещений в решетке и
квантования электромагнитного поля. Да и сам термин фонон отражает близкую
аналогию с фотоном. В связи с этим по аналогии с фотонами мы можем говорить
о корпускулярной природе фононов. В рамках такого описания мы можем
говорить об эмиссии/создании и поглощении/уничтожении фононов и т. д.
Очевидно, что такое описание базируется на операторах рождения и уничтожения
гармонического осциллятора (смотрите дополнение 1.Г)
Поскольку число фононов, которые могут существовать в моде п, не является
ограниченным, фононная заселенность определяется той же самой статистикой
заселенности, которая характеризует фотоны, что делает их бозонами. При
термодинамическом равновесии (при температуре 7) среднее число фононов в моде дается таким
образом соотношением:
6.Б.2. Фрелиховское взаимодействие
Фононы представляют собой нестационарное возмущение периодического потенциала
кристалла, определяющего электронные состояния в зонах. Такое возмущение
естественно приводит к возможности рассеяния электронов из одного состояния в другое в
соответствии с золотым правилом Ферми. В неполярном полупроводнике (таком, как Si)
потенциал взаимодействия, связывающий электроны с фононами, в своей основе имеет тот
факт, что искажения решетки изменяют зонную структуру пропорционально амплитуде
относительного смещения атомов. Например, локальное сжатие из-за акустической
волны приводит к локальному увеличению ширины запрещенной зоны и возрастанию
энергии состояний в зоне проводимости (смотрите рис. 6.Б.4). В адиабатическом
приближении электрон в этом случае подвергается воздействию потенциала, пропорционального
амплитуде деформации а этот потенциал может затем индуцировать переходы, т. е. элект-
ро-фононные столкновения.
Естественно, что такие процессы (называемые рассеянием на деформационном
потенциале) имеют место также и в полярных полупроводниках (например, в GaAs),
с:
6.Б. Оптические фононы и фрелиховское взаимодействие 239
Зона проводимости
(Т)
Валентная зона
Рис. 6.Б.4. Индуцированное фононами изменение запрещенной зоны (называемое
деформационным потенциалом) действует на электроны как потенциал
рассеивающего центра.
но в этом случае проявляются дополнительные взаимодействия из-за того факта,
что фононы создают поляризационные и электростатические поля, следующие за
фононом. В случае акустических фононов мы говорим о пьезоэлектрическом
эффекте. В случае оптических фононов электростатическое поле приводит к электрон-
фононному взаимодействию, называемому взаимодействием Фрелиха.
Фрелиховское взаимодействие оказывает более сильное влияние по сравнению с
деформационным потенциалом, поэтому оно и обсуждается в этом разделе как иллюстрация
электрон-фононного взаимодействия.
Поскольку кристалл является полярным, в этом случае осуществляется перенос
заряда г от атомов х к атомам у. Таким образом, деформация, вызванная фононом, приводит к
поляризации:
Р = е*(х-у)у F.Б.23)
При этом величина заряда составляет р = —V • Р. Для оптического фонона с волновым
вектором q мы имеем:
р(г, /) = -е* у iq • (X - Y) exp(iq г - ia>4t) F.Б.24)
Из этого выражения мы видим, что LO-фононы могут индуцировать заряд. В этом
последнем случае уравнение Пуассона дает нам электростатический потенциал:
Кша(г, 0 = -f-^-±-{Х - Y)exp(iq • г - mj) F.Б.25)
Это и есть тот потенциал, с которым электрон может взаимодействовать. Матричный
элемент, который описывает взаимодействие между начальным электронным состоянием к и
конечным состоянием к' есть:
-ее* N X -Y . 1
dr =
F.Б.26)
При этом квадрат его модуля дается выражением:
- eVq(r)\k')f = 4^-^ tJlA<^/(k, k') F.Б.27)
Здесь Д есть символ Кронеккера, а интеграл перекрытия тот же самый, что был
введен ранее при обсуждении примесного рассеяния (уравнение F.33)). Перед тем,
W240 Дополнения к главе 6
как мы сможем использовать золотое правило Ферми, нам необходимо определить
е'иХ- Y.
Для определения е* мы используем следующий аргумент: в нашей модели Т0-
фононы обладают частотой ^ = ylBk/mnd), амплитуда колебаний (как реакция на
воздействие осциллирующего поля с частотой со) вблизи охто дается соотношением:
-со2 (Х- Y) = -mndco2TO(X- Y) + e* E F.Б.28)
Это, в свою очередь, определяет поляризацию:
Р = !^L—* F.Б.29)
'"red*' (<»т ~ (О2)
При этом проницаемость дается выражением:
е(а>)= еое„ + -^ F.Б.30)
m^V (a>lo -со2)
В частности, «статическая» проницаемость при со« соТО составляет:
еоеЛ = ео£„ + тг-Y- F.Б.31
В случае LO-фононов поле возрастает в результате поля наведенной поляризации
—е* (X— Y)(N/V)/eoe^ что приводит к дополнительной восстанавливающей силы:
Y)+^-(X -Y)+e*E F.Б.32)
При этом реакция системы определяется соотношением:
Р e*2N/mK(iV e*2N/mndV
F.Б.ЗЗ)
E \q)j0 + (е*2 N I еое„тпЛУ)- со1 ] (<aL2o -co2)
Частота coLO превышает сото. Таким образом, мы можем определить эффективный заряд е:
— = Q)jO€0(fst - £„)= (^ог~ X^lo ~ ^то ) F.Б.34)
В то же самое время мы получаем соотношение Лиддейна—Закса—Теллера:
^L = bL F.Б.35)
Так, что:
F.Б.36)
И наконец, амплитуда моды может быть определена из принципа соответствия, делая
классическую энергию моды эквивалентной числу фононов в моде (Уравнения F.Б.20) и
F.Б.21)):
£.<« = yW^Lol* -Y\2N = nqhcoLO F.Б.37)
В этом случае результат для скорости перехода, близкий к окончательному,
принимает вид:
5abs(k -> k') = ^-|(k|- eVg\k'p[E(k') - E(k) - hcoq] F<Б>38)
)-b(oq]
К|к'-к|2'
6. Б. Оптические фононы и фрелиховское взаимодействие
Этот результат относится к столкновению, при котором LO-фонон
поглощается, а его энергия передается электрону. Ранее мы говорили об использовании
уравнения F.Б.37). В действительности, при корректной квантово-механичес-
кой трактовке этой проблемы мы должны были бы выразить оператор X— Y
через операторы рождения и уничтожения, соответствующие гамильтониану в
F. Б. 20). После чего процедура становится полностью аналогичной электрон-
фотонному взаимодействию, рассмотренному в разделе 3.5.1. Таким образом
неудивительно обнаружить, что выражение F.Б.38) остается действительным для
поглощения фононов. В случае эмиссии фононов мы должны заменить nqnanq+ 1,
что соответствует сумме стимулированного и спонтанного излучения фонона:
Интересно отметить, что включение стимулированного излучения обеспечивает
детальный баланс при термодинамическом равновесии:
SJk -> k')/eq(k)[l -
= S Jk -> k')/eq(k')[l ~/eq(k)]
F.Б.40)
При этом /удается распределением Бозе—Эйнштейна F.Б.22), afcq
определяется распределением Ферми—Дирака E.38). В этом случае разностный поток частиц
между этими двумя состояниями равен нулю.
Исходя из уравнений F.Б.38) и F.Б.39), мы можем рассчитать полную скорость
рассеяния из-за фрелиховского взаимодействия с участием оптических фононов.
t -> к') F.Б.41)
Используя аппроксимацию, что /(к, 10 =1, мы находим:
■ч
-кп&к'
2т
8\\ h2k'2 /2т)-(п2к2 /2т \± ha>,
к +к' -Ikk'jn
При этом к'2 = к2 ± 2 mhcoop/h2, что, в конце концов, дает:
nq\n
+hcoo
F.Б.43)
Рисунок F.Б.5) демонстрирует зависимость Л от Е для GaAs. Естественно, что
эмиссия фононов имеет место только выше определенного энергетического порога
Е> hco из-за того факта, что после излучения фонона электрон обязательно
должен обладать только положительной остаточной энергией. Таким образом, мы
видим, что электрон-фононное взаимодействие является чрезвычайно эффективным
в рассеянии избыточной энергии электрона (на временной шкале процесс
происходит в течение временного интервала порядка 100 фс). Таким образом, это
взаимодействие играет фундаментальную роль в механизмах оптической релаксации.
Важно также отметить, что для рассеяния (неупругого и анизотропного),
происходящего через фрелиховское взаимодействие, в общем случае мы не можем
определить время релаксации. Таким образом, расчет подвижности требует более
сложного решения (по сравнению с F.22)) уравнения Больцмана.
242 Дополнения к главе 6
10 хЮ1
I
о
о
о
а
о
*:
О
,
/* • • • —
/
1.1.
1 ¥
■"-—-—
—— полная
.... эмиссия
поглощение
_
100
400
500
200 300
Энергия ( мэВ)
Рис. 6.Б.5. Скорость рассеяния на оптических фононах в GaAs при Т= 300 К. Энергия
оптических фононов составляет 36 мэВ, £st = 12,85, еж = 10,88.
Литература
В.К. Ridley, Quantum Processes in Semiconductors, Claredon Press,Oxford A988).
6.B. Лавинный пробой
Если электрическое поле, приложенное к полупроводнику, значительно превышает поле
скорости насыщения, часть из электронов будет способна приобрести дополнительное
количество энергии по отношению к минимуму зоны проводимости, большее ширины
запрещенной зоны Е. В этих условиях становится возможным процесс ударной ионизации.
Электрон взаимодействует со всеми другими электронами в валентной зоне за счет электрон-
электронного взаимодействия, при этом он может возбудить через запрещенную зону
другой электрон, что соответствует генерации электронно-дырочной пары (процесс
генерации). В этом процессе сохраняются энергия и квазиимпульс. Перед
столкновением мы имеем электрон в состоянии к. с энергией Ес(к) и электрон в состоянии -
кА с энергией Ev (кА). После столкновения в зоне проводимости имеются два
электрона в состояниях kj и к2 при этом законы сохранения могут быть записаны (смотрите
обратный процесс на рис. 6.Г. 1):
F.В.1)
Для того, чтобы определить энергетический порог этого процесса, используем
аппроксимацию параболической зоны Ес(к.) = Eg + fi2k2/2me и Ev(kh) = — fi2kh2/2mh,
а также предположим, что эффективные массы составляют для электронов те и для
дырок mh и выполняются соотношения:
' 1+ F.В.2)
2т,
2mh
Мы можем убедиться в том, что минимум начальной энергии реализуется,
когда все импульсы ориентированы в одном и том же направлении. Более изящно
можно определить этот минимум (с использованием метода Лагранжа),
минимизируя функцию:
6. В. Лавинный пробой
F.В.З)
где Я есть множитель Лагранжа. Беря производную от kv /c2 и кл, мы находим, что:
2 к к к
-A. = J±L. = Jh- = b- F.B.4)
П е с h
Отсюда мы определяем минимальную начальную энергию:
= 6 в 5
2wc, J 1 + (m, / mh )
Это выражение приводит к порогам ударной ионизации слегка выше Eg в случае
тяжелых дырок, но к величине порядка 3/2£^ в том случае, когда те, mh близки друг
другу. Таким образом порог ниже в случае генерации тяжелых дырок.
Из соображений симметрии аналогичный процесс, при котором начальной частицей
является дырка, дает тот же самый результат, что и в предыдущем случае при
соответствующей замене те на mh. В то же время мы должны четко представлять, что в
рассматриваемом диапазоне энергии использование параболического приближения не является
достаточно корректным.
Как только первичный электрон генерировал электронно-дырочную пару, он будет вновь
ускоряться электрическим полем, что делает возможным его участие в последующих актах
генерации пар. Подобным же образом после достаточного ускорения в электрическом поле
каждая из вторичных частиц, в свою очередь, будет способна играть роль первичных частиц
и участвовать в процессе генерации пар. Основным результатом такого процесса является
то, что полная концентрация свободных носителей в структуре возрастает геометрическим
образом. Такая ситуация в полупроводнике называется пробоем и сопровождается
возрастанием концентрации свободных носителей и увеличением проводимости. На практике, мы
определяем коэффициенты ионизации ап и ар (которые в дальнейшем будем
полагать равными) как число вторичных пар, генерированных первичным электроном при
пробеге электроном 1 см среды в направлении приложенного поля. Естественно, что
эти коэффициенты зависят от напряженности поля F. Таким образом, при
перемещении через область сильного поля 0 < х < w первичный электрон сможет генерировать:
Ns = \an{Fyix F.B.6)
вторичных пар. Вторичные и последующие частицы могут генерировать полное число
электронов в этой области (до тех пор, пока Ns < 1), определяемое соотношением:
Nw = 1 + Ns + Ns2 + N* +... = —l-— F.B.7)
Если электрон входит в область при х = 0, на выходе из области при х = w будет Nw
электронов. Мы определяем коэффициент умножения Мп для электронов как отношение
выходного тока и тока на входе в область сильного поля. Аналогичным образом мы
можем определить Мр для дырок как у @) = Mpjp(w), где дырки входят в область в точке
w и покидают ее в точке 0. Рисунок 6.В. 1 иллюстрирует явление лавинного пробоя.
Наиболее простая модель для определения коэффициентов ионизации
предложена Шокли, и она известна под очаровательным названием модели счастливого
электрона. Поскольку лишь электроны, которые обладают энергией больше пороговой,
определяемой F.В.5), будут способны запустить лавинный механизм, таких
электронов будет очень немного, так как по большей части электроны будут растрачивать
свою энергию в столкновениях еще до того, как из-за ускорения они приобретут
пороговую энергию. Обозначим через Яор длину свободного пробега электрона до
столкновения с оптическим фононом (для простоты предположим, что она не зави-
|( 244 Дополнения к главе 6
-О'#-
-е¥
О w х
Рис. 6.В.1. Иллюстрация процесса умножения носителей за счет ударной ионизации. Под
влиянием сильного приложенного поля Гъ область сильного поля в точке х = О
входит одиночная частица, в то время как Мп электронов выходят из области
сильного поля.
сит от энергии), а через Л. обозначим среднюю длину свободного пробега до
соударения с другим электроном (в предположении, что пороговая энергия уже достигнута).
Наконец, предположим, что каждое столкновение сопровождается падением
скорости электрона до нуля. Для того, чтобы приобрести пороговую энергию Е., электрон
должен пройти минимальное расстояние х, определяемое Е. = efxr Вероятность того,
что электрон сможет сделать это без рассеяния на оптических фононах составляет:
F.В.8)
Как только кинетическая энергия электрона превысит порог ионизации
(смотрите рис. 6. В.2), средняя длина свободного пробега Л будет определяться совместным
проявлением двух механизмов 1/А = 1/Д + 1/Лор. Вероятность того, что первым актом
столкновения, испытываемого электроном, является ударная ионизация (а не
рассеяние на фононе решетки) составляет таким образом Л/Л.. Если же первым процессом
будет столкновение с фононом, скорость электрона упадет до нуля, и он должен
будет вновь наращивать энергию с самого начала. Для такого «холодного старта»
вероятность ионизации будет составлять:
Энергия
Рис. 6.В.2. Модель Шокли для определения коэффициента ионизации а\ первичный
электрон приобретает энергию, достаточную для создания вторичной
электронно-дырочной пары.
6. В. Лавинный пробой
л-А.
Е,
F.В.9)
Если мы определим аор как число столкновений с фононами на длине пробега в
1 см, баланс между энергией, передаваемой электрическим полем, и энергией,
рассеиваемой в процессах ионизации и излучения фононов, может быть записан в виде:
eF =
F.В.10)
где счесть коэффициент ионизации, который мы ищем. В этом случае число актов набора
энергии электронами из состояния остановки (после соударений) составляет ап + агор, что
дает число столкновений на длине в 1 см:
Устраняя аор в F.В.10) и F.В.11), получаем:
eFPi
F.В.11)
F.В.12)
где мы воспользовались тем фактом, что Е ор<< Е. (-50 мэВ и -1 эВ
соответственно). Повторная подстановка F.В.9) в этом случае дает окончательный результат,
иллюстрируемый рисунком 6.В.З:
F.В.13)
Рис. 6.В.З. Зависимость коэффициента ионизации а от напряженности приложенного поля
в соответствии с уравнением F.В.13) для кремния. Е. = 1,8 эВ, Л^ = 10 нм,
Я. =200 нм.
За исключением случаев очень сильных полей F мы можем пренебречь вторым
членом в знаменателе, что позволяет нам переписать F.В. 13) в виде:
ап =-^— eFexp %- I F.B.13)
Коэффициент ударной
ионизации
Несмотря на крайнюю упрощенность этой модели выражение F.В. 14) успешно
воспроизводит экспериментально наблюдаемые зависимости ап от напряженности
приложенного поля.
246 Дополнения к главе 6
Литература
J.S. Blakemore, Semiconductors Statistics, Dover, New York A987).
6.Г. Оже-рекомбинация
Процессом, обратным ударной ионизации, является Оже-рекомбинация. В этом
случае электрон и дырка рекомбинируют, а высвобождаемая энергия передается
другому электрону или дырке. Схематично для сильно упрощенной зонной
структуры эти процессы иллюстрирует рисунок 6. Г. 1.
Рассмотрение эффекта в случае слегка более реалистичной зонной структуры,
включающей зоны легких и тяжелых дырок, привело бы к увеличению числа
возможных Оже-процессов за счет того, что второй дыркой могла бы быть либо
легкая, либо тяжелая дырка, при этом одновременно возможны были бы процессы как
в той же самой зоне, так и между различными валентными подзонами.
Равным образом рис. 6.Г.1 показывает, каким образом законы сохранения
полной энергии и импульса ограничивают комбинации возможных начальных и
конечных состояний. Например, рекомбинация электрона на дне зоны проводимости
и дырки в вершине валентной зоны не является разрешенным Оже-процессом, так
как вторая частица не может совершить вертикальный переход.
Качественно также очевидно, что поскольку в Оже-процессе участвуют 3
частицы, он должен превалировать в условиях повышенной концентрации электронов и
дырок. Как правило, это имеет место в случае узкозонных полупроводников или в
системах с сильным отклонением от термодинамического равновесия (например, при
больших уровнях оптической накачки или инжекции тока, как это имеет место в
полупроводниковых лазерах).
Единственной моделью, которая дает надежду получить аналитическое
описание Оже-рекомбинации (и тем самым дать некую физическую интерпретацию),
является модель с двумя параболическими зонами, электроны и дырки которых
обладают эффективными массами соответственно тс и mv. Предположим, что
электроны могут достичь равновесия друг с другом, а дырки могут сделать то же самое
в течение времени, меньшего характеристического времени рекомбинации. Мы
предположим также, что распределение частиц остается невырожденным. В этом
случае концентрация электронов определяется соотношением:
а б
Рис. 6.ГЛ. Два возможных процессов Оже-рекомбинации: (а) электрон с импульсом
kj рекомбинирует с дыркой кл, а другой электрон с к2 получает
высвобожденную энергию и переводится в состояние к3 (СНСС); (б) аналогичный
процесс с участием двух дырок и одного электрона (СННН).
6. Г. Оже-рекомбинация 247
n = Nc exp - ±£-
kBT
В то же время концентрация дырок дается соотношением:
p = N, exp
F.Г.1)
k.T
F.Г.2)
где jun (jup) есть квазиуровень Ферми для электронов (дырок). В самом деле, как мы видели
разделе 5.6.4, эти уравнения определяют /лп и jup при равновесии jun = jup = /^.Гипотеза
квазиравновесия для электронов (дырок) означает, что вероятность занятия электронного
состояния к с энергией ес дается (в предположении параболичности зон и того, что
энергия зависит только от модуля волнового вектора к):
2me
F.Г.З)
fc(k) = exp
к„Т
В случае дырок аналогичное выражение имеет вид:
кЙТ
F.Г.4)
при этом:
2mv
Скорость рекомбинации с учетом процесса (смотрите рис. 6.Г. 1л), при котором
начальные состояния включают два электрона с Ц и к2 и дырку с кЛ, а конечное
состояние соответствует одиночному электрону с к3, должна быть умножена на
весовой множитель вероятности заселенности состояний кр к2, кА (и где можно
предположить, что состояние к3 является незанятым с вероятностью 1):
, к2, к3) = ехр - —
квТ
п р
exp
k22 +(mc/mv)kl I
F.Г.5)
И вновь отметим, что этот процесс должен быть разрешен законом сохранения
импульса, т. е.:
Ц + Ц-Ц^Ц F.Г.6)
а также законом сохранения полной энергии:
ec(k[)+£c(k2)-£v(kh)= £с(*з) F.Г.7л)
Таким образом:
((B48 Дополнения к главе 6
— \kl+ kM/mX2 ~ *з2 ]+ Eg = 0 F.Г.76)
2mc
Таким образом, взаимодействие слабо зависит от к,, Ц, кА, наиболее вероятный
процесс определяется максимизацией Р(к{, к2, kh), при этом константы определяются
законами сохранения.
Для того, чтобы найти максимальное значение, используем ту же процедуру,
что и в дополнении 6.В, и используем метод множителей Лагранжа для нахождения
максимума функции:
F = Р(к„ к2, кн)- г\^\_К +к2 + Ьпс/тХ - к^ + Es - Afc +к2-к„- к,)
F.Г.8)
Таким образом:
F.Г.9)
При этом оптимальная величина имеет место при:
к2=к{,кИ=-?±к{ F.Г.10)
тс
Закон сохранения импульса дает:
После того, как к2, kh9 k3 определены в функции kv эта последняя величина
получается из закона сохранения энергии, что в результате дает:
Таким образом, максимальная вероятность составляет:
)
или:

Вероятность Оже-рекомбинации (СНСС)
Это позволяет определить максимальную вероятность при термодинамическом
равновесии в виде:
«Зеркальный» процесс, в котором участвуют две дырки и один электрон может быть
получен заменой n<r*p,ju<r> l/ju, Nc <-> Nv что дает:
6. Г, Оже-рекомбинация
Вероятность Оже-рекомбинации (СННН)
В большинстве полупроводников // = mjmv < 1, при этом сравнение соответствующих
вероятностей показывает, что при сравнимых концентрациях электронов и дырок (п и р),
доминировать будет первый процесс.
Максимальные вероятности F. Г. 13)—F. Г. 16) описывают существенные особенности
зависимости Оже-рекомбинации от температуры и концентрации носителей. Вблизи
равновесия вероятности F. Г. 14) и F. Г. 16) показывают, что этот эффект значителен в
узкозонных полупроводниках и при повышенных температурах. При фиксированной
температуре и ширине запрещенной зоны скорости рекомбинации зависят, как мы и могли бы этого
ожидать, от концентрации пир:
Яснее = Сснсс„2 ^ Лсн„„ = СснтПр2 FТЛ7)
где Ссннн есть коэффициент, связанный с вероятностью Ро, определяемой F.Г. 14).
В условиях равновесия мы находим, что /^снсс = Сснссл0л.2, т. е.:
дснсс = ^снсс П^_Р_ F.Г.18)
Для обратных процессов создание электронно-дырочной пары электроном с
достаточной энергией пропорционально п и определяется (следуя той же самой схеме
рассуждений) соотношением:
Gc =GOC— F.Г.19)
и поскольку Goc= /^снсс,мы можем переписать выражение ддя рекомбинационного
баланса в виде:
= RCHCC -Gc =GOC — (ПР~П') F.Г.20)
«о { "? ;
Оценка коэффициентов Сснсс, Ссннн сложна и не сопровождается особой
дополнительной информацией с учетом того, что реальная зонная структура лишь в первом
приближении может быть представлена двухзонной моделью. Таким образом, здесь мы
не будем ставить себе целью определение этих величин. Тем не менее мы
представим уравнение Б.Л. Гельмонта, (ЖЭТФ 48, 268 A978)) для времени жизни
электрона г = ло//?снсс в условиях термодинамического равновесия:
Рисунок 6.Г.2 показывает, что время жизни электрона в собственном полупроводнике
с малой шириной запрещенной зоны сильно зависит от температуры из-за вероятности Ро
в уравнении F.Г. 14).
Вдали от состояния термодинамического равновесия, как показывает
ограниченное расширение F.Г.20), скорость г, связанная с Оже-процессом,
характеризуется квадратичной зависимостью от концентрации носителей, т. е. г = CAuge/*2-
При этом коэффициент пропорциональности соответствует коэффициенту Оже.
Рисунок 6.Г.З показывает экспериментальные значения коэффициента Оже,
определенные при комнатной температуре в двух случаях, важных для инфракрасного де-
250 Дополнения к главе 6
10"° -
100
150 200 250
Температура (К)
300
Рис. 6.Г.2. Рассчитанное время жизни электрона в собственном полупроводнике с
малой шириной запрещенной зоны Е. Использованные параметры относятся
' ' .Jbcx= 15%.
| 100 200 300 400 500 600 700
Ширина запрещенной зоны (МэВ)
Рис. 6.Г.З. Коэффициент Оже для HgCdTe и InAsSb при комнатной температуре в
функции ширины запрещенной зоны (с вариациями ширины запрещенной
зоны, определенными модификацией состава твердого раствора).
тектирования: Hg^Cd, _ хТе и In As1 _ xSbx. Ширина запрещенной зоны в этих двух
важных системах твердых растворов является функцией их состава х. Рисунок 6.Г.З
подтверждает экспоненциальную зависимость коэффициента Оже от ширины
запрещенной зоны.
Литература
J.S. Blakemore, Semiconductor Statistics, Dover, New York A987).
P.T. Landsberg, Recombination in Semiconductors, Cambridge University Press, Cambridge
A991).
ГЛАВА 7
ОПТИЧЕСКИЕ СВОЙСТВА
ПОЛУПРОВОДНИКОВ
7.1. Введение
В главах 1—3 мы описали различные механизмы взаимодействия между
электромагнитной волной и двухуровневой квантовой системой. В то же время мы кратко
упомянули, что эти же результаты могут быть тривиально обобщены на системы,
обладающие произвольным числом дискретных состояний. В главе 5 мы видели,
каким образом электроны в кристаллическом твердом теле и, в частности (с
учетом нашей основной цели) в полупроводнике, распределены по энергетическим
зонам, при этом их можно классифицировать в соответствии с непрерывно
изменяющимся индексом: волновым вектором к. В этой главе мы представим
математический аппарат, который позволит нам учесть взаимодействия между
излучением и этими непрерывно распределенными состояниями. После чего мы будем в
состоянии описать взаимодействия между объемными полупроводниковыми
материалами и излучением.
7.2. Дипольные моменты в прямозонных
полуп роводн и ках
Рассмотрим объем V кристаллического полупроводника, в котором собственные
функции h^c энергиями £лк даются функциями Блоха—Фуке, введенными в E.12):
"ikr =(r|^k) G.1)
Напоминаем, что к есть волновой вектор собственного состояния,
принадлежащего первой зоне Бриллюэна полупроводника и обозначающий положение состояния в
«-ной энергетической зоне в направлении ek = k/k (смотрите рис. 5.2 и 5.4). Функции
ип к(г) обладают периодичностью кристаллической решетки (т. е. для каждого вектора
решетки г.: ип к(г + г.) = ип .(г)). Более того, эти функции нормированы на объем
элементарной ячейки К, т. е. ]„ |мяк(г)|2с13г = V.. Как уже объяснялось в дополнении 1.А,
мы нормируем стационарные функции по отношению к виртуальному ящику объема
V= NV., при этом fK|*Fj2d3r =1, что приводит к квазиквантованию волновых векторов
к.Напоминаем, что наиболее общепринятая процедура, используемая при квазикван-
товании в кристаллических твердых телах, состоит в использовании циклических
граничных условий Борна—фон Кармана, приведенных в E.10). Наконец, важным
моментом, достойным упоминания (а также полезным во многих случаях), является то, что
пространственная вариация волновых функций e-lkr очень слаба по сравнению с той,
которая возникает из-за атомных волновых функций ип к(г) (смотрите рис. 5.3).
Другими словами, е-1кг действует как огибающая для блоховских функций.
На полупроводник действует электромагнитная волна, для которой
гамильтониан возмущения для взаимодействия (смотрите C.13)) может быть записан в виде:
, /)= ^cos(kop • г - cot) = -qE • f cos(kop r - cot) G.2)
Глава 7. Оптические свойства полупроводников
где г — оператор положения, кор — волновой вектор излучения, а Е —
напряженность электрического поля. В этом случае гамильтониан оптического
взаимодействия будет связывать два состояния \Ч*п к) и 14^, к,). Уравнения A.82) и A.83)
позволяют рассчитать скорость вероятности (с) того, что электрон с волновым
вектором к из зоны п попадет в состояние к' зоны п':
(ha> = Е,л, - ЕпЛ) G.3)
Напоминаем, что векторы к квазиквантованы. Энергетическая зависимость дельта-
функции Дирака выражает требование сохранения энергии:
Теперь рассчитаем матричный элемент Wn k n, v\
= ~у~ JJj<^)eik'r(r)e-ik-r^(r)e-ikrd3r G.5)
Этот последний интеграл может быть упрощен, если заметить, что функция е1^ ~ ^ "k) r
изменяется очень медленно по сравнению с произведением двух функций ип к(г). Таким
образом, мы можем переписать интеграл в G.5) следующим образом:
Cell i
«;,,(r)r«n,k(r)d3r G.6)
а интеграл I в G.6) может быть записан в виде:
I = JJJ«;,k.(R)(R + i*K>k(R)d3R =jjju*^(R)Runk(R)d3R G.7)
Cell / CeU 0
где R перекрывает пространство элементарной ячейки в области около 0. Член с г. в
интеграле может быть устранен из G.7), поскольку блоховские функции ортонормиро-
ваны для к ф к'. В результате этого этот интеграл не зависит от /-той ячейки, в пределах
которой производится его оценка.В этом случае уравнение G.6) приобретает вид:
кор-к) G.8)
где функция Кронеккера в последнем члене выражает требование сохранения момента
при электрон-фотонном взаимодействии:
k^f + k^ G.9а)
Сохранение момента
при оптических переходах
Волновые векторы фотонов в видимом и близким к видимому спектральных
диапазонах сильно отличаются друг от друга: кор = 2л/Л ~ 104 — 106 см, тогда как
типичные волновые векторы в зоне Бриллюэна по порядку величины составляют
к — 2л/а или 108 см (напоминаем, что а есть постоянная решетки). Таким образом
волновой вектор излучения является пренебрежимо малым по сравнению с этим же
параметром для электронов в каждой из различных энергетических зон, так что:
к'«к G.96)
Оптические переходы
являются «вертикальными»
Рисунок 7.1 иллюстрирует тот факт, что оптические переходы в зонной
диаграмме должны иметь место при постоянной величине к. Именно в этом смысле
такие переходы называют вертикальными. Очевидно, что это правило для переходов
может быть реализовано, если зонная структура имеет прямой характер, т. е. если
экстремумы валентной зоны и зоны проводимости выровнены по вертикали в зоне
7.2. Дипольные моменты в прямозонных полупроводниках 253
св
Рис. 7.1. Оптические переходы между
состояниями зоны проводимости и
валентной зоны имеют место при постоянной
величине к. Такие переходы называют
«вертикальными».
-ik r
-ik r
VB
Бриллюэна. Ситуация с переходами в непрямой зонной структуре более сложна и
не рассматривается в этой книге. Таким образом, в будущем мы сможем устранить
индекс к' из G.8).
Начиная с этого момента и далее мы ограничимся оптическими переходами
между валентной зоной и зоной проводимости. Будем обозначать через и^ и ил
периодические компоненты блоховских функций соответственно в зоне
проводимости и валентной зоне. В этом случае дипольный матричный элемент WJk) для
переходов между валентной зоной и зоной проводимости принимает вид:
Wv c(k) = -q
rj(k' - kop - k)
G.10)
г =
Дипольный матричный элемент для
переходов валентная зона -» зона проводимости
Теперь мы можем использовать C.9.6) для того, чтобы связать матричные
элементы операторов оптического взаимодействия А р и D Е:
m0cok
G.Ш)
г =
где т0 масса электрона в вакууме, a h wk есть энергетический зазор между двумя
состояниями в зоне проводимости и валентной зоне. Мы видели в дополнении 5.В,
что pw может быть получен исходя из параметра Кейна Р. Эта формула
чрезвычайно полезна, так как величина Р практически постоянна в соединениях III—V
(смотрите таблицу 7.1), что делает G.10) достаточно предсказуемым. Более того,
используя теорию Кейна, мы можем легко показать, что в первом порядке по к, матричные
элементы G.11л) являются постоянными. Уравнение, связывающее pvc с параметром
Кейна Р, может быть найдено в литературе в таком количестве различных форм,
сколь велико и число определений этого параметра. В E.В. 18) мы использовали
предположение, что <г>Р2 является параметром, гомогенным по энергии». Другие
авторы используют предположение, что «Р есть параметр, гомогенный по скорости, а
Глава 7. Оптические свойства полупроводников
третьи, предполагают, что этот параметр гомогенен по импульсу».В нашем рассуждении
мы предпочитаем использовать энергию Кейна Ер (= Р2), что является единогласно
признаваемым параметром B0—25 эВ) и это приводит к следующему результату:
G.116)
Дипольный матричный элемент
и энергия Кейна
где Eg есть ширина запрещенной зоны. Также популярным в литературе
параметром является матричный элемент xvc. Это понятие вводится с тем, чтобы учесть тот
факт, что в оптических переходах принимают участие только подзоны легких и
тяжелых дырок, а не спин-орбитально отщепленная подзона, которая отстоит
достаточно далеко по энергии. Мы могли бы использовать элементы перехода,
введенные в E.В.22), но идея, лежащая в основе этих расчетов, достаточно проста: только
две трети силы осциллятора (т. е. две зоны из трех) принимают участие в переходе,
что приводит к:
2 1 Й Ер
X — £_
J .с,, тп
G.11*)
В таблице 7.1 приведены соответствующие параметры Eg, E^ mjm^ rw для основных
полупроводников, используемых в оптоэлектронных применениях. Отметим, что в случае
узкозонных полупроводников дипольный матричный элемент становится очень большим
в сравнении с межатомным расстоянием, а электронные волновые функции становятся
все более делокализованными по мере того, как уменьшается ширина запрещенной зоны.
В этом смысле принято говорить о том, что полупроводники становятся все более
квантовыми по мере уменьшения ширины их запрещенной зоны.
Табл. 7.1. Величина Eg (ширины запрещенной зоны), тс /т0 (эффективной массы
электронов), энергии Кейна Ри дипольного матричного элемента оптического
перехода гж для различных полупроводников (из книги: G. Bastard, Wave
Mechanics Applied to Semiconductor Heterostructures, Wiley, New York A991))
£(эВ)
mJmo
Ер(эВ)
GaAs
1,5192
0,0665
22,71
6,14
InP
1,4236
0,079
17
5,67
GaSb
0,811
0,0405
22,88
11,5
InAs
0,418
0,023
21,11
21,5
InSb
0,2352
0,0139
22,49
39,5
Пример
Энергия Кейна Ер в GaAs составляет 22,7 эВ и соответствует кейновской скорости:
Вх1,6х109 Кл
"= 122,7 В xl,i
V 2хО,9>
2х0,9х10-30 кг
= 1,42хЮ6 м/с
Матричный элемент гус дается G.116) и равен:
rvc = 1,05 х 104 Дж с х 1,42 х 106 м сA,5 В х 1,6 х 109 Кл) = 6,14 А.
Элемент х входит в расчеты поглощения и равен г х VB/3) или 5,0 А.
7.3. Оптическая восприимчивость полупроводника
7.3. Оптическая восприимчивость полупроводника
Теперь мы можем рассчитать оптическую восприимчивость, связанную с
переходами из валентной зоны в зону проводимости. Рассмотрим полупроводниковый
кристалл объемом К в условиях квазиквантования. Предполагается, что структура
валентной зоны и зоны проводимости является параболической и описывается
соответствующими эффективными массами mv и тс.При условии, что оптические
переходы являются вертикальными, попробуем найти оптическую восприимчивость
Zk(co), связанную с переходами при постоянной величине к между валентной зоной
и зоной проводимости. Уравнения G.4) и G.(9) дают связь между валентной зоной
£(к) и зоной проводимости £(к) в условиях связи через оптический переход
(смотрите рис. 7.1):
^f( )Eg G.12)
Ec(k)Ev(k) ^f( +
2 [тс
где к есть модуль вектора к. Для упрощения G.12) полезно ввести приведенную
эффективную массу:
— = — + — G.13)
mr mc mv
Приведенная эффективная масса
Безразмерная оптическая восприимчивость, связанная с переходом между
квазидискретными уровнями Ev(k) и isc(k), в этом случае дается C.26):
[со - coAk)]T2-i [N _
£оь [со- coyc(k)]2T2 + 1
где xvc(k) (= xvc в соответствии с нашим предположением о независимости диполь-
ных матричных элементов от к) есть элемент перехода в направлении Ох,
выбранном произвольно для упрощения обозначений, covc(k) = (Ec(k) — Ev(k))/h и Т2 есть
время релаксации электронов в зонах. Nc(k) и Nv(k) представляют концентрации
носителей (см~3) на уровнях Ес и Ev. В этом случае полная восприимчивость
определяется суммированием членов восприимчивости G.14я) по волновым векторам к
зонной структуры, т. е.:
2хж(к)гТ [eo-eovc(k)]T2-i
[yv (k)
[co-covc(k)\T2 + 1
где множитель 2 связан с тем фактом, что для каждого вектора к имеются 2
спиновых состояния. Предположим, что объем виртуального ящика достаточно большой,
чтобы суммирование заменить интегрированием по к:
'dE GЛ5)
Правило эквивалентности между
суммированием по к и интегрированием по к и энергии Е
где плотность р(к) выражена в 1/(см~3), р(Е) — в 1/Дж, а множитель 2
обусловлен спиновым вырождением. В изотропной среде микроскопические плотности
Nc(k) и Nv(k) в G.14) определяются pc(k)d3k и /?v(k)d3k, где рс(к) и pv(k) равны и
даются E.17), при этом рс(к) = pv(k) = 2К/8;г3 = У/4я3 (мы умножили результат
на 2 для того, чтобы учесть вырождение по спину, при этом напоминаем, что V
есть объем кристалла). К этим членам мы должны добавить выражение,
соответствующее термическому квазиравновесию: а именно мы должны ввести
функции Ферми—Дирака fc(Ec(k)) и/у (Ev (k)), описывающие вероятности
заселенности для уровней Ес(к) и £v(k) и приведенные в E.38) раздела 5.6:
Глава 7. Оптические свойства полупроводников
, GЛби)
f = -
1 + F (?-*'*)'kT
EFc и EFv есть квазиуровни Ферми для электронов и дырок (заметьте, что в
данном случае^ отличается от E.44), поскольку здесь мы используем вероятность того,
что состояние валентной зоны занято электроном). В этом случае бесконечно
малую разность плотности Nv— Ncb G.14) для элемента d3k можно заменить на:
Nv-Ne+> p#klfv[Ev(k)]{l-fc[Ec(k)]} -fc [Ec(k)]{l -fv[Ev(k)]}] =
G.166)
= pdWv[Ev(k))-fc[Ec(k)]}
Таким образом, оптическая восприимчивость получается интегрированием G.14) по
первой зоне Бриллюэна или:
^^(k>|7'/ G.17)
[а>-а>„(к)]2Т22+1
Мы предполагаем, что теории Кейна (смотрите дополнение 5.В) матричный
элемент xvc не зависит от к. Требование сохранения энергии может быть записано с
использованием G.4), G.12) и G.13) в виде:
G.18)
£ п2к2
v 2mv
Поскольку волновые векторы к и энергии фотонов h co^ связаны, мы можем
проинтегрировать G.17) по частотному интервалу падающих фотонов с использованием
выражений E.19) и E.20):
„ = —f —~ I We ~ Eg /^)l/2^^vc G.19я)
2л { п j
или вновь:
\3/2
2л
\3/2
G.196)
Р;(ЮЛ
2л
Комбинированная плотность состояний (Дж~1 см)
Выражение G.19) описывает комбинированную плотность состояний,
связанную через энергию фотона hco. Подставляя последнее выражение в интеграл G.17),
мы получаем основное соотношение настоящего раздела:
"А' G20)
{a-ajTt +1
Оптическая восприимчивость, связанная с
межзонным переходом в полупроводнике
7.3. Оптическая восприимчивость полупроводника 257
В этом выражении связанные энергии Ev и Ес являются функциями h со
посредством соотношений в G.18). Коэффициент поглощения связан с мнимой частью
оптической восприимчивости через C.36), т. е.:
«(»)=-£-Хы G-21)
или
^] l/f\
^]ЛЮ]( f\ ,_2 G.22)
Последнюю формулу легко упростить, если заметить, что лоренциан ведет себя
как функция Дирака в сравнении с более медленно меняющимися функциями под
знаком интеграла. В результате мы получаем коэффициент поглощения (в см) в виде:
а(р)= **'*> Pj(co)\fMco) - /,(йо>)] G.23)
или вновь:
а(а>) = -у(ф) = а0 (<*>)(/„{ho)- ft (ha,)) G.24)
Поглощение и усиление
в полупроводнике (см)
где у(со) есть усиление полупроводниковой среды, a aQ(co) есть поглощение
опустошенной зоны проводимости, при этом:
3 /2
Поглощение опустошенной
зоны проводимости (см~1)
Функции fc(h со) nfv(hco) являются функциями Ферми—Дирака:
1 + exp \Ec(fio))- EF \/ kT }
G.256)
1 + exp §Ev(tta>)- EF ]/ kT }
G.25*)
mv g
Уравнение G.24) показывает, что поглощение в прямозонных полупроводниках для
фотонов с энергией, большей ширины запрещенной зоны, возрастает как ^{fico — 2?)
(смотрите рис. 7.2). Уравнения G.23)—G.24) позволяют описать оптические характеристики
полупроводника в условиях отклонения от термодинамического равновесия.
Условие оптического усиления (т. е. а(со) < 0) дается соотношением:
fc(hco)-fv(hco)>0 (
или иначе с учетом G.256) и G.25<?):
EFc-EFv>hco G.266)
Условие Бертрана—Дюррафура
Глава 7. Оптические свойства полупроводников
hv
Рис. 7.2. Представленные рисунки показывают эволюцию кривых поглощения и
усиления в функции положения квазиуровня Ферми. Тонированные (жирные)
линии соответствуют слабому (сильному) отклонению от равновесия. В этом
случае среда поглощает все фотоны с энергией, превышающей ширину
запрещенной зоны. Как только энергетический интервал между квазиуровнями
Ферми превышает ширину запрещенной зоны, все фотоны, обладающие
энергией в диапазоне между Eg и EF -Efv, начинают усиливаться (условие Берна-
ра—Дюррафура).
Это последнее уравнение утверждает, что усиливаться будут лишь те фотоны,
которые обладают энергией, меньшей энергетического зазора между
квазиуровнями Ферми. Эти квазиуровни связаны с неравновесной заселенностью N
условием, полученным в разделе 5.6:
i
= \Рс{Е)-
1
-йЕ
G.27)
Это выражение относится к квазиуровню Ферми для электронов EFc, и
аналогичная формула имеет место для квазиуровня дырок. В условиях положительного
усиления кривая, описываемая G.23), называется кривой усиления в
полупроводнике. Рисунок 7.2 иллюстрирует эволюцию кривой усиления в функции
возрастающего отклонения от термодинамического равновесия.
7.4. Поглощение и спонтанное излучение
7.4. Поглощение и спонтанное излучение
Из главы 3 мы знаем, что подход, основанный на оптической восприимчивости не
позволяет нам учесть спонтанное излучение. Естественным методом трактовки
такого эффекта является использование скоростных уравнений Эйнштейна. Мы
рассматривали эту теорию в разделе 3.6 применительно к широкополосной
электромагнитной волне. Мы вновь воспроизведем указанный подход по ряду причин: во-
первых, он представляет очень тонкий расчет (следите за размерностью), имеющий
большое практическое значение, во-вторых, в силу исторических причин в случае
полупроводников используются другие обозначения и, наконец, в-третьих, в
данном случае этот подход используется в другом контексте: теперь мы имеем дело с
уширенным энергетическим спектром (впрочем мы уже упоминали об
эквивалентности широкополосной волны и энергетического спектра уширенного перехода.)
Рассмотрим в полупроводнике объемом V уровень Ev (k) в валентной зоне и
уровень Ес(к) в зоне проводимости при определенном значении к, имея в виду в
дальнейшем перейти к квазиквантованию. Как мы видели в разделе 3.6, в случае
электромагнитной волны с широким спектральным распределением pph( h со) скорость
оптического перехода gvc(c~l) no всему объему К и между уровнями Ес и Ev
пропорциональна вероятности того, что состояние Ev занято, а состояние Ес является пустым.
g (к) = В f(E)[\ -f(E)]pAhv) G.28)
где /?ph (Дж) есть плотность фотонов на единицу энергии в объеме V, a Bvc (Дж с)
есть скорость перехода в расчете на один фотон в резонаторе, определяемая
золотым правилом Ферми (смотрите C.76)—C.77)) в виде:
= JLq2E2x2c G.29)
где Ео есть электрическое поле, связанное с одним фотоном в объеме V (величина Bvc
дается для одного фотона в резонаторе!) и определяемое B.77):
fico = — щ £0Eq V G.30л)
2 ор
или
£2 = 2Ьт G.306)
Из этого следует:
d _ nQ2xla> _ nq1 Ер п лП
где мы использовали G.116). Обратите внимание на присутствие члена К в
знаменателе: это следует из делокализованной природы блоховских волновых функций,
которая требует, чтобы мы рассматривали в качестве объема взаимодействия полный
объем кристалла К (смотрите дополнение 1.А). Напоминаем, что сохранение энергии
требует выполнение соотношения hco = hcovc— Evc(k) = Ec(k) — Ev(k). В то же время
имеются два отличия от условий, которые предполагались в разделе 3.6. Во-первых,
функции^ и/у, приведенные в G.25а) и G.256), обеспечивают описание
неравновесных явлений с использованием квазиуровней Ферми и, во-вторых, коэффициент
Эйнштейна Bvc на этот раз выражается в единицах Дж см (мы предлагаем читателю
в качестве самостоятельного упражнения проверить размерность величины Bvc в G.31)).
Аналогичным образом скорость стимулированного излучения дается соотношением:
gjk) = BJJEc)[l - fv(E)]pJhv) G.32)
К этому, естественно, мы должны добавить скорость спонтанного излучения gj*0" (см),
которая не зависит от плотности фотонов в полупроводнике и дается выражением:
£;-(к) = AJc(E)[\ -ДЕ)] G.33)
Глава 7. Оптические свойства полупроводников
Acv есть скорость спонтанного перехода в объеме V. Для начала рассмотрим случай
термодинамического равновесия. Плотность фотонов на единицу энергии в объеме
К дается спектром излучения черного тела в Дж с-1м~3 (уравнение B.91)), который
следует разделить на hv с тем, чтобы выразить этот параметр в виде плотности
числа частиц), а не в виде плотности энергии) и вновь — на h с тем, чтобы
выразить этот параметр в единицах энергии, а не частоты:
Подобным же образом в равновесии распределения Ферми—Дирака идентичны для
двух зон (fc =fv =f и Efc = EFv = Ef).
Стационарное условие для состояния термодинамического равновесия может быть
записано таким же образом, как и в случае (З.В.4):
BJ{E^~ ПЕСЬЛЕК)- В„/{ЕЛ\- f{Ev)\yfh{EKh ACJ{EC\\- f{Ev)] G.35а)
или иначе:
*»<Е?У = 6а G.356)
\] B,rtxp(E,,./kT)-B,,.
Это может быть справедливым при любых температурах только в том случае, когда
коэффициенты Эйнштейна Bcv, Вж и Ап связаны соотношением:
ВК=В„ G.36а)
Acr = *<E)V В„ G.366)
Эти уравнения аналогичны C.77) и C.78) за исключением того, что Всуи Вп вьфажены
не в тех же единицах. Здесь хотелось бы подчеркнуть концепцию, лежащую в основе
подхода Эйнштейна, а именно: хотя соотношения между коэффициентами А и i?
устанавливаются для термодинамического равновесия, они, будучи собственными характеристиками
системы, остаются справедливыми во всех случаях, включая даже сильное отклонение от
термодинамического равновесия.
Теперь мы можем заменить В^ в G.36) на выражение, приведенное для этого
параметра в G.31), что позволяет найти:
А„ = — G.37я)
где rR есть излучательное время жизни, определяемое выражением:
1 q x^i
rR ксъ
%Pa>?c a no^gEP
he0 ЪпсъП2£^тв
G.376)
Излучательное время жизни
в полупроводнике
Отметим, что в излучательном времени жизни как в полупроводниках, так и
атомах проявляется та же тенденция. Чем больше величина запрещенной зоны, тем
короче становится излучательное время жизни и тем тяжелее становится добиться
инверсии заселенности в такой системе. Такой характер проявляется, например,
при переходе от полупроводников с шириной запрещенной зоны, соответствующей
инфракрасному излучению (например GaAs), к широкозонным полупроводникам
(например GaN).
Теперь мы можем пойти вперед и рассчитать скорость поглощения rabs(k)(c)
для произвольного волнового вектора к, обусловленного конкуренцией переходов
с —> v и v —> с.
7.4. Поглощение и спонтанное излучение
-fJE)]Peh(hv) ~ BcJc{E)[\ - fSE)]pph(hv) G.38)
или:
г.Jk) = i?J/v(£) -/c(£)]pph(* v) G.39)
где Ev и /£, есть состояния, связанные через энергию фотона hv и приведенные в
G.18)" и G*25).
Теперь рассмотрим принципиально другую ситуацию. Найдем поглощение
монохроматической волны с частотой ц падающей на кристалл (т. е. в данном случае
pph есть дельта-функция Дирака S(E — hv) — в резонаторе объемом К имеется
единственный фотон). Поглощение в объеме К обусловлено переходами по всей зоне
Бриллюэна и (смотрите G.15)) определяется выражением:
J = |pc/-abs(k)d3k
G.40)
С учетом требования по сохранению энергии G.18) и преобразования переменных в
G.19) это приводит к скорости поглощения в виде:
\ ] G.41)
(Заметьте: объемный член V будет устранен членом 1/Кв В^ что является наградой за
квазиквантование.)
Коэффициент поглощения a(h v) получается из анализа эксперимента,
иллюстрируемого рисунком 7.3. В рассматриваемом случае фотон с энергией fi впадает на
полупроводниковую пластину с поверхностью Sn толщиной Az. Энергия, поглощаемая в течение
времени At составляет RabshcoAt (при объеме К= SAz), а энергия, пересекающая
поверхность есть hcoc/nopAt. Отношение этих двух величин есть просто a(hv)Az и
оно может быть записано в виде:
/ ч _
мощность, поглощенная в единице объема _ R^Jico
мощность, падающая на единицу поверхности ticoc / по
Или иначе с учетом G.41) и G.31):
)- fc(hv)]
G.42)
G.43)
Это выражение в точности соответствует уравнению G.22), полученному при
использовании формализма матрицы плотности, если вспомнить, что плотности на
единицу частоты и энергии связаны друг с другом соотношением pfjtv) = Pj(co)/h.
Понятно, что мы предприняли эти усилия не только для того, чтобы
подтвердить соответствие формализма матрицы плотности и скоростных уравнений Эйн-
VWWWV
Az
Рис. 7.3. Экспериментальная геометрия для
определения коэффициента поглощения.
Глава 7. Оптические свойства полупроводников
штейна. Используя такой подход мы дополнительно получили в наше
распоряжение средство для расчета скорости спонтанной эмиссии Rspon(hv) из-за
распределения носителей в условиях термодинамического квазиравновесия в
полупроводнике. Эта скорость определяется суммированием G.33) по зоне Бриллюэна:
Язроп (*v)= 2£ rspon(k) = 2]£ —!—/c(k)[l - fv(k)]S(Ee - Ev = hv) G.44)
k k TR(k)
При этом суммирование проводится по всем волновым векторам к, удовлетворяющим
условию сохранения энергии (выражаемому дельта-функцией Дирака S), а именно:
Используя эквивалентность G.15) и G19), находим:
Л5Ро„ (hv) = J/-spon (£)Pj(E)8(E = hv)lE = /-spon (hv)Pj(hv) G.46)
0
откуда получаем:
*spon (*O= —Pj(hv)fc[Ec(hv)}{\ ~ fv[EvQ>v)]} G.47)
Спектральное распределение скорости излучатель-
ной рекомбинации в полупроводнике (с~1 см~3 Дж)
В этой формуле мы узнаем выражение типа n/rR, полученное для атомов (смотрите
главу 4). С использованием G.376) это выражение может быть записано в
следующем виде:
G-48)
Деля выражение G.48) на формулу для поглощения G.43), получаем соотношение
между поглощением и спонтанной эмиссией, которое остается справедливым для всех
термодинамически квазиравновесных ситуаций:
Kpon("v)= cc{hv) hv/kT G.49)
he e -1
Уравнение Ван Рузбрека—Шокли
Уравнение G.49) позволяет рассчитать спектр спонтанного излучения Rspon{hv),
исходя из спектра поглощения, и оно представляет собой ничто иное, как
состояние микроравновесия для фотона с энергией hv между спонтанной эмиссией и
поглощением, обусловленных спектром черного тела.
Попробуем теперь определить спектральное распределение Rspon(hv) спонтанного
излучения полупроводника вблизи термодинамического равновесия. Функции
Ферми—Дирака в G.41) могут быть аппроксимированы функциями Больцмана:
1-/,(£,)-ехр -
кТ
G.50)
EF - Ev
кТ
Следовательно:
f| G.51)
7.5. Коэффициент бимолекулярной рекомбинации
где AEf есть зазор между квазиуровнями Ферми AEf = Efc - EFv. Таким образом, мы
приходим к спектральному распределению R (hv):
G.52а)
К1
Спектральное распределение скорости
спонтанной эмиссии (с~1 см~3 Дж~1)
При этом константа Kspon с учетом G.47) дается выражением:
к*°п -~^ЧГ р\ кт
G.526)
Рисунок 7.4 иллюстрирует зависимость скорости спонтанной эмиссии от
энергии излучаемых фотонов. Отметим, что вся мощность излучения распределена в
пределах интервала от 0 до 1,8£Гвыше порога поглощения.
Рис. 7.4. Спектральное распределение скорости спонтанной эмиссии. Полуширина
спектра составляет величину порядка 2кТ.
Уравнение G.526) показывает, что мощность оптического излучения возрастает
как exp (AjE1^), т. е. она возрастает тем больше, чем сильнее выводится
полупроводник из состояния термодинамического равновесия.
Пример
Рассчитаем коэффициент поглощения а(Е) и скорость спонтанной эмиссии гЛдля
GaAs:
mv = 0,46aw,
mc = 0,067/т^
xvc = 3,2 A
"OP= 3,6
В соответствии с G.25л) коэффициент поглощения составляет:
При этом
G.53)
А аЬс =
Глава 7. Оптические свойства полупроводников
Таким образом,
К^ = A, 6 х 109 КлM/2 х 3,2 х 10~10 мJ х B х 0,058 х 0,9 х Ю'30K'2/
/ @,8 х 10 м х 8,85 х 102 Ф м'1 х A,05 х 104K х 3,6)
или КлЫ = 12 000 см эВ-'/2.
Таким образом, для фотона с энергией, превышающей ширину запрещенной
зоны на 0,01 эВ, коэффициент поглощения составляет 1200 см.
В этом случае излучательное время жизни составляет:
G.54)
tR ЛС'ПН£О
Таким образом:
\/rR = A,5 ВK х A,6 x 109 КлM х C,2 x 100 мJ х 3,6/
/ C,14 x C x 108 м cK x A,05 x 104 Дж сL x 8,85 x 102 Ф м)
или rR — 0,7 не.
Обратите внимание на то, что хх не является величиной, полученной из теории Кейна (табл.
7.1). Эта величина была выбрана подбором исходя из наилучшего соответствия с
экспериментальными данными по поглощению. Это же лишний раз вскрывает тот факт, что двухзонная
модель параболических зон Кейна является упрощенной, поскольку она не учитывает непа-
раболичность зон, анизотропию валентных подзон и т. д.
7.5. Коэффициент бимолекулярной рекомбинации
Уравнение G.44), которое было описано в последнем разделе, выражает
распределение скорости переходов (см с Дж) в функции энергии фотонов для двух
неравновесных распределений носителей с использованием соответствующих
квазиуровней Ферми. Теперь найдем полную скорость рекомбинации для фотонов всех
энергий, т. е. используем интегрирование распределения G.44) по hv\
где произведение двух распределений Ферми—Дирака дается G.51) или:
jEF-EF)/kT "r
^U(*)
G.55)
G.56)
Теперь используем выражение для комбинированной плотности состояний G.19tf)
и получим:
(е, -Eh )/kT , /л Л3/2 ~
Т« 2Ж'[П' ] ' G 57)
Это уравнение может быть сильно упрощено с учетом того, что в приведенном
выше уравнении G.57) мы узнаем эффективную плотность состояний,
приведенную в E.42) и E.43):
7.5. Коэффициент бимолекулярной рекомбинации
где мы заменили эффективную массу в зоне проводимости на приведенную
эффективную массу тг, при этом:
/jspon =J_jv.e (*..-*-.-Омг G59)
* R
С учетом выражений E.42)—E.45) для эффективной плотности состояний в двух
зонах, а также концентрации носителей в функции энергии Ферми, уравнение G.59)
принимает вид:
R = J— np
РОП тл NCNV
Ъчо последнее уравнение лучше известно в виде:
Дзроп = Впр
G.60)
3/2
G.61)
G.62)
В-1 NJ - » К
г„ NeNr TRNc{mv)
Скорость излучательной рекомбинации
(см~3 с) и коэффициент излучательной
бимолекулярной рекомбинации (см с~1)
где В есть коэффициент бимолекулярной рекомбинации. В таблице 7.2
представлены экспериментально определенные значения коэффициента В для ряда наиболее
важных полупроводниковых соединений III—V.
Табл. 7.2. Коэффициенты бимолекулярной рекомбинации для различных прямозон-
ных полупроводников (по данным V.P. Varshni, Phys. Stat. Sol. 19, 459 A967))
Материал
GaAs
GaSb
InP
InAs
InSb
В (см3 с1)
7,2 х Ю-10
2,4 х Ю0
1,3 х 10"9
8,5 х 10"»
4,6 х 101
Пример
Для GaAs эффективная плотность состояний в зоне проводимости составляет TV = 4,3 х 1017 см 3
(раздел 5.6.1) и излучательное время жизни rR равно 7 х 10~10 с. Приведенная масса есть
1/A/0,067) + A/0,50) = 0,059. Коэффициент бимолекулярной рекомбинации В в этом
случае составляет 1/G х Ю0 с х 4,3 х 1017 см) х @,059/0,50K/2 или 1,34 х Ю'10 см3 с,
что достаточно близко к экспериментальной величине ~10~10 см3 с.
В более общем случае коэффициент бимолекулярной рекомбинации может быть
рассчитан с использованием выражения для Nc в G.62) и выражений для
эффективных масс тги mv, приведенных в E.В. 19) и E.В.27) в рамках теории Кейна.
Принимая энергию Кейна постоянной в соединениях III—V и равной -20 эВ мы, таким
образом, можем вывести величину коэффициента В в функции ширины
запрещенной зоны соединений III—V. На рис. 7.5 приведено сравнение результатов этой
простой теории с экспериментальными данными, приведенными в табл. 7.2.
f( 266 Глава 7. Оптические свойства полупроводников
Рис. 7.5. Коэффициенты бимолеклярной рекомбинации для различных
полупроводников III—V. Сплошная линия представляет собой обобщенную зависимость,
полученную с использованием G.62) в предположении о том, что энергия
Кейна постоянна и составляет 20 эВ для всех полупроводников. Точки на
рисунке соответствуют экспериментально полученным данным.
Мы можем сделать заключение о том, что соответствие в данном случае вполне
удовлетворительно. Таким образом, данная теория обладает достаточным
потенциалом для прогнозирования и может быть еще более улучшена за счет учета
дополнительных вкладов от спин-орбитально отщепленной зоны и т. д.
Выражение G.61) представляет собой закон действующих масс, электроны и дырки
рекомбинируют индивидуально друг с другом, при этом скорость рекомбинации
определенного типа носителей, очевидно, пропорциональна концентрации носителей другого
типа. Предположим, что обычно встречающаяся ситуация состоит в слабом смещении
системы из состояния равновесия. В этом случае равновесные концентрации носителей л0
и р0 связаны друг с другом законом действующих масс nj>0 = я.2, где п. есть собственная
концентрация носителей E.49). В этом случае неравновесные концентрации носителей
определяются соотношениями:
п = п0 + An
р=ро
G.63)
где предполагается, что An и Ар малы по сравнению с концентрацией основных
носителей, при этом (для обеспечения нейтральности заряда) An = Ар. В этом
случае дополнительная скорость рекомбинации составляет:
= В(пр -
В(п0 + ро)Ап
G.64)
При этом скорость излучательной рекомбинации неравновесных носителей равна:
G.65)
Arad ~ .
1
1
BN
dop
Время излучательной рекомбинации
в полупроводнике
где Ndop есть уровень легирования полупроводника. Время излучательной
рекомбинации может быть также записано в виде:
3/2
G.66)
7.6. Условия оптического усиления в полупроводниках
Таким образом, время излучательной рекомбинации tnd достаточно близко к
спонтанному времени жизни тю т. е составляет величину порядка наносекунд. К
сожалению, эти два понятия часто путают.
Пример
Для кристалла GaAs, легированного до концентрации 1017 см, эффективная
плотность состояний в зоне проводимости составляет TV. = 4,3 х 1017 см
(раздел 5.6.1), время спонтанной эмиссии rR равно 7 х 100 с и приведенная
эффективная масса равна 1/A/0,067) + A/0,50) = 0,059. В этом случае излучательное
время жизни составляет:
/rad = 7 х 100 с х D,3 х 1017 см-3/1017 см) х @,5/0,059K/2 или tnd = 5 не
7.6. Условия оптического усиления в полупроводниках
Анализ, проведенный в разделе 7.3 показал, что полупроводник, выведенный из
состояния термодинамического равновесия, может обеспечить условия
оптического усиления фотонов с энергией, удовлетворяющей условию Бернара—Дюррафура
G.266). Таким образом, представляется важным раскрыть особенности
эксперимента, обеспечивающие реализацию этого условия.
Предположим, что в неравновесных условиях вводится значительное число
носителей (Ал и Ар) Так, что положение квазиуровней Ферми дается соотношениями:
G.67)
UTF
Kl t[/2
где Fl/: есть функция, обратная интегральной функции Ферми—Дирака порядка 1/2,
определяемой (смотрите раздел 5.6) как:
°г V1/2
Предположим, что полупроводник слегка легирован и что п = р » п0 и р0. В
этом случае материал более не будет поглощать фотоны с энергией hv — Eg в том
случае, когда неравновесная концентрация носителей wtrans будет удовлетворять
следующему условию прозрачности (смотрите G.626)):
G.69)
Условие прозрачности
для полупроводника
Рисунок 7.6 демонстрирует разность EFc — EFv в функции неравновесной
концентрации носителей п. Концентрация прозрачности достигается, когда EFc — EFv = Eg, что
эквивалентно условию прозрачности G.69)
Пример
Программа MATHEMATICA, приведенная ниже, дает пример поведения
квазиуровней Ферми в GaAs в функции неравновесной концентрации носителей.
Условие прозрачности реализуется при nttans = 1,2 х 1018 см.
W268 Глава 7. Оптические свойства полупроводников
Рис. 7.6. Зависимость
энергетического зазора между
квазиуровнями Ферми от неравновесной
концентрации носителей
заряда GaAs. Порог прозрачности
удовлетворяет условию Берна-
pa—Дюррафура для hv = Eg.
-150
0.0 0.5 1.0 1.5
концентрация носителей (х 1018см~3)
Gamm32=Sqrt[N[Pi]]/2
F[x_, u_]=Sqrt[x]/( 1 +Exp[x-u])
Tifermi=Table[{Ninegrate[f[x,u],{x,0,lnfJnJty}]/gamm32,u},{u,-5,5,0.2}]
lfermi=lnterpolation[tifermi]
Nc=4.7*107(*in cm-3*)
Nv=7 10~18(*in cm-3*)
Efc[nJ=ifermi[n/Nc]
Etv[pj=jfermj[p/Nv]
deltaef[xj=25.9*(efc[x]+efv[x])
Plot[deltaef[x],{x,10-16,2~18}]
Выше порога прозрачности среда начинает усиливать те фотоны, которые обладают
энергией, удовлетворяющей условию Бернара—Дюррафура. В этом случае спектр
усиления дается соотношением:
y(hv)= Kabs(hv - Eg)[/2\fc(hv)- fv(hv)] G.70)
где Kabs дается G.526), а функции Ферми—Дирака fc(hv) nfv(hv) определяют
заселенность тех уровней в зоне проводимости и валентной зоне, которые
удовлетворяют условию Ес — Ev = hv и которые даются соотношениями G.25а) и G.256).
Рисунок 7.7. показывает, каким образом кривая усиления изменяется в функции
неравновесной концентрации носителей в GaAs. Чем больше превышение
концентрации носителей порога прозрачности, тем шире становится кривая усиления.
Рисунок 7.8 показывает, каким образом максимальное усиление изменяется в
функции неравновесной концентрации носителей. После достижения прозрачности
максимальное усиление увеличивается линейно с возрастанием плотности заряда
над порогом. Это чисто феноменологическое соотношение очень полезно при
моделировании полупроводниковых лазеров (смотрите главу 13).
Пример —
Ниже приведена программа MATEMATICA, описывающая поведение усиления в
неравновесном полупроводнике. Рекомендуем читателю потренироваться в
использовании этой программы с применением численных постоянных для различных
полупроводников, приведенных в таблице приложения (стр. 588).
Gamm32=Sqrt[N[Pi]]/2;
F[x_,uJ=Sqrt[x]/A+Exp{x-u]);
tifermJ^abletiNJntegratefffx.ul^x.OJnfinity}]^!!! m32,u} ,11,-5,5,0.2}]
ifermi =Table[{Nintegrate[f[x,u],{x,0,lnfinity}]gamm32,u},{u,-5,5,0.2}]
ifermi=lnterpolation[tifermi];
7.6. Условия оптического усиления в полупроводниках
Рис. 7.7. Изменение кривой
усиления в GaAs в функции
концентрации
электронно-дырочных пар. При концентрации
выше 1,2 х 1018 см среда
обеспечивает оптическое усиление
в области энергий фотонов,
удовлетворяющих условию
Бернара—Д юррафура.
400
300
I
хЮ18ст
300 -
200 -
100 -
1.58
п(хЮ18см 3)
Рис. 7.8. Изменение максимума кривой
усиления в GaAs в функции
концентрации электронно-дырочных пар.
kb=8.63 10" -5;Т=300;
Nc=4.7* 10" 17 (*in cm-3);Nv=7. 10" 18 (*in cm-3*);
Eg=1.5;mc=0.067;mv=0.46;Kabs=12000;
mr=1/A/mc+1/mv);
n=1.2 10" 18;
nc=n/Nc;efc=25.9 10"-3*ifermi[nc]
nv=n/Nv;efv=25.9 10" -3*ifermi[nc]
nv=n/Nv;efv=25.9 10" -3*ifermi[nv]
Ec=mr/mc*(hnu-Eg);
Ev=mr/mv*(hnu-Eg);
fc=1/(Exp[Ec-efc)/kb*T)]+1);
fv=1/(exp[Ev+efv)/kb*T)]+1);
gain-Kabs*(hnu-Eg)A/2)*(fc-fv);
plot12=Plot[gain,{hnu,1.5>1.6}]
Литература
A. Kireev, Physique des Semiconducteurs, MIR, Moscow A975).
J.I. Pankove, Optical Processes in Semiconductors, Dover Publications, New York A971).
B.K. Ridley, Quantum Proccesses in Semiconductors, Clarendon Press, Oxford A988).
B. Sapoval and C. Hermann, Physic of Semiconductors, Springer, Berlin A985).
K. Seeger, Semiconductor Physics, 3-rd Edn, Springer, Berlin A985).
P. Yu and M. Cardona, Fundamentals of Semiconductors, Springer, Berlin A995).
ДОПОЛНЕНИЯ
К ГЛАВЕ 7
7.А. Модуляторы электропоглощения
на эффекте Франца—Келдыша
Когда мы прикладываем к полупроводнику статическое электрическое поле, бло-
ховские волновые функции уже не представляют стационарные состояния
кристалла, т. к. потенциал более не обладает периодичностью межатомного расстояния.
Соответствующее изменение в волновых функциях оказывает существенное
влияние на оптическое поглощение. В данном случае полупроводник может поглощать
фотоны с энергией h со, меньшей ширины запрещенной зоны Eg. Более того, выше
запрещенной зоны спектр проявляет осцилляции, накладывающиеся на обычный
характер зависимости (hco— Eg)l/2, реализующийся в условиях F= 0. Это и есть т. н.
эффект Франца—Келдыша. Как мы увидим позже это явление эффективно
используется в электромодуляторах. Начнем с того, что представим формализм,
позволяющий описать этот эффект.
Произвольно предположим, что электрическое поле ориентировано в направлении ь
В этом случае уравнение Шредингера приобретает вид:
f— + Vc(T)-eFz\r{T) =
0 J
мы можем разложить волновую функцию у/ в базисе блоховских функций \пк) = ип k(r)eikr
(решения уравнения в отсутствие электрического поля) в виде:
4k(r) G.A.2)
Спроецируем результирующее уравнение на базис функций |А/К>, что дает:
eN(k)aN(k)-eF^(NK\ z \nk)an(k) = EaN{k) G.A.3)
«k
Второй член в последнем уравнении, обусловленный полем, может быть
преобразован следующим образом:
j "iKr *
и
_Y f_dk f- "iKr * - ikr — iSfl/1-4 GA*4)
-Jdr,iKrw;
Последний член в этом выражении исключается, т. к. интеграл по kz является
периодической функцией по kz с периодом 2n/az, где az есть постоянная элементарной ячейки. С
учетом периодичности unk(r) по г и ортогональности базиса другие члены имеют вид:
7.А. Модуляторы электропоглощения на эффекте Франца—Келдыша 271
1а„(к)Дк
G.А.5)
При этом:
В этом случае уравнение Шредингера с коэффициентами ajk) приобретает вид:
- \eF
К) G.A.6)
Уравнение Шредингера для кристалла
в присутствие электрического поля
Последнее уравнение возникает во всех случаях, связанных с наложением
электростатического поля на кристаллический потенциал, как это имеет место в
эффекте туннелирования через запрещенную зону (эффект Зенера).
С использованием подхода теории возмущений найдем решение, близкое к £^@);
сначала мы можем пренебречь влиянием членов, обусловленных зонами cn*N(B этом случае
зоны являются несвязанными). Член zNfP остающийся в сумме, может быть перенесен
направо. В то же время не будем пренебрегать им и будем надеяться на то, что aN(K) будет
играть важную роль только при К = 0 и ZN/Jfi) = 0 для экстремума зоны N.
При Е= eJiO) решение G.А.6) имеет вид:
а„(К) = а„(К,, К,) = а„(Кц, 0)ехр — f [E -eN(K')]dK'z =
[eF {
= aN(Kv 0)exp
eF
Kz
G.A.7)
Мы ввели эффективную массу тмддя TV-ной зоны и Kj = (Кх, К^. В действительности,
сделанные аппроксимации являются теми аппроксимациями подхода эффективной массы, которые
мы более детально изучим в Главе 8. Теперь мы уже может рассчитать следующую функцию:
Es.aJKr)tKl G.A.8)
Она представляет собой ничто иное, как огибающую функцию, описывающую
изменение волновой функции стационарного состояния в направлении электрического
поля. С этой целью используем следующую формулу (смотрите уравнение A0.4.32) Аб-
ромовича и Стегуна):
>s(^3 + xt)dt G.A.9)
Таким образом мы получаем следующее выражение для огибающей функции:
ip 0)АЛ\
2mN
h2e2f2
i/з
~eFz\
G.А.10)
Огибающая функция
для электрона в зоне N
Дополнения к главе 7
Рис. 7.А.1. Функция Эйри.
-0.6
-10
В представленном выражении Ai(^) есть функция Эйри, которая по определению
есть решение уравнения:
d2Ai
dz
Эта функция стремится к нулю, когда z
вид этой функции. В действительности:
л/ \ 1
2 -zM(z) = 0 G.A.11)
=>. Рисунок 7.А. 1 иллюстрирует общий
.3/2
При z < 0 функция осциллирует с уменьшающимся периодом:
1
-йп|-|*+Т
G.А.12)
G.А.13)
С первого взгляда решение G.А. 10) может показаться несколько сложным. Однако
мы увидим, что поведение функции легко может быть понято. Сначала мы отметим,
что аргумент функции Эйри в G.А. 10) равен 0 для zo = (Е — е^О) — h2JC2/2rnN)/eF. При
Z < Zq функция уменьшается экспоненциально. Рис. 7.А.2 показывает, что этот
эффект аналогичен туннельному эффекту, когда волновая функция проникает в
запрещенную зону полупроводника. При z > Zo функция осциллирует все более и более
быстро, что соответствует увеличению кинетической энергии (смотрите рис. 7.1).
Более того, решения для других энергий — те же самые за исключением того, что
они являются транслированными на Az0 = AE/eF. Одним из следствий этого
свойства является то, что нормировочная константа aN@) не зависит от К, или Е.
Рис. 7.А.2. В присутствии
электрического поля волновые
функции С электронов и дырок
перекрываются даже в том случае, если
они разделены по энергии на
интервал, меньший размера
запрещенной зоны Eg. Это
обеспечивает возможность оптического
поглощения фотонов с энергией,
меньшей ширины запрещенной
зоны.
ф
hv
7.А. Модуляторы электропоглощения на эффекте Франца—Келдыша 21Г3
Теперь мы можем описать квантовые эффекты, связанные с поглощением,
имеющие место в полупроводниках в условиях приложенного электрического поля.
Рисунок 7.А.2 показывает две электронные волновые функции в валентной зоне.
Решения для дырок в валентной зоне эквивалентны решениям для электронов: нам
нужно лишь заменить те на — mh, где mh есть (положительная) масса дырок. Как
следствие этого направление движения частиц в поле изменяется. Мы видим
также, как электроны (и дырки) могут перемещаться через запрещенную зону за счет
туннелирования. Вероятность проявления этого (зенеровского) эффекта связана с
интегралом перекрытия между экспоненциальной волновой функцией и
обращенной к ней валентной зоной.
Аналогичным образом мы можем догадаться, что можно перевести электрон из
валентной зоны в зону проводимости за счет поглощения фотона, даже если его
энергия h со меньше £\ Для этого необходимо лишь, чтобы две волновые функции
имели ненулевое перекрытие. При фиксированной величине hco это перекрытие
уменьшается экспоненциально по мере того, как F —> 0.
Говоря более точно, скорость перехода между состоянием |Кц, Е{) в валентной
зоне и состоянием |Кц, Е2) в зоне проводимости дается золотым правилом Ферми:
S(\ -> 2) = ^-|B|еЕ. • r|l)|2 S(E2 -Ex- hco) G.A.14)
Если мы подставим в это последнее выражение волновую функцию,
полученную в G.А. 10), мы найдем аналогично G.10) оптический матричный элемент:
<(КгК(Кг) G.А.15)
К.
В этом выражении частью, которая изменяется по отношению к случаю с F= 0, является
сумма:
G.А.16)
где тг — приведенная масса. Из соотношения G.А.9) мы вновь получаем функцию Эйри:
^wr I i Г7 гу г? п Лп I G.A.17)
Существенным моментом является то, что Iz отличается от 0, когда Е2~ Ех —hco
меньше, чем Е. Именно этот член ответственен за эффект Франца—Келдыша. Для
расчета полной скорости перехода на заданной частоте нам необходимо
просуммировать по всем начальным состояниям, т. е. по всем Кц и Е19 при этом энергия
конечного состояния Е2 составляет Ех + h со. Для этого мы временно опустим
константы и вновь подставим их позже при стыковке полученных результатов с
формулой при F= 0. Вводя характеристическую энергию Франца—Келдыша:
G. А. 18а)
К" е л )
а также безразмерную переменную:
S=hCU~pEs G.A.186)
получаем для суммы по К..:
Р
> -г
Дополнения к главе 7
Последний интеграл можно проверить, беря его производную и используя
уравнение для определения Ad(z): Ai"(z) = zAi(z).
При F —> 0 поглощение в функции h со должно согласовываться с ранее
полученным результатом (уравнение G.24)):
a(hco, F = 0)=abJhco- Eg
GА19)
При /" -> 0 и hco < Eg9 £—> -oo G.A.18) стремится к нулю, как этот и должно
быть. При Z1—> 0, hco >Eg, £-> ©о мы должны использовать асимптотическую форму
(уравнение G.А.13), что приводит к:
к
G.А.20)
Приведенная зависимость имеет такой же характер, как и G.А. 19). Сравнение G.А. 19) и
G.А.20) определяет, таким образом, окончательный результат:
")= аьр1/2п[К\'2(- £)+ £Ai2(- £)] G.А.21)
Поглощение в присутствии
электрического поля
Рисунок 7.А.З иллюстрирует особенности поглощения в полупроводнике в
условиях приложенного электрического поля.
Для фотонов с энергией меньше ширины запрещенной зоны наблюдается
ненулевой коэффициент поглощения, в то время, как при hco> Eg наблюдаются
осцилляции поглощения в функции энергии фотонов.
10°
10"
10"'
i-з
10"
10"
10"
10"
/-
/
/
■ / ■
3.5
3.0
еГ 2.5
^2.0
^ 1.5
1.0
0.5
ПО
-4 -2 0
-4 -2 0
8 10
Ч 5
Рис. 7.А.З. Поглощение в условиях электрического поля в функции энергетического
интервала между энергией фотонов и шириной запрещенной зоны £ = (hco- E^/ft
где /?= (h2e2F2/2mr)l/2. Характеристика для области энергий меньше
ширины запрещенной зоны (левый рисунок) представлена в
логарифмическом масштабе.
Пример
Для приложенного электрического поля с напряженностью F = 10 кВ/см и
mr = memh(me + mh)= 0,059m0 (в случае GaAs) мы получаем характеристическую
энергию Франца—Келдыша величиной:
Р =
2тг
(l,05xl0-34J(l06J
2х 0,059 х9,1 х 10-3| х 1,6 х 10
эВ = 8,6 мэВ
7.А. Модуляторы электропоглощения на эффекте Франца—Келдыша
В этом случае поглощение при h со — Eg — —8,6 мэВ составляет (смотрите рис. 7.А.З)
J[— 1) = 0,022 или 2,2% от той величины, которая была бы при hco — Eg = +8,6 мэВ в
отсутствии приложенного поля.
Этот эффект используется в модуляторах на эффекте Франца — Келдыша.
Основной принцип их функционирования достаточно прост (смотрите рис. 7.А.4). На
полупроводниковый волновод (с шириной запрещенной зоны Eg) наносится
металлический электрод для формирования барьера Шоттки с полупроводником (см. главу 10).
При приложении разности потенциалов V между этим верхним электродом и
омическим контактом с тыльной стороны полупроводника мы вводим электрическое
поле напряженностью F= V/d, где d — расстояние между верхним и нижним
контактами (для минимизации какого-либо падения напряжения из-за эффектов
пространственного заряда уровень легирования полупроводника выбирается достаточно
низким). Приложение разности потенциалов величиной 5 В к межконтактному зазору
величиной 1 мкм приводит к напряженности электрического поля 50 кВ/см, что
соответствует характеристической энергии /? = 25 мэВ. В результате этого фотоны,
распространяющиеся в волноводе с энергией Eg — 25 мэВ будут испытывать
поглощение, в 100 раз большее по сравнению со случаем отсутствия поля. Из этого легко
видно, каким образом мы могли бы использовать такой прибор для преобразования
электрического (изменяющегося во времени) сигнала в оптический сигнал.
Такие приборы называются модуляторами электропоглощения на эффекте
Франца—Келдыша. Модуляторы этого типа являются чрезвычайно быстродействующими
(с максимальной рабочей частотой, лежащей в диапазоне десятков ГГц), так как
для своего функционирования они не требуют пространственного смещения
электрических зарядов. Что не имеет места, например, в случае SEED-модуляторов
(приборов на основе собственного электрооптического эффекта, смотрите дополнение 8.В).
a v=ov
v
Out
\/=5V
t
hv
свет
a
n_n_
ВЫХОД
t
Рис. 7Л.4. Функционирование электрооптического модулятора на эффекте Франца-
Келдыша.
Литература
М. Abramovich and I.A.Stegin, Handbook of Mathematical Functions, New York<
Dover A970).
H. Haug and S.W. Koch, Theory of the Optical and Electronic Properties of Semiconductors,
Singapore, World Scientific A993).
J.I. Pankove, Optical Processes in Semiconductors, Dover Publications, New York A971).
Дополнения к главе 7
7.Б. Коэффициент оптического преломления
полупроводников
Как оказывается, знание коэффициента оптического преломления
полупроводников имеет фундаментальное значение для реализации оптоэлектронных приборов.
В то же время эта тема оказывается достаточно сложной, поскольку используемые
модели существенно различаются в зависимости от рассматриваемой длины волны.
В частности, в этом смысле мы различаем два спектральных диапазона.
7.Б.1. Средний и дальний ИК-диапазоны
Взаимодействие между полупроводником и электромагнитной волной в среднем и
дальнем инфракрасном диапазонах вводит в действие оптические фононы материала
(смотрите Дополнение 6. Б). Режим дальнего ИК-диапазона называется областью остаточных
лучей, где среда становится чрезвычайно поглощающей и дисперсионной. Например, для
GaAs этот диапазон располагается в области 30 мкм.
В этом спектральном диапазоне поглощение и коэффициент оптического
преломления хорошо описываются моделью гармонических осцилляторов с собственными
частотами, равными частотам поперечных оптических фононов (vTO). Эта модель использует
четыре параметра: статическую диэлектрическую постоянную 8s диэлектрическую
постоянную при бесконечно большой частоте £те, резонансную частоту vT0 и коэффициент
затухания у. Простое расширение модели Лоренца дает в этом случае выражение для
диэлектрической постоянной в виде:
1 2 V ор ор / °°\0 оо/ \ • • /
В GaAs энергия оптических фононов составляет h vTO = 33,25 мэВ, а соответствующие
диэлектрические постоянные равны 8ж = 10,88 и ss - ет =1,97, а коэффициент затухания
есть у~ vTO/133. Вдали от резонанса (для энергий фотонов более 33 мэВ) выражение G.Б.1)
может быть упрощено, что дает:
]1/2
Уравнение Зеллмайера
В таблице 7.Б.1 приведены различные параметры, необходимые для
проведения этих расчетов применительно к системе GaAs/AlGaAs.
Табл. 7.Б.1. Диэлектрические постоянные и энергии поперечных оптических фононов
в функции состава твердых растворов Alx Gat _x As
Статическая диэлектрическая постоянная, es
Высокочастотная диэлектрическая
постоянная, £х
Энергия оптических фононов, h vTO
13,18—3,12х
10,89-2,73 х
33,29-0,64*-!, 16 х2
В действительности существует целый ряд феноменологических поправок к
формуле Зелмайера, при этом наиболее точная формула для A^Ga^^As (при hv в
единицах эВ) имеет вид:
7.Б. Коэффициент оптического преломления полупроводников 277
7,10 +
3,78
1,97
\-0,\S0(hvJ [C0,08/*v)f-l]
- 0,528 jc
G.Б.26)
Рисунок 7.Б.1 демонстрирует изменение коэффициента оптического
преломления GaAs в диапазоне от 5 до 12 мкм.
I
Ф
a
t—
ф
3.26
7 8 9 10
Длина волны (мкм)
11
12
Рис. 7.Б.1. Коэффициент оптического преломления в средней ИК-области для GaAs,
полученный с использованием расширенного уравнения Зеллмайера.
7.Б.2. Диапазон вблизи края запрещенной зоны
В оптических свойствах материалов в рассматриваемом диапазоне доминирует процессы,
связанные с полосой поглощения полупроводников. Простейшим подходом,
учитывающим этот процесс, является модель Вепля и Дидоменико. Этот подход заключается в
рассмотрении переходов между валентной зоной и зоной проводимости в виде единого ос-
цилляторного перехода с резонансной частотой vw и силой осциллятора nEJI (по
историческим причинам Ed называется энергией дисперсии). В этом случае уравнение Зеллмайера
может быть записано в виде:
= 1 +
G.Б.З)
Это соотношение выполняется удивительно хорошо для целого ряда
полупроводников и изоляторов. Тем не менее согласие между теорией и экспериментом оказывается
недостаточным для оптоэлектронных применений, в которых принципиальную важность
имеет прецизионный контроль оптических параметров. В связи с этим мы обратимся вновь
к более феноменологическому подходу.
Для этого мы вспомним, что действительная е{ и мнимая е2 части диэлектрической
постоянной связаны соотношением Крамерса—Кронига:
G.Б.4)
где PV обозначает «главное значение». Отметим, что интеграл в G.Б.4) показывает,
что хотя поглощение и вводит в действие диапазон энергий, связанных с энергией
фотона, на действительную часть диэлектрической постоянной влияет вся зонная
структура, что делает расчет более сложным. Уравнение G.Б.4) может быть
представлено в виде ограниченного ряда:
й£'
G.Б.5)
278 Дополнения к главе 7
или в другом виде:
где моменты М. даются формулой:
_{ +М_ъЕ2 +М_5Е4 + ...
= -{et(E)E'd£
к J
G.Б.6д)
G.Б.66)
Таким образом, мы ищем выражение для £2(Е), которое представляет собой просто
поглощение в материале. Существуют различные модели, которые страдают
определенной степенью произвольности, так как они включают в себя феноменологические
коррекции кривой поглощения в полупроводниках (как правило, достаточно сложные). Здесь
же мы ограничимся моделью Афромовича, так как она является одной из наиболее
пригодных для прикладных целей.
Эта модель использует аппроксимацию е2(Е) в виде функции:
€2(Е)
_ \tjE , Eg < Е < Ej
О, в других случаях
G.Б.7)
Вскоре мы увидим, как параметры модели связаны с Еео и Ed. Рис. 7. Б.2
демонстрируют, насколько хорошо эта формула описывает GaAs.
Это последнее уравнение показывает, каким образом можно рассчитать моменты М_х
2л
G.Б.8)
Сравнивая G.Б.З) с G.Б.6), мы видим, каким образом параметры rj и ^связаны с
дисперсионной энергией Ed и эффективной энергией осциллятора Есо:
л
2
Ed
- Е]
G.Б.9)
50
20
10
5
2
1
0.5
0.2
n 1
1
-
-
— /*
/у'
е
- (г
i
GaAs.
J
У/
уУ
у^
1.424
1
/^
/ = 36.1 '
ю = 3.65
У
У
1 1
V
-
-
Ef = 4.96
. \!. Г
1.5
5 6
Рис. 7.Б.2. е2 в функции энергии фотонов в GaAs и его аппроксимация соотношением
G.Б.7) (воспроизведенная по Solid State comm. 15, М.А. Afromowitz. Refractive
index of Gaj^Al^As, p. 59 A974), с разрешения Elzevier Science).
7.Б. Коэффициент оптического преломления полупроводников 279
В самом деле, подставляя формулу для е2 G.Б.7) в соотношение Крамерса—
Кронига, мы в конце концов получаем:
G.Б.10)
Соотношение Афромовича
Система уравнений G.Б.8), G.Б.9) и G.Б. 10) позволяет рассчитать
коэффициент преломления различных полупроводников (хорошо согласующиеся с
экспериментальными значениями), как только определены значения Eg, Еео, Ed В таблице
7.Б.2 представлены значения этих параметров для трех трехкомпонентных
соединений: AlGaAs, GaAsP и GalnP.
Табл. 7.Б.2. Эффективная энергия осциллятора £ о, энергия дисперсии Ed и ширина
запрещенной зоны Eg для различных полупроводниковых твердых растворов
* о ОВ)
EdCB)
Eg (эВ)
<Ч_хА1хАз
3,65 + 0,871* + 0,179х2
36,1 -2,45*
1,424+ 1,266л: + 0,26х2
GaAs^P
3,65 +0,721*+ 0,139х2
36,1 +0,35jc
1,441 + 1,091* + 0,2 Ъс2
С*,Ь1§.ХР
3,391 + 0,524* + 0,595*2
28,91 +7,54*
1,34 +0,668*+ 0,758*2
На рис. 7.Б.З. представлены результаты расчета коэффициента оптического
преломления в диапазоне составов твердых растворов AlGaAs.
1.3 1.4 1.5 1.6
Энергия фотона (эВ)
1.7
1.8
Рис. 7.Б.З. Коэффициент оптического поглощения в функции энергии фотонов для
различных значений состава AlGaAs, полученный с использованием
формулы Афромовича G.Б. 10).
Литература
М.А. Afromovitz, Solid State Comm.15, 59 A974).
J.S. Blakemore, /. Appl Phys. 53, R 123 A982).
S.H. Wemple and M. DiDomenico, Phys. Rev. B3,1338 A971).
Дополнения к главе 7
7.В. Поглощение на свободных носителях
Одним из наиболее поразительных аспектов полупроводников является
способность их электронов либо поглощать, либо излучать свет в процессе челночных
переходов между зоной проводимости и валентной зоной, которые обычно
называются межзонными переходами. В то же время существует другой тип оптических
переходов с участием состояний в пределах одной зоны, называемых внутризонны-
ми переходами.
Рассмотрим полупроводник с коэффициентом преломления пор (еоп 2ор = е).
Поглощение, обусловленное свободными носителями учитывается
электропроводностью а. Пусть полупроводник находится под воздействием
электромагнитной волны Е с частотой со, распространяющейся вдоль направления z и падающей
на поверхность при z =0. Эта волна вызывает протекание в объеме
электрического тока с плотностью j = crE. В этой первой части предположим, что
электропроводность не зависит от частоты со. В полупроводнике электромагнитная волна
является решением уравнений Максвелла (смотрите B.1)):
at G.B.1)
dt
где D есть вектор смещения, связанный с электрическим полем Е и поляризацией Р
соотношением:
D = е0Е + Р = е0Е + ео^Е = £Е G.В.2)
Как мы уже видели в главе 2, система уравнений G. В. 1) дополняется уравнением V • В = О,
а также в предположении нейтральности среды — законом Пуассона V • Е = 0. При
использовании G.В.1), G. В.2) и этих двух нулевых дивергенций уравнения
Максвелла приводят к простому волновому уравнению:
Г721? dE d'E (n D i\
V Е = //ост —- + juo€ —- G.В.З)
d> d/~
Дисперсионное соотношение co(k), связывающее волновой вектор и частоту, может
быть получено подстановкой волнового уравнения Е = EQQi(a)t~kz) G.B.3), что дает:
k2 =ju0£OJ-icoju0o GB-4)
Таким образом, мы приходим к двум различным режимам, зависящим от
относительной амплитуды действительной и мнимой частей G.В.4).
Сильная проводимость (а» есо)
В этом случае в G.В.4) доминирует мнимая часть, при этом волновой вектор дается
соотношением:
Мы видим также, что амплитуда волны уменьшается экспоненциально с
коэффициентом поглощения, определяемым двойным корнем квадратным от G.В.5). Величина,
обратная этому коэффициенту, приводит к характеристической длине, называемой глубиной
скин-эффекта S, и она корректно отражает расстояние, на котором волна поглощается
свободными носителями (рис. 7.В.1):
Глубина скин-эффекта
7. В. Поглощение на свободных носителях
ИК
свч
скин слои
кремний
Рис. 7.В.1. Под действием засветки пластина крепления становится сильнопроводя-
щей и экранизирующей СВЧ-волну на глубину скин-слоя. Часть сигнала
поглощается на этой глубине, а другая — отражается.
Пример
Предположим, что мы хотим сконструировать планарный отражатель для радара на
основе кремния (eSi = 13), работающий в т. н. ^-полосе, т. е. в области 10 ГГц
(смотрите рис. 7.В.1). В темновых условиях кремниевый обладает очень большим
удельным сопротивлением (р > 1000 Ом см). В условиях засветки его проводимость
резко возрастает. Неравенство а » есо удовлетворяется, как только удельное
сопротивление рстановится меньше, чем 1/Bл-х 10ю с х 13 х 8,85 х 10~14 Ф см) или
14 Ом см. Такой величины легко добиться за счет засветки. Говоря более точно,
давайте рассмотрим кремниевый слой (с подвижностью ju = 1000 см2 В с,
временем жизни носителей г= 1 мс и толщиной 1 мкм), используемый в качестве
отражающего слоя на частоте 10 ГГц. Во-первых, для того, чтобы отражать радарную
волну эффективно, глубина скин-эффекта должна быть меньше толщины слоя
кремния или а > 1/B х 1,2 х 10~6 Гн м х 2ях х 10 с х 102 м2), т. е. 6,6 х 106 Ом м. Это
удельное сопротивление соответствует концентрации фотогенерированных
носителей п = a/q^i или 4 х 1020 электронов на см. Для этого, в свою очередь, требуется
плотность мощности падающего излучения Р (= ndhv/r) на уровне 6,4 Вт см для
фотонов с энергией 1 эВ.
Слабая проводимость (а« ет)
В этом случае G.В.4) приобретает вид:
^) Щ^) G-в-7)
Мы видим, что волна поглощается (Eoe~KZ) и что ее интенсивность /ослабляется
с константой ослабления a(I0t~2KZ = Ioe~az):
а = ^-а G.В.8)
"op
где Zo есть вакуумный импеданс (Zo = (//0/£:0I/2 = 377 Ом). В действительности, в
последнем выражении мало пользы, так как оно не учитывает динамики
электронов, т. е. оно предполагает, что электропроводность является функцией
мгновенной величины напряженности электрического поля, что, как правило, не имеет
места. В связи с этим мы представим более корректную модель, которая учитывает
время реакции электронного газа и которая называется моделью Друде.
Рассмотрим газ свободных электронов с концентрацией я, состоящий из
электронов с эффективной массой me{f (смотрите главу 5). В главе 6 мы видели, что
Дополнения к главе 7
полная зонная структура материала может быть учтена с использованием понятия
эффективной массы и что динамическое поведение электрона может быть описано
уравнением:
m^v + Hb&L-qEit) G.B.9)
где v есть скорость электрона, а т есть среднее время между столкновениями. Если
приложенное поле постоянно E(t) = Ео, скорость также будет постоянной и
определяемой соотношением v0 = qrEJm^ при этом плотность электрического тока,
возникающего из-за общего движения газа, составляет у0 = nqv0 = сг0Е0. Таким образом,
электропроводность составляет а0 = nq2r/m^ что является тем же результатом,
который мы нашли уже ранее в разделе 6.2. Если поле является электромагнитным типа
Eeia>t, то в этом случае уравнение G.В.9) показывает, что проводимость а (со) зависит
от частоты в соответствии с соотношением:
<j(a,)=_J?<L_ G.B.10)
\ + w
Дисперсионное соотношение G.В.4), описывающее связь между волновым
вектором к и частотой со, остается действительным при замене а на приведенное выше
выражение для а (со). Таким образом, мы сразу получаем выражение для
поглощения (более точное по сравнению с соотношением G.В.8)):
а = Л f G.B.11)
пор 1 + (cotJ
Произведение Zocro по размерности соответствует обратной длине. В
кристаллических полупроводниках, время столкновений, как правило, лежит в диапазоне
0,1—10 пс, и произведение сот составляет для оптического диапазона очень
большую величину. Таким образом, выражение G.В.11) может быть упрощено до вида:
а= Z? nq2% G.B.12)
4ж пор mefrr
Модель Друде для поглощения
на свободных носителях
Пример
Брусок кремния (пор = 3,6, weff = 0,321aw0) легирован до концентрации 1020 см или
1026 м~3. При этом уровне легирования среднее время столкновений г составляет
10~14 с. Этот результат приводит к проводимости:
ли 0,321 х 0,9 х 10 -30 кг
или удельная проводимость составляет величину порядка 1 м Ом см.
Коэффициент поглощения излучения на длине волны 10 мкм B х 1014 с) дается G.В. 11) и
составляет:
а= ZQo0 =377Омх8,8х104Ом-' м'1 =
а M
njanJ 3,6x4
Таким образом, ИК-излучение поглощается на глубине порядка 0,4 мкм.
В то же время эта очень простая модель обладает рядом недостатков:
• модель предсказывает спектральную зависимость типа Л2 для коэффициента
поглощения, что не подтверждается экспериментом. В общем случае,
коэффициент поглощения яг пропорционален степенной зависимости Л с показателем,
отличным от 2 (а = const х Лр, где р изменяется в диапазоне 1,5—3);
7. В. Поглощение на свободных носителях
• модель ничего не говорит о микроскопической природе процесса поглощения на
свободных носителях (взаимодействие с примесями, акустическими фононами и т. д.).
Для решения этих проблем необходимо обратиться к квантово-механической
трактовке. Одновременно мы должны осознавать, что квантово-механический
анализ будет сопряжен с рядом трудностей, которые надо преодолеть прежде, чем он
сможет предложить удовлетворительное описание поглощения свободным
электронным газом. Рисунок 7. В.2 один из таких аспектов рассмотрения.
Рис. 7.В.2. Поглощение фотона в
одной зоне возможно только в случае
участия механизма рассеяния, который
может обеспечить необходимое
сохранение импульса между начальным и
конечным состояниями.
Как мы видели в начале главы, матричный элемент, описывающий связь между
зонным электроном и электромагнитной волной является ненулевым только для
практически вертикальных переходов, при которых сохраняется волновой вектор к.
Поскольку квазисвободные электроны распределены по параболической зоне
проводимости полупроводника, то доступных состояний «над» этой зоной, которые
могли бы принять возбужденный электрон не имеется. Другими словами, мы не
можем одновременно удовлетворить условия сохранения импульса (к = к') и
энергии (h2k21 2/weff + hv = h2k2/2me{r). Таким образом, нам необходимо другое
взаимодействие для обеспечения дополнительного импульса с тем, чтобы возвратить
возбужденный электрон обратно в зону проводимости.
Для этого мы располагаем всеми механизмами, описанными в главе 6 (примеси,
оптические фононы и т. д.) В качестве примера рассмотрим взаимодействие с
оптическими фононами, описываемое гамильтонианом взаимодействия l/2(//pheifttf + к. с).
Поскольку этот переход требует участия двух одновременных возбуждений, мы
должны использовать теорию возмущений второго порядка, к которой мы
прикоснулись в дополнении З.Б. Уравнение (З.Б.26) дало нам скорость перехода в секунду
между начальным |/) и конечным |/) состояниями:
■/)-?
(f\Hjn)(n\Hji)
Е. ~ Е.
G.В.13)
Эта формула использовалась в контексте двухфотонного поглощения. Здесь же мы
имеем Ярег = #ор + #ph и соответствующие члены имеют вид:
/ „ I -^-ш- I \ / I .■»■ I Л / л I т-ш- I \ / I •- ш- I Л 2
■'>■?
£, - £.
£, - £.
8(Ет) G.В.14)
Два другие члена в сумме соответствуют двухфотонному поглощению (в виде
членов типа (i\Hop\n) (n\Hop\f)) и двухфононного рассеяния (в виде членов типа
(/|#рЬ|л) </i|#ph|/>). Естественно, такие переходы не обеспечивают одновременное
сохранение энергии и импульса. В интегральном виде закон сохранения
энергии в процессе различных переходов второго порядка может быть выражен в
виде:
Дополнения к главе 7
S(Etot)=s(Ef-Ei-hcoop±ha)ph)
G.В.15)
в зависимости от того участвует ли в процессе поглощение или излучение фононов.
Хотя принцип, лежащий в основе этих вычислений, понятен, на практике
суммирование по промежуточным состояниям достаточно утомительно. Этот расчет
может быть изучен по книге Ридли A988).
С учетом сложности этих квантовых моделей часто используется
феноменологические формулы, полученные из эксперимента. Поглощение на свободных
носителях может быть описано соотношением:
G.В.16)
а = к Г^(см)] U(mkm)T
1 10" \[ 9 J
где Ка есть параметр, зависящий от материала и приведенный в таблице 7.В.1 для
различных полупроводников.
Табл. 7.В.1. Коэффициенты, необходимые для расчетов поглощения на свободных
носителях (H.Y. Fan, Semiconductors and Semimetals, vol. 3, R.K.
Willardson and A.C. Beer, eds.,Academic Press, New York A967), Ch. 9) no
формуле G.В. 16)
Материал
GaAs
InP
GaSb
InAs
InSb
AlSb
N(x 1017 см'3)
1-5
0,4-4
0,5
0,3-8
1-3
0,4-4
К
3
4
6
4,7
2,3
15
P
3
2,5
3,5
3
2
2
На рисунке 7.В.З представлены коэффициенты поглощения ряда
полупроводниковых материалов, важных для оптоэлектронных применений (GaAs, InP и
GaSb), в функции концентрации свободных электронов и для двух практически
важных длин волн: 1,55 мкм (для телекоммуникационных целей) и 10 мкм (для
оптических оборонных применений).
Мы видим, что паразитное поглощение может быть значительным и его следует
учитывать при расчетах порогов лазерной генерации.
Поглощение на свободных носителях приводит к изменению As в
полупроводниковых материалах. Для определения амплитуды этого эффекта нам необходимо
только ввести выражение G.В. 10) в дисперсионное соотношение G.В.4) и
просуммировать действительные части к2. В этом случае мы находим:
Ае = —
со:
со
G.В.17)
где со есть плазменная частота электронного газа, определяемая соотношением:
1
со: =
"eff
G.В.18)
Плазменная частота
Это изменение показателя преломления используется в электро-оптических
модуляторах. Как показано на рис. 7.В.4, электромагнитная волна каналируется облас-
7.В. Поглощение на свободных носителях
2 0.01
на длине волны 1,55 мкм
ю1
2 34567 2 34567
ю17 ю18
Концентрация электронов (см~ )
Рис. 7.В.З. Коэффициенты поглощения на свободных носителях в функции
концентрации электронов, рассчитанные по G.В.16) с использованием величин,
приведенных в таблице 7.В.1, для GaAs, InP и GaSb и для длин волн 1,55
мкм и 10 мкм.
золна
V
область пространственного
заряда
вход
света
зеркала
инжектированные свободные
носители
волна
вход
света
Рис. 7.В.4. Функционирование модулятора на свободных носителях.
тью пространственного заряда (смотрите главу 10), расположенной между двумя
зеркалами, находящимся с двух сторон волновода.
Этот волновод длиной L ведет себя как резонатор Фабри—Перо с
пропусканием, определяемым (9.Г.21). Интуитивно понятно, что волновод пропускает
излучение с волновым вектором к, когда kL = тп (включенное состояние) и
блокирует излучение, когда kL = Bт + \)ж/2 (выключенное состояние). Под влиянием
приложенного извне напряжения электроны инжектируются в область простран-
(ft 286 Дополнения к главе 7
^^УА
ственного заряда и модулируют е в соответствии с G.В.17), что переводит волновод
из включенного в выключенное состояние. Напряжение, необходимое для
переключения состояния модулятора, дается соотношением:
k(V0FF)-k(V0N)=±- G.B.19)
Это соотношение с учетом дисперсионного соотношения к = со^/2/с = 2япор/А0, где Ло есть
длина волны в вакууме, может быть записано в виде:
А€ = ~f ^ G'В-20)
Пример
Рассмотрим волновод на основе InP (пор = 3,5, /weff = 0,077m0). Мы хотим определить
длину волновода для его переключения на длине волны Ло = 1,55 мкм при инжек-
ции в область пространственного заряда 1017 носителей/см3. Плазменная частота со
электронного газа дается G. В. 18) и составляет:
102
На длине волны 1,55 мкм частота составляет 1,2 х 1015 с, что приводит к
изменению е величиной Ае = — 3 х 10~3. В этом случае необходимая длина прибора в
соответствии с G.В.20) составляет:
L = 3,5 х 1,55 х 10 мм/B х 3 х 10) = 0,9 мм
Литература
N.W. Ashcroft and N.D. Mermin, Solid State Physycs, Holt, Rinehart, and Winston,
New York A976).
J.I. Pankove, Optical Processes in Semiconductors, Dover Publications, New York A971).
B.K. Ridley, Quantum Proccesses in Semiconductors, Claredon Press, Oxford A988).
ГЛАВА 8
ПОЛУПРОВОДНИКОВЫЕ
ГЕТЕРОСТРУКТУРЫ
И КВАНТОВЫЕ ЯМЫ
8.1. Введение
В главе 5 мы уже видели, что принципиально важной характеристикой
полупроводникового материала является существование запрещенных энергетических зон или,
запрещенных зон, отделяющих богатую электронами валентную зону от бедной электронами зоны
проводимости. При этом как запрещенная, так и разрешенные энергетические зоны,
определяются объемным потенциалом кристаллического материала.
В основе проектирования зонных структур лежит гетеропереход, реализуемый при
синтезе одного полупроводникового слоя на другом. Для некоторых специально
выбранных полупроводников, обладающих совместимыми кристаллическими
структурами и постоянными решетки, можно достичь эпитаксиального выращивания одного
материала на другом. В этом случае расположение атомов второго материала образует
виртуально совершенное продолжение лежащей ниже кристаллической решетки. Из
тщательно подобранных условий композиционный переход между двумя материалами
может быть сделан практически идеально резким (т. е. во многих случаях
протяженность гетерограниц может составлять величину в пределах монослойной шкалы).
Вдали от гетероперехода и в глубине объема двух материалов электроны
подвержены воздействию объемных потенциалов (запрещенных зон и зонной
структуры), характерных для каждого из образующих объемных материалов.
Количественное описание такого изменения потенциала требует расчетов на атомном уровне.
Расчеты такого уровня (проводимые численными методами с использованием
компьютеров) являются чрезвычайно сложными и лежат вне основного содержания
настоящей книги. Тем не менее, такие расчеты показывают, что в масштабе
нескольких атомных слоев вблизи границы раздела имеет место перенос
электрического заряда, который, в свою очередь, создает зарядовый диполь границы раздела,
ответственный за резкий скачок электростатического потенциала на границе
раздела, который накладывается на кристаллический потенциал. По обе стороны от
переходной области (на протяжении нескольких монослоев) электроны обладают
характеристиками образующих систему полупроводников (запрещенные зоны,
эффективные массы и т. д.). В то же время относительное положение валентных зон
определяется процессом переноса заряда. С макроскопической точки зрения мы
можем рассматривать гетеропереход как систему, для которой нарушается
непрерывность валентной зоны или имеет место разрыв валентной зоны AEv. Для наших
целей будем считать, что AEv является параметром (определяемым
экспериментально или предсказываемым более детализированными теоретическими моделями),
который зависит исключительно от пары материалов, образующих гетеропереход.
Как только становится известным разрыв валентной зоны, разрыв зоны
проводимости АЕс может быть тривиально определен с использованием наших знаний о
ширине запрещенной зоны объемных материалов. При этом важно отметить, что с
учетом химической природы зарядового диполя границы раздела, его влияние
ограничено сравнительно ограниченным числом химических связей, которые
перекрывают гетерограницу.
Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
В рассматриваемом случае возможны три типа структур (смотрите рис. 8.1): в
первом случае вся запрещенная зона более узкозонного полупроводника находится
в пределах зоны проводимости и валентной зоны более широкозонного
полупроводника (в данном случае имеют место гетероструктуры типа 7); в альтернативном
варианте один из разрывов зон может быть больше различия ширины запрещенной
зоны двух полупроводниковых материалов (гетероструктуры типа II) и, наконец,
величина одного из разрывов может быть больше ширины запрещенной зоны
наиболее широкозонного полупроводника (гетероструктуры типа III).
1 2
Е1
9
'П.
а тип I
1
i
Ir
r
♦
2
E'i
б тип
В ТИП I
Рис. 8.1. Три типа гетероструктур, реализуемые в системе из двух полупроводников,
обладающих шириной запрещенной зоны Egl и /Г,2, Ее и £,, обозначают
соответственно зону проводимости и валентную зону.
Для электрона в зоне проводимости гетероструктуры зонный разрыв
представляет, по сути, скачок потенциальной энергии в области гетероперехода. При
заданной полной энергии Eiot электрон будет обладать кинетической энергией Etot—Ecl в
полупроводнике 1 и кинетической энергией Ехо—Ес2 в полупроводнике 2, где Ес.
есть энергия дна зоны проводимости полупроводника /. В результате, осаждая
последовательность полупроводниковых слоев (каждый из которых имеет
соответствующую толщину и состав) можно сформировать любой необходимый профиль
потенциала вдоль направления роста кристалла. При этом наши возможности
принципиально ограничены набором доступных материалов и возможностью их
эпитаксиального выращивания. Понятно, что кристаллические структуры
материалов должны иметь практически идентичные постоянные решетки. В противном
случае полупроводник, осажденный на первый слой, будет подвержен очень
большой энергии упругой деформации, приспособиться к которой кристалл сможет
только в том случае, когда толщина слоя останется малой. За пределами области
критической толщины напряжение в эпитаксиальных слоях будет релаксировать, разрывая
практически совершенную кристалличность структуры и ухудшая оптоэлектронные
свойства, которые в других условиях могут быть обеспечены этими материалами.
Например, в случае InAs лишь немного менее двух монослоев могут быть эпитак-
сиально осаждены на GaAs до того, как начнется процесс релаксации с
образованием трехмерных островков.
На рисунке 8.2 показана связь между шириной запрещенной зоны и
постоянной решетки для различных объемных материалов. Требование точного
соответствия постоянных решетки для различных объемных полупроводников делит
8.2. Формализм огибающей функции 289jj)
Ч-.
AIP ZnS^.;S; ~" Cdo^no.sTe
ZnTe
AiSb \
7""*"*-v CdTe*
4.0
§ 3.0
СО
g_CN 2.0
О s
т а
0 с
а
1 1.0
0.0
5.4 5.6 5.8 6.0 6.2 6.4 6.6
постоянная решетки (А)
Рис. 8.2. Связь между шириной запрещенной зоны и постоянной решетки различных
объемных полупроводников.
эти полупроводники на пять отчетливо выраженных групп с точки зрения
совместимости по постоянной решетки. Среди этих материалов наиболее
контролируемыми являются твердые растворы GaAs/Al^Ga^^As, при этом могут быть
получены материалы с любым содержанием А1, поскольку постоянная решетки
существенно не изменяется с составом х. Двумя другими важными системами являются
GaxInj_xAs Р1 _ и AMrij.^As, которые могут быть получены осаждением на
подложки InP, а также InASj _х $Ъх и Al;cGaI _ х Sb на подложках InP и lnAs{_x Sb и
AlxGa, _x Sb на подложках GaSb. И, наконец, постоянные решетки Hgt _xCd xTe
хорошо соответствуют осаждению на подложки CdTe, а также они обеспечивают
возможность получения материалов с шириной запрещенной зоны, изменяющейся от
видимой области спектра вплоть до нуля и возможность получения материалов с
отрицательной запрещенной зоной, что свидетельствует о поведении этого
материала как полуметалла в этом диапазоне составов.
8.2. Формализм огибающей функции
Волновые функции электрона в гетеропереходе можно описать с использованием
формализма огибающей функции. Эта аппроксимация формально идентична той,
которая используется для описания распространения электромагнитной волны в
неоднородной среде, как например, в случае волновода в (9.27) или в нелинейной
оптике, как в A2.21). Данный раздел является достаточно проблемным и читатель
может просто принять (8.17) на веру и перейти к другому разделу.
Теперь мы выведем аппроксимацию огибающей функции для полупроводника,
обладающего периодическим потенциалом F(r), отражающим кристаллическую
периодичность решетки. Обсудим простой случай электрона в зоне проводимости гетерос-
труктуры — более сложная проблема, связанная с вырождением валентной зоны будет
оставлена до дополнения 8.Г.
Ш 290 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
Г\Г\Г\Г\Г\Г\Г\Г\
Цг)
Рис. 8.3. Потенциал, действующий на электрон, состоит из кристаллического
потенциала и внешенго потенциала, представленного изогнутой линией.
Рассмотрим потенциал VJj), медленно изменяющийся по г, как это показано на
рис. 8.3. Гамильтониан электрона, задаваемый этой комбинацией потенциалов, в
этом случае может быть записан в виде:
2т0
Для У(г) = 0 решения уравнения Шредингера Ну/ = Еу/ представляют собой
блоховские функции \п, к) (смотрите главу 5):
При этом должно удовлетворяться уравнение:
(8.2)
где О, есть объем кристалла, п — индекс зоны, а ип к(г) обладает периодичностью решетки.
Соответствующая энергия есть еп к.
При Уф О разложим решения уравнения Шредингера (8.1) по набору волновых
функций базиса в виде блоховских функций:
~~ 4е'кЧк(г) (8-3)
(8.4)
Поскольку волновая функция Блоха является решением задачи для «кристалла с нулевым
потенциалом», это последнее выражение может быть переписано в виде:
,ке*Чк(г) (8.5)
После этого спроецируем это выражение на волну |M£) = £2~1/2eikr и М£. В этом
случае, используя ортогональность блоховских волновых функций, получаем
эквивалентное выражение для уравнения Шредингера:
«к о
4k(r)dr =
- eN
(8.6)
Вплоть до настоящего момента мы не допустили никаких изъянов в нашем
выводе. Таким образом, вполне разумным представляется подумать над тем, какие
аппроксимации необходимы для упрощения приведенного выше выражения. В связи
с этим заметим, что если К(г) является постоянной величиной, то левая часть будет
8.2. Формализм огибающей функции 291
представлять Фурье-образ величины ^Л(т)иш(т) и она будет зависеть только от
кристалла.
Тот факт, что К(г) изменяется очень медленно, означает, что Фурье-образ,
определяемый выражением:
(8.7)
К, =-|-|V(r)e-""dr
равен нулю за исключением значений q, очень малых по сравнению с радиусом зоны Брил-
люэна. При подстановке (8.7) в (8.6) возникает следующий член:
^^f^(Kk() (8.8)
Этот член будет практически равен нулю для постоянной величины V. Поскольку
функции иж и ипк являются периодическими, мы можем положить, что г = R. + г', где R
обозначает положение ячейки /, a f ограничен объемом элементарной ячейки. Этот приводит к
следующей сумме по г.
(89)
"<*" cell
где символ Jcell подчеркивает, что интефал берется по элементарной ячейке, а Ак есть
дельта-функция Кронеккера. В этом выражении мы предположили, что к и К лежат
внутри зоны Бриллюэна. Если бы они были вблизи края зоны Бриллюэна, то мы
учли бы процесс, при котором k + q — К = G, где G есть вектор обратной решетки.
Учет этих эффектов вряд ли привнес бы что-то новое в наше рассмотрение.
Вновь используем тот факт, что только очень малые векторы q дают вклад в
потенциал, при этом разлагая огибающий интеграл для периодических частей бло-
ховских волновых функций по q:
7Г ^<гХк+ч(гЖ ^ [w^(rXK(r)dr4^
"cell i "cell c{n "cell c{n
l (8.10)
= ANn + -—q • Мж(г'^Лк(гЖ
b^ceU c^u
Ортогональность волновых функций м^им^ при том же самом волновом
векторе К имеет место из-за ортогональности блоховских функций различных состояний.
(Заметьте! Для различных волновых векторов периодические части не являются
ортогональными). Простейшая аппроксимация состоит в сохранении только первого
члена, что позволяет выделить каждую из различных зон в уравнении (8.6). С учетом
(8.9) и (8.10) уравнение Шредингера в обратном пространстве принимает вид:
X ^+/q = EaNK (8.11)
4
Введем огибающую функцию:
Определение огибающей функции
В реальном пространстве мы можем записать (8.11) в виде:
/[B92 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
XiK r ^-i iK г ~ ^ iK r
К Kq К
Или вновь в другом виде:
a eiKr + V Keiqr V a eiKr -
з ч к к (8.14)
Поскольку связанными через (8.11) являются только компоненты, близкие к К, мы
можем представить дисперсионное соотношение для зоны еж в виде ряда по К Для более
важного случая с К = 0 мы вводим эффективную массу т *N зоны TV:
h2 К2
£nk=£no+-z-t- (8-15)
2mN
При этом для упрощения рассмотрения будем предполагать ее изотропной.
Подставляя (8.15) в (8.14), мы находим:
г d3K
£no + ~ |^ке =£*оСЛ*) 7^г2^(г) (8.16)
Это позволяет нам получить награду за наши усилия, а именно — уравнение Шредингера
ддя огибающей функции:
+ К(г)Ъ(г) = (£-^0)^(г) (8.17)
4
2mN J
Уравнение Шредингера
для огибающей функции
Это уравнение представляет собой основной результат настоящей главы. Оно
показывает, что роль эффективной массы намного шире той, которую она играла в
контексте рассмотрения, проведенного в главах 5 и 6: в случае потенциала V(r),
слабо изменяющегося по отношению к кристаллическому потенциалу, волновая
функция электрона в зоне проводимости N является, таким образом, волновой функцией
частицы, обладающей эффективной массой, связанной с зоной N и подверженной
воздействию потенциала К(г). Все влияние материала учитывается в уравнении
Шредингера (8.17) эффективной массой m*N и энергией ет зоны ./Упри К = 0.
В случае этой принятой аппроксимации полная волновая функция имеет вид:
(8.18)
При этом решение, соответствующее потенциалу V= 0 есть:
уЛ-е*'иж(г) (8.19)
Оно отличается от точного решения заменой в (8.3) #м(г) на ит (г).
В случае гетероперехода, для которого внешний потенциал К(г) претерпевает
разрыв на протяжении области атомарного масштаба, вывод, который нам
предстоит сделать, уже не будет строго справедливым. Если, однако, мы будем искать
состояния, близкие по энергии к зоне проводимости, то мы сможем
аппроксимировать решения по обе стороны гетероперехода соотношениями (8.17) и (8.18) и
использовать блоховские функции ит(г), характерные для каждого материала. Для
получения стационарного состояния электрона в гетероструктуре, мы должны
будем «сшить» оба решения на границе раздела (смотрите раздел 1.3.1). Начнем с
того, что волновые функции должны быть непрерывными:
ит@+) (8.20)
8.3. Квантовая яма
где знаки «±» относятся к материалам слева и справа от границы раздела при z = 0.
В этом уравнении огибающая функция изменяется очень слабо в пределах ячейки
перед границей раздела, при этом если мы используем среднюю величину (8.20) по
этой ячейке, то получим:
ИДО") = &@+) (8.21)
Точное решение должно обеспечивать сохранение потока вероятности через
границу раздела. Как было показано в разделе 1.3, поток вероятности дается
соотношением:
j = -ir-^(r)V^(r) - f*,(r)Vf *(r)l (8.22)
mN\
Сохранение потока вероятности при пересечении границы раздела приводит к уравнению
непрерывности:
Это последнее условие может быть легко включено в рассматриваемый формализм
при использовании записи уравнения Шредингера для огибающей функции в виде:
- V -4 V + V(r) \С„(т) = (Е- eN0)CAr) (8-24)
где т *N (г)учитывает изменение эффективной массы при переходе от одного
материала к другому.
Мы должны отметить, что этот достаточно эвристический подход скрывает ряд
важных проблем. Мы ограничили нашу аппроксимацию простой зоной, где эффективная
масса не зависит от К, т. е. параболической зоной (смотрите (8.15)). В том случае,
когда фигурирующие энергии £иА К(г) значительны, это предположение не является
допустимым. Мы предположили также, что зона N является невырожденной при К = 0,
что явно не имеет места для валентных зон. Эти два аспекта (параболичность и
вырождение) связаны друг с другом. Вывод огибающих функций в рамках многозонной
трактовки будет основной (и проблемной) темой дополнения 8.Г. На время мы
просто продекларируем, что аппроксимация огибающей функции в (8.18) вместе с
соответствующим уравнением Шредингера (8.24) достаточны для квантового
описания электрона в гетероструктуре.
8.3. Квантовая яма
С использованием двух гетеропереходов теперь становится возможной реализация
одномерного профиля потенциала вдоль направления роста для электронов,
соответствующего квантовой яме, исследованной в главе 1.
Рис. 8.4 демонстрирует наиболее изученную к настоящему времени структуру с
квантовой ямой, состоящую из слоя квантовой ямы GaAs, заключенного между
двумя более широкозонными барьерными слоями AlxGaj _xAs. При х < 0,4 разрыв
зоны проводимости пропорционален содержанию А1, так что АЕс ~ х х 836 мэВ.
Подбирая содержание А1 и толщину слоя GaAs в процессе роста, мы можем
создать квантово-размерную структуру, обладающую электронными свойствами,
соответствующими требованиям пользователя — на практике это называется
квантовой инженерией.
Для электронов в зоне проводимости слои AlGaAs образуют потенциальные барьеры
высотой VB = AEc. В этом случае уравнение Шредингера приобретает вид:
- V—К— Vf (г) + V(z)C (г) = Ear) (8-25)
2т (z)
|( 294 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
направление роста
Рис. 8.4. Потенциальная яма возникает, когда слой GaAs выращивается между двумя
более широкозонными барьерными слоями AlxGa, _xAs. Когда ширина слоя
ямы достаточно мала, движение электронов в квантовой яме становится
квантованным в направлении роста, при этом разрешенные энергетические
уровни, соответствующие движению в этом направлении, становятся
дискретными. В плоскости, параллельной границам раздела, движение электронов
остается неограниченным. В результате этого полная электронная волновая функция
дается произведением огибающей функции (решение одномерного уравнения
Шредингера) и периодических блоховских функций ипк (обусловленных
периодичностью кристаллической решетки), а также плоских волн, описывающих
свободное движение в плоскости, параллельной границам раздела.
При этом величина V(z) равна нулю в яме иКвв барьерах. Как эффективная масса,
так и потенциал зависят только от z, в то время как в направлениях х и у
(параллельно границам раздела) эффективные потенциалы не изменяются.
Следовательно фг) может быть записана в виде:
Яг) = £K(*)exp(iKR) или R = (х, у) и К = (кх, ку) (8.26)
В этом выражении огибающая волновая функция представляет свободное
движение электронов в плоскости, параллельной границам раздела, a CnK(z) определяется
одномерным уравнением Шредингера:
h2
= E{nK(z)
(8.27)
Обозначая эффективные массы в яме и барьере соответственно как mw и /ив, находим:
,Л) (8.28)
Для малых ^корректировка «потенциальной энергии» из-за изменения эффективной
массы пренебрежимо мала. Практически во всех случаях ей пренебрегают из тех
соображений, что функция £nK(z) в этом случае становится независящей от К и подчиняющейся
простому уравнению:
:„(*)= *„Ш
Н2К2
(8.29)
8.3. Квантовая яма
Если бы эффективная масса не зависела от материала, это уравнение было бы
тем же самым, что и уравнение, полученное для квантовой ямы, исследованной в
главе 1. Поскольку как эффективные массы, так и потенциалы постоянны в
областях, разделенных гетеробарьерами, решение (8.29) получить нетрудно.
Рассмотрим границу раздела при z — L/2 для е < VB в области ямы. Решением
является комбинация двух плоских волн:
C(z)=a ek{z-L/2)-btAk{z-Ln\ z < L/2 (8.30)
При этом h2k2/2mw = е.
В области барьера для z > L/2 допустимое решение содержит затухающую экспоненту:
C(z)=ct-K{z-L/2\ z> L/2 (8.31)
с h2k2/2mB = VB- e.
Используя условия непрерывности при z = L/2, мы находим:
А = е-'" = {mw/mB)c-iK
a (mw /тв)с + \к
С учетом (8.30) выражение (8.32) говорит нам о том, что электронная волновая
функция сдвинута по фазе на 2ф в результате отражения от границы раздела при z = L/2. В этом
случае 0 дается соотношением:
sin ф = -j - ^ (8.33)
С учетом того, что область ямы начинается у границы раздела при z — ~L/2, фаза
плоской волны, распространяющейся слева по направлению к границе раздела
справа, увеличивается на kL, при этом отражение увеличивает фазу на 2ф, при этом
обратный проход отраженной волны к — L/2 приводит опять к добавлению kL.
Наконец, отражение при z = —L/2 обусловливает второй фазовый сдвиг величиной 2ф.
Для стационарного состояния полный фазовый сдвиг после полного цикла
обращения должен быть равен 2пж, где п есть целое число. Это приводит к условию, что
2ф= пп— kL или вновь:
a(8.34)
f ТГ7Т = п
* Ufo/^M'+Kj " х k
0
при этом h2k*/2mw = VB
Графическое решение на рис. 8.5 показывает, каким образом это условие выполняется
для нескольких значений mB/mw.
При mw = тв решения на рис. 8.5 эквивалентны тем, которые представлены на
рис. 1.2.
В этом случае энергия стационарного состояния, которое мы можем
обозначить как |яК) в соответствии с (8.29), дается соотношением:
(8-35)
где еп представляют собой дискретные значения энергии и решения (8.29), а К является
непрерывной величиной в плоскости (Кх, К). Эти состояния организованы в виде подзон, как это
показано на рис. 8.6. Каждая подзона включает в себя ансамбль электронных
состояний, обладающих тем же самым состоянием квантованного движения,
перпендикулярного границам раздела, а также непрерывно изменяющимися волновыми
векторами К, соответствующими их беспрепятственному движению в плоскости. Для
описания ансамбля электронов, занимающих такую зонную структуру, используется понятие
двумерного электронного газа.
|( 296 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
2.0
1.5
^ 1.0
0.5
0.0
Рис. 8.5. Графическое решение (8.34).
Решения даются точками пересечения
наклонных линий п — kL/я и
функций arcsin.
0.0
0.2
0.4 0.6
klk0
0.8
1.0
Рис. 8.6. Квантово-размерная
структура (а), показывающая две подзоны в яме
с соответствующими огибающими
функциями (перпендикулярными границам
раздела) и энергетические спектры (б).
2 «2
1 fc1
< ►
Важно отметить, что волновые функции по-прежнему допускают разделение
переменных, поскольку потенциал зависит только от z- Форма V(z) имеет значение
только при определении энергетических минимумов подзон еп. Энергия еп
называется также энергией ограничения. Таким образом, концепции подзон и энергий
ограничения остаются справедливыми во много большем числе систем по сравнению с
рассмотренной здесь симметричной квантовой ямой.
8.4. Плотность состояний и статистика системы
с квантовой ямой
В каждой подзоне электронные состояния содержат компоненту в виде плоской
волны в направлении, параллельном границам раздела. Как это уже неоднократно
делалось для трехмерного континуума (смотрите Дополнение 1.А, раздел 5.3, ...) и
сейчас включим двумерную квантовую яму в плоскость за счет использования
макроскопической прямоугольной области с площадью А = Lx Ly. Граничные условия
на краях этой прямоугольной области (или иначе — «виртуального ящика») вводят
квазиквантование допустимых значений импульса fi К. В соответствии с
цикличными граничными условиями Борна—фон Кармана (смотрите раздел 5.2):
8А, Плотность состояний и статистика системы с квантовой ямой
y/(x,y,z)=y(x+ Lx,y,z)
y/(x,y,z)=y(x,y + Ly,z)
Применительно к волновым функциям в (8.26) это условие означает:
(8.36)
К - (к К \-
К - [Кх, Ку)-
2ту
(8.37)
где пх и п являются целыми числами. Если мы будем представлять допустимые
значения К в виде точек на плоскости (рис. 8.7), то в этом случае каждое состояние
будет занимать площадь BжJ/Ьх Ly, при этом плотность состояний в этом
двумерном пространстве К будет постоянной, т. е. Z)(K) = gA/BnJ.
Рис. 8.7. Квазиквантованные значения для
К = BmJLx, 2mJLy) представляются
точками в плоскости обратного пространства.
Состояния, обладающие энергией менее Ео,
заключены в круг радиуса Ко (уравнение (8.39)).
В последнем выражении было учтено вырождение по спину gs = 2, так как
каждое состояние К допускает два решения с противоположными спинами.
Нам часто приходится вычислять суммы функций /, зависящих только от
энергии состояний:
У f[E(K)U J^
jf(E)Dn(E)dE
(8.38)
Здесь Dn(E) представляет собой плотность состояний в я-ной подзоне. В
предположении параболичного характера дисперсии, подобного уравнению (8.35), число
состояний Nn(E0) с энергией меньше Ео будет равно числу состояний с волновым
вектором К, лежащим внутри окружности радиуса Ко = Bmw(E0 — £п)/Н2У/2' как это и
показано на рис. 8.7, т. е. при Ео > е\
N
Таким образом, плотность состояний в подзоне является постоянной:
(8.39)
еп) (8.40)
При Е< £пне имеется допустимых состояний и Dn{E) = 0, что отражается функцией
Хэвисайда в.
В этом случае плотность состояний в системе дается суммой плотности
состояний для каждой подзоны.
(8.41а)
Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
E i{
Рис. 8.8. Подзоны и плотность состояний
для двумерной структуры.
D(E)
Эта функция имеет ступенчатую форму (рис. 8.8), при этом высота ступеньки
является константой материала. В то же время положение ступенек зависит от
конкретной величины ет и, таким образом, от потенциала, ограничивающего электроны в
дискретных подзонах. Часто используется двумерная плотность состояний p2D в
расчете на одну подзону и единицу площади (эВ см), которая определяется
соотношением:
p2D = ^Р = ^\ (8.416)
Двумерная плотность состояний
При термодинамическом равновесии вероятность того, что электрон занимает
состояние с энергией ЕпК, по-прежнему определяется статистикой Ферми:
ч 1
exp[(EnK-EF)/kBT]
(8.42)
где EF есть энергия Ферми. Поверхностная концентрация пп электронов в подзоне
п, таким образом, составляет:
я. =
= nc
(8.43)
Критическая концентрация
где пс есть критическая концентрация носителей в подзоне. Полная поверхностная
концентрация носителей в системе в этом случае определяется соотношением:
*, = Xп» (8-44)
Уравнения (8.43)—(8.44) определяют ns в функции EFn Т. Они позволяют однозначно
определить уровень Ферми, если известна величина ns.
Если энергетический зазор между самыми нижними уровнями превышает тепловую
энергию (т. е. е2 — ех » квТ), а концентрация ns не слишком велика, то заселена
будет лишь одна подзона и мы можем выразить ns и EF в виде:
(8.45)
П5
8.5. Оптические межзонные переходы в квантовой яме 299
Уравнение (8.45) показывает, что в двумерном электронном газе имеет место
переход от вырожденного к невырожденному режимам. В том случае, когда ns » пс,
мы получаем условия вырожденного электронного газа, для которого:
(8.46)
Fl
PlD
В случае невырожденного режима ns« яс, при этом:
= п exp -
ex-EF
(8.47)
На рис. 8.9 в линейном и логарифмическом масштабах представлены зависимости ns(E).
10
1
0.1
0.01
П ПП1
-
-
-8
/
/
/
i . i
-4 0
№f-*i)
-
-
-
. i .
4 8
/квт
-8-4 0 4 8
а (£F-E1)//CBT
Рис. 8.9. Плотность состояний в подзоне в функции положения уровня Ферми Efb
линейном (а) и логарифмическом (б) масштабах.
Пример
Рассчитаем плотность состояний и критическую концентрацию для квантовой ямы
GaAs.
Эффективная масса тс в GaAs составляет 0,067ая0, что приводит к плотности р2£>:
0,067 х 0,9 х 100
p2D = 1,6хЮ-19 Кл
3,14x(l,05xl04 Джс]Р
= 2,78хЮ13 эВ1 см
13 эВ1 см
(8.47)
В этом случае критическая концентрация составляет пс = рю х 25,9 мэВ или 7,2 х 1011 см.
Таким образом, квантовая яма, легированная до уровня 1012 см, является
вырожденной. Разность между положением уровня Ферми и энергией ограничения в этом случае
составляет:
EF-ex =1012 см-2/B,78х1013 эВ-1 СМ-2)=36мэВ
8.5. Оптические межзонные переходы в квантовой яме
8.5.1. Дырочные состояния в валентных зонах
Пара материалов, образующих гетероструктуру типа I, может быть использована
для реализации квантовой ямы для электронов зоны проводимости. В валентной
зоне профиль потенциала, воспринимаемый электронами, представляет собой об-
f( 300 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
W
ращенную яму. Если мы используем (чрезвычайно) упрощающую
аппроксимацию валентной зоны в виде двух параболических зон (одной для тяжелых дырок с
эффективной массой mhh < 0 и другой — для легких дырок с эффективной массой
mlh < 0), то с использованием аппроксимации огибающей функции получаем два
следующие уравнения Шредингера:
(8.48)
dz 2m*h{z)dz
При этом потенциал имеет вид:
V(z)=0,-±<Z<±
V(z)=-VB=-AEf, |<|
(8.49)
Трехмерные решения этих уравнений Шредингера имеют вид:
/ГЛЛ _ /Г j_ chh л. ^ К
2тш
nhh
i2K2
Ih
(8.50)
Здесь: £v есть максимум валентной зоны для материала ямы, а массы и собственные
энергии еп отрицательны. Совершенно понятно (смотрите рис. 5. 13), мы можем
рассматривать эту проблему с использованием положительных масс, заменив при этом
знаки как у масс, так и у собственных энергий. В уравнении Шредингера это
соответствует замене V(z) -> —V(z) и еп -> — еп. В этом случае потенциал ямы является
потенциалом ограничения для дырок (в этом случае направление отсчета
положительной энергии направлено вниз на рис. 8.10), а кривая дисперсии соответствую-
объемный
материал
яма
V(z)
т*<0
i 1
-V(z)
/77* > О
Рис. 8.10. Слева — потенциал, действующий на электрон в валентной зоне, становится
ямой для дырок. Справа — потенциал ям приводит к снятию вырождения
валентной зоны вследствии различия эффективных масс легких и тяжелых дырок.
8.5. Оптические межзонные переходы в квантовой яме
щих подзон для дырок, подобно случаю электронов проводимости на рис. 8.6,
носит вогнутый характер.
В рамках этой модели основным эффектом квантовой ямы является снятие
вырождения между зонами легких и тяжелых дырок в центре зоны Бриллюэна из-
за различия эффективных масс (|£яАА| < кл/л|). (В действительности же структура
подзон является намного более сложной (мы возвратимся к этому аспекту в
дополнении 8.Г). Использованная здесь простая модель аналогична модели, которую мы
применили для оценки оптических свойств объемных полупроводников, когда мы
пренебрегали анизотропией эффективной массы в валентной зоне.
8.5.2. Оптические переходы между валентной зоной
и зоной проводимости
Сейчас нас будут интересовать переходы между различными состояниями в квантовой яме
под влиянием синусоидально изменяющегося во времени возмущения, например,
электромагнитной волны. Можно представить себе три типа переходов: (I) — межзонный
переход, при котором электрон в валентной подзоне может быть возбужден в подзону
проводимости; (II) — межподзонный переход, при котором электрон перемещается из одной
подзоны в другую, оставаясь в той же самой зоне; (III) — внутриподзонный переход, при
котором электрон переходит в различные состояния К в пределах той же самой подзоны п.
Последний тип перехода может иметь место вследствие процесса рассеяния,
как это уже обсуждалось в контексте поглощения на свободных носителях в
дополнении 7. В. В этом случае для осуществления необходимого обмена импульсами
между электроном и решеткой требуется взаимодействие с фононом или примесью
(смотрите рис. 7.В.2). Два другие типа переходов для случая взаимодействия с
электромагнитной волной представлены на рис. 8.11. Новым моментом, вводимым
двумерным аспектом квантово-размерной системы, является то, что межподзонные
оптические переходы являются разрешенными в первом порядке. Очевидно, что в
объемном материале такой процесс запрещен. Этот важный механизм мы будем
обсуждать в следующем разделе.
В случае межзонных переходов мы можем рассчитать скорость перехода,
используя золотое правило Ферми. Рассмотрим волну, проходящую через яму:
межподзонные
переходы
межзонные
переходы
hh2
а б
Рис. 8.11. Оптические переходы в пространстве К являются вертикальными.
Представлены 2 типа переходов: слева — в обратном пространстве (а), справа — в
реальном пространстве (б).
wT 3 0 2 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
Е(г, 0 = Eq cos(q • г - cot) = ^Eq exp[i(q. г - o>t)]+ ±EJ exp[- i(q r - <af)] (8.51)
Потенциал взаимодействия электрического диполя (смотрите раздел 3.2 и
дополнение З.Г) электронов в квантовой яме есть:
V4(r9 t) = -eEr = -|Eq • г exp[i(q • г - cot)]+ к. с. (8.52)
Скорость перехода из состояния ц/"пК в валентной зоне в состояние ^к, в зоне
проводимости в соответствии с золотым правилом дается соотношением:
S(nK -> /яК') = ^-e2|(mK'|Eq • r|/iK)|£(£mY - ^к - Л<») (8.53)
По сравнению с объемным случаем (смотрите уравнение G.10)) в
рассматриваемой ситуации имеет место изменение дипольного матричного элемента:
К% • г|лК) = ^-Jc*UK*o(r)e-iK'REq . re*'CUKo(r)e-iKRdr (8.54)
Идя по тому же пути, как это уже неоднократно делалось в этой главе, и учитывая, что
огибающая функция изменяется медленно по сравнению с постоянной решетки, мы
можем выделить быстро и медленно изменяющиеся части, положив г = f + (R, z), где f
принадлежит элементарной ячейке, а г. = (R, z) обозначает положение /-той
элементарной ячейки. В этом случае интеграл превращается в сумму по /:
i.
f * rwr i(K+q-K')r' f * ii
dr исОтъа • г wv0(r )e + E • г dr uc0(r )uvOr
J ' J
(8.55)
i(K+q-K') if
где az есть постоянная решетки в направлении z. Последнее приведенное уравнение
не поддавалось бы трактовке, если бы не наше умение сделать определенные
упрощающие предположения. Начнем с того, что заметим в сумме по R. проявление
закона сохранения для параллельных компонент импульса К+ q — К' = 0.
Поскольку волновым вектором излучения можно пренебречь по сравнению с волновыми
векторами электрона К и К" в зоне Бриллюэна, это требование к импульсу
учитывается дельта-функцией Кронеккера Ак к,, что приводит к ненулевому вкладу только
для К = К'. По этой же самой причине сумма по z( может быть заменена
интегралом, что приводит к следующему выражению для первого интеграла:
:'(z)£;№dz (8.56)
В этом выражении мы обнаруживаем матричный элемент rvc для г перехода между
валентной зоной и зоной проводимости.
В дополнение к этому, если протяженность волновых функций (~ толщине квантовой
ямы) очень мала по сравнению с длиной волны Л, то в этом случае мы просто имеем:
I{= AKKEq.r Jm,c\n,v) (8.57a)
при этом
(т, с | я, v) = J£•(#;(*)»* (8-576)
Во второй части уравнения (8.55) экспоненциальное выражение под знаком
интеграла является практически константой, т. к. Д»д,аКи К' далеки от края зоны Бриллюэна
(в противном случае аппроксимация огибающей функции не действительна), при этом
ортогональность блоховских функций устраняет этот член.
Таким образом, скорость перехода составляет:
8.5. Оптические межзонные переходы в квантовой яме 303 JJ)
5(иК -> тК') = 4^|Е„ • rvc|2|(m, с \ п, v)\2S(Es - йа>)Дкк. (8.58а)
При этом:
„ е П2К2 , ,| П2К2 „ „ h2K2 h2K2 /
В связи с этим отметим, во-первых, что сохранение полной энергии вводит порог для
оптического поглощения hco > £threshold =Е + £„ + К1 > ^- Таким образом, порог
оптического поглощения в квантовой яме испытывает коротковолновый сдвиг по
сравнению с поглощением объемного полупроводника на величину, равную сумме
энергий ограничения в зоне проводимости и валентной зоне. Этот
коротковолновый сдвиг используется для определения физических параметров квантовой ямы
(состав барьеров, толщина ямы ...). Скорость генерации электронно-дырочных пар
равна числу переходов в секунду:
G = 77 = SS(nK "* ^)/;(K)[l-/;(K)] (8.59)
В этом выражении вероятности заселенности обеспечивают присутствие электрона в
начальном состоянии \п, v) и незаполненное конечное состояние \т, с). Сохранение энергии
и параллельной компоненты импульса определяют К как функцию энергии фотонов:
п2к2 { \ \ Л п2к2 . _. с . vi /fi,m
2 [тс \mv\J 2mr * I I
Здесь: тгестъ приведенная масса. При термодинамическом равновесии в качестве
следствия получаем:
1
(Е,.-\е; -e;{h<o)-EF
+ ехр
> (8.61)
1 + ехр i^r I
(8.62)
/и.
Для переходов между валентной подзоной п и подзоной проводимости m мы можем
просуммировать по К:
С. = ^-|Е, • rro|-|(«, v | и, с)\ х -^ //(К)[1 - f.4K)\S ?-^- + £,hreshold
2h А к 2mr
«, v | пг
, с)\- х f М!1^/
' J BяJ
|q wf|( | , )\ /Л)[ fm4»] \
2» ' ' ' J BяJ [ 2mr
или
дипольный момент плотность состояний вероятность заселенности
1C 04 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
Это выражение мы можем вновь переписать в виде:
ле1
v | т, i
(8.636)
Скорость межзонных переходов
для квантовой ямы (с1 см)
В этом выражении можно увидеть произведение дипольного момента и элемента
перекрытия (п, v \т, с), комбинированную плотность состояний для двумерного
случая, mr/h2, а также соответствующую статистику заселенности. Таким образом,
скорость генерации Gmn является произведением коэффициентов статистики/ш и/й,
которые зависят от температуры, положения уровня Ферми и скорости генерации
G° = I,GJ}n, что имело бы место в случае, когда fm(l — fn) было бы равно единице и
зависело лишь от структуры. Это иллюстрируется рисунком 8.12.
гг|Е-г
vc\
Рис. 8.12. Скорость генерации в собственной квантовой яме ступенчатого профиля.
Всякий раз, когда становится возможным новый подзонный переход при
заданной энергии поглощения, скорость генерации возрастает на ступеньку.
Порог генерации пары располагается по шкале энергий выше
эквивалентной запрещенной зоны объемного материала.
Перекрытие огибающих функций \(т, с\п, v)|2 позволяет ввести правила отбора.
Например, в симметричной квантовой яме переходы между подзонами с различной
четностью запрещены. В случае подзон, лежащих глубоко в яме, огибающие
функции для электронов и дырок практически идентичны так, что возможны только
переходы между состояниями, обладающими одинаковыми индексами (т = п).
Анализ, проведенный для переходов, индуцированных поглощением, между
валентной зоной и зоной проводимости дает совершенно те же результаты для
стимулированного излучения (в этом случае участвуют переходы между зоной
проводимости и валентной зоной) за исключением статистики заселенности.
Стимулированная рекомбинация за счет поля имеет вид:
тп " ~ Jn Y^/J/m V1®) (о.64)
При этом баланс генерации—рекомбинации из-за поля имеет вид:
2Ь
)|/;(^)-/;M] (8-65)
Баланс скорости оптической генерации-
рекомбинации для квантовой ямы (с~1 см~2)
И, наконец, вспомним, что для двух блоховских функций с собственными
состояниями, имеющими одинаковые к в различных зонах, справедливо
соотношение:
8.6. Оптические межподзонные переходы в квантовой яме
(иск | [Я, г] \ил) = (Еск -
1" / II \
(8.66)
т0
Как было показано ранее в главе 7, матричный элемент rvc может быть выражен
через матричный элемент Кейна, использованный в дополнении 5.В в рамках к • р-
метода:
\П
(8.67)
Egm0
Мы можем задуматься над тем, следует ли заменять член Eg в (8.67) на со в выражениях
для скорости генерации, чтобы учесть фотоны с энергией, превышающей ширину
запрещенной зоны. Однако, мы не должны слишком много требовать от аппроксимации
огибающей функции, которая применима лишь до тех пор, пока \tico— E^/Eg« 1.
Тот факт, что вырождение валентной зоны приводит к возникновению отличных друг
от друга подзон тяжелых и легких дырок имеет в качестве следствия то, что матричный
элемент rvc зависит от типа перехода. С использованием волновых функций дырок
дополнения 5.В читатель может убедиться в справедливости правил отбора,
приведенных в таблице 8.1.
Табл. 8.1. Изменение ориентации электрического поля по отношению к квантовой
яме приводит к правилам отбора для переходов rw в уравнении (8.65)
равным величине г^ в объемном материале, умноженной на коэффициент,
приведенный в таблице
hh-^e
lh-^e
ТМ (E\\z)
0
V2/V3
ТЕ (E±z)
1/V2
1/л/6
В частности, переходы между электронной подзоной и подзоной тяжелых
дырок запрещены для ТМ-поляризации (т. е. для электрического поля,
перпендикулярного границам квантовой ямы — смотрите главу 9).
8.6. Оптические межподзонные переходы
в квантовой яме
При межподзонном переходе начальное и конечное состояния электрона принадлежат
одной и той же зоне. Это приводит к правилам отбора и характеру, полностью отличным
от тех, что наблюдаются при межзонных переходах. Для конкретизации давайте
предположим, что этой зоной является зона проводимости (смотрите рис. 8.11). В этом случае
начальными и конечными состояниями являются:
i
(8.68)
При этом в них входят те же самые блоховские функции ujr).
Золотое правило Ферми вновь дает нам скорость перехода, индуцированного
электромагнитным полем (уравнение (8.53)). Для матричного элемента
единственное различие между уравнениями (8.54) и (8.55) заключается в том, что начальное
состояние также находится в зоне проводимости.
([C06 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
(8.69)
Здесь сумма по R., очеввдно, связана с сохранением импульса в параллельном
направлении. В том, что касается первого интеграла, матричный элемент f в данном случае
равен нулю, так как uj?) преобразуется как 1 при операциях кубической симметрии
кристаллической решетки.
Второй интеграл в (8.69) в этом случае дает £2сс11, когда изменение экспоненциального
члена пренебрежимо мало в пределах элементарной ячейки. В результате, нам остается
сумма:
При этом ее, в свою очередь, можно обратить в интеграл в направлении z
Поскольку огибающие функции ортогональны, этот последний интеграл приводит
к межподзонному правилу отбора, гласящему, что переход может вызвать только
Е -компонента (смотрите рис. 8.13).
Интеграл (8.71) может быть записан в виде:
h =
Это приводит к скорости перехода:
S(nK
-%г\*ЛтН»$*.-е.-
(8.72)
(8.73в)
wvwm
1
-6/2 d/2
Рис. 8.13. Квантовая яма с двумя связанными состояниями (а) и соответствующие
дисперсионные кривые полной энергии £ (б), приводящие к наличию столь
большого количества подзон. Поскольку подзоны параллельны, переходы при
постоянном К приводят к энергетическим резонансом (т. е. переходы с одной и
той же энергией имеют место в широком диапазоне значений К между
парами подзон).
8.6. Оптические межподзонные переходы в квантовой яме 307
9
Рис. 8.14. Зависимость скорости возбуждения фундаментальной подзоны от энергии
фотонов. Подзоны в квантовой яме приводят к дискретным переходам
(переходы из связанного состояния в связанное состояние). Над барьерами
подзоны формируют континуум и могут участвовать в переходах между
континуумом и связанными состояниями.
Заметим, что в этом последнем выражении аргумент в ^-функции Дирака более
не зависит от К, поскольку подзоны параллельны (рис. 8.14). Таким образом, даже
если оптические переходы приводят к взаимодействию между светом и делокализо-
ванными электронными состояниями в среде (о чем свидетельствует
существование энергетической подзоны), это взаимодействие тем не менее является
резонансным, как если бы система обладала дискретными уровнями1.
Энергия фотонов, резонансная с уровнями в квантовой яме определяется
соотношением:
tlG) = £„-£„
(8.736)
Для установления скорости электронных переходов из одной подзоны в другую
должны быть применены статистические соображения, как это уже имело место в случае
межзонных переходов. В результате этого скорость возбуждения—релаксации может быть
получена суммированием по К:
G = [ЦА =\У\ S(nK -> mK')[/;(K) - /.(К)] (8.74)
Поскольку S(nK —> тК') не зависит от К результат получается особенно простым:
dt ' 2» *'
(8.75)
Скорость оптической
генерации—рекомбинации (с~1 см~2)
Здесь: ппи пт — соответственно концентрации электронов в подзонах пит.
Зависимость Got энергии фотонов представлена на рис. 8.15, и она существенно
отличается от зависимости, приведенной на рис. 8.12 для межзонных переходов. В (8.75)
мы узнаем также выражения A.86) и C.63), установленные в процессе обсуждения
атомных переходов между дискретными уровнями. Такие переходы между
связанными состояниями в квантовой яме называются переходами из связанного в
связанное состояние.
Над барьером подзоны не образуют дискретный спектр. В этом случае
огибающие функции являются протяженными, а энергетические уровни свободными. Их
можно классифицировать по компоненте kz их волнового вектора в барьере:
|Г308 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
падающий свет
квантовая
пружина'
свободное
движение
\
- ^Х,У
\
Рис. 8.15. При межподзонных переходах лишь компонента электрического поля,
перпендикулярная квантовым ямам, может оптически взаимодействовать с
«квантовыми осцилляторами», возникающими из-за допустимого смещения. В то
же время для параллельной компоненты поля остается возможность слабого
взаимодействия со свободным двумерным электронным газом.
1 " / ч 4K'.R)i/e0(r)
(8.76)
2mR
Теория скорости возбуждения следует из простого обобщения (8.75) при замене
суммирования по т на интегрирование по kz (смотрите Дополнение 1 А):
G =
(8.77)
Мы предположили, что заселенность состояний в барьере п^ пренебрежимо мала.
Заметим, что при всех энергиях фотонов h со > VB — еп явно возможными являются
переходы из подзоны п в континуум. Эта ситуация аналогична явлению
фотоионизации, которого мы касались в дополнении 1.А и к которой вновь более детально
возвратимся в главе 11 при изучении квантово-размерных детекторов.
8.7. Оптическое поглощение и угол падения
Зная скорости оптических переходов для различных механизмов (межзонного, межподзон-
ного), мы теперь уже в состоянии перейти к расчету коэффициентов поглощения для
квантовых ям, используя при этом принцип: каждый переход соответствует поглощению фотона.
Начнем же с предложения сводки характеристик для каждого из этих типов переходов.
8.7.1. Сводка по скоростям межзонных
и межподзонных переходов
Рисунок 8.16. суммирует качественные характеристики скорости межзонных и
межподзонных переходов, определенные в двух предыдущих разделах. Существенным моментом
является то, что межподзонные переходы приводят к резонансному характеру спектров
поглощения для фотонов с энергией, равной энергетическому интервалу между
параллельными подзонами.
С другой стороны, межзонные переходы приводят к ступенчатому характеру спектров
поглощения, при этом каждая ступень соответствует порогу перехода «спаренных»
электронной и дырочной подзон.
8.7. Оптическое поглощение и угол падения 309
межподзонные
переходы
Рис. 8.16. Спектры поглощения фотонов при межзонных и межподзонных переходах
качественно отличаются друг от друга. Поскольку электронные подзоны
параллельны, все переходы между двумя электронными подзонами имеют
место при одной и той же энергии. В случае межзонных переходов спектры
поглощения приобретают ступенчатый характер, при этом каждая ступень
соответствует энергии перехода вследствие связи между определенными
дырочными подзонами.
Дипольные моменты, определяющие силу осцилляторов для переходов, также
имеют различную природу, как это иллюстрируется рисунком 8.17.
При межзонных переходах дипольный момент возникает как результат набора
атомных диполей между блоховскими функциями (смотрите (8.57)). Эффективный
дипольный матричный элемент reff = rjjn, c\n, v) имеет размеры порядка 0,6 нм в GaAs, если
(т, с\п, v) = 1. В альтернативном случае при межподзонных переходах диполь является
результатом ортогональности огибающих функций (смотрите (8.75)). Эффективный
дипольный матричный элемент reff = (m \z\n) в этом случае имеет размер порядка 5 нм для
очень глубокой квантовой ямы GaAs / AlAs толщиной 8 нм. Таким образом, для данного
объемного полупроводника, дипольные матричные элементы для межподзонных переходов
могут быть существенно больше тех, которые соответствуют межзонным переходам.
а переход
б переход
е2
Рис. 8.17. Дипольные моменты переходов являются результатом взаимодействия либо (а)
диполей различных блоховских функций (межзонные переходы), либо (б)
диполей между различными огибающими функциями (межподзонные переходы).
((( 310 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
8.7.2. Влияние угла падения
Принцип в основе этого расчета идентичен тому, который был представлен для
случая объемного полупроводника (смотрите уравнение G.42)) с добавлением ряда
тонких моментов для учета двумерной природы квантово-размерной системы. Мы
могли бы поинтересоваться, почему следует ожидать, что коэффициент
поглощения будет изменяться в зависимости от того, падает ли излучение перпендикулярно
или под углом к квантовой яме. Сейчас мы представим детальное описание
механизмов поглощения излучения, имеющих место в квантовой яме.
Баланасная скорость перехода G(см~2 с) соответствует поглощенной мощности W
электромагнитной волны, равной:
W =
см1]
(8.78)
Среда, содержащая квантовую яму, является по сути неизотропной. Для расчета
поглощения, испытываемого волной, проходящей через среду, мы, таким образом,
должны учесть геометрию и пространственную протяженность пучка излучения
(смотрите рис. 8.18).
Рис. 8.18 иллюстрирует общий случай. Плоская волна с распределением потока,
определяемым Ф(/*), встречает на своем пути квантовую яму, перекрывающую угол 0по
отношению к направлению распространения. В этом случае амплитуда
электрического поля определяется соотношением:
, / \ 1 |„
(8.79)
Здесь: п{со) есть коэффициент преломления и Zo = (juje^l/2 есть вакуумный
импеданс. Энергия, пересекающая структуру за одну секунду составляет:
(8.80)
Рис. 8.18. Электромагнитная волна с распределением интенсивности Ф(г)
распространяется через среду и встречает на своем пути квантовую яму длиной L,
ориентированную под углом в к направлению распространения.
8.7. Оптическое поглощение и угол падения 31 I
Полная скорость поглощения в квантовой яме, нормированная на энергию
падающего излучения Жп, в этом случаен составляет:
L/г
w
1
I cose/2
-Lcose/2
Ф(О)
(8.81)
Здесь геометрия задачи заключена в соотношении интегралов. Вспомним, что как
скорость генерации, так и интенсивность F пропорциональны \Eq\2. Таким образом,
коэффициент зависит только от поляризации поля по отношению к яме.
Из последнего выражения (рис. 8.19) следуют два граничные случая:
1. Если перетяжка пучка излучения настолько мала, что полный поток пересекает яму,
два интеграла равны друг другу, при этом коэффициент поглощения arQW составляет:
w
ha>G[Eq(O))
O@)cos^
[на квантовую яму]
(8.82)
Отметим, что ширина ямы в явном виде не входит в это выражение для
поглощения. Скорость поглощения не зависит от ширины ямы и является безразмерной
(выраженная в процентах). С другой стороны, угол ^входит в (8.82) и также в выражение для
скорости перехода G в соответствии с правилами отбора, приведенными в Таблице 8.1.
2. Если перетяжка пучка излучения велика, что, в частности, имеет место в
случае в = л/2, и интенсивность не изменяется в яме, поглощение составляет:
W ho)G[EAO)] г
Ф(О)
(8.83)
'QW
-иг
Ф(г)
QW
а б
Рис. 8.19. Два предельных случая для поглощения. В первом случае поглощение не
зависит от глубины ямы, а во втором — зависит.
If 312 Глава 8. Полупроводниковые гетероструктуры и квантовые ямы
Здесь мы ввели коэффициент ограничения:
г _ [ЕДО)|2 <у
(8.84)
где JQW есть толщина ямы, а Г есть доля волны, которая «видит» поглощающую
среду.
В этой геометрии представляется естественным ввести коэффициент поглощения
квантовой ямы с использованием выражения:
1 dWm _ fta>g[E,@)] г Г ,
а ^7 1 a -} lCM
dx Ф@)
}lCM J @.65)
</QW
Коэффициент поглощения для
параллельного распространения в яме
Сейчас мы уже можем рассчитать коэффициент поглощения aQW с
использованием выражений для скоростей различных переходов G, которые мы установили в
(8.75) для межподзонных переходов.
Начнем с межзонных переходов. С учетом выражений (8.65), (8.79) и (8.82)
поглощение для квантовой ямы дается вкладами переходов, связанных с участием
различных пар участвующих подзон:
^ ||)кЧМ] (8.86в)
При этом коэффициенты поглощения для каждого перехода (смотрите уравнение
(8.75) составляют:
Вклад межзонных переходов п -> m
для поглощения квантовой ямы (%)
В случае межподзонных переходов поглощение между переходами с участием
различных подзон описывается соотношением:
Это дает для каждого перехода (смотрите (8.75)):
\№) (8-876)
Вклад от межподзонных переходов п -> т
в поглощение квантовой ямы (%)
В этом последнем выражении, как мы напоминаем, S есть 8-функция,
выраженная в Дж, которая может быть заменена на лоренциан, если переход уширен
по какой- то особой причине. Более того, мы отмечаем, что rfqz = Е /|2£ | есть вектор
поляризации электромагнитной волны и rj = sin# — его компонента вдоль оси
роста квантовой ямы. При п = 1 и т = 2 (8.876) идентично соотношениям C.37) и
C.39) для оптического поглощения в двухуровневой системе, полученным с
использованием формализма матрицы плотности. Это подчеркивает глубокую
аналогию между внутриподзонными переходами в полупроводниках и переходами в
атомной физике.
В соотношениях (8.866) и (8.876) мы видим существенно различный характер
угловой зависимости для каждого из этих типов механизмов. Более примечатель-
8.7. Оптическое поглощение и угол падения
ным является то, что межподзонное поглощение раскрывает характеристическую
зависимость от sin20 и, таким образом, оно характеризуется нулевым значением
при нормальном падении @=0). Как мы увидим позже в главе 11, это имеет очень
важные последствия для квантово-размерных фотодетекторов.
Пример
1. Межподзонное поглощение в квантовой яме GaAs.
Для фундаментальных переходов hh{—e{ в квантовой яме GaAs мы можем считать
перекрытие огибающих функций равным единице. Для электромагнитной волны,
падающей по нормали к квантовой яме межзонное поглощение дается формулой (8.866) и мы
находим для h *у=1,5 эВ:
Ю-31 кг 377 Ом Г 1 t
QW * 3 I \\1а ш\'с\ / \3
п т\">У ' F,58х Ю-16 эВс)
Здесь мы использовали правила отбора из таблицы 8.1, a rcv величина объемного
поглощения, приведенная в таблице 7.1.
2. Межподзонное поглощение в квантовой яме GaAs.
Рассмотрим глубокую квантовую яму GaAs, позволяющую нам
аппроксимировать низко лежащие состояния бесконечной прямоугольной ямой той же ширины.
Предположим, что ширина и уровень легирования ям составляют соответственно
10 нм и 1012 см~2, при этом температура достаточно низка так, чтобы занятым был
только основной уровень. Зазор между двумя уровнями вблизи дна ямы дается
соотношением A.49) или:
Я12=D-1)
16
2 0,067 х 0,9 х 10-30 кгхA0"8 м)
Дипольный матричный элемент определяется соотношением (З.Г.24):
|| ^я = 0,18а = 1,8 нм
И наконец, межподзонное поглощение в резонансе для волны, падающей под
углом 45°, дается выражением (8.876). Предполагая уширение йГ, равным 10 мэВ,
заменим ^-функцию на 1/(/гйГ) так, что:
1 0,169 377 Ом A,6х1019Сх1,8хЮ-9 мJ 1П16 _2 Q 1Л_3
= х-? х х— ^Ю16 м ~ 8x10 j
ЮбхЮ^Джс 0.01 3.3 2
Литература
G. Bastard, Wave Mechanics Applied tj Semiconductor Heterostructures,Wuey, New
York A991).
S.L. Chuang, Physics of Optoelectronc Devices, Wiley Interscience, New York A995).
C. Weisbuch and B. Vinter, Quantum Semiconductur Structures, Academic Press, Boston A991).
ДОПОЛНЕНИЯ
К ГЛАВЕ 8
8.А. Квантовые нити и ящики
Мы уже видели, что полупроводники могут использоваться для создания квантово-раз-
мерных структур, которые действуют таким образом, что ограничивают движение
носителей в направлении z (в направлении роста). Если движение ограничено еще и в другом
направлении (например, х) движение электронов в структуре останется свободным
только в одном остающемся направлении у. В таком случае мы можем эффективно
сформировать электронный волновод.
В технологическом смысле существуют два общих подхода для реализации
такого двойного ограничения (смотрите рис. 8.А. 1):
1. Для поперечного сегментирования квантовой ямы в в виде нитей может
использоваться литография.
2. Для этой же цели может использоваться отрицательное напряжение,
приложенное к металлическому затвору очень малых размеров. За счет увеличения
электронного потенциала под контактами мы создаем параллельные линейные
области обеднения в квантовой яме за исключением области, лежащей под
пространством, разделяющим контакты. При увеличении амплитуды приложенного
напряжения поперечный размер электронного волновода может быть уменьшен до
пределов отсечки, когда от канала в яме ничего не остается.
Очевидно, что уравнение Шредингера для огибающей функции у/(т),
описывающей электронные состояния в квантовой нити, имеет вид:
(8.А.1)
металл
зона обеднения
Рис. 8.А.1. Методы, используемые для
формирования квантовых нитей.
Формирование ультрамалой меза-структу-
ры с использованием литографии (а)
и задание поперечной симметричной
геометрии обеднения за счет
приложения потенциала к соответствующим
образом текстурированным
металлическим контактам (б).
8.Л. Квантовые нити и ящики
Потенциал V(x, z), управляющий процессами в такой квантовой нити,
сохраняет трансляционную симметрию в у-направлении. Таким образом волновая
функция yAj) допускает выделение плоской волны только в у-направлении, т. е.:
Функция £(х, z) удовлетворяет двумерному уравнению Шредингера:
(8.А.2)
(8.А.З)
В общем случае эти уравнения описывают одномерные подзоны с дискретными
связанными состояниями |/) в двух измерениях, а также свободное движение в
направлении у. Для заданной подзоны / энергия состояния (/, ку) есть:
(8.А.4)
Обобщая ход рассуждений, иллюстрируемый рис. 8.6., можно рассчитать плотность
состояний в подзоне, накладывая периодические пределы в направлении у
d(jc)=1A- (8.A.5)
Напоминаем, что gs есть коэффициент спинового вырождения (gs = 2). Плотность
состояний по энергии можно легко найти, записав плотность dn. в пределах бесконечно малого
интервала энергии dE\
dn. = D.(E)dE= 2D.(k)dky (8.А.6я)
В это выражение входит коэффициент 2, поскольку для заданной энергии Е имеются 2
значения ку, определяемые (8.А.4). Плотность состояний по энергии в этом случае дается
выражением:
dkr
m
Kb X2(E-E,)
(8.A.66)
Это выражение характеризуется сингулярностью при Е = Е. (смотрите рис. 8.А.2).
Для решения (8.А.З) в общем случае используются численные методы или
аппроксимации. Тем не менее, если мы представим потенциал в виде прямоугольной
нити размерами Lx x Ly, характеризуемый бесконечными барьерами, решение
может быть легко получено разделением переменных:
3D
2D
D(E)
D(E)
D(E)
OD
D(E)
E
Рис. 8.А.2. Плотность состояний в системах с размерностью, изменяющейся от 3 до 0.
Как видно, общий характер зависимости D(E) радикально зависит от
размерности ограничения. Для D(E) используются единицы [эВ1 см -° ], где
D — число измерений, вдоль которых частицы не испытывают ограничения.
((C16 Дополнения к главе 8
, z)= £,,„.(*> z)= ir T sin -7—sin -у- (8А7)
Здесь пх= 1, 2, 3, ..., nz= I, 2, 3, ... Энергия квантового ограничения,
соответствующая одномерной подзоне (пх, п), находится тривиально:
^.,=0^14 + ^-1 (8-А.8)
Мы видим, что если Lx» Lz уровни пх формируют лестницу с маленькими
ступеньками внутри уровней, что следует из разделения ямы на подзоны по ак В альтернативном
случае, когда Lx = Lz два набора уровней не могут разрешиться, при этом многие уровни
являются вырожденными.
Теперь мы можем распространить этот ход рассуждений вплоть до нулевой
размерности. Потенциал, ограничивающий электроны в трех измерениях, способен создать
полностью связанные состояниями, обладающие дискретным спектром. В этом
случае мы можем говорить о квантовом ящике, квантовой точке или даже об
искусственном атоме. Квантовые точки можно формировать с удивительной легкостью,
осаждая полупроводник с постоянной решетки, сильно отличающейся от этого же
параметра подложки другого состава. Необходимая величина рассогласования
постоянных решетки приводит к крайне малой критической толщине, как это имеет
место в случае InAs, осаждаемого на GaAs.B этом случае InAs формирует
маленькие островки на подложке GaAs, что приводит к квантовым ящикам
пирамидальной формы с высотой и шириной нанометрового размера. Рисунок 8.А.2
суммирует результаты для плотности состояний для систем с размерностью 3, 2, 1 и 0.
Литература
С. Weisbuch and В. Vinter, Quantum Semiconductor Structures, Academic Press, Boston A991).
8.Б. Экситоны
Наша трактовка полупроводников вплоть до настоящего момента покоилась на одноэлек-
тронной аппроксимации. В действительности же полупроводник состоит из колоссального
ансамбля взаимодействующих атомных ядер и электронов. С учетом этого
результативность этой простой аппроксимации может считаться просто удивительной. В
действительности полупроводник представляет собой систему с определенным фундаментальным
состоянием. То, что мы наблюдаем, есть возбуждение этой системы и ее отход от этого
фундаментального состояния. То, что мы называли «энергией электрона» в действительности
выражает разность энергии системы с одним дополнительным электроном и системы в
основном состоянии (без дополнительного электрона). Подобным же образом «энергия
дырки» соответствует разности энергии системы в основном состоянии и энергии
системы при удалении электрона.
Оправдание того, почему такие возбуждения могут быть удовлетворительно
аппроксимированы одночастичными уравнениями Шредингера, является одной из проблем,
которые лучше всего решаются в рамках теории многих тел. В значительной степени
успешность этой аппроксимации определяется формой кристаллического потенциала, который
мы лишь едва очертили. Оказывается, что этот потенциал должен учитывать ядерные ку-
лоновские потенциалы и их экранировку электронами за счет того, что известно
как обменно-корреляционный потенциал Vxc. Этот потенциал описывает энергию,
которую может получить система за счет коррелированного движения электронов.
Такая корреляция в движении приводит к некоторому увеличению среднего
расстояния между электронами, что приводит к уменьшению кулоновской энергии
из-за электрон-электронного взаимодействия. Основной урок, который из этого
8.Б. Экситоны
следует, заключается в том, что для многих типов возбуждений одноэлектронная
аппроксимация является вполне разумной при условии, что кристаллический
потенциал выбран достаточно удачно.
В расчетах поглощения электромагнитной волны, проведенных в главах 7 и 8,
предполагалось, что возбуждение системы, сохраняющее число частиц, может быть
записано в виде суммы возбуждений, соответствующих генерации
электронно-дырочных пар в системе. В процессе обмена между электромагнитной волной и
полупроводником полная энергия сохраняется. Фотон исчезает и электронная система
возбуждается (генерация электронно-дырочной пары) в состояние, расположенное
выше на величину энергии, которую несет фотон. Однако, в этом возбужденном
состоянии корреляция электронных движений отличается от той, которая
характерна для основного состояния. Это приводит к качественным изменениям в
возбужденных состояниях, выходящим за пределы количественных эффектов,
рассматриваемых в рамках одноэлектронного описания. И вновь для того, чтобы показать
возможность представления этой корреляции в виде взаимодействия между дыркой
с положительным зарядом и массой (+е и mh) и электроном с массой те и
отрицательным зарядом, следует прибегнуть к теории многих тел. Однако, демонстрация
этого результата потребовала бы слишком больших усилий и к тому же она выходит
за рамки настоящей книги.
8.Б.1. Трехмерные экситоны
Попытаемся описать состояние электронно-дырочной пары с учетом взаимодействия их
противоположных зарядов. Очевидно, что нам необходимо двухчастичное состояние, т. е.
являющееся результатом тензорного произведения (смотрите уравнение B.48))
электронного и дырочного состояний. Двухчастичная волновая функция может быть представлена
в виде ряда по блоховским функциям для электронов и дырок:
<Кг„ г2) = ^гХС(к" к2)е'к' Ч,(г.)е'к'Ч2(г2) = ХС(к" Мк» к>> (8Б1)
В этом случае состояние двух частиц дается решением двухчастичного уравнения Шредингера:
) (8.Б.2)
Давайте подставим в это последнее уравнение (8.Б.1) и спроецируем результат на
Ц, к2), что дает:
+ ^+К^-W, к2) + Ус(к; к;)(к„ к2|к(Г1 -г2)|к;, к;) = яс(к„ к2) (8.б.з)
Используя тот факт, что потенциал взаимодействия медленно изменяется по
отношению к размерам элементарной ячейки, используем тот же ход рассуждений, что и
ранее и (смело!) введем огибающую функцию с тем, чтобы упростить матричный
элемент:
i(k-2-k2-k;+
(8.Б.4)
п -к2-к2-к1+К1 .-, k;) = -Ak,_k2_qK(q)
Здесь:
= —[dreiqrK(r) (8.Б.5)
/1 1 It,/ 4I1/ 1/\ 1 fj л ^-k.Mr.-r,)
(кр к2 \V(t{ - г2)|к;, к'2) = — di^dr.e К(г, - г2)е
318 Дополнения к главе 8
Это выражение представляет собой Фурье-образ кулоновского взаимодействия. Для
получения (8.Б.4) мы предположили, что периодические части блоховских
функций не зависят от к.
В этом случае мы можем записать уравнение Шредингера (З.Б.З) в виде:
к2) + У K(q)C(k, -q,k2 + q) = EC(kl9 k2) (8.Б.6)
Поскольку kj + k2 сохраняется в члене взаимодействия, представляется
целесообразным провести замену переменных kj и Ц на новые переменные Кик, где:
к к. к2
н (8.Б.7)
к- = ^К + кик^1К-к
Здесь М= те + mh есть полная масса, а \/тг = (\/те) + A//яА) определяет
приведенную массу тг. С этими новыми переменными мы имеем:
К К) - с(к, к)
Ц - q, k2 +q) = С(К, k + q)
При этом уравнение Шредингера приобретает вид:
' к>+ У ^(q)C(K, к + q) = £C(K, к) (8.Б.9)
J
Сумма по q обусловлена взаимодействием между электроном и дыркой и касается только
второго члена аргумента для С. Это означает, что ЦК, к) допускает разделение переменных и
может быть записано в виде С(К, k) =y(K)g(k), где g(k) должно подчиняться соотношению:
q) = Eg{k) (8*Б-10)
Теперь мы можем ввести огибающую функцию для относительного движения:
В этом выражении мы узнаем определение, эквивалентное (8.12). Используем ту же
процедуру, что и при получении из (8.14) уравнения (8.17), что дает уравнение Шредингера
(8.10) в реальном пространстве:
J^L\ (8.Б.12)
2mr ov ' wow [ 2N
В этом выражении мы узнаем уравнение Шредингера для атома водорода (или лучше
сказать, для позитрония\). В этом случае допустимые величины энергии составляют:
Е =£ i *2*2 КУ* п = \ 2
2М (8.Б.13)
Здесь: Ry есть энергия ионизации s-состояния атома водорода. Эта величина известна как
Ридберг и она равна 13,6 эВ. Как мы это могли и ожидать, взаимодействие между
электроном и дыркой создает дискретные состояния в запрещенной зоне, через которые электрон
и дырка связываются друг с другом (с точки зрения их относительного движения),
сохраняя при этом свободу перемещаться по кристаллу как пара. Член h2K2/2Mсоответствует
кинетической энергии, связанной со свободным движением центра масс двух частиц. При
энергии, большей Eg + h2K2/2M, мы имеем континуум разрешенных энергетических со-
8. Б. Экситоны
стояний. Этот континуум соответствует возбуждению системы, которое приводит к
эффективному освобождению электрона и дырки от их взаимной связи. Рисунок
8.Б.1 иллюстрирует спектр возбуждения полупроводника.
Взаимодействие системы с электромагнитной волной сохраняет полную
энергию и импульс. Это означает, что К = q ~ 0, где q есть волновой вектор фотона.
Таким образом спектр поглощения содержит ряд дискретных линий в запрещенной
зоне, а также область континуума при h со > Eg.
Помимо проявления дискретных линий в спектрах поглощения электронно-
дырочная корреляция в полупроводниках имеет и другие следствия. Поглощение
континуума также увеличивается вблизи края запрещенной зоны. В результате этого
поглощение в функции энергии фотона проявляет разрыв вместо более мягкой
зависимости вида (hco— E)l/2, рассчитанной в Главе 7. Этот эффект, описываемый
коэффициентом Зоммерфельда, обусловлен пространственным перекрытием волновых
функций электрона и дырки вследствие взаимодействия, которое стремится
приблизить обе частицы друг к другу. На рис. 8.Б.2 приведено сравнение усиленного
поглощения вследствие экситонных состояний с поглощением в рамках одноэлек-
тронной модели.
Пример
1. Экситоны в GaAs.
В случае GaAs мы имеем те = 0,067aw0, mhh = 0,5 lm0 и е = 12£0. Энергия связи экситона
для п — 1 составляет:
Е Це*.
тАе
Мы видим, что величина Ев мала по сравнению с А^Гпри комнатной
температуре. В результате этого связанным экситон может оставаться только при очень
низких температурах. Среднее расстояние между электроном и дыркой в экситон-
ном состоянии с п = 1 составляет (по аналогии с боровским радиусом в атоме
водорода):
0,052 нм = 10,6нм
Рис. 8.Б.1. Спектр возбуждения
полупроводника отражает присутствие связанных
экситонных состояний в запрещенной зоне.
Связь с фотоном, имеющим волновой
вектор q, обеспечивает сохранение полной
энергии и импульса. Таким образом, спектр
поглощения состоит из набора дискретных
линий, за которыми следует континуум.
= cq
>■ к
3 20 Дополнения к главе 8
поглощение
Рис. 8.Б.2. Экситонная корреляция между электроном и дыркой модифицирует спектр
поглощения. По сравнению с «некоррелированным» спектром (тонкая
линия) в энергетической зависимости поглощения проявляются резкие экси-
тонные резонансы в области ниже края запрещенной зоны, а также резкое
возрастание поглощения в области слегка выше края поглощения.
Это согласуется с предположением о медленно меняющейся огибающей функции
по сравнению с размерами элементарной ячейки.
2. Экситоны в GaN
Для широкозонного полупроводника, каким является GaN, £,= 34 эВ, те = 0,22т0,
mhh ~ то и £ = 9,8f0, при этом приведенная масса составляет 0,18 т0, Ев =26 мэВ и
а*в = 2,8 нм. В результате этого экситонные эффекты намного более важны в
широкозонных полупроводниках. При комнатной температуре доля 1 — ехр(—26/25,9)
или 64% генерированных экситонов останется в связанном состоянии.
8.Б.2. Двумерные экситоны
Мы видели, что в квантовой яме движение электронов может быть ограничено в
пределах области размером в несколько нанометров, т. е. на расстоянии, значительно
меньшем боровского радиуса трехмерного экситона. Следствием этого ограничения
является то, что зоны квантуются в виде подзон, разделенных интервалом в
несколько десятков мэВ, что превышает энергию связи трехмерного экситона.
Применительно к корреляции между электронами в основной зоне проводимости и дырками
в основной валентной зоне кулоновское взаимодействие может иметь место только в
направлении, параллельном границам раздела. По сравнению с потенциалом
ограничения кулоновский потенциал не играет существенной роли в перпендикулярном
направлении. В этом случае экситонная волновая функция представляет собой:
K2)C1c(^)eiKlRl^o(r1)CU2)elK2R^,,o(r2) (8.Б.14)
к,, к.
Здесь векторы R и К обозначают движение, параллельное границам раздела. Используя те
же самые преобразования, что и в предыдущем разделе, получаем уравнение Шредингера,
управляющее движением частиц в плоскости:
(8.Б.15)
(8.Б.16)
-e, -£l-Eg k(R)
При этом эффективный потенциал взаимодействия есть:
e2k,c(z,)\2\C(z,)\
^ff(R) =
-z2]2
8. Б. Экситоны
Эта последняя аппроксимация действительна в предельном случае, когда
огибающие функции характеризуются пренебрежимо малой протяженностью по
сравнению с экситонным радиусом. Решение этого уравнения для «двумерного
водородного атома» дает следующие собственные энергии:
В этом выражении используется та же самая эффективная константа Ридберга, которая
была определена в последнем разделе.
поглощение
fico
+ «2
б
1.0
ф 0.6
ф
I 0.4
0.2
0.0 -
Ч [50 Periods
N 10nm GaAs
[i0nmAI03Ga07As
I
I
1.40 1.45
1.50 1.55 1.60 1.65
энергия фотона (эВ)
1.70 1.75
Рис. 8.Б.З. Спектр поглощения квантовой ямы, модифицированного корреляцией
электронов и дырок, т. е. присутствием экситонов. По сравнению с процессом,
в котором участвуют лишь свободные электронно-дырочные пары (тонкие
линии), экситоны приводят к возникновению дискретных линий ниже края
эффективной ширины запрещенной зоны, при этом каждая ступенька,
обусловленная поглощением континуума, деформируется узким экситонным
пиком (а). Этот результат выглядит особенно выразительно в
экспериментах по квантовым ямам различной толщины (б) (по данным D.S. Chemla,
and DA. В.Miller, Adv. Phys. 38,89 A989), перепечатано с разрешения Taylor
& Francis Ltd. Http: www.co.uk/journals).
322 Дополнения к главе 8
Таким образом, двумерный экситон обладает энергией связи, в четыре раза
большей по сравнению с эквивалентным трехмерным экситоном.
Пример
Рассмотрим квантовую яму GaAs шириной 5 нм. В предыдущем примере мы
видели, что энергия связи трехмерных экситонов в GaAs составляет 5,6 мэВ. В этом
примере ширина ямы намного меньше боровского радиуса экситона а*в = 10,6 нм,
при этом энергия связи составляет 4 х Ев или 22,4 мэВ. В результате этого
существенная доля ансамбля экситонов E8%) останется в связанном состоянии при
комнатной температуре. Соответственно в этом случае экситонные особенности в
явном виде проявляются в полощении и люминесценции этих квантовых ям
(смотрите рис. 8.Б.З).
В более реалистичном случае, когда пространственной протяженностью волновых
функций g(z) и g(z) по сравнению с я* полностью пренебречь нельзя, эффективное
взаимодействие ослабляется по сравнению с чисто двумерным случаем, при этом энергия
связи экситонов плавно уменьшается в направлении энергии связи трехмерных
экситонов. Количественная трактовка этого эффекта требует, чтобы, помимо основных
зон учитывались бы также и другие подзоны. Разумное описание этого
промежуточного режима возможно только с использованием численных методов.
Как и в трехмерном случае, корреляция между электроном и дыркой
кардинально модифицирует спектр поглощения квантовых ям. В области ниже края
эффективной запрещенной зоны Eg + е{ + е* спектр содержит дискретные линии. В
области выше края зоны наблюдается увеличение поглощения по сравнению со
случаем свободных электронов и дырок. Рисунок 8.Б.З качественно иллюстрирует
модификацию спектров поглощения.
Литература
R.J. Elliott, Phys. Rev., 108, 1384 A957).
Н. Haug and S.W. Koch, Quantum Theory of the Optical and Electronic Properties of
Semiconductors, World Scientific, New York A990).
S. Smitt-Rink, D.S. Chemla, and DA. Miller, adv. Phys. 38, 89 A989).
8.B. Квантово-размерный эффект Штарка и модуляторы
с собственным электрооптическим эффектом
В дополнении 1.В мы уже видели, каким образом электрическое поле /%
приложенное перпендикулярно квантовой яме будет смещать энергетические уровни в яме
(или уровни, которые, как мы теперь знаем, соответствуют дну подзон). Этот
квантово-размерный эффект Штарка может использоваться в модуляторах
электропоглощения. В этом случае приложенное напряжение модулирует интенсивность
проходящего пучка излучения.
Для рассмотрения этого эффекта выберем частоту излучения таким образом,
чтобы при F = 0 энергия фотона соответствовала области прямо под краем
эффективной ширины запрещенной зоны квантовой ямы:
Av <£,+<(())+£/@) (8.В.1)
В этих условиях излучение не поглощается ямой (смотрите рис. 8.В. 1).
С использованием простой модели дополнения 1.В находим, что уровень е*
снижается в соответствии с уравнением A.В.2):
8.В. Квантово-размерный эффект Штарка 323
J
вход
выход
JUUUL
выход
в '
Рис. 8.В.1. Принцип функционирования модулятора на основе квантово-размерного
эффекта Штарка.
При этом в случае очень глубокой ямы (уравнение A.В.4)):
Ъ л П
Основной дырочный уровень смещается аналогичным образом:
*;и=*;(о)-4^4-2
(8.В.З)
(8.В.4)
ч я h
При этом эффективная ширина запрещенной зоны (рис. 8.В.2) уменьшается
(длинноволновый сдвиг) в соответствии с:
Е (F)=F Г01 Г e2jL4MF> (8B5)
*,effV ) g,eflfL J 35Л6 h2
Здесь М = те + тА. При фиксированной величине Av0 эффективная ширина
запрещенной зоны может стать меньше hv0, и яма будет поглощать излучение пучка.
Край поглощения является очень резким (рис. 8.10 или 8.Б.З) В результате этого
Рис. 8.В.2. Под воздействием
электрического поля F эффективная ширина
запрещенной зоны и связанный с ней край
поглощения уменьшаются по энергии. В
результате этого фотоны с энергией, которая
изначально была меньше края
запрещенной зоны при нулевом поле (а), будут
поглощаться квантовой ямой при
приложении поля (б).
У
r,eff
к
@)
\
i
г
Дополнения к главе 8
слабая модуляция электрического поля приводит к сильной модуляции
пропускаемого света. Амплитуда модуляции может быть увеличена последовательным
введением нескольких квантовых ям.
Пример
В случае квантовой ямы GaAs шириной L = 200 А при приложении поля с
напряженностью F— 10 кВ/см находим:
^м^ОбУ + О^ДхЮ-31 кг /in6R _lV __„
xiiu dm ) e — z,/
K.h Z ^ x(iqB
1 * ' 3V A,05х10-34ДжсJ
Для длин волн порядка 1,5 мкм это соответствует длиноволновому сдвигу края
поглощения величиной АЛ/Л = АЕ/Е или 5 нм.
Из уравнения (8.В.5) видно, что квантово-размерный эффект Штарка
проявляет очень сильную зависимость от ширины ямы L. Хотя этому эффекту
благоприятствует большая ширина ямы, его амплитуду нельзя произвольно увеличивать за
счет возрастания ширины ямы. Ограничение возникает из-за того, что перекрытие
электронной и дырочной волновых функций (локализованных на
противоположных границах раздела из-за приложенного поля) становится все меньше по мере
возрастания ширины ямы. Это, в свою очередь, приводит к уменьшению
поглощения (уравнение (8.636)).
В пределе широкой ямы подзоны данной зоны сближаются до тех пор, пока
становится уже невозможно их различить одну от другой, при этом квантво-раз-
мерный эффект переходит в эффект Франца—Келдыша, изученный в дополнении
7.А. Можно было бы спросить себя, а какой из этих двух механизмов способен
обеспечить лучшие функциональные характеристики модулятора. Преимуществом,
предоставляемым квантовыми ямами является то, что высокий уровень
поглощения гарантируется состоянием поглощения, т. к. как электроны, так и дырки
локализуются в пределах той же самой ямы. В альтернативном варианте эффект
Франца—Келдыша сопровождается сравнительно слабым поглощением в состоянии
«блокирования излучения». Это связано с тем, что экспоненциальный спад края
запрещенной зоны всегда остается достаточно слабым (смотрите рис. 7.А.З).
Другим преимуществом, обеспечиваемым квантово-размерным эффектом Штарка,
является то, что ширина квантовой ямы может быть оптимизирована (в процессе
роста) с учетом специфической длины волны модулируемого излучения.
Еще одно явление, обусловленное квантово-размерным эффектом Штарка,
является то, что квантовая яма под влиянием электрического поля ведет себя как
фотопроводник. Электроны и дырки, фотогенерированные в процессе поглощения, могут
покинуть яму либо вследствие теплового выброса в надбарьерную область, либо
вследствие туннелирования через потенциальные барьеры (смотрите рис. 8.В.Зя). После
чего электрическое поле вытягивает носители из структуры, вызывая протекание
фототока, который в первом приближении пропорционален произведению
поглощения на поток излучения. Комбинированное использование квантово-размерного
эффекта Штарка и фотопроводимости приводит к реализации прибора с акронимом
«SEED» или прибора с собственным электро-оптинеским эффектом.
Принцип функционирования SEED-прибора иллюстрируется рисунком 8.В.З.
Мы включаем модулятор электропоглощения в цепь смещения с
последовательным сопротивлением R. Электрическое смещение модулятора в этом случае
приводит к тому, что энергия фотона начинает превышать положение экситонного
пика, связанного с основным переходом, что приводит к сильному поглощению.
В этом случае SEED-прибор находится в состоянии сильного поглощения (смотрите
рис. 8.В.1). При малом уровне мощности падающего излучения Р.п фототок
/также остается малым. По мере увеличения мощности оптического излучения фото-
8. Г. Валентные подзоны
'out
Рис. 8.В.З. Принцип функционирования SEED-прибора. Под
влиянием электрического поля носители освобождаются из
квантовой ямы, например, за счет туннелирования (а).
Структура, содержащая квантовые ямы, электрически смещается
цепью с последовательным сопротивлением RF). Реакция
структуры на действие электрической цепи заключается в резком
уменьшении выходного сигнала, когда мощность входного
излучения превышает определенное пороговое значение (в).
ток также возрастает, что приводит к скачку падения напряжения на
сопротивлении KSEED. В результате этого падение напряжения на модуляторе также падает,
что сопровождается уменьшением напряженности поля FSEED в квантовой яме,
приводящим к ослаблению поглощения (т. к. ослабление поле сопровождается
коротковолновым сдвигом края поглощения). Как только падение напряжения на
SEED-приборе достаточно упадет, прибор переходит в состояние слабого
поглощения. Это, однако, приводит к уменьшению фототока, что способствует
восстановлению состояния сильного поглощения SEED-прибора. Ниже этот цикл
суммируется в следующем виде:
ahia.
FSEED I => коротковолновый сдвиг :
II:
v T
KSEED '
F Т ■
rSEED '
длинноволн овый сдвиг
Таким образом, SEED-прибор обладает двумя стабильными состояниями при
заданном уровне мощности падающего излучения, включение которых
определяется предысторией ранее проводившейся засветки. Режим бистабильности, в
пределах которого SEED проявляет такой характер, может использоваться, например, в
элементах оптической памяти.
Если в дополнение к этому мы заменим внешнее сопротивление вторым
SEED-прибором, то станет возможным объединять такие элементы в цепи, способные осуществлять
логические операции с использоанием комбинированных пучков излучения.
Литература
S. Schmitt-Rink, D.S. Chemla, and D.A. Miller, Adv. Phys.3S A989).
8.Г. Валентные подзоны
В разделе 8.3 мы уже видели, каким образом электронное ограничение
потенциалом ямы приводит к сдвигу минимума зоны проводимости и проявлению
квантовой энергии ограничения. В случае валентной зоны мы уже не можем
использовать ту же аппроксимацию. Уровни у потолка валентной зоны являются
вырожденными по отношению к подзонам легких и тяжелых дырок в центре зоны
Бриллюэна. В дополнении 1.Б мы уже видели, что возмущение может приводить к
снятию выврождения уровней. И в этом случае мы смогли решить задачу, устано-
3 26 Дополнения к главе 8
вив векторное подпространство, перекрываемое вырожденными состояниями, а также
изучая влияние возмущения на это подпространство. Сейчас мы покажем, каким
образом можно расширить этот подход с тем, чтобы включить в него
аппроксимацию огибающей функции для набора зон.
Основной идеей, лежащей в основе этой аппроксимации, является предположение о
том, что волновые функции дырок могут быть представлены в виде ряда:
Здесь: ип0 есть волновые функции в центре зоны Бриллюэна для различных
дырочных подзон (т. е. п — 1 для тяжелых дырок и п = 2 для легких дырок), а £п есть
огибающая функция, которая изменяется в пределах существенно большего
масштаба длин по сравнению с постоянной решетки. При рассмотрении в пределах
многих элементарных ячеек уравнение (8.Г.1) показывает, что мы находимся в
векторном подпространстве, образованном вырожденными дырочными зонами.
Уравнение Шредингера для \j/ всегда может быть выражено в виде:
(8.Г.2)
Здесь К есть кристаллический потенциал, a Vx есть внешний потенциал. Это
уравнение можно записать также и в виде:
2/Ил
(Р<Г„)[Р"„о(г)]
(8.Г.З)
Здесь мы использовали тот факт, что ип0 представляют собой стационарные
состояния кристалла при к = 0 с энергией еп0. Подобно тому, как это уже неоднократно
делалось на протяжении этой главы, спроецируем это уравнение на известный
базис. Для этого умножим это уравнение на u*NQ и проинтегрируем по всему
пространству. Изменение £п в пределах постоянной решетки пренебрежимо мало,
поэтому мы можем привести интегралы к более удобному виду, следуя методу,
использованному в (8.55). Ортогональность блоховских функций в пределах каждой
ячейки приводит к следующему уравнению для £п:
материал 1
материал 3
Рис. 8.Г.1. Валентные зоны в квантовой яме.
8.Г. Валентные подзоны 327 jft
- ^0)^(г) (8.Г.4)
Здесь Р^ = (uj^u^) есть матричный элемент, связывающий TV-ную и я-ную зоны в рамках
к • р-теории (смотрите Дополнение 5. В).
Мы видим, что (8.Г.4) является тем же самым матричным уравнением, полученным
при рассмотрении к • р-теории (смотрите E.В. 10), если мы заменим к на оператор р и
введем в диагональ матрицы внешний потенциал. Для потенциала V(z), изменяющегося только
в одном направлении, Kj останется хорошим квантовым числом, при этом огибающая
функция может быть представлена в виде £(г) = (l/V>4)^K(^)exp(iK|( • R), который приводит
уравнение к системе связанных дифференциальных уравнений относительно £,K(z):
[Е-'лк^м <8Г51
Здесь мы использовали тот факт, что плоская волна в направлении, перпендикулярном z,
диагонализирует к • р-матрицу с собственными энергиями £^Щ, 0).
В прямоугольной квантовой яме (смотрите рис. 8.Г.1) PNn и б^(Кц, 0) являются
постоянными в каждом материале.Влияние потенциала V(z) заключается в
возникновении разрывов зон, которые мы учитываем, накладывая на волновые функции и
поток вероятность условия непрерывности на границах раздела (смотрите раздел 8.2).
Мы видим, что в каждом материале решение (8.Г.5) соответствует энергии Ев виде:
<Г„ = але!*-г+/?„е-^ (8.Г.6)
Здесь кп есть комплексное число, которое является решением уравнения:
ej&r кп) = Е (8.Г.7)
т. е. кп есть поперечный волновой вектор, при котором зона п имеет энергию Е.
Следует отметить, что для энергии в пределах запрещенной зоны и над потолком
валентных зон уравнение (8. Г.7) имеет чисто мнимое решение кп = шп (смотрите, например,
уравнение E.В.25)). В объеме такое решение является недопустимым, т. к. оно расходится
на бесконечности. Однако, в случае туннельного эффекта такое решение может
возникнуть в виде затухающей волны в конечной или полубесконечной области пространства.
Рисунок 8.Г.2 иллюстрирует этот принцип для двух дырочных подзон в двух материалах
для энергии, близкой к валентной зоне.
В барьерном материале для двух валентных зон, Е > ^(Кр 0) возможно только
затухающее решение. Если между — L/2 <z<L/2 заключен узкозонный материал, решение для
Z < -L/2 должно содержать яглA) = 0 в разложении (8.Г.6). При z > L/2 только /?C) = 0 дает
возможное решение. В материале ямы Е< £/(Кц, 0) без каких-либо ограничений на
коэффициенты. На границах раздела условия непрерывности волновых функций, следующие
из (8.Г.5), например при z — Z_ = ~L/2, имеют вид:
а^е*- = а™**"*- + ^2)e**<- (8.Г.8)
Аналогичное уравнение для условия непрерывности производной волновой функции
имеет вид:
m°1' ' (8.Г.9)
Как мы видим из (8.Г.9) влияние границ раздела заключается в перемешивании
компонент легких и тяжелых дырок, хотя эти компоненты являются независимыми
Дополнения к главе 8
к
A)
(iK
£1<Х
Ti^»
-j >^
/
у^^ к = \ к
<ч&—►
^^ к
X
\
B)
е2
B)\
£2
/
/
\
а материал барьера б материал ямы
Рис. 8.Г.2. Вблизи валентной зоны значения к, при которых е{к) =Е являются
действительными при Е, лежащей ниже потолка валентной зоны, и
действительными при Е, лежащей выше. Рисунок показывает, каким образом
волновые векторы, входящие в уравнения (8.Г.6)—(8.Г.9),определяются для
заданной энергии Е, определяемой Кц =0.
-40
-60 -
-80 -
-100
-120
-140
-160
0.05
0.10
-0.10 -0.05 0.00
К„ (А)
Рис. 8.Г.З. Валентные подзоны квантовой ямы, соответствующие движению,
параллельному границам раздела, являются непараболическими. В данных рас-
счетах предполагалось, что ширина ям составляет 12 нм, глубина — 44 мэВ,
а высота барьеров — 70 мэВ.
в каждом материале. Четыре соотношения (8.Г.8)—(8.Г.9) для N= 1 (тяжелые
дырки) и N= 2 (легкие дырки) определяют четыре коэффициента для материала
квантовой ямы в функции двух коэффициентов в материале барьера при z > L/2.
Граничные условия на границе раздела при z+ = L/2 определяют четыре коэффициента
для затухающих волн в материале барьера. В этом случае мы должны искать
энергии и коэффициенты ягяA), устраняющие коэффициенты а®\ После этого нам
остается только определить нормировочный коэффициент для волновой функции.
Хотя методология расчета и ясна, сами расчеты должны проводиться
численными методами. Некоторые из иллюстрирующих примеров приведены на рис. 8.Г.З.
Очевидно (что и не удивительно), что дисперсионные кривые каждой подзоны
значительно отклоняются от простых парабол.
ГЛАВА 9
ВОЛНОВОДЫ
9.1. Введение
Одной из основных целей оптоэлектроники является использование фотонов в
качестве элементарных битов для переноса и обработки информации. Однако до того,
как электроны будут лишены своей привилегированной роли в интегральных
электронных схемах, должны быть разработаны средства, которые позволили бы
фотонам распространяться по определенным областям, где они могли бы участвовать в
выполнении логических или аналоговых операций. Волноводы дают метод
захвата света в локальных областях распространения, способных выполнять функцию
оптических межсоединений. Вторым преимуществом волноводов является то, что
они предоставляют средство для усиления взаимодействия между светом и средой
за счет концентрации плотности оптической энергии в пределах узких каналов. Это
является предметом первостепенной важности в приборах, основанных на
нелинейно-оптическом взаимодействии со средой (например, в электрооптических
модуляторах, оптике с преобразованием частоты и т. д. ...), а также при максимизации
эффективности лазерных диодов.
Пример
Непрерывное излучение мощности в десять мВт можно легко каналировать по
волноводу шириной 3 мкм и толщиной 0,2 мкм. Это приводит к плотности мощности
на единицу поверхности:
Р = 10 Вт /C х 10 х 2 х 10 см2 )= 1,6 МВт см2
Эта величина представляет собой значительную плотность мощности. Мы можем
сравнить ее с максимальными уровнями электрической мощности, переносимыми
по электронным цепям. Эта величина в типичном случае соответствует плотности
тока в 1 МА см~2 (этот предел возникает вследствие электромиграции атомов в
металлических межсоединениях) при напряжении в 1 В, что приводит к плотности
мощности величиной в 1 МВт/см2. Следует также отметить, что пиковая плотность
мощности топтической энергии, переносимой волноводами, может быть увеличена
в импульсном режиме вплоть до 1 ГВт/см2.
9.2. Геометрический подход к волноводам
Интерпретацию волноводного распространения света мы начнем с рассмотрения
распространения световых пучков. Этот подход позволит нам быстро подойти к
интуитивному пониманию концепций, лежащих в основе этого явления.
Рассмотрим слой сердцевины, сформированный из диэлектрического материала
толщиной d и коэффициентом преломления п{, заключенный между двумя очень
толстыми (в идеальном случае бесконечными) ограничивающими слоями с
коэффициентом преломления пг Световой пучок внутри среды 1 образует угол 0х' по
отношению к нормали к плоскости, разделяющей слои. Затем этот луч за счет
преломления переходит в среду 2 под углом в\ к нормали (смотрите левую часть
рисунка 9.1л).
330 Глава 9. Волноводы
Рис. 9.1. Лучевое представление условий, приводящих к оптическому ограничению
света волноводом (а). Числовая апертура волновода дается максимальным
синусом угла входа для пучка, входящего из воздушной среды (б).
Вспоминая основные результаты Декарта—Снелля—Френеля, мы можем
сделать следующие выводы:
• углы в\ и в\ связаны друг с другом соотношением:
я, sin в[ = п, sin
(9.1)
• если пх > п2 световая волна в среде 1 полностью отражается, если она падает под
критическим углом 6'с (полное внутреннее отражение)^ определяемое соотношением:
efc = arcsin -^
и I
(9.2)
• если поляризация волны является поперечной электрической (ТЕ), т. е. если
поляризация электрического поля параллельна плоскостям слоев, волна отражается и ее фаза
сдвигается по отношению к падающей волне на угол фг, лежащий между Оиж:
cos0,'
sin20,
1/2
(9.3)
Здесь: 0, = я/2 — в\. Заметим, что как общее правило мы сохраняем символ ' для
обозначения компоненты, соответствующей углу в, т. е. в' = л/2 — в.
Правая сторона рис. 9.1л описывает ситуацию, соответствующую полному
внутреннему отражению, когда волна становится распространяющейся при условии, что
в\ > 6'с. В то же время мы не должны полагать, что любая электромагнитная волна,
удовлетворяющая последнему условию будет волноводной. В действительности же
каждое отражение между границами раздела между двумя различными средами будет
приводить к дефазировке волны, что будет приводить к ее деструктивной
интерференции с самой собой, за исключением случая синфазности волны с волнами,
возникшими в результате предшествующих отражений. Это последнее условие хорошо
иллюстрируется рисунком 9.1 а. Проследим два последовательных отражения от двух
границ раздела в трех точках /0, 1Х и /2. Явно видно, что волна в точке /2 является
9.2. Геометрический подход к волноводам
результатом, по крайней мере, двух других волн: волны, которая не испытала
отражение и которая соответствует смещению IQM, а также другой волны, испытавшей
два отражения, прошедшей расстояние 101{ + /,/, и получившей вследствие двух
отражений фазовый сдвиг Bф). Эти две компоненты характеризуются разностью расстояний
распространения /,/2 - 1{М= IJ2 - IlI2cos20l = 2sin201/1/2 = 2sin201 x d/cos&c = = 2dsin<91 и
фазовым сдвигом 2фг, что приводит к дефазировке величиной 2kdsm6{ — 2фг, где к есть
волновой вектор, a 2mJA0 есть длина волны электромагнитной волны в вакууме.
Фазовые сдвиги из-за многократных отражений будут приводить к деструктивной
интерференции, если только они не будут кратны 2я, в результате чего мы приходим
к условию самосогласования локализованной волны:
2ппх
-2фг = 2лт
(9.4)
Теперь нам остается только подставить это последнее условие в формулу Френеля
(9.3) с тем, чтобы поучить:
. Gm,d . л тк
tan —l— sin 0, ——
sin2 ^с
sin2 (9,
1/2
(9.5)
Уравнение (9.5) с неизвестной величиной sin#, позволяет определить различные углы
9т, обеспечивающие волноводное распространение волн в волноводе. При этом мы не
забываем, что фазовый сдвиг 0гимеет величину в пределах от 0 до я: Рисунок 9.2
иллюстрирует графический метод получения допустимых решений этого уравнения. Когда sin^
изменяется в пределах интервала 0 —> sin#c, член в правой стороне периодически проходит
через +оо -> 0, тогда как член в левой стороне периодически проходит через 0 -^ +«>
каждые XJ2nxd. Кроме того рисунок. 9.2 позволяет рассчитать количество Nm вол-
новодных мод, распространение которых возможно в волноводе. Их будет столько,
сколько периодов содержится в интервале 0 -» sin#c или %mej{XJ2n{d). Таким
образом, мы находим:
(9-6)
Число разрешенных ТЕ-мод
в симметричном волноводе
Здесь Int-функция целого числа, a NA есть числовая апертура волновода,
определяемая с использованием соотношения (9.2) в виде:
0.5
Рис. 9.2. Графическое решение уравнения (9.5) для условий, соответствующих
приведенному ниже примеру.
Глава 9. Волноводы
NA = (л2 - nJ-y'1
(9.7)
Числовая апертура волновода
Рисунок 9.1£ показывает, что числовая апертура представляет собой синус
входного угла волновода для лучей, падающих из воздушной среды. В том случае, когда
числовая апертура больше 1, входной угол составляет я/2. Уравнения (9.6) и (9.7)
показывают, что по аналогии с одномерной ямой, которая всегда обладает
связанным состоянием, симметричный волновод всегда имеет, по крайней мере, одну
разрешенную ТЕ-моду. Кроме того, уравнение (9.6) позволяет сформулировать
условие одномодового волновода:
1
2NA
(9.8)
Аналогичный ход рассуждений может быть использован для ТМ-мод (с
соответствующей системой уравнений Френеля) и обобщен на случай несимметричных волноводов.
В то же время более предпочтительным нам представляется использование более
эффективного подхода, основанного на использовании уравнений Максвелла.
Пример
Рассмотрим волновод на основе слоя InGaAs (я, = 3,9), заключенного между двумя слоями
AlGaAs (п2 = 3,0). Числовая апертура волновода составляет NA =C^ — 3,02I/2 = 2,49.
В том случае, когда толщина слоя InGaAs составляет 1 мкм, волновод будет иметь
пять разрешенных мод на длине волны 0,9 мкм.
9.3. Колебательный подход к волноводам
Вспомним, что электрическое поле электромагнитной волны в нейтральной среде (j = 0 и
р = 0) с коэффициентом преломления п(т) является решением волнового уравнения,
следующего из уравнений Максвелла (смотрите Главу 2):
V2E(r, t) - //0г0А72(г)|^Е(г, 0 =
(9.9)
Предположим, что волна имеет радиальную частоту со, т. е. что поле Е определяется
формулой:
Е(г, t) = Re[E(r)eift"]
Это выражение приводит к уравнению Гельмгольца для амплитуды Е(г):
(9.10)
0 (9.11)
Здесь к есть модуль волнового вектора к, связанный с со вакуумным дисперсионным
соотношением к = со/с. Рассмотрим частный случай с волной, распространяющейся
вдоль оси Oz (рис. 9.3).
х
Рис. 9.3. Геометрия планарного
волновода.
-d
9.3. Колебательный подход к волноводам
В этом случае мы можем представить поле в виде E(r, t) = Е(х,
уравнение (9.11) может быть записано следующим образом:
~[&, при этом
(9.12)
Заметим, что условие одинаковости константы распространения Р в среде 1 и
среде 2 соответствует условию самосогласования, приведенному в разделе 9.2.
Наконец, предположим, что волна не изменяется вдоль направления у, т. е. что д/Эу = 0.
В этом случае возможно разделение уравнения (9.12) на три уравнения:
4-т
дх
-Р2)е{х)= 0, для х > 0
^У Е(х)+ {к2п2 - р2 )Е(х) = 0, для -d < х < 0
Эх
Эх
(9.13)
э2
дх2
Е(х)+ {k2nl- р2 )Е(х)= 0, для х < -d
Напомним, что п{ > п2. На этой стадии рассмотрения мы можем проанализировать
различные решения (9.13), исследуя влияние различных значений кп. и /Усмотрите рисунок 9.4).
Если /3 > knv то к2п? —/^является отрицательной величиной независимо от
величины х, решения (9.13) экспоненциально расходятся, что соответствует
нефизическому решению.
Если кпх > Р > knv то амплитуда Е (х) в волноводе является синусоидальной
функцией, а за пределами волновода — экспоненциально затухающей функцией.
Этот случай соответствует волноводным модам, которые мы определим позже,
введя соответствующие граничные условия.
Наконец, если Р < кп2, то решения будут синусоидальными повсюду и волна
будет выходить из волновода. Такая ситуация соответствует случаю утекающих мод,
когда падающий световой пучок входит в волновод таким образом, что
эффективный угол в волноводе превышает критический угол полного внутреннего
отражения. На время оставим эти утекающие моды, которые в действительности могут
запрещенная
область
кпЛ
волноводные
моды
I континиум
а б
Рис. 9.4. Различные электромагнитные режимы в волноводе аналогичны различным
электронным состояниям в квантовой яме: рисунок (а) показывает
пространственное изменение коэффициента преломления л(г), а также изменение
амплитуды поля; рисунок {б) иллюстрирует разрешенные значения константы
распространения Д
Глава 9. Волноводы
быть использованы в ряде интересных практических применениях. Теперь же
более детально исследуем решения (9.12) для ТЕ- и ТМ-мод.
Поперечные электрические (ТЕ) волны
В рассматриваемом случае электрическое поле ориентировано вдоль оси Оу. Обозначим
его амплитуду как Е(х), т. t.E(x, z) = Re[£(^)ei(fitf "^J. При этом магнитное поле
/?определяется уравнением Ленца—Максвелла (V х Е = —дЪ/dt), которое дает:
со v
Из уравнений Максвелла мы знаем, что электрическое поле Еу(х) и магнитное поле
Врс) (т. е. первая производная Еу) непрерывны на обеих границах раздела при х = 0 и х=-d.
Отметим, что эти уравнения распространения, полученные из (9.12), вместе с
граничными условиями формально идентичны уравнениям Шредингера, которые приводят к
квантованию электронных энергетических состояний в квантовых ямах, описываемых
потенциалом V(x) (раздел 1.4). Указанное соответствие имеет вид:
со с п(т)~ <г^ r-V(j)
Е{т) <-> у/(г)
Рисунок 9.4 иллюстрирует эту аналогию квантовой ямы и волновода.
Утекающие моды соответствуют континууму несвязанных состояний над квантовой ямой
тогда, как волноводные моды концептуально эквивалентны связанным состояниям
в квантовой яме. Отметим к тому же, что форма (глубина) ямы зависит от частоты
со, как это показано в соотношениях соответствия, приведенных выше.
Граничные условия для (9.13) имеют вид:
Еу{х)непрерывна при х = О и х = -d
— Ev(x)непрерывна при х = О и х = -d
При этом процедура получения решений (9.13) аналогична случаю квантовой ямы (раздел
1.4). Желая получить пространственную зависимость амплитуды волны, предположим'.
А ехр (- кх ) для х > О
Bcos(ax)+ С sin (ах) для - d <х < О (9.16)
D ехр [к(х + d)\ для х < -d
Здесь: к — константа оптического ослабления вне волновода. Этот параметр эквивалентен
длине туннельного ослабления в квантовой механике. Начнем с введения условия
самосогласования, представленного в (9.13), что дает:
+сс =пк
-к2 =п]к2 (9Л7а-в)
к = со/с
9.3. Колебательный подход к волноводам 335
а = п k sin 0
пЛк
1 р = п^к cos в
Рис. 9.5. Графическое представление условий, приводящих к волноводному эффекту.
Нам остается записать граничные условия (9.15):
• при х = 0:
А = В
• при х = — ±
asm
D = A\cos(ad)+—sm(ad)\
in(ad)- Kcos(ad)= к \cos(ad)+— sin(ad)\
Это последнее условие дает параметры волноводной волны:
tg(ad) =
2ка
1 Т
а - к
2 2 2 2
Р +а =щк
2 2 2 2
р -к = г^к
к = со /с
(9.18)
Система уравнений, определяющих
ТЕ-моды в симметричном волноводе
Таким образом, задача заключается в нахождении при заданной радиальной
частоте со и толщине d константы распространения Д которая удовлетворяет
одновременно всем условиям (9.18) и приводит к точному уравнению относительно Д
полностью эквивалентному (9.5). Этот подход может быть обобщен на случай
волновода произвольной формы. Ниже мы приводим программу MATHEMATICA,
которая может быть использована для получения решений для асимметричного
волновода.
Глава 9. Волноводы
Пример
Обобщение (9.18) на случай асимметричного волновода немедленно приводит к:
/ ,\ К-у + К-,
tg(ad)=-j—-2 ъ—
а\\-\ k2rc31 a
2 2 2 2
р + а = п{к
2 2 2 2
р -к2 =п2к
2 2 2 2
р - к3 = п3 к
Здесь использована обычная система обозначений. Рассмотрим волновод с сердцевиной
на основе слоя GaAs толщиной 0,3 мкм (л1 = 3,3), заключенного с одной стороны между
ограничивающим слоем AlAs (п2 = 2,7) и воздухом (п3 = 1). В расчетах будем пренебрегать
собственной дисперсией в этих средах.
Lambda=0.9;t=.3;Bet=.;
N3=1;n1=3.3;n2=2.7;
K=2*N[Pi]/Lambda;
kt=k*t;
Bett=Bet*t;
ht=Sqrt[(nr2*kr2-BetT2)];
qt=Sqrt[(-n3'x2*kr+Bett'N2)];
pt=Sqrt[(-n2~2*kr2+BetT2)];
f[Bet__]:Tan[ht]-(qt+pt)/(ht-pt*qt/ht);
Plot[f[Bet],{Bet,10,50}];
Sol=FindRoot[f[Bet]= =0,{Bet,21}];
Neff=Bett*Lambda/B*N[Pi])/.sol
При этом получаем, что константа распространения составляет 21,3 мкм, а
эффективный коэффициент преломления neff =3,1267.
Представляется интересным для частного случая симметричного волновода
установить связь между геометрическим подходом раздела 9.1 и колебательным подходом,
используемым в настоящем разделе.Для этого достаточно заметить, что вектор
распространения в волноводе есть @, ±п{к cos#m, njcsmej. Затем, учитывая (9.18), получаем
рт =nlkcos0m
ат = п{к cos вт (9.19)
/ 2 2
Кт = Л,Л1 COS 0m-COS вс
Эквивалентность геометрического
и колебательного подходов
Эти соотношения представляют собой ничто другое как (9.5), и они хорошо
поддаются графической интерпретации, как это показано на рис. 9.6. Мы видим,
что нулевой порядок (минимальное значение 0J приводит к максимальному
коэффициенту ослабления кт, т. е. к максимально локализованной моде.
Теперь нам остается нормировать амплитуду электромагнитной волны в
волноводе, т. е. найти величину константы А в (9.16). В ее определении имеется
определенная степень произвола, так как мы не уточнили размеры поперечной
протяженности Оу. Обычный в таких случаях подход заключается в таком выборе А, чтобы
нормированное поле Еу соответствовало мощности в 1 Вт на длине волновода в 1 м
(вдоль Оу). В этом случае условие нормировки может быть записано в виде:
9.3. Колебательный подход к волноводам
Рис. 9.6. Дисперсионные кривые для
волновода в недесперсионной среде с
пх = 2, п2 = 1,5 и «з = 1. ТЕ (ТМ)-моды
показаны сплошными (пунктирными)
линиями.
S = —
(9.20)
В этом последнем уравнении мы использовали соотношение (9.14)
(горизонтальная черта показывает, что данная величина усредняется по времени; р0 есть
единичная нормированная мощность, соответствующая 1 Вт/м, а т есть индекс ТЕ-
моды в волноводе). Мы рекомендуем использовать р0 для того, чтобы уравнения
были однородными, что имеет первостепенную важность, например, при
рассмотрении эффектов нелинейной оптики (смотрите дополнение 9.В)! При
использовании выражения (9.16) для полевых и граничных условий уравнение (9.20) дает:
= 2а„
<oju о
1/2
(9.21)
В качестве последнего замечания отметим, что поскольку функции Еут(х)
являются решениями линейных дифференциальных уравнений (т. е. собственными
векторами дифференциального оператора (9.12)), они взаимно ортогональны. Говоря
более точно, с учетом условия нормировки (9.20) функции Е™(х) удовлетворяют
уравнению:
(9.22)
Таким образом, если волновод является абсолютно ограничивающим (т. е. если njn2 —> «>)
моды могут быть записаны в виде:
Мода т в абсолютно
ограничивающем волноводе
Давайте специально выпишем для этого случая несколько очень полезных
аппроксимаций для коэффициентов а и к (т =1):
338 Глава 9. Волноводы
л
а ~ —
d
(9.236)
/2 2Л"
Поперечные магнитные (ТМ) волны
В рассматриваемом случае компоненты электромагнитного поля могут быть
разделены, при этом поперечная магнитная компонента может быть записана в виде:
Ву(х, z, /)= Re[£»ei(u"-*> J (9.24)
В то же время электрическое поле Е, определяемое V х В = l/(n.cJdE/dt, может быть
записано в виде:
(9.25)
Здесь п. есть коэффициент оптического преломления среды /. Собственные ТМ-моды в
волноводе получаются при наложении условий непрерывности для полевых компонент Ву
и Ez на обеих границах раздела (это мы оставляем читателю в качестве упражнения). Это
приводит к следующему результату:
(926)
= о)/сиеп=\^- I
Система уравнений, определяющих
ТМ-моды в симметричном волноводе
Для каждой комбинации величин частоты со и толщины d мы получаем
многочисленные разрешенные значения для константы распространения /3 различных
мод. Общепринятое представление различных мод в волноводе заключается в
отображении дисперсионной кривой лс1ГЦ), где Azeff есть эффективный коэффициент
оптического преломления для волновода, определяемый как яе(Г = J3c/co.
Рисунок 9.7 показывает дисперсионную кривую для теоретического волновода с
я, = 2, п2 = 1,5 и л3 = 1 в функции d/A0. Как явно видно из этого рисунка, имеется
несколько возможных решений, т. е. возможны несколько решений, при этом
волноводы по своей природе являются, таким образом, многомодовыми. Позже мы
увидим, что для большинства применений предпочтительными являются одномодовые
волноводы. В этом случае одномодовое распространение гарантируется при
удовлетворении условия (9.8), т. е. когда отношение d/A0 меньше NA/2. Из рисунка 9.7 мы
также можем заключить, что волновод естественно вводит дисперсию, т. к. всегда
существует разброс между максимальными значениями п{ и пг Этот фактор обычно
называется модовой дисперсией волновода. Эта компонента дисперсии дает свой вклад
в естественную дисперсию, определяемую материалами, образующими волновод.
9.4. Оптическое ограничение
0.90 1.00
1.10 1.20 1.30
длина волны, мкм
1.40 1.50
Рис. 9.7. Дисперсия в волноводе, содержащем слой сердцевины толщиной 0,5 мкм,
заключенный между двумя слоями Al0 jGaQ^ толщиной 1,0 мкм.
Возникающая естественным образом дисперсия из образующих волновод материалов
дает свой вклад в дисперсию из-за геометрии волновода.(С разрешения
A. Fiore. LCR. THALES.).
Рисунок 9.8 демонстрирует результат полного расчета для системы AlGaAs с
использованием дисперсионных соотношений Афромовича, приведенных в
дополнении 7. Б. Мы увидим, что эта дисперсия приводит к отрицательным эффектам в
нелинейно-оптических волноводах.
1.0
0.8
0.6
0.4
0.2
0.0
уменьшающийся
порядок
0.0
0.2
0.4
0.6
0.8
1.0
sin0m/sin0c
Рис. 9.8. Зависимость коэффициента ограничения оптического волновода от sin 6J
/sin вс. Волноводные моды с малыми индексами (малая величина sin 0m)
обеспечивают лучшее оптическое ограничение.
9.4. Оптическое ограничение
Представляется важным оценить количество энергии, эффективно каналируемой
или захваченной волноводом между точками 0 и — d. Это количество энергии
описывается с использованием коэффициента ограничения G, определяемого как:
]\Е(хJ6х
^d
]\E(XJdx
(9.27)
Глава 9. Волноводы
Для того, чтобы ознакомиться с этой концепцией, рассчитаем коэффициент
ограничения для моды т симметричного волновода. Благодаря симметрии задачи
(9.27) может быть записано в виде:
Г =1-
(9.28)
Или с учетом (9.16) и (9.22):
Г =i
2ктеощ0
(9.29)
После чего мы подставим в (9.29) различные геометрические выражения для Ат, @т и кт,
полученные в (9.19) и (9.21), что дает:
Г =1-
sin
sin'
; Sin 9C -Sin вт I
. = !--
(9.30л)
Здесь ЛГесть соотношение sin 6^/sin 6J. и мы напоминаем, что Л^ есть число
допустимых мод волновода. Рис. 9.9 представляет изменение коэффициента
ограничения для типичного волновода в функции sin 6m /sin вс.
Отметим, что эта последняя величина возрастает с увеличением индекса моды, при
этом, как видно из рисунка, максимальным ограничением при минимальном
порядке моды. Таким образом, ТЕ0 и ТМ0 моды волновода испытывают наиболее
эффективное волноводное распространение. Этот факт используется при
конструировании многих оптоэлектронных приборов (например, лазеров, модуляторов и т. д.)
Естественно, что разработчик волноводов будет предпочитать использование
одномодовых волноводов. Ограниченное разложение (9.30я) приводит к крайне
полезной аппроксимации для ТЕ0:
Го = т^т>где/) =
(9.306)
2+ZJ
Демонстрацию справедливости этого соотношения мы оставляем читателю в качестве
задачи.
0.8
0.6
0.4
0.2
0.0
. точное решение(9.30а)
— аппсжсимси 1ия Г9.306)
0.0 0.1 0.2
толщина, мкм
0.3
0.4
Рис. 9.9. Сравнение значений коэффициента ограничения G, полученных с
использованием точного метода (9.30л) и аппроксимации (9.306) для длины волны
1,55 мкм в волноводе на основе GaSb/AlGaSb, описанного в примере.
9.5. Взаимодействие между волноводными модами: теория связанных мод
Пример
Рассмотрим волновод, состоящий из слоя сердцевины на основе GaSb толщиной
0,2 мкм, а также из ограничивающих слоев AlGaSb. Пренебрежем собственной
дисперсией этих материалов и примем пх = 3,837 для коэффициента оптического
преломления GaSb и п2 = 3,589 для аналогичного параметра Al; GaSb. Числовая
апертура NA волновода составляет, таким образом, 1,36. Число мод на длине волны
1,55 мкм дается (9.6) и составляет N — IntB x 0,2 х 1,36/1,55) +1 = 1. Таким
образом, рассматриваемый волновод является одномодовым, и мы можем использовать
выражение (9.306) для определения коэффициента ограничения для ТЕ0-моды в
волноводе. При этом мы получаем D = 1,10 и Го = 0,38.
Программа MATH EM ATI CA, приведенная ниже, позволяет сравнить значения
коэффициентов ограничения, полученные с использованием точного метода (9.30я)
и аппроксимации (9.306) применительно к описанной выше системе. Полученные
таким образом результаты иллюстрируются рис. 9.9 и они подтверждают
действенность аппроксимации (9.306).
Lamda=1.55;t=.
n1=3.837;n2=3.589;ON=Sqrt{nr2-n2~2};
ninit=(n1+n2)/2;
k=2*N[Pi]/Lambda;
Bet=2*N[Pi]*neff/Lambda;alpha=Sqrt[(nr2*k^2-Ber2)];
kappa=Sqrt[(-n2~2*k~2+Ber2)];
fct=Tan[alpha*t]-2*kappa*alpha/(alpha~2-kapa~2);
tab=Table[{,sol=FindRoot[fct,{neff,ninit}];
gamma=Abs[1 -(пГ2-пегГ2)/(пГ2-п2~2)/
A+k*t/2*Sqrt[nefT2-n2])/.sol} ,{t,.O1 ,.4,01}];
plot1=UstPlot[tab]
dis=2*N[Pi]*t*ON/Lambda;
plot2=Plot[dis~2/B+dis~2),{t,0,4}]
Show[plot1,plot2]
9.5. Взаимодействие между волноводными
модами: теория связанных мод
Волноводные моды представляют собой собственные состояния
электромагнитного поля в волноводе. Они образуют полный базис (вместе излучательными
состояниями, которые могут распространяться в волноводе, но которыми мы пока будем
пренебрегать), в рамках которого мы можем использовать разложение по
возмущениям. Такие возмущения могут иметь много источников: гофрирование волновода
(хаотичное или периодическое), нелинейные взаимодействия (например,
генерация второй гармоники) или, возможно, присутствие второго волновода,
расположенного столь близко, что становится возможной связь за счет фотонного туннели-
рования. Все эти возмущения можно рассмотреть в рамках очень эффективного
формализма, известного под названием теории связанных мод. Эта теория очень
похожа на теорию возмущений в квантовой механике.
Начнем же мы с уравнений Максвелла в среде:
(9.31)
Здесь D есть вектор смещения:
Глава 9. Волноводы
D(r, t) = *0E(r, 0 + зд(г)Е(г, t) + Pper(r, 0 = *г)Е(г, 0 + Ppcr(r, t) (9.32)
В этой последней формуле е(т) = я2 (г) есть диэлектрическая постоянная для
различных материалов, образующих волновод A,2, ...) и Ррег есть возмущающая
поляризация, которая исключает диэлектрический отклик различных слоев
(поскольку он включен в я(г)). В этом случае уравнения (9.31) приобретают вид:
2 2
V2E(r) - juoe(r)-^-E(r) = ju0 ^т
dt
т
dt
*, О
(9.33)
Уравнение распространения с возмущающим
поляризационным источником
Это уравнение образует базис для трактовки с использованием метода
возмущений различных эффектов в волноводах (рассеяние, дифракция, ...), и оно играет
центральную роль в оптоэлектронике (смотрите, например, главу 12). Для того,
чтобы не усложнять чрезмерно систему обозначений, мы не будем рассматривать
изменения по у, но будем интересоваться амплитудой электрического поля вдоль
еу, которую мы будем обозначать как £(г, /)• В этом случае дифференциальный
оператор V2 есть (Э2/дх2) + (d2/dz2).Roj\z Е(т, t) может быть разложено по базису
волноводных мод Em(r, t) = еуЕт(х)&{@'~м или:
^ 'x\x{p*~PmZ) + к. с.
(9.35)
Мы напоминаем, что здесь каждая мода должна удовлетворять уравнению:
Члены Ат представляют собой амплитуды волноводной волны, изменяющиеся
вдоль z вследствие влияния возмущений. С учетом нормировки (9.20) квадрат
модуля | Ат |2 есть оптическая мощность моды т на единицу ширины волновода. В
отсутствие возмущений члены Ат не зависят от z- Подставляя (9.34) в (9.33), мы
получаем:
(9.36)
к. с. =
Здесь Рурет есть компонента вектора возмущающей поляризации в направлении Оу.
Заметим, что первая сумма равна нулю с учетом (9.36). Мы также используем
аппроксимацию, когда амплитуда волны слабо изменяется (аппроксимация
огибающей функции). Это позволяет нам записать:
«А,
(9.37)
Аппроксимация огибающей
функции
В этом случае (9.36) принимает вид:
Э
2-* ~ Рт ъ?J
+ к- с. = Mo ^tW О
(9.38)
После чего умножим это выражение на E^z), и возьмем интеграл, что эквивалентно
проецированию (9.33) на собственный базис волновода. Используя условия орто-
нормальности (9.22) после перегруппировки подобных членов мы получаем:
9.5. Взаимодействие между волноводными модами: теория связанных мод
де ,,е ...... __±_|1 Jfc <,, ,)В,С«*ж <9.39,
Уравнение связанных мод
для возмущающей поляризации
Мы напоминаем, что здесь р0 есть константа нормировки (р0 = 1 Вт/м). В этом
последнем уравнении Af и А~ есть амплитуды моды /, распространяющейся в
направлениях +z и — z соответственно. Уравнение (9.39) описывает, каким образом
возмущающая поляризация PpeT(r, t) может индуцировать перенос энергии между
различными собственными модами резонатора. Часто возмущающая поляризация
является функцией других возмущенных мод и (9.39) (или уравнение связанных мод)
вызывает их связь. Это очень эффективный формализм с широкой областью
применения. Мы будем использовать его для описания функционирования оптических
согласователей (дополнение 9.Б), лазеров с распределенной обратной связью
(Дополнение 13.А), а также оптического преобразования частоты в нелинейных
волноводах (дополнение 9. В).
Литература
S.L. Chuang, Physics of semiconductor Devices, Wiley Intrescience, New York A995).
D. Marcuse, Theory of Dielectric Optical Waveguides, Academic Press, New York A974).
B.A. Saleh and M.C. Teich, Fundamentals of Phjtjnics, Wiley Interscience, New York A991).
A Yariv, Quantum Electronics, Wiley, New York A989).
ДОПОЛНЕНИЯ
К ГЛАВЕ 9
9.А. Оптическое взаимодействие между волноводами:
электрооптические переключатели
В разделе 9.3 мы видели, что электромагнитная волна, захваченная слоем сердцевины
волновода обладает затухающей компонентой в ограничивающем слое (смотрите рис.
9.4). Если поблизости от первого волновода располагается второй волновод,
способный ограничивать волну той же самой частоты, при этом перекрытие с затухающей
компонентой волны значительно, то ограниченная волна будет переходить через
ограничивающий слой во второй волновод. Этот эффект аналогичен электронному тунне-
лированию через барьеры в квантовой механике. Формализм связанных мод особенно
хорошо приспособлен для описания связи этого типа между волноводами.
Рассмотрим два волновода (смотрите рис. 9.А. 1). Первый {правый) волновод
содержит слой сердцевины с показателем преломления nR, помещенный между
двумя ограничивающими слоями с коэффициентом преломления п. Второй
волновод, расположенный на расстоянии D налево от первого, содержит слой
сердцевины с коэффициентом преломления nL, расположенным между слоями того же
барьерного материала, что и правый волновод. Два волновода были изготовлены
так, что если бы они были разделены бесконечным расстоянием, каждый из них
обладал бы единственной основной собственной модой, обладающей
компонентой электрического поля вдоль Оу, при этом каждая из компонент ER{x, z, t) и
EL{x, z, t) были бы решениями уравнений типа (9.13) вида:
(9.А.1)
При приложении друг к другу каждый из волноводов будет действовать
возмущающим образом на другой волновод.
Следуя принципам,
изложенным в разделе 9.4 и
идентичным тем, которые
были получены в рамках
стационарной теории
возмущений в квантовой
механике (смотрите, например,
дополнение 1.Б), мы можем
записать новые моды для
связанной системы в виде
линейной комбинации фун-
п
■ * -ntT;
п
"я
п
Рис. 9.АЛ. Геометрия
связанных волноводов (а). Волна,
локализованная исключительно в
левом волноводе (б). Волна,
связанная в двух волноводах (г).
9.А. Оптическое взаимодействие между волноводами
даментальных собственных мод для каждого изолированного волновода (так же как
это было в случае квантовых ям, мы будем пренебрегать модами более высокого
порядка):
Е(х, z, t)= -[AR(z)ER(x)el{u)t~p*z) + AL{z]EL{z)^{(Ot~PtZ) + к. с] (9.А.2)
2
Если волноводы бесконечно отдалены друг от друга, амплитуды AR(z) и AL(z)
являются константами. Приближение двух волноводов до минимального зазора
индуцирует обмен энергией между ними, приводя к изменению амплитуд AR(z) и AL(z).
Для правого волновода возмущением /wper будет поляризация левого волновода из-за
синхронного возбуждения нового поля Е(х, z, t), определяемого (9.2) или:
PR(x 7 t)-F \n2(x)-n2 \f(x 7 t) (9 АЗ^
Здесь: nL(x) есть функция, равная nL в левом волноводе и п в других точках.
При рассмотрении задачи о распространении волны в одном направлении уравнение
связанных мод может быть записано в виде:
[с0£°
4р0
левый
волновод (9. А. 4)
левый
волновод
В формуле (9.А.4) первый член в интеграле с правой стороны не играет особой роли.
Его влияние ограничивается малой коррекцией константы распространения PR. В то же
время, второй член обеспечивает связь между двумя волноводами. В этом случае
уравнение (9.А.4) и его эквивалент для левого волновода приобретают вид:
-AR=
AL
Здесь мы ввели фазовый сдвиг А0между двумя волноводами, определяемый:
AJ3=J3L-/3R (9.A.6)
а также интегралы перекрытия между двумя волнами, определяемые соотношениями:
4 Ро левый
полиовоп (9.А.7)
Уравнения (9.А.5) являются классическими уравнениями связанных
маятников, и они полностью эквивалентны уравнениям Раби, обсуждавшимся в
дополнении 1.Д. Эти уравнения могут быть решены при введении пробных функций вида
еа/. Предположим, что амплитуды на входе каждого волновода равны AL@) = Ао и
AR@) = 0.
В случае симметричных волноводов мы предположим, что g^ = gLR = g.
Решения (9.А.5) могут быть записаны в виде:
f( 346 Дополнения к главе 9
(9A8)
AL(z)= Ле-'(л*/2)| cosj^ + i^-sin^
При этом:
Уровни оптической мощности в волноводах в этом случае равны:
(9.A.9)
7 (9.А.10)
IL(z) = /», - Л(г)
Здесь /*0 мощность излучения, падающего на вход левого волновода. Уравнение (9.А. 10)
богато информацией. Во-первых, оно показывает, что энергия волны осциллирует
между двумя волноводами по всему расстоянию распространения с пространственным
периодом Atians, называемым расстоянием переноса (смотрите рис. 9.А.2), определяемым
соAtians
отношением:
Я -
trans
2л
(9А11)
В дополнение к этому максимальная доля энергии, которая может быть перенесена из
одного волновода в другой, составляет:
g
(9-А-12)
Так же, как это было и в случае осцилляции Раби, нас не удивляет то, что
энергия может полностью перераспределяться между волноводами в процессе
осцилляции, пока фазы согласованы, т. е. до тех пор, пока:
Рис. 9.А.2. Мощность волны распространяется и распределяется между двумя
связанными волноводами. Расстояние, на котором осуществляется
перераспределение мощности, есть расстояние переноса Atnm.
9.А. Оптическое взаимодействие между волноводами
Afi = fiL - fiR = О (9.А.13)
Условие согласования фаз
между двумя волноводами
Таким образом, волноводы могут выполнять функцию оптических
переключателей (тем более тогда, когда они идентичны). Рассчитаем константу переноса к
для двух Г£0-волн и случая, когда nR = nL = nv Поля EL(x) и ER(x) определяются
(9.16). Интегралы перекрытия (9.А.7) могут быть легко рассчитаны:
f cos(oxl4.e-^-*>djc (9A.14)
BL есть амплитуда волны в левом волноводе, центр которого принят за точку отсчета (это
объясняет, что интеграл берется от — d/2 до d/2), a AR есть амплитуда затухающей волны,
исходящей из правого волновода. Напоминаем, что электрические поля Е(х) изменяются
в двух волноводах как cos (ах) и как с~кх — в ограничивающих слоях. Эти
амплитуды приведены в (9.21), что дает:
g = Л а~ * е-^ (9.А.15)
т^ а2 + к2 d + 2/к
Изменение е""^ оправдывает определение константы к как константы фотонного тун-
нелирования между двумя волноводами.
Пример
Рассмотрим два волновода со слоями сердцевины на основе InGaAs (я, = 3,5) и
ограничивающими барьерными слоями на основе InALAs (n2 = 3,3). Ширина
волноводов составляет 0,6 мкм. Коэффициенты а и к получаются с использованием
программы MATHEMATICA, приведенной ниже:
Lambda =1.55=0.6;(*micron*))
n1=3.5;n2=3.3;
k=2*N[Pi]/Lambda;
Bet=2*N[Pi]*neff/Lambda;
alpha=Sqrt[(nr2*Ber2];
kappa=Sqrt[(-n2~*k~2+Ber2)];
Plot[fct,[neff,n2,n1}];
sol=FindRoot[fct= = 0,[neff,3.43}];
alpha /.sol(microrf-1*)
kappa/.soKfmicron^-i *)
Из этих расчетов мы получаем а= 2,97 мкм ик = 3,67 мкм. Если два волновода
разделены расстоянием 1 мкм, коэффициент связи удается формулой (9.А. 16) и
составляет 4,6 х 10~3 мкм. Таким образом, длина переноса Atrans по порядку величины составляет
2/= 1,ЗММ.
Этот механизм переноса энергии между связанными волноводами используется в
электрооптических модуляторах, как это иллюстрируется рис. 9.А.З. В рассматриваемом
случае два идентичных волновода изготавливаются с использованием
электрооптической сердцевины с коэффициентом преломления, изменяющимся в зависимости от
напряженности приложенного поля в соответствии с соотношением:
An = n3rF (9.A.16)
Здесь г — электрооптический коэффициент, в типичном случае равный нескольким
пм В в полупроводниках (г = 1,6 пм В и пъг = 59 пм В в GaAs), при этом
изменение An величиной 5 х 10~4 может быть легко получено при полевой модуля-
348 Дополнения к главе 9
Рис. 9.А.З. Схематическое представление
электрооптического модулятора, основанного на связанных волноводах.
ции амплитудой 100 кВ см. Длина волновода выбирается таким образом, что при
нулевом электрическом поле (два волновода идентичны и А/? = 0) вся энергия
левого волновода передается в правый волновод у конца обоих волноводов, т. е.
при gL = л/2. На левый волновод наносится металлический электрод для того,
чтобы при приложении электрического поля F происходило изменение как
коэффициента преломления, так и константы распространения /?. Это приводит к
фазовому сдвигу между двумя волноводами AJ3(F). Мощность выходного излучения на
выходе правого волновода в этом случае является функцией электрического поля,
определяемой (9.А. 10) или:
Ш)
sin
J
1/2
(9.А.17)
Мощность оптического излучения будет практически полностью перенесена в
левый волновод (IR(L) = 0) при приложении достаточно сильного электрического
поля F, такого что:
диффузия Zn
Si,:Njt
металлизация
усилителя
1пР(р+
имплантация н+
InPn.i.d.
■дложка 1пР
.■ i г \изация
•■ ■! акта
- ■■ .' лновод
GalnAsPi/. г- змкм)
ВОЛНОВОД
GalnAsP (/1 = 1,3 мкм)
усилительная секция
Рис. 9.А.4. Реализация переключателя на связанных волноводах. Это схематичное
представление показывает переключатель 2x2, интегрированный с оптическим
усилителем. (С разрешения N Vodjdany @LCR/THALES).
9. Б. Брэгговские волноводы
<Jbn (9.A.18)
Для оценки необходимой напряженности поля мы можем грубо
предположить, что изменение коэффициента преломления AnL, определяемое (9.16),
влияет на константу распространения как j3L = 2лпе///Л0 (мы напоминаем, что Ло
есть вакуумная длина волны и псп есть эффективный коэффициент преломления
в волноводе) так, что А/3 = 2яАп/Л0. В этом случае условие (9.18) определяет
напряжение переключения при условии, что Ane{((F) = (V3/2)(A0/L). При длине
волновода 2 мм и длине волны 1 мкм нам необходимо обеспечить изменение An
величиной 4 х 10, что соответствует полю переключения 100 кВ см или 10 В
для волновода толщиной 1 мкм. Рисунок 9.А.4 иллюстрирует реальную
реализацию такого электрооптического модулятора. Поскольку для функционирования
этого прибора не требуется перемещения зарядов, емкостные эффекты в
действительности дают нулевой вклад, и времена переключения крайне малы.
Максимальная частота модуляции для этого типа приборов превышает 10 ГГц.
Литература
A. Yariv, Quantum Electronics, Wiley, New York A989).
9.Б. Брэгговские волноводы
Мы увидим, каким образом уравнение связанных мод (9.39) позволит нам изучить
поведение волноводной волны в оптическом волноводе, гофрированном с
периодом L (смотрите рис. 9.Б.1). В том случае, когда длина периода гофра равна длине
волны распространяющегося излучения (т. е. 2л//?), гофрированная часть
волновода действует как брэгговский отражатель (смотрите дополнение 9.Г.1). Эта
ситуация, относящаяся к распространению фотонов, аналогична случаю,
рассмотренному в главе 5, относящемуся к электронам в твердых телах (приводящему к
образованию разрешенных энергетических зон). Брэгговская решетка может быть
представлена периодической модуляцией относительной проницаемости. Для
начала предположим что эта модуляция изменяется синусоидально как:
Возмущающая поляризация, вызванная этой модуляцией, дается в этом случае
выражением:
Ррм!=£0А£(г)£(г,0 (9.Б.2)
Электромагнитное поле в волноводе E(r, t) может быть разложено по базису
собственных волноводных функций, как это описывается (9.34). С использованием
(9.Б.1) и (9.Б.2) возмущающая поляризация может быть записана в виде:
m{z)Em^)^m±{2n/K))l + к. с (9.Б.З)
Подставим теперь (9.Б.З) в уравнение связанных мод (9.39), заменяя производную
— со2, при этом получаем:
(9Б4)
W3 5 0 Дополнения к главе 9
Л
Рис. 9.Б.1. Геометрия брэгговского волновода.
Мы благоразумно сохранили две противонаправленные моды А+ и А~, т. к. мы
ожидаем их связь за счет гофра в виде дифракционной решетки. Уравнение (9.Б.4)
связывает различные амплитуды Am(z) через связанные дифференциальные
уравнения. Мы можем избежать массы ненужной работы, исследуя это уравнение. В (9.Б.4)
введены два типа констант распространения:
Эти константы связывают дА~/дг с Ат. Кроме того:
Эти константы связывают dA'/dz с А*.
Первый случай нас не интересует, хотя он и обеспечивает возможность
рассмотрения задач, связанных с дифракцией Фраунгофера в ближнем поле. В то же
время нас интересует второй случай, устанавливающий связь между падающей
волной с индексом / справа со второй волной с индексом т слева. Говоря более точно,
мы имеем дело со специальным случаем / = /я, т. е. случаем, соответствующим
отражению. В (9.Б.4) мы сохраняем только те члены, для которых рассогласование
фаз 2Д/? близко к нулю, поскольку только эти члены, в конце концов, будут
интерферировать конструктивно. Это фазовое рассогласование дается соотношением:
Ар = Д-— (9.Б.5)
Л
Фазовое рассогласование
в брэгговском волноводе
Это последнее условие может интерпретироваться как условие сохранения
полного волнового вектора. Периодическая решетка обеспечивает волновой вектор -
2я/А, который вычитается из волнового вектора падающей волны /?,+ и генерирует
волновой вектор, соответствующий отраженной волне j3f (смотрите рис. 9.Б.2). В
этом случае уравнение (9.Б.4) может быть разделено на два связанных уравнения:
Рис. 9.Б.2. Интерпретация условия
согласования по фазе брэгговского
волновода с использованием концепции
сохранения волновых векторов.
9. Б. Брэгговские волноводы 3 51
2л
Л
±
Здесь константа связи g дается выражением:
(9.Б.6я)
Уравнения связанных мод
брэгговского волновода
(9.Б.66)
О (9.Б.7)
Это означает, что суммарная оптическая мощность двух мод остается постоянной.
Связанные уравнения (9.Б.6) можно решить стандартными методами, а
именно: подставляя одно из уравнений в другое, что, например, дает:
«A, L
Исходя из (9.Б.6) можно легко показать, что:
Ал/ -g2A,+ = о
(9.Б.8)
Амплитуды А* и Af являются, таким образом, линейными комбинациями
экспонент аргументов:
Я = iA/5 ± S
Здесь десть дискриминант (9.Б.8):
(9.Б.9*)
(9.Б.96)
Для получения полного решения наложим граничные условия на амплитуды в
волноводе. Волна падает слева с амплитудой Ао на вход дифракционной решетки
(z — 0) (смотрите рис. 9.Б.1). В то же время никакая волна не падает слева на выход
волновода при z = L. В этом случае граничные условия имеют вид А\ @) = Ао и
A~(L) = 0, при этом решения (9.Б.6) легко находятся в виде:
g
A~(z)=A-A
sh(SL)+S ch(SL)
e-**sh[s(z-L)]
+\Afxi
(9.B.10fl)
- L)]- \
- If
^^J~^iAfish(SL)+Sch(SLr
Поведение обеих волн носит особенно простой характер, когда
удовлетворяется брэгговское условие (А/? = 0), т. е. когда волновой вектор решетки равен
коэффициенту л/Л волноводной волны. В этом случае решение (Э.ЬЛОа) принимает
простой вид:
3 5 2 Дополнения к главе 9
ch (SL )
Рисунок 9.Б.1 иллюстрирует для этого случая поведение квадрата амплитуд (т.
е. оптической мощности на единицу ширины волновода) в функции расстояния.
Падающая волна Af экспоненциально затухает в области решетки, порождая
отраженную волну А~. В том случае, когда произведение SL достаточно велико, т. е.
если решетка достаточно эффективна, ^,"@) по порядку величины близка к Ло,
тогда как Af(L) « 0. В этом случае перенос энергии является полным, и область
решетки ведет себя как брэгговский отражатель.
Этот брэгговский отражатель обладает характерной для него спектральной шириной
полосы, определяемой требованием, чтобы Sбыло действительной величиной, т. е. с
учетом (9.Б.9я):
71 п / \ 71
--g<Pl(co)< —
Л Л
(9.Б.11)
Спектральная ширина полосы
брэгговского отражателя
Таким образом, ширина полосы, выраженная в волновых числах, составляет
2g. Рис. 9.Б.З дает типичный пример пропускания брэгговского волновода,
описываемого соотношением:
Sch{SL)+\AJ3sh(S L
(9.Б.12в)
Условие (9.Б. 11) так же, как выражение для пропускания волновода (9.Б.12я)
показывает, что произведение gL управляет максимальной эффективностью
брэгговского волновода. В резонансе при А/? = 0 пропускание дается формулой:
Т =
1
(9.Б.126)
ch (SL)
Если коэффициент связи g мал, брэгговский волновод должен иметь достаточно
большую длину с тем, чтобы выполнялось неравенство gL» 1. Для понимания роли
различных параметров (а также того, каким образом их следует комбинировать для
обеспечения эффективного брэгговского волновода) мы попытаемся вывести
выражение для эффективности волновода с сильным ограничением.
Рассмотрим волновод толщиной d и коэффициентами преломления ^£1 и у1е2
соответственно для слоев сердцевины и ограничения (смотрите рис. 9.Б.1). В
предположении распространения 7!£0-волны в волноводе с сильным ограничением (9.13)
дает для величины, обратной длине волны, а и глубины туннельного
проникновения к следующие аппроксимирующие выражения (смотрите (9.236)):
1
0.8
0.6
Рис. 9.Б.З. Зависимости
коэффициентов пропускания и отражения
брэгговского волновода от нормированного
рассогласования фаз kfi/g для gL =2.
9. В. Преобразование частоты в нелинейных волноводах
л
-7
(9.Б.13)
fe2)
а Яп
В этом случае нормировочный коэффициент волноводной волны (9.21) составляет:
№- (9.Б.14)
d
В том случае, когда решетка сформирована на расстоянии D от сердцевины и имеет
амплитуду модуляции h (смотрите рис. 9.Б.1), константа связи в соответствии с (9.Б.66)
имеет вид:
D+h
g -—Ч-Ж. \ А ъ &х (9.Б.15)
8рЛ J
го D
При этом с учетом (9.Б. 13) и (9.Б14):
71 £м (XJi\e~lKD
Это последнее выражение показывает, что эффективность брэгговского волновода
определяется эффектом фотонного туннелирования (т. е. ocq~2kD).
Пример
Найдем произведение gL для волновода на основе GaAs со следующими параметрами:
п{ = 3,3, п2 = 3 и ем — 3
Ло= 1 мкм, d = 0,5 мкм, D = 0,2 мкм и h = 0,1 мкм.
Волновое число а составляет тг/d или 6,28 мкм, при этом константа фотонного
туннелирования к дается (9.Б. 13) и составляет C,32 — 32I/2а = 8,63 мкм. В этом
случае произведение gL определяется с использованием (9.Б. 16) или:
4 3C,32-32)[ 0,5 J d d
Для получения величины gL порядка 1 нам необходима длина волновода 200d
или 100 мкм.
Литература
S.L. Chuang, Physics of Optoelectronic Devices, Wiley Interscience, New York A995).
A. Yariv, Quantum Electrvnics, Wiley, New York A989).
9.B. Преобразование частоты
в нелинейных волноводах
Как мы увидим в главе 12, полупроводники обладают нелинейной
восприимчивостью второго порядка, большей, чем у большинства других материалов. Напомним,
что в такой среде вторая гармоника нелинейной поляризации Р2(О генерируется
двумя волнами с частотой со в соответствии с соотношением:
354 Дополнения к главе 9
Эту формулу можно понять следующим образом: электромагнитное поле,
поляризованное в направлении / взаимодействует со второй волной, поляризованной
вдоль оси у, что приводит к нелинейной поляризации вдоль оси к. Таким образом,
X является тензорной величиной. Более того, действительная часть поляризации
представляет собой действительную часть (9.В.1).
Как мы увидим в этом Дополнении существует большой интерес в использовании
волноводов для осуществления оптического преобразования частоты с использованием
оптической нелинейности в полупроводниках. Первой причиной этого является то, что
оптическое ограничение в волноводах приводит к значительным амплитудам
электромагнитного поля даже при умеренных уровнях оптической мощности. Вторая причина
заключается в возможности решения проблем, связанных с рассогласованием фаз,
с использованием современной технологии микрообработки.
Используя как геометрию, так и систему обозначений главы 9 (смотрите рис. 9.3),
исследуем два следующих случая.
9.В.1. Режим с входящей ТЕ-модой
и выходящей ТЕ-модой
В этом случае будем предполагать, что одиночная волноводная ТЕ-волна взаимодействует
сама с собой таким образом, что амплитуда дается соотношением:
, z, 0= -
к. с
]
(9.В.2)
Здесь: Ef есть решение волноводного уравнения (9.13), Af(z) учитывает изменение
амплитуды пучка накачки (с частотой со) вдоль волновода, а /За ТЕ есть константа
а ТЕ
распространения 77?-волны с частотой со в волноводе, определяемая решением (9.13).
При устранении членов по со — со (что соответствует оптическому выпрямлению)
нелинейная поляризация на частоте 2со в (9.В.1) принимает вид:
Р£ (*. <> 0= ^\К" (*, г)е-'B"'-2'- "г) + к. с] (9.В.Зв)
С использованием (9.В.2) получаем:
Р^(х, z)= eoX^U;(z)E;(x)]2 (9.B.36)
Анализируя следствия, которые влечет за собой введение нелинейной
поляризации в уравнение связанных мод (9.23), мы видим, что член источника 2со
обуславливает генерацию волн с частотой 2со. Уравнение (9.39) позволяет рассчитать
изменение амплитуды волны 2со в волноводе. При рассмотрении только тех волн,
которые распространяются направо, формула (9.39) приобретает вид:
dz
7 J
2сор0 Э/2 i
+ к. c.
}E?°(x)dx
(9.B.4)
Рис. 9.В.1. Конфигурация генерации второй
гармонизации ТЕ—ТЕ.
9. В. Преобразование частоты в нелинейных волноводах
Здесь Р1ш ТЕ есть константа распространения волны 2со в волноводе.
Используя обозначение для эффективного коэффициента преломления, мы видим, что
p2w ТЕ =пе{{Bа)Jсо /с. Еу2а)(х) есть волноводная мода на частоте 2со. Функция/(х)
представляет изменение нелинейной восприимчивости по всему волноводу.
Например, в том случае, когда нелинейным является только материал сердцевины,
f{x) является ступенчатой функцией. В этом случае уравнение (9.В.4)
приобретает упрощенный вид:
z (9.B.5)
Здесь: Syy есть интеграл перекрытия мод Еу с самими собой, определяемый формулой:
(9.В.6)
(9.В.7)
В то же время <?/? представляет собой рассогласование фаз:
Уравнение (9.В.5) описывает перенос энергии между фундаментальной волной
и ее гармониками. Для упрощения предстоящего обсуждения предположим, что
эффективность преобразования мала. Тогда можно предполагать, что амплитуда Аю
(z) постоянна поперек волновода и равна своей величине на входе волновода (А£).
В этом случае уравнение (9. В.5) может быть проинтегрировано:
Ро
IS/3L
е -1
dpL
(9.В.8)
Вспоминая, что условия нормировки (9.20)—(9.22) устанавливают, что квадрат
модуля амплитуды |Л|2 мод в волноводе есть ничто иное, как мощность излучения,
введенного в моду на единицу ширины волновода, мы получаем эффективность
преобразования в волноводе в виде:
sin с
(9.B.9)
IT) 4 { 2 ,
В этой последней формуле уровни мощности Ру выражены в Вт на единицу
ширины волновода. Рассмотрим изменение эффективности преобразования по длине
волновода L. Нелинейная среда извлекает энергию из пучка накачки и передает ее
второй гармонике, при этом периодически по длине волновода имеет место
обратный процесс. В результате этого максимально достижимая эффективность
достигается на конце длины взаимодействия, которую называют (правда, не совсем
уместно) длиной когерентности и которую мы называем длиной согласования фаз:
Длина согласования фаз в волноводе
Эта величина возрастает (так же, как и максимальная эффективность) по мере
уменьшения дисперсии волновода. Позже мы увидим, что для искусственного
получения согласования фаз могут быть использованы определенные методы. В этом
случае функция главного синуса (sine) в (9.В.9) равна единице, при этом
преобразование частоты может происходить конструктивно по всей длине волновода, что
приводит к параболической зависимости (по L2) эффективности преобразования.
Теперь мы придадим более физический вид выражению (9. В.9). Для этого мы
должны рассчитать интеграл перекрытия Syy. С этой целью сделаем несколько
упрощающих аппроксимаций:
fl( 356 Дополнения к главе 9
• Только материал сердцевины является нелинейным, а функция Дх) является
ступенчатой.
• Волноводы являются бесконечно ограничивающими, а моды — синусоидальными,
как в (9.23), т. е.:
!?;(*)= 2
В этом случае интеграл перекрытия может быть записан в виде:
s
( d )
или:
(9.В.Щ
d nix
В последнем выражении использовано предположение, что neff(aj) ~ weff Bco).
Подставляя это последнее уравнение в (9.В.9), мы, в конце концов, получаем величину
эффективности преобразования частоты для абсолютно ограничивающего
нелинейного волновода для случая без обеднения пучка накачки (т. е. для А" = const):
Р/ {Зл ' nl \dl\ \ 2
Эффективность преобразования
в нелинейном волноводе
Здесь: Zo есть вакуумный импеданс величиной 377 Ом. Обратите внимание! В
последнем уравнении уровни мощности Р выражены в Вт м по ширине
волновода, а / есть ширина волновода. В случае согласования фаз эффективность
преобразования определяется соотношением:
(9.B.136)
Это уравнение вскрывает существенное препятствие (порядка 10~20 для типичных
значений х1о) и уровней мощности) для достижения разумного значения
эффективности и одновременно объясняет привлекательность волноводов с точки зрения их
использования при преобразовании частоты. Благодаря оптическому ограничению
в волноводах электромагнитные поля могут быть значительными даже при
сравнительно невысоких уровнях мощности, что приводит к осязаемой эффективности
преобразования.
Пример
Предполагая, что задача согласования фаз решена, рассмотрим волновод на основе
GaAs (х2 « 100 пм В и neff » 3) длиной 2 мм, толщиной 0,5 мкм и шириной 2 мкм.
При введении в волновод оптического излучения мощностью 10 мВт на длине
волны Ло = 2 мкм эффективность преобразования составит:
4,Зх10-2°Bх10+3мкм/2мкм|A02пмВ-7A0-2Вт/@,5х10^хм2))/33,т.е.16%
Квазифазовое согласование
Мы видели, что условия согласования по фазе выполняются, когда есть дисперсия
между волной накачки на частоте со и гармоникой на частоте 2со (т. е. /За)« /32(о).
9. В. Преобразование частоты в нелинейных волноводах
Однако, мы знаем, что в полупроводниках зонная структура приводит к
существенной дисперсии и что эта дисперсия существенно усиливается в волноводах
(смотрите рис. 9.7). Могло бы показаться, что согласование фаз по своей природе
невозможно в объемных полупроводниках. Однако, как оказывается, можно прибегнуть
к услугам технологии, чтобы пространственно свойства этих материалов могли бы
достичь такого состояния, которое называется квазифазовым согласованием.
При первом интуитивном подходе предположим, что мы можем модулировать
величину нелинейной восприимчивости периодическим образом вдоль волновода:
(9.B.14)
В этом случае уравнение связанных мод (9. В.4) изменяется незначительно: член в
экспоненте под знаком интеграла становится равным iBcot — {2/За ТЕ ± 2/A)z). При этом
все теоретические выкладки для эффективности преобразования остаются
прежними за исключением того, что член фазового рассогласования становится равным:
SP = Pi*te-W*te±— (9.В.15)
Л
Условие, приводящее к квазифазовому согласованию может быть записано в виде:
Аа,ТЕ-2&.ТЕ=^ (9.В.16)
Условие квазифазового
согласования
Рисунок 9.В.2 дает интерпретацию этого условия. Волновой вектор решетки
Bяг/Л) добавляет к этому волну накачки, что приводит к эквивалентности с
волновым вектором гармоники.
С технологической точки зрения это может быть осуществлено за счет
использования пространственного разрушения оптической нелинейности периодическим
образом с использованием ионной имплантации, методов кристаллического роста,
примесной диффузии и т. д. В этом случае выражение для нелинейности может
быть записано в следующем виде:
*£4 + У sinfzl (9.B.17)
В уравнении связанных мод (9.В.4) лишь один член, соответствующий условию
квазифазового согласования будет давать ненулевой вклад:
(9-В.18)
Таким образом, фазовое согласование может быть получено при длине гофра,
равной Л (п = 1, первый порядок), ЗЛ (п = 3, третий порядок) и т. д. Очень простой
расчет показывает, что для фазового согласования первого порядка эффективность
преобразования частоты остается той же самой, что величина, определяемая (9.В.13я):
Рис. 9.В.2. Интерпретация условий
квазисогласования фазы с использованием вол- 2 я
новых векторов. ~д"~
358 Дополнения к главе 9
/Ceff
У
(9.В.19)
Гофрирование, обеспечивающее фазовое согласование более высокого
порядка, приводит к еще меньшей эффективной нелинейной восприимчивости.
Рисунок 9.В.З. иллюстрирует физический принцип, лежащий в основе
квазифазового согласования. В пределах последовательных интервалов, каждый из
которых перекрывает Лрт, нелинейные диполи устраняются, при этом подавляется
механизм, ответственный за деструктивную интерференцию.
преобразованная
мощность
квазифазовое
согласование
без фазового соглосования
Рис. 9.В.З. Метод квазифазового согласования для оптического преобразования
частоты в нелинейном волноводе. Оптическая нелинейность попеременно
устраняется или оставляется неизменной в пределах последовательных
интервалов, каждый из которых перекрывает одну длину когерентности.
9.В.2. Режим с входящей ТЕ-модой
и выходящей ТМ-модой
В рассматриваемом случае нелинейная поляризация волновода принимает вид:
С(*> z)= eoZ%[A;(z)E;(x)]2
(9.B.20)
Этот член не равен нулю только если нелинейный тензорный элемент тоже не
равен нулю, что определяется симметрией полупроводникового кристалла.
Рисунок 9.В.4 показывает, каким образом происходит нелинейное взаимодействие. В
рассматриваемом случае расчет может быть проведен совершенно так же, как и в
предыдущем разделе, что позволяет нам записать:
plo>
16
»i
"LJ ( p» Л. JSBL
%——\ —^- Sin C2\ -!—-
r \dl 2
(9.В.21)
I TE ^ ^/t, j fteff у Ы1 J
На этот раз фазовое рассогласование определяется формулой:
9. Г. Резонаторы Фабри—Перо и брэгговскые отражатели
Рис. 9.В.4. Конфигурация генерации второй
гармоники ТЕ—ТЕ.
(9.В.22)
Уравнение (9.В.22) иллюстрирует другую возможность, основанную двулучепре-
ломлением в волноводе. В этом случае в волноводе достаточно обеспечить условие:
neff [2о))= nefr [со) (9.В.23)
Рисунок 9.В.5 демонстрирует такой волновод с квазифазовым согласованием,
реализованный с использованием гетероструктуры GaAs/AlGaAs/Al2O3.
800
1000
1200
1400
1600
частота, иэВ
Рис. 9.В.5. Модовое фазовое согласование в волноводе, реализованное с
использованием гетероструктуры GaAs/AlGaAs/Al О (С разрешения A. Fiort @LCR/
THALES.).
Литература
A. Fiore, V. Berger, E. Rosencher, P. Bravetti and J. Nagle,Nature, 391, 463 A998).
S. Someckh and A. Yariv, Appl. Phys. Lett. 21,140 A972).
J.P. van der Ziel, Appl Phys. Lett. 26, 60 A975).
9.Г. Резонаторы Фабри—Перо
и брэгговские отражатели
Оптическая обратная связь, обеспечиваемая зеркалами, является обязательной для
установления лазерных колебаний в оптическом резонаторе. Мы видели, что для
того, чтобы в резонаторе установился лазерный режим, должны быть выполнены два
условия: одно условие накладывается на усиление D.21 я), а другое — на фазу D.24).
Это последнее условие означало, что лазерные моды должны были быть
собственными модами оптического резонатора. Для задания резонатора могут использоваться
два типа зеркал — металлические зеркала и диэлектрические зеркала.
Диэлектрические зеркала особенно важны в полупроводниковых лазерах, в особенности, в
поверхностно-излучающих лазерах с вертикальным резонатором (VCSELs). Формализм,
используемый при описании распространения волны в слоистой среде идентичен тому,
360 Дополнения к главе 9
который описывает распространение волны в слоистом волноводе. Таким образом,
это дополнение удачно вписывается в главу, посвященную волноводам.
Для начала рассмотрим электромагнитную волну с частотой со =2яу,
распространяющуюся в двух средах A и 2) с общей границей раздела при z = 0 (смотрите
рис. 9.Г.1). Амплитуды волны в каждой среде определяются действительной частью
выражения:
Реальные волны, безусловно, имеют вид Re(i?(£)eiu")- Индекс R показывает, что
амплитуда соответствует волне, движущейся направо (е1^'-^) в то время, как
индекс L соответствует волне, движущейся налево (ei(a" + kz)). После этого запишем
уравнения Френеля, устанавливающие непрерывность электрического и магнитного
полей на границах раздела. Поскольку В = к х Е/со (смотрите B.17а—г)) и k. = 2m./AQi
где AQ есть длина волны в вакууме, а п. — коэффициент преломления в среде /, эти два
условия при z = 0 приобретают вид:
F + F - F + F
^ R\ ^ ^ L\ * u R2 ^ u 12
к F — к F — к F к F
(9.Г.2)
Предположим, что волна падает слева, т. е., что EL2 = 0, при этом система
уравнений (9. Г.2) может быть легко решена, что дает:
ER2 =*,2£/П (9ГЗ)
При этом:
л, +и2
(9.Г.4)
Ра -_^-"i
п, + п-,
Интерпретация (9.Г.З) очень проста. г12 есть коэффициент пропускания для
волны, идущей из среды 1 в среду 2, тогда как рп есть коэффициент отражения той
же волны от среды 2. Отметим несколько важных моментов. Во-первых, тп ф г21,
тогда какpl2= —р21. Также сразу отметим, что:
т г + п2 — \ Г9Г^
t'12*'21 г\2 — yj.l. .JJ
Это есть ничто иное, как констатация непрерывности потока вектора Пойнтинга через
границу раздела.
Теперь обобщим наши обозначения на случай описания двух границ раздела,
при этом / — 1 и / представляют многослойную диэлектрическую структуру с
границами, расположенными при zr Обозначим через ER ., EL . амплитуды справа и
z=0
1
~Я2
*►
-12
Рис. 9.Г.1. Распространение волны через
границу раздела.
9. Г. Резонаторы Фабри—Перо и брэгговские отражатели
рядом с границей раздела / — 1//, а через Е'R ., Е' L / — амплитуды волны слева и
рядом с границей раздела /// + 1 (смотрите рис. 9.Г.2). Уравнения непрерывности
(9.Г.2) могут быть представлены в матричной форме:
(9.Г.6)
(9.Г.7)
При этом передаточная матрица Р дается выражением:
Заметим, что с учетом (9.Г.4) и (9.Г.5) детерминант Р._{ . = n./n._v
Распространение волны в слое / учитывается с использованием константы распространения к.
или:
Здесь D. — дефазирующая матрица:
о
о
(9.Г.8)
(9.Г.9)
При этом ф. = А:./ = 2mi.l./A0 выражает дефазировку волны в слое / толщиной /.
Таким образом, для набора из N произвольных диэлектрических слоев,
электрические поля в средах 1 и N связаны соотношением:
[Е;]= PnD2P23 ... £„_,/>„-,. Л^]= SlN[^A (9.Г.10)
Матрица распространения S
Матрица S{ N есть матрица распространения. Рассматриваемое представление
также называется формализмом S-матрицы. Поскольку она является
произведением нескольких матриц, ее детерминант является произведением их
детерминантов, и он равен nN/nv Таким образом, детерминант не зависит от различных сред,
разделяющих среду 1 от среды N. Представляют интерес также и обозначения в
(9.Г. 10), так как они позволяют «распространить» граничные условия на всю
структуру. Рассматриваемый формализм идентичен тому, который был развит в главе 1
для получения собственных состояний квантовой ямы.
Если мы захотим отыскать коэффициент пропускания тш коэффициент отражения
plN для всей структуры, а также ее пропускание TlN и отражение RlN, нам будет
нужно лишь наложить граничное условие EL N = 0, которое означает, что никакая
другая волна не идет слева, что приводит к выражениям:
Pin =
(9.Г.11)
"Я/И
Рис. 9.Г.2. Иллюстрация формализма матрицы распространения S.
362 Дополнения к главе 9
tlN =-LnTlN=^-\rlN\2 (9.Г.12)
Отметим, что RlN +TlN = (\SX2\2 + nJnJ/lSj2 = 1, поскольку det(S) = njnv Это
последнее равенство означает, что световой поток сохраняется, и это само по себе
поддерживает нас в нашем рассмотрении!
9.Г.1. Резонатор Фабри—Перо
Сейчас мы применим этот формализм к простой задаче, связанной с резонатором
Фабри—Перо (смотрите рис. 9.Г.З). Он состоит из диэлектрической пленки
толщиной lcav, покрытой двумя тонкими металлическими слоями. Говоря более точно, эта
система содержит пять сред (вакуум -> металл -> диэлектрик -^ металл -» вакуум).
Полностью эта задача может быть решена при введении комплексного показателя
преломления для металла и предположении, что его действительная часть
стремится к —©о. Решение этой задачи оставляется читателю. Мы же рассмотрим систему,
состоящую из трех сред (вакуум = 1 -> диэлектрик = 2 -> вакуум = 3, при этом
металлические слои учитываются с использованием матриц переноса Рп и Р21,
определяемых соотношениями:
e 1 r'21"^W< i J (9ТЛЗ)
Одним из многих свойств металлических пленок, которое читатель может
вывести сам в качестве упражнения, является то, что в противоположность диэлектрикам,
коэффициенты г12 и г21 равны. Член &в отражает вклад дефазировки, обусловленной
металлическим зеркалом (в = п в случае совершенного зеркала), а коэффициент
отражения р0 близок к единице и учитывает большое отражение зеркал. Матрица
распространения 5I3 = PnD2P23 может быть легко рассчитана из соотношения:
Это соотношение приводит к пропусканию TFP резонатора Фабри—Перо
(смотрите (9.Г.12):
т _ 1Т12Т21| /Q р 1СЧ
Таким образом, мы вводим полный коэффициент дефазировки S = 2(ф — 0),
пропускание (Т = |г12|2) и отражение (R = р2) зеркала. Таким образом, полное пропускание
зеркала, т. е. доля интенсивности излучения, падающего слева, которое пересекает
резонатор, составляет:
ГРР = =-^ (9.Г.16)
FP \ + R2 -2RcosS
Мы напоминаем, что фаза ^определяется формулой:
(9.Г.17)
В том случае, когда длина волны излучения, падающего на резонатор,
изменяется, пропускание осциллирует между минимальным 7\п и максимальным Гтах
значениями, определяемыми:
9.Г. Резонаторы Фабри—Перо и брэгговские отражатели 363
cav
WVWVW
металлические
зеркала
Рис. 9.Г.З. Резонатор Фабри—Перо.
max
A - rY
Если бы зеркала были абсолютно совершенными (R + Т + А = 1 с
коэффициентом поглощения зеркала А = 0) мы бы получили Гтах = 1, т. е. вся энергия
прошла бы через резонатор. Это могло бы показаться удивительным, как если бы
мы сдвигали два зеркала со слабым пропусканием Т, и полное пропускание
комбинированной системы (при определенном зазоре) оказалось бы равным 1 вместо Т2,
что мы могли бы ожидать! Этот эффект является результатом конструктивной
интерференции, что является типичным для волновых явлений. Аналогичный эффект
проявляется в случае резонансного туннелирования электронов через двойные
квантовые барьеры.
Подставляя (9.Г. 18) в выражение для пропускания резонатора (9.Г. 16), мы
получаем:
1 (9.Г.19)
Т - Т
1 FP "" 'm
l+Csin2(£/2)
где С — контраст резонатора, определяемый формулой:
7LV , 4 Я
С =
-1 =•
(9.Г.20)
Tmin 0 - яJ
Вблизи резонанса резонатора (S~ 2тя, где т — целое число) (9.Г.19) принимает вид
лоренциана:
^FP e ^max "
\Av
(9.Г.21)
Пропускание резонатора Фабри—Перо
Здесь A v частотный интервал между оптическими модами, a F есть зеркальность
резонатора, определяемая формулой:
364 Дополнения к главе 9
F = tc-^- (9.Г.22)
1 — /V
Зеркальность резонатора
Зеркальность по порядку величины составляет я/Г для R « 1. Рисунок 9.Г.4
представляет зависимость TF? от частоты излучения. Спектральная зависимость
пропускания резонатора проявляет ряд максимумов, разделенных частотными интервалами:
Av =
(9.Г.23)
v I Av
Рис. 9.Г.4. Спектр пропускания
резонатора Фабри—Перо с
зеркальностью F = 10.
Эта величина представляет собой межмодовый интервал резонатора (или свободный
спектральный диапазон) с полушириной:
Sv=-
(9.Г.24)
Именно благодаря этому параметру F можно интерпретировать как меру
зеркальности.
В случае идеального зеркала {в = я) резонансы имеют место при толщине
резонатора:
А.
(9.Г.25)
Здесь т есть целое число. Таким образом резонансный резонатор Фабри—Перо
есть устройство полуволнового типа. Интерпретация резонанса Фабри—Перо
приведена на рис. 9. Г. 5. На этой диаграмме амплитуды и относительные фазы
различных распространяющихся полей представляются векторами Френеля или фазора-
ми. В условиях вне резонанса векторы, соответствующие отраженным волнам,
складываются (круговым образом), при этом их сумма равна нулю. Все происходит
таким образом, как если бы два металлических зеркала вели себя независимо друг
от друга и обладали бы пропусканием Т при полном пропускании пары зеркал Т2.
а б в
Рис. 9.Г.5. Когда резонатор Фабри—Перо находится вне резонанса сложение векторов
Френеля происходит по круговой траектории (а). При приближении к
резонансу фазовый сдвиг между каждым вектором становится кратным 2я, при
этом отдельные векторы Френеля выстраиваются, что приводит к
пропусканию, близкому к единице (б). Это последнее условие реализуется в
полуволновом резонаторе.
9. Г. Резонаторы Фабри—Перо и брэгговские отражатели
С другой стороны, по мере того как толщина диэлектрического слоя
приближается к полуволновому значению, разность фаз между отдельными фазорами
становится кратным 2лг (т. е. они начинают выстраиваться вдоль одного направления),
при этом они суммируются (интерферируют) конструктивно.
Рассчитаем теперь комплексную амплитуду электрического поля внутри
резонатора, считая зеркала идеальными. Это можно сделать используя [Е2] = Р23[Е3], а
также (9.Г.1), т. е.:
-rk~lkz -Poe+iMe-2i>] (9.Г.26я)
Амплитуда поля внутри резонатора есть модуль (9.Г.26я) (это не является
тривиальным результатом и мы оставляем это доказательство читателю в качестве
упражнения). Рисунок 9.Г.6 показывает распределение электрического поля в
резонаторе. Отметим проявление эффекта резонанса, приводящего к увеличению
максимальной напряженности поля внутри резонатора. Мы можем легко найти
максимальную напряженность поля, предполагая, что в резонансе (т. е. при ф = я
и р0 «1) электрическое поле (9.Г.26д) приближается к стоячей синусоидальной
волне, спадающей до нуля у зеркал при z = 0 и z = /cav при к = я/1сгу. Максимальная
напряженность поля имеет место при z = / v /2 или:
1-Ро
(9.Г.266)
Или с учетом (9.Г.5) и (9.Г.21):
(9S.26e)
Таким образом интенсивность излучения посередине резонатора усиливается в
4/Г раз по сравнению с входящим потоком, при этом коэффициент 1/Т обусловлен
коэффициентом отражения зеркала, а коэффициент 4 возникает вследствие
конструктивной интерференции двух волн, распространяющихся в противоположных
направлениях. Энергия, запасенная в резонаторе, получается интегрированием
синусоидального распределения, т. е.:
Е -I
Jsi
sin k2zdz =
(9.Г.27)
Здесь S есть площадь резонатора. Эту величину следует сравнить с энергией,
теряемой за цикл, что соответствует интегральному фотонному потоку за цикл.
Отношение этих двух величин, коэффициент качества резонатора Q, определяемый (9.Г.27)
и (9.Г.23), может быть записано в виде:
Рис. 9.Г.6. Увеличение внутреннего поля резонатора как следствие уменьшения
коэффициента пропускания Т.
366 Дополнения к главе 9
„ запасенная энергия „ v /n r лоч
С/= = t -— (УЛ.Щ
расход энергии за один цикл Av
Коэффициент качества и зеркальность
резонатора для волны с частотой v
Эта величина связана с фотонным временем жизни соотношением:
Q = 2kvic (9.Г.29)
Это соотношение устанавливает связь между тс и F.
Пример
1. Рассмотрим резонатор Фабри—Перо, содержащий диэлектрический стержень
длиной 50 см с коэффициентом преломления 1,5. Металлические зеркала, наносимые
на оба конца стержня, обладают коэффициентом отражения Я = 99% и
пропусканием Т= 1 - Я = 10~3. В этом случае зеркальность резонатора есть F — яЯ/Т = 3140.
Межмодовый интервал есть 3 х 108 м с~!/C х 0,5 м) или 2 х 108 Гц. Для длины волны
1 мкм (v= 3 х 10м Гц) коэффициент качества Q = 3,14 х 103 х 3 х 1014 Гц/2 х 108 Гц
или Q = 5 х 109! В действительности такой величины трудно добиться, так как
трудно обеспечить необходимую степень параллельности зеркал при достаточно
большом расстоянии между ними.
2. Теперь рассмотрим резонатор, реализованный с использованием слоя AlGaAs
толщиной 0,25 мкм и п = 3. Длина резонансной волны в резонаторе в этом случае
составляет Ао = 2яор/сау или 1,5 мкм. На обе стороны слоя AlGaAs наносятся
металлические зеркала, обладающие коэффициентом отражения Я = 99,9% и пропусканием
Т= 1 - Я = 10~3. В этом случае зеркальность резонатора рассчитывается аналогично
предыдущему примеру, F = яЯ/Т = 3140. В то время как в рассматриваемом случае
межмодовый интервал составляет 3 х 108 м с~УB х 3 х 0,25 х 10~6 м) или 1,5 1014 Гц. В
этом случае коэффициент качества есть 3,14 х 103 х 2 х 1014 Гц /1,5 х 1014 Гц или Q= 4200.
9.Г.2. Брэгговские зеркала
Рассмотрим теперь последовательность двойных слоев, сформированных
чередованием слоев на основе среды 1 и 2. Сейчас нас будет интересовать матрица
распространения S между правыми границами среды 1 в пределах двух последовательных
двойных слоев (смотрите рис. 9.Г.7):
S = PnD2P1{D, (9.Г.30)
При этом:
Здесь: r12, r21 и рп = —p2l определяются (9.Г.4). В этом случае матрицу Sлегко найти:
*-±
При этом г2 = т12т21. Эта £ — матрица принимает особенно простой вид, когда слои 1
и 2 являются четвертьволновыми, т. е. фх = ф2 = я/2 или в другой записи /cav . = тяА/4п.,
где т являются целыми числами:
Я1 + Р2 2,1
9.Г. Резонаторы Фабри—Перо и брэгговские отражатели 367
Е\
Е\
Рис. 9.Г.7. Геометрия и соответствующая элементарная матрица распространения для
брэгговского зеркала.
Эта матрица имеет собственные значения:
(9.Г.34)
Ее собственные векторы имеют вид:
Это сразу приводит к диагонализации (9.Г.ЗЗ):
S = Г1 МТ, при этом М =-Ы
7
Ы +Р
и Г =
о
(9.Г.35)
(9.Г.36)
В этом случае матрица распространения для серии из N двойных слоев имеет вид:
SN =T-'MNT = —
2N
О
о
При этом коэффициент отражения, определяемый (9.Г. 12), есть:
(9.Г.37)
(9.Г.38)
Или, с учетом (9.Г.4):
(9.Г.39)
Коэффициент отражения последовательности
из N двойных диэлектрических слоев
Здесь мы произвольно предположили, что п{ > п2. Мы видим, что по мере того, как
число слоев возрастает, коэффициент отражения стремится к единице, что и реализует
брэгговское зеркало.
368 Дополнения к главе 9
Мы были бы в праве предполагать, что брэгговское отражение такого рода
представляет собой сильно резонансное явление и что условия на длину волны,
обеспечивающие R = 1 в лучшем случае должны были быть очень суровыми.
Фактически же такое предположение очень далеко от истинного. В
действительности в полной аналогии с результатами по зонной структуре, полученными в
главе 5, для электронов в кристаллических твердых телах и в рассматриваемом
случае формируются запрещенные зоны (или зоны непрозрачности) для
распространения излучения.
Мы можем обобщить подход, использованный выше, для описания условий
вне резонанса (хотя это и объемная задача). Здесь же мы только оценим число N
двойных слоев, необходимое для формирования зоны непрозрачности АЛ, такой что
1 -R < 10"":
81пЮ^-^ 2LogZ!L_^ + Log4 M)
л ". +м ъ N A
Когда число двойных слоев N стремится к бесконечности, зона непрозрачности
стремится к своему пределу, определяемому соотношением:
\1/2
(9.Г.41)
Пример
Мы хотим получить брэгговское зеркало на основе двойных слоев GaAs/AlGaAs,
отражающее на пиковой длине волны Л = 1 мкм. Коэффициенты оптического
преломления GaAs и AlAs равны соответственно 3,30 и 2,9. В этом случае
необходимая четвертьволновая толщина составляет /GaAs = 757 Е и /A1As = 862 А для
двух материалов. Для серии из 20 двойных слоев коэффициент отражения
зеркала составит:
Д15 = [(l - 0,87840 )/(l + 0,87840 )]2 = 97,8%
Это в свою очередь, потребует эпитаксиального выращивания структуры с
полной толщиной 20 х 1578 А или 3,1 мкм. Предполагая, что типичная скорость
эпитаксиального выращивания составляет ~1 мкм/час, находим, что синтез такой
структуры потребует немногим более 3 часов.
Ширина полосы непрозрачности, которая при этом будет реализована,
определяется (9.Г.41):
АЛ/ Я = 4 I к [0,44 /6,36 In C,40 / 2,96 )]1/2 или АХ = 0,116 мкм.
Рисунок 9. Г. 8 показывает спектр отражения R(A) для системы из 20 двойных
слоев, рассчитанный с использованием программы MATHEMATICA, приведенной
ниже.
Мы видим, что ширина полос непрозрачности близка к значению,
рассчитанному выше.
x=.;1.(*mm*)
п1=3.3;п2=2.9;|1 = |/D*п1);|2Н/D*п2;
r12=(n1-n2)/(n1+n2);t12=2n1/(n1+n2);
r21=(n2-n1)/(n1+n2);t21=2n2/(n1+n2);
А=Аггау[а,{2,2};а[1,1]=1.;а[1,2]=г12;а[2,1]=г12;а[2,2]=1.;М12=АД12;
B=Array[bl{2l2}]b[1,1]=1.;b[1,2]=r21;b[2f1]=r21;b[2f2]=1.;M21=BA21;
R=Table[{x,D1=Array[d1,{2,2}];D2=Array[d2,{2>2}];
d1[1,2]=0;d1[2J]=0;d1[U]=N[Exp[-|*2W
9.Г. Резонаторы Фабри—Перо и брэгговские отражатели 369
л
• •
i
•
Л-
F
1 .
г
0.8
0.6
0.4
0.2
•
* * ж
• \ ж
• /
• • • f
• \ •
• • •
0.85
0.9
0.95
1.05
1.1
1.15
Л(мкм)
Рис. 9.Г.8. Спектр отражения брэгговского зеркала с параметрами, приведенными в
примере.
d2[1,2]=0;d2[2J]=0;[1J]=N[Exp[4*2*PJ*n2*|2/x]];d2[2,2]=N{Exp[|*2*Pi*n2*12/x]];
S= D2.M21.D1.M12;Sp=MatixPower[S,20];Spp=M12.Sp;
r=Abs[Spp[[1,2]]/Spp[[2>2]]]},{x,.85J1.15J.001}];
ListPlot[R]
Литература
G. Bruhat, Optique, 6h Edn, Masson, Paris A992).
M.V. Klein and Т.Е. Furtak, Optics, John Wiley, New York A986).
P. Yeh, Optical Waves in Layered Media, Wiley Interscience, New York A988).
ГЛАВА 10
ОСНОВЫ ФИЗИКИ
ПРИБОРОВ
10.1. Введение
Полупроводники представляют собой материалы, которые крайне чувствительны к
внешним воздействиям (например, к освещению, электрическим полям, тепловым
градиентам, ...)• Эта их особенность используется в широкой гамме полупроводниковых
приборов. Типичная реакция полупроводника на такие воздействия будет раскрыта в
дальнейшем. До сих же пор мы ввели две характеристические длины экранирования. Одной из них
была глубина обеднения F.68):
A0.1)
Эта характеристика определяет расстояние, на протяжении которого потенциал Кэкра-
нируется фиксированным зарядом с плотностью ND (как правило состоящим из
ионизированных легирующих атомов). Одновременно мы ввели длинуДебая F.25):
(Ю.2)
Эта характеристика определяет расстояние, на котором потенциал экранируется
подвижными зарядами с концентрацией п0. Напомним, что е есть заряд электрона,
е есть диэлектрическая проницаемость полупроводника, кв — постоянная Больцма-
на, а Т — температура. Нижняя граница доступного диапазона уровней легирования
полупроводников ограничена фоновой концентрацией электрически активных
примесей, вводимых в образец в процессе его синтеза и обработки (для Si и GaAs эта
нижняя граница составляет соответственно ~108 см и 1014 см). Верхняя граница
определяется уровнем вырождения (порогом металлического характера переноса) при
ND > Nc или Nv в зависимости от того, какой тип (п или р) имеет материал (смотрите
главу 5). Как видно, эти характеристические длины варьируются от 0,1 до 10 мкм для
уровней легирования соответственно в диапазоне от 1018 см до 10м см. Указанный
нижний предел величиной 0,1 мкм определяет типичные размеры микроэлектронных
компонентов. В этой главе мы изучим несколько структур, которые помимо их
пригодности для оптоэлектроники как таковой, образуют основу современной электроники.
10.2. Поверхностные явления
На поверхности полупроводника нарушается периодичность кристаллического
потенциала. Каждый атом на поверхности связан со стороны полупроводника с
лежащими ниже атомами объема, тогда как электронные волновые функции с вакуумной
стороны границы раздела являются несвязанными и распространяются в свободное
пространство. Такие незавершенные поверхностные состояния называются
свободными связями. Эти два эффекта приводят к формированию электронных состояний в
запрещенной зоне объемного материала вблизи поверхности (смотрите дополнение
5.Г). В действительности такие локализованные поверхностные состояния непре-
10.2. Поверхностные явления
рывно распределены по запрещенной зоне и образуют в ней континуум. Для того,
чтобы характеризовать этот континуум, введем характеристический уровень ф0 над
потолком валентной зоны, который обладает следующим свойством: когда
поверхностные состояния заняты вплоть до уровня ф0, поверхность является электрически
нейтральной. С использованием полупроводниковой терминологии можно сказать,
что состояния ниже ф0 ведут себя как доноры (поскольку они нейтральны, когда
заняты электронами), тогда как состояния выше ф0 проявляют характеристики
акцепторов (поскольку они становятся отрицательно заряженными, будучи занятыми
электронами). В действительности поверхность всегда подвержена воздействию
окружающей атмосферы и очень вероятным является то, что примеси,
адсорбированные поверхностью будут давать свой вклад в заселенность локализованных
состояний в запрещенной зоне. Однако этот вклад может быть включен в определение ф0.
Например, на поверхности полупроводника /t-типа проводимости положение
уровня Ферми определяется легирующими примесями внутри материала. При
термодинамическом равновесии положение уровня Ферми неизменно по всей
структуре. На поверхности поверхностные уровни должны быть заполнены вплоть до
уровня Ферми, что приводит к формированию поверхностного заряда:
а = -eNj[EF -ф0- £v@)] (Ю.З)
Здесь Nx (см эВ-1) есть плотность поверхностных состояний, которая для простоты
предполагается здесь постоянной по зоне, а £у@)есть положение валентной зоны на
поверхности (смотрите рис. 10.1).
Поскольку структура в целом нейтральна, этот поверхностный заряд должен быть
скомпенсирован пространственным зарядом в полупроводнике, распределенным по области
обеднения (смотрите рис. 10.1). В противоположность поверхностному заряду,
распределенному в области толщиной порядка атомного монослоя, глубина обеднения L является
макроскопической величиной. Падение электростатического потенциала в этой области
пространственного заряда было описано в главе 6 и определяется уравнением F.69):
Vd=LlNoL2 =J-cjL (Ю.4)
Здесь сгесть заряд области обеднения. Таким образом, положение зоны
проводимости на поверхности составляет Ес@) = Ес(°°) + eVd, и оно представляет собой
внутренний потенциальный барьер, мешающий электронам покинуть объем
полупроводника. Падение потенциала можно получить подстановкой A0.4) в A0.3):
вакуум полупроводник
заряженный
Рис. 10.1. Поверхностные
состояния между уровнем
Ферми и ф0 создают
поверхностный заряд, который
компенсируется пространственным
зарядом в области обеднения.
Глава 10. Основы физики приборов
I e_
2~e
или:
1 е
1 е
A0.5)
A0.6)
В пределе очень больших концентраций поверхностных состояний Vd перестает
зависеть от Nj. При этом уровень Ферми на поверхности становится, таким образом,
фиксированным при Ev@) + ф0 и его положение определяется выражением:
)~ EF = eVd
A0.7)
В этом случае толщина области обеднения равна соответствующей глубине обеднения для
потенциала V^
Проанализируем теперь поведение металлического слоя, осажденного на
полупроводник. Сначала мы отметим, что прежде, чем электрон сможет покинуть полупроводник и
перейти в вакуум, электрон на дне зоны проводимости у поверхности должен преодолеть
барьер zs. Этот параметр называется электронным сродством полупроводника и он
выражает энергию, удерживающую электроны в материале (смотрите рис. 10.2).
В качестве мысленного эксперимента представим себе, что мы придвигаем металл
ближе к поверхности полупроводника. Поскольку металл не имеет запрещенной зоны,
его сродство равно работе выхода из металла фт (т. е. разности энергии между уровнем Ферми
и вакуумом). Если мы закоротим эти два материала внешним проводом, уровни Ферми
выравнятся. Это произойдет вследствие переноса заряда между полупроводником и
металлом, что приведет к разнице потенциальной энергии между внутренними объемами
двух этих материалов. В металле, обладающем колоссальным количеством
свободных электронов A022—1023 см) перенесенный заряд ограничен в пределах
поверхностного слоя с толщиной, определяемой длиной Дебая, называемой также длиной
Томаса—Ферми в металлах. Поскольку в металлах эта величина крайне мала, этот
поверхностный слой может быть представлен как поверхностный заряд.
Со стороны полупроводника распределение перенесенного заряда может быть
описано с использованием двух моделей.
металл
вакуум
полупроводник
£ Рис. 10.2. В состоянии
с термодинамического рав-
zFs новесия между металлом
и полупроводником
имеет место перенос заряда,
что приводит к
выравниванию положения уровня
Ev Ферми. Распределение
этого заряда определяет
высоту барьера Шотки фв.
10.3. Переход с барьером Шотки
1. Модель Шотки. В отсутствие поверхностных состояний заряд формируется
только в пределах слоя обеднения. По мере того, как расстояние между двумя
материалами стремится к нулю, зона проводимости фиксируется на уровне:
Есф)=Фт~Х5 A0-8)
Это уравнение означает, что на границе раздела нет заряда. При этом падение
потенциала на области обеднения составляет:
eVd = Ес§)- Ес(оо)=фт - zs - E(oo) A0.9)
Здесь: величина Ес(<х>) определяется уровнем легирования. Это и есть модель Шотки.
2. Модель Бардина. В противоположном пределе, когда плотность
поверхностных состояний велика, переносимый заряд может быть легко обеспечен за счет
освобождения достаточного количества поверхностных состояний без существенного
влияния на полупроводниковые зоны. В этом случае величина eVd полностью
определяется ф0 и не зависит от типа осаждаемого металла. Это есть модель Бардина.
В рамках обеих моделей высотой барьера Шотки называется энергия:
ефв = Ec@)-EF A0.10)
В рамках первой модели фв зависит от металла, но не от уровня легирования
полупроводника. В модели Бардина фв не зависит ни от металла, ни от уровня
легирования полупроводника.
На практике экспериментальные результаты соответствуют промежуточной между
двумя моделями ситуации, при этом более часто они все-таки согласуются с
моделью Бардина. Более того, после осаждения металла возможна модификация
поверхностных состояний за счет химической связи между двумя типами материалов,
при этом как фв, так и ф0 начинают зависеть от металла. Суммируя изложенное,
можно сказать, что высота барьера Шотки зависит от пары металл/полупроводник,
но при этом указанная зависимость намного слабее той, которая предсказывается
моделью Шотки. При последующем рассмотрении мы будем предполагать, что фв
слабо зависит от пары металл/полупроводник и не зависит от уровня легирования,
при этом величины убудут браться из эксперимента.
Как говорят, пара металл/полупроводник образует контакт Шотки к
полупроводнику. Мы увидим, что такой тип контакта действует как выпрямляющий контакт
(т. е. обеспечивает преимущественное токопротекание в одном направлении), что
является важной характеристикой, используемой в диодах Шотки. Такие же
приборы находят свое применение в качестве приемников оптического излучения.
10.3. Переход с барьером Шотки
При контактировании металла и полупроводника более не существует барьера между
каждым из этих материалов и вакуумом, при этом электрон с энергией, превышающей высоту
барьера Ес@) может перемещаться между металлом и полупроводником. При
термодинамическом равновесии концентрация электронов у поверхности, обусловленная
полупроводником, описывается классическим выражением:
m0)=7vrexp £-1-^ — = Nр ехр - , A0.11)
к Т \ к Т \
При большой высоте барьера фв по сравнению с квТэгт концентрация, естественно,
очень мала по сравнению с концентрацией носителей заряда внутри полупроводника:
-"^"GLexpf-Srl A0-12)
Глава 10. Основы физики приборов
dcc
Среди поверхностных электронов с концентрацией п @) половина имеет
компоненту скорости, направленную к металлу, а другая половина имеет компоненту
скорости, направленную к полупроводнику. Средняя скорость электронов,
направленных к металлу, составляет:
A0.13)
Это соответствует плотности тока:
A0.14)
До тех пор, пока система находится в равновесии, этот ток полностью
компенсируется током, протекающим в противоположном направлении от металла к полупроводнику:
Если мы приложим напряжение 0арр, то получим (смотрите рис. 10.3):
О015)
EF m = EF s -ефарр A0.16)
Здесь предполагалось, что уровни Ферми располагаются вдали от перехода. В металле
проводимость столь велика, что никакое падение напряжения невозможно и, таким образом,
Ес@) остается на уровне EF т + ефв. Таким образом, приложенный потенциал ограничен
областью полупроводника, которая должна так модифицировать область обеднения,
чтобы падение потенциала стало равным Ес@) — £ (°°) = eVd — ефарр.
Примечание: такая модуляция длины обеднения L с приложенным напряжением приводит к
емкости С, определяемой приращением заряда из-за изменения приложенного напряжения йфа :
d^pp = V
eeN r
€
Т
A0.17)
"Vapp ----- ■ '
Эта емкость есть функция приложенного напряжения — свойство широко используемым
в ВЧ-применениях. Таким образом, барьер Шотки действует как варактор, характеризуемый
переменным реактивным сопротивлением. Если приложенный сигнал является суммой
сигнала с малой амплитудой с частотой cos и амплитудой К, а локальный генератор обладает
частотой со0 = 0M - Асо и амплитудой VQ » К, реактивный ток будет обладать компонентой на
разностной частоте Асо. Этот ток может быть записан в виде (Q = NJL):
металл
полупроводник
Рис. 10.3. Переход Шотки при
приложении прямого напряжения фарр.
Область обеднения сужается, при
этом концентрация электронов со
стороны полупроводника
возрастает, приводя к потоку электронов из
полупроводника в металл.
арр/
10.3. Переход с барьером Шотки
*Q_ = ^О_^Фщ. = с@) \ Vd d0app е
<*t <* A* d/ \Vd- фарр d/
^(Л\ К cos (a)nt)+ V. cosCooj)],,, . / \ ., .
= -C@1 1 + -3 v ° ^ J ^-^ (Ko«o 81пЦ/)+ Ks^5 si
A0.18)
Этот ток содержит компоненту с частотой Лгу:
d/ d^app d/ 2 Kj 2
В общем случае, в токе диода содержатся все частоты со0 ± со0, со0 ± cos, cos ± й>0.Таким
образом, варактор преобразует высокочастотный сигнал с частотой cos в сигнал с
промежуточной или низкой частотой cos — со0. Следовательно, такой прибор является полезным при
гетеродинном детектировании. Подобно другим нелинейным приборам варактор также реализует
функции удвоения частоты и выпрямления с частотой cos — со0. Позже мы возвратимся к этому
при рассмотрений концепций нелинейной оптики.
С металлической стороны границы раздела ничего не изменилось. Перед
электронами стоит тот же барьер, который надо преодолеть, чтобы войти в
полупроводник, при этом плотность тока из металла в полупроводник остается равной:
В то же время со стороны полупроводника происходит изменение барьера.
И именно такая асимметричная реакция полупроводника и металла приводит к
выпрямительным характеристикам диода. Для упрощения расчетов
предположим, что диффузионный перенос (и следовательно подвижность) очень велик в
полупроводнике. Кроме того, мы предположим, что перенос электронов
приведет лишь к незначительному возмущению равновесного состояния
полупроводника. В этом случае концентрация носителей с полупроводниковой стороны
перехода составит:
«@)= ",е
При этом плотность тока, направленного к металлу, будет равна:
В этом случае результирующий ток через структуру составит:
A0.23)
Вольт-амперная характеристика диода Шотки
При этом плотность тока насыщения /^ дается выражением:
Постоянная А* называется константой Ричардсона. В предположении
эффективной массы тс = т0 ее величина составляет А = 120 А см К. Типичный график
в соответствии с A0.24) показан на рис. 10.4.
Глава 10. Основы физики приборов
1000
800
600
400
200 -
0 -
-10 -5
-
1
]
-
Рис. 10.4. Вольт-амперная характеристика
диода Шотки.
Пример
Для перехода А1—GaAs фв =0,7 В. В этом
случае плотность тока насыщения при
комнатной температуре составляет:
тг
--p- |=120хО,067хЗОО х
xexd - —'— |А см 2 = 0,5 мк А
СМ
В случае диода с площадью 100х 100 мкм2
10 максимальный обратный ток есть |/J =
= 0,05 нА. При приложенном
напряжении фарр = 0,2 В прямой ток составляет:
/ =
мка
При фарр = 0,4 В его величина равна / = 0,44 мА. Сопротивление диода /^ при фар = О
равно:
JL
kBT = 0,025
ejM ,5x10-
- Ом см2 =50 кОм см2
Для детального учета характеристик реальных диодов Шотки к идеальной
модели следует добавить ряд коррекций. Во-первых, электронный перенос в области
обеднения может быть ограничен способностью полупроводника переносить электроны,
когда коэффициент их диффузии мал. Другими словами, при прямом смещении их
концентрация л@) будет меньше равновесного значения для полупроводника
(уравнение A0.21), при этом величина инжектированого в металл потока будет
уменьшена. Это должно приводить к модификации коэффициента перед экспонентойу8а1 в
/— ^-характеристиках, в то время как зависимость от ф^ остается неизменной.
Более того, высота барьера может быть уменьшена из-за заряда изображения.
Электрон, покидающий металл, поляризует электронный газ в металле.
Результирующее при этом сродство электрона к металлу, известное из электростатики,
может быть представлено в виде притяжения этого электрона к одиночному
виртуальному заряду изображения Vlm(z) - —eVD£Bz)), где z есть расстояние между
электроном и поверхностью металла. Это приводит к добавлению члена —eFz к потенциалу
области обеднения, что приводит к уменьшению максимума этого потенциала по
отношению к фв: Vmax = фв — (eF/4s)l/2. Таким образом, полная высота барьера
уменьшается, что приводит к увеличению/^ и проявлению зависимости плотности тока
от напряженности поля F (от приложенного напряжения). К тому же, если
напряженность F очень велика, что имеет место в случае сильно легированного
полупроводника даже при малых приложенных напряжениях, электроны могут пересекать
переход за счет туннелирования, при этом Вольт-амперные характеристики становятся
линейными. В этом случае переход называется омическим контактом.
И наконец, источником дополнительного тока может быть и ряд паразитных
процессов (генерация электронно-дырочных пар в области пространственного
заряда, токи утечки по периметру контакта и т. д.). Эти процессы сильно зависят от
особенностей конкретного процесса изготовления контактов. На практике эти па-
10.4. р—п-переход
разитные эффекты учитываются введением коэффициента идеальности л, который
всегда >1, что является проявлением природного закона Мэрфи, и который
определяется из измерения характеристик контакта:
Н^Н <io-25)
Диод Шотки идеален, когда п = 1.
10.4. р—п-переход
р—«-переход образуется легированным полупроводником /?-типа с одной стороны
перехода и легированным полупроводником л-типа с другой стороны перехода. /— К-харак-
теристика для тока пересекающего такой переход в функции приложенного
напряжения, который проявляет выпрямляющий характер подобно тому, как это
было в случае диода Шотки. В то же время процесс, ответственный за это, имеет
другой характер.
Начнем с рассмотрения резкого/?—п-перехода в условиях термодинамического
равновесия (т. е. перехода, в котором тип легирования изменяется в пределах очень малого
расстояния по сравнению с протяженностью области пространственного заряда —
смотрите рисунок 10.5). При z > 0 полупроводник имеет р-тип проводимости с постоянной
концентрацией акцепторов NA. Вдали от перехода уровень Ферми располагается,
вблизи валентной зоны, и концентрация дырок в валентной зоне есть рр = NA, где
индекс «р» обозначает р-сторону перехода. К тому же, вследствие теплового равновесия
мы имеем пр = nf и концентрация электронов составляет п = я.2 /NA, при этом они
являются неосновными носителями при условии, что пр« NA. С «-стороны перехода (при z < 0)
полупроводник легирован донорами до постоянного уровня ND. Таким образом, вдали от
перехода уровень Ферми располагается вблизи зоны проводимости, при этом
концентрации основных носителей-электронов и неосновных носителей-дырок составляют
соответственно пп = NDupn = nf/ND« пп.
Вдоль перехода концентрация дырок не может изменяться скачком от рп до рр.
Следовательно, существует область около z = 0, где p(z) < рр = NA. Аналогичным
образом, в случае электронов мы также имеем область, где n(z) < пп = ND. В
условиях равновесия всегда выполняется n(z)p(z) = я,2, но сумма концентраций
подвижного заряда будет намного меньше концентраций фиксированных ионизированных
атомов примеси. Таким образом, область обеднения характеризуется плотностью
заряда ~eNA с /ьстороны перехода и положительным зарядом eND с «-стороны
перехода. Дипольный слой ответственен за формирование электростатического
потенциала по обе стороны перехода. В условиях равновесия этот потенциал
обеспечивает выравнивание уровней Ферми электронов и дырок. Он всегда существует в
условиях равновесия и поэтому называется встроенным потенциалом, при этом его
величина определяется выражением:
К = (EF - £Д - (EF - £,), = Е,- kj lnf-^-1 (Ю.26)
Здесь мы использовали E.52) и E.54) для расчета положения уровней Ферми в функции
уровней легирования.
Физическая причина возникновения потенциального барьера заключается в
следующем. Если мы представим себе, что мы приводим в контакт и- и /ьобласти
полупроводника, то основные носители с обеих сторон перехода будут
диффундировать в другую область (т. е. в область, где они присутствуют в качестве
неосновных носителей), как это и следовало ожидать из закона Фика. В отсутствие какого-
либо противодействующего механизма как электроны, так и дырки продолжали бы
диффундировать до тех пор, пока их концентрации не стали бы постоянными по
Глава 10. Основы физики приборов
о.
Q)
Ec(z)
I
о
концентрация \/
электронов V
полная концентрация А
носителей ^Ч\
-wn
f ю15
Зю10
ю5
10е
о
* ю-5
; концентрация
; дырок
концентрация
электронов
концентрация
дырок
Рис. 10.5. Диод с р—«-переходом в состоянии термодинамического равновесия.
Потенциал, создаваемый дипольным зарядом в области обеднения между dn и
dpi приподнимает зоны со стороны р по сравнению с я-стороной.
Одновременно потенциал удерживает большинство электронов в области z < 0 и
большинство дырок в области z > 0.
всей структуре. Однако, заряженные атомы легирующей примеси
противодействуют этому механизму. По мере того, как все большее число носителей переходит на
другую сторону перехода, амплитуда пространственного заряда, сформированного
остаточными ионизированными атомами примеси, увеличивается, что создает
энергетический барьер, который препятствует и, в конце концов, прекращает
дальнейшую диффузию носителей. Таким образом, мы видим, что диффузия носителей
будет играть доминирующую роль в работе р—«-диода. Именно по этой причине
встроенное поле иногда называют диффузионным потенциалом. Мимоходом еще раз
отметим эффективность концепции уровня Ферми. Этот параметр определяет
электронное сродство в каждом из материалов и учитывает химические потенциалы,
электростатические потенциалы и т. д. Результирующим распределением будет то,
которое обеспечивает постоянное положение уровня Ферми по всей структуре.
Теперь мы уже можем идти вперед и рассчитать электростатический потенциал
<p(z) или, что проще, рассчитать потенциальную энергию электронов V(z) = -eflzY
Используем аппроксимацию области обеднения, поскольку она существенно упро-
10.4. р—п -переход 379
щает расчеты — т. е. мы пренебрежем влиянием носителей на распределение
потенциала в области пространственного заряда.
Таким образом, в интервале —dn < z < О, уравнение Пуассона имеет вид:
■± = —ND A0.27)
t*Z £
При этом его решение представляет собой:
V(z)= Vn +—ND(z + dJ A0.28)
В /^-области при 0 < z < d уравнение Пуассона имеет вид:
При этом соответствующее решение определяется выражением:
A0.30)
У перехода, расположенного при z = 0,физическая непрерывность потенциала
и его первой производной, т. е. электрического поля, приводит к следующим
условиям:
NDdn = NAd,
При этом, поскольку Ур~Уп~У^ решения приобретают вид:
d'¥ A0-32)
^2=^-^г
Присутствие потенциала смещает зоны в полупроводнике, поскольку энергия
электронов увеличивается вдоль структуры в каждой точке на величину — есЦт) = V(z)'.
Ec(zh Ec(~Wn)+V(z)-Vn <10J3>
= Ec(z)-Eg = EXWp)+V(z)-Vf
ем:
y(z)-vn
Исходя из этой конфигурации энергетических зон для Ec(z) и Ev(z), мы можем
рассчитать концентрации электронов и дырок:
В частности, мы находим, что:
A035)
Глава 10. Основы физики приборов
Таким образом, для условий термодинамического равновесия мы определили:
вид потенциала V(z), зонную диаграмму для Ec{z) и Ev(z), ширину областей
пространственного заряда и концентрации носителей в каждой точке.
Пример
Рассмотрим р—«-переход на основе GaAs, каждая область которого легирована до уровня
ND = NA= 1017 см. Отыщем диффузионный потенциал Уы и электрическое поле в
переходе при z — 0. Из уравнения A0.26) мы имеем:
При этом dn = dp = 92 нм. Таким образом, слой обеднения очень тонок. Максимальная
напряженность поля имеет место при z = 0 и она равна:
Ясно, что в условиях равновесия через структуру не будет протекать ток. Вне
области обеднения не существует ни электрическое поле, ни градиент концентрации
носителей. С другой стороны, в области обеднения имеется сильное электрическое поле, а
также значительный градиент концентрации носителей. Постоянное положение уровня
Ферми по всей структуре гарантирует, что все компоненты тока будут взаимно
компенсироваться, если диффузионный профиль будет таким, как он описывается A0.34). Перед
тем, как перейти к рассмотрению приложения напряжения к структуре, полезно
представлять себе порядок различных параметрических длин, которые характеризуют
переход. Область, определяемая z < 0, представляет собой колоссальный резервуар
свободных электронов, сдерживаемых потенциалом области обеднения. Лишь незначительная
концентрация неосновных электронов может просочиться в /^-область перехода.
Подобным же образом область z > 0 образует резервуар для дырок, сдерживаемый
потенциалом области обеднения. Наконец, в нейтральных областях увеличенная концентрация
основных носителей обеспечивав высокий уровень проводимости, что приводит к
нулевому электрическому полю в этой области. Таким образом, потенциал остается
постоянным по обе стороны области обеднения даже в условиях не очень сильных токов.
Приложение слабого прямого смещения фарр (т. е. такого, которое уменьшает
высоту барьера) приводит к энергетическому зазору между уровнями Ферми по обе
стороны области обеднения (смотрите рис. 10.6):
Е,., = £,..-*„ A0-36)
В нейтральных областях потенциал остается постоянным, при этом
единственной областью, в которой возможно изменение падения напряжения, является
сужающийся обедненный слой. Этот эффект может быть учтен заменой в A0.31) F
на К - ефарр, что дает:
A0.37)
В резервуаре электронов потенциал при dp понижается до уровня К - ефт.
Поскольку область обеднения узка, мы можем предположить, что электронный
резервуар будет в равновесии вплоть до dp. Таким образом, концентрация электронов в
соответствии с A0.34) и A0.35) есть:
10.4. р—п-переход 3 81
(а)
-Fn
а
ф
о
&арр
концентрация
электронов
Рис. 10.6. Под влиянием прямого приложенного поля фярр область обеднения
сжимается, потенциальный барьер между п- и ^-областями уменьшается, а
концентрация носителей возрастает (жирные линии). Эти носители рекомбиниру-
ют с основными носителями, что обеспечивает протекание тока в структуре.
п(d ) = пп ехр -
Условие Шокли
Мы напоминаем, что п = nf/NA есть равновесная концентрация неосновных
носителей. Уравнение A0.38) имеет фундаментальное значение с точки зрения
описания р—«-перехода и оно называется условием Шокли. При z — d имеется
избыток электронов по сравнению с равновесным значением пр. Этот избыток
электронов должен быть удален через /ьконтакт (при z — W на рис. 10.5) или за счет
рекомбинации с дырками в области dp < z < Wp. В обоих случаях возникает ток
между переходом и /^-контактом. Важно помнить, что до тех пор, пока ефарр < Уъ.
электроны останутся неосновными носителями с концентрацией на несколько
порядков меньшей по сравнению с концентрацией дырок и, как следствие,
нейтральность заряда в р-области останется сравнительно ненарушенной из-за инжекции
электронов. И как результат, отсутствует поле, способное удалить электроны из
этой области (т. е. в обратном направлении!). Таким образом, единственной
возможностью переноса является диффузия. В этом случае уравнение переноса
электронов (смотрите F.60)) имеет достаточно простой вид:
A0.39)
Э/ dz п Bz т„
В стационарном состоянии имеет место уравнение:
A0.40)
Здесь Dn есть коэффициент диффузии для электронов в р-области, а тп есть их
время жизни до рекомбинации с дырками. Введем диффузионную длину:
382 Глава 10. Основы физики приборов
A. =JdT
A0.41)
Диффузионная длина
При этом с учетом An(z) = n(z) — пр уравнение может быть записано в виде:
A0.42)
Условие Шокли (уравнение A0.38)) позволяет рассчитать An на краю области обеднения:
An(dp)=n lexp
k.T
-1
A0.43а)
В том, что касается второго ограничивающего условия, мы будем моделировать
контакт при z = Wp временем жизни, которое настолько мало, что электроны и дырки
находятся в термодинамическом равновесии с уровнем Ферми-контакта. Так, что:
При этом решение для An(z) есть:
An(z)= An(dp)-
sinh
sinh
При этом имеют место два предельных случая:
К
A0.436)
A0.44)
«w.
A0.45)
An(z)= An(dp)\ I -
Wp
Первый предельный случай соответствует ситуации, когда ни один из
инжектированных электронов не может достичь контакта, поскольку они уже проре-
комбинировали с дырками. В этом случае полный ток должен сохраняться, и по
мере того, как мы удаляемся от перехода (т. е. z увеличивается в направлении от
dp к IV) электронный поток постепенно заменяется дырочным с тем, чтобы
поддержать процессы рекомбинации. Во втором предельном случае диффузионная
длина достаточно велика настолько, что все электроны, инжектированные при
Z — dp достигают Wp, не рекомбинируя с дырками.
Во обоих случаях полный ток, генерируемый инжекцией электронов, является
диффузионным током при z = dp (положительным, если он направлен от /^-области
к п-области), т. е.:
d/;| = eD^
An(dp)-
cosh I "^^
sinh
H^n -dn
A0.46)
-coth
^„ -flf.
exp
exp
kRT
Здесь: jns есть предел диффузионного тока для электронов, который определяется
выражением:
10.4. р—п-переход
Jns =
nneD,
A0.47)
Условие, выполнение которого необходимо для справедливости этой теории,
заключается в том, что область обеднения должна быть достаточно узкой с тем,
чтобы не имели место ни процессы генерации, ни рекомбинации
электронно-дырочных пар. Помимо всего прочего это означает, что Ln» dn + dp.
Ход рассуждений, использованный применительно к инжекции неосновных
электронов в ^-область, равным образом применим к инжекции дырок в «-область.
Потенциальный барьер для дырок при z = ~dn уменьшается таким образом, что
концентрация дырок составляет:
A0.48)
При этом уравнение диффузии для неосновных дырок в «-области (—Wn<z< ~d)
в этом случае имеет вид:
d2Ap Ар(г)_Л
dz2
A0.49)
Здесь: Lp2 = Drp есть квадрат диффузионной длины дырок в «-области. Решение
последнего уравнения с граничными условиями при z — ~ Wn и z — ~dn аналогично
A0.44) и приводит к следующему уравнению для концентрации избыточных дырок:
inhl-
sinh
Ap(z)=Ap(-dn) Л
sinh
A0.50)
Таким образом, ток, обусловленный инжекцией дырок в область я-типа составляет:
-1
При этом предел диффузионного тока для дырок составляет:
A0.51)
Р„ейр
pneDp
W_-d_
_ eD
= lv
«/
No
. N
A0.52)
Полный ток в «-области при z является, таким образом, суммой трех
компонент: электронного тока на основе электронов, инжектированных в р-область тока
электронов, рекомбинирующих с дырками, инжектированными в «-область, а
также тока дырок, инжектированных в «-область. В любом месте /^-области
проявляются аналогичные три процесса.
Полный ток, проходящий через структуру, является, суммой A0.46) и A0.51)
токов, инжектированных с двух сторон области обеднения:
= л
Js = L + Jps
A0.53)
Вольт-амперная характеристика р—n-диода
Глава 10. Основы физики приборов
Мы обсудили случай, когда ефарр > О, при котором инжектируются неосновные
носители. При ефарр < 0 в условиях обратного смещения уравнения остаются теми
же самыми за исключением того, что вместо избытка неосновных носителей в
данном случае имеет место их дефицит, способствующий генерации электронно-
дырочных пар в нейтральных областях. Вольт-амперные характеристики
по-прежнему описываются уравнением A0.53), но при этом ефарр < 0.
Пример
Для перехода на основе GaAs мы имеем NA = ND = 1017 см~3. Если подвижность
электронов в р-области составляет jun = 5000 см2 В с при аналогичном параметре для
дырок в я-области ju = 800 см2 В с, то мы находим с использованием соотношения
Эйнштейна Dn = jukBT/e = 5000 х 0,025 см2 с = 125 см2 с и Dp = 20 см2 с. При
времени жизни носителей тп = г = 1 не диффузионные длины составляют Ln = 3,5 мкм
и L = 1,4 мкм, что явно намного больше области обеднения. Собственная
концентрация носителей определяется E.49) и составляет п. = 1,8 х 106 см~3. Таким образом, диод
с большой толщиной обладает следующими пределами диффузионного тока:
• _ п}eDn _ (l,8xl012Jx 1,6x10~19 х 125x10 А_1Й ш_18 А
jns — — — 1,0 х Ш
NALn 1023 х3,5x10~6 м2 см2
. = nfeDp = (l?8xl012Jxl,6xlQ-19x20xl0-4 _A_ = 07xl0~18 -A-
ps NDLp 1023 xl,4xlO m2 см2
Таким образом плотность обратного тока составляет^ = 2,5 х 10~18 А см~2, а сопротивление
диода при фарр = 0 есть:
фарр
J]1 0,025
2,5x10
Омсм2=10,6Омсм2
Приведенные значения предельных токов очень малы. В действительности же
при рассматриваемых условиях в измеряемых токах доминируют токи утечки,
связанные с дефектами (смотрите дополнение 10 Б).
Выражение для Вольт-амперной характеристики (уравнение A0.53))
заслуживает нескольких завершающих комментариев:
1. Зависимость от фарр имеет тот же самый характер, что и в случае диодов Шотки.
В то же время различие в коэффициентах отражает тот факт, что характеристика
определяется одновременным проявлением ряда механизмов. Диод Шотки является
униполярным прибором, в котором протекание тока определяется переносом
основных носителей. В то же время р—я-диод является биполярным прибором, в котором
перенос носителей контролируется неосновными носителями в каждой области.
2. р—л-диод является лучшим выпрямительным прибором, когда
диффузионные токи минимальны. Широкозонные полупроводники (с малой величиной nf) с
высоким уровнем легирования и большими временами жизни наиболее
благоприятны для решения проблемы, связанной с диффузионными токами.
3. При использовании сильно асимметричной схемы легирования (например, NA » Лу
весь ток является результатом инжекции электронов в/ьобласть в то время, как инжекция
дырок минимизирована. Аналогичный эффект может быть также достигнут за счет
использования различных материалов для формирования р—«-гетероперехода, в
котором nf изменяется по обе стороны перехода (смотрите дополнение 10.А).
Литература
Kwok К. Ng, Complete Guide to Semiconductor Devices, McGaw Hill, New York, A995).
S.M. Sze, Physics of Semiconductor Devices, New York A981).
ДОПОЛНЕНИЯ
К ГЛАВЕ 10
10.А. Несколько вариантов диодов
10.А.1. Диод с р—п-гетеропереходом
Диод с гетеропереходом — это р—л-диод, в котором р-н п- области задаются
полупроводниками с различной шириной запрещенной зоны. Начнем с рассмотрения
структуры, представленной на рисунке 10.А.1, до того, как в обеих областях установится
термодинамическое равновесие. В этом случае каждый материал обладает своим
уровнем Ферми. Полупроводниковые гетеропереходы были рассмотрены в главе 8. Как
было установлено, в такой структуре разрыв ширины запрещенной зоны
распределяется на разрывы зоны проводимости АЕс и валентной зоны AEv, при этом его
протяженность измеряется в пределах атомарной шкалы. Так как указанные разрывы
имеют химическую природу, они не изменяются при переходе материалов к состоянию
равновесия. Как это имеет место в случае любого полупроводникового перехода, при
термодинамическом равновесии основные носители диффундируют в области, где
они становятся неосновными до тех пор, пока не произойдет выравнивание уровней
Ферми. На рис. 10.А.1 выравнивание уровней Ферми с обеих сторон структуры
приводит к возникновению внутреннего потенциала, определяемого выражением:
V - Е{1) - Е{2) - Е{{) -к Г In с I
W D )
к Ti
= £г<2) + АЕС - квТ In
NCNV
NDNA
= Е™ - A£v - квТ In
NCNV
A0.A.1)
Q.
CD
@
-A)
-d)
AEr
rB)
v
Q.
Рис. 10.А.1. Диод с /7—«-гетеропереходом. A) — легированный материал л-типа, а
B) — легированный материал /?-типа. Зонная диаграмма до (а) и после (б)
установления термодинамического равновесия.
Дополнения к главе 10
При этом уравнение Пуассона и результаты, полученные для толщины области
обеднения (A0.26)—A0.31)) остаются неизменными. В то же время внутренний
потенциал определяется A0.А.1).
И опять зоны следуют за потенциалом, показанным для равновесной структуры
на рис. 10.А.1. Понятно, что приложение внешнего потенциала к этой структуре
описывается той же самой теорией переноса неосновных носителей с
использованием соотношений A0.44) и A0.49) с тем важным отличием, что на этот раз:
Рп =
Т?~ и пр =
ТрA0.А.2)
В данном случае собственные концентрации различны для каждого материала. Для
симметрично легированной структуры (ND = NA) концентрация неосновных носителей в
материале с большей шириной запрещенной зоны меньше, чем в материале с меньшей
шириной запрещенной зоны (т. е. п2.1 « n2j2 т. к. л.2 ос е -£/ВД. В результате этого ток
неосновных носителей, инжектированных в материал с большей шириной запрещенной
зоны (дырки в материале 1), сильно уменьшается по сравнению со случаем гомоперехода.
10.А.2. р—/—П-ДИОД
Другим типом диода, играющим очень важную роль в оптоэлектронике, является
р—/—я-диод, в котором слаболегированная область заключена между
сильнолегированными областями р- и «-типа (смотрите рис. 10.А.2). Встроенный потенциал
всегда определяется положением уровней Ферми в областях р- и л-типа, т. е.:
A0.А.З)
ех
Ф
Рис. 10.А.2. Зонная
диаграмма /?—/—я-диода при
термодинамическом равновесии.
Потенциал V(z) определяется уравнением Пуассона, который в аппроксимации
области обеднения (смотрите рис. 10.А.2) есть:
d2V
dz2
d2V
dz2
d2V
При этом решения имеют вид:
2N
•ND9 d{-d2 < z
d2
A0.A.4)
e
£
d2<z<d2+dp
A0.A.5)
10.А. Несколько вариантов диодов 387
Здесь длины обеднения d и d определяются К. = V — V или:
п р х ы р п
"Ddn = ^V,^
A0.А.6)
В пределе, когда d2 — d{ » dn,d, решение имеет простой вид:
d2 A0.A.7)
< dx
Это есть ничто иное, как линейное падение потенциала между двумя
сильнолегированными областями «- и /ьтипа. После чего система ведет себя как простой
конденсатор с металлическими обкладками, при этом постоянное электрическое поле
в собственной области определяется соотношением F — VhJ(d2 — */,).
Приложение обратного напряжения к этой структуре приводит просто к увеличению
напряженности поля F:
F= V«+efa»\ (Ю.А.8)
d2-dx
Имеется много применений p—i— «-диодов. Так как эта структура характеризуется
постоянным электрическим полем в собственной области, она используется как
базовая структура для оптоэлектронных компонентов, требующих модуляции
однородного поля (т. е. электрооптические модуляторы на основе эффекта Штарка
(дополнение 8.В) или Франца—Келдыша (дополнение 7.А). Наиболее важным
является использование р—/— «-диода в качестве высокочастотного фотоприемника.
Быстрый фотоотклик этих приборов имеет двойственную природу. Во-первых,
динамическая емкость р—/— «-диода (С = eA/(d2 — dx)) намного меньше по
сравнению со сравнимым р—«-переходом (С = eA/L, где L есть ширина области
обеднения).Таким образом. RС-постоянная намного меньше в случае р—/—«-прибора,
что обеспечивает возможность детектирования ВЧ-сигналов. В дополнение к этому
собственная область может быть сделана с достаточно большой толщиной, с
тем чтобы поглотить практически все излучение. В результате этого
поглощение, имеющее место в нейтральных областях, сводится до минимума. Это, в
свою очередь, уменьшает вклад фотогенерации в диффузионный ток и
эффективно устраняет вклад времени жизни неосновных носителей в полный
динамический отклик фотодиода (смотрите раздел 11.4).
Достаточно небольших усилий, чтобы определить ограничения такой картины
«постоянного поля» в собственной области p—i— «-диода. Остаточный (фоновый)
уровень легирования в собственной области никогда не является полностью
нулевым, при этом, если длина обеднения Lres, соответствующая этому остаточному
уровню легирования, меньше d2 — dv поле не может оставаться постоянным, и оно
будет экранироваться пространственным зарядом, связанным с ионизированными
легирующими примесями. Эта длина обеднения существенно зависит от качества
материала. Другой предел связан непосредственно с собственной концентрацией
носителей «. в полупроводнике. Определяющим параметром в данном случае
является длина Дебая, соответствующая «.. Если d2 — d{ > lD, то свободные носители
будут экранировать поле, и структура «выродится» в систему с двумя переходами и
областью нулевого поля между ними. Поскольку lD зависит от температуры, в
особенности, через «., становится невозможным поддерживать поле в пределах достаточно
большой длины в узкозонном полупроводнике при окружающей температуре.
388 Дополнения к главе 10
Пример
1. Найдем максимальный допустимый уровень легирования, который позволил бы
нам реализовать/7—/—я-диод, работающий при напряжении V » Vbi. Пусть
толщина собственной области составляет D. Из A0.1) мы имеем:
Ц^ A0А9)
еи~
В Si при напряжении 100 В и ширине обеднения 50 мкм {е = eQer и ег— 12) мы
должны обеспечить ND < 5 х 1018 см.
2. Найдем максимальную рабочую температуру для р—/—я-диода на основе InAs с
толщиной собственной области D. В таком узкозонном полупроводнике (Eg = 0,36 эВ)
ограничение следует из собственной концентрации носителей при комнатной
температуре, определяемой E.49). Связанная с этим длина Дебая в этом случае составляет:
=еЕ /4кйТ A0.А.10)
\[ v
Эффективные плотности состояний Nc и Додаются E.46) при эффективных массах
mjme = 0,023 и mjme = 0,4 или Nc = 8,7 х 1016 (Т/300I5 см~3 и Nv = 6,3 х 1018 см
(Т/300I'5. Требование, чтобы lD > D при D = 5 мкм приводит к Ттах = 159 К.
10.Б. Ток утечки диода
Теория /— V-характеристик р—«-диодов, представленная в разделе 10.3, использует
два допущения:
1. Область обеднения узка по сравнению с диффузионными длинами.
2. В области обеднения не происходит ни генерации, ни рекомбинации пар.
Результаты, следующие из этой теории, находятся в разумном согласии с
экспериментальными данными, полученными для полупроводниковых диодов с
умеренными значениями ширины запрещенной зоны (< 1 эВ) в условиях слабого уровня
инжекции, когда нельзя пренебрегать концентрацией неосновных носителей при
комнатной температуре. В случае широкозонных материалов имеется существенный
вклад в диффузионный ток от генерационно-рекомбинационных процессов в
области обеднения, при этом во многих случаях эта компонента доминирует.
Мы видели, что условие Шокли A0.38), предполагающее, что носители в
области обеднения остаются в равновесии с их соответствующими областями,
определяет концентрации носителей в области обеднения:
A0.Б.1)
При этом К — К = Уы ~ ефарр. Напомним, что пп и рр есть концентрации основных
носителей по обе стороны перехода.
Предположим теперь, что ловушечные центры в материале лежат вблизи
середины запрещенной зоны и приводят к генерации типа процесса Шокли—Рида-
Холла и рекомбинации (смотрите раздел 6.5). Результирующая скорость процесса
генерации электронно-дырочных пар в этом случае дается выражением F.56):
_ = ^1 =
Б
Здесь пх и /?, есть концентрации, определяемые энергией захвата Ети пх=р{= л.для
ловушечных центров вблизи ширины запрещенной зоны. Выражение A0. Б.2) по-
10. Б. Ток утечки диода
казывает, что как только пр ф nf (это, как правило, имеет место в области
пространственного заряда смещенного диода), будет иметь место генерация (пр < nf) или
рекомбинация (пр > nf) электронно-дырочных пар.
В условиях обратного смещения (пр < nf — смотрите рис. 10.Б. 1) практически
повсюду в области обеднения мы будем иметь p(z) < п. и п (z) < п. при этом
уравнение A0.Б.2) приводит к генерационному току:
л = -А
AО.б.з)
Он связан с тем, что электроны и дырки быстро удаляются из области обеднения
доминирующим здесь сильным полем.
Рис. 10.Б.1. Механизм генерации электронно-дырочных пар дефектами в области
пространственного заряда.
Этот ток следует сравнить с предельным диффузионным током:
= enfDn en?Dp
J S \т j \т г
A0.Б.4)
Отношение jg/js пропорционально п~1, из чего мы видим важную роль, которую
играет (по сравнению с диффузионным током) генерационный ток в
широкозонных полупроводниках. Сумма этих двух компонент дает вклад в ток утечки обратно
смещенного перехода (смотрите рис. 10.Б.2). Поскольку собственная концентрация
носителей п. пропорциональна exp(—Eg/2k7), мы видим, 4toj's °c exp(-Eg/k7), в то
время каку^ <* txp(—Eg/2kT). Таким образом, генерационно-рекомбинационный
ток преобладает при высоких температурах.
Пример
Для диода на основе GaAs, рассмотренного в последнем примере раздела 10.2, мы
находим, что при обратном смещении величиной в —1 В. толщина области обеднения
составляет:
dn+dp= 92 нм
= 123 нм
W3 90 Дополнения к главе 10
In J
t
i диффузионный
ток -Eg/ kBT
6
генерационно -
рекомбинационный -Ед/2кдТ
ток
1/Г
Рис. 10.Б.2. Ток утечки диода в функции температуры.
При условии, что т Оп + тОр = 10 не генерационный ток составляет:
. 1,6х10-'9х1,8х1012х123х10-9 А
10x10"
м
= 3,5x10-'° Асм"
Эта компонента тока превышает диффузионную компоненту на несколько (восемь!)
порядков величины.
Таким образом, вр—/—«-диоде важность генерационного тока возрастает по мере
увеличения толщины собственной области. Этот темновой ток в фотодиодах играет
центральную роль в определении интегральных функциональных характеристик этого типа
приборов (смотрите главу 11).
В более общем случае произвольного смешения мы имеем:
n(z)p(z)-n,.
A0.Б.5)
п, dz
Мы можем получить аппроксимацию верхнего предела для этого интеграла, если мы
оценим максимум подынтегрального выражения: в рассматриваемом случае знаменатель
обладает минимумом при V= V ,так что:
A0.Б.6)
При подстановке этого выражения находим:
Л-г =
A0.Б.7)
10. Б. Ток утечки диода
Эта последняя аппроксимация действительна только при ефарр > квТ, т. е. в условиях
прямого смещения.
Мы видим, что характеристики диода, в котором доминирует генерационно-
рекомбинационный ток, имеют тот же самый вид, что и в классическом случае со
следующими важными отличиями: коэффициент и предел генерационно-рекомбинац-
тонного тока имеют другую величину, поскольку знаменатель в экспоненте равен
2квТвместо А^Г.Именно это оправдывает, то что мы можем записать
I—V-характеристики реального диода в виде:
Здесь.д, ток насыщения, есть сумма лимитирующих токов, а коэффициент идеальности п
заключен между 1 и 2 (близок к 1, когда доминирует диффузионный ток, и к 2, когда
доминирует генерационно-рекомбинационный ток)
В заключение суммируем три главных механизма, определяющих времена жизни
носителей в полупроводниках и, токи утечки диодов, изготовленных из этих
материалов:
1. Излучательная рекомбинация. Излучательная рекомбинация электронов и дырок
очень эффективна в материалах с прямой структурой энергетических зон. Выражение для
времени жизни носителей, определяемое G.65) может быть получено из рис. 7.5. При
типичных уровнях легирования величина этого параметра может варьироваться от
приблизительно 10 не (в GaAs) до 100 не (в InSb).
2. Примесная рекомбинация {рекомбинация Шокли—Рида). Этот механизм был описан в
разделе 6.5., при этом выражение для времени жизни дается F.59):
-UcrSRvthW, A0.Б.9)
Здесь: Nt — концентрация дефектов, vth — тепловая скорость носителей,
определяемая соотношением (mv2/2) = mcv2xh = kT/Ак, при этом, например, в GaAs
vth = 107 х G/300I/2 см с. Поперечные сечения захвата crSR обычно соответствуют
площади, перекрываемой волновыми функциями (т. е. имеют порядок 10~15 см2).
Таким образом, концентрация дефектов 1015 см в GaAs приводит к времени
жизни порядка 100 не.
3. Оже—рекомбинация. Природа этого механизма подробно рассматривалась в
дополнении 6.Г, при этом выражение для времени жизни тА. в собственном материале дается
F.Г.21). В материале, легированном до концентрации ND, время жизни может быть
получено из F. Г. 20):
^J (Ю.Б.10)
Этот механизм доминирует в токах утечки диодов на основе узкозонных полупроводников
при комнатной температуре (т. е. InAs, InSb, HgCdTe и т. д.).
ГЛАВА 11
ПОЛУПРОВОДНИКОВЫЕ
ФОТОПРИЕМНИКИ
11.1. Введение
Еще в 1850 году Антуан Сезар Беккерель обнаружил, что некоторые материалы
генерируют ток под воздействием светового потока. Но понадобилось много
времени вплоть до 1935 года прежде, чем была разработана квантовая теория
конденсированных сред, которая могла удовлетворительно описать это явление. Тем не
менее, несмотря на нехватку теоретических представлений об этих эмпирических
наблюдениях, из этих материалов стали изготовляться фотоприемники, которые
стали использоваться в фотографии и военных применениях, связанных с ИК-
детектированием.
Общие фундаментальные принципы, лежащие в основе функционирования
фотоприемников, иллюстрируются рис. 11.1. В отсутствие фотовозбуждения
носители заряда в этих материалах не проводят ток в силу ряда причин: либо они
находятся в зоне, где они не могут принимать участие в проводимости (например,
в заполненной валентной зоне) (а), либо они блокированы потенциальным
барьером (б) как в детекторе Шотки или же захвачены связанными квантовыми
состояниями, как это, например, имеет место в примесных фотопроводниках или кванто-
во-размерных фотоприемниках.
• •••♦
(а) (б) (в)
Рис. 11.1. Три типа квантового детектирования, основанные на межзонных переходах,
генерирующих электронно-дырочные пары (я), внутренней фотоэмиссии
выше потенциального барьера (б) и переходах из связанного состояния в
континуум (в).
В основе фотодетектирования лежат оптически возбуждаемые переходы
между двумя ансамблями квантовых уровней, одни из которых являются
проводящими, а другие — изолирующими. Именно по этой причине полупроводниковые
фотоприемники иногда называют квантовыми детекторами.
В соответствии с рисунком 11.1 в разделах 11.3 и 11.4 рассматриваются
фотоприемники типа (а) (фотопроводниковые и фотовольтаические приемники), в то
время как раздел 11.5 посвящен фотоприемникам с внутренней фотоэмиссией, а
раздел 11.6 рассматривает квантово-размерные фотоприемники типа (в).
Мы увидим, что все эти типы фотоприемников обладают общей
характеристикой. Их функциональные возможности (в частности, обнаружительная способность
D\ которая будет рассмотрена позже) изменяются с рабочей температурой как
квадратный корень от t~hv/kT, где hv — минимальная энергия детектируемых фотонов.
11.2. Распределение носителей в фотовозбужденном полупроводнике
Мы увидим, что это может интерпретироваться и как утверждение: «если
детектируются фотоны с энергией hv, то этот процесс будет сопровождаться и комбинацией
фононов с такой же средней энергией».
11.2. Распределение носителей
в фотовозбужденном полупроводнике
Сложность механизмов фотовозбуждения обусловлена множеством различных
характеристических длин, управляющих электрон-фотонным взаимодействием в
среде. Во-первых, эти процессы зависят от глубины поглощения, которая по порядку
величины составляет несколько а~1 (смотрите разделы 7.3 и 7.4). Затем, важную
роль играют диффузионные длины неосновных носителей (глава 10),
определяющие расстояние, на котором носители эффективно участвуют в механизмах
детектирования. И, наконец, есть еще и размеры области пространственного заряда,
имеющие особое значение в фотовольтаических приемниках. Все эти
характеристические длины имеют практически тот же порядок величины — от нескольких
микрометров до нескольких десятков микрометров. Таким образом, ни одним из
этих механизмов нельзя пренебрегать в пользу каких-либо других. В большинстве
случаев для описания механизмов детектирования необходимо прибегать к полным
уравнениям для полупроводников (уравнения F.60) и F.61)). В этом разделе мы
опишем эти уравнения, не прибегая к их решению во всей их полноте — такая
работа была бы возможна, но утомительна и привела бы к результатам
ограниченной полезности. В то же время они будут полезны для читателя при условии их
соответствующего упрощения применительно к особенностям решаемой задачи.
Мы ограничимся одномерной трактовкой (вдоль оси Oz распространения света) и
пренебрежем проблемами, возникающими из-за неоднородной засветки и т. д.
Для начала отметим, что световой поток в среде убывает экспоненциально в
соответствии с соотношением:
<S>(z)=<&oeaz A1.1)
Здесь Фо есть поток фотонов, падающий на поверхность. В свою очередь,
коэффициент поглощения является функцией энергии фотонов, как это уже объяснялось в
главах 7 и 8. Рисунок 11.2 демонстрирует спектральные зависимости коэффициента
поглощения a(hv) для ряда полупроводников, имеющих особое значение для опто-
электроники. Отметим различный характер спектральной зависимости a(hv) для
прямозонных (GaAs, InAs, InSb) и непрямозонных полупроводников подобно Si,
который проявляет менее резкий край оптического поглощения по сравнению с пря-
мозонными материалами.
длина волны (мкм)
_, 5 3 21.5 1 0.7 0.5 0.4 0.35
о
I
InSb
С
/ /GaP
i / i
6
5
4
3
2
12 3 4
энергия фотонов
Рис. 11.2. Спектральные зависимости коэффициента поглощения ряда полупроводников.
394 Глава 11. Полупроводниковые фотоприемники
Фотоны, поглощенные полупроводниками, генерируют электронно-дырочные
пары с концентрацией An = п — п0 и Ар — р — р0 при скорости генерации,
определяемой соотношением:
Gopfcb^V"* (И.2)
После рождения носители заряда ожидают два варианта дальнейшего развития
событий. Либо они рекомбинируют друг с другом с характеристическим временем
жизни г (г для электронов и г для дырок), либо они будут удалены электрическим
полем или диффузией к омическим контактам. Уравнения F.60) и F.61), которые
описывают эти механизмы, имеют вид:
Ар
Здесь плотности тока электронов (Jn) и дырок (/) составляют:
—- = Dn —п + пиЕ
q dz
A1.4л)
Р _ __П J±_ ,
q Pdz
A1.46)
При этом коэффициенты /г и D есть подвижности и коэффициенты диффузии
для соответствующих типов носителей. В таблице 1.1. приведены характеристики
переноса этих материалов, а именно: типичные рекомбинационные времена жизни
(которые, естественно, могут зависеть от засветки), подвижности, значения
ширины запрещенной зоны и диэлектрические постоянные.
Табл. 11.1. Значения рекомбинационного времени жизни г, подвижности junn //,,
ширины запрещенной зоны при 300 К и диэлектрических постоянных для
ряда важных полупроводников
Материал
Si
Ge
GaAs
InAs
InSb
г (с)
10
ю-2
10
10
ю-7
М„ (см2 В с)
1350
3900
8500
33000
105
Mp (см2 В с)
480
1900
400
460
1700
Eg (эВ)
1,12
0,67
1,42
0,36
0,18
er
11,8
16
13,2
14,6
17,7
К этим уравнениям мы должны добавить уравнение Пуассона, позволяющее
нам рассчитать электрическое поле в функции постоянной плотности заряда,
обусловленного легирующими примесями, а также концентрации фотогенерированных
носителей, т. е.:
A1.5)
Здесь е есть диэлектрическая постоянная материала (при этом е = eQer, а ег —
относительная диэлектрическая проницаемость), a Nd+ и N~ есть концентрации легиру-
11.2. Распределение носителей в фотовозбужденном полупроводнике
ющих примесей. В состоянии равновесия (т. е. в отсутствие засветки) и в объеме
материала N/ + р0 = N~ + /i0.
Уравнение A1.5) позволяет понять, каким образом эффективность
фотодетектирования фотодиода изменяется при больших уровнях засветки, когда, например,
Аи ~ Nd. Важно отметить, что характеристическое время, называемое
диэлектрическим временем релаксации, в течение которого материал сохраняет электрическую
нейтральность, достаточно мало (rdiel = е/а « 10~12 с, где а есть проводимость
материала). Таким образом, среда будет электрически нейтральной, т. е.:
A1.6)
Последнее уравнение, несмотря на свой простой вид, имеет очень важные
следствия с точки зрения динамики фотоприемника. Во-первых, поскольку носители
рекомбинируют парно, это означает, что рекомбинационные времена должны быть
равными (г = г = т). В свою очередь, это возможно только, если механизмы
зависят тем или иным образом от п и р. Другим следствием равенства A1.6) является то,
что внутреннее поле должно установиться прежде, чем это условие может быть
наложено на A1.3), A1,4) и A1.5). Мы могли бы еще более усложнить приведенную
выше таблицу за счет введения механизмов захвата для каждого типа носителей,
пространственной неоднородности и т. д.
Начнем с упрощения системы, которую пытаемся исследовать. Предположим,
что материал фотоприемника имеет преимущественно /ьтип проводимости (р » р0,
при этом, как мы увидим дальше, этот случай представляет интерес с прикладной
точки зрения), а также то, что не прикладывается никакое электрическое поле E(z).
Мы всегда можем пренебречь всеми эффектами, связанными с сохранением
нейтральности заряда, как, например, возникновением внутреннего поля — эта
нейтральность гарантируется основной легирующей примесью. Подставляя A1.4д) в
(П.Зя), мы получаем:
2
A1.7)
рекомбинашя диффузия
Решением этого уравнения является сумма частных решений, включая член
источника, а также общее решение без члена источника, т. е.:
A1.8)
1 - \аь0 )
Здесь: LD есть диффузионная длина электронов LD = V(Z)z), а константы А и В
определяются граничными условиями, специфичными для каждой определенной
задачи. Эти условия могут быть нескольких типов:
Поверхностная рекомбинация S (в единицах см с) при z = Zo накладывает
условие:
SAnl =D(—An) (И.9)
u° ld* U
Омический контакт, т. е. граница раздела, где рекомбинация неосновных
носителей заряда мгновенна (омический р+ контакт к материалу /ьтипа накладывает
условие на концентрацию неосновных носителей п в виде пр = л.2, т. е. п ~ 0) так, что:
An\z__Zo~0 A1.10л)
Область пространственного заряда, начинающаяся при z — Zq, т. е. область, из
которой удаляются все носители, вновь приводит к:
A/il =0 (Н-Юб)
Глава 11. Полупроводниковые фотоприемники
Проанализируем, например, случай с бесконечно толстым образцом (d » LD и 1/я).
Когда z -> °°, An -> 0. Коэффициент А в этом случае получается с использованием
граничных условий при z — 0. Предположим, что омический контакт отсутствует и
электроны могут свободно рекомбинировать на поверхности (z = 0) со скоростью
50. Уравнения A1.8) и A1.9) сразу дают распределение фотогенерированных
носителей An(z):
An(z)=-
A1.11)
Как можно было бы ожидать, концентрация носителей на поверхности
становится нулевой при скорости рекомбинации, стремящейся к бесконечности
(смотрите рис. 11.3). Если, с другой стороны, поверхность полупроводника
пассивирована (т. е. плотность поверхностных состояний равна нулю), то 50 = 0 и количество
носителей, генерированных во всем объеме, дается интегралом A1.11):
Antot = J An{z)dz =
A1.12)
Последнее выражение можно прочитать как АпХоХ/т= Фо, т. е. полный поток
падающих фотонов Fo преобразуется в поток носителей АпХоХ/т.
14x10
о
О 5 10 15
расстояние (мкм)
Рис. 11.3. Распределение фотогенерированных носителей при потоке фотонов
Фо = 1018 см~2, коэффициенте диффузии 1 см2 с, диффузионной длине 10 мкм
и коэффициенте поглощения 104 см, а также для различных значений
скорости поверхностной рекомбинации S.
Другой очень простой случай связан с рассмотрением образца толщиной </, по
которому ток не может протекать через поверхности входа и выхода излучения
(например, это фотопроводник, в котором направление распространения
электрического тока перпендикулярно потоку фотонов): в предположении отсутствия
внешнего электрического поля это означает, что Jn = DndAn/dz ~ 0 при z = 0 и при z = d.
Интегрирование A1.7) немедленно приводит к полной поверхностной
концентрации фотоносителей A«tot, генерированных в объеме:
A«tot=O0r(l-
A1.13)
Отношение потока генерированных носителей Antoi/rn потока падающих
фотонов Фо выражает эффективность преобразования потока фотонов в поток
носителей. Этот отношение есть внутренняя квантовая эффективность tj. фотоприемника,
которая в данном случае определяется выражением:
11.3. Фотопроводники
"Л
77/ =
Внутренняя квантовая
эффективность фотоприемника
Одновременно с внутренней квантовой эффективностью должны быть учтены
и потери. Наиболее важные из них, как правило, связаны с потерями фотонов за
счет оптического отражения от поверхности, т. е. rjop = 1 — R. Этот коэффициент
оптической эффективности особенно мал в случае границы раздела необработанной
полупроводниковой поверхности и воздуха, поскольку коэффициент преломления
полупроводника л1с значителен, a R = (я1с — 1J/(я1с + IJ. Так, в случае Si nx = 3,4, что
приводит к R = 0,3 и 77ор = 1 — R = 0,7. Таким образом, полная эффективность, как
правило, близка к:
г] = Wop = A - R>fc -е-*) A1.146)
Для уменьшения потерь на отражение на границе раздела
полупроводник/воздух в широком спектральном диапазоне часто используются антиотражающие
покрытия. Рисунок 11.4 суммирует различные факторы, влияющие на полную
эффективность фотоприемника.
отражение
Рис. 11.4. Из всего падающего потока фотонов Фо только часть, изображаемая на
рисунке серой областью и соответствующая фотонам, поглощенным на
глубине d, может участвовать в фотогенерации носителей.
Пример
Найдем распределение носителей в полупроводнике с коэффициентом
поглощения а= 104 см. Предположим также, что материал характеризуется подвижностью
носителей 40 см2 В с и рекомбинационным временем жизни 10~6 с. Эти
параметры приводят к коэффициенту диффузии, определяемому соотношением
Эйнштейна Dn — (kT/q)fin величиной в 40 см2 В с х 25,9 мВ или 1 см2 с, при этом
диффузионная длина (Dnr)l/2 составляет 10 мкм. Таким образом, понятно, что в
соотношении A1.1) а доминирует над 1/1, при этом распределение Дл(г) прежде всего зависит
от относительной величины SJDn и а. Рисунок 11.3 иллюстрирует распределения
Дл(г) для различных значений скорости поверхностной рекомбинации So.
11.3. Фотопроводники
11.3.1. Обнаружительная способность фотодиода
Сконцентрируем теперь наше внимание на поведении идеального
фотопроводника, изготовленного из однородного полупроводникового материала определенного
типа (для определенности />-типа) толщиной d, шириной w и длиной / (смотрите
рисунок 11.5). Как это имеет место в подавляющем большинстве случаев (за ис-
Глава 11. Полупроводниковые фотоприемники
Рис. 11.5. Геометрия
фотопроводникового приемника
излучения.
Ш
ключением квантово-размерных фотоприемников — смотрите раздел 11.5). Потоки
фотонов и носителей заряда перпендикулярны друг другу. Поток фотонов падает на
поверхность полупроводника в направлении Oz. Фотоны в световом потоке
обладают энергией hv, большей ширины запрещенной зоны Eg9 и они поглощаются в
соответствии с определенной зависимостью а от h v. С двух сторон приемника
делаются контакты (смотрите рис. 11.5), позволяющие:
1. Прикладывать электрическое поле Е параллельно поверхности (вдоль оси Ох).
2. Выводить носители, т. е. эффективно и без ограничений обеспечивать
электрическую нейтральность материала.
Как мы только что видели, при пренебрежении потоком носителей через
верхнюю и нижнюю поверхности поверхностная концентрация носителей определяется
равенством двух потоков Antot/r= т]Ф0. Это соответствует предположению о том, что
диффузионная длина настолько велика, что неоднородностями Дл(г) можно
пренебречь, при этом объемная концентрация An(z) = Ал = const дается соотношением:
Ап Щ A1.15)
а
Под влиянием поперечного электрического поля Е, связанного с внешней
разностью потенциалов V(E = V/l), по структуре начинает протекать ток с плотностью
yph = AnqjunE и полной амплитудой /ph = yphwd, m. к. площадь сечения, пересекаемого
шоком составляет wd.
Iph =rjqMnTуФ0Г A1.16)
С другой стороны, (этот более тонкий подход к фотопроводникам был
разработан А. Роузом), фотонный поток пересекает сечение площадью wl. Таким образом,
представляется разумным нормировать ток /ph на мощность излучения Р^ = /ivO0rv/,
падающего на поверхность с площадью wl, что приводит к фоточувствительности
91 приемника излучения:
= "ТП77 A117)
Из этой формулы видна важность произведения //яг, задающего
фоточувствительность приемника излучения. Фактически лишь в этой формуле для фототока
проявляются собственные характеристики полупроводника. Произведение /лпт (см2 В)
используется как критерий качества материала для фотоприемника. Выражение
A1.17) может быть также записано в виде:
(Ш8)
Фоточувствительность
фотопроводника (А/Вт)
11.3. Фотопроводники
Здесь: g есть коэффициент усиления фотопроводимости, определяемый
соотношением:
A1.19)
О ' tr r-« jr
rtr iinE junV
rtr есть время переноса электронов, перемещающихся между двумя контактами.
Отметим, что фоточувствительность приемника излучения в функции длины волны
может быть представлена в виде:
= rjg
А (мкм )
1,24
A1.20)
Рисунок 11.6 демонстрирует спектральную характеристику
фоточувствительности ЩЛ) широкополосных квантовых приемников излучения.
Выражение для усиления фотопроводимости легко понять. Оно представляет
собой отношение электронного потока, создаваемого вдоль оси Ох, и потока
фотонов в направлении Oz. Первым удивительным наблюдением является то, что
этот член может быть больше единицы, т. е. оно создает ложное (!) представление
о том, что единичный фотон может породить несколько электронно-дырочных
пар без привлечения эффекта лавинного умножения и т. п. Был предложен ряд
интерпретаций, позволяющих разрешить этот парадокс. Первое объяснение,
предложенное А. Роузом, заключается в том, что можно представить себе, что перед
тем, как исчезнуть в результате рекомбинации, электрон может несколько раз
пройти по цепи. Таким образом, один и тот же электрон может несколько раз
участвовать в процессе формирования тока. Другое объяснение заключается в
том, что полупроводниковая среда накапливает электронно-дырочные пары в
процессе засветки, а контакты обеспечивают все необходимое для обеспечения
электрической нейтральности.
Пример
Рассмотрим слой InSb толщиной 3 мкм, длиной /= 1 мм и шириной w = 100 мкм.
Мы хотим определить фоточувствительность этого приемника излучения на длине
волны 6 мкм при приложенном напряжении 10 В (что соответствует
напряженности электрического поля 102 В см~1), предполагая, что квантовая эффективность
прибора rj составляет 60%. Подвижность носителей в InSb приведена в таблице 11.1 и
составляет 105 см2 В с, что приводит к времени переноса rtr = 10 см/A05 х 102 см с) или
10~8 с. Поскольку время жизни носителей составляет 10~7 с, мы находим, что
усиление фотопроводимости g составляет 10/10"8 = 10. В таком случае
фоточувствительность есть 0,6 х 10 х 6 мкм/A,24 мкм эВ) или 30 А/Вт.
А-Вт )
Рис. 11.6. Спектральная зависимость
фоточувствительности фотопроводника.
Линейное изменение фоточувствительности с
длиной волны является следствием того, что
число фотонов, обеспечивающих мощность
излучения в 1 Вт, увеличивается с Л.
Общий вид спектральной зависимости
характерен для широкополосных квантовых
приемников излучения.
Глава 11. Полупроводниковые фотоприемники
11.3.2. Обнаружительная способность фотопроводника
Как это уже обсуждается в дополнениях 11.А и 11.Б, в основе возникновения шумов
в фотопроводниках лежат три механизма. Этими тремя механизмами являются:
тепловой шум iR, генерационно-рекомбинационный шум iGR, а также фотонный шум
(или дробовой шум, связанный со случайными флуктуациями числа фотонов,
попадающих на приемник излучения), представляемый соотношениями A1.А.27), A1.А.38)
и A1.Б.6). Предположим, что имеет место случай, когда характеристики диода не
ограничены фотонным шумом, т. е. приемник излучения не находится в ВЫР-режи-
ме (смотрите дополнение 11.Б). В этом случае шум, генерируемый самим
приемником излучения при приложении напряжения, превышающего kT/q, есть:
4 = 4^Av + 4^/0Av = М— + gv\v « 4qgI0Av A1.21)
К Ry q j
Напомним, что /0 есть темновой ток, /^-сопротивление фотопроводника, a Av —
ширина полосы интегрирования, определяемая соотношением Av= l/2fint, где t.mt есть
время интегрирования, a g — усиление фотопроводимости. Отношение сигнал/шум
is/iN в этом случае дается соотношением:
; о? р
S / N =^-= . ™ A1.22)
h ^4qgIAv
Введем эквивалентную мощность шума (NEP), которая представляет собой
мощность в пределе детектирования, соответствующую отношению сигнал/шум,
равному 1. Из A1.22) мы получаем NEP для фотопроводника:
A1.23)
Эквивалентная мощность шума
Из последней формулы видно, что этот параметр не является независимым
от измерительной системы, т. е. он не позволяет классифицировать материалы
для приемников излучения с использованием некоего коэффициента качества.
Для нормировки A1.23) заметим, что NEP является функцией ширины полосы
вида V(Av), а также (с учетом того, что /0 = J0A) — функцией квадратного корня
площади поверхности образца у1А. В связи с этим мы вводим такой параметр,
как обнаружительная способность D\ которая в общем виде определяется
следующим образом:
Связь между обнаружительной
способностью (см Гц1/2 Вт~1) и NEP
Нестандартной (варварской) единицей измерения обнаружительной
способности является Гц1/2 Вт, которая в цивилизованном мире называется также
джонсом. Теперь мы уже можем рассчитать обнаружительную способность
фотопроводника:
Л* - f * A1.25)
/4У
Примечание: /0 есть плотность темпового тока, протекающего между двумя
электродами, нормированная на площадь поверхности, на которую падает свет\ Таким
образом, плотность тока для полупроводника /ьтипа дается соотношением:
Jo=qpoJUpE^ A1.26)
11.3. Фотопроводники
Здесь р0 — концентрация носителей в отсутствие засветки, а Е — электрическое
поле между двумя контактами. Выражение A1.25) может быть представлено в
следующем виде:
Г~Г~~ A1.27)
Если бы мы взяли полупроводник я-типа, отношение /лп /jup должно было бы
быть заменено на мр/мп << Мп/мр> чт0 привело бы к уменьшению обнаружительной
способности. Большое различие между подвижностью неосновных носителей
(электронов) и подвижностью основных носителей является существенным фактором
для достижения высокой обнаружительной способности фотопроводниковых
приемников излучения. Поскольку /7=1 — £~ad> мы видим, что существует
оптимальная величина отношения rj/yld, близкая к 0,66 V<z Таким образом, максимальная
оптическая эффективность полупроводника с точки зрения обнаружительной
способности составляет 66%. Следовательно, максимальная обнаружительная
способность определяется выражением:
A1.28)
0 jup
Максимальная обнаружительная
способность фотопроводника
Это выражение интересно тем, что в нем D* является функцией только
параметров материала и длины волны. Таким образом, мы видим, что обнаружительная
способность материала возрастает по мере уменьшения темновой концентрации
носителей р0. В то же время приемники инфракрасного (ИК) излучения,
работающие в пределах атмосферных «окон прозрачности» в спектральных
диапазонах 3—5 мкм и 5—12 мкм (смотрите дополнение 2.Б) обязательно должны
иметь ширину запрещенной зоны соответственно порядка 250 и 120 мэВ.
Уравнение E.49) говорит нам о том, что при обычных температурах (т. е.
при kT/q > 25 мэВ), значения собственной концентрации носителей л.,
обусловленные тепловым возбуждением электронов через запрещенную зону,
значительны (п. » 1016 см~3), что приводит к слабой обнаружительной
способности. Таким образом для того, чтобы продвинуть спектры фоточувствительности
в более длинноволновую область, квантовые приемники излучения следует
охлаждать до низких температур. Рисунок 11.Б.4 дает сравнение
обнаружительной способности для ряда материалов, что зримым образом демонстрирует
отмеченное выше.
Приведенный ниже пример иллюстрирует использование выражения A1.28) для
определения обнаружительной способности.
Пример
Предположим, что мы хотим определить обнаружительную способность
фотопроводника на основе InSb. При комнатной температуре собственная
концентрация носителей, рассчитанная в соответствии с E.49), составляет 1016 см. Для
улучшения функциональных характеристик приемника излучения он должен
работать при достаточно низкой температуре с тем, чтобы поддерживать
концентрацию свободных носителей р0 на уровне 10м см. Предполагая, что
коэффициент поглощения а составляет 104 см, а также используя параметры,
приведенные в таблице 11.1, мы получаем обнаружительную способность на длине
волны 6,6 мкм @,2 эВ):
0,2х1,6хЮ~19 Дж V 4х1014см 1700
105 пс 1Л11 _ 1/2 D _
х-—=2,5хЮп смГц1/2 Вт
Iff 402 Глава 11. Полупроводниковые фотоприемники
После чего рассчитаем эквивалентную мощность шума (NEP), соответствующую
размерам области детектирования 50 х 50 мкм2, при времени интегрирования 10 мс,
т. е. при A v = 50 Гц:
= 50xl0-4V50ru1/2/2,5xl011 джонс=0,14 пА
11.3.3. Время отклика фотопроводника
Время отклика фотопроводника, подверженного воздействию нестационарного
оптического сигнала Gop(t), может быть получено из (И.Зя, б). Существенные
характеристики в рассматриваемом случае могут быть легко получены в
предположении однородного освещения. Интегрируя (П.Зя) по толщине материала (от 0 до d
как в A1.14я)) и учитывая квантовую эффективность, мы немедленно приходим к
динамическому уравнению:
Аи,,
A1.29)
Ряд возможных случаев иллюстрируется рисунком 11.7:
• Световой импульс прямоугольной формы с началом при / = 0 и окончанием при t— T« т
(рис. 11.7я), Уравнение A1.29) показывает, что в этом случае отклик материала
будет мгновенным, но не будет сопровождаться усилением: в материале сразу
устанавливается концентрация Afltot, при этом она определяется полным числом
поглощенных фотонов Anlot = r]Go Т. После окончания импульса концентрация
спадает экспоненциально с характеристическим временем жизни т.
• Световой импульс прямоугольной формы и большой длительности с началом при / = О
(рис. 11.76). В этом случае концентрация носителей дается A1.29) в виде:
Дл!ос =
A1.30)
Таким образом, время отклика фотопроводника равно времени жизни носителей
в материале.
• Синусоидально изменяющаяся засветка Gop(t) = Gopsincot. Интегрирование A1.29)
следует сразу и приводит к синусоидальному отклику Afltot@ = Anxot(co)sm(cot + ф),
при этом:
A1.31)
Таким образом, фотопроводник ведет себя как полосовой фильтр с частотой
отсечки 1/2ят.
ор
7«т
-'ор
Л2)
Рис. 11.7. Временная эволюция отклика фотопроводника при импульсной засветке
(а), резком прерывании засветки (б) и синусоидально модулированной
засветке (в).
11.4. Фотоволыпаические приемники излучения
Эти три результата дают представление об особой дилемме, стоящей перед
фотопроводниками. Материалы с большей обнаружительной способностью
одновременно обладают большими временами жизни носителей и худшими временными
характеристиками.
Рисунок 11.8 показывает частотную зависимость 91 фотопроводника для двух
различных времен жизни носителей. Этот результат является иллюстрацией
утверждения: максимальное усиление х ширина полосы = const.
<
0.01
10
10°
частота (с )
Рис. 11.8. Частотные характеристики фотопроводников с различными временами
жизни носителей заряда. Для фотопроводников произведение усиления на
ширину полосы есть постоянная величина.
11.4. Фотовольтаические приемники излучения
Одной из проблем, связанных с использованием фотопроводниковых приемников
излучения, является их низкий импеданс. По своей природе фотопроводник
является фоточувствительным резистором. Поскольку для электрического усиления
предпочтителен большой импеданс, комбинация элементов фотодетектирования и
усиления образует импедансный мостик, приводящий к ухудшению характеристик
фотоприемника. Это не имеет места в случае фотодиода.
Фотоволыпаический приемник излучения использует выпрямляющие
характеристики р—«-диода или перехода Шотки для обеспечения большого импеданса и для
разделения электронно-дырочных пар, генерируемых процессами поглощения.
Таким образом, именно внутреннее поле в диоде ответственно за циркуляцию тока.
Рисунок 11.9 иллюстрирует функционирование фотодиода.
В качестве примера мы взяли р+—«-диод, в котором основная часть падения
встроенного потенциала имеет место в материале «-типа (смотрите раздел 10.4).
Излучение входит через верхнюю поверхность и пересекает р+-область, которая
предполагается достаточно тонкой, чтобы пренебречь поглощением в этом слое.
Фотоны поглощаются в «-области и порождают электронно-дырочные пары в
области пространственного заряда (SCR) и в объеме материала. Пары, фотогенериро-
ванные в SCR немедленно разделяются внутренним электрическим полем, которое
удаляет дырки по направлению к поверхности, что и образует генерированный фо-
тоток — JG. Пары, генерированные вне SCR диффундируют по структуре, при
этом некоторая их часть способна достичь SCR и пройти через процесс разделения
заряда, что приводит к плотности диффузионного тока Jdifr
Эти две компоненты обусловливают плотность полного фототока /ph, который
суммируется с темновым током:
-\)-Jf
A1.32)
/(D04 Глава 11. Полупроводниковые фотоприемники
рекомбинация
хЛЛЛЛЛЛЛ^
хЛЛЛЛЛЛЛ^
W
область пространственного
область
дифузионная
область
полупрозрачный
металл
металлический
контакт
Рис. 11.9. Иллюстрация функционирования фотодиода: зонная диаграмма (а),
геометрия поглощения (б) и типичная конструкция прибора (в).
Здесь: Ум1 есть ток насыщения диода, определяемый A0.24) для случая диода Шот-
ки, и ограниченный диффузией дырочный ток р+—я-диода, определяемый A0.52).
Кесть потенциал, приложенный к диоду. Рисунок 11.10 иллюстрирует
характеристики диода в условиях освещения. В рассматриваемом случае возможны два
режима детектирования:
• Режим фототока. Диод может быть введен в схему с очень малым импедансом,
например, включен последовательно с амперметром или с низкоомным
резистором, к которому параллельно подключен вольтметр, как это показано на рис.
11.10а. В этом случае измеряемый ток дается выражением A1.32).
• Режим фотонапряжения. В данном случае диод включается в схему с высоким
импедансом (/= 0). При этом, как показывает A0.32) на выводах диода
появляется напряжение Vph. В обращенной форме напряжение Vph выражается в виде:
A1.33)
11.4. Фотоволыпаические приемники излучения
Рис. 11.10. Два режима функционирования фотовольтаического приемника
излучения: режим фототока (а) и режим фотонапряжения (б).
Расчет плотности фототока /ph следует из уравнений, приведенных в разделе
11.3. Такой расчет представляет собой хорошее упражнение, позволяющее
ознакомиться с применением различных граничных условий A1.10). Давайте начнем с
расчета тока JG в области пространственного заряда, т. е. между z = 0 и z = W.
В SCR плотность избыточного заряда An имеет нулевое значение, т. к. все носители
мгновенно удаляются из этой области, при этом динамическое уравнение A1.3а)
принимает вид:
——JG = -аФе' A1.34)
Я &Z
Плотность тока JG мы получаем, интегрируя A1.34) в области от 0 до We
учетом того, что электронный ток не может протекать из />+-области, поскольку
концентрация электронов может быть равна только нулю (пр+ = и.2) так, что JG @) = 0,
при этом:
A1.35)
Это есть электронный ток, который пересекает границу раздела между SCR и
нейтральной областью при z > W.
Вклад диффузионного тока получается из дифференциальных уравнений A1.3а)
или A1.7), которые в стационарном состоянии в качестве решения допускают A1.8),
что мы можем записать в виде:
An(z)= Ae~z/lD +Bez/lD +^~
-e~az A1.36)
В данном случае учитывается, что поток фотонов при z = W составляет только Фое~аЖ.
Мы можем предположить, что образец имеет достаточно большую толщину так,
что В = 0. Более того, любой электрон при z = Wнемедленно удаляется
электрическим полем, накладываемым граничным условием A1.106) An(W) = 0 так, что:
A1.37)
Глава 11. Полупроводниковые фотоприемники
Плотность диффузионного тока при z = W дается соотношением:
A1.38)
Так что:
Для достаточно распространенного условия aW ~ 1 вклады JG и Jm
(соответственно A1.35) и A1.39)) сравнимы по величине так, что ни одним из этих членов
нельзя пренебречь. В этом случае полный фототок дается соотношением:
A1.40)
Эта формула показывает, что малая квантовая эффективность области
пространственного заряда SCR может быть компенсирована в случае большой
диффузионной длины, т. е. то, что область пространственного заряда пропускает, может быть
компенсировано диффузионной областью. Как и в случае фотопроводника
выражение A1.40) может быть представлено в виде:
Я = Я—L- A1.41)
hv/q
Или в другой записи:
я = 4iKM_) A1<42)
1,24
При этом полная квантовая эффективность rj дается выражением:
AМЗ)
Таким образом, эта формула очень похожа на A1.18). Однако, мы замечаем
отсутствие усиления фотопроводимости, что эквивалентно утверждению о том, что
усиление g в случае фотодиода равно единице.
Пример
В кремнии я-типа проводимости, легированном до уровня 1016 см при
напряжении на переходе Уы = 1 В, SCR имеет протяженность в 1 мкм. В соответствии с
рисунком 11.2 коэффициент поглощения а = 104 см при энергии квантов 2 эВ.
В этом случае эффективность SCR I — t~aW составляет 64%. С другой стороны,
диффузионная длина есть yl((kT/q)junr) или 500 мкм (смотрите таблицу 1.1), что
приводит к величине квантовой эффективности, в которой доминируют потери на
отражение A — R).
11.4.1. Обнаружительная способность фотодиода
Как это обсуждается в дополнениях 11.А и 11.Б, за шум в фотовольтаических
приемниках излучения ответствены два механизма: генерационный шум (без участия
рекомбинации) iG A1.A.38) и шум, связанный с флуктуациями появления фотонов
A1.Б.6). И вновь мы предположим, что в шуме приемника излучения не
доминирует компонента, связанная с фотонами (т. е. что приемник излучения
функционирует не в BLIP-режиме (смотрите дополнение И.Б). В этом случае шум, связанный с
самим приемником излучения, описывается выражением:
il = 2qI0Av = 207.A + e«"'*r )\v A1.44)
11.4. Фотоволыпаические приемники излучения
Здесь: 1Ш есть ток насыщения фотодиода. В выражении A1.44) подразумевается,
что знак «плюс» имеет место вследствие того, что прямой и обратный вклады
взаимно компенсируются при К= 0, в то время как их соответствующие вклады в шум
являются аддитивными. В этом случае отношение сигнал/шум (S/N) определяется
выражением:
При этом выражение для эквивалентной мощности шума принимает вид:
AL46)
Мы вновь вводим обнаружительную способность IT, т. к. она позволяет нам
избавиться от параметров, не присущих системе, а именно: от площади А,
связывающей ток /ю1 с плотностью тока JMt (/sat = AJJ) и поток Фо с мощностью падающего
излучения Р.тс (Р.тс = АФопу), а также от ширины полосы частоты измерений Av:
D* = -. -2 A1.47в)
Jf v'a')
На этот раз мы также подчеркиваем, что область детектирования и переноса — это
одно и то же. При этом направления потоков фотонов и электронов параллельны.
Мы могли бы подумать, что следует подать смещение на диод (V< 0) для того,
чтобы уменьшить коэффициент tqV/kT и улучшить обнаружительную способность
фотодиода. Однако, такое смещение часто приводит к дополнительному шуму (ток
периферийной утечки и т. п.) в регистрируемом сигнале. При нулевом
приложенном поле (К= 0) выражение (И.47я) приобретает вид:
D* = —2 pi - A1.476)
hv/q гт^
Заметим, что:
Здесь: RA (Ом см2) есть произведение сопротивления перехода и его площади.
С учетом этого выражение для обнаружительной способности может быть
записано в другом виде:
°*=1Г~гШг AL49)
hv/q \4kT
Обнаружительная способность
фотодиода
Рисунок 11.11 показывает, каким образом обнаружительная способность D*
изменяется в функции произведения RA при различных температурах и длине волны
детектирования 5 мкм (/*v=250 мэВ) при квантовой эффективности 50%.
Эта последняя формула достаточно предсказуема в связи с выражением для
плотности токау^ в переходе AО.Б.4д), т. е.:
Мы напоминаем, что здесь Dp, LDp и тр есть коэффициент диффузии, диффузионная
длина и время жизни неосновных носителей заряда (дырок) с «-стороны перехода;
ND есть уровень легирования: п. есть собственная концентрация носителей,
определяемая соотношением E.49): Е — ширина запрещенной зоны материала приемни-
((D08 Глава 11. Полупроводниковые фотоприемники
"J2
10~4 10 10~2 10 10° 101 102 103 104
ЯЛ (Ом/см)
Рис. 11.11. Изменение обнаружите л ьной способности фотодиода на длине волны
5 мкм в функции RA (предполагается, что кванитовая эффективность
составляет :
ка излучения: Nc и Nv есть эффективные плотности состояний в зоне проводимости
и валентной зоне, определяемые E.46). Таким образом, вне режима BLIP обнару-
жительная способность приемника излучения изменяется как t~Eg/2kT, что
подчеркивает важность функционирования этих приборов при низкой температуре. Мы
также можем использовать A0.Б.З), если в токе утечки диода доминируют генерацион-
но-рекомбинационные процессы с участием примесей.
Пример
Мы хотим рассчитать произведение RA и обнаружительную способность фотодиода
на основе InSb я-типа проводимости, легированного до уровня 1016 см, при
температуре 150 К. Пренебрежем температурной зависимостью ширины запрещенной
зоны. Таблица 11.1 дает нам коэффициент диффузии при 150 К (kT/q = 13 мэВ)
или 1700 х 13 х 10 = 22 см2 с. Уравнения E.46) дают плотности состояний Nc и N
для тс = 0,0145 и mv = 0,4aw0, а именно: Nc= 1,5 х 1016 см~3 и Nv = 2,2 х 1018 см. Ток
насыщения идеального диода определяется A1.50) или:
i
22 см2с-] 1,5хЮ16 х 2,2x10'
Ю-7 с
101
.CM-3e-o.i8/o.oi3 = 7,6 х Ю-3 А см"
=1,6хЮ-19Ас
Произведение RA определяется из (kT/q)^ и составляет 1,7 Ом см2. В этом
случае при полной квантовой эффективности rj = 0,5 обнаружительная
способность составляет:
/)* =
0,5
1
= 2,8хЮ10 см Гц1/2 Вт"
0,25 эВ V4xl,6xlOl9^i 7,6 х Ю-3 А см"
На рис. 11.12 показана температурная зависимость обнаружительной
способности D* этого прибора. Из этого графика ясно видно, насколько выгодным является
функционирование приемников инфракрасного излучения при низкой температуре.
11.4.2. Время отклика фотодиода
Время отклика фотодиода может быть получено из решения динамических
уравнений A1.3) и A1.4). Хотя расчет сам по себе достаточно утомителен, о его
результате достаточно легко догадаться. В полный временной отклик фотодиода
дают вклад 3 постоянные времени, каждая из которых обусловлена особым
физическим эффектом:
'100
11.4. Фотовольтаические приемники излучения
120 140 160
рабочая температура (К)
180
200
• Постоянная времени из-за диффузионного тока. Ясно, что эта постоянная есть
ничто иное как время жизни носителей т. Она изменяется в диапазоне от 10~4 с
в кремнии до 10~8 с в GaAs (это соответствует ширине полосы, изменяющейся
от 10 кГц до 100 МГц). Во многих случаях (например, в телекоммуникационных
применениях) такая величина постоянной времени является неприемлемой.
• Емкостная постоянная времени. Область пространственного заряда приводит к
емкости Cd, определяемой A0.17):
С - А \ У8^ D _ jdl
A1.51)
Напоминаем, что е = еоег есть проницаемость среды, Кы — встроенный потенциал
(Vbi = УО=ФВ~ (Ес — EF) для перехода Шотки, как это иллюстрируется рис. 10.2 или
как это определяется A0.25) в случае р—«-перехода, И^есть толщина области
обеднения, a ND-уровень легирования. В режиме быстрого функционирования эта емкость,
включенная последовательно с согласованной цепью с импедансом У? = 50 Ом,
приводит к верхней границе частоты, определяемой \/2тгЯС.
Пример
В случае типичного приемника излучения с площадью в 1 мм2, легированного до
уровня 1015 см, и при потенциале Vbi — V= 10 В мы получаем область
пространственного заряда шириной W = 3,6 мкм и емкость 30 пФ. При нагрузке 50 Ом
частота отсечки приемника излучения составит 1/2тгЯС = ПО МГц.
• Постоянная времени из-за переноса носителей через область пространственного
заряда. Протяженность SCR при приложении потенциала в 1 В составляет величину
порядка 1 мкм, при этом напряженность электрического поля в этой области
составляет 104 В см. Даже в материале со сравнительно малой подвижностью
(например, /а = 102 см2 В с) это соответствует скорости 106 см с и таким
образом времени пролета носителей 100 пс и частоте отсечки 10 ГГц.
Первые два ограничения являются неприемлемыми для большинства
телекоммуникационных применений, требующих ширины полосы частот в десятки ГГц
или более того. Предназначенные для этих применений р—i—я-диоды (смотрите
рис. 11.13) обладают собственной областью с большой шириной W, заключенной
между сильнолегированными областями п- и /?-типа проводимости.
Эти диоды были рассмотрены в разделе 10.2 (смотрите зонную диаграмму на
рис. 10.А.2). Такая приборная структура обладает рядом преимуществ:
Глава 11. Полупроводниковые фотоприемники
хЛЛЛЛЛЛЛ^
хЛЛЛЛЛЛЛ^
хЛЛЛЛЛЛЛ^
W
0 область пространственного заряда
Рис. 11.13. Функционирование р—/—я-перехода.
• Она обладает малой емкостью Cd = Ae/Ww, таким образом, увеличенной частотой
отсечки.
• Вклад диффузионного тока /diff пренебрежимо мал (aW» 1 в A1.40)) так же, как
и влияние постоянной времени г на время отклика диода. Динамические
характеристики прибора в этом случае определяются генерационным током в SCR.
Пример
Для типичного приемника излучения с площадью фоточувствительной
поверхности 0,01 мм2 на основе материала, легированного до концентрации 1014 см~3 и при
потенциале V= 100 В, мы находим ширину SCR W— 36 мкм. Если нас устраивает
ширина собственной области 10 мкм, то мы приходим к емкости 0,1 пФ. При
последовательном соединении с цепью, имеющей импеданс 50 Ом, приемник
излучения будет обладать частотой отсечки XjlnRC или 30 ГГц. В этом случае средняя
напряженность электрического поля составит 102 В/10 мкм или 105 В см. Это
приведет к времени переноса в 10 мкм на 107 см с~1 или 100 пс, при этом частота
отсечки составит 10 ГГц.
11.5. Фотоприемник с внутренней эмиссией
Функционирование фотодиода Шотки с внутренней фотоэмиссией иллюстрируется
рисунком 11.14. Как это уже подробно обсуждалось в разделе 10.3, положение
потенциального барьера фш, естественно, заключено между уровнем Ферми
металлического слоя и дном зоны проводимости полупроводника. Сейчас мы рассмотрим
световой пучок, распространяющийся через полупроводник и состоящий из
фотонов с энергией h v, меньшей ширины запрещенной зоны полупроводника, что
делает полупроводник практически прозрачным для электромагнитного излучения). Свет
поглощается металлическим слоем, передавая свою энергию «морю» электронов.
77.5. Фотоприемник с внутренней эмиссией
металл
полупроводник
оптический резонатор
Рис. 11.14. Функционирование фотодиода Шотки с внутренней эмиссией.
После чего электроны могут эмиттироваться в полупроводник через
потенциальный барьер. Это непосредственно приводит к частоте отсечки прибора:
К =
мкм
A1.52)
Квантовый выход этих структур достаточно низок, поскольку в металле
электроны теряют свою энергию на очень малых расстояниях. В самом деле, средняя
длина баллистического переноса LB для большинства металлов лежит в интервале от
50 до 100 А. Коэффициент поглощения металлов дается величиной, обратной
глубине скин-эффекта S (смотрите G.В.6)): для металла с удельным сопротивлением
порядка 10 мкОм см это приводит к глубине скин-эффекта S величиной 200 А в
инфракрасной области спектрального диапазона, при этом коэффициент
поглощения составляет a=l/S= 5 х 105 см. Таким образом, нам следует ожидать
эффективность преобразования фотонов в горячие электроны в металле на уроне 1 — t~aL\
т. е. в диапазоне 10—20%. Для увеличения поглощения структуру
металл/полупроводник обычно помещают внутри резонатора (смотрите рис. 11.14).
Более того, не все горячие электроны, возбужденные выше барьера будут
обязательно компенсированы за счет полупроводника, т. к. они должны
распространяться в определенном направлении. Это иллюстрируется рисунком 11.15.
Рассмотрим те электроны, которые обладают полной энергией Е и
относительным импульсом Р ~ Е1/2 над уровнем Ферми металла. Горячие электроны, у
которых импульсы ориентированы под углом в относительно нормали к поверхности
границы раздела обладают компонентой импульса Pcostfn, таким образом,
энергией Е cos20 в соответствующем направлении (в направлении Oz). Априори они рав-
((Г412 Глава 11. Полупроводниковые фотоприемники
Q = 4л
= 2jtA-cosfl)
а ' б
Рис. 11.15. Функционирование фотодиода Шотки с внутренней эмиссией.
ным образом распределены по отношению к углу в. Таким образом, в пределах
телесного угла 4л* лишь часть всего ансамбля электронов Р(Е) будет способна
преодолеть потенциальный барьер (смотрите рис. 11.15):
р(Е)__ 2,A - cos »)_!-»./£)'" A1.53)
4л 2
Предположим, что плотность состояний в металле рт (см эВ) есть
постоянная величина. В этом случае электронный поток, эффективно переносимый в
полупроводник составит:
hv
■^-= \pmP(E)dE =-
hv
A1.54)
Внутренний квантовый выход дается отношением потока iph/q и поглощенного
потока фотонов р hv, т. е.:
\'/2
Это выражение приводит к полному квантовому выходу г/:
ч1 /2
A1.55)
A1.56)
Мы должны отметить, что выражение A1.56), полученное в рамках
использованного подхода, является чрезвычайно простым и не воспроизводится в
эксперименте. Учитывая, что плотность состояний в трехмерной металлической среде
изменяется как рос yJE (смотрите, например, уравнение E.20)) и принимая во
внимание принцип исключения Паули для металла, мы могли бы найти:
1 /, , v
/Ш1 О Г I V THIS /
$EFhv
Здесь: EF есть энергия Ферми в металле. Это последнее выражение подтверждается
экспериментально и известно как закон Фаулера. Рисунок 11.16 показывает, что
эффективность внутренней эмиссии диода на основе Si/IrSi подчиняется закону
Фаулера. К тому же выражение A1.55) приводит к разумным результатам при hv ~ ф .
11.6. Квантово-размерные фотоприемники
Я(мкм)
0.20
0.15
0.10
0.05
10 6 4 3
ill I
- V = 0.129 эВ
^ Сл = 0.096 эВ~]
^ ;/
2
i
/
1 ,
1.5
• • •
i .
1
i
:
-
-
,= 2В -
i
0.2
0.4
0.6
0.8
1.0
hv (эВ)
Рис. 11.16. График Фаулера для квантового выхода в фотодиоде Шотки с внутренней
эмиссией на основе Si/ IrSi (по данным В. I. Tsaur, M. M. Weeks R. Trubiano,
P.W. Pelegrini, and Т. R. Yew, IEEE Electron. Dev. Lett. EDL-9, 650 (У 1988 IEEE).
Уравнение A1.56) объясняет, почему по своей природе диоды Шотки не
являются хорошими приемниками излучения. Во-первых, из-за малой средней
баллистической длины пробега горячих электронов в металлах внешний квантовый выход
мал, как мы уже отмечали это в начале настоящего раздела (т. е. ~ 10%). К тому же
в области на 10% выше частоты отсечки, т. е. при hv~ \,\фт5 внутренний квантовый
выход составляет всего 10~3, что приводит к полному квантовому выходу 10~4, что,
мягко говоря, не впечатляет!
Тем не менее, этот тип приемников излучения добился определенного успеха в
тепловизионной индустрии, так как в этих приборах диапазон детектируемых длин
волн определяется не столько полупроводниковым материалом, сколько высотой
барьера между металлом и полупроводником. Кремний (исключительный
полупроводниковый материал для микроэлектроники!) в рассматриваемом случае может
использоваться одновременно для изготовления интегральных фотоприемных
матриц и схем обработки сигнала. В этом случае единственной проблемой является
выбор хорошей пары Si/металл. Например, приборы на основе /ьтипа Si/PtSi
обладают длинноволновой границей отсечки при 5,6 мкм. С использованием таких
приборов были изготовлены фотоприемные матрицы форматом 1024 х 1024 пикселей,
что позволило добиться ИК-отображения с высоким разрешением (несмотря на
низкую обнаружительную способность).
11.6. Квантово-размерные фотоприемники
В разделе 8.6 мы уже видели, каким образом квантование движения электронов в
направлении, перпендикулярном границам раздела в квантовых ямах, например,
на основе системы GaAs/Alx Gal _xAs приводит к появлению энергетических
подзон. Если такие квантовые ямы имеют «-тип проводимости (с эффективной
двумерной концентрацией ps, выраженной в см), в соответствии со статистикой
Ферми—Дирака дополнительные электроны начинают заполнять эти подзоны,
начиная с основной подзоны еу В том случае, когда фотоны падают на квантовую яму,
они обладают преимущественными возможностями для реализации электронных
переходов между подзонами проводимости.
(ц 414 Глава 11. Полупроводниковые фотоприемники
^-^
Возможно проявление двух типов оптических переходов:
• Переходы между связанными состояниями е{ —> е2 (переходы из связанного
состояния в связанное состояние). В разделе 8.6 мы видели, что такие переходы
приводят к практически моноэнергетическим особенностям поглощения, а именно
поглощаются только фотоны с энергией в пределах спектрально уширенного (на
величину ИГ) распределения в окрестности Hv=s2 — е{ = е12.
В этом случае коэффициент поглощения в квантовой яме дается (8.876):
а - —~ Ps—~~? (г—7—nf/(?) A1.57fl)
П nsc (en -hvj + (йГ/
Мы напоминаем, что Zo есть вакуумный импеданс C77 Ом), пх — коэффициент
преломления полупроводника, zn — дипольный матричный элемент
(аппроксимация этого параметра приведена в З.Г.24) и его типичная величина имеет порядок 1
нм), q есть угол между осью освещения вектором нормали квантовой ямы. Как видно
из раздела 8.7.2 функция f(q) изменяется как sin2#/cos#AO тех пор, пока поперечное
сечение светового пучка поверхности детектора остается в пределах его поверхности.
Зависимость sin2^ следует из правил отбора для кц, как это поясняется рис. 8.13.
• Переходы из связанного в свободное состояние. Они доминируют, когда имеется
лишь одна подзона в квантовой яме (смотрите (З.Г.27)). В этом случае переходы
происходят между локализованными состояниями в квантовой яме
(энергетический зазор между барьером и дном зоны проводимости составляет ех = Ес — £,).
В этом случае коэффициент поглощения дается интегралом A1.57а), который
берется состояниями континумма \kz) в зоне проводимости барьера. Состояния Щ
обладают энергией Ef= h kz2/2mc над дном зоны проводимости барьера, где тс -
эффективная масса в зоне проводимости. В дополнении 1.А мы видели все
сложности, связанные с нормировкой состояний континуума и необходимостью
введения вирутального ящика шириной ЬГк1 для того, чтобы осуществить такую
нормировку. Для расчета поглощения в квантовых ямах, связанного с переходами из
связанного в свободное состояние, мы должны ввести следующий интеграл:
nq1 Zo , С Luct I/, i i л|2 tiY I я ,
« = —a—H—KM^I1)! 7 —42 d
-(hv-ex)
" 'V7 /1... „ \ . /+.r^V
A1.576)
2mc
Мы напоминаем, что здесь Z,fict /я — одномерная плотность состояний импульса в
континууме (смотрите дополнение 1.А. Выражение A1.576) может быть
представлено в виде, более пригодном для расчетов за счет введения дипольного объема z(E)\
который возникает как предел /,fict|(A:Jz|l)|2 при Luct —><*>, с последующим
интегрированием по энергии конечных состояний Ef, что приводит к выражению:
а = jaD(hv, E,)lEff@) A1.58a)
о
Здесь: aD есть дифференциальное поглощение, определяемое следующим образом:
A1.58б)
Тонкие линии на рисунке 11.17 представляют энергии е2 — е{ межподзонных
переходов между связанными состояниями в квантовых ямах на основе GaAs/AlxGa, ^As
в функции содержания А1 х, а также толщины ямы.
Жирная линия представляет геометрическое место точек, соответствующих
концентрации и толщине, приводящих к квазирезонансной ситуации, когда
энергия первого возбужденного состояния е2 располагается как раз на уровне вершины
11.6. Квантово-размерные фотоприемники
квантовой ямы (и соответственно у дна барьера). Именно такая конфигурация и
используется в квантово-размерных фотоприемниках.
Безусловно, в такой ситуации структура обладает двойным преимуществом: сила
осцилляторов для таких переходов все еще играет важную роль, что очень близко к
ситуации с переходами между связанными состояниями, и в то же время
возбуждаемый электрон может свободно распространяться по возбужденному состоянию,
что аналогично характеру переходов между свободными и связанными
состояниями. Таким образом, рис. 11.17 показывает, что мы можем подобрать параметры
квантовой ямы и условие квазирезонанса будет обеспечено в спектральном
диапазоне от 5 до 20 мкм, т. е. перекрывать часть дальней ИК-области спектра.
Аналогичным образом средняя ИК-область спектра может быть освоена с
использованием квантовых ям на основе InGaAs/AlGaAs.
Электроны, возбужденные в континуум барьера, удаляются электрическим полем,
что приводит к фототоку. Электрическое поле Е возникает за счет приложения
соответствующего внешнего смещения, например, через два сильнолегированных
контактных слоя GaAs. Такая структура приемника излучения с набором квантовых ям
представлена на рис. 11.18. Мы увидим, что увеличение числа квантовых ям приводит к
тривиальному повышению полного уровня поглощения света, а также к увеличению
полной квантовой эффективности и обнаружительной способности прибора.
При достаточно низких температурах электроны захватываются в основной кван-
тово-размерной подзоне, и в идеальном случае система становится изолирующей. Под
влиянием потока фотонов электроны фотоионизируются из квантовых ям и попадают
в барьерные области, что приводит к фототоку, который может быть измерен
амперметром. На рисунке 11.19 показаны рассчитанный (с использованием A1.58)) и
измеренный спектры поглощения приемника излучения с набором квантовых ям. Следует
отметить что по сравнению с другими типами полупроводниковых фотоприемников,
квантово-размерные приборы являются узкополосными приемниками излучения*.
. см
Uj
Alx Ga1_xAs GaAs
10
15
20
30
60
80
100
120
d (ангстрем)
Рис. 11.17. Энергии переходов в квантовых ямах GaAs/AlxGa1 _ xAs между связанными
состояниями (тонкие линии), между свободными и связанными
состояниями (затемненная область) и между связанными и квазирезонансными
состояниями (жирные кривые).
* Прим. ред.: строго говоря узкополостным спектром фоточувствительности обладает
достаточно широкий круг не только квантово-размерных фотоприемников.
Глава 11. Полупроводниковые фотоприемники
фотовозбужденный электрон
фототок
расстояние
Рис. 11.18. Схема функционирования приемника излучения с набором квантовых ям.
0 00
100
120
160
энергия (МэВ)
Рис. 11.19. Экспериментальный и расчетный спектры поглощения приемника
излучения с набором квантовых ям в планарной волноводной геометрии (в= 90°).
(С разрешения F. LucOTHALES).
Для описания работы квантово-размерных приемников излучения могут быть
использованы две модели (рис. 11.20)
• Модель фотопроводника (рис. 11.20<з). Скорость генерации на квадратный
сантиметр в одиночной квантовой яме с коэффициентом поглощения ar1QW под
воздействием потока фотонов Фо есть:
Gop=/WQW*0 (П.59)
Здесь рв есть вероятность того, что фотовозбужденный электрон будет возбужден в
континуум барьера и удален электрическим полем. В стационарном состоянии эта
скорость может быть компенсирована скоростью захвата, которая поддерживает
заполнение квантовых ям электронами. В этом случае скорость рекомбинации
определяется соотношением:
R = £^- A1.60)
11.6. Квантово-размерные фотоприемники 417
Рис. 11.20. Две модели для описания переноса электронов через приемник излучения
с набором квантовых ям: модель фотопроводимости (а) и фотоэмиссии (б).
Здесь г есть время захвата электрона в барьере квантовой ямой, a p2D — двумерная
плотность фотовозбужденных носителей. Во время захвата ^доминируют
взаимодействия Фрелиха (смотрите дополнение 6.Б) и его типичное значение лежит в
диапазоне от 1 до 10 пс. Предположение о равенстве друг другу A1.59) и A1.60)
определяет двумерную плотность p2D. Трехмерная концентрация носителей p3D
может быть получена в предположении о том, что носители однородно распределены
по барьерному материалу с толщиной L так, что:
Ло= —= Z A1.61)
Следуя той же самой схеме рассуждений, как и в разделе 11.2, мы находим, что
фоточувствительность приемника излучения с набором квантовых ям есть:
1
hv Iq
A1.62)
Здесь: ^1QW есть квантовая эффективность одиночной квантовой ямы, ти — время
переноса электрона в барьере толщиной L со скоростью vd = juE, a G1QW есть
однопроходное усиление фотопроводимости. Мы видим, что в этом последнем
выражении чувствительность приемника излучения не зависит от числа квантовых ям.
Этот достаточно удивительный результат есть следствие сохранения
электрического тока. С другой стороны, мы увидим, что обнаружительная способность прибора
с N квантовыми ямами пропорциональна V7V.
• Модель фотоэмиссии (рис. 11.206). При использовании этой модели ток
определяется тем условием, что в стационарном состоянии поток носителей, захваченный
квантовыми ямами рс /ph /q находится в точном балансе с потоком фотоионизиро-
ванных электронов вне ямы ре #1QWO0. Коэффициент рс есть вероятность захвата
для электрона, пересекающего квантовую яму. Полагая оба потока равными,
получаем для фоточувствительности приемника излучения:
Рс
A1.63)
Мы видим, что выражения для чувствительности квантово-размерного
приемника излучения, получаемые в рамках каждой модели, идентичны, если:
Глава 11. Полупроводниковые фотоприемники
— =vA A1.64)
Рс L
Это последнее выражение связывает время захвата квантовой ямы с
вероятностью захвата электрона, пересекающего квантовую яму.
Пример
Рассмотрим квантово-размерную структуру, подверженную воздействию
электрического поля, возбуждаемого разностью потенциалов в 1 В на расстоянии в
1 мкм, т. е. с напряженностью 104 В см. Подвижность носителей в барьере
составляет 102 см2 В с при толщине барьера L между последовательными
квантовыми ямами 25 нм и времени захвата тс= 10 пс. В этом случае скорость vd
составляет 106 см с, а вероятность захвата рс равна 0, 25. В этом случае усиление
фотопроводимости квантовой ямы <71QW в предположении вероятности ионизации
ре = 1 составляет 4.
При использовании согласователя с дифракционной решеткой коэффициент
поглощения для типичной квантовой ямы составляет or1QW = 1% на длине волны
Л = 10,6 мкм A17 мэВ). В этом случае фоточувствительность такого квантово-
размерного приемника излучения составляет В = 4 х 10~2/0,117 = 0,34 А Вт.
Обращаясь к аспектам, связанным с обнаружительной способностью, мы
видим, что шум приемника излучения с 7V квантовыми ямами определяется A1.А.42):
i*R=2qI0B-pe)-±- A1.65)
Темновой ток /0 может быть получен, если мы сначала рассчитаем
концентрацию p2D th термически активированных носителей в барьере зоны проводимости.
Ранее мы видели (8.43), что эта концентрация определяется выражением:
A1.66)
p3D я iife)d£ = 1Ь|£.е<
L 7th" J L 7th"
Ec
Здесь пс есть критическая концентрация (8.43) в зоне проводимости, а уровень
Ферми EF получается, если предположить, что квантовые ямы легированы до
концентрации ps так, что (смотрите 8.45):
При этом Ес — Егестъ энергетический зазор между уровнем барьера и уровнем
Ферми. Для квазирезонансного приемника излучения при пумы должны иметь:
EC-EF =hv-(EF-£l)=hv fis-y A1.676)
тс /7th
Темновой ток получаем, положив /0 = AJ0 = Aqp3D thvd, при этом выражение для
обнаружительной способности (в предположении ре » 1)дается в виде:
D* * * - A1.68)
pB)J/N
Так что:
D' ш 2Ж.- £! — A1.69)
ч \ т„кТ -((e -
Обнаружительная способность
квантово-размерной структуры
11.6. Квантово-размерные фотоприемники
Из этого выражения мы и получаем выше упомянутую зависимость от ViV.
Последнее уравнение показывает также, что, если мы увеличиваем уровень легирования
квантовых ям, мы можем ожидать улучшения квантовой эффективности за счет
увеличения alQW (смотрите A1.58)). Однако, высота теплового барьера Ес — EF
уменьшается в соответствии с A1.676). Таким образом, существуют компромиссные
условия, оптимизирующие обнаружительную способность A1.69).
Рисунок 11.21 демонстрирует температурную зависимость обнаружительной
способности на длине волны 8,5 мкм для квазирезонансного приемника излучения.
В рассматриваемом случае мы наблюдаем зависимость еЛ1//2*г, типичную для всех
квантовых приемников излучения.
Рис. 11.21. Температурная
зависимость обнаружительной
способности квантово-размерной
структуры (N = 50) в предположении
квантовой эффективности 1% на
квантовую яму.
80
120 160 200
температура (К)
240
Широко распространенный интерес к квантово-размерным приемникам
излучения обусловлен двумя принципиальными преимуществами:
• Длина волны фотодетектирования может быть подобрана по желанию. Для этого
необходимо только выбрать определенные значения толщины квантовой ямы и
содержание А1 в барьере в процессе синтеза (этот аспект проектирования
называется квантовой инженерией).
• Стандартные методы микрообработки наиболее хорошо подходят для
производства крупноформатных матриц приемников излучения, которые в отличие от
диодов Шотки обладают хорошей обнаружительной способностью.
Наконец, заметим, что поскольку квантово-размерные приемники
излучения не могут регистрировать излучение при нормальном угле падения, то
должен быть найден способ, обеспечивающий эффективное участие фотонов в меж-
подзонных переходах. Это может быть достигнуто за счет формирования
решеточного устройства ввода на поверхности приемника излучения травлением
(смотрите рис. 11.22).
Пример
Рассчитаем обнаружительную способность для квантово-размерной структуры при
77 К в предположении следующих физических параметров:
lQW
hv= 0,155 эВ (Л= 8 мкм)
N= 50
Рс = 0,25
vd = 106 см с
mjnh2 = 2,78 х 1013 эВ'1 см и«с = 7,2х 1011 G/300) см
1= 250 А
ps = 5 х 10й см
В этом случае уровень Ферми дается соотношением A1.676):
((D20 Глава 11. Полупроводниковые фотоприемники
контакт пикселя
общий контакт
падающее ИК-излучение
подложка GaAs
контактные слои GaAs
контакты
слой MQW
диэлектрический слой
Рис. 11.22. Одиночный пиксель матрицы приемников излучения с набором квантовых
ям. Решеточное устройство ввода перенаправляет перпендикулярно
падающее излучение для увеличения перекрытия с разрешенными межподзон-
ными переходами.
£,-£> =0,155эВ-5х10и /2,78хЮ13 эВ = 0,155-0,018эВ = 137мэВ
При этом обнаружительная способность определяется выражением A1.69):
ю-2
D =
0,138 х 1,6 х 109 Дж
л/50
4x0,25x10* см с-х7,2хЮ"(Г/ЗОО)см-'с.(ц,/мь1от)
250хЮ~8см
или 3 х 1011 см Гц1/2 Вт при 77 К.
11.7. Лавинные фотоприемники
В лавинном фотодиоде усиление достигается за счет использования умножения
электронно-дырочных пар для увеличения числа фотогенерированных носителей.
Ударная ионизация была описана в дополнении 6.В, где коэффициент умножения ап
определялся как число вторичных электронно-дырочных пар andx9 генерированных
электроном при прохождении расстояния dx в условиях электрического поля.
Аналогичным образом коэффициент ар описывает количество пар, генерированных
дыркой. Эти коэффициенты сильно зависят от напряженности поля, будучи
пренебрежимо малыми в слабых полях (смотрите рис. 6.В.З). В лавинном фотодиоде
мы можем получить сильное поле при приложении значительного обратного
смещения к р—/—я-структуре (смотрите рис. 11.23).
Таким образом, имеются три возможных источника тока, проходящего через
такой диод (с площадью поперечного сечения А): первичная генерация
(термическая или обусловленная поглощением фотонов) AqGdx в слое толщиной cbc; ударная
11.7. Лавинные фотоприемники 421
ионизация, обусловленная электронами ocnlndx и ударная ионизация,
обусловленная дырками ар1дх. Эти механизмы приводят к следующим уравнениям для
стационарного тока:
A1.70)
dx
= «Л +
Непрерывность полного тока / = 1п + / обеспечивается этими уравнениями,
при этом, заменяя / во втором уравнении, мы получаем:
Это уравнение обладает общим решением:
A1.71)
A1.72)
Константа С зависит от граничных условий у контактов: п при х=0ир при х = L.
В идеальном случае я-контакт не может инжектировать дырки In(L) = 0, а р-кон-
такт не может инжектировать электроны и 7@) = 0. Из условия сохранения
полного тока следует, что / = /я@) = / (L) так, что:
= AqG
an-apQxp[(an-ap)L]
гния следует, чтс
>му на коэффищ
ехр[(а„-ар)ь\-\
A1.73)
Как мы видим, из этого последнего уравнения следует, что результирующий ток I/Aq
равен генерационному току G, умноженному на коэффициент М, определяемый как:
A1.74)
AqGL L а„ -арехр[(ал - ocp)L\
Коэффициент умножения
генерационного тока
В частном случае, когда ап = ар = а выражение для коэффициента умножения
упрощается:
Рис. 11.23. В лавинном диоде фотогенериро-
ванная электронно-дырочная пара за счет
ударной ионизации создает вторичные пары.
Глава 11. Полупроводниковые фотоприемники
М =
1
При заданной напряженности поля A1.74) накладывает предел на длину
области умножения. Если L возрастает до значения, обращающего знаменатель в ноль
(рис. 11.24), коэффициент умножения возрастает до бесконечности, при этом
бесконечно малый уровень генерации носителей приводит к лавинообразному
процессу, который закорачивает диодную цепь. Такой всплеск тока действительности
может разрушить диод, если только он не ограничивается где-либо в цепи. Уравнение
A1.74) также показывает, что идеальным материалом для получения большого
коэффициента умножения в собственной области должен был бы быть материал, в
котором коэффициенты ионизации электронов и дырок (ап и ар) были бы как
можно более близки друг к другу. Однако как мы увидим в дополнении 11.А.5 это
могло быть достигнуто за счет намного более важного усиления шума и, таким
образом, привело бы к ухудшению обнаружительной способности.
Здесь мы видим, что лавинный механизм приводит к усилению
фотопроводимости, но по принципиально другим причинам, чем тем, которые приводят к
усилению в фотопроводнике. В дополнении 11.А.5 мы увидим, что лавинные фотодиоды
обладают дополнительными источниками шума, возникающими вследствие
лавинного процесса.
Для реализации лавинного эффекта может быть использован ряд возможных
геометрий. Собственная область, например, может использоваться для поглощения
света и лавинного усиления сигнала. Мы можем также реализовать поглощение
света в области слабого поля (т. е. в одной из контактных областей) и использовать
для лавинного умножения только лавинную область. В действительности, если
поглощение фотонов создает неравновесную концентрацию носителей в контактных
областях п- и /ьтипа, часть этих носителей будет диффундировать к области
лавинного умножения, приводя к инжекционному току (дырочному току при jc = 0 и
электронному току при х = L). В фотодиодах с разделением областей поглощения и
умножения для формирования области лавинного умножения используется
широкозонный полупроводник, в то время как для области поглощения используется
узкозонный полупроводник.
Рассмотрим в качестве примера электронный ток In(L), инжектированный из
^-контакта при х = L. В A1.70)—A1.72) мы имеем G = 0, при этом изменяются
100
12 3 4 5
anL
Рис. 11.24. Коэффициент умножения в соответствии с A1.74) для ряда различных
значений отношения ajap.
11.7. Лавинные фотоприемники 423 jH
граничные условия при х = L. В этом случае общее решение A1.72) с граничным
условием 7@) = 0 имеет вид:
/,(*)=-^—{1-ехр [-(«„-«,>]} A1.76)
При х = L мы имеем:
/ = /„(!)+ /,(!)= /„(!)+ -^—{1 - ехр [- (ая - «,)l] } A1.77)
ая - ар
Из этого мы получаем коэффициент умножения тока электронной инжекции:
Мп — = — р —г- A1.78)
Коэффициент умножения для
инжектированных электронов
Аналогичным образом мы получаем коэффициент умножения дырочной инжекции:
/ДО) а„-а,ехр[(а„-а,)/,]
Коэффициент умножения для
инжектированных дырок
Как и в случае коэффициента умножения М для тока объемной генерации, эти
коэффициенты умножения инжектированных носителей расходятся, если ап1
достигает определенного порога (смотрите рис. 11.24).
Лавинные фотодиоды широко используются для детектирования слабых
сигналов, при этом для детектирования излучения с длиной волны менее 1 мкм наиболее
широко используются приемники излучения на основе кремния. В
телекоммуникационных областях применения ддя детектирования сигналов на длине волны 1,55 мкм
используются приемники излучения на основе InGaAs.
Литература
R.J. Keyes, ed., Optical and Infratrd detectors^ Topics in Physics Vol. 19, 2nd Edn,
Springer Verlag, Berlin A980).
H. Mathieu, Physique des Semiconduteurs et des Composant Electronigue, Masson,
Paris A987).
G.H. Rieke, Detection of light: Fom the Ultraviolet to the Submillimeter, Cambridge
University Press, Cabridge A994).
A. Rose, Cocepts in Photoconductivity and Allied Problems, Willy Intersience, New
York A963).
S.M. Sze, Physics of semiconductor devices, Wiley interscience, New York A981).
Литература по квантово-размерным фотоприемикам
B. Levin, /. Appl Phys. 74, Rl- R81 A993).
E. Rosencher, B. Vinter, F. Luc, L. Thibadeau, P. Bois, and J. Nagle, IEEE
J. Quantum Electron. QE -30, 2875 A994).
ДОПОЛНЕНИЯ
К ГЛАВЕ 11
11 .А. Шум фотоприемника
В дополнениях З.А. и 4.Г мы обратились к некоторым аспектам теории шумов для
того, чтобы учесть статистические свойства света. Поскольку понятие «отношение
сигнал/шум» является основополагающим для детектирования света (и сигнала!),
мы в этом разделе продвинем дальше математический формализм теории шумов.
Здесь рассматриваются также и физические механизмы, ответственные за
генерацию шума в приемниках излучения.
Перед тем, как приступить к достижению основных целей настоящего
дополнения, нам хотелось бы рассмотреть достаточно простой (и достаточно далекий от
строгости) аргумент, который позволит нам быстро вывести формулу для
генерационного шума, что и является целью этого дополнения. Такая схема рассмотрения
будет нам полезна как концептуальная путеводная нить до тех пор, пока мы не
разработаем более точную теорию.
Рассмотрим поток фотонов Ф, падающий на приемник излучения с квантовой
эффективностью г] в течение времени Г (смотрите рисунок 11.А.1). Это
характеристическое время есть время интегрирования приемника излучения, которое также
составляет l/2Av, где Av есть ширина полосы детектирования. В течение этого
временного интервала создается N фотоэлектронов. TV есть случайное число со
средним значением, определяемым N = 77ФГИ, если 7V флуктуирует в соответствии с
распределением Пуассона, дисперсия этой величины определяется как а* = N. Ток
фотогенерации может быть оценен числом носителей, создаваемых за единицу
времени, как / = qN/T.B этом случае среднее значение и дисперсия фототока
даются соотношениями:
/ = / =
qN
A1.А.1)
Таким образом, мы получаем формулу A1.А.38), связывающую среднюю
величину тока и его дисперсию, Теперь мы проведем указанный вывод более корректно.
фотоны
электроны —•-
мощность шума в полосе Л V
Рис. 11.А.1. Шум в процессе детектирования (а) и соответствующий спектр шума в
фотогенерированном токе (б).
11 Л. Шум фотоприемника
11.А.1. Флуктуации
Рассмотрим ток i(t), циркулирующий по цепи. В реальной ситуации этот ток
флуктуирует около среднего значения, соответствующего уровню сигнала.
Наблюдателю, лишенному каких-либо средств обработки сигнала (например, интегрирования
сигнала и т. п.), этот шум помешает зарегистрировать сигнал с уровнем, меньшим
амплитуды хаотичных флукутаций. В связи с этим мы теперь разработаем
физический и математический инструментарий, позволяющий нам количественно работать
с этой простой, но фундаментальной шумовой моделью.
В рассматриваемом случае ток i(t) является примером случайного
(стохастического) процесса. Случайный процесс есть функция, являющаяся следствием
случайной выборки /(/, £)> где f есть случайная переменная (смотрите рис. 4.Г.2). Говоря
более точно, такой процесс описывается набором функций /(/, f), —«> < t < °°,
связанных с распределением вероятности /(О? гДе/(О — вероятность
проявления функции /(/, £). Как обычно, мы определяем среднее по ансамблю в виде
(/@) = li(t9 OfiOdCn </2@> = ti2b, C)f(C)d£ Для стационарных стохастических
процессов, а лишь эти процессы мы и будем здесь рассматривать, это среднее не
зависит от t. Более того, мы дадим новое определение i(t), вычитая среднее
значение (/(/)) (которое фактически соответствует сигналу) из флуктуирующего тока так,
что среднее значение (/(/)) будет равно нулю. Это делается из соображений
удобства, так как облегчает многие последующие выражения.
Хотя простые средние значения не зависят от времени, временные аспекты
флуктуации при этом не исчезают. Ток в момент времени t{ может иметь различную
величину в момент времени t Этот эффект называется памятью стохастического
процесса. Мера этой памяти может быть найдена с использованием
автокорреляционной функции для /, которая является средним i(t)i(t{) по ансамблю:
s.Q, O= (''MO) = j'(>; f >(',; <Г)/(<ГК (п.А.2)
Идея, лежащая в основе A1.А.2) заключается в том, что, если процесс не
обладает памятью, тогда i(t) и /(/,) являются независимыми случайными переменными и
среднее от произведения равно произведению средних, что превращает A1.А.2) в
ноль. В случае стационарных процессов функция S.. зависит только от разницы
т= t{ — t. Более того, очевидно, что мы имеем S.^r) = S..(— z).
Фурье-образ автокорреляционной функции называется спектром мощности /:
Su(co)= j
Спектр мощности i(t)
Мы можем лучше понять причину того, почему мы называем это спектром
мощности, рассчитав квадрат тока i(t) в течение большого временного
интервала Т. Ток, стробированный в интервале от —Т/2 до Т/2, мы можем разложить в
ряд Фурье:
(П.А.4)
1 Т..
1 Г
/ (О):) = /
т J
При этом мы получаем для квадрата тока:
J\k
Дополнения к главе 11
Это выражение позволяет получить среднее по времени от квадрата
рассматриваемой величины:
Т/2
Т _т/2
Последнее соотношение есть ничто иное, как теорема Парсеваля. Подставляя
выражение для i(a)k) в это последнее выражение, мы находим:
7V2
-т/2
I Т/2 2 772 772
\± \i(t)c-^ d/ = ^T- fdie^' — \i(f)i(f
\T J/2 к Tj/2 T J/2
Этот последний интеграл представляет среднее по времени от переменной
i(t)i(t + z). Если среднее по ансамблю для этого интеграла в пределе Т -> «> равно
автокорреляционной функции 5..(t), то в этом случае такой процесс называется
эргодинеским процессом. В дальнейшем мы будем предполагать, что механизмы
фотодетектирования являются эргодическими процессами. Можно показать, что это
свойство удовлетворяется, если интеграл от tS..(z) сходится.
Таким образом, следствие эргодичности для A1.А.7) заключается в следующем:
772
В пределе при Т^><*> имеет место:
(Т/2 \
Urn I J/'(f)lr\ = ]?£Ш= fs.№ (ПА.9)
-Т/2 I -оо -оо
Здесь мы преобразовали сумму в интеграл, учитывая, что Асок = 2я/ Т и используя
соотношение:
X/fV(«) (ПАЮ)
Уравнение A1.А.9) означает, что полное среднее i2(t) распределено по частотному
спектру, определяемому S(v), при этом, поскольку мы не делаем различия между
положительными и отрицательными частотами (смотрите рис. 11.А.1), мощность
по полосе положительных частот А уесть:
Tv2 = ^(-v)+S(v)]av = 2S(y)Av (ПАП)
Средняя мощность
в полосе частот А у
Для проведения расчетов нам необходимо извлечь из спектра мощности шума еще
одно важное свойство. Рассмотрим передаточную функцию линейного фильтра h(co),
которая преобразует сигнал ixn(co) в выходной сигнал iout(co) — h(u))iin(co). В
соответствии с теоремой свертки мы имеем:
Теперь найдем функцию корреляции между /out и /in:
SM) = (U (>>„ (f -r) = j h(t'Xim (t - t% (f - r))d/' = J h(f%(r - f)lf = *(r;^(r)
A1.A.13)
Автокорреляционная функция для / определяется умножением A1А12) на / (/ + ft
11 Л. Шум фотоприемника 427 j)
*(- г)Ч,(- т)
A1.A.14)
Или вновь:
Это выражение позволяет получить Фурье-образ в виде:
Преобразование спектра
мощности фильтром
Этот важный результат позволяет восстановить A1.А.11) на фоне средней
мощности шума, поскольку фильтр (\h{co)\ = 1, если со{< со < со{ + Асо и h(co) = 0 при других
частотах) передает мощность S(cq)&cd. В дополнение к этому это уравнение
показывает, что расчет распространения шума в линейной цепи полностью аналогичен
распространению обычного сигнала, если мы представим шум в виде амплитудного
источника iv, квадрат амплитуды которого дается A1.А.11). Вооружившись этими
общими результатами, мы можем теперь обратиться к проблеме идентификации
физической природы шума приемника излучения.
Пример
Для простой интегрирующей цепи на рис. 11.А.2 мы легко находим:
{(о) 1 + ion
В этом случае показано, что, если спектр шумового источника на входе есть S..(co),
то спектр мощности на выходе есть:
Рис. 11.А.2. Интегрирующая цепь.
Таким образом, фильтр значительно ослабляет шум за счет устранения части
спектра мощности выше со = 1/г. Чем больше величина т, тем больше и величина
фильтрации.
11.А.2. Физическая природа шума
В полупроводниковом образце, включенном в цепь короткого замыкания,
мгновенный циркулирующий ток, сохраняется повсюду в цепи и определяется выражением:
<> A
Здесь Аи V относятся соответственно к площади и объему образца, а сумма по п
берется по всем N носителям в образце. В среднем этот ток равен нулю. Однако,
((D28 Дополнения к главе 11
поскольку скорость и число носителей может флуктуировать, в общем случае,
в любой момент времени /'(/) отличается от того, чтобы быть точно равным нулю.
Таким образом, эти отклонения от нуля ответственны за шум тока (смотрите рис.
11.А.З). В последнем уравнении проявляются два источника шума:
• Скорость каждого носителя может флуктуировать из-за рассеяния или теплового
движения. Это является источником теплового шума (называемого также шумом
Джонсона или Найквиста).
• Число носителей может флуктуировать либо из-за генерационно-рекомбинаци-
онных процессов (что называется генерационно-рекомбинационным шумом) или же
из-за того факта, что каждый контакт может в какой-то момент инжектировать
или захватывать один электрон с обязательным интервалом между каждым
событием (т. н. дробовой шум).
х
\
Рис. 11.А.З. Хаотическое движение свободных носителей в полупроводнике вызывает
флуктуации тока в цепи.
Поскольку эти механизмы отличаются друг от друга, их можно рассматривать
как независимые и некоррелированные источники шума.
11.А.З. Тепловой шум
Для расчета теплового шума мы вначале рассмотрим электрон в полупроводнике, в
котором нет ни поля, ни градиента концентрации носителей. Эволюцию функции
распределения такого электрона дает уравнение Больцмана (смотрите главу 6):
A1.А.18)
Здесь /(v, /) есть вероятность того, что в момент времени / электрон обладает
скоростью v (уравнение F.7)). Мы использовали аппроксимацию времени релаксации
для интеграла столкновений (уравнение F.12)).^(у)есть распределение Максвелла
при термодинамическом равновесии.
Решение этого уравнения получить достаточно просто:
' П - ехр - —
1 I Т<
A1.А. 19)
Если мы фиксируем скорость в момент времени на величине v0, то в этом
случае мы имеем/(v0) = S(\ — v0) и (И.А. 19) дает причинную функцию распределения, т.
е. вероятность того, что скорость в момент времени t составляет v при условии, что
в момент времени / = О она равна v0:
Комбинированная функция распределения, т. е. вероятность того, что скорость
составляет v в момент времени / и v0 в момент времени t — 0, соответственно есть:
11.А. Шум фотоприемника А1Я
/(v, f; v0, 0)= fo(\o)S (v - vjexp
1-exp
A1.A.21)
Из этого комбинированного распределения мы получаем автокорреляционную
функцию для vx при t > 0:
S^t) = JdvdvovxvOx/(v, /; v0, 0)= Jdv0v02JC/0(v0)expf- ^y)]+ ° (H-A.22)
В том, что касается стационарных процессов, мы имеем SJ^t) = S^—t). Более того,
если бы г была просто постоянной величиной, то интегрирование A1.А.22) дало бы:
Sl(t)=—txp --Li A1.A.23)
Спектр мощности шума есть Фурье-образ:
Это дает:
A1.А.24)
A1.А.25)
При этом в комбинации с A1.А.26) мы получаем:
Для обычных электронных частот сотс « 1 (г имеют величину порядка пс), при
этом с использованием F.16) мы находим для подвижности:
Sxx(co)=2 — ju A1.A.26)
Далее, каждый электрон дает вклад в ток —qvJL, и поскольку движение
электронов является некоррелированным для спектра мощности /, мы имеем:
^
A1.А.28)
Компонента теплового тока
в спектре шума тока
Здесь: G = \/R есть проводимость полупроводника. Связь между флуктуациями,
описываемая токовой автокорреляционной функцией S.. и проводимостью G
является частным случаем достаточно общей флуктуационно-диссипативной теоремы.
Связь между линейным откликом G и флуктуациями / показывает, что диссипатив-
ные процессы не могут существовать без флуктуации или шума. Таким образом,
невозможно измерить отклик системы в условиях возмущения без того, чтобы сама
система не была бы источником шума.
Применяя соотношение A1.А.11) для мощности в полосе частот Ац
обусловленной тепловым шумом, мы находим:
£ = AkTGAv = ^f-Av A1.A.29)
к
Тепловой шум в полосе частот Av
Это последнее выражение может быть интерпретировано следующим образом:
тепловая мощность Ri*, рассеиваемая на резисторе R в полосе частот A v
эквивалентна средней тепловой энергии 4кТ, рассеиваемой в течение времени Av.
Дополнения к главе 11
Пример
Найдем стандартную дисперсию тока из-за теплового шума при 300 К в резисторе
номиналом в 50 Ом при интегрировании сигнала в течение 1 мс. Спектральная
ширина составляет 103 Гц, при этом выражение A1.А.29) дает VD х 1,3 х 10~23 Дж К х
х 300 К х 103 Гц/50 Ом) или 0,57 нА. Этот ток далек от того, чтобы быть
пренебрежимо малым.
11 .А.4. Генерационно-рекомбинационный шум
Процесс электронно-дырочной генерации не создает абсолютно постоянный ток,
т. к. электроны и дырки несут дискретные заряды, а момент их рождения является
случайным. В этом случае флуктуации тока возникают из-за флуктуации
концентрации свободных носителей в полупроводнике. Из A1.А. 17) мы видим, что для
того, чтобы флуктуации концентрации генерировали флуктуации тока, средняя
скорость носителей должна быть отличной от нуля. В противоположность
тепловому току генерационно-рекомбинационный шум присутствуют только в том случае,
когда ток имеет ненулевое значение. Это, в свою очередь, требует того, чтобы в
полупроводнике были электрическое поле или градиент концентрации носителей.
Проследим «судьбу» электрона, возникшего в момент времени tk и
путешествующего со скоростью v, вплоть до его «трагического исчезновения» из зоны
проводимости вследствие рекомбинации в более поздний момент времени tk + rk
(смотрите рис. 11.А.4). Вклад этого события '/:' в ток цепи составляет ik(t — tk), где:
_<£, 0</<-rA
[О, / < О или тк < t
Таким образом, полный ток составляет:
Мы можем записать средний ток в виде:
A1.А.30)
A1.А.31)
A1A32)
Здесь N есть скорость генерации и (г) — среднее время жизни электрона. Такой
процесс генерации может иметь разнообразную физическую природу: генерация на
Рис. 11.А.4. Электрон, возникший в диоде, генерирует ток во время своего движения
к/^-контакту; с дыркой происходит то же самое в л-контакте (а). В
фотопроводнике возникший электрон рекомбинирует с дыркой в
полупроводнике (б).
11.А. Шум фотоприемника
примесном центре (как это имеет место в случае механизма Шокли—Рида,
исследованного в разделе 6.5), эффект Оже (смотрите дополнение 6.Г), межзонная
термоэлектрическая эмиссия (смотрите дополнение 10. Б) или поглощение фотона. Во
всех этих случаях мы можем предполагать, что распределение времен
возникновения электронов следует распределению Пуассона, т. е., что отсутствует временная
корреляция между событиями создания электронов.
В соответствии с нашей теперь уже хорошо отработанной процедурой спектр
мощности генерированного тока есть:
"j( ik(t - /J£ /,(г - Л e-'-dr A1.A.33)
Это выражение может быть рассчитано с использованием Фурье-образа для
элементарного вклада ik:
'*(>->*)= f — /*(*>) е-'е--'*
J In
A1.А.34)
}
Это выражение, будучи вставлено в A1.30), дает:
d(ox
2л
A1.А.35)
В этом усреднении сумм мы имеем два различных случая:
• Поскольку времена создания и жизни электронов не являются
коррелированными при к Ф I каждая сумма принимает вид'.
В интеграле (И.А.35) для Su эти средние величины дают квадрат среднего тока.
• При к = /, когда среднее от двойной суммы в A1.А.35) может быть записано в виде:
£ ik (со, X
Это выражение приводит к простому результату для автокорреляционной
функции флуктуации тока:
A1.A.38)
Используя уравнение A1.А32) для среднего тока, мы получаем следующий результат:
При этом усиление g имеет вид: A1.А. 39)
g = -
L rtr
Дополнения к главе 11
Здесь: усиление фотопроводимости было введено в разделе 11.3, a rtr есть время
переноса электрона через генерационно-рекомбинационную область. В этом
случае мы получаем следующий общий результат для генерационно-рекомбинационно-
го шума:
^-Av A1.A.40)
Генерационно-реком-
бинационный шум
Таким образом, как это и предсказывалось, этот вид шума присутствует только
при событии, связанном с ненулевым средним током. В связи с этим выражением
особый интерес представляют три случая:
1. Фотодиод без рекомбинации. В этом случае распределение времен жизни
имеет особенно простой вид. Создаваемый электрон будет иметь время жизни rtr,
которое позволит ему дойти до /^-контакта, где он мгновенно рекомбинирует. Таким
образом, мы имеем g = 1 и (г2) = (гJ при отсутствии каких-либо флуктуации по г.
В этом случае рассматриваемый процесс представляет собой в чистом виде
генерационный шум:
I;=2qlAv A1.A.41)
Генерационный шум
Пример
Предполагая, что ток с амплитудой в 1 нА пересекает фотодиод, а ширина
полосы составляет 1 кГц A1.А.41), мы приходим к генерационному шуму с
амплитудой VB х 1,6 х 109С х 10"9 А х 10 Гц) или 0,56 пА.
2. Фотопроводник с рекомбинацией. Мы можем предположить, что излучатель-
ное время жизни носителей распределено в соответствии с процессом Пуассона:
A1.А.42)
Среди прочего это соотношение обладает тем свойством, что (г2) = 2(гJ.Это
приводит к генерационно-рекомбинациолнному шуму:
1?=4qglAv A1.A.43)
Генерационно-реком-
бинационный шум
Генерационно-рекомбинационный шум может рассматриваться как
генерационный шум 2q(l/g)Av, усиленный с коэффициентом усиления g, к которому
добавляется рекомбинационный шум. В фотодиоде рекомбинационный шум равен нулю:
в то же время в фотопроводнике это шум того же типа, что и генерационный шум.
Это, в свою очередь, приводит к удвоению генерационного шума и ответственно за
появление коэффициента 4 в уравнении A1.А.43).
3. Шум генерации-захвата в квантово-размерных фотоприемниках. Как мы
видели, когда электрон пересекает квантово-размерную структуру, он может быть
захвачен с вероятностью рс. Вероятность того, что электрон будет захвачен после того,
как он пройдет п ям за пределами той ямы, из которой он был изначально
фотовозбужден, составляет рс{\ — рс)п~1, при этом средние времена жизни составляют:
'4*- A1.А.44)
11.А. Шум фотоприемника
Здесь Lw есть расстояние между последовательными ямами. Шум,
соответствующий A1.А.40), в этом случае составляет:
1? =2B- pjgglAv A1.A.45)
Генерационно-рекомбинационный
шум в структуре с набором ям
При этом два предела имеют вид:
• рс -> 1 (фотодиодный предел, т. к. захват электрона близлежащей квантовой ямой
неизбежен),
• рс -> 0 (фотопроводниковый предел, т. к. вероятность захвата является пуассонов-
ским процессом, поскольку электрон пересечет много ям до того, как он будет
захвачен).
Мы напоминаем, что g = l/pcN, где N есть число квантовых ям.
11 .А.5. Шум умножения
В разделе 11.7 мы видели, каким образом генерационный шум в лавинных диодах
умножается за счет ударной ионизации. Поскольку генерационный ток также
является источником шума, мы можем ожидать, что этот шум должен усиливаться при
лавинном умножении. Однако, процесс ударной ионизации является также и
случайным процессом и дает свой вклад в полный шум. Для описания шума в
лавинном приемнике излучения нам необходимо обобщить уравнения раздела 11.7 с тем,
чтобы мы могли найти ток 1(х0), обусловленный источником генерационного шума
qGAAxS (х — х0), расположенного при х = х0, 0 < х0 < L. В этом случае уравнение
A1.70) может быть записано в виде:
—L = ajn + ар1р + qGAAxS(x - х0)
A1.А.46)
- —- = ajn+ aplp + qGAAxS(x - х0)
При этом граничные условия имеют вид /@) = In(L) = 0. Для полного тока 7(х0)
решение для 1р, использующее эти граничные условия, имеет вид:
A1.А.47)
х0 < х < L
Здесь: Дог = «^A — к) = ая — ар и к = ар/ап.
При х = х0 интегрированием A1 .А.46) вблизи х = х0 мы получаем:
/,(<; х0)- /,fo; xo)= qGAbx A1-A.48)
Это позволяет нам определить 1(х0):
l(xo)= qGAAx АаеДаХ° = qGAAxM(x0)
ап -
Здесь коэффициент умножения М теперь уже зависит от х0:
М(*о)= \-k£Z (HA.50)
Дополнения к главе 11
Из A1.А. 49) можно сделать заключение, что за счет умножения
генерационный источник при х0 дает ток в цепи, который в М(х0) раз превышает первичный
генерационный ток. Таким образом, мы можем рассматривать область умножения
как фильтр в том смысле, как это использовалось при изложении раздела 11.АЛ,
поскольку он обладает передаточной функцией вида М(х0). Мы также видим, что
коэффициенты умножения, выведенные в разделе 11.7, в ряде частных случаев
принимают следующий вид:
1. Инжекция при х = 0:
1 - к
2. Инжекция при х = L:
1 - к
3. Однородная объемная генерация:
A1А52)
j
(Н.А.53)
qGAdx,
Тот факт, что лавинная область ведет себя как линейный фильтр, важен с точки
зрения расчета шума. С учетом A1.А. 16) мы знаем спектр шума на выходе фильтра
в |Л/(хо)|2 раз отличается от входного спектра шума. Поскольку источники в
различных точках х0 являются независимыми, достаточно рассчитать полный шум в виде
вкладов ото всех источников и умножить результат на М(х0J.
В каждой точке имеются три генерационных источника, обладающие
соответствующим шумом:
£,=2qAvaJn(x0)Ax A1.A.54)
~tp=2qAvapIp(x0)Ax
Здесь: G(xo)A\x есть скорость термической и оптической генерации, ап1п(х0)сстъ
генерационный ток, возникающий из-за электронных столкновений, а яг/р(*0)
соответствует току, создаваемому дырками. / (jc0) и / Ц) есть соответственно средние
электронный и дырочный токи. Случай, связанный с инжекцией электронов или
дырок через контакты, может быть описан заменой qG(xo)AAx на ln(L)S(x0 — L) или 1п@)8
(х0), что приводит к инжекционному шуму:
& = 2qAvln(L)S (х0 - l)= 2qAvlp@)S (x0) A1.A.55)
В этом случае полный шум приемника излучения есть:
0 ° A1.А.56)
Рассмотрим теперь три следующих случая:
1. Объемная генерация, т. е. G(x0) = G, 0 < jc0 < 1. В соответствии с A1.74) мы
имеем / = qGALM и:
11.А. Шум фотоприемника
Ip(x)=qAG
anLM
Да
A1.А.57)
Подставляя эти уравнения в (И.А.56) и используя выражения для М, приведенные
в A1.74), мы находим:
# = 2qAvAqG(\ + а„ЬМ)\ Л/26с)е-ДахсЬс =
J (И.А.58я)
= IqAvAqGLM (l + anLM^ + apLM)= iqAvIM V + anLMkl + aPLM)
Ki
Это выражение может быть также переписано в виде:
f = 2qAvlMF(M)
A1.А.586)
Таким образом, шум состоит из генерационного шума, умноженного на
коэффициент лавинного умножения М, играющего ту же роль, что и g в
фотопроводнике (смотрите A1.А.43), при этом коэффициент умножения шума F(M) описывает
вклад в шум, обусловленный лавинным процессом. На рисунке 11.А. 5 показана
зависимость этого коэффициента от произведения anL. Заметим, что этот
коэффициент минимален, когда к = 0 или \/к = 0, но ассимптотически пропорционален
М, когда два коэффициента ионизации имеют одно и то же значение. Таким
образом, для получения приемников излучения с высокими функциональными
характеристиками, необходимо подбирать материалы и конфигурации смещения, при
которых доминирует какой-либо один из этих коэффициентов.
2. Электронная инжекция, т. е. qG(x0) = In(L)S(x0 — L). В этом случае мы имеем
/= МI (L) и в соответствии с уравнениями A1.76)—A1.78):
100
Рис. 11.А.5. Коэффициент умножения шума в соответствии с уравнением A1.А.54) для
различных значений ап/ар.
f( 436 Дополнения к главе 11
/»=/-/,(*)
A1.А.59)
После подстановки в уравнение A1.А.55) и упрощения (заметьте, что eAflfi =
= М /A - к + кМ\) это дает:
= 2gAvIn(L] Ml
A1.А.60)
-к) 2
1 м„
Этот результат может быть интерпретирован аналогично предыдущему случаю.
Более того, мы ясно видим, что коэффициент умножения шума минимален при к = О
и резко возрастает по мере приближения ап к ар.
3. Дырочная инжекция, т. е. qG(x0) = Ip@) J(x0). Этот случай может быть выведен
из предыдущего с использованием замены In(L) на /@), ап на ар и, таким образом,
к на 1/к, что дает:
tf = 2qAvIMpF(Mp)
A1.А.61)
Этот случай представляет практический интерес только тогда, когда ар » ап.
В заключение этого раздела еще раз отметим, что имеется ряд источников шума,
поведение которых суммировано на рисунке 11.А.6. Важно подчеркнуть: мы
обнаружили, что:
• фотонный шум за счет механизма детектирования преобразуется в
фотоэлектронный шум, при этом, как мы видели в этом разделе, его «судьба» та же самая, что
г—i
Щ фотонный шум щ
сигнал
£ схемный шум ^
II .
фотоэлектронный J Ц фотонный шум Ц
детектируемый
шум
сигнал
g или Н
g или Н
схемный шум
р z 4
% усиления Щ,
| фотоэлектронный 1
щ шум щ
детектируемый
шум
усиление
а Ц б
Рис. 11.А.6. Различные источники шума фотодетектирования в фотодиоде (а) или
в приемнике с внутренним усилением (фотопроводник или
лавинный прибор) (б).
11.А. Шум фотоприемника
и у сигнала, т. е. он «страдает» из-за тех же самых квантовых потерь (rj < 1) и
претерпевает то же самое усиление (g в случае фотопроводников и М в случае
лавинных фотодиодов), что и детектируемый сигнал.
• шум усиления обладает специфическим характером в том, что касается лавинных
приемников излучения с коэффициентом f{M), описываемым A1.А.586);
• шум цепи считывания (т. е. усилитель, интегратор и т. д.) не зависит от усиления
фотопроводимости;
Таким образом, понятно, что можно получить выигрыш от внутреннего
усиления (усиление фотопроводимости с коэффициентом g или лавинное умножение с
коэффициентом М) перед тем, как использовать электронное усиление.
Говоря более точно, если шум усилителя есть <7атр1. (А Гц1/2) отношение сигнал/
шум для полной электронной цепи дается выражениями A1.73) и A1.А.586):
S I N =
MAq 7}Ф с
A1.А.62)
Здесь: А есть площадь поверхности, Фо — поток фотонов, a rj — квантовая
эффективность приемника излучения. Этот результат следует сравнить с отношением
сигнал/шум, полученным для случая использования фотодиода в той же самой цепи
регистрации, т. е.:
S/N =
A1.А.63)
Теперь мы сравним отношение сигнал/шум для фотодиода и кремниевого
лавинного диода с к = сс/ап = 0,1 и anL= 3. В этом случае М = 100 и F{M) =12
(смотрите рис. 11.24 и 11.А.5). На рисунке 11.А.7 приведено сравнение A1.А.62) с
A1.А.63). Отметим, что использование лавинного фотодиода обладает
преимуществами при малых уровнях сигнала, когда мы хотим отделить шум детектирования
от шума усилителя. Говоря более точно, это есть случай, когда:
t 1ОЭ
ф
о
101
10
101
101'
ю1
9 1
поток излучения (фотон см с )
Рис. 11.А.7. Сравнение отношения сигнал/шум двух диодных фотоприемников с
площадью 1 мм2 при полосе частот 50 Гц.
Дополнения к главе 11
1-1/М2
Ф° F{M)-\ 2q2An F(MJq2Arj
Таким образом, если мы предположим, что световой сигнал образован фотонами
с энергией 1 эВ и он детектируется с использованием приемника излучения
площадью в 1 мм2 и с квантовой эффективностью 0,5 при шуме усилителя 0,1 пА Гц~1/2, то
это приводит к предельному потоку 3,2 х 1012 фотонов см с. Таким образом, для
мощности падающего излучения менее 0,5 мкВт лавинный фотоприемник
излучения был бы исключительным приемником излучения.
Литература
R.J. Keyes, Ed., Optical and Infrared Detecyors, Topics in Physics Vol. 19, 2nd,Springer
Verlag, Berlin A980).
R.J. Mclntyre, IEEE trans. Electron Dev. ED-19, 164 A966).
A. Papoulis, Probability, Random variables, and Stochastic Processes, McGraw-Hill,
New York A965).
11.Б. Пределы обнаружительной способности:
функциональные характеристики,
ограниченные фоном (BLIP)
Как мы видели в дополнении 11.А, шумы всех приемников излучения
накладываются на идеальный сигнал. Таким образом, нас интересует детектируемый сигнал
(например, в виде фототока i), т. к. мы можем выделить его на уровне фона,
определяемого шумовым током /л. Таким образом, задача детектирования сигнала
заключается в достижении максимально возможного отношения сигнал/шум:
S/N=± A1.Б.1)
В общем случае сигнал is (А) является произведением фоточувствительности
<Н (А/Вт) и мощности падающего излучения Рпс (Вт). В этом случае шум in
принимает вид in = (^мА/^Дуу/^смотрите дополнение 11.А), где и есть константа B или 4
в зависимости от того, какой используется тип фотовольтаического приемника или
фотопроводника с коэффициентом усиления g); А есть площадь приемника
излучения; Jd — плотность тока, обусловленного фоном, a Av — ширина полосы
измерительной системы, т. е. 2//int, где /int есть время интегрирования системы измерения.
В этом случае отношение сигнал/шум есть:
S/N = . ^"с A1.Б.2)
y]uqAJdAv
Минимальная детектируемая мощность есть та, которая соответствует
отношению сигнал/шум, равному 1. Эта величина называется мощностью, эквивалентной
мощности шума (NEP) и она определяется соотношением:
NEP =
Мощность, эквивалентная
мощности шума
Это последнее выражение показывает, что функциональные характеристики
приемника излучения с точки зрения NEP зависит от A vh площади приемника
излучения. Эти две зависимости являются ничем другим, как следствием закона больших
чисел /и/V/w, где т есть число детектируемых событий в определенном спектраль-
11. Б. Пределы обнаружительной способности
ном диапазоне. Для проведения сравнения различных технологий приемников
излучения введем параметр, более соответствующий собственным
характеристикам, для оценки функционирования, а именно обнаружительной способности D\
определяемой как:
или:
/)* = /х A1.Б.5)
Зависимость обнаружительной
способности (см2 Гц1/2 Вт)
от плотности тока Jd
Сейчас самое время дать определение плотности фонового тока Jd. У этого тока
могут быть два источника возникновения:
• Собственная причина обусловлена тем фактом, что приемник излучения собирает
излучение черного тела от окружающей среды при температуре Тв. Эта
компонента шума дается соотношением:
(И.Б.бя)
• Здесь т](Л) есть квантовая эффективность приемника излучения для фотонов с
длинами волны Л; Лх и Л2 которые определяют спектральный диапазон
детектирования; g есть коэффициент усиления фотопроводимости (g = 1 для фотодиода);
(йФв(Л)/6Л)АЛ — поток фотонов в спектральном диапазоне АД (йФ^йЛ в единицах
см~2 с мкм)- Этот последний параметр может быть выражен через излучатель-
ную способность черного тела, приведенную в дополнении 2. Б в виде:
— = -y-7f- (П.Б.бб)
Здесь: с — скорость света.
• Другой причиной, связанной с самим приемником излучения является темповой
ток, связывающий проводимость за счет свободных электронов в
фотопроводниках (смотрите уравнение A1.26)), или же ток утечки /м1 фотодиодов (смотрите
уравнение A1.44)). Для более явного изложения этих положений рассмотрим шум
в обратно смещенном (К< 0) фотодиоде (коэффициент eqVT =0 в A1.44) и и = 2).
В этом случае полная обнаружительная способность на длине волны Ло при
температуре фона Тв дается выражением:
- A1.Б.7)
Полная обнаружительная
способность фотодиода
Сюда мы включили зависимость плотности тока /м1 от температуры приемника
излучения rdet (смотрите уравнение A1.50). По мере уменьшения температуры
приемника излучения /м1 уменьшается экспоненциально (как erEJkT^). Из этого
последнего выражения ясно видно, что существует температура функционирования, ниже
которой бесполезно дальше охлаждать приемник излучения. При этом в
функциональных характеристиках системы преобладает фоновый ток и мы можем сказать,
что в данном случае приемник излучения находится в BLIP-режиме (смотрите рис.
440 Дополнения к главе 11
,е-Ед/2кТ
qr)<p
BLIP
Рис. 11.Б.1. Определение температуры ВЫР-режима.
11.Б.1, иллюстрирующий инфракрасное функционирование приемника излучения,
ограниченное фоном). Температура, необходимая для достижения ВЫР-режима Твир
дается выражением:
A1.Б.8)
Температура BLIP-режима
Уравнение A1.Б.7) позволяет рассчитать пределы обнаружительной
способности фотодиода:
Т U
1 в)~
1
hv /q
2l/2q
-11/2
cU
(П.Б.9я)
Для нахождения фундаментального предела обнаружительной способности,
связанного с излучением черного тела, на длине волны отсечки Ло (где обнаружитель-
ная способность максимальна), положим г]{Л) = 1 для Л в диапазоне между Л1 = 0 и X
= Л2, что приводит к следующему выражению:
Обнаружительная способность
в BLIP-режиме
Рисунок 11.Б.2 иллюстрирует эти фундаментальные пределы в функции длины
волны детектирования Л для температуры фона Тв = 300 К. Предел
обнаружительной способности при комнатной температуре значительно снижается, т. к. длина
волны детектирования возрастает до примерно 8 мкм. Это связано с изменением
спектральной характеристики излучательной способности черного тела при
температуре 300 К с максимумом вблизи 10 мкм (смотрите рис. 11.Б.2). Линейное
возрастание £>вЫР тах для Л > 8 мкм происходит вследствие того, что число фотонов,
необходимое для достижения энергии в 1 Вт, возрастает по мере увеличения Л.
В реальном аппаратурном применении приемник излучения «наблюдает» через
объектив какую-либо деталь изображения в присутствии фона (смотрите рис. 11.Б.З).
Если поверхности, окружающие приемник излучения, охлаждаются, то поток чер-
11. Б. Пределы обнаружительной способности
ю
о
о
о
С
О
Сч
2
1
'й 1
Л
~~3
о
П11
9
8
7
А
10
15
длина волны (мкм)
Рис. 11.Б.2. Зависимость предела обнаружительной способности идеального
фотодиода (rj = 1) от длины волны детектирования.
Т «Та
Рис. 11.Б.З. В системе инфракрасного детектирования экранировка от потока
излучения черного тела осуществляется за счет охлаждения оболочки
приемника излучения. Приемник излучения регистрирует фон в пределах
входного угла ф.
ного тела при температуре Тв, принимаемый приемником излучения, уменьшается
как sin20, где ф — входной угол апертуры.
Таким образом, шум, связанный с потоком излучения черного тела Фв
уменьшается как sin2^. В этом случае обнаружительная способность системы в BLIP-
режиме дается выражением:
л* B т \
П A Т Л\- ^BLIP \Л0» i В )
sin ф
A1.Б.10)
Таким образом, мы видим, что обнаружительная способность в BLIP-режиме
может быть значительно увеличена за счет уменьшения входного угла приемника
излучения. В общем случае у входа фотоприемного модуля на
расстоянии/помещается линза с диаметром D, при этом расстояние/соответствует фокусному
расстоянию линзы. В этом случае отношение f/D определяет т. н./— число (FN) системы
tgф= 1/B х FN). Поскольку sinV= l/(l+l/tg2^), уравнение A1.Б.10) можно
переписать в виде:
4FN2/)B*LIP
(Яо, Тв)
A1.Б.11)
Дополнения к главе 11
Часто инфракрасные приемники излучения используются для получения
теплового изображения объекта на непрерывном фоне теплового шума (смотрите рис.
11.Б.З). В этом случае возникает разумный вопрос о том, какова минимальная
величина теплового контраста, разрешение которого способен обеспечить приемник
излучения. На самом же деле ответ достаточно прост. Это есть разность
температур, эквивалентная мощности шума (NETD), которая определяется изменением
температуры, приводящим к отношению сигнал/шум, равному 1, (т. е. таким
изменением, которое приводит к мощности излучения, равной NEP в соответствии с
A1.Б.З)). На рис. 11.Б.4 представлены зависимости D\A0, TB = 300 К) для ряда
квантовых приемников излучения. Из B.Б.12) следует, что изменение температуры
А Г черного тела приводит к изменению СДА^АГизлучательной способности
абсолютно черного тела dR/dA в спектральном диапазоне АД (Cd выражено в Вт см~2 К).
В этом случае NETD может быть записано в виде:
NEP = NETD x-^- f 4т = Q(AA)NETD
<\Т J ал
ля
Это дает зависимость NETD от обнаружительной способности IX:
NETD =
С,(АЯ) D* (d/dT)j(dR/dX)dX
A1.Б.12)
A1.Б.13)
Рис. 11.Б.5 иллюстрирует связь между разностью температуры, эквивалентной
мощности шума, NETD и обнаружительной способностью для приемника излуче-
|lnsb77K
идеальный фотовольтаическии детектор
1 2 3 4 5 6 7 8 9 10 11 12 13 14
InAs 300 К
х-а .
Рис. 11.Б.4. Графики обнаружительной способности различных квантовых
приемников излучения.
11. Б. Пределы обнаружительной способности
£0.01 -
0.001
10'
Обнаружительная способность (см Гц1/2 Вт~1)
Рис. 11.Б.5. Связь между NETD и обнаружительной способностью в двух
спектральных диапазонах для приемника излучения размером 40 х 40 мкм2 при
ширине полосы 50 Гц и FN =1.
ния размером 40 х 40 мкм2 с шириной полосы 50 Гц. Из представленного рисунка
видно, что возможно разрешение исключительно малых тепловых контрастов.
Пример —
Ниже приведена программа MATHEMATICA для расчета разности температуры,
эквивалентной мощности шума, для приемника излучения на спектральный
диапазон 3—5 мкм с площадью фоточувствительной поверхности 40 х 40 мкм2 при
ширине полосы 50 Гц и/-числе.//1*
('universal constants*)
с=2.988 10 ~8 Г m/s*);
k= 1.381<T-23(\J/K*);
h = 6.625 1(T-34(* J.s*);
hb = h/B*3.1416);
mO = 0.91 10~ -30 (*kg*);
('Wavelength Band in mm *)
lambda 1 =3;lambda2=5;
(*Blackbody as a function of temperature*)
temp =.; lambda =.;
emm. =2*3.1416*h*c~2*(lambda*1(T -6)-5/(Exp[h*c/((lambda*1(T-
6)*k*temp)]-1)
emm = emm * 10 ~-6 (* W/irT2/mm*);
contr = D [emm, temp];(*contrast used in the NETD calculation*)
temp = 300 (*Blackbody temperature*);
(*Differential contrast over the spectral band*)
cc = Nintegrate[ contr, {lambda.lambda 1, lambda 2}] (*W/rrT2/K*)
*10 =-4(* W/cnrT2/K*);;
df =-50;A = 16 1(T(*cm2 *);dies =1;
NEDT =Sqrt[df/Adet/cc*A]4*dies~2);
Plot[NEDT,{1(T10,1(ni}]
Результаты этих расчетов представлены на рис. 11.Б.5.
Литература
G. Gaussoigues and S.Chomet, Infrared Thermography, Kluwer, Boston A993).
R.J. Keyes, Ed. Optical and Infrared Detectors, Topics in Physics Vol. 19, 2nd Edn,
Springer Verlaqg, Berlin A980).
ГЛАВА 12
ПРЕОБРАЗОВАНИЕ
ОПТИЧЕСКОЙ ЧАСТОТЫ
12.1. Введение
Одним из наиболее впечатляющих достижений волновой оптики является ее
успех в обеспечении последовательного и согласованного описания взаимодействий
между электромагнитными волнами и материей (газами, твердыми телами и т. д.)
Уравнения Максвелла, описывающие распространение света, а также уравнения
Лапласа—Лоренца, описывающие члены-источники, связанные со светом, в
совокупности позволяют учесть эффекты преломления, рассеяния и дифракции света
в конденсированных средах. Мягко говоря, просто поражает, что такая теория
учитывает сложные взаимодействия электромагнитной волны с огромным
ансамблем атомов (каждый из которых может быть аппроксимирован индивидуальным
гармоническим осциллятором) за счет использования коэффициента оптического
преломления пор. В предельной выразительности понятия коэффициента
оптического преломления можно найти определенную аналогию с эффективной массой в
теории твердого тела.
При описании всех этих эффектов электромагнитная волна с круговой
частотой со вызывает колебательное движение свободных частиц с той же самой
частотой, что, в свою очередь, приводит к переизлучению на той же самой частоте. Это
является следствием линейного характера уравнений, которые мы до сих пор
использовали. В этой главе мы увидим, что нелинейные среды (т. е. материалы,
реакция которых на внешнее возбуждение содержит нелинейные члены) могут быть
использованы для преобразования частоты, примером чего являются, генерация
второй гармоники и оптические параметрические генераторы.
12.2. Механическое описание генерации
второй гармоники
Как мы теперь уже знаем, механическая модель упруго связанного электрона
успешно описывает ряд оптических эффектов таких, как спектральную дисперсию
(дополнение 7.Б). Сейчас же мы попробуем установить поведение электрона,
подверженного воздействию ограничивающего потенциала, содержащего
неквадратичные члены более высокого порядка. Для упрощения предположим, что
ограничивающий потенциал U(x) является одномерным, при этом он может быть записан в
виде (смотрите рисунок 12.1):
тф+тОх A2.1)
Здесь coQ есть собственная частота колебаний осциллятора в линейном режиме,
т — масса электрона в вакууме, a D есть коэ4)фициент нелинейности (в единицах м с~2).
Эта система подвергается воздействию дипольной электродвижущей силы:
F = qEcos(ax)=^(eiu*+K. с.) A2.2)
2т
12.2. Механическое описание генерации второй гармоники 445
V(x)
Р - е у{0)Е
Рис. 12.1. Электрон, ограниченный асимметричным потенциалом и возбуждаемый
электромагнитным полем Е cos cot (д), испытывает ангармонические
колебания около своей точки равновесия (б). Его движение содержит
постоянную компоненту (в) и компоненту при 2со (г), которые порождают
соответственно постоянную поляризацию (оптическое выпрямление) и генерацию
сигнала второй гармоники.
Как обычно, здесь к. с. означает комплексно сопряженную величину. Таким образом,
движение частицы x(t) подчиняется следующему дифференциальному уравнению:
х + ук + о$х + Dx2 = У—
2т
+ к. с
.)
A2.3)
Здесь: у есть коэффициент трения частицы, который определяет ширину
соответствующего оптического перехода (смотрите дополнение ЗА). Поскольку,
очевидно, что движение частицы должно быть периодическим (с частотой со и ее
соответствующими гармониками), то мы можем провести гармонический анализ x(t),
записав этот параметр в виде:
+ x2ei2ft* +... + к. с.)
A2.4)
Временно предположим, что х0 = 0, т. е., что в системе отсутствует постоянная
наведенная поляризация. Однако позже мы увидим, что соответствующий член
может существовать, что приводит к эффекту оптического выпрямления. Подставляя
A2.4) в A2.3), получаем:
f( 446 Глава 12. Преобразование оптической частоты
_ SL (х^ + к. с.)- 2а}(х2&2** + к. с.)+ ^- foe1" + к. с.)+ icoy{x2e2af + к. с.)+
+ ^£ foe1" + к. с.)+ ^- fa2** + к. с.)+ j (к?е21вг + 2х^'ш + A2.5)
* + х2х* + 2ххх2еш + x22e4iu* + к. с.)= ^(eiu* + к. с.)
На первый взгляд эта формула может показаться сложной, но, как это часто
имеет место в нелинейной оптике, она может быть существенно упрощена за счет
группировки подобных членов.
Сначала мы рассмотрим линейный отклик, т. е. члены при eifi", и пренебрежем
ими в D. При этом для со- со0 мы сразу находим:
х = qE \ - qE 1 A2.6)
1 т (fol - аJ)+ iary 2сот (со0 - оо)+ iy/2
Движение, описываемое соотношением x{(t) = хр** + к. с, приводит к линейной
поляризации среды:
/?(/)= ^^@= NqxAe" + к. с.) A2.7)
где 7V есть объемная плотность систем, взаимодействующих с волной. В этом
случае мы можем провести идентификацию каждого члена в выражении A2.7) для
линейной восприимчивости, приведенной в C.24):
^•{Х1т)£кш + к.с.) A2.8)
Это приводит к следующему выражению:
<<о) _ Nq2 1 A2.9)
1 2соте0 (со0 -со)+\у/2
Этот последний результат эквивалентен тому, который получается в классической
модели Лоренца в рамках квантовой механики, рассмотренной в главах 2 и 3.
Используя в наших рассуждениях метод индукции, мы определим нелинейную
восприимчивость второго рода как:
/>(/)= ^(хB2й))Е2ё2а" + к. с.)= -^(х2е2Ш + к. с.) A2.10)
Член с х2 обусловлен нелинейным квадратичным членом Dx2 в A2.3). Его
выражение может быть получено из A2.5) из идентификации членов при е21й":
х2(г4оJ + 2iary + co2,)= —Dx2 A2.11я)
Из последнего выражения мы видим, что именно член jc2 обусловливает движение
электрона с частотой 2со. Используя A2.6), мы находим:
х2 = -■
24 т2со3 К<уо ~" ф) + '^У I ^\ Lv^o ~ 2co)+ B/3)i/J
После подстановки этого последнего уравнения в A2.10) мы можем найти
восприимчивость второго порядка в виде:
iy/2]2[(oH - 2e)+ B/3)iy]
12.2. Механическое описание генерации второй гармоники
В этом месте несколько моментов заслуживает упоминания. Во-первых, система
является дважды резонансной при со = со0 и при со = 2со0. В дополнение к этому из
сравнения A2.12) и A2.9) мы видим, что эта модель предсказывает следующую
связь между линейной и нелинейной восприимчивостью:
Хг
mD
Как следует из A2.13) параметр Si2m) (называемый параметром Миллера)
должен быть аналогичен во всех материалах, что в значительной степени имеет
место. В таблице 12.1 представлены значения нелинейной восприимчивости второго
рода для различных полупроводников. Взглянув на эту таблицу, мы отмечаем, что
^«3-8х 109SI.
Таблица 12.1. Коэффициенты оптического преломления на фундаментальной длине
волны 10,6 мкм n2a)i на частоте второй гармоники 5,3 мкм, квадратичная
восприимчивость Хг и параметры Миллера для ряда полупроводников
(значения п2т и £МШег для InSb не определены)
Материал
InSb
InAs
GaSb
GaAs
CdTe
ZnTe
ZnSe
3,95
3,49
3,8
3,27
2,69
2,69
2,42
"I*
?
3,54
3,82
3,30
2,71
2,70
2,43
Хг (ПМ В)
1634
419
628
368
168
90
78
*umJW SI>
9
2,8
3,2
5,4
6,4
4,7
8,6
Теперь сконструируем чрезвычайно грубую модель для несимметричного
кристалла, которая позволит нам получить величину Д исходя из фундаментальных
констант. Для этого предположим, что электроны в таком кристалле подвержены
воздействию притягивающего потенциала, обусловленного ядром с зарядом 2д и
вторым ядром с зарядом q, удаленным на расстояние а от первого ядра. Этот
потенциал может быть записан в виде:
A2.14)
а - х
Вблизи минимума этот потенциал может быть разложен в ряд:
[а
A2.15)
В этом случае коэффициент нелинейности в A2.1) получается отождествлением
подобных членов, что дает:
A2.16)
Глава 12. Преобразование оптической частоты
Полагая, что типичное межатомное расстояние а составляет 5 А, мы находим,
что D = 2 х 1041 м с, а это приводит к параметру Миллера #2<ы) величиной 6 х 109 SI
для концентрации N атомов величиной 6 х 1028 атомов/м3 (смотрите уравнение
A2.13)). Наша простая модель, приписывающая природу оптической
нелинейности в материале асимметрии атомных потенциалов, образующих среду атомов,
приводит к результатам, согласующимся с экспериментально определенными
величинами. В дополнении 12.А мы представляем более последовательный кванто-
во-механический вывод, основанный на формализме матрицы плотности.
Наконец, очевидным является то, что величина х2 по своей природе является
тензором. Если фундаментальная волна обладает компонентами (Ех, Е, /?), волна второй
гармоники будет обладать компонентами (Рх, Ру, Р^, которые, в более общем случае,
будут определяться квадратичными комбинациями компонент Е, Е и Е, а именно:
х у z
р,
р
Z J
El
Е]
Е\
EyEz
^z^x
ЕХЕУ
A2.17)
Тензоры Z22t0) обладают свойствами, которые сильно зависят от симметрии
рассматриваемого кристалла. Сейчас мы не будем вдаваться в подробности
классификации этих различных типов симметрии, а ограничимся описанием различных оп-
тоэлектронных приборов, использующих нелинейные свойства этих материалов.
12.3. Электромагнитное описание нелинейной
квадратичной оптической восприимчивости
Ангармоническое смещение электронов в нелинейном материале, подвергнутом
возбуждению электромагнитной волны, приводит к излучению света с частотами
2со, Ъсо... Расчет оптического излучения из-за нелинейных членов-источников
учитывается подобно случаю линейной оптики с использованием эффективного
формализма в виде уравнений Максвелла. Напомним уравнения Максвелла в
отсутствие свободных зарядов (р = 0) и тока проводимости (j = 0):
VE = O
VB = O
VxE = --^-l
A2.18)
Здесь Р есть вектор поляризации и сумма членов линейной поляризации Р,,
определяемых A2.8) или Pz = е0(п2ор — 1) Е (при п\ = 1 + xL> a также нелинейной
поляризации, определяемой, например A2.10). Система уравнений A2.18) может
быть записана в более компактном виде:
^E = ,0^Pnl A2.19)
Уравнение распространения с членом источника
12.3. Электромагнитное описание ...
Для упрощения системы обозначений и концентрации нашего внимания на
основных концепциях предположим, что система имеет одномерный характер и
что все электромагнитные волны распространяются вдоль оси Оь
Как это показано на рис. 12.2, мы рассмотрим электромагнитные волны с
частотами co.(i = 1,2 и 3 при соъ > со2 > а){), которые распространяются в нелинейном
кристалле. Эти три волны могут быть описаны огибающими функциями, т. е. они
могут быть записаны в виде:
к. с
]
'\/\/\/\/\/\/\/\>> a)
A2.20)
Рис. 12.2. В среде, характеризуемой, нелинейной оптической восприимчивостью xv три
волны с частотами cov co2 и соъ в процессе распространения могут
обмениваться энергией через посредство квадратичных поляризационных членов.
Напоминаем, что аппроксимация огибающей функции предполагает, что
вариации амплитуды Е. (z) малы по сравнению с масштабом соответствующих длин
волн А. = 2л:/к., а именно:
Аппроксимация огибающей функции
Более того, решения линейных уравнений Максвелла (без членов источника как в
A2.19)) приводят к следующим дисперсионным соотношениям:
A2.22)
Эти три волны взаимодействуют в кристалле посредством нелинейной
поляризации. Предположим, что вектор нелинейной поляризации ориентирован вдоль оси
Оу, при этом мы будем рассматривать лишь его модуль РЛ. Нелинейный член
источника, в свою очередь, включает члены в E^z, fyE, которые будут генерировать
волны с круговой частотой со3= а){+ сог Аналогичным образом, члены источника в
E^iz, t)E^(z, t) (или E^iz, f)E°\z9 t) будут генерировать волны с частотой сох = соъ — со2
(или со2 = о)ъ~ со^. Таким образом мы ожидаем проявление трех механизмов:
механизм А:
механизм Б:
механизм В:
+ со2 суммарная частота
— со2 разностная частота
— со. разностная частота
Например, нелинейный член источника, соответствующий механизму Б,
получается непосредственным обобщением A2.10):
0=
к. с]
A2.23)
На этой стадии рассмотрения важно отметить, что присутствие членов e+ifi)/ или e~ifi>«'
во временной зависимости будет сопровождаться соответственно членами E.(z) или
E.\z) в огибающей функции. Более того, понятно, что нет оснований приравнивать
нелинейную восприимчивость х{аъ~щ) восприимчивости генерации второй
гармоники %{е02). Тем не менее, для того чтобы сохранять простоту обозначений, мы будем
записывать восприимчивость в общем виде xY
Глава 12. Преобразование оптической частоты
Теперь нам остается лишь подставить выражение для нелинейной поляризации
A2.23) в качестве члена источника в уравнения Максвелла A2.19). Рассчитаем
каждый из членов этих уравнений: Первый член может быть записан в виде:
{л
d*2 ' J A2.24)
= -\ \—Е, - 2ik — Е, - k}E, |е'<<»/-*.О + к. с. - -\ \ - 2i/fc, — Ех + h}E, ]e'W-*,O + к. с.
2 I dz2 dz J 2 I dz I
Здесь мы использовали аппроксимацию огибающей функции A2.21). Таким
образом, уравнение распространения A2.19) может быть записано в виде:
- -\ 2\кх — Ех + к}Ех ] е«-*-*.О + к. с. =
A2.25)
Поскольку со{ =к1с/п1 и со= соъ — cov это уравнение может быть упрощено и записано
более компактно в виде:
{кх Jl^e-»** + к. с. = Ьё^^еХ*-*^* + к. с] A2.26)
Теперь мы уже можем учесть изменение комплексной амплитуды Ex(z) в
материале (в функции эволюции амплитуд двух волн источника E2(z) и
E3(z)),описывающей механизм генерации разностной частоты сох— со3— сог
Очевидно, что два других механизма соъ = сох + со2 и со2 = соъ — сох происходят одновременно
с этим процессом. Амплитуды Ex(z)9 E2(z) и E3(z) связаны друг с другом через
следующую систему дифференциальных уравнений:
G)l=aK-aJ<->—Ex=
Е2 ixXE%t»* A2.27)
<оъ = сох + со2 о ^-Еъ = -i^
Параметрические взаимодействия
второго порядка
Мы оставляем читателю возможность самостоятельного вывода двух последних
уравнений в A2.27). Отметим, что добавляемые частоты +а). приводят к члену Е. в
A2.27), тогда как вычитаемые частоты — cOj дают члены Е* с правой стороны
уравнения. &к есть рассогласование фаз, определяемое как:
Ак = къ-к1- к2 A2.28)
Рассогласование фаз
12.4. Оптическая генерация второй гармоники
Сейчас мы опишем специфический случай, когда со = (ох = со2 и тъ = 2со. Эта
ситуация соответствует оптической генерации второй гармоники.^ этом случае уравнение
A2.27) приобретает вид:
12.4. Оптическая генерация второй гармоники
со
a-iA*Z
Л Е1@ — ~l
dz
CO
nlfc
A2.29)
В этих уравнениях видно новое
обозначение для Еш. В основе появления члена ДА;
лежит то, что поле источника Р1ш
синхронно с полем Ею (которое его и генерирует),
которое имеет скорость распространения,
определяемую с/пш, в то время как поле Е1ш
обладает своей скоростью распространения
в соответствии с п2ш (смотрите рис. 12.3).
На время предположим, что
эффективность нелинейного преобразования мала и
соответственно Ea(z) остается практически
постоянной по объему взаимодействия, т.
е. что Ea(z) = Ео. Полный расчет
приводится в дополнении 12. В. Второе
дифференциальное уравнение в A2.29) может быть
легко проинтегрировано вдоль траектории
взаимодействия (на длине нелинейного
кристалла от 0 до L), что позволяет найти:
Lc
Рис. 12.3. Природа возникновения разности
фаз между полем нелинейной поляризации
РBсо) и полем второй гармоники ЕBсо).
- 1
A2.30)
Мы можем применить метод, использованный ранее в A.77) для
нестационарных возмущений, который включает в себя умножение числителя и знаменателя в
A2.30) на e-lA*L/2, что приводит к:
A2.31)
В общем случае, нас более интересует оптическая мощность, преобразованная
в излучение второй гармоники, связанной с амплитудой Е2т соотношением:
pi.=-^-"i*\Elm{Lt A2.32)
zZ0
Здесь Zo — вакуумный импеданс (Zo = (juo/£o)l/2 = 377 Ом). В этом случае
эффективность преобразования второй гармоники есть:
р z3
Jjsl = 2 ° (сое у LYsinc
A2.33)
Выход процесса генерации
второй гармоники
Это последнее уравнение выявляет роль, которую играет рассогласование фаз Ак.
Если этот член равен нулю, то эффективность преобразования возрастает
квадратично с длиной взаимодействия L (sine @) = 1), при этом происходит постоянный
обмен энергией между фундаментальной волной и волной второй гармоники вдоль
траектории взаимодействия вплоть до истощения мощности накачки (смотрите
дополнение 12.В.). С другой стороны, если Ак не равно нулю, то эффективность
изменяется как sin2 (AkL/2) и периодически осциллирует вдоль траектории
взаимодействия (смотрите рис. 12.4). В этом случае во время распространения по
кристаллу энергия периодически передается от волны к волне. Длина Lc, на протяжении
которой энергетический перенос достигает максимума, определяется AkLc = я, т. е.:
Глава 12. Преобразование оптической частоты
24
20
16
12
8
4
0
Согласование
по фазе
Без согласования
по фазе
0.0 0.5 1.0 1.5
2.0 2.5 3.0 3.5 4.0 4.5 5.0
LILr
Рис. 12.4. Изменение мощности сигнала второй гармоники Р1т в функции расстояния
распространения в нелинейной среде для согласованных и
несогласованных по фазе случаев.
4=77— S <12-34)
4(*->О
Длина фазового рассогласования
Здесь Ло есть длина фундаментальной электромагнитной волны в вакууме. Этот
параметр Lc в литературе некорректно называется длиной когерентности. Очевидно, что
существование такой длины максимального преобразования связано с естественной
дисперсией, имеющей место в нелинейном материале (исключение составляют резо-
нансы материала, где дисперсия может быть аномальной), где пBсо) > п(со). Анализ
A2.29) и A2.30) позволяет понять осцилляционную природу энергетического обмена
между фундаментальной волной и ее второй гармоникой. Можно показать, что при
Z < Lc работа, совершаемая волной с частотой со над диполями с частотой 2со,
положительна тогда, когда при Lc< z <2Lc имеет место обратная ситуация.
Пример
Мы хотим использовать кристалл GaAs для преобразования пучка излучения с
длиной волны 10,6 мкм в излучение с длиной волны 5,3 мкм. GaAs — это материал с
очень сильной нелинейной восприимчивостью на длине волны 10,6 мкм.
Предположим, что в этой экспериментальной конфигурации %г = 100 пм В. При этом,
другие необходимые нам константы составляют:
п E,3 мкм) - п A0,6 мкм) = 2,5 х 10
(смотрите соотношение Зеллмайера в дополнении 7.Б).
«E,3 мкм) ~ яA0,6 мкм) ~ 3.
В этом случае оптимальная длина для достижения максимальной
эффективности преобразования дается соотношением Lc = 10,6 мкм/D х 2,5 х 10~2) = 10,6 мкм.
При этом достижимая эффективность составляет:
= 2 х
-1 ]х
мВ-
т. е.:
p..
см
)
В предположении Рш— 1 МВт см2 эффективность преобразования составляет
всего 105, что является разочаровывающим обстоятельством. Причиной такой
малой эффективности является рассогласование фаз, ограничивающее эффективную
дину взаимодействия на уровне 100 мкм.
12.5. Соотношения Мэнли—Роу
Рисунок 12.5 иллюстрирует различные экспериментальные конфигурации для
реализации удвоения оптической частоты: а) кристалл удвоения частоты может быть
помещен за пределами лазерного резонатора, б) для использования преимуществ
оптической обратной связи кристалл удвоения частоты может быть располагаться и
внутри оптического резонатора (смотрите дополнение 12.Д), в) и, наконец, очень
компактная (микрокристальная) конфигурация может быть реализована за счет
нанесения зеркал на обе стороны расположенного рядом YAG и слои кристалла
удвоения частоты, так как в этом случае для накачки структуры может быть
использован лазерный диод.
Nd:YAG
Nd:YAG
NLC
Рис. 12.5. Различные конфигурации для генерации второй гармоники на длине волны
530 нм с использованием лазера на основе Nd: YAG на длину волны 1,06 мкм.
Нелинейный кристалл (NLC), помещенный вне оптического резонатора и
ориентированный таким образом, чтобы обеспечивать угловое
согласование фаз (я), внутрирезонаторное преобразование с использованием NLC,
ориентированное таким образом, чтобы обеспечивать угловое согласование
фаз (б)у микрокристальное преобразование с использованием зеркал,
нанесенных на обе поверхности слоев Nd: YAG и NLC.
12.5. Соотношения Мэнли—Роу
Анализ A2.27) выявляет недостаток эстетической симметрии между
представленными уравнениями (присутствие различных со. и п. в каждом уравнении). Для того,
чтобы сделать эти уравнения симметричными, Мэнли и Роу предложили ввести
следующие величины:
Г~ , A2.35)
Эти модифицированные амплитуды интересно использовать по той причине, что
они непосредственно связаны с потоком фотонов Фш. с энергией h со.. В
действительности, мощность излучения дается выражением:
-co.W
A2.36)
|( 454 Глава 12. Преобразование оптической частоты
Так, что:
0
При этом в этих выражениях не появляются ни со., ни п.. Подставляя вновь
введенные амплитуды в уравнения преобразования A2.27), мы получаем более
симметричную систему:
сох = соъ - со2 <-> —- Д = -\кАъА2е~Ш1
dz
со2 = соъ - сох <-> —А2 = -i/cA*Де^ A2.38)
dz
со3 = сох + со2 <-> —Д = -\
dz
Нелинейные уравнения связи
между потоками фотонов
Здесь: к — коэффициент нелинейной связи:
A2.39)
пхп2пъ
Уравнение A2.39) будет особенно эффективным, если мы можем
предположить, что материал не обладает дисперсией (т. е., что Ьк = 0). Как мы увидим далее,
это условие может быть реализовано за счет использования техники
искусственного согласования фаз. Сейчас же мы продемонстрируем преимущество A2.38) по
сравнению с A2.27), Для этого мы умножим каждое уравнение в A2.38) на А] и
прибавим к нему его комплексно сопряженное выражение. Тогда мы получим:
Д — Д + Ах — Д = -\кАх А2 А3 + \кАхА2Аъ
dz dz
А2—А2+А2 — Ах = -\кАх А2 Аъ + \кАхА2Аъ A2.40)
dz dz
Аъ—-Аъл-Аъ—-А->> = -\кАхА2Аъ + \кАх А2 Аъ
dz dz
Это приводит к уравнениям Мэнли—Роу:
|2)(Kr) A2.41)
Уравнения Мэнли—Роу отражают тот факт, что поток фотонов сохраняется. Таким
образом, в эксперименте с суммированием частоты фотоны с энергией h соъ могут
возникать только за счет числа образующих их фотонов с энергией hco{n h coT Иначе говоря,
соотношения Мэнли—Роу вскрывают асимметрию энергетического обмена. В случае
процесса генерации разностной частоты (со{ = соъ — со2) мы видим, что фотоны с энергией
h соъ поглощаются и создаются фотоны с энергией Ь со2 даже, если они уже
присутствуют. Мы возвратимся к этому аспекту позже (смотрите раздел 12.8).
Таким образом, мы видим, что процесс преобразования частоты можно
интерпретировать в рамках корпускулярного подхода. Фотоны с энергией %cov hcov Ьщ
не могут обмениваться энергией за исключением случаев, когда их энергия, как и
импульс частиц сохраняются при взаимодействии (смотрите рис. 12.6):
Ьсох + hco2 = hco3 A2.42)
к + к = к
Законы сохранения энергии
и импульса для фотонов
12.6. Параметрическое усиление 455
со
Рис. 12.6. Условия переноса энергии между тремя волнами cov cov соъ во время
взаимодействия в нелинейной среде могут интерпретироваться с использованием
законов сохранения энергии и импульса, управляющих фотонами,
образующими волны.
12.6. Параметрическое усиление
Уравнение A2.38) показывает, что можно усилить сигнал с частотой сох {сигнальный
пучок) за счет нелинейного взаимодействия со вторичной волной с частотой соъ
(пучком накачки) (смотрите рис. 12.7). Как и следовало ожидать из законов
сохранения A2.42) в этом процессе возникает третий пучок с частотой со2 (называемый
холостым пучком).
Для упрощения указанных расчетов сделаем те же упрощения, как и при
рассмотрении генерации второй гармоники. А также предположим, что на амплитуду
пучка накачки A3(z) не влияет нелинейное взаимодействие. Другими словами,
предполагается, что эффективность преобразования мала (что имеет хорошие
основания, как это показано в примере раздела 12.3, а также будет показано далее).
В такой ситуации мы говорим о необедненном пучке накачки. Полный расчет
приведен в дополнении 12.В.
В рамках такой аппроксимации A2.38) принимает простой вид:
(О
(ПАЗ)
Рис. 12.7. При параметрическом усилении падающий сигнал с частотой со{ усиливается
по мере распространения в нелинейной среде за счет нелинейного
квадратичного взаимодействия с пучком накачки с частотой соу Сохранение
энергии фотонов требует возникновения сопровождающего пучка с частотой сог
|( 456 Глава 12. Преобразование оптической частоты
Здесь параметрическое усиление g (в см) дается соотношением:
A2.44)
ntn2n3 2 с \ щп2
А3 и Е3 являются постоянными амплитудами пучка накачки. Решение этой системы
дифференциальных уравнений A2.43) является тривиальным. Мы находим':
A,(z) =
A2.45)
A2(z)= A2@)ch(gz)- Ы,(О)%пЫ
Предположим, что при z — 0 отсутствует инжекция сопровождающего пучка, т. е.
А2@) = 0. Эволюция сигнального и холостого пучков может быть записана в виде:
A2.46)
Эти две волны испытывают экспоненциальное усиление в функции длины
распространения в среде (как это имеет место в случае лазерного усиления) — такая
ситуация называется параметрическим усилением. Рисунок 12.7 иллюстрирует
изменение уровня мощности Еш для различных волн в среде.
Пример
Мы хотим усилить излучение на длине волны 10,6 мкм в кристалле GaAs, который
мы будем предполагать согласованным по фазе (т. е., что Ак = 0 — позже мы увидим,
каким образом это может быть достигнуто на практике). Предположим, что в
специальной конфигурации, используемой в эксперименте, х2 = Ю0 пм В.
Рассчитаем параметрическое усиление в кристалле, предполагая плотность мощности
накачки РюЪ на длине волны 5,3 мкм, равной 5 МВт см.
Соответствующая амплитуда электрического поля есть:
£3 = B^о/"орI/2 = Bх5x10'° Вт м^х377Ом/3I/2 =3,5x10* В м-'
Таким образом, параметрическое усиление g = %2/2с х со/по х Е3 или:
g = (l010MB-1)/Fxl08MC-1)xl,8xl014c1x3,5xl06 В м"'/3 = 0,35 см'1.
Эта величина достаточно мала, учитывая достаточно большую мощность накачки.
Следует отметить, что уравнение A2.38) утверждает, что невозможно усилить
сигнал с частотой cov используя накачивающие пучки со{ или со2 с меньшей частотой.
В действительности, в предположении необедненного пучка накачки Ax(z) — Лх
рассуждение, аналогичное проведенному ранее, показывает, что, если соъ< cov то
изменения амплитуды сигнала A3(z) будут синусоидальными (как cos(gz)) и
неэкспоненциальными. С математической точки зрения это является причиной присутствия
Е. или Е* в нелинейных связанных уравнениях в зависимости от того, увеличиваем
ли мы или уменьшаем частоту (смотрите уравнение A2.38)) — а именно на этом мы
настаивали ранее. С физической точки зрения это следует из того факта, что в
соответствии с соотношениями Мэнли—Роу, каждый фотон cov аннигилирующий для
рождения фотона со3, будет сопровождаться поглощением фотона со2. А такие фотоны
отсутствуют в системе! К этому аспекту мы возвратимся позже в разделе 12.8.
1 ch = cosh, sh = sinh
12.7. Оптические параметрические генераторы
12.7. Оптические параметрические генераторы
Как было показано в предыдущем разделе, оптическое усиление, связанное с
параметрическим усилением, достаточно слабо. Таким образом, от экспериментальной
конфигурации, представленной на рис. 12.7,мы не можем ожидать достаточной
эффективности преобразования. Эта ситуация полностью аналогична той, которую
мы встречали в разделе 4.4 в ходе нашего изучения лазерного усиления. В связи с
этим воспользуемся тем же самым приемом, который позволил нам добиться
лазерных колебаний даже в слабо усиливающей среде, а именно — обратной
оптической связью.
В этом случае мы помещаем нелинейный кристалл в центр оптического
резонатора Фабри—Перо (смотрите дополнение 9.Г), содержащего два зеркала с
комплексными коэффициентами отражения ге и г при этом г. — (ЯI/2ёф1 (где / = е или s
соответственно для входа или выхода системы). Я. есть коэффициенты отражения,
а ф. соответствующие фазовые сдвиги (ф. = п для металлических зеркал).
Исследуем два различных случая (смотрите рис. 12.8):
1. Генератор с простым резонансом. В этом случае зеркала обладают
коэффициентами отражения, близкими к единице для сигнальной волны, но фактически
нулевыми для холостой волны.
2. Генератор с двойным резонансом. В этом случае зеркала обладают
коэффициентами отражения, близкими к единице как для сигнальной, так и для холостой
волны.
В обоих случаях зеркала, удовлетворяющие этим требованиям могут быть
получены за счет нанесения многослойных диэлектрических композиций
(смотрите дополнение 9.Г). При последующем рассмотрении мощность накачки
будет предполагаться необедненной. Полный анализ будет приведен в
дополнении 12.Е.
QJ3
0)л
Рис. 12.8. Принцип функционирования оптического параметрического генератора
(ОРО). Нелинейный кристалл заключен в резонаторе между двумя
зеркалами Ме и Ms. В том случае, когда параметрическое усиление, которое
сигнальная волна со{ извлекает из пучка накачки o)v превышает резонатор-
ные потери, система начинает генерировать на частоте cov Мы можем
добиться, чтобы генерация была только на частоте cov используя резонаторы
с простым резонансом (а) или одновременно как на частоте соу
сигнальной, так и дополнительной со2 волны, используя резонатор с двойным
резонансом.
Глава 12. Преобразование оптической частоты
12.7.1. Оптические параметрические генераторы
с простым резонансом (SROPO)
Рассматриваемый случай подобен случаю лазерного резонатора. Во избежание
бесполезного повторения предположим, как это было сделано в разделе 4.4, что
активный кристалл заполняет все пространство между двумя зеркалами (т. е., что L
является одновременно длиной активного кристалла и оптического резонатора).
Поскольку резонатор не является резонансным для дополнительной волны, амплитуда
A2(z) остается малой и коэффициент усиления для волны при одиночном проходе
дается соотношением A2.46) в виде cosh(gL) даже после многих проходов.
Рассмотрим сигнальный пучок с малой амплитудой ах (идущий от входного
зеркала Ме и направленный к выходному зеркалу М), подверженный
параметрическому усилению с использованием пучка накачки с частотой соъ (смотрите рис.
12.8я). Будучи у выходного зеркала сигнальная волна имеет комплексную
амплитуду cosh(g£)e~ikiL. Затем волна отражается, при этом ее амплитуда становится
равной a{rs cosh(gZ,)e'*iL, и она путешествует по кристаллу в обратном направлении.
В этом случае волны со{ и соъ распространяются в противоположных
направлениях, и условие согласования фаз не может быть удовлетворено, при этом в
результате прохода усиление отсутствует. В этом случае амплитуда волны, когда она
возвращается к входному зеркалу Ме, имеет вид a/s cosh(gZ)e2/A:^. Наконец,
сигнальная волна испытывает второе отражение на входном зеркале и ее амплитуда
становится равной axrjrs cosh(g2)e-2/*iL и т. д.
В этом случае сигнальная волна в резонаторе при z = 0 является суммой
вкладов за счет многих проходов:
Д @) = ^{l + rersch(gL)e-™>L + [rersch(gL)e-™^]2 + ...} A2.47)
Или:
Л.Ф)= ^-т A2.48)
1 - rer,ch (gL )е-2»м
Система начинает спонтанно генерировать, как только знаменатель в A2.48)
становится равным нулю, т. е. при выполнении двух условий:
^L-k.L^m^, /и = 0,1,2... A2.496)
Первое условие свидетельствует о том, что система обладает пороговым усилением
threshold' выше которого она начинает спонтанно генерировать на частоте сог Таким
образом, оптический параметрический генератор «разбивает» фотон с частотой сог
на два фотона (аI9 со2) такие, что (ох + аJ = соу Понятно, что, как и в случае
лазерных колебаний, параметрические колебания возникают из квантового шума в
резонаторе. Поскольку усиление, как правило, мало, cosh(gZ) « 1 + (gLJ/2 и условие
A2.49я) при Re = Rs = R « 1 сводится к:
8*™^L « JTHt A2.50)
Порог SROPO
Последнее условие означает, что система начинает генерировать как только
усиление резонатора начинает превышать его потери A — R)l/2 из-за пропускания зеркал.
Второе условие является отражением ограничения по фазе, фиксирующего моды,
разрешенные в резонаторе. Тем не менее, мы можем задаться вопросом, на какой
же волне начнет генерировать система, если он накачивается на частоте сог В самом
деле, в противоположность лазерным колебаниям, частота генерации определяется
12.7. Оптические параметрические генераторы
не атомными переходами. Все пары (cov co2), удовлетворяющие соотношению cdx + со2 =
(ov априори являются допустимыми. К тому же в макроскопическом кристалле с
размерами >1 мм фазовые условия не являются жесткими условиями отбора и как
таковые не позволяют выбрать какие-то определенные пары (оI9 со2). В дополнении
12.Б мы увидим, что именно условия согласования по фазе (Ц + к2 = к3)
определяют конкретную частоту сог В общем случае это условие может быть получено
поворотом кристалла в определенную кристаллографическую ориентацию,
обеспечивающую удовлетворение фазового условия (Ц + Ц = к3) для требуемой частоты сог
Пример
Мы хотим возбудить генерацию в резонаторе на основе кристаллического GaAs,
согласованного по фазе на длине волны 9 мкм при накачке пучком на длине волны 5 мкм.
Кристалл GaAs длиной 5 мм обладает нелинейной восприимчивостью 100 пм В. Оба
торца кристаллического резонатора покрыты зеркалами с коэффициентом отражения
98%, При этом мы хотим узнать уровень пороговой мощности накачки для
накачивающего пучка, инициирующего оптическую параметрическую генерацию в структуре.
Длина дополнительной волны есть 1/A/5 — 1/9)мкм или 11,9 мкм. В этом случае
частоты сигнальной и дополнительной волн составляют соответственно 2,1 х 1014
и 1,6 х 1014 с.
Порог параметрического усиления системы определяется A2.50):
Sthresho,d = Л х A - 0,98)/2 /0,5 см = 0,4 см
Пороговое параметрическое усиление соответствует электрическому полю
накачки, определяемому A2.44):
10-10 м В(бхЮ8 мс-')хB,1х1014 c'xl,6xlO14 с~1I/2 х{
Таким образом, мощность накачки у порога генерации составляет:
^threshold = l/BZ0>op£32,thresho.d = 6 МВт СМ
Эта величина значительна.
12.7.2. Оптические параметрические генераторы
с двойным резонансом (DROPO)
В рассматриваемом случае дополнительная волна со2 также испытывает оптическую
обратную связь от зеркал и уже не является пренебрежимо малой по сравнению с
сигнальной волной сох. Таким образом, мы пришли к подтверждению формализма,
представленного в дополнении 9. Г и использованного для описания
распространения оптической волны в резонаторе Фабри—Перо. Обозначим как гх и г2 (г. = (ЯI/2е[ф1
для i = 1,2) коэффициенты отражения двух зеркал (которые предполагаются
идентичными на входе и выходе) соответственно для сигнальной и дополнительной
волн. Введем вектор комплексной амплитуды A(z):
Ax(z)t-U
A2*(z)e«
Распространение дополнительной и сигнальной волн между входным и
выходным зеркалами, описываемое системой уравнений A2.45), может быть
представлено в матричной форме:
W460 Глава 12. Преобразование оптической частоты
АЛЩ = МА@) A2.52)
Здесь: М есть матрица:
_i sh (gl)eik>L ch (gL ) e1
Ал обозначает амплитудный вектор, распространяющийся направо. Как только
волна приходит к выходному зеркалу, часть излучения отражается, что
описывается вектором:
-[: :■]
AL(L) = RMA(O), при этом R = 0 r*\ A2.54)
Здесь: AL соответствует комплексной амплитуде, направленной налево. Как и в
предыдущем случае, сигнальная и дополнительная волна не могут
взаимодействовать с волной накачки в этом направлении распространения, так как они не могут
удовлетворять условию фазового согласования A2.42). В этом случае амплитудный
вектор AL перед отражением имеет вид:
Ге*'1 О I
А£@) = LRMA@), при этом L = n _iM A2.55)
I I
Наконец, сигнальная и дополнительная волны отражаются у входного зеркала, при
этом амплитудный вектор принимает вид:
АЛ@) = RLMA(O) A2.56)
Условие генерации может быть получено из требования, что сумма всех этих
вкладов расходится, как это и было в предыдущем случае. Мы могли бы потребовать
также, чтобы все эти волны идентично воспроизводились при z = 0 (условие,
эквивалентное первому), т. е. что АЛ@) = А@). Это требование накладывает условие:
det(RLRM - Id) = 0 A2.57)
Здесь: Id есть матрица тождества формата 2x2. Это последнее условие получается
путем перемножения матриц, что приводит к выражению:
Оценка детерминанта не вызывает особых проблем и приводит к условию:
Здесь члены дефазировки Аф. определяются соотношением:
Аф1=2(к1.Ь-ф1} / = 1,2 A2.60)
Уравнение A2.59) дает нетривиальное решение только в том случае, когда
удовлетворяются следующие три условия:
кхЬ-фх - тп
ф2 = пп A2.61)
Первые два условия в A2.61) есть ничто иное, как условия стоячей волны в
резонаторе для сигнальной и холостой волны. Третье условие показывает, что резо-
12.8. Суммарная частота, разностная частота и параметрическое усиление 461 jj)
ss^x/j
натор устанавливает параметрические колебания для двух волн, как только
параметрическое усиление для двух волн g превысит потери на зеркалах Rx и В^. Как и
в случае простого резонатора, мы имеем cosh(gZ) « 1 + (gthreshold£J/2 и R{ « Л, » 1, где
threshold есть параметрическое усиление у порога генерации. Это пороговое усиление
дается соотношением:
Stlueshold L - V(l-*.Xl-*J A2.62)
Порог DROPO
Последнее приведенное выражение следует сравнить с условием A2.50) для
резонатора с простым резонансом. Конфигурация с двойным резонансом уменьшает
порог генерации на коэффициент:
р _ ^threshold, простой резонанс _ I 2 ,~у ^<ъ\
^threshold, двойной резонанс V ~" "**2
Пример
Теперь мы рассчитаем порог генерации ОРО, описанного в разделе 12.6.1, т. е. для
кристалла GaAs длиной 5 мм, согласованного по фазе с волной 9 мкм и
накачиваемого пучком на длине волны 5 мкм. Оба торца кристалла на этот раз покрыты
зеркалами с коэффициентом отражения 98 и 99,8% соответственно для сигнальной
и холостой волн. Мы хотим найти пороговую мощность, необходимую, чтобы
инициировать параметрическую генерацию в структуре.
Порог генерации уменьшается на коэффициент F, определяемый A2.63):
/т = [2/Bх10-3)]1/2илив31раз
Таким образом, оптическая мощность у порога генерации есть:
=6/31 МВт см или 190 кВт см
Теперь мы обобщим некоторые из особенностей, связанных с явлением
параметрической генерации:
• Все пары частот (cov со2), удовлетворяющие условию сох + со2 = cov где соъ есть
частота генерации накачивающего пучка, могут генерироваться ОРО.
Конкретный выбор пары частот, которая испытает эффект ОРО, определяется
стационарными фазовыми условиями A2.496) и A2.61) (для начала заметим, что резонатор-
ные зеркала должны быть тщательно подобраны) и, в особенности, условием
сохранения импульса участвующих в процессе фотонов A2.42). Мы можем изменить
пару (cov со2) и, таким образом, длины волн, генерируемых ОРО за счет изменения
условий фазового согласования (например, изменяя ориентацию нелинейного
кристалла). На практике ОРО используется как перестраиваемый источник
излучения (смотрите дополнение 12.Б).
• Как это было в случае лазеров, параметрические колебания возникают из шума в
резонаторе. Этот шум является следствием не спонтанной эмиссии, а квантового
шума в резонаторе (смотрите раздел 2.5).
12.8. Суммарная частота, разностная частота
и параметрическое усиление
В начале раздела 12.2 мы видели, что взаимодействие между тремя волнами с
частотами cov oJ и о)ъ в кристалле, обладающем нелинейной восприимчивостью
второго порядка, приведет к генерации суммарной и разностной частот. К тому же мы
только что видели, что в этом случае могут возникнуть параметрические колеба-
Глава 12. Преобразование оптической частоты
ния. Сейчас пора провести различие между этими различными режимами. В связи
с этим мы рассмотрим две волны с круговыми частотами со2 (накачка) и сох (сигнал),
падающие на нелинейный кристалл. Предположим со2 > cov Уравнение A2.38)
указывает на три процесса, которые мы можем ожидать:
Генерация разностной частоты (DFG) со'ъ = сь2 — сох
Предположим, что ориентация кристалла была выбрана таким образом, чтобы
удовлетворить условию фазового согласования DFG, а именно Ак = \ — к{ — к'3 = 0.
После небольших изменений в обозначениях два соответствующие уравнения A2.38)
могут быть записаны в виде:
d . *
"d * A164)
щ = со2 - со'ъ <-> — Аъ = -ig*2Ax
Здесь: g2 = кА2 и эту величину можно считать действительной. Эта система может
быть тривиально решена с тем, чтобы получить эффективность преобразования,
соответствующую отношению преобразованной мощности P3(L) к мощности
падающего сигнала Р{@):
г» / г \ /
A2.65)
Энергия передается от сигнальной волны сох волне с разностной частотой со'3 и
волне накачки со2. В терминах числа фотонов (смотрите главу 2) это может быть
записано как |/ip nv n'3) -> \п{ — 1, п2 + 1, п\ — 1). В конце пути L = n/2g2 процесс
передачи энергии меняет свое направление и фотоны волн с частотами со\ и т2
рекомбинируют, усиливая сигнальные фотоны с частотой cov что может быть
записано как |лр nv п\) -> \пх + 1, п2 — 1, л'3 — 1) (смотрите рис. 12.9). Как следствие
этого, в параметрических взаимодействиях могут проявляться процессы
«расщепления» фотонов и рекомбинации. В дополнении 12.Е мы увидим, что
превалирующий механизм зависит от относительной фазы каждой волны по отношению к
другим волнам.
Заметим, что даже при максимальной эффективности преобразования (т. е. при
gL = л/2) эффективность преобразования не может превысить единицу:
л/2д
Рис. 12.9. Различные процессы переноса энергии, участвующие в процессе генерации
разностной частоты в нелинейной среде.
12.8. Суммарная частота, разностная частота и параметрическое усиление
Это последнее выражение напоминает нам о том факте, что параметрическое
преобразование фотона с энергией h сох в фотон с меньшей энергией h со \ не может
происходить с эффективностью, большей ti(o\lna)v При малой величине
эффективности по сравнению с единицей A2.65) может быть записано в более простом
виде, если мы заметим, что:
i^^ A2.67)
С использованием A2.44) для выражения g2 в функции электрического поля Е2 и
A2.32) для выражения Е2 в функции мощности на единицу поверхности Р2 это дает:
@х2гJ A2.68)
2пхп2пъ
Эффективность преобразования
для оптических частот
Таким образом, мы приходим к выражению, аналогичному уравнению A2.33),
полученному в контексте генерации второй гармоники.
Генерация суммарной частоты (SFG) (оъ — тг + сох
Сейчас мы вновь предположим, что ориентация кристалла была выбрана таким
образом, чтобы удовлетворить условию согласования фаз в процессе SFG, а именно:
Лк = Ц + Ц - Ц= 0. В этом случае два соответствующие уравнения A2.38) принимают вид:
d * A269)
щ = соъ - й\ <-> — Д = -ig*2A3
Как и ранее, эта система уравнений может быть тривиально решена. При этом
полученный результат будет носить характер, идентичный приведенному ранее в
A2.65). Однако, на этот раз энергия переносится от сигнальной волны и волны
накачки к волне с суммарной частотой соу На языке числа фотонов это
записывается в виде |aip п2, пг) -> \п1 — 1, п2 — 1, п3 + 1). В конце пути L = n/2g2 процесс
переноса энергии меняет свое направление и фотоны волны суммарной частоты соъ
«фрагментируются» в фотоны с частотой со2 и сох Этот процесс может быть записан
в виде |яр п2, п3) -> \ttj + 1, п2 + 1, пъ — 1) (смотрите рис. 12.10).
Уравнение A2.69) очень похоже на A2.64) при обсуждении процесса генерации
разностной частоты. Таким образом, выражение A2.68) имеет тот же вид и для
процесса генерации суммарной частоты. В дополнение к этому в рассматриваемом
случае максимальная эффективность определяется выражением:
A2 70)
Таким образом, эта эффективность может превышать единицу. В этом факте
нет ничего необычного, т. к. увеличение мощности пучка из-за преобразования
фотонов с энергией hcox ъ фотоны с меньшей энергией псоъ происходит за счет
фотонов пучка накачки.
Таким образом, какой из двух процессов (генерации суммарной или
разностной частоты) будет иметь место, определяется тем, какое из двух условий
согласования фаз (соответственно к3 = Ц + Ц или к'3 = к'2 — kt) реализуется.
|Г464 Глава 12. Преобразование оптической частоты
п12д
Рис. 12.10. Различные процессы переноса энергии при генерации суммарной частоты
в нелинейной среде.
Параметрическая генерация
Этот случай отличается от двух, рассмотренных выше. При параметрической
генерации фотоны пучка накачки с энергией hco2 спонтанно «расщепляются» в пары
фотонов с меньшей энергией hco{ и hco\ (смотрите рис. 12.11). Под словом
«спонтанно» в данном случае подразумевается то, что рождение фотонов с энергиями
происходит без какого-либо воздействия извне.
По аналогии с D.28л, б) из раздела 4.6 по лазерной генерации, а также с учетом
уравнений Мэнли—Роу, мы могли бы сделать заключение, что выходная мощность
параметрического генератора дается выражением:
со.
со.
со,
-1
A2.71)
НЕПРАВИЛЬНО!
Здесь
2, threshold
определяется условиями генерации A2.50) или A2.62). Это
уравнение является следствием ложной интуиции и хотя используется многими авторами,
оно никогда не подтверждается экспериментально, т. е. оно действенно лишь в
Рис. 12.11. Процесс переноса энергии при параметрической генерации.
12.8. Суммарная частота, разностная частота и параметрическое усиление
очень ограниченном диапазоне. В действительности ситуация намного более
сложная, и она обсуждается в дополнении 12.Е (смотрите уравнения 12.Е.20) и A2.Е.ЗЗ).
Спонтанное рождение фотонов с энергией hcoxvifi co'y которые необходимы для
«затравки» ОРО-генерации, связано с параметрической флуоресценцией. Это
физическое явление не может быть описано в рамках классического подхода,
разработанного выше (это подобно тупику, к которому мы в свое время пришли при
обсуждении лазерной генерации, что продиктовало необходимость введения в нашу
модель спонтанной эмиссии — смотрите главу 4). Рисунок 12.12 иллюстрирует
условия, при которых может наблюдаться рассматриваемый эффект. Поток накачки
с фотонами, имеющими энергию h co2 и волновым вектором к2, падает на
нелинейный кристалл. На одной оси с падающим пучком мы поместили детектор,
чувствительный только к фотонам с энергией псо{и h со'ъ. Диаграмма направленности
экспериментальной системы такова, что могут детектироваться лишь фотоны,
возникающие в нелинейном кристалле и обладающие волновым вектором к2 в пределах
dk (смотрите рис. 12.12).
В процессе параметрического взаимодействия может быть спонтанно создан
ансамбль фотонных пар (hcov hco3) с hco{ + Ьо)ъ— hcor Поскольку в этом процессе
преобразования частоты должен сохраняться импульс, детектироваться будут лишь
пары фотонов с полным импульсом Ц + к '3 и в пределах входной апертуры
приемника излучения. Именно эта параметрическая флуоресценция ответственна за
запуск параметрической генерации.
Детектор
Рис. 12.12. Принцип, лежащий в основе параметрической генерации. Фотоны с
энергией h co2 спонтанно «расщепляются» в нелинейном кристалле на пары
фотонов с энергией Й &>, и Й co\ (а). Детектируются лишь те пары,
ориентированные по направлению к детектору и удовлетворяющие сохранению
импульса в пределах dkF).
Литература
R.W. Boyd, Non Linear Optics, Academic Press, Boston A972).
P. Butcher and D. Cotter, The Elements of Nonlinear Optics, Cambridge University
Press, Cambridge A990).
Y.S. Shen, The Principles of Non Linear Optics, Wiley, New York A984).
R.L. Sutherland, Handbook of Nonlinear Optics, Marcel Dekker Inc., New York A996).
A. Yariv, Quantum Electronics, 3rd Edn, Wiley, New York A989).
ДОПОЛНЕНИЯ
К ГЛАВЕ 12
12.А. Квантовая модель квадратичной нелинейной
восприимчивости
В разделе 12.2 в рамках механической модели нелинейной оптики мы смогли
увидеть, каким образом нелинейная восприимчивость второго порядка возникает
вследствие асимметрии механических потенциалов A2.1), ограничивающих движение
электронов, которое возбуждается электромагнитными волнами. Хотя интуитивно
эта модель кажется продуктивной, она находится в сильном противоречии с кван-
тово-механической природой электронов в среде. В связи с этим мы предлагаем
здесь вывод квантового подхода. Очень эффективный и прогностический
формализм, который нам предстоит разработать, основан на подходе матрицы плотности,
представленном в разделе 1.7.
Рассмотрим квантовую систему, описываемую гамильтонианом Но и
обладающую спектром дискретных невырожденных состояний |/> с энергией Е. такой, что
H0\i) = E\i). Примеры таких систем показаны на рис. 12.А.1. В условиях теплового
равновесия соответствующая матрица плотности представляет собой диагонализи-
рованную матрицу р0 с диагональными элементами /?..@) = п., равными заселенности
уровней Е. в соответствии со статистикой Ферми—Дирака. Плотность заселенности
выражается в единицах «см» или «см» в зависимости от того двумерная или
трехмерная системы рассматриваются. После чего система возбуждается
электромагнитной волной с электрическим полем, которое имеет вид:
E(t)=
A2.А.1)
В рамках дипольной D • Р-аппроксимации (смотрите главу 3) взаимодействие
между квантовой системой и электромагнитным полем описывается гамильтониа-
г
i
мввнвм
Рис. 12.А.1. Несколько примеров асимметричных квантовых систем, основанных на
квантовых ямах.
12.А. Квантовая модель квадратичной нелинейной восприимчивости
ном H(t) = —qzE(t). Под влиянием этого нестационарного возмущения эволюция
элементов р.. матрицы плотности описывается уравнением Шредингера:
J A
0(), р],-Г,(р-р<°>), A2.A.2)
Для упрощения мы предположим, что для описания системы нам требуются только
две скорости релаксации Г..: Г, = \/Т{ для / = j есть скорость релаксации
заселенности (неупругий механизм), т. е. скорость выхода электрона из возбужденного
состояния, а также Г2 = \/Т2 — недиагональная скорость релаксации или константа
дефазировки, соответствующая упругому рассеянию электронных фаз по различным
состояниям. Матрица плотности может быть представлена в виде ряда по
электрическому полю в следующем виде:
5> A2.A.3)
п
При этом:
21!!, р'"'], A2.А.4)
{[ор] рГ}
dt \h \ti
Член порядка п(р(п)) действует в дифференциальном уравнении по р(п+1) как
член источника. Следуя рекуррентной последовательности, мы видим, что вклад
электрического поля E{t) в дипольный матричный элемент р.}п) является
полиномом порядка п. В этом случае электрическая поляризация в направлении Oz дается
средней величиной оператора qz полученного, как и другая наблюдаемая величина —
(смотрите раздел 1.7) оценкой шпура pqz:
Z*p« A2A-5)
k
Таким образом, вклад матрицы плотности порядка п в электронную
поляризацию является поляризацией я-ного порядка:
P(n)(t)=Tr(p(n)qz) A2.A.6)
В этом случае первые два элемента в разложении электронной поляризации P(t)
системы получаются из члена полинома:
P(t)= еоХ11)Ё*ш + eoX%E2t2i" + к. с.
Здесь: %{1), Х?\ш и х0B) есть соответственно линейная и квадратичные
восприимчивости (для процессов генерации второй гармоники и оптического выпрямления). Член
по 2о) связан с произведением членов по eifi" и eifi" в то время, как постоянный член
является результатом произведения ei<M/ и e~ift". Член х0B) порождает постоянное
электрическое поле под влиянием электромагнитной волны, что соответствует явлению
оптического выпрямления, и в этой книге мы не будем его более касаться. Нас
интересует лишь член генерации второй гармоники 2со (или в более общем случае пса),
т. е. выражения р(п) вида:
p(")(t)= p(">(tf>)eimaf + /5(w>(- (o)eineot A2.A.8)
В A2.А.4) мы можем заменить член dp.fn+ l)/dt на i(n + \)cop.jn+ 1}. Более того,
поскольку гамильтониан Яо является диагональным в базиое, сформированном его
стационарными состояниями |/), мы имеем:
™)АНо)>, = fo - Е,)(Р^\ A2.А.9)
Это приводит к упрощенному варианту рекуррентного соотношения в A2.А.4):
468 Дополнения к главе 12
A2А10)
Здесь: ял. = (Е.— E)/h есть боровская частота. Начнем с применения рекуррентного
соотношения A2.А.10) для п = 0. Это сразу дает:
при этом:
Здесь Zj, есть матричный элемент zv ~ (i\z\j)- Подставляя это выражение в A2.А.5)
и A2.А.6), мы получаем линейную поляризацию:
/*<«>=■£У Ы2("'-"Л е A2А13)
П Tk kcQ+Q)ki)-\Tki]
В условиях слабой освещенности и при разумных температурах (кТ < Еп — Е{)
заселенным будет только уровень |/>, и, таким образом, только члены i или к = 1
дают вклад в линейную восприимчивость. Сравнивая это выражение с уравнением
A2.А.7), мы находим, что линейная восприимчивостть определяется выражением:
Это позволяет нам получить коэффициент поглощения как а = oAmtfl)/n с, т. е.:
а =
r'opc0u
или вновь:
A2.А.16)
Здесь fkl = 2т(Ек — E^zxk/fi2 есть сила осциллятора для перехода |1) —> \к), что
воспроизводит результат, полученный в главе 3, а именно, уравнение C.41).
Следующая итерация (п = 1) дает нам квадратичную восприимчивость. Таким
образом, начнем с элемента второго порядка матрицы плотности:
При этом р2^2) определяется A2.А.10):
[??Л = —, ! An, P0)ljE A2.A.18)
ЛBа»+®,-ir,)
Проведем итерацию, подставляя A2.А. 12) для р0) в последнее выражение, при
этом находим:
W..={у y ^
" * й2 B© + а, - \ТЦ) | V [(« + «v )- in- J ' К» + «h )- ir,/]J
Затем используем шпур оператора р B)qz для того, чтобы найти электронную
поляризацию второго порядка PB)(t) (смотрите A2.А.6). Для определения квадратичной
12.А. Квантовая модель квадратичной нелинейной восприимчивости
восприимчивости нам нужно лишь использовать уравнение A2.А.17), при этом (после
исполнения нескольких акробатических номеров с индексами!) мы находим:
A2.А.20)
Несмотря на свой несколько сложный вид эта формула позволяет рассчитать
квадратичную оптическую восприимчивость для любой квантовой системы, при
этом особый интерес для нас представляют следующие два случая:
• Двухуровневая система. При пренебрежении антирезонансными членами в A2.А.20)
в суммировании остаются лишь два члена, а именно те члены со + со.., для которых
co.j > 0. Это дает для квадратичной восприимчивости:
£0П2 {со - co1{ - \T2 %2co - co2X - \T2
Здесь: Sn = B|z|2) — (l|z|l) = z22 n
ствие переходов с уровня |1) на уровень |2>. Мы сразу видим, что, если система
обладает инверсионной симметрией (или говоря более точно, если электроны на
двух уровнях обладают тем же самым средним положением zn = z22), то
квадратичная восприимчивость сводится на нет. Вторым моментом является то, что
квадратичная восприимчивость максимальна, когда достигает максимума
произведение z{\Sir Для достижения максимума квадратичной восприимчивости
необходимо, чтобы средние положения волновых функций, описывающих состояния
|1) и |2) были бы разнесены друг относительно друга на максимально возможное
расстояние (zl2 максимально). Взаимный компромисс между этими двумя
противоречивыми требованиями может быть достигнут путем квантовой инженерии
молекул и квантовых ям для конкретных применений нелинейной оптики. Вдали от
резонанса (соп » со) выражение A2.А.21) может быть записано в виде:
у B) _ Я \ni ~ п2 A^i~2^i2 ) П2А22)
£0 [Псо2[ I qj
Квадратичная восприимчивость
двухуровневой системы
Величина в числителе представляет собой величину заряда в асимметричном объеме
Zl2Sn. Из этой формулы мы видим, что квадратичная восприимчивость
выражается в единицах мВ (а на практике в единицах пм В)- Хотя это выражение и не
было получено в контексте физики полупроводников, оно тем не менее дает
полезную информацию по поведению этих материалов, поскольку можно
рассматривать зону проводимости и валентную зоны как если бы они представлялись
двумя различными энергетическими уровнями, разделенными по энергии на Eg.
Предполагая (в рамках данного рассмотрения) постоянными матричные
элементы zjJ9 мы видим, что можно ожидать изменение нелинейной восприимчивости
полупроводников как l/£g2. Рисунок 12.А.2 иллюстрирует квадратичную
нелинейную восприимчивость х2 Дда различных полупроводников на длине волны 10,6 мкм
в функции ширины их запрещенной зоны Eg. Зависимость, предсказываемая
A2.А.22), удивительно хорошо выполняется несмотря на упрощенность модели,
которую мы использовали и которая не учитывает изменяющуюся ионность
химической связи и т. д.
• Трехуровневая система. В случае трехуровневой системы с постоянным
энергетическим зазором (Е2 — Ех = Еъ — Е2 = fiQ) выражение A2.А.20) обладает четким
максимумом, соответствующим двойному резонансу со- соп~ со2Ъ ~ О,. В
рассматриваемом случае в сумме A2.А.2) доминирует один член:
Дополнения к главе 12
1000
100
.. • InSb
8-
6 '•
4
2
GaSb
DO
5 InAs
• GaAs
CdTe '•••...
ZnSe
5 6 7
8 9
Рис. 12.А.2. Квадратичная
оптическая восприимчивость
различных полупроводников на
длине волны 10,6 мкм в
функции ширины запрещенной
зоны.
%2(о ~
1
Eg(eV)
Ъ(Щ -п2)
эВ
еХ
-п- ir2
-2Q- \Г2
A2.А.23)
И вновь, понятно, что произведение Zl2z23z3l равно нулю, если система
асимметрична. Вблизи резонанса (co~Q) квадратичная восприимчивость принимает вид:
уB)
/С 2<у,
_ q (я, - n2)(zl2Z,3Z3l)
A2.А.24)
Выражения A2.А.22) для нерезонансной системы и A2.А.24) для резонансной
системы обеспечивают достаточно надежное предсказание величины нелинейной
квадратичной восприимчивости в квантовых системах, таких как молекулы или
асимметричные квантовые ямы.
Пример
1. Асимметричные молекулы. Выражение A2.А.22) позволяет рассчитать порядок
величины нелинейной восприимчивости в среде, образованной молекулами с
резонансом Ьо)п вблизи 2 эВ с концентрацией 1028 молекул/м3, а также матричными
элементами zn = 1 А и 8п = 0,1 А. Отношение q/eQ составляет 1,8 х 10"8 В м.
Среднее число молекул в z22Sn составляет таким образом 10 х A0~10J х 10~п или 10~3.
ZB) = 1,8 х 10"8 В м х 10/4 В2 = 4,5 пм В
Эта величина есть именно то, что приблизительно было обнаружено при
исследовании неоптимизированных асимметричных молекул.
2. Асимметричные квантовые ямы. В главе 8 мы видели, что оптические межпод-
зонные переходы в квантовой яме могут быть описаны как переходы между
дискретными энергетическими уровнями. В этом случае электроны обладают
эффективной массой, связанной с их подзоной. В процесс можно ввести асимметричные
композиционные градиенты в квантовых ямах с тем, чтобы обеспечить
асимметричность ограничивающих потенциалов (смотрите 12.А.1).
В качестве примера возьмем квантовые ямы со слоями GaAs толщиной 6 нм и
Al01Ga09As толщиной 4,5 нм, разделенных барьерами Al04Ga06As толщиной 30 нм.
Квантовые ямы легированы до уровня 2 х 1017 см, при этом коэффициент
заполнения составляет У4. Для расчета энергетических уровней Ev Ev Ev получаемых как
решения одномерного уравнения Шредингера ((р*/2т* + V(z))\i> = E\i), а также
матричных элементов ziv z^ и z3V может быть использована очень простая
программа MATHEMATICA. Эта система была спроектирована таким образом, чтобы
обеспечить эквивалентность переходов Е2 — Ех и Еъ — Е2 с энергией перехода,
эквивалентной длине волны 10,6 мкм. Матричные элементы zl2 z^ и z3l составляют
соответственно 2,1, 3,0 и 0,38 мкм. Отметим, что эти матричные элементы превышают
соответствующие значения для молекул. Это связано с малой эффективной массой
электронов в GaAs. Поскольку система является дважды резонансной для расчета
12. Б. Способы реализации фазового согласования в полупроводниках
восприимчивости при резонансе может быть использовано соотношение A2.24).
Мы находим, что:
уB) _
Л2й), max
1,6 х IP'19 Кл 2 х 1023 м3 / 4 х B,4 х 1027 м3)
8,85 х КГ12 Фм"
(ю-2 в]
= 22 000 пм В A2.А.24)
В заключение следует отметить, что значительные по амплитуде нелинейные
оптические эффекты могут быть реализованы в дважды резонансных системах.
Экспериментальные данные, представленные на рис. 12.А.З подтверждают
резонансную природу этого нелинейного оптического эффекта.
15 14 13 12 11 10 9 8
0.25
0.2
g 0.15
о
с
О)
I 0.1
ф
о
6 0.05
поглощение f
2f- генерация
теоретическая
кривая
i !x ■У/. 111
150
100
50
I
О
8
сг
ГО
80
90
100 110 120 130 140 150 160
Рис. 12.А.З. Процессы поглощения и генерации второй гармоники излучения в
дважды резонансных квантовых ямах (Из Е. Rosencher and P. Bois, Phys. Rev., В
44, 11 315 A991) и P. BOucaud, et al. Appl. Phys. Lett. 57, 215 A990)).
Литература
P. Butcher and D. Cotter, The Elements of Nonlinear Optjcs, Cambridge University
Press, Cambridge A990).
J.L. Oudar and J. Zyss, Phys. Rev. A 26, 2016 A982).
E. Rosencher and P. Bois, Phys. Rev. В 44,11 315 A991).
Y.S. Sen, The Principles of Non Linear Optics, Whiley, New York A984).
12.Б. Способы реализации фазового согласования
в полупроводниках
На протяжении изложения мы видели, что очень низкая эффективность имеет
место, когда не удовлетворяются условия согласования фазы (смотрите, например,
A2.33)). Вообще говоря этот критерий невозможно удовлетворить в любом
заданном материале, т. к. он требует отсутствия оптической дисперсии во всем
используемом частотном диапазоне. В случае генерации второй гармоники условие
согласования фазы можно записать в виде:
п{1со) = п(бо)
A2.Б.1)
Для того, чтобы это условие было удовлетворено, максимальная длина
преобразования Lc A2.34) должна быть бесконечной. Естественно, все материалы (и в
особенности полупроводники) обладают дисперсией. Тот факт, что более узкозонные
полупроводники, обладающие все большей нелинейной восприимчивостью второ-
Дополнения к главе 12
го порядка (смотрите A2.А.22), одновременно проявляют все более сильные
дисперсионные характеристики (смотрите дополнение 7.Б), является, по меньшей мере,
неблагоприятным моментом.
К счастью, есть несколько путей решения этой проблемы. Опишем два
наиболее используемых метода:
• согласование фаз в режиме двулучепреломления;
• квазифазовое согласование.
12.Б.1. Согласование фаз в режиме двулучепреломления
Многие кристаллические материалы (и среди них некоторые полупроводники)
обладают анизотропными оптическими свойствами благодаря своей кристаллической
структуре. В этом разделе мы ограничим наше рассмотрение одноосными
кристаллами — кристаллами, обладающими осью симметрии, относительно которой любая
элементарная операция симметрии не приводит к изменению кристалла
(например, поворот на я/3, л/4 и т. д.). Предположим для определенности, что эта ось
(называемая оптической осью) лежит в направлении Oz. Из элементарной теории
оптики мы знаем, что такой кристалл является двулунепреломляющим, т. е.
коэффициент оптического преломления не является одним и тем же параметром для всех
направлений распространения. Говоря более точно, электромагнитная волна,
распространяющаяся вдоль оси Oz характеризуется коэффициентом преломления по
(индекс «О» обозначает обыкновенную волну) тогда, как волна, распространяющаяся
в любом другом направлении в плоскости Оху, характеризуется другим
коэффициентом преломления пе (индекс «е» обозначает необыкновенную волну)
Более того, из оптики нам известно, что при любом направлении
распространения электромагнитной волны возможны лишь два главных направления
поляризации, а именно: волна, поляризованная вдоль одного из этих главных
направлений поляризации, останется линейно поляризованной во время своего
распространения через кристалл. Эти два главных направления геометрически определяются
так, как это показано на рис. 12.Б.1. С этой целью рассмотрим эллипсоид
коэффициента преломления, определяемый геометрическим местом точек {х, у, z), для
которых справедливо соотношение:
— + ^- + ^- = 1 A2.Б.2)
«О П1 Пе
Пусть распространяющаяся волна имеет волновой вектор к. Без потери общности
мы можем предположить, что волновой вектор лежит в плоскости Oyz. Пересечение
плоскости, перпендикулярной к, с эллипсоидом коэффициента преломления дает
нам эллипс (смотрите рис. 12.Б.1). Две главные оси, одной из которых является ось
Ох, и являются двумя главными направлениями поляризации, при этом величина
двух главных осей этого эллипса дает коэффициент преломления для каждой
поляризации. Из рисунка 12.Б.1 понятно, что коэффициент преломления вдоль оси Ох не
зависит от угла в, и он всегда равен п\ это — обычная поляризация. С другой стороны,
второе разрешенное направление поляризации {необыкновенная поляризация,
соответствующая волновому вектору к) характеризуется коэффициентом преломления пе,
который зависит от угла в и определяется простым соотношением:
1 = cos2 6 | sin2 6 A2.Б.З)
Если обыкновенный коэффициент преломления п0 меньше необыкновенного
коэффициента преломления пе, то эллипсоид будет узким по экватору и в этом случае
кристалл есть положительный одноосный материал. В противоположном случае, когда
п0 > иДкак это показано на рис. 12.Б. 1) кристалл представляет собой
отрицательный одноосный материал.
12. Б. Способы реализации фазового согласования в полупроводниках
Ось распространения
Направление
необыкновенного
луча
Рис. 12.Б.1. Определение двух
разрешенных направлений поляризации в
Направление х * среде с двулучепреломлением. Один из
обыкновенного двух коэффициентов преломления (пе)
луча зависит от угла в между волновым
вектором и оптической осью. Этот
рисунок соответствует ситуации в т. н.
отрицательной одноосной среде.
Фазовое согласование в режиме двулучепреломления использует эту оптическую
анизотропию. В этом случае при определенных условиях можно обеспечить равенство
коэффициента преломления п(со) в одном главном направлении и пBсо) в другом
направлении. Говоря более точно, хотя в общем случае мы имеем пBсо, в) > п(со, в), мы
можем, используя отрицательный одноосный материал, обеспечить:
neBco,es)=n0(co)
A2.Б.4)
В случае положительного материала мы должны использовать поBсо) = пе(со, в).
Для решения этого уравнения перейдем к плоскости Oyz и попробуем найти угол 0,
который удовлетворяет этому уравнению. Рассмотрим нормальный эллипс
необыкновенных коэффициентов преломления, образованный геометрическим местом точек М,
для которых ОМ@) = пе(со, в) и который дает сферу обыкновенных коэффициентов
преломления, точки которой Мудовлетворяют соотношению ОМ(в) = по(со, в).
Рисунок 12. Б.2 показывает, что нормальный эллипс коэффициентов преломления может
быть получен из индекса коэффициентов преломления вращением на л/2. Добавим к
этому рисунку нормальные эллипсоиды коэффициента преломления,
соответствующие частоте 2со. Пересечение между сферой по(со) и эллипсом пеBсо, в) задает конус
относительно оптической оси, вдоль которого имеет место согласование фаз между
волной со и ее второй гармоникой 2со (смотрите также рисунок 12.Б.З).
Понятно, что решение существует только тогда, когда по(со) > пеBсо) > пе(со), т. е.
при наличии существенного двулучепреломления. Используя равенства A2Б.З) и
A2.Б4), мы видим, что угол <9 определяется условием:
1
я»2
cos 2 6S sin26c
пеBа>J
A2.Б.5)
Или вновь:
ft V ft V A2Б6)
Согласование фаз в режиме двулучепреломления
#474 Дополнения к главе 12
пр{2ь). в)
\
\
/ \
f
J
/
Рис. 12.1
Ось согласования
по фазе
, в)
т
Рис. 12.Б.2. Графтческий метод вывода
условия согласования фаз обыкновенной
волны (частоты со) и необыкновенного
луча второй гармоники Bсо) для
отрицательной одноосной среды.
Это последнее уравнение позволяет прямо рассчитать угол фазового согласования,
как только становятся известными дисперсионные соотношения для каждой
поляризации. Большинство из них может быть получено из уравнений Зеллмайера
(уравнение G.Б.2) или Афромовича (уравнение G.Б.10)) соответственно для
широкозонных и узкозонных полупроводников. После того, как становится известен угол
фазового согласования, нам остается рассчитать величину квадратичной оптической
восприимчивости с использованием уравнения A2.17). Понятно, что результат будет
Ось согласования по
фазе на частоте со
Рис. 12 Б.З. Метод согласования
фаз с использованием двулучепре-
ломления, иллюстрируемый
эллипсоидами коэффициента
преломления при со и 2@ для
отрицательной одноосной среды.
12. Б. Способы реализации фазового согласования в полупроводниках
зависеть от различных ненулевых членов тензора х^ш) и> таким образом, от
симметрии кристалла. Читатель может найти описание всех соответствующих тензоров в
справочном пособии по нелинейной оптике, таком как книга Сазерленда A996).
Пример
Ниобат лития является одним из наиболее популярных нелинейно-оптических
материалов. Это не полупроводник, а скорее изолятор типа оксида металла^ который
обладает сильным двулучепреломлением и, таким образом, он хорошо пригоден для
реализации фазового согласования. Обыкновенный и необыкновенный коэффициенты
преломления этого материала даются зависимостями типа соотношений Зеллмайера:
В
п2 = А-
С-Я2
-DA2
При этом:
"о
А
4,5820
4,9048
В
0,099169
0,11768
С
0,044432
0,04750
D
0,21950
0,027169
Рисунок 12. Б.4 иллюстрирует дисперсионные зависимости этого материала.
Мы хотим согласовать по фазе кристалл ниобата лития для того, чтобы
добиться удвоения частоты излучения лазера на основе Nd: YAG на длине волны 1,3 мкм
и получить световой пучок на длине волны 0,65 мкм. Таким образом, нам надо
решить уравнение A2.Б.6). Приведенная ниже программа MATHEMATICA может
быть использована для решения задач подобного рода.
ae=4.820;be=0,099169;c=0.044432;de=0.021950;
ao=4.9048;bo==0.117768;co=0/4750;do=0.027169; ne2[IJ:=ae - Ье/(се-Г2
ne[l_]:Sqrt[ne2[l]
по21_]::ао-Ьо/(со-Г2)- с!о*Г2
no(l_]:Sqrt[no2[l]]
Funct=A ./no2[l]-1 ./ne2[l/2]-1 ./nO2[l/2];
theta =ArcSin[Funct]*180/Pi;
N[theta]/.1/3
ParametricPlotHthetaJMU.1,3.5}]
I
Ш
о
5
Q.
С
h-
I
0)
s
If
s
C5
О
Рис. 12.Б.4. Дисперсионные
кривые ниобата лития.
0.4
0.6 0.8 1.0
Длина волны (мкм)
Фазовое согласование параметрических колебаний в режиме двулучепреломле-
ния может быть реализовано с использованием тех же самых принципов. Однако в
Дополнения к главе 12
этом случае нам необходимо удовлетворить требования по сохранению как энергии,
так и импульса фотонов. В случае пучка накачки на частоте cov а также сигнального
и холостого пучков с частотами ох и со2 условия в A2.42) могут быть записаны в виде:
со2 =
A2.Б.7я)
Поскольку njnz и п2/п3 меньше 1, оптическая дисперсия вновь будет
препятствовать фазовому согласованию, если только с помощью какого-либо приема
(например, использования двулучепреломления) ее не удастся скомпенсировать. В
отрицательном одноосном материале (пе < п0) естественно выбирать конфигурацию,
в которой сигнальная и дополнительная волны имеют обычную поляризацию,
а волна накачки — необыкновенную поляризацию так, чтобы отношения п0(со)/пе(сог)
и п0(со2)/пе(со3) делали два уравнения в A2.Б.7а) совместимыми. Такая ситуация
соответствует т. н. еоо-конфигурации, при этом:
[по(щ)~ пХ^со, =[пе(со,)- по(щ)]ц A2.Б.76)
В этом случае оба члена положительны. Угол фазового согласования в5
определяется уравнением:
пМц + n0{oh)oh = ne{oh, 0s)co, A2.Б.8)
Здесь: изменение пе в функции Сдается выражением A2.Б.З). Таким образом, за счет
параметрического взаимодействия (или «расщепления») может быть получена любая
частота оI в том случае, когда следующее выражение допускает решение 0s((o):
sin 0r
"еМ.
v-1/2
A2.Б.9)
Рисунок 12. Б.5 демонстрирует изменение длины волны сигнальной и холостой
волн в функции угла фазового согласования в для пучка накачки на длине волны
1,06 мкм в кристалле ниобата лития LiNbO3. Возможны и другие конфигурации
фазового согласования (например, еое, оео...), при этом заинтересованному читателю
рекомендуется более детально ознакомиться со специальной литературой по этому вопросу.
Пример _ .
Диаграмма фазового согласования для нелинейного материала представляет собой
набор пар (для сигнальной и дополнительной волн), которые могут генерироваться
при заданной длине волны накачки в функции такого параметра, как угол в между
4.0
45.5
46.0 46.5 47.0
Угол к оси Oz
47.5 48.0
Рис. 12.Б.5. Угловая
зависимость фазового согласования
для ниобата лития на длине
волны 1,064 мкм. (С
разрешения Т. DebuisschertOTHALES).
12. Б. Способы реализации фазового согласования в полупроводниках
волной и оптической осью кристалла. Программа MATH EM ATI С А, приведенная
ниже может быть использована для решения уравнения A2.Б.9) (дисперсионные
кривые имеют тот же самый вид, что и в предыдущем примере)
ae=4.5820;be=0.099169;ce=0.044432;de=0.021950;
ao=4.9048;bo=0.11768;co=0.04750;do=0.027169;
ne2[lJ:ae-be/(ce-r2)-de*r2;ne[l_]:=Sqrt[ne2(l)];
no2[l_]:=ao-bo/(co-r2)-do*r2;no[l_]:=Sqrt[no2[l]];
Н=(Aр/11)*по[11]+Aр/12)*по[12Г2;
f2=1/f1-1/no2[lp];
f3= 1/ne2[lp]-1/no[lp];
fctopo=Sqrt[f2/f3];theta=ArcSJn[fctopo]*N[180/Pi];
ParametricPlotfithetaJI}, {11,1.5,4.}]
При наличии средств для обеспечения фазового согласования в режиме двулу-
чепреломления реализация оптического параметрического генератора (ОРО) как
спектрально перестраиваемого источника когерентного излучения становится
очевидной (смотрите рис. 12.Б.6). Лазерный резонатор обеспечивает мощный пучок
излучения с частотой сог Этот пучок в дальнейшем претерпевает параметрическое
взаимодействие с нелинейным кристаллом внутри резонатора с одиночным или
двойным резонансом. Зеркала ОРО проектируются таким образом, чтобы
обеспечить повышенный коэффициент отражения в требуемом спектральном диапазоне
перестройки для сигнального и холостого пучков. Перестройка длины волны ОРО
осуществляется поворотом кристалла с тем, чтобы найти угол фазового
согласования, требуемый для получения необходимой частоты сигнала о)х (уравнение A2.Б.9)).
12.Б.2. Квазифазовое согласование
В основе этого подхода лежит поиск средств для пространственной модуляции
оптической нелинейности с некоторым периодом (Л), что приводит к
квазиволновому вектору К = 2л/А, необходимому для удовлетворения требования по сохранению
волнового вектора (подобно тому, как это имеет место в дифракционной теории).
Условие квазифазового согласования заключается в обеспечении условий для
проявления такого квазиволнового вектора, с участием которого выполняется
соотношение к~ — 2к = К.
2(о со
Эту концепцию легко понять, возвратившись к уравнению A2.29), описывающему
в аппроксимации необедненного пучка (Ew = const) эволюцию поля второй гармоники
Е2а) в процессе ее распространения через нелинейную среду. К этому уравнению,
однако, мы добавим пространственное изменение х(z), которое мы запишем в виде:
OFO
1
0
0)
ш
Я= 1
Рис. 12.Б.6. Схематическое представление Я = 1
конфигурации спектрально
перестраиваемого ОРО с двойным резонансом. Я = О
Я
я
я
= 0
1
1
CD
(О
(О
f( 478 Глава 12. Преобразование оптической частоты
Здесь: f(z) есть периодическая функция, осциллирующая между —1 и +1. В этом
случае мы получаем:
<*Z n2(oc
Напряженность преобразованного поля E2w в конце пути распространения L в этом
случае составляет:
»С О
Разлагая J(z) в ряд Фурье с периодом Л, получаем:
В этом случае уравнение A2.Б. 12) дает:
L
E2m(L)= -i^LE2X fn \e^-ln«z A2.Б.14)
"г«С п {
В этом последнем уравнении мы ясно видим ту роль, которую играет
периодическая модуляция восприимчивости. Предположим, что существует такое целое число
я, при котором выполняется соотношение:
*2.-2*.=— A2.Б.15)
Л
В этом случае лишь один член в A2.Б. 14) не равен нулю при больших значениях L,
что приводит к выражению:
Сравнивая A2. Б. 15) с выражением для длины максимального преобразования
Ьс A2.34), мы находим, что периоды модуляции кратны параметру Lc,
определяемому соотношением:
A = 2nLc A2.Б.17)
Выражение A2. Б. 16) показывает, что среда ведет себя таким образом, как будто она
удовлетворяет фазовому согласованию, но при этом эффективная нелинейная
восприимчивость дается выражением:
Xf =\fn\f A2.Б.18)
Здесь: fn есть член ряда Фурье для периодической функции f(z), определяемый
выражением:
является синусоидальной функцией (J(z) = sin2^;0\), то/, =fx = 1/2 и
Z2ff = X2/2- Более реалистичный подход основан на модуляции нелинейной
восприимчивости за счет периодического обращения направления нелинейности таким
образом, что fl(z) = +1 между 0 и Л/2 и —1 между Л/2 и Л (смотрите рис. 12.Б.7). В
этом случае интегрирование A2. Б. 19) следует непосредственно и дает:
yefr = —у A2.Б.20)
л
12. В. Обеднение накачки при параметрических взаимодействиях
Рис. 12.Б.7.
Квазифазовое согласование с
использованием
последовательности
попеременно ориентированных
слоев GaAs. Каждый из
слоев обладает
толщиной, равной длине
фазового рассогласования
на требуемой длине
волны.
Полное согласование
по фазе
Квазисогласование по
фазе
Рассогласование
по фазе
GaAs
Рисунок 12.Б.7 иллюстрирует механизм квазифазового согласования.
Направление нелинейности инвертируется до того, как начнется процесс перекачки
энергии от волны второй гармоники к фундаментальной волне. Этот тип квазифазового
согласования обеспечивает ряд физических систем. В среднем инфракрасном
диапазоне можно использовать последовательность слоев GaAs с чередующейся
кристаллографической ориентацией (т. е. с переходом от ориентации A10) к
ориентации A, 1, 0» на каждой длине фазового рассогласования Lc (что составляет 106 мкм
для удвоения частоты на длине волны 10,6 мкм с преобразованием в излучение с
длиной волны 5,3 мкм). В ближней инфракрасной области (для реализации
голубого излучения за счет удвоения частоты излучения лазерного диода на основе GaAs с
длиной волны 805 нм) возможно использование обращения доменов в ферроэлек-
трических материалах.
Литература
Методы преобразования частоты:
A.Yariv, Quantum Electronics, 3rd Edn, Wiley, New York A999).
R. L. Sutherland, Handbook of Nonlinear Optics, Marcel Dekker Inc., New York A996).
Двулучепреломление:
M. Born and E. Wolf, Principles of Optics, 6th Edn, Pergamon Press, Oxford A980).
J. M. Perez, Optique, 4eme edition, Masson, Paris A997).
12.B. Обеднение накачки при параметрических
взаимодействиях
Во время нашего рассмотрения параметрического взаимодействия в главе 12
предполагалось, что эффективность преобразования между пучком накачки, с одной
стороны, а также сигнальной и холостой волнами, с другой стороны, настолько
Дополнения к главе 12
низка, что мы можем пренебречь любым ослаблением интенсивности пучка
накачки (т. е. как предполагалось в разделе 12.3, E(z) = Ео). В действительности же в
настоящее время для некоторых ОРО-материалов реальным является уровень
эффективности, превышающий 50%. Поскольку энергия должна сохраняться в
процессе параметрического взаимодействия, возникновение нелинейных волн должно
происходить за счет энергии пучка накачки. Однако точное описание ослабления
интенсивности пучка накачки требует более точного учета параметрических
взаимодействий. Наиболее примечательным является то, что по мере рассмотрения
материала этого раздела мы обнаруживаем первичную роль, которую играют в
параметрических взаимодействиях относительные фазы различных волн. В главе
12 этот аспект проблем был априори недостижим из-за нашей начальной посылки
упростить задачу за счет аппроксимации постоянного уровня пучка накачки.
Наше рассмотрение мы начнем со случая согласованного по фазе (Ак = 0)
процесса генерации второй гармоники (со + со — 2со):
— А(О = -[кА*й)А2о)
Zd (П.ВАа)
Alto = ~1Л:Ду
dz
Как мы напоминаем, здесь: к есть параметр нелинейной связи, определяемый
выражением:
2 с [nln2co J
Для учета фазовых эффектов введем переменные:
A2.В.2)
После подстановки в A2.В. 1) и приведения подобных членов мы приходим к
системе связанных дифференциальных уравнений:
— щ - кихи2 sin (#2 - 20,)
— и2= ки] sinB0, - 92)
dz A2.B.3)
— 0, = -ки2 cos@2 - 20,)
dz
— в2 = -к£-cosB0, -02)
dz u2
Эти уравнения могут быть существенно упрощены, если будут найдены их
инварианты (или константы движения). Первый инвариант получается из
комбинации первых двух уравнений A2.В.З), что дает:
"AzJ +«2feJ = «b2 = const A2.B.4)
Это выражение есть ничто иное, как выражение закона сохранения энергии.
Второй инвариант получается делением уравнений по du./dz на уравнения по
dOjdz и введением члена относительной фазы 0= 20, — 02, что дает:
d6,
1
Лщ
I + _
= cot0
12. В. Обеднение накачки при параметрических взаимодействиях
1
du2
A2.В.5)
Эти два уравнения A2.В.5) могут быть скомбинированы с тем, чтобы получить
одно уравнение:
uf(z)u2(z)cos
(9@)= Г
A2.В.6)
Здесь Г есть константа, определяемая граничными условиями. Это последнее
уравнение показывает, каким образом в процессе нелинейного взаимодействия в
кристалле изменяется разность фаз между двумя волнами. Если предположить, что
начальная амплитуда волны второй гармоники на входе нелинейного кристалла равна
нулю (т. е., что амплитуда обратной связи равна нулю), то м2@) = 0 и константа Г
равна нулю. При z > 0 A2.В.6) удовлетворяется для ненулевой падающей волны,
если только 0(z) — const = Bт + \)ж/2. В этом случае и0 в уравнении сохранения
энергии есть амплитуда волны накачки на входе нелинейной среды, при этом
уравнение для амплитуды u2(z) принимает вид:
— и2 = к(и20-и22)
dz
A2.В.7)
Уравнение A2.В.7) может быть легко проинтегрировано, что дает эволюцию
амплитуды в нелинейной среде:
Здесь:
i/2(O=i/otanh U-
: есть длина преобразования частоты:
1 с л3/:
A2.В.8я)
A2.В.86)
кип
Длина преобразования частоты
Здесь: п~пш~ п2(о, Iесть мощность падающего излучения, aZ0- вакуумный
импеданс C77 Ом). Рисунок 12.В. 1 демонстрирует изменение нормированной
интенсивности («j/«0J и (и2/и0J в функции нормированного расстояния z/%.
Заметим, что после распространения на расстояние, примерно равное длине
преобразования, 50% энергии волны накачки будет преобразовано в излучение
второй гармоники.
„ 1.0
m 0.8
s
о
I
0.6
0.4
02
о
0.0
4 V I
0 12 3 4 5
Нормированное расстояние z/£
Рис. 12.В.1. Эволюция нормированной интенсивности волн накачки и второй
гармоники в функции расстояния распространения, нормированного на длину
преобразования в нелинейной среде.
482 Дополнения к главе 12
Пример
Рассмотрим кристалл с нелинейной восприимчивостью 10 пм В коэффициентом
преломления 1,5. Мощность падающей волны на длине волны Л = 1 мкм составляет
10 кВт в пределах площади 1 мм2. В этом случае уравнение A2.В.86) дает:
2 и3/2
$я = 8,2 х 103 —4в JL или 1?5 см. A2.В.8*)
\Z2jpm В1 V Вт м-
Рассмотрим теперь более общий случай, затрагивающий трехволновое
параметрическое взаимодействие соъ = тх + со2. Исходя из A2.38) и обобщая предыдущую
замену переменных (т. е. Ak = ukeWk),получаем следующую систему связанных
нелинейных уравнений:
— щ = кщщьтд
dz
— щ =KU]u3sin0
dz
— щ =-щи2ьтв
Z A2.B.9)
d й - *r uiu
d^l=~%
dz щ
0 = -fc-L^.cOS9
dz Щ
Здесь фаза 0 определяется соотношением: в= въ — в2 — ву Отыскивая, как и
прежде, инварианты, мы легко находим:
Это является отражением закона сохранения энергии. Одновременно с этим получаем:
",k)«2fe)«3fe)cos 0(z)= Г A2.В.11)
Последнее соотношение отражает сохранение фазы.
Теперь мы уже в состоянии приступить к обсуждению вопроса, который
оставили в стороне в главе 12. А именно: если на входе нелинейного кристалла имеются три
волны (ov co2 и (ov то каким образом система решает, какую из следующих
последовательностей следует реализовать: со{ + й>2 -»cov со3 — ^ —> со2 или со3— со2-* со^ Ответ
на этот вопрос дается относительными фазами различных волн. Говоря более точно,
в этом случае будет проводиться отбор различных механизмов (генерация
суммарной, разностной частот, параметрическое усиление) в соответствии с граничными
условиями, определяемыми различными законами сохранения A2.В.10) и A2.В.11).
Возьмем в качестве примера генерацию суммарной частоты (SFG), для которой
два граничные условия имеют вид:
«i@)= "и, = «т «2@)= 0 = «23, «з@)= 0 И Т. О. COS0(O= 0 A2.В.12)
В этом случае дифференциальное уравнение относительно иъ имеет вид:
12. В. Обеднение накачки при параметрических взаимодействиях
dZ =
dU,
A2.В.13)
Здесь: z — нормированное расстояние Z = z/£{, %{ — длина преобразования для
волны cov U3 есть нормированная амплитуда U3 =«3/w2o> a m есть соотношение
первоначальных амплитуд т = (и20/и10J. Решение дифференциального уравнения
A2.В.13) может быть выражено с использованием (малоизвестной!) функции
численного анализа, а именно — эллиптической функции Якоби, sn(z) (смотрите также
дополнение 12.Е). В связи с тем, что математическая природа и значение этой
функции не входит в круг вопросов, рассматриваемых в настоящей книге, для
наших целей будет достаточно только отметить, что она протабулирована и
приводится в современных электронных справочных изданиях. В этом случае интеграл
A2.В. 13) дается формулой:
-4
dx
- тх
Или:
В этом случае решения, дающие амплитуды трех волн, имеют вид:
A2.В.14)
A2.В.15)
и (VY - и2 -и2 sn2f — -^- I
«2VW - 0 «20ЬП р 9 ^Г I
{ SI Ul0 j
A2.В.16)
Рисунок 12.В.2 иллюстрирует эволюцию нормированнной интенсивности
различных волн и{/и10, и2/и10 и м3/"ю в предположении, что соотношение интенсивно-
стей т = 1/3. Мы видим, что функция Якоби sn(z) является периодической.
Физическая природа такой модуляции заключена в периодическом обмене энергией между
волнами накачки и SFG. Как только волна суммарной частоты со3 полностью
истощит волну накачки с частотой cov начнется обратный процесс, и волна соъ вновь
начнет усиливаться за счет волны суммарной частоты.
1.0
|
0.8
0.6
Рис. 12.В.2.
Изменение интенсивности к
накачивающей вол- i 04
ны (a)j и со2) и волны л
суммарной частоты о
в)ъ в функции норми- s о.2
рованного расстоя- о.
ния при соотноше- х
ниии интенсивности 0.0
т = (м20/и10J, равном 0
1/3.
uA(z) =u;0-u220sr\(z,m)
u3(zJ=u220sr\(z,mJ
2 3 4
Нормированное расстояние
Дополнения к главе 12
Представленный формализм точно описывает механизм энергетического
обмена между различными волнами и выявляет роль, которую играют относительные
фазы. Рисунок 12.В.2 показывает, каким образом энергия волн накачки тх и со2
комбинируется с тем, чтобы сформировать волну суммарной частоты со3 вплоть до
полного истощения неосновной волны со2 когда начинается обратный процесс
реконструкции волны со2 за счет волн со{ и со3 и т. д.
Литература
М. Abramovitz and I. Stegun, Handbook of Mathematical Tables, Dover Publications,
New York A970).
J.A. Armstrong, N. Bloembergen, J. Ducuing, and P. s. Pershan, Phys. Rev. 127, 1918
A962).
Y.S. Shen, The Physics of Nonlinear Optics, Wiley, New York A984).
12.Г. Спектральные и временные характеристики
оптических параметрических генераторов
Оптическая параметрическая генерация (ОРО) имеет много общего с лазерной
генерацией. В обоих случаях обратная оптическая связь, обусловленная зеркалами,
приводит к генерации и устанавливает условия для амплитуды усиления по
отношению к резонаторным потерям и резонаторным длинам волн. В этом разделе мы
сконцентрируем наше внимание на двух аспектах, которые специфичны для ОРО,
а именно их спектры усиления и динамические характеристики.
Параметрическое усиление определяется геометрическими факторами
применительно к условию фазового согласования, что контрастирует с лазерами, где
усиление имеет место через квантовые переходы, происходящие с участием
дискретных атомов или в пределах зонной структуры кристалла. Именно из-за этого ОРО
являются исключительно полезными в качестве перестраиваемых когерентных
источников излучения для спектроскопических исследований атмосферы, биологии
и т. д. Уравнение A2.33) показывает, что эффективность преобразования для
параметрического процесса такого, как со3 -> со{ + со2 зависит от фазового
рассогласования Ак =к3 — кх — к2 и пропорциональна sinc2(A&Z/2), где L есть длина нелинейного
материала. Таким образом, полуширина кривой усиления (т. е. спектральная
восприимчивость) дается выражением:
AkL = ±n A2.Г.1)
При точном согласовании фаз фотоны в коллинеарной геометрии
удовлетворяют двойным условиям сохранения как энергии, так и импульса:
— = — + —
^ Л ^ A2.Г.2)
А£ _
2я Л$ Л
В этом последнем уравнении мы не уточнили тип использованного фазового
согласования. Это может быть конфигурация типа е —» о + о, в случае которой п3 — пе(Л2),
пх = по(Ах) и п2 = по(Л2) или это может быть конфигурация другого типа. Более того,
в случае квазифазового согласования с периодом Л к уравнению фазового
согласования должен быть добавлен волновой вектор 2л/Л. Таким образом мы будем
искать, какое влияние на вектор Ак будут оказывать изменения АЛ{. При
фиксированной длине волны Л3 изменения сигнальной и холостой волн связаны через
производную первого уравнения в A2.Г.2):
12.Г. Спектральные и временные характеристики... 485
М. = _Дф_ A2.Г.З)
Влияние рассматриваемого фактора на фазовое рассогласование может быть
выявлено дифференцированием второго уравнения в A2.Г.2):
\ Я;
С учетом A2.Г.1) и A2.Г.З) это последнее уравнение приводит к полуширине
кривой усиления:
Спектральная восприимчивость ОРО
Отметим, что чем ближе мы приближаемся к условию вырождения (т. е. сох ~ со2),
тем шире будет кривая усиления. Такой характер иллюстрируется следующим ниже
примером, а также рисунком 12.Г.1. В ряде случаев желательно добиться
максимально узкой кривой усиления (как например в случае одномодовых ОРО). В этом случае
становится необходимым использовать конфигурации с различными поляризациями
сигнальной и холостой волн (т. е. конфигурации типа е -> е + о, называемые
параметрическими взаимодействиями второго рода). В том случае, когда поляризации
сигнальной и холостой волн идентичны, такой случай относится к типу I.
Пример
С учетом кривых Зеллмайера для ниобата лития, приведенных в дополнении 12.Б,
приведенная ниже программа позволяет рассчитать зависимость ширины полосы
от длины волны сигнала при длине волны накачки 1,064 мкм.
ae=4.5820;be=0.099169;ce=0.044432;de=0.0211950;
ao=4.9048;bo=0.11768;co=0.04750;do=0.027169;
ne2[l_]:=ae-be/(ce-r2)-de*r2;ne[l_]:Sqrt[ne2[l]];
L=104;
=11, пс
Г|12
Plot[AA,, {11,1.5,2}]
АЯ = Absl — (по[11] = no[l2] + dn[l2]l2 -dn[H]H)-1
Таким образом, разрешенные резонаторные моды в ОРО, попадающие в контур
спектра усиления нелинейного кристалла, будут испытывать усиление. При этом,
отклик ОРО будет жестко зависеть от типа резонанса внутри резонатора.
Первый случай затрагивает ОРО, в котором резонансна только сигнальная
волна о){ (т. е. в данном случае имеет место случай ОРО с одиночным резонансом,
или случай SROPO, иллюстрируемый рисунком 12.Г.2). Усиливаются все
разрешенные частоты vlm — mc/2n{Lcay, разделенные свободным спектральным
интервалом (A vFSR = c/2/i,Z,cav), что соответствует числу мод N =2(AAl/Al)(LcaJAl), способных
принимать участие в генерации. Принимая АЯ, = 0,01 мкм, Я, =1,6 мкм и Lcav = 4 см,
получаем, что число разрешенных мод составляет 312. В режиме непрерывного
функционирования (непрерывный ОРО) из-за конкуренции мод (смотрите
дополнение 13.Д) будет генерироваться лишь одна мода, наиболее близкая к пику кривой
усиления. В этом случае перестройка частоты возможна за счет изменения длины
резонатора. Частота генерации изменяется линейно и непрерывно со смещением
резонаторных мод вплоть до того момента, когда прилегающая мода не станет наи-
Дополнения к главе 12
I
ш
с;
о
CD
014
0.12
СЮ
\ 0.08
'о.Об
004
0.02
1
1.5 16 17 1.8
Длина волны сигнала (мкм)
1.9
2.0
Рис. 12.Г.1. Зависимость кривой длины усиления при параметрической генерации в
нистате лития с длиной волны накачки 1,069 мкм.
более близкой к максимуму кривой усиления. Когда это происходит, колебания
«перескакивают» на соседнюю моду (что является типичным для ОРО в
непрерывном режиме (смотрите рис. 12.Г.2)). Таким образом эффективный диапазон точной
перестройки равен свободному спектральному интервалу.
В дважды резонансном ОРО (DROPO) моды определяются двумя условиями:
• собственные моды со1т и со2т перекрываются контуром кривой усиления ОРО.
Эти два условия могут быть представлены в виде диаграммы Джиордмэйна—
Миллера (смотрите рис. 12.Г.З). Оси частот сигнальной и холостой волн
ориентированы в противоположных направлениях и располагаются таким образом, чтобы
любая пара частот со1т и со2т на одной вертикальной линии складывались, чтобы дать
частоту накачки соу Таким образом, будут способны генерировать лишь те пары мод
со1т и со2т, которые перекрываются в пределах их соответствующей ширины линии
(Ля/ = &coFSR/F., где / = 1,2, a F. есть зеркальность резонатора на частоте со). С учетом
дисперсии нелинейной среды зазор между модами со1т и со2т будет изменяться в
зависимости от частоты, и лишь немногие моды будут способны перекрываться в
пределах кривой усиления (даже в импульсных условиях — смотрите рис. 12.Г.З).
Таким образом, DROPO по своей природе более благоприятствует одномодовой
генерации по сравнению с SROPO. С другой стороны, эти приборы имеют
тенденцию быть менее стабильными. Одной из причин такой нестабильности является
эффект группирования мод. Если кривая усиления достаточно широка (что часто
имеет место!), то пара несоседних резонаторных мод может оказаться более близко
Параметрическое
усиление
Моды
сигнала
VFSR
Длина резонатора
Рис. 12.Г.2. Спектральная
перестройка SROPO: все моды,
лежащие внутри контура
кривой усиления способны к
генерации. В режиме
непрерывной генерации генерирует
лишь мода, ближайшая к
максимуму кривой усиления (а).
Изменение длины резонатора
обеспечивает частотную
перестройку в пределах
свободного спектрального интервала.
12.Г. Спектральные и временные характеристики...
Рис. 12.Г.З. Диаграмма Джи-
ордмэйна—Миллера для
DROPO. Генерировать могут
лишь моды, которые
перекрываются контуром кривой
усиления (а). В общем случае
моды проявляют тенденцию
группироваться, при этом
частоты генерации ОРО
флуктуируют между этими
различными значениями. В результате
этого DROPO проявляет
тенденцию к неустойчивости (б).
Моды
сигнала
Длина резонатора
расположенной, чем пара соседних мод (смотрите рис. 12.Г.З). В этом случае
частота генерации будет флуктуировать между этими двумя модами, что приведет к
нестабильности выходных характеристик ОРО.
Как правило, параметрическое усиление в нелинейном кристалле достаточно слабо
и линейно увеличивается с ростом уровня накачки. Таким образом, очень выгодно
использовать ОРО в импульсном режиме, когда для накачки нелинейного кристалла
используются импульсы с высокой пиковой интенсивностью (например,
генерируемые лазером с переключением добротности). В связи с этим приступим к описанию
переходных характеристик ОРО в импульсном наносекундном режиме, т. е. режиме,
когда длительность импульсов соответствует времени жизни резонаторных фотонов.
Для этой цели попробуем описать эволюцию амплитуд различных волн в
процессе обращения фотонов в резонаторе (в промежутке между tn и tn+ {). Более того,
сделаем следующие допущения:
• Относительные фазы волн таковы, что константа движения в пределах структур
Г = 0, т. е. cos в = 0. Это означает, что различные фазы остаются постоянными в
нелинейном кристалле (смотрите A2.В.9)).
• Предполагается, что параметрическое усиление достаточно слабо настолько, что
A2.В.9) может быть линеаризовано.
При этих двух допущениях A2.В.9) может быть записано в виде:
A2.Г.6)
<со--;(!)- f,■(!}.-(!
f
В ОРО волны о), направляются в обратном направлении зеркалами с полным
коэффициентом отражения г. (который временно предполагается действительным) ко
входу резонатора так, что новые входные сигналы в моменты времени tn + 1 равны:
A2.Г.7)
Дополнения к главе 12
Здесь: f(f) есть накачивающее электрическое поле на входе ОРО. В момент времени
/ + j амплитуды волны посередине нелинейного кристалла в этом случае составляют:
Введем теперь новое обозначение я//,) = u"(L/2). В этом случае приращения
амплитуды различных волн в процессе кругового обращения в резонаторе
составляют:
^ф)(|) A2.Г.9)
Здесь: TRT есть время кругового обращения в резонаторе, т. е. TRT = 2L/c. В этом
случае уравнение A2.Г.6) может быть записано в виде:
—*,(/)=-^-
Динамические уравнения ОРО
Эти уравнения описывают динамическое поведение ОРО. В этом случае
различные величины, присутствующие в A2.Г. 10) даются выражениями:
1 1 - г,
RT A2.Г.11)
Величины а. являются действительными волновыми амплитудами посередине
нелинейного кристалла, связанные с фотонными потоками через соотношение
A2.37), т. е. Ф. = af/2hZ0. Эти величины, однако, могут быть отрицательными (что
соответствует 6= -л/2 в A2.В.9)), поскольку они описывают колебательный
перенос энергии между различными модами в процессе их взаимодействия в
нелинейном кристалле. Здесь ДО представляет член источника накачки ОРО (по
амплитуде), у. представляют собой различные нелинейные члены связи, а г. — времена
жизни фотонов с различными частотами в резонаторе.
Для детального описания однорезонансного ОРО (SROPO) мы должны
сделать предположение о том, что обратная связь по отношению к сигнальной и
холостой вол-нам отсутствует так, что г2 = гъ = 0. В A2.Г. 10) время жизни для
холостой волны может считаться пренебрежимо малым по сравнению с
сигнальным временем жизни (т{= TRT/(l — г,) и продолжительностью импульса накачки,
которое, как правило, составляет несколько наносекунд. Это аналогично тому,
что dajdt = 0 так, что:
12.Г. Спектральные и временные характеристики... 489
— (
Динамические уравнения SROPO
При этом g2 = kL/2.
Теперь представляет интерес решить A2.Г. 10) в общем случае (SROPO, DROPO)
для стационарных условий, т. е. при/(/)=/= const и da./dt= 0. Уравнение A2.Г.10)
приводит к:
Как и в случае лазерных уравнений D.34) и D.35), это уравнение допускает два
типа решений:
• Ниже порога. Фотонные потоки сигнальной и холостой волн равны нулю (а{ — а2 — 0),
а амплитуда потока фотонов накачки в резонаторе возрастает линейно в функции
амплитуды накачки (а3 =/г3).
• Выше порога. Фотонный поток накачки фиксируется на своем пороговом
значении, определяемом Лъ threshold = аъ2thrcshold = \/{у{т{у2г^). Фотонный поток сигнальной
волны определяется вторым уравнением A2.Г. 13):
4 = а\ = I
J threshold
Здесь: порог задается выражением/threshold = аъ threShoi</T3# Это означает, что пороговая
мощность накачки DROPO пропорциональна 1/Т{Т2, где Т. — коэффициент
пропускания зеркала, который мы уже определили A2.62).
Уравнение A2. Г. 14) предполагает также, что мощность выходного сигнала Р{
пропорциональна ^Р3/Р3 threshold ~ 1, как это иллюстрируется рисунком 12.Г.4. Эта
зависимость явно отличается от линейной зависимости P.m — Pout для лазеров. Этот
момент, как правило, опускается многими аваторами, и он будет более детально
обсуждаться в дополнении 12.Е.
Следующий ниже рисунок 12.Г.4 иллюстрирует временную эволюцию DROPO,
как это описывается выражением A2.Г. 10). Рисунок 12.Г.5 показывает временную
эволюцию накачивающей волны на выходе резонатора ОРО, полученную исходя из
этих уравнений. Начиная с уровня параметрического флуоресцентного шума,
сигнальная волна возрастает экспоненциально, при этом сигнальная и холостая волны
быстро истощают мощность пучка накачки.
Пример
Исследуем временную эволюцию DROPO, накачиваемого импульсами гауссовской
формы. Уравнения нормированы и решены с использованием программы
MATHEMATICA. Мы видим, что сигнал не может возрастать без предварительной
«затравки» малым количеством фотонов источника, поставляемых
параметрической флуоресценцией.
g=5;t=2;eq1 = ap'[ t ]= = E^V - ap[t] -g as[t] ac[t];
eq2 = as' [t] = = -as[t] + g ac [t] ap [t];
eq3 = ac' [t] = g as[t] ap[t];
sol = NDSolve[{eq1, eq2,eq3, ap[-5] = = 0, as [-5] = = 0.001, ac [ -5] = = 0.001},
W 490 Дополнения к главе 12
ОТ 2
Накачка на входе
Сигнал на
выходе
Накачка в резонаторе
Рис.12.Г.4. Отклик ОРО в функции квадратного корня от мощности накачки.
i
о
I
CD
0.8
0,
0.4
0.2
0.0
-
-
/
/
/
1 1
♦***"" жч#
У v
/ у
/Обедненная *
f накачка ^^J
1
V
х
\ Накачка на входе
:Л /
А4- /
\ ^—:
-4
-2
0
Время
Рис. 12.Г.5. Временной
профиль амплитуд
накачивающей и сигнальной
импульсных волн в ОРО,
полученный с
использованием уравнений
связанных мод A2.Г.10).
{ap[t], as[t], [ac[t]}, {t,-5,5}];
P1 = Plot[Evaluate [t]/. sol,{t,-5,5}],
PlotStyle ©RGBcolor [1, 0, 0], DisplayFunction ® Identity];
P3 = Plot[Evaluate[as [t] /. sol, {t, - 5,5}], PlotStyle ® RGBColor[0, 0, 1],
DisplayFunction ® Identity];
Литература
J.A. Giordmaine and R.C. Miller, Phys. Rev. Lett 14, 973 A965).
Y.S. Shen, The Physics of Nonlinear Optics, Wiley, New York A984).
12.Д. Параметрические взаимодействия
в лазерных резонаторах
Как следует из A2.33) или A2.68) эффективность параметрического
преобразования пропорциональна интенсивности пучка накачки. Таким образом, было бы вы-
12.Д. Параметрические взаимодействия в лазерных резонаторах
годно, чтобы параметрическое взаимодействие могло иметь место в оптическом
резонаторе самого накачивающего лазера, поскольку интенсивность пучка накачки
в 1/Траз (где Г пропускание зеркала) больше выходной мощности накачки
(смотрите дополнение 9.Г.) В связи с этим исследуем эффективность внутрирезонатор-
ного преобразования частоты. Для того, чтобы упростить наш подход и выделить
наиболее важные аспекты рассматриваемой проблемы, предположим, что:
1. Соображения согласования фазы были учтены адекватным выбором
резонатора, что позволяет нам сфокусировать наше внимание исключительно на числе
фотонов в резонаторе.
2. Амплитуды волн в резонаторе не зависят от положения: эта аппроксимация
представляется разумной в том случае, когда зеркальность резонатора на частотах со
и 2со больше нескольких единиц.
3. Вся среда характеризуется одним коэффициентом преломления, что
позволяет пренебречь влиянием вариации эффекта преломления.
Разработаем теперь формализм для внутрирезонаторного удвоения частоты.
Необходимая для этого конфигурация эксперимента и соответствующие
обозначения иллюстрируются рисунком 12.Д.1. Предположим, что параметрическое
усиление достаточно слабо с тем, чтобы оправдать аппроксимацию необедненного пучка
(смотрите раздел 12.3). В течение временного интервала dt энергия Ра и Р2(о,
содержащаяся в со- и 2со-волнах, покидающих нелинейную среду, связана с числом
фотонов Р2 на частоте 2со и Ру на частоте со следующими соотношениями:
1 SL A2.Д.1)
Здесь d — скорость света в среде, £ — сечение пучка по нормали, a L — полная
длина резонатора. Скорость изменения числа фотонов из-за нелинейного
взаимодействия, определяется соотношениями:
ь*
A2.Д.2)
Здесь, как мы напоминаем, для генерации одного фотона с частотой 2со
необходимы два фотона с частотой со. Напомним, что для того, чтобы найти выражение для
Кп1, с одной стороны, мощность циркулирующая по резонатору и скорость обмена
числом фотонов связаны соотношением:
Рис. 12.Д.1.
Конфигурация метода удвоения
частоты.
0 14
0.12
СЮ
0.08
0.06
004
0.02
" Лазер
Нелинейный
кристалл
1.5
1.6
1.9
2.0
492 Дополнения к главе 12
S
С другой стороны, интенсивности Рю и Р2о) определяются A2.33):
Р2л = VP; A2Л4в)
Здесь rj — эффективность преобразования (в м2 Вт):
^У A2.Д.46)
В пренебрежении обеднением пучка накачки в кристалле коэффициент Кп1
получается из A2. Г.З) и A2.Г.4):
Обратим теперь наше внимание на реакцию внутрирезонаторной лазерной среды.
Временная эволюция среды в отсутствие эффекта удвоения частоты
определяется D.34) и D.35), при этом мы должны учитывать, что лазерная среда занимает
лишь часть резонатора.
Ayv = r2(yvo-AO-#,w,
dt A2.Д.6а)
Здесь: N — число атомов в состоянии инверсной заселенности, а /Г —
коэффициент линейной связи:
*, = ^ A2.Д.66)
В отсутствие какого-либо параметрического взаимодействия мы немедленно
приходим к стационарному поведению системы. Если число атомов N меньше
пороговой величины NthTcshold, то число фотонов Рх будет равно нулю и N= NQ
(пропорционально мощности накачки). В противоположной ситуации Добудет
фиксировано на уровне 7Vthreshold:
л/
1У threshold
При этом число фотонов Рх будет даваться соотношением:
/> = />„>-1) A2.Д.76)
Здесь: Psat = V2/Kl = SL/ccro т2 есть число фотонов насыщения, а г — нормированная
скорость накачки г = NJNihnAioXd (смотрите раздел 4.6), теперь нам остается только
свести вместе эти два механизма (усиление и преобразование частоты) для того,
чтобы описать процесс в резонаторе:
N T2(NON)
±Р^К,МРх-Г^Р{-Кп,Р? A2.Д-8)
В стационарном состоянии второе уравнение системы дает возможность
установить связь между числом инвертированных атомов с числом фотонов Р,:
ДР, A2.Д.9Д)
12.Д. Параметрические взаимодействия в лазерных резонаторах
При этом:
/?=^- A2.Д.96)
Таким образом, инверсная плотность более не является фиксированной! Это
происходит из-за того, что фотоны с частотой со не насыщают лазерные переходы, т.
к. они устраняются из резонатора за счет превращения в фотоны с частотой 2со.
При подстановке A2.Д9) в первое уравнение A2.Д.8) число фотонов Рх будет
даваться решением квадратного уравнения:
Здесь: есть отношение и = Г2/Гсау1 и Y= Pi/Nthteshold (смотрите D.36)). Число фотонов
Г 2Р2, покидающих резонатор, в этом случае дается третьим уравнением системы
A2.Д.8), т. е.:
is
Г Р — nl N2 Yl
1 cav 2 л 2 ~ ^ J Y threshold J
•»/>У]
A2.ДЛ2)
ИЛИ
Эта последняя величина существенно зависит от параметра и/3= А^АГ
который представляет собой ничто иное, как нелинейный параметр,
нормированный на линейные параметры. Анализ A2.Д.12) показывает, что коэффициент
нелинейности КпХ можно выбрать для достижения оптимальной эффективности и это
для каждого уровня накачки г; достаточно, чтобы и/3 = 1т. е. при коэффициенте
нелинейности, определяемом соотношением:
Это последнее уравнение показывает, что оптимальный уровень нелинейной
связи имеет место, когда нелинейные потери при насыщении (Кор1Р^
соответствуют линейным резонаторным потерям. Таким образом, мы видим, что представляет
интерес минимизация линейных потерь для того, чтобы свести к минимуму длину
нелинейного кристалла. Оптимальный поток фотонов с энергией 2со, который
может покинуть резонатор, составляет:
Гс„ ,/», = - Гст , Рш (V7 - 1 J A2.Д. 14)
Заметим, что этот поток пропорционален (Vr — 1J;за пределами порога
основная часть энергии накачки преобразуется в фотоны с частотой 2со, при этом
поток фотонов с частотой 2со становится пропорциональным V/*. Таким образом,
резонатор ведет себя практически как идеальный преобразователь частоты.
Рисунок 12.Д.2 показывает изменения нормализованной инверсной заселенности
X = N/Nthrtshold и нормированного потока Z = ^2/^Ьге5Ьо1с1 фотонов с частотой 2со в
функции скорости накачки г. На этом рисунке четко видны уход от состояния
фиксации инверсной заселенности X, а также зависимость вида (Vr — IJ числа
фотонов Z с частотой 2со.
Временная зависимость сигнала, полученная с помощью A2.Д.8) и в
пренебрежении членом спонтанной эмиссии T2(N0 ~ N) во время импульса, может быть
записана в виде:
— X ~-XY
d/
W494 Дополнения к главе 12
з.о
2.5
2.0
1.5
1.0
0.5
0.0 HU- ■ - —,
/^^^ Фиксация
£т -
X
i
^^
I
2 3
Скорость накачки
Рис. 12.Д.2. Изменение
нормированного числа атомов усиливающей
среды в возбужденном состоянии X,
а также нормированного
фотонного потока Z с частотой 2 со в
функции скорости накачки г.
at 2
Рисунок 12.Д.З демонстрирует временную зависимость фотонного потока с
частотой 2со, полученную с использованием дифференциальных уравнений A2.Д. 15).
Как и ранее (смотрите раздел 4.6.2), в рассматриваемом случае необходима
«затравка» для стимулирования эффекта спонтанного излучения (параметрической
флуоресценции). Рисунок 12.Д.З демонстрирует также, что в случае большой величины
коэффициентов связи (/?> 1) длительность импульсов становится большой, но при
этом интегральная величина (энергия импульса) остается неизменной. Это —
хорошая новость: она означает, что малые нелинейности тонких нелинейно-оптических
кристаллов достаточны для обеспечения хорошей SHG-эффективности. И в
действительности, внутрирезонаторные SHG на длину волны 1,06 мкм с
использованием лазера на основе YAG стали подлинной «рабочей лошадкой» современных
мощных лазеров видимого диапазона, которые смогли полностью заменить ионные
газовые лазеры.
Пример
Приведенная ниже программа MATHEMATICA дает расчет импульсного процесса,
описываемого A2.Д.15).
xi=10; b=1;
eq1=y[t] = = y[t]*(x[t]-1)-b y[t]-2;
eq2=x'[t] = =-x[t]*y[t];
sol=NDSolve[{eq1,eq2,x[0] = = xi,y[0] = = 0.001 },{x[t],y[t]},{t,0.,50}];
plot2=Plot[Evaluate[by[t]^2/sol,{t,0,50}],Plotstyle->
{RGBColor[.5>0,.5]},PlotRange->{0,1},DJsplayFunctJon->ldentity];
о
h
£ о
5
2 4 6
Нормированное время
Рис. 12.Д.З. Временная
зависимость сигнала второй
гармоники для различных
значений Р отношения
нелинейного и линейного
коэффициентов.
12.Е. Характеристики непрерывных параметрических генераторов...
Литература
J.A. Murray, /. Appl. Phys., 41, 609 A970).
R.G. SmithJEEEJ. Quantum Electron. 6,215 A970).
12.E. Характеристики непрерывных параметрических
генераторов в непрерывном режиме
Вплоть до настоящего характеристики ОРО анализировались в предположении
слабой эффективности частотного преобразования. Это позволило нам предположить,
что пучок накачки остается необедненным и, таким образом, очень удобно
упростить теоретические выкладки. В действительности же, как мы теперь увидим, эта
аппроксимация очень плохо оправдывается (сообщалось о достижении
эффективности преобразования выше 93%!), и сейчас мы попытаемся вывести
характеристики ОРО без использования этой аппроксимации.
Для этой цели вспомним уравнения распространения для фаз и амплитуд
различных полей (смотрите рис. 12.В.9):
и \Z ) = ки -у \7 ) и ■> \Z )sin ф \Z ) A2.E.I a)
d z
— w2(O= KuXz)^,(z)sin ф^) A2.Е.16)
— uAz)= -Kul(z)u2(z)sm ф^) A2.E.1#)
d^
A.^(z)= tfilzM^i^cos ф(г) A2.Е.1г)
C0S фк) (i2i)
u7(z)
Ы^}С0$ фЬ) (П.ЕЛе)
фзA) фЬ)
dz u,(z)
Здесь: ф= фъ— ф{ — ф2 есть относительный нелинейный фазовый сдвиг, а к —
нелинейный коэффициент связи, определяемый соотношением к = (z^/lcjico^co^n^n^2.
Из соотношения A2.ЕЛ) можно получить четыре величины, которые постоянны в
процессе распространения (при этом три из них являются независимыми):
Г = uXz)u2(z)u3(z)cos 4>(z) A2.Е.2я)
щ = u2(ZJ + u3(ZJ A2.E.26)
m3=ul(zj-u2(zy A2.Е.2г)
Эти константы распространения определяются граничными условиями. Более того,
закон сохранения энергии может быть легко записан в виде:
axux{zj + a2u2{zf + u3(ZJ = ^£- = Рс A2.Е.З)
соъ
Здесь: а. = со./со3 — есть квантовые дефекты ОРО, а Рс — полная оптическая
мощность, циркулирующая по резонатору.
(ft 496 Дополнения к главе 12
^=^
Резонатор обеспечивает эффект обратной связи применительно к различным
рециркулирующим полям, что приводит к следующим стационарным
самосогласованным уравнениям для полевых амплитуд Е. между входом при z = 0 и выходом
кристалла при z = L:
A2.E.4)
Здесь: V/?. и 0. есть коэффициент отражения и дефазпровка, вызванная зеркалом,
соответственно для сигнальной и холостой волн; L! есть длина резонатора за
пределами кристалла для моды /. С другой стороны, A2.Е.2) и A2.Е.З) гарантирует, что
входная и выходная мощности равны и определяются формулой:
= 2Z^ = ц2 = 2 + A _ ^ 2 + A _ ^ ^ 2 = 2 Е
Здесь: м/0 = м@) и и/£ = и.A).
В том случае, когда ОРО работает выше порога в стационарном режиме,
частоты генерации сигнальной и холостой волн определяются соотношением
сохранения энергии со{ = со2 + со3, а также уравнением кругового обращения A2.Е.4) для
различных полевых амплитуд. В результате этого, характеристики частотной
перестройки ОРО сильно зависят от величины и резонансной природы различных
полей в резонаторе, как мы увидим это ниже. Теперь мы исследуем решения этих
связанных уравнений соответственно в конфигурациях SROPO и DROPO.
12.Е.1. ОРО с одиночным резонансном
Таким образом, для конфигурации SROPO мы предположим, что коэффициент
отражения для холостой волны равен нулю, т. е., что г2 = 0. В этом случае
самосогласованные уравнения записываются в виде:
i/,@)=r,i/1(L) A2.E.6fl)
и2@)=0 A2.Е.66)
rt(O)-a(l)=*I+A:II + ^ A2.E.6*)
При этом мы помним, что полная фаза электрического поля в нелинейном
кристалле составляет 0{(z) + k{z. Условие A2.Е.6) означает, что константа движения Г
есть Г = 0 в A2.Е.2я) и, таким образом, поскольку ux(L)u2(L)uz(L) ф 0 выше порога,
то cos^(z) = 0. Таким образом, порог достигается, как только фаза </>(z) идентична
(л/2) + рл, где р есть целое число. Знак sin^ (т. е. четность р) имеет большое
значение в A2.Е.1<2—в): он говорит о том, вливается или ли энергия накачки в сигнал или
наоборот.
Из A2. ЕЛ г— е) можно заключить, что три фазы 0.(z) (/ = 1, 2, 3) являются по
отдельности постоянными и, в частности, что фх(Ь) = ^,@). В этом случае
уравнение A2.Е.6#) имеет простое следствие:
kxL + — £.' + &! = 2тл, где т есть целое число A2.Е.7я)
с
Таким образом, мы вновь получаем в нашем общем случае простое и интуитивное
условие, что SROPO генерирует только тогда, когда сигнальное поле резонансно в
резонаторе, что и определяет гребенку возможных сигнальных частот сох или продольных мод
подобно тому, как это имеет место в лазере, что дается точным уравнением:
Щ=т 2лС A2.Е.76)
L + пщ )Ь
Теперь, используя A2.Е6я) и A2.Е.66), уравнения сохранения потока A2.Е.2),
получаем:
12.Е. Характеристики непрерывных параметрических генераторов... 497
Щ = «зо = An A2.Е.8я)
тъ = и20 = Rxu2XL = и2и - u\L A2.Е.86)
«il+< = Riuh+Pb A2.Е.8*)
Здесь: амплитуды сигнальной и накачивающей волн на входе кристалла
(соответственно u3L и ulL) должны быть определены в функции входной мощности иъ\. На
время предполагая, что энергия перетекает от накачки к сигнальной волне,
получаем для формулы A2.Е.16), описывающей эволюцию холостой волны, следующее
выражение:
j-u2 = к^-иЦт,+и1) A2.Е.9)
Это выражение может быть формально проинтегрировано, что дает:
kL
= Г d A2.E.10)
Это последнее выражение представляет собой хорошо известное решение в виде
обратных функций Якоби:
u2(b)= i
-^Ч A2.Е.11)
Представляется не бесполезным напомнить следующее определение обратных
функций Якоби:
Обратная функция Якоби
В этом случае использование условия сохранения потока для накачки в пределах
всей длины кристалла (уравнение 12.Е.86) приводит к следующей записи (A2.Е. 11):
Уравнение A2.Е.13) является точным и оно дает величину амплитуды сигнала на
выходе кристалла в функции входной мощности р.п.
Давайте сначала найдем порог генерации SROPO: в этом случае амплитуда
сигнала u.L -^ О при ненулевой амплитуде накачки и30 ф 0. Поскольку sn(ix|/w) ~ i sinh(x),
когда т -> 0, из A2.Е.13) можно получить величину нормированной пороговой
накачки р:
pg=
Эта есть как раз та величина, которая получается в линейной теории
SROPO(ypaBHeHne A2.49); очевидно, что эта теория верна в том случае, когда
сигнал имеет исчезающе малую амплитуду в кристалле. При введении нормированных
переменных X = рт /ps и Y = u?L /ps точное уравнение, дающее нормированную
мощность сигнала Уна выходе кристалла в функции нормированной входной
мощности X, принимает вид:
sn> icosh ' L/yU/f.-L =i__L A2.E.15)
Дополнения к главе 12
Нормированная выходная мощность сигнала Y' есть произведение Уна
пропускание зеркала, т. е.:
Г=A-Л1)Г A2.Е.16)
Уравнение A2.ЕЛ 5) выполняется для любой величины мощности накачки и
его решение зависит от одного единственного параметра: коэффициента
отражения для сигнала Ry Оно легко решается с использованием компьютерной
программы. В качестве примера на рисунке 12. ЕЛ приведены кривые зависимости У от X
(т. е. характеристики нормированной величины Pout — Pin) для коэффициента
отражения для сигнала Rx = 90%.
В случае больших значений коэффициента отражения зеркал, т. е., когда
8 = 1 - R{ -> 0, из A2.ЕЛ 5) может быть получено ассимптотическое выражение.
С использованием аппроксимации cosh'^l/^l — 8) « V<?A2.E.15) может быть
записано в виде:
A2.Е.17)
Ассимптотическую величину этого последнего выражения достаточно сложно
определить, в случае, когда 8 -> 0. Можно показать, что как только коэффициент
отражения превысит 80%, A2.ЕЛ 7) станет хорошо аппроксимироваться
универсальным соотношением, которое не зависит от коэффициента отражения:
X ~—£_ A2.Е.18)
sin2 л/Г
Вблизи порога (Х~ 1) с использованием разложения в ряд Тейлора это выражение
можно записать в следующем виде:
A2.Е.19)
Это выражение при выходной мощности на частоте cov которая дается выражением
1 out, 1
A — R)cqu?J2Z' приводит к соотношению:
7
6
5
4
3
2
10
7
6
5
4
3
2
1
| Я, = 0.9
-
-
-
; DROPO
-
я ^Г
/
/ ....
DROPO
(Я2 = 0.9)
. ..1 \
(Я2 =
/
/
/
/
/
•
= 0.2)х /
/
#
/SROPO (Я2
i
i
i
•
i
i
■ ы ■■■■■!
-
-
= 0)
-
-
■
я
■
10
5 6 7 8 9
100
Рис. 12.ДЛ. Связь между РоШ и P.v для ОРО с простым резонансом (/?, = 0,9), ОРО с
двойным резонатором (R{ = R2 = 0,9) и DROPO (/?, = 0,9, Л, = 0,2).
12.Е. Характеристики непрерывных параметрических генераторов...
±™± = в±±\ p=--l A2.E.20)
щ co3 v Ps
Характеристики SROPO
в непрерывном режиме
Коэффициент пропорциональности 6 в A2.Е.20) является достаточно
неожиданным, но он может быть выведен прямо с учетом того, что сигнальное поле Е{
практически фиксировано в резонаторе и что поля Е3 и Е2 соответственно накачки
и холостой волны представляются косинусной и синусной функциями положения
в резонаторе.
Внимательный анализ A2.ЕЛ 5) показывает, что выходная мощность может быть
полностью обедненной (u3L = 0 или, что эквивалентно, Х= Y') при входной
мощности р , определяемой соотношением:
iKLyfp^ = sn
A2.Е.21)
Это выражение после проведения утомительных операций алгебры эллиптических
функций приводит к следующей формуле:
V _ ^sat _
Здесь К есть эллиптический интеграл
-К2 -
Я
A2.Е.22)
Рисунок 12.Е.2 иллюстрирует изменение интенсивности насыщения Xsat в функции
коэффициента отражения Rr Численное исследование показывает, что Xsat слабо
зависит от R (в диапазоне от 0,5 до 0,99), т. е. Хш « 1Р@) = (л/2J « 2,4. Для входной
мощности, большей этой величины, часть мощности сигнальной и холостой волн
преобразуется в кристалле обратно в мощность накачки. Таким образом, входная
мощность р^х есть оптимальная мощность накачки, для которой эффективность
ОРО составляет 100%, т. е. вся входная мощность накачки преобразуется в
сигнальную и холостую волны.
Рис. 12.Е.2. Нормированная
мощность насыщения ОРО в
функции различной величины
коэффициента отражения
зеркала. При этих значениях
эффективность ОРО составляет 100%.
Одновременно при такой
входной мощности происходит
полное истощение пучка накачки.
2
О
1
3
о
4.0
3.5
3.0
2.5
2.0
1.5
0.0
DROPO (Ri
0.2 0.4 0.6 0.8 1.0
Коэффициент отражения зеркала
Дополнения к главе 12
12.Е.2. ОРО с двойным резонансом:
сбалансированный DROPO
В случае DROPO самосогласованные уравнения принимают вид:
Ul@)= rlUl(L) A2.Е.23*)
u2@)=r2u2(L) A2.E.236)
()() ^ A2.Е.23*)
2т1х A2.Е.23г)
С
Здесь мы предусмотрели возможность того, что имеется две различные длины
резонатора для сигнальной и холостой волн (L{\ L2'). В том, что касается фазовых
условий, следует отметить, что ни одна из волн (сигнальная, холостая, накачки) выше
порога не исчезают в любой точке кристалла; это означает, что константа
движения Г может принимать любое ненулевое значение: таким образом, нет никаких
ограничений на величину относительной фазы ^(z).
Относительно амплитудных условий A2.Е.23я) и A2.236) можно сказать, что
уравнение сохранения потока приводит к выражению:
A-Л,)«,аJ = A-Л2)«2аJ A2.Е.24)
Это выражение есть ничто иное, как равенство фотонных потоков сигнальной и
холостой волн на выходе ОРО.
Для простоты мы сначала предположим, что оба коэффициента отражения
равны, т. е. R{ = R2 (например, в случае вырождения): такая ситуация относится к
случаю сбалансированного DROPO. В этом случае u{(z) = u2(z) — u(z) и ф{{£) = </>2(z).
Уравнение A2.Е.23#) приводит к фазовому условию:
Я +/clL + ^--2ml7r = O2 + k2L + ^^-2m27i: = 5ф A2.Е.25)
с с
В рассматриваемом случае система может генерировать в условиях разбаланса,
так как обе части A2.Е.25) необязательно равны нулю. Однако, уходы фаз
^сигнальной и холостой волн должны быть равны по отношению резонансу холодного
резонатора (8ф = 0). Условие A2.Е.25) совместно с сохранением энергии фотонов
(о{ + со2 = а)ъ дают точное уравнение, накладывающее требование, чтобы заданные
значения частоты сигнальной и холостой волн выбирались из «гребенки»
возможных величин, зависящих от двух целых величины /я, и тг Эта «гребенка»
непрерывно транслируется вдоль частотной оси при изменении отстройки 8ф.
Уравнения A2. ЕЛ я—в) показывают, что перенос энергии между накачивающим и
параметрическими волнами максимален при sin^(^) = 0, что означает нулевое
значение константы Г. В этом частном случае, аналогичном SROPO, индивидуальные фазы
fi.(z) постоянны по кристаллу и отстройка 8ф равна нулю. Можно показать и обратное
(а именно: нулевая отстройка приводит к нулевому значению константы Г). Это и есть
случай точного двойного резонанса для сигнальной и холостой волн в резонаторе. На
практике такая ситуация реализуется настройкой длин L[w Ь2'пг. резонанс, как в двух-
резонаторном ОЯОРО.Однако, можно показать, что DROPO может генерировать и в
случае, когда это условие не выполняется, но при этом будет иметь место больший
порог по сравнению со случаем точного резонанса. Держа в уме последнее
ограничение, предположим, что мы имеем дело с точным двойным резонансом так, что Г = 0.
Поскольку т3 = 0, уравнение сохранения мощности A2.Е.2г) в данном случае
имеет вид:
рс = u(ZJ + u3(zJ A2.E.26)
12.Е. Характеристики непрерывных параметрических генераторов...
В этом случае эволюция сигнальной волны описывается выражением:
kL = | „d</ ^ч A2.Е.27)
A2.Е.28)
И в этом случае порог вновь достигается, когда холостая волна uL -> 0 при рс ф 0.
Это дает пороговую мощность для сбалансированного DROPO:
Здесь uL = u(L). Это выражение тривиально интегрируется, что дает:
, ( 1 1 ,
log -— +log
c = log —
\R
A2.Е.29)
В данном случае внутрирезонаторный поток рс связан с р.т и uL соотношением
A2.Е.26), т. е. рс = р.п + Ru*. С использованием тех же самых обозначений, как и в
случае SROPO (X= pjpc и Y= и?/р) выражение для Pout — Р.п A2.Е.28) может быть
записано в нормированном виде:
log
IX + RY +ypT-(\-R)Y
= logl-4=\LlX + RY -l)
A2.E.30)
Уравнение A2.Е.30) действительно только в том случае, когда выходной сигнал Y'
меньше потока накачки, т. е. Y' = A — R)Y< X. Равенство Y' — ^достигается при
мощности насыщения р^, определяемой A2.Е.30), т. е.:
i l + i^i-
рм = Ps(l- R)
A2.Е.31)
При этой величине мощность накачки иЪ1 равна нулю. Вариация
нормализованной мощности насыщения в функции коэффициента отражения зеркал R— Rx — R^
показана на рисунке 12.Е.2, где приводится сравнение с аналогичной величиной для
SROPO. Рисунок показывает, что при коэффициенте отражения R в диапазоне от 0,9
до 1 величина psat составляет около 4ps. При этой величине, т. е. в четыре раза выше
порога, эффективность ОРО составляет 100%. При входной мощности выше этой
величины происходит обращение мощности излучения сигнальной волны в
мощность излучения накачки: в этом случае <p(z) изменяется от л/2 до —л/2 A2.Е. 18).
Этот расчет может быть доведен до логического конца, но он оставляется читателю в
качестве упражнения.
В этом случае рисунок 12. ЕЛ показывает характеристики Pout — Р.т
сбалансированного DROPO для случая, когда коэффициент отражения составляет 90% как для
сигнальной, так и для холостой волны. Можно разложить A2.Е.30) в ряд с тем,
чтобы получить универсальное соотношение для вырожденного DROPO, которое
выполняется ниже насыщения, как только коэффициент отражения начинает
превышать 90%:
1 A2.Е.32)
A2.Е.ЗЗ)
Это выражение может быть представлено в другом виде:
Характеристики Р.т — PMt
сбалансированного DROPO
502 Дополнения к главе 12
Совершенно понятно, что эффективность ОРО равна 1, когда Р.п = Р^х = 4Ps,
что согласуется с A2.Е.31).
12.Е.З. Оптический параметрический генератор (ОРО)
с двойным резонансом: общий случай
И наконец, кратко приведем ниже уравнения, описывающие DROPO в общем
режиме (R{ ф R2), которые имеют значение для практических применений, но
которые достаточно утомительно выводить. В предположении реализации
точного двойного резонанса (Г = 0) и при комбинировании A2.Е.16) и A2.Е.2)
получаем:
KL =
^D
A2.E.34)
Здесь: с учетом соотношения сохранения потока A2. Е.34) константы т{ и т2
определяются соотношением:
Щ =
- R7
A2.E.35*)
A2.E.356)
При использовании функций Якоби, определенных в A2.Е.12) уравнение A2.Е.34)
может быть записано в виде:
R2u22L = sn
>4L
A2.E.36)
-sn iJ/f.
1-/?,
Rx-R2
\-R{
Это последнее уравнение приводит к уравнению A2.Е.13) для случая SROPO
(R2 = 0). Выражение для пороговой мощности ps легко получается при u2L = О,
а именно:
= log
A2.E.37)
Эта формула несколько отличается от обычного выражения, полученного в
уравнении A2.61). И вновь ОРО достигает оптимального условия функционирования
(эффективность = 100%), когда выполняется условие р.п = A — R^u*^ а именно:
sn
1 -
- R,
1 -
A2.Е.38)
-sn 1л/лТ
1 -
1 -
Это выражение позволяет проследить изменение нормированной величины
мощности насыщения Х^х в функции коэффициентов отражения R{ и &,, а именно в области
между случаями SROPO и DROPO (смотрите рис. 12.Е.2). Зависимость
нормированной величины Р — Р имеет, к сожалению, достаточно тяжеловесный вид:
12.Е. Характеристики непрерывных параметрических генераторов...
sn"
1-Я
я-я
Я-
R2Y
-sn"
1-Я
R2Y
A2.Е.39)
В качестве компенсации за тяжеловесность выражения из этой формулы с
некоторыми алгебраическими могут быть получены формулы для всех
экспериментальных случаев, рассмотренных выше, при этом может быть получено выражение для
случая DROPO. Рисунок 12. ЕЛ демонстрирует численные результаты для
характеристик Pout — Рь, полученных для Rx = 90% при коэффициенте отражения /^ = 20%.
Литература
М. Abramovich and I. Stegun, Handbook of Mathematical Tables, Dover Publications,
New York A970).
E. Rosencher and C. Fabre, JOSA В (to be published 2001).
ГЛАВА 13
СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ
И ЛАЗЕРНЫЕ ДИОДЫ
13.1. Введение
В главе 6 мы видели, что полупроводник, выводимый из состояния
термодинамического равновесия, в том случае, когда возбужденные носители заряда могут ре-
комбинировать друг с другом, может излучать свет (в дополнение к излучению
черного тела). К тому же мы установили условие Бернара—Дюррафура, которому
должны удовлетворять энергетические распределения. Сейчас мы покажем, каким
образом эффект излучения света может быть использован в
электролюминесцентных диодах (называемых иначе светоизлучающими диодами или СИД), а также в
лазерных диодах. Рассмотрение этого вопроса потребует использование
содержания, по крайней мере, пяти предыдущих глав:
• главы 4, описывающей лазерные колебания;
• главы 7, рассматривающей различные механизмы оптического излучения в
полупроводниках;
• главы 8, описывающей физику полупроводниковых гетероструктур и квантово-
размерных структур;
• главы 9, рассматривающей волноводные эффекты в оптических гетероструктурах;
• главы 10, описывающей механизмы инжекции в р—я-диодах.
Данная глава достаточно сложна (и в то же время она является и
вдохновляющей!), т. к. затрагивает многие физические концепции, разработанные в рамках
этой книги. При частом использовании материала, разработанного в других главах
мы, тем не менее, найдем время для повторения ряда ключевых концепций с тем,
чтобы при прохождении этой главы читатель не наталкивался на чрезмерное
количество препятствий.
13.2. Электрическая инжекция
и неравновесная концентрация носителей
Обычно излучение света в полупроводнике происходит вследствие
электронно-дырочной рекомбинации в областях, где они обладают концентрацией, избыточной
по сравнению с уровнями, допускаемыми и термодинамическим равновесием.
Единственным исключением в рассматриваемом случае является униполярный квантово-
каскадный лазер, который мы рассмотрим в дополнении 13.И.
Естественно, электронно-дырочная рекомбинация имеет место в прямо
смещенном р—я-переходе, где, как мы увидим, неосновные носители заряда могут
сосуществовать с основными носителями на расстояниях порядка LD (т. е.
диффузионной длины). Этот эффект известен как электрическая инжекция (глава 10). Мы
рассмотрим такой переход, в котором сходятся электронный (JJq) и дырочный (JJq)
потоки (здесь Je и Jh обозначают плотности тока электронов и дырок, a q есть
величина заряда электрона). С учетом требования по электронейтральности мы
имеем Je = Jh = J (смотрите рис. 13.1).
13.2. Электрическая инжекция и неравновесная концентрация носителей
Рис. 13.1. Оптическое излучение в
полупроводнике имеет место в результате
рекомбинации электронно-дырочных пар в
областях, где сосуществуют оба типа
носителей (как это имеет место в р—я-пе- J
реходе). е
р—n-переход
Сейчас проблема заключается в том, чтобы определить объемную плотность
неравновесных носителей пе и nh в переходе. Это позволит нам рассчитать
положение квазиуровней Ферми G.67), скорости стимулированной G.41) и спонтанной
G.47) эмиссии в структуре. Для этого достаточно записать для стационарных
условий, что полная скорость рекомбинации Rioi (см с) в объеме V точно
соответствует падающему потоку носителей, проходящих через поверхность £, т. е.
VRtot = SJJq = SJJq = SJ/q. Исключительно с целью упрощения необходимых
обозначений мы предположим, что уровень легирования вблизи перехода
пренебрежимо мал по сравнению с неравновесной концентрацией носителей. Это обеспечива-
ет выполнение п = пи
п.
Полная скорость рекомбинации Rtot, компенсирующей поток, входящий в
область перехода, отражает вклады, по крайней мере, четырех различных механизмов,
рассмотренных в предыдущих главах, а именно:
• безызлучательной рекомбинации со скоростью Лпп из-за присутствия глубоких
уровней дефектов, поверхностных дефектов,... (смотрите раздел 6.5 и дополнение 5.Г);
• спонтанной излучательной рекомбинации со скоростью Вп2, где В есть
коэффициент бимолекулярной рекомбинации, определяемый G.61) и G.62);
• Оже-рекомбинации со скоростью CAugn3, исследованной в дополнении 6. Г;
• стимулированного излучения со скоростью RstNph, где Rst (= Rahs) есть
коэффициент стимулированного излучения G.41), a Nph есть плотность фотонов.
Для начала сконцентрируем свое внимание на поведении прибора намного ниже
порога, т. е. будем пренебрегать стимулированным излучением GVph = 0). В этом
случае концентрация носителей определяется стационарным условием:
^ = 1±- = ±.= Атп+Вп2+СА„еп> A3.1)
qd qd qd
Здесь d = V/S есть эффективная толщина перехода, т. е. расстояние, в пределах
которого имеет место рекомбинация. Очевидно, что в A3.1) рекомбинационные
члены не эквивалентны. Первый и последний члены не генерируют свет (т. е. они
являются безызлучательными) тогда, как второй член описывает спонтанную
эмиссию в структуре. В связи с этим перегруппируем эти члены следующим образом:
A3.2)
J__J_ J_
'tot 'nr 'rad
Здесь: /rad, tni и ttot соответственно излунательное, безызлдунательное и полное времена
жизни. В этом случае неравновесная концентрация носителей определяется
соотношением:
Глава 13. Светоизлучающие диоды и лазерные диоды
п =
qd
A3.3)
Эта очень простая формула является одним из основных результатов настоящей
главы. Заметим:
• Полное рекомбинационное время ftot зависит от концентрации носителей и,
таким образом, от условий функционирования. Зачастую этот параметр
определяется остаточным уровнем легирования (в этом случаем мы будем заменять
концентрацию носителей п в A3.3) на уровень легирования Л^). В большинстве
случаев этот параметр будет константой, определяемой экспериментом.
• Член Оже-рекомбинации CAugn2 зависит от концентрации носителей и его
значение все более возрастает по мере увеличения концентрации.
• При заданной плотности тока неравновесная концентрация носителей резко
возрастает по мере уменьшения толщины активной области. В случае гомоперехода
эта толщина d определяется LDn + LDp, где диффузионные длины неосновных
носителей LDn (электронов в /ьобласти) и LDp (дырок в я-области) определяются
A0.41) и, как правило, равны величине, лежащей в диапазоне от 1 до 10 мкм
(смотрите рис. 13.2).
Определив неравновесную концентрацию носителей в A3.3), с использованием
G.67), мы можем рассчитать положение квазиуровней Ферми для каждого из типов
носителей.
При выполнении этого возникают три возможные случая:
• спонтанная эмиссия доминирует над стимулированной эмиссией, и диод
функционирует в электролюминесцентном или СИД-режиме;
• среда инвертирована (смотрите критерий Бернара—Дюррафура в G.266) и G.69)),
но при этом резонаторные потери превышают усиление среды, при этом диод
функционирует в режиме оптического усиления (этот режим соответствует
суперлюминесцентному диоду);
• стимулированная эмиссия доминирует над спонтанным излучением, а
резонаторные потери точно компенсируются усилением среды, приводя
функционирование прибора в режим лазерной генерации (это соответствует лазерному диоду).
В течение некоторого времени нас будет интересовать первый из упомянутых
выше случаев.
Fn OOOOO
•iff
п,Р
Рис. 13.2. При заданном потоке носителей концентрация эленктронно-дырочных пар
намного больше в гетеропереходе (б), чем в гомопереходе (д), где более
эффективна диффузия носителей.
13.3. Электролюминесцентные диоды
Пример
Пусть при определенных условиях гетероструктура Al0 25Ga0 75As/GaAs толщиной
d = 10 нм обладает полным рекомбинационным временем жизни величиной 5 не.
Ток величиной 1 мА, пересекающий сечение перехода 10 мкм х 100 мкм приводит
к неравновесной концентрации носителей A3.3):
п = \0~3A х 5 х 10"9 с /(Ю см2 х 1,6х 10"9 Кл х 10 см) = 3,1 х 1018 см
Поскольку эта концентрация носителей превышает эффективную плотность
состояний в зоне проводимости Nc = 4,3 х 1017 см, электронный газ будет
вырожденным, и в этом случае положение квазиуровня Ферми для электронов E.566)
составит:
EFn -Ес = (l,05xl(T34 ДжJ/Bх0,067х0,9х10-30 кг)C^x3,1x1024 мJ/3/1,6х1(Г19 Кл = 116мэВ
Соответственно концентрация дырок р (= п) меньше эффективной плотности
состояний в валентной зоне Nv = 1,3 х 1019 см, при этом положение квазуровня
Ферми, определяемое E.47), составит:
EFp - Ev = 0,0259 эВх ln(l,3x 109 /Зх 1018)= 38 мэВ
В рассматриваемом случае энергетический зазор между электронным и дырочным
квазиуровнями превышает ширину запрещенной зоны, т. е.:
(EFn - Ес)- (EFp - Ev)=\\6 - 38 мэВ > 0
При этом в соответствии с критерием Бернара—Дюррафура система инвертирована.
13.3. Электролюминесцентные диоды
13.3.1. Электролюминесценция
При появлении избыточных носителей в области перехода, они распределяются по
зоне проводимости и валентной зоне, занимая все более высокие энергетические
уровни (смотрите рис. 13.3). При использовании модели с единственной валентной
подзоной распределения носителей могут быть записаны с использованием квази-
уровней Ферми (смотрите раздел 7.6) EFc (для электронов в зоне проводимости) и
EEv (в валентной зоне):
A3.4)
п
N~v
Здесь Fl/2 есть величина, обратная интегралу Ферми—Дирака Fl/2, определяемому
формулой:
1 °% ,.1/2
A3.5)
Как это уже обсуждалось в разделе 7.4, это отклонение от равновесия,
описываемое квазиуровнями Ферми для электронов и дырок, вызывает усиление
спонтанной эмиссиии со спектральным распределением скорости Rspon(hv) в единицу
времени в единичном объеме и энергетическом интервале (для фотонов с энергией
hv), описываемым G.47):
Глава 13. Светоизлучающие диоды и лазерные диоды
СВ
VB
Рис. 13.3. Оптические переходы в
полупроводнике являются вертикальными
(т. е. с сохранением к) по энергии.
Состояния Ec(hv) и Ev(hv) соединены друг с
другом оптическими переходами с
участием фотонов с энергией hv. СВ-зона
проводимости, VB-валентная зона.
—
A3.6)
Для величин, появляющихся в этом выражения мы еще раз напоминаем их
определения, приведенные в главе 6:
• rR есть спонтанное излучательное время жизни в излучающем материале, которое
можно предполагать относительно не зависящим от энергии излучаемых
фотонов. Эта величина является характеристикой данного материала, и она зависит от
физических параметров этого материала (эффективных масс носителей,
матричных элементов Кейна и т. д.), как это описывается G.376).
• p.(hv) есть комбинированная плотность состояний G.19). Этот параметр учитывает число
состояний, удовлетворяющих требованиям сохранения энергии hv = EcQs) — Ev(k) и
квазиимпульса (постоянное значение к) для переходов между состояниями с
энергией Ev(k) в валентной зоне и Ес(к) в зоне проводимости (смотрите рис. 13.3).
• fc {hv) и fv(hv) есть функции Ферми—Дирака, описывающие заселенность
состояний, связанных оптическими переходами, т. е. удовлетворяющих G.256, в):
/»=■
1 + ехр
)- EFc
кТ
A3.7а)
mr
1
(E(hv)-£Fv
+ ехр[ кт
A3.76)
13.3. Электролюминесцентные диоды
Как правило, в случае электролюминесцентных диодов концентрация
избыточных носителей достаточна мала, что оправдывает аппроксимацию функций
Ферми—Дирака функциями Больцмана, что соответствует тому, что квазиуровни
Ферми далеки от экстремумов зон. Как было показано в главе 7, в этом случае
спектральная зависимость скорости спонтанной эмиссии может быть существенно
упрощена, что дает (смотрите 7.52а):
hv - Eg
kT
Здесь Kspon определяется формулой:
-ехр -
кТ
A3.8)
A3.9)
При этом AEF есть энергетический зазор между квазиуровнями Ферми AEF = EFc - EFv.
Очевидно, что по мере возрастания концентрации избыточных носителей п
множители ехр (EFJkT) и ехр (—EJkT) также возрастают, приводя к тому, что
спектральная зависимость скорости Rspon(hv) пропорциональна я2, что и неудивительно.
Форма спектральной линии спонтанной эмиссии определяется A3.8). Тривиальным
образом можно показать, что максимальная интенсивность излучения достигается
при /zvpeak = Eg + кТ/2, при этом полуширина линии составляет Ahv~
1,8/:Т(смотрите рис. 13.4).
Поскольку /lpeak и /zvpeak связаны соотношением Лреак(мкм) = l,24//*vpeak (эВ), мы
сразу находим, что на шкале длин волн полуширина АЛ связана с пиковой длиной
волны следующим выражением:
АЛ = 1,45ДреакА:Г A3.10)
На рисунке 13.5 представлены спектральные распределения плотности
излучения СИД, изготовленных на основе различных полупроводников. Как и
предсказывается формулой A3.10), спектры излучения становятся уже (на шкале длин волн)
по мере изменения энергии излучения от инфракрасного к ультрафиолетовому
диапазону спектра.
Рис. 13.4. Спектральное распределение скорости спонтанной эмиссии. Полуширина
спектра составляет величину порядка 1,ЪкТ.
ufs 10 Глава 13. Светоизлучающие диоды и лазерные диоды
3 18
4 0 3.513 0 2.5 2.0 1.61 15
10
УФ*
►ИК
GaAs014P086
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
Л (мкм)
Рис. 13.5. Спектральные распределения излучения СИД на основе различных
полупроводников. Спектральная полуширина пропорциональна Д2сак, как это
предсказывается формулой A3.10). (Из книги S.Sze: Physics of Semiconductor
Devices, copyright © Wiley Interscience, New York A981).
13.3.2. Внутренняя и внешняя эффективность СИД
Сместим теперь центр нашего внимания со спектрального распределения Rspon(hv)
излученной энергии на полную интенсивность Rspon, соответствующую оценке
интеграла A3.6) по полной зонной структуре полупроводника. Такое интегрирование
уже было проведено в разделе 7.5. Сейчас же мы уже способны показать, что
скорость излучательной рекомбинации в случае, когда концентрации носителей
далеки от вырождения (как это имеет место в случае СИД), дается (смотрите G.62) и
G.65) соотношением:
Л*ро„ = Вп.п„ = у- A3.11)
'rad
Здесь: frad есть время жизни излучательной рекомбинации, а В — коэффициент
бимолекулярной рекомбинации, связанный с излучательным временем rR в
соответствии с G.62). В этом случае полный поток фотонов Ф, генерируемый объемом
перехода V принимает особенно простой вид:
Ф = Rspon L = JLd A3.12)
^ 'rad
Введем теперь коэффициент rj., определяемый соотношением:
*" 1 A3.13)
/„
rad / ' nr
Внутренняя квантовая эффективность
Этот коэффициент rj. есть внутренняя квантовая эффективность СИД. Он
определяет процентную долю электронно-дырочных пар, способных освободить свою
запасенную энергию в виде излучаемых фотонов сразу после акта рекомбинации. С
учетом A3.3) мы видим, что поток излучаемых фотонов определяется соотношением:
Ф = /7, —
A3.14)
13.3. Электролюминесцентные диоды
Это последнее уравнение ясно показывает ту роль, которую играет внутренняя
квантовая эффективность в том, что касается эффективного преобразования потока
носителей J/q в поток фотонов Ф.
Несмотря на это далеко не весь свет, излучаемый р—«-переходом, способен
покинуть полупроводник. В действительности, электролюминесцентное излучение
является не направленным, а характеризуется ламбертовской диаграммой
направленности. Рисунок 13.6 иллюстрирует все оптические механизмы, дающие вклад в
уменьшение полной эффективности СИД:
• б^-лучи (т. е. лучи, составляющие малый угол с вектором нормали к поверхности)
проходят через полупроводниковый материал, который поглощает определенную
долю излучаемого света. Очевидно, что это поглощение может быть уменьшено в
гетеропереходе за счет соответствующего выбора для п- и /^-областей, образующих
гетеропереход полупроводников с шириной запрещенной зоны, превышающей
энергию фотонов, генерируемых структурой. Тем не менее, все равно небольшая доля
малоугловых лучей излучения будет испытывать частичное отражение от границы
раздела полупроводник/воздушная среда. Доля ndicl перпендикулярно падающего
света, пропускаемого границей раздела (т. е. диэлектрическая эффективность),
дается уравнением Френеля:
wdiei = 1 ""Н2 7v~ = 7 S£Tu" A3.15)
Здесь пх есть коэффициент оптического преломления полупроводникового
материала. В случае GaAs (пх = 3,6) эффективность пропускания составляет 0,7.
Эта эффективность возрастает по мере уменьшения оптического коэффициента
преломления полупроводника (т. е. в случае диодов, излучающих на более
коротких длинах волн). Это, например, было подтверждено в случае светоизлуча-
ющих диодов на основе GaN, излучающих в голубой области спектра, для
которых пк = 2,3 и /7dieI = 0,85.
• 02-лучи, излучаемые за пределами конуса, задаваемого критическим углом #,
отражаются полностью. Если бы процесс на этом бы и закончился, то
эффективность СИД была бы катастрофически мала. В рассматриваемом случае доля
излучаемого света составила бы только 4%! В действительности же ситуацию улучшает
то, что известно как эффект рециклирования фотонов. Часть фотонов, отраженных
обратно, поглощается с образованием электронно-дырочных пар и, как следствие,
имеется некая вероятность, что они смогут пройти через границу раздела
полупроводник/воздух после повторного излучения. Комбинация всех этих процессов
определяет эффективность пропускания rjt, которая, будучи умножена на
внутреннюю квантовую эффективность, дает долю электронно-дырочных пар,
преобразуемых в фотоны, способные покинуть СИД. Внешняя мощность излучения Pcxt
в этом случае дается произведением вышедшего из СИД фотонного потока на
энергию излученных фотонов:
A3.16)
Рис. 13.6. Лучи, составляющие угол вх относительно к нормам и поверхности СИД,
испытывают частичное френелевское отражение таким образом, что при
больших углах в2 имеет место полное отражение.
Глава 13. Светоизлучающие диоды и лазерные диоды
Здесь: rjcxt есть внешняя квантовая эффективность, определяемая как rjext = 77Д.
В практике принято использовать такую величину как энергетическую отдачу
91 (Вт А) для СИД, определяемую как отношение плотности мощности
излучения и плотности тока прямого смещения /*, т. е. 91 = Pext/J:
*=ЛС« — = ПС«^ A3.17)
Энергетическая отдача СИД (Вт А)
на определенной длине волны
Теперь мы можем поставить вопрос об энергетической эффективности
электролюминесцентного диода. В том случае, когда последовательное сопротивление
мало, прямое напряжение смещения, необходимое для получения эмиссии, будет
связано с шириной запрещенной зоны, т. е. hv/q. В этом случае электрическая
мощность, прикладываемая к диоду, составляет /х hv/q. Уравнение A3.16) дает
нам энергетическую эффективность диода PtJ(J х hv/q) или ~77ext. Таким образом
энергетическая эффективность тесно связана с внешней квантовой
эффективностью rjcxt (в пределах учета влияния последовательного сопротивления), т. е. в
пределах порядка 20%. Эту величину можно сравнить с энергетической эффективностью
лампы накаливания в видимой области спектра на уровне 1%, в которой остальная
часть энергии (99%) рассеивается в виде тепла.
Примеры
1. СИД на основе GaAs/Al0 25Ga0 75As излучает на пиковой длине волны 0,87 мкм.
Его внутренняя квантовая эффективность составляет 50%, а диэлектрическая
эффективность равна 20%. Таким образом энергетическая отдача СИД составляет:
91 = 0,5x0,2x1,24 мкм/0,87 мкм = 0,14 ВтА1
В предположении тока накачки 20 мА мощность оптического излучения
составит 2,8 мВт.
2. Диод на основе InGaN/GaN излучает на пиковой длине волны 0,4 мкм.
Внутренняя квантовая эффективность составляет 50% в то время, как диэлектрическая
эффективность составляет 40% (коэффициент оптического преломления GaN
составляет 2,3). В этом случае энергетическая отдача диода составляет:
91 = 0,5 х 0,4 х 1,24 мкм / 0,4 мкм = 0,62 ВтА1
При токе накачки 20 мА внешняя мощность излучения СИД составит 12,4 мВт, что
явно больше, чем в случае СИД на основе GaAs/AlGaAs*.
3. Коэффициент бимолекулярной рекомбинации В для GaAs приведен в
таблице 7.1 раздела 7.5 (В = 7,2 х 10~10 см3 с). В предположении, что уровень
легирования гетероструктуры составляет ND = 2 х 1017 см постоянная времени излучатель-
ной рекомбинации /rad, определяемое G,65), составит frad = \/BND =7 не.
Предполагая, что безызлучательное время жизни составляет 5 не, находим, что внутренняя
квантовая эффективность в рассматриваемом случае составит 42%.
13.3.3. Несколько приборных вопросов
В настоящее время имеются три основные области применения СИД:
индикаторные панели, подсветка, системы передачи информации с умеренной скоростью
передачи. Эти приборы достаточно экономичны, поскольку могут производиться с
использованием массовой технологии. Рисунок 13.7 иллюстрирует типичную конст-
Прим. ред.: В данном случае под /понимается прямой ток смещения, а не его плотность.
13.3. Электролюминесцентные диоды 513
Контакт
аАз.. Р.
Контакт
Рис. 13.7. Приборная структура СИД с прозрачной подложкой.
рукцию электролюминесцентного диода. В данном случае слои GaAsx Pl _х эпитак-
сиально выращиваются на подложке GaP. При этом состав х изменяется от 0 (GaP)
до х = 0,35 (£,(GaAs0 35Р0 65) = 0,62 эВ)*, что обеспечивает условия постепенного
согласования постоянных решетки между подложкой и электролюминесцентным
слоем. После синтеза структуры на ее поверхность осаждается SiO2, и она текстури-
руется с использованием стандартной литографической техники для вскрытия окон
в диэлектрическом слое. После этого проводится диффузия акцепторной примеси
через окна в SiO2, и, наконец, металлические слои осаждаются на верхнюю
поверхность (это обеспечивает контакт с материалом /ьтипа) и на тыльную сторону
подложки. Поскольку GaP прозрачен для излучаемого света, свет,
распространяющийся по направлению к подложке, отражается металлизацией обратно в направлении
к поверхности. Это приводит к увеличению внешней квантовой эффективности
электролюминесцентного диода. Все, что остается сделать — это разрезать
пластину на кристаллы (или чипы) и индивидуально смонтировать их в корпусах со свето-
выводящим окном. Предполагая, что типичные размеры поверхности кристалла
СИД составляют 100 х 100 мкм2, мы можем ожидать получение около 200 000
дискретных приборов из пластины с площадью поверхности 20 см2 (т. е., выражаясь на
«микроэлектронном жаргоне», из двухдюймовой пластины).
Процесс спонтанной эмиссии в полупроводнике является изотропным, .при этом
диаграмма направленности излучения имеет ламбертовский характер (т. е.
изменяется в соответствии с cos# — смотрите рисунок 13.8д). Обычно для усиления
направленности и увеличения силы света СИД в его корпус обычно встраивается
параболическая линза из эпоксидной смолы (смотрите рис. 13.8).
Рис. 13.8. Диаграмма направленности электролюминесцентного излучения имеет
ламбертовский характер (а). Для увеличения яркости СИД они корпусируются
с использованием параболических линз из эпоксидной смолы (б).
* Прим. ред.: для GaAsO35Po 65:N Eg = 2 эВ.
Глава 13. Светоизлучающие диоды и лазерные диоды
И наконец, времена отклика СИД равны полному рекомбинационному
времени ftot. Как отмечается в специальной литературе по этому вопросу, эти времена
лежат в диапазоне от 1 до 50 не, что соответствует сравнительно скромной
величине частот порядка нескольких сотен МГц.
13.4. Оптическое усиление в диодах с гетеропереходами
В разделе 13.3 основное внимание уделялось спонтанному излучению. Однако в
главе 7 мы видели, что в том случае, когда полупроводник выводится
возбуждением достаточно сильно из состояния термодинамического возбуждения, становится
возможным достижение инверсии заселенности между электронами в зоне
проводимости и дырками в валентной зоне. Тогда мы даже сумели получить условие
прозрачности, т. е. концентрацию заряженных носителей «transp в зонах,
необходимую для того, чтобы материал был эффективно прозрачен для излучения, и при
превышении которой материал проявляет усиление (смотрите G.69)). На языке тока
электрической инжекции A3.3) это означает, что материал становится прозрачным,
когда он возбуждается плотностью тока прозрачности Jtransp, определяемой:
A3.18)
Здесь: Nc и Nv есть соответственно эффективные плотности состояний в зоне
проводимости и валентной зоне. При возбуждении выше этого порога прозрачности
усиление будут испытывать фотоны с энергией hv, удовлетворяющей критерию
Бернара—Дюррафура:
Eg <hv <EFc-EFv A3.19)
В контексте оптической восприимчивости усиление среды с усилением y(hv) было
рассчитано в разделе 7.3 при обсуждении скоростных уравнений. Эти результаты
настолько важны, что мы должны воспроизвести их здесь. Усиление дается формулой:
y{hv)= a0(co[fcQiv)- /v(/*v)]) A3.20a)
Здесь а0 есть поглощение пустой зоны проводимости (т. е. в условиях нулевого
тока), определяемое выражением:
\3/2
" ^ A3.206)
Напоминаем, что^ nfv есть функции Ферми—Дирака, определяемые A3.7),
a xvc есть матричный элемент, определяемый G.11), тг — приведенная
эффективная масса G.13), nsc — коэффициент оптического преломления
полупроводника, а Яо — длина электромагнитной волны с частотой со в вакууме.
Уравнение A3.20а) может быть также записано в форме, которая лучше
напоминает аналогичные уравнения для лазерных атомарных переходов, введенных в
главе 4:
A3.20*)
Понятно, что в A3.20#) множитель Pj(hv)(fc — f) играет роль g(hv)(N2 ~ N{)b
уравнениях для лазера на атомных переходах.
Таким образом, по мере того, как плотность тока /, протекающего через диод
становится все более важной, увеличивается и концентрация носителей,
определяемая A3.3). Это приводит к тому, что квазиуровни Ферми, определяемые A3.4), все
больше и больше проникают в зоны, что приводит ко все большей и более
широкой кривой усиления A3.20я) — смотрите рисунок 13.9. Рисунок 13.10 показывает
13.4. Оптическое усиление в диодах с гетеропереходами
hv
Рис. 13.9. Инверсия заселенности и оптическое усиление в полупроводниковой среде.
Этот рисунок иллюстрирует уравнение( 13.20) и представляет две зоны,
участвующие в процессе (а). Рисунок (б) показывает соответствующие
распределения Ферми—Дирака для квазиуровней Ферми в зоне проводимости и
валентной зоне. Рисунок (в) показывает кривую усиления среды (сплошная
жирная линия), являющуюся произведением коэффициента поглощения
ao(hv) (бледная линия) и коэффициента заполнения}^ — fv (жирная линия).
Символы А и □ обозначают фотоны с энергией, соответственно
удовлетворяющей и не удовлетворяющей условию Бернара—Дюррафура. СВ и VB —
соответственно зона проводимости и валентная зона.
Глава 13. Светоизлучающие диоды и лазерные диоды
-200
1.50
1.52
1.54
1.56
1.58
/7У(ЭВ)
Рис. 13.10. Зависимости усиления от плотности тока инжекции для гетероструктуры
GaAs/AlGaAs толщиной 100 нм в предположении, что излучательное
время жизни составляет 5 не при внутренней квантовой эффективности 0,5,
что соответствует ttot = 2,5 не. В данном случае плотность тока
прозрачности составляет 760 А см.
результирующие кривые усиления для разных уровней тока инжекции. Как нам уже
известно из раздела 7.7 и рисунка 7.7, максимальное усиление утах (являющееся
одним из наиболее важных параметров этих кривых, поскольку лишь ближайшие к утах
моды будут генерировать) возрастает практически линейно с увеличением
концентрации носителей п в области выше порога прозрачности ntiua . Общепринятым
является использование для сложной зависимости утах от п линейной аппроксимации:
Утах — У0
transp
-1
A3.21)
Здесь: параметр у0 выбирают методом оптимального подбора. При
концентрации п в диапазоне от 0 до «transp среда является поглощающей. При п > nXmnsp материал
становится прозрачным и зависимость утах от п хорошо воспроизводится.
Уравнение A3.3) позволяет нам переписать это выражение в виде зависимости
от плотности тока /. В этом случае максимальное усиление утах дается выражением:
Утях ~~ /о
— 1
A3.22а)
Здесь: плотность тока прозрачности определяется A3.18) и связана с Htransp
соотношением:
qd
A3.226)
Пример
Рассмотрим усиление, обеспечиваемое лазерным диодом на основе двойного
гетероперехода GaAs/AlGaAs. Из экспериментов установлено, что время жизни из-
лучательной рекомбинации frad составляет 5 не. Из рисунка 7.7 следует, что
пороговая концентрация носителей, соответствующая прозрачности п , составляет
1,2 х 1018 см 3. Предположим, что диод обладает квантовой эффективностью
толщина его активной области d составляет 100 нм, ширина и длина
соответственно равны 10 и 300 мкм. В этом случае пороговая плотность тока
прозрачности /transp составляет:
13.5. Лазерные диоды с двойным гетеропереходом
Рис. 13.11. Изменение максимального
усиления полупроводникового перехода в
функции плотности тока инжекции в
рамках модели линейной аппроксимации.
'max
I
I
Q.
transp
Amnsp = 1,6 x 1019 Кл x 10 см x 1,2 x 1018 см /(o,5 x 5 x 10~9 c) = 760 Асм или 23 мА
При концентрации носителей п= 2,4 х 1018 см~3 (что соответствует уровню, вдвое
большему порога, и току инжекции 46 мА) максимальное усиление составляет 300 см.
Это приводит к усилению G в структуре величиной ехрC х 102 см х 3 х 10~2 см)
или 8100.
Полупроводниковые оптические усилители (SOA) используются в качестве
усилительных каскадов на выходе лазерных диодов (в этом случае их обычно называют
монолитными оптическими усилителями — МОРА). В рассматриваемом случае одна
из проблем заключается в том, чтобы они находились в режиме лазерной
генерации. С этой целью для устранения обратной оптической связи на выходные окна
наносятся антиотражающие покрытия (R < 106). Более того для максимального
извлечения энергии из этих приборов их резонаторам придается рупорная форма.
Это делает резонатор нестабильным, что препятствует формированию
стационарных оптических мод в спектральном диапазоне усиления (смотрите рисунок 13.12).
13.5. Лазерные диоды с двойным гетеропереходом
13.5.1. Лазерный порог
Полупроводниковый р—«-переход, возбужденный до уровня выше порога
прозрачности, будет способен усиливать те электромагнитные моды (т. е. фотоны),
которые удовлетворяют критерию Бернара—Дюррафура. Как это описывалось в разделе
4.4, в среде будут наблюдаться лазерные колебания, если в ней обеспечены условия
обратной оптической связи. Существует ряд методов, обеспечивающих
необходимую обратную связь, которые описаны в дополнении 13.А. Простейший из них
заключается в использовании естественного зеркала в виде границы
полупроводник/воздух. В этом случае полупроводниковый резонатор получают скалыванием
полупроводникового кристалла в двух различных местах вдоль той же самой
кристаллографической плоскости, что обеспечивает идеально параллельные зеркала
(смотрите рис. 13.13). Граница раздела полупроводник/воздух обеспечивает
диэлектрическое зеркало с коэффициентом Rm, определяемым соотношением:
A3.23)
Глава 13. Светоизлучающие диоды и лазерные диоды
n
p
• •
о
с
о
о
о о
та
о о
о
с
У
\
г\Л/\/\Р>
Антиотражающее покрытие
Рис. 13.12. Функционирование оптического полупроводникового усилителя (SOA).
Падающая волна, например, от выходного лазерного диода, усиливается
прямосмещенным переходом (а). Одной из проблем при проектировании
SOA является необходимость получения прибора с высоким усилением без
режима собственной лазерной генерации. С этой целью для
предотвращения возможности формирования стационарных оптических мод на длине
волны усиления используются антиотражающие покрытия и рупорная
геометрия прибора.
В случае GaAs, nx = 3,6 и коэффициент отражения составляет Rm = 0,32. Эта
величина может показаться малой по сравнению с параметрами зеркал,
используемых в других типах лазеров (например, в газовых, ионных лазерах,...). Однако
усиление, обеспечиваемое полупроводниковыми лазерами (вплоть до нескольких тысяч
см), представляется значительным по сравнению с уровнями, обеспечиваемыми
альтернативными лазерными средами. И как результат этого, использование сильно
отражающих зеркал не является обязательным требованием для наблюдения
лазерной генерации в полупроводниковых приборах. Физическую природу такого
большого усиления в полупроводниках можно вскрыть, сравнив выражения для усиления
в конденсированной (fij<hv)(fc -/)Л2/Ъятк) и атомной (g(hv)(N2 - ЛГ)Д2/8/ггЛ) средах:
• Концентрация имеющихся центров излучения (несколько 1018 см) намного
превосходит уровни, достижимые в газовых средах A015 см).
• Оптические поперечные сечения также намного больше для электронов в зонах
по сравнению с электронами на атомных орбиталях. Таким образом, на длине
волны ~1 мкм в ионных или газовых лазерах типичное излучательное время жиз-
13.5. Лазерные диоды с двойным гетеропереходом
U
Рис. 13.13. Конфигурация полупроводникового инжекционного лазера с двумя
зеркалами, полученными скалыванием.
ни составляет величину порядка 1 мс, в то время как в полупроводниках этот
параметр составляет величину порядка нескольких наносекунд. Это связано с де-
локализованной природой электронов проводимости в конденсированной среде.
В разделе 4.4 мы видели, что лазерные колебания возникают, когда усиление
усиливающей среды стремится превысить резонаторные потери в оптическом
резонаторе.
Имеется несколько типов потерь:
• Собственные потери ат как следствие потери фотонов при прохождении через
зеркала (до некоторой степени необходимые, так как свет должен иметь
возможность покинуть резонатор!). Это описывается соотношением D.216) в виде:
1
" 2L П
RmXR
A3.24а)
Здесь мы допустили возможность того, что зеркала имеют различные
коэффициенты отражения (Rml и Rm2). В случае, когда одно из зеркал является полностью
отражающим, порог генерации уменьшается. L есть длина резонатора.
Паразитные потери а как результат поглощения свободных носителей в
контактных слоях, вследствие рассеяния на шероховатости поверхности и т. д.
В этом случае условие достижения лазерного порога D.216) принимает вид:
A3.246)
^threshold ~^P^lfR R
Это последнее выражение не учитывает тот факт, что усиленные моды (фотоны)
должны удовлетворять уравнениям Максвелла в гетеропереходе. Соответственно
такая структура ведет себя как волновод. В двойной гетероструктуре потенциальные
барьеры, обладающие большей шириной запрещенной зоны по сравнению с кван-
тово-размерным материалом, характеризуются меньшим коэффициентом
преломления так, что электромагнитные волны остаются захваченными в среде с большим
коэффициентом преломления (и, что более важно, остаются в области усиления —
смотрите рис. 13.14)). В главе 9 (мы видели, что электромагнитное поле ограничено
в структуре вдоль оси Ох, перпендикулярной к границам раздела, и что
коэффициент распространения /? зависит от индексов поперечной моды (смотрите,
например, (9.13)). Доля энергии, эффективно присутствующей в области усиления,
дается коэффициентом ограничения Г (9.27):
Глава 13. Светоизлучающие диоды и лазерные диоды
-►*
-с/ О
Рис. 13.14. Электронно-дырочная рекомбинация имеет место в области с наименьшей
шириной запрещенной зоны и соответственно с наибольшим
коэффициентом преломления. Таким образом, помимо обеспечения усиления,
узкозонный полупроводник является также и областью оптического
ограничения для усиленных оптических мод.
Г =
]\Е(х)\гдх
A3.25)
Таким образом, только доля Г электромагнитной энергии испытывает усиление
(смотрите также раздел 8.7.2) в предположении, что как барьеры, так и ямы
характеризуются теми же самыми потерями. Таким образом, выражение для лазерного
порога модифицируется и приобретает вид:
/threshold
)=r\a>+2L
RmlRm2
= -(ар+ат) A3.26а)
Пороговое условие для лазера
с гетеропереходом
Сконцентрируем теперь наше внимание на максимальном усилении,
определяемом A3.22а). Это последнее выражение может быть представлено в более четком
виде с использованием плотности порогового тока /ШгеЛо|<|:
qdnt
1
1
1
A3.266)
Поскольку коэффициент ограничения Г падает с уменьшением толщины
двойной гетероструктуры d (смотрите (9.30), мы видим, что существует оптимальная
13.5. Лазерные диоды с двойным гетеропереходом
величина d. Эта ситуация иллюстрируется рисунком 13.15 в сравнении с
аналогичной зависимостью для лазерного диода на основе гомоперехода. Большая разница в
величине плотности порогового тока, с одной стороны, является результатом
слабого оптического ограничения в лазерах с гомопереходом, а с другой стороны —
результатом уменьшения объема материала в более тонких гетероструктурах,
который должен быть инвертирован (смотрите рис. 13.2).
СО
о
о
с
о
с;
Гомопереход
Двойной
гетеропереход
Толщина активной области d
Рис. 13.15. Зависимость плотности порогового тока от толщины активной области d.
По своей природе гетеропереходы характеризуются более низкой
плотностью порогового тока вследствие лучшего перекрытия оптической моды и
среды усиления, а также вследствие усиленного ограничения носителей.
Пример
Рассмотрим лазерный диод с гетеропереходом на основе GaAs/AKjaj _x As с
толщиной */ямы 100 нм. Излучательное время жизни составляет 5 не, а внутренняя
квантовая эффективность у порога равна 50%. Резонатор диода имеет длину и ширину
соответственно 500 и 5 мкм, а также полностью отражающее зеркало. Содержание
А1х в барьерах достаточно велико, чтобы обеспечить коэффициент ограничения Г = 1.
В этом случае потери на зеркале ат составляют:
ат = 1пA/0,32)/Bх5х10 см)= 11,4 см
Предположим, что паразитные потери ар составляют 10 см, что приводит к
аш = 21,4 см. Система перейдет в режим лазерной генерации, как только
максимальное усиление утах в прямо смещенном диоде превысит atot. Применительно к
рис. 13.10 это соответствует плотности порогового тока /threshold== 800 А см (или с
учетом площади поверхности прибора пороговый ток /thrcshold составит 20 мА).
Фотонное время жизни в полупроводниковом резонаторе определяется
выражением (смотрите D.23я, б)):
1
A3.27)
2L RmlRm2
Здесь: d = c/nop есть скорость света в материале. В предположении нулевых
паразитных потерь, типичной длине резонатора L = 500 мкм и коэффициентов
отражения зеркал 1 и 0,32 находим фотонное время жизни 5 пс. Таким образом, мы
делаем вывод о том, что следствием слабой оптической обратной связи является
очень короткое время жизни фотонов в резонаторе.
Глава 13. Светоизлучающие диоды и лазерные диоды
13.5.2. Выходная мощность
До тех пор, пока порог прозрачности не достигнут, прибор ведет себя точно так
же, как СИД, высвобождая свою оптическую энергию по всем возможным
направлениям. В области между порогом прозрачности и началом лазерной
генерации (/trans < J < ^lhreshold) стимулированное излучение доминирует над спонтанной
эмиссией. В этом случае излучательная эмиссия приобретает направленность, т. к.
усиление еп способствует излучению вдоль направления, близкого к оси диода (в
этом случае диод называется суперлюминесцентным). Как только максимум кривой
усиления утах достигает порогового значения ^hreshold, электромагнитные моды (как
мы увидим далее), соответствующие этому максимуму, будут усиливаться вдоль слоя,
заключенного между двумя гетеропереходами. Когда этот порог превышается,
концентрации носителей в переходе становятся фиксированными на своей пороговой
величине «threshold (смотрите D.22я, б)). В этом случае удовлетворяется условие A3.26),
требующее равенства резонаторных потерь и усиления. Все дополнительные
носители (в действительности же только их часть, определяемая внутренней квантовой
эффективностью rj) будут сразу рекомбинировать вследствие эффекта
стимулированного излучения. Однако, как мы увидим, по мере того, как Jt становится больше
d, квантовая эффективность быстро стремится к единице.
Эксперименты показывают, что при возбуждении за пределами лазерного
порога полупроводник ведет себя как однородная среда (смотрите раздел 4.6). В этом
случае фотонный поток может быть получен в предположении равенства усиления
насыщения и резонаторных потерь y(hv) = yQ(hv)/(l + Ф/Ф5а()(смотрите D.10)). Это
приводит к D.26л, 6) или D.28я, в). Мы вновь получим этот результат, однако,
теперь применительно к частному случаю полупроводниковой среды.
Возвратимся к скоростным уравнениям A3.1), связывающим плотность тока /
и концентрацию носителей п, при этом на этот раз мы не забудем включить
скорость стимулированного излучения Rsts:
-L. = АЛп + Вп2 + CAug«3 + Rss A3.28)
Здесь s — объемная плотность фотонов в резонаторе. Выше лазерного порога усиление
среды фиксируется на пороговой величине ^hreshol так же, как и концентрации
носителей (т. е. п — flthreshold). В этом случае уравнение A3.28) может быть записано в виде:
— = "threshold + Rsxs A3.29я)
Я** ^"threshold
Здесь rthreshoId определяется выражением:
'™ = , . п * _., A3.296)
лпг Ч- ^"threshold
Введем теперь плотность порогового тока Jt
threshold*
•'threshold = ^threshold A3.30)
^threshold
При подстановке этого выражения в A3.29) приходим к Rsts = (/— ^hreshow)/^- Для
того, чтобы найти скорость стимулированного излучения Rsi, вспомним, что
скорость изменения заселенности dn/dt вследствие конкуренции между поглощением
и стимулированным излучением дается выражением dn/dt = c'ys = Rsts (смотрите
C.72л)). Как только усиление фиксируется, скорость стимулированного излучения
становится равной Rst = ^hresholdc'. Подставляя это последнее выражение в A3.29), мы
получаем концентрацию фотонов в резонаторе:
S = —Г—[ 7{j - AhreshoU ) A3-31Л)
Я" 7 threshold C
13.5. Лазерные диоды с двойным гетеропереходом
Это последнее выражение показывает, что выше порога весь ток «поглощается»
стимулированным излучением. В основе тока утечки могут лежать сложные
механизмы с участием безызлучательных каналов таких, как поверхностная
рекомбинация (смотрите главу 10), баллистических электронов, распространяющихся по гете-
роструктуре без рекомбинации и т. д. Для учета этих механизмов введем
внутреннюю квантовую эффективность rj., что позволяет нам переписать A3.31л) в виде:
s т(«/ - Лизиса ) A3.316)
В этом случае выходная лазерная мощность Pout определяется либо D.29а), либо
D.30л). Мы вновь получим этот результат, записав выходную мощность в виде
произведения: плотности фотонов в резонаторе s, энергии фотонов hv,
эффективного объема моды Lwd/Г и скорости ухода фотонов из резонатора cfocm.R этом
случае использование обозначений наятоящей главы дает для выходной мощности
следующее выражение:
р _ (энергия ^плотность ^эффективный )(скорсть ухода). (h\ (\ \ j w^_\ (с>п \ ло >у)\
^out - \фотона А фотонов А объем моды А фотонов /~ \nv) \s) г *т' \М-**)
С учетом A3.26) и A3.31) мы окончательно получаем:
рм = п,-Ь——0 - /*«** ) A3.33)
ат + ар q
Здесь / есть ток / = JLw так, что:
Р~ =»7« у (/-/*«*«) A3-34)
Зависимость выходной мощности
лазерного диода от тока накачки
В этом последнем выражении внешняя квантовая эффективность rjext дается
выражением:
<хт \n(\/Rm)
^ext = rii — = Vi \ 7 A3.35)
Теперь мы введем чрезвычайно важный параметр полупроводниковых
лазерных диодов, а именно: дифференциальную квантовую эффективность rjd. Этот
параметр представляет собой изменение выходящего фотонного потока dPout/hv из-за
изменения плотности тока диода dJ/q:
dPM/hv
"''^77 <13J6>
С учетом A3.34) и A3.35) мы можем записать:
""' A337->
В рамках этого простого подхода квантовые эффективности rj&xt и rjd
эквивалентны, т. к. Pout(J) является линейной зависимостью. Разумеется, такая ситуация не
носит общий характер. Общепринятая практика при оценке характеристик
полупроводниковых лазеров заключается в построении зависимости rj~l в функции
длины лазерного резонатора L (для этого скалыванием получают лазеры различной
длины и производится их индивидуальное измерение). После чего с
использованием уравнения A3.37а) определяется внутренняя квантовая эффективность rj. и
паразитные потри ар для конкретных приборов (смотрите рис. 13.17).
((E24 Глава 13. Светоизлучающие диоды и лазерные диоды
<ё
О
о:
Ш
ps = 4d — (/ - 'threshold)
threshold
Рис. 13.16. Характеристика P(F) лазерного диода. Объяснение феномена насыщения
приведено в дополнении 13.Е.
II
it
* о
If
Длина резонатора L
Рис. 13.17. Величина, обратная квантовой эффективности в функции длины
лазерного резонатора.
Уравнение A3.34) определяет оптическую мощность лазера. Представляется
интересным сравнить эту выходную мощность с электрической мощностью,
вводимой в диод. В предположении отсутствия какого-либо паразитного сопротивления
напряжение, необходимое для получения необходимого тока инжекции, будет
определяться шириной запрещенной зоны Eg/q или F« hv/q. В этом случае
электрическая мощность есть Ре1 = IV — hv/q так, что:
A3.376)
Это последнее соотношение определяет КПД прибора. До тех пор, пока структура
будет обладать хорошей квантовой эффективностью и будет возбуждаться
существенно выше порога, полупроводниковые лазеры будут характеризоваться
прекрасной эффективностью преобразования электрической энергии в оптическую (в
особенности это выглядит наглядно в сравнении с газовыми лазерами, в которых
типичная величина эффективности составляет менее
13.6. Квантово-размерные лазерные диоды
Пример
Возвращаясь к примеру из раздела 13.5.1, рассмотрим лазерный диод на основе
GaAs/AKjaj _xAs (с d = 100 нм, Г = 1, tnd = 5 не, rjf = 0,5 и L = 500 мкм. Однако в
этом случае будем предполагать, что прибор обладает двумя зеркалами с Rm = 0,32.
При этом мы находим, что потери на двух зеркалах составляют а = 1п( 1/0,32)/
/E х 10 см) = 22,8 см.
В предположении, что паразитные потери ^составляют 10 см полные потери
аш составят 32,8 см. Это приведет к дифференциальной квантовой
эффективности у порога rje величиной 0,5 х 22,8/32,8 или 35%.
13.6. Квантово-размерные лазерные диоды
13.6.1. Оптическое усиление в квантово-размерной
структуре: общий случай
В предыдущем разделе мы видели, что пороговый ток в значительной степени
пропорционален толщине активной области лазерного диода (т. е. ширине
потенциальной ямы, сформированной двойным гетеропереходом). Для дальнейшего
уменьшения порогового тока, естественно, необходимо еще более уменьшать размер
активной области вплоть до шкалы квантовых размеров (т. е. использовать
потенциальные ямы, которые настолько узки, что они способны ограничивать и
квантовать движение носителей в направлениях, перпендикулярных границам
раздела). Какое-то время мы уже посвятили исследованию физики таких квантовых ям
в главе 8. Напомним теперь некоторые важные результаты этой главы.
Электронные и дырочные волновые функции в квантовых ямах определяются
произведением трех членов: периодической части блоховских волновых функций,
обусловленных тем фактом, что носители принадлежат экстремумам конкретной
полупроводниковой зоны (мс(г) для электронов, uv(r) для дырок при к = 0 в случае
модели с одной валентной подзоной с экстремумом при Г); части, описывающей
свободное движение носителей параллельно границам раздела квантовых ям (eik«ri,
где Гц и kj. есть соответственно положение и волновые векторы волны в плоскости
квантовой ямы); части, описывающей квантование движения в направлении,
перпендикулярном гетерограницам. Таким образом, волновые функции электронных
состояний в подзоне п и тяжелые дырочные состояния в подзоне т могут быть
записаны в виде:
Огибающие функции en(z) и ЛЛт(^)описывают одномерные состояния с
энергиями еп и hh и являются решениями одномерных уравнений Шредингера:
A3.39)
Здесь Ve(z) и Vhh(z) есть потенциалы электронов и тяжелых дырок (смотрите рис.
13.18). Напоминаем, что на таких диаграммах увеличению энергии соответствует
направление вверх для электронов и вниз — для дырок. Эта концепция может быть
расширена на случай подзоны легких дырок спин-орбитальной подзоны, что
вызывает существенное усложнение необходимых обозначений (в связи с этим в насто-
Глава 13. Светоизлучающие диоды и лазерные диоды
Е(к)
Плотность состояний
Fc
Рис. 13.18. Зонная структура, подзоны ДЦ) и плотности состояний в квантовой яме.
ящей главе мы не будем рассматривать такие подзоны). Уравнения A3.38) и A3.39)
показывают, что электроны и дырки распределены по энергетическим подзонам
(которые, в дополнение ко всему, смещены параллельно друг к другу для
различных типов носителей), Экстремумы этих подзон (еп и hhj определяются
уравнениями Шредингера A3.39) и их положение составляет (смотрите рис. 13.18):
2тс
A3.40)
hhm{kt) = шт
1ти
Плотность состояний в каждой подзоне постоянна, означая, что концентрации
электронов и тяжелых дырок есть (смотрите (8.41а, б):
7ih
- hhm)
A3.41)
Здесь Яесть функция Хэвисайда.
Межзонные оптические переходы соединяют состояния с идентичными к...
Таким образом, фотон с энергией h v соединяет состояния в подзоне проводимости п
с состояниями в валентной подзоне т, связанные соотношением:
h v = Eg
hhm
2тг
A3.42)
Здесь тг есть приведенная эффективная масса, определяемая \/тг = \/тс + 1//яЛА
(смотрите рис. 13.18). В такой системе оптическое усиление для электромагнитной
волны с частотой п было рассчитано в разделе 8.7. Оно было получено
суммированием вкладов из-за оптических переходов между валентными подзонами т и
подзонами зоны проводимости п с волновым вектором, лежащим в интервале от к до
к + йк. Это приводит к плотности инверсии носителей:
13.6. Квантово-размерные лазерные диоды
d(Nc -КГ = Р2°М{Г:[Ес(к)]- f:[Ev{k)} }dk A3.43)
d
Усиление y(hv) может быть получено интегрированием по к вклада A3.43) в
оптическую восприимчивость и суммированием по всем участвующим подзонам.
Этот результат получен в виде соотношения (8.86), но здесь мы перепишем его в
виде, более пригодном для настоящего обсуждения:
r(*v)= a2D £ InAfcn{hv)- fvm(hv)]o(hv -Eg-en- hhm) A3.44)
Здесь In m есть интегралы перекрытия |(я|аи)|2, &fcn nfvm есть распределения Ферми в
подзонах пит:
ехр {[Ec"(hv)- Ef\/ кТ}
A3.45а)
m.
/m(Av)=-
+ cxp{[E:(hv)-EFv]kT}
A3.456)
^()
Коэффициент поглощения a2D (см) есть поглощение квантовой ямы с
нулевой заселенностью (т. е. в условиях нулевого тока) и он определяется
соотношением:
221тг A3.46а)
Здесь Ло есть длина волны в вакууме. Как это уже достатоно подробно обсуждалось
в разделе 8.7.2, A3.46я) представляет коэффициент ослабления для света при
нормальном падении, проходящий через квантовую яму толщиной d. Таким образом,
коэффициент a2D выражается в единицах см. Концепция длины ослабления в
квантовой яме не является особенно удовлетворительной. Поскольку толщина
квантовой ямы очень мала по сравнению с длиной ослабления l/or2D, ослабление,
определяемое da2D, не зависит от толщины квантовой ямы (строго говоря это имеет место,
если только в квантовой яме имеется единственный локализованный уровень).
В связи с этим используем скорость ослабления в расчете на одну яму
(безразмерную величину) A2D = da2D, определяемую (8.866):
2nq2x2vcmr A3.466)
2D " Л^о*2
Коэффициент ослабления
для одной квантовой ямы
Эта формула подразумевает использование впечатляюще больших параметров.
Для того, чтобы выразить A2D через параметры близкой величины,введем два
следующих энергетических параметра: межзонную энергию Evc = h kvc2/2mr, где kvc есть
волновой вектор kvc = 2n/xvc, и электростатическую энергию Estat = q2/4n£0AQ. В этом
случае скорость ослабления принимает вид:
= ]б£1 £^ A3.47)
Глава 13. Светоизлучающие диоды и лазерные диоды
Это последнее уравнение позволяет быстро оценить скорости ослабления в
квантовых ямах с использованием параметров аналогичной величины. Следующий ниже
пример иллюстрирует удобство использования указанного выражения.
Пример
Рассмотрим скорость ослабления для квантовой ямы на основе GaAs. Напомним
используемые параметры для GaAs:
тс = 0,067we; mv = 0,46/w,; mr = 0,058/we
xw = 6,14 E/V2 = 4,3 E (смотрите таблицы 7.1 и 8.1)
"sc= 3>3
Ao = 0,8 мкм
Уравнение A3.466) приводит к коэффициенту ослабления:
А = 2л-A,6хЮ-19 КлJD,3 х10-'° мJх 0,058 х 0,9 xlQ-20 кг Q 6%
0,8х10 м х 3,3 х 8,85 хЮ2 Фм х (l,05x 104 Дж с2)
Этот расчет, мягко говоря, утомителен! Все, что это в действительности означает, так
это то, что единицы системы MKSM не приспособлены идеально для решения
подобных задач. Это, в свою очередь, является еще одним поводом для того, чтобы
переписать A3.47) с использованием более легко манипулируемых параметров.
Определив Evc = 3,99 эВ и Estat =1,8 мэВ, мы легко получаем тот же самый результат.
13.6.2. Порог прозрачности
Рассмотрим р—я-диод с одиночной квантовой ямой (смотрите рис. 13.19). При
прямом смещении этого диода инжектированные носители аккумулируются в
квантовой яме. Концентрация носителей на единицу площади ns может быть получена
по аналогии с A3.13), т. е.:
л. = Ps = — A3.48)
При достаточно большом токе мы получаем инверсию заселенности, что
приводит к прозрачности квантовой ямы (смотрите рис. 13.20). В окрестности
прозрачности квазиуровни Ферми начинают проникать в подзоны. При этом в процесс
вовлечены только подзоны с п =/и = 1, при этом усиление может быть записано
просто в виде:
)- fv](hv)\e(hv - Eg-ex-hhx) A3.49)
Оптическое усиление вследствие
первого перехода е1 - hh^
qV
Рис. 13.19. Прямо смещенный р—я-диод с одиночной квантовой ямой.
13.6. Квантово-размерные лазерные диоды 529
I
Область усиления
I
a(rtv)
-a2D(/7v)
a(hv) r
Рис. 13.20. По мере того, как квантовые ямы заполняются электронно-дырочными
парами, квазиуровни Ферми поднимаются внутри подзон. Как только
энергетический зазор между двумя квазиуровнями Ферми превысит ширину
запрещенной зоны, фотоны, удовлетворяющие условию Бернара—Дюрра-
фура, начинают усиливаться: зонная диаграмма (а), подзонная структура
(б), соответствующие распределения Ферми—Дирака (в) и кривая
усиления в квантовой яме (г).
Понятно, что эффекты уширения могут быть учтены в виде свертки с
использованием функции Лоренца:
A3.50)
f[ 530 Глава 13. Светоизлучающие диоды и лазерные диоды
Эти выражения могут быть рассчитаны точно, если вспомнить, что p2D и p2D hh есть
константы, определяемые A3.41). Таким образом, для электронов A3.50)
записывается в виде:
п5 = Ргъ.е \ ТГ^ v ,dE A3.51)
E?+e\ + exp[(E-EF)/kT]
Здесь мы предположили, что энергия у потолка валентной зоны равна нулю. При
использовании обозначений (Е — Efc) и exp (Eg + е{ - Efc)/kT = uc это последнее
выражение принимает вид:
я, = p2Ix.*rJ^f^d« = p2D.,Arinfl + J-l A3.52)
Так, что:
iii \ ^ Fc ~ Е' — е,
ns = nc In I + exp * L
. Г. { hh, - EFr
ns = я. In 1 + exp lkT f>
A3.53)
Здесь пс и nv есть двумерные критические концентрации, определяемые
соотношениями:
"с =
A3.54)
Мы увидим, что концентрации прозрачности и порога могут быть выражены в
виде произведения этих двумерных критических концентраций на коэффициент,
близкий к 1 (как правило, в интервале от 1 до 5).
Такой метод расчета усиления заключается в следующем: при заданной
плотности тока /мы находим концентрацию носителей, определяемую A3.48), затем
определяем квазиуровни Ферми в соответствии с A3.53) и, наконец, с помощью
A3.49) и функций Ферми A3.45) находим усиление. Рисунок 13.21 демонстрирует
кривую усиления A3.48) в функции энергии фотонов при возрастающей
концентрации носителей. Отметим резкое увеличение усиления при hv > Eg + ех + hhv
Такой характер является более резким по сравнению со случаем регулярного
гетероперехода и он связан со ступенчатым профилем плотности состояний в
двумерной структуре (в противоположность зависимости V/s, проявляющейся в
трехмерных структурах). Таким образом, максимальное усиление ymax достигается, когда
Av= Eg + el + hhv т. е.:
Eg
7^ = cx2D\f:(hv = Eg+ei+ hh,)- fj(hv = Eg+el+ AAj A3.55)
Уравнения A3.53) и A3.45) позволяют простым образом связать величину функции
Ферми с концентрацией носителей п:
\+txvlEFc-Eg-e{)/kT\
Аналогичным образом:
A3.5бв)
e-Pjnt = fifa) A3.566)
В этом случае A3.55) может быть записано в виде:
13.6. Квантово-размерные лазерные диоды 531 j|
fr, Fr
h\>
F~ r
Рис. 13.21. Изменение кривой усиления для квантово-размерного лазера при
возрастающем уровне накачки. Пунктирные кривые показывают величну
усиления при нулевой температуре. Жирная (слабая) линии соответствуют
сильным (слабым) уровням накачки.
= а.
A3.57)
Максимальное усиление квантовой ямы в
функции концентрации носителей (см ~1)
Здесь: Rcv (= mhh/mj есть отношение эффективных масс носителей в зоне
проводимости и валентной зоне. Рисунок 13.22 демонстрирует изменение максимального
усиления в функции приведенной поверхностной концентрации njnc при R = 6,8
(для GaAs) и R = 1. Мы видим, что усиление быстро возрастает, как только
достигается условие прозрачности, но оно быстро насыщается. Это происходит из-за
двумерного характера состояний. Из A3.57) следует, что порог прозрачности
достигается, как только максимальное усиление становится положительным, т. е.
когда достигается порог прозрачности пи:
7 ~ »U I "с
-. 1
A3.58)
0 2 4 6 8
Нормированная поверхностная концентрация
Рис. 13.22. Нормированное (по отношению к поглощению a2D) усиление в функции
нормированной (по отношению к двумерной критической концентрации
носителей пс) поверхностной концентрации носителей.
Глава 13. Светоизлучающие диоды и лазерные диоды
При Rcv = 1 мы имеем nit = лс1пB). Ток прозрачности всегда связан с пс через
численный коэффициент, близкий к 1. Это объясняет важность концепции
двумерной критической концентрации носителей пс. Рисунок 13.22 демонстрирует условие
прозрачности для различных значений Rcv. Отметим важность четкого согласования
эффективных масс носителей в зоне проводимости и валентной зоне. Это и
является одной из причин мотивации выращивать напряженные лазерные структуры (мы
исследуем эти структуры в дополнении 13.Б).
Следует отметить, что в литературе изменение максимального усиления утах в
функции концентрации носителей часто принимается в виде логарифмической
зависимости:
[f) A3-59)
Здесь константа у0 зависит только от отношения эффективных масс Rcv и
получается процедурой подгонки (смотрите ниже). Эта последняя формула приводит к
характеру поведения, близкому к предсказываемому формулой A3.57) для величин п,
которые приближаются к порогу прозрачности. Это уравнение обладает тем
преимуществом, что оно простым образом вводит порог прозрачности в формулу
усиления. Заметьте отличие от подобного, но линейного соотношения A3.21) для
трехмерных лазерных диодов.
Пример
1. Используем следующую программу MAHEMATICA для подтверждения
эквивалентности A3.57) и A3.59):
f=1-Exp[-x] - Exp[-x/R]
R=6.8
plot1=Plot[f,{x,.5,5}]
FindRoot[f= =0,{x,1}]
xO=x/.%
plot2=Plot[0.48*g,{x,.5,5}]
Show[plot1,plot2]
Рисунок 13.23 дает сравнение этих двух выражений. С использованием
процедуры подгонки мы находим, что у0 = 0,48 a2D.
2. В случае GaAs плотности двумерных состояний есть:
Рю,е = mjTth2 = 2,8xl013 см эВ
Рыл = тНИ/ш2 = 1,9х1014 см2 эВ
о
п/пс
Рис. 13.23. Сравнение величин утах, полученных с использованием точной формулы
A3.57) (сплошная кривая) и аппроксимации A3.59) (пунктирная кривая).
13.6. Квантово-размерные лазерные диоды
Критическая двумерная концентрация носителей в зоне проводимости есть
пс = p2D kT или 2,8 х 1013 см~2 эВ1 х 0,0259 эВ =7,25 х 1011 см. Рисунок 13.22
показывает, что в GaAs ntr = 1,6 пс = 1,6 х 10 см. В квантовой яме толщиной 100 Е
это соответствует пороговой концентрации прозрачности 1,16 х 10 см. Этот
результат очень близок к тому, который получается для объемного материала. В
действительности преимущество использования квантовых ям заключается не в
уменьшении пороговой концентрации носителей, а скорее в уменьшении плотности тока
прозрачности и, следовательно, в уменьшении пороговой плотности тока.
В действительности кривая усиления квантово-размерного лазера очень
сложна. По мере того, как в квантовых ямах увеличиваются концентрации носителей,
электроны и дырки начинают заселять все более высоко лежащие энергетические
состояния в подзонах, что приводит сложным переходам: сначала к ех—/j/jj-nepexo-
дам, затем к e2—hh2-переходам и т. д. Рисунок 13.24 показывает результаты расчета,
учитывающего все эти переходы.
X
CD
с;
о
200
100
-100
-200
-300
-400
1400 1500 1600 1700 1800 1900 2000
Энергия (мэВ)
Рис. 13.24. Модовое усиление (т. е. произведение усиления на коэффициент
ограничения Г) для квантово-размерного лазера при двух различных значениях
концентрации носителей. В условиях более высоких уровней инжекции
тока могут наблюдаться как e—hhv так и е2—/*/*2-переходы (С разрешения
A.Fily@THALES)
13.6.3. Лазерный порог квантово-размерного лазера
Рисунок 13.25 демонстрирует конфигурацию квантово-размерного лазера со
слоями раздельного ограничения как для носителей, так и для фотонов (называемого
лазером на основе гетероструктуры с раздельным ограничением или SCH — лазером).
В рассматриваемом случае для ограничения фотонов, генерируемых квантовой ямой
AHjtej _ xAs/GaAs, она введена в резонатор с меньшим коэффициентом
преломления (также выполненный на основе Al^ Ga2 .^As, но с у > х). Электромагнитное поле
усиливается вдоль квантово-размерного слоя. Как это описано в разделе 13.5.1,
(смотрите A3.26)), слабое перекрытие между волноводной волной и квантовой ямой
приводит к уменьшению усиления от ^до уГ, где Г есть коэффициент оптического
ограничения, определяемый A3.25). С учетом A3.59) условие получения лазерных
колебаний в квантово-размерном лазере может быть записано:
f( 534 Глава 13. Светоизлунающие диоды и лазерные диоды
AlxGai-xAs
Рис. 13.25. Профили оптической моды, энергетических зон для лазера на основе кван-
тово-размерной гетероструктуры.
A3.60)
Здесь в соответствии с принятой системой обозначений ар есть паразитное
поглощение, L — длина резонатора, a Rml и Rm2 — коэффициенты отражения зеркал.
Коэффициент ограничения дается отношением Г = d/dmode, где dmode есть
протяженность пространства, занимаемого оптической модой (смотрите рис. 13.25 и раздел
9.4). Плотность порогового тока ^threshold в этом случае дается A3.38). В
предположении, что время ftot зависит от п очень слабо (что в действительности является очень
грубым приближением) характеристика усиление — ток описывается выражением:
A3.61^)
Логарифмическая аппроксимация
оптического усиления квантовой ямы (см~1)
Понятно, что в этом выражении плотность тока прозрачности Ju (А см)
описывается соотношением:
*tnt
A3.616)
Пример
Используем ту же самую физическую систему,которая уже использовалась в двух
предыдущих разделах, а именно: квантовую яму GaAs толщиной 100 А. Длина
резонатора составляет 500 мкм, при этом коэффициенты отражения зеркал равны
R= 100% и R= 32%. Паразитные потери составляют 10 см. Таким образом,
пороговое усиление, определяемое ар — 1/21п(/?5), составляет 21,4 см. Ширина моды Jmode
равна 5000 А. Эффективное усиление Fa2D = A2D/dmode есть 0,55 х 10/5000 А или
110 см. Для определения лазерного порогового тока нам необходимо найти
отношение п/пс, при котором 1 — ехр(—п/п) — ехр(—п/пс R) = 21,4/110 или п = 1,3 х 1012 см
13.6. Квантово-размерные лазерные диоды
(R = 6,8 и пс = 7,25 х 1011 см~2). Предполагая, что время жизни составляет 5 не,
площадь поверхности равна 5 х 500 мкм2, мы находим, что пороговый ток
составляет 1 мА, т. е. в 10 раз меньше того, который получается в лазере на основе гетеро-
структуре, рассмотренном в разделе 13.5.1.
13.6.4. Правила масштабирования для лазеров
с набором квантовых ям
Сравним теперь поведение лазеров с гетеропереходом и одиночной квантовой ямой.
Как отмечалось в предыдущих разделах, требуемые концентрации носителей при
порогах прозрачности и лазерной генерации практически идентичны вне
зависимости, рассматривается объемный полупроводниковый лазер или квантово-размерный
лазер. С другой стороны, необходимые плотности тока уменьшаются
пропорционально d, ширине области усиления. К тому же мы заметили, что в квантово-размер-
ной системе усиление возрастает более резко в функции тока возбуждения
вследствие одномерного характера плотности состояний (смотрите рисунки 13.10 и 13.22).
С нижней стороны оптическое усиление в лазерах с одиночной квантовой ямой
насыщается более быстро в функции тока накачки (по крайней мере, до тех пор пока
не включатся другие квантово-размерные переходы типа e2—hh2); в то же время в
объемных полупроводниковых лазерах на основе гетероструктур усиление будет
продолжать расти. Эти особенности в суммарном виде представлены на рис. 13.26.
Теперь мы уже в состоянии поставить вопрос о том, каково должно быть
количество квантовых ям NQW для того, чтобы свести пороговый ток до минимума.
Понятно, что по мере того, как возрастает количество квантовых ям NQW (что
соответствует включению набора квантовых ям в то, что называется структурой с набором
квантовых ям), тем больше будет усиление и тем легче будут компенсироваться
потери. С другой стороны, если число ям слишком велико, то необходимый
пороговый ток будет возрастать пропорционально iVQW. Таким образом, существует
некое оптимальное число квантовых ям, являющееся результатом компромисса
между этими противодействующими факторами.
Для определения этого оптимального числа зададим следующие параметры:
• G{ — максимальное усиление лазера с одиночной квантовой ямой:
= Ту, In
A3.62)
Усиление
Гетеропереход
Ток
Js^
Рис. 13.26. Сравнение кривых усиление—ток для объемных и квантово-размерных
лазеров.
((E36 Глава 13. Светоизлучающие диоды и лазерные диоды
Здесь /tr , есть плотность тока прозрачности для одиночной квантовой ямы, a Jx
есть плотность тока накачки структуры.
G^ есть усиление структуры, аналогичной предыдущей, но обладающей N
квантовыми ямами. В предположении, что связь с электромагнитными волнами
идентична для всех ям, находим:
GN = NG, = NTy0 In -fi-
A3.63)
Если JN есть плотность тока накачки для структуры с набором квантовых ям, мы
должны иметь:
JN =
= NJl
A3.64)
Подставляя в A3.63) величину J{, приведенную в A3.64), получаем изменение
оптического усиления в функции числа квантовых ям N:
A3.65)
На рисунке A3.27) приведено сравнение кривых усиление—ток (GN),
полученных для числа квантовых ям N= 1, 2, 3 и 4. Видно, что порог прозрачности
увеличивается пропорционально N.
Рис. 13.27. Нормированное усиление для структуры с N квантовыми ямами в функции
нормированной плотности тока (нормированной к плотности тока
прозрачности лазеров с одиночной квантовой ямой). Плотность порогового тока
возрастает пропорционально N.
Плотность порогового тока получается, если предположить, что усиление A3.65)
равно потерям A3.60), т. е.:
-^^exp
л
1
NTy0
1
A3.66)
Здесь мы ввели квантовую эффективность rj. Это последнее выражение позволяет
оптимизировать многие аспекты лазерных резонаторов с набором квантовых ям.
Оптимальное число квантовых ям может быть получено, если мы положим UJJ&N = 0, что
приводит к:
-Jj-fe.+ i
In-
1
fa D+ In
[Гуо{ р 2L RmlRm
резонаторы ые потери
усиление одиночной квантовой ямы
A3.67)
13.7. Динамические аспекты лазерных диодов
Здесь Int — функция целого числа. Интерпретация этой последней формулы
достаточно прозрачна. Ток /thrcshold N есть произведение A3.66) на Lw (где w есть ширина
структуры) и обладает минимумом в функции длины резонатора. Оптимальная длина
получается из производной /threshold no L, что дает:
^idc A3681
Пример
Рассмотрим лазер с набором квантовых ям и следующими характеристиками:
Параметры одиночной квантовой ямы: Г = 0,1; уо= 100 см.
Параметры резонатора: ар = 10 см, Rml = 1, Rm2 = 0,32.
В предположении резонатора длиной 500 мкм мы получаем потери 21,4 см и
усиление на квантовую яму, равное 10 см. Оптимальное число квантовых ям Nopt
равно 3.
В случае резонатора с одиночной квантовой ямой его оптимальная длина равна
570 мкм.
13.7. Динамические аспекты лазерных диодов
Динамические характеристики лазерных диодов могут быть исследованы с
использованием процедуры, аналогичной подходу, использованному в разделе 4.7.
Однако, лазерные диоды вводят новые характеристики, которые должны быть
включены в связанные динамические уравнения D.34) и D.35). Модифицируем эти
уравнения с тем, чтобы включить в них особенности, связанные с функционированием
лазерного диода:
dn J п
ds s A3-69)
-j^= c'g(n)s(n - пиУ - j-
Динамические уравнения
полупроводникового лазерного резонатора
Первые два члена в первом уравнении описывают поступление электронно-
дырочных пар вследствие тока инжекции, а также потери пар из-за всех рекомби-
национных механизмов за исключением стимулированного излучения. Третий член
отражает вклад стимулированного излучения, и он равен концентрации фотонов в
резонаторе (см), умноженной на произведение g(n)(n — л1г)(где (я — ntr) дает
коррекцию на необходимую концентрацию прозрачности полупроводникового
лазера); d — с/пх есть групповая скорость фотонов в полупроводнике, через которую
можно установить соотношение между фотонным потоком и концентрацией
(смотрите главу 4). Член g(n) (см~Усм~3 или см2) описывает изменение динамического
усиления в функции концентрации носителей:
g(n)=%- A3.70*)
dn
Этот параметр является также характеристическим наклоном кривой g(n) смотрите
рис. 7.8 для лазеров с гетеропереходами и рисунок 13.22 для квантово-размерных
лазеров). В случае лазеров с гетеропереходами это усиление является константой,
определяемой A3.21):
A3.706)
Глава 13. Светоизлучающие диоды и лазерные диоды
Здесь п = njd. Сравнивая A3.69) с D.1), мы находим, что динамическое усиление
есть понятие, очень близкое к оптическому поперечному сечению сгор в атомной
физике. Не было бы преувеличением рассматривать динамическое усиление как
поперечное оптическое сечение для каждого электрона в полупроводниковой среде, Мы
увидим, что это оптическое поперечное сечение в случае полупроводников
значительно: несколько 10~16 см2 в сравнении с 10~19 см2 в легированных ионами (Сг, Nd,
...) лазерах. Это и объясняет очень большие усилительные характеристики
полупроводниковых лазеров.
Во втором уравнении A3.69) третий член отражает создание фотона в волновод-
ной моде (и следовательно, с влиянием Г). Второй член отражает резонаторные
потери (рассеяние света, потери на зеркалах и т. д.) через эффективное фотонное
время жизни г, которое, как мы напоминаем, равняется (смотрите D.24) и A3.27):
c'[xp + (\/2L)\n(\/RmlRm2)] A3.71)
Расчет динамических характеристик лазерного диода проводится по
традиционным правилам (смотрите раздел 4.7). Предположим, что усиление g(ri) = g не
зависит от п для малых сигналов. Обозначим через п0 и s0 соответственно
концентрации электронов и плотности фотонов в стационарном состоянии. Они
определяются стационарными решениями A3.69):
1_
A3.72)
С использованием этих уравнений мы вновь легко приходим к результатам,
полученным в A3.34) для мощности лазерного излучения в функции тока
возбуждения. На самом деле нас интересует малосигнальная динамическая
характеристика при токовой модуляции J = Jo + SJ (при SJ « Jo). Таким образом, мы
записываем концентрации пар носителей и плотности фотонов в виде п = по + Snu
s = s0 + Ss. Пренебрегая членами второго порядка, мы находим следующую систему
дифференциальных уравнений в малосигнальном пределе:
dSn Sj - ( 1 /lie
d/ qd [txox 6oJ Гтс
A3.73)
dSs _ , e
— = Tcgs0Sn
Здесь мы использовали A3.72). Исследуем теперь гармонический отклик системы,
принимая:
Sj = Re\Sj(to)eiM\; Sn = Re [Sn(co)el(Ot\; Ss = Re [Ss(u))el<of\ A3.74)
В этом случае система дифференциальных уравнений A3.73) приводит к:
&(а»)= (Sj / qd)Yc'g
*о - со2 + [A / txox )+ c'gs0\\co + c'gs0 /тс
В этом случае малосигнальный отклик дается выражением:
rc)Y + ИЙ ЛJ+ <
Этот отклик максимален на частоте релаксации coR:
A3.76)
13.7. Динамические аспекты лазерных диодов
A3.77л)
Частота релаксации
полупроводникового лазера
При этом коэффициент демпфирования ГЛ определяется выражением:
^ \тс<о\ A3.776)
Физическая причина колебаний и релаксации обсуждалась ранее в разделе
4.7.1. Эти явления соответствуют колебательному обмену энергией между
электронно-дырочными парами и фотонной заселенностью, охваченными
взаимодействием через стимулированное излучение. Говоря более точно, по мере того, как
увеличивается плотность электронно-дырочных пар, также возрастает и
усиление, которое запускает механизм увеличения фотонной плотности, что приводит
к увеличенной скорости стимулированного излучения, которое уменьшает
концентрацию носителей (за счет рекомбинации), приводя к колебаниям этих
параметров. Релаксация происходит из-за потери фотонов (за счет паразитного
поглощения или за счет потерь на зеркалах), что описывается г, как в A3.776). Рисунок
11.28 демонстрирует частотную характеристику полупроводникового лазера.
Характер поведения, предсказываемый выражением A3.76), воспроизводится
экспериментально, демонстрируя начальное возрастание до максимальной величины с
последующим спадом пропорционально /~2. Уравнение A3.77а) предсказывает
также увеличение релаксационной частоты с возрастанием тока накачки с учетом
зависимости fR от s01/2. Наконец, мы отмечаем, что максимальная частота
эксплуатации (т. е. частота, при которой вблизи fR\Ss{co)\ = \Ss@)\) возрастает с
увеличением наклона g(n) (или g(J)). Таким образом, квантово-размерные лазеры
обладают существенным преимуществом перед объемными лазерами с учетом их
лучшего динамического усиления.
10
о
-10
-20
m
%-*
-40
-50
-60
-70
'.
: I 4*
" I 1 • •
r
....
j :
1 ' ■
i i
j _ _ L_
!
i !
. |
1 . 1 _
rNL ! i
i 1
j
| j
. _| . . J ,
i
i
10 15 20 25
Частота (ГГц)
30
35
40
Рис. 13.28. Частотная характеристика лазерного диода на основе InGaAsP/InP (С
разрешения E/Goutain@THALES).
Глава 13. Светоизлучающие диоды и лазерные диоды
Пример
Найдем частоту релаксации гетеролазера на основе GaAs/AlGaAs. Необходимые
для этого параметры есть:
Выходная мощность, РоиХ = 10 мВт
Энергия фотонов hv= 1,4 эВ
Коэффициенты отражения выходных зеркал, Rml = I, Rm2 = 0,32
Площадь области оптической моды А = wdmode, где w (ширина
резонатора) = 2 мкм и dmodc (эффективная глубина моды) = 0,1 мкм, что
дает А = 2 х 10"9 см2.
Длина резонатора L = 200 мкм
Паразитные потери ар = 10 см
Коэффициент оптического преломления пх = 3,3
Квантовая эффективность /7=1
Динамическое усиление g, определяемое рис. 7.8, есть 3 х 10~16 см2
Фотонная плотность s0 определяется A3.32), что мы перепишем здесь в виде:
^й. = A-/?)-£_ йою0 A3.78)
Это приводит к фотонной плотности sQ величиной 3,6 х 1015 см~3. Фотонное
время жизни в резонаторе есть \/d{ap - 1/21п(/?)) или 2,8 пс. Таким образом,
релаксационная частота есть:
зхЮ10/3,Зхсм с-'хЗхКГ16 см2хЗ,6х1015 см п . __
—■ гвш^-с =9'4 ГГц
13.8. Характеристики излучения лазерного диода
13.8.1. Спектральное распределение
Рисунок 13.29 показывает спектральное распределение излучения лазерного диода
при различных токах накачки. Ниже порога (рис. 13.29а) спектральное
распределение излучения следует за кривой усиления среды и модулируется разрешенными
модами Фабри—Перо в резонаторе (смотрите рис. 4.9). Поскольку резонатор,
использованный в рассматриваемом эксперименте, имел длину 300 мкм, а пиковая
длина волны Л составляла 0,85 мкм, ожидаемый межмодовый интервал (АЛ = Л2/2 nxL или
0,36 нм) находился в соответствии с экспериментом. На рис. 13.295 моды, которые
испытывают усиление, превышающее пороговое условие, приводят к лазерной
генерации. Поскольку механизмы внутризонного рассеяния чрезвычайно быстры @,1 пс),
в полупроводниках проявляется тенденция вести себя как однородная среда, что
способствует одномодовой эмиссии. В то же время ряд конкурирующих
механизмов (например, выжигание спектрального провала, выжигание пространственного
провала (смотрите главу 4), шнурование) может вызвать многомодовое излучение.
Часто для обеспечения одномодового функционирования в приборную
структуру встраиваются распределенные брэгговские зеркала. Такие приборы известны
как лазеры с распределенной обратной связью (DFB) и они являются предметом
дополнения 13.А. Другой возможностью является уменьшение размеров резонатора
таким образом, чтобы межмодовый интервал превысил ширину кривой усиления.
С учетом типичной ширины усиления АЛ величиной 100 нм приходим к длине
резонатора L = Л2/2порАЛ или 1 мкм. Такие короткие резонаторы могут быть
сформированы с использованием геометрии вдоль оси эпитаксиального роста. Прибо-
13.8. Характеристики излучения лазерного диода
-10
-50
/ = 30 m A
Г=296К
Энергия (эВ)
8800
Длина волны (Е)
8400
8200
3
|
1.4
1.5
Энергия (эВ)
Рис. 13.29. Спектр излучения лазерного диода на основе GaAs/Al018 Ga0 82 As ниже (а)
и выше (б) лазерного порога. (С разрешения Е. Goutain@THALES).
ры, изготовленные с использованием такой геометрии, называются поверхностно-
излучающими лазерами с вертикальным резонатором (VCSEL) и они исследуются в
дополнении 13. В.
Вспомним, наконец, что свет, излученный лазерным диодом ниже порога
прозрачности, является некогерентным (смотрите главу 4). Действительно, торцевые СИД
являются лазерными диодами с уровнем усиления ниже порога лазерной генерации.
В определенных случаях на грани кристаллов лазерных диодов специально
наносятся антиотражающие покрытия с тем, чтобы подавить оптическую обратную связь и
«удержать» приборы от лазерной генерации в условиях высокого уровня тока инжек-
ции. Тем не менее, как только приборы возбуждаются за пределами порога
прозрачности, стимулированное излучение начинает доминировать над спонтанной
эмиссией. В этом режиме СИД излучают чрезвычайно яркую (хотя и некогерентную)
электролюминесценцию. Такие приборы называются суперлюминесцентными диодами.
Глава 13. Светоизлучающие диоды и лазерные диоды
13.8.2. Пространственное распределение
Расчет пространственного распределения энергии люминесценции, излучаемой
лазерным диодом, достаточно сложен, требующий применения численных
методов, которые мы рассмотрим ниже. Наиболее часто используется аппроксимация
дальнего поля. Напомним сейчас эту аппроксимацию.
Распределение зарядов, колеблющихся с частотой со приводит к амплитудному
распределению электрического поля Enf (г') (Enf есть ближнее поле) в пределах
малой апертуры в плоскости z = 0, где г' направлен вдоль основной оси апертуры
излучения (смотрите рис. 13.30). Дальнее поле Eff в точке, удаленной на г от
апертуры, есть Фурье-образ ближнего поля, а именно:
Jdr'eikr[-2nxEnf(r')]
A3.79)
Здесь п есть единичный вектор, направленный по нормали к апертуре, ur—
единичный вектор в направлении г и к = со/сит есть вакуумный волновой вектор в
направлении г (смотрите рис. рис. 13.30).
В этом случае излученная мощность дается соотношением P(r) = (\/2)Z0\Eff(r)\2,
где Zo есть вакуумный импеданс (Zo = 377 Ом). Особый интерес представляет
пространственное распределение интенсивности излучения вдоль двух направлений:
• Вдоль оси роста. В этом случае угловое распределение (в функции 0±) дается
выражением:
1/2 d/2
J J eiA
-1/2 -d/2
(*', y')dx'dy'
A3.80)
Здесь /есть эффективная ширина моды (смотрите рис. 13.31). В лазерной волновод-
ной структуре волноводное поле распределено, в основном, между —dmodj2 и +dmodj2.
Принимая в качестве ближнего поля Ej(x, у) функцию С(х, dmo6j2) x С (у, 1/2), где
С(х, а) = 1 между — а и +а и 0 в других местах, можем записать Фурье-образ
A3.80) в виде:
Рис. 13.30. Диаграмма для расчета распределения дальнего поля полупроводникового
лазера.
13.8. Характеристики излучения лазерного диода
' mode
Рис. 13.31. Угловое распределение света, выходящего из фундаментальной моды
полупроводникового волновода.
A3.81)
Таким образом, мы видим, что вся энергия заключена между углами +AJ2dmodc и
—A0/2Jmode. Этот результат может быть получен при аппроксимации ограниченной
моды в виде гауссовского пучка шириной IV = dmodc/2 (смотрите 4.Д.5)). В этом
случае расходимость пучка составляет hJnW^ = 2Я(/яг/тос1е ~ \/2dmode.
• Направление, параллельное границам раздела. В этом случае угловое распределение
описывается соотношением:
1/2 d/2 2
/>ff(r) ос cos2 By J J e-i*eta*'y'£nf (*', jc')dx'djc' A3.82)
-1/2 -d/2
При этом расходимость пучка составляет kJ2L
Выражения A3.80) и A3.82) чрезвычайно полезны, поскольку они позволяют
трактовать более общие случаи по сравнению с рассмотренной выше
аппроксимацией. Рис. 13.31 обобщает полученные результаты. В случае мод более высокого
порядка реализуются угловые распределения с увеличенной дисперсией и
соответственно ослабленной амплитудой.
В случае типичной лазерной структуры шириной 5 мкм и эффективной модо-
вой шириной dmodt = 1 мкм угловая расходимость вдоль оси роста имеет величину
порядка A мкм/1 мкм) рад или 60 ° и A мкм/5 мкм) рад или 10° вдоль направления,
параллельного гетерограницам. Таким образом, пространственное распределение
излучения из полупроводника по своей природе, в общем случае, является
эллиптическим с преобладанием угловой расходимости вдоль оси роста. Это означает
необходимость использования корректирующей оптики в тех областях
применения, которые требуют использования соответствующим образом коллимированных
световых пучков (например, при использовании лазеров в системах с компакт-
дисками, при эффективном вводе излучения в оптические волокна и т. д.).
Литература
Н.С. Casey Jr and M. В. Panish, Heterostructure Lasers, Part A: Fundamental Principles,
Academic Press, New York A978).
S.L. Chuang, Physics of Optoelectronic Devices, Willey Interscience, New York A995).
A. Yariv, Quantum Electronics, Wiley, New York A989).
ДОПОЛНЕНИЯ
К ГЛАВЕ 13
13.А. Лазеры с распределенной обратной связью
(DFB-лазеры)
Как это уже обсуждалось в разделе 13.8, полупроводниковые лазеры могут
генерировать одновременно на большом количестве продольных мод. Однако, такое мно-
гомодовое функционирование нежелательно в целом ряде применений, поскольку
оно приводит к: временному уширению в оптических волокнах, проблемам
коллимации пучка и т. д. Таким образом, в таких случаях за счет использования зеркал с
большой спектральной селективностью выгодно выбрать одиночную моду, которая
испытает лазерное усиление. Такие зеркала могут быть реализованы за счет
использования распределенной обратной связи. В данном случае идея заключается в
том, чтобы встроить в лазерный резонатор модулированную волноводную
структуру с периодом Л (смотрите рис. 13.А.1). Такое периодическое возмущение,
аналогичное брэгговскому зеркалу (смотрите дополнение 9. Г), действует подобно
фильтру с очень большой селективностью. Формализм для описания оптической моды в
пространственно модулированном волноводе был представлен в дополнении 9.Б.
Сейчас же мы напомним основные результаты.
Обозначим соответственно как Af(z) и >4;~(<:)амплитуды оптических мод /с
константой распространения Д, распространяющихся направо и налево.
Периодическое возмущение приводит к энергетическому обмену между волнами,
распространяющимися налево и направо, как это описывается системой уравнений (9Б.6):
dz
dz
Здесь Д/? есть член рассогласования фаз, определяемый соотношением:
A3.А.1)
Ap = pf- — A3.А.2)
Только моды /с АР« 0 могут распространяться в структуре. Обозначим как сов и
Рв частоты и константы распространения, которые удовлетворяют брэгговскому
условию АР = 0. Константа связи g (не путайте с усилением!), которая описывает
- Л U
z=0
= L
Alo.5Gaa5As
т_гил_
A!Q 3Ga0 7As
GaAs
Ai0 3Ga0 7As
Рис. 13.А.1. Поперечное
сечение лазера с
распределенной обратной связью.
Содержание А1 на диаграмме носит
условный характер,
предполагающий возможный состав
слоев.
13.Л. Лазеры с распределенной обратной связью (DFB-лазеры)
эффективность связи между волнами, распространяющимися налево и направо,
может быть записана (9. Б.66) в виде:
1м(*)Е,(хJйх A3.А.З)
Здесь со есть частота электромагнитной волны, sM(x) — функция относительной
(модулированной) проницаемости в области дифракционной решетки, Et(x) есть
распределение электрического поля для моды /, а р0 — есть нормировочная
константа, необходимая для получения однородного уравнения (р0 = 1 Вт м). С
учетом наличия усиливающей среды (с коэффициентом усиления у) A3.А.1)
принимает модифицированный вид:
±A- = \gA;e-2^-7Ai
A3.А.4)
dz
Для решения этой системы уравнений проведем преобразование переменных:
А; = а;е~к
A3.А.5)
а; = а;е*
Это приводит к новой системе уравнений:
±а; = \galtW»*
dz A3.A.6)
f
Формально, система A3.А.6) аналогична системе уравнений A3.А.1) с учетом
преобразования А/?—> А/? + \у.
Таким образом, можно использовать результат дополнения 9. Б. Для этого нам
необходимо детализировать граничные условия для амплитуд в волноводе.
Предположим, что волна с амплитудой я,+@) = а0 падает слева на вход дифракционной
решетки (z = 0, смотрите рис. 13.А.1), при этом никакая волна не падает справа на
выход волновода (z = L) так, что a~(L) =0. В этом случае, уравнение (9.Б. 10) может
быть записано в виде1:
«7(Z)- " L))+ Scb (PL)'"**** [S(Z - L)]
A3.A.7)
[S(z - L)]}
° i(A£ + \y)sh(SL)+ Sch(SL)
На этот раз здесь коэффициент Сдается (смотрите (9Б.96) соотношением:
ё = ylg' + b-iApJ A3.A.8)
Присутствие в экспоненте члена ±yz учитывает усиление в волноводе.
Знаменатели в A3.А.7) выражают зеркальность периодической модуляции. Знаменатели в
этом выражении исчезают, если:
Jcosh SL = (y- iA£)sinh SL A3.А.9я)
Пороговое условие для DFB-лазера
sh = sinh, ch = cosh.
Дополнения к главе 13
В действительности, если это последнее условие удовлетворяется, система
обеспечит ненулевой отклик даже при нулевом входе A2) — это и есть то, что
характеризует лазерную генерацию. Для того, чтобы понять следствия этого условия для
требований на усиление и согласование фаз, проанализируем A3.А.9) для брэггов-
ской частоты сов, т. е. для А/3 = 0:
A3.А.96)
Когда усиление g стремится к бесконечности обе стороны этого последнего
уравнения стремятся к единице, но при этом одна сторона от 1+, а другая от 1~. Понятно,
что A3.А.96) не может быть удовлетворено и Ар = 0 более не определяет
распространяющуюся моду, т. е. усиление вводит новые условия для согласования фаз. Таким
образом, необходимо решать уравнение A3.А.9) в комплексной плоскости.
Рисунок 13.А.2 показывает контурный график \/\ScoshSL — (у — iA/?)sinh&L|2 для
gL = 0,5. Чрезвычайно полезная программа MATH EM ATI CA, используемая для
получения этого графика, приводится ниже:
gL=0,5;
deltal_=Sqrt [д1_~2+(у-1*хГ2];
Den=1/Abs[deltaL*Cosh[deltaL]-(y-l*xSinh[deltaL]];
ContourPlot[Den, {x,0f15),{y,0,6},PlotPoints - > 100
ContourShadlng — > False, AspectRatio ->7]
Отметим, что произведение усиление—длина yL, необходимое для достижения
порога, возрастает по мере отклонения от брэггвского условия ApL= 0. Это
означает, что распределенная обратная связь благоприятствует только малым
отклонениям от брэгговского условия. Для того, чтобы лучше понять это поведение решим
это уравнение для случая сильного усиления, т. е. у» g.
Уравнение A3.А.9) может быть переписано в виде:
е = ■
A3.А.10я)
Это выражение может быть преобразовано следующим образом:
14
Рис. 13.А.2. Контурный график A3.А.9) в плоскости ApL — yL Решения этого
уравнения располагаются в центрах замкнутых кривых.
13.А. Лазеры с распределенной обратной связью (DFB-лазеры)
I * )
Поскольку из A3.А.8) мы имеем:
A3 А. 106)
8 ., .. « i * . м * . A3A.10*)
у-\Ар \ [y-iApj
Начнем с анализа фазовых требований для A ЗА. 106), обеспечивающих
возможность осцилляции моды /:
2arctan М. + 2АД1- g2^>L = Bт + \)я
2/52
A3.А.11)
Как только усиление у становится достаточно большим по сравнению с
разностью фаз, соотношение A3.А.11) значительно упрощается, что дает:
Ap,L
Генерационными модами, наиболее близкими к брэгговской моде, являются
те, которые соответствуют т = 0, т. е. A/?0L = я/2 или т = — 1 или A/3QL = —я/2 и
которые не слишком сильно отличаются от тех, которые мы наблюдаем на
рисунке 13.А.2 (A/30L « 2). Для того, чтобы выразить это условие через разрешенные
длины волн, необходимо вспомнить, что Р{ — 2я72еП./Л, где «eff есть эффективный
коэффициент преломления для моды / (смотрите главу 9), а также, что брэгговская
длина волны Лв = 2лейЛ является резонансной длиной волны для дифракционной
решетки. При использовании A3.А.2) две моды, ближайшие к брэгговским
условиям, есть:
2ке(Г 1 _ 1
Яо Л " 2L
A ЗА. 13а)
2п* 1 1
Я., Л 2L
Или, поскольку 1/L « 1/Л:
A3А.136)
Я, - Ав ~ A2cff —
Спектральный зазор между двумя допустимыми модами составляет:
Это тот же самый результат, что мы получили для случая двух зеркал, разделенных
расстоянием L.
Если следовать A3 А. 106), то условие усиления при пороге дается соотношением:
4 (У,^)+ (/» + !/2)V A3А.15)
Ш2
Уравнение A3 А. 15) является точной функцией у., при этом рисунок 13А.З дает
точки, удовлентворяющие A3А. 15) в предположении gL = 0,5. Понятно, что
распределенная обратная связь способствует фундаментальным модам (/ = 0, —1),
результатом чего является то, что лазеры с распределенной ОС в значительной
степени благоприятствуют лазерной генерации на одиночной продольной моде.
Дополнения к главе 13
1400 -
Рис. 13.А.З. Решения уравнений A3.А.15) для произведения gL{ = 0,5, дающие
усиление, необходимое для генерации мод т = 0, 1 и 2. Видно, что наиболее
благоприятные условия имеют место для моды т = 0, наиболее близкой
условиям Брэгга.
В пренебрежении паразитными потерями ар условие лазерного порога
реализуется при ythKSholdL « 2. Выражение A3.26я) ythKshM = ~l/2\n(RmlRJ показывает, что эта
оптическая обратная связь соответствует коэффициентам отражения зеркал,
определяемым RmlRm2 = е~4 = 0,02. Это совсем недалеко от величин порога, необходимых
для лазеров с резонаторными зеркалами, полученными скалыванием, при этом для
границ раздела GaAs/воздух RmlRm2 = 0,322 = 0,1. Понятно, что усиление у порога
threshold м°жет быть уменьшено за счет константы связи g, что соответствовало бы
использованию зеркал с большими значениями коэффициентов отражения.
Константа связи может быть увеличена за счет приближения дифракционных решеток
ближе к активной области лазера. Это может приводить к значительным потерям,
так как слишком близкое приближение дифракционной решетки к активной
области будет приводить к дифракции света в излучательные («утекающие») волновод-
ные моды. В общем случае оптимизация такой структуры требует использования
численного моделирования.
13.Б. Лазеры с напряженными квантовыми ямами
Максимальное усиление утах для усиливающей среды с квантовыми ямами, как
было получено в A3.57), составляет:
= а,
_е-"/"< -е"/л^ ) A3.Б.1)
Здесь a2D есть поглощение холодного резонатора для среды (т. е. в условиях
отсутствия инжекции носителей, /= 0), определяемое A3.46); ns есть двумерная
концентрация носителей (в см~2) в зоне проводимости и валентной зоны квантовой ямы;
пс есть критическая двумерная концентрация в зоне проводимости (уравнение A3.54));
Rcv есть соотношение эффективных масс mv/mc, где mv есть эффективная масса
состояний в первой валентной зоне, заполненной током инжекции. В главе 13
обоснованно предполагалось, что эта подзона является подзоной тяжелых дырок (с
эффективной массой mhh), поскольку, как мы видели в главе 8, снятие вырождения
приводит к тому, что эта подзона располагается выше других (т. е. выше подзоны
легких дырок и спин-орбитально отщепленной подзоны). Таким образом, как
показано на рисунке 13.23, как концентрация прозрачности, так и ток прозрачности
уменьшаются в соответствии с убыванием отношения эффективных масс. Рисунок
13. Б. Лазеры с напряженными квантовыми ямами
13.21 объясняет этот эффект: при эквивалентной концентрации носителей
квазиуровень Ферми более легко проникает в валентную подзону в том случае, когда
эффективная масса (и следовательно, связанная с ней эффективная плотность
состояний) становится меньше. Другими словами, чем меньше эффективная масса в
валентной подзоне, тем легче выполняется условие Бернара—Дюррафура.
Таким образом, нас интересует возможность использования как можно меньших
эффективных масс. Однако, в рамках конкретной полупроводниковой системы
такая гибкость подхода не возможна, поскольку всегда доминирует подзона тяжелых
дырок. В связи с этим Яблоновичем и Кейном был предложен способ
инвертирования подзон легких и тяжелых дырок с использованием механического напряжения
с целью уменьшения тока прозрачности в лазерных диодах с полупроводниковыми
квантовыми ямами. Это может быть реализовано за счет встраивания слоев
напряженных квантовых ям в приборную структуру.
Рассмотрим в качестве примера квантовую яму In, _^GauAs/InP с составом и,
который отуклоняется от значения, соответствующего точному согласованию
постоянных решетки с подложкой InP (т. е. d а = а0 — а(и) = 0 для и = 0,468). В
процессе синтеза подложка InP вынуждает растущий слой InGaAs принимать
такую же конфигурацию, как если бы это было продолжением решетки InP. В случае
несогласованных по постоянной решетке слоев такая модификация возможна до
тех пор, пока энергия упругого напряжения остается меньше энергии связи InGaAs/
InP. Толщина слоя, при которой обе энергии становятся равными друг другу,
называется критической толщиной /..
При толщине слоя, меньшей /., механическое напряжение из-за
рассогласования постоянных решетки является тензором с элементами, определяемыми
соотношением:
о-о - р - ** - ао~а(и)
t — t w — t - —
a aa
A3.Б.2)
Здесь: Ох и Оу являются двумя направлениями в плоскости квантовой ямы, a Oz
лежит вдоль направления роста. Модуль Пуассона а (равный ~1/3) для
большинства полупроводников III—V, фигурирует в A3.Б.2) и описывает упругость среды.
Когда а(и) > а0 потенциальная яма является упруго сжатой, а когда а(и) < а0, она
является растянуто напряженной (смотрите рисунок 13.Б.1).
Сжатие Растяжение
О О С- "'.- О '.; ',} •' ';. ■."„• ■".; ,",, .,'
О О С О О О ■■ г; Д О О О <Г , ."•
Рис. 13.Б.1. В том случае, когда постоянная решетки объемного lnl _uGa;/As при
конкретной величине и больше аналогичной величины для InP, этот
материал, будучи эпитаксиально выращен на подложке InP, будет сжато
напряжен. В противном случае при а (и) < а0 выращенный слой InGaAs будет
растянуто напряжен. Это заключение имеет место только в том случае,
когда толщина слоя для конкретного состава слоя Int _MGawAs остается
меньше критической толщины 1с.
Дополнения к главе 13
Механическое напряжение в InGaAs заставляет образующие слой атомы
занимать положения, которые являются для них недоступными в ненапряженной
структуре. В результате этого интегралы перекрытия между атомными орбиталя-
ми, а также зонная структура напряженного InGaAs отличаются от аналогичных
характеристик ненапряженного материала.
В отсутствие напряжения ширина запрещенной зоны In,_MGauAs при
температуре 300 К определяется выражением:
Eg(u)= 0,324 + 0,7и + 0,4«2(эВ) A3.Б.З)
Член квадратичной коррекции, который добавляется к обычной линейной
интерполяции между значениями ширины InAs и GaAs, называется параметром
кривизны. В условиях напряжения расчет напряжения показывает, что дно зоны
проводимости сдвигается на 8Е\
A3-Б.4)
Здесь ес есть деформационный потенциал зоны проводимости и он зачастую имеет
отрицательное значение (ес = —5 эВ для GaAs). Аналогичным образом, потолок
валентной зоны также сдвигается по энергии, но при этом величина сдвига
различна для подзон легких и тяжелых дырок:
SEhh(u)=-P(u)-Q(u)
A3.Б.5а)
6Elh(u)=-P(u)+Q(u)
При этом:
A3.Б.56)
2 ч~ » «' s a0 { \-о
Здесь ev и es есть соответственно деформационный потенциал и деформационный
потенциал сдвига для InGaAs (ev = 1,2 эВ и es = —1,8 эВ). Выражение A3.Б.5я) с
физическими константами, приведенными выше, показывает, что в условиях
растягивающего напряжения, происходит обращение положения подзон легких и
тяжелых дырок по отношению друг к другу в пределах зонной структуры. Рисунок
13.Б.2 обобщает различные возможности.
Таким образом, одним из основных аспектов влияния напряжения является
снятие вырождения подзон легких и тяжелых дырок при к = 0 для объемного InGaAs.
Ситуация несколько усложняется в случае квантовых ям, так как снятие вырождения
из-за квантово-размерного эффекта проявляется в более сильной степени в случае
легких дырок, чем в случае тяжелых дырок. Инверсия положения подзон легких и
тяжелых дырок является результатом тонкого равновесия между этими двумя
механизмами снятия вырождения. Рисунок 13.Б.З иллюстрирует подзонную структуру,
полученную для квантовой ямы InGaAs /InP, в функции механического напряжения.
В действительности же влияние этого эффекта на ток прозрачности не так
внушительно (несколько десятков процентов), но, тем не менее, оно может быть
значительным в случае длинноволновых приборов (а именно приборов для
телекоммуникационных применений, работающих на длине волны 1,55 мкм).
Пример
(Просмотрите для справки первую таблицу).
13. Б. Лазеры с напряженными квантовыми ямами
Ehh j
E
Ih
\
Сжатие Отсутствие Растяжение
напряжения
а(и) > aQ а(и) = а0 a(i/) < а0
Рис. 13.Б.2. В зависимости от знака и амплитуды механического напряжения системы
In, _ u Gaw As/InP подзона легких дырок может находиться ниже, на уровне
или выше подзоны тяжелых дырок.
Рассмотрим квантовую яму In047 Ga053 As/InP толщиной ПО А. Поскольку
я@,53) < я@,47) квантовая яма является растянуто напряженной. В
действительности, из линейной интерполяции следует:
alnAs = 6,0584 A; *GaAs = 5,6533 А
a @,53) = 0,53 х 5,6533 А + 0,47 х 6,0584 А = 5,8437 А
Поскольку я1пР = 5,8688 A, Sa/a0 = [a0 - a(u)]/a0 = 4,277 х 10
Эффективные массы также могут быть получены с использованием линейной
интерполяции между InAs и GaAs:
тс = 0,53 х 0,067 + 0,47 х 0,023 = 0,0463
mhh = 0,53 х 0,5 + 0,47 х 0,4 = 0,453
тш = 0,53 х 0,087 + 0,47 х 0,026 = 0,0583
Это приводит к RcJth = mhh/mc = 9,78 и Rc ш = тш/тс = 1,259.
Ширина запрещенной зоны ненапряженного объемного InGaAs определяется
A3.Б.З) и составляет Eg = 0,807 эВ. Механические и физические параметры
системы есть:
<т= 0,33, ес = -6,2 эВ, ev = 1,1 эВ, es = -1,7 эВ
Таким образом, зона проводимости смещается на 2 х (—6,2) х 4,277 х 10 эВ =
= —0,053 эВ. Коэффициенты Р@,53) и 6@,53) есть соответственно -2 х 1,1 эВ х
х 4, 277 х 10 эВ = -9,4 мэВ и 2 х 1,7 эВ х 4, 277 х 10~3 эВ = 14,5 мэВ. Смещение
валентных подзон легких и тяжелых дырок из-за механического напряжения
определяется A3.Б.4), т. е. SEh= -Р ~ 0 = —5,1 мэВ и 8 Elh = -Р + Q = +23,9 мэВ
(смотрите рис. 13.Б.4).
Таким образом, подзона легких дырок lhx поднимается выше подзоны тяжелых
дырок hhv В этом случае эффективная ширина запрещенной зоны определяется
энергетическим зазором ех — lh{ = 0,800 эВ, обеспечивая лазерное излучение на
длине волны Л = 1,55 мкм.
Дополнения к главе 13
hh
/7/7,
Ih -
Сжатие
hh
hh,
Ih '
Ih
hh
hh,
Отсутствие
напряжения
Напряжение
Рис. 13.Б.З. По мере того, как механическое напряжение меняет свой характер от
сжимающего до растягивающего подзона легких дырок постепенно
сдвигается из положения ниже hh2 к положению выше hhv
Уменьшение концентрации носителей в режиме прозрачности можно оценить,
сравнив решения уравнения A3.Б.1) для Rc hh и Rc /Лили (п/п)с hh = 1,79 и (п/пс)с ш = 0,78.
Такое сравнение показывает, что в рассматриваемом случае концентрация в
режиме прозрачности уменьшается в 2,3 раза.
Для излучения на длине волны 1,55 мкм толщина ненапряженной квантовой
ямы должна быть порядка 60 А. Выигрыш в токе прозрачности для напряженной
структуры по сравнению с ненапряженной составит всего 60/110 х 2,3 или 1,3 раза,
что согласуется с экспериментом.
Литература
S.L. Chuang, Physics of Optoelectronic Devices, Wiley Interscience, New York A995).
E. Yablonovich and E.O. Kane, /. Lightwave TecchnoL LT-4, 504 A986).
13. В. Поверхностно-излучающие лазеры с вертикальным резонатором (VCSEL)
-20
0.40
0.60
0.45 0.50 0.55
Состав InGaAs
Рис. 13.Б.4. Изменение положения подзон тяжелых и легких дырок в системе 1
13.В. Поверхностно-излучающие лазеры с вертикальным
резонатором (VCSEL)
Полупроводниковые лазеры с торцевым выводом излучения представляют ряд
неудобств. Начать с того, что в них проявляется тенденция к многомодовому
характеру генерации (что, в принципе, связано с пространственным
выжиганием провала — смотрите рис. 4.11). Это, в свою очередь, приводит к генерации
шума, в основном из-за переключения мод вследствие малых тепловых
флуктуации. В дополнение к этому лазерное излучение является расходящимся, что
вызывает серьезные технологические проблемы, например, при их эффективном
согласовании с оптическими волокнами (смотрите рис. 13.31). Некоторые из этих
неудобств могут быть обойдены при использовании поверхностно-излучающих лазеров
с вертикальным резонатором (VCSEL, что произносится как «виксел»).
Лежащая в основе прибора концепция достаточно проста. Лазерный резонатор
формируется вдоль направления роста структуры, что обеспечивает
контролируемое осаждение чрезвычайно тонких слоев (толщиной менее микрометра) и
практически идеально (с точностью до монослоя) параллельных резонаторным зеркалам.
Зеркала представляют собой брэгговские отражатели, сформированные эпитакси-
альным наращиванием чередующихся полупроводниковых слоев соответствующей
толщины и состава. Металлические зеркала не используются по ряду причин:
невозможным является эпитаксиальное нанесение достаточно совершенных
металлических слоев на полупроводники III—V, металлы поглощают ИК-излучение, что
отрицательно сказалось бы на пороговых токах в этих приборах*. Рисунок 13.В.1
показывает типичный VCSEL, состоящий: из резонатора Фабри—Перо (смотрите
дополнение 9.Г), задаваемого нижним брэгговским зеркалом с N{ парами
четвертьволновых слоев GaAs/AlAs «-типа, обладающим очень большим (>99,9%)
коэффициентом отражения, из полуволнового A/2) резонатора, а также из верхнего брэг-
говского зеркала из N2 пар четвертьволновых слоев GaAs/AlAs /ьтипа, обладающего
большим (-99%) коэффициентом отражения.
13.В.1. Условия достижения порога в VCSEL
Функциональные характеристики VCSEL мы можем легко оценить, отправляясь от
ряда простых рассмотрений. VCSEL может быть аппроксимирован резонатором
* Прим. ред.: Это утверждение не совсем корректно, т. к. нанесение полупрозрачных
металлических зеркал на поверхность полупроводниковых слоев возможно и используется в технологии ЛД.
Дополнения к главе 13
Брэгговское зеркало
Резонатор
Брэгговское зеркало
"eft
Рис. 13.В.1. VCSEL, состоящий из квантовых ям, выращенных в резонаторе Фабри—
Перо, заключенных между двумя брэгговскими зеркалами. Рисунок
показывает распределение электромагнитного поля в резонаторе.
Фабри—Перо толщиной L = \/2пх, заключенным между двумя металлическими
зеркалами. В этом случае межмодовый интервал составляет Ду = c'/2L = с'/А(с' =c/«sc),
т. е. Ahv= 1,6 эВ для L = 0,16 мкм и в предположении типичных величин /15с = 3и
Л — 1 мкм. Поскольку этот межмодовый интервал намного больше ширины полосы
усиления, лазер работает на одиночной продольной моде (смотрите рис. 13.В.2).
В этом случае порог лазерной генерации дается выражением:
j
ln
Здесь Rml, Tml, Rm2 и Tm2 есть соответственно коэффициенты отражения и
пропускания для верхнего и нижнего зеркал, ар есть паразитное поглощение, Г —
коэффициент перекрытия между электромагнитной волной и квантовой ямой. Lc{f —
эффективная длина резонатора: в VCSEL она включает в себя расстояние, на которое
волна проникает в брэгговское зеркало или, иначе говоря, на которое фотоны
проникают в зеркала за счет туннелирования. Расчет Z,eff и не является простым, но
величина этого параметра не является первостепенным фактором в нашей попытке
оценить функциональные характеристики VCSEL.
Принципиальные аспекты VCSEL в сжатом виде заключены в A3.В. 1): хотя
коэффициент перекрытия Г достаточно мал, это может быть компенсировано
использованием зеркал с малым пропусканием. У нас есть возможность оценить
каждый из приведенных параметров. Коэффициенты пропускания Тт брэгговских
зеркал были рассчитаны в дополнении 9.Г (смотрите (9.Г.39)):
71 = 1-
A3.В.2)
Здесь «j и п2 коэффициенты преломления слоев, образующих брэгговские зеркала.
Коэффициент перекрытия Г определяется интегралом:
13.В. Поверхностно-излучающие лазеры с вертикальным резонатором (VCSEL) 555
Пропускание
QW
ВМ
99.9°
Рис. 13.В.2. В VCSEL межмодовый интервал намного больше ширины спектра
усиления. Таким образом, VCSEL будет генерировать лазерное излучение на
одиночной продольной моде.
d/2
j
г =
_ -d/2
A3.В.З)
Здесь d — толщина активной области. Для оценки этого интеграла мы
использовали аппроксимацию (9.Г.26), заключающуюся в том, что поле E(z) рассматривается
как стационарная волна:
(^\ L^/2<z<Leff/2 A3.B.4)
В других областях E(z) =0. В рамках этой аппроксимации мы пренебрегаем
электромагнитным полем за пределами расстояния туннелирования фотонов в брэгговс-
ких зеркалах. В этом случае интеграл A3.Г.З) легко рассчитать:
Г =
dEl
A3.В.5)
Это приводит к:
A3.В.6)
Здесь: г] = 2 для аппроксимации A3.Б.4), но в общем случае имеет значение в
диапазоне от 1 до 2. Интеграл A3.В.З) показывает важность расположения уси-
Дополнения к главе 13
лителя по отношению к пучности электромагнитной волны. Если бы квантовая
яма располагалась в узле электромагнитной волны, то эффективное усиление Ту
было бы равно нулю. Этот результат мог бы быть получен с использованием
соотношения D. В. 12) (полученного при изучении электромагнитных лазерных
уравнений в дополнении 4.В) т. е. с применением A3.В.4) для E(z) как для
единственной допустимой моды резонатора. При подстановке A3.В.5) в A3.В. 1) и
пренебрежении паразитными потерями находим, что необходимое усиление у
порога составляет:
Тт\
Тт2 =
threshold
A3.В.7)
Пороговое условие для VCSEL
Теперь мы можем определить типичные условия функционирования VCSEL.
Сконцентрируем свое внимание на системе GaAs/AlGaAs, поскольку она является
наиболее употребимой системой для изготовления таких приборов. Предположим,
что активной областью нашего VCSEL является квантовая яма толщиной 100 А
(d = 10~6 см). Предположим, что мы хотим добиться, чтобы пороговый ток для
прибора с площадью активной области 30 х 30 мкм2 составил 1,2 мА (т. е., что
плотность порогового тока /threshold =136 А/см2). В предположении, что время жизни
составляет 1,6 не это приводит к двумерной концентрации носителей ns = Jihse^oXdtxJq
или 1,36 х 1012 см (смотрите A3.3)). В этом случае пороговое усиление дается
A3.57) и составляет:
с\
A3.В.8)
Здесь коэффициенты a2Bd = A2D = 0,55%, пс = 7,25 х 1011 см~2, a Rcv = 6,8
получен в примере раздела 13.6.1. Это приводит к *tyhreshold = 4,9 х C10~4ar2D, т. е.
threshold = 490 см. В этом случае уравнение A3.В.7) дает сумму Т + Т вели-
чиной 9,8 х 10. Полагая
Т =
1 ml
Tm2 и используя A3.В.2), мы видим, что мы
можем выбрать набор, состоящий из 30 пар слоев GaAs/AlAs для нижнего
зеркала и 30 пар слоев для верхнего зеркала (в дальнейшем будем полагать Л « 1 мкм,
пх = 3,4 и п2 = 2,96).
Рисунок 13.В.З показывает расчетное убывание порогового тока в функции числа
пар слоев в брэгговских зеркалах.
DO
е
е
о
Q.
О
25 30 35 40
Число пар слоев брэгговских зеркал
45
Рис. 13.В.З. Изменение порогового тока VCSEL на основе GaAs/AlAs в функции числа
пар слоев в брэгговских зеркалах (S = 30 х 30 мкм2).
13.Г. Тепловые аспекты лазерных диодов и мощных приборов
13.В.2. Функционирование VCSEL
В дополнение к одномодовому функционированию VCSEL обладают и другими
преимуществами такими, как низкие пороговые токи и уменьшенная расходимость
пучка излучения. Расходимость выходного пучка может быть легко рассчитана с
использованием выражения D.Д.5) для гауссовских пучков:
^ A3.В.9)
Здесь Wo — ширина выходного пучка. Для VCSEL диаметром 10 мкм (или Wo = 5 мкм),
работающего на длине волны 1 мкм мы получаем расходимость величиной 1/ 5 к радиан
или 4° по всем направлениям.
Малый пороговый ток в первую очередь является результатом малого объема
материала, который надо инвертировать. В случае лазера с реберным волноводом и без
антиотражающих покрытий граней для получения достаточного усиления в общем
случае необходимы резонаторы длиной 200 мкм. В предположении, что толщина квантовой
ямы составляет 100 Е при ширине прибора 3 мкм, это соответствует активному объему
6 мкм3. Эту величину следует сравнить с объемом активной области VCSEL,
составляющим 100 Е х A0 мкмJ или 1 мкм3. Еще большего уменьшения порогового тока можно
добиться за счет оксидирования боковых граней прибора с тем, чтобы усилить
электрическое и оптическое ограничение. VCSEL с резонатором диаметром 3 мкм,
изготовленные таким образом, обладали пороговым током порядка нескольких мкА (при этом
указанная величина соответствует плотности тока порядка 100 А см).
Литература
Специальный выпуск по полупроводниковым лазерам, IEEEJ. Quantum Electron.
June A991).
13.Г. Тепловые аспекты лазерных диодов
и мощных приборов
Одной из особенностью лазерных диодов по сравнению с газовыми или ионными
лазерами с твердотельной матрицей (как например Nd: YAG) является то, что
активный объем, в котором носители рекомбинируют (излучательно или другим
образом), занимает незначительную часть структуры. Таким образом, лазерный диод
с квантовой эффективностью rj = 1 — £ < 1 рассеивает в виде тепла £Р от полной
мощности в малом объеме материала. Это может приводить к существенному
нагреву материала, что может привести к нарушению функциональных
характеристик прибора и, в конечном результате, к его отказу (химическая деградация,
расплавление и т. д.). Сейчас мы изложим краткий теоретический подход, в рамках
которого мы сможем исследовать нагрев и его влияние на характеристики лазебр-
ных диодов. Для простоты ограничимся одномерной моделью.
Нашей исходной точкой будет закон Ньютона—Флика, устанавливающий, что
тепловой поток Ф (Вт) через границу материала, обладающего неоднородным
распределением температуры (смотрите рис. 13.Г.1), пропорционален температурному
градиенту в данном месте:
Ф(х) = -kVT(x) A3.Г.1)
Закон Ньютона—Флика
Здесь к есть теплопроводность в Вт см К. Этот тепловой поток приводит к
изменению внутренней энергии Еш (Дж см) каждого элемента объема, которое
может быть выражено с точки зрения сохранения энергии в следующем виде:
558 Дополнения к главе 13
т
т+
f
Внутренняя
AT
энергия =
рсТ
Рис. 13.Г.1. Иллюстрация закона
Ньютона—Флика.
Поток
I
^Т) = 0 A3.Г.2)
at
С использованием термодинамики эта внутренняя энергия может быть записана
в виде:
Е* = рс,Т A3.Г.З)
Здесь: р есть удельный вес (г см), ас - удельная теплоемкость материала (Дж К г).
Если среда обладает внутренними тепловыми источниками, распределенными в
соответствии с S(x, t) (Вт см), то система уравнений A3.Г.1)—A3.Г.З) приводит к тепловому
уравнению Фурье.
dt Эх2 рср
Тепловое уравнение Фурье
Здесь D есть коэффициент теплопроводности (см2 с), определяемый выражением:
/> = — A3.Г.5)
Рср
Коэффициент теплопроводности
Найдем теперь решения уравнения Фурье для двух показательных примеров,
которые позволят нам лучше понять тепловые характеристики лазерных диодов.
Эмиссионная поверхность в бесконечной среде: переходная характеристика
Этот пример описывает переходную характеристику лазерного диода в отсутствие
теплоотвода. Определим эффективную поверхность теплового источника,
включающего все диссипативные механизмы в структуре (омические контакты,
поглощение на свободных носителях, безызлучательная рекомбинация и т. д.) после
воздействия токового импульса:
S(x9t)=£PS(x)Ht(t) A3.Г.6)
Здесь S(x) есть 8 — функция Дирака (см1), a HT(t) — ступенчатая функция, равная
1 между 0 и г и нулю в других областях (безразмерный параметр). Для любого
момента времени t изменение наклона Т(х) в любом месте эмиссионной
поверхности может быть получено интегрированием A3.Г.4) в интервале между — е и +е с
учетом того, что Г должно быть непрерывным при х = 0:
*L dx - d\^_ dx = lLHr(f)ls(pc)dx A3.Г.7)
Э/ I dx2 pcp J
Или иначе:
13.Г. Тепловые аспекты лазерных диодов и мощных приборов 559
L
дх
РСР
A3.Г.8)
Здесь мы предположили, что среда симметричная относительно точки х — 0. Это
последнее выражение означает, что тепловой поток %Р распределяется равным
образом по обе стороны перехода. При этом он равен Dd Т/дх.
Для решения A3.Г.4) определим временную функцию преобразования Лапласа:
D— f (*,*)- sf (x,s)= -H-S(x)\ 1 "e"J I A3.Г.9)
Эх2 pcp L s j
Здесь член в квадратных скобках представляет собой преобразование Лапласа
ступенчатой функции. Однородное решение для левой стороны уравнения имеет вид
(для х > 0):
f (x, s)= A(s)e-^7Tx A3.Г.10)
Функция A(s) может быть получена из условия A3.Г.8) в виде:
A(s)=- ^/>г_1"<;"" A3.Г.11)
2 pcpy!D s
Это позволяет нам переписать временную зависимость преобразования Лапласа
для распределения температуры:
1 £ О , 1 <±-st
A3.Г.12)
Имеется и обратное преобразование Лапласа для этого последнего выражения,
но оно достаточно сложно, как мы увидим это несколько позже. В течение
некоторого времени нас будет интересовать прежде всего нагрев перехода, т. е. ситуация
при х = 0. Обратное преобразование Лапласа A3.Г. 12) для х = 0 тривиально и оно
определяется выражением:
Таким образом максимальная температура Ттйх достигается в конце токового
импульса (при t = т), что и неудивительно:
Записав A3.Г. 14), мы ввели энергию светового импульса Е = Рти длину
теплопроводности LD = (£)тI/2. В записи с использованием указанных параметров A3.Г. 14)
становится понятным: имеющий место нагрев является результатом диссипации
количества теплоты £Ер в слое материала толщиной L^n, Это уравнение также
показывает, что в данной конфигурации диода имеет место постоянный нагрев
диода в функции длительности импульса г, что неизбежно приведет к разрушению
прибора, если импульс будет достаточно длинным. Таким образом, необходимо
искать способы отвода тепла от области перехода. Рисунок 13.Г.2 иллюстрирует
полное решение для теплового распределения в функции времени, что дается
обратным распределением Лапласа A3.Г.12), а именно:
A3.Г.15)
Дополнения к главе 13
10 15
Расстояние (см)
20*10
-з
Рис. 13.Г.2. Зависимость перегрева в ЛД на основе GaAs от расстояния от перехода в
различные моменты времени после окончания теплового импульса
амплитуды 200 Вт/см2 длительностью 100 мкс.
Здесь erfc есть дополнительная функция ошибок 1-erf для условий, приведенных в
следующем ниже примере.
Пример
Используемые физические постоянные для GaAs из таблицы 13.Г. 1 есть:
р = 5,32 г см
ср = 0,35 Дж Г1 К
к = 0,46 Вт см К
D = 0,25 см2 с'1
В случае диода, рассеивающего количество тепла £Р (Вт см) при длительности
импульса г (мкс) увеличение температуры составит:
Т^ =6x10 "<<?/> (г (мкс ))К2
Таблица 13.Г.1. Тепловые константы для GaAs и InP: р есть удельный вес, ср —
удельная теплоемкость, к — теплопроводность, a D — коэффициент
тепловой диффузии
Материал
GaAs
InP
р (г см'3)
5,32
4,787
ср (Дж г1 К1)
0,35
0,34
к (Вт см К1)
0,46
0,67
D (см~2 с1)
0,25
0,41
Пусть лазерная линейка мощностью 100 Вт имеет ширину 1 см и длину 500 мкм.
В предположении коэффициента нагрева £ равного 10%, тепловая нагрузка
составит %Р = 2 х 102 Вт см. Импульс длительностью в 1 мс приведет к увеличению
температуры на 3,8 К в то время как после 1 секунды перегрев увеличивается до 120 К,
что приводит к необратимому разрушению лазерного диода.
Тепловое рассеяние с двух сторон перехода при непрерывном функционировании
Для предотвращения теплового перегрева с двух сторон перехода должны
размещаться теплоотводы, например, в точках х = +L и х = —L. Тепловое уравнение
13.Г. Тепловые аспекты лазерных диодов и мощных приборов
A3.Г.4), описывающее тепловую характеристику прибора, остается тем же
самым за исключением того, что теперь используются другие граничные условия
(T(L, t) = T(—L, i) = О для любого момента времени t). В предположении, что
такая система обладает стационарным решением, стационарное уравнение
Фурье для Т может быть записано в виде:
д2Тж =
дх2 к
Благодаря первому интегралу в A3.Г.8) это последнее уравнение может быть
проинтегрировано без особых трудностей, что дает Т(х) = (gP/2fc)(L — х) для х > 0.
Стационарное падение температуры между источником и теплоотводом, таким
образом, является линейной функцией. При этом повышение температуры перехода
по отношению к теплоотводу составляет:
-S(x)
A3.Г.16)
2к
A3.Г.17)
Это соотношение может быть интерпретировано как способность теплоотвода
отводить мощность £Р/2 на расстоянии L с учетом теплопроводности материала к.
В общем случае A3.Г. 17) может быть записано в виде:
ДГтах = Rth4P A3.Г. 18)
Здесь Rth есть тепловое сопротивление системы (см2 К Вт).
В случае теплоотвода, расположенного на расстоянии L от перехода (смотрите
рис. 13.Г.З), тепловое сопротивление дается A3.Г. 18) и составляет:
«■4
A3.Г.19)
Тепловое сопротивление для теплоотвода,
расположенного на расстоянии L
от перехода (см2 К Вт~1)
Пример
В продолжение предыдущего примера рассчитаем стационарное возрастание
температуры для того же самого перехода, но на этот раз в присутствии теплоотвода,
расположенного на расстоянии 5 мкм от перехода. Тепловое сопротивление в
рассматриваемом случае составляет 5 х 10~4 см/0,46 Вт см К или 1,1 х 10~3 см2 К Вт.
Рис. 13.Г.З. Присутствие стационарного теплоотвода, расположенного на расстоянии
X, определяет стационарную температуру перехода.
Дополнения к главе 13
Соответствующее возрастание температуры АГтах равно 2 х 102 Вт см х 1,1 х 10~3 см2
К Вт или 0,22 К. Сравнение этой величины с полученным ранее значением 3,8 К
дает представление о преимуществах использования теплоотводов.
Помимо опасности расплавления лазерного диода существует еще целый ряд
других неблагоприятных следствий, связанных с неконтролируемым увеличением
температуры перехода. Во-первых, с учетом теплового расширения
полупроводников их ширина запрещенной зоны уменьшается с увеличением температуры, при
этом длина волны излучения смещается в длинноволновую область спектра. Для
типичного лазерного диода на основе GaAs/AlGaAs скорость температурного
смещения длины волны излучения составляет приблизительно 3,2 Е К. Это может
оказать самое негативное влияние в тех областях применения, когда лазерные
диоды используются для накачки лазерного материала; в этом случае длинноволновый
сдвиг приводит к ослаблению перекрытия между спектром излучения лазерного
диода и поперечным оптическим сечением ионов (смотрите дополнение 4.Д).
Другим эффектом, связанным с увеличением температуры, является
увеличение полного порогового тока /threshold. Физические механизмы этого многочисленны
(эффект Оже, тепловая активация механизмов безызлучательной рекомбинации).
Зависимость /.
от температуры прибора может быть промоделирована с
использованием феноменологического соотношения:
'threshold ~~ * О1
>Т/Т0
A3.Г.20)
Здесь феноменологический параметр То называется характеристической
температурой лазера. Простым правилом, связанным с этим параметром является то, что,
чем больше ширина запрещенной зоны и чем глубже квантовые ямы, тем будет
выше соответствующая характеристическая температура То и тем более
стабильным относительно изменений температуры будет прибор. В таблице 13.Г.2
приведены типичные значения То, полученные для различных полупроводниковых
систем. Лазерные диоды, изготовленные на основе гетероструктур GaAs/AlGaAs
обладают характеристическим температурами порядка 100 К тогда, как лазеры
среднего ИК-диапазона на основе InGaSb/InAs обладают величиной То порядка
30 К, означая, что эти приборы способны функционировать лишь при низких
температурах.
Таблица 13.Г.2. Характеристические температуры лазерных диодов на основе
различных полупроводниковых систем.
Гетероструктуры
GaN/InGaN
GaAs/AlGaAs
InGaAs/GaAs
InGaAs/AlGaAs/InP
InGaSb/InAs/GaSb
Длина волны (мкм)
0,40
0,85
0,98
1,55
3-4
Г0(К)
180
150
90
60
35
На рисунке 13.Г.4 представлены максимальные рабочие температуры лазерных
диодов с длиной волны излучения в диапазоне от 1,5 до 5,5 мкм.
13.Д. Спонтанная эмиссия в полупроводниковых лазерах
500
400
300
200
100
1.5 2 2.5 3 3.5 4 4.5 5 5.5
Длина волны (мкм)
Рис. 13.Г.4. Максимальные рабочие температуры для полупроводниковых лазеров,
излучающих в диапазоне от 1,5 до 5,5 мкм: квантово-размерные
структуры типа I на основе соединений III—V Sb, квантово-размерные гете-
роструктуры типа II и III на основе соединений III—V Sb, солей
свинца, HgCdTe, а также квантово-каскадные лазеры (частное сообщение
A. Jouillie).
• а
- DO
Г
".... I ....
D
■
ш
од ■
I .... I
с
i
ш
I ,
. 1 I . .
в ffl
п
■
□
. . . 1. .
1 1 1 1 1 1 1
- :
ш ■
д
. . 1 . . . ."
13.Д. Спонтанная эмиссия в полупроводниковых лазерах
При предыдущем рассмотрении мы пренебрегали влиянием спонтанной эмиссии
на характеристики полупроводниковых лазеров. В связи с тем, что полупроводники
обеспечивают большое усиление, имеет место и значительное усиление
спонтанной эмиссии (что называется ASE или усиленной спонтанной эмиссией). В свою
очередь, оказывается, что ASE играет фундаментальную роль в определении основных
характеристик лазерных диодов. В связи с этим настоящий раздел посвящен
исследованию влияния этого эффекта на функционирование лазерного диода.
Система уравнений A3.69) описывает связь между концентрацией носителей п
и плотностью фотонов s в резонаторе. Как мы отмечали в разделе 4.А, для учета
спонтанной эмиссии, нам необходимо только добавить член (независимый от
числа фотонов s) для дополнительной скорости Rspon генерации фотонов. В этом случае
уравнение A3.69) принимает вид:
&п J
ds
ds A3ДЛ)
— = c'gs (n - ntT)T - ycs + Rspon
d/
Скорость излучательной рекомбинации была рассчитана в главе 7 и дается
уравнением G.61): Rspon = ysponn. Здесь ^spon есть скорость спонтанной эмиссии,
определяемая yspon = Вр, где р (= я, если мы по-прежнему считаем, что излучатель-
ная рекомбинация имеет место в нелегированной области) есть концентрация
дырок, а В — коэффициент бимолекулярной рекомбинации. Тем не менее, мы
должны учесть, что не все фотоны, излученные в активной области переходят в
волноводные моды (смотрите рис. 13.Д.1). Только доля /? спонтанно излученных
фотонов (называемых коэффициентом спонтанной эмиссии) переходит в волновод и
усиливается. Расчет для получения этого коэффициента /3 достаточно сложен и не
является достаточно надежным. В связи с этим, общепринятая практика
заключается в том, чтобы рассматривать /?в качестве подбираемого параметра (т. е.
определяемого согласованием кривых), при этом его величина лежит в диапазоне между
10~4 и 10~5 для реберных волноводных лазеров.
564 Дополнения к главе 13
Волноводный слой
Сердцевина
Волноводный слой
Активный слой
Рис. 13.Д.1. Только лишь часть /? излученных структурой фотонов переходит в волно-
водную моду и испытывает усиление.
В стационарном состоянии выражение A3.Д.1) определяет концентрации
электронов и фотонов:
s =
Ус -
-Tc'g(n-nu)'
A3.Д.2)
qd
Первое их этих двух уравнений является особенно полезным и оно отражает
тот факт, что лазерные колебания возникают из спонтанной эмиссии, как только
усиление превысит резонаторные потери. В этом случае пороговая концентрация
"threshold Дается выражением:
Tc'g
A3.Д.З)
п
= —; у =
= 1 +
ОЗ.Д.4)
Второе уравнение в A3.Д.2) может быть выражено более кратко за счет
введения безразмерных переменных:
— и а = thresh
JU ",r
Здесь /tr= qdyXoXnx— плотность тока прозрачности. Таким образом, мы
устанавливаем четкую связь между концентрацией носителей и током накачки, которая может
быть записана в компактном виде:
_ + ^ifc0 A3.Д.5)
Г а - х
Здесь г] — квантовая эффективность, определяемая как г] = yspon/yXoX = rtot/r n. Для
того, чтобы найти зависимость s(J) плотности фотонов от тока накачки, нам
необходимо только решить это уравнение и подставить его в первое уравнение A3.Д.2),
что дает:
ус а-х
Уравнения A3.Д.5) и A3.Д.6) являются двумя параметрическими уравнениями по
х, которые позволят нам рассчитать характеристики s(J). Если /3 = 0, то мы вновь
получаем характеристику лазерного диода, подробно описанную в главе 13, в
соответствии с которой концентрация носителей п увеличивалась пропорционально
электрическому току / = qyXoXdn в области ниже порога и резко фиксировалась на
уровне п = пхт в области выше порога. Если /3 ф 0, то зависимость носит более
плавный характер, описываемый рисунком 13.Д.2.
13.Д. Спонтанная эмиссия в полупроводниковых лазерах
Рис. 13.Д.2. Изменение плотности фотонов s (нормированной к пороговой
концентрации носителей пи) в функции плотности тока накачки (нормированной
к плотности тока прозрачности /tr) для различных значений
коэффициента спонтанной эмиссии Д Другие используемые параметры приведены в
примере, который приводится ниже.
Пример
Кривые на рис. 13.Д.2 были рассчитаны в предположении квантовой эффективности
rj = 0,5, резонаторного времени жизни тс = 2 пс, времени жизни спонтанной эмиссии
rsPon = ^ не, коэффициента ограничения Г = 0,5, концентрации носителей в режиме
прозрачности пХх =1,25 х 1018 см и динамического усиления g =2,5 х 10~16 см2 или
а= 1,352. Программа MATHEMATICA, приводимая ниже, может быть
использована для получения лазерных характеристик ниже порога.
beta=.;gamma =0,5;tauc=1/2B.10~n2);taus=1/B.1(T-9);
eta=0.5;g=2.5 1(T-16;ntr =1.25 10" 18;пор=3.3;
с=3.107пор;
alpha =1+tauc/(gamma)*c'*g*ntr);
R=taus/tauc;
Betap=(alpha -1)*R;
Eq1 =yp = = alpha*zp/(zp+betap)+beta/betap*zp*
(alpha*zp/(zp+betap)-1)
sol=Last[Solve[eq1 ,zp)];
t=zp/.sol;
Needs[ "Graphics'Graphlca"']
Beta =1(T1-4;
ploti = LogPlot[t,{yp,.01,2}]
beta =10~-3;
plot2=LogPlot[yp,.01,2]
plot 3=LogPlot[t,{yp,.01,2]
Show[plot1,plot2,plot3]
Дополнения к главе 13
Рисунок 13.Д.2 может быть интерпретирован следующим образом: ниже порога
фотоны спонтанно переходят в волноводную моду резонатора (в этом режиме
лазерный диод ведет себя как СИД). Выше порога плотность фотонов существенно
возрастает (как это описывалось ранее в дополнении 4.А). Более того, как видно из
рисунка 13.Д.2 пороговый эффект становится все более мягким по мере того, как
коэффициент /Устремится к 1.
Эта картина была еще более уточнена Yamamoto с сотрудниками. Этот автор
отметил, что само по себе динамическое усиление g дается g = j3S/rspon, где S есть
площадь поверхности образца. При подстановке этого выражения в A3.Д.5) и A3.Д6)
ему удалось показать, что по мере того, как /? стремится к 1, лазерный порог
стремится к нулю. Из этого наблюдения возникала концепция лазера с нулевым порогом,
в котором все спонтанно излученные фотоны дают вклад в лазерную эмиссию в
режиме усиления.
Представляется интересным использовать настоящую модель для описания
многомодового характера полупроводниковых лазеров вблизи порога. Для этого
предположим, что в резонаторе одновременно существует т мод. Эти моды
характеризуются межмодовым частотным интервалом A vcav = d/2L. Таким образом,
каждая из т мод описывается уравнением типа A3.Д.1) с учетом дополнительной
возможности, что параметры g и /3 изменяются в соответствии с модовым
коэффициентом преломления:
d/ qd tot
dsm _ , A3-Д'7>
d/
Лазерные уравнения
для однородного усиления
Отметим, что в этих уравнениях все моды характеризуются одной и той же
инверсией заселенности п, которая, по определению, означает, что лазерная среда
предполагается однородной. Предположим, что кривая усиления имеет вид лорен-
циана, смотрите рис. 13.Д.З:
g =
1 + [(v -vo)/Av]2
So 1-
Д v
A3.Д.8)
Очевидно, как это следует из глав 7 и 13, полупроводниковые усиливающие
среды по своей природе обладают более сложными кривыми усиления. Таким
образом, эта формула предлагает лишь аппроксимацию более точной ситуации (в то
же время она достаточно хорошо согласуется с экспериментом). При записи пол-
Усиление
А
\
V-M v0 vm VM
Рис. 13.Д.З. Аппроксимация параболической огибающей кривой усиления для
полупроводникового лазера. Число усиленных мод составляет 2М + 1.
13.Д. Спонтанная эмиссия в полупроводниковых лазерах
ного числа мод в виде 2М + 1 (при М= А v/Д vcav), т. е. для тех мод, для которых g > О,
уравнение A3.Д.8) дает коэффициенты усиления для каждой из мод т (где т
изменяется от — М до + М):
A3.Д.9)
Система уравнений A3.Д.7) может быть решена точно таким же образом, как и
до сих пор, что приводит к точному выражению для нормированной плотности
тока у =J/Jtt в функции нормированной концентрации носителей х = п/пх\
'-("/л/J A3Л10в)
-!-х{х-\)\ - ;■ —л
Г mrri (а - 1)- (х - 1) [1 - (т I М )г \
В предположении, что 2М + 1 мод могут стремиться к бесконечности, это
последнее уравнение может быть записано иначе в виде:
Х~ &и A3.Д.106)
Г J[(a-l/x-l)-l]+n:
Это уравнение может быть точно решено, что дает:
у = x + 2^^-x[i(l + f2)arctanfil-lj A3.Д.Ш)
При этом е определяется как:
е^ A3
х-1
Эти уравнения следует интерпретировать с использованием абсолютных
значений комплексных величин, если е2 < 0. Аналогичным образом, плотность фотонов
sm для моды т получается в соответствии со стационарной величиной второго
уравнения A3.Д7), т. е.:
. х-1f m
а-х{М
A3.ДЛ2)
Здесь s0 есть плотность фотонов в максимуме кривой усиления, определяемая
A3.Д.6) или:
7с <* - X
Здесь для упрощения рассмотрения мы предположили, что коэффициент
спонтанной эмиссии /3 не зависит от моды.
Такой подход позволяет сделать ряд заключений. Начнем с того, что хотя мы
предположили, что система однородно уширена, мы замечаем (смотрите рис. 13.Д.4),
что в резонаторе может существовать несколько лазерных мод. Излучение этих мод
вводится в действие спонтанной эмиссией (что описывается Д заметим, что, если
Р = 0, то sm = 0). Более того, по мере того, как ток накачки становится большим
(у -> оо)? нормированная концентрация носителей х стремится к а и становится
фиксированной. В то время, как плотность фотонов s0 в центральной моде
стремится к бесконечности, плотность фотонов в моде m насыщается в соответствии с
соотношением:
ус а-\\пг
A3.ДЛ4)
Дополнения к главе 13
10
г1 -
-
10
10"' -
10"
1 1
-
р = ю-4
-
1
/
\
У
i
1 I I V—
^^^~ т = 0
т= 1
/77=2
/77 = 5
1 1 1
0.5
1.0 1.5
2.0
J/Jtr
2.5 3.0
3.5
Рис. 13.Д.4. Изменение плотности фотонов sm моды т (нормированной к
концентрации носителей в режиме прозрачности /itr) в функции плотности тока
накачки / (нормированной к плотности тока прозрачности /tr) для
коэффициента спонтанной эмиссии Р — 10. Другие используемые параметры
приведены в следующем ниже примере.
Таким образом, интенсивность поперечных мод спадает до нуля по сравнению
с интенсивностью центральной моды. Такой характер зависимости
воспроизводится экспериментально и приводится на рис. 13.Д.5.
Пример
Как развитие предыдущего примера программа MATHEMATICA, приведенная ниже,
может быть использована для расчета характеристик многомодового лазера в
функции тока накачки вблизи порога.
М=10;
beta=1(T-3;
x=alpha-u;
z=betap*(alpha/u-1);
eps=Sqrt[u/ (alpha-1-u)];
y=Abs[x+2*beta*(A+eps^2)/eps*ArcTan[1/eps]-1)];
m=1;
z1=z*1/A-H((x-1)/(alpha-x)*(m/M)^2));
tabley1=Table[{y,z1},{u, КГ-6,1(Г-4,1(Г-6}];
tabley2=Table[{y,z1},{u,10^-4J10'4-2,10'x-4}];
1ааЬ1еуЗ=ТаЬ1е[{у,г1},{и,10Л-2,1., 1СГ-2}];
tablep=Join[tableyp1,tableyp2,tableyp3];
p2=LogListPlot[tablepy]
Литература
G.P. Agrawal and N. K. Dutta, Long Wavelength Semiconductor Lasers, Van Nostrand
Reinhold, New York A986).
G. Bjork and Y. Yamamoto, IEEE J. Quantum Electron. QE. 27, 2386 A991).
13.Е. Насыщение усиления и К-фактор 569
о
I
ф
„ill,
.А
i
ill
in
Ро = 11.7 mW
Ро = 8.1 mW
Ро = 4.6 mW
Ро = 1.75 mW
Illln
Ро = 0.82 mW
8200
8300
8400
Рис. 13.Д.5. Спектр продольных мод лазера на основе гетеростурктуры InGaAs/InP
при различных токах накачки (Из статьи W. Streifer, D.R. Scifres, and R.D.
Bumham, Appl Phys. Lett. 40, 305 A982)).
13.E. Насыщение усиления и К-фактор
В главе 14 (уравнение D.10)) мы видели, что усиление в газовых или ионных
лазерах является насыщаемым, т. е. усиление в функции плотности фотонов s в
резонаторе может быть записано в виде y(s) = yj(\ + s/sj), где у0 есть усиление холодного
резонатора (см)- Это насыщение приводит к стабилизации лазерного усиления до
его стационарного значения (смотрите рис. 4.6). В предположении, что потери у
порога ас (= \/dr) равны приведенному выше уравнению для y(s) можно получить
плотность фотонов в функции тока накачки. Указанное насыщение имеет место
вследствие конкуренции между скоростью накачки R и двумя участвующими
механизмами обеднения возбужденного уровня, а именно: стимулированной эмиссией
и рекомбинацией носителей (излучательной или безызлучательной). Тот же самый
эффект имеет место в полупроводниковых лазерах, в которых эти два последние
механизма включают в себя межзонные переходы (смотрите рис. 13.ЕЛ). Мы легко
находим, что плотность насыщения фотонов составляет ss mttr=:l/dgtt inter> где d есть
скорость света в материале, g — дифференциальное усиление и tt inter = ftot — время
жизни внутризонной рекомбинации (смотрите уравнение A3.69))! "сравнивая это
Дополнения к главе 13
Рис. 13.Е.1. Межзонный и внутризонный
механизмы релаксации, приводящие к временам
релаксации ttintei и tt intra: СВ-зона
проводимости, VB-валентная зона.
выражение с D.9), мы видим подобие того, какую роль играет дифференциальное
сечение g в полупроводниковых лазерах и оптическое поперечное сечение аор в
атомных лазерах.
Это межзонное насыщение является насыщением только с точки зрения
мощности в оптических усилителях (как, например, в МОРА). Однако, в лазерных диодах
выходная мощность в рамках этого подхода остается линейной функцией тока
накачки. Принимая типичные значения с' = 1010 см с, g = 10~15 см2 и f.nter = 1 не, мы
получаем плотность внутризонного насыщения на уровне 1014 см~3. Имеется еще и
другой механизм насыщения, связанный с внутризонной релаксацией (смотрите главу
6 и рисунок 13.ЕЛ). Характеристические времена релаксации составляют величину
порядка пикосекунд (/.ntra = 1 пс). С использованием выражения ss intra = \/c/gtt intra это
приводит к плотности внутризонного насыщения порядка ss intra = 1017 см~3. Этот
последний тип насыщения может рассматриваться в динамических уравнениях
полупроводниковых лазеров как мгновенный и он дается другим выражением:
1 + ES
или:
у(п, s)= y(n)(l-£s)
A3.Е.16)
Здесь € есть коэффициент подавления усиления и он составляет величину порядка
нескольких 1017 см~3. Таким образом, плотность фотонов всегда мала по сравнению
с \/е. В связи с этим мы будем использовать вторую формулу A3.Е.16) так она
приводит к более простым результатам.
Для включения этого нового эффекта в описание функционирования лазера
вновь возвратимся к A3.69) и включим в эту формулу выражение для насыщенного
усиления A3.Е.16) т. е.:
dn J „
— = Ушп ~ <?
d/ qd
A3.Е.2)
^=[rG(n,s)-yc]s
dt
Здесь: G(n, s) = c'y(n, s) есть скорость эмиссии (с) тогда, как ус = 1/г и ytot — l//tot
есть соответственно скорость резонаторных потерь и скорость безызлучатель-
ной рекомбинации. Для иллюстрации влияния члена насыщения е на стацио-
)s
13.Е. Насыщение усиления и К-фактор 57IJn
нарные характеристики лазера выберем модель для усиления лазерной среды в
виде у(п) = g(n — «tr), где, как мы напоминаем, пи есть концентрация в режиме
прозрачности.
В стационарном состоянии число фотонов s0 определяется нетривиальным
решением системы уравнений A3.Е.2), полученным с учетом dn/dt = ds/dt =0 для
qd ttni
A3.Е.З)
Tc'g(n0 -ntT)(\ -€so)= —
Устраняя п0 из обоих уравнений, мы получаем уравнение второй степени:
s i
°
- Ttc (J J
Здесь мы использовали для /threshold выражение:
_qd_
. Ч threshold
' tnt
qd
A3.E.4)
A3.E.5)
В том случае, когда е мало, мы вновь возвращаемся к ситуации, описанной в
A3.72), т. е. к линейной зависимости s от плотности тока /, как только /превысит
^threshold* К°гда плотность тока / становится большой настолько, что более нельзя
пренебрегать es0 по сравнению с 1, зависимость плотности фотонов s0 становится
сублинейной, как это и следует из (легко получаемого) решения уравнения второй
степени A3.Е.4). Рисунок 13.Е.2 иллюстрирует результирующую зависимость
мощности излучения от тока накачки.
Динамические характеристики лазера могут быть получены из записи п = п0 + Sn,
J = Jo + SJ и s = s0 + Ss, где изменения параметров a (n, J или s) являются
гармоническими функциями вида ~Sa&ot. Рекомбинационный член G(n, s) = cfgo(n — nt)(\ — es)
может быть представлен в виде разложения:
= G0+ GnSn + Gs6s
A3.Е.6я)
Линейная
зависимость
Насыщение
'threshold
Рис. 13.Е.2. Характеристическая зависимость выходной мощности от тока инжекции
для лазерного диода, возбуждаемого за пределами линейного режима.
[(E72 Дополнения к главе 13
Здесь члены разложения определяются формулой:
Gn =c'g0; Gs = -ес'}0
A3.E.66)
Таким образом, мы проводим разложение A3.Е.2), удерживая лишь члены
первого порядка и используя условия равновесия A3.Е.З), которые могут быть
записаны здесь в виде GG0 = ус и JJqd = ytotn0 + Goso, что дает:
A3.E.7)
Ц- = Sn(ico + Г„)+ Ss(G5s0 + Go)
qd
SnTGns0 = Ss(ia)-rGss0)= S(io)+rs)
В это выражение мы ввели члены затухания:
Г„ = ?tot + c'goso; Ts = еГс'м A3.Е.8)
Здесь Гп есть коэффициент затухания, уже полученный в разделе 13.7 (уравнение
A3.76)), который описывает потери в системе (а именно, утечку фотонов из
резонатора и безызлучательную рекомбинацию носителей). Гз представляет собой
новый член, связанный с насыщением. Система уравнений A3.Е.7) может быть
просто решена подобно A3.75), что приводит к динамической характеристике
лазерного диода:
Ss
TGnsJqd
A3.Е.9)
SJ (ico + Tn)(\co + Г,) + TGnGas0
Здесь мы пренебрегли GssQ по сравнению с Go. С учетом того, что нас интересует
только амплитудная характеристика лазерного диода, A3.Е.9) может быть
представлено в виде:
A3.Е.10)
qd
(Г„Г5 + TGnGoso)- со2
Г5)
Это выражение может быть аппроксимировано в виде:
-III,
qd
В это выражение мы ввели следующие параметры:
• (угловую) частоту релаксации coR, определяемую:
• Гя или коэффициент затухания лазерного диода:
A3.Е.11)
A3.Е.12)
A3.Е.13)
Этот коэффициент мы выражаем как функцию резонансной частоты f в виде:
A3.Е.14)
В это выражение входит коэффициент К, представляющий собой временной (в
общем случае) параметр, выражаемый в не и определяемый выражением:
A3.Е.15)
Выражения A3.Е.11)—A3.Е.15) показывают, что кривые резонансной
релаксации уширяются пропорционально параметру Гл, который, в свою очередь, возрас-
13. Е. Насыщение усиления и К-фактор
тает более быстро с внутренней плотностью фотонов s0 (т. е. с внутренней
мощностью) по сравнению с тем, как это предсказывается простой теорией раздела 13.7
(смотрите рис. 13.Е.З). Экспериментальный график «ширины резонанса ГЛ в
функции резонансной частоты fR' позволяет определить время жизни носителей ftot и
коэффициент подавления усиления е. Экспериментальные данные, приведенные
на рис. 13.Е.4 ясно показывают, что на коэффициент к доминирующее влияние
оказывает эффект насыщения усиления. В предположении, что типичная величина
е составляет 5 х 107 см3, e/cfg0 равняется 5 х 107 см3/C х 106 см2 х 9 х 109 см с)
или 18 пс, что явно преобладает над резонаторным временем жизни г (порядка 1—2 пс)
в выражении для коэффициента АГA3.Е.15).
4 6
Частота (ГГц)
10
Рис. 13.Е.З. Расчетная частотная характеристика лазерного диода с параметрами,
приведенными в таблице 13.Е.1. В результате насыщения максимальная
мощность излучения лазерного диода, при этом резонансные релаксационные
кривые начинают уширяться.
Таблица 13.Е.1. Значения параметров, использованных при расчетах, представленных
на рис. 13.Е.З.
Выходная мощность
Длина волны
Длина резонатора
Ширина резонатора
Ширина моды
Полная ширина ямы
Объем моды
Активный объем
А*
hv
L
Z
mode
d
active
0,8 эВ
250 mkm
2 mkm
0,2 mkm
0,05 mkm
1,2 x 100cm3
2,5 x 101 см3
Л— 1,55 mkm
У-». = LZd^
Г-ь. = LZd
^574 Дополнения к главе 13
о
о
^ 6
■ 125-160 цт
• 200 цт
▼ 200 |лт R2 = 0.8
rlf20 = 0.32 х 10"9s
10
15
20 25
30
^Р((ГГцJ мВт)
Рис. 13.Е.4. Зависимость ширины резонанса Гя частотной характеристики лазерного
диода от частоты резонанса / Наклон характеристики есть коэффициент
к, позволяющей определить коэффициент подавления засиления е, при
этом точка пересечения этой линии с осью ординат дает время жизни
носителей.
Продолжение табл. 13.Е.1
Выходная мощность
Коэффициент перекрытия
Коэффициент преломления
Коэффициент отражения
зеркал
Коэффициент спонтанной
эмиссии
Коэффициент поглощения
зеркал
Коэффициент паразитного
поглощения
Г
"so
к
р
ат
0,1
3,4
0,3
5 х 10
48 см
20 см
с' = с/пк
^ = ("sc-lO(«sc+lJ
сст = -\n(RJ/L
13.Ж. Шум и ширина полосы лазерного диода 575
Продолжение табл. 13.ЕЛ
Выходная мощность
Характеристики фотонов:
плотность (см)
число
время жизни
Дифференциальное усиление
Концентрация в режиме
прозрачности
Пороговая концентрация
Количество носителей у
порога
Коэффициент стимулиро-
ваного излучения
Безызлучательное время
жизни
Излучательное время жизни
Скорость спонтанной эмиссии
Коэффициент насыщения
Коэффициент затухания
Характеристики релаксации:
частота
затухание
so
So
So
п
Ns
В
'tot
Tn6
spon
e
fR
3,6 x lO^w
1,6 ПС
2,5 x 106 см2
1 x 1018 см
3,7 x 1018 см
9,2 x 107
100 cm3c"'
2hc
2,7 hc
1,7 x HFc
10~17 см
E + 6,6/>mWI08C-'
l,9xlO^mW)c-'
3,2 x 10'(/>mW)'/2 с
1,3 xlO'/^
Pmv = sovmob*hvac'/2
1/r = (am + ap)c/nx
rS0 (", " wtr) = (««+ aP)
^= «^active
Cd = Bng
'"spon"" ^^activc/ 7rad"~ ^spon ^acUve
Г„ - l/'lo, + Cgoso
a)R = 2*tR = (cv;«-()
Г, =(Г„ + Ts)/2
13.Ж. Шум и ширина полосы лазерного диода
Вы видели в дополнении 4.Г, каким образом спонтанная эмиссия, будучи
результатом квантового перехода и, таким образом, непредсказуемой, может быть
представлена в рамках динамических лазерных уравнений виде ланжевеновских сил. Эти
силы являются хаотичными временными процессами (или стохастическими
процессами), обладающими амплитудой автокорреляционной функции вследствии
согласования (смотрите 4.Г. 126) динамических уравнений D.Г.З) со скоростными
уравнениями D.А.13). В этом последнем случае спонтанная эмиссия учитывается
заменой члена эмиссии с*оо sn на член Ccrop(s + \)п. Таким образом, для переменных
случайной амплитуды / и фазы ф получаются два несвязанные дифференциальные
уравнения (смотрите D.Г.15)). Тот же самый формализм может быть использован и
в случае лазерных диодов. Однако, в этом случае рассчитанная спектральная
полуширина оказывается намного уже наблюдаемой экспериментально. Этот феномен
был успешно объяснен С. Генри, заметившим, что полупроводниковый лазерный
Дополнения к главе 13
диод является рассогласованным лазерным резонатором из-за того, что случайные
переменные амплитуды и фазы коррелируют друг с другом за счет связанных
изменений усиления и коэффициента оптического преломления. Другими словами,
флуктуации коэффициента оптического преломления полупроводника также приводят к
флуктуациям резонансной волны резонатора, что обуславливает уширение
лазерной линии. Этот эффект является уникальным для полупроводниковых
материалов. Наш анализ продолжим рассмотрением модели С. Генри.
Предчувствуя важность влияния относительной проницаемости на
распространение электромагнитного поля, мы более не можем ограничиваться изучением
электромагнитных флуктуации в одной точке (например, при х = 0), как это имело
место в D.Г.З). Таким образом, начнем с описания электромагнитного поля с
использованием понятия случайной нестационарной огибающей (смотрите 4.Г.14)):
Будем искать уравнение Ланжевена для лазерной среды с относительной
проницаемостью ех, которому эта нестационарная огибающая может удовлетворять.
Запишем волновое уравнение:
£f£fc')=^r|Usc£fc>) A3.Ж.2)
В рамках аппроксимации нестационарной огибающей функции членом d1E/dt1
можно пренебречь, при этом A3.Ж.1) и A3.Ж.2) приводят к:
A3-Ж.З)
Здесь, по определению, относительная проницаемость еж есть:
*« = («sc + Щт У A3.Ж.4)
Параметры пх и п1т обозначают соответственно действительную и мнимую части
коэффициентов преломления. Действительная часть коэффициента преломления
связана с коэффициентом распространения к выражением:
£=-%sc=4 A3.Ж.5)
с с
Мнимая часть коэффициента п1т описывает затухание амплитуды волны в
полупроводниковой среде. Коэффициент поглощения, определяемый C.36) в этом
случае может быть записан в виде:
<* = 2j"lm A3.Ж.6)
(Напоминаем, что в данном случае амплитуда будет изменяться как е~а/2*, а
мощность как е").
В лазерной среде эффективный коэффициент поглощения а в
действительности является результатом конкуренции, с одной стороны, между паразитным
поглощением ар и потерями на зеркалах ат (ат = — \/2L\n(RxR^ и ас = ар +сст, а с другой
стороны — усилением ^так, что:
f«,m=|(«c-r) A3-Ж.7)
У лазерного порога усиление уравновешивает потери так, что п1т = 0 и
коэффициент оптического поглощения становится чисто действительным. Несмотря на
это, флуктуации числа носителей An приводят к флуктуациям проницаемости £,
что описывается соотношением:
£sc = (nsc + AnR + [Ап1тУ « nl + 2i«scA/iIm(l - iJ3e) A3.Ж.8)
13.Ж. Шум и ширина полосы лазерного диода
Здесь /Зе есть коэффициент уширения, определяемый соотношением:
A3.Ж.9)
Коэффициент уширения
Подставляя выражение для еж A3.Ж.8) в уравнение A3.Ж.З), используя A3.Ж.5)
и сохраняя только члены первого порядка, мы находим, что огибающая функция
E{t) является решением дифференциального уравнения:
A3.Ж.10)
dt x
Это уравнение может быть также записано в виде:
-ч -v/ у~ К~с I /V *ге/~\'/ О A3.Ж.11)
Читатель легко узнает это уравнение, поскольку оно идентично D.Г.З), в
котором пренебрегалось влиянием флуктуации на проницаемость еж, за исключением
дополнительного коэффициента умножения A — \/Зе), который учитывает
флуктуации €ж.
Коэффициент J3e равен нулю для атомных переходов, как это имеет место в
данном случае; лазерная генерация имеет место в пике лоренцовской кривой
усиления, где Дяк равно нулю (смотрите рис. 13.Ж.1). Соотношение Крамерса—Кро-
нига утверждает, что действительная часть коэффициента преломления nR
пропорциональна производной коэффициента поглощения, что само по себе связано с п1т.
С другой стороны, в конденсированных средах кривая усиления более не носит
лоренцовский характер и даже в максимуме усиления AnR не равно нулю (смотрите
рис. 13.Ж.1).
N
N + 31
Рис. 13.Ж.1. В атомных системах изменение коэффициента оптического преломления
в функции концентрации носителей A«R/A7V равно нулю с учетом
лоренцовской кривой усиления (а). В полупроводниковой среде кривая
усиления асимметрична, при этом AnR/AN не равно нулю, что приводит к
ненулевому коэффициенту уширения линии излучения AnR/Anlm.
Дополнения к главе 13
В соответствии с формализмом, развитым в дополнении 4. Г. введем ланжеве-
новскую силу /*(/), возбуждающую электрическое поле в соответствии с
соотношением:
Э/2 2
Вводя подобно дополнению 4.Г, интенсивность /и фазу ф, мы можем разделить это
дифференциальное уравнение на два:
— 1 +с'(ас -уI = 2y[TRe[F(t)e-*] A3.Ж.Ш)
d/
Теперь добавим к этим уравнениям изменение числа носителей п и возвратимся
к обозначениям, введенным в дополнении 13.Е. (смотрите рис. 13.Е.2). При этом мы
получаем ланжевеновские уравнения для полупроводниковой лазерной среды:
fa-\to-7c)P.-W A3.Ж.146)
±n + ru,n + Gs = ±±J + Fii(t) A3.Ж.14*)
at qd at
Лаежевеновские уравнения
для полупроводникового лазера
В дополнение к D.Г. 15) мы добавили к динамическому уравнению для числа
фотонов s A3.Ж. 14а) детерминистский член спонтанной рекомбинации Rspon
таким образом, чтобы среднее значение члена (Fs(t)) было равно нулю. Этот член
Rspon (см~3) есть скорость излучательной рекомбинации, полученная в разделе 7.5
и уже введенная в дополнении 13.Д: Rspon = PBnp — /3n/rrad, где В есть
коэффициент излучательной рекомбинации, rad — излучательное время жизни (смотрите
уравнение G.61)), а /?есть коэффициент спонтанной эмиссии (смотрите
дополнение 13.Е).
Нам по-прежнему необходимо определить автокорреляционные функции для
ланжевеновских функций Fs(t), Fn{t) и FJ(t). Процедура расчета в данном случае
такая же, как и та, что использовалась в дополнении 4. Г. Поскольку их вывод
достаточно сложен, мы ограничимся итоговыми результатами:
(Р.ЪУ.Ъ') = 2DaS(f - t'); п„ = Rspon s A3.Ж.15*)
(РЛУЛ'У) = 2DmSQ - /'); Dm = /?spon s + ушН A3.Ж.156)
(ГЛУ.Ъ')' 2DKS(t-t'y, D» = Ь^ A3.Ж.15*)
45
Здесь мы пренебрегли перекрестными членами по Dsn. Достаточно полное
описание этого последнего расчета можно найти в работе С. Генри A982).
13.Ж.1. Уширение линии излучения
Интегрирование последнего уравнения A3.Ж.146) дает:
«К>о)= -^ fi.it - '.)+ I4(«)d« <13Ж16)
2 {
13.Ж. Шум и ширина полосы лазерного диода
Здесь мы использовали тот факт, что в стационарном состоянии Г G — ус = Rs Js0
(уравнение A3.Ж.14д)). Выполняя тот же самый расчет, что и в дополнении 4.Г\мы
получаем ширину линии излучения A v:
d+^ A3Ж17)
Ширина линии излучения
полупроводникового лазера
Здесь Pout есть мощность излучения лазера, теперь мы понимаем справедливость
понятия «коэффициента уширения линии излучения». При типичной величине /? = 5
при комнатной температуре ширина линии излучения увеличивается в 26 раз по
сравнению с величиной, полученной из соотношения Шавлова—Таунса A4.Г.31).
Пример
Рассмотрим резонатор полупроводникового лазера (hv= 1 эВ) длиной 300 мкм с
коэффициентом паразитных потерь ар = 10 см и двумя зеркалами с
коэффициентом отражения 0,3. В этом случае коэффициент потерь на зеркалах составляет
1/C х 10~2 см) х 1пО,3 или 40 см. Если полупроводник обладает коэффициентом
оптического преломления, равным 3,3, фотонное время жизни г— \/dac в этом
случае составляет 3,3/C х 10ю см с х 50 см) или 2,2 пс. В предположении, что
выходная мощность прибора составляет 1 мВт, а величина /? равна 5, находим, что
лазерный диод будет обладать шириной линии излучения:
1,6хЮ9Дж L -2\ Ллг\ъяг
Av = —-— Р A + 52 )= 140 МГц
2я-B,2х10-12 сJ10 Вт
13.Ж.2. Относительная интенсивность шума (RIN)
и баланс оптической связи
Для того, чтобы определить амплитуду шума в лазерных диодах, являющегося
следствием флуктуации силы Ланжевена проведем разложение A3.Ж. 14л) и A3.Ж.14<?)
аналогично тому, как это было сделано в дополнении 13.Е (смотрите A3.Е.7).
Поскольку нас не интересуют флуктуации тока, мы можем положить в этих
уравнениях SJ = 0, что приводит к:
(io) + rn)dn + G0Ss = Fn
A3.Ж.18)
TGns0Sn + (\о) + TsMs = Fs
Здесь Fnn Fs есть Фурье-образы ланжевеновских сил. Напомним, однако, что эти
Фурье-образы не обладают математическим существованием сами по себе, но
являются промежуточным шагом в расчете, как это было уже показано в дополнении 4.Г.
Лишь параметры
(Fs(tJ) = (F,F,')tf = 2DM и (F.(tJ) =
в действительности определены и представляют собой мощность шума в
полосе А/.
Система уравнений A3.Ж.18) может быть сразу решена, что дает:
Дисперсия {SsSs*) величины Ss может быть получена в виде:
Дополнения к главе 13
'■'■■>
A3.Ж.20)
Здесь релаксационная частота coR и коэффициент затухания Гк уже были введены
соответственно в A3.Е.12) и A3.Е.13).
Определим отношение дисперсии (Ss2) и s2 как относительную интенсивность
шума (RIN). Величина RIN соотносится с A3.Ж.20) в соответствии с соотношением:
RIN =
A3.Ж.21)
С учетом выражения для дисперсии A3.Ж.15) выражение для RIN может быть
записано в виде:
RIN = 2 *«" ^ + Г-^+ ^ГС^°5° ^ fl + r'ot ^ 7 ^ 5°) A3 Ж
{l>J BTy
Относительная интенсивность шума
или RIN для лазерного диода
Размерный анализ этого отношения показывает, что RIN выражается в
единицах Гц, что согласуется с определением A3.Ж.21). Поскольку эта величина, как
правило, мала, принято выражать ее в дБ Гц. Относительные флуктуации
интенсивности (Ss2)/s02 в полосе А/могут быть получены из формулы:
= 10
RINdB /10
А/ = RIN А/
Таким образом, RINdB для -160дБ Гц соответствует RIN величиной 106 Гц.
Рис. 13.Ж.2 показывает результаты расчета RIN с использованием уравнения
A3.Ж.22). Параметры, использованные в этих расчетах для типичного лазерного
диода, используемого в телекоммуникационных применениях, представлены в
таблице 13.Е.1. Несколько моментов, следующих из полученных результатов,
заслуживают внимания:
• шум максимален в резонансе, что является также и общим результатом теории
электрических цепей;
• шум ослабляется по мере возрастания тока инжекции и лазерной мощности;
• уровень шума резко падает при малых частотах модуляции.
-110
-160
10
2 4 6
Частота (ГГц)
Рис. 13.Ж.2. Расчетные частотные зависимости относительной интенсивности шума
(RIN) для типичного лазерного диода на длину волны 1,55 мкм,
полученные с использованием параметров, приведенных в таблице 13.Е.1.
13.Ж. Шум и ширина полосы лазерного диода
Интересное предельное условие для RIN имеет место при очень низких частотах
модуляции (со = 0) и больших плотностях фотонов s0 Wgoso » ytot и для Rsps0 » nsytot):
RIN « 2 ^"^ A3.Ж.226)
Мы напоминаем, что здесь г есть время жизни фотонов в резонаторе. Для
типичных параметров лазерных диодов, приведенных в таблице 13.ЕЛ мы
находим, что при мощности излучения 1 мВт величина RIN составляет 2 х 1,7 х 1012 с х
х A,6 х 102 сJ/3,6 х 104 = 2,4 х 106 Гц или -156 дБ.
Параметр RIN является существенным для расчета оптического бюджета в
телекоммуникационных применениях. Ток i(t), генерируемый в фотоприемнике
лазерным сигналом P(t) дается A1.18) или A1.41):
A3.Ж.23)
п\
Здесь г) есть полная эффективность с учетом потерь в оптической линии связи и
фотоприемнике (смотрите рис. 13.Ж.З). Флуктуации P(t) также приведут к
флуктуации полного тока диода. С учетом соотношения пропорциональности A3.Ж.23)
относительная дисперсия (Ai(tJ)/i2 тока идентична относительной дисперсии
сигнала (P(tJ)/P2 от лазерного диода. Как мы уже показывали при рассмотрении ряда
случаев (смотрите дополнения 4.Г и 11.А), дисперсия временных флуктуации и
частотный спектр флуктуации S(f) (т. е. средняя мощность шума в частотном
интервале А/) связаны соотношением:
(AP(tj) = j AP(tJdt = J Sp(f)df = Sp(f)Af A3.Ж.24)
Это соотношение позволяет связать дисперсию шума фотоприемника с RIN
лазерного диода:
RIN =
A3.Ж.25)
i2Af i2 P2 s2
Таким образом, при расчете оптического бюджета A3.Ж.25) позволяет
рассчитать шум фотодетектирования при приеме сигнала, обусловленный лазерным
диодом. RIN лазерного диода следует сравнить с другими компонентами шума,
обусловленными самим фотоприемником (с использованием концепции обнаружитель-
ной способности, рассмотренной в дополнении 11.Б), а также оптическим волокном
(поляризационный шум, шум усиления и т. д.)
Оптический
сигнал
Усилитель
Лазерный диод
Фотоприемник
Рис. 13.Ж.З. Иллюстрация оптического бюджета в оптических
телекоммуникационных системах.
Дополнения к главе 13
Пример
Рассмотрим лазерный диод с приборными параметрами, приведенными в таблице
13.Е.1. В предположении мощности излучения Ро = 3 мВт и частоте модуляции
1 ГГц (Д/ = Ю9 Гц) лазерный диод будет обладать RIN, равным —150 дБ (смотрите
рис. 13.Ж.2). Если полная эффективность линии связи составляет tj = 0,1, то фото-
Рп Л1Зх10Вт
При этом относительная амплитуда флуктуации тока фотоприемника в этом случае
составит:
Это означает, что величина дисперсии составляет 10 х /0 или 3,7 х 10~7 А.
Литература
G.P. Agrawal and N.K. Dutta, Long Wavelength Semiconductor Lasers, Van Nostrand
Reinhold, New York A986).
C.H. Henry, IEEEJ. Quantum Electron. QE18, 259 A982).
C.H. Henry, IEEEJ. Quantum Electron. QE19, 1391 A983).
13.3. Униполярные квантово-каскадные лазеры
Одной из характерных особенностей полупроводниковых лазерных диодов
является то, что в прямо смещенном диоде принимают участие два типа носителей
(электроны и дырки). Это делает традиционные лазерные диоды биполярными приборами.
Существует и другой класс лазеров, функционирование которых базируется
исключительно на электронах — это т. н. униполярные квантово-каскадные лазеры. В
данном случае в основе работы прибора лежит идея использовать межподзонные
переходы в квантовых ямах (смотрите раздел 11.6). Точно также как межподзонное
поглощение может использоваться в квантово-размерных фотоприемниках, в этом
типе лазера используется межподзонное усиление. Принципиальные концепции,
обеспечивающие функционирование прибора, иллюстрируются рисунком 13.3.1.
• Квантово-каскадный лазер является четырехуровневым лазером. Электроны с
уровня |4) (в действительности с уровня |1>, принадлежащего прилегающей квантовой
яме) туннелируют через материал барьера на уровень |3> квантовой ямы. Из-за
существования минизонных запрещенных зон (что является следствием
периодичности потенциальных барьеров квантовых ям, действующих как «электронная
брэгговская решетка») туннелирование электронов в состояния континуума
затруднено и они могут лишь рекомбинировать в квантовых ямах (рис. 13.3.\а).
• Для обеспечения того, чтобы время жизни тп для перехода |2) —> |1) было
значительно меньше времени жизни г32 для |3> -> |2) (т. е. требование инверсии
заселенности — смотрите главу 4) энергетический зазор Е12 делается резонансным по
отношению к энергии фононов в материале матрицы (Еп = hcuop = 34 мэВ для
GaAs, смотрите дополнение 6.Б), что приводит к тп = 0,4 пс (рис. 13.3.16).
• Переход |3) -» |2> должен сопровождаться передачей значительного квазиимпульса
q в виде эмиссии оптических фононов так, чтобы время жизни г32 было насколько
возможно большим (смотрите дополнение 6.Б и уравнение F.Б.39), где было
показано, что скорость перехода изменяется как l/q2) (рис. 13.3.16).
• Материал барьера, разделяющего квантовые ямы, должен быть приблизительно
такого состава и толщины, чтобы под влиянием электрического поля уровень |1) в
13.3. Униполярные квантово-каскадные лазеры
одной яме находился в резонансном состоянии с уровнем |3) в прилегающей и
более низко расположенной квантовой яме (рис. 13.3.16).
При выполнении всех этих условий мы получаем сложную структуру,
показанную на рисунке 13.3.2. Приборная структура проектируется таким образом, чтобы
матричные элементы zn боли как можно большими. При этом распределение
потенциала в условиях электрического поля приобретает ступенчатый характер и
электроны проходят через нее каскадным образом (отсюда и название этого типа
лазера). В нижней части каждого каскада этой структуры электрон генерирует фотон.
Активная
область
Рис. 13.3.1. Схематичное представление межподзонных переходов в квантово-
каскадном лазере с квантовой ямой (а). Условие передачи квазиимпульса на Е(к)-
диаграмме (б). Условия смещения, обеспечивающие резонансное тунне-
лирование между последовательными квантовыми ямами (в).
Инжектирующий барьер
Запрещенная
минизона
!l
Минизона
Рис. 13.3.2. Зонная структура
квантово-каскадного лазера
(С. Sirtori@THALES).
Активная
область
Дополнения к главе 13
При наличии оптической обратной связи становится возможной и лазерная
генерация на этих переходах. Рассчитаем функциональные характеристики квантово-
каскадного лазера при следующих параметрах прибора:
• длина волны излучения Л = 9,3 мкм при излучательном времени жизни гк = 60 не
(смотрите уравнения C.69) и C.71));
• время жизни на уровне |2) есть т2 = 0,23 пс (включая одновременное проявление
эффектов с участием оптических фононов и туннелирования);
• время туннелирования на уровне |3) составляет т3 = 1,5 пс, что приводит к
квантовой эффективности туннелирования rj = t3/tr или 2,5 х 10~3(смотрите уравнение
A3.13));
• длина резонатора составляет 1 мм;
• эффективный оптический коэффициент преломления в волноводе составляет
nsc = 3,26, что приводит к коэффициенту отражения Rm = 0,28 и коэффициенту
потерь на зеркалах am: 1/LlnR = 18 см;
• коэффициент паразитного поглощения ар = 45 см из-за эффекта поглощения на
свободных носителях, которое очень эффективано в области достаточно больших
длин волн (смотрите дополнение 7.В и уравнение G.В. 12), при этом ар
пропорционально Л2);
• коэффициент ограничения для N квантовых ям Гп определяется ЛТ15 где Г{= d/dmodc
коэффициент ограничения одиночной квантовой ямы (где d — толщина
квантовой ямы, a dmodc — ширина моды) так, что Гп = 0,233 для 25 ям.
В рассматриваемом случае условие лазерной генерации получается при
равенстве усиления и потерь у порога A3.26):
r>thrcsho.d =<*я+а, A3.3.1)
Это приводит к усилению квантовых ям, равному 190 см. Усиление у (см) из-за
межподзонных переходов |3) —> |2) определяется либо (8.876), либо A1.57) и составляет:
У = feill^^LA^ A3.з.2)
й п^ ЙГ„ d
Здесь */толщина квантовой ямы A0 нм), Zo — вакуумный импеданс C77 Ом), #Г32
есть уширение перехода (типичное значение составляет 10 мэВ), hv— резонансная
энергия фотона A30 мэВ) и г1Ъ — дипольный матричный элемент (порядка 2 нм).
Это приводит к пороговой концентрации 2 х 1010 см — малой величине по
сравнению с аналогичным параметром для лазеров на межзонных переходах (>1012 см).
Это различие является результатом большой величине сил осциллятора, связанной
с межподзонными переходами. Концентрация инверсии Ап32 = пъ — п2 связана с
током накачки соотношением A3.3):
Таким образом, мы приходим к пороговой плотности тока 5 кА см. Такая
большая величина пороговой плотности тока связана с малым временем жизни
возбужденного состояния. Тем не менее, несмотря на большие пороговые, токи
квантово-каскадные лазеры обладают рядом преимуществ. Тремя основными
преимуществами являются:
• Эти лазеры могут быть спроектированы таким образом, чтобы они работали на
любой фиксированной длине волны в диапазоне между 4 и 13 мкм в рамках
одной и той же полупроводниковой системы. Это может быть реализовано с
использованием зонной инженерии, как это было описано в главе 8.
• Выходная мощность излучения квантово-каскадного лазера с 7V квантовыми ямами
чрезвычайно велика (несколько сотен мВт), поскольку каждый электрон может
привести к излучению в общей сложности N фотонов (по одному на каждую яму).
С использованием A3.34) полная мощность излучения может быть записана в виде:
13.И. Конкуренция мод: перекрестные модуляторы
Л. = :
— (/"/th
)
A3.3.4)
Понятно, что поскольку приложенное напряжение пропорциональна Nx hvKYlJX
прибора Pout/Pel остается неизменным (смотрите A3.376).
Как мы видели на рисунке 13.Г.4, максимальные рабочие температуры
определяются Оже-рекомбинацией. Однако механизм Оже виртуально не существует при
межподзонных переходах, поскольку подзоны параллельны (смотрите
дополнение 6.Г и рис. 6.Г.1). В результате этого характеристические температуры То для
межподзонных лазебров достаточно велики. Например, для лазера, излучающего
на длине волны 9,3 мкм То= 140 К. Таким образом, квантово = каскадные лазеры
могут работать в импульсном режиме на таких больших длинах волн вплоть до
комнатной температуры (смотрите рис. 13.Ж.З).
400 -
^ 300 -
§; 200 -
ф
ф
с
Q)
100 -
5 10 20
Длина волны (мкм)
Рис. 13.3.3. Максимальные рабочие температуры квантово-каскадных лазеров,
функционирующих на различных длинах волн.
Литература
J. Faist, F. Capasso, D.L. Sivco, С. Sirtori, A.L. Hutchinson, and A.Y. Cho, Science
264, 553 A994).
C. Sirtoni, J. Sivco, A.L. Hutchinson, and A.Y. Cho, IEEEJ. Quantum Electron. QE-33,
89 A997).
13.И. Конкуренция мод: перекрестные модуляторы
В дополнении 11.Д мы видели, что вблизи порога полупроводниковый лазер может
генерировать в многомодовом режиме несмотря на то. что усиливающая среда
является однородной. При достаточно сильном возбуждении настолько выше порога,
что спонтанной эмиссией можно пренебречь по сравнению со стимулированным
излучением, лазер, в конце концов, вновь приобретает одномодовый характер. Сейчас
мы изучим этот феномен более детально. Мы покажем, что этот эффект может
быть понят с учетом перекрестного насыщения, при этом мы увидим, каким
образом этот эффект используется в оптоээлектронных приборах, а именно в
модуляторах с перекрестным усилением.
Мы начнем с A3.Д.7), дающего динамические уравнения для лазерного
резонатора в многомодовом режиме. Для упрощения расчетов предположим, что лазер
функционирует в режиме намного выше уровня прозрачности так, что п » nti и
величиной Rspon можно пренебречь, при этом существуют лишь две моды. В этом
случае уравнение A3.Д.7) может быть записано в виде:
Дополнения к главе 13
&п
A3.И.1)
Напоминаем, что s и п есть соответственно концентрация электронов и плотность
фотонов, / — плотность тока накачки, d —толщина активной области; ttot — полное
рекомбинационное время жизни; г — время жизни фотонов в резонаторе; g. —
динамическое усиление; d — скорость света в среде, а Г — коэффициент ограничения.
В стационарном состоянии 13.11) дает концентрацию электронно-дырочных пар:
п = - ; ^—; A3.И.2)
1 + с£Л* +cgts
Здесь: п0 = JtioX/qd есть концентрация электронно-дырочных пар холодного
резонатора, что приводит к усилению среды G. для моды / в виде:
G,n
G, =■
€ 2S2
A3.И.З)
Здесь G.o = Yc'g. n0 есть усиление холодного резонатора и в. = cfg. /tot. Как и в
дополнении 11.Е и в соответствии с общепринятой практикой члены в обозначают
величину, обратную плотности насыщения фотонов 5Mt для которой величина усиления
уменьшается вдвое (смотрите главу 2). В последнем уравнении A3.13) мы видели,
что усиление на одной длине волны может быть насыщено пучком накачки на
различных длинах волн. Этот эффект используется в модуляторах с перекрестаным
усилением. Рассмотрим и объясним сейчас функционирование этого прибора.
Рассматриваемый прибор способен преобразовывать модулированный сигнал с
длиной волны Я2 в модулированный сигнал с длиной волны Лг В завершение этого
полупроводниковый оптический усилитель (типа МОРА) накачивается
непрерывным пучком на длине волны Л2 с интенсивностью, приближающейся к плотности
насыщения (смотрите рис. 13.ИЛ). Дополнительный сигнал на длине волны Лх
насыщает среду (смотрите 13.3.3), при этом на длине волны Л2 наблюдается
ослабление усиления. Таким образом выходная мощность на длине волны Д2уменьшается,
когда увеличивается входная мощность на длине волны Лг Таким образом, сигнал,
изначально передаваемый на длине волны Л19 отображается «негативно» в световом
пучке на длине волны Л2 (смотрите рис. 13.И. 16).
Дадим теперь краткое описание динамического поведения этого лазера с
учетом конкуренции мод 1 и 2. Для этого мы предположим, что лазерное усиление G
находится в стационарном режиме в то время, как оптические моды не находятся в
этом режиме. Это приводит к ftot < г, что имеет место в лазерах на основе атомных
переходов, но не в полупроводниковых лазерах. Хотя и нет особой необходимости
МОРА
w
Рис. 13.И.1. Функционирование модулятора с перекрестным усилением.
13.И. Конкуренция мод: перекрестные модуляторы
в такой аппроксимации, без нее будут скрыты физические аспекты
рассматриваемой задачи, которые мы хотели бы представить в явном виде.
Подставляя выражение для насыщенного усиления A3.И.3) в A3.ИЛ), получаем:
s Si ? / = 1,2
адед г/ ' A3.И.4)
Предположим, что среда слегка насыщена (что предполагает es. « 1), обеспечивая
ограниченное разложение A3.14):
s2 = a2s2 - 621v2 ~ K2sl A3.И.5)
В это последнее выражение мы ввели следующий параметр:
<*i = G/o > к, = Gi£i> ва = G,ej
гс ОЗ.И.бя)
Эти члены есть ничто иное, как полное усиление (являющееся результатом
конкуренции между резонаторным усилением и потерями, членом автонасыщения и
членом автоперекрестного насыщения). В контексте аппроксимации A3.И.5) мы
видим, что имеются два стационарные решения для плотности фотонов для этих двух
уравнений:
(a, -k.s, -<91252>, =0
(<*2-<V. ~k2s2 >2 =0
A3.И.66)
Легко показать, что линии а. = ks. + O.JS. не пересекаются. Таким образом,
решения лежат в точках пересечения линий, определяемых условием A3.И.66), и
осей координат, как это представлено на рис. 13.И.2: точка A (s20= 0 и slQ = а{/к{) и
точка В (sl0 = 0 и s20 — а2/к2). Мы увидим, что только одна из этих двух точек дает
устойчивое решение A3.И.5).
Вблизи точки А ддя плотности фотонов может быть записано разложение в
виде s2 = 8s2 и s20 = а2/к2. После чего дифференциальные уравнения линеаризуются
и могут быть записаны в матричном виде:
В'
G21 *1
Рис. 13.И.2. Из двух стационарных решений уравнения конкуренции мод A3.И.5),
показанных кружками, стабильной является лишь с большим значением
усиления (т. е. наиболее далеко отстоящая от начала).
Дополнения к главе 13
AC,
Мы видим, что решение будет устойчивым только, если:
а2<в21^- A3.И.8)
к{
С учетом определений A3.3.6) это соответствует условию:
Gl0 > G20 A3.И.9)
Другими словами, хотя положительное усиление в резонаторе имеет место
для обеих длин волн, предпочтительной для лазера в стационарном состоянии
будет генерация на моде с наибольшим усилением (отсюда и термин
конкуренция мод). Используя тот же самый формализм, мы могли бы показать, что
неоднородно уширенная среда будет характеризоваться многомодовым
стационарным функционированием.
Литература
G. Grynberg. A. Aspect, and С. Fabre, Introductionaux aux lasers et a loptique quantique,
Ellipses, Paris A997).
A.E. Siegman, Lasers, University Science Book, Mill Valley, CA A986).
I. Valiente, J.C. Simon, and M. LeLigne, Electron Lett., 29, 502 A993).
Литература
Общие сведения по свойствам полупроводниковых материалов приведены в:
К.Н. Hellwege, ed., Landolt-Bornstein Numerical Data and Functional Relationships in
Sccience and Technology, Springer, Berlin.
O. Madelung, ed., Semiconductorsr, Group IV Elements and 111-V Compunds, in Data in
Science and Technology, Springer, Berlin. A196).
Recent review works:
B.L. Wiess, ed., EMIS Dataviews Series, INSPEC, London.
Свойства основных полупроводниковых
Si
Ge
GaAs
AlAs
InAs
материалов
GaP
InP
GaSb
InSb
Ширина запрещенной зоны
Eg (эВ)
@т=о к
@г=ок
Постоянная решетки, А
Диэл. постоянная, e^Je^
непрямая
1,170
1,124
5,43095
11,9
непрямая
0,744
0,664
5,64613
16,2
прямая
1,519
1,424
5,6533
13,1
непрямая
2,229
2,17
5,6600
10,06
прямая
0,418
0,354
6,0583
15,15
прямая
2,350
2,272
5,4505
11,1
прямая
1,424
1,344
5,8688
12,56
прямая
0,70
6,096
15,69
прямая
0,236
0,18
6,4794
16,8
Эффективная масса
Электронная продольная
Электронная поперечная, mel/mQ
Тяжелых дырок, mhh /m0
Легких дырок, mjh/m0
0,9163
0,1905
0,537
0,153
1,59
0,0823
0,284
0,043
0,067
0,50
0,087
0,15(Г)
0,79
0,15
0,023
0,40
0,026
0,254
4,8
0,67
0,17
0,073
0,60
0,12
0,047
0,8
0,05
0,014
0,42
0,016
Параметры Латтинджера
п
Уъ
Собственная концентрация,
я (см~3)
4,25
0,32
1,45
1,5 х 1010
13,4
4,3
5,7
2,4 х 1013
7,0
2,3
2,9
1,8 х 106
3,45
0,68
1,3
20,4
8,3
9,1
1,3 х 1015
4,05
0,49
1,25
3,0 х 106
5,04
1,6
2,4
1,2 х Ю8
13,3
4,4
6,2
4,3 х 1012
40,1
18,1
19,2
2,0 х 1016
Подвижность
Электронов, //е (см2/В с)
Дырок, juh (см2/В с)
1450
370
3900
1800
8000
400
400
100
30000
480
200
150
5000
180
5000
1500
80000
1500
§
со
CD
Заявки на книги присылайте по адресу:
125319 Москва, а/я 594
Издательство «Техносфера»
e-mail: knigi@technosphera.ru
sales@technosphera.ru
факс: @95) 956 33 46
В заявке обязательно указывайте
свой почтовый адрес!
Подробная информация о книгах на сайте
http://www.technosphera.ru
Э. Розеншер, Б. Винтер
Оптоэлектроника
Компьютерная верстка — НА. Попова
Дизайн книжных серий — СЮ. Биричев
Ответственный за выпуск — Л.Ф. Соловейчик
Формат 70 х 100/16. Печать офсетная.
Гарнитура Ньютон
Печл. 37. Тираж 2000 экз. Зак. № 10644
Бумага офсет № 1, плотность 65 г/м.2
Издательство «Техносфера»
Москва, ул. Тверская, дом 10 строение 3
Диапозитивы изготовлены ООО «Европолиграфик»
Отпечатано в ППП «Типография «Наука»
Академиздатцентра «Наука» РАН,
121099 Москва, Шубинский пер., 6