Автор: Шведов А.С.
Теги: денежное обращение банковское дело биржи экономика отдельных стран экономика мирового океана экономика
ISBN: 5-7598-0066-3
Год: 1999
Текст
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ВЫСШАЯ ШКОЛА ЭКОНОМИКИ
А.С.Шведов
ТЕОРИЯ
ЭФФЕКТИВНЫХ
ПОРТФЕЛЕЙ
ЦЕННЫХ БУМАГ
Пособие для студентов,
изучающих портфельную теорию
и теорию финансовых деривативов
ft
Москва 1999
УДК 336.76
ББК 65.9(2)26
Ш 34
Рекомендовано редакционно-издательским советом
Государственного университета - Высшей школы экономики
Рецензенты: кандидат физ.-мат. наук, доцент В.Б.Демидович,
доктор физ.-мат. наук, профессор В.И.Ротарь
ISBN 5-7598-0066-3
© ГУ ВШЭ, 1999
© А.С.Шведов. 1999
Содержание
Введение............................................. 4
§1 . Основные понятия и моделирование риска ......... 9
§2 . Игра на повышение и игра на понижение. Позиции
“быка” и “медведя”............................. 19
§3 . Эффективный фронт и эффективные портфели.. 25
§4 . Оптимальный портфель при возможности заимство-
вания и одалживания............................ 44
§5 . Упрощенные методы нахождения эффективных порт-
фелей. Использование индексов.................. 53
§6 . Анализ полезности.............................. 65
§7 . Другие вопросы, связанные с уменьшением риска . 82
§8 . Модель оценки фондовых активов................. 96
§9 . Исследование структуры эффективного фронта .... 108
§10 . Вычислительные процедуры для нахождения эффек-
тивных портфелей.............................. 116
Библиографический список .......................... 139
Предметный указатель .............................. 142
Введение
Теория эффективных портфелей направлена на решение
практической задачи о рассредоточении капитала по раз-
личным видам ценных бумаг в условиях неопределенности.
Основные положения этой теории были разработаны аме-
риканским математиком Г.Марковицем при подготовке его
докторской диссертации в 1950 - 1951 годах. На основе дис-
сертации им была написана книга [10]1, до сих пор остаю-
щаяся важным учебником по портфельной теории. Сущест-
венный вклад в данную теорию был сделан другим аме-
риканским математиком -- Дж.Тобином, который устано-
вил существование оптимального портфеля среди множест-
ва эффективных портфелей. Работы Г.Марковица привлек-
ли внимание многих математиков и специалистов по ценным
бумагам и вызвали большое число обсуждений и публика-
ций. Блестящее изложение построенной теории дано в моно-
графии [14] У .Шарпом, который также внес в создание этого
направления значительный вклад. Позднее все три упомяну-
тых математика стали лауреатами Нобелевских премий по
экономике. Дж.Тобин получил Нобелевскую премию в 1981
году, а Г.Марковиц и У.Шарп - в 1990 году.
Современная математика - это тысячи различных тео-
рий, очень непохожих друг на друга и имеющих непохожие
судьбы. Одни из математических теорий относительно про-
зрачны, другие невообразимо сложны, одни стремительно
развиваются, другие по разным причинам не развиваются
*См. библиографический список.
Введение
5
совсем или развиваются очень слабо, одни известны всем,
кто занимается математикой, другие почти забыты. Каж-
дая из этих теорий неповторима по своей красоте, в каж-
дую вложены чьи-то души, таланты, лучшие годы жизни.
Однако далеко не все теории имеют практические приложе-
ния. И даже среди тех математических теорий, про которые
можно сказать, что они используются в практике, лишь не-
многие стали действительно уникальными инструментами
и приносят большие реальные результаты, в том числе и
для людей, от математики совершенно далеких. Место дру-
гих математических теорий в прикладных областях менее
важно, третьих - еще более скромно, о возможности приме-
нения четвертых говорят лишь небольшие группы матема-
тиков. Конечно, у разных людей могут быть разные точки
зрения на то, какое место занимает та или иная математи-
ческая теория на этой шкале, и место это может меняться
со временем как в одну, так и в другую сторону.
Ни в коем случае нельзя считать, что те из математичес-
ких теорий, которые не используются в практике, бесполез-
ны. Они необходимы с точки зрения внутренней логики нау-
ки. Никто не знает, на какой ветке вырастет золотое яблоко,
а различные теории не только сильно между собой связаны,
но часто и само деление математического направления на
отдельные теории очень условно.
Практическое значение теории эффективных портфелей,
которая является математической теорией, для рассредото-
чения вкладов, увеличения прибыли и снижения риска очень
велико. В [11] использование этой теории названо революци-
ей для фондового рынка.
И после 1970 года, когда вышла книга Шарпа [14], многие
авторы обращались к изложению различных сторон теории
6
эффективных портфелей2. В последние годы было издано не-
сколько книг на русском языке, в которых освещен ряд по-
ложений теории эффективных портфелей3. Однако ни одна
из этих книг не содержит достаточно подробное изложение
данной теории. Настоящее издание в какой-то степени вос-
полняет этот пробел.
Никакая теория не может охватить все особенности
практической ситуации. Так и рекомендации по рассредото-
чению капитала, получаемые из теории эффективных пор-
тфелей, являются рекомендациями, а не директивами. Соот-
ношение математических методов, которым посвящена эта
книга, и других методов анализа в работе реального финан-
сового института может быть достаточно сложным4. Отме-
тим, что теория эффективных портфелей - это далеко не
единственная математическая теория, которая использует-
ся в настоящее время для выработки решений на фондовых
рынках. Существуют другие математические теории, роль
которых при управлении капиталом не меньше, чем роль
теории эффективных портфелей. Но в этой книге мы их не
рассматриваем.
В книге содержится изложение ставших уже классичес-
кими идей и результатов теории эффективных портфелей. В
§1 обсуждается возможность математического моделирова-
ния риска, дается определение доходности, перечисляются
используемые в дальнейшем понятия из теории вероятнос-
тей. В §2 описаны две основные операции на рассматрива-
емом идеальном рынке: покупка и выпуск ценных бумаг. В
23десь можно назвать книги [1], [2], [3], [8], [9], [12] и многие другие.
Наиболее важные оригинальные статьи собраны в [13].
3Например, [16], [18], [22], [24], [28], [30], [34], [37].
4См., наир.: Поиск. 1997. 8 - 14 марта; [37], с. 199 - 201.
Введение
7
§3 изучаются портфели ценных бумаг. Доходность портфеля
рассматривается как случайная величина, и портфели оце-
ниваются по математическому ожиданию Е и стандартному
отклонению <т этой случайной величины. Портфель называ-
ется эффективным, если из тех же ценных бумаг и при тех
же ограничениях на их пропорции нельзя составить другой
портфель, который имел бы такое же математическое ожи-
дание доходности Е и меньшее стандартное отклонение а. В
§4 рассмотрен частный, но важный случай, когда среди цен-
ных бумаг, из которых создается портфель, присутствует
безрисковая ценная бумага. Тогда среди эффективных порт-
фелей может быть выделен оптимальный портфель.
Относительно случайных величин, которые представ-
ляют собой доходности ценных бумаг, при практическом
построении эффективных портфелей должны быть сдела-
ны некоторые дополнительные предположения. Один из су-
ществующих подходов, связанный с использованием индек-
сов рынка, описан в §5. В §6 применительно к портфельной
теории рассматривается метод принятия решений, основан-
ный на максимизации ожидаемой полезности. В §7 обсуж-
дается влияние риска на темп роста капитала, даются при-
меры уменьшения риска путем включения в портфель спе-
кулятивной ценной бумаги и путем выпуска ценных бумаг.
Здесь же обсуждается еще один способ уменьшения риска
портфеля, связанный с использованием деривативов5. В §8
рассматривается применение теории эффективных портфе-
лей для оценки фондовых активов.
В §9 и 10 используется несколько более сложный мате-
матический аппарат, чем в остальной части книги. Естес-
5Иногда деривативы называют также производными финансовыми
инструментами.
твенно, первые 8 параграфов могут быть прочитаны без
привлечения этого материала. В §9 при некоторых допол-
нительных предположениях доказано, что множество точек
на плоскости (а, Е), отвечающих эффективным портфелям,
состоит из нескольких кусков кривых второго порядка (или
из куска одной кривой). В §10 описан метод построения мно-
жества эффективных портфелей. В основе этого метода ле-
жит решение задач математического программирования. За
исключением самых простых случаев, данный метод может
быть реализован только при помощи компьютеров 6.
Далеко не все вопросы, относящиеся к теории эффектив-
ных портфелей, затронуты в этой книге. Например, нами со-
всем не обсуждается возможность учета асимметрии в рас-
пределении доходностей при выборе портфеля. Нашей целью
было дать изложение основ теории эффективных портфелей,
а не обрисовать современное состояние данной теории.
Автор благодарен своим коллегам из Государственно-
го университета - Высшей школы экономики Э.Б.Ершову,
Г.Г.Канторовичу, Е.В.Коссовой, Т.А.Ратниковой, А.Г.Шо-
ломицкому, которые читали рукопись книги и сделали мно-
го полезных замечаний. Разумеется, ответственность за все
остающиеся неточности лежит на авторе.
Для чтения этой книги требуется определенная подготов-
ка по теории вероятностей и математической статистике, по
аналитической геометрии и по математическому анализу, а
для чтения §9 и 10 - еще и по линейной алгебре7.
6Существует большое число компьютерных программ, которые
включают алгоритмы построения эффективных портфелей. Некоторые
из этих программ описаны, например, в [18].
7Все необходимые сведения по этим предметам содержатся, напри-
мер, в [38], [31], [20] и [26].
§ 1. Основные понятия и
моделирование риска
При управлении капиталом средства могут вкладываться
в акции, в недвижимость, направляться на покупку ино-
странной валюты или другого имущества. Дадим опреде-
ление доходности, которая является важным показателем
эффективности капиталовложений. Рассмотрим период вре-
мени (t, t + Af), Ai > 0. Пусть St - стоимость некоторого
имущества, например акции, в момент времени Л St+At -
стоимость того же имущества в момент времени (t+Af); D -
доход, полученный от владения имуществом в этот период
времени. Тогда
доходность =
•S't+At — St + D
Мы считаем, что St > 0, St+^t > 0. Хотя мы и назвали
D доходом, для нас несущественно, положительно D, отри-
цательно или равно 0. Если имуществом являются акции, то
D - это дивиденды, выплаченные в рассматриваемый пери-
од времени, и в этом случае D > 0. Из определения видно,
что доходность может быть как положительным, так и от-
рицательным числом, или равняться О8.
С точки зрения математической теории, которая излага-
ется в этой книге, виды имущества, между которыми рас-
8Более академическим термином является не “доходность”, а, на-
пример, “норма дохода”, “ставка дохода” или “ставка прибыли”. Од-
нако практики чаще называют данную величину доходностью.
10
Теория эффективных портфелей ценных бумаг
средоточен капитал, несущественны. Важны только доход-
ности для различных видов имущества, а также то, как эти
доходности могут изменяться и как они связаны между со-
бой. Поэтому в дальнейшем мы будем говорить о рассредо-
точении капитала по различным видам ценных бумаг. Это
делается с единственной целью упростить изложение. Ника-
кие отличительные особенности ценных бумаг по сравнению
с другими видами имущества нами не используются.
Мы будем рассматривать идеальный рынок, где выпол-
няются следующие условия. Предполагается, что все цен-
ные бумаги абсолютно ликвидны и бесконечно делимы. Это
означает, что в любой момент времени можно купить или
продать любое количество каких угодно ценных бумаг и да-
же сколь угодно малую долю любой ценной бумаги. Цена
покупки совпадает с ценой продажи. Расходы на покрытие
трансакционных издержек и уплату налогов в расчет не при-
нимаются.
Кому-то сделанные предположения могут показаться
слишком далекими от реальной жизни. Однако именно тео-
рия, построенная при указанных предположениях, является
базовой. Изменение в той или иной форме этих предположе-
ний приводит к усложнению теории и к приближению ее к
реальной жизни.
Допустим, что цель управления заключается в том, что-
бы к моменту времени (t + Ai) путем вложения средств в
ценные бумаги максимально увеличить капитал, имеющий-
ся в момент времени tQ. Если бы доходности для всех цен-
ных бумаг были предсказуемы абсолютно точно, то вопрос о *
9 Это простейшая постановка задачи. Определение цели может быть
и более сложным, например, если Д/ велико. Мы коснемся этого во-
проса в §7.
§1. Основные понятия
11
рассредоточении капитала не возникал бы. Нужно было бы
просто вложить все средства, как собственные, так и, если
это возможно, заемные, в ценные бумаги с максимальной
доходностью.
Однако точная предсказуемость доходностей не входит
в число исходных предположений. Поэтому вопрос о спо-
собах рассредоточения капитала возникает и должен быть
изучен. При этом должна быть рассмотрена связь между
ожидаемыми прибылями и размерами риска при различных
возможных стратегиях.
Прежде чем переходить к моделированию риска матема-
тическими средствами, необходимо понять, что такое риск.
В словаре русского языка С.И.Ожегова риск определяет-
ся как “возможная опасность”. Правомерно ли измерять
эту опасность одним числом, например в каких-то денеж-
ных единицах? В рамках рассматриваемой теории мы даем
утвердительный ответ на этот вопрос. Измеряя опасность
одним числом или набором чисел, мы в определенной сте-
пени упрощаем ситуацию и делаем ее более доступной для
анализа математическими средствами.
Но даже при таком соглашении существуют очень раз-
ные подходы к изучению риска10. Невозможно, да и, навер-
но, не нужно примирить все точки зрения и дать какой-то
унифицированный метод описания риска. Мы сосредоточим
внимание на том подходе к моделированию риска, который
был предложен Г.Марковицем и который будет использо-
ваться нами в дальнейшем.
10Например, подходы, принятые в [4], или в [7], или в [19], или в [29],
это перечисление можно было бы и продолжить, совсем не похожи друг
на друга.
12
Теория эффективных портфелей ценных бумаг
Различные исходы, которые могут возникнуть после
принятия решения, можно сравнивать между собой по раз-
мерам приобретений или потерь. Но эти размеры приоб-
ретений или потерь должны быть увязаны с вероятностя-
ми соответствующих исходов. Для того чтобы сделать это,
необходимо использовать математический аппарат теории
вероятностей. Описанию математического аппарата теории
вероятностей посвящено большое количество учебников, и
приводимое в этом параграфе краткое пояснение некоторых
терминов ни в коем случае не претендует на то, чтобы эти
учебники заменить.
Пусть на рынке существует п видов ценных бумаг. До-
ходность каждой ценной бумаги будем считать случайной
величиной; для у-й ценной бумаги обозначим эту случай-
ную величину Rj. (Обозначение R происходит от англий-
ского слова return - доход, прибыль).
Вопрос о том, что такое случайная величина, подробно
рассмотрен в [38]. Здесь мы напомним только, что так на-
зывается числовая функция, определенная на множестве до-
статочно общего вида и обладающая рядом свойств. Каждой
случайной величине Rj ставятся в соответствие два числа.
Одно из этих чисел называется математическим ожиданием
случайной величины Rj и обозначается E(Rj). Математи-
ческое ожидание может пониматься как в некотором смыс-
ле среднее значение данной числовой функции. Другое чис-
ло показывает, насколько сильно значения числовой функ-
ции в разных точках отличаются от ее среднего значения.
Это число называется дисперсией случайной величины Rj и
обозначается D(Rj)11. Точные определения математическо-
11 Существуют случайные величины, у которых не определена дис-
персия, а возможно, и математическое ожидание. Нами такие случай-
§1. Основные понятия
13
го ожидания и дисперсии случайной величины могут быть
найдены в курсах теории вероятностей, и мы приводить эти
определения не будем. Дисперсия любой случайной величи-
ны неотрицательна. Чем больше дисперсия, тем больше раз-
брос значений случайной величины. В частности, нулевая
дисперсия означает, что случайная величина как числовая
функция принимает только одно значение (которое в этом
случае, конечно, является ее средним значением)12. Часто
вместо дисперсии удобно использовать другую меру разбро-
са случайной величины, называемую стандартным отклоне-
нием. Стандартное отклонение случайной величины опреде-
ляется, как квадратный корень из ее дисперсии. Мы будем
использовать для математического ожидания и стандартно-
го отклонения доходности (Ду) обозначения
Ej = Д(Д>), се,- =
Каждой паре случайных величин Ri и Rj ставится в
соответствие число, называемое ковариацией этих случай-
ных величин. Строгого определения ковариации, так же как
строгого определения математического ожидания и диспер-
сии, мы давать не будем. Скажем только, что ковариация
двух случайных величин показывает степень их зависимос-
ти. Если случайные величины независимы, то их ковариа-
ция равна нулю. Положительная ковариация случайных ве-
личин означает, что отклонение одной из этих случайных
ные величины для моделирования доходностей ценных бумаг исполь-
зоваться не будут.
1аНа самом деле это не совсем так. Ради строгого построения ма-
тематической теории следует принять, что случайная величина с ну-
левой дисперсией может принимать и другие значения, кроме своего
среднего значения, но вероятность этого равна нулю. Однако рассмот-
рение таких тонкостей выходит за рамки этой книги.
14
Теория эффективных портфелей ценных бумаг
величин в большую сторону от своего среднего значения вы-
зывает отклонение другой случайной величины от ее сред-
него значения также скорее в большую сторону, чем в мень-
шую. Отрицательная ковариация случайных величин озна-
чает, что отклонение одной из этих случайных величин в
большую сторону от своего среднего значения вызывает от-
клонение другой случайной величины от ее среднего значе-
ния скорее в меньшую сторону, чем в большую. Для кова-
риации случайных величин выполняются соотношения
| Cov(Ri, Rj) |< ffi • €Tj-, Cov(Rj. Rj) = a2.
Если crj > 0 и cTj > 0, то величина
Cov(Ri, Rj)
называется корреляцией случайных величин Rj и Rj. Мы
будем пользоваться обозначением
Cij = Cov(Ri, Rj).
Будем считать, что капитал в момент времени t равен
1, и обозначим через Xj средства, направленные на покупку
j-й ценной бумаги. Должно выполняться соотношение
Возможно, Xj < 0 при некоторых j. Это означает, что со-
ответствующие ценные бумаги не куплены, а проданы без
покрытия на срок или, что то же самое, выпущены, и полу-
ченные при этом средства вложены в другие ценные бумаги.
§1. Основные понятия
15
Подробнее о том, что такое продажа без покрытия на срок,
будет сказано в §2. Определение набора чисел Xi, Хг,... ,хп
-.это и есть решение задачи о рассредоточении капитала.
Доходность портфеля ценных бумаг, определяемого на-
бором чисел Xi, Х2,..., хп, обозначим через R, случайная ве-
личина R имеет вид
R = 5? xj &з-
j=i
Тогда математическое ожидание и дисперсия случайной ве-
личины R определяются по следующим формулам:
E(R) = £ xi E(Ri), D{R) = Е Cov№, RA-
3=1 г=13=1
Для математического ожидания и стандартного откло-
нения доходности R будем использовать обозначения
Е = E(R), а =
Число Е будем называть ожидаемой доходностью портфе-
ля. Риском для портфеля называется стандартное отклоне-
ние а. Называя стандартное отклонение а риском, мы под-
разумеваем, что оно является математической моделью для
риска. Иногда нам будет удобнее считать математической
моделью риска не стандартное отклонение <т, а дисперсию
• Мы будем пользоваться обеими этими возможностями
без специальных оговорок.
Правильность (или хотя бы допустимость) выбора та-
кой математической модели, как модели для риска, неоче-
видна. Конечно, большое стандартное отклонение <т, т. е.
большой разброс, большая неопределенность в доходностях,
16
Теория эффективных портфелей ценных бумаг
- это большая опасность проигрыша. Но это и большая воз-
можность выигрыша. Почему же мы говорим, что <т - это
математическая модель, именно для возможной опасности?
К этому вопросу мы будем возвращаться на протяже-
нии всей книги, постепенно добавляя аргументы в поль-
зу утверждения, что стандартное отклонение <т правильнее
считать математической моделью возможной опасности, а
не математической моделью возможных достижений.
Чтобы определить ожидаемую доходность портфеля Е и
риск <т, надо знать ожидаемые доходности всех ценных бу-
маг E(Rj) п ковариации доходностей Cov(Ri, Rj). Как луч-
ше на практике найти ожидаемые доходности и ковариа-
ции доходностей различных ценных бумаг - это достаточно
сложный вопрос. Один из простейших способов состоит в
следующем. Пусть для любой ценной бумаги известны до-
ходности за L прошедших периодов времени, каждый про-
тяженностью St:
R^\R{p,...,R{^.
1 L
Тогда можно принять за E(Rj) величину ~ 57 > а за
1 L
Cov{Ri, Rj) - величину -—- } - E(Ri))(R^} - E(Rj)).
L 1 i=i
Возможны и другие способы расчета ожидаемых доходнос-
тей и ковариаций доходностей ценных бумаг, при которых
ожидаемая доходность Е и риск <т будут, естественно, дру-
гими.
Преимуществом описанного подхода, при котором риск
моделируется одним числом <т, являются простота и нагляд-
ность. И как мы уже говорили, этот подход, впервые исполь-
зованный Г.Марковицем, оказался весьма продуктивным.
§1. Основные понятия
17
Но нельзя забывать о том, что при сведении всей неопреде-
ленности к одному числу значительный пласт информации
оказывается потерянным. Потери первого вида вызваны са-
мим решением о применении математических средств, ко-
торые, конечно, не могут передать все многообразие окру-
жающей жизни. (Любые попытки сделать это приводят к
чему-то невообразимо громоздкому и абсолютно ненужно-
му.) Потери второго вида связаны с тем, что в рамках са-
мой математики существуют значительно более совершен-
ные (но и более сложные) конструкции для моделирования
риска. Однако возможность их применения ограничена уже
тем, что для их понимания и использования требуется зна-
чительно более длительная и глубокая математическая под-
готовка, чем для понимания риска, как стандартного откло-
нения случайной величины, обозначающей доходность.
Чтобы закончить обсуждение этого вопроса, приведем
следующую цитату. “Ни от одной меры риска нельзя ожи-
дать, что она будет показывать точные результаты в любых
обстоятельствах. Стандартное отклонение доказало свою
эффективность в большинстве ситуаций, с которыми стал-
киваются практики.”13
Следующий пример, принадлежащий Дж.Тобину14, по-
казывает, что математическое ожидание и стандартное от-
клонение доходности несут в себе далеко не всю информа-
цию о портфеле. В таблице 1.1 для нескольких портфелей
показаны возможные доходности и вероятности получения
таких доходностей.
13См.: [37], с. 181, раздел “Альтернативные меры риска”.
14См.: Tobin J. The theory of portfolio selection //The theory of interest
rates Eds. F.H.Hahn, F.P.R.Brechling. L.: Macmillan and Co., Ltd., 1965.
Chap. 1.
18
Теория эффективных портфелей ценных бумаг
Таблица 1.1
Портфель Доходности Вероятности Е сг
А 0.15 0.12 0-09 0.333 0.333 0.333 0.12 0.025
В 0.24 0.12 0.00 0.333 0.333 0.333 0.12 0.098
С 0.34 0.12 -0.10 0.1 0.8 0.1 0.12 0.098
D 0.14 0.06 -0.02 0.333 0.333 0.333 0.06 0.065
Е 0.1429 -1.0 0.98 0.02 0.12 0.160
F 1.2421 0.0971 0.02 0.98 0.12 0.160
Мы видим из таблицы 1.1, что при одной и той же ожи-
даемой доходности Е = 0.12 портфель А с а = 0.025 яв-
ляется менее рискованным, чем портфель В с <т = 0.098. У
портфелей В ти С оказались одинаковыми обе характеристи-
ки Е и а, хотя возможные доходности и вероятности таких
доходностей у этих портфелей разные. Легко понять, что
портфель D однозначно хуже и портфеля А и портфеля В.
При этом по паре чисел Е и <т можно сказать, что портфель
D хуже портфеля А. Но, зная только Ела, сказать, что
портфель D хуже портфеля В, нельзя. У портфелей ЕлР
одинаковы обе характеристики Виа, хотя для портфеля Е
возможна потеря всего капитала с вероятностью 0.02, а для
портфеля F возможно увеличение капитала больше, чем в
два раза, с той же вероятностью.
§ 2. Игра на повышение и игра на
понижение. Позиции “быка” и
“медведя”
Предположим, что в момент времени t один из участников
рынка ценных бумаг, которого мы будем называть вкладчи-
ком, совершает сделку с каким-то другим участником этого
рынка. Эта сделка может быть одного из следующих двух
видов: покупка ценной бумаги или продажа ценной бумаги
без покрытия на срок. В чем содержание и смысл этих сде-
лок, мы объясним чуть позже, когда будем рассматривать
длинные и короткие позиции. Сделка должна быть завер-
шена в момент времени (t + At). Допустим пока, что доход
D, получаемый от владения ценной бумагой в период време-
ни (t, t + At), равен 0. Для акций это означает, что в этот
период времени не выплачиваются дивиденды.
Длинная позиция - это позиция при игре на повышение
стоимости ценной бумаги. Вкладчик, занявший длинную по-
зицию, покупает ценную бумагу в момент времени t, когда
ее стоимость равна St, и продает данную ценную бумагу в
момент времени (t + At), когда ее стоимость равна
При игре на повышение вкладчик предполагает, что сто-
имость ценной бумаги увеличится. На рис. 2.1 на горизон-
тальной оси отложена стоимость ценной бумаги St+ы, а на
вертикальной оси - средства (St+at —St), получаемые вклад-
чиком в результате сделки. Если St+&t > St, то игра на
повышение была успешной. (Мы пренебрегаем инфляцией,
20
Теория эффективных портфелей ценных бумаг
например, считая At малым, пренебрегаем трансакционны-
ми издержками и т.п.) Вкладчик, играющий на повышение,
называется “быком”.
Рис. 2.1. Средства, получаемые вкладчиком при игре на
повышение, в зависимости от стоимости ценной бумаги в мо-
мент закрытия позиции
Короткая позиция - это позиция при игре на понижение
стоимости ценной бумаги. При игре на понижение вкладчик
предполагает, что стоимость ценной бумаги уменьшится. В
момент времени t вкладчик получает от партнера по сдел-
ке средства, равные стоимости ценной бумаги St. В момент
времени (t + At) вкладчик должен купить эту ценную бума-
гу, стоимость которой в это время равна St+&t, и передать
ее партнеру по сделке или просто передать ему соответству-
§2. Позиции “быка” и “медведя”
21
ющую сумму, что при принятых нами условиях идеального
рынка одно и то же. На рис. 2.2 на горизонтальной оси от-
ложена стоимость ценной бумаги St+At, а на вертикальной
оси - средства (St — получаемые вкладчиком в ре-
зультате сделки. Если St+^t < St, то игра на понижение
была успешной. Вкладчик, играющий на понижение, назы-
вается “медведем”15. Про вкладчика, занявшего короткую
позицию, говорят, что он продал ценную бумагу без покры-
тия на срок или что он выпустил ценную бумагу.
Рис. 2.2. Средства, получаемые вкладчиком при игре на
понижение, в зависимости от стоимости ценной бумаги в мо-
мент закрытия позиции
15Мы следуем традиции, принятой в американской экономической
литературе, и используем слово “вкладчик” (investor) даже в тех слу-
чаях, когда, казалось бы, уместнее было слово “игрок” (gambler).
22
Теория эффективных портфелей ценных бумаг
В описанных сделках момент времени t называется мо-
ментом открытия позиции, а момент времени (t + Ai) - мо-
ментом закрытия позиции.
Конечно, изложенная схема является упрощенной и со-
ответствует принятым нами условиям идеального рынка.
Предположим также, что вкладчик может полностью распо-
ряжаться средствами, полученными им от продажи ценных
бумаг без покрытия на срок. В действительности, процеду-
ра продажи ценных бумаг без покрытия на срок может быть
более сложной16.
Сделанное в начале параграфа допущение D — 0 не
является принципиальным и может быть отброшено, если
принять, что вкладчик, продавший ценную бумагу без по-
крытия на срок, обязан выплачивать покупателю доход, по-
лучаемый от владения ценной бумагой в период времени
(£,£ + Д£). Для простоты изложения мы предположили, что
момент закрытия позиции (t + Д£) заранее определен. Но это
требование может быть ослаблено.
Сказанное может быть выражено в виде таблицы 2.1.
Таблица 2.1
Открытие позиции Закрытие позиции
Длинная позиция Покупка ценной бумаги Продажа ценной бумаги
Короткая позиция Продажа ценной бумаги без покрытия на срок Завершающая покупка ценной бумаги
При наличии коротких позиций доходность портфеля мо-
жет принимать сколь угодно большие значения. Предполо-
жим, что доходности двух ценных бумаг предсказуемы точ-
16См.,напр.: [2], с. 72 - 73.
§2. Позиции “быка” и “медведя” 23
но и равны соответственно 0.1 и 0.25. Пусть при собствен-
ном капитале, равном 1, вкладчик выпустил первую ценную
бумагу на сумму X (X > 0) и купил вторую ценную бумагу
на сумму (X + 1). Тогда доходность портфеля будет равна
R = -X • 0.1 + (X + 1) • 0.25 = X • 0.15 + 0.25,
т. е. может быть сколь угодно большой, если X - большое
положительное число. Ясно, что при наличии неопределен-
ности подобная стратегия является весьма рискованной.
Если на рынке имеется п видов ценных бумаг, то вы-
бор портфеля ценных бумаг - это определение набора чисел
Xi, х2,.. -, жп, удовлетворяющих условию
f> = i-
з=1
Если Xj > 0, то Xj - это средства, направленные вклад-
чиком на покупку у-й ценной бумаги. Если Xj < 0, то (—ж3)
- это средства, полученные вкладчиком от выпуска у-й цен-
ной бумаги. Если Xj = 0, то у-я ценная бумага не включается
в портфель вкладчика.
Следующий пример, принадлежащий У.Шарпу [14], поз-
воляет лучше понять, что такое игра на понижение. Пусть у
мистера А есть фруктовое дерево, находящееся в его собст-
венности (или 1000 фруктовых деревьев). Мистер А заклю-
чил контракт с мистером Б о том, что каждый раз после
сбора урожая определенную часть выручки мистер А отдает
мистеру Б. Передаваемые суммы не являются заранее опре-
деленными, они зависят и от собранного урожая, и от спроса
на данные плоды. Мистер В заключил контракт с мистером
Г о том, что он будет выплачивать ему те же самые суммы и
24
Теория эффективных портфелей ценных бумаг
в те же самые сроки, что и мистер А мистеру Б. Первый кон-
тракт в [14] называется фондовым активом ~ это контракт
между вкладчиком (мистером Б) и “внешним миром” (мис-
тером А). Второй контракт в [14] называется финансовой
ценной бумагой - это контракт между двумя вкладчиками,
мистерами В л Г. Вкладчики В л Г заняли длинную пози-
цию в отношении данной ценной бумаги. Вкладчик В занял
короткую позицию в отношении данной ценной бумаги, т.
е. он считает, что дерево мистера А не даст хорошего уро-
жая или что плоды не будут пользоваться спросом. С точки
зрения рассматриваемой нами теории, позиции вкладчика Б
и вкладчика Г совершенно одинаковы, и не имеет никакого
значения, что первый из них заключил контракт с “внеш-
ним миром”, а второй - с некоторым другим вкладчиком.
Разумеется, следует считать, что мистер В безусловно вы-
полняет свои обязательства, а мистер А заранее объявляет
размер дивидендов.
В реальной жизни продажа ценных бумаг без покрытия
на срок не так бесспорна с этической точки зрения, как
покупка или обычная продажа ценных бумаг. Существует
точка зрения, что подобный капитал является фиктивно-
спекулятивным и играет отрицательную роль17. Но, по мне-
нию многих экономистов, право вкладчика играть на пони-
жение так же важно для свободного рынка, как право играть
на повышение.
17См., напр.: Российская газета. 1997. И июля. С. 8.
§ 3. Эффективный фронт и
эффективные портфели
Напомним, что на рынке существует п видов ценных бу-
маг, доходность j-й ценной бумаги является случайной ве-
личиной Rj. В этом параграфе мы будем считать, что все
ценные бумаги являются рисковыми, т. е. D(Rj) > 0 при
j — 1,2, Наличие безрисковых ценных бумаг, т. е.
ценных бумаг с точно предсказуемой доходностью, меняет
ситуацию. Портфели, куда включаются безрисковые ценные
бумаги, будут рассмотрены в §4.
Начнем со случая п = 2, т. е. когда портфель составляет-
ся из двух видов ценных бумаг. Для каждой из ценных бумаг
известны ожидаемые доходности и Е? и стандартные от-
клонения доходностей ai и сг2. Портфели с какими ожидае-
мыми доходностями Е и с какими стандартными отклонени-
ями доходностей а могут быть получены путем комбинации
этих двух ценных бумаг? Будем использовать следующие
обозначения:
Ж1 = р, ж2 = 1 — р.
Тогда для портфеля, определяемого парой чисел Ж1,ж2, до-
ходность
R — pRi + (1 — /1)Я2.
Отсюда ожидаемая доходность
Е = pEi + (1 — д)Е2,
Дисперсия
= м2#(Я1) + (1 - м)2£>(й2) + 2/1(1 - /i)Cov(7?1, Я2) =
26
Теория эффективных портфелей ценных бумаг
— //2СТ2 + (1 — Д)2(?2 + 2//(1 — /1)р12<Т1(Т2,
где pi2 - корреляция случайных величин Ri и 7?,2.
Напомним, что корреляция по абсолютной величине не
может превосходить 1, т. е. —1 < р12 < 1.
Полученные уравнения для Е и ст2 при изменении р от
—оо до +оо определяют некоторую кривую на плоскости
(а, Е). Будем считать, что Ei У Е2. поскольку при Ег — Е2
все точки интересующей нас кривой находятся на прямой
Е = Ei. Из уравнения для Е находим
Е — Е2
Ei~E2
Подставляя это выражение в уравнение для ст2, видим,
что изучаемая кривая является кривой второго порядка на
плоскости (ст, -Е), уравнение которой имеет вид
—(Ei — Е2)2 • ст2 +
+((<71 — ^г)2 + 2 (1 — Р12) Ст! ст2) • Е2 +
+2((Ei + Е2) рг2 Ст1 ст2 - Е2ст2 - Егст2) • Е +
+(Е2а2 + Е2а2 — 2Е1Е2р12 ctj ст2) = 0.
При классификации кривых второго порядка основную роль
играет знак определителя матрицы, составленной из коэф-
фициентов при членах второго порядка (см., например, [25],
с. 64 - 65). В данном случае эта матрица имеет вид
( -(Ei - Е2У 0 \
у О (<71 — СТ2)2 + 2 (1 — Р12) <71 СТ2 у
При Ст1 У ст2 или /912 < 1 определитель этой матрицы отри-
цателен, т. е. данная кривая является гиперболой или парой
пересекающихся прямых. Если cti = ст2 и р12 = 1, то, как
§3. Эффективный фронт
27
нетрудно увидеть, все точки интересующей нас кривой на-
ходятся на прямой а — (Т2-
Более детальный анализ показывает, что данная кривая
является гиперболой при —1 < р12 < 1 и явЛяется парой
прямых при /?12 = ±1. Подробно теория кривых второго по-
рядка на плоскости описана, например, в [31].
Рис. 3.1. Возможные сочетания рисков и ожидаемых до-
ходностей для портфелей, составленных из двух ценных бумаг
На рис. 3.1 показаны возможные виды зависимости ст
от Е для портфеля, составленного из двух ценных бумаг,
28
Теория эффективных портфелей ценных бумаг
когда корреляция р12 равна соответственно 1, 0.33, -0.33,
-1. Приведены только части кривых, отвечающие значени-
ям 0 < р < 1, <т > 0.
Рис. 3.2. Некоторые возможные сочетания рисков и ожи-
даемых доходностей для портфелей, составленных из трех цен-
ных бумаг
Добавим к двум рассматриваемым ценным бумагам еще
одну ценную бумагу 3 (см. рис. 3.2) и ограничимся пока рас-
смотрением портфелей с хг > 0, х2 > 0, хз > 0. На рис. 3.2
изображен случай, когда корреляции доходностей для лю-
бых двух ценных бумаг по абсолютной величине меньше 1,
и кривые, соединяющие соответствующие точки, являются
кусками гипербол. Рассмотрим портфель А, который состо-
ит из равных долей ценных бумаг 1 и 2. Мы можем считать,
§3. Эффективный фронт
29
что портфель А является новой ценной бумагой, доходность
которой имеет вид
Ra = 0.5 • Я1 + 0.5 • R2.
Рассмотрим портфель В, который состоит из равных долей
А и ценной бумаги 3. Доходность портфеля В имеет вид
Rg = 0.5 Ra “Ь 0.5 • R3 — 0.25 • Ri -Ь 0.25 • R2 + 0.5 • Rs-
В приведенном примере мы брали равные доли ценных
бумаг 1 и 2 для составления портфеля А и равные доли А и
ценной бумаги 3 для составления портфеля В. Но мы могли
брать и не равные, а какие-то другие доли. В этом случае
положение точки В на плоскости (ст, В) было бы другим.
Рассмотрим множество тех точек В на плоскости (ст, Е),
координаты которых являются стандартным отклонением
и математическим ожиданием доходности портфеля, опре-
деляемого каким-нибудь набором чисел «1, х2, «з, таким, что
Xi + х2 + Хз = 1, ®1 >0, «2 > О, Хз > 0.
Обозначим множество всех таких точек через Q. Опре-
делим подмножество Qo множества Q. Точка Во с координа-
тами (ст0, Во), принадлежащая множеству Q, входит в под-
множество Qo, если она обладает следующими двумя свой-
ствами.
1. Для любой другой точки В, принадлежащей множес-
тву Q и имеющей координаты (ст, Во), выполняется условие
Ст > Сто.
2. Для любой другой точки В, принадлежащей множес-
тву Q и имеющей координаты (сто, В), выполняется условие
В < Bq.
30
Теория эффективных портфеле!! ценных бумаг
Подмножество Qo называется эффективным фронтом.
Портфель, определяемый набором чисел хг, ж2, ®з, называет-
ся эффективным, если соответствующая ему точка В при-
надлежит эффективному фронту Qo. На рис. 3.3 сплошной
линией изображен эффективный фронт, а кружками показа-
ны точки, соответствующие нескольким другим портфелям.
Рис. 3.3. Точки, отвечающие портфелям с ожидаемой до-
ходностью Е и риском <г (показаны кружками), и эффективный
фронт (показан сплошной линией)
Эффективный фронт является вогнутой кривой.
Напомним, что действительная функция f(x), определен-
ная на некотором отрезке, называется вогнутой, если для
любых значений аргумента х и у и для любого а, 0 < а < 1,
§3. Эффективный фронт
31
выполняется условие
f(ax + (1 - а)у) > af (ж) + (1 - a)f (у).
Функция называется выпуклой, если для любых х и у и для
любого а, 0 < а < 1, выполняется условие
f(ax + (1 - а)у) < а/(ж) + (1 - а)/(у).
Если рассматриваемая функция является дважды непре-
рывно дифференцируемой, то условие вогнутости равно-
сильно тому, что при всех х выполняется условие f"(x) < 0.
Условие выпуклости в этом случае равносильно тому, что
при всех х выполняется условие f"(x) > 0.
Говоря, что эффективный фронт является вогнутой кри-
вой, мы имеем в виду, что он является графиком вогнутой
функции аргумента а.
Рис. 3.4. Недопустимая форма эффективного фронта
(сплошная линия)
32
Теория эффективных портфелей ценных бумаг
Действительно, допустим, что эффективный фронт име-
ет форму, показанную на рис.3.4, т. е. не является вогнутым.
Точками А, В и С показаны три эффективных портфеля. Из
портфелей А тя. В можно составить портфель D, который
имеет то же стандартное отклонение ст, что и портфель С,
но большую ожидаемую доходность Е, т. е. портфель С не
является эффективным.
Мы дети формальное определение эффективного фрон-
та. Но почему именно эффективные портфели должны быть
привлекательны для вкладчиков? То, что портфели с боль-
шей ожидаемой доходностью привлекательнее, чем портфе-
ли с меньшей ожидаемой доходностью, не вызывает сомне-
ний. Но почему при одной и той же ожидаемой доходности
портфели с меньшим стандартным отклонением доходнос-
ти привлекательнее, чем портфели с большим стандартным
отклонением? Здесь мы скажем только, что большинство
вкладчиков не любит неопределенность. Подробно данный
вопрос будет обсуждаться в §6 и 7.
Теперь вместо портфеля из трех видов ценных бумаг рас-
смотрим портфель из п видов ценных бумаг. Через Q обозна-
чим множество тех точек В, координаты которых (а, Е) яв-
ляются стандартным отклонением и математическим ожи-
данием доходности портфеля, определяемого каким-нибудь
набором чисел Xi, х2,..., хп, таким,что
Ж1 + ж2 + ... + ®п = 1, Ж1 > к, Х2 > 12,. • •, Хп > 1п. (3.1)
Здесь li, 12,..., 1п - некоторые действительные числа.
Если Ц < 0, то по г-й ценной бумаге вкладчиком мо-
жет быть занята как длинная, так и короткая позиция, а
(—li) - это отношение суммы, которую вкладчику допуска-
ется получить от выпуска г-й ценной бумаги, к его собствен-
§3. Эффективный фронт
33
ному капиталу. Если Ц - большое по абсолютной величине
отрицательное число, то фактически это означает, что от-
сутствуют ограничения на выпуск г-й ценной бумаги. Если
Ц = 0, то по г-й ценной бумаге вкладчиком может быть заня-
та только длинная позиция. Если Ц > 0, то вкладчик должен
направить соответствующую часть капитала на покупку г-й
ценной бумаги.
Эффективный фронт Qo для п видов ценных бумаг опре-
деляется точно так же, как и для трех видов ценных бумаг.
Пример. Рассмотрим набор из 6 ценных бумаг. Пусть
ожидаемые доходности Ej этих ценных бумаг равны
( 0.040700 0.046400 0.070500 0.099400 0.085700 0.125000 ).
Пусть ковариации доходностей Cij равны
/ 0.000189 0.000103 0.000102 0.000370 0.000081 0.000037
0.000103 0.000377 0.000460 0.000146 0.000342 0.000225
0.000102 0.000460 0.000612 0.000131 0.000409 0.000358
0.000370 0.000146 0.000131 0.000808 0.000160 0.000087
0.000081 0.000342 0.000409 0.000160 0.000425 0.000194
\ 0.000037 0.000225 0.000358 0.000087 0.000194 0.000407
На рис. 3.5 приведены три рассчитанных эффективных
фронта. Эффективный фронт а рассчитан при условии, что
выпуск каждой из 6 рассматриваемых ценных бумаг разре-
шен. но ограничен. Средства, полученные от выпуска каж-
дой ценной бумаги, не должны превышать 30% собственного
капитала вкладчика:
/1 _ 12 — 13 _ /4 — /5 — Iq = —0.3.
То, что ограничения в 30% для всех ценных бумаг сов-
падают, не имеет принципиального значения. Эти ограни-
чения могли бы быть и разными для разных ценных бумаг.
34
Теория эффективных портфелей ценных бумаг
Эффективный фронт b рассчитан при условии, что выпуск
ценных бумаг не разрешен:
li = h = 1з — Ц ~ I5 — 1& = 0.
Эффективный фронт с рассчитан при условии, что не толь-
ко выпуск ценных бумаг не разрешен, но вкладчик обязан
вложить в каждую из ценных бумаг не менее 10% собствен-
ного капитала:
ll — = I3 — I4 — I5 — Iq — 0.1.
Рис. 3.5. Примеры эффективных фронтов для одного и то-
го же набора ценных бумаг при различных ограничениях на па-
раметры портфеля
Ясно, что набор возможных портфелей для случая а ши-
ре, чем набор возможных портфелей для случая Ь. В свою
§3. Эффективный фронт
35
очередь, набор возможных портфелей для случая b шире,
чем набор возможных портфелей для случая с. Поэтому эф-
фективный фронт а проходит не ниже, чем эффективный
фронт Ь, который, в свою очередь, проходит не ниже, чем
эффективный фронт с. На рис. 3.5 показан случай, когда
данные эффективные фронты не пересекаются; При другом
наборе ценных бумаг эффективный фронт а может, напри-
мер, частично совпадать с эффективным фронтом Ь.
Мы вплотную подошли к задаче математического опи-
сания эффективных портфелей и эффективных фронтов, но,
прежде чем заниматься этой задачей, следует сделать еще
одно добавление.
На переменные ж1? ж2,..., хп наложены ограничения (3.1).
При составлении портфелей могут возникать и другие огра-
ничения на эти переменные вида равенств или вида нера-
венств, выражающие собой те или иные дополнительные
условия. Например, ограничения могут иметь вид
х5 — 0.2,
или
Зж2 — ж8 = 0,
или
жб < 0.14,
или
ж3 + ж7 > 0.5.
Эти ограничения означают, что в ценные бумаги пятого ви-
да должно быть вложено ровно 20% средств; в ценные бу-
маги восьмого вида - втрое больше средств, чем в ценные
бумаги второго вида; в ценные бумаги шестого вида может
быть вложено не более 14% средств; по крайней мере 50%
36
Теория эффективных портфелей ценных бумаг
средств должно быть вложено в ценные бумаги третьего и
седьмого вида. Под средствами здесь везде имеются в виду
собственные средства вкладчика.
Все ограничения, которые мы будем рассматривать, име-
ют следующий вид. В правой части равенства или нера-
венства стоит некоторое число, а в левой части - линейная
функция от переменных Xi, х2,..., хп. Ограничения с нели-
нейными функциями, например, такие, как
• х2 < 0.5
или
— «4 = о,
нами рассматриваться не будут.
Ограничения вида неравенств, входящие в условие (3.1),
мы оставим в существующем виде, а все остальные огра-
ничения вида неравенств заменим на ограничения вида ра-
венств при помощи следующего стандартного приема. В до-
полнение к переменным Xi, х2, ,хп введем вспомогатель-
ные переменные sn+i,хп+2.... ,хх. При помощи этих пере-
менных ограничения вида неравенств заменим на ограни-
чения вида равенств. Например, ограничения х& < 0.14 и
жз + ж? > 0.5 примут вид
xq 4* ®n+i — 0.14, ®n+i > 0,
и
х3 + х7 - хп+2 = 0.5, жп+2 > 0.
Если ограничений вида неравенств, которые нужно за-
менять на ограничения вида равенств, нет, то, естествен-
но, вспомогательные переменные не вводятся и считается
N = п.
§3. Эффективный фронт
37
Теперь все ограничения задачи можно записать в виде
i=l
(3.2)
®1 — ^1, _ ^2, • • • ~ ®п4-1 0, ®п+2 > 0, • • • 1 %N > О*
В число ограничений вида равенств из (3.2) мы включаем и
ограничение
»=i
Ограничения вида равенств из (3.2) мы будем часто запи-
сывать в виде
Ах = Ь,
где х - JV-мерный вектор, b - m-мерный вектор, А - матрица
размера т х N.
Рис. 3.6. Эффективный фронт на плоскости (а, Е) и соот-
ветствующий ему эффективный фронт на плоскости (V, Е)
38
Теория эффективных портфелей ценных бумаг
Работать с построенными эффективными фронтами
удобнее на плоскости (<т, Е). однако строить эффективные
фронты удобнее на плоскости (У,Е), где V = а2 (обозна-
чение V происходит от английского слова variance - дис-
персия). Мы определили эффективный фронт как кривую
на плоскости (<т, Е). Образ этой кривой на плоскости (V, Е)
при отображении V = <т2, Е = Е мы будем также назы-
вать эффективным фронтом (см. рис. 3.6). Зная эффектив-
ный фронт на одной из плоскостей (<т, Е) или (V, Е), нетруд-
но определить его на другой плоскости.
На плоскости (V, Е), так же как и на плоскости (<т, Е), эф-
фективный фронт является кривой, выпуклой вверх. Можно
даже сказать, что на плоскости (V, Е) эта кривая более вы-
пукла, чем на плоскости (<т, Е) (не будем пытаться придать
этим словам строгий смысл - сделать это не очень сложно,
но введение соответствующих понятий не является для нас
необходимым). В частности, на плоскости (<т, Е) эффектив-
ный фронт может содержать прямолинейные участки. На
плоскости (V, Е) прямолинейных участков на эффективном
фронте быть не может.
Напомним, что если портфель определяется набором чи-
сел Ж1, Ж2, .. -, хп, то математическое ожидание доходности
имеет вид
п
£< = УЗ хз Ej,
J=i
где Ej = E(Rj'), а дисперсия доходности имеет вид
V = £ S xi xi Cih
j=l
где Cjj = Cov(Ri, Rj).
§3. Эффективный фронт
39
Пусть Л > 0 - некоторое число. Рассмотрим на плоскости
(V, Е) прямые
-ХЕ + V = а,
отвечающие различным а (см. рис. 3.7). (Дисперсия случай-
ной величины, конечно, не может быть отрицательным чис-
лом, но мы можем в данном случае рассматривать эффек-
тивный фронт просто как кривую на плоскости (V, Е).)
Рис. 3.7. Эффективный фронт и семейство прямых — ХЕ+
+V = а для некоторого А > О
Пока а является отрицательным числом, большим по
абсолютной величине, прямая —ХЕ + V = а не пересека-
ется с эффективным фронтом. При увеличении а прямая
—ХЕ + V — а приближается к эффективному фронту. На-
40
Теория эффективных портфелей ценных бумаг
конец, при каком-то а происходит соприкосновение (на рис.
3.7 соприкосновение происходит при а = а2). В ~ это точка
соприкосновения данной прямой с эффективным фронтом.
Рис. 3.8. Эффективный фронт и соприкасающиеся с ним
прямые —ХЕ + V = а при различных X
Как определить то значение а, при котором происходит
соприкосновение? Это минимальное из всех а, при которых
на прямой — ХЕ + V = а есть точка с координатами (Eq, Vo),
где Eq - ожидаемая доходность одного из рассматриваемых
§3. Эффективный фронт
41
портфелей, a Vo - дисперсия доходности этого портфеля. Та-
ким образом, надо найти минимальное значение выражения
п п п
-л хз + 22 £Xi хэ Cii, (3-3)
j=l i=l j=l
которое может быть достигнуто при жх, ж2,..., жп, удовле-
творяющих условиям (3.2).
На самом деле нас интересует не столько само минималь-
ное значение а, при котором прямая —АЕ + V = а и эффек-
тивный фронт имеют общую точку, сколько тот набор чисел
Ж1,ж2,..., жп, при котором это минимальное значение а до-
стигается. Этот набор чисел ®i, ж2,..., хп определяет один
из эффективных портфелей. Обозначим этот набор
®(Л) = (Ж1(Л), ж2(А),..., ж„(А)).
При изменении А от 0 до +оо точка соприкосновения описы-
вает весь эффективный фронт (см. рис. 3.8).
При А = 0 набор чисел ж (А) определяет эффективный
портфель с минимальным возможным риском. При увеличе-
нии А для эффективного портфеля, определяемого набором
чисел ж (А), увеличивается и математическое ожидание до-
ходности Е, и дисперсия доходности V. При А = оо набор
чисел ж(А) определяет эффективный портфель с максималь-
но возможной ожидаемой доходностью.
На рис. 3.9 показан возможный вид графиков функций
®i(A), ж2(А), • • •, ®п(^), когда выпуск ценных бумаг не раз-
решен. (Приведен случай, когда существуют такие 4 ценные
бумаги, что при любом А эффективный портфель не содер-
жит других ценных бумаг кроме этих четырех.)
Каждая из функций ж4(А) является непрерывной кусочно-
линейной функцией. Это означает, что графики функций со-
стоят из отрезков прямых линий. Те точки А, в которых
42
Теория эффективных портфелей ценных бумаг
какая-либо из функций я»(А) испытывает разрыв производ-
ной, называются угловыми точками. На рис. 3.9 это точки
А1, А2, Аз, А4. В число угловых точек также включается точ-
ка А = 0. Эффективные портфели, соответствующие угло-
вым точкам А, называются угловыми портфелями.
Рис. 3.9. Функции Ж1(А), ж2(А), ж3(А), ж4(А), определяющие
при каждом А состав одного из эффективных портфелей
Мы сказали, что функции ®i(A), ж2(А),..., жп(А) могут
быть непрерывными кусочно-линейными функциями. Оста-
ются два вопроса. Почему они могут быть такими? Могут
ли эти функции иметь какой-либо другой вид? Структура
эффективного фронта будет рассмотрена в §9, где приведе-
ны условия (достаточно общего вида), при соблюдении ко-
§3. Эффективный фронт
43
торых функции жх(А), ж2(А),..., жп(А) являются непрерыв-
ными и кусочно-линейными. С практической точки зрения
можно сказать, что эти функции всегда являются непрерыв-
ными и кусочно-линейными18. Один из алгоритмов постро-
ения функций ®i(А), ж2(А), ..., жп(А), предназначенный для
реализации на компьютере, описан в §10.
То, что некоторые точки А названы угловыми, не озна-
чает, что в соответствующих местах эффективный фронт,
как кривая на плоскости (<т, Е), имеет излом. Хотя излом
и возможен. Например, если бы на рис. 3.9 между точками
Ai и А2 графики всех функций жДА) были горизонтальными
отрезками, то эффективный фронт имел бы излом.
Если мы знаем, например, наборы чисел ж(А1) и «(Аг),
определяющие два соседних угловых портфеля, то мы мо-
жем определить эффективные портфели, отвечающие всем
А между Ai и А2, по формулам
жг(Л) = "Г—rXi^ + Г—
i — 1,2,...,те, Ai < А < А2.
На плоскости (V, Е) эффективный фронт состоит из кусков
парабол, а на плоскости (<т, Е) - из кусков гипербол и отрез-
ков прямых.
Если в условии (3.2) отсутствуют все ограничения на
выпуск ценных бумаг (т. е. = Z2 = • • = In = —оо) и от-
сутствуют все ограничения вида неравенств (т. е. N = п),
то задача имеет более простое решение. В этом случае функ-
ции Ж1(А), ж2(А), ..., жп(А) являются не кусочно-линейными,
а линейными.
18См., напр.: [37], с. 221 - 225.
§ 4. Оптимальный портфель при
возможности заимствования и
одалживания
Допустим, что кроме п видов рисковых ценных бумаг, о ко-
торых говорилось в §3, на рынке существует безрисковая
ценная бумага. Доходность безрисковой ценной бумаги обо-
значим Rf- (Обозначение F происходит от английского сло-
ва free - свободный, в данном случае - свободный от риска).
Для единства стиля доходность Rf следовало бы считать
случайной величиной. Но эта случайная величина принима-
ет только одно значение, никакого риска с этой ценной бу-
магой не связано. Это означает, что дисперсия D(Rp} — 0, а
математическое ожидание E(Rp) равно тому значению, ко-
торое данная случайная величина принимает. Нам следова-
ло бы ввести обозначение Ер = E(Rp). Но в экономической
литературе вместо Ер используется обозначение Rp. И мы
с этого момента будем поступать так же, считая Rf числом.
Рассмотрим портфель А, составленный каким-то спосо-
бом из п рисковых ценных бумаг. Зафиксируем //, 0 < ц < 1,
и составим новый портфель, состоящий на ц • 100 % из без-
рисковой ценной бумаги и на (1 -р) • 100 % из портфеля А.
Доходность этого портфеля имеет вид
R = д • Rf + (1 - д) • Ra.
Отсюда ожидаемая доходность полученного портфеля
Е — ц • Rf + (1 - д) • Еа (4.1)
§4. Оптимальный портфель
45
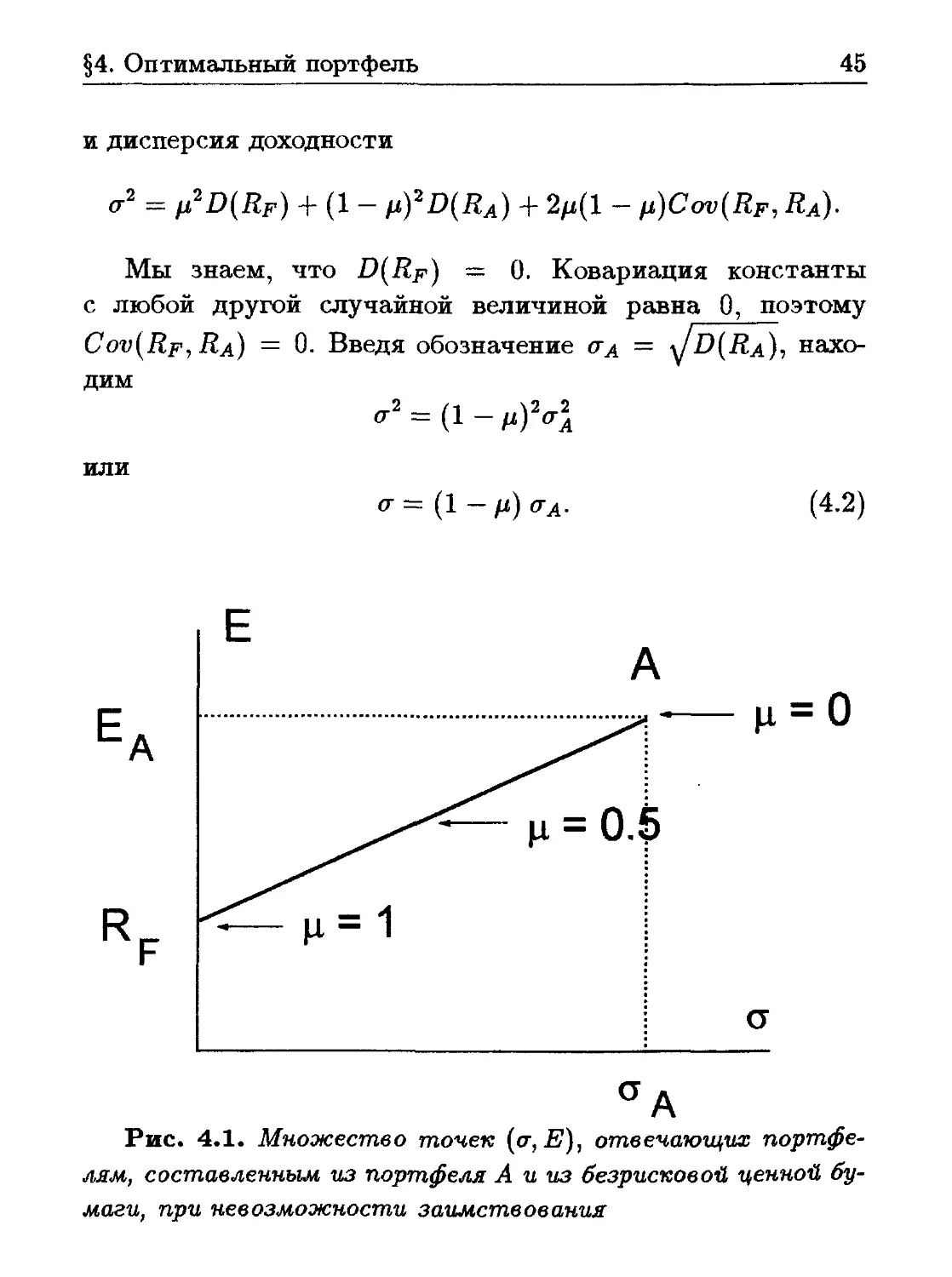
и дисперсия доходности
<т2 — }j,2D(Rf) + (1 — p.)2D(RA) + 2/z(l — ii)Cov(Rf, Ra)-
Мы знаем, что D(Rf) — 0. Ковариация константы
с любой другой случайной величиной равна 0, поэтому
Cov(Rf-> Ra) = 0- Введя обозначение аА = \^D(RA), нахо-
дим
а2 = (1 - М)2а2
или
<r = (1 - д) ал.
(4.2)
Рис. 4.1. Множество точек (а,Е), отвечающих портфе-
лям, составленным из портфеля А и из безрисковой ценной бу-
маги, при невозможности заимствования
46
Теория эффективных портфелей ценных бумаг
На рис. 4.1 показаны ожидаемые доходности Е и риски
а полученных портфелей при различных //. Из уравнений
(4.1) и (4.2) видно, что этим портфелям на плоскости (а, Е)
соответствует отрезок прямой линии.
Рис. 4.2. Множество точек (а,Е), отвечающих портфе-
лям, составленным из портфеля А и из безрисковой ценной бу-
маги, при возможности заимствования
Теперь будем считать, что вкладчик может не только
дать, но и взять любой заем, причем по одной и той же про-
центной ставке Rp. Тогда одалживание или заимствование
можно представлять как покупку или выпуск безрисковой
ценной бумаги. Рассмотренный выше случай ц > 0 соот-
ветствует покупке безрисковой ценной бумаги. Выпуску без-
§4. Оптимальный портфель
47
рисковой ценной бумаги и вложению полученных средств в
портфель А соответствует случай ц < 0. Из уравнений (4.1)
и (4.2) видно, что получающимся при этом портфелям на
плоскости (ст, Е) соответствует полупрямая (см. рис. 4.2).
Из уравнения (4.2) находим
1 - И = а/аА.
Тогда из уравнения (4.1) следует, что
Е = fl - —) Rf + — Еа
V «’’а/ &а
или
Е = Rf + а. (4.3)
(Та
Уравнение (4.3) - это уравнение прямой, изображенной
на рис. 4.2. Отметим, что эта прямая проходит через точ-
ку с координатами (<тд, ЕА). Слева от точки А лежат точки,
соответствующие комбинациям портфеля А с купленной без-
рисковой ценной бумагой. Справа от точки А лежат точки,
соответствующие комбинациям портфеля А с выпущенной
безрисковой ценной бумагой.
До сих пор портфель А был выбран произвольно. Теперь
остановимся на том, как выбрать портфель А наилучшим
образом. На рис. 4.3 для трех эффективных портфелей А, В
и С изображены прямые
р о . еа - Rf
Ь — Rp ------------<т,
(та
E = Rf + — ~ Rf а,
(ТВ
48 Теория эффективных портфелей ценных бумаг
E = RF + а.
На рис. 4.3 А - это точка с координатами (ад, Ед), В -
точка с координатами (ав, Ев), С - точка с координатами
(ас, Ес)-
Рис. 4.3. Эффективный фронт для портфелей из рисковых
ценных бумаг (кривая линия) и возможные сочетания риска и
ожидаемой доходности при добавлении в рисковый портфель
безрисковой ценной бумаги
При принятом нами критерии комбинации безрисковой
ценной бумаги и портфеля В лучше, чем комбинации без-
рисковой ценной бумаги и портфеля А, поскольку они дают
большую ожидаемую доходность при одном и том же рис-
ке. Комбинации безрисковой ценной бумаги и портфеля С
§4. Оптимальный портфель
49
еще лучше. Рассмотрим портфель (7, для которого значение
коэффициента
Ес — Rf
<?С
является максимальным среди всех возможных портфелей.
Очевидно, что этот портфель эффективный.
Все вкладчики, которые имеют одинаковое суждение об
эффективном фронте и о безрисковой процентной ставке Rf
и которые руководствуются правилом минимизации риска
при некоторой, определенной каждым из них для себя, ожи-
даемой доходности портфеля, выберут портфель С (состо-
ящий только из рисковых ценных бумаг) с максимальным
значением коэффициента (4.4). Те вкладчики, которые ме-
нее расположены к риску, вложат часть своих средств в без-
рисковые ценные бумаги. Их портфелям на рис. 4.3 соответ-
ствуют точки верхней прямой, лежащие левее точки С. Те
вкладчики, которые более расположены к риску, выпустят
безрисковые ценные бумаги. Их портфелям на рис. 4.3 соот-
ветствуют точки верхней прямой, лежащие правее точки С.
Важно то, что и те, и другие выберут портфель С с мак-
симальным значением коэффициента (4.4), т. е. способ со-
ставления портфеля из рисковых ценных бумаг не зависит
от того, производит ли вкладчик заимствование или одал-
живание и в каких размерах. Этот результат называется
теоремой о разделении19.
19Строго говоря, на эффективном фронте может быть больше одной
точки С с максимальным значением коэффициента (4.4). До §8, где
рассматривается модель оценки фондовых активов, мы не будем ис-
пользовать единственность портфеля с максимальным значением ко-
эффициента (4.4). Практически случаи, когда подобный портфель не-
единственен, редки. Аргументация, почему такие случаи могут быть
исключены из рассмотрения при изучении модели оценки фондовых
50
Теория эффективных портфелей ценных бумаг
Мы сказали, что одни вкладчики менее расположены к
риску, а другие вкладчики более расположены к риску. В
§6 при обсуждении полезности будет введено понятие нерас-
положенности к риску, и среди вкладчиков будут выделены
нерасположенные к риску, безразличные к риску и склонные
к риску. В рамках этих определений и те вкладчики, кого
мы назвали менее расположенными к риску, и те вкладчики,
кого мы назвали более расположенными к риску, являются
вкладчиками, нерасположенными к риску20.
Портфель С, для которого достигается максимальное
значение коэффициента (4.4), называется оптимальным.
Замечание. Название “оптимальный” для портфеля с
максимальной величиной коэффициента (4.4) является об-
щепринятым, но несколько дезориентирующим. Дело в том,
что доходность портфеля С, который мы назвали оптималь-
ным, может с вероятностью, близкой к 1, быть меньше до-
ходности некоторого другого портфеля D. Подобная ситуа-
ция описана в [33], с. 165 - 166. Это может произойти, на-
пример, в следующем случае. На рис. 4.4 слева изображе-
на функция распределения доходности портфеля С, а спра-
ва - функция распределения доходности портфеля D. При
этом, конечно, с практической точки зрения сам по себе пор-
тфель С хуже портфеля D. Но за счет достаточно малень-
кого стандартного отклонения ас величина коэффициента
активов, приведена, например, в работе: Fama E.F. Risk, Return and
Equilibrium: Some Clarifying Comments // J. of Finance. V. 23 (March
1968). P. 29 - 40 (см.также [13], c. 559 - 571). Мы не будем эту аргумен-
тацию повторять.
20Поэтому правильнее было бы вместо “менее расположенные к рис-
ку” говорить “сильнее нерасположенные к риску”, а вместо “более рас-
положенные к риску” - “слабее нерасположенные к риску”. Но пока
такое нагромождение отрицаний кажется неоправданным.
§4. Оптимальный портфель
51
(4.4) для портфеля С может оказаться больше, чем для пор-
тфеля D. Почему же тогда портфель С называется опти-
мальным? Дело в том, что путем комбинации портфеля С
и безрискового актива можно построить портфель с доход-
ностью R = ц • R? + (! — //)• Rc, который при некотором
р, < 0 обладает тем же риском (стандартным отклонением
доходности), что и портфель D, но большей ожидаемой до-
ходностью. По принятым критериям такой портфель лучше,
чем портфель D.
Рис. 4.4. Возможный вид функций распределения случайных
величин, обозначающих доходность
Кривая, изображенная на рис. 4.3, является эффектив-
ным фронтом для портфелей, составленных из п рисковых
ценных бумаг. Рассматривая портфели, состоящие из п рис-
ковых и одной безрисковой ценной бумаги, можно точно так
же ввести понятие эффективного фронта. В этом случае эф-
фективным фронтом будет полупрямая R?C, изображенная
на рис. 4.3 (при отсутствии ограничений на заимствование
средств) или некоторый отрезок этой прямой (если такие
ограничения есть).
52
Теория эффективных портфелей ценных бумаг
Рассмотрим также вопрос о том, как будет выглядеть
эффективный фронт, если процентная ставка Rp\ по ко-
торой вкладчик может дать безрисковый заем (например,
купив государственные ценные бумаги) ниже процентной
ставки , по которой вкладчик может взять заем. Эффек-
тивный фронт для этого случая изображен сплошной линией
на рис. 4.5. Он состоит из отрезка прямой линии, соединяю-
щего точку с вертикальной осью, из части криволиней-
ного эффективного фронта между точками и С1'2'1 (эф-
фективного фронта, соответствующего портфелям, состав-
ленным только из рисковых ценных бумаг), и из полупрямой
(или отрезка), расположенной правее точки С^.
Рис. 4.5. Эффективный фронт для случая, когда безриско-
вое заимствование производится по более высокой процентной
ставке, чем безрисковое одалживание
§ 5. Упрощенные методы
нахождения эффективных
портфелей. Использование
индексов
Одним из наших основных предположений является рас-
смотрение доходностей ценных бумаг как случайных вели-
чин 7?i, Яг, • • 1 Rn- Но при построении эффективных фрон-
тов используется не вся информация об этих случайных
величинах, а только следующие числовые характеристи-
ки случайных величин: математические ожидания E(Ri),
дисперсии P(jRj), ковариации Cov(Ri, Rj). В §1 был описан
только простейший способ определения этих числовых ха-
рактеристик по известным в предыдущие периоды значени-
ям доходностей рассматриваемых ценных бумаг.
Вопросу о том, как находить числовые характеристики
случайных величин, нужные для построения эффективных
фронтов, посвящено большое количество работ. Обзор неко-
торых из этих работ и сравнительный анализ существую-
щих методов можно найти, например, в [2].
Опишем один из распространенных практических подхо-
дов к построению случайных величин Rly R2, ., Rn- Этот
подход имеет название модель с одним индексом.
Пусть случайная величина Rm обозначает доходность
индекса рынка. (Обозначение М происходит от английского
слова market - рынок.)
54
Теория эффективных портфелей ценных бумаг
Индекс рынка - это набор ценных бумаг, используемый
для определения ситуации на данном рынке фондовых ак-
тивов путем расчета усредненной стоимости этих ценных
бумаг21. Можно даже сказать, что индекс рынка - это набор
ценных бумаг в совокупности со способом расчета их усред-
ненной стоимости. Иногда сокращенно индексом называют
саму усредненную стоимость.
Доходность индекса рынка может рассматриваться как
усредненная доходность входящих в данный индекс ценных
бумаг. При том, что мы рассматриваем рынок, состоящий
из п видов ценных бумаг, возможно, например, следующее
определение этой случайной величины:
Rm = —y^Rj.
Мы привели последнюю формулу только для иллюстрации.
Использоваться в дальнейшем она не будет22.
Если речь идет о рынке акций в США, то в качестве
индекса рынка может быть использован, например, индекс
Доу - Джонса или индекс агентства “Стандард энд Пур”.
В модели с одним индексом предполагается, что Rm -
это общий фактор, и зависимость линейна, т. е. случайные
“Определение индекса см. [37], с. 982. Распространено также дру-
гое определение, когда под индексом понимается не сам набор ценных
бумаг, а некоторая характеристика этого набора.
22В §8 мы будем обозначать через Rm доходность рыночного порт-
феля, т. е. портфеля, состоящего из всех акций, имеющихся на рынке,
и тогда последняя формула оказывается вообще неправильной. Но в
этом параграфе возможна большая свобода в выборе случайной вели-
чины Rm, поскольку рыночный портфель, конечно, является индексом
рынка, но индекс рынка может быть определен и по-другому.
§5. Использование индексов
55
величины 7?i, Т?25 • • •, Rn, Rm обладают следующим свойст-
вом. При каждом i = 1,2,... ,п существуют числа и &
такие, что для случайных величин £{, определяемых урав-
нениями
Ri — о:» + Мм + £», (5-1)
выполняются следующие условия. При всех i
E(ti) = 0, Cov(£i, Rm) — 0, (5.2)
и при i j
Cov(£i,£j) = 0. (5.3)
Для оценки чисел оч и fa по известным значениям доход-
ностей в различные моменты времени может быть исполь-
зован аппарат регрессионного анализа (см., например, [38]).
Эти числа называются коэффициентами Альфа и Бета для
данной ценной бумаги. Особенно важную роль при анализе
рынка и выработке решений играют коэффициенты Бета.
Условие (5.3) является очень сильным упрощением и
основной характеристикой модели с одним индексом. Оно
означает, что единственная причина, по которой доходнос-
ти различных ценных бумаг меняются взаимосвязанно, - это
изменение индекса Rm- Если исключить влияние этого ин-
декса, то доходности различных ценных бумаг становятся
независимыми, и изменение любой из них никак не связа-
но с изменением всех остальных. Например, модель с одним
индексом не может передать того, что доходности ценных
бумаг, относящихся к различным отраслям промышленнос-
ти, могут изменяться по-разному, а внутри одной отрасли
- более или менее согласованно. Для преодоления этого не-
достатка используются модели с несколькими индексами, о
которых будет сказано в конце данного параграфа.
56
Теория эффективных портфелей ценных бумаг
Будем пользоваться обозначениями
а? = D(£i), а2м = Р(ЗД, = Е&), Сц = Cov(Ri, Rj).
В частности, Сц — D(Ri). Из условий (5.1), (5.2) и (5.3)
следует, что
Сц = Р? + of, (5-4)
Сц = Pi Pj <r2M при i ± j. (5.5)
Формула (5.4) показывает,что дисперсия доходности г-й
ценной бумаги Сц, которую мы рассматриваем как матема-
тическую модель риска, складывается из двух частей. Эти
слагаемые могут трактоваться как риск, связанный с общим
состоянием рынка и с коэффициентом Бета данной ценной
бумаги, Р2 (Уmi ъ риск, относящийся только к данной цен-
ной бумаге, а2. Риск р2 &м называется систематическим
риском. Риск а2 называется несистематическим риском.
Напомним, что портфель ценных бумаг определяется на-
бором чисел «1, «2, • • •, ®п, таких, что
i=l
Математическое ожидание доходности портфеля
Дисперсия доходности портфеля
= 52 52 Х* х3 Сц- (5-7)
i=l 3=1
§5. Использование индексов
57
Из (5.1) и (5.2) получаем
Е = 52^ аг 4- (3i E(Rm)-
i=i i=i
Из (5.4) и (5.5) получаем
°2 = Z Z х5 & 05 aM + ibxi ai-
i=i j=i i=i
Отсюда легко увидеть, что
°2 = (sXi 0i] [£ x5 aM + S ai •
\i=l / \j=l / i=l
Если определить коэффициент Бета для портфеля
0 = S Xi 0<>
г=1
ТО
п
2 __ х>2 2 . z»2 „2
а - 0 ам + 2_sxi ai-
i=i
Рассмотрев, например, случай ®i = х2 = ... = хп = 1/п,
нетрудно увидеть, что сумма
n 1 /1 п \
77, п \ п /
г=1 \ г=1 /
стремится к нулю при увеличении п, если дисперсии всех
случайных величин ei ограничены сверху одним и тем же
числом. Поэтому при больших п риск хорошо рассредото-
ченного портфеля определяется систематическими рисками
58
Теория эффективных портфелей ценных бумаг
входящих в портфель ценных бумаг и приближенно может
быть представлен в виде
_2 _ /32 _2
а -Р ам-
Теперь мы можем дать хотя и менее строгое, но относя-
щееся к более общим ситуациям, чем только модель с одним
индексом, определение систематического и несистематичес-
кого рисков. Тот риск, который потенциально может быть
исключен при помощи рассредоточения капитала по различ-
ным видам ценных бумаг, называется несистематическим.
Тот риск, который нельзя исключить путем рассредоточе-
ния капитала, называется систематическим.
В §4 было показано, что при возможности покупки и вы-
пуска безрисковой ценной бумаги с доходностью Rp на эф-
фективном фронте можно выделить оптимальный портфель.
В некоторых случаях набор чисел Xi, ж2, • • •, хп, который
определяет оптимальный портфель, может быть найден при
помощи явных формул. Проведем разбор одного из таких
примеров.
Будем считать, что используется модель с одним ин-
дексом, дисперсии и ковариации доходностей ценных бу-
маг определяются по формулам (5.4) и (5.5). При построе-
нии эффективного фронта на определяющие портфель числа
»1, Жг,..., накладываются ограничения вида равенств и
неравенств
N
, OijX» — bj, j — 1,2,...,т, Xi > /i, a>2 > • 2-n > In-
(5.8)
Будем считать, что отсутствуют все ограничения на выпуск
ценных бумаг (т. е. Ц = = ... = 1п — — оо) и вообще
§5. Использование индексов
59
отсутствуют все ограничения вида неравенств, т. е. N = п
(мы уже неявно предположили это, не включив в условия
(5.8) вспомогательные переменные ®n+i,..., ж^).
Будем считать, что в условиях (5.8) т = 1 и единствен-
ное ограничение вида равенств - это обычное условие
Xi + Х2 + . . . + хп = 1.
В конце §3 мы говорили, что при таких ограничениях эф-
фективный фронт на плоскости (а, Е) является частью ги-
перболы или частью прямой линии. Будем считать, что иде-
альной корреляции доходностей нет, и эффективный фронт
является частью гиперболы.
Положим
2 у-'П Pi(^i ~ Rf)
Д — .
в? '
14-я2. Vn t-L
_ Pi (Ei- Rf \ • _ 1 о
У* 2 I /о ’ z — 1; 2;..., п;
X Pi /
Xi = =^—~, i = l,2, ...,n. (5.9)
Zaj-i Уз
Мы покажем, что набор чисел a?i, х2, • • •, хп, определяе-
мый по формулам (5.9), соответствует оптимальному пор-
тфелю. Читатель, не заинтересованный в математических
подробностях, может опустить приводимое ниже доказа-
тельство.
60
Теория эффективных портфелей ценных бумаг
В §4 было показано, что если набор чисел ®i, ж2,.. ., хп
определяет оптимальный портфель, то именно при этих зна-
чениях ®i, ж2,..., жп достигает максимума функция
, Е — Rp
,ж2,...,жп) = ------,
6F
где Ена как функции Ж1, ж2,..., хп определяются по форму-
лам (5.6) и (5.7). Поскольку речь идет об отыскании услов-
ного максимума, составим функцию Лагранжа
1(Ж1, ж2, . . . , Хп, А) = 0(®1, ж2, . . . , Жп)-А-(Ж1 + ®2 + . . , + ®п-1).
Необходимое условие максимума - это равенство нулю част-
ных производных:
^ = 0, ^ = о, .... ^ = 0.
UX\ 0X2 охп
После дифференцирования получаем систему уравнений
Ек ’ I J2 52
\i=l j—1
((\ S/2
n n \
5252л*ж^) =
i=l j=l /
к = 1,2,..., n.
Домножив k-e уравнение на хь и сложив все эти уравнения,
получаем
§5. Использование индексов
61
У словие
dL
дхк
принимает вид
£х((Е{-Яг)
i-1
п
• 52 Xi^ik + — Rf) = 0.
»=1
Введем обозначение
а =
Е — Rf
а2
Тогда числа х?,..., жп, соответствующие оптимальному
портфелю, должны удовлетворять системе уравнений
я • ' XiCik = Ek Rf, к ~ 1) 2,..., п.
г=1
Введем обозначение
yi = a-Xi, г = 1,2,...,п.
Тогда величины У1, у2, • • •, Уп удовлетворяют системе линей-
ных алгебраических уравнений
5 у У&гк = Ek Rf, = 1, 2, . . . , П.
г=1
62
Теория эффективных портфелей ценных бумаг
Воспользовавшись формулами (5.4) и (5.5), получаем
п
Ук<т% + ^Уг&/Зк(Гм = Ек-Rf, к = 1,2,... ,п.
i=i
Отсюда
Ек~Кр <т‘м \ , , о
Ук 2 „2 I / -> У*Р{ I , к — 1, 2, . . . , П,
ак ak V=i /
или
Рк I &к HF 2 / V /э 1 I 7 in
yfc=~2l'—Ъ-------<Гм-\2^Уг& , к = 1,2,... ,п.
17 к \ Рк \»=1 / /
(5.10)
Каждое из уравнений (5.10) определяет величину yk неявно,
так как эта величина входит и в левую, и в правую часть
уравнения. Чтобы получить явные выражения для ук, ум-
ножим каждое из уравнений (5.10) на /Зк и сложим все эти
уравнения. Тогда
f v5 я — v5 ^к ^к ~ а2 (V5 Я V5
У. УкРк 1 = 2^---Z2------ам 2> УкРк I ’ 2> Тг •
\fc=l / к=1 ак \fc=i / к=1 ак
Отсюда
^(Ei-Rf)
( п \ <У^
I S Vi0k I = —-----Я2
' i+’m-e4
i=l
Подставляя это выражение в (5.10), получаем
(Зк (Ek - Rf Л , _ 9
Ук — 2 I о " / ’ — 1, 2, • • • , П.
ак \ Рк /
§5. Использование индексов
63
Из этого и из условия yi = а • х± при i = 1,2,..., п следует,
что набор чисел (5.9) определяет оптимальный портфель.
Отметим, что для оптимального портфеля а > 0. Поэ-
тому при любом i числа ж» и у» имеют один и тот же знак.
Ограничимся рассмотрением случая
X?! > 0, &>0,...,£n>0.
Из полученных формул можно сделать следующий вывод.
При составлении оптимального портфеля г-я ценная бумага
должна быть куплена, если
Ei — Rf л
(в этом случае > 0 и st- > 0) и г-я ценная бумага должна
быть выпущена, если
Ei — Rf
-------< А
(в этом случае у, < 0 и ж,- < 0). Отметим, что от вели-
Ei — Rp
чины отношения ------- зависит не только то, должна ли
Рг
быть г-я ценная бумага куплена или выпущена, но и то, в
какой пропорции данная ценная бумага должна входить в
оптимальный портфель.
Найдя оптимальные портфели при двух различных зна-
чениях процентной ставки Rf, можно восстановить весь
эффективный фронт. Это следует из линейности функций
ж1(А),ж2(А), ..., жп(А), рассмотренных в §3.
На этом мы закончим рассмотрение примера, когда при
использовании модели с одним индексом числа Ж1, ж2, • • •, ®п,
64
Теория эффективных портфелей ценных бумаг
определяющие оптимальный портфель, могут быть найде-
ны по явным формулам. Отметим, что и в более общих си-
туациях решение вопроса о включении г-й ценной бумаги
в портфель существенно зависит от величины отношения
Ei — Rf
Модель с несколькими индексами - это естественное об-
общение модели с одним индексом. Пусть мы рассматрива-
ем к индексов, которым соответствуют случайные величины
/1,12,. , Ik- При каждом i = 1,2,... ,п считаем, что спра-
ведливо уравнение
Ri = ai 4- fliylx 4- + • •. + fliklk + £i,
где свойства случайных величин Е{ аналогичны свойствам
этих же случайных величин в модели с одним индексом. Тог-
да формулы для дисперсий и ковариаций сходны с форму-
лами (5.4) и (5.5). Основные затруднения вызывает вопрос
о том, какие именно индексы выбирать для включения в
модель и приводит ли увеличение числа индексов к улуч-
шению модели. Но рассмотрение этого вопроса выходит за
рамки данной книги.
§ 6. Анализ полезности
Изложение портфельной теории часто строится так, что по-
нятие полезности привлекается при рассмотрении большин-
ства вопросов. Мы пошли по другому пути, который также
используется достаточно часто, собрав вопросы, связанные
с полезностью, в одном параграфе.
Доходность (по крайней мере, теоретически) может быть
любым действительным числом (если мы допускаем, что
доход может быть отрицательным). Пусть на множестве
действительных чисел определена монотонно возрастающая
66
Теория эффективных портфелей ценных бумаг
обычно достаточно гладкая функция U, которую мы будем
называть функцией полезности (см. рис. 6.1). (Обозначение
U происходит от английского слова utility - полезность.)
Рассматривается следующая задача: определить портфель
из ценных бумаг, для которого математическое ожидание
случайной величины U(R) максимально. Случайная величи-
на R, как и раньше, означает доходность портфеля ценных
бумаг. Этот подход к составлению портфелей ценных бумаг
имеет название максимизация ожидаемой полезности.
Если рассмотреть функцию
=a + bU(R), Ь>0,
то
EtU^R)) = a + bE(U(R))
и максимум E(Ui(R)) достигается для того же портфеля,
что и максимум E(U(R)). Поэтому без уменьшения общнос-
ти можно ограничиться рассмотрением функций U, таких,
что
П(-1) = -1, (7(0) = 0.
Никогда не следует усложнять дело без необходимости.
Почему нельзя ограничиться рассмотрением случайной ве-
личины (7(7?) = R, т. е. считать, что полезность равна
или пропорциональна доходности, и не вводить еще один
термин? Среди рассматриваемых нами функций (7(г) при-
сутствует и функция U(г) = г, однако, как будет показано
ниже, другие функции полезности позволяют лучше пере-
дать поведение реального вкладчика, чем функция полез-
ности (7(г) = г.
Функция (7(г), график которой изображен на рис. 6.1,
§6. Анализ полезности
67
является строго вогнутой23. Если эта функция дважды не-
прерывно дифференцируема, то U"(г) < 0 при любом дейст-
вительном г. Вкладчик, составляющий портфель так, чтобы
достигался максимум ожидаемой полезности, когда функция
U(r) вогнутая, называется вкладчиком, нерасположенным к
риску, или вкладчиком с нерасположенностью к риску.
Рис. 6.2. Линейная функция полезности
Функция U(r), график которой изображен на рис. 6.2, яв-
ляется линейной, т. е. U"(r) = 0 при любом действительном
г. Вкладчик, составляющий портфель так, чтобы достигал-
ся максимум ожидаемой полезности, когда функция U(r) ли-
нейная, называется вкладчиком, безразличным к риску.
230пределение вогнутой функции приведено в §3.
68
Теория эффективных портфелей ценных бумаг
Функция Z7(r), график которой изображен на рис. 6.3. яв-
ляется строго выпуклой. Если эта функция дважды непре-
рывно дифференцируема, то U"(r) > 0 при любом действи-
тельном г. Вкладчик, составляющий портфель так, чтобы
достигался максимум ожидаемой полезности, когда функция
и(г) выпуклая, называется вкладчиком, склонным к риску.
Поясним эти определения на примере. Пусть у вкладчика
есть две возможности. Первая возможность состоит в том.
чтобы вложить свой капитал в ценные бумаги, у которых
доходность
-Г1
Г2
с вероятностью 0.5,
с вероятностью 0.5,
§6. Анализ полезности
69
П и г2 положительные числа, т. е. с вероятностью 0.5 капи-
тал уменьшается и с вероятностью 0.5 он возрастает. Вто-
рая возможность состоит в том, чтобы не вкладывать ка-
питал ни в какие ценные бумаги. При выборе второй воз-
можности доходность равна 0 и полезность, следовательно,
также равна 0. Выбирая между этими двумя возможностями
и максимизируя ожидаемую полезность, вкладчик выберет
первую возможность, если
E(U(R)) = Щ-п) 0.5 + 1Г(г2) • 0.5 > 0.
Вкладчик может выбрать как первую, так и вторую воз-
можность, если
£/(—Г1) • 0.5 + U(r2) • 0.5 = 0,
и выберет вторую возможность, если
U(-ri) • 0.5 + tZ(r2) • 0.5 < 0.
Если функция полезности является вогнутой, т. е. мы
имеем дело с вкладчиком, нерасположенным к риску, то
условие
tf(-n) + Шт,) > о (6.1)
может выполняться только при г2 > ту. Поэтому, если
вкладчик, нерасположенный к риску, выбрал первую воз-
можность, т. е. вложил свой капитал в рассматриваемые
ценные бумаги, это означает, что r2 > г1- При равновероят-
ных выигрыше и проигрыше вкладчик, нерасположенный к
риску, будет играть только если размер выигрыша больше
размера проигрыша, причем больше на определенную ве-
личину, зависящую от вида функции полезности. Действи-
тельно, условие (6.1) для вогнутой функции U выполняется
70
Теория эффективных портфелей ценных бумаг
не при всех r2 > ri, а только при r2 > > ri. Величина
зависит от выбранной функции полезности U. Вкладчик,
нерасположенный к риску, не будет вкладывать капитал в
ценные бумаги, если E(R) = 0.
Если функция полезности является линейной функцией
(7(г) = г, т. е. мы имеем дело с вкладчиком, безразличным
к риску, то условие (6.1) выполняется при г2 > г^. Этот
вкладчик выбирает первую возможность (т. е. вкладывает
капитал в ценные бумаги) при г2 > п, может выбрать как
первую, так и вторую возможность при г2 — ri, и выбирает
вторую возможность при r2 < ri. Вкладчик, безразличный к
риску, не будет вкладывать капитал в ценные бумаги, если
E(R) < 0.
Если функция полезности является выпуклой, т. е. мы
имеем дело с вкладчиком, склонным к риску, то существу-
ет г2 < ri, такое, что условие (6.1) выполняется при любом
Г2 > ^2 и не выполняется при г2 < г2- Этот вкладчик выбе-
рет первую возможность (т. е. купит рассматриваемые цен-
ные бумаги) при т2 > г2, может выбрать как первую, так
И вторую ВОЗМОЖНОСТЬ при Г2 = Г2 и выберет вторую воз-
можность при г2 < г2- Вкладчик, склонный к риску, может
вложить свой капитал в ценные бумаги даже при E{R) < 0.
В рассмотренном примере присутствуют три типа пове-
дения вкладчика: нерасположенность к риску, безразличие
к риску и склонность к риску. Наиболее близким к поведе-
нию реального вкладчика среди этих трех типов является
нерасположенность к риску.
Нерасположенность к риску означает, что вкладчик дол-
жен получить компенсацию за присутствие риска. В §3 мы
приняли в качестве отправной точки, что, при одной и
той же ожидаемой доходности, портфели с меньшим стан-
§6. Анализ полезности
71
дартным отклонением привлекательнее, чем портфели с
большим стандартным отклонением. Там мы сказали толь-
ко, что большинство вкладчиков не любят неопределен-
ность. Но этот ответ является не до конца убедительным,
поскольку большее стандартное отклонение предполагает
больший разброс, как в сторону проигрыша, так и в сторо-
ну выигрыша. Теперь мы можем добавить, что для вклад-
чика, нерасположенного к риску, отрицательные отклонения
уменьшают ожидаемую полезность сильнее, чем увеличива-
ют ее такие же по величине и вероятности положительные
отклонения.
В качестве примера рассмотрим портфель А с доходнос-
тью
_ Г 0.1 — д'л с вероятностью 0.5,
1 0.1 + с вероятностью 0.5,
и портфель В с доходностью
0.1 — 8в с вероятностью 0.5,
0.1 + 8в с вероятностью 0.5,
причем 0 < 8а < 8в-
Покажем, что из свойств строго вогнутых функций сле-
дует, что E(U(RA)) > E(U(Rb))- Имеем
E(U(Ra)) = 0.5(7(0.1 - <5л) + 7(0.1 + <М),
E(U(RB)) = 0.5(7(0.1 - 8В) + 17(0.1 + 8В)).
Если функция U строго вогнутая, то весь график функ-
ции U(R) на интервале (0.1 — <£в,0.1 + 8в) лежит выше
хорды, соединяющей точки (0.1 — 8в, ZZ(0.1 — <£g)) и (0.1 +
+8b,U(0.1 + 8в))- Т. е. середина хорды, соединяющей точки
(0.1 - 8А, £7(0.1 - и (0-1 + 8а, 7(0.1 + <$д)), лежит выше
72
Теория эффективных портфелей ценных бумаг
середины первой хорды. Это и означает, что E(U(Ra)) >
> E(U(RB)).
Поэтому вкладчик, нерасположенный к риску, максими-
зируя ожидаемую полезность, выберет портфель А, для ко-
торого стандартное отклонение доходности меньше, а не
портфель В, для которого стандартное отклонение доход-
ности больше.
Рис. 6.4. Функция полезности вогнутая при г < р и выпук-
лая при г > р
Возможны функции полезности и более сложного ви-
да, чем вогнутые, линейные или выпуклые. Например, на
рис. 6.4 приведен график функции полезности, которая во-
гнута при г < р и выпукла при г > р. Такая функция по-
лезности характеризует поведение вкладчика, которое яв-
§6. Анализ полезности
73
ляется нерасположенностью к риску в отношении отрица-
тельных и не очень больших положительных г, но данный
вкладчик придает существенное значение возможности зна-
чительного выигрыша. Подробное изложение теории полез-
ности можно найти в [35].
Рис. 6.5. Кривые безразличия для вогнутой квадратичной
функции полезности
В качестве примера рассмотрим случай, когда функция
полезности U(r) имеет вид
U{r) ~ а г2 + (а + 1)т. (6-2)
Эта функция полезности является вогнутой при а < 0, ли-
нейной при а = 0, выпуклой при а > 0 и удовлетворяет
условиям
С7(-1) = -1, [7(0) = 0.
74
Теория эффективных портфелей ценных бумаг
Рис. 6.6. Кривые безразличия для выпуклой квадратичной
функции полезности
Воспользовавшись формулой
Е(Я2) = (Е(Я))2 + D(R)
и обозначениями
Е = E(R), а2 = D(R),
получаем
E(U(R)) = а Е2 + (а + 1) Е + аа2.
При различных с рассмотрим на плоскости (<т, Е) кривые
а Е2 + (а + 1) Е + а а2 = с. (6.3)
§6. Анализ полезности
75
Чтобы построить портфель с максимальной ожидаемой
полезностью, нужно выбрать кривую с максимальным с, ко-
торая пересекалась бы со множеством точек на плоскости
(ст, Е), отвечающих возможным портфелям. Затем нужно
выбрать портфель, у которого риск а и ожидаемая доход-
ность Е совпадают с координатами (<т, Е) найденной точки
пересечения.
Рис. 6.7. Определение портфеля А из рисковых ценных бу-
маг путем максимизации ожидаемой полезности
При а = 0 семейство кривых (6.3) - это семейство гори-
зонтальных прямых
Е = с,
76
Теория эффективных портфелей ценных бумаг
а при фиксированном а / 0 и при
с /1 а+1\2
_+ >0
а \2 а /
- это семейство окружностей на плоскости (а, Е)
1 а + 1\2
2а/
1 а+ 1\2
2а/
+ а2
с
= —И
а
На рис. 6.5 (при а = —0.2) и 6.6 (при а = 0.2) изображе-
ны по три окружности из каждого семейства, отвечающие
различным с.
Ограничимся рассмотрением вкладчиков, нерасположен-
ных к риску, т. е. вкладчиков с вогнутой функцией полез-
ности (6.2). Будем считать, что а < 0 и а фиксированно.
Пусть портфели составляются из п рисковых ценных бу-
маг при наличии каких-то ограничений. На рис. 6.7 пока-
заны эффективный фронт и одна из окружностей, заданная
уравнением (6.3). Эта окружность пересекается с эффектив-
ным фронтом в единственной точке А. Если мы увеличим
с, то радиус окружности, заданной уравнением (6.3), умень-
шится, и эта окружность не будет пересекаться с эффектив-
ным фронтом. Таким образом, путем максимизации ожидае-
мой полезности из всего множества эффективных портфелей
выбирается тот портфель, которому соответствует точка А
на плоскости (а, Е). Этот портфель зависит от выбранного
значения а при определении функции полезности в (6.2).
Если к п рисковым ценным бумагам добавлена безрис-
ковая ценная бумага с доходностью Rp, которую можно как
продавать, так и выпускать, то, как было показано в §4,
эффективный фронт располагается на прямой линии (см.
рис. 6.8). Точка С соответствует оптимальному портфелю
§6. Анализ полезности
77
из рисковых ценных бумаг. На этом эффективном фронте,
как и в случае, когда рассматриваются портфели, состо-
ящие только из рисковых ценных бумаг, можно выделить
портфель с максимальной ожидаемой полезностью, которо-
му на рис. 6.8 соответствует точка А. В данном случае функ-
цией полезности определяется размер средств, которые сле-
дует заимствовать или одолжить, т. е. направить на выпуск
или покупку безрисковой ценной бумаги.
Рис. 6.8. Определение портфеля А из рисковых и безриско-
вой ценных бумаг путем максимизации ожидаемой полезности
Первым шагом в создании теории полезности стало ре-
шение задачи о Санкт-Петербургском парадоксе. Этот па-
радокс был обнаружен в XVIII веке Н.Бернулли, а объ-
78
Теория эффективных портфелей ценных бумаг
яснение было дано Д.Бернулли24, работавшим в те годы в
Санкт-Петербурге. Отсюда и произошло название “Санкт-
Петербургский парадокс”.
Задача Н.Бернулли имеет следующий вид. Определить,
сколько должен заплатить Павел Петру за возможность
сыграть в следующую игру. Игра заключается в бросании
монеты и прекращается при первом появлении герба. Если
герб выпадает при первом броске, то Петр платит Павлу
один дукат. Если при первом броске выпадает решетка, а
при втором - герб, то Петр платит Павлу 2 дуката. Если
при первых двух бросках выпадают решетки, а при третьем
- герб, то 4 дуката, и т.д. Если впервые герб выпадает при
n-м броске, то Петр платит Павлу 2П-1 дукатов.
Возможные исходы игры, вероятности этих исходов и со-
ответствующие выигрыши Павла приведены в таблице 6.1.
Таблица 6.1
Исход Вероятность исхода Выигрыш Павла
Г 1/2 1
РГ 1/4 2
РРГ 1/8 4
. . .
Р ... РГ п раз l/2n+1 2П
. , * . . .
Пусть случайная величина X обозначает выигрыш Пав-
ла. Найдем ее математическое ожидание.
ад = 1-1+2.1+... + 2».Аг+...=
24Bernoulli D. Specimen Theoriae Novae de Mensura Sortie.
Commentarii Academiae scientiarum imperialis petropolitanae, vol. 5,
1738; перепечатано: Exposition of a New Theory on the Measurement
of Risk. Econometrica, January 1954, 23 - 36.
§6. Анализ полезности
79
1 1 1
— г + т +•••+„ + ••- = оо.
Ы 4U Ai
Таким образом, “по справедливости” Павел должен запла-
тить Петру за возможность сыграть в такую игру беско-
нечно большую сумму денег, и, разумеется, Павел должен
соглашаться играть за любую конечную сумму денег, кото-
рую назовет Петр.
Парадокс заключается в следующем. Представьте себя
на месте Павла. Сколько Вы заплатите за возможность сыг-
рать в такую игру? Вряд ли больше 2-3 (конечно, не дука-
тов, а современных денежных единиц, но суть дела от этого
не меняется). Очень азартный человек может заплатить за
возможность сыграть в такую игру 5 - 7, но едва ли больше.
Во всяком случае, сколь угодно большую сумму не заплатит
никто. В чем же здесь дело?
Д.Бернулли предложил следующее решение. Оценивать
эту игру следует не по математическому ожиданию случай-
ной величины X, а по математическому ожиданию случай-
ной величины U(X), где U(x) = log ж, и сравнивать E(U(X))
с U(P), где Р - плата за игру. Говоря современным язы-
ком, Д.Бернулли ввел функцию полезности С7(ж) и потребо-
вал, чтобы ожидаемая полезность выигрыша была не мень-
ше, чем полезность суммы, заплаченной за игру25. Функ-
ция полезности С7(ж) является монотонно возрастающей. То,
что эта функция является вогнутой, передает нерасположен-
ность к риску. Для того чтобы определить сумму, больше
которой Павел не должен платить за участие в игре, найдем
253десь мы используем немного другой подход, чем в начале пара-
графа. Полезность определяется не как функция от доходности, а как
функция от стоимости имущества. Эти два подхода являются близки-
ми и взаимосвязанными.
80
Теория эффективных портфелей ценных бумаг
математическое ожидание случайной величины U(X).
OQ -1
E((7(X)) = £log2“-1.i =
n=l Z
= f(»-l)log2.1=log2.f ^1.
n=l Z n=l 2
Покажем, что
f —= 1-
±-! 2n
n=l
Отсюда будет следовать, что E(U(X)) = log 2 = 17(2). Та-
ким образом, при функции полезности U(x) = log (ж) Павел
должен играть, если Петр потребовал с него за возможность
сыграть в данную игру меньше 2 дукатов, и не должен иг-
рать, если Петр потребовал с него больше 2 дукатов.
Имеем
§6. Анализ полезности
81
Независимо от Д.Бернулли решение задачи Н.Бернулли
примерно в то же время было предложено Г.Крамером, ко-
торый использовал функцию полезности U(x) = у/х и полу-
чил, что математическое ожидание полезности выигрыша
равно полезности суммы, которая несколько больше 2 дука-
тов (см. [8]).
§ 7. Другие вопросы, связанные с
уменьшением риска
В этом параграфе приведено несколько примеров, показы-
вающих, что уменьшение стандартного отклонения доход-
ности носит позитивный характер, а также за счет чего это
уменьшение может быть достигнуто.
До сих пор мы говорили о доходности за один период вре-
мени (t, t + At). Теперь мы коснемся вопроса, как изменяется
стоимость ценной бумаги или стоимость портфеля за к пери-
одов времени (t,t+At), (t+Ai,t+2At), (t+(fe—l)At,t+A:At).
Еще раз подчеркнем, что приводимый ниже материал - это
несколько примеров. Все они носят очень упрощенный ха-
рактер и не претендуют на роль исчерпывающего анализа
многопериодной задачи.
Если речь идет о портфеле, то мы считаем, что его со-
став не изменяется с момента времени t до момента време-
ни (t + A:At). Введем случайные величины Gj, 6?2, • • •, Gk- Gi
- это доходность рассматриваемой ценной бумаги или рас-
сматриваемого портфеля за период времени (t + (г — l)At, t +
-|-tAt), i = 1,2,... ,k. Раньше мы обозначали доходность че-
рез R. В этом параграфе нам удобнее изменить обозначение.
Определим случайную величину
G = [(1 + G,) (1 + ед •... • (1 + Gt)]1'* - 1,
которую назовем темпом роста капитала.
Поясним данное определение. Пусть g,gi,g2, ,9k -
значения, принимаемые случайными величинами G. Gi,Gz,
§7. Вопросы, связанные с уменьшением риска
83
..., Gk- Если стоимость рассматриваемой ценной бумаги
или портфеля в момент t равна St, то чему будет равна сто-
имость этой ценной бумаги или портфеля St+k&t в момент
времени (t + A:At)? Допустим, что для каждого i (1 < i <к)
доход D, полученный от владения ценной бумагой в период
времени (t 4- (г — 1)Д£, t + гД£), равен нулю. Тогда
St+kAt — St • (1 + 5i) • (1 + 52) •...(!+ 5fc).
Если бы доходность для любого из к периодов равнялась
одному и тому же числу д, то при каком значении д была
бы получена та же стоимость ценной бумаги или портфеля
S't+fcAt? Для этого нужно, чтобы выполнялось равенство
(1 + д)к = (1 + 51) (1 + 5г) • • • • • (1 + 5fe)-
Исходя из полученной формулы и дано определение случай-
ной величины G.
Будем считать, что все случайные величины С?1,С?2,
..., Gk имеют одинаковые математические ожидания и оди-
наковые дисперсии. Позднее мы сделаем предположение, что
эти случайные величины еще и независимы.
Посмотрим, как связан темп роста капитала с мате-
матическим ожиданием и дисперсией случайных величин
Gi, G2, • , Gk- Введем обозначения
Е= E(GI) = ... = E(Gb), <r! = O(G,) = ... = P(G»).
(7.1)
Найдем приближенное выражение для log (1 + G) (log -
это логарифм по основанию е). Имеем
l°g (1 + G) ~ --(log (1 + Gi) +log (1 + 672)+- • .+log (1 + Gk))-
К
84
Теория эффективных портфелей ценных бумаг
Воспользовавшись при i = 1,2, ...,к формулой Тейлора и
отбросив члены третьего и более высоких порядков малости,
получаем log (1 + Gi) & Gi — 0.5 G2. Отсюда
log (1 + G) ~ —“(Gi + GaH-.. .4-Gfc) —— 0.5(G!i + G!2 + . . .+G>).
К к
Считая G > — 1, введем функцию полезности
{7(G) = log (1 + G),
эта функция является монотонно возрастающей и вогнутой.
Имеем
E(U(G)) « |• RGJ + E(G2) + ... + E(Gk))~
К
— 1 0.5 (E(GJ) + E(G^) + ... + E(G|)).
Воспользуемся тем, что
£?((??) = E(Gi)2 + D(Gi), i = l,2,...,fc.
При помощи (7.1) получаем
E(U(G)) « Е - 0.5 Е2 - 0.5 о2.
Функция Е — 0.5 Е2 является монотонно возрастающей при
Е < I26. Поэтому из полученной формулы можно сделать
26Отбросив члены третьего и более высоких порядков малости пос-
ле применения формулы Тейлора, мы неявно предположили, что слу-
чайные величины G, в основном принимают значения между -0.3 и
0.3. Условие Е < 1 при этом, конечно, выполняется. Отметим рабо-
ту: Hakansson N.H. Capital Growth and the Mean-Variance Approach
to Portfolio Selection / / Journal of Financial and Quantitative Analysis.
1971. V.6. P. 517 - 557. В этой работе рассматриваются примеры, в
которых доходность за один период может быть больше 1; результаты
в этом случае носят другой характер.
§7. Вопросы, связанные с уменьшением риска
85
вывод, что темп роста капитала возрастает с возрастанием
ожидаемой доходности за один период Е. Этот вывод, ко-
нечно, не является неожиданным. Из этой формулы можно
также сделать вывод, что темп роста капитала убывает с
возрастанием риска а. Этот вывод является менее очевид-
ным.
Связан ли последний вывод с конкретным видом функ-
ции полезности 17? Не повлияло ли на результат то, что мы
воспользовались приближенной формулой для log (1 + Gj)?
Ниже приведены другие подтверждения того, что темп рос-
та капитала убывает с возрастанием риска а. Это является
еще одним аргументом в пользу утверждения, что при одной
и той же ожидаемой доходности (за один период) портфели
с меньшим стандартным отклонением привлекательнее для
вкладчика, чем портфели с большим стандартным отклоне-
нием.
Остановимся на случае к = 2. Пусть gi = т + е, gi —
— г — £, £ > 0. Тогда
9 = \/(1 + 51) • (1 + 5г) - 1 = ^(1 +т)2 - £2 - 1.
Мы приходим к тем же выводам, что и раньше: д возрастает
с возрастанием т и убывает с возрастанием £.
Еще одну проверку сделанного вывода, что темп роста
капитала уменьшается при возрастании риска, проведем с
помощью метода Монте - Карло. Будем считать, что каж-
дая из случайных величин Gi равномерно распределена на
отрезке [г-7,т + 7]. Тогда E(Gi) = г, D(Gi) - 72/3, * =
= 1,2,..., к.
Сделаем предположение, что случайные величины Gi, G2,
... ,Gk независимы. Используя датчик случайных чисел,
найдем числа Zi,Z2,-.., z^, которые являются значениями
86
Теория эффективных портфелей ценных бумаг
независимых случайных величин Zj, Z2,.... Z&, каждая из
которых равномерно распределена на отрезке [0,1]. Поло-
жим = ((1 + #1) • (1 + #2) • ... • (1 + дкУ)1/к - 1, где
gi = г + 27 (zi — 0.5), i = 1,2,..., к. Вместо использовав-
шегося ранее обозначения д мы теперь используем обозна-
чение д(к\ чтобы подчеркнуть, какое количество периодов
рассматривается.
Пусть г = 0.1, к = 50. Рассмотрим следующие четыре
значения 7 : 7 = 0.1, 7 — 0.2, 7 = 0.4, 7 = 0.8.
Таблица 7.1
Номер расчета 7 = 0.1 7 = 0.2 7 = 0.4 7 = 0.8
1 0.094752 0.086164 0.058661 -0.047038
2 0.087713 0.072024 0.029672 -0.113036
3 0.103610 0.104244 0.096145 0.033427
4 0.102123 0.101259 0.090304 0.023957
5 0.098004 0.093076 0.073583 -0.018544
6 0.103159 0.103824 0.097636 0.051568
7 0.095150 0.086755 0.058810 -0.053454
8 0.111273 0.119523 0.126549 0.093927
9 0.112802 0.123007 0.135315 0.120162
10 0.102236 0.100846 0.086822 0.003617
11 0.094037 0.085163 0.058311 -0.039967
12 0.087207 0.071495 0.030957 -0.095093
13 0.091323 0.079820 0.047812 -0.062776
14 0.098256 0.093536 0.074744 -0.009545
15 0.101482 0.100020 0.087876 0.018939
16 0.082554 0.061757 0.009413 -0.151392
17 0.088205 0.073075 0.032438 -0.099698
18 0.092594 0.081744 0.048797 -0.077906
19 0.099322 0.095075 0.075535 -0.017526
20 0.092913 0.083406 0.056632 -0.036430
§7. Вопросы, связанные с уменьшением риска
87
В таблицах 7.1 и 7.2 приведены результаты 20 расчетов
темпов роста капитала и соответствующих этим темпам
роста величин капитала в конце последнего периода. Эти
результаты отвечают различным, полученным при помощи
датчика случайных чисел наборам Zi, z2,..., Zk- В таблице
7.1 при разных 7 показаны полученные темпы роста капи-
тала
Из 20 испытаний в 16 испытаниях наибольшие значения
д получены при 7 = 0.1, в 2 испытаниях (в третьем и в
шестом) наибольшие значения д получены при 7 = 0.2, в 2
испытаниях (в восьмом и в девятом) наибольшие значения
д TLony4ffBH при 7 — 0.4, и ни в одном испытании - при
7 = 0.8. Больше того, при 7 = 0.8 в 13 испытаниях получены
отрицательные значения темпа роста капитала.
В таблице 7.2 для тех же расчетов приведены значения
величин (1 + </(5()))50. Они показывают, во что превращается
капитал, равный 1 в начале первого периода, к концу 50-го
периода.
Полученные результаты можно представить себе так. В
начальный момент времени t рассматриваются 20 одинако-
вых Вселенных. В каждой Вселенной существуют 4 ценные
бумаги с одинаковыми математическими ожиданиями до-
ходностей, равными 0.1, т. е. средний прирост стоимости
каждой ценной бумаги в каждой Вселенной за один период
составляет 10%. Но дисперсии доходностей (т. е. риски) для
каждой из 4 ценных бумаг различны. В нашем примере они
составляют 0.12/3, 0.22/3, 0.42/3, 0.82/3; эти 4 числа оди-
наковы для всех Вселенных. В момент времени t в каждой
из Вселенных в каждую ценную бумагу вкладывается одна
денежная единица. В таблице 7.2 показано, во что превраща-
ется эта денежная единица через 50 периодов; каждая строка
88
Теория эффективных портфелей ценных бумаг
соответствует одной из Вселенных и показывает стоимость
соответствующей ценной бумаги27.
Таблица 7.2
Номер расчета 7 = 0.1 7 = 0.2 7 = 0.4 7 = 0.8
1 92.424467 62.340748 17.291933 0.089902
2 66.946124 32.376543 4.314589 0.002485
3 138.286731 142.313831 98.491210 5.176053
4 129.270420 124.298892 75.400557 3.266593
5 107.201047 85.609438 34.816705 0.392238
6 135.490324 139.632061 105.419341 12.355815
7 94.120448 64.060532 17.414352 0.064135
8 195.448588 282.916913 386.815160 89.006419
9 209.364502 330.457838 569.915828 291.094048
10 129.937942 121.989981 64.255623 1.197825
11 89.454381 59.530602 17.008435 0.130109
12 65.405578 31.586904 4.592289 0.006764
13 79.006086 46.511440 10.331419 0.039099
14 108.438151 87.430092 36.749584 0.619071
15 125.563325 117.497991 67.448502 2.555156
16 52.781897 20.010122 1.597496 0.000273
17 68.476405 34.001832 4.934118 0.005241
18 83.743317 50.841084 10.828487 0.017328
19 113.828654 93.796845 38.125833 0.413103
20 84.973403 54.898025 15.710257 0.156375
27В приведенном примере доходности ценных бумаг в разных Все-
ленных независимы и независимы внутри одной Вселенной для раз-
ных периодов времени. Для одного периода внутри одной Вселенной
доходности д, различных ценных бумаг определяются одним и тем же
числом z,-, но с разными 7. При рассмотрении примера, когда доходнос-
ти всех четырех ценных бумаг независимы также для каждого перио-
да времени внутри каждой Вселенной, результаты носят аналогичный
характер.
§7. Вопросы, связанные с уменьшением риска
89
В 16 Вселенных наилучшие результаты дали вклады в
ценные бумаги с минимальным риском, и ни в одной Вселен-
ной наилучшие результаты не дали вклады в ценные бумаги
с максимальным риском. При вкладах в наиболее рискован-
ные ценные бумаги в большинстве Вселенных начальный
капитал не только не увеличился, но даже уменьшился.
Из результатов этих расчетов следует тот же вывод, что
и из примеров, рассмотренных ранее в настоящем парагра-
фе: при увеличении риска (в данном случае при увеличении
7) темп роста капитала снижается?8.
Следует сделать вывод, что поговорка “Риск - благород-
ное дело” не относится к управлению капиталом.
Из таблицы 7.1 видно, что даже при 7 = 0.1 в большинст-
ве испытаний темп роста капитала оказался ниже 10%. Это
закономерно, так как отрицательные отклонения доходнос-
тей от среднего значения оказывают более сильное действие,
чем такие же по величине положительные отклонения. При
7 = 0.8 только в одном испытании темп роста капитала
оказался больше 10%.
Рассмотренные примеры добавляют еще один аргумент
в пользу утверждения, что при одной и той же ожидаемой
доходности портфели с меньшим стандартным отклонением 28
28То, что при вложении в наиболее рискованные ценные бумаги в
большинстве случаев начальный капитал не увеличился, а уменьшил-
ся, не должно вызывать удивления. Рассмотрим более простой пример.
Пусть в четные периоды доходность равна (0.1 4- е), а в нечетные пе-
риоды (0.1 — е). Тогда средняя доходность за 50 периодов равна 0.1.
Капитал, равный 1, за 2 периода превращается в капитал, равный
(1.21 — £2), т. е. при £ < д/0-21 он увеличивается, а при £ > \/0.21 -
уменьшается. Например, при е = 0.9 капитал, равный 1, за 50 перио-
дов превращается в 0.425 « 0.0000000001. И это при среднем приросте
10% за период.
90
Теория эффективных портфелей ценных бумаг
предпочтительнее для вкладчика, чем портфели с большим
стандартным отклонением.
Эти примеры не призваны заменить серьезный анализ
проблем управления капиталом в течение нескольких пери-
одов, когда в конце каждого периода часть средств направ-
ляется на потребление, полезность определяется функцией
общего вида, состав портфеля в течение рассматриваемого
времени не обязан быть постоянным, от периода к перио-
ду меняется распределение доходностей для каждой ценной
бумаги, вырабатываемые рекомендации зависят от размера
капитала, и т.д. Данным вопросам уделено большое внима-
ние со стороны математиков29.
Приведем теперь пример из другой области, показыва-
ющий, что включение в портфель высокорискованной цен-
ной бумаги может не увеличить, а уменьшить риск пор-
тфеля за счет того, что изменение доходности этой ценной
29См., напр.: Elton Е., Gruber М. On the Optimality of Some
Multiperiod Portfolio Selection Criteria //J. of Business. V. 47. N 2 (April
1974). P. 231 - 243; Fama E.F. Multiperiod Consumption - Investment
Decisions // Amer. Econ. Review. V. 60. N 1 (1970). P. 163 - 174;
Hakansson N.H. Multiperiod Mean-Variance Analysis.' Toward a General
Theory of Portfolio Choice // J. of Finance. V.26. N 4 (1971). P. 857
- 884; Hakansson N.H. Optimal Investment and Consumption Strategies
under Risk for a Class of Utility Functions // Econometrica. V.38. N 5
(September 1970). P. 587 - 607; Mossin J. Optimal Multiperiod Portfolio
Policies // J. of Business. V. 41 (April 1968). P. 215 - 229; Samuelson
P.A. The ’Fallacy’ of Maximizing the Geometric Mean in Long Sequences
of Investing or Gambling // Proceedings of the National Academy of
Sciences of the U.S.A. 1971. V.68. N 10. P. 2493 - 2496; Stapleton R.,
Subrahmanyam M. Multi - Period Equilibrium Asset Pricing Model //
Econometrica. V. 46. N 5 (1978). P. 1077 - 1096; Stevens G. On Tobin’s
Multiperiod Portfolio Theorem // Review of Economic Studies. V.39. N
120 (1972) V. 461 - 468.
§7. Вопросы, связанные с уменьшением риска
91
бумаги слабо связано с изменением доходностей большин-
ства других ценных бумаг. Данный пример принадлежит
Г.Марковицу [10].
Пусть вкладчик решил направить свой капитал на по-
купку в равных долях 200 ценных бумаг, т. е.
1
«1 = «2 = . . • = «199 = «200 = ZZ7T-
Вкладчик уже выбрал 199 ценных бумаг. Доходность каж-
дой из них имеет дисперсию V, а ковариация доходностей
для любой пары этих ценных бумаг равна 0.5 V. В качестве
200-й ценной бумаги вкладчиком может быть выбрана ли-
бо ценная бумага А, либо ценная бумага В. Ценная бумага
А аналогична выбранным 199 ценным бумагам. Дисперсия
доходности ценной бумаги А равна V, и ковариация ее доход-
ности с доходностью любой из 199 выбранных ценных бумаг
равна 0.5 V. Ценная бумага В является высокорискованной,
дисперсия ее доходности равна 100 V. В то же время доход-
ность ценной бумаги В благодаря ее спекулятивному харак-
теру практически не связана с общим состоянием рынка и
с доходностями других ценных бумаг. Поэтому ковариации
доходности ценной бумаги В с доходностями выбранных 199
ценных бумаг равны 0.
Дисперсия доходности портфеля, составленного из 200
ценных бумаг, равна
200 200
X? X? xixjC{j =
i—1 j—1
199 199 199
^2^2 XjXjCjj “h 200*4“
i=l j=l i=l
92
Теория эффективных портфелей ценных бумаг
199
+ У ®200®jC,200j + ®200®200С,200 200-
J=1
199
Первое слагаемое в правой части равно • V, его величина
не зависит от того, будет добавлена в портфель ценная бу-
мага А или ценная бумага В. При добавлении ценной бумаги
А сумма трех последних слагаемых правой части равна
2 • 199 • 0.5 • V + V _ 1
40000 ~ 200 ‘ V'
При добавлении ценной бумаги В сумма трех последних сла-
гаемых правой части равна
100 • V _ 1
40000 “ 400 ’
Таким образом, при добавлении высокорискованной цен-
ной бумаги В дисперсия доходности портфеля оказывает-
ся меньше, чем при добавлении традиционной ценной бума-
ги А.
В данном примере сумма трех последних слагаемых не-
велика по сравнению с первым слагаемым, но этот пример
хорошо показывает роль ковариаций. Если бы в первом сла-
гаемом правой части все ковариации, не являющиеся дис-
199
персиями, были равны 0, то оно было бы равно не • V, а
199
------- V, т. е. было бы в 100 раз меньше.
40000 ’
Существует также возможность уменьшения риска пор-
тфеля путем выпуска ценных бумаг. Пусть портфели со-
ставляются из п рисковых ценных бумаг. Мы уже неодно-
кратно сталкивались с тем, что множество возможных пор-
тфелей (и, следовательно, эффективный фронт) зависит не
§7. Вопросы, связанные с уменьшением риска
93
только от доходностей этих ценных бумаг, но и от тех огра-
ничений вида равенств и вида неравенств, которые наложе-
ны на определяющие портфели наборы чисел, ®i, ж2, • • 5 ®п-
Рассмотрим два эффективных фронта. Будем считать, что
ограничения вида равенств в обоих случаях имеют один и
тот же вид
Ах — Ь,
а ограничения вида неравенств различны. Первый эффек-
тивный фронт строится при ограничениях вида неравенств
> 0, «2 > о,. • • ,хп > 0. (7.2)
Второй эффективный фронт строится при ограничениях ви-
да неравенств
®1 > — ОО, «2 > —оо,..., хп > —оо. (7.3)
На каждом из этих двух эффективных фронтов выбе-
рем портфели с минимальными (для данного фронта) дис-
персиями доходностей. Естественно, что данные эффектив-
ные портфели обладают и минимальными для своего эф-
фективного фронта математическими ожиданиями доход-
ностей. Доходность выбранного портфеля с первого эффек-
тивного фронта обозначим Д', а доходность выбранного пор-
тфеля со второго эффективного фронта обозначим R". Оче-
видно, что
D(R") < D(R'),
так как множество возможных портфелей при ограничени-
ях (7.3) шире, чем при ограничениях (7.2). Могут ли встре-
титься такие случаи, когда
Р(Д") < Р( Д') ?
94
Теория эффективных портфелей ценных бумаг
Ответ на этот вопрос положителен. Может оказаться (но
это не всегда так), что на втором эффективном фронте су-
ществует портфель с доходностью R, такой, что
E(R) > E(R'), D(R) < D(E)
(см., например, рис. 3.5).
Риск портфеля можно также уменьшить, включая в пор-
тфель финансовые деривативы. Примерами деривативов яв-
ляются опционы, фьючерсы, свопы. К сожалению, основные
учебники по деривативам, такие, как [5], [6], [15], на русс-
кий язык не переведены. Из имеющейся на русском языке
литературы можно назвать книги [17], [23]30.
Пусть, например, рассматриваемые п рисковых ценных
бумаг - это различные акции. Кроме акций рассмотрим еще
к опционов на какие-то из этих акций. Опционом называ-
ется право купить или право продать некоторую акцию в
течение определенного срока по определенной цене. В дан-
ном случае для нас несущественно, какие именно опционы
рассматриваются.
Пусть параметры портфелей из акций х1у ®2, • • •, ®п удов-
летворяют условиям (3.1). Для каждого такого портфеля
можно рассчитать ожидаемую доходность Е и стандартное
отклонение доходности (риск) а. Как и в §3, множество всех
таких точек на плоскости (<т, Е) обозначим через Q.
Пусть числа ®i, • • •, ®n+i, • • •, xn+k являются пара-
метрами портфелей из акций и опционов и удовлетворяют
условиям
+ а?2 + • • • + Xn+k = 1
30Упомянем также обзор: Шведов А.С. О математических методах,
используемых при работе с опционами // Эконом, журнал Высшей
школы экономики. Т.2. Вып.З (1998). С. 385 - 409.
§7. Вопросы, связанные с уменьшением риска
95
при «1 > Zi, ... хп > 1п,хп+1 >0, ... хп+к > 0. Вместо
условий хп+1 >0, ..., хп+к > 0 можно было наложить,
например, условия xn+i > —оо, • •, хп+к > —оо. Для нас
важно только, чтобы среди допустимых были портфели с
параметрами жп+1 = 0, ..., хп+к = 0, являющиеся портфе-
лями из одних акций.
Для каждого портфеля из акций и опционов можно рас-
считать ожидаемую доходность Е и риск а. Множество всех
таких точек на плоскости (<т, Е) обозначим через Q. Оче-
видно, что Q С Q. При фиксированном Eq обозначим через
<т(Е0) наименьшее значение координаты а для всех точек с
координатами (<т, Ео) из множества Q. Через а(Е0) обозна-
чим наименьшее значение координаты а для всех точек с ко-
ординатами (ст, Eq) из множества Q. В силу условия Q С Q
выполняется соотношение a (Eq) < <т( Ео). Т. е. за счет вклю-
чения в портфель опционов может быть достигнуто умень-
шение риска портфеля при фиксированной ожидаемой доход-
ности. А привести к увеличению риска при фиксированной
ожидаемой доходности включение в портфель опционов не
может. Расчеты показывают, что такое уменьшение риска
действительно происходит.
§ 8. Модель оценки фондовых
активов
После того как основные положения теории эффективных
портфелей были разработаны, следующим важнейшим с
точки зрения практических приложений шагом явилось соз-
дание модели оценки фондовых активов. Эта модель позво-
ляет сделать заключение, является тот или другой фондо-
вый актив недооцененным или переоцененным, и дать со-
ответствующую количественную оценку. Существует боль-
шое число разновидностей этой модели. Некоторые из этих
разновидностей описаны, например, в [2]. Там же дан их
сравнительный анализ й приведены результаты тестов, по-
казывающие, насколько хорошо данные модели соответ-
ствуют реальному рынку ценных бумаг в США. Мы да-
дим описание только самой первой, наиболее простой моде-
ли оценки фондовых активов, которая является тем не менее
одной из самых распространенных. Создание модели оцен-
ки фондовых активов связано с именами Шарпа, Линтнера,
Моссина31. Нельзя сказать, что отношение всех специалис-
тов к этой модели одинаково положительное32. Однако даже
31Sharpe W.F. Capital Asset Prices: A Theory of Market Equilibrium
under Conditions of Risk // Journal of Finance. 1964. V.19. P. 425 - 442
(см. также [13], c. 543 - 558); Lintner J. Security Prices, Risk and Maximal
Gains from Diversification // Journal of Finance. 1965. V.20. P. 587 - 615;
Mossin J. Equilibrium in a Capital Asset Market // Econometrica. 1966.
V. 34. P. 768 - 783.
32См., напр.: Fama E.F., French K.R. The CAPM is Wanted, Dead or
Alive // J. of Finance. 1996. V. 51. N 5. P. 1947 - 1958.
§8. Модель оценки фондовых активов
97
тот факт, что данный подход пытаются оспорить в течение
больше чем тридцати лет, и число публикаций, связанных
с моделью оценки фондовых активов, не уменьшается, гово-
рит о важности этой модели.
Модель оценки фондовых активов дает соотношение, ко-
торому должны удовлетворять ожидаемая доходность и ко-
эффициент Бета33 для любой ценной бумаги или портфеля
ценных бумаг. Выводится это соотношение в рамках рас-
сматриваемого идеального рынка ценных бумаг, но оказы-
вается хорошо передающим реальную ситуацию. Если для
некоторого фондового актива (ценной бумаги или портфеля
ценных бумаг) ожидаемая доходность ниже, чем та, которая
получается из этого соотношения при коэффициенте Бета,
соответствующем данному фондовому активу, это означает,
что данный фондовый актив является переоцененным. Если
для некоторого фондового актива ожидаемая доходность вы-
ше, чем та, которая получается из этого соотношения при
коэффициенте Бета, соответствующем данному фондовому
активу, это означает, что данный фондовый актив является
недооцененным.
Для вывода соотношения, которому должны удовлетво-
рять ожидаемая доходность и коэффициент Бета любого
фондового актива, делаются все те предположения, которые
мы делали раньше. Предполагается, что все ценные бума-
ги абсолютно ликвидны и бесконечно делимы, цена покупки
330пределение коэффициента Бета для ценной бумаги в рамках мо-
дели с одним индексом дано в §5. В этом параграфе мы не предпо-
лагаем, что доходности различных ценных бумаг после исключения
зависимости каждой из них от доходности индекса рынка становят-
ся независимыми между собой. Однако приводимое ниже определение
коэффициента Бета для ценной бумаги достаточно похоже на опреде-
ление, данное в §5.
98
Теория эффективных портфелей ценных бумаг
совпадает с ценой продажи. Расходы на покрытие трансак-
ционных издержек и уплату налогов в расчет не принима-
ются.
Возможно заимствование и одалживание в неограничен-
ных размерах по одной и той же процентной ставке Rf-
Кроме того, делаются следующие дополнительные пред-
положения.
Все вкладчики одинаковым образом определили период
времени (t,t + At), по которому рассчитываются доходнос-
ти. Мнения всех вкладчиков относительно ожидаемых до-
ходностей всех ценных бумаг, дисперсий и ковариаций до-
ходностей совпадают. Все вкладчики принимают решения
исходя только из ожидаемых доходностей имеющихся цен-
ных бумаг, дисперсий доходностей и ковариаций доходнос-
тей.
Никто из вкладчиков в отдельности не может вызвать
изменение цен фондовых активов (и, следовательно, доход-
ностей) своими действиями. Но все вкладчики сообща опре-
деляют цены фондовых активов своими действиями.
Наконец, предположим, что рынок находится в равнове-
сии. Для периода времени (t + At, t + 2At) ожидаемые доход-
ности всех ценных бумаг, дисперсии и ковариации доходнос-
тей такие же, как и для периода времени (t, t + At)34.
Кроме безрисковой ценной бумаги на рынке существует
п рисковых ценных бумаг. Портфель из п рисковых ценных
34Равновесие может пониматься как набор стационарных случай-
ных процессов, используемых в качестве математической модели; см.,
напр.: Сох J.C-, Ingersoll J.E., Ross S.A. An Intertemporal General
Equilibrium Model of Asset Prices // Econometrica. 1985. V.53. N 2. P.
363 - 384.
§8. Модель оценки фондовых активов
99
бумаг определяется набором чисел ®i, ®2,..., хп, таких, что
Х1 + ж2 + ... + хп = 1.
Будем считать, что нет других ограничений вида равенств
и нет никаких ограничений вида неравенств, т. е.
«1 > —оо, «2 > —оо,
ОО
ценных бумаг (кривая линия) и линия рынка капитала (прямая
линия)
На рис. 8.1 гиперболой показан эффективный фронт для
портфелей, состоящих только из рисковых ценных бумаг.
Прямой линией показан эффективный фронт для портфелей,
100
Теория эффективных портфелей ценных бумаг
состоящих из рисковых и безрисковой ценных бумаг. По-
скольку все вкладчики одинаково рассчитали эти два фрон-
та, портфели всех вкладчиков соответствуют точкам, нахо-
дящимся на построенной прямой линии.
В §4 портфель М, соответствующий точке касания пря-
мой и гиперболы, был назван оптимальным. Те вкладчики,
портфелям которых соответствуют точки, находящиеся на
прямой левее точки М, купили безрисковую ценную бума-
гу, т. е. произвели одалживание. Те вкладчики, портфелям
которых соответствуют точки, находящиеся на прямой пра-
вее точки М, выпустили безрисковую ценную бумагу, т. е.
произвели заимствование. Вкладчики, портфелям которых
соответствует точка М, не включили в свои портфели без-
рисковую ценную бумагу.
Но соотношение рисковых ценных бумаг в портфелях у
всех вкладчиков одинаково. Оно определяется набором чи-
сел Ж1, ж2,..., жп, отвечающим портфелю М.
Что можно сказать о числах ж15 ж2,..., ж„, отвечающих
портфелю М ? Пусть общее количество рисковых ценных
бумаг г-го вида на рынке составляет Qi, а цена одной ценной
бумаги г-го вида равна Pi. Тогда в рыночном портфеле, т.е.
в портфеле, состоящем из всех ценных бумаг, имеющихся на
рынке, доля ценных бумаг г-го вида составляет
м =
1 Pi Qi-
Но своему составу оптимальный портфель М должен совпа-
дать с рыночным портфелем, так как все рисковые ценные
бумаги присутствуют у вкладчиков только в виде портфеля
М, и все ценные бумаги, которые есть на рынке, распреде-
лены между вкладчиками.
§8. Модель оценки фондовых активов
101
Сделанное заключение, что оптимальный портфель М по
своему составу совпадает с рыночным портфелем, является
правильным, но оно требует некоторых пояснений. Состав
оптимального портфеля М рассчитывается по определен-
ным формулам. Может ли оказаться, что при некотором i
рассчитанное значение Xi окажется, например, меньше, чем
х^1 Ч Это будет означать, что спрос на г-ю ценную бумагу
недостаточен, т. е. ее цена слишком велика. В такой ситу-
ации цена г-й ценной бумаги будет уменьшаться. Со време-
нем это приведет к увеличению спроса на данную ценную
бумагу, что вызовет увеличение ее цены и увеличение до-
ходности, пока данная ценная бумага не станет достаточно
привлекательной для вкладчиков для включения ее в пор-
тфель М в нужном количестве. Аналогично, если окажет-
ся, что при некотором г рассчитанное значение Xi больше,
чем ж^, это будет означать, что спрос на г-ю ценную бума-
гу избыточен. За этим последует увеличение ее цены. Это
приведет к уменьшению спроса на данную ценную бумагу,
что вызовет уменьшение ее цены и уменьшение доходности.
Поэтому в состоянии равновесия оптимальный портфель М
определяется набором чисел х^, ж^,..., х™.
Данное пояснение является упрощенным даже с точки
зрения сделанных нами предположений. Мы не уточнили,
какому моменту времени соответствуют цены Pi, Pz,..., Рп-
Мы не стали учитывать того, что доходности определяются
не только ценами, но и другими доходами, связанными с вла-
дением данными ценными бумагами. Тем не менее описан-
ный механизм в определенной степени передает сущность
этих процессов.
Сделанное заключение, что все вкладчики составляют
портфель из рисковых ценных бумаг одним и тем же спосо-
102
Теория эффективных портфелей ценных бумаг
бом, является внутренним результатом нашей теории. При
помощи этого заключения мы выведем соотношение между
ожидаемой доходностью и коэффициентом Бета для любого
фондового актива.
Прямая на рис. 8.1, касательная к эффективному фронту,
называется линией рынка капитала. Обозначим через Ем
ожидаемую доходность рыночного портфеля М, а через ам
- стандартное отклонение доходности рыночного портфеля.
Тогда уравнение линии рынка капитала имеет вид
Е = Rf + . а.
Ем — Ер
Коэффициент ------называется рыночной ценой риска.
Вывод соотношения между ожидаемой доходнос-
тью фондового актива и систематическим риском.
Воспользуемся теми выкладками, которые были проведены
в §5. Если набор чисел xi, х2, ..., хп определяет оптималь-
ный портфель М, то при этих xi, ж2,..., хп достигает мак-
симума функция
6>(ж1,я;2,...,а;п) =
Е — Rp
а
где
Е = £ х{ Е^ а2 == 52 У2 «J Cij.
i—1 г—1 j—1
Как и раньше, Ei — E(Ri), Cij = Cov(Ri, Rj) и, в частности,
Сц = D(Ri). Ri - это случайная величина, обозначающая
доходность г-й ценной бумаги.
§8. Модель оценки фондовых активов
103
В §5 было показано, что числа Xi, х2,..., хп, отвечающие
оптимальному портфелю М, должны удовлетворять системе
уравнений
п
а • ' XiC^ — Ек RF, к — 1,2,..., zi,
i=l
где a - некоторое число, не зависящее от к. В §5 было полу-
чено выражение для а. Ниже мы найдем выражение для а
другим способом.
Заметим, что
Y^XiCik = ^XiCov(Ri^Rk) = Cov(^XiRi,Rk) = Cov(RM,Rk),
t=l i=l i=l
где случайная величина Rm - это доходность оптимального
портфеля М. Условие
а • Cov(Rm, Rk) — E(Rk) — Rf
выполняется при всех к = 1,2,..., п, т. е. для любой ценной
бумаги. Следовательно, это условие выполняется для любой
линейной комбинации случайных величин Ri, R2,..., Rn-
Поэтому, если R - доходность произвольного портфеля, со-
ставленного из рассматриваемых ценных бумаг, то
а • Cov(RM, R) = E(R) - Rf.
В частности, при R = Rm получаем
а ' &м ~ Ем ~ Rf-
откуда
Ем - Rf
ам
а =
104
Теория эффективных портфелей ценных бумаг
Подставляя найденное значение а, получаем соотношение
E(R) = Rf + Em~Rf . Cov(Rm, R). (8.1)
ам
Формула (8.1) и есть то соотношение, которое мы хотели
получить. Введем обозначение
= Cov(RM, Я)
Р 2
Величина /З2 называется систематическим риском,
а величина (<т2 — (З2 а^) - несистематическим риском. Эти
определения находятся в соответствии с определениями §5,
где мы рассматривали модель с одним индексом. Соотноше-
ние (8.1) может быть записано также в виде
E(R) = RF + (3- (Ем -Rf). (8.2)
Как связаны систематический риск (3 • ам и риск а —
Корреляция случайных величин Rm и R определяется по
формуле
Сот(Ям,Я) = -°Г(Дм,Д).
<ТМ • а
Из определения коэффициента Бета следует, что
(3 • ам = Cor(RM, R) • а.
Напомним, что корреляция любых двух случайных величин
по абсолютной величине не превосходит 1. Поэтому
-о- < (3 ам < <?
§8. Модель оценки фондовых активов
105
Отсюда следует, что несистематический риск не может
быть отрицательным числом.
Замечание. Многие результаты этого параграфа похо-
жи на результаты §5, однако это сходство является скорее
внешним. В §5 мы считали, что доходности Ri определяют-
ся по формуле (5.1), т. е. каждая из случайных величин Ri
как-то зависит от Rm, при этом никакой зависимости между
доходностями различных ценных бумаг больше нет. В этом
параграфе мы не накладываем подобного ограничения. С
другой стороны, определенная в этом параграфе доходность
рыночного портфеля Rm, конечно, может использоваться в
качестве доходности индекса рынка. Но в §5 требования к
случайной величине Rm были меньшие.
1
Рис. 8.2. Линия рынка ценных бумаг
106
Теория эффективных портфелей денных бумаг
На рис. 8.2 на плоскости (/3, Е) показана прямая, опре-
деляемая уравнением (8.2). Эта прямая называется линией
рынка ценных бумаг. Мы доказали в рамках построенной на-
ми теории, что для любого фондового актива коэффициент
/3 и ожидаемая доходность Е связаны формулой (8.2), т. е.
соответствующая точка на плоскости (/3, Е) должна лежать
на линии рынка ценных бумаг.
Практически это означает следующее. Пусть для неко-
торого фондового актива определены Е (ожидаемая доход-
ность) и /3 (коэффициент Бета). Если соответствующая точ-
ка лежит выше линии рынка ценных бумаг, то данный фон-
довый актив является недооцененным, поскольку его ожида-
емая доходность слишком высока по отношению к система-
тическому риску. Если соответствующая точка лежит ниже
линии рынка ценных бумаг, то соответствующий фондовый
актив является переоцененным.
Для определения ожидаемой доходности могут исполь-
зоваться различные методы оценивания и прогнозирования.
Основной математический инструмент для определения ко-
эффициента Бета - регрессионный анализ. В странах с раз-
витым фондовым рынком имеются специальные службы, ко-
торые регулярно рассчитывают и публикуют коэффициен-
ты Бета для различных ценных бумаг. При этом коэффици-
енты Бета для одной и той же ценной бумаги, полученные
разными службами, могут несколько различаться. Это свя-
зано с тем, что разные службы используют различные ин-
дексы, различные варианты регрессионного метода. Различ-
ными могут быть и исходные данные для нахождения значе-
ний доходности. В одних случаях это еженедельные данные,
в других - ежемесячные данные35.
35См. [37], с. 521 - 522'
§8. Модель оценки фондовых активов
107
Пусть (3 - коэффициент Бета некоторого портфеля, т.е.
/3 = Pi, где /317/?2, • • ,Рп ~ коэффициенты Бета
имеющихся рисковых ценных бумаг, а числа ®i, ®2, • • ,хп
определяют состав портфеля. Если /3 > 1, то данный пор-
тфель называется агрессивным. Если (3 < 1, то данный
портфель называется оборонительным. По формуле (8.2)
Е = Rf + (3 • (Ем — Rf), где Е - ожидаемая доходность пор-
тфеля. При благоприятных изменениях рынка, т. е. при рос-
те Ем, ожидаемая доходность агрессивного портфеля растет
быстрее, чем Ем- При неблагоприятных изменениях рынка,
т. е. при уменьшении Ем, ожидаемая доходность оборони-
тельного портфеля уменьшается медленнее, чем Ем- Эта
ситуация показана на рис. 8.3.
Рис. 8.3. Изменение ожидаемой доходности портфеля Е
в зависимости от ожидаемой доходности рыночного порт-
феля Ем
§ 9. Исследование структуры
эффективного фронта
В §3 было показано, что при составлении портфелей из п
рисковых ценных бумаг с соблюдением ограничений (3.2)
эффективными являются те и только те портфели, парамет-
ры которых ®i, ®25 • •, ®п доставляют минимум квадратич-
ной форме (3.3) при каком-нибудь А > 0. В этом параграфе
мы наложим некоторые условия, в частности, мы потребу-
ем, чтобы при каждом А > 0 существовал только один век-
тор Ж1(А), ®г(А),..., ®п(А), удовлетворяющий условиям (3.2)
и доставляющий минимум квадратичной форме (З.З)36. При
соблюдении этих условий мы докажем, что каждая из функ-
ций а^(А), где i = 1,..., п, как функция аргумента А, являет-
ся непрерывной и кусочно-линейной. Отсюда, в частности,
следует, что на плоскости (<т, Е) эффективный фронт состо-
ит из частей гипербол и/или частей прямых. Эффективный
фронт на плоскости (V, Е) при этом состоит из частей па-
рабол.
Перепишем задачу (3.2), (3.3) из §3 немного в другой
форме. При любом А > 0 надо найти ДГ-мерный вектор
X = (®1, ®2, • • ч ®п)5 при котором функция
Я N N
+ (9.1)
i=l »=1 j=l
36Подобные условия являются общепринятыми при рассмотрении
данных вопросов (см., например, [14]). С практической точки зрения
эти условия вполне приемлемы.
§9. Структура эффективного фронта
109
достигает своего минимального значения. Координаты век-
тора х должны удовлетворять условиям
я
= j = 1,2, ...,тп,
(9.2)
> 0, ®2 > 0,... xjf > 0.
Т. е. функция (9.1) минимизируется на множестве векто-
ров, удовлетворяющих условиям (9.2).
Коэффициенты линейной формы из (9.1) Ei, Е?,..., Е^
могут быть произвольными, а квадратичная форма явля-
ется неотрицательно определенной. Это означает, что для
любого ЛГ-мерного вектора х — (®i, ж2,..., ®#)
я я
^ij > 0.
»=1 j=l
Задачи такого типа называются задачами квадратично-
го программирования.
Чтобы связать эту задачу с задачей (3.3), (3.2) из §3,
можно считать, что при п < N выполняются условия Ei = 0,
если i > п, и Cij = 0, если i > п или j > п.
На первый взгляд условие (9.2) кажется менее общим,
чем аналогичное условие (3.2) из §3, так как здесь нижними
границами для всех переменных являются нули, а в §3 ниж-
ними границами, по крайней мере, для части переменных,
могли быть произвольные числа. Но сделанное упрощение
не является существенным. Мы могли и в условии (9.2) в
качестве нижних границ взять произвольные числа, а затем
сделать преобразования типа сдвигов, положив, например,
х^ — Х{ li. i — 1,2,..., 7i,* х^ — ж,’, i — п -j-1,..., 2V.
110
Теория эффективных портфелей ценных бумаг
При этом изменились бы коэффициенты линейной формы из
(9.1) и правые части в уравнениях (9.2), но это не имеет
принципиального значения. Мы не стали делать этих пре-
образований, чтобы не вводить новых обозначений.
Пусть и — m-мерный вектор. Определим функцию
.№ 2V N m / ДО \
$(», и) = -а 52 ^»+5212хз ^+52 Uk (h - 52 а*х*) •
t=l i—l j=l к=1 \ i—l /
Основным инструментом исследования в этом параграфе
является следующая теорема, принадлежащая Куну и Так-
керу.
Теорема. TV-мерный вектор ж, удовлетворяющий усло-
виям (9.2), тогда и только тогда является решением зада-
чи квадратичного программирования (9.1) - (9.2), когда су-
ществует тп-мерный вектор й такой, что
дФ
——(ж, й)>0, г = 1,2,..., Я; (9.3)
OXi
дФ
(ж,й) = 0, «= 1,2,...,7V. (9.4)
OXi
Доказательство теоремы Куна - Таккера можно найти,
например, в [27], [Зб]37.
При А > 0 решение задачи квадратичного программиро-
вания (9.1), (9.2) обозначим через ж(А). Сделаем следующее
предположение.
Условие 1. При любом А > 0 решение ж (А) задачи квад-
ратичного программирования (9.1), (9.2) существует и един-
ственно.
37На самом деле теоремой Куна - Таккера называется существенно
более общее утверждение. Но мы сформулировали эту теорему в той
общности, в какой она нам будет нужна.
§9. Структура эффективного фронта
111
На основании теоремы Куна - Таккера при любом
А > О существует вектор и(А) такой, что условия (9.3) и
(9.4) выполняются при х — ж(А), й = и(Л). Сделаем еще
одно предположение.
Условие 2. При любом А > О вектор и(Л) единственен.
Зафиксируем Л > 0; ж(Л) = (жг(А),..., ж^(А)) - реше-
ние задачи квадратичного программирования (9.1), (9.2).
Индексы г, для которых жДА) > 0, назовем внутренними.
Индексы г, для которых ж^(А) = 0, назовем внешними33.
а) внутренний индекс i
б) внешний индекс i
Рис. 9.1. Графики функции Ф(г,и), как функции от Xi,
вблизи точки (®(А),и(А))
На рис. 9.1 приведены графики функций Ф(ж,и), когда
все переменные, кроме х^, фиксированны и равны соответ-
ствующим координатам векторов ж(А) и и(А). Ветви пара-
38Разумеется, тот индекс i, который при одном А является внутрен-
ним, при другом А может быть внешним.
112
Теория эффективных портфелей ценных бумаг
бол направлены вверх в силу неотрицательной определен-
ности квадратичной формы SjLi xi xj Этот рису-
нок помогает понять смысл условий (9.3) и (9.4).
Определение. Рассмотрим некоторую точку Ао > 0.
Пусть выполняются следующие три условия.
1. Существует число £ > 0 такое, что при всех А, при-
надлежащих интервалу (Ао — £, Ао + £), и при любом внут-
реннем по отношению к Ао индексе i
Tj(A) > 0.
2. Существует число £ > 0 такое, что при всех А, принад-
лежащих интервалу (Ао — £, Ао + £), и при любом внешнем
по отношению к Ао индексе i
Xj(A) = 0.
3. Если индекс i внешний по отношению к Ао, то
ЭФ
—(т(Ао),и(Ао))>0.
их.
Тогда точку Ао будем называть неугловой.
Те точки А, которые не являются неугловыми, будем на-
зывать угловыми. В число угловых точек включается также
точка А = 0. Для примера, изображенного на рис. 3.9, угло-
выми заведомо являются точки Aj, Аг, A3, А4.
В §3 мы утверждали, что функции ж;(А), соответству-
ющие эффективным портфелям, являются непрерывными и
кусочно-линейными. Ниже мы докажем теорему, из которой
это утверждение легко следует, если сделать еще одно пред-
положение.
§9. Структура эффективного фронта
113
Условие 3. Множество угловых точек конечно.
Теорема. Если точка Ло неугловая, то существуют чис-
ла
, С2, . . . , С/у, d\, С?2 •>•••> dm
til существует число е > 0 такие, что при любом Л, при-
надлежащем интервалу (Ло — е, Ло + е), координаты векто-
ров ж(Л) и и(Л) имеют вид
жДЛ) - ®i(A0) + ^(Л - Ао), г = 1,2,..., JV;
ufc(A) = ufc(Ao) + dk(X - Ao), к = 1,2,... ,тп.
Доказательство. Как мы и говорили, доказательство
построено на теореме Куна - Таккера. Причем мы сначала
воспользуемся тем, что условия (9.3) и (9.4) необходимы для
того, чтобы вектор ж, удовлетворяющий условиям (9.2), был
решением задачи (9.1), (9.2), а потом тем, что эти условия
достаточны.
На основании уравнений (9.4), (9.2) составим систему из
(N + т) линейных алгебраических уравнений относительно
(N + т) неизвестных Ж1, ж2,..., • • • ,ит- Правую
часть во всех уравнениях будем записывать в виде много-
члена первой степени от Л.
Воспользуемся тем, что
"X (ж, 1а) А -|- 2 Xj Cij t — 1,2,. • •, -У.
5=1 fc=l
(9.5)
Для внешних по отношению к Ао индексов i уравнение
(9.4) запишем в виде
Xi = 0 + 0 • А.
(9.6)
114
Теория эффективных портфелей пенных бумаг
Для внутренних по отношению к Ао индексов i уравнение
(9.4) запишем в виде
N т
£ 2 СИ xi ~ Е a^k = Ъ + (9.7)
j=i k=i
Оставшиеся т уравнений (9.2) имеют вид
N
^2aikXi — bk + 0 • А, к = 1,2,(9.8)
i=i
В силу условий 1 и 2 и теоремы Куна - Таккера компонен-
ты векторов ®(Ао) и м(А0) являются единственным решени-
ем системы линейных алгебраических уравнений (9.6) - (9.8)
при А — Ао. Поэтому определитель матрицы данной систе-
мы (а сама матрица не зависит от А, от А зависит только
правая часть) отличен от нуля. Применяя метод последо-
вательного исключения неизвестных (см., например, [26]),
получаем, что при любом А решение системы (9.6) - (9.8)
имеет вид
Xi = oti 4- Д- А, г = 1,2, ...,ЛГ;
(9-9)
Mfc=7fc-HfcA, к = 1,2,... ,т,
где a,, /3i, 7fc, 6к - некоторые числа.
Осталось показать, что при А, близких к Ао, величины
(9.9) удовлетворяют условиям (9.3) и (9.4) теоремы Куна -
Таккера, и поэтому при этих А величины ж,, определяемые
в (9.9), являются решением задачи (9.1), (9.2).
Согласно определению неугловой точки для внешних по
отношению к Ао индексов i
дФ
£-(ж(Ао),н(Ао))>0.
§9. Структура эффективного фронта
115
Но из (9.5) и (9.9) следует, что
дФ
^(Ж(А),и(А)) = £+^А,
где - некоторые числа. Поэтому для внешних по отно-
шению к Ао индексов i в некоторой окрестности точки Ао
дФ
—(я(А),и(А)) > 0.
OXi
Для внутренних по отношению к Ао индексов i
дФ
—(Ж(А),и(А)) = 0
в силу уравнений (9.7). Поэтому условия (9.3) выполняются.
Условия (9.4) выполняются в силу (9.6) и (9.7).
Теорема доказана.
§ 10. Вычислительные процедуры
для нахождения эффективных
портфелей
В этом параграфе описан один из существующих способов
построения эффективных портфелей. Описание разделено
на три части. В первой части изложены основные идеи сим-
плексного метода для решения задач линейного программи-
рования. Здесь вводятся некоторые необходимые для даль-
нейшего понятия, эта часть приведена для того, чтобы сде-
лать изложение замкнутым. Во второй части описан сим-
плексный метод для решения задач квадратичного програм-
мирования. При этом задача квадратичного программиро-
вания сводится к задаче, похожей на задачу линейного про-
граммирования, но с нелинейным ограничением на перемен-
ные. В третьей части излагается метод критических линий,
предназначенный для построения эффективных портфелей.
При применении метода критических линий приходится не-
сколько раз решать задачу квадратичного программирова-
ния.
Нужно ли разбираться с тем, как устроены алгоритмы,
если существует большое число компьютерных программ,
удобных для использования, в которых эти алгоритмы реа-
лизованы? Это все равно, что спрашивать, нужно ли знать
географию, если существуют извозчики. Мы стоим на той
точке зрения, что хотя извозчики, конечно, нужны, но гео-
графию все-таки тоже знать надо. Использование чужих
Вычислительные процедуры
117
компьютерных программ ставит исследователя под тот по-
толок, который разработчик программы для него опреде-
лил, если у исследователя нет хорошо прокомментированно-
го полного исходного текста программы. Но разбираться с
таким текстом часто труднее, чем написать свою програм-
му. Незнание алгоритмов, предназначенных для решения ба-
зовой задачи, делает невозможным рассмотрение практи-
ческих ситуаций, в которых необходимы не сами эти ал-
горитмы, а некоторые их модификации. Для рассматривае-
мого круга вопросов такой практической ситуацией может
быть наличие существенной асимметрии в распределении
доходностей39.
1. Симплексный метод для решения задач линей-
ного программирования. Задача линейного програм-
мирования формулируется следующим образом40. Пусть
с1; C2,.. •, cq - некоторые действительные числа. Среди всех
д-мерных векторов х — (®i, ®2, • • •, ®9), удовлетворяющих
приводимым ниже условиям (10.2) и (10.3), требуется найти
тот (или один из тех), для которого значения функции
L(x) = хз (Ю-1)
j=i
является максимальным. Условия, которым должны удовле-
творять вектора ж, имеют следующий вид. Во-первых, су-
ществуют р-мерные вектора Do, Di, D2, .., Dq такие, что
39См., напр.: Chunhachinda Р., Dandapani К., Hamid S., Prakash
A.J. Portfolio selection and skewness: Evidence from international stock
markets // J. of Banking and Finance. V. 21. N 2 (1997). P. 143 - 167.
40Нашей целью является решить при всех А > 0 семейство задач
(9.1), (9.2) из §9. Связь задач линейного программирования с этими
задачами станет понятна во второй части настоящего параграфа.
118
Теория эффективных портфелей ценных бумаг
координаты вектора х удовлетворяют соотношению
ч
xi Dj — Dq. (10.2)
j=i
Условия (10.2) - это система р линейных алгебраических
уравнений относительно q неизвестных. Считается, что
р < q. Во-вторых, координаты векторов ж неотрицательны:
жх > 0, ж2 > 0, ..., xq > 0. (10.3)
Множество векторов ж, удовлетворяющих условиям (10.2)
и (10.3), называется многогранным множеством задачи
линейного программирования. Обозначим это множество
через Г.
На рис. 10.1 показано, как могут выглядеть множества
Г для случая q = 3. Рисунок 10.1, а соответствует значению
р = 1; множеством Г является треугольник АВС. Рисунки
10.1, б, в соответствуют значению р — 2; множествами Г
являются отрезки АВ.
Множество Г может быть как ограниченным, так и не-
ограниченным. (Все множества Г, показанные на рис. 10.1,
являются ограниченными.) Если множество Г ограничен-
ное, то задача линейного программирования всегда имеет
решение. Если множество Г неограниченное, то задача ли-
нейного программирования может или иметь решение, или
не иметь решения.
Нетрудно понять, что если задача линейного програм-
мирования имеет решение, то среди тех точек ж, удовле-
творяющих условиям (10.2) и (10.3), для которых значение
функции £(ж) является максимальным, присутствует хотя
бы одна вершина множества Г. Поэтому задача линейного
§10. Вычислительные процедуры
119
программирования может быть решена путем перебора вер-
шин множества Г.
в
Рис. 10.1. Примеры многогранных множеств задач линей-
ного программирования
120
Теория эффективных портфелей ценных бумаг
Глядя на рис. 10.1, отвечающий случаю q = 3, можно по-
думать, что задача перебора является совсем простой. Од-
нако это не так, и при больших q решение задачи линейно-
го программирования требует применения достаточно слож-
ных математических методов.
Описание этих методов дано, например, в [21], [27], [39];
там же можно найти доказательства приводимых ниже
утверждений. Мы не будем рассматривать все сложные слу-
чаи и все варианты, а дадим описание только основной схе-
мы симплексного метода для решения задач линейного про-
граммирования. Хотя это описание содержится во многих
книгах, мы все же приведем его, поскольку без этого будет
невозможно изложить симплексный метод для решения за-
дач квадратичного программирования.
Будем предполагать, что выполняется следующее усло-
вие.
Условие невырожденности. Все вершины множест-
ва Г имеют р положительных координат и (g — р) нулевых
координат.
Множества Г, изображенные на рис. 10.1, а, б, удовле-
творяют условию невырожденности. Множество Г, изобра-
женное на рис. 10.1, в, условию невырожденности не удов-
летворяет, так как у точки В две нулевые координаты, а
q — р = 3 — 2 = 1.
Симплексный метод решения задачи линейного програм-
мирования состоит из двух этапов.
Этап 1. Нахождение одной из вершин многогранного
множества Г.
Этап 2. Последовательное “улучшение” вершины мно-
жества Г, т. е. переход от найденной вершины к некоторой
другой вершине, для которой значение функции L больше.
§10. Вычислительные процедуры
121
Невозможность такого перехода означает, что либо найдено
решение задачи линейного программирования, либо уста-
новлено, что задача линейного программирования неразре-
шима, т. е. функция Z(«) на множестве Г принимает сколь
угодно большие значения (это возможно лишь в случае, если
множество Г является неограниченным).
Мы начнем с описания этапа 2, считая, что некоторая
вершина х множества Г известна.
Если вершина х = (ж1; х2,..., ж9) множества Г извест-
на, то в силу условия невырожденности из набора чисел
(1,2,..., q) можно выбрать р чисел ^i, s2,..., sp, таких, что
Xj > 0, если j равно одному из чисел з2,..., зр, и Xj = 0,
если j не равно ни одному из этих чисел.
Лемма, р-мерные вектора DS1, Di2,..., DSp линейно не-
зависимы.
Доказательство. Предположим противное. Тогда су-
ществуют числа а2, .., ар не все равные нулю, такие, что
р
DSi = 0.
»=i
Построим q-мерный вектор у = (У1,У2, • • • ,Уд) следующим
способом
{at-, если j = Si при некотором i
0, если j не совпадает ни с одним из чисел
Тогда
<j
£ Уз Dj = 0.
i=i
Выберем £ > 0 так, что при любом i = 1,2,... ,р
хч ~£yei >0 и хв. +Eyei > 0.
122
Теория эффективных портфелей ценных бумаг
Это возможно сделать в силу условия х,. > 0 при i —
= 1,2, ...,р. Тогда точки х' = (® — еу) и х" — (х + су)
принадлежат множеству Г, поскольку координаты каждой
из них удовлетворяют условиям (10.2) и (10.3).
С другой стороны,
х =0.5 х' + 0.5 х".
Но множество Г является выпуклым, и его вершина не мо-
жет быть серединой отрезка, соединяющего две другие точ-
ки этого множества.
Лемма доказана.
Линейно независимые вектора D„,, DS2,..., Dfy, постро-
енные по вершине х множества Г, называются базисом этой
вершины. Разложим каждый из векторов _D0, Pi, D2,..., Dq
по векторам базиса:
р
(Ю.4)
Рассматривая это разложение при j = 0, легко сделать
следующий вывод. Зная вектор Ро и базис вершины, можно
однозначно восстановить координаты этой вершины. Дей-
ствительно, сравнивая формулы (10.4) и (10.2), видим, что
7»о — x»ii i = 1>2,... , р. Отметим, что в силу условия невы-
рожденности 7^0 > 0 при i = 1,2,... ,р.
При j = 1,2,... ,q введем обозначения
р
~ ~ сз "Ь •
г=1
Здесь ci, с2,..., сд - коэффициенты из (10.1).
§10. Вычислительные процедуры
123
Зная коэффициенты 7^ и величины Aj, можно опреде-
лить, какая из следующих трех ситуаций имеет место.
1. Рассматриваемая вершина х является решением зада-
чи линейного программирования.
2. Задача линейного программирования не имеет реше-
ния.
3. Перебор вершин следует продолжить.
Ответ имеет следующий вид.
1. Если > 0 при любом j = 1,2,..., q, то вершина х
является решением задачи линейного программирования.
2. Если существует j такое, что Aj < 0, и все соот-
ветствующие данному j коэффициенты 7,5 неположительны,
т. е.
7ij < 0 при г = 1,2,...,р,
то задача линейного программирования неразрешима, т. е.
при ограничениях (10.2), (10.3) линейная функция £(ж),
определяемая в (10.1), может принимать сколь угодно боль-
шие значения.
3. Если Aj < 0 для некоторых индексов j, и для каждого
такого у, по крайней мере, одно из чисел 7^ положительно,
то существует вершина у множества Г, для которой £(у) >
> L(x).
Эта вершина у может быть найдена следующим образом.
Зафиксируем некоторое к, для которого Аа, < 0. Например,
можно выбрать к так, чтобы Да, было наименьшим из всех
Aj. Среди всех индексов i (1 < i < р), для которых 7^ > 0,
выберем тот индекс (обозначим его через г), для которого
7го
Угк
= min
i
'liO
Используя условие невырожденности, можно показать, что
124
Теория эффективных портфелей ценных бумаг
после того как к выбрано, г выбирается однозначно. Постро-
им набор векторов
-^«1 > • • • 5 ^г-1 5 ^k-, Dgr+1 Dgp-
Можно показать, что этот набор векторов является базисом
некоторой вершины у, для которой справедливо соотноше-
ние L(y) > L(x).
Книги, в которых можно найти доказательства приве-
денных утверждений, были указаны выше.
Мы описали этап 2 симплексного метода, но должны опи-
сать еще этап 1, т. е. дать метод определения вершины мно-
жества Г, с которой начинается перебор. Это можно сде-
лать, решив следующую вспомогательную задачу линейно-
го программирования.
Требуется найти (q + р)-мерный вектор х, для которого
значение функции
р
является максимальным. Координаты вектора х должны
быть неотрицательными и удовлетворять системе линейных
алгебраических уравнений
&ij xj “Ь xq+i dio, i 1, 2, . . . ,р.
Через dij обозначены координаты векторов Dj из условия
(10.2) при j = 0,1,2,... , q. Мы можем считать, что df0 > 0
при i = 1,2,... ,р. (Этого всегда можно добиться, умножив
некоторые из уравнений (10.2) на —1.) В качестве вершины,
§10. Вычислительные процедуры
125
с которой начинается перебор при решении вспомогатель-
ной задачи линейного программирования, берется точка с
координатами
Xq — 0, Xq-j-i — ПрИ Z — 1, 2, . . ,р.
Решение вспомогательной задачи всегда может быть
найдено, поскольку функция М(х) ограничена сверху ну-
лем. Если найден (д + р)-мерный вектор ж, являющийся ре-
шением вспомогательной задачи, для которого М(х) = 0, то
последние р координат этого вектора нулевые, а первые q ко-
ординат удовлетворяют системе линейных алгебраических
уравнений (10.2), и соответствующий g-мерный вектор яв-
ляется вершиной множества Г исходной задачи линейного
программирования. Если для найденного решения вспомо-
гательной задачи М(ж) < 0, то это означает, что система
условий (10.2), (10.3) исходной задачи несовместна.
При изложении симплексного метода нами несколько раз
использовалось условие невырожденности. В практических
ситуациях условие невырожденности может нарушаться.
Тем не менее задачи линейного программирования можно
решать симплексным методом и в этих случаях, иногда не
обращая внимания на вырожденность, а если это не прохо-
дит, то используя те или другие модификации алгоритма41.
Мы искали вектор ж, при котором функция £(ж), опреде-
ленная в (10.1), принимает максимальное значение. Но мо-
жет быть и так, что нам нужно найти вектор ж, при кото-
ром функция £(ж) принимает минимальное значение. Что-
бы найти такой вектор ж, можно воспользоваться уже по-
лученными расчетными формулами. Вектор ж, при котором
41О решении задач линейного программирования при нарушении
условия невырожденности см., например, [21], [27], [39].
126
Теория эффективных портфелей ценных бумаг
достигает максимального значения функция — lbj=i cj xj-> ~
это тот вектор, при котором достигает минимального зна-
чения функция L(x).
2. Симплексный метод для решения задач квадра-
тичного программирования. В §3 и 9 мы сталкивались с
задачей квадратичного программирования. Сформулируем
ее еще раз. Пусть даны TV-мерный вектор Р и матрица С
размера N X N. Матрица С является симметричной, т. е.
Су = Cji при любых i и j. Кроме того, матрица С явля-
ется неотрицательно определенной. Это означает, что для
любого TV-мерного вектора х — (®i, х2,... ждг) справедливо
неравенство
N
£ 22Xi хз са °-
i=i j—i
Среди всех TV-мерных векторов, удовлетворяющих при-
водимым ниже условиям (10.6) и (10.7), требуется найти тот
(или один из тех), для которого значение функции
X N N
f(x) = 22R + 22 22хэ (ю.5)
г=1j—1
является минимальным. Условия, которым должны удовле-
творять вектора х, имеют следующий вид. Во-первых, су-
ществуют m-мерные вектора В, Ai, А2, . An такие, что
координаты вектора х удовлетворяют соотношению
N
= (10.6)
7=1
Условие (10.6) - это система т линейных алгебраических
уравнений относительно N неизвестных. Считается, что
§10. Вычислительные процедуры
127
т < N. Условие (10.6) будем записывать также в виде
Ах — В,
где А - матрица размера N х т. Во-вторых, координаты
векторов х неотрицательны:
Ж1 > 0, х2 > 0,..., xN > 0. (10.7)
Для решения задач квадратичного программирования
разработано много различных методов (см., например, [27],
[32], [36]). Вольф42 предложил метод, в котором задача квад-
ратичного программирования сводится к задаче, похожей на
задачу линейного программирования, но содержащей нели-
нейное ограничение. (Это ограничение приведено ниже как
условие (10.9).) Для решения данной задачи используется
симплексный метод. Ниже приведено описание этого подхо-
да.
Через А' обозначим матрицу, полученную транспониро-
ванием матрицы А. Скалярное произведение d-мерных век-
торов х = (жь х2,..., xd) и у = (yi,y2, • • ,yd) будем обозна-
чать (ж,у) :
d
(Х,У) = ^хз Уг
Теорема. Пусть координаты У-мерного вектора ж удов-
летворяют условиям (10.6) и (10.7) и пусть существуют
m-мерный вектор и — («1, и2,..., мт] и TV-мерный вектор
V = (^1,^2,. . . ,V/y), для которого
> 0, v2 > 0,... ,vN > 0, (10.8)
42Wolfe Р. The Simplex Method for Quadratic Programming / /
Econometrica. V. 27. 1959. P. 382 - 398.
128
Теория эффективных портфелей ценных бумаг
такие, что выполняются соотношения
(г?,ж) = 0 (10.9)
и
2 С х - v + А'и + Р = 0. (10.10)
Тогда х является решением задачи квадратичного програм-
мирования (10.5) - (10.7), т. е. значение функции F в данной
точке х не больше, чем в любой другой точке, удовлетворя-
ющей условиям (10.6) и (10.7).
Доказательство. Пусть у - некоторый jV-мерный век-
тор, удовлетворяющей условиям (10.6) и (10.7). Мы пока-
жем, что F(y) > F(x). Из неотрицательной определенности
матрицы С следует, что
(t/- ж, C(t/- ж)) > 0.
Отсюда следует, что
О/, Су) + (ж, Сх) > (ж, Су) + (у, Сх) = 2 (ж, Су).
Получаем
(у, Су) - (ж,Сж) > 2 (х.С(у — ж)) = 2 (Сх,у — ж).
Поэтому
F(y) - F(x) = (Р, у - ж) + (у, Су) - (ж, Сх) >
> (Р + 2 Сх,у - ж).
В силу (10.10)
Р + 2 Сх — v — А'и
§10. Вычислительные процедуры 129
и
F(y) ~ F(x) > (и - А'и, у -х)~
= (v, У) ~ (и,ж) - (А'и, У) + МЧ ®) =
= {у, у) - (и, ж) - (и, Ау) + (и, Аж) = (и, у) > 0.
Последнее неравенство следует из того, что координаты век-
торов v и у неотрицательны. При предпоследнем переходе
использовалось (10.9) и то, что
Аж = Ау = В.
Теорема доказана.
В силу доказанной теоремы для решения задачи квадра-
тичного программирования (10.5) - (10.7) достаточно найти
какие-нибудь вектора и, v и ж, удовлетворяющие условиям
(10.7) - (10.9) и системе линейных алгебраических уравне-
ний
Аж = В,
(10.11)
, 2 Сх — v + А'и — —Р.
При найденном ж будет достигаться самое меньшее значение
функции F, какое только возможно при соблюдении условий
(10.6) и (10.7).
Для определения векторов it, v и ж, удовлетворяющих
условиям (10.7) - (10.9) и системе линейных алгебраичес-
ких уравнений (10.11), необходимо решить еще одну задачу
линейного программирования, к описанию которой мы пе-
реходим.
В этой задаче р = N + т, q = 3 N А 2 т. (/-мерный
вектор имеет вид
(ж, v, u2, z),
130
Теория эффективных портфелей ценных бумаг
где х, v и z - Димерные вектора, а и1 и и2 - тп-мерные век-
тора; координаты всех этих векторов неотрицательны. Сис-
тема ограничений из р линейных уравнений относительно q
неизвестных имеет вид
Ах
(10.12)
2Сх - v + А1 и1 — А'и2 + Gz =-Р.
G - это диагональная матрица размера N х N, точный вид
которой приведен ниже, а искать максимум будем для функ-
ции
L(x, v, и1, и2, z) = — zx — z2 — ... — z#.
Если найденный максимум функции L будет равен 0, это
будет означать, что
zi ~ z2 = ... = zN = 0,
1 2
а вектора ж, v и и = и — и удовлетворяют системе уравне-
ний (10.11) и условиям (10.7), (10.8). Пока оставим в стороне
вопрос о выполнении условия (10.9).
Теперь дадим точное описание матрицы G. Она констру-
ируется таким образом, чтобы было возможно построить
исходный ^-мерный вектор (х^и^и2, z) с неотрицатель-
ными координатами, удовлетворяющий системе уравнений
(10.12). С этого вектора будет начат перебор при решении
задачи линейного программирования симплексным методом.
Сначала найдем какой-нибудь Димерный вектор х° с неот-
рицательными координатами, удовлетворяющий условию
Ах° = В.
§10. Вычислительные процедуры
131
Это можно сделать, решив вспомогательную задачу линей-
ного программирования, рассмотренную в конце первой час-
ти данного параграфа. Будем предполагать, что у исходно-
го ^-мерного вектора составляющие v = 0 и и1 = и2 = 0.
Положим
N
Si = -Pi-Y,Ciix4, ; = 1,2,...,ЛГ.
»=1
Будем считать, что матрица G диагональная, т. е. все эле-
менты, расположенные вне главной диагонали матрицы,
равны 0, и обозначим элементы, стоящие на главной диа-
гонали этой матрицы, через (7ц, (7гг, • • •, Gjfjf. Положим
G . _ J 1,
“ 1 -1,
если Sj > 0,
если 6j < 0
при j =
Если определить TV-мерный вектор z° = (z°, z^- • • •, z#)
при помощи равенства = | |, то координаты этого векто-
ра неотрицательны, и ^-мерный вектор (ж0, v, u1, u2, z°) (на-
помним, что v = 0, и1 = и2 = 0) удовлетворяет системе
уравнений (10.12). Все координаты этого 5-мерного векто-
ра неотрицательны, а положительных координат у него не
больше, чем р. Поэтому соответствующая точка является
вершиной многогранного множества задачи линейного про-
граммирования, и с этой вершины может быть начат пе-
ребор при поиске максимума функции .Цж,^,^1,^2, г) сим-
плексным методом.
Для построенного исходного 5-мерного вектора
(ж0, 0, 0,0, z°)
132
Теория эффективных портфелей ценных бумаг
выполняется также условие (10.9), поскольку v = 0. В силу
неотрицательности координат векторов х и v условие (10.9)
может быть записано в следующей комбинаторной форме:
если Xj > 0, то Vj — 0;
если Vj > 0, то Xj = 0;
j — 1,2,..., N. Поэтому для выполнения условия (10.9) в
симплексный метод достаточно добавить следующее огра-
ничение:
если при некотором j, 1 < j' < N. в базис входит столбец
Dj, то при продолжении перебора вершин в базис не может
быть включен столбец Dj+w;
если при некотором j, 1 < j < N, в базис входит стол-
бец Dj+wy то при продолжении перебора вершин в базис не
может быть включен столбец Dj.
Как и для задач линейного программирования, для задач
квадратичного программирования требуется накладывать
некоторые условия невырожденности, которые гарантируют
сходимость симплексного метода (см., например, [36]). Но
практически применение симплексного метода может ока-
заться успешным и в тех случаях, когда эти условия не вы-
полнены.
3. Метод критических линий для построения эф-
фективных фронтов. В начале §9 сформулирована задача
квадратичного программирования, решив которую, можно
найти эффективный портфель, соответствующий некоторо-
му значению параметра Л. При изменении А от 0 до +оо
таким образом описывается весь эффективный фронт. При
фиксированном А задача квадратичного программирования
может быть решена симплексным или каким-нибудь другим
§10. Вычислительные процедуры
133
методом. Но применить подобный метод бесконечное коли-
чество раз, чтобы найти эффективный портфель при любом
Л, нельзя.
Ниже описан метод, позволяющий построить весь эффек-
тивный фронт, решив задачу квадратичного программиро-
вания лишь конечное число раз. Этот метод называется ме-
тодом критических линий. Он был предложен в [10] и усо-
вершенствован в [14]. Иногда его называют методом Марко-
вица - Шарпа.
Будем предполагать, что имеют место допущения 1, 2
и 3, сделанные в §9. Тогда достаточно построить эффек-
тивные портфели, решив соответствующие задачи квад-
ратичного программирования, только для угловых Л. При
всех остальных А величины «1(A), ж2(А),..., sjy(A), опреде-
ляющие эффективные портфели, могут быть построены пу-
тем линейной интерполяции по А между соседними угловы-
ми точками, поскольку, как было доказано в §9, функции
«1(A), «2(A),..., «м(А) являются непрерывными и кусочно-
линейными, графики этих функций могут иметь изломы
только в угловых точках.
Но как определить, какие А являются угловыми? Метод
критических линий предназначен для отыскания угловых
точек А.
Прежде чем переходить к изложению этого метода, сде-
лаем одно замечание. Эффективный портфель с минималь-
ным стандартным отклонением может быть найден путем
решения задачи квадратичного программирования (9.1),
(9.2) из §9 при А = 0. Изначально неизвестно, какое А отвеча-
ет эффективному портфелю с максимальной ожидаемой до-
ходностью. Но мы можем определить сам этот портфель, ре-
шив следующую задачу линейного программирования. Най-
134
Теория эффективных портфелей ценных бумаг
ти максимальное значение функции
N
'ZxiEi
»=i
при ограничениях (9.2) из §9. Знание этого эффективного
портфеля позволяет установить Л, отвечающее эффектив-
ному портфелю с максимальной ожидаемой доходностью.
Действительно, если оказалось, что некоторый найденный
эффективный портфель, соответствующий какой-то угловой
точке Л, совпадает с эффективным портфелем с максималь-
ной ожидаемой доходностью, то мы можем утверждать, что
данное А и есть то А, которое отвечает эффективному пор-
тфелю с максимальной ожидаемой доходностью. Значение А,
отвечающее эффективному портфелю с максимальной ожи-
даемой доходностью, обозначим Л.
Пусть Ао - некоторая неугловая точка, 0 < Ао < Л. Метод
критических линий позволяет найти две ближайшие к Ао
угловые точки а и Ь, такие, что а < Ао < Ь.
Решим задачу квадратичного программирования (9.1),
(9.2) из §9 при А = Aq. Напомним, что индексы i, (1 < i < TV),
для которых ж,(А0) > 0, называются внутренними. Индек-
сы г, (1 < i < TV), для которых «;(Ао) = 0, называются
внешними. Все индексы i делятся на внутренние и внешние,
поскольку переменные не могут быть отрицательными.
В §9 составлена система линейных алгебраических урав-
нений (9.6) - (9.8), которой должны удовлетворять функции
®j(A) и ujt(A) при всех А, достаточно близких к Ао. Здесь
j = 1,2,..., N и к = 1,2,..., т. Уравнения (9.6) записыва-
ются для внешних индексов г, а уравнения (9.7) - для внут-
ренних.
§10. Вычислительные процедуры
135
Будем использовать формулы, справедливость которых
была установлена в §9. Для внутренних индексов г :
Xi = oii + Д А.
Для внешних индексов i :
5Ф
—(ж(А),и(А)) = ^i + T}i А.
Числа определяются при решении системы линейных
алгебраических уравнений (9.6) - (9.8). Для определения чи-
сел Ci->4i привлекается также формула (9.5).
На основании определения неугловой точки для внутрен-
них индексов i
ai + Д Ао > 0.
Для внешних индексов i
Ci + r]i Ао > 0.
Идея метода критических линий очень проста. Интервал
(а, Ь) - это наибольший из интервалов, содержащих точку
Ао, и таких, что для любого А, принадлежащего (а,Ь), вы-
полняются следующие неравенства. Для внутренних индек-
сов i
оь+&Х> 0,
для внешних индексов i
Ci + Ъ А > о,
(см. рис. 10.2). Т. е. в качестве а нужно взять наибольшую
точку, меньшую Ао, в которой либо для некоторого внутрен-
него индекса i
сц + fa а = 0,
136
Теория эффективных портфелей ценных бумаг
либо для некоторого внешнего индекса i
& + T]i а = 0.
Разумеется, следует положить а = 0, если окажется, что
положительных а, обладающих указанным свойством, нет.
Аналогично определяется и точка Ь.
Рис. 10.2. Определение интервала (а, Ь) методом крити-
ческих линий. Графики прямых oy + Pi X для внутренних индек-
сов г (верхняя часть рисунка) и графики прямых & + ту X для
внешних индексов i (нижняя часть рисунка)
Эффективные фронты, относящиеся к примеру из §3 и
приведенные на рис. 3.5, рассчитаны методом, описанным в
настоящем параграфе. В таблице 10.1 показаны параметры
угловых портфелей для эффективного фронта а.
§10- Вычислительные процедуры
137
Таблица 10.1
®2 Х4 ®5 356
1.019959 0.001720 -0.300000 -0.300000 0.260616 0.317705
0.966880 -0.300000 -0.300000 -0.300000 0.462422 0.470698
0.870690 -0.300000 -0.300000 -0.300000 0.466397 0.562913
-0.300000 -0.300000 -0.300000 0.365471 0.552674 0.981856
-0.300000 -0.300000 -0.300000 0.361536 -0.300000 1.838464
-0.300000 -0.300000 -0.300000 -0.300000 -0.300000 2.500000
Таблица 10.2 содержит параметры А, <т и Е для этих уг-
ловых портфелей.
Таблица 10.2
А (7 Е
0.000000 0.007431 0.052670
0.001200 0.008208 0.072929
0.002366 0.009030 0.080881
0.006035 0.020256 0.159144
0.025379 0.030631 0.192755
0.079119 0.042698 0.209690
В таблице 10.3 показаны параметры угловых портфелей
для эффективного фронта Ь.
Таблица 10.3
®2
0.660125 0.000000 0.000000 0.000000 0.098259 0.241616
0.373510 0.000000 0.000000 0.000000 0.110105 0.516385
0.000000 0.000000 0.000000 0.212319 0.137631 0.650049
0.000000 0.000000 0.000000 0.211684 0.000000 0.788316
0.000000 0.000000 0.000000 0.000000 0.000000 1.000000
138
Теория эффективных портфелей ценных бумаг
Графики функций ajx(A), ж4(А), ж5(А), ж6(А) приведены на
рис. 3.9. Таблица 10.4 содержит параметры А, а и Е для
этих угловых портфелей.
Таблица 10.4
А (Т Е
0.000000 0.011913 0.065490
0.003476 0.013532 0.089186
0.004647 0.016868 0.114156
0.007769 0.017838 0.119581
0.024965 0.020171 0.125000
В таблице 10.5 показаны параметры угловых портфелей
для эффективного фронта с.
Таблица 10.5
Х2 хз Х5
0.465003 0.100000 0.100000 0.100000 0.100000 0.134997
0.162093 0.100000 0.100000 0.100000 0.100000 0.437907
0.100000 0.100000 0.100000 0.100000 0.100000 0.500000
Таблица 10.6 содержит параметры А, а и Е для этих уг-
ловых портфелей.
Таблица 10.6
А (Т Е
0.000000 0.013875 0.066000
0.003750 0.015504 0.091536
0.006914 0.016187 0.096770
Библиографический список
[1] Bawa V.S., Brown S.J., Klein R.W. Estimation Risk
and Optimal Portfolio Choice. Amsterdam: Elsevier - North
Holland Publ., 1979.
[2] Elton E., Gruber M. Modern Portfolio Theory and
Investment Analysis. N.Y.: Wiley, 1987.
[3] Fama E.F., Miller M.H. The Theory of Finance. N.Y.:
Holt, Rinehart and Winston, 1972.
[4] Heerwaarden A. Ordering of Risks. Theory and Actuarial
Applications. Amsterdam: Tinbergen Institute, 1991.
[5] Hull J.C. Options, Futures and Other Derivatives. 3d
edition. Englewood Cliffs (N.J.): Prentice Hall, 1997.
[6] Jarrow R., Rudd A. Option Pricing. Homewood (Ш.):
Dow Jones - Irwin, 1983.
[7] Laffont J.J. The Economics of Uncertainty and Information
Cambridge (Mass.): MIT Press, 1989.
[8] Levy H., Sarnat M. Investment and Portfolio Analysis.
N.Y.: Wiley, 1972.
[9] Levy H., Sarnat M. Capital Investment and Financial
Decisions. Englewood Cliffs (N.J.): Prentice - Hall, 1978.
[10] Markowitz H.M. Portfolio Selection: Efficient Diversifica-
tion of Investments. N.Y.: Wiley, 1959.
[11] Mathematical Finance / Eds. M.H.A.Davis, D.Duffie,
W.H.Fleming, S.E.Shreve. N.Y.: Springer-Verlag, 1995.
[12] Reilly F.K. Investment Analysis and Portfolio Manage-
ment. Chicago: Dryden Press, 1979.
[13] Security Evaluation and Portfolio Analysis / Eds. E.Elton,
M.Gruber. Englewood Cliffs (N.J.): Prentice - Hall, 1972.
140
Теория эффективных портфелей ценных бумаг
[14] Sharpe W.F. Portfolio Theory and Capital Markets.
N.Y.: McGraw-Hill, 1970.
[15] Wilmott P., Howison S., Dewynne J. The mathematics
of financial derivatives. A student introduction. Cambridge:
Cambridge Univ. Press, 1995.
[16] Брейли P., Майерс С. Принципы корпоративных фи-
нансов. M.: Олимп - Бизнес, 1997.
[17] Буренин А.Н. Рынки производных финансовых ин-
струментов. М.: Инфра-М, 1996.
[18] Гитман Л.Дж., Джонк М.Д. Основы инвестирова-
ния. М.: Дело, 1997.
[19] Глазунов В.Н. Финансовый анализ и оценка риска ре-
альных инвестиций. М.: Финстатинформ, 1997.
[20] Ильин В.А., Позняк Э.Г. Основы математического
анализа. 4.1. М.: Наука, 1982.
[21] Карманов В.Г. Математическое программирование.
М.: Наука, 1975.
[22] Касимов Ю.Ф. Основы теории оптимального портфе-
ля ценных бумаг. М.: Филинъ, 1998.
[23] Колб Р.У. Финансовые деривативы. М.: Филинъ, 1997.
[24] Количественные методы финансового анализа / Под
ред. С.В.Брауна, М.П.Крицмена. М.: Инфра-М, 1996.
[25] Корн Г., Корн Т. Справочник по математике для на-
учных работников и инженеров. М.: Наука, 1974.
[26] Курош А.Г. Курс высшей алгебры. М.: Наука, 1971.
[27] Кюнци Г.П., Крелле В. Нелинейное программирова-
ние. М.: Сов. радио, 1965.
[28] Меньшиков И.С. Финансовый анализ ценных бумаг.
М.: Финансы и статистика, 1998.
[29] Нуреев Р.М. Курс микроэкономики. М.: Норма -
Инфра-М, 1998.
Библиографический список
141
[30] Первозванский А.А., Первозванская Т.Ю. Финан-
совый рынок: расчет и риск. М.: Инфра-М, 1994.
[31] Погорелов А.В. Аналитическая геометрия. М.: Наука,
1968.
[32] Пшеничный Б.Н., Данилин Ю.М. Численные ме-
тоды в экстремальных задачах. М.: Наука, 1975.
[33] Ротарь В.И. Теория вероятностей. М.: Высшая школа,
1992.
[34] Рынок ценных бумаг / Под ред. В.А.Галанова, А.И.Ба-
сова. М.: Финансы и статистика, 1996.
[35] Фон Нейман Дж., Моргенштерн О. Теория игр и
экономическое поведение. М.: Наука, 1970.
[36] Хедли Дж. Нелинейное и динамическое программиро-
вание. М.: Мир, 1967.
[37] Шарп У.Ф., Александер Г.Дж., Бэйли Дж.В. Ин-
вестиции. М.: Инфра-М, 1997.
[38] Шведов А.С. Теория вероятностей и математическая
статистика. М.: Высшая школа экономики, 1995.
[39] Юдин Д.Б., Гольштейн Е.Г. Линейное программи-
рование. М.: Наука, 1969.