0 Ш И KJ ш @
НОВОЕ
В ЖИЗНИ, НАУКЕ, ТЕХНИКЕ
СЕРИЯ МАТЕМАТИКА, КИБЕРНЕТИКА
9'7Э .
И. Г. Башмакова СТАНОВЛЕНИЕ АЛГЕБРЫ
НОВОЕ В ЖИЗНИ, НАУКЕ, ТЕХНИКЕ
И. Г. Башмакова,
доктор физико-математических наук, профессор
Серия	СТАНОВЛЕНИЕ
«Математика,	mrrrni 1
кибернетика»,	АЛ ГсЬг Ы
№ 9, 1979 г.
(ИЗ ИСТОРИИ МАТЕМАТИЧЕСКИХ ИДЕЙ) Издается ежемесячно с 1967 г,
Издательство «Знание» Москва 1979
22.1г БЗЗ
Башмакова И. Г.
ВЗЗ Становление алгебры (из истории математический идей). М., «Знание», 1979.
64 с. (Новое в жизни, науке, технике. Серия «Мате* матика, кибернетика». 9. Издается ежемесячно в 1967 г.)
Научные истины лучше воспринимаются и усваиваются человеком, если они подаются в тесной связи с жизнью, в процессе их становления и развития, порой противоречивого и драматического.
В брошюре рассказывается о развитии некоторых алгебраических идей и о создании буквенного исчисления, которое стало языком современной математики.
Матерйал рассчитан на широкий круг читателей.
20201
22.1г
© Издательство «Знание», 4979 г.
ПРЕДИСЛОВИЕ
Настоящей брошюрой в этой серии начинается систематическое печатание работ под общим названием «из истории математических идей». Само их название показывает, что специальное внимание в таких работах будет обращено не на биографии выдающихся математиков, а на факты биографии самой математики.
История математических идей представляет интерес не только для тех, кто занимается историей науки, но и для всех, кто использует математику, а также интересуется ею самой и ее философскими проблемами. Знание фактов истории науки, ее связей с актуальными задачами различных эпох исключительно важно для учителей средних школ и преподавателей вузов, поскольку оно дает возможность выяснить происхождение понятий, основных идей науки, постановок задач и методов исследования. Вдобавок история позволяет выяснить и вопросы, связанные с разработкой математической символики, которая не только открывает возможность в краткой и удобной форме записывать математическую информацию, но и автоматизировать производство математических операций.
Последнее утверждение требует небольшого разъяснения. В науке необходимы ясность и точность выражения мысли. Язык науки не должен создавать дополнительных трудностей при восприятии сообщаемой информации. Идеи и факты при передаче не должны допускать разночтений. Обычная речь, житейский язык не обладают этим качеством. А без него не может быть науки как системы знаний, не может быть уверенности в том, что определенное утверждение всеми понимается одинаково и что в процессе рассуждений оно не подвергается искажению. Вот почему математика вынуждена разрабатывать собственный язык, максимально точно передающий свойственные ей
особенности. Об этом прекрасно сказал известный французский физик Луи де Бройль: «Где можно применить математический подход к проблемам, наука вынуждена пользоваться особым языком, символическим языком, своего рода стенографией абстрактной мысли, формулы которой, когда они правильно записаны, по-видимому, не оставляют места ни для какой неопределенности, ни для какого неточного истолкования»*.
Следует заметйть, что математическая символика не только не оставляет места для неточности выражения мысли и расплывчатого истолкования написанного, но позволяет также кратко записывать необходимую информацию и автоматизировать проведение тех действий, которые необходимы для получения выводов.
Рассмотрим такой простой пример. Известно, что в строительной механике, геодезии, экономике, организации производства и других направлениях теоретической и при-1 кладной науки часто требуется решать системы линейных алгебраических уравнений с соответствующим числом неизвестных. С помощью привычной алгебраической символики необходимые действия осуществляются по определенным правилам, не зависящим от числа неизвестных. Для двух-трех неизвестных это доступно каждому школьнику VI—VII класса. Нет необходимости при переходе от одной задачи к другой производить какие-то специальные рассуждения — они выполнены раз и навсегда для всех подобных систем. Применение набора стандартных правил позволяет не только решить каждую такую задачу без затруднений принципиального порядка, но даже поручить это автомату — электронной вычислительной машине.
Мы прекрасно знаем, как затруднено решение простейших алгебраических задач чисто арифметическими методами. При таком решении каждая задача требует особых рассуждений, специального подхода, значительного умственного напряжения. Для математики и ее применений одного разговорного языка недостаточно — требуется специально разработанный символический язык, приспособленный к классу решаемых вопросов. Именно в связи с этим уже в наши дни пришлось затратить много усилий на выработку языков программирования математических й логических задач при постановке их решения на ЭВМ.
♦ Луи де Б р о й л ь, По тропам науки. М., ИЛ, 1962, с. 326,
Настоящая брошюра посвящена одной из старейших областей математики — алгебре. С элементами алгебраических знаний знакомятся все, кто обучается в средней школе. Эти знания становятся позднее фундаментом при изучении математическрго анализа, линейной алгебры й других частей курса математики любого высшего учебного заведения, в котором дается дополнительное математическое образование. Вот те причины, в силу которых мы начинаем издание книжек «из истории математических идей» именно с истории алгебры.
Автор брошюры ограничивается рассмотрением лишь четырех моментов из истории алгебры — алгебраические знания Древнего Вавилона, геометрическую алгебру Древней Греции, зарождение буквенной символики и вклад в алгебраическую мысль французского математика Виета. Разные эпохи, разные подходы и разные задачи. Каждая из рассмотренных эпох внесла свой вклад в формирование алгебры и свой неповторимый вклад в историю алгебраической мысли. Каждый очерк читается как вполне законченное целое.	,
Сто тридцать лет назад в Мессопотамии археологами была найдена древнейшая библиотека в развалинах города Ниневии. Четыре года спустя была раскопана библиотека Ашшурбанипала. Сотни тысяч глиняных табличек с клинописными записями хранятся в* крупнейших музеях мира. Удалось разгадать древний язык и письменность. Культура прошлого стала достоянием науки.
Выяснилось, что. в далеком Двуречье почти за две тысячи лет до нашего летосчисления были составлены таблицы умножения, квадратов последовательных целых чисел и некоторые другие. Но что самое удивительное, так это умение решать квадратные уравнения. Для решения квадратных уравнений древние народы Мессопотамии разработали систему действий, эквивалентную формуле, которой мы пользуемся для разыскания корней квадратного уравнения. При этом удивительно то, что ни в одной табличке не были найдены рассуждения, приведшие к используемому алгоритму. Найденные глиняные таблички скорее могут быть названы ученическими тетрадями и школьными пособиями, чем монографиями, излагающими накопленные знания. ,До сих пор еще нет окончательных представлений о том, как древние вавилоняне пришли к своим открытиям. Предлагаемые реконструкции их рассуждений являются только правдоподобными, но далеко не окончательными.
Несомненно, что читатели с интересом познакомятся с первым очерком И. Г. Башмаковой.
Следующие два очерка посвящены математике Древней Греции. При этом речь идет не только о частных результатах, но и о гораздо большем — о превращении математики из «сборника рецептов» в развитую научную дисциплину с собственным предметом и методом исследования. Именно в Древней Греции математика стала дедуктивной дисциплиной, в которой из небольшого числа исходных положений — аксиом и постулатов — выводились многочисленные Следствия — теоремы. В течение многих столетий греческое построение геометрии, нашедшее в труде Евклида свое высшее выражение, служило образцом для развития математики. И снова возникает вопрос большого методологического значения: какие причины привели математиков Древней Греции к дедуктивному построению геометрии? В одном из докладов, который был подготовлен мной и И. Б. Погребысским, мы высказали мысль о том, что отход от деспотической формы правления к ограниченно демократической, когда правитель должен был обосновывать перед общим собранием свободных граждан принимаемые решения, мог послужить толчком для развития и построения научных знаний.
Второй очерк дает представление о своеобразном построении алгебры древними греками — геометрической алгебре, явившейся следствием открытия пифагорейцами несоизмеримых отрезков, т. е. таких, отношения которых не могут быть выражены никакими отношениями целых чисел. Пифагорейцы пришли к выводу, что геометрические величины имеют более общую природу, чем числа, и поэтому в основу математики следует положить не арифметику, а геометрию.
Позволив первоначально получить значительное ко--личество важных результатов, геометрическая алгебра в дальнейшем сделалась помехой, так как даже уравнение третьей степени ее методами решено быть не могло. Но тем не менее геометрическая алгебра сыграла очень большую роль в развитии математики.
Третий очерк в основном посвящен творчеству величайшего алгебраиста древности —Диофанта Александрийского, алгебраический формализм которого составляет особый этап в развитии алгебры. В своей работе «Арифметика» он расширил числовую область до поля рациональных чисел, •ввел алгебраическую символику для первых шести поло
жительных и отрицательных степеней неизвестного, для обозначения вычитания и равенства. .
Последний, четвертый, очерк рассказывает о математике европейского средневековья и эпохи Возрождения, усовершенствовании алгебраической символики, первых крупных успехах — решении уравнений третьей и четвертой степени.
Большой и продуктивный период в развитии'алгебры связан с именем Ф. Виета. Именно он сделал особенно .много, чтобы в алгебре появилась система символов, облегчающая производство необходимых преобразований и вычислений. . .
Несколько лет назад И. Г. Башмакова, изучая труды Ф. Виета, обратила внимание на своеобразное исчисление треугольников, введенное и разработанное им; Простое сравнение с формулами Муавра для умножения и возведения в степень комплексных чисел показало тождественность формул в исчислении Виета и работе Муавра. Это интересное историческое открытие нашло отражение в четвертом очерке.
Теперь несколько слов об авторе. Изабелла Григорьевна Башмакова — профессор Московского университета. Несколько лет назад она была избрана членом международной академии по истории науки. Ее основные научные результаты относятся к математике Древней Греции и истории алгебры.
Академик АН УССР Б. В. ГНЕДЕНКО
1. АЛГЕБРА ДРЕВНЕГО ВАВИЛОНА
1. В середине прошлого века из Мессопотамии во Францию и Британию начали поступать глиняные таблички, покрытые вытесненными на них клиньями, или «клинописью». В 1849—1850 гг. в развалинах древнего города Ниневии Лейярд нашел дворцовую библиотеку, а в 1853 г. Хормузд Рассам открыл библиотеку Ашшурбанипала. 20 000 табличек из этих раскопок хранятся сейчас в Британском музее. С тех пор таблички поступали в музеи сотнями и тысячами, и теперь их насчитывается около 500 000. Правда, большинство из табличек оказались разрозненными в результате спекуляции ими, которой занимались как местные жители, так и приехавшие со всех концов мира авантюристы. Так что работа ученых над табличками чрезвычайно затруднилась. Начало одного текста может теперь храниться в Лондоне, середина — в Нью-Йорке, а конец — в Париже. Расшифровка текстов шла медленно.
Оказалось, что среди табличек имеются и «математические». Они были расшифрованы только в 1929—1930 гг. Это открыло неведомый до того мир древней математики Двуречья. Здесь особые заслуги принадлежат О. Нейгебау-еру, работа которого, появившаяся в 30-х годах нашего столетия, положила начало бурному потоку исследований. Здесь следует отметить видного французского ассириолога Ф. Тюро-Данжена, который первым начал систематическую публикацию текстов. (Его дело затем было-продолжено А. Саксом, О. Нейгебауером, Э. М. Бройнсом.) У нас в Союзе исследованием математики Двуречья занимались М. Я. Выгодский, И. Н. Веселовский, А. А. Вай-ман.
При изучении математических табличек оказалось, что по содержанию они делятся на два класса: 1) «тексты-таблицы» (например, содержащие таблицы умножения или
В	•
таблицы квадратов) и 2) «тексты-задачники», содержащие формулировки и решение задач.
Все эти тексты, как оказалось, относятся к двум резко ограниченным и далеко отстоящим друг от друга периодам: большая часть их является «древневавилонской», т. е. относится ко времени династии Хаммурапи (1800—1600 гг. до н. э.), другая, меньшая часть, была составлена в эпоху Селевкидов (III—I вв. до н. э.), т. е. относится уже к эпохе эллинизма. За время, разделяющее оба периода, изменились язык и форма написания знаков, что и позволило провести строгую датировку табличек, однако математическое содержание текстов осталось в основном тем же.
Но всего удивительнее оказался тот факт, что большинство «текстов-задач» являлись задачами на квадратные уравнения! Вавилоняне за две тысячи лет до н. э. умели решать квадратные уравнения и делать алгебрайческие преобразования! Это было поразительное открытие, заставившее отнести начало алгебры не к V в. до и. э., как думали раньше, а к XVIII в.!
Прежде чем переходить к рассмотрению вавилонских задач, скажем несколько слов о «текстах-таблицах».
Для обозначения всех чисел вавилоняне пользовались только двумя знаками: вертикальным и горизонтальным клиньями. Эти знаки вдавливались палочкой в глину, а затем дощечка из глины обжигалась. Как же удавалось обходиться только двумя знаками?
Все числа от 1 до 9 записывались с помощью соответствующего числа вертикальных клиньев (рис. 1). Число 10 записывалось с помощью горизонтального клина. Затем все числа до 59 получались комбинацией этих двух клиньев, см., например, число 23. Число 60 снова записывалось с помощью вертикального клина, так что изображенная на рис. 1 последняя запись могла означать число 60+23=83. Мы пишем «могла означать», так как запись эта могла быть прочитана многими способами: она могла означать 1+23Х Хб0~*=1|;р или, например, 602+23=3623 и вообще 60*+ +23-60*1, где k^k.
Такая неоднозначность записи объяснялась тем, что у вавилонян не было нуля. Правда, в эпоху Селевкидов появился специальный разделительный знак, который ставился, если в середине числа был пропущен шестидесятеричный разряд, но в конце числа этот знак никогда не ставился.
Сделаем выводы:
1)	Система нумерации вавилонян была позиционной, так как числовое значение одного и того же знака определялось не только его формой, но и положением, которое он занимал в записи числа.
2)	Основанием системы служило число 60. Откуда взялось такое число? Обычно нумерации имеют основанием 10— число пальцев на руках, иногда 20 (следы такой системы сохранились во французском и в скандинавских языках). Но как могло получиться 60? На этот счет существует много гипотез, ни одна из которых не является более убеди- • тельной, чем все остальные. Итак, это пока неизвестно.
3)	В системе не было нуля, поэтому запись не имела абсолютного характера. Какому числу на самом деле отвечала запись, приходилось определять из контекста.
Неудобства, связанные с отсутствием нуля, искупались до некоторой степени тем, что вавилоняне имели возможность сразу единообразным способом записывать и целые числа, и шестидесятеричные дроби. То есть вместе с позиционной системой у них имелись и систематические дроби.
Но при таком большом основании, как 60, довольно трудно выучить таблицу умножения! Мы учим ее до 9x9, а вавилонским детям пришлось бы доходить до 59x59. Но, к их счастью, это им не было нужно. При раскопках
Рис, J
нашли такое количество «таблиц умножения», что, по-видимому, их изготовляли массам# для школьников и они ими пользовались при решении задач точно так же, как мы теперь пользуемся таблицами логарифмов. Это — один из видов наиболее часто встречающихся таблиц.
Другой вид связан с операцией деления. Чтобы разделить число на число N, вавилоняне всегда брали число ему обратное 7V'=-^- и умножали М на N'. Поэтому у них большое распространение получили и «таблицы обратных величин». Количество и тех и других говорит о том, что они применялись для преподавания, что в Вавилоне должны были быть школы, в которых обучались дети. Кроме названных таблиц, имелись еще таблицы квадратов натуральных чисел, таблицы кубов, а также таблицы квадратных корней (в шестидесятеричных дробях), чисел п34~па и др. Таких таблиц было меньше. Видимо, их применяли уже в специальных случаях.
Заметим, что следы вавилонской нумерации сохранились и до сих пор: мы делим час на 60 минут, а минуту — на 60 секунд, т. е. считаем время по шестидесятеричной системе. То же мы делаем при делении окружности на градусы, минуты и секунды. Такая традиция перешла к нам из астрономии. Вавилоняне первыми проводили систематические наблюдения звездного неба, составляли календарь, вычисляли периоды обращения Луны и планет, могли предсказывать солнечные и лунные затмения. Эти астрономические знания впоследствии перешли к грекам, которые вместе с астрономическими таблицами заимствовали и шестидеся--теричную нумерацию. Ею пользовался и знаменитый астроном Лтолемей (II в. н. э.) в своем фундаментальном труде, известном под арабизированным названием «Альмагест».
Еще позднее,, в VIII—IX вв., этот труд был переведен на арабский язык, а. вместе с ним в обиход и арабских астрономов вошла вавилонская шестидесятеричная нумерация. Отсюда она проникла в Европу. Только в XV—XVI вв. появились десятичные дроби и начали вытеснять шестидесятеричные. Однако, как мы видели, отголоски шестидесятеричной нумерации дошли и до нас.
II. Какие же задачи решали вавилонские школьники? Существуют тексты с большим количеством однотипных задач, в которых нужно найти «длину» и «ширину» или «множимое» и его обратную величину — «множитель», для которых задана сумма или разность.
Вот одна из таких «канонических» задач:
Задача 1. «Множимое и множитель 2; 30», т. ё. даны две. взаимно обратные величины: «множимое» — х и «множитель» — х (хх=1) и х+х=2; 30. Транскрипция 2; 30 означает, что мы имеем дело с числом 2|§. Для облегчения чтения в дальнейшем мы будем записывать все числа в нашей десятичной позиционной системе. Таким образом, учащемуся предложена система:
х + х= 2,5, хх— 1.
Далее в тексте описывается, какие операции нужно сделать для нахождения решения. Для того чтобы нам было легче следить за действиями вавилонского вычислителя, мы будем записывать их с помощью буквенной символики:
{х 4- х = а;
-	’	(О
хх = Ь.
Эта система эквивалентна уравнению г®—аН-6=0. Итак:
1)	«На 0,5 умножь : 1,25» (т. е. а-0,5=а/2).
2)	«1,25 на 1,25 умножь : 1,5625» (т. е. а/2-а/2=а2/4).
3)	«1 вычти отсюда : 0,5625» (т. е. (а/2)2—Ь).
4)	«Что на что надо умножить, чтобы получить 0,5625?: 0,75» (т. еУ (а/2)2 - Ь-
5)	«0,75 к 1,25 прибавь : 2 — множимое» (т. е. х — а/2-\-+V(a/2)*-b.
6)	«0,75 от 1,25 вычти : 0,5 — множитель» (т. е. х — а/2— -V(a/2)*-b.
Мы видим, что школьнику дается рецепт или, если угодно, алгоритм для решения системы (1), равносильный хорошо известной нашей формуле. То, что мы записываем в виде формулы, вавилоняне задавали как строго определенную последовательность операций. Но как же было получено такое решение?	<j
Прежде чем попытаться ответить на этот вопрос, рассмотрим некоторые другие задачи.
Чтобы школьник лучше усвоил способ решения, в таблицах приводится большое количество однотипных задач, 12
причем имеющих, как правило, одни и те же ответы. Это задачи, которые мы бы записали с помощью уравнений:
(х±у=а;
I xy=b.
Это — канонические системы. Но затем задачи усложняются. Предлагаются задачи, которые еще нужно свести к каноническим. Вот пример одной из них:
Задача 2. «Длина, ширина. Длину и ширину я перемножил и площадь получил. Затем избыток длины над шириной я прибавил к площади: 183 получилось у меня. Затем я длину и ширину сложил : 27. Спрашивается длина, ширина и площадь».
Итак, предложена система:
Г(х—У)+ху= 183;
U+t/=27.	(2)
Решение: «Ты сделаешь так», и далее приводится следующая последовательность операций: 1)27+183=210.
2) 27+2=29.
3)29X0,5=14,5.
4)14,5X14,5=210,25.
5)210,25—210=0,25.
6) «Что на что надо умножить, чтобы получить 0,25? : 0,5». 7) 14,5+0,5=15 —длина.
8)	14,5—0,5=14 — ширина.
9)	«Отними 2, которое ты прибавил к 27, от ширины 14; 12 — истинная ширина».
10)	«15 — длину, 12 — ширину я перемножил, 180— площадь».
В чем же смысл этого решения? Проанализировав действия вавилонского вычислителя, можно заметить, что, начиная с пункта 3) и до пункта 8), он пользуется алгоритмом для решения системы:
|ни=210;
|и+о=29.
Из пункта 9) мы узнаем, что х=н=15, a y—v—2= = 14—2=12. Кроме того, мы знаем, что 210 — это сумма 183 и 27, а 29 — это сумма 27 и 2. Итак, вавилонский математик с самого начала сложил уравнения системы (2):
ху+(х—у) = 183 х+у=27 i хг/+2х=210, или x(t/+2)=210.
Обозначив у+2 через v, можно получить:
№=210, х+у=х+г/+2=27+2=29,.
т. е. получить именно ту систему, которую решает вавилонский математик в пунктах 3)—8).
Наша реконструкция потребовала от нас умения складывать выражения (х—у) и (х+у), а также умения выносить в выражении ху-\-2х множитель х «за скобки». Можно ли предполагать, что вавилонские математики умели проделывать такие операции?
На этот вопрос следует ответить утвердительно. Рассматриваемая ниже задача 3 показывает, что они знали даже такие формулы:
(а+&)2=а2+2а&+Я
Задача 3. Площадь двух моих квадратов я сложил: 1825, сторона второго квадрата равна 2/3 стороны первого и еще 5GAR*, т. е.
х2 + у2 = 1825; -
2	, -
у =§х+5.
Чтобы подставить у в первое уравнение, необходимо воспользоваться следующей формулой:
/2	/2\2 2 । о 2 г» । го
5Х+ 5) = 5 х2+ 2-х-5х + 52.
/ \&] &
Тогда для х получаем квадратное уравнение:  ах2+2Ьх=с,
где а = l-f-^j2; & = |-5; с =25.
В тексте сначала вычислены коэффициенты а, b, с, a затем найдены:
х = а-1 (У" ас + Ь2 —
♦ GAR — мера длины,
0 = |л+5.
.О
III. Нас, естественно, интересуют два весьма трудных вопроса:
1) была ли у вавилонян алгебра?
2) как возникли те задачи, которые мы находим в вавилонских текстах?
Чтобы ответить на первый из этих вопросов, надо уяснить, что мы понимаем под алгеброй.
Современная алгебра понимается как учение об операциях над произвольными математическими объектами (обозначаемыми буквами), причем операции эти, как правило, являются «законами композиции» (или бинарными отношениями), позволяющими двум объектам из одного множества ставить в соответствие третий объект из этого же множества. Такими «законами композиции» могут быть сложение, умножение чисел или, например, сложение векторов.
Если, например, заданы, некоторое множество М объектов {а, 0, у, б...} и для них некоторый закон композиции ®, обладающий свойствами:
1)	если а € М и 0 С М,- то а®0 6 М,
2)	а®(0®у)=(а®₽)®у (ассоциативность),
3)	существует элемент е, такой, что для любого а а®е=е®а=а,
4)	для всякого а СМ существует такое а'СМ, что а®а'=а'®а=е,
то множество М называется группой (группа — одна из алгебраических структур).
Итак, вопрос о наличии алгебры в Древнем Вавилоне сводится к двум основным вопросам: 1) была ли у вавилонян буквенная символика? 2) знали ли они законы арифметических операций (законы композиции)?
Мы настолько привыкли к буквенному исчислению, что нам без него сейчас трудно даже представить математику. А между тем буквенное исчисление было создано лишь в конце XVI в. До этого, по крайней мере на протяжении 34 веков, математика существовала и развивалась без такого исчисления, т. е. без формул!
Разберем характерные черты буквенных обозначений, посмотрим, чего мы достигаем, вводя символы. В чем, н«> пример, принципиальная разница в записи:
(а+6)2=а2+62+2аб
и в фр-азе. «Квадрат суммы двух количеств равен квадрату первого количества, плюс квадрат второго количёст-ва, плюс удвоенное произведение первого на второе»?
Конечно, первая запись короче. Но дело не только и не столько в этом. Дело в том, что над словами не определены никакие математические операции, мы не можем их складывать или умножать друг на друга. С символами же мы можем оперировать — и это главное. Например, подставляя вместо Ь сумму p+q, мы получаем:
[a+(p+<7)l2=a2+(p+<7)a+2«(p+7);=a2+P2+^+2w+ 4-2ар+2о7.
Причём новая формула получена чисто механически, без привлечения логических рассуждений, а только с помощью правил исчисления. Лейбниц писал, что буквенное исчисление «разгружает воображение».
Теперь мы можем сказать, что буквенной символики у вавилонян не было. У них имелись специальные термины для слов «длина», «ширина», «множимое» и «множитель», причем это были шумерские слова, которые ярко выделялись среди прочего, текста. (Шумеры были древними обитателями Двуречия. ОколоXXIII в. до.н. э. они были завоеваны и, по-видимому, ассимилированы семитическим племенем — аккадянами.) Эти слова как будто играют роль символов, но с ними никогда не оперируют (нет даже правил их переноса из одной части, уравнения в другую).
Перейдем теперь к вопросу об общих законах арифметики у вавилонян.
Прежде всего, как могли вавилоняне найти алгоритм решения системы;
(х+у=а;
(ху=Ь?
Вероятно, они рассуждали так: если бы х = у = 11 то а* г. ,	, а»	а
ху «= . Если о Ф f то пусть х превосходит % на некото-
• а
рую величину, а у — меньше <j на ту же величину:
х==1+г;
a
У = 2~г-Тогда х+у—а, ху = /~\2 —г2==6.
Откуда находим: г= — b, а затем х и у. Если ва-
вилоняне рассуждали именно так, то они должны были знать, что (а+^)(а—Ь)=а2—Ь2. И они действительно знали эту формулу! Задача 2, которую мы привели, показывает их умение выносить общий множитель за скобки и делать подстановку, а задача 3, что им’была известна формула (а+b)2. Другие задачи, о которых мы, правда, не говорили, показывают, что вавилоняне знали и формулу для (а—Ь)2. Итак, вавилонские математики знали общие законы операций сложения и умножения и пользовались ими.
Далее, они применяли эти законы для получения формулы решения квадратного уравнения, и наконец, для преобразования более сложных уравнений к каноническим.
Все это приводит нас к выводу, что в вавилонской математике XIX—XVIII вв. до н. э., несмотря на отсутствие символики, появились элементы алгебры.
Как же все-таки возникли задачи на квадратные уравнения? При измерении полей, естественно, возникает такая задача: измерены длина и ширина поля, найти его площадь. Но никогда не возникнет задача: известны площадь и периметр участка, найти его стороны.
Мы полагаем, что задачи последнего типа появились в результате научного анализа применяемых методов. Пусть мы знаем длину х и ширину у, тогда мы можем вычислить полупериметр х+у и площадь ху. Как проверить, правилен ли наш результат? Можно ли сделать «проверку», т. е. по данным ху и х+у найти х, yi Возможно, таким образом могла возникнуть первая «обратная задача», которыми так богато последующее развитие математики.
Разберем этот вопрос подробнее. В своей книге по истории математики в средние века А. П. Юшкевич охарактеризовал задачи. на «обращение» следующим образом: «В плане более отвлеченного развития происходило обращение ряда задач — практически данные величины принимались за искомые, а искомые — за данные; это явилось
2 Серия «Математика» № 9
17
одной из предпосылок разработки алгебраических приемов»*.
Приведем несколько примеров:
Прямая задача 1. Дана сторона квадрата а. Найти площадь у=а2. Для ее решения надо заданное число а умножить само на себя.
Обратная к задаче!. Дана площадь квадрата Ь. Найти его сторону.
Теперь у—Ь — заданная величина, а сторона квадрата х — искомая: х2=Ь.
Для решения задачи надо из заданного числа b извлечь квадратный корень: х = У Ь.
Прямая задача! Дайы стороны прямоугольника а и Ь. Найти его площадь S.
Задача решается при помощи умножения:
S=ab.
Как поставить обратную задачу? Если просто задать площадь S и потребовать определения сторон х и у, то задача будет неопределенной. Доопределить ее можно двумя способами:
1-я обратная к задаче2. Дана площадь прямоугольника S и одна из сторон у=а. Найти другую сторону, т. е. ax=S.
И решение задачи сводится к делению: x=S/a.
2-я обратная н задаче 2. Дана площадь прямоугольника 3 и-сумма (или разность) двух его сторон, т. е. '
xy=S\ x±y=b.
В этом случае задача сводится к эквивалентному квадратному уравнению:
г2+6г±5=0.
Последняя задача является принципиальна более сложной, чем первоначальная прямая или 1-я обратная к ней. Ее анализ и привел вавилонских математиков почти за 4 тыс. лет до наших дней к открытию формулы решения квадратных уравнений. При этом, как мы видели, использовались алгебраические преобразования. .
* А. П. Юшкевич. История математики в средние века. М., 1961, е. 11ю
2. ГЕОМЕТРИЧЕСКАЯ АЛГЕБРА ДРЕВНЕЙ ГРЕЦИИ .
I. VI—V вв. до н. э. ознаменовались для Греции великими событиями: там впервые в истории человечества было создано демократическое государство, возникли трагедия и комедия и, наконец, была создана математика как абстрактная теоретическая наука.
Каждое из этих событий имело неоценимое значение для всей истории и культуры человечества, а появление всех трех граничило с чудом. Оно и получило название «греческого чуда».
Нам здесь особенно важно, что именно в это время воз-' никла математика как абстрактная наука, основанная на системе доказательств. Такое преобразование математической науки из рецептурной, какой она была в Египте и Вавилоне, в. доказательную произошло, как утверждают все античные авторы, в школе Пифагора, который около 530 г. до н. э. переехал с острова Самос, своей родины, в Кротон (Южная Италия), где и основал пифагорейский союз — братство, преследовавшее политические, морально-этические и научные цели.
Знаменитый философ —неоплатоник Прокл (V в. н. э.) в своих комментариях к «Началам» Евклида писал: «...Пифагор преобразовал эту мудрость (т. е. математические знания. — Я. Б.) в форму свободного учения. Он рассматривал начала геометрии абстрактным образом и получал ее теоремы не материальным, а интеллектуальным способом.
Это он открыл учение об иррациональностях и построении космических тел».
Систематическое введение доказательств в математику стимулировало ее быстрое развитие. В Греции V—III вв. до н. э. были созданы первые математические теории: построены система евклидовой геометрии, элементарная теория чисел, теория конических сечений (т. е. кривых 2-го порядка), первая теория действительных чисел и элементы теории пределов.
Здесь уместно будет сказать несколько слов о роли доказательств в нашей науке. Обычно говорят, что доказательство служит для установления истинности того или иного математического предложения. Это, конечно, верно. Но дело не только в этом. Доказательства выявляют связи между математическими предложениями, позволяют установить, от каких посылок это предложение зависит. Так,
например, предложения «внешний угол треугольника больше каждого внутреннего, с ним не смежного» и «сумма углов треугольника равна 2d», которые при первом знакомстве кажутся сходными, на самом деле зависят от совершенно различных посылок. Первое из них не зависит от аксиомы параллельности, оно верно в так называемой «абсолютной геометрии» (оно верно и в геометрии Лобачевского), а второе существенно зависит от аксиомы параллельности и в геометрии Лобачевского не имеет места. Таким образом, доказательства дают нам возможность классифицировать и «упорядочивать» математические предложения. Поэтому некоторые особенно важные предложения имеют иногда много различных доказательств (так, Гаусс дал 8 различных доказательств квадратичному закону взаимности, а теперь их известно более 40). Ученые ищут новые доказательства неттотому, что сомневаются в старых, а потому, что хотят найти наиболее «естественные» доказательства или установить связи рассматриваемой теоремы с другими частями математики.
Но вернемся к «ранним» пифагорейцам (т. е. жившим в VI — начале V в. до н. э.). Никаких текстов от них не дошло. Кроме того, по традиции они приписывали все свои открытия «самому», т. е. Пифагору, о котором уже при жизни ходили загадочные легенды. Кто на самом деле был автором ранних теорий, узнать нельзя, поэтому мы будем говорить о «математике пифагорейцев», пользуясь сведениями, которые можно почерпнуть из сочинений Платона и Аристотеля, а также из отрывков трудов математиков-пифагорейцев конца V в. до н. э., таких, как Архит из Та-рента и Феодор из Кирены.
Пифагорейцы делили математику на четыре части: арифметику, геометрию, астрономию и гармонию (учение о музыке); При этом, как свидетельствует Архит, «первой» из них была арифметика; она лежала в основе и геометрии, и астрономии, и гармонии.
Числом пифагорейцы называли «множество единиц», т. е. числами они признавали только целые положительные (или натуральные) числа. Единица Е была материей чисел, она считалась неделимой, поэтому ни о каких «частях» ее ~ Е говорить было нельзя. Дроби осмысливались в теоретических сочинениях как «отношение чисел», вместо того чтобы говорить о Е, они рассматривали отношение
двух целых чисел — тЕ : пЕ. Таким образом возникла первая теория «пар чисел». По существу, это означало, что в арифметику были введены положительные рациональные числа.
Пифагорейцы первоначально полагали, что рациональных чисел достаточно для обоснования учения о подобии. Они считали, что все отрезки соизмеримы, поэтому, если надо найти отношение отрезков АВ и CD, то надо найти их общую меру F. Тогда АВ—pF, CD=qF и АВ : CD — = pF : qF = р : q.
В гармонии пифагорейцы также обнаружили, что «созвучными» будут музыкальные интервалы, отвечающие струнам, длины которых имеют отношение 1 : 2 (октава), 2 : 3 (квинта), 3 : 4 (кварта). Эти открытия привели пифагорейцев к мысли, что «все есть число», что все закономерности мира можно выразить с помощью целых чисел й их отношений. Вот что об этом писал Аристотель:
«Так называемые пифагорейцы были первые, занимавшиеся науками (та ратгщата). Поскольку в дальнейшем они. узнали, что отношения и законы музыкальной гармонии основываются на числах, а также все остальные (предметы) походят на числа... то они высказали мнение, что элементы чисел являются элементами всех вещей и что весь мир в целом является гармонией и' числом» (Аристотель ^Метафизика А5, 985в»).
Платон в «Государстве» пишет, что арифметика есть «учение о четных и нечетных числах». Отрывок из этого древнего учения содержится в IX книге «Начал» (предл. 21—34). Ко времени Евклида было уже доказано, что произведение двух целых чисел АВ тогда и только тогда может делиться на простое число р, если по крайней мере один из сомножителей А или В делится на р. Исходя из этой теоремы, можно доказать, что любое натуральное число АГ однозначно представимо в виде произведения простых:
,	jV=Ofti ..,р\
1 Г 2 S
Пифагорейцы доказали аналогичные теоремы не для любого простого числа р, а для наименьшего простого, т. е. для р=2. Они доказали, что произведение АВ может быть четным (т. е. делиться на 2) тогда и только тогда, если по крайней мере одно из чисел А или В — четно. Отсюда
следовало, что каждое целое N однозначно представимо в виде:
#=2*УХ,
где — нечетно. Исходя из своего учения, пифагорейцы находили «совершенные числа», т. е. равные сумме своих делителей. Они доказали, что если 1+2+...+2я=р — простое, то 2пр будет числом совершенным. Так, при п=1, р=3, 2р=6 — совершенное, при и=2, р=7— простое, значит 22-7=28— совершенное и т. д.
B XVIII в. великий математик Леонард Эйлер доказал, что никаких других четных совершенных чисел, кроме найденных пифагорейцами, не существует.
Но эта первая «арифметизация» математики вскоре потерпела крах. В'самой пифагорейской школе было сделано открытие, показывающее, что существуют «несоизмеримые отрезки», т. е. такие, отношение которых не может быть выражено с помощью целых чисел.	j
Первыми найденными отрезками такого рода были сто- I рона и диагональ квадрата. Аристотель писал: «Если бы I сторона и диагональ квадрата были соизмеримы, то нечет-ное число равнялось бы четному».	1
В «Началах» Евклида в конце X книги имеется дока- в зательство, в точности соответствующее словам Аристотеля. ♦ Оно опирается на «теорему Пифагора», которую умели доказывать пифагорейцы, и на «учение о четных и нечетных».
Вкратце воспроизведем это наиболее древнее известное нам доказательство.
Пусть АВГД — квадрат и пусть сторона и диагональ его соизмеримы (рис. 2): .
АГ:АВ=т : n,	(1)
где т и п не являются оба четными, иначе их можно было бы сократить на 2.
Из (1) следует, что
(АГ)2: (АВ)2 = т2: п2.'
Но по теореме Пифагора (АГ)2 = 2(АВ)2, следовательно, щ2=2п2,	(2)
значит т? — четно. Из учения о четных и нечетных следует, что в этом случае и т — четно (так как произведение

двух нечетных чисел нечетно). Но тогда п — нечетно. Поскольку т — четно, то т—2/. Подставляя т в (2), получим: 4/2=2п2, или п2=2/2, т. е. п2— четно, следовательно, и п должно быть четным, что приводит к противоречию.
Открытие, несоизмеримости означало, что целых чисел и их отношений недостаточно для выражения отношений любых двух отрезков, что с помощью одних только рациональных чисел нельзя строить метрическую геометрию. Это-то и поразило греков.
В диалоге Платона «Законы» афинянин говорит, что поздно узнал о несоизмеримости и что до этого он был подобен неразумному животному. Аристотель писал в «Метафизике»: «...Все начинают с изумления, обстоит ли дело именно так, как «недоумевают», например, про загадочные самодвижущиеся игрушки, или «сходным образом» в отношении солнцеворотов, или несоизмеримости диагонали; ибо у всех, «кто еще не рассмотрел причину», вызывает удивление, если что-нибудь нельзя измерить самою малою мерою».
Вскоре были найдены и другие несоизмеримые отрезки. Так, согласно Платону, Феодор из Кирены показал, что стороны квадратов с площадями 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 несоизмеримы со стороной единичного квадрата, а его юный высокоодаренный ученик — Теэтет доказал, что если площадь квадрата выражается любым целым неквадратным числом N, то сторона его несоизмерима с единицей. Иными словами, было установлено, что если N=^a?, то VN не выражается никаким рациональным числом, что он — иррационален.
Итак, целых чисел и их отношений оказалось недостаточно для выражения отношений геометрических величин. Арифметика в том виде, в каком она была в то время, не могла служить основой, для геометрии.
Какой же мог быть выход из создавшегося кризиса? Расширить числовую область? На той ранней стадии развития математики это вряд ли было возможно. Но как же быть? Может быть, вовсе отказаться от построения абстрактной науки, которая преподносит такие странные сюрпризы? Но и этого пифагорейцы делать не хотели: слишком прекрасными и стройными были их теории.
И вот, пифагорейцы пришли к мысли, что поскольку геометрические величины имеют более общую природу, чем числа, то в основу математики надо положить не арифметику, а геометрию, Это был настоящий революционный переворот, который на первых порах принес богатые плоды. Геометрическое облачение придало всей классической греческой математике необыкновенную красоту и монолитность. При этом и учение о решении уравнений, да и сама арифметика приобрели геометрическую форму. «Геометрическая алгебра» нам хорошо известна, так как она изложена во II и частично в I книгах «Начал» Евклида,. Сей? .час мы дадим, о ней представление и нашим читателям. ,
II. «Геометрической алгеброй» мы теперь называем ту часть античной математики, в которой было построено прямое исчисление отрезков и площадей.
Сложение отрезков осуществлялось геометрически — путем приставления одного к другому, вычитание — путай выкидывания из большего отрезка части, равной меньшему. Операция вычитания была возможна лишь тогда, когда вы-, читаемое не превосходило уменьшаемого. Произведением двух отрезков назывался построенный на них прямоугольник. Разумеется, не имело смысла говорить о сложений прямоугольника и отрезка. Поэтому исчисление, определенное в геометрической алгебре, было «ступенчатым». Первую ступень составляли отрезки, вторую— площади, которые обычно задавались в виде треугольников или прямоугольников, третью — объемы.
Это позволило впервые в истории устанавливать в общем виде алгебраические тождества. Так, тождество
(а+Ь)г^аг+Ь2+2аЬ
было установлено с помощью фигуры, изображенной на рис. 3, в которой АЕ=а, a BE=t.
Рис. 3
Справедливость тождества была этим установлена для любых а и b независимо от их конкретных величин и независимо от того, являются ли они соизмеримыми или нет.
С помощью «геометрической алгебры» стало возможным -изучение общих свойств алгебраических операций.
Так, в I предложении II книги Евклид доказывает, что прямоугольник, заключенный между двумя отрезками, будет равен сумме прямоугольников, заключенных между одним из этих отрезков и прямыми, параллельными ему и рассекающими прямоугольник на части (рис. 4).
Таким образом, если а=а1+аа+а3, то bd^biai+ai+aa)^ =6а>4-Ьа2+6а8.
"С нашей точки зрения, это предложение устанавливает закон дистрибутивности умножения по отношению к сложению. Удивительно, что еще в III в. до н. э. Евклид заменил этот закон и счел необходимым его обосновать!
Рис. 4
Задачи, эквивалентные квадратным уравнениям, формулировались как задачи на «приложение площадей». Первая из них гласила: приложить к данному отрезку а заданную площадь 3 так, чтобы «недостаток» был квадратом. . .
Пусть ДВ=а и S — площадь, заданная в виде треугольника (рис. 5). Надо было «приложить» S к АВ так,, чтобы AAtDC=S, а прямоугольник АуВВ^Р — «недостаток» — был квадратом. Если обозначить AiB=x, то задаче будет отвечать уравнение:
х(а—x)=S.
По-гречески «недостаток» называется словом «эллейп-сие», поэтому такое приложение площадей получило название эллиптического.
Заметим, что дреь.'е рассматривали уравнение элЛип-са относительно его вершины *, т. е. в наших обозначениях оно имеет вид:
y2=kx{a—х), поэтому и соответствующая кривая получила название эллипса.
В «Началах» отмечается, что задача возможна при S^-y- поскольку max х(а — х) — -^~,
4	0 < х < а	4
* Аполлоний записывал это уравнение геометрически — с помощью геометрической алгебры,
а. К
Рис. 6
Другая задача была двойственна первой: приложить к данному отрезку а данную площадь S так, чтобы «избыток» был квадратом. Эта задача эквивалентна решению уравнения:
x(a+x)=S.
«Избыток» по-гречески будет «хиперболе», поэтому и задача получила название гиперболической (отсюда же и название гипербола для кривой tf=kx(a+x)).
К двум рассмотренным нами задачам добавлялась еще третья: преобразовать данный прямоугольник ab в квадрат х2, т. е. требовалось решить уравнение:
х*—аЬ.
Решение всех трех-задач основывалось на преобразовании произведений ab, х(а—х) и х(а+х) в разность двух квадратов, для чего применялось тождество:
.	(а-\-Ь\2 (а — Ь\2
= )'
Оно устанавливалось геометрически (см. рис. 6).
Пусть АВ=а, BD=b, AC=CD =	, ВС =	—
Тогда, как нетрудно видеть, прямоугольник ABMAi равновелик «гномону» (угольнику), получающемуся, если из квадрата на CD вычесть квадрат на СВ. Действительно, прямоугольники АСС^Ах и BDKJ равны между собой,
а часть СВМСг — общая обеим фигурам (на рисунке она заштрихована дважды).
Таким образом, х2 записывался с помощью разности квадратов:
2	/& И- Ь\% (а —»Ь\2
Геометрически х представлялся в виде катета прямо-о ct Ц- ь
угольного треугольника с гипотенузой —£— и другим катетом Такой треугольник было нетрудно построить, проводя из С, как из центра окружность радиусом АС (рис. 7), и восстанавливая из В перпендикуляр BJ к AD. ‘ Так как (BJ)* = (CJ)2 - (СВ)2 = (АС)2 - (СВ)2 =	—
/ u — о\*	г> г
— (—у) , ТО X—BJ.
Зададимся теперь вопросом: какой класс задач можно было решать с помощью «геометрической алгебры»?
Нетрудно видеть, что «разрешимыми» этим методом будут те и только те задачи, которые можно свести к последовательному решению конечного числа квадратных урав1-нений. Так, например, ребро правильного додекаэдра а ==—У"13) может быть получено в результате решения уравнений: .
у2—2k2y(mA-n)-\-ki(m+n)2—4тп—0;
х2—у,
где D — диаметр описанной сферы, k = -g- (т= 15, и= 13.
И наоборот, всякая задача, которую можно решить построением с помощью циркуля и линейки, сводится к последовательному решению квадратных уравнений.
Действительно, все такие построения состоят из следующих элементов: проведение прямой через две точки, нахождение точек пересечения двух прямых, прямой и окружности, двух окружностей. Как нетрудно видеть, все эти точки пересечений можно найти в результате решения либо линейного, либо квадратного уравнений.
Пусть исходные величины лежат в некотором поле * К. Решение линейного уравнения не выведет нас из этого поля. А вот при решении квадратного уравнения
х2+ох—b	(1)
мы получим, вообще говоря, величины, не принадлежащие исходному полю:
xli2=-|±j/’(|y+d=P± у?:
Наименьшим полем, содержащим корни уравнения (1), будет поле, состоящее из величин г + где r,s, q € К. Пусть это наименьшее поле будет /С (V^).
, При дальнейших построениях мы будем оперировать уже . величинами из Kj. Если нам снова придется решать квадратное уравнение
x2+a1x=fe1£ alt bi € Ki,	(2)
то корни его Xi, 2 = Pi ± Vqi
уже, вообще говоря, не лежат в Ki- Величины г, 4- s1 Уqv, где гъ qi £ Ki составят новое поле — К2, минимальное из полей, содержащих корни уравнения (2), и т. д. Таким образом, каждому построению в геометрии Евклида будет отвечать конечная цепочка квадратных уравнений (линейные можно не учитывать):
x2+ax=b, а, Ь £ К, x2+a1x=b1, alt
* Полем называется множество, замкнутое относительно четырех арифметических действий: сложение, умножение, вычитание и деление, обладающих обычными свойствами.
причем коэффициенты каждого последующего уравнения принадлежат полю, содержащему корни предыдущего.
Таким образом, задачи, сводящиеся к решению одного или нескольких квадратных уравнении, и геометрия циркуля и линейки связаны между собой самым тесным образом.
Однако уже в V в. до н. э. в греческой математике появились задачи, которые не могли быть "решены средствами классической геометрической алгебры. Иными словами, появились первые «неразрешимые» задачи. Обычно их насчитывают три и называют знаменитыми задачами древности: задачи удвоения куба, трисекции угла и квадратуры круга. Все три задачи имеют очень длинную историю: две из них были решены лишь’в 30-х годах XIX в., а третья — только в конце его. Впоследствии к этим задачам была присоединена и четвертая: узнать, какие многоугольники с простым числом сторон могут быть построены циркулем и линейкой? Древние умели строить правильные 3- и 5-угольники. Вопрос состоит в том, чтобы узнать, можно ли построить правильный 7-угольник, а если нет, то существуют ли еще правильные многоугольники, которые допускают построен ие циркулем и линейкой? Ответ на этот вопрос был получен только в самом конце XVIII в. молодым К. Ф. Га-. уСсом.
Рассмотрим подробно первую из знаменитых задач. Она формулируется так: построить куб, объем которого был бы в 2 раза больше объема заданного куба, или в наших обозначениях: х3=2а3.	’	_
Задача эта была настолько популярной, что о ней сложили легенду. Рассказывали, что на острове Делос вспыхнула чума. Оракул, спрошенный о том, как избавиться от этого бедствия, ответил, что надо увеличить вдвое жертвенник, имевший форму куба. Поэтому задача об удвоении куба носит еще название делосской.
Естественно, что удвоение куба пытались осуществить с помощью того алгоритма, который уже имелся, т. е. с помощью построений циркулем и линейкой. В переводе на язык алгебры это означало, чтоу^ пытались представить в виде конечной комбинации квадратных корней. Это сделать не удавалось. Тогда началось тщательное, исследование задачи. Гиппократ Хиоский (V в до н. э.) обобщил её и свел к отысканию двух средних пропорциональных между заданными величинами. Пусть задан прямоугольный па-30
раллелепипед а2Ь (всегда можно предполагать, что основание уже преобразовано в квадрат), требуется преобразовать его в куб: xs=p2fe.
Решение задачи, как показал Гиппократ, эквивалентно нахождению таких двух вели чин х и у, что
а _х_у х~у~Ь-
Если Ь—2а, то х как раз равняется ребру удвоенного куба. Вскоре Архит из Тарента показал, что эти величины можно найти, рассмотрев пересечение трех поверхностей: тора (у которого внутренний круг имеет нулевой радиус), конуса и цилиндра. Это решение скорее доказывало существование двух средних между любыми двумя величий нами, чем давало эффективный способ их нахождения. В существовании поверхностей, полученных вращением, окружностей и скольжением прямых по окружности, древние не сомневались. Пересечение таких поверхностей и давало решение. Дальнейшие попытки ученых были направлены к нахождению способа построения двух средних между двумя заданными величинами. Для этого обратились к тем геометрическим местам, которые получаются из пропорции Гиппократа:
ау=х2 и xy—ab.
Пересечение этих двух «мест» и давало решение задачи. Однако исследование «мест» было Делом отнюдь нелегким. Прежде всего надо было установить, являются ли эти «места» непрерывными кривыми (тогда можно говорить о точке их пересечения) или представляют дискретный ряд точек. Только Менехму (вторая половина IV в. до н. э.) удалось представить эти «места» как плоские сечения конусов вращения. Менехм рассмотрел три рода конусов вращения: прямоугольные конуса, тупоугольные и остроугольные. ► Проводя сечения плоскостью, перпендикулярной к образующей, он получил три рода кривых, которые мы теперь называем соответственно параболой, гиперболой и эллипсом. Эти названия кривым дал Аполлоний (III в. до н. э.).
i До этого их так и называли сечениями прямоугольного, тупоугольного и остроугольного конуса. После такого стереометрического определения Менехм переходил к выводу планиметрических свойств полученных сечений и в дальнейшем оперировал только с этими планиметрическими
свойствами, равносильными нашим уравнениям (например, py=xt для параболы).
Для чего же нужно было это стереометрическое определение? По-видимому, как и в решении Архита, оно служило для доказательства существования и непрерывности рассматриваемых геометрических мест*.
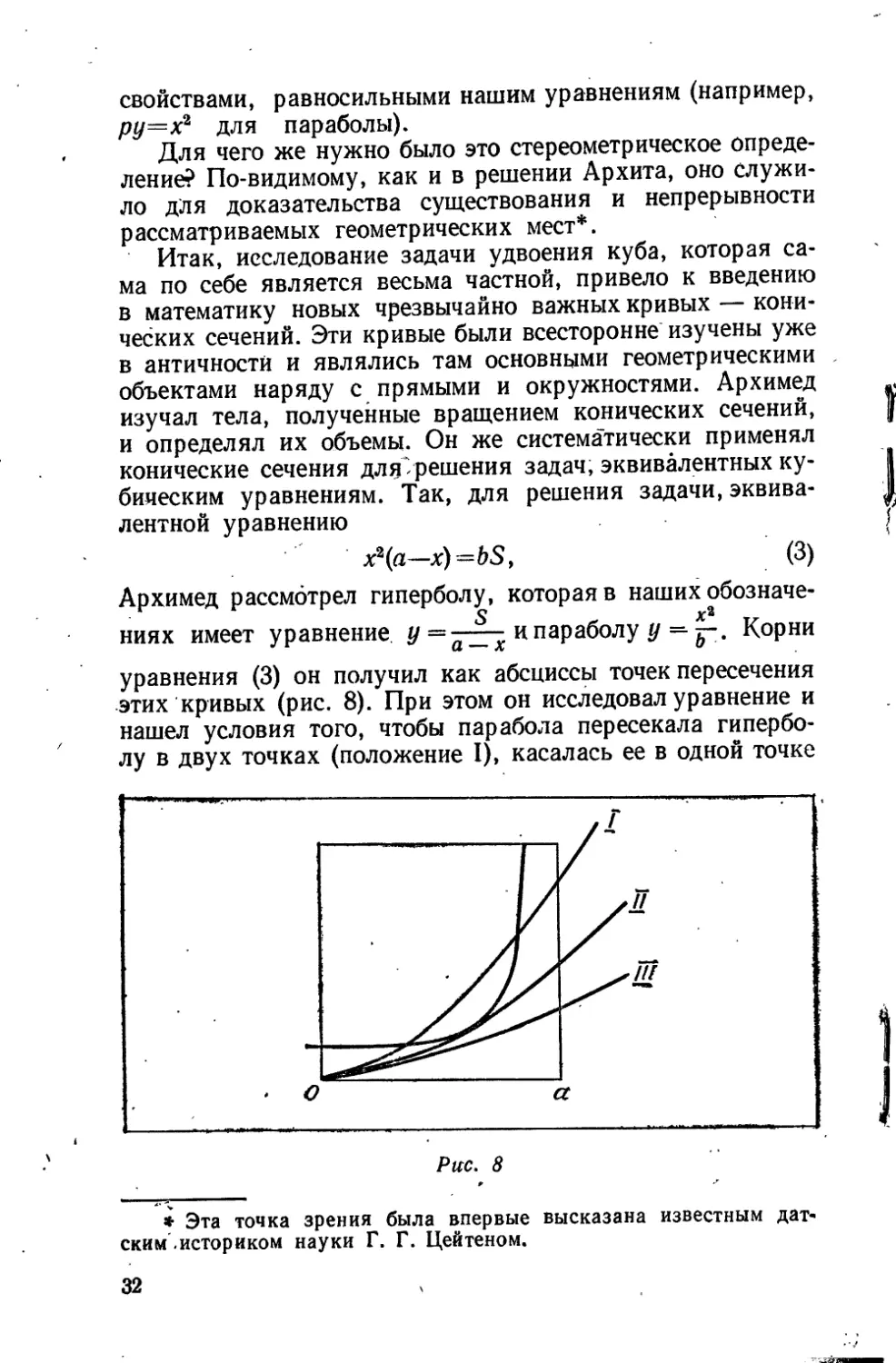
Итак, исследование задачи удвоения куба, которая сама по себе является весьма частной, привело к введению в математику новых чрезвычайно важных кривых — конических сечений. Эти кривые были всесторонне изучены уже в античности и являлись там основными геометрическими объектами наряду с прямыми и окружностями. Архимед изучал тела, полученные вращением конических сечений, и определял их объемы. Он же систематически применял конические сечения для"решения задач, эквивалентных кубическим уравнениям. Так, для решения задачи, эквивалентной уравнению
х2(а—x)=bSt	(3)
Архимед рассмотрел гиперболу, которая в наших обозначе-
S	х2
ниях имеет уравнение у и параболу у = Корни уравнения (3) он получил как абсциссы точек пересечения этих кривых (рис. 8). При этом он исследовал уравнение и нашел условия того, чтобы парабола пересекала гиперболу в двух точках (положение I), касалась ее в одной точке
Рис. 8
* Эта точка зрения была впервые высказана известным датским .историком науки Г. Г. Цейтеном.
(положение II) и не имела с ней ни одной общей точки при (положение III).
Уже простейшее кубическое уравнение, как мы видим, не могло быть решено средствами геометрической алгебры.
. Уравнение степени п>4 нельзя было даже представить непосредственно с помощью равенств площадей или объемов. Здесь приходилось прибегать к «обходному пути», привлекая сложный и неудобный аппарат пропорций. Кроме того, геометрический язык был тормозом для расширения понятия числа. В геометрической алгебре не было места для отрицательных чисел, не говоря уже о мнимых.
Таким образом, геометрическая алгебра, позволившая на первых порах получить большие тактические преимущества перед числовой .алгеброй Вавилона (доказательство тождеств, общее решение квадратных уравнений и исследование их), при дальнейшем развитии математики сделалась помехой. Она, подобно панцирю, сковывала живой организм математики и не позволяла ему правильно расти. Можно сказать, что если с точки зрения тактики она и была полезна, то с точки зрения стратегии означала некое тупиковое направление. j
Для дальнейшего развития всей математики, в том числе и самой алгебры, необходимо было отказаться от геометрического языка и искать новый более общий и более гибкий. Правильный путь, ведущий к построению такого языка, был найден в первые века нашей эры, о чем мы и расскажем в следующем очерке.
3. РОЖДЕНИЕ БУКВЕННОЙ АЛГЕБРЫ
I. II—I вв. до н. э. были временем стремительного возвышения Рима, который покорял и обращал в провинции одно за другим эллинистические государства, города и союзы городов материковой Греции. В 30-гг. до н. э. пало последнее из эллинистических государств — Египет, и была основана Римская империя.
В результате этого положение бывших эллинистических государств коренным образом меняется. С одной стороны, прекращаются разорительные войны и прямой разбой, что приводит к более устойчивому экономическому положению, но, с другой — эллинистические государства теряют самостоятельность и, по образному выражению Плутарха, всегда сознают, что над их головой занесен «римский сапог».
И все же греческая наука вновь оживает. В первые века н. э. Александрия остается научным и культурным центром древнего мира. Рим никогда не мог сравниться с ней в этом отношении. По существу, он так и не приобщился к глубинам эллинской мысли. Римляне с презрением относились к математике и друг'йм абстрактным наукам, ценя только узко практические знания. Но и этим должны были заниматься греки^ сирийцы и другие покоренные народы, а не римляне, уделом которых была власть над миром. Как писал Вергилий:
Тоньше другие ковать будут жизнью дышащую бронзу, — Верю тому, — создадут из мрамора лики живые, Красноречивее будут в судах, движение неба Тростью начертят своей и вычислят звезд восхожденья, Ты же, римлянин, знай, как надо народами править. ,
Конец I и II в. и. э. обычно называют греческим возрождением, имея в виду, что это было временем жизни и творчества таких великих писателей, как Плутарх и Лукиан. Но такой же расцвет мы наблюдаем и в естественных науках: в I в. в Александрии работал прекрасный математик и талантливый инженер-изобретатель Герои, который первым открыл движущую силу пара, в конце века — математик и астроном- Менелай, создатель системы геометрии и тригонометрии на сфере (первой системы неевклидовой геометрии), а во II в.— знаменитый астроном и математик Клавдий Птолемей, создавший геоцентрическую модель Солнечной системы (она просуществовала вплоть до XV— XVI вв.). Уже в творчестве этих ученых наметился поворот к вычислительной математике, к расширению понятия числа, к отказу от геометрической алгебры.
Эти тенденции проявились с особой силой в творчестве величайшего алгебраиста древности Диофанта Александрийского, о жизни которого мы почти ничего не знаем. Правда, в Палатинской антологии, составленной ученым грамматиком и арифметиком Метродором Византийским (IV в. н. э.), сохранилась эпитафия, которая гласит:
Прах Диофанта гробница покоит: дивись ей — и камень Мудрым- искусством его- скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком, И половину шестой встретил с пушком, на щеках. -Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец. Только полжизни отцовской возлюбленный сын его прожил-Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе.
Тут и увидел предел жизни печальной своей *.
Отсюда нетрудно подсчитать, что Диофант прожил 84 года. Однако для этого вовсе не нужно владеть «мудрым искусством его». Достаточно уметь решать уравнение 1-й степени с одним неизвестным, а это умели делать египетские писцы еще за 18 веков до н. э.
На этом наши сведения о Диофанте кончаются. Однако его творчество сыграло настолько большую роль в истории алгебры, что ученые потратили немало усилий, чтобы определить время его жизни. Проследим за ходом их рас-суждений. Прежде всего известно, что Теон Александрийский в своих комментариях к. «Альмагесту» Клавдия Птолемея привел отрывок из сочинений Диофанта. Поскольку деятельность Теона падает на вторую половину IV в. н. э., очевидно, Диофант не мог-жить позднее середины IV в. Этим определяется верхний предел промежутка возможного времени жизни Диофанта. С другой стороны, сам Диофант в своей работе «О многоугольных числах» дважды упомина- ' ет Гипсикла, математика, жившего в Александрии в середине II в. до н. э. Итак, нижним пределом является вторая половина II в. до н. э. Таким образом, получаем промежуток в 500 лет!
Сузить этот промежуток попытался П. Таннери, известный историк науки, издатель критически проанализированного текста сочинений Диофанта, который теперь принят в качестве канонического. В библиотеке Эскуриала он нашел отрывок из письма Михаила Пселла, византийского ученого XI в., текст которого был искажен при переписках. После восстановления Таннери один из отрывков письма может быть переведен так: «Что касается этого египетского метода, то Диофант рассмотрел его более точно и ученнейший Анатолий, после того как собрал наиболее важные части этой науки, посвятил их своему другу Диофанту». Известно, что Анатолий Александрийский составил «Введение в арифметику» в десяти частях, фрагменты из которой дошли до нас в передаче Ямблиха (IV в. н. э.). Известный историк церкви Евсевий (IV в. н. э.) также упоминает Анатолия и превозносит его за глубокие познания в арифметике, геометрии и астрономии. Но Анатолий жил в Александрии в середине III в. н. э., а в 270 г. покинул
* Приведенный перевод с древнегреческого принадлежит С. П. Боброву.
ее, чтобы принять сан епископа Лаодикийского. Таким образом, если Таннери правильно прочел письмо Пселла, то Диофант жил в середине III в. н. э.
Эго подтверждается еще и тем что сама «Арифметика» Диофанта посвящена «достопочтенному Дионисию», который, как это видно из введения к I книге, интересовался наукой о числах и ее преподаванием. Между тем с 231 по 247 г. во главе Александрийского христианского училища для юношества был Дионисий, ставший в 247 г. епископом Александрийским. По предположению Таннери именно ему и была посвящена «Арифметика».
Поэтому обычно теперь считают, что Диофант жил около 250 г. Однако существуют свидетельства, правда, весьма поздние, которые ставят эту дату под сомнение. Дело в том, что первым европейским математиком, серьезно изучавшим «Арифметику» Диофанта, был Рафаэль Бомбелли. В предисловии к своей «Алгебре» (1572 г.) Бомбелли писал, чт > он нашел в библиотеке Ватикана замечательную руко-пи ь, посвященную науке о- числах, составленную «неким Диофантом, греческим автором, жившим в эпоху Антонина Пия». Эту же дату повторяют затем Виет, Ферма и другие ученые XVI—XVII вв.
Но Антонин Пий был римским императором в середине II в. н. э., т. е. время жизни Диофанта -отодвигается на 100 лет назад, и он оказывается современником астронома Клавдия Птолемея и деятелем «греческого возрождения».
Откуда же почерпнул свои сведения Бомбелли? Это абсолютно неизвестно. Можно только предположить,. что он читал в библиотеке Ватикана какие-то дополнения к рукописи Диофанта, которые были с тех пор утеряны. Быть может, новые находки на арабском Востоке или в  недрах европейских библиотек прояснят этот вопрос. Пока что наиболее вероятным временем жизни Диофанта представляется столетие с середины II в. по середину III в. н. э.
Основным произведением Диофанта была «Арифметика», которая, как он сам об этом пишет, была разделена на 13 книг. Из них до нас дошли 6 книг на древнегреческом языке, а недавно были найдены и опубликованы еще 4 книги в арабском переводе, которые также приписываются Диофанту.
«Арифметика» явилась поворотным пунктом в развитии алгебры и теории чисе^. Именно в ней произошел окончательный отказ от геометрической алгебры. Но это вовсе не означало, что алгебра вернулась к тому состоянию, ко
торое было у нее в Вавилоне; Нет, в «Арифметике» алгебра обрела новый язык, гораздо более оперативный и удобный, чем язык геометрии. Именно здесь родилась буквенная алгебра.
Введение к «Арифметике» представляет собой краткий трактат по алгебре. Оно начинается с описания символики. Диофант называет неизвестное «числом» (’apiOpos) и применяет для него знак 6, который уже встречался у Герона и в мичиганском папирусе (II в. н. э.). Возможно, что этот знак представляет последнюю букву в слове ’apt'&poS, т. е. это «концевая сигма». Дело в том, что греки пользовались алфавитной нумерацией, т. е. все буквы их алфавита имели числовые значения; первые девять букв а, р ,..., Ф означали числа 1, 2, ..., 9; следующие девять букв i, х,...— последовательные десятки: 10, 20, ..., 90, наконец, последние 9 букв — сотни от 100 до 900*. Над буквами, означающими числа, сверху, ставили черточку, чтобы не спутать их со словами. Например, число 121 в греческой записи выглядело так: рха. При этом буква a — «сигма»— имела числовое значение 200, но в конце слова она записывалась иначе, а Именно: S. Этот-то знак, не имеющий числового значения, и мог быть взят для обозначения неизвестного. После этого Диофант вводит 6 положительных и 6 отрицательных степеней неизвестного. Символы для положительных степеней являются сокращениями их греческих названий. Квадрат неизвестного (динамис — сила, степень) Диофант обозначает символом AY, куб (кубос— куб)—KY, четвертую степень (динамодинамис — квадрато-квадрат)— AYA, пятую степень (динамокубос — квадрато-куб)— AKY, шестую степень (кубокубос — дубо-куб) — KYK.
Отрицательные степени Диофант определяет как дроби с числителем единица и знаменателем, равным соответствующей степени неизвестного. Для отрицательных степеней вводится знак, напоминающий косой крест, который добавляется справа к символу соответствующей положительной степени.
У Диофанта есть также специальный символ для неизвестного в нулевой степени, М, который он (так же как современный алгебраист) не отождествляет с числом 1. Например, многочлен (1 •х2-Ы0х+1-х°), который мы запи-
* Поскольку в греческом алфавите всего 24 буквы, то к нему. для нужд нумерации добавляли еще 3 «архаические буквы» — «вау», «коппа» и «сампи».
сываем обычно более кратко х*4-1 Ох-Н, отождествляя 1-х2 с х2 и 1-х° с 1, в символике Диофанта выглядит следующим образом:
AYagiMa.^
Отождествления йаГс а у Диофанта нет и не может быть. Это происходит из-за того, что Диофант не ввел специальных знаков для сложения и умножения. Их отсутствие восполняется строго определенным порядком записи степеней неизвестного и коэффициентов, при котором коэффициент всегда следует за знаком степени. При этом для того чтобы свободный член не сливался с коэффициентом при старшей степени, необходим символ для нулевой степени неизвестного, выступающий в роли знакоразделителя.
Помимо перечисленных символов, Диофант употребляет еще знак □ для неопределенного квадрата.
Заметим, что введение шести первых степеней неизвестного означало решающий Щаг на пути построения алгебры, независимой от геометрии. Ведь только три первые _ степени неизвестного е, ДY и KY могли быть истолкованы геометрически как образы в трехмерном пространстве. Введя четвертую, пятую и шестую степени, а также обратные к ним величины, Диофант решительно порвал с классической геометрической алгеброй. Этот шаг, по-видимому, оставался непонятым многими из его современников и многими из последующих ученых. Так, Папп Александрийский писал (конец III в. н. э.): «Нельзя говорить о данном отношении какого-нибудь предмета, построенного на четырех прямых, к предмету, построенному на остальных, потому что не существует ничего, что заключало бы больше, чем три измерения. Однако незадолго до нас стали позволять себе выражаться подобным образом, не указывая, впрочем, при этом на что-либо сколько-нибудь вразумительное».
После введения символов для степеней неизвестного Диофант формулирует правила умножения хт на хп, где |m|<6, |п|<6; |/п+п| <6, которые в наших обозначениях* можно записать как хтхп—хт+п.
. При этом он выделяет два правила, носящих совершенно общий характер.
* .Мы будем в дальнейшем пользоваться для обозначения степеней* неизвестного современными знаками.
1. «Всякий вид (eiSoS), умноженный на одноименную с ним часть, производит единицу», т. е. произведение степени хт на обратную ей величину х~т дает 1.
2. «Так как единица остается всегда неизменной, то умноженный на нее вид остается тем же видом», т. е. существует такой элемент 1, что для каждого т
хт-1=хт.
Нетрудно видеть, что здесь впервые в явном виде выделены основные теоретико-групповые свойства операциц умножения.
Приходится только удивляться глубине проникновения Диофанта в алгебраическую суть вопроса.
Наконец, Диофант вводит знак Ж (который он сам характеризует как «перевернутую и укороченную букву "ф), отвечающий нашему знаку «минус». О нем мы будем говорить подробнее в следующем пункте. Сейчас скажем только, что при записи многочленов или'уравнений Диофант выписывает сначала подряд все положительные члены, а затем после знака Д — все отрицательные. Например, многочлен
х8—2х2+10х—3 в записи Диофанта выглядел бы так: . •	.	г .
К
(здесь а=1, 0=2, у=3, i=10),
При записи уравнений Диофант применяет знак равенства Ча, представляющий собой две первые буквы слова Чао? — равный. Например, уравнение-х3=2—х в его записи будет
КасбМрМа
—
В конце введения формулируются правила преобразования уравнений, попавшие в Европу через арабов и получившие поэтому арабизированные названия «ал-джебр» и «ал-мукабала». Эти правила разрешают прибавление к обеим частям уравнения одинаковых членов и приведение подобных членов.
Таким образом мы видим, что во введении к «Арифмети-ке» Диофант изложил в аксиоматической форме основные алгебраические понятия и элементы алгебраической символики, т. е. теоретические основы той части математики,
которая в дальнейшем получила название алгебры, а не арифметики.
Однако анализ решений задач позволяет обнаружить в самой «Арифметике» более широкие теоретические основания, чем те, которые явно изложены во введении. Прежде всего это относится' к числовой области Диофанта.
II. Числовая область Диофанта. Во введении дается традиционное определение числа как некоторого количества или множества единиц. В дальнейшем при решении задач под числом уже понимается любое положительное рациональное число. Решение задачи Диофант всегда ищет в области положительных рациональных чисел. В то же время когда возникает угроза получения отрицательного, или иррационального решения, Диофант, чтобы прийти именно к положительному и рациональному, решению; проводит дополнительный анализ условий задачи. Часто этот анализ сложнее й тоньше самого способа решения. Таким образом, казалось бы, напрашивается вывод, к которому' обычно приходили исследователи «Арифметики», что Диофант работает в области положительных рациональных чисел. С этим нельзя согласиться в полной мере, Верно лишь то, что Диофант ищет решения* задач в области положительных рациональных чисел.
Как хорошо известно, одних положительных рациональных чисел недостаточно для построения алгебры. Действительно, для этого нужна область, в которой можно беспрепятственно производить все четыре действия арифметики, т. е. поле.
Как же мог построить свою алгебру Диофант?
Мы постараемся показать, что он ввел отрицательные числа, свободно оперировал с ними, хотя они еще и не получили у него права гражданства.
Действительно, в определении (IX) введения он сформулировал правило знаков:
«(IX) Недостаток (ZsupiS), умноженный на недостаток, дает наличие (unap|ie); недостаток же, умноженный на наличие, дает недостаток; знак же для недостатка — Л-, укороченное и опрокинутое вниз ф».
Здесь словом «недостаток» переведено греческое слово Xeupis. Это слово — специальный математический термин, в обычных словарях оно отсутствует. Произведено оно от глагола Xeijtto, одним из значений которого является «недоставать», «не хватать». Поэтому в русском переводе был
чис-них
для
выбран термин «недостаток». Поль Таннери в своем z классическом издании «Арифметики» Диофанта переводит термин Aeit|ng на латынь словом «.minus» — меньше, а термин vnapJjig, означающий по-гречески «существование», «бытие», а во множественном числе — «имущество» — словом «plus» — больше. Во введении к «Ариф-метике» twiapSjig является специальным термином для обозначения положительного числа. Заметим еще, что Xeeipig нельзя переводить словом «вычитаемое», как это иногда делают, так как вычитание Диофант обозначает словами, производными от глагола a<paipe<o — отнимать. К тому же правило (IX) он приводит до рассмот- рения многочленов.
Таким образом, Диофант вводит отрицательные ла, по существу, аксиоматически, формулируя для «правило знаков»:
(—)Х(—) = (+); <-)Х(+Ь(-).
Диофант 'не определяет специальных правил
сложения и вычитания отрицательных чисел, но пользуется ими при оперировании с многочленами, имеющими как положительные, так и отрицательные коэффициенты. Так, например, в ходе решения задачи III. 8 «Арифметики» Диофанту требуется из x2-}-4x-t-l вычесть 2x4-7. В результате он получает х24-2х—6. Здесь Диофанту для вычитания многочленов необходимо произвести вычитание их свободных членов 1—7=—6, т. е. из меньшего числа вычесть большее, что невозможно без введения отрицательных чисел. Другой интересный пример мы находим в задаче VI. 14, по ходу решения которой из 54 вычитается 90—15х2 и получается 15х2—36. Здесь, кроме того, что из меньшего числа вычитается большее (54—90=—36), производится также вычитание одночлена (—15х2). При этом Диофант, очевидно, пользуется правилом —(—а)=а. Это показывает, что он владел правилами знаков не только для умножения, но и для вычитания. Последние, видимо, были достаточно хорошо известны, так как Диофант не счел нужным их специально формулировать.
Наконец, отрицательные числа неявно встречаются и в промежуточных вычислениях. Например, в задаче 11.11
Диофант полагает сторону некоторого квадрата равной х^-2, при этом в решении участвует только квадрат (х—2)2, а не его сторона. В конце задачи Диофант, решая уравнение относительно х, находит х=15/8. Легко видеть, что тогда выражение х—2=—1/8<0. Это, однако, не смущает Диофанта, так как для нахождения решения задачи он оперирует со значением квадрата (—1/8)3, т. е. с положительным числом, 1/64. Аналогичная ситуация имеет место в задачах II. 11—13, 20, 21, 23, 28, 29, 32 и многих других.
Таким образом, хотя решения задач по традиции ищутся в области положительных рациональных чисел, в ходе решения задач Диофант вводит отрицательные числа и оперирует с ними, расширяя тем самым числовую область до поля рациональных чисел.
III. Выяснив, что представляет собой числовая область Диофанта, мы теперь рассмотрим возможности его алгебраической символики.
С помощью описанных им во введении алгебраических символов Диофант может записать, во-первых, любой многочлен от неизвестного х, степень которого <6, и, во-вторых любой многочлен от х-1, степень которого также <6. При решении некоторых задач Диофант работает и с рациональными функциями от х, степень числителей и знаменателей которых <6.
Мы видим, что символика Диофанта характеризуется, во-первых, ограничением на число неизвестных и, во-вторых, на величину степени. Возникает вопрос: насколько каждое из этих ограничений существенно?
Начнем с ограничения на степень. Диофант вводит символику только для первых «шести степеней неизвестного. Разумеется, ограничение именно шестой степенью не принципиально. Число 6 выбрано в качестве верхней границы для вводимых степеней, видимо, потому, что многочленами большей степени Диофанту просто не приходится пользоваться.
Уже в арабских книгах «Арифметики» встречаются 8-я и 9-я степени неизвестного, которые, возможно, были добавлены кем-нибудь из комментаторов.
Теперь мы перейдем к другому важному ограничению — на число неизвестных.
Алгебра Диофанта на первый взгляд есть алгебра рациональных функций от одного неизвестного. Но большинство его задач сводятся к неопределенным уравнениям от 42
многих неизвестных (часто пяти, шести и больше). Например, задача II.8 формулируется так: «Разложить заданный квадрат на два квадрата». Для ее записи в виде уравнения необходимо два неизвестных: х2+^=а2.
Задача III. 19 эквивалентна системе:
(*1 + Х2 + Х3 + х4)2 + Xi = yl,
(xi + х2 + х3 + х4)2 — Xi = г1, i — 1,2,3,4,
т. е. в записи должно участвовать 12 неизвестных. Как же Диофант записывает эти уравнения и оперирует с ними?
Уже в математике Древнего Вавилона решение алгебраической задачи с конкретными числовыми Данными служило одновременно двум различным целям: получению численного решения задачи и демонстрации общего приема решения целого класса однотипных задач. Как мы видели, имелся класс задач на отыскание «длины» и «ширины», если заданы сумма (или разность) их и «площадь», т. е. произведение «длины» на «ширину». При этом составлялись группы таких задач, имеющих одни и те же, заранее подобранные ответы. Это делалось для того, чтобы выпуклее показать общность алгоритма их решения. Действительно, в этом случае центр тяжести переносился на сам алгоритм, так как численные ответы были заранее известны и могли служить только для проверки правильности применяемого способа' решения.	~
В «Арифметике» Диофанта роль числовых параметров существенно расширяется. Обычно для решения задачи Диофант представляет все искомые числа как рациональные функции от одного неизвестного и параметров. Параметрам, правда, придаются конкретные числовые значения, но при этом, как правило, Диофант оговаривает, что они могли бы быть и любыми другими числами. Эти-то параметры и играют в «Арифметике» роль дополнительных переменных.
Так, при решении задачи II.8 (формулировку см. ранее) Диофант принимает а2=16, один из искомых квадратов берет в качестве неизвестного t2 (мы применяем для простоты более привычные нам обозначения), а сторону второго составляет «из некоторого количества t минус столько единиц, сколько их найдется в стороне 16-ти, пусть это будет 2/—4», т. е. Диофант хочет положить второй квадрат рав
ным (kt—а)2, но поскольку у пего нет знаков ни для произвольного параметра k, ни для заданного произвольного числа а, он, объяснив, что k — произвольно, а а — сторона заданного квадрата, берет 2t-^~ 4, где 2 есть и число «2», и символ для произвольного, рационального числа.
Сделаем подстановку Диофанта:
P+(kt—а)2=а2.
Откуда
. 2ak
_ »61 ,,	ht	„	б3 — 1Г 121
5|; I/	kt	a	fe2_|_ j I - 5 .
Однако иногда оказывается, что произвольно выбран- J ныё значения для параметров не годятся, т. е. основное ' неизвестное получается отрицательным и иррациональным. Тогда оказывается необходимым предварительное исследо- ! вание задачи для выяснения того, какие ограничения еле- ] дует наложить на выбор параметров.	4 I
Так, например, задача IV.8 сводится к системе:	|
'	x? + x2 = !/3,
xt+x2=y,	' '
при решении которой Диофант полагает: xz=t, xk—$t> где 0=2.
Из второго уравнения он находит:
а из первого
*___
(0+1)3- 03 /
Поскольку 0=2, то /2=1/19, т. е. t — иррационально. Диофант анализир.ует, как t2 составлено из параметра 0, иначе говоря, находит/2=/-1 (0), где f (0)=(0+1)3—03, откуда делает вывод, что исходная система будет иметь рациональное решение, если
(0+1)8—03=П.
Он берет 0 в качестве нового неизвестного 0=г (обозначает его той же буквой, что и первоначальное) и получает вспомогательное уравнение:
Зг2+Зг+1 = П.
, Решая это последнее уравнение своим методом, т. е. полагая □ =#?— I)2, Диофант получает:
г .3 + 2*	f
*	*2 — 3»
другими словами, это означает, что параметр Р можно выбирать только из класса чисел
3 + 2*
*2—3*
Отметим, что знаком £ (см. стр. 37) в процессе решения-одной и той же задачи Диофант может обозначать последовательно различные неизвестные. Так, в рассмотренной за даче s — это сначала прибавляемое число х2, а затем неизвестное во вспомогательном уравнении.
Замечательно, что Диофант часто сознательно выбирает для несвободных параметров числа, которые не приводят к решению, чтобы показать, как надо проводить анализ задачи.
То обстоятельство, что Диофант смотрит на параметры не как на конкретные числа, а, скорее, как на символы, ярко подтверждается при решении задач Ш.10 и III,11. Рассмотрим первую из них:
*	1X2+0 = у?;
*	2X3+0 = 02;
*	3*1 + a=yl.
Диофант принимает а=12 и полагает fa-e, (8=5), тогда х1х2=ь2—а, и он принимает Xi=(e2—а)/, х2=1//. Этим первое уравнение обращается в тождество. Затем он полагает у2=Ь, (6=4), тогда х2х8=62—а, но x2=W, значит х3=(62—a)t. Остается удовлетворить третьему уравнению:
(82—а) (6а—а)Р+а=у*.
При выбранных Диофантом параметрах получаем:
52/2+12=//2.
Это уравнение имеет рациональное решение /=1, z/3=8, а значит, оно имеет и бесконечно много других рациональных решений, которые могут быть найдены методом, изложенным во II книге «Арифметики». Но Диофант как будто не замечает этого. Ведь существование решения уравнения
при <5=4 и е=5 получилось чисто случайно! И Диофант ищет общие условия, которые надо наложить на параметры 8 и 6, чтобы было обеспечено существование рационального решения.
Таким образом, в алгебраическом формализме Диофанта наряду со знаками для неизвестного и его степеней большую роль играют знаки конкретных чисел, которые несут дополнительную нагрузку, выполняя функцию параметров. При этом они могут служить:
1). знаками свободных параметров,
2) знаками для несвободных параметров (параметров, удовлетворяющих некоторым дополнительным условиям).
Алгебраический формализм Диофанта представляет, как мы думаем, особый этап в развитии алгебры, характеризующийся тем, что отсутствие нескольких неизвестных и буквенных обозначений для параметров компенсируется по-лифункциональным использованием* знаков для единственного неизвестного и его степеней и знаков для конкретных чисел. Этот этап, начало которому было положено «Арифметикой» Диофанта, продолжался .вплоть до второй половины XVI в. Только в это время в алгебре были введены сначала знаки для второгр, третьего и т. д. неизвестных (Бомбелли и Стевин), а затем'знаки для параметров и буквенное исчисление (Ф. Виет).
Развитие алгебры показало, что алгебраический формализм Диофанта, хотя и менее мощный, чем современный, способствовал замечательным успехам как в изучении диофантовых уравнений, так и позднее, в решении определенных уравнений 3-й и 4-й степеней.
Здесь уместно обратить внимание читателя на тот факт, что основной проблемой, при исследовании которой развивались -и совершенствовались метода алгебры, была не проблема решения уравнений в радикалах, которая 'занимала сравнительно мало места, а проблема решения неопределенных уравнений. Мы видели, что именно с ней было связано первое введение буквенной символики, возникновение алгебраического формализма, о котором мы писали, а также расширение понятия числа до поля всех рациональных чисел. Мы покажем, что и дальнейшее развитие алгебры вплоть до Введения буквенного исчисления было связано с исследованием неопределенных уравнений.
4. СОЗДАНИЕ БУКВЕННОГО ИСЧИСЛЕНИЯ
I. Диофант был последним великим математиком древности. После него работали только более или менее талантливые комментаторы. Но вскоре и такие работы прекратились. Античная наука и культура погасли вместе с гибелью всего античного общества. Факел знания был передан на Восток. В течение более восьми веков (VII—XV вв.) научные исследования велись народами, населявшими Иран, Среднюю Азию, Малую Азию, Северную Африку. В VII— VIII вв. они были объединены в Арабский халифат, и хотя огромное государство арабов, оказалось недолговечным и вскоре распалось иа части, господствующим научным языком стал арабский.
В VIII в. в Багдадском Доме мудрости работала целая коллегия переводчиков и комментаторов. Были переведены «Начала» Евклида, многие сочинения Архимеда, философские трактаты Аристотеля.
Математики стран Востока познакомились с «Арифметикой» Диофанта, которая была переведена на арабский язык в начале X в., и усвоили содержащиеся там алгебраические методы. Ал-Караджи (X в.) в своей книге «Ал-Фах-ри» ввел бесконечный ряд степеней неизвестного, заметив, что степени образуют цепь пропорций, которую мы можем записать так: 1 : х=х : х2=хг:х3=...
К этому ряду добавляется, как и у Диофанта, ряд «частей», т. е. отрицательных степеней неизвестного:
___L.L_
X • X2 X2  Xs — X* • X* ~~ ' • •
Алгебра в это время уже воспринимается как самостоятельная наука — наука, о решении уравнений. Однако ученые стран арабского Востока совершенно отказались от пользования буквенной символикой. Название неизвестного и его степеней они записывали е помощью специальных слов. Например, неизвестные они называли «вещью»— шай (что потом было переведено на итальянский и получило название «сова»). Нередко в научных трактатах даже числа записывались не символами (цифрами), а словами. Поэтому-то с точки зрения создания исчисления математика стран арабского Востока ничего не дала.
Другим крупным научным центром была Византия (Константинополь), где хранились, тщательно переписывались и комментировались древнегреческие рукописи.
Из научных центров арабского Востока и Византии ; начиная с X—XII вв. научная мысль стала проникать ; в Европу. В XI—XII вв. здесь переводили на латынь Евклида, Архимеда и Аристотеля.
Первым Крупным математиком Европы был Леонардо Пизанский (или Фибоначчи) (1180—1240). Он родился в богатом торговом городе — республике Пизе (откуда и происходит добавок «пизанский») и юношей жил в Алжире, где его отец был торговым консулом. Леонардо познакомился с десятичной позиционной системой счисления, принятой у арабов, и с их алгеброй. Он путешествовал по Египту, Сирии, Провансу и Сицилии и, вернувшись домой в Пизу, издал там в 1202 г. книгу «Liber abaci», в которой изложил десятичную позиционную систему и правила арифметических действий в ней, арифметику, геометрию и алгебру. Для своего времени это была замечательная книга, равной которой не появлялось в ближайшие 250 лет.
Достаточно сказать, что в ней решались квадратные уравнения, рассматривались арифметическая и геометрическая прогрессии и был введен и исследован знаменитый ряд Фибоначчи:
1, 1, 2, 3, 5, 8, ....
члены которого удовлетворяют соотношению: «П‘И=^П~ЬЫП—!•
Однако, ничего не зная о символике Диофанта и его методах, Леонардо не пользовался алгебраическим языком.
В .Европе буквенные обозначения для неизвестного и его степеней начали применять только в XV в., после того как пала Византия и греческие ученые переехали на Запад. Но в Византии пользовались не системой обозначений Диофанта, основанной на аддативном принципе, а неудобной системой, описанной у византийского ученого Михаила Пселла (XI в.) и восходящей, по-видимому, к Анатолию, другу и корреспонденту Диофанта. Эта система была основана на мультипликативном- принципе, т. е. квадрато-куб означал в ней 6-ю степень, а кубо-куб — 9-ю. 5-я степень, которую нельзя было представить в виде произведения 2“ и 3₽ , называлась «первой невыразимой», 7-я —«второй невыразимой». Приведем для примера обозначения, которые употреблял Лука Пачоли (ок. 1445-ок, 1515) в своей знаменитой книге «Сумма знаний по арифметике, геометрии, отношениям и пропорциям», которая 48.
была напечатана в Венеции в 1494 г. (это была первая печатная книга по математике). Вот эта таблица:
х°—га° — [питего] х—со — Icosa ] х2—се— [сел so] х3—си [cubo] х*—се се— [cetiso de censo I х5—par°— [primo relate] x°—ce cu — [censo de cubo] x7—2°r°— [secundo relate] x°—ce ce ce— [censo de censo de censo] ,	x®—cu cu— [cubo de cubo]
xl0—cep°r9— [censo de primo re la to]
x29—9	— [nono rela to 1
finis
Мы видим, что Лука распространил обозначения на первые 29 степеней неизвестного, причем 9 из них оказались «невыразимыми» (relate — это, по-видимому, ошибочный .
перевод греческого термина aXoyo’s—«невыразимый», прочитанный как о Xoyos —«отношение»). Никаких символов для отрицательных степеней неизвестного у него нет.- За-' то он вводит обозначения для действий:
Р т
R
R3
В4или RR
Аналогичные обозначения применяли и так называемые «коссисты»— математики-алгебраисты Германии и Чехии. Наиболее известный из них Иоганн Видман (1460 г.— первая половина XVI в.) ввел для сложения и вычитания знаки-|-и—, которые быстро вытеснили итальянские обозначения р и т.
Наконец, Рафаэль Бомбелли (Италия) ц Симон Стеввд (Нидерланды) ввели новые обозначения для степеней неиз* вестного, в которых подчеркивалась однородность ряда степеней* Например, х, х*, х*. ... БомСюлди обозначал символами	я Стевин
Так что многочлен х’— 10х+5 в записи Бомбелли выглядел так: Й/й 10^55.
Стевин ввел обозначения в для второго неизвестного н его Степеней:
а также для третьего: ter. ф, ter.ter..
Однако никому из математиков до Виета (1540—1603) не пришло в голову ввести обозначения для произвольных постоянных величин, входящих в задачу. Поэтому формул, к- которым мы так привыкли в математике, до Виета не было.
II. Между тем европейская алгебра в XVI в. добилась первых крупных успехов — были решены в радикалах уравнения 3 и 4 степеней. Эти задачи много веков представлялись неразрешимыми. Еще Лука Пачоли в своей «Сумме» сравнивал их с квадратурой круга.
С решением кубических уравнений была связана целая история, наполненная/ интригами, коварством и обманом. Мы не будем здесь на ней останавливаться, отсылая любознательных читателей к интересной брошюре С. С. Демидова*, изданной в этой же серии. Скажем только, что формулы для решения уравнения
x>Jrpx=q, р, <?>0,	(1)
были впервые, по-видимому, найдены профессором университета в Болонье Сципионом дель-Ферро (1456—1526), который не публиковал своего открытия, затем вновь в 1535 г. самостоятельно получены Никколо Тартальей (1500—1557), а впервые опубликованы они были в 1545 г. в книге Дж. Кардано «Ars magna» (т. е. «Великое искусство»— этим именем
* Принцип такого обозначения также содержался у Пселла, который называл х — первым числом, х2— вторым числом, х8 — третьим и т. д..
♦ См.: С. С. Демидов. У истоков современной алгебры. М., «Знание», 1971,
тогда называли алгебру) и с тех пор носят название формул Кардано. Н. Тарталья решил и уравнение вида:
x3=px+q, р, <7>0.	(2)
Он пришел к формулам, которые в современных обозначениях выглядят так:
<3>
Если ^)2~ (F)3 <'(^> то в Ф0РмУле (3) под квадратным корнем оказывается отрицательное число, что не позволяло найти корень х уравнения (2). Этот случай получил назвав ние «неприводимого». Он послужил камнем преткновения и для Тартальи, и для Кардано.
Читатель может уДивиться: ведь и при решении квадратного уравнения
х2+Ьх+с—0	(4)
Ь*	TZ
может случиться, что^—с<0_ Какие же новые трудности принесла формула (3)?
Дело в том, что при — с < 0 уравнение (4) не имеет действительных корней. Оба корня его будут комплексными сопряженными числами:
т. е. можно сформулировать следующее ограничение: для того чтобы корни уравнения (4) были действительными; нужно, чтобы
; D-gy-oo:
Напротив того, 1в случае	< 0 оказалось, что
уравнение (2) имеет действительный корень. И дажетри действительных корня! Это можно видеть из примера уравнения №= 15x4-4.	,(2')
Уравнение (2') имеет корень х=4.
Два другие его корня можно найти, решая квадратное уравнение:
£=^x^ = x* + 4x+1 = q, -
X — 4
Его корнями будут: х1== — 2 +]/Зих2 = — 2—Уз.
Итак, исходное уравнение имеет три действительных корня:
4,—2 + У"3,—2 — УЗ. Между тем — (•£] =4—125 == \ л /	’ \ о ]
= -121<0.
. Именно это обстоятельство и смущало математиков XVI в.
Оно же побудило Рафаэля Бомбелли — математика и инженера ввести новые числа.
Рафаэль Бомбелли готовил к изданию свою «Алгебру», когда один из его друзей сообщил ему, что в Ватиканской библиотеке имеется замечательная античная рукопись по алгебре. Ознакомившись с ней, Бомбелли немедленно начал переводить ее, чтобы «обогатить мир произведением такой важности». Эта рукопись являлась списком «Арифметики» Диофанта. Перевод ее Бомбелли так и не закончил, зато в его «Алгебре», опубликованной в 1572 г., появились 143 задачи из «Арифметики» (всего в ней 189 задач), методы решения которых он хорошо усвоил. Извлек он из «Арифметики» и способ введения новых чисел. В своей «Алгебре» он сначала вводит отрицательные числа (тепо), которые многими в то время квалифицировались как «ложные». Делает он это тем же способом, что и Диофант, т. е. определяя над ними правила действий при помощи таблицы:
Piu via piu fa р1й.	>
Meno via meno fa piu.
‘	Piu via meno fa meno.
Meno via piu fa meno.
Корень квадратный из отрицательного числа, как замечает Бомбелли, не может быть ни положительным, ни отрицательным числом. Эти «софистические» числа Бомбелли называет «piu di meno», т. е. плюс из минуса (+У—1),
/	J___
или «meno di тепо», т. е. минус из минуса (—у—1), н
также вводит их аксиоматически, определяя правила действий с ними:
Piu di meno via piu di meno, fa meno.
Piil di meno via meno di meno, fa piu. Meno di meno via pit! di meno, fa piu..
Meno di meno via meno di meno, fa meno.
(т. e. в наших обозначениях (-H) (+0=—1; (+0 <—i)~ =4-1 и т. д.).
Никакой интерпретации новым числам Бомбелли не дает. Он рассматривает их как формальные символы, о которых ничего неизвестно, кроме правил (5).
С помощью этих чисел Бомбелли удалось разъяснить неприводимый случай.
Если дано уравнение (2'), то
Но как нашел Бомбелли (2-|-03=24-1Н, т. ё.
- >/’2+ТП = 2 4-(.
Он знал также, что если
у' 4 4- В» = а 4- Р0 то V A —Bi = а — pl, поэтому х=24-14-2—1=4—«мнимые» компоненты у ничто' жаются и корень оказывается действительным. Это, конеч* но, не было «решением» уравнения (2) в общем случае, так как алгебраически нельзя найти yf А 4- Bi , т. е. найти а и Р такие, что а 4- ip = У4 4- Bi, но это объясняло, в чём состоит механизм получения решения.
Заметим, что введенные Бомбелли мнимые числа имели для математики огромное значение, гораздо большее, чем задача, благодаря которой они возникли.
Однако в течение двух столетий мнимые компоненты воспринимались математиками как удобные символы, которые применялись только в промежуточных выкладках, а результат всегда формулировался для «настоящих», т. е. действительных чисел. Лишь в начале XIX в. положение дел изменилось и комплексные числа получили права гражданства, но еще раньше, а именно в творчестве Виета, появилось новое исчисление, «исчисление треугольников», с успехом заменившее оперирование с комплексными числами.
Таким образом, как линия развития алгебраической символики, так и линия развития понятия числа подводит нас к творчеству замечательного французского математи-ка — Франсуа Виета.
III. Франсуа Виет родился в 1540 г. в городе Фонтене-ле-Конт, в 60 км от ла-Рошели — знаменитой крепости гугенотов. Виет был сыном прокурора и сам избрал карьеру юриста. По окончании курса в г. Пуатье он начал заниматься юридической практикой в родном городе. Но уже через четыре года поступил секретарем и домашним учителем к знатному дворянину-гугеноту де-Партеней. Виет занимался с его 12-летней дочерью Екатериной космогонией и очень увлекся изучением астрономии и тригонометрии. Уже в это время, по-видимому, он выразил sin пх и cos пх в виде многочленов от siru и cos х. После смерти де-Пар-тенея и замужества Екатерины Виет последовал за своей ученицей в Париж. В 1571 г. мы находим его там советником парламента. Вскоре Виет получил видную придворную должность и стал тайным советником королей сначала Генриха III, а затем Генриха IV.
В это время Виет оказал французскому двору крупную услугу. Испания и подвластная ей территория Нидерландов были разделены враждебной Францией. Переписка с Нидерландами велась с помощью особого шифра, который содержал более 500 знаков. Эти знаки к тому же время от времени изменялись. Французы часто перехватывали Письма в Нидерланды, но долгое время не могли их расшифровать. Только когда это дело поручили Виету, он'быстро нашел ключ к шифру, и в течение двух лет французы знали о всех планах и сложных интригах испанского двора. Впоследствии испанцы обвиняли Генриха IV в том, что на его службе находится дьйвол.
Виет жил в эпоху кровопролитных религиозных войн.
Вопрос о том, был ли сам Виет католиком или гугенотом, остается темным. Нам1 известно только, что его связь со знатными и активными деятелями-гугенотами (первый муж Екатерины Партенёй был убит в Варфоломеевскую ночь, второй — принц де-Роган — являлся одним из признанных гугенотских вождей, сама Екатерина играла видную роль при защите ла-Рошели) привела к тому, что по настоянию ярых католиков—герцогов Гизов Виет был отстранен от должности в конце 1584 г. и вновь приглашен ее занять в начале 1589 г. (после разрыва короля с Гизами). Эти четыре года оказались чрезвычайно плодотворными для
творчества Виета. Все это время он работал над большим трудом «Искусство анализа» или «Новая алгебра». Рассказывают, что Виет, работая, мог просиживать за письменным столом по трое суток подряд, иногда только подпирая голову рукой и забываясь сном на несколько минут. И все же труд не был завершен.
Но главное было написано. И это главное переделало всю математику Нового времени.
В 1646 г. сочинения Виета были собраны его учениками и изданы в Лейдене. Первые два из этих сочинений, носящие заглавия 1) «Введение в аналитическое искусство» (In artem analiticem I^agoge.) и 2) «Предварительные замечания к видовой логистике» (Ad logisticam speciosam notae priores.), и будут нас здесь интересовать.
В первом из них Виет ставит своей целью создать, новую алгебру, т. е. такое аналитическое искусство, которое обладало бы строгостью геометрии древних, но позволяло бы «хорошо производить математические операции». С этой целью он делит все величины на «ступени», К первой из них относятся «длины» или величины одного измерения, их можно между собой складывать и вычитать из большей меньшую. Произведение двух величин 1-й ступени принадлежит уже 2-й ступени, которая содержит «площади» или величины двух измерений. >
Мы видим, что в этом Виет следовал «геометрической алгебре» древних. Но Виет рассмотрел бесконечно много «ступеней». Если обозначить множество величин n-й ступени Виета через R^t то множество всех его величин будет:
и... и /?«.и ...
Для величин, принадлежащих одной и той же ступени R£, определены сложение и вычитание меньшей величины из большей. Если же aQR". и то для них определено умножение и сф £1?^+'*. Если п>т, то определено и деление, причем
Все величины этих «ступеней» Виет обозначил согласными буквами алфавита: В, С, D. Неизвестные, которые тоже располагаются по ступеням (к принадлежат п-е степени неизвестных), он обозначил гласными буквами: А, Е, I.
Таким образом, он построил первое буквенное исчисление, которое, однако, отличалось от современного. Для
составления уравнений, например, нужно было соблюдать «принцип однородности», т. е. следить, чтобы все его члены принадлежали одной и той же ступени. Например, уравнение
x8+3Bx=D
в записи Виета выглядело бы так:
A cubus+B piano 3 in A aequari D solido.
«В piano» означает, что BfzR+> a «D solido», что
Итак, это первое буквенное исчисление дало возможность записывать уравнение с произвольными буквенными коэффициентами, а также записывать и выводить алгебраические тождества.
Выводу необходимого запаса формул—тождеств посвящено второе сочинение. Там, например, выводятся соотношения:
(B±D)2=B2±2BD+D2,
(B±D)3^B3±3B2D+3BD2±D3 и т. д. до (B±D)8.
Было ли это существенно?
Мы уже говорили, что основное преимущество символов состоит не только в том, что они позволяют сократить запись, а главным образом в том, что для них могут быть определены математические операции, сложения, вычитания, умножения, деления, для них можно определить правила раскрытия скобок и подстановок. Поэтому-то буквенное исчисление позволяет заменить часть мыслительных операций чисто механическими вычислениями. А такая «механизация» мыслительных операций делает уже возможным замену их работой машины.
IV. Последняя часть «предварительных замечаний к видовой логистике» носит название «Порождение треугольников» (Genesis triangulorum). В нем как раз и строится исчисление треугольников, эквивалентное оперированию с комплексными числами.
В основе «исчисления треугольников» лежит; формула, известная еще Диофанту:
(х2+у2) (u2+v2)—(xu—yv)2+(xv+yu)2= = (xu-\-yv)2+(xv+yu)2.
Из нее Диофант выводил, что если некоторые числа р и q представимы суммами двух квадратов, то их произведение 66
будет представимо в том же виде двумя различными способами. Например: 5=12+22, 13=224-32, -
5-13=65=42+72=82+12.
Эту формулу в общем виде доказал Леонардо Пизанский в своей «Книге квадратов» (1225).
Виет выводит формулу алгебраически, пользуясь своим буквенным исчислением, а затем ставит задачу: из двух прямоугольных треугольников с рациональными сторонами составить третий, у которого все стороны рациональны, а гипотенуза равна произведению гипотенуз составляющих треугольников..
Если первый составляющий треугольник имеет стороны (х, у, г), где х— основание, у — высота, az — гипотенуза, а второй — стороны (и, v, w), то из них можно составить два новых прямоугольных треугольника, удовлетворяющих условию задачи:
1) (|xu—yvf, xv+yu, zui);
2) (xu+yv, | xv—yu\, zw) (рис. 9).
Виет отмечает, что если <р — острый угол при основании треугольника (х, у, г),аф— острый угол при основании треугольника (и, v,.w), то угол при основании первого со-
ставного треугольника будет ф-Нф,. а второго — ф—ф (в предположении, что ф+ф<л;/2, ф—ф>0>.
Композицию треугольников Виета можно интерпретировать как операцию умножения комплексных чисел. Поставим в соответствие прямоугольному треугольнику (х, у, г) комплексное число a—x+iy,. причем |а|2=х2+г/2, Arg а=ф. Тогда первая операция Виета равносильна перемножению чисел а=х+1у и f>=u+iv, (|р \г=и2++, Arg р= =Ф):
сф=(х-Ну) (u+iv)—(xu—yv)+i (xo+yu),
причем |ap|2=|a|2- |P|2 =zW, т.,е. произведению чисел сф отвечает первый составной треугольник Виета (|хи— #у|, xv+yut zw). Как отмечает Виет, Arg (aj})=Arg а+ +Arg р.
Что же соответствует второй операций Виета? Легко видеть, что это будет произведение а и числа сопряженного Р, т. е.
ар=(х-(-й/) (и—iv)=(xu+yv)+i (uy—vx).
Это отвечает треугольнику (xu+yv, \иу—vx\, zw). При-
чем Arg (ap)=Arg a+Arg p=Arga—Arg p. Таким образом, не вводя явно никаких «мнимостей», Виет построил исчисление, эквивалентное исчислению комплексных чисел.
Виет применил это исчисление для получения треугольника, получающегося n-кратным умножением треугольника а=(х, у, г) самого на себя, иначе говоря, для вывода формулы (x+iy)n. Виет последовательно находит*: a2=a®1a=(x2—у2, 2ху, a8=a®1a2=(x3—Зху2, Зх2у—у3, г8);
a4=a®1as=(x4—5х2у2+у\ 4+у—4ху3, z4);
a6=a®1a4==(x5—10х8г/’4-5хг/4, 5х*у—lOxy+i/5, г®).
Затем он формулирует общее правило: для определения основания и высоты треугольника ап, полученного n-кратным умножением а=(х, у, г) на себя, необходимо образо-вать п-ю степень бинома х+у и «полученные отдельные однородные члены последовательно разделить на две части, и в обеих первые члены взяты положительными, а затем отрицательными» и т. д.; тогда «первая часть будет подобна основанию (искомого) прямоугольного треугольника, а
* Здесь — композиция, соответствующая первой операции Виета.	'
вторая — высоте. Гипотенуза же подобна той же степени гипотенузы (исходного) прямоугольного треугольника».
Треугольник а=(х, у, г) Виет называет треугольником угла <p=Arg (x+iy), а* (имеет двойной угол при основании)— треугольником угла 2<р, а8—3<р, а4—4ф и т. д.
Итак, Виет предлагает следующую процедуру: надо возвести бином х+у в n-ю степень:
(х+у)п = хп + пх»-1 у + ”(”~° х«-V +
1 ‘Х'и
Тогда
' а" = 17х" — *	* xn~21/2 4-.. .^ '
(их"-1 у —п{п~^Лз~^ хп~3у3+•••)»2”]>
что в точности отвечает нашей формуле:
(х + iy)n = х“— *	xn-21/2 +... 4-1 (их"-1 у 
п(п —1)(п —2) з 3 ,	\
12-3 Х
В которой сгруппированы действительные, а затем чисто мнимые члены.
Но Виет на этом не останавливается. Он замечает, что каждый из треугольников а2, а8, ... может быть охарактеризован острым углом при основании 2<р, 3<р, ... и гипотенузой, т. е. a2=(z2, 2<р), а8=(г3, 3<р), ...
Основание и-го треугольника xn—zn-cos пф, а высота z/n=z"sin п<р, или в современных обозначениях
\г (cos ф4~« sin ф)]п=гп(со8 n<p-f-t sin Пф)*.
Одновременно он получает формулы для выражения cos «ф и sin пф через степени cos ф и sin ф.
V. Свое «исчисление» Виет прщ^енил для решения задач Диофанта и для исследования «неприводимого» случая.
В задаче 9 книги II Диофант рассматривает уравнение
х24-^=а24-^¥=П
* Это и есть так называемая формула Муавра (XVIII в)
и решает его для а=2, Ь—3. Для этого он делает подстановки
х=<4-2,
y=kt—3.
Тогда х2+^=(/га+1) /»-(6й—4) <4-13=13
при k=2, <=8/5, х=18/5, z/= 1/5
Виет уже знал это решение и воспроизвел его в своем сочинении «Зететика» (так Виет называл учение о решении уравнений), но после этого привел и другое решение: пусть (р, q, г)— прямоугольный треугольник с целыми рациональными сторонами, т. е.
ра4-^=г8
(например, (3, 4, 5) или (5, 12, 13). Виет применяет к этому треугольнику и к треугольнику (а, b, У а2 4- &а) свои композиции и ®4:
(а, b, Уа* + Ь*)	(р, q, г) =
= (| ар — bq |, aq 4- bp, г У а8 4- 62),
(a'b, Уа84-Н ®2 (р, q, г) =
= [ар 4- bq, | aq — bp |, г Уа2 4- 62).
Затем Виет берет треугольник, подобный полученному, с гипотенузой г. Его катеты будут в первом случае:
= I ар — Ьд\
= ад + Ьр
У г а во втором:
у  ар+Ьд г >
' .. 1«<7—М ' У г
И в обоих случаях х2+у2—а2+Ь2.
По существу, Виет применяет здесь композицию ктре. угольникам [а, Ь, Уа2 4- Ь2) и^-^-, у~, 1)т. е. с нашей то-60
чки з рения правило умножения числа а=а+Ы на число Р = ~- + ~ i модуль которого |₽|=1.
Тогда	~
Виет показывает, что оба способа решения приводят к одинаковым результатам.
Что касается исследования «неприводимого» случая, то идея Виета состояла в сведении его к задаче трисекции угла. Пусть дано уравнение
x*=px+q
”УСТЬ ®2 - (г)3< °-
Его всегда можно представить в виде:' к '	х8=3г2х+аг2,
а так как (аг2/2)2<г8, то, а2<4г2 и й<2г, поэтому а можно всегда записать так: a=2r sin и. Тогда x=2r sin %-, т. е. уравнение сведется к уравнению трисекции угла, которое получается из способа возведения a=(cos <р, sin <р, 1) в 3-ю степень. Нетрудно видеть, что
а8=(со83ф—3 cos <р sin2q>, 3 cos2<p sin q>—sin*<p, 1)=^ =(cos Зф, sin Зф, 1).
Отсюда sin 3ф=3 со52ф sin ф—sin3 ф.
Или, обозначая sin ф=х, Зф=и, получим: sin и—Зх—4Х3, т. е. 2 sin и=3 (2х)~—(2х)3.
Обозначая далее 2х=—у, 2 sin и=а, найдем #8=3у4га. Отсюда видно, что все три корня в этом случае — вещественные.
Аналогичным методом Виет решил и знаменитую задачу нидерландца Адриана ван Роумена, посланную им в виде вызова математикам всего мира. Рассказывая об этом вызове королю Генриху IV, нидерландский посланник добавил, что к французским математикам ван Роумен не обращается, так как таковых во Франции, видимо, нет.
«И все же,— возразил король,— у меня есть математик и весьма выдающийся. Позовите Виета». Виет прочел письмо ван Роумена, в котором треббвалось решить уравнение
45х—3795х3+9534х5-
45х48+х45=а
при
»-/ >r-VW> •
Сохранились сведения о том, что Виет сразу же- нашел один корень, а на следующее утро представил еще 22 решения этого уравнения.
Виет увидел, что предложенное а является стороной вписанного в круг правильного 15-угольника, т. е. является хордой, стягивающей дугу в •^•=24°. Коэффициенты при х44, х43, .... х показывали, что дело идет о делении этого угла на 45 равных частей, т. е. одним из решений будет:
_	24°	4°
2 Sln Г45 = 2 SinТб'
Остальные положительные решения будут иметь вид:
2 sin (-Ig-t."'36!)0 /1=1,2.22. '
Оставшиеся еще 22 решения будут отрицательными, поэтому Виет их не учитывал.
Ответ Виета был опубликован в 1594 г. (на следующий год после постановки задачи) и принес ему мировую славу.
я» *	*	*7
Буквенное исчисление Виета было первым, позволившим заменить часть мыслительных операций механическими. С этих пор в математику входят формулы. Сначала, как мы видели, это было сделано в алгебре, но вскоре буквенное исчисление было построено и в математическом анализе, а именно, дифференциальное и интегральное исчисление, которое в XVII в. часто называли алгеброй бесконечного. Теперь имеются исчисления, специально построенные для геометрии (векторное и тензорное), исчисления высказываний и предложений в математической логике и многие другие, создаваемые специально для нужд тех или иных математических и даже технических задач.
ЛИТЕРАТУРА
Башмакова И. Г., Славутин Е. И. Исчисление треугольников Ф. Виета и исследование диофантовых уравнений. ИМИ, вып. XXI, М., «Наука», 1976.
Бу р б а к и Н. Очерки по истории математики. Перев. И. Г. Башмаковой под ред. К. А. Рыбникова. М., «Мир», 1963.
Ван-дер-Варден Б. Л. Пробуждающаяся наука. Пе-рев, И. И. Веселовского. М., Физматгиз, 1959.
Диофант. Арифметика. Перев. И. И. Веселовского, редакция и комментарии И. Г. Башмаковой. М., «Наука», 1974.
Евклид. Начала. Перев. и комментарии Д. Д. Мордухай-Болтовского, т. 1—3. М. — Л., 1948—1950.
История математики с древнейших времен до начала нового времени. Под ред. А. П/ Юшкевича. М., «Наука», 1970.
Нейгебауэр О. Точные науки в древности. Перев. Е. В. Гохман. Редакция и предисловие А. П. Юшкевича. М., «Наука», 1968.
Хрестоматия по истории математики под ред. А. П. Юшкевича. т. I. М., «Просвещение», 1976.
Юшкевич А. П. История математики в средние века. Гос. изд-во физ.-мат. лит. М.> 1961.
СОДЕРЖАНИЕ
Предисловие	3
1.	Алгебра Древнего Вавилона................... 8
2.	Геометрическая алгебра Древней Греции . .	19
3.	Рождение буквенной алгебры ...<«	33
4.	Создание буквенного исчисления ......	47
Литература . . .....................«	* . .	63
Изабелла Григорьевна БАШМАКОВА СТАНОВЛЕНИЕ АЛГЕБРЫ (Из истории математических идей)
Главный отраслевой редактор В. П. Демьянов Редактор Г. Г. Карвовский. Мл. редактор Т. Г. И н * ш а к о в а. Обложка художника Л. П. Р о м а с е н к о. Худож. редактор М. А. Бабичева. Техн, редактор А. М. Красавина. Корректор В. В. Каночкина
ИБ № 1684
Т-15538. Индекс заказа 94309, Сдано в набор 11.07.79 г. Подписано к печати 22.08.79 г« Формат бумаги 84Х1081/м- Бумага типографская № 3. Бум. л. !< Печ. л. 2. Усл, пфч. л. 3,36.	Уч.-изд. л. 3,13, Тираж 38 040 >кз,
।	Издательство «Знание». 101835, ГСП Москва, Центр, проезд Серова,
д, 4, Заказ 1636, Цена 11 коп.
Чеховский полиграфический комбинат Союзполиграфпрома Государственного комитета СССР
I	по делам издательств, полиграфии и книжной торговли
г, Чехов Московской области.


11 когт.	Индекс 70096