Автор: Фридлендер Б.И. Хаиров Р.А.
Теги: методичка задачи по математике высшая математика дискретная математика
Год: 2007
Текст
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Б.И. ФРИДЛЕНДЕР, Р.А. ХАЙРОВ
ГРАФЫ
Утверждено редакционно-издательским советом института
в качестве учебно-методического пособия
по дисциплине «Дискретная математика»
*10059045*
Москва 2007
ЗАДАЧА 1
Алгоритм поиска кратчайшего пути между двумя вершинами
(Дейкстры)
Рассмотрим две вершины л и / в |рафет все дуги которого имеют
неотрицательные веса
Пусть имеются /и вершин, близких к вершине s. Близость любой
вершины х к вершине 5 определяется кратчайшим путем из х в s (рис. 1.(1,
то есть известны кратчайшие пути, соединяющие s с выделенными m
вершинами. Найдем близкую к я новую fffl+l^-ю вершину. Окрасим в
черный цвет вершину $ и /и близких к д вершин. Построим для каждой
неокрашенной вершины у пути, непосредственно соединяют ие с помощью
дуг fx yj каждую окрашенную вершину х с у. Выберем из этих путей
кратчайший и будем условно считать его кратчайшим путем из вершины 5
в вершину у.Та из неокрашенных вершин у, которая имеет наименьшее
расстояние до m вершин х, будет условно считаться кратчайшим
расстоянием из вершины j до верш ины у.
Рис. L1
Выбираем из множества у ближайшую к j (т"Н)-ю вершину, для
которой условно кратчайший путь у-.у имеет наименьшую величину. Это
означает, что кратчайший путь из д в fm+lj-ю вершину должен проходить
только через окрашенные вершины из числа m вершин.
Повторяя процедуру увеличения числа окрашенных вершин,
приходим к вершине / и тем самым находим оптимальный путь из / в 5.
Отсюда получаем алгоритм:
Шаг I. Вначале все вершины и дуги не окрашены. В ходе алгоритма
каждой вершине присваивается число й?(х), равное кратчайшему пути из х
в 5, где х-окрашенная вершина.’ Полагаем j|s)= 0 ;с/(х) = <® для всех х,
отличных от 5.
•5-
Щаг 2г Для каждой неокрашенной вершины пересчитать величину
d(x);
d[x}= min|rf(jc),d(j)+
Если rf(x) = oo для веся неокрашенных вершин, закончить процедуру
алгоритма: в исходном графе отсутствуют пути из вершины з в
неокрашенные вершины. В противном случае окрасить ту из вершин х, для
которой величина й?(х) является наименьшей. Кроме того, окрасить дугу,
ведущую в выбранную на данном шаге вершину х
Положить у-х.
Шаг 3, Еслну=/, закончить процедуру, так как кратчайший пугь из s
в ( найден и проходит через окрашенные дуги. В противном случае
перейти к шагу 2.
Пояснение.
Каждый раз, когда окрашивается вершина, окрашивается и одна
дуга.
Поэтому на каждом этапе к каждой окрашенной вершине подходит
только одна дуга. Следовательно, окрашенные дуги образуют дерево с
корнем в вершине з. Единственный путь от s к вершине х по этому дереву
является кратчайшим путем. Очевидно, что кратчайший путь из любых
двух вершин дерева проходит по направленным ветвям построенного
дерева.
Если не фиксировать з;онечную вершину Л го описанный алгоритм
позволит построить дерево с направленными ветвями, покрывающими
весь граф. Кратчайший пугь от корневой вершины до любой вершины
графа проходит по ветвям построенного остова.
Пример. Найти кратчайший путь между вершинами ди/ весового
графа, приведенного на рис. 1.2.
Рис. 1.2
Шаг 1. Окрашена вершина s. dis)- 0; </(х)=® для всех вершин, не
совпадающих с з.
Шаг 2. £-=‘i
rf(a)=min{c/(aX*Z(s)+ м($5я)}=nainfco,0+3}=3
</(£>)- Цу,&)} - min{a>,0 + 2} = 2
rflс) = и(з,с)}=min{co,0+7} = 7
d (e) = min{d(e), dfc) 4- Цз, e)J=min ^c.,0 + 4} - 4
-6-
d (A ) = m i n ДА), d (a) + h(s 5 A)} = mi п{жяО + сД = тс
Д/)= тш{Д/), Д.г)+ = min{cc,0+<jo}= тс
Так как </(£•) = 2 является минимальной величиной из величин
ДД, Д&).Де),Дс)3 ДА).Д/), то вершина & окрашивается, как и дуга fjrfj/.
Строящееся дерево кратчайших путей состоит из дуги ф&Л
Шаг 3. так как вершина t не окрашена, то переходим к шагу 2.
Шаг 2. (у=Д
Да) = тпш{Дак с?0) 4- H0sfl)}= min {3,2 4- тс} = 3
Де) = тгДДс), Д/?)+ и(/>,€)}= min (7,2 + 3} = 5
Де)= min|rf(4rf(b)+ w(h,cj}= m n{4,2 + oo|= 4
fl* (A ) = тт{ДА ), ДД+ w(fr, A)} = m in {тс, 2+тс)=co
Д0= пнл{Д/),Дд)+ ДЛ*/))=тш{тс,2+7} = 9
Так как ДД является миним£л£йой величиной из величин ДД, Дс),
Де), ДА), Д/), то вершину ст, как и ребро окрашиваем. Текущее
•ерево состоит из двух дуг
Шаг 3. Так как вершина / не окрашена, переходим к шагу 2.
Шаг 2. (ужл>
Дс) = m in {ДД (fl) + Да, с) J = min {5,3 + тс) = 5
Де) = ппп{ДД До)4- Да, е)} = min{43 4- тс} = 4
ДА)= тт{ДА),Дд)4- и(а,А)) = тш{тс,3 + 2}= 5
Д/) = mi п{2/ (f Да)+ До j)} = min {9Т3 + тс} = 9
Так как Де) является минимальным из {ДДД^ДА^Д^/го вершина
<ге'» окрашивается вместе с дугой Текущее дерево состоит из ipex
ребер:
Шаг 3. Так как вершина / не окрашена* переходим к шагу 2.
Шаг 2, £р=Д
Дс) = пнДДД Де)+ Дс, ^)} = min {5,4 +«>} = 5
ДА) = mi п{ДА ), Де) + ДА, e)J ?= min (5,4 + х>} = 5
Дг) = min{^ (/), J (е) + Д/, e)J = min {9,4 4- 5} = 9
Обратим внимание^ что Дс) и ДА) одинаковы, равны пяти. Это
означает, что вес маршрутов и одинаков. Поэтому, какую из
вершин закрасить* t? или А* не имеет значения. Выбираем для окраски
вершину с и ребро с/ Теперь текущее дерево состоит из четырех ребер:
Шаг З.Так как вершина t не окрашена, переходим к шагу 2.
Шаг 2. (у=с)
б?(А)= и(Л,с)|- тиц5,5 + 2} == 5
J (/) - nrin{t/(/ )>*/ (г)+и(/, с)} = min {9Т5 + со}=9
Так как минимальна из 4М и 4')> то закрашиваем вершину и
ребро (д к). Текущее дерево состоит из пяти ребер:
Шаг 2.
Закрашиваем вершину / и ребро f 1), Получаем текущее дерево,
которое и является решением задачи: кратчайший путь из вершины j к
вершине t состоит из дуг (од! и (X? и hmcci длину 34*2+/—б.
Построен! юс дерево является и покрывающим остовым деревом, так
как проходит через все семь вершин.
Заметим, что если бы в процессе решения мы закрасили вершину к* а
не с, то полученное дерево остовом не было бы, хотя отв г был бы таким
же.
(2], [Ю].
-S-
Задача 1
Алгоритм Дейкстры
-9-
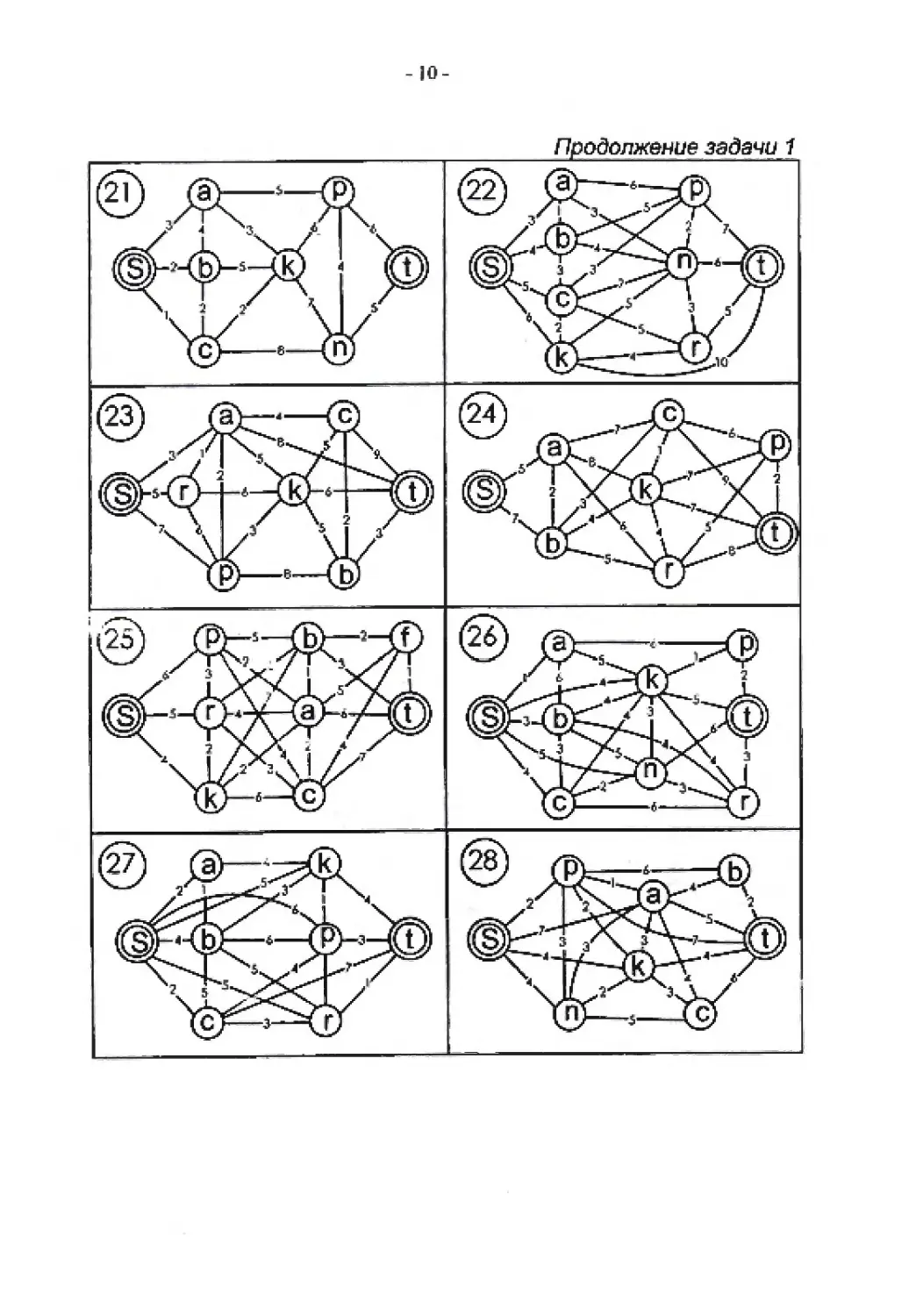
Продолжение задачи 1
- 10-
Продолжение задачи 1
ЗАДАЧА 2
- Il -
Определение оптимального расстояния между вершинами
ациклического графа
Между шестью городами А, В, С, D, Е, F последовательно
установлена связь. В каждом городе имеются пункты связи, всего 14
пунктов. Пункты в каждом городе между собой нс связаны.
IV------м- ТИ
В городе А пункт 1, в городе В - пункты 2 и 3, аналогично в С * 4, 5,
6;в1Э-7,8,9,10; вЕ- U,12,13;bF-14.
Приведен весовой граф, все ребер которою означает цену сообщения
от одной вершины до другой (или километраж, или стоимость сообщения).
Требуется найти такой маршрут между начальной вершиной 1 и
конечной вершиной 14, чтобы суммарный вес маршрута был
минимальным. Зялячя решается поэтапно. Всего имеется пять этапов (I, II»
Ш, IV, V). Решение проводится двумя ходами: сначала делается обратный
код (VIV-III-11-I) и затем прямой ход (1-П-Ш-1V V), которым
соответствует направлению.
Обратный ход. Для каждого этапа обратного хода (начиная с эта
VI составляем подграф, для которого записываем матрицу смежности
V IV ш
10 4 5 6
U 12 13
12
13
8 2 1 СО
3 2 3 1
СО 4 5 8
«о
10
«j
I
2
2
3
Начиная с этапа V, рассматриваем последовательно возможные
ребра, через которые могут проходить искомые маршруты. На этапе V эти
маршруты могут проходить из вершин 11,12, 13 веса4, 5 и I.
V
11 12 13
14
На этапе IV ребро (7,11) имеет вес 8, и если маршрут следует через
это ребро, то обший вес пути из вершины 7 до вершины 14 равен 8+4=12.
Все полученные цифры-расстояния от вершин 7,8,9 и 10 заносятся
соответственно в каждую клетку снизу от косой черты. Далее выбираем из
этих цифр в каждом столбце наименьшее значение. Например, во втором
столбце наименьшей цифрой будет 5, и отмечаем эти значения кружками
IV
7 8 9 10
Составляем подграф для этапа III. Его матрица смежности
составляется аналогично матрице этапа IV. Величины расстояний от
вершин 4, 5 и б до вершины 14 соответственно равны 8,7 и 9.
-13-
Составляем матрицу смежности подграфа лапа
вычислений получаем минимальные расстояния от вершин
Бертины 34, которые равны соответственно 10и9.
Л
II. После
2 и 3 до
Составляем матрицу смежности подграфа этапа 1. В результате
получены два равных ответа: кратчайший путь из вершины 2 и 3 до
вершины 14 равные 12.
Для тс го, чтобы узнать маршрут, следует сделать «прямой ход». Из
последней матрицы сначала выберем начало пути из вершины L к вершине
2. Далее из матрицы этапа И выбираем вершину 5, в которой кратчайшее
расстояние до вершины 14, равное 10, отмечено кружком. В следующей
матрице HI выбираем вершину 10, так как в столбце 5 в последней строке в
кружочке стоит наименьшее расстояние до вершины 14, равное 7.
Аналогично в матрице IV находим следующую вершину 12. Тем самым
определен кратчайший путь 1-2-5- 10-12-14. Вес кратчайшего пути равен
2+3+1+1+5=12. Второй кратчайший путь 1^3-4-8-13-14 также имеет вес
12.То есть имеются два одинаковых минимума
[18], [1].
Задача 2
Поэтапно найти маршрут с наименьшим весом
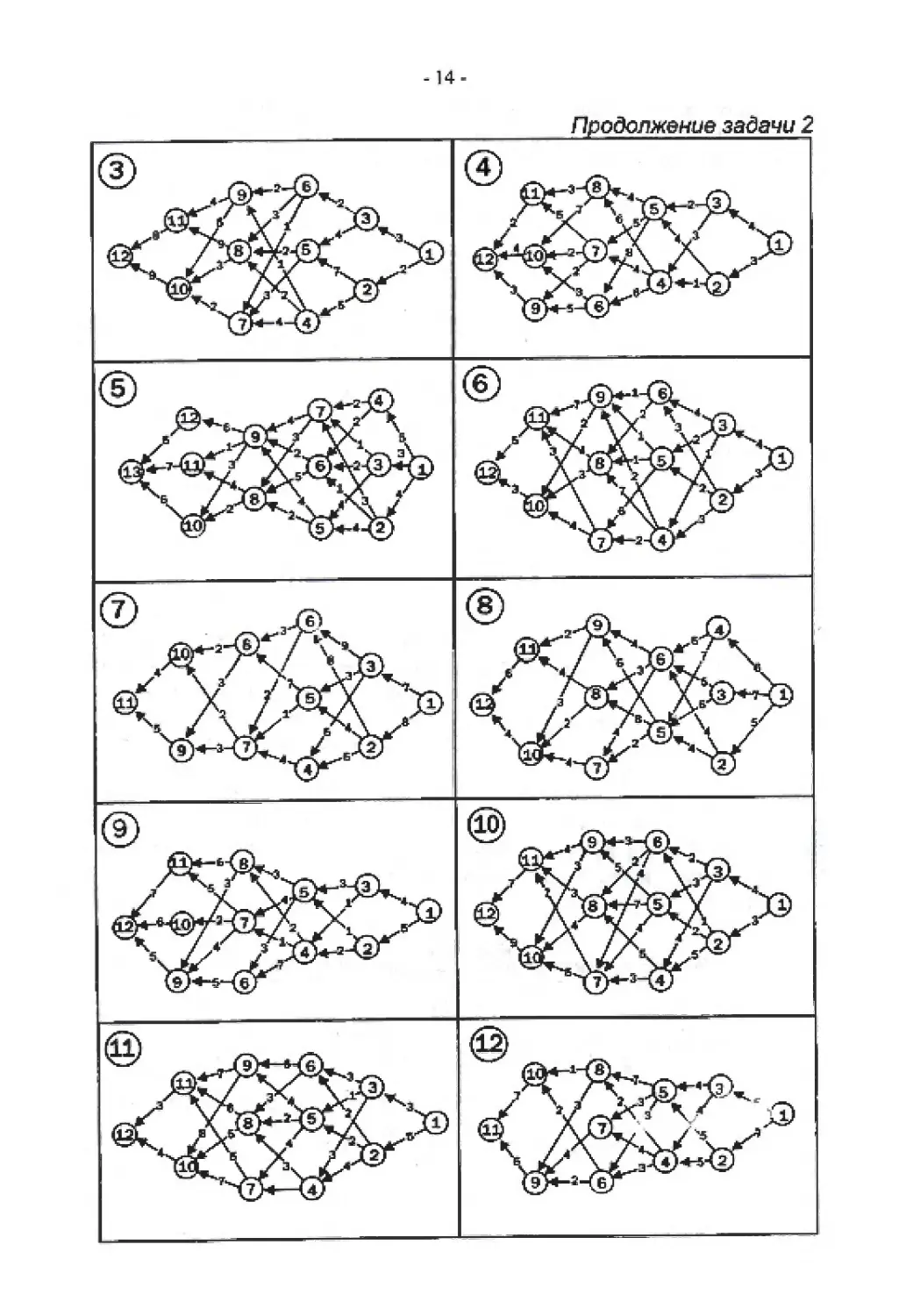
- 14-
Продалжение задачи 2
15-
Продолжение задачи 2
-16-
Продолжение задачи 2
- 17-
ЗАДАЧА 3
Метод ветвей и границ (Задача коммивояжера)
Коммивояжеру требуется посетить каждый город области и
возвратиться в исходный пункт, Предполагается, что каждый город он
посетит только один раз. Коммивояжер стремится выбрать такой путь при
котором длина маршрута или время пути, или стоимость пути были бы
минимальны. Задача эта может быть сформулирована как задача по
определению оптимального гамильтонова цикла на направленном весовом
графе, вершины которого соответствуют городам, а ребра
коммуникациям, соединяющим пары городов. Причем веса ребер
) равны расстояниям между городами. Эти веса могут быть не
коммутативны, то есть IFtXpjr-)* . Мы оудем рассматривать
полный направленный граф. Если между какими-то двумя вершинами
отсутствует FF, то направленное расстояние между ними считаем равным
бесконечности.
Оптимальный маршрут не обязательно должен быть гамильтоновым
контуром, Например граф, приведенный на рис. 3.1, имеет только один
гамильтоьов контур, Т| — х3 — ач“ Jq j общая длина которого равна
1+1+10=12. Между тем оптимальный путь х, -х2-х3-х2 имеет длину
1+1 +1+1“4,
Если для любых трех вершин «рафа выполняется неравенство
треугольника IFfx^Xy/2 И^Ч.г^ + И^д^Л то решением задачи
коммивояжера является оптимальный гамильтонов контур. Если
неравенство треугольника не выполняется, то для решения задачи
расстояние И-Yx..xJ следует заменить меньшим расстоянием
I'/fx^x^ > + JFfx ,х J. В частности, на графе рис. 3.1 вес ребра FFfXpXjJ
следует уменьшить с 10 до 2,
Пример. Полный весовой направленный граф с л-4, т—!± приведен
на рис. 3.2. Каждая вершина инцидентна с ребрами.
Половина этик ребер имеет направления, исходящие из вершин, а
половина - входящие в вершину. Каждое ребро имеет вес, или
«расстояние» между вершинами, указанный числом рядом с каждым
Рис. 3.1
Рис. 3.2
- 18-
Составляем матрицу расстояний НЧх,^), приведенную на рис. 3.3.
Строение этой матрицы аналогично строению матрицы смежности.
Х|
X,
А‘з
л4
Х| Xj Xj х^
СО 4 2 6
3 Ж 2 4
2 2 СО 6
3 5 5 со
только вместо единиц и нулей проставлены веса
то есть направленные расстояния от
вершины х, до вершины лу Стропа г является
индексом вершины, из которой исходит ребро*
столбец/ - индекс вершины, в котирую направлено
ребро.
Рис. 3.3
XJ Хд *1 х« *1
X. =0 4 2 1 6 2 ! со 2 0 4 х, ад 2 0 Хй
1 х, 3 OQ 7 и 1 оО 0 2 х, 1 ад 0 0
2 2 2 ад 6 5 0 0 У 2 ад 2 4 । ю х> о ' 0 ад 2
г "» J 5 S « 3 0 D 0 3 X. 0 2 2 ад
Л,=: 2+2‘i i'2+З =9 1+0+0+2- =9 ШШ
Рис 3-4-а Рис д 3.4-6 Рис. 3.4-г г
Можно проверить, что все неравенства треугольников для матрицы
на рис. 3.3. выполняются и искать оптимальный путь коммивояжера
следует среди ^мильтоновых контуров. Гамильтоновых контуров
.........хт ) возможно построить в количестве п!, так как число
различных перестановок л чисел равно л Л
Рассмотрим какую-нибудь строчку х4] матрицы расстоянии
|иух(>х^. Уменьшим все элементы этой строчки на число й. Это будет
означать, что общая длина пути во всех л/ возможных гамильтоновых
контуров тоже будет уменьшена на й, так как в каждом контуре
обязательно совершается только оди н путь из вершины гх^. Если этот
контур был минимальным, то таковым он и останется, только его общий
вес тоже уменьшится на Л. Выбираем в каждой строке i минимальное
значение FFfxr.x ) при всех значениях и вычитаем эта значения
соответственно из каждой строки матрицы Общая длина
каждого контура уменьшится на Л, = й, + Л, +...+й„, и в каждой строке
новой весовой матрицы появится хотя бы одни нуль. В нашем примере
(рис. 3.4-а) эти минимальные значения fFfXpX^J в строчках равны 2; 2; 2;
3, которые и записываем справа от новой таблицы весов (рис. 3.4-а).
Общий вес каждого контура уменьшится на fr( ~2+2+2+3=9.
-19-
То же самое можно проделать со всеми значениями весов по
столбцам матрицы, так как уменьшение всех элементов столбцов х7
матрицы на некоторую величину соответствует тому, что все ребра,
входящие в вершину ху, будут уменьшены на эту величину. Определяем в
столбцах примера минимальные значения весов ребер и складываем их,
получаем А2 - = О+(ЖН2=2. После вычитания из каждого элемента
столбца величины Л, имеем в нашем примере новую матрицу (рис. 3.4-в)
(изменен только последний столбец). В полученной матрице в каждой
строке и в каждом столбце обязательно присутствует хотя бы один нуль.
Как уже обсуждалось выше, оптимальный гамильтонов контур с
полученной матрицей весов будет таким же, как оптимальный контур
исходной данной матрицы, но вес этого контура будет на
Л меньше. Значит /*=11 является храшшей в том
смысле, что вес искомого оптимального гамильтонова контура будет нс
меньше й=41. Это число Л называется константой приведения.
Выбираем первое ребро оптимального контура, причем это ребро
соответствует ячейке полученной матрицы с нулевым значением.
Таких нулей в матрице шесть: fx]rx3>, fx2JXjJ, (%.х4Л (%,xj, J
и (x^xj). Для определенности рассмотрим ребро (xt,xj. Найденная граница
возрастает с А=11 до 11+2-13, то есть гамильтонов цикл, не содержащий
ребро fxlzXj J, будет иметь вес не менее 13.
Найдя аналогично для каждого нуля матрицы на рис. 3.4-в значения
суммы минимальных элементов в строке и столбце, получаем таблицу на
рис. 3.5, в которой над нулями записаны полученные после сложения
числа. Для выбора правильного ребра с нулевым весом из числа этих
ребер применяем процесс ветвления. Наибольшее значение из полученных
цифр {2Ю;2;0;2;2} равно двум.
Рис. 3.5
Выбираем из ребер с наибольшим одинаковым весом любое, пусть
это будет ребро (xt,x3). Обозначим через z цикл Гамильтона и через у (г) -
границу суммы всех весов подмножества г. В нашем случае y(z)=L 1. Если
-20-
оставить а множестве z ребро то y(z)=l 1+2=13. Этот факт
выражается в форме |рафа.
Y^)=il
Черта 13 означает, что ребро (1,3) из множества z нс убирается.
Такой процесс сравнения называется ветвлением, а сам метод носит
название метода ветвей и границ. Вычеркнем из матрицы (рис. 3.5) первую
строку и третий столбец. Этот процесс стягивания матрицы по дуге fx|(xj
приводит к ноной матрице.
0 Если ребро (хрх^) входит в искомый цикл
Гамильтона, то это означает, что в ячейку
0 fследует 3ai нсать не 0, а «, что и было
сделано. Далее с сокращенной матрицей
и следует произвести ту же процедуру, что и с
исходной матрицей. Находим для нее константу
приведения й - + й2, она оказывается нулевой, так как в каждой строке и
в каждом столбце присутствует нуль, поэтому Л=0, Каждому нулю
соответствуют суммы тш значений элементов строки и mm значений
элементов столбца, которые записываются над косой чертой в
соответствующих клетках. Далее находим max значение и s этих цифр, и
если этот max оказался в ячейке (xr х; J, то это ребро будет принадлежать
искомому циклу. В рассматриваемой задаче - это ребро fx3,x^ с
соответствующим значением четыре.
Запишем новую сокращенную матрицу без третьей строки и
второго столбца. Очевиден конечный результат. Последние
два ребра цикла fx2,x4> и fx4,xj.
Ответ: искомый цикл Xpjj-xj-x^-Xp
Проверка: 2+2+4+3=11.
-21 -
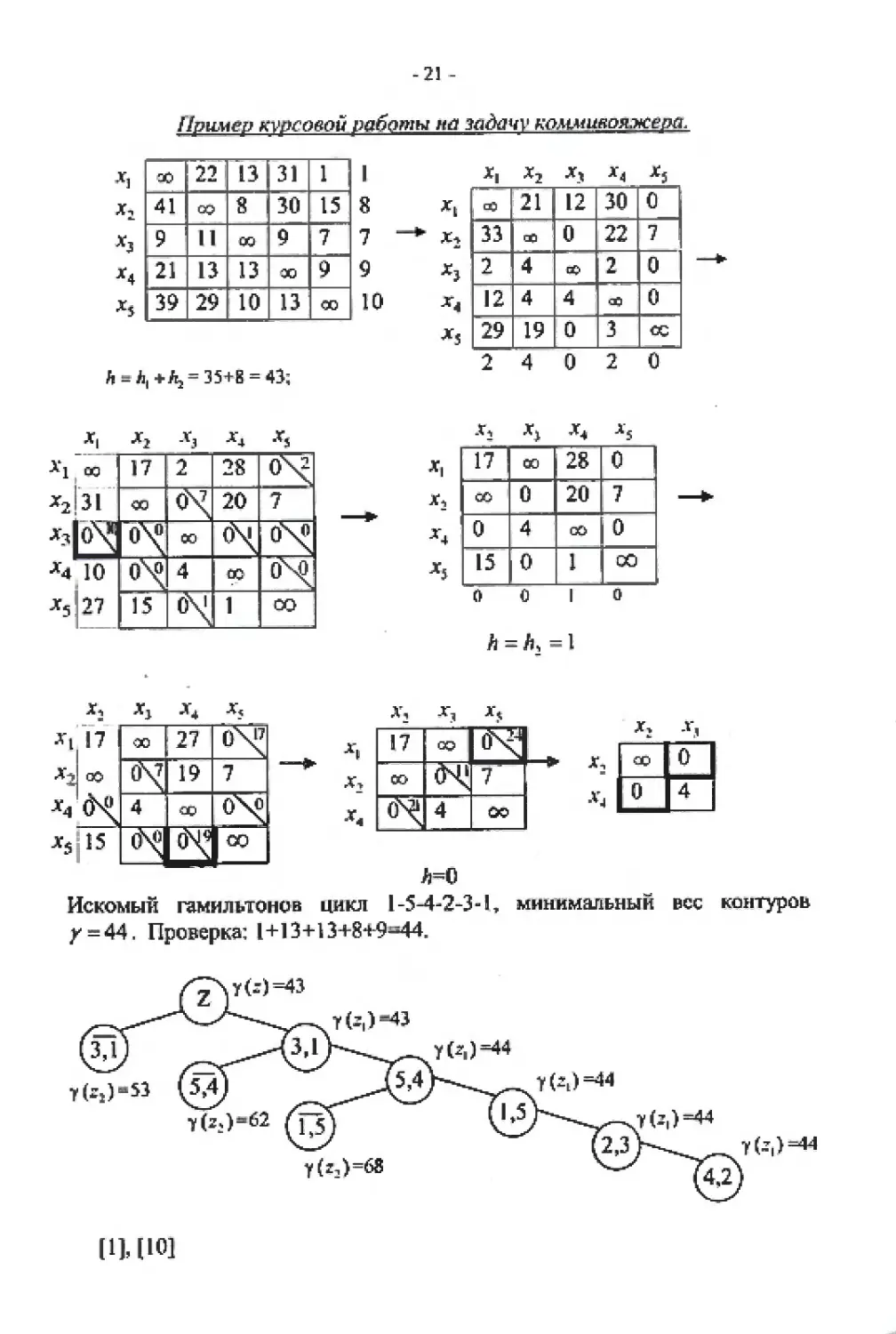
Пример курсовой работы на задачу коммивояжера.
*1 з& 22 13 31 1 1
Хп 41 а? 8 30 15 8
,9 11 СО 9 7 7
*4 21 13 13 00 9 9
*S 39 29 То 13 00 10
Х| Х2 Х> х4 х5
1 °9 21 12 30 0
33 □0 0 22 7
2 4 сО 2 0
12 4 4 о0 0
'29 19 0 3 ОС
2 4 0 2 0
Л,+/^ = 35+8 = 43;
х3 х* х4 х5
17 СО 28 0
3Q 0 20 7
0 4 СО 0
15 1° 1 00
0 0 10
Л = Л, = I
*г -h
Л-0
Искомый гамильтонов цикл 1-5-4-2-3-L минимальный вес контуров
у = 44. Проверка: l+13+l 3+8+9М4.
[1Ц101
-22-
Задача 3
Коммивояжера
© Х| Xj Xj Xi X3 (7) Xi Xi /Э Jtj. x> CD A-jj Xj Xj X| Xj
Х| QO 4 1 38 13 28 Xi DC 10 18 ib 4 Xi □0 1 5 3 7 6
13 се 11 10 12 Xj 34 QO 41 J 28 6 Xj 10 00 6 9 7
Xj 21 11 оо , 1 31 Xj 23 8 DO 48 8 Xj 3 2 QO 4 6
Л* 2. 8 8 38 oo 13 XI 25 27 30 □0 7 Xi 8 15 11 С» 1
Х3 9 । 8 17 6 CO Xj 11 I J 7 14 ОС Xj 9 7 6 10 0 c
(7) Х| X, □с Xj 13 Хз 17 Xi 12 Xj 14 (D X| X| ОС Л 2 !4 Xl 35 Xi —1 3 Xj 11 CD Xl X| oc- Хг 28 Xl 4 Xl X 20 1 s 1_
х? в оо 17 12 xj 38 00 36 19 8 Xj 18 oo 4 3 3 1
Хз 9 33 ОС 19 45 Xj 14 13 00 9 9 X.t 40 6 00 23 4
Х| 9 14 32 Cc 41 Xi 34 311 17 00 8 Xl 41 22 13 00 1 ]
А I 2 г* ₽- 25 3 SO Xi 2 11 11 7 00 Xj 9 1 5 4 0 0
(7) Х| Xj Xd X5 (T) Xi Xj Xj jq Xj CD X| X; Xj Xl Xq
Xj О& 18 33 47 10 Xi •co 10 18 7 9 JC| co 30 46 19 2
Xj 3 О' Об 14 43! 10 X? 29 ОС 39 14 5 10 00 19 3 2
Xj в 9 ОС- 24 12 Xj 30 20 co 0 10 Xj 2 15 co 36 0
Л 23 2 32 00- 13 xj 11 26 36 ОС 6 Xl 26 22 30 00 4
х< 15 11 12 16 oo JTs 10 11 9 8 DO xs 3 4 3 2 ! =
ио) Х| X; Xj x> Xj Xi л Xj Xl X*5 (D Xi Xj Xj Xj Xj
х4 оо 2 11 3 I 2 Xl 00 35 I 2 17 43 Xi 00 35 10 5 2 5
1 5 се з ; 5 1 3 Хг 17 ОС ll 8 12 24 Xj 0 00 30 10 2 1(У
Xj 2 4 оэ 2 1 Xj 14 14 co 9 11 Xj 7 18 DO 9 г С,
X, 1 3 5 DC 7 Xs 33 19 11 5 00 42 Xi 6 7 8. ос
х5 5 1 2 3 JK4 X5 23 34 15 1 00 Xj 15 40 30 6 c »
(!з) Х| Хг Xj Xi Xj (u) Xi J Сз J JQ Xj CD Xl Xj Xj Xi J Ci
Х| со 9 10 7 1 8 X| co 3 36 9 22 Xi QO 31 41 16 7 p
Х2 14 ОО 15 12 23 хг 40 ОС 17 5 28 Xj 12 co 20 9 1 IT
Хз 9 33 -CO 18 43 Xj 20 8 00 6 10 Xj 21 31 00 1 1 1
X 13 8 23 ОС 33 X 13 1 1 16 DC- 13 Xi 27 12 37 60
X; il 13 33 1 23 3 DO i x3 41 15 33 । 2 , 00 Xj 10 9 8 7 « Xl
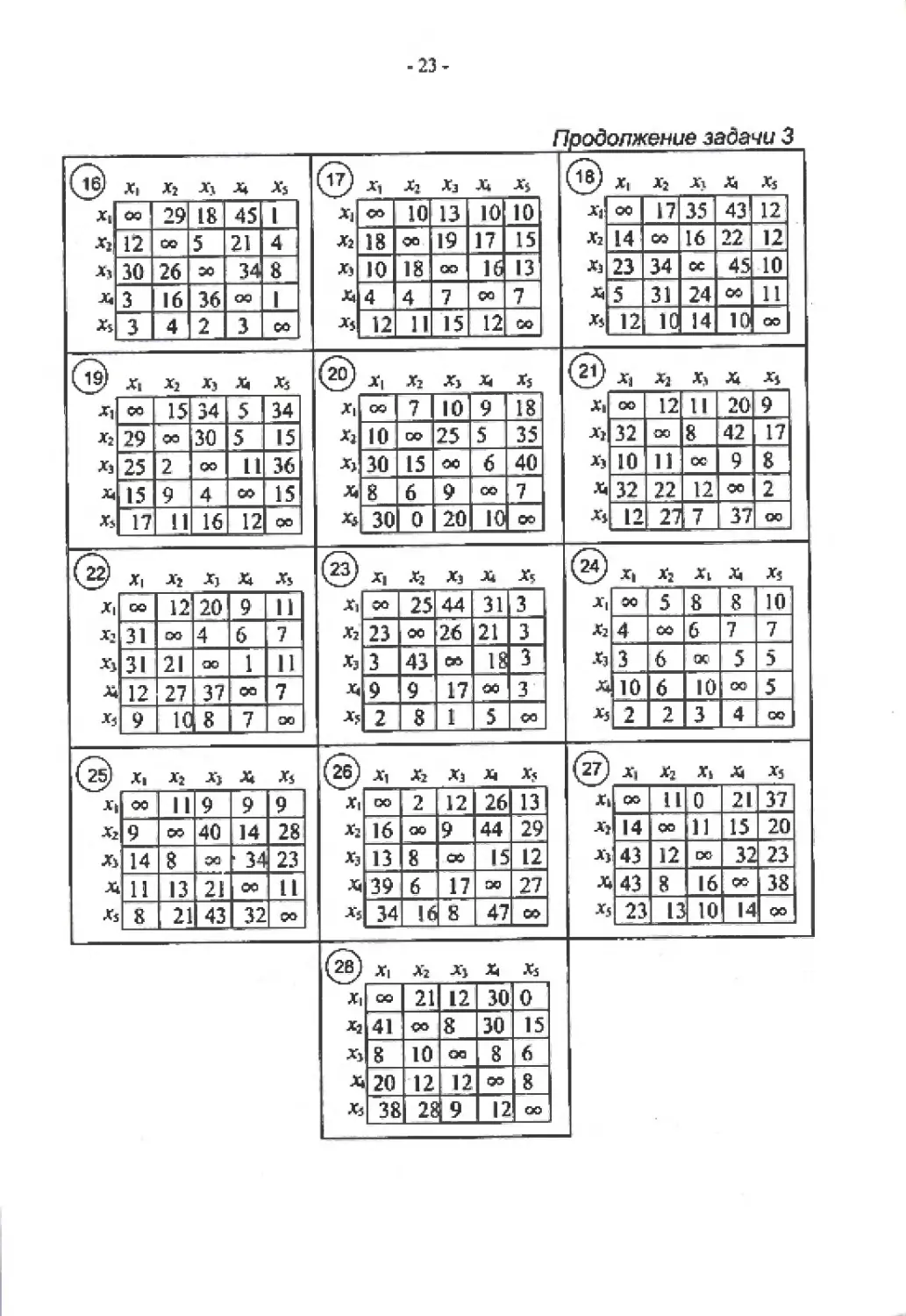
-23-
(Те) Xi x2 Хл x* xs Xj Xj •Лч Xs (w) Xi Xi Хг Х| х3
*1 OQ 29 IB 45 1 Л) да 10 13 10 J0l Х| да 17 35 431 12
Xj 12 да 5 21 4 I Xi 1 8 да 19 17 15 х2 14! да 16 22 12
30 26 ЭО 34 8 Xj 10 18 DO 16 13 Ха 23 34 да 45 10
JQ 3 16 36 « 1 Xi 4 4 7 да 7 Jtj 5 31 24 да п
Xs 3 4 2 3 ©a x5 12 11 15 12 да Xs 12 10 14 10 да
MS) Xi x2 X3 АЙ X3 (20) jf 1 x2 X) Xi (21) Xi X3 X? JQ Xs
Xi Сй 15 34 5 34 Xi OQ 7 10 9 1 18 Xi да 12 И 20 9
X-i 29 да 30 5 15 Xj 10 DO 25 5 35 Xj 32 DO 8 42 17
*3 25 2 DO 11 36 Xj 30 15 да 6 40 Xj 10 11 да 9 8
Xi 15 9 4 » 15 № 8 6 9 00 7 Xi 32 22 12 да 2
Xs 17 11 16 12 да X» 30 0 | 20 10 да Xs 12 27 7 37 да
(j^j?) fi Xi x> Xi xs (2) J Cl x3 Хз JQ Хч (24) Xi Xi Xi Х| х3
, Xi OQ 12 20 9 11 X! да 25 44 31 3 Xi да 5 8 8 10
X2 31 DO- 4 6 I7 1 *2 23 да 26 21 3 Xi 4 да 6 7 7
Xj 31 21 DO 1 11 *3 3 43 да 18 3 X3 3 6 Ж 5 5
ьа 1 2 27 37 ©a 7 X| 9 9 17 да 3 10 6 10 да 5
Xi 9 10 I8 7 да Хч 2 8 1 5 да X3 2 2 3 4 да
l@ Ci Xi Xj Д xs (2) Xj x2 Ха Х| х? (27) X| x2 Xi Xi Хз
X| Ф0 II 9 9 9 Xi DO 1 2 12 26 13 X| ! да U 0 21 37
x3 9 ОФ 40 14 28 x2 16 да 9 44 29 Xj 14 да 11 15 20
Xj 14 8 ЭС 34 23 Xj 1 3 8 да 15 12 X) 43 12 да 32 23
X i 1 [1 13 21 «11 Xi 39 6 17 да 27 X i 43 8 16 QC* 38
Xj 8 ' 21 43 32 да Xs 34 u 8 47 да Xj 23 13 10 14 да
|(гв) Xi Xj Xj Х| Х3
Xi GO 21 12 30 0
Xi 41. да 8 30 15
Xj 8 10 ОС 8 6
» 20 12 12 да 8
x3 38 21 ! 9 12 да
-24-
ЗАДАЧА 4
Потоки в сетях
Сетью называется ориентированный связный граф G с множеством
вершин # = {х,Х|,хг,х^...,хл,/} и множеством ориентированных ребер,
называемых дугами |(x,,xpj. Каждой дуге придается вес C(xltx,)Z0,
называемый пропускной способностью дуга.
Граф содержит две вершины s н t, где s называется источником или
входом, a t - стоком или выходом, а остальные вершины {х|(х2,Хз(...,хя}
называются промежугочн ыми (рис. 4.1).
На множестве дуг определена функция f(xt,Xj). Если х- начало
дуги, а у- конец дуги, то f(xy) называется потоком через дугу. Функция/
всегда неотрицательная и целочисленная. Если это не удовлетворяет
точности расчета, всегда можно изменить масштаб в измерении величины
потока. Свойства функции /:
1. {О 5 f( ху) £ С( хуД поток не превышает пропускной
способности.
2- f(xy) = Q где Е* и ££- множество дуг
fx .r jefi; О у M E*
входящих и исходящих из вершины х. Из этих двух соотношений удобно
представить, что по дугам сети движется несжимаемая жидкость, которую
дуги пропускают только в одном направлении с ограничением пропускной
способности. Из свойства 2 следует закон сохранения потока жидкости.
Отсюда явствует, что суммарный поток из вершины я истока
X /^У) равен суммарному потоку, входящему в сток ffsyj .
Ф/еЕг" («УЛЕГ
Эта величина называется величиной потока сети и обозначается через и .
Составим простой путь из £ в f (без циклов). Каждая дуга этого пути имеет
свою пропускную способность CfXpXj^. Выберем из всех
-2S-
неотрицательных значений CfxpXyJ этого простого пути наименьшее
Значение и обозначим его через И. Составим поток по этому пути, в
котором все функции f(xirXj) будут одинаковыми, равными К В каждом
простом пути величина истока через любую дугу /fxpxp одинакова.
Известна теорема, что любой поток в сети от истока s до стока f можно
представить в форме суммы простых /или элементарных/ потоков. Если
вершины хр и xf связаны несколькими дугами в одном направлении, то их
нужно «склеить» в одну дугу? а также суммировать для этой дуги
величины ограничений х,хр.
Разрез сети, отделяющий вершины s и 7? определяется двумя
подмножествами вершин X и Xt причем A г>А = 0. seA,
teX, XuX = N.
Число CfX.AJ называется пропускной способностью разреза,
равной сумме входящих в разрез дуг с направлением от у кг. Очевидно,
что любой простой путь из s к г обязательно должен нечетное число раз
пройти через дуги разреза. Величина У произвольного потока остается
постоянной в каком бы разрезе се ^вычисляли. Учитывая, что множество
всех разрезов О1раничен0 и что каждому разрезу соответствует число
C/A\AJ, то всегда можно найти минимум этих чисел. Такой разрез
называется минимальным.
TgopgjHg ’Ф'ор^о-Ф'длксрсО'мд. Для любой сети максимальная
величина потока из J в / равна минимальной пропускной способности
разреза, отделяющего s от t
гпеоре.мы^ 1. Поток (. является максимальным тогда и
только тогда, когда нет ни одного пути, увеличивающего поток. Дуга
f(xirXj) называется насыщенным _ потоком f(GJ? тели
/f) = C(xt ,Xj), и свободной от потока, если f(XItXj ) = 0.
2. Разрез (Х.Х) минимален в том, и только в том случае,^если
каждый максимальный поток /(G) насыщает все дуги разреза (Х>Х) и
оставляет свободными все дуги разреза f X,X).
Рис 4.2
-26-
Примср. На каждой дуге сети на рис. 4,2 проставлено число С(х„х^),
равное пропускной способности. Построим возможные разрезы сети и
определим для каждого разреза С(А',Х). Далее найдем минимальный
разрез min С(А\ А). Из приведенных при разрезах цифр следует, что
minC(A\A) = 15. Согласно теореме Фор да-Фал керсона максимальный поток
ИЗ 5 В I ранен И = 15.
Минимальный разрез, проходящий через дуги (х, хД0гх2) и fsxjj,
согласно следствию 2 теоремы Форда-Фалкерсона, определяет
максимальный поток, и при этом все дуги^ разреза насыщены, то_ссть
/(х.Л^Ш^х,), если дуги принадлежат (W), и /(хл,х,) - в случае (Ал А).
В нашем примере /(хрд^) = 7. /(.*3х2)=5, /(д\х3) = 3. В сумме они равны 15.
Суммируя эти потоки, получаем граф сети на рис. 43 Подбором дуг можно
убедиться, что этот поток /(G) состоит из суммы четырех простых
потоков:
х»
^\7;7
Рис 4.3
При каждой дуге проставлены две цифры: первая Cfxpxp, вторая
Memo# рдсетд/лжкй дешенкя задача
и л< дксаииодьис^и
Алгоритм состоит из последовательных шагов. К жлый шаг дает
увеличение потока на некоторое целое число. На каждом шаге
производятся две операции: А и В. Алгоритм может начинаться с нулевого
потока, но можно начать с очевидного простого потока. Так начинается
операция «А». Вторая операция «В» приводит либо к новому потоку
-27-
болыпсй величины, либо к тому, что поток максимален, то есть существует
разрез, все дуги которого насыщены.
Операция «А» (приписывание меток к вершинам)
Каждая метка записывается около вершин сети и имеет вид (я > г)
или (лГ д £J ,где £• - тоже натуральные числа.
Во время операции «А» каждый узел находился в одном из трех
состояний:
1. Узел не помечен.
2. Помечен и просмотрен.
3. Помечен и не просмотрен.
Сначала источник 5 получает пометку (-»'*)» после чего источник
помечен и просмотрен, а все остальные вершины не просмотрены и не
помечены. Пусть некоторый узел помечен (я*. £(Все соседние узлы у
получают пометки (х+,yjy, если только f(xfy) < С(хлу) (рис.4.4).
vU.€(y2))
W* *
Рис. 4.4
Тогда £(y) = min[e(x).C(x.y)-f(x.y)] (такие узлы «у» теперь
помечены и не просмотрены).
Если же соседний непомеченный узел определяет направление дуги
от у к я, то есть, если /(у,х)>0, то метка у вершины у имеет вид
(х'.с(у)), где г(у) -mi'n|zY
Такие узлы с<у» теперь помечены и не просмотрены, а узел «х» после
этого помечен и просмотрен. Это первая часть шага повторяется до тех
пор, пока нс окажется помеченным сток f, или пока нельзя будет больше
пометить ни одного узла, а сток останется непомеченным. В первом случае
переходим к операции «В», а во втором шаги алгоритма закончены.
Операция «В>> (изменение потока)
После операции «А» сток t имеет пометку (у\ или (у
Если пометка (у*, ф, то /(y,t) заменяется на f(y,t) + £(t)
Если имеется пометка (у\#6МЛто ffhy) заменяется на
f(t,y )-£(!).
Затем в любом из этих случаев следует переход к рассмотрению узла «у».
Далее аналогично: если узел «у» имеет пометку (х\#(у7), то /(х.уЛ
зяменяслся на /(x.y) + ^G), а если он имеет пометку (х"тг’^)),то /Сь-г)
заменяется ня /Yr aj-s/f)+ и далее следует перейти к рассмотрению
узла л\ Обратим внимание на то, что в последовательных операциях «В»
исток в каждой луге изменяется на одну и ту же величину t(f)£ 0t то есть
при каждом таге исток сети /(G) увеличивается ня g(t)r Когда мы
достигнем источника S, изменение /fG) прекращается и следует стереть
уже ненужные пометки при всех узлах и перейти к новой операции «А»
нового следующего шага.
Алгоритм заключается в поиске по шшям простых путей из s в t
увеличивающих поток. На каждом шаге должен происходить «прорыв»
жидкости от истока х к стоку г Если же после операции «А» нс достигнут
сток, то исток был максимальным. Приписывание некоторому узлу х
пометки соответствует выделению пути из я, который может оказаться
начальным отрезком, увеличивающим общий ноток.
Пример. Методом расстановки пометок найдем максимальный поток
сети, фаф которой приведен на рис. 4.1,
Для облегчения расчетов составим таблицу формул операций «А» и
«В»,_____________________
Операция «А»
Для метки (х\г(у)):Дг,у)>0; £(y) = mit{€(x).C(x.y)-f(x,y)] (4.1)
Для метки (х ^y) = mwtfxA./ify,x)J (4.2)
Операция «В»
Если метка при «у» имеет вид то Дху) заменяется на
[/(Х>’) + ^Л| (4.3)
Нели метка при «у» имеет вид - (х~,е(у)), то Дуд) заменяется на
[/’(у,х)-ф>| (4.4)
Задаемся начальным нулевым потоком
Рис. 4.5
-29-
Операция «Ап Пометим источник $(-,~). Здесь £=*-. Это означает,
что остаточная пропускная способность равна бесконечности. Тем самым
узел 5 помечен. Пометим соседние утлы. Например, по формуле (4.1)
найдем метку узла х3. Так как J1-. Л
Поэтому X/ZJJ- Аналогично и
хдуй). Узлы и л, помечены и не просмотрены (рис. 4.5).
Просмотрим узел Xj. Соседом узла является сток /. Найдем метку стока.
f« = min[F(AH^Ix/)-/(v)]=mm(3315-0) = 3. Поэтому ДД и произошел
прорыв потока по простому пути s-x3 -г.
Операция «В», По формуле (43) новый поток па дугах найденного
простого маршрута увеличивается на £. Потоки в остальных дугах
остались прежними, то есть нулевыми.
Шаг2
Вернемся к узлу Xj, который был помечен и нс просмотрен (рис. 4.6).
Рис. 4.6
Операция «Ап
Находим метку узла х4 по формуле (4.1):
xX^,m^]AQxlxJ-/fxlxj]=x4^/7-0^ = xJxl7/. По той же
формуле (4.1) проставляем последовательно метки в узлах дч. х3 и г. Все
эти узлы сети расположены на простом пути 5 — т3 -х4 — х2 -х3 -г. Из
меток на этих узлах (sfXjfs* ,8Д ,7)л ,7/ х3,7 XI, следует
что минимальное значение всех остаточных пропускных способностей
равно семи.
Операция «В»
Из формулы (4.3) находим новые потоки в дугах.
-зе-
/(%/>3 + 7 = 10. f(XixJ = 0+7 = 7; /^xJ = 0 + 7 = 7;
/<^> = 0 + 7 = 7; /fjxJ=0+7 = 7,
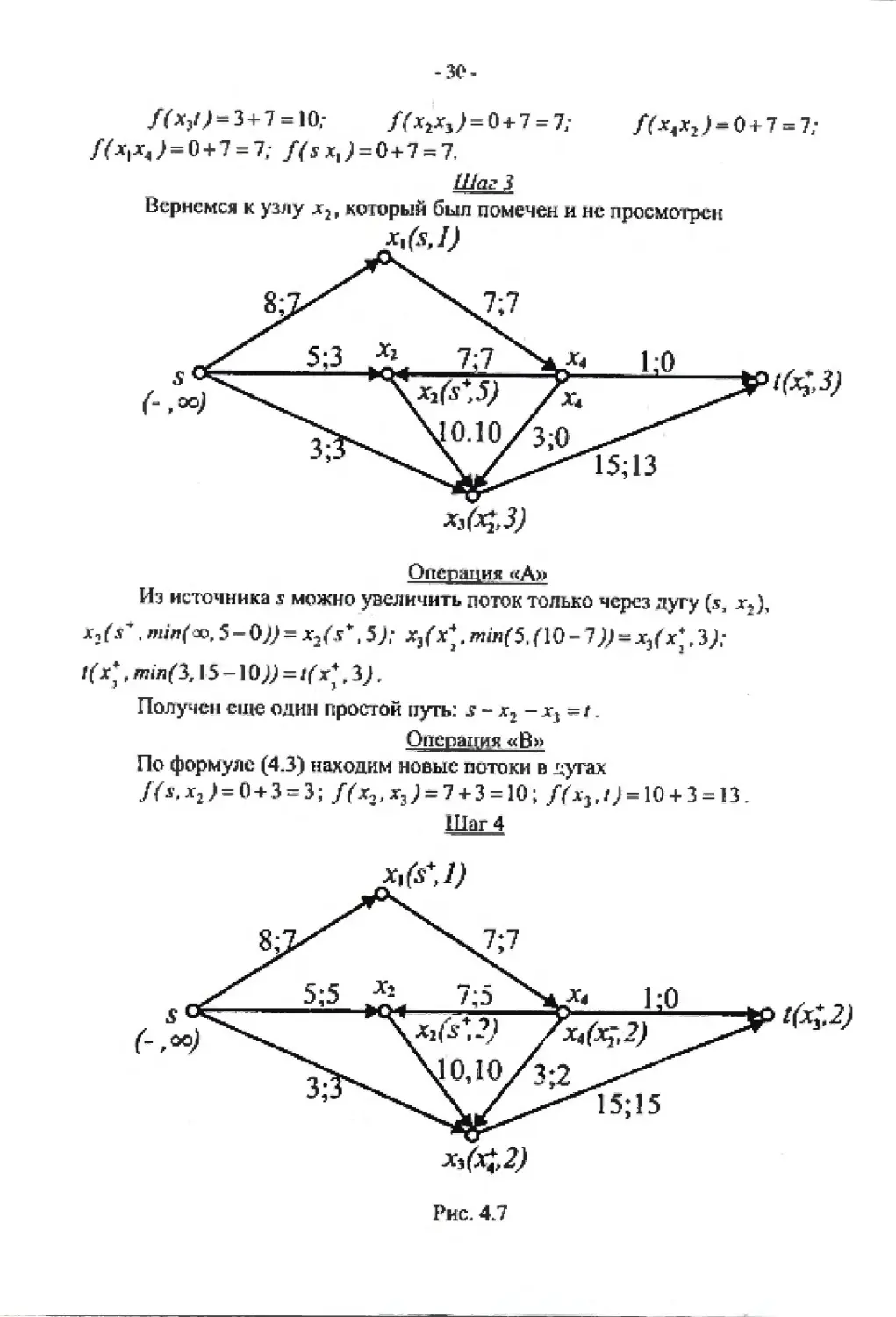
Шаг J
Вернемся к узлу л2, который был помечен и нс просмотре»
Операция «А»
Из источника s можно увеличить поток только через дугу (j3
Л, 5-0)) = х/Г, 5): х3(х*. min(5, <Ю - 7J> л,(Х, 3/-
f (Г, mmf 3,15 -10)) = t (x*, 3).
Получен еще один простой путь: - хг - xi = t.
Операция «В»
По формуле (4.3) находим новые потоки в дугах
f(s.x1) = 0 + 3 = '}-, /(x2,x3J = 7 + 3 = 10; ffxjj) = 10 + 3 = 13.
Шаг 4
хз(*;>2)
Рис. 4.7
-31 -
Операция «А»
Из источника s можно увеличить» поток только через дугу (л> х2).
Проставим метку х2Л?*Рлпя6юл5-3j)-fa+ .2/ x4fah гтш(2,.7 = fa2J2^
। so формуле (4.2). х5 (%, /яiл( 2.3 - = ( х4,2 }. * (х , mwi f 2J 5 -13 ,) = ( х3 ,2 )
Операция ^В»
/7х3г/> = <13 + 29 = 15 формула (4.3), /<х4. х3) =( 0 +2> = 2,
/<х4. х2 > = <7 - 2; = 5 по по формуле (4.4)
Больше увеличить поток невозможно! 'гак как дуги (х3,/) и (хрх4)
насыщены. Из графа следует, что Ияйй. = J 5 -
Выделим дуги с насыщенным потоком. Это (X|.t4 ), fa х2), fax^J,
fx-iXy) и </х3>. Просматривая эти дуги, составляем минимальное
сечение, проходящее через дуги <Х|Х4 ), fa x2J и fax2_). В иных задачах
таких сечений может быть несколько,
(Я (14 [10]
Пример решения задачи 4
Для заданного графа сети (рис. 4.9), найти максимальный ноток и
минимальный разрез.
Задачу решить методом расстановок пометок Форда-Фалкерсона.
Следует заметить, что построение простых ну гей по тагам неоднозначно,
и хотя ответ и разрезы минимальною сечения одни и тс же, простые
потоки различные.
Рис. 4,9
Эго показано двумя решениями данной задачи одним и тем же
алгоритмом. Сравнение этих решений приведено на рис. 4Л0 и рис. 4.11.
Отсюда видно различие простых потоков* составляющих максимальный
поток Г,=27. Простые потоки отмечены толстыми ребрами.
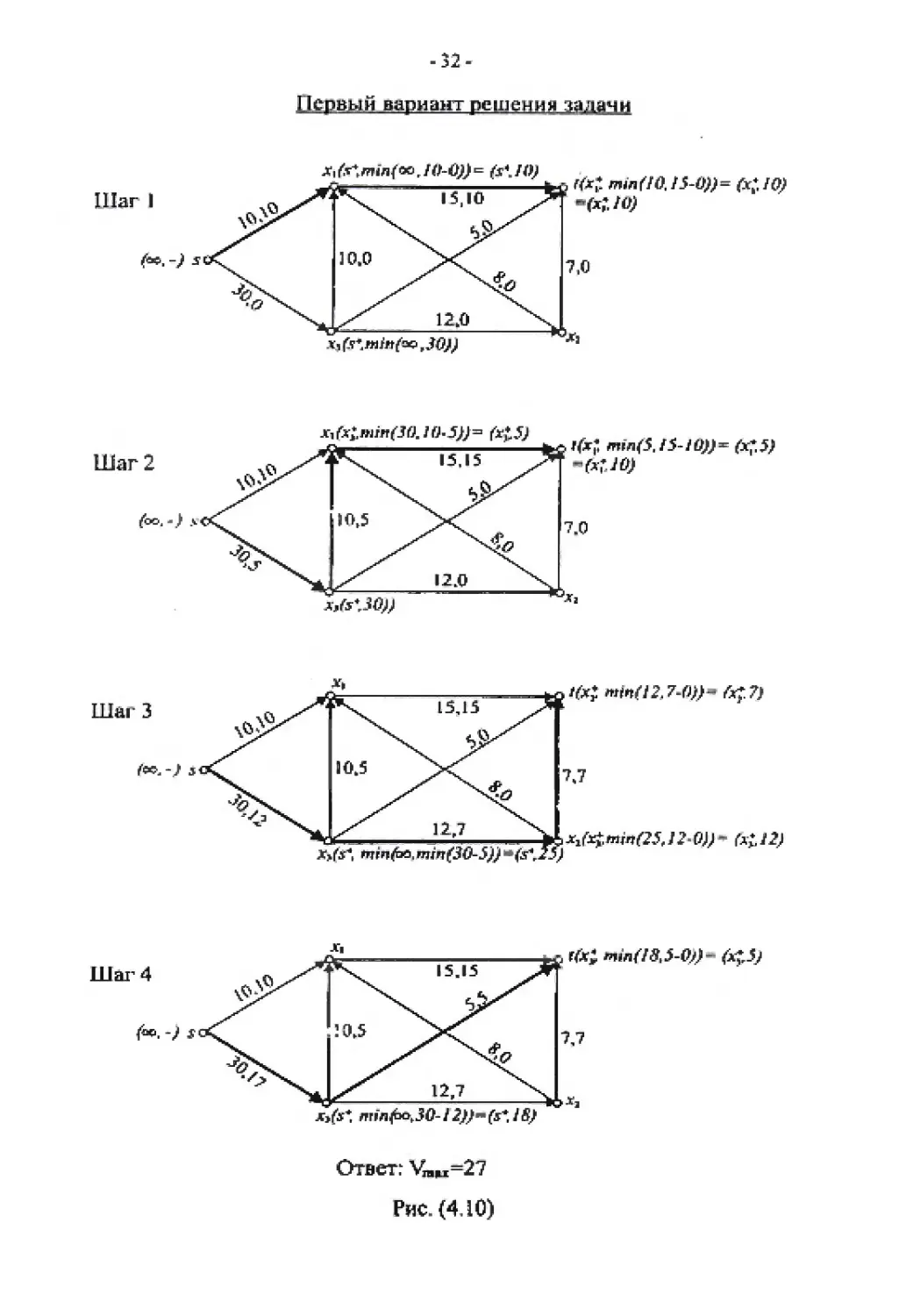
Цервой вариант peingHHH задачи
Ответ: УгаЯ1=27
Рис. (4.10)
-33-
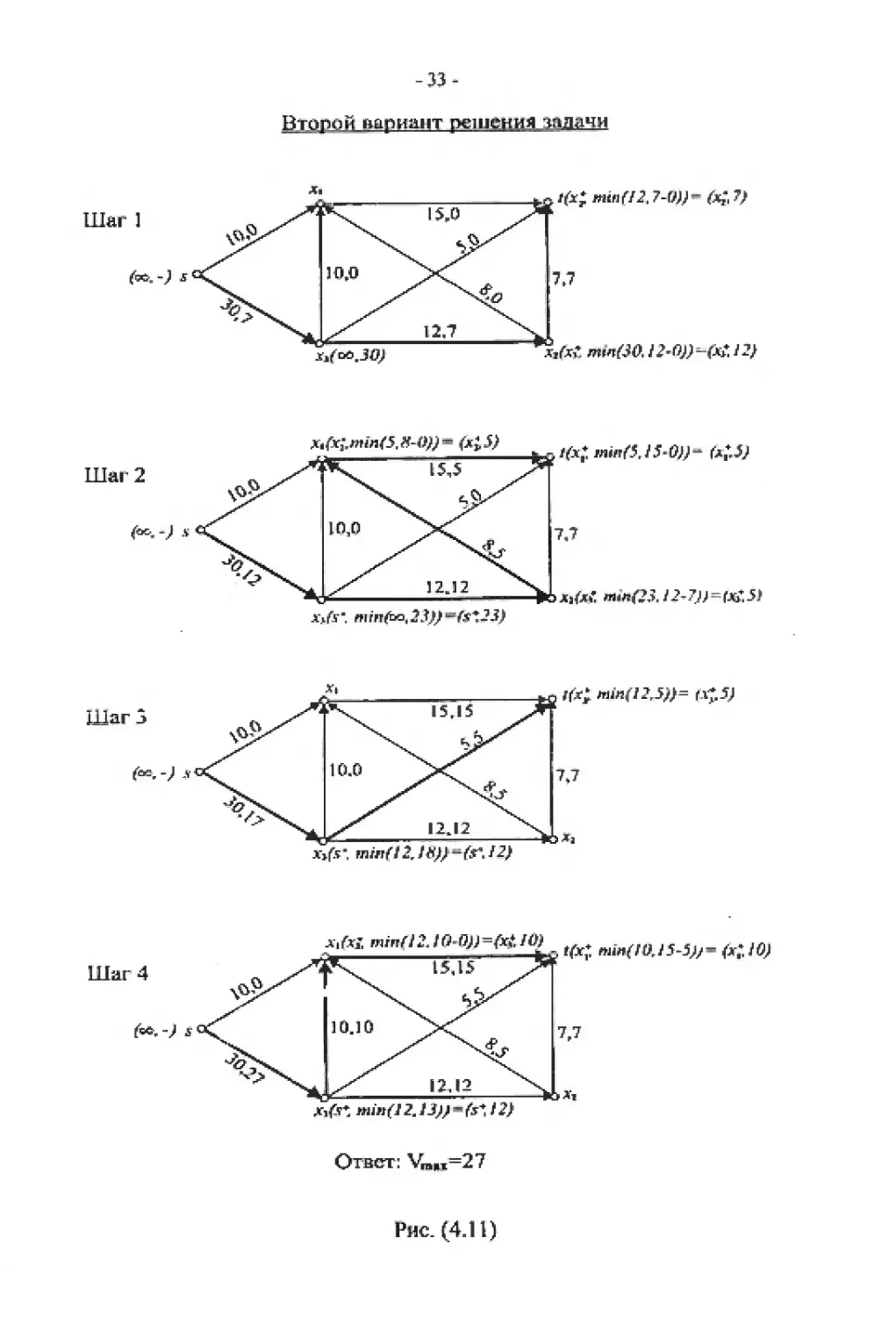
Второй вариант решения
д*!л£5, ЗМЭД (л5) Шаг 2 „ 15,5 X ** -X 12J2 - x/r", ffi рг^Ьо, 23ДО "<s*2 J) Xi Шаг j f4 l5,|S (ocr -J .yo/X 10.0 X. "/X. I2J2 Alft", minf f 2, - ^r. /2) At ft£ mjft<7 2. / 0'0)J = Atf /< Шаг 4 ft x^T\ 15,15 x' f"&cr - j ji °CL J 0. J 0 >s. 1212 Xj£rt J«j»f12. U}/ - fr* / 2J1 |hd^x* wwrf5JJ“t^“ fa|*-^ 7,7 ^O Wjh*. rtirtf?,?. / 2-7JJ = fAb 5) min(lJr5^= M* 5J 7J ^6 Ла jLo tpr* /5-5>/ж 7,7
Рис. (4.11)
34-
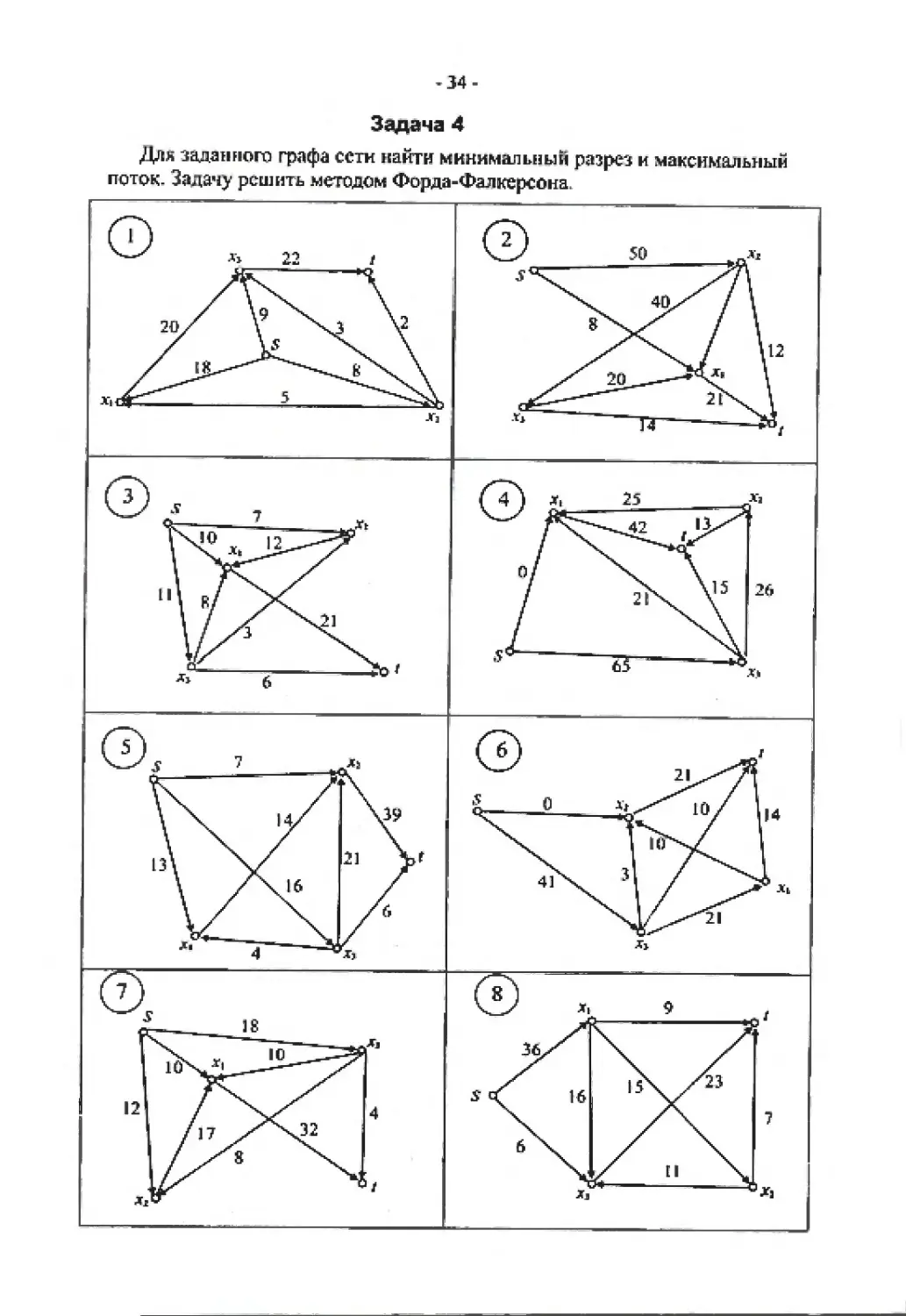
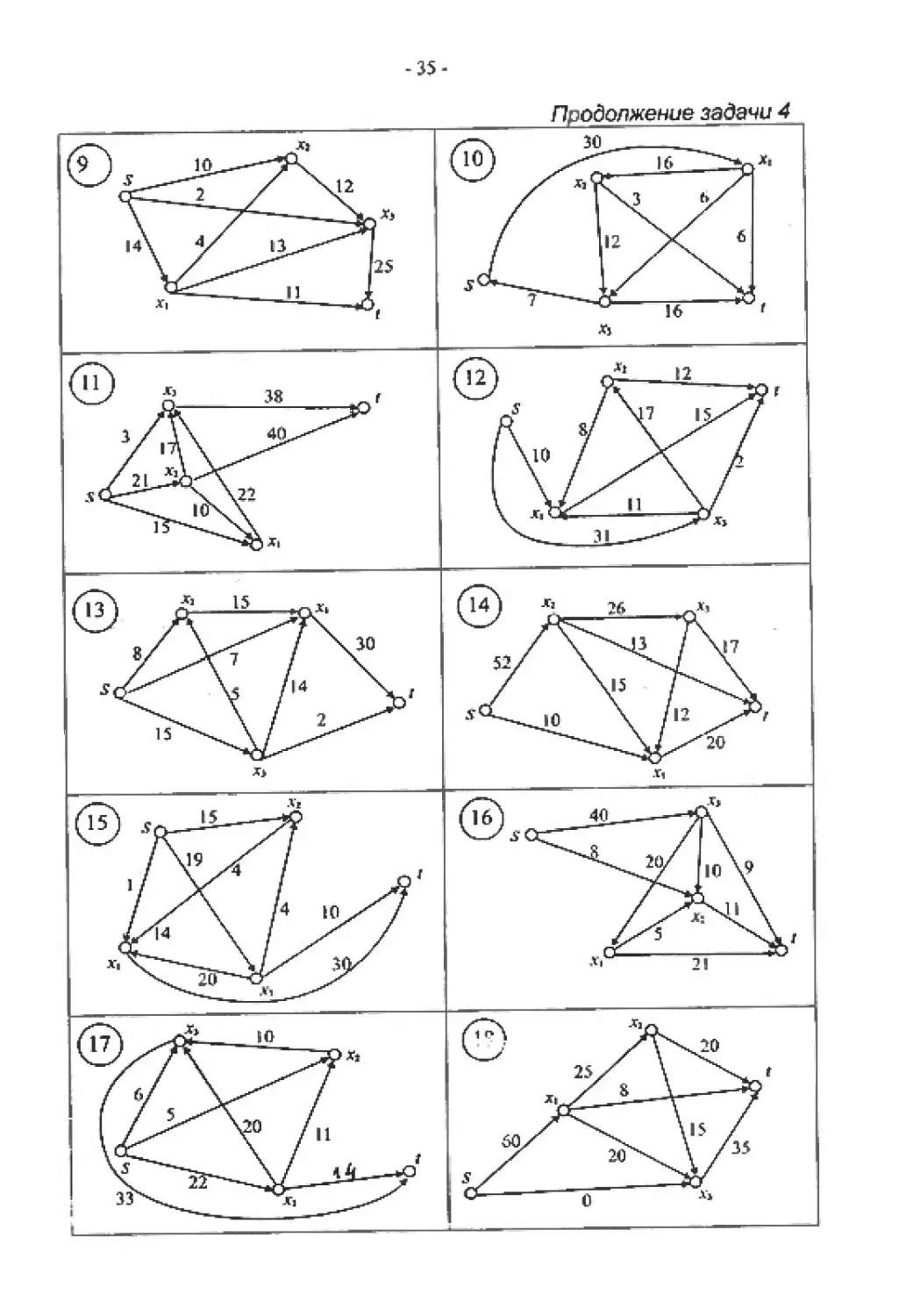
Задача 4
Для задан нот графа сети найти минимальный разрез и максимальный
поток. Задачу решить методом Форда Фалкерсона.
-35-
Продолжение задачи 4
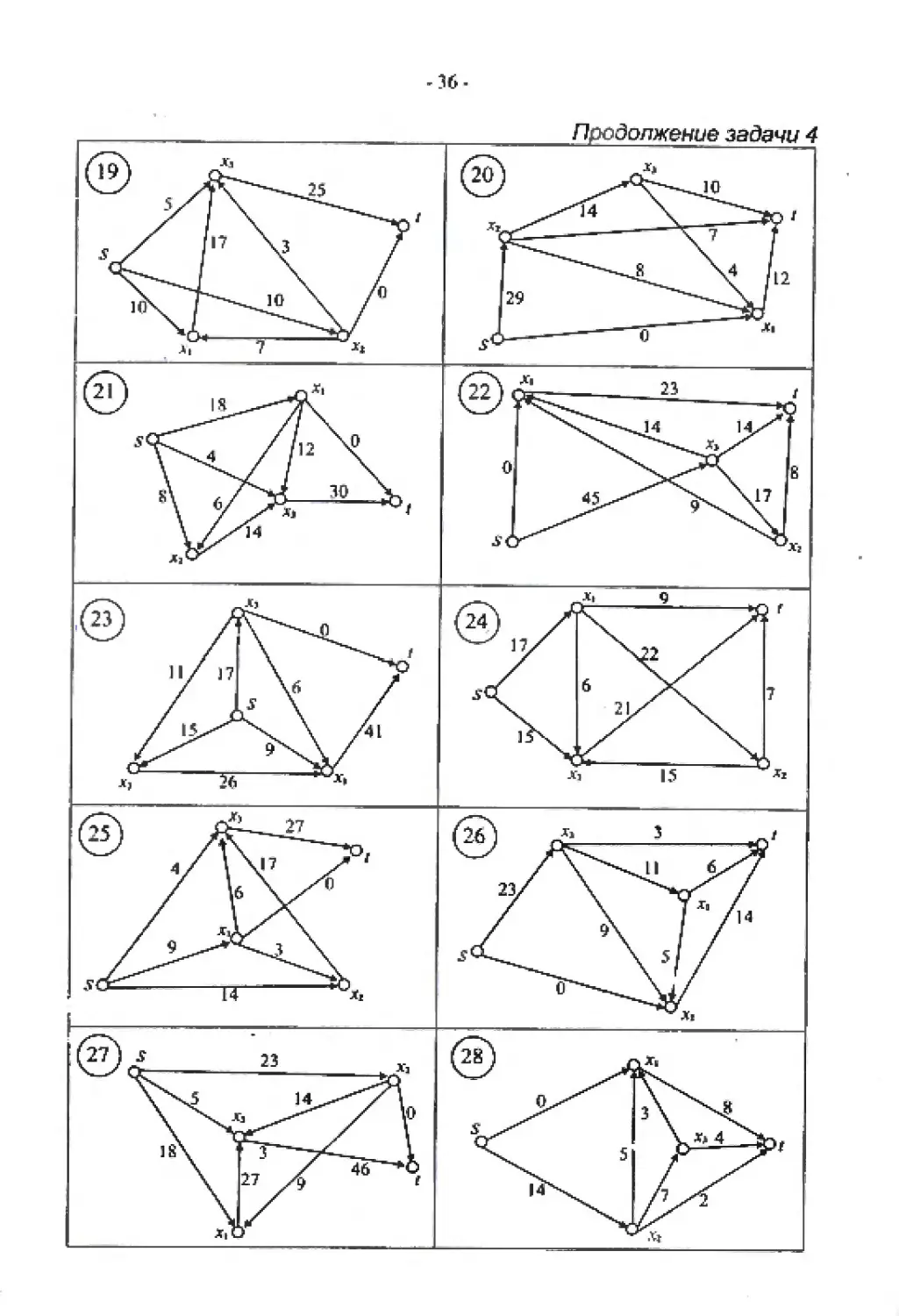
-36-
Продолжение задачи 4
-37 -
ЗАДАЧА 5
По заданному чертежу графа определить основные его
матрицы (А. В, К Ф)
Составить матрицы инцидснций «Л», смежности
фундаментальных циклов «Ф» и фундаментальных разрезов «Я» но
заданному графу. Покажем решение задачи на примере: (рис. 5.1),
Дан орграф (ориентированный граф) G с числом вершин п-5 и
числом дуг, равным ?п=7ь Остов графа отмечен толстыми линиями дуг;
число ветвей остова равно л-2 =5-2 =4. Число хорд m-n 11 -7-5+2 -3.
Составим матрицу инцидснций Л =
порядка (5x7).
L ес™ К является шчоодм дуги
О, если вершина* Р' и дуга нсия^идемтиы
- L гели дершшде является концолг дуги /у-
Нули в матрице не проставлялись. Если бы граф был нс
ориентир званным, то матрица «Л» имела бы такой же вид, но единицы
были бы без минусов. Обратим внимание, что каждый столбец состоит из
двук отличных от нуля ячеек.
Составим матрицу смежности «В» порядка (5x5) по правилу:
-1, если вершимы и Р, смежные. то гать свяэляы дугой
7- = 5 0. если i * j и К и П яс
V Г J
степени вершины F,, если: = j
-38-
Проверьте справедливость формулы 2? = /1 Л? , где
транспонированная матрица инциденций.
Составим мафицу фундаментален ыхлазреги] в /С
Матрица фундаментальных разрезов имеет (л-/) строк и (лл-л+/)
столбцов. Число фундаментальных разрезов равно числу ветвей остова.
I, сеч и гИ-ра /г лриллАчежмва / - лгу разрезуи «р,|"гята|*иЛ
а/ше/аяацшл разреза
t.'v = < - L ft-.frw дуга фмлайаяжтда у - .му разрезу w ее орпсятсл^ш
w разреза
0. №,w <Эуга I »tr пршшдпеэ/сит j—му разрезу
Положительное направление разреза совпадает с направлением ветви,
через которую проходит разрез.
В случае неориентированного графа вместо (-1) ставятся единицы.
Составим матрицу фундаментальных циклов Ф
Направление цикла определяется направлением хорды, входящей в
цикл. Всего фундаментальных циклов в рассматриваемой задаче три, по
В случае неориентированного графа в его матрице Ф все отрицательные
элементы проставляются положительными числами.
-39-
Правильность составления матриц и разрезов можно проверить,
воспользовавшись ортогональностью матриц и разрезов матриц Л и Ф ,
где Фг- транспонированная матрица фундаментальных циклов: К Ф -О,
Здесь нуль - нулевая матрица порядка (4x3), Проверка ортогональности
сводится к нахождению скалярных произведений строк матриц А" и Ф. Эти
строки называются соответственно векторами разрезов и векторами
циклов.
Например, найдем сумму произведений третьей строки матрицы А
и второй строки матрицы Ф: (0110010)(01001(-1)0)<Н1
Скалярное произведение второй строки матрицы АЛ и первой строки
матрицы Ф: ((-!)(-! Х-1)0100)( 1СЮ(-1)100>С-1 уьО4Ю-НН-1-Н)-Н)-О.
115]
Задача 5
матрицы фундаментальных разрезов и фундаментальных циклов.
Проверьте их ортогональность_____________
-40-
-41-
ЗАДАЧА6
По заданной матрице инццденций составить список хорд и
ветвей графа и построить граф
Ci Ci ёз с* ев Ci Cic Cm С12 е«я
1
2
3
4
5
6
7
&
Пример L Рассмотрим матрицу инциденций графа с л=8 вершинами
(строками) и т=13 ребрами (столбцами).
Последовательно рассматриваем ребра: #|, £3, Л4---* Дяя
любого взятого последовательного ребра решается вопрос, включить его в
остов или включить в список хорд. Параллельно строится остов графа:
если ребро становится ветвью, то его вносят в построение остова; если
ребро образует цикл, то его исключают из рассмотрения и заносят в список
хорд. В наших задачах остов содержит я-1=8-1=7 ветвей.
Алгоритм Шаг L Выбрать очередное ребро . Если оно образует
никл с ранее построенными ветвями» то следует занести его в список хорд
и вывести из рассмотрения.
Шаг 2. Выбрать из следующего столбца очередное ребро ^ч|.
Возможны четыре случая:
а) Вершины принадлежат одному и тому же связному подграфу,
тогда ребро становится хордой.
б) Только одна вершина принадлежит связному подграфу, тогда это
ребро становится ветвью.
в) Ни одна из вершин не принадлежит подграфу» тогда это ребро
становится ветвью и является началом подграфа остова.
г) Концевые вершины принадлежат различным несвязным
подграфам остова. Такое ребро является ветвью.
Шаг 3. Если все вершины образуют связный граф с w-L ветвями и
все m ребер просмотрены, процесс окончен. В противном случае следует
перейти к шагу 2.
Ребра включенные в остов (смг таблицу 6.1 и рис. 6.1).
е< С2 Cj с* Са е? ед Ci© 1 ^11 0» еп
1-6 4-7 1-3 4-3 — 2-7 । “ 7-8 «Г и™ 5-8 —
-42-
(J)); erf®—®);
Список хорд:
e&(CD---@)1 erf®
Cirf®—®); Cii((2)—®); eirfd)—(D)‘
Ребра Ребра, включенные а остов Подграф остова 1 Подграф остова 2 Подграф остова 3
С| -Ц- ®i
4- сд
+
-|-
*q Pj Ci
! Ц-. r*i UJ Д'
4- CJ e4 *S «6 «J
м. 1 «1 *1 CT
►J5 .b ft b
^10 — чГ e чГ 1 r-J
ен •W e* i?! ?л ₽4 £\ 4?,
e, *4 *s‘i ci
gl) <м c, e7 e,«, es et e,
Замечание. Аналогично задаче 6 решается задача о нахождении
остова весового графа с минимальным общим весом. Для этого следует
составить нстътй список ребер графа (<q, .-•) в порядке
возрастания веса ребер и построить новую матрицу инциденцкй с этим
новым порядком столбцов. А дальше ветви остова находятся так же, как в
задаче 6.
ПОМ 15]
-43 -
Задача 6
1? => с> с* es е* вт е« е. с,0 e,i он е« Qj е, е» ei е* «о <ч Ст е* е( е10 Си йт с«
-44-
-45-
Лройолжание задачи 6
(11) ei е* Сз е* е? е» ей eifl Си си си (Ц) Ci са еа е* Cs с* е? сз с* ею с« ею Сн
®) е< еа £1 е* cs ел ет с* с* ею си ен e« (Я) й са сз с< о с* с» си Сц С|Я ен
-46-
ЗАДАЧА 7
По заданной матрице инцаденций графа -алгебраически
построить матрицы смежности, фундаментальных разрезов,
фундаментальных циклов
Рассмотрим четыре вида матриц, ассоциированных с простыми
неориентированными графами без петель.
Матрицы инциденций Л порядка (тхл)
Матрицы смежности В порядка (их/?)
Матрицы фундаментальных циклов Ф порядка (тм?)
Матрицы фу ндамся стальных разрезов порядка («- 1хт), л - число
вершин графа, m - число ребер графа, v=m-ii+l число хорд, (лЛ) - число
ветвей графа.
Постановка задачи. По заданной матрице инциденций Я построить
матрицу смсжеяости, матрицу фундаментальных разрезов и матрицу
фундаментальных циклов.
Задачу решить алгебраически.
Столбцы матрицы Л пронумерованы специальным образом; первые
номера столбцов соответствуют хордам. Всего таких начальных столбцов
1й=/Л-л+1 -
Задача решается алгебраически, что означает, что все известные из
курса линейной алгебры алгебраические понятия, такие как линейная
зависимость, методы нахождения обратной матрицы, линейные
пространства и др., выполняются по модулю два. Это называется двоичной
арифметикой. В ней определены только две операции - сложение и
умножение:
[0 + 0 = 0
- 0 + 1=И+0 = 1
1 + 1^0
го-о = о
я 01 = ТО = 0
1-1 = 1
Операция вычитания отсутствует, как и отрицательные числа.
Пример. НаЙдсм двумя способами обратную матрицу М
Аой
м= но
1 О 0J
I. Находим М 1 методом присоединенной матрицы.
Находим определитель |Л/| разложением па элементам 1-й строки
|Л/| = 1
I о
00
1 1
10
= 1(1 0 + 0-0)+ 0(10+ 10) +
+ 1(1-0 + 11) = 10+0-0+11 «0+0+1=!
-47-
Так как |л/|*0, то ранг матрицы равен трем и обратная матрица
существует.
Al 5^22 Л2Э
ЧА| Аз Аз>
где - алгебраические дополнения
элементов матрицы М, а индекс «Т» - индекс транспонирования.
Следовательно, обратная матрица равна
foonr
010
гооГ
011
J01,
2, Обратные матрицы больших, порядков проще находить
методом элементарных преобразований строк. В алгебре матриц часто
применяются блочные матрицы., то сеть разбиение матриц на
прямоугольные блоки, разделенные вертикальными и горизонтальными
чертами.
А/-3 -
Л<П Л/|,
1
& » л
Составим матрицу из двух блоков: Л/ и Е, где £ - единичная
матрица:
Л«Ж= ПО
/10 0
X
10 0"
010
001,
Далее применим метод элементарного преобразования строк
(метод Гаусса) с целью получить в левом блоке единичную матрицу, в в
правом - матрицу М~1:
<100 ООЙ
110 010
.101 100
X г
Меняем местами 1-ю и 3-ю строки.
л
1 О
1 1
-4Е-
G oo
I 10
4ooi
о о г
010
101?
Складываем по модулю два 1-ю и 3-ю строки.
'10 0 0 0 Г
010 011
к0 01 101,
Складываем по модулю два 1-ю и 2-ю строки .
Получили матрицу из двух блоков. В левом блоке получена
единичная матрица. А в правом - искомая матрица Л/ 1.
Ранг матрицы инциденций равен п-1. Это следует из того, что в
каждом столбце матрицы Л поставлены две единицы, то есть четное число.
Если в матрице Я сложить все строки, то получим нулевую строку. Отсюда
любая строка является линейной комбинацией других строк. Запишем
матрицу 4 без последней строки и обозначим ее через Я. Ранг матрицы >3
равен («-IK С помощью матрицы Я можно найти матрицы
фундамшпальных циклов Ф и фундаментальных разрезов К, Известна
теорема, что любой разрез графа и любой цикл имеют четное число
пересечений, то есть имеют четное число общих ребер, Отсюда следует
ортогональность матриц Фг и А?
Фг-А=0.
Так как первые v столбцов матрицы фундаментальных циклов
образуют единичную матрицу, то очевидно, что матрица Ф состоит из двух
блоков:
Ф-Е| Ф]2 .
Аналогично, так как последние л-l столбцов матрицы
фундаментальных разрезов образуют единичную подматрицу (эти столбцы
соответствуют ветвям графа), то Я? может быть представлена в форме двух
блоков:
A.JE,
где Е - единичная матрица порядка (л’1), а Ап - порядка (п-1) ‘V.
Учитывая ортогональность матриц Ф и получаем
/Г+ф|2М),
Ф Кт
= (Е|Ф]2)-(КИ |£)- ЧЕ|Ф,
поэтому .А г = -Ф12=Ф|2(гпос12).
Зная одну из матриц Ам или Ф12, добавлял встсгвующии блок
единичной матрицы, просто получить другую матрицу; из Atl получаем
Ф|2» ИЗ Ф|2~ Кц-
Прсдставим матрицу Я в форме двух последовательных блоков:
-49-
>4 - j4||j Л|21
причем блок л,, имеет v столбцов, а (л-1) столбцом. Очевидно,
что блок Л|2 - невырожденная квадратная матрица порядка (л-1).
Покажем, что если столбцы матрицы Л, Ф и А записаны с одним и
тем же порядком ребер, соответствующим некоторому одному остову
(сначала хорды, затем ветви), то =Ф12=А21А| н /^Аз^Ф^Е, |дс
= Ail Аг; Ф12; А= А|।|Е.
Докажем справедливость равенства ^|]=Ф^И А'з ^ц- Рассмотрим
любую строчку i матрицы инцидеицин Эта строчка содержит единицы в
тех столбцах, номера которых определяют ребра, инцидентные с Аой
вершиной. Если из трафа убрать эти ребра, то определится разрез,
оставляющий с одной стороны изолированную / ~ую вершину, а с другой
стороны - все остальные вершины с инцидентными им ребрами.
Рассмотрим любую строку матрицы циклов и найдем пересечение строки i
матрицы Л и строки J матрицы Ф. Учитывая, что число пересечений
любого цикла с любым разрезом четно, получаем нулевую сумму
произведений строки / и строки у. Отсюда следует , что матрица J и Фг
ортогональны: /1ФТ=М1 Воспользовавшись формулами /f^AilA*» и
ФГ^-А, „случаем АФГ = (Ап \А12)(-^г')=А11Е+А{2Ф[2=А^+Л,2Ф^=0,
Ф|2 Ф12
Умножаем обе части равенства слева на , получаем A^Ai4^!^*
Отсюда Ф|2=“ А~з A i = Al* Ai Этим доказаны оба соотношения
^n=^i2=А2А1 и Доказано, что зная Л, можно алгебраически найти
матрицы К и Ф.
Покажем, что матрица смежности В может быть найдена по
формуле 2?- Л .
Элемент матрицы равен единице, если вершина связана
ребром с вершиной «2. Рассмотрим множество ребер, инцидентных с
вершиной /( и множество ребер, инцидентных с вершиной /2. Если эти
вершины связаны ребром* то в строках q и А матрицы Л и столбце,
соответствующем этому ребру, проставлены единицы. В других столбцах
таких общих единиц не будет. Это означает, что сумма произведений
элементов строк и г2 равна единице. Если же вершины iL и г2 не связаны
ребром, то сумма произведений равна нулю. Отсюда следует, что
произведение матриц равно матрице смежности 5. Матрица В
симметричная , так как А Ат = ЛГЛ и по главной диагонали имеет нули.
-50-
Задача 7
По заданий матрице ннциденций Л найти матрицу смежности Л,
матрицу фундаментальных, разрезов К и матрицу фундаментальных циклов
ф. Задачу решить алгебраически. [15]
Пример задачи.?.
Задана матрица ннциденций порядка (5x6)
11 1
1 1 1
1 1 -1 ш
1 1 1 1
1 1
е2 es ее-
I
Л=
3
4
5
По формуле Я=ЛЛГ находим матрицу смежности. Произведение матриц
выполняется в двоичной арифметике по модулю два.
Находим обратную матрицу Л^1 методом элементарных преобразований
Л|2|£
1-ю строку ставим на место 2-й, а вторую на место 1-й.
-51 -
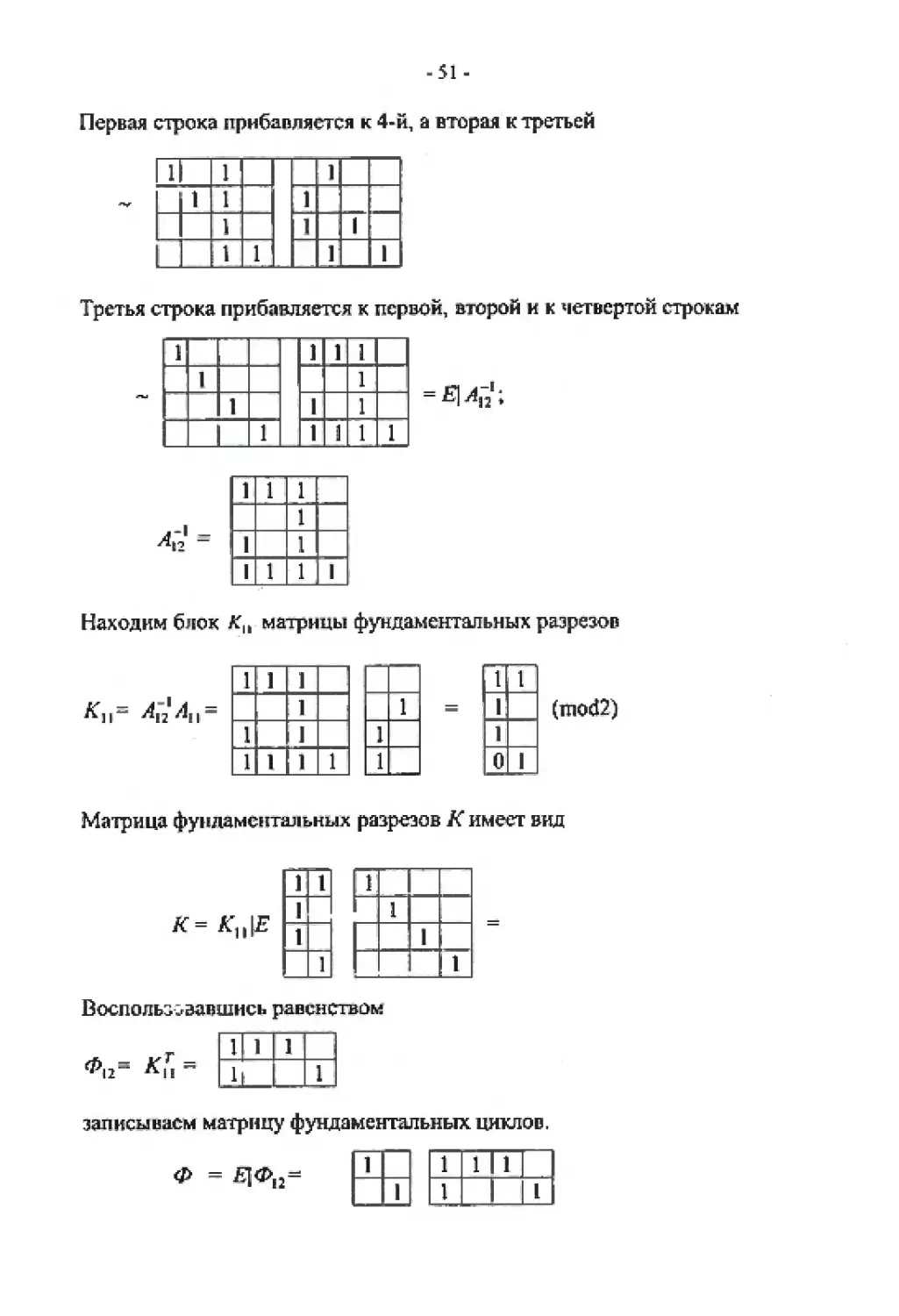
Первая строка прибавляется к 4-й, а вторая к третьей
Третья строка прибавляется к первой, второй и к четвертой строкам
1-|.
12 *
Находим блок К|Ь матрицы фундаментальных разрезов
(mod2)
Матрица фундаментальных разрезов Л" имеет вид
Воспользовавшись равенством
записываем матрицу фундаментальных циклов.
Ф = Я]Ф(2-
-52.
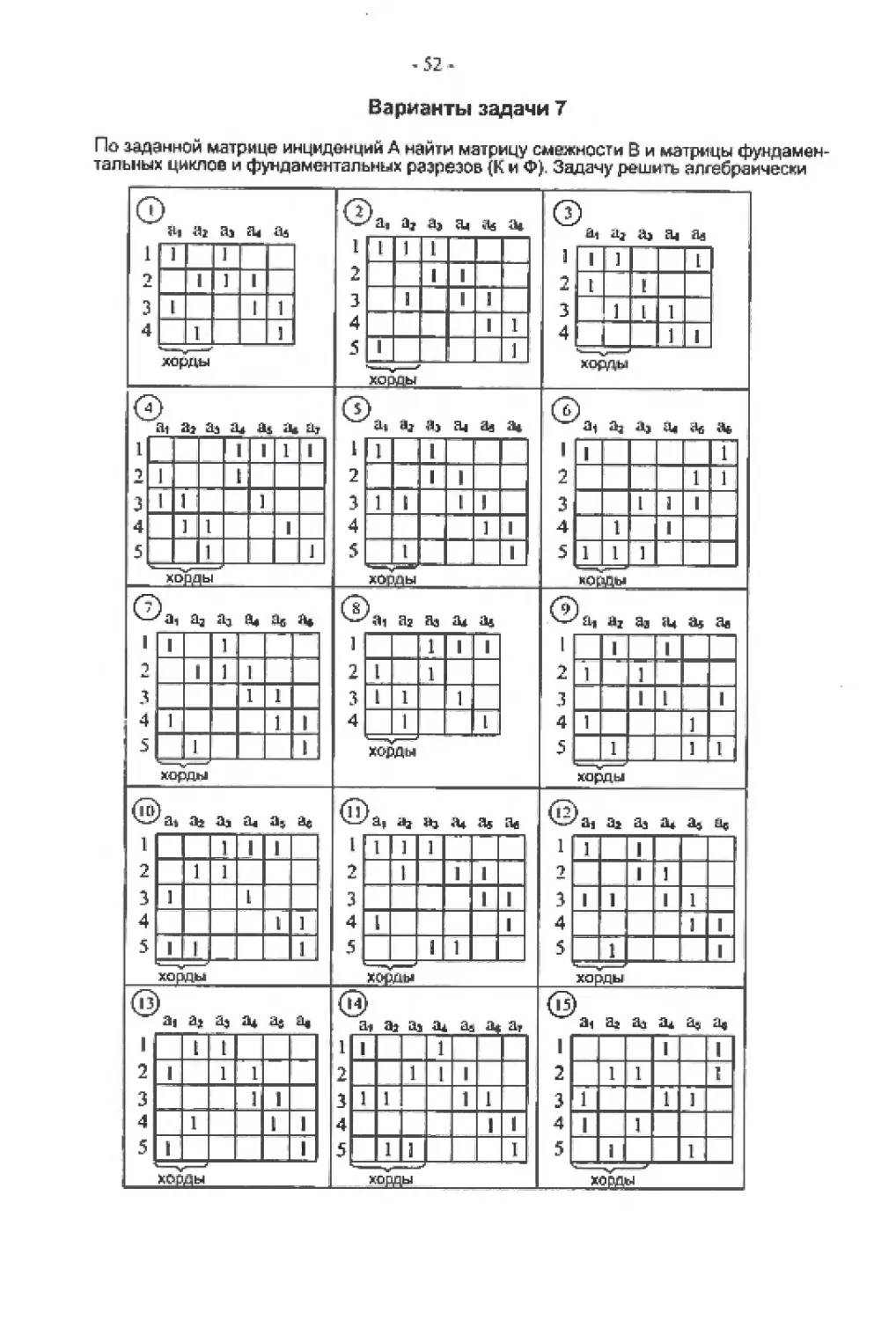
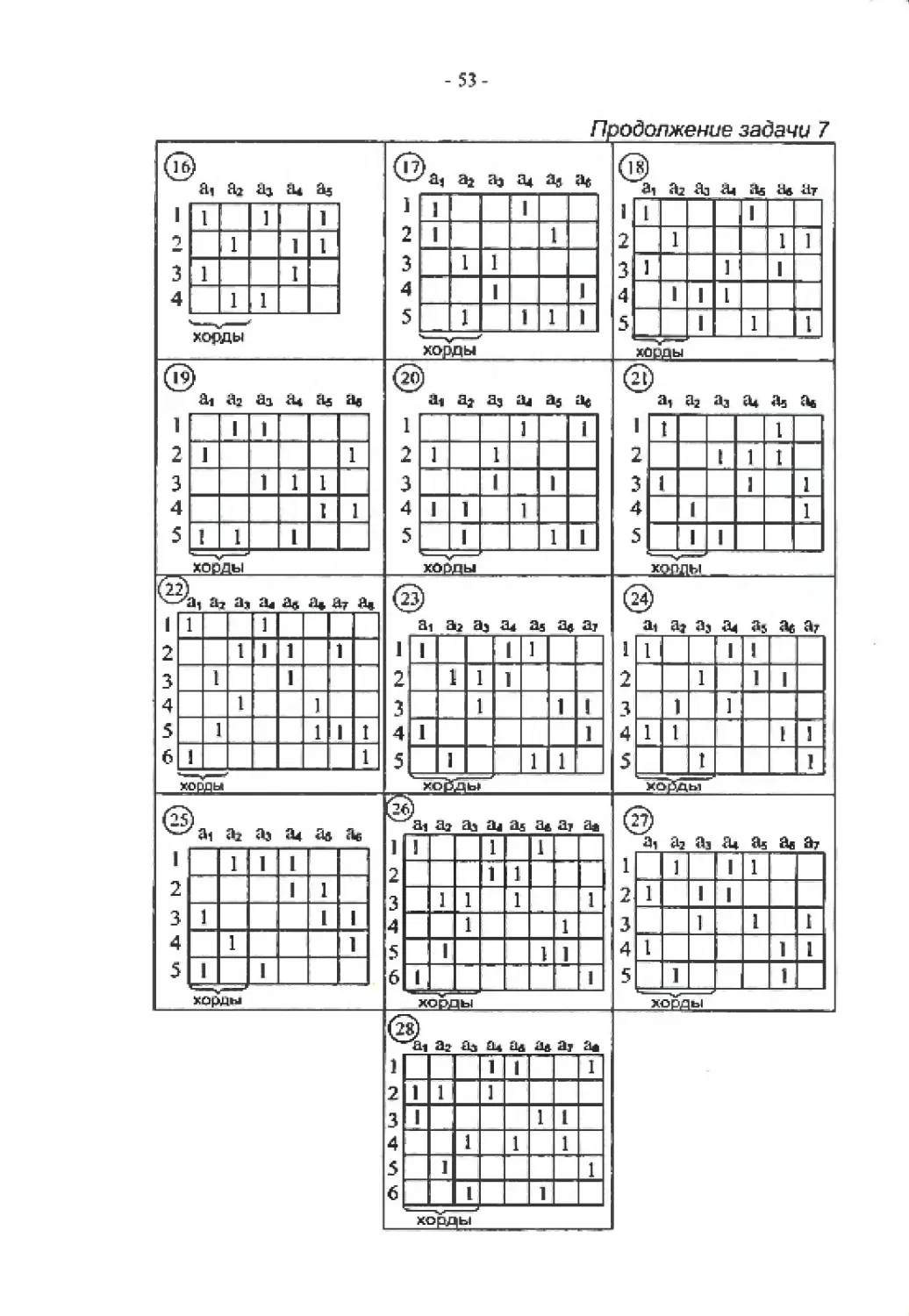
Варианты задачи 7
По заданной матрице инцидснций А найти матрицу смежности В и матрицы фундамен-
тальных циклов и фундаментальных разрезов (К и Ф). Задачу решить алгебраически
хорды
хорды
хорды
хорды
хорды
- 53-
-54-
ЗАДАЧА8
Планарные графы
Часто важно знать, возможно ли начертить граф на плоскости так.
чтобы его ребра не пересекались, точнее, имели бы общие точки только в
вершинах графа. Это важно во многих задачах электроники, транспортных
задачах. Например, при изготовлении печатных электрических схем, при
нанесении на изоляционный материал токопроводящих материалов. Так
как проводники не изолированы, то не должны пересекаться.
Плоским графом называется граф, в котором никакие два различных
ребра не имеют пересечений. Любой граф, изоморфный плоскому графу,
называется планарным графом.
Легко показать, что если строить граф в трехмерном пространстве,
то любой граф можно построить без пересечений ребер, но если строить
граф на плоскости - это не так. Например, полный двудольный граф /Г33
(рис.8.1) не является планарным, без пересечений его нельзя уложить на
плоскость. Но если из девяти ребер графа одно любое ребро убрать,
граф можно уложить на плоскость, он станет планарным.
Рис, 8,2
Полный граф с пятью вершинами 1С5> приведенный на рис. 8-2.
также не допускает плоской реализации.
Гранью плоского графа называется часть плоскости, любые две
точки которой могут быть соединены непрерывной кривой, не
пересекающей ребра графа. Граница грани- множество ребер и вершин,
принадлежащих этой грани. Например, на рис. 8.3. приведен граф с тремя
гранями: Г,, А. Гэ. Грань Л называется внешней гранью, содержащей
бесконечно удаленную точ Внешняя грань есть у всякого планарного
графа и притом всегда одна. Остальные грани называются внутренними
-55-
Рис. 8.3
Рис. 8.4
Графическое представление графов разнообразно, Например, любую
внутреннюю грань можно сделать внешней: на рис. 8.4 грань - внешняя,
а Г5 - внутренняя, не так* как на рис. 8.3, хотя эти графы практически
одинаковы* изоморфны.
Обозначим через п число вершин (рафа* через w - число ребер, через
/ - число граней. Для всякого планарного
Эйлера: n-m+f=2.
графа справедлива формула
Доказательство Построим в связном плоском графе любое остовное
дерево с количеством ветвей, равным л-2. Количество хорд равно
цикломатическому числу н=лг-л+/, Если добавить к ветвям остова одну
хорду, то полученный подграф будет иметь две грани: одну грань
внешнюю, а вторая грань добавится с введением хорды. Учитывая, что
таких добавленных к остову хорд будет v=w-n+/F получаем общее число
граней:/=У4-у=/Отсюда формула Эйлера имеет вид п-т +/и2.
Формула Эйлера справедлива для любою выпуклого многогранника
(куба, тетраэдра и др.)* а следовательно и для любой проекции выпуклого
многогранника на плоскость, лишь бы разные вершины многогранника не
проектировались на плоскость в одну точку.
Например, вершины и ребра куба проектируются в планарный граф
(рис. 8,5), Этот граф изоморфен плоскому графу на рис. 8.6. Этот плоский
храф> как и куб, имеет восемь вершин, двенадцать ребер и шесть граней:
л -7tt+/=$-/2+6-2.
Рис, 8.5 Рис, 8.6
Докажем, что граф А"33 (рис 8.1) непланарен. Предположим, что он
планарен и справедлива формула Эйлера. Тогда число его граней должно
равняться /=яьл+2=Р“б+2=5. Эти пять граней следующие: /4152/, /5263/,
/4163/, /4162/, /6342/, так как каждая грань ограничена четырьмя ребрами.
-56-
Вссги границ у всех граней, вместе взятых, 4/М-5-20. С другой стироны
каждое ребро граничит с двумя гранями, то есть всех границ должно быть
2тп-2я9=18. Раз 20 * 18» граф не планарен.
Докажем что граф /<5 (рис. 8.2) не планарен. Предположим» граф
планарен, Тогда число его граней по формуле Эйлера должно быть равно
/=д:-л+2=/0-5+2=7. Эти семь граней должны быть треугольниками: /125/,
/124/» /125/»/134/,/135/,/145/» /234/, /235/,/245А/345/.
Всего Cj =
3/2/
-10 треугольников. Каждая грань ограничена тремя
ребрами. Всего таких границ 3^=3 7=21. Каждое ребро граничит с двумя
разными гранями. Всего таких границ 2^=240=20. Так как 20^21» то
наше предположение, что граф планарен» неверно.
Критерии планарн
Подразбиение ребра ef xirx^) состоит в замене ребра двумя ребрами
и где z - новая вершина. Два графа называются
гемеоморфными, если оба они могут быть получены из одного того же
графа подразбиением его ребер.
Критерий Понтрягина - Куратковского. Граф планарен тогда и
только тогда, тогда он не содержит подграфов, гомеоморфных и A\v
Если Я3 или являются подграфами, то граф не планарен. Например»
граф на рис. 8.7 не планарен» так как каждая его вершина инциндентна с
четырьмя ребрами, то есть является графом .
Пример, На рис. 8.8 приведен граф Петерсона» содержащей подграф
В этом можно убедиться» сделав обратное подразбиение ребер,
инциндентаых с вершинами» закрашенными в черный цвет» и сравнить с
графом на рис.8.9.
Рис. 8.8 Рис. 8.9
-57-
представляет собой процесс последовательного включения в
предварительно уложенный плоский подграф Gj сег-мснта S/ Сегмент 5,
является плоским подграфом графа G в форме цепи, концы которой
являются вершинами, принадлежащими 1рафу СР Эти вершины на концах
цепи называются контактными и обозначаются не кружочками, а
квадратиками. Сегмент Sf укладывается в >рань и контактные
вершины сливаются с соответствующими вершинами грани. После
укладки 1рань разбивается на дне грани. В начале процесса укладки в
качестве G| выбирают подграф G в форме простого цикла, содсржаще1'о
возможно большее число вершин графа G. Сегменты 5 получаются
разбиением на компоненты графа G- GP Это могут быть отдельные ребра с
контактными вершинами на концах или цепи, дополненные вершинами,
отсутствующими в G . Предполагается, что в графе G отсутствуют точки
сочленения и мое гы и что всегда в каждом сегменте присутствуют не
менее двух контактных вершин,
Два сегмента S;l н 53 называются конфликтующими, если они оба не
могут уложиться в одну грань одновременно. Случается, что сегмент
может быть уложен в нескольких гранях ( 1 г| £ 2 ), но если это помешает
укладке новой грани на следующем шаге, следует вернугься и
пересмотреть выбор грани, стараясь избежать конфликтующих сегментов,
алгоритм укладки графа на плоскость.
I. Выберем простой цикл из графа G и уложим его на плоскость.
Обозначим его через Cq.
II. Найдем грани графа G| и сегменты относительно Gp если
множество сегментов пусто, то перейдем к п. VIIL
JIL Для каждого сегмента S определим на графе G| множество
граней FfS).
IV , Если существует сегмент 5, который невозможно уложить нив
одну из граней (иначе, если |/YjJ] = 0), то граф G непланарен. Конец. В
противном случае перейти к п. V.
V . Если есть сегмент S, для которого существует единственная
допустимая грань F, то перейти к п. VII. Иначе - к п. VI.
VL Для некоторого сегмента 5 с несколькими допустимыми
гранями выбираем одну F. «
VIL Если cei мент S имеет вид 1В^Т\а , то выделяем из него цепь
L вида и помещаем L в грань F. Заменяем G, на G| и
перейдем к п.Ц,
VIII . Построена укладка G, графа G на плоскости. Конец,
-58-
Пример решения курсовой задачи 8
По заданному графу G (рис. 8.10) провести его плоскую укладку или
доказать его непланарностъ.
Рис. 8Л0
Известно, что у планарного графа всегда /м < Зя - 6 при я>3. Но
заметим, что это не означает, что все непланарные графы удовлетворяют
неравенству например, у непланарного графа Язг В нашей задаче
п=6, т»41; 11 <3-6-6= 12.
1. Строим граф G] в виде простого цикла, стараясь включить в него
возможно большее число вершин, чтобы уменьшить число сегментов:
1’2’6-5-4’3-1. Всего шесть ребер
Рис.8.12. Подграф G, и его сегменты ня 2-м шаге алгоритма
-59-
Рис. 8.13. подграф G| и сегменты на 3-м шаге алгоритма.
Рис. 8.14. Подграф <7| и сегменты на 4-м шаге алгоритма.
6
Рис 8.15. Подграф и сегмент на 5-м шаге алгоритма
Рис. 8.16. Укладка графа <71( приведенного на рис. 8.10
По формуле Эйлера проверяем число граней:/=л1-й+2=1 1-6+2“7
[2], [151, [101
-60-
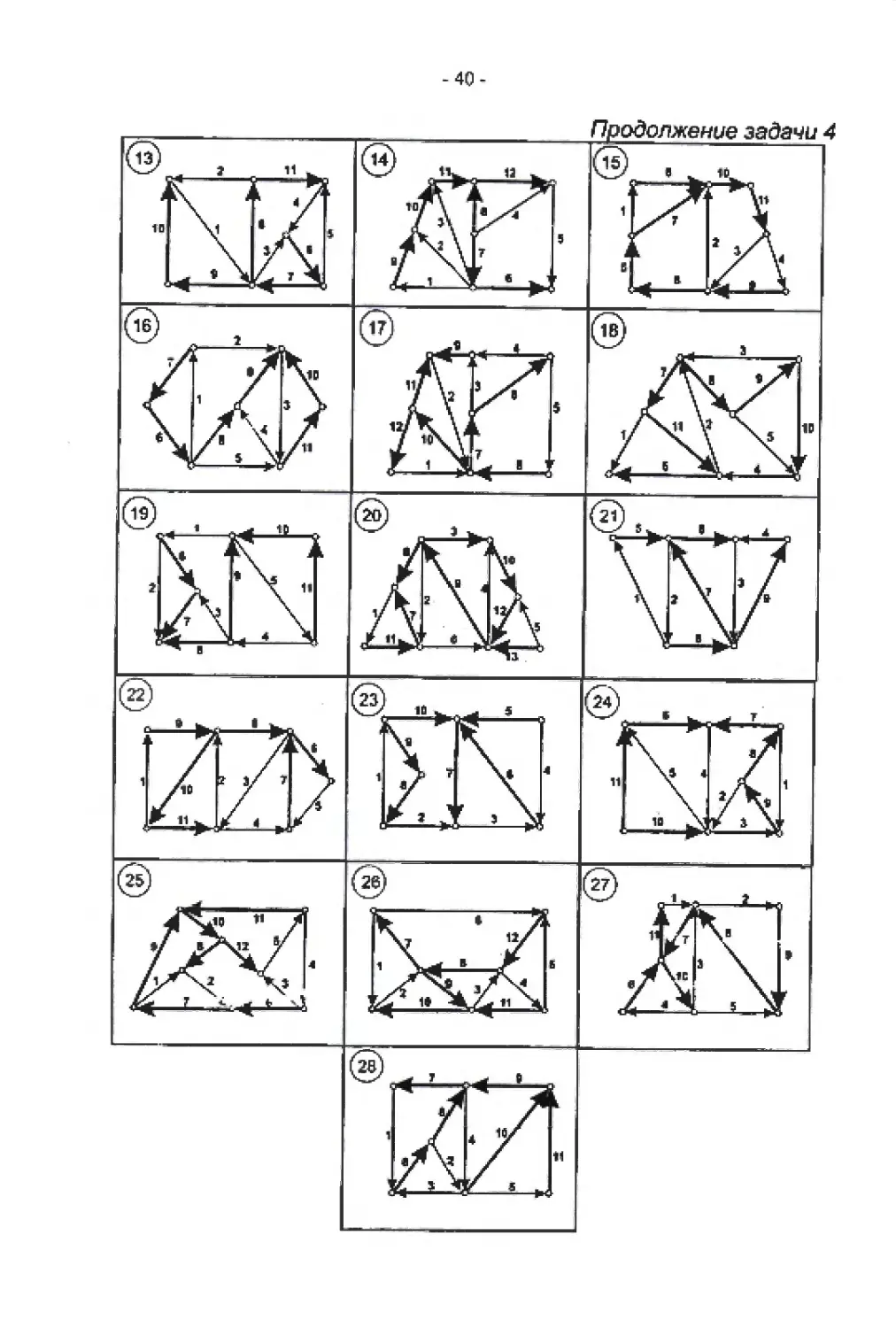
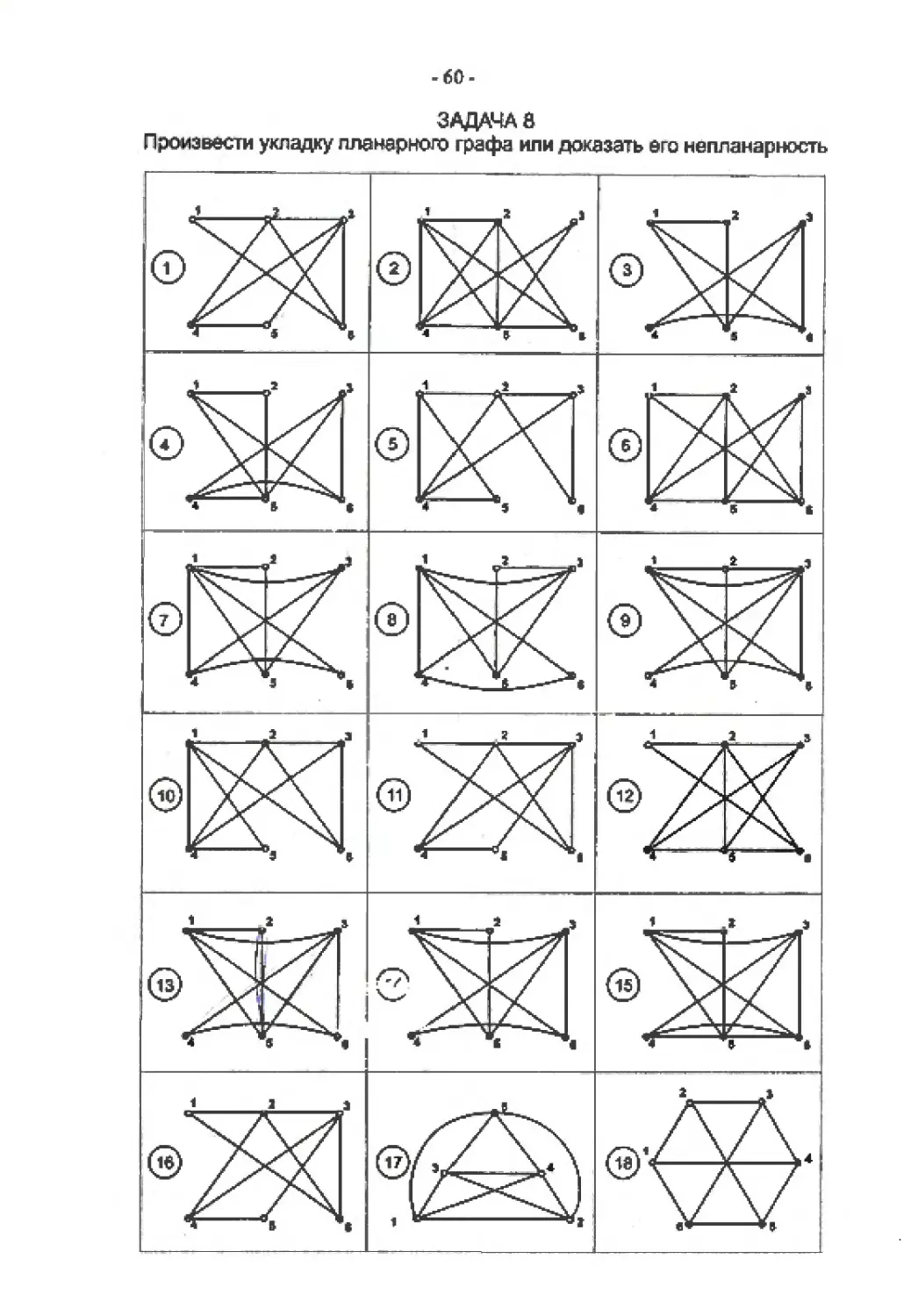
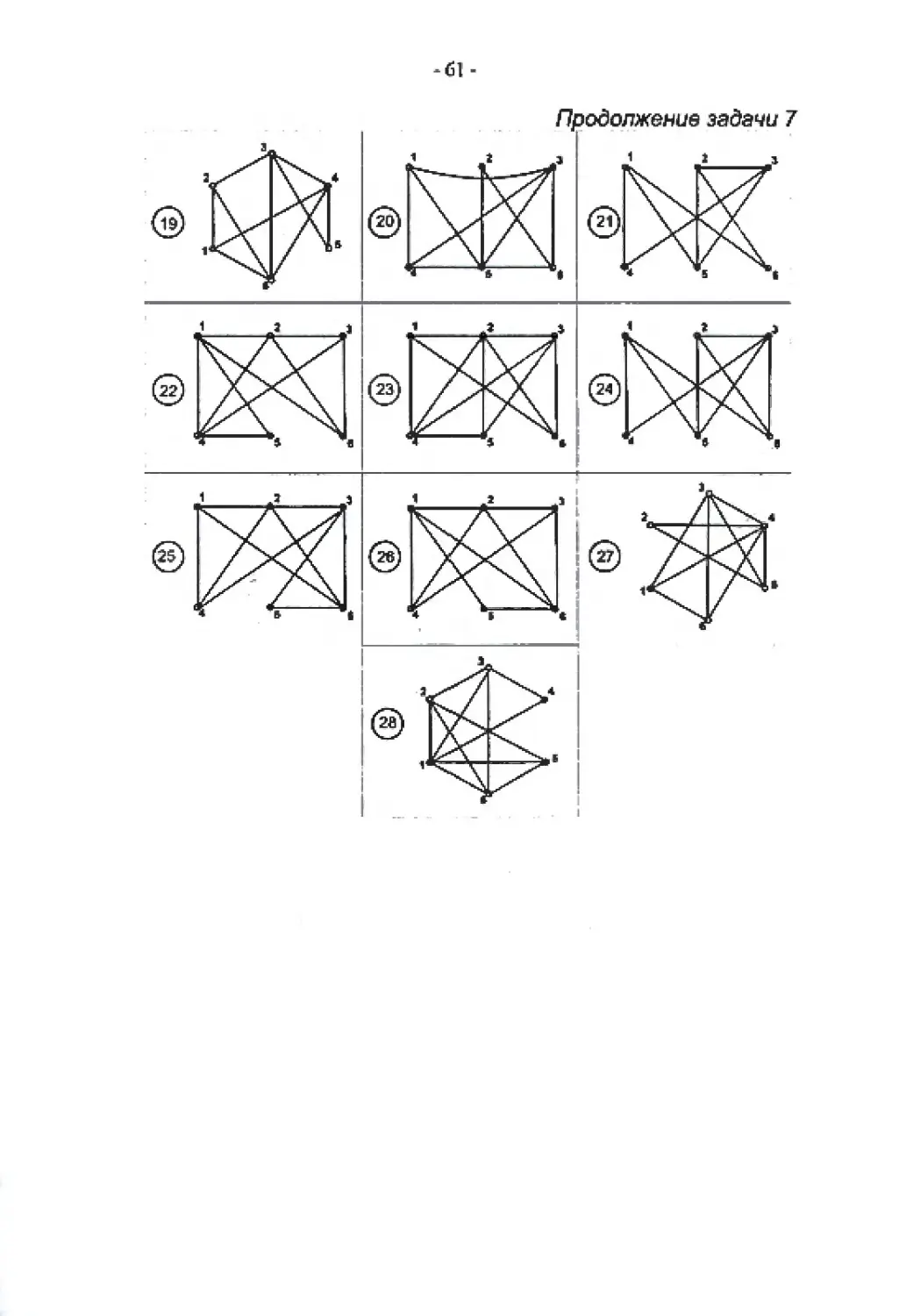
ЗАДАЧА 8
Произвести укладку планарного графа или доказать его непланарнооть
-61
Продолжение задачи 7
-62-
ЗАДАЧА9
Электрические сети
Рассмотрим связные графы без петель. Электрическая сеть есть
неориентированный граф* ребрами которого являются электрические
элементы:
1. Олшческме деления
2. Яидукгоивиост и
3. £лгкослш
► /Тяссиетш с элементы
1. Лэдердторы лдевд
2. Источники напряжения
®k(t)
® шо
Ллтяаеные зл&иемлты
Основная задача электрических цепей - найти в каждом ребре ток
jfО и напряжение UftJ, где t - время. Между током и напряжением в
каждом элементе имеется своя зависимость:
UK(t) = RiR(i)- ic(t) = C^-, UL(t) = L^^.
dt dt
Эти зависимости в пассивных элементах рассматриваются в
линейной постановке, Это означает, что /?, С и £ являются постоянными
положительными коэффициентами, независящими от i(f) и Uff).
Поясним связь между и Uc (ic(t) = С).
Пусть - величина заряда в конденсаторе, q зависит от напряжения
между пластинами конденсатора. Количество электричества q
пропорциональна напряжению q = CUc . Если эта зависимость линейна, то
С равно изменению при изменении подводимого напряжения t/c на
единицу. Емкость «С» равна тангенсу угла наклона прямой на графике
рис, 9.1.
Рис. 9.1
-63-
Продифференцируем по времени зависимость q( t) - CC/f 0
Учитывая, что ток через конденсатор равен
*сО)~
dt
f получаем
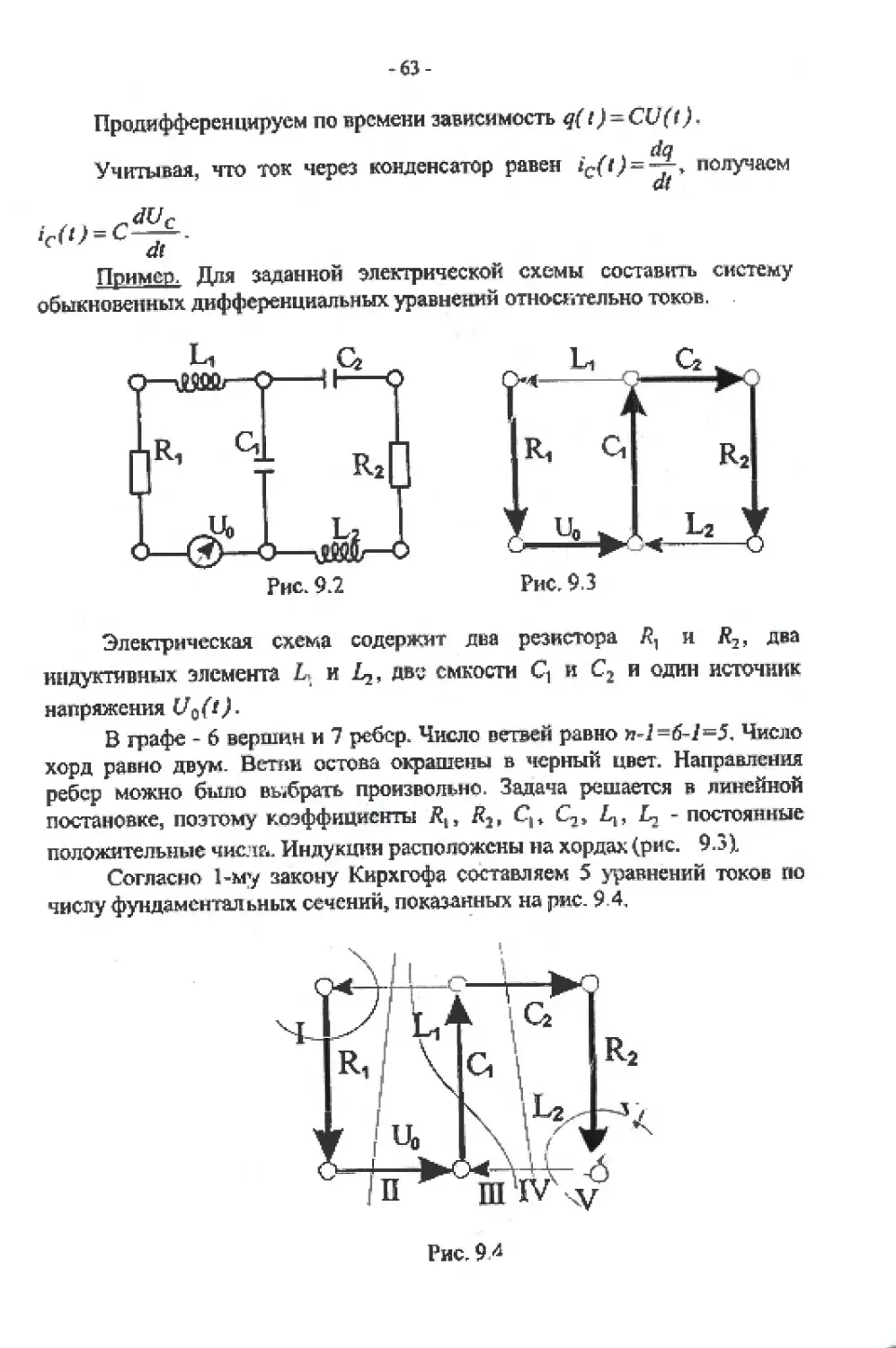
Пример. Для заданной электрической схемы составить систему
обыкновенных дифференциальных уравнений относительно токов.
Рис. 9.2
Рис, 9.3
Электрическая схема содержит два резистора Л, и /?2, два
индуктивных элемента L. и две емкости С| и С2 и один источник
напряжения
В графе - 6 вершин и 7 ребер. Число ветвей равно »-2=6-7=5, Число
хорд равно двум- Ветви остова окрашены в черный цвет. Направления
ребер можно было выбрать произвольно. Задача решается в линейной
постановке, поэтому коэффициенты Ср 2q, 2^ - постоянные
положительные числа. Индукции расположены на хордах (рис. 9.31
Согласно 1-му закону Кнрхгофа составляем 5 уравнений токов по
числу фундаментальных сечений, показанных на рис. 9.4.
Рис, 94
-64-
Разрез I /л-^=0
Разрез Я - = О
’ Разрез Я/ - <А + 1С1 - /^ = О (9.1)
Разрез IV iCi -iLi = О
| Разрез V гл -= О
Согласно 2-му закону Кирхгофа составляем два уравнения
напряжений, соответствующих двум фундаментальным циклам,
показанным на рис. 9.5.
Рис. 9.5
коняк р 1 U* +14 + (7 4- = О
контур IJ U + (Л + t7 +U. =0 (9 2)
ь- I '-‘S нг
Число уравнений относительно токов и напряжений в сумме равно
числу ребер графа, Такая система уравнений называется гибридной.
Воспользовавшись зависимостями между токами и напряжениями в
пассивных элементах схемы
ил = Лгд; 07 = L^; (9.3)
преобразуем уравнения, полученные из фундаментальных циклов 1 и II.
Получилось два интегро-дифференциальных уравнения.
Продифференцируем их по времени /, Получаем два обыкновенных
дифференциальных линейны?; уравнения с постоянными коэффициентами
второго порядка:
г
11г., If, . di, t94)
С] Р<^ + с J dt + R'SKi + ^2 - 0
(Р-.5)
-65-
И так, получили систему из семи уравнений отнск ителыго токов в
семи ребрах схемы, пять из которых - алгебраические и два -
дифференциальные уравнения второго порядка: (9.1) и (9.5)
Дополнительные замечания
1. Если ребра схемы содержат только омические сопротивления и
источники напряжений, зависящих от времени то система уравнений
принимает алгебраическую форму и численно решается методом Гаусса
для каждого требуемого момента времени.
2. Если требуется решить систему уравнений численно на ЭВМ, то
следует вместо напряжений и токов в емкостных и индуктивных элементах
принять за новые переменные заряды и ф? и нотокоскоплення
индуктивностей у/, и ул и при составлении системы уравнений по закону
Кирхгофа воспользоваться соотношениями:
Учитывая также уравнения (9.1)
= = получаем четыре
уравнения первого порядка в нормальной форме:
— --UD(t)- — (т.е. и. = -R.i. -UD-Ue)
dl 1 D С, l£| 0 q
^2 _ Я\ ftp *3
ftsL-a^vl (т.е.,с
'2
(т.е. ic = it
с»
dt
После интегрирования их (явным или неявным методом) можно
численным дифференцированием получить искомые фуикпии = ^-;
1
_. ^Л , г. <7| ?-> (М.
- —; U. = и функции Ц- U.. = ^; t. =
>с' " <й
т - i-2-
3, Заметим, что описанный в замечании 2 метод широко применяется
при решении электрических схем с нелинейными элементами , напри мер
схем на полупроводниках,
[Щ [19]
-66-
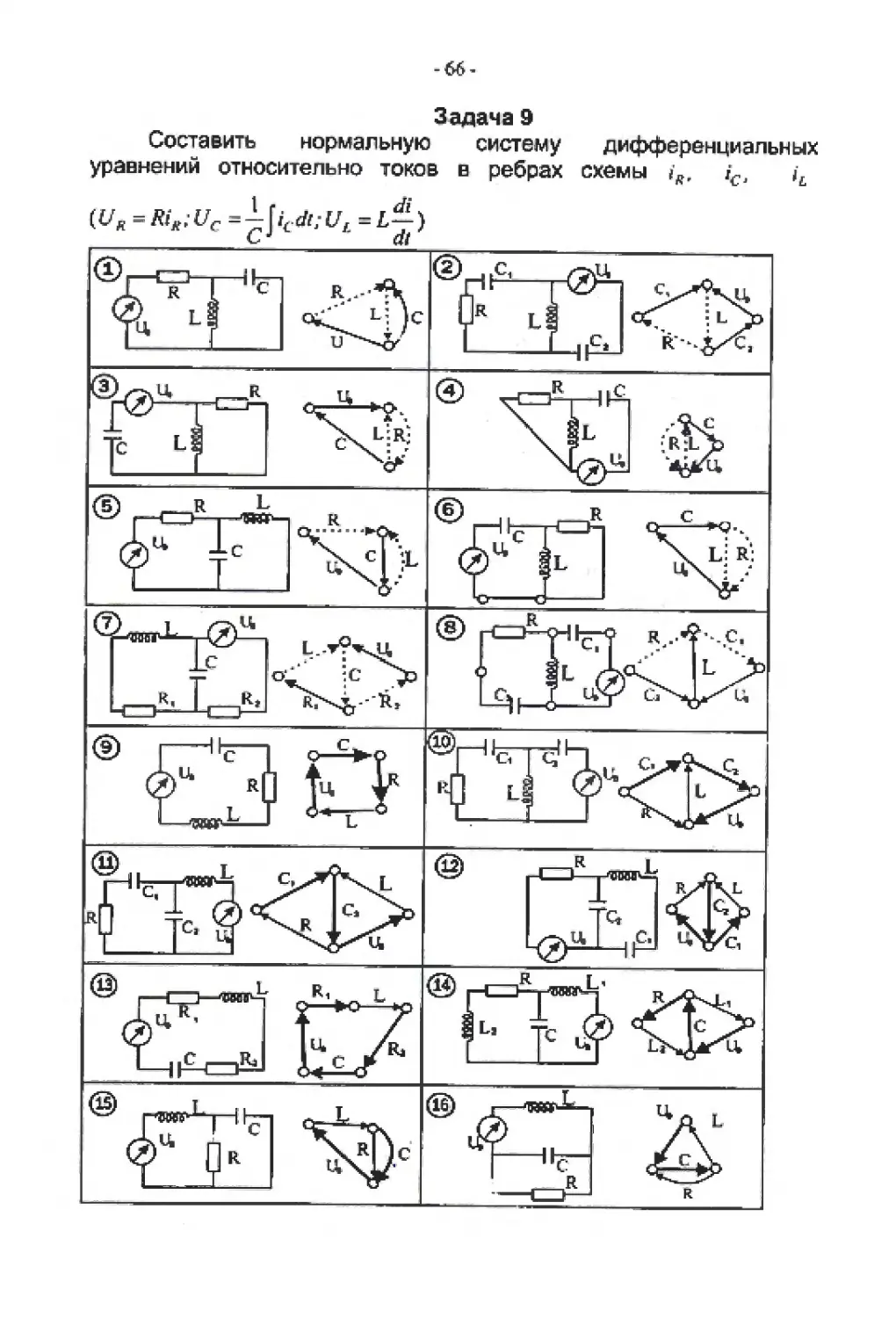
Задача 9
Составить нормальную систему дифференциальных
уравнений относительно токов в ребрах схемы i„, ir l
-67-
68-
ЗАДАЧА 10
Построение двойственной схемы
Рассмотрим плоский связный граф. Гранью его называется
множество точек, каждая пара которых может быть соединена
непрерывной кривой из этого множества. Граница грани - это множество
вершин н ребер, принадлежащих этой грани. Число граней графа
обозначим через/
Если л - число вершин, m - число ребер, то число граней можно
вычислить по формуле Эйлера л-то+/=2, причем в число / включается и
внешняя грань, содержащая бесконечно удаленную точку.
Пример (рис. ЮЛ).
Рис. 10.1
Ь)
Заметим, что формула Эйлера справедлива не только для плоских
графов, но и для множества выпуклых пространственных многогранников.
Например, куб имеет 8 вершин, 12 ребер и 6 граней:
/2+б-2.Такне многогранники могут быть вписаны один в другой так:
каждая вершина вписанного многогранника расположена на грани
описанного. Вписаюгый многогранник также получается выпуклым.
Например, на рисунке 10.2 показано, как в куб вписан октаэдр.
Аналогично в октаэдр можно вписать куб. Такие пространственные
фигуры называются двойственными или дуальными. Число вершин одной
из фигур равно числу граней другой; число ребер одинаково:
jf = п; л = /; /и — т.
Рис. 10.2
-69-
Если спроектировать куб на плоскость, то получаем плоский граф
(рис. 10.3, в).
Если спроектировать куб вместе с вписанным октаэдром, получим
два плоских графа: один - с вершинами И2 Fj И6 И7 Кв и другой - с
вершинами 1,2,3, /> (рис. 10.3, с). Граф - проекция октаэдра приведена на
рис, ЮЗ, с. Плоские графы 10.3, в и 10.3, с тоже называются
двойственными.
Рис. 103
Пример построения двойственного графа для данного графа
приведен на рис. 10.4, а.
Плоский граф имеет 5 вершин, две грани, 5 ребер. Одна из граней -
внешняя. Выбираем внутри каждой грани произвольную точку и
помещаем в эти точки вершины двойственного графа. Далее строим ребра
двойственного графа так, чтобы они были инцидентны с вершинами в двух
соседних гранях исходного графа и пересекали каждое ребро графа G
только один раз. Двойственный граф на рис. Ю.4, а) показан пунктиром, и
отдельно - на рис. 10.4, в. Из построения следует, что висячему ребру в
двойственном графе соответствует петля.
Рис. 10.4
Построенные в примерах двойственные графы плоские. Они взаимно
однозначно определяют друг друга с точностью до изоморфизма.
Изоморфизм заключается в том, что каждый из графов может иметь на
плоскости различное расположение вершин и формы ребер.
Пусть имеем два двойственных графа G и 5 < Подмножество ребер
из G образует простой цикл тогда и только тогда, когда соответствующее
множество ребер в G образует разрез. Действительно, если простой цикл в
G ограничивает одну штг. несколько граней, тогда удаление ребер*
-70-
составляющих этот цикл, соответствует удалению ребер трафа й + которые
пересекают ребра цикла графа CZ А удаление этих ребер из графа 5
соответствует образованию отдельной компоненты с вершинами,
находящимися внутри цикла. В частности, внутри цикла
F| - И2 - графа G (рис, 103), который определяет
единственную грань, находится единственная вершина 6, принадлежащая
графу (7.
После удаления ребер L6, 2-6, 3-6, 4-6 в графе G образуется новая
компонента (квадрат), убранные ребра являются разрезом.
Приведем обобщение этого частного примера. Множество
фундаментальных циклов в G отображается в й в множество
фундаментальных разрезов, а множество фундаментальных разрезов в G
отображается в множество фундаментальных циклов в 5, Все планарные
графы имеют свои двойственные, чего нельзя утверждать про непланарные
графы. Например, и имеют двойственных графов.
Двойственность встречается в математических формулах, в
физических явлениях. В частности* между электрическим напряжением
U(t) и токами в 1(У в различных электрических схемах наблюдается одна и
та же зависимость - прямая пропорциональность, Такне схемы называются
дуальными или двойственными, Приведем' пример двух электрических
схем (рис. 10.5).
Рис. 10.5
В схеме рис. 10.5, а - источник Э.Д.С* последовательно с ним
включены омическое сопротивление Л, индуктивность Z н емкость С
Схема рис. 10.5^. состоит из источника тока и трех параллельных
ветвей: проводимости g, емкости С н индуктивности £. граф на
рис. 10.5, а содержит три ветви я одну хорду. Поэтому можно построить
одни фундаментальный цикл и три фундаментальных разреза. Граф в
схеме в) имеет две вершины, одну ветвь и три хорды. В схеме а) токи во
всех четырех элементах одинаковы, что следует из Ьго закона Кирхгофа.
На основании 2-го закона Кирхгофа приравниваем нулю алгебраическую
сумму потенциалов элементов г /?, L, С:
yDfO=/?i+Z^+lp<ft.
ill с *
-7]
После дифференцирования этого интегро-дифференциального уравнения
получаем дифференциальное линейное уравнение 2-го порядка с
1 юстоянн ыми коэффициентам и:
Л । L^1' I '
Jf d/ ff/2 С
В схеме в) имеется один фундаментальный разрез, проходящий через все
четыре ребра с элементами g, С, £. Из 1-го закона Кирхгофа
следует, что сумма токов, проходящих во всех элементах этого
фундаментального резерва, равна нулю: ^/0 = То есть
После дифферс нцирования, как
дифференциальное ура вненис
и в схеме а), получаем линейное
2-го порядка с постоянными
коэффициент ами
4/р ! £
dt ~S dt dt2 V
Сравнивая уравнения для токов в схеме а) и для напряжений в схеме в),
приходим к выводу, чз о в случае пропорциональности коэффициентов
/e = g;£ = C;C = E и функций = законы изменения токов в
схеме а) и напряжений в схеме в) будут одинаковыми. Такие
электрические схемы называются дуальными или двойственными, Если
построить для данной электрической схемы граф (7. для зрафа (7 построить
двойственный граф G, на каждом ребре графа G поместить электрический
/7 । х 7/и - -
элемент, выполняя равенства (t) - > W U - ~ -
А = —; L = —; С = —, то получим дуальную схему.
а а а
Пусть граф G будет ориентированным, т.с, пусть заданы
положительные направления токов. Тогда положительные направления
токов на каждом ребре двойственного графа <7 должны быть согласованы
с направлением соответствующих ребер графа £7. Когда грани графа (7
пронумерованы* то внутри х-й грани находится к-я вершина двойственного
графа. Обход ребер по границе к-й [рани считается положительным* если
Он происходит по часовой стрелке. Тогда направление на эквивалентном
ребре должно быть положительно, если ток направлен к к-му углу.
Например, на рис. 10.6 приведена грань графа G - к с вершиной к графа G
н па границе грани выбраны положительные направления ребер.
Тогда ребра, исходящие из к-й вершины, получат направления, показанные
на рис. 10.6.
- 72-
РиС- 10.6
Элементы Элементы
исходной дуальном
схемы схемы
Табл, 10,1
R С L U(t) i(t)
— = — = — = —— = —— = const = йг
g L C i(t) U(t)
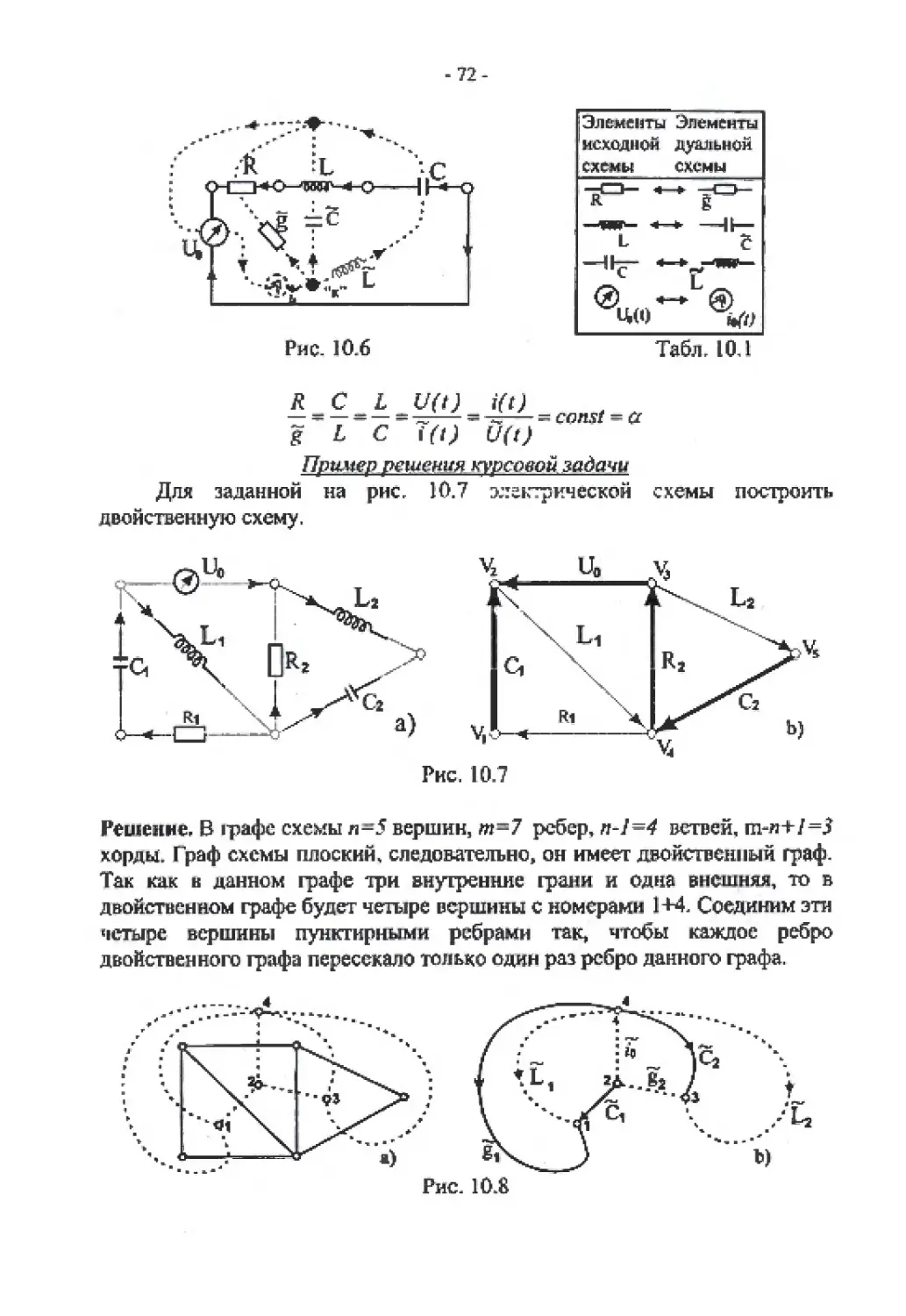
Пример решения курсовой задачи
Для заданной на рис, 10.7 электрической схемы построить
двойственную схему.
Рис. 10.7
Решение. В граф : схемы л-5 вершин, т-7 ребер, л-/=4 ветвей, nwi+/=J
хорды. Граф схемы плоский, следовательно, он имеет двойственный граф.
Так как в данном графе три внутренние граня и одна внешняя, то в
двойственном графе будет четыре вершины с номерами 1+4. Соединим эти
четыре вершины пунктирными ребрами так, чтобы каждое ребро
двойственного графа пересекало только один раз ребро данного графа.
Рис. 10.8
-73-
Такнх ребер тоже будет семь. Получим двойственный граф (рис. 10.8). Три
хорды графа на рис. 10Д в отображаются натри ветви остова отмеченного
краской на рис. 10.8,в. А четыре ветви остова на рис. 10.7, в отображаются
на хорды графа на рис. 10.8,в : 4-1,2-4,2-3,43 Отсюда очевидно взаимное
соответствие фундаментальных циклов и фундаментальных разрезов.
[17]
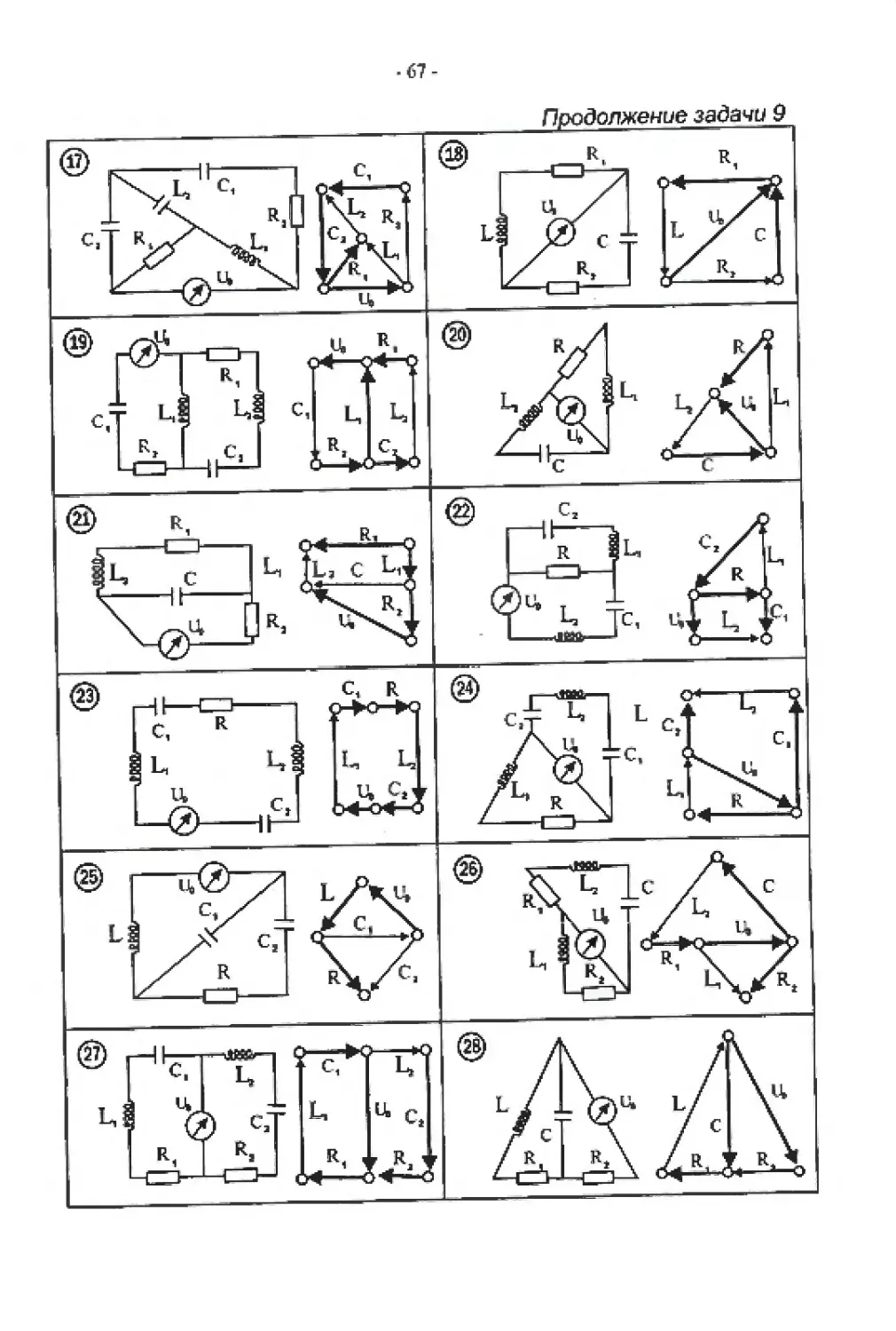
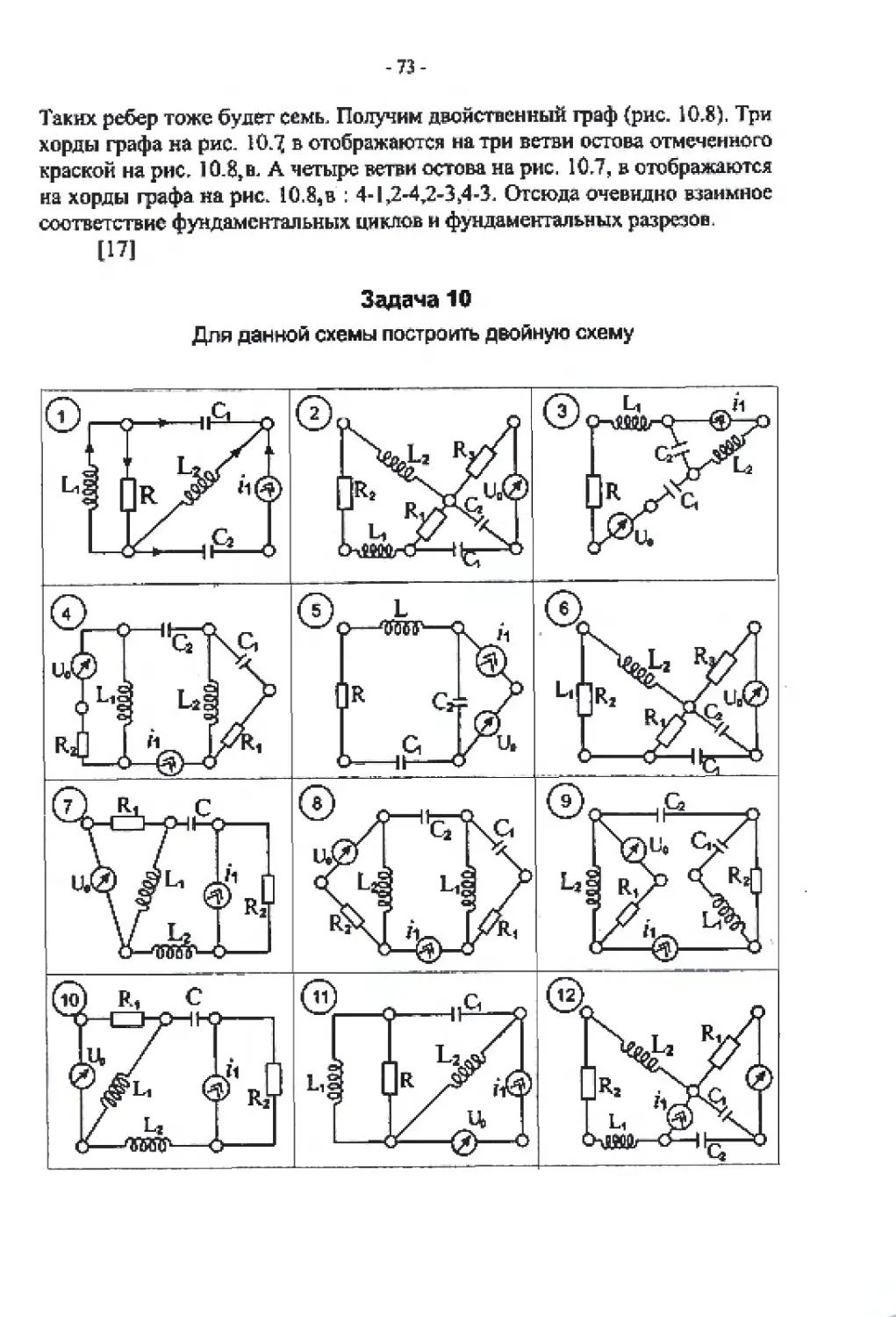
Задача 10
Для данной схемы построить двойную схему
-74’
-75-
БИБЛИОГРАФИЧЕСКИЙ СПИСОК:
I. Белов В,В., Воробьев В.М., Шаталов В.Е. Теория графов. М.:
Высшая школа, 1976.
2. Емеличсв В. А., Мельников О.ML, С арканов В. И., Тышкевич
В.И. М.; Наука,1980.
3. Харари Ф. Теория «рафоа. Мл Мир» 1973.
4. Татт У. Теория графов. М.: Мир, 1988.
5. Форд Л- Фалкерсон Д. Потоки в сетях. М. 1966.
6. Матханов ILH. Основы анализа электрических цепей.
Нелинейные цепи. М: Высшая школа, 1986.
7. Нефедов В.И., Осипова В.Л. Курс дискретной математики. Мг:
МАИ, 1992.
8. Кузнецов О.П, Дискретная математика для инженеров. СпБ.:
Лань, 2005.
9. Судоплатов С.В., Овчинникова Е.В, Дискретная математика.
НГТУ, М., 2006.
10. 1 Паноре в С.Д. Дискретная математика. Курс лекций и
практических занятий. СпБ.: ВХВ, 2006.
11. В. Белов» С. Авдошин. Методические указания по курсу
дискретной математики. МИЭМ. М., 1980, 1983.
12. В. Белов» В.Н. Жихарев Методические указания к курсовым и
лабораториям работам но дисциплине алгоритмы дискретной
математики. МИЭМ.М., 1988.
13. С. Сетпу; М.Б. Рид Линейные графы и электрические цепи. М.:
Высшая школа, 1971.
14. Татт. Теория фафов. М.: Мир, 1988.
15. М. Свами» К. Тхулаеираман. Графы, сети, алгоритмы. М.: Мир»
1988,
16. О. Орс. Теория [рафов М.: Наука, 1980.
17, Р, Уилсон. Введение в теорию графов. М.: Мир, ! 977.
18, В. Ли некий. Комбинаторика для программистов. М.: Мир, 1988.
19. В.Г. Феофанов. Вычислительная математика. Численные методы
решения линейных и нелинейных уравнений. СпБ.: 1982.